БАКАЛАВР • МАГИСТР
Под редакцией Ф. П. Васильева
МЕТОДЫ
ОПТИМИЗАЦИИ
УЧЕБНИК и ПРАКТИКУМ
\
^Ч
II НИ ||„т..II ИИ И
МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ имени
М. В. ЛОМОНОСОВА
Еюрэйт
издательство
УМО ВО рекомендует
biblio-online.ru

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ имени М. В. ЛОМОНОСОВА
МЕТОДЫ
ОПТИМИЗАЦИИ
УЧЕБНИК И ПРАКТИКУМ
ДЛЯ БАКАЛАВРИАТА И МАГИСТРАТУРЫ
Под редакцией профессора,
доктора физико-математических наук Ф. П. Васильева
Рекомендовано Учебно-методическим отделом
высшего образования в качестве учебника для студентов
высших учебных заведений, обучающихся по естественнонаучным
направлениям и специальностям
Книга доступна в электронной библиотечной системе
biblio-online.ru
kMd
Москва- Юрайт-2016

УДК 51-3(075.8)
ББК 22.1я73
М54
Ответственный редактор:
Васильев Федор Павлович — профессор, доктор физико-математических наук,
профессор кафедры оптимального управления факультета вычислительной
математики и кибернетики Московского государственного университета имени М. В.
Ломоносова.
Авторы:
Потапов Михаил Михайлович — профессор, доктор физико-математических наук,
профессор кафедры оптимального управления факультета вычислительной
математики и кибернетики Московского государственного университета имени М. В.
Ломоносова;
Будак Борис Александрович — кандидат физико-математических наук,
преподаватель кафедры оптимального управления факультета вычислительной математики
и кибернетики Московского государственного университета имени М. В. Ломоносова;
Артемьева Людмила Анатольевна — кандидат физико-математических наук,
преподаватель кафедры оптимального управления факультета вычислительной
математики и кибернетики Московского государственного университета имени М. В.
Ломоносова.
Рецензенты:
Арутюнов А. В. — доктор физико-математических наук, профессор, заведующий
кафедрой нелинейного анализа и оптимизации факультета физико-математических
и естественных наук Российского университета дружбы народов;
Куржанский А. Б. — академик Российской академии наук, доктор
физико-математических наук, заслуженный профессор Московского государственного университета
имени М. В. Ломоносова.
Методы оптимизации : учебник и практикум для бакалавриата и магистратуры /
М54 под ред. Ф. П. Васильева. — М.: Издательство Юрайт, 2016. — 375 с. — Серия :
Бакалавр и магистр. Академический курс.
ISBN 978-5-9916-6157-7
В учебнике излагаются наиболее известные и часто используемые на практике
методы поиска экстремума (максимума, минимума) функций конечного числа
переменных, объясняются идейные, эвристические соображения, лежащие в основе
каждого метода, исследуется их сходимость, обсуждаются вычислительные аспекты,
области применимости методов, их достоинства и недостатки. Рассмотрены также
методы решения задач оптимального управления процессами, описываемыми
системами обыкновенных дифференциальных уравнений. Основной текст книги
соответствует типовой программе для бакалавров. Выделенный звездочками
дополнительный текст рассчитан на обучающихся в магистратуре и читателей, заинтересованных
в углубленном изучении предмета. Учебник содержит достаточно большое
количество разобранных примеров и упражнений для самостоятельной работы студентов.
Соответствует актуальным требованиям Федерального государственного
образовательного стандарта высшего образования.
Для бакалавров и магистров технических вузов.
УДК 51-3(075.8)
ББК22.1я73
т-^J/^* Все права защищены. Никакая часть данной книги не может быть воспроизведена
I Ж в какой бы то ни было форме без письменного разрешения владельцев авторских прав.
Delphi Law Сотралу Правовую поддержку издательства обеспечивает юридическая компания «Дельфи».
© Коллектив авторов, 2015
ISBN 978-5-9916-6157-7 © ООО «Издательство Юрайт», 2016

Оглавление
Обозначения 7
Предисловие 11
Глава 1. Введение в оптимизацию. Классический метод 15
1.1. Постановка задачи 15
1.1.1. Задача минимизации 15
1.1.2. Задача максимизации 20
1.2. Теоремы Вейерштрасса 22
1.2.1. Классическая теорема 22
1.2.2. Обобщенная теорема Вейерштрасса 25
1.2.3. Теорема Вейерштрасса для некомпактных множеств 30
1.3. Задачи безусловной оптимизации. Классический метод 32
1.3.1. Описание метода 32
1.3.2. Примеры 38
1.4. Задачи на условный экстремум. Правило множителей Лагранжа 40
1.4.1. Постановка задачи. Необходимое условие оптимальности
на выпуклом множестве 40
1.4.2. Правило множителей Лагранжа в задачах с ограничениями
типа равенств 43
1.4.3. Правило множителей Лагранжа в общем случае 45
1.4.4. Достаточные условия оптимальности 47
1.4.5. Примеры 50
1.4.6. Экономический смысл множителей Лагранжа 60
1.5. Метод штрафных функций 61
1.5.1. Описание метода 61
1.5.2. Сходимость метода 64
1.5.3. Недостатки и достоинства метода 69
1.6. Обоснование правила множителей Лагранжа 70
1.7. Вспомогательные предложения 73
1.7.1. Формулы конечных приращений 73
1.7.2. Леммы о числовых последовательностях 75
Упражнения 76
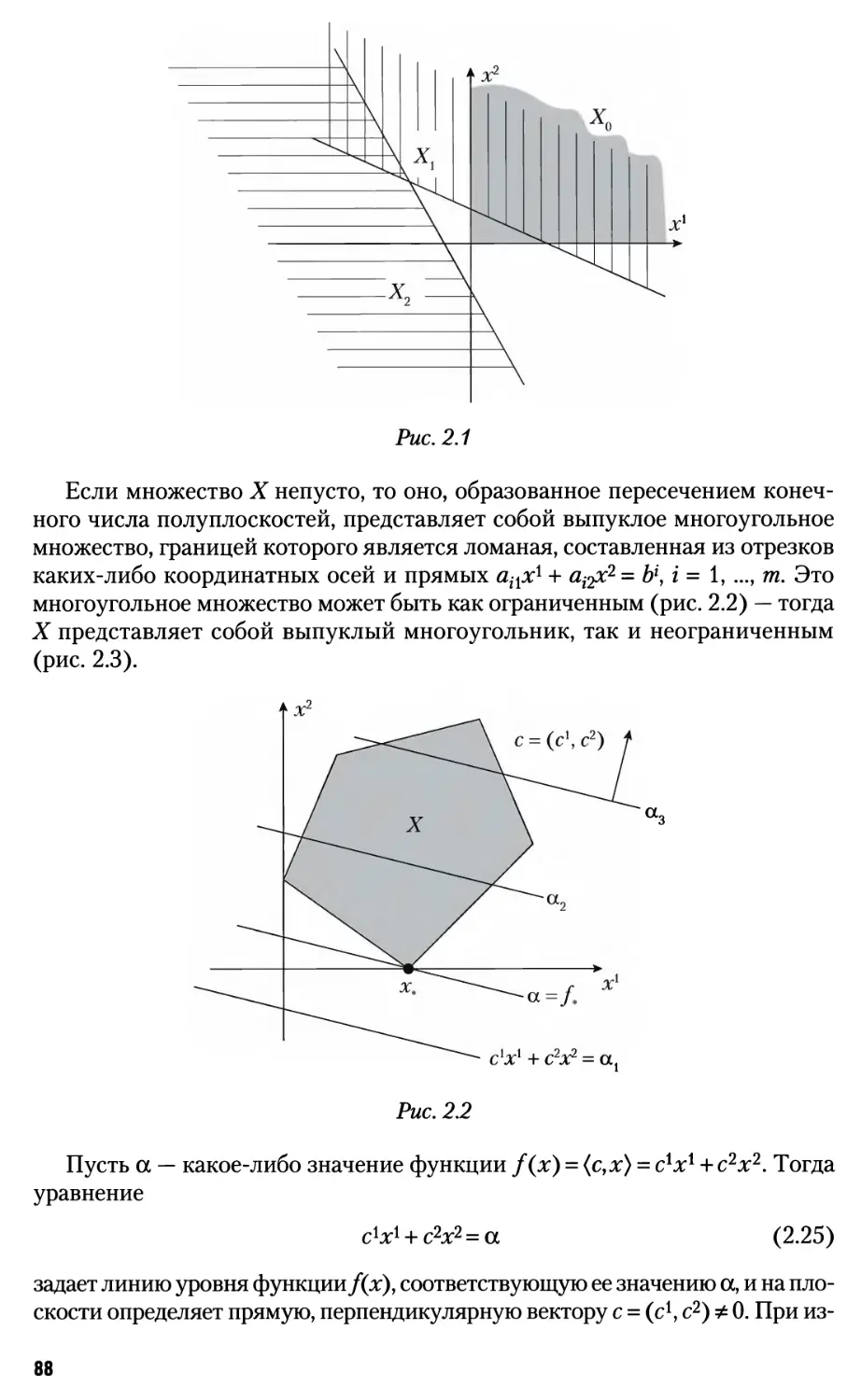
Глава 2. Линейное программирование 81
2.1. Постановка задачи 81
2.1.1. Общая задача линейного программирования 81
2.1.2. Примеры 83
2.1.3. Каноническая задача 85
2.1.4. Основная задача 86
3

2.2. Геометрическая интерпретация задачи линейного программирования 87
2.3. Угловые точки в канонической задаче 91
2.4. Симплекс-метод 94
2.4.1. Приведенная задача 94
2.4.2. Описание симплекс-метода 97
2.4.3. Примеры 107
2.4.4. Конечность метода в невырожденной задаче 109
2.5.* Антициклин 112
2.5.1. Пример 112
2.5.2. Лексикографическое упорядочение векторов 114
2.5.3. Лексикографический антициклин 116
2.5.4. Симплекс-метод в канонической задаче максимизации 121
2.6. Поиск начальной угловой точки 122
2.7. Теорема Вейерштрасса в линейном программировании 126
2.8. Теоремы двойственности 127
Упражнения 137
Глава 3. Элементы выпуклого анализа 140
3.1. Выпуклые функции 140
3.1.1. Понятие выпуклой функции 140
3.1.2. Критерии выпуклости 143
3.1.3. Свойства точек минимума выпуклых функций 146
3.1.4. Другие свойства выпуклых функций 148
3.2. Сильно выпуклые функции 151
3.2.1. Понятие сильно выпуклой функции 151
3.2.2. Критерии сильной выпуклости 153
3.3. Метрическая проекция 157
3.4. Теорема Куна — Таккера 164
3.5. Теорема Куна — Таккера для многогранного множества 171
3.6.* Двойственные задачи. Примеры 174
Упражнения 183
Глава 4. Методы минимизации функций 186
4.1. Методы минимизации функций одной переменной 186
4.1.1. Метод деления отрезка пополам 187
4.1.2. Метод золотого сечения 188
4.1.3. Метод ломаных 190
4.1.4. Метод покрытия 194
4.1.5. Метод касательных 198
4.2. Градиентный метод 198
4.2.1. Описание процесса. Выбор шага, проблемы старта и остановки 198
4.2.2. Сходимость метода скорейшего спуска для сильно выпуклых
функций 202
4.2.3. Траектория процесса. Непрерывный аналог градиентного метода 205
4.3. Метод проекции градиента 208
4.3.1. Описание процесса. Варианты выбора шага 208
4.3.2. Сходимость метода для сильно выпуклых функций 209
4

4.4. Метод условного градиента 211
4.4.1. Идея линейной аппроксимации и варианты ее реализации 211
4.4.2. Сходимость метода 214
4.5. Метод Ньютона 216
4.5.1. Описание процесса. Варианты выбора шага 216
4.5.2. Сходимость классического метода Ньютона для сильно
выпуклых функций 217
4.5.3. Сходимость метода Ньютона с переменным шагом для сильно
выпуклых функций 220
4.6.* Метод переменной метрики 223
4.6.1. Описание процесса. G-проекция 223
4.6.2. Сходимость метода переменной метрики для выпуклых функций ....227
4.6.3. Непрерывный вариант метода переменной метрики 230
4.7.* Квазиньютоновские методы 233
4.8. Метод покоординатного спуска 245
4.8.1. Основная версия метода для задач без ограничений 245
4.8.2. Другие варианты метода покоординатного спуска 247
4.9. Метод покрытия для функции многих переменных 249
4.10.* Метод модифицированных функций Лагранжа 252
4.11.* Экстраградиентный метод 259
4.11.1. Описание процесса 259
4.11.2. Сходимость экстраградиентного метода 260
Упражнения 264
Глава 5. Принцип максимума Понтрягина 266
5.1. Постановка задачи оптимального управления 266
5.1.1. Примеры постановок задач оптимального управления 266
5.1.2. Допустимые управления 269
5.1.3. Задача Коши 270
5.1.4. Постановка задачи 274
5.2. Принцип максимума в задаче оптимального управления
со свободным правым концом 277
5.2.1. Формулировка принципа максимума 277
5.2.2. Краевая задача принципа максимума 278
5.2.3. Доказательство принципа максимума Понтрягина 283
5.3.* Принцип максимума (общий случай) 287
5.3.1. Формулировка принципа максимума в общем случае 287
5.3.2. Краевая задача принципа максимума в общем случае 289
5.3.3. Общие граничные условия 291
5.4.* Примеры 293
5.5.* Принцип максимума и классическое вариационное исчисление 305
Упражнения 309
Глава 6. Динамическое программирование 313
6.1. Принцип оптимальности 313
6.2. Схема Беллмана 315
6.2.1. Разностная аппроксимация задачи оптимального управления 315
6.2.2. Уравнение Беллмана 316
5

6.2.3. Вычислительная схема 319
6.2.4. Синтезирующая функция 321
6.2.5. Оценка погрешности 322
6.2.6. Построение минимизирующих последовательностей 324
6.2.7. Приложение к задачам конечномерной оптимизации 325
6.2.8. Замечания к схеме Беллмана 326
6.3.* Проблема синтеза для систем с непрерывным временем 327
6.3.1. Задача Коши — Беллмана 328
6.3.2. Примеры 331
6.3.3. Приближенный метод 334
6.3.4. Оценка погрешности 337
6.4.* Контрпримеры 339
6.5.* Применение метода динамического программирования к задачам
дискретной оптимизации 342
Упражнения 346
Практикум 349
Литература 363
Ответы к упражнениям 366
Предметный указатель 372

Обозначения
R — числовая ось
[a; b] = {xe R : а < х < Ь) — отрезок
(a; b) = {xe R : а < х < Ь) — интервал
(а; Ь] = {х е R : а < х < Ь), [а; Ь) = {х е R : а < х < Ь) — полуинтервалы
Шп — и-мерное линейное пространство векторов-столбцов х с
координатами Я1', 1=1, ..., П
хт =(х1,...,хп) — вектор-строка, полученная транспонированием
вектора-столбца х
j_
Ы|р = £ИР \, 1 <р < °°, IUL = тахЦ — нормы вектора хвМ.п
U=l
\<i<n
En — и-мерное евклидово пространство, представляющее собой про-
п
странство Rn , оснащенное скалярным произведением (х, у) = ^х1у1
\\Х\\ = \\Х\\2=\\Х\\ЕП
— евклидова норма вектора
U=l
{ev ..., еп} — ортонормированный базис пространства Еп, где е{ - (О, ...,
О, 1, 0, ..., 0)т — вектор-столбец, i-я координата которого равна единице,
а остальные равны нулю, г - 1,..., п
Л =
41
\.атп,1
\п
*тпуп J
= {щj, i = \,...,m; j = l,...,n} =
С „ \
\anj
= (Д.-. А,)-
матрица размера тпхпс элементами а^ где а{ = (aiX,..., ain) — i-я строка матрицы
A, Aj = (ay,..., amj)T —j-vi столбец матрицы А
Ат =
а,
14
Kai,n
ыл
а,
( лтЛ
= (aj,...,aj) =
7П,П J
А1
v^y
матрица размера пхтп,
полученная транспонированием матрицы А размера тпхп
I„=(ev...,en) =
^
V п )
— единичная матрица и-го порядка со столбцами
е1> •••» еп
detA — определитель квадратной матрицы А
Л-1 — обратная матрица для квадратной матрицы А с detA Ф О
гапкЛ — ранг матрицы А

n
Ax = ((Ax)1, ..., (Ах)т)т, где (Ax)1 = ^atjXJ, * = 1> •••> m> ~ произведение
7=1
матрицы размера m x n на вектор хе Еп
\\a\\ = max || Ax\\Em — норма (операторная норма) матрицы А размера тхп
ЫЕп ^1
АВ — произведение матрицы А = {аф размера тхп на матрицу В = {by}
размера пх q, его результатом является матрица С = {Су} размера тх q
п
с элементами с$ = X ЩФш^ * = 1> •••> mJ- 1> •••> Ч
k=i
А > О — неотрицательно определенная симметричная матрица, т.е.
(Ах, х)>0 для всех хе Еп
А > О — положительно определенная симметричная матрица, т.е.
(Ах, х)>0 для всех хе Еп,хфО
А < 0 — неположительно определенная матрица, т.е. (~А) > О
А < О — отрицательно определенная матрица, т.е. (~А) > О
х = (х1,..., хР)Т > 0 — неотрицательный вектор, т.е. х1 > О для всех г = 1,..., п
х = (х1,..., хп)т > 0 — положительный вектор, т.е. х1 > О для всех i = 1,..., п
х = (х1,..., хпУ > (у1,..., z/w)T — вектор х не меньше вектора у, т.е. х - у > О
л: = (х1,..., xw)T > (у1,..., уп)т — вектор х больше вектора у, т.е. х - у > О
£^? = {х е Еп\ х > 0} — неотрицательный ортант пространства Еп
х+ =(х\,...,хг1У, где х\ = max{0;.r*}, г = 1, ..., п, — проекция вектора х
на неотрицательный ортант пространства Еп
х = (х1, ..., хп)т > 0 — лексикографически положительный вектор, т.е.
х^Ои первая ненулевая координата этого вектора положительна
х = (х1,..., хп)т > (у1,..., уп)т — вектор х лексикографически больше
вектора у, т.е. х - у > 0
х* =lexmin^ — лексикографический минимум множества векторов {xt,
ieM
г е М), т.е. для каждого номера г е М либо х{ >- х*, либо х{ = х*
S = S(v,B) = \ — симплекс-таблица угловой точки v с базисом В, где
Г = (IY ..., Гг)т, Г, = (уя, Y,.lf..., yin), i = 1,..., г, Д = (А0, Ах,..., Д„)
ГгЛ]
5 =
чА/
>-0 — лексикографически положительная симплекс-таблица, т.е.
Г, > 0 для всех i = 1,..., г
11 - ' *
>-59 =
I До /
— симплекс-таблица Sx лексикографически больше
симплекс-таблицы 52, т.е. А{ > А2
X — замыкание множества X
ТрХ — граничные точки множества X
intX — внутренние точки множества X
dimX — размерность множества X
Хи Y — объединение двух множеств X и Y
X nY— пересечение двух множеств X и Y
X + Y — сумма двух множеств X и Y
8

X \ Y — разность двух множеств X и Y
оХ — произведение числа а на множество X
X х Y — прямое (декартово) произведение двух множеств X и Y
0 — пустое множество
р(х,Х) = inf \х - у\ — расстояние от точки х до множества X
уеХ
0(v, е) = {х е Еп\ \\х - v\\ < е} — 6-окрестность точки v, представляющая
собой открытый шар радиуса 6 > 0 с центром в точке v
S(v, К) = {х е Еп\ \\х - v\\ < R) — замкнутый шар радиуса R с центром
в точке v
L1 — ортогональное дополнение подпространства 1с£й
Px(z) — проекция точки z е Еп на множество X
P§(z) — G-проекция точки z e Епнг множество X
f(x) —> min, x e X, — краткая символическая запись задачи минимизации
функции f(x) на множестве X
/* = inf f(x) — точная нижняя грань функции f(x) на множестве X
хеХ
X* = {х g X: f(x) = /* > -°°} — множество точек минимума функции f(x)
наХ
f(x) —> max, x e X — краткая символическая запись задачи
максимизации функции f(x) на множестве X
/* =sup/(x) — точная верхняя грань функции/(х) на множестве X
хеХ
X* = {х е X: f(x) = /* < +°°} — множество точек максимума функции/(х)
наХ
. = f'xi (x) = fxi (x) — частная производная функции/(х) =/(х1,..., хп)
в точке х по переменной х\ г = 1,..., п
f'(x) = ,..., "1 = grad/(x) — градиент функции f(x) в точке х
у дх1 дхп J
^ . = f£xj (x) = fxixj (x) — частная производная второго порядка
по переменным х\ од функции/(х) =/(х1,..., хп) в точке х, i,j = 1,..., п
f'(x) — вторая производная функции f(x) в точке х, она является ква-
дратнои матрицей п-то порядка с элементами ^ ., i,j = 1,..., п
oxloxJ
df(x) v f(x + te)-f(x) , r/ ч
у = hm ■:L^ — — производная функции j(x) в точке х
ае ^^+о ^
по направлению е, || в || = 1
dx(t)
x(t) = —-^- — первая производная функции x(t) по времени t
at
d2x(t)
x(t) = —To — вторая производная функции x(t) по времени t
at1
lim xk — предел последовательности {xk} = (xv x2,..., xk,...)
k—>oo
lim xk — верхний предел последовательности {xk}
k—>oo

lim xk — нижний предел последовательности {xk}
k—>oo
lim f(x) — предел функции f(x) при х —» a
X—H2
lim f(x) — верхний предел функции f(x) при х —> a
x—>a
lim /(x) — нижний предел функции f(x) при х —» я
/(я + 0) = lim /(x) — предел функции /(х) одной переменной x
*->a+0
при стремлении х к точке а справа
f(a-0)= lim /(x) — предел функции f(x) одной переменной х
*->а-0
при стремлении х к точке а слева
0(t) — величина, определенная в окрестности точки t = О и такая, что
0(0
t < С при всех достаточно малых t, где С — некоторая неотрицательная
постоянная
o(t) — величина, определенная в окрестности точки t = 0 и такая, что
£->0 t
С(Х) — пространство непрерывных на замкнутом ограниченном
множестве X функций/(х) с нормой |/|с = тах|/(х)|
СХ(Х) — пространство непрерывно дифференцируемых на множестве X
функций
С2(Х) — пространство дважды непрерывно дифференцируемых на
множестве X функций
С1{(Х) — пространство непрерывно дифференцируемых на множестве
X функций, градиент f(x) которых удовлетворяет условию Липшица на X
Q(I) — множество функций, удовлетворяющих на множестве X
условию Липшица с константой L
Н = Н(х, г/, t, V, а0) — функция Гамильтона — Понтрягина
/ = l(x, y,t. Г, а) — малый Лагранжиан
£ = £(х, К) — функция Лагранжа в общей форме
L = L(x, X) — функция Лагранжа в нормальной форме
М = М(х, X) — модифицированная функция Лагранжа
V — квантор общности
3 — квантор существования
g — знак принадлежности
с — знак строгого включения одного множества в другое
с — знак нестрогого включения одного множества в другое
def
= — знак определения, используется при введении объектов

Предисловие
Первые задачи геометрического содержания, связанные с отысканием
наименьших и наибольших величин, появились еще в древние времена.
Развитие промышленности в XVII—XVIII вв. привело к необходимости
исследования более сложных задач на экстремум и к появлению
вариационного исчисления. Однако лишь в XX в. при огромном размахе
производства и осознании ограниченности ресурсов Земли во весь рост встала
задача оптимального использования энергии, материалов, рабочего
времени, большую актуальность приобрели вопросы наилучшего в том или
ином смысле управления различными процессами физики, техники,
экономики и др.
Сюда относятся, например, задача организации производства с целью
получения максимальной прибыли при заданных затратах ресурсов, задача
оптимальной организации перевозок при ограниченном количестве
транспортных средств, задача минимизации издержек (отходов) производства,
задача оптимального размещения объектов производства, оптимального
использования посевной площади, оптимального управления запасами,
оптимальной организации работы пунктов массового обслуживания,
выбора оптимальных сроков сезонного производства, задача управления
системой гидростанций и водохранилищ с целью получения
максимального количества электроэнергии, задача о космическом перелете из одной
точки пространства в другую наибыстрейшим образом или с наименьшими
затратами энергии, задача о быстрейшем нагреве или остывании металла
до заданного температурного режима, задача о наилучшем гашении
вибраций и многие другие задачи.
На математическом языке такие задачи, называемые задачами
оптимизации, могут быть сформулированы как задачи отыскания экстремума
(минимума или максимума) некоторой функции (функционала) f(x)
на заданном множестве X из некоторого пространства. Функцию f(x)
принято называть целевой функцией, а ее аргумент х часто называют
параметром управления или допустимой точкой, множество X — допустимым
множеством. Значение целевой функции f(x) выражает собой качество
(цену) допустимой точки х. Требование принадлежности точки х
множеству X выражает собой наличие некоторых ограничений, вытекающих,
например, из законов сохранения энергии, ограниченности имеющихся
ресурсов, возможностей технической реализации управления,
нежелательности каких-либо запрещенных (аварийных) состояний и т.п.
Сразу же заметим, что на практике формулировка задач оптимизации,
составление целевой функции/(х) и множества X являются сложной
проблемой, требующей больших знаний в предметной области, материальных
11

затрат по сбору и анализу информации, постановке необходимых
экспериментов и т.п. Обсуждение возникающих здесь вопросов является
предметом особой области знаний, называемой математическим моделированием,
и выводит нас за рамки настоящего учебного пособия. Чтобы читатель
имел некоторое представление об этой сложной работе по формулировке
задач оптимизации, в гл. 2 будут приведены примеры линейных задач
оптимизации.
В общем случае, говоря о задаче оптимизации, мы будем подразумевать,
что известны целевая функция f(x), допустимое множество X и цель, т.е.
ищется ли минимум или максимум функции. Далее возникает проблема:
как искать экстремум функции f(x) на множестве X? Если множество X
содержит небольшое число точек, то задачу оптимизации можно решить
относительно просто: достаточно вычислить значения целевой функции
в этих точках и, сравнивая их по величине, простым перебором найти
экстремальное (минимальное или максимальное) значение и указать точку,
где этот экстремум достигается. Однако если число точек в X велико
и даже, возможно, бесконечно, то такой метод простого перебора не под
силу современным вычислительным средствам. Как искать экстремум
в такой ситуации? Ясно, что нужны специальные методы оптимизации,
нужна теория таких методов, нужна наука.
Читатель отчасти уже знаком с классическим методом
оптимизации, основанном на дифференциальном исчислении, который излагается
в основных курсах по математическому анализу. В настоящее время
теория оптимизации обогатилась фундаментальными результатами,
полученными по таким направлениям, как линейное программирование, выпуклое
программирование, динамическое программирование, стохастическое
программирование, дискретная оптимизация, теория оптимального
управления процессами, описываемыми дифференциальными уравнениями, и др.
Потребности практики способствовали бурному развитию методов
решения задач оптимизации. Появление современных вычислительных средств,
компьютеров сделало возможным эффективное решение многих важных
прикладных задач оптимизации, которые ранее из-за своей сложности
казались недоступными, появились пакеты программ оптимизации.
В настоящем учебнике излагаются элементы теории оптимизации,
а также основы наиболее часто используемых на практике методов
приближенного решения задач оптимизации и краткая характеристика этих
методов. Усилия авторов были направлены на поиск наиболее экономных
схем изложения, упрощение доказательств, чтобы сделать материал более
доступным, не снижая уровня строгости.
Руководствуясь этими методическими соображениями, авторы вынесли
в первую главу метод штрафных функций, для изложения и понимания
которого, по сути, достаточно знания свойств непрерывных функций
многих переменных из классического математического анализа. Это дало нам
возможность в первой же главе с помощью аппарата штрафных функций
дать простое доказательство важнейшего в теории оптимизации правила
множителей Лагранжа. Во второй главе дается элементарное
изложение основ линейного программирования с привлечением минимального
12

математического аппарата, опираясь лишь на самые первичные понятия
из линейной алгебры, такие как матрица, определитель, линейная
зависимость и независимость векторов, ранг матрицы, произведение матриц,
обратная матрица, не предполагая знания довольно сложной теории
выпуклых многогранных множеств. И в последующих главах авторы
старались уделить методическим аспектам большое внимание, стремясь полнее
и проще излагать основные факты теории и методов оптимизации.
К сожалению, ограниченный объем книги не позволяет уделить
внимание таким важным разделам теории и методов оптимизации, как
дискретная оптимизация, стохастическая оптимизация, вопросам устойчивости
вычислительных алгоритмов, методам решения неустойчивых задач, задач
большой размерности и др.
Материал книги для своего понимания требует лишь знания основ
математического анализа, линейной алгебры, элементов теории
обыкновенных дифференциальных уравнений в объеме стандартных курсов
бакалавриата и магистратуры технических вузов. В книге выделены основной
и дополнительный тексты. Основной текст описывает материал
действующей типовой программы «бакалавр-магистр». Дополнительный текст,
служащий для более углубленного усвоения материала и предназначенный
магистрам, в оглавлении и в заголовках внутри книги помечен символом *.
О содержании книги можно судить по оглавлению. В книге
значительное место занимает иллюстративный материал, примеры задач с разбором
решений. В конце каждой главы приведены вопросы и упражнения
теоретического характера, а в конце учебника отдельным блоком представлен
практикум — задачи для самостоятельной работы студентов.
При составлении заданий практикума к гл. 1,2 мы пользовались
упражнениями из задачника [5], к гл. 5, 6 идеи заданий заимствованы из книги [15].
При работе над книгой авторы опирались на свой опыт работы со
студентами на факультете ВМК МГУ имени М. В. Ломоносова. В книге широко
использованы материалы монографии Ф. П. Васильева [12], касающиеся
конечномерных задач и методов их решения, а также задач оптимального
управления процессами, описываемыми обыкновенными
дифференциальными уравнениями. Эту книгу можно считать продолжением настоящего
учебника.
По рассматриваемой в учебнике проблематике имеется обширная
литература. Список литературы в конце учебника отражает лишь некоторые
источники, которые были непосредственно использованы при написании
книги или близко примыкают к ней, расширяя и дополняя ее содержание.
Авторы выражают глубокую благодарность А. В. Тимохову за
материалы, которые были существенно использованы при составлении
заданий по практикуму к гл. 1—3, а также В. Ю. Королеву за полезные советы
по содержанию книги.
В результате освоения дисциплины у студента должны формироваться
следующие профессиональные компетенции:
знать
• классификацию задач оптимизации (задачи безусловной и условной
оптимизации; классическую задачу на условный экстремум; задачи матема-
13

тического, выпуклого, линейного программирования; задачи оптимального
управления);
• основные положения теории оптимизации (теория необходимых
и достаточных условий оптимальности для конечномерных задач, правило
множителей Лагранжа, теория двойственности задач линейного
программирования, принцип максимума Понтрягина в оптимальном управлении
и др.);
• элементы выпуклого анализа как основы современной теории
оптимизации;
• классификацию численных методов оптимизации (конечношаговые
и бесконечношаговые методы, методы условной и безусловной
оптимизации, методы нулевого, первого и второго порядков);
• понятийный аппарат численных методов оптимизации (итерация
метода, начальная точка, направление убывания, критерий останова,
сходимость метода);
уметь
• аналитически решать простейшие нелинейные задачи оптимизации,
используя теорию необходимых и достаточных условий оптимальности;
• аналитически решать простейшие задачи линейного
программирования, используя симплекс-метод;
• строить прикладные модели, сводящиеся к задачам оптимизации;
• анализировать характеристики прикладной задачи оптимизации
(целевую функцию, допустимое множество) на предмет ее отнесения
к конкретному классу задач;
• выбирать адекватный численный метод решения прикладной задачи
оптимизации (с последующим обращением к соответствующим
библиотекам компьютерных программ);
владеть
• навыками решения задач оптимизации;
• материалом дисциплины на уровне, позволяющем формулировать,
исследовать и решать прикладные задачи оптимизации.
Авторы будут признательны читателям за советы и критические
замечания по содержанию книги.

Глава 1
ВВЕДЕНИЕ В ОПТИМИЗАЦИЮ.
КЛАССИЧЕСКИЙ МЕТОД
1.1. Постановка задачи
1.1.1. Задача минимизации
Перед тем как начать изложение теории оптимизации, введем
некоторые обозначения и напомним определения из линейной алгебры и
математического анализа [9, 22, 29, 31]. Через Шп будем обозначать и-мерное
вещественное линейное пространство, состоящее из вектор-столбцов
ytl
\л )
. У =
, z =
с действительными координатами я1', у\ z\ г - 1,..., п\ сумма х + у двух
вектор-столбцов и произведение со: вектор-столбца х на действительное число
авМй определяются обычным образом:
гх1 + у1'
, ах =
Вектор-столбец
о= ...
W
называется нулевым. Вектор-строку, полученную транспонированием
вектор-столбца х, обозначим через хт = (х{,...,хп). Там, где не могут
возникнуть недоразумения, вектор-столбец из Шп или соответствующую ему
вектор-строку для краткости мы часто будем называть просто вектором или
точкой, а знак транспонирования «т» будем опускать.
п
Если в Rn ввести скалярное произведение двух векторов (х,у) = ^х1у\
*=1
х,уеЖп, то Шп превращается в и-мерное евклидово пространство, которое
будем обозначать через Еп. Если {х, г/) = 0, то векторы х и у называются
ортогональными. Это скалярное произведение порождает норму (длину)
вектора в Еп, которую вычисляют по формуле
15

Ы|= (x,x)V2 =
Величину
р(х,у) = \\х-у\\ =
V>1
,2^
называют евклидовым расстоянием между точками х, у е Еп.
Для любых трех точек x,y,ze En справедливо неравенство
||;c-y||<||jc-z|| + ||z-y||,
называемое неравенством треугольника. Когда важно подчеркнуть, что
скалярное произведение, норма, расстояние взяты именно в Еп, мы будем
писать (х,у)ЕП, ||х||£Я,||х-у||£11.
В Еп справедливо неравенство Коти — Буняковского
(х, у) < \\х\\ • || у Цдля \/х,уе Еп,
причем неравенство превращается в равенство тогда и только тогда, когда
векторы х, у коллинеарны, т.е. х = ау при некотором а.
Иногда мы будем пользоваться и другими нормами векторов из Mw,
такими как
(п И1/р
\г=1 )
\<i<nx
Как известно, в конечномерных пространствах все нормы
эквивалентны. Это значит, что если ||-||7, \\п — две нормы в Rn, то существуют
такие положительные числа тх и т2, что /wjlx ||7 < ||х\п < т2||#||/для любого
х е Rn. Отсюда следует, что если последовательность {xk} сходится к точке
х в какой-либо норме ||-||/, т.е. \\xk - x\\j —> 0 при k —> °о, то эта
последовательность будет сходиться кхив любой другой норме ||||/7, в частности
\%ь ~*11 = max m -х{\ —> 0, что равносильно покоординатной сходимости.
11 ||о° 1<1<я' * '
В основном мы будем работать в евклидовом пространстве Еп. Перейдем
к постановке задач оптимизации.
Пусть X — некоторое известное множество из и-мерного евклидова
пространства En, a f(x) = /(х1,..., хп) — функция, определенная на этом
множестве. Кратко задачу оптимизации будем записывать следующим образом:
/(х)—>min, xeX. (1.1)
Поясним, что подразумевается под задачей (1.1). Начнем с того, что
напомним некоторые определения из классического математического
анализа [22, 29].
Определение 1.1. Точку х* е X будем называть точкой минимума функции
f(x) на множестве X, если f(x*) < f(x) для всех хе X; величину f(x*) назовем
наименьшим значением/(г) на X и обозначим minf(x) = /* = f(x*). Множе-
хеХ
ство всех точек минимума функции/(г) на X будем обозначать через X*.
16

В зависимости от свойств множества X и функции f(x) множество X*
может содержать одну, несколько и даже бесконечно много точек, а также
возможны случаи, когда множество X* пусто. Поясним это на примерах.
Пусть
21Ы1
/(*) = _£Е!!_ х = (х\...,хп)еЕп.
1+1Ы1
График этой функции при п = 1 изображен на рис. 1.1.
На множестве Хх = Еп минимальное значение этой функции равно нулю:
/*=/(0) = 0, множество X* точек минимума состоит из единственной точки х*=0.
На множестве Х2 = {х е Еп: \\х\\ > 1} функция f(x) не имеет минимального значения,
так как/(х) > 0 при всех х е Х2, причем на последовательности xk, k= 1,2,...,
функция стремится к нулю: lim/(x^) = 0, но равенство/(х) = 0 невозможно ни в одной
точке х е Х2, так что Х2* = 0.
Пример 1.2
Пусть
[ 1
г, ч и-м,еслих*О,
[1,еслих = 0;
График этой функции при п = 1 изображен на рис. 1.2.
У\
Рис. 12
На множествах Хх = Еп или Х2 ={х е Еп :\\х\\> 1} функция/(х) принимает строго
положительные значения, множество точек ее минимума пусто.
17

Если X = Х3 ={х еЕ»:\\х\\< 1/2}, то/.=1, Х3* = {х = 0}.
ЕслиХ = Х4={хе Еп : ||х||<2}, то/ =-, Х4* = {ig Х4 : ||х|| = 2} — я-мерная сфера
с центром в точке х = 0 (при п = 1 Х4* — это две точки х* = 2 и х* = -2).
Если Х = Х5= {хе & : ||х|| < 1}, то/* = 1, Х5*= {хе Х5: ||х|| = 1} и {х = 0}.
Пример 1.3
Пусть
// ч Jsin2 ~
/(х)= \х j
[О прих = 0.
График этой функции изображен на рис. 1.3.
при х > 0,
3 2
Рис. 13
На множестве X = Xt = {х: 1 < х < 2} /* = 0, Xt* = {x* =1}.
f 1 | 11
Если X = Х2 = \ х: — < х < 1 к то/* = 0, Х2* состоит из трех точек xt = —, х2 = —, х3 = 1.
ЕслиХ = Х3 = {х:0< 1}, то/* = 0,Х3*= xgX3:x = -,wgn|u{x = 0}.
Пример 1.4
Пусть /(х) = In х, X = {х е Я1: 0 < х < 1}.
Здесь
(рис. 1.4).
Здесь X* = 0, для последовательности х^ =—, k = 1, 2, ..., имеем lim/(x^) = -
Pwc. 14
18

Определение 1.2. Функция/(х) называется ограниченной снизу на
множестве X, если существует такое число М0, что f(x) > М0 для всех х е X.
Функция f(x) не ограничена снизу на X, если существует
последовательность {xk} е X, для которой lim f(x) = -°°.
£->оо
В примерах 1.1—1.3 функции ограничены снизу на рассматриваемых
множествах. В примере функция не ограничена снизу, хотя и принимает
конечные значения во всех точках из X
В тех случаях, когда X* = 0, естественным обобщением понятия
наименьшего значения функции на множестве является понятие точной
нижней грани функции.
Определение 1.3. Пусть функция/(х) ограничена снизу на
множестве X. Тогда число /* называют точной нижней гранью или инфимумом
f(x) на X, если
1) /* < f(x) при всех х е X;
2) для любого сколь угодно малого числа 6 > 0 найдется точка х£е X
такая, что f(x£) < /* + 6.
Точную нижнюю грань f(x) на X будем обозначать через inf f(x) = /*.
хеХ
Если функция f(x) не ограничена снизу на X, то в качестве точной нижней
грани f(x) на X принимается /* = -°°.
В примерах 1.1 и 1.2/* = 0, а множество X* может быть пустым или
непустым в зависимости от множества X; в примере 1.4 f* = -°о, X* = 0.
Если X* Ф 0, то, очевидно, точная нижняя грань Дт) на X совпадает с
наименьшим значением этой функции на X, т.е. inf f(x) = minf(x). В этом слу-
хеХ хеХ
чае говорят, что функция f(x) достигает своей точной нижней грани в
каждой из точек х* е X*. Подчеркнем, что inf f(x) = f* всегда существует [22,29],
хеХ
причем если f(x) ограничена снизу на X числом М0, то f* > М0 > -«>, и /* = -«>,
еслиДг) не ограничена снизу X Заметим, что если функция достигает
некоторой своей нижней грани, то эта нижняя грань необходимо будет и точной
нижней гранью функции, поэтому в дальнейшем в тексте мы в некоторых
случаях для краткости будем говорить «функция достигает своей нижней
грани».
После введенных определений можем уточнить постановку задачи (1.1).
Здесь обычно различают задачи двух типов. К первому типу относят задачи,
в которых требуется определить величину /* = inf f(x) — точную нижнюю
хеХ
грань функции/(х) на множестве X. В таких задачах возможно, что X* = 0.
В задачах второго типа ищется не только величина /«, но и какая-либо
точках* е X*, в которой достигается точная нижняя грань, — здесь уже
подразумевается, что X* Ф 0. Если множество X* состоит более чем из одной
точки, то здесь возможны уточнения постановки задачи (1.1). Например,
нужно искать точку х* е X*, которая ближе всего расположена к заданной
точке х0.
Возможна и более широкая постановка задачи минимизации второго
типа, когда ищутся не только точки минимума в смысле определения 1.1,
но и точки так называемого локального минимума.
19

Определение 1.4. Точках* е X называется точкой локального минимума
функции/(х) на множестве Xсо значением/*=f(x*), если существует такая
малая 6-окрестность 0(х*, г) = {хе Еп : \\х -х*\\ < е} точки х», что fix*) <f(x)
для всех х е X п 0(х*, б). Если при некотором 6 > 0 равенство f(x*) = f(x)
для х е X п 0(х*, б) возможно только при х = х*, то х* называют точкой
строгого локального минимума.
Для функции, график которой изображен на рис. 1.5, точки х0, х2, х4
являются точками строгого локального минимума, а в точках х,
удовлетворяющих неравенствам х5 < х < х6 и х8 < х < х9, реализуется нестрогий
локальный минимум. Других точек локального минимума у данной
функции нет.
a — xQ хх х2 х3 х4 х5 х6 х7 х8 х9 о — х10 х
Рис. 15
Точки локального минимума, в которых минимум достигается в смысле
определения 1.1, в литературе часто называют точками глобального
минимума или точками абсолютного минимума функции f(x) на множестве X.
Для функции, изображенной на рис. 1.5, X* = {х2} и [х8; х9] — точки
глобального минимума.
1.1.2. Задача максимизации
Перейдем к обсуждению постановки задачи максимизации, которую
кратко будем записывать так:
f(x) —> max, x e X. (1.2)
Для пояснения постановки задачи (1.2), как и в случае задачи
минимизации (1.1), нам понадобятся некоторые определения.
Определение 1.5. Точку х* е X будем называть точкой максимума
функции f(x) на множестве X, если f(x*) > f(x) для всех х е X; величину
f(x*) назовем наибольшим или максимальным значением f(x) на X и
обозначим тах/(х) = /(х*) = /*. Множество всех точек максимума/(х) на X
хеХ
будем обозначать через X*.
Определение 1.6. Функция f(x) называется ограниченной сверху
на множестве X, если существует такое число Mv что f(x) < Мх для всех
х g X. Функция f(x) не ограничена сверху на X, если найдется
последовательность {xk} g Xтакая, что lim fixk) = +°°. Если функция ограничена на X
k—>oo
и сверху, и снизу, то она называется ограниченной на X.
20

Определение 1.7. Пусть функция/(г) ограничена сверху на
множестве X. Тогда число /* называется точной верхней гранью или супремумом
f(x) на X, если:
1) /* >f(x) при всех хе X;
2) для любого сколь угодно малого числа 6 > 0 найдется точка хе е X
такая, что f(xE) > /* - е.
Точную верхнюю грань/(х) на X будем обозначать через sup/(x) = /*.
хеХ
Если функция f(x) не ограничена сверху на X, то в качестве точной
верхней грани f(x) на X принимается /* = +°°.
Если X* Ф 0, то, очевидно, точная верхняя грань f(x) на X совпадает
с максимальным значением этой функции на X, т.е. sup/(.r) = max/(.r).
хеХ хеХ
В этом случае говорят, что функция/(г) на X достигает своей точной
верхней грани в точке х* е X*. Подчеркнем, что sup/(x) = /* всегда существует
хеХ
[22, 29], причем еслиДг) ограничена сверху на Xчислом Мь то/* <МХ<
< +°°, и/* = +°°, если/(х) не ограничена сверху на X. Выражение тах/(х)
хеХ
не всегда имеет смысл. Справедливы соображения, аналогичные
высказанным ранее: если функция достигает какой-то своей верхней грани, то эта
верхняя грань необходимо будет точной верхней гранью.
Для иллюстрации сказанного обратимся к функциям f(x) и
множествам X из примеров 1.1—1.4, но задачи минимизации в них заменим
задачами максимизации.
В примере 1.1 для обоих множеств Хх = Еп, Х2 = {\\х\\ > 1} максимальное
значение функции f(x) равно /* = 1, X* = {Цх|| = 1} — n-мерная сфера
радиуса 1 с центром х = О (при п = 1 это две точки х* = 1 и х* = -1), что следует
из неравенства
21Ы1 (Ы-1)2
1+Ы12" 1+Ы12
l-f(x) = l—^j=KU*\ Z ^0 VxeE",
которое при |д:| = 1 обращается в равенство/(х) = 1 =/*.
В примере 1.2 на множестве X = Х2 = {\\х\\ > 1} максимальное
значение равно/*=1, множество X* = {\\х\\ = 1}; для остальных множеств/* = +°°,
Х*=0.
Г 2
В примере 1.3 на множестве X = [0; +°°) имеем /* = 1, X* =\ х = —-—,
I 2« + 1
6 = 0,1,...}.
В примере 1.4 /* = 0, X* = {х = 1}.
В задачах максимизации (1.2) также можно различать задачи двух
типов: в задаче первого типа ищется величина/*, а в задачах второго типа
ищутся/* и какая-либо точка максимумах* такая, чтоДг*) =/*.
Задачи (1.1), (1.2) тесно связаны между собой равенством
sup/(*) = -inf (-/(*)), (1.3)
хеХ xsX
21

из которого следует, что всякая задача максимизации функции f(x) на X
равносильна задаче минимизации
def
g(.r)->min, хеХ, g(x)=-f(x). (1.4)
Отсюда ясно, что методы, разработанные для решения задач
минимизации, нетрудно переформулировать и использовать для решения задач
максимизации. Поэтому в дальнейшем мы в основном будем исследовать
задачу минимизации (1.1).
Сказанное относится и к задачам поиска точек локального максимума
функции f(x) на множестве X.
Определение 1.8. х*е X называется точкой локального максимума
функции f(x) на множестве X со значением /* = f(x*), если существует такая
малая 6-окрестность 0(х*, г)={х е Еп :\\х- х*\ < е} точки х*, что/(х*) >f(x)
для всех х е X п 0(х*, г). Если при некотором 6 > 0 равенство/(х) =f(x*)
для х е X п 0(х*, е) возможно только при х = х*, то х* называют точкой
строгого локального максимума.
Точки локального максимума, в которых максимум достигается
в смысле определения 1.5, часто называют точками глобального максимума
или точками абсолютного максимума функции f(x) на множестве X.
Для функции, график которой изображен на рис. 1.5, точки xv x3, х7,
х10 являются точками строгого локального максимума, а в точках х,
удовлетворяющих неравенствам х5 < х < х6 и х8 < х < х9, реализуется нестрогий
локальный максимум; х3, х7 — точки глобального максимума. Других точек
локального максимума у нее нет. Обращаем внимание читателя на то, что
все точки х из интервалов (х5, х6) и (х8, х9) одновременно являются как
точками локального минимума, так и точками локального максимума.
Множество всех точек локального минимума или максимума функции
на множестве X принято называть точками локального экстремума
функции на этом множестве или, проще, точками экстремума. Если мы хотим
найти все точки экстремума (как минимума, так и максимума), то,
объединяя постановки задач (1.1), (1.2), кратко будем писать
f(x) —> extr, x g X.
Функцию/(х) в задачах (1.1), (1.2) часто называют целевой функцией,
множество X — допустимым множеством, точки х е X — допустимыми
точками.
1.2. Теоремы Вейерштрасса
1.2.1. Классическая теорема
Как мы видели в простейших примерах 1.1—1.4, функция/(х) может
быть ограниченной или неограниченной сверху или снизу на множестве X,
множество точек ее экстремума может быть пустым или непустым.
Приведем теорему Вейерштрасса из классического математического анализа,
в которой даются достаточные условия на целевую функцию f(x) и
допустимое множество X, гарантирующие конечность точной нижней и точной
верхней граней и непустоту множества точек экстремума f(x) на X. Сна-
22

чала напомним некоторые определения и факты из математического
анализа [20, 22, 29].
Определение 1.9 Пусть {xk} = (xv x2, ..., xk, ...) — некоторая
последовательность точек из Еп. Последовательность {xk} называется
ограниченной, если существует такое число М > 0, что \\xk\\ < М для всех А = 1, 2, ... .
Последовательность {xk} называется неограниченной, если существует ее
подпоследовательность {xk } такая, что limlbty | = +°°- Точка v называется
' /->ооН 'II
предельной точкой последовательности {xk}, если существует ее
подпоследовательность {xk }, сходящаяся к v.
Согласно теореме Больцано — Вейерштрасса [20, 22, 29] всякая
ограниченная последовательность {xk} e Еп имеет хотя бы одну предельную точку.
Определение 1.10. Множество X с Еп называется ограниченным, если
существует число М > 0 такое, что || х || < М для всех х е X. Множество X
называется неограниченным, если существует последовательность {xk} e X
такая, что lim \хЛ = -н».
Определение 1.11. Точка v e Еп называется предельной точкой
множества X, если любая ее е-окрестность 0(v, е) = {х е Еп : || х - v || < е} содержит
точку w е X, отличную от v (w Ф v).
Из этого определения следует, что точка v будет предельной точкой
множества X тогда и только тогда, когда существует последовательность
{xk} е X, хкФ v, k = 1, 2,..., сходящаяся к точке v. Предельная точка
множества X может как принадлежать X, так и не принадлежать ему.
Определение 1.12. Точка v называется внутренней точкой множествах,
если существует ее е-окрестность 0(р, б) = {х е Еп : \\х - v\\ < г}, которая
целиком принадлежит множеству X. Если найдется е-окрестность точки v,
которая не содержит ни одной точки из X, то v назовем внешней точкой
множества X. Если любая е-окрестность точки v содержит как точки из X,
так и точки, не принадлежащие X, то v называется граничной точкой
множества X. Наконец, возможно, что точка v принадлежит множеству X,
но существует е-окрестность этой точки, не содержащая никакой другой
точки этого множества. Такая точка v называется изолированной точкой
множества X.
Совокупность всех внутренних точек множества X будем обозначать
через intX, совокупность всех граничных точек — через ГрХ
Уточним, что изолированная точка v множества X является его
граничной точкой, причем она является предельной точкой единственной
последовательности элементов множества X, а именно {xk= v), k = 1, 2,... .
Внутренние точки множества и его граничные точки, не являющиеся
изолированными, будут предельными точками множества X, а внешние и
изолированные точки множества X не являются его предельными точками.
Определение 1.13. Множество Хс£я называется замкнутым, если оно
содержит все свои предельные точки.
Из вышесказанного вытекает, что замкнутое множество является
объединением всех своих внутренних и граничных (включая изолированные)
точек. В частности, множество, состоящее только из изолированных точек,
является замкнутым.
23

Определение 1.14. Множество ХсР такое, что каждая
последовательность {xk} e X обладает хотя бы одной предельной в смысле
определения 1.11 точкой, лежащей в X, называется компактным.
Из теоремы Больцано — Вейерштрасса и определений 1.9—1.12 следует,
что в Еп компактными являются все замкнутые ограниченные множества
и только они (т.е любое компактное множество из Еп ограничено и
содержит все свои предельные точки).
Примерами компактных множеств в пространстве Еп являются
следующие:
• п-мерный шар радиуса R с центром в точке х0 е Еп
• n-мерная сфера Х= {хе Еп : ||х - х0\\ = R};
• и-мерный параллелепипед X = {х е Еп : а{< х{< biy г = 1, ..., п), где ai9
Ъ{, а{ < Ъ{, г = 1,..., п — заданные числа;
• отрезок X = [и, v] = {х е Еп : х = ха = аи + (1 - сс)а, 0 < ос < 1},
соединяющий точки и, v g Еп\
• множество X = {х е Еп : ||#||(||#|| - 1)(||^|| - 2) < 0}, являющееся
объединением кольца 1 < || х || < 2 и изолированной точки 0.
Примерами некомпактных множеств являются следующие замкнутые,
но неограниченные множества:
• все пространство X = Еп\
def
• неотрицательный ортант X-Е1^ = {х е Еп\ х1 > 0,..., хп > 0};
• гиперплоскость X = {х е Еп : (с, х) = у}, где у — заданное число, с е Еп,
сфО — заданный вектор, который называют нормальным вектором
гиперплоскости;
• полупространство X = {х е Еп : (с, х) < у} или X = {х е Еп : (с, х) > у};
• прямая X = {х g Еп : х = x(t) =x0+td,-°o<t< +°°}, проходящая через
точку х0, с направляющим вектором d e En, d*0;
• лучX = {хе Еп:х = x(t) = x0+td,t> 0}.
Открытый луч X = {х g En:x = x(t) =x0+td,t>0}H открытый n-мерный
шар X = {х е Еп: || х - х0 \\ < R} также являются некомпактными множествами.
Определение 1.15. Пусть функция/(х) определена на множестве X с Еп.
Говорят, что функция f(x) непрерывна в точке х е X, если для любой
последовательности {xk} e X, сходящейся к точке х, справедливо равенство
\imf(xk) = f(x). Функцию/(х) называют непрерывной на множестве X,
k—>oo
если она непрерывна в каждой точке этого множества.
Приведем формулировку теоремы Вейерштрасса для непрерывных
функций в том виде, как она дается в обычных курсах математического
анализа [20, 22, 29].
Теорема 1.1. Пусть X — компактное множество из Еп, функция f(x)
определена и непрерывна на X. Тогда
/* = inf/(x)>-oo, X*={xeX:f(x) = f*}*0;
хеХ
Г = supf(x)<-ко, Г={хеX:f(x) = f*}*0.
хеХ
24

1.2.2. Обобщенная теорема Вейерштрасса
Теорема 1.1 дает достаточные условия разрешимости одновременно как
задачи минимизации (1.1), так и задачи максимизации (1.2).
Между тем на простейших примерах 1.1—1.4 мы видели, что эти задачи
не всегда разрешимы одновременно. Это обстоятельство наводит на мысль
о том, что условия теоремы 1.1, гарантирующие одновременную
разрешимость задач (1.1), (1.2), по-видимому, являются слишком жесткими.
Внимательный анализ теоремы 1.1 показывает, что условие непрерывности
целевой функции/(х) можно существенно ослабить. Оказывается, для
разрешимости задачи минимизации достаточно полунепрерывности снизу
функции /(г), для задачи максимизации — ее полунепрерывности сверху.
Дадим строгое определение этих понятий. Предварительно введем понятие
нижнего и верхнего пределов последовательности.
Определение 1.16. Число а называется нижним {верхним) пределом
ограниченной снизу (сверху) числовой последовательности {ak}, если:
1) существует хотя бы одна подпоследовательность {ak }, сходящаяся
к а;
2) все предельные точки последовательности {ak} не меньше (не больше)
числа а, т.е. число а является наименьшей (наибольшей) предельной
точкой последовательности {ak}.
Нижний и верхний пределы будем обозначать lim ak и lim ak соответ-
ственно.
Иначе говоря, а — нижний (верхний) предел последовательности {ak},
если для любого 6 > 0:
1) существует номер N такой, что ak > а - е (ak < а + е) для всех k > N;
2) для любого номера т найдется номер km> m такой, что ak <a + e
(%^-е).
В том случае, когда {ak} не ограничена снизу (сверху), то по
определению принимают lim ak=-°o (lim ak = -н»); в частности, если lim ak = -©о, то
lim ak = -оо; (если lim ak = +°°, то lim ak = +°°).
Например:
• если ak= (-1)*, k = 1, 2,..., то Итя^ =-1, \imak =1;
• если ak= (-l)kk, k= 1,2,..., то lim ak = -oo, Hm ak = +oo;
• если ak= [1 + (-l)k]k, k = 1, 2,..., то hmak =0, \imak = +oo;
• если ak= hrx, k= 1,2,..., то lim ak = lim ak = 0.
Важно заметить, что нижний и верхний пределы (конечные или
бесконечные), в отличие от обычного предела, у любой последовательности
всегда существуют. Для того чтобы последовательность {ak} имела обычный
предел, необходимо и достаточно, чтобы lim ak = lim ak=a; тогда lim ak = a.
£—>oo k—>°o k—>°o
Определение 1.17. Пусть функция/(х) определена на множестве X с Еп.
Говорят, что функция f(x) полунепрерывна снизу {сверху) в точке х е X,
25

если для любой последовательности {xk} e X, сходящейся к точке х, имеет
место соотношение lim f(xk)> f(x) (lim f(xk)< f(x)). Функцию/(х) назы-
вают полунепрерывной снизу (сверху) на множестве X, если она
полунепрерывна снизу (сверху) в каждой точке этого множества.
На рис. 1.6 изображены графики функций, не непрерывных, но
полунепрерывных снизу в точке а, на рис. 1.7 — не непрерывных, но
полунепрерывных сверху в точке а. Функция, график которой изображен на рис. 1.8,
не является в точке а ни полунепрерывной снизу, ни полунепрерывной
сверху.
»t
Рис. 1.6
У\
Рис. 1.7
Рис. 1.8
Предлагаем читателю доказать, что функция f(x) полунепрерывна
снизу (сверху) в точке х е X тогда и только тогда, когда для любого 6 > О
существует 8 > 0 такое, что для всех у е X таких, что ||у - х\\ < 8,
справедливо неравенство f(y) > f(x) - г if (у) < f(x) + б). Нетрудно убедиться, что
функция непрерывна в точке х тогда и только тогда, когда она в этой точке
полунепрерывна и снизу, и сверху.
26

Пусть Х= {х g Еп : ||х|| < 1} — «-мерный единичный шар;/(х) = ||х|| при 0 < ||х|| < 1
и/(0) = а. Тогда при а < О функция/(х) будет полунепрерывна снизу на X, при а > О —
полунепрерывна сверху на X; при а = О — непрерывна на X
Пример 1.6
Пусть X = (-©о; +°о),
/(*) =
sin—, х>0,
-х, х<0,
1<2, Х = 0.
Тогда при а<-\ эта функция будет полунепрерывной снизу на X, при я > 1 —
полунепрерывной сверху, при | а \ < 1 в точке х = О эта функция не будет
полунепрерывной ни снизу, ни сверху.
Установим связь между свойством полунепрерывности снизу функции
и замкнутостью множеств
М(с) = {хе X: f(x) <c},c = const,
называемых множествами Лебега функции f(x) на множестве X.
Лемма 1.1. Пусть X — замкнутое множество из Еп. Тогда для того чтобы
функция f(x) была полунепрерывна снизу на X, необходимо и достаточно,
чтобы множество Лебега М(с) было замкнутым при всех с (пустое
множество считается замкнутым по определению). В частности, еслиДг)
полунепрерывна снизу на X, то множество X* точек минимума/(х) на X замкнуто.
Доказательство
Необходимость. Пусть f(x) полунепрерывна снизу на X. Возьмем
произвольное число с, будем полагать, что М(с) Ф 0. Рассмотрим какую-либо
предельную точку w множества М(с). Тогда существует последовательность
{xk} g M(c), сходящаяся к w. В силу замкнутости X точка we Х.Из того, что
f(xk) < с, k = 1, 2,..., с учетом полунепрерывности снизу/(х) в точке w имеем
f(w) < lim f(xk) < с, т.е. w e M(c). Замкнутость М(с) доказана. В частности,
k—>оо
множество X* = {х е X:f(x) < f* = inf f(x)} замкнуто.
Достаточность. Пусть для некоторой функции f(x) множество М(с)
замкнуто при любом с. Возьмем произвольные 6 > 0, х е X и
последовательность {xk} е X, сходящуюся к точкех. Пусть lim f(xk)-a- lim f(xk ).
£->оо /И->оо т
Тогда f(xk ) < а + 6, т.е. xk е М(а + б) для всех достаточно больших
номеров km. Но множество М(а + б) замкнуто по условию, а точка х является
пределом для {xk }. Следовательно, х е М(а + б), т.е. f(x) < а + 6. В силу
произвольности 6 > 0 отсюда имеем f(x)<a= lim f(xk). ■
k—>oo
Ниже мы приведем несколько расширенную формулировку теоремы
Вейерштрасса для полунепрерывных функций, используя понятия
минимизирующей или максимизирующей последовательностей. Дело в том, что
27

на практике точно определить координаты точки экстремума удается лишь
в редких случаях, если даже их существование гарантировано строгими
утверждениями типа теоремы 1.1. Ниже мы увидим, что все
итерационные методы оптимизации, по сути, представляют из себя описание правил
построения минимизирующей и максимизирующей последовательностей.
Определение 1.18. Последовательность {xk} e X называется
минимизирующей (максимизирующей) для функции f(x) на множестве X, если
Jim /(**)= inf /(*) = /* (Jim f(xk) = sup/(x) = /*).
Из определения и существования нижней (верхней) грани функции
f(x) на множестве X следует, что хотя бы одна минимизирующая
(максимизирующая) последовательность гарантированно существует. В самом
деле, если /* = -«>, то найдется последовательность {xk} e X такая, что
lim f(xk) = -©о = /*. Если/*> -©о, то согласно определению 1.3 нижней грани
£->оо
для любого номера k > О существует точка xk, для которой
/.</(*,)</,+р k = l,2,....
Отсюда следует, что \imf(xk) = f*. Аналогично, опираясь на определе-
k—>oo
ние 1.7 верхней грани, можно построить максимизирующую
последовательность.
Определение 1.19. Скажем, что последовательность {xk} сходится
к непустому множеству X, если Нтр(х^,Х) = 0, где р(и,Х) = inf \\u-x\\ —
k—>оо ХЕХ
расстояние от точки и е Еп до множества X.
Лемма 1.2. Пусть X — произвольное непустое множество из Еп,
р(г/, X) = inf \\и - х\\ — расстояние от точки и е Еп до множества X. Тогда
хеХ
справедливо неравенство
\p(u,X)-p(v,XJ[<\\u-v\\ \/u,veEn. (1.5)
Доказательство
Прежде всего из соотношений р(г/, w) = \\и - w\\ > 0 и р(г/,Х)<||г/-гИ|
(w g X) следует, что функция р(г/, X) неотрицательна и конечна во всех
точках и е Еп. Возьмем произвольное число 6 > 0. По определению нижней
грани для любых и, v е Еп найдутся точки uv vE e X такие, что
р(г/, X) < р(г/, и£) < р(г/, X) + 8, р(р, X) < p(v, v£) < p(v, X) + 8.
Из этих неравенств с помощью неравенства треугольника р(г/, vE) < р(г/, v) +
+ p(v, v£) и того, что р(г/, X) < р(г/, vE), имеем
р(г/, X) - р(р, X) < р(г/, v£) - p(v, v£) + e< р(г/, v) + 8.
Аналогично получается неравенство
р(г/, X) - p(v, X) > р(г/, щ ) - 8 - р(я, щ ) > -р(г/, и) - 8.
28

Объединяя последние два неравенства, имеем | р(г/, X) - p(v, X)\ <
< р(г/, v) + 8. Отсюда, переходя к пределу при 8 —» +0, получаем требуемое
неравенство. ■
Из неравенства (1.5) следует, что lim p(vk, X) = p(v, X) для любой после-
£->оо
довательности {vk}, сходящейся к точке v, т.е. функция р(и, X) непрерывна
по и в любой точке v e Еп.
Теперь мы можем сформулировать и доказать расширенную теорему
Вейерштрасса.
Теорема 1.2. Пусть X — компактное множество из Еп, а функция f(x)
определена и полунепрерывна снизу (сверху) на X. Тогда
/• = inf/(*) > — (/* = sup/(x) < +oo),
хеХ хеХ
множество X* = {х е X:f(x) = /*} (X* ={хе X:f(x) = /*}) непусто,
компактно и любая минимизирующая (максимизирующая) последовательность
сходится к X* (X*).
Доказательство
Рассмотрим вариант теоремы, касающийся задачи минимизации. Как
было показано выше, гарантированно существует хотя бы одна
минимизирующая последовательность {xk}, т.е. xke X,k= \, 2, ..., lim f(xk) = /*. Рас-
£->оо
смотрим любую из них. Так как X — компактное множество, то {xk} имеет
хотя бы одну предельную точку и все ее предельные точки принадлежат X.
Возьмем любую предельную точку х* этой последовательности. Тогда
существует подпоследовательность {xk }, сходящаяся к точке х*.
Пользуясь свойством нижней грани /* и полунепрерывностью снизу функции
f(x) в точке х*, имеем /* < f(x*)< lim f(xk ) = lim f(xk) = /*, т.е. f(x*) = /*.
Отсюда следует, что /* > -oo, X* Ф 0, а любая предельная точка любой
минимизирующей последовательности лежит в X*.
Докажем, что X* компактно. Возьмем любую последовательность {vk}e X*.
Так как {vk} e X — компактному множеству, то существует ее
подпоследовательность {vk }, сходящаяся к некоторой точке v* e X. Но {vk} —
минимизирующая последовательность, так как f(vk) = /*, k = 1, 2,.... По доказанному
выше тогда и* е X*, значит, X* — компактно.
Наконец, покажем, что любая минимизирующая последовательность
{xk} сходится к X*. Так как p(xk, X*) = inf p(xk, x) > 0, k = 1, 2,..., то ясно, что
хеХ*
Итр(^,Х*)>0. Пусть Нтр(х^,Х*)= lim p(xk ,Х*) = я<+оо. В силу ком-
пактности X из {xk } можно выбрать подпоследовательность, сходящуюся
к некоторой точке х*. Не умаляя общности, можем считать, что сама
последовательность {xk } сходится к х* (чтобы не переходить к тройной
индексации). Согласно лемме 1.2 функция р(х, X*) непрерывна по переменной х,
поэтому lim p(xk , X*) = р(х*, Х*) = а. Однако по доказанному ранее х* е X*.
т—>оо т
Тогда а - р(х*, X*) = 0. Это значит, что lim p(xk, X*) = lim p(xk, X*) = 0. Сле-
довательно, предел Нтр(х^,Х*) существует и равен нулю.
k—>oo
29

Вариант этой теоремы, относящийся к задаче максимизации f(x) на X,
доказывается аналогично и опирается на соотношения (1.3), (1.4).
Теорема 1.2 доказана. ■
В теореме 1.2 сформулированы достаточные условия, гарантирующие,
что в задачах (1.1), (1.2) нижняя и верхняя грани целевой функции/(х)
на допустимом множестве X достигаются хотя бы в одной точке.
Разумеется, отдельные утверждения этой теоремы остаются справедливыми
и при нарушении некоторых ее условий, о чем свидетельствуют при-
2\\х\\
меры 1.1—1.4. В частности, в примере 1.1 функция f(x) = непре-
1+Ыг
рывна на множестве Хх = Еп, но это множество не является компактным
(оно замкнуто, но не ограничено). Тем не менее здесь /* = О, X* = {х = 0} Ф 0,
т.е. часть утверждений теоремы 1.2 справедлива, однако существуют
минимизирующие последовательности
, R = 1, Z,..., Xfe = \ку лс,..., к), R = 1, Z,...,
первая из которых сходится к X*, а вторая — нет.
1.2.3. Теорема Вейерштрасса для некомпактных множеств
Заметим, что в теоремах 1.1, 1.2 условие компактности множества X
является довольно жестким. Приведем две теоремы, которые также будем
называть теоремами Вейерштрасса, но в которых компактность
множества X не предполагается, зато функция f(x), кроме полунепрерывности
на X, удовлетворяет некоторым дополнительным требованиям.
Теорема 1.3. Пусть X — непустое замкнутое множество из Еп, функция
f(x) полунепрерывна снизу (сверху) наХи для некоторой точки v e X
множество Лебега
M(v) = {xeX: f(x) < f(v)} (M,(v) = {xeX: f(x) > f(v)})
ограничено. Тогда /* > -°° (/* < +°°), множество X* (X*) непусто, компактно
и содержится в множестве M(v) (M{(v)), любая минимизирующая
(максимизирующая) последовательность {xk}, принадлежащая множеству M(v)
(Mf (а)), сходится к множеству X*.
Доказательство
Рассмотрим вариант этой теоремы, касающийся задачи минимизации.
По определению множества M(v) имеем: f(x) > f(v) при всех х е X \ M(v)
и f(x) < f(v) при всех х е M(v). Это значит, что на X \ M(v) функция f(x)
не может достигать своей нижней грани на X и для доказательства теоремы
достаточно рассмотреть функцию f(x) на множестве M(v).
По лемме 1.1 множество M(v) замкнуто, из его замкнутости и
ограниченности следует его компактность. Применяя к эквивалентной исходной
задаче минимизации
f(x) —> min, x e M(v)
теорему 1.2, получим все утверждения теоремы, относящиеся к задаче
минимизации функции f(x) на множестве X. Подчеркнем, что в этой теоре-
30
г(1)_

ме утверждается сходимость к X* только тех минимизирующих
последовательностей {xk}, которые принадлежат M(v). В случае f(v) > /* условие
{xk} е M(v) можно не оговаривать, так для любой минимизирующей
последовательности {xk} найдется номер k0 такой, чтоДл^) <f(v) для всех k > k0,
т.е. xk g M(v) при k > k$. Если же f(v) = /*, то X* = M(v), и в этом случае
могут существовать минимизирующие последовательности, которые не
принадлежат M(v) и не сходятся к X*. Для обоснования этого факта достаточно
вернуться к примеру 1.1 и положить v = 0. Тогда, очевидно, M(v) = {0},
последовательность xk= (k, k,..., k), & = 1, 2,..., будет минимизирующей, не
содержащейся в M(v) и не сходящейся к X*.
Вариант теоремы 1.3, касающийся задачи максимизации функции/(х)
на множестве X, доказывается и комментируется аналогично, с опорой
на соотношения (1.3), (1.4), связывающие задачи минимизации и
максимизации. ■
Теорема 1.4. Пусть X — непустое замкнутое множество из Еп, функция
f(x) полунепрерывна снизу (сверху) на X и для любой последовательности
{xk} e X такой, что lim \хЛ = +°°, справедливо равенство
limf(xk) = +оо (lim f(xk) = -~).
k—>°o k—>°o
Тогда /* > -°° (/* < +°°), множество X* (X*) непусто, компактно и любая
минимизирующая (максимизирующая) последовательность {xk} сходится
кХ*(Х*).
Доказательство
Рассмотрим вариант теоремы, касающийся задачи минимизации.
Заметим, что если множество X ограничено, то все утверждения теоремы
следуют из теоремы 1.2. Поэтому пусть X неограничено, т.е. существует хотя
бы одна последовательность {vk} е X такая, что lim lb J = +«>. Тогда согласно
условию теоремы lim/(^) = +oo. Возьмем какую-либо точку v e X такую,
£->оо
что f(v) > f* (например, можно принять v - vk при достаточно большом k),
и рассмотрим множество Лебега M(v) = {х е X : f(x) < f(v)}. Допустим,
что множество M(v) неограничено, тогда существует последовательность
{wk} e M(v) такая, что lim|UJ + °°. В этом случае Нт/(г^) = +°°, что про-
тиворечит неравенству f(wk)<f(v)<+o°, вытекающему из включения
wke M(v), k=\,2,.... Таким образом, множество M(v) ограничено. Отсюда
и из теоремы 1.3 следуют все утверждения теоремы 1.4.
Для задачи максимизации доказательство проводится аналогично. ■
Еще одно обобщение теоремы Вейерштрасса можно найти в
упражнении 1.17 к этой главе.
Следует заметить, что теоремы 1.1—1.4 Вейерштрасса неконструктивны:
они лишь утверждают, что величины /* или /* конечны, а множества X*, X*
непусты, но они не содержат в себе методы вычисления указанных
величин, нахождения точек экстремума. Тем не менее ценность этих теорем
в том, что они гарантируют разрешимость задач оптимизации (1.1), (1.2).
Более того, они подсказывают, что одним из методов получения прибли-
31

женного решения этих задач является построение минимизирующих
(максимизирующих) последовательностей. Конкретные способы этих
построений будут рассмотрены в гл. 4.
1.3. Задачи безусловной оптимизации. Классический метод
1.3.1. Описание метода
Рассмотрим задачу поиска локального или глобального экстремума
гладкой функции многих переменных на всем пространстве Еп. Такую
задачу принято называть задачей на безусловный экстремум или задачей
безусловной оптимизации. В этом термине отражен тот факт, что на
переменные х = (х1,..., хп) никакие дополнительные ограничения в такой задаче
не накладываются. Если необходимо искать только точки минимума или
точки максимума, то такую задачу называют задачей безусловной
минимизации или безусловной максимизации соответственно.
Задачи безусловной оптимизации часто возникают при обработке
результатов экспериментов, измерений, наблюдений за какими-либо
физическими, экономическими процессами. Предположим, что
наблюдаемый процесс характеризуется набором параметров х = (х1, х2, ..., х*) е Еп,
а результатом является действительное число у. Пусть проведено т
наблюдений и получены числа ур соответствующие параметрам Xj =(xj,...,xp,
7=1,..., т. Точная зависимость между х и у нам неизвестна, но имеющийся
у нас опыт наблюдений дает нам основание предполагать, что эта
зависимость описывается функцией вида у = ф(х, а), зависящей от числовых
параметров а = (av ..., as). Тогда естественно попытаться подобрать параметры а
так, чтобы зависимость указанного вида наилучшим образом
аппроксимировала результаты наблюдений уь ..., ут. В качестве меры точности
наблюдений часто берут функцию
т
f(a)=l(yj-q>(xpa))2. (1-6)
7=1
Наилучшим считается такое значение параметров а = (av ..., as) e Es,
при котором функция f(x) принимает наименьшее значение на Es.
Обработка результатов наблюдений на основе минимизации функции (1.6)
называется методом наименьших квадратов.
В качестве аппроксимирующей функции ф(х, а) в формуле (1.6) нередко
берут линейную функцию (s = п):
ф(х, а) = {а, х) = аххх +... + а^12. (1.7)
Во многих экономико-математических моделях вводится понятие
производственной функции у = ф(х, а), где у — объем производства, х = (х1, ...,
хп) — вектор используемых ресурсов. Наиболее известным примером
производственной функции служит функция Кобба — Дугласа
y = AY[(xJ)aJ =A(x1)ai(x2)a2 '...-{хп)ап, ^ = const>0.
7=1
32

При построении такой функции для конкретного экономического
объекта числовые параметры аь ..., ап оценивают по статистическим данным
о значениях у и х = (х1,..., хп) за предыдущие периоды времени.
В качестве меры точности наблюдений вместо функции (1.6) могут быть
использованы и другие функции, например
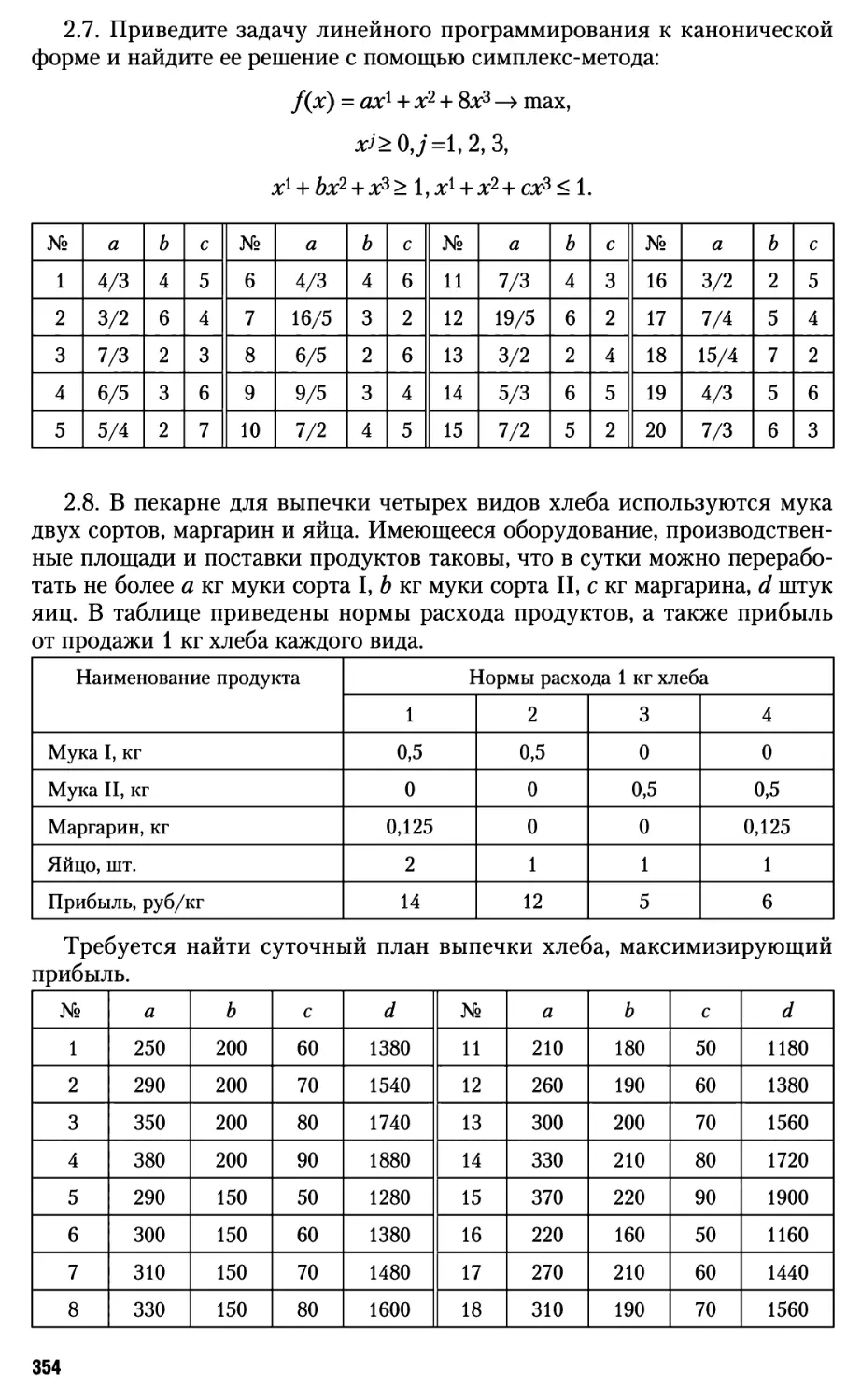
j.
( т Лр
/(*) = 2(У;-Ф(*;>я))р ,р>1,или/(й)=тах|г/,-ф(х-,й)|. (1.8)
Задачи минимизаций функций (1.6)—(1.8) по переменной а на
множестве Es являются задачами безусловной оптимизации.
Кратко изложим классический метод поиска решения задач на
безусловный экстремум, подразумевая под этим тот подход к ним, который основан
на дифференциальном исчислении функций многих переменных и обычно
излагается в учебниках по математическому анализу [22, 29].
Сначала напомним некоторые понятия и факты.
Определение 1.20. Пусть функция/(х) определена в некоторой малой
6-окрестности 0(х, е) = {v е Еп : \\v -х\\ < г} точки х. Говорят, что функция
f(x) дифференцируема в точке х, если существует вектор f\x) e Еп такой,
что приращение функции можно представить в виде
д/(х) = f(x + А) - f{x) = </'(*)> h) + о(й, x) \/h : \\h\\ < e, (1.9)
где o(h, x) — величина, бесконечно малая более высокого порядка, чем || h ||,
|о(А,х)|
что означает lim ' „ ., ' = 0. Вектор f'(x) называется первой производной
11а||->о \\п\\
или градиентом функции / в точке х.
Условие (1.9) однозначно определяет градиент /'(*)> причем
ВДх)
/'(х) = (/;1(х),...,/;„(^))т, где К(х) = Ц£1, i = i,...,n. (1.10)
Таким образом, если функция дифференцируема в точке х, то она
необходимо обладает частными производными в этой точке. Обратное, однако,
неверно: наличие частных производных для функций многих переменных
(п > 2) не гарантирует дифференцируемость функции. Например, функция
fix1, x2) = vk1*2! имеет частные производные
/;,(0,0)= lim ^ ^^ = 0;
JO-(0 + Ar2)|-Vo^O
/;2(0,0)= lim Я-± -^ = 0,
х Д*2-»0 ДГ2
однако для этой функции не выполнено равенство (1.9) при h = (/г1, /г2),
А1 = А2;
J(0+^)(0+^)| = \hy I = 4-llAll ф о(||А||).
33

В этом примере частные производные в точке (0; 0) терпят разрыв.
Достаточным условием дифференцируемости функции/в точке л: является
существование и непрерывность частных производных в этой точке [22, 29].
Если функция дифференцируема в каждой точке множества X, то ее
часто называют гладкой на X. Если производная f\x) существует и
непрерывна в каждой точке хе Х,то функцию/(х) называют непрерывно
дифференцируемой на множестве X. Напомним, что функция, дифференцируемая
в точке х, непрерывна в этой точке.
Определение 1.21. Пусть функция/(х) определена и дифференцируема
во всех точках некоторой е-окрестности точки х. Говорят, что функция/(х)
дважды дифференцируема в точке х, если существует матрица f"(x)
размера п х п такая, что
/'(* + Л) - /'(*) = f'\x)h + ox (А, х) \/h: \\h\\ < е,
(1.11)
i lk(A>*)l
где Km -—й-jj—- = 0. Матрица j(x) называется второй производной, или
||А||—>о \\п\\
гессианом, функции / в точке х.
Условие (1.11) однозначно определяет вторую производную/"(г), причем
7*1*1 С*) fx'lx2(X) - fx'lxn(X)
f'2Y\(x) /'L2CO - Jr2Yn(X)
/"(*)=
Э2/(*)_ Э (df(x)
= {fZrj(x),i,j = U,n}, (1.12)
Jxnxn \X)j
3 (
Э/(*)
Эх1'
вторая частная производ-
где Л- ,•(#) =— =—г, . ,
•/*'*;V ' dxldxJ дх1^ dxJ ) dxJ\
ная функции/(х) по переменным дг1', хК Известно [22, 29], что/"(.г) —
симметричная матрица.
Если функция f(x) дифференцируема в некоторой е-окрестности
точки х, а в самой точке х существует ее вторая производная, то
справедлива формула Тейлора
f(x + h)-f(x)= {f'(x),h)+-{f"(x)Kh) + o2(Kx) VA:||A||<e, (1.13)
где lim
W-x>
\o2(h,x)\
! r—0. Остаточный член в формуле Тейлора взят в форме
Пеано — этого нам будет достаточно в дальнейшем. Заметим попутно, что
другие формы остаточного члена, уточняющие его оценку, накладывают
на функцию/(г) более жесткие условия [22, 29].
Квадратичную форму
d2f(x) = (f"(x)h,h)= %Щ^к*Ы
i j=i oxlaxJ
переменной h = (Л1, ..., hn) e En называют вторым дифференциалом
функции / в точке х. Если функция дважды дифференцируема в каждой точке
34

множества X, то ее часто называют дважды гладкой на X. Если вторая
производная f'(x) существует и непрерывна в каждой точке х е X, то
функцию/(х) называют дважды непрерывно дифференцируемой на множестве X.
Определение 1.22. Пусть А = {а^ i,j = 1,..., п} — симметричная матрица
п
размера п х п, (Ah,h) = £ а^Ы — соответствующая ей квадратичная
форма. Говорят, что матрица А положительно (неотрицательно)
определена на Еп и обозначают А > О (А > 0), если
(Ah,h)>0 ((Ah,h)> 0) \/heEn,h*0 (\/heEn).
Аналогично матрица А отрицательно (неположительно) определена
на Еп, т.е. А < 0 (А < 0), если
(Ah,h)<0 ((Ah,h)<0) \/heEn,hФ0 (\/heEn).
Перейдем к изложению необходимых и достаточных условий
оптимальности в задачах на безусловный экстремум.
Теорема 1.5 (необходимое условие экстремума). Пусть х* — точка
локального экстремума (минимума или максимума) функции f(x) на Еп,
a f(x) дифференцируема в точке х*. Тогда
/'(*.) = <>. (1.14)
Если/(х) дифференцируема в некоторой г-окрестности 0(х*, б) точки х*
и дважды дифференцируема в точке х*, то /"(**)>0 в точке локального
минимума и f"(x*)< 0 в точке локального максимума.
Доказательство
Пусть для определенности х* — точка локального минимума
функции f(x) на Еп. Это значит, что существует 8-окрестность 0(х*,Ь) точки х*
такая, что f(x) > f(x*) \/х е 0(х*, 8). Отсюда и из формулы (1.9) при х = х*,
h = -tf'(x*), 0 < t < t0, где число t0 столь мало, что t0 \f'(x*)\\ < 8, имеем
0 < </'(*.)." */'(*•)> + o(t) = -t\fXx. )f + o(t).
Разделим это неравенство на t > 0 и затем устремим t —» +0. Получим
-|/'(**)| > 0, что возможно только при выполнении равенства (1.14).
Далее, пусть/(х) дифференцируема в окрестности 0(х*,е) и дважды
дифференцируема в точке х*. Зафиксируем произвольное h e Еп и
возьмем t0> 0 столь малым, что t0 \\h\\ < г. Тогда х = х* + th e 0(х*,г) и из формулы
(1.13) с учетом уже доказанного равенства (1.14) имеем
0<f(x. +th)-f(x*) = -(f"(x*)th,th) + o(t2) \/t:0<t<t0.
Разделив это неравенство на t2 и устремив t —»+0, находим 0 < (f"(x* )h, h)
V h g En. Согласно определению 1.22 это значит, что /"(#*) >0. Так как
точка локального максимума функции f(x) является точкой локального
минимума функции (-f(x)), то, применяя уже доказанные утверждения
теоремы к функции (-f(x)), получим, что если х* — точка локального
максимума/^) на Еп, то f'(x*) = 0, f"(x*) < 0. ■
35

Определение 1.23. Точка v, удовлетворяющая уравнению f'(v) = О,
называется стационарной точкой функции/(х).
Из теоремы 1.5 следует, что в задаче безусловной оптимизации только
стационарные точки могут быть точками экстремума дифференцируемой
на Еп функции. Однако стационарная точка не всегда является точкой
экстремума. Более того, даже если в стационарной точке v выполняется
условие f"(v) > О (f"(v) < 0), то и это не значит, что точка v непременно
является точкой локального минимума (максимума). Можно уверенно сказать
лишь одно: если функция/(х) дифференцируема на Еп, то ее стационарные
точки, и только они, являются подозрительными на экстремум.
Пример 1.7
Пусть/(w) = х4 - г/4, и = (х, у) е Е2. Очевидно, v = (0; 0) — единственная
стационарная точка функции/, в ней матрица f'(v) нулевая и является как неотрицательно,
так и неположительно определенной. Однако в любой е-окрестности точки v = 0
существуют точки х = (е, 0) и у = (0, е), в которых/(х) >f(v) = 0 и f(y) <f(v) = 0, т.е. v = 0
не является точкой экстремума.
Этот пример показывает, что условия экстремума, сформулированные
в теореме 1.5, являются лишь необходимыми, но в общем случае этих
условий недостаточно для наличия экстремума. Тем не менее оказывается, что,
несколько усилив условия теоремы 1.5, можно получить условия,
достаточные для наличия экстремума.
Теорема 1.6. Пусть функция f(x) дифференцируема в окрестности 0(р, б)
стационарной точки v этой функции и дважды дифференцируема в точке v.
Тогда если f"(v) > 0,mo v — точка строгого локального минимума функции
f(x), а если/"(р) <0,mov — точка строгого локального максимума. Если
квадратичная форма {f"(v)h, h) принимает значения разных знаков, то в точке v
функция не имеет ни локального минимума, ни локального максимума.
Доказательство
Пусть в точке v выполнены условия f'(v) = 0, f"(v) > 0, но v не является
точкой строгого локального минимума. Тогда существует последовательность
{xk} такая, чтохкФ v, {xk} —»v,f(xk) <f(v). Точки xk можно представить в виде
xk=v + tkdk, где dk = и— л-, tk = \xk - v\ —»0 при k —»°°.
\\хк-Щ
Так как || dk || = 1, то, выбирая при необходимости подпоследовательность
согласно теореме Больцано — Вейерштрасса, можем считать, что {dk} —» d0,
|| d0\\ = 1. Тогда, полагая в формуле (1.13) х = v, h = tkdk, имеем
0>f(xk)-f(v) = ±t%(f"(v)dk,dk) + o(tZ), k = i,2,... ■
Разделим это неравенство на t\ и устремим k —> °о. Получим
(f"(v)d0,d0)<0, что противоречит условию f"(v) > 0. Следовательно, v —
точка строгого локального минимума функции/(х). Аналогично
доказывается, что если f'(v) = 0, f\v) < 0, то v — точка строгого локального
максимума.
36

Наконец, пусть f'(v) = 0 и существуют точки hv h2^0 такие, что
</»V ^><0< </»/*2, h>). (1.15)
Тогда согласно формуле (1.13)
2 n
2 w v^,»., ■ ^2
>0
при всех достаточно малых L Это значит, что в рассматриваемом случае
(1.15) в любой окрестности точки v найдутся точки, в которых значения
функции f(x) могут быть как меньше, так и больше f(v). Следовательно,
v не является точкой локального экстремума этой функции. Теорема 1.6
доказана. ■
Замечание 1.1. Для выяснения знакоопределенности квадратичных
п
форм (Ah, h)= Yj aJtW существуют различные алгебраические критерии
[9,31].
Определение 1.24. Главными минорами матрицы А называются
определители
\i2 **=det
ат - ат
ат '" ат
1 < ц < i2 <... < ц < п, k = \,..., п.
Главными угловыми минорами называются определители А12 ь k=l,..., п.
Для иллюстрации возможностей применения достаточных условий
экстремума мы будем использовать критерий Сильвестра: для того чтобы
выполнялось А > 0, необходимо и достаточно, чтобы все главные миноры
матрицы А были неотрицательны; для того чтобы выполнялось А > 0,
необходимо и достаточно, чтобы все главные угловые миноры матрицы А были
положительны.
Кроме этого, сформулируем критерии знакоопределенности
симметричной матрицы А в терминах собственных чисел этой матрицы.
Напомним, что собственным числом матрицы А называется решение X уравнения
det|Л - Х1п\ = 0, где /„ — единичная матрица размера пх п. Известно, что
если матрица А симметричная, то у нее существует п действительных
собственных чисел Xv X2, ..., Хп (с учетом их кратности). Для того чтобы
симметричная матрица А была неотрицательно (положительно) определена,
необходимо и достаточно, чтобы все собственные числа матрицы А были
неотрицательны (положительны). Квадратичная форма (Ah, h) знакопере-
менна тогда и только тогда, когда у матрицы А имеется хотя бы одно
положительное и хотя бы одно отрицательное собственное число.
Итак, классический метод исследования дважды гладкой функции
f(x) на экстремум на всем пространстве Еп опирается на теоремы 1.5 и 1.6
и заключается в следующем.
37

1. С помощью необходимого условия f\x) = О ищутся все точки,
подозрительные на экстремум.
2. Найденные стационарные точки проверяются на экстремум с
помощью достаточных условий, т.е. проводится исследование
знакоопределенности в них матрицы вторых производных f"(x).
В том случае, когда в стационарной точке v квадратичная форма
{f"(v)h,h) не меняет знака при всех h e Еп, но может равняться нулю
при некоторых h Ф 0, то для выяснения поведения функции в окрестности
точки v можно привлечь старшие производные и связанные с ними формы
более высокого порядка:
dmf(v) = Ъ^г-г-Щ (Л1)* • • .фпУп,
где суммирование проводится по всем целым гь ..., гт таким, что 0 < г{ < т,
i = 1, ..., и, г{ + г2 + ... + гп=т. Однако на практике исследование характера
стационарных точек с помощью форм dmf(v), m > 3, почти не применяется
из-за его громоздкости.
Если описанным выше способом удается выявить все точки
локального минимума (максимума) функции /(г), то для определения
глобального минимума (максимума) этой функции на всем пространстве Еп нужно
сделать две вещи: перебрать все найденные точки и из них выбрать точку
(точки) с наименьшим (наибольшим) значением функции (если
найденных точек конечное количество, то такая точка, одна или несколько,
обязательно существует), затем проверить, может ли функция принимать
значения, меньшие (большие), чем в этой точке. Если нет, то эта точка (точки)
и будет точкой глобального минимума (максимума).
1.3.2. Примеры
Рассмотрим примеры исследования функций на экстремум.
Пример 1.8
Пусть f(u) = —x2 -cosy, и = (х, у) G Е2.
Для исследования этой функции на экстремум применим классический метод.
Из системы уравнений
f\u) = grad/(M) = (f'x(x, у) =x,f'y(x, у) = sin у) = (0,0)
найдем стационарные точки щ= (xk= 0, yk = nk), k = 0, ±1,.... Вторая производная
f" =1 f» =0
J xx x J xy w
1Л*=о fm=cosy
в точке щ равна
'"^-(J cd
1 0
\
о (-i>
-nk
Если k = 2m — четное число, то f"(uk) =
(1 0
>0 по критерию Сильвестра,
поскольку ее главные миноры равны 1. Значит, согласно теореме 1.6 все
стационарные точки и2т= (0, 2nm), m = 0, ±1,... будут точками строгого локального минимума.
38

Более того, поскольку/(w) > -1 для всех и из Еп, то все эти точки являются точками
глобального минимума со значением /* =/(w2m) = -l.
(\ о Л
Если же k = 2т + 1 — нечетное число, то /"(w2m+i) = Л не знакоопределена
[у -1J
в силу того, что ее главные миноры равны 1 и -1. Поэтому точки и2т+\ не являются
точками экстремума рассматриваемой функции.
Этот пример интересен тем, что функция f(u) имеет бесконечно много
локальных (точнее, глобальных) минимумов, но не имеет ни одного
локального максимума.
Пример 1.9
Пусть в пространстве Еп даныр точек х{ = (х/,..., х?\ i = 1,...,р, и требуется найти
точку х е Еп, сумма квадратов расстояний от которой до этих данных точек
минимальна.
Эта задача равносильна задаче минимизации функции /(#) = 2£||*~*i| на ^п-
Функцию f(x) удобнее представить в виде
!=1
9 Р 0 1 Р
f(x) = p\\x\\ -2р{х,х0) + %\\хА ,гдех0=—2>f.
i=\ Pi=\
Отсюда очевидно, что f'(x) = 2р(х - х0) и х0 — единственная стационарная
точка. Вторая производная f"(x) = 2plw где /„ — единичная матрица размера п х п.
Следовательно, (f"(x0)h,h) = 2p\\h\\ >0 при всех h e En,h*0. Значит, по теореме 1.6
х0 — точка строгого локального минимума.
Однако здесь можно сказать больше: х0 — точка глобального минимума функции
f(x) на ЕР. В самом деле, рассматриваемая функция такова, что lim f(x) = -и». Тогда
Ы|-»+оо
по теореме 1.4 множество X* точек глобального минимума/(х) на ЕР непусто, а по
теореме 1.5 любая точка х* из X* является стационарной точкой. Поскольку здесь
имеется единственная стационарная точка х0, то х0 е X*. Следовательно,
*•={*<>}. /•=/(*o)=-p|WI2+Shf-
i=\
Заметим, что при исследовании этой несложной задачи можно было
обойтись и без привлечения теоремы 1.4, поскольку здесь/(х) - f(x0) =
=р||.г-.г0||2>0длявсех.ге Еп. Ясно также, что в этой задаче/* = sup /(х) = -н»,
хеЕп
т.е. задача максимизации функции f(x) на Еп не имеет решения.
Приме
Решим задачу безусловной минимизации
f(u)=x3 + y3-3xy^>min, u = (x,y)E E2.
(бх -3)
Для рассматриваемой функции f'iu) = (Зх2 - Зу, Зу2 - Зх), f"(u) = rt . .
1,-3 бг/J
Стационарными являются точки щ = (1, 1), и2= (0, 0). Применение критерия
(6 -3^|
Сильвестра дает следующие результаты: /"(wi)= 0 >0, поэтому щ — точка
I"3 6)
39

(О -3
строгого локального минимума; квадратичная форма с матрицей f"(u2) = \
V 3 °/
не является знакоопределенной, значит, и2 не является точкой экстремума. В этом
примере функция имеет один локальный минимум, но он не является глобальным;
здесь /* =-«>, минимизирующей последовательностью будет щ= (-&, 0), k = 1, 2, ... .
Нетрудно убедиться, что для этой функции /* =-н».
Рассмотрим задачу безусловной минимизации
/00 = — —+ #4->min, и = (х,у)еЕ2.
4 5
Здесь J'(и) = (*з - Х2, 4г/3), /"(w) =
Г3х2-2х 0
0 12г/2
г0 0
0 0
Стационарных точек две: и0= (0, 0), и{ = (1, 0). В них/(м0) = 0, f"(u0) =
/<«,>=4/"<«•>=(£ I
Пользуясь теоремами 1.5,1.6, мы не можем уверенно сказать, достигается ли в этих
точках какой-либо экстремум, и придется как-то учесть конкретные особенности
рассматриваемой задачи. Для того чтобы распознать характер экстремума в точке и0,
вычислим значения целевой функции в точках ие = (хе = е, уг = 0), ve = (хе = 0, уе = е)
при малых е > 0. Имеем:
/(We) = -e4--e3=e2
1 1
4£"3
<0; f(ve) = e*>0.
Это значит, что в любой окрестности точки и0 = (0, 0) функция может
принимать как положительные, так и отрицательные значения, т.е. точка щ не является
точкой экстремума.
Чтобы понять, что творится в точке щ, во-первых, заметим, что /* = sup f(u) = -н»,
и, во-вторых, обратимся к теоремам 1.3,1.4 Вейерштрасса. Условия этих теорем в
рассматриваемой задаче выполнены, в чем легко убедиться, отдельно рассмотрев слага-
1 1
емые —х4 —х3 и уА функции/(w). Отсюда выводим: нижняя грань /* = inf f(u) > -оо
4 3 иеЕ2
достигается в какой-то точке и*. Но согласно теореме 1.5 такая точка должна быть
стационарной. Из предыдущего вытекает, что такой точкой может быть лишь
и* = щ = (1,0). Впрочем, это можно подтвердить и непосредственно:
/(")-/(",) = ^(*-l)W+2* + l)+t/4=^(*-l)2
1
х+з
2
+ 9
+ #4>0 УиеЕ2.
J
1.4. Задачи на условный экстремум. Правило множителей Лагранжа
1.4.1. Постановка задачи.
Необходимое условие оптимальности на выпуклом множестве
В приложениях задачи на безусловный экстремум встречаются
сравнительно редко. Дело в том, что в практических задачах переменные, как пра-
40

вило, не могут быть совершенно произвольными и должны удовлетворять
некоторым дополнительным условиям, выражающим, например, условия
неотрицательности тех или иных переменных, условия ограниченности
используемых ресурсов, ограничения на параметры конструкции системы,
условия нормировки и т.п. Иначе говоря, переменные х = (х1,..., хп) должны
принадлежать некоторому заданному множеству X е Еп. Тогда чтобы
подчеркнуть, что экстремум функции ищется при условии х е X Ф Еп, часто
говорят о задаче на условный экстремум. В случае, когда ищутся только
точки минимума или точки максимума, говорят о задаче условной
минимизации или условной максимизации соответственно.
В таких задачах мы также будем рассматривать точки локального
минимума и максимума, но теперь будем их различать по тому, являются ли они
внутренними для множества X или граничными.
Изолированную точку можно по определению считать как точкой
строгого локального минимума, так и точкой строгого локального максимума.
В предыдущем параграфе мы рассмотрели задачу безусловной
оптимизации, когда допустимое множество X = Еп состояло лишь из внутренних
точек. Если дважды дифференцируемая функция f(x) на множестве X
имеет точку локального минимума (максимума) х*, являющуюся
внутренней точкой множества X, то необходимо выполняются условия
/'(*.) = О, f"(x*)>0 (/"(**)^0), (1.16)
что доказывается точно так же, как в теореме 1.5. Однако, если х* —
граничная точка множества X, то эти условия, вообще говоря, не выполняются.
Например, элементарная функция/(х) = -х2 на отрезке X = {х е Е1:1 < х < 2}
имеет глобальный минимум в точке х* =2, но /'(2) = -4, /"(2) = -2. Как
очевидно, условия (1.16) не выполняются. Следовательно, необходимые
и достаточные условия экстремума в задаче
f(x)->extr,xe ХфЕп (117)
должны иметь другую форму, отличную от теоремы 1.5.
Сначала приведем необходимые условия оптимальности для задачи
(1.17), когда X — выпуклое множество из Еп.
Определение 1.25. Множество X называется выпуклым, если для любых
точек х, у е X точка ха = х + а(у - х) = ау + (1 - а)х принадлежит X
при всех а, 0 < а < 1. Иначе говоря, множество X выпукло, если отрезок
[х, у] = {ха = х + а(у - х), 0 < а < 1}, соединяющий любые две точки х, у
из множества X, целиком лежит в X.
Примерами выпуклых множеств в Еп являются рассмотренные ранее
и-мерный шар, и-мерный параллелепипед, гиперплоскость,
полупространство, неотрицательный ортант, прямая, луч. Сфера {хе Еп: ||х\\ = R} —
невыпуклое множество.
Теорема 1.7. Пусть в задаче (1.17) множество X выпукло, х* е X — точка
локального минимума (максимума) функции f(x) на X, пусть в этой точке
функция f(x) дифференцируема. Тогда необходимо выполняется неравенство
(f'(x*),x-x*)>0 ((f'(x*),x-x*)<0) \/xeX. (1.18)
Если х* g intX, то неравенство (1.18) равносильно условию f'(x*) = 0.
41

Доказательство
Пусть х* е X — точка локального минимума в задаче (1.17). Рассмотрим
произвольную точку х из X, тогда в силу выпуклости множества X точки
ха -х* +а(х-х*), а е [0; 1], тоже в нем содержатся. Поэтому при любых
a е [0; а0], где а0 > 0 — достаточно малое число, с учетом
дифференцируемое™ функции f(x) в точке х* имеем
0 < f(x* + а(х -х*))- f(x*) = a(f'(x*), x - х*) + о(сс),
или
0<</'(**),*-**>+— Vcte(0;a0].
Отсюда, переходя к пределу при a —» +0, получим условие (1.18).
Если х* е intX, то для любого е е Еп найдется е0 > 0 такое, что
х = х*+еееХ при всех е, |е|<е0- Полагая в формуле (1.18) х = х*+ее,
получим г{/'(х*), е) > 0 при всех е, | е | < е0, что возможно только при (/'(«**)>е) = 0-
Пользуясь произволом в выборе е, можем взять е = f'(x*), что приводит
к равенству f\x*) = 0.
Аналогично рассматривается случай, когда х* — точка локального
максимума. ■
Условие (1.18) имеет простой геометрический смысл. Как известно [22,
29], для гладкой функции производная по направлению единичной длины
е равна
ое £->о t
Полагая е - ■» Jx-x*), мы приходим к тому, что в точке экстремума
\\Х X*
производная по направлению е неотрицательна, если х* — точка локального
минимума, и неположительна, если х* — точка локального максимума, что
означает невозможность убывания или соответственно возрастания
функции по направлениям, ведущим из точки х* в множество X.
Неравенство (1.18), как и условие стационарности f'(x*) = 0, в задачах
безусловной оптимизации может быть записано в виде системы уравнений,
из которой можно определить точки, подозрительные на экстремум.
Поясним это на примере.
Пример 1.12
Рассмотрим задачу
def
/(*)-> extr,xeX = £? ={х = (х\...,хп)еЕп: х{ >0,...,хи >0},
предполагая, что функция f(x) дифференцируема на Е^.
Сначала рассмотрим задачу поиска точек локального минимума. Покажем, что
тогда условие (1.18)
{f'(x*),x-x*) = f,f'j(x*)(xJ-x!)>0 VxeE? (1.19)
42

равносильно системе
x*=(xl,xl...,x?)EE",xif^(x*) = 0, i = l,...,я,
с дополнительным требованием: если xi=0, то /',(х*)>0. Для обоснования этого
факта зафиксируем произвольный номер i, 1 < г < п, и в неравенстве (1.19) положим
х = (xl..., xt\ х\ xi+\..., *.я),
где х* — произвольное неотрицательное число. Будем иметь
%(х*)(х{-х1)>0 \/х{>0.
Такое неравенство при xl>0 справедливо только в случае /',(х*) = 0, если же
xi = О, то в точке минимума /', (х*) > 0.
Это означает, что точка хеЕ% может быть подозрительной на минимум в этой
задаче, только если она является решением системы п уравнений с п неизвестными
*'/;,(*) = 0, 1 = 1,..., я,
и дополнительным условием: х1> 0, г = 1, ..., п, и /',(х)>0, если х{- 0. Аналогично
убеждаемся, что подозрительные на максимум точки удовлетворяют этой же системе
с дополнительным условием х1> 0, i = 1,..., я, и /',(х)<0, если х1= 0.
В общем случае в задаче (1.17) для множества X с гладкой границей
неравенство (1.18) также может быть записано в виде уравнений f\ (x*) = 0,
i=l, ..., п, если х* eintX, или системы, составленной из условий
принадлежности х* границе множества X и условий равенства нулю
производных функции f(x) по некоторым касательным направлениям к границе
в точке х*. Однако полученные на этом пути системы, как правило, весьма
сложны и неудобны для практического использования.
1.4.2. Правило множителей Лагранжа
в задачах с ограничениями типа равенств
Для исследования задач на условный экстремум имеются другие,
более удобные методы, одним из которых является правило множителей
Лагранжа. Изложим это правило для следующей задачи:
f(x) —»extr, x e X,
(1 20)
X = {xeX0:gj(x)<0J = lJ...Jm;gj(x) = 0J = m + lJ...Jm + s}J
где Х0 — заданное выпуклое множество из Еп, функции /(г), gfix),j = 1, ...,
т + 5, определены на Х0. Условия gj(x) < 0, j = 1,..., т, в задаче (1.20)
принято называть ограничениями типа неравенств, условия gj(x) = 0J = т + 1,...,
m + s, — ограничениями типа равенств. Здесь не исключаются возможности,
когда отсутствуют ограничения типа неравенств (т = 0) или равенств (s = 0).
Возможно также, когда отсутствуют ограничения обоих типов (m = s = 0), т.е.
X = Х0 и задача (1.20) превращается в (1.17). Если т = s = 0, Х0 = Еп, то из
задачи (1.20) получим задачу безусловной оптимизации из параграфа 1.3.
Для описания правила множителей Лагранжа для задачи (1.20) введем
функцию
_ m+s
£(х,X) = V(*)+ S bjgjW (1-21)
43

переменных х = (х1, ..., хп) е Х0, X = (X0,Xv...,Xm+s) = (X0,X)eEm+s+1,
называемую функцией Лагранжа задачи (1.20). Переменные Х0, Xv ..., Xm+S
называются множителями Лагранжа. Будем говорить, что множитель Х0
соответствует целевой функции/(х), множитель Xj, 1 <j <m + s, соответствует
ограничению из задачи (1.20), задаваемому функцией gfix).
Перейдем к формулировке необходимых условий экстремума для задачи
(1.20). Начнем с классической задачи на условный экстремум, традиционно
рассматриваемой в математическом анализе [22, 29] в разделе,
посвященном неявным функциям:
/(r)->extr,xe X={xe Еп \gx(x) = 0,...,gs(x) = 0}. (1-22)
Эта задача является частным случаем задачи (1.20) при т = 0, Х0= Еп.
Допустим, что систему уравнений
gj(x) = 0J=l,...,s, (1.23)
удалось преобразовать к виду
х1 = ф!(ля+1,..., хп),..., хР= фр(ля+1,..., хп), (1-24)
выразив из (1.23) какие-то р переменных (для простоты обозначений мы
считаем, что это переменные х1,..., хР) через остальные. Тогда задачу (1.22)
на условный экстремум можно свести к задаче на безусловный экстремум
функции
g(xP+\ ..., хп) =/(9t(xP+1,..., хп),.., фр(ля+1,..., хп), хР+\ ..., хп)
переменных (xP+i, ..., хп) е Еп~р, и полученную задачу можно исследовать
по описанной в параграфе 1.3 схеме. Однако этот подход имеет
ограниченное применение, так как явное выражение вида (1.23) одной группы
переменных через остальные удается получить лишь в редких случаях.
Сформулируем правило множителей Лагранжа для задачи (1.22).
Справедлива следующая теорема.
Теорема 1.8. Пусть х* — точка локального экстремума (минимума или
максимума) функции f(x) на множестве X из задачи (1.21). Пусть функция
f(x) дифференцируема в точке х*, функции gx(x), ..., gs(x) непрерывно
дифференцируемы в некоторой окрестности точки х*. Тогда необходимо
существуют число Х*0 и вектор X* = (Х\,..., X*s) e Es такие, что
х* =(Xixv---Xs)=(X*0X)*o,
д£(хХ)
дх1
Э/(^)^^ГЭ^*)_Л ,_, о (1.25)
7=1
-^♦£Ч^-*.--' ,
или, короче,
Г Ф0, £'х(х„Г) = Х£/'(*0+ X Vjg'jix,) = 0. (1.26)
Если градиенты g[(x*), ...,g's(x.) линейно независимы, то Х*0 Ф 0.
44

Таким образом, в теореме 1.8 утверждается, что всякая точка
локального экстремума х* задачи (1.22) необходимо удовлетворяет равенству
£х(х,Х) = 0 при некотором подходящим образом выбранном
нетривиальном наборе множителей X*. В этой теореме использованы лишь первые
производные функций /(г), gj(x), поэтому условия (1.25), (1.26) принято
называть необходимыми условиями экстремума первого порядка задачи (1.22).
Из теоремы 1.8 следует, что подозрительными на локальный экстремум
(минимум или максимум) могут быть лишь точки х* е_Еп, для которых
существуют множители Лагранжа X такие, что пара (#•, X) является
решением системы
V'(*)+2M;(*) = 0, g7(x) = 0,; = l,...,5, Х = (Х0,Х)фО. (1.27)
7=1
Эта система состоит из п + s скалярных уравнений сп + s + 1
неизвестным
(х, X) = (х, Х0, Х) = (х ,...,хп, Х0, Х^..., Xs).
Нетрудно видеть, что если набор (х,Х) — решение системы (1.27), то
набор (х, - X) тоже будет ее решением. Более того, набор (х, аХ) при любом
ос Ф 0 также будет решением этой системы. Это значит, что условие X Ф О
можно заменить каким-либо условием нормировки и к системе (1.27)
добавить, например, уравнение
Ш|2=^+Ш2=2Х? = 1. (1.28)
7=0
В результате мы получим систему (1.27), (1.28) п + s + 1 уравнений
cw + 5+l неизвестным. При любом фиксированном способе нормировки,
гарантирующем условие X Ф 0, из системы (1.27) мы получим одно и то же
множество точек х*, подозрительных на локальный экстремум. На
практике вместо условия (1.28) часто рассматривают систему (1.27),
поочередно добавляя к ней условия Х0 = 1 и Х0 = 0 Д = (Xv ..., Xs) Ф 0.
1.4.3. Правило множителей Лагранжа в общем случае
Теперь сформулируем правило множителей Лагранжа для общей задачи
(1.20). Функция Лагранжа в этой задаче имеет тот же вид (1.21).
Теорема 1.9. Пусть Х0 — выпуклое множество, х* е X — точка локального
минимума (максимума) задачи (1.20), функции /(г), gi(x), ..., gm+s(x)
непрерывно дифференцируемы в некоторой окрестности точки х*. Тогда
необходимо существуют множители Лагранжа X* = (Х*0, Х\,..., X*m+S) такие, что
Х**0, Х*0>0 (Хо<0), Х;>0,...Д;>0; (1.29)
(£'х(х*Х\х-х*)>0 \/хеХ0; (1.30)
Х&(х.) = 0, j = U.,m. (1.31)
Равенства (1.31) называют условиями дополняющей нежесткости или,
короче, условием дополнительности.
45

Замечание 1.2. Если х* — внутренняя точка Х0 (например, если Х0 = Еп),
то неравенство (1.30) равносильно условию
_ m+s
j£(*.f V)=x;/'(*.)+ 2 ад(*.)=о. (i.32)
7=1
Замечание 1.3. В сформулированной теореме, в отличие от теоремы 1.8,
появились условия на знаки множителей Лагранжа Х0, Xv ..., Хт. Это
случилось, во-первых, потому, что в общей задаче (1.20) на условный
экстремум появились ограничения типа неравенств, записанные в виде gfix) < 0,
7=1,..., т. Ничто не мешало написать какие-то из этих ограничений в виде
hj(x) > 0, но тогда пришлось бы внести в формулировку теоремы несколько
измененное правило знаков на множители Лагранжа. Однако эти
изменения не носят принципиального характера, так как любые ограничения вида
h(x) > 0 можно записать в виде g(x) = -h(x) < 0. Во-вторых, в теореме 1.9
правило выбора знаков множителя Х0 дает нам возможность различать
задачи минимизации и максимизации и в то же время позволяет
единообразно изучать задачи на экстремум.
Кстати, уже в формулировке теоремы 1.7 мы могли записать условия
экстремума (1.18) в виде (X0f'(x*),x-x*)>0 V х е X, где Х0 > 0 в задаче
минимизации, Х0 < 0 в задаче максимизации, но в теореме 1.7 особой
необходимости в введении множителя Х0 еще не было. Можно также отметить,
что указанная выше связь (1.3), (1.4) между задачами минимизации и
максимизации подчеркивает естественность приведенного в теореме 1.9
правила выбора знака Х0.
Заметим, что теорема 1.9 охватывает утверждения теорем 1.7, 1.8.
В самом деле, если в задаче (1.20) отсутствуют ограничения типа равенств
и неравенств (s = т = 0), т.е. X = Х0, то условия (1.29)—(1.32)
превращаются в утверждения теоремы 1.7. Если Х0 = Еп и отсутствуют ограничения
типа неравенств (т = 0), то из условий (1.29)—(1.32) следуют утверждения
(1.25), (1.26) теоремы 1.8.
Доказательство теоремы 1.9 будет приведено ниже в параграфе 1.6 после
изложения метода штрафных функций.
Из теоремы 1.9 следует, что подозрительными на экстремум могут быть
лишь точки хеХ, для которых существуют множители Лагранжа X такие,
что пара (х, X) является решением системы
X G -Aq,
\(£'х(х,1),у-х)>0 УуеХ0,
hjgj(x) = 0,gj(x)<0, j = l,...,rn, (1.33)
Я;(х) = 0, j = m + l,...,m+s,
[l = (\0,Xl,...,\m+s)*0,\l>0,...,\m>0,
причем Х0 > 0 в случае точки локального минимума, Х0 < 0 в случае
точки локального максимума. Нетрудно заметить, что если (х, X) — решение
системы (1.33), то (х,аХ) при любом а > 0 также будет решением этой
системы. Это значит, что условие X Ф 0 в системе (1.33) можно заменить, как
46

и в системе (1.27), условием нормировки (1.28) или исследовать систему
(1.33), последовательно полагая в ней Х0= 1 в случае локального
минимума, Х0= -1 в случае локального максимума; отдельно выделить случай
Х0= 0, (kv ..., Хт) Ф 0. Решение системы (1.33) часто называют критической
точкой задачи (1.20).
Подчеркнем, что, приступая к решению задачи на экстремум с помощью
теоремы 1.9, прежде всего надо проверить, записана ли постановка задачи
в каноническом виде (1.20), правильно записать функцию Лагранжа (1.21)
и далее разобраться со знаками множителей Лагранжа.
1.4.4. Достаточные условия оптимальности
Определив решения системы (1.33) с учетом условий нормировки,
получим множество точек, подозрительных на экстремум в задаче (1.20),
и соответствующие им множители Лагранжа. Для выяснения того, будет
ли в найденной точке х* в действительности реализовываться локальный
минимум или максимум, нужно провести дополнительное исследование
свойств целевой функции в окрестности точки х* с учетом ограничений,
задающих множество X. Здесь может быть полезна информация,
вытекающая из теорем 1.2—1.4 Вейерштрасса, из геометрических, физических,
экономических и тому подобных соображений. Для анализа характера
экстремума критической точки можно использовать достаточные условия
экстремума, основанные на знакоопределенности второй производной
функции Лагранжа. Приведем одно из таких условий (теорема 1.10), для его
формулировки нам понадобится следующее определение.
Определение 1.26. Ограничение типа неравенства gj(x) < 0 назовем
активным в точке х*, если gj(x*) = 0. Множество всех активных
ограничений далее будем обозначать через I(x*) = {j\ l<j<m,gj(x*) = 0}.
Теорема 1.10. Пусть в задаче (1.20) множество Х0 выпукло, функции f(x),
gi(x), ..., gm+s(x) дифференцируемы в некоторой окрестности точки х*еХ
и дважды дифференцируемы в этой точке, набор (х*, V) = (х*, (К*0, X*))
является решением системы (1.33), причем \*Q>0 (k*0 < 0), и кроме того,
(£'^(x*X)kh)>0 (1.34)
для всех he En,h*0, удовлетворяющих условиям
W'(*O,A>£0f (1.35)
<g;.(**),/*><o v/e/(**), (1.36)
(g'j(x*),h) = 0, j = m + l,...,m + s. (1.37)
Тогда в точке х* реализуется строгий локальный минимум {максимум)
функции f(x) на множестве X.
Сразу же заметим, что теорема 1.10 является обобщением теоремы 1.6,
выражающей достаточные условия строгого локального экстремума в
задачах безусловной оптимизации.
Доказательство
Если х* — изолированная точка множествах, то по определению х* будет
точкой строгого локального экстремума. Поэтому далее будем предпола-
47

гать, что х* не является изолированной точкой множества X. Допустим, что
Х*0 >0, выполнено условие (1.34), но точка х* не является точкой строгого
локального минимума. Тогда найдется последовательность {xk} e Х0 такая,
что
xk±x.,gj(xk)<OJ = l,...,m,gj(xk) = 0,j = m + l,...,m + s,
f(xk)<f(x*),k = l,2,..., X\mxk=x*. ^ ' '
k—>oo
Точки xk можем представить в виде
xk =x*+tkhk,rjiehk =й-^ ^77, tk = ||x£-.r*|—>0при&—>«>.
\xk-x*\
Так как \\hk\\ = 1, k = 1, 2, ..., то, выбирая при необходимости
подпоследовательность согласно теореме Больцано — Вейерштрасса [22, 29], можем
считать, что {/^}—>/ь ||/z*|| = 1. С учетом условий (1.38) и
дифференцируемое™ функций/(х), gj(x) в точке х* имеем
0>f(xk)-f(x*) = tk(f'(x*),hk) + o(tk);
0>gj(xk)-gj(x,) = tk(g'j(x,),hk) + o(tk)jel(x,);
0 = gj(xk)-gj(x,) = tk(gj(x,Xhk) + o(tk% j = rn + i...,m + s,k = i2,....
Разделив эти соотношения на tk > О и устремив k —> °°, получим
</'(**)Л><о, (я;(^)Л><о,;е/(х#), <£;(**)Л>=о,
7 = /и +1,..., т + 5, \h* II = 1.
Отсюда и из условия Xq >0 следует, что К — решение системы (1.35)—
(1.37), причем к Ф 0. Тогда согласно условию (1.34)
(^(х*,Х*)/г*Л)>0.
С другой стороны, учитывая условия (1.38), неравенства \*0 >0, X*- >0,
j = 1,..., т, условия (1.31) и gj(x*) = 0J = т + 1,..., /я + s, а также тот факт,
что f(xk)<f(x*), k = 1, 2,..., имеем
_ /И /7Z+S
А*4д>х;/(*А)+2%-(*4)+ I x;g,.(*t)£X5/(*t)£x;/(*.)=
7=1 7=ш+1
=КА*-)+1Щ(х*)+ £ х&(*.)= А**. **), ^=1,2,....
7=1 j=m+l
Отсюда с помощью формулы Тейлора (1.13) с учетом неравенства (1.30)
находим
0>£(xk,X*)-£(x*,X*) = (£'x(x*,'k*),xk-x*)+— (£/xx(x*yX*)(xk - х*)у xk - х*) +
^|**-*.|2)Ц^^^ £ = 1,2,....
Разделив это неравенство на t\ и устремив £ —> °°, получим
48

что противоречит условию (1.34). Следовательно, х* — точка строгого
локального минимума задачи (1.20).
Аналогично доказывается, что если Х0 < 0, неравенство (1.34) выполнено
при условиях (1.35)—(1.37), то х* — точка строгого локального максимума
задачи (1.20). ■
Замечание 1.4. Подчеркнем, что приведенные в теореме 1.10 условия,
когда в подозрительной на экстремум точке х* реализуется строгий
локальный минимум или максимум, являются достаточными, но не необходимыми.
В ней предполагается, что проведен предварительный анализ множителей
Лагранжа X* = (Х*0,Х*) точки х*, подозрительной на экстремум, и найден
«хороший» набор множителей, у которых компонента Х*0 имеет
определенный знак или, возможно, Х*0 =0, и выполняются условия (1.34)—(1.38).
Такой анализ необходим, так как не всякое решение (х* Д*) системы (1.33)
обладает «хорошими», т.е. удовлетворяющими (1.34)—(1.38) свойствами.
Более того, может оказаться так, что «хорошие» множители не существуют,
и теорема 1.10 попросту не работает, неприменима. Этот факт будет
проиллюстрирован в приводимых ниже примерах 1.13, 1.14, 1.17, 1.18.
Отдельно остановимся на случае «хорошего» набора (Х*0,Х*),
соответствующего точке х*, когда Х*0 =0. Тогда по теореме 1.10 точка х* является
как точкой строгого локального минимума, так и точкой строгого
локального максимума, т.е. одновременно выполняются неравенства f(x*)<f(x)
и f(x*)> f(x) для всех хеХпО£(х*), где ОДх*) = {хе£и:|х-л:*|<е} —
6-окрестность точки х*. С первого взгляда может показаться, что так
не бывает. Увы, бывает! Но в одном единственном случае, когда таких точек л:
нет, т.е. множество XnOe(i*) = {x*} состоит из единственной точки х*. Иначе
говоря, х* — изолированная точка множества X (см. ниже пример 1.19).
Так как задача (1.22) является частным случаем задачи (1.20) при т = 0,
Х0 = Еп, то теорема 1.10 применима и к задаче (1.22). При этом ее
формулировка может быть несколько упрощена. Поскольку в задаче (1.22)
ограничения типа неравенств отсутствуют, то 1(х*) = 0 и условие (1.36)
теряет смысл. Кроме того, Х0 = Еп, поэтому неравенство (1.30) может быть
заменено условием (1.26). Это значит, что систему (1.33) можно
заменить системой (1.27). Наконец, покажем, что требование (1.35) можно без
ущерба исключить.
Допустим, что в задаче (1.22) неравенство (1.34) справедливо для всех
/г, удовлетворяющих условиям (1.35), (1.37) при Х*0 > 0. По доказанному это
значит, что х* — точка строгого локального минимума. Убедимся, что тогда
при т = 0, Х0= Еп неравенство (1.34) будет справедливо и в том случае,
когда Х*0 < 0, т.е. когда (f'(x*), h) > 0. Возьмем вектор а = -h, для него
выполнены соотношения
я*0, (g'j(x,),a) = (g'j(x*X-h) = -(g'j(x,Xh) = 0, ; = l,...,s,
</'(*.). а) = </'(*.)." h) = -</'(**), h) > 0.
По сделанному допущению для такого вектора а верно (£^ (х*, X* )а, а) > 0.
Но тогда
СО*., X* Я h) = (££(х., Х')(-а), (-а)) = (££(х, 1')а, а) > 0.
49

Это значит, что при т = О, Х0 = Еп неравенство (1.34) остается
справедливым для всех h, удовлетворяющих условиям (1.35), (1.37), независимо
от знака множителя Х*0. Следовательно, условие (1.35) в формулировке
теоремы 1.10 для случая задачи (1.22) может быть опущено.
Таким образом, переформулируя теорему 1.10 применительно к задаче
(1.22), получаем следующую теорему.
Теорема 1.11. Пусть в задаче (1.22) функции f(x), gi(x),..., gs(x)
дифференцируемы в некоторой окрестности точки х*еХ и дважды
дифференцируемы в этой точке, набор (х*, V) = (х*, \*0, XJ,..., X*) является решением
системы (1.27), причем XJ > 0 (k*Q < 0) и, кроме того,
U£(x*,X*)/a>>0 (1.39)
для всех he Еп,1гФ0, удовлетворяющих условиям
<£/(*•).А> = 0, ; = 1,...,5. (1.40)
Тогда в точке х* реализуется строгий локальный минимум {максимум)
в задаче (1.22).
1.4.5. Примеры
Для иллюстрации теорем 1.7—1.11 рассмотрим несколько примеров.
Пример 1.13
Пусть на «-мерной единичной сфере Х= {хе Еп : ||х||2= 1} требуется найти точку,
сумма квадратов расстояний от которой до р заданных точек хь х2, ..., хр была бы
минимальной или максимальной. Иначе говоря, нужно решить задачу
/(*) = £\\х~xif ->extr> xeX = {xeEn\ g(x) = \\xf -1 = 0}.
z=l
Аналогичная задача в случае Х-Еп была рассмотрена в примере 1.9. Действуя,
как и тогда, представим целевую функцию в виде
f(x) = p\\xf -2p(x,x0) + th( =
i=\
= р\\х-х0(-р\\х0( + Ъ\\хг(, *o=-5>r
Применим к этой задаче теорему 1.8. Составим функцию Лагранжа:
£(x,I) = X0f(x) + X(\\x\\2-l), хеЕп,1 = (Х0,Х)еЕ2.
Система (1.27) здесь имеет вид
£'х(х,1) = 2рХ0(х-х0) + 2Лх = 0, 1Ы|2=1,(Х0Д)^0. (1.41)
Если Х0 = 0, то X Ф 0, поэтому из первого уравнения следует х = 0. Но тогда
условие ||х||2 = 1 не выполнено. Стало быть, Х0Ф 0, и, считая, что х0Ф 0, из системы (1.41)
находим две точки, подозрительные на экстремум, и соответствующие им
множители Лагранжа:
щ = А, *о*0, X, =рХофг0|-1); (1.42)
v, =-А Х0 *0, Х2=-Мо(|ко|| + 1)- (1-43)
Ы
50

Пример 1.14
Найдем условные экстремумы в задаче
/(w) = 3(x3+#3)->extr, u = (x,y)eX = {ueE2:g(u) = l-x-4y = 0}.
Составим функцию Лагранжа этой задачи:
£(и,Х) = £(х,у,Х0,Х) = ЗХ0(х3+у3) + Х(1-х-4у), иеЕ2,Х = (Х0,Х)еЕ2.
Система (1.27) здесь имеет вид
£'х(х,у,Х0,Х) = 9Х0х2-Х = 0, £'у(х,у,Х0,Х) = 9Х0у2-4Х = 0, (Х0Д)*0, х + 4у = 1.
При Х0 = 0 эта система не имеет решения, поэтому можем принять Х0 = 1 и Х0 =
= -1. У системы будет две пары решений:
(12} 1
(щ,Х1) = (х1,у1,Х0,Х1):щ=\х1 =-,у{=- Д0=1Д1=-;
Л 9
'Я'0 = 1Д2=—;
1
1 2
(м2, А.2) = (х2, г/2 Д0, А.2): м2 = | х2 = —, у2 = —
— 12
(1/!,^) = (^1^1 ДО Да)1 Wl =| *1 = д»У1 = g
Д0--1Д3 --—;
("2»^4) = (^2»y2»^0»^4>: U2 =
1 2
^2=-у.У2=у
До -~1Д4 _~
49'
Таким образом, подозрительными на экстремум будут только точки щ, и2. Для
того чтобы воспользоваться достаточными условиями, выпишем вторую
производную функции Лагранжа:
ЛО*>*/ЛД) £'^(х,у,Х0,Х)) fl8V О л
V
^;а("Д)=
О 18Х0г/
и систему (1.37) для вектора h =
К
, учитывая, что g'(u) =
-1
(g'(u,),h) = -hl -4*2=0.
'-4^
Любое ее решение имеет вид А =
<i?;„(Ml)X1)A,A) =
<-С(игД4)А.А> =
Согласно теореме 1.11 отсюда имеем: щ =
1 2
, £ G (-©о, -и»). Поэтому для таких h
= 36t2 >0 W*0;
252
t2>0 Vt*0.
—,— | — точка строгого локального
У У ,
минимума; и2=\ —,— | — точка строгого локального максимума.
Еще раз отметим, что условия теоремы 1.11 не являются необходимыми._В этом
примере точке строгого локального минимума их помимо «хорошего» набора Хх
соответствует и набор Х3, не отвечающий условиям теоремы (в нем Х0 = -1):
(£'^(ubl3)h,h) =
-2 0 У-4П r-4t
0 -4
= -36£2<0 V**0.
52

Для выяснения характера возможного экстремума в этих точках привлечем
теорему 1.11. Вторая производная функции Лагранжа равна
£Ь(х, X) = £^{х, V X) = 2(рХ0 + Х)1п,
где /„ — единичная матрица размера пхп.С учетом соотношений (1.42), (1.43)
соответственно имеем
£'хх (v\ Д 0' ^1) = 2/Ло \\Х01| In >
Отсюда следует
(£^иХ01Хх)к,к) = 2рХ0\\х0\\Щ2 >0, VX0 >0,VAe£w,A*0;
{£^(v2, Х0, Х2)А, А) = -2рХ0|^о|НН|2 > 0» v^o < 0, VA e £w, A * 0.
В частности, эти неравенства выполняются при всех А Ф 0, удовлетворяющим
условию (1.37):
<g'(^),A) = 2<^,A> = 0, 1 = 1,2.
Согласно теореме 1.11 это означает, что точка vx является точкой строгого
локального минимума, v2 — точкой строгого локального максимума. Попутно отметим, что
если бы мы попытались узнать характер экстремума в точках vb v2, используя
множители Лагранжа Х{, Х2 из соотношений (1.42), (1.43) при Х0 < 0 и Х0 > 0
соответственно, мы убедились бы, что условия теоремы 1.11 не выполнены.
Можно высказать более сильное утверждение: точки vx и v2 являются точками
строгого глобального минимума и максимума функции f(x) на множестве X
соответственно. Для его обоснования нужно обратиться к теореме 1.2 Вейерштрасса,
согласно которой функция f(x) на множестве X достигает своих точной нижней
и точной верхней граней, причем эти точки глобального экстремума, конечно же,
являются решениями системы (1.41), которая при х0Ф 0 имеет всего два решения
v{ и v2. Следовательно, одна из этих точек является точкой глобального минимума,
другая — точкой глобального максимума. Вычислив и сравнив значения f(v{),f(v2),
нетрудно убедиться, что vx — точка глобального минимума, v2 —точка глобального
максимума со значениями
M) = /*=p-2l>f
/(02) = /*=P + 2HU
*|| II2
=i
+
!=1
+
!=1
Так как прих0Ф 0 у функции/(х) других точек экстремума на Xнет, Tof(v{) <f(x)
Ухе X,x*v{,h f(x) <f(v2) Ухе X,x*v2, т.е. экстремумы строгие.
Осталось рассмотреть случай х0= 0. Тогда системе (1.41) удовлетворяют все точки
х е X, им соответствует один и тот же набор множителей Лагранжа Х0 Ф 0Д = -рк$.
Это значит, что при х0= 0 нам не удалось извлечь из теоремы 1.8 никакой полезной
информации — все точки единичной сферы как были, так и остались
подозрительными на экстремум. К тому же здесь для всех А из В1 будет {£^(х, X)h, h) = 0. Однако
чтобы разобраться в сложившейся ситуации, достаточно вычислить значение функ-
р п
ции f(x) при х0 = 0, х е Еп. Получим f(x) = р + S|K| = const V х е X. Таким обра-
!=1
зом, при х0 = 0 задача становится тривиальной: все точки х е X являются точками
абсолютного минимума (или максимума).
51

Аналогичные соображения можно высказать и про точку и2 и набор Х2.
Подчеркнем существенность того момента, что условие {£uU(u*, X*)h, h) > 0 должно
выполняться лишь для тех й, которые удовлетворяют условиям (gf(w*), h) = 0: матрица
£uU{u2lXA) знакопеременная, неравенство {££u(u2,XA)h,h)>0 не могло выполняться
при всех h g Еп.
Остается заметить, что для последовательностей щ= (1 - 4k, k), vk= (1 + 4k, -k) e X
имеем f(uk) —> -«>, f(vk) —> +°° при & —> <». Это значит, что в рассматриваемой задаче
/* = inf f (и) = -<*>, f* = sup/(w) = +°°, так что глобальный минимум и максимум
не достигаются.
В этом примере тот же результат нетрудно получить другим путем. А именно,
можно было из условия g(u) = х + 4у-1=0 получить х = 1 - 4у, затем перейти к
эквивалентной задаче на безусловный экстремум q(y) =/(1 - 4у, у) = 3[(1 - 4у)3 + у3] —>
—> extr, ye Е{,и применить к ней классический метод, изложенный в параграфе 1.3.
Рассмотрим задачу
/(и) =*-> extr, и = (х, у) е Х= {и е E2:g(u)=x3-y2 = 0}. (1.44)
Функция Лагранжа этой задачи
£(и,Х) = £(х,у,Х0,Х) = Х0х + Х(х3-у2), и = (х,у)еЕ2, Х = (Х0,Х)еЕ2.
Система (1.27) имеет вид
£'х(х, уД0Д) = *0 + ЗХх2 = 0, £'у(х, уД0Д) = -2Ху = 0,
х3-г/2=0, Х = (Х0,Х)±0.
Из этой системы находим единственную точку и* = (0,0), подозрительную на
экстремум. Ей соответствуют наборы множителей Лагранжа вида X* = (X*0 = ОД) Д е 2?1,
**0.
Для выяснения характера экстремума точки и* попробуем применить теорему 1.11.
Уравнению (g'(u*), h) = (0, h) = 0 удовлетворяют любые he E2. Однако на Е2 матрица
не является знакоопределенной ни при каком X, теорема 1.11 здесь не работает. Тем
не менее несложно догадаться, что в задаче (1.44) и* — точка строгого глобального
минимума. В самом деле, с учетом равенства х3 - у2 = 0 имеем f(u) = x = (y2 )^3 >0 = f(u*) = f*
при всех и = (х, у) Ф 0. Верхняя грань здесь /* = -и».
Исследуем на условный экстремум задачу
/(x) = lh:-d|2->extr, xEX = {xeEn:\\xf<l}, (1.45)
где а — заданная точка из ЕР.
В простейшем случае, когда а = 0, очевидно, функция f(x) достигает своей
нижней грани /* = 0 на X в точке х = а = 0, своей верхней грани /* = 1 — в точках хе X
таких, что ||д:|| = 1. Пусть а Ф 0. Для поиска точек экстремума в этом случае
воспользуемся теоремой 1.9. Введем функцию Лагранжа
£(x,X) = X0\\x-af +X(\\xf -1), Х = Д0Д)е£2Д>0.
53

Первая и вторая производные этой функции равны
£'х(х,Х) = 2Х0(х-а) + 2Хх; £'хх(х,Х) = 2(Х0 + Х)1п,
где 1п — единичная матрица размера п х п. Система (1.33) здесь имеет вид
Д0 + Х)х = Х0а, X(\\xf -1) = О, Ы|2 < 1, X = (Х0 Д) Ф ОД > 0.
(1.46)
Нетрудно показать, что если (х, Х0, X) — решение системы (1.46), то Х0Ф 0. Тогда
из системы (1.46) вытекает
^о II II2
х = -—^—а; \\х\\ =
Х0 + Х
^Xq+Xj
Ы2<1;
X(\\xf-l) = X
г
\
yX0+Xj
Waf-1
= 0, Х = (Х0Д), Х0*0, Х>0.
Из соотношений (1.48) следует, что либо X = 0, либо
Ал + А
вом из этих случаев имеем
во втором —
х = а, |И1<1, Х = (Х0,0), Х0*0,
= 1Г1Г, х = ±/й, Х0*0,Х>0.
\\а\\ \\а\\
Ал + А
(1.47)
(1.48)
|в|| = 1Д>0. Впер-
(1.49)
(1.50)
Все это можно подытожить следующим образом. Если || а \\ > 1, то система (1.47)-
(1.48) имеет два набора решений
х = Т1,Х0,Х = Х0(\\а\\-1)
\\а\\
(Х\,Х{)-
(х2Д2) = х = -Д|Д0Д = -Х0(1Н1 + 1)
а если \\а\\ < 1, то — три набора решений
, Х0>0;
, ^о<0,
(х{,Х{) = \ х = Т1,Х0,Х = Х0(\\а\\-1)\, Х0<0;
У \\а\\ J
(х2Д2)= х = -Д|Д0Д = -Х0(Ы1 + 1) , Х0<0;
У \\а\\ J
(х3,Х3) = (х = а,Х0,Х = 0),Х0 *0.
Таким образом, в задаче (1.45) подозрительными на экстремум являются лишь
точки х{ = -л—м, х2 =—п—.г, х3 = а. Для дальнейших исследований будем пользоваться
Ы\ \\а\\
теоремой 1.10.
Если || а || > 1, то точка хх = -л—л- и ее множители Лагранжа Х0 > ОД = Х0(\\ а \\ - 1) > 0
\\а\\
таковы, что £'ж(х{, Х{) = 2(Х0 + Х)1п = 2Х0 \\a\\ln > 0; для точки х2 = —п—л- и ее множите-
IMI
лей Лагранжа Х0< ОД = -Х0(\\а|| + 1) > 0 имеем £,хх{хъ Х2) = 2(Х0 + X)In = -2X0 \\a\\ln > 0.
Отсюда и из теоремы 1.10 следует, что точка хх = -п—п- — точка строгого локального
\\а\\
а
минимума, а точка х2 = —»—п- — точка строгого локального максимума.
IMI
54

Если 0 < || а || < 1, то для точки х2 = —п—л- с наборами множителей Лагранжа Х0 < О,
Ml
^ = ~^о(11 я || + 1) > 0 находим £^(х2у Х2) = 2(Х0 + Х)1п = -2Х0 \\a\\ln > О, т.е. она является
точкой строгого локального максимума. Точках3 = я в этом случае, очевидно,
является точкой строгого глобального минимума, равного нулю. Остается разобраться
с точкой хх = n-ji с множителями Лагранжа Х0< ОД = Х0(\\а\\- 1). Для нее получаем
£'ж(х\> ^-l) = 2(^o + Wn = ^-0 Wa\\ln < 0, и теорема 1.10 нам помочь не может.
При || а || = 1 точка х{ совпадает с точкой х3, а в случае || а \\ < 1 оказывается, что
в ней при п > 1 не реализуется ни локальный максимум, ни локальный минимум,
так как в любой ее окрестности найдутся точки шара X = {х е ЕР : ||х|| < 1}, в которых
значения функции/(х) будут как меньше/(Xj), так и больше/(Xj). Точнее говоря,
при || а || < 1 внутренние точки шара Хх = {х е Е2 : ||х - а\\ < 1 - ||я||} (рис. 1.9)
принадлежат шару X, и в них/(х) </(х1), а в точках вне шара Х1? но принадлежащих X,
будет/(х) >f(x{). При п = 1 точках! будет точкой строгого локального максимума.
Рис. 1.9
Остается заметить, что согласно теореме 1.1 Вейерштрасса в задаче (1.45) нижняя
и верхняя грани достигаются хотя бы в одной точке, а в силу теоремы 1.9 таковыми
могут являться лишь точки Xj, x2, х3. Отсюда и из проделанного исследования
вытекает, что перечисленные точки являются точками строгого глобального экстремума.
Этот пример отражает один любопытный момент: свойства задачи поиска
экстремумов зависят не только от функции и множества, но и от
размерности пространства, в котором она поставлена.
Пример 1.17
Исследуем на условный экстремум задачу
f(u)=x2 + y2->extr,и = (х,у)е Х={и = (х,у)е X0,g(u)=x + y-2<0},
где Х0 = {и = (х, у) g Е2: х > 1, у > 0}.
Для этой задачи функция Лагранжа имеет вид
(1.51)
£(и,Х) = £(х,у,Х0Л) = Х0(х2+у2)+Х(х+у-2), (х,у)еХ0, Х = (Х0,Х)*0, Х>0.
Ее градиент и вторая производная имеют вид
£'и(и,X) = (2Х0* + Х,2Х0у + X), £'^(и, X) =
2Хп 0 "|
— ZAq12.
0 2Х0)
Согласно теореме 1.9 точки экстремума в задаче (1.51) являются решением
системы (1.33), которая здесь запишется в виде
{£^(u,X),v-u) = (2X0x + X)(v{-x) + (2X0y + X)(v2-y)>0 Vv = (vvv2)eX0', (1.52)
55

Х(х + у-2) = 0, Х = (Х0Д)*0, ^>0. (1.53)
В неравенстве (1.52), как и в примере 1.12, будем различать два случая: и е int X0
hug ГрХ0. В результате система (1.52), (1.53) распадается на следующие подсистемы:
х>1, у>0, £^и,Х) = (2Х0х + Х,2Х0у + Х) = (0,0),
Х(* + у-2) = 0, (Х0,Х)фО, ^0,
* = 1, ^(м,Х) = 2Х0у + Х = 0, Х(* + у-2) = 0, (^0Д)*0, X>0, (1.55)
у = 0, i£(tt,X) = 2X0* + X = 0, Х(х + у-2) = 0, (Х0,Х)фО, X>0. (1.56)
Во всех подсистемах вариант А.0 = 0 влечет за собой X = 0, что противоречит
условию X = (Х0,Х)фО. Поэтому в системах (1.54)—(1.56) Х0Ф0. Нетрудно убедиться, что
система (1.54) не имеет решения. Система (1.55) имеет два семейства решений: щ =
= (х= 1,у = 0),Х0Ф0,Х = 0; и2 = (х = 1,у= 1)Д0<0Д = —2Я0 > 0. Система (1.56) имеет
одно семейство решений: и3 = (х = 2, у = 0), Х0 < 0Д = -АХ0 > 0.
Таким образом, в рассматриваемой задаче подозрительными на экстремум
являются три точки: их = (1, 0), и2 = (1, 1), и3 = (2, 0). Для выяснения характера
экстремума в этих точках попробуем применить теорему 1.10. Точка щ = (1,0) имеет
«хороший» набор множителей Лагранжа X = (Х0 = 1Д = 0). Тогда (££u(uvX)h, h) = 2\\h\\ > 0
при всех h g Е2, h Ф 0, в частности, это верно и для й, удовлетворяющим условиям
(1.35)—(1.37). Стало быть, их — точка строгого локального минимума. В точках и2 и щ
теорема 1.10 не работает, так как Х0< 0 и {£„и(щ Д)й,й) = -2|й| <0 при всех h e Е2,
h Ф 0, i = 2, 3. Поэтому придется привлекать иные соображения. Значения целевой
функции в точках щ, и2, щ таковы:
/(и,) = 1 </(и2) = 2 </(«з) = 4. (1.57)
Согласно теореме Вейерштрасса 1.1, на компактном множестве X
рассматриваемая целевая функция f(u) =x2 + у2 достигает своей точной нижней и точной верхней
граней хотя бы в одной точке, и эти точки необходимо являются решением системы
(1.52), (1.53). Отсюда и из соотношений (1.57) следует, что щ = (1,0) — точка
глобального минимума (что уже показано ранее), щ=(2, 0) — точка глобального максимума.
Для выяснения характера экстремума в точке и2= (1,1) рассмотрим две последо-
1 А 1
вательности:vk = xk = 1,ук =1~т \wk = xk =1 + т>Ук ~^~Т \>^~ 1» 2,.... Эти последо
/v J V fC /v ,
вательности принадлежат множеству X и сходятся к точке и2, причем
/(^) = l + fl4l <f(u2)<f(wk) = 2 + -°
k
F'
Следовательно, точка и2= (1, 1) не является точкой экстремума.
Пример 1.18
Исследуем на условный экстремум задачу
f(u) = x2+y2+z2^> extr, и = (х, у, z) е X,
X = {uEX0,g{(u) = xy = 0,g2(u) = x2-y2=0},
где Х0 = {и = (х, у, z) g Е? : z > 1}.
Воспользуемся теоремой 1.9. Функция Лагранжа для этой задачи имеет вид
£(и,Х) = Х0(х2 + у2 + z2) + Xxxy + Х2(х2 - у2),
u = (x,y,z)GX0,X = (X0, XvX2)gE3.
(1.58)
56

Ее градиент равен
ЩиЛ) = (£'х(иЛ),ЩиЛ),£'2(и,1) =
= (2Х0х + Хху + 2Х2х, 2Х0у + Х{х - 2Х2у, 2X0z),
ее вторая производная имеет вид
(2(Х0 +Х2) Х{ О л
^>,Х) = К 2(Х0-Х2) О
{ О О 2X0J
Точки экстремума в этой задаче в силу теоремы 1.9 являются решением системы
(1.33), которая принимает вид
<^(!й),0-И>=^^ (160)
\/v = (vvv2,v3)eX0;
ху = 0, х2-у2=0, X = (X0,XvX2)±0. (1.61)
В неравенстве (1.60), как и в примерах 1.12, 1.17, будем различать случаи
ие intX0={w = (x,2/,2) :z> 1} и we ГрХ0 = {и = (х,у,z) :z= l}.
Тогда система (1.60), (1.61) распадется на две подсистемы: если и е intX0, то
£'и(щ X) = (2Х0х + Хху + 2Х2х, 2Х0у + Ххх - 2Х2у, 2X0z) = (0,0,0), 1 б2
ху = 0, х2-у2=0, 2>1, Х = (Х0,Х{1Х2)±0;
и если и е ГрХ0, то
i?;(w,X) = 2^0x + ^12/ + 2^2x = 0, £'y(u,X) = 2X0y + Xxx-2X2y = 0,
ху = 0, х2-у2=0, 2 = 1, X = (^0,^,^2)^0, (1'63)
причем частная производная £'г(и, X) = 2X0z\ = 2X0 должна быть неотрицательна,
если и = (х, у, 1) — точка локального минимума, и неположительна, если и = (х,
г/, 1) — точка локального максимума.
Уравнения ху = 0, х2 - у2 = 0 из этих подсистем приводят нас к равенствам х = 0, у = 0,
поэтому из системы (1.62) следует, что подозрительными на экстремум будут точки
щ = (0,0,2), 2 > 1 с соответствующими им семействами наборов множителей Лагранжа
Х0 = 0, (Аф А.2) Ф 0. Из системы (1.63) находим подозрительную точку и2 = (0,0,1),
соответствующими ей множителями Лагранжа будет любой набор X = (Х0, XvX2)*0.
Если для выяснения характера экстремума точек щ, и2 мы попробуем применить
теорему 1.10, то обнаружим, что у точки щ нет «хороших» множителей Лагранжа,
удовлетворяющих условиям (1.34)—(1.37). У точки и2 «хорошими» множителями
являются, например, множители X = X* = (Х*0,0,0) с любым Х*0 > 0 и £'ии(и2, Х*) = 2Х*013 > 0,
так что и2 — точка строгого локального минимума.
Остается заметить, что полное решение рассматриваемой задачи (1.58) проще
было получить, вовсе не привлекая теоремы 1.9, 1.10. Дело в том, что множество X
здесь состоит только из точек и = (0, 0, 2), z > 1 и, по сути, задача сводится к задаче
поиска экстремума функции одной переменной p(z) = z2 на множестве z > 1. Отсюда
следует, что в задаче (1.58) в точке и2- (0, 0, 1) достигается глобальный минимум
/* =1, других точек экстремума нет; /* =+°о.
Пример 1.19
Рассмотрим задачу на условный экстремум
/(м) = х->extr, ueX = {u = (x,y)eE2:gx(u) = x2 + y2-l = 0,g2(u) = x3 + y3-l = 0}.
57

i&(«a)=
Функция Лагранжа этой задачи имеет вид
£(и,Х) = Х0х + Хх(х2 + у2-1) + Х2(х3 + у3-1), и = (х,у)еЕ2,Х = (Х0,Х1,Х2)еЕ3.
Ее градиент и вторая производная равны
£'и(ц, X) = (Х0 + 2Ххх + 3^2х2,2Хху + 3^2г/2),
Тч_(г2Х1 + 6Х2л: О "J
О 2\1+6\2У)
Для решения этой задачи воспользуемся теоремой 1.11. Записывая систему (1.27),
имеем
Х0 + 2Ххх + ЗХ2х2 = 0, 2Хху + ЗХ2у2 = 0,
х2+у2=1, х3+у3=1, Х = (Х0,Хх,Х2)±0.
Есть два решения этой системы. Первое их них — точка щ = (0, 1), ей
соответствуют множители ЛагранжаX = (Х0 = 0,Х{,Х2), где 2ХХ + ЗХ2 = 0. Среди них есть
«хорошие» множители, удовлетворяющие условиям (1.39), (1.40), например можно
рассмотреть набор X* = (Х0 =0,Х{= 3, Х2 = -2). В самом деле, для решений системы (1.40)
<£(«!),*> = 2*2= 0, <Й(«1).А> = ЗА2=0> h = (fh,h2)*0
Г 6 0У^^
имеем
£|).«е>а
<4К«,Л>.*Н ^
Отсюда и из теоремы 1.11 следует, что точка щ = (0; 1) является одновременно
как точкой строгого локального минимума, так и строгого локального максимума
со значением целевой функции/(г/j) = 0, что в силу замечания 1.4 возможно только
в случае, когда щ — изолированная точка множества X.
Аналогично доказывается, что второе решение системы (1.64) и2 = (1, 0) с
соответствующими ему множителями Лагранжа X = (Х0, Х{, Х2), где Х0 + 2ХХ + ЗХ2 = 0 при
X = X* = (Х0 =0,Х{= 3,Х2 = -2) является изолированной точкой экстремума функции
f(u) со значением f(u2) = 1.
Пример 1.20
Рассмотрим задачу на условный экстремум
/(*) = {Ах, х) -> extr, х е X = {х е Е*: ||xf = 1}, (1.65)
где Л — симметричная матрица размера пхп.
Составим функцию Лагранжа:
£(х, X) = Х0{Ах, х) + Х(1 - Ы12), * е Р», X = (Х0 А) е £2.
Ее градиент равен ^(х, X) = 2А.0Аг - 2Ал:.
Система (1.27) в этом примере имеет вид
Х0Ах-Хх = 0,\\х\\2=1,(Х0,Х)*0. (1.66)
Нетрудно видеть, что случай Х0= 0 здесь невозможен, поэтому в (1.66) остается
принять Х0= ±1. Достаточно рассмотреть вариант Х0= 1, это приведет нас к системе
Лх = Ах,И|2=1, (1.67)
которая представляет собой подробно исследованную в линейной алгебре [9, 31]
задачу на собственные векторы и собственные значения матрицы Л. Как известно,
58

у любой симметричной матрицы все п собственных значений Х{,..., Хп действительны.
Пусть они упорядочены в порядке возрастания:
Х{<Х2<...<Хп, (1.68)
а х{, ..., хп — соответствующие им нормированные собственные векторы. Пары
(х{, Х{), ..., (хп, Хп) будут представлять собой все решения системы (1.67), поэтому
точки хь ..., хп, и только они, являются подозрительными на экстремум задачи (1.65).
К ней применима теорема 1.1 Вейерштрасса, согласно которой функция/(х) на
множестве X достигает конечных верхней и нижней граней хотя бы в одной точке,
причем в силу теоремы 1.8 все эти точки в паре со своими множителями Лагранжа
являются решением системы (1.67). Заметим, что
f(xf) = (Axt, x{) = (XfX^Xi) = Xf\\xi\l = 1, i = 1,..., п.
Отсюда и из соотношений (1.68) вытекает
f(xx) = Xx<f(x2) = X2<...<f(xn) = Xn.
Это значит, что точка хх является точкой глобального минимума задачи (1.65),
хп — точкой ее глобального максимума. В этом примере удалось обойтись без
применения достаточных условий оптимальности.
Отметим, что в последнем примере нами фактически доказано
следующее утверждение: для всеххтаких, что ||х\\ = 1, справедливо Хх < {Ах,х) < Хп,
или
Xx\\xf <{Ax,x)<Xn\\xf \/хеЕп. (1.69)
Левое неравенство (1.69) означает, что матрица Л положительно
(неотрицательно) определена тогда и только тогда, когда Хх > 0 (кх > 0).
Замечание 1.5. В примерах 1.15, 1.18, 1.19 мы встретились с задачами,
в которых подозрительными на экстремум оказались точки, у которых
все или некоторые множители Лагранжа X = (Х0, X) Ф 0 имели компоненты
Х0 = 0. Обращаем внимание читателя на то, что необходимое условие
экстремума (теоремы 1.8,1.9) при Х0 = 0 вовсе не содержит какую-либо
информацию о целевой функции. Так, например, система (1.27) в задаче (1.22)
при Х0 = 0 имеет вид
iXjgr(x) = 0, gj(x) = 0, ; = l,...,s; X = (Xv...,Xs)*0. (1.70)
7=1
В задаче (1.20) система (1.33) при Х0 = 0 превращается в систему
(m+s \
yZ\gAxXy-xj>0\/yeX0;Xjgj(x) = Oy gj(x)<0J = l,...,m
gj(x) = 0, j = m + l,...,m + s; X = (Xv...,Xm+s)*0, Х1>0у...уХт>0.
Приходится признать, что если множество Х0 и функции gi(x), ...,
gs(x), задающие множество X, обладают специфическими свойствами
(1.70), (1.71), то компоненты х всякого решения (х,Х) систем (1.27), (1.33)
при Х0 = ОД = (Xv ..., hm+s) Ф 0 автоматически становятся подозрительными
на экстремум, какой бы ни была целевая функция/(х).
59

Задачи (1.20), (1.22), в которых системы (1.70), (1.71) имеют решение,
часто называют анормальными задачами. Любопытно заметить, что в
анормальной задаче (1.22) условие (1.70) имеет простой геометрический смысл
и означает, что в точкехе Xградиентыg[(x),...,g's(x) линейно зависимы.
Читатель, желающий углубиться в теорию анормальных и иных задач,
ознакомиться с более тонкими необходимыми и достаточными условиями
оптимальности, найдет много интересного в специальной литературе (см.,
например, [2, 12]).
Заметим, что с помощью изложенных выше необходимых и
достаточных условий экстремума лишь в редких задачах удается найти и
полностью проанализировать все точки экстремума. Поэтому может создаться
впечатление, что эти условия имеют лишь теоретическое значение. Однако
это не так. Как мы увидим ниже, многочисленные методы оптимизации
в той или иной степени представляют собой итерационные процессы,
подсказанные условиями экстремума и предназначенные для решения систем
уравнений и неравенств, составляющих суть этих условий. Нередко даже
беглый теоретический анализ условий оптимальности позволяет получить
немало полезной информации о свойствах решений конкретной задачи,
которая может быть использована при конструировании и реализации
численных методов.
1.4.6. Экономический смысл множителей Лагранжа
Как правило, множители Лагранжа имеют вполне определенную
интерпретацию, связанную с содержательным смыслом исходной
оптимизационной задачи. Следуя работе [36], приведем одну из возможных
интерпретаций, в которой множители Лагранжа играют роль цен на ресурсы.
Предположим, что на некотором предприятии изготавливается п
видов продукции и пусть xJJ = 1, 2, ..., п, — в принципе возможные
количества выпуска продукции j-го вида. Пусть f(x) — функция, значениями
которой является прибыль от реализации произведенной продукции
х = (х1, х2, ..., хп). Пусть в процессе производства используются т видов
сырья и на изготовление продукта х расходуется gt(x) единиц сырья i-го
типа, г - 1, 2,..., т. Предположим, что в распоряжении предприятия имеется
Ы единиц сырья i-го вида, и предприятие с целью извлечения
максимальной выгоды может как докупать на рынке недостающее для производства
сырье, так и продавать его излишки, незадействованные в производстве.
Пусть р{> 0, г - 1, 2, ..., т, — рыночная цена единицы сырья i-го типа,
a h = (A1, h2, ..., hm) e Em — вектор, координатами которого являются
объемы i-го сырья Ы, запланированные предприятием к покупке или
продаже. Будем считать, что положительные значения (Ы > 0) соответствуют
покупке сырья, а отрицательные (Ы< 0) — его продаже. В данных условиях,
разумеется, учитывающих далеко не все экономические факторы, задача
максимизации прибыли предприятия может быть сформулирована в виде
/(*)-</?,/*>->шах, ^>0,; = 1,...,и, &(*)<#+#, i = l,...,w, (1.72)
где р = (pv p2,..., рт) — вектор действующих рыночных цен на ресурсы, а (х,
К) g Еп+т — принятый предприятием план выпуска продукции и покупки-
60

продажи сырья. Запишем задачу (1.72) в общей форме (1.20), в которой
отсутствуют ограничения типа равенств:
F(x, К) = -f(x) + (р, /z) —> min, (x, h)eX0,
Gi(x,h) = gi(x)-hi<bi, i = l,...,/7z, (1.73)
X0 = {(x,h)eEn+m:xi >0J = 1,...,n).
Предположим, что функции/(г) и g£x), г - 1,..., /и, моделирующие
соответственно доходность производства и расход ресурсов, являются
непрерывно дифференцируемыми по х. Тогда для оптимального решения (x*,h*)
задачи (1.73) справедливы все утверждения теоремы 1.9. Предположим
дополнительно, что отличен от нуля множитель Лагранжа \*0 > 0,
отвечающий за доходность экономической деятельности предприятия. Это
позволяет после соответствующей перенормировки считать, что Х*0 = 1 и
использовать теорему 1.9 с классической функцией Лагранжа, в которой Х0= 1:
т
£(x,h,X) = F(x,h) + "ZhGi(*>h), Х = (Х1Д2,...ДЯ|).
Утверждение (1.30) этой теоремы примет вид
(^(х,к)(х*^^*)Л^^)-(х,Л))Еп+т ^0, (x,h)eXQ. (1.74)
Поскольку в неравенстве (1.74) вариации по h ведутся по всему
пространству Ет, то, зафиксировав х-х*, из (1.74) можно извлечь равенство
нулю частной производной функции Лагранжа по h, аналогичное
соотношению (1.32) из замечания 1.2:
т
4(ьЛДО = Шй) + ЕЩ(^й)=0. (1.75)
1=1
Зависимость h в рассматриваемом нами случае линейная, так что
покоординатная запись уравнения (1.75) оказывается совсем простой:
р{-Х*=0, г = 1,2,...,/тг,
и означает, что оптимальные значения X* множителей Лагранжа в точности
совпадают с действующими ценами р{ на ресурсы.
1.5. Метод штрафных функций
1.5.1. Описание метода
Метод штрафных функций является одним из наиболее простых
и широко применяемых методов решения задач минимизации. Основная
идея метода заключается в сведении исходной задачи
f(x) —> min, x e X (1-76)
к последовательности задач минимизации
ФДх) —> min, х е X0,k= 1,2,..., (1-77)
61

где Ф^(х) — некоторая вспомогательная функция, а множество Х0
содержит X. При этом функция Ф^(х) подбирается так, чтобы она с ростом
номера k мало отличалась от исходной функции f(x) на множестве X и
быстро возрастала на множестве Х0 \ X. Можно ожидать, что быстрый рост
функции Ф/г(х) вне X приведет к тому, что при больших k нижняя грань
этой функции на Х0 будет достигаться в точках множества X или близких
ко множеству X, и решение задачи (1.77) будет приближаться к решению
задачи (1.76). Кроме того, как увидим ниже, имеется достаточно широкий
произвол в выборе функций Ф^х) и множества Х0 для задач (1.77), и
можно надеяться на то, что задачи (1.77) удастся составить более простыми
по сравнению с исходной задачей (1.76) и допускающими применение
несложных методов минимизации.
Определение 1.27. Последовательность функций {Pk(x)}, k = 1, 2, ...,
определенных и неотрицательных на множестве Х0, содержащем
множество X, называют штрафом или штрафной функцией множества X на
множестве Х0, если
[О, хеХ,
Km/1<*)=' '.у
£_>оо l+OO, XSXq\X.
Из этого определения очевидно, что при больших номерах k за
нарушение условия х е X приходится «платить» большой штраф, в то время как
при любом фиксированном х е X штрафная функция представляет собой
бесконечно малую величину при k —» °°.
Для любого множества X<zEn можно указать сколько угодно различных
штрафных функций. Например, если {Ak} — какая-либо положительная
последовательность, lim Ak = -н», то можно взять
k—>oo
Pk(x) = Akp(x,X),xe En = X0,k=l,2,...,
где р(х,Х) = inf \х - у\ — расстояние от точки х до множества X, или
уеХ
[О, хеХ,
Pk(x)-\Ak\\x-xlxtX, *-U~'
где х — какая-либо точка из X. Приведем другие примеры штрафных
функций, когда в (1.77) множество X имеет вид
Х = {хеЕп:хе XQ,gt(x) < 0, г = 1,..., т\g((x) = 0, г = т +1,..., m + s}, (1.78)
где Х0 — заданное непустое множество из Еп (не исключен случай Х0 = Еп),
функции /(г), &(х), г = 1,..., т + 5, определены на Х0. В качестве штрафной
функции этого множества можно взять
т m+s
Pk(x) = AkP(x), P(x) = ^(max{gi(x);0})P+ X \gi(x)\p, xeX0, (1.79)
1=1 i=m+l
где Ak> 0, k = 1, 2,..., lim Ak = -H», ap > 1 — фиксированное число.
k—>°o
Если ввести обозначения
fmax{g,-(.r);0}, i = l,...,/7z,
62

то функцию (1.79) кратко можно записать в виде
m+s
Pk(x) = AkP(x% P(x)=Z(gt(*))p> *zX0. (1.81)
i=l
Функцию Р(х) мы также будем называть штрафной функцией
множества (1.78), подразумевая при этом, что после умножения на Ak> О,
lim Ak = -и», она превратится в штрафную функцию в смысле определе-
k—>oo
ния 1.27. Величины Ak из формулы (1.81) будем называть штрафными
коэффициентами. Заметим, что существуют и другие штрафные функции
множества (1.78). Например, можно взять
m+s
A(*)=Z4b<#(*))ft. *е*о> * = t2,...f (1.82)
i=l
где Pi > 1, Aki> О, lim Aki = +©o, i = 1, ..., m + s; здесь каждое ограничение
из множества (1.78) имеет свой штрафной коэффициент. Весьма широкий
класс штрафных функций множества (1.78) дает следующая конструкция:
m+s
где <p,-(g) — произвольная функция, определенная при g > О, такая, что
Ф;(0) = 0, (Pj(g) > 0 при g > О, г = 1, ..., m + s. При необходимости можно
выбрать функции <p,-(g) так, чтобы штрафная функция Р^(х) обладала
различными полезными свойствами, такими как, например, непрерывность,
гладкость, выпуклость, простота вычисления значений функции и нужных
производных и т.п.
Возможны и другие конструкции штрафных функций множества (1.78).
Приведем еще два конкретных примера штрафной функции:
( m+s \Ak
( m m+s \
Pk(x) = A£l Sexp(4kgf.(x))+ J exp(4g?(*)) , *eX0,
где Л^ > 0, k = 1, 2,..., lim Ak = +°o.
£->oo
Допустим, что некоторое множество Х0, содержащее X, а также
штрафная функция {Pk(x)} множества X на Х0 уже выбраны. Предполагая, что
функция f(x) определена на Х0, введем функции
Ф*(*) =/(*) + ^*(*)> л: е X0,k = 1, 2,... (1.83)
и рассмотрим последовательность задач (1.77) с функциями (1.83). Будем
считать, что
0^=infO^(x)>-oo, 6 = 1,2,.... (1.84)
хо
Если здесь при каждом 6=1,2,... нижняя грань достигается, то условия
Фк(хк) = Фк*, xkeX0, (1.85)
63

определяют последовательность {xk}. Однако точно определить хк из
условий (1.85) удается лишь в редких случаях. Кроме того, нижняя грань в
формуле (1.84) при некоторых или даже всех k= 1,2,... может и не достигаться.
Поэтому будем считать, что при каждом k = 1, 2,... с помощью какого-либо
метода минимизации найдена точка хк, определяемая условиями
Ч^Хц, Фк(хк)<Фк*+гк, (1.86)
где {гк} — некоторая заданная последовательность, гк> О, k = 1,2,..., lim гк = О
k—>oo
(если хк удовлетворяет условиям (1.85), то в условиях (1.86)
допускается возможность гк= 0). Отметим, что, вообще говоря, не исключен случай
Хк£ X.
Таким образом, метод штрафных функций описан.
Подчеркнем, что дальнейшее изложение не зависит от того, каким именно
методом будет найдена точка л^ из условий (1.86). Описанию и
исследованию конкретных методов решения задач типа (1.86) будет посвящена гл. 4
настоящей книги, здесь же мы ограничимся предположением, что имеется
достаточно эффективный метод определения такой точки хк.
1.5.2. Сходимость метода
Так как lim Рк(х) = +°° при х е Х0\ X, то можно ожидать, что для широ-
£->оо
кого класса задач (1.76) последовательность {хк}, определяемая условиями
(1.86), будет приближаться к множеству X и будут справедливы равенства
\imf(xk) = f*, limp(j^,X*) = 0. (1.87)
k—¥°° k—¥°°
Прежде чем переходить к теоремам сходимости метода штрафных
функций, рассмотрим несколько примеров.
Пример 1.21
Пусть требуется решить задачу
f(u) = х2+ху + у2^> min, и е X = {и = (х, у) е Е2 :х + у - 2 = 0}.
В качестве штрафной функции возьмем Р^{и) = k(x + у - 2)2 и положим
Фк(и)=х2 + ху + у2 + к(х + у-2)2,ие X0 = E2,k = 1,2,....
Функция ФДм) при каждом фиксированном k = 1, 2, ... достигает своей нижней
грани на Е2 в точке щ = (xk, yk), которая определяется уравнениями
**h^ = 2xk + yk + 2k(xk + yk-2) = 0;
^^hl = xk + 2yk+2k(xk+yk-2) = 0.
ду
Отсюда получаем
Щ =
f Ak Ak л
3 + Ak'3 + Ak
\2k
k k Ak + Ъ £2 *V '
При k —> oo будем иметь uk^>u*= (1,1), Ф^щ) —» 3. Нетрудно видеть, что и* —
решение исходной задачи. В самом деле,
64

Отсюда при и е X имеем f(u) > 3 = f(u*) = f* = lim Фк(щ). Таким образом, в рас-
смотренном примере метод штрафных функций сходится.
Пример 1.22
Рассмотрим задачу
f(x) = е~х —>min, хеХ = {хеЕ{:g(x) = хе~х = 0}.
Здесь Х = {0} = Х*, /*=1. Возьмем штрафную функцию Рк(х) = kg2(x) = &г2е-2*
и положим
Фк(х) = е-*+ fccV2*, х е X0 = ЕК
Так как Фк(х) > 0 при всех х е Е1, lim Ф^(х) = 0, то Ф^* = inf Ф^(х) = 0. В качестве
точки xk, удовлетворяющей условиям (1.86) при гк= e~k+ k2e~2k, здесь можно взять
xk = k, k= 1,2,.... Получим lim/(x^) = 0</*=l, limp(xk,X*) = +«>. Этот пример пока-
зывает, что метод штрафных функций не всегда сходится.
Попробуем применить метод штрафных функций к задаче
&00=*/2<о,
f(u) = (х -1)2 - у —> min, w g X = j w = (х, г/, 2) е Х0 = Е3: g2(u) = -z< 0,
[ g3(w) = *2-^0J
Нетрудно видеть, что здесь /* = 1, X* = X = {и = (0,0, z): z > 0}. Возьмем штрафную
функцию Pk(x) = k[gt(u) + (g$(u))2 +(gj(w))2], тогда
Ф^(х) = (х-1)2-г/ + ^2+*(тах{-2;0})2+*(тах{х2-г/2;0})2, меХ0 =£3,£ = 1,2,....
Очевидно, что при всех и из Е3 Фк(и)>тт(-у + ку2) =—-, причем если взять
( \ Л 1 1
точку щ = 1,—,2& , то Фк(ик) =—-. Следовательно, Ф**=—7г>-00' ^ = 1» 2, ...,
и точка м^ удовлетворяет условию (1.86) при е^ = 0. Однако имеем
1
lim /(W,)=lim|-— | = 0 </.=!;
*->оо^ 2k
(
р(щ, Х*)= inf p(uk, и) = inf
иеХ>
2>0
4^1 +(2*-^)2
V/2 Г / 1 ^'/2
1 + (2*
, К — 1, Z, ...,
поэтому lim p(w^, X*) = 1, т.е. метод штрафов не сходится. В этой задаче функции /(м),
£i(w)> &(w)> &(w) являются полиномами, множество X выпукло, нижняя грань Ф^*
достигается.
Приведем пример задачи, в которой возможен случай Ф^* = -«>, & = 1, 2,....
65

Пример 1.24
Пусть
f(x) = -x2 -> min, xgX = {xgX0=E{: g(x) = Ы < 0}.
Здесь /* =0, X* =X = {0}. Возьмем штрафную функцию Pk(x) = k\x\, тогда ясно,
что ФДх) = -х2 + k \х\, Фи* = inf Фк(х) = -оо, k = 1, 2,..., и условие (1.86) теряет смысл.
В то же время если в этой задаче взять, например, Pk(x) = (k + l)|x|2, то имеем
Фк(х) = -х2 + (k + 1)х2, Ф^* = 0 > -оо, причем нижняя грань достигается в точке xk = 0,
3
k = 1, 2,.... Можно взять Pk(x) = k\x\4, Ф*(х) = -х2 + fct4, тогдаФ^* = -—тг, эта нижняя
16«
грань достигается в точках xk =±—т=, А = 1, 2,....
В обоих случаях lim f(xk) = /*, lim p(x^, X*) = 0, метод штрафов сходится.
&-»<» &-»<»
Итак, приведенные примеры показали, что попытки применять метод
штрафов могут приводить к различным результатам. Тем не менее можно
заметить, что некоторые соотношения выполнены во всех примерах.
Сформулируем и докажем соответствующее утверждение.
Теорема 1.12. Пусть функции f(x), gj(x), i = 1, ..., m + s, определены
на множестве Х0, функция Фк(х) имеет вид (1.81), (1.83) и для нее
выполнено условие (1.84), последовательность {xk} определена условиями (1.86).
Тогда
Ш/(хк)^Фк(хк)=Шф^^/.. (1.88)
Если, кроме того, /** = inf f(x) > -°°, то
m+s
Р(Ч)= 1 (gt(*k))p=0(A^), k = l,2,...; (1.89)
limgl-(^)<0, i = l,...,m; \imgi(xk) = 0, i = m + l,...,m + s. (1.90)
k—¥°° k—¥°°
Доказательство
Как очевидно из формул (1.80), (1.81),
Р(х) = 0 Мхе Х;Р(х)>0\/хе Х0\Х.
Поэтому, с учетом выражения (1.83),
/(х) = Фк(х)\/хе Х,/(х)<Фк(х)=Лх)+АкР(х)\/хе Х0. (1.91)
Переходя в (1.91) к нижней грани по соответствующим множествам,
получим
def
inf f{x) = /• = inf Фк(х); inf f{x) = /** < inf Фк(х) = Фк*. (1.92)
xeX xeX xeXq xeXq
Так как Xс Х0, то inf Фк(х) > inf Фк(х) = Фк*. Отсюда и из соотношений
xeX xeXq
(1.92) следует
/**<Ф** </*,£= 1,2,.... (1.93)

Поскольку Ф^* >-°°, k = 1, 2, ..., и последовательность {xk} определена
условием (1.86), тогда из (1.86), (1.91), (1.93) имеем
/**</(хк)<Фк(хк)<Фк*+гк</*+гк, £ = 1,2,.... (1.94)
Из соотношений (1.94) при k —> °° с учетом равенства lim гк = 0 полу-
k—>oo
чаем неравенства (1.88).
Пусть теперь/** >-°°. Тогда из неравенств (1.93) следует, что/* >Ф^* >-°°.
Отсюда и из неравенств (1.94) находим
0<АкР(хк)<Фк(хк)-/(хк)</*+гк~и £ = 1,2,..., (1.95)
или 0 < Р(*£)<(/*+supe^-/**)^1, k = 1, 2, ... . Оценка (1.89) доказана.
Из нее следует, что ИтР(хк) = 0 или limg^(^) = 0, i = 1, ..., т + s. Вспо-
&—>оо k—>°о
миная определение (1.80) для g+C^), отсюда получим соотношения (1.90).
Теорема доказана. ■
Примеры 1.22,1.23 показывают, что в общем случае неравенства в (1.88)
могут быть строгими. Приведем достаточные условия справедливости
равенств (1.87).
Теорема 1.13. Пусть Х0 — замкнутое множество из Еп, функции
/(*)> &(*)> •••> &«(*)> l&i+i(*)l> •••> \gm+ix)\ полунепрерывны снизу на Х0,
/** = inf f(x) > -оо. Пусть последовательность {хк}, определяемая условиями
хо
(1.81), (1.83), (1.86), имеет хотя бы одну предельную точку. Тогда все
предельные точки {xk} принадлежат множеству X* точек минимума задачи
(1.76), (1.78). Если, кроме того, множество
Хь = {х:хеХ0, g?(x)<8J = l,...,m + s} (1.96)
ограничено хотя бы при одном значении 8 > 0, то для последовательности
{xk} выполняются равенства (1.87).
Доказательство
При сделанных предположениях для последовательности {xk}
соотношения (1.88)—(1.90) сохраняют силу. Пусть а* — какая-либо предельная точка
последовательности {хк}, пусть {xk } —»v*. Заметим, что а* е Х0 в силу
замкнутости Х0. Тогда с учетом полунепрерывности снизу указанных в
условии теоремы функций из соотношений (1.90) получим
й(о.) < Hm gt(xy ) < lim gt(xk) < 0, г = 1,..., щ
|g,(a*)|<lim|g^)|= lim \gt(xk)\= 0, i = m + l,...,m + s.
П—>оо «—>°°
Следовательно, a* g X. Тогда с учетом соотношения (1.88) имеем
/* < /(р.)< Ит f(xk )< jto /(**)</*,
т.е. lim /(x^ ) = f(v*) = /*, что означает v* e X*.
Я->оо я
67

Наконец, пусть множество (1.96) ограничено при некотором 8 > 0.
Из соотношений (1.90) следует, что {xk} е Хь для всех k > k0. Это
означает, что {xk} имеет хотя бы одну предельную точку. Но, как было выше
показано, все предельные точки {xk} принадлежат X*. Следовательно,
limp(^,X*) = 0. Из тех же рассуждений и неравенств (1.88) вытекает
Первое
вое равенство (1.87). Теорема доказана. ■
Для иллюстрации теоремы 1.13 рассмотрим следующий пример.
Пример 1.25
Пусть дана задача f(x) = е~х —> min, х е X = {х е Ех: g(x) = х = 0}.
Здесь /* = 1, X = X* = {0}. Функции/(х), g(x) непрерывны на замкнутом множестве
Х0 = Е1, /** = inf е~х = 0, множество Хь = {х е Е1 : \х\ < 5} ограничено при любом 5 > 0.
Е1
Таким образом, все условия теоремы 1.13 выполнены. Положим Р(х) = (g(x))2 = x2,
Ak = k, тогда
Фк(х) = е-х+ kx*,xeP,k = l, 2,....
Нетрудно видеть, что Ф^* = inf Ф^(х) > 0. Пусть {е^} — произвольная
последовательность неотрицательных чисел, стремящаяся к нулю. Определим точку xk из условия
(1.86): Ф^(х^)<Ф^*+е^, k = 1, 2, ... . Для получаемой таким образом
последовательности {xk} согласно теореме 1.13 имеют место равенства (1.87).
Обращаем внимание читателя, что рассмотренные в примерах 1.22
и 1.25 задачи по существу одинаковые: минимизируется одна и та же
функция е~х на одном и том же множестве X = {0}, и отличие состоит лишь в том,
что в примере 1.22 множество X задается ограничениями g(x) = хе~х= 0,
а в примере 1.25 — g(x) = х = 0. Тем не менее в примере 1.22 метод
штрафных функций расходится, в примере 1.25 сходится.
Отсюда заключаем, что для сходимости метода штрафных функций
важное значение имеет способ задания множества X: ограничения,
задающие множество X, и штрафные функции этого множества должны быть
как-то согласованы с минимизируемой функцией/(х).
Определение 1.28. Скажем, что задача (1.76), (1.78) имеет
согласованную постановку на множестве Х0, если для любой последовательности
{xk} e Х0, для которой
limg^(^) = 0, i = l,...,/rc + s, (1-97)
£->оо
имеет место соотношение
Щп/(**)>/,= inf/(*)• (1.98)
k—>oo X
Отметим, что в примере 1.25 задача имеет согласованную постановку
на Е1, а в примере 1.22 такой согласованности нет.
Теорема 1.14. Пусть Ф^х) =f(x) + A^ipc), где Р(х) определена формулой
(1.81), пусть Ф^* = inf Ф^(х), k = 1, 2,.... Тогда для того чтобы
Хо
НтФ^=/*, (1.99)
68

необходимо, чтобы задача (1.76), (1.78) имела согласованную постановку
на множестве Х0. Если /** = inf f(x) > -°°, то согласованной постановки за-
хо
дачи (1.76), (1.78) на Х0 достаточно для справедливости равенства (1.99).
Доказательство
Необходимость. Пусть имеет место равенство (1.99). Возьмем
произвольную последовательность {хп} е Х0, удовлетворяющую условиям (1.97).
Тогда lim P(xn) = 0 и справедливы неравенства
<&k*<<&k(xn)<f(xn) + AkP(xn), £,и = 1,2,....
Отсюда при п —> оо получим Ф^* < lim f(xn) при всех А = 1, 2, ... . Пере-
П—>°о
ходя здесь к пределу при k —» °°, с учетом равенства (1.99) будем иметь
1щ/(xw)> lim Ф^*=/*,
что и требовалось.
Достаточность. Пусть /** >-«>, задача (1.76), (1.78) имеет
согласованную постановку на множестве Х0. Поскольку Ф^(х) > f(x) при всех х е Х0,
то Ф^* > /** > -©о и имеет смысл говорить о последовательностях,
удовлетворяющих условиям (1.86). Возьмем одну из таких последовательностей
{xk}. Согласно теореме 1.12 тогда справедливы соотношения (1.88)—(1.90).
Заметим, что соотношение (1.90) равносильно (1.97), откуда следует
соотношение (1.98).
Наконец, из соотношений (1.91), (1.98) получим lim f(xk)= lim Ф^* = /*.
Теорема 1.14 доказана. ■ ~*°° ~*°°
1.5.3. Недостатки и достоинства метода
Рассмотренный выше метод штрафных функций дает простую и
универсальную схему решения задач минимизации на множествах, не
совпадающих со всем пространством, и часто применяется на практике. Поскольку
имеется достаточно богатый выбор штрафных функций, то при
составлении функции Ф/г(х) можно постараться обеспечить нужную гладкость этой
функции, выпуклость, подумать об удобствах вычисления значений
функции и требуемых ее производных и т.п. Так, например, если функции gi(x)
будут г раз непрерывно дифференцируемы на множестве Х0, то при любом
р > г функция (1.81) также будет г раз непрерывно дифференцируема наХ0.
Если в функции (1.81) р = 1, то из непрерывности &(х), г - 1,..., т + 5,
следует непрерывность Р^{х) на Х0, но гладкости Р^{х) в этом случае ожидать
не приходится.
Кроме того, имеется определенная свобода в выборе множества Х0
для задачи (1.77): в задании множества (1.78) всегда можно отнести
к множеству Х0 наиболее простые ограничения (например, Х0 может быть
шаром или параллелепипедом в Еп, совпадать с полупространством или со
всем пространством Еп и т.д.), а остальные ограничения оформить в виде
gt(x) < 0 или gj(x) = 0 и учесть их с помощью штрафной функции. Поэтому
можно надеяться на то, что вспомогательные задачи (1.77), (1.83) удастся
69

сформировать более простыми, более удобными для применения
известных методов минимизации, чем это возможно в исходной задаче (1.76).
Следует заметить, что хотя сама схема метода штрафных функций
довольно проста, но при практическом использовании этого метода
для решения конкретных задач минимизации могут встретиться серьезные
трудности. Дело в том, что для получения хорошего приближения
решения задачи (1.76) номер k в (1.77), (1.83) (или штрафной коэффициент Ak
в (1.81)) приходится брать достаточно большим. А с увеличением номера k
свойства функции Ф^(х) = f(x) + P^ipc), x e Х0, оказывается, во многих
случаях начинают ухудшаться: малое изменение некоторых переменных может
привезти к резкому изменению значений функции Ф^х) и, наоборот,
изменение переменных, «слабо связанных» с параметром Ak, может вызывать
небольшие изменения функции Ф^х). Это обстоятельство может привести
к тому, что при больших k методы минимизации, используемые для
решения задачи (1.77), будут плохо сходиться и определение точки xk,
удовлетворяющей условиям (1.86), с возрастанием k может потребовать все
большего и большего объема вычислительной работы (см. упражнение 3 гл. 4).
Поэтому при практическом применении метода штрафных функций
вспомогательные задачи (1.77) обычно решают лишь для таких номеров k
(возможно, больших), для которых удается обеспечить достаточно быстрое
убывание функции Ф^х) и достаточную близость получаемых точек к
множеству X при небольшом объеме вычислительной работы. Если полученное
на этом пути приближение к решению задачи (1.76) недостаточно хорошее,
то привлекают более тонкие и, вообще говоря, более трудоемкие методы
минимизации, стараясь при этом получше использовать ту информацию,
которая получена с помощью метода штрафных функций.
1.6. Обоснование правила множителей Лагранжа
Опираясь на метод штрафных функций, можно дать простое
доказательство правила множителей Лагранжа, изложенного выше в параграфе 1.4.
Напомним, что там мы рассматривали задачу
f(x) —> extr, x e X,
(1.100)
X = {xeX0:gj(x)<0J = lJ...Jm;gj(x) = 0J = m + l,...Jm + s}J
где Х0 — заданное выпуклое множество из Еп, функции /(г), gi(x),..., gm+s(x)
определены на Х0. Для исследования этой задачи была введена функция
Лагранжа
_ rn+s _
£(х,Х) = Х0/(х)+Ъ^М1 хеХ0,Х = (Х0,Х)еЕ™+^. (1.101)
7=1
Правило множителей Лагранжа было сформулировано в виде
теоремы 1.9. Имея в виду, что задачи минимизации и максимизации тесно
связаны условиями (1.3), (1.4), мы ограничимся доказательством лишь части
теоремы 1.9, касающейся задачи минимизации, дополнительно потребовав
замкнутость множества Х0.
70

Теорема 1.15. Пусть Х0 — выпуклое замкнутое множество, х*еХ —
точка локального минимума задачи (1.100), функции f(x), g^(x), ..., gm+s(x)
непрерывно дифференцируемы в некоторой окрестности точки х*. Тогда
необходимо существуют множители Лагранжа \* = (К*0,..., X*m+S) такие, что:
Х**0, Хо>0, Х;>0,...Д;>0; (1.Ю2)
(£'х(х*,Х*),х-х*)>0 \/хеХ0; (1.103)
\*jgj(x*) = 0, j = l,...,m. (1.104)
Доказательство
Введем функцию goC*) = /(*) + |*-**| > х е ^о> а также рассмотрим
множество W0 = Х0 n S(x*, у), где 5(х*, у) = {х е Еп: | jc - х* | < у}, у > 0. Так как
х* — точка локального минимума функции f(x) на X, то при достаточно
малых у < 1 будет справедливо f(x)>f(x*) \/xeXnS(x*,y). Рассмотрим
вспомогательную задачу минимизации
g0(x)->min, xeW, (1105)
W = {xeW0:gt(x)<0, i = l,...,m; gt(x) = 0, i = /7z + l,...,77z + s}.
Таккак g0(.r)>/(x)>/(х*)привсеххе W,x Фx*,причем g0 (x*) = f(x*),то
ясно, что х* — единственное решение задачи (1.105) и g0* = inf g0(x) = f(x*).
xeW
Применим к задаче (1.105) метод штрафных функций, а именно, введем
функцию
т m+s
Ф*(*) = £о(*)+£Х(тах<&(*);0})2+& £ g?(x), xeX0.
Так как W0 — компактное множество, функции g0(x), Ф^(х), k= 1,2, ...
непрерывны на нем, то
§о* = inf g0(*) > -°°> ф** = i!}f Ф*(*) > "°°
XEWq XEWq
и существует точкаxke W0 такая, чтоФ^(х^) = Ф^*. Далее, в силу
ограниченности множества W0 его подмножество W(S) = {xeWQ: gf(x)< 8, i = 1,...,m + s}
тоже ограничено при всех 8 > 0. По теореме 1.13 тогда
Ит|хЛ-дг.| = 0, \img0(xk) = g0*=f(x*)=\imf(xk). (1.106)
Применяя теорему 1.7 к задаче Ф^(х) —»inf, x g W0, имеем
<Ф£(^),*-^>>0 V*eW0. (1.107)
Покажем, что неравенство (1.107) на самом деле верно для всех х е Х0
при всех достаточно больших номерах k. Возьмем произвольную точку
хе Х0и рассмотрим точки xka = xk+ a(x-xk), 0 < а < 1. Так какХ0 —
выпуклое множество, то xka е Х0. Далее,
71

С учетом соотношений (1.106) имеем
и и Y и и Y
Р£_хч1 о ^k>k^\ a\x-xk\<+- Va,0<a<a0 =а0(х)<1.
Поэтому |^a-^*|<Y» T-e- хкаеЩ V^>^q, Va, 0<a<a0, и в формуле
(1.107) можем положить х = xka. Получим (Ф'к(хк), а(х-xk)) >0 при всех
а, 0 < а < а0 = а0(х), k > k0. Сокращая это неравенство на a > 0, получаем
(&k(xk),x-xk)>0 VxeX0,V&>V (1.108)
Подставим в неравенство (1.108) явное выражение для производной:
т m+s
**(**) = f'(xk) + 2(xk -x.)+Z%max{gi(xky,0}g'i(xk)+ £ 2к&(хк)£(хк).
i=l i=m+l
Будем иметь
(m+s \
f\xk) + 2(xk-x.)+ ^iiikg;(xkXx-xk)>0 ViEX0,Vi>^ (1.109)
[2&max{&(^);0}>0, i = l,...,m,
ik \2kgt(xk% i = 77Z + l,...,77Z + S.
/ _._ \l/2
/ m+s \ '
Разделим неравенство (1.109) на
m+s
1+ £ \tfk >1. Получим
V i=l )
(W4**) + 2X0*(**-*0+ ЪЬгл£Ы>х-Хк)*0 VxeX0,V^>^,(1.111)
где
m+s \ '
\k~
причем в силу выражения (1.110) \k- 0, i = 1,..., /и при всех & > k$. Заметим,
что последовательность {^ =(Х0^,...,Х|Я+5^)} ограничена, так как А^| = 1.
Пользуясь теоремой Больцано — Вейерштрасса и выбирая jipn
необходимости подпоследовательность, можем считать, что {^}—>X = (X0,...,Xm+5),
ще Х{> 0, г - 0, 1,..., т, IWI = 1. Как видим, условия (1.102) для полученного
X выполнены. Так как/'(.г), g[(x) непрерывны и {xk}^> x* в силу
соотношений (1.106), то из неравенства (1.111) при k —> °° получим неравенство
(1.103).
Наконец, если gj(x*) = 0, то \igi(x*) = 0. Если же &(**)< 0 пРи
некотором i, 1 <г<т, тоg,-(^) < 0 при всехk>ki>k{). Тогда из выражения (1.110)
видно, что \iik = 0, и поэтому Xik = 0 для любого k > kv При k —» оо отсюда
имеем Х,-= 0 при &(х*)<0, так что снова \&(х*) = 0. Равенства (1.104)
получены, теорема 1.15 доказана. ■
Другое доказательство этой теоремы при несколько ослабленных
требованиях на задачу (1.100), основанное на теоремах о неявных функциях
и теоремах отделимости выпуклых множеств, см., например, в [5, 12].
72

1.7. Вспомогательные предложения
Ниже приводятся некоторые формулы и другие сведения, которые нам
понадобятся в дальнейшем. При первом чтении настоящей книги этот
материал можно пропустить и возвращаться к нему по мере надобности
при наличии ссылок.
1.7.1. Формулы конечных приращений
Для гладких на отрезке [а; Ь] функций в курсе математического анализа
обычно доказывается формула конечных приращений Лагранжа
f(b)-f{a)=f\%)(b-a),
где £ — некоторая точка из интервала (а; Ь). Ниже приводятся некоторые
обобщения этой формулы для функций многих переменных. Будем
пользоваться общепринятыми обозначениями: С{(Х) — множество всех
функций, непрерывно дифференцируемых на множестве X; С*(Х) — множество
всех функций, дважды непрерывно дифференцируемых на множестве X.
Возьмем какую-либо функцию /(г), определенную на множестве X с Еп.
Пусть точки х, х + h е X таковы, что h Ф О, х + th е X при всех t, О < t < 1.
Тогда можно рассматривать функцию одной переменной g(t) = f(x + th)
при t g [0; 1]. Оказывается, если f(x) е Ср(Х) при р = 1 или р = 2, то
g(t) g O[0; 1], причем
g*(t) = (f'(x + th),h), g'Xt) = (f'\x + tK)h,hX 0<£<1. (1.112)
В самом деле, если, например, f(x)e (^(Х), то, заменив в формуле (1.13)
х на х + th, h на Nth, получим
g(t + АО - g(t) = At(f'(x + th), h) + Ute)2(f"(x + th)h, h) + o(\ At\2).
Такое разложение с учетом того, что g(t) e (?[(); 1], указывает на
справедливость формул (1.112).
Для дважды дифференцируемой функции одной переменной имеют
место формулы
g(0 - g(0) = g'(Q,t)t = J g'(x)dx = g'(0)t+\g"(Q2t)t* ■
о l
g'(t)-g'(0) = g"(Q3t)t, О^Эз.Эз <1.
Полагая в этих формулах t = 1 и пользуясь равенствами (1.112),
получаем различные формулы для конечных приращений функции многих
переменных:
/(х + Ь)-/(х) = (Г(хЩЬ),Ь) = КГ(х + Ж),Ьу, (1.113)
о
f(x + h)-f(x) = (fXx),h) + ±(f'Xx + e2h)h,hy, (1.114)
73

(1.115)
</'(*+A) - f\x), h) = (f"(x + Q3h)h, h),
где 0 < 0^02,63 < 1. Далее, так как
4-f'(x + th) = f"(x + th)h, 0<t<l,
at
то, интегрируя это векторное равенство, имеем
1 Л
f\x+h)- f\x) = lf"(x+th)hdt = lf"(x + th)dt
о U
Поскольку градиенты f'(x + К) и f'(x) в случае, когда переменная х
имеет размерность два или выше, представляют собой векторы, то аналог
этой формулы, использующий промежуточную точку, неверен. Так,
например, если рассмотреть вектор-функцию
к (1.116)
h(t) =
cost
то
h(2n)-h(0) =
(О
(О
1ъ
(О} , ( cost
Ф2пк'(х) = 2п\
v°y
v-siniy
ни при каком т е (0; 2тт). Для вектор-функций h(x) можно утверждать
лишь, что
||А'(*)-А'(У)||* sup |ЛЧт)|Н|л:-у|.
те[х,у]
Подчеркнем еще раз, что в формулах (1.112)—(1.116)
подразумевается, что точки х, х + h принадлежат множеству X вместе с отрезком х + th,
0 < t < 1. В частности, эти формулы верны на любых выпуклых множествах.
Приведем одно простое утверждение, основанное на формуле (1.113).
При описании и исследовании методов минимизации нам часто придется
иметь дело с функциями, градиент которых удовлетворяет условию Липшица.
Определение 1.29. Пусть/(х) е СХ(Х). Скажем, что градиент f'(x) этой
функции удовлетворяет условию Липшица на множестве X с постоянной
L > 0, если
\\Пх)-Пу)\<Ь\х-у\ \/х,уеХ. (1.117)
Класс таких функций будем обозначать через СХ1(Х).
Лемма 1.3. Пусть X — выпуклое множество, f(x) e Ci{(X). Тогда
при всех х, у е X
\Kx)-f{y)-(f\y),x-y)\<^\x-yf.
Доказательство
Используя формулу (1.113), имеем
1
/(*) " /(*/) " </'(*/), х - у) = \{f'(y+t(x - у)) - f'(y), х - у).
о
(1.118)
74

Пользуясь неравенством Коши — Буняковского и тем, что модуль
интеграла не превосходит интеграла модуля, с учетом условия (1.117) получим
|У(лг) - У (г/) - <У 41/), ^ - г/>| < / |<У Чг/ + ^С^ -1/)) - У Чг/), ^ - г/>|^ <
о
^ JII/Чу+*С^ - у» - /Чу)! - Ik - у||Л ^ J£||jc - yf t Л=4lk - yf -
о о l
Лемма доказана. ■
1.7.2. Леммы о числовых последовательностях
Приведем несколько лемм о числовых последовательностях, которые
нам пригодятся при оценке скорости сходимости различных итерационных
методов минимизации.
Лемма 1.4. Пусть числовая последовательность {ak} такова, что
ak+1<ak+8k, 8*>0, 6 = 0,1,..., £ 8* <+<*>. (1.119)
Тогда существует lim ak < +°°. Если {ak} ограничена еще и снизу, то lim ak
k—>°° k—>°°
конечен.
Заметим, что если 8k= 0, k = 0,1,..., то последовательность {ak} не
возрастает и лемма 1.4 превращается в хорошо известное утверждение о пределе
монотонной последовательности.
Доказательство
Суммируя первое из неравенств (1.119), имеем
т-\ ею
вт£в*+Х8,-£в* + Е8,- (1.120)
i=k i-k
при всех т > k > 0. Пусть
lim ak = lim ak ,kn< kn+1, n = 0,1,...; lim kn = oo.
£_>oo Я->°о П W->°o
oo
Положив в соотношении (1.120) k = kw получим am<ak + 5i 8,- V m > kn.
i=kn
oo
Следовательно, lim am<ak + X 8,- для всех п = 1, 2,.... Отсюда при и —> oo
m^°° n i=kn
имеем lim am < lim ak = lim am. Но всегда lim am < lim am, поэтому lim am =
= lim am. Отсюда следует существование предела {ak}. Далее, при k = 0
т—>оо
из соотношения (1.120) следует ограниченность {ak} сверху. Поэтому если
{ak} ограничена еще и снизу, то lim ak конечен.
k—>оо
Лемма 1.5. Пусть числовая последовательность {bk} такова, что
bk+l>bk-bk, bk>0, £ = 0,1,..., S54<4«».
A=0
75

Тогда существует lim bk > -оо. Если {bk} ограничена еще и сверху, то
k—>°о
lim bk конечен.
k—>°о
Эта лемма сводится к лемме 1.4, если принять bk= -ak, k = О, 1,....
Лемма 1.6. Пусть числовая последовательность {ak} и неотрицательное
число А таковы, что
ak>0,k = Oy l,...;ak-ak+1>Aal &>^>0. (1.121)
Тогда ak = 0(&-1), А = 1, 2,..., т.е. найдется постоянная В > О такая, что
0<^<5^"1Д=1,2,.... (1.122)
Доказательство
Если ат= О при некотором m>k§, то из соотношений (1.121) следует,
что я^= О ПРИ всехк>гПуИ оценка (1.122) становится тривиальной — в ней
достаточно взять B = mmaxai. Поэтому пусть ап> О при всех n>k$. Тогда
\<i<m
из соотношений (1.121) имеем
—-—-^"^+1>-^л>л>о, n>v
Суммируя эти неравенства по п от k0 до некоторого k -1 > ^, с учетом
положительности чисел я^ получаем
>A(k-k^)^ — >A(k-k^)<^ak< &>V
fl* % ak Акк-bo)
Но -—— <—— при k > k0l поэтому 0<ak < ^ . Если 1<&<£q, to
k-Rq k Ak
у
§<ak<-j- max ak. Остается в (1.122) принять В = max{(^Q + 1)Л-1; k$ max ak).
k \<k<kQ \<k<kQ
Упражнения
1.1. Найдите верхний и нижний пределы последовательности ап =
= sin — , где т — фиксированное натуральное число.
1
1.2. Пусть /(x) = arctg— (x Ф 0). Как надо доопределить эту функцию
х
при х = 0, чтобы она стала полунепрерывной снизу или сверху на (-°°, +°°)?
1.3. Приведите примеры, показывающие, что в задаче минимизации
(максимизации) условия компактности множества X и
полунепрерывности снизу (сверху) функции/(х) по совокупности аргументов, достаточные
для достижимости точной нижней (верхней) грани, существенны.
1.4. Пусть полунепрерывная снизу функция имеет точку глобального
минимума на множестве Еп. Следует ли отсюда, что эта функция имеет
точку глобального минимума на любом замкнутом множестве из Еп?
Указание. Рассмотрите функцию из примера 1.1.
76

1.5. Пусть полунепрерывные снизу функции/и g имеют точки
глобального минимума на замкнутом множестве X с Еп. Следует ли отсюда, что
сумма/ + g также достигает глобального минимума на X?
Указание. Рассмотрите функции /(х) = -, g(x) = -, а е Еп,
1+ЫГ 1+ЫГ
аФО.
1.6. Пусть X — замкнутое множество из Еп. Докажите, что для любой
точки у е Еп найдется хотя бы одна точка х* е X, ближайшая к у.
Указание. Примените к задаче минимизации р(г/, X) = \у - х|| —> min, х е X,
теорему 1.3.
1.7. Выясните, будет ли произвольная минимизирующая
последовательность сходиться к множеству точек минимума функции f(u) на
множестве X, если:
а) X = {и = (х, у) е Е2: х > О, у > 0, х + 2у < 1}, f(u) =x + y;
б)Х=^,/(х) = ||х||(1 + ||х2||)-1;
b)X = £*/(*HW|2.
1.8. Найдите точки экстремума на всем пространстве Е2 функций:
1 1
a) f(x,y) = -x4 +-х3-х2 +siny;
6)f(x,y)=x* + y*-2x2;
в) /(х, у) = ху\п(х2 + г/2), (х, у) Ф (0, 0), /(0, 0) = 0.
1.9. Исследуйте на экстремум на пространстве Еп (п > 2) функцию
(ау х) + Ь
/(х) = —f , где ае Еп> Ъ е (-«>, +оо) фиксированы.
1.10. Пусть/(х) — непрерывная на^1 функция одной переменной.
Докажите, что между любыми двумя ее точками локального минимума лежит
по крайней мере одна точка локального максимума. Для случая Еп,п>2,
подобный результат неверен: рассмотрите упражнение 1.11.
1.11. Покажите, что функция/(w) = хех- (1 + e*)cos у> и = (х, у) е Е1,
имеет бесконечно много локальных минимумов, но не имеет ни одного
локального максимума.
1.12. Пусть функция/(х) одной переменной имеет производную порядка
т - 1 в некоторой е-окрестности 0(х*,е) точки х* и производную порядка т
в самой точке х*, причем
f'(x*) = f"(x*) = ... = f(™-V(x*) = 0. (1.123)
Докажите, что
а) если х* — точка локального минимума/на 0(w*,e) и т = 2/ + 1, то
необходимо f(m\x*) = 0;
б) если х* — точка локального минимума / на 0(гг*,е) и т = 2/, то
/<™)(х*)>0;
в) если т = 2/ и /(™)(х*)>0, то х* — точка строгого локального
минимума/.
Переформулируйте утверждения а) — в) для точек локального
максимума.
77

1.13. Пусть х* — точка строгого локального минимума бесконечно
дифференцируемой функции /(х) одной переменной. Можно ли тогда
утверждать, что /<w)(x*)*0 хотя бы при одном т> т.е. цепочка равенств (1.123)
оборвется на каком-то номере ml
IV1/*2, х Ф О,
Указание. Рассмотрите пример: f(x) = \
[О, х = 0.
1.14. Пусть х* — точка строгого минимума функции/на Е1. Можно ли
утверждать, что/убывает в некоторой левой полуокрестности х* и
возрастает в некоторой правой полуокрестности х*?
2х + х sin— х Ф 0
Указание. Рассмотрите функцию /(х) = 1 х'
[о, х = 0.
1.15. В точке и0= (0, 0) функция/(и) переменной и = (х,у) е Е2 имеет
локальный минимум вдоль каждой прямой, проходящей через точку и0.
Можно ли утверждать, что в точке щ реализуется локальный минимум
функции f(u)?
Указание. Рассмотрите функцию f(u) = 2т4 - Зх2у + у2= (х2 - у)(2х2 - у)
при u = td\/ d = (б/1, d2) Ф 0, t е Ми при и = (х, г/), где х2 < у < 2х2.
1.16. С помощью правила множителей Лагранжа решите задачи:
1
а) f(u) = x-—y2 —>extr, иеХ = {и = (х,у)еЕ2: х2+у2 <1};
б) f(u) = х - у2 —> extr, и е X = {и = (х, у) е Е2: х2 + у2 < 1};
в) f(u) = x2+y^> extr, и е X = {и = (х, у) е Е2: х2 + у2 < 1, х > 0, у > 0};
г) f(u) = е*~у ~Х~У^> extr, и е X = {и = (х, у)е Е2: х + у < 1, х > 0, у >0};
д) f(u) = xsinг/ —> extr, гг е X = {гг = (х, г/) е £2: Зх2 -4cosг/-1 = 0};
е) /(г/) = xz/z —> extr, и е X = {и = (х, у, z) e Е3: х2 + у2 +z2 < 1};
ж) f(u) = xyz —>extr, и е X = {гг = (х, г/, z) е £3: х2 + г/2 + z2 = 1, х + г/ + z = 0};
з) /00 = xz/z —> extr, ueX = {u = (xyyyz)eE3:x2+y2+z2 =l,x + z/ + z = l};
H)/(w)=S(xf)2^extr,weX = |w = (x1,...,xw)e£'w:|;xi=l| (n>2);
i=l I i=l J
к) f(u)=fJaixi^extr1ueX = \u = (x\...1xn)eEn:fJ(xi)2=l\ (n>2).
1.17. Функция/(х), определенная на множестве Хе Еп, называется
бесконечно растущей {бесконечно убывающей) на X, если для любой
последовательности {xk} е X такой, что либо lim|xJ = °°, либо limx^ = хеХ\Х,
&->оо" &->оо
справедливо lim/(x£) = +<*> (lim f(xh) = -qq).
Докажите, что если X — произвольное множество в Епу а /(х) —
бесконечно растущая (убывающая) полунепрерывная снизу (сверху) функция
наX, то глобальное решение задачи/(х) —> min (max),xe Xсуществует.
Указание. Рассмотрите произвольную минимизирующую
последовательность и ее предельные точки, воспользуйтесь методом доказательства
от противного.
78

1.18. Решите задачи:
1
а) /(х) = х+ >extr, хеХ = Ех;
х
А
б) f(u) = xy+—+ >extr, и = (х,у)еХ = Е2, аЪ Ф 0;
х у
111
в) /(&) = —+—+——> extr, и е X = {и = (х> у, z) е Е3: xz/z = 2;x, z/,z>0};
х1 у1 z1
111
г) f(u) = —г+—г+—т~> extr,и е X = {и = (х, г/, z) е £3: х + г/ + z = 3; х, г/, z >
х2 г/2 z2
>0}.
1.19. Найдите экстремумы функции/(гг) = х*х2 + х2х3 +... + х"-1^ на
множествах:
а) Х={и = (х\ ...,xw)e Еп : х* + ...+xw = 1};
б) X={w = (x!, ...,xw)e £w: x* + ... +xw= 1,х'>0, z=l,..., и}.
1.20. Исследуйте на экстремум задачу
f(u) = хп + yn + zn^> extr, и е X={u = (x,y1z)e X0: хг/ = 0,х2-г/2 = 0},
где Х0 = {и = (х, г/, z) e f3: z > -1}; и — натуральное число.
1.21. Пользуясь теоремами 1.8—1.11, исследуйте на экстремум задачу
/(х) —> extr, х е X, где/(х) е С2^1)* a множество X имеет вид:
а) Х={хе £i:x2=0};
6)Х={хе £i:x3<0,x2 = 0};
в)Х={хе F:x2<0,x2 = 0}.
1.22. С помощью правила множителей Лагранжа найдите решение
задачи
f(u) = х —> extr, ие X = {и = (х, у) е Е2: х > 0, 0 < у < х2, х2 + у2 < 1}.
1.23. С помощью правила множителей Лагранжа найдите решение
задачи
/(x) = ||x-a||2->extr,xeX={xe En: ||х||2(||х||2- 1)(||х||2-4) <0},яе Еп.
1.24. Докажите, что если х* = (xi, x?,..., х?) — точка минимума в задаче
/(х) —> extr, х е X = {х = (х1, х2,..., хп): а^ < xi < bjy j = 1,..., и},
где/(х) е Сх(Еп), а^< bj,j = 1, ..., п — заданные числа, то /^(х*) = 0, если
cij <xl < by f'xj(x*) >0, если xl = а^ /^ (х*) <0, если xl = by
1.25. Примените метод штрафных функций к задачам
а) f(u) = х2 + г/2 —> min, ие X = {и = (х, у) е Е2: g(u) = -х - у + 1 < 0} или
ие Х={и = (х,у) е Е2: g(u) = -х - у + 1 = 0};
б) /(и) = ху —> min, we X = {w = (х, у) е f2: х2 + у2 < 25} или и е X =
= {гг = (х,г/)е#:х2 + г/2 = 25};
в) Аи) =x2 + y2 + z2^> min, ие X = {и = (х, г/, z) e f2: х + г/ + z + 1 < 0}.
1.26. Пусть/(х) = е-2*, а множество Х={хе Е1:0<х<1] задано
ограничениями: g(x) = |х| + |х- 1| - 1 = 0, либо#(х) = е~*(|х| + |х- 1| - 1) = 0, либо
gi(x) = -х < 0, g2(x) = х - 1 < 0. Выясните, в каких случаях задача/(х) —>
—> min, х е X, имеет согласованную постановку на Е1.
79

1.27. Пусть {Pk(x)} — штрафная функция некоторого множествах Пусть
функция ф(£) определена при t > О, ф(0) = 0, причем ф(£) —> 0 при t —> О,
ф(£) —> ©о при t —> ©о. Покажите, что тогда {(p(Pk(x))} является штрафной
функцией множества X
1.28. Примените метод штрафных функций к задаче
f(u) = x2 + (l - ;а/)2 —> min, и е X={u = (xyy)e E2:g(u) = x-a = 0}>
исследуйте его сходимость при различных значениях параметра а.

Глава 2
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Под линейным программированием понимается раздел теории
оптимизации, в котором изучаются задачи минимизации или максимизации
линейных функций на множествах, заданных системами линейных равенств
и неравенств.
2.1. Постановка задачи
2.1.1. Общая задача линейного программирования
Общей задачей линейного программирования принято называть задачу
минимизации или максимизации линейной функции
f(x) = с1*1 + с2х2 +... + спхп (2.1)
и-мерной переменной х = (г1, х2,..., хп) при условиях
xk>0, kel+; (2.2)
\anx1+a12x2+... + alnxn <b{,
(2.3)
[amlx1+am2x2+... + amnxn<bm;
am+l,lX +am+l,2X +- + ат+1,пХП =Ьт+ >
(2.4)
[am+s,lX +am+s,2X +- + am+s,nxn = bm+s.
Здесь n,mns — заданные числа, п — натуральное, m,s — целые
неотрицательные; С, а$, Ъ\ i= 1,2,..., т + s,j = 1,2,..., п — заданные вещественные
числа, 7+ с {1, 2, ..., п} — заданное подмножество номеров. Обязательное
присутствие в постановке задачи всех без исключения ограничений (2.1)—
(2.4) не требуется, так что допускаются случаи 7+ = 0 и случаи, когда
отсутствуют ограничения типа равенств (s = 0) или типа неравенств (т = 0).
Как уже отмечалось выше, между задачами минимизации и
максимизации нет принципиальной разницы и каждая из них легко сводится к
другой, поэтому далее изложение будем вести для задач линейного
программирования, записанных в форме задачи минимизации. Если ввести векторы
с = (с1, с2,..., с"), а{ - (ай1 а а,..., a in), х = (х1, х2,..., хп), то задачу (2.1)—(2.4)
можно кратко записать так:
f(x) = (с, х) —> min, х е X,
81

X = \xeEn:xk>01keI+1
Ц,х><#, z = l,...,m; j
(ai1x) = bi1 i = m + l1...1m + s\
где через (•, •) обозначено скалярные произведения соответствующих векторов.
Приведем еще одну форму матрично-векторной записи задачи (2.1)—(2.4).
Предварительно договоримся о некоторых обозначениях. Если для каких-
либо двух векторов х = (г1, х2,..., хр), у = (г/1, г/2,..., уР) справедливы неравен-
ствахР>уР при всех г = 1, ...,р, то будем кратко писать: х>у. Тогда, например,
неравенство х > О означает, что х* > О для всех г = 1,..., р.
Не умаляя общности дальнейших рассмотрений, можем считать, что
переменные х1, х2,..., хР- перенумерованы так, что 7+ = {1, 2,..., щ}, 0<щ<п(щ = 0
соответствует случаю 1+ = 0). Отдельно выделяя неотрицательные
координаты, вектор х можем представить так: х = (х1, х2), хх = (х{, х\,..., xf1) e Е\
х2 = (х\,х\,...,х%2)еЕп2,xt >0,щ + п2 = п. Используя принятые обозначения,
задачу (2.1)—(2.4) можем записать в следующем виде:
f{x) = (q, X!) + (с2, х2) —> min, x e X, (2.5)
X = \x = (xlyX2):x1eEniyx2eEn2y
А \х\ + \чхч — Ь\ >
Xl>0\, (2.6)
где Ау — матрицы размером m{ x я-, Ъ{ е Е"Ч, d е £^", zj = 1, 2; 7^ = m;m2 = s:
Ап =
а
и
Ч»!
а,
тп\
Р А2 -
Л21 -
ат+\,1
а,
тп,щ J
ГП+\,Щ
1их+\
а
\п
я,
я,
m+sA
а
5^22 -
h =
кЬт;
m+s,ni J
ГЬт+Л
т,щ+\ •" um
ат+\,щ+\ •*• am+\,n
;b2 =
Um+s
\U J
yam+s,ni+l
;q =
сщ
an
(гЩ+\\
» C2 ~
Cnl
cn
Множество представимое в виде соотношений (2.5)—(2.6), называется
многогранным множеством.
Подчеркнем, что в соотношении (2.6) и всюду ниже в произведениях
вида Anxly Ai2x2y Аху Ву> ... матриц AiV Ai2y A 5, ... на соответствующие
векторы х1у х2, х, у будем подразумевать, что х1у х2, х, у — это векторы-столбцы
подходящей размерности, хотя для экономии места, как мы уже делали
выше, часто будем записывать эти векторы в виде строки.
Укажем еще одну форму записи множества (2.6):
Х = \
Щ п2
2j Л11х1 + 2j Ау2рс2 < 0j,
x = (xv х2): х{ е Eni, х2 е Еп2,k=1 k=1 x{>0
Уj ^2\X\ ~^~ 2j **TlXtl = 2>
где Ajj — k-ik столбец матрицы А$.
82

Точку х* е X назовем точкой минимума функции (с, х) на множестве X
или, короче, решением задачи (2.5), (2.6), если (с, х*) = inf (с, х).
хеХ
2.1.2. Примеры
Приведем ряд конкретных примеров постановок задач вида (2.5), (2.6).
Пример 2.
Пусть на некотором предприятии изготавливаются п видов продукции из т видов
сырья. Известно, что на изготовление одной единицы продукции j-ro вида нужно
dy единиц сырья i-ro вида. В распоряжении предприятия имеется Ь{ единиц сырья
i-го вида. Известно также, что на каждой единице продукции j-го вида предприятие
получает с; единиц прибыли. Требуется определить, сколько единиц хх, х2,..., хп
каждого вида продукции должно изготовить предприятие, чтобы обеспечить себе
максимальную прибыль.
Если предприятие наметит себе план производства х = (л:1, х2,..., х"), то оно
израсходует апхх + ... + а{гр^ единиц сырья г-го вида и получит сххх + ... + с^71 единиц
прибыли. Ясно также, что все величины xi, i = 1,..., п, неотрицательны. Поэтому мы
приходим к следующей задаче линейного программирования: максимизировать функцию
f(x) = сххх + ... + Сгрс71 при ограничениях хх > О,..., хп > О, апхх + ... + airpcn < bl, i = 1,..., т.
Поскольку задача максимизации функции f(x) равносильна задаче минимизации
функции -fix), то с учетом введенных выше обозначений сформулированную задачу
линейного программирования можно кратко записать в виде
f(x) = (-с, х) -> min, хе X = {хе Еп: х>0, Ах <Ь).
Ясно, что задача (2.7) является частным случаем задачи (2.5), (2.6).
(2.7)
Пример 2.2 (задача о рационе)
Предположим, что есть п продуктов питания (хлеб, молоко, мясо, крупа,
картофель и т.п.) и Cj,j = 1, 2, ..., п — цены этих продуктов. Предположим, что в
соответствии с медицинскими требованиями выбрано т значимых для здоровья полезных
веществ (углеводы, белки, жиры, витамины и т.п.) и известно, что количество f-ro
полезного вещества в единице^-го продукта составляет atj, г = 1,2,..., т, а минимально
допустимая норма его потребления равна b\ i = 1, 2, ..., т. Тогда задача
минимизации расходов на питание с соблюдением установленных медицинских норм может
быть сформулирована в виде
f(x) = (с,х)->min, xeX = \xeEn:x>0, J)ayxJ >Ъ1, i = 1,...,т>,
где х = (хх, х2, ..., Xй) — планируемый рацион, в котором j-й продукт содержится
в количестве XJ.
;юкании посевной площади)
Пусть под посев р культур отведено г земельных участков площадью
соответственно в bv ..., br гектаров. Известно, что средняя урожайность г'-й культуры
на^'-м участке составляет ау- ц/га, а прибыль за один центнер i-й культуры
составляет с{ руб. Требуется определить, какую площадь на каждом участке следует
отвести под каждую из культур, чтобы получить максимальную прибыль, если по плану
должно быть собрано не менее d{ центнеров i-й культуры.
83

Обозначим через utj площадь, которую планируется отвести под f-ю культуру
на^'-м участке. Тогда
uXj + ... + upj=bp ; = l,...,r. (2.8)
Ожидаемый средний урожай f-й культуры со всех участков равен апип +... + ainuin
центнеров. Поскольку согласно плану должно быть произведено не менее d{
центнеров f-й культуры, то
апип +... + ainuin>dv i = 1, ...,р. (2.9)
Ожидаемая прибыль за урожай f-й культуры равна ct(anun + ... + ainuin)} а за
урожай всех культур —
JJci(anui^..^ainuin) = f(u). (2.10)
Таким образом, приходим к задаче максимизации функции (2.10) (или
минимизации функции -f(u)) при условиях (2.8), (2.9) и естественных ограничениях и^ > 0,
f = 1, ...,р,;= 1,..., г.
Если в полученной задаче умножить соотношения (2.9) на (-1) и переменные utj
переобозначить через хх, х2,..., х", то мы придем к задаче вида (2.1)—(2.4).
Пример 1Л (грс
Пусть имеется г карьеров, где добывается песок, и р потребителей песка
(например, кирпичные заводы). В f-м карьере ежесуточно добывается а{ тонн песка, а^-му
потребителю ежесуточно требуется bj тонн песка. Пусть ctj — стоимость перевозки
одной тонны песка с f-ro карьера j-му потребителю. Требуется составить план
перевозок песка так, чтобы общая стоимость перевозок была минимальной.
Обозначим через utj планируемое количество тонн песка, поставляемое из f-ro
карьера j-му потребителю. Тогда с f-ro карьера будет вывезено
un+... + uip=at, 1 = 1,..., г, (2.11)
тонн песка, j-му потребителю доставлено
uXj^...^urj=bj, ; = l,...,p, (2.12)
тонн песка, а стоимость перевозок будет равна
f(u)=iicijUij. (2.13)
j=U=\
Естественно требовать, чтобы
^>0, f = l,...,r,; = l,...,p. (2.14)
В результате мы получили задачу минимизации функции (2.13) при условиях
(2.11), (2.12), (2.14), которая, очевидно, является частным случаем общей задачи
линейного программирования (2.1)—(2.4).
К задачам типа (2.1)—(2.4) сводятся также и многие другие прикладные
задачи технико-экономического содержания.
Следует заметить, что приведенные выше примеры задач линейного
программирования, вообще говоря, представляют лишь приближенную,
упрощенную математическую модель реальных задач. Вполне может оказаться,
84

что принятая математическая модель, обычно составляемая на основе
приближенных данных о реальном моделируемом явлении (объекте, процессе),
не охватывает какие-либо важные существенные стороны исследуемого
явления и приводит к результатам, существенно расходящимся с
реальностью. В этом случае математическая модель должна быть изменена,
доработана с учетом вновь поступившей информации, а получаемые при анализе
усовершенствованной модели данные должны снова и снова критически
сопоставляться с реальными данными и использоваться для выяснения
границ применимости модели. Математическая модель лишь при высокой
степени адекватности моделируемому явлению может быть использована
для более глубокого анализа явления и проникновения в его сущность,
для выработки целенаправленного управления.
Практика показала, что задачи линейного программирования вида (2.5)
вполне пригодны для достаточно адекватного описания, исследования
и анализа и многих других (разумеется, далеко не всех) реальных явлений,
процессов и ситуаций в экономике, технике и хозяйственной
деятельности. Кроме того, задачи линейного программирования нередко возникают
в качестве подзадач на определенных этапах решения более сложных
оптимизационных проблем. В настоящее время теория и методы линейного
программирования являются одними из наиболее изученных и разработанных
разделов в теории и методах оптимизации. Приступим к более детальному
рассмотрению этих задач.
2.1.3. Каноническая задача
Из общей задачи (2.5), (2.6) линейного программирования обычно
выделяют так называемую каноническую задачу
f(x) = (с,х) —> min, хе X = {хе Еп\ х >О,Ах = Ь), (2.15)
в которой т = О,7+ = {1, 2,..., и}, А21 = А; А22 = 0; q = с; с2 = 0;b2 = b,a
матрицы АП1АХ2 и вектор Ъх отсутствуют.
Задача (2.15) привлекательна тем, что при ее исследовании, разработке
методов ее решения можно пользоваться хорошо известной из
линейной алгебры теорией систем линейных алгебраических уравнений.
Замечательно также и то, что методы, созданные для решения канонической
задачи (2.15), нетрудно модифицировать и применять для решения общей
задачи линейного программирования (2.5), (2.6). Дело в том, что задача
(2.5), (2.6), оказывается, сама равносильна некоторой канонической задаче.
Покажем это.
Для того чтобы легче было понять последующие построения, прежде
всего заметим, что любое действительное число а можно представить
в виде разности двух неотрицательных чисел: а = а+- а~> где а+ = тах{0; а} >
> 0, а~= тах{0; -а} > 0. Отсюда следует, что вектор х2 =(х\у...ух22) можно
представить в виде разности неотрицательных векторов
x2=z1-z2, zx = max{0;x2)>0, z2 = max{0;-x2}>0, (2.16)
где операция взятия максимума проводится покоординатно:
zx = (z{,..., zf2), z{ = max{0; x{}, z2 = (z\,..., z22), z{ = max{0; -x{}, ; = 1,..., n2.
85

Далее заметим, что ограничения Ах < Ъ типа неравенств можно записать
в виде ограничений типа равенств Ах + v = b, добавив сюда неравенство
v > 0; ясно, что точка х будет решением неравенства Ах < Ъ тогда и только
тогда, когда (х, v) — решение системы Ax + v = byv>0. Отсюда следует, что,
вводя переменную
v = b1-Anx1-A12x2>0, (2.17)
ограничение Апхх+АХ2х2 <Ьхс учетом равенств (2.16) можно представить
в равносильном виде
Anxt+A12x2 +v = Anx1+A12z1 + (-A12)z2+v = bv 0^0.
Ограничение A21xt+A22x2 = Ъ2 с учетом равенств (2.16) запишем таким
образом:
А2Ххх + A22z2 + (-A22)z2 + 0 • v = Ь2.
Учитывая эти соображения, в пространстве новых переменных w = (хь
zv z2, v), xx eEni, zx eEn2, z2 еЕп2, veEmi, рассмотрим следующую
равносильную (2.5), (2.6) каноническую задачу:
g(w) = (cvx1) + (c2yz1) + (-c2yz2) + (0,v)^>mmy weW, (2.18)
W = L = (xl,zi,z2,vy.W>0, УхЛ\+(а!2ъ-Ь\> <219>
где / — единичная матрица размера т1 х тх. Оказывается, задачи (2.5), (2.6)
и (2.18), (2.19) обе одновременно имеют или не имеют решения, причем,
зная какое-либо решение одной из этих задач, нетрудно получить решение
другой задачи.
2.1.4. Основная задача
В линейном программировании наряду с канонической задачей (2.15)
принято также выделять и так называемую основную (или стандартную)
задачу:
/(*) = <c,*>->min, xeX = {x>0:Ax<b}y (2.20)
получающуюся из общей задачи (2.5), (2.6) при т = s, 7+ = {1, 2, ..., и}. Это
объясняется тем, что в приложениях большое число линейных
математических моделей изначально естественным образом записывается в виде
задачи (2.20) (см., например, задачу (2.7)). Следует также отметить, что
задача (2.20) весьма удобна для геометрических интерпретаций, делающих
наглядными многие понятия и методы линейного программирования.
Если ввести дополнительные переменные v = (я1, ..., vm) посредством
соотношений
v = b-Ax, v>0, (2.21)
то задачу (2.20) в пространстве Еп+т переменных z = (x, v) можно записать
в канонической форме

g(z) = <</,z>->min, zeZ = {z = (x,v)>0,Cz = Ax + Imv = b}, (2.22)
где d = (с, 0) e En+m; С = (Л, Im ); Im — единичная матрица размера т х т.
Задачи (2.20), (2.22) равносильны, и, зная решение х* е X* задачи (2.20),jno
формуле (2.21) нетрудно получить решение задачи (2.22) z* =(x*,v* =b-Ax*)y
и обратно, если z* = (x*, v*) е Z*, то х* е X*.
С другой стороны, каноническую задачу (2.15) нетрудно записать
в форме основной задачи. В самом деле, если ограничения типа равенств
Ах = Ъ заменить на равносильную систему двух неравенств Ах < Ъ, Ах > Ъ,
то тогда задачу (2.15) можно записать в следующем виде:
(Ах<Ъ }
х>0: ' \ = {x>0:Cx<g}y (2.23)
Заметим, что задачи (2.15), (2.23) равносильны.
Как видим, все три формы задач линейного программирования — общая
задача (2.5), (2.6), каноническая (2.15), основная (2.20) — тесно связаны
между собой, и простыми преобразованиями от одной формы легко
перейти к другой. Поэтому если мы научимся решать одну из этих задач, то тем
самым будем уметь решать задачу линейного программирования,
записанную в любой другой форме. Заметим однако, что изложенные приемы
сведения задач (2.5), (2.6), (2.15), (2.20) к канонической или основной задаче
могут привести к чрезмерному увеличению размерности переменных или
числа ограничений. Поэтому методы решения задач линейного
программирования обычно разрабатывают для задач (2.15) или (2.20) как более
простых для исследования, а затем, учитывая указанную связь между
задачами (2.5), (2.6), (2.15), (2.20), модифицируют полученные методы
применительно к другим классам задач линейного программирования, стараясь,
по возможности, не увеличивать их размерность.
2.2. Геометрическая интерпретация задачи
линейного программирования
Кратко остановимся на геометрическом смысле задачи линейного
программирования. Рассмотрим задачу (2.20) при п = 2:
f(x) = с1*1 + с2х2 —> min, xeX,
. (2.24)
хеХ = {х = (х1,х2):х1 >0,х2 >0,айхх + ai2x2 <bl, i = l,...,m}.
Введем множества Х0={х = (х1, х2): х1 > 0, х2 > 0} = Е2 —
неотрицательный квадрант плоскости; Xi={x = (x1,x2):ailx1+ai2x2<bi} —
полуплоскость, образуемая прямой апх{ + ai2x2 = Ъ\ i = 1, ..., т. Ясно, что
множество X является пересечением множеств Х0, Х1у ..., Хт. Может случиться,
что это пересечение пусто (рис. 2.1), — тогда задача (2.24) теряет смысл.
87

Рис. 2.1
Если множество X непусто, то оно, образованное пересечением
конечного числа полуплоскостей, представляет собой выпуклое многоугольное
множество, границей которого является ломаная, составленная из отрезков
каких-либо координатных осей и прямых а^х1 + ai2x2 = Ъ\ г = 1, ..., т. Это
многоугольное множество может быть как ограниченным (рис. 2.2) — тогда
X представляет собой выпуклый многоугольник, так и неограниченным
(рис. 2.3).
Рис. 2.2
Пусть а — какое-либо значение функции f(x) = (с,х) = сххх + с2х2. Тогда
уравнение
cW + c2x2 = a (2.25)
задает линию уровня функции /(г), соответствующую ее значению а, и на
плоскости определяет прямую, перпендикулярную вектору с = (с1, с2) Ф 0. При из-

менении а от -оо до -и» прямая (2.25), смещаясь параллельно самой себе,
«зачертит» («заметет») всю плоскость. При этом вектор с — градиент функции
f{x) — указывает направление, в котором следует смещать прямую (2.25),
чтобы увеличивать значение функции /(х) = (с, х). Может случиться, что
при изменении а от -оо до -и» прямая (2.25) при некотором значении а = /*
впервые коснется X и будет иметь с X общую точку х* (на рис. 2.2—2.5 прямая
(2.25) представлена при а = ах < /* < а2 < а3). Ясно, что (с, х*) = /* = inf(c, x),
т.е. точка х* — решение задачи (2.24).
Рис. 2.3
Возможен случай, когда прямая (2.25) при первом касании с
многоугольником X будет иметь не одну общую точку с X, а целую сторону
(рис. 2.4, 2.5). Это может случиться, если X имеет сторону,
перпендикулярную вектору с.
Рис. 2.4
89

a=fm cixi + c2x2 = al
Рис. 2.5
Если многоугольное множество X неограничено, то наряду со случаями,
когда при первом касании прямая (2.25) будет иметь с X одну общую
точку х* (см. рис. 2.3) или сторону (см. рис. 2.5), возможна ситуация, когда
прямая (2.25) при всех а < Oq < +°° имеет общую точку с X (рис. 2.6). Тогда
inf(с, х) =-°о (первого касания прямой (2.25) с X нет), т.е. задача (2.24)
не имеет решения.
Рис. 2.6
Из рассмотренных случаев задачи (2.24) очевидно, что задача
линейного программирования может не иметь ни одного решения (см. рис. 2.1,
2.6), иметь лишь одно решение (см. рис. 2.2, 2.3), может иметь бесконечно
много решений (см. рис. 2.4, 2.5), при этом множество решений может быть
неограниченным (см. рис. 2.5).
90

Аналогично можно показать, что множество X в задаче (2.20) при п = 3
является многогранным множеством, и дать геометрическую
интерпретацию этой задачи. Предлагаем читателю самостоятельно рассмотреть этот
случай, а также исследовать задачу (2.15) при п = 2, 3.
2.3. Угловые точки в канонической задаче
На примере рассмотренной выше задачи (2.24) нетрудно усмотреть, что
если она имеет решение, то среди решений найдется хотя бы одна угловая
точка (вершина) многоугольного множества X. Ниже мы увидим, что это
не случайно: и в более общей задаче линейного программирования,
оказывается, нижняя грань функции (с, х) на X достигается в угловой точке
множества.
Определение 2.1. Точка v множества X называется угловой точкой
(вершиной, крайней точкой, экстремальной точкой) множества X, если
представление v = avt + (1 - a)v2 при vt, v2 e X и 0 < а < 1 возможно лишь
при vx = v2. Иначе говоря, v — угловая точка множества X, если она не
является внутренней точкой никакого отрезка, принадлежащего множеству X.
Например, угловыми точками многоугольника на плоскости или
параллелепипеда в пространстве являются их вершины; все граничные точки
шара будут его угловыми точками; при п > 2 замкнутое полупространство
или пересечение двух замкнутых полупространств не имеют ни одной
угловой точки.
В задачах линейного программирования понятие угловой точки играет
фундаментальную роль и лежит в основе многих методов решения таких
задач. В дальнейшем мы будем подробно исследовать каноническую задачу
(2.15). Поэтому начнем с изучения свойств угловых точек множества
X = {х е Еп\ х > 0, Ах = Ь}, (2.26)
где А — матрица размера т х и, А Ф 0, Ъ — вектор из Ет. Ниже будет
показано, что множество (2.26), если оно непусто, имеет хотя бы одну угловую
точку. Возникает вопрос: как узнать, будет ли та или иная точка множества
(2.26) угловой точкой? Приведем один достаточно простой алгебраический
критерий угловой точки множества (2.26). Для этого вначале обозначим^'-й
столбец матрицы А через Aj и запишем систему уравнений Ах = Ъ в
следующей эквивалентной форме:
A1x1 + ...+Arpcn=b. (2.27)
Теорема 2.1. Пусть множество X задано условиями (226), А Ф 0, ранг
матрицы А равен г. Для того чтобы точка v = (v1> ..., vn) e X была
угловой точкой множества X, необходимо и достаточно, чтобы существовали
номера jb ...,jv 1 <ji< n, 1= 1,..., г, такие, что
Ahvh+... + AJrvir=b; Ы=0, j*jp, /? = l,...,r, (2.28)
причем столбцы Aj ,..., Aj линейно независимы.
91

Доказательство
Необходимость. Пусть v — угловая точка множества X. Если v = О, то
из условия 0 е X следует, что Ъ = 0. Поскольку А Ф 0, то г = rank А > 1
и существуют линейно независимые столбцы Л • ,..., Л . Отсюда имеем
А: -0 + ... + Aj -0 = 0. Для случая v = 0 соотношения (2.28) доказаны.
Пусть теперь v Ф 0 и пусть v^,...,v^ — все положительные координаты
точки v. Так как и е X, то остальные ее координаты равны нулю. Отсюда
и из условия Av = b с учетом представления (2.27) имеем
Ahvh+... + AJkv>k=b 0>=O, ./*./,, р = 1,...,*. (2.29)
Покажем, что столбцы Л;- ,..., Л;- линейно независимы. Пусть при
некоторых аь ..., ak имеет место равенство
щАк+... + акАк=0. (2.30)
Возьмем точку v+ = (v{,..., v^) с координатами а+р = v*p + еос^, ^ = 0 при^ Ф
*jp> Р = 1» •••> ^> и точку а_ = (и!,...,vl) с координатами и^ = vjp -гару v[=0
upnj Ф]р, р = 1,..., k. Поскольку vjp > 0, р = 1,..., &, то при достаточно малых
е > 0 будем иметь v+ >0>v_> 0.
Кроме того, умножая равенство (2.30) на е или -е и складывая с суммой
(2.29), приходим к равенствам Av+ = b, Av_= b. Таким образом, v+, v_e X.
Очевидно, что v = (v+ + v_)/2, т.е. справедливо равенство v = av+ + (1 - a)v_
при а = 1/2. По определению угловой точки это возможно лишь при v+ =
= v_=v,a это в свою очередь означает, что at = ... = ak = 0. Таким образом,
равенство (2.30) возможно только при а{ = ... = ak= 0. Линейная
независимость столбцов Aj ,..., Aj доказана, отсюда следует, что к < г.
Если k = г, то соотношения (2.29) равносильны (2.28). Если k < г, то
добавим к столбцам Aj ,...,Aj новые столбцы Лу ,..., Aj матрицы А так,
чтобы система столбцов А , ...,А- ,Л,- ,...,Л,- была линейно независи-
Л Jk Jk+\ Js
мой, а при добавлении любого другого столбца Aj эта система становилась
линейно зависимой. Тогда система Л ,..., Л образует некоторый базис
линейной оболочки векторов Аь ..., Ап, размерность которой равна рангу
матрицы Л, так что s = г = rank Л. Добавив к первому равенству (2.29)
столбцы Aj ,...,Aj , умноженные соответственно на иЛ+i =0,...,^ =0,
из равенства (2.29) получим соотношения (2.28). Тем самым необходимость
доказана.
Достаточность. Пусть некоторая точка v = (a1, ..., vn) удовлетворяет
условиям (2.28), где Aj ,..., Aj линейно независимы, г = rank Л. Пусть
v = ол)х + (1 - a)v2 при некоторых vt, v2 e X, 0 < а < 1. Покажем, что такое
представление возможно только при vt = v2 = v. Сразу же заметим, что если
для какого-то j е {1, ..., п} xi- 0, то из этого представления с учетом
неравенств 0 < а < 1, v[ > 0, vJ21 > 0 получим 0 < av{ + (1 - a)v{ = vJ = 0, что возможно
лишь при v{=v2= vi = 0. Таким образом, для получения равенства v = vx = v2
остается еще доказать, что v{ = v2 = vi и при тех^', для которых xi> 0.
По условию (2.28) у точки v положительными могут быть лишь
координаты иЛ,..., vir. Произведя при необходимости перенумерацию переменных,
92

будем считать, что Ы* > 0,..., vh > 0, v^+\ = 0,..., v^ = О (случаи k = О или k = г
здесь не исключаются). Тогда соотношение (2.27) можно переписать в виде
A: vh +... + A; vik =b. Кроме того, учитывая, что по доказанному v{ = v2 = 0
при всех j Ф]р,р=\, ..., ky равенства Av{= Ъ также можно записать в виде
AjV-1 +... + Aj v{k =b, i = 1, 2. Вспомним, что векторы Aj ,...,Aj линейно
независимы. Поэтому вектор Ъ может линейно выражаться через Л ,..., Л
единственным способом. Это значит, что v*p =vtp = v2 дляр = 1,..., k. Тем
самым установлено, что v = vt = v2. Следовательно, v — угловая точка
множества X. ■
Определение 2.2. Систему векторов Л; ,..., Л; , входящих в первое
из равенств (2.28), называют базисом угловой точки v, а соответствующие
им переменные vh,..., v^ — базисными координатами угловой точки v. Если
все базисные координаты угловой точки положительны, то такую
угловую точку называют невырожденной. Если же среди базисных координат
vh,...,vJr хотя бы одна равна нулю, то такая угловая точка называется
вырожденной. При фиксированном базисе Aj ,..., Aj переменные вместо
xh,...,xJr называются базисными переменными угловой точки, а остальные
переменные од — небазисными {свободными) переменными.
Из теоремы 2.1 следует, что невырожденная угловая точка обладает
единственным базисом, его составляют столбцы с теми номерами, которым
соответствуют положительные координаты угловой точки. Если угловая
точка вырожденная, то она может обладать несколькими базисами. В самом
деле, если г>л > 0,..., яА > 0, k < г = rank Д а остальные координаты х$
угловой точки v равны нулю, то, как очевидно из доказательства теоремы 2.1,
в базис такой точки обязательно войдут столбцы Л; ,..., Л; , а остальные
базисные столбцы Aj ,..., Aj , входящие в представление (2.z8), могут быть
выбраны, вообще говоря, различными способами.
Поскольку из п столбцов матрицы А можно выбрать г линейно
независимых столбцов не более чем Сгп способами (Сгп — число сочетаний из п
элементов по г), то из теоремы 2.1 следует, что число угловых точек
множества (2.26) конечно.
Пример 2.5
Найдем все угловые точки множества
Х = {х = (х\х2,х3,хАеЕА:х>0, хх + х2 + Зх3 + хА = 3, хх-х2 + х3 + 2хА = 1}.
Для этого обозначим
А =
ГЛ ( \ \ (ъ\ (\\ (о
1
А2 =
1
-1
А3 =
3
Ч1/
АА =
1
V2,
Ь =
Ясно, что ранг матрицы А = (АХ\А2\А3\А4) равен двум. Согласно теореме 2.1 нам
надо рассмотреть все наборы (Aj ,Aj ), 1 <jx <j2 ^ 4, состоящие из двух ее линейно
независимых столбцов, решить системы Л v^ + A:j)ti = b, после чего дополнить
полученные базисные координаты vh, v& точки v нулями.
Всего имеется С| = 6 пар столбцов: (Аь Л2), (Аь Л3), (Аь Л4), (Л2, А3), (Л2, Л4),
(Л3, АА). Каждая из них является линейно независимой. Проделав необходимые
вычисления, мы получим, что точки vx = (2, 1, 0, 0) и v2 = (0, 5/3, 0, 4/3) являются
93

невырожденными угловыми точками множества X, точке vx соответствует базис Лх,
Л2, а точке v2 — базис Л2, Л4\ угловая точка v3= (О, 0, 1,0) вырожденная и ей
соответствуют базисы Av Л3, Аъ Л3 и А3, Л4\ точка vA = (5, 0, 0, -2), сооветствующая набору
(Ль Л4), не является угловой для множества X, так как vA £ X (у нее есть
отрицательные координаты).
2.4. Симплекс-метод
2.4.1. Приведенная задача
Будем рассматривать каноническую задачу
/(x) = (c,x)^min, хеХ = {хеЕп:х>0,Ах = Ь}у (2.31)
где Л — ненулевая матрица размера тхп;се Еп\Ъ e Ет. Ниже будет
показано, что всякое непустое множество X из (2.31) имеет хотя бы одну
угловую точку и, кроме того, если inf (с, х) = /* > -«>, то эта точная нижняя грань
хеХ
достигается хотя бы в одной угловой точке множества X. Отсюда следует,
что задачу (2.31) можно попытаться решить следующим образом: сначала
найти все угловые точки множества X, пользуясь, например,
конструкциями теоремы 2.1, затем вычислить значение функции f(x) = (c,x) в каждой
из угловых точек, число которых, как мы знаем, конечно, и определить
наименьшее из них. Однако такой подход к решению задачи (2.31)
практически не применяется, так как уже в задачах не очень большой размерности
число угловых точек может быть столь большим, что простой перебор всех
их может оказаться невозможным за разумное время даже при
использовании самых лучших современных компьютеров.
Тем не менее идея перебора угловых точек множества оказалась весьма
плодотворной и послужила основой ряда методов решения канонической
и других задач линейного программирования. Одним из таких методов
является так называемый симплекс-метод. Название этого метода связано с тем,
что он впервые разрабатывался применительно к задачам линейного
программирования, в которых множество X представляло собой симплекс в Еп\
Х = \х = (х\...,хп):х>01 |>'=l|.
Затем метод был обобщен на случай более общих множеств X, но
первоначальное название за ним так и сохранилось; в литературе этот метод
часто называют еще методом последовательного улучшения плана.
При реализации симплекс-метода осуществляется упорядоченный
(направленный) перебор угловых точек множества X, при котором
значение функции (с, х) убывает при переходе от одной угловой точки к другой,
что позволит, перебрав, быть может, лишь относительно небольшое число
угловых точек, выяснить, имеет ли задача (2.31) решение, и, если имеет, то
найти его.
Перейдем к описанию симплекс-метода для решения канонической
задачи (2.31).
94

По условию 1 = rank А < min{m; n}. Предположим, что из системы (Лх)* =
= b\ i = 1,..., т исключены линейно зависимые уравнения, т.е. г = т, матрица Л
имеет размеры г х п.
Тогда, как известно, г < п. Если г = п, то система Ах = Ъ будет иметь
единственное решение х0 и множество X либо будет пустым (если не
соблюдается ограничение х0 > 0), либо состоит из одной точки (если х0 > 0) — в этом
случае задача (2.31) становится малосодержательной. Поэтому будем
считать, что г < п. Тогда систему Ах = Ъ можем записать в виде
\апх1+... + а1пхп =Ь{>
\arixx+... + arnxn =br,
г = т<п.
(2.32)
Пусть известна некоторая угловая точка v = (я1, v2, ..., vn) множества X
с базисом Aj yAj_,..., Л/ • Матрицу 5 = (Л; , Л; ,..., Л; ), столбцами которой
являются базисные векторы, будем называть базисной матрицей или
просто базисом. Через I(v) = {jiy ...,jr} обозначим номера базисных переменных
или, короче, базисные номера. Перенумеровав переменные, можем считать,
что I(v) = {1,2,..., г}; тогда столбцы Аь Л2,..., Аг матрицы Л составляют базис
точки v, а х1, х2,..., хг — ее базисные переменные. Обозначим
(гЛ
х =
хг ,
В =
V =
Hi
fv^
v*ry
с =
Гс^
rr
vc J
AJ=
Hj
\avj
l\r
\ar\
a,
= (AI4|...|4).
•rr J
Тогда систему (2.32) можно кратко переписать в виде
b = A1x1+... + Arxr+Ar+1xr+1+... + Anxn=Bx+ £ \xk. (2.33)
k=r+l
Так как столбцы Аь ..., Аг линейно независимы, то detB Ф 0 и,
следовательно, существует обратная матрица Б-1. Кроме того, вспомним, что
согласно теореме 2.1 небазисные координаты угловой точки v заведомо
равны нулю, так что v =
о
, где v > 0. Отсюда и из системы (2.33) следует,
что базисные координаты v удовлетворяют системе Bv=b, откуда имеем
v = B~1b. Умножая систему (2.33) на Б-1 слева, получим следующее
соотношение между базисными переменными х и небазисными переменными
\Т+1 у№
•Л/ J • • • J щЛ* %
k=r+\
(2.34)
Обозначим {В~хАкУ = у{ k — i-я координата вектора-столбца yk = B~lAk.
Тогда систему уравнений (2.34) можно записать в покоординатной форме:
95

vx = xx
nl —
rl
V1 - X
Vs =
if - xr + у.
+ Yi,r+i*r+1 +... +Yijfc** +... +Yifn*n>
+ Y*>+i*r+1 + ••• +Y,\*** + ... + Y*>*w,
*5 +Y5,r+i*r+1 + .- + Y,,*** +... +У,,я^я.
!Xr+1 +... + Yr,^ +... + Yr,w^w.
(2.35)
r,r+
Систему B~xAx = B~xb, полученную умножением исходной системы
Аг = 6 на матрицу Б-1 слева, называют приведенной системой угловой точки v
с базисной матрицей В. Системы (2.34) и (2.35), таким образом,
представляют собой различные формы записи приведенной системы точки v с
базисом В = (Аи ..., Аг). Подчеркнем, что из невырожденности матрицы В следует,
что системы (2.34), (2.35) равносильны исходной системе (2.32) или (2.33).
п
Пользуясь равенством x-v- ^ B~xAjXJy вытекающим из системы
j=r+\
(2.34), значения функции/(х) выразим через небазисные переменные:
f(x) = (c,x) + tcjXJ=lcyV- £Я"ЦхЛ+ f,CjXJ =
j=r+l \ j=r+l I j=r+l
или, короче,
= <с,5>- 2 «c,B-*Aj)-Cj)xi9
j=r+\
f(x) = f(v)- J А^Л
j=r+\
(2.36)
где учтено, что (c,v) = (c,v) = fip), и использованы обозначения
Ду=<с,В-Ц.>-су = £с^-с,., ; = 1, ...,«• (2.37)
1=1
Выражение (2.36) будем называть приведенной формой целевой функции,
соответствующей угловой точке v с базисом В.
Входящие в (2.35), (2.36) величины yik, v-v A; удобно записать в виде
табл. 2.1, которую принято называть симплекс-таблицей угловой точки v
с базисом В = (Аь ..., Аг).
Таблица 2.1
г,
г,
г,
гг
д
Б
*i
х>
Л?
дгг
У
i)i
Я''
Vs
V
№
я-1
1
0
0
0
0
X4
0
1
0
0
0
Xs
0
0
1
0
0
хг
0
0
0
1
0
лг^1
Yi.ru
Ytr+i
Ys.r+i
Yr,r+1
Аг+i
д^
Ya
Y«
Ys*
Yn*
A*
X>
Yy
Y-V
Ysj
YV
A,
ЛГ"
Yi,„
Y,-,„
Ys,n
Ъ,п
A„
96

В столбце Б этой таблицы перечислены базисные переменные х1, ..., хг
точки v, в столбце V размещены значения базисных переменных v = В~ХЪ
угловой точки v; в столбцахх^ находятся координаты yik = {В~ХА^)\ i = 1,..., г
векторов yk = В-^А^ k = 1, ..., п; в столбцах базисных переменных х1, ..., хг
отражены равенства B~xAj= epj = 1,..., г, вытекающие из определения
обратной матрицы Б-1; здесь е; —j-й столбец единичной матрицы размера гхг.
В крайнем левом столбце для удобства изложения приведены
обозначения для строк симплекс-таблицы: Г19 Г2,..., Гп> Д. Так, например, в строке
1> (&, О,..., 0,1, 0,..., О, Yiif+i,..., Y,>)
записана вся информация, по которой удобно воспроизвести
соответствующее г-е уравнение системы (2.35), и наоборот, зная г-е уравнение этой
системы, легко можно восстановить строку Гг. В строке А помещены
величины А0 = f(v) = (с, v), A1?..., Дя, связанные с минимизируемой функцией
/(х) = (с, х) формулами (2.36), (2.37); в этой строке отражено, что для
базисных номеров
Aj = (с, ej)-cJ = cJ -cJ = 0, j = 1,..., г.
По строке А = (J{p), 0, ..., О, Аг+1, ..., Aw) симплекс-таблицы легко
воспроизвести формулу (2.36) и обратно, используя формулу (2.36), несложно
восстановить строку А. Из формул
y0=v=B-% yj=B-iAj9 Ь0=<с,В-Щ = /(р), bj=<fi9B-iAj)-ci
для величин, заполняющих симплекс-таблицу, следует, что эта таблица
однозначно определяется заданием векторов с, Ь, матрицы А и базисной
матрицы В угловой точки v.
После сделанных преобразований каноническую задачу (2.31) теперь
можно сформулировать в следующей равносильной, так называемой
приведенной форме: минимизировать функцию (2.36) при условиях (2.35)
и соблюдении неравенства х > 0.
2.4.2. Описание симплекс-метода
Рассмотрим получившуюся приведенную форму задачи (2.31). Следует
сразу заметить, что приведенная форма не проще исходной задачи, но тем
не менее в новой ее формулировке с явным разделением базисных и
небазисных переменных, оказывается, легче проследить за тем, как изменяется
функция/(х) при изменении небазисных переменных, и можно попытаться
выбрать эти переменные так, чтобы в новой точке w e X было f(w) <f(v).
Однако если мы начнем изменять все небазисные переменные сразу, то
вряд ли сможем проследить и за изменением функции /(х), и за
соблюдением ограничений х > 0. Поэтому мы попробуем изменить лишь одну
из небазисных переменных, скажем, переменную х^, г +1 < k < и, остальные
небазисные переменные положим равными нулю, а базисные
переменные будем определять из уравнений (2.35). Иначе говоря, новую точку
w = (w1,..., wn) будем искать среди точек с координатами
wi =Т)Х -Ya**>->^' =vi -yilkxk,...,wr =vr -yrJkxk,
wr+1 = 0,..., wk~x = 0, wk = xk > 0, wk+1 = 0,..., wn = 0.
97

В такой точке w согласно формуле (2.36) значение функции f(w) равно
f(w) = f(v)-Akxk, xk>0. (2.39)
Наша ближайшая задача: выбрать номер k, r + \<k<n, и величину я* > О
так, чтобы новая точка (2.38) удовлетворяла требованиям Aw = b, w> О,
f(w) < f(v) (в идеале хотелось бы получить f(w) < f(v)). Что касается
первого требования Aw = b, то здесь проблем нет: точка (2.38) при любом
выборе номера k и величины xk, очевидно, является решением системы
(2.35) и равносильной ей системы (2.32). Анализируя знаки величин А^,
Уф нетрудно выяснить, можно ли удовлетворить оставшимся двум
требованиям w > 0 и f(w) < f (v)> и указать правило выбора нужного номера к
и нужной величины xk > 0. Такой анализ приведет к рассмотрению трех
взаимоисключающих друг друга случаев.
Случай I. Справедливы неравенства
Aj=(c,B-iAj)-Cj£0, ; = r + l,...,n, (2.40)
т.е. в нижней строке симплекс-таблицы 2.1 все А;, 1 <j < и, неположительны.
Как очевидно из соотношений (2.38), (2.39), при выполнении условия
xk > 0 тогда невозможно добиться неравенства f(w) < f(v) ни при каких к,
r+l<k<n.B лучшем случае, при xk= 0, получим w = v,f(w) =f(v). Однако
это обстоятельство не должно огорчать нас, так как оказывается, что
при выполнении условий (2.40) рассматриваемая точка v является
решением задачи (2.31). В самом деле, для любой точки х е X = {х>0 : Ах = Ь)
с учетом представления (2.34) и неравенств (2.40) имеем
/(*) = <с,*>+ £ сЫ>(с,х)+ £ <с,5-1Л;х>) =
j=r+l j=r+l
= Iс, х + £ Я"1 AjxJ \ = (с, v) = f(v).
Таким образом,/(х) >f(v) при всех хе X, т.е. v — решение задачи (2.31).
Случай П. Существует номер k> г + 1 < k < и, такой, что
А^>0,уа<0,г=1,...,г,т.е.у^ = 5-1^<0. (2.41)
Это значит, что в k-м столбце симплекс-таблицы (см. табл. 2.1) над
величиной А^> 0 нет ни одного положительного числа у#. В этом случае при всех
yk > 0 точка wy определяемая формулами (2.38), будет иметь
неотрицательные координаты и, следовательно, будет принадлежать множеству X. Тогда,
как очевидно из (2.39),
f(w) =f(v) - Afpcb —> -оо при xt* —> +оо.
Это значит, что /* = inf f(x) = -оо, т.е. задача (2.31) не имеет решения.
хеХ
Случай III. Существует номер k, г + 1 < k < п, ддя которого А^ > 0, причем
для каждого такого номера k найдется номер г, 1 < г < г, что у# > 0, или, иначе
говоря, в каждом k-м столбце симплекс-таблицы над величиной А^> 0 имеется
хотя бы одно положительное число Уф что можно кратко записать в виде
V Д*> 0 3 г е {1,..., г} : yuk> 0. (2.42)
98

Для точки w, определяемой формулами (2.38), согласно равенству (2.39)
здесь будет справедливо f(w) =f(v) - ДЛя*(я) ^f(v) при любом д&> 0.
Остается лишь позаботиться о выполнении условия w > 0. В рассматриваемом
случае множество номеров
Ik(v) = {i:l <i<r, yik>O}*0.
Если i £ Ik(v)> т.е. yik < 0, то как ясно из формул (2.38), wl = v{ - y^xt1 >
>vj>0 при любом выборе з&> 0. Если же yik> 0, то при xk > min (vj/yik)
ielk(v)
величина wl = v{ - Уц?& станет отрицательной хотя бы для одного номера
г е Ik(v).
Таким образом, для обеспечения условия w > 0 для точек, определяемых
формулами (2.38), здесь нужно xk взять так, чтобы 0<xk < min (vj/yik).
ielk(v)
Пусть
min— = —, seh(v). (2.43)
Так как множество 4(a) непусто и конечно, то хотя бы один такой номер
s существует. Величину ysk, где номера k> s определяются условиями (2.42),
(2.43), называют разрешающим (ведущим) элементом симплекс-таблицы.
Зафиксируем один из разрешающих элементов ysk табл. 2.1 и в
формулах (2.38), (2.39) положим я* = vs/ysk. Получим точку w = (w1,..., wn) с
координатами
wx=vx- Yijfc —,... ,wl = vl - yik —,... ,ws~x = Vs-1 - ys_ik —,
l S,k I S,k I S,k
Vs Vs Vs
ws = vs - ysk = 0,ws+1 = vs+1 - ys+lk , ...,wr =vr - yrk , (2.44)
У s,k *s,k *s,k
wr+i = 0,..., да*"1 =0,wk= —,wk+i = 0,..., wn = 0,
и значение функции f(x) в этой точке
f(w) = (c,w) = f<p)-*k—- (2-45)
Ys,k
По построению точка w с координатами (2.44) принадлежит
множеству X. Покажем, что w — угловая точка множества X с базисом
А^ ..., As_i, Ak, As+i>..., Av (2.46)
получающимся из базиса точки v заменой столбца As на Ak. Учитывая, что
ws=wr"rX =... = wk~x = wk+1 =... = wn=0,
условие Aw = b можно записать в виде
A xwx +... + A^w5-1 + Л5+1г^+1 +... + AjWr+ Akwk = b.

Согласно теореме 2.1 остается показать, что система векторов (2.46)
линейно независима. Пусть для некоторых чисел а1у ..., а5-1, а5+1, ..., ar ak
оказалось, что
щАх+... + as_xAs_x + сс5+1Л5+1 +... + аЛ+ М*= °- (2-47)
г г
Поскольку Ak=BB~xAk = yZAi(B~1Ak)i = XY/uA' to из равенства (2.47)
i=l i=l
следует
Е 0CfA+^SYaA= S (ос/+ос^а)Л+ос^,И5=0-
1=1,1>5 1=1 1=1, I>5
Но система Ах, ..., Л5, ..., Аг является базисом точки v и,
следовательно, линейно независима. Тогда последнее равенство возможно лишь
при осг + ос^ = 0, i = 1, ..., г, i Ф s; аку8к = 0. Но у5,* > 0 как разрешающий
элемент, поэтому ak= 0. А тогда все остальные а{= 0, i = 1,..., r,i*s. Таким
образом, равенство (2.47) возможно лишь при at = ... = а5-1 = а5+1 = ... = аг=
= ak = 0. Это значит, что система (2.46) линейно независима.
Тем самым показано, что точка w, определяемая формулами (2.44),
является угловой точкой множества X с базисом (2.46), х1,..., х5-1, xky xs+1,...,
xr — ее базисные переменные, причем f(w) <f(v)> так как в формуле (2.45)
A*>0,Y5,*>0,^>0.
Замечание 2.1. Полезно подчеркнуть, что при доказательстве того, что
точка w является угловой точкой, мы нигде не пользовались тем, что А^ > 0.
Это означает, что независимо от знака А^ формулы (2.43), (2.44)
позволяют перейти от одной угловой точки v множества X к другой его угловой
точке w, лишь бы Ik(v) Ф 0, Vs > 0. Если Vs = 0, то формулы (2.43), (2.44)
дают ту же угловую точку, т.е. w = v, но при этом происходит замена базиса
Аь ..., Аг на базис (2.46).
Теперь обсудим правила заполнения симплекс-таблицы точки w
(табл. 2.2), постараемся понять, как связаны симплекс-таблицы точек v
и w. Как и в табл. 2.1, в столбце Б укажем базисные переменные х1,..., х5-1,
xky xs+1,..., хг точки w, в столбце V — соответствующие значения wx,..., г^-1,
wk, ws+1> ..., wr ее базисных координат, вычисленных по формулам (2.44).
В столбцах xi нам нужно поместить координаты у,- ■ вектора у; = 5_1Л;, где
В'1 — матрица, обратная к матрице В = (Д |... | As_x \ Ak \ As+1 \... \АГ).
Следует, однако, заметить, что обращение матриц, их умножение
являются довольно трудоемкими операциями, поэтому вычисление координат
вектора у., опирающееся на его определение, может потребовать большого
объема вычислений. В связи с этим полезно вспомнить, что вектор у-
совпадает со столбцом коэффициентов при переменной xi в приведенной
системе В~1Ь = В~1Аху соответствующей угловой точке w с базисом (2.46).
К счастью, имея приведенную систему (2.35) для угловой точки v, из нее
нетрудно получить такую систему и для точки w. Покажем, как это
делается. С этой целью разделим 5-е уравнение системы (2.35) на разрешающий
элемент у5^> 0; учитывая, что в силу формул (2.44) wk=vs/ysk, получим
7)s i k-\ v • n Y •
»*= — = —**+ X ^-xi+xk+ £ ^-xi. (2.48)
Ys,k ys,k j=r+iYs,k j=k+iYs,k
100

ь
"й
+
Ъ
i
%
ъ
+
"к
ъ
1
"к
Ъ
^
ю
R^
1>^
1?^
-4
о
Т
7
о
о
\>?
о
о
ч—1
*Э
**
С
R,
IS^
-ч
о
*ч
1?^
о
о
1г^
о
•ч—i
о
"&
■*
и
R
т
1^
1^
5
1^
о
1^
7
1^
о
о
«о
1>2
-
О
о
1ь
1.
J
R,
1^
1^
-ч
1^
-
1>5"
к.
1^
О
о
«а
1^
О
О
о
3
"*
иГ
R
1^
1^
5
7
i^
о
7
X
1^
о
•ч—1
7
1^
о
о
о
+
+
"+
R
1^"
7
о
-ч
1>Ь
1^"
•ч—1
о
\£
о
о
о
к.
^
U
R
К
К
7
•«4
К
о
7
•«4
К
7
к.
К
о
о
«о
К
о
о
о
<
101

Из этого уравнения можно выразить переменную xk через остальные
переменные:
71s 1 П V .
xk=- —xs- £ l*±xi, (2.49)
Ys,k Ys,k j=r+\ ys,k
после чего подставить ее в другие уравнения системы. Это даст нам
г \
vi=xi+ £ Yy*'+Y,\*
j=r+l
j*k
Ys,k
я*- X —*7
Ys,k Ys,k j=r+i Ys,k
(.ILL
V 4s,k j
(
Xs + X
j=r+l
Yy-Ya
Yc*
Л
*>,
откуда с учетом формул (2.44) получим
w'
У$,к
( .111
Ys,k
Xs + Ё
j=r+\
(
Yy-Yfjfc
Y,f*.
^
x>, i = l,...,r,i*s. (2.50)
Система г уравнений (2.48), (2.50) относительно неизвестных х1, х2,..., xn
равносильна системам (2.35), (2.32) и представляет собой приведенную
систему для угловой точки w. Отсюда следует, что в строке Г5 табл. 2.2
согласно равенству (2.48) мы должны записать величины ysj9j = 0, 1,..., и,
определяемые формулами
v* _
1 _
у Q=wk=-^—f у =-^,у .=0, ; = l,...,5-l,5 + l,...,r;
Vs,k ' 4s,k ''
_ _ Y •
Ys* = t 7»/=-^» > = r + l,...,A-l,A + l,...,n.
YS,A
(2.51)
В других строках Гг, i * 5, табл. 2.2, в силу формул (2.44), (2.50) следует
поместить величины у{) J = 0, 1,..., и, определяемые формулами
Yif0 = о"" = tf - Ya —> Y,\,- = t Y,\, = ——> Y,-j = 0> l<j<r,j*i,j* s;
Ys,k Ys,k
— — Y ■
Ya = °> Y,-j = Y,-j " Y,\* —> J = r +1,..., * -1, * +1,..., n.
(2.52)
Наконец, заполним строку А табл. 2.2. С этой целью подставим
переменную oft из выражения (2.49) в формулу (2.36), тогда с учетом формулы
(2.45) получим следующее выражение значения функции f(x) через
небазисные переменные точки w\
f(x) = №- 2 Ajx>-Ak
j=r+\
xs- 2/ — xJ
Ys,k Ys,k j=r+i Ys,k
(
= /(»)-
Л
V Ys,k j
xs- X
(
j=r+\
A A ' S J
bj-bk —
1
Ys,k
xK
(2.53)
)
102

Из формулы (2.53) следует, что в строке А табл. 2.2 должны быть
записаны величины A J = 0, 1,..., и, вычисленные по формулам
A,=f(w) = f(v)-Ak —, А,=-ДА—, А,=0, l<j<rj*s;
Ys,k Ys,k ^254^
Д*=0, А=А-А^-^-, j = r + l,...,k-l,k + l,...,n.
Ys,k
Таким образом, симплекс-таблица угловой точки w с базисом (2.46)
полностью заполнена. Несложный анализ формул (2.51), (2.52), (2.54)
с учетом конкретных числовых значений у^, у,-,-, А, А в базисных столбцах
табл. 2.1, 2.2 показывает, что элементы этих таблиц связаны следующими
простыми соотношениями:
l<i<r,i*sJj = 0,l,...,n.
Если элементы и строки табл. 2.1 обозначить через у^(р), Aj(v)> Гг(а),
А(и), а элементы и строки табл. 2.2 — через y^iw), Aj(w), Г((т), A(w), то
соотношения (2.55) можно записать в векторной форме:
Уз*(Р) Ys,k(v)
A(w) = A(v)-Ak(v)-Fs^
(2.56)
Y,jfc(»)
Соотношения (2.55) и (2.56) описывают один шаг известного метода
Гаусса — Жордана [9, 31], соответствующий исключению переменной я*
из всех строк симплекс-таблицы, кроме строки Г5, в которой переменная я*
остается с коэффициентом у8^{гю) = 1-
Итак, один шаг симплекс-метода, заключающийся в переходе от одной
угловой точки v множества X к другой угловой точке w, описан. Этот
шаг формально можно истолковать как переход от одной симплекс-
таблицы (табл. 2.1) к другой симплекс-таблице (табл. 2.2) по формулам
(2.55) или (2.56), где номера k,sn разрешающий элемент ySfk = Ys,k(v)
выбираются из условий (2.42), (2.43).
Формулы перехода (2.55), (2.56) были получены в предположении, что
множество номеров базисных переменных угловой точки v имеет
специальный вид I(v) = {1,2, ..., г}, что соответствует табл. 2.1. Конечно, путем
перенумерации переменных всегда можно добиться, чтобы множество I(v)
имело указанный вид, но это связано с дополнительной обработкой
числовых массивов, усложняет программную реализацию симплекс-метода
на компьютере. Однако нетрудно убедиться, что можно обойтись без
какой-либо перенумерации переменных, а формулы перехода (2.55), (2.56)
остаются справедливыми для угловых точек с любым множеством
базисных номеров.
В самом деле, пусть номера базисных переменных начальной точки v
образуют множество I(v) = {j\,j^ ->Л-}- Заметим, что в процессе примене-
103

ния симплекс-метода множество I(v) обновляется на каждом шаге и нельзя
ожидать, что номера^,Л* ->Л- из этого множества будут упорядочены,
скажем, в порядке монотонного возрастания или убывания (так, например,
в табл. 2.2, в отличие от табл. 2.1, монотонность номеров базисных
переменных в столбце Б уже нарушена). Однако это обстоятельство нашим
дальнейшим рассуждениям никак не помешает. Обозначим
х-
fxh^
kx'tj
V =
^Л
Л
с =
Uh^
AJ=
(„ \
у%;
в=
а
1Л
У%
Ч
а
Vr J
= (Ah\AJ2\...\Ajr);
(2.57)
(2.58)
yk=yk(v) = B^Ak, yQ=y0(v) = B-% уц=у(Л(и) = (В-%У; (2.59)
Y,,o = Y«,o(*0 = (В~1ЬУ, г = 1,..., r, k = 1,..., n. (2.60)
Так как В^В = B~\Ah |...| Ajr) = (B^ |... | B^AJr) = (e, |...|er) = I - еди-
ничная матрица размера г х г, то у;. = B~xAj. =et для всех i = 1, ..., г. Кроме
того, согласно теореме 2.1
Bv = Ajvh +... + Ajr vir = b; vi = 0, j<£ I(v),
поэтому v=B~xb = y0l vii =(В-{ЬУ = Y/,o> i = 1, ..., ry vl= 0, j ё I(v). Умножая
n
систему Ax = ^JAixi =b слева на матрицу Б-1, как и при выводе системы
i=l
(2.34), (2.35), получим приведенную систему угловой точки v с базисом 5
в векторной форме
0<v = B-4 = y0=x+ X (B-1Ak}xk = fiykxk
или в покоординатной форме
vJi=yi0=xJi+ £ Y;^ = £Yi***> i = l,...,r.
te/(») ' k=\
(2.61)
По аналогии с формулами (2.36), (2.37) для целевой функции получим
ее приведенную форму
f(x) = (c,x) + X cJxJ=lc,v- X В~1А,хА + X dxi =
jel(v) \ jel(v) I jel(v)
= (c,v)~ 2 «c,B-U,>-^>'.
Это выражение можно переписать в виде
До =/(*)+ I AiX*=/(x)+SA4x*,
(2.62)
104

где приняты обозначения
До=/(0) = <с,0>,
Ak=(c,B-iAk)-ck=(c,yk)-ck = tcJiyifk-ck, & = 1,2,...,и,
(2.63)
i=l
причем учтено, что для всех k =jjE I(v) величина Ak= 0, поскольку
ДЛ = (с, Я"1 ЛЛ)-сЛ = (с,е,-)-сЛ = сЛ -сЛ =0, i = 1,..., г.
Информацию из формул (2.58)—(2.63) об угловой точке v с базисом
В = (Aj ,..., Aj ) удобно записать в виде новой симплекс-таблицы (табл. 2.3):
строка Г{ в ней соответствует z'-му уравнению (2.61), строка А —
представлению (2.62) для целевой функции.
Таблица 23
Г,
Г;
Г,
Гг
Д
Б
х\
*>i
XJS
xJr
V
Yi,o
Yi,o
Ys,o
Yr,o
Ao
x^
Yi.i
Yi,i
Y*i
Yr.i
Ai
X*
Yi,i
Yy
Isi
Yr,«
A,-
**
Ъ,к
Уц
Ys,*
Уг,к
A*
Xh
Yu,=0
^=1
Ysjf=0
Yr,;;=0
Д,=0
ЛЯ
Yi„
Yi»
Ys,n
Уг,п
Аи
Отметим, что в столбце базисной переменной х->< вектор у, = б*(
т.е. Y/j. = 0 при всех IФ i, \ < I < r, ytj. = 1; в нижней строке этого столбца
Д,-. = 0. Симплекс-таблицу 2.3 можно кратко записать в виде матрицы
(
S = (v,B) =
Yo Yi
VAo Ai
Y»
A.
rr
размера (r+ 1) x (n + 1), где столбцы у* подматрицы Г =
V
vVry
и элементы
строки А вычисляются по стандартным формулам
Vk=B-iAk, Ak=(c,B-iAk)-ck=(cyyk)-ck, £ = 0,1,...,и; (2.64)
здесь для единообразия формул принято Ъ = Л0, предполагается, что с0 = 0,
остальные обозначения взяты из (2.57)—(2.60).
Опишем один шаг симплекс-метода в общем случае. По аналогии с
формулами (2.40)—(2.42) рассмотрим три взаимоисключающие возможности.
Случай I. Справедливы неравенства
Aj=(cyB-iAj)-cJ<0y ; = !,..., и, (2.65)
105

т.е. в нижней строке симплекс-таблицы 2.3 все величины Д1?..., Ап
неположительны. Тогда с учетом равносильности систем (2.32) и (2.61) для
любой точки х е X имеем
f(x) = (c,x)+ S dx)>{c,x)+ X <c,B-My>^ =
\ ;«/(о) /
Это значит, что v — решение задачи (2.31).
Случай П. Существует номер k > О, k £ I(v), такой, что
Д*>0, yk=B~iAk<0, (2.66)
т.е. в k-м столбце симплекс-таблицы 2.3 над Д^ > 0 нет ни одной
положительной величины yik. Тогда точка х = x(t) = (х1,..., X") с координатами
xk -vh -yikt, i = 1,...,г; xk = t, xi = 0, j£I(v), jФk,
будет принадлежать множеству X при всех t > 0. Отсюда и из выражения
(2.62) следует, что f(x(t)) = f(v) - Akt —> -°° при t —> +°°. Это значит, что
/* = inf f(x) = -оо, т.е. задача (2.31) не имеет решения.
хеХ
Случай III. Существует номер k>0,k£ I(v), для которого Д^> 0, причем
для каждого такого номера к найдется такой номер г, 1 < i < г, что yik > 0,
или, короче,
УД4>0 3уа=(В-1Л]1)'->0. (2.67)
Это значит, что в каждом k-м столбце симплекс-таблицы 2.3 над
величиной Д^ > 0 имеется хотя бы одно положительное число yik. Тогда выберем
номер s и разрешающий элемент ysk > 0 из условий
minM = M, selk(v) = {i:l<i<r,yik>0}. (2.68)
fe/*<*>Y,\* Ys,k
Далее, рассуждая так же, как выше (см. формулы (2.44)—(2.46) и
пояснения к ним), убеждаемся, что точка w = (w1,..., wn) с координатами
Wh = Vh -уц = yi0 -уц —^y i = 1,...,ryi*s; wis = 0;
Уз,к Уз,к (2 69)
7)Js Yen •
wk= = -^-; wJ=0,jeI(v)J*k,
Vs,k Уз,к
принадлежит множеству Х, является угловой точкой этого множества с
базисом
(Ак,...,А^,Ак,А^,...,А^) = В. (2.70)
Значение функции f(x) в этой точке равно
/(а0 = /(г;)-Д* —= Д0-Д*М. (2.71)
4s,k 4s,k
106

Замечание 2.1 с очевидными изменениями сохраняет силу в
рассматриваемом общем случае. Приведенная система точки w выводится так же, как
система (2.48), (2.50), и имеет вид
1
wk= X]s+ £ -±Lxj+xky
WJi = Xh +
Уз,к
( .1IA
Ys,k
j£l(v) YS,k
(
(2.72)
Yfj-Ya
12±
Ys,k
xK
а аналогичное (2.53) выражение для функции f(x) выглядит следующим
образом:
( кЛ ( » Л
/(*) = /(»)-
4s,k
Xjs - X
А; "А*
±sj_
Ys,k
be J.
(2.73)
Нетрудно видеть, что если I(v) = {1,2, ..., г}, то формулы (2.68)—(2.73)
переходят в соответствующие формулы (2.43)—(2.46), (2.48), (2.50),
(2.53). Анализируя коэффициенты при переменных х1, х2, ..., хп в
выражениях (2.72), (2.73), получаем аналогичные (2.51), (2.52), (2.54) формулы
для величин, которые должны находиться в строках Ti(w)y i = 1, 2, ..., г,
A(w) симплекс-таблицы точки w, и убеждаемся в том, что переход от
симплекс-таблицы точки v с базисом B = (Aj ,...,Aj ) к симплекс-таблице
точки w с базисом (2.70) совершается по тем же формулам (2.55), (2.56),
где номера k, s определяются из условий (2.67), (2.68).
2.4.3. Примеры
Рассмотрим каноническую задачу линейного программирования
f(x) = Юл:2 - х3 + Ах4 + х5 -» min, xeX,
Х = {х = (х1,х2,х3,х4,х5)>0: хх + 2х3 + х4=2,2хх -х3 + х5 = 3,-хх + х2 + х3 = 1}.
Уравнения, задающие это множество, можно записать в виде
3
=
'Г
2
х1 +
0
х2 +
'2"
-1
г3 +
Y
0
ХА +
1
Как и выше, столбец из коэффициентов при переменной у> будем обозначать
через Д. Нетрудно видеть, что выписанная система уравнений является
приведенной системой для угловой точки v0 = (0, 1, 0, 2, 3) с базисом Аъ Л4, Л5\ здесь
1(*>о) = {/1 = 4 J2 = 5 J3 = 2Ь В = (Л4> Л5> AlY
Внесем коэффициенты этой системы в строки Гь Г2, Г3 симплекс-таблицы
точки v0. Пользуясь формулами (2.63), (2.64), вычислим значения величин AjJ = 0,
1, ..., 5 и впишем их в строку А табл. 2.4. В этой строке величина А3> 0, а в столбце
х3 имеются положительные элементы Yi,3= 2, Уз,з= 1- ^то значит> что в точке v0
реализовались условия (2.67). Определим номер s из условия (2.68):
107

• Ко Y3,ol • f2 ll .
пищ —•—•-=£- V = пищ —; -} = 1.
[Y1.3 Y3,3J 12 lj
Таблица 2.4
Ti
r2
r3
A
Б
X4
X*
X2
V
2
3
1
21
*i
1
2
-1
-4
ЛГ2
0
0
1
0
X3
2
-1
Ш
18
*<
1
0
0
0
л:5
0
1
0
0
Как видим, здесь минимум достигается сразу при двух значениях s = 1 и s = 3. Для
определенности возьмем 5 = 3. Тогда разрешающим элементом будет Уз,з= 1: Л = 3,5 = 3.
В табл. 2.4 и в последующих таблицах разрешающий элемент будем помещать в
квадратик. В соответствии с выбранным разрешающим элементом переменную х& = х2
и столбец А: = А2 будем выводить из базиса, и заменим их переменной х3 и столбцом
А3 соответственно. Согласно формуле (2.56) разделим строку Г3 на Уз,з= 1 и
полученные величины внесем в строку Г3 табл. 2.5. Затем будем последовательно умножать
строку Г3табл. 2.5 на величиныУ\з= 2,y2t3 = ~1> А3 = 18, получившиеся строки вычтем
соответственно из строк Гь Г2, А табл. 2.4 и результат вычитания внесем в строки 1\,
Г2, А табл. 2.5. Таким образом, придем к симплекс-таблице 2.5 следующей угловой
точки vx = (0, 0, 1, 0, 4) с базисом Вх = (Л4, Л5, А3), со множеством базисных номеров
Kv\) = {/i = 4,Уг = 5,./з = 3} и со значением функции/^) = 3 <f(v0) = 21.
Таблица 25
г4
г2
Гз
д
Б
X*
jfi
хъ
V
0
4
1
3
*i
1
1
-1
14
X2
-2
1
1
-18
X3
0
0
1
0
*<
1
0
0
0
л:5
0
1
0
0
В строке А табл. 2.5 величина А{ = 14 > 0, в столбце хх имеются положительные
элементы Yi.i = 3, Y2,i = 1» те- снова реализовались условия (2.67). Пользуясь
правилом (2.68), имеем
. /О 41 _
min^—; — г = 0,
l3*lj
исходя из чего однозначно определяем номер s = 1 и разрешающий элемент Yi.i = 3.
Это значит, что переменную xh =хАи столбец А: = АА мы выводим из базиса и
заменяем их переменной хх и столбцом Ах соответственно. По формулам (2.56)
вычислим симплекс-таблицу 2.6 следующей угловой точки v2 = (0, 0, 1, 0, 4) с базисом
В2 = (Аь Л5, А3), со множеством I(v2) = {j\ = 1J2 = 5J3 = 3} и со значением функции
f(v2) = 3 =/(^i). В строке А этой таблицы среди величин А1? ..., А5 нет
положительных. Это значит, что реализовался случай (2.65), точка v2 = (0, 0, 1,0, 4) является
решением рассматриваемой задачи, /* =f(v2) = 3.
Заметим, что точки vx и v2 совпадают и различаются лишь базисами. Выясняется,
что еще в табл. 2.5 мы, оказывается, уже получили решение задачи, но не смогли это
распознать и вынуждены были сделать еще один шаг симплекс-метода.
108

Таблица 2.6
г4
г2
Гз
д
Б
*i
Х5
X3
V
0
4
1
3
*i
1
0
0
0
*2
-2/3
5/3
1/3
-26/3
X3
0
0
1
0
X*
1/3
-1/3
1/3
-14/3
X5
0
1
0
0
Пример 2.7
Рассмотрим еще одну задачу:
f(x) = хх + х2 - х3 - хА + х5 —> min, xeX,
X = {х = (хх, х2, х3, хА, х5) > 0: хх - х3 + хА + х5 = 1, х2 + х3 - х4 + х5 = 1}.
Нетрудно видеть, что v0= (1, 1, 0, 0, 0) — угловая точка с базисом В0= (Ль А2),
со множеством I(v0) = {jx = 1J2 = 2} и система уравнений, задающая множество, уже
записана в приведенной форме.
Таблица 2.7 представляет собой симплекс-таблицу точки v0. В строке А имеется
несколько положительных величин А3= А4 = А5 = 1. В качестве разрешающего
элемента выберем величину Уг.з = 1 из столбца х3. По формулам (2.56) при s = 2, k = 3
совершим переход к симплекс-таблице 2.8 угловой точки vx = (2, 0, 1, 0, 0) с базисом
Вх = (Ах, Л3), со множеством I(vx) = {jx = lj2 = 3}.
Таблица 2.7
Б
Xх
X2
V
1
1
2
Xх
1
0
0
X2
0
1
0
X3
-1
ш
1
*<
1
-1
1
X5
1
1
1
В строке А табл. 2.8 имеется величина А4 = 2 > 0, но столбец х4 не содержит
положительных элементов. Это значит, что реализовался случай (2.66). Следовательно,
/* = -оо, рассматриваемая задача не имеет решения.
Таблица 2.8
Xх
X3
2
1
1
1
0
0
1
1
-1
0
1
0
0
-1
2
2
1
0
Подобно тому как это сделано в табл. 2.7, 2.8, в последующих
симплекс-таблицах мы иногда будем опускать обозначения строк или столбцов, полагая, что
читатель уже привык к обозначениям.
2.4.4. Конечность метода в невырожденной задаче
Из вышеизложенного следует, что, имея какую-либо начальную
угловую точку v0 множества X, с помощью симплекс-метода последовательно
109

переходя от одной угловой точки к другой, можно построить
последовательность угловых точек и0, vi9 ..., vp9 ... . Согласно формуле (2.41) на
каждом шаге имеем
Л^-Л»,)-^»^.
ysjt\PP)
где bk(vp) > О, ysJt(vp) > О, ys0(vp) = vJp ^ °- Отсюда следует, что
/(i;0)>M)>...>/(^)>.... (2.74)
Процесс получения последовательностей {и }, \f(vp)} в дальнейшем
будем кратко называть симплекс-процессом.
Заметим, что в примерах 2.6, 2.7 симплекс-процесс завершился за
конечное число шагов выполнением одного из условий (2.65) или (2.66). Однако
всегда ли это будет так? Возможно, существуют канонические задачи,
для которых симплекс-процесс может неограниченно продолжаться? Для
ответа на этот принципиально важный вопрос внимательнее
проанализируем описанный симплекс-процесс. Прежде всего заметим, что поскольку
варианты (2.65)—(2.67) изменения знаков величин Ak(v)y Уц(р)
исчерпывают все возможности и взаимоисключают друг друга, то
симплекс-процесс может быть бесконечным лишь в том случае, когда на каждом шаге
этого процесса будут реализовываться условия (2.67).
Каждая реализация условий (2.67) связана с переходом от одной
угловой точки к другой угловой точке, от одной симплекс-таблицы к другой
симплекс-таблице. Это значит, что всякий бесконечный симплекс-процесс
порождает последовательности угловых точек {ор}, их базисов {Вр},
симплекс-таблиц {Sp}y где Sp является симплекс-таблицей точки vp с базисом Вр,
причем, как очевидно из формулы (2.74), соответствующая
последовательность {f(vp)} не возрастает. Поскольку угловых точек и их базисов в задаче
(2.31) конечное число, то конечно и множество симплекс-таблиц этой
задачи. Отсюда следует, что симплекс-процесс может быть бесконечным
лишь в том случае, когда хотя бы одна из симплекс-таблиц 5,
соответствующая некоторой угловой точке v с базисом 5, будет повторяться бесконечно
много раз. Это значит, что найдется бесконечная подпоследовательность
номеров {р/}: рх <р2 < ... < р,< ... такая, что vp[ = v, Bp[ = Я, Spi = 5, f(vpi) = f(p)
при всех /=1,2,.... В силу (2.74) это возможно лишь тогда, когда
f(vp) = const \/p>pt. (2.75)
Таким образом, необходимым условием бесконечности
симплекс-процесса является условие (2.75), которое должно выполняться начиная
с некоторого номера pv Посмотрим, когда это возможно. Начнем с
выяснения того, когда f(w) =f(v) и когда f(w) <f(v)> где угловая точка w
получена из угловой точки v в результате одного шага симплекс-метода. В силу
условий (2.67)—(2.68) Ak(v) > О, Y*,^) > 0 и, кроме того, ySio(v) = vJs ^0 как
базисная переменная угловой точки v. Отсюда и из формулы (2.71)
следует, что f(w) =f(v) тогда и только тогда, когда v^ = 0, т.е. v — вырожденная
угловая точка. Такое явление мы наблюдали в примере 2.6 при переходе
110

от табл. 2.5 к табл. 2.6. Таким образом, среди канонических задач имеет
смысл выделять задачи вырожденные и невырожденные.
Определение 2.3. Задачу (2.31) называют вырожденной или
невырожденной соответственно тогда, когда множество X в этой задаче содержит
хотя бы одну вырожденную угловую точку или не содержит таковые.
Покажем, что в невырожденных задачах (2.31) симплекс-процесс всегда
конечен. В самом деле, в таких задачах все базисные координаты угловой
точки v будут положительны. Поэтому какими ни были номера к, s,
определяемые из условий (2.37), (2.38), всегда^ > 0 и согласно (2.74) тогда f(w) <f(v).
Отсюда следует, что в невырожденных задачах симплекс-процесс
порождает такую последовательность угловых точек и0, vb ..., vp,..., для которых
M)>/(0i)>~>/(0,)>-- (2-76)
Поскольку угловых точек конечное число и из-за строгих неравенств
они повторяться в симплекс-процессе не могут, то этот процесс закончится
на каком-то шаге выполнением условия либо (2.65), либо (2.66). Впрочем,
конечность симплекс-процесса здесь вытекает и из несовместимости
соотношений (2.75), (2.76). Таким образом, доказана следующая теорема.
Теорема 2.2. Пусть в канонической задаче (2.31) множество X
непусто и невырождено, гапкЛ = г = т < п, пусть v0 — произвольная угловая
точка этого множества. Тогда симплекс-процесс, начинающийся с точки v0
при выборе разрешающего элемента ysk из условий (2.67), (2.68), завершится
за конечное число шагов нахождением некоторой угловой точки vp
множества X, в которой реализуются условия либо (2.65), либо (2.66), причем
в случае (2.65) vp — решение задачи (2.31), f(pp) = f* >-°°, в случае (2.66)
задача (2.31) не имеет решения, /* = -°°.
Заметим, что хотя теорема 2.2 справедлива при любом выборе
номеров k, s из условий (2.67), (2.68), но продолжительность симплекс-процесса
и последняя точка vp могут существенно зависеть от выбора этих номеров.
Интересно отметить, что если номер k из условий (2.67) как-то уже выбран
и зафиксирован, то в невырожденных задачах номер s условием (2.68)
определяется однозначно: для невырожденной угловой точки w = (w1, ...,
wn) с базисом (2.70) координаты wh > 0 для г\Ф s, 1 < г < г. Из формул (2.69)
следует, что vh - ЧуР**/Ч8& > 0 или v*x/4i,k > v*s /4s,k Для всех z G h(v)> * * 5>
так что минимум в левой части условия (2.68) будет достигаться на
единственном номере s e 1^(р)-
Отсюда вытекает, что условие (2.68) может неоднозначно определять
номер s лишь в вырожденных задачах. Кстати говоря, если в (2.68)
минимум достигается хотя бы на двух номерах 5, / е 4(я), s ф /, то в силу (2.69),
wis = wii = 0, т.е. угловая точка w непременно будет вырожденной (так
случилось в табл. 2.4,2.5). Конечно, точка w может быть вырожденной и в том
случае, когда условие (2.68) однозначно определяет номер s e 4(a), Для которого
z)Js = 0 (это значит, что точка v вырожденная); тогда в силу (2.69) у точки w
базисная координата х$= 0 (см. табл. 2.5, 2.6). Впрочем, если
selk(v), vb=0, (2.77)
то минимум в условии (2.68) равен нулю и будет достигаться именно
на этом номере s (и на всех других номерах / е 4(a), для которых vh = 0),
111

и согласно формулам (2.69), (2.71) тогда w = v, f(w) = f(v). Это значит,
что при выполнении условий (2.77) мы сделаем один шаг симплекс-метода
и останемся в той же точке w = v, лишь заменив один ее базис В = (А: ,..., Aj )
на другой базис (2.70) (именно так случилось в табл. 2.5, 2.6). Здесь
возникает естественный вопрос: при выполнении условий (2.77) не может ли
привести дальнейшее применение симплекс-метода к бесконечному
перебору базисов угловой точки v, не может ли здесь реализоваться
бесконечный симплекс-процесс? Оказывается, так вполне может быть.
2.5.* Антициклин
2.5.1. Пример
Приведем пример вырожденной задачи, в которой симплекс-процесс
приводит к так называемому зацикливанию, заключающемуся в
бесконечном циклическом переборе базисов одной и той же угловой точки.
Пример 2.8
Рассмотрим каноническую задачу
f(x)=xx-xA-x5 + x6^>min,xe X,
(2.78)
где
Х = \х = (х\х2,...,х7)>0: -2х* + х2 + х*-Зх5 + 4х6=0Л. (2.79)
-Зл:1 + х3 + АхА - 2х5 + х6 = 0 J
Нетрудно видеть, что точка v0= (0, 0, 0, 0, 0, 0,1) является угловой точкой с
базисом (А7, А2, А3) = В0, система (2.79) представляет собой приведенную систему этой
точки. Образуем симплекс-процесс, взяв в качестве начальной точку v0 с указанным
базисом. В табл. 2.9—2.15 приведены результаты вычислений для первых точек v0,
vx,..., v7; в квадратиках указаны разрешающие элементы этих таблиц. В табл. 2.9,2.11,
2.13 разрешающий элемент условием (2.68) определяется неоднозначно, в табл. 2.10,
2.12, 2.14 разрешающий элемент находится однозначно.
Таблица 2.9
1\
г2
Г3
А
Б
Х?
*2
X3
V
1
0
0
0
*1
1
-2
-3
-1
*2
0
1
0
0
X3
0
0
1
0
*<
1
ш
4
1
*5
1
-3
-2
1
ofi
1
4
1
-1
X7
1
0
0
0
Таблица 2.10
X7
X*
X3
1
0
0
0
3
-2
1
1
-1
1
-4
-1
0
0
1
0
0
1
0
0
4
-3
10
4
-3
4
-15
-5
1
0
0
0
112

Таблица 2.11
xi
X*
X*
1
0
0
0
0
0
1
0
7/5
-3/5
-4/5
-1/5
-3/5
2/5
1/5
-1/5
0
1
0
0
-2
s
2
2
6
-2
-3
-2
1
0
0
0
Таблица 2.12
xi
X*
X*
1
0
0
0
0
0
1
0
1/5
-3/5
2/5
1
1/5
2/5
-3/5
-1
2
1
-2
-2
0
1
0
0
2
-2
Ш
2
1
0
0
0
Таблица 2.13
X1
*5
jfi
1
0
0
0
-2
2
1
-2
-3/5
[Щ
2/5
1/5
7/5
-4/5
-3/5
1/5
6
-3
-2
2
0
1
0
0
0
0
1
0
1
0
0
0
Таблица 2.14
Х1
*2
3*
1
0
0
0
4
10
-3
-4
0
1
0
0
-1
-4
ш
1
-3
-15
4
5
3
5
-2
-1
0
0
1
0
1
0
0
0
Таблица 2.15
Б
*7
X*
х*
V
1
0
0
0
X*
1
-2
-3
-1
*2
0
1
0
0
X3
0
0
1
0
*<
1
Q
4
1
*5
1
-3
-2
1
я*
1
4
1
-1
ЛГ?
1
0
0
0
Как очевидно, табл. 2.9 и 2.15 совпадают, и поэтому если на следующих шагах
продолжать выбор тех же разрешающих элементов в том же порядке, то придем к
бесконечному симплекс-процессу, в котором будет осуществляться циклический
перебор базисов точки v0 в следующем порядке:
(Л7, А2, Л3) -> (Л7, Л4, Л3) -> (Л7, Л4, Л0 -> (Л7, Л5, Лj)-»
-> (Л7, Л5, Л6) -> (Л7, Л2, Л6) -> (Л7, Л2, Л3)
и т.д. Любопытно отметить, что длина цикла в задачах линейного
программирования меньше шести не бывает.
113

Этот пример показывает, что описанный выше симплекс-метод
действительно может привести к бесконечному симплекс-процессу и с его
помощью может быть решена не всякая каноническая задача (2.31). Если
функция f(x) = (с, х) принимает одинаковые значения в нескольких
вырожденных угловых точках, то, по-видимому, возможны более сложные
бесконечные симплекс-процессы, в частности, явления зацикливания с участием
в цикле базисов различных таких точек.
2.5.2. Лексикографическое упорядочение векторов
Можно ли избежать зацикливания при работе симплекс-метода или,
точнее, появления бесконечных симплекс-процессов? Нельзя ли
уточнить правило (2.67), (2.68) выбора разрешающего элемента так, чтобы
для любой задачи (2.31) симплекс-процесс, начинающийся с произвольной
начальной угловой точки, завершался за конечное число шагов
реализацией одного из условий (2.65) или (2.66)? Положительный ответ на эти
вопросы имеет важное значение для обоснования симплекс-метода и
означал бы, что можно, по крайней мере в принципе, решить любую задачу
линейного программирования симплекс-методом.
Определение 2.4. Любое правило выбора разрешающего элемента,
уточняющее правило (2.67), (2.68), с помощью которого можно избежать
зацикливания или, точнее, появления бесконечного симплекс-процесса во
всякой канонической задаче (2.31), назовем антициклином.
На практике правило (2.67), (2.68) нередко уточняют следующим
образом: среди номеров k, удовлетворяющих условиям (2.67), выбирают тот,
для которого А^ принимает максимальное значение, а если таких номеров
несколько, то берут минимальный из них, и затем после такой фиксации
номера k берут номер s минимально возможным из условий (2.68). Такое
уточнение правил (2.67), (2.68) действительно гарантирует
однозначность выбора разрешающего элемента ysk, выглядит вполне естественным
и в примере 2.8, как легко проверить, на самом деле позволяет избежать
зацикливания. Однако в общем случае в классе канонических задач
линейного программирования такое уточнение правила (2.67), (2.68) не спасает
от зацикливания и, следовательно, не может служить антициклином. Это
говорит о том, что построение антициклина — дело тонкое, и с первого
взгляда неясно даже, существуют ли они. К счастью, антициклины
существуют, и к настоящему времени уже созданы различные и не очень
сложные антициклины (см., например, работы [4, 5, 12, 36]).
Остановимся на одном из них [4]. Для описания этого антициклина нам
понадобится понятие лексикографического упорядочения конечномерного
пространства.
Определение 2.5. Говорят, что вектор х = (г1,..., х1) е R1
лексикографически положителен (отрицателен), и обозначают х > О (х < 0), если х Ф 0
и первая ненулевая координата вектора х положительна (отрицательна).
Говорят, что вектор ig R1 лексикографически больше (меньше) вектора
у g Ш1уи пишут х > у (х < у)> если х - у > 0 (х - у -< 0).
Другими словами, запись х > 0 означает, что существует номер р, 1 <
<р<1, такой, что х1 = ... = хр-{ = 0, хР> 0, остальные координаты хр+1у ..., &
114

могут быть любыми. Лексикографическое неравенство х > у означает
существование такого номера р, что 1 < р < /, х1 = г/1,..., хр~{ = уР-{, хР > уР.
Для любых Ху у g W выполнено одно и только одно из соотношений:
х > у,х < у или х = у. Ясно, что отношение > транзитивно, т.е. если х > г/,
у > z, то х > г. Упорядочение векторов в их лексикографическом убывании
(или возрастании) вполне аналогично упорядочению слов в словарях, что
и объясняет присутствие слова «лексикографический» в определении 2.5.
Перечислим несколько важных для дальнейшего изложения материала
свойств лексикографического отношения > (эти свойства несложно
вывести, опираясь на определение 2.5):
1) если х > О, то ах > О для всех а > 0;
2) если х > у, то ах > ау для всех а > 0;
3) если х > 0, у > 0, то х + ау > 0 для всех а > 0;
4) если х> 0, тоу > у -ах для всех а > 0 и у е R1.
Определение 2.6. Пусть М0 — некоторое (конечное или бесконечное)
множество целых чисел (номеров), пусть G = {yi=(y},...,yli)eRl, ieM0}.
Вектор ys, se M0 называется лексикографическим минимумом множества G,
если для всех г е М0 либо у{ > ys, либо у{ = ys. Лексикографический
минимум будем обозначать ys = lexminz/f.
ieM0
Лемма 2.1. Пусть М0 — конечное множество номеров, и пусть в
заданном множестве G = {у{ е Rl, i e М0} все векторы различны. Тогда
лексикографический минимум множества G достигается на единственном векторе
ys g G, т.е. ys < у{ для всех г е М0, i Ф s. Для определения номера s нужно
последовательно рассматривать множества
М0, Mt ={s:se М0, у\ = minу\),..., М = {s: se M v yps = min yf)
до тех пор, пока не будет обнаружено множество Mv, 0 < v < /, состоящее
из единственного номера 5, который и будет искомым.
Доказательство
В простейшем случае, когда множество М0 состоит из
единственного номера 5, по определению ys — искомый вектор. Если М0 содержит
более одного номера, строим множество Mv Если М1 содержит лишь один
номер 5, то у\ < у\ для всех г е М0, г Ф 5, и ясно, что ys = lexminz/^. Если М1
ieMo
содержит по крайней мере два номера, то процесс продолжается.
Пусть уже построены множества М0 з Мх з ... з Мр9 р<1, причем
множества М0, ..., Mp_t содержат более одного номера. Если Мр состоит из
единственного номера 5, то ys — искомый вектор. Если Мр содержит более одного
номера, то строим множество Мр+1 и т.д. В крайнем случае, когда множества
М0,..., Мм окажутся состоящими более чем из одного номера, этот процесс
закончится построением множества М/ = {seM[_1: y[ = min y\). Если бы
множество Mi содержало два различных номера 5, q> то у векторов г/5, yq все
координаты были бы одинаковыми, т.е. ys = yq. Однако по условию леммы
в множестве G нет двух одинаковых векторов. Следовательно, М/ состоит
из единственного номера 5, причем ys = lexminz/^. Лемма доказана. ■
/еМ0
115

2.5.3. Лексикографический антициклин
Г А
Опираясь на отношение > между векторами, введем отношения >-, >-
на множестве симплекс-таблиц. Не стремясь к общности построений, мы
можем ограничиться следующим определением, достаточным для
дальнейших рассмотрений.
Определение 2.7 Симплекс-таблицу S = S(v> В) угловой точки v с бази-
г
сом В назовем лексикографически положительной и будем обозначать 5V0,
если для всех г = 1,..., г строка Г{= (yi0, yitl,..., yin) > 0 (см. табл. 2.3). Будем
говорить, что симплекс-таблица St = S(vly Bx) лексикографически больше
А
другой симплекс-таблицы S2 = S(v2l B2) и будем обозначать S^S2, если
строка А = Д1 =(А^,..., Ajj) таблицы St лексикографически больше строки
А = А2 = (А§,..., А2) таблицы S2.
Для примера укажем, что табл. 2.4—2.8, 2.13 лексикографически
положительны, табл. 2.9—2.12, 2.14, 2.15 не являются таковыми; симплекс-
таблица 2.12 лексикографически больше симплекс-таблицы 2.11.
Используя введенные лексикографические понятия, перейдем к
описанию обещанного антициклина. Напомним, что применение симплекс-
метода во всякой невырожденной задаче приводит к построению
последовательности угловых точек и0, vt, ..., vp9 ... со свойством (2.76). Так как
в симплекс-таблице точки vp первое число в строке А равно f(vp)> то
согласно определению 2.6 свойство (2.76) будет означать, что
соответствующие этим точкам симплекс-таблицы 50, Sly..., Sp,... таковы, что
А А А А
50>-51>-..>5р >-.... (2.80)
При написании цепочки лексикографических неравенств (2.80) мы учли
А А А
транзитивность отношения >- для симплекс-таблиц: если StyS2, 52^53, то
А
St yS3. Так как симплекс-таблиц конечное число, а в цепочке (2.80)
повторение таблиц невозможно, то еще раз убеждаемся в конечности
симплекс-процесса в невырожденных задачах. В вырожденных задачах
последовательность \f(vp)} обладает, вообще говоря, лишь свойством (2.74),
а свойство (2.80), как очевидно из примера 2.8 (см. табл. 2.9—2.15), может
не выполняться. Возникает идея: нельзя ли как-то дополнить правило
(2.67), (2.68) выбора разрешающего элемента так, чтобы и в вырожденных
задачах получались последовательности симплекс-таблиц со свойством
(2.80)? Реализация этой идеи приведет нас к антициклину.
Пусть v — какая-либо угловая точка множествах с базисом В = (А: ,...,А- )
и с симплекс-таблицей S = S(v, 5), пусть это будет табл. 2.3. Предположим,
что таблица S удовлетворяет условиям (2.67) и уже зафиксирован какой-
либо номер k ё I(v), k > 0, из (2.67). Выберем номер s и разрешающий
элемент ysk из условия
-^- = lexmin^-, selk(v) = {i: 1 <i<г, yik >0}. (2.81)
ys,k fe/*<°> yuk
116

С помощью леммы 2.1 убедимся, что условие (2.81) однозначно
определяет номер s. Для этого нам надо показать, что множество
[ г. 1
G = \ yi; = —-, i e Ik(v) = М0 \ состоит из различных векторов. Допустим, что
[ Ya J
два вектора из этого множества оказались равными:
Г Г
— = ——, p,kelk(v), рФк
Ъ,к УРл
у.,
Тогда Г, =——Г„, т.е. строки Г„ Г„ в матрице
Vp,k
r = (YolYil-lY„) = (5-16|B-4|...|B-4) = 5-1(6M)
пропорциональны. Множество X непусто, поэтому система (2.32) совместна,
и тогда согласно теореме Кронекера — Капелли [9] rank (b\A) = rank A-r.
Отсюда и из невырожденности матрицы Б-1 следует, что гапкГ = гапкЛ = г.
Это значит, что строки Г1у..., Гг матрицы Г образуют линейно независимую
систему векторов, и никакие строки Г,-, Гр в этой матрице
пропорциональными не могут быть. Полученное противоречие показывает, что множество G
состоит из различных векторов. Согласно лемме 2.1 условие (2.81)
однозначно определяет номер s e 4(а)> причем для его практического
нахождения можно воспользоваться конструкциями, указанными в этой лемме.
Важно заметить, что лексикографическое правило (2.81) выбора
разрешающего элемента не отменяет ранее сформулированное правило (2.67),
(2.68), а, наоборот, включает его в себя, дополняет и уточняет его. В самом
деле, в соответствии с конструкциями леммы 2.1 для поиска номера s
из условия (2.81) мы в первую очередь образуем множество
М1= \seM0 =Ik(v): M = minMl
которое в точности совпадает с множеством номеров 5, определяемых
условием (2.68). Отсюда, кстати, следует, что если множество Мх состоит
из единственного номера (так будет, например, в невырожденных задачах),
то оба правила (2.67)—(2.68) и (2.81) определяют один и тот же номер 5,
один и тот же разрешающий элемент ysk. Если же Мх содержит более
одного номера, то правило (2.81) устраняет возможную в вырожденных задачах
неоднозначность в выборе разрешающего элемента при пользовании
правилом (2.67)—(2.68). Итак, выберем номера k, s и разрешающий элемент
yStk=ys,k(v) из условий (2.67), (2.81) и по правилам (2.56) совершим переход
от симплекс-таблицы S(v, В) угловой точки v с базисом В к
симплекс-таблице S(w, В) угловой точки w с координатами (2.69) и с базисом (2.70).
Лемма 2.2. Пусть симплекс-таблица S(v, В) угловой точки v с базисом
г
В лексикографически положительна, т.е. S(p, 5)^0, пусть в точке v
реализовался случай (2.67). Пусть, далее, разрешающий элемент ysk определен
с помощью лексикографического правила (2.81), осуществлен переход
117

к следующей точке w с базисом В по правилам (2.56) и получена симплекс-
таблица S(w, В). Тогда
_ г а _
S(w,B)>0, S(v,B)>S(w,B). (2.82)
Доказательство
г
В самом деле, если S(p, 5)^0, то по определению 2.7 в этой симплекс-
таблице строки Гг= rt(v) > 0, i = 1,..., г. Тогда из правил (2.56), неравенства
ysk = ysj,(v ) > 0 и свойства 1) отношения > следует, что Г (w) = —^^-^0.
Y,jfc(»)
Пусть теперь i * 5. Тогда либо yik> 0, либо yik < 0. Если у^> 0, то i e Ik(v)
и согласно правилу (2.81) имеем
Г,-(р) у Г,(р)
Y,-,*(o) Y,,*(o)
В силу правил (2.56) и свойства 2) отношения > тогда
Vs,k(v)
т.е.
rI.(»)=rj(o)-^^r,(0)^o.
Если гi4 < 0, то а = _lbii!Z > о и
Ys,a(°)
Г,.(да) = Г,.(о) + Г,(»)
Ygfo)
Y,jt(o).
>0
в силу свойства 3) отношения >. Таким образом, Г;(да) > 0 для всех i = 1,..., г,
_ г
а это означает, что симплекс-таблица S(w, В)у0.
Наконец, из того, что Vs(w))~0, Ak = Ak(v) > 0, из формулы (2.56)
для строки A(w) и свойства 4) отношения > имеем
A(v)>A(v)-Ak(v)rs(w) = A(w).
А _
Это значит, что S(p, B)yS(w> В). Лексикографические неравенства (2.82)
доказаны. ■
Теперь посмотрим, к какому симплекс-процессу приведет применение
правил (2.67), (2.81). Пусть у нас имеется некоторая угловая точка v0 с бази-
г
сом 50, с симплекс-таблицей 50^0. Пользуясь правилами (2.67), (2.81),
(2.56), организуем симплекс-процесс, начинающийся с точки г>0, и получим
последовательности угловых точек {vp}> их базисов {Вр}> симплекс-таблиц
{Sp}> где Sp — симплекс-таблица точки vp с базисом Вр. Согласно лемме 2.2
последовательность {Sp} удовлетворяет лексикографическим неравенствам
(2.80), в чем легко убедиться с помощью математической индукции, осно-
118

г
вываясь на неравенствах (2.82) и 50 ^0. Так как в цепочке неравенств (2.80)
повторение симплекс-таблиц невозможно в силу транзитивности отноше-
А
ния >- и в задаче (2.31) множество симплекс-таблиц конечно, то такой
симплекс-процесс закончится на каком-то шаге реализацией одного из условий
(2.65) или (2.66). Это значит, что правило выбора разрешающего элемента
по формулам (2.67), (2.81) является антициклином. Тем самым доказана
следующая теорема.
Теорема 2.3. Пусть в канонической задаче (2.31) гапкЛ = г=т<п,
множество X непусто, v0 — какая-либо угловая точка этого множества с сим-
r
плекс-таблицей 50^0. Тогда симплекс-процесс, начинающийся с точки v0,
при выборе разрешающего элемента ysk из условий (2.67), (2.81) завершится
за конечное число шагов определением некоторой угловой точки vp
множества X, в которой реализуются условия либо (2.65), либо (2.66), причем
в случае (2.65) f(vp) = /* > -°°, vp — решение задачи (2.31), а в случае (2.66)
задача (2.31) не имеет решения, /* = -оо.
Построенный антициклин (2.67), (2.81) обоснован при условии, что
г
начальная симплекс-таблица 50^0. Но это условие нельзя считать
серьезным требованием к антициклину, так как, переставив некоторые из
базисных столбцов и соответствующим образом перенумеровав переменные,
любую симплекс-таблицу 50 легко сделать лексикографически
положительной. В самом деле, нетрудно видеть, что если угловая точка v с базисом
В = (А:,..., Aj ) невырожденная, то ее симплекс-таблица S > 0, так как тогда
(см. табл. 2.3) Y/,o = v^ > 0 и, следовательно, Г{ > 0 при всех i = 1,..., г.
Если точка v вырожденная, то Y;,o = 0 хотя бы для одного номера г,
1 < г < г, и первый отличный от нуля элемент в строке Yi может оказаться
отрицательным. Тогда Г{ < 0 (см., например, строки Г2, Г3 табл. 2.9).
Впрочем, такой «недостаток» строки Гг легко исправить, если соответствующий
базисный столбец хЬ симплекс-таблицы переставить между столбцами V
и х1. Такая перестановка, равносильная перенумерации переменных,
приведет к тому, что в строке Г{ сразу после величины у^о = 0 окажется
величина у,-,у = 1 и будет Гг > 0, а на лексикографической положительности или
отрицательности других строк это не отразится, так как ysj. = 0 при всех
s Ф 1, 1 < s < г. Отсюда ясно, что, последовательно переставляя указанным
образом базисные столбцы xh для всех строк Г/ -< 0, нетрудно добиться,
чтобы симплекс-таблица стала лексикографически положительной.
Так, например, в табл. 2.9 для этого достаточно переставить столбцы
х2, х3 между столбцами Vn х1. К тому же такую операцию с
перестановкой столбцов и перенумерацией переменных нужно сделать самое большее
один раз в самом начале симплекс-процесса. Впрочем, операцию с
перестановкой столбцов и перенумерацией переменных можно явно и не делать,
если эту операцию учесть при порядке формирования множеств Мх, М2,...,
указанных в лемме 2.1 и используемых при поиске номера s из условия
(2.81). Более того, можно доказать, что условия (2.67), (2.81) являются
г
антициклином и без требования 50 ^0.
119

Заметим также, что антициклин (2.67), (2.81) оставляет некоторый
произвол в организации симплекс-процесса из-за того, что условие (2.67)
определяет номер k, вообще говоря, неоднозначно. Для устранения
указанной неоднозначности к правилу (2.67), (2.81) можно сделать дополнение,
руководствуясь какими-либо другими соображениями, например, можно
выбирать минимальный или максимальный номер k, удовлетворяющий
условиям (2.67).
Пример 2.9
Для иллюстрации изложенного антициклина (2.67), (2.81) рассмотрим задачу
(2.78), (2.79), в которой, как обнаружилось выше, использование правила (2.67), (2.68)
выбора разрешающего элемента может привести к зацикливанию.
Сначала симплекс-таблицу 2.9 начальной угловой точки v0= (0,0, 0,0,0, 0,1)
сделаем лексикографически положительной, переставив базисные столбцы х2, х3 между
столбцами Vw xx\ в результате придем к табл. 2.16, в которой сохранена
первоначальная нумерация переменных.
Таблица 2.16
1\
г2
Г3
А
Б
X7
X2
X3
V
1
0
0
0
X2
0
1
0
0
X3
0
0
1
0
*1
1
-2
-3
-1
X*
1
1
Ш
1
*5
1
-3
-2
1
jfi
1
4
1
-1
X7
1
0
0
0
В строке А табл. 2.16 величина А4 = 1 > 0 и весь столбец х4 заполнен
положительными числами: 71,4 = 1> Y2.4 = 1> Уз,4 = 4. Таким образом, получаем, что условия (2.67)
здесь выполнены и I4(v0) = {1, 2, 3}. Для применения лексикографического правила
(2.81) выпишем следующие строки:
-^ = (1,0,0,1,1,1,1,1), -^. = (0,1,0,-2,1,-3,4,0), ii =
0,0,
1
[ 2 4
Yl,4 Y2)4 Y3)4
Последовательно сравнивая по величине их координаты, легко находим
указанные в лемме 2.1 множества Мх = {2; 3}, М3= {3}, искомый номер 5 = 3, так что здесь
, . frt г2 г31 г3
lex rnin^ —^, —^, —^- г = —^-.
lYl,4 Y2)4 Y3,4J Y3,4
Понятно, что те же множества Mv M2 и номер 5 = 3 можно было получить
непосредственно из табл. 2.9, просматривая ее столбцы в таком порядке: V, х2, х3, хх, х4,
х5, х6, х7. Итак, разрешающим элементом является 73,4 = 4. Далее по формулам (2.56)
в базис вводим переменную х4 и выводим из базиса х3. В результате придем к
симплекс-таблице 2.17 угловой точки vx, совпадающей с v0, но имеющей другой базис
(Л7, Аъ Л4).
Таблица 2.17
Х1
X*
X*
1
0
0
0
0
1
0
0
-1/4
-1/4
1/4
-1/4
7/4
-5/4
-3/4
-1/4
0
0
1
0
|3/2|
-5/2
-1/2
3/2
3/4
15/4
1/4
-5/4
1
0
0
0
120

В этой таблице разрешающим элементом может быть лишь величина Yi,5 = 3/2.
Из базиса выведем переменную х7, заменив ее х5, по формулам (2.56) получим
табл. 2.18.
Таблица 2.18
Х5
X*
X*
2/3
5/3
1/3
-1
0
1
0
0
-1/6
-2/3
1/6
0
7/6
5/3
-1/6
-1
0
0
1
0
1
0
0
0
1/2
5
1/2
-2
2/3
5/3
1/3
-1
В ее строке А все величины Л,-, 1 < i < 7, неположительны, реализовались
условия (2.65). Симплекс-процесс на этом заканчивается, найденная невырожденная
угловая точка v2 = (О, 5/3, 0, 1/3, 2/3, 0, 0) является решением задачи (2.78), (2.79),
Заметим, что хотя среди задач линейного программирования
вырожденные задачи встречаются довольно часто, но тем не менее на основе всего
практического опыта применения симплекс-метода к таким задачам
сложилось убеждение, что вероятность получения бесконечных
симплекс-процессов ничтожно мала. Добавим также, что использование антициклина
на каждом шаге симплекс-метода может привести к заметному
увеличению машинного времени ЭВМ, требующегося для решения задачи.
Поэтому на практике чаще всего пользуются упрощенным правилом выбора
номеров k и s из условий (2.67), (2.68), беря, например, наименьшие или
наибольшие номера, удовлетворяющие этим условиям.
Из сказанного следует, что наличие симплекс-метода, снабженного
антициклином, для практики, видимо, не является слишком актуальным,
но в теоретическом плане это принципиально важно и ставит симплекс-
метод на надежный математический фундамент.
2.5.4. Симплекс-метод в канонической задаче максимизации
Кратко остановимся на применении симплекс-метода для решения
канонической задачи максимизации:
f(x) = (с, х) —> max, х е X = {х е Еп : х > 0, Ах = Ь), (2.83)
где А — ненулевая матрица размера г х и, с е Еп, Ъ е Ету г = rank Л < п.
Конечно, эту задачу можно свести к равносильной задаче минимизации
g(x) = -f(x) —> min, x E X, и к ней применить описанный выше симплекс-
метод без каких-либо изменений. В то же время нетрудно несколько
видоизменить симплекс-метод и приспособить его для непосредственного
применения к задаче (2.83).
Легко понять, посмотрев на формулы (2.36), (2.39) и (2.62), что
при решении задачи максимизации (2.83) нас прежде всего будут
интересовать величины А^ < 0, и мы естественно придем к рассмотрению следующих
трех случаев, аналогичных случаям (2.65)—(2.67).
Случай I. В нижней строке симплекс-таблицы 2.3 все Аь ..., Ап
неотрицательны. Исходная угловая точка v является решением задачи (2.83).
121

Случай П. В нижней строке симплекс-таблицы 2.3 найдется величина
Д^ < О, 1 < k < и, и находящийся над ней столбец yk неположителен. Тогда
/* = sup(i% х) = -и», задача (2.83) не имеет решения.
хеХ
Случай III. В нижней строке симплекс-таблицы 2.3 имеются величины
Ak<0y 1 < k <пу причем в каждом столбце над величиной А^ < 0 найдется
хотя бы одно число yik> 0.
Тогда фиксируем один из таких номеров к с А^ < 0 и выбираем
разрешающий элемент ysk по правилу (2.68) или, точнее, (2.81), а затем по
формулам (2.69) совершаем переход от угловой точки v с базисом В к точке w,
которая согласно замечанию 2.1 также будет угловой точкой множества X
с базисом By имеющим вид (2.70), причем f(w) >f(v). Один шаг симплекс-
метода для задачи (2.83) описан. Как и выше, можем считать, что исходная
г
симплекс-таблица S(v,B)>-0. Тогда будут справедливы следующие
лексикографические неравенства, аналогичные неравенствам (2.82):
_ г а _
S(WyB)y0y S(VyB)<S(WyB).
Отсюда следует, что симплекс-процесс для задачи (2.83) будет
конечным и закончится реализацией одного из случаев I или П.
Все высказанные здесь утверждения, касающиеся задачи (2.83),
доказываются совершенно так же, как и аналогичные утверждения, касающиеся
задачи (2.31). Предлагаем читателю убедиться в этом самостоятельно.
2.6. Поиск начальной угловой точки
Выше мы подробно изложили симплекс-метод для канонической задачи:
f(x) = (с, х) —> min, хg X = {х = (х1,...,хп)>0,Ах = 6}, (2.84)
где А — матрица размера тхпу с е Еп, Ъ е Е™, в предположении, что
множество X непусто и известна какая-либо его угловая точка, т = r= rankA
Покажем, как избавиться от этих ограничений. Нас будут интересовать
следующие вопросы:
1) Как распознать пусто или непусто множество X, и если оно непусто,
то имеет ли оно хотя бы одну угловую точку?
2) Как найти эту угловую точку, ее базис?
Ниже на них будут даны ответы. Замечательно то, что для этого будет
использован сам изложенный выше симплекс-метод с антициклином.
Оказывается, по исходной задаче (2.84) легко можно составить новую
вспомогательную каноническую задачу, к которой очень удобно применить
симплекс-метод, и в зависимости от того, чем закончится
симплекс-процесс для вспомогательной задачи, можно будет сказать, пусто или непусто
множество Ху найти его угловую точку. Этот метод поиска начальной
угловой точки в литературе часто называют методом искусственного базиса.
Можем считать, что матрица А Ф 0, так как при А = 0 либо X = Е^ = {х > 0},
либо X = 0, и задача (2.84) становится малосодержательной. Будем также
122

считать, что в (2.84) вектор Ъ > О, так как если Ы < О при некотором г, 1 < г <
< т, то соответствующее г-е уравнение (Ах)1 = Ы системы Ах = Ъ можно
умножить на (-1). Наряду с основными переменными х = (г1,..., хп) введем
вспомогательные (искусственные) переменные и = (и1,..., ит) и в
пространстве Еп+т переменных у = (и> х) = (м1, ..., ит, х1, ..., хп) рассмотрим
следующую каноническую задачу линейного программирования:
g(y) = и1 + и2 +... + ит = (1т,и) —>min, yeY,
Y = {y = (u,x)eEn+m:y>0, Cy = u + Ax = b},
(2.85)
где 1т= (1, ..., 1) g Em\ С = (Im, A); Im — единичная матрица размера тхт.
Систему Су = и + Ах = Ъ перепишем в покоординатной форме:
Ь1 -их + ах 1х1 + ... + at :XJ +... + alnxn,
b* - и1 + апхх +... + а$хз +... + ainxn,
Ът = um+aTnlx1+... + amjxJ +... + amnxn.
(2.86)
При и1 = ... = ит = О система (2.86) превращается в систему Ах = Ъ.
Множество Y непусто: оно содержит, например, точку z0 = (b, 0) > 0. Более того,
с помощью теоремы 2.1 легко убедиться, что точка z0 является угловой
точкой множества Ус базисом (е1у..., ет) = 1т. Система (2.86) является
приведенной системой этой точки, rank С = т. Для целевой функции
приведенная форма равна
g(y) = (lmyb-Ax) = g(z0)-(ATlm1x)1
где АТ — транспонированная матрица А. Теперь симплекс-таблица точки z0
составляется просто (табл. 2.19): в столбце Б находятся базисные
координаты и1 у..., и™, в столбце V— вектор Yo= Ь, в столбцах и1,..., и™
вспомогательных переменных записаны векторы y[=ev..., y'm = ew B столбцах х1,..., хп
основных переменных расположены векторы Yi =Im^i= ^i>-> Yn = ^пЛп = ^п-
Таблица 2.19
г,
г,
гт
д
Б
v>
и'
ит
V
Ы
Ы
Ът
Ао
и1
1
0
0
0
и'
0
1
0
0
ит
0
0
1
0
X1
«и
Щ\
ат\
Ai
3)
aV
ач
amj
Д;
хп
а\п
ain
атп
А,
Элементы строки А легко вычисляются по формулам (2.63), которые
применительно к задаче (2.85) дадут следующее: величины Д{,..., Д^, соот-
123

ветствующие базисным переменным и1,..., ит, равны нулю, а величины А0,
A1?..., Ап равны сумме элементов соответствующих столбцов V, х1,..., хп:
ТП ТП
i=l i=\
Привлекательно также и то, что симплекс-таблица 2.19
лексикографически положительна и поэтому здесь удобно применять симплекс-метод
с антициклином (2.81).
Поскольку g(y) > О при всех у е F, то g* = inf g(y) > 0 и случай g*=-°°
здесь невозможен. Поэтому, взяв в качестве начальной точку z0, с помощью
симплекс-метода с антициклином за конечное число шагов найдем
угловую точку z* =(w*,a*) множества F, являющуюся решением задачи (2.85):
g(z*) = g* > 0. Имеются две возможности: или g(z*) > 0 или g{z*) = 0.
Если g(z*) = ul +... + иР > 0, то и* Ф 0 и, оказывается, множество Xв (2.84)
будет пустым. В самом деле, если существует хотя бы одна точка х0 е X, то
точка у0 = (0, х0) принадлежит множеству Y и, кроме того, тогда g(z/0) = 0»
что противоречит неравенствам g(#o)-£(z*) = £* >0- Таким образом, при
g(z*) = g* > 0 множество X пусто, и задача (2.84) не имеет смысла.
Пусть теперь g(z*) = ul +... + vS1 = 0. Тогда и* = 0 и z* = (0, о»). Кроме того,
по построению z* = (0, v*) — угловая точка множества Y. Покажем, что тогда
v* будет угловой точкой множества X. Прежде всего ясно, что из z* > 0
следует v* > 0, а из Сг* = Ъ имеем Ао* = Ъ. Это значит, что v* e X. Далее
рассмотрим представление
v* =оа1+(1-а)х2, 0<а<1;^,^2 е^> (2.87)
и покажем, что оно возможно лишь при v*=xt= х2. Точки ух = (0, х{), у2 =
= (0, х2)У очевидно, принадлежат Y. Тогда представление (2.87) можно
переписать в виде z* =ау1 +(1-ос)г/2> 0 < а < 1. Но z* — угловая точка
множества Y. Поэтому последнее равенство для z* возможно лишь при z*=yx= y2.
Отсюда следует, что v*=xt= x2. Таким образом, v* — угловая точка
множества X.
Тем самым получен критерий непустоты множества X: если g* > 0, то
X = 0, если g* = 0, то X Ф 0, и доказана важная теорема.
Теорема 2.4. Если множество X - {х е Еп : х > 0, Ах = Ь) непусто, то оно
имеет хотя бы одну угловую точку.
Итак, доказана принципиальная возможность использования симплекс-
метода, оснащенного антициклином, для решения произвольной
канонической задачи. Подчеркнем, что теорема 2.4 доказана без ограничительного
предположения г = гапкЛ = т. Найденная методом искусственного базиса
угловая точка v* множества X вполне может быть использована как
начальная при применении симплекс-метода в исходной задаче (2.84). Зная
координаты точки v*, можно определить номера базисных переменных и ранг
матрицы Л, пользуясь известным методом Гаусса — Жордана [9, 31].
Напомним, что положительные координаты точки v* заведомо являются
базисными (см. доказательство теоремы 2.1). Не вдаваясь в детали,
скажем, что, опираясь на симплекс-таблицу угловой точки z* = (0, v*), которая
124

получится на заверщающем этапе симплекс-процесса для вспомогательной
задачи (2.85), можно значительно облегчить поиск базиса точки v* [11].
Приведем еще две теоремы, касающиеся канонической задачи, в
доказательстве которых симплекс-метод также играет существенную роль.
Теорема 2.5 Если задача (2.84) разрешима, то среди ее решений
найдется хотя бы одна угловая точка множества X.
Доказательство
По условию теоремы X Ф 0 и существует точка v*eX такая, что
(с, v*) = f*> -оо. По теореме 2.4 тогда множество X имеет хотя бы одну
угловую точку. Отправляясь от одной из этих угловых точек, с помощью
симплекс-метода с антициклином за конечное число шагов придем к угловой
точке х*9 которая является решением задачи (2.84). Теорема 2.5 доказана. ■
Теорема 2.6. Для того чтобы каноническая задача (2.84) была
разрешима, т.е. существовала точка х*еХ такая, что (с,х*) = inf(c,х) = /* >-°°,
необходимо и достаточно, чтобы:
1) множество X было непустым;
2) функция f(x) = (с, х) была ограничена снизу на X.
Доказательство
Необходимость очевидна. Достаточность. Из того, что X Ф 0, по
теореме 2.4 имеем существование угловой точки множества X. Принимая эту
точку за начальную, будем решать задачу (2.84) с помощью симплекс-
метода, снабженного антициклином. Так как по условию /* >-°°, то
случай (2.66) здесь невозможен, и симплекс-процесс завершится за конечное
число шагов реализацией случая (2.65) и отысканием точки х*, являющейся
решением задачи (2.84). Теорема 2.6 доказана. ■
На этом мы заканчиваем изложение симплекс-метода для
канонической задачи (2.84). Учитывая возможность сведения общей задачи
линейного программирования к канонической задаче, можно сказать, что
симплекс-метод является универсальным методом решения задач линейного
программирования. Конечно, компьютерная реализация описанной выше
схемы симплекс-метода требует огромной дополнительной работы: надо
выбрать подходящую модификацию метода, изучить влияние погрешности
на симплекс-процесс, организовать хранение исходной и текущей
информации о задаче и т.п.
Симплекс-метод относится к так называемым конечным методам,
позволяющим найти решение задачи линейного программирования или
обнаружить ее нерешаемость за конечное число арифметических действий.
Это число, конечно, зависит от размерностей т, п задачи (2.84). Известен
пример задачи линейного программирования с п переменными и т = 2п
ограничениями, для решения которого требуется не менее 2п - 1 шагов
симплекс-метода, и, следовательно, число арифметических операций,
необходимых для получения решения, не меньше 2п [11]. Отсюда следует, что
количество вычислений для решения «плохих» задач линейного
программирования симплекс-методом оценивается экспоненциальной функцией
параметров т, п размерности задачи, и уже при не очень больших т, п
решение таких задач симплекс-методом невозможно за обозримое время
даже на самых мощных компьютерах. Как принято говорить, на классе
125

задач линейного программирования симплекс-метод имеет
экспоненциальную сложность (см., например, работу [11]). Однако вопреки такому
пессимистическому выводу в практических задачах симплекс-метод показывает
высокую эффективность, причем в абсолютном большинстве реальных
задач количество необходимых арифметических операций имеет порядок
п2т. Причина этого удивительного явления пока еще не выяснена.
В последнее время появились методы, имеющие полиномиальную
сложность [11]. Так называются конечные методы, для которых число
элементарных операций, необходимых для получения решения задачи линейного
программирования с нужной точностью, не превышает некоторого
полинома от размерностей т, п задачи (2.84). Эти методы в самом деле
эффективнее симплекс-метода на «плохих» искусственно придуманных
задачах линейного программирования, но на реальных задачах пока не могут
успешно конкурировать с ним. На практике симплекс-метод и его
модификации по-прежнему остаются основным методом линейного
программирования.
2.7. Теорема Вейерштрасса в линейном программировании
Одну теорему Вейерштрасса о достижении нижней грани в
канонической задаче мы уже привели — это теорема 2.6. Убедимся, что она
справедлива и в общем случае. А именно, рассмотрим общую задачу линейного
программирования
f(x) = (с, х) = (q, xt) + (с2, х2) —> min, х = (х1у х2)е X, (2.88)
IJ\\ а Х\ т J\\ nXn S Da ,
x = (xl,x2):xieEni,x2eEn2 u * _, *i^0[, (2.89)
21*^1 22*^2 — 2* I
где Ay — матрицы размера т{ х rip Cj e EnJ, Ъ{ е Е™*, i,j=l,2. Как и выше,
будем обозначать /* = inf /(х), подразумевая при этом, что X Ф 0. Для слу-
хеХ
чая, когда /* >-°°, введем множество X* ={ieX:/(i) = /*}. Напоминаем,
что задача (2.88), (2.89) называется разрешимой, если X* Ф 0; каждую
точку х* е X* называют решением этой задачи.
Приведем теорему существования решения задачи (2.88), (2.89),
которая дополняет теоремы Вейерштрасса из параграфа 1.2 и характеризует
специфику задач линейного программирования.
Теорема 2.7. Задача (2.88), (2.89) разрешима тогда и только тогда,
когда Хф0 и целевая функция f(x) ограничена снизу на X, т.е. /* > -оо.
Доказательство
Необходимость очевидна, так как условие X* Ф 0 предполагает, что
X Ф 0 и /* > -оо. Достаточность. Пусть X Ф 0, /* > -оо. Покажем, что тогда
X* Ф 0. Задачу (2.88), (2.89) запишем в канонической форме:
f(x) = (с, х) -> min, х е X = {х е Еп: Ах = b, x > 0}, (2.90)
при этом се Еп\ Ъ е Ет\ А — матрица размера ту. п. Как и в параграфе 2.1,
положим
126

x2 = z1- z2, z{ = max{0; x2}, z2 = max{0; -x2}, v-bx- Anxt - A 12x2,
и в пространстве переменных w = (xly zb z2, v) e E<?, q = n{ + 2n2 + ть
рассмотрим задачу
g(w) = (cvx1) + (c2,z1) + (-c2,z2) +(0y v)^>miny weWy (2.91)
f A 1x1 + Ao^ + (-A2)z2 + /m a = Ы,1
Wr = Jwe^:w>0, и 1 12 1 12 2 ' / (2.92)
[ A21xt +A22zt +(-A22)z2 +0v = b2, J
где Im — единичная матрица размера mt x mv Задача (2.91), (2.92)
совпадает с задачей (2.90), если принять
с = (q,c2,-c2,0)eEny b = (bvb2)eEm, A =
[ Ап А12 -А12 1Щ\
КА21 А22 -А22 0
где А — матрица размера т х и, т = т1 + т2, п - q = п{ + 2п2 + mv Рассуждая
от противного, несложно доказать, что из Хф 0, /* > -«> следует, что W±-0,
g* = inf g(w)>-oo. Тогда по теореме 2.5, примененной к канонической за-
weW
даче (2.91), (2.92), множество W* = {we W: g(w) = g*}*0.
Возьмем произвольную точку w* = (xr, z1#, z2*, v*) e W*. Тогда в силу
проведенных построений точка х* = (х1#, х2* = zr - z2*) — решение задачи (2.88),
(2.89), т.е. X* Ф 0. Теорема 2.7 доказана. ■
Нетрудно видеть, что для нелинейных задач такая теорема неверна.
Например, задача f(x) = е~х —> min, х Е X = {х Е Е1 : х > 0} не имеет
решения, хотя в ней /* = 0 > -©о.
Следствие2.1. Задача максимизации (d, х) —> max,xe Xимеет решение
тогда и только тогда, когда X Ф 0 и функция (d, x) ограничена сверху на X.
Для того чтобы убедиться в справедливости этого утверждения,
достаточно заметить, что такая задача максимизации равносильна задаче (2.88),
(2.89) с с = -d, и воспользоваться теоремой 2.7.
2.8. Теоремы двойственности
Прежде чем переходить к изложению так называемых теорем
двойственности, докажем несколько важных лемм.
Лемма 2.3. Для того чтобы некоторая точка х* из множества X была
решением канонической задачи (2.90), т.е. х* е X*, необходимо и
достаточно существования точки X* = (к\у..., Х*т)ЕЕт такой, что
ЛтГ+с>0, {с,х*) = -{ЪХ\ (2.93)
где АТ— матрица, полученная транспонированием матрицы А.
Доказательство
Необходимость. Возьмем произвольную точку х* е X*. Покажем, что
тогда необходимо существует точка X* е Ет со свойствами (2.93).
Сначала рассмотрим случай т = г = rank А. Применим к задаче (2.90)
симплекс-метод с антициклином. По условию /(х*) = /* > -«>, поэтому сим-
127

плекс-процесс закончится обнаружением некоторой угловой точки v*
множества X с базисом B = (Aj ,...,Aj ), /(а*) = /*, причем будут выполняться
неравенства (2.65):
Дл=<с,В"14к>-с*<0, & = 1,2,...,и, (2.94)
где с" = (сл,...,с^). Положим X* = -(Б_1)тс\ Пользуясь известным из
линейной алгебры тождеством (Мх,у) = (х,Мту), справедливым для любых
х е Еп, у е 2?11 и любых матриц М размера m x и, из соотношений (2.94)
имеем
0^AA=<(B-1)Tc>4fe>-c*=4V>4fe>-^ ^ = l,2,...,n.
В векторной форме эти неравенства можно записать в виде АТХ* +с > 0.
Далее вспомним, что у угловой точки v* базисные координаты хк =(w?1,...,
vlr) = B~xb, а небазисные координаты равны нулю. Поэтому
(с, *.> = /.= (с, и.) = (с, а> = (с, 5"^) = ((Я"1)7^ Ь) = -(Ь, Г).
Таким образом, искомая точка А* со свойствами (2.93) найдена.
Случай гп = r= ranL4 рассмотрен. Пусть теперь m>r= rankA Тогда в системе
уравнений Ах = Ь> которую можем записать в виде (а{ух) = Ь\ i = 1, ..., m>
где щ — строки матрицы Д имеются ровно г линейно независимых
уравнений. Перенумеровав уравнения, можем считать, что первые г уравнений
этой системы линейно независимы, а остальные уравнения с номерами
г = г + 1, ..., m линейно выражаются через первые г базисных
уравнений. Удаление линейно зависимых уравнений приведет к равносильной
системе Ах = Ь, где А — матрица, состоящая из строк аь аъ..., аг матрицы Д
Ъ = (б1,..., br), и задача (2.90) сведется к равносильной канонической задаче
f(x) = (с,х) —>min, xeX = {x>0, Ах = Ь}.
В этой задаче число уравнений равно г = rank Л, и по доказанному
существует точка А* = (к\у..., А*)е Ег такая, что
ЛтХ*+с>0, {с,х*) = -{ЬХ\ (2.95)
Рассмотрим точку X* = (Х*,0)еЕт, полученную добавлением к
координатам X* нулевых координат Х*г+1 = 0,..., Х*т = 0. Тогда из соотношений (2.95)
следует, что АТХ* +с > 0, (с,х*) = -(Ь,Х*). Необходимость доказана.
Достаточность. Пусть для каких-либо точек 1*е1Д*еР выполнены
соотношения (2.93). Тогда для всеххе Xимеем
0 < (х, АТХ* + с) = (с, х) + (Аг, X*) = (с, х) + (Ьу X*) = (с, х) - (с, х*).
Это значит, что х* е X*. Лемма 2.3 доказана. ■
Лемму 2.3 нетрудно обобщить на случай общей задачи линейного
программирования (2.88), (2.89).
Лемма 2.4. Для того чтобы некоторая точка х* =(х1*,х2*) из
множества (2.89) была решением задачи (2.88), (2.89), необходимо и достаточно,
чтобы существовала точка X* = (к\, Х*2), Х\ е Е**, Х2 е Ет2> такая, что
128

A^+Aj^+c^O, Л1т2Х;+Л2т2Г2+с2=0, Х;>0; (2.96)
(cvx1*) + (c2,x2*) = -(bvX*1)-(b2,X2)y (2.97)
где AI — матрица, полученная транспонированием матрицы Ац.
Доказательство
Возьмем любую точку х* =(xt*yx2*) из множества X*, тогда точка w* =
= ух^*у z^*y z2*y v*)y где Za* = maxjuj х2*)\ z2* = maxjuj Ху*/ > ^* = i ii^i* -/a-iо^з*'
является решением задачи (2.91), (2.92), причем g(w*) = g*=f*= f(x*).
Применяя лемму 2.3 к канонической задаче (2.91), (2.92), заключаем, что это
возможно тогда и только тогда, когда существует точка X* =(^Д2), Х[ еЕ™!,
Х*2 е Ет2, такая, что
ЛтГ+с =
ATi
А~2
-Л12
/
Л21
AJ2
-AJ2
° J
+
М
c2
-c2
l°J
/
=
V
^41 1 21 2 ^1
12 1 ~^~ 22 2 ~^~ ^2
-A12^\ - A22^2 ~ C2
>0;
Учитывая, что x2*=z1*-z2*, эти соотношения нетрудно переписать
в равносильном виде (2.96), (2.97). Лемма 2.4 доказана. ■
С задачей (2.88), (2.89) тесно связана задача линейного
программирования
\|/(Х) = -(bv Xt)-(b2> Х2) —> max, X = (Xv X2) e Л;
(2.98)
Л
которая называется двойственной задачей по отношению к исходной задаче
(2.88), (2.89), переменные X = (kly Х2) называются двойственными
переменными по отношению к исходным переменным х = (хь х2).
Будем обозначать \|/* = sup\|/(X), Л* = {к е Л: \|/(Х) = \|/*}. Как видим,
двойка
ственная задача (2.98), (2.99) однозначно определяется по элементам q, c2,
Ъь Ъ2, А1Ь Л12, Л21, Л22 исходной задачи (2.88), (2.89).
Лемма 2.5. Если в задачах (2.88), (2.89) и (2.98), (2.99) множества X
и Л непусты, то величины /* = inf/(x), \|/* =sup\|/(X) конечны и справед-
х&х ХеА
ливо неравенство
\|/*</*. (2.100)
Доказательство
Возьмем произвольные хеХДеЛ. Тогда справедлива следующая цепочка
неравенств, вытекающая из определений (2.89) и (2.99) множеств X и Л:
f(x)-\\f(X) = (cvx1) + (c2yx2) + (bvX1) + (b2yX2)>
^ \Слу Ха) т \С2, Х2/ т \^i \Х\ т /хл2Х2у Л|/ ~г \./i2jXj ~г ./i22X2, А2/ =
= (cl+Aflkl +AJik2,xi) + (c2 +Д12А1 +y4j2A2,x2> >0. (2.101)
129

Таким образом,
/(*)>\|f(X) VxeX, ХеЛ. (2.102)
Последовательно переходя в неравенстве (2.102) сначала к нижней
грани по х е X, затем к верхней грани по X е Л, убеждаемся, что величины
/*, \|/* конечны и удовлетворяют неравенству (2.100). Лемма 2.5 доказана. ■
Выясним, как выглядит задача, двойственная по отношению к
двойственной задаче (2.98)—(2.99). Замечательно, что эта задача, оказывается,
с точностью до эквивалентной формы совпадает с исходной задачей (2.88),
(2.89). Чтобы убедиться в этом, перепишем задачу (2.98)—(2.99) в
равносильном виде как задачу минимизации:
-y\f(k) = (bt, Xt) + (b2,X2> —> min, Xe Л,
[ (-A2)^l+(-^22)^2=C2> J
по форме совпадающую с исходной задачей (2.88), (2.89), и затем,
пользуясь тем же правилом, с помощью которого была сконструирована
двойственная задача (2.98), (2.99) на основе исходной задачи (2.88), (2.89),
составим двойственную задачу к задаче (2.103). Обозначив двойственные
к X = (Аф Х2) переменные через х = (хх, х2), придем к следующей задаче:
-(q, xt)-(с2, х2) —> max, x = (xt, х2)еМ,
Г ххеЕъ,(-АЪУхх+(-АЪУх2+Ъх>Ь 1 (2.104)
\ v * 2) x2eEn2,(-Aj1)Tx1+(-AJ2)Tx2+b2=0, 1 J
являющейся двойственной по отношению к задаче (2.103). Так как(-А£)т =
= -Ay, i,j = 1, 2, то нетрудно видеть, что М = X и задача (2.104)
равносильна задаче (2.88)—(2.89). Таким образом, с учетом сделанных
эквивалентных переходов от задачи (2.98)-(2.99) к задаче (2.103), от (2.104) к (2.88),
(2.89), можем сказать, что задача, двойственная по отношению к
двойственной задаче (2.98)—(2.99), совпадает с исходной задачей (2.88), (2.89), и,
следовательно, задачи (2.88)—(2.89) и (2.98)—(2.99) образуют пару
взаимодвойственных задач.
Оказывается, параллельное изучение взаимодвойственных задач
способствует более глубокому пониманию природы этих задач, оказывается
полезным при разработке методов их решения, обогащает теорию
линейного программирования. Связь между взаимодвойственными задачами
(2.88)—(2.89) и (2.98)—(2.99) отражена в следующих теоремах,
называемых теоремами двойственности.
Теорема 2.8. Задача (2.88), (2.89) имеет решение тогда и только тогда,
когда имеет решение двойственная к ней задача (2.98), (2.99). Иначе говоря,
взаимодвойственные задачи линейного программирования либо обе
одновременно разрешимы, либо ни одна из них: не имеет решения. Если задачи
(2.88)—(2.89) и (2.98)—(2.99) разрешимы, то значения их: экстремумов
совпадают, т.е.
/*=y*. (2.105)
130

Доказательство
Пусть задача (2.88)—(2.89) имеет решение, т.е. X* Ф 0. Возьмем любую
точку х* е X*. Согласно лемме 2.4 тогда существует точка X* е Л, для
которой справедливо равенство (2.97). Таким образом, Л Ф 0, и, кроме того,
/* =f(x*) = \\f(k*)<\\f*. Отсюда и из (2.100) следует /* =f(x*) = \|/(X*) = \|/*,
т.е. X* е Л*. Таким образом, из разрешимости задачи (2.88)—(2.89) следует
разрешимость двойственной к ней задачи (2.98)—(2.99). Так как задача
(2.88)—(2.89), в свою очередь, является двойственной к двойственной
задаче (2.98)—(2.99), то из разрешимости задачи (2.98)—(2.99) следует
разрешимость задачи (2.88), (2.89), причем \|/* = /*. Теорема 2.8 доказана. ■
Теорема 2.9. Взаимодвойственные задачи (2.88)—(2.89) и (2.98)—
(2.99) имеют решение тогда и только тогда, когда существуют точки
х* = (хр, х2*), А* = (XJ, А2) такие у что
х*еХ, ГеЛ, /(*.) = ¥(**). (2.106)
Соотношения (2.106) справедливы для всех точек х* е X*, А* е Л* и только
для них.
Доказательство
Необходимость. Пусть задачи (2.88)—(2.89) и (2.98)—(2.99) разрешимы,
т.е. Х*Ф0, Л* Ф0. Возьмем любые точки х*еХ*, Х*еЛ*. Это означает,
что /(х*) = /*, \|/(А*) = \|Л Но согласно теореме 2.8 тогда /* =\|/*, поэтому
/(x*) = \|/(V). Таким образом, в качестве точек х*Д*, удовлетворяющих
условиям (2.106), можно взять любые точки из множеств X*, Л*.
Достаточность. Пусть для каких-то точек х*=(х1*,х2*Х ^*=(^Д2)
выполняются соотношения (2.106). Это значит, что множества X и Л
непусты и по лемме 2.5 тогда /* >-«>, \|/* <+оо. Отсюда, из теоремы 2.7 и
следствия к ней следует, что задачи (2.88)—(2.89) и (2.98)—(2.99) разрешимы,
т.е. X* Ф 0, Л* Ф 0. Согласно теореме 2.8 тогда /* = \|Л Отсюда и из
соотношений (2.106) имеем /* </(х*) = \|/(Х*)<\|/* =/*. Это значит, что все
неравенства здесь обращаются в равенства, т.е. /(х*) = /*, \|/(Х*) = \|/*, и,
следовательно, х* е X*, А* е Л*. Теорема 2.9 доказана. ■
Замечание 2.2. Условия (2.106) равносильны условиям
х*еХ, ГеЛ, f(x*)<yQC). (2.107)
В самом деле, совмещая неравенство из (2.107) с неравенством (2.102)
при х = х*Д = V, приходим к равенству f(x*) = \|/(Х*).
Теорема 2.10. Взаимодвойственные задачи (2.88)—(2.89) и (2.98)—(2.99)
имеют решение тогда и только тогда, когда существуют точки х* = (х1#, х2*),
А* = (XJ, Х2) такие, что
х, е X, X* е Л, x{*(Afx\\ +AJtX*2 +ct)J =0, j = 1,..., nv
(к\У(bt -Anxt* -А12х2*У =0, i = 1,..., mt.
Соотношения (2.108), называемые условиями дополняющей
нежесткости, справедливы для всех точек х* е X*, X* е Л* и только для них.
Доказательство
Необходимость. Пусть задачи (2.88)—(2.89) и (2.98)—(2.99) имеют
решение. Согласно теореме 2.9 тогда условия (2.106) справедливы при всех
131

х*еХ*, Л*еЛ*. В частности, /(х*)-\|/(А*) = 0. Отсюда и из соотношения
(2.101) заключаем, что при х = х*Д = V все неравенства в (2.101) обращаются
в равенство, что с учетом ограничений (2.89), (2.99) возможно только при
(Л1т1Х;+Л2т1Г2+с1,х1*)= ^(A^+AJ^+qyxi* =0. (2.109)
В силу (2.89), (2.99) каждое слагаемое в сумме (2.109) неотрицательно.
Поэтому из (2.109) следуют первые равенства (2.108). Для доказательства
остальных равенств (2.108) воспользуемся неравенствами
f(x)-y(X) = (c11x1) + (c2lx2) + (bvX1) + (b2,X2)>
>(-А11к1-А21к2ух1) + (-А12к1 -A22k2,x2) + (bvX1) + (b2>X2) =
= (b1-Anx1-A12x2, ^i> + (Ь2 -А21х{ -Л22х2, Х2) >0 Vxе ХДе Л, (2.110)
аналогичными (2.101) и также вытекающими из определений (2.89), (2.99)
множеств X, Л. Из (2.110) при х = х* Д = А* с учетом равенства (2.106) имеем
щ
(Ь1-Апх1*-А12х2*Х1) = 1(Ь1-Апх1*-А12х2*У(Х\У=0. (2.111)
Из неотрицательности каждого слагаемого в сумме (2.111) следует
вторая группа равенств (2.108).
Достаточность. Пусть для каких-то точек х* =(хг,х2*), X* =(Х[УХ2)
выполнены условия (2.108). Тогда для них справедливы равенства (2.109),
(2.111). Отсюда и из (2.89), (2.99) следует, что в (2.110) при х = х*Д = Х*
все неравенства обращаются в равенства и, следовательно, f(x*) = \\f(k*).
Таким образом, точки х*, X* удовлетворяют условиям (2.106). Согласно
теореме 2.9 тогда х* е X*, X* е Л*. Теорема 2.10 доказана. ■
Покажем, что двойственные переменные в задачах линейного
программирования можно истолковать как обобщение понятия множителей
Лагранжа, используемых в классическом анализе при исследовании задач
на условный экстремум (см. параграф 1.4). Введем функцию
L(x, X) = (q, xt) + (с2, х2) + (kv Апх{ + Л12х2 - Ьх) +
+ (Х2,А21х1+А22х2-Ь2) (2.112)
переменных
xeX0={x = (xv х2): xt е Eni, х2 е Eni, xt > 0},
XeA0={X = (XlyX2yi1eEm^X2eEm21X1>0}.
Эта функция называется функцией Лагранжа задачи (2.88)—(2.89),
двойственные переменные X = (кь Х2) называются множителями Лагранжа,
причем Xt > 0 — множители, соответствующие ограничениям типа
неравенств в определении множества (2.89), Х2 — множители, соответствующие
ограничениям типа равенств. Пользуясь тождеством (A^Xj, X,-) = (xj, А^Х{),
функцию (2.112) можно записать в виде
L(xyX) = (-bvX1) + (-b2yX2) + (xvA?1X1+Aj1X2+c1) +
+ (x2,A?2X1+Aj2X2+c2). (2.113)
132

Определение 2.8. Точка (х*Д*)еХ0 хЛ0 называется седловой точкой
функции Лагранжа, если
L(x*,X)<L(x*X)<L(xX) VxeX0, ХеА0. (2.114)
Теорема 2.11. Взаимодвойственные задачи линейного программирования
(2.88), (2.89) и (2.98), (2.99) имеют решение тогда и только тогда, когда
существует пара точек х*=(х1*,х2*)еХ0> X* = (Х*1уХ*2)еА0> образующая
седловую точку (х*Д*) функции Лагранжа. Точка (х*,Х*)еХ0 хЛ0 будет
седловой точкой тогда и только тогда, когда х* е X*, X* е Л*, т.е.
множество седловых точек функции Лагранжа совпадает со множеством X* х Л*.
Справедливы равенства
Цх,Д*) = /,=/(х,) = \|/(Г) = \|/* V(x*,?t*)eX*xA*. (2.115)
Доказательство
Необходимость. Пусть задачи (2.88), (2.89) и (2.98), (2.99) имеют
решение. Возьмем произвольную точку (х*, V), где х* е X*, X* е Л*. Согласно
теоремам 2.8—2.10 тогда
f(x*) = y(X*) = /*=\|Л (x*1A?1X\+Aj1X2+c1) = 01
а также A21xt* + А22х2* = Ъ2, AJ2X\ + AJ2X2 + c2 = 0 по определению множеств X,
Л. С учетом перечисленных равенств из представлений (2.112)—(2.113)
при х = х*, Х = Х* получим равенства (2.115). Кроме того, из (2.113) при
X = X* имеем
L(xy X*) = \\f(X* ) + (xv А^Х\ + AJtX*2 + q) Ух е Х0.
Отсюда и из уже доказанных равенств (2.115) следует, что
L(x,X*)-L(x*1X*) = (x1,A?1X*1+Aj1X2+c1)>0 \/хеХ0.
Правое неравенство (2.114) доказано. Далее, из (2.112) при х = х* имеем
1(х*, X) = f(x*) + (Xt, Дххх* + АХ2х2* -bx) \/ХеА0.
Отсюда и из (2.115) следует левое неравенство (2.114):
1(х*Д*)- 1(х*, X) = (XvЪх -Апх^ -АХ2х2*) > 0 MXe Л0.
Тем самым установлено, что любая точка (х*, X*) е X* х Л* является
седловой точкой функции Лагранжа.
Достаточность. Пусть (х*Д*)еХ*хЛ* — какая-либо седловая точка
функции (2.112). Покажем, что тогда х* еХ*, X* еЛ*, т.е. задачи (2.88)—
(2.89) и (2.98)-(2.99) разрешимы. С учетом представлений (2.112)—(2.113)
функции Лагранжа перепишем неравенства (2.114) в развернутом виде:
f(x*) + (Xi, Апх±* +А12х2* -Ь\) + (Х2уА21х^ +А22х2* -Ь2)<
<L(x,yX")<\\f(X*) + (xvA^1Xl+AJ1X2+c1) + (x2yA^ (2.116)
\/хеХ0,ХеА0.
133

При любом действительном t точка X = (к{ = О, Х2 = £(^21хг + ^22х2* ~ ^))
лежит в множестве Л0. Подставив эту точку в неравенства (2.116), из левого
неравенства имеем
^ЦЛз^+^^з*-^! -Ц**Д* )-/(**) VteR.
Разделим обе части этого неравенства на t, считая t > О, и устремим t —> -н».
Получим \А2iXp + А22х2* - Ь21 < 0, что возможно только при А21х{*+А22х2* = Ъ2.
Далее положим в неравенствах (2.116) \ = (кх = (О,..., О, \\, О,..., 0), Х2 = 0),
считая Х\ > 0. Это даст нам
Ц{Апх^+Апхт-Ь^)1 < ЦдьД* )-/(*.) \/Х\ >0.
Разделив это неравенство на Х\ > 0 и устремив XJ —> +°°, при каждом
г - 1, ..., п{ получим (Апх{* +А12х2*-ЬхУ <0, т.е. Апх{* +А12х2* <Ь{.
Следовательно, х*еХ.
Аналогичными рассуждениями, полагая в неравенствах (2.116) сначала
х = (х{ = 0,х2 = t{A^2X\ + AJ2\*2 + c2)), ^eR,
затем
х = (xt = (0,..., 0, х{, 0,..., 0), х2 = 0), х\ > 0,
устанавливаем, что X* е Л. Таким образом, показано, что всякая седло-
вая точка (х*Д*) функции (2.112) принадлежит X х Л. Наконец, положив
в(2.116)х=(х1 = 0,х2 = 0)Д = (Х1 = 0Д2 = 0),получим/(х*)^ 1(х*Д*)<\|/(Х*).
С другой стороны, для любых точек х* е X Д* е Л справедливо неравенство
(2.102): f(x*)>\\f(k*). Следовательно, /(х*) = \|/(Х*). Это значит, что точки
х*Д* удовлетворяют всем условиям (2.106).
В силу теоремы 2.9 тогда х* е X*, X* е Л*. Тем самым показано, что все сед-
ловые точки функции Лагранжа принадлежат множеству X* х Л*. С другой
стороны, выше было установлено, что каждая точка из X* х Л* является сед-
ловой. Следовательно, множество седловых точек функции Лагранжа задачи
(2.88)—(2.89) совпадает со множеством X* хЛ*. Теорема 2.11 доказана. ■
В следующей теореме вопросы разрешимости и неразрешимости
взаимодвойственных задач обсуждаются в терминах пустоты или непустоты
множеств X, Л. Предварительно отметим, что согласно теореме 2.7 и
следствия к ней неразрешимость задачи (2.88)—(2.89) означает, что либо Х= 0,
либо X Ф 0, но /* = -°о, а для двойственной задачи (2.98)—(2.99)
неразрешимость равносильна тому, что либо Л = 0, либо Л Ф 0, но \|/* = -и».
Теорема 2.12. Справедливы следующие утверждения а—г):
а) взаимодвойственные задачи (2.88), (2.89) и (2.98), (2.99) разрешимы
тогда и только тогда, когда множества X и Л непусты одновременно',
б) в задаче (2.88)—(2.89) X Ф 0, /* >-оо тогда и только тогда, когда
в задаче (2.98)-(2.99) Л Ф 0, у* < +<*>;
в) если в задаче (2.88)—(2.89) Хф 0, /* =-«>, то в двойственной задаче
(2.98)—(2.99) Л = 0; обратно', если Л Ф 0, \|/* = -и», то X = 0;
г) если в задаче (2.88)-(2.89) X Ф 0, а в задаче (2.98)-(2.99) А = 0,то
/* = -°о; обратно: если X = 0, Л Ф 0, то \|/* = -и».
134

Доказательство
а) Если задачи (2.88)—(2.89) и (2.98)—(2.99) разрешимы, то, конечно,
X Ф 0, Л Ф 0. Обратно, если X Ф 0, Л Ф 0, то из леммы 2.5 следует, что
/* >-<», \|/* <+оо, и разрешимость задач (2.88)—(2.89) и (2.98)—(2.99)
вытекает из теоремы 2.7 и следствия к ней.
б) Пусть в задаче (2.88)—(2.89) Хф0,/*> -оо. Тогда согласно теореме 2.7
задача (2.88)—(2.89) разрешима, а по теореме 2.8 разрешима и
двойственная задача (2.98)—(2.99), т. е. Л Ф 0, \|/* < +оо. Обратно: из Л * 0, \|/* < -н»
следует разрешимость задачи (2.98)—(2.99), поэтому разрешима и
двойственная к ней задача (2.88)—(2.89), так что Хф0у /* > -оо.
в) Это утверждение легко доказывается рассуждениями от противного.
Пусть Хф0> /* = -оо, но Л Ф 0. Согласно утверждению б) тогда обе задачи
(2.88)—(2.89) и (2.98)—(2.99) имеют решение и /* >-«>, что противоречит
условию. Аналогично доказывается, что если Л Ф 0, \|/* = -н», то X = 0.
г) Пусть X * 0, Л = 0, но /* > -оо. Тогда в силу утверждения б) Л Ф 0,
\|/* < +оо, что противоречит условию Л = 0. Аналогично убеждаемся, что
если X = 0, Л * 0, то \|/* = -и». Теорема 2.12 доказана. ■
Следующий пример показывает, что возможен случай, когда во
взаимодвойственных задачах (2.88)—(2.89) и (2.98)—(2.99) оба множества X
и Л пусты.
Пример 2.10
Пусть исходная задача имеет вид
f(x) = xx-2x2-+mm, хеХ = {х = (х\х2)>0:х*-х2 = 1, хх-х2 = 2).
Тогда двойственная задача будет выглядеть так:
\|/(Х) = -Х1-2Х2^тах, ХбЛ = {Х = (Х1Д2):Х1+Х2>-1| Хх+Х2<-2}.
Ясно, что X = 0, Л = 0.
Приведенные выше теоремы двойственности часто позволяют
получить содержательную информацию о рассматриваемой задаче линейного
программирования, иногда на этом пути удается провести полное
исследование задачи и даже получить ее решение. Для иллюстрации рассмотрим
задачу линейного программирования, не содержащую ограничения типа
неравенств.
Рассмотрим задачу
f(x) = (с, х) —> min, х е X = {х е Еп: Ах = Ь},
где А — матрица размера т xn.ee Еп,Ье Е™. Эта задача является частным случаем
задачи (2.88)—(2.89), когда пх = 0,п2= п, тх = 0,т2= т, Л22 = А,Ь2= Ь, матрицы Лп,
АХ2,А2Х,Ъ\ отсутствуют. Двойственной к ней является задача
\\f(X) = -(b, X>->max, ХеА = {ХеЕт:АТХ + с = 0}.
Если Хф 0, /* > -оо, то согласно теореме 2.12 Л Ф 0, \|/* < -и» и, следовательно,
вектор с представим в виде с = -АТХ0, где Х0 е А. Но тогда
135

f(x) = (с, x) = -{ЛТХ0} х) = -(X0, Ax) = -(X0, b) = const
при всех х е X, так что X* = X. Аналогично если х0е X, то b = Ax0 и
\\f(X) = -{b, X) = -(Ах0, X) = -(х0, АТХ) = (х0, с) = const Vk e Л,
так что \|/* = (х0, с) = /*, Л* = Л. Как видим, задачи линейного программирования без
ограничений типа неравенств малосодержательны и большого интереса не
представляют.
В заключение докажем еще одну теорему, известную в литературе под
названием теоремы Фаркаша. Эта теорема имеет важные приложения
в выпуклом анализе, теории экстремальных задач и может быть легко
доказана на основе приведенных выше теорем двойственности.
Теорема 2.13. Пусть множества X, Л определены согласно
формулам (2.89), (2.99), X Ф 0, пусть а — заданное число. Тогда для того чтобы
неравенство f(x) = (cvx1) + (c2>x2)>a было справедливо для всех х = (х1у
х2) е Ху необходимо и достаточно, чтобы А Ф 0 и существовала точка
X* = (k*v Х2)е Л такая, что \|/(Х*) = -(bv XJ) -(b2> X^) > а.
Доказательство
Необходимость. Пусть X Ф 0 и f(x) > а при всех х е X. Тогда ясно, что
/* = inf f(x)>а>-оо, и в силу теоремы 2.7 задача (2.88)—(2.89) имеет реше-
хеХ
ние. Согласно теореме 2.8 двойственная задача (2.98)—(2.99) также будет
разрешима, т.е. Л Ф 0 и найдется точка X* е Л, для которой
\|/(Х*) = sup\|/(X) = \|/* = /* > а.
Достаточность.ПустьХ*0,Л*0иточкаХ* е Л такова, что \|/(Х*) >я.Тогда
с помощью неравенства (2.102) при Х = Х* имеем /(х)>\|/(Х*)>я при всех
х е X. Теорема 2.13 доказана. ■
В приложениях часто используется следующий частный вариант
теоремы Фаркаша.
Теорема 2.14. Пусть А1у А2 — матрицы размера mt x и, т2х п, вектор
с е Еп. Тогда для того чтобы для всех х таких, что Atx < 0, А2х = 0, было
справедливо неравенство (с, х) > 0, необходимо и достаточно, чтобы
существовала точка X* = (XJ, Х^), XJ е Emi, X[ > ОД2 е Ет2, такая, что
c = -Aj'k\-Ajr2. (2.117)
Доказательство
Положим
Х={хе Еп:А1х<0,А2х = 0};
A = {X = (XvX2):X1eEm^X2eEm2yA^X1+AJX2+c = 0}.
Эти множества являются частными случаями множеств X, Л из (2.89),
(2.99) при Ап = 0, А12 = Ах, А21 = 0, А22 = А2, Ъх - 0, Ъ2 = 0, сх = 0, с2 = с.
Здесь X Ф 0, так как 0 е X. Отсюда и из теоремы 2.13 при а = 0
следует утверждение теоремы 2.14, причем в качестве искомой точки
136

X* = (X\, X*2) можно взять любую точку X* е Л. Попутно отметим, что здесь
\\f(k) = О = \|/* =/* = /(0)</(х) при всех х е Ху X е Л, Л* =Л, а равенство
(2.117) вытекает из принадлежности точки X* множеству Л. Теорема 2.14
доказана. ■
Упражнения
2.1. Задачу
f(x) = х1 + х2 + х4 —> min, х е X,
Х={х=(х\х2,х3,х*): х1>0ух3>0ух^<1ух1 + х2<1ух1 + х3>1}
запишите в виде канонической задачи.
2.2. При каких значениях параметра а задача
f(x) = х1 + ах2 —> min, iel,
X={x=(x\x2):x>0,xi-x2>l,xi + 2x2>4}
имеет решение? Не имеет решения? Имеет единственное решение?
Результат изобразите графически.
2.3. Для данных множеств найдите все угловые точки и их базисы:
а) X = {х = (х1, х2, х3, х4, х5) : х > О, А{х{ + А^х:2 + Л3х3 + ААх^ + Л5х5 = Ь), где
( \\ (\\ (\\ (\\ (Q\ л (\\
А =
к-h
;ДН
; До -
V1/
> Ai —
v°y
;4 =
v1.
;*>=
V1/
б) Х= {хе Еп\х> О, х1 + х2 + ... + хп = 1} (симплекс).
2.4. Пусть X = {xeEn:(ai,x)<bi, z = l,...,m}, где а{ — заданные векторы
из Еп\ Ы — заданные числа, i = 1,..., т. Докажите, что точка v е X является
угловой точкой множества X тогда и только тогда, когда обращаются в
точные равенства не менее чем п из неравенств (aiyv)<biy среди которых есть
п линейно независимых. Докажите, что при т < п это множество не имеет
угловых точек.
2.5. Рассмотрите задачу
/(х) = -х1 + 6х2 + х3 + 2Х4 + х5 —>extr,хе X,
где X — множество из пункта а) упражнения 2.3. Перебором угловых
точек множества X найдите максимальное и минимальное значения целевой
функции. Примените к этой задаче симплекс-метод, беря в качестве
начальной различные угловые точки множества X.
2.6. Рассмотрите задачу
/(х) = х1 + 4х2 + х5 —>extr,хе X,
Х={х=(х1,х2,х3,х4,х5)>0:х1 + х2 + х3 + х4 + 2х5=2,х1-х3 + 2х4 + х5=1}.
Найдите решение этой задачи двумя способами: перебором угловых
точек и симплекс-методом.
137

2.7. С помощью симплекс-метода решите задачи:
а) /(х) = х1 + х2 + х3 + х4 —> min, ie X, X = {х = (х1, х2, х3, х4) > 0 :
2х1 + х2-хЗ + х4=3,-2х1 + х2 + х3-х4 = -1};
б) /(х) = х1 - х2 + х3 - х4 —> min, х е X, X = {х = (х1, х2, х3, х4) > 0 :
х1 + х2 + х3 + х4= 1};
в) Ах) =х{ + 2х3 + х5 —> min, х е X,
[ х1+х2+х3+х4 +х5 =5,
X = j х = (х1, х2,х3, х4, х5)> 0: х2 +х3 + х4 -х5 = 2,
I х3 - х4 + х5 = 1
г) /С*) = Зх1 + 4х2 + Зх3 - х4 - 2х5 - х6 —> min, x e X,
[ 2Х1 + Зх2 + 4х3 - х4 - 2х5 - Зх6 = 24,]
Х_ J у. — / у\ у2 уЗ уА у-5\ > О* -v-1 _i_ *)у-2 _ ^-3 _ ^-4 _ *)у-5 _|_ ^-6 — О
I уО у\) — Q
I Л> Л> — \J
Д) Ах) = х1 - х2 + х3 + х5 —> min, х g X,
|д;1 _|_ х2 — X3 — X4 + Х^ = 1, 1
* = (*1.*2.*3'*4'*5)^ft_xi+23C2+JC3_2x4_x5a;2j;
е) /(х) = х1 + 2х2 - х3 - х4 - х5 —> max, x e X,
х1+х2+3х3+4х4=12,1
X = ^ х = (х1, х2, х3, х4, х5) > 0:
х1-х2+х3-х4 <2
(предварительно приведите эту задачу к каноническому виду);
ж)/(х) = х1 + х2 + х3 + х4 —> max, х е X, X = {х = (х1, х2, х3, х4) > 0
х1 + х2 + Зх3 + 4Х4 = 12, х1 - х2 + х3 - х4 = 2};
з) /(х) = х1 + Зх2 + 2х3 + 4Х4 - 2х5 -> min, x e X,
Х =
-х1+х3-2х4=-2,
х = (х1,х2,х3,х4,х5)>0: х2-х3+х4-2х5 =0,
2х1+х2+5х4+х5=7
(возьмите в качестве стартовой угловой точки х0= (3, 1, 1, 0, 0)).
2.8. Проверьте, что в задаче
/(х) =х3-х4 + х5 + х6—>max,xe X,
где
Х =
о
tfJ +
'0Л
v°y
х2 +
у — /у 1 -уz уо <v*4 ^5 yb yl Л > Q
*Л/ у*Л/ у JX/ • *Л/ у %Л/ у %Л/ у %Л/ у *Л/ ш ^— ^*У
4 4-1 -2
4
v1.
'-2Л
х3 +
-3
v1;
х4 +
П;
х5 +
1
V1,
х6 +
'0\
0
V1,
х7 =
V
vb
симплекс-метод может привести к зацикливанию: при выборе в качестве
стартовой угловой точки v0= (1, 1, 0, 0, 0, 0, 1), можно получить
циклическую последовательность угловых точек с базисами (А1у А2, А7), (Л3, А2,
138

Л7), (Л3, А1у Л7), (Л5, Аь Л7), (Л5, Л6, Л7), (Аь Л3, Л7), (Л1? Л2, Л7). Решите эту
задачу с помощью антициклина.
2.9. Найдите начальную угловую точку методом искусственного базиса,
после чего с помощью симплекс-метода решите задачи
a) /(х) = 2х* + х2 - х3 + Зх4 - 2х5 —> min, x e X,
х = (х1, х2, х3, х4, х5) > О,
(3\ (9) (9Л
Х =
5
V1,
x4 +
'2Л
1
V1/
х2 +
ч°,
х3 +
v3y
х4 +
v°y
X5 =
'30^
19
v3y
б) /(*) = х1 - х2 + 2х3 + Зх4 - х5 -» min, л: € X,
х = (х1, х2, х3, л:4, х5) > 0,
Х = \
1
Xi +
m
-i
x2 +
Г1л
о
v1.
x3 +
m
-i
л:4 +
Г1Л
0
X5 =
' 1 ^
2

Глава 3
ЭЛЕМЕНТЫ ВЫПУКЛОГО АНАЛИЗА
В этой главе изучаются свойства выпуклых, строго выпуклых и сильно
выпуклых функций. Выпуклый анализ играет фундаментальную роль
в теории и методах оптимизации.
3.1. Выпуклые функции
3.1.1. Понятие выпуклой функции
Напомним определение выпуклого множества.
Определение 3.1. Множество X из пространства Еп называется
выпуклым, если для любых и, v е Xточкаха= аи + (1 - a)v принадлежит
множеству X при всех ае [0; 1].
Иными словами, множество X выпукло, если оно вместе с любыми
двумя точками и, v, ему принадлежащими, целиком содержит отрезок, их
соединяющий. Так, например, на рис. 3.1 множество Xt выпукло, а
множество Х2 невыпукло.
Рис. 3.1
Ясно, что все пространство Еп образует выпуклое множество. Пустое
множество и множество, состоящее из одной точки, также будем считать
выпуклыми. Тогда из определения 3.1 непосредственно следует, что
пересечение любого числа выпуклых множеств является выпуклым
множеством.
Примерами простейших выпуклых множеств являются шар,
гиперплоскость, полупространство. Также являются выпуклыми многогранные
множества, рассмотренные в гл. 2:
X = {xeEn:x>0,Ax = (<)b}y Х = {хеЕп :Ax = byAx<b}.
Определение 3.2. Функция /(г), определенная на выпуклом множестве
X с Епу называется выпуклой на этом множестве, если
140

f(au + (1 - a)v) < af(u) + (1 - a)f(v)
(3.1)
при всех UjVS X,ae [0; 1]. Если в формуле (3.1) при и Ф v равенство будет
только при ос = 0иос=1,то функция/(х) называется строго выпуклой на X.
Определение 3.3. Функцию/(х) называют вогнутой {строго вогнутой)
на выпуклом множестве X, если функция {-fix)) выпукла (строго выпукла)
наХ
Из этих определений непосредственно вытекает, что если Хх с Х2
и функция f(x) выпукла (строго выпукла) на Х2, то она будет выпуклой
(строго выпуклой) на Xt; если/(х) вогнута (строго вогнута) на Х2, то она
будет вогнутой (строго вогнутой) на Xt.
Иногда в литературе выпуклые функции называют выпуклыми вниз,
а вогнутые — выпуклыми вверх. Геометрическим смыслом выпуклости
(вогнутости) является тот факт, что хорда, соединяющая две точки
графика функции, лежит не ниже (не выше) его. Для строго выпуклой (строго
вогнутой) функции эта хорда (за исключением концов) будет лежать строго
выше (строго ниже) графика. Пользуясь методом математической
индукции, нетрудно показать, что для любой выпуклой функции f(x) на
выпуклом множестве X имеет место неравенство Йенсена
( т \ т
/ ХаЛ. <Хаг./(*;) Vm = l,2,...,
Kiml J i-1
m
Vx{ e X,a{ > 0, i = 1,..., m, £аг- = 1.
(3.2)
Отметим, что одна и та же функция на каких-то одних множествах
может быть выпуклой, а на каких-то других — нет. Если множество X пусто
или состоит из одной точки, то любую функцию на таком множестве нам
будет удобно считать выпуклой (или вогнутой) по определению.
Подчеркнем также, что всюду, если не оговорено противное, мы будем
рассматривать лишь функции, принимающие конечные значения во всех точках
области определения.
Примерами выпуклой функции на всем пространстве Еп служат
линейная функция f(x) = (с, х) и норма/(х) = ||х||. Отметим, что линейная
функция f(x) = (CyX) одновременно является и вогнутой на Еп. На рис. 3.2,
3.4—3.7, 3.11, 3.12 приведены примеры различных выпуклых на указанных
множествах X функций одной переменной, на рис. 3.3,3.8—3.10 — вогнутых.
у = 2-х2
Рис. 3.2
Рис.33
141

X = F
y = ex
Рис. 3.4
y = \x - 1| + \x+ 11— 3
X=E]
Рис. 35
2-#,л;<2
1,* = 2
^=[-2,3]
Рис. 3.7
У =
-1-л;,л;<0
-1,0<*<3
tx = 3
-j—►
Рис. 3.8
Х=[0,п]
y = smx
Рис. 3.9
i = 4x
y = smx
X=[0,W)
X=[-n,0]
Рис. 3.10
Рис. 3.11

t
Х=[0,-н»)
у = -In x
iV^^
Рис. 3.12
3.1.2. Критерии выпуклости
Даже для несложной функции одной переменной f(x)=ex исследование
выпуклости с помощью определения является не очень-то простой
задачей, поэтому необходимо иметь более удобные способы проведения такого
исследования. Сформулируем и докажем критерии выпуклости
дифференцируемой функции.
Теорема 3.1 (критерии выпуклости первого порядка). Пусть X —
выпуклое множество из пространства En,f(x) e С1(Х). Функция f(x)
является выпуклой на множестве X тогда и только тогда, когда справедливо
неравенство
f(u)>f(v) + (f'(v),u-v) \/u,veX (3.3)
или неравенство
(f'(u)-f'(v),u-v)Z0 \/u,veX. (3.4)
Доказательство
Сначала покажем, что из выпуклости/(х) на множестве X следует
неравенство (3.3). Возьмем произвольные u,ve Хи некоторое ае (0; 1]. Тогда
по определению выпуклости
f(au + (1 - a)v) < af(u) + (1 - a)f(v) ^ a(f(u) -f(v)) >f(au + (1 - a)v) -f(v).
Применяя формулу конечных приращений (1.113), получаем
f(au + (1 - a)v) -f(v) = (f'(v + Qa(u - v)), a(u - v)),
и приходим к соотношению
а(/(м) -f(v)) > <f'(v + Qa(u - v)), a(u - v)) V а е (0; 1].
Поделим его на а > 0 и перейдем к пределу при а —> 0 + 0. Тогда
в силу непрерывности/'^) на множестве X и того, что 0 е [0; 1], имеем
f'(v + Qa(u - v)) —> f'(v), и потому
f(u)-f(v)Z(f'(p)9u-v) Mu,veX.
Теперь покажем, что из неравенства (3.3) вытекает неравенство (3.4).
Для произвольных u, v e Хв силу (3.3) выполнены неравенства
/(и) > № + {f'{v), u - v); f(v) >f(u) + (/'(«), v-u).
143

Складывая их, находим
f(u) + f(v)>f(u) + f(v) + (f'(v),u-v) + (f'(u),v-u)^
<^(f/(u)-f/(v)1u-v)>0 \/u,veX.
Наконец, докажем, что из неравенства (3.4) следует выпуклость
функции/(х) на множестве X. Рассмотрим произвольные w, v е X, а е [0; 1]
и обозначим w = ом + (1 - a)v. Отметим, что тогда и - w = (1 - а)(и - v)>
v-w- a(v - и). Нам надо проверить выполнение неравенства af(u) + (1 -
- Oi)f(v) - f(w) > 0. Пользуясь формулой конечных приращений (1.113),
запишем цепь равенств:
а/(гО + (1-а)/(г0-/(^
1 1
= а J (f'(w + t(u - w), u^w )dt + (1 - a)\ (f'(w + t(v - w)), г^хю )dt =
0 (l-a)(u-v) 0 a(v-u)
1 1
= a(l-a)j(fXw + t(l-a)(u-v))1u-v)dt + a(l-a)j(f\w + ta(v-u))1v-u)dt =
о о
l
= cc(l - a)J (f'(w + £(1 - a)(u -v))- f\w + ta(v -u)),u- v)dt Vm, veX,\/ae [0; 1].
о
Обозначим w + t(l - a)(u - v) = p e X,w + ta(v - u) = q e X. Заметим,
что тогда;? - q = t(u-v) и потому в силу неравенства (3.4)
1
j(f'(w + t(l-a)(u-v))-f'(w + ta(v-u))1u-v)dt =
о
= ]kf'(p)-f'(q),(p-<l))dt>0.
о1
Но тогда, с учетом того что ос(1 - а) > 0 при всех а е [0; 1], имеем
а/00 + (1" сО/(0) -/(») > 0 V и, v e X, Va е [0; 1],
что и требовалось доказать. ■
Внимательно проанализировав доказательство этой теоремы, мы
получаем следующее следствие.
Следствие 3.1. Если X — выпуклое множество из пространства Еп,
f(x) е СХ(Х), то из справедливости утверждения f(u)>f(v) + {f'(v),u-v)
V w, v e X,u*v, или утверждения (f'(u)-f'(p),u-v)>0 V и, v e X,u*v,
вытекает строгая выпуклость функции f(x) на множестве X.
Эквивалентность выпуклости неравенству (3.3) в литературе обычно
называют теоремой о касательной плоскости. Ее геометрический смысл
очень прост: график гладкой выпуклой на множестве X функции лежит
не ниже касательной, проведенной к нему в произвольной точке
множества X. Неравенство (3.4) для функции одной переменной также имеет
очевидную интерпретацию и фактически представляет собой условие
неубывания производной f'(x). Для функции многих переменных говорить
о неубывании уже не приходится, но все равно, по инерции,
эквивалентность выпуклости неравенству (3.4) зачастую называют теоремой о
монотонности градиента.
144

Для того чтобы доказать критерии выпуклости, использующие вторую
производную, нам понадобится одно важное свойство выпуклых множеств.
Лемма 3.1. Пусть X — выпуклое множество, intX Ф 0, и0 е intX, v е ГрХ
Тогда для всех ос е (0; 1] точка va=v + а(щ-v)e intX
Доказательство
Так как и0 е intX, то некоторая ее 8-окрестность 0(щ, 8) = {и: \ и - щ\ <
< 8} целиком принадлежит X. Возьмем произвольное ос е(0; 1] и
покажем, что окрестность 0(vw ос8) = {и : | и - va \ < ос8} точки va
принадлежит X. Для этого возьмем произвольную точку и е 0(vw a8) и положим
1
w = u0+—(u-va) (рис. 3.13).
Рис. 3.13
1 1
Поскольку |и>-Ио| = —||м-0„|<— 8а = 8, то w е 0(щ> 8) сХ Из опреде-
м и ан и а
ления точки w имеем представление
и = va+a(w -u0) = v + a(u0-v) + a(w - u0) = aw + (l- a)v,
где v,w e Хи0<а<1. Тогда и е X в силу выпуклости X Тем самым
показано, что произвольная точка и из 0(vw oc8) принадлежит X
Следовательно, va — внутренняя точка множества X. ■
Теорема 3.2 (критерии выпуклости второго порядка). Пусть X —
выпуклое множество из пространства Еп, intX Ф 0, f(x) e С2(Х). Функция
f(x) является выпуклой на множестве X тогда и только тогда, когда
справедливо утверждение
</"(*)А,А>>0 VxeX, \/heEn. (3.5)
Доказательство
Достаточность. Возьмем произвольные и, v e X, тогда по формуле
конечных приращений (1.115)
{fXu)-fXv\u-v) = {f\v + Q(u-v))(u-v\u-vl 0e[O;1].
Так как v + Q(u - v) e X из-за выпуклости X, a h = и - v е £п, то в силу
формулы (3.5)
(f"(v + Q(u - v))(u -v),u-v)> 0,
следовательно, и (f'(u)-f'(v),u-v)>0. По теореме 3.1 из этого
неравенства вытекает выпуклость f(x) на X
145

Необходимость. Пусть/(х) выпукла на X, тогда по теореме 3.1 верно
неравенство (3.4). Рассмотрим сначала внутреннюю точку х g intX. Взяв
произвольное h g En, мы можем утверждать, что для всех достаточно малых
е > 0 точка х + eh лежит в множестве X Поэтому
(f'(x + eh) - f'(x), x + eh-x)>0.
Но по формуле конечных приращений (1.115)
(f'(x + eh) - f'(x), x + eh-x) = {f"(x + 0ех)е/г, е/г),
стало быть, (/"(.г + 0е/г)е/г, е/г)>0. Сокращая левую и правую части этого
неравенства на е2 > 0 и переходя к пределу при е —> 0 + 0, с учетом
непрерывности f"(x) на X имеем {f"(x)h, h)>0 Мхе intX, V h е En, т.е.
выполнено (3.5).
Теперь рассмотрим граничную точку х множества X. Возьмем любую
1
точку v g intX и построим последовательность точек xk = x+—(v-x).
k
По лемме 3.1 точки xkl k = 1, 2,..., будут внутренними точками множества X,
и при этом \xk - х\ —> 0. Тогда, как мы уже доказали, для любого he En
выполнено {f"(xk)h,h)>0. Переходя в этом неравенстве к пределу при к —> °°,
с учетом непрерывности f\x) получаем (f"(x)h, h) > 0 V h e Еп.Ш
Из приведенного доказательства теоремы 3.2 и следствия к теореме 3.1
вытекает следующее следствие.
Следствие 3.2. Если X — выпуклое множество из пространства Еп,
f(x) е С2(Х)У то из справедливости утверждения (f"(x)h,h)>0 V х е X,
V h е Епукф0 вытекает строгая выпуклость функции f(x) на множестве X.
Отметим, что условие intX Ф 0 в теореме 3.2 не может быть ослаблено.
Для этого рассмотрим такой пример. Пусть X = {и = (х, у) е Е2 : у = 0},
f(u) =x2- у2. Ясно, что множество X представляет из себя прямую на
координатной плоскости и не имеет внутренних точек. С помощью определения
нетрудно убедиться, что f(x) является выпуклой и даже строго выпуклой
функцией на X, но для всех х из X выполнено
</-<***>-((о ЖНЗН-2*
что меньше нуля, если взять hx = 0, h2 = 1.
3.1.3. Свойства точек минимума выпуклых функций
Теперь перейдем к изучению задач минимизации выпуклых функций
на выпуклых множествах. Такие задачи будем кратко называть выпуклыми
задачами. Начнем с обоснования того факта, что выпуклая функция
многих переменных не может иметь на выпуклом множестве точек локального
минимума, отличных от точек глобального минимума.
Теорема 3.3. Пусть X — непустое выпуклое множество из
пространства Еп, функция f(x) определена и выпукла на X. Тогда любая точка
локального минимума f(x) на множестве X является ее точкой глобального
минимума, а множество
146

X. = {xeX:f(x) = f. = mff(x)}
xeX
выпукло.
Если, кроме того, функция /(х) является строго выпуклой на X, то
множество X* состоит не более чем из одного элемента.
Доказательство
Предположим, что х* является точкой локального минимума функции
f{x) на множестве X. Это означает, что существует такое е0 > 0, что для всех
точек множества X, удовлетворяющих неравенству |х-х*|<е0,
справедливо /(х)>/(х*)«
Рассмотрим произвольную точку х множества X и положим ха = ах +
+(1 - ос)х*. Ясно, что при 0 < а < min \ Т,—-—й , 1 \ точка ха в силу выпуклости
[||х-х*|| J
множества X тоже в нем содержится и, кроме того, /(ха) > /(х*), поскольку
|ха -х*|<е0. Пользуясь определением выпуклости функции/(х), имеем
/(ха)<а/(х) + (1-а)/(х*)^а(/(х)-/(х*))>/(ха)-/(х*).
Поскольку правая часть последнего неравенства неотрицательна, а а > О,
мы получаем /(х) > /(х*) для любого х g X, что и означает, что х* — точка
глобального минимума функции /(х) на множестве X, /(х*) = /*.
Далее возможно два случая. Если множество X* пусто или состоит
из одной точки, то оно выпукло. Если же это не так, то рассмотрим две
произвольных точки хь х2 множества X* с X. Для произвольного ос g [0; 1]
точка х = осх! + (1 - ос)х2 лежит в множестве X в силу его выпуклости, и,
кроме того,
/(аг1+(1-а)х2)<а/(х1) + (1-а)/(х2) = а/*+(1-а)/*=/*,
поэтому /(ах1+(1-а)х2) = /*, что означает xgX*. Выпуклость
множества X* доказана.
Наконец, если функция /(х) является строго выпуклой на X, поступим
аналогично. Пусть xvx2 g X* с X, xt Ф х2. Тогда для всех ае (0; 1) точка
х = OCX! + (1 - ос)х2 лежит в множестве X в силу его выпуклости, но
/(аг1+(1-а)х2)<а/(х1) + (1-а)/(х2) = а/*+(1-а)/*=/*,
что невозможно. Значит, множество X* содержит не более одного элемента.
Теорема доказана. ■
Заметим, что даже строгая выпуклость функции /(х) не гарантирует
непустоту множества X*, что можно подтвердить элементарным
примером. Положим X = Е1, f(x) = ех (см. рис. 3.4). Поскольку при всех х из Е1
fix) = ех>0, то f(x) по следствию 3.1 из теоремы 3.1 строго выпукла на Е1.
Ясно, что /* = 0, но fix) > 0 при всех х g E1, поэтому X* = 0.
В завершение этого параграфа сформулируем и докажем необходимые
и достаточные условия минимума выпуклой функции.
Теорема 3.4 (критерий оптимальности для выпуклых задач). Пусть
X — выпуклое множество из пространства Еп, функция fix) выпукла и
непрерывно дифференцируема на X. Тогда если множество X* = {х е X: fix) = f* =
147

= inf f(x)} непусто, то х* е X* тогда и только тогда, когда справедливо
хеХ
неравенство
(f'(x*),x-x*)>0 \/хеХ.
(3.6)
Кроме того, если х* е intX, то х* е X* тогда и только тогда, когда
Доказательство
Тот факт, что из х* е X* вытекает неравенство (3.6), доказан в теореме 1.7;
случай х* е intX разобран там же. С другой стороны, если функция f(x)
является выпуклой и непрерывно дифференцируемой на множестве X,
a (f'(x*), х-х*) > О V х е X, или /'(#*) = 0, то, применяя теорему 3.1,
получим
f(x)-f(x*)>(f'(x*),x-x*)>0 УхеХ.
Значит, при всех х из X f(x) > f(x*), x* e X*. Теорема доказана. ■
Итак, мы получили, что выпуклые функции обладают несколькими
полезными с точки зрения минимизации свойствами. Во-первых, для них
не существует проблемы локальности минимума, и, во-вторых, достаточное
условие минимума не требует вычисления второй производной. Более того,
при изучении в следующих главах вопросов сходимости итерационных
методов минимизации станет ясно, что выпуклость функции f(x) является одним
из главных свойств, обеспечивающих эту сходимость. Для невыпуклых
функций задача поиска точек минимума гораздо сложнее, чем для
выпуклых. Докажем еще несколько арифметических свойств выпуклых функций,
полезных для исследования выпуклости и обоснования некоторых фактов.
3.1.4. Другие свойства выпуклых функций
Понятия выпуклой функции и выпуклого множества неразделимо
связаны друг с другом. В частности, с помощью выпуклых функций можно
описывать выпуклые множества, что вытекает из того, что надграфик любой
выпуклой функции является выпуклым множеством. Дадим
соответствующее определение и докажем этот несложный геометрический факт:
Определение 3.4. Надграфиком (или эпиграфом) функции/(х),
определенной на множестве X с Еп, называется множество (рис. 3.14)
epi/ = {{и, v) e En+1 :ueX,v> f(x)}.
epi/
У=/(х)
a | b
Рис. 3.14
148

Теорема 3.5. Для того чтобы функция /(г), определенная на выпуклом
множестве X, была выпуклой на нем, необходимо и достаточно, чтобы ее
надграфик был выпуклым множеством.
Доказательство
Необходимость. Пусть функция f(x) выпукла на выпуклом множестве X.
Возьмем две произвольные точки wt = (щ, vt), w2 = (и2, v2) e epi/ и
составим их выпуклую комбинацию wa = awx + (1 - a)w2 = (olu1 + (1 - a)u2,
avx + (1 - a)v2), 0 < a < 1. Из выпуклости множества X вытекает, что иа =
= ащ + (1 - а)и2 е X. С другой стороны, из выпуклости функции /(г) следует,
что f(ua) < af(u{) + (1 - a)f(u2) ^ av{ + (1 - oc)i;2. Таким образом, wae epi/
при всех a e [0; 1]. Выпуклость epi/доказана.
Достаточность. Пусть epi/ — выпуклое множество. Возьмем
произвольные щ, и2е Xи a e [0; 1]. Тогда wx = (ux,f(ux)), w2- (u2,f(u2)) g epi/.
В силу выпуклости epi/ точка wa = awt + (1 - a)w2 = (aut + (1 - a)u2,
af(ui) + (1 ~ a)f(u2)) тоже лежит в epi/. Но тогда по определению надгра-
фикаДаг^! + (1 - а)и2) < а/(щ) + (1 - ос)/(гг2)- Выпуклость/(х) доказана. ■
Теперь покажем, что любое множество Лебега выпуклой функции
является выпуклым.
Теорема 3.6. Пусть X — выпуклое множество, а функция f(x) выпукла
на X. Тогда множество М(с) = {хеХ: f(x) < с} выпукло при любом с.
Доказательство
Сначала заметим, что множество М(с) может оказаться пустым или
состоять из одной точки. Тогда оно выпукло по определению. Если же
оно состоит более чем из одной точки, то, рассматривая произвольные и,
v е М(с), а е [0; 1] и пользуясь выпуклостью множествах и функции/(х),
имеем
аи + (1 - a)v е X, f(au + (1 - a)v) < af(u) + (1 - a)f(v) < ас + (1 - a)c = с,
т.е. аи + (1 - a)v e M(c), поэтому М(с) выпукло. ■
Следствие 3.3. Пусть Х0 — выпуклое множество, функции g^x), i =
= 1,..., т, выпуклы на Х0, функции gj(x), i = m + 1, ..., т + s, заданы
формулами gj(x) = (aiyx) - b{, где а{ — заданные векторы из Еп, Ъ{ — заданные числа.
Тогда выпукло множество
Х = {хеХ0 :gi(x)<0,i = l,...,m; gj(x) = 0, i = m + l,...,m + s}.
Доказательство
В силу теоремы 3.6 множества Х{ ={хеХ0:gj(x) < 0} выпуклы при всех
г = 1, ..., т. Множества Y{ ={хеХ0 \{а{,х)-Ъ{ =0}, г = т + 1, ..., т + s, также
выпуклы, что можно установить с помощью определения или получить
из теоремы 3.6, заметив, что Y{= V{ n W{, где Vi={xeX0:(ai,x)-bi<0},
Wi={xeX^\ b{ - {a{, x) < 0}. Линейные функции (at, и) - Ъ{ и Ъ{ - (а{, и)
выпуклы, стало быть, V{ и W{ выпуклы, но тогда выпуклы и Y{, г = т + 1,..., m + s.
Значит, множество X тоже будет выпуклым, так как оно является
пересечением выпуклых множеств Хь ..., Хт, Ym+1,..., Ym+S. ■
Заметим, что обратное к теореме 3.6 утверждение неверно: из
выпуклости множества Лебега М(с) при любом с не следует выпуклость функции
149

f{x). Например, множество М(с) = {хе [0; + °°): у/х < с} выпукло при любом
с (при с < 0 оно пусто, при с > 0 оно представляет из себя отрезок [0; с2]),
но функция f(x) = у/х не выпукла (и даже строго вогнута) как на [0; +°°),
так и на любом выпуклом множестве, содержащемся в [0; +«>).
Теперь обсудим простейшие арифметические свойства выпуклых
функций.
Теорема 3.7. Если функции f(x)y г = 1,..., т, выпуклы на выпуклом
множестве X, то функция f(x) = а^^х)+ ... + a^J^x) выпукла на этом множестве
при любых а{> 0, г = 1,..., т.
Доказательство
Рассмотрим произвольные и, v е X и некоторое а е [0; 1]. Тогда в силу
выпуклости функций fix)
fiau + (1 - a)v) = atfiau + (1 - a)v) +... + amfmiau + (1 - a)v) <
<a1iaf1iu) + il-a)fiv)) + ... + amiafmiu) + il-a)fm^
= a(Vi(tt) + ... + aw/w^
что и требовалось доказать. ■
Теорема 3.8. Пусть fix), ie I — произвольное семейство функций,
конечных и выпуклых на выпуклом множестве X, и пусть fix) = sup/(x), x e X.
iel
Тогда функция fix) выпукла на X.
Доказательство
Возьмем произвольные точки и, v е X, некоторое a e [0; 1] и положим иа=
= ом + (1 - a)v. Для каждого фиксированного г е / функция fix) выпукла
на X, поэтому
/(Ma)<a/;(W)+(l-a)y;.(r;)<a/(W)+(l-a)/(i;) Vi€ /.
Переходя в левой части этих неравенств к верхней грани по г е /, получим
fiua)<afiu) + il-a)fiv) Vae[0;l].
Выпуклость функции fix) доказана. ■
Отметим, что хотя каждая из функций fix), i e /, принимает конечное
значение в каждой точке хеХ,в каких-то точках хе X возможно/(х) = -и».
Несмотря на это, доказанное утверждение, очевидно, сохраняет силу.
Теорема 3.9. Пусть функция hit) одной переменной выпукла и не
убывает на отрезке [а; Ь] iвoзмoжнocmь а = -°° или Ъ = +°° здесь не
исключается). Пусть функция gix) выпукла на выпуклом множестве X с Еп> причем
gix)e [a; b] при всеххе X. Тогда функция fix) = higix)) выпукла на X.
Доказательство
Возьмем произвольные и> v е X и a e [0; 1]. Тогда
fiau + (1 - a)v) = higiau + (1 - a)v)) < hiagiu) + (1 - a)g(p)) <
<ahigiu)) + il-a)higiv)) = afiu) + il-<*)f(v),
что и требовалось доказать. ■
Следствие 3.4. 1. Пусть функция gix) выпукла на выпуклом
множестве X. Тогда функция g^ix) = max{g(x); 0} выпукла на X.
150

2. Если функция g(x) выпукла и неотрицательна на выпуклом
множестве X, то функция/(х) = (g(x))P выпукла на Xпри всех/? > 1.
3. Если функция g(x) выпукла на выпуклом множестве X, то при всех
р > 1 функция/(х) = (max{0; g(x)})P = (g+(u))P выпукла на X.
4. Если функция g(x) выпукла на выпуклом множестве X, g(x) < О
при всех х е X, то функции/(х) = -(g(x))~19f(x) = (max{-ln(-g(x)); 0})p,
р > 1, выпуклы на X.
3.2. Сильно выпуклые функции
Как было отмечено в параграфе 3.1, выпуклая и даже строго выпуклая
функция может не достигать своей точной нижней грани на выпуклом
замкнутом множестве. Тем не менее существует подкласс выпуклых функций,
для которых такое невозможно.
3.2.1. Понятие сильно выпуклой функции
Определение 3.5. Функция/(х), определенная на выпуклом множестве
X с Еп> называется сильно выпуклой на этом множестве, если существует
такая константа к> 0, что
f(au + (1 - a)v) < of (и) + (1 - a)f(v) - усс(1 - а) \\и - vf (3.7)
при всех u,veX, всех а е [0; 1]. Отметим, что если неравенство (3.7)
верно при к- х0, то оно будет верно и для всех х€ (0; х0). Максимальная
из констант к, обеспечивающих выполнение неравенства (3.7), называется
константой сильной выпуклости функции f(x) на множестве X. Функция,
получающаяся умножением сильно выпуклой на -1, называется сильно
вогнутой.
Из этого определения следует, что сильно выпуклая на множестве X
функция является на нем строго выпуклой и тем более выпуклой.
Типичным примером сильно выпуклой на всем пространстве Еп служит функция
f(x) = (х,х) = \\х\\ . Для нее неравенство (3.7) превращается в тождественное
равенство сх=2:
|ш/ + (1-а)а| =а|м|| +(l-cc)lkl -a(l-a)\\u-v\\ ._
\/u,veEn, Vcce[0;l].
Далеко не всякая выпуклая функция будет сильно выпуклой.
Например, линейная функция f(x) = (с, х) выпукла на Еп, но не сильно выпукла,
в чем можно легко убедиться прямой проверкой определения.
Легко показать, что сумма выпуклой на выпуклом множестве X
функции и сильно выпуклой с константой к на том же множестве функции
будет сильно выпуклой функцией на X с той же константой к. Если f(x)
сильно выпукла на X с константой к, то функция g(x) = af(x) при любом
а = const > 0 будет сильно выпуклой на X с константой а к.
Изучим свойства множеств Лебега сильно выпуклой функции.
151

Теорема 3.10. Пусть X — выпуклое замкнутое множество, а
функция f(x) сильно выпукла и полунепрерывна снизу на X. Тогда множество
M(v) = {xeX:f(x)<f(v)} непусто, выпукло, замкнуто и ограничено
при любом v e X.
Доказательство
Множество М(р) непусто, так как v e М(р), и выпукло по теореме 3.6.
Для обоснования замкнутости множества М(р) рассмотрим
произвольную последовательность {xk} точек множества М(р), сходящуюся к
некоторой точке х. Поскольку множество X замкнуто и все xk содержатся
в М(р) сХ,тоихе X А так как функция/(х) полунепрерывна снизу на X
nf(xk) <f(v) при всех k = 1, 2,..., то
f(x)<\jmf(xk)<f(v),
k—»°о
поэтому хе М(р).
Чтобы доказать ограниченность множества М(р), положим M(v) = MtKj М2,
где Мх={хе М(р)\ \\х - v\\ < 2}, М2={хе M(v): \\x - v\\ > 2}.
Множество М1 непусто (v e Мх), содержится в шаре радиуса 2 и поэтому
ограничено. Также оно замкнуто как пересечение замкнутых множеств
М(р) и шара. Значит, оно компактно. Тогда по теореме 1.2 Вейерштрасса,
/** = inf f(x) > -оо.
Если множество М2 пусто, то М(р) = Мх ограничено. В противном
случае рассмотрим произвольную точку х е М2. Возьмем у = v + а(х - v), где
1 1
0 < а = и м < —. Ясно, что
II*-в! 2
\\У
-v\\ = \\a(x-v)\\ = j—|IU-dl = l,
поэтому у е Мх. Пользуясь определением сильной выпуклости функции/(х),
имеем
/(*/) < af(x) + (1 - a)f(v)-^а(1 - а)\\х - vf о
«|a(l-a)IU-d|2 <a(f(x)-f(v))+(f(v)-f(y)).
1
Учитывая, что f(y) > /**, 1 - a > — и f(x) < f(v) в силу того, что хе М2а
с М(р), получаем
f * lk-dl2</(,)-/^IU-dl<4<^>-^>,
4 \\x-v\\ x
т.е. точка х удалена от v не более чем на константу, что и означает
ограниченность множества М2. Значит, и множество М(р) ограничено как
объединение ограниченных множеств. Теорема доказана. ■
Теперь докажем основное утверждение, устанавливающее свойства
задачи минимизации сильно выпуклой функции.
152

Теорема 3.11 (Вейерштрасса). Пусть X — выпуклое замкнутое
множество из пространства Еп> функция f(x) является сильно выпуклой с
константой к и полунепрерывной снизу на X. Тогда /* = inf f(x) > -°°, множе-
хеХ
ство решений X* ={xeX:f(x) = f*} непусто и состоит из единственного
элемента х* и справедливо неравенство
^\\x-x*f<f(x)-f(x*) \/хеХ. (3.9)
Доказательство
Возьмем произвольную точку v из множества X и рассмотрим
множество Лебега M(v) = {xeX: f(x) < f(v)}.
Сразу заметим, что задачи минимизации функции f(x) на множестве X
и множестве М(р) эквивалентны, т.е. точные нижние грани и множества,
на которых они достигаются, совпадают. По теореме 3.10 множество M(v)
непусто, замкнуто и ограничено, что дает нам его компактность. Так как
функция/(х) полунепрерывна снизу на М(р) с X, то по теореме 1.2
Вейерштрасса /* = inf f(x) = inf f(x) > -oo, X*={xe X\f(x) = /*} Ф 0. Из силь-
xeM(v) xeX
ной выпуклости f(x) вытекает ее строгая выпуклость, поэтому по
теореме 3.3 множество X* состоит из единственной точки х*.
Далее, рассматривая произвольные 1б1иае (0;1]и записывая
определение сильной выпуклости, получаем
/(ост + (1 - а)х*) < af(x) + (1 - a)f(x*) a(l - a) \x - x* | <=>
«ya(l-a)|x-x*| <a(f(x)-f(x*)) + (f(x*)-f(ax + (l-a)x*)).
Так как множество X выпукло, х,х* е X, то и ах + (l-a)x* e X. Поэтому
справедливо неравенство f(x*) - /(ост + (1 - а)х*) < 0. Тогда имеем
ja(l-a)\\x-x*f <a(f(x)-f(x*)) Vae(0;l], MxeX.
Сокращая это неравенство на a > 0 и переходя после этого к пределу
при a —> 0 + 0, получим неравенство (3.9). Теорема доказана. ■
3.2.2. Критерии сильной выпуклости
Начнем с доказательства простого вспомогательного утверждения.
Лемма 3.2. Пусть X — выпуклое множество. Функция f(x) сильно
выпукла на X с константой к > 0 тогда и только тогда, когда функция
g(x) = f(x) |Ы| выпукла на X.
Доказательство
Учитывая равенство (3.8), прямой проверкой мы убеждаемся в том, что
для любых г/, v e X, a e [0; 1] неравенства
g(au + (1 - a)v) < ag(u) + (1 - a)g(v)
153

и
f(au + (1 - a)v) < af(u) + (1 - a)f(v) - уcc(l - сс)||г/ - of
эквивалентны. ■
Теорема 3.12 (критерии сильной выпуклости первого порядка). Пусть
X — выпуклое множество из пространства Еп> f(x)e C1(X). Функция f(x)
является сильно выпуклой с константой к > 0 на множестве X тогда
и только тогда, когда справедливо утверждение
f(u)>f(v) + (fXv)yu-v)+^\\u-vf \/u,veX, (3.10)
или утверждение
{fXu)-f\v\u-v)>Au-vf Vu,veX. (3.11)
Доказательство
Сначала заметим, что для сильно выпуклой функции h(x) = \\x\\
неравенство (3.10) будет выполнено как равенство при я =2:
\\uf=\\vtH2v,u-v)+\\u-vt.
Рассмотрим функцию g(x) = f(x)—— Ы1 . С учетом вышесказанного мы
можем записать такую цепь соотношений:
g(u) > g(v) + (g'(v)y u-v)<^> g(u) + у\\uf > g(p) + уlldl2 + (g'(v) + md,u-v) +
+f Ik - dl2 + f (Ы12 - 1Ы12 - <2t;, г/ - ^> - ||гг - d|2 ) «
<^f{u)>f{v) + {f\v\u-v) + ^\\u-vf.
Поэтому, с одной стороны, неравенство g(u) > g(v) + (g'(v), u-v) Vw, veX
эквивалентно неравенству (3.10), но, с другой стороны, по теореме 3.1
оно эквивалентно выпуклости функции g(x) на множестве X, которая
по лемме 3.2, в свою очередь, равносильна сильной выпуклости с
константой к на множестве X функции/(х).
Рассуждая аналогично, имеем
<g'(w) - g'(v), u-v)>0a (g'(u) + ки- g'(v) -kv,u-v)>k \\u - v\\ <=>
<*{fXu)-f'(v),u-v)>x\\u-vf.
Поэтому неравенство {g'(u)-g'(v),u-v)>0 Vw,veX эквивалентно как
неравенству (3.11), так и, по теореме 3.1, выпуклости функции g(x) на
множестве Ху которая по лемме 3.2, в свою очередь, равносильна сильной
выпуклости с константой хна множестве X функции f(x). ■
Теорема 3.13 (критерий сильной выпуклости второго порядка). Пусть
X — выпуклое множество из пространства Еп, intX* 0,/(x) е С2(Х).
Функция f(x) является сильно выпуклой с константой к > 0 на множестве X
тогда и только тогда, когда справедливо утверждение
(f"(x)h,h)>x\\hf VxeXyheE". (3.12)
154

Доказательство
Для функции g(x) = f(x)—— \\х\\ справедливо g"(x) = f"(x)-я1п, где
4 — единичная матрица размера п х п. Отсюда ясно, что неравенство (3.12)
равносильно неравенству
(g"(x)h, h)>0 VxeXyheE".
Таким образом, по теореме 3.2 функция g(x) будет выпуклой на X.
Но тогда по лемме 3.2 функция/(х) будет сильно выпуклой с константой к
на X. Теорема доказана. ■
Стоит отметить, что неравенство (3.12) эквивалентно
положительной определенности матрицы вторых производных f"(x). При
выполнении условия f(x) e С?(Х) она будет симметричной, и для исследования
ее на положительную определенность удобно пользоваться критерием
Сильвестра. Напомним, что он заключается в следующем: симметричная
матрица положительно определена тогда и только тогда, когда все ее
главные угловые миноры положительны.
Проиллюстрируем возможность применения критериев выпуклости
и сильной выпуклости на нескольких примерах.
Пример 3.1
Пусть g(x) = (с, х), где сер- заданный вектор. Тогда g'(x) = си
(g'(u)-g'(v),u-v) = (c-c,u-v) = 0 Vu,veEn.
Из этого вытекает, что линейная функция g(x) в силу теоремы 3.1 будет
выпуклой на всем пространстве Еп (и, как следствие, на любом выпуклом множестве
из Еп), поскольку выполнено неравенство (3.4). Также очевидно, что неравенство
(3.11) при и Ф v не выполнено ни при каком к> О, поэтому по теореме 3.12 g(x)
не является сильно выпуклой ни на каком выпуклом множестве из Еп, содержащем
более одной точки.
ример 3.2
Исследуем на выпуклость и сильную выпуклость квадратичную функцию типа
невязки
Mx) = \\Ax-bf, (3.13)
где А — заданная матрица размера тхп,Ье Ет — заданный вектор. Напомним, что
термин «невязка» используется, например, при решении системы линейных
уравнений Ах = Ь: если взять какую-то точку х0, то вектор Лх0 - Ь называется невязкой,
равенство невязки нулю означает, что х0 — решение системы. Сначала с помощью
определения найдем первую и вторую производные функции (3.13). Рассматривая
ее приращение, получаем
Mx + h)-Mx) = \\A(x + h)-b( -\\Ax-bf =
= \\Лх - bf + 2(Лх - b, Ah) + \\Ahf - \\Ах - bf = (2ЛТ (Ах - Ь), К) + \\Ahf.
Ясно, что 0 < \\Ah\\ < \\a\\ \\h\\ , поэтому \\Ah\\ = o(\\h\\) при h —> 0 и, следовательно,
f({x) = 2AT(Ax-b). После этого, записывая приращение градиента f{(x), находим
f{(x + И) - f{(x) = 2Ат(А(х + И) - b) - 2AT(Ax -b) = 2ATAh,
из чего вытекает f{(x) = 2АТА.
155

Поскольку вторая производная f" не зависит от х, то мы можем воспользоваться
теоремами 3.2 и 3.13 для одновременного исследования выпуклости и сильной
выпуклости функции fi(x) на всех выпуклых множествах с непустой внутренностью из Е1,
в том числе и на всем пространстве Е1. Имеем
{f"(x)K h) = (2ATAh, h) = 2{Ah, Ah) = 2\\Ah\\2 Vx, heEn.
Очевидно, что при всехх, h из Еп справедливо (f"(x)h,h)>0, т.е. верно
неравенство (3.5), поэтому fi(x) в силу теоремы 3.1 будет выпуклой на всем пространстве
Еп (и, как следствие, на любом выпуклом множестве из Еп).
Для исследования сильной выпуклости функции f\(x) придется привлечь более
тонкие соображения. Неравенство (3.12) для нее превращается в неравенство
2||i4A|2>x|A|2 VheE". (3.14)
Покажем, что оно будет справедливо в том и только в том случае, когда
Ли*О VA*0. (3.15)
Очевидно, что из справедливости неравенства (3.14) вытекает условие (3.15). Для
обоснования обратного утверждения предположим, что условие (3.14) нарушается,
т.е. существует последовательность ненулевых векторов {fk} е Еп такая, что К } —> О
Ш
при k —> ©о. Переходя к векторам hk = уутг, мы получим, что Ц/^Ц = 1 при всех k = 1, 2,...
НЛП
и, кроме того, ЦЛ/^Ц—>0 при k —> «>. Последовательность {hk} ограничена,
следовательно, из нее можно выделить подпоследовательность {hk }, сходящуюся к вектору
А0, причем в силу непрерывности нормы |^| = 1 и ||Л/го| = 0, из чего вытекает
равенство Ah0= 0, т.е. неравенство (3.15) тоже неверно. Это означает, что при выполне-
нии неравенства (3.15) выражение -й-й- ограничено снизу некоторым
положительным числом е0, и неравенство (3.14) выполнено для >с = 2е§.
Для получения точного выражения для константы сильной выпуклости
перепишем неравенство (3.14) в виде (2ATAh,h) >кШ. Матрица2АТА всегда является
симметричной и неотрицательно определенной. Следуя рассуждениям из примера 1.20,
мы получим, что неравенство (3.14) будет справедливо тогда и только тогда, когда
все собственные числа матрицы 2АТА положительны, константой сильной
выпуклости функции fi(x) будет минимальное из них.
Итак, квадратичная функция (3.13) будет сильно выпукла на любом выпуклом
множестве с непустой внутренностью тогда и только тогда, когда выполнено условие (3.15).
Пример 3.3
Рассмотрим квадратичную функцию общего вида
f2(x) = (Ax,x)-(c,x) + d, (3.16)
где А — заданная матрица размера пхп,се En,de R известны. Отметим, что
рассмотренная в предыдущем примере функция (3.13) может быть сведена к виду (3.16):
\\Ах - bf =(Ax-b,Ax-b) = (АтАх, х) - 2(ATb, x) + \\bf.
Как и в предыдущем примере, начнем с нахождения первой и второй
производных функции /2(х). Записывая ее приращение, имеем
f2(x + И) - f2(x) = (А(х + А), х + И) - (с, х + И) - {Ах, х) + (с, х) =
= ((A + AT)x-c,h) + (Ah,h),
156

откуда, с учетом того что 0 < \{Ah,h)\ < |л|• |й|| = о(||й|), находим /2'(#) = (А + Ат)х-с.
Далее, рассмотрев приращение градиента
Д(х + к)-Д(х) = [(А + Ат)(х + к)-с]-[(А + Ат)х-с] = (А + Ат)к,
получаем Д{х) = А-\- Ат. Для исследования этой функции на выпуклость и сильную
выпуклость, как и в предыдущем примере, воспользуемся теоремами 3.2 и 3.13. Ясно, что
(fi'(x)h,h) = ((A + AT)h,h) Vx,heEn.
Из полученного представления очевидно, что неравенство (3.5) будет справедливо
в том и только в том случае, когда симметричная матрица А + Ат будет
неотрицательно определенной, что эквивалентно тому, что все ее собственные числа
неотрицательны. Неравенство (3.14) будет выполняться тогда и только тогда, когда матрица
А + Ат будет положительно определенной, что эквивалентно положительности всех
ее собственных чисел (см. пример 1.20, неравенство (1.69)). Константой сильной
выпуклости функции f2(x) будет минимальное собственное число матрицы А + АТ.
Итак, квадратичная функция общего вида (3.16) будет выпуклой (сильно
выпуклой) на всем пространстве Еп (и на любом выпуклом множестве с непустой
внутренностью из Еп) тогда и только тогда, когда матрица А + Ат неотрицательно
(положительно) определена.
3.3. Метрическая проекция
В этом параграфе будет рассмотрено понятие метрической проекции.
Оно понадобится в дальнейшем, при изложении итерационных методов
минимизации.
Определение 3.6. Метрической проекцией точки х е Рна множество
1с£" называется ближайшая кхточка множестваX, т.е. такая точка/?, что
реХ, \\р - х\\ = inf \\u - х\\.
иеХ
Проекцию точки х на множество X мы будем обозначать через Рхх.
Понятно, что если х е X, то Рхх = х. Если же точка х не лежит в X, то ее
проекция на X может быть не единственна или не существовать, что можно
проиллюстрировать простыми примерами:
Пример 3.4
В пространстве Е1 рассмотрим множество Х= (-1,1). Покажем, что не существует
1
проекции точки х = 2 на множество X. Рассмотрев точки uk=l-—eX,k=l,2, ...,
k
мы видим, что \щ -х\ = 1 + у. Также ясно, что для любого иизХ\и-х\> 1. Поэтому
k
inf \u-х\ = 1, но в X нет точек и таких, что I и - х\ = 1.
иеХ
Пример 3.5
Пусть X = {х е Еп : \\х\\ = 1} — единичная сфера. Очевидно, что проекцией нуля
0 = (0, 0, ..., 0) на множество X является любой из элементов множества X, так как
для всехие Xсправедливо\\и-0|| = 1.
157

Отметим, что в примере 3.4 проекция не существовала из-за
незамкнутости множества X, а в примере 3.5 проекция оказалась не единственна
из-за невыпуклости множества X. Сформулируем и докажем утверждение,
содержащее достаточные условия существования и единственности
проекции.
Теорема 3.14 (о существовании и единственности метрической
проекции). Пусть X — замкнутое множество из пространства Еп. Тогда
для любой точки х е Еп существует ее метрическая проекция на
множество X. Если множество X еще и выпукло, то эта проекция будет
единственной.
Доказательство
Из определения метрической проекции и неотрицательности
расстояния вытекает, что если точка р является проекцией точки х на
множество X, то р будет решением задачи минимизации
g(w) = ||w-x|| -^min, иеХ,
и, более того, если рассмотреть некоторую точку v из X и соответствующее
ей множество Лебега М(р) = {ие X: \\и - х\\ < \\v - х\\ }, то р также будет и
решением задачи минимизации
g(tt) = l|tt-jc|| -^min, ueM(v). (3.17)
Функция g(u) является непрерывной, и, как было показано в
предыдущем параграфе, является сильно выпуклой на всем пространстве Еп.
Значит, по теореме 3.10 множество М(р) является в любом случае
ограниченным; если множество X замкнуто, то множество М(р) тоже замкнуто, а если
множество X выпукло, то множество М(р) тоже выпукло.
Таким образом, если множество X замкнуто, то задача (3.17)
представляет собой задачу минимизации непрерывной функции на замкнутом
и ограниченном, т.е. компактном множестве, и поэтому она
гарантированно имеет решение по теореме 1.2 Вейерштрасса. Если же множество X
выпукло и замкнуто, то задача (3.17) представляет собой задачу
минимизации непрерывной сильно выпуклой функции на выпуклом замкнутом
множестве, которая имеет, причем единственное, решение по теореме 3.11. ■
Теорема 3.15 (характеристическое свойство метрической проекции).
Пусть Хс£"- выпуклое замкнутое множество. Точка р будет являться
метрической проекцией точки х на множество X тогда и только тогда,
когда выполнено неравенство
(р-х,и-р)>0 \/иеХ. (3.18)
Доказательство
В доказательстве теоремы 3.14 было показано, чтор является решением
задачи минимизации сильно выпуклой непрерывной функции g(u) = \\и - х\\
на выпуклом замкнутом множестве X. По теореме 3.4 это равносильно
выполнению неравенства
(g'(p),u-p)>0 УиеХ.
158

Осталось заметить, что g'(u) = 2(и - х), g'(p) = 2(р - х). Теорема
доказана. ■
Теорема 3.15 имеет простой геометрический смысл (рис. 3.15): вектор
р - х должен образовывать острый или прямой угол с любым вектором
вида и - р, где и е X.
Рис. 3.15
Теорема 3.16 (о нестрогой сжимаемости проективного отображения).
Пусть IcP- выпуклое замкнутое множество. Тогда для любыххь х2 е Еп
справедливо
lPxxi~Pxx2l-\\xi~x2b (3.19)
т.е. расстояние между проекциями двух произвольных точек на X не
превосходит расстояния между этими точками.
Доказательство
Обозначим рх = Рх хь р2 = Рх хъ Тогда по теореме 3.15
(р1-х1уи-р1)>0 УиеХ; (р2-х2уи-р2)>0 УиеХ.
Подставляя в первое из этих соотношений и = р2е Х> а во второе —
u=pte Xy имеем
(р1-х1ур2-р1)>0; (p2-x2ypt-p2)>0.
Складывая эти неравенства, получим
(Р\ ~Р2> P\-Pl) ^ (Р\~Р2> *1 "*2>>
откуда, пользуясь неравенством Коши — Буняковского, находим
\\Pl-P2(^\\Pl-P2\\'\\Xl-X2\l
В случае \рх -р2\ = ^ утверждение теоремы, очевидно, верно. В
противном случае мы можем последнее соотношение сократить на эту величину,
что даст нам нужный результат. Теорема доказана. ■
Проиллюстрируем приведенные теоремы на примерах, выведя явные
формулы для проецирования на некоторые множества из Еп.
159

Пример 3.6
Выведем формулу для проекции на я-мерный параллелепипед
X = {x = (x\...,xn)eEn:ai<xi<^i,i = l,...,n},
где af, Pf, af < Pf — заданные числа, i = 1, ..., п. Его выпуклость и замкнутость
элементарно проверяются с помощью определений. Пусть х= (х{,..., хп) g X. Положим
р = (р\ ...,рп), где
р< =
af, х*<а0
ft, xf>Pf, i = l,...,n.
х1, af<xf<Pf,
Тогда (pf - х*)(и1-р1) > 0 для всех и1', af < wf < Pf, i = 1,..., п. Отсюда, суммируя по г
от 1 до я, получаем (р-х, и-р)>0 для всех и е X. Следовательно, по теореме 3.15
построенная точка р является проекцией точки х на множество X. В случае когда
х е X, как было отмечено ранее, Рхх = х.
Пример 3.7
Рассмотрим проецирование на гиперплоскость
Н = {хеЕп:(с,х) = а}, сеЕп,сфО, аеШ.
С помощью определения нетрудно убедиться, что гиперплоскость является
выпуклым и замкнутым множеством, поэтому проекция на нее любой точки существует
и единственна. Для вывода явной формулы проекции можно использовать
геометрические соображения, фактически, надо всего лишь опустить на гиперплоскость
перпендикуляр. Известно, что вектор с является нормальным вектором
гиперплоскости, поэтому проекцию р произвольной точки х следует искать в виде р = х + tc, где
t — некоторое число (рис. 3.16). В силу того чтор е Я, имеем
и и2 , v а-(с,х)
(с, р) = a <=> (с, х + tc) = а <=> t \\с\\ = a-(c,x)<^>t = -
wr
(с, х) = а
Рис. 3.16
Итак,
р = Рнх = х+ \ 'с.
(3.20)
Теперь строго обоснуем этот результат, применив теорему 3.15. Подставляя
полученную формулу (3.20) в утверждение этой теоремы, имеем
. а-(с,х) а-(с,х)
(р-Х,и-р) = [Х + ^-^5 С-X,U-X —^ С ) =
а-(с,х)
idr wr
а-(с,х) А (а-(с,х)
(с, и) - (с, х) —2—(с, с) | =
•«с, и)-а).
160

Но если ие Я, то (с, и) = а, стало быть, (р - х, и - р) = 0 при всех ие Н. Неравенство
из утверждения теоремы выполнено, справедливость формулы (3.20) установлена.
Рассуждая аналогично, можно получить формулы для метрической проекции
на полупространство HS = {хе Еп: (с, х) < а):
Phsx~
х +
a-(cfx)
у2
ху если (с, х) < а
с, если (с, х) > а,
(3.21)
и слой F = {xeEn:a<(c,x)<P}:
PFx =
а-(с,х)
х+——-—с, если (с, х) < а,
х +
Р-<с,*>
У2
х, если а < (с, х) < р.
с, если (с, х) > Р,
(3.22)
Их справедливость устанавливается точно так же, как и в случае гиперплоскости.
Пример 3.8
Рассмотрим проектирование на шар В = {х е Еп: \х - х0| < R}, x0 e En> R> 0.
Шар, так же как и гиперплоскость, является выпуклым и замкнутым множеством,
стало быть, проекция на него любой точки существует и единственна. Геометрические
соображения, привлекаемые для получения формулы проекции на шар, достаточно
очевидны: точка, уже лежащая в шаре, совпадает со своей проекцией, а точка х>
лежащая вне шара, спроецируется в пересечение/? (рис. 3.17) границы шара с прямой,
содержащей х и центр шара. Показать, что это пересечение является ближайшей к х
точкой, очень просто.
Рис. 3.17
Ясно, что проекцией на шар точки, лежащей вне шара, может быть только точка,
лежащая на его границе. Рассматривая произвольную точку q с границы шара, в силу
неравенства треугольника имеем
||х-^||>||х-х0||-||^-х0|| = ||х-р|| + ||р-х0||-||^-х0|| =
= \\x-p\\ + R-R = \\x-pl
т.е. р — ближайшая к х граничная точка шара. Наконец, вектор р есть сумма
вектора х0 и вектора длины R, коллинеарного вектору х - х0. Таким образом, формула
для проекции на шар выглядит так:
R
*о-'
р = Рвх =
Хп+1
\х-х0\\
[х,если|х-х0|<#.
(х - х0 ), если \х - х01 > R,
(3.23)
161

Для строгого обоснования вышеприведенных рассуждений воспользуемся
теоремой 3.15 о характеристическом свойстве метрической проекции. Рассмотрим
произвольную точку х, не лежащую в шаре Д что означает |х-х0|>#. Подставляя
формулу (3.23) для проекции на шар в неравенство (3.18), имеем
(p-X,U-p) = ((x0-x) + T, гЛх-Х0),и-Х0-ъ м(*-*о)/ =
II IIv
\\Х Х[
о II
_|х-Х0|-ДГ R Л_
-—и и— \Х0-Х,и-Х0)- и гЛХ0-Х,Х-Х0) -
р-*о| I р-*о| )
II II ({хо-х'и-хо) + Щх~хоЬ'
Р-хо||
Заметим, что если ие В, то |г/-х0||<# и по неравенству Коши — Буняковского
\Xq X, Ы Хг\) ^ \\Ы Xq • \\Х Xq ^ лх \\Х Xq .
Из этого следует, что (р - х, и - р) > О при всех и е В, справедливость полученной
формулы для проектирования на шар (3.23) установлена.
Пример 3.9
Выведем формулу для проекции на множество
Р = \х = (х1,х2,...,хп)еЕп :х1 > J(xk)2 [,
k=2
-и»
граница ГрРкоторого задается формулой F(x) = £ (xk)2 - х1 = О и представляет собой
k=2
обобщение параболоида вращения z = х2 + у2 из ЕР.
Для обоснования выпуклости и замкнутости множества Р поступим следующим
образом: заметим, что оно представляет из себя множество Лебега М(0) функции
F(x). Она является непрерывной на всем Еп, и, кроме того, F'(x) = (-1,2х2,2х3,..., 2хп),
(FXu)-FXv),u-v) = ((0,2(u2-v2),...,2(un-vn)),(u{-v\u2-v2,...,un-vn)) =
= 2J^(uk-vk)2>0 Vu,veEn,
k=2
поэтому по теореме 3.1 функция F(x) выпукла на всем Еп и, следовательно, по
теореме 3.6 и лемме 1.1 множество Р выпукло и замкнуто. Таким образом, по теореме 3.14
для любого хе Еп существует, причем единственная, его проекция на множество Р.
Покажем, как вывести формулу для проектирования на него, привлекая
геометрические соображения. Возьмем точку х = (х1, х2, ..., хп), не лежащую в множестве Р,
п
т.е. хх < Yj (xk)2, будем полагать, что/? = РРх. Ясно, чтор принадлежит границе ГрР
k=2
множества Р, т.е. F(p) = О, и является основанием перпендикуляра, опущенного из х
на ГрР (рис. 3.18).
Поскольку параболоид симметричен относительно оси xv то точка р лежит
на отрезке, концами которого являются точки х и х = (р0,0,0,..., 0), где р0 —
некоторое неотрицательное число. Поэтому р = Хх + (1 - Х)х, 0 < X < 1. В то же время из
математического анализа [22, 29] известно, что вектор F'(x0) является нормальным
вектором в точке х0 к поверхности, заданной уравнением F(x) = 0. Стало быть, условием
того, чтор есть основание перпендикуляра, опущенного из точки х на ГрР, будет
коллинеарность векторов F'(p) их-х, т.е. F'(p) = \i(x-х).
162

+ xn
Переходя к координатам, имеем
р = (Хх1 + (1 - Х)р0, Хх2, Хх3,..., Ххп );
F\p) = (-1,2Хх2,2Хх3у..., 2Ххп);
х-х = (Хх{ - Хр0, Хх2, Хх3,..., Ххп).
Из условия F'(p) = \i(x - х) находим \х = 2; -1 = 2(Ххх - Хр0), что дает нам р0=х{+ —.
ZK
После этого воспользуемся тем, что
РеГрР^№+(1-Х)р0=Х2Ъ(хк)2,
k=2
откуда следует
^Л *=2 U=2
X3 = (2*(-1)A. + 1.
(3.24)
Это уравнение относительно X является кубическим. Отметим, что у него
п
при выполнении неравенства х1 < £ (xk)2 обязательно есть, причем единственный,
k=2
корень на (0; 1), не имеет особого смысла выписывать явную формулу для него.
Подытожим: для любого х = (х{, х2,..., хп) е Ё1
р = РРх =
л^еслих1^ £(х*)2,
k=2
[х1*—-,Хх2,Хх3,...,Ххп 1есляхх< £(х*)2,
\ 2л J k=2
(3.25)
где X — корень уравнения (3.24), лежащий на интервале (0; 1).
Проверим правильность этих рассуждений с помощью теоремы 3.15 о
характеристическом свойстве проекции. Возьмем любые и = (г/1, и2,..., ип) е Р, х = (х1, х2у...,
хп) g РУ тогда
р-х = (Х-1)(~,х2,х3,...,хЛ,
и-р = \ их-хх — ,и2-Хх2,и3-Хх3,...,ип-Ххп \;
I 2X )
(р-х,и-р) = {Х-\){-^-и^^+^-+±и^-Х±{х^Л
I IK Ik Ак1 k=2 k=2
1-Х
X-l
Mi-2>*)2+$>*-X**)2 \+^-± (2дг»-1)Х + 1-2 £(**)2
2Х i. 4=2 А=2 ) ™г I U=2
X3
163

Заметим, что первое слагаемое из правой части последнего соотношения неотри-
п
цательно, так как О < X < 1, и1 - £ (uk)2 > О, второе же слагаемое равно нулю в силу
k=2
формулы (3.25). Поэтому (р - х, и - р) > О при всех ие Р, выведенная нами формула
(3.25) обоснована.
Завершим изложение свойств метрической проекции формулировкой еще
одного критерия оптимальности, представляющего собой несколько
переформулированную теорему 3.4.
Теорема 3.17 (проекционная форма критерия оптимальности). Пусть
X — выпуклое замкнутое множество, X* — множество точек минимума
функции f(x) на X. Если х* е X* uf(x) дифференцируема в точке х*, то
необходимо выполняется равенство
x*=Px(x*-af'(x*)) Vcc>0. (3.26)
Если, кроме того, f(x) непрерывно дифференцируема и выпукла на X, то
всякая точка х*, удовлетворяющая уравнению (3.26), принадлежит
множеству X*.
Доказательство
Согласно теореме 3.15 равенство (3.26) эквивалентно неравенству
(х* - (х* - af'(x*)), и - х*) > 0 УиеХу
откуда с учетом положительности а имеем (f'(x*),u-x*)>0 для всех
ие X. Таким образом, условия (3.26) и (3.6) эквивалентны. Отсюда и из
теорем 1.7, 3.4 следует утверждение этой теоремы. ■
3.4. Теорема Куна - Таккера
В этом параграфе мы рассмотрим условия оптимальности для задач
выпуклого программирования. Под выпуклым программированием
понимается раздел теории экстремальных задач, в котором изучаются задачи
минимизации выпуклых функций f(x) на выпуклых множествах X (или
максимизации вогнутых функций на выпуклых множествах).
Оказывается, что для таких задач можно сформулировать не только
необходимые, но и достаточные условия экстремума в терминах первых
производных, т.е. критерий принадлежности некоторой точки множеству
X* ={х* el:/(i*)= inf f(x) = f*}. Одним из таких утверждений в теории
хеХ
выпуклого программирования является теорема о седловой точке функции
Лагранжа, известная в литературе под названием теоремы Куна — Таккера.
Однако изложение материала мы начнем с рассмотрения общей
постановки задачи условной минимизации (см. параграф 1.4):
f(x) —> min, x e X,
Х = {хеХ0сЕ»: gl(x) < 0,..., gm(x) < 0; gm+1(x) = 0,..., gm+s(x) = 0}, (3*27)
где множество Х0 задано, функции/(х), gi(x)> ..., gm+s(x) определены и
конечны на Х0. Введем функцию
164

L(xy X) =f(x) + Xtgt(x) +... + Xmgm(x) + Xm+1gm+1(x) + ...+Xm+Sgm+S(x\ (3.28)
называемую нормальной функцией Лагранжа. Она получается из общей
функции Лагранжа £(х, X) (см. формулу (1.21)) при Х0= 1. Ее переменные
х и X могут принимать значения из множеств Х0 и
Л0= {X = (Хь ..., Xm+S) 6 £>»+*: Рц > О,..., Лт> 0} (3.29)
соответственно.
Определение 3.7. Точку (х*,Х*) называют седловой точкой функции
L(x, X) на Х0 х Л0, если
(**Д*)еХ0хЛ0, L(x*yX)<L(x*yX*)<L(xyX*) VxeX0, ХеЛ0. (3.30)
Прежде чем переходить к выяснению связи между седловой точкой
нормальной функции Лагранжа и решением задачи (3.27), дадим другую,
равносильную (3.30), формулировку определения ее седловой точки.
Лемма 33. Для того чтобы точка (х*Д*) была седловой точкой
нормальной функции Лагранжа (3.28) на Х0 х Л0, необходимо и достаточно,
чтобы выполнялись следующие условия:
1)х*еХ; 2)L(x*,X*)<L(xX) УхеХ0; 3)X*gf(x*) = 0y i = l,...,m. (3.31)
Доказательство
Необходимость. Пусть (х*Д*) е Х0х Л0 — седловая точка нормальной
функции Лагранжа (3.28) на Х0 х Л0. Тогда второе из условий (3.31) уже
выполнено. Остается показать, что первое и третье условия оттуда тоже
выполнены. Для этого перепишем левое неравенство (3.30) с учетом
конкретного вида нормальной функции Лагранжа:
f(x,) + X1g1(x,) + ... + Xm+sgm+s(x,)<f(x,) +
+ Kei(x*) + - + K+sem+s(x*) VAeA0,
откуда имеем
(X\-X1)g1(x,) + ... + (X*m-Xm)gm(x,) +
4K+i-K+i)gm+i(^) + ''' + (K+s-K+s)gm+s(^)^ VXeA0. (3.32)
Возьмем точку X = (Xly ..., Xs), где Xj = X*j +1 при некоторому, 1 <j<m,
и Xt =Х* при всех остальных г = 1, ..., т + s (i *j). Из определения (3.29)
множества Л0 и из того, что X* е Л0, следует, что выбранная точка X е Л0.
Из формулы (3.32) при таком X получим -gj(x*) > 0, т.е. gj(x*) < 0 при всех
j= 1,..., т.
Далее, пусть X = (Х1у ..., Xm+S) — точка с координатами Xj =X*j +gj(x*)
при некоторому, т + 1 <j < т + 5, и Хг-=Х\ при всех г = 1, ..., т + 5, i Ф j.
Ясно, что и эта точка X содержится в Aq, поэтому из формулы (3.32) имеем
-(gj(x*))2 > 0, т. е. gj(x*) = 0 при всех j = т + 1,..., т + s. Значит, выполнены
все соотношения из определения (3.27) множества X, и точка х* е X.
Теперь возьмем точку X = (Х1у ..., Xm+S) с координатами Xj= 0 при
некоторому, 1 <j <т, иХ(= X* при всех остальных г - 1, ..., т + 5, г Ф]. Такая
точка также принадлежит множеству Л0, поэтому из формулы (3.32) мы
165

находим 0 < X*jgj(x*). Но X*- > 0, и мы показали, что gj(x*) <О при j = 1,..., т,
поэтому последнее неравенство возможно лишь при X*jgj(x*) = Oj = 1,..., т.
Все соотношения (3.31) получены.
Достаточность. Пусть для некоторой точки (х*Д*)еХ0хЛ0
выполнены соотношения (3.31). Это значит, что неравенство L(x*yX*)<L(xyX*)
V х е Х0 из определения седловой точки выполнено, и нам надо всего лишь
показать, что для всех X е А0 верно L(x*> X) < L(x*, А*), т.е.
ЧКп+1 ~ К+\ )gm+l (*• ) + • - + (K+s ~ K+s )gm+s (Х* ) ^ ° V А Е Л0.
Кроме того, х* е X, поэтому g{ (х*) = 0, т + 1 < г < т + s, а также X]gt (х*) = О,
i=l,..., т. С учетом этого интересующее нас неравенство принимает вид
-Xxgx{x,)-...-Xmgm{x,)>Q VAeA0.
Но так как X е Л0, то А»! > 0, ..., Хт > О, а так как х* е X, то gi(x*) < 0,...,
gm(x*)<0. Поэтому неравенство справедливо, точка (х*Д*) — седловая.
Лемма доказана. ■
Подчеркнем, что в лемме 3.3 от множества Х0 и функций f(x), gi(x),
г = 1, ..., т + 5, не требуется никаких особых свойств — здесь важно только
то, что Х0* 0 и функции/(х), &(х), i=l, ..., т + 5, определены и конечны
наХ0.
Если сделать дополнительные предположения о выпуклости и
гладкости задачи (3.27), то лемму 3.3 можно переформулировать в
альтернативной, так называемой дифференциальной форме.
Лемма 3.4. Пусть в задаче (3.27) множество Х0 выпукло, функции ^(х),...,
gm(x) выпуклы на Х0, функции g{(x) = (aiy x) + biyi = m+ 1,..., т + s —
линейные и, кроме того, функции/(х), g\(x),..., gm(x) дифференцируемы на
множестве Х0. Тогда для того чтобы точка (х*> X*) была седловой точкой
нормальной функции Лагранжа (3.28) на Х0 х Aq, необходимо и достаточно, чтобы
(m+s \
Г(х*)+^Х*^'((х*)ух-х*)>0 \/хеХ0; (3.33)
XJgf-(*0 = 0, i = 1,..., щ х, е X. (3.34)
Доказательство
При сделанных предположениях нормальная функция Лагранжа (3.28)
выпукла и дифференцируема на множестве Х0 при каждом X е Л0. Поэтому
условие (3.33) согласно теореме 3.4 равносильно второму из условий (3.31).
Условия (3.34) совпадают с оставшимися из условий (3.31). ■
Теперь выясним, как связаны между собой седловая точка нормальной
функции Лагранжа и решение задачи (3.27).
Теорема 3.18. Пусть (х*Д*) — седловая точка нормальной функции
Лагранжа на Х0х Л0. Тогда i*el*, /(х*) = 1(х*Д*) = /*, иными словами,
точка х* является решением задачи (3.27).
Доказательство
В силу леммы 3.3 для пары (х*, V) выполнены условия (3.31), поэтому
х* еХ. Кроме того, A*gf(x*) = 0, i = 1, ..., т, и gi(x*) = 0, г - т + 1, ..., т + s,
166

из чего вытекает Цх*, Х*) = /(#*), и неравенство L(x*> Х*)< L(x> X*) Ухе Х0
перепишется в виде
m+s
f(x*)<L(xX) = f(x)+Zrigi(x) VxeX0. (3.35)
i=l
В частности, это верно и для всех х е X. Но если х е X, то g((x) < 0 и
Х\ > О при i = 1,..., га, a gt(x) = О при i = т + 1,..., га + 5. Поэтому
77Z+S
Хх;&(*)*о vxex.
i=l
С учетом этого из формулы (3.35) мы находим, что f(x*)< L(x, Х*)< f(x)
при всех х е X, т.е. х* е X*. Теорема доказана. ■
Заметим, что теорема 3.18, как и лемма 3.3, доказана без каких-либо
предположений о структуре множества Х0 и свойствах функций/(х), &(х),
г - 1,..., m + s.
Возникает вопрос: во всякой ли задаче вида (3.27) нормальная
функция Лагранжа имеет седловую точку? Только что доказанная теорема 3.18
позволяет понять, что ответ отрицательный: если множество решений X*
пусто, то нормальная функция Лагранжа такой задачи не может иметь
седловую точку. Более того, даже в выпуклых задачах с X* Ф 0 нельзя
утверждать наличие седловой точки.
Рассмотрим выпуклую задачу
/(*) = -*-> min, xeX = {xeEl:x>0,g(x) = x2<0}.
Здесь Х0 = [0; -и») — выпуклое множество, функции f(x) и g(x) выпуклы на Х0,
X = {0} — выпуклое множество, /* =0, X* =Х = {0}. Нормальная функция Лагранжа
для этой задачи имеет вид
L(x,X) = -x + Xx2, xeX0,XeA0=[0; + oo).
По теореме 3.18 седловой точкой такой функции на Х0х Aq может являться только
точка вида (х*=0,Х*). Но тогда неравенство L(x*,X*)<L(x,X*) УхеХ0 не может
выполняться, так как L(x*, X*) = 0, a L(x, X*) может принимать отрицательные значе-
( 1 А 1
ния: при V=0 1(1, 0) = -1, априХ*>0 L\ -ггтД*
2Х*
АХ*'
Таким образом, для существования седловой точки на задачу (3.27)
кроме условий выпуклости должны быть наложены какие-то
дополнительные ограничения. Поясним возникающие здесь проблемы на примере
несколько упрощенной постановки задачи условной минимизации
/(*)->min, xeX = {xeX0cE»:g1(x)<0,...,gm(x)<0}, (3.36)
где Х0 — заданное выпуклое множество; функции/(х), gi(x),..., gm(x)
определены, конечны и выпуклы на Х0. От исходной постановки (3.27) она
отличается требованиями выпуклости и отсутствием ограничений-равенств.
Заметим, что в силу следствия 3.3 из теоремы 3.6 множество X будет
выпуклым, поэтому такая задача будет выпуклой.
167

Предположим, что существует точка х0е X такая, что
g1(x0)<0,...,gm(x0)<0. (3.37)
Это требование к задаче (3.36) принято называть условием Слейтера,
а точку х0 — слейтеровой точкой. В выпуклой задаче вместо условий (3.37)
достаточно потребовать для каждого г = 1,..., т существования точки х{ е X
такой, что gi(xi) < О, г - 1, ..., т. Тогда в качестве х0 из (3.37) можно взять
т
х0 = Yjaixv ai> 0, oq + ос2 + ... + ocm = 1, поскольку тогда в силу неравенства
Йенсена (3.2) и того, что из х-х е X вытекает gj(xt) < О J = 1,..., т, справедливо
т
gj(.x0)u2Щё^х{)<ajgj(Xj)<О, j = 1,...,т.
Может показаться, что если g((x) = О при каком-то г, то точка х лежит
на границе множества X, а для внутренних точек множества X выполнено
gt(x) < 0, г = 1,..., т. Это не так, что можно проиллюстрировать на
следующем примере.
Рассмотрим задачу
f(x) = х-»min, xeX = {xeX0=Eu.g(x)<0},
где g(x) = х2 при х < 0 и g(x) = 0 при х > 0. Нетрудно показать, что функции/(х) и g(x)
выпуклы на Х0, так что задача выпукла. Здесь X = [0; -и»), X* = {0}, /* =0. Ясно, что
все точки х > 0 являются внутренними для множества X, но g(x) = 0 \/х > 0, и
условие Слейтера (3.37) заведомо не может выполняться. Убедимся, что нормальная
функция Лагранжа для этой задачи L(x, X) = х + Xg(x) не имеет седловой точки
на Х0 х Л0, где А$ = [0; -и»). Согласно теореме 3.18 седловыми могут быть лишь точки
вида (х* = 0Д > 0). Однако неравенство 1(0, X) = 0 = /* < 1(х, X) не может выполняться
при всех х е 2Г1 ни при каком X > 0. Действительно, если X = 0, то L(x,X) = х < 0 V х < 0;
если X > 0, то L(x, X) = х + Хх2 < 0 при всех х е (-Х; 0).
Итак, мы показали, что если в выпуклой задаче не выполнено условие
Слейтера, то нормальная функция Лагранжа может и не иметь седловой
точки. Оказывается, что выполнение этого условия является гарантом
наличия седловой точки, что и докажем.
Теорема 3.19 (Куна — Танкера). Пусть в задаче (3.36) множество Х0
выпукло, функции f(x), gi(x), i = 1,..., т, выпуклы на Х0 и выполнено условие
Слейтера (3.37). Пусть, кроме того, множество X* точек минимума
функции f(x) на множестве X непусто. Тогда для каждой точки х* е X*
необходимо существуют множители Лагранжа
г=(х;,...д;)ел0={Хе^:х1>о,...дш>о}
такие, что пара (х*, X*) образует седловую точку нормальной функции
Лагранжа на множестве Х0 х Л0.
Доказательство
Для простоты доказательства введем дополнительное предположение
о непрерывной дифференцируемости функций/(х), gi(x),..., gm(x) на мно-
168

жестве Х0. Тогда мы можем воспользоваться теоремой 1.9, согласно
которой для любой точки х* € X» найдется набор X* = (Х*0, Х*и..., Х*т) такой, что
(£х(х.,Х*),х-х*)>0 УхеХ0, (3.38)
Г ФО, Х"0 > О, XI > 0,..., Х*т >0; X-gi(x.) = 0, j = 1,..., т, (3.39)
т
где £(х, X) = X0f(x) + X\gi(x)- Поскольку множители Xq, Aj, ..., Хт неотри-
цательны, а функции/(х), gi(x),..., gm(x) выпуклы на множестве Х0,
функция £(х, X*) будет выпуклой на Х0. Тогда по теореме 3.4 из неравенства
(3.38) вытекает, что £(х*, Х*)< £(х, X*) при всех х е Х0. Подробнее запишем
это неравенство и воспользуемся условиями (3.39):
т
£(х*у Г ) = XJ/(*.) + S XJftOO = Kf(x*) <
m
<£(xX) = Kf(x) + ^X;gi(x) VieI0. (3.40)
i=l
Покажем, что Aq >0. В самом деле, если Х*0 =0, то среди
неотрицательных чисел XJ,...,Х^ в силу соотношений (3.39) есть строго положительное.
Взяв в качестве х в соотношении (3.40) слейтерову точку х0> мы полу-
т
чаем 0<Y,X*gi(x0)y что неверно из-за отрицательности чисел g\(x0)y ...,
i=l
gm(x0). Тогда мы можем считать, что Х*0 = 1 (если это не так, то мы можем
вектор X* поделить на Х*0 — условия (3.38) и (3.39) останутся
выполненными, а в новом векторе множителей Лагранжа будет Х*0 = 1). Но это
означает, что и для нормальной функции Лагранжа справедливо неравенство
L(x*,X*)<L(x,X*) для всех х е Х0, т.е. выполнено одно из неравенств
из определения седловой точки.
Далее, так как i*eX*cX, то g((x*)<0, г - 1,..., т, и для любого набора
неотрицательных чисел X = (Х1у..., Хт) с учетом условий (3.39) мы имеем
т т
SXI.ft(^)^o=s^ft(^)-
i=l i=l
Добавляя к обеим частям этого неравенства f(x*) мы получаем
L(x*,X)<L(x*,X*) при всех X е Л0, т.е. выполнено и второе неравенство
из определения седловой точки. Теорема Куна — Таккера доказана. ■
Доказательство, не требующее предположения непрерывной
дифференцируемое™ функций/(х), gi(x)y..., gm(x)y и более общие варианты теоремы
Куна — Таккера можно найти в работе [12].
Разберем еще один пример, показывающий, что условие Слейтера
является лишь достаточным, но не необходимым условием существования
седловой точки нормальной функции Лагранжа для выпуклой задачи.
Рассмотрим выпуклую задачу
f(x) = х-»min, xeX = {xeEu.x>0,g(x) = x2<0}.
169

Здесь, как и в примере 3.10, Х0= [0; -н») — выпуклое множество, функции/(х)
и g(x) выпуклы на Х0, X = {0} — выпуклое множество, /* = 0, X* = X = {0}. Нормальная
функция Лагранжа для этой задачи принимает вид
L(x, X) = х + Хх2, х е Х0 Д е Л0 = [0; + «>),
и имеет на Х0 х Л0 семейство седловых точек (х* = ОД* > 0). Действительно,
Дх*Д*) = 0<1(хД*) = х(1 + Гх) VxeX0=[0; + oo).
Условие Слейтера же в этой задаче, очевидно, не выполнено, так как g(0) = 0.
Объединим лемму 3.3, теоремы 3.18 и 3.19 и сформулируем
утверждение, удобное для использования на практике.
Теорема 3.20. Пусть в задаче (3.36) множество Х0 выпукло, функции
f(x), gi(x), i = 1, ..., т выпуклы на Х0 и выполнено условие Слейтера (3.37).
Пусть, кроме того, множество X* точек минимума функции f(x) на
множестве X непусто. Тогда для каждой точки х* е X* необходимо существуют
множители Лагранжа X* = (Х[,...,Х*т) такие, что выполнены условия:
L(x*, Х*)< L(x, V) Ухе Х0 (принцип минимума); (3.41)
Х[ > 0,..., ^4^0 (неотрицательность множителей Лагранжа); (3.42)
X\gx (х*) = 0,..., Kmgm (х*) = 0 (условия дополняющей нежесткости). (3.43)
Кроме того, если для пары (х*, X*) выполнены условия (3.41)—(3.43) и х* е
е X, то х* е X*.
Проиллюстрируем применение этой теоремы на следующем примере.
Пример 3.13
Рассмотрим выпуклую задачу
f(x) = \\xf -> min, х € X = {х € Еп: (с, х) > 1}.
Фактически она представляет собой поиск ближайшей к началу координат точки
полупространства и эквивалентна задаче проектирования на гиперплоскость. В этом
примере Х0 = Еп — выпуклое множество, f(x) = \\х\\ — выпуклая и даже сильно
выпуклая на Еп функция, g(x) = l-(c,x) — выпуклая на Еп функция. Нормальная
функция Лагранжа этой задачи имеет вид
L(x, X) = \\xf + X(l - (с, х», х е Еп, X е Л0 = [0; + «>).
2
В качестве слейтеровой точки возьмем х0 = —^с. Значит, применима теорема 3.20,
\\с\\
и нам надо найти решение (х*, X*) системы
L(x*X)<L(xX) VxeEn,
\\1-(с,х)) = 0,
Г>0,
удовлетворяющее условию х* е X. Оно и будет решением задачи. Поскольку при всех
X* > 0 нормальная функция Лагранжа выпукла и дифференцируема по х, то
первое неравенство из этой системы по теореме 3.4 эквивалентно условию Lx(x*,X*) = 0.
Тогда мы имеем
170

2x*-X*c = 0,
V(l-<<;,*.» = О,
X*>0.
Из первого уравнения вытекает, что х*=—Х*с, и, подставляя это во второе
( 1 .. I|2S 2
уравнение, получаем X 1—X \\с\\ . Отсюда имеем два решения: X = 0, х*=0
2
/
и X* = —г", х* = —т. Очевидно, что х* = 0 не лежит в множестве X, поэтому первая
пара — посторонняя. Решением задачи будет х* = —-г. Этот результат совпадает
lldl
с результатом, который можно получить с помощью явной формулы (3.20)
проецирования на гиперплоскость.
3.5. Теорема Куна - Таккера для многогранного множества
В этом параграфе мы приведем еще один вариант теоремы Куна —
Таккера для задачи условной минимизации выпуклой функции/(х) на
многогранном множестве вида
Г 24(х) = (а4,х)-к <0, г = 1,...,7я; 1
f(x)^mm,xeX = \хеХ0: ^ } " ' 1 .' ' ' , (3.44)
где Х0, в свою очередь, является многогранным множеством и задается
в виде
X0={xeEn:(Ci,x)<di,i = l,...,p; (ciyx) = diyi = p + ly...yp + q}; (3.45)
а{, с{ е Еп — заданные векторы; bi9 d{ — заданные числа. Мотивация
выделения отдельного множества Х0, заданного ограничениями такого же сорта,
как и X, заключается в том, что совершенно необязательно учитывать
абсолютно все ограничения с помощью функции Лагранжа, может оказаться,
что часть из них вполне приемлема. Так, например, в приведенной
постановке возможны следующие случаи:
Х0=Е«, Х0=Е?, Х0={х = (х\...,хп): *<>0, ге/с{1,...,я}},
X0={x = (x1,...,x»y.ai<xi<h,i = l,...,n},
где осг, Р; — заданные величины, а( < (Зг, i = 1, ..., п, не исключен вариант,
когда некоторые а(= -°° или Р; = -н». Все эти множества имеют достаточно
простую структуру, пригодную для минимизации на них функции
Лагранжа с помощью аналитических соображений или несложных итерационных
методов.
Для дальнейшего изложения материала нам понадобится следующее
определение.
Определение 3.8. Пусть X — некоторое множество из Еп, х — точка
из множества X. Направление е Ф 0 называется возможным в точке х, если
существует число t0 > 0 такое, что х + te e X при всех t, 0<t<t0. Иначе
171

говоря, достаточно малое перемещение из точки х по возможному
направлению не выводит за пределы множества X.
Очевидно, если х е intX, то любое направление е Ф О является
возможным в этой точке. В граничных точках множества возможное направление
может и не существовать, что легко подтвердить на примере.
Пример 3.14
Пусть X = {и = (х, у)е Е2: х > О, х2 < у < 2х2}. Точка (0; 0) является граничной
точкой этого множества. Выберем произвольное направление е = (е{, е2), оно будет
возможным, если х + te = (tev te2) попадет в множество X при всех t e [0; t0]. Ясно, что
случаи ех < 0 или е2 < 0 невозможны, при ех = 0, е2 > 0 имеем 0 < te2 < 0, что неверно
при всех t > 0. Если е{ >0,е2= 0, то должно выполняться t2e\ < 0 — это также неверно
при всех t > 0, наконец, если ех > 0, е2 > 0, то должно быть верно te2 < 2t2e\ — но это
не так при t е 0; —^- . Таким образом, в точке (0; 0) нет возможных направлений.
Для выпуклых множеств X, содержащих не менее двух точек,
приведенная в примере 3.14 ситуация невозможна: в любой точке и такого
выпуклого множества X имеется хотя бы одно возможное направление, причем
все возможные направления в этой точке имеют вид е - y(v - и), где у > 0,
v e X,v*u.
Для многогранного множества несложно дать полное описание всех
возможных направлений в любой его точке, сформулируем и докажем
соответствующее утверждение.
Лемма 3.5. Множество возможных направлений множества X,
описанного формулами (3.44), (3.45), в любой его точке х* имеет вид
[ (aiye)<0Jeri; (aiye) = 0J = m + ly...ym + s-]
К = К(х*) = <ееЕп:е*0у v Л . т# , v Л . л \у
{ (ciye)<0yiel2; (ciye) = 0y г = p + ly...yp + q J
где I[ = {i: \<i<my (aiyx*) = b{}y Г2 = {i: \<i<py (ciyx*) = d{) — множества
активных индексов в точке х*у т.е. множества индексов, для которых
ограничения-неравенства выполняются как равенства.
Доказательство
Пусть е = (е1, ..., еп) Ф 0 — произвольное возможное направление
множества X в точке х*. Согласно определению возможного направления тогда
существует такое число t0> 0, что x = x*+teeXy т.е.
{aiyx*+te)<biy г = 1,...,/тг; {aiyx*+te) = biy i = m + ly...ym + s;
(q,x* + te)<diyi = 1,...,p; (c(yx* + te) = diyi = p + ly...,p + qy
при всех ty 0 < t < t0. С учетом того, что х*еХуи определения множеств ГХу
Г2 активных индексов точки х* из формулировки леммы сразу получаем
ее К.
Верно и обратное: если ее Ку то е — возможное направление в точке х*.
В самом деле, пусть ее К. Тогда для i e I* имеем (aiy x* + te) = bt + t(aiy e) < Ъ{
при всех t > 0, а если i € 1[У 1 < i < ту то (aiy х*)< Ъ{ и найдется такое t0 > 0, что
(а(у х* + te) < Ъ{ при 0 < t < t0. Если т +1 < i < т + sy то (aiy х* + te) = Ъ{ при всех t
Аналогично, взяв при необходимости t0 > 0 еще меньшим, убедимся, что
172

выполняются и остальные соотношения (3.46), так что х* +te е X, 0 < t < t0.
Лемма доказана. ■
Теорема 3.21. Пусть в задаче (3.44), (3.45) Х0 — многогранное
множество из Еп, функция f(x) выпукла на Х0 и дифференцируема в точке х* е X*.
Тогда существуют множители Лагранжа
г=(х;,...д;+5)ел0={Хе£^:х1>о,...дш>о}
такие у что пара (х*> А*) образует седловую точку нормальной функции
Лагранжа (3.28).
Доказательство
Согласно теореме 3.4 для того, чтобы в задаче (3.44), (3.45) х* е X*,
необходимо и достаточно выполнения неравенства
(f'(x.),x-x.)>0 УхеХ. (3.47)
Рассмотрим произвольную точку х* е X*, возьмем любое е е К. Тогда
по лемме 3.5 существует t0 > О такое, что x = x*+teeX при всех t e (0; t0].
Подставив такую точку х в неравенство (3.47), получим (/'(#*), te)>0,
из чего с учетом положительности t следует (f'(x*)> e)>0.
По теореме Фаркаша 2.12 тогда найдутся числа Х\ > 0, г е 1[, Х*т+1,..., X*m+S,
\i* > 0, г е Гъ \i*p+1,..., \i*p+q такие, что
m+s p+q
/'<*•) = " X K<h ~ X КЩ - I Щ-с,- - I Ц*с,.. (3.48)
le/J" i=m+l iel*2 i=p+l
Доопределив X* = 0 при i e {1,..., m)\I*v получим точку X* = (k*v..., X*m+S)e
e Л0. Отсюда, учитывая определение множества 1[ и условие х* е X* с X,
имеем
X*((ai,x*)-bi) = ),*gi(x*) = 0, i = l,...,m + s, (3.49)
а равенство (3.48) можем переписать в виде
m+s p+q
/'(*•)+ I K"i = - X tib - I \CiCi. (3.50)
Нормальная функция Лагранжа в рассматриваемой задаче (3.44), (3.45)
имеет вид
m+s
1(*Д) = /(*)+ X \({ацх)-Ь{\ хеХ0, ХеА0.
i=i
В силу выпуклости функции /(х) на Х0 справедливо неравенство
f(x)-f(x*)>(f'(x*),x-x*), х е Х0 (теорема 3.1). Пользуясь этим фактом,
определением множества 1*ъ условием \i* >0, iel^, и равенством (3.50),
для каждого х е Х0 получаем
77Z+S / 77Z+S \
Дхд*)-1(х*д*)=/(х)-/(х*)+ X ^(я*,*-^) >(/'(**)+ Х^-» *-**)=
1=1 \ 1=1 /
173

т.е. L(x*,X*)<L(x,X*) \/хеХ0. Отсюда и из формулы (3.49) с помощью
леммы 3.3 имеем, что (х*Д*) — седловая точка нормальной функции Ла-
гранжа. Теорема доказана. ■
Замечание 3.1. Если f(x) = (с, х), то из теоремы 3.21 вытекает теорема 2.11
для задач линейного программирования. Однако принятая здесь схема
изложения не позволяет считать теорему 2.11 следствием теоремы 3.21,
так как при ее доказательстве была существенно использована теорема
Фаркаша 2.12, которая в свою очередь (как, впрочем, и сама теорема 2.11)
получена как следствие доказанных в параграфе 2.8 утверждений. Следует
также отметить, что множество (3.44), вообще говоря, не содержит слейте-
ровых точек.
3.6.* Двойственные задачи. Примеры
Вернемся к общей задаче условной минимизации
/(*)-> min, xeX,
X = {xeX0QE-:gl(x)<Oy...ygm(x)<0;gm+1(x) = Oy...ygm+s(x) = 0}
и выпишем для этой задачи нормальную функцию Лагранжа
Ц*Л) = /(*) + Х1я1(*) + ... + Хтя^ (3.52)
х е Х0, X е А0 = {X = (Xlf..., Xm+S): Xt > О,..., Хт > 0}. (3.53)
Оказывается, что эту задачу можно переформулировать. Введем
функцию
ф(х) = sup L(xy X). (3.54)
ХеА0
m+s
Ее можно вычислить явно. Ясно, что если i е I, то J \&i(x)-®
при всех X е Л0, причем равенство здесь реализуется при X = (0,..., 0) е Л0.
Если жехе Х0\Х, то найдется номер г такой, что либо l<i<mng((x) > 0,
либо m + \<i<m + SYL g((x) Ф 0, так что подходящим выбором X е Л0 сумму
m+s
X \§i(x) можно сделать сколь угодно большой. Таким образом,
i=i
, ч \/(х),еслихеХ,
ф(х) = <
[-и», если х е Х0 \ X.
Отсюда следует, что inf ф(х)= inf f(x) и задачу (3.51) можно перепи-
хеХ0 хеХ
сать в равносильном виде
ф(х)-> min, xeX0. (3.55)
Будем предполагать, что /* = inf f(x)>-«>, X* = \хеХ\ f(x) = /*}ф0.
хеХ L J
Тогда в задаче (3.55) минимальное значение ф* функции ф(х) на множестве
Х0 будет равно /* и будет достигаться на том же множестве X*.
174

Отметим, что задача (3.55) состоит из двух последовательных этапов:
сначала мы максимизируем функцию Лагранжа (3.52) по переменной X
на множестве Л0, после чего полученную функцию ф(х) мы минимизируем
по переменной х на множестве Х0. Возникает вполне естественный вопрос:
а что будет, если в этом процессе поменять местами операции
максимизации по X и минимизации по х? Более подробно выражаясь, введем функцию
\\f(X) = inf L(xy X), X е Л0, (3.56)
xeX0
и рассмотрим задачу
—> max, Л Е Л0. (3.57)
Задачу (3.57) называют двойственной задачей к задаче (3.55) или
к исходной основной задаче (3.51), переменную X = (Х1у ..., Xm+S) называют
двойственной переменной в отличие от исходной, основной переменной
х = (х1,..., хп), \|/(Х) — двойственной функцией.
При формулировке задач вида (3.51) мы обычно подразумеваем, что
функции/(х), gi(x), г = 1, ..., т + s, принимают конечные значения во всех
точках множества Х0. Поэтому \\f(X) < +«> при любом фиксированном
X е Л0. Но формула (3.56) не исключает возможности появления значений
1|/(Х) = -оо при некоторых X е Л0. Имея в виду это обстоятельство, задачу
(3.57) нетрудно записать в привычной форме
\|/(X)->max, XeA = {XeEm+s:XeA0,\\f(X)>-oo}, (3.58)
рассматривая лишь те точки, где значения функции \\f(X) конечны.
Обозначим
\|/* = sup \|/(Х) = sup\|/(X), Л* = {X е Л0: \|/(Х) = \|/*} = {X е Л: \|/(Х) = \|/*}. (3.59)
ХеА0 ХеА
Теперь установим ряд свойств двойственной задачи. Во-первых, она
гарантированно является задачей выпуклого программирования,
независимо от того, была ли выпуклой или нет задача (3.51). В самом деле,
функция -L(x> X) линейна и, следовательно, выпукла по X на выпуклом
множестве Л0, поэтому по теореме 3.8 функция
-\|/(Х) = sup (-I(x, X))
хеХ0
выпукла на Л0. Это эквивалентно тому, что функция \|/(Х) вогнута на Л0, т.е.
^(оЛ1 + (1 - а)Х2) > тКА1) + (1 - сс)\|/(А2)
для всех а е [0; 1] и всех X1, X2 е Л0. Но тогда если X1, X2 е Л0 и ^(Х1) >
> -о©, \|/(Х2) > -со, то и ^(аХ1 + (1 - а)Х2) > -о© V а е [0; 1]. Это значит, что
множество Л в задаче (3.58) также выпукло.
Стало быть, задачи (3.57), (3.58), записанные в равносильном виде
-\|/(Х) —> min, X е Л0, или -\|/(Х) —> min, X е Л, (3.60)
представляют собой задачи выпуклого программирования. Благодаря
этому обстоятельству исследовать двойственную задачу нередко бывает про-
175

ще, чем исходную. Но зачем это делать? Какую информацию мы можем
получить об исходной задаче (3.51), изучая двойственную задачу?
Оказывается, задачи (3.55) и (3.57) и, следовательно, задачи (3.51) и (3.58) тесно
связаны между собой и параллельное их исследование зачастую позволяет
полнее изучить каждую из них, наметить новые подходы к их решению.
Докажем утверждение, описывающее связь между двойственными задачами.
Теорема 3.22. Для функций (р(х) и \|/(Х), определенных формулами (3.54)
и (3.56), справедливо соотношение
\|/(Х) < \|/* = supinf L(xy X) < ф* = inf supL(x> X) < (p(x) Ух е Х0, УХ e Л0. (3.61)
л0 xo xo л0
Для того чтобы X* Ф 0, Л* Ф 0, \|/* = ф*, необходимо и достаточно, чтобы
функция L(xy X) имела седловую точку на Х0 х Л0. Множество этих седловых
точек совпадает с множеством X* х Л*.
Доказательство
Из формулы (3.56) следует, что
\\f(X) = inf L(xy X) < L(xy X) УХ e Л0, Vi6l0.
xeX0
Отсюда и из формулы (3.54) имеем
\|/* = sup \\f(k) < sup L(x, X) = ф(х) Vi6l0.
XeAq XeAq
Переходя к нижней грани по х е Х0в этом неравенстве, получаем \|/* < ф*.
Неравенство (3.61) доказано.
Далее, пусть X* Ф0, Л* Ф0, \|/* = ф*. Возьмем произвольные i*el* и
X* е Л* и покажем, что (х*> X*) — седловая точка функции Лагранжа (3.52).
Ясно, что
\|/* = \|/Д*) = inf L(x, Х*)< L(x*y Х*)< sup L(x*y X) = q>(x*) = ф*.
xeX0 XeA0
Но так как мы предположили, что \|/* = ф*, то эти неравенства
превращаются в равенства:
L(x*y Х*) = inf L(x, Х*) = sup L(x*y X).
хеХ0 ХеА0
Отсюда имеем неравенства (3.30), т.е. (х*Д*) — седловая точка. Тем
самым показано, что X* х Л* принадлежит множеству седловых точек
функции L(xy X) на Х0 х Л0.
Наконец, предположим, что (х*> Х*)еХ0хА0 — седловая точка функции
L(x, X) на Х0 х Л0. Исходя из определения (3.30), имеем L(x*y X) < L(x*y X*)
\/Х е Л0. Значит,
sup L(x*> X) = ф(х*) = L(x*> X*).
ХеА0
Кроме того, L(x*, X*)< L(x, X*) Ухе Х0, так что
L(x* Д*) = inf L(xy X*) = \|/(X*),
хеХ0
176

откуда и из неравенства (3.61) следует
1(х*, X*) = \|/(Г) < \|/* < ф* < ф(х*) = 1(х*, V),
т.е. \|/(Х*) = \|/* = ф* = ф(х*). Это значит, что \|/* = ф*, X* е Л*, х* е X* и, кроме
того, что множество седловых точек функции L(x, X) на Х0 х Л0
принадлежит множеству X* х Л*. Теорема доказана. ■
Сформулируем два полезных следствия из теоремы 3.22.
Следствие 3.5. Следующие четыре утверждения равносильны:
1) (х* Д*) е Х0 х Л0 — седловая точка функции L(x, X) на Х0 х Л0;
2) Х**0,Л**0,\|/*=ф*;
3) существуют точки х* е Х0, X* е Л0 такие, что ф(х*) = \|/(Х*);
4) справедливо равенство max inf L(x, X) = min sup L(x, X).
XeA0 xeX0 xeX0 XeA(j
Напоминаем, что когда пишут max или min, то гарантируется
достижение соответствующей верхней или нижней грани.
Следствие 3.6. Если (х*, X*) и (г/*, \i*) e X0 x Л0 — седловые точки
функции L(x, X) на Х0х Л0, то (х*,ц*), (г/*Д*) также являются седловыми
точками этой функции на Х0 х Л0, причем
L(x*> \x) = L(y*y X*) = L(x*> X*) = L(y*y ц*) = ф* = \|/*.
Из этого следствия вытекает, что при решении выпуклой задачи с
помощью правила множителей Лагранжа для всех х* е X* можно взять один
и тот же набор X*.
Не следует думать, что если (х*, X*) е Х0 х Л0 — седловая точка функции
L(x, X) наХ0х Л0, то и точки (г/, \х) е Х0х Л0, для которых 1(г/, \i) = L(x*> X*)>
также будут седловыми точками. Так, например, функция L(x, X) = Xx имеет
единственную седловую точку (х*Д*) = (0;0) на Е1 x E1, L(x*yX*) = 0. Для
точек вида (г/, 0) или (0, ц) значение рассматриваемой функции также
равно нулю, но седловыми они не являются. В общем случае можно лишь
утверждать, что
Х*сХ(Г) = {хеХ0:Цх,Г) = Цх*,Г)};
Л* с А(х*) = {X е Л0: L(x*y X) = L(x*y X*)},
где множества X*, Л* есть множества решений задач (3.55) и (3.57)
соответственно.
Замечание 3.2. Отметим, что в определении 3.7 седловой точки, в
формулировке и доказательстве теоремы 3.22 и в следствиях 3.5, 3.6 нигде
не использовано, что рассматриваемая функция L(x> X) является функцией
Лагранжа какой-либо задачи условной минимизации вида (3.27). Поэтому
эта теорема и ее следствия справедливы и в том случае, когда
рассматриваются произвольные множества Х0, Л0, любая функция L(x, X),
определенная на Х0 х Л0, и строится пара задач
ф(х) = sup L(x, X) —» min, xeX0; \\f(X) = inf L(x, X) —» max, X e A0.
XeA0 xeX0
Теорема 3.22 играет важную роль в теории игр.
Проиллюстрируем теорему 3.22 несколькими примерами.
177

Пример 3.15
Рассмотрим задачу
f(x) = hx-af^>mm, хеХ = {хеХ0 =Еп: Ах = Ъ), (3.62)
где А — заданная матрица размера т х п\ а е Еп, Ь е Ет — известны. Сразу
заметим, что эта задача равносильна задаче проектирования точки а на множество X.
В силу теорем 3.11, 3.14 она имеет, причем единственное, решение х*. Опишем метод
его поиска, основанный на переходе к двойственной задаче. Нормальная функция
Лагранжа для рассматриваемой задачи
L(x,X) = -||* - at +<X, Ъ -Ах), хеЕп,ХеА0=Ет (3.63)
сильно выпукла по х на Еп при каждом X е ЕР1 и согласно теореме 3.11 достигает своей
точной нижней грани в единственной точке х(Х). В силу теоремы 3.4 точка х(Х)
является решением уравнения L'(x,Х) = х-а-АТХ = О, откуда находим
х(Х) = а + АтХ. (3.64)
Значит, двойственная задача может быть выписана явно:
V(X) = infL(x,X) = L(x(X),X) = --\\ATxf +{X,b-ATa)->max, XeA0 = Em. (3.65)
En 2
Функция \|/(Х) вогнута, дифференцируема на Em, ее производная равна
ц'(Х) = -ААтХ + Ь-Ата.
Отсюда и из теоремы 3.4, примененной к выпуклой функции -\|/(Х), следует, что
решение X* двойственной задачи (3.65) удовлетворяет системе линейных
алгебраических уравнений
ААТХ = Ь-Аа. (3.66)
Ниже в примерах мы увидим, что двойственная задача не всегда имеет решение.
Поэтому необходимо объяснить, почему система (3.66) имеет хотя бы одно решение.
Здесь можно воспользоваться теоремой 3.21, согласно которой функция Лагранжа
(3.63) имеет седловую точку. Поэтому мы можем задействовать следствие 3.5
теоремы 3.22, которое дает нам X* Ф&, X* *0, /* =\|Л Это значит, что система (3.66)
имеет хотя бы одно решение X*. После этого по формуле (3.64) находится решение
х* = х(Х*) = а + АТХ* задачи (3.62).
Таким образом, переход к двойственной задаче позволил свести исходную задачу
к хорошо известной задаче (3.66) из области линейной алгебры.
В гл. 2 были рассмотрены двойственные задачи линейного
программирования, приведены теоремы двойственности, причем двойственная задача
была введена аксиоматически, без объяснения, откуда она появилась.
Покажем, что к ней можно прийти с помощью изложенной в этом
параграфе техники.
Рассмотрим общую задачу линейного программирования
/(x) = (c1,x1) + (c2,x2)^min, xeX,
(о.57)
X = {х = (xv x2)e Eni х Еп2: х{ > 0, А11х1 + Апх2 -Ь{<0, А21х{ + А22х2 -Ь2= 0},
178

где q е Eni, с2 е Eni, b{ e Emi, b2 e Emz — заданные векторы; матрицы Ау- также заданы
и имеют размерность mfx rip i,j = 1, 2. Нормальная функция Лагранжа этой задачи
имеет следующий вид:
L(x, X) = (q, хх) + (с2, х2) + X М(А Л + \гхг ~ h)1 + £ М(^гЛ + ^22*2 ~ ^У»
х = (хх,х2)еХ0=Е?хЕп2,Х = (Х1..Л?1Х2,..Л%2)еЛ0=Е?хЕт2.
Введя обозначения Х{ = (Х\,...,Х™1), Х2 = (Х12,...,Х21), ее можно переписать в более
коротком виде
L>yX, К) = \Cj, Xj/ + \^2' *^2/ "^ \^1» 11*^1 "^ -^12*^2 — 1/ "^ \^2» 21*^1 "^ -^22*^2 — j£/'
Нетрудно получить, что функция ф(х) = sup L(x, X), х е Х0, определяемая согласно
Х€Л0
формуле (3.54), в нашем случае имеет вид
[{с*, х*) + (со, Хп), если х е X,
Ф(х)= 4lf i; Ч2 ^\ v (3.68)
[+оо, еслихеХ0\Х.
Для вычисления функции \|/(Х), определяемой по формуле (3.56), удобнее
представить нормальную функцию Лагранжа в следующем виде:
L(x, X) = (-bv X{) + (-b2, X2) + (xv А[{Х{ + А%ХХ2 + q) +
+ (х2,Л1Г2^1+^22^2+С2)' *€^0> ^еЛ0-
Отсюда вытекает, что
^Н^ЛЫ^ДДеслиХеЛ, (3.69)
[-«>, если X е Л0 \ Л,
где
Л = {X = (Х{,Х2)е£mi х£т2: Xj >0, AJ{XX + Л£Х2 + q >0, А{2Х{ + Л£2Х2 + с2 = 0}.
Из полученных выражений (3.68), (3.69) для функций ф(х), \|/(Х) следует, что
задача ф(х) —> min, x e Х0, равносильна исходной задаче (3.67), а двойственная к ней
задача \\f(X) —> max, X e Aq, равносильна задаче вида (3.57)
x\f(X) = -(bvXl)-(b2,X2)^>m<ix, XeA. (3.70)
Это и есть двойственная задача, рассмотренная в гл. 2.
Теорема Куна — Таккера, теорема 3.22 являются обобщением теорем
для задач линейного программирования, изложенных в параграфе 2.8,
на нелинейные задачи оптимизации. Однако сразу заметим, что не все
утверждения, справедливые для задач линейного программирования,
допускают обобщения на нелинейные задачи. Так, например, из того, что
исходная нелинейная задача оптимизации имеет решение, не следует, что
двойственная к ней задача будет также иметь решение. Кроме того, нельзя
утверждать, что двойственная к двойственной задаче будет равносильна
исходной задаче. Для невыпуклых задач эта неравносильность очевидна,
так как ранее нами было показано, что двойственную задачу всегда можно
записать в виде выпуклой задачи, и поэтому двойственная к двойственной
задаче может быть равносильна исходной, только если исходная задача —
выпуклая. Но даже требование выпуклости исходной задачи не спа-
179

сает положение, причем даже в тех случаях, когда нормальная функция
Лагранжа исходной задачи имеет седловую точку. Поясним эти
рассуждения на примерах.
Пример 3.17
Рассмотрим выпуклую задачу
f(x) = -x->min, хеХ = {хеЕи.х>0,g(x) = х2<0}.
Здесь Х0 = [0; -и»), X = {0}, /* =0, X* =Х = {0}. Нормальная функция Лагранжа
для этой задачи имеет вид
L(x, Х) = -х + Хх2, х е Х0,Х е Л0 = [0; + «>).
1
Функция x\f(X) = inf L(x, Х) = —- при X > 0 и \(/(0) = -«>. Соответственно,
двойственно АХ
ная задача (3.58) имеет вид
\у(Х) = > max, X е Л = (0; + °°).
АХ
Множество Л — открытое, \|/* = /* = 0, но Л* = 0 Ф X*. Из этого вытекает, что L(x, X)
не имеет седловой точки на Х0 х Л0.
Пример 3.18
Рассмотрим задачу
f(x) = е~х-»min, хеХ = {хеЕи. g(x) = хе~х = 0}.
Здесь Х0 = Е{, X = {0}, /* = 1, X* = X = {0}. Запишем для этой задачи нормальную
функцию Лагранжа:
L(x,X) = е~х + Ххе~х, хеХ0,ХеА0=ЕК
Функция \|/(Х) = inf L(x, X) = Xexpl —— при X < 0, \|/(0) = 0 и ц(Х) = -«> при X > 0.
Двойственная задача (3.58) имеет вид
[ —
ц(Х) = \Хек пРиХ<0>->тах, ХеЛ = (-оо;0].
[0приЛ = 0
Множество Л — замкнутое, \|/* = 0 < /*, Л* = {0}. И в этом примере 1(х, X) не имеет
седловой точки на Х0 х Лф.
Пример 3.19
Рассмотрим выпуклую задачу
f(x) = -7*i*2 ~~> т*п> xeX = {x = (xvх2)еЕ2: хх >0,х2 >0,g(x) = x{<0}.
Здесь X0 = {x = (xvx2)eE2:x{>0,x2>0} = E2,X = {(0,tXt>0},f*=0,X*=X.
Нормальная функция Лагранжа для этой задачи имеет вид
L(x, X) = -7*i*2 + ^*i> * € Х0 Д е Л0 = [0; + с»).
180

Ясно, что функция \|/(Л) = inf L(x,X) = -«> для всех X > О, поэтому в этом примере
хеЕ%
двойственная задача бессмысленна.
Пример 3.20
Рассмотрим выпуклую задачу
/(*) = \\xf->min, хеХ = {хеЕп:g(x) = \\xf-1 < 0}.
Здесь Х0 = En, f* = 0, x* = (0,0,..., 0). Нормальная функция Лагранжа выглядит так:
Цх, X) = Ы|2 + X(\\xf -1) = (1 + Х)Ы|2 - X, х е Х0Д е Л0 = [0; + «>).
Очевидно, что \\f(X) = inf ДхД) = -X при всех X е А*. Таким образом, двойствен-
хеЕп
ная задача (3.58) имеет вид x\f(X) = -X —> max, X е Л = [0; -и»). Здесь \|/* = 0 = /*, Л* = {0};
седловой точкой нормальной функции Лагранжа будет (х*, X*) = ((0,0,..., 0), 0).
В примере 3.20 двойственная задача получилась задачей линейного
программирования. Как было показано в параграфе 2.5*, тогда двойственная
к двойственной задаче будет также задачей линейного программирования,
и она вовсе не совпадает с исходной нелинейной задачей.
Пример 3.21
Рассмотрим задачу так называемого геометрического программирования:
g(x) = yZci(xx)an~-(xr)air ->min, xeX = intEl, (3.71)
i=\
где intEZ = {x = (x1,...,xr):x1>0,...,xr >0}; c{> 0, atj, i = 1, ..., nj = 1, ..., r, — заданные
числа. Функция/(х) из (3.71) называется позиномом. Примером позинома может
служить функция Кобба — Дугласа, упомянутая в параграфе 1.3.
Для исследования этой задачи удобнее перейти к новым переменным и = (щ,...,
Ur+n) по формулам
г
щ = 1пх*, г = 1,..., г; ur+i = -Ъ{ + £ a¥ujt Ъ{ = -lncf, г = 1,..., п, (3.72)
и переписать ее в эквивалентном виде:
п
f(u) = Xeur+i -»min, ueU,
i=\
U = \ueEr+n: £я^м, -wr+f-b{ = 0, i = 1,...,я[.
(3.73)
Отметим, что функция f(u) выпукла на Е^*1, U — многогранное множество.
Составим нормальную функцию Лагранжа для этой задачи:
L(u,X) = £eur+i+%Xi
i=\
i=\
ЪЪЪ-иы-Ь \ =
= S(el^-MrH-XIA-)+2; S^-X,- \ир ueU0 = E™, XeA0 = E«.
С помощью классического метода нетрудно показать, что нижняя грань функции
ф(г) = е2 - Xtz - Хр{ переменной z на числовой оси равна ф* = Х{ - Х{ In Х{ - Х{Ь{, причем
181

при Xj> О она достигается в точке z* = -ln^; функция ^1пЛг при Х{= О здесь считается
доопределенной по непрерывности нулем. Отсюда, опираясь на линейность
функции L(u, X) по переменным щ,..., uv получаем
\|/(Х)= inf L(u,X) =
ueEr+n
yZ(Xi-XilnXi-Xibi\XeE^.'ZaijXi=OJ = l,...,r,
-oo при других X.
Поэтому двойственная задача (3.58) здесь будет иметь вид
п
\|/(Х) = X O^i - \ In Xt - Xfo ) -»max, X e Л,
i=\
A = \X = (Xx,..^n)eE«:ZaijXi=OJ = l,...,r\.
(3.74)
Если здесь верхняя грань достигается в точке X* Ф О, то задачу (3.74) можно
записать в более простой форме. А именно, учитывая, что любую точку X = (Х{,..., Хп) Ф О
можно представить в виде X = ац, где
п Х-
задачу (3.74) перепишем сначала в терминах переменных (а, ц):
^i(oc,|li) = \|/(ац) = £а(|И; - ц, 1па^ - цД) =
= а 1 - 1П0С + 2(|LLf 1пСг - jLlf lnjLl,)
—>max, (а^еЛ^
A1 = Ua,|ii):a>0,|iie^,X^ = l,S^^=0,; = l,...,r[.
Далее, пользуясь классическим методом поиска экстремума, нетрудно получить,
>0 (здесь принято 0°= 1) доставляет функции xj/^a, ц) мак-
что число а* = П
i=\
а-1
симальное значение по a > 0 при фиксированном jul е Е%, причем xj/^a*, ц) = П
Тогда двойственная задача (3.74) перепишется в следующем виде:
г#л
\^i )
A2=\\i = (\iv...,\in)eE!l:fJiii=l,fJaij\ii=0J = l,...,r\.
i=\
i=\
(3.75)
Если jli* = (jLiJ,...,|Li*)eint2i^ — решение задачи (3.75), то, полагая X* = a*\i*, где
( \ъ
—7 , иг+1*=Х*{, i = 1, ..., я, из системы линейных алгебраических уравне-
ний (3.72) можно найти щш,...,иГш, откуда имеем решение х* =(xl =eur,...,xl =еиг*)
исходной задачи (3.71). Задача (3.75) часто бывает проще задачи (3.71). Переход
к двойственной задаче особенно эффективным оказывается тогда, когда множество
Л2 в задаче (3.75) состоит из единственной точки ц*, которая и будет решением этой
задачи.

Упражнения
3.1. Исследуйте на выпуклость, вогнутость, сильную выпуклость,
сильную вогнутость функции одной переменной в области их определения:
a) /(*) = *3; б) Ах) = х*\ в) /(*) = -1шг, г) /(*) = -; д) /(*) = е™\
х
3.2. Выясните, при каких значениях параметров будут выпуклыми,
вогнутыми, сильно выпуклыми, сильно вогнутыми на указанных
множествах функции:
а) Ах) = ах2+Ьх + СуХ= (-оо; +оо);
6)Ах)=хр1Х=(0;+оо);
в) Ах) = (х2-тХ= (-со; +оо), пеN;
г) Ах) = (sin х+1)р,Х= (-я; 0), р > 0;
д)/(х) = |1пх|р,Х1 = (0;1],Х2=[1;4-),Х3=(0;4-),р>0.
3.3. С помощью теоремы 3.2 докажите, что на указанных множествах
будут выпуклы функции:
а) f(u) = ^jl + x2+y2, и = (х,у) е U= E2;
6)f(u) = —yU={u = (x,y)eE2: y>0}.
У
3.4. Выясните, при каких значениях параметров будут выпуклыми,
вогнутыми, сильно выпуклыми, сильно вогнутыми на указанных
множествах функции нескольких переменных:
а) Аи) =Qx2 + 2bxy + су2, и - (х, у) е U = Е1;
6)Au)=xPyq, U={u = (xyy)e E2: х>0уу>0};
в)/(10 = Ми|М =
r)f(u) = (Au,u),A =
fa
\b
1°
fa
b
,0
b
a
b
b
a
b
°1
b
aj
°)
b\
a]
и = (xy y, z) e U= E3;
u = (x,y>z) e U= E3.
3.5. Исследуйте на выпуклость и сильную выпуклость на всем
пространстве Еп функцию f(x) = \\х\\ - (с, х)2, где с е Еп — заданный вектор.
3.6. Исследуйте на выпуклость и сильную выпуклость в зависимости
от параметра X > 0 функцию /(х) = |Ы| -Х|Ы| на множествах Хх = Еп>
Х2={хе Еп:(с,х) > 1}, где с е Еп — заданный ненулевой вектор.
3.7. Приведите пример выпуклых на Е1 функций/(х) ng(x) таких, что их
суперпозиция h(x) =A§(X)) не будет выпуклой на области ее определения.
3.8. Приведите пример вогнутой на множестве X функции Ах) такой,
что функция \АХ)\ выпукла на X.
3.9. Пусть Ах) и g(x) — выпуклые на X функции. Будет ли их
произведение выпуклым на X?
3.10. X с Еп — выпуклое множество. Докажите, что расстояние
р(хуХ) = inf || у - х || от точки х до множества X является выпуклой функ-
уеХ
цией переменной х на всем пространстве Еп.
183

3.11. Пусть U с Еп — выпуклое множество, intC/ Ф 0, функция f(x)
выпукла и принимает конечные значения на U. Докажите, что она
непрерывна на intC/. Приведите пример выпуклой функции, имеющей точки
разрыва на границе Гр U множества U.
-, если у Ф О,
является выпуклой
3.12. Докажите, что функция f(u) = 1 у
[О, если у = О
на множестве U = {и = (х, у) е Е2 : у > 0} и {(0; 0)} и полунепрерывной
снизу на нем. Проверьте, что она не будет полунепрерывной сверху в точке
(0; 0) и, более того, для любого а > 0 существует такая последовательность
{щ} -» (0; 0), что lim f(uk) = a.
&->оо
3.13. Докажите, что если выпуклая функция непрерывна и ограничена
сверху на Еп, то она является постоянной.
3.14. Докажите, что выпуклая функция, отличная от постоянной, может
достигать своей точной верхней грани на выпуклом множестве только в его
граничных точках.
3.15. Может ли выпуклая функция на выпуклом замкнутом
ограниченном множестве иметь много локальных максимумов, и при этом не
достигать своей точной верхней грани на нем? Рассмотрите пример
1
U = {u = (x,y)eE2:x2+y2<l}, f(u) =
-, w=(i;0),
л 1
1--, и = щ =
(
•-*
26-1
k2
0 в остальных точках.
3.16. Решите выпуклые задачи безусловной минимизации:
а) f(u) = х2 - ху + у2 + 3\х - у - 2| —> min, и = (хуу) е Е2;
б) f(u) = х2 + у2 + 4 тах{х; у} —> min, и = (х, у) е Е2.
3.17. Пусть X = {х е Еп: (q, х) > 1, (с2, х) > 1}, q, с2 Ф 0, (q, c2) = 0. Найдите
проекцию нулевого вектора (0,..., 0) на множество X.
3.18. Пусть А, В — выпуклые множества из Еп, Ет соответственно, пусть
' I - (Ра(<*))
е Ет+п. Докажите, что Pz (z ) =
Z = AxB,z =
fa\
Л
Рв(Ь)
3.19. Выведите формулу для проекции на множество
X = {(x1,...yxn)eEn:x1>yj(x2)2+... + (xn)2}.
Сравните полученный результат с результатом примера 3.9.
3.20. Постройте двойственные задачи к задачам:
а) Аи) = х\ + 2х2 + 2х3 + хА + х5 —» min, и е U, U = {и- (хь х2, х3, хА, х5) >
> 0 : хх + х2 + х3 + хА + 2х5 = 2; хх -х3 + 2хА + х5= 1};
я| • i f я ■ 1
б) f(u)=Yax1 -ai: -* т*п> w E ^=iw=(**> •••> *я)Е £": X** = о г> где^ Е R»
i = 1,..., я (cm. [36, с 185, пример 3.1]).
Найдите решения исходных и двойственных к ним задач.
184

3.21. Пусть в задаче (3.51) множество Х0 выпукло, функции g\(x), ...,
gjx) выпуклы на Х0, функцииgm+1(x),..., gm+s(x) линейны: g((x) = (а{, х) + Ъ{,
at e En, 6feM,i = m+l,..., т + s. Докажите, что тогда множество X из (3.51)
выпукло. Докажите, что штрафная функция
т m+s
ад = Х(тах{&(*),0})Р+ S \gi(x)\P,xeX0yp>l
i=l i=m+l
выпукла на Х0.
3.22. Пусть функция Лагранжа задачи (3.51) имеет седловую точку
(х*> V). Докажите, что тогда
m+s.
а) /* <f(x)+ X |^i|g/4x)> т-е- заДача (3.51) имеет согласованную поста-
i=i
новку (см. определение 1.28);
б) задача (3.51) равносильна задаче со штрафами
m+s
Ф(х, А) = f(x) + Л £ gf (x) -> min, А > max{| XJ |,..., | X*m+S |},
т.е.ттФ(х,А) = Ф.=/.,Х*(А) = {хеХ0:Ф(х,А) = Ф.} = Х*.
xeX0

Глава 4
МЕТОДЫ МИНИМИЗАЦИИ ФУНКЦИЙ
Выше, в гл. 2, был рассмотрен симплекс-метод для решения задач
линейного программирования. Перейдем к изложению других методов
минимизации функций конечного числа переменных, не предполагая линейности
рассматриваемых задач.
К настоящему времени разработано и исследовано большое число
методов минимизации функций многих переменных. Мы ниже остановимся
на некоторых наиболее известных и часто используемых на практике
методах минимизации, будет дано краткое описание каждого из
рассматриваемых методов, исследованы вопросы сходимости, обсуждены некоторые
вычислительные аспекты этих методов. При этом мы ограничимся
рассмотрением лишь одного-двух основных вариантов излагаемых методов, чтобы
ознакомить читателя с основами этих методов, полагая, что знание основ
методов облегчит читателю изучение литературы, позволит ему без особого
труда понять суть того или иного метода и выбрать подходящий вариант
метода или самому разработать более удобные его модификации, лучше
приспособленные для решения интересующего читателя класса задач.
4.1. Методы минимизации функций одной переменной
Рассмотрим задачу минимизации функции одной переменной на отрезке
/(x)^min, xeX = {xeE1:a<x<b}. (4.1)
Может показаться, что эта задача проста и здесь вполне можно
обойтись обобщением классического метода, рассмотренного в гл. 1, а именно,
мы, решая уравнение f'(x) = О, находим какие-то точки, подозрительные
на экстремум, к этим точкам добавляем концы отрезка х = а, х = Ь, а также
точки, где производная f'(x) не существует. Затем для выяснения характера
экстремума в отобранных точках исследуем поведение целевой функции
в окрестности этих точек. Возможно, здесь нам помогут теоремы Вейерш-
трасса 1.2—1.4, теоремы 3.3, 3.4, не исключено, что нам придется
придумывать специальные приемы, основанные на явном виде функции f(x). Это
непростая работа. Также следует отметить, что поиск корней уравнения
f'(x) = О может оказаться задачей, по сложности не уступающей исходной
задаче (4.1). Так что в большинстве случаев обобщением классического
метода здесь не обойтись.
Обсудим несколько известных методов поиска приближенного решения
задачи (4.1).
186

4.1.1. Метод деления отрезка пополам
Простейшим методом минимизации функции одной переменной,
не требующим вычисления производной, является метод деления отрезка
пополам. Опишем его, предполагая, что минимизируемая функция f(x)
унимодальна на отрезке [а; Ь].
Определение 4.1. Функцию/(х) назовем унимодальной на отрезке [а; Ь]>
если она непрерывна на нем и существуют числа а, Р (а < а < Р < Ь) такие,
что:
1) f(x) строго монотонно убывает при а < х < а (если а < ос);
2) f(x) строго монотонно возрастает при Р < х < b (если Р < Ь);
3) f(x) = /* = inf f(x) при а < х < Р, так что X* = [ос; Р].
хе[а,Ь]
Случаи, когда один или два из отрезков [а; ос], [а; Р], [Р; Ь] вырождаются
в точку, здесь не исключаются. В частности, если а = Р, то функцию f(x)
назовем строго унимодальной на отрезке [а; Ь].
Поиск минимума функции/(х) на [а; Ь] начинается с выбора двух точек
хх = {а + Ъ - 8)/2 их2=(а + Ь + 5)/2, где 8 — постоянная, являющаяся
параметром метода, 0 < 8 < b - а. Величина 8 выбирается нами и может
определяться целесообразным количеством верных десятичных знаков при
задании аргумента х. В частности, ясно, что 8 не может быть меньше машинного
нуля ЭВМ, используемой при решении рассматриваемой задачи. Точки хь
х2 расположены симметрично на отрезке [а; Ь] относительно его середины
и при малых 8 делят его почти пополам — этим и объясняется название
метода.
После выбора точек х1у х2 вычисляются значения f(x1)yf(x2) и
сравниваются между собой. ЕслиД^) <f(x2), то полагают ах = a, bt = х2; если же
f(xi) >f(x2)> то полагают ах = хь bx = b. Поскольку/(х) унимодальна на [а;
Ь], то ясно, что отрезок [aly bt] имеет общую точку с множеством X* точек
минимума f(x) на [а; Ь] и его длина в любом случае равна
, b-a-Ъ с
щ -а< = + 8.
1 * 2
Далее процесс продолжается аналогичным образом: пусть отрезок [ak_t;
bk_x], имеющий непустое пересечение с X*, уже известен, и пусть
^_1-а,_1=^^+5>5(А>2).
Тогда берем точки x2k_x = (ak_t + bk_x - 8)/2, x2k= (ak_t + bk_x + 8)/2,
расположенные на отрезке [ak_t; bk_t] симметрично относительно его середины,
и вычисляем значения функции f(x2k_x),f(x2£). Если/(х2^_1) <f(x2k)> то
полагаем ak=ak_b bk = x2k; если же/(^_!) >f(x2k), то полагаем ak = x2k_b bk=bk_t.
Длина получившегося отрезка [ak; bk] равна bk- ak= (b - a - b)/2k +Ь>Ь
u[ak;bk]nX* *0.
Если количество вычислений значений минимизируемой функции
ничем не ограничено, то описанный процесс деления отрезка пополам
можно продолжать до тех пор, пока не получится отрезок [ak; bk] длины
bk- ak<E, где е — заданная точность поиска точки минимума в задаче (4.1),
187

e > 8. Отсюда имеем, что k > log2[(fe - а - 5)/(е - 8)]. Поскольку каждый
шаг метода деления пополам требует двух вычислений значений функции,
то нам требуется всего n = 2k> 2\og2[(b -а-5)/(е-8)] таких вычислений.
После определения отрезка [ak; bk] в качестве приближенного
решения задачи можно взять точку x = x2k_t при f(x2k_t) ^ f(^2k) и % = x2k
при f(x2k-i) > f(x2k)- Значение f(x) может служить приближением для
/* = inf f(x). При таком выборе точки х будет допущена погрешность
хе[а,Ь]
p(x,X*)<max{bk-x;x-ak} = (b-a-b)/2k. Можно поступить по-другому
и в качестве приближенного решения предложить точку v = (ak + bk)/2
с погрешностью p(v,X*)<(bk-ak)/2 = (b-a-S)/2k+1 +8/2, при
достаточно малых 8 погрешность для точки v будет меньше погрешности
для точки х.
Однако в этом случае придется провести еще одно дополнительное
вычисление значения функции в точке v и принять f(v) = /*. Увы, на
практике нередко встречаются функции, нахождение значения которых в
каждой точке связано с большим объемом вычислений или дорогостоящими
экспериментами, наблюдениями; понятно, что здесь приходится дорожить
каждым вычислением значения минимизируемой функции. В таких
ситуациях возможно даже, что число п, определяющее количество вычислений
значений функции, заранее жестко задано и превышение его недопустимо.
Из предыдущего следует, что методом деления отрезка пополам с
помощью п = 2k вычислений значений функции можно определить точку
минимума унимодальной функции на отрезке [а; Ь] в лучшем случае с
точностью (b - a)/2k+1.
В заключение отметим, что метод деления отрезка пополам без
изменений можно применять для минимизации функций, не являющихся
унимодальными. Однако в этом случае нельзя гарантировать, что найденное
решение будет достаточно хорошим приближением к глобальному
минимуму.
4.1.2. Метод золотого сечения
Перейдем к описанию метода минимизации унимодальной функции
на отрезке, столь же простого, как метод деления отрезка пополам, но
позволяющего решить задачу с требуемой точностью при меньшем количестве
вычислений значений функции, а именно, к методу золотого сечения.
Как известно, золотым сечением отрезка называется деление отрезка
на две неравные части так, чтобы отношение длины всего отрезка к длине
большей части равнялось отношению длины большей части к длине
меньшей части отрезка.
Нетрудно проверить, что золотое сечение отрезка [а; Ь] производится
двумя точками
Xl=a+?——(b-a) = a + 0y381966011(b-a);
x2=a+^—±(b-a) = a + 0,618033989(b-a),
188

расположенными симметрично относительно середины отрезка, причем а <
<хх<х2<Ь,
b-xt xt-a x2-a b-x2 2
Замечательно здесь то, что точка хх в свою очередь производит золотое
сечение отрезка [а; х2], так как х2 - хх < хх - а = Ъ - х2 и (х2 - a)/(xt - а) =
= (xt - а)/(х2-хх). Аналогично, точках2 производит золотое сечение отрезка
\х{, Ь]. Опираясь на это свойство золотого сечения, можно предложить
следующий метод минимизации унимодальной функции/(х) на отрезке [а; Ь].
Положим ах = ayb1 = b. На отрезке [at; bt] возьмем точки хь х2,
производящие золотое сечение, и вычислим значения f(xx),f(x2). Далее, если/^)
< f(x2), то примем а2 = аь Ъ2 = х2, х2 = х{, если же f(xt) > f(x2)> то примем
а2 = хь Ъ2 = Ьь х2 = х2. Поскольку функция f(x) унимодальна на [а; Ь]> то
отрезок [а2; Ь2] имеет хотя бы одну общую точку с множеством X* точек
минимума функции/(х) на [а; Ь]. Кроме того, Ъ2-а2
и весьма важно то, что внутри [а2; Ь2] содержится точка х2 с вычисленным
значением функции f(x2) = min{f(x1);f(x2)}y которая производит золотое
сечение отрезка [а2; Ь2].
Далее, пусть уже определены точки х1у ..., хп_х (п > 3), в них
вычислены значения функции f(xt), ..., f(xn_t), найден отрезок [ап_х\ Ьп_х]
такой, что [an_1;bn_i]nX**0> bn_1-an_1 =
fS-iT2
(b-a), и известна
точка хп_ь производящая золотое сечение отрезка [ап_{, Ьп_х] и такая, что
f(xn_t)= min f(x(). Тогда в качестве следующей точки возьмем точку
l<i<n-l
хп =an_1+bn_1-xn_v также производящую золотое сечение отрезка [ап_1у
6„_i], и вычислим значение f(xn).
Пусть для определенности ап_х <хп< хп_х < Ьп_х (случай хп_х < хп
рассматривается аналогично). Если f(xn)<f(xn_x), то полагаем ап= ап_ь
bn=xn_v хп =хп; если же f(xn)>f(xn_x), то полагаем ап = хп, Ъп = Ьп_ь
хп=хп_1. Новый отрезок [ап; Ьп] таков, что [ап;Ьп]пХ*Ф0, Ъп - ап =
1 (Ь-а), точка хп производит золотое сечение отрезка [ап; Ьп]
и f(xn ) = min{f(xn ); f(xn_t)} = min f(x().
\<i<n
Если число вычислений значений функции f(x) заранее не ограничено,
то описанный процесс можно продолжать, например, до тех пор, пока
не выполнится неравенство Ьп- ап< е, где е — заданная точность
нахождения приближенного решения задачи (4.1). Если же число вычислений
значений функции/(х) заранее жестко задано и равно п, то процесс на этом
заканчивается и в качестве решения задачи второго типа можно принять
пару х = хп, fix), где f(x) является приближением для /* = inf f(x),
xe[a;b]
а точка х служит приближением для множества X* с погрешностью
189

75-1 Гл/5-lT
p(x,X*)<max{bn-xn;xn-an} = ——(Ьп-ап) = \——\ (b-a) = An.
A V Z J
Вспомним, что с помощью метода деления отрезка пополам за п = 2k
вычислений значений функции f(x) в аналогичном случае мы получили
точку х с погрешностью
,_ v..b-a-Ъ Ъ-а
Р<<х>х*^^7^<^72=вп'
n \ Гл/5-lY
Отсюда имеем —^ = —^~
Вп { л/2
= (0,87)" — очевидно, что уже при
небольших п преимущество метода золотого сечения перед методом деления
отрезка пополам становится ощутимым.
Кратко обсудим возможности численной реализации метода золотого
сечения. Заметим, что число в машинном представлении неизбежно
будет задано приближенно, поэтому первые точки хь х2 будут найдены
с погрешностью. В дальнейшем если на отрезке [ап; Ьп], содержащем точку
хп с предыдущего шага, при выборе следующей точки хп+1 на каждой
итерации пользоваться симметричной формулой хп+1 =ап+Ьп-хп>то
погрешности, поначалу допущенные на первом шаге, могут быстро накапливаться,
и метод начнет порождать точки, далекие от ожидаемых точек при работе
с точными данными. Поэтому на практике на каждом шаге метода в
качестве точки хп+1 лучше взять ту из точек an+(3->J5)(bn-an)/2 или
ап +(V5 -l)(bn -ап)/2, которая наиболее удалена от хп (здесь под л/5
подразумевается какое-то из приближений этого числа). Этот простой прием
делает метод более устойчивым и позволяет избежать быстрого нарастания
погрешностей.
4.1.3. Метод ломаных
Описанные выше методы часто приходится применять без априорного
знания о том, что минимизируемая функция является унимодальной.
Однако в этом случае погрешности в определении минимального значения
и точек минимума функции могут быть значительными. Например,
применение этих методов к минимизации непрерывных на отрезке функций
приведет, вообще говоря, лишь в окрестность точки локального минимума,
в которой значение функции может сильно отличаться от искомого
минимального значения на отрезке. Поэтому представляется важной разработка
методов поиска глобального минимума, позволяющих строить
минимизирующие последовательности и получить приближенное решение задач
минимизации первого и второго типов для функций, не обязательно
унимодальных. Здесь мы рассмотрим один из таких методов для класса
функций, удовлетворяющих условию Липшица.
Напомним, что функция/(х) удовлетворяет условию Липшица на отрезке
[а; Ь], если существует постоянная L > 0 такая, что
\f{x)-f{y)\<L\x-y\ Ух,уе[а;Ь]. (4.2)
190

Постоянную L называют постоянной Липшица функции f(x) на отрезке
[а; Ь].
Условие (4.2) имеет простой геометрический смысл: оно означает, что
угловой коэффициент (тангенс угла наклона) . — , хорды, соеди-
1*-у|
няющей точки (х> f(x)) и (г/, /(г/)) графика функции, не превышает
постоянной L для всех точек х, у е [а; Ь]. Из формулы (4.2) следует, что
функция/(х) непрерывна на отрезке [а; Ь], так что по теореме 1.2 множество X*
точек минимума/(х) на [а; Ь] непусто.
Теорема 4.1. Пусть функция f(x) непрерывна на отрезке [а; Ь] и на
каждом отрезке [а(; ai+1], i = 1, ..., т, где ах = а> ат+1 = Ь> удовлетворяет
условию (4.2) с постоянной Ц. Тогда f(x) удовлетворяет условию (4.2) на всем
отрезке с постоянной L = max L.
l<i<m
Доказательство
Возьмем две произвольные точки х, у е [а; Ь]. Пусть ар<х<ар+1>
as<y< as+1 при некоторых р, s е {1,2,..., т}> p<s.B случае р = s очевидно,
что \f(x) - f(y)\ < Lp \x - у\ < L \х - у\. Если р < s, то
|/W-/(y)|=^
+ /(«s ) " /(#) ^Lp\X~ ар+11+ LP+1 |flP+l " аР+2| + - + Ls-\ \as-\ ~as\ + Ls \as -У\^
^L(ap+1-x + ap+2-ap+1+... + as-as_1+y-as) = L\x-y\y
что и требовалось доказать. ■
Теорема 4.2. Пусть функция f(x) дифференцируема на отрезке [а; Ь]
и ее производная f\x) ограничена на этом отрезке. Тогда f(x)
удовлетворяет условию (4.2) с постоянной L = sup |/'(*)!•
хе[а,Ь]
Доказательство
По формуле конечных приращений (1.113) для любых точек х, у е [а; Ь]
имеем/(х) -f(y) =f'(y + 6(x - у))(х - г/), 0 < 6 < 1. Отсюда и из
ограниченности f'(x) следует утверждение теоремы. ■
Перейдем к описанию метода ломаных. Пусть функция f(x)
удовлетворяет условию (4.2) на отрезке [а; Ь]. Зафиксируем какую-либо точку
у е [а; Ь] и определим функцию g(x, у) = f(y) - L\x - у\ переменной х
(а<х< Ь). Очевидно, что функция g(x, у) кусочно-линейна на [а; Ь]> и
график ее представляет собой ломаную линию, составленную из отрезков
двух прямых, имеющих угловые коэффициенты L и -L и пересекающихся
в точке (y>f(y)). Кроме того, в силу условия (4.2)
f(x)-g(xyy) = f(x)-f(y) + L\x-y\>L\x-y\-\f(x)-f(y)\>0 \/xyye[a;b],
т.е.
g(x,y) = f(y)-L\x-y\<f(x) \/xe[a;b]y (4.3)
причем g(y, у) = f(y). Это значит, что график функции f(x) лежит выше
ломаной g(x, у) при всех х е [а; Ь] и имеет с ней общую точку (y>f(y)).
191

Свойство (4.3) ломаной g(x> у) можно использовать для построения
следующего метода, который и называется методом ломаных. Этот метод
начинается с выбора произвольной точки х0 е [а; Ь] и составления функции
g(x,x0) = f(x0)-L\x-x0\=p0(x).
Следующая точка хх определяется из условий
Po(*i) = min p0(x), ххе[а\Ъ\
хе[а,Ь]
Очевидно, что х1 = а или х1 = Ъ. Далее берется новая функция
Pi(x) = max{g(x, xt); p0(x)}> очередная точка х2 находится из условий
Pi(x2) = т^п Pi(x)> x2 e ia'y Н Далее процесс продолжается таким же
образа; Ь]
зом, а именно, пусть точки х0> х1у..., хп, я > 1, уже известны, тогда
составляется функция
Рп (х) = max{g(x, хп ); рп_х (х)} = max g(x, x{),
0<г<п
и следующая точка хп+1 определяется условиями
Pn(xn+i)= mini pn(x),xn+1e [a;b]. (4.4)
хе[а; b]
Если минимум рп(х) на [а; Ь] достигается в нескольких точках, то в
качестве хп+1 можно взять любую из них. Метод ломаных описан. Его
применение проиллюстрировано на рис. 4.1, на котором график функции/(х)
изображен жирной линией, ломаная ABC — часть графика функции g(x, x0) =
= Ро(х), отрезок DE — часть графика функции g(x, xt), ломаная ABFD —
график функции Р\(х)> ломаная PQR — часть графика функции g(x> x2)>
ломаная ABSPTD — график функции р2(х)> отрезок KL — часть графика
функции g(x, x3), ломаная KMBSPTD — график функции р3(х).
Рис. 4.1
192

Очевидно, что рп(х) является кусочно-линейной функцией, и график ее
представляет собой непрерывную ломаную линию, состоящую из отрезков
прямых с угловыми наклонами L или -L. Из теоремы 4.1 следует, чторп{х)
удовлетворяет условию (4.2) с той же постоянной L, что и функция/(х).
Ясно также, что
pn_t(x)= max g(x,xi)<maxg(x,xi) = pn(x),xe [a;b]. (4.5)
0<i<n-l 0<i<n
Кроме того, согласно формуле (4.3) справедливо неравенство g(x, x() <
<f(x) при всех х е [a; b], i = О, 1,..., п, поэтому
рп(х)<f(x) Vxe[a,b],n = 0,l,.... (4.6)
Таким образом, на каждом шаге метода ломаных задача минимизации
функции f(x) заменяется более простой задачей минимизации кусочно-
линейной функции рп(х), которая приближает f(x) снизу, причем в силу
соотношения (4.5), последовательность \рп(х)} неубывает при любом фик-
сированнном х е [а; Ь]. Докажем теорему о сходимости метода ломаных.
Теорема 4.3. Пусть f(x) — произвольная функция, удовлетворяющая
на отрезке [а; Ь] условию (4.2). Тогда последовательность {хп}, полученная
с помощью описанного метода ломаных, такова, что:
1) lim f(xn)= lim pn(xn+1) = /* = inf f(x), причем справедлива оценка
я—><» я—>«> хе[а,Ь]
0<f(xn+1)-f* <f(xn+1)-pn(xn+1), я = 0,1,...; (4.7)
2) {хп} сходится к множеству X* точек минимума функции f{ос) на [а; Ь],
т.е. lim р(хп, X*) = 0.
Я—>°о
Доказательство
Возьмем произвольную точку х* е X*. С учетом условий (4.4) и
неравенств (4.5), (4.6) имеем
Pn-l(Xn) = ™*Pn-l(x) ^ Pn-l(Xn+l) ^ Pn(Xn+l) =
xe[a;b]
= шп ря(.х)йря(х.)й/(х*) = /„
xe[a;b]
т.е. последовательность \рп(хп+1)} неубывает и ограничена сверху. Отсюда
сразу следует оценка (4.7) и существование предела lim pn(xn+1) = p* </*.
Я—><»
Покажем, что /?*=/*.
Последовательность {хп} ограничена и по теореме Больцано — Вейерш-
трасса обладает хотя бы одной предельной точкой. Пусть v* — какая-либо
предельная точка последовательности {хп}. Тогда существует ее
подпоследовательность {хщ}, сходящаяся к v*. Заметим, что/(^) = g(xiy x() <рп{х^) <
<f(xt), т. е./(х() =pn(xi) при всех г - 0, 1,..., п. Тогда
0 ^ Рп (*,■) " min рп (х) = f{xi) - рп (хп+1) = рп (х{) - рп (хп+1 )<L\xi- xn+11
хе[а,Ь]
при всех п = 1, 2, ..., i = 0, 1, ..., п. Принимая здесь п = nk- 1, i = nk_x <
<nk-\, получаем0</(*„w)-Pnk-i(xnk)^L\x4_x ~x4 ik = 2> 3,.... Отсюда
при & —> °° имеем
193

/. < /(о.) = lim f(xnk{) = hmp^x^ ) = p*< /.,
т.е. \imf(xn)=\impnl(xn) = p*=f*. Пользуясь тем, что рассуждения
проведены для произвольной предельной точки v* последовательности
{хп}> убеждаемся в справедливости первого утверждения теоремы. Второе
утверждение следует из теоремы 1.1. ■
Таким образом, с помощью метода ломаных можно получить решение
задач минимизации первого и второго типов для функций,
удовлетворяющих условию (4.2). Проста и удобна для практического использования
формула (4.7), дающая оценку неизвестной погрешности f(xn+i)-f* через
известные величины, вычисляемые в процессе реализации метода
ломаных. Этот метод не требует унимодальности минимизируемой функции, и,
более того, функция может иметь сколько угодно точек локального
экстремума на рассматриваемом отрезке. На каждом шаге метода ломаных нужно
минимизировать кусочно линейную функцию рп(х)> что может быть
сделано простым перебором известных вершин ломаной рп(х)> причем здесь
перебор существенно упрощается благодаря тому, что ломаная рп(х)
отличается от ломаной pn_i(x) не более чем двумя новыми вершинами. К
достоинству метода относится и то, что он сходится при любом выборе
начальной точки х0.
Далее будет рассмотрен другой метод, по своей идее близкий к методу
ломаных, но более удобный для реализации на компьютере.
4.1.4. Метод покрытия
Обозначим через Q(L) класс функций, удовлетворяющих условию
Липшица (4.2) на отрезке [а; Ь] с одной и той же для всех функций этого класса
постоянной L > 0. Для функций f=f(x) e Q(L) будем рассматривать задачу
минимизации первого типа, когда ищется величина /* = inf f(x). Для
xe[a,b]
решения этой задачи можно пользоваться методами, которые заключаются
в выборе точек хь ..., хп, а<х1<...<хп< Ъ, вычислении значений функции
f(xt)y ..., f(xn) и определении величины /(хк)=тт/(х()> принимаемой
\<i<n
за приближение к /*.
Возникает вопрос: как выбрать метод так, чтобы при достаточно
больших п было верно
min/(*,)</*+е V/(*)eQ(L), (4.8)
\<i<n
где е > 0 — заданная точность? Ниже будет изложено несколько методов
решения поставленной задачи (4.8). В каждом из этих методов
определенным образом строится некоторая система отрезков, покрывающих
исходный отрезок [а; 6], и вычисляются значения функции в подходящим
образом выбранных точках этих отрезков. Поэтому излагаемые ниже методы
принято называть методами покрытия.
Простейшим методом для решения задачи (4.8) может служить метод
равномерного перебора, когда точки хь ..., хп выбираются по правилу
194

x1=a+—, xi+1=xi+h = x1+ih, z = l,...,n-%xn =mm{x1+(n-l)h;b}, (4.9)
где h = шаг метода, а число п определяется условием xn_i <b — < xx +
+ (n-l)h.
Теорема 4.4. Метод равномерного перебора (4.9) решает задачу (4.8)
2е
на классе Q(L). Если h> —, то существует функция f(x) е Q(I), для
которой метод (4.9) не решает задачу (4.8).
Доказательство
Пусть f = f(x) — произвольная функция из Q(L). С учетом неравенства
(4.3) для любого х е [х( - /г/2; х{ + /г/2] имеем
Lh
f(x)>f(xi)-L\x-xi\>f(xi)-—>mmf(xi)-e, г = 1,...,я.
Z \<i<n
Так как система отрезков [х(- /г/2; х{+ /г/2], г = 1, ..., п, покрывает
весь отрезок [а; Ь]> т.е. всякая точка х из [а; Ь] принадлежит одному
из отрезков этой системы, то из предыдущего неравенства следует, что
f(x) > min f(xt) - е для всех х е [а; Ь]. Поэтому /* > min f(x{) - е для любой
\<i<n \<i<n
2е
функции f=f(x) e Q(L)y что равносильно неравенству (4.8). Если h > —, то,
Lh
например, для функции/(х) = Lx метод (4.9) дает тт(Ьх{)-Ьа = — > е. ■
\<i<n 2
Метод равномерного перебора (4.9) относится к пассивным методам,
когда точки хь ..., хп задаются все одновременно до начала вычислений
значений функции. На классе Q(L) можно предложить такой же простой,
но более эффективный последовательный метод перебора, когда выбор
точки х-г при каждом г > 2 производится с учетом вычислений значения
функции в предыдущих точках хь ..., хм, и задачу (4.8) удается решить,
вообще говоря, за меньшее количество вычислений значений функции, чем
методом (4.9).
А именно, следуя работе [19], положим
х1-а +—> xi+1
= a + -y xi+1=xi+h + J l/—L,z = l,...,w-2,
Li
xn =mini^
(4.10)
2e
где h = —, F{ = min/(x7), а число п определяется условием
L i<j<t J
Xn_x<b-\<xn_x+h+f^l-F"-\
Теорема 4.5. Метод последовательного перебора (4.10) решает задачу
(4.8) на классе Q(L).
195

Доказательство
Пусть f = f(x) — произвольная функция из Q(L). С учетом неравенства
(4.3) для всех х е [xf; х( + /г/2 + (f(x() - F^/L] имеем
Кх)>_Кхд-1[\,М^±ув,-^В.-г.
Аналогично для всеххе [х(- /г/2; xt] получим f(x) > f(xf) - Lh/2 >Fn-E.
Поскольку система отрезков [xt- /г/2; х{+ h/2 + (f(xt) - Ft)/L]y i = 1, ..., n,
покрывает весь отрезок [а; Ь], то из предыдущих неравенств следует, что
f(x) >Fn-e при всеххе [а; Ь]. Тогда f*>Fn-e при всех/=/(х) е Q(L), что
равносильно неравенству (4.8). ■
В худшем случае, когда, например, функция f(x) постоянна или
монотонно убывает на [а; Ь] и, следовательно, Fi=minf(xj) = f(xi), метод
(4.10) превращается в метод (4.9), и для решения задачи (4.8) тогда
потребуется Nt~-— вычислений значений функции. В самом лучшем
2е
случае, когда f(x) = А + L(x - В), где А, В — постоянные, имеем Ft = /(х(),
х{ =x1+(2i~1 -1)/г, i=l, ..., п - 2, и для решения задачи (4.8) понадобится
всего N2 ~ 1 + log2 — вычислений значений функции. И вообще, если
/(хг) > Fj при каком-либо г, то xi+1 - xt > /г, и поэтому число п вычислений
значений функции, необходимое для решения задачи (4.8), будет, вообще
говоря, меньше Л^ и больше N2.
Заметим также, что метод (4.10) идейно примыкает к методу
ломаных, но при этом выгодно отличается простотой реализации. Недостатком
метода (4.10), как и метода ломаных, является необходимость априорного
знания постоянной L из условия (4.2).
Далее изложим еще один вариант метода покрытия для решения задачи
(4.8). Пусть зафиксирована сетка точек (4.9) с шагом h = 2e/L Выберем две
произвольные точки vb v2 этой сетки, вычислим значения f(px),f(v^)
минимизируемой функции и положим Fx =f(vt), F2 = тЭД; /(^2)} = minl/^);
f(v2)}. Имеются две возможности: либо F2 = f(v2) < Fly либо F2 = Fx <f(v2).
Если F2< Fb то из дальнейших рассмотрений исключаем точку v± вместе
F — F
с теми точками Хх сетки (4.9), для которых |jr7- — ^1 < — -, не вычисляя
значений f(Xj). Если F2= Fb то исключаем точку v2 вместе с точками Xj
сетки (4.9), для которых \xj -v2\< -— -. Начальный шаг метода описан.
Опишем общий шаг. Пусть в точках vb v2, ..., vk сетки (4.9) уже
вычислены значения функции f(vt), f(v2), ..., f(vk), найдена величина
Fk = mm{Fk_{, f(vk)} = min/(^), и пусть vh — та из точек vb v2,..., vh в кото-
\<i<k Jk
рой Fk =f(vj) = minf(vi). Далее возьмем любую точку vk+1 сетки (4.9), ко-
Jk \<i<k
торая на предыдущих шагах не исключалась и в которой еще не
вычислялось значение функции f(x). Вычислим f(vk+1) и найдем величину
Fk+1 =min{^;/(^+1)}= min /(р{). После этого имеются две возможности:
\<i<k+\
196

либо Fk+1 =f(vk+1) < Fh либо Fk+1 = Fk<f(vk+1). В первом случае, когда Fk+1 <
< Fky из дальнейших рассмотрений исключим точку Vj и вместе с нею те
точки Xj сетки (4.9), для которых
\Xj-Vjk\<Z^±. (4.11)
Заметим, что некоторые из этих точек могли оказаться исключенными
уже на предыдущих шагах. Для нас здесь важно лишь то, что среди
исключенных точек заведомо нет таких, в которых значение функции f(x) было
бы меньше, чем Fk+1. В самом деле, прежде всего f(Vj ) = Fk>Fk+1. Для
остальных исключенных точек Xj имеем
f{xj)-FM=f{xj)-f{vh) + Fk-FM>-L\xrvh\ + Fk-FM>0
в силу формул (4.3) и (4.11). Таким образом, без дополнительных
вычислений значений функции f(x) мы сумели выяснить, что исключенные точки
не являются перспективными с точки зрения получения в них значений
функции, меньших Fk+1.
Рассмотрим вторую возможность, когда Fk+1 = Fk <f(vk+1). Тогда из
дальнейшего перебора исключаем точку vk+1 вместе с точками Xj сетки (4.9),
для которых
\xj-vM\<f(Vk^-Fk. (4.12)
Нетрудно убедиться, что и в этом случае в исключенных точках
значения функции не могут быть меньше Fk+1. В самом деле, здесь
f(xj)-Fk+i=f(xj)-Fk=f(xj)-f(vM)+f(PM)-Fk *
>-L\xj-vk+i\ + f(vk+i)-Fk>0
в силу формул (4.2) и (4.12). Общий шаг метода описан.
Так как на каждом шаге метода берется новая точка сетки (4.9),
которая еще не исключена из перебора и в которой значение функции/(х) еще
не вычислялось, то ясно, что на каком-то шаге такие точки будут
исчерпаны и описанный процесс закончится за N шагов, N<n, перебором точек
vb v2,..., vNсетки (4.9) и вычислением величины FN = min f(v{) = min/(#,-).
\<i<N \<i<n
Теорема 4.6. Пусть f(x) — произвольная функция из класса Q(L), и пусть
сетка точек {хь ..., хп} определена согласно (4.9). Тогда найденная методом
последовательного перебора (4.11), (4.12) величина FN = minF(xi) решает
\<i<n
задачу (4.8).
Доказательство
Так как система отрезков [xt- h/2; х{+к/2\, i = 1,..., п, образует покрытие
отрезка [а; Ь], то для любой точки х е [а; Ь] найдется точка Xj сетки (4.9)
такая, что \х - х ■ I < h / 2. Тогда
Lh
f(x) = f(x)-f(Xj) + f(Xj)>-L\x-xj\ + FN>-^FN=FN-E
для любого х е [а; Ь]. Следовательно, /* >Fn-e> т.е. выполняется
неравенство (4.8). Теорема 4.6 доказана. ■
197

Метод (4.11), (4.12), как и метод (4.10), в худшем случае может
превратиться в метод простого перебора точек сетки (4.9). В то же время ясно, что
для многих функций f(x) e Q(L) этот метод гораздо эффективнее метода
простого перебора, так как если величины Fk- Fk+1,f(vk+1) - Fk в формулах
(4.11), (4.12) достаточно большие, то многие точки сетки (4.9) могут оказаться
исключенными из перебора без вычисления в них значений функции. В
параграфе 4.9 будет описан метод покрытия для функции многих переменных.
4.1.5. Метод касательных
Пусть функция/(х) выпукла и дифференцируема на отрезке [а; Ь],
удовлетворяет условию Липшица и унимодальна на [а; Ь]. Тогда для
минимизации/^) на [а; Ь] применимы почти все описанные выше методы, в
частности метод ломаных. Однако если значения функции f(x) и ее производной
f'(x) вычисляются достаточно просто, то здесь можно предложить другой,
вообще говоря, более эффективный вариант метода ломаных, когда в
качестве звеньев ломаных берутся отрезки касательных к графику f(x) в
соответствующих точках, — метод касательных.
Зафиксируем какую-либо точку v e [a; b] и определим функцию
g(x,v) = f(v) + f'(v)(x-v), а<х<Ъ.
Согласно теореме 3.1 g(x, v) <f(x) Ухе [a; b]. В качестве начального
приближения возьмем любую точку х0 е [а; Ь] (например, х0 = а)> составим
функцию Pq(x) = g(x, х0) и определим точку хх е [а; Ь] из условия
Po(*i)= min J90(*), xxe[a\b\.
xe[a,b]
Ясно, что при/'(х0) * 0 получим либо хх = а, либо хх = Ъ. Далее построим
новую функцию Pi(x) = max{p0(x); g(x, хх)} и следующую точку х2 е [а; Ь]
найдем из условия
А(*2> = min. А(*), х2 е [а; Ь]
хе[а,Ь\
и т.д. Если точки х0, xv ..., хп, п > 1, уже известны, то составляем очередную
функцию pn(x) = max{pn_1(x);g(xyxn)} = mzxg(xyxi) и следующую точ-
0<i<n
ку хп+1 определяем из условий рп(хп+1)= min pn(x)> xn+1 e [a; b]. Метод
хе[а;Ь]
касательных описан. Теорема о его сходимости во многом повторяет
теорему о сходимости метода ломаных.
Описанные выше методы ломаных, покрытия, касательных основаны
на существовании простых кусочно-линейных функций,
аппроксимирующих целевую функцию снизу. Аналогично можно строить методы
минимизации, когда целевая функция может быть аппроксимирована снизу
кусочно-полиномиальными или другими функциями.
4.2. Градиентный метод
4.2.1. Описание процесса. Выбор шага, проблемы старта и остановки
Будем рассматривать задачу
/(*)->min,xe X = E«, (4.13)
198

предполагая, что функция f(x) непрерывно дифференцируема на Еп, т.е.
f(x) e 0(Еп). Согласно определению 1.20 дифференцируемой функции
f(x + h)-f(x) = (f'(x)yh) + o(hyx), Hmo^p = 0. (4.14)
Если f'(x) Ф 0, то при достаточно малых || h || главная часть
приращения (4.14) будет определяться величиной (f'(x)yh). В силу неравенства
Коши — Буняковского
-1/Хх)1Щ*(/'(х),к)£\ПхЦЩ,
причем если f'(x) Ф 0, то правое неравенство превращается в равенство
только в слусае h = af'(x), а левое неравенство — только если h = -af'(x), где
а — произвольное неотрицательное число. Отсюда ясно, что при f'(x) Ф 0
направление наибыстрейшего возрастания функции/(х) в точке х
совпадает с направлением ее градиента f\x), а направление наибыстрейшего
убывания — с направлением антиградиента (-fix)).
Это замечательное свойство градиента лежит в основе ряда
итерационных методов минимизации функций. Одним из таких методов является
градиентный метод, к описанию которого мы переходим. Этот метод, как
и все итерационные методы, предполагает выбор начального
приближения — некоторой точки х0. Общих правил выбора точки х0 в
градиентном методе, как, впрочем, и в других методах, к сожалению, нет. Обычно
начальное приближение х0 стараются выбрать поближе к искомому
оптимальному решению х*> учитывая имеющуюся априорную информацию
о его местоположении. Будем считать, что некоторая начальная точка х0
уже выбрана. Тогда градиентный метод заключается в построении
последовательности {xk} по правилу
**+i =**-<**/'(**)> <**>0, А = 0,1,.... (4.15)
Числа ak из формулы (4.15) часто называют длиной шага или просто
шагом градиентного метода. Если f\xk) Ф 0, то при достаточно малых
ak > 0 гарантируется убывание: f(xk+1) <f(xk). В самом деле, из формулы
(4.14) при всех достаточно малых ak> 0 имеем
f(xk+0-f(xk) = ak\-\\f\xk)f+^
<0.
Если/Х^) = 0, то#£ — стационарная точка. В этом случае процесс (4.15)
прекращается, и при необходимости проводится дополнительное
исследование поведения функции в окрестности точки xk для выяснения того,
достигается ли в этой точке минимум функции f(x) или не достигается.
В частности, если/(х) — выпуклая функция, то согласно теореме 3.4 в
стационарной точке всегда достигается минимум.
Существуют различные способы выбора величины щ в методе (4.15).
В зависимости от способа выбора щ можно получить различные
варианты градиентного метода. Укажем несколько наиболее употребительных
на практике способов выбора ak.
199

1. На луче х = xk - af'(xk), a > О, направленном из точки xk по
антиградиенту, введем функцию одной переменной
gk(V) = f(xk-af'(xk)), сс>0,
и определим ak как точку ее минимума:
a^argming^cc). (4.16)
a>0
Метод (4.15), (4.16) принято называть методом скорейшего спуска.
При/Х^) * 0 согласно формуле (1.112) имеемg£(0) = -Ц/Ч**)! < 0, поэтому
нижняя грань в соотношении (4.16) может достигаться только при ak> 0.
Приведем пример, когда шаг спуска ak, определяемый условием (4.16),
может быть выписан в явном виде.
Пример 4.1
Пусть функция f(x) является квадратичной:
f(x) = ±(Ax,x)-(b,x), (4.17)
где Л — симметричная положительно определенная матрица размера пхп\Ь —
некоторый вектор из Еп. Выше, в примере 3.2, было доказано, что эта функция сильно
выпукла и ее производные вычисляются по формулам f'(x) = Ax-b,f'\x) = Л, поэтому
метод (4.15) примет вид
**+i = xk ~ v-kiAxk ~ b), k = 0,1,...,
и будет представлять собой хорошо известный итерационный метод решения системы
линейных алгебраических уравнений Ах = Ь. Для определения значения о^ из
условий (4.18) запишем явное выражение функции
gk(a) = f(xk)-a\\nxkf +^.{Af\xk), f'(xk))
и приравняем к нулю ее производную:
g'k(a) = -\\f'(xk)f + a(Af'(xk), f'(xk)) = 0.
При f'(xk) Ф 0 это условие выполняется при положительном значении
* (Af'(xk),f'(xk)) (A(Axk-b),Axk-b)
а поскольку функция g^(a) сильно выпукла, то найденное о^ будет искомым
решением одномерной оптимизационной задачи (4.16).
Разумеется, точное определение значения (4.16) шага скорейшего
спуска не всегда возможно. Кроме того, нижняя грань в формуле (4.16)
при некоторых k может и не достигаться. Поэтому на практике обычно
используют значения ak, приближенно удовлетворяющие условиям (4.16).
Можно, например, выбрать ak из условий
gk*<gk(ak)<gk.+5k, 5*>0, £5,=5<~ (4.18)
200

или из условий
gk*<gk(ak)<(l-Xk)gk(0) + Xkgk*y 0<X*<Xk<l. (4.19)
Величины 6ky Xk из условий (4.18), (4.19) характеризуют погрешность
выполнения условия (4.16): чем ближе 6k к нулю или Xk к единице, тем
точнее оно выполняется. При поиске ak из условий (4.18), (4.19) можно
пользоваться различными методами минимизации функций одной
переменной, в том числе и изложенными в параграфе 4.1.
Следует также заметить, что антиградиент (-f'(xk)) указывает
направление быстрейшего спуска лишь в достаточно малой окрестности точки xk,
и если функция/(х) меняется быстро, то в следующей точке xk+1
направление антиградиента (~f'(xk+1)) может сильно отличаться от (-f'(xk)). К тому
же и сами антиградиенты часто бывают известны лишь приближенно, так
что далеко не всегда целесообразно расходовать вычислительные ресурсы
на уточнение приближенного значения ak.
2. На практике нередко довольствуются нахождением какого-либо
ak> 0, обеспечивающего монотонное убывание: f(xk+1) <f(xk). С этой целью
выбирают какую-либо постоянную а > 0, после чего в методе (4.15) на
каждой итерации сначала берут щ = а и проверяют условие монотонности.
В случае его нарушения шаг ak=a дробят до тех пор, пока оно не
выполнится. Если потребности в дроблении а не возникает, можно проверить,
нельзя ли увеличить значение а с соблюдением условия монотонности.
3. Если функция/(х) е Сх^(Еп), т.е./(х)е С1 (Еп) и градиент f'(x)
удовлетворяет условию Липшица
\f\x)-f\y)\<Цх-у\\ Ух,уеЕ",
причем константа L > 0 известна, то в методе (4.15) в качестве щ может
быть взято любое число, удовлетворяющее условиям
°<e°Sa'-IT2? (420)
где е0, е — положительные числа, являющиеся параметрами метода. В
частности, при е = 1/2, е0= 1/1 получим метод (4.15) с постоянным шагом
ak = 1/1. Понятно, что при больших значениях L такой шаг становится
слишком мелким и в результате, несмотря на отсутствие в методе (4.15),
(4.20) процедуры одномерной минимизации (4.16), его преимущество
перед методом скорейшего спуска практически теряется. Вопросы
сходимости метода (4.15), (4.20) будут рассмотрены в следующем параграфе.
4. Возможен выбор ak из условия [23, 40]
f(xk)-f(xk-akf'(xk))>zak\\f'(xk)f, e>0. (4.21)
Для удовлетворения условия (4.21) сначала обычно берут некоторое
число ak = а > 0 (одно и то же на всех итерациях; например, ak = 1), а затем
при необходимости дробят его, т.е. изменяют по закону ak= Х*а> г - 0, 1, ...,
0 < X < 1, до тех пор, пока впервые не выполнится условие (4.21). Такой
способ определения ak в литературе часто называют выбором шага по Армихо [9].
201

5. Возможно априорное задание шагов ак из условий
сс*>0, 6 = 0,1,..., £сс*=°о, £сс2<°о (4.22)
Эти условия будут выполнены, если взять, например, ak=c(k + 1)_а, где
с = const > 0, а = const е (1/2; 1]. Априорный выбор (4.22) очень прост
в реализации, но не гарантирует выполнения условия монотонности
f(xk+i) <f(xk)> и> вообще говоря, в таком варианте градиентный метод
сходится медленно.
6. В тех случаях, когда заранее известна нижняя грань /* = inf f(x) > -«>,
хеЕп
в методе (4.15) можно взять абсциссу
точки пересечения прямой / = /* с касательной к кривой / = gk(a) =
=/(**-«/'(**))в точке (0; а(о».
Допустим, что шаги ак в методе (4.15) как-то выбраны (например, одним
из перечисленных выше способов). Тогда на практике итерации (4.15)
продолжают до тех пор, пока не выполнится некоторый критерий окончания
счета. Для этого часто используют следующие критерии:
\\xk-xk+1\\<e; \f(xk)-f(xk+1)\<e; \\f'(xk)\\<e;
|/(^+i)-/(^)|^e|K+i-^|; \Яхк)-/(хк+1)\Цхк-хк+1\\<г,
где е > 0 — заданное число. Иногда заранее задают число итераций;
возможны различные сочетания этих и других критериев. Разумеется, к этим
критериям завершения вычислений надо относиться критически,
поскольку они могут выполняться и вдали от искомого решения. К сожалению,
надежных критериев окончания процесса работы метода, которые
гарантировали бы получение решения задачи (4.13) с требуемой точностью, и
применимых к широкому классу задач, пока нет. Сделанное замечание о
критериях окончания счета относится и к другим излагаемым ниже методам.
4.2.2. Сходимость метода скорейшего спуска
для сильно выпуклых функций
При теоретическом исследовании свойств сходимости метода
предполагается, что процесс (4.15) бесконечный и мы имеем дело с двумя
последовательностями {хк} е Епу {f(xk)}> k = 0y l,.... Главными здесь обычно
являются вопросы об асимптотическом поведении этих последовательностей
и выполнении предельных соотношений
lim/(*,) = /*, limp(^,X*) = 0, (4.23)
k—>оо Л—>оо
а также об оценках скорости сходимости в формулах (4.23). Для
положительного ответа на эти вопросы на функцию f(x) кроме условия
f(x) e Сх(Еп) приходится накладывать дополнительные более жесткие
202

ограничения. В следующей теореме для определенности рассматривается
процесс (4.15) с выбором шага ak по правилу скорейшего спуска (4.16).
Теорема 4.7. Пусть функция f(x) принадлежит классу Схх{Еп) {см.
определение 1.29), т.е. ее градиент f (х) удовлетворяет условию Липшица
(1.117) с константой L > 0. Пусть также f{ос) сильно выпукла на Еп с
константой сильной выпуклости к> 0. Тогда для любой начальной точки х0 е Еп
последовательные приближения xk, вырабатываемые методом скорейшего
спуска (4.15), (4.16), обладают свойствами сходимости (4.23) и
выполняются следующие оценки:
0 < f(xk)-f*<(f(x0)-f*)qk, (4.24)
\\xk-x4*^(f(xQ)-f.}qb, £ = 0,1,..., (4.25)
где х* — точка минимума f(x) на Еп, q = 1 - я/L, 0 < # < 1.
Доказательство
Функция/(х) сильно выпукла, поэтому согласно теореме 3.11 нижняя
грань /* конечна и достигается в единственной точке х*. Из формулы (3.10)
при v = xky и = х* имеем
ak=f(xk)-f{x.)Z(fXxk),xk-x.)~ixk-x.f^Xxkifa-x4-
для всех k = 0, 1, ... . Для оценки разности ak+1 - ak сначала учтем правило
(4.16):
ам~Ч= Kxk+\)"/(**)*/(**~<*/'(**))"/(**) v«^°.
а затем, поскольку fix) е С1'1(Еп), воспользуемся утверждением леммы 1.3,
подставив в него х = хк - af'(xk), у = хк:
2(1
«*+i-«**!/'(** >1 -а2-а
л
Va>0.
Взяв здесь конкретное а = 1Д, > 0, доставляющее минимум правой
части, получим оценку
aM-ak<-M\f\xk)f
2V
Отсюда и из формулы (4.26) следует рекуррентное соотношение
( Л
я*+1^ 1-j Wk=gak, 6 = 0,1,...,
а из него — оценка (4.24). Вторая оценка (4.25) следует непосредственно
из оценки (4.24) и свойства (3.9) сильно выпуклых функций. В заключение
отметим, что условие 0 < q < 1, важное для содержательности утверждений
теоремы, выполняется для всех сильно выпуклых функций класса С1<1(Еп),
203

так как для таких функций всегда к < L, что очевидно из двусторонней
оценки
х|*-у| <{f\x)-f\y\x-y)<L\x-y\ Vx,yeEn.
Теорема 4.7 доказана. ■
Замечание 4.1. При наличии оценок вида (4.24), (4.25) со значением
q е (0; 1) скорость сходимости итераций к оптимальному решению по
функции (4.24) и по аргументу (4.25) принято называть линейной скоростью
или сходимостью со скоростью геометрической прогрессии. В теореме 4.7
линейная скорость сходимости метода скорейшего спуска была установлена
при весьма жестких требованиях к функции f(x), одним из которых было
условие ее сильной выпуклости. Некоторые утверждения о сходимости
со скоростью ниже линейной при ослабленных требованиях к f(x) можно
найти, например, в работе [12].
К невыпуклым функциям градиентные процедуры следует применять
с большой осторожностью, поскольку они становятся весьма
чувствительными к выбору начального приближения и могут сходиться как к точкам
локального минимума, так и к стационарным точкам функции, не
являющимися оптимальными даже в локальном смысле. Приведем
соответствующий пример.
Рассмотрим задачу безусловной минимизации невыпуклой функции в
пространстве Е2:
f(u) = х2 + (у2 -1)2 —> min, и = (х, у)еЕ2.
Понятно, что точная нижняя грань /* = 0 и достигается в двух точках {х* = 0; у* = ±1).
Применим к задаче метод скорейшего спуска (4.15), (4.16), взяв в качестве
начального приближения любую точку и0 = (х0, у0 = 0), лежащую на оси х. Градиент
функции равен/'(и) = (2xr, 4у(у2- 1)), поэтому f'(u0) = (2r0; 0),
g0(a) = f(u0-af'(u0)) = (l-2a)2x2+l
и в соответствии с правилом (4.16) при х0 Ф 0 получаем а0 = 1/2, а при х0 = 0 можно
взять любое а0 > 0. В любом случае следующее приближение окажется равным
w1 = w0-a0//(w0) = (0;0).
В этой точке градиент функции равен нулю: /'(wi) = (0; 0), поэтому процесс
останавливается, однако найденное приближение щ = (0; 0) не является ни
решением исходной задачи, ни даже точкой локального минимума, так как/(0; 0) = 1,
а при малых е > 0 значения функции в соседних точках вида щ = (х = 0; у = ±е) будут
меньше: /(we) = (е2- 1)2</(щ) = 1. Заметим, что при старте из позиций и0= (х0= 0;
г/0), у0 * 0, у0 Ф ±1, находящихся на оси г/, метод скорейшего спуска за один шаг
приведет нас к одному из оптимальных решений. Действительно, в данном случае
/'(ио) = (0; 4г/0(у2 -1)), g0(a) = {у*[1 -Щу$ - 1)р - 1р
и минимальным значением функции g0(a) окажется g0* = 0. При решении уравнения
g0(a) = 0 сначала разложим на множители разность квадратов:
{у0[1 - 4а(у2 -1)]+1}{у0[1 - 4а(у02 -1)] -1} = 0,
204

а затем поделим обе части уравнения на (г/0 + 1)0/о~ 1) * 0:
[1-4аг/0(г/0-1)][1-4аг/0(г/0 + 1)] = 0.
Отсюда имеем две точки минимума функции g0(a): ao± = №Уо(Уо - О]-1- При \у0\ >
> 1 оба эти значения положительны, т.е. допустимы. Выбор а0+ приведет нас в щ =
= (0; 1)е X*, а выбор а0_ — в щ = (0; -1)е X* При 0 < у0 < 1 допустимым будет только
а0+ > 0, приводящее в щ = (0; 1), а при -1 < г/0 < 0 — только а0_ > 0, приводящее в щ =
= (0; -1).
4.2.3. Траектория процесса.
Непрерывный аналог градиентного метода
Метод скорейшего спуска имеет простой геометрический смысл: точка
xk+ly определяемая условиями (4.15), (4.16), лежит на луче Lk= {х е Еп :
х = xk - (xf'(xk)y a > 0} в точке его касания поверхности уровня Г^+1 =
= {х е Еп : f(x) = f(xk+1)}> а сам луч Lk перпендикулярен к поверхности
Рис. 42 Рис. 43
В самом деле, пусть х = x(t)> a < t < b> — некоторое параметрическое
уравнение кривой, принадлежащей Г^, т.е. f(x(t)) = f(xk) = const, a<t<b,
dx
причем x(t0) = xk. Тогда (f(x(t)))'t = (f'(x(t))y x(t)) = 0, a < t < b, где x = —.
at
В частности, при t = t0 имеем (f'(xk)> x(t0)) = 0. Это означает, что градиент
(или антиградиент) f'(xk) перпендикулярен к касательному направлению
поверхности уровня Г^ в точке xk> или, иначе говоря, луч Lk
перпендикулярен к Г^. Перемещения из точек xk в следующие позиции xk+1 происходят
по направлениям антиградиентов (-f'(xk)); из условия (4.16) при ak> 0
получаем
eki-Щ) = -<f'(xk - akf'(xk)), /'(**)> = -(f\xk+l), f\xk)) = 0,
что означает ортогональность градиентов с соседними номерами, а также
и факт касания направления спуска Lk из точки xk с поверхностью
уровня Гк+1у соответствующей очередному приближению xk+1. Таким образом,
движение итерационного процесса метода скорейшего спуска происходит
по ломаной линии со взаимно перпендикулярными соседними звеньями.
205

Чем ближе поверхности уровня функции f(x) к сферам, тем выше
скорость сходимости метода скорейшего спуска. Это очевидно и из оценок
(4.24), (4.25), которые уточняются при уменьшении параметра q = 1 - яг/L,
т.е. при приближении отношения к/L к единице.
Заметим, что у квадратичной функции вида f(x) = а \\х\\ + (Ь> х) + с,а>0,
поверхностями уровня являются именно сферы, х= L, q = О и метод
скорейшего спуска будет сходиться к точке минимума х* за один шаг из любого
начального приближения х0.
Если же к «: I, то поверхности уровня функции f(x) сильно вытянуты
(см. рис. 4.3). Такие функции принято называть овражными, примеры
таких функций см. в упражнениях 4.2, 4.3 к этой главе. У таких функций
небольшие вариации некоторых переменных, характеризующих «склон
оврага», приводят к резкому изменению значений, а от остальных
переменных, задающих направление «дна оврага», их значения зависят слабо.
Поскольку значение q оказывается близким к единице, ухудшаются
теоретические оценки скорости сходимости (4.24), (4.25), а при неудачном
выборе стартовой точки х0 (см. рис. 4.3) приближение к решению может
существенно замедлиться из-за мелкошаговых перемещений итераций xk
в направлениях, близких к поперечным ко «дну оврага».
Для ускорения сходимости градиентного метода на классе овражных
функций разработан ряд эвристических приемов, с некоторыми из
которых можно ознакомиться в работе [12].
Остановимся на непрерывном варианте градиентного метода. В этом
методе вместо итерационного процесса (4.15) за основу берется задача
Коти для системы дифференциальных уравнений [17]:
x\t) = -a(t)f\x(t)\ t>0; х(0) = х0. (4.27)
Ее решение x(t), £ > О, является непрерывным аналогом
последовательности приближений {xk}, k = О, 1, ..., из метода (4.15), а заданная функция
a(t) > 0 — аналогом шагов ak. Система (4.27) описывает движение
материальной точки в силовом поле, задаваемом антиградиентом {-fix)), со
скоростью x'(t)> пропорциональной антиградиенту. Сразу заметим, что
итерационный процесс (4.15) представляет собой известный метод ломаных
Эйлера для приближенного решения задачи Коши (4.27) [6]. При
условиях, близких к условиям теоремы 4.7, траектории x(t) системы (4.27)
при t —> -и» будут притягиваться ко множеству X* точек минимума задачи
(4.13). В каждой из таких точек х* el* выполняется условие
стационарности f'(x*) = 0, поэтому все они являются точками равновесия
(стационарными решениями) системы (4.27). Приведем соответствующую теорему
о сходимости.
Теорема 4.8. Пусть функция f(x) е С11(Еп) и сильно выпукла на Еп
с констатной сильной выпуклости х>0>а множитель a(t) из правой части
дифференциального уравнения (4.27) непрерывен notuj a(t)dt = +°°. Тогда
о
траектория x(t) системы (4.27), выходящая из любой стартовой точки
206

x0 e En, сходится к единственной точке минимума х* функции f(x) на Еп,
причем справедлива оценка
( t \
\x(i) - х* || < |х0 - х* || ехр -я\ ос(т)б/т
V о
V£>0.
(4.28)
Доказательство
Прежде всего заметим, что по теореме 3.11 точка минимума х* функции
f(x) на Еп существует и единственна, а по теореме 3.4 имеем f'(x*) = 0.
Введем функцию
V(t) = ±\\x(t)-x.(,
t>0.
(4.29)
С учетом формул (4.27) и (3.11) имеем
V \t) = ((t) - х,, *'(*)> = -a(t)(f'(x(t)) - /'(**), x(t) -x*)<
< -xa(t)\\x(t) - x,f = -2xa(t)V(t) W > 0.
( ft X\
Отсюда следует, что —
at
V(t) ехр 2х{а(т)б/т
V о
< 0 при всех t > 0. Инте-
1 и ||2
грируя это неравенство от 0 до текущего t и учитывая, что V(0) = —\\х0 -х*\\ ,
получим
0<V(t)<V(0)exp
-2х|а(т)б/т
о
-~^\\хо~х*
ехр
-2х|а(т)б/т
о
что равносильно оценке (4.28). Теорема доказана. ■
Замечание 4.2. Пользуясь терминологией, принятой в теории
дифференциальных уравнений [17], решение х* задачи минимизации (4.13) можно
назвать глобальным аттрактором системы дифференциальных
уравнений (4.27), притягивающим к себе все ее траектории. Можно также
сказать, что х* — это асимптотически устойчивое по Ляпунову положение
равновесия этой системы. Для доказательства по существу мы
использовали второй метод Ляпунова, а в качестве функции Ляпунова взяли
функцию (4.29). При исследовании свойств сходимости методов
минимизации второй метод Ляпунова (или его дискретный аналог) используются
довольно часто; при этом в качестве функций Ляпунова наряду с
функцией (4.29) берут также функции V(t) = f(x(t))-f*y V(t) = \\f'(x(t))\\ и др.
Заметим также, что в случае a(t) = ос0 > 0 траекториии x(t) будут
притягиваться к оптимальному решению х* с экспоненциальной скоростью:
\x(t) - х* || < ||х0 - х* || ехр(-хос01) W > 0.
Непрерывные методы минимизации привлекательны тем, что для
приближенного решения возникающих здесь задач Коши наряду с методом
Эйлера могут быть использованы более точные методы Адамса, Рунге —
Кутта и др. [6], которые приведут к отличным от метода (4.15) дискретным
версиям градиентного метода, возможно, более быстрым и эффективным.
207

В заключение отметим, что по мере приближения к искомому решению
х* практическая скорость сходимости градиентных процессов обычно
снижается. Это связано с тем, что в окрестности точки минимума градиент
f'(xk) близок к нулю, главная линейная часть приращения f(xk)-f(x*)>
на базе которой выбирается направление спуска, становится малой,
уменьшаются расстояния между соседними итерациями \\xk+1 - xk\\ и
усиливается влияние неизбежных погрешностей вычислений. Поэтому вблизи
точки минимума стараются по возможности использовать более точные
и, вообще говоря, более трудоемкие процедуры, учитывающие не только
линейные, но и квадратичные части приращений, как это делается,
например, в методе Ньютона (см. параграф 4.5).
4.3. Метод проекции градиента
4.3.1. Описание процесса. Варианты выбора шага
Будем рассматривать задачу условной минимизации
f(x) -> min, jelcP, (4.30)
в которой множество X допустимых элементов х необязательно совпадает
со всем пространством Еп> а функция/(х) е СХ(Х). Чтобы учесть
присутствующие в постановке задачи (4.30) ограничения, можно взять за
основу итерационную схему (4.15) и дополнить ее операцией проектирования
на допустимое множество X (см. определение проекции 3.6). В результате
мы придем к так называемому методу проекции градиента.
А именно, пусть х0е X — некоторое начальное приближение. Далее
будем строить последовательность {xk} по правилу
**+! = Px(Xk-*kf'(Xk))> k = 0,1,..., (4.31)
где ak — положительная величина. Если X — выпуклое замкнутое
множество и способ выбора {ak} задан, то в силу теоремы 3.14
последовательность {xk} будет однозначно определяться условием (4.31). В частности,
при X = Еп метод (4.31) превратится в градиентный метод.
Если на некоторой итерации оказалось xk+1 = xk (например, это
случится при/'(я)ь) = 0), то процесс (4.31) прекращают. В этом случае точках^
удовлетворяет необходимому условию оптимальности xk = P^xk- OLkf'(xk))
(см. теорему 3.17), и для выяснения того, является ли в
действительности xk решением задачи (4.30) или нет, при необходимости нужно
провести дополнительное исследование поведения функции f(x) в окрестности
точки xk. В частности, если f(x) — выпуклая функция, то такая точка xk
является решением задачи (4.30).
В зависимости от способа выбора ak в формуле (4.31) можно получить
различные варианты метода проекции градиента. Укажем несколько
наиболее употребительных на практике способов выбора ak.
1. Введем функцию g^(a) = f{P^xk - af'(xk)) переменной a > 0 и
определим щ из условий
&(«*) = inffifeCa^g*., a*>0. (4.32)
208

Понятно, что при X = Еп метод (4.31), (4.32) превратится в метод
скорейшего спуска. Точное значение щ из условий (4.32) удается найти лишь
в редких случаях, поэтому на практике обычно пользуются
приближенными условиями типа (4.18) или (4.19).
2. Иногда довольствуются нахождением какого-либо ak > О,
обеспечивающего условие монотонности: f(xk+1) <f(xk). Для этого обычно
выбирают некоторую постоянную а > 0 и в методе (4.31) на каждой итерации
берут сначала ak = ос, а затем при необходимости уменьшают это значение
до момента выполнения условия монотонности.
3. Если функция f(x) принадлежит классу CXi{X) и константа
Липшица L для градиента f'(x) известна, то в условии (4.31) в качестве шага ak
можно взять любое число, удовлетворяющее условиям
°<е°-а'-1Т2? <433>
где е0 > 0, е > 0 — параметры метода.
4. Возможен выбор шага ak из условия
f(xk)-f(Px(xk-akfXxk)))>e\\xk-Px(xk-akf'(xk))(, (4.34)
где е > 0 — параметр метода. На практике для определения такого ak можно
сначала взять некоторое а^= а (например, а = 1) и дробить его до тех пор,
пока не выполнится условие (4.34). Для функций/(х) е СХХ{Х)
выполнения условия (4.34) можно добиться за конечное число дроблений.
5. Возможно априорное задание шагов ak из условий
сс*>0, 6 = 0,1,..., £а*=+~, Ха2<+~, (4.35)
k=0 k=0
например ak= (k + 1)_1, k = 0, 1,....
Заметим, что описанные здесь варианты метода (4.31) при X = Еп
переходят в соответствующие варианты градиентного метода,
описанные в параграфе 4.2. Если X Ф Еп, то трудоемкость описанных вариантов
метода проекции градиента напрямую зависит от трудоемкости операции
проецирования на данное множество X. На множества X простой
структуры — шар, параллелепипед, гиперплоскость, полупространство или их
несложные сочетания (см. примеры 3.6—3.8) — проецирование реализуется
без затруднений. Если же отыскание проекций на X требует значительных
вычислительных затрат, то эффективность метода проекции градиента
заметно снижается.
4.3.2. Сходимость метода для сильно выпуклых функций
Приведем утверждение о сходимости метода проекции градиента
с постоянным шагом при условиях, близких к условиям теоремы 4.7.
Теорема 4.9. Пусть X — выпуклое замкнутое множество, а функция f(x)
принадлежит классу С11{Х) {см. определение 1.29) с константой Липшица
I > 0 и сильно выпукла на X с константой сильной выпуклости к> 0. Тогда
для любой начальной точки х0е X приближения xk> вырабатываемые мето-
209

дом проекции градиента (4.31) с постоянным шагом ak= ос, 0 < а < IkLt2,
сходятся к единственному решению х* задачи (4.30), причем справедлива
оценка
\xk-x.\<qk(a)\x0-x.\, & = 0,1,..., (4.36)
в которой q(a) = у 1 - 2ха + 12а2, 0 < q(a) < 1.
Доказательство
Введем отображение
Ax = Px(x-af'(x))y
действующее из Хв X. По теореме 3.16 о нестрогой сжимаемости
проективного отображения имеем
|И*-Лу|2 ^ =
= Ik - у( + ос21/'(*) - f\y)f - 2а (f'(x) - /'(у), х-у) \/х,уе X.
Отсюда с учетом свойства (3.11) сильно выпуклой функции/(х) и
условия Липшица для ее градиента получаем оценку
\\Ах - Ayf < (1 + а2!2 - 2ма)\\х - yf = q2(a)\\x - yf \/x, yeX,
или
ЦЛх - Лг/|| < ^(a)||x - г/|| \/х,уеХ. (4.37)
Так как 0 < a < 2xZr2, то значения q(a) е (0; 1). Такое отображение А
называется сжимающим с коэффициентом сжатия q = q(a) е (0; 1). Метод
(4.31) с учетом введенного отображения можно кратко переписать в виде
xk+1=Axky & = 0,1,.... (4.38)
Отсюда и из соотношения (4.37) имеем
\\xk+i -xk\\ = Vх k - Axk_t I < q(a) \\xk - xk_t \\ <
<q\a)\\xk_1-xk_2\\<...<qk(a)\\x1-x0\[
Тогда для любых натуральных k> m> k < т> имеем
\Хт ~Xk\- \Хт " Хт-\ \ + \Хт-\ " Хт-2 \ + - + \Xk+\ ~Xk\\-
<(qm-\a) + qm-\a) + ... + qk(a))\\xt-x0\\< ^q_ (^ 1К-*о|.
Правая часть последнего неравенства стремится к нулю при k,m^>°°.
Это означает, что последовательность {xk} фундаментальная, поэтому она
сходится к некоторой точке х* [22, 29]. В силу замкнутости множества X
точка х* е X. Пользуясь непрерывностью проективного отображения
(теорема 3.16), из соотношения (4.38) получаем
х* = Ах* = Рх(х* - а/'(х*)).
В силу теоремы 3.17 это значит, что х* el*. Наконец, из сжимаемости
отображения А выводится и линейная скорость сходимости метода (4.36)
со знаменателем геометрической прогрессии q = q(a):
210

\\xk -x*\\ = \\Axk_t -Ax*\< q(a)\xk_x -x*\ = q(a)\\Axk_2 -Ax*\<
<q2(a)\\xk_2-x*\\<...<qk(a)\\x0-x*l 4 = 0,1,....
Теорема 4.9 доказана. ■
Замечание 43. Оценка (4.36) свидетельствует о линейной скорости
сходимости метода проекции градиента с постоянным шагом а е (0;
2яЬ~2) из любого начального приближения х0е X. Наименьшее из соот-
ветствующих значений q(a) достигается при выборе а = а* = я1г2 и равно
q(a*) = ^Jl->c2L~2. Сравнивая формулы (4.36) и (4.25), можно оценить,
насколько градиентный метод с постоянным шагом а*, в который
превращается процесс (4.31) в случае X = Еп> уступает по скорости сходимости
методу скорейшего спуска. Главными показателями при сравнении
являются знаменатели соответствующих геометрических прогрессий g(ou) и
Jq = yJl-x/L:
q(a*) = ^\-к2172 = yll-x/Lyjl + x/L = yfeyll + x/L > yjq.
Заметим, что при к / L «: 1 градиентный метод с постоянным шагом,
в котором к тому же отсутствует процедура одномерной минимизации
по а, проигрывает методу скорейшего спуска не так уж и много. Другие
варианты теорем о сходимости метода проекции градиента, в том числе
при менее жестких требованиях к функции/(х), можно найти в работе [12].
4.4. Метод условного градиента
4.4.1. Идея линейной аппроксимации и варианты ее реализации
Этот метод используется для решения задач условной минимизации
/(*)-> min,*e X, (4.39)
гладких функций/(х) е СХ(Х) на выпуклых замкнутых ограниченных
множествах X с: Еп.В основе его конструкции лежит важная в теоретическом
и практическом плане идея аппроксимации заданной функции/(х) на
каждой итерации другими, более простыми функциями. В методе условного
градиента в качестве таковых берутся простейшие линейные
аппроксимации. Пустьх0е X — некоторое начальное приближение. Если k-e
приближение xk e X уже найдено, вместо самой функции f(x) рассматривается ее
линейное приближение
и решается вспомогательная задача минимизации функции fk(x) на
множестве X.
fk(x)^minyxeX. (4.40)
Пусть xk — одно из решений задачи (4.40), т.е.
xkeX, fk(xk) = minfk(x). (4.41)
хеХ
211

Так как множество X замкнуто и ограничено, а линейная функция
fk(x) непрерывна, то такая точка xk всегда существует по теореме Вейер-
штрасса 1.1. Если у задачи (4.40) точек минимума много, в качестве
вспомогательной точки xk берется любая из них. Следующее (k + l)-e
приближение вычисляется по правилу
xk+1=xk+ak(xk-xk)y 0<ссЛ<1. (4.42)
В силу выпуклости множества X всегда xk+1 e X. Описанная процедура
(4.40)—(4.42) называется методом условного градиента. Шаги ak в условии
(4.42) можно выбирать различными способами; некоторые из них будут
описаны ниже.
Заметим, что если
\ 4 о (aiyx)<b:yi = ly...ym; }
X = \x = (x\x2y...yx«)eE«:x*>0yi = ly...yn' ' . " ' ,
[ (ai9 x) = biyi = m + ly..., m + sj
то задача (4.40) превратится в задачу линейного программирования,
которая может быть решена за конечное число шагов симплекс-методом,
описанным в гл. 2. Если окажется, что xk = xk (это возможно, например, в
случае, когда f'(xk) = 0), то независимо от способа выбора ak в (4.42) получим
xk+i= xk- Согласно теореме 1.7 это означает, что точка xk удовлетворяет
необходимому условию минимума в задаче (4.39). В этом случае итерации
прекращаются, и при необходимости проводится дополнительное
исследование точки xk. В частности, если f(x) выпукла, то согласно теореме 3.4
точка xk будет решением, т.е. хкеХ*и задача (4.39) решена.
Укажем случаи, когда решение задачи (4.41) находится явно. Если X —
я-мерный параллелепипед:
X = {x = (x1,...,xny.ai<xi<$i,i = l9...,n},
п
то функция fk(x) = f(Xk) + Yjf'xi (xk)(xi ~XD достигает своей нижней грани
i=i
на X в точке xk = (х\,..., Щ) с координатами Щ = а( при /^ (xk)> 0, х\ - 0,-
при /',- (xk) < 0, а в случае /',- (xk) = 0 в качестве х\ можно взять любое число
из отрезка [оу PJ (обычно берут Щ = а(> х[ = 0,- или х\ - (а( +Pf)/2).
Если X = {х е Еп \ \\х - v0\\} — шар радиуса R с центром в точке а0, то
точное решение xk задачи (4.41) легко находится с помощью неравенства
Коши — Буняковского:
**=*о-я|И**)Г7'(**).
Разумеется, так просто найти точное вспомогательное приближение xk
удается далеко не всегда, и задачу (4.41) часто приходится решать
приближенно, определяя xk из условий
xkeX, fk(xk)<mmfk(x) + Ek, Ek>0, lime^=0.
xeX &->oo
Укажем неколько наиболее употребительных способов выбора шага ak
в условии (4.42).
212

1. Величина ос^ может выбираться из условий
a*=argming£(a), gk(a) = f(xk+a(xk-xk)). (4.43)
0<a<l
Заметим, что для важного в приложениях класса квадратичных и сильно
выпуклых функций f(x) задачу одномерной минимизации (4.43) можно
решить явно. Действительно, пусть, как и в примере 4.1, функция имеет
вид (4.17), а именно,
1
f(x) = -(Axyx)-(byx)y
где А — симметричная положительно определенная матрица размера п х п>
Ъ е Еп. Тогда f'(xk) = Axk-b. Пользуясь формулой (1.13), в которой в силу
квадратичное™/(х) остаточный член равен нулю, запишем явное
выражение для функции g^(a):
&(ос) = /(^) + а(//(^),^-^)+у<л(^-^^^-^)-
Если (A(xk-xk),xk -xk) = 0y то xk =xk, и тогда, как отмечалось выше,
xk еХ*. Если же (A(xk -xk)> xk -xk) > О, то наименьшее значение
квадратичной функции gk(o<) будет достигаться при
„ _ <fX*k)>Xk-Xk)
ak* - ~777=~
(A(xk-xk)yxk-xk)
При выборе вспомогательного приближения xk по правилу (4.41)
значение 0С£* неотрицательно, поэтому с учетом имеющегося ограничения 0 < a <
< 1 получаем окончательно ak = min{a^*; l}.
В общем случае точное решение одномерной задачи минимизации (4.43)
или затруднительно, или невозможно, поэтому на практике обычно
используют приближенные решения этой задачи, определяемые из условий
0<сс,<1, gk(ak)<gk*+Sk, 8А>0, £5,=5<оо
k=o
или
0<a*<l, gk(ak)<(l-Xk)gk(0) + Xkgk., 0<X<Xk<l.
При этом могут привлекаться различные методы минимизации
функций одной переменной, в том числе и методы, описанные в параграфе 4.1.
2. Если/(х) е CXi{X) и известна константа Липшица L градиента f'(x)>
то возможен выбор ak в формуле (4.42) из условий
<**
^:J<.P*|/*(**)|
= пипк1;—! г1
Xk-*k\
{AAA)
где е0 < pk < — -, е0, е — параметры метода, 0 < е0 < 1.
213

3. Другой способ выбора ak — это ак=Х^, где г0 — минимальный
из номеров г > О, удовлетворяющих условию
/(хк)-/(хк+Х1(хк-хк))>Х1г\/к(хк)\,
где Х,г — параметры метода, 0<Х<1,0<е<1.
4. Величины ак в формуле (4.42) можно априорно задавать из условий
оо
0<сс*<1, lima^=0, Xa*=4~, (4.45)
например ак= (k + 1)_1, k = О, 1, ... . Такой выбор ак очень прост для
реализации на компьютере, но, вообще говоря, не гарантирует выполнения
условия монотонности f(xk+1) <f(xk).
5. Возможны и другие способы выбора ак. Например, можно на каждом
шаге сначала полагать ак= 1, а затем при необходимости дробить ак до тех
пор, пока не выполнится условие монотонности f(xk+1) <f(xk).
4.4.2. Сходимость метода
Остановимся на сходимости метода условного градиента при выборе
шага ак по правилу (4.43).
Теорема 4.10. Пусть множество X с Еп выпукло, замкнуто и
ограничено, а функция f(x) е СХХ{Х) и выпукла на X. Тогда для любого начального
приближения х0е X последовательность {хк}, вырабатываемая методом
(4.41)—(4.43), обладает следующими свойствами сходимости:
limp(^,X*) = 0, 0<f(xk)-f*<^-, 6 = 1,2,..., C = const>0. (4.46)
&->оо k
Если, кроме того, f(x) сильно выпукла на X с константой сильной
выпуклости к, то
\хк-х*\<^, 6 = 1,2,.... (4.47)
Доказательство
При сделанных предположениях множество X компактно, а
функция/(х) непрерывна на X, поэтому по теореме Вейерштрасса 1.1 /* >-°°
и Х**0. Последовательность значений функции ограничена снизу:
f(xk)>f*, а выбор ак по правилу (4.43) гарантирует ее монотонное
невозрастание:/^) >f(xk+1), к = 0, 1, ..., значит, эта последовательность имеет
предел и, следовательно,
lim(/(^)-/(^+1)) = 0. (4.48)
Из условия (4.43) следует, что
/(**+i) = ek(<*k) = §k* ^ f(*k + ъ(хк -хк)) Vaе [0; 1].
Ограниченное множество X имеет конечный диаметр
d- sup ||w-dl<+°°.
u,veX
214

Используем его значение для оценки разности f(xk) -f(xk+1) с помощью
утверждения (1.118) леммы 1.3:
/(**) " Д**+1) ^ /(**) " f(*k + a(*k ~xk))^ -«</'(** )>^ " **)"
- \\*k ~ 4 f ^ -«</'(** )^л - ^л > - a2— (4.49)
при всех a e [0; 1], всех & = 0, 1, .... Отсюда при всех 0 < a < 1 следует
неравенство
0<-(fXxk),xk-xk)<f(Xk)~f(Xk+i) + a^, 6 = 0,1,....
С учетом формулы (4.48) при фиксированных a e (0; 1] перейдем
в этом неравенстве к пределу при k —> °°, а затем — к пределу при a —> 0.
В результате получим соотношение
lim(f'(xk),xk-xk) = 0. (4.50)
Свойство (3.3) выпуклых функций из теоремы 3.1 и определение
(4.41) вспомогательных точек xk позволяют оценить текущие уклонения
ak =f(xk)-f* до минимального значения функции:
0<ak=f(xk)-f(x.)<(fXxk),xk-x.)<(f'(xk),xk-xk) (4.51)
Здесь х* е X* — одно из оптимальных решений. Отсюда и из
соотношения (4.50) следует сходимость процесса по функции: f(xk)^> /*, а
значит, и сходимость по аргументу (см. теорему 1.2): p(xk,X*)^>0. Заметим,
что неравенство (4.51) может служить полезной апостериорной оценкой
при практическом применении метода условного градиента. Из неравенств
(4.49) и (4.51) следует оценка
Ld2
ak - ak+1 > aak - a2 —- Va e [0; 1], k = 0,1,.... (4.52)
Полагая в этом неравенстве a = 1, находим ak+1 <Ld2 /2, k = 0, 1, ... .
Максимальное значение правой части неравенства (4.52) на всей числовой
прямой -оо < a < +°° достигается в точке
- ak
но поскольку мы только что показали, что ak <Ld2/2, k = 1, 2, ..., то
значения ak е [0,1/2] при k > 1, так что их можно подставлять в формулу (4.52).
Сделав это, получим неравенства
а2
ak~ak+1-~2Ld*' k = X>2>~"
Таким образом, последовательность {ak} удовлетворяет условиям
леммы 1.6, из которой следует оценка (4.46). Наконец, оценка (4.47)
вытекает из свойства (3.9) сильно выпуклых функций и оценки (4.46). Теорема
доказана. ■
215

4.5. Метод Ньютона
4.5.1. Описание процесса. Варианты выбора шага
Будем рассматривать задачу условной минимизации
/(*) -> min, jelcP, (4.53)
в которой множество X допустимых элементов х необязательно
совпадает со всем пространством Еп, а функция f(x) e (^(Х). Итерационная
последовательность для метода Ньютона строится так же, как и для метода
условного градиента, однако вместо главной линейной части приращения
f(x) -f(xk) здесь берется его квадратичная часть. А именно, если известно
приближение xk> то для нахождения следующего приближения xk+1 мы
сначала находим вспомогательную точку xk e X из условия
xkeX, fk(xk) = minfk(x)y
хеХ
где
1
fk(x) = (fXxk)>x-xk)+^(f'\Xk)(x-xk)>x-xk)> (4.54)
после чего вычисляем xk+1 по формуле
xk+1=xk+ak(xk-xk). (4.55)
Величина ak е [0; 1] называется шагом метода Ньютона. В случае Х = Еп
в предположении положительной определенности матрицы ff\x^) точка xk
может быть явно вычислена по формуле
**=**-СГ(**))-7'(**). (4.56)
Этот результат вытекает из того, что положительная определенность
матрицы f"(Xk) гарантирует как ее обратимость, так и сильную выпуклость
квадратичной функции/^(х) (ясно, что Д'(х) = f"(xk) и выполнены
условия теоремы 3.12). Но тогда необходимым и достаточным условием
минимума на Еп дифференцируемой на всем Еп квадратичной функции fk(x)
будет условие
Mx) = f'(xk)+f"(xk)(x-xk) = 0,
из которого элементарно вытекает равенство (4.56). Отметим, что в случае
отсутствия положительной определенности матрицы $"(х£) задача поиска
точки xk может иметь много решений или быть вообще неразрешимой.
Достаточными условиями ее однозначной разрешимости будут
положительная определенность матрицы $"(х£) в совокупности с выпуклостью и
замкнутостью множества X (см. теорему 3.12).
Если в условии (4.54) на некоторой итерации оказалось xk = xk, то
необходимо выполняется условие
(f£(xk)yx-xk) = (f'(xk)yx-xk)>0 VxeX,
что в силу теоремы 1.7 будет и необходимым условием минимума функции
f(x) на X. Поэтому процесс (4.54), (4.55) надо остановить, и для выяснения
216

того, является ли в действительности xk решением задачи (4.53) или нет,
при необходимости нужно провести дополнительное исследование
поведения функции f(x) в окрестности точки xk. В частности, если f(x) —
выпуклая функция, то такая точка xk является решением задачи (4.53) в силу
теоремы 3.4.
В зависимости от способа выбора ak в формуле (4.55) можно получить
различные варианты метода Ньютона. Кратко обсудим некоторые из них.
1. Если взять ak = 1, то xk+1 = xk, и мы получаем так называемый
классический метод Ньютона. Он имеет квадратичную скорость сходимости, но,
как будет показано ниже, сходится лишь локально.
2. Можно ввести функцию gk(ti) = f(Xk +a(xk-xk)) переменной а е
е [0; 1] и определить ak из условий
&(<**)= n}ing^(a) = gP, a*e[0;l]. (4.57)
ае[0;1]
Такой способ приводит нас к гибриду методов скорейшего спуска
и Ньютона. Точное значение ak из условий (4.57) удается найти лишь
в редких случаях, поэтому на практике обычно пользуются
приближенными условиями ak е [0; 1], gk(ak)<gk* +е, где параметр е > 0 мы
выбираем сами.
3. Возможен выбор шага ak = Хт, где т — минимальное целое
неотрицательное число, обеспечивающее справедливость неравенства
f(xk)-Kxk+7,™(xk-xk))>h.™ \fk(xk)\, (4.58)
где X е (0; 1) — параметр метода. Как будет показано ниже, такой вариант
метода уже обладает свойством глобальной сходимости с квадратичной
скоростью.
Если функция fk(x) из условия (4.54) сильно выпукла, а X = Еп или
X задается линейными ограничениями типа равенств или неравенств, то
процедура вычисления точки xk оказывается не очень трудной. Однако
задача (4.54) в общем случае может оказаться весьма сложной и
сравнимой по объему требуемой для решения вычислительной работы с
исходной задачей (4.53). Метод Ньютона обычно применяют в тех случаях, когда
вычисление производных f'(x), f"(x) не представляет особых трудностей
и вспомогательная задача (4.54) решается достаточно просто.
Достоинством метода Ньютона является высокая скорость сходимости. Поэтому
хотя трудоемкость каждой итерации этого метода, вообще говоря, выше,
чем в методах первого порядка, но общий объем вычислительной работы,
необходимой для решения задачи (4.53) с требуемой точностью, при
применении метода Ньютона может оказаться меньше, чем при применении
других, более простых методов.
4.5.2. Сходимость классического метода Ньютона
для сильно выпуклых функций
Приведем утверждение о сходимости классического метода Ньютона
(4.55), когда ak = 1, xk+1 = xk.
217

Теорема 4.11. Пусть функция f(x) определена и является сильно
выпуклой с константой к > О на выпуклом замкнутом множестве X с непустой
внутренностью из пространства Епу f(x) e С2(Х), f"(x) удовлетворяет
на X условию Липшица с константой L > О, т.е.
\\f"(x)-f"(y)\\<L\\x-y\\ \/x,yeX. (4.59)
Пусть {xk} — последовательность, полученная классическим методом
Ньютона при некотором начальном приближении х0 е X, удовлетворяющем
соотношению
Я = 1^\\хо-х*\\<1>
где х* — решение задачи (4.53). Тогда она сходится к х*> причем
\\xk-x4<^q2k, 6 = 0,1,2,....
Доказательство
При выполнении условий теоремы задача минимизации (4.53)
удовлетворяет всем требованиям теоремы 3.11, поэтому ее решение х* существует
и единственно. Далее, как уже упоминалось выше, Д\х) = f"(xk). Так
как функция f(x) является сильно выпуклой на X, a intX Ф 0, то по
теореме 3.13 (f"(x)h, h) > яУг\ при всех х е X, h е Еп. В силу того что xk е X,
справедливо неравенство {f"(xk)h, h) > x||/z|| для любого h e En> а это
означает, что (fk'(x)h> h) > x||/z|| при всех х е X, h е Еп, поэтому функция fk(x)
также является сильно выпуклой на X с константой к. Стало быть, и задача
нахождения точки xk тоже удовлетворяет всем требованиям теоремы 3.11,
xk существует и единственна. Итак, при выполнении условий
доказываемой теоремы классический метод Ньютона определен корректно.
Теперь воспользуемся теоремой 3.4 (критерием оптимальности)
для исходной задачи и для задачи поиска xk = xk+{.
{f\x*),x-x*)>Q УхеХ;
(fk(xk+i \х-xk+i) = </'(**) + f'\xk)(**+!-xk\x-xk+1> > 0 \/хеX.
Подставляя в первое из этих неравенств xk+1 е X, а во второе х*еХ
и складывая полученные соотношения, имеем
(f(x,)-f(xk)-r(xk)(xk+1-xk)yxk+1-x,)>0^
** </'(*•) - /'(**)> xk+i ~ x*)" </"(** )(*• ~ xk )> xk+i ~x*)^
^ (f'Xxk )(xk+i ~ x*)>xk+i ~ x* )•
Оценим левую и правую части полученного неравенства. Для этого
воспользуемся формулой конечных приращений, неравенством Коши — Буня-
ковского, условием (4.59) и критерием сильной выпуклости:
(IXх*) ~ f\xk )> xk+i ~х*)~ {f"(xk )(x* ~ xk )>xk+i ~х*) =
218

1
= I(f"(xk + t(x* -xk))(*• -xk)> xk+i -x*)dt-(f"(xkXх* -xk)> xk+i -*•) =
0
1
= \((f"(Xk+t(x*-xk))-f"(Xk))(x*-xk)> xk+i-x*)dt ^
0
1 £ 2
<$L\\t(x*-xk)\\-\\x*-xk\[\\xk+i-x.\\dt = -\\x. -xk\\ -\\хк+1-х.\\;
о L
(f"(xk)(xk+i -x.),xk+1-x.) >x\\xk+1-x.\\ .
С учетом этих оценок мы получаем
II 11^ II II ^ II 11^ II II ^ II 11^ и — с\ л о
— р* — Хи\ • №>+i ~~ X* ^ УС №>+i ~~ ХЛ <=> p^+i ~~ X* S ——№> ~ Х*\\ , к — U, 1, Z,... .
2II 2х
Отсюда уже нетрудно вывести нужный результат, используя метод
математической индукции. Действительно, при k = О с учетом
соотношения q = —\х0 -хЛ<1 имеем
и и L и м2 2я 9 2>с 2i
\\х1 - *• Р^Ро"х*\\ = ~Y<12 = ~^Т •
т-г и и ^ 2х 0k
Предполагая по индукции, что \\xk -х*\\ < —ql , выводим
\2 о
LX 2£+i
и и I и м2 I f 2>f о*
=т«
Теорема доказана. ■
Замечание 4.4. Оценка |^+1-х*|<-—1^-^*| свидетельствует о
квадратичной скорости сходимости классического метода Ньютона. К
сожалению, за тривиальный способ выбора шага ak приходится расплачиваться
тем, что начальное приближение х0 должно быть близко к решению задачи
х*> которое мы, естественно, заранее не знаем. Существенность этого
требования подтверждается таким примером: рассмотрим функцию
/(*) =
-х4+- 1+- \х2, \х\<&,
453 21, 5
х2 3
— + 2|х|--8, |*|>8,
где х е Е1, а 8 е (0; 2) — фиксированное число. Нетрудно видеть, что
f(x) e (^(Е1) и, кроме того, f"(x) > 1 при всех ie f1, так что/(х) сильно
выпукла на Е1. Далее, ясно, что /* = 0, х* = 0. В качестве начального
приближения возьмем х0 = 8. Применяя классический метод Ньютона, мы
получим последовательность xk= (-l)k • 2, k = 1, 2, ..., которая расходится, хотя
начальное приближение х0 отличается от х* = 0 на число 8, которое может
быть сколь угодно малым.
219

Исходя из этих соображений, классический метод Ньютона часто
применяют на завершающем этапе поиска минимума, когда с помощью более
грубых, менее трудоемких методов уже найдена некоторая точка,
достаточно близкая к точке минимума.
4.5.3. Сходимость метода Ньютона с переменным шагом
для сильно выпуклых функций
Перейдем к рассмотрению метода (4.54), (4.55) с выбором шага ak=Xmy
где т — минимальное целое неотрицательное число, для которого
выполняется неравенство (4.58). Покажем, что такой способ выбора шага
гарантирует сходимость метода Ньютона при любом выборе начального
приближения, в отличие от классического метода Ньютона.
Теорема 4.12. Пусть функция f(x) определена и является сильно
выпуклой с константой к > О на выпуклом замкнутом множестве X с
непустой внутренностью из пространства Еп, f(x)e C2(X)> f"(x)
удовлетворяет условию Липшица (4.59), существует такая константа М > О, что
при всех х е X, h e Еп. Тогда последовательность {xk}>
получаемая методом Ньютона (4.54), (4.55), (4.58), при любом начальном
приближении х0е X существует и сходится к точке х* — единственному
решению задачи (4.53), причем найдется номер k0 такой, что при всехk>k§
будет справедливо ak = 1 г/, кроме того,
\\xk-x4<^-q2k, k = k0,k0+l,.... (4.60)
Доказательство
Рассуждая так же, как и при доказательстве теоремы 4.11, мы получаем
существование единственного решения х* задачи (4.53), сильную
выпуклость с константой хна X функции/Дх) из условия (4.54) и
существование и единственность точки xk е X, удовлетворяющей условиям (4.54).
Тогда по теореме 1.7 для всех k = 0, 1,... справедливо
(f^xk),x-xk) = {fXxk) + f"(xk)(xk-xk),x-xk)>0 VxeX. (AM)
Если оказалось, что xk=xk, то из неравенства (4.61) вытекает
(f'(xk)yx-xk)>0, х е X. В силу выпуклости функции/(х) по теореме 3.4
отсюда следует, что xk=xk= хь т.е. задача (4.53) решена. Если же xk Ф xk,
то fk(Xk)<fk(xk) = ®- Покажем, что тогда существует хотя бы один номер
т > 0, для которого выполняется условие (4.58). Для этого возьмем
произвольное число а е [0; 1] и положим ха = xk+a(xk-xk). Отсюда и из
выпуклости fk(x) получаем
fk(xa)<afk(xk) + (l-a)fk(xk) = afk(xk)<0.
Пользуясь формулой Тейлора, приращение А/ = f(xa) - f(xk) можно
представить в виде
л
А/= </'(**)> а(х* -xk))+-^f"(xk+Qa(xk -xk))a(xk-xk),a(xk -xk)} =
= fk(xa)+Y{(f"(xk + ^(Xk-xk))-f''(xk))(xk-xk),xk -xk), (4.62)
220

где 0 < 0 < 1. Учитывая, что в силу выпуклости множества X точка
xk+Qa(xk-xk) тоже в нем содержится, по условию теоремы имеем
(f"(xk + Qa(xk-xk))(xk-xk),xk-xk)<M\\xk-xk\ ,
— — II— l|2
кроме того, по теореме 3.13 (f"(xk)(xk -xk),xk-xk)> x\xk -xk\ > О,
поэтому из формулы (4.62) вытекает
^f = f(xa)-f(xk)<afk(xk)+—^-\\xk-xkf.
Так как xk — точка минимума сильно выпуклой функции fk(x) на X, то
согласно теореме Вейерштрасса 3.11
\\xk -xkf <l(fk(Xk)-fk(xk)) = l\fk(xk)\, (4.63)
11 м ус К
и мы приходим к неравенству
¥ = f(xa)-f(xk)<-a\fk(xk)\+^-\fk(xk)\, 0<сс<1. (4.64)
Отметим, что в силу критерия сильной выпуклости и условия теоремы
при всех х е X, h е Еп справедливо x\\h\\ <(f"(x)hyh)<M\\h\\ , поэтому
х < М. Возьмем произвольное а, удовлетворяющее условиям
0< <а< <—. (4.65)
2М 2М 2 v '
Отсюда и из неравенства (4.64) будем иметь
f(Xk)-f(Xa) = f(Xk)-f(xk+a(xk-xk))>
^ос11-^1|Л(^)|>-а|Л(^)|
при всех а, удовлетворяющих условиям (4.65). Возьмем такой номер п > 1,
для которого Хп < < Хп~х. Тогда ясно, что
2М
2М 2М
Значит, ос = Хп удовлетворяет условиям (4.65), и, следовательно,
при а = Хп будет справедливо неравенство (4.66). Это значит, что при г - п
выполняется условие (4.58). Тогда существует наименьшее число т,
0<т<п, удовлетворяющее неравенству (4.58). Приняв в соотношении
(4.55) ak=Xmy получим следующее приближение xk+1.
Тем самым показано, что последовательность {xk}, генерируемая методом
Ньютона с рассматриваемым способом выбора шага, при любом начальном
приближении существует. Из формулы (4.58) имеем
л
f(xk)-f(xk+i)>-^ak\fk(xk)\, £ = 0,1,....
221

Учитывая, что ak = Хт > Хп > , отсюда находим
f(xk)-f(xM)>^\fk(xk% £ = 0,1,.... (4.67)
Таким образом, при всех k = О, 1, ... справедливо соотношение/^) >
> f(xk+i) > /*. Тогда существует \imf(xk)>f*> откуда следует, что
\im(f(xk)- f(xk+1)) = 0. Но тогда из неравенства (4.67) вытекает, что и
&—>оо
lim fk(Xk) = 0, откуда с помощью соотношения (4.63) находим
&—>оо
lim I**-х4|| = 0. (4.68)
В силу того что при всех k = О, 1, ... выполнено f(xk) > f(xk+1), все
члены последовательности {xk} лежат в множестве Лебега М(х0) =
= {xeX:f(x)<f(x0)}. Для сильно выпуклых непрерывных функций
множество М(х0) замкнуто и ограничено, поэтому последовательность {xk}
имеет хотя бы одну предельную точку, причем все ее предельные точки
лежат в М(х0) с X
Пусть ги — произвольная предельная точка {xk} и пусть {xk }—>a*.
С учетом равенства (4.68) и условия/(х) е С2(Х) из соотношения (4.61)
при k = km^> оо получим (f (v*),x-v*)>0 для всех х е X. Согласно
теореме 3.4 тогда v*=x* — точка минимума функции/(х) на X. Следовательно,
\\mf(xk)= lim f(xk ) = f(x*) = f*, т.е. {xk} — минимизирующая ПОСЛеДОВа-
^оо 77Z—>«> т
тельность. Отсюда и из теоремы 3.4 следует, что {^}—> х*.
Вернемся к неравенству (4.62). С учетом неравенства Коши — Буняков-
ского и условия Липшица (4.59) из него следует
/(^а)-/(^)^аЛ(^)+^|еа(^-^)|-|^-^| <afk(xk)+—\\xk-xk\\ ,
а е [0; 1], k = 0, 1, ... . Еще раз используя соотношение (4.63), приходим
к неравенству
/(^)-/(^)^-а|Л(^)|+^|Л(^)|1К-^1- 0*а£1.
В силу равенства (4.68) и того, что {xk}^> x*, существует номер k0 такой,
что —\xk -xk\ < — при всех k > k^ и, кроме того, q = —Ita, -хЛ< 1. Тогда мы
имеем
/(^)-/(^a)^a|A(^)(l-a^lK-^|]^a[l-f]|A(^)|
при всех a е [0; 1] и k>k§. В частности, при a = 1 отсюда заключаем, что
условие (4.58) выполнено при m = 0, и, следовательно, ak= X°= 1, xk+1 =xk
при каждом k > k$. Таким образом, начиная с номера k = k0 этот вариант
222

метода Ньютона превращается в классический метод Ньютона с
начальным приближением Хи, удовлетворяющим условию теоремы 4.11. Отсюда
следует оценка (4.60), что и требовалось доказать. ■
Рассмотренный вариант выбора шага в методе Ньютона ненамного
сложнее варианта ak= 1, причем скорость сходимости остается той же,
а начальное приближение можно брать любым. При наличии эффективных
методов минимизации квадратичной функции fk(x) на множестве X этот
метод можно с успехом применять для минимизации достаточно гладких
функций.
4.6.* Метод переменной метрики
4.6.1. Описание процесса. G-проекция
Идея метода переменной метрики основана на известных свойствах
антиградиента: вектор -f'(x) является направлением скорейшего
убывания функции f(x) в точке х, и, кроме того, он ортогонален поверхности
уровня, определяемой уравнением f(x) = f(x).
Так как для выпуклой функции множества, ограниченные
поверхностями уровня, будут выпуклыми, то из геометрических соображений
становится ясно, что в таком случае поворот антиградиента на острый угол
даст нам новый вектор, задающий направление убывания функции, причем
движение в этом направлении может быть более выгодным с точки зрения
минимизации функции f(x). На рис. 4.4 изображено семейство
поверхностей уровня некоторой выпуклой функции/(х), х = (х1у х2)у и показана
примерная траектория движения метода в идеализированном случае:
предполагается, что мы заранее знаем точку минимума х* и каждый раз дово-
рачиваем антиградиент на некоторый угол так, чтобы двигаться по прямой
в точку х*.
Рис. 4.4
Заметно, что на каждой итерации угол получается разный, и эти
соображения для задачи безусловной минимизации выпуклой функции f(x)
223

на всем пространстве Еп приводят нас к итерационной схеме: х0е Еп —
задано,
*A+i = xk-u*kHkfXxk\ k = О,1,..., (4.69)
где ak > О, k = О, 1,..., — шаг метода; Hk — положительно определенные
матрицы, т.е. (Hkx, х)>0 при всех х е Еп, k = О, 1, ... . Это неравенство
гарантирует остроту угла между векторами -f'(xk) и -Hkf\xk). Подчеркнем, что
мы можем лишь полагать, что при достаточно малых положительных щ
будет выполняться f(xk+1) <f(xk). Выбор же той или иной матрицы Hk
может оказаться как удачным, так и неудачным: при решении задачи
минимизации, как правило, совершенно неясно, как следует поворачивать
вектор -f'(xk) для ускорения сходимости.
На эти геометрические соображения можно взглянуть и с другой
стороны. Известно, что любая симметричная положительно определенная
матрица G размера п х п задает в пространстве Еп новое скалярное
произведение
(xyy)G=(Gxyy), х,уеЕп,
соответствующую норму \\x\\G=y](Gx,x) и метрику Рс(#, у) =
= yj{G(x-y),x-y). Такую метрику мы будем кратко называть G-метрикой.
Тогда итерационный процесс можно описать следующим образом: на
каждом шаге мы с помощью симметричной положительно определенной
матрицы Gk меняем метрику пространства, т.е. задаем преобразование
координат x = yjGkx. В этих новых координатах поверхности уровня функции
f(x) примут другой вид, в том числе может получиться так, что они станут
близки к сферам с центром в точке минимума х* = ->jGkx*. Текущая точка
xk перейдет в точку xk, функция f(x) перейдет в функцию g(x) = /(у^*)>
и будет вполне естественным сделать шаг метода по формуле
*k+l =xk~akg/(^k)y
что с учетом формулы дифференцирования сложного отображения можно
переписать в виде Т^Л+i =y^kxk~ak(y^k)~1f/(xk)- Домножая обе части
на (yJGk )_1, имеем
xM=xk-akG-k'nxk). (4.70)
Эта формула отличается от формулы (4.69) лишь тем, что в нее
входит обратная матрица G^1. Так как матрица, обратная к симметричной
положительно определенной матрице, тоже симметрична и положительно
определена, то для случая безусловной минимизации никакой разницы
в предлагаемых итерационных схемах (4.69) и (4.70) нет. Эти рассуждения
и объясняют название метода — метод переменной метрики.
В дальнейшем мы будем придерживаться схемы, в которую входит
обратная матрица, и вместо Gk будем писать G(xk), подчеркивая тем самым,
что на каждом шаге выбор матрицы Gk= G(xk) зависит от точки xk и свойств
функции f(x).
224

Для задачи условной минимизации дифференцируемой функции f(x)
/(*)->min;xe Ic£", (4.71)
предлагается действовать следующим образом. Пусть х0е X — некоторое
начальное приближение. Далее будем строить последовательность {xk}
по правилу
Ч+х = -Рх(Ч\ч-akG-Kxk)f'(xk)), k = О,1,2,.... (4.72)
где ak > О, k = О, 1, ..., — шаг метода; G(xk), k = О, 1, ..., — симметричные
положительно определенные матрицы размера п х п; V£ — операция
G-проецирования на множество X. Дадим ее строгое определение.
Определение 4.2. Пусть G — симметричная положительно
определенная матрица размера п х п. G-проекцией точки хе £ина множество 1с£й
называется ближайшая в смысле G-метрики к х точка множества X, т.е.
такая точка р, что
реX, (G(p-х),р-х) = min(G(u-х),и-х).
иеХ
Для G-проекции будем использовать обозначение p = Vx%. Приведем
утверждение, описывающее свойства операции G-проецирования.
Теорема 4.13. Пусть X — выпуклое замкнутое множество из Еп, G —
симметричная матрица размера пхп, числа тиМ таковы, что
0<т<М, m\\xf<(Gx,x)<M\\xf MxeX.
Тогда:
1) для любого хиз Еп существует, причем единственная, его G-проекция
p = Vgx на множество X;
2) Р = V%x тогда и только тогда, когда (G(p-x),u-p)>0 \/иеХ;
3) если Pi=Vx xi> Pi-^x хъ то \Р\ ~Pi\- —IK ~х21-
Доказательство
Заметим, что вторая производная функции г (и) = Pq(u, x) равна 2G, что
в совокупности с условием т\\х\\ ^ (Gx, х) при всех х е X означает ее
сильную выпуклость на множестве X. Таким образом, задача минимизации этой
функции на выпуклом замкнутом множестве X в силу теоремы Вейерш-
трасса 3.11 имеет, причем единственное, решение/?.
Далее, градиент функции г(и) равен 2G(u - х). Поскольку р
минимизирует функцию г(и) на множестве X, то по критерию
оптимальности 3.4 для выпуклых функций (г'(р),и-р)>0 при всех и е X, т.е.
(G(p-х),и-р)>0 при всех и е X.
В силу только что доказанного утверждения из того, что рх и р2
являются G-проекциями точек хх и х2 на множество X соответственно, вытекает
{G(px-xx),u-px)>Q VueX; (G(p2-x2),v-p2)>0 \/veX.
Полагая и=р2е X,v=pte X, имеем
(G(p1-x1),p2-p1)>0; (G(p2-x2),p1-p2)>0.
225

Складывая эти неравенства, получим
(G(x1-x2)yp1-p2)>(G(p1-p2)yp1-p2)y
откуда с учетом неравенства Коши — Буняковского и того, что т\\х\\ <
< (Gxy х) < М\\х\\ при всех х е Х> следует
т\р\ -Pit AG(<x\ -^2)INIa -#>MMlh -^INIa -ftll-
В случае \\р1 - p2\\ = 0 утверждение З доказываемой теоремы, очевидно,
верно. В противном случае мы можем поделить обе части последнего
соотношения на \\р1 -р2Ц что даст нам нужный результат. Теорема доказана. ■
Операция G-проецирования обобщает операцию метрического
проецирования, рассмотренную в параграфе 3.3: если положить G = 1п, где 1п —
единичная матрица размера п х п, то из теоремы 4.13 будут следовать
теоремы 3.14-3.16.
Таким образом, если в задаче (4.71) X — выпуклое замкнутое множество,
матрицы G(xk) симметричны, существуют такие положительные числа т
и М, 0 < т < М, что при любом k = 0, 1,... справедливо
ти|Ы|2 < (G(xk)x, x) < M\\xf Ух е X, (4.73)
а способ выбора ос^ > 0 задан, то последовательность {xk}> генерируемая
методом (4.72), будет определяться однозначно. Отметим, что для случая
Х=Еп уравнения (4.72) примут вид (4.70).
Метод переменной метрики, как очевидно из уравнений (4.72) или
(4.70), имеет два параметра: набор чисел ос^> 0 и набор матриц G(xk).
Отметим, что при желании можно обозначить G(xk) = akG(xk)> и перейти к
уравнениям с одним параметром G(xk).
Вообще говоря, вопрос выбора на каждом шаге матрицы G(xk) весьма
непрост. Понятно, что в случае G(xk) = In, k = 0, 1, ..., метод переменной
метрики превратится в метод проекции градиента, а в случае сильной
выпуклости функции/(х) можно положить G(xk) = f"(xk)> k = 0, 1, ..., что
приведет нас к варианту метода Ньютона, на каждом шаге которого
приближение xk+1 находится как решение задачи
1
fk(x) = ak(fXxk)yx-xk)+-(f\xk)(x-xk)yx-xk)^>mmy xeX.
Поскольку fk\x) = f"(xk)> то Для каждого k = 0, 1,... функция fk(x) будет
сильно выпуклой на X. Записывая критерий оптимальности для нее,
получим (fk(xk+1)> х-xk+1) > 0 при всех хе X, т.е.
(akf'(xk) + f'\xk )(xk+1 -xk\x- xk+1) > 0 VieX.
Это неравенство в силу теоремы 4.13 эквивалентно уравнению (4.72)
nPHG(xk)=f"(xk).
На практике обычно ищут матрицы G(xk) достаточно простой
структуры (диагональные, трехдиагональные, разреженные), ввиду того что
при решении задачи условной минимизации возникает необходимость их
226

обращения. Можно рассматривать матрицы поворота, явный вид которых
известен из курса линейной алгебры. В конечном счете определяющим
фактором их выбора является максимальное упрощение процесса
вычисления обратной матрицы G~1(xk) и процедуры нахождения G-проекции.
Следует сказать, что проблема конструктивного выбора матрицы G(xk)
в методе (4.72) пока еще мало изучена.
4.6.2. Сходимость метода переменной метрики
для выпуклых функций
Перейдем к обсуждению достаточных условий сходимости метода
переменной метрики.
Теорема 4.14. Пусть X — выпуклое замкнутое множество из Еп> f(x)
выпукла и непрерывно дифференцируема на Х> градиент f\x)
удовлетворяет условию Липшица с константой L > О, т.е.
\r{x)-f'{y)\<L\x-y\ Vx,yeX.
Пусть, кроме того, при некотором х0 е X множество М(х0) =
= {хеХ: f(x) < f(x0)} ограничено; матрицы G(xk) для любого k = О,1,...
симметричны и удовлетворяют условию (4.73). Наконец, пусть шаг ak
удовлетворяет условию
0<e0<ak<j?L, (4.74)
где е0 > 0, е > 0 — параметры метода. Тогда для последовательности {xk}>
полученной методом (4.72) при начальном приближении х0, выполнено
lim/(**) = /*, limp(^,X*) = 0, (4.75)
причем справедлива оценка
О <f(xk)-/*<%, C0=const>0, £ = 1,2,.... (4.76)
k
Доказательство
Сразу отметим, что в силу свойств множества Лебега и непрерывности
функции f(x) множество М(х0) замкнуто, и это в сочетании с его
ограниченностью дает его компактность. Тогда по теореме Вейерштрасса 1.2
inf f(x) = inf f(x) = f* > -co.
X M(x0)
Воспользуемся леммой 1.3, которая утверждает, что при сделанных
предположениях справедливо неравенство
L 1
|/(*) - Яу) ~ </'(*/)> х-у)\< -\\х - у\\ Ух, уеХ.
Полагая в нем у = xk,x = xk+l, имеем
f(xk)-f(xk+i)>(f'(xk),xk-xk+l)—-\\xk-xk+l\\ , 6 = 0,1,.... (4.77)
227

С другой стороны, из уравнения метода (4.72) и теоремы 4.13 следует,
что
{G{xk)[xk+x-{xk-akG~\xk)f\xk))lx-xk+x)>0 \/хеХ.
Перепишем это неравенство в виде
1
{fXxk),x-xk+])>—{G(xk)(xk-xk+i),x-xk+]) VxgX, £ = 0,1,.... (4.78)
ак
Отсюда при х = хк с учетом условия (4.73) вытекает
1 77Z II 1|2
(f'(xk)>xk~xk+i)-~~(G(xk)(xk-xk+1)1 xk -xk+i)>—\\xk-xk+i\\ ,
ак ак
£ = 0,1,...,
что в сочетании с тем, что градиент f'(x) удовлетворяет условию Липшица,
дает
f(xk)-f(xk+i)>l^—g iK-^+if' * = 0Л....
Далее, из этого соотношения и условий (4.74) на шаг метода находим
f(xk)-f(xk+l)>^\\xk-xk+lf, k = 0,l,..., (4.79)
что означает неубывание последовательности {f(xk)}. Так кж/(хк) >/* > -<»,
то существует конечный предел lim f(xk)> f* и, следовательно, \im(f(xk)-
k—>°° k—>°°
-f(xk+i)) = 0. Отсюда и из неравенства (4.79) предельным переходом
получаем lim \\хк - хк+1 II = 0.
к—»°°
Теперь еще раз воспользуемся ограниченностью множества М(х0). Так
как согласно неравенству (4.79) f(xk+1)<f(xk)<...<f(x0), то хке М(х0)
при всех к = 0, 1, .... По теореме Больцано — Вейерштрасса
ограниченная последовательность {хк} имеет хотя бы одну предельную точку. Пусть
х — произвольная предельная точка {хк} и {хк } —> х. Множество М(х0)
замкнуто, поэтому xeM(x0)(zX. По доказанному, lim|x^+1-x^| = 0,
значит, и {хк +i}—>х. Фиксируя в соотношении (4.78) ^f) оизвольное х е X
и переходя к пределу при к = кт —> °°, с учетом условий (4.73), неравенства
Коши — Буняковского и непрерывности f\x) получим
{f'(x\x-x)= \im(f'(xk \x-xk +i)>
т^оо т т
-^-^\\С(хО(х^-хо\[\\х-хЫ\^
> lim \\хк +i-xk \\'\\х-хк +i\\> i-i hm it +\~хк =0,
т^оо ак И т ШИ II т И 60 го->~11 Rrn+i *m|l
стало быть, по критерию оптимальности для выпуклых задач (теорема 3.4)
хеХ*.
228

Возьмем произвольную точку х* е X*. Из критерия выпуклости
(теорема 3.1) имеем
0<ak=f(xk)-f(x.)<(f'(xk),xk-x.) =
= <f'(Xk)>xk-xk+i)-(f'(xk)>x*-xk+i)> * = 0Л....
Пользуясь неравенством (4.78) при х = х*> условием (4.74) выбора ос^,
компактностью множества М(х0) и непрерывностью ||/'(*)||> отсюда
находим
1
0<ak<(f'(xk),xk-xk+1) (G(xk)(xk-xk+i),x*-xk+i)<
ak
А
- !/'(** )| • Ik* - хм II+—р(.*к )(** - хм )|| • Ik* - хм I ^
й !/'(** )| • Ik* - xm I+—Ik* - хм II • Ik* - хм II *
- k*-x*+i
e0
( .. и м и А и и
sup ||/'(*)||+— sup k*~x\\ \=^iIk*~xk+i\\> k=o,\,...
M(x0) 60 M(x0) J
Из этого соотношения и неравенства (4.79) следует ak-ak+1 >—Ci1a\ =
= Аа%, k = О, 1, ... . Отсюда с помощью леммы 1.6 придем к оценке (4.76).
Это означает, что последовательность {f(xk)} минимизирующая, т.е. первое
из равенств (4.75) выполнено. Второе равенство (4.75) вытекает из
теоремы 1.3. Теорема доказана. ■
Также отметим, что если при сделанных в теореме предположениях
функция f(x) является еще и сильно выпуклой на множестве X с
константой х, то по теореме Вейерштрасса 3.11 будет справедливо соотношение
\\xk-x4<f^, k = l,2,...
где х* — единственное решение задачи (4.71).
Замечание 4.5. Как было отмечено выше, полагая G(xk) = In или
G(xk) =f"(xk), k = О,1,..., мы получим варианты метода проекции градиента
и метода Ньютона. Приведем теоремы об их сходимости, непосредственно
вытекающие из теоремы 4.14.
Следствие 4.1. Пусть X — выпуклое замкнутое множество из Еп, f(x)
выпукла и непрерывно дифференцируема на X, градиент f'(x)
удовлетворяет на X условию Липшица с константой L > 0. Пусть, кроме того,
при некотором х0е Xмножество М(х0) = {хеХ: f(x)< f(x0)} ограничено,
2
а шаг ak удовлетворяет условию 0<е0 <ak < , к - 0, 1, ..., где е0 > 0,
Li i t
е > 0 — параметры метода. Тогда для последовательности {xk}>
генерируемой при начальном приближении х0 уравнениями xk+i =Px(xk ~akf'(xk))>
k = 0, 1,..., выполнено
limp(^,X*) = 0; 0<f(xk)-/*<-$-, C0 =const>0, 4 = 1,2,....
229

Следствие 4.2. Пусть X — выпуклое замкнутое множество из Еп,
intX Ф 0, f(x) сильно выпукла с константой к и дважды непрерывно
дифференцируема на X, градиент f'(x) удовлетворяет на X условию Липшица
с константой L > О, а шаг ak удовлетворяет условию 0 < е0 < ak < , k = О,
Lit
1, ..., где е0> 0, е > 0 — параметры метода. Тогда для последовательности
{xk}, генерируемой при произвольном начальном приближении х0 е X
уравнениями
1
xk+i E x> fk(xk+i) = ™lfk(x)> k = 0,\,...,
хеХ
справедливо
b-MJf.
С0 = const > 0, k = 1,2,...,
где х* — единственная точка абсолютного минимума функции f(x) на X.
При выводе следствия 4.2 необходимо учесть, что для сильно выпуклой
непрерывной функции множество Лебега М(х0) замкнуто и ограничено
при любом х0 g X, точки xk, k = О, 1, ..., в нем содержатся, откуда с учетом
непрерывности/"(.г) следует ограниченность ||/^(^)||, k = О, 1,..., и
выполнение условия x\\h\\ < {f"(xk)h, h) < М||/г|| при всех h e Еп, k = 0, 1,....
4.6.3. Непрерывный вариант метода переменной метрики
Следуя схеме, рассмотренной в подпараграфе 4.2.3, предложим
непрерывный вариант метода переменной метрики. Рассмотрим систему
дифференциальных уравнений
х(0) = х0,
где a(t) > 0 — заданная функция; G(x(t)) — симметричная положительно
определенная матрица при всех t > 0. Перед тем как обсуждать свойства
этой системы, докажем еще одно утверждение, связанное с G-проекцией.
Теорема 4.15. Пусть X — выпуклое замкнутое множество, X* —
множество точек минимума функции f(x) на X. Если х*еХ* и функция f(x)
дифференцируема в точке х*, то для любой симметричной положительно
определенной матрицы G размера пхп необходимо выполняется равенство
x*=V§(x*-aG~xf'(x*)) Vcc>0. (4.81)
Если, кроме того, f(x) выпукла на X, то всякая точка х*,
удовлетворяющая равенству (4.81), принадлежит X*.
Доказательство
В силу теоремы 4.13 равенство (4.81) эквивалентно неравенству
(G(x,-(x,-aG-1f(x,)),x-x,)>0 VxeX,
которое можно переписать в виде
(af'(x*), х - х*) > 0 \/х е X,
230

что для всех а > 0 равносильно неравенству (f'(x*), х-х*) >0, х е X.
Отсюда и из теорем 1.7, 3.4 следует утверждение этой теоремы. ■
Замечание 4.6. Только что доказанная теорема 4.15 представляет собой
обобщение теоремы 3.17.
Согласно теореме 4.15 решение х* задачи (4.71) удовлетворяет при t > О
уравнению (4.81) при а = a(t) > 0. Это значит, что каждая точка х* еХ*
является точкой равновесия (стационарным решением) системы (4.80).
Можно надеяться, что при некоторых ограничениях на функции/(х), a(t)
и матрицу G(x) траектория x(t) системы (4.80) при больших t
приближается к множеству X*. Если X = Еп, то при всех х е Еп Т>х(х) = х, и (4.80)
превращается в систему
x(t) = -a(t)(G(x(t)))-if'(xm t>0,
х(0) = х0.
Если Хф Еп, то уравнение (4.80) в силу теоремы 4.13 эквивалентно
неравенству
(G(x(t))[x(t) + x(t) - (x(t) - a(t)(G(x(t)))-if'(x(t)))l x - (x(t) + x(t))) > 0
\/xeX,t>0,
которое после упрощений принимает вид
(G(x(t))x(t) + a(t)f'(x(t)), x - x(t) - x(t)) > 0 \/x e X, t > 0. (4.83)
Отсюда ясно, что при G(x) = In методы (4.82) и (4.80) превращаются
в непрерывный вариант градиентного метода (4.27) и метода проекции
градиента соответственно. В случае когда/(х) е С2(Еп) и сильно выпукла
на Еп, полагая G(x) =f"(x), можно получить непрерывный вариант метода
Ньютона. Приведем теорему о сходимости метода (4.80).
Теорема 4.16. Пусть X — выпуклое замкнутое множество, функция
f(x) g Сх(Еп) и выпукла на Еп, /* > -°о, X* Ф 0; функция a(t) > ос0 > 0
непрерывно дифференцируема и ос'(0 ^ 0 при всех t>0; матрица G(x)
симметрична, и существует сильно выпуклая на Еп с константой к > 0 функция
\у(х) е С1^) такая, что \\f"(x) = G(x) при всех х е Еп. Пусть траектория
системы (4.80) с начальным условием х(0) = х0 определена при всех t>0.
Тогда существует точка v* = v*(x0)e X* такая, что
lim x(t) = v*, lim f(x(t)) = f(v*) = /*, lim x(t) = 0.
t—>°° t—>°° t—>°°
Доказательство
Рассмотрим произвольную точку х* е X*. Тогда в силу критерия
оптимальности (теорема 3.4) для всех х е X справедливо (f'(x*), х - х*) > 0.
Примем в этом неравенстве х = x(t) + x(t) e X, умножим его на a(t) > 0 и
сложим с неравенством (4.83) при у = х*. Это даст нам
(G(x(t))x(t) + a(t)(f'(x(t)) - f\x*)), х, - x(t) - x(t)) > 0,
что равносильно неравенству
(G(x(t))x(t), x(t)) + (G(x(t))x(t), x(t) - x* > + a(t)(f'(x(t)) -
- f\x*), x(t)) + a(t)(f'(x(t)) - f\x*), x(t) - x, > < 0 V^ > 0, Vx* g X*.
(4.84)
231

По условию теоремы существует функция \\f(x) такая, что \\f"(x) = G(x)
при всех х е Еп, поэтому
—(\|/(х*) - \|/(х(0) + <\|/'(*(0)> *(t) ~ x*» =
= (y"(x(t))x(t), x(t) - х,) = (G(x(t))x(t), x(t) - x, >.
Кроме того,
^(f(x(t))-f(x,)-(fXx.),x(t)-x,)) = (f'(x(t))-f'(x*),m),
и в силу выпуклости функции/(х) на Еп и теоремы 3.1
(f'(x(t))-f'(x*),x(t)-x*)>0 W>0. (4.85)
Тогда из неравенства (4.84) следует
(G(x(t))x(t), x(t)) + 4т(У(х*) " ¥(*(*)) + <¥'(*(*))> x(f) - х,» +
+ <х(О^(/(^(О)-/(^)-<//(^),лг(О-^»^0 W>0,V*.eX,.
Интегрируя это неравенство на произвольном отрезке [т; t], получим
t t
\{G{x{s))x{s), x(s))ds + (\|/(х*) - \\f(x(s)) + (y'(x(s)), x(s) - x*» _ +
T
+а(0(/(^))-/(ь)-(/'(ь)д(5)-ь})[;;-
- Ja'(5)(/(x(s))-/(x.)-<//(x.),x(s)-x.»flb^0 W>x>0, Vx. eX..
T
Из выпуклости функции f(x) на f72 и сильной выпуклости \|/(х) на Еп
по теоремам 3.1, 3.12, 3.13 вытекает
f(x(t))-f(x*)-(f'(x*),x(t)-x*)>0 W>0,Vx*gX*;
\|/(х*)-\\f(x(t)) + <\|f'(*(*))> x(t)-х*)^к\x(t)-x, f Vt > 0, Vx* g X*;
<С(х(ОЖО, *(*)> ^ *|*(*)f v* ^ 0.
Все это с учетом соотношений a(t) > 0, a'(0 ^ 0 дает нам
xj||x(5)| <is + x|x(£)-**| <у(х*)-\у(х(т)) + (\у'(х(т)),х(т)-х*) +
+ a(T)(f(x(T))-f(x*)-(f'(x*), х(т)-х.)) = v(x, x.) (4.86)
W>t>0,Vx*gX*.
II , ч l|2 V(0,X*) Л +Г,, , .,2 , V(0,X*)
Это означает, что \\x(t) -хЛ < при всех t > 0 и I ш £) at < .
К Q К
Поэтому существует последовательность {£,-} —> +°о такая, что {x(t{)}—>v*,
{х(Ъ)} —> 0. Так как множество X замкнуто, x(t) + x(t)e X при всех t > 0, то
lim (£(£,-) + x(t{ )) = v*eX.
i—»-н»
232

Положим в неравенстве (4.83) t = t{. Тогда при z —> °° с учетом
соотношения lim a(t{) = ос(°о) > ос0 > О имеем
i—»oo
а(соХ/'(&»), х - v*> > О \fx € X.
Согласно критерию оптимальности (теорема 3.4) тогда v* е X». Из соот-
ношения (4.86) при х* =v*>x = t{ следует \x(t) -vA < —v при всех t > 0.
Переходя здесь к пределу при £, £,- —> -н», имеем lim х(£) = v*. Тогда
lim /(*(*)) = Яги) = /♦, lim f'(x(t)) = /'(о.).
Наконец, с учетом неравенства (4.84) при х* = v* имеем
к\\x(t)f < (G(x(t))x(t), x(t)) < (G(x(t))x(t), v, - x(t)) - a(t)(f'(x(t)) -
-nv.),x(t)) + a(t){nx(t))-f'(v.),v.-x(t))<
^ |G(x(0)| I*(t)|| ||o. -х(0||+a(0|/'(^(0)-/'(w.)|| И*)|| ^
<|ir(0|(|G(x(0)||h-x(0|+a(0|/^(0)-/4^)|N
^^dGWO)|h-^)|| + a(0||/4^))-//(o.)||)2+|:|i:(()||2 W>0,
откуда вытекает
\mf <^(iG(x(t))\\\\v*-^(0|+a(0|/'WO)-/'(fO|)2 W>0.
Отсюда при t —> +00 следует, что lim i:(£) = 0. Теорема доказана.
4.7.* Квазиньютоновские методы
Еще раз подчеркнем, что все вышеперечисленные варианты метода
Ньютона могут быть эффективно использованы лишь тогда, когда матрица
вторых производных f"(x^) легко вычисляется и все последующие
вспомогательные задачи решаются достаточно просто. Желание преодолеть
возникающие здесь трудности привело к появлению так называемых
квазиньютоновских методов. Основным их достоинством является тот факт, что
они имеют высокую скорость сходимости, не сильно уступающую методу
Ньютона, но при этом не требуют на каждом шаге вычислять обратную
матрицу вторых производных.
Для простоты изложения будем рассматривать задачу безусловной
минимизации
f(x) —> min, х е Еп,
и предполагать, что/(х) е С1^). Общая итерационная схема
квазиньютоновского метода выглядит так: выбираются начальное приближение х0 е Еп
233

и матрица Н0 размера п х и, дальнейшие вычисления проводятся по
формулам
xM=xk-tkHkf'(xk), Hk+i=U(xhHk), £ = 0,1,2,..., (4.87)
где tk — некоторые числа, а функция U(xk, Hk) такова, что
последовательность матриц {Hk} размера п х п удовлетворяет так называемому
квазиньютоновскому условию
HkM\4+x)-f\xk)) = xk+i-xk, £ = 0,1,2,.... (4.88)
Это условие фактически является требованием того, что матрица Hk+i
в определенном смысле аппроксимирует обратные матрицы вторых
производных (f"(xk+i))-x и (/""(Jty))"1: если воспользоваться для
функции/формулой конечных приращений, то
f'(xk+1)-f'(xk) = f"(xk + e(**+i -**))(**+i -*k)> ве[0;1],
что в случае невырожденности матрицы /"(#) может быть переписано
в виде
(/"(** +6(^+1 -xk)))-i(J'(xk+i)-f'(xk)) = xk+1 -xk.
Сравнивая это уравнение с квазиньютоновским условием (4.88), мы
убеждаемся, что матрицы Hk+1 и (f//(xk+Q(xk+i-xk)))~i удовлетворяют
одному и тому же соотношению, в которое входят приращения аргумента
и градиента функции/. Именно этот факт и позволяет обеспечить высокую
скорость квазиньютоновских методов.
Возникает естественный вопрос: как на каждом шаге строить матрицы
Hk+V k = 0, 1,2,...? Ясно, что при работе с итерационной схемой
квазиньютоновского метода мы на каждом шаге сначала по известным xk, Hk находим
xk+i, после чего вычисляем приращения градиента f'(xk+i) -f'(xk) и
аргумента xk+1 - xk и приходим к необходимости решить систему из п
уравнений (4.88), в которую входит п2 неизвестных элементов матрицы Hk+i.
Очевидно, что такая система имеет бесконечно много решений, и
возникает вопрос о какой-то их структуризации. Кроме того, совершенно неясно,
все ли они будут позволять существенно улучшить значение функционала
при переходе к xk+2 или нет. Исчерпывающий ответ на эти вопросы вряд ли
существует, однако выделить некоторые способы построения «удачных»
матриц Hk+i вполне возможно.
Мы рассмотрим простейший из таких способов. Напомним, что векторы
х{ и градиенты /'(•*;) являются вектор-столбцами, т.е. имеют размерность
п х 1. Предлагается итеративно переходить от матрицы Hk к матрице Hk+1
с помощью формулы
Hk+1=HkH(xk+1-xk)-Hk(f\xk+1)-f(xk))] \ (4.89)
ak v/ \xk+i)-j \xk))
где вектор-столбец dk, вообще говоря, зависящий от xk и Hh на каждом шаге
выбирается так, чтобы число dj(f'(xk+1)- f'(xk)) не равнялось нулю.
234

Отметим, что при таком способе вычисления Hk+1 квазиньютоновское
условие (4.88) выполнено, в чем можно легко убедиться прямой проверкой.
Формула (4.89) задает так называемое семейство квазиньютоновских
методов ранга один. Такое название является вполне естественным следствием
того, что так называемая матрица поправки
.„_„ „ ((*M-*t)-gt(/'(*bi)-/'(*t))KT
4H'="W~"4 W<^,)-/'(*»)>
имеет ранг, равный единице, в силу того что она является произведением
вектор-столбца на вектор-строку. Векторы dk можно трактовать как
параметризацию этого семейства: каждый конкретный способ их выбора задает
соответствующий ему квазиньютоновский метод.
Наиболее известным методом ранга один является метод Бройдена,
который получается, если в уравнениях (4.87) положить tk= 1, k = 0, 1, ...,
а в уравнениях (4.89) на каждом шаге брать dk=f'(xk+i) -f'(xk)> что
приводит нас к такой схеме: пусть начальное приближение х0 е Еп, и матрица Я0
размера пхп известны, тогда
xk+i=xk-Hkf'(xk), £ = 0,1,...; (4.90)
(zk-Hkyk)yJ^ k = 01^ (491)
\\ Г* s ч Г§ • ч К-
VkVk
где zk = xk+i - xk, yk = f'(xk+i) ~f'(xk)- Если подставить так введенные
величины zk и yk в формулу (4.91), то она примет вид
Hkr(xk+i)(fXxk+l)-fXxk)y
\\f'(xk+l)-f'(xk)f
Перед тем как приступать к изложению результатов о сходимости
метода Бройдена, введем некоторые необходимые понятия и докажем
несколько вспомогательных утверждений.
Пусть А — матрица размера пхп. Напомним, что нормой (операторной
нормой) матрицы \\А\\ называется число [29]
IUI| = max!^.
хеЕп \\Х\\
Лемма4.1 (Банаха). Пусть А,В — матрицы размерапхпиА
невырождена. Тогда если \\А-Ш\ < 1, то матрица А + В тоже невырождена, причем
II/HI
|(Л+В)"'|£г™- <492)
Доказательство
т
Обозначим С = -А~ХВ и рассмотрим семейство матриц Sm = £ Ck, m = 0,
1, ..., где С°= 1п — единичная матрица. Заметим, что ||с||<|и_1||-||5||<1. Так
как ||С*|| < ||с|| при всех k = 0, 1,..., то для любых целых неотрицательных т,
/, т < /, выполнено
235

II с с II —
\k=m+\
< i ihi< i \\c\kM^,
k=m+\ k=m+\ 1-lib ||
поэтому \St -Sm\—>О при /, m —> °°. Таким образом, матричная
последовательность {Sm} — фундаментальная, из чего вытекает ее сходимость к
некоторой матрице S. Кроме того,
Sm\\ =
2 с*
\k=0
<Sl№xlkf< i
k=o k=o 1-IICII
/и = 0,1,...,
значит,
,и|Ы|<
i
i-И
Также воспользуемся тем, что справедливы равенства
Sm(In-C) = (In-C)Sm=In-C^, m = 0,l,....
Переходя в них к пределу при т —> °°, с учетом того, что из || С\\ < 1
следует || О711| —> 0 при т —> «э, т.е. матричная последовательность {С171} сходится
к нулевой матрице, имеем S(In- С) = (In- C)S = In, поэтому S = (1п- С)-1 =
= (4 + Л-1/*)-1, матрица 1п + А'1 В невырождена, ее определитель отличен
от нуля. Так как определитель произведения матриц равен произведению
их определителей и 1п + А~ХВ = А~{(А + 5), то и определитель матрицы А + В
тоже отличен от нуля, А + В — невырождена. Наконец,
||(Л + Б)-1| = |(Л(/й+Л-1Б))-1| = ||(/и+Л-15)-М-1|<|и-1|.|5||<
„ IU-Ч „ IU-4I
-i-IU-ifiiri-IU-i|.|Bir
Лемма Банаха доказана. ■
Помимо леммы Банаха нам понадобится норма Фробениуса матрицы А
размера пхп, представляющая собой обобщение обычной нормы вектора
на случай матрицы:
iuii, =
( п п \l
114
С помощью непосредственных вычислений несложно убедиться в
справедливости следующих свойств этой нормы: если А — произвольная
матрица размера пхп, то
lUlJ = tr(ATA) = t(ATA)a, IUII ^IUIf ; \AxyT\F = 1^ 1Ы1 v*> Уе £п> (493>
«=i
\\A(In-xyT)(F=\\AfF-2yTATAx + \\Axt\\y( Vx,yeE". (4.94)
Теперь перейдем к обоснованию теоремы о сходимости метода Бройдена.
Теорема 4.17. Пусть функция f(x) дважды непрерывно
дифференцируема и сильно выпукла с константой >с в некоторой окрестности
X = {хе Еп: \х-х*| <С} точки х*у f'(x*) = 0 и существует число К>0 такое,
что выполнено неравенство
\\f"(x)-f"(x*)\\^K\\x-x*\\ \/xeX. (4.95)
236

Тогда метод, определяемый уравнениями (4.90), (4.91), локально и
сверхлинейно сходится к х*> что означает, что существуют такие е, 8 > 0, что
из справедливости неравенств |х0-х*|<е, |#0-(/"(x*))_1|F <8
(локальность) вытекает
lim К-^1 тг = 0 (сверхлинейность).
k^>°o pck-x*\
Доказательство
Начнем с обоснования того, что при сделанных предположениях
для всех uyveX справедливо неравенство
\fXu)-f\v)-f'Xx*)(u-v)\<Km^ (4.96)
и, кроме того, существует такое положительное число р, что
Ни - v\\ < \f'(u) - f'(v)\\ <p\\u- v\\ Vm, veX. (4.97)
р
Для этого заметим, что для любого ае [0; 1], любых х, у е Еп
справедливо
far + (1 - a)y| < а|Ы1 + (1 - а)|у| < тах{Ы1; |г/|}.
Интегрируя обе части этого соотношения по а от 0 до 1, имеем
1
/far + (1 -a)y\da < тах{Ы1; |г/|} Vx, у е Еп. (4.98)
о
Далее, пользуясь формулой конечных приращений (1.116), для любых
uyveX имеем
1 1
\\f'Xv + t(u-v))(u-v)dt-\f'Xx*)(u-v)dt\
о о
\\f'(u)-f'(v)-f"(x*)(u-v)\\ =
= JtTfa + t(u - v)) - /"(*. ))(u - v)dt\ < \\\f"(v + t(u - v)) - f"(x*)|| • ||и - v\\dt <
llo II о
1 1
<K\\u-v\\j\\v + t(u-v)-x*\\dt = K\\u-v\\j\\t(u-x^
о о
Применяя соотношение (4.98) к подынтегральному выражению в
правой части, положив x = u-x*,y = v-x*, получаем
\\1'(Ц) ~ Г(Р) ~ f"(x* )(и - v)\\ < К тах{| и -х.\\; \\v - х* |} \\и - v\\.
Неравенство (4.96) доказано. Для доказательства двойного неравенства
(4.97) воспользуемся непрерывностью отображения/"(х) и сильной
выпуклостью f(x). Поскольку множество X замкнуто и ограничено, то
существует такая константа М, что |/"(*)| - М для всех хе X. Тогда по формуле
конечных приращений с учетом выпуклости X
\\f'(u)-f'(v)\<M\\u-v\\ \/u,veX,
237

\\ЩЧ<1
и, кроме того, по теореме 3.12 и неравенству Коши — Буняковского
>г ||ы - dl2 ^ <УЧ«> - УЧ»). м - »> ^ ||УЧм) - УЧ»)|| - Им - dl ^ Af Им - dl2 -
Сокращая это неравенство на \\и - v\\ и полагая р = тах{М; 1 / к), мы
получаем неравенство (4.97).
В силу выполнения условия теоремы матрица f"(x*) будет
положительно определенной и невырожденной, а х* будет точкой минимума
функции/(х) наX. Возьмем произвольное положительное re (0; 1) и выберем
числа е = е(г) и 8 = Ь(г) так, что
е<С; 25|/"(*0|<г; Kp|(/''(*.))i|e<5(l-r);
Кг(2Ь+\\(Г(х,))-^)+2ЦГ(х4^г.
Ясно, что это можно сделать, взяв их достаточно малыми. Возьмем
любую пару (х0, Я0) такую, что |х0-х*|<е, ^-(/''(.г*))-1!^ <8. Тогда
с учетом свойств нормы Фробениуса (4.93) \\Н0 - (/" (х.))-1| < 8 и, поскольку
5||/"(.**)| < г/2 < 1 в силу соотношений (4.99), то по лемме Банаха 4.1,
полагая Л = (/"(•** ))_1> В = Н0 -(/"(•** ))_1> мы имеем невырожденность матрицы
Я0 и оценку
1№)|
1-г/2 '
Пользуясь уравнениями (4.90) и тем, что f'(x*) = 0, имеем
Х\ ~ х* = хо ~ -"о/ v*0/ — х* =
= -H0(fXxo)-fXx-)-f"(x*)(x0-x,)) + (In-Hof"(x.))(x0-x.).
Положив в неравенстве (4.96) в качестве и и v точки х0е X и х* е X
соответственно, находим
1х1-х4фоШ'(*о)-/'(*•)-f"(.x-X*o-x4+Pn -Я0/"(*.)|Н|*0 -х*\\<
<Кг\\Н0\[\\х0 -*.|+|/"(х.)||-|Я0 -(f"(x*))-f\\x0-x4<
<(^е|Я0|+5|/"(д:.)|)|ко-^|-
Но поскольку
||Я0|<|(/''(х.))-1|+|Я0-(Г(^))-1И5+|(/"(хО)-1|,
то, учитывая соотношения (4.99), мы получаем ||^ — лг* || < г||jr0 — jf* ||.
Дальнейшее доказательство проведем по индукции. Предположим, что удалось
провести k > 0 итераций метода, точка xk+i найдена, справедливы
соотношения
\\Нт-(Г\х,))-%<2Цхт+1-х4<г\\хт-х4 Vm = 0,l,...,£.
Покажем, что тогда либо xk+1 = х*, либо матрица Hk+i и точка xk+2 могут
II 1|2
быть найдены с помощью формул (4.90), (4.91) (знаменатель yji/k -\Уи\
дроби в формуле (4.91) окажется отличен от нуля), причем
\\НМ-(Г(х*)У% <25,\\xk+2-x*\\<г\\хм-х.\.
238

Из предположения индукции следует, что |xm+1-x*|<rm+1|x0-x*|<
<rm+1e<C, m = 0, 1, ..., ky поэтому точки хь х2>..., xk+1 принадлежат
множеству X. Пользуясь неравенством (4.97), имеем
л
l^l = |A^+i)-/4^)||^-K+i-^|.
Отсюда следует, что случай yk = 0 возможен, только если xk+i = xk, что
с учетом формулы (4.90) эквивалентно равенству Н^\хк) = 0. Так как
\\Hk-(f"(*•))-% £2&, то в силу свойства (4.93) ^-(/'Ч**))-1!^,
и поскольку из (4.99) вытекает 28||/"(.г*)||<г<1, то по лемме Банаха 4.1,
полагая A = (f"(x*))~1y B = Hk-(f/\x*))~iy мы имеем невырожденность
матрицы Hk и оценку
К'1^.
Значит, уравнение Н^\х£) - 0 имеет только нулевое решение, т.е.
f'(xk) = 0. Но тогда
o = \\f\xk)-f\x4>-\\xk-x,l
поэтому xk+1 =xk= x*, и метод останавливается, найдя точку минимума.
В противном случае укФ 0, матрица Hk+i и точкаxk+2 могут быть вычислены
по формулам (4.90), (4.91). Для всех т = 0,1,..., k справедливо соотношение
K+i -cr(*»))if=\ня+(Zm -н™Ут)уТт -(/-(х.))-1
|| УтпУгп
(Ят-(/"(хО)-1)
L-
УтУ1^
УтУт J
\\{гт-{Пх,))^ут)у1
УтУп
Оценим правую часть этого соотношения. Для обработки первого
слагаемого воспользуемся формулой (4.94), взяв в ней Л = Ят-(/'Хг*))-1,
х=у и= Ут = Ут .
л Ут> У Т „ „о*
УтУт \\Ут\\
\\(Нт-(Г(х,)у1)
'»-..т
УтУ1
УтУп
=\\Hm-(f "(**))-%-
- 2-%[Нт -(Г(х.)У^[Нт -(Г(х.)УЧут +\[Нт -(Г'(х.)У1]ут\\
I2 \\Уп
\\Уп
II II4
\\Ут\
п и2 \\Hm-(f"(x.))-4ymf
-\\nm~U Кх*)) \\F " ~2 -
= ят-(/"(^.))-1
a(i \[Hn-{f'Xx.)y\yf Л
\\Нт-(Г(х,))-^\\у
1|2 и ||2
llf w^m I
239

Для оценки второго слагаемого воспользуемся неравенством (4.96)
при и = хт+1 g Xy v = хт g X и свойствами нормы Фробениуса (4.93)
ддяА=1п,х = 2т-(/,Хх*)Г1Ут,У = ^- = -М^:
УтУт \Ут\
|[г,-(Г(*.))г1у,]ут| \\гт-(Г(х*)ГхУт\Ы_
1J~^~ 1J II II
II УтУт ||f |Z/m||
\\Г(хт+0-Г(хт)\\
По предположению индукции ||xm+1-x*|<r||xm-x*|<|xm-x*|, кроме
того, в силу неравенства (4.97) „ п " m+1—-^—гг<р, стало быть,
\\f'(xm+l)-f'(xm)\\
кгп-(Пх.))-1ут)уЛ <Кр1(Г(Хт)у1Ц \\
|| УтУт \\р
Пользуясь этими оценками, для всех т = О, 1,..., k имеем
К+1 -(/"(*.))if ^ ТГё^Ця, -(/"(x.))-i|f+
+ iCp|(/"(x.))-1||K-^|,
где
_\\(Hm-(f"(x*))-i)yn
(4.100)
e„=i
Jm
\\Нт-{Пх,))-%\ут
<1.
Загрубим эти неравенства при всех т = 0, 1, ..., k, заменив множители
>/l-0^ на 1, и сложим их. С учетом того, что ||xm-x*|<rm|x0-x*|<rme,
и соотношения (4.99), получим
К, -</»<*.»-1Ия„ -</w|f+**yl's
s5^p|(/-<^))-|ea28
Положив в лемме Банаха 4.1 Л = (/"(**))-1> B = Hk+i-(f"(x*))~1, мы
получим, что матрица Я^+1 невырождена и
*й|^-
Наконец, рассуждая так же, как и ранее, находим
xk+2 -x*= xk+l - Hk+if'(xk+1)- х* =
= ~Hk+i [f'(xk+l) - f'(x.) - /"(** )(xk+l - x»)]+(In - Hk+lf"(x* ))(xk+l - x»),
240

поэтому с учетом неравенства (4.96)
IK+2 -x4*JlpMllfXxiHrl)-fxx.)-f"(x.xxM -х.ц+
+\\1п-нмгхх4-\\*м-Ф
<Ke\\HM\\-\\xk+i -*.|+|/"(х.)|-||яы -(/"(^))-1|NK+i -х4*
<(Хе|ЯА+1|+8|/"(^)|)|К+1-^|-
Так как
K+J * №(х.)г*\+\нм-(Г(х.)г11 ^
<25+|(/"(*»))i|,
то, учитывая соотношение (4.99), мы получаем \xk+2 -х*\<r\xk+x -х*\.
Индукционный переход завершен. Итак, мы показали, что либо на какой-то
итерации получится f'(xk) = 0 (это критерий остановки метода), что
эквивалентно условию xk =х*, либо с помощью уравнений (4.90), (4.91) будет
получено две последовательности {xk}, {Hk} такие, что для всех k = 0, 1,2,...
справедливо
xkeX; \\xM-x.\\<r\\xk-x4; 1нк-(Г(х.)У%*2&;
1я-1|<И*>1. (4Л01)
^h+i-^k\\4fXxk+l)-fXxk)\\<p\\xk+l-xk\\. (4.102)
Отметим, что сходимость метода Бройдена к х* с линейной
скоростью нами уже установлена, так как из соотношений (4.101) следует
|х^-х*|<г^|х0-х*|. Для доказательства сверхлинейной сходимости
вернемся к неравенствам (4.100). Теперь можно утверждать, что они
справедливы при всех т = 0, 1,.... Заметим, что vl-я < 1 — для всех а < 1, поэтому
их можно переписать в виде
^\\нт -(ГХх.)У% <\\нт -(Г(х.)У% -
-К+1 -(Г(.х.))-%+icP|(/"(^))-ilh h> -*.ц.
Суммируя эти неравенства по т от 0 до произвольного N, находим
\ £ Ъ\ня -(Г(х*))-%<\\н0 -(ГХх*)У% -\\HN+i -(f'Xx*))-% +
, Кр\\(Г(х.))-\ ,, *р|(Г(*ОН|е
1-Г " " 1-Г
-и» .. ..
Это значит, что ряд £ 6JL \Нт -(/'Ч**))"1) L СХ°ДИТСЯ> поэтому
т=0
Um Ql\\Hk -(f'Xx*)T% =0. (4.103)
241

Подставляя сюда выражение для 0^, имеем
\LHk-(f"(x.))-t)yk(
lim "v " SJ x " "K\ = 0.
Hk-(f"(x*))-l\
£_>noll тт , Г„, чч < II II l|2
IIF'
Из этого с учетом неравенства (4.101) |#£-(/%r*))_1| <28 вытекает,
что и
JH-^-^U (4,04)
Из формул (4.90) имеем
ЩУк = Hkf'(xk+l)-Hkf'(xk) = Hkf'(xk+l) + xk+i -xk,
стало быть,
(Я4-(/"(х.))-1)У*=Я4/'(^*+1)-(/"(х.))-1(У*-Г(х.)г*).
Отсюда с помощью неравенства (4.96) получаем соотношение
||/'(хА+1 )|| < ||iyft-i || [||(//А - (/"(х*) )"! )2/А ||+1(/"(^ ))"11| • ||^ - /'Ч^* )гА ||] =
= |Я,-1||[|(Я,-(/"(^))-1)^| + |(/"(^))-1|х
*1/Ххы)-/'(.хк)-Г(х.Ххм-хк%]й
<\\щЩ(нк -(/"(х.))-1)^|+^|(/"(^))-1||К -*-|-|*ы-**|]-
Разделив его на |^|| = |/4^+i)~/4^)|» c учетом соотношений (4.101)
имеем
0<lim И*ы)| <f- И^)! <
k^\\fXxk+l)-f'(xk)\\ *-и.|/'(*ы)-/'(**Я
^ кГ(*.И lim 1як-(Г(х.)гчук\ |
1_Г *_>„ |у4|
Первый предел из правой части этого неравенства равен нулю в силу
равенства (4.104). Пользуясь неравенством (4.102), имеем |jty+1-jty|<
< p|/4^+i)~/4^)|- Кроме того, xk -х* —> 0, стало быть и
Шп 11/^1)» -о
k4\f'(xk+0-f'(xk)\\
Наконец, в силу соотношения (4.97)
|/'(**+i)| = |/'(^+i)-/'(^)| ^ ЧхМ-х*1
|/'(^+i)-/'(^)|^p|K+i-^INp(IK+i-^I+IK-^I)^
<р(1+г)\\хк-х*\\,
242

поэтому
o<iimlfcizfJ<iim р|/'<^.)|| =0.
Теорема доказана. ■
В качестве еще одного примера квазиньютоновского метода ранга один
рассмотрим метод МакКормика, который получается, если в формуле (4.87)
положить tk= 1, а в формуле (4.89) на каждом шаге брать dk=xk+i -xk.
Выпишем его схему. Пусть начальное приближение х0е Епи матрица Я0 размера
п х п известны, тогда дальнейшие вычисления проводятся по формулам
xk+i=xk-Hkf'(xk\ £ = 0,1,...; (4.105)
Hk+i = Hk + (Zk~HTkyk)Z^ , £ = 0,1,..., (4.106)
ЧУк
где zk = xk+1 - xk, yk = f'(xk+x) -f'(xk). Приведем без доказательства
утверждение о его сходимости.
Теорема 4.18. Пусть функция f(x) и точка х* удовлетворяют условиям
теоремы 4.17. Тогда метод МакКормика (4.105), (4.106) локально и
сверхлинейно сходится к х*у т.е. существуют такие е, 8 > 0, что из \х0 -х*\\ < е,
|Я0 -(///(^*))~1|/г -S вытекает
k^°° \\Xk~X*\\
Отметим, что можно утверждать локальную сверлинейную сходимость
целого семейства методов ранга один, в которых на каждом шаге векторы dk
выбираются равными Nyk, где N — произвольная симметричная
положительно определенная матрица размера пхп.
Теперь еще раз вернемся к обсуждениям того момента, что матрицы Hk
в определенном смысле аппроксимируют матрицу (/"(•%£) )-1- Для дважды
дифференцируемой функции матрица вторых производных и обратная
к ней симметричны, поэтому хотелось бы пользоваться их симметричными
аппроксимациями. Однако матрицы Hk, получаемые в методах Бройдена
и МакКормика, будут несимметричны. Несложные рассуждения
показывают, что единственный способ получения квазиньютоновского метода
ранга один, гарантирующего симметричность матриц Hk> таков: матрица Я0
выбирается симметричной, затем на каждом шаге полагаем dk= zk- H$k.
Но такой метод не обладает свойством локальной сходимости, т.е. может
случиться так, что, выбирая х0 и Я0 сколь угодно близкими к х* и (/"(•** ))-1
соответственно, мы не получим последовательность {xk}> сходящуюся к х*.
Приведем соответствующий пример.
Пример 4.3
Рассмотрим функцию f(x) = — Ы| , х = (xvx2)T e E2. Для задачи ее минимизации
на Е2 имеем х* = (0,0)т, /* = 0,
243

f'(x) = x,f"(x) = (f"(x))-^
В качестве начального приближения х0 и матрицы Я0 берем
{ г ^
Хк =
1 + 8
^
v 1-е/
'1 + е О Л
О 1-е
Выбирая 8 близким к нулю, мы можем сделать нормы |д:0 - х»| и |#0 -(/"(*))_1|F
сколь угодно малыми. Однако
z0=x{-x0 = -H0f'(x0) = 8(1 + 8)I ; г/о = /'(*i)" /'(*о) = х\ ~хо = 2о5
dQ = 20 - Н0у0 = 20 - #0Z0 = 82(1 + 8)
1
Очевидно, что d^y0 = 0, и мы даже не можем выполнить один шаг метода,
несмотря на близость начального приближения к решению задачи.
Эти трудности можно преодолеть, рассматривая квазиньютоновские
методы ранга два. Кратко обсудим их вид. Пусть начальное приближение
х0 g Еп и матрица Я0 размера п х п заданы, дальнейшие вычисления
проводятся по формулам
Hk+i =Hk +
xk+i-xk-Hkf'(xk)>
(Ч -НкУк)^ + dk(zk -нкУкУ yk(zk~Hkyk)dkdk
djyk
idjykf
где zk = xk+1- xky yk=f'(Xk+i) ~f'(xk)> a векторы dk являются параметрами
метода и на каждом шаге в зависимости от xk, Hk выбираются каким-то
определенным способом. Нетрудно убедиться, что такая формула дает матрицу
Hk+1, удовлетворяющую квазиньютоновскому условию (4.88), причем ранг
матрицы поправки AHk= Hk+1 - Hk теперь окажется равным двум. Более
того, если матрица Hk была симметричной, то и матрица Hk+1 тоже
окажется симметричной.
Конкретными примерами методов ранга два являются метод Грин-
стадта, в котором берут dk = yk, и метод BFGS (Бройдена — Флетчера —
Гольдфарба — Шанно), в котором полагают dk = zk. Достаточные условия их
сходимости описывает следующая теорема.
Теорема 4.19. Пусть функция f(x) и точка х* удовлетворяют
условиям теоремы 4.17. Тогда методы BFGS и Гринстадта локально и
сверхлинейно сходятся к х*> т.е. существуют такие е, 8 > 0, что из |г0 -х*| < е,
|#0 -(/"С**))"1!^ -5 вытекает
Более глубоко познакомиться с теорией и примерами
квазиньютоновских методов читатель может в работе [18].
244

4.8. Метод покоординатного спуска
В предыдущих параграфах мы рассмотрели методы, которые для своей
реализации требуют вычисления первых или вторых производных
целевой функции. Однако в практических задачах нередко встречаются случаи,
когда либо эта функция не обладает нужной гладкостью, либо
вычисление ее производных с нужной точностью является слишком трудоемким.
В таких случаях желательно иметь методы минимизации, для реализации
которых достаточно уметь вычислять лишь значения функции. Одним
из таких методов является метод покоординатного спуска.
4.8.1. Основная версия метода для задач без ограничений
Рассмотрим задачу минимизации функции общего вида на всем
пространстве:
/(*)->min,xE Х = Еп. (4.107)
Выберем в пространстве Еп некоторый базис {e,-}f=1, например
стандартный базис из единичных координатных векторов е{- (0,..., 0,1, 0,..., 0), г = 1,
2, ..., и, у которых i-я координата равна единице, а все остальные
координаты равны нулю. При реализации метода будет производиться
циклический перебор этих базисных векторов, поэтому для удобства описания
итерационного процесса (теоретически бесконечного) выстроим их в единую
бесконечную последовательность
Ро = еьР\ = еъ •••> Рп-\ = *п> Рп = еь рп+1 = еъ ..., р2п_х = еп, р2п = еь .... (4.108)
Перед запуском метода выбирается некоторая стартовая точка х0 е Еп>
стартовый шаг ос0 > 0 и коэффициент дробления шага X е (0; 1). Допустим,
что на k-и итерации найдено k-e приближение xk и текущее значение шага
равно ak > 0. Для определения очередного приближения выполняются
следующие действия. Берется базисный вектор pk и вычисляется значение
функции в точке х = xk + CLfpk. Проверяется условие:
если/(х*+ ag>k) <f(xk\ то xk+1 = xk+ ед, ak+1 = ak (4.109)
и процесс продолжается из точки xk+1 со следующим по порядку базисным
направлением pk+1. Если/(х^+ ос^) >f(xk)> то вычисляется значение
функции в противоположной точке х = xk - CLjpk. Проверяется условие:
если/(х*- ag)k) <f(xk)y то xk+1 = xk- ag)h ak+1 = ak (4.110)
и переходим к следующей итерации с очередным базисным вектором pk+i.
Будем называть (k + 1)-ю итерацию удачной, если переход от xk к xk+1
произошел по одному из условий (4.109) или (4.110) и сопровождался строгим
убыванием значения функции. Если же f(xk - ос^) > f(xk)> т.е. нарушены
оба условия (4.109) и (4.110), назовем (k + 1)-ю итерацию неудачной.
Дальнейшие действия зависят от предыстории. В процессе вычислений ведется
подсчет числа неудачных итераций, случившихся подряд. Если их общее
245

количество вместе с неудачей на текущем (k + 1)-м шаге еще не достигло
и, то полагают
Xk+i=*k> ak+i=<*k (4.111)
и переходят к очередному базисному направлению pk+1. Если же все п - 1
итерации, предшествующие неудаче, зафиксированной на (£+1)-м шаге,
также были неудачными, то производится дробление шага ak с априорно
выбранным коэффициентом А е (0; 1):
Xk+i=*k> ak+i=^k (4.112)
и проверка основных условий (4.109) и (4.110) продолжается на более
мелкой сетке. Достаточные условия сходимости описанного варианта метода
покоординатного спуска содержит следующая теорема.
Теорема 4.20. Пусть функция f(x) выпукла на Еп и принадлежит
классу С1(Еп), а начальное приближение х0 таково, что множество
M(x0) = {xeEn:f(x)<f(x0)} ограничено. Тогда последовательность xk,
вырабатываемая методом (4.108)—(4.112), сходится и по функции,
и по аргументу:
lim/(**) = /., limp(^,X*) = 0. (4.113)
k—»°о k—»°о
Доказательство
Согласно теореме 1.3 имеем /* > -©о, X* Ф 0. Из описания метода (4.108)—
(4.112) следует монотонность: f(xk+i) <f(xk), k = 0, 1, ..., поэтому при всех
k = 0, 1,... xkg M(x0) и существует lim f(xk)> /*.
k—»°о
Покажем, что lim ak = 0, т.е. моментов дробления шага метода будет бес-
конечно много. Допустим противное: пусть последнее дробление
состоялось на N-м шаге, после чего процесс вычислений (бесконечный)
продолжается с фиксированным шагом а^= а^= а > 0, k = N, N+ 1,.... Рассмотрим
в пространстве Еп дискретную решетку (сетку) Ма с одним и тем же
равномерным шагом а > 0 по всем координатным направлениям и поместим
точку xN в один из ее узлов. Из описания метода покоординатного спуска
следует, что все следующие приближения xk являются узлами этой самой
решетки, т.е. xk e Ma V k> Nn остаются в пределах ограниченного
множества М(х0), в котором может находиться лишь конечное число узлов сетки
Ма. Но при перемещении по конечному множеству узлов невозможно
бесконечное число раз наблюдать строгое убывание значений функции, без
которого обязательно произошло бы дробление шага. Полученное
противоречие показывает, что процесс дробления ak бесконечен и lim ak = 0.
k—»°°
Пусть k±<k2< ... <km< ... — номера тех итераций, на которых длина шага
ak дробится. В соответствии с описанной процедурой (4.108)—(4.112) этим
дроблениям предшествуют серии ровно из п неудачных итераций по всем
базисным направлениям:
Л^+«Атег)>/(^), /(^-aftme,)>/(^), i = l,2,.... (4.114)
246

Из последовательности точек xk , принадлежащих ограниченному
множеству М(х0)у можно выбрать сходящуюся подпоследовательность. Без
умаления общности можем считать, что сама последовательность {xk }
сходится к некоторой точке х*. С помощью формулы конечных приращений
из неравенств (4.114) для всех г = 1, 2,... имеем
</Хч, +ет<ЧЛМК *0' </'К, -в^тв,.),ег.)(-а^)>0 (4.115)
при некоторых 0+, 0~ е[0;1], т = 1, 2, ... . Поделим неравенства (4.115) на
ak > О, после чего перейдем в них к пределу при т —> °°. С учетом условия
f'(x) g С(Еп) непрерывности градиента, ограниченности значений 0± и
сходимости ak —> 0 получим соотношения
</'(**),*,->>0, </'(**),е*>^0, z = l,2,...,n.
Так как {ez}f=1 — базис в Еп, то отсюда следует, что f'(x*) = 0, а поскольку
функция f(x) выпукла, то точка х* является одной из точек минимума:
х* еХ*. Получается, что подпоследовательность {xk } является
минимизирующей: lim f(xk ) = f(x*) = f*. Отсюда и из монотонности последова-
т—>°° m
тельности \f(xk)} следует, что минимизирующей является и вся
последовательность {xk}: \imf(xk) = f*, т.е. первое из утверждений (4.113) доказано.
k—»°о
Второе утверждение о сходимости по аргументу по теореме 1.3 следует
из сходимости по функции и ограниченности множества М(х0). Теорема
доказана. ■
Заметим, что при реализации описанного варианта метода
покоординатного спуска не используются значения градиентов минимизируемой
функции, однако в условии теоремы 4.20 присутствует требование гладкости
этой функции. Приведем пример, показывающий, что при отсутствии
гладкости без усиления остальных условий теоремы 4.20 сходимость метода
покоординатного спуска гарантировать нельзя.
Рассмотрим двумерную задачу минимизации
f(u) = (х-1)2 + (у -1)2 + 2\х - у\ —> min, и = (х, у)еЕ2.
Функция/непрерывна, сильно выпукла, ограничена снизу на всем пространстве Е2,
достигает своей нижней грани /* = 0 в единственной точке и* = (х* = 1, у* = 1) и на
прямой у = х не является дифференцируемой. Нетрудно проверить, что при выборе в Е2
стандартных базисных направлений ех = (1,0), е2 = (0,1) в случае запуска метода
покоординатного спуска из начала координат щ = (0; 0) независимо от выбора стартового
шага ос0 > 0 процесс зациклится в начальной точке: щ = и0= (0; 0), k = 1,2,..., и
сходимости к решению задачи минимизации не будет ни по функции, ни по аргументу:
f(uk)-f*=f(u0)-f* = 2, \uk-u*\=\u0-u*\=y/2, * = 1Д....
4.8.2. Другие варианты метода покоординатного спуска
Описанный выше метод покоординатного спуска нетрудно
адаптировать для решения задач минимизации на выпуклых замкнутых множествах
247

X(zEn несложной структуры с непустой внутренностью int Хф&.
Рассмотрим для примера задачу минимизации на параллелепипеде:
/(х)—>min, xeX = {x = (xi,...yxn)eEn: аг;<хг! <A»-,i = l,...,n}, (4.116)
где аь Ъ{ — заданные числа, а{< biy г = 1,..., п. Пусть на k-и итерации найдено
очередное приближениеxke Xс шагом а^>0и выбрано очередное
базисное направление pk. Проверяется условие:
если^ + а^е X^f{xk + ag)k)<f{xk), Toxk+x = xk+ag)hak+x = ak. (4.117)
Если хотя бы одно из двух условий (4.117) нарушено, организуется
проверка ПРОТИВОПОЛОЖНОЙ ТОЧКИ Xk - OLfPk-
ecmxk-ag>ke Xnf(xk-alpk)<f(xk)yToxk+1 = xk-akPhak+1 = ak. (АЛ18)
Если нарушены и условия (4.117), и условия (4.118), то (k + 1)-я
итерация считается неудачной и дальнейшие вычисления выполняются по
правилам (4.111), (4.112), (4.117), (4.118). Сформулируем утверждение о
сходимости описанного процесса. Его доказательство можно найти в работе
[12].
Теорема 4.21. Пусть функция f(x) выпукла на множестве X вида (4.116)
и принадлежит классу С1(Х). Тогда при любом выборе начального
приближения х0 g X и стартового шага ос0 > 0 последовательность xk,
вырабатываемая методом (4.111), (4.112), (4.117), (4.118), сходится к решению
задачи (4.116) и по функции, и по аргументу:
lim f(xk) = /• = inf /(*), lim p(xh X*) = 0.
k—»°° xeX k—»°°
Существуют и другие варианты метода покоординатного спуска. Так,
вместо стандартного базиса из единичных координатных векторов,
который использовался в формуле (4.108), можно взять в Еп произвольный
базис {ef-}f=1, не обязательно ортонормированный. При этом останутся
в силе утверждения обеих теорем 4.20 и 4.21, правда, «покоординатным
спуском» соответствующий итерационный процесс можно будет назвать
с некоторой натяжкой. Кстати, если в примере 4.3 с негладкой функцией
f(x) в качестве базисных направлений вместо стандартных координатных
взять векторы ех = (1, 1), е2= (-1, 1), то из того же самого начального
приближения щ = (0; 0) для любого стартового шага ос0 > 0 последовательность
{xk} будет сходиться к решению задачи.
Вместо процедуры дробления для определения значения шага ak можно,
как и в методе скорейшего спуска, решать вспомогательную задачу
одномерной минимизации типа (4.16):
a* = argming£(cc), gk(a) = f(xk+apk), (4.119)
-оо<а<-и»
и в качестве следующего приближения брать точку
xk+i=xk+apk, £ = 0,1,.... (4.120)
248

Этот подход эффективен в тех случаях, когда задачу (4.119) можно
решиь явно, в частности в случае сильно выпуклых квадратичных
функций вида
f(x) = ±(Ax,x)-(b,x), (4.121)
где А — симметричная положительно определенная матрица размера пхп,
Ъ g Еп. Заметим, что для таких функций метод (4.119), (4.120) превращате-
ся в хорошо известный из линейной алгебры итерационный метод Зейде-
ля [6], которым в данном случае решается система линейных
алгебраических уравнений f'(x) = Ах- Ъ = 0.
Хотя скорость сходимости метода покоординатного спуска, вообще
говоря, невысокая, благодаря простоте каждой итерации и скромным
требованиям к гладкости минимизируемой функции этот метод довольно
широко применяется на практике. Существуют и другие методы
минимизации, использующие лишь значения функции и не требующие для своей
реализации вычисления производных. Например, используя вместо
производных их разностные аппроксимации, можно построить модификации
методов, описанных в предыдущих параграфах, при реализации которых
будут задействованы лишь значения функции в подходящим образом
выбранных точках. Другой подход для минимизации негладких функций,
основанный лишь на вычислении значений функции, дает метод покрытия,
который будет рассмотрен ниже в параграфе 4.9.
4.9. Метод покрытия для функции многих переменных
Опишем еще один метод минимизации, основанный лишь на
вычислении значений целевой функции без привлечения значений каких-либо ее
производных. Речь пойдет о методах покрытия, одномерный вариант
которых был изложен в параграфе 4.1. Эти методы служат для минимизации
функций, удовлетворяющих условию Липшица. Заметим, что такие задачи
в общем случае являются многоэкстремальными, т.е. в них могут
существовать точки локального минимума, отличные от точек глобального
минимума. Большинство методов, описанных выше в этой главе, при их
применении к многоэкстремальным задачам скорее всего нам помогут найти
лишь какую-либо точку локального минимума, расположенную
поблизости от начальной точки. Поэтому эти методы часто называют локальными
методами. На практике для решения многоэкстремальных задач локальные
методы обычно используются следующим образом: на множестве задают
некоторую сетку точек и, выбирая в качестве начального приближения
точки этой сетки, с помощью того или иного локального метода находят
локальные минимумы функции, а затем, сравнивая полученные
результаты, определяют ее глобальный минимум. Однако ясно, что такой подход
к решению многоэкстремальных задач весьма трудоемок и не всегда
приводит к цели. Поэтому представляют большой интерес методы поиска
глобального минимума в многоэкстремальных задачах.
249

Перейдем к изложению одного из методов покрытия, которые служат
для решения многоэкстремальных задач с целевой функцией,
удовлетворяющей условию Липшица. Ограничимся рассмотрением задачи
минимизации на параллелепипеде:
f(x)->min, xeTI = {x = (х1,...,хп): а{ <х{ <biy г = 1,...,и}, (4.122)
где а{, Ъ{ — заданные числа, а{ < Ъ{, а функция f(x) удовлетворяет условию
\f(x)-f(y)\<L\\x-y\l \/x,yeIIy (4.123)
где L = const > 0, \х-г/L = max)*1' -у1'). В правой части неравенства (4.123)
можно было поставить любую другую норму \х -у\ 1 < р < -н», например
евклидову норму \х - г/||, как это мы неоднократно делали выше, когда
требовали выполнения условия Липшица от функции или ее производных.
В силу эквивалентности норм в Еп условие Липшица в любой норме может
быть сведено к виду (4.123). А норма \х - г/L здесь привлекает нас тем, что
такие множества, как параллелепипед, куб, удобно описывать с помощью
именно такой нормы. Так, например, множество
{хеЕп:\\х-х0\\ж<к/2} = {хеЕп:\х1-х10\<к/2^ = 1,...,п}
представляет собой куб с центром в точке х0, ребром длины h и с
гранями, параллельными осям координат. Именно такими кубами мы будем
покрывать параллелепипед П. Кроме того, использование нормы Ц-IL позволит
нам изложить многомерный вариант метода покрытия для решения задачи
(4.122) так же просто, как в одномерном случае.
На параллелепипеде П введем многомерную сетку Щ, состоящую из
совокупности точек вида X; А = (xl, xf, ...,х/,..., х7} ), j-я координата х3{
которых при каждому = 1,..., п образована по правилу (ср. с параграфом 4.1):
х]т ._i = х{ + (mj - 2)h, xJm. = min{x/ + (ти,- - l)h; bj},
где h = шаг метода, а натуральное число mj определяется двойным
неравенством х3т _х <bj — <x{ +(mj-l)h. В качестве приближения нижней
грани /* в задаче (4.122) можно взять величину min/te { ) = Fh, которую
Щ
можно найти с помощью простого перебора всех значений функции f(x)
по точкам сетки Щ. Имеет место следующая теорема.
Теорема 4.22. Для любой функции f(x), удовлетворяющей условию
(4.123), справедлива оценка
/*<^</#+е. (4.124)
250

Доказательство
Кубы IL л ={хеЕпЛх-Х;Л | ^h/2} с центрами X: л ellh
покрывают весь параллелепипед П. Это означает, что для любой точкиigII
найдется куб IL г , содержащий эту точку. Отсюда и из условия (4.123) имеем
/(x)^/(xJi.j;)-l||x-x^L^FA-l| = FA-e УхеП.
Переходя здесь к нижней грани по х е П, приходим к оценке (4.124). ■
Метод простого перебора предполагает, что в каждой точке сетки Ylh
вычислены значения функции f(x), которые в определенном порядке
перебираются с целью определения величины Fh. Однако, как и в
одномерном случае, нетрудно указать более эффективные способы
определения величины Fh, которые, вообще говоря, не предполагают вычисления
значений функции/(х) во всех точках сетки Щ и перебора всех точек этой
сетки.
Опишем один из таких методов последовательного перебора. На
первом шаге выбирается произвольная точка v{ e Щ, вычисляется значение
f(vx) и полагается Fx = f(vx). Допустим, что в точках vb v2, ..., vk сетки Ylh
уже вычислены значения функции f(v{), ..., f(vk) и найдена величина
Fk = mmf(vi) = mm{Fk_1;f(vk)}, k > 2. Через vh обозначим ту из точек
\<i<k Jk
vx,..., vk, в которой Fk = f(Pj ). Далее возьмем любую из точек vk+i e Щ,
которая в предыдущих шагах не исключалась из рассмотрения и в которой еще
не вычислялось значение функции/(х). Вычислим значение f(vk+i) и
величину Fk+1=mm{Fk;f(vk+1)}= min f(v{). Имеются две возможности: либо
Fk+i=f(vk+i) < Fh либо Fk+i = Fk<f(vk+i). В первом случае, когда Fk+i < Fk,
полагаем Vj = vk+1 и из дальнейшего перебора исключаем точку Vj и
вместе с нею все точки х{ х е ПЛ, для которых
Кл-^И^г11- (4125>
Заметим, что некоторые из этих точек могли оказаться исключенными
из перебора уже на предыдущих шагах. Для нас важно лишь то, что среди
исключенных точек заведомо нет таких, в которых значение функции f(x)
было бы меньше, чем Fk+1.B самом деле, справедливо f(Pjk) = Fk > Fk+i. Для
остальных исключенных точек X: , , не зная значения f(xit , ), можем ска-
зать, что
f(^.jJ-Fk+i=f(xi,.jJ-f(%) + Fk-Fk+i^
в силу соотношений (4.123) и (4.125). Рассмотрим вторую возможность:
Fk+1 = Fk <f(vk+1). Тогда полагаем Vj =Vj и из дальнейшего перебора
исключаем точку vk+1 вместе с точками х{ { е ПЛ, для которых
Ki-4*/(p*f~f*- <4126>
251

Нетрудно убедиться, что и в этом случае в исключенных точках
значения функции не могут быть меньше Fk+1. Действительно, здесь
f(Xi,jn)-Fk+i =Яхк^)-/<Рк+1)+/<Ры)-Ъ *
^-L\\xh.jn-vM\\ + f(4+i)-Fk^
в силу соотношений (4.123) и (4.126). Общий шаг метода описан.
Так как на каждом шаге метода берется новая точка сетки Щ,
которая еще не исключалась из перебора и в которой значение функции f(x)
еще не вычислялось, то ясно, что на каком-то шаге описанного процесса
перебора такая новая точка не найдется и процесс закончится за N шагов,
N<mi-m2-...-mn> перебором точек vb ..., vN сетки Ylh и определением
величины FN = min f(vt) = min f(x;j ) = Fh. В силу теоремы 4.22 величина Fh
удовлетворяет неравенствам (4.124).
Как и в одномерном случае, нетрудно привести примеры, когда
изложенный метод покрытия может превратиться в метод простого перебора
точек сетки Щ. В то же время ясно, что если величины Fk- Fk+i,f(vk+]) - Fk
в формулах (4.125), (4.126) достаточно большие, то многие точки сетки ПЛ
будут исключены из перебора без вычисления в них значения функции.
4.10.* Метод модифицированных функций Лагранжа
Рассмотрим задачу
/(*)-> min, хеХ, (4 127)
X = {xeX0<zE»: g{(x) < О,..., gm(x) < 0; gm+i(x) = 0,..., gm+s(x) = 0},
где/(х), g\(x),..., gm+s(x) — заданные функции, определенные на множестве
Х0. Пусть /* > -°о, X* Ф 0. Для выпуклой задачи (4.127) при различных
дополнительных предположениях в параграфе 3.4 было установлено, что
найдутся множители Лагранжа
Г = (Х\,...,\*m+s)e А0 = {\е£»«: X, >0,....Хт >0}
такие, что пара (х*Д*), где х* еХ*, образует седловую точку нормальной
функции Лагранжа
m+s
L(x,X) = f(x)+ZKgi(x)> xzXo> ^Л0, (4.128)
i=l
т.е.
1(х*Д)<Цх*,Г) = /*<1(х,Г) VxgX0, VXgA0. (4.129)
Была также доказана справедливость обратного утверждения: если
(х*, X*) g Х0 х Л0 является седловой точкой функции (4.128), то х* е X*.
Основываясь на этих фактах, можно предложить различные методы
решения задачи (4.127), сводящиеся к поиску седловой точки функции
Лагранжа. Например, здесь естественным образом напрашивается итераци-
252

онный процесс, представляющий собой метод проекции градиента по
каждой из переменныххик (спуск по переменнойхи подъем — по К):
xk+1=PXo(xk-akL'x(xhXk)), k = Q i
h+i = \ (h + akL{(xk, Xk)) = PAq (Xk + akg(xk))y
где
L'x(x,X) = (L'x t (хД),..., Un (хД)),
Ц,(х, X) = (L{{ (x, A),..., L{m+s (x, A)) = (&(*),..., gm+5(x)) = g(x);
длину шага ak в процессе (4.130) можно выбирать из тех же соображений,
как это делалось выше в параграфе 4.2. Заметим, что проекция любой точки
X g Em+S на множество Л0 вычисляется явно по формуле РА (к) = (\ily...,\im+s)y
где
|ьц =max{\;0}, z = l,...,m; Цг=\, z = m + l,...,m + s.
Однако этот метод может не сходиться к решению исходной задачи, что
покажем на несложном примере.
Пример 4.5
Пусть/(х) = 0, X = {х е Е\ : g^x) = л: < 0}. Нормальная функция Лагранжа этой
задачи имеет вид
L(x,\) = x\, xeX0=E1, ^еЛ0=[0; + «>).
У нее на Х0 х Aq есть единственная седловая точка (х* ,Х*) = (0; 0). Запишем
уравнения процесса (4.130):
xk+\ =xk~ ak^k, ^k+\ =^k+ akxh k = 0,1,....
Но тогда
поэтому вне зависимости от выбора начального приближения (х0, Х0) Ф 0 и длины
шага 0С£ > 0 процесс расходится.
Пример 4.5 иллюстрирует, что попытка напрямую использовать
для поиска седловой точки функции Лагранжа изложенные выше методы,
пригодные для решения задач оптимизации, может оказаться неудачной.
Дело в том, что функция Лагранжа (4.128) по переменной \ не очень хорошо
«устроена». Чтобы преодолеть возникающие здесь трудности, можно
попытаться видоизменить функцию Лагранжа, строить так называемые
модифицированные функции Лагранжа, которые имеют то же множество седловых
точек, что и функция (4.128), но при этом обладают лучшими свойствами.
Такие функции, оказывается, существуют и могут быть использованы как
для поиска седловой точки функции (4.128), так и для решения задачи
(4.127). Мы рассмотрим один из возможных здесь подходов.
Ограничимся рассмотрением следующей задачи:
/(*)->min, xeX = {xeX0QEn:g1(x)<0y...ygTn(x)<0}, (4.131)
253

где f(x), g(x) = (g\(x), ..., gm(x)) — заданные функции класса СХ(Х0). Для
сокращения записи мы будем пользоваться векторными неравенствами:
если а е Ет, то запись а > (<) 0 означает, что щ > (<) 0, г - 1,..., ш,
неравенство а>(<)Ь для а,ЬеЕт будем трактовать как неравенство а - Ъ > (<) 0.
Например, с учетом этих обозначений систему неравенств gi(x) < 0, ...,
gm(x) < 0 можно записать в виде g(x) < 0.
Наряду с классической функцией Лагранжа задачи (4.131)
L(x,X) = f(x) + (g(x),X)1 xeX0, ХеА0={ХеЕ™:Х>0} = Е™ (4.132)
рассмотрим следующую модифицированную функцию Лагранжа:
M(x^) = f(x) + ±\\(X + Ag(x)y(-±\\xf (4.133)
переменных х е Х0,Хе Л0, где А — произвольная фиксированная
положительная константа; в формуле (4.133) принято обозначение
а+=РЕ?(а) = (а{,...,а]п)у ^=тахЦ;0}, z = l,...,m, (4.134)
— проекция точки ае Ет на положительный ортант Е™.
Нетрудно видеть, что функция cp(z) = (max{z; О})2 = (z+)2 одной
переменной непрерывно дифференцируема на всей числовой оси Е1, причем
(p'(;z) = 2max{z;0} = 2z+.
Отсюда следует, что если/(х), g(x) e С{(Х0), то функция (4.133)
непрерывно дифференцируема по х и X, причем
м;оа)=/'<*)+№ (х)у(\+лё(х)]\
1 хеХ0ДеЛ0, (4.135)
M{(x,\) = j\(\ + Ag(x)y-\l
где g'(x) =
дх1 '" дхп
dgm(x) dgm(x)
дх1 '" дхп ,
— матрица Якоби размера т х и, у
которой в 1-й строке J-м столбце стоит число g{j(x) = * . , г = 1,..., mj = 1,..., и,
а матрица (g'(x))T получена транспонированием g'(x). Далее, пользуясь
теоремами 3.8, 3.9 и следствиями из них, нетрудно показать, что если Х0 —
выпуклое множество и функции f(x), g\(x), ..., gm(x) выпуклы на Х0, то
функция М(х, X) выпукла по переменной х на множестве Х0 при любом
фиксированном X е Л0.
Отметим также, хотя это ниже явно не будет использовано, что
функция М(х, X) является вогнутой по переменной X на множестве Л0 = Е™
при любом фиксированном х е Х0 — в этом проще всего убедиться,
доказав неравенство (Мх(х,Х)-Мх(х, |ы)Д-|и)<0 для всех X, |i e Л0 и затем
воспользовавшись теоремой 3.1.
254

Перейдем к описанию метода решения задачи (4.131), использующего
функцию М(х, X). В качестве начального приближения возьмем любые
точки х0 е Х0, Х0 е Л0. Пусть k-e приближение xk e X0, Xk e Л0 уже известно.
Составим функцию
1 2
Ф*(*) = —1*-**| + аМ(х,Хк), хеХ0, (4.136)
где а — некоторое положительное число, являющееся параметром метода.
Предположим, что существует точка vk, удовлетворяющая условиям
vkeX0, Фк(рк) = тшФк(х). (4.137)
хеХ0
В качестве следующего приближения примем xk+i = vk. После этого
приближение Хк+1 находится по формуле
Xk+i=(Xk+Ag(xk+i))+. (4.138)
Описанный метод (4.137), (4.138) кратко будем называть методом
модифицированных функций Лагранжа. Для исследования его сходимости нам
понадобятся некоторые свойства функции а+, определенной равенствами
(4.134). Из теоремы 3.16 следует, что
\\а+-Ь+\\<\\а-Ь\\ \/а,ЬеЕп. (4.139)
Далее, система соотношений
g = (&,..., gm)< О, Х = (Х1,...Дт)>0, Х&=0, 1 = 1,...,m, (4.140)
эквивалентна равенству
X = (X + Ag)+ (4.141)
при любых постоянных А > 0. В самом деле, если выполняются
соотношения (4.140), то для каждого г = 1,..., т либо g{ = 0, X,- > 0, либо X,- = 0, g,-< 0.
В каждом из этих случаев, очевидно, равенство (4.141) верно. Таким
образом, из равенства (4.140) следует равенство (4.141). Докажем обратное.
Пусть имеет место равенство (4.141). Распишем его покоординатно:
Xf = (Хг- + Ag{)+ = max{Xz- + Ag{; 0}, г = 1,..., т.
Отсюда ясно, что Хг > 0 при всех г = 1,..., ш, т.е. X > 0. Если при каком-то
г е {1, ..., т} Хг = 0, то X^g; = 0 и, кроме того, 0 = (0 + Ag{)+y откуда следует
gi < 0. Если Хг > 0, то 0 < Хг = (Хг + А&)+, что возможно лишь при g{ = 0. Итак,
Kei = 0, z = 1,..., m, g< 0. Эквивалентность равенств (4.140) и (4.141)
доказана.
Далее, пользуясь определением (4.134) функции а+, нетрудно получить,
что для любых а, Ъ е Ет
(а+,а) = (а+,а+), (a\b)<(a\b+),
откуда вытекает
255

(a+-b+,a-b) = (a+,a) + (b+,b)-(a+,b)-(b+,a)>
>(a+1a+) + (b+,b+)-(a+1b+)-(b+1a+) = (a+-b+1a+-b+)1
т.е.
(a+-b+,a-b)>(a+-b+,a+-b+) = \\a+-b+f \/a,beEm. (4.142)
Теорема 4.23. Пусть Х0 — выпуклое замкнутое множество из Еп,
заданные функции f(x), g\(x), ..., gm(x) класса С1(Х0) выпуклы на Х0,
/* >-«>, X* Ф&, функция Лагранжа (4.132) имеет хотя бы одну седловую
точку (х;Х*)еХ0 хЛ0 в смысле неравенств (4.129). Тогда
последовательность {(xk, X^)}, получаемая методом (4.137), (4.138) при любом выборе
начального приближения (х0, Х0) е Х0 х Л0 и любых фиксированных
параметрах а > О, А > О, существует и сходится к некоторой седловой точке
функции Лагранжа (4.132).
Доказательство
При сделанных предположениях функция М(х, X) выпукла по
переменной х g Х0 при всех X g Л0, А > 0, поэтому при любых xk e X0, Xk е Л0, а > О,
А > 0 функция Ф^(х), определяемая формулой (4.136), сильно выпукла наХ0
с константой сильной выпуклости >с- 1. Отсюда и из теоремы 3.11 следует,
что точка vk = xk+i, удовлетворяющая условиям (4.137), существует и
определяется однозначно. Таким образом, при выполнении условий теоремы
последовательность {(xk, Xk)} существует и имеются достаточно
эффективные способы реализации каждой итерации метода (4.137), (4.138).
Возьмем произвольную седловую точку (х*Д*)еХ0хЛ0 функции
(4.132). Согласно лемме 3.4 ее существование эквивалентно соотношениям
(f'(x*) + (g'(x*))TX*,x-x*)>0 \/xeX0; (4.143)
g(**)<0, Г>0, Х;&(х0 = 0, z = l,...,m. (4.144)
В силу эквивалентности соотношений (4.140), (4.141), условия (4.144)
можно переписать в следующей равносильной форме:
X*=(X*+Ag(x*))+. (4.145)
Из сотношения (4.143) с учетом равенства (4.145) имеем
(fXx.) + (g\x.))T(Xm +Ag(x.))+,x-x.)>0 \/xeX0. (4.146)
Далее, из условия (4.137) и теоремы 3.4 следует, что
<*£(**+i)>*-**+i>^° VxgX0.
Отсюда с учетом формулы (4.135) получим
<**+i-**+a/4**+i) + ^ /4147ч
\/хеХ0. К ' }
Примем в формуле (4.146) х = xk+1, k = 0, 1, ..., умножим полученные
неравенства на а > 0 и сложим с неравенством (4.147) при х = х*. Это даст
нам соотношения
256

+<a(g'(^+i))T(^ + Ag(xk+l)y -a(g'(x.)y(Xm+Ag(x.)y,x* -xk+l)>0.
Отсюда для всех k = О, 1,... имеем
-a<( V + Ag(x.))+, g'(*« )(**+i - x. )>+a(f'(xM ) - /'(*.), x*+1 - x. >. (4.148)
Так как функции/(л:), g,-(:r) выпуклы, то согласно теореме 3.1
(f'(xk+i)-f'(x,),xk+i-x.)>0;
g'(xk+i Xxk+i -X')* g(xk+1) - g(x.) > g'(x* )(xk+l - x*).
Отсюда и из неравенства (4.148) следует
<**+i -**»*• -**и> ^<*«Л* + Л#(%и))+ -Q-* + Ag(x*))+,g(xk+l)-g(x*)) =
= ^((Xk + Ag(xk+l)y-(X* + Ag(x.)y, «Xk + Ag(xk+l))-\k)-(X* + Ag(x.))-\y
К правой части этой оценки применим неравенство (4.142). С учетом
формулы (4.138), определяющей точку Xk+1, и равенства (4.145) получим
(xk+1 -xk,x.- xk+1) > j((Xk + Ag(xk+1))+ -
- (Г + Ag(x*)yy [(Xk + Ag(xk+1))+ -h\- № + 4g(x<))+ " V]> >
-"7^+i~^ >^m~^~^*+^*) = ~t^+i~^ >^k+i-^k)> A = 0,1,...,
т.е.
<*Л+1 -x^, x* -*Л+1)+— (ХЛ+1 -Xk,X* -Xk+i) > 0, & = 0,1,...,
откуда, воспользовавшись тождеством
2<«-i,c-a> = ||i-c||2-k-i||2-||c-d|2, (4.149)
справедливым для любых векторов а, Ь, с из произвольного евклидова
пространства, находим
II II2 alh i*ll2^ll II2
||Х^-Х*|| + — \\Ak-A\\ >\\Xk+1-Xk\\ +
л £ = 0,1,.... (4.150)
«II2 a/Hi i II2 Hi i*ll2\
^+i~x*|| +T4r*+i~A*ll +lr*+i~A II J>
Суммируя эти неравенства по k от 0 до произвольного N, получим
||2 ОС и. . *||2
N
(
11 U|h 1*11 V» II ¥ Ulh 1 \Г \г*
+ Т11Л^+1~Л11 +2^ ||^+1"^|| + ~7|г*+1~Л*11 \-
А
k=o
п2 а.
V
Л1
<|х0-х#|2+^0-Г|2. (4.151)
257

Это значит, что ряды ^ |дгл+1 -х^| и ^ Ц^+i ~^| сходятся, и поэтому
Jim \\xk+i -xk\\ = 0, lim \\Xk+i - Xk\\ = 0. (4.152)
Кроме того, из соотношения (4.151) следует, что последовательности
{xk}, {kk} ограничены, значит, по теореме Больцано — Вейерштрасса из них
можно выделить подпоследовательности {хЛ, {^.}, сходящиеся к
некоторым точкам v* eEn, \i* eEm. Тогда в силу равенств (4.152)
последовательности {xl+1}, {X^.+i} также сходятся к тем же точкам.
Переходя в формуле (4.138) к пределу при k = k{•—> °°, получим
\С = (\С + Ag(v*))+. В силу соотношений (4.140), (4.141) это равенство
эквивалентно соотношениям
g(v*)<0, ц*>0, ц*&(г;*) = 0, z = l,...,m. (4.153)
Далее, переходя к пределу при k = k{—> «э в неравенстве (4.147), получим
<а/Ч^) + ос(яЧ^))т|ы*^-^>^0 VxgX0,
или, что равносильно
(L'x(v*y\i)yx-v*)>0 \/xeX0.
Отсюда в силу теоремы 3.4 имеем
L(v*,\i*)<L(xy\i*) \/хе Х0. (4.154)
Из формул (4.153), (4.154) и леммы 3.3 следует, что (а*,м*) — седловая
точка функции L(x, X). Неравенство (4.150), справедливое для всех седло-
вых точек (х*, V), будет верным и для точки (а*, ц*), что дает нам
н и2 °4h *ii2oi и2 °Чк *н2 и и2
Ir-41 +71Г*"*1! -р*+1"л1 +7^+1"^i +F*+i"x*ll +
°4h ч II2 ^11 II2 °4h *ll L п а
Это значит, что последовательность j|x^ -а*| +— |Х^ — jlx* || > монотонна.
У нее есть подпоследовательность с номерами k = k{1 которая сходится
к нулю. Следовательно, и сама она монотонно стремится к нулю. Таким
образом, последовательность (xk> Xk), полученная методом (4.137), (4.138),
сходится к седловой точке (v*> \i*), так что последовательность {xk} сходится
к v* — решению задачи (4.131) (теорема 3.18). ■
Метод модифицированных функций Лагранжа мы изложили в
предположении, что задача минимизации (4.137) решается точно. На практике,
конечно, приходится решать эту задачу приближенно. Например, точку
xk+1 можно определять из условий
xk+ieX0, Фк(хк+1)< inf Ф*(*) + 52,
хеХ0
оо
где^ 8# < °°- Сходимость подобного метода изложена в работе [12].
258

4.11.* Экстраградиентный метод
Покажем, что, несколько усложнив схему градиентного метода, можно
получить сходящийся метод решения задач выпуклого программирования,
используя классическую нормальную функцию Лагранжа. Этот метод
будем называть экстраполяционным градиентным или, короче,
экстраградиентным методом. В нем наряду с градиентными шагами будут
присутствовать так называемые прогнозные шаги, что оправдывает присутствие
в названии этого метода слова «экстраполяционный».
4.11.1. Описание процесса
Рассмотрим задачу условной минимизации
/(*) -> min, х g X = {х g X0: gt(x) < О,..., gm(x) < 0},
(4.155)
где Х0 — выпуклое замкнутое множество из Еп> a g(x) = (gi(x),..., gm(x))T —
функция из C^Xq), г - 1,..., т. Нормальная функция Лагранжа этой задачи
def
(4.156)
1(хД) = /(*) + <A, g(x)>, xeX0, XeA0 = Ef.
Она имеет производные
^ = 4(*,X) = /(i)UV(*); ^^ = Li(x,\) = g(x), (4.157)
где g'(x) =
3gi(*)
Эх1
дхп
dgm(x) dgm(x)
, х € Х0, — матрица Якоби.
Эх1 '" Эх"
Опишем один шаг экстраградиентного метода. Пусть начальное
приближение (х0, Xq) € Х0 х Aq задано. Для перехода от &-го приближения (xk, Xk),
k > 0, к (k + 1)-му сначала делаем прогнозный шаг
4=PXo(xk-^Lx(xk,Xk)) = PXo(xk-^fX4)+4g,(xk));
XJk=PAo(X4+pigi(x4>X4)) = />Ao(Xit+fig(x4))>
затем основной шаг
Xk+i=Px0(Xk-№Ax-k,h)) = PXo(xk-№\W + 4gXxk));
(4.158)
(4.159)
где р > 0 — параметр метода. Запишем метод (4.158), (4.159) в кратком
виде. Для этого введем обозначения
2 =
4*7
^«(L^X)) (/'(*)+ ХТ*'(*У
-Lx(x,X)
к
Z = X0xA0czEn+m.
-g(x)
(4.160)
259

Заметим, что оператор проектирования точки z -
вычисляется по формуле (см. упражнение 3.18)
на множество Z
Pzz =
Поэтому метод (4.158), (4.159) можем кратко записать так:
*о=(*оЛ); Zk=pz(4-№k)> zk+i=pz(zk-W*k)> * = 0Л.... (4.161)
4.11.2. Сходимость экстраградиентного метода
Сходимость экстраградиентного метода (4.161) будем доказывать,
предполагая, что выполнены следующие условия I—V:
I. Множество Х0 с Еп выпукло, замкнуто.
П. Функции/(х), gi(x), ..., gm(x) выпуклы и непрерывно
дифференцируемы на Х0.
III. Для любого ограниченного подмножества Хх множества Х0
существует постоянная М = М(Х{) > О такая, что
||Я(^) - Жг/)|| < Л^ ||^ - г/||; ||/Ч^) ~ /Чг/)|| < Л^ ||^ - г/||;
\\g\x)-g'(y)\\ < М\х-у\ Vx, yeXx.
(4.162)
IV. Нормальная функция Лагранжа L(x, К) (4.156) задачи (4.155) имеет
( хЛ
g Z, т.е.
седловую точку s* =
4xv
1(х*Д)<1(х*Д*)<Ц*Д*) VxgX0, ХеА0=Е™. (4.163)
Множество всех седловых точек функции L(x> X) будем обозначать
через 5*.
Для формулировки условия V нам понадобится множество
S0 = \z =
1*7
;Z:||z-Zo|<4(||z#-z0| + |^0|)t4L (4.164)
где z0 =
(х^
eZ — начальная точка процесса (4.161), z* — какая-либо сед-
ловая точка функции L(x, К).
Множество 50 (4.164) выпукло, замкнуто, ограничено, и на нем
отображение Л из (4.160) удовлетворяет условию Липшица с некоторой
константой L0:
lAz-Ayl^LoWz-yl Vz,yeS0 (4.165)
— это вытекает из условия (4.162) при Хх = {х е Х0: \х-х0^ < Rq}.
Подчеркнем, что множество Z = Х0 х Ef не ограничено и, как очевидно из формул
(4.160), отображение А не будет удовлетворять условию Липшица на Z.
260

Теперь можем сформулировать условие V.
V. Будем предполагать, что параметр Р в методе (4.161) выбран из условия
0<P<min — ;1 . (4.166)
Теорема 4.24. Пусть выполнены условия I—V. Тогда метод (4.161),
(4.166) при любом начальном приближении z0e Z порождает
последовательности {zk}, {zk}> которые принадлежат множеству S0 из (4.164) и
монотонно сходятся к некоторой седловой точке 5* =
('г ^
g S0 функции Лагранжа
(4.156) с первой компонентой х* еХ, являющейся решением задачи (4.155).
Для доказательства этой теоремы нам понадобятся следующие две леммы.
Лемма 4.2. Пусть выполнены условия I, П. Тогда точка s* =
\Х V
из Z
будет седловой точкой функции (4.156) тогда и только тогда, когда
выполняется неравенство
<As*,z-s*>>0 \/zeZ. (4.167)
Доказательство
Функция L(x, X) выпукла по переменной х на Х0 при каждом X е Е+т>
вогнута (линейна) по переменной ХеЕ™ при каждом х е Х0. Согласно
теореме 3.4 тогда правое и левое неравенства (4.163) соответственно
выполняются тогда и только тогда, когда
(L'x(x*,X*),x-x*)>0 \/хеХ0; <-!{(**,Г)Д-Г>>0 \/ХеЕ™.
Сложив эти неравенства, придем к формуле (4.167). ■
Лемма 4.3. Пусть выполнены условия I, П. Тогда отображение А
из (4.160) является монотонным, т.е.
(Az-Ay,z-y)>0 \/z,yeZ. (4.168)
Доказательство
Так как функция L(x, X) дифференцируема по х, X, выпукла по х, вогнута
по X, то в силу теоремы 3.1 имеем
{L'x(x, X),x-y)> L{х, X) - L(y, X); (L'x(г/, р),у-х)> L(y, p) - 1(х, р);
<-!{(*, Х),Х-р)> L(xy р)-L(x, X); <-I£(y, p)y p-X)> L(y, X)-L(y, p)y
при всех х, у g Х0, Х,р е Е™. Сложив эти неравенства, получим
<i;(x>x)-i;(y>p)>x-y>+<-ii(x>x)-(-ii(y>p))>x-p>^o>
что равносильно (4.168). ■
Замечание 4.7. Выше мы уже встречались с монотонными
отображениями — это градиент выпуклой функции (теорема 3.1). Однако здесь
отображение А из (4.160) в отличие от упомянутых случаев не является
градиентом какой-либо функции.
Перейдем к доказательству теоремы.
261

Доказательство теоремы 4.24. Сначала убедимся, что
последовательности {zk}, {zk}> порождаемые методом (4.161), таковы, что
zkeS0, 2^g50, |z£-s*!<|z0-s*| \/s*eS*, Л = 0,1,.... (4.169)
Воспользуемся методом математической индукции. Заметим, что
Н^Ь —^о|| = ||^^<^о —Р-^^о> —^^<^o>||^lko —Р-^^о — ^о|| = Р||^^о||^^о-
Отсюда и из формулы (4.164) очевидно, что при k = 0 соотношения
(4.169) выполнены. Сделаем индуктивное предположение: пусть
соотношения (4.169) справедливы при некотором k > 0, и докажем, что они будут
выполняться для следующего номера k + 1.
Пользуясь характеристическим свойством проекции (теорема 3.15),
равенства (4.161) запишем в виде эквивалентных им неравенств
(zk-zk+$Azkyz-zk)>0;
(Zk+i-Zk+fiAzk'Z-Zk+i)^0 VzeZ, £ = 0,1,.... (4.170)
В первом неравенстве (4.170) возьмем z = zk+1> во втором z = s* и сложим
получившиеся неравенства. Тогда
(4-zk'zk+\-4) + (zk+\-zk's*-zk+\)+ ,^ 171ч
+ $(Azhzk+1-zk) + $(Azkys*-zk+i)>0.
Пользуясь тождеством (4.149), преобразуем первые два слагаемых
из неравенства (4.171):
/- -ч-1/!! II2 II- II2 II - II2\
\zk~zkyzk+i~zk/-^\\\zk+i~zk\\ ~\\zk~zk\\ ~\\zk+i~zk\\ У>
(zk+i~zh** -**+i> = 2<1* -zk(-\\zk+i-Zk( ~\\s* ~zk+i(y
С учетом этого из неравенства (4.171) имеем
и и2 ^н и2 и- и2 и и2
If*+i-*II ^1И*-*11 -p*-z*l -|f*+i-^I +
+ 2V(Azk-Azk,zk+1-zk) + 2V(Azk-As*,s*-zk) + 2^^ (4.172)
Из неравенств (4.167), (4.168) при z = Ik,y = s* следует, что
(As*,s*-zk)<0; (Azk-As*,s*-zk)<0. (4.173)
Кроме того, в силу индуктивного предположения (4.169) zk,Ik e50,
поэтому в формуле (4.165) можем принять z- zk>y = Jk. Тогда
(Azk-Azk,zk+i-zk)<Lq\zk-zk\-\zM-zk\<-Lq\zk-zk\ +-Ц\zk+i-zk\\ .
Из неравенства (4.172) с учетом этого факта и соотношений (4.173),
(4.166), (4.169) имеем
Ь+1 S.( <\zk -5.f +(-1 + Р10)фА -Zk( +\\zk+l -Zk()<
<|z*-s.|2<|20-s.|2 Vs»eS». (4.174)
262

В частности, в соотношении (4.174) в качестве s* можем взять седловую
точку z* из определения (4.164) множества 50. Тогда
b+i-*f Фо-*|2-
Следовательно,
IK+i-2o||^IK+i-2*|| + lk*-2o||^2lk*-2o||^^- (4.175)
Это значит, что zk+i e 50. Теперь в формуле (4.165) можем принять
2 = Ч+ьУ = zo е $о> что приведет к неравенству
IN+i-^oMA)|ki-2o|- (4-176)
Напомним, что проекционное отображение обладает свойством
нестрогой сжимаемости (теорема 3.16). Отсюда и из соотношений (4.161), (4.166),
(4.175)-(4.176) имеем
fe+i -2б| = \\Pz(zM-№k+l)-Pzz0\\ < \\zM -$Azk+l -z0\\ <
<\\zk+i -$Azk+l -z0\\<\\zk+i -z0\\ + p\\Azk+l - Az0\\ + $\\Az0\\<
<(1+р10)||2,+1-г0||+р||Л20||<4||г.-20||+||^0||</го,
так что Jk+i eS0. Таким образом, мы убедились, что соотношения (4.169)
справедливы для следующего номера k + 1 и, следовательно, для всех k = О,
1,.... Индуктивное доказательство соотношений (4.169) закончено.
Из (4.169) следует, что неравенства (4.174) верны для всех k = О, 1, ... .
Суммируя их по k от 0 до некоторого N, получим
Ikjv+i-^f+(i-pa>)S(lk*-53fe||2+lkA+i-^fj^lko-^*ll2» w=u,...,
°° II _ ||2 °° и _ m2
где (1 - pi0) > 0 в силу (4.166). Это значит, что ряды £ \\zk -zk\\ , J) \\zk+1 - zk||
сходятся, и поэтому
Hb-i*|=o, Hki-^N- (4Л77)
Последовательность {zk} e 50 ограничена, и по теореме Больцано — Вей-
ерштрасса из нее можно выделить подпоследовательность {z^},
сходящуюся к некоторой точке s* eS0. С учетом равенств (4.177) можно показать,
что подпоследовательности {zl}, {zki+1} также сходятся к той же точке s*.
Тогда, переходя в неравенствах (4.170) к пределу при £ = £г—> °°, получим
(As*, z - s*) > 0 при всех z e Z. В силу леммы 4.2 это значит, что 5* =
Г г- Л
л*
€5.-
седловая точка функции (4.156). Взяв в формуле (4.174) s. = s., придем
к неравенствам
Ь+1-5.|<|2А-5.|, £ = 0,1,.... (4.178)
Отсюда следует, что \zk -s.| < \zk. -s.| при всех k > k{, и поэтому
0< lim \zh -s*II< lim \zh -s*II<\\zt -s*\\ = 0.
— ii и k^j\ и || *, у
263

Это значит, что lim \zk -5* =0, т.е. вся последовательность zk сходится
к седловои точке s* =
(хЛ
, причем, как очевидно из (4.178), эта сходимость
монотонная. Согласно теореме 3.18 точка х*еХ и является решением
задачи 4.155. Теорема доказана. ■
Замечание 4.8. Величина R0 из определения (4.164) множества 50 и,
следовательно, постоянная L0 из (4.165) зависят от седловои точки z* и нам
неизвестны. Поэтому выбор параметра Р из условия (4.166) не является
конструктивным и имеет скорее теоретическое значение. Тем не менее
условие (4.166) подсказывает нам, что если Р выбрать достаточно малым,
то метод (4.161) будет сходиться. Это значит, что на практике величину
Р можно получить дроблением какой-нибудь начальной величины Р0 > 0
(например, Р0= 1) за конечное число шагов.
Упражнения
4.1. Найдите явное выражение для шага ak метода скорейшего
спуска (4.15), (4.16) для задачи минимизации квадратичной функции
f(x) = \\Ах - b\\ на всем пространстве Еп, где А — матрица размера т х и,
Ъ g Еп. Сформулируйте требования к матрице Л, гарантирующие линейную
скорость сходимости вида (4.24), (4.25).
4.2. Примените метод скорейшего спуска для минимизации функций
f(u) =х2 + ау2, и = (х, у) g E1, и f(u) = х2 + у2 + az2, и = (х> у, z) e i£, при
различном выборе начального приближения и0 и в предположении, что
коэффициент а »1.
4.3. Примените метод штрафных функций к задаче условной
минимизации
f(u) =x2 + y2^> min, и = (х,у)е Х= {(х, у) е Е2 : х < 0},
взяв в качестве штрафной функции ФДх, у) = х2 + у2 + k(max{x; О})2, (х, у) е
g £2, А = 1, 2,....
Убедитесь, что функции Ф^(х, у) при больших k становятся овражными
и градиентный метод, примененный к задаче Ф^(х, у) —> min, (х, у) е Е1,
может сходиться медленно. Покажите, что в исходной задаче нормальная
функция Лагранжа имеет седловую точку. Докажите, что исходная задача
имеет согласованную постановку.
4.4. Примените метод проекции градиента с постоянным шагом к
следующей задаче условной минимизации в пространстве Е2:
/(w) = (x-l)2+(z/ + l)2^min, u = (x,y)eX = E2 = {(x,yy.x>0,y>0}.
Для этого найдите константу сильной выпуклости к функции/(w),
константу Липшица L ее градиента f\u) и возьмите в качестве шага спуска
значение а* = кЕг2 из замечания 4.3. В качестве начального приближения
возьмите произвольную точку щ =(х0,у0)еЕ2. Найдите следующие при-
264

ближения щ= (xk, yk), k = 1, 2,.... Остановите процесс при первом
попадании щ в множество решений задачи U*.
4.5. Примените метод условного градиента (4.41)—(4.43) к следующей
задаче условной минимизации в пространстве Е2:
/(г/) = х2+2г/2->тт, иеХ = {и = (хуу)еЕ2:2<х<Ау -1<г/<1}.
В качестве начального приближения возьмите произвольную точку и0 =
= (х0у у0) g X и найдите следующие приближения uk= (xk, yk), k = 1, 2, ...,
в случаях, когда г/0 < 0, г/0 = 0 и г/0 > 0. Остановите процесс при первом
попадании щ = (xky yk) в множество решений задачи U*.
4.6. Примените классический метод Ньютона к задаче безусловной
минимизации в пространстве Е2:
f(u) = 2х2 - Аху + Зг/2 - Ах - 2г/ —> min, и = (х, у) е X = Е2.
Убедитесь, что он сойдется за один шаг к решению ги =(х* =А,у* =3)
этой задачи.
4.7. Примените классический метод Ньютона к задаче условной
минимизации в пространстве Еп\
/(х) = |[(х1-1)2+(х2)2+... + (^)2]2-
- [(х1)2 +(х2 -I)2 +(х3)2 +... + (х")2] -> min,
хеХ = {х = (х\...ухп)еЕп:х1+х2>2}.
Взяв в качестве начального проближения х0 = (2, 0, 0, ..., 0), сделайте
один шаг классического метода Ньютона, найдите следующее
приближение xv
4.8. Нарисуйте линии уровня f(x) = С = const функции из примера 4.4
и дайте графическое объяснение причины расходимости основного
варианта метода покоординатного спуска (4.108)—(4.112) при выборе
начальных приближений вида и0 = (а, а), аф 1, находящихся на линии у = х
разрыва производной.
4.9. Докажите, что в задаче минимизации квадратичной сильной
выпуклой функции вида (4.121) на всем пространстве Еп процесс (4.119), (4.120)
сходится из любого начального приближения х0 е Еп.

Глава 5
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
В этой главе рассматриваются задачи оптимального управления
процессами, описываемыми системами обыкновенных дифференциальных
уравнений. Этот класс экстремальных задач существенно отличается
от рассмотренных выше: если в задачах минимизации функции конечного
числа переменных искомая точка минимума являлась точкой и-мерного
пространства, то в задачах оптимального управления искомая точка
минимума представляет собой функцию, принадлежащую некоторому
бесконечномерному функциональному пространству [29]. Такие задачи имеют
многочисленные приложения в механике космического полета, в вопросах
управления электроприводами, химическими или ядерными реакторами,
виброзащиты и т.д.
Эффективным средством исследования задач оптимального управления
является принцип максимума Понтрягина, представляющий собой
необходимое условие оптимальности в таких задачах. Принцип максимума,
открытый коллективом российских математиков во главе с академиком
Л. С. Понтрягиным, представляет собой одно из крупных достижений
современной математики и является краеугольным камнем
современной математической теории оптимального управления. Принцип
максимума Понтрягина существенно обобщает и развивает основные
результаты классического вариационного исчисления, созданного Л. Эйлером,
Ж. Л. Лагранжем и другими выдающимися математиками прошлого.
Появление принципа максимума стимулировало последующее бурное развитие
теории экстремальных задач и методов их решения.
5.1. Постановка задачи оптимального управления
5.1.1. Примеры постановок задач оптимального управления
Приведем несколько конкретных задач оптимального управления.
Движение плоского маятника, подвешенного к точке опоры при помощи жесткого
невесомого стержня (рис. 5.1), как известно, описывается уравнением
/ё + ЪЪ + mgl sin 6 = М(т),
где / — длина жесткого стержня маятника; т — масса, сосредоточенная в конце
стержня; / = тР — момент инерции; Ъ > О — коэффициент демпфирования; g —
гравитационная постоянная (ускорение силы тяжести); 0 = 0(т) — угол отклонения
стержня от точки устойчивого равновесия; т — время; М(т) — внешний управляю-
266

щий момент. Если сделать замену переменной t = zJmgl/I, то это уравнение можно
привести к виду
ср н- Рф н- sin ф = г/(^),
(5.1)
где
Ф=Ф(0=е
\rngl I V /
М
\rngl
mgl
Рис. 5.1
Обозначим x(t) = ф(£) (угол отклонения маятника), x2(t) = ф(£) (скорость маятника).
Тогда уравнение (5.1) запишется в виде системы двух уравнений первого порядка:
x\t) = x2(t)\ x2(t) = -$x2(t)-smx{(t) + u(t). (5.2)
Пусть в начальный момент t = О маятник отклонился на угол хх(0) = х^ и имеет
начальную скорость х2(0) = х%. Будем также считать, что функция u(t)
(управляющий момент, выбор которого может влиять на движение маятника) удовлетворяет
ограничению
|w(0|^Y = const>0 W>0.
(5.3)
Для примера 5.1 возможны следующие постановки задач оптимального
управления: выбрать управление u(t)> удовлетворяющее условиям (5.3),
так, чтобы:
1) за минимальное время Г остановить маятник в одной из точек
устойчивого равновесия, т.е. добиться выполнения условий
x1(T) = 2nk, х2(Т) = 0 (5.4)
при некотором k, k = О, ±1,... (задача быстродействия);
2) за минимальное время Г добиться выполнения условия
(х\Т))2+(х2(Т))2<г,
где е > 0 — заданное число;
3) к заданному моменту времени Т какая-либо из величин
т т
(х\Т))2+(х2(Т))2, \(x\t))2dt, \(x\t))2+(x2(t))2dt,
о о
max \xx(t% maxllxHOl; l*2(Ol)
o<t<r ' о<*<г '
принимала минимально возможное значение;
267

4) в заданный момент Г выполнялось равенство х2(Т) = 0, а величина
хх(Т) была максимально возможной (задача о накоплении возмущений);
5) к заданному моменту Г добиться выполнения условий (5.4) и мини-
т
мизировать величину ju2(t)dt (условие (5.3) здесь может быть опущено).
о
Если колебание маятника ограничено какими-либо упорами, то в
перечисленных задачах нужно еще требовать выполнения условия вида
|x1(0|^|bi = const>0 W>0.
На управление u(t) вместо условия (5.3) (или наряду с условием (5.3)
могут накладываться ограничения вида
т
ju2(t)dt<R = const >0.
о
При изучении малых колебаний маятника часто полагают sincp * ф. Тогда
уравнение (5.1) и эквивалентная ему система (5.2) становятся линейными
и будут иметь вид
(р + Рф + (р = г/(£)
и, соответственно,
x\t) = x2(t)\ x2(t) = -$x2(t)-x\t) + u(t).
Как известно, движение центра масс космического аппарата и расход массы
описывается системой дифференциальных уравнений
f = v, v = ^- + F, G = -gq, 0<t<T, (5.5)
где t — время; г = r(t) =(r{(t), r2(t), r3(t)) — радиус-вектор центра масс космического
аппарата; v = v(t) = (v{(t), v2(t), v3(t)) — скорость центра масс; G = G(t) — текущий
вес космического аппарата; g — коэффициент пропорциональности между массой
и весом; р =p(t) = (P\(t),p2(t),p3(t)) — вектор тяги двигателя; q = q(t) — расход
рабочего вещества; F= F(r, t) = (Fv F2, F3) — вектор ускорения от гравитационных сил.
В каждый момент времени t движение космического аппарата характеризуется
величинами r(t), v(t), G(t), называемыми фазовыми координатами. Пусть в
начальный момент t = 0 фазовые координаты аппарата известны:
r(0) = r0,v(0) = v0,G(0) = G0. (5.6)
Величины q = q(t), p = p(t) являются управлением: задавая их по-разному,
можно получить различные фазовые траектории (решения) задачи (5.5), (5.6).
Конструктивные возможности аппарата, ограниченность ресурсов рабочего
вещества накладывают на управление q(t), p(t) ограничения, например, вида
т
pmin<|p(Ol<Pmax, qmin<q(t)<qm,x Ше[0;Т] или j q*(t)dt < R = const >0.
о
Кроме того, на фазовые координаты задачи (5.5), (5.6) могут накладываться
некоторые ограничения, вытекающие, например, из условий того, чтобы вес аппарата был
268

не меньше определенной величины или траектория полета проходила вне
определенных областей космического пространства (областей повышенной радиации) и др.
Для примера 5.2 возникают задачи выбора управлений q(t), p(t) так,
чтобы управления и соответствующие им траектории задачи (5.5), (5.6)
удовлетворяли всем наложенным ограничениям, и кроме того, достигалась
та или иная цель. Например, здесь возможны следующие задачи:
1) попасть в заданную точку или область космического пространства
за минимальное время;
2) к заданному моменту времени попасть в заданную область
пространства с заданной скоростью (например, совершить мягкую посадку) и с
максимальным весом аппарата или минимальной затратой энергии;
3) достичь определенной скорости за минимальное время и т.п.
5.1.2. Допустимые управления
Приведенные в примерах 5.1, 5.2 задачи являются частным случаем
более общей задачи оптимального управления, к формулировке которой
мы переходим.
Пусть движение некоторого управляемого объекта (течение
управляемого процесса, изменение управляемой системы) описывается
обыкновенными дифференциальными уравнениями
«Л/ ~~ J \ «Л/ , «Л/ , •••, •Л' , 1л> , 1л> , •••, 1л> I, If ~~ J., •••, »*■,
которые в векторной форме можно записать в виде
x = f(x,u,t), (5.7)
где t — время, х = (х1, х2, ..., хп) — величины, характеризующие движение
объекта в зависимости от времени и называемые фазовыми координатами
объекта; и = (и1, и2, ..., иг) — параметры управления («положение рулей»
объекта), выбором которых можно влиять на движение объекта; / = (Д
р, -,fn)', функции/(х, w, t), г - 1,..., п, описывающие внутреннее устройство
объекта и учитывающие различные внешние факторы, предполагаются
известными.
Для того чтобы фазовые координаты объекта (процесса, системы) (5.7)
были определены в виде функций времени х = x(t) на некотором отрезке
t0<t<T, необходимо в начальный момент времени t0 задать начальное
условие x(t0) = х0 и параметры управления и = (и1, г/2, ..., иг) как функции
времени и = u(t) при t e [t0; 7]. Тогда фазовые координаты х = x(t) будут
определяться как решение следующей задачи Коти [17]:
x(t) = f(x(t),u(t),t), t0<t<Ty (5.8)
x(t0)=x0. (5.9)
Нетрудно видеть, что функции и = u(t), называемые управлениями,
должны удовлетворять определенным требованиям непрерывности,
гладкости, так как, с одной стороны, при слишком «плохих» (слишком
«разрывных») u(t) задача (5.8), (5.9) может не иметь смысла, с другой — слишком
269

«хорошая» функция u(t) не будет иметь физического смысла управления.
В большинстве прикладных задач в качестве управлений и = u(t) могут
быть взяты кусочно-непрерывные функции.
Например, в задаче из примера 5.2 двигатель космического аппарата
на каких-то участках полета может быть выключенным, может быть
включенным, т.е. управления p(t)> q(t) могут терпеть разрыв. Напомним [29],
что функция u(t) называется кусочно-непрерывной на отрезке [t0; 7], если
u(t) непрерывна во всех точках t e [t0; 7], за исключением, быть может,
лишь конечного числа точек t0 < т{ < ... < тр < Т, в которых функция u(t)
может терпеть разрывы типа скачка, т.е. существуют конечные пределы
lim u(t) = u(xi-0); lim г/(О = и(тг+0), (5.10)
но, вообще говоря, и(т{ - 0) Ф и(т{ + 0), г - 1, ..., р. В точках тг, г - 1, ..., р>
функция и может быть определена или не определена.
Далее, как очевидно из примеров 5.1, 5.2, значения управлений в
каждый момент времени не могут быть произвольными и подчиняются
некоторым ограничениям. Мы будем рассматривать такие ограничения, которые
можно описать условием
u(t)e V\/te [t0;T\y (5.11)
где V — заданное множество из Ег. Например, в случае ограничений (5.3)
из примера 5.1 множество Vимеет вид V = {и е Е1: \и\ <у}. Случай V= Er
также не исключается.
Кусочно-непрерывное управление и = u(t), t0<t<T, удовлетворяющее
условию (5.11) в точках его непрерывности, будем называть допустимым
управлением.
5.1.3. Задача Коши
Пусть заданы точка х0 е Еп> множество V из Ег и некоторое кусочно-
непрерывное управление и = u(t), t0<t<T> удовлетворяющее условиям
(5.11). Рассмотрим задачу Коши (5.8), (5.9). Сразу же возникают
следующие вопросы: что понимается под решением этой задачи? существует ли
оно? единственно ли?
В классических учебниках по дифференциальным уравнениям обычно
рассматривается задача Коши [17]:
x(t) = g(x(t)yt),a<t<b; x(a) = х0, (5.12)
где вектор-функция g(x, t), x e En,te [a; b], непрерывна по совокупности
(х, t) g Еп х [а; Ь]. Решением этой задачи называется функция х = x(t),
которая определена, непрерывно дифференцируема на отрезке [а; Ь] и всюду
на этом отрезке удовлетворяет условим (5.12). Здесь подразумевается, что
существуют конечные пределы
lim x(t) = x(a + 0) = x(a) = x0; lim x(t) = х(а + 0) = lim g(x(t)yt) = g(x0>t0);
£-»a+0 £-»a+0 £-»a+0
lim x(t) = x(b-0); lim x(t) = x(b - 0) = lim g(x(t)yt) = g(x(b-0)yb).
t^>b-0 t^>b-0 t^>b-0
270

Приведем одну из стандартных теорем, посвященную проблеме
существования и единственности решения задачи (5.12) [17].
Теорема 5.1. Пусть функция g(x, t) при каждом х е Еп непрерывна по t
на отрезке [а; Ь] и удовлетворяет условию Липшица
\g(x,t)-g(y,t)\<L\x-y\ Vx,yeEn, te[a;b], Z = const>0. (5.13)
Тогда задача Коти (5.12) имеет, притом единственное, решение x(t),
определенное на всем отрезке [а; Ь].
Однако сразу заметим, что эту теорему мы не сможем без оговорок
применить к задаче (5.8), (5.9). Дело в том, что у нас управление u(t) является
кусочно-непрерывной функцией и правая часть уравнения (5.8) f(x(t)> u(t)>
t) = g(x, t) может иметь разрывы по переменной t> что неизбежно влечет
за собой разрывы в его левой части. Отсюда ясно, что понятие решения
задачи Коши (5.8), (5.9) требует уточнения.
Будем предполагать, что функция/(х, и, t) непрерывна по совокупности
своих аргументов (х, и, t) на Епх Vx [t0; 7], управление и = u(t) является
кусочно-непрерывной на отрезке [t0; Т\ функцией и имеет разрывы вида
(5.10) первого рода [29] в точках тг, г = 1, ..., р, T0=t0<x1< ... <тр< тр+1 = Т,
а в точках непрерывности удовлетворяет условию (5.11).
Определение 5.1. Решением задачи Коши (5.8), (5.9) назовем
функцию х = x(t), которая непрерывна на отрезке [t0; 7], x(t0) = x0, а на каждом
частичном интервале (тг; тг+1), г = 0, 1, ..., р, имеет непрерывные
производные и удовлетворяет уравнению (5.8); кроме того, существуют конечные
пределы
lim x(t) = x(xi-0), z = l,...,j9 + l; lim х(£) = *(тг+0), z = 0,l,..., р. (5.14)
Такая функция является кусочно-гладкой.
Теорема 5.2. Пусть функция /(х, w, t) такова, что удовлетворяет
условию Липшица по переменной х.
\\f(x,u,t)-f(y,u,t)\\<L\\x-y\\ \/(x,u,t),(y,u,t)zE«xVx[t0;Tl (5.15)
непрерывна по (и, t) на Vx [t0; Т] при каждом х е Е, управление и = u(t)
кусочно-непрерывно на [t0; Т] с разрывами в точках тг, г - 1, ..., р> и
удовлетворяет условию (5.11). Тогда при любом выборе начальной точки х0 е Еп
задача Коши (5.8), (5.9) имеет, причем единственное, решение х = x(t),
определенное на всем отрезке [t0; 7].
Доказательство
На отрезке [t0 = т0; xj непрерывности управления u(t) рассмотрим
задачу Коши
4(t) = f(x0(t),u(t),t), x0<t<T{, х0(х0) = х0. (5.16)
Эта задача при a- t0 = x0, Ъ - т^ х(а) - х0, g(x, t) = f(x, u(t), t)
превращается в задачу (5.12). Нетрудно заметить, что при выполнении условий
теоремы 5.2 будут выполнены и условия теоремы 5.1. Поэтому, применяя
теорему 5.1 к задаче (5.16), получим, что задача Коши (5.16) имеет, при-
271

чем единственное, решение x0(t), определенное на всем отрезке [т0; xj.
При этом существуют конечные пределы
lim x0(t) = х0(т0+0) = х0(т0) = x0; lim x0(t) = x0(xi-0);
lim i:0(0 = i:o(Xo+0) = /(x0,w(T0+0),^0);
£-»т0+0
lim x0(t) = x0(Ti-0) = f(x0(Ti-0),u(Ti-0),Ti).
На следующем отрезке [т^ т2] непрерывности управления u(t)
рассмотрим задачу Коши
ii(t) = f(xi(t)iu(t%t)9Ti<t<T2; х1(т1) = х0(т1-0). (5.17)
Применяя к ней теорему 5.1 при а = т1у Ъ - т2, х(а) - х0(т{ - 0), g(x, t) =f(x,
u(t)y t)y получим, что и эта задача Коши имеет единственное решение xt(t)y
T1<t<x2co свойствами:
lim x1(t) = xi(Ti+0) = x1(T1) = x0(Ti-0); lim xx(t) = xx(x2-0y
t^Ti+0 £-»т2-0
lim xx(t) = xx(tx + 0) = f(xx(xx + 0), u(x{ + 0), т{);
t^Xx+0
lim xx(t) = x{(t2 -0) = f(x{(x2 -0), u(x2 -0), x2).
£-»т2-0
Далее, действуя аналогично, можем последовательно найти функции
x0(t), xt(t),..., x^i(t) на отрезках [т0; xj,..., [тм; тг] и затем перейти к отрезку
[тг; т/+1] и рассмотреть следующую задачу Коши:
*,■(*) = f(Xi(t),u(t),О, T^«xi+i; xj(Tj) = ^-1(Tj-0). (5.18)
С помощью той же теоремы 5.1 убеждаемся, что задача Коши (5.18)
также имеет единственное решение x^t) и существуют конечные пределы
\imxi(t) = xfa + 0) = х{(х{) = x^iTi-O); lim *,-(*) = х{(хм -0);
xf+0 Tf+1-0
lim x{ (t) = x{ (г,- + 0) = f(x{ (x,- + 0), и(х,- + 0), x,-);
lim *,.(*) = ii(Ti+1 -0) = /(^(tw-0), m(x,-+1 -0),xi+1).
*->Tf+1-0
Этот процесс заканчивается на отрезке [tp; tp+1=T\ нахождением
последней функции xp(t), t g [т^; 7].
Далее мы можем определить функцию x(t), t0<t<T, которая на
каждом из частичных отрезков [тг; т/+1], г = 0, 1, ..., р, совпадает с
соответствующей функцией x{(t). Нетрудно заметить, что такая функция непрерывна
на отрезке [t0; 7]. В самом деле, на стыках t = тг частичных отрезков
функции x{(t) обладают свойством
*,-(*i + 0) = xfc ) = Jw(Tf - 0),
272

так что х(т{ + 0) = х(т{) = х(т{ - 0), т.е. x(t) непрерывна в точках t = i{, г - 1,
2,..., р. В остальных точках t0<t< Г функция x(t) непрерывно
дифференцируема и, как очевидно из формул (5.16)—(5.18), удовлетворяет уравнению
(5.8). Конечные пределы (5.14) также существуют. Таким образом,
построенная функция x(t), t0<t<T, является решением задачи Коши (5.8), (5.9).
Оно единственно, что вытекает из теоремы 5.1, последовательно
применяемой к задачам (5.18), г - 0, 1,..., р. Теорема 5.2 доказана. ■
Для функции x(t), составленной из кусков xf(t)y t e [тг; тг+1], являющихся
решением соответствующих задач Коши, справедливо равенство
t i-\ 0+i t
x(t) - x0 = J x(x)dx = X J Xj (x)rfx + J x(x)dx =
i-\ 0+1 t
= £ \ f(Xj(T)yu(T)yT)dx + Jf(xi(x)yu(T)yT)dx =
j=o tj t{
= )f(x(x)yu(T)yT)dx \/t,t0^t<tp+i = T. (5.19)
Это значит, что решение x(t) задачи Коши (5.8), (5.9) является
непрерывным решением интегрального уравнения
t
x(t)= \f(x(T),u(T),T)dx + x0, te[t0;T]. (5.20)
'о
Верно и обратное: если x(t), t e [t0; T] — непрерывное решение
интегрального уравнения (5.20), то оно является решением задачи (5.8), (5.9).
В самом деле, если t — точка непрерывности функции /(х(т), и(т), т), то
по теореме о дифференцировании интеграла с переменным верхним
пределом [29] правая часть формулы (5.20) дифференцируема в этой точке,
причем
dt
= f(x(t),u(t),t). (5.21)
J/(x(t),w(t),t>/t
Тогда дифференцируема в точке t и левая часть уравнения (5.20),
и с учетом формулы (5.21) имеем
x(t) = f(x(t),u(t),t). (5.22)
Это значит, что на каждом интервале (тг; тг+1), г - 0, 1,..., р, непрерывное
решение уравнения (5.20) удовлетворяет дифференциальному уравнению
(5.8). Кроме того, из соотношения (5.22) следуют равенства (5.14).
Таким образом, функция x(t), t e [t0; 7], является решением задачи
Коши (5.8), (5.9) тогда и только тогда, когда x(t) — непрерывное решение
интегрального уравнения (5.20), т.е. мы получили другое, интегральное,
определение решения задачи Коши (5.8), (5.9). Отсюда и из теоремы 5.2
следует, что интегральное уравнение (5.20) имеет единственное
непрерывное решение.
Замечание 5.1. Формула (5.19) остается справедливой, если функция
/(х(т), и(х)у т) в точках разрыва тг, г - 1, ..., р, принимает любые конечные
273

значения или вовсе не определена в них — это обстоятельство никак не
влияет ни на существование, ни на значения интегралов в формулах (5.19),
(5.20). Это означает, что кусочно-непрерывное управление и = u(t) в точках
разрыва может принимать любые конечные значения, необязательно
принадлежащие множеству V (5.11), или вовсе не определено, что не влияет
на траекторию x(t) задачи Коши (5.8), (5.9).
5.1.4. Постановка задачи
Вернемся к постановке задачи оптимального управления. Решение
задачи Коши (5.8), (5.9) будем называть траекторией, соответствующей
допустимому управлению и = u(t) и начальному условию х0, и будем далее
обозначать через х = x(t; и, х0). Начальную точку х = x(t0; и, х0) = х0 будем
называть левым концом траектории, t0 — начальным моментом, х(Т; и,
х0) — правым концом траектории, Т — конечным моментом. В тех случаях,
когда из контекста ясно, какому допустимому управлению или начальному
условию соответствует траектория, будем пользоваться более короткими
обозначениями х = x(t; и), x(t; х0) или просто х = x(t), t0<t<T.
Будем предполагать, что начальный момент t0 и левый конец
траектории x(t0), конечный момент Г и правый конец х(Т) должны удовлетворять
условиям
x(t0)eS0(t0), *ое©о> ^(Г)е51(Г), Тев{, (5.23)
где 0О, ©! — заданные множества на числовой оси М = {£:-<»<£<+©о}
(не исключается возможность, что 0О =R или @{ = М); S0(t0), S^T) —
заданные множества из Еп.
В задачах оптимального управления принята следующая
классификация концевых условий (5.23). Если множество 0О состоит из единственной
точки t0, то начальный момент называется закрепленным, если Q{ состоит
из единственной точки Т, то конечный момент называют закрепленным.
Если множество S0(t0) (или S^T)) состоит из одной точки и не зависит
от t0, т.е. S(t0) = {x0} (или соответственно S^T) = {x^), то левый (правый)
конец траектории называют закрепленным. Если S(t0) = Еп, t0 e 0О (или
S^T) = Еп, Те ©t), то левый (правый) конец траектории называют
свободным. В остальных случаях левый (правый) конец траектории называют
подвижным.
Наряду с ограничениями (5.23) на концах траектории, как мы видели
в примерах 5.1, 5.2, могут быть и другие дополнительные ограничения
на траекторию вида
x(t)e G(t),t0<t<T, (5.24)
где G(t) — заданные множества из Еп. Условия (5.24) называются
фазовыми ограничениями. Конечно, граничные условия (5.23) также можно
отнести к фазовым ограничениям, но они выделены отдельно, важны сами
по себе и более просты для исследования.
После введения перечисленных выше терминов несколько уточним
некоторые обозначения.
274

В учебной литературе символом f(x) часто обозначают как значение
функции / в точке х, так и саму функцию, которая представляет собой
отображение, ставящее каждой точке х из области определения функции
/
точку у из области значений функции: х—> у. Отдавая дань традициям, мы
до сих пор пользовались и будем пользоваться этим не вполне
определенным символом/(х) в тех случаях, когда из контекста нетрудно понять, идет
ли речь о функции как об отображении [29] или о ее значении в
конкретной точке х. Однако в тех случаях, когда обозначение f(x) может привести
к недоразумениям, за значением функции в точке х будем сохранять
обозначение f(x)y а саму функцию как отображение будем обозначать через
/(•) или просто/. Так, например, если и = u(t), t e [t0; T] — допустимое
управление, воспринимаемое в целом как отображение, то будем его
обозначать через и(-), a u(t) = (ux(t), ..., ur(t)) есть значение этого управления
в точке t, и включение u(t) e V означает, что значения u(t) этой функции
принадлежит множеству V с Ег.
Аналогично х(-; и(-), х0), или, короче, х(), — это траектория (решение)
задачи Коши (5.8), (5.9), соответствующая управлению и(-) и начальной
точке х0 в смысле определения 5.1, ах(£; и(-), х0) или, короче, x(t), — это
значение (xx(t)y..., xn(t)) траектории в точке t, как например, в формуле (5.24).
Пусть заданы множества 0О, ®{ с R, Va Er, S0(t0), S{(T) e En.
Следующий набор
(u('),x('),XtyX(T),ttyT)
назовем допустимым, если и(-) — допустимое управление, х() = х(- ; и(-),
х0) — траектория системы (5.8), (5.9), такая что
x(t0)eS0(t0), x(T)eS{(n Ьев0, Тевх.
Пусть множество допустимых наборов непусто и на этом множестве
задана целевая функция или, как будем говорить, функционал
/ = /("О. *(•)» х0, х(Т), t0,T) =
т
= jf°(x(r,u(-),x0),u^)^)dT+^(x0,x(T),t0,T), (5.25)
где f°(x, и, t), g°(x0, y,t,T) — заданные функции переменных хе Е",ие V,
t0e 0O, Те evx0e S0(t0),ye S^T).
Будем рассматривать задачу
J = Д"0). *()> *о> *(Т)> *0'Т)^> min> (5-26)
при условиях
x(t) = f(x(t),u(t),t), t0<t<T; (5.27)
x(t0) = x0e S0(t0), x(T)€ 51(Г), t0 е в0, Те Gi; (5.28)
u(t)eV, t0<t<T. (5.29)
Задача оптимального управления сформулирована. Еще раз подчеркнем,
что здесь подразумевается, что управление и(-) — кусочно-непрерывная
275

функция, которая в точках своей непрерывности удовлетворяет условию
(5.29), х() = х(-у и, х0) — решение задачи Коши (5.8), (5.9) в смысле
определения 5.1, удовлетворяющее условиям (5.28). Мы ограничимся
рассмотрением лишь задач минимизации, так как задача максимизации/ всегда
может быть сведена к эквивалентной задаче минимизации (-J). Если
в формулах (5.25)—(5.29) fx(x, и, t) = 1, g°(x0, yytyT) = О, то/= Т-10 — в этом
случае задачу (5.26)—(5.29) называют задачей быстродействия.
Обозначим
/* = inf Ди(-), *(•), *<>, х(Т), £0, Г),
где нижняя грань берется по всем допустимым наборам (5.27)—(5.29).
Допустимый набор (и (•), х (•), х0,х(Т), t0, T) назовем оптимальным решением
задачи (5.25)—(5.29), и*(-) — оптимальным управлением, х*() —
оптимальной траекторией, если
J\u*\/> x*v)> Хо*>х*\*)> ^о*> Т*) = J*.
Целевую функцию (5.25) выше мы назвали функционалом. Видимо, это
следует кратко пояснить. Во-первых, это дань традициям — так называлась
целевая функция в классическом вариационном исчислении, из которого
выросла современная теория оптимального управления [33]. Во-вторых,
употребляя термин «функционал», мы желаем подчеркнуть, что задача
оптимального управления все же отличается от задачи минимизации
функций конечного числа переменных х е Еп, которую мы рассматривали выше.
Дело в том, что допустимые наборы (5.27)—(5.29), на которых определен
функционал (5.25), в отличие от гл. 1—4 не принадлежат конечномерному
пространству, а являются элементом бесконечномерного функционального
пространства. Так, например, у нас управление и(-) — это элемент
функционального пространства, состоящего из кусочно-непрерывных r-мерных
вектор-функций, траектория х() — элемент пространства непрерывных
функций, имеющих кусочно-непрерывные производные. В задачах оптимального
управления мы имеем дело с новыми объектами, такими как управление,
траектория, имеющими более сложную природу по сравнению с элементами
из Еп. По этой причине методы оптимизации, изложенные в гл. 1—4,
напрямую не применимы для решения задач оптимального управления, требуют
доработки, дополнительного переосмысливания, привлечения новых идей.
В рамках настоящей книги мы не имеем возможности подробнее
останавливаться на определении, что такое функциональное пространство, как
обобщаются понятия функции, функционала, градиента и т.п., и отсылаем
интересующегося читателя к анализу более высокого уровня, называемому
функциональным анализом, к его приложениям [1,12,14, 29, 38]. Мы
остановимся лишь на тех методах решения задач оптимального управления
(5.25)—(5.29), которые для своего понимания требуют лишь знания основ
математического анализа, линейной алгебры, обыкновенных
дифференциальных уравнений в объеме стандартных курсов технических вузов. Одним
из таких методов является принцип максимума Понтрягина, к изложению
которого мы переходим. О другом методе решения таких задач речь пойдет
в следующей главе.
276

5.2. Принцип максимума в задаче оптимального управления
со свободным правым концом
5.2.1. Формулировка принципа максимума
Сначала рассмотрим сравнительно простой вариант задачи
оптимального управления (5.25)—(5.29), а именно
J(u) = J f\x(t), u(t), t)dt + g°(x(T)) -> min;
'о
x(t) = f(x(t),u(t),0, t0<t<T; x(t0) = x0;
u = u(t)eV, t0<t<T,
(5.30)
(5.31)
(5.32)
где/°(х, и, t),f(x, и, t) = (/{(ху и, t), ...,fn(x, и, t)), g°(y) — заданные функции
переменных x = (x1,..., xn) e En,ye En, и = (и1,..., ur); V — заданное
множество из Er\ t0, T — заданные моменты времени; х0 — заданная точка из Еп.
Предполагается, что допустимое управление и = и(-) —
кусочно-непрерывная функция со свойством (5.32); траектория х = х() = х(- , и, х0) задачи
Коши (5.31) существует на всем отрезке [t0; 7] при любых допустимых и(-).
На правый конец х(Т) траекторий никакие условия не накладываются,
поэтому задача называется задачей со свободным правым концом.
Для формулировки принципа максимума введем функцию
Я(х,и,UV) = -7°(*>и,*) + <¥,/(х,и,0> = -/°(*>и,0+ £УгЛ(х>Ъt), (5.33)
i=l
где \|/ = (х^,..., \\fn) — вспомогательные переменные. Эту функцию называют
функцией Гамильтона — Понтрягина. Предположим, что функции fi(x, и,
t),j = 0, 1, ..., и, g°(x) дифференцируемы по х. Тогда функция Я(х, w, t, \|/)
также дифференцируема по х, причем
дН (дН дН | дН ТТ, rCi, . Д г|- .
Эх
Эх1 '" Эх71
Эх'
7=1
Эту формулу можно записать в следующей векторно-матричной форме:
— = Я^(х, w, U V) = -/?(*> ", t) + (Jx(x, г/, 0)т ¥>
ох
где f% = (/°t,..., f°n) = grad/0; T — знак транспонирования;
(5.34)
fx(x,u,t) =
(f\
f"
l ^
z1
J vn
Jx" J
grad/1 "\
grad/"
Каждому допустимому набору (и(), х()) задачи Коши (5.31) поставим
в соответствие задачу Коши
ч>(0=-
дН
дх
, t0<t<T,
(5.35)
u=u(t), x=x(t; и, xq )
277

V(7>-^-
Ъу
(5.36)
\x=x(T;u,xq)
называемую сопряженной к (5.31) задачей. Как очевидно из формул (5.34),
система (5.35) линейна по \|/ и ее коэффициенты кусочно-непрерывны
по переменной t. Поэтому можно предположить, что правая часть
системы (5.35) удовлетворяет условию Липшица по \|/. А тогда существование
решения задачи Коши (5.35), (5.36) можно доказать, непрерывно склеивая
решения задач Коши, аналогичные задачам (5.16)—(5.18).
Теперь мы можем сформулировать необходимое условие
оптимальности для задачи (5.30)—(5.32) — принцип максимума Понтрягина.
Теорема 5.3. Пусть функции f*(x, w, t), f(x, и, t), g°(x) и все их
частные производные по переменным х непрерывны по совокупности аргументов
(х, u,t)eEnxVx[t0; Г], где V — замыкание V. Пусть и = и(-) — оптимальное
управление, х = х(- ; и) — оптимальная траектория задачи (5.30)—(5.32).
Тогда для всех точек t e [t0; 7], являющихся точками непрерывности
управления u(t), функция H(x(t; и), v, t, \\f(t; и)) переменной v = (и1,..., vr)
необходимо достигает своей верхней грани на множестве V при v = u(t), т.е.
max H(x(t; и), v, t, \\f(t; u)) = H(x(t; u), u(t)> t, \\f(t; u)). (5.37)
veV
Здесь функция Н(х, и, t, \\f) определена согласно (533), \|/ = \\f(t; и) —
решение задачи Коши (5.35), (5.36).
Центральное место в теореме 5.3 занимает условие максимума (5.37):
оказывается, что если и(-) — оптимальное управление, х() — оптимальная
траектория, то тогда функция H(x(t), v, t, \|/(0) конечного числа переменных
v = (а1, ..., vr) будет достигать своего максимума на V именно при и = u(t)
в моменты времени t e [t0; T\ непрерывности управления и(-). Поэтому
теорему 5.3, дающую необходимое условие оптимальности, принято называть
принципом максимума Понтрягина для задачи со свободным правым концом.
5.2.2. Краевая задача принципа максимума
Прежде чем доказывать теорему 5.3, зададимся вопросом: какая польза
от этой теоремы? Что хорошего можно ожидать от равенства (5.37)? Ведь
в (5.37) нет ничего известного, мы не знаем ни оптимальное управление
и(-), ни соответствующую ему траекторию х(), ни соответствующую им
новую функцию \|/(£; и). Как развязать этот запутанный узел?
Оказывается, не все тут так уж страшно. Здесь обычно поступают
следующим образом. Составляют функцию Н(х, и, t, \\f) согласно формуле (5.33)
и рассматривают ее как функцию г переменных и = (г/1, ..., ur) e V, считая
остальные переменные (х, t, \\f) параметрами. Затем при каждом
фиксированном наборе (х, U V) решают конечномерную задачу максимизации
Я(х, г/, t, \|/) —> max, и е V, (5.38)
и находят функцию
и = и(х, t, \|/) g V, (5.39)
278

на которой достигается верхняя грань в задаче (5.38), т.е.
Н(х, и(х, t, \|/), t, \|/) = sup Н(х, v, t, \|/). (5.40)
veV
Если исходная задача оптимального управления (5.30)—(5.32) имеет
решение, то, как следует из соотношения (5.37), функция (5.39) определена
на непустом множестве.
Допустим, что функция (5.39) нам уже известна. Тогда можем
рассмотреть следующую систему из 2п дифференциальных уравнений
[х = fix, uix, t, \i/), t\
tn<t<T, (5.41)
\у/ = -Н'х (х, и(х, t, У)ХУ),
относительно неизвестных (х(), \|/()) = К')- Как известно [17], общее
решение системы (5.41) зависит, вообще говоря, от 2п произвольных
числовых параметров и для определения этих параметров нам нужно иметь 2п
соотношений. Для этих целей нам служат 2п краевых условий
*(*о) = *о. V(T) = -^(x(T)), (5.42)
взятых из формул (5.31), (5.36).
Итак, основываясь на теореме 5.3, от исходной задачи (5.30)—(5.32) мы
пришли к краевой задаче, состоящей из условия максимума (5.40), системы
дифференциальных уравнений (5.41) и условий (5.42). Такую краевую
задачу принято называть краевой задачей принципа максимума.
Можно ожидать, что имеется лишь конечное число отдельных
изолированных функций z(t) = (x(t), \\f(t))y t0<t<T, удовлетворяющих условиям
(5.41), (5.42). Возьмем одну из таких функций z(t) и подставим ее в (5.39).
Получим функцию
u = u(t) = u(x(t),t,W(t)), t0<t<T. (5.43)
Пусть эта функция оказалась кусочно-непрерывной на [£0; 7]. Из
формул (5.39), (5.40), (5.43) следует, что полученное таким образом управление
u(t), t0<t<T, удовлетворяет условию максимума (5.37) и, следовательно,
согласно теореме 5.3 может претендовать на роль оптимального
управления задачи (5.30)—(5.32), а функция x(t) = x(t\ w(-), x0), t0 < t < Г, — на роль
оптимальной траектории этой задачи.
Таким образом, опираясь на принцип максимума, мы свели исходную
задачу поиска управления в бесконечномерном функциональном
пространстве к более «легкой» знакомой нам конечномерной задаче максимизации
(5.38) и к такому знакомому объекту вычислительной математики [6], как
краевая задача вида (5.41), (5.42).
Для иллюстрации сказанного рассмотрим несколько примеров задач
оптимального управления со свободным правым концом, посмотрим, как
выглядит краевая задача принципа максимума в конкретных случаях.
279

Требуется минимизировать функционал
J(u) = ±](x2(t) + u2(t))dt
при условиях x(t) = -ax(t) + u(t),0<t<T\ x(0) = x0.
Здесь x0, a > 0, T> 0 — заданные постоянные; V = E1; правый конец траектории
свободный. Составим функцию Гамильтона — Понтрягина Н = -(х2 + и2)/2 + \\f(-ax +
+ и) и выпишем сопряженную систему
\\f = -H'x=x + a\\f, 0<t<T.
Функция Н = -(х2 + и2)/2 + \\f(-ax + и) достигает своей верхней грани по и на V= E{
при и = \|/, и краевая задача принципа максимума запишется в виде
x = -ax + \\f, \\f = a\\f + x; x(0) = x0, \|/(Г) = 0.
Решив эту задачу, находим, что подозрительным на оптимальность является
управление
efo _ e2\Te-kt
u(t) = y(t) = x0- 0<t<T,
(k-a) + (k + a)eZK1
где X = yja2 +1, и оно действительно является оптимальным [12].
Пример 5.4
Требуется минимизировать функционал
J(u) = ](u2(t)-x(t))dt
о
при условиях x(t) = u(t), 0 < t < 4; х(0) = 0, u(t) — кусочно-непрерывное управление,
\u(t)\<10<t<4.
Эта задача получается из задачи (5.30)—(5.32) при п = 1, г = 1, t0= 0, Т= 4,
f°(x,u,t) = u2-x, f(x,u,t) = u, g°(x) = 0,
хо=0, V = {ueE*:\u\<l}.
Функция Гамильтона — Понтрягина здесь имеет вид Н(х, w, t, \\f) = -и2 + х + \\ш.
Задача (5.38) равносильна задаче
-и2 + \\fu —»max, | и \ < 1,
решение которой выглядит так:
[+1,если\|/>2,
и = u(\\f) = J -1, если \|/ < -2, (5.44)
-\|/,если|\|/|<2.
2 ' '
Сопряженная задача (5.35), (5.36) в этом примере имеет вид
\|/(£) = -Я;=-1,0<£<4, \|/(4) = 0.
Теперь можем выписать краевую задачу принципа максимума (5.41), (5.42):
*(*) = и0|г). \j/(0 = -l; ^(0) = 0, \|/(4) = 0. (5.45)
280

Отсюда имеем \\f(t) = -t + 4, 0 < t < 4. Тогда в силу решения (5.44)
[1,если0<£<2,
u(t) =
-(4-£),если2<£<4.
Этому управлению соответствует траектория
кесли0<£<2,
x(t) = \ 1
--=-(4-£)2 + 3,если2<£<4.
Краевая задача принципа максимума (5.45) решена. Найденные управление u(t)
и траектория x(t) являются подозрительными на оптимальность. Можно показать
[12], что они действительно являются оптимальными.
Минимизируем функционал
J(u) = U{u2(t)-x2(t))dt
1 о
при условиях x(t) = u(t), О < t < 2л; х(0) = 1, | u(t) |< 1.
Здесь п = 1, г = 1, £0 = О, Т = 2тт, х0 = 1, f°(x, и, t) = u2- x2, f(x, и, t) = и, g°(x) = О,
V = Е{. Функция Гамильтона — Понтрягина такова:
Н(х, и, t, \|/) = -—(и2 - х2) + \\ш.
Максимум этой функции по и при и е Е{ достигается при и = \|/. Сопряженная
задача имеет вид
y(t) = -H'x=-x(t),0<t<2n; \|/(2я) = 0.
Выпишем краевую задачу принципа максимума:
x(t) = \\f(tX V(t) = -x(t)', *(0) = 1, \|/(27i) = 0.
Нетрудно проверить, что эта задача имеет единственное решение
x(t) = cos t, \\f(t) = - sin t, 0<t<2n.
Согласно формуле (5.43) получаем u(t) = \\f(t) = sint. Подозрительные на
оптимальность управление и траектория получены:
u(t) = - sin t, x(t) = cos t, 0<t<2n.
Им соответствует значение функционала
л2п л2п
J(u) = ±j(sin2t-cos2t)dt = j-j(-cos2t)dt = 0.
2 о 2 0
Однако теорема 5.3 дает лишь необходимое условие оптимальности. Поэтому
неплохо бы убедиться, действительно ли найденные управление и траектория
являются оптимальными. Возьмем, например, последовательность um(t) = mcos—, m = 1, 2,
.... Ей соответствуют траектории xm(t) = 2msm—+1, и значения функционала J(um) =
= n(-3m2 - 2) - 16/72 —» -оо при m —» оо. Следовательно,/* = -«>, задача не имеет
решения.
281

Пусть движение материальной точки описывается дифференциальным уравнением
x(t) = u(t), 0<t<T,
где Т > 0 — заданный момент времени; и = u(t) — кусочно-непрерывное
управление (внешняя сила), \u(t)\ < 1. Пусть в начальный момент t0= 0 известны начальное
положение х(0) = х0 точки и ее начальная скорость х(0) = х0. Нашей задачей
является нахождение допустимого управления и = u(t), 0<t<T, такого, чтобы
функционал J(u) = (х(Т))2 + (х(Т))2 принимал минимальное значение. Здесь мы хотим
переместить нашу материальную точку как можно ближе к точке х = 0 с как можно меньшей
скоростью, ожидая, что если время Т достаточно большое, то она окажется в точке
х = 0 с нулевой скоростью.
Применим к этой задаче принцип максимума. Сначала преобразуем ее и запишем
в виде задачи (5.30)—(5.32). С этой целью введем переменные xx(t) = x(t), x2(t) = x(t),
0<t<T, и, полагая в (5.30)-(5.32)
f *
x =
./=
U "
'хф?
придем к следующей равносильной задаче оптимального управления:
J(u) = (х\Т))2 + (х2(Т))2 -> min (5.46)
при условиях
x\t) = x2(t), x2(t) = u(t), 0<t<T; x(0) = x0; (5.47)
u(t)eV = {ueEu.\u\<\), 0<t<T. (5.48)
Функция Гамильтона — Понтрягина здесь имеет вид H(x,u,t,\\f) = \\f1x2+\\f2u,
сопряженная задача Коши выглядит так:
ФЧО = -H'xi = 0, \\f2(t) = -Я;2 =-yv0<t<T;
щ(Т) = -2хЧПу2(Т) = -2х2(Т).
Задача максимизации (5.37) здесь равносильна задаче
\\f2u —» max, и е У,
которая легко решается и приводит к явной формуле
[ 1, если \|/2 > 0,
и = sgn\|/2 = \ -1, если \|/2 < 0, (5.49)
I Vw e V, если \|/2 = 0.
Таким образом, краевая задача принципа максимума (5.40)—(5.42) в
рассматриваемой задаче (5.46)—(5.48) имеет вид
х* = х2, х2 = sgn\|/2, щ = 0,\j/2 = -щ, 0<t<T,
*(0) = *о, у(Т) = -2х(Т).
Можно показать, что задача (5.46)—(5.48) имеет решение [12], поэтому краевая
задача (5.50) согласно теореме 5.3 также имеет решение. Если (x(t), \\f(t)), 0<t<T —
решение задачи (5.50), то формула (5.49) дает формулу для управления,
подозрительного на оптимальность:
и = u(t) = sgn \|/2(0, 0 < t < Т.
К сожалению, решение краевой задачи (5.50) в аналитической форме получить
не удается. Для поиска ее решения можно использовать известные методы решения

краевых задач [6]. Следует сразу же оговориться, что известные методы решения
краевых задач зачастую излагаются в предположении, что в системах вида (5.41),
(5.42) правые части дифференциальных уравнений являются достаточно гладкими.
Однако в краевых задачах принципа максимума, как ясно из формул (5.50), правые
части уравнений могут быть разрывными. Это обстоятельство затрудняет численное
решение краевых задач принципа максимума, требует серьезной доработки,
модификации известных численных методов.
5.2.3. Доказательство принципа максимума Понтрягина
Вернемся к теореме 5.3. Мы ее докажем при несколько более жестких
требованиях на входные данные задачи (5.30)—(5.32), чем это указано
в ее формулировке. Полное ее доказательство, требующее развития более
сложного математического аппарата, более тонких рассуждений, читатель
найдет в работах [1, 33].
Сначала докажем, что траектория задачи (5.31) мало меняется при малом
изменении управления и(-) и начального условия х0, предполагая, что
вектор-функция f(x, и, t) непрерывна по совокупности своих аргументов
и удовлетворяет условию Липшица по совокупности переменных (х, и):
\\f(x + Ax,u + h,t)- f(x, и, 0|| ^ ДИ Д*1 + 11%
V(x + bx,u + h,t),(x,u,t)eEnxVx[t0;T], l = const>0.
Для этого нам понадобится одно утверждение, известное в литературе
как неравенство Гронуолла.
Лемма 5.1. Пусть функция (p(t) непрерывна на отрезке [t0; 7] и
удовлетворяет условию
t
0<(f>(t)<aj(f>(x)dx + k t0<t<T, я,6 = const>0, (5.52)
'о
тогда
0<(p(0<6efl<'-4 t0<t<T. (5.53)
Доказательство
t
Положим R(t) = a\ ф(т)б/т. Заметим, что R(t0) = 0, R(t) > 0, а также
to
R(t) = a<p(t), t0 < t < Т. С учетом условия (5.52) имеем
R(t)<aR(t) + abaR(t)-aR(t)<aby t0<t<T.
Умножив обе части последнего неравенства на е~а^~^\ получим
^-{R{t)e-a^-^)<аЬе-а«-*о\ t0<t<T.
at
Отсюда, интегрируя это неравенство на [£0; t] с учетом равенства
R(t0) = 0, находим
£(0<6efl('-'o)-6.
Из этой оценки и из (5.52) вытекает требуемое неравенство (5.53). ■
283

Лемма 5.2. Пусть вектор-функция f(x, и, t) непрерывна по
совокупности (х, и, t) на Еп xVx[t0;T] и удовлетворяет условию (5.51). Тогда
т
max |#(£; u + h,x0+ Ах0 ) - х(£; и, х0 )|| < С01Дх01 + Q J |й(0|^ (5.54)
где х(- ; и, х0) согласно нашим обозначениям — решение задачи Коши
(5.31), соответствующее допустимому управлению и = и(-) и начальному
условию х0; С0 = eL(r-'o); Сх = С01.
Доказательство
Существование траекторий x(t; u> x0)> x(t; u + hyx0 +Ax0) следует из
теоремы 5.1. Из формулы (5.20) имеем
Ax(t) = x(t; и + h, x0 + Дх0 ) - x(t; u> х0 ) =
t
= \ (/(х(т; u + h,x0+ Ах0 ), и(х) + /г(т), т) - f(x(x; и, х0 ), и(т), т))б/т + Дх0.
'о
Отсюда с учетом условия Липшица (5.51) получаем
t t т
\bx{t)\ < L J (||Дх(т)| + |Л(т)|)Л + ||Дх0| < L.) |Дх(т)|</т + 1 J |Л(т)|</т + |д*ь|.
Это неравенство запишется в виде (5.52), если принять
т
Ф(0 = |Ах(0|; а = Ц b = LJ\\h(T)\\dT + \\Ax0\\.
'о
Отсюда и из леммы 5.1 следует оценка (5.54). ■
Теорему 5.3 будем доказывать в предположении, что наряду с условием
(5.51) условию Липшица будут удовлетворять частные производные f£, fx,
g? функций/0,/, g°:
\f$(x + Ax,u + h,t)~ /°(*, и, 0|| ^ Ц1М1 + 1% (5-55)
|/x (x + Дх, г/ + К t) - fx (x, г/, *)| < Ц1М1 + \\h\\); (5.56)
||g0(x + Ax)-g°(x)|<l||Ax|| (5.57)
при всех (х + Дх, и + /г, £)> (*> w, t) g £ x Vx [t0; 7], где I = const > 0. В
условиях (5.51), (5.55)—(5.57) каждая функция в действительности имеет свою
константу Липшица, но в теоретических рассуждениях конкретные
значения этих констант нам не нужны, поэтому для упрощения изложения под L
подразумевается максимальная из них.
Доказательство теоремы 5.3. Пусть и = и(-) — оптимальное
управление, х = х(- ; и) — оптимальная траектория задачи (5.30)—(5.32). Тогда
по определению оптимального управления для любой
кусочно-непрерывной функции h(t), t0<t<T, такой что u(t) + h(t) e V во всех точках ее
непрерывности, A/(w) =J(u + К) ~J(u) > 0. Подставляя сюда явное
выражение для функционала/, имеем
284

4Д w) = J (/° (*(т; и + h), и(т) + /г(т), т) - /° (х(т; и), г/(т), т))/т +
'о
+g(x(T; u + h))- g(x(T; и)) > 0. (5.58)
Здесь x(t; u + h) — решение задачи Коши (5.31), соответствующее
допустимому управлению и(-) + /*(•)• Приращение
Ax(t) = x(t; u + h)- x(t; и), t0<t<T,
удовлетворяет условиям
^0) = f(x(t) + Ax(t), u(t) + h(t), t)-f(x(t),u(t), t), (5 59)
t0<t<T, Ax(t0) = 0.
Из условий (5.59) и леммы 5.2 следует оценка
\\Ах(фС{1\\Кт)\\с1т \/te[t0;T]. (5.60)
'о
Пользуясь формулой конечных приращений (1.113)
g°(x(T) + Ax(T))-g°(x(T)) = (!g(x(T) + QiAx(T)),Ax(T)), 0<91<1,
перепишем формулу (5.58) в виде
А/(«) = j (f°(x(t)+Ах(т), и(х)+h(x), т) - f°(x(x), и(х), x))dx +
to
HgUximAxiTV+^O, (5.61)
где
R, =(gUx(T) + e1Ax(r))-gO(x(r)), Ax(T)). (5.62)
Учитывая условие Липшица (5.57) и оценку (5.60), при t = Г имеем
|^|< 1|Ах(Г)| < LC\ \||/г(т)||б/т . (5.63)
Vo J
Преобразуем второе слагаемое из правой части формулы (5.61).
Вспомним, что функция \|/ = \|/(£; и) = \\f(t) — решение задачи Коши (5.34), (5.36):
V(0 = -H'x(x(t),u(t),UV(0). t0<t<T; V(D = -й(х(Г)).
Отсюда с учетом условий (5.59) получаем
(g°x(x(T)), Ах(Т)) = -<V(T), Дх(Г)> = - J -|<V(0, *x(t))dt - <V(<b), Д*(*о)> =
И
dAx(£)\
•J (v(0.^r2)+<v(0. Д*(0> k = J <я;(х(0, «(О. *,v(0). Д*(0>*-
- J (v(0> /(*(0+MO. «(0+hit), t) - f(x(t), u(t), t))dt.
k>
285

Подставив полученное выражение в формулу (5.61) и переписав ее
с помощью функции Гамильтона — Понтрягина в виде
т
AJ(U) = -j (H(x(t) + Ax(t)y u(t) + h(t), ty V(0) " H(x(t), u(t), t, \\f(t)))dt +
T
+j(H'x(x(t)yu(t)yty\|/(0),A*(0>^ + £i -°> (5-64)
а также учитывая, что по формуле конечных приращений
Н(х + Axyu + hyty\\f)- Н(ху иу ty \|/) =
= Н(х + Дх, u + hyty \\f)-H(xy u + hyty \|/) + Н(ху u + hyty \\f)-H(xyuyty\\f) =
= (Нх(х + 02Дх,u + hyty\|/), Дх) + H(xyu + hyty\\f)-H(xyuyty\|/), 0<02 < 1,
находим
т
4Ди) = - \ (H(x(t)y u(t) + h(t), ty \|/(0) - H(x(t)y u(t)y ty y(t)))dt + /с^ч
t0 (5.65)
где
т
R2=-j(Hx (x(t) + 02 Ax(0, u(t) + h(t)y ty \|/(0) -
- Hx(x(t)y u(t)y ty \\f(t))y Ax(t))dt.
Из формулы (5.34), условий Липшица (5.55), (5.56) и оценки (5.60)
следует, что
т
\R2\<L(1+ max |г|Г<^;г/)|)J<||Лаг<0||2н-1|^^<0||-||/г<0||)^^^
(т Л2
<С2\ j\\h(t)\\dt\ , (5.66)
vo J
где С2 = const > 0. Объединяя оценки (5.63), (5.66), получаем
(т У
|^+/^|<С3 J|A(0|* , C3=const>0, (5.67)
v'o J
где постоянная С3 зависит от и(-)у но не зависит от h(-).
Пусть t — точка непрерывности управления u(t), пусть число е > 0 столь
мало, что [t; t + е] с [t0; 7] и u(t) непрерывно на [ty t + е], и пусть а —
произвольная точка из V. Положим
v ' [0 при Tu[t;t+e]. v y
Приращение вида (5.68) называется игольчатой вариацией (рис. 5.2).
286

Рис. 5.2
Тогда управление u(t) + h(t) кусочно-непрерывно и u(t) + h(t) е V. Отсюда
и из формул (5.65)—(5.68) имеем
О < Д/(и) < С3 J \\v - и(х)\\ dx
t+e
+ J (Н(х(х;и),v,х,\|/(т;и))-Н(х(х;и),и(х),х,\|/(т;u)))dx. (5.69)
t
Учитывая, что функция
g(x) = Н(х(х; и), v, х, \|/(т; и)) - Н(х(х; и), и(х), х, \|/(т, и))
непрерывна на отрезке [t, t + e], с помощью теоремы о среднем и
неравенства Коши — Буняковского из соотношения (5.69) получаем
t+E „
О < AJ(u) < -eg(t+63е)+Съг J \\v - и(х)\\ dx, 0 < 63 < 1.
Разделим это неравенство на е > 0 и устремим е —» +0. Получим 0 < -g(t),
или
g(t) = H(x(t; и), v, t, \|/(£; и)) - H(x(t; и), u(t), t, y(t; и)) < 0 V» € V,
что равносильно соотношению (5.37). Принцип максимума для задачи
(5.30)-(5.32) доказан. ■
5.3.* Принцип максимума (общий случай)
5.3.1. Формулировка принципа максимума в общем случае
Рассмотрим следующую задачу оптимального управления с более
общим граничным режимом на правом конце траектории:
J(u(-),x(-),x0,t0,T)= lf°(x(t),u(t),t)dt + g°(x(T),T)^mm; (5.70)
to
x{t) = f(x(t),u{t),t), t0<t<T, x(t0) = x0; (5.71)
gJ(x, T) < 0, ; = 1,. ..,m, 1
v ' 1 gJ(x,T) = 0J = m+l,...,m+s\
u = u(t)eV, t0<t<T.
(5.72)
(5.73)
287

Здесь g(x, T),j = О, 1, ..., m + s — заданные
непрерывно-дифференцируемые функции переменных (х,Т)еЕп xQ{, не исключаются случаи, когда
в условиях (5.72) отсутствуют ограничения типа неравенств (т = 0), типа
равенств (s = 0), возможно также, что s = т = 0, S^T) = Еп, когда правый
конец свободен; остальные обозначения в формулах (5.70)—(5.73) те же,
что и в задаче (5.30)—(5.32).
Для формулировки принципа максимума введем функции
Щх, и, t, W,a0) = ~aof°(x> u> *) + <¥> /(*> ы> 0>; (5.74)
/(*, Т, а) = a0g0(x, T) + axg\x, T) + ... + am+sg™+s(x, Т), (5.75)
где \|/ = (\\fv ..., \\fn), a = (а0, ах, ..., am+s) — вспомогательные переменные;
далее функцию Щх, и, t, \|/, а0), как и выше в формуле (5.33), будем
называть функцией Гамильтона — Понтрягина, функцию 1{х, Т, а) — малым
лагранжианом.
Каждому допустимому набору (и(-), х()) и моменту Г задачи (5.70)—
(5.73) поставим в соответствие систему дифференциальных уравнений
. _ дН
ах
, t0<t<T. (5.76)
u=u(t), x=x(t;u)
Сформулируем теорему, выражающую необходимое условие
оптимальности — принцип максимума Понтрягина для задачи (5.70)—(5.73).
Теорема 5.4. Пусть функции Р(х, и, t), f(x, и, t), g°(x, Т), ..., g™+5(x, T)
и их частные производные по переменным х непрерывны по совокупности
своих аргументов при всех хеЕп,иeV, te[t0;T],T е&{. Пусть, кроме того,
конечный момент времени Т задан, и = и(-) — оптимальное управление,
х = х(- ; и) — оптимальная траектория задачи (5.70)—(5.73). Тогда
необходимо существуют вектор-функция \|/ = \\f(t) = (\|/i(0> •••> Wn(t))> t0<t<T,
и числа а0, ах,..., ат+5такие, что \|/ = \\f(t) является решением системы (5.76),
соответствующей оптимальному набору (и(-), х(-; и), а0);
а = (а0, ах,..., am+s) * 0, а0> 0, ах > 0,..., ат > 0; (5.77)
при всех t g [t0; 7], являющихся точками непрерывности оптимального
управления и(-), функция H(x(t; и), v, t, \\f(t), a ) переменной v = (v1, ..., vr)
достигает своей точной верхней грани на множестве V при v = u(t), т.е.
max H(x(t; и), v, t, \\f(t), a0) = H(x(t; u), u(t), t, \\f(t), a0 ); (5.78)
veV
и справедливы равенства
dl(x, T; a)
V(T) = -
дх
; (5.79)
\х=х(Т;и)
ajgJ(x(r;u),T) = 0, j = l,...,m. (5.80)
Если же конечный момент Тне закреплен и также определяется из
условия минимума функционала (5.70) (как, например, в задаче быстродей-
288

ствия), а функции g>(x> T)yj = 0> 1, ..., m + s, непрерывно дифференцируемы
поТ е ©!, то
dl(x, T: а)
Щх(Т;и),и(Т-0),ТМПа0)= У '
дТ
(5.81)
х=х(Т;и)
Условия (5.79), (5.81) называются условиями трансверсальности;
условие (5.80) — условием дополнительности.
Доказательство этой теоремы, представляющей собой принцип
максимума Понтрягина для задачи (5.70)—(5.73), можно найти, например,
в работе [12].
Из непрерывности функций x(t; и), \\f(t) и из соотношения (5.78)
следует, что функция
Я(0 = supH(x(t; u),v,t,W)>я о )> te[t0;T],
veV
непрерывна всюду, где непрерывно оптимальное управление и(-). Можно
доказать [12, 33], что на самом деле функция H(t) определена и
непрерывна всюду на отрезке [t0; 7], причем в точках t разрыва управления и(-)
справедливо равенство
H(t) = H(x(t; w), u(t ± 0), t, \|/(0, a ). (5.82)
5.3.2. Краевая задача принципа максимума в общем случае
Пользуясь схемой, изложенной в предыдущем параграфе, теорему 5.4
можно применить для практического решения задачи (5.70)—(5.73).
А именно, сначала решаем конечномерную задачу максимизации функции
(5.74)
Н(х, и, t, \|/, а ) —> max, и е V, (5.83)
считая, что (х>t>\\f,a0)eEn x[t0;T]xEn х(-оо; + оо) являются параметрами,
и определяем функцию
и = и(х,t,\|/,а)е V, (5.84)
на которой достигается верхняя грань в задаче (5.83). Далее составляем
систему из 2п дифференциальных уравнений
[ X = fix, U(X, t, \|/, Ял )> t), - -
j\ > \ > >v> oj> j> t0<t<Ty (5.85)
[\j/(0 = -H'x(x, u(x, t, V> Яо)> Ь V> tfo)>
относительно неизвестных (x(-), \|/()). Для определения 2п параметров,
от которых зависит общее решение системы (5.85) [17], а также т + s + 2
параметров а0, аь ..., am+s, Т нам нужно 2п + m + s + 2 условия. Из формул
(5.71), (5.72), (5.79)—(5.81) имеем:
*0о) = *о, ¥(Г) = -Э/(Х(2,Г,Д); (5.86)
ajgJ(x(T;u),T) = 0J = l,...,m, gJ(x(T;u),T) = 0J = m + l,...,m + s; (5.87)
289

Н(х(Т; и), и(Т - 0), Г, Х|/(Г), а0 ) = д1(х(?^Т>а\ (5.88)
— всего 2п + m + 5 + 1 условие. Наконец заметим, что функции Н(х, и, t, \|/,
я0), /(х, Г, л), определенные при помощи формул (5.74), (5.75), линейны
и однородны относительно параметров (а, \|/) = (я0, я^ ..., am+s, \\fv ..., уД т.е.
Н(ху и, ty а\|/, аа0 ) = осЯ(х, w, t, \|/, я0 ), /(х, Г, ая) = а/(х, Г, a) Voc > 0.
Это означает, что если набор {а, \|/) удовлетворяет условиям теоремы 5.4,
то этим условиям удовлетворяет и набор (оса, а\|/) при любом а > 0. Иначе
говоря, теорема 5.4 определяет набор {а, \|/) лишь с точностью до
положительного множителя, и этим множителем мы можем распорядиться по
своему усмотрению. Например, опираясь на первое из условий (5.77), можно
выписать уравнение
II и9 m+s
Ml =Z*? = 1. (5.89)
В результате мы получим краевую задачу, состоящую из задачи
максимизации (5.83), системы дифференциальных уравнений (5.85), условий
(5.86)—(5.89). Эту краевую задачу называют краевой задачей принципа
максимума задачи оптимального управления (5.70)—(5.73). Разумеется, ее
надо еще решать совместно с неравенствами
а0 >0,ах >0,...,ат >0; g'(x(T))<0J = l,...,т. (5.90)
Если в задаче (5.70)—(5.73) момент Г задан, то условие (5.88) в краевой
задаче отсутствует.
На практике вместо условия (5.89) часто рассматривают задачу (5.83)—
(5.88), поочередно добавляя к ней условия а0= 1 иа0=0, (av ..., am+s) Ф 0.
Заметим, что функция (5.84) может иметь разрывы, быть многозначной,
что серьезно осложняет исследование и численное решение краевой задачи
принципа максимума. Если удастся ее решить и получить функции (x(t), \|/(0)
и параметры а0, аь ..., am+s, T, то согласно формуле (5.84) мы найдем и
управление и = u(t) = u(x(t), ty \\f(t)> a0\ удовлетворяющее принципу максимума и,
следовательно, подозрительное на оптимальность в задаче (5.70)—(5.73).
Отметим, что если в задаче (5.70)—(5.73) правый конец свободен, т.е.
m = s = 0, St(T) = Епу то малый лагранжиан (5.85) имеет вид 1(х> Г, а) =
= <2og°(x, Г), условие трансверсальности (5.79) запишется в виде
wn n dS°(x(T),T)
¥(7>-a° д~х •
Так как в силу условий (5.77) а = а0 Ф 0, а0 > 0, то условие нормировки
превратится в равенство а0= 1. Отсюда следует, что теорема 5.3 является
следствием теоремы 5.4 при фиксированном Г, а условие (5.79) — это
условие трансверсальности в задаче (5.30)—(5.32).
Посмотрим, как выглядит условие трансверсальности в задаче (5.70)—
(5.73), когда правый конец траектории закреплен, т.е.
x(r) = x1=(x11,x12,...,xf), (5.91)
290

что соответствует случаю ограничений-равенств вида gj(x) = xi -х{ =0,
7=1,..., п. Тогда малый лагранжиан здесь примет вид
п
l(x, a) = a0g°(x, T) + X uj(xj ~ х{ ),
7=1
а условия трансверсальности будут выглядеть так:
W) = ^0х(х(П Т) + (Щ, "2> •••> ая), (5.92)
Н(х(П и(Т - 0), Г, \|/(Г), я0) = аоё*(х(Т), П (5.93)
Условие (5.77) здесь можно заменить равносильным условием
я0+|у(Г)|*0, я0^0. (5.94)
В самом деле, если условие (5.94) не выполняется, то а0= 0, \|/(Г) = 0.
А тогда в силу (5.92) (а1у а2> ...^я) = 0, следовательно, а = (а0> аь ..., ап) = 0,
что противоречит условию (5.77). Это значит, что для задачи (5.70), (5.71),
(5.73), (5.91) выполняется условие (5.94). Верно и обратное: из условий
(5.92), (5.94) следует условие (5.77).
Таким образом, краевая задача принципа максимума для задачи (5.70),
(5.71), (5.73), (5.91) состоит из системы (5.85), краевых условий
*(*о) = хо> х(т) = xv (5.95)
условий трансверсальности (5.92), (5.93), неравенства а0> 0 и условия
нормировки
00+1x1/(7)1 = 1. (5.96)
Так как неизвестные параметры аь ..., ап входят лишь в условие
трансверсальности (5.92) и не входят в условия (5.85), (5.95), (5.96), то эти
параметры и условие (5.92) можно исключить из дальнейшего рассмотрения.
5.3.3. Общие граничные условия
В приложениях нередко возникают задачи, в которых левый и правый
концы траектории должны выбираться согласованно, в зависимости друг
от друга. Это требование можно записать в виде
(x(t0),x(T))eS(t0yT), t0ee0yTeSly
где S(t0, Т) при каждом (£0, Т)е©0х 01 представляет собой заданное
множество из Еп х Еп. Примером такого множества является
[ gJ(xyyyt0,T) = 0y i = m + ly...ym + s\
где£7(х, y,t,T) — заданные функции переменных (х, г/, t, Т)еЕпхЕпх@0х @{.
В задаче (5.70)—(5.73) мы имели более простой случай: S(t0, Т) = S(t0) x S{(T)y
где множество S0(t0) = {x-x0 =0} состоит из одной точки, S^T) взято
из формулы (5.72).
291

Рассмотрим задачу оптимального управления
J(u()yx()yx0,x(T),t0J) =
т
= j f\x(t), u(t), t)dt + g°(x(t0), х(Т), t0, Т) -> min (5.98)
'о
при условиях
*(t) = f(x(t)yu(t),0, t0<t<T; (5.99)
(40),1(Г))е%,Г); (5.100)
u(t)eV, te[t0;T], (5.101)
где S(t0> T) — множество, определенное формулой (5.97). Включение (5.101)
понимается так же, как и в задаче (5.26)—(5.29). Далее предполагается, что
в (5.75) вместо g(xy T) берутся функции g(xy y> t0> T) из (5.97); сопряженная
система (5.76) имеет тот же вид.
Теорема 5.5. Пусть функции f°(x, и, t),f(x, и, t), gi(x> y> t> Г) и их
производные f£, fx, gJx, gJy, gJt , gj, j = 1, ...,jn + 5, непрерывны по
совокупности аргументов при x e En, у e En> ueV> t e [t0; 7], t0 e0O, Te©t. Пусть
и = u(-) - оптимальное управление, x(- ; и) — оптимальная
траектория задачи (5.98)—(5.101). Тогда необходимо существуют
вектор-функция \|/ = \\f(t) = (\|/i(0> —j V/z(0)» t0<t<T, и числа а0, аь ..., ат+5такие, что
\|/ = \\f(t) является решением системы (5.76), соответствующей
оптимальному набору (и(-), х(-; и), а0);
а = (а0,а{,..., am+s)Ф 0, а0 >0, ах > 0,..., ат > 0; (5.102)
при всех t g [t0; 7], являющихся точками непрерывности оптимального
управления и(-), функция H(x(t; и), v> t, \\f(t)> a ) переменной v = (я1, ..., vr)
достигает своей точной верхней грани на множестве V при v = u(t), т.е.
maxH(x(t; и), v, t, \\f(t), a0) = H(x(t; и), u(t), t, \\f(t), a0);
veV
и справедливы равенства
dl(x,y,t0,T)
Wo) = ~
дх
/=*(f)
, v(T)=-
dl(x,y,t0,T)
dy
:=x(to)
/=*(f)
(условия трансверсальности);
ujgj(x(t0),x(T),t0,T) = 0, j = 1,...,m,
(условие дополнительности);
dl(x,y,tj)\
H(x(t0)y u(t0 +0), t0, \\f(t0)y a0) = -
Н(х(Т),и(Т-0),ТМПао) =
dt
dl(x, y, t, T)
x=x(t0),y=x(T),t=t0
dT
(5.103)
(5.104)
(5.105)
(5.106)
(5.107)
\x=x(t0),y=x(T),t=t0
(условия трансверсальности по времени).
292

Если ^закреплено, то условие (5.106) отсутствует, если Тзакреплено,
то условие (5.107) отсутствует.
Доказательство этой теоремы см., например, в работе [12].
Основываясь на теореме 5.5, нетрудно сформулировать краевую задачу
принципа максимума, соответствующую задаче (5.98)—(5.101), используя
ту же схему, как и выше в задаче (5.70)—(5.73).
Если в задаче (5.98)—(5.102) правый конец свободен, т.е. функции gJ,
j = 1,..., т + s не зависят от у, то второе условие (5.104) трансверсальности,
как и в задачах (5.30)—(5.32), (5.70)—(5.73) будет иметь вид
V(T) = -g°y(x(t0),x(T),t0,T);
аналогично если в задаче (5.98)—(5.101) левый конец свободен, т.е.
функции g,j = 1, ..., т + 5, не зависят от х, то первое условие (5.104)
трансверсальности имеет вид
Если в задаче (5.98)—(5.101) правый конец закреплен, т.е. т = 0, а
ограничения-равенства имеют вид gi = yi -x{ =0,j = l, ..., п, то второе
равенство из (5.104) можно не учитывать в краевой задаче принципа максимума,
заменив его условием х(Т) = х1, причем условие а Ф 0 нужно заменить
условием нормировки а0 +|\|/(Г)| = 1.
Аналогично, если в задаче (5.98)—(5.101) левый конец закреплен, т.е.
m = 0, gi = xi -x^= 0,j = 1,..., п, то первое неравенство из (5.104) можно
опустить, заменив его условиемx(t0) =х0и условием нормировкиа0 + |\|/(*о)|= ^
Заметим, что выше мы ограничились изложением принципа максимума
для задач, когда отсутствуют фазовые ограничения, множество V не
зависит от времени и фазовых переменных, процесс описывается системами
обыкновенных дифференциальных уравнений. Более общие постановки
задач оптимального управления исследовались, например, в работах [1—3,
12, 14, 15, 33, 38].
5.4.* Примеры
Для иллюстрации теорем 5.4, 5.5 рассмотрим конкретные примеры задач
оптимального управления с более сложными краевыми условиями.
Пример 5.7
Рассмотрим задачу минимизации функционала
J(u) = )(u\t) + x\t))dt
о
при следующих условиях: x(t) = u(t),0<t<T, x(0) = x(T) = 0.
Здесь момент Т> 0 задан; V= E{. В этой задаче нетрудно угадать ответ: пара u(t) =
= 0, x(t) = 0 является единственным решением. Продемонстрируем изложенную выше
схему использования принципа максимума.
Выпишем функцию Гамильтона — Понтрягина: Н(х, и,\у,а) = -а0(и2 + х2) + \\fu
и сопряженную систему \j/ = -Н'х = 2а0х. Если а0 = 0, то функция Н = \\ш может дости-
293

гать своей точной верхней грани на множестве V = Ех лишь при \|/ = 0 (в
противном случае Н* = +°°). Однако соотношения а0= \|/ = 0 противоречат условию (5.96).
Следовательно, а0 > 0. Тогда можем считать, что а0= 1. В этом случае функция
Н = -и2 - х2 + \\fu достигает верхней грани на Е\ при и = \|//2. С учетом этого краевая
задача принципа максимума запишется в виде
x = \\f/2,y = 2x,0<t<T; x(0) = x(T) = 0.
Она имеет единственное решение x(t) = \\f(t) = 0,0<t<T. Тогда u(t) = \\f(t)/2 = 0,
0 < t < Т. Это и есть уже известное нам оптимальное управление.
Перейдем к рассмотрению более интересной задачи оптимального
управления, которая в зависимости от величины конечного момента Т
имеет единственное решение, или имеет бесконечно много решений, или
не имеет решения. Эта задача любопытна также и тем, что даже в том
случае, когда она не имеет решения, краевая задача принципа максимума будет
иметь одно или даже бесконечно много решений.
Пример 5.8
Пусть требуется минимизировать функционал
J(u) = ](u2(t)-x2(t))dt
о
при условиях x(t) = u(t),0<t<T, x(0) = x(T) = 0, Т> 0 известно (сравните с
примером 5.5).
Функция Гамильтона — Понтрягина здесь имеет вид
Я = -а0(и2 - х2) + \|Ш,
сопряженная система такая:
\j/ = -Н'х = -2а0х.
Если а0 = 0, то Н = \\fu достигает своей точной верхней грани (так же как и в
предыдущем примере) на V = Ех лишь при \|/ = 0, что противоречит условию (5.96).
Следовательно, а0 > 0, можно считать, что а0 = 1. Тогда Н = х2-и2 + \\ши точная
верхняя грань Н по переменной и е Е1 достигается при и = \|//2. Краевая задача
принципа максимума имеет вид
ir = \|//2,\j/ = -2x,0<£<7\ x(0) = x(T) = 0.
Общее решение этой системы задается формулой
x(t) = Csint + D cos t, \\f(t) = 2C cos t - 2D sin t,
где C,D — произвольные постоянные. С учетом условия д;(0) = 0 отсюда имеем D = 0,
и тогда x(t) = Csint, \\f(t) = 2Ccos£. Условие х(Т) = 0 приводит к равенству Csin T= 0.
Возможно, что Тф nk, k = 1, 2,...; тогда С = 0 и краевая задача принципа максимума
будет иметь единственное решение x(t) = 0, \\f(t) = 0, 0 < t < Т, а управлением,
подозрительным на оптимальность, будет u(t) = \\f(t)/2 = 0, 0 < t < Т. Если же Т = nk, где
k — целое положительное число, то краевая задача принципа максимума имеет целое
семейство решений x(t) = Csint, \\f(t) = 2Ccost, зависящих от одного параметра С,
и управлений, подозрительных на оптимальность, будет бесконечно много:
u(t) = Ccost, 0<t<T.
Спрашивается: будут ли найденные управления оптимальными? Оказывается,
ответ на этот вопрос зависит от величины Т. Рассмотрим случаи Г>тти0<Г<тт.
294

1. Случай Т> тт. Покажем, что тогда inf J(u) = -©о. Для этого возьмем
последовательность управлений и соответствующих им траекторий
wm=wm(0 = ^rCOSy, *m = Xm(t) = TWSHly, 0 < t < Г, Ш = 1, 2,... .
Тогда
.. . ? 1_ „frf Л
► -оо, 772—»+оо.
7(Мт)=/(м2(0_х2(0^=1Гот2
о z
Следовательно, при Т > тт рассматриваемая задача оптимального управления
не имеет решения. В то же время краевая задача принципа максимума при всех Т> тт
разрешима, причем при Т = nk, k = 2, 3, ..., она имеет бесконечно много решений,
при остальных Т > тт — единственное решение.
2. Случай 0 < Т < тт. Тогда для любых кусочно-непрерывных функций v(t),
для которых существует решение x(t) задачи x(t) = v(t), О < t < Т, х(0) = х(Т) = О,
по теореме об интегрировании по частям несобственного интеграла имеем
i2±(t)x(t)ctgtdt=(ctgtd(x2(t)) = lim xHt)ctgt\t=t2 + t?^dt=t?^dt,
о о fi^o+o 6 ''='! J0sin2£ J0sin2£
в силу того что lim x2(t)ctgt = О, а в случае Г= тт еще и lim x2(£)ctg£ = 0 (эти факты
можно без труда обосновать, применив правило Лопиталя). Пользуясь выведенным
соотношением и тем, что x(t) = v(t), находим
j(v)Jj(v2(t)-xHt))dt = ](vHt) + xHt)ctg4-^]lt =
о оК sm2t)
т т
= j(v2(t)-2x(t)x(t)ctgt + x2(t)ctg2t)dt = j(v(t)-x(t)ctgt)2dt>0.
о о
Итак,/(а) > 0, а на управлениях u(t) = О при Т< тт и u(t) = Ccost при Г= тт будем
иметьУ(гг) = 0. Таким образом, при Т< тт рассматриваемая задача оптимального
управления имеет единственное решение, при Т = тт — бесконечное количество решений,
причем все решения найдены с помощью принципа максимума.
Пусть материальная точка у (маленькая тележка) движется по закону y(t) = u(t),
где u(t) — кусочно-непрерывное управление (внешняя сила), | u(t)\ < 1, 0 < £ < Г. Если
ввести функции x{(t) = y(t) и x2(t) = y(t), то это уравнение в пространстве
переменных х = (л:1, х2) можно записать в равносильном виде
Необходимо найти такое допустимое управление, чтобы точка из заданного
состояния х(0) = х0 =(xl,xl) перешла в конечное состояние х(Т) = (0, 0) за минимальное
время Г (сравните с примером 5.6).
Сформулированная в этом примере задача быстродействия является частным
случаем задачи (5.70)—(5.73), где
J{u, Т) = J1A, /о = 1)в°-0,/ = (х2, и), х(0) = х0 = (хЪ,х$),
о (э.шу;
x(T) = (0,0),m = 0,s = 2, У = {иеЕ1:\и\<1).
295

Пользуясь теоремой 5.4, запишем краевую задачу принципа максимума. Функция
Гамильтона — Понтрягина (5.74) здесь имеет вид
Н(х, и, \|/, а0 ) = -а0 • 1 + \\f{x2 + \|/2 и,
малый лагранжиан (5.75)
1(х, Т,а) = а00 + аххх + а2х2,
сопряженная система (5.76)
Условие максимума (5.78), (5.83) здесь равносильно задаче \\f2u —» max, и е V,
откуда следует, что
[+1, если\|/2(£)>0,
u = u(t) = sgn\\f2(t) = \-l, если\|/2(О<0, (5.110)
[VweF, если\|/2(0 = 0.
Таким образом, система (5.85) в рассматриваемой задаче быстродействия (5.109)
имеет вид
хх = х2,х2 = sgn\|/2,\j/t = 0,\j/2 = -\\fv 0<t<T. (5.111)
Граничные условия в этой системе получаются из соотношений (5.109) и
условий трансверсальности (5.79), (5.81):
хЩ = хЪ х2ф) = х1 *ЧГ) = 0, х2(Т) = 0; (5.112)
^(T) = -^L = -av V2(r) = -A = -fl2; (5.113)
Н(х(П и(П У(Г), *b) = -*о + ЩСПхНТ) + х|/2(Г)г/(Г) = Ц = 0. (5.114)
К системе (5.111)—(5.114) нужно добавить условия нормировки
0 = 0 или я= 1, (5.115)
вытекающие из условий (5.77): (я0, аь а2) * 0, а0> 0, m = 0.
Совокупность условий (5.111)—(5.115) составляет краевую задачу принципа
максимума задачи быстродействия (5.108)—(5.109). Ниже будет получено
аналитическое решение этой задачи. Предварительно изучим поведение системы (5.108), когда
u(t) = 1 или u(t) = -l,t>0. Сначала рассмотрим задачу Коши
x\t) = x2(t), x2(t) = l, t>0, хЩ = х1 х2(0) = х§. (5.116)
Ее решение выписывается явно:
x\t) = ^-t2+txl+xlx2(t) = t + xl t>0. (5.117)
Заметим, что
*Чо4<' + *о)2-^+*Ц(*2<0)2-^+< (5.118)
Это значит, что решение задачи Коши (5.116) в фазовой плоскости (л:1, х2) лежит
на параболе (рис. 5.3)
хЦос^+С,, Сх=~{х1У+х1 (5.119)
296

Рис. 53
Стрелка на рис. 5.3 указывает направления движения на параболе по траектории
(5.117) и отражает возрастание координаты x2(t) с ростом t > 0.
Аналогично, при и = u(t) = -l имеем задачу Коши
x\t) = x2(t),x2(t) = -U>0, *Ч0) = xlx2(0) = xl
Ее решение также находится явно, оно имеет вид
(5.120)
x^(t) = -^2+tx2+xl=~(t-x§)2+^ + xlx2(t) = -t + xl t>0, (5.121)
и в фазовой плоскости (х1, х2) лежит на параболе (рис. 5.4)
(5.122)
Рис. 5.4
Вернемся к краевой задаче (5.111)—(5.115) принципа максимума. Сначала
рассмотрим случай а0= 0. Тогда из условия трансверсальности (5.114) с учетом
равенствах^ Т) = 0 и формулы (5.110) имеем
у2(7>(Г) = V2(7>gm|/2(r) =| щ(Т) \= 0,
297

стало быть, \|/2(Г) = 0. Отсюда и из (5.111) следует
у {(t) = C3= const, \\f 2(t) = C3(T-t), 0<t<T. (5.123)
Если Съ = 0, то Wi(t) = 0, \|/2(0 = 0, что при а0 = 0 противоречит условию (5.94).
Следовательно, Съ Ф 0. Если С3 > 0, то u(t) = sgn\|/2(0 = 1,0 < t < Т, и мы приходим к системе
(5.116); если Съ < 0, то u(t) = sgn\|/2(0 = -1,0 < t < Т, мы приходим к системе (5.120).
Как очевидно из формул (5.116)—(5.119), при u(t) = l,0<t<T,B финальную точку
х(Т) = 0 траектория приходит лишь в специальном случае, когда начальное условие
х0 =(xq,xI) и момент времени Г связаны условием (рис. 5.5, часть параболы АО)
\{xlf=xl xl=-T<Q.
(5.124)
)
о
к
^Ч U=\
V^\
Xх
\л
Рис. 55
Аналогично из формул (5.120)—(5.122) при u(t) = -1, 0<t<T, следует, что
в финальную точку х(Т) = 0 траектория приходит в специальном случае, когда
(рис. 5.6, часть параболы ВО)
~(дг02)2=4<0, х$=Т>0.
(5.125)
и = -1
х2
О
298
Рис. 5.6

Таким образом, при а0= 0 краевая задача (5.111)—(5.115) принципа максимума
выделяет подозрительные на оптимальность управления ux(t) = 1,0 < t < Г, и (t) = -1,
О < t < Т, и соответствующие им траектории x(t, щ), x(t; и2) с начальными точками х0
из условий (5.124) и (5.125) соответственно.
Рассмотрим случай, когда а0 = 1. Тогда из условия трансверсальности (5.114)
с учетом равенства х2(Т) = 0 и формулы (5.110) имеем
Х|/2(Г)г/(Г) = x|/2(7>gm|/2(r) =| Х|/2(Г) |= 1,
т.е. \|/2(Г) = 1 или \|/2(Г) = -1. Отсюда и из (5.111) следует, что
\\f2(t) = C4(T-t) + lMH\\f2(t) = C4(T-t)-l, 0<t<T, C4=const. (5.126)
Случай Q = 0 связан с управлениями u(t) = 1, u(t) = -1,0 < t < Т и, по сути, уже
рассмотрен выше в соотношениях (5.124), (5.125). Если С4Ф 0, то, как очевидно из
формул (5.126), линейная функция щ(£) может обратиться в нуль лишь в одной точке
t = т. С учетом формулы (5.110) это означает, что для произвольных начальных точек
х0, отличных от задаваемых условиями (5.124), (5.125), оптимальными могут быть
лишь управления
или
щ{1) =
u2(t) =
1,
-1,
1,
0<£<т,
x<t<T
0<t<x,
x<t<T.
(5.127)
(5.128)
В силу замечания 5.1 (с. 273) интерес для нас представляет лишь случай 0 < т < Т.
Пусть начальная точка х0 лежит ниже кривой ЛОВ (рис. 5.7). Покажем, что тогда
существует единственное управление, которое при подходящем выборе т, Г переводит
точку х0 в точку х(Т) = 0 и является решением краевой задачи (5.111)—(5.115)
принципа максимума. В самом деле, управление u{(t) = 1 порождает траекторию (5.117),
лежащую на параболе (5.119), и эта траектория в некоторый момент т пересечется
с кривой ВО. Если в этот момент переключиться на управление u{(t) = -1, t > т,
траектория попадет на кривую ОВ и, как в случае (5.125), в момент Т = x2(z) по
кривой ВО придет в финальную точку х(Т) = 0.
Рис. 5.7
Аналогично показывается, что если точка х0 лежит выше кривой ЛОВ (рис. 5.8), то
управление (5.128) при подходящем выборе т, Г переводит точку х0 в точку х(Т) = 0.
299

А именно, при и = u(t) = -1, t> О, происходит движение по параболе (5.122) до момента
т пересечения этой параболы с кривой АО, затем происходит переключение на
управление u(t) = 1, t > т, и при Т= х2(т) траектория по кривой АО достигает точки х(Т) = 0.
Рис. 5.8
Краевая задача (5.111)—(5.115) принципа максимума для задачи быстродействия
(5.108) полностью исследована. Выяснилось, что оптимальными могут быть лишь
управления u(t) = 1 или u(t) = -l,0<t<T, когда начальные точки х0удовлетворяют
специальным условиям (5.124) или (5.125) соответственно, в остальных случаях,
когда начальная точка х0 расположена ниже кривой АОВ или выше АОВ,
оптимальными могут быть лишь управления вида (5.127) или (5.128) соответственно. Эти
управления действительно являются оптимальными [1, 12, 14, 15, 24].
Заметим, что формулы (5.127), (5.128) (при т = 0 эти же формулы
соответствуют случаю а0 = 0) представляют оптимальное управление задачи
(5.108) как функцию времени. Такие управления часто называют
программным управлением.
Проведенное подробное исследование задачи (5.108) позволяет
записать оптимальное управление как функцию фазовых координат х = (х1, х2):
Г1, если точка х лежит ниже кривой АОВ или на дуге АО,
u=-u(x>)=-\ (5.129}
[-1, если точка х лежит выше кривой АОВ или на дуге ОВ.
Такая функция и(х) называется синтезирующей функцией, а задача
построения синтезирующей функции — задачей синтеза. В практических
задачах оптимального управления использование синтезирующей
функции может оказаться предпочтительнее по сравнению с программным
управлением. Можно себе представить, что в задаче (5.108) движущаяся
тележка снабжена измерительным устройством, позволяющим «узнавать»
координаты тележки (х1, х2) в любой момент времени. Тогда, зная эти
координаты и формулу (5.129), можно установить рули тележки в
состояние «1» или «-1», обеспечивая оптимальное (по быстродействию)
движение тележки. В общем случае синтезирующая функция удобна и тем, что
300

с ее помощью можно осуществлять коррекцию траектории в условиях,
когда на оптимальное движение процесса влияют какие-либо
возмущающие факторы, ошибки измерений. Следует сказать, что задача синтеза
весьма сложна, ее решение в явном виде удается найти в редких случаях.
Один из методов получения приближенного решения этой задачи будет
рассмотрен в гл. 6.
Требуется перевести точку х = (х1, х2) из состояния х0 = (2, -2) на множество
5t = {xeE2:g1(x) = x1 = 0} быстрейшим образом, предполагая, что движение точки
подчиняется уравнениям
x{(t) = x2(t),x2(t) = u(t), t>0,
причем u(t) e V = {и е Е1: | и |< 1}.
Как и в предыдущем примере, здесь Н = -a0+\\f{x2 + \\f2u, малый лагранжиан
l(x, T, а) = а0+ аххх, сопряженная система имеет вид \j/t = 0, \j/2 = -\\fv откуда следует,
что
\\fx(t) = C, \\f2(t) = -Ct + D, С, D = const.
Условия трансверсальности здесь дают
щ(Т) = -а{, \|/2(Г) = 0, -а0+щ(Т)х2(Т) + у2(Т)и(Т) = Н\(=т=0.
Следовательно, \\f2(t) = С(Т - t), 0<t<T. Заметим, что здесь С Ф 0, так как
при С = 0 получим \\fx(t) = \|/2(0 = 0, 0<t<T, а тогда ах = 0, из условия H\t=T=0
вытекает а0 = 0 — противоречие с условием (5.77). Итак, С Ф 0, \\f(t) = С(Т - t) Ф 0
при 0 < t < Т. Максимизируя функцию Н по и таким, что | и \ < 1, имеем
u(t) = sgn\\f2(t) = sgnC, 0<t<T.
Подозрительными на оптимальность здесь могут быть лишь управления u(t) = 1
или u(t) = -l,0<t<T. Если u(t) = 1, то из краевой задачи
*i = х2, х2 = 1, 0 < t <Т; х{(0) = 2, х2(0) = -2, х\Т) = 0
получим Т= 2, xx(t) = -(t-2)2, x2(t) = t-2, 0<t<2. Если u(t) = -1, то из задачи
i;i = х2, х2 = -1, 0 < t < Г; х\0) = 2, х2(0) = -2, х^Т) = 0
будемиметьГ = л/8-2,х1(О = 4-^ + 2)2,х2(О = -^-2,0<^<>/8-2.
Таким образом, краевая задача принципа максимума здесь дает два решения.
Однако лишь управление u(t) = -1, 0<t<T = \/8-2, может претендовать на
оптимальность, так как Т = 2 > >/8 - 2, управление u(t) = 1,0 < t < Т заведомо неоптимально.
Рассмотрим задачу минимизации функционала
J {и) = \{{u\t))2 + (u2(t))2)dt + *Ч1) + *2(1) (5.130)
о
при условиях
x\t) = u\t), x2(t) = u2(t), 0<t<l,
хЧ0) = 0, ^2(0) = 0, хЧ1)<0, ((х2(1))2-хЧ1)<0,
где и = u(t) = ((wKO, u2(t))).
(5.131)
301

Эта задача является частным случаем задачи (5.70)—(5.73) при п = г = 2, t0 = 0,
T=l,m = 2,s = 0,V=E2,x=(x\x2),y = (y\y2),
/° = (ux)2+(u2)2,f(x,u,t) = u, g°(x,y) = y{ + y2, g{(x,y) = y\ g2(x,y) = -yx+(y2)2,
левый конец траектории закреплен. Из условий (5.131) очевидно, что правый конец
любой допустимой траектории этой задачи удовлетворяет равенствам х{(1) = 0,
1 2
х2(1) = 0. Тогда J(u) = j\\u(t)\\dt>0 для всех допустимых управлений. Поскольку
о
и = u(t) = 0 — допустимое управление и/(0) = 0, то J* = 0, u(t) = 0 — единственное
оптимальное управление задачи (5.130), (5.131).
Воспользуемся принципом максимума. Функция Гамильтона — Понтрягина
Я = -а0[(и{)2 + (и2)2] + \\f{u{ + \\f2u2
не зависит от х, поэтому сопряженная система имеет вид х^ =0 \j/2=0, 0 < t < 1.
Следовательно, \|/i(0 = q, \|/2(0 = c2, c{,c2 — константы. Далее выпишем малый
лагранжиан:
1(х,у,а) = а0(у1+у2) + аУ+а2[-у{+(у2)2]
и сопряженную систему с условиями на а0, av a2:
-\|/i(l) = а0Л + а{Л+а2-(-1) = а0+а1-а2; (5.132)
-\\f2(i) = a0l + a{0 + a2-2x2(i) = a0; (5.133)
а$+а?+а$ = 1, а0 >0, щ >0, а2 >0. (5.134)
Покажем, что в этой задаче а0 = 0. В самом деле, если а0 > 0, то можем
воспользоваться условием нормировки а0 = 1. Тогда функция Н = -\\и\\ + (\|/, и) достигает своего
максимума на V = Е2 в точке и = \|//2 = с/2, с = (q, c2). Соответствующая траектория
x{t) = {x\t) = ^cxUx2{t) = ^c2t\
может удовлетворять условию х(1) = 0 лишь при ct = с2 = 0. Таким образом, \\f(t) = 0,
0 < t < 1. Из условия (5.133) тогда следует, что а0 = 0, что противоречит равенству
а0= 1. Следовательно, я0= 0.
Но тогда линейная функция Н = (\|/, и) на Е2 может иметь конечный максимум
(который, кстати, должен достигаться на оптимальном управлении u(t) = 0) лишь
при \|/ = \\f(t) = с = 0. Из условий (5.132)—(5.134), учитывая, что а0= 0, получаем а{ =
= а2 > 0. Таким образом, краевая задача принципа максимума здесь дает
а = (а0 =0,ax=d,a2=d), d>0, \\f(t) = 0,0<t<l.
Как видим, в этой задаче функция Н тождественно равна нулю, и условие
максимума (5.78) не дает возможности отыскать оптимальное управление и = u(t) = 0,
0<£<1.
Говорят, что оптимальное управление и(-) является особым на отрезке
[а; Р] с [t; 7], если H(x(t)> и, t, \|/(£), а0) при t е [а; Р] не зависит от и. В этом
случае условие (5.78) для набора (х = x(t), t,\\f = \\f(t), а0) при t e [a; P]
не дает никакой полезной информации об оптимальном управлении.
В частности, когда нарушается условие (5.96), т.е. а0 = 0, \\f(t) = 0yt0<t<Ty
мы имеем дело с одним из типичных случаев появления особого
управления на всем отрезке [£0; 7] — в этом случае из определения (5.74) функции
Гамильтона — Понтрягина следует, что Н= 0 и, следовательно, любое допу-
302

стимое управление удовлетворяет условию максимума (5.78). Так
случилось в только что рассмотренном примере 5.11.
Приведем пример задачи оптимального управления со свободным
правым концом, когда оптимальное управление является особым не на всем
отрезке [t0; Т\.
Требуется минимизировать функционал
1
J(u) = \x\t)dt (5.135)
о
при условиях x(t) = u(t), О < t < 1, х(0) = х0,и = u(t) — кусочно-непрерывное
управление, u(t) е V= {we E: \u\ < 1}.
Выпишем функцию Гамильтона — Понтрягина:
Н(х, и, \\f) = -x2 + \\fu.
В силу теоремы 5.3 сопряженная задача имеет вид
\\f(t) = -Н'х = 2x(t\ О < t < 1, \|/(1) = О,
а условие максимума (5.37) дает
и = u(t) = sgn\|/(£).
Краевая задача принципа максимума запишется следующим образом:
x(t) = sgn\\f(t),\\f(t) = 2x(t),0<t<T, x(0) = x0,\|/(l) = 0.
Здесь уместно вспомнить, что величина (5.135) выражает площадь
криволинейной трапеции Ш, х): 0 < t < 1, 0 < х < х2(щ. Отсюда ясно, что эта площадь будет
уменьшаться, если график решения задачи Коши x(t) = u(t), x(t) = х0, \ u(t)\ < 1 по
возможности будет приближаться к числовой оси. Это значит, что при х0 > 1 оптимальными
в этой задаче будет управление u(t) = -1, 0<£< 1, и соответствующая траектория
x(t) = -t + x0; функция \\f(t) = -t2 + 2x0t + 1 - 2х0 в этом случае меньше нуля при всех
te [0; 1], и, как и положено, согласно принципу максимума u(t) = sgnx\f(t) = -1. Далее,
если 0 < х0 < 1, то оптимальными будут управление
[-1, 0<£<х0,
w [0, х0<^<1
и соответствующие ему траектория и функция \\f(t)
\-t + x0, 0<t<x0, \-t2 + 2x0t-x$ = -(t-x0)2, 0<t<x0,
X(t) = \0, x0<t<i W) = \0, x0<t<l,
причем u(t) = sgnx\f(t), что снова согласуется с принципом максимума. Однако
на отрезке [х0; 1] функция H(x(t), и, \|/(0) = 0 и достигает своего максимума при | и \ < 1
не только при и = 0, но и в любой другой точке этого отрезка. Это значит, что
управление u(t) = 0 при t е [х0; 1] является особым, его значение однозначно не
определяется условием максимума, и это значение мы определили исходя из геометрических
соображений.Если х0 = 0, то оптимальны u(t) = 0, x(t) = 0, x\f(t) = 0, 0 < t < 1. Если же
-1 < Xq < 0, то оптимальна тройка
[1, 0<£<-х0, \t + x0, 0<t<-xo,
u(t) = \' °А x(t) = \n ° ^°
[0, -х0<^<1, [0, -х0<£<1,
\t2+2x0t + x$=(t + x0)2, 0<t<-x0,
W)[09 -x0<t<l.
303

Как видим, при -1<х0 < О управление u(t) = О на отрезке -х0 <t<\также
является особым. Наконец, если х0 < -1, то оптимальны
u(t) = 1, x(t) = t + x0, \\f(t) = t2 + 2x0t -1 - 2x0 > 0,
и опять все соответствует принципу максимума: u(t) = sgnx\f(t) = 1, 0 < t < 1.
В следующих примерах будет показано, как выписывается краевая
задача принципа максимума для некоторых задач оптимального
управления движением математического маятника.
Пример 5.13
Рассмотрим задачу оптимального управления математическим маятником со
свободным правым концом (5.2), (5.3), а именно
J (и) = (х\Т))2 + (х2(Т))2 -> min (5.136)
при условиях
x{(t) = x2(tlx2(t) = -smx\t)-^x2(t) + u(t),0<t<T, х(0) = х0; (5.137)
u(t)eV = {ueEx:\u\<l}, (5.138)
где х = (хх, х2) — фазовые координаты, х0 = (х^, х%) — заданная точка, Т> 0 —
заданный момент времени.
В этой задаче правый конец траектории свободен, /° = 0, g°0/) = (г/1)2 + О/2)2-
Выпишем функцию Гамильтона — Понтрягина:
Н(х, и, \|/) = \\fxx2 + \|/2(-sinxx - fix2 + и)
и сопряженную систему:
\\fx=-H'xl=\\f2cosxx, \|/2 = -Я^2=-\|/1+р\|/2, 0<t<T. (5.139)
Из условий (5.36) имеем
Щ(Т) = -§11(х(Т)) = -2х\Т)> ч/2(Г) = -ё«2(х(Г)) = -2^(Г). (5.140)
Из условия максимума функции Н по переменной и с учетом ограничения | и \ < 1
следует, что и = sgn\|/2. Тогда краевая задача принципа максимума запишется в виде
хх=х2, ir2=-sinx1-P^2+sgn\|/2, \\fx=\\f2cosxx, \j/2 =-\|/1 + P\|/2, 0<t<T; (5.141)
х(0) = х0, щ(Т) = -2хх(П щ(Т) = -2х2(Т). (5.142)
Если краевая задача (5.141), (5.142) имеет решение (x(t), \\f(t)), 0<t<T, причем
\|/2(£) обращается в нуль в конечном числе точек, то функция u(t) = sgn\\f2(t) будет
управлением, подозрительным на оптимальность в задаче (5.136)—(5.138).
Как и в примере 5.6, явное решение краевой задачи (5.141) в аналитической форме
получить не удается, приходится искать ее решение численными методами [6].
Заметим, что если для некоторого управления v = v(-) из (5.138) решение задачи
Коши х(-; v) (5.137) таково, чтох(Т; v) = 0, toJ(v) = 0. Это значит, что v(-) —
оптимальное управление в задаче (5.136)—(5.138). Любопытно, что это управление является
особым — его нельзя получить из принципа максимума. В самом деле, при х(Т; v) = 0
из формул (5.139), (5.140) следует \\f(t; v) = 0}0<t<T}3. тогда H(x(t\ v), и, \\f(t, v)) = 0,
0 < t < T, при всех и е V и условие (5.37) не суживает исходное множество
управлений, подозрительных на оптимальность.

Пример 5.14
Рассмотрим задачу минимизации функционала
J(u) = ]u2(t)dt
о
при условиях
x\t) = x2(t),x2(t) = -smx\t)-fix2(t) + u(t),Q<t<T, x(0) = x0,
u(t)eV = {ueEu.\u\<l}
и закрепленном правом конце х(Т) = О, Т> О — задано.
Здесь V=Ei,
Н = -а0и2 + \\f{x2 + \|/2(-sinx{ - fix2 + w),
сопряженная система имеет вид (5.139). В случае а0= О функция Я может
достигать своей верхней грани на Ех лишь при \|/2 = 0. Но если \|/2(0 = 0, 0 < t < Г, то
из второго уравнения (5.139) получим \|/1(^) = 0, что противоречит условию (5.96).
Таким образом, можем положить а0= 1. Тогда из условия максимума функции
Н по переменной и е Е получим и = \|/2/2. Краевая задача принципа максимума
будет иметь вид
*(0) = *0,*(7>0.
Пример
Рассмотрим задачу быстрейшего перевода точки х = (х{, х2) из состояния х0 Ф 0
в начало координат (0; 0), предполагая, что движение точки подчиняется условиям
(5.137)-(5.138).
Здесь У°= 1, g°= 0; функция Гамильтона — Понтрягина имеет вид
Я = -а0 + \\f{x2 + \|/2(-sinxx - fix2 + w), a0 > 0. (5.143)
Отсюда ясно, что сопряженная система будет иметь вид (5.139), а условие
максимума функции Н по переменной и при ограничениях | и \ < 1 выделит
функцию и = sgn\|/2. Краевая задача принципа максимума в этом случае будет состоять
из системы (5.141), граничных условий х(0) = х0, х(Т) = 0, условия трансверсальности
H\t=T=-a0 + y2(T)u(T) = 0
и условия (5.96). Отметим, что в этой задаче \|/2(£) Ф 0. В самом деле, если бы \|/2(£) = 0,
то из формулы (5.139) будем иметь \\f^(t) = 0, а из условия H\t=T=0 получим а0= 0,
что противоречит (5.96).
5.5.* Принцип максимума
и классическое вариационное исчисление
Основной задачей классического вариационного исчисления, как известно
[1, 12, 14, 15], является следующая задача: среди всех непрерывных
кривых х = x(t0), t0<t<T> имеющих кусочно-непрерывные производные x(t)
305

и удовлетворяющих условиям x(t0) е S0, x(T) e S{, найти такую, которая
доставляет функции (функционалу)
т
J=jf°(x(t)1x(t)1t)dt
минимальное значение. Здесь x(t) = (xx(t),..., xn(t)), S0 и 5t — заданные
множества в Еп. Будем предполагать, что функция/Хх, и, t) непрерывна и
имеет непрерывные производные f£, /w°, /Д f$, /^, /w°w при (х, и, t) е ЕпхЕпх
х [t0; ©о). Далее в этом параграфе для простоты мы ограничимся
рассмотрением случая закрепленного левого конца: x(t0) = x0, t0 задано, а правый
конец х(Т) либо закреплен: х(Т) = хь Г задано, либо свободный: Sx = Еп, Т
задано, либо является подвижным и лежит на заданной гладкой кривой
Sl=Sl(T) = {yeE":g(y,T) = y-<p(T) = 0}, Ге(-»;+~).
Обозначим x(t) = u(t) и запишем рассматриваемую задачу в
эквивалентном виде как задачу оптимального управления:
т
J (и) = J P(x(t),u(t),t)dt -> min,
'о
x(t) = u(t),to<t<T, x(t0) = x0,x(T)eSt(T).
Для исследования этой задачи воспользуемся принципом максимума
Понтрягина. Выпишем функцию Гамильтона — Понтрягина:
Н(х, и, t, \|/, a0) = -a0f°(x, и, t) + (\|/, и) (5.144)
и сопряженную систему:
y\f = -H'x=a0f£(x,u,t), a0>0. (5.145)
Для решения (u(t)> x(t))> t0<t<T, рассматриваемой задачи должно
выполняться необходимое условие
H(x(t),u(t),UW),во) = SUPH(x(t)>u>t>V(0>«o)> t0<t<T, (5.146)
иеЕп
где \\f(t) — решение системы (5.145) при и = u(t), x = x(t; и), t0<t<T. Так
как в данном случае множество V совпадает со всем пространством Еп, то
условие (5.146) может соблюдаться лишь в стационарной точке, т.е.
Hu=-a0f*(x(t),u(t),t) + W) = 0, t0<t<T. (5.147)
Отсюда ясно, что а0 Ф О, так как при а0 = О из формулы (5.147) получаем
\|/(£) = 0, что противоречит теореме 5.4. Следовательно, можно считать, что а0=
= 1. Тогда соотношения (5.144)—(5.147) перепишутся соответственно в виде
H(x,u,t,x\f) = -f°(x,u,t)+ (\|/,w); (5.148)
№ = f2(x(t),u(t\t), t0<t<T; (5.149)
H(x(t)yu(t),t,\|/(0) = supH(x(t)yu,t,\|/(0), t0<t<T; (5.150)
ueEn
V(t) = f°(x(t),u(t),t), t0<t<T. (5.151)
306

Из уравнения (5.149) имеем
t
С учетом соотношения (5.151) отсюда получаем
f2(x(t),u(t),t)= ]f?(x(T),u(T),T)dT + y(to)> t0<t<T. (5.152)
'о
Уравнение (5.152) называется уравнением Эйлера в интегральной форме]
заметим, что здесь u(t) = x(t), t0<t<T. Если уравнение (5.152)
продифференцировать по t, то получим уравнение Эйлера классического
вариационного исчисления в дифференциальной форме
^(f<*(x(t),u(t),t))-f?(x(t),u(t),t) = oy u(t) = x(t)y t0<t<T.
at
Далее, необходимым условием для достижения функцией H(x(t), u(t)> t>
\|/(0) максимума при и = u(t) является неположительность квадратичной
формы
t HXj(x(t)Mt),tMt)Mj
при любых £ = (£t, £2> •••> £m)> t0<t<T. Отсюда, учитывая выражение (5.148)
для Я, имеем
tf!v(mMt),t№j*0 \/$eE\ t0<t<T. (5.153)
Условие (5.153) называется необходимым условием Лежандра. В
частности, при п = 1 оно принимает вид
Шх(!),и(!),№, t0<t<T.
Теперь выведем необходимое условие Вейерштрасса. Для этого
перепишем условие (5.150) с учетом (5.148), (5.151) таким образом:
0 < H(x(t)y u(t), U W)) ~ H(x(t), v, t, \|/(0) =
= P(x(t\ v, t)-f\x(t), u(t), t)-(v-u(t), /2(x(t), u(t), t)). (5.154)
Это неравенство будет справедливо при любых v е Е, t e [t0; Т\, если
пара (u(t), x(t)), t0<t<T, является решением исходной задачи. Введем
в рассмотрение функцию
E(t,x,u,v) = f°(x1v1t)-f0(x,u,t)-(v-u,f2(x,u,t)), (5.155)
называемую функцией Вейерштрасса. Известное в классическом
вариационном исчислении необходимое условие Вейерштрасса
E(t,x(t),u(t),v)>0, t0<t<TyveEn,
как видим, является следствием неравенства (5.154). Далее заметим (см.
формулу (5.82)), что функции \\f(t) и H(t)= sup H(x(t),u,t,x\f(t),a0) непре-
иеЕп
307

рывны на отрезке [t0; Т\. Поэтому с учетом соотношений (5.148), (5.150),
(5.151) имеем
(fu0(x(t),u(t),t))t=0,
««(О, /°(*(0. <t), t)) - f\x(t), u(t), t))t = 0, ° '
Здесь принято обозначение (z(t))t=z(t + 0) - z(t - 0). Поскольку
равенства (5.156) выполнены при всех t,t$<t<T, то они сохраняют силу, в
частности, и в те моменты t, когда функция x(t) может иметь излом, т.е.
производная x(t) терпит разрыв. Таким образом, если учесть связь u(t) = x(t),
условия (5.156) превращаются в известные из классического
вариационного исчисления условия Эрдмана — Вейерштрасса в точках излома
кривой x(t), t0<t<T.
Теперь перейдем к рассмотрению условий на правом конце
оптимальной кривой x(t)y t0<t<T. Если конец х(Т) свободен, то в силу условия
(5.36) тогда\|/(Г) = 0. Отсюда с учетом выражения (5.151) имеем
/»(х(Т)МПТ) = 0. (5.157)
Если правый конец х(Т) подвижен, точнее,
x(T)eS1(T) = {yeE«:gJ(y1T) = yJ-q>j(T) = 01 ; = l,...,n},
то согласно условиям (5.79) существуют постоянные аь ..., ап такие, что
Ч{(Т) = -£а^(х(Т),Т) = -ъ;
}=\ у
Щх(Т), и(Т), Т, у(Г))= £ ajgj(x(T), T) = -t<tj%(T) =
j=\ j=\
= Е¥,(7>/Г) = <¥(Г),ф(Г)>.
Так как H(x,u,t,y) = (y,u)-f°(x,u,t) и y(t) выражается формулой
(5.151), то последнее равенство можно переписать так:
fO(x(T), и(Т), Т)+</»(*(Г), и(Т), Т), ф(Г) - и(Т)) = 0. (5.158)
Условия (5.157), (5.158) при учете связи x(t) = u(t) выражают собой
известные в классическом вариационном исчислении условия
трансверсальности для свободного и соответственно подвижного правого конца.
Таким образом, в случае V = Еп из принципа максимума следуют все
основные необходимые условия, известные в классическом вариационном
исчислении. Однако, если V — замкнутое множество иУ*Еп, то
соотношение (5.147), вообще говоря, не выполняется. Более того, имеются примеры,
когда и условие Вейерштрасса в этом случае не имеет места [33].
Условие максимума (5.78), являясь естественным обобщением
условия Вейерштрасса из классического вариационного исчисления, имеет то
существенное преимущество перед условием Вейерштрасса, что оно
применимо для любого (в частности, и замкнутого) множества Ve En и для более
общих задач. Заметим, что случай замкнутого множества наиболее интере-
308

сен в прикладных вопросах, поскольку значения оптимальных управлении
чаще всего лежат на границе множества V.
Упражнения
5.1. Найдите оптимальное управление в задаче
з
J (и) = j (x(t) + и2 (t))dt -> min, x(t) = u(t), 0 < t < 3,
о
если:
a) V = {ueEl:\u\<l},x(0) = 0;
6)V = {ueEu.\u\<l},x(3) = 0;
B)V = {ueEu. \u\ < 1}, x(0) = 0, x(3) = 0;
r) V = {u e Ey: |u| < 1/2}, x(0) = 0, x(3) = 0.
5.2. Найдите оптимальное управление в задаче
2
J (и) = \u2(t)dt —> min,
где
\x\t) = x2(t), (хЩ) (2) (х\2)) (0)
~ ~ ' ' х2(0)
x2(t) = u(t),
0
х2(2)
Л
5.3. Найдите решение краевой задачи принципа максимума, если
р(0=*2(0.
а функционал имеет вид
0<t<2,
гх1(0)л
k*2(0),
У
^42)"
l*2(2)J
Jx(u) = J(w2(0 + 12x40)* -> min.
о
5.4. Примените принцип максимума для решения задачи
J (и) = J х1 (£)<# —> min,
fx1(0=^2(0.
х2(0=«(0-
0<£<4, \u(t)\<\
при условиях:
а) х2(0) = 0, xi(4) = 0, х2(4) = 0;
б) xi(0) = 0, х2(4) = 0;
в)хЧ4) = 0,х2(4)=0.
5.5. Задача быстродействия является частным случаем задачи (5.70)—
(5.73), причем в функции (5.70) можно принять как/° = 1, g°(T) = 0, так
w.f>= 0, g°(T) = Т. Убедитесь, что обе формализации задачи быстродействия
приведут к одной и той же краевой задаче принципа максимума.
5.6. Найдите решение задачи быстродействия (5.108) в случае х(0) =
= (1;0),х(Г) = (0;0).
309

5.7. Решите задачу быстродействия
\xl(t) = x2(t),
\x2(t) = u(f),
J(u) = Г ->min, . v ; Д " 0<t<T,
при условиях:
а) хЧО) = 1, ^2(0) = 0, дгЧГ) = 5, дг2(Г) = 0, | и \ < 1;
б) дгЧО) = 1, *2(0) = 1, *2(Г) = 0, | и | < 1;
в) *i(0) = 4, *2(0) = 1, *2(Г) = 0, | и \ < 1.
5.8. Решите задачу
J(u) = ]u2(t)dt^ min, \*!® = *®' 0<^<1,
при условиях:
а) *Ч0) = 0, х2(0) = О, *i(l) = 1, х2(1) = 0;
б) *Ч0) = 0, х2(0) = 0, х\\) = О, х2(1) = 1;
в) *i(0) = 2, *2(0) = 0, *i(l) = 0, х2(1) = 0.
5.9. Решите задачу
Л") = \[u2(t)-(x\t))2\lt -> min,
о
[x2(t) = u(t),
5.10. Решите задачу
Лм) = ^2(1)->шт, x(t) = u(t)y0<t<ly х(0) = х0,
и = u(t) — кусочно-непрерывное управление, \u(t)\ < 1, 0 < t < 1.
Убедитесь, что при | х | > 1 задача имеет единственное оптимальное управление
u(t) = -1,0<£<1,а при | лг0| < 1 оптимальных управлений бесконечно много.
Указание. При |jr0| < 1 рассмотрите управления
-1 npn0<t<x0 <1,
uk(t) =
1 при x0+ih<t<x0+\ г + — /г,
-1 при*0+ *+— \h<t<x0+(i + i)h, г = 0,...,£-1,/г =——-,
k = 2, 3, ..., и покажите, что управление uk(t) при каждом k > 2 является
решением этой задачи.
5.11. Приведите пример задачи оптимального управления, которая сама
не имеет решения, но при этом краевая задача принципа максимума имеет
решение.
Указание. Рассмотрите задачу
т
J(u) = \(u2(t)-x2(t))dt->min, x(t) = u(t),0<t<T, х(0) = 0,х(Т) = 0.
о
310

Убедитесь, что при Т Ф nk, T > п краевая задача принципа максимума
имеет единственное решение, при Т = nk, k = 2, 3, ..., — бесконечно много
решений.
5.12. Приведите пример задачи оптимального управления, не имеющей
решения, у которой краевая задача принципа максимума также не имеет
решения.
Указание. Рассмотрите задачу
1
J(u) = j(x2(t)-u2(t))dt^>min, x(t) = u(t),0<t<l, x(0) = 0,
о
u(t) — кусочно-непрерывная функция, u(t) е V = {и е Е{-\ и |< 1} V t е [0; 1].
Покажите, что J(u) > -1 при всех допустимых управлениях, в качестве
минимизирующей последовательности возьмите
uk(t) =
1, при{<£<!+—,
k k 2k £ = 2,3,....
, i 1 ^i + 1 . Л. L л
-1, при- + —-<t<—-, z = 0,l,...,£-l,
k Ik k
5.13. Минимизируйте функционал
т
J(u) = ju2(t)(u(t)-i)2dt
о
при условиях
x(t) = u(t),0<t<T, х(0) = 0,х(Т) = 1, u(t)eV = {ueE1:0<u<l}.
Покажите, что:
а) при 0 < Т < 1 задача не имеет решения;
б) при Т= 1 задача имеет единственное решение u(t) = 1, /* = 0;
в) при Т> 1 /* = 0, имеется бесконечно много оптимальных управлений
вида
u(t) =
N
1,если^Е[^;6г.]с[0;Г], i = l,...,N, JJ(bi-ai) = \,
i=l
0, в остальных точках t е [0; Г],
[яг;Ь{]п[а^;bj] = 0, г Ф j. Примените принцип максимума к этой задаче.
5.14. Минимизируйте функционал
1
J(u) = jsmu(t)dt
о
при условиях
Покажите, что оптимальному управлению u(t) = 0, 0<^<1в принципе
максимума соответствует лишь а0 = 0.
311

5.15. Сформулируйте краевую задачу принципа максимума для задачи
быстрейшего перевода математического маятника (5.137)—(5.138) из точки
x(0) = x0=(xl,x$) в точку x(T) = t(xl(T),x2(T)), удовлетворяющую
условиям (е > 0 — заданное число):
a)\\x(T)f=t2;
б)|*(Г)|<е;
в) х^Т) = 0,\х2(Т)\<е;
г) \xi(T)\<e,x2(T) = 0;
д)|хЧГ)|<е,|х2(Г)|<е.

Глава 6
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Метод динамического программирования широко применяется
для решения задач оптимизации, имеющих специальную структуру.
Термин «динамическое программирование» был введен американским
математиком Р. Беллманом, который поначалу разрабатывал его для решения
задач оптимального управления процессами, динамика которых
описывалась обыкновенными дифференциальными уравнениями, а затем
распространил этот метод и на другие классы оптимизационных задач. Следует
сказать, что идеи, на которых основывается метод динамического
программирования, были известны давно, в частности они интенсивно развивались
русским математиком А. А. Марковым в теории вероятностей (марковские
процессы).
Мы не будем пытаться охарактеризовать этот метод в общем виде,
поскольку трудно унифицировать его многочисленные модификации,
привязанные к конкретным приложениям, и отошлем читателя к книгам [7,12,
27, 30, 36] и приведенным в них библиографическим источникам. Здесь
мы ограничимся изложением схемы Беллмана для задачи оптимального
управления с фазовыми ограничениями, обсудим ее применение к задаче
синтеза, а также рассмотрим приложения метода к некоторым классам
конечномерных задачам оптимизации.
6.1. Принцип оптимальности
Рассмотрим следующую задачу оптимального управления:
Ди()у *(•), *ь, Т, х0) = J f\x(t\ u(t), t)dt + Ф(*(Г)) -> inf; (6.1)
'о
x(t) = f(x(t),u(t),t), t0<t<Ty x(t0) = x0; (6.2)
x(t)eG(t), t0<t<T; (6.3)
и = u(t)e V(t), t0<t<T; u(t) — кусочно-непрерывная функция; (6.4)
моменты времени t0> T будем считать заданными (описание обозначений
см. в параграфе 5.1).
Заметим, что в отличие от задачи (5.98)—(5.101) в задаче (6.1)—(6.4)
граничные условия проще, но зато имеются фазовые ограничения (6.3) и
множество V = V(t) в (6.4) зависит от времени. Принцип максимума в таких
задачах, как правило, приводит к довольно сложной краевой задаче [2, 3,
12], и может оказаться, что для поиска оптимального решения выгоднее
313

применять метод динамического программирования, к изложению
которого мы переходим. Этот метод основывается на принципе оптимальности,
который мы сейчас уточним применительно к задаче (6.1)—(6.4). Пусть
(u*(t),x*(t)), t0<t<T, — оптимальное решение задачи (6.1)—(6.4) и пусть
tx — произвольный промежуточный момент времени: t0 < tx < Т. Рассмотрим
задачу оптимального управления на промежутке tx<t<T\
т
J(u(), *(•), tv Т, хх) = J P(x(t), u(t), t)dt + Ф(х(Т)) -> inf;
x(t) = f(x(t),u(t\t), tx<t<T; (6.5)
x(tt) = xv x(t)eG(t), t{<t<T;
и = u(t) e V(t), t{ < t < T, u(t) — кусочно-непрерывная функция.
При ^^hi^ х0 задача (6.5) превращается в исходную задачу (6.1)—
(6.4), так что можно говорить о погружении исходной задачи в семейство
задач (6.5), зависящее от параметров tx и хх. Задачу (6.5) можно
рассматривать как самостоятельную задачу оптимального управления, в которой
значения tx и хх выбраны независимо от исходной постановки (6.1)—(6.4).
Если же такую связь установить, выбрав в задаче (6.5) в качестве стартовой
точки х{ фазовые координаты x*(tt) оптимальной траектории задачи (6.1)—
(6.4) в момент tx, то будет справедлив принцип оптимальности, который
гласит: оптимальным решением задачи (6.5) при х{=х*(^) является
сужение (u*(t)>x*(t)), tx<t<T, на отрезок [tt; T\ оптимального решения
задачи (6.1)—(6.4). Покажем это.
Допустим, что задача (6.5) с начальной точкой хх =x*(t{) имеет
оптимальное решение (&**(£),#**(£)), tx<t<T, отличное от (u*(t)yx*(t)), t{<t<Ty
такое что
J(u**(), ***(•), tv Г, x*(tt)) < J( и. (•), *•(•), tv Г, x*(t{)). (6.6)
Определим управление
_ __ \u*(t),t0<t<tv
и* =u*(t) = \ / ч „
v ' \u**(t), tx<t<T.
Этому управлению соответствует траектория х* = x(t\u*), t0<t<T.
Нетрудно заметить, что пара функций (й* (£),#*(£)), t0<t<T> является
допустимой в задаче (6.1)—(6.4), причем х*(Т) = х**(Т) и в силу (6.6)
ЛВД, ВД, t0, Т, х0)= J f°(x*(t)y ш(0, t)dt + jf°(x*(t), ш(0, t)dt +
h т
+ Ф(х*(Т)) = J /°(**(0> w*(0, t)dt + J/°(x**(0, u**(t\ t)dt + <S>(x**(T)) <
<J(u*(-),x*(-),t0,T,x0),
что противоречит оптимальности пары (u*(t),x*(t)), t0<t<T. Таким
образом, справедливость сформулированного принципа оптимальности
установлена.
314

Спрашивается: зачем нужна задача (6.5), какую полезную
информацию можно извлечь из приведенного и почти очевидного принципа
оптимальности? Оказывается, опираясь на сформулированный принцип
оптимальности, задачу (6.1)—(6.4) можно свести к специальной задаче Коши
для уравнений с частными производными, играющей такую же роль, какую
играет краевая задача принципа максимума в задаче (5.70)—(5.73).
Следует заметить, что сформулированный выше принцип
оптимальности справедлив не для всякой задачи оптимального управления.
Например, в задаче (5.98)—(5.101), в которой условия на левом и правом концах
связаны условием вида (5.97), принцип оптимальности может и не
выполняться. Соответствующие примеры будут приведены ниже в параграфе 6.4.
6.2. Схема Беллмана
6.2.1. Разностная аппроксимация
задачи оптимального управления
Чтобы несколько упростить изложение метода динамического
программирования и сделать его более алгоритмичным, мы сначала рассмотрим
применение принципа оптимальности не к задаче (6.1)—(6.4) напрямую,
а к ее разностной аппроксимации. А именно, разобьем отрезок [t0; Т\ на N
частей точками t0 < t± < ... < tN_± < tN= Г и, приняв эти точки в качестве
узловых, заменим интеграл в формуле (6.1) квадратурной формулой
прямоугольников, а дифференциальные уравнения (6.2) — разностными
уравнениями с помощью явной схемы Эйлера [6]. В результате придем к следующей
дискретной (разностной) задаче оптимального управления:
/0(^K-lo)=sV(^.«i)+*(^)->inf; (6.7)
хм=Р{(х{,щ), z = 0,...,JV-l, х0=х; (6.8)
xteGif z = 0,...,JV (6.9)
[ui]0=(u0,uv...,uN_1): щеУ{, z = 0,...,JV-l, (6.10)
где F?(x,u) = /°(х,и,^Щ+1 -Ь), Fi(x, и) = х + f(x, и, t)(ti+i - t{), G{ = G(t{)9
V{= Vfa). Заметим, что задачи вида (6.7)—(6.10) имеют также и
самостоятельный интерес и могут возникать при непосредственном моделировании
управляемых дискретных (импульсных) процессов [13].
Если задать какое-либо дискретное управление [и{]0 = (и0, иь ..., им_{)
и начальное условие х0 = х е G0, то система (6.8) однозначно определяет
соответствующую дискретную траекторию [х{]0 = [х{(х; [щ]0)]0 = (х0, хь ...,
xN). Зафиксируем некоторое х е G0 и через А0(^) обозначим множество
управлений [щ]0 таких, что:
1) выполнены условия (6.10);
2) дискретная траектория [xj0, соответствующая управлению [щ]0
и выбранному начальному условию х0 = х, удовлетворяет
ограничениям (6.9).
315

Пару ([wj0, Mo)> состоящую из управления и траектории, будем
называть допустимой для задачи (6.7)—(6.10) или, короче, допустимой парой,
если эта пара удовлетворяет всем условиям (6.8)—(6.10) или, иначе говоря,
Шое До(*)-
Множество А0(х) может быть пустым или непустым. Если А0(х) = 0
при всех х е G0, то условия (6.8)—(6.10) несовместны и функция (6.7)
будет определена на пустом множестве. Поэтому, чтобы задача (6.7)—(6.10)
имела смысл, естественно предполагать, что существует хотя бы одна точка
х е G0, для которой А0(х) * 0. Обозначим Х0 = {х е G0: A0(#) * 0}. Тогда
задача (6.7)—(6.10) может быть сформулирована совсем кратко:
минимизировать функцию 10(х, [щ]0) на множестве [щ]0 е А0(х), х е Х0.
Положим
!*о= in| r inf 10(хЛщ]оУ
Допустимую пару ([w*]0,[x*]0) назовем решением задачи (6.7)—(6.10),
если Iq(xq,[u*]0) = Iq; при этом компоненту [и*]0 назовем оптимальным
управлением, а компоненту [х*]0 — оптимальной траекторией задачи (6.7)—
(6.10).
Задача (6.7)—(6.10) представляет собой задачу минимизации функции
n + Nr переменных х, u0l иь ..., uN_b и для ее решения в принципе могут быть
использованы методы, описанные в гл. 1—5. Однако в практических
задачах число n + Nr обычно бывает столь большим, что непосредственная
реализация методов гл. 1—5 становится технически сложной. Дополнительные
трудности вызывает и неявное описание множеств А0(х), Х0, на которых
минимизируется функция I0(x> [wj0). Для преодоления этих трудностей
и используется метод динамического программирования, с помощью
которого задача (6.7)—(6.10) большого числа переменных сводится к конечной
последовательности задач минимизации меньшей размерности.
6.2.2. Уравнение Беллмана
Для изложения метода динамического программирования нам
понадобятся следующие вспомогательные задачи:
1к(ху[и{]к) = ^РН^и{) + Ф(хм)^т{; (6.11)
Ык
хм = р1(хцЩ)> i = k,...,N-l, xk=x\ (6.12)
x{eG{, z = &,..., AT; (6.13)
[ui]k=(uhuk+v...yuN_1)\ u{eV{, i = k,...,N-l, (6.14)
зависящие от целочисленного параметра k> 0<k<N-l> и точки х e Gk.
При k = 0 задача (6.11)—(6.14) превращается в исходную задачу (6.7)—
(6.10). Через А^(х) обозначим множество всех управлений [щ]к,
удовлетворяющих условиям (6.14) и таких, что соответствующие им траектории
ixi\k= (xk = х> xk+i> •••> xn)> определяемые условиями (6.12), удовлетворяют
фазовым ограничениям (6.13). Пару ([и{]к, [х{]к) назовем допустимой парой
316

для задачи (6.11)—(6.14), если [и^е Ak(x). Допустимую пару ([w*]^,[x*]^)
будем называть решением задачи (6.11)—(6.14) при фиксированном х е Gk>
если
Компоненту [u*]k этого решения назовем оптимальным управлением,
а компоненту [x*]k — оптимальной траекторией задачи (6.11)—(6.14).
Используя семейство задач (6.11)—(6.14), сформулируем принцип
оптимальности для разностной задачи (6.7)—(6.10): если [и*]0=(щ,...,и*м_1),
[xq] = (xq, ..., x*N_{) — оптимальные управление и траектория задачи (6.7)—
(6.10), то в задаче (6.11)—(6.14) при xk =x*k оптимальными будут
управление [u*]k = (u*k,..., uN_x) и траектория [x*]k = (x*k,..., x*N_{). Справедливость
сформулированного принципа нетрудно доказать с помощью
рассуждений, аналогичных уже применявшимся выше при сравнении решений
задач (6.1)—(6.4) и (6.5), а сам этот принцип является основой
последующих рассмотрений.
Если Х0Ф 0, то для любого ky0<k<N-l> множество Ak(x) Ф 0 хотя бы
для одного х е Gk. Введем функцию
Bk(x)= inf Ых,[щ\), £ = 0,1,...,ЛГ-1,
называемую функцией Беллмана задачи (6.7)—(6.10). Областью
определения функции Bk(x) является множество Xk= {x e Gk: A^(x) Ф 0}. Покажем,
что функция Беллмана задачи (6.7)—(6.10) удовлетворяет некоторым
рекуррентным соотношениям, называемым уравнением Беллмана.
Теорема 6.1. Функция Беллмана задачи (6.7)—(6.10) необходимо
является решением уравнения
Bk(x)= inf (FHx,u) + Bk+x(Fk(x,u))\ xeXk, & = 0,1,...,ЛГ-1, (6.15)
ueDk(x)
в котором
Вн(х) = Ф(х),хе GN, (6.16)
a Dk(x) — множество всех тех и е Vk, для которых существует хотя бы
одно управление [щ]к е Ak(x) с компонентой uk = и. Верно и обратное:
функция Bk(x), х е Xk, k = 0, 1, ..., N- 1, определяемая условиями (6.15), (6.16),
является функцией Беллмана задачи (6.7)—(6.10).
Доказательство
Будем предполагать, что нижние грани в определении функции
Беллмана и в уравнении Беллмана (6.15) конечны.
Необходимость. По определению функции Беллмана имеем соотношения
Bk(x)= inf 1к(х,[и{]к)ухе Xhk = 0,1,...,ЛГ- 1;
л* 00
В^х) = Ф(х)у х е GN.
Покажем, что значения функций Bk(x) связаны рекуррентными
соотношениями (6.15). Непосредственно из определения очевидно, что мно-
317

жества Dk(x) и Ak(x) пусты или непусты одновременно, а поскольку xk+i =
= Fk(x, и) у то для непустоты этих множеств необходимо и достаточно, чтобы
Ak+1(Fk(x> и)) Ф 0. Справедливость соотношения (6.15) при k = N- 1
вытекает из условия Вц(х) = Ф(х) и представления
IN-i(x> kki) = Fn-i(*> и) + Ф(Рм_х(ху и))у
верного для любого
и е DN_{(x) = AN_i(x) = {u:ue VN_b xN= FN_x(xy и) e GN,xe G^}.
Докажем (6.15) при 0 < k < N- 1. Для этого сначала убедимся в том, что
Bk(x)< inf \F*(x,u) + Bk+x(Fk(x,u))l xeXk. (6.17)
ueDk(x)
Под действием произвольного управления и е Dk(x) дискретная
траектория перемещается из точки xk=x в точку xk+i = Fk(x> и), для которой Ak+1(xk+1) Ф
Ф 0. По определению нижней грани Bk+1(xk+1)= inf Ik+\(xk+\Aui\k+\)
Ak+\(xk+0
для любого е > 0 найдется управление [uf ]^+1 е &k+i(xk+i) такое, что
Bk+i(*k+i) ^ h+i(xk+v Kki) ^ Bk+1(xk+1) + e.
Поскольку [щ]к = {и, м|+1,..., и%_{)е &k(x)> то
Bk(x) ^ h(x> [Щ]к) = Fk(x> u) + h+i(xk+i> К ]*+i) ^
<F^(xyu) + Bk+1(xk+1) + e = F^(xyu) + Bk+1(Fk(xyu)) + e.
В силу произвольности и е Dk(x) и величины е > 0 отсюда следует
неравенство (6.17).
С другой стороны, по определению нижней грани inf 1^х\щ\) = В^{х)
для каждого е > 0 найдется такое управление [vf]k eAk(x), что Bk(x)<
<Ik(x,[vf]k)<Bk(x) + e. Если взять фрагмент этого управления [^f]^+i =
= (^|+1,...,^_i), действующий от момента k + 1, то [^]|+1 eAk+1(Fk(x,vl))
и поэтому
F£(x,*k)+BM(Fk(x,*№
= h(x,[vf]k)<Bk(x) + E.
Так как v\ е Dk(x)> то отсюда имеем
inf [Fk\x, и) + Bk+1(Fk(x, и))] < Bk(x) + e,
ueDk(x)
а тогда в силу произвольности е > О
inf [Fk\x,u) + Bk+i(Fk(x,u))]<Bk(x), xeXk.
ueDk(x)
Отсюда и из (6.17) следует равенство (6.15).
Достаточность. Пусть функции Bk(x), x e Xk, k = О, 1, ..., N - 1,
определены из условий (6.15), (6.16). Покажем, что при каждом х е Хких
значения Bk(x) равны нижним граням функций (6.11) по переменным [щ]к
при соблюдении условий (6.12)—(6.14). Отметим, что из условий (6.15),
318

(6.16) функции Bk(x), x e Xk, k = О, 1, ..., N, определяются однозначно.
С другой стороны, как было установлено выше, функции inf 4(^,[ц]^),
Д*(*)
х е Xk также удовлетворяют условиям (6.15), (6.16). Тогда из
единственности решения системы (6.15), (6.16) следует, что Bk(x)= inf Ik(xAui\k)i
Д*(*)
х е Xk, k = 0, 1,..., N-1. Теорема 6.1 доказана. ■
6.2.3. Вычислительная схема
Пользуясь условиями (6.15), (6.16), можно последовательно
определить функции Bk(x) и их области определения Xk, двигаясь в направлении
убывания номера k от N к 0. Функция В^{х) = Ф(х) и множество XN= GN
известны. Если найдены функция Bk+i(x) и множество Xk+V k < N - 1,
то для определения Bk(x) нужно решить задачу минимизации функции
ф(х, u) = F£(x, u) + Bk+i(Fk(x, и)) переменных и = (и1, ..., иг) на известном
множестве Dk(x) = {и: и е Vk> Fk(x> и) е Xk+1}. Здесь могут быть
использованы методы гл. 1—5. Функция Bk(x) определена в точке х тогда и только
тогда, когда Dk(x) Ф 0. Таким образом, при определении значений
функции Bk(x) одновременно находится и область ее определения Xk= {xr. x е Gk>
Dk(x) Ф 0} = {х: х е Gk, Ak(x) Ф 0}. Так как Ak(x) Ф 0 хотя бы при одном
хе Gk,TO Xk* 0, k = N, N- 1,..., 1,0.
Предположим, что нам удалось найти функции Bk(x) из условий (6.15),
(6.16) и, кроме того, пусть также известны функции щ(х) е Dk(x), x е Xk,
k = 0j 1,..., N- 1, на которых достигается нижняя грань в правой части
условия (6.15). Тогда, оказывается, решения задач (6.7)—(6.10) и (6.11)—(6.14)
выписываются совсем просто. А именно, оптимальное управление [и*]0
и соответствующая траектория [х*]0 для задачи (6.7)—(6.10) определяются
следующим образом: сначала из условия
inf B0(x) = B0(4) (6.18)
хеХ0
находят Xq е Х0, затем последовательно полагают
Щ -Щ\хъ)1 х\ -ЛЛ^О'^оЛ и\ -ui\xi)> ,n >iq\
Х2 -Г\\Х\>Щ)> —9 XN ~ ^N-l\xN-VuN-l)-
Оптимальное управление [u*]k и траектория [x*]k для задачи (6.11)—
(6.14) определяются аналогично:
xk = х, uk= uk(xk)y xk+i = Fk(xk>uk),..., xN = Рм_{(хм_1уun_x). (6.20)
Для доказательства этих утверждений введем вспомогательные функции
R^^^B^iF^uV-BiW + Ff^u), г = 0,1,...,ЛГ-1, (6.21)
и перепишем уравнения Беллмана (6.15) в терминах R{:
inf Rk(x,u) = Rk(x,uk(x)) = 0, i = 0,l,...,JV-l. (6.22)
ueDk(x)
С помощью функций R^Xy и) значения функции (6.11) на любом
управлении [ui\k е Ak(x) и х е Xk записываются в виде
319

h(^Ui]k) = Nf! Rii^u^ + B^x) (6.23)
i=k
при всех k = 0, 1,..., N- 1. В самом деле, учитывая равенство В^{х) = Ф(х),
из (6.12), (6.21) получим
f Ri(xi9ui)= f [Вм(хьд-В{(х{) + 1*(х{,щ)] =
i=k i=k
= 5^(%)-^(i)/f^(i,Ml.) = ^(i,K.y-B^(4
i=k
что равносильно (6.23).
Теорема 6.2. Пусть найдены функции Bk(x) из (6.15)—(6.16) и их
области определения Xk, а также функции и = uk(x), x e Xk, k = 0, 1, ..., N - 1,
на которых достигается нижняя грань в уравнении (6.15) или (6.22), и пусть
Xq определена условием (6.18). Тогда оптимальное управление [и*]0 и
траектория [х*]0 для задачи (6.7)—(6.10) определяются соотношениями (6.18)—
(6.19).
Доказательство
Из определения и(х), [и*]0, [х*]0 и эквивалентности форм (6.15) и (6.22)
записи уравнения Беллмана имеем
Ri(xlui) = Ri(xi,ui(xi))= inf. ад,и) = 0, i = 0,l,...,iV-l. (6.24)
ueDi(Xi)
Возьмем произвольную точку х е Х0, произвольное управление
[щ]0 е А0(^) и соответствующую им траекторию [х{]0 из (6.8). Так как
ще Dfai), то из уравнения (6.22) и определения щ(х) следует неравенство
11{(х{ущ)> inf Ri(xiyu) = Ri(xi,ui(xi)) = 0y i = 0,l,..., JV-l. (6.25)
ueDi(Xi)
С помощью формулы (6.23) при k = 0 с учетом соотношений (6.18),
(6.24), (6.25) получаем
N-1
1о(хЛщ]о)-1о(х*оЛщ]о)= X [Ri(Xv4)-Ri(xlu*)] + B0(x)-B0(x*0)>0
для любых хе Х0и [щ]0 е A0(#), что и требовалось доказать. ■
Теорема 6.3. Пусть известны Bk(x), x e Xk из (6.15), (6.16), а также
функции uk(x), на которых достигается нижняя грань в уравнении (6.15)
или (6.22). Тогда оптимальное управление [u*]k и траектория [x*]k
для задачи (6.11)—(6.14) определяются формулами (6.20).
Доказательство
Возьмем произвольное управление [щ]к е А^(х) и соответствующую
траекторию [x^k из (6.12). Соотношения (6.24), (6.25) остаются
справедливыми и здесь при всех i = k,..., N-1. Отсюда с помощью (6.23) получим
N-1
4(^КЬ)"4(^к*Ь)= X №(^^г)-^(х;,гг*)]>0,
i=k
что и требовалось доказать. ■
320

6.2.4. Синтезирующая функция
В теории оптимального управления и ее приложениях важное место
занимает так называемая проблема синтеза, заключающаяся в построении
функции и = uk(x), выражающей собой оптимальное управление при
условии, что в момент k объект находится в точке х фазового пространства.
Такая функция uk(x) называется синтезирующей.
Теорема 6.3 показывает, что решение уравнения Беллмана (6.15)
равносильно решению проблемы синтеза для задачи (6.7)—(6.10).
Действительно, та функция щ(х), на которой достигается нижняя грань в (6.15),
является синтезирующей, так как если в момент k объект находится в точке
х е Xk, то дальнейшее оптимальное движение объекта определяется
условиями xi+1 = F{(xiy щ(х{)), г = k,..., N- 1, xk = х, а если х g Xk, то Ak(x) = 0 и тогда
движение с соблюдением условий (6.12)—(6.14) невозможно. Достаточные
условия существования функции Беллмана и синтезирующей функции
для задачи (6.7)—(6.10) даются в следующей теореме.
Теорема 6.4. Пусть множества Gk, k = 0, 1,..., N, замкнуты, множества
Vk, k = 0, 1,..., N, замкнуты и ограничены, функция F£(x,u) полунепрерывна
снизу, а функция Fk(x, и) непрерывна по совокупности аргументов (х, и)
при х е Gk,ue Vk, k = 0, 1,..., N- 1, Ф(х) полунепрерывна снизу на
множестве GN. Тогда множества Xk, k = 0, 1, ..., N, замкнуты, множества Dk(x),
k = 0, 1, ..., N - 1, замкнуты и ограничены равномерно по х е Xk, нижняя
грань в правой части уравнения (6.15) достигается хотя бы при одном
и = щ(х) е Dk(x) и функция Bk(x) полунепрерывна снизу на Xk,k = 0, 1,..., N.
Доказательство
По условию множество GN= XN замкнуто, а функция Ф(х) = 5^(х)
полунепрерывна снизу на XN. Сделаем индуктивное предположение: пусть
множество Xk+1 замкнуто, а функция Bk+1(x) полунепрерывна снизу на Xk+1
при некотором k, 0 < k < N - 1. Докажем, что тогда Xk замкнуто и на Xk
справедливы все утверждения теоремы. Так как Dk(x) = {и: и е Vk, Fk(x,
и) е Xk+]} (zVknVk ограничено, то Dk(x) ограничено равномерно по х е Xk.
Докажем замкнутость Dk(x) при любом фиксированном х е Xk. Пусть
vm e Dk(x), т = 1,2, ..., vm —> v при т —> «>. Это значит, что vm e Vk, Fk(x,
vm) e Xk+i, m = 1, 2, .... Из замкнутости Vk, Xk+i и непрерывности Fk(x, v)
имеем: v e Vk, lim Fk(x, vm) = Fk(x, v)e Xk+1, т.е. v e Dk(x). Замкнутость Dk(x)
m—>°°
доказана.
Покажем замкнутость множества Xk = {х: х е Gk, Dk(x) Ф 0}. Пусть
ут е Xk, т = 1, 2, ..., г/ш —> у при т —> ©о. Из замкнутости Gk следует, что
у е Gk. Остается убедиться в том, что Dk(y) Ф 0. Так как Dk(ym) Ф 0, то
существует такое vm e Vk, что Fk(ym, vm) e Xk+1, m = 1, 2, .... В силу
компактности Vm из последовательности {vm} можно выбрать подпоследовательность
\Рт } —*v G Vk ПРИ Р ~^ °°- Поскольку множество Xk+1 замкнуто, а функция
Fk(x, и) непрерывна, то lim Fk(ym , vm ) = Fk(y, v)e Xk+1, т.е. v e Dk(y). Таким
p—»oo P P
образом, Dk(y) Ф 0 и, следовательно, множество Xk замкнуто.
Из непрерывности Fk(x, и) и полунепрерывности снизу F®(x, и) и Bk+1(x)
следует, что функция ф(х, u) = F^(x, u) + Bk+i(Fk(x, и)) полунепрерывна
321

снизу по (ху и) при х е Xk> и е Dk(x). Поскольку множество Dk(x)
замкнуто и ограничено, то в силу теоремы 1.2 функция ф(х, и) при
каждом фиксированном х е Xk достигает своей нижней грани на Dk(x) хотя
бы в одной точке и = uk(x) е Dk(x) и в силу уравнения Беллмана (6.15)
Bk(x) = inf Mx,u) = q>(x,uk(x)).
ueDk(x)
Остается доказать полунепрерывность снизу функции Bk(x) на
множестве Xk. Пусть ху уте Хь ут^хирит^ ~, Bk(ym) = ср(утУ uk(ym)). Так
как uk(ym) е Dk(ym) е Vk> то в силу компактности Vk последовательность
{щ(Ут)> т = 1» 2, ...} имеет хотя бы одну предельную точку v е Vk. Будем
считать, что сама последовательность {uk(ym)} —> v при т —> «>. Поскольку
функция Fk(xy и) непрерывна, множество Xk+1 замкнуто и, кроме того,
Fk(ltm> vk(ym)) E Xk+i> T0 lim Fk(ym>vk(ym)) = Fk(y>v)eXk+v Эт0 значит, что
т—>°о
v E Dk(x), и тогда
Hm Bk(ym)= Ит ф(уте, щ(ут))> ср(х, v)> inf <р(*, и) = Bk(x).
Полунепрерывность Bk(x) на Х^ доказана, что и требовалось. ■
6.2.5. Оценка погрешности
Нетрудно привести примеры задач типа (6.7)—(6.10), когда
нижняя грань в уравнении (6.15) или (6.18) не достигается. В таких задачах,
конечно, приходится пользоваться величинами, лишь приближенно
реализующими нижнюю грань в уравнениях (6.15), (6.18). Но даже в том
случае, когда нижняя грань в них достигается, получить точные
выражения для функций Bk(x)y щ(х) и точки Xq из этих уравнений часто бывает
затруднительно. Поэтому на практике приходится иметь дело и с
приближенными данными, и с приближенными решениями. Некоторое
представление о величине погрешности, возникающей при приближенном решении
задачи (6.7)—(6.10), дает приводимая ниже оценка.
Пусть К{(х) — приближенное значение функции Беллмана Bf(x), i = 0,
1,..., N По аналогии с (6.21) введем функции
Si(x,u) = Ki+i(Fi(x,u))-Ki(x) + Ff>(x,u), z = 0,...,JV-l, (6.26)
и, кроме того, положим
s^x) = Ф(х) - Кц(х)у х е GN. (6.27)
Возьмем произвольную допустимую пару [wj0= (Mo» иь •••> un-i)> ixi\o =
= (х0у хь ..., xN_{) задачи (6.7)-(6.10). Тогдах0е Х0, [и{]0е А0(х0)у ще £>,<*,•),
i = 0, 1,..., N- 1. Учитывая условие (6.8), из соотношений (6.26) имеем
Si(xiyui) = Ki+1(xi+1)-Ki(xi) + FP(xiyui)y i = 0,...,tf-l.
Суммируя эти равенства по i от 0 до N - 1, с помощью (6.27) получим
формулу
N-1
1о(хоЛщ]о)= X ^(х1ущ) + 5м(хм) + К0(х0У (6.28)
i=0
322

Если К{(х) = В{(х), то s^x) = 0 и (6.28) превратится в знакомую нам
формулу (6.23) при k = 0.
Предположим, что каким-либо образом найдены некоторое
управление [Щ]0 и соответствующая ему траектория [х{]0> удовлетворяющие
условиям (6.8)—(6.10), т.е. х0 еХ0, [щ]0 е Д0(Г0), щ еЬ((х{), г = 0, 1, ..., N - 1.
Тогда согласно формуле (6.28) имеем
_ _ N~{ _ _ _ _
1о(хоЛщ]о)= X Si(xi1ui) + sN(xN) + K0(x0)1
откуда для любых х0 е Х0, [щ]0 е Aq(^o) получаем
-10(х0,[щ]0) + 10(х0у[щ]0) =
N-1 _ _ _ _
= X [-^(^^г) + 5Дхг,ггг)]-5^(^) + 5^(^)-^0(х0) + ,К:0(х0). (6.29)
i=0
Учитывая, что Г0,х0еХ0,[Ц]0еД0(Г0), [щ]0е А0(х0),(х1ущ)е ХгхЦ(хг),
перейдем в формуле (6.29) к нижней грани по (х0, [щ]0):
_ _ N-1 _ _
0</0(Г0,[г7г]0)-/о< S [Si(*i>ui)- inl i^f А(х,и)] +
+sN (xN ) - inf sN (x) + K0 (x0 ) - inf K0 (x). (6.30)
xN x0
Полученные неравенства представляют собой оценку погрешности,
которая будет допущена при выборе |Д]о>[^] в качестве приближенного
решения задачи (6.7)—(6.10).
Если К{(х) = В{(х), i = 0, 1,..., N, то S{(x, и) = R{(xy и), s^{x) = 0 и из
формулы (6.22) будет следовать, что inf R{{x,u) = 0 для всех х е Xi9 так что
ueDi(x)
inf inf R{(x,u) = 0. Тем самым при К{(х) = В{(х) из оценки (6.30) получим
xeXi ueDi(x)
более компактную оценку
0</о(Го^Ц]о)-^о^Ё^№^/) + 50(Г0)-^50(х). (6.31)
Из оценки (6.31) следует, что чем точнее элементы щ(х) е Аг(х), х0 е Х0
приближают значения R{(x, щ(х)) к inf Ri(x,u) = 0, х е Х{, и значение
ueDi(x)
Щ(Хо) ~ к inf 50(х), тем лучше строящиеся затем по правилам
хо
Щ — uo\xo)i xi = -ч)(■*"()» ио)' ui = wi(^i)> •••> xn = Fn-i\xn-v un-\)
управление [щ] и траектория [х{] будут приближать значение /о(^о>1Д]о)
к точной нижней грани /q.
Заметим, что на практике конструктивное описание множеств Xi9 D{(x)
часто отсутствует и если в правой части оценки (6.30) вместо Х{ и D{(x)
взять более доступные множества G{ и V{ соответственно, то тогда правая
часть (6.30) может только увеличиться и вместо (6.30) мы получим более
грубую апостериорную оценку погрешности
323

0<10(х0,[щ]0)-Г0 < X ^(ЗД)- inf inf S(x,u)] +
i=0 xeGiueVi(x)
+sN(xN)-mfsN(x) + K0(x0)-mfK0(x). (6.32)
GN G0
6.2.6. Построение минимизирующих последовательностей
Оценка (6.30) полезна также и тем, что она указывает пути получения
достаточных условий оптимальности для задачи (6.7)—(6.10).
Теорема 6.5. Для того чтобы управление [щ]0 и траектория [х{]0,
удовлетворяющие условиям (6.8)—(6.10), были решением задачи (6.7)—(6.10),
достаточно, чтобы существовали функции К{(х), г = 0, 1, ..., N, такие, что
для функций Sf(x, и) и %(х), определяемых формулами (6.26), (6.27),
выполняются соотношения
Si(xi,ui)=inf inf Si(x,u) = Simin, z = 0,l,...,JV-l; (6.33)
xeXj ueDi(x)
sn(xn) = inf%(x) = sNmin; K0(x0) = infK0(x) = K0m[n. (6.34)
xN x0
Доказательство
Справедливость утверждения теоремы следует из того, что при
выполнении условий (6.33), (6.34) правая часть оценки (6.30) обращается в нуль,
атогда/0(Г0,[^]0) = /о. ■
С помощью оценки (6.30) нетрудно также получить условия,
достаточные для того, чтобы та или иная последовательность допустимых пар
управлений и траекторий была минимизирующей для задачи (6.7)—(6.10).
Теорема 6.6. Пусть последовательность управлений [щт]0 и
траекторий [xim]0, m=l,2,..., удовлетворяет условиям (6.8)—(6.10). Для того чтобы
выполнялось соотношение
lim I0(x0m, [щт]0) = Г0, (6.35)
т—>°°
достаточно существования функций Kt(x), i = 0, 1,..., N, таких, что
\imSi(xim,uim) = Simin, i = 0,l,...,JV-l, (6.36)
т—>°°
\imsN(xNm) = lim K0(x0m) = KQmin, (6.37)
где St min, sNmin, K0 min определены в формулах (6.33), (6.34).
Доказательство
Подставим в оценку (6.30) на место [щ]0 и [х{]0 соответственно [uim]0
и [хгш]0, после чего перейдем к пределу при т —> «>. С учетом
условий (6.36)—(6.37) получим равенство (6.35). ■
Всякую функцию К{(х), г = 0, 1, ..., N, удовлетворяющую условиям
теоремы 6.5 или теоремы 6.6, назовем функцией Кротова [28] задачи (6.7)—
(6.10), соответствующей допустимой паре [щ]0, [х{]0 или соответственно
последовательности допустимых пар [uim]0, [xim]0, m = 1, 2,....
324

Заметим, что если существует хотя бы одна функция Кротова К((х),
г = 0, 1,..., N, то функция К{(х) + ц, i = 0, 1,..., N, при любых осг также
является функцией Кротова. Это дает возможность без ограничения общности
считать, что в теоремах 6.5, 6.6 Simin = 0, i = 0,1,..., N- 1, %min = 0, ибо в
противном случае функцию Kt(x) можно заменить на К{(х) + ос,-, где
ai = $Шп +^i+l,min + — + ^JV-l,min» 1 = 1,..., N-1, (XN =SNmin.
Таким образом, функция Кротова для допустимой пары ([Ц]0, [^;]о) или
последовательности ([uim]0y [xim]0), m = 1, 2, ..., согласно теоремам 6.5, 6.6
удовлетворяет условиям
Si(xyu) = Ki+1(Fi(xyu))-Ki(x) + Fi\x,u)>0,
ueDi(x)1xeXi1 i = 0,..., JV-1;
sN(x) = -KN(x) + <b(x)>0, xeXN=GN, K0(x)>K0min, xeX0, (6.39)
причем неравенства (6.38), (6.39) обращаются в равенства при и = щ, х = х{
или при и = щт, х = xim в пределе при m —> «>.
Сравнение соотношений (6.38), (6.39) с соотношениями (6.15), (6.16),
(6.18), (6.22) показывает, что функция Беллмана всегда является
функцией Кротова, а обратное, вообще говоря, неверно. Заметим также, что с
помощью функции Кротова удается установить оптимальность допустимых
пар, не решая проблемы синтеза, так как согласно условиям (6.38), (6.39)
функция К{(х) выбирается с учетом индивидуальных свойств конкретной
допустимой пары управления и траектории (или последовательности пар),
подозрительных на оптимальность.
6.2.7. Приложение к задачам конечномерной оптимизации
Остановимся на одном специальном классе задач минимизации
функций большого числа переменных, которые с помощью метода
динамического программирования могут быть сведены к последовательности задач
минимизации функций меньшего числа переменных. А именно, пусть
решается задача минимизации
N-1
1о([щ\>) = 1о(Щ>Щ>->им-\) = X У50(«О->пип; (6.40)
щеУ{, г = 0,1,...,ЛГ-1; (6.41)
XWOO^', j = l,..,p; S1g/(«f) = W. j = P + l,..,n, (6.42)
i=0 i=0
где V{ — заданные множества из Er\ fi°(u)> g-(u)> ueViy — заданные
функции; У — заданные числа. В простейшем случае, когда г = 1 и
f?(ui) = ciui, g{(ui) = aijui, V^fae^1:^ >0}, г = 1,...,ЛГ-1, j = l,...,ny
задача (6.40)—(6.42) превращается в задачу линейного программирования:
X f?(ui) = c0u0+... + cN_iuN_i^>mm1 щ>0, i = 0,l,...,JV-l;
325

N-l N-l
X Оцщ < У, j = 1,..., p; X aijui =&, j = p + l,..., n.
Задачу (6.40)—(6.42) нетрудно записать в форме задачи (6.7)—(6.10).
Для этого введем переменные xi9 i = 0, 1,..., N, как решение системы
xk+i = xk + gk(uk)>k = 0,1,..., N- 1,х0 = 0, (6.43)
где gk(u) = (gl(u),...,g%(u))T, xk =(*],...,х£)т, k = 0, 1,..., ЛГ. Так как из систе-
N-1
мы (6.43) следует, что xN = X §k(uk)> T0 ограничения (6.42) равносильны
условию
%gGjv={i:igP, jr./ <Ы,] = \,...,р; xi =Ы,] = р + \,...,п). (6.44)
Таким образом, задача (6.40)—(6.42) эквивалентна задаче
минимизации функции (6.40) при условиях (6.41), (6.43), (6.44) и является частным
случаем задачи (6.7)—(6.10) при следующих данных: Fi°(x,u) = fV(u), F{(x,
и) = х + gi(u), Ф(х) = 0, G{ - Еп, г - 1,..., N- 1; G0= {0}, GN определено
соотношением (6.44). Это значит, что для исследования задачи (6.40)—(6.42)
может быть применен метод динамического программирования,
изложенный выше. Пользуясь введенными ранее обозначениями, можем переписать
уравнение Беллмана (6.15), (6.16) применительно к задаче (6.40)—(6.42):
Bk(x)= inf fA°(")+iW(*+&("))]>
ueDk(x)
xeXk, 6 = 0,1,...,N-l, BN(x) = 0.
Если ограничения (6.42) отсутствуют, то GN= En и в данной формуле
можно положить Dk(x) = Vkl k = 0, 1, ..., N-l. Этими уравнениями можно
пользоваться для решения задачи (6.40)—(6.42), как это показано выше
в подпараграфе 6.2.3.
Подчеркнем, что в задаче (6.40)—(6.42) функция и ограничения имеют
весьма специальный вид — это обстоятельство было весьма существенно
для применения метода динамического программирования. Другие классы
подобных задач описаны, например, в работах [7, 30].
6.2.8. Замечания к схеме Беллмана
Изложенный выше метод динамического программирования является
достаточно эффективным средством решения задач вида (6.7)—(6.10). С его
помощью исходная задача сводится к последовательности
вспомогательных и, вообще говоря, более простых задач минимизации функций
меньшего числа переменных для определения Bk(x), щ(х) (см. условия (6.15),
(6.16). Метод динамического программирования относится к классу
методов декомпозиции — так называются методы минимизации, которые
позволяют задачи большой размерности свести к задачам меньшей размерности;
подробнее о методах декомпозиции см., например, в работе [39].
Этот метод дает значительный выигрыш в объеме вычислений по
сравнению с простым перебором всевозможных допустимых управлений и тра-
326

екторий, поскольку при определении Bk(x)> щ(х) рассматриваются лишь
такие управления, которые переводят точку х е Gk в точку xk+1 = F(x> и) е
е Gk+ly а дальнейшее движение из точки xk+1 осуществляется по
оптимальной траектории, при этом неоптимальные траектории вовсе не
рассматриваются. Указанные достоинства метода динамического
программирования, простота схемы, применимость к задачам оптимального управления
с фазовыми ограничениями делают этот метод весьма привлекательным,
и его широко используют при решении задач типа (6.7)—(6.10). Что
касается задачи (6.1)—(6.4), с которой мы начали изложение, то можно
показать, что при некоторых ограничениях решение дискретной задачи (6.7)—
(6.10) при lim max (ti+1 -t{) = 0 будет приближаться в некотором смысле
ЛГ->ооО<г'<ЛГ-1
к решению задачи (6.1)—(6.4).
Заметим, что аналитическое выражение для Bk(x)> щ(х) на множестве
х е Xk удается найти редко, и на практике приходится ограничиваться
приближенным вычислением Bk(x), uk(x) в некоторых заранее выбранных
узловых точках множества Xk. Однако согласно условию (6.15) при
вычислении Bk(x) нужно знать значение Bk+1(Fk(x, и)) при некоторых и> и здесь
вполне возможны случаи, когда точка xk+1 = Fk(x, и) не будет принадлежать
заранее выбранному множеству узловых точек из Xk+i, а нужное значение
Bk+i(xk+i) еще не будет вычислено. Если же мы захотим вычислить
недостающее значение Bk+i(xk+i), то здесь могут понадобиться значения ранее
вычисленных функций Bk+2(x), ..., В^{х) в новых дополнительных точках,
а для этого в свою очередь придется еще более расширить множества
узловых точек в Xk+i, Xk+2, ... и т.д. На практике в таких случаях недостающее
значение Bk+i(x) получают с помощью интерполяции по значениям Bk+i(x)
в близлежащих узловых точках, что, как правило, приводит к снижению
точности. Заметим также, что принятый выше способ аппроксимации
задачи (6.1)—(6.4) с помощью разностной задачи (6.7)—(6.10) довольно
груб, поскольку опирается на простейший метод ломаных Эйлера для
интегрирования дифференциальных уравнений и квадратурную формулу
прямоугольников. Другие способы аппроксимации этой задачи, которые
не требуют интерполяции и оставляют достаточную свободу при выборе
способа аппроксимации задачи (6.1)—(6.4) см., например, в работе [12].
6.3.* Проблема синтеза для систем с непрерывным временем
Выше мы кратко рассмотрели проблему синтеза для задачи (6.7)—(6.10)
с дискретным временем. Рассмотрим проблему синтеза для задачи (6.1)—
(6.4) с непрерывно меняющимся временем. Проблема синтеза
для задачи (6.1)—(6.4) заключается в построении функции и = и(х, t),
называемой синтезирующей функцией этой задачи и представляющей
собой значение оптимального управления при условии, что в момент t
система (6.2) находится в точке х, т.е. x(t) = x. Умение решать проблему
синтеза крайне важно в различных прикладных задачах оптимального
управления. В самом деле, если известна синтезирующая функция и(х> t)>
то техническое осуществление оптимального хода процесса может быть
327

произведено по следующей схеме, называемой схемой с обратной связью.
С измерительного прибора, замеряющего в каждый момент t фазовое
состояние x(i), на ЭВМ или какое-либо другое вычислительное средство
подается величина x(t)> вычисляется значение управления u(t) = u(x(t)> t)>
после чего найденное значение u(t) оптимального управления передается
на исполнительный механизм, непосредственно реализующий требуемое
течение управляемого процесса.
6.3.1. Задача Коши — Беллмана
Проблема синтеза для задачи (6.1)—(6.4) сводится к определению
управления w*(x) = u*(x,x,t) из условий
№ *> «О) = J /°(*С0, м(т), тут + Ф(*(Г)) -> inf; (6.45)
t
х(х) = f(x(x),w(x),т), t<x<T, x(t) = x; (6.46)
x(t)eG(t), t<x<T; (6.47)
и = u(x)e V(t), t<x<T; u(x) — кусочно-непрерывная функция, (6.48)
где х — произвольная точка множества G(t), at — произвольный
фиксированный момент времени, t0<t<T. Заметим, что при t = t0 задача (6.45)—
(6.48) превращается в исходную задачу (6.1)—(6.4).
Обозначим через Д(х, t) множество всех управлений w(x), t<x<T,
удовлетворяющих условиям (6.48) и таких, что соответствующая траектория
х(х) = х(т, и), t < т < Г, системы (6.46) определена на всем отрезке [t; T\
и удовлетворяет фазовому ограничению (6.47). Положим
X(t) = {х: х е G(t), A(x, t) Ф 0}.
Пару (и(т), х(т)), t < т < Т назовем допустимой парой задачи (6.45)—
(6.48), если x(t) = х е X(t), управление и(-) е А(х, t) и х() является
траекторией системы (6.46), соответствующей управлению и(-). Аналогично
пару (и(т), х(х)), t0 < т < Т будем называть допустимой парой исходной
задачи (6.1)—(6.4), если x(t0) =x0e X(t0), u(-) е А(х0, t0) и выполнены все
соотношения (6.2)—(6.4). Допустимую пару (и*(т),х*(т)), t < т < Г, задачи
(6.45)—(6.48) будем называть оптимальным решением этой задачи, если
J(t, х, &*(•)) = inf J(t, x, u(-)), при этом &*(•) будем называть оптимальным
А(д:,0
управлением, а х*() — оптимальной траекторией задачи (6.45)—(6.48).
Зная оптимальное управление гг*(т) = и*(т,х,£) задачи (6.45)—(6.48)
при всех тех (х, t), x е G(t), t$<t<T, при которых эта задача имеет решение,
нетрудно получить синтезирующую функцию задачи (6.1)—(6.4):
достаточно положить u(x,t) = u*(t,x,t). Однако получить явное аналитическое
выражение для оптимального управления и*(т, x,t) задачи (6.45)—(6.48)
удается лишь в редких случаях, поэтому желательно иметь другие подходы
к решению проблемы синтеза.
Вспомним, что при решении проблемы синтеза для дискретных систем
важную роль играло уравнение Беллмана (6.15), (6.16). Оказывается, ана-
328

логичное уравнение может быть получено и для задачи (6.45)—(6.48).
Введем функцию
B(x,t) = inf J(t,x,u(-))> (6.49)
Д(*,0
называемую функцией Беллмана задачи (6.1)—(6.4). Если задача (6.1)—
(6.4) удовлетворяет некоторым ограничениям и функция В(х, t)
непрерывно дифференцируема, то можно показать, что функция Беллмана
удовлетворяет следующим условиям, называемым уравнением Беллмана задачи
(6.1)-(6.4):
inf ((Вх(х, t), f(xy и, t)) + Bt(x, t) + f°(x, и, t)) = О,
ueD(x,t) (6.50)
xeX(t), t0<t<T;
B(x, T) = Ф(х), x e X(T) = G(T), (6.51)
где Bjr=(B1,...,B„), В i9 Bt— частные производные функции В(х, t),
a D(x, t) — множество всех тех и е V(t), для которых существует хотя бы
одно управление и(-) е А(х, t) со значением u(t) = u(t-0) = и. Задачу (6.50),
(6.51) будем называть задачей Коти — Беллмана.
Изложим эвристические соображения, приводящие к
соотношениям (6.50), (6.51). С этой целью воспроизведем уравнения (6.15), (6.16):
inf [BM(Fk(x,u))-Bk(x) + Fg(x,u)] = Q, xeXk, & = 0,1,...,ЛГ-1; (6.52)
ueD(x,t)
Вм(х) = Ф(х)у xeXN=GN. (6.53)
Вспомним обозначения, связывающие задачи (6.1)—(6.4) и (6.7)—(6.10):
F£(x,и) = (tk+i-tk)f°(xyи,tk), Fk(xyи) = x + (tk+i-tk)f(x,и,tk),
и подставим их в соотношения (6.52), (6.53), исключив индекс k, приняв
tk =t,M = tk+1 - th tN= Г, Bk(x) = В(х, t), Bk+1(y) = B(y, t + АО, Dk(x) = D(x, t),
Xk = X(t). Тогда соотношения (6.52), (6.53) могут быть переписаны в
следующей безындексной форме:
inf [В(х + Mf(x,и,О,t + M)-В(х,t) + Atf°(x,и,t)] = 0, хеX(t), t0<t<T;
ueD(x,t)
В(х,Т) = Ф(х), xeX(T) = G(T).
Поделив первое из этих равенств на At и совершив формальный
предельный переход при At —> 0, придем к соотношениям (6.50)—(6.51).
Разумеется, приведенные рассуждения не претендуют на строгость и служат лишь
наводящими соображениями при получении соотношений (6.50)—(6.51).
Заметим, что уравнение (6.50) является дифференциальным
уравнением в частных производных первого порядка, левая часть которого
осложнена взятием нижней грани.
Под решением задачи (6.50)—(6.51) мы будем понимать функцию
В(х, t), которая определена и непрерывна при всех (х, t), x е X(t), t0<t<Ty
обладает кусочно-непрерывными частными производными Вх, Bt,
удовлетворяет уравнению (6.50) всюду, где существуют эти производные, удовлет-
329

воряет условию (6.51) и, кроме того, для любой допустимой пары (и(-)>
х()) задачи (6.45)—(6.48) при всех х е X(t) nt0<t< Г функция 5(х(т), т)
переменной т имеет кусочно-непрерывную производную на отрезке [t; 7].
Теорема 6.7. Пусть В(х, t) — решение задачи (6.50), (6.51) и, кроме того,
пусть нижняя грань в левой части (6.50) достигается на кусочно
непрерывной функции и(х, t) е D(x, t), x е X(t), t0<t<T Тогда и(х> t) является
синтезирующей функцией задачи (6.1)—(6.4).
Доказательство
Возьмем произвольные t, t0 < t < Т, и х е X(t). Пусть функция х*(т), t0 < т <
< Г является решением задачи Коши
х(т) = f(x(x),и(х(т),т),т), t0<x<T; x(t) = х,
и пусть х*(т) е Х(х) при всех те [t; Т\. Положим ш(т) = гг(х*(т), т) t0 < т <
< Т Ясно, что &*(•) е А(х, t) и (к*(-), #*(•)) — допустимая пара задачи (6.45)—
(6.48). Покажем, что пара(&*(•),х*()) является оптимальным решением
задачи (6.45)-(6.48).
Заметим, что для любой допустимой пары (и(-), х()) задачи (6.45)—
(6.48) справедлива формула
т
J(t, х, и(-)) = J R(x(t), w(t), x)dx + B(x, t), (6.54)
t
где
R(xy и, t) = (Bx (x, t), f(xy u, t)) + Bt (x, t) + /° (x, u, t). (6.55)
В самом деле, по условию функция 5(х(т), т) переменной т непрерывна
и имеет кусочно-непрерывную производную. Тогда в силу уравнения (6.46)
имеем
dB(x(x),x) = _
dx
всюду на [t; T\ за исключением, быть может, конечного числа точек.
Интегрируя это тождество по т на [t; T\ и учитывая формулу (6.51), получим
т т
Ф(х(Т)) - В(х, t) = \ R(x(x), м(т), x)dx - J /°(х(т), м(т), x)dx,
t t
что равносильно формуле (6.54). Заметим, что формула (6.54) является
непрерывным аналогом формулы (6.23).
В терминах функции R из (6.55) уравнение (6.50) можно записать в
краткой форме inf R(x, и, т) = 0. Отсюда и из определения функции и(х, т)
ueD(x,x)
имеем
R(xy и(ху т), т) = 0 = inf R(xy и, т) < R(x> и, т) (6.56)
ueD(x,x)
для всех и е D(x, т), х е Х(т), t<x<T Если (и(-), х()) — допустимая пара
задачи (6.45)—(6.48), тох(т) е Х(т), и(т) = и(т + 0) = ие D(x(x),т), t<т< Г,
поэтому из соотношения (6.56) получаем
330

R(x*(t),и(*.(т)),t) = R(x*(t),u.(t),t) = 0 <R(x(t),m(t),t), t<x<T, (6.57)
для любой допустимой пары задачи (6.45)—(6.48). Отсюда и из
формулы (6.54) с учетом условия x*(t) = x(t) = x имеем
т
М х, и(-))-№ х, и.0) = /ВДт), и(т), тут > 0 (6.58)
t
для всех допустимых пар (и(-), х()) задачи (6.45)—(6.48).
Из соотношений (6.54), (6.57), (6.58) следует, что
J(t,x,u())= inf J(t,x,u()) = B(x,t).
A(x,t)
Тем самым доказано, что функция В(х, t), определяемая
соотношениями (6.50), (6.51), в самом деле является функцией Беллмана задачи (6.1)—
(6.4), а функция и(ху t)> на которой достигается нижняя грань в левой
части соотношения (6.50), является синтезирующей для этой задачи. ■
С помощью функций В(х, t), и(х, t) нетрудно получить решение
и для исходной задачи (6.1)—(6.4). А именно, верна следующая теорема.
Теорема 6.8. Пусть В(х, t) — решение задачи (6.50)—(6.51) и пусть
нижняя грань в левой части соотношения (6.50) достигается на кусочно-
непрерывной функции и(х, t). Кроме того, пусть точка х*0 е X(t0) определена
из условия
B(x*0,t0)= inf B(x,t0), (6.59)
xeX(t0)
а пара (&*(•), #*(•)) является допустимой парой задачи (6.1)—(6.4), причем
х*() — это решение задачи Коши
х(т) = /(х(т),гг(х(т),т),т), t0<x<T; x(t0) = x*0,
а и*(х) = и(х*(т)>х). Тогда пара (&*(•), •**()) является оптимальным решением
задачи (6.1)—(6.4), т.е.
Д£0,Хо,ш(-))= inf inf J(t0,x,u()) = J*.
xeX(t0)u(-)eA(x,to)
Доказательство
Возьмем произвольную допустимую пару (и(т), х(х)), t0 < т < Г,
x(t0) = x0e X(t0) задачи (6.1)—(6.4). Из формулы (6.54) и неравенств (6.57)
при t = t0c учетом условия (6.59) имеем
т
J(t0,x0,u(-))-J(t0,x*0,u*(-))=[R(x(x),u(T),T)dT + B(x0,t0)- inf B(x,t0)>0,
t0 xeX«o)
что и требовалось доказать. ■
6.3.2. Примеры
Рассмотрим несколько примеров задач оптимального управления,
в которых удается явно выписать функцию Беллмана (6.49) и
синтезирующую функцию.
331

Пример 6.1
Решается задача минимизации
1
J(и) = \х2(t)dt->inf, x(t) = u(t), 0 < £ < 1, x(0) = x0, \u(t)|< 1.
0
Эта задача уже исследовалась выше с помощью принципа максимума Понтрягина.
Для вычисления функции Беллмана В(х, t) (6.49) запишем задачу (6.45)—(6.48):
1
J(t, х, м(.)) = J x2(x)dx -> min,
t (b.bO)
x(i) = w(t), t < x < 1, x(t) = x, G(t) = El, V = {u e Ex: \u\ < 1}.
Рассуждая так же, как и в примере 5.12, убеждаемся, что оптимальное программное
управление и соответствующая ему траектория в задаче (6.60) имеют следующий вид:
при t<z<l,x>l-t и(т) = -1, х(т) = -т + х + t\
при t<i<x + t, 0<x<\-t м(т) = -1, х(т) = -т + х +1;
при x + t<T<\yQ<x<\-t и(т) = 0, х(т) = 0;
при £<т<1,х=0 и(т) = 0, х(т) = 0;
при t<i<-x+U -\+t<x<0 w(t) = 1, х(т) = i + x-t\
при -x + t<T<l,-l+t<x<0 w(t) = 0, х(т) = 0;
при £<т<1,х<<-1+£ м(т) = 1, х(т) = т + х - £.
Значения функции Беллмана при 0 < t < 1 будут равны
B(x,t) =
(х + £-1)3), x>\-t,
4/ 3
з(*
—, 0<х<1-£,
3
3'
-1 + £<х<0,
в,(*,*)=
я,(*,о=
,-(-*3 + (*-£ + 1)3), xZ-1 + t,
а при £ = 1, как ясно из соотношения (6.50), имеем В(х, 1) = 0, х е Ех. Приведем
выражения для ее производных:
\x2-(x + t-l)2>0, x>l-t,
\х2>0, 0<x<l-t,
\-х2<0, -1 + £<х<0,
\-x2+(x-t + \)2<0, x<\ + t\
Нетрудно проверить, что функция В(х, t) является решением задачи Коши —
Беллмана (6.50), (6.51) при/= и,/° = х2, Ф(х) = 0, X(t) = E{. Синтезирующая
функция равна
[-1, х>0,
и = и(х) = -sgnBx (x, t) = \l, x<0,
0, х = 0.
-(x + t-1)2, x>l-t,
0, -\ + t<x<\-t,
-(x-t + 1)2, x<-l + t.
Пример 6.2
Пусть точка (х1, х2) на плоскости Е2 движется по закону
x\t) = x2(t\ x2(t) = u(t), 0<t<T, \u(t)\<l.
Требуется найти такое кусочно-непрерывное управление, которое переводит
точку х из заданного начального состояния x(0) = (Xq, xfi) в конечное состояние
х(Т) = (0; 0) за минимальное время Т.
332

Эта задача исследовалась выше с помощью принципа максимума (см. пример 5.9),
были найдены оптимальное программное управление, синтезирующая функция.
Проверим, как эти результаты согласуются с тем, что можно получить, применяя
метод динамического программирования.
В рассматриваемой задаче функция Беллмана В(х, t) выражает собой
оптимальное время перевода точки х- (хх, х2), находящейся в момент времени t в положении
x(t) =х,в начало координат. Иначе говоря, В(х, £) — это минимальное значение функции
J(t, х, */(•)) = J1A, /°=1,
(6.61)
при условиях
х\х) = х2(т), х2(т) = м(т), t < т < Т; x\t) = х\ x2(t) = х2;
\E2,t<z<T,
[0,т = Г,
и(т)eV = {ueE{: \и\ < 1}, t<x<T, и(т) — кусочно-непрерывная функция.
/ = (х2,и),х(т)еС(т) =
(6.62)
Здесь х е Е2 — произвольная точка, a t > О — произвольный момент времени.
Задача (6.61), (6.62) аналогична задаче (6.45)—(6.48), но здесь момент Т заранее
не задан и подлежит определению из условия минимума. Заметим, что при t = О эта
задача превращается в задачу (5.109). Выше было установлено, что в задаче (6.61),
(6.62) важную роль играет кривая ЛОВ (см. рис. 5.6, 5.7), составленная из кусков
параболы (5.124) х1 = Ux2)2, х2 < 0 и (5.125) х1 = ~(х2)2, х2>0.
Было показано, что если точка х = (х1, х2) расположена ниже кривой ЛОВ, то
оптимальное управление имеет вид
и(т) = 1 при t < т < £, и(т) = -1 при £ < т
и ему соответствует оптимальная траектория х(т) = (х{(т), х2(х))\
(6.63)
х\т) =
х2(т) =
-т2 + тх2+х{, t<T<L
2
_1Т2+Т2^ + Х2^)) + Х1(^_^2_^2(^^<Т<Г;
(6.64)
-Т + 5 + *2©, $<t<T,
и вполне определенное значение параметра £ = -х2 + J—(х2)2 - хх.
Если точка х = (хх, х2) расположена выше кривой ЛОВ, то оптимальное
управление имеет вид
м(т) = -1 при t < т < £, и(т) = 1 при £ < т, (6.65)
и ему соответствует оптимальная траектория х(т) = (^(т), х2(т)):
--Х2+ХХ2+ХХ, £<Т<£,
2
^Т2+Т(Ч + Х2^)) + Х1(^) + ^2_^2(^Д<Т<Г>
2,T4_J * + *2>^^
хЧт)
W \T-^ + x2(£),^<t<T,
со значением £, = х2+ J—(x2 )2 + х1.
(6.66)
333

Если начальная точка х лежит на кривой АО (5.124) или на кривой ОВ (5.125),
то в формулах (6.63)—(6.66) надо принять £ = L
Из формул (6.64), (6.66) и условия х(Т) = О находим решение задачи (6.61)—
(6.62): минимальное время Т* = Т*(х, t) = В(х, t) будет равно
B(x,t) =
$-хЧ® = 2$-х*=х* + 2^(^У
2+ХХ,
если точка х расположена выше кривой ЛОВ или на кривой ОВ;
-х> = -х*+2^(х
(6.67)
2)2-х\
если точка х расположена ниже кривой ЛОВ или на кривой ЛО.
Получаем, функция Беллмана в рассматриваемой задаче быстродействия от
времени t не зависит, непрерывна по х на Е2 во всех точках, кроме точек кривой ЛОВ,
и имеет в области непрерывности частные производные Bt(x) = 0иВх=(В {,В 2):
ВАх)=
1
\\{хгУ+хх
, В,(х) = 1 +
¥
-, если х лежит выше АОВ;
2)2 + ^
ВЛх) = -
$$**-•
-, В2(х) = -1+
{{
=■, еслих лежит ниже ЛОВ.
(х*У
242 _г1
Отсюда имеем
inf ((Bx, f) + Bt+f°) = inf «В»*2 + Blu +1» =
|и|<1 |и|<1
inf
|И|<1
inf
|и|<1
—х -+ 1 + -1
W + 1
= 0, если х лежит выше ЛОВ,
-j -+ -l+-j
^_(Х2)2_Х1 у ^(x2)2_xlJ
W + 1
= 0, если х лежит ниже ЛОВ,
причем нижняя грань здесь достигается при
[-1, если х выше ЛОВ,
u = -sgnBx2(x) =
+1, если х ниже ЛОВ.
(6.68)
Таким образом, вне кривой ЛОВ уравнение (6.50) выполняется, функция (6.68) —
синтезирующая. Кроме того, при t = Т из соотношений (6.61)—(6.62) следует, что
B(x)\xeG(T)= B(0) = 0, так что можно считать, что условие (6.51) также выполняется.
На кривой ЛОВ метод динамического программирования в рассматриваемой задаче
не работает [33].
6.3.3. Приближенный метод
Согласно теореме 6.7 для решения рассматриваемой проблемы синтеза
достаточно найти решение задачи (6.50), (6.51) при различных х, t.
Обсудим, как это можно сделать. Прежде всего заметим, что конструктивное
описание множеств X(t)> D(x> t)> входящих в формулировку задачи (6.50),
(6.51), часто отсутствует, и поэтому на практике вместо задачи (6.50), (6.51)
334

обычно пользуются следующей «приближенной», но более
конструктивной задачей:
inf ((Вх (ху t)y f(xy иу t)) + Bt (ху t) + /°(х, uyt)) = О,
ueV^ (6.69)
xeG(t)y t0<t<Ty В(хуТ) = Ф(х)у xeG(T)y
получающейся из задачи (6.50)—(6.51) заменой D(x, t)y X(t) на V(t), G(t)
соответственно. Конечно, здесь надо помнить, что задача (6.69) может и не иметь
решения, в то время как задача (6.50)—(6.51) может оказаться разрешимой.
Достаточно удобными и эффективными при решении задачи (6.50)—
(6.51) или задачи (6.69), по-видимому, являются методы, основанные
на рекуррентных соотношениях (6.15)—(6.16), представляющих собой
некоторую дискретную аппроксимацию задач (6.50)—(6.51) и (6.69)
и содержащих функции Bk(x), являющиеся приближениями для В(х, tk).
Существуют и другие подходы. Предположим, что удалось получить явное
выражение и = и(ху ty Bx) для точки иу в которой достигается нижняя грань
inf ((Bx,f(x,u,t)) + f°(x,u,t))
ueV(t)
при фиксированных значениях параметров (ху t, Bx). Подставив такое
выражение и = и(ху ty Bx) в формулу (6.69), приходим к следующей задаче Коши:
Bt + ((ВХУ f{x, иу t)) + f°(xy иу t))\u=u(xXBx)= 0,
xeG(t)y t0<t<Ty В(хуТ) = Ф(х)у xeG(T)y
для нелинейного уравнения с частными производными первого порядка.
Для численного решения этой задачи Коши можно пользоваться
известным арсеналом методов — разностными методами, методом характеристик,
методом прямых и т.п. [6].
Иногда удается найти решение В(ху t) задачи (6.69) в виде многочлена
по переменным х1,..., хп с неопределенными коэффициентами, зависящими
от времени:
ГП\ 1712 тп
B(x,t)= X 2...2 ^.Л(0(*1)М*яУ».
При подстановке этого выражения для В(ху t) в формулу (6.69) получим
дифференциальное уравнение для определения коэффициентов \|/г л (t)\
щ щ
Bt(x,t)= 2 - I ^h.jn(t)(x')4...(x"yn =
ц=0 i„=0
= inf F(v0_0(0. ••..¥«,...« (ty,x\...,x",u,t), xeG(t), t0<t<T, (6.70)
ueV(t) Y n
с дополнительными условиями вида
щ щ
I ••• I Ч\.4,(Т)(х1)ч...(х"У« =Ф(х), xeG(T). (6.71)
i1=0 in=0
Если Ф(х)у inf Fy в свою очередь, являются многочленами относительно
V(t)
хху ..., хпу то, приравняв коэффициенты при одинаковых степенях в соот-
335

ношениях (6.70), (6.71), получим задачу Коши для системы
обыкновенных дифференциальных уравнений относительно \|/^_,- (t). Для решения
задачи Коши можно использовать различные численные методы: Эйлера,
Адамса, Рунге — Кутта и т.д. [61. Если Ф(х) или inf F не являются мно-
V(t)
гочленами относительно х1, ..., хп, то условия (6.70), (6.71) не могут быть,
вообще говоря, удовлетворены во всей области G(t)> t0<t<T,ни при каком
выборе N = (т1 + 1) • ... • (тп+ 1) коэффициентов \|/г л (t). В этом случае
можно задать в области G(t) N кривых £i(£)>..., £#(0 и определять \\fajn(t)
из условия удовлетворения равенств (6.70), (6.71) не всюду в G(t)> а лишь
на этих кривых. Этот подход приводит к задаче Коши для системы
обыкновенных дифференциальных уравнений, не разрешенных относительно
производной \|ь л (t) (отметим, что эти производные в уравнение будут
входить линейно). Кривые ^(0> •••> £n(0 обычно выбирают так, чтобы они
имели достаточно простое аналитическое выражение (например, семейство
прямых, параллельных осям координат, семейство парабол и т.п.) и
задавали достаточно густую сетку в области G(t)> t0<t<T. Для иллюстрации
вышесказанного приведем пример.
Пример 6.3
Рассматривается задача минимизации:
т
J (и) = J u\t)dt + Хх2(Т) -> min,
о
x = u(t), 0<t<T, x(0) = x0, u(t) — кусочно-непрерывная функция
при заданных значениях Т> 0, х0Д > 0. Здесь G(t) = Е{, V(t) = Е{, 0 < t < Т.
Задача (6.69) в рассматриваемом случае имеет вид
inf[Bx(x,t)u + Bt(x,t) + u2] = 0, xeE\ 0<t<T; (6.72)
иеЕ{
В(х,Т) = Хх2, хеЕК (6.73)
Нижняя грань в соотношении (6.72) достигается при и = -Вх/2, поэтому
уравнение (6.72) перепишется так:
Bt(x,t)-B2(x,t)/4 = 0, xeE\ 0<t<T. (6.74)
Функцию В(х, t) будем искать в виде многочлена переменной т.
В(х, t) = \\f0(t) + Wi(t)x + \\f2(t)x2.
Подставив это выражение в соотношения (6.73), (6.74), получим
\j/0+\j/1x + \j/2x2-(\|/1+2\|/2x)2/4 = 0, xeE\ 0<t<T,
\\f0(T) + \\f{(T)x + x\f2(T)x2=Xx2, xeEK
Приравнивая коэффициенты при одинаковых степенях х, придем к следующей
задаче Коши:
\j/0-\|/?/4 = 0, xj/i-x|/iX|/2=0, \j/2-\|/^=0, 0<t<T,
Х|/0(Г) = 0, щ(Т) = 0, у2(Т) = Х,
которая легко решается аналитически:
¥о(0^0, X|/t(O = 0, У2(0=1_Х(^_Г)-
336

Таким образом, в этом примере явно находятся и функция Беллмана, и
синтезирующая функция:
B(x,t) = — , w(x,0 = -—= — , xeE\ 0<t<T.
6.3.4. Оценка погрешности
Предположим, что с помощью того или иного метода нам удалось
получить некоторое приближенное решение В(х, t) задачи (6.50)—(6.51)
или (6.69). Если это решение получено разностным методом (например,
методами параграфа 6.2) на какой-то дискретной сетке точек, то
доопределим ее (например, интерполяцией или с помощью сплайнов) во всех точках
области G(t), 0 < t < Т, до некоторой непрерывной кусочно-гладкой функции
В(х, t). Тогда функцию и = и(х, t), на которой реализуется точная или
приближенная нижняя грань функции R(x> u> t) из соотношения (6.55) на
множестве D(x, t) или V(t), можем принять в качестве приближенного решения
проблемы синтеза для задачи (6.1)—(6.4). Это значит, что приближенное
решение (й(-),х()), задачи (6.45)—(6.48) будем определять из условий
х(х) = /(Г(х),и(Г(х),х),х), t<x<T, x(T) = x,
(Ь./Ь)
ЭДеС(х), й(т) = и(ЭД,т), t<x<T. '
Приближенное решение исходной задачи (6.1)—(6.4) находится
аналогично: сначала определяем точку Г0, на которой точно или приближенно
реализуется нижняя грань функции В(х, t0) на множестве X(t0) или G(t0),
а затем, решая задачу (6.75) при t = t0, x = x0, находим траекторию х(т)
и управление й(х) = и(х(т)), t0<x<T. Найденную пару (й(-), х()) принимаем
за приближенное решение задачи (6.1)—(6.4). Приведем оценку
возникающей при этом погрешности. Пусть К(х, t) — какая-либо функция, которая
определена и непрерывна при всех х е X(t), t0<t<T, обладает кусочно-
непрерывными производными Кх, Kt и такова, что для любой допустимой
пары (&(•), *(•))> задачи (6.45)—(6.48) при всеххе X(t), t0<t<T, функция
К(х(т), х) переменной х является кусочно-гладкой или абсолютно
непрерывной на [t; T\. На практике в качестве функции К(х> t) обычно берут
какое-либо приближенное решение В(х, t) задачи (6.50)—(6.51) или (6.69).
По аналогии с формулой (6.55) введем функцию
S(x, и, t) = (Кх(х, t), f(x, и, t)) + Kt(x, t) + f°(x, и, t), _ч
(b./b)
xeX(t), t0<t<T,
и, кроме того, положим
s(xy T) = Ф(х) - К(х, Т)ухе G(T). (6.77)
Возьмем произвольную допустимую пару (и(-)> х()) задачи (6.45)—
(6.48). В силу уравнения (6.46) тогда имеем
dK(x(x),x)
dx
■ = S(x(t), м(т), t) - /°(*(т), w(x), x), t0<x<T.
337

Учитывая непрерывность и кусочную гладкость функции К(х(т), т),
проинтегрируем это тождество по т от t до Т:
т
J(t, х, и(.)) = \ S(x(x), и(т), тут + 5(х(Г), Г) + К(х, t). (6.78)
Если К(х, t) = B(x, t), то S(x, и, т) = R(x, и, т), s(x, Г) = 0 и эта формула
превратится в формулу (6.54).
Предположим, что каким-то образом получена пара(й(т), Г(т)), £ < т < Г,
удовлетворяющая условиям (6.47), (6.48) и уравнению (6.46) с начальным
условием x(t) = xe X(t). Тогда согласно равенству (6.78)
т
J(t, х, й()) - J(t, х, и{-)) = J [S( *(т), й(т), т) - 5(х(т), и(т), т)]Лт +
t
+[s(x(T), T) - s(x(T), Г)] + [К(х, t) - К(х, О] (6.79)
для любой допустимой пары (и(-), х()) задачи (6.45)—(6.48). Из
соотношения (6.79) уже нетрудно получить требуемые оценки погрешности для
задач (6.45)-(6.48) и (6.1)-(6.4). Обозначим
^minCO= inf inf S(x,w,t),
xeX(x)ueD(x,T)
5min= inf s(x,T), Knin(t)= inf K(x,t), (6.80)
xeX(t) xeX(t)
и предположим, что (г7(),х()) — некоторая допустимая пара
задачи (6.45)—(6.48), которую мы хотим взять в качестве приближенного
решения. Учитывая, что для любой допустимой пары (&(•)> х()) задачи (6.45)—
(6.48) имеют место включения x(t) = х е X(t), u(-)eA(xyt)> х(т) е Х(т),
и(т) е D(x(t), t), t < т < Г, из соотношений (6.79), (6.80) получим искомую
оценку погрешности
0<Л*,х,й())- inf J(t,x,u(-))^
A(x,t)
/l(S(x(x)M^)^)-Smi^))dTHs(W),T)-smin) + K(x,t)-Kmin(t). (6.81)
t
Если же (й(т),Г(т)), t0 < т < Г, — допустимая пара задачи (6.1)—(6.4),
которая берется за приближенное решение, и x(t0) = x0> то из соотношений
(6.79), (6.80) имеем такую оценку погрешности:
0<J(t0,x0,u(-))- inf inf J(t0,x,u(-))<
xeX(t0)u()eA(x,t0)
4(ВДт),ВД,т)-5т^^ (6.82)
'о
+ К(х0 ,t0)- Kmin (t0 ).
Если K(x, t) = В(х, t), то S(x, и, t) = R(x, и, t), s(x, T) = 0 и, кроме того,
из соотношения (6.56) следует, что inf R(x, u,t) = 0 при всех x е X(t), так
ueD(x,t)
338

что inf inf R(x, и, t) = 0. Поэтому при K(x, t) = В(х, t) из соотношений
xeX(t)ueD(x,t)
(6.81), (6.82) соответственно получим
0 < М х, Ч')) ~ inf J(t, х, м(0) <
u()eA(x,t)
Т
<\R(x(x),u(x),x)dx + B(x,t)- inf B(x,t); (6.83)
Jt xeX(t)
0<J(t0,x0,u(-))- inf inf J(t0,xyu(-))<
xeX(t0)u()eA(x,t0)
T
< \R(x(x)1u(x)1x)dx + B(x0lt0)- inf B(x,t0). (6.84)
Из оценок (6.83), (6.84) следует, что если определить й(х> t) e A(x, t)>
xeX(t) так, чтобы значение R(x, й(х, t), t) было поближе к inf R(x, и, t),
значение В(х, t) — поближе к inf B(x, t), а затем найти пару (г7(т), х(х))
xeX(t)
из условий
t(x) = f(x(x)yй(х(х)ут)т), х(х)еG(x), t<x<T, x(t) = х, й(х) = й(х(х)>т),
то величина J(t, x, й(-)) (в случае задачи (6.1)—(6.4) величина J(t0, J0, й(-))
будет мало отличаться от искомого оптимального значения, а функция
й(х, t) будет хорошим приближением для синтезирующей функции.
Заметим, что оценки (6.82), (6.84) являются аналогами оценок (6.30) и (6.31).
Заметим также, что в приложениях могут оказаться удобнее более грубые
оценки, получающиеся после замены в соотношениях (6.81)—(6.84)
неконструктивно определенных множеств А(х, t) и X(t) множествами V(t) и G(t)
соответственно.
6.4.* Контрпримеры
Как уже отмечалось выше, принцип оптимальности справедлив не для
всякой непрерывной или дискретной задачи оптимального управления.
Приведем примеры, показывающие, какие именно нарушения этого принципа
могут возникнуть, если в исходных оптимизационных задач присутствуют
ограничения, отличные от принятых в (6.1)—(6.4) или (6.7)—(6.10).
Пример 6.А
Рассмотрим задачу управления вида
J(t0,u) = x2(T)^>min, x(t) = u(t), |м(*)|<1, t0<t<T, x(t0)-x(T) = l (6.85)
с заданными значениями t0< T начального и конечного моментов времени. Если
в задаче (6.85) существует допустимая траектория x(t), то
т т т
\ = x{tQ)-x{T) = -\x{x)dx = -\u{x)dx<\\i{x)\dx<T-tQ.
t0 t0 t0
Это значит, что при Т- t0 < 1 в задаче (6.85) нет ни допустимых траекторий, ни
оптимальных решений. Если же Т-10> 1, то среди допустимых траекторий имеется
339

траектория x*(i) со свойством х*(Т) = 0. Она также должна удовлетворять начальному
условию x*(t0) = 1. В таком случае допустимое кусочно-постоянное управление вида
u*(t) = -1, t0 < t < t0 +1, u*(t) = 0, t0 +1 < t < T, (6.86)
порождает допустимую траекторию x*(t) перехода из начального состояния x*(t0) = 1
в конечное состояние х*(Т) = 0:
x*(t) = -t + l, t0<t<t0 + l, x*(t) = 0, t0 + l<t<T.
Заметим, что J(u*) = J* = 0, значит, пара (u*(t), x*(t)) является оптимальным
решением задачи (6.85). Рассмотрим для задачи (6.85) семейство задач вида (6.5),
зависящих от параметра tvt{<t<T:
J(tvu) = x2(T)^>min, x(t) = u(t), |w(^)|< 1, tx<t<T, x(tx)-x(T) = l. (6.87)
При tx = t0 эта задача превращается в задачу (6.85), но для нее, в отличие от задачи
(6.1)—(6.4), уже невозможно сформулировать принцип оптимальности в
прежнем виде, поскольку для значений параметра tv близких к Г, а именно: Т - tx< 1,
у задачи (6.87) не будет не только оптимальных, но даже и допустимых управлений.
Пример 6.5
Рассмотрим следующую конкретную дискретную задачу оптимального
управления типа (6.7)—(6.10), в которой поточечные ограничения (6.10) на управления
замещены интегральными :
I0(x,[ui]0) = x2N^>inf;
xi+i=xi+ui, z = 0,1,...,ЛГ-1, х0=х; (6.88)
N-\
K]o=(W0>wl>-> uN-\Y %U?<1,
i=0
а остальные элементы конструкции постановки (6.7)—(6.10) не нарушены: Ff(x, и) = 0,
Ф(х) = х2, Ff(x, и) = w, G{ = E1, dimxf = dimw, = 1.
С помощью правила множителей Лагранжа задачу (6.88) можно решить явно.
Выразим в соотношениях (6.88) значениеxNчерез [и]0= (м0, щ, ..., w#-i) и запишем
задачу в форме (1.20) задачи минимизации функции N переменных [wj0= (w0, щ,...,
un-\) c единственным ограничением типа неравенства:
1о(х>[щ\о) =
N-\
х+ X Щ
i=Q
N-\
'inf. go(K]o)=E"^l-
i=0
(6.89)
Задача (6.89) представляет собой проблему минимизации непрерывной функции
на замкнутом ограниченном множестве ЛГ-мерного евклидова пространства, поэтому
в этой задаче минимум (как, впрочем, и максимум) обязательно достигается. Для
определения точки минимума рассмотрим функцию Лагранжа:
L([MJ0,X) = X0
х+ X Щ
i=0 )
+ *1
(N-\
\luf-l
V i=0
, Х = (Х0,ХХ), Х0>0,ХХ>0,
запишем необходимые условия оптимальности в форме (1.32) из замечания 1.2 к
теореме 1.9:
2X0Lr+ £ Uj + 2X^=0, f = 0,1 AT —1, X0 >0,Xt >0, X*0, (6.90)
и присоединим к ним условия допустимости и условия дополняющей нежесткости (1.31):
N-\ (N-\ \
5>?<1, ХЛ 2«?-1 =0. (6.91)
i=0 V *=0 )
340

При ^0= 0 в силу того, что Х{ > 0, условия (6.90) и (6.91) оказываются
несовместными, поэтому будем считать, что Х0 = 1. Если при этом Х{ = 0, то из условий (6.90)
и (6.91) следует соотношение
г2 =
ЛМ
л
;=0
ЛГ-1
= luj\ < £l2 I"]
j=0
N-\
>0
<N-1 = N. (6.92)
Получается, что для стартовых точек х, удовлетворяющих условию (6.92),
имеющихся управляющих ресурсов достаточно для того, чтобы обеспечить перевод
дискретного процесса (6.88) в конечное нулевое состояние xN = 0. Предположим теперь,
что условие (6.92) нарушено, т.е. х2 > N. Тогда обязательно Х{ > 0 и из (6.90) будет
следовать, что у оптимального управления [и*]0 все компоненты щ будут одинаковыми:
U: =-
N + X{
Из условий дополняющей нежесткости находим значение множителя Лагранжа
Х{ = \x\yjN - N и выражаем компоненты оптимального управления и оптимальной
траектории непосредственно через х и N
х
Щ=~. , /—> * = 0,1,...,ЛГ-1,
MJ" (6.93)
*шй,хЧй) "-"■l--N-
Предположим, что начальная точка процесса х расположена вдали от нуля и
условие (6.92) нарушено с запасом, а именно: х2 > AN Тогда условие (6.92) будет
нарушаться и для всех без исключения текущих положений х* оптимальной траектории:
хр >N, i = 0, 1, ..., N. Рассмотрим для задачи (6.88) семейство задач типа (6.11)—
(6.14), зависящих от целочисленного параметра k = 0, 1,..., N- 1:
Ik(x,[ui]k) = x2N^'mi;
xi+x=xi + ui, i = k,...,N-l, xk = x; (6.94)
[Ui\k=(uk,uk+v...,uN_xy. 5>?<1.
i=k
В формулировке принципа оптимальности в задачах (6.11)—(6.14)
предполагалось, что стартовая точка х процесса (6.12) совпадает с положением х\
оптимальной траектории, поэтому возьмем в задаче (6.94) х = х*ки найдем оптимальное
решение [w/]^,[x*]^ задачи (6.94). Для стартовой точки х\ нарушено условие типа (6.92):
x*k2 >N>N-k, поэтому задача (6.94) будет иметь единственное оптимальное
решение, имеющее подобную соотношениям (6.93) структуру:
*
и' = 5 , i = k,k+l,...,N-l,
\xl\fiTk'
^ui^-ih
i = k,k+l,...,N.
Подставляя на место х\ их явное выражение из соотношений (6.93), получим
щ= р -, i = k,k + l,...,N-l. (6.95)
1 \x\y[N^k
Сопоставляя соотношения (6.93) и (6.95), заключаем, что сужения
оптимальных управлений[щ]0задачи (6.88) на промежуток i = k, k + 1,..., N- 1 не совпадают
с оптимальными управлениями [u*t]k для задач (6.94) ни при каких k = 1, 2,..., N- 1,
т.е. принцип оптимальности нарушается.
341

Пример 6.6
Рассмотрим задачу оптимального управления типа (6.1)—(6.4), являющуюся
непрерывным аналогом задачи (6.88) из предыдущего примера 6.5:
г
J(t0,u) = x2(T)-> min, x(t) = u(t), t0<t<T, x(t0) = x, \u2{t)dt<\. (6.96)
'о
Единственным, но важным отличием задачи (6.96) от (6.1)—(6.4) является
присутствие в постановке задачи (6.96) интегральных ограничений на управления. Для
строгого обоснования приводимых ниже выводов требуется знакомство с
понятиями измеримых и интегрируемых по Лебегу функций, а также с определением диф-
ференцирумости и формулировкой правила множителей Лагранжа в
бесконечномерном гильбертовом пространстве. Заинтересованным читателям, желающим
разобраться в этих вопросах, порекомендуем книги [12, 29], а здесь ограничимся кратким
изложением основных результатов, полностью аналогичных тем, которые были
подробно описаны в примере 6.5.
Аналогом условия (6.92) будет неравенствох2 < Т-10, а прих2>T-t0y задачи (6.96)
будет существовать единственное оптимальное решение u*(t), x*(t), аналогичное
соотношениям соотношениям (6.93):
х х( t-t ^
t0<t<T. (6.97)
Если начальная точка процесса х расположена вдали от нуля, так что х2 >
> 4(Г- t0), то, как ясно из соотношений (6.97), для всех промежуточных положений
x*(i) оптимальной траектории будет выполняться неравенствоx2(t)>T-t0,t0<t<T.
Рассмотрим семейство задач типа (6.5), зависящих от параметра tb t0 < tx < Т:
т
J(tvи) = х2(Т)->min, x(t) = u(t), t{<t<T, x(t{) = x, Ju\t)dt< 1. (6.98)
h
Найдем оптимальное управление u*(i) в задаче (6.98) при х = x*(t{), как это
делается в формулировке принципа оптимальности:
u*(t) = £ -, tx<t<T. (6.99)
\x\yJT-ti
Как и в предыдущем примере, непосредственно из соотношений (6.97) и (6.99)
очевидно, что сужение оптимального управления u*(t) на промежуток tx < t < Т не
совпадает с оптимальным управлением u*(t) задачи (6.98) при выборе стартовой позиции
х = x*(t{), т.е. принцип оптимальности нарушается, а «виновником» этого нарушения
являются присутствующие в задаче (6.96) ограничения на управления интегрального
типа, не вписывающиеся в постановку задачи (6.1)—(6.4).
6.5.* Применение метода динамического программирования
к задачам дискретной оптимизации
Выше мы изложили один из вариантов метода динамического
программирования. Существует большое количество модификаций этого метода,
основанных на различных формулировках принципа оптимальности,
учитывающих структуру и специфические особенности конкретных классов
задач оптимизации. Мы здесь не будем пытаться охарактеризовать метод
динамического программирования в общем случае, отсылая читателя
342

к имеющейся обширной литературе (см., например, [7, 12, 27, 28, 30, 36]),
и ограничимся рассмотрением некоторых задач дискретной оптимизации.
Так принято называть задачи оптимизации, в которых допустимое
множество U состоит из точек и = (и1, ..., ип) с координатами, принимающими
отдельные дискретные (например, целочисленные) значения.
Типичным примером такой задачи является классическая задача о
рюкзаке. Пусть имеется N предметов и пусть а{ > 0 — вес, а с{ > 0 — ценность
г-го предмета, i = 1,..., N. Требуется загрузить рюкзак, выдерживающий вес
Ь, набором предметов, суммарная ценность которых максимальна. Введем
переменную щ, принимающую значение 1, если j-й предмет грузится в
рюкзак, и 0 — в противном случае, г = 1,2,..., N. Тогда задачу о рюкзаке можно
сформулировать в следующем виде:
N
jx(uv..., uN)=Y>ciui ->max; (б.юо)
N
^а{щ<Ь, tt,=0vl, z = l,...,JV. (6.101)
В этой задаче допустимое множество состоит из конечного числа
элементов, и в принципе ее решение можно получить простым перебором. Однако
даже при сравнительно небольших N такой перебор практически
неосуществим из-за слишком большого объема вычислительной работы. Из-за
дискретности допустимого множества здесь неприемлемы многие
известные методы (например, градиентный метод, метод Ньютона), не работают
известные условия оптимальности. Поэтому для решения задач дискретной
оптимизации приходится создавать специальные методы [7, 27, 30, 36].
На примере задачи о рюкзаке покажем, что для ее решения можно
использовать метод динамического программирования. Переменные щ, ..., ип
в задаче (6.100), (6.101) назовем управлением системы. Введем переменные
k
xk =b-^aiui1 k = l,...,N,
которые будем называть состоянием системы. Нетрудно убедиться, что
состояние системы удовлетворяет условиям
def
xk = xk_x-akuk, k = \,2,...,N, x0 = b; (6.102)
N
b = x0>x1>...>xN=b-'Zaiui>0. (6.103)
i=l
Исходную задачу (6.100), (6.101) вложим в семейство задач того же типа:
N N
Jk(ukl...,uN)=1£сметах, ^а{щ<хк_х, & = ЛГ,ЛГ-1,...,1, (6.104)
i=k i=k
где щ=0\/ 1, г = k,..., N. Максимальное значение функции/^г^, •••> щ) в
задаче (6.104) назовем функцией Беллмана и обозначим
Bk(xk-i) = max/^tt*,..., uN). (6.105)
343

Если на k-м шаге при решении задачи (6.104) выбрано некоторое
управление uky траектория перейдет из состояния xk_x в состояние xk = xk_{ - akuk.
Принцип оптимальности гласит: при любом выборе uk на последующих
шагах управления uk+i, uk+2,..., % должны выбираться так, чтобы функция
Jk+i(uk+i> •••> un) достигала своего максимального значения Bk+1(xk)> и,
следовательно, при выборе щ нужно позаботиться о том, чтобы совокупный
набор (щ, uk+v ..., uN), полученный добавлением элемента uk к
оптимальному набору (щ+1у ..., uN)y приводил бы к максимальному значению Bk(xk_x).
Иначе говоря, функция Беллмана должна удовлетворять условиям,
называемым уравнением Беллмана:
Bk(xk-0 = ^ах {ckuk+Bk+x(xk_x-akuk)}, k = 1,2,...,N, (6.106)
0<uk<lxk_{/akj
def
^+i(^) = 0, (6.107)
где \xk_±/a^\ — целая часть числа xk_±/ak. Напомним, что управление uk
принимает всего два значения: щ= 0 V 1, поэтому условие 0k<uk< \xk_Ja^
в соотношении (6.106) равносильно системе неравенств xk = xk_x - akuk> 0
или 0<akuk <xk_b k = 0, 1,..., N. Равенства (6.106), (6.107) являются
следствием сформулированного выше принципа оптимальности и
доказываются с помощью рассуждений, использованных при выводе уравнений (6.15),
(6.16); в данном случае эти рассуждения даже упрощаются, так как
допустимое множество в задачах (6.104) состоит из конечного числа элементов,
и максимум в (6.105) достигается.
В задаче (6.106) допустимое множество состоит из одного или двух
элементов, и вычисление значений функции Bk(xk_{) не представляет
трудностей. Начинать нужно с построения множества XN_{ состояний, состоящего
N-1
из точек xN_{ = Ъ- X я,-м,-, где щ= 0 или щ= 1, так что
xn-\ = \xn-\ :b,b-l,...,6-max\0; £ Щ [[•
Далее вычисляем значения функции Беллмана
BN (xN_{) = max cNxN = max{xN •0 = 0,cN-l = cN}\/ xN_{ e XN_{
и определяем точки им*(хм_{)> xN_x е XN_b в которых этот максимум
достигается. Если уже вычислены Bk+1(xk)> uk+i*(xk)> xke Xk> то находим
множество состояний
X^_1=|^_1:6,6-l,...,6-maxJ0;X«^+1*(^)l .
По формуле (6.106), сравнивая величины Bk+X(xk_x) и ck+ Bk+1(xk_t - ak),
определяем Bk(xk_x), uk_1*(xk_1) V xk_x e Xk_x и т.д. до номера k = 1, пока
не будут определены множества Х0, Вх(хц), щ*(х0) Vi0g X0. Далее идем
обратным ходом и последовательно определяем точку х0* е Х0, в которой
В\(х0*)= max В{(х0), управление щ* = щ*(х0*), величины х1*=х0*-а1щ*,
х0еХ0
344

2\*^"l*/ — niaX Jjn\pC\)i Hn* — ^9*V*^"l*)i*^2* — X\* Clntlo*)•••>X\r_i* — ^N—1* ^N—l^N—l**
xxeXx
BN(xN_{*) = max Вм(хм_{), uN*=uN*(xN_1*). Решением задачи (6.100),
xN-\eXN-\
(6.101) будет набор и* = (щ*, и2*>..., uN*), тах^(щ,..., uN) = BN(xN_{*).
Для иллюстрации вышеизложенного рассмотрим пример задачи о
рюкзаке:
Ji(uv и2, и3, и4) = и{ + и2 + Зг/3 + 2гг4 —> max
при условиях щ +2и2 + 2и3 + щ < 4, щ; = 0 V 1, г = 1,..., 4. Множество Х3
состояний х3 = 4 - г^ - 2и2 - 2и3 содержит элементы Х3 = {4, 3, 2, 1, 0}, поэтому
[2прих3= 4,3,2,1, [1 при х3=4,3,2,1,
54(хо)= max 2м4=1Л Л w4*w) = L
4V 3/ о<и4<[*3] [0прих3=0; 4 v 3/ [0 при х3=0.
Далее находим
Х2={х2=4-щ- 2и2 :4,3,2,1}, 53 (х2 ) = max (Зи3 + В4 (4 - 2г/3 )),
0<и3<[х2/2]
В3(х2) = 5 при х2=4,3, 52(х2 = 2) = 3, 52(х2=2) = 3, 52(х2=1) = 2,
II при jr2 = 4,3,2,
0 при х2 = 1,
Xi = {xi=A-ui:4,3}, 52(х1) = max (и2 + В3(х{ - 2и2)),
0<и2<[х{/2]
В2(х{) = 5 при хх = 4,3,
и2* (xt = 4) = 1, и2* (xt = 3) = 0,
Х0={х0=4}, Bt(x0)= max (щ+В^А-щ)), Bt(A) = 6, m1.=m1(x0=4) = 1.
o<Wi<l*oJ
Обратным ходом находим:
А (*о*) = тах А (хо )> хо* = 4, В{ (х0* = 4) = 6,
х0еХ0
щ* = щ*(4) = 1, xt* = х0* -щ* = 4-1 = 3, B2(xt* = 3) = 5, и2* = u2*(xt* = 3) = 0,
Х2* = Х\ * — АЫ2* = О — U = О, .Do \^2* = О) = О, ^3* = ^3* \*^9* = х = *
х3* = х2* -2г/3* =3-2 = 1, 54(х3* = 1) = 2, гг4* = щ*(х3* = 1) = 1.
Отсюда получаем решение задачи: щ* = 1, и2* = 0, щ* = 1, щ* = 1, т.е. в
рюкзак нужно взять предметы с номерами 1, 3, 4; ценность взятых предметов
максимальна и равна Bt(A) = 1 • 1+2-0 + 3- 1 + 2- 1 = 6.
Кратко остановимся еще на одной классической задаче дискретного
программирования, известной как задача коммивояжера. Имеется N
городов, пронумерованных числами 0,1,...., N- 1. Для любой пары городов (ij)
задано расстояние с^ между ними. Выехав из исходного города, комммивоя-
жер должен вернуться в него, побывав во всех остальных городах ровно
по одному разу. Требуется найти маршрут наименьшей длины или
наименьшей стоимости.
345

Без ограничения общности можем считать, что любой маршрут начинается
и заканчивается в городе с номером 0. Чтобы запретить переезды вида (г, г),
будем считать, что си= -к», г = 1, 2, ..., п. Предполагать, что с$= Ср
необязательно. Таким образом, задача коммивояжера сводится к задаче минимизации
J(u) = c0h +ci{i2 +... + ciN_i0 ->min (6.108)
на множестве U допустимых маршрутов и = (0, it, z2, ..., iN_i, 0), где (it, ...,
iN-\) — произвольна перестановка чисел 1,..., N- 1. Заметим, что
постановки вида (6.108) возникают при описании практически важных задач
оптимизации стоимости или времени доставки готовой продукции заказчикам,
а также при моделировании многих других практически важных процессов
с целью их оптимизации.
Обозначим через Вк_{(0, *i, ..., ik) функцию Беллмана, выражающую
длину кратчайшего из путей, соединяющих города 0 и ik и проходящих
в произвольном порядке через города it, ..., ik, предполагая, что числа 0,
iv ...., ik попарно различны при k < N - 1. Принцип оптимальности
применительно к задаче (6.108) можно сформулировать следующим образом:
поведение оптимально, если какими бы ни были решение на первом шаге
и состояние процесса после первого шага, последующие решения должны
быть оптимальными. Из этого принципа вытекает, что функция Беллмана
при всех k = 0, 1,..., N- 1 удовлетворяет уравнениям
ЯЛ(0, iv..., ik, ik+i) = mini^O, i2,..., ik, ц) + сг^+1;
B^^9ii9i39...9ik9i2) + ciAbl; (6io9)
^ft-i(0> h> h> 4> •••» h> h) + ci3ik+x '•> -5
bm№^ 1^*)+^}.
Другие примеры применения метода динамического программирования
к задачам дискретной оптимизации и обсуждения возникающих при этом
достаточно сложных проблем читатель найдет, например, в работах [4, 27,
30, 36].
Упражнения
6.1. Найдите функцию Беллмана и синтезирующую функцию в задаче
J(u) = x2(l)^>mm, x(t) = u(t), 0<t<l, х(0) = х0,
где и = u(t), §<t<\, — кусочно-непрерывная функция, u(t) e Vcz E1.
Рассмотрите случаи:
а) V=[0;1];
б) V= [-1; 1].
6.2. Найдите синтезирующую функцию в задаче быстродействия, в
которой требуется перевести точку х(0) = х в точку х(Т) = 0 за минимальное
время Г, соблюдая условия:
x(t) = ax(t) + u(t), \u(t)\<ly 0<t<Ty х(0) = ху
где а = const > 0, \х\ < \/а.
346

Указание. Убедитесь, что в этой задаче функция Беллмана равна
4
В(х) = —1п(1-яЫ), Ы < У а.
а
6.3. Найдите функцию Беллмана и синтезируюущую функцию в задаче
перевода точки х = (х1, х2) в точку х(Т) = (0; 1) за минимальное время Т
при условиях:
xi(t) = x2(t), x2(t) = u(t), x(0) = (x\x2), \u(t)\<ly 0<t<T.
6.4. Найдите функцию Беллмана для задачи
т
J(t0, х0, и(-)) = J ((a(t), *(*)> + Ъ{ц, О М + <с> х(т)) ->min;
о
x(t) = A(t)x(t) + B(t)u(t), u(t)eV(t), t0<t£T, x(t0) = x0
с кусочно-непрерывными управлениями и = u(t). Считаются заданными
моменты времени t0, Т, матрицы A(t)> B(t) порядка п х п, п х г
соответственно, скалярные функции a(t), b(u, t), векторы с, х0 е Еп и множества
V(t)czEryt0<t<T.
Указание. Требуемую функцию Беллмана В(х> t) ищите в виде
скалярного произведения В(х, t) = (\\f(t), x), а для определения значений функции
\|/(0> t0<t<T, составьте соответствующую задачу Коши.
6.5. Найдите функцию Беллмана для задачи
J(u)= S ({а{,х{) + Ь{(щ)) + {с,Хи)^>тт\
xM=Aixi+Ci(ui), щеЦ, i = 0,...,Nvx0=a,
в которой считаются известными векторы а{, с, а, матрицы Д порядка пхп,
функции С{(и) = (C/(w),...,Cf(w)), bj(u) переменной ие У{^Еги множества
v;,i = o, 1 лг-1.
Указание. Функцию Беллмана ищите в виде скалярного произведения
Bk(x) = (\\fklx),k = 01 1,..., ЛГ.
6.6. Найдите решение задачи о рюкзаке методом динамического
программирования:
а) Зщ + 2и2+и3+2щ^таху2и1 + и2+2и3+щ<4уи1=0 V 1,1=1,2,3,4;
б) 2их + и2+ и3+ 2и4 + Аи5 —> max, щ + 2и2 + 2щ + Ъщ + и5 < 7, щ = 0 V 1,
i= 1,2,3,4,5.
6.7. Методом динамического программирования найдите решение
задачи коммивояжера для пяти городов с матрицей расстояний [27]
foo 4 5 2 9]
3 - 3 4 8
6 4 оо 1 7 .
3 2 5 - 8
8 9 6 8 оо
347

6.8. Методом динамического программирования решите задачу
линейного программирования в пространстве Е5:
f(x) = Зх1 + 2х3 + х4 + xs -> extr,
х=(х1,х2,х3,хА,х5)е Х={х>0,х1 + х2 + х3 + хА = 1у-х{ + 2х2 + х3 + х5= 1}.

Практикум
К главе 1
1.1. Найдите все значения параметров Ьш, при которых квадратичная
функция/(х, у) = kx2 + 2axy + b2y2 + сх+ту имеет точку глобального
минимума на Е2.
№
1
2
3
4
5
а
2
1
3
4
5
Ъ
3
8
4
5
2
с
6
-1
6
-8
10
№
6
7
8
9
10
а
1
3
5
2
4
Ъ
4
2
3
5
3
с
-2
9
5
-4
-12
№
И
12
13
14
15
а
5
1
4
2
3
6
2
4
5
3
7
с
15
-3
-4
8
6
№
16
17
18
19
20
а
4
5
3
1
2
6
3
6
4
3
5
с
16
-10
-15
4
-2
1.2. Найдите точки глобального максимума функции/(х, г/) = х2 + ш/2
на множестве X = {(х, у) е Е2 :\х\ + Ь\у\}. Нарисуйте линии уровня/(х, у) =
= const.
№
1
2
3
4
5
а
3
1
5
2
1
Ъ
2
2
2
3
3
с
4
3
2
4
3
№
6
7
8
9
10
а
5
10
1
3
20
Ъ
3
3
4
4
4
с
2
4
1
2
3
№
И
12
13
14
15
а
2
1/2
4/5
12
8
Ъ
1
1
1
3
3
с
3
2
1
6
4
№
16
17
18
19
20
а
6
1
5
20
30
b
2
2
2
5
5
с
9
4
5
10
20
1.3. Найдите все значения параметра к, при которых функция/(х, г/) =
= ах - у имеет точку глобального минимума на множестве X = {(х, у) е
€ F
№
1
2
3
4
5
: -х + Ь\х
а
6
7
8
3
5
6
3
2
4
1
2
| + с]
с
5
2
3
1
4
, и найдите эту точку.
№
6
7
8
9
10
а
4
7
9
10
2
6
2
3
4
3
1
с
2
3
5
4
1
№
И
12
13
14
15
а
8
10
4
6
8
b
2
4
1
2
3
с
4
1
5
3
2
№
16
17
18
19
20
а
6
9
5
9
10
b
1
2
1
3
2
с
3
1
2
5
4
349

1.4. Найдите точку глобального минимума функции/(х, у) = ах2 + 2ху +
+ by2 -2х-3у на пространстве Е2.
№
1
2
3
4
5
а
b
2
3
4 |
5
6
№
6
7
8
9
10
а
2
2
2
2
2
6
1
2
3
4
5
№
11
12
13
14
15
а
3
3
3
3
3
Ь
1
2
3
4
5
№
16
17
18
19
20
а
4
4
4
4
4
Ь
1
2
3
4
5
1.5. Найдите точки экстремума функции f(x,y) = e~(x2+y2)(ax2+by2)
на пространстве Е2.
№
1
2
3
4
5
а
1
7
1
8
1
Ь
2
3
4
5
6
№
6
7
8
9
10
а
8
2
2
7
2
Ь
3
4
5
6
7
№
И
12
13
14
15
а
9
3
3
7
3
6
1
5
1
2
6
№
16
17
18
19
20
А
4
6
4
1
5
Ъ
1
7
3
5
6
1.6. Найдите точки экстремума функции/(х, у) = х3у2(ах + Ьу + с) на
пространстве Е2.
№
1
2
3
4
5
а
-4
-3
-1
-5
-1
Ь
-1
-1
1
-1
-1
с
1
9
3
4
7
№
6
7
8
9
10
а
-2
-4
-2
-4
-2
6
-1
1
-1
-1
1
с
3
2
8
4
6
ГйГ
и
12
13
14
15
а
-5
-1
-1
-3
-4
Ъ
-1
1
-1
1
1
с
5
2
9
8
5
№
16
17
18
19
20
а
-3
-2
-9
-2
-2
6
-1
-1
1
-1
1
с
7
2
3
1
9
1.7. Найдите точки экстремума функции f(x, у) = ах + by при условии
х2 + у2 = с2.
№
1
2
3
4
1 5
а
2
4
-3
-2
2
6
-3
1
4
1
3
с
5
3
2
1
4
No.
6
7
8
9
10
а
7
-2
-1
-4
-2
6
2
6
7
-1
-3
с
4
2
5
3
1
№
11
12
13
14
15
а
-2
5
-5
-7
1
Ъ
-5
-3
-1
-1
-7
с
5
1
2
4
3
№
16
17
18
19
1 20
а
5
-1
2
-5
1
Ь
1
5
5
3
7
с
3
1
2
5
4
350

1.8. Найдите точки экстремума функции f(x, у) = ах2 + 2ху + by2
при выполнении условия Ах2 + су2 = 9.
№
1
2
3
4
5
а
1
3
1
1
1
6
1
4
1
2
1
с
3
5
2
6
1
№
6
7
8
9
10
а
3
5
3
7
5
b
2
4
5
9
2
с
2
3
6
5
1
№
И
12
13
14
15
а
5
5
9
9
3
6
8
3
3
7
6
с
6
2
1
3
7
№
16
17
18
19
20
А |
7 |
13
7 |
9
7 |
Ъ
4
4
И
5
13
с
2
1
6
2
7
1.9. Найдите точки экстремума функции f(x, у) = ах3 + Ьуг при условии
х2 + у2 = с2.
№
1
2
3
4
5
а
3
7
1
7
3
6
2
3
2
2
4
с
2
3
5
1
2
№
6
7
8
9
10
а
3
4
1
5
3
6
1
3
4
2
5
с
3
4
5
2
1
№
И
12
13
14
15
а
1
4
5
2
2
Ъ
8
1
3
5
1
с
1
5
4
3
2
№
16
17
18
19
20
а
2
2
8
1
3
Ъ
3
7
1
3
7
с
4
1
2
5
3
К главе 2
2.1. Решите с помощью симплекс-метода каноническую задачу
линейного программирования
f(x) =хх + ах2 - 2х3 + х4 + 2х5 - х£ —> max,
^>0j=l,...,6,
-х1 + х2 + х3+(6-6)х4+(с+1)х5 + .%6=3,
2*1 + x2 + 2x3- 2(6 + 3)^+ (2c + 1)*5 + Sjfi= 6,
3x1 + x2 + 2x3-3(6 + 2)^+(2c+l)x5 + 6jt6=6,
взяв в качестве начальной точки v0= (0, 0, 3, 0, 0, 0) с базисом (Av А2, Л3).
№
1
2
3
4
5
а
-1
-3
-4
-5
-2
6
4
3
2
1
5
с
5
4
3
2
1
№
6
7
8
9
10
а
-5
-4
-1
-2
-3
6
4
3
2
1
5
с
1
2
3
4
5J
№
11
12
13
14
15
а
-2
-3
-4
-1
-5
Ь
3
4
5
2
1
с
2
3
4
5
1
№
16
17
18
19
20
а
-4
-3
-2
-1
-6
Ь
4
3
2
1
5
с
4
3
2
1
5
2.2. Решите с помощью симплекс-метода каноническую задачу
линейного программирования
f(x) = ах1 + х3+ 5х5 + fix6 —> max,
351

xJ>0,j=l,...,6,
2х1 + х* + х*+(Ь + 1)х* + (с-3)х5-2х$ = 1,
Зх1 + Зх2 + х* + Ьх*+ (с - 12)*5- 11^=3,
-хх + 2х2 - *з - ф + 3)х* - (с + 11 )х5 - 12л* = 2,
взяв в качестве начальной точки v0= (О, 1, 0, 0, 0, 0) с базисом (А1г А2, А3).
№
1
2
3
4
5
а
-4
-6
-3
-7
-9
Ь
2
3
2
4
3
с
2
2
1
2
1
№
6
7
8
9
10
а
-4
-7
-8
-5
-8
b
3
5
6
4
7
с
3
3
2
1
5
№
11
12
13
14
15
а
-7
-5
-6
-4
-9
b
6
3
5
3
6
с
4
2
5
1
3
№
16
17
18
19
20
а
-6
-7
-5
-8
-7
Ь
4
2
4
5
3
с
2
2
3
1
1
2.3. Решите симплекс-методом каноническую задачу линейного
программирования
f(x) = -х1 - Зх2 + х3 + х4 —> min,
*;>0j=l,...,4,
axi-x2 + x3 + bx4= 120,
х1 + х2-х3 + х4 = 0,
х1 + х2 + х3+схА= 120,
предварительно найдя какую-либо угловую точку.
№
1
2
3
4
5
а
1
3
5
7
9
6
2
5
8
11
14
с
2
2
2
2
2
Г~№
6
7
8
9
10
а
1
2
3
4
5
6
5
8
11
14
17
с
5
5
5
5
5
№
И
12
13
14
15
а
1
3
5
7
9
Ь
0
1
2
3
4
с
0
0
0
0
0
№
16
17
18
19
20
а
1
2
3
4
5
b
3
5
7
9
11
с
3
3
3
3
3
2.4. С помощью симплекс-метода решите каноническую задачу
линейного программирования
f(x) =хх-х2 + х3- Зх5 —> max,
^>0j=l,...,5,
2х{ -х2 +х3 -хА Xs = 1,
6 + 1
-2х1 + х2 + хА-х5 = а,
-хх +х2-х3 + х4 + Xs = 8,
с + 1
предварительно найдя какую-либо угловую точку.
352

№
1
2
3
4
5
a
1
2
3
4
5
6
1
1
1
1
2
с
2
2
2
2
2
№
6
7
8
9
10
a
6
7
2
4
6
ft
2
2
1
1
1
с
2
2
3
3
3
№
11
12
13
14
15
a
2
4
6
3
6
ft
2
2
2
1
1
с
3
3
3
4
4
№
16
17
18
19
20
a
3
6
3
6
3
ft
2
2
3
3
4
с
4
4
4
4
4
2.5. Решите симплекс-методом задачу
fix) = -х1 + х2 + х3 - ах4 —> min,
x)>0,j=l,...,A,
-х1 + 2х2-х3 + хА<2,
bxl + x2 + x3-2xi<12,
2xl + cx2 + 4x3 + 2x4<6,
предварительно приведя ее к каноническому виду.
№
1
2
3
4
5
а
2
3
4
7
8
6
3
1
2
2
3
с
-1
1
-1
3
4
Г~№
6
7
8
9
10
а
5
4
6
2
5
6
2
3
1
2
3
с
3
6
5
2
7
№
11
12
13
14
15
а
2
3
5
7
6
6
1
3
2
1
3
с
2
4
-1
5
8
№
16
17
18
19
20
а
3
4
3
4
5
b
3
1
1
1
2
с
1
2
0
3
6
2.6. Приведите пример таких значений параметров р и q, при которых
задача
f(x) = ах{ + Ьх2 —> max,
xi>0,xi + px2< l1xi-x2>q\
а) имеет пустое допустимое множество X;
б) имеет бесконечную верхнюю грань /* =sup/(x);
х
в) имеет единственное решение;
г) имеет бесконечно много решений.
№
1
2
3
4
5
а
3
3
2
8
3
b
5
7
3
3
4
№
6
7
8
9
10
а
2
6
3
5
4
Ъ
1
5
7
8
7
№
11
12
13
1 14
15
а
7
7
3
5
5
6
3
4
2
3
6
№
16
17
18
19
20
а
2
5
2
7
3
6
5
2
7
2
1
353

2.7. Приведите задачу линейного программирования к канонической
форме и найдите ее решение с помощью симплекс-метода:
f(x) = ах1 + х2 + 8х3 —> max,
xJ>0J =1,2,3,
хх + bx2 + х3 > 1, х1 + х2 + ex3 < 1.
№
1
2
3
4
5
a
4/3
3/2
7/3
6/5
5/4
b
4
6
2
3
2
с
5
4
3
6
7
№
6
7
8
9
10
a
4/3
16/5
6/5
9/5
7/2
6
4
3
2
3
4
с
6
2
6
4
5
№
11
12
13
14
15
a
7/3
19/5
3/2
5/3
7/2
b
4
6
2
6
5
с
3
2
4
5
2
№
16
17
18
19
20
a
3/2
7/4
15/4
4/3
7/3
b
2
5
7
5
6
с
5
4
2
6
3
2.8. В пекарне для выпечки четырех видов хлеба используются мука
двух сортов, маргарин и яйца. Имеющееся оборудование,
производственные площади и поставки продуктов таковы, что в сутки можно
переработать не более а кг муки сорта I, b кг муки сорта И, с кг маргарина, d штук
яиц. В таблице приведены нормы расхода продуктов, а также прибыль
от продажи 1 кг хлеба каждого вида.
Наименование продукта
Мука I, кг
Мука II, кг
Маргарин, кг
Яйцо, шт.
Прибыль, руб/кг
Нормы расхода 1 кг хлеба
1
0,5
0
0,125
2
14
2
0,5
0
0
1
12
3
0
0,5
0
1
5
4
0
0,5
0,125
1
6
Требуется найти суточный план выпечки хлеба, максимизирующий
прибыль.
№
1
2
3
4
5
6
7
8
а
250
290
350
380
290
300
310
330
Ъ
200
200
200
200
150
150
150
150
с
60
70
80
90
50
60
70
80
d
1380
1540
1740
1880
1280
1380
1480
1600
№
11
12
13
14
15
16
17
18
а
210
260
300
330
370
220
270
310
Ъ
180
190
200
210
220
160
210
190
с
50
60
70
80
90
50
60
70
d
1180
1380
1560
1720
1900
1160
1440
1560
354

Окончание таблицы
№
9
10
а
400
240
Ь
150
100
с
90
50
d
1820
1080
№
19
20
а
340
390
Ъ
200
180
с
80
90
d
1720
1860
2.9. Строителям требуются комплекты досок, каждый из которых
состоит из а досок длиной 1,5 м и Ъ досок длиной 0,6 м. Как следует
распилить с четырехметровых досок, чтобы получить наибольшее число
указанных комплектов?
№
1
2
3
4
5
а
1
1
1
1
2
Ъ
3
3
3
3
5
с
660
720
780
840
660
№
6
7
8
9
10
а
2
2
2
3
3
Ъ
5
5
5
7
7
с
770
880
990
640
800
№
И
12
13
14
15
а
3
3
3
3
4
Ь
7
8
8
8
9
с
960
510
680
850
600
№
16
17
18
19
20
а
4
4
4
4
4
6
9
9
9
9
9
с
630
660
690
720
750
К главе 3
3.1. Докажите, что множество X = {(х, у) е Е2 : ах2 + Ьху + су2 <0,у> 0}
является
№
1
2
3
4
5
а
2
3
2
2
4
выпуклым конусом и и
b
-7
4
-5
-5
-15
с
6
-4
2
3
9
№
6
7
8
9
10
а
4
5
5
3
3
Ь
-5
-13
-17
-1
-8
зобр
с
-6
6
6
-4
4
азите его на плоскости
№
11
12
13
14
15
а
2
3
3
5
5
b
1
1
-1
-8
-2
с
-3
-4
-2
-4
-3
№
16
17
18
19
20
(х,у)
а
6
2
2
6
4
1.
6
-1
7
-3
1
-5
с
-5
3
-5
-5
-6
3.2. Изобразите на плоскости сумму двух выпуклых множеств: отрезка
X = [хь х2], где xt = (4, а), х2 = (4, 3), и
1) круга Хх = {х = (х\ х2) € В : (х1 - Ь)2 + (х2 - с)2 < 1};
2) квадратаХ2= {х = (х\х2)е Е2 : {х1- Ь\ < 1, \х2- с\ < 1};
3)
№
1
2
3
4
5
треугольника А3 с
а
1
0
-1
2
0
ft
2
3
4
2
3
с
1
2
3
1
2
№
6
7
8
9
10
вершинами (
а
-2
1
0
-1
2
ft
4
3
2
3
4
с
3
1
2
3
1
-2;-
№
11
12
13
14
15
1).(1
а
0
-2
1
0
-1
Ь),
b
2
3
4
2
3
(3;-
с
1
2
3
3
1
с).
№
16
17
18
19
1 20
а
2
1
0
-1
2
ft
4
2
3
4
2
с
2
3
1
2
3
355

3.3. Найдите минимальное значение параметра А,, при котором выпукло
множество X = {(х, у) е Е2 : (ах2 + 1)г/, у > X).
№
1
2
3
4
5
а
2
1
4
5
3
Ь
1
5
2
1
4
№
6
7
8
9
10
а
1
5
3
4
2
6
2
3
1
5
3
№
11
12
13
14
15
а
2
1
3
5
4
Ь
2
3
2
2
3
№
16
17
18
19
20
а
4
5
1
2
3
6
4
4
1
4
3
3.4. В пространстве Е4 найдите проекцию начала координат на
множество X = {х = (х1, х2, х3, х4) е Е4 : х1 + ах2 -х4 = Ь,х1 + ах3 + х4 = с}.
№
1
2
3
4
5
а
2
2
2
2
2
b
9
9
-9
-9
9
с
6
-6
6
-6
9
№
6
7
8
9
10
а
2
2
2
2
2
b
9
-9
-9
9
9
с
-9
9
-9
18
-18
№
И
12
13
14
15
а
b
6
6
-6
-6
6
с
6
-6
6
-6
9
№
16
17
18
19
20
а
b
6
-6
-6
6
6
с
-9
9
-9
12
-12
3.5. На параболе 2у = сх2 найдите точку, ближайшую к точке х0 = (а; Ь)
№
1
2
3
4
5
а
2
9
8V3
9
4~2
S
9
Ь
-5
-1
-3
-7
3
2
с
1
2
-2
-1
1
4
-1
№
6
7
8
9
10
а
4
2ч/б
9
4л/з
3
1
3
ь
10
2
9
7
2
9
2
с
1
4
1
1
3
1
2
1
3
№
И
12
13
14
15
а
-1
2ч/б
3
2V3
9
4
2n/3
9
6
5
2
6
3
4
7
4
3
с
1
1
3
4
1
1
2
№
16
17
18
19
20
а
1
5
4^6
9
4л/з
9
л/2"
8
2n/3
3
b
1
2
-4
3
2
7
8
-9
с
-5
1
2
-2
-2
1
6
3.6. С помощью теоремы Куна — Таккера решите выпуклую задачу
минимизации
f(u) = ах2 + Ъху + су2 —>min, we X = {и = (х,у) е Е2: х2 + у2<\,х + у>\).
№
1
2
а
1
4
ft
1
4
с
3
3
№
6
7
а
2
20
Ь
3
4
с
2
11
ГЙь
11
12
а
4
9
ft
5
6
с
2
5 J
No.
16
L^7
а
5
27
ft
4
3
с
1
11
356

Окончание таблицы
№
3
4
5
а
Ь
2
11
Ь
-2
-4
-8
с
2
5
6
Но.
8
9
10
а
16
1
12
Ь
-4
-2
-6
с
7
3
7
№
13
14
15
а
11
1
12
Ь
-2
-2
-4
с
3
5
13
№
18
19
20
а
5
3
7
ft
-2
-10
-6
с
1
19
12
3.7. С помощью теоремы Куна — Таккера решите выпуклую задачу
минимизации
/(") =
№
1
2
3
4
5
а
14
-30
16
-18
-8
Х-(
Ъ
15
-7
15
12
И
%\ + \
R
13>/2
25
17
20
10
у-Ь
№
6
7
8
9
10
| —> min, и € X = {и
а
5
8
16
-16
-6
Ь
15
-7
8
-14
-4
Л
13
6л/2
17
20
-5
№
И
12
13
14
15
= (х
а
3
-10
9
-10
-3
»У)€
6
5
14
16
-30
10
Е £2;
R
6
9л/2
15
26
9
х2 +
№
16
17
18
19
20
У2<
а
-9
-9
-12
24
-7
R2}.
Ъ
10
-И
11
-13
-6
R 1
16
7л/2
15
36
5л/2
3.8. С помощью теоремы Куна — Таккера решите выпуклую задачу
минимизации
f(u) = (х - а)2 + (у - Ь)2 —> min, и е Х= {и- (х,у) е Е2 : |х| + |г/|<7?}.
№
1
2
3
4
5
а
8
-6
12
-8
4
6
И
-И
4
-15
15
/г
7
8
9
10
11
№
6
7
8
9
10
а
2
-2
-5
3
-15
Ь
15
-13
15
-18
4
К
7
8
9
10
11
№
11
12
13
14
15
а
-4
7
-5
3
-3
Ь
9
-8
13
-10
-14
R
7
8
9
10
11
№
16
17
18
19
20
а
-11
14
-12
14
16
Ь
-3
-1
2
3
-5
R
1
8
9
10
И
К главе 4
4.1. Для решения задачи условной минимизации
f{x) = \\х-af ->min, xeX = {xeEn: \\xf <2(6,х), \\bf <(b,*>},
где а> Ъ — заданные векторы из Еп> воспользуйтесь методом проекции
градиента с постоянным шагом ak= 1, взяв в качестве начального приближения
х0 = Ъ. Остановите процесс при первом попадании в множество решений.
№
1
2
3
а
(1,1,1,1)
(2, -1,1, 0, 1)
(1,3,1,2)
Ъ
(1,-3,1,1)
(0,1,3,0,-2)
(0,-1,1,1)
№
И
12
13
а
(1,2,0,1)
(3, 0, 1, 0, -1)
(2, 1, 3, 0)
Ъ
(-1,1,2,-1)
(-1, -1, 2, 0, -1)
(1,1,-1,3)
357

Окончание таблицы
№
4
Ь
6
7
8
9
10
а
(2,-1,3,1,1)
(1,2,3,-1)
(2, -3, 1, 1, -1)
(1,0,2,-2)
(2, 0, -1, 2, 1)
(1,-1,-1,-1)
(3, -2, 0, 0, 1)
Ь
(1,-1,-1,1,-1)
(-1, 2, 0, 3)
(1,0,-1,-1,0)
(2, 0, -3, -2)
(0, 3, -3, -1, -1)
(0, 2, -3, 1)
(-1, 0, 2, 0, 3)
№
14
15
16
17
18
19
20
а
(3,1,1, 0, 2)
(1,-3,3,0)
(-2, 1, 1, 2, 1)
(2, 2, -2,1)
(3,-1,1,1,1)
(1,2,-3,0)
(-1,1,1,-1,1)
Ь
(1,0,-1,2,-1)
(3, 2, 1, 1)
(1,3,-1,-1,2)
(-2, 1, -1, 0)
(-1, 0, 0, 1, 2)
(-3, 0, -1, 2)
(2, 1, 1, 1, 1)
4.2. Для решения задачи условной минимизации
f(x) = \\х-af ->min, хеХ = {хеЕп: \\xf <2{b,x), \\bf <(b,*>},
где a> b — заданные векторы из Еп, воспользуйтесь методом условного
градиента, взяв в качестве начального приближения х0 = Ъ. Остановите
процесс при первом попадании в множество решений.
№
1
2
3
4
5
6
7
8
9
10
а
(1,1,1,1)
(2, -1, 1, 0, 1)
(1,3,2,1)
(2, -1, 3, 1, 1)
(-1,2,3,-1)
(2, -3, 1, -1, -1)
(1,0,-2,-2)
(-2,0,-1,2,1)
(3,-1,-1,-1)
(3, -2, 0, 0,1)
Ъ
(1,-3,-1,3)
(0, -1, 2, 0, -3)
(0,-1,1,1)
(1,-1,-1,-1,1)
(1, 2, 0, 3)
(-1,0,1,-1,0)
(2, 0, 3, -2)
(0, 3, 3, -1, -1)
(0, 2, -3, 1)
(-1,0,0,2,3)
№
И
12
13
14
15
16
17
18
19
20
а
(1,2,0,1)
(3, 0, 1, 0, -1)
(1,2,3,0)
(3, 1, 1, 0, 2)
(1,-3,3,0)
(-2, 1, 1, 0, 1)
(2,-2,-2,1)
(3, 2, 0, 1, 1)
(1,-2,-3,0)
(-1,-1,1,-1,1)
Ъ
(-1,1,3,-1)
(-1, 2, 1, 0, -2)
(1,1,-1,3)
(1,0,-1,3,-1)
(3, 1, 0, 3)
(1,3,-1,-1,0)
(-2,-1,-1,0)
(-1, 0, 0, 1, 2)
(-3, 0, -1, 2)
(2,-1,1,1,1)
4.3. Для решения задачи безусловной минимизации
/(x) = («,x)4+2|U-6||2^min, хеХ = Еп,
где a, b — заданные векторы из Еп, воспользуйтесь классическим методом
1
Ньютона, взяв в качестве начального приближения х0 =—Ь. Остановите
процесс при первом попадании в множество решений.
№
1
а
уз з з)
ь
(3,-1,1,-2)
№
11
а
(5 4 2 2'
{Г Г 7'7,
Ъ
(0, -1, 7, 2)
358

Окончание таблицы
№
2
3
4
5
6
7
8
9
10
а
V
13 1 i 1Л
4'4'2' 4'4j
(2 2 1 4"|
U'5' 5'5j
V
2 2 3 2 2
5'5'5' 5' 5
I 7'U'7'7J
(5 3 11 5"j
U'8' 4'8' 8j
Г2 4 5 2^
\j'T 7' 7J
ч 5'5' 5' '5j
( l l l П
t 2'2' 2' 2j
fl 1 113")
1,2*4' 4'4'4j
b
(-2, 4, -1, 2, -2)
(5, -2, 0,1)
(0,5,0,-1,1)
(1,3,2,7)
(1,4,-2,0,1)
(7,-1,0,-2)
(0,5,2,-2,1)
(-3,1,2,-2)
(2,4,3,3,0)
№
12
13
14
15
16
17
18
19
20
a
Г 3 5 1 1 1
{ 4'8'8' 8' 8
f1 1 1 *1
[2' 2'2' 2)
л
f 424 3 2Л
{ 7'7'T Г!)
1, 3 3 3)
(2 16 2 2"!
[7' 7'7'7'7j
U 2 1 2]
U' 5'5' 5)
( 3 1 17 1
{ 8'8' 8'8' 4
л
HI)
U 4 1 4N
1,7' 7' '7' 7,
b
(2, 0, 1, 4, 1)
(2,4,-1,1)
(2, -7, 1, 0, 2)
(6, 1, 3, -1)
(-1, 2, 0, -7, 2)
(-2, 5, 2, -3)
(4,-1,1,0,1)
(-7, 2, -1, 2)
(2, 2, -3, -14, 0)
К главе 5
5.1. Пользуясь принципом максимума Понтрягина, найдите
оптимальное управление в задаче
т
J {и) = J (мл:1 (t) + (u(t))2 )dt -> min
при условиях
(хЛ
х =
( y\
, x(t) =
х(0) =
V J
(хЩ^
U2(0)
x\t)) (x2(t))
yh
x2(t)
, x(T) =
u(t)
(a\ ._ (x\T)\ ГОЛ
x\T)
, 0<t<T;
, V = EK
Л
№
1
2
3
4
5
6
Г
1
2
3
2
1
2
M
4
4
4
8
-4
-4
a
1
1
0
0
0
1
b
0
0
1
1
1
0
No.
9
10
11
12
13
14
T
1
2
3
2
1
2
M
4
4
4
8
-4
-4
a
0
0
1
1
1
0
b
1
1
0
0
0
1
No.
17
18
19
20
21
22
T
1
2
3
2
1
2
M
4
4
4
8
-4
-4
a
ft
359

Окончание таблицы
№
7
8
Г
1
2
М
-4
-8
а
0
1
*
1
о
Но.
15
16
Г
2
1
М
-8
4
а
0
1
6
1
1
№
23
24
Т
2
3
Ц
-8
-2
а
1
1
6
1
1
5.2. Пользуясь принципом максимума, найдите управление и
соответствующую траекторию, подозрительную на оптимальность, если
т
J (и) = J (ax(t) + и2 (t))dt —> min,
о
при условиях
x(t) = u(t),0<t<T, x(0) = 0,
u(t) — кусочно-непрерывное управление, такое что | u(t)\ < у при всех t е [0;
т\.
№
1
2
3
4
5
6
7
а
2
-2
3
-3
1
-1
3
т
2
2
1
3
3
3
2
Y
2
№
8
9
10
И
12
13
14
а
-3
2
-2
2
-2
4
-4
Г
2
3
3
2
2
1
1
Y
2
2
2
3/2
3/2
3/2
3/2
№
15
16
17
18
19
20
а
1
-1
3
-3
3
-1
т
3
3
1
1
3
3
Y
1/2
1/2
1/2
1/2
1
1
5.3. Примените принцип максимума в задаче быстродействия
J (и) = Т —¥ min при условиях
\x\t) = u(t),
х1(0) = а, х2(Т) = Ь, х2(0) = 0, х2(Т) = 0,
управление u(t) — кусочно-непрерывное, | u(t)\ < у при всех t е [0; Г].
No.
1
2
3
4
5
6
а
1
2
1
3
2
3
6
2
1
3
1
3
2
Y
No.
7
8
9
10
11
12
а
1
2
1
3
2
3
Ъ
2
1
3
1
3
2
Y
2
2
2
2
2
2
№
13
14
15
16
17
18
а
3
4
2
4
1
4
6
4
3
4
2
4
1
Y
No.
19
20
21
22
23
24
а
3
4
2
4
1
4
Ъ
4
3
4
2
4
1
Y
2
2
2
2
2
2
360

К главе 6
6.1. Пользуясь методом динамического программирования, найдите
решение задачи минимизации
при условиях
№
1
2
3
4
5
«1
1
1
2
-1
1
я2
1
2
1
1
2
*fe
«3
2
1
1
2
-1
*!=■
№
6
7
8
9
10
л t х^ , vX
«1
1
-1
-2
-1
-1
а2
-1
-2
1
-1
2
<1},г =
«3
-2
1
-1
2
-1
№
11
12
13
14
15
1, ...,
ах
2
-2
-2
3
1
ЛГ+1
а2
2
2
-1
1
3
, полагая
«3
2
-2
-1
1
1
No.
16
17
18
19
20
N =
ах
1
3
2
2
-3
3.
а2
-3
-1
-1
-1
1
«3
1
1
1
-1
1
6.2. Для задачи быстрейшего перевода точки х =
Гх^
V J
в точку х(Т) =
при условиях хх(t) = х2(О,х2(t) = u(t\0<t<T, |u(t)|< 1:
1) с помощью принципа максимума Понтрягина найдите оптимальное
программное управление;
2) вычислите функцию Беллмана;
3) укажите синтезирующую функцию.
№
а
Ъ
1
1
1
2
1
0
3
0
1
4
1
-1
5
-1
1
6
-1
0
7
0
-1
8
-1
-1
9
1
2
10
2
1
11
2
0
12
0
2
13
-1
2
14
2
-1
15
-2
0
16
0
-2
17
-2
-1
18
-1
-2
6.3. Имеются пункты (i,j), i = 1,..., m j = 1,..., n,m<n, соединенные
дорогами. Предполагается, что из каждого пункта (i,j), 1 < z < m - 1, l<j<n-l,
можно проехать либо на «север» в пункт (г +1 j), удаленный от пункта (i,j)
на расстояние с^, либо на «восток» в пункт (ij +1), удаленный от пункта
(i,j) на расстояние Ъц. Других дорог, по которым можно выехать из пункта
(i,j), нет. Из «пограничных» пунктов (rn,j), 1 <j<n- 1, можно выехать
только на «восток» в пункт (mj +1), удаленный от пункта (m, j) на
расстояние bmj, а из пунктов (г, гг), 1 < г < m - 1, можно выехать только на «север»
в пункт (/+ 1, п)у удаленный от пункта (г, п) на расстояние cin. Требуется
с помощью метода динамического программирования указать кратчайший
путь из любого пункта (i,j) в «финальный» пункт (т, п).
Найдите синтезирующую функцию, если m = 5, п = 10,
citj = \щ +;(-1У4 j = *> -> 4> J = *> ->10;
buj = \щ -г*(-1У4 * = t-..,5,j = 1,...,9,
число d равно 2 или 3, варианты чисел av a2, а3, а4> а5 приведены в таблице.
361

№
1
2
3
4
5
6
7
8
9
10
«l
10
9
8
7
16
5
14
3
12
11
a2
4
1
9
11
5
13
6
13
2
3
«3
7
5
2
12
7
9
11
5
16
12
Ч
13
7
6
3
8
10
12
7
8
4
a5
2
15
1
7
4
16
13
17
9
5
№
И
12
13
14
15
16
17
18
19
20
«l
3
12
9
14
5
15
6
16
7
17
a2
13
5
14
6
15
3
16
4
17
4
"з
6
14
7
15
3
16
4
17
5
12
Ч
14
7
15
3
16
4
17
5
12
2
«5.
7
15
3
16
4
17
5
12
2
18

Литература
1. Алексееву В. М., Тихомиров В. М., Фомин С. В. Оптимальное
управление / В. М. Алексеев, В. М. Тихомиров, С. В. Фомин. — М.: Наука, 1979.
2. Арутюнову А. В. Принцип максимума Понтрягина: доказательство
и приложения / А. В. Арутюнов, Г. Г. Магарил-Ильяев, В. М.
Тихомиров. — М.: Факториал-Пресс, 2005.
3. Арутюнову А. В. Условия экстремума. Анормальные и вырожденные
задачи / А. В. Арутюнов. — М.: Факториал Пресс, 1997.
4. Ашманову С. А. Линейное программирование / С. А. Ашманов. — М. :
Наука, 1981.
5. Ашманов, С. А. Теория оптимизации в задачах и приложениях /
С. А. Ашманов, А. В. Тимохов. — СПб.; М.; Краснодар : Лань, 2012.
6. Бахвалов, Н. С. Численные методы / Н. С. Бахвалов, Н. П. Жидков,
Г. М. Кобельков. - М.: Наука, 1987.
7. БеллмаНу Р. Динамическое программирование / Р. Беллман. — М. :
Издательство иностранной литературы, 1960.
8. БлагодатскиХу В. И. Введение в оптимальное управление / В. И. Бла-
годатских. — М.: Высшая школа, 2001.
9. Бурмистрова, Е. Б. Линейная алгебра / Е. Б. Бурмистрова, С. Г.
Лобанов. - М.: Юрайт, 2014.
10. Васин, А. А. Теория игр и модели математической экономики /
А. А. Васин, В. В. Морозов. - М.: МАКС Пресс, 2008.
11. Васильев, Ф. П. Линейное программирование / Ф. П. Васильев,
A. Ю. Иваницкий. — М.: Факториал Пресс, 2008.
12. Васильеву Ф. П. Методы оптимизации. Т. I, II / Ф. П. Васильев. —
М. :МЦНМО, 2011.
13. ГайшуНу И. В. Системы с дискретным временем / И. В. Гайшун. —
Минск : Институт математики НАН Белоруссии, 2001.
14. Галееву Э. М. Оптимальное управление / Э. М. Галеев [и др.]. — М. :
МЦНМО, 2008.
15. Галеев, Э. М. Оптимизация: теория, примеры, задачи / Э. М. Галеев,
B. М. Тихомиров. - М.: URSS, 2000.
16. Гончаров, В. А. Методы оптимизации / В. А. Гончаров. — М.: Юрайт,
2014.
17. Денисов, А. М., Разгулин, А. В. Обыкновенные дифференциальные
уравнения. — М.: МАКС Пресс, 2009.
18. ДенниСу Дж. Численные методы безусловной оптимизации и
решения нелинейных уравнений / Дж. Деннис, Р. Шнабель. — М.: Мир, 1988.
19. Евтушенко, Ю. Г Методы решения экстремальных задач и их
применение в системах оптимизации / Ю. Г. Евтушенко. — М.: Наука, 1982.
363

20. Зорин, В. А. Математический анализ / В. А. Зорич. — М.: МЦНМО,
2007.
21. Измаилов, А. Ф. Численные методы оптимизации / А. Ф. Измаилов,
М. В. Солодов. — М.: Физматлит, 2008.
22. Ильин, В. А. Математический анализ : комплект в 2 ч. : учебник
для бакалавров / В. А. Ильин, В. А. Садовничий, Б. X. Сендов. — М. :
Юрайт, 2013.
23. Карманов, В. Г. Математическое программирование / В. Г.
Карманов. — М.: Физматлит, 2000.
24. Киселев, Ю. Н. Оптимальное управление. Линейная теория и
приложения / Ю. Н. Киселев, С. Н. Аввакумов, М. В. Орлов. — М.: МАКС Пресс,
2007.
25. Краснощеков, П. С. Оптимизация в автоматизированном
проектировании / П. С. Краснощеков, В. В. Морозов, Н. М. Попов. — М. : МАКС
Пресс, 2008.
26. Коннов, И. В. Нелинейная оптимизация и вариационные
неравенства / И. В. Коннов. — Казань : Издательство Казанского университета,
2013.
27. Корнеенко, В. П. Методы оптимизации / В. П. Корнеенко. — М. :
Высшая школа, 2007.
28. Кротов, В. Ф. Методы и задачи оптимального управления / В. Ф.
Кротов, В. И. Гурман. - М.: Наука, 1973.
29. Кудрявцев, Л. Д. Курс математического анализа : комплект в 3 т :
учебник для бакалавров / Л. Д. Кудрявцев. — М.: Юрайт, 2014.
30. Мину, М. Математическое программирование. Теория и алгоритмы /
М. Мину. - М.: Наука, 1990.
31. Орлова, И. В. Линейная алгебра и аналитическая геометрия для
экономистов / И. В. Орлова, В. В. Угрозов, Е. С. Филонова. — М. : Юрайт,
2014.
32. Поляк, Б. Т. Введение в оптимизацию / Б. Т. Поляк. — М. : Наука,
1983.
33. Понтрягин, Л. С. Математическая теория оптимальных процессов /
Л. С. Понтрягин [и др.]. — М.: Наука, 1976.
34. Срочко, В. А. Итерационные методы решения задач оптимального
управления / В. А. Срочко. — М.: Физматлит, 2000.
35. Стрекаловский, А. С. Элементы невыпуклой оптимизации /
A. С. Стрекаловский. — Новосибирск : Наука, 2003.
36. Тимохов, А. В. Методы оптимизации : учебник и практикум для
бакалавриата и магистратуры / А. В. Тимохов, А. Г. Сухарев, В. В. Федоров. —
М.: Юрайт, 2014.
37. Тихонов, А. Н. Методы решения некорректных задач / А. Н. Тихонов,
B. Я. Арсенин. - М.: Наука, 1979.
38. Фурсиков, А. В. Оптимальное управление распределенными
системами. Теория и приложения / А. В. Фурсиков. — Новосибирск : Научная
книга, 1999.
39. Цурков, В. И. Декомпозиция в задачах большой размерности /
В. И. Цурков. - М.: Наука, 1981.
364

40. Bertsecas, D. P. Nonlinear programming / D. P. Bertsecas. — Belmont:
Athena, 1999.
41. Bonnans, J. F. Pertutbation analysis of optimization problems /
J. F. Bonnans, A. Shapiro. — N. Y.: Springer, 2000.
42. Bonnans, J. F. Numerical optimization. Theoretical and practical
aspects /J. F. Bonnans [et al.]. — Berlin : Springer, 2006.
43. Burachik, R. S. Set-valued mappings and enlarhements of monotone
operators / R. S. Burachik, A. N. Iusem. — N. Y.: Springer, 2008.
44. Dontchev, A. L. Implicit functions and solution mappings / A. L. Dontchev,
R. T. Rockafellar. - N. Y.: Springer, 2009.
45. Izmailov, A. F. Newton-type methods for optimization and variational
problems / A. F. Izmailov, M. V. Solodov. — N. Y.: Springer, 2014.
46. Nesterov, Yu. Introductory lectures on convex optimization. A basic
course / Yu. Nesterov. — Boston : Cluwer, 2004 (русское издание:
Нестеров, Ю. Е. Введение в выпуклую оптимизацию / Ю. Е. Нестеров. — М. :
МЦНМО, 2010).
47. Nosedal,J. Numerical optimization /J. Nosedal, S. J. Wright. — N. Y. :
Springer, 2006.
48. Strongin, R. G. Global optimization with non-convex constraints.
Segnential and parallel algorithms / R. G. Strongin, Y. D. Sergeyev. — Boston :
Cluwer, 2000.

Ответы к упражнениям
Глава 1
1.1. Если т = 2k, то Hm<2w=-1, \iman=l; Если т = 2k - 1, то
л. . f 7lk Л 7Г- . f 7lk
hm я„ = -sin —— , hm я„ = sin
n—»°°
2k —1) я->°о I 2& —1
1.2. При /(0)<— функция/(х) будет полунепрерывной снизу на (-«>;
я
-к»); при /(0) > — функция/(х) будет полунепрерывной сверху на (-©о; +°°).
1.3. В задаче f(x) = \пх —> min, x e (0; 1) функция /(х) непрерывна
на X, X — не компактно, /* = -°о,Х* = 0; если положить g(x) = -х при х < 0,
g(x) = х2 + 1 при х > 0, то в задаче g(x) = —> min, х е [-1; 1] функция g(x)
не полунепрерывна снизу в х = 0, X — компактно, /* = 0,Х* = 0.
1.4. Не следует.
1.5. Не следует.
1.7. а) Будет; б) не будет; в) будет.
1.8. а) Точки локального минимума ulk =
f п
x = l,y = -— + 2nk\, точки
глобального минимума u2k=\ x = -2,y = -— + 2nk |, k е Z, точки локального
максимума u3k =
x = 0,y = — + 2nk \ykeZ;
б) точки глобального минимума их = (х = 1, у = 0), и2 = (х = -1, у = 0),
точек локального или глобального максимума нет;
в) точки локального минимума щ 2 =
( 1 .о
x = ±-j=,y = ±-r=
v V2e V2e
, точки локаль-
ного максимума щ 4 = \х = ±-т^. У = +—f=
V v2e v2e
1.9. Если6<0,то/. = -yjiaf+b*,X, = у-аI;если6>0,то/. = -Щ,X, = 0;
если Ь = 0, то при о = 0 /* = 0, X* = Еп, при аФО /» = -|Ы1, X. = 0.
1.13. Нет.
1.14. Нет.
1.15. Нет.
1.16. а) Точка глобального минимума щ = (х = -1, у = 0), точка
глобального максимума и2 = (х = 1, у = 0);
366

б) точки глобального минимума щ 2 =
( 1 ^
точка глобального максимума щ = (х = 1, у = 0);
точка локального минимума и4 = (х = -1, у = 0);
в) точка глобального минимума их = (х = 0, у = 0);
точка глобального максимума и2 =
s
Х = ~2'У = \
\
г) точка глобального минимума щ = (х = 0, у = 1);
точка глобального максимума и2 = (х = 1, у = 0);
д) точки глобального минимумаuik = х = ±1, г/ = +— + 2я& , & е Z;
( к Л
точки глобального максимумаи2^ = х = ±1, г/ = ±— + 2я& , £ е Z;
V 3 J
е) точки глобального минимума:
"1 =
1
1
1
Л
*=~7з^=7з'2=7з
1 1 1
Щ=\ X = -j=,y = -j=,Z = —
(
точки глобального максимума:
,U2={x=S'y=~S'z=Sf
^ ( 1 11
, Щ=\ Х = т=,У = /=>2 = ~~
Я"' S' Д.
Uc =
х =
1
1
у=—/=.2=—
1
S'*- S S
fU6={x=~S'y=S'z=~Sf
U7={x=~S'y=~S'z=S.
ж) точки глобального минимума:
, Щ — \ X — —^-, у — —^, 2 — у—
Щ =
___2_ _J_
Х=~Я'У=Я'2=Я
J_ __L
S'y=S'
u3=\ x = -j=,y = —,z = -
2
, ы2 =
S'*~S S.
x=S'y=~S'z=S)'
sf
точки глобального максимума:
J -A -_ ! - О
J_ __J_ __2^
j6,y=~S'z=S
з) точки глобального минимума:
f \ 2 2\ (2
x=~S'y=S'z=~S.
u, =
^ = -—, г/ = —, г = — |, м2 =
x=3'y=~3'z=V'
2 2 1
Uz=\x = -,y = -,z = --\,
точки глобального максимума:
щ = (x = 1, у = 0, z = 0), u5 = (x = 0, у = 1, z = 0), u6 = (x = 0, у = 0, z = 1);
367

и) точка глобального минимума ги = —,—,...,— , точек локального или
уп п п)
глобального максимума нет, /* = -н»;
к) точка глобального минимума щ = - тгтг, точка глобального максимума
а
и2 = imF» где а = \аь •••> °я)-
Ml
1.18. а) х* =1 — точка строгого локального минимума, х* =-1 — точка
строгого локального максимума, /* = -°°, /* = +°°;
б) при яб > 0 и* = \ х* = ?/—, г/* = ?/—
^ V о \ а
— точка строгого локального
минимума, /* =-°°, /* =+оо, при ab < 0 и* =
2 Ж
х*=п>у*=п
— точка
строгого локального максимума, /* = -°°, /* = +°°;
в) и* = (х* = v2, г/* = у2, г* = v2) — точка глобального минимума, /* = +°°;
г) и* = (х* = 1, у* = 1, г* = 1) — точка глобального минимума, /* = -к».
fi О
1.19. а) При п = 2 точка глобального максимума и* = —, — , точек
локального или глобального минимума нет, /* = -°°, при п = 3 точки глобального
* Г1 и Л
максимума и = —»*» — И, точек лока
нет, /* = -©о, при п > 4 /* = -©о, /* = -к»;
максимума и* =\—,t, —1\, точек локального или глобального минимума
б) некоторые точки глобального максимума и* =
г
О,...,0,^,0,...,О ,
некоторые точки глобального минимума и* = (0,..., 0,1,0,..., 0).
1.20. Если п — четное, то ги =(х* =0, г/* =0, г* =0) — точка глобального
минимума, и* = (х* = 0, г/* = 0, г* = -1) — точка локального максимума, точек
глобального максимума нет; если п — нечетное, то ги = (х* = 0, г/* = 0, z* = —1) —
точка глобального минимума, точек локального или глобального
максимума нет.
1.21. х = 0 — изолированная точка экстремума.
1.22. их = (х = 0, у = 0) — точка глобального минимума, и2 = (х = 1,
у = 0) — точка глобального максимума.
1.23. При а = 0 х = 0 — точка глобального минимума, сфера || х || = 1 — точки
локального минимума, сфера \х\ = 2 — точки глобального максимума; при
0<\\а\\< — х=0 — точка глобального минимума, х-й—й — точка локального
2 ||а||
минимума, х = -2й—г, — точка глобального максимума; при ||а|| = — 1=0и
Ш 2
х - й—м — точки глобального минимума, х = -2-п—» — точка глобального мак-
1Ы1 1Ы1
симума; при — < ||а|| < 1 х = -л—и — точка глобального минимума, х = 0 — изо-
368

лированная точка экстремума, х = -2тг-» — точка глобального максимума;
IMI
при 1<||я||<2х = я — точка глобального минимума, х = 0 — изолированная
точка экстремума, х = -2тг-л- — точка глобального максимума; при ||а|| > 2
IMI
х = 2й—|г — точка глобального минимума, х = 0 — изолированная точка экс-
N1
тремума, х = -2й—й — точка глобального максимума.
IMI
Глава 2
2.3. v{ = (1/3, 2/3, 0, 0, 0) — угловая точка с базисом (А{, А2); v2 = (0, 0,
1, 0, 0) — вырожденная угловая точка, ее базисы (Л3, А{)у (Л3, А2), (А3> Л4),
(Л3, А5); v3 = (1, 0, 0, 0, 2) с базисом (At, Л5), vA = (0, 1/2, 0, 1/2, 0) с базисом
(Л2, Л4), v5= (0, 0, 0, 1, 1) с базисом (Л4, А5); базисным парам (А{, Л4), (Л2,
Л5) соответствуют точки не из X.
2.5. Минимальное значение /* = 1 достигается на множестве,
представляющем собой отрезок [v2j v3] = {av2 + (1 - ol)v3> 0 < a < 1}, где v2 = (0, 0, 1,0,
0) — вырожденная угловая точка, v3 = (1, 0, 0, 0, 2); максимальное значение
/* = 4 достигается в единственной точке v4 = (0, 1/2, 0, 1/2, 0);
/•=1 = /(о2) = /(^)</(^) = 3</(о1) = у</(04) = /-=4.
2.6. Угловые точки: vx = (1, 1, 0, 0, 0), v2 = (3/2, 0, 1/2, 0, 0), v3 = (0, 3/2,
0, 1/2, 0), vA = (0, 0, 1, 1, 0), v5 = (0, 0, 0, 0, 1);
/.=/(о4) = 0</(о5) = 1</(о2) = 3/2</(О1) = 5</(^) = 6.
2.7. а) х* = (1,1,0,0), /* = 2; б) X* = [xv x2] = {axt +(1-a)*2}, ^i = (0,1, 0, 0),
*2 = (0,0,0, 1),/*=-1;в)х*=(0,3,0,1/2,3/2),/*=3/2;г)х*=(1,2,7,0,0,4);
д) X Ф 0 (например, (0, 1 + а, 0, я, 0) е X V я > 0), но /* = -~, поскольку,
например, /(0, 1 + а, 0, я, 0) —> -оо при а —> ©о; е) х* =(7,5,0,0,0), /* =17;
ж) х* = (7,5,0,0), /* = 12; з) х* = (0,1,0,1,1), /* = 5.
2.9. а) х, = (0,3,8,0,0), /* = -5; б) X = 0.
Глава 3
3.1. а) Ни выпукла, ни вогнута; б) выпукла, не сильно выпукла; в)
выпукла, не сильно выпукла; г) ни выпукла, ни вогнута; д) ни выпукла, ни
вогнута.
3.2. а) При а > 0 сильно выпукла, х = 2а; при а < 0 сильно вогнута,
к = 2а; при а = 0 выпукла и вогнута, не сильно выпукла, не сильно
вогнута; б) при р е (-«>; 0] и [1; 2) и (2; +«>) выпукла, не сильно выпукла;
при р е (0; 1) вогнута, не сильно вогнута; при р = 2 сильно выпукла, к = 2;
в) при п = 1 сильно выпукла, х = 2; при п > 2 ни выпукла, ни вогнута;
г) при 0 < р < 1 ни выпукла, ни вогнута; при р > 1 выпукла, но не сильно
выпукла; д) наХ{ при 0 <р< 1 ни выпукла, ни вогнута; при \<р<2 сильно
выпукла; при р > 2 выпукла, но не сильно выпукла; на Х2 при ре (0; 1]
369

вогнута, но не сильно вогнута; при р > 1 ни выпукла, ни вогнута; на Х3 ни
выпукла, ни вогнута ни при каких р.
3.4. а) При а > 0, о 0, ас - Ъ2 > 0 сильно выпукла, к = а + с - у/(а - с)2 + АЬ2;
при а < 0, с < 0, ас - Ъ2 > 0 сильно вогнута, к = а + с + ^(а - с)2 + 4б2; при а > О,
с>0уас = Ь2 выпукла, но не сильно выпукла; при а< 0, с< 0, ас = Ъ2 вогнута,
но не сильно вогнута; при а = b = 0, с > 0 или 6 = с = О, а > 0 выпукла,
но не сильно выпукла; при а = b = 0, с < 0 или b = с = 0, а < 0 вогнута,
но не сильно вогнута; при а = Ъ = с = 0 выпукла и вогнута; ни выпукла,
ни вогнута в иных случаях; б) выпукла, но не сильно выпукла в случае
р(р - 1) > 0, qiq - 1) > 0, pqil - р - q) > 0; вогнута, но не сильно вогнута
в случае 0 < р < 1,0<д< 1, р + q < 1;ни выпукла, ни вогнута в
остальных случаях; в) сильно выпукла, если а Ф 0, а2 Ф 2Ь2; выпукла в остальных
случаях; г) при а > 0, а2 > 2Ь2 сильно выпукла; при а < 0, а2 > 2Ь2 сильно
вогнута; при а > 0, а2 = 2Ъ2 выпукла, но не сильно выпукла; при а < 0,
а2 = 2Ъ2 вогнута, но не сильно вогнута; при а = Ь = 0 выпукла и вогнута; ни
выпукла, ни вогнута в остальных случаях.
3.5. Если || с || < 1, то сильно выпукла, к= 2(1 - ||с||); если ||с|| = 1, то
выпукла, но не сильно выпукла; ни выпукла, ни вогнута, если ||с|| > 1.
3.6. На множестве Х{ ни выпукла, ни вогнута при всех X > 0; на Х2
сильно выпукла в случае А,||с||2 < 2; выпукла, но не сильно выпукла в
случае X || с ||2 = 2; ни выпукла, ни вогнута, если X \\ с \\2 > 2.
3.7.fix)=x2,gix)=x2-l.
3.8. fix) = -e*.
3.9. Нет, например fix) = х, gix) = х2.
3.11.Х=[-1; 1],/(х)=х2,если-1<х<1,/(±1) = 2.
3.16. а) и* = ix* =\,у*= -1), /* = 3; б) ги = (х* = -1,у* = -1), /* = -2.
3.17. "
Ikill hi
2*
3.18.
Рхх =
[о, еслих1 <-ylix2)2+... + ixn)2,
ху ecjmxx>^ix2)2+... + ixn)2,
x1+^lix2)2+... + jxn)2 x1+^lix2)2+... + jxn)2
2 ' 2^ix2)2+... + ixn)2
x1+yljx2)2+... + jxn)2 лп
2^ix2)2+... + ixn)2
xn
, иначе.
3.19. а) В исходной задаче и* =(0,0,0,0,1), /* =1, двойственная задача
имеет вид \\f(k) = -2Х{ -Х2^> sup, X = (kv X2) : -Xt + X2 < -2, -2Х{ -Х2 < 1,
-Х{ -2\2 < 1, для нее Л* ={^ = (^,^2): ^+2^ =-1,^ >-1/3}, \|/*=1;
б) в исходной задаче X* ={х = (х*1,х*2,...,х?): xl -a{ -a{A, i = l,2,...,n}, где
А = ах + а2 +... + ап1 а{ > 0, г - 1, 2,..., п, а{ + а2 +... + ап = 1, /* =| Л |,
двойственная задача имеет вид \\f(k) = Xiax + a2 + ... + ап) —> sup, X е [-1; 1], для нее
\|/* = | Л |, Л* = [-1; 1] в случае Л = 0, иначе Л* = (к* = sgnA}.
370

Глава 5
5.1.а)и(0 =
-1, 0<£<1,
||(*-3), 1<£<3;
б)ы(0 =
в) И(*) = ^ЦА 0 < £< 3; г) «(() =
-, 0<£<2,
1, 2<t<3;
1 1
2 2 2
2 2
5.2. u(t) = 3(t-l).
5.3.u(t) = -3t2 + 6t-2.
5.4. а) Ы(0 = Г1°2<^<4. 6) "(0 = 1- 0 < t< 4; в) «(f) = -1, 0 < t< 4.
5.6.u(0 = -
5.7. a)w(0 = -
б)м(0 = -1,0<^<1 = Г.;
f-1, 0<t<l,
[l, l<t<2 = Z.
[-1, 0<t<2,
[l, 1<^<4 = Г,;
в)м(0=-1, 0<^<4 = Г..
5.8. a) u(t) = -Ylt + 6, 0 < t <1; 6) u(t) = 24t - 12; в) u(t) = \2t -4.
5.9. u(t) = -smt, 0 < t <7i.
Глава 6
6.1. а) Функция Беллмана B(x, t) = x2 при х > О, B(x £) = 0 при -1 + t <
< О, В(х, t) = (1 - t + х)2 при лг < -1 +1, синтезирующая функция и(х, t) = О
при х > О, и(х 0=1 ПРИ ^ < 0; б) функция Беллмана В(х, t) = (t + x - I)2
при лг> 1 - t, B(x, t) = 0 при -l+t<x<l-t, В(х, t) = (1 + х- t)2 при х<
< -1 +1, синтезирующая функция и(х, t) = -\ при х > О, и(х £) = 0 при х = 0;
и(х 0 = 1 ПРИ л: < 0, или, короче, и(х, t) = sgn x
6.2. и(х) = sgn х
6.3. и(х1, х2) = -1, если точка х = (хх, х2) лежит выше и правее кривой ABC,
и(хх, х2) = 1, если точка х = (л:1, л:2) лежит ниже и левее кривой ABC.
Кривая ABC составлена из фрагментов двух парабол. Дуга АВ является частью
11 11
параболы л:1 =— (л:2)2 —, а дуга ВС — частью параболы х1 =-—(х2)2 +—,
расположенной во второй четверти х1 < 0, х2 > 0.
6.6. а)/тах = 6,щ = 1, и2 = 1,щ = 1, щ = 0; б)/тах = 9,щ = 1, и2 = 1,щ = 0,
щ = 1, щ = 1.
6.7. Оптимальный маршрут 3—> 4 —> 2 —> 1 —» 5 —» 3, его длина 1 + 2 +
+ 3 + 9 + 6 = 21.
6.8./тах = 5, *тах = (1, 0, 0, 0, 2),/min = 1/2, xmin = (0, 1/2, 0, 1/2, 0).

Предметный указатель
А
Антициклин 114
Б
Базисная матрица 95
Базисные координаты угловой
точки 93
Базисные переменные 93
Базис угловой точки 93
В
Вектор лексикографически
отрицательный 114
Вектор лексикографически
положительный 114
Вторая производная (гессиан) 34
Г
Гиперплоскость 24
Главный минор квадратной
матрицы 37
Главный угловой минор квадратной
матрицы 37
Градиент 33
д
Двойственные переменные 175
Допустимая пара 316, 328
3
Задача анормальная 60
Задача быстродействия 276
Задача второго типа 19, 21
Задача выпуклая 146
Задача двойственная 175
Задача классического
вариационного исчисления 305
Задача коммивояжера 345
Задача Коши 206, 269
Задача Коши — Беллмана 329
Задача линейного
программирования вырожденная 111
Задача линейного
программирования двойственная 129
Задача линейного
программирования каноническая 85
Задача линейного
программирования невырожденная 111
Задача линейного
программирования общая 81
Задача линейного
программирования основная (стандартная) 86
Задача оптимального управления
275
Задача оптимального управления
с закрепленным
— временем 274
— концом 274
Задача оптимального управления
со свободным концом 274
Задача оптимального управления
с подвижным концом 274
Задача оптимального управления
с фазовыми ограничениями 274
Задача о рюкзаке 343
Задача первого типа 19, 21
Задача синтеза 300
Задача сопряженная 278
Задача с согласованной
постановкой 68
Зацикливание 112
Значение функции наибольшее
(максимальное) 20
Значение функции наименьшее
(минимальное) 16
Золотое сечение отрезка 188
372

и
Игольчатая вариация 286
Краевая задача принципа
максимума 290
Критерий Сильвестра 37, 155
Критерий сильной выпуклости 154
Л
Лексикографический минимум 115
Лексикографическое правило 117
Луч 24
М
Малый лагранжиан 288
Матрица, определенная
неотрицательно 35
Матрица, определенная
неположительно 35
Матрица, определенная
отрицательно 35
Матрица, определенная
положительно 35
Метод Бройдена 235
Метод Гаусса — Жор дана 103
Метод градиентный 199
Метод градиентный непрерывный
(дифференциальный) 206
Метод декомпозиции 326
Метод деления отрезка пополам
187
Метод золотого сечения 188
Метод искусственного базиса 122
Метод касательных 198
Метод квазиньютоновский 233
Метод квазиньютоновский ранга
два 244
Метод квазиньютоновский ранга
один 235
Метод классический 33
Метод локальный 249
Метод ломаных 191
Метод модифицированных
функций Лагранжа 255
Метод наименьших квадратов 32
Метод Ньютона 216
Метод переменной метрики 223
Метод покоординатного спуска 245
Метод покрытия 194, 250
Метод последовательного перебора
195
Метод последовательного
улучшения плана 94
Метод проекции градиента 208
Метод равномерного перебора 194
Метод скорейшего спуска 200
Метод условного градиента 211
Метод штрафных функций 61
Метод экстраполяционный
градиентный 259
Множество выпуклое 41
Множество допустимое 22
Множество замкнутое 23
Множество компактное 24
Множество многогранное 82
Множество неограниченное 23
Множество ограниченное 23
Множитель Лагранжа 44
Н
Надграфик (эпиграф) функции 148
Направление возможное 171
Неравенство Гронуолла 283
Неравенство Йенсена 141
Неравенство Коши — Буняковского
16
Неравенство треугольника 16
Нижний предел последовательности
25
Норма вектора 15
Норма матрицы операторная 235
Норма матрицы Фробениуса 236
О
Ограничения активные 47
Ограничения типа неравенств 43
Ограничения типа равенств 43
Ограничения фазовые 274
Окрестность точки 20
Ортант неотрицательный 24
Ортогональные вектора 15
Отрезок 24
П
Параллелепипед 24
Переменная метрика (G-метрика)
224
373

Позином 181
Полупространство 24
Последовательность
максимизирующая 28
Последовательность
минимизирующая 28
Постоянная Липшица 74
Постоянная сильной выпуклости
151
Приведенная система угловой точки
96
Приведенная форма целевой
функции 96
Принцип максимума 278
Принцип оптимальности 314, 344
Проблема синтеза 327
Программирование выпуклое 164
Программирование геометрическое
181
Программирование динамическое
313
Производная по направлению 42
Прямая 24
Р
Разностная аппроксимация 315
Разрешающий элемент 99
Расстояние между точками 16
Решение задачи Коши 270
Решение оптимальное 276
С
Симплекс 94
Симплекс-метод 94
Симплекс-таблица 96
Скорость сходимости
сверхлинейная 237
Скорость сходимости квадратичная
219
Скорость сходимости линейная 204
Сложность полиномиальная 126
Сложность экспоненциальная 126
Сфера 24
Т
Теорема Вейерштрасса 22
Теорема Куна — Таккера 168
Теорема Фаркаша 136
Точка глобального (абсолютного)
минимума 20
Точка внешняя 23
Точка внутренняя 23
Точка глобального (абсолютного)
максимума 20, 22
Точка глобального (абсолютного)
минимума 16
Точка граничная 23
Точка допустимая 22
Точка изолированная 23
Точка критическая 47
Точка локального максимума 22
Точка локального минимума 20
Точка локального экстремума 22
Точка множества предельная 23
Точка подозрительная на экстремум
36
Точка последовательности
предельная 23
Точка седловая 133,165
Точка елейтерова 168
Точка стационарная 36
Точка строгого локального
максимума 22
Точка строгого локального
минимума 20
Точка угловая 91
Точка угловая вырожденная 93
Точка угловая невырожденная 93
Точка экстремума 22
Точная верхняя грань 21
Точная нижняя грань 19
Траектория (решение) задачи Коши
274
Траектория (решение) задачи Коши
оптимальная 276
У
Управление допустимое 270
Управление оптимальное 276
Управление особое 302
Управление программное 300
Уравнение Беллмана 317, 329
Уравнение Эйлера 307
Условие Вейерштрасса 307
374

дополнительности (допол-
нежесткости) 45, 289, 292
достаточное оптимально-
Лежандра 307
Слейтера 168
трансверсальности 289
Эрдмана — Вейерштрасса
трансверсальности 292
Условие
няющей
Условие
сти 47
Условие
Условие
Условие
Условие
308
Условия
Ф
Фазовые координаты 268
Фазовые ограничения 274
Формулы конечных приращений
73
Функционал 276
Функция Лагранжа нормальная
165
Функция Беллмана 317, 329
Функция Вейерштрасса 307
Функция вогнутая 141
Функция выпуклая 141
Функция Гамильтона — Понтряги-
на 277
Функция гладкая 32
Функция дважды
дифференцируемая 34
Функция дважды непрерывно
дифференцируемая 35
Функция двойственная 175
Функция дифференцируемая 33
Функция Кобба — Дугласа 32
Функция Кротова 324
Функция кусочно-гладкая 271
Функция кусочно-непрерывная 270
Функция Лагранжа 44
Функция Лагранжа
модифицированная 254
Функция Ляпунова 207
Функция непрерывная 24
Функция непрерывно
дифференцируемая (дважды гладкая) 34
Функция ограниченная 20
Функция ограниченная сверху 20
Функция ограниченная снизу 19
Функция полунепрерывная сверху
25
Функция полунепрерывная снизу
25
Функция производственная 32
Функция сильно вогнутая 151
Функция сильно выпуклая 151
Функция синтезирующая 300,321,
327
Функция строго вогнутая 141
Функция строго выпуклая 141
Функция, удовлетворяющая
условию Липшица 74
Функция унимодальная 187
Функция целевая 22
Функция штрафная 62
Ш
Шар 24
Штрафной коэффициент 63

Наши книги можно приобрести:
Учебным заведениям и библиотекам:
в отделе по работе с вузами
тел.: (495) 744-00-12, e-mail: vuz@urait.ru
Частным лицам:
список магазинов смотрите на сайте urait.ru
в разделе «Частным лицам»
Магазинам и корпоративным клиентам:
в отделе продаж
тел.: (495) 744-00-12, e-mail: sales@urait.ru
Отзывы об издании присылайте в редакцию
e-mail: red@urait.ru
Новые издания и дополнительные материалы доступны
в электронной библиотечной системе «Юрайт»
biblio-online.ru
Учебное издание
МЕТОДЫ ОПТИМИЗАЦИИ
Учебник и практикум для бакалавриата и магистратуры
Под редакцией профессора,
доктора физико-математических наук Ф. П. Васильева
Формат 70x100 Vie-
Гарнитура «Petersburg». Печать цифровая.
Усл. печ. л. 29,06. Тираж 1000 экз. Заказ № 7837, 20 экз.
ООО «Издательство Юрайт»
111123, г. Москва, ул. Плеханова, д. 4а.
Тел.: (495) 744-00-12. E-mail: izdat@urait.ru, www.urait.ru