THE MATHEMATICAL THEORY
OF BLACK HOLES
S. Chandrasekhar
University of Chicago
Clarendon Press Oxford
Oxford University Press New York
1983

С.Чандрасекар
МАТЕМАТИЧЕСКАЯ
ТЕОРИЯ
ЧЕРНЫХ ДЫР
В 2-х частях
Часть 2
Перевод с английского
канд. физ.-мат. наук В. А. Березина
под редакцией
д-ра физ.-мат. наук Д. В. Гальцова
Москва «Мир» 1986

ББК 22.632
418
УДК 52+53
Чандрасекар С.
418 Математическая теория черных дыр: В 2-х ч. Ч. 2. Пер.
с англ. —М.: Мир, 1986, 355 с, ил.
Вторая часть книги посвящена исследованию вращающихся черных дыр,
описываемых метрикой Керра. Вслед за выводом решения Керра и изложением
основных теорем о его свойствах дается подробный анализ геодезических, описы-
описывающих траектории массивных и безмассовых частиц. Проводится исчерпывающее
исследование электромагнитных и гравитационных возмущений поля Керра в рам-
рамках формализма Ньюмена—Пенроуза. Рассматривается массивное поле спина 1/2
на фоне геометрии Керра с изложением основ спинорного анализа в искривленном
пространстве-времени. Приводятся альтернативные подходы к описанию воз-
возмущений черных дыр, построению более общих решений и попыткам обобщения
изложенных результатов на случай вращающихся заряженных черных дыр.
Рассчитана на физиков и астрофизиков-теоретиков, может служить учебным
пособием для студентов и аспирантов этих специальностей.
„ 1704020000-276 еА ос , ББК 22.632
4 041@1)-86 54~86' Ч- 1
Редакция литературы по астрономии, геофизике
и космическим исследованиям
Originally published in English under title
«The Mathematical Theory of Black Holes»
© Oxford University Press 1983
© перевод на русский язык, «Мир», 1986,

Глава 6
МЕТРИКА КЕРРА
51. Введение
Здесь мы начинаем изучение решения Керра. Как утвер-
утверждалось в прологе, это единственное решение уравнений общей
теории относительности, описывающее все возможные черные
дыры, которые только могут возникнуть при гравитационном
коллапсе объектов звездной массы, и это единственный пример,
когда физическая теория дает точное описание макроскопического
объекта. По большому счету предыдущие главы — лишь прелю-
прелюдия к исследованию, к которому мы сейчас приступаем.
«В литературе нет конструктивного аналитического вывода
метрики [Керра], адекватного ее физическому смыслу, и даже
прямая проверка этого решения уравнений Эйнштейна связана
с громоздкими вычислениями» [Ландау и Лифшиц] *. Вопреки
этому утверждению, мы увидим, что после выписывания уравне-
уравнений и их упрощения вывод метрики Керра осуществляется до-
довольно просто на основе разумных математических и физических
предположений.
В данной главе, помимо вывода метрики Керра и установления
ее единственности, будет дано описание пространства-времени,
задаваемого этой метрикой, в формализме Ньюмена—Пенроуза,
откуда с очевидностью будет следовать, что метрика Керра при-
принадлежит к типу D по классификации Петрова.
52. Уравнения для стационарного
и аксиально-симметричного
вакуумного пространства-времени
В гл. 2 (§11) было показано, что метрика стационарного
аксиально-симметричного пространства-времени может быть за-
записана в виде
ds2 = e2v {dtf - ё1^ (dcp - со dtJ - е2^ (dx2J - е2^ (dr3J, A)
где v, г|), |л2, |л3 и со — функции только координат х2 и х3, причем
остается возможность наложить координатное условие на \i% и ji3.
* Л. Д. Ландау, Е, М, Лифщиц, Теория поля, — М,; Наука, 1973, § 104,
с, 411, — Прим, ред,

Глава 6. Метрика Керра
Если выбрать тетраду так, чтобы базисные 1-формы имели
вид
со0 = ev d/, со1 = е* (d<p - со dt), со2 = еМх2, со3 = е»* dx3, B)
то, используя выражения для компонент тензора Римана, приве-
приведенные в гл. 2 (уравнения G5)), получаем следующие выражения
для не равных нулю компонент:
/?Ш2 = +е-*-»' (e*-*V.2). 2 + е-*"ф. 3^2,3 + V/^^V 2,
#.з.з = 4-е-*** (е**^. з). з + <f 2li'i|>. 2fi3,2 + VA2l"-V3,
/?10I0 = -<f2^, 2v. 2 - в№"ч>. 3V. 3 - V/*-2V2V2 + <f2*V3);
#2323 = +<f'^•[(^•-•V 3). з + (^>з, 2). 2],
#2020 = -e-M'-v (e^'v. 2),2 - e-2^v, 3fx2, з +
#3030 = -^^-v (e^'v. 3). 3 - e-^'v, 2li3,2 +
Rim = +e~^ (e*-»V. 2), 3 - e-»*-»^ 3^ 2 + ifif*-w-*>at 2co, 3,
+^-2^-vco, 2 (t|5,2 - V,v. 2) + V2e"^-V (e*""'©. 2). 2 +
+ V^2|i>-V«». 3^2.3,
+e*-2|i'-V 3 (Ф. 3 - V»v. 3) + V.e"'1'-* (e^'co. 3). 3 +
#3002 = +е-*-»> (^'%,2)#3-^^^,з}г3.2-3//*"^3^.2со,3,
#12зо = +xke-»°-v (e*-**®. 2), 3 + V^'^^V 3 Bt|5,2 - ^3> 2 - v, 2),
#.302 = -V2e-^-v («*-•*•©. 3), 2 - Vie*"*1''114-V 2 Bф. 3 - w, 3 - v. 3),
#.O23 - -Ч*-*-»' [(e*-\ 3). 3 - (e*-v©. 2). з1- C)
Кроме того, следующие компоненты тензора Римана равны нулю:
#1210 = #1310 = #1223 = #1СЯ2 = #1002 = #1003 = #2330 — #3220 = 0- D)
Компоненты тензоров Риччи и Эйнштейна представляют собой
некоторые линейные комбинации компонент тензора Римана
(указанные в уравнениях G5) гл. 2). Полагая их равными нулю,
получаем уравнения для метрики стационарного аксиально-
симметричного пространства-времени. Достаточно для наших
целей рассмотреть следующие уравнения:
е'21Хг [v, 22 + v, 2 (i|j + v - ц2 + И-з), г] +
+ е~^ [v, 33 + v, з (ф + v + ц2 - Цз). з] =
= + Vй" [e-2|i'(«», 2f + е** К зJ] (#оо = 0), E)
е-2»> №, 22 + t, 2 A> + V - ^2 + |*3), |] +

52. Уравнения для стационарного пространства-времени
+ v _|_ ^ _ ^), 8] =
(со, 2J + <г2^ ((о, 3J] (Rn = 0), F)
+i»^, Ш) 3), з = О G?и = 0), G)
V).2 М%3 - (* + Чз^3,2 + Ф>2Ф,3 + V,2V,3 =
= V2^-2v42«,3 (#» = O), (8)
V), зз + (Ф + V)K (V - |i8),, + Ч>,,1Ы +
+ в"*' [V, , ft + Ц,), , + ф, 2(i3( 2] =
= _i/4e2*-2v[е-2^2 (о,, 2J _ е-*»* (со, 3J] (G22 = 0), (9)
v), 22 + (г|) + v), 2 (v - (г2), 2 + ф, ,i|), J +
v[е-2^К2J - е-^ (@,3J] (G33 = 0). A0)
Полагая
P=^+v, A1)
можно переписать уравнения E) и F) в следующем виде:
= V2^-v [&*-»* (со, 2J + ^--^ (со,зJ], A2)
(eP+ii.-»i, г|), 2), 2 + (^+^^з г|), 3), з =
= —V2^-v [^-^(ш, 2J + ^-^з (о)}3J]. A3)
Складывая и вычитая эти уравнения, получаем
[е^'И.аЬ + [^2"ДзИ,з],з = 0, A4)
[еР+и,-и. (ф - v),2],2 + И+^"^(г|) - v),3),3 =
= ~^-v[^3-^2(co,2J + ^2-^ (со,3J]. A5)
Если сложить уравнения (9) и A0), то получим уравнение
A4), если же эти уравнения вычесть друг из друга, приходим
к уравнению
4е№ (Р, 2J4 2 + г|), 2v 2) - 4е»*-»* (Р,3^2,з + ^,3v,3) -
= 2e-V {Из-д2 И,2],2 - [е»*-*> И,3],з} -
- e2^-?v[e»*-»> (co,2J - е**-»* (со>3J]. A6)
Можно предложить следующий порядок действий при иссле-
исследовании вышеприведенных уравнений.
Прежде всего, используя калибровочную свободу, наложим
на функции |л2 и |Л3 координатное условие: функция
е2 <**.-»*.)'= А (х2, х3) A7)
должна иметь некоторый удобный для дальнейших выкладок
вид. Теперь уравнение A4) становится уравнением для функции

Глава 6. Метрика Керра
Р = яр -\-v. Решение его не представляет трудностей. Действи-
Действительно, ниже в п. б будет показано, что функция ехр (Р) может
рассматриваться в качестве одной из координат (другими сло-
словами, ее можно включить в определение координаты). Уравнения
G) и A5) теперь представляют пару связанных уравнений для
функций г|}—v и со, и решение этой системы уравнений является
центральной задачей теории стационарных аксиально-симме-
аксиально-симметричных решений уравнений Эйнштейна.
Смысл проведенных преобразований становится ясным, если
записать метрику A) в виде
ds2 = е* [х (dtJ - (Их) (dcp - со d/J] — Д-1/2вд2+Дз [(d*2J + A (dx3J],
A8)
где
Функцию А, как уже говорилось, можно выбрать произвольно;
уравнение для р может быть решено независимо от других, а
основной задачей является решение уравнений для х и <*>, причем
решение для функции |л2 -|- М'з получается в квадратурах, если
известны функции % и со (это будет подробно показано ниже).
Отметим важный факт: функция ехр (—2Р) есть детерминант
метрики двумерного пространства, натянутого на векторы d/dt
и д/дср.
Кроме того, уравнения для функций х и ю также обладают
важным свойством. Если переписать уравнение G) в виде
[е»г-»л (С0| 2J ^_ ^2-М.з (о), 3JJ B0)
и использовать уравнение A5), получим
v),3]},3 = 0. B1)
Последнее уравнение можно переписать в виде
со2^ ,], 8 = 0. B2)
Сравнение уравнений G) и B1) показывает, что функции со и
X2—со2 формально удовлетворяют одному и тому же уравнению.
а. Сопряженные метрики. Важной особенностью уравнений,
описывающих метрику стационарного аксиально-симметричного
пространства-времени, является возможность, зная одно решение,
получать другие решения. Например, если метрику A8) под-
подвергнуть преобразованию
<p-+—it, B3)

52. Уравнения для стационарного пространства-времени 9
то в результате получим
X(d/J - (l/x)(d<p - cod02->(l/x)(d02 +
+ B(о/х) At dcp - [(x2 - co2)/x] (dcpJ =
= {%(dtf-(l!x)(dq)-&dtn B4)
& = co/(f - со2), x = K/(f - со2). B5)
Никакие другие метрические коэффициенты не изменяются при
этом преобразовании. Заключаем, что если (х, со) есть решения
интересующих нас уравнений, то (х, со) также есть решения
тех же уравнений. Это утверждение будет явным образом про-
проверено в § 53: оно является следствием того, что функции со и
X2—со2 удовлетворяют одному\ тому же уравнению.
Назовем (х, со) и (х, со) сопряженными решениями, а преобра-
преобразование B3) — сопряжением.
б. Преобразование Папапетру. В калибровке
Ш = ^з = М" А = 1 B6)
метрика A8) принимает следующий вид:
ds2 = # [х (d/2) - A/х) (dcp - со d/J] - е^ [(d*2J + (dx3J], B7)
причем функция ехр (Р) удовлетворяет уравнению
И, асе-0 (а = 2,3). B8)
Мы можем теперь использовать тот факт, что ехр (Р) удовлет-
удовлетворяет двумерному уравнению Лапласа, чтобы рассматривать
эту функцию двух переменных в качестве новой координаты.
Рассмотрим координатное преобразование
(х\ х3)->(р, г), B9)
е^ [(dx2J + (dx3J] ->/ (р, z) [(dpJ + (dzJ]. C0)
Ясно, что такое преобразование координат возможно, если
(Р,2J +(г,2J = (р,зJ +(г,зJ,
Р, 2Р, 3 +2, 2*. 3 = 0. C1)
Этим условиям можно удовлетворить, положив
Р, 2 = +2, 3, Р, 3 = —2, 2- C2)
Очевидно, уравнения C2) удовлетворяются вследствие уравнения
Р,а* = 0 (р=*Р). C3)
Следовательно, функцию ехр (Р) = р можно выбрать в ка-
качестве одной из координат; при этом метрика B7) принимает вид
ds2 = р ft (d/J - A/х) (dcp - со dtf] —
-<?* [(dpJ +(dzJl, C4)
где х. со и |л — функции риг. Будем говорить, что метрика за-
записана в форме Папапетру.

10 Глава 6. Метрика Керра
53. Выбор калибровки и приведение уравнений
к стандартному виду
Конкретный выбор калибровки, который будет сделан ниже,
не приводит к какой-либо потере общности и на данном этапе он
не является строго необходимым. Однако этот выбор дает нам
физическое обоснование поиска метрики определенного вида.
Удобно выбрать полярный угол 0 (угол с осью симметрии)
в качестве пространственной координаты л:3. (Ниже в настоящей
главе мы заменим угол 0 на функцию cos 0 в качестве независи-
независимой переменной.)
Будем предполагать, что метрика допускает горизонт событий,
который определим как гладкую двумерную изотропную поверх-
поверхность, натянутую на касательные векторы d/dt и д/дц —
«векторы Киллинга» пространства-времени.
Пусть уравнение, задающее горизонт событий, имеет вид
N (х\ х3) = 0, C5)
согласующийся с предполагаемой стационарностью и аксиальной
симметрией пространства-времени. Поверхность горизонта изо-
изотропна, следовательно,
g4NtiN,, = 0. C6)
В выбранной нами метрике уравнение C6) дает
exp {2Qx3 - |х,)} (ЛГ,ГJ + (Л^,еJ== 0, C7)
где г — х2. Вследствие калибровочной свободы можно предпо-
предположить, что
ехр{2([г3-[г2))-А(г), C8)
где А (г)— некоторая функция переменной г, которую пока оста-
оставим неопределенной. Из уравнения C7) теперь следует, что
условие изотропии поверхности принимает вид
Д(г) = 0. C9)
Второе условие в определении горизонта — изотропная поверх-
поверхность должна быть натянута на векторы d/dt и д/дф — требует,
чтобы f детерминант метрики подпространства (t, ф) равнялся
нулю на поверхности А (г) = 0:
е^ = 0 (Д (г) =0). D0)
Поскольку вид функции А еще не задан, без потери общности
можно предположить
r, 0), D1)

53. Выбор калибровки и приведение уравнений 11
где / (г, Э) — некоторая функция гиб, регулярная на поверх-
поверхности Л (г) = 0 и на оси 0 = 0. Но мы предположим, что функ-
функция ехр ф) имеет более специальный вид
efi = Д1/2/ @), D2)
т. е. что эта функция допускает разделение переменных г и 0.
Если функции ехр (|л3 — |л2) и ехр (|3) удовлетворяют уравне-
уравнениям C8) и D2), то уравнение A4) для функции ехр (Р) прини-
принимает вид
[Д1/2(Д>/2)(ДГ + A//) /, 9е = 0, D3)
Требования регулярности на оси и выпуклости горизонта дают
А,гг = 2, / = sin 6. D4)
Подходящее решение для А имеет вид
Л - г2 — 2Мг + а\ D5)
где М и а — постоянные*. (Ниже мы покажем, что эти постоян-
постоянные есть не что иное, как масса и удельный момент количества
движения черной дыры.)
Таким образом, в выбранной нами калибровке, которая сов-
совместима с существованием горизонта событий, имеем
е^-иш = Д1/?, е$ = A1/2 sin 0, D6)
где А дается уравнением D5).
Очевидно, что сделанный выбор решений для ехр (pi3 — М^)
и ехр (Р) не ведет к потере общности, поскольку метрика имеет
форму Папапетру, если
р = *Р = A1/2 sin 0, z = (г — М) cos 0. D7)
Если, кроме того, вместо координаты 0 ввести переменную
(обозначавшуюся индексом 3)
jut, = oos ©, D8)
то уравнения A5) и G) приводятся соответственно к виду
IД (^ 2J + б (o)j зJ ^ D9)
[^e2 <*-v> со, 2], 2 + [бе2 <*-*) со, 3], з = 0, E0)
где
б = 1 — ^ = sin2 0. E1)
* Следует отметить, что хотя М и а появились как постоянные интегриро-
интегрирования, (М2 — а2 )и Д инвариантны относительно преобразования (Ксантопулос)
М -> М' = (М2 - а2I/2/р, а -> af = q (M2 -
где р и q — постоянные и р2 + q2 = 1.

12 Глава 6. Метрика Керра
Пусть х определяется уравнением A9). Тогда уравнения D9)
и E0) можно записать следующим образом:
+ «(».Л E2)
(¦?•••)..+(v-4.-0- E3)
или иначе
X 1(АХ,2). 2 +Fх. зЫ =
= А 1(х, 2J + (<о, 2J1 + б [(х, 3J + ((о, зJ1, E4)
X Кд<о, г), г + (бм, з), 3] = 2Ах, 2«, 2 + 2Ь%, з», з- E5)
Полагая теперь
X = х + (о, Г = х-«. E6)
получаем пару симметричных уравнений:
•V2(X + Y) [(АХ, 2)J +FХK)K] =
= Д(Х,2J + б(ХKJ, E7)
V2 (X + П КАК, 2), 2 + (бГ, 3), 3] = А (^, 2J + S (Г, 3J. E8)
Уравнения (8) и A6) (определяющие р2 -+- (х3) после некото-
некоторых элементарных преобразований приобретают вид
—(ц/б) (^з + Ца), 2 + К' — Л1)/Л ] (Из + (ig), з =
= [21 {X + Yf) (X, 2Y, з + Y, SX, 3), E9)
2(r—M) (ns + (i2), 2 + 2ц (p3 + (x2), з =
= [4/(X + ГJ] (АХ, 2Г, 2 - 6X, ,K, 3) -
— 3 l(r — MJ — A I/A +(}i2 +6)/6. F0)
Теперь очевидно, что если решены уравнения E7) и E8) для
функций X и У, решение для (ц2 + ц3) получается из уравне-
уравнений E9) и F0) в квадратурах.
Уравнения E7)—F0) могут быть записаны в более симметрич-
симметричном виде, если вместо г ввести новую переменную
т] =(/¦ — М)/(М2 — а2)'/2, А = (М2 — а2) (т)8 — 1). F1)
Имеем
= (ri2-D(X,nJ + A - ц2) (X, ,J; F2)
V2 (X + Y) {[(rf - 1) Y, „], , + [A - р2) Г,,»], ^} =
= (Г12-1)(Г,,J + A - (Xя) (К, „)8, F3)
~ Т=^ ^3 + ^-1 + 1р~г (!*» + Ив), ii =
= [2/(Х + ГJ] (X, ЧК, й + Г, „X, й), F4)

53. Выбор калибровки и приведение уравнений 13
2т) (Из + Иг), т) + 2и (Из + Иг), ц =
= [4/(Х + 7J] l(ri2 - 1) X, п?, „ -
- A - и2) X, „Г, J - 3/(т!2 - 1) + 1/A - и2)- F5)
Преобразования
X = A + F)/(l - F), К = A + G)/(l - G) F6)
позволяют привести уравнения F2) и F3) к удобному виду
A — FG) {[(л» — 1) F, Д„ + [(l-|is)FfJflt} =
= -2G [(rf - 1) (F, nJ + A - и2) (F, „J L F7)
A - FG) {Ift8 - 1) G, Д „ + [A - и2) G, Д ,} =
= _2F [(yf - 1) (G, nf + A - и2) (G, йJ]. F8)
Метрические функции % и со связаны с функциями F и G сле-
следующим образом:
х = A _ FG)/(i - F) A - G),
со - (F — G)/(l — F) A — G). F9)
Теперь нетрудно усмотреть, что уравнения F7) и F8) допу-
допускают простое решение
F = —pri — фг,, G = —/?т] + q\i, G0)
где /? и q — действительные постоянные, подчиняющиеся условию
р2-<72=1. G0')
а. Некоторые свойства уравнений для X и Y. Пусть (X, Y) —
решение уравнений F2) и F3). Тогда
1. (К, X) также есть решение. При этом % остается неизмен-
неизменным, а со меняет знак — тривиальное изменение, эквивалентное
замене ф ->—ф.
2. (X + с, Y — с), где с — произвольная постоянная, также
является решением. В этом случае % снова остается неизменным,
в то время как со -> со -{-2с — снова тривиальное изменение,
соответствующее преобразованию ф ->¦ ф — 2ct.
3. (X, Y'1) и (Y'1, X) также представляют решения.
Этот факт следует из инвариантности уравнений F7) и F8) отно-
относительно одновременного изменения знаков функций F и G (что
соответствует замене X и Y обратными величинами X и Y).
Новые решения имеют важное значение. Чтобы убедиться в этом,
выразим метрические коэффициенты, соответствующие новым ре-
решениям (обозначим их % и со) через метрические коэффициенты %
и со, соответствующие старым решениям:
X ) — XY ~ х2 - оJ '
X

14 Глава 6. Метрика Керра
Сравнение с уравнением B5) показывает, что решения, получен-
полученные из (X, Y), являются сопряженными к решениям, полу-
полученным из (X, Y). Таким образом, преобразование (X, Y) ->
-> (X, Y'1) эквивалентно сопряжению.
4. Комбинируя результаты п. 1—3, получаем, что если (X, Y)
есть решение, то решением является и комбинация
[X/(l +cX), K/(l —cY)h
где с — произвольная постоянная. Но в результате мы не полу-
получаем никаких действительно новых решений, помимо сопря-
сопряжения.
б. Альтернативные формы уравнений. Вернемся к уравне-
уравнениям G), A2) и A3). В выбранной нами калибровке и при выбран-
выбранном решении для ехр ф) эти уравнения принимают следующий
вид:
^^) ^Д^) -0, G2)
, г
2
[(A sin 0) v,г], г + [(sin 0) v, 0], е = +(^/2А sin 0) [А (со, гJ + (со, еJ],
G3)
[(A sin Э) г|), r], r f [(sin 9) ф, в], в = ~(^4ф/2A sin Э) [А (со, гJ + (со, еJ].
G4)
Из уравнения G2) следует, что решение для со может быть
получено, если известен вид «потенциала» Y. Действительно,
если
г4*©, r/sin Q = Г, е, e4^co, 0/A sin Э = -Г, г, G5)
следовательно,
со, Г = +в^^, е sin 0, со, е - ~в-^Г г A sin 0. G6)
Условие интегрируемости последнего уравнения имеет вид
(е~^ АГ г), г + A/sin 9) (e-^Y, 0 sin 0), е = 0, G7)
поэтому уравнение G4) можно следующим образом переписать
через Y:
(Аг|), г), Г + A/sin Э) (г|), е sin Э), 0 = -У2<г** [(Г 0J + А (Г, гJ]. G8)
Полагая теперь
X = е2* G9)
и возвращаясь к переменным т] и [х, получаем уравнения
1(т|» - 1)Х лди + [A - Ю*,ц/*и =
= ~A/Х2) [(л2 - 1) (Г, ,J + A - fx2) (Г, ,J], (80)
[(Л2- 1)Г г/Х2],, + [A -^)Г,,/Х2и = 0. (81)*
* Поскольку нам не придется использовать одновременно уравнения F2)
и F3) и уравнения (80) и (81), одни и те же обозначения X и К для разных вели-
величин не должны вызывать недоразумений.

53. Выбор калибровки и приведение уравнений 15
Поведение решений уравнений (80) и (81) при ц ->оо, совме-
совместимое с требованием, чтобы пространство-время было асимпто-
асимптотически плоским, может быть найдено следующим образом.
Сейчас для наших целей достаточно знать, что требование,
чтобы пространство-время было асимптотически плоским, приво-
приводит к следующему асимптотическому поведению метрических
коэффициентов:
e2v_^i -2М*/г + О(г2), со->2///-3 + О(/-4) при г->оо, (82)
где М* (не обязательно равное М в определении А — см. сноску
на с. 11)—масса, а / — момент количества движения источ-
источника. Легко видеть, что выписанные асимптотики совместны
с уравнением G3) и, как будет показано ниже, они также сов-
совместны с уравнениями (80) и (81).
Перепишем асимптотики через переменную г\:
e2v -> 1 - 2М*/(/И2 - а2I/2 т| + О (тр2),
со -> J/(M2 - а2р тK + О (л).
Поскольку
e2^+2v = Хе2* = А A — (J,2) = (М2 - a2) (rf - 1) A - \i2), (84)
приходим к выводу, что
X-*(M2-a2)(l -\i2)rf[l +2M*/(M2-a2I/2ri] + O(l). (85)
Из уравнения (81) теперь следует асимптотика для Y:
Г->2/|АC-ц2) + О (л), (86)
а из уравнений G5) и (85) следует, что со имеет требуемую асимпто-
асимптотику со -> 2Jr~z (г -> оо).
в. Уравнение Эрнста. Эрнст ввел другую форму записи основ-
основных уравнений, сыгравшую основную роль в исследованиях,
целью которых было нахождение всех стационарных аксиально-
симметричных решений уравнений Эйнштейна в пустоте. Кроме
того, уравнение Эрнста позволяет наиболее просто и кратчай-
кратчайшим путем вывести метрику Керра.
Прежде всего отметим, что уравнение E3) позволяет получить
функцию со из потенциала Ф:
Ф, 2 = (б/Х2) со, з, Ф, з = -(А/Х2) со, 2. (87)
Потенциал Ф удовлетворяет уравнению
а уравнение E2), записанное через потенциал Ф, принимает
следующий вид:
[A (In х), *], 2 + [б (In х), з1, з = (Х2/Д) (Ф, зJ +
+ (» (Ф, 2J- (89)

16 Глава 6. Метрика Керра
Полагая
Y = (Лб)«/2/Х, (90)
находим, что уравнения (88) и (89) могут быть приведены к виду
(ср. с уравнениями E4) и E5))
Y КАТ, а), 2 + (бЧ'. з), .1 = А К*, 2J - (Ф, 2J1 +
+ 6 [0Р,,)*-(Ф,,)а1, (91)
? [(АФ, 2), , + FФ, ,),,] = 2Д?, 2Ф, 2 + 2б?, 3Ф, з- (92)
Можно представить функции ? иФ как действительную и мни-
мнимую части комплексной функции
Z = W +1Ф (93)
и объединить уравнения (91) и (92) в одно уравнение
Re(Z)[(AZ, 2),2 + FZ 3),з] = A(Z>aJ + 6(Z,8)a. (94)
По своей структуре уравнение (94) похоже на систему уравне-
уравнений E7) и E8) для функций X и Y. Следовательно, уравнение (94)
должно обладать свойствами, аналогичными перечисленным выше
в разд. а. Именно, если Z есть решение, то решением является
и функция Z, решением также является функция Z/(l -f- icZ),
где с — произвольная действительная постоянная. Преобразо-
Преобразование Z->Z/A -f- icZ) эквивалентно так называемому «преобра-
«преобразованию Эйлера». В отличие от рассмотренных выше преобразова-
преобразований для решений X и Y преобразование Эйлера приводит к су-
существенно новым решениям, поскольку переход от Z к метри-
метрическим функциям связан с операцией интегрирования.
Преобразование
Z = -A + ЕI{\ - Е) (95)
(аналогичное преобразованию F6)) приводит уравнение (94)
к следующему виду:
A-ЕЕ*) [(Д?,,)>а+F?,зЫ =
= -2Е* [А (Е, 2J + б (Е, 3J ]. (96)
Это и есть уравнение Эрнста.
Мы видели, что с решением (%, со) связано сопряженное ре-
решение
X = Х/(Х2 -«2), со = со/(х2 - со2). (97)
Аналогично можно вывести и сопряженное уравнение Эрнста.
Вводя определения
W = (МУ'2/% = ef+v (х2 — со2)/х = e2v — coV*, (98)
Ф 2 = (б/х2) 5,з = (Ф2/А) 5,,, Ф,з = -(А/?) 5,2 = -(Ф2/б) S, 2,
(99)
Z = • V + Я> = —A + ?)/(! - ?), A00)

54. Вывод метрики Керра 17
получаем
A - ??*)[(Д? 2), 2 + F? з),3] = -2?* [А (?, 2J + б (?,3J]. A01)
Снова вводя переменные г) и |х, имеем
A - ??*) {[(л2 - 1)?, Д л + [A - [х2)Ё, Д ^} =
= -2?* [ОJ - 1) (?, ,J + A - jx2) (? ,J]. A02)
Метрические функции t иФ следующим образом выражаются
через функцию Е:
?-ReZ- —A -??*)/|1 -?|2, Ф = lmZ = i(E-E*)/\l ~Ё\2.
A03)
54. Вывод метрики Керра
Нетрудно проверить, что уравнение Эрнста A02) допускает
элементарное решение (аналогичное решению G0) уравнений F7)
и F8))
Е = —рц — iqp, A04)
где
р* +q2 = 1 A05)
и р и q — действительные постоянные (выбор знаков р и q в ре-
решении A04) продиктован соображениями удобства для дальней-
дальнейшего изложения). Соответствующее решение для Z имеет вид
Z =
1 + /7Г1 + if/jU
Разделяя мнимую и действительную части Z, получаем
1 + 2/7Г] + р V + ^/2^2 (РЛ + 1 J + ^72^2
ф = ?^
Выраженные через переменную г эти величины становятся
равными
f=
[(г - М) + (М2 — а2I/2/р]2 + [^2 (М2 — а2)/р2] fx2 '
ф = 2[д{М*-а*Iр]у
[(г - М) + (УИ2 - а2I/2/р] + [^ (М2 - а2)/р2] ^ w
Если в согласии с условием A05) выбрять
р = (м2 — а2)]/2Ш ? = а/УЙ A10)

18 Глава 6. Метрика Керра
то решения для У и Ф существенно упрощаются:
f = (д _ аЧ)/р\ Ф = 2аМ\х/р\ A11)
Далее, вследствие уравнения (99) имеем
ф9 2 = —4аМг|х/р4 - 0Г2/Д) со, з = [(Л — а26J/р4Д ]со, 8,
Ф, з - BяМ/р4) (г2 - а2^2) = -(Т*/в) ш 2 -
= — [(А — а26J/р46]со, 2. A13)
Следовательно,
2 — а2|и2) б
©,8-— (Д__а2бJ »
и решение для со имеет вид
со 2аМг6
Получаем также (ср. с уравнением (98))
Y = е2Ъ (Х2 _ ^2) = e2v _ ^е^ = (А — а?б)/р2. A16)
Используя предыдущее уравнение, можем записать
® = д7Г^5 (X2 - со2) - —-г- е-3*. A17)
Из уравнений A16) и A17) теперь следует
е2^ (А — а26)/р2 - ^Э — (о2е4^ = б (Ар4 — 4a2MV2S)/p4. A18)
Здесь мы использовали выражение ехр B|3) = А6. Решения для со
и ехр B\f>), которые получаются из уравнений A17) и A18), можно
записать в простом виде с помощью следующих легко проверяе-
проверяемых тождеств:
Цг* + a2) =F а (Д6I/*] (А1/2 ± ад1/2) = р2А^2 ± 2аМг&^2, A19)
22 (А — а2б) = р4А — 4а2М2г2б, A20)
где
22 - (г2 +а2J —а2 Аб. A21)
Из уравнения A18) получаем, воспользовавшись тождеством A20):
ехр Bф) - б22/р2, A22)
а из уравнения A17) теперь следует
со = 2аМг/22. A23)

Ц, 54. Вывод метрики Керра 19
|}меем также
i ехр Bv) - ехр B|3 — 2^) - р2А/22, A24)
- % = ехр (—г|) +v) = р2 А1/2/B2б1/2). A25)
Из уравнений A23) и A25) находим, используя тождество A19)
Л1/2 flfi/
'2 ( }
Наконец, завершая решение, вернемся к уравнениям E9) и
F0). Редукция этих уравнений облегчается следующими форму-
формулами, дающими выражения для производных функций X и Y:
s 2 —
L, з =
_
'2 "
Используя предыдущие формулы, уравнения E9) и F0) сведем
к следующему виду:
—(цз + (Х2), 2И-/б + (Из + ^2), з(/" — М)/А =
= и [(г — М) (р2 + 2а2б) — 2гА]/(р2 Аб), A29)
2{г — М) (из + 1*а), 2 + 2и (Из + ^2), з =
= 4 — 2 (г — МJ/А — 4rM/p2. A30)
Легко убедиться, что функция
ехр (из + И2) = Р2/А1/2 A31)
является решением этих уравнений, и поскольку ехр (из — Иг) =
= А1/2 (в выбранной нами калибровке), то решения для ехр (из)
и ехр (иг) по отдельности имеют следующий вид:
ехр Bщ) = р7Д; ехр Bи3) = р2. A32)
Теперь мы завершили решение уравнений для всех метриче-
метрических коэффициентов и можем выписать метрику:
ds2 = р2 (Д/22) (d/J - B2/р2) [d<p - BaMr/22) d/)]2 sin2 6 -
-(P2/A)(drJ-p2(d0J. A33)

20 Глава 6. Метрика Керра
Это и есть метрика Керра. Выпишем ковариантный и контра-
вариантный метрические тензоры
1— 2Мг/р2 0 0 2aMr sin2 0/р2
О
0
0
0
2aMrsin2O/p2
22/р2А
0
0
-Р2/А
0
0
0
-Л/Р
0
0
-Р2
0 —
0
2 0
-1/р2
A34)
2аМг/р2А
0 • A35)
2aMr/p2A 0 0 — (A-a2sin26)/p2Asin2e
Заметим, что при а = О метрика Керра A33) сводится к мет-
метрике Шварцшильда в стандартной записи. Кроме того, из асимпто-
асимптотического поведения
. e2v _+ i _ 2M/r + О (г2), е2* -^г2 sin2 0 + О (г),
со ^2аМ1г3 +О(/-4), в3»*» ->г2 +0 (г). A36)
е-2цг _^ 1 _ 2М/г + О (г-2) (г -»- оо)
различных метрических коэффициентов видно, что метрика рр
приближается к метрике Шварцшильда при г->оо. Отсюда мы
заключаем, что метрика Керра асимптотически плоская, а па-
параметр М следует отождествить с массой черной дыры. Из асимпто-
асимптотического поведения функции со (со ->2аУИг~3), которая опреде-
определяет увлечение инерциальной системы отсчета, следует, что а
нужно отождествить с удельным моментом количества движения
черной дыры (т. е. моментом единицы массы).
Отметим, наконец, следующие алгебраические соотношения
между метрическими функциями, которые в дальнейшем ока-
окажутся полезными:
а — (г2 + а2) со - а Ар2/22,
1 — <ш sin2 0 = (г2 + а2) р2/22. A37)
а. Тетрадные компоненты тензора Римана. В принципе
нетрудно подставить различные метрические коэффициенты мет-
метрики Керра в выражения, выписанные в уравнении C), и полу-
получить компоненты тензора Римана. Вычисления можно упростить,
заметив прежде всего, что помимо равных нулю компонент, при-
приведенных в формулах D), и циклического тождества
^1230 + ^1302 + ^1023 = 0 A38)

54. Вывод метрики Керра 21
имеются еще следующие соотношения, которые являются след-
следствием равенства нулю тензора Риччи:
А*1213 — A3002I A*i330 — А*122(Ь
А0202 ~ А1313» А0303 == А1212» A«^)
^2323 = А*Ю10 = А*0202 ~Ь А*0303-
Выпишем далее производные различных метрических функций
М>2, е = — a2 sin Э cos 9/р2 = \x3i е; [х3, 2 = Г^Р2\
(V* + |Аз), 2 = 2г/р2 — (г — М)/А; (\х2 + jx3), е =
= —2а2 sin 0 cos 9/р2;
ф, 2 - [2г (г2 + а2) — а2 (г — М) sin2 0 ]/22 — г/р2 -
= -v, 2 + (г - М)/А;
i|>, е = ctg 6 + а2 A/р2 — А/22) sin Э cos Э =
- —v, з + ctg Э;
ф, 29 = 2а2 {-(г - М)/22 + (А/24) [2г (г2 + а2) -
— а2 (г — М) sin2 Э ] — r/p4} sin e cos 0 - —v, 2б;
i|>, ее = —cosec2 Э — а2 A cos 20/22 —
—2а4 A2 sin2 Э cos2 9/24 + а2 cos 20/р2 +
+ Ы sin2 Э cos2 9/р4 = —V, ее — cosec2 9;
@> е = +4а3Мг A sin 9 cos 9/24;
со, 2 - —2аМ [(г2 + а2) (Зг2 — а2) —
— а2 (г2 — а2) sin29]/24. A40)
Теперь нетрудно получить следующие формулы:
#102з = - [(AS)>/2/4рУ] (X, 3У, 2 - X 2У, 3) -
- —аМ cos 9 (Зг2 - а2 cos2 9)/р6 - -(/?la80 + #iso2)>
^12зо - ^1302 = B2 sin 9/2р4) [-со, г (\х2 + |х3), е -
- со, е (|х2 + Из), г + е-4%4гЧ r/sin 9), е sin 9 +
+ в^ (е^со, е/А sin 9), r A sin 9] =
= — 3 (аМ cos 9/р6) (Зг2 - a2 cos2 9) 2~2 [(г2 + а2J + а2А sin2 9],
#2323 =(Д1/2/Р2)[Кз/Д1/2),8 + (И8,2А1/2),2] =
- Mr (г2 - За2 cos2 9)/р6 = R02Q2 + Яозоз - -Rmw,
= —2 (Мг/р6) (г2 - За2 cos2 9) (ЗаД'/2/22) (г2 + a2) sin 9,

22 Глава 6. Метрика Керра
2#шз = (A'/V) ГCф + v), 32 + Зф, Зг[>, 2 + v, ,v, 2 -
— (Ц + v), гИ-2, з — (Зф + v), зИз, г 1 =
= —2 (аМ cos 0/р6) (Зг2 — а2 cos2 9) (За Д1/2/^2) (г2 + а2) sin 9,
3#шз — #зозо = ег^ Щ, зз + v, зз + 3 (г|>, 3J + (v, 3J -
- (Зф + v), з[х3, з1 + в11' Cip + v), 2ц3> 2 =
= —(Мг/р6) (г2 — За2 cos2 9) 2~2 [5 (г2 + а2J + а2 А sin2 9 ]. A41)
Наконец, с помощью соотношений A38) и A39) получаем
#Ю23 = —аМ cos 9 (Зг2 — a2 cos2 9)/pe,
#12зо = — (аМ cos 9/р6) (Зг2 — a2 cos2 9) 2'2 [(г2 + а2J +
+ 2а2 A sin2 9],
#1302 = _|_(ам cos 9/р6) (Зг2 — a2 cos2 9) 2 [2 (г2 + а2J +
+ а2 A sin2 0],
—#зоо2 = #i2i3 = —{аМ cos 9/pe) (Зг2 — а2 cos2 9) х
X (За Д»/2/22) (г2 + а2) sin 9,
-#i22o = #1ззо = -(Мг/р6) (г2 — За2 cos2 9) (За А'/2/22) х
X (г2 + а2) sin 9,
-#юю = #2323 = +(Мг/рв) (г2 — За2 cos2 9) = Я0202 + Я0303,
—#1з13 = #0202 = +(М/7р6) (г2 — За2 cos2 9) 2 х
X [2 (г2 +а2J +а2 A sin2 9],
-#i2i2 = #о3оз = -(Mr/p6) (r2 — За2 cos2 9) 2 х
X [(г2 + а2J + 2а2 A sin2 9]. A42)
Замечаем, что не равные нулю компоненты тензора Римана
становятся сингулярными только при 9 = я/2 и г = 0; следо-
следовательно, это единственная сингулярность пространства-вре-
пространства-времени Керра.
55. Единственность метрики Керра;
теоремы Робинсона и Картера
Мы видели, что метрика Керра, заданная на стационарном
аксиально-симметричном асимптотически плоском пространстве-
времени, обладающем выпуклым гладким горизонтом событий,
характеризуется только двумя параметрами — массой М и мо-
моментом количества движения (/ = аМ). Единственность метрики
Керра для описания черных дыр следует из теоремы Робинсона,

55. Единственность метрики Керра 23
которая гласит: стационарные аксиально-симметричные реше-
решения уравнений Эйнштейна в пустоте, имеющие гладкий и выпук-
выпуклый горизонт событий, являющиеся асимптотически плоскими и
регулярными вне горизонта, однозначно определяются заданием
двух и только двух параметров — массы и момента количества
движения.-
Доказательство теоремы Робинсона основано на использо-
использовании тождества (см. уравнение A56) ниже), которое выводится
из уравнений (ср. с уравнениями (80) и (81)):
Е = 0, F = 0, A43)
где
Е (X, У) = [(л2 - 1)Х, Ц/Х), л + ft* - 1) У! ,Д2 +
+ [A-^)Х^/Х],^ + A-^)Г^/Х2, A44)
F (X, У) = [(л2 - 1) У, ,/*2], ч + [A - И2) У, »1Х\ »¦ A45)
Напомним, что при выводе уравнений (80) и (81) мы исполь-
использовали калибровочный произвол, чтобы горизонт событий соот-
соответствовал значению rj = 1. Кроме того, из выражений A44)
и A45) для операторов Е и F ясно, что если (X, У) представляет
решение уравнений, то (сХ9 сУ), где с — произвольная действи-
действительная постоянная, также будет их решением. Следовательно,
не теряя общности, мы можем предположить, что интересующие
нас решения X имеют на бесконечности одинаковое асимптоти-
асимптотическое поведение (ср. с уравнением (85))
X -+ A - [г2) Л2 + О fa) (Л -* оо). A46)
Это ограничение на решения эквивалентно рассмотрению решений
с одинаковой массой.
Соответствующие асимптотики для Y имеют вид (ср. с уравне-
уравнением (86))
У -+2J\i C -\i2) +0 (rf1) (л -+ оо), A47)
где J—момент количества движения.
Помимо того что решения X и Y должны обладать асимптоти-
асимптотиками A46) и A47), в соответствии с условием, чтобы пространство-
время было асимптотически плоским, потребуем, чтобыX и Убыли
гладкими и регулярными на оси ([г = ±1) и на горизонте (л = 1),
а также были регулярными вне горизонта (л > 1). Казалось бы,
можно найти |несколько решений с одинаковым значением У,
удовлетворяющих вышеприведенным требованиям. Теорема Ро-
Робинсона утверждает, однако, что для каждого значения J су-
существует не более одного решения. Доказательство проводится от
противного: если существуют два решения (Хь Yx) и (Х2, Уа)
для одного значения У, то они должны совпадать.

24 Глава 6. Метрика Керра
Предположим, что существуют два решения (Хъ Уг) и (Х2, Y2)f
принадлежащие одному и тому же значению У, и, следуя Робин-
Робинсону, рассмотрим функционал
00 1
R = j J [(Хг/Х2) (У2 ~ YJ F (Хъ YJ +
1 -1
+ (Х2/Х0 (Y1 - У2) F (X2, Y2) +
+ A/2Х,Х2) [(У2 - У,J + (Xl - X2)] Е (X,, К,) +
+ A/2Х,Х2) [(Y2 - У,J + (X2 - ХШ Е (Х2, Y2)) их] dfx. A48)
Вследствие уравнений, которым удовлетворяют пары (Xi, Yi)
и (Х2, Y2), функционал R должен тождественно равняться нулю.
Мы, однако, покажем, что единственно в силу определений опе-
операторов Е и F и граничных условий, наложенных на решения,
функционал R может быть сведен к интегралу от положительно
определенного выражения. Приведение функционала к такому
виду опирается на два элементарных алгебраических тождества,
составляющих содержание следующих лемм Робинсона.
ЛЕММЫ РОБИНСОНА:
I.
[Х2 (Y2 - У,) YU1] + X, (Х,Х2>Т1 - Х2ХЬ ,) ]2 +
?) [X! (Y2 - У,) Y2.n + X2 (X,X2ll1 - X.X,,,,)]2 =
= A/2Х?Х2)(У2-У1J(У1,г1)
2
+ A/2Х1Х^)(У2-У,J(У2,Г1J +
+ (UX\Xt) (У2 - Ух) (У2 + УО. ч (ХхХ,, ч - Х,ХХ, „). A49)
II.
?|) [(Х2 + X,) (X,r2tT1 - X2YUr]) -
-(У2-У1)(Х1Х2,Т)+Х2Х1,Л)Р +
|) [(Х2 - Xi) (Х,У2.г, + Х2У1>Т1) —
(У2 - YJ (ХХХ2) „ + Х2Х!, „) ? =
i) (У2 - У,J (Х,Х2>Л + Х2Х,1Г1J -
- A/X\XI) (Y2 - Yi) (У2 - У,), „ (Х,Х2, п + Х2Х,,,) +
+ (V2XUD {(xi + xi) x
x[Xj (У2>Г1J + Xi (УЬг,J] - 4Х2Х|У,,11Уг.Г1}. A50)

55. Единственность метрики Керра 25
Два других тождества получаются заменой производных по х\
производными по [х.
Поскольку производные по г\ (г]-члены) и производные по \л
(jx-члены) входят в выражения для ?и^и, следовательно, в функ-
функционал R, совершенно симметрично (если не считать замену мно-
множителя (г]2 — 1) множителем (\i2 — 1)) проведем выкладки только
для г]-членов. Ясно, что для [г-членов получится аналогичный ре-
результат.
В функционале R проинтегрируем по частям те члены, в ко-
которых в качестве множителя стоит функция F. Что касается чле-
членов с функцией Е в функционале, то проинтегрируем по частям
только те слагаемые, в которые множителем входят выражения,
взятые в квадратные скобки в определении функции R (ср. с урав-
уравнением A44)). Проинтегрированные г]-члены имеют следующий
вид:
(г]2 - 1) {(Y, - Г2), ч (К, - Yx) +
+ A/2ХЛ) [(У2 - Yxf (X2XljT1 + ХхХг, ,) +
+ {Xl - Х\) (Х2Х{, л - XiX2, л) 1) =
- V, (г]2 - 1) {- A/ХгХ2) [(Y2 - Y{))\ +
+ A/X\XI) (Y2 - Yxf (X2XU л + X,X2i л) +
i) (Xl - Xl) (X2Xi., - XiX2. л)} =
U. A51)
Объединяя их с подобными же членами, появляющимися при
интегрировании по частям [г-членов, имеем
1
Вследствие требований гладкости функций X и Y на горизонте
и на оси значения выражений в фигурных скобках, вычисленные
на оси (|х = ±1) и на горизонте (ц = 1), равны нулю, а требуе-
требуемое асимптотическое поведение A46) и A47) решений на беско-
бесконечности приводит к тому, что
A53)*
* В действительности эти члены имеют порядок О (п~5), если принять во
внимание член порядка О (г\ х) в уравнении A46) (ср. с уравнением (85)).

26 Глава 6. Метрика Керра
Следовательно, поверхностный интеграл A52) равен нулю.
Оставшиеся после интегрирования по частям г]-члены в объем-
объемном интеграле с точностью до множителя (ц2 — 1) равны
(l/2X?X2) [(У2 - У,J + Х% - X2] (У, „J
+ х2 - xi] (Y2,11J - (yu ,,/х2) [(x,/x2) (Y2 - у,)], „
_(Х1,Г1/Х,)К1/2Х1Х2)[(У2-У1)Чх1-Х2:]),Т)
n/xi) [(х2/х,) (у2 - к,)]. „ -
-(Х2. V^2) {A/2X,X2) [(У2 - У,J + X? - Xi]}, „ =
= A/2Х?Х2) (У2 - Г,J 0Y лJ + 0/2X2%) (У2 - Г,J(Г2,,/ +
+ A/Х,Х2) [(Г2 - Г,), „]2 + A/Х2Х°2) (Y2 - Г,) (Г2 + Г,). „ х
х (х,х2. „ - х2х,, ч) - (l/xfxl) (у2 - г,) (г2 - у,), т, х
Х(Х2Х,, ч + Х,Х2, ^) - A/Х?Х!) (Х,Х,, „ - Х2Х2, ,)х
X(Х,Х2, л - Х2Х,. „) + A/2Х?Х|) (Xf - X2) {Xl[(X,. „J +
+ (rI.11J]-xH(x2,tlJ+(y2,riJ]} +
|) (У2 - Y{f (X,X2> „ + Х2Х,. „J. A54)
Замечаем, что некоторые члены в правых частях уравнений A54)
и A49) (лемма I Робинсона) являются общими. Исключая их,
находим после некоторых перегруппировок
A/2Х?Х|) [Х2(У2 - У,) У,, „ + X, (X,X2, „ - Х2Х,, „)]2 +
i) [X, (У2 - У,) У2, „ + Х2(Х,Х2, „ - Х2Х,, ч)]2 -
? (Х2, ,J + Xl (X,, riJ -
- 2XlX3Xi.riX2, „] + A/X,X2) [(У,, лJ + (У2, ,J - 2YX, ,У2,,] -
- A/Х2Х22) (У2 - У,) (У2 - У,), л (Х2Х,. „ + Х,Х2, „) -
- (l/X\Xl) ((X2 + XI) X,, „Х2, ч - Х,Х2 [(X,. nf + (Х2, лJ]) +
+ (l/2X?Xi) (У2 - У,J (Х2Х,, „ + Х,Х2. ,J +
-f A/2X?X|) (Xl - X2) {Х^ [(X,. ,J + (У,, ,,J] -
?11J + (УГ2.Т1J]}. A55)
Многие члены в 3, 4, 6 и 8-й строках сокращаются, а оставшиеся
в точности равны членам в правой части уравнений A50), состав-
составляющего содержание леммы II Робинсона. Таким образом, г)-
члены в подынтегральном выражении с точностью до опущенного
нами множителя (ц2 — 1) равны положительно определенным

55. Единственность метрики Керра 27
выражениям, входящим в тождества лемм Робинсона. Подобный
же вклад в подынтегральное выражение дадут и ji-члены. В ре-
результате получаем
00 -fl
J J Aг1с1иA/4Х^)[(г,2-1)B[Х2(Г2-У1)Г1,Г) +
1 -1
+ x1(x1x2)T)-x2x1,T))F +
+ 2 [Хг (r2 - y,) y2, „ + x2 (XtX,, „ - ад,/ +
, „ - Х2УМ) - (У2 - У х) (ХгХ2> „ + X2Xh „)]« +
- Xj) (Х,У1# „ + XxYt, „) - (Ka - КО x
+ XtXuJ?\ + A - И2) |2 [X2 (F2 - Ух) r1)lt +
- X2Xl5 / + 2 [Xx (Г2 - Yj) Г2) № + X2 (ХД2, ц -
)> + [(X2 + X,) (X^ - XaYuJ - (Y2 - Yi) X
+ X2Xb д)]2 + [(X2 - Xt) (X^, № + X,Y2, J -
- (F2 - УО (Х!Ха, ц + ХЛ, д)]2}] = 0. A56)
Из уравнения A56) следует, что каждое из восьми положительно
определенных выражений, стоящих под знаком интеграла, должно
быть тождественно равно нулю. Следовательно,
(Уа - У0 (Х,Х2, а + XtXlt а) = (Х2 + Хг) х
X (ХхУ,, .- Х2ГЬ „) = (Х2 - Хх) (Х2УЬ e + X,Y2, a), A57)
^2 (^2 — ^l) ^1, а — —^1 (^1^2, а — ^2^1, а)»
П) ^2, а - -Х2 (XA, а - Х2Хи а), A58)
где а = т), (х. Равенство двух выражений в правой части уравне-
уравнения A57) требует, чтобы
X2iY2.a = XlYUa. A59)
Используя этот результат, находим, что равенство первых
двух выражений A57) дает
х,х2 (к2 - Y1)t а - (к2 - yx) (ад а +х2хи а) - о
(а = л> р). A60)
Уравнение A60) можно переписать и в другом виде
[(Г2 - rj/XAl, а = 0 (а = т|, |i). A61)
Поскольку функции Y± и Y2 равны в асимптотике при г\ -> оо,
из уравнения A61) следует
Га = Yx. A62)

28 Глава 6. Метрика Керра
Из уравнений A58) (любого из них) следует теперь
(Xi/X2),« = 0 (а = т|, V). A63)
И снова из равенства асимптотик Хг и Х2 при ц -> оо получаем
Х1 = Х2. A64)
Отсюда следует единственность решения для заданных значений
М (вследствие выбранной нами нормировки решений) и J.
Поскольку метрика Керра удовлетворяет граничным условиям
теоремы Робинсона и представляет собой решение для данных зна-
значений М и J (<М2), следовательно, это единственное решение
для заданных значений М и J. Другими словами, открытие Керра
дало доказательство существования решения, удовлетворяю-
удовлетворяющего требованиям теоремы Робинсона!
Представляют интерес два специальных случая тождества
Робинсона A56).
Рассмотрим сначала случай «близколежащих решений» (X, Y)
и (X + 6Х, Y + б У), т. е. квазистационарные аксиально-сим-
аксиально-симметричные возмущения, оставляющие неизменными массу и мо-
момент количества движения. Считая 6Х и б К величинами первого
порядка малости (какими и надлежит быть возмущениям!), полу-
получим, линеаризуя уравнение A56), следующее тождество:
dt] dfx A/X*) {(n2 - 1) [(X,,6X -Yt1i6Y- X6X,„)» +
+ (X. „6Г + Y, 46X - Х6Г, ,J + (X, Л6Г - Y, „6X)«] +
+ A - ц2) [(X, ибХ - У, Ц8Г - ХбХ, „J +
(X, №бГ + Y, ^6Х - ХбГ, цJ + (X, цбГ - Г, ^6ХJ]} = 0, A65)
которое эквивалентно тождеству, впервые полученному Карте-
Картером. Из уравнения A65) следует (так же как и при доказательстве
теоремы Робинсона), что
6Х = 0, 8Y = 0. A66)
Другими словами, в решении Керра не существует квазистацио-
квазистационарных и аксиально-симметричных возмущений, при которых
масса и момент количества движения оставались бы неизменными.
Это утверждение можно выразить и иначе: вдоль последователь-
ности решении КерРа не может быть точек бифуркаций. Послед-
Последнее утверждение составляет содержание теоремы Картера, ко-
которая была доказана до того, как Робинсои получил общий ре-
результат,

56. Описание в формализме Ньюмена—Пенроуза 29
Рассмотрим теперь случай невращающейся черной дыры,
когда Y = 0. Тождество Робинсона в этом случае сводится к вы-
выражению
oo-f-l
J J [(r12-l)(X1X2iT1-X2X1,^ +
I -1
+ A - |i2) (X{X2, » - X2XU J] [(XT + Xl)/XUl] dridfi = 0, A67)
где Хг и Х2 — два решения для одной и той же массы. Отсюда
следует, что
Хх = Х2. A68)
Другими словами, в предположении аксиальной симметрии
невращающаяся черная дыра определяется однозначно зада-
заданием массы. Этот результат, но без предположения об аксиаль-
аксиальной симметрии, является содержанием теоремы Израэля, которая
гласит: метрика Шварцшильда является единственным решением,
описывающим невращающиеся черные дыры.
56. Описание пространства-времени Керра
в формализме Ньюмена — Пенроуза
Описание пространства-времени Керра в формализме Нью-
Ньюмена— Пенроуза начнем с построения изотропной тетрады. В гл. 7
(§ 636) будет показано, что в пространстве-времени Керра су-
существует простой класс изотропных геодезических, касательные
векторы к которым равны
? , ъ=±Е> 1Г = 0' -ё-=(а/Л)Я. 069)
где Е — постоянная. Выберем действительные изотропные век-
векторы 1 и п вдоль этих геодезических и добавим к ним комплекс-
комплексный изотропный вектор т, такой, что он ортогонален к векто-
векторам 1 и т. В результате получим следующий базис:
/< = A/А) (г2 + a2, +A, 0, а),
п* = A/2р2) (г2 + а2, —Л, 0, а), A70)
т1 = A/р/2) (ш sin 0, 0, 1, i cosec 0),
где
р = г + w cos 6, р* = /- —iacose. A71)
[К сожалению, буква р используется для обозначения различных
величин: как спиновый коэффициент в выражении р2 = г2 +
+ a2 cos2 0, и теперь еще как р и р*. Чаще всего это не будет вы-
вызывать недоразумений, но в некоторых случаях нам придется
различать спиновый коэффициент и величины, определенные урав*

30 Глава 6. Метрика Керра
нением A71). Поэтому спиновый коэффициент в таких случаях мы
будем обозначать р. Но р2 всегда будет обозначать р2 = г2 +
+ a2 cos2 в.]
Вектор 1 имеет аффинную параметризацию в отличие от век-
векторов пит, которые параметризованы так, чтобы удовлетворить
требуемым условиям нормировки
Ьп = 1, mm = - 1. A72)
Ковариантные компоненты базисных векторов равны
/. = A/Д)(Л, -р2, 0, -a A sin2 0),
щ = A/2р2) (Д, +р2, 0, —a Д sin2 0), A73)
mt = (l//2p) (m sin 0, 0, —p2, —i (r2 + a2) sin 0).
Спиновые коэффициенты, определяемые уравнениями B86)
гл. 1, в выбранном нами базисе удобнее всего вычислить с по-
помощью Я-символов (гл. 1, уравнение B65)). Отличные от нуля
^-символы равны
^122 = —[(/•- М) р2 - г Д 1/р4, Я243 - — А/2р2р,
^132 = + \/~2iar sin 0/р2р, ^324 — —^ A C0S 9/р4,
A74)
Ji134 = —2ш cos 07p2, ?i334 = +{ia + r cos0) cosec 0/т/"р2,
^2i3 = — К2а2 sin 0 cos 0/р2р, ^34i = —1/р-
Для спиновых коэффициентов получаются следующие выражения:
х = а — ^ = v — e = 0,
р = —1/р*, р = ctg 0/2/2"p,
л = ш sin 0//2 (р*J, т = —ia sin 0//2p2, A75)
ц = —Д/2р2р*, у = р + (г — М)/2р2, а - л — р*.
Равенство нулю спиновых коэффициентов х, аД и v показы-
показывает, что конгруэнция изотропных геодезических 1 и п бессдви-
бессдвиговая. Из теоремы Гольдберга—Сакса теперь следует, что про-
пространство-время Керра принадлежит к типу D по классифика-
классификации Петрова.
Из теоремы Гольдберга—Сакса следует также, что в выбран-
выбранном нами базисе вейлевские скаляры Wo, tplt Y3 и ?4 равны нулю.
Это можно проверить и прямыми вычислениями, свертывая не
равные нулю компоненты тензора Римана, перечисленные в урав-
уравнениях A42), с векторами 1, n, m и m в соответствии с определе-
определениями этих скаляров.

56. Описание в формализме Ньюмена—Пенроуза
31
Поскольку в уравнениях A42) компоненты тензора Римана
приведены в тетрадном базисе, удобно выразить и базисные век-
векторы через тетрадные компоненты, подвергнув их преобразованию
ё* О О О
- со^ е'Ф О О
О 0 е^ О
О 0 0 е**
Находим
) = \ev (г2 + а2)/А,
= \ev (r2 + а2)/2р2,
А/222,
A76)
0},
0},
т<»> = (teva sin 9//2р,
(r2 + a2)/(/2p22sin0), 0, gn./i/2p}.
A77)
При вычислении были использованы соотношения A37).
Используя вышеприведенное представление базисных векторов
и уравнения D) и A39), получаем, например,
— % = RVQrslPm4rms =
pqrs
#2020 [(l2m0J - (№)*] + 2Я1330 [(I2J m°ml - (m8J Z0/1]
2/?зоо2 [I4°mo/n3 + I4lmlm?] + 2#23
+ 2R2ml4°m1m3 + 2Rm
= (P4/Ap2) {- #0101 + I(r2 + a2J/22] #озоз -
- (a2 A sin2 6/22) ?0202 _ [Ba A'/2/22) (r2 + a2) sin 9] #1330j +
+ (Ф4/АР2) |+ #2301 + 1(Г2 + a2J/2*] #2!03 +
+ (a2 A sin2 9/22) ^2013 + {Ba A'/2/22)(r2 + a2) sin 9] #3002|. A78)
Подставляя теперь компоненты тензора Римана из уравнения A42),
находим
% = 0, A79)
что и требовалось доказать. Подобным же образом проверяется
равенство нулю вейлевских скаляров Ть W3 и 4V
Значение единственного не равного нулю вейлевского ска-
скаляра ^ можно получить свертыванием тензора Римана с соот-
соответствующими векторами изотропного базиса согласно опреде-
определению. Получаем при этом
= Rpgr,lpmfnrjh* =
= #
0101
#
озоз
m
112]
n°ihl -
#
- Z2n21 m812]
0202
m°
- Pn1

32 Глава 6. Метрика Керра
+ #1ззо [12п2 (т1т° + rhltn°) - (/Vz° + /W) | т312] +
+ #зоо2 [l2n°m°m3 + l°n2tn°m3 + l2nlmlm3 + IWmW] +
+ #23oi [/2m3 (Az°mx - /Лп0) + д2т3 (^m1 - Pm0)] +
+ #2103 [l2n°mlm3 + IWm1!?!3) + #2013 [lln2m3m° + 12пгт3т°] =
= V2 I + #0101 + [(/* + fl2J/S2J #0303 - (a2 A sin29/23) #0202 _
- [Ba Д»/2/22) (Г2 + a2) sin 9] /?1330} +
+ (f/2) {~ #2301 + [(/* + ^)/22] #2i03 +
+ (a2 A sin29/22) R20l3 + [Ba A1/2/^2) (r* + a2) sin 9] R3m\ =
= - (Mr/p6) (r2 -- 3a2 cos2 9) - (iaM cos Э/р6) C/-2 - a2 cos29) =
= - Af/(p*K. A80)
На этом мы закончим описание пространства-времени Керра
в формализме Ньюмена — Пентроуза, продемонстрировавшее, что
эта метрика является алгебраически специальной.
57. Метрика в форме Керра—Шилда
Способ вывода метрики Керра, описанный нами в § 52—54,
отличается от использованного Керром в оригинальной работе.
Керр искал решения уравнений Эйнштейна специального вида,
пригодного для описания алгебраически специальных много-
многообразий. Эта форма метрики в настоящее время называется фор-
формой Керра—Шилда и имеет вид
где г\ц — метрика плоского пространства-времени, а 1 — изотроп-
изотропный по отношению к этой метрике вектор. Метрика Керра при-
принадлежит к этому классу. Оказывается, именно в форме Керра—
Шилда наиболее явно проявляется структура пространства-
времени Керра. Исследованию структуры пространства-времени
Керра мы предпошлем доказательство того, что метрика вида
A81) с необходимостью принадлежит к типу 11 по классифика-
классификации Петрова. В дальнейшем изложении мы следуем Ксантопу-
лосу.
Сначала некоторые предварительные замечания.
Рассмотрим многообразие, на котором заданы две метрики
gil и g'ij. Пусть V/ и V't — операторы ковариантного дифферен-
дифференцирования относительно каждой из метрик. Для ковариантного
вектора ^, определенного на многообразии, должно существо-
существовать соотношение вида
V& - Vilj - СГД«, , A82)

57. Метрика в форме Керра—Шилда 33
где коэффициенты С") обладают всеми свойствами симметричной
связности. Например, должно выполняться соотношение
it j = \il j — Lijl rn-f-Liml i A00)
для тензора Т) типа A,1). С помощью этих формул можно найти
связь тензоров Римана, вычисленных для каждой из двух метрик
(использовав при этом тождество Риччи):
= 2V[(- (VnU - Cl k\m) -
- 2Cn[in {Vnlk - Cmnk\m) - 2CI lt (Vnln - C% a\m). A84)
После некоторых упрощений (используя симметрию коэффициен-
коэффициентов С™ по индексам i и /) получаем соотношение
R'mm = Яф - 2V[*C?j k + 2Cnk yCJl я. A85)
Соответствующее выражение для тензоров Риччи получается
сверткой:
R'th = /?,л - 2Vt^] л + 2С1 [t-C] n. A86)
При исследовании метрики Керра—Шилда A81) мы будем
отождествлять нештрихованную и штрихованную метрики в пре-
предыдущих формулах с метриками
% и gij = r\ij + liljy A87)
где, как уже говорилось, lt — изотропный вектор относительно
метрики r\ijy т. е.
/' = т|% /'/| = 0. A88)
Вводя определение
g'/= т)</-/<//, A89)
находим, что
*"*/* = (Ч'7 ~ Щ Ы + ///*) = Ь[. A90)
Другими словами, определенный таким образом тензор gll дей-
действительно является контравариантной формой тензора gtj. Более
того,
= 1'. A91)
Следовательно, индекс изотропного вектора может подниматься
и опускаться как с помощью тензора ц, так и тензора g. Отсюда
следует, что вектор 1 является изотропным и по отношению к мет-
метрике g. (Однако в общем случае поднятие и опускание
осуществляется только метрикой ц.)
2 Чандрасекар С, т. 2

34 Глава 6. Метрика Керра
Ниже мы получим явное выражение для связности С/7}. По-
Поскольку оператор Vi определен через символы Кристоффеля,
вычисленные на основе метрики gtj,
0. A92)
Но это же выражение можно вычислить и с помощью уравне-
уравнения A83). Имеем
Vjgik = Vigjk - CTjgmk ~ C%gim = О- A93)
С другой стороны,
Vjfoft = V, (ън + W = Vj (W- A94)
Следовательно,
Vt- (l;lk) = Cjfem* + Cftg/«. A95)
Из последнего выражения получаем (точно так же, как полу-
получаются выражения для символов Кристоффеля из условия ра-
равенства нулю ковариантной производной метрического тензора)
= 72 [V/ (Ijk) + V/ (lkh) - Vk (Ittj)]. A96)
Свертывая последнее соотношение с тензором gkn, имеем (вслед-
(вследствие соотношения A90))
С?] = V* (Л*" - Л") IV/ (Ijlk) + V/ </*/*) - Vft (/,/;•)]• A97)
Это соотношение можно несколько упростить, если вспомнить,
что вектор 1 изотропный:
С?, = V. [V/ (//Г) + V/ (Цп) - Vn (lilf) + lnlk Vk (Щ]. A98)
Свертывая уравнение A98) по индексам п и /, получаем
С% = 0. A99)
Подобным же образом находим
КСЪ = - Va/« V" (/,-//) - - V. (*А Vя// + ///„ Vя/,), B00)
iic?i = 42(iniivJi + iiiiv<n- B01)
Определив вектор X соотношением
Xj^l'Vtlj, B02)
можно переписать соотношения B00) и B01) следующим образом:
ОД = - Va </*Х7 + //X,), l'C?j = + V2 (/"X, + l,Xn) ¦ B03)
Кроме того, должно выполняться равенство
UXj = 0. B04)

57. Метрика в форме Керра—Шилда 35
Предположим теперь, что метрика gtj является решением
уравнений Эйнштейна в пустоте. Тогда тензор Риччи R\j дол-
должен быть равен нулю. Но тензор Rtj также равен нулю, по-
поскольку метрика г\и по предположению есть метрика плоского
пространства-времени. Поэтому вследствие уравнения A86)
должны выполняться следующие равенства:
О = — 2V[iCm] k + %Ck[iCm] n = ~' S/iCmk + S/mCTk + CfcjCmn ~~
- CnkmCTn = VmC?k - CIA B05)
где для получения окончательного ответа было использовано
уравнение A99). Свертывая теперь уравнение B05) с тензором /'/*
и используя соотношения B03) и B04), получаем
о = - ? [vm (i'c?k) - c?k vJI + (ikcnkm) (ilc?n) =
= - xl4k vm (imxh + xHh) + v, (imx* + /'x») vjt +
+1/4 (inxm + /mx«) (i"Xn + inx») = - v»/*/" vmxft +
+ V2Xi/'" Vm/' = + lUXhlm Vjk + ViXtX' = XtX*. B06)
Следовательно, X — изотропный вектор, и, поскольку он также
ортогонален изотропному вектору I, они должны быть пропор-
пропорциональны. Поэтому можно написать
Xj =*/,, B07)
где ф — некоторая функция пропорциональности. В силу опре-
определения B02) вектора Xj имеем
X1 = l'VilJ = 4>li. B08)
Таким образом, вектор 1 определяет конгруэнцию изотропных
геодезических. Наконец, объединяя уравнения B03) и B07), полу-
получаем соотношения
lnCni} = -Щь 11Спч = +фГг1;. B09)
Вернемся теперь к уравнению A85) и свернем его с тензо-
тензором 1!1т. Поскольку тензор Rij™ равен нулю (вследствие того
что метрика к\ц по предположению является метрикой плоского
пространства-времени), имеем
l4mR'iikm = Vlm (v)C?k - VtCTk + CnkiC% - CnkjC?n). B10)
Легко убедиться, что все члены в правой части, кроме первого,
равны нулю вследствие уравнений B09). Следовательно,
lUmRl/km = Vlm VjCTk = V [V/ (LCTk) - CTk Vjlm] =
= -/' V/ (ФЩ - С%ф1т= - (I1 Vj-ф -f ф2) Ub B11)
2*

36 Глава 6. Метрика Керра
где для получения окончательного ответа мы снова воспользова-
воспользовались уравнениями B09). Поскольку индекс вектора 1 может под-
подниматься и опускаться и метрикой ц, и метрикой g, полученное
соотношение можно переписать в следующем виде:
RijkmVlm =Hltlk9 где Я - -(/''Vj-ф + ф2). B12)
Напомним еще раз, что 1 представляет конгруэнцию изотропных
геодезических.
Из уравнения B12) следует, что
Rum [Л]/'/ - - #/,/[*/„] = 0. B13)
В гл. 1 (уравнение C85)) было дано определение пространства-
времени типа II по классификации Петрова. Нетрудно видеть,
что соотношение B13) в точности совпадает с этим определением,
причем 1 есть главное изотропное направление.
а. Приведение метрики Керра к форме Керра — Шилда. Нач-
Начнем с конгруэнции изотропных векторов ), определенных урав-
уравнением A69). Выбирая Е = 1, получаем
ctt - [(г2 + a2)/A] dl)
dr = dX, d9 -0, dy=(a/A)dl. B14)
Вместо t и ф введем новые переменные
du =dt — [(r2 + a2)/A] dr, dф = dcp — (a/A) dr. B15)
В этих новых координатах изотропная геодезическая выглядит
следующим образом:
/' =@, 1,0,0). B16)
Чтобы выразить метрику через новые переменные, удобно сна-
сначала записать ее в виде
ds2 = (Д/р2) Ш — a sin2 9 dy]2 —
— (sin2 е/р2) [(г2 + a2) dy — a dt]2 — (р2/А) (drJ - р2 (d0J. B17)
Прямая подстановка соотношений B15) теперь дает
ds2 = (A/p2) (du ~ a sin2 в dфJ - (sin2 9/р2) [(г2 + а2) dф - a du]2 +
+ 2dr (du — а dф sin2 9) — р2 (d9J. B18)
Соответствующий метрический тензор имеет вид
(«) (г) (в) (ф)
1 - 2УИг/р2 1 0 2aMr sin2 9/р2
1 0 0 —asin2e
0 0 —р2 0
(gtj) =
2aMr sin2 9/р2 —а sin2 9 0 —I2 sin2 9/р2
B19)

57. Метрика в форме Керра—Шилда 37
Дальнейшей перегруппировкой членов можно привести ме-
метрику B18) к виду
ds2 =[(du + drJ — (drJ — p2 (d9J — (r2 -f a2) sin2 0 ЩJ —
— 2a sin2 Э dr Aф] — B/Wr/p2) (du — a sin2 9 dфJ. B20)
Поскольку ковариантцые компоненты вектора 1 равны
- h -(I, 0, 0, —a sin2 9), B21)
можно записать метрику следующим образом:
ds* = [(d*0J - (drJ — р2 (d0J — (г2 + a2) sin2 9 (dyJ —
— 2а sin2 0 dr dcp] — BMr/p2) /,/, dx1 d*'\ B22)
где
dx° = du + dr. B23)
Теперь покажем, что часть метрики B22), заключенная в ква-
квадратные скобки, представляет метрику плоского пространства-
Времени. Таким образом, мы привели метрику Керра к виду
Керра — Шилда, и, следовательно, тот факт, что метрика яв-
является алгебраически специальной, становится частью ее опре-
определения.
Можно теперь проверить, что подстановки
^ = (rcosq)-f-tf sin (p)sin 9, у = (г sin ф — a cos ф) sin 9,
х2 +у2 = (г2 + a2) sin2 9, z - г cos 9 B24)
Приводят часть метрики B22), заключенную в квадратные скобки,
К виду метрики плоского пространства-времени:
I (dx0J — (dxJ — (dr/J — (dzJ. B25)
Выпишем явный вид метрики Керра в новых координатах. Имеем
а§2 = (^ _ ((kJ _ (dyJ _ (d2J _[2Мг7(л4 + a2z2)] |d*° —
i- l/(r2 + а2) [г (xdx+y dy) + а (х dy — у dx)] — (z/r) dz\2y B26)
где в соответствии с подстановками B24) величина г2 неявно опре-
определяется уравнением
Л4 _ Г2 (^2 +у2 +Z2 _ fl2) _ a2^2 _ Q B27)
Метрика B26) явным образом аналитична всюду, кроме по-
поверхностей
- х* +у* +z* =a2, z -0. B28)
Другими словами, метрика имеет кольцевую сингулярность в пло-
плоскости (ху у). Ниже в § 58 мы исследуем структуру этой сингуляр-
сингулярности подробнее. Здесь же заметим, что Керр в своей оригиналь-
оригинальной статье получил метрику именно в форме B26).

38 Глава 6. Метрика Керра
58. Структура пространства-времени Керра
Необходимо остановиться подробнее на двух вопросах, свя-
связанных со структурой пространства-времени Керра — обсудить
природу изотропных гиперповерхностей и структуру сингуляр-
сингулярности при г = О и 0 = я/2.
Рассмотрим сначала изотропные гиперповерхности, располо-
расположение которых определяется нулями функции Д (г):
Д (г) = г2 — 2Мг + а2 = О, B29)
г = г+ = М + (М2 — а2I/2, г = г, = М-(М2 — а2I'2. B30)
Эти корни действительны, положительны и различны, если а2 <
< Л!3. Будем предполагать, что это неравенство выполнено.
Поскольку
Д >0 при г >г+| г </•_,
Д <0 при г. <r <r+,
ясно, что, как и в случае пространства-времени Рейсснера —
Нордстрема, нужно различать три области:
А при г < rj, В при г_ < г < /-+; С при г > г+. B32)
(Ниже мы увидим, что область А можно распространить на
все отрицательные значения г, даже если область С распростра-
распространяется на все положительные значения г.) Мы увидим, что, как
и в геометрии Рейсснера — Нордстрема, поверхность г = г+
представляет собой горизонт событий, а поверхность г = г„ —
горизонт Коши.
Мы уже указывали, что в пространстве-времени Керра не
равные нулю компоненты тензора Римана (перечисленные в урав-
уравнениях A42)) расходятся только при г = 0 и Э = я/2 и что это
единственная сингулярность геометрии Керра. Поскольку рас-
расходимость на поверхности г — 0 появляется только при значении
Э = я/2, ясно, что структура сингулярности не может быть
такой же, как структура сингулярности при г — 0 в метриках
Шварцшильда и Рейсснера — Нордстрема. Чтобы понять струк-
структуру сингулярности пространства-времени Керра, нужно прежде
всего устранить произвол, вносимый системой координат (г, 9, ср)
на поверхности г = 0. Этот произвол был устранен выбором
«декартовых» координат (х, у, г) в п. 57, а. В метрике B26), запи-
записанной в этих координатах, величина г2 задавалась неявно урав-
уравнением B27), связывающим координаты х, у и z, причем
х2 +у2 =(r2 +a2) sin2 9. B33)
Поверхности постоянного г являются ссфокуснымн эллипсоидами,
главные оси которых совпадают с осями координат. Эти эллипсо-
эллипсоиды при г = 0 вырождаются в диск
х2 + у2 < a2, z = 0. B34)

58. Структура пространства-времени Керра
Точка (г = 0, 0 = я/2) соответствует, таким образом, кольцу
х2 +у2 =а2, 2 -0, B35)
и сингулярность вдоль этого кольца есть единственная сингуляр-
сингулярность пространства-времени Керра.
Точки внутри кольца B35) имеют координаты г — О, я/2 >
>9>0и0<ф< 2я. Поверхности постоянного 0 пересекают
диск и выходят с другой его стороны, поэтому мы имеем право
распространить область изменения г на все отрицательные
const
(г<6)
<г>0)
Сингулярность
Карта [x,z]
Карта [x',zr]
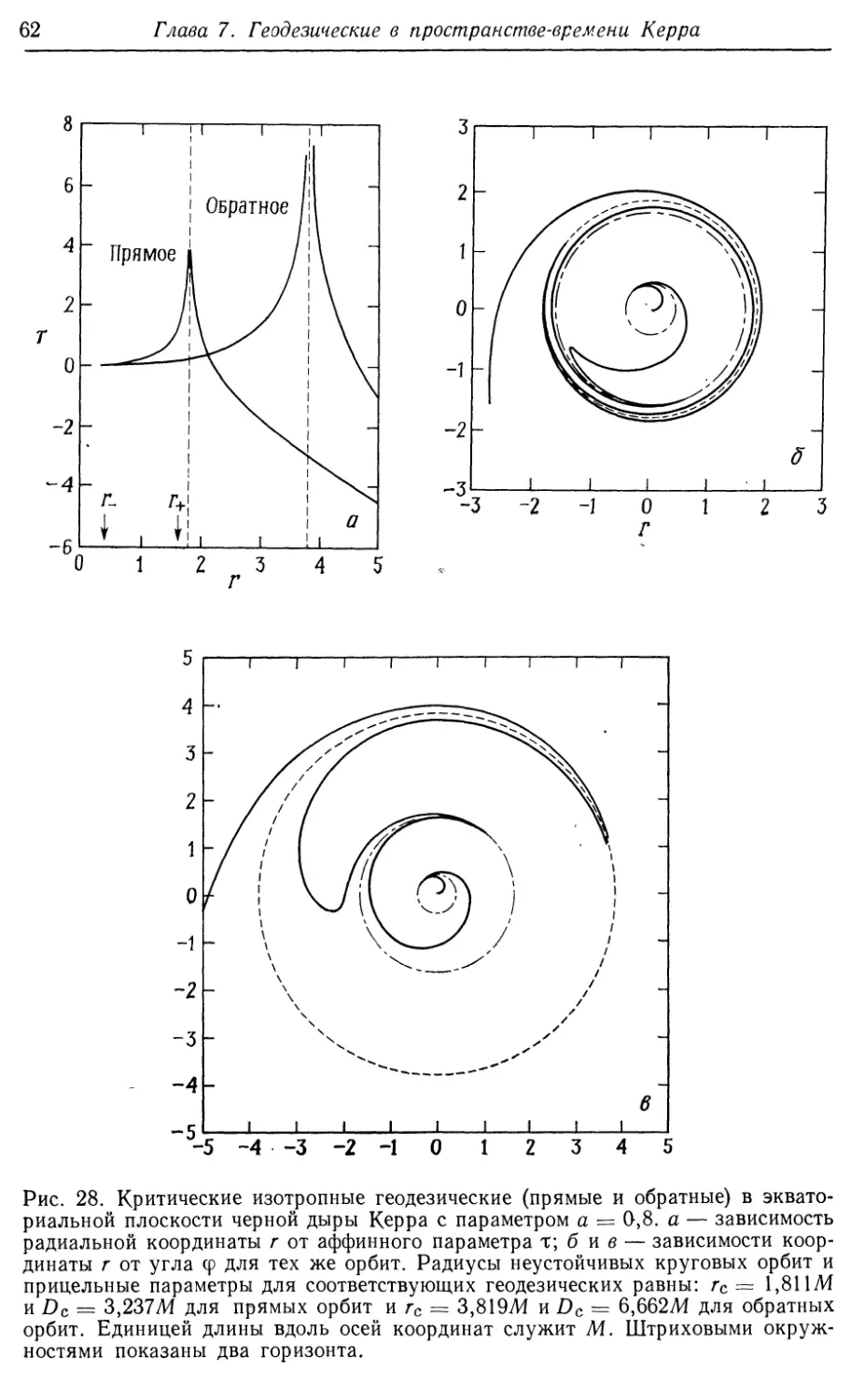
Рис. 25. Кольцевая сингулярность метрики Керра в экваториальной плоскости.
Структура сингулярности проясняется, если метрика записана в «декартовых
координатах» в виде B26), когда кривые постоянного г становятся софокусными
эллипсоидами вращения, а кривые постоянного 6 — софокусными гиперболои-
гиперболоидами. Аналитическое продолжение на все отрицательные значения г получается
приклеиванием к диску (х2 + у2 ^.а2; г = 0) другого диска в карте (*', у\ г')
и соответствующим отождествлением точек, которое описано в тексте и показано
на рисунке. На рисунке показаны сечения у = 0 и у1 = 0 плоскостей дисков.
значения. Другими словами, мы аналитически продолжаем функ-
функцию г, определяемую уравнением B27), на все отрицательные
значения. Мы завершим это аналитическое продолжение тем, что
введем вторую карту (х', у', z') и отождествим точки на верхней
части диска с координатами х и у в карте (х, у, г) с точками на
нижней части диска, имеющими те же координаты, но в карте
(х\ у', z'). Подобным же образом отождествим точки на нижней
стороне диска в карте (х, у, г) с точками на верхней стороне диска
в карте (х', у\ z') (рис. 25). Расширение первоначального много-
многообразия в этом случае аналогично расширению комплексной
плоскости до совокупности римановых поверхностей для пред-
представления аналитических функций, имеющих сингулярности.
В таком расширенном многообразии величина г в области Л,
определенной неравенствами B32), может принимать любые отри-
отрицательные значения.
Метрика B26), продленная на все расширенное многообразие,
имеет в карте (xf, у', z') тот же вид, что и в карте (х, у, z), за исклю-

40 Глава 6. Метрика Керра
чением того, что теперь г принимает отрицательные значения.
Следовательно, в (*', у\ г')-карте члены в фигурных скобках
в метрике B26) появляются с множителем -{-2MrsI(r* -\-a2z2).
При больших отрицательных значениях г пространство снова ста-
становится асимптотически плоским, но с отрицательной массой
в качестве источника.
Займемся теперь устранением координатных сингулярностей
при г+ и г_. Поскольку в пространстве-времени Керра векторы 1
и п, определяющие главные изотропные конгруэнции, не орто-
ортогональны семейству гиперповерхностей, их нельзя использовать
как основу для построения несингулярных координат, как это
делалось при исследовании метрик Шварцшильда и Рейсснера —
Нордстрема. Полезно поэтому поначалу ограничиться рассмотре-
рассмотрением двумерного (г, ^-многообразия вдоль оси симметрии и по-
показать, что природа горизонтов по существу та же, что и в про-
пространстве-времени Рейсснера — Нордстрема, и что многообразие
может быть расширено аналогичным образом.
На оси симметрии при 6=0 метрика Керра сводится к виду
ds2 - (Д/(г2 + a2)) (dt - ((г + а2)/А) dr) (dt + (г2 + а2) dr/Д). B36)
Определяя изотропные координаты
и = f — г*, v = t + л*, B37)
где
г* = J (г2 + а2) dr/Д = г +[D + а2)/(л+ - г-)) In | г - г+ | -
_ [(rL + а2)/(/> - г-)] In | г - г_ |, B38)
получае!М
ds2 =[Д/(г2 + а2)] Аи дп. B39)
Подстановка B37) относится к областям Л и С (ср. с уравне-
уравнениями D6) и D8) гл. 5). В области В величина Д отрицательна,
поэтому следует положить
и - г* +t, v = ^ — Л B40)
При этом метрика принимает следующий вид:
ds2 =[| Д \1{г2 +а2)] du dv. B41)
При таком выборе изотропных координат части многообразия
во всех трех областях могут быть представлены «блоками», изоб-
изображенными на рис. 26. Границы блоков отождествляются ука-
указанным выше образом. Областям Л, В и С соответствуют области
А', В' и С, получаемые из первых преобразованием и ->—и
и v -> —и, «опрокидывающими» световые конусы. Максимальное
аналитическое продолжение (г, ^-многообразия затем получается
склеиванием вместе копий шести блоков без нарушения аналитич-
аналитичности, т. е. так, чтобы края блоков покрывались или (и, л)-картой,
или (и, л)-картой (за исключением углов блоков). Результирующая

=-оо\ t=+oo
/•=-00; f=-oo
Г=Г+У /-=
Овласть Л
Овласть 5
Область С
Рис. 26. Различные области пространства-времени Керра вдоль оси 6 = 0. Объяснение см. в тексте.

42
Глава 6. Метрика Керра
Рис. 27. Максимальное аналитическое продолжение пространства-времени Керра
для 6 = 0 получается путем склеивания блоков, показанных на рис. 26, анало-
аналогично тому, как это было сделано для пространства-времени Рейсснера—Норд-
стрема и показано на рис. 14.
«лестница» показана на рис. 27; она может быть продолжена
бесконечно в обе стороны.
Аналитическое описание максимально расширенного простран-
пространства-времени на оси симметрии может быть получено совершенно
аналогично случаю пространства-времени Рейсснера — Норд-
стрема.
В областях А и С положим
а в области В —
где
tg U = — е~аи, tg V = +e+av,
tg U = +е+аи, tg V = +e+av,
a =(r+-r-)/2D +a2),
B42)
B43)
B44)
а и и v в подстановках B42) и B43) имеют то же значение, что
и в уравнениях B37) и B40). Теперь метрика принимает «уни-
«универсальный» вид
ds2 - —D | Л |/а2) cosec 2U cosec 2V dU dV, B45)

58. Структура пространства-времени Керра 43
где г определяется неявно уравнениями
I g2ar \[ _ [+ I \г _ ,~ -р ^ ^ < ^) B46)
Р = (г! + а2)/D + а2) = г_/г+. B47)
Выбор координатных осей вдоль изотропных геодезических
на рис. 26 и 27 позволяет наглядно представить структуру про-
пространства-времени. Ясно, что разделительная линия г = г+ яв-
является горизонтом событий, а линия г — г_ есть горизонт Коши.
Смысл этих понятий был подробно выяснен в предыдущих главах.
Устранить координатные сингулярности в общем случае еди-
единым образом и в то же время получить максимальное аналити-
аналитическое расширение полного многообразия гораздо труднее. Труд-
Трудности возникают из-за того, что и координата /, и координата ф
проявляют сингулярное поведение по мере приближения к гори-
горизонту вдоль изотропных (или времениподобных) геодезических
(см. § 61). По этой причине простая замена координат, которая
была бы удовлетворительной на обоих горизонтах одновременно,
оказывается неосуществимой и мы вынуждены исследовать гори-
горизонт событий и горизонт Коши по отдельности.
Рассмотрим сначала преобразования координат, которые поз-
позволяют Гладко пересечь горизонт событий.
Начнем с того, что запишем метрику в виде (ср. с уравнением
B17))
ds2 = (А/р2) (dt — a sin2 9 dфJ - (sin2 9/р2) [(г2 + а2) dф — a dt]2—
- (Р2/А) (drJ - р2 (d9J, B48)
и положим, как и выше,
и = / — /*, v = t + r#, B49)
где г* определена уравнением B38). Но вдобавок вместо коорди-
координаты ф введем новую угловую координату
Ф+ - Ф — at/2Mr+, B50)
где индекс « -j- » подчеркивает, что сейчас нас интересует гладкое
пересечение горизонта событий. (Введение новой угловой пере-
переменной, зависящей от того, какой горизонт мы пересекаем, яв-
является существенной особенностью исследований, связанных с про-
пространством-временем Керра.)
Делая замену переменной, получаем
dt — a sin2 9 dф = [p+/(r+ + a2)] dt — a sin2 9 dq)+ —
= [р;/2 (г2 + а2)] {Аи + dv) — a sin2 9 dф+, B51)
где
pl = rl + a2 cos2 9. B52)

44 Глава 6. Метрика Rep pa
Подобным же образом находим
{г2 + a2) dq> - a dt =(г2 + а2) с1ф+ + [а(г2 - г2)/2(г2 + а2)] (da + du),
B53)
dr =[A/2 (r2 + а2)] (du — da). B54)
Подставляя выражения B51), B53) и B54) в уравнение B48),
после некоторых упрощений получаем
ds2 = (Д/2р2)[р4+/(г2 + а2J + pV(r2 + а2J] du dv — р2 (d9J -
— (sin2 e/p2) [(г2 + а2) d9+ + а ((г2 — г2)/2 (г2 + а2)) (du + dv)]2 -
- (а2 A sin2 9/4р2) [Р2/(г; + а2) + Р2/(г2 + а2)] [(г2 - г\)!{г\ + а2) X
X (г2 + а2)] [(daJ + (d^J] + (а A sin2 9/р2) [а sin2 9 d9+ -
+a2)]d9+. B55)
Чтобы включить четыре соприкасающиеся области Г, 1Г, I и II
на рис. 27 в одну координатную окрестность, определим, как
и прежде, новые координаты
tg U+ = — е~а+и = — е-а+*е+а+г*,
tg V+ = fe+a+t; = +e+a+'e+a+r* ' ^
a+ =(r+-rj/2(rj +a2). B57)
Тогда
da = — B/a+) cosec 2f/+ d(/+, dy - + B/a+) cosec 2 У+ d У+. B58)
Подставляя эти выражения для da и dv в уравнение B55), получим
метрику в требуемом виде, причем г задается неявно следующим
уравнением в координатах U+ и V+:
tg U+ tg V+ = —е2^ \r-r+\\r-r_ |-Э+, B59)
где
Р+ = г>+. B60)
Рассмотрим теперь подстановки, необходимые для гладкого
пересечения горизонта Коши:
и =r* +t, v =r* — U B61)
Ф, = Ф — at/2Mr_. B62)
Результирующая форма метрики может быть получена из урав-
уравнения B55) заменой индекса «+» индексом «—», а также da на —d^
и dv на du. Преобразования, аналогичные преобразованиям
B56)—B60), имеют вид
tg U_ = е+а-и = е+а- с-*+о, tg V_ = e+a-v = ^+a- с*-'), B63)
da = B/a.) cosec 2f/. d(/., dy = B/aJ cosec 2K_ dK.,
a_ = (r. - r+)/2 (rl +a2), B64)

58. Структура пространства-времени Rep pa 45
и г определяется неявно через U_ и Vj.
tg ?/« tg V_ = e2<*-' | г — r_ 11 г — r+ |-P-, B65)
где
P. =r+/r.. B66)
Нетрудно проверить, что метрика, записанная в координатах
(?/+, V+) и (?/_, V_), аналитична всюду, кроме точек с сингуляр-
сингулярной кривизной, где величина р2 становится равной нулю.
В гл. 7 будет показано, что в максимально расширенном много-
многообразии все времениподобные и изотропные геодезические имеют
бесконечную аффинную длину (как при продолжении в прошлое,
так и при продолжении в будущее), кроме тех геодезических,
которые обрываются в сингулярности; другими словами, расши-
расширенное пространство-время является геодезически полным.
а. Эргосфера. Помимо принципиального различия в структуре
сингулярностей метрики Керра, с одной стороны, и метрик Шварц-
шильда и Рейсснера — Нордстрема — с другой, есть еще одна
особенность, которая отличает метрику Керра от двух других
метрик. Это различие связано с тем, что в пространстве-времени
Керра в отличие от пространства-времени Шварцшильда или
Рейсснера — Нордстрема горизонт событий не совпадает с по-
поверхностью
gtt =l- 2Мг/р2 = 0, B67)
или в более подробной записи
г2 — 2Mr + a2 cos2 9 = А - a2 sin2 9 = 0. B68)
Внешняя по отношению к горизонту событий поверхность
г = Ге (9) = М + (М2 — a2 cos2 9I/2, B69)
на которой становится равным нулю метрический коэффициент gtt,
называется эргосферой. Она совпадает с горизонтом событий только
на полюсах 9 = 0 и 9 = я.
Эргосфера — это поверхность стационарного предела в том
смысле, что она является внутренней границей области, на кото-
которой мировая линия частицы dt = 0 времениподобна. Этот факт
становится ясным, если посмотреть, к каким следствиям приводит
очевидное требование
<1; B70)
где
(Q _ о) B71)

46 Глава 6. Метрика Керра
есть ф-компонента 3-скорости в ортонормированной тетрадной
системе отсчета, рассмотренной в § 52. Для геометрии Керра
неравенство B70) дает (ср. с уравнением A25))
| Q - со | < ev~^ = р2 Д1/2/22в1/2. B72)
Отсюда следует, что
Qmax - (о ± р2 Д1/2/2261/2 = BaAfr6'/2 4= р2 Д1/2)/^1/2. B73)
min
Тождества A19)—A21) позволяют переписать предыдущее выра-
выражение следующим образом:
д/±аб/
"max = ± г/ о . о\ /л«\1/21 «1/с-> ' (^' V
min l(r + а~) ± a (A6)l/Z] б17"
В частности, снова используя тождества A19)—A21), получаем
_ Л/-^/2 = _ А-аЧ 5
min f(r2 + fl2)fl(A6I/2]61/2 [р2А1/2 + 2а^б1/2]б1/2 ' ^ ^
Поскольку внутри эргосферы
А — аЧ < 0, B76)
заключаем, что
Qmln > 0 B77а)
внутри эргосферы и
Qmm = 0 (r = re (9)) B776)
на самой эргосфере. Этот результат находится в согласии со
сделанным выше утверждением, основанным на равенстве нулю
метрического коэффициента gtt на эргосфере, что эргосфера есть
поверхность стационарного предела.
Тот факт, что внутри эргосферы не может существовать ста-
стационарный наблюдатель, разумеется, не запрещает существование
в этой области (г+ < г < ге (8)) времениподобных траекторий,
которые могут уходить на бесконечность. Эта часть пространства,
таким образом, имеет двустороннюю связь с внешним простран-
пространством. Ниже, в §65, мы увидим, что существование такой конеч-
конечной области пространства между горизонтом событий и поверх-
поверхностью стационарного предела ведет к важным следствиям:
допустимы процессы, например так называемый процесс Пенро-
уза, которые приводят к извлечению вращательной энергии
черной дыры.

Библиографические замечания 47
В заключение выпишем для будущих ссылок выражение для
площади поверхности горизонта событий:
Я 2Я
Площадь поверхности = J j (geegW)r=r+ d9 dcp =
о о
Я 2я
= J j [(sin2 e/p2) ((г2 + a2J - а2 A sin2 9 } 9J/2r+ d0 d<p =
О О
= 4я (г*. + а2) = 8пМг+ == 8л7И Ш + (М2 — а2I'2]. B78)
Библиографические замечания
Керр опубликовал свое открытие в виде короткого письма (датированного
26 июля 1963 г.)
1. Kerr R. P. Phys. Rev. Lett., 11, 237—238, September 1, 1963 и сделал сооб-
сообщение на семинаре несколько месяцев спустя A6—18 декабря 1963 г.):
2. Kerr R. P. In: Quasistellar Sources and Gravitational Collapse, eds. I. Robin-
Robinson, E. Schuking, University of Chicago Press, Chicago, 1965, pp. 99—103.
Несмотря на малый объем, оригинальное сообщение удивительно полно пере-
перечисляет основные особенности решения. Но в этом сообщении нет даже намека
на способ получения решения, который был описан примерно два года спустя
в работах
3. Kerr R. Р.у SchieldA. InrComitato Nazionale per le Manifestazioni Celebrative
Del IV Centenario della Nascita di Galileo Galilei, Atti del Convegno Sulla
Relativita Generale: Problemi Dell'Energia E Onde Gravitazionali, ed. G. Bar-
bera, Florence, 1965, pp. 1—12,
4. Kerr R. P., Schild A. In: Proceedings of Symposia in Applied Mathematics,
17, 199—209, American Math. Soc, 1965.
Однако авторы предупреждают читателя в работе [3], что «вычисления, приво-
приводящие к этим результатам, никоим образом нельзя назвать простыми».
§ 52. Литература, посвященная исследованиям стационарного аксиально-
симметричного пространства-времени обширна; об объеме библиографии можно
судить по обзору
5. Kinnersley W. In: General Relativity and Gravitation, eds. G. Shaviv, J. Rosen,
John Wiley and Sons, Inc., New York, 1975, pp. 109—135.
После написания этого обзора были достигнуты впечатляющие успехи. Но здесь
мы касаемся общей теории лишь в той степени, в какой это необходимо, чтобы
создать основу для простого вывода решения Керра. f%
Хотя уравнения данного параграфа были получены в качестве частных
случаев уравнений гл. 2, они по существу в том же виде содержались в работе
6. Chandrasekhar S., Friedman J. L. Astrophys. J., 175, 379—405, 1972.
Преобразование, названное нами преобразованием Папапетру, описано в ра-
работах
7. Papapetrou A. Ann. d. Physik, F) 12, 309—315, 1953,
8. Papapetrou A. Ann. d'l Iustitut Henri Poincare, Section A, 4, 83—105, 1966.
§ 53. В этом параграфе мы в основном следуем работе
9. Chandrasekhar S. Proc. Roy. Soc. (London), A 358, 406—420, 1978.
Уравнение Эрнста получено в работах
10. Ernst F. J. Phys. Rev., 167, 1175—1178, 1968,
11. Ernst F. J. Phys. Rev., 168, 1415—1417, 1968.
См. также
12. Xanthopoulos В. С Proc. Roy. Soc. (London), A 365, 381—411, 1979.
§ 55. Основные работы, в которых исследовался вопрос о единственности
Пространства-времени Керра, следующие;

48 Глава 6. Метрика Керра
13. Carter В. Phys. Rev. Lett., 26, 331—333, 1972,
14. Robinson D. С. Phys. Rev. Lett., 34, 905—906, 1975.
См. также
15. Carter B. In: Black Holes, eds. C. De Witt, B. S. De Witt, Gordon and Breach
Science Publishers, New York, 1973,
16. Carter B. In: General Relativity — An Einstein Centenary Survey, eds.
S. W. Hawking,*W. Israel, Cambridge, England, 1979, Ch. 6, pp. 294—369.
Доказательство теоремы Израэля (выведенной в настоящем параграфе как спе-
специальный случай теоремы Робинсона при более ограничивающих предположе-
предположениях, чем в оригинальной работе Израэля) приведено в работе
17. Israel W. Phys. Rev., 164, 1776—1779, 1968.
§ 56. Для этого параграфа важной является работа
18. Kinnersley W. J. Math. Phys., 10, 1195—1203, 1969.
§ 57. Пространство-время «Керра—Шилда» было введено в работах [3, 4].
Основные идеи, использованные при изложении, взяты из работы.
19. Xanthopoulos В. С. J. Math. Phys., 19, 1607—1609, 1978.
§ 58. Основные работы по структуре пространства-времени Керра сле-
следующие:
20. Carter В. Phys. Rev., 141, 1242—1247, 1966,
21. Boyer R. //., Lindquist R. W. J. Math. Phys., 8, 265—281, 1967,
22. Carter B. Phys. Rev., 174, 1559—1570, 1968.
Координаты, в которых мы получили решение Керра, часто называют координа-
координатами Бойера—Линдквиста; они были введены в работе [21].

Глава 7
ГЕОДЕЗИЧЕСКИЕ
В ПРОСТРАНСТВЕ-ВРЕМЕНИ КЕРРА
59. Введение
Эта глава посвящена изучению геодезических в простран-
пространстве-времени Керра. Необходимость выделения этого материала
в отдельную главу вызвана несколькими причинами: помимо
того что описание геодезических позволяет выявить существенные
черты пространства-времени (например, уместность продолжения
многообразия на отрицательные значения радиальной коорди-
координаты г), открытая Картером возможность разделения переменных
в уравнении Гамильтона — Якоби оказалась первым из того
множества свойств метрики Керра, которые создали вокруг нее
некий ореол чуда. Кроме того, изучение геодезических показывает
возможность (впервые открытую Пенроузом) извлечения энергии
из черной дыры Керра, выявляя таким образом процесс, о кото-
котором никто и не подозревал. В то же-время изучение геодезических
пространства-времени Керра позволяет обнаружить некоторые
общие и совершенно неожиданные свойства многообразий, при-
принадлежащих типу D по классификации Петрова. Мы начнем
изложение с установления одного из этих свойств.
60. Теоремы об интегралах геодезического движения
в пространстве-времени типа D
по классификации Петрова
В гл. 1 (п. 9, в) было показано, что в пространстве-времени
типа D по классификации Петрова главные изотропные кон-
конгруэнции являются геодезическими и бессдвиговыми и что в изо-
изотропном тетрадном базисе A, n, rn, m), в котором векторы 1 и п
задают главные изотропные направления, спиновые .коэффи-
.коэффициенты х, сг, X и v, а также вейлевские скаляры 4V Wlf W3 и ?4
равны нулю:
y.=or=A,=v=0, A)
Wo = W, = Y3 = ?4 =, 0. B)
Если к тому же векторное поле 1 имеет аффинную параметризацию
(что мы и будем предполагать), то спиновый коэффициент е также
равен нулю:
е = 0. C)

50 Глава 7. Геодезические в пространстве-времени Керра
Наконец, из тождеств Бианки (гл. 1, уравнения C21)) получаем
следующие уравнения для не равного нулю вейлевского ска-
скаляра 4V-
D In ?2 = +3р; б In ?2 = +3т;
Л In W2 = —3|х; б* In ?2 - —Зя, ^
где D, Л, б и б* — производные по направлению вдоль векто-
векторов 1, n, m и m соответственно.
Метрический тензор g^-, записанный через координаты векто-
векторов 1, n, m и m в координатном базисе, имеет следующий вид
(гл. 1, уравнение B46)):
Su = hrij + Ijtii ~ mitfij — mjtnh E)
а ковариантные производные векторов 1, п и m равны (гл. 1,
уравнение C57))
'/; * = + (Y + Y*) ^ ~ («* -f Р) /у*/ - (а + Р*) ^/^^ ~
— ntfijlf — T*mjli ~\- ptfijtrii + p^trijtrii; F)
«у; * = - (Y + Y*) Л//* -Ь (а* + Р)"А' + (« + Р*) *№ +
+ n^tfijuj -f ят;-я^ — \inijfhi — [х*т7-тг; G)
^/; / = + (Y - Y*) т/^' + (а* - Р) т/^^ + (I3* - °0 т/т^ +
(8)
(Предыдущие соотношения выполняются только в пространстве-
времени типа D по классификации Петрова, поскольку при вы-
выводе их были использованы соотношения A) и C).)
Пусть к и f — два произвольных вектора, тогда в соответствии
с уравнением E) имеем
k-f = giW = (k-1) (f n) + (k-n) (f .1) - (km) (f m) - (km) (f-m),
(9)
-(k.m)(k-m)], A0)
-(k.mN-(k-mN*. A1)
Сфэрмулируем и докажем основную теорему (Уокер и Пен-
роуз):
ТЕОРЕМА 1. Если k—аффинно параметризованная изо-
изотропная геодезическая, а вектор i ортогонален к и параллельно
переносится вдоль этой геодезической, то в пространстве-времени
типа D по классификации Петрова величина
Ks = klf! (Ьп/ — Ijtii — mifhj -f- mcmf) ЧТ1/3 =
- klf Bищ - 2mimi - gii) Y2~1/3 -
-2[(k.l)(f.n)-(k.m)(f.m)]Y2-1/3 A2)

60. Теоремы об интегралах 51
сохраняется вдоль геодезической, т. е.
№& =0. A3)
Эта теорема допускает более общую формулировку: простран-
пространство-время типа D по классификации Петрова допускает кон-
конформный тензор Киллинга.
Доказательство. Предположения теоремы об изотропности
и аффинной параметризации геодезической к, об ортогональности
ей вектора f и параллельном распространении вектора f вдоль к
требуют выполнения следующих соотношений:
#V^ = 0. k'Vifj = O, A4)
(kl)(kn)-(km)(km) = 0, A5)
(k-l)(f-n) + (k-n)(f-l)-(k-m)(f.in)-(k-m)(f.m) = O. A6)
Поскольку
k'Vi {[(k-l)(f.n) - (k.m)(f -m)] V/3) =
= ?L71/3 ( kl V, [(k ¦!) (f • n) - (k • m) (f ¦ m)] +
-L[(kl)(f-n)-(k.m)(f-m)]/j'VIln?2-1/3}, A7)
для доказательства теоремы требуется показать, что
?<Vj[(k-lj(fn) -(km)(fm)] =
= - [(k • 1) (f • n) - (k • m) (f • m)] kl V,- In ?2~'/3. A8)
Распишем подробно левую часть уравнения A8), воспользовав-
воспользовавшись уравнением A4):
= (f • n) k'k'lj; i + (k• 1) k{ffn/; i - (f -m) k'ktmj; i — (k• m) k{fim,.,,. A9)
Подставляя вместо ковариантных производных //; ,• и т. д. выра-
выражения F)—(8), получаем после упрощения следующее соотноше-
соотношение:
Jfe'Vi[(k-l)(rn)-(k-m)(f.m)] =
= р [+ (f • n) (k• т) (к• т) - (f_m) (к• п) (к• т)] +
+ x[-(f.n)(k.m)(k-l)-f (f-iH)(k-n)jk.l)] f
+ (k.m)(k.in)(f.l)J +
)(f.m)-(k.m>(k.n)(f.|)]. B0)
Уравнения D) и A1) позволяют получить для левой части урав-
уравнения A8) следующее выражение:
— [(к • 1) (f • п) - (к • m) (f • т)] kl V,- In ?2~'/3 =

52 Глава 7. Геодезические в пространствб-времени Керри
)-(k.m)(f.m)] X
X [+р(к-п)-|х(к-1)-т(к.т) + я(к.щ)]. B1)
Равенство A8) (которое и составляет утверждение доказываемой
теоремы) подсказывает нам, что члены в правой части уравнения
B0) должны быть равны выражению в последних двух строчках
уравнения B1). Проверим, что это действительно так. Рассмотрим,
например, те члены в уравнении B0), которые появляются в пра-
правой части со спиновым коэффициентом |я в виде множителя. Вслед-
Вследствие уравнений A5) и A6) имеем
+ (k.m)(k.m)(f.I) = -(k.l)[(k.l)(f.n)-(k.m)(f.m)]. B2)
Очевидно, что это выражение равно соответствующему выраже-
выражению (со спиновым коэффициентом \i в виде множителя) в урав-
уравнении B1). Подобным же образом устанавливаются и другие
равенства. Сохранение Ks при перенесении вдоль аффинно пара-
параметризованной изотропной геодезической, таким образом, до-
доказано.
ТЕОРЕМА 2. Если к — аффинно параметризованная геодези-
геодезическая в пространстве-времени типа D по классификации Пет-
Петрова, то величина
/С = 21Y2 |-2/з (к • 1) (к • п) — Q | к |2 = 21V21-2/3 (к - т) (к - т) —
-(Q-|^2|-2/3)|k|2 B3)
сохраняется при перенесении вдоль к в том и только в том случае,
если существует скаляр Q, удовлетворяющий следующим уравне-
уравнениям:
DQ = D\W21/3, AQ = Л | ^2|/3, 6Q - 6*Q - 0. B4)
Доказательство. Заметим сначала, что эквивалентность двух
форм записи величины К в формулировке теоремы следует из
уравнения A0).
Сохранение К при перенесении вдоль геодезической к требует,
чтобы
(k • О (к • п) | ^ I'*] = | к р k*4tQ, B5)
поскольку величина |к|2 сохраняется. Вследствие уравнения A1)
правая часть уравнения B5) может быть переписана в следующем
виде:
к2 j ^ v^Q = I к I2 [(к • n) DQ + (к -1) AQ —
-(k.mNQ-(k.m)8*Q]. B6)

60. Теоремы об интегралах 63
Левая часть уравнения B5) равна
= 21 ?21/3 W V* (к. 1) (к • п) + (к • 1) (к • п) Ы V* In | W2 |/3]. B7)
С другой стороны, вследствие соотношений D), а также вследствие
того, что к является геодезической, имеем
) Л—(k-mN- (k-mN*]x
X AпТ2 + In Y?) = - [(k.n)(p + p*) - (k.l)fti + Ю -
— (k.iii)(T —ji*)-(k-m)(T* —ji)], B8)
kl Vr (kl) (kn) = (k-n) J№7/: i + (k-l)fcW/i/;,. B9)
Подставляя теперь уравнения B8) и B9) в уравнение B7), а также
выражения F) и G) для ковариантных производных /;-; { и П/; t-,
находим
= 21 ?2 |/з |f(k.п) (р + р*) - (к• 1) (ц + [i*)] [(к• ш) (к-Ъ) -
= | к |2 [(к • n) D | W2 |-2/з + (к • 1) А | ?2 |-2/з], C0)
причем последнее равенство получается с учетом соотношений D).
Сравнение этого равенства с правой частью уравнения B6) при-
приводит к соотношениям B4), что и требовалось доказать.
СЛЕДСТВИЕ 1. В произвольном пространстве-времени типа D
по классификации Петрова каждой изотропной геодезической к
соответствует интеграл движения
Ко = 2 |ТЯ |-2/3 (к • ш) (к. т) = 2 | У2 |-2/з (к. 1) (к. п). C1)
Это сразу же следует из доказанной теоремы, поскольку для
изотропной геодезической |к|2 —0, и поэтому для справедли-
справедливости теоремы в этом случае ни одно из требований B4) не является
необходимым.
СЛЕДСТВИЕ 2. Постоянная /Со в следствии 1 с точностью
до множителя равна квадрату модуля комплексной постоянной Ks
из теоремы 1.
Доказательство. Из уравнения A2) следует, что
KSK*S = 41W21-2/3 [(к • 1) (f • п) - (к • m) (f • т)] х
X[(k.l)(f.n)-(k-m)(f.m)]> C2)
а из уравнения A6) —
|/(s|2=_4|?2|-2/3[(k.l)(f.n)-(k.m)(f.m)]x
C3)

54 Глава 7. Геодезические в пространстве-времени Керра
Раскрывая скобки и упрощая с помощью тождеств A5) и A6)
(примененных несколько раз), получаем
= - 4 | W2 |-2/з {(k. m) (k ^h) (f n)(f l) + (k- mJ (f mJ -
-(km)(f.m)[(km)(f m) + (km) (f m)]} -
= -4|4^2|-2/3(k.m)(k.m)[(f.n)(f.l)-(f.m)(f.m)] =
= - 4 | W21/2 (k • m) (k • m) | f |2. C4)
При параллельном переносе f величина |f |2 остается постоянной
вдоль геодезической к, откуда и следует доказываемое утвер-
утверждение.
СЛЕДСТВИЕ 3. В метрике Керра существует сохраняющаяся
величина указанного в теореме 2 вида.
Если выбрать систему координат, принятую нами в гл. 6
(уравнение A80)), то получаем
| ?2|'/3 - М/Зр2 = М/3 (г2 + a2 cos2 9). C5)
Мы удовлетворим условиям теоремы, если положим
Q = M-2/V2. C6)
Следовательно, в геометрии Керра величины
/С = 2р2 (к -1) (к - п) — г21 к |2,
К = 2р2 (к • т) (к • т) + а2 | к |2 cos2 9 C7)
являются интегралами движения.
Два интеграла C7) могут рассматриваться как независимые,
поскольку их эквивалентность вытекает из постоянства вели-
величины |к|2, что можно интерпретировать как закон сохранения
массы покоя.
ТЕОРЕМА 3. Для существования в пространстве-времени
типа D интеграла геодезического движения, рассматриваемого
в теореме 2, необходимо и достаточно, чтобы спиновые коэффи-
коэффициенты р, т, |я и я были связаны соотношениями
р/р* = jx/fx* - т/я* - я/т*. C8)
Доказательство. По условию теоремы 2 существование интег-
интеграла геодезического движения вида B3) для пространства-времени
типа D но классификации Петрова связано с существованием
скаляра Q, обладающего следующими свойствами:
DO - Df, AQ = Д/, SQ - S*Q - 0, C9)

60. Теоремы об интегралах 55
где для удобства введено обозначение
/НЧМ/3. D0)
Тождества Бианки D) для вейлевского скаляра W2, записанные
через функцию /, принимают следующий вид:
Df = -(р + Р*) /; б/ = (я* - т) /;
D1)
А/ = +(|i + fx*) /; б*/ = (я - т*) /.
Для доказательства теоремы нужно подействовать коммута-
коммутационными соотношениями (гл. 1, §8, в) на скаляр Q, а затем
получить следствия требований C9), согласованные с. уравне-
уравнениями D1). Для пространства-времени типа D коммутационные
соотношения с учетом соотношений A) и C) принимают следующий
вид:
6*6 — бб* = ([I* — ц) D + (р* — р) А + (а — р*) б +
+ (Р-а*N*.
AD - DA = (У + у*) D - (т* + я) б - (т + я*) б*,
D2)
8D — ?>б = (а* + Р — я*) D — р*б,
бЛ — Лб = (т — а* — р) А + (Ц - Y - Y*) б.
Действуя этими соотношениями на скаляр Q, получаем, восполь-
воспользовавшись требованиями C9):
(]i* - ц) D/ + (Р* - Р) А/ = 0, D3)
(&D-DA)f = (y+y*)Df, D4)
6?>/ = (а* + р — я*) Z)/, D5)
б А/ = (т - а* - р) А/. D6)
Воспользуемся теперь соотношениями D1). Уравнение D3) сразу
же приводит к соотношению
(fx* - |i) (р + р*) = (р* - р) (|i + |i*), D7)
которое после упрощения может быть записано в виде
pfi* = р*ц, или р/р* = \il\i*. D8)
Вычисляя, далее, левую часть уравнения D4) с помощью соотно-
соотношений D2), получаем
(т* + я) б/ + (т + я*) б*/ - 0. D9)
Вследствие соотношений D1) имеем
(т* + я) (т — я*) f (т + я*) (т* — я) - 0. E0)
После упрощения уравнение E0) принимает вид
тт* —яя* — 0, или т/я* = я/т*. E1)

56 Глаза 7. Геодезические в пространстве-времени Керра
Получить следствия из уравнений D5) и D6) немного труднее.
Прежде всего приведем с помощью уравнений D1) уравнения D5)
и D6) к следующему виду:
б In (р + р*) - (а* + C — 2я* + т) = б In p +
+ 6 In (l + p*/p), E2)
6 In (fx + \i*) = Bт — я* — а* — C) - б In |x +
+ б In (I +\i*/\i). E3)
Поскольку вследствие уравнения D8) р/р* = (я/pi*, то, вычитая
уравнение E3) из уравнения E2), получаем
б In р — б In у, - 2а* + 2C — я* — т, E4)
или в другом виде
бр — рб In ц = Bа* + 2C — я* — т) р. E5)
С другой стороны, из тождества Риччи (гл. 1, уравнение C10л))
следует, что
бр = р(а* + р + т)-тр*. E6)
Исключая с помощью этого соотношения бр из уравнения E5),
получаем, снова воспользовавшись уравнением D8):
—б|я - (а* + р — я* — 2т) ц + т|я*. E7)
Но тождество Риччи (гл. 1, уравнение C10н)) дает
—6fx* = (а* + Р + я*) ii* — я>. E8)
Складывая уравнения E7) и E8), получаем
-б ([х + [X*) = (а* + C - 2я* — 2т) (х +
+(а* +р +т +я*)^1*. E9)
С другой стороны, мы имеем соотношение (ср. с уравнением E3))
-б (р + ii*) = -Bт - я* - а* - р) (ц + ^*). F0)
Из сравнения уравнений E9) и F0) находим
tji* — я*|1 = 0, или т/я* = |л/|л*. F1)
Комбинируя уравнения D8), E1) и F1), получаем соотношения
C5), что и следовало доказать.
Оказывается, что соотношениям C5) в действительности удо-
удовлетворяют большинство метрик типа D по классификации Пет-
Петрова.
61. Геодезические в экваториальной плоскости
Ясно, что геодезические в экваториальной плоскости могут
быть описаны практически так же, как и геодезические в про-
пространстве-времени Щварцщильда или Рейсснера — Нордстрема;

61. Геодезические б экваториальной плоскости 5?
существования интегралов энергии и момента количества движе-
движения оказывается достаточным для сведения задачи к квадратурам.
Но при этом имеются два существенных различия. Во-первых,
следует различать прямые и обратные орбиты, т. е. орбиты, дви-
движение по которым вокруг оси симметрии совпадает или противо-
противоположно вращению черной дыры. И, во-вторых, координата ф,
так же как и координата t, не является подходящей координатой
для описания того, что же «в действительности» видит сопутству-
сопутствующий наблюдатель. Траектория, приближающаяся к горизонту
(при гЛ или при г_), будет делать бесконечное число оборотов
вокруг черной дыры, и чтобы пересечь горизонт, ей понадобится
бесконечное время t, но ни то ни другое не происходит с сопут-
сопутствующим наблюдателем.
Лагранжиан для движений в экваториальной плоскости (этим
движениям соответствует 9 = 0, 8 = const = я/2) равен
2S = A — 2M/r) i2 -Ь 4аЛИф/г — г2г2/Д — [(г2 + а2) +
+ 2а2М/г]ф2, F2)
откуда следуют выражения для обобщенных импульсов
pt = A — 2M/r) t + 2аМу/г = Е = const, F3)
— /?ф = — 2аМ11г + [(г2 +а2) + 2а2М/г] ф = L = const, F4)
—рг - г2г/А, F5)
где точка над буквой обозначает дифференцирование по аффин-
аффинному параметру т. (Постоянство р% и /?ф следует из того, что лаг-
лагранжиан не зависит от t и ф, а это в свою очередь проявление
стационарности и аксиальной симметрии геометрии Керра.)
Гамильтониан имеет следующий вид:
Ж - ptt + /?фф + ргг — 2 - 72 A — 2Mlr) t2 + 2aMty/r —
— r2r2/2A — V2(/-2 + a2 + 2a2Mlr) ф2. F6)
Отсутствие в гамильтониане явной зависимости от координаты /
приводит к постоянству гамильтониана
2Ж - [A — 2Mlr)i + 2aMq>/r]t — [(г2 + а2 + 2а2М/г) ф —
— 2aMt/r] ф — г2г2/Д - El — /лр — г2г2/Д = бх = const. F7)
Без потери общности можно положить
бх = 1 F8а)
для времени подобных геодезических и
6Х = 0 F86)
для изотропных геодезических. (При этом в случае времениподоб-
ных геодезических Е следует интерпретировать как удельную
энергию, т. е. энергию на единицу массы.)

58 Глава 7. Геодезические в пространстве-времени Керрй
Решая уравнения F3) и F4) для фи/, получаем
ф = A/Д) [A _ 2M/r) L + 2аМЕ/г), F9)
/ - A/Л) [(г2 + а2 + 2a2M/r) Е - 2aMLIr]. G0)
Подставляя эти решения во второе равенство в уравнении F7),
получаем радиальное уравнение
гЧ2 = г2Е2 + BМ/г) (аЕ — LJ + (а2Е2 ~ L2) — 8XA. G1)
а. Изотропные геодезические. Как уже упоминалось, для изо-
изотропных геодезических 82 = 0, и радиальное уравнение G1)
принимает следующий вид:
г2 - Е2 + BМ/г3) (L — аЕJ — (L2 — а2Е2)/г2. G2)
В дальнейшем нам будет удобно характеризовать геодезиче-
геодезические прицельным параметром
D = LIE G3)
вместо L.
Отметим прежде всего, что геодезические с прицельным пара-
параметром
?> = a (L = аЕ) G4)
играют ту же роль, что и радиальные геодезические в геометриях
Шварцшильда и Рейсснера — Нордстрема. Действительно, в этом
случае уравнения F9), G0) и G2) сводятся к уравнениям
г = ± ?, t = (г2 + а2) ?/Д, ф = а?/Д. G5)
Радиальная координата линейно зависит от аффинного параметра,
а уравнения для t и ф можно переписать следующим образом:
dt/dr - ± (г2 + а2)/Д, dyldr - ± а/А. G6)
Решения этих уравнений имеют следующий вид (ср. с уравнением
B38) гл. 6):
±t = r + [(г; + а2)/(г+— г.) ] In l(r/r+) - 1] -
- [(г + а2)/(г+ - r_) ] In [(г/г.) — 1) ],
G7)
±Ф - 1а/(г+ - г.) ] In l(r/r+) - 1 ] -
- la/(r+ —rj] In [(r/rj - 1].
При приближении к горизонтам г+ и г_ значения координат t
и ф стремятся к ±оо, на что мы уже обращали внимание.
Как будет показано ниже, изотропные геодезические, описы-
описываемые уравнениями G6), принадлежат к главным изотропным
конгруэнциям геодезических, лежащим в экваториальной
плоскости.

61. Геодезические в экваториальной плоскости 59
Ясно, что в общем случае нужно различать, как и в шварц-
шильдовой геометрии, орбиты с прицельным параметром, большим
или меньшим некоторого критического значения Dc (которое
в свою очередь разное для орбит с прямым и обратным движе-
движением). Если значение прицельного параметра равно критиче-
критическому, то среди решений уравнений геодезических будет неустой-
неустойчивая круговая орбита некоторого радиуса гс. Если D > Dc,
то мы получим орбиты двух типов: орбиты первого рода, начина-
начинающиеся на бесконечности, будут иметь в перицентре значение
г > гс, орбиты же второго рода, для которых г в апоцентре
меньше гс, будут обрываться в сингулярности при г = О (и 9 =
= я/2). При D = Dc орбиты первого и второго рода сливаются,
навиваясь бесконечное число раз на неустойчивую круговую
орбиту радиуса г = гс. Если же D < Dc, то орбиты могут быть
только одного типа: начинаясь на бесконечности, они пересекают
оба горизонта и обрываются в сингулярности.
Неустойчивая круговая «фотонная орбита» радиуса гс описы-
описывается следующими уравнениями (ср. с уравнением G2)):
Е2 + BM/r?) (L - аЕJ — (L2 — а2Е2)/г\ = 0, G8)
—FM/rAc) (L — aEf + B1 rl) (L2 — а2Е2) - 0. G9)
Из уравнения G9) следует, что
гс = ЗМ (L — aE)/(L + аЕ) = ЗМ (Dc — a)/(Dc + a). (80)
Подставляя это соотношение в уравнение G8), находим
?3 = A/27УИ2) (I +aE)*/(L — аЕ) =
= (Е2/27М2) (Д. + afl{D0 —a), (81)
откуда получаем
(Dc +af =27M2(Dc-~a). (82) *
Полагая
y^Dc+a, (83)
получаем кубическое уравнение
у3 — 27М2у + 54аМ2 = 0. (84)
Орбитам с прямым вращением соответствует псложительное
значение а > 0, а орбитам с обратным вращением — отрицатель-
отрицательное значение а < 0. Если а > 0, то
у = —6М cos (О + 120°), (85)
где
cos 30 = а/М, Dc = у — а, гс = ЗМ A — 2а/у),
* Из уравнений (80) и (82) легко вывести соотношение D2C = Зг^ + а2, яв-
являющееся простым обобщением результата, получаемого в шварцшильдовом
пределе а = 0.

60 Глава 7. Геодезические в пространстве-времени Керра
а в случае —а —\а\ > 0 имеем
у =6М cos ft, cos 30 = | a \/M, Dc = у + | a |,
rc =ЗЛ1 A +2|a|/y). (86)
Нетрудно проверить, что
rc =4Mcos2* =2M {1 +cos [B/3) arccos (±a/M)]), (87)
где верхний знак соответствует обратным орбитам, а нижний —
прямым орбитам.
Из уравнений (85) и (86) находим
а=0 Dc=3/3"Af, rc=3Af, (88)
а = М Dc = 2М гс = М (прямые орбиты), (89)
а =—М Dc =7Му гс = 4М (обратные орбиты).
Вернемся теперь к уравнениям, описывающим орбиты с кри-
критическим значением прицельного параметра Д.. Выражение в пра-
правой части уравнения G2) имеет двойной корень, и поэтому его
можно представить в виде
й2 = ME2 (Dc - af и" {и - исJ Bи + ис), (90)
где
и = 1/г, ис = 1/гс = (Dc + а)/ЗМ (Dc - a). (91)
Уравнение (90) интегрируется:
[Е (Dc — а) М1'2) х = ± J и~2(и — ис)-г Bи + ис)~^2 du =
= ±{Mul) \Bu + ис)Щи + Cuc)-V2 In | [Bи + ucfi2 -
- (ЗисI'2 V lBu + ucyi2 + {Ъису1Ц). (92)
Чтобы получить траектории геодезических с критическим значе-
значением прицельного параметра, лежащих в экваториальной пло-
плоскости, можно объединить уравнение (90) с уравнением
ф = [Еи2/3 (а2и2 — 2Ми + 1) ис] [3Dcuc — 2 (Dc -fa) w], (93)
которое прямо следует из уравнения F9), в результате чего полу-
получим уравнение
«L = пр. + „)/«¦«,(«V -Ши + 1)-^» + «У. ¦ (94)
L = пр. + „)/«¦«,(«V -Ши + 1)-^
Интегрирование дает
a2 (Dc + a) J (u — u+) (u - u_) (u - uc) Bu + uc)l/2> '
, М1'2 г [3Dcuc-2(Dc + a)u]du g
""a2 (Dc + a) J (u — u+) (u - u_) (u - uc) Bu + uc)l/2> ' '

$> 61. Геодезические в экваториальной плоскости 61
где и± = \1г±. Интеграл в правой части выражения (95) является
элементарным и может быть вычислен в явном виде. Окончатель-
Окончательный результат содержит элементарные дроби и очень громоздкий,
поэтому мы не будем его здесь выписывать.
На рис. 28 показаны орбиты, вычисленные с помощью уравне-
уравнений (92) и (95). Ясно видны уже описанные выше особенности этих
орбит. Характер орбит общего вида в экваториальной плоскости
нетрудно понять из представленных графиков орбит с критиче-
критическим значением прицельного параметра.
б. Времениподобные геодезические. При описании времени-
подобных геодезических уравнения F9) и G0) для ф и I остаются
неизменными, но уравнение G2) следует заменить уравнением
Ч2 = — А + r2E2 + BM/r) (L — aEf — (L2 — а2?2), (96)
:где Е — энергия единицы массы частицы, описывающей данную
траекторию.
/. Специальный случай L =аЕ. Представляет интерес поведе-
поведение времени подобных геодезических с L = аЕ, а также изотроп-
изотропных геодезических с прицельным параметром D = а при пере-
перетечении горизонтов, характерное для орбит общего вида.
Если L = аЕ, то уравнение (96) принимает вид
, г2г2 = (Е2 — 1) г2 + 2Мг — а2, (97)
1 уравнения для ф и I остаются такими же, как и для изотропных
Геодезических (ср. с уравнениями G5)):
ф = а?/Д, I = Е (г2 + а2)/Д. (98)
Интегрирование уравнения (97) приводит к следующему резуль-
результату:
> = (Я2 —I) A(Е2 — 1) г2 +2Мг — а2]1'2 —
;_Л4(?2 — I)-1/2 In {{(Е2 — \) г2 +2Мг — а2]1'2 +
] +Г (?2 __ !I/2 + ЩЕ2 _ 1I/2})э (99)
иногда Е2 > 1, и
'- = — A — Е2)-1 {[—A — Е2) г2 + 2Мг — а211/2 +
| + A — Е2у1!2 arcsin [М — A — Е2) г VIM2 —
% —а2 A —Б2)]1/2!, A00)
<огда Е2 < 1. (Заметим, что выписанные выражения справедливы
Только при а2 < М2.)

62
Глава 7. Геодезические в пространстве-времени Керра
-3 -2
-
/
/
7 I
-
-
i
j
/
/ >
/ /
/ f
' I
\
\
\
\
\
\
i
i i i
f
\ x ^
1 1 1
^ )
J j
у
I 1
\
\
\
z
/
I
_
-
-
_
-
6
1
-5 -4-3-2-1
1
Рис. 28. Критические изотропные геодезические (прямые и обратные) в эквато-
экваториальной плоскости черной дыры Керра с параметром а = 0,8. а — зависимость
радиальной координаты г от аффинного параметра т; б и в — зависимости коор-
координаты г от угла ф для тех же орбит. Радиусы неустойчивых круговых орбит и
прицельные параметры для соответствующих геодезических равны: гс = 1,81 \М
и Dc = 3,237М для прямых орбит и гс = 3,819М и Dc = 6,662M для обратных
орбит. Единицей длины вдоль осей координат служит М. Штриховыми окруж-
окружностями показаны два горизонта.

61. Геодезические в экваториальной плоскости
63
Чтобы получить уравнение траектории, нужно объединить
уравнения для г и ф, и в результате имеем
dw/d<p = ±(а/Е) (и — и+) (и — и.) [(Е2 — 1) + 2Ми —
-А2]1/2, A01)
где и = 1/г и и± = 1/г±. Интегрирование дает следующее ре-
решение:
Ф = [а (и+ - и.)] (In \2Е [Е2Ц + 2 (М - а2и+) 1+ - а2]1/2 +
+ 2 (М — Л+)} — In {2E [Е2Ц + 2 (М — aV) L —
— а211/2 + 2?2L + 2 (М — а2^)}), . A02)
где
?+ = (и — ^±)-
A03)
Рис. 29. Пример неограниченной времениподобной геодезической с L = аЕ
в экваториальной плоскости черной дыры Керра при а = 0,8. На рисунке изобра-
изображена орбита, для которой Е = 1,4. Единицей длины вдоль осей координат слу-
служит М; штриховыми окружностями показаны два горизонта.
Пример орбиты, вычисленной на основе уравнения A02), показан
на рис. 29.
2. Круговые орбиты. Рассмотрим теперь радиальное уравнение
(96) в общем случае. Вводя новую переменную и (= 1/г), обратную
к радиусу, получаем уравнение
u~W = —(а2и2 — 2Ми + 1) + Е2 + 2М (L — аЕJиъ —
— (L2 -а2Е2) и2.
A04)

64 Глава 7. Геодезические в пространстве-времени Керра
Как и в случае геометрии Шварцшильда и Рейсснера — Норд-
стрема, круговые орбиты играют важную роль в классификации
орбит. Кроме того, они представляют собой простые примеры,
на которых легко увидеть основные особенности поведения гео-
геодезических.
Найдем значения L и Е, которые соответствуют круговой
орбите некоторого заданного радиуса г = Ми. При этих значе-
значениях L и Е кубический многочлен в правой части уравнения
A04) должен иметь двойной корень. Выпишем условия существо-
существования этого двойного корня:
—(а2и2 — 2Ми + 1) + Е2 + 2Мх2иъ — {х2 + 2аЕх) и2 = 0, A05)
—(а2и — М) + ЗМх2и2 — (х2 + 2аЕх) и = 0, A06)
где
х = L —аЕ. A07)
Из уравнений A05) и A06) следуют соотношения
Е2 = A — Ми) + Мх2и\ A08)
2ахЕи = х2 (ЗМи — \) и — (а2и — М). A09)
Исключая из этих соотношений Е, получаем следующее квадрат-
квадратное уравнение для х:
х*и2 [{ЗМи — IJ — 4а2Ми*] —
—2х2и [{ЗМи — 1) {а2и — М) — 2а2и {Ми — 1) ] +
+ {а2и — МJ = 0. (ПО)
Дискриминант {Ь2 — \ас)\\ этого уравнения равен
4д2М Л2иа, где Д„ = а2и2 — 2Ми + 1. A11)
Если ввести обозначения
{ЗМи — IJ — \агМи* = Q+Q_, A12)
где
Q± = 1 — ЗМи ± 2а (М^3I/2, (ИЗ)
то решение уравнения {ПО) можно записать в особенно простом
виде
х2и2 - (Q±AU - Q+QJIQ+Q- = (Д» - Q+VQ+. A14)
С другой стороны, как легко проверить,
ди — Q^ = u {аи'*2 ± М1'2J. A15)
Следовательно,
X - — (tf^1/2 ±

61. Геодезические в экваториальной плоскости 65
Как станет ясно ниже, верхний знак в этой формуле соответ-
соответствует обратным орбитам, а нижний — прямым орбитам. Этого
соглашения о знаках мы будем придерживаться и далее.
Подставляя решение A16) для х в уравнение A08), находим
Е = [1 — 2Ми 4= a {Mu)xl2]IQ^2. A17)
Этому значению Е соответствует следующее значение L:
I == пЕ +х = ТМ1/2 1а2и2 + 1 ± 2а (MuzI/2V(uQtI/2. A18)
Как уже объяснялось и как явствует из вывода формул A17)
и A18), Е и L есть соответственно энергия и момент количества
движения на единицу массы частицы, описывающей круговую
.орбиту, обратный радиус которой равен и. Из уравнений A17)
и A18) и из уравнений F9) и G0) получаются следующие выра-
выражения для угловой скорости Q и скорости вращения ()
od(p L — 2Mux (L
" ~~ 6t ~ (г* + а*)Е — 2аМхи ~~ A + а%2) ? — 2аМих*
e*-v (Q — a,) = (Г2 +а2 + 2Ma2lr) Q/Д1/2 — 2аМ/(г А1/2).
A20)
Подставляя сюда значение х, получаем окончательные выра-
выражения *
Q = +(Мы3I/2/[1 q= а (Мы3I/2], A21)
Интересно отметить, что условие существования неустойчивой
'^круговой изотропной геодезической можно получить, рассма-
рассматривая предел Е -> оо уравнения A17), когда
1 QT = 1 — ЗМи =F 2a (M^3I/2 - 0 A23)
щ, следовательно,
I г3/2 — ЗУИг1/2 =F гаУИ1/2 - 0. A24)
Прямая проверка показывает, что решение этого кубического
уравнения для г1/2 согласуется со значением, которое дает урав-
уравнение (87).
? Вернемся к исследованию круговых орбит. Пусть L и Е при-
принимают значения, соответствующие круговой орбите, обратный
!•¦.-
¦ * Для получения этих выражений удобно использовать следующие соот-
соотношения:
! L — 2Мих = =F
A + А2) Е - 2аМхи3 =Ац[1Та
3 Чандрасекар С, т. 2

66 Глава 7. Геодезические б пространстве-времени Керра
радиус которой равен и = ис, т. е. значения L и Е даются форму-
формулами A17) и A18), если в них положить и = ис. Значения L, Еу х
и т. д., соответствующие данному значению иСУ будем отмечать
индексом с. Кубический многочлен в правой части уравнения
A04) при и = ис допускает двойной корень, следовательно, это
уравнение можно привести к виду
и-й* = 2М (Lc - aEcf (и - ис? [и + 2ис - ^U-aE^ ] • <125>
Подставляя Lc и Ес из уравнений A17) и A18), находим
A2 — а2Е! + а2)/2Мх2 =
= [1 + За2и2с ± 4а (Мм?I/2]/2 (аи1/2 ± M1/2f A26)
и, следовательно,
Uc __ (Ll _ a2E2c + а2)/2Мх2с = ~^J2{au\12 ± М1/2J. A27)
Уравнение A25) может быть переписано в более простом виде
и2 = 2MxW (и — исJ (и — и.), A28)
и. = ~ис + Д«с/2 {аи\12 ± М1/2J. A29)
Ясно, что значение и% определяет обратный радиус орбиты
второго рода, связанной с устойчивой круговой орбитой, обрат-
обратный радиус которой равен ис. Решение уравнения A28) имеет вид
%={хс BМр)-1 J и-2 (и - Uc)-1 (и - и*)/2 da. A30)
Для получения траектории уравнение A28) нужно объединить
с уравнением
ф2 = (u2/ku) (Lc — 2Мхси). A31)
В результате получаем
= 1 Г (Lc — 2Мхси) Ли ,j32,
Ф xca2BM)l/2 J (и — и+)(и-и_)(и-ис)(и-и*I/2
Орбиты второго рода, вычисленные с помощью уравнения A30),
показаны на рис. 30.
Ясно, что круговая орбита становится неустойчивой при
и^ = и0. Это условие можно записать, используя уравнение A29),
следующим образом:
4ис (аи\12 ± М1Г?J = А„с = а2и2 - 2Мис + 1. A33)
Расписывая это уравнение и опуская (ставший уже ненужным)
индекс с, получаем следующее уравнение:
За2*/2 + 6Ми ± 8а (Ми*I*2 — 1=0. A34)

61. Геодезические в экваториальной плоскости
67
Переписывая его через пере-
переменную г, имеем
Г2 _ QMr =F 8a (MrI/2 —
— За2 = 0. A35)
Это биквадратное уравнение
для г1/2 можно стандартным спо-
способом свести к квадратному
уравнению
г — 2qr1'2 — 2М ch ft/ch 3ft =F
=F гаМ1/2/^ — Af = 0, A36)
где
о -
±т
Г- j
\ ,
Прямое
Обратное
i
Г . а
q* =4M (ch ft/ch 3ft) sh2 ft. A37)
Геодезическая, описывающая
движение частицы, энергия и
момент количества движения +
которой соответствуют неустой-
неустойчивой круговой орбите, может
быть получена из уравнений
A30) и A32), в которых нужно
лросто положить ис = и%. При-
Пример такой орбиты показан на
рис. 31.
Круговые орбиты, которые
формально получаются из урав-
уравнений A17) и A18) и радиус ко-
которых меньше значения, опре-
определяемого уравнением A35),
являются времениподобными
аналогами (в случае Е2 > 1)
неустойчивых изотропных гео-
геодезических, рассмотренных в
п. 61, а. Это следует из рас-
рассмотренного выше предельного
перехода Е2 -> с».
Помимо предельного случая
?2 _> оо, интересно рассмотреть
и другой предельный случай
орбиты с Е2 = 1, которая яв-
является переходной между свя-
связанными и несвязанными орби-
орбитами и соответствует движению частицы, падающей по направ-
направлению к черной дыре с бесконечности из состояния покоя.
3*
-60
Рис. 30. Примеры орбит второго рода,
связанных с устойчивыми круговыми
орбитами радиуса а — 20М и б —
9,5М. Параметры изображенных орбит
следующие:
гс Е L Орбиты
20 0,9780 4,7222 Прямая
0,8911 —4,9981 Обратная
9,5 0,9503 3,4153 Прямая
0,9605 —4,1243 Обратная

68
Глава 7. Геодезические в пространстве-времени Керра
Из~ уравнений A08) и A16) получаем следующее уравнение
для радиуса круговой переходной орбиты:
A38)
I'2]. A39)
1 = X2U2 = (W/Q:p) (аи1/2 ±
которое может быть переписано в виде
Q* = 1 — ЗМи 4= 2а (Ми?I'2 = и [а2и + М ± 2а
300
200 -
±Г
100
-100
Обратное
] Прямое
Рис. 31. Прямые и обратные переходные круговые орбиты в пространстве-вре-
пространстве-времени Керра с а = 0,8.
Это последнее уравнение можно упростить
[аи ± 2 (МиI'2 Р = 1
и получить следующее решение:
г = 2М ±а +2(М2 ± а
A40)
A41)
Круговая орбита с данным значением радиуса является огиба-
огибающей траекторий частиц, начинающих движение на бесконеч-
бесконечности из состояния покоя. Пример переходной траектории по-
показан на рис. 32.
При исследовании изотропных и времени подобных геодези-
геодезических мы встретились с предельными круговыми орбитами трех
типов: неустойчивой фотонной орбитой, последней устойчивой
времениподобной орбитой и переходной орбитой, граничной между
связанными и несвязанными орбитами. Зависимость радиусов
этих орбит от отношения а/М показана на рис. 33. Отметим,
что радиусы всех трех типов прямых орбит стремятся к М в пре-
пределе а -> М. Более тщательное исследование поведения радиусов
по мере приближения к этому пределу приводит к результатам,
представленным в табл, 7,

61. Геодезические в экваториальной плоскости
69
Рис. 32. Примеры критических пе-
переходных ограниченных орбит пря-
прямых и обратных с Е2 = 1, начина-
начинающихся из бесконечности из состоя-
состояния покоя. (На рис. 30—32 в силу
условия о знаках аффинный пара-
параметр вдоль прямых и обратных
орбит изменяется в противополож-
противоположных направлениях.)
10
0 -
-20
О
Г- Г+
Прямое '
Л
1 Обратное 1
1 i
2 4
Г
1.0
а/М
Радиусы предельных круговых орбит
Рис. 33. Зависимость радиу-
радиусов круговых экваториаль-
чых орбит вокруг черной
^ыры Керра от параметра- а.
Штриховые и пунктирные
кривые (для прямых и об-
обратных орбит) соответствуют
границе устойчивости (ms),
связанности (mb) и положе-
положению фотонных орбит (ph).
Сплошными линиями обозна-
обозначены горизонт событий г+ и
экваториальная граница эрго-
сферы, которая всегда лежит
на расстоянии 2М.
Таблица 7
Прямая орбита
а = М A — б) (б ->
Обратная орбита
М
гтЪ
ЗМ
AM
6M
М[\+
4М
C+2 \Г2) М
Ж

70 Глава 7. Геодезические в пространстве-времени Керра
Совпадение трех предельных радиусов для прямых орбит
при а -> М в действительности «иллюзорно», поскольку собствен-
собственные расстояния между ними стремятся к ненулевым пределам.
В самом деле, если
а = М A — б), г+ - М [1 + B6I/2] + О (б3/2), A42)
то собственное расстояние между г = М A + е) и г+ равно
Г=М A+8)
j > M In [(е2 - 26I/2 + е]/B6р. A43)
Если взять значения е, приведенные в табл. 7, то получим
(>ph — >V)co6ctb. расст -> V2M In 3 При 8 = (86/3I'2;
(ГтЬ — Г+)собств. расст -* ЛПп (l + /У) при 8 = 261/2; A44)
(rrt - Г+Hобств. расст -* М In (^б"-1/6) ПРИ 8 = DвI/3.
Тот факт, что собственные расстояния стремятся к ненулевым
пределам при а-> М, является следствием произвола в выборе
радиальной координаты в пределе а-+М. С этим связан также
и другой факт: энергия частицы на последней устойчивой круговой
орбите не стремится к бесконечности в пределе а2 ->¦ М2 — 0,
как можно было бы ожидать из совпадения радиуса орбиты с ра-
радиусом горизонта. Действительно, в случае а = М энергия ча-
частицы на круговой прямой орбите, обратный радиус которой
равен и, определяется выражением (ср. с уравнением A17))
с / лл\ l—2Mu + (Mu)/ /t;R4
?d,rect (a - М) = [хШи + 2\м1„12 . A45)
которое при стремлении радиуса орбиты к радиусу горизонта
снаружи и изнутри, т. е. при и ->¦ М =F 0, стремится к разным
пределам:
(а = М) -> ±3~1** (и -+ М-1 т 0). A46)
Предельное значение Е = 3~1/2 при r-+ M + 0, когда а =
= УИ, имеет важное значение — это максимальное значение энер-
энергии (на единицу массы), которое может иметь частица на устой-
устойчивой круговой орбите в геометрии Керра при а2 <С М2.
Ниже, в § 66, мы рассмотрим следствия, к которым приводит
обнаруженная нами разрывность функции Е в пределе г -^ М ± 0
при а =М.
62. Общее уравнение геодезических и разделение
переменных в уравнении Гамильтона—Якоби
В общем случае геодезическое движение в стационарном ак-
аксиально-симметричном пространстве-времени допускает два инте-

€2. Общее уравнение геодезических 71
грала движения: момент количества движения относительно оси
симметрии и энергию. Кроме того, вследствие параллельного
перемещения 4-вектора скорости вдоль геодезической должна
сохраняться его норма. Вообще говоря, существования этих
трех интегралов движения еще недостаточно для сведения реше-
решения уравнений геодезического движения к квадратурам. Воз-
Возможность такого сведения была обнаружена Картером, явным
'.образом выполнившим разделение переменных уравнения Гамиль-
Гамильтона—Якоби и доказавшим существование еще одной сохраня-
сохраняющейся величины. Вслед за Картером Уокер и Пенроуз пока-
:заяи, что любое пространство-время типа D по классификации
^Петрова обладает комформным тензорным полем Килинга (и,
^следовательно, сохраняющейся комплексной величиной /Cs, кото-
которая фигурировала в теореме 1 § 60 для случая изотропных гео-
геодезических), а также показали, что в геометрии Керра вдобавок
^существует интеграл /С, который был введен нами в следствии 3
-теоремы 2. В данном же параграфе мы проведем редукцию урав-
шений геодезических в общем случае с учетом этих результатов.
В общем случае лагранжиан имеет следующий вид:
22* = (i — 2Мг/р2) I2 + DaMr sin2 9/р2) *ф — (р2/Д) г2 — р2е2 —
_ (г2 + а2 + 2a2Mr sin2 9/р2) (sin2 9) ф2. A47)
Из лагранжиана получаем следующие интегралы энергии и мо-
момента количества движения:
+Pt = A — 2Мг/р2) / + BaMr sin2 9/р2) ф = Е = const, A48)
—Ар = — BaMr sin2 9/р2) I + (г2 + а2 +
+ 2а2Mr sin2 9/р2) (sin2 9) ф == Lz = const. A49)
*jКроме того, имеются еще интегралы (ср. с уравнениями C7))
2р2 (к -1) (к • п) — г21 к |2 = /С, A50)
2p2(k.m)(k-m) + a2cos29|k|2 = /С, A51)
тде1, п, m и m — базисные изотропные векторы. Интегралы A50)
и AS1) можно рассматривать как независимые, поскольку это
предполагает сохранение величины | к |2. Как обычно, положим
| к |2 = 6г = 1 A52а)
для времениподобных геодезических и
|к|2 = бх = 0 A526)
для изотропных геодезических. В нашем случае
*' = (U Л е, Ф). A53)

72 Глава 7. Геодезические в продтранстбе-времени Керрй
Явный вид интегралов A50) и A51) в геометрии Керра можно
найти, воспользовавшись выражениями из гл. 6 (уравнения A73))
для изотропных базисных векторов:
A/А) [М — (аЛ sin2 Э) ф ]2 — (р4/А) г2 — б^2 - К, A54)
l(a sin Э) I — (г2 + a2) (sin Э) ф ]2 + р4е2 + бха2 cos2 Э = К. A55)
С другой стороны, из уравнений A48) и A49) следует, что
(a sin 6) I — [(г2 + a2) sin Э ] ф =аЕ sin Э — Lz cosec Э, A56)
At — (aA sin2 в) ф = (г2 + а2) ? — aLz. A57)
Подставляя эти выражения в уравнения A54) и A55), получаем
следующие уравнения:
A/А) [(г2 +а2) Е — aLz ]2 - (р4/А) г2 — бгг2 - /С, A58)
(аЕ sin Э — Lz cosec ЭJ + р492 + бха2 cos2 Э = /С, A59)
которые можно переписать иначе:
р?2 = [(/Я + а2) ? _ aLj2 _ д Fir2 + ^)f A60)
р402 = _ (а? sin е _ Lz cosec еJ + (_бха2 cos2 6 + К). A61)
Уравнения же A56) и A57) дают дополнительную пару уравнений
p2t = B2? — 2aMrL2)/A, A62)
р2ф = A/А) [2аМгЕ + (р2 — 2Mr) Lz cosec2 в]. A63)
Теперь уже очевидно, что решение уравнений геодезических
сводится к квадратурам.
В дальнейшем окажется полезной следующая форма записи
уравнения A61):
р*02 = [к — (iz _ аЕJ ] — la2 Fi — Е2) + L\ cosec2 в ] cos2 в.
A64)
а. Разделение переменных в уравнении Гамильтона — Якоби
и альтернативный вывод основных уравнений. Как уже указыва-
указывалось, существование четвертой сохраняющейся при движении
вдоль геодезической величины было впервые доказано Карте-
Картером, когда он продемонстрировал возможность разделения пере-
переменных в уравнении Гамильтона — Якоби. В то время это откры-
открытие оказалось полной неожиданностью и навело на мысль, что
и другие уравнения математической физики должны допускать
разделение переменных. Так оно и оказалось в действительности,
как мы увидим ниже в гл. 8—10. Мы считаем полезным показать,
следуя Картеру, возможность разделения переменных в урав-

62. Общее уравнение геодезических 73
нении Гамильтона — Якоби как первое звено в цепи замечатель-
замечательных свойств геометрии Керра.
Уравнение Гамильтона — Якоби, описывающее движение
вдоль геодезической в пространстве-времени с метрикой g'/,
имеет следующий вид:
2?=«"^-|г A65)
где 5 — функция Гамильтона. Подставляя сюда коэффициенты
метрики Керра (гл. 6, уравнение A35)), получаем
- [(А - rfsin«e)/p«Asin«e] (|^J - (Д/р2) Dг) (
A66)
Удобно переписать это уравнение следующим образом:
[«sin-в -?¦ +|L]2 - (A/P2)(-f-J -
A67)
Предполагая, что переменные могут быть разделены, будем
искать решение уравнения A67) в виде
S = V26it - Et + L2cp + Sr (г) + Se (в), A68)
где Sr и Sq — функции только указанных нижним индексом
переменных. Теперь уравнение A67) принимает вид
62р2 = A/Д) [(г2 + а2) Е - aLzJ - A/sin2 0) (аЕ sin2 0 - Lzf -
069)
С помощью тождества
(аЕ sin2 6 - Lzf cosec2 6 = {L\ cosec2 8 - a2?2) cos2 0 + (Lz - aEf
A70)
уравнение A69) может быть переписано следующим образом:
{ А (-^J - A/Д) [(г2 + а2) Е- aLzf + (Lt - aEf + V*} +
+ / (-^-J + (LI cosec2 9 - a2?2) cos2 9 + 6,a2 cos2 9 j = 0. A71)

74 Глава 7. Геодезические в пространстве-времени Керра
Возможность разделения переменных теперь очевидна, и мы имет
А DfJ = <1/А) № +а2)Е ~ aL*? - Ю + (^ - аЕ?+б^
A72>
jk У = Q - (L§ cosec2 9 - #2?2 + »,а8) cos2 0, A73)
где # — постоянная разделения. Вводи сокращенные обозна-
обозначения
R = [(Г2 + а2) ? - aL2]2 - Д [^ + (Lz - aEf + в^2], A74)
в = Q - [a2 (8i - Е2) + L2 cosec2 9) cos2 6\ A76)
мы можем следующим образом записать решение для функции 5::
г е
S = VAt - Et + 1гф + J /?1/2 (r) A" dr + J 61 /*(в)<Ю. A76)
Основные уравнения движения могут быть получены из реше-
решения A76) для 5 стандартной процедурой приравнивая нулю част-
частных производных функции S по различным постоянным интетра-
лам движения (Q, Ьъ Е и Lz в нашем случае). Действительно,
уравнение
-Ц- = i/s J д-i д-1/2 dRldQ dr + Va J в-1/2 ae/aC de = О A77)
приводит к соотношению
г
A78)
а равенство нулю других частных производных приводит к соот-
соотношениям
г е ;
% = j (г2//?1/?) dr + a2 j в-1/2 cos20 d6, A79)
г е
J
е
* = Vi J Д-1^-1^ 5/?/дЛ dr + Va j в~1/2 де/дЕ d0 =
= хЕ + 2М j г [г2Е - a (Lz - аЕ)\ Д-»/?-»/« dr, A80)
г в
ф = —va J д-'я-1'2 a^/^L2 dr - va J в-1
= а I [(r2 + а2) Е - aL,] A-*R-V2 dr + J (I, cosec2 8 - aE) %-W d6,
A81)

ёЗ. Изотропные геодезические 78
которые получаются после упрощения с использованием урав-
уравнения A78).
Теперь нетрудно проверить, что уравнения A78)—A81) пол-
полностью эквивалентны системе уравнений A60)—A63), если по-
положить
Q = К - {1г - аЕ)*. A82)
В частности, при таком отождествлении постоянных правые
части уравнений A60) и A64) совпадают с определениями вели*
чин R и в в уравнениях A74) и A75) соответственно, а соотно-
соотношение A78) является очевидным следствием уравнений A60)
и A64). Наши основные уравнения теперь принимают вид:
#; р4&2 = в, A83)
ф = A/д) [2аМгЕ + (р2 — 2Mr) L cosec* в],
рЧ = A/Д) B2? — 2aMrLz), A84)
где
R = ?V4 + (а2Е2 -Ц-С?)г2 + 2Мг [Q + (Lz - аЕJ] -
-Лг-б^Д, A85)
0 == ? + (а2Е2 - II cosec2 0) cos2 9 - Ьха2 cos2 0. A86)
Удобно собрать вместе различные формулы для тензорных
и тетрадных компонент 4-вектора импульса. Имеем
-Ре = Р2Р* =
ф = BaMr sin2 0/р2) р* - (г2 + а2 + 2a?Mr sin2 0/p2)(sin20) р<* = -LZ,
A87)
pf = A - 2Mr/p2) p^ + BaMr sin2 0/р2) р* = Е;
pit) = Р@ = e-v(? - coL2) = e+vp',
pr, A88)
63. Изотропные геодезические
При рассмотрении орбит общего вида, не лежащих в одной
плоскости, ограничимся описанием проекции этих орбит на
плоскость (г, 0), поскольку зависимость от координат / и ф по
сути такая же, как и для орбит в экваториальной плоскости.
Для изотропных геодезических бх = 0, и поэтому удобно умень-
уменьшить число параметров, вводя комбинации
I = LJE, г) = QIE*. A89)

% Глава 7. Геодезические в пространстве-времени Керра
Кроме того, вместо R/E2 и ®/Е2 будем писать R и 9:
Я ^ г* + (а* _ gi _ Л) r* + 2iW [ti + F — аJ] г.— А|, A90)
9 =* п + а2 cos2 0 — ?2 ctg2 в. A91)
Единственный Параметр — прицельный параметр ?), с по-
Мощью которого классифицировались орбиты для изотропных
геодезических в экваториальной плоскости, теперь заменяется
двумя параметрами I и т). Параметры ? и т) связаны с «небесными
координатами» аир объекта, которые фиксируются наблюда-
наблюдателем на бесконечности, очень простыми соотношениями. С по-
помощью выражений A88) получаем следующие соотношения:
а = {rpW/pV>)r+oo = gcosec0o,
где 0О — угловая координата наблюдателя на бесконечности.
Координата а — видимое расстояние от источника света до оси
симметрии в направлении, перпендикулярном лучу зрения, а
координата р — видимое расстояние от источника света до его
проекции на экваториальную плоскость в направлении, перпен-
перпендикулярном лучу зрения.
Проекция орбиты на плоскость (г, 0) описывается уравнением
г 0
f R-V2 &г = [ в/2 d8, A93)
г. в,
где гг и 0* — некоторые заданные начальные значения коорди-
-нат г и 0. Следует также заметить, что, хотя знаки /?1/2 и в1/2
могут быть выбраны независимо друг от друга, необходимо строго
придерживаться сделанного однажды выбора.
а. Движение по координате 0. Рассмотрим сначала движение
по координате 0, определяемое интегралом от 6~1/2 в уравне-
уравнении A93), поскольку уже это позволит нам получить некоторую
информацию о характере орбит. Действительно, требование
неотрицательности функции в накладывает ограничения на
постоянные \ и г\:
г) +(а-?J2>0. A94)
Это неравенство становится очевидным, если записать функцию в
в виде
0 = т| + (а — IJ — (a sin 0 — I cosec 0J. A95)
Удобно заменить переменную 0 переменной ^ = cos 0 и вме-
вместо интеграла по 0 в уравнении A93) рассматривать интеграл
>jT1/2djA, v A96)

63. Изотропные Геодезические 77
где
вц =± ti — (|* +1| — a2) jia — aV4. A97)
Поскольку
ti при |jl = 0, 0 < я/2,
k-P<0 при ,1=1, 0 = 0, A98)
нужно отдельно изучать случай г) > 0 и г] < 0. Если rj > 0,
то из условия в^ ^ 0 следует, что |li2 должно быть в пределах
между [а2 = 0и некоторым значением ^тах, т. е. 0 <: \i? < Цтах,
если же г) < 0, то 0 < ^2 <: \i2 < ц* < 1 (при этом не исключено,
что такой интервал вообще не существует). Другими словами,
в случае г\ > 0 орбиты будут пересекать экваториальную пло-
плоскость и симметрично осциллировать около нее, а в случае
г] < 0 орбиты не могут пересекать экваториальную плоскость
и полностью лежат внутри конуса, причем и ось симметрии
@ = 0), и ортогональное к ней направление @ = я/2) лежат
вне этого конуса. Случай г\ = 0 нужно исследовать отдельно.
Нетрудно выписать сразу же явные выражения для интег-
интеграла /^ во всех трех случаях: т) > 0, г\ = 0 и ц <0. Имеем
1) ti > 0: в^ = а2 ([л2. + ji3) (j4 - ^i2) @ < jx2 < ц^), A99)
где
VL = (l/2a?) {[(? + г, - a2J + 4a2r,]1/2 + (f + r, - a2)),
следовательно,
I 6j71/2d[x = a(^4_ + ^2_)~1/2F (i|), Л), B01)
k2 = \i%l(\i+ + ^t?_), cosi|) =
2) r) = 0:
6^ = (a2-g2)^-aV @ < tx2 < ^ах), B02)
где
nLx = 1-Г/«2 (|5I2<M2)>
следовательно,
^max
] e?/2dv= -(а2-ГГ1/2АгсЬ(^тах). B03)
I*
3) л < 0:
B04)
= (l/2a2) ((| t, | + a2 - |2) ± [(IЦ | + «2 - tf - 4a2 h iFb
B05)

?8 Глава 7. Геодезические ё проОпранСШё-времени Керрй
следовательно,
м-
J e^dfx = (\la\L+)F (t|>, k)t B06)
Где
o<isi<M-hl1/
В уравнениях B01) и B06) F (ip, /г) обозначает эллиптический
интеграл Якоби первого рода.
б. Главные изотропные конгруэнции. Из уравнений A94)
и A95) следует, что случай
г) + {а - If = 0 B07)
отличается тем, что условие 6^ ^ 0 выполняется, только если
9 = е0 = const, I = a sin2 0O, B08)
причем при 0 = 00 в^ = 0. Из уравнения B07) теперь вытекает.,
что
т) = —a2 cos4 80. B09)
Подставляя эти значения g и ц в уравнение A90), находим
# = (г2 + a2 cos2 0ОJ?2, B10)
где мы восстановили опущенный прежде множитель Е2. Из урав-
уравнения A83) теперь получаем
г = ±Е. B11)
Подобным же образом из уравнений A84) находим
ф = а?/Л, i = (г2 + а2) ?/Д. B12)
Следовательно, эти специальные изотропные геодезические опи-
описываются уравнениями
«¦=л±*.е, 4- = ±е, -^-=о, 4^ = 4-^- B13)
dT Д ' dx dx dx A v '
Полученные уравнения определяют бессдвиговые изотропные
конгруэнции, которые были использованы в гл. 6 (§ 56) для
построения изотропного базиса при описании пространства-
времени Керра в формализме Ньюмена — Пенроуза и доказатель-
доказательства принадлежности этой метрики к типу D по классификации
Петрова,
в. Движение по координате г. Обратимся теперь к изучению
радиального движения, определяемого интегралом от R~l/2 в урав-
уравнении A93).

63. Изотропные геодезические 79
Как и в случае орбит, лежащих в экваториальной плоскости,
рассмотренных в § 61, существуют орбиты, которые пересекают
горизонт событий, и орбиты, не пересекающие горизонт. Для
орбит в экваториальной плоскости это различие определялось
тем, меньше или больше прицельный параметр D некоторого
критического значения Dc, причем орбиты с прицельным пара-
параметром, в точности равным Dc, представляли неустойчивую
круговую орбиту. Подобным же образом, в рассматриваемом
общем случае различие определяется тем, лежат ли значения
интегралов движения I и г) по одну или по другую сторону от
некоторого критического геометрического места точек (?в, г\8)
в плоскости (I, г)), причем орбиты, интегралы движения вдоль
которых лежат на самом геометрическом месте точек, являются
неустойчивыми с г = const. Геометрическое место точек (?e> r\s)
играет в общем случае ту же роль, что и прицельный параметр De
для орбит в экваториальной плоскости.
Неустойчивые орбиты постоянного радиуса описываются урав-
уравнениями
# = г* + (а2 — I2 — г)) г2 +2М [г) + (I - аJ] г — а\ = О,
B14)
dR/dr = 4г3 + 2 (а2 — I2 — г\) г + 2М [г\ +A — аJ] = 0, B15)
откуда следуют соотношения
Зг4 + Г2а2 _ ц (Г2 _ Д2) = Г2|2| . B16)
г4 — а2Мг + г) (а2 — Mr) = Mr (g2 — 2ag). B17)
Эти уравнения можно разрешить относительно ^ и т). Действи-
Действительно, исключая параметр г), получаем
а2 (Г _ М) I2 — 2аМ {г2 — а2) I —
— (г2 + а2) [г (г2 + а2) — М (Зг2 — а2) ] = 0. B18)
Дискриминант получившегося квадратного уравнения равен
aV2A2, B19)
следовательно, решение уравнения B18) имеет следующий вид:
I = [М (г2 — а2) ± rAVa (г — М). B20)
Если в решении B20) выбрать верхний знак, т. е. если
I = (г2 +а2)/а, B21)
то из уравнения B16) находим следующее решение для т):
г) = —гЧа2. B22)
Полученные решения для | и ц удовлетворяют соотношению
т, + (а - |J = 0, B23)

Глава 7. Геодезические в пространстве-времени Керра
которое несовместимо с нашим требованием, чтобы орбита не
лежала в экваториальной плоскости, поскольку в п. 63, б было
показано, что это соотношение приводит к условию Э = const.
Следовательно, в уравнении B20) нужно выбирать нижний знак.
Имеем поэтому
I = [М (г2 — а2) —
—гА)/а (г — М), B24)
Рис. 34. Геометрическое место точек (s
T]s), определяющее интегралы движения
трехмерных орбит постоянного радиуса
вокруг черной дыры Керра с а = 0,8. Еди-
Единица длины вдоль оси абсцисс равна М.
Из уравнения B25) следует, что ц = 0, когда
4а2М - г (г — ЗМJ,
ц = г3 На2М — г(г —
— ЗМJ]/а2 (г — МJ =
= г3 [4МА — г(г —
— МJ]/а2 (г — МJ. B25)
Эти уравнения определяют
в параметрическом виде гео-
геометрическое место критиче-
критических точек (?в> кN) (рис. 34).
В п. 63, а мы видели, что
характер орбиты зависит от
того, больше, равна нулю
или меньше нуля величина ц.
Мы должны, следовательно,
различать эти три случая.
следовательно, когда
±2аМ1'2 = г3/2
B26)
B27)
Но это уравнение совпадает с уравнением A24), которое опреде-
определяет радиусы неустойчивых круговых фотонных прямых и обрат-
обратных орбит, лежащих в экваториальной плоскости. Обозначим
радиусы этих неустойчивых фотонных орбит г$ и Грь*: Тогда ясно,
что
B28)
г]>0 при г
л = 0 при г = г$, г =
т|<0 при r+<r<r{p+h\
Решения для движения по координате Э, соответствующие
трем случаям, приведенным в B28), были даны в п. 63, а. Из этих
решений следует, что не существует орбит постоянного радиуса
при т) < 0, поскольку, чтобы величины \х2±, определенные урав-
уравнением B05), были положительны, необходимо вьшоднецие т-

63. Изотропные геодезические 81
равенств 0 < I < а — | ц |1/2 и | т] | < а2, а эти неравенства
(как легко проверить) не могут быть удовлетворены при значе-
значениях I и т|, задаваемых уравнениями B24) и B25).
Важно также отметить, что при г) = 0 орбиты целиком лежат
в экваториальной плоскости, потому что в этом случае из урав-
уравнения B16) следует, что I2 = Зг2 + я2, а это в точности совпадает
с уравнением, приведенным в сноске к уравнению (82) (напом-
(напомним, что I (= LJa) имеет тот же смысл, что и D (= Lid) ранее).
Вернемся теперь к исследованию движения по координате г.
Пусть | и г) принимают значения \s и t]s, соответствующие орбите
постоянного радиуса rs, т. е. пусть %s и r\s — значения, опреде-
определяемые уравнениями B24) и B25) для г = г8. При таком выборе
постоянных движения г. есть двойной корень уравнения R = О,
и можно показать, что функция R сводится к виду
R = (r- rsf (r2 + 2rrs ~ aV.2). B29)
а интеграл, который мы должны рассматривать, равен
f R-i/2 dr = | (г - г.) (г2 + 2rrs - аЧ/г2)~ dr. B30)
Из этого уравнения следует, что траектория состоит из двух
частей: внешней и внутренней относительно г = г8. Поскольку
t]s > 0, эта траектория будет обрываться прежде, чем достигнет
г = 0, потому что больший из двух корней уравнения
г2 + 2гг5-яЧ/г52 = 0, B31)
равный
-г. + (г* + a2r]s/^I/2 = -г, + 2 (М Ars)I/2/(rs - М), B32)
положителен и, как
а2 < М\
Полагая теперь
и вычисляя интеграл
орбиты на плоскость
Je^I/2dfi = ±c-I/2ln
с
можно
B30),
(г, Э =
12 И1
= 3rl-
показать
получаем
• arcos \x)
+ 4rsx 4-
- a\tlr\
, меньше ra
уравнение
сх2)]х/2 + 2сх
(>0).
при условии
B33)
для проекции
c + 4rs], B34)
B35)
Интеграл по ^ в правой части уравнения дается выражением B01).
Примеры траекторий, вычисленных на основе уравнения B34),
показаны на рис. 35.
Хотя мы рассмотрели только такие орбиты, для которых
интегралы движения лежат на геометрическом месте критических
точек (ls, r|s), ясно, как они должны выглядеть и в общем случае?
§ Чандрасекар С.

82
Глава 7. Геодезические в пространстве-времени Керра
-6 х В
Рис. 35. Критические изотропные геодезиче-
геодезические в плоскости (/*, 0) для трех пар значений
параметров: а — rs = 1,85, r\s = 1,6524; б —
rs = 3,75, r]s = 4,9087; в — rs = 3,0, r\s =
= 27,0. Эти орбиты не достигают сингуляр-
сингулярности. Единица длины вдоль осей координат
равна М, а параметр решения Керра а ра-
равен 0,8.
когда значения интегра-
интегралов движения сосредото-
сосредоточены с той или с другой
стороны от этой7критиче-
этой7критической кривой: две части
траектории по мере при-
приближения к сфере г = rs
с одной или с другой сто-
стороны будут или разде-
разделяться на две несвязные
части (которые мы назвали
орбитами первого и вто-
второго рода), или объеди-
объединяться в одну непрерыв-
непрерывную траекторию.
Представляет интерес
случай т) = 0. Как мы
видели, орбиты постоян-
постоянного радиуса г = г±ъ при
т) = 0 лежат целиком в
экваториальной плоско-
плоскости. Все орбиты в эква-
экваториальной плоскости так-
также характеризуются ра-
равенством нулю постоян-
постоянной Картера. Но не все
орбиты с т] = 0 лежат
в экваториальной плоско-
плоскости, потому что при т) = 0
движение по координате г
в общем случае опреде-
определяется интегралом (ср.
с уравнением B14))
-tJ]}-x/2<ir, B36)
а движение по коорди-
координате 0 определяется
уравнением B03). Инте-
Интеграл B36) можно свести
к эллиптическому инте-
интегралу Якоби, и, следов^*

6$. Изотропные геодезические
83
тельно, траектории в плоскости (г, 0) описываются уравне-
уравнением
(а* - p)-i/2 Arch (fi/fxmax) - ± (АВ)-*/' F (г|>, Л), B37)
где
IW - A - WI/2, k" - [(Л + ВJ
cos i|> = [(А - В) г + гхА]/[(А + В)г + гхА],
sh 30 = [27 M2 (a - g)/(a + ?K]1/3.
Эти траектории существуют только при I < а. Для орбит в эква-
экваториальной плоскости ограничение ? < а эквивалентно огра-
ограничению!) <: а (см. опреде-
определения D и ? в уравнениях
G3) и A89)). Существование
трехмерных орбит с г\ = О
и I < а — это проявление
неустойчивости орбит с при-
прицельным параметром D < а,
лежащих в экваториальной
плоскости. Ясно также, что
все эти траектории обрыва-
обрываются в сингулярности и не
имеют естественного продол-
продолжения в область отрица-
отрицательных значений г (см.
Рис. 36. Пример изотропной геодезиче-
геодезической с х\ = 0 в плоскости (г, 0). Это един-
единственный тип орбит, не лежащих в эква-
экваториальной плоскости, которые обры-
обрываются в сингулярности. Единица длины
вдоль координатных осей равна М, а па-
параметр Керра а равен 0,8.
рис. 36, на котором показаны
примеры траекторий, вычи-
вычисленных на основе уравне-
уравнения B37)).
Наконец, рассмотрим класс орбит с г\ < 0. Эти орбиты инте-
интересны потому, что они естественным образом продолжаются
в область отрицательных значений г, делая ^гем самым расшире-
расширение многообразия физически необходимым. Однако условия
появления таких орбит очень жесткие: |т]|<а2 и 0 < | ? | <:
< | а | — | т] |1/2. Уравнения движения вдоль таких траекторий
по координатам гиб были численно проинтегрированы Г. Туми
и результаты показаны на рис. 37.
г. Случай а = М. Хотя мы и решили (вопреки общеприня-
общепринятому мнению) не уделять специально внимания исследованию
предельного случая а = УИ, в данном разделе мы кратко рассмо-
рассмотрим соотношения, полученные в предыдущем разделе, в пре-
пределе a = М. (Напомним, что в п. 61, б, обсуждая уравнение A42),'
мы уже отметили неприемлемость координаты г для описания

Глава 7. Геодезические в проОпрансше-врёмени Керрй
Рис. 37. Два примера орбит с отрицательным
значением т), которые продолжаются в об-
область отрицательных значений г: а — т] =
= —0,3 и ? = —0,05; б — т] = —0,3 и ? =
= —0,07. Угловая координата 0 для этих
орбит заключена в пределах между 0mln
и Этах. Хотя в плоскости (/*, 0) эти орбиты
проходят через нуль, они в действительности
не проходят через сингулярность: в коорди-
координатах Керра—Шилда (рис. 25) они плавно
проходят сквозь диск, обходя сингулярность.
(Параметр Керра а выбран равным 0,8.)
явлений вблизи горизонта
событий, когда а -> М.)
В пределе а — М урав-
уравнения B24) и B25) при-
принимают вид
+М*)Ш9
DЛГ — г),
B38)
и мы можем получить
явное (а не параметриче-
параметрическое) выражение для гео-
геометрического места кри-
критических точек т] (I). Дей-
Действительно, разрешая пер-
первое из уравнений B38)
относительно г, получаем
r(l) = M +BM2 — Miy2.
B39)
Подставим затем это зна-
значение в выражение для х\\
ц (I) = (ИМ7) [М +
+ B7И2 — Miy^f [37И —
— BУИ2 — MlI'2]. B40)
Напомним, что
а = +1 cosec 0О,
р = (т, + a2 cos2 60 —
- I2 ctg2 бор. B41)
Видимая форма черной
дыры для наблюдателя на
бесконечности опреде-
определяется проекцией крити-
критической кривой на «небес-
«небесную сферу» точно так же,
как неустойчивая круго-
круговая орбита радиуса 37И
(с критическим прицель-
прицельным параметром 3 i/~3 M)
определяет форму черной
дыры Шварцшильда. В на-
нашем примере просто пред-
представить геометрическое

63. Изотропные геодезические
место критических точек (|, х\) в виде замкнутой кривой в пло-
скости (а, р). Для наблюдателя в экваториальной плоскости,
смотрящего на черную дыру из бесконечности, видимая форма
атой черной дыры будет определяться соотношением
К
B42)
Получающаяся кривая показана на рис. 38.
д. Изменение направления поляризации при движении вдоль
изотропной геодезической. Обычно в общей теории относитель-
относительности распространение света
описывается на языке гео-
геометрической оптики. При та-
таком описании основным по-
понятием является понятие
световых лучей, определяемых
как траектории, ортогональ-
ортогональные к световым фронтам. Бо-
Более точно, световой луч есть
кривая в пространстве-вре-
пространстве-времени, касательный вектор
к которой в каждой точке
указывает в направлении
усредненного вектора Умо-
ва — Пойнтинга. Эти кри-
кривые, часто называемые траек-
траекториями фотонов, являются
изотропными геодезическими
общей теории относительно-
относительности. При изучении ИЗОТрОП- Рис. 38. Такой видит экстремальную чер-
ных геодезических в настоя- "Ую ДЫРУ КеРРа (а = м) удаленный на-
тттрй гпяпр и п ппрттктллштыу блюдатель в экваториальной плоскости,
щей главе и в предыдущих если черная дыра находится перед источ.
главах мы Придерживались ником освещения и угловой размер этого
именно такой точки Зрения. источника больше углового размера чер-
Поляоизаиия является н°й Дыры. Единица длины вдоль осей а
другой Характеристикой све- ?ав^(мРеДеЛеННЫХ уРавнениями <241»
та, и эта характеристика
важна для астрофизических исследований как раз при изуче-
изучении черных дыр. Дело в том, что следует ожидать, что
излучение, идущее от аккреционных дисков, окружающих
черные дыры, поляризовано. И поэтому возникает вопрос, как
связана поляризация излучения, принимаемого удаленным на-
наблюдателем, с состоянием поляризации излучения, покидающего
аккреционный диск. Ответить на этот вопрос довольно просто.
Состояние поляризации описывается направлением электриче-
электрического вектора в плоскости, перпендикулярной направлению
распространения, т. е. перпендикулярной вектору к, а электри-

86 Глава 7. Геодезические б пространстве-времени Керра _
ческий вектор, ортогональный к, переносится параллельно вдоль
светового луча, т. е. вдоль изотропной геодезической, описы-
описываемой вектором к. При такой постановке задачи ясно, что в гео-
геометрии Керра нужно просто отождествить вектор f в формули*
ровке теоремы Уокера — Пенроуза в § 60 с вектором электриче*
ского поля и воспользоваться сохранением комплексной вели-
величины Ks при движении вдоль изотропной геодезической (вели-
(величина К8 определена уравнением A2)).
В пространстве-времени Керра вейлевский скаляр Ч^ равен
(см. уравнение A80) гл. 6)
?2 = — М (г — la cos 6)-3, B43)
и интеграл Уокера — Пенроуза становится равным
[(kl) (f n) — (k-n) (f-1) -(k.m)(f-m) + (k-m)(f.m)](r-tecose)=»
= K% + tKv B44)
Подставляя сюда выражения для базисных векторов (уравне-
(уравнение A73) гл. 6), находим
_ _ Н- а {krf<* - W sin2 0 = А, B45)
(km) (f.m) - (km) (f.m) =*
= i [(r2 + a2) {№f* - №f>) - a (ktfe ~ fee/0I sin 0 = IB. B46)
Используя введенные выше обозначения Л и В, можно следующим
образом записать закон сохранения (умножив на (г -f ia cos 0)
уравнение B44)):
р2 (Л + 1В) = (г + ia cos 0) (/Са + iKi). B47)
Приравнивая в этом уравнении действительные и мнимые части
слева и справа, получаем
Л = (l/p2)(^-^icos0), B48)
В = A/р2) (Кгг + аК2 cos 0). B49)
Кроме того, условие ортогональности векторов к и f приводит
к следующему соотношению:
A - 2Мг/р2) k*f* + BaMr sin2 0/р2) (&р + *ф/') - рЩ* -
- (р2/А) Щг - (г2 + а2 + 2a2Mr sin2 0/р2) №р sin2 0 = 0. B50)
И наконец, уравнения геодезических A83) и A84) дают
= A/А) [(г2 + а2J — а2Д sin2 9 — 2аМгЦ
= A/А) \2aMr + (р2 — 2Mr) | cosec2 6]. * *
Компоненты вектора к определяются из уравнений B51), а урав-
уравнения B48)—B50) определяют компоненты вектора f, причем

63. Изотропные геодезические 87
трех уравнений как раз достаточно для этой цели, поскольку
•вектор f определен с точностью до слагаемого, пропорциональ-
пропорционального изотропному вектору к.
Предыдущие уравнения интересуют нас лишь постольку,
поскольку они связывают направление вектора f, задаваемого
какой-либо физической теорией, в некоторой точке вблизи чер-
черной дыры с направлением вектора f на бесконечности. Поэтому
достаточно рассмотреть асимптотики решения уравнений
B48)—B50).
Из уравнения B51), как можно показать, получаются следую-
следующие асимптотики компонент вектора к:
Ав _> р/r2, &ф -> (Цг2) cosec2 90, B52)
где
p2 = л + a2 C0S2 Qo _ g2 ctg2 6() B53)
(ср. с уравнением A92)). Поскольку вектор f определен лишь
с точностью до слагаемого, пропорционального изотропному
вектору к, можно без потери общности положить
f* = 0. B54)
Условие ортогональности B50) теперь дает
—гЩ* - krfr - г2 sin2 %k<?fv = 0 (r-+oo), B55)
откуда получаем, используя уравнения B52):
fr = _p/e _ ipm B56)
Подобным же образом из уравнений B48) и B49) следуют асимп-
асимптотики
; jr 1 п Qin2 а Яф — /^ г—1 ^9^7V
/ -f- a Sin tJo/4' — Д2Г , \^д')
[г2 (А0/в — Ае/ф) - ар] sin 90 = /d/-1. B58)
^Исключая с помощью уравнения B56) компоненту fr из уравне-
уравнения B57) и подставляя выражения для компонент kQ и № из урав-
уравнений B52), получаем
г- —Р/е — (| — a sin2 60) /ф = /СаГ, B59)
I (| cosec 90 — a sin 0О) /е — р sin 60/ф = Кгг~х. B60)
1Вводя обозначение
г 7 = I cosec 60 — я sin 0О, B61)
^получаем
I Р/е + 7 sin Эо/ф = —К2г~К 7/е — Р sin 90/ф = +/С!/—1. B62)
эти уравнения относительно /е и /*, находим
f» sin 90 = — (p/Ci + Y^)/r(P2 + У2),

88 Глава 7. Геодезические в пространстве-времени Керра
Если обозначить через <?Ге и <?Гф компоненты вектора напря-
напряженности электрического поля <? в поперечной плоскости, ко-
которая определяет состояние поляризации на бесконечности, то
%v = — r sin Go/*, <Гв = — /f>, B64)
и из уравнений B63) следует, что
%* = (р^ + УК2)/Ф2 + 72), ^е = (Р/С, - Ytfi)/(P2 + Y2).
B65)
Выбором нормировки вектора <S нетрудно добиться выполнения
соотношения
К\ + К22 = 1. B66)
В этом случае (^Гф, <?Ге) — единичный вектор в поперечной пло-
плоскости, определяющей состояние поляризации, причем пара-
параметры Стокса (нормированные на единичную интенсивность),
обычно используемые для описания состояния поляризации,
могут быть легко выражены через вектор (<?Гф, <?Ге).
64. Времениподобные геодезические
При исследовании времениподобных геодезических в уравне-
уравнениях A85) и A86) можно положить бх = 1, и уравнение, опреде-
определяющее проекцию геодезической на плоскость (г, 0), снова имеет
вид
г 0
e-i/2d9, B67)
но теперь функции R к @ определяются следующим образом:
# = г4 + (а2 — I2 — л) г2 + 2М [г] + (I — аJ] г —
— а2ц — г2Д/?2, B68)
в = п + а2 A — ?) cos2 0 — I2 ctg2 0, B69)
где % = LJE, г] = QIE2, а ? — энергия на единицу массы.
Мы здесь написали R и в вместо RIE2 и в/?2.
а. Движение по координате 9. Рассмотрим сначала движение
по координате 0, определяемое интегралом от функции в/2,
и заменим, как и прежде, переменную 0 переменной \i = cos 0.
Правая часть уравнения B67) тогда принимает вид
B70)
где
ви = t, _ [|« + т] — а2 A — Е~г) ] f — а2 A — Е~2) ц4. B71)

64. Времениподобные геодезические
Очевидно, нужно различать три случая: связанные орбиты
с Е2 < 1, переходные орбиты с Е2 = 1 и несвязанные орбиты
с ?2 > 1.
В случае связанных орбит с ?2 < 1 удобно заменить а2 выра-
выражением
а2 = а2 (Е~2 — 1) > 0 B72)
и записать функцию ©р, в виде
% = Л - а2 + Л + а2) fi2 + ccV4. B73)
Из этого выражения для 6^ и требований, чтобы б^^О и 0 <
< (х2 <: 1, следует, что отрицательные значения т] запрещены,
а область изменения ц,2 начинается от нуля и простирается до
меньшего из двух корней уравнения
Л — (I2 + Л + а2) ц2 + «V = 0 (л > 0). B74)
Интеграл B70) теперь может быть стандартным образом сведен
к эллиптическому интегралу первого рода. Имеем
f 
I
= a ([(D tf) (, ^Г^ D+) (¦,
о
B75)
где
p2± = (l/2a2) j(|2 + Tj + a2) ± [(|2 + t] + a2J — 4a2-n]i/2},
'; B76)
k = [x_/[x_j_, sin \|) = (i/ji-,. B77)
? Для переходных орбит с Е2 = 1 получаем
; @^ = Л ~ а2 + Л) (х2. B78)
И снова отрицательные значения т] запрещены, а соответству-
соответствующий интеграл равен
| м-
i
| В случае же несвязанных орбит с ?2 > 1 применимы резуль-
результаты исследования изотропных геодезических в п. 63, а, если а2
вменить выражением
а2 = а2 A — ?) > 0. B80)
Итак, связанные и переходные орбиты должны с необходи-
необходимостью пересекать экваториальную плоскость и осциллировать
тносительно нее, а несвязанные орбиты очень похожи на изо-
ропные геодезические: существуют орбиты с ц > 0, пересека-
пересекающие экваториальную плоскость, орбиты с ц < 0, не пересека-
мдие экваториальную плоскость, лежащие внутри конуса и

90 Глава 7\ Геодезические ё пространстве-времени Кйрра
продолжаемые в области отрицательных значений г, и суще-
существуют орбиты с t) = 0.
б. Движение по координате г. Переходя к исследованию
движения по координате г, определяемого интегралом от функ-
функции R~1/2, рассмотрим в соответствии с уже ставшей стандартной
процедурой специальный класс.орбит, которые не только пред-
представляют основу для их классификации, но и являются простыми
орбитами, уравнения для которых легко интегрируются, и в то же
время достаточно хорошо иллюстрируют общие особенности гео-
геодезических. В рассматриваемом случае этими специальными орби-
орбитами являются такие, для которых радиальная координата оста-
остается постоянной. Это осуществляется при условии выполнения
следующих соотношений:
/? = 0> dR/dr = 0. B81)
Ограничения на интегралы движения |, г) и Е2, следующие из.
условий B81), можно получить в точности так же, как и в п. 63, ву
за исключением того, что теперь нужно в определении R добавить
член —/*2Л/?2. Следуя по проторенному пути, находим, что урав-
уравнения B16) и B17) заменяются уравнениями
Зг4 + г2а2 — ц{г2 — а2) — (r/ЕJ (Зг2 — 4Мг + а2) = г2?2, B82I
г4 — а2Мг + х\ (а2 — Mr) — (rs/E2) (r — М) = гМ (I2 — 2а?).
B83)
Как и прежде, нужно разрешить эти уравнения относительно-
? и л-
Исключая т] из уравнений B82) и B83), получаем вместо»
уравнения B18)
а2 (г — М) I2 — 2аМ (г2 — а2) I —
— {(г2 + а2) [г (г2 + а2) — М (Зг2 — а2) ] — гА2/?2} = 0. B84)
Решение этого уравнения имеет^ вид (ср. с уравнением B20));
| = а-\ (г _ л|)-1 (Af (г2 - а2)± гД [1 - Е~2 A - М/г)]1/2}, B85)
? соответствующее решение для г) есть (ср. с уравнением B25))
х\а2 (г—М) = г3 (г — М)~г Ш2М — г (г — ЗМJ] +
+ {НЕJ [г (г — 2МJ — а2М ] —
— 2г3М (г — iM)-xA {1 ± [1 — A — Mlr)IE2Yi*). B86)
Геометрическое место этих критических точек, определяющих
критическую кривую, показано на рис. 39.
Пусть теперь интегралы движения ? и ц принимают зна-
^чения \s и r]s, соответствующие движению частицы с энергией Е
мг единицу массы по орбите постоянного радиуса rs, т. е. пусть

64. Времениподобные геодезические
91
?s и r)s принимают значения, задаваемые уравнениями B85)
и B86) при заданном значении г = rs и заданной энергии ?.
(Разумеется, необходимо, чтобы для выбранных значений rs
и ?2 величина r]s была положительной в случае ограниченных
и переходных орбит.) Если интегралы движения выбраны ука-
указанным образом, то rs является двойным корнем уравнения R = О
и, следовательно, функцию R можно представить в виде
B87)
B88)
~~a\/r2s].
Полагая теперь
х = (г - г,),
видим, что интеграл, кото-
который мы должны приравнять
тому или другому выраже-
выражению для интеграла
2dm B89)
найденному выше в п. 64, а,
равен
= - Jd*{(l —
B90)
Рис. 39. Геометрическое место точек (?в,
г|з), определяемое уравнениями B85) и
B86), для переходных ограниченных вре-
мениподобных орбит с Е2 = 1,0. Единица
длины вдоль оси абсцисс равна М, а па-
параметр Керра а выбран равным 0,8.
Это элементарный интеграл, значения которого легко выписать
для каждого из трех случаев Е2 > 1, Е2 = 1 и Е2 < 1. Действи-
Действительно, вводя определение
\ F(x) = а + $х + ух2, B91)
где а, р и у — коэффициенты квадратичной формы по х, которая
появляется в интеграле B90), находим
: ± 7-1/2 In [2 (yF)V2 + 27л: + И при у > 0,
±7^1/2ArshB7JC+p)JD-1/2 при 7>0, Z)>0,
=F (—У)/2 arcsin B7^ X Р) (—Я)-1/2 при 7<0, D < 0,
B92)
^ D = - 4 {[rs A - Я-2) + M/E*f + (aV/i) A - ?)Ь B93)
;, Примеры орбит, вычисленных на основе этих уравнений,
Доказаны на рис. 40.

92
Глава 7. Геодезические в пространстве-времени Керра
Как и в случае изотропных геодезических, орбиты постоян-
постоянного радиуса, соответствующие г\ = 0, обязательно лежат в эква-
экваториальной плоскости.
Это сразу же следует из
уравнений B82) и B83),
которые при т) = 0 сво-
сводятся к следующим урав-
уравнениям:
Зг2 + а2 — {Зг2 ~ A Mr +
г3 — г2 (г — М)/Е2 =
= М (I — а2), B94)
а эти уравнения совпа-
совпадают в точности с урав-
уравнениями A08) и A09), опи-
описывающими круговые ор-
орбиты в экваториальной
плоскости.
65. Процесс Пенроуза
Выше (п. 58, а) мы об-
обращали внимание на важ-
важное значение поверхности,
на которой компонента
метрики gtt обращается
в нуль, и на то, что в гео-
геометрии Керра эта поверх-
поверхность не совпадает с го-
горизонтом событий, за ис-
исключением полюсов. В то-
тороидальном пространстве
между этими двумя по-
поверхностями, т. е. в эрго-
сфере, вектор Киллинга
dldt становится простран-
ственноподобным и точно
также становится про-
странственноподобной со-
сохраняющаяся компонента
Рх 4-вектора импульса.
Энергия частицы в этой области пространства, измеряемая наблю-
наблюдателем на бесконечности, может быть отрицательной. Последнее
обстоятельство имеет важные следствия: становится возможным,
как показал впервые Пенроуз, физический процесс, приводящий
-5--
Рис. 40. Критические переходные времени-
подобные геодезические в плоскости (г,
0), описываемые уравнениями B79) и B92)
для трех значений rs: а — 2,154; б —
4,0; в — 5,44. Единица длины вдоль коорди-
координатных осей равна М, а значение параметра
Керра а выбрано равным 0,8.

65. Процесс Пенроуза 93
к извлечению энергии и момента количества движения из черной
дыры. В настоящем параграфе мы изучим природу таких процес-
процессов и найдем ограничение на количество энергии, которую можно
извлечь из черной дыры.
Найдем прежде всего предельное значение энергии, которую
может иметь частица в заданной точке пространства. Этот предел
мы получим, приравняв нулю кинетическую энергию, пропор-
пропорциональную г2. Тогда из уравнений A83) и A85) следует
[г (г2 + а2) + 2а2М] Е2 - 4aMLzE - L\ (r - 2Af) -
- (V + Qlr) A = 0. B95)
Разрешая уравнение B95) относительно Еу получаем
Е = (г (г2 + а2) + 2О:М)-> BaMLz ± Д1/2 \t2L\ +
+ [г (г» + а*) + ММ] (б,г + ?r-i)}1/2). B96)
Разрешив его относительно Lz, получим следующее выражение:
1г = [1/(г - 2Л1)] {— 2аМ? ± А1/2 [г2?2 -
-(r-2Af)(e1r + <?r-0l1/2}- B97)
При выводе этих соотношений было использовано тождество
Аг2 — 4а2М2 = [г2 (г2 + а2) + 2а2Мг] A — 2М/г). B98)
Из уравнения B96) можно получить условия, при которых
энергия Е, измеренная наблюдателем на бесконечности, может
быть отрицательной. Прежде всего важно отметить, что частица
единичной массы, находящаяся на бесконечности в состоянии
|юкоя, должна иметь энергию Е = 1 в соответствии с принятым
йами соглашением. Чтобы удовлетворить этому требованию,
Ьужно выбрать положительный знак в правоц части уравне-
уравнения B96). Теперь очевидно, что необходимыми условиями выпол-
выполнения неравенства Е < 0 являются следующие:
I Lz < 0, B99)
| 4а2М2Ц > A {r2Ll + [г2 (г2 + а2) + 2a2Mr] {bx f фг2)}. C00)
Б- помощью тождества B98) последнее неравенство может быть
рриведено к виду
| LJ + A Fj + ?/г2)} <0. C01)
следует, что ? <0 в том и только в том случае, если
Lz<0 и (г - 2М)< - (Ar/LD(в! + С/г2). C02)

94 Глава 7. Геодезические в пространстве-времени Керра
Следовательно, только частицы, направление вращения которых
вокруг черной дыры противоположно вращению самой черной
дыры, могут иметь отрицательную энергию, а в экваториальной
плоскости, кроме того, необходимо, чтобы г < 2М, т. е. частицы
должны находиться в эргосфере.
а. Процесс, предложенный Пенроузом. Пенроуз предложил
следующий процесс, иллюстрирующий возможность извлечения
энергии из керровской черной дыры.
Частица, двигаясь по геодезической из состояния покоя на
бесконечности, попадает в экваториальную плоскость в точке
г (<2УИ), которая является ее точкой поворота (т. е. в этой точке
г = 0). В точке г частица распадается на два фотона, один из кото-
которых уходит в черную дыру, пересекая горизонт событий, и «те-
«теряется», а другой вылетает на бесконечность. Рассмотрим случай,
когда фотон, пересекающий горизонт событий, имеет отрицатель-
отрицательную энергию, а энергия фотона, уходящего на бесконечность,
больше, чем энергия частицы, пришедшей с бесконечности.
Пусть
El0) = l, L[z°\ Ea\ Lzl\ E{2) и Lz2) C03)
обозначают энергию и момент количества движения соответственно
частицы, приходящей из бесконечности, и фотонов, один из кото-
которых пересекает горизонт событий, а второй уходит на бесконеч-
бесконечность.
Поскольку частица приходит в точку г, двигаясь по времени-
иодобной геодезической, и г есть точка поворота ее траектории,
то Uz°" можно найти из уравнения B97), если в нем положить
Ьх = 1, Е = 1 и Q = 0. Получаем таким образом:
If =: [1/(г - 2М)][— 2аМ + BМгДI/2] = а@). C04)
Подобным же образом, полагая бх = Q = 0 и выбирая соответ-
соответственно отрицательный и положительный знаки в уравнении B97),
можно получить соотношения между энергией и моментом коли-
количества движения фотона, пересекающего горизонт событий (от-
(отрицательный знак), и фотона, уходящего на бесконечность (по-
(положительный знак):
L<1} = [1/(г - 2М)] (— 2аМ - гА1/2) Е{{) = осA)?A), C05)
= [1/(г - 2М)] (- 2аМ + гД1/2)^B) = аB'?B). C06)
Законы сохранения энергии и момента количества движения
требуют, чтобы выполнялись соотношения
1, C07)
= Li0) = a@). C08)

65. Процесс Пенроузй 95
Из этих уравнений можно найти значения
?A) = (а@) _ аB))ДаA) _ аB))э
?B) = (аA) _ а@))/(аA) _ аB))в C09)
Подставляя значения а@), а(П и аB) из уравнений C04)—C06),
получаем
L ±). C10)
Фотон, уходящий на бесконечность, будет иметь энергию, боль-
большую, чем энергия частицы ?<0) — 1, если г < 2М (как мы и по-
постулировали). Выигрыш в энергии АЕ равен
АЕ = -^-[BМ/гУ^ - 1]= - ЕМ. C11)
Из уравнения C11) следует, что максимальный выигрыш в энер-
энергии в рассматриваемом процессе достигается тогда, когда точка
поворота траектории частицы находится на горизонте событий.
Следовательно,
^I/2-1]. C12>
Поскольку минимальное значение г+ равно М (когда а2 = М2),
АЕ < (/2 — 1)/2 - 0,207. C13)
Поучительно вывести это неравенство и другим способом.
Введем с этой целью понятие «неприводимой массы»
Mir = -I" (r% + Ф)Ч* = (Mrj2)W. C14)
Ниже в п. 65, г будет дано объяснение этому названию. Неравен-
Неравенство C12) теперь можно переписать следующим образом:
AE<-±-(M/Mlr-\). C15)
Из уравнения B96) можно вывести более общее неравенство.
Именно, из уравнения следует, что
[г (г2 + а2) + 2а2М ] Е — 2aMLz ^ 0. C16)
В частности,
[Г (Г2 _|_ а?.\ _|_ 2а?М] Е - 2aMLz ^ 0. C17)
Но
г+ (г\ + а2) + 2а2М = 2М {г\ + а2) = 4М2г+. C18)
Следовательно,
2Mr+E — aLz ^> 0. C19)
В п. 65, г мы еще вернемся к этому неравенству.

§6 Глава 7. Геодезические в пространстве-времени Керра
б. Неравенство Уолда. Существуют ограничения на энергию,
которая может быть извлечена из черной дыры посредством
процесса Пенроуза. Мы выведем два неравенства (впервые полу-
полученные Уолдом и Бардином, Прессом и Тьюкольским), которые
выявляют причины этих ограничений.
По аналогии с процессом, рассмотренным в предыдущем раз-
разделе, предположим, что частица, имеющая 4-скорость Vi и удель-
удельную энергию Еу распадается. Пусть е — удельная энергия, а
и1 — 4-вектор скорости одного из фрагментов. Будем искать пре-
пределы на величину е.
Выберем ортонормированную тетрадную систему е\а), в ко-
которой вектор W совпадает с вектором тетрады е[0)У а остальные
(пространственноподобные) базисные векторы обозначим е\а) (а =
= 1, 2, 3), т.е.
*[„) = ?/' и е[а)(а=1, 2, 3). C20)
В этой системе имеем
+ o<e>*fe)), C21)
где v(a> — пространственные компоненты 3-вектора скорости фраг-
фрагмента; кроме того,
Y = (l-MV/2> M2=t>(a4>). C22)
Предположим теперь, что пространство-время допускает вре-
мениподобный вектор Киллинга ? = д/дх°у и пусть его пред-
представление в выбранной нами тетраде имеет следующий вид:
h = 6@I/* + tia)ef\ ? = g<°>?/' + lia)elay C23)
Отсюда следует, что
Е = bW = g@) = VUt = V°), C24)
goo = 1% = ?Bo)-?(a)g(a) = E2 - | g |2. C25)
Получаем, таким образом, соотношение
m2=?(a)?(a)=?2-?oo. C26)
Из представления C21) 4-скорости фрагмента имеем
е = ltui = у (g@) + u(«)g(a)) = Y (E -f 11; 11 g | cos *), C27)
где О — угол между трехмерными векторами и<а> и ?(а). С помощью
соотношения C26) уравнение C27) можно переписать следующим
образом:
е = уЕ + у | v | (?2 - gooI/2 cos •». C28)
Из этого соотношения сразу же следует неравенство Уолда
уЕ - у | v | (?2 - gooI/2 < е < уЕ + y I w I (E2 - Ы1/2- C29)

65. Процесс ПенроуЬй
В геометрии Керра внутри эргосферы
goo = 1 - 2Мг/р2 < 0, C30)
причем нижний предел равен —1 и достигается на горизонте
событий при а = М и 9 = я/2. Следовательно, в геометрии Керра
всегда выполняется неравенство
II/2 < е < уЕ + у \v\ (E\+ 1I/2. C31)
Мы видели, что максимальная энергия, которую может иметь
частица, двигающаяся по устойчивой круговой орбите, равна
(см. уравнение A46))
?тах = 3->/2. C32)
Следовательно, чтобы величина г была отрицательна, необхо-
необходимо, чтобы
\v\>E/(E2 + 1)*/2 = 1/2. C33)
Другими словами, прежде чем какое-либо извлечение энергии
посредством процесса Пенроуза станет возможным, частица
должна приобрести релятивистскую энергию.
Интересно сравнить неравенство C31) с неравенством, которое
получилось бы в рамках специальной теории относительности
при, отсутствии преимуществ, которые дает эргосфера:
уЕ — y\v\ (?2 — II/2 < е < уЕ + y\v\ (?2 — 1I/2. C34)
Отсюда ясно, что эргосфера не дает слишком больших преиму-
преимуществ по сравнению с обычными процессами, описываемыми
специальной теорией относительности.
в. Неравенство Бардина — Пресса — Тьюкольского. Предполо-
Предположим теперь, что две частицы с удельными энергиями Е+ и ?_,
двигаясь каждая по своей орбите, сталкиваются в некоторой
точке. Каков нижний предел на величину относительной трех-
трехмерной скорости \w\ этих частиц?
Выберем такую ортонормированную тетраду
е\о) = и\ е\а) («=1, 2, 3), C35)
в которой трехмерные скорости частиц в точке пересечения орбит
равны по величине и противоположны по знаку, так что
М = 2М/A+М2), \v\2 = vWv{a). C36)
Для 4-скоростей ul и uL двух частиц в момент столкновения полу-
получаем в выбранной системе отсчета следующее представление:
< = Y W + v^e\a)), ul = у (Ul - iW(a)), C37)
где
у = A_|0р)-«/2. C38)
4 Чандрасекар С, т. 2

98 Глава 7. Геодезические в пространстве-времени Керра
Предположим теперь, что пространство-время допускает вре-
мениподобный вектор Киллинга lt (= д/дх°), имеющий следующее
представление в выбранной тетрадной системе:
6'»!<»)?/'+ 6(«>4„ i,=WA- + i(P)e!P) (|<О)=1(о,). C39)
Тогда по определению
goo = tit = ^@)^@) - lia)ta) = Й» - 16 Г, C40)
так что
|Б|8 = Йо>-«Гоо- C41)
Удельные энергии двух частиц в момент столкновения равны
Е+ = Ьи\ = у (g@, + l>(a)g(a)) = У F(О, + | V | | g | COS О),
?_. = hut = v F@, - ^(а)?<а)) = V (Б@) - I v 11Б | cos 0), C42)
где * — угол между 3-векторами ?(а> и и(а). Из предыдущих
уравнений следует, что
Y6(o, - (?+ + ?-)/2, Y | v 11 g | cos О - (?+ - Е-)/2. C43)
Отсюда получаем соотношение
(Е+ - Л-,J = 4T2M2|||2cos2# =1»|2DY2|@) - 4YVoo]cos2^ =
= | у |2 [(Е+ + ?_J - 4у^оо] cos2 0, C44)
при выводе которого использованы соотношения C41) и C43).
Из уравнения C44) следует очевидное неравенство
(Е+ - EJ < | v |2 [(?+ + ?.J - 4y*?Too]- C45)
Вспоминая определение у (формула C22)), перепишем его в виде
\v 2
1 1
или иначе
-\v\UE+ + E
Корни этого
[(
Следовательно
\v\l
[(Е+ -f ?_J —
квадратного
El - Ы1/2 ±
>
^\(El-gooy/l
4^оо/A — 1 ^ |2)] ^ (?+ — Е_у
i + El-2goo)-(E+-E_r
трехчлена относительно
(El — gooI/2]2/(?+ + ?-J-
2-(El-gw>)l/2\/(E+ + E_),
\ C46)
^0. C47)
| v |2 равны
C48)
C49)
и искомый нижний предел \w\ следует из уравнения C36). По-
Получившееся неравенство называется неравенством Бардина —¦
Пресса — Тьюкольского.
Если частица с энергией Е+ движется по устойчивой круговой
орбите в экваториальной плоскости пространства-времени Керра,
то ее максимальная энергия (как мы видели) равна 3~1/2. При

65. Процесс Пенроуза 99
наиболее выгодных условиях, т. е. при значениях g00 = —1
и Е_ = 0, неравенство C49) дает
M>[(l+4"I/2- l]/3=2-1/3, C50)
а соответствующее неравенство для \w\ имеет вид
М^Х' C51)
в полном согласии с результатом C33), полученным из неравен-
неравенства Уолда.
Основной вывод, следующий из неравенств Уолда и Бардина —
Пресса — Тьюкольского, таков: чтобы извлечь значительную
энергию посредством процесса Пенроуза, нужно сначала разо-
разогнать осколки частицы до скоростей, превышающих половину
скорости света, под действием гидродинамических или каких-
либо других сил. Конкретный пример, рассмотренный в п. 65, а,
подтверждает это заключение.
г. Обратимое извлечение энергии. Вернемся к неравенству
C19), полученному в п. 65, а. Это неравенство превращается
в равенство, только если рассматриваемый процесс происходит
на горизонте событий. В общем случае выигрыш в энергии ЬМ (=Е)
и выигрыш в моменте количества движения б/ (=LZ) подчиняются
неравенству (частица, пересекающая горизонт, имеет отрица-
отрицательную энергию —Е и момент количества движения —L2):
2г+МЬМ ^ abJ. C52)
Если предположить, что процесс происходит «адиабатически»,
так что черная дыра снова описывается метрикой Керра, но с дру-
другими параметрами, то
8J = б (аМ) = МЬа + аЬМу C53)
и неравенство C52) дает
{2Мг+ - а2) ЬМ = г\ЬМ ^> МаЬа. C54)
По определению неприводимой массы М\г (формула C14))
имеем
M2ir = Мг+12 = М [М + (М2 - а2I/2]/2. C55)
Следовательно,
8Mb = {г\ЬМ - МаЬа)/2 (М2 - а2I/2. C56)
Таким образом, неравенство C54) эквивалентно ограничению
6М?Г^О. C57)
Другими словами, не существует непрерывного процесса, который
приводил бы к уменьшению неприводимой массы черной дыры, —
4*

100 Глава 7. Геодезические в пространстве-времени Керра
этот результат оправдывает термин «неприводимая масса». По-
Поскольку площадь поверхности горизонта событий пропорцио-
пропорциональна квадрату неприводимой массы (ср. с уравнением B78)
гл. 6):
Площадь поверхности = 4л (г\ + а2) = 16яМ?г, C58)
полученный результат можно сформулировать иначе: не суще-
существует непрерывного процесса, который приводил бы к уменьше-
уменьшению площади поверхности черной дыры. Более общее утвержде-
утверждение, что никакими взаимодействиями между черными дырами
нельзя уменьшить сумму площадей их поверхностей, называется
теоремой Хокинга. Наше рассмотрение применимо, однако,
только к бесконечно малым процессам, в которых участвует
только одна черная дыра Керра.
Поскольку самое большее, чего мы можем достичь, это сохра-
сохранить неприводимую массу неизменной, процессы, в которых
неприводимая масса остается постоянной, называются обрати-
обратимыми. Можно также отметить, что из определения C55) следует
соотношение
М2 = М?г + /2/4М?г. C59)
Поскольку УИ?г не может уменьшаться, можно интерпретировать
второй член «/2/4Mjv как вклад кинетической энергии вращения
в квадрат инертной массы черной дыры. Посредством процесса
Пенроуза извлекается из черной дыры именно эта энергия вра-
вращения.
. Еще один результат, имеющий общий интерес, следует из рас-
рассмотрения действия процесса Пенроуза на экстремальную чер-
черную дыру, для которой а = М и г+ = М. В этом случае нера-
неравенство C54) дает
М8М 2* аба, или б (УИ2 — а2) ^ 0. C60)
Другими словами, черная дыра при этом перемещается вниз
по последовательности решений Керра к меньшим значениям
а2/М2 и перестает быть экстремальной. Таким образом, голая
сингулярность (решение с а2 > М2) не может быть создана бес-
бесконечно малыми процессами типа рассмотренных выше. Остается
открытым вопрос, можно ли получить голую сингулярность с по-
помощью нелинейного «взрывного» процесса. Предположение о том,
что голая сингулярность не может быть создана в пространстве-
времени, в котором первоначально не было голых сингулярностей,
составляет содержание гипотезы космической цензуры, выска-
высказанной Пенроузом.
66. Геодезические в пространстве-времени Керра с а2 > М2
Поскольку мы интересуемся в основном черными дырами, мы
ограничились изучением метрик Керра с а2 < М2, так как только
такое пространство-время обладает горизонтом событий и опи-

66. Геодезические с а2 > М2 101
сывает черную дыру. Если а2 >М2, то горизонты исчезают и
остается только кольцевая сингулярность. Фактически остается
только голая сингулярность. Считается, что голые сингулярности
в природе не существуют: гипотеза космической цензуры запре-
запрещает их появление в результате обычных процессов. Тем не ме-
менее чрезвычайно интересно знать, что собой представляет про-
пространство-время с голыми сингулярностями и имеются ли суще-
существенные различия в том, как проявляются многообразия с голыми
сингулярностями и многообразия с сингулярностями, спрятан-
спрятанными под горизонтами событий. Сравнительное изучение геоде-
геодезических в пространстве-времени Керра с а2 < М2 и в простран-
пространстве-времени Керра с а2 > М2, возможно, позволит понять,
каковы могут быть эти различия.
а. Изотропные геодезические. Заметим прежде всего, что су-
существенные особенности изотропных геодезических зависят от
того, выполнено неравенство а2 < М2 или неравенство а2 > М2.
Действительно, в п. 61, а было показано, что в случае а2 <С М2
изотропные геодезические в экваториальной плоскости имеют
различное поведение в зависимости от того, больше или меньше
их прицельный параметр некоторого критического значения Df
(верхний знак относится к обратным орбитам, а нижний — к пря-
прямым орбитам): орбиты, начинающиеся на бесконечности и име-
имеющие прицельный параметр D >D?, после прохождения пери-
перицентра снова уходят на бесконечность, в то время как орбиты
с D << DT обрываются в сингулярности. Но в случае а2 >М2
такое различие имеет место только для обратных орбит; все прямые
орбиты, начинающиеся на бесконечности и имеющие прицельный
параметр D >а, снова уходят на бесконечность. Подобное раз-
различие связано с тем, существуют или нет неустойчивые круговые
фотонные орбиты. Радиусы этих неустойчивых круговых фотон-
фотонных орбит определяются действительными положительными кор-
корнями кубического уравнения относительно г1/2 (ср. с уравне-
уравнением A24)):
^ = гз/2 _ ЗМг\/2 зр 2аМ1/2 = 0, C61)
^а в случае а2 >УИ2 это уравнение, если выбрать положительный
знак, что соответствует прямым орбитам, не имеет ни одного дей-
действительного положительного корня. Однако если выбрать отри-
отрицательный знак, соответствующий обратным орбитам, то уравне-
уравнение C61) допускает корень (ср. с уравнением (87))
h4 C62)
= \а\1М.

102 Глава 7. Геодезические в пространстве-времени Керра
Соответствующий прицельный параметр, связанный с этой не-
неустойчивой круговой обратной орбитой, равен
?><-> = М Fch О + ch 3*). C63)
Что касается орбит постоянного радиуса, не лежащих в эква-
экваториальной плоскости (неплоских орбит), то к ним полностью
применено сказанное в п. 63, а. В частности, орбиты с т]>0
(rs<Cf{ph) пересекают экваториальную плоскость и не попадают
на сингулярность, а орбиты с ц << 0 (включающие обратные ор-
орбиты с rs > /ph\ а также все прямые орбиты) заключены внутри
конуса, причем направления 0 = 0 и 0 = л/2 лежат вне этого
конуса и имеют точку поворота при некотором отрицательном
значении г. (Случай т) = 0 возможен только для обратной орбиты
crs = /ph*.) Однако для орбит с ц < 0 есть одно важное отличие.
В случае а2 <С М2 орбиты, имеющие точку поворота в области
отрицательных значений г, не могут вернуться в мир, который
они покинули: существование горизонтов заставляет их мигри-
мигрировать в другие миры. Но в случае а2 >> УИ2 горизонтов нет, и
траектории, имеющие точку поворота в области отрицательных г,
могут вернуться в мир положительных г, неся информацию о «чу-
«чудесных приключениях» во время этого путешествия (см. п. 66, в).
б. Времениподобные геодезические. Интересные особенности,
возникающие при переходе через «барьер» а2 = УИ2, были впервые
изучены де Феличе. Рассмотрим, следуя ему, выражение (ср.
с уравнением A17)):
[ (зУ/2&\ C64)
которое связывает значения энергий прямых орбит (+) и обрат-
обратных орбит (—) с заданным значением обратного радиуса и (=11 г).
Сейчас мы интересуемся только прямыми орбитами, поскольку
обратные орбиты ограничены требованием Q_ ^ 0, т. е. радиусом
круговой фотонной обратной орбиты (который, как мы видели,
существует при всех значениях а2), а для прямых орбит такого
ограничения нет.
Уже отмечалось, что для прямых орбит функция ?(+) в слу-
случае а = М имеет разрыв при г -+ М ± 0 (ср. с уравнением A46)):
?(+) _> +3-1/2 (г-+М± 0). C65)
Существование разрыва является следствием произвола в выборе
радиальной координаты г в точке г = М при а2 = УИ2. Мы же
здесь рассмотрим поведение функции ?<+> при г < УИ. Из урав-
уравнения C64) следует, что функция Е{+) будет иметь нуль, если
уравнение
гз/2 _ 2Мг1'2 + аУИ1/2 = 0 C66)

66. Геодезические с а2 > Л12 ЮЗ
допускает действительный положительный корень г1/2. В случае
а = М уравнение C66) допускает два таких корня
и г1/2 - V2 (/5" - 1) УИ1/2, C67)
другими словами,
r = M и r = VaC-/5")Af = 0,38197iM. C68)
Следовательно, функция Е{+) отрицательна в интервале
V2 C - /5~) М<г<М (?<+) < 0), C69)
и, значит, в интервале C69) при а2 = М2 существует устойчивая
круговая орбита с отрицательной энергией. Такие устойчивые
круговые орбиты с отрицательной энергией существуют и при
а2 > М2, но только если
C2/27J М2 > а2 >М2. C70)
Это утверждение является следствием существования у уравне-
уравнения C66)
г3/2 - 2/Wr1/2 + C2/27I/2 М3/2 = 0 C71)
двух совпадающих корней при а2/М2 = 32/27:
г1/2 = BМ/3I/2, или г - 2/3 М, C72)
причем при \а\ > C2/37I/2 М = 1,088УИ положительные дей-
действительные корни отсутствуют вовсе.
Обсуждение неплоских времениподобных геодезических, про-
проведенное в § 64, полностью приложимо и для случая а2 > УИ2.
И снова особый интерес представляют орбиты с г\ < 0, поскольку
они возвращаются в область положительных значений г после
посещения области с отрицательными значениями г; этим орби-
орбитам посвящен следующий раздел.
в. Нарушение принципа причинности. Одной из основных
особенностей пространства-времени с сингулярностями является
возможность существования областей, в которых нарушается
принцип причинности в том смысле, что в этих областях могут
быть замкнутые времен и подобные кривые, что позволяет буду-
будущему влиять на прошлое — такое свойство по общему убеждению
нефизично. В пространстве-времени Керра, расширенного вклю-
включением области с отрицательными значениями г, принцип причин-
причинности определенно нарушается там, где ?фф >0, а координата ф
становится времениподобной.
Граница области, в которой координата ср времениподобна,
определяется уравнением
22 = (г2 + а2J — а2 А sin2 9 -
= (г2 + а2) (г2 + a2 cos2 9) + 2Ma*r sin2 9 - 0; C73)

104 Глава 7. Геодезические в пространстве-времени Керрй
это уравнение может удовлетворяться только отрицательными
значениями г. Полагая х = —г с целью избежать двусмыслен-
двусмысленности, можем переписать уравнение C73) в следующем виде:
(*2 + а2J • за / \ /очл\
1 ! '- == sirr В (х = —г) 1о74)
а* (х2 + а2 + 2Мх) * '' к '
Очевидно, что из этого уравнения следует
fl2 (JC2 + fl2 f 2Мх) < }' ^375)
и это неравенство накладывает ограничение на область измене-
изменения х:
0 < х < хтах, C76)
где
Jfmax ^ Bа//3") sh [V8 Arsh C yWM/a)} C77)
есть положительный корень уравнения
х3 + а2х — 2Ма2 = 0. C78)
В частности,
0 < х < М при а2 = М2,
0 < х < 1,2878М при а2 - ЗМ2. C79)
Подобным же образом получается ограничение на область
изменения 0
sin2 9mln < sin2 в < 1, C80)
C81)
Минимум в выражении в правой части достигается при х = zMy
где z — положительный корень уравнения
(г + IK — C — а2/М2) (z + 1) + 2 A — а2/М2) = 0. C82)
Приведем некоторые примеры*
raln = 55,75°- (я =
г - VT- 1, sin29min = 0,9080, 9min = 65,25° (а = М /3"). C83)
Таким образом, уравнение C74), определяющее границу об-
области, в которой может нарушаться принцип причинности, на-
накладывает довольно жесткие условия на область изменения (—г)
и 9.
Хотя при а2< М2 области, в которых координата ср стано-
становится времениподобной, существуют при всех значениях а2 >0,
эти области не обмениваются с внешним миром никакими сигна-

Библиографические замечания 105
лами, и мы можем не очень беспокоиться по этому поводу. Но
мы не можем оставаться бесстрастными, когда а2 > М2 и не су-
существует горизонтов событий и поэтому область, в которой ко-
координата ф времениподобна, причинно связана с внешним простран-
пространством. Интересен в этой связи вопрос, может ли нарушаться
принцип причинности (в каком-либо смысле) при движении вдоль
времениподобных (или изотропных) геодезических. Если такое
нарушение возможно, то оно может иметь место только при дви-
движении вдоль неограниченных геодезических с к] < 0, которые
имеют точку поворота в области отрицательных значений г.
Поскольку (ср. с уравнениями A79) и A80))
г е
/ = j r2R~V4r + а2 J в-1/2 cos29 d0 +
+ 2М \ г [г2 - а (? - а)] Д R^'2 dr, C84)
то, для того чтобы принцип причинности нарушался, отрицатель-
отрицательный вклад последнего интеграла от той части орбиты, которая
проходит в области отрицательных значений г (и который может
быть максимизирован выбором такой орбиты, для которой выраже-
выражение а (? — а) отрицательно и точка поворота лежит в области,
где координата ср времениподобна), должен компенсировать по-
положительный вклад всех трех интегралов от той части геодезиче-
геодезической, которая лежит в области положительных значений г. Для
получения окончательного ответа нужны дополнительные рас-
расчеты.
Библиографические замечания
Проведенное Картером разделение переменных в уравнении Гамильтона—
Якоби сделало возможным полное аналитическое исследование геодезических
в пространстве-времени Керра:
1. Carter В. Phys. Rev., 174, 1559—1571, 1968.
См. также работу
2. Carter В. Commun. Math. Phys., 10, 280—310, 1968.
§ 60. При изложении материала мы нарушили хронологическую последова-
последовательность событий и начали с исследования интеграла движения для изотропных
геодезических (допускаемого произвольным пространством-временем типа D).
Существование этого интеграла было открыто Уокером и Пенроузом:
3. Walker AT, Penrose R. Commun. Math. Phys., 18, 265—274, 1970.
Уокер и Пенроуз нашли также интеграл движения, аналогичный открытому
Картером для времениподобных геодезических для частного случая метрики
Керра.
Изложение в тексте отличается от изложения этого вопроса Уокером и Пен-
Пенроузом, которые использовали спинорный формализм. Наше изложение более
прямое и упрощенное. Однако его преимущество в том, что оно дает простые
необходимые и достаточные условия, выраженные через спинорные коэффи-
коэффициенты, существования интегралов движения для времениподобных геодезиче-
геодезических типа интеграла Картера в пространстве-времени типа D по классификации
Петрова.

106 Глава 7. Геодезические в пространстве-времени Керра
Теорема 1 доказана совместно с Б. Ксантопулосом.
Оказывается, условия, эквивалентные условиям теоремы 3, содержались
в работах Хаузера и Мальхиота (хотя автор не смог разобраться в их обозна-
обозначениях):
4. Hauser /., Malhiot R. J. J. Math. Phys., 16, 150—152, 1975,
5. Hauser /., Malhiot R. J. J. Math. Phys., 16, 1625—1629, 1975,
6. Hauser /., Malhiot R. J. J. Math. Phys., 17, 1306—1312, 1976.
§ 61. Геодезические в экваториальной плоскости черной дыры Керра ши-
широко обсуждались в литературе. Полный список работ см. в обзоре
7. Sharp N. A. General Relativity and Gravitation, 10, 659—670, 1979.
При написании книги автор пользовался следующими работами:
8. de Felice F. II Nuovo Cimento, 57B, 351—388, 1968,
9. Bardeen J. M., Press W. H., Teukolsky S. A. Astrophys. J., 178, 347—369,
1972,
10. Bardeen J. M.y Press W. //., Teukolsky S. A. Astrophys. J., 161, 103—109,
1970,
11. Bardeen J. M., Press W. Я., Teukolsky S. A. In: Black Holes, ed. С De Witt,
B. S. De Witt, Gordon and Breach, New York, 1973, p. 241—289.
Обычно процедура исследования геодезических в пространстве-времени Керра
состоит в следующем: начинают с общих уравнений движения (выведенных
нами в п. 62, а), а затем рассматривают орбиты в экваториальной плоскости
как частный случай. Для нахождения геодезических в экваториальной плоско-
плоскости, разумеется, не нужны общие уравнения движения: их можно исследовать
независимо, как это и сделано в тексте.
Иллюстрации геодезических как в этом, так и в последующих параграфах
были подготовлены Г. Туми, которому автор выражает свою признательность.
§ 62. Доступное изложение вопроса см. в книгах:
12. Misner С. W.y Thome К. 5., Wheeler J. A. Gravitation, W. H. Freeman and
Co., San Francisco, 1970. [Имеется перевод: Ч. Мизнер, К. Торн, Дж. Уилер.
Гравитация. — М.: Мир, 1977.],
13. Stewart Л, Walker M. Springer Tracts in Modern Physics, 69, 69—115, 1973.
§ 63 и 64. Из множества статей, посвященных геодезическим в пространстве-
времени Керра, наиболее полезны, по мнению автора, следующие
14. Bardeen J. M. In: Black Holes, ed. С. DeWitt, В. S. DeWitt, Gordon and
Breach, New York, 1973, p. 215—239,
15. de Felice F.t Calvani M. II Nuovo Cim., 10B, 447—458, 1972,
16. Calvani M., de Felice F. General Relativity and Gravitation, 9, 889—902,
1978.
См. также работы
17. Boyer R. #., Lindquist R. W. J. Math. Phys., 8, 265-281, 1967,
18. Wilkins D. С Phys. Rev. D5, 814—822, 1972,
19. Cunningham С. 7\, Bardeen J. M. Astrophys. J., 183, 237—264, 1973,
20. Cunningham С. 7\, Bardeen J, M. Astrophys. J., 202, 788—802, 1975,
21. Cunningham С. Г., Bardeen J. M. Astrophys. J., 208, 534—549, 1976.
Применение комплексного интеграла Уокера—Пенроуза к исследованию изме-
изменения направления поляризации при движении вдоль изотропных геодезических
восходит к работам Старка и Коннорса:
22. Connors P. A., Stark R. F., Nature, 269, 128—129, 1977,
23. Stark R. F., Connors P. A. Nature, 266, 429—430, 1977,
24. Connors P. Л., Piran Г., Stark R. F. Astrophys. J., 235, 224-^244, 1980.
Исследование, проведенное нами в п. 63, д, является развернутым изложением
статьи [22].
§ 65. Возможность физических процессов, которые в принципе позволяют
извлекать вращательную энергию из черной дыры, была впервые продемонстри-
продемонстрирована в работе
25. Penrose /?., Floyd R. M. Nature Phys. Sci., 229, 177—179, 1971.
В этой же работе была установлена также «теорема о площади поверхности»
горизонта, правда, на конкретном примере.

библиографические замечания lot
Более подробное исследование процессов Пенроуза содержится в работах:
26. Christodoulou D. Investigations in gravitational collapse and the physics of
black holes, Ph. D. dissertation, Princeton University, Princeton, N. J., 1971;
Phys. Rev. Lett., 25, 1596—1597, 1970,
27. Christodoulou D., Ruffini R. Phys. Rev. D4, 3552—3555, 1971.
Понятие неприводимой массы было введено в работе [26].
Пределы на величину энергии, которую можно извлечь из черной дыры
посредством процесса Пенроуза, были получены Бардином, Прессом и Тьюколь-
ским в работе [9], а также Уолдом в работах
28. Wald R. M. Astrophys. J., 191, 231—233, 1974,
29. Wald R. M. Ann. Phys., 82, 548—556, 1974.
См. также работу
30. Piran Г., Shaham J. Phys. Rev. D16, 1615—1635, 1977.
§ 66. Геодезические в пространстве-времени Керра в случае а2 > М2 и
возможность нарушения принципа причинности в этом пространстве-времени
наиболее обстоятельно исследовались де Феличе и его сотрудниками:
31. de Felice F. Astron. Astrophys., 34, 15—19, 1974,
32. de Felice F. Astron. Astrophys., 45, 65—68, 1975,
33. de Felice F., Caluani M., Nobili L. II Nuovo Cim., 26 B, 1 — 15, 1975,
34. Caluani M., de Felice /\, Muchotrzeb В., Salmistraro F. General Relativity
and Gravitation, 9, 155—163, 1977,
35. de Felice F. Nature, 273, 429—431, 1978,
36. de Felice F., Calvani M. General Relativity and Gravitation, 10, 335—343,
1979.
В тексте мы попытались суммировать основные результаты перечисленных работ.

Глава 8
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
В ГЕОМЕТРИИ КЕРРА
67. Введение
Изучение черных дыр Шварцшильда и Рейсснера—Нордстрема
показало, что понимание структуры пространства-времени углуб-
углубляется и существенно обогащается в результате изучения реакции
метрики на внешние возмущения. Поскольку внешние возмуще-
возмущения могут быть представлены в общем случае в виде падающих
волн различного типа, изучение возмущений по существу сводится
к исследованию распространения волн разных типов в простран-
пространстве-времени черной дыры и, в частности, к изучению поглощения
и рассеяния этих волн. Хотя сформулированная таким образом
задача имеет физическую основу, ее решение раскрывает анали-
аналитическое богатство исследуемого пространства-времени, часто
весьма неожиданное. В случае пространства-времени Керра это
богатство проявляется практически с самого начала исследования.
Поскольку пространство-время, описывающее черную дыру
Керра, стационарно и аксиально-симметрично, естественно
ожидать, что общее возмущение можно представить в виде супер-
суперпозиции волн различной частоты а и периода 2тп (т = 0, 1, 2 ...)
по координате ф. Другими словами, можно было бы ожидать,
что исследование возмущений сведется к исследованию суперпо-
суперпозиции различных мод, зависимость которых от времени и коорди-
координаты ф имеет вид
exp {i (at -f m<p)}, A)
где т — целое число, которое может быть положительным, отри-
отрицательным или нулем. Вряд ли кто-нибудь ожидал, что зависи-
зависимость амплитуды этих волн от других двух переменных гиб
может быть также факторизована. Но в 1971 г. Тьюкольский по-
показал, что это дальнейшее разделение переменных может быть
достигнуто, если уравнения для безмассовых частиц — фотонов,
гравитонов и двухкомпонентных нейтрино — записать в форма-
формализме Ньюмена — Пенроуза, причем базисные векторы выбрать
так, как в § 56. И оказывается, что эта неожиданная возможность
разделения переменных основных уравнений математической
физики является своего рода заклинанием типа «Сезам, от-
откройся!» для преодоления последующих препятствий.
В настоящей главе мы начинаем изучение электромагнитных
возмущений черной дыры Керра, описываемых уравнениями

68. Определения и лёммЫ 109
Максвелла, и исследование распространения электромагнитных
волн. Теория достаточно проста, что позволяет сделать изложение
полным и замкнутым. Это изложение послужит прообразом для
изучения других полей.
68. Определения и леммы
Предположим в согласии с формулировкой задачи об иссле-
исследовании возмущений в § 67 и аналогично подходу к такой же
задаче для метрик Шварцшильда и Рейсснера — Нордстрема, что
возмущения можно разложить на моды, зависимость которых от
времени и координаты ф определяется уравнением A). Общий
множитель вида A) во всех величинах, описывающих возмуще-
возмущения, мы будем опускать, при этом все символы будут обозначать
соответствующие амплитуды.
Базисные векторы A, n, m, т), заданные уравнениями A70)—
A73) гл. 6, рассматриваемые как касательные векторы, действу-
действующие на функции, зависимость которых от / и ф имеет вид A),
становятся дифференциальными операторами:
1 = D = <250, п = д = -(Д/2р2) 2>J,
B)
где
®п = дг + //С/А + 2п (г — М)/Д,
Я>\ = дг - iKlk + 2п (г - М)/Д, C)
К = (г2 -f a2) g -f am, Q = ао sin 9 -f m cosec 0, D)
р = г -f ia cos 0, р* = г — ш cos 0, р2 = г2 -f a2 cos2 0. E)
Заметим, что 2Е)п и 2b\ являются чисто радиальными операто-
операторами, а 3?п и 3?п — чисто угловыми операторами. Ясно, что при
действии на «фоновые» величины (не зависящие от / и ф) опера-
операторы 2D и 3? сводятся к операторам дг и <90 соответственно.
Дифференциальные операторы, которые мы сейчас определили,
удовлетворяют целому ряду элементарных тождеств, которые
нам придется часто использовать в этой и последующих главах.
Поэтому мы соберем их вместе и представим в виде серии лемм
(ср. с уравнениями B27)—B29) гл. 4).
ЛЕММА 1.
9?п @) = —2* (я - 0), 3>1 = (®п)\
(sin 0) 2n+i = 2п sin 9, (sin 0) 2*п+\ = &l sin 0, F)

110 Глава 8. Электромагнитные волны 6 геометрии Керра
ЛЕММА 2.
C> + т/р*) B + ima sin 9/р*) = (S + i/ла sin 9/р*) @ + m/p*), G)
где iZ) может быть любым из операторов 2Ьп и 2&\, 3! — любым
из операторов 3! п и 3S\, am — постоянная (обычно положитель-
положительное или отрицательное целое число).
ЛЕММА 3.
&п+1&п+2 • • • &п+т (/ COS 9) = (COS 9) 3?п+1 . . . 3?n+mf -
-(msin9)^n+2...^n+w/, (8)
где / — произвольная гладкая функция 9, а операторы 5?п можно
заменить операторами 3?\.
ЛЕММА 4.
Пусть / (9) и g (9) — две произвольные функции 9, заданные
на интервале 0 < 9 < я, тогда
я л
J g (Snf) sin 9 d9 = - J / Bln+ig) sin 9 d9. (9)
о о
И наконец, отметим два элементарных тождества, играющие
решающую роль во многих преобразованиях, приводящих к упро-
упрощению формул:
QQ _i_ q ctg 9 = 2аа cos 9, К — aQ sin 9 = p2a. A0)
69. Уравнения Максвелла: редукция
и разделение переменных
Уравнения Максвелла в геометрии Керра можно получить,
подставляя в уравнения C30)—C33) гл. 1 спиновые коэффициенты,
перечисленные в гл. 6 (уравнения A75)) и производные по направ-
направлению из уравнений B). В результате имеем
(г.
Эти уравнения принимают более простой и более симметричный
вид, если записать их через новые переменные
Фо = ?о, Ф^^уХ Ф2 = 2</>2(р*J. A2)

69. Уравнения Максвелла 111
Получаем
(И)
A5)
A6)
а. Редукция уравнений для Фо и Ф2 и разделение переменных.
Очевидно, что коммутативность операторов (^0+ 1/р*) и B?% +
+ ia sin 0/р*) (вследствие леммы 2 § 68) позволяет исключить Фх
из уравнений A3) и A6) и получить уравнение только для функ-
функции Фо
, ia sin 9 \ / г„ ia sin 9
К
^Г)(Д>?-^Г)]ФО = О. A7)
Подобным же образом коммутативность операторов C?0 -j-
+ ш sin 0/р*) и A {S>\ + 1/р*) позволяет исключить Фх из урав-
уравнений A4) и A5) и получить уравнение только для функции Ф^
К
ia sin 9 \ / ^+ ia sin 9
о+ + ^г)(^о-^г)]Ф2 = О. A8)
Уравнение A7) можно упростить с помощью следующих легко
проверяемых тождеств:
21К
р* '
2ia sin 9
Q A9)
и соотношения
К — aQ sin 0 - р2а. B0)
Получаем
[AS)iS)i + S^o^i — 2ta (r + ш cos 0)] Фо = 0. B1)
Подобная же редукция уравнения A8) дает:
Dp + 2ч&\ + 2io (r + fa cos 0)] Ф2 = 0. B2)

112 Глава 8. Электромагнитные волны в геометрии Керра
Уравнения B1) и B2) явно допускают разделение переменных.
Действительно, подстановки
Фо = /?+i (г) S+1 F), Ф2 = /?_! (г) S..x F), B3)
где R±1 (г) и S±1 F) — функции соответственно только перемен-
переменных гиб, приводят к разделению переменных в уравнениях B1)
и B2), в результате чего получаем следующие две пары уравне-
уравнений:
3>\ — 2ior) R+l = XR+l, B4)
+ 2ао cos 6) S+i = — XS+{; B5)
\S>q + 2ior) /?_i =XR-i, B6)
(^o^i* - 2ao cos 6) S-j = —XS-i, B7)
где X — постоянная разделения.
Заметим, что постоянная разделения одна и та же и для урав-
уравнения B1), и для уравнения B2). Причина этого та же, что и
в аналогичной задаче гл. 4 (уравнения B48) и B50)), где мы дали
объяснение этому факту.
Уравнения, эквивалентные уравнениям B4)—B7), были впер-
впервые получены Тьюкольским. Мы будем называть их уравнениями
Тьюкольского.
Заметим, также, что из сравнения уравнения B6) с уравне-
уравнением B4), записанным в виде
Л Oirrr\ А Р 1 A D (ЪЯЛ
'О — ZfrOT) /_\/\+i — Л L\i\+i , V-^^V
следует, что функции R_x и AR+i удовлетворяют комплексно-
сопряженным уравнениям, а функции S+1 F) и S_x F) удовлетво-
удовлетворяют паре уравнений, каждое из которых может быть получено
из другого заменой 6 на я — 6.
70. Тождества Тьюкольского — Старобинского
Расцепление уравнений A3)—A6) и получение пары незави-
независимых уравнений с разделяющимися переменными для функ-
функций Фо и Ф2 решает задачу только отчасти, потому что, помимо
того что еще не получено решение для функции Фь нужно опре-
определить относительную нормировку функций Фо и Ф2. Решение
последней проблемы в некотором смысле имеет более фундамен-
фундаментальное значение: решение любой задачи линейной теории воз-
возмущений должно определяться с точностью до одного общего
коэффициента пропорциональности. В данном случае требуется,
чтобы при заданной амплитуде, например, функции Фо, решение
для функции Ф2 определялось однозначно, и обратно (не допу-
допускается даже произвол в виде коэффициента пропорциональности),

70. Тождества Тьюкольского—Старобинского 113
Когда Фо и Ф2 представлены в виде B3), то решения для функ-
функций 5+1 F) и S_x F) могут быть сделаны однозначными, если
на каждую из них наложить требование нормировки на единицу:
J s2+1 sin e de = j 52_i sinede = 1. B9)
о о
Однако относительная нормировка радиальных функций R+i
и R_i остается при этом неизвестной.
Для полного решения уравнений Максвелла требуется, как
будет видно, тщательный анализ уравнений B4)—B8) и соотноше-
соотношений между решениями R+1 и Rnl и между решениями S+1 и S_b
вытекающих из этих уравнений. Такой анализ был сделан Старо-
бинским и Тьюкольским и привел к некоторым замечательным
тождествам, которые являются основными для создания полной
теории. Ниже мы получим эти тождества (правда не в том виде,
в каком они были первоначально сформулированы).
ТЕОРЕМА 1. Выражение ts.SD^^R^x лишь коэффициен-
коэффициентом пропорциональности отличается от функции Ai?+i, а вы-
выражение kSDtSDtA/?+i лишь коэффициентом пропорциональности
отличается от функции R_v
Доказательство. Действуя оператором 2H?>0 на уравнение*
B6), которому удовлетворяет функция R_i, получаем
-i f 2roZHR_]) -f
D\ - 2ior) &o&oR-\ • C0)
Следовательно, функция Ж)^2Ь^_Х удовлетворяет тому же самому
уравнению, что и функция R+1, и первая часть теоремы доказана.
В то же время результат предыдущих вычислений эквивалентен
установлению справедливости следующего тождества:
\ - 2ior) ?>о&о- C1)
Тождество, комплексно-сопряженное этому, имеет вид
®\®1 (Д2)о2)о - 2ior) = (А2>?2>! + 2tarr) S5o^o • C2)
Отсюда следует справедливость второй части теоремы.

114 Глава 8. Электромагнитные волны в геометрии Керра
СЛЕДСТВИЕ. Подходящим выбором относительной норми-
нормировки функций Д#+1 и R_x можно добиться того, чтобы
, C3)
,, C4)
где <& — постоянная, которая может быть комплексной *.
Ясно, что требуемую относительную нормировку легко обеспе-
обеспечить, поскольку функции Д7?+1 и R_x удовлетворяют комплексно-
сопряженным уравнениям.
ТЕОРЕМА 2. Если относительная нормировка функций kR+1
и R_i выбрана так, что удовлетворяются уравнения C3) и C4),
то квадрат модуля постоянной & равен
|<g>|2 = х2 — 4а2а2, а2 = а2 + ami о. C5)
Доказательство. Действуя оператором Д^о^о на уравнение
C3), получаем
Д2>?2>?А2>о2>оД-1 = «* Д^о^о ДЯ-и • C6)
В силу уравнения C4) последнее равенство можно переписать
следующим образом:
HSDtSDt Д^о^оЯ-i = | ^ Г R-x • C7)
Следовательно, по модулю операторного равенства
Д2>?2>о + 2шг - К = О
мы имеем соотношение
Д-^J^J Д^о^о = | V Г, C8)
откуда значение l^l2 можно получить прямым вычислением ле-
левой части тождества. Имеем
50 + 4«т 0
>о^о (А, - 2шг) + 4ira Д^5о+^о + 4ia Д^50- C9)
С другой стороны,
- г Д^5^о + 2Д^0 - 2»/С. D0)
Б § 71 будет показано, что W — действительная постоянная.

70. Тождества Тьюкольского—Старобинского 115
С помощью этого последнего соотношения можно привести резуль-
результат в уравнении C9) к виду
2iro) &2)tg)o - 4а/С =
= (К + 2tVa) (А, - 2iro) - 4а [(г2 + а2) а + am] =
= Х2- 4а2о2 - 4аот = | V |2, D1)
что и доказывает требуемое тождество.
ТЕОРЕМА 3. Выражение S'oS'iS+i только коэффициентом
пропорциональности отличается от функции 5_ь а выражение
SS\S\S-\ только коэффициентом пропорциональности отличается
от функции S+1.
Доказательство. Действуя оператором SqSx на уравнение B5),
которому удовлетворяет функция 5+ь получаем
~№03?{S+l = S?Q3?X (StSx + 2ао cos 6) S+l =
= gvgi2?tS?{S+x + 2ao (cos 9) ^O^i5+I - 4aa (sin 6) 5^,5+1. D2)
Последовательно преобразуя это выражение, находим
S^i^o^i = ^o^i (^о - 2Q) 2?i =
- 2*о (^i + 20) ^o^i - 2^0^iQ^i- =
Х ^oQ - Q ctg 6) Sx =
(aa cos 6 + m ctg 6 cosec 6) S\ —
- 2Sо [Q^o^i + (^cr cos 6 — m ctg 6 cosec 6) Sx] =
- S0S\SqSx - 4aa (cos 6) ^q^i + 4aa (sin 6) Sx. D3)
Объединяя результаты редукции D2) и D3), получаем
( D4)
Таким образом, выражение i^i^S+i удовлетворяет уравнению
B7), которому удовлетворяет и функция S_b и, следовательно,
первая часть теоремы доказана. В то же время результат преды-
предыдущих преобразований эквивалентен установлению справедли-
справедливости тождества
2W Bto + 2aacos6) = {3?ъЯ?\ - 2aacos6) 2q&x. D5)
Сопряжение этого соотношения (получаемое заменой 6 на я — 6),
т. е. уравнение
\ - 2aacos6) = {S\SX + 2aa cos б) 2%2\, D6)

116 Глава 8. ЭлектромаёнШпные волны ё геометрии Керрй
показывает, что справедлива и вторая часть теоремы.
Теорема 3, очевидно, эквивалентна доказательству существо-
существования соотношений вида'
i?oi?iS+I = AS-!, 2\2\S-x = D2S+l, D7)
где Dx и D2 — две действительные постоянные.
ТЕОРЕМА 4. Если обе функции S+1 F) и 5_х @) нормиро-
нормированы на единицу, то в соотношениях D7) D1 = D2 и, следовательно,
2?02?{S+l = DS-u gt&TS-x = DS+{. D8)
Доказательство. Метод доказательства состоит в применении
леммы 4 к обоим нормировочным интегралам B9). Действительно,
л л
d\ - d\ \ sU sin e de = J (sws+i) (S^iS+i) sin e de =
о о
n
- j (&t2\2b2xS+x) S+l sin 6 d6. D9)
0
С другой стороны,
S?lS?\S?QgxS+x = Dx3?tS?\S-x = D{D2S+x, E0)
и уравнение D9) дает
л
D\ = DxD2 J Six sin 6 d9 = D{D2, E1)
о
поскольку функция S+i также по предположению нормирована
на единицу. Равенство коэффициентов Dx и D2 следует из этого
последнего соотношения.
ТЕОРЕМА 5. Постоянная D в теореме 4 равна
D* = X2 — 4а2а2 - |^|2. E2)
Доказательство. Из уравнения E0) и равенства Dx = D2(~D)
следует, что для доказательства теоремы требуется прямым вы-
вычислением установить, что
S?tS?\S?QSx - ^ -- 4aV E3)
с точностью до операторного равенства
Заметим прежде всего, что
2\%'о - (&х - Щ {Set + 2Q) - 5?x2l + 4aacos6 E4)
и, следовательно,
2\2\2ъ&х = 3?t {&xSet + 4ш cos в) S'i =
= 2?tS?x (—X - 2аа cos 6) + 4яст (cos 6) S\SEx - 4ао (sin 6) Sx • E5)

70. Тождества Тьюкольского—Старобинскогд - И?
С другой стороны, вследствие леммы 3 из § 68 имеем
S\SX cos 6 = (cos 6) S%SX - (sin 0) (^i + S\) =
= (cos 6) SlSx - 2 (sin 6) Sx + 2Q sin 6. E6)
Объединяя полученные равенства, приходим к требуемому ре-
результату
2%2\2ъ2\ = - (* + 2ш cos 6) 2%&х - 4aoQ sin 6 =
= (k -f 2ao cos 6) (k — 2ao cos 6) — 4ao (ao sin 6 + m cosec 6) sin 6 =
- X2 - 4a2o2 - 4шт = К2 - 4a2o2 = D2 = \ V |2. E7)
Мы будем называть ^ и D постоянными Старобинского.
Вернемся теперь к уравнениям C3) и C4). Введем обозначе-
обозначения Р+1 и Р_г для функций Л#+1 и /?_! соответственно, если их
относительная нормировка совместна с этими уравнениями. Таким
образом, будем писать
. E8)
Первое из этих уравнений может быть переписано в виде
&P+l = A^o^qP-! - A B>J + 2f/C/A) ^оЯ_1 -
= A?>t?>0P-i + 2i№oP-\- E9)
Используя уравнение для функции P_b получаем отсюда
<&Р+1 = (Х- 2wr) Р_г + 2/7С2У-1- F0)
Подобным же образом из второго из уравнений E8) находим
^*Р_! = (Я + 2tor)P+l - 2iK®lP+\- F1)
Уравнения F0) и F1) позволяют выразить производные функций
Р+1 и Я_1 через сами эти функции:
"ТГ = + -Г" Р^ ~ Ж № + 2tor>Р-1 - ^-ib
-%- = - 1«-р_1 + -?- [(К - 2iar)P_l - VP
Следует отметить, что мы еще не знаем по отдельности действи-
действительную и мнимую части V, хотя знаем ее абсолютное значение.
Этот пробел будет ликвидирован в § 71.
Подобным же образом из уравнений D8) находим, что если
обе функции 5+i и 5_х нормированы на единицу, то
^fS-i = - A/2Q) [(Я - 2шcos6M.! + DS+l], (g3
^XS+1 = + A /2Q) [(X + 2ao cos 6) S+1 + DS_t].
Очевидно также, что эти уравнения позволяют выразить производ-
производные функций S+1 и 5_! через сами эти функции.

118 Глава 8. Электромагнитные волны в геометрии Керра
71. Завершение построения решения
Для полного окончания решения уравнений Максвелла, кроме
разделения переменных в уравнениях для функций Фо и Ф2,
необходимо определить их относительную нормировку. Если мы
выберем радиальные функции Ai?+i и R_t равными соответственно
функциям Р+1 и Р_г (что согласуется с уравнениями E8)), а функ-
функции 5+i и S_i нормируем на единицу (в согласии с уравнениями
D8)), то нам остается определить численный множитель, на кото-
который нужно умножить, например, функцию Ф2 = P_iS_b если
функция АФ0 выбрана равной P+iS+1. Этот множитель можно
найти только из уравнения, которое прямо связывает функции Фо
и Ф2. Такое уравнение может быть получено исключением функ-
функции Фх из уравнений A3) и A4) с помощью леммы 2 из § 68. Дей-
Действительно, действуя оператором (SQ -f- to sin 6/p*) на уравне-
уравнение A3), а оператором CH -j- 1/p*) на уравнение A4) и складывая
результаты, получаем:
(So + ia sin е/р*) (Sx - ia sin 9/p*) Фо =
= @о+1/р*)@о-1/р*)Ф2. F4)
После упрощения это уравнение принимает следующий вид
S0S1O0 - 0О2>ОФ2. F5)
Если решения для Фо и Ф2 даются уравнениями B3), то уравне-
уравнение F5), требует, чтобы
B>oS>iS+i)/S-i = (b&o&oR-i)/bR+i. F6)
Если теперь предположить, что обе функции S+1 и S_x норми-
нормированы на единицу, то из уравнения D8) следует:
Д2>оЗД-1 = ЯАЯ+1. F7)
В этом последнем уравнении можно отождествить функции R_t
и Р_г и функции Л#+1 и Р+1, т. е.
Я.1 = Р-ъ A^+i = Р+ъ F8)
если
9 - ^* = D = (X2 - 4а2а2)!/2. F9)
В силу равенства E2) из последнего уравнения следует, что ^ —
действительная постоянная и что можно не делать различия
между ^ и ^* (например, в уравнениях F0)—F2)).
Теперь мы можем определить функции </>0 и, </>2 (см. уравне-
уравнения A2) и B3)):
bto = P+iS+u ^2 = [l/2(p*J]P.iS.1. G0)
Таким образом, соотношение F5) не только позволяет определить
относительную нормировку решений ф0 и </>2, но и однозначно
определяет постоянную Ф.
а. Решение для функции фг. Нам осталось получить решение
для скаляра Фх.

71. Завершение построения решения 119
Определим прежде всего функции
_l-P_l),
+1-P+i),
/+1 (в) = A/9») [(cos в) ^fS_, + (sin в) S_, ],
/-i (в) = (I/*) [(cos9) 2>XS+1 + (sin в) S+1].
Используя тождества Тьюкольского—Старобинского, можно про-
проверить, что функции g± (г) и /± @) удовлетворяют дифференциаль-
дифференциальным уравнениям
A?>og+i = rP+i; 2Я/+1 = S+1cos 0;
A?>tg-i = г/3-,; 2tf_x = S_! cos 0. G2)
Запишем теперь уравнение A3) в виде
А2>0 (р*Фх) = (р*^! - ia sin 0) АФ0. G3)
и подставим вместо функции АФ0 решение P+1S+1. Используя
формулы G1) и тождества, доказанные в § 70, можно переписать
это уравнение следующим образом:
о (р*Фх) = (/¦/>+,) ^i5+1 - ш/>+1 [(cos 0) <?XS+1 + (sin 0) S+1) =
50P-i) /-x- G4)
Мы получили, таким образом, соотношение
®0 (р*Ф,) = 2>о (g+i^iS+l - iaf_,2>oP-i). G5)
Аналогично из уравнения A4) получаем
2о (Р*ФО = [(/¦ - ia cos 0) ^о - 1 ] ^_iS_t =
= (r&oP-i - P-i) 5-i - ia (&0P-1) (cos 0) S_x =
= g+i^0^iS+i - ia {p,P_x) 3?4_ъ G6)
ИЛИ
^o (p*Oi) = ^o fe^Ai - tW-iW-i). G7)
Сравнивая уравнения G5) и G7), заключаем, что требуемое ре-
решение для Фх имеет вид
Р*Ф! = g+x (r) 5VS+1 @) - iaU @) ^oP-i (О- G8) *
* Строго говоря, к частному решению уравнения G8) нужно прибавить
решение Р соответствующих однородных уравнений
&0 (Р) = ^0 (Р) = 0.
Но решение
Р = const X exp [—ia (/¦„ + ш cos 6)] ctgm F/2),
где г^ определяется уравнением (см. уравнение A00) ниже)
dr* = (г2 + a2) dr/A (а2 = а2 + ат/о)
и сингулярно при 0-0 и 6 = л/2, и поэтому мы не включили его в решение
для р*Фх.

120 Глава 8. Электромагнитные волны в геометрии Керра
Производя аналогичные действия с уравнениями A5) и A6),
найдем, что решение для Фх можно получить и в другом виде
-р*Ф! = g_x (г) 2\S-X F) - iaf+l F) 2>tP+l (г). G9)
Сравнение решений G8) и G9) приводит к интересному тож-
тождеству
g+i&iS+i + ?_! 2?S_! - ia (/-i ФоЯ-i + /+1 &%Р+{).я (80)
Прежде чем заняться проверкой этого тождества, заметим, что
комбинируя решения G8) и G9), мы можем записать решение для
</>х в более симметричной форме
фг = Ф^/Ур* = [/274 (Р*J] [(ff+i#iS+1 - er-^fS-O -
- ia (/-i 2У>-1 - /+i &%Р+1)]. (81)
б. Проверка тождества (80). Выражения для g*±i (r) и /±i (б)
могут быть с помощью уравнений F0), F1) и F3) переписаны
в виде комбинаций функций Р±\ (г) и S±\ (Э):
g+1 = A/297С) [(tVX - 2а2а) P_t - i
[-(irk + 2aV> P+
—X cos 6 + 2a2a/a) 5_x - ^5+1 cos 6], ( ^
/_x - A/2^C) [(+X cos 6 + 2a2a/a) S+1 + «PS.x cos9].
Теперь тождество (80) проверить легко.
б. Решение для векторного потенциала. В данном разделе мы
покажем, как из найденных решений для максвелловских скаля-
скаляров </>0, </>х и ф2 можно получить в явном виде решение лля вектор-
векторного потенциала А.
Начнем с выражения
Fn^djAt-dtAj (83)
и выразим скаляры ф0 и <j>t через векторный потенциал А. Имеем
<*„ = Ftjl'mi = I'm/ (djAi - dtAj) = VbAt - mJDA} =
= (l//2"p) ll2%Ai - tn'^oAj =
= A/yTp) ^J [(r2 + a2) Л,/А + Лг + (a/A) Лф] -
- (l/-/TpJ>0(iaAtslnQ + Ae + iA4casixQ), (84)
^>2 = m'n' (djAt — diAj) = m' ДЛг — я'8*Л> =
= - (ml A/2p2) ^)о+Л,- - (nV/2"p*) ZoA, =
= - (l/p2p*2 /2") {A^)J (-шЛ, sin 0 + AQ - Мф cosec 0) +
+ <?0[-ДЛг + (/-2 + а2)Л + аДр]). (85)

71. Завершение построения решения 121
Полагая теперь
ДF+1 = (г2 + a2) At + ААГ + аЛф> AF_i = (г2 + а2) Л, - ДЛГ + aAv,
G+1 = шЛ{ sin Э + Ав -f 1'ЛФ cosec Э,
G_! = — iaAt sin 6 + А& — /Лф cosec Э, (86)
перепишем уравнения (84) и (85) с помощью решений G0) для
скаляров ф0 и <j>2 и определений G2) в следующем виде:
A//2~) BtfAF+, - A0oG+1) = (г + fa cos в) P+[S+1 =
= S+, A0o?+i -h iaP+i ^o/+., (87)
(r + w cos в) P_,S_i =
V ^o/-. • (88)
Эти уравнения легко разрешить относительно функций
и G±i. Находим
0Н+1) /2",
AF_, = (-iaP.if-i +) /
где функции #+i и Я_1( введенные здесь как произвольные, как
мы сейчас покажем, на самом деле не являются независимыми.
Имея решения для F±l и G±i, мы можем решить уравнения
(86) для компонент векторного потенциала. Находим
- (Д/2) (F+l - F_,) = (iafV
Я_,), (90)
Я+1 + ^оЯ-,), (91)
= V. [А (^1 + ^-i) + ia (G+1 - G_x) sin 9] =
- g^S^) sin 0] +
+1 - ^оЯ-i) sin в], (92)
p'A, = - V. [aA (F+i + Z7-!) sin2 G + / (z-2 + a2) (G+1 - G_x) sin 9] =
= - (i//Y) [a2 (P+1f+l - P^U) sin2 G -
- (r2 + a2) (?+1S+1 - g^Sj) sin 6] -
- (l//2~) [a (A2>0H+l - А^Я.,) sin2e +
+ i (r2 + a2) (&tH+ - 2Vf_,) sin 6]. (93)

122 Глава 8. Электромагнитные волны в геометрии Керра
Как уже упоминалось, существует ограничение на выбор
функций Н+1 и Я_х: его можно найти, вычисляя фг через А и
сравнивая результат с решением (81). Вычислим ф± через вектор-
векторный потенциал:
фг = i/2 ум + m^mi) FtJ = V2 (IW + fh
= - (A/2p2) I'ablAi - nf?oAj +
+ (mV/2"p) i?o4 - (mV/2~P*) ^ОЛУ -
- (Vap2) [iKAr - (r2 + a2) At, r - ^Лф, г - QAQ -
- i (aAt,e sin2 9 + Лф, е) cosec 9]. (94)
Подставляя теперь выражения для компонент А из уравнений
(90)—(93) и приравнивая получающееся выражение решению (81)
для </>ь находим, произведя упрощения:
^pT = 0. (95)
Этим уравнением определяется свобода в выборе калибровки
векторного потенциала. Оно напоминает кулоновскую калибровку.
72. Преобразование уравнений Тьюкольского
к стандартному виду
Рассмотрим вместо уравнений B6) и B8) более общие урав-
уравнения
[Д0Н s \®1 - 2 B | s | - 1) юг] P+l s | = XP+l s „ (96)
[ti2Dt\ s \&о + 2 B1 s | - 1) far] P-i s i = ХР_, s,, (97) *
описывающие безмассовые поля спина \s\. Действительно, в слу-
случае \s\ = 1 уравнения сводятся к уравнениям B6) и B8), описы-
описывающим фотоны со спином 1, а в гл. 9 и 10 мы увидим, что в слу-
случае | s | = 2 и 1/2 эти уравнения описывают соответственно рас-
распространение гравитационных волн и двухкомпонентных ней-
нейтрино.
Поскольку функции P+\s\ иР-isi удовлетворяют комплексно-
сопряженным уравнениям, достаточно рассмотреть уразнение
только для функции P+|S|. Кроме того, из соображений удобства
будем писать просто s вместо |s|, понимая, что s следует считать
положительным и принимающим значения 2, 1 и 1/2. Будем рас-
рассматривать, таким образом, уравнение
o+ - 2 Bs - 1) юг] P+S = XP+S. (98)
Здесь Р+. s | и Р_| s | обозначают функции &SR+S и R_s для которых мы не
будем предполагать какую-либо специальную относительную нормировку.

72. Преобразование уравнений Тьюкольского 123
В этом уравнении величина m входит в операторы ЗЬ и 35+ явно
через выражение
B 2
Покажем теперь, как исключить явную зависимость от m подхо-
подходящей заменой переменных.
Во-первых, введем вместо г новую независимую переменную
г#, определяемую уравнением
тНт^т. <100>
где
02 = Г2 + а2> а2 = а2 + ат/а A01)
Вследствие того что величина а2 может быть отрицательной (когда
пг отрицательно, а а ->0), ясно, что соотношение между г* и г,
вытекающее из уравнения A00), может при некоторых обстоя-
обстоятельствах стать двухзначным. В свое время мы рассмотрим,
как поступать в таком случае, а пока изучим формальные след-
следствия предлагаемой замены переменных.
Непосредственным следствием перехода к новой независимой
переменной г* является более простая запись операторов &0
и2H+:
2>о = (со7д) Л+, Я>% = (со7Д) Л_, A02)
где, как обычно,
Простота обусловлена тем, что в силу определения A01)
имеем
К = са2а. A04)
Во-вторых, изменим вдобавок зависимую переменную:
у = |u2|-e+i/2p+s# (Ю5)
В случае целых значений s это преобразование сингулярно, если
в интересующей нас области изменения со2 величина г должна
менять знак — об этом речь впереди.
После замены переменных уравнение (98) принимает вид
А<-]со2 {Л+ [(co2/As) Л_ (| со2 |S-1/2F)]} -
- 2 Bs - 1) tor | ш2 \S-^2Y - X | со2 \S~^2Y = 0. A06)
Расписывая его, получаем
Л
»"* [тег (-f^i •'Iм")]1'-
- [2 Bs - 1) iar | ш2 Is/2 + % \ ©2 Is/2] Y = 0. A07)

124 Глава 8. Электромагнитные волны в геометрии Керра
Если ввести определения
р=I?:1п '~^~ = "ё"[2гА - й* {г - M)l A08)
A09)
то уравнение A07) можно привести к виду
Л2Г +РЛ„У — QY = 0, (ПО)
с которым мы уже встречались при изучении возмущений шварц-
шильдовской черной дыры (гл. 4, уравнение B84)).
а. Зависимость г* от г. Интегрируя уравнение A00), полу-
получаем соотношение
+). (ill)
При изучении внешних возмущений керровской черной дыры нам
не нужно знать, что «происходит» под горизонтом событий г = г+.
Поэтому мы рассмотрим зависимость г* от г только при г > г+.
Из уравнения A11) с очевидностью следует, что зависимость
г* от г однозначна при г > г+, если
г% + а2 = 2Мг+ — а2 + а2 = 2Мг+ + ат/о > 0. A12)
При выполнении этого неравенства
г^ -> + оо при г -> оо,
г^ -> —оо при г -> г+ + 0.
и г^ является монотонной функцией г. Полагая для отрицатель-
отрицательных т
as = —am/2Mr+ (т < 0) A14)
и помня, что мы условились считать а положительным, заключаем,
что, до тех пор пока а > оьУ зависимость г% от г однозначна вне го-
горизонта событий и г% может принимать любые значения на всей
числовой оси (—оо, +оо). Но если 0 < а < as и г\ + а2 < 0,
то зависимость г% от г двузначна, причем г# -> + оо как при
г -> оо, так и при г -> г+ + 0. В последнем случае в окрестности
г = | а | поведение г% таково:
r^r^(\a\) + (\a\!A{a{)(r-\a\r + O((r~\a\n 015)
Точно так же в случае 0 < cr < os функции Р и Q в уравне-
уравнении (ПО) становятся сингулярными при г = |а|. Следовательно,

73. Общая теория преобразований 125
в этих случаях уравнение нужно рассматривать раздельно для
двух ветвей зависимости г^ от г, а именно для |а| <г < оо и
г+ <г <|а|.
Мы покажем в § 74 и 79, что в интервале 0 < а < as коэффи-
коэффициент отражения для падающих волн с целым спином превышаешь
единицу. Это явление называется супер радиацией и является ана-
аналогом процесса Пенроуза для волн.Мы рассмотрим природу супер-
суперрадиации в § 75, а здесь хотим обратить внимание на сходство
неравенства
2Mr+a < —am A16)
(эквивалентного условию а < os) с неравенством C52) гл. 7;
эти неравенства в точности совпадут, если отождествить ho с 8М,
а Атс б/, где h — постоянная Планка.
В заключение отметим, что а2 становится отрицательным,
прежде чем о становится равным os:
а2 < 0 при о <: ас = —т/а, A17)
причем а2 = 0, когда колебания в волне происходят в такт с вра-
вращением черной дыры (будем называть такую частоту «согласован-
«согласованной»). В интервале os < о < GС, несмотря на то что а2 < О,
тем не менее г\ + а2 > 0 и зависимость г* от г остается одно-
однозначной.
73. Общая теория преобразований и редукция
к одномерному волновому уравнению
В предыдущем параграфе мы привели общее уравнение Тью-
кольского (98) к виду (ПО), полностью совпадающему с уравне-
уравнениями формализма Ньюмена—Пенроуза, которые появлялись
в § 20 при изучении возмущений шварцшильдовской черной дыры.
Поэтому, так же как и ранее, будем искать преобразование, по-
посредством которого уравнение A10) сведется к одномерному
Ьолновому уравнению вида
A2Z - VZ, A18)
|где V — потенциал, подлежащий определению.
i Развиваемая здесь теория отличается от формализма, разви-
развитого в § 30, только в одном отношении: функции Р теперь опре-
определены иначе (ср. уравнение A08) с уравнением B86) гл. 4).
удет однако удобнее записать все основные формулы в том виде,
каком они нам понадобятся.
Предположим, что функция Y связана с функцией Z следующим
^отношением (ср. с уравнениями B87) и B88) гл. 4):
Y = /A+A+Z+ WA+Z, A19)

126 Глава 8. Электромагнитные волны в геометрии Керра
где / и W — некоторые функции г*, которые следует найти.
Уравнение A19) может быть также записано в виде
Y = fVZ + ГЛ+Z, A20)
где
Т = W + 2/а/. A21)
Действуя оператором Л_ на уравнение A19) и используя
тот факт, что функция Z по предположению удовлетворяет урав-
уравнению A18), находим (ср. с уравнениями B90) — B92) гл. 4)
A_Y = - (As/«4s) PZ + RA+Z, A22)
где
(-A7co4s) P (О = -±-fV + WV, A23)
R = fV + dr/dr*. A24)
Потребуем теперь, чтобы функция У, определяемая уравне-
уравнением A19), удовлетворяла уравнению (ПО) вследствие уравнения
A18). Повторяя выкладки § 30 гл. 4, получаем уравнения (ср.
с уравнениями B98) и B99) гл. 4)
A26)
Можно проверить, что уравнения A22)—A26) допускают
интеграл
(co47As) RfV + РГ = К = const. A27)
Этот интеграл позволяет обратить уравнения A20) и A22):
(A8/©48) KZ = RY — ТЛ_Г, A28)
KA+Z = РГ + E4s/As) VfA_Y. A29)
Уравнения A20), A22), A28) и A29) являются необходимыми
и достаточными условиями того, что из уравнения (ПО) вследствие
уравнений A23) — A26) следует уравнение A18), и обратно.
Поскольку уравнения A22)—A26) допускают интеграл A27),
достаточно рассмотреть следующие уравнения:
-- dT/dr*, A30)
(.31)
R(R- dT/dr,) + (A754s) |5Г = (Д7645) K, A32)
(R -Qf)V= (A7S40 dp/dr^. A33)

73. Общая теория преобразований 127
Отметим, что уравнение A32) есть другая форма записи интеграла
A27), в котором ffV заменено на R — 7\г* в соответствии с урав-
уравнением A30).
Уравнения A30)—A33) дают четыре уравнения для пяти
функций /, р, Rf T и V. Имеется, таким образом, значительная
свобода для поиска нужных нам решений этих уравнений. Однако
для конкретных функций Q, которые следуют из уравнения A09)
при s = 1/2, 1 и 2, оказывается, можно написать решения уравне-
уравнений в явном виде. Можно преобразовать уравнение A10) к одно-
одномерному волновому уравнению и найти явное выражение для
потенциала V.
Предположим, что уравнение A10) преобразуется в одномер-
одномерное волновое уравнение вида A18) и пусть Z1n Z2 — два независи-
независимых решения этого уравнения. Их вронскиан, очевидно, будет
постоянным (ср. с уравнением C54) и последующими уравне-
уравнениями гл. 4):
[Z1? Z2]r, = const; A34)
здесь при вычислении вронскиана производные берутся по пере-
переменной г*, на что и указывает индекс. Если частота о принадлежит
интервалу частот, которому соответствует суперрадиация, то
при интерпретации соотношения A34) следует соблюдать осто-
осторожность, потому что в этом случае, как будет показано, потен-
потенциал V сингулярен (так же как и функции Р и Q в уравнении
(ПО)) при г = | сх | > г+. Как указывалось выше, в этих случаях
уравнение нужно рассматривать раздельно для двух ветвей функ-
функции г% от г. Вронскианы двух независимых решений будут по-
постоянными по отдельности для каждой ветви, но не обязательно
одинаковыми. С другой стороны, если два рассматриваемых ре-
решения Zx и Z2 соответствуют двум различным решениям уравне-
уравнений Тьюкольского, то вронскианы [Zlf Z2]r* для двух ветвей
должны быть связаны друг с другом, и эту связь можно найти
следующим образом.
Пусть У\ и Y2 соответствуют двум решениям Zx и Z2. Тогда
[Ylt Kalr. = УЛ-Уг ~ ПЛ-П. A35)
Подставляя теперь вместо Y и Л_ Y выражения A20) и A22), на-
находим:
I^i, Y*lr. = [#/V + (A7u4s)pT] B,A+22 - Z^Z,). A36)
Поскольку первый сомножитель в правой части пропорционален
интегралу A27), получаем
lYlt YA, - ~/C(A7S4e) [Zlt Z2]v A37)
Но из уравнения A05) следует, что
[Уг, У21, = - I й2 \-i2s-l) [Pg (I), Ps BIч =
= -А (-6* | б2128)'1 [P. A), Р$ B)]„ A38)

12$ Глава S. Электромагнитные волны в геометрии Керра
где Ps A) и Ps B) — независимые решения уравнения Тьюколь-
ского, из которых получены решения Y± и Y2. Объединяя уравне-
уравнения A37) и A38), получаем
K[Zl9 Z2]r+ = _Д1--|!рг[РвA)> PsB)], A39)
Поскольку уравнение Тьюкольского не может иметь сингуляр-
сингулярности в интервале г+ < г < оо, из уравнения A39) следует, что
когда а2 < 0 и г+ < |а|, т. е. когда имеет место суперрадиация
и 0 < а < а6. Таким образом, в случае s = 1 и 2 при пересечении
сингулярности г = |а|(>г+) меняется лишь знак вронскиана
[Zb Z2]r+, в случае же s = 112 вронскиан [1Ъ Z?]r+ сохраняет
свое значение.
До сих пор наше рассмотрение касалось только уравнения
A10) для функции P+s. Что меняется для комплексно-сопряжен-
комплексно-сопряженного уравнения для функции P_s? Когда приходится использовать
оба уравнения, оказывается удобным различать соответствующие
решения Y комплексно-сопряженных уравнений, вводя обозна-
обозначения К(+а) и F(~a). Уравнения для них будем писать в виде
Л2у(±а) + РАту{±а) - QY{±G) = 0. A41)
И если мы будем искать преобразование, приводящее урав-
уравнение для Y{'0) к одному волновому уравнению для функ-
функции Z(~a) (функции К(+а) соответствует решение Z(+a) вол-
волнового уравнения), действуя по аналогии с преобразованием
уравнения для функции 5/(+ст), то найдем, что все уравнения оста-
останутся справедливыми, если в них поменять знак а всюду, где он
входит явным образом, и это замечание относится, в частности,
и к уравнениям A30)—A33). Следует, однако, отметить, что а2
остается неизменным в обеих системах уравнений, потому что
«комплексное сопряжение» требует одновременного изменения
знаков а и т, например операторы &п и &\ являются комплексно-
сопряженными только при таком одновременном изменении зна-
знаков а и т.
74. Потенциальные барьеры для падающих
электромагнитных волн
В двух предыдущих параграфах, рассматривая преобразование
уравнения Тьюкольского к одномерному волновому уравнению,
мы обращали внимание на сингулярность соответствующих пре-
преобразований, когда зависимость г* от г становится двузначной
в интервале частот 0 < а < as, в котором имеет место суперра-

74. Потенциальные барьеры для падающих волн 129
диация и связанные с этим сингулярности полученных потенциа-
потенциалов при г = |а| (>г+), но не исследовали этот вопрос подробно.
В этом параграфе мы проясним данный вопрос в связи с исследо-
исследованием электромагнитных возмущений (s = 1). К счастью, в этом
случае решения различных уравнений достаточно просты, так
что имеется возможность выделить и разрешить отдельные
аспекты проблемы.
В случае s = 1 уравнения A09) и A30)—A33) принимают
следующий вид:
Q = (А/со4) (X — а2Д/со4), A42)
R—fV = dT/dr» A43)
R (R — dT/drJ + (А/со4) рГ - (А/со4) /С, A45)
RV — QfV = (А/со4) dp/dr^, A46)
Покажем, что эти уравнения допускают решения, совместные
с требованиями
Т = const, R = ?Д/оL, A47)
где ^ — еще одна постоянная. При этих предположениях урав-
уравнение A44) дает
р = г/а? — Г (X — а2 А/со4). A48)
Подставляя в уравнение A45) это решение для р и предполагаемый
вид Ry находим
q2 (А/й4) + Т [2ioq — Т (X — а2 А/со4) ] = К. A49)
Из этого уравнения следует:
q2 = -Га2, ^ = ±*Та, A50)
/С = 2/а^Г — Г2Х = —Г2 (X ± 2аа) - const, A51)
что нам и требуется. И наконец, уравнение A46) дает
±*<у-®=*ткШ' A52)
или, иначе,
т/ n.Ad/A\ А Г. 9A_...2d/A\]
A53)
Таким образом, уравнения A43)—(И6) действительно имеют ре-
решения, совместные с требованиями A47), если Q определяется
уравнением A42). Заметим также, что решение для V не зависит
5 Чандоасекао С. т. 2

130 Глава 8. Электромагнитные волны в геометрии Керра
от выбора постоянной Т и что, кроме того, мы получили два раз-
различных решения, соответствующие выбору того или иного знака
в уравнении A53) и, наконец, что функция V является комплекс-
комплексной при о > ос ( = —пг/а).
Поскольку в решения для R, р и К величина Т входит в ка-
качестве простого масштабного множителя, можно без потери общ-
общности положить
Т = 2/а. A54)
В этом случае
# = +2(та А/со4; К = 4а2 (к ± 2<та),
Р - —2/а (А, — а2Д/со4 ± 2оа), A55)
а уравнения, связывающие решения уравнений (ПО) и A18)
в случае s = 1, принимают вид
Y - +2аа (А/со4) Z + 2/aA+Z, A56)
A^Y = 2/а (А/со4) (X — а2 (А/со4) ± 2аа) Z н= 2аа (А/со4) A+Z,
A57)
/CZ - =F2oaY — 2ia (coVA) Л_К, A58)
A:A+Z = —2/а (к — а2 А/со4 ± 2аа) Y =f 2ааЛ.Г. A59)
Два решения уравнений A56)—A59), получающиеся при раз-
разном выборе знаков, которые мы будем обозначать Z+ (верхний
знак) и Z_ (нижний знак), очень просто связаны между собой
(точно так же, как очень просто связаны решения, описывающие
аксиальные и полярные возмущения черных дыр Шварцшильда
и Рейсснера—Нордстрема). Действительно, подставляя в соот-
соотношение
K+Z+ - — 2oaY — 2/а (со4/А) А_У A60)
выражения, связывающие функции Y и A_Y с функцией Z_,
получаем
K+Z+ = —2аа [+2аа (А/са4) Z_ + 2/gA+ZJ -
- 2/а [2/а (А, - а2Д/а>4 - 2aa)Z_ + 2aaA+Z_]. A61)
После упрощения уравнение A61) принимает вид
K+Z+ = 4a2 (X - 2a2A/co4 - 2aa) Z_ - 8/a2aA+Z_. A62)
Таким образом, если известно решение Z_, относящееся к потен-
потенциалу К_, то можно получить решение Z+, соответствующее по-
потенциалу V+. В частности, из уравнения A62) следует, что
K+Z+ — K_Z_ - 8/aa2A+Z_ (r — оо, г -> г+ + 0). A63)
а. Связь между решениями Z{+G) и Z(~a). В предыдущем
параграфе мы ввели верхние индексы, чтобы различать решения

74. Потенциальные барьеры для падающих волн 131
уравнения Тьюкольского (ПО) Y{+G) и комплексно-сопряженного
ему уравнения Y{'0) (см. уравнение A4h)). Этим решениям соот-
соответствуют решения одномерных волновых уравнений Z(+a) и
Z{~G). Подставляя в уравнения A43)—A46) выражения A54)
и A55), но с обратным знаком а, найдем, что функции Z(+a) и
Z(~a) удовлетворяют одному и тому же уравнению с потенциалом
A53):
A2Z{±G) = VZ{±G). A64
Поскольку при а > ас = —т/а потенциалы V комплексны,
в этих случаях функции Z(+a) и Z{'G) в отличие от функций Y{+G)
и Y{'G) не удовлетворяют комплексно-сопряженным уравнениям.
Если выбрать в качестве Z(+a) решение уравнения с потен-
потенциалом
К, =-^т А, — а2-^- — taco2 -r- -^ ) A65)
+ со4 L W4 dr \ со4 / J v '
(т. е. решение, обозначенное Z+ в уравнениях A60)—A63)),
то получим следующие соотношения:
T{±G) = ±2/a; R{±G) = +2aaA/co4,
— a2 A/ca4 ± 2aa), A66)
4G2(A ±2aa),
а уравнения, связывающие решения Z(+a) и Z(~a), имеют вид
F(±a) = zp 2aa (Д/со4) Z(±a) +2taA±Z(±a), A67)
A-F(±a) = ±2w (A/co4) (X - a2 A/©4 ± 2aa) Z(±a) q=
=F2aa(A/co4)A±Z(±a), A68)
K{±G)Z{±O) = =F2aaF(±a) н= 2ш(со4/Д) АтГ(±а), A69)
A70)
(Заметим, что если выбрать верхние знаки и в уравнениях A56)—
A59) и A67)—A70), то они просто совпадут, как и должно быть
в силу определений.)
Если следовать процедуре, использованной при установлении
связи между решениями Z+ и Z_ (уравнения A60)—A63)), то из
уравнений A67)—A70) получим следующую связь между реше-
решениями Z(+a) и комплексно-сопряженным решению Z(~a)-
K{+a)Z{+G) = 4о2(Х - 2сс2 Д/со4 - 2aa) [Z('a)]* - 8iao2A+ [Z('a)]*.
A71)
5*

132 Глава 8. Электромагнитные волны в геометрии Керра
Асимптотики функций Z^a* и Y^±o\ совместные с асимптотиками функции
V+= (А/со4) [I — а2А/со4 - toco2 d (A/co4)/drl
Z(+a) exp [+ior*] exp [—tor*]
Z("a) exp I—tor*] [(I + 2aa)/(k — 2aa) ] exp [-War,. ]
(> _4a2 exp [+ior# ] [~(k + 2aa)/r2] exp [—far* ]
_4o2 exp [+iarj — (A, + 2aa) Д exp [—iorj Z~+2 [52 + i (r+
y(-<0 _4a2 exp [-шг, ] — (k + 2aa) exp [+/аг# ]/г2
У("а) —4a2 exp [—iorj — (k + 2aa) Д exp [+/аг#] со^2 [со2 — i (г+ — му<з]
~1
В частности, при г->оо, г -> г+ + О
^(±a)z(±a) _ K(Ta) [z(Ta)]* _ 8
Можно отметить еще соотношение (см. уравнение F9))
б. Асимптотическое поведение решений. Потенциал К, опре-
определенный уравнением A53), спадает экспоненциально по г* на
горизонте событий при г -> г+ + 0 и убывает пропорционально Г2
при г -> со. Таким образом, если частота а лежит вне интервала
суперрадиации, потенциал является короткодействующим, инте-
интеграл по всей области изменения г% конечен и всегда веществен.
Если же частота лежит в интервале суперрадиации, то потенциал
имеет сингулярность при г = \а\ > г+ (см. п. 75,/? ниже) но
поведение на горизонте и на бесконечности не меняется. Следова-
Следовательно, во всех случаях решения волновых уравнений имеют
следующую асимптотику:
Z -> exp [±ior^] (г -> оо, г -> г+ + 0). A74)
Подставляя эти выражения в уравнения A56)—A59) и A67)—
A70), можно найти соответствующее поведение на асимптотике
для функции Y (и, следовательно, также для решений уравнения
Тьюкольского). Кроме того, уравнения A63) и A72) позволяют
связать асимптотики решений, принадлежащих двум потенциа-
потенциалам, и асимптотики решений Z(+a) и Z(~a), принадлежащих
одному и тому же потенциалу.
Действительно, из соотношения A63) следует, что решения
для Z_, имеющие соответственно асимптотики при г -> оо и г ->
-> г+ + 0:
Zi+a) -> exp [—far,], Zl+0) — exp [+torj, A75)

74. Потенциальные барьеры для падающих волн 133
Таблица 8
для потенциала V,
}-°s!°)]
V_ =(Д/со4) [\ - а2А/со4 + ia(b2 d (A/co4)/dr]
ехр I+шг* ] [(Я + 2аа)/(Я — 2аа) ] ехр [—гаг* ] г* -> ± оо
ехр [—шг* ] ехр [+шг*] г* -> ± оо
—4а2 ехр [+шг* ] [— (Я + 2аа)/г2] ехр [—ior* ] r-> + ос
—4а ехр[+гаг^] —(Я+2аа)Лехр[—ior#] со [со^ + l (r+—MWa] л->г +0
—4а2 ехр [—ior* ] — (к + 2аа) ехр [+?аг* ]/г2 г -+¦ + оо
—4а2 ехр [—гаг*] — (Я+ 2аа) А ехр [i'cr^] со [оУ; — г (г — MJ/a] r-+r++ 0
приводят к решениям Zi+a) со следующим асимптотическим пове-
поведением:
/мп\ \ [(^ ~ 2аа)/(Я + 2ааI ехр [—iorA при г —> оо,
+ ~^ I г . • 1 \ r\ (I'D)
{ expl+iarj при г—»г+ + 0.
Подобным же образом находим, с помощью соотношения A72),
что решения для Z{+°\ имеющие асимптотики
.(-a) J expl+tarj при
+ ^ ( ехр[—шг^] при
приводят к решениям для 2++а) со следующим асимптотическим
поведением:
, — 2ао)/(к + 2aa)] exp [—шг%] при
+ \ expl+ior] при
В табл. 8 приводится сводка асимптотик для функций 2(±а) и
F(±a), полученных из асимптотики exp (i/orj для функции
Z++a), принадлежащей потенциалу V+.
Подчеркнем, что при выводе соотношений A56)—A59) и A67)—
A70) не делалось никаких предположений об относительной нор-
нормировке функций F(+a) и F("o). Эта относительная нормировка,
по сути дела, определена в табл. 8, поскольку приведенные здесь
асимптотики для функций F(+a) и F("a) были получены в пред-
предположении, что функция Z(+a), принадлежащая потенциалу V+,
имеет асимптотики exp [+ior+] и ехр [—iart] при г -> оо и г ->
-> г+ + 0.

134 Глава 8. Электромагнитные волны в геометрии Керра
75. Задача об отражении и прохождении волн
После формального сведения уравнений Тьюкольского (в слу-
случае s = 1) к форме одномерных волновых уравнений перейдем
к задаче их использования для нахождения коэффициентов отра-
отражения и прохождения падающих электромагнитных волн. Сразу
же оговоримся: хотя сведение основных уравнений к одномерным
волновым уравнениям предполагает, естественно, исследовать
далее задачу о проникновении через барьер, следует еще показать,
что коэффициенты отражения и прохождения, появляющиеся
в такой задаче, имеют отношение к реальным физическим про-
процессам. Отложим решение этого и других вопросов физической
интерпретации до § 76, а сейчас продолжим формальное исследо-
исследование уравнений.
Рассматривая задачу об отражении и прохождении потенциаль-
потенциального барьера, заданного уравнением A53), будем различать три
случая: о > ас (= —т/а), когда а2 > 0; а8 < а < ас, когда
а2 < 0, но г? > | а |; и 0 < а < as, когда а2 < 0 и r+ < | а |.
а. Случай а > ас (= —т/а) при а2 > 0. Поскольку а2 > 0,
зависимость г* от г однозначна во всей интересующей нас области
изменения г, а потенциалы V± из табл. 8 ограничены и коротко-
действующи. Поэтому волновое уравнение A64) допускает ре-
решения, удовлетворяющие следующим граничным условиям:
ехр 1+iorJ + А{+0) ехр [—iorJ при г#—* + °°>
B++o) ехр [+юг%] при /•*-> — со,
, _. f exo \—iorJ 4-
} ехр [—farj + Л[о) ехр [ + torj при
+5+ ехр[—mr#] при г*—> — со.
Здесь введен нижний индекс «+», чтобы подчеркнуть, что рас-
рассматриваются решения, соответствующие потенциалу V+.
Поскольку и Zl+(J),H Z[~o) удовлетворяют волновым урав-
уравнениям с одинаковыми потенциалами V+, коэффициенты отраже-
отражения и прохождения
R = A{:o)A{;Q\ T = B{+a)Bta) A81)
будут подчиняться закону сохранения
..^•V- R + T=l. A82)
С другой сторсшы,. соотношения между асимптотиками решений
Zl+CT)H Z(~a), приведенные в табл. 8, дают
^~0) = ТЗШНЛГ'Г. Bi"a) =Ш+О)Г- A83)

75. Задача об отражении и прохождении волн 135
Тогда выражения для R и Т в уравнении A81), могут быть пере-
переписаны в виде
к-2аа
(+а)|2
A84)
Отсюда следует, что R и Т вещественны. Важность выражений
A84) для R и Т, однако, в том, что для получения решений с раз-
различными асимптотиками A79) и A80) не нужно дважды интегри-
интегрировать волновое уравнение: достаточно проинтегрировать его
лишь один раз, например в случае граничных условий A79).
Выражения A84) для R и Т справедливы только для решений,
соответствующих потенциалу V+. Если рассмотреть решения,
соответствующие потенциалу К_, то получим следующие соот-
соотношения:
ё12> T=|Bi+T A85)
С другой стороны, соотношения из табл. 8 дают
.(-кг) R(+o) __ R(+o)
Следовательно, соотношения A84) и A85) дают одинаковые коэф-
коэффициенты отражения и прохождения.
Вышеприведенное исследование проясняет, как нужно моди-
модифицировать стандартные методы решения задачи прохождения
через одномерный действительный потенциальный барьер для
случая, когда потенциалы комплексны, а решения, удовлетворя-
удовлетворяющие комплексно-сопряженным граничным условиям, сами не
являются комплексно-сопряженными функциями.
б. Случай as < а < ас. В этом случае а2 < 0, но r+ > | а |.
Следовательно, в нужной области изменения г зависимость г#
от г остается однозначной. С другой стороны, вследствие мни-
мнимости а потенциал A53) становится вещественным:
где
со2 - г2 — | а |2, | а |2 - —а2. A88)
Потенциалы вдобавок ограниченны и короткодействующи, по-
поэтому применима теория проникновения через одномерные потен-
потенциальные барьеры, известная из элементарной квантовой меха-
механики. Следует, однако, отметить, что потенциалы V+ и V_ приво-
приводят к одинаковым коэффициентам отражения и коэффициентам,
прохождения. Причина этого в том, что соответствующие ампли-

136
Глава 8, Электромагнитные волны в геометрии Керра
0,6 г
0,4-
0,2-
-0,2
i
0,38
0.38,
0,358
—-—.
О7366
1 1 1
0,368
i
Ц
0,
64
6s
-2
Рис. 41. Потенциальные барьеры для падающих на черную дыру Керра (а =
плексных потенциалов, соответствующих значениям / = 1 и т = — 1. У кри
потенциалов V+ и V_ в интервале частот ас ^ а ^ os. У кривых указаны соот
туды отраженных и прошедших волн связаны соотношениями
(ср. с уравнением A86))
л _ h-2i\a\o л о _ д
A89)
и поэтому
|Л+|2 = |Л-|2, |B+|2 = |BJ2. A90)
Хотя потенциалы, задаваемые уравнением A87), ограниченны
при а > aSi они становятся сингулярными на горизонте в пре-

75. Задача об отражении и прохождении волн
137
-0,2-
= 0,95) электромагнитных волн; а — действительные, б — мнимые части ком-
ых указаны соответствующие значения ас. в и г — семейство действительных
етствующие значения а.
деле а -> as -f- 0, поэтому падающим волнам становится все труд-
труднее проникать через барьер по мере приближения частоты а
к значению as (см. рис. 41, на котором показано семейство потен-
потенциалов в интервале частот as < а < ас). В результате следует
ожидать, что
R->1, T->-0 при a->-Gs + 0. A91)
Эгот аргумент, хотя и находится в согласии с нашим предсказа-
предсказанием, что при о = os начинается суперрадиация и, следовательно,

138 Глава 8. Электромагнитные волны в геометрии Керра
коэффициент отражения становится больше единицы, т. е. R > 1,
не является строгим, как будет видно из результатов п. 105, а.
Но в следующем разделе мы покажем, что для а < as действи-
действительно R > 1, а непрерывность требует, чтобы R = 1 при а =
в. Случай 0 < cr < as. Как было показано, если сг < as и
г\ — | а |2 < 0, функция г* от г достигает минимума при г = \ а \
и стремится к +°° как ПРИ г -> °°> так и при г -> г+ -f 0. Поэтому
нужно отдельно рассматривать решения для двух ветвей функции
г# (г), которые, начинаясь с г = | а|, идут или к г->оо, или
к г -> r+ -f- 0- Рассматривать отдельно решения для двух ветвей
нас заставляет также и тот факт, что потенциалы A87) имеют
сингулярности при г = |а|. Действительно, переписывая выра-
выражение для потенциалов V± в виде
V± = (А/й4) [X + (А/й4) [ а | (| а | T4r) =F 21 а | (г — АГ)/Й2], A92)
находим, что в окрестности г = | а| функции V± имеют следующее
поведение:
16|а|2(г-|а|L. A93)
Отложим на время решение вопроса о том, каким образом сингу-
сингулярность в потенциале при г = | а| следует учитывать при на-
нахождении решения волнового уравнения, здесь же отметим, что
граничные условия, которые должны быть наложены на решения
волнового уравнения, остаются прежними, именно:
j , r,
I B± exp [+ iorj при Л(.->оо, r->r+ + 0,
где индексы «±» введены для различения решений, соответству-
соответствующих потенциалам^1/+ или V_. Может возникнуть вопрос, почему
волна, приближающаяся к горизонту вдоль ветви r% -> -f °°
и г -> г+ -\- 0, должна иметь зависимость exp [-ficrr^], так же
как и волна, приближающаяся к горизонту вдоль ветви г* -> —оо
и г -> r+ -f- 0 в случае а > as. Мы рассмотрим этот вопрос в § 76,
а сейчас продолжим исследование, приняв граничные усло-
условия A94).
Даже с этими граничными условиями мы должны принять
во внимание следующее важное обстоятельство: в соответствии
с уравнением A46) при пересечении сингулярности при г = | а \
знак вронскиана [Z, Z* ]Гш должен измениться. Поэтому, вводя
обычные определения
К = |Л+|2, Т = |?±|2, A95)
получим теперь следующий закон сохранения:
R-T=l. A96)

75. Задача об отражении и прохождении волн 139
Следовательно, в интервале частот 0 < о < as величина коэффи-
коэффициента отражения больше единицы, т.е. R >1. Это явление
называется суперрадиацией.
Остается выяснить, как можно получить решение волнового
уравнения, удовлетворяющее граничным условиям A94), надле-
надлежащим образом учитывающее сингулярность A93) в потенциалах
при г = | а|. Для этого нужно исследовать поведение Z вблизи
сингулярности. Непосредственные вычисления показывают, что
в окрестности точки г = \ а | существуют два независимых реше-
решения для Z, имеющих следующее поведение:
2+~|(г-|а|)Г и |(г-|а|)Г Для V+9
Z_ ~ \(г - | а |)|5/2 и |(г - | а \)\-V* для VL,
а общее решение для Z вблизи | а | является линейной комбинацией
указанных решений.
Метод решения волнового уравнения с граничными условиями
A94) следующий. Начнем с решения для Z+ (соответствующего
потенциалу V+), имеющего асимптотику
Z+-> exp [-f/crrj (г* -> -f°° вдоль ветви г -> г+ +0), A98)
и продолжим интегрирование от горизонта в направлении возра-
возрастания г (но при этом в направлении убывания г*). В случае
приближения к сингулярности при г = | а | слева (по г) решение
будет стремиться к определенной линейной комбинации рассмо-
рассмотренных выше фундаментальных решений вблизи сингулярности.
Пусть эта линейная комбинация имеет вид (ср. с уравнением
A97)) при /'->|а| — О
• Z+-^C1(|a|-r)»/» + C2(|a|-r)^> A99)
где Сх и С2 — постоянные, которые будут найдены в процессе
интегрирования. Требование изменения знака вронскиана [Z+,
Z+K в точке г = | а \ приводит к тому, что при г -> | а \ -\- О
подходящая линейная комбинация имеет вид
Z+ -> iCx (r - | a |f/2 - iC2 (r - | a \)^ (r -+ \ a \ + 0). B00)
С помощью выражения для Z+ можно теперь продолжить интегри-
интегрирование в направлении возрастания как г, так и г* вдоль ветви
г _> -j-ao. Таким путем найдем в конце концов, что при г -> оо
решение имеет асимптотику
?+->CfnCexp[+for#] + Crefexp[— for#] (г#-^ оо, г-*- оо), B01)
где С1пс и Cref — постоянные, которые определятся в процессе
интегрирования. Поскольку решение, с которого мы начинали
интегрирование, соответствует прошедшей волне единичной ам-
амплитуды при приближении к горизонту, ясно, что искомые коэф-

140
Глава 8. Электромагнитные волны в геометрии Керра
фициенты отражения и прохождения равны
R4Cref|2/|Cinc|2, T = |Clnc|-*. B02)
Определенные таким образом коэффициенты R и Т будут удовле-
удовлетворять закону сохранения A96).
На рис. 42 изображено решение для Z (в данном примере это
стоячая волна), полученное непосредственным интегрированием
уравнения для Z+, соответствующего значению частоты а =
V2
0,8
0,4
Z 0
-0,4
-0,8
-
-
"\
. \
^ ;
20 ,
/
/
/ 30
\
АО \
-
-
50
Рис. 42. Иллюстрация решения волнового уравнения для Z, представляющего
стоячую электромагнитную волну (/= — m =+1) с частотой суперрадиации
(а = gs/2) в поле черной дыры Керра (а = 0,95). Часть кривой, помеченная
цифрой 1, представляет действительную амплитуду волны в интервале оо >
> г > | а |, а часть кривой, помеченная цифрой 2, представляет мнимую ампли-
амплитуду волны — мнимую в силу уравнения B00) — в интервале | а | > г > г+.
Точка поворота лежит при г* = 8,707.
В табл. 9 приведены коэффициенты отражения и прохождения
для электромагнитных волн различной частоты, падающих на
керровскую черную дыру с а = 0,95.
Таблица 9
Коэффициенты отражения электромагнитных волн, падающих на керровскую
черную дыру со= 0,95 A=1, т= —1)
а
0,325000
0,345000
0,350000
0,365593
0,375593
0,385593
0,395593
°/°s
0,8979
0,9531
0,9669
1,0100
1,0376
1,0653
1,0929
R
1,02428
1,01919
1,01565
0,99241
0,96100
0,90807
0,82563
а
0,405593
0,415593
0,425593
0,435593
0,445593
0,455593
o/os
1,1205
1,1481
1,1758
1,2034
1,2310
1,2586
R
0,70998
0,56810
0,41943
0,28686
0,18435
0,11332

76. Дальнейшее развитие теории 141
76. Дальнейшее развитие теории
и физическая интерпретация
Как говорилось в начале § 75, нам нужно установить, яв-
являются ли коэффициенты отражения и прохождения, полученные
из одномерных волновых уравнений для функций Z(±or), теми
физическими величинами, которые описывают взаимодействие
черной дыры Керра с падающими электромагнитными волнами.
Но прежде чем начать обсуждение этих вопросов физической ин-
интерпретации, необходимо показать, как те же самые коэффици-
коэффициенты отражения и прохождения получаются из уравнений Тью-
Тьюкольского при наложении подходящих граничных условий.
Напомним прежде всего, что (ср. с уравнением A2))
Фо = Фо = #+iS+i ехр [| (ot + тф)],
2 (р*J ф2 = Ф2 = fl^S.! ехр [ i(ot + тФ)],
где мы восстановили множители, описывающие зависимость от
времени и угла ср. Функции Тьюкольского R+l и R_x в свою очередь
связаны с функциями У<+а) и У(~а) соотношениями (ср. с уравне-
уравнением A05))
R
где
со2 = г2 + а2 + ami а. B05)
Во избежание произвола ограничимся рассмотрением случая
сг > as (когда а2 > 0) и исследованием решений Z(±or), соответ-
соответствующих потенциалу К, и удовлетворяющих граничным усло-
условиям A79) и A80). Эти ограничения не повлекут потери общности:
изменения, необходимые при изучении случая а2 < 0 и решений
Z(±(J), соответствующих потенциалу К_, незначительны и в основ-
основном формальные.
Из асимптотик, приведенных в табл. 8, находим, что гра-
граничные условия, которым удовлетворяют решения У<±а), полу-
получающиеся из уравнения A67) и граничных условий A79) и A80)
для решений Z(+±o), имеют следующий вид:
( — 4а2 ехр [+ шг#] — (к + 2аа) Л(+а> ехр [— ior#]/r2 при г-> оо,
"^ 1 - 4а2В<+а> ехр [+ шг#] при г-> г+ + 0,
B06)
— (Я -(- 2аа) ехр [+ ior%]/r2 — 4а2Л(~а) ехр [— tor*] при г ->¦ оо,
- (X + 2ста) В("а> А ехр [+ wr#] со;2 [со2 - i (r+ - М)/о]'1 при
B07)

142
Глава 8. Электромагнитные волны в геометрии Керра
Напомним, что
[Л<+°>]* - [(К -
2аа)]
B08)
(см. уравнение A83)). Из соотношений B04) теперь следует, что
соответствующие решения радиальных уравнений Тьюксльского
удовлетворяют следующим граничным условиям:
при г
\ при
[—tarj при r-
/?!r1ansAexp[+ iarj при
Из сравнения с уравнениями B06) и B07) получаем
Rl+\c = — 4а2, RlX = — (к -\- 2аа),
-о,
B09)
B10)
R^r5 = - 4a2 (й2+I/? B(+c) ^lr,ans = - [Ct + 2аа) (й2+I/2/Я'] В("а).
B11)
В уравнении B11) были использованы следующие обозначения:
l -os/o), B12)
= (Ш-rl/o*) (а - as) [(о - <js) + i (M2 - аУ*/2Мг+]. B13)
Из соотношений B11) теперь следует:
?(ref) 2 16а4
p(inc)
16 а4
)(inc)
(A,
¦|А(-°)|3.
B14)
Вследствие связи Л(+а> и Л(~а) (уравнения B08)) получаем
Я2 — 4а2а2
16а4
16а4
Я2 __ 4а2а2
B15)
Согласно уравнению A81), коэффициент отражения R может
быть задан одной из двух следующих формул:
16а4
№ - 4а2а2
(ref)
+\
(inc)
+1
8 — 4а2а2
16а4
R(jnc)
B16)

76. Дальнейшее развитие теории
143
Подобным же образом находим два выражения для коэффициента
прохождения Т:
т = | в^ |2 = 4^
(trans)
<+1
(inc)
+
2Mr+ (o — a,)
p
(trans)
T = I B<-°> |2 =
5,1
n(trans)
R(jnc)
(8MV:/a') (a - os) [(a - asJ -f (M1 - a')/4M Y+]
(inc)
o(lrans)
, B17)
. B18)
Из закона сохранения A82) теперь вытекают два соотношения:
4G4
(ref) I2
1 I
8Mr+(o-os)
(trans)|2
(inc)|2
16o4
4MVJ
X
фактически эквивалентные тождеству A39), которому удовлетво-
удовлетворяют вронскианы, что несложно показать, если воспользоваться
тождествами Тьюкольского—Старобинского.
Хотя мы и ограничились случаем а2 > 0, легко убедиться,
что формулы B16) и B17) справедливы в общем случае без каких-
либо ограничений. Заметим также, что в согласии с результатом,
полученным в п. 75, ву
Т <0 при or < as, B21)
т. е., как и предсказывалось, имеет место суперрадиация.
а. Следствия условия унитарности. Ясно, что мы должны
прийти к тем же самым коэффициентам отражения и прохожде-
прохождения R и Т, если будем искать решения для Z(±a), удовлетворя-
удовлетворяющие граничным условиям
J С^ ехр [— ior*] + ехр [+ iorJ при г -+ г+ + О,
С<-*> ехр [+ ior] + ехр [— ior*] при г^г+~\- О,
D(-a>exp [+ iorj при г->оо
вместо граничных условий A79) и A80).
Вместо соотношений A83) теперь получим
[С(+р)]*
с(-а)
B24)

144
Глава 8. Электромагнитные волны в геометрии Керра
а коэффициенты отражения и прохождения будут равны
1 X + 2ао 1
D
к±2ао
т =
С(±о)
B25)
B26)
Имея решения для Z(±a), удовлетворяющие граничным усло-
условиям B19) и B20), можно теперь показать, как и в случае, рас-
рассмотренном выше, что соответствующие решения уравнений
Тьюкольского удовлетворяют следующим граничным условиям:
!\пс>ехр[—ior^] + /?^ef)exp [+ от*]/А при r-*r+ + 0>
/?+tirans) ехр [—ior%]/r3 при r-^оо,
B27)
pone) exp [_. iar^ _|_ ^ret) д ехр [+ ier*] при r->-r+ + 0,
' B28)
где
#$<= = _ [(Я + 2ao) F2+I/2///]C(+0), ^1!,пс) = - 4a2 (S2+I/2 C(-a),
Из предыдущих уравнений находим, что коэффициенты отраже-
отражения и прохождения теперь равны
Х2 __
16а4 | И |2
л.2
16а4 I Я I2
«I
B30)
B31)
Наконец, обратим внимание на то, что асимптотики решений
уравнений Тьюкольского R+1 и R_± можно было бы получить
по известному асимптотическому поведению ехр (±ior*) решений
Z(±a) одномерных волновых уравнений. Эти асимптотики, кото-
которые можно «вычитать» из первых строчек уравнений B09), B10),
B27) и B28), получаются также и из самих уравнений Тьюколь-
Тьюкольского, но путь от этих асимптотик к выражениям B16)—B18)
и B30)—B31) для коэффициентов отражения и прохождения не
является ни прямым, ни легким (см. п. 76, б).
б. Прямое вычисление потока излучения на бесконечности и
на горизонте событий. Понятия отражения и прохождения волн
через потенциальный барьер при наличии связанного с этими про-
процессами закона сохранения столь естественны, что не могут

76. Дальнейшее развитие теории 145
не иметь простой физической интерпретации. Это мы неявно пред-
предполагали, начиная с § 75. Покажем теперь, что это действи-
действительно так.
Для этого нужно вернуться к выражению для тензора энер-
энергии-импульса (в данном случае тензора энергии-импульса максвел-
ловского поля) и установить следующие факты. Во-первых, нужно
показать, что при г -> оо существует предел
lim r2Tu B32)
Г->-ОО
т. е. компонента Т\ тензора энергии-импульса на больших рас-
расстояниях убывает как 1/г2, что соответствует картине распростра-
распространения волны и, кроме того, что поток энергии на бесконечности
(в единицу времени и в единице телесного угла), вычисленный
для уходящих (т. е. отраженных) и для приходящих (т. е. па-
падающих) волн, равный по определению
^ = limr2n, B33)
приводит в точности к полученным ранее значениям коэффи-
коэффициента отражения R. Во-вторых, требуется показать, что на гори-
горизонте величина
T\t(t)^-i B34)
(где \ (/) — времениподобный вектор Киллинга фонового про-
пространства-времени, a dS/—элемент трехмерной поверхности
горизонта, ортогональный радиальному направлению внутрь),
вычисленная надлежащим образом, приводит к тому же значению
коэффициента прохождения Т, что и выведенное выше.
Выраженный через максвелловские скаляры тензор энергии-
импульса в формализме Ньюмена—Пенроуза имеет следующий
вид (ср. с уравнением C39) гл. 5):
= {фофоПсП! f </>2</>2*Ц- + Ц\ф\ Uuni) + ЩьЩ)\ —
+ Комплексно-сопряженные члены. B35)
Подставляя сюда для базисных векторов выражения из гл. 6
(уравнения A70) и A73)), получаем, что величина, которая нам
нужна для вычисления коэффициента отражения R, равна
lim (г2/2л) (- 74Мо + frfr*). B36)
Г->оо
Для скаляров ф0 и </>2 имеем решения (ср. с уравнениями G0))
ф0 - /?+1S+1, ф2 = [1/2 (р*J] R^S^ B37)
где угловые функции S+1 и S_x нормированы на единицу, а от-
относительная нормировка радиальных функций R+1 и R^x согла-

146 Глава 8. Электромагнитные волны в геометрии Керра
суется с уравнениями C3) и C4), следовательно, мы знаем все
величины, входящие в уравнение B36). Отсюда находим, что
поток энергии на бесконечности равен
i;_ / 2/o^^ / i/ o2 Гп(^)п("°I i /т/л«-4\ о2 г t->(+cf) t->(—cj)ti /ooo\
= lim \r /2n) {— /40+1 LK+i K+i J-j-(l/4r j o_i La-i a-i Jj. (zoo)
Г -> 00
Формулы B09) и B10) показывают, что уравнения Тьюкольского
допускают решения, для которых предел B38) существует. Дей-
Действительно, учитывая определения коэффициентов R(+\nc) и R(?*f)
в формулах B09) и B10), имеем
d2?(inc)
dtdQ /_ 2я 4
B39)
d2?<ref> \ 5^ 1
J ) ll
dtdQ l~2n
(ref, +o) D(ref, -a
Подставляя для коэффициентов 7?^пс' +a) и т. д. выражения B11),
находим из предыдущих уравнений после интегрирования по
углам коэффициент отражения
R = Л(+а>Л(-а>, B40)
что находится в согласии с выражением A81), выведенным при
исследовании одномерных волновых уравнений для функций Z(±a).
Для вычисления потока энергии B34) через горизонт событий
выражение для тензора энергии-импульса в базисе, которым мы
пользовались до сих пор (определенном формулами A70) и A71)
гл. 6), не годится, поскольку вектор 1 сингулярен на горизонте
(где А равно нулю). Чтобы найти базис, свободный от сингуляр-
ностей, мы, следуя Хартлю и Хокингу, подвергнем базис, опре-
определяемый формулой A70) гл. 6, вращению из класса III (п. 8, ж),
для которого А = 2 (г2 -f a2)/A. Это вращение не влияет на век-
векторы m и т, в то время как векторы 1 и п переходят в векторы
1 , д 1 г 1 А л а 1
-*- 2 (г2 + а2) [ 2 ' 2 (а2 + а2) ' ' 2 (а2 + a2) J '
B41)
_ г (г2 + Д2J (г2 + Д2) п (г2 + а2) 1
П~ L ^ ' Р2 ' ' Р2А J '
Вдобавок перейдем к координатам Керра—Шилда (п. 57, а),
произведя преобразование
dv = dt + [(г2 +а2)/А] dr, d$ = dcp + (a/Д) dr. B42)
Выбор этой системы координат удобен при исследовании потока
излучения, направленного внутрь, а выбор координат, определяе-

76. Дальнейшее разбитие теории 147
мый уравнениями B15) гл. 6, удобен для исследования излучения,
направленного наружу. Изотропные векторы 1(ШУ) и п^ИН}> но-
нового базиса равны
А 0 — 1 п<"">-Го - г2 + а2 0 ol
B43)
Заметим что этот базис не имеет особенностей на горизонте собы-
событий будущего, т. е. для наблюдателей, падающих внутрь.
Элемент трехмерной поверхности горизонта, нормальный к ра-
радиальному направлению внутрь, равен
dS/ - l(jHHJMr+ sin 6 d6 dф dv. B44)
Это выражение следует из вида метрики в координатах Керра—
Шилда (уравнение B19), гл. 6), а также из уравнения B72) гл. 6.
Поскольку якобиан преобразования равен единице, т. е.
д (ф, v)/d (ф, /) = 1, можно также написать-
dSy = l{jHHJMr+ sin 6 d6 dф dt. B45)
Вследствии стационарности и аксиальной симметрии простран-
пространство-время Керра имеет времениподобный вектор Киллинга
? (t) (— dldt = d/dv) и аксиальный вектор Киллинга ? (ф) (= д/ду =
= д/дф). Поэтому для любого поля, тензор энергии-импульса
которого хорошо определен, мы можем определить векторы
потока
Т1Г(О> 7Ч?(Ф), - B46)
связанные с законами сохранения энергии и момента количества
движения. При этом потоки энергии и момента количества дви-
движения через элемент двумерной поверхности, образованный пере-
пересечением горизонта и двух поверхностей постоянного значения
координаты у, разделенных расстоянием dv, соответственно равны
d? = Т& @ dS/f dLz = Til' (Ф) dSy. B47)
Подставляя для d2/ выражение из уравнения B45), получаем
для потока энергии и момента количества движения в черную
дыру через горизонт событий выражения
B49)
Из уравнения B43) теперь следует, что на горизонте (где А = 0)
\<нн) = i (t) + (a/2Mr+) | (ф). B50)

148 Глава 8. Электромагнитные волны в геометрии Керра
Из уравнений B48) и B49) получаем
\dtdQjr+^ 2Mr+ \dtdQ )r+~ + lJ ' { }
С другой стороны, для выбранных нами зависимостей возмущений
от t и ф имеем
д . д /осо\
-дг = 1а> w = tm' B52)
и из сравнения выражений для dE и dLz в уравнении B47) сле-
следует, что
dLz = (т/о) dE. B53)
Вследствие этого из уравнения B51) получаем
/ 1 J — ^ ( d2? \ = 2Mr Т- .цнщщнн)} B54)
Вспоминая теперь, что os = —ат/2Мг+, находим,
(J^L) = ™I^- Т пнн)щнну,ш B55)
\ dt dQ //•+ а — os lJ v '
Из уравнения B35) для Ttj имеем
Tijl(HH)iliHHU = A/2п) ф(онн)^""\ B56)
Максвелловский скаляр ф0 в базисе, в котором были получены
уравнения B37), связан со скаляром <j>@HH\ вычисленным в ба-
базисе, заданном уравнением B43), соотношением
ф«*н) = ^о!2(г" +а2). B57)
Поэтому из уравнения B55) получаем
(°~°s) '2^^°' B58)
Подставляя решение для </>0, находим
Из асимптотического вида R+1 на горизонте (формула B09))
следует, что
— tl 2 Г D(trans, +g) D(trans, -a)i
ч dtdQ Jr+- 2я 8Mr+(o-os) LK+^ K+i J<
Теперь ясно, что уравнение B60) вместе с выражением B39) для
(d?<inc)/d/ dQ)oo дает то же значение для коэффициента прохожде-
прохождения Т, что было получено выше (см. соотношения B17) и B19)).
Мы убедились теперь в том, что коэффициенты отражения и
прохождения, определенные в § 75, имеют именно тот физический
смысл, который мы им приписывали.

76. Дальнейшее разбитие теории 149
в. Дальнейшее развитие теории. Для полноты картины нужно
выяснить несколько вопросов, касающихся правильных гранич-
граничных условий на горизонте для максвелловского скаляра </>0.
Решение для R+1 в уравнении B09), подходящее для описания
входящих волн на горизонте, имеет следующую асимптотику:
R+1 -> А ехр [ +ior# ] при г -> г+ + 0. B61)
Это решение сингулярнэ, и поэтому возникает вопрос, почему оно
допустимо. Это решение действительно допустимо, потому что
сингулярность появляется только вследствие неудачного выбора
базиса (векторы которого не определены на горизонте), в котором
был вычислен максвелловскии скаляр </>0. Именно по этой причине
нам пришлось перейти к несингулярному базису Хартля—Хо-
кинга в предыдущем разделе (уравнение B45)). Как следует из
уравнения B57), в базисе Хартля—Хокинга максвелловскии
скаляр </>0 умножается на А/2 (г2 -\- а2) ( = А/4УИг+ на горизонте)
и этот множитель устраняет сингулярность из выражения B61).
Другой вопрос связан с представлением входящих волн на
горизонте функцией ехр (ior*). Следует иметь в виду, что перемен-
переменная г* неявно содержит зависимость от частоты а. Для нахожде-
нахождения явной зависимости от or удобно перейти к переменной г</\
определяемой уравнением (ср. с уравнением A00))
~ r2 + a2 dr • К^Ч
После интегрирования этого выражения получаем
r^ =r + [2Mr+/(r+-r_)][ln(r/r+- I)-in (г/г. - 1)] при г>г+.
B63)
Зависимость г[с) от г в отличие от зависимости г* от г всегда
однозначна (именно поэтому обычно ее и предпочитают исполь-
использовать):
г[с) ^-\-оо при г-^оо, г[с)->—оо при r->r+-f- 0. B64)
Из сравнения уравнений A11) и B63) следует, что, хотя г* ->
-> г[с) при г->оо, при приближении к горизонту
г, -* A + ат/2Мг+о) г</> = A - aja) г</> при {г-+г+-\- 0). B65)
В соответствии с этим выбранное нами представление для входя-
входящих волн на горизонте имеет следующий вид:
ехр [i (о - os) г<Я + Ш\ = ехр [i (kr^ + ot)], B66)
где
k = о — as. B67)
Таким образом, групповая скорость волн на горизонте равна
vgT = —do/dk - —1. B68)

150 Глава 8. Электромагнитные волны в геометрии Керра
Для фазовой же скорости получаем выражение
yph = —a/k = — (l — as/a)-\ B69)
Следовательно, наблюдатель в любой локальной системе отсчета
будет видеть волны, идущие к горизонту (со скоростью света!),
но это не всегда так для наблюдателя на бесконечности, который
регистрирует фазовую скорость. Для наблюдателя на бесконеч-
бесконечности волны, описываемые уравнением B66), будут представ-
представляться движущимися по направлению к черной дыре, только если
о > os, но если о лежит в интервале частот, супер радиации
этот наблюдатель будет видеть волны, исходящие из черной
дыры, что и свидетельствует о супер радиации. Во всяком случае,
единственное физическое требование, которое нужно накладывать
на входящие волны, —это отрицательность групповой скорости,
этому требованию удовлетворяет представление B66).
Итак, асимптотика B61) решений для /?+1, представляющих
входящие волны на горизонте, полностью удовлетворяет всем
физическим требованиям. Примечательно, что выбор перемен-
переменной г% и следующий за этим анализ, оказывается, обеспечили
все необходимые свойства.
77. Общие замечания
Решение уравнений Максвелла, проведенное в предыдущих
параграфах, дает первое впечатление об аналитическом богатстве
пространства-времени Керра. Здесь мы кратко повторим основные
моменты.
В определенном смысле наиболее замечательным фактом яв-
является возможность разделения переменных в уравнениях, за-
записанных в формализме Ньюмена—Пенроуза. Это сразу же рас-
раскрывает преимущество записи уравнений в такой системе отсчета,
которая на фундаментальном уровне учитывает и использует
алгебраическую структуру пространства-времени. Заслуживает
внимания также то обстоятельство, что при разделении перемен-
переменных появляются новые функции, отличные от всех известных ранее
трансцендентных функций классического анализа. В частности,
угловые функции параметрически зависят от частоты сг. Это
становится очевидным, если переписать уравнение для S+1 (9)
в развернутой форме:
-Д-р -4- ( sin 9 -^r-) + [к - 2аат - a2a2 sin2 9 + 2аа cos 9 -
sin и ao \ ciu /
- (m2 + 1 + 2m cos 9)/sin2 9] S+1 = 0. B70)
(Уравнение для S_x (9) получается просто изменением знака
членов с cos 9 в уравнении B30).) Только в случае равенства
нулю а (или а) функция S+1 @) сводится к классической транс-
трансцендентной функции — к функциям Гегенбауэра или, как их

77. Общие замечания 151
часто называют, спиновым гармоникам. Появление параметра аа
в угловых функциях означает, что нельзя обсуждать вопросы
устойчивости на основании только структуры радиальных
функций.
Удивляет не только возможность разделения переменных
в уравнениях. Появление пары функций (которые мы обозначили
индексами +1 и —1)> связанных между собой посредством то-
тождеств Тьюкольского—Старобинского, также окутано тайной.
Конкретно имеется в виду следующее: если обе угловые функции
нормированы на единицу, то S+1 F) = S_± (я — 0). Но почему
эта «дискретная симметрия», возможно, и «понятная», должна
присутствовать в тождествах Тьюкольского—Старобинского?
Тот же вопрос возникает и в отношении радиальных функций Д#+1
и /?_!, которые удовлетворяют комплексно-сопряженным урав-
уравнениям. Важным, а также и необходимым, каким оно появляется
в нашем исследовании, следствием тождеств Тьюкольского—
Старобинского является и то, что производные функций R+1
и /?_! и 5+1 и 5_х могут быть представлены в виде линейных ком-
комбинаций соответственно функций R+1 и R_± и S+1 и S_±. И наиболее
таинственным является тождество, связывающее постоянные Ста-
Старобинского для радиальных и угловых функций.
Много вопросов возникает и в теории преобразований, разви-
развитой в § 73. Является ли, например, значимым тот факт, что функ-
функции У<±а> связаны «дуальным» преобразованием, приводящим
к паре потенциалов, которые дают одни и те же коэффициенты
отражения и коэффициенты прохождения? В случае простран-
пространства-времени Шварцшильда или Рейсснера—Нордстрема суще-
существование дуальных преобразований было связано с наличием
физически различных классов возмущений (аксиальных и поляр-
полярных). Существует ли соответствующее физическое разделение
возмущений и для пространства-времени Керра?
Есть и другие аспекты, относящиеся уже к деталям. Например,
элементарная теория проникновения через барьер, знакомая
из квантовой механики, поворачивается здесь новой гранью:
как может комплексный потенциал описывать упругое рассеяние
и как действительные потенциалы с сингулярностями приводят
к суперрадиации.
Исследуя в следующей главе гравитационные возмущения, мы
увидим, что все описанные особенности метрики Керра и многие
другие возникнут в еще более пышном обрамлении.
Библиографические замечания
Расцепление уравнений и разделение переменных в уравнениях Ньюмена—
Пенроуза, описывающих максвелловские и вейловские скаляры, было впервые
обнаружено Тыокольским и опубликовано в статье
1. Teukolsky 5. Л. Phys. Rev. Lett., 29, 1114—1118, 1972.

152 Глава 8. Электромагнитные волны в геометрии Керра
Открытие Тьюкольского способствовало дальнейшему развитию теории керров-
ских черных дыр. Более подробное изложение содержится в работе
2. Teukolsky S. A. Astrophys. J., 185, 635—649, 1973.
Приложение к задаче об отражении, прохождении и усилении волн керровской
черной дырой рассматривалось в статьях
3. Старобинский А. А., Чурилов С. М. ЖЭТФ, 65, 3—8, 1973,
4. Press W. #., Teukolsky S. A. Astrophys. J., 185, 649—673, 1973.
В статьях [3, 4] содержатся тождества, которые мы назвали тождествами Тью-
Тьюкольского—Старобинского. Близкие вопросы рассматривались также в статье
5. Bekenstein J. D. Phys. Rev. D7, 949—953, 1973.
Изложение в настоящей главе почти исключительно основано на следующих
работах:
6. Chandrasekhar S. Proc. Roy. Soc. (London), A348, 39—55, 1976,
7. Chandrasekhar S. Proc. Roy. Soc. (London), A349, 1—8, 1976,
8. Chandrasekhar S. Proc. Roy. Soc. (London), A358, 421—437 (Appendix A, 434—
437), 1978.
См. также
9. Chandrasekhar S., Detweller S. Proc. Roy. Soc. (London), A352, 325—338 (Appen-
(Appendix A., 335—338), 1977.
Теория преобразований, изложенная в § 74, по существу впервые была развита
в работе
10. Chandrasekhar S., Detweiler S. Proc. Roy. Soc. (London), A345, 145—167,
1975.
В статье
11. Chandrasekhar S. In: General Relativity, An Eistein Centenary Survey (§§ 7.5,
7.81—7.84), ed. S. W. Hawking, W. Israel, Cambridge, England, 1979
содержится обзор полученных результатов (рассматриваемых с несколько иной
позиции).
§ 73—75. Изложение этих параграфов основано на работах [6, 7]. Альтер-
Альтернативный подход см. в статье
12. Detweiler S. Proc. Roy. Soc. (London), 349, 217—230, 1976.
§ 76, б, в. Содержание близко к изложению в работах Пресса и Тьюколь-
Тьюкольского [2, 4]. См. также статью
13. Hawking S., Hartle J. В. Commun. Math. Phys., 27, 283—290, 1972.
Другой подход к исследованию уравнений Максвелла в геометрии Керра содер-
содержится в работах
14. Cohen J. M.9 Kegeles L. S. Phys. Rev. D10, 1070—1084, 1974,
15. Chrzanowski P. L. Phys. Rev. Dll, 2042—2062, 1975,
16. Chrzanowski P. L. Phys. Rev. D13, 806—818, 1976.
Здесь можно объяснить, почему автор предпочел первоначальную версию фор-
формализма Ньюмена—Пенроуза в противовес более поздней и более симметричной
версии, предложенной в
17. Geroch R.y Held A., Penrose R. J. Math. Phys., 14, 874—881, 1973.
Причина в том, что если бы мы предпочли эту более позднюю версию, то при-
пришлось бы заменить базис, принятый нами в гл. 5 (уравнение A70)), на более сим-
симметричный:
B)V2B a2, Д,0, а),
п1' = BР2ДГ1/2(г2 + а2, Л, 0, -а),
т< = Bр2)~1/2 (ш sin 6, 0, 1, i cosec 6),
где р2 = г2 + a2 cos2 9. Этот базис можно также получить, подвергнув первона-
первоначальный базис вращению из класса III (гл. 1, уравнение C47)). Вследствие этого
ни один из векторов 1 или п не имел бы аффинной параметризации. Кроме того,
в этом новом базисе мы должны все время работать с выражением (г + a cos 6) '
вместо более элегантного алгебраически и более простого для формальных вы-
выкладок выражения (г ± ia cos 0). И наконец, в гл. 9 станет совершенно оче-
очевидно, что основные сложности проблемы лежат гораздо глубже и не могут быть
устранены так просто.

Глава 9
ГРАВИТАЦИОННЫЕ ВОЗМУЩЕНИЯ
КЕРРОВСКОЙ ЧЕРНОЙ ДЫРЫ
78. Введение
Эта глава посвящена теории гравитационных возмущений
керровской черной дыры. Объект исследования довольно сложный
и поэтому изложение, несмотря на значительный объем, едва ли
представляет собой нечто большее, чем просто набросок.
Начнем с краткой постановки задачи.
При описании пространства-времени Керра в формализме
Ньюмена—Пенроуза (гл. 6, § 56) в выбранном базисе изотропных
тетрад A, n, m, m) вейлевские скаляры ?0, ?], ?3 и ?4 и спиновые
коэффициенты х, сг, у, v и 8 равны нулю. Равенство нулю этих
величин отражает специальный алгебраический характер (тип D
по классификации Петрова) пространства-времени Керра, бес-
сдвиговость главных изотропных направлений 1 и п, а также
аффинную параметризацию изотропной геодезической 1. Спиновые
коэффициенты р, т, ^, я, а, р и 7, а также вейлевский скаляр W2
не равны нулю, их значения были вычислены в гл. 6 (уравнения
A75) и A80)).
Если керровская черная дыра возмущена каким-либо грави-
гравитационным воздействием, например падающими гравитационными
волнами, то величины, которые были равны нулю в стационарном
состоянии, вообще говоря, уже не равны нулю, но становятся
величинами первого порядка малости, а величины, которые были
отличны от нуля в стационарном состоянии, получат приращения
первого порядка малости. Следовательно, гравитационное воз-
возмущение описывается величинами
Ч'о, Vl9 W3, W,, х, а, К v, A)
1A), nA),mA),mA), B)
где индекс A) во втором наборе величин указывает на то, что это
приращения первого порядка малости к невозмущенным значе-
значениям соответствующих величин в стационарном состоянии. Для
величин из первого набора соответствующий индекс не нужен,
поскольку они в стационарном состоянии равны нулю. (Заметим,
что спиновый коэффициент е не включен в первый набор, поскольку
равенство нулю этого коэффициента в стационарном состоянии

154 Глава 9. Гравитационные возмущения черной дыры
не является следствием алгебраического характера простран-
пространства-времени.)
Задача состоит в том, чтобы определить два набора величин
A) и B). Мы увидим, что эта задача естественным образом де-
делится на две части: определение величин из первого набора и
определение величин из второго набора. Первой части посвя-
посвящены § 79—81, а второй части — § 82—95. При этом теория пер-
первой и второй задач составляет единое целое.
79. Редукция и расцепление уравнений
для вейлевских скаляров Wo, Wl9 W3 и Ч^
Как уже упоминалось в гл. 4 (п. 29, а), среди уравнений Нью-
Ньюмена—Пенроуза имеется система из шести уравнений, линейных
и однородных относительно величин %, Ч^, ?3, Ч^, х, tf, X и v,
равных нулю в фоновой геометрии. Это четыре из тождеств Бианки
(гл. 1, уравнения C21а), C21г), C21д) и C21з)) и два из тождеств
Риччи (гл. 1, уравнения C106) и (ЗЮк)):
(б* _ 4а + я) Yo — (D — 2е — 4р) ?х - Зх?2,
(Л - 4v + р) % - (б - 4т - 2C) Уг = За?2, C)
(D — р — р* — Зе + е*) а — (б — т + я* — а* — 30) х - %,
(D + 41 - р) ?4 - (б* + 4я + 2а) ^F3 = -ЗЯ?2,
(б + 4р - т) Т4 - (Л + 2? + 4^) ?3 - -3V?2, D)
(Л + (г + |х* + 3v — V*) Я — (б* + За + 6* + я - т*) v -
= -%,
Мы рассматривали эти уравнения в гл. 4 (§ 29) при исследовании
возмущений шварцшильдовой черной дыры.
Уравнения C) и D) уже линеаризованы, поскольку величины
^Fo, Y1( х и а в уравнениях C) и величины ?4, ?3, X и v в уравне-
уравнениях D) уже появляются величинами первого порядка малости,
поэтому можно заменить все другие величины (включая операторы
производных по направлениям) их невозмущенными значениями.
Эти уравнения обладают еще одним важным свойством: они пред-
представляют собой полностью расцепленные две системы из трех
уравнений относительно величин %, Ч^, х и а, с одной стороны,
и величин Чг4, XF3, X и v, с другой стороны. Отсюда следует, что реше-
решения для каждого из двух наборов величин являются независи-
независимыми.
Будем предполагать, как и ранее, что возмущения имеют сле-
следующую зависимость от t и ср:
exp [iat + Шф}, E)
где а — постоянная (в большинстве случаев действительная и
положительная), am — целое число (положительное, отрица-

79. Редукция и расцепление уравнений 155
тельное или нуль). Действие базисных векторов 1, n, m и m (гл. 6,
уравнения A70)—A73)), рассматриваемых как касательные век-
векторы, на функции с вышеуказанной зависимостью от / и <р описы-
описывается дифференциальными операторами, определенными в § 68
гл. 8. В частности, мы будем опускать множитель E) во всех
величинах, описывающих возмущения, так что соответствующие
символы будут описывать амплитуды.
Как мы уже убедились, различные спиновые коэффициенты
(исключая х, а, X и v), a также вейлевский скаляр ?2 в уравне-
уравнениях C) и D) можно заменить значениями A75) и A80) из гл. 6,
а дифференциальные операторы — выражениями B)—E) из гл. 8.
Результирующие уравнения принимают простой и симметрич-
симметричный вид, если записать их через новые функции
ф0 = %, ог = ч^р
й = х//2(р*)8, s-ap/(P*J, F)
/ = fcp*/2, n = vp2//2i
После некоторых преобразований уравнения C) и D) принимают
следующий вид:
{2г — Зш sin е/р*) Фо — (<25О + 3/р*) Фг = — 6Mk, G)
А (Ф* - 3/р*) Фо + (St, + Зш sin е/р*) Ф1 = -f 6Afs, (8)
(^0 + 3/р*) s - {2tx + Зш sin е/р*) й = рФ0/(р*J; (9)
(SD0 — 3/р*) Ф4 — B_г + Ыа sin е/р*) Ф3 = +6М/, A0)
B\ — Зш sin е/р*) Ф4 + А (^^ + 3/р*) Ф3 = + 6Мд, A1)
A (&tx + 3/р*) / + {?_, + Зш sin е/р*) я = рФ4/(р*J. A2)
Расцепление уравнений в двух системах G)—(9) и A0)—A2)
можно продолжить аналогично тому, как это было сделано в гл. 8
(уравнения A3)—A6)). Действительно, можно исключить Фх из
уравнений G) и (8), подействовав на уравнение G) оператором
(??±г + Зш sin е/р*), а на уравнение (8) — оператором CH +
+ 3/р*), а затем сложив получившиеся уравнения. Правая часть
результирующего выражения с точностью до множителя 6М
совпадает с левой частью уравнения (9). Получаем окончательно
уравнение для Фо
1Х + Ыа sin е/р*) C?2 - Ыа sin 6/р*) +
+ (S>Q + 3/р*) А (Щ - 3/р*)] Фо = 6МрФи/(р*J- A3)

156 Глава 9. Гравитационные возмущения черной дыры
Подобным же образом из уравнений A0)—A2) получается урав-
уравнение для Ф4
+ Зш sin 9/p*) B\ - Зш sin 9/p*) -f
+ A (®tx + 3/p*) (S>0 - 3/p*)] Ф4 = 6Л4рФ4/(р*J. A4)
Распишем подробно две группы членов в левой части уравне-
уравнения A3):
A {2Dl + 3/р*) B>\ - 3/р*) =
= L2b&% + F/р*) [— iK + {г - М)] - 6Д/(р*J, A5)
B1Х + Зш sin 9/p*) (Se2 - Зш sin 9/p*) -
= SetxS2 + Fш sin 9/p*) (Q + ctg 9) + 6а2 sin2 9/(p*)a. A6)
Если подставить эти выражения в уравнение A3) и воспользо-
воспользоваться элементарными тождествами из гл. 8 (уравнение A0)),
то получим уравнение
[А&.Щ + ^1^2 - бит (г + to cos 9)J Фо = 0. A7)
Аналогично уравнение A4) приводится к виду
[ДФ+^о + 2^2* + Ыа {г -1- шcos 9)] Ф4 = 0. A8)
Уравнения A7) и A8), очевидно, допускают разделение пере-
переменных. Действительно, подстановки
Фо - R+* (r) S+2 (в), Ф4 = R_« (r) S_2 (в), A9)
где R±2(r) и S+2(9)—функции только указанных переменных,
приводят к следующим двум парам уравнений:
(ДФ^ - Ыаг) R+2 = XR+2, B0)
B±г22 + 6шт cos 9) S+2 - - KS+2, B1)
(Д^+^о + 6^) ^-2 = ^-2» B2)
(^.^J - 6aa cos 9) S_2 - - ^5.2. B3)
Заметим (снова!), что при разделении переменных в уравнениях
A7) и A8) мы использовали одну и ту же постоянную разделения.
Причины этого мы уже обсуждали.
Уравнения, эквивалентные уравнениям B0)—B3), были впер-
впервые выведены Тьюкольским, и мы будем называть их уравнениями
Тьюкольского.
Заметим, что уравнение B0) может быть переписано в виде
(A^.^J— Ыаг) Д2Я+2 - X№R+2. B4)
Следовательно, функции А2/?+2 и R_2 (подобно функциям Д??+1
и R_x в гл. 8) удовлетворяют комплексно-сопряженным уравне-
уравнениям. Заметим также, что уравнения B2) и B4) совпадают с урав-
уравнениями соответственно (96) и (97) гл. 8 при \s\ = 2, т. е. эти
уравнения описывают гравитоны со спином 2.

80. Выбор калибровка 157
80. Выбор калибровки и решения
для спиновых коэффициентов к, а, X и v
В общем случае линеаризованные уравнения, описывающие воз-
возмущения, должны быть совместны с произволом в выборе тетрад-
тетрадной системы отсчета и в выборе координат. Более точно, мы имеем
шесть степеней свободы, связанных с локальными бесконечно
малыми вращениями локальной тетрады, и четыре степени сво-
свободы, связанные с бесконечно малыми координатными преобра-
преобразованиями; всего десять калибровочных степеней свободы. Мы
можем использовать этот произвол так, как нам будет удобно.
Как объяснялось в гл. 4 (§ 29, б), в линейной теории возму-
возмущений вейлевские скаляры Wo и ?4 являются калибровочно
инвариантными величинами в отличие от скаляров Л?1 и W3. Сле-
Следовательно, можно выбрать такую калибровку (т. е. подвергнуть
тетрадный изотропный базис бесконечно малому вращению),
в которой вейлевские скаляры Ч^ и Ws становятся равными нулю,
не затрагивая при этом скаляры lF0 и 4V
Если выбрать калибровку, в которой }?1 и *?3 равны нулю, то
соответствующие решения для коэффициентов ?, s, / и п сразу же
получаются из уравнений G), (8), A0) и A1). Возвращаясь к пер-
первоначальным переменным (спиновым коэффициентам) и, а, X и v,
имеем
х = -(/2/6М) (р*J R+2 B% - Зш sin e/p*) S+2, B5)
а = +A/6УИр) (р*J S+2A (Щ — 3/р*) #+2, B6)
Х=+ B/6Мр*M_2 B>0 - 3/р*) Я_2, B7)
v = (/2/6Мр2) R-2 (&2 - Зшэш е/р*) 5_2. B8)
Следует отметить, что мы еще не зафиксировали относительную
нормировку функций Фо (= R+2S+2) и Ф4 (= /?_2S_2), и поэтому
есть соответствующая неоднозначность в решениях для к и а
относительно решений для К и v.
а. Призрачная калибровка. Помимо калибровки, в которой
вейлевские скаляры }?1 и *?3 становятся равными нулю, можно
выбрать и другие калибровки. В частности, можно выбрать ка-
калибровку, в которой восстанавливается недостающая явная сим-
симметрия уравнений G)—(9) и A0)—A2). Имеется в виду следующее.
При рассмотрении, например, уравнений G)—(9) мы видели,
что из первой пары мэжно исключить скаляр Фх, а последнее
уравнение оказывается «правильным» соотношением между k
и s, что позволило получить отдельное уравнение для ска-
скаляра Фо. Точно так же первая пара уравнений позволяет
исключить скаляр Фо, если использовать коммутативность опера-
операторов (i?2 — 3i sin 9/р*) и Д(^9 —3/р*), но теперь у нас нет
«правильного» соотношения между k и s для получения отдельного

158 Глава 9. Гравитационные возмущения черной дыры
уравнения для скаляра Фх. Используя калибровочный произвол,
можно подвергнуть локальную возмущенную тетраду бесконечно
малому вращению и исправить ситуацию, добавив (ad hoc?) не-
необходимое соотношение. Действительно, добавив уравнение
А (Ф$ - 3/р*) k + {22 ~ Sia sin e/p*) s = [2р/(р*J] Фь B9)
мы можем получить отдельное уравнение для скаляра Фх
+ {&2 - Зш sin 0/р*) {St. х + 3m sin 8/p')] 0>i =
= [12Мр/(р'J] Ф,. C0)
Упрощая это уравнение, имеем
[Д2#2>о + ^2^-i - бит (г + ia cos 6)] Ф, = 0. C1)
Ясно, что последнее уравнение допускает разделение переменных;
в результате подстановки
Фх - Я+1 (г) S+1 (в) C2)
(введение нижнего индекса +1 Для этих функций станет понятно
из дальнейшего) придем к следующей паре уравнений:
(ЛйJ+^о - Шг) R+l = (^A) - 2) R+ ь C3)
(^2^-i + 6aacos9) S+i = - (А,A) - 2) S+i- C4)
С помощью легко проверяемых тождеств
A2>j2>o = A^i^i" + 4/ra - 2, SV^-i = ^o^i - 4штcos 9 + 2
C5)
перепишем уравнения C4) и C3) в виде
(A2>i2tf - 2tor) /?+i = ^A)/?+i, C6)
(S?S^1 + 2aacoseM+1 = -^A)S+1. C7)
Но точно такие же уравнения были выведены в гл. 8 (§ 69) для
максвелловского скаляра ф0 (гл. 8, уравнения B4) и,B5)).
Аналогичным образом, дополняя уравнения A0)—A2) соот-
соотношением
B>о - 3/р*) п - B?\ - 3tesln e/p*) / - [2р/(р*)°1 Фз, C8)
можно получить отдельное уравнение для вейлевского скаляра Ф3,
которое допускает разделение переменных и позволяет, следова-
следовательно, представить скаляр Ф3 в виде произведения R^ (r) Sel (9),
где R_± (r) и S_! (9) удовлетворяют паре уравнений B6) и B7)
из гл. 8 для максвелловского скаляра Ф2.
Таким образом, в калибровке, которая восстанавливает сим-
симметрию уравнений G)—A2), вейлевские скаляры Wx и Ws удовле-

81. Тождества Тьюкольского—Старобинскоёо 159
творяют тем же уравнениям, что и максвелловские скаляры </>0
и ф2у описывающие распространение электромагнитных волн
в геометрии Керра. В гл. 11 (§ 111) мы покажем, что в калибровке,
которая окажется наиболее подходящей для исследования воз-
возмущений заряженной черной дыры Керра—Ньюмена, снова по-
появятся уравнения B9) и C8), которые в настоящем параграфе
были постулированы из соображений симметрии.
81. Тождества Тьюкольского—Старобинского
Функции А2/?+2 и R_2 и функции S+2 и S_2 удовлетворяют
тождествам, аналогичным полученным в гл. 8 (§ 70). Доказатель-
Доказательство этих новых тождеств (в отличие от установленных в § 70)
требует гораздо более сложных алгебраических преобразований.
Но ввиду их решающей роли для построения полной теории мы,
помимо формулировок, укажем основные этапы доказательств.
ТЕОРЕМА 1. Функция
лишь постоянным множителем отличается от функции Л2/?+2,
а функция
лишь постоянным множителем отличается от функции /?_2.
Доказательство. В силу уравнений B2) и B4), которым удо-
удовлетворяют функции R_2 и Л2/?+2, теорема эквивалентна установ-
установлению справедливости тождества
2^o®o2)o2)o, C9)
а также комплексно-сопряженного тождества.
Доказательство тождества C9) состоит в последовательной
редукции его левой части; главные моменты этого процесса сле-
следующие:
6 (г - ЛГ) 2>о - 2iK@o - lOiar + 4] g)^®^ -
j - Ыог) &ъЗ)ъ?)ъ?)ъ. D0)

160 Глава 9. Гравитационные возмущения черной дыры
СЛЕДСТВИЕ. Выбором относительной нормировки функций
R+2 и R_2 можно добиться выполнения соотношений
, D1)
2, D2)
где *& —некоторая комплексная постоянная.
Указанная относительная нормировка действительно может
быть найдена, поскольку функции А2/?+2 и ?L2 удовлетворяют
комплексно-сопряженным уравнениям.
ТЕОРЕМА 2. Если относительная нормировка функций А2/?+2
и R_2 выбрана так, что удовлетворяются уравнения D1) и D2),
то квадрат модуля постоянной %? равен
= А,2 (X + 2J — 8о*Х [ее2 Efc + 6) — 12а2] +
+ 144а4сс4 + 144G2Л12, D3)
D4)
Доказательство. Очевидным следствием уравнений D1) и D2)
является соотношение
tfSDtSDtSDt&t A2^)o^o3)o^oR-2 = \V\2 #-2- D5)
Таким образом, по модулю операторного соотношения
имеем
ДЭД^о'^о^о А2^)о2)о^о^о = | ^ Г, D6)
и значение D3) для |^|2 должно следовать из прямого вычисления
левой части, хотя это и не простая задача.
Установим прежде всего, что по модулю операторного равенства
)-\3)о + Gior = h справедливы следующие тождества:
ъ = 2(iK +г- М) ®0+(К — 6iar)9 D7)
ooo [/С (t/C + г - Af) + (К + 2 + 2игг) А] йH +
+ 2iK (X - 6iar) - 6taA, D8)
A*?>0?Hg>02H = {— 8iK [К2 + (г - MJJ +
+ [4//C (Я + 2) + 8tar (г — M) ] А — 8/aA2| S>0 +
+ [(А, + 2 + 2tar) (к — 6tcrr) — 12/a (IK — r + M)} A +
+ 4i/C (iK — r + M) (I — 6iar) = A03H + Bo. D9)
Затем четыре раза последовательно подействуем оператором 3I. \
на тождество D9) и воспользуемся рекуррентным соотношением
StiLx (Ап?H + Вп) = (Ап, г + Вп) ®ъ +
+ A/А) [(к - Ыог) Ап - 2 (iK + г - М) ВЛ + АВп> г) =
= Лп+12>о + Я„+1. E0)

81. Тождества Тьюкольского—Старобинского 161
Получаем
Аг = [Х(Х +2) + 4шг (А, + 3) + 12aV2 — 12ш (i? + г — М) ] А +
+ 4i/C (t/C + r — М) (А, + 6iar), E1)
Бх = 2i/C (X2 + 36aV2) — 12iofcA;
Л2 = —8ia (X + 6iar) A — 24ta [/B + (r — MJ] +
+ 2 (iK + r — M) (X + 6t<rr) (A, + 2 + 2tar), E2)
B2 = (A,2 + 36ff2r2) (A, + 2 + 2iar) + I2ia (X — 6iar) (iK — r + M);
A3 = 48a2A + (X + 6iar) [(A, + 2J + 4a2r2] —
— 12ia (r — M)(X + 2 — 2tarr) — 4a/( GA, + 6 + 18/<v), E3)
Bs = —6ia (X + 6iar) (A, + 2 + 2iar) + 72a2 (iK — r + M);
B4 = (i/A) {%* (К + 2J — 8о2Х la2 EA, + 6) — 12а2] +
+ 144а2 (М2 + а2а4)}. E4)
Последняя строчка и дает нам значение постоянной Старобинского
Важно отметить, что мы определили только значение квадрата
модуля l^l2, а аргумент этого числа пока остается неизвестным.
ТЕОРЕМА 3. Функция
оС> ^XoZs Q°& \°& 2*^+2
лишь постоянным множителем отличается от функции S^2»
а функция
лишь постоянным множителем отличается от функции 5+2.
Доказательство. Очевидно, теорема эквивалентна доказатель-
доказательству тождества
2-Х2ъ<?\2ъ B>-i2f2 + 6aacos 0) =
= {2-\2% - 6aa cos 0) S-XSqS\S2 E5)
и сопряженного ему, получаемого заменой 0 на я — 0.
Последовательно преобразуя левую часть тождества E5),
имеем
COS0) =
Г Ср Q? СО Q?3? \ О/7ГР rr\Q A OP Q?
— |_<Х — \°& 0~? 1 eZT о ~Т~ ^au LUo DoZ/ — \3s о —
6 Чандрасекар С , т. 2

162 Глава 9. Гравитационные возмущения черной дыры
- 12ао sin 0 +
= [?-Х2ь2\ - 2aacos02'_, + 2^_, - 4a0sin0] 2ъ2\2* =
= {SB-\9E\ - 6aacos0) 2-&ъ2\&* E6)
При этом были использованы следующие тождества:
U + 2,
E7)
= 2?\3?-! - 4aa cos 9 - 2,
4aasin 9.
Последний шаг преобразований E6) устанавливает справедливость
тождества E5) и, следовательно, справедливость теоремы.
Альтернативная формулировка теоремы 3 состоит в утвержде-
утверждении справедливости соотношений вида
b E8)
где Dx и D2 — две действительные постоянные.
ТЕОРЕМА 4. Если функции 5+2 (9) и S_2 (9) нормированы
на единицу, то в соотношениях E8) D± = D2 и
^_i^o^i^2S+2 = D5_2, 2U&t2\2tS-2 = DS+2. E9)
Доказательство. Доказательство следует из теоремы 4 гл. 8,
если четыре раза последовательно применить лемму 4 (§ 68) к нор-
нормировочному интегралу
о
Л
= \ B?-lg?o
о
\
о
я
\
О
я
= D, D2 \ 5+2 sin 0 de = Dx D2, F0)
о
откуда и следует равенство Dx и D2.
ТЕОРЕМА 5. Постоянная D в теореме 3 равна
D* = X2 (К + 2J — 8о21 [а2 Eк + 6) — 12а3] +
+ 144a4a4 = |^|2 — Шо2М2. F1)

81. Тождества Тьюкольского—Старобинского 163
Доказательство. Величина D2 должна получаться в результате
прямого вычисления тождества
&-i&o&i&2 = D\ F2)
справедливого по модулю операторного равенства
5Li52 + 6aacos 9 = — X
и следующего,из уравнений E8) (это тождество фактически было
использовано в предпоследней строчке преобразований F0)).
Прямое вычисление тождества F2) является непростой задачей.
Мы здесь представим только основные этапы этого вычисления.
Прежде всего с помощью рекуррентного соотношения
&п2% = — (X + баи cos 9) + Ш + (п + 1) ctg в] 5>2 X
X mod 5*115*2 + бао cos 9 = —X F3)
находим
SPxSe2 = — (X + баа cos 9) + 2 (Q + ctg 9) 5?2, F4)
2f02?12>2 = [бае sin 9 — 2Q (X + бас cos 9) ] +
+ [_ (А, + 2) — 2аа cos 9 + 4Q (Q + ctg 9) ] 5\>, F5)
2f^1S>0S?12>2 = (X + бао cos 9) (X + 2 — 4Q2 +
+ 4Q ctg 9 — 2аа cos 9) + 12аа (Q sin 9 — cos 9) +
+ [8aa cosec 9 — 4Q (X + 2 — 2Q2 + 2 ctg2 9) ] S2. F6)
Затем подействуем на тождество F6) последовательно операторами
<2?2, 5*i", 2^0 и 5*1-1. Воспользовавшись рекуррентным соотноше-
соотношением
^ (Л + В?2) = [(л — 2) Л ctg 9 — 2<?Л + ^.е —
— В (X + баа cos 9) ] + [(п + 1) В ctg 9 + Я,е + 4 ] 52, F7)
находим последовательно
3?Х?-\5Бъ5?\?<1 = 2Q (Х2 — 36а2а2 cos2 9) - 12ааЯ sin 9 +
+ {4Q [Заа sin 9 — (Q + ctg 9) (Я, — баа cos 9) ] +
+ Я (X + 2) — 4^ш cos 9 — 12aV cos2 9} &2, F8)
5>?5>j5>_i5>o5>i2>2 = 4аа(Х2- 36а2аcos29) cos 9+
+ (X + баа cos 9) {l2aaQ sin 9 — [X (X + 2) — 4tam cos 9 —
— 12flV cos2 9]} + {4 (X - 6ao cos 9) (Q - 4aoQ cos 9 - 2aa cosec 9)+

164 Глава 9. Гравитационные возмущения черной дыры
+ 2Q (X2 - 36aV cos2 9) - 24aoQ2 sin 9 +
+ 2 [X (X + 2) - 4Xao cos 9 - 12aV cos2 9] ctg 9} 22ч F9)
= 6шт (X2 -\-2X- 8aoXcos9 + I2a2o2cos2 9 - \2aoQ sin 9) sin 9 +
- (X - 6aa cos 9) (X2 + 2X- 4aa cos 9 - 4a2a2 cos2 9) -
— 2 (X + 6aa cos 9) (X — 4шт cos 9) -f
+ 4шт<2 F + 7X - 18шт cos 9) sin 9} g2 G0)
и, наконец,
= X2(X + 2J — 8g2X [a2 EX + 6) — 12a2] + 144aV = D2. G1)
а. Сводка полезных формул. Будем писать
^ Р+2, R-2 = Я_2, G2)
если радиальные функции R+2 и /?-2 имеют относительную нор-
нормировку, требуемую уравнениями D1) и D2).
Ясно, что с помощью установленных тождеств можно выразить
(ср. с гл. 8, § 70) производные функций Тьюкольского (как ра-
радиальных, так и угловых) через сами эти функции.
Поскольку уравнение D9) справедливо по модулю уравнения,
которому удовлетворяет функция Р_2, оно представляет собой
редуцированную форму уравнения
A30o^o^oiZVP-2 = A^P+2, G3)
в котором все производные высших порядков были исключены
с помощью уравнения второго порядка, которому удовлетворяет
функция Р_2. Таким образом, уравнение D9) и комплексно-со-
комплексно-сопряженное к нему позволяют выразить производные функций
Р+2 и Р_2 в виДе линейных комбинаций функций Р+2 и Р_2. Находим
*- = А
—??-) - iA2] P+2, G4)
где
<е = V± + /У2, Гх - X (X + 2) — 12a2a2, Г2 - \2аМ\ G5)
Лх = + ДГХ — 4ХК2 + 24a/C (a2 — Mr),
А2 - — АГ2 — 4А, [К (г — М) + гаА] + 24огК2 = —V2Blir,
G6)

81. Тождества Тьюкольского—Старобинского 165
В± = —8/С [К2 + (г - Mf] + 4А [К (А, + 2) +
+ 2аг (г — ЛГ) ] — 8аД2 - — 8К3 + 8К (а2 — М2) —
— 8аД (а2 — Mr) + 4XK&.
Аналогичным образом из уравнений E8) и F6) находим
Pi^S+a = О5.2 — К + а2) S+2, G7)
где
рх = 8Q3 — 8Q ctg2 9 — 4 (X + 2) Q -f 8аа cosec 9,
ах = I (X + 2) — 12а2а2 + 24aaQ cosec 9 — 4A,Q2,
а2 = —24aoQ2 cos 9 + 4X (Q ctg 9 + аа cos 9). G8)
Объединяя уравнение G7) с «присоединенным» к нему уравнением,
получаем следующую пару уравнений:
Pi d(S+2d|S-2) = -(«, + 2рх ctg 0) (S+2 + 5_2) -
- («х + PiQ + О) (S+2 - S_2),
_ D) E+2 + 5_2) _
-(a2 + 2plCtg9)E+2-5_2).
Уравнения G4) и G9) играют существенную роль в последующем
развитии теории.
б. «.Скобочные-» обозначения. Для сокращенной записи громозд-
громоздких уравнений, которые появляются в развиваемой нами теории,
удобно ввести специальные обозначения:
[Р]* = Р+2 ± P.2; [S]* = S+2 ± S_2> (80)
= 2>tP+2 ± 2>oP-2, [&&P]* = 3>t3>lP+2 ± ^o^oP-2;
(81)
= s2s+2 d= ^2+5_2; [S'S'S]* = ^,^2s+2 ± ^^2+5_2.
(82)
Следующие уравнения являются элементарными следствиями
'введенных определений:
(83)
(f/C/A) [^5P]T, (84)
T - 2 [Sf ctg 0, (85)
- [2'S]±ctg 0. (86)

166 Глава 9. Гравитационные возмущения черной дыры
В этих обозначениях уравнение D7) и комплексно-сопряжен-
комплексно-сопряженное к нему принимают вид
= - 2iK [SDPf + 2 (г - ЛГ) [3)Р\- +
+ b[P]± + 6ior[Pf9 (87)
а уравнение F4) и присоединенное к нему записываются следу-
следующим образом:
[&ZS]* = 2Q [SSf + 2 [ZS]* ctgQ-k [Sf - 6ao [Sf cos9. (88)
Фактически эти уравнения являются уравнениями Тьюкольского
для нормированных функций.
82. Возмущения метрики; постановка задачи
При исследовании возмущений пространства-времени основной
интерес представляют изменения, вызванные возмущениями ме-
метрических коэффициентов. В формализме Ньюмена—Пенроуза
эти изменения прямо связаны с изменениями изотропных векторов
базиса. Обозначим эти приращения 1A), nA), mA) и тA). Кроме
того, важны также изменения спиновых коэффициентов и вейлев-
вейлевских скаляров. Таким образом, мы должны рассмотреть величины,
перечисленные в начале настоящей главы (величины B)). Но
прежде чем сформулировать точно, чего же мы хотим, перечислим,
что мы уже знаем и что остается еще неизвестным.
В § 79 были получены точные решения для величин, пере-
перечисленных в списке A). В частности, в калибровке, в которой
^ = ?3 = 0, (89)
решения для спиновых коэффициентов х, а, у и v даются фор-
формулами B5)—B8). Решения для вейлевских скаляров ?0 и ?4
(которые не зависят вообще от выбора калибровки) записаны
через функции Тьюкольского R±2 и S±2:
% = Д+25+2, ^4 = R-*SJ(p*)*. (90)
Напомним, что если угловые функции 5+2 и 5_2 нормированы на
единицу, а радиальные функции А2/?+2 и R_2 выбраны равными
функциям Р+2 и Р_2 (см. уравнения D1) и D2)), то неизвестным
остается коэффициент пропорциональности либо для скаляра WOi
либо для скаляра Чг4. Можно напомнить, что в аналогичной
ситуации при решении уравнений Максвелла в гл. 8 (§71) подоб-
подобная неопределенность допускала простое разрешение, поскольку
уравнения для максвелловских скаляров ф0 и </>2 в отличие от
уравнений G)—A2) не были полностью расцеплены. Наконец,
помимо относительной нормировки решений для ?0 и ?4 неиз-
неизвестным остается еще аргумент постоянной Старобинского.

82. Возмущения метрики; постановка задачи 16?
а. Матричное представление возмущений базисных векторов.
Удобно ввести специальный индекс для нумерации базисных
векторов A, n, m, т). Полагая
11 = 1, р = п, I3 - т, I4 ="й, (91)
мы можем записать возмущение ltA) базисного вектора I1 в виде
линейной комбинации невозмущенных базисных векторов V:
li(l) = A)V. (92)
Тогда возмущения базисных векторов полностью описываются
матрицей А.
Поскольку векторы I1 и I2 действительны, а векторы I3 и I4
комплексны, то матричные элементы Л|, А\, А\ и А\ действительны,
а остальные матричные элементы комплексны; кроме того, ма-
матричные элементы, которые отличаются перестановкой индек-
индексов 3 и 4, являются комплексно-сопряженными. Вследствие этого
определение матрицы А требует 16 действительных функций.
В последующем анализе окажется удобным использовать
вместо недиагональных элементов А\ (I Ф /) следующие величины,
пропорциональные этим матричным элементам:
4?; F\ = (l/p)A\;
= (л/2Р2р) 4; Fl
Ft = (A/2p2p) At; { '
Мы увидим также, что важную роль играют следующие комби-
комбинации:
F = Fl±F\; Bt = (F3i + Fl) + (Fi + Ft);
G = Fl + F\\ J32 = (F\ + Fl) - (Ft + Ft)i
H = F\-Fl\ C,=(Fi + F§)-(Fi + F42); (94)
J = F\~Ft; C2 = (Fl-Fl)-(Fl-Fl);
U = A\ + A\\ V = A\ + A\.
Оказывается,
Fl, F\, U, V, F, G, Si действительны,
B.2, Ci, Co чисто мнимые,
F\ и Fl F\ и F? (i = l, 2), F\ и F\, (95)
H ц J комплексно-сопряженные.

168 Глава 9. Гравитационные возмущения черной дыры
б. Возмущения метрических коэффициентов. Как мы уже
утверждали, центральной задачей в теории возмущений геометрии
пространства-времени является определение нормальных мод
возмущений метрических коэффициентов. Эти метрические воз-
возмущения связаны с возмущениями изотропных базисных векторов
соотношениями (ср. с уравнениями B46) гл. 1)
^v (I) = /V A) + /|4 AV _ mn~v A) _ -». (l)mv +
+ Г A)^ + №A) - mv A) m^ - mWA). (96)
Вычисляя различные компоненты g^v{l) в соответствии с выше-
вышеприведенной формулой и используя уравнение (92) настоящей
главы и уравнение A70) гл. 6, находим
a2
) + «2 № + f з) sm2 e
+ (/2/Д) to (r2 + a2) (Cj + B2) sin 9,
8Г 0) = - (А/р2) (Л1, + Л22) + (Д/р2) (Fl + F?),
= (а2/Р2Д) (А\ + Л2.) - A/р2) (Л? + At) cosec2 0 +
+ («2/р2Д) (Fl + F2) + (F| + /1) cosec2 0 +
+ (/2/Д) to (Ci + Bi) cosec 0,
- <" = _ (r2 + a2) (f« - F2)/p2 + ia sin 0 (Я - J - C2)//2,
<e A) (| - Fj) sin 0 + (r* + a2) (F + G - В,)Д/>/2,
= to
+ (//A /2) [(r2 + a2) + a2 sin2 0] (d + B2) cosec 0,
/ф О) = _ (a/p2) (/?' _ tf) + (,-//2) (Я - J - C2) cosec 0,
ge* о = j (Fl - Ft) cosec 0 + (a/A /2) (F + G - B,). (97)
Итак, возмущения метрических коэффициентов зависят только
от следующих 10 комбинаций матричных элементов матрицы А:
l±F2u
A\~\-Al Al-\-At, Fl±F
H — J — C2, F + G — Blt F — G +J +H. (98)

83. Линеаризация тождеств Бианки 169
в. Сводка подлежащих определению величин, имеющихся для
этого уравнений и допустимого калибровочного произвола. Вели-
Величины, перечисленные в списках A) и B), требуют для своего опре-
определения десять действительных функций для описания пяти ком-
комплексных вейлевских скаляров, 24 действительных функций для
описания 12 комплексных спиновых коэффициентов и 16 действи-
действительных функций для описания матрицы А: всего 50 действитель-
действительных функций. Используя свободу в выборе калибровки, мы
можем наложить 10 калибровочных условий. Из этих десяти сте-
степеней свободы шесть соответствуют выбору локальной тетрадной
системы отсчета, а четыре являются следствием общей ковариант-
ковариантности теории.
Как было подробно показано в гл. 1 (§8), формализм Нью-
Ньюмена—Пенроуза дает три системы уравнений: тождества Бианки,
коммутационные соотношения и тождества Риччи. Считая, что
каждое комплексное уравнение эквивалентно двум действитель-
действительным уравнениям, имеем 16 уравнений, представляющих тождества
Бианки (для вакуумных полей, которые мы здесь рассматри-
рассматриваем), 24 уравнения, представляющих коммутационные соотно-
соотношения, и 36 уравнений, представляющих тождества Риччи (или
только 20, если мы учтем 16 исключающих соотношений — урав-
уравнения C11) гл. 1). Следовательно, у нас есть 76 уравнений для
определения 50 действительных функций, на которые мы можем
вдобавок наложить 10 калибровочных условий.
Мы уже использовали четыре из шести тетрадных степеней
свободы, предположив, что
% = ?3 = 0 (99)
и получив отсюда решения B5)—B8) для спиновых коэффициентов
х, сг, А, и v. Используем теперь две из четырех координатных
степеней свободы, предположив, что возмущение вейлевского
скаляра Ч^ также равно нулю, т. е.
?21) - 0. A00)
После этого у нас есть еще четыре калибровочные степени свободы.
83. Линеаризация остальных тождеств Бианки
Четыре из восьми тождеств Бианки (уравнения C) и D))
мы уже использовали. Оставшиеся четыре тождества (уравнения
C216), C21 в), C21е) и C21 ж) гл. 1) имеют вид
если пренебречь величинами второго порядка малости Wo, хЧ^,
v^Fq и сгЧ^. Уравнения A01) обладают замечательным свойством:

170 Глава 9. Гравитационные возмущения черной дыры
в калибровке Л?1 = х?3 = 0 они формально совпадают с уравне-
уравнениями в стационарном случае и справедливы с точностью до
величин первого порядка малости (включительно).
Поскольку W2 = —М (р*)~3 и мы выбрали такую систему
координат, в которой Ч^1* = 0, линеаризованные уравнения A01)
имеют следующий вид:
pA)=-i1A)lnp*; RA> =i2A)lnp*;
тA) 13(|Iпр*; nA)=-fl4A)lnp*. A02)
Используя соотношения
I1 In р* = D In р* = (р*)-1; I2 In р* = Д In р* = ji;
13 1 — * ci~* i4i~* с*1~* г \ /
lnp = о In p = — т; I lnp =o lnp = -(-п
и матричное соотношение
\1 A) = А',11, A04)
получаем развернутую запись уравнений A02):
р<" = - (A\Jf + А^ - Air + А\п) = - M(I)/p*,
|xA) = + {AW + Ah - Ah + A\n) = AMB)/2P2p% A05)
x(I> = - (AW + A\n-Ah + A\n) = - MC),
nA) = + (A\/f + A*aV. - A\x + AU) = (p/p*) MD),
где
MB) =-Al + Fi + iay'2(p/A)GsinQ,
MC) = Я + (ia sin 0//2) (F34 + A\i p2),
MD) = J + (fa sin 0//2) (Fj + At/p2).
Приведем здесь для дальнейших ссылок уравнения, которые
являются следствием уравнений A05):

84. Линеаризация коммутационных соотношений 171 ,
Итак, тождества Бианки A01) позволяют выразить возмущения
спиновых коэффициентов р, т, ц и п через возмущения базисной
тетрады, если выбрать калибровку, в которой 4>о{) = 0.
84. Линеаризация коммутационных соотношений.
Три системы уравнений
В краткой «скобочной» записи коммутационные соотношения
принимают следующий вид:
[l'f 1/]=CJ[/1*, A08)
где 1 (в качестве касательных векторов) следует интерпретиро-
интерпретировать как производные по направлениям, а структурные кон-
константы CLJ выражаются через спиновые коэффициенты (урав-
(уравнения C07) гл. 1). Значения спиновых коэффициентов даны
в гл. 6 (уравнения A75)), при этом структурные константы в ста-
стационарной фоновой метрике равны
С? = у + 7* = ~ 'Л/Р4 + (/- - Щ1?~\ Cf =a* -f р - я* = 0;
q1 = e -f е* = 0; С:]1 = х = 0;
Cf - - (г* + я) = —/2шг sin 9/р2р*; Cf = - (р* -f е - 8*) = 1/р;
С;1 = - (т + я*; = + /2шг sin 9/p2p; CJ1 = — а = 0;
Cf = - v* = 0; С;я = [х* - (г - шА cos 9/р4;
A09)
Cf = т - а* - р = /2а2 sin 9 cos 9/p2p; Cf = р* - р = 2ш cos 9/р2;
Cf = ii - у + 7* = ~ Д/2р2р; Cf = а - р* = - (p*ctg9—
— ш sin в)/(р*>2 >^2;
Cf = X* = 0; Cf = P - а* = + (pctg9 +
+ ia sin 9)/p2 -/2.
С помощью уравнения (92) линеаризованные уравнения A08)
можно переписать в виде
Ш\ 1'1 + [1\ A'k\k) = dM^lm + cil\m, A10)
где с1т — возмущения фоновых значений Ст. Расписывая урав-
уравнение (ПО), получаем
AicXr + А{С'Х + (\сА'т) Г - AМ^) Г = Ci'^l" + 47lm. A11)
Вследствие линейной независимости вектора 1 имеем
\lAL - \'Alm = А№т - А[С% + C'jAm + с'Л. A12)

172 Глава 9. Гравитационные возмущения черной дыры
Уравнение A12) по многим причинам является основным урав-
уравнением теории: оно дает основную систему неоднородных уравне-
уравнений для элементов матрицы А и, кроме того, неоднородные члены
прямо связаны с возмущениями спиновых коэффициентов.
Двадцать четыре уравнения A12) могут быть сгруппированы
в три системы по восемь уравнений каждая.
Из уравнений A09) следует, что
с» = - (т + я*)'"; с» = + (р* -
с? + ^ = + (т - я*)(П; с? + с? = -
;
*)(П; с? + с? = -(р + р*)т; ( '
С помощью уравнений A05) можно выписать систему из восьми
уравнений, в которых неоднородные члены, следующие из членов
с1Л в уравнении A12), выражаются через элементы матрицы А.
Следовательно, уравнения A12) дают систему восьми однородных
уравнений для элементов матрицы А. Эту систему назовем си-
системой I.
Далее,
С*'* —— л/• а1 <т* />3^ л?^** ^32 ___ 0 sfc
5_ л» С4 U» С1 V > С4 Л
С4^ з— V** Г1^^ П** Г1 л;* /°^ 7
у ~— /w , О.» —— W , Li V, С/ q /V •
Но уже есть явные решения (уравнения B5)—B8)) для спиновых
коэффициентов х, аД и v через функции Тьюкольского (оставим
в стороне неизвестную еще относительную нормировку функций
R+2 и /?_2). Следовательно, уравнение A12) дает еще одну систему
восьми уравнений для элементов матрицы А, в которой неоднород-
неоднородные члены можно считать известными. Будем называть ее систе-
системой II.
Две системы уравнений — система I и система II — содержат
вместе 16 уравнений для 16 функций, необходимых для определе-
определения матрицы А. Однако мы увидим ниже, что этих уравнений не-
недостаточно для определения матрицы А: их нужно дополнить
линеаризованными тождествами Риччи.
И снова из соотношений A09) следует, что
с*1 - cf - 2 (а* - р)A1 - (т + я*)A),
с\х ~ cf = 2 (а + Р*)A) - (т* + я)п\
с^ __. cf = 2 (у - y*)U) - (fx - |и*)A), ( '

84. Линеаризация коммутационных соотношений 173
С учетом этого мы можем выписать еще одну систему из восьми
уравнений (систему III), в которой неоднородные члены прямо
связаны с возмущениями оставшихся спиновых коэффициентов а,
р\ у и е. Следовательно, если матрица А уже определена, эта
система уравнений будет служить для завершения решения.
Выпишем теперь все три системы уравнений в явном виде.
Следует, однако, отметить, что приведение уравнений к виду,
который дается ниже, отнюдь не простая задача.
СИСТЕМА I
2t>tF\ + SD0Fl = - irT sin 8 + Bw cos 9/p2) / B1, 3),
2>tF\ + 2HFl = + irT sin 9 - Bia cos 8/p2) H B1,4),
2?\F\ - SS\F\ = iAT cos 0 - Biar sin 6/p2) G D3, 1),
2y.Fl - 2\F\ = iAT cos 8 + Biar sin 9/p2) F D3, 2),
= Tia (F\ + F2) cos 8 C1,1) + C2, 2),
D1,1)+ D2, 2),
,Fj + p23?\F\ =
C1,3)+ D1, 4),
= + 2iar(F4-F?)sin9 C2, 3) + D2, 4), A16)
где
T = (/2/p4)a(t/-y), О' = Л1 + Л2, К = Лз+Л44. A17)
СИСТЕМА II
A/-/2) p2^oF2 - ^-ip4/7? - 2(ap2f4Cos8 = V2Apx C1, 2),
A//2) p2^o^2 - 5>-ip4F2 + 2/ap2F3 cos 8 = V2Ap V D1, 2),
A//2) i?l,p4fl - 1/2p2A^>0p2/74 + /2iarp2F2 sin 8 =
= -V2A(pJa C1,4),
A//2) ^_ip4F3 - 1/2р2А^ор2/?з - / 2/arp2F2 sin 8 =
= -V2A(p*)V D1,3),
A//2) p2^oF? + ^>lip4F? - 2('ap2F2cos9 = - Bp4p/A) v* C2, 1),
A//2) p2^0Fl + 0i,p4Fl + 2шр2^1со5 9 = - Bp4p7A) v D2, 1),

174 Глава 9. Гравитационные возмущения черной дыры
l/l/2) SUpFl -f (Р2/2) b&tfFl - /2mrp2F? sin 8 =
= p2(p)V C2,4),
A/,/2) 2-^F\ + V2P2A^>oP2F3 +/ 2<arp2F4 sin 9 =
= P2(P*J^ D2,3). A18)
СИСТЕМА III
- [1/p2 (p*K] S>U [p4 (p Y Л] + Bm cos 0/p*) (Fj - F2,) +
+ (l/2/p*)iflslnepF3 + [l/2/(p'J]'asine^4 D1, 1) — D2, 2),
2 (e - e*)<«> = (/2/Ap2) <?_, (P4Fl) - (/2/Ap2) <?t, (p4^) -
- 2>0 (^44 - Al) + B |/2/A) iar sin в (F| + F$) D1, 4) - C1, 3),
2(t-tT>=[1'/2(p7]^-.[(p7^]-
- [MY 2 (p*L) ^1, [(pL Fi) - (A/2p2) ^ (Л1 - At) +
+ BmA cos 9/p4) (F2 - Л2) - (/ 2/p2) iar sin в (F? + F?)
D2, 3) - C2, 3),
(T + ?T> = Л22 ^ (^) + (/2/P2) /or sin Э (F? - Ff) -
- (A/2p2) <2>о+Л! - ^HЛ2 B1,1),
(e + e*)A) = + B /2/A) iar sin 0 (F| - Ft) -
- B /2/A) a2 sin Э cos 0F - x/2 AiZ)? (Л^/р2) - фйА\ B1, 2),
(a _ p')<«> = _ B/acose/p-) {F\ - F23) - У + (l//2p*) ^0^ -
- A /2) ^f (Л|/р) - [Л44//2 (p*J] (p*ctg Э - ia sin 9) D3, 3)
A19)
(Уравнения для (a* + P)A> и (a* — P)A> не были включены сюда,
поскольку они сразу же следуют из уравнений для (а -|~ Р**)A) и
(а - р*)О>.)
85. Редукция системы I
Исключая величину Т из первых четырех уравнений системы
I (уравнения A16)), получаем пару уравнений
3b\F + @oG = Bia cos 9/p2) (J - Я), A20)
&\H - S\J = - Biars\nQ/p2) {F + G), . A21)
где F, G, J и Н определены уравнениями (94).

85. Редукция сисщемы 1 175
Вычитая далее уравнение B1, 4) из уравнения B1, 3) и скла-
складывая уравнения D3, 1) и D3, 2) получаем другую пару уравне-
уравнений
®t{F\ - F\) + ?>№ - Fl) = - 2irT sin 9 + B*acos9/p2) (/ + #),
A22)
- + 2/ AT cos 9 + Biar sin 9/p2) (F - G). A23)
Подобным же образом, складывая и вычитая соответствующие
уравнения, мы можем заменить вторую группу из четырех урав-
уравнений системы I эквивалентной системой
®о (F? + Fl) - &t (Fl + F|) = Bm cos 8/p2) C, + (/2/p2) dU/dQ,
^o(F?-Fl)-a)J(Fi-Fj) =
= - Bш cos 0/p2) (F + G)~ (/2/p2) Q^. A24)
*,(Fi + F!) + Stf(Fj+FD =
= Bшг sin 8/p2) (/ - Я) + (/2/p2) iKV,
S?x (F\ - Ff) + Set {F\ - Fl) = (liar sin 0/p2) B2 + (/2/p2) AdV/dr.
Полезно переписать уравнения A22)—A24) в альтернативной
форме
(г/С/А) С2 = dCJdr + 2trT sin 6 - Bia cos 6/p2) (/ + Я), A25)
Qfix = - (д/dQ + ctg 6) B2 + 2/ AT cos 9 + Bшг/р2) sin 0 (F - G),
A26)
(//(/A) Sx = Bm cos 6/p2) Cx - д (J + Я)/дг + (/2/p2) di//ae, A27)
(t/C/A) S2 = - Biacos e/p2) (F + G) + <3 (У - Я)/5г - (/2/p2) QU,
A28)
QCx = - Bwrsin e/p2) (/ - H) +
4- (d/d8 + ctg 0) {F + G)~ (/2/p2) iKV, A29)
QC2 = - Biarsin 0/p2) 52 + (d/a64-ctg 0) (F - G) - (/2/p2) AdV/dr,
A30)
где 5i, B2, Cx и С3 определены уравнениями (94).
Можно показать, что не все из восьми уравнений A20), A21)
и A25)—A30) являются независимыми: уравнения A27) и A30),
например, могут быть выведены из остальных шести уравнений.
Заключаем отсюда, что только шесть из восьми уравнений системы
I являются независимыми. В качестве основных уравнений выбе-

176 Глава 9. Гравитационные возмущения черной дыры
рем A27)—A30) и уравнения A20) и A21). Последние два уравне-
уравнения могут быть записаны и в другом виде:
(ШЛ) (F-G)=d(F + G)ldr - Bia cos 0/p2) (J - Я), A31)
Q(J + H) = (д/dQ + ctg Э) {J -H)~ Biar sin 0/p2) (F + G). A32)
Из уравнений A27)—A32) следует, что величины Blt В2, Си
С2, F — G и J + Я могут быть выражены через величины F -\- G,
/ — Я, ?/ и V. В конце концов окажется, что функции U и V
остаются неопределенными; их можно положить, например, рав-
равными нулю, использовав тем самым две из оставшихся четырех
калибровочных степеней свободы.
Ниже также выяснится, что уравнения A31) и A32) играют
самую важную роль в дальнейшем развитии теории.
86. Редукция системы II; условие интегрируемости
ая уравнения, можно
дующими четырьмя
- Ft) + 2mp2F cos 6 =
Складывая и вычитая уравнения, можно заменить систему II
(уравнения A18)) следующими четырьмя парами уравнений:
A33a)
/2Qp2F2 - S>!lP4 (F? - Fl) + 2/ap2G cos 0 = - Bp4/A) (p*v - pV);
/2p2 (dFl/dQ) - ^)_lP4 (Fl + Ft) +
+ 2шр2 (Fl - F\) cos 0 = V* A (p'x* -f px), A336)
/2p2 (dFJ/dQ) + ^V № + Ft) + 2шр2 (F| - F42) cos 0 =
= - Bp4/A) (P*v + pv*);
- iKp'Fl + A//2) ^?,p4 (Fi + FJ) - /2шгр2Я sin 0 =
= (PJ (P2^* - Acr/2),
A33b)
- iKp'Fl -\- A//2) S'.jp4 (F3 + Fl) + /2шгр2/ sin 0 =
= (p*J(P2X-Aa*/2);
- p2 A EP2F43/ar) + A//2) ^!lP4 (Fl - F2) +
+ /2шгр2 (F? + Fl) sin 0 = - (pJ (p2k* + Aa/2),
A33r)
-p2 A (ap2F^/ar) + A//2) ^_lP4 (Fj - F|) -
- /2tarp2 (F4 -f Fj) sin 0 = - (p*J (p\ + Aa72).

86. Редукция системы II 177
Далее, складывая уравнения в каждой-из четырех пар A33) и
воспользовавшись соотношениями A27)—A30) для дальнейшей
редукции, получим четыре уравнения:
(Q//2) {F\ + tf - t/) + А'/2а [р2 (/ - Я)/А1/2]/аг =
= A /2р2) [(А/2) (р*х* - рх) - Bр*/Д) (P*v - pv*)], A34)
A//2) a (Fl + f i - u)№ + д1/2а [P2 (/ + Я)/д1/2]/аг =
= (l/2p2) [(A/2) (p*x* + px) - Bp*/A) (P*v + pv*)], A35)
- (iKl/2) [P2 (f? -t- f?) + v] + a [P2 (f + o)]/ae =
= (l//2p2) [(PJ (p2^* - Aa/2) + (p*J (p2X - Acr*/2)], A36)
(A//2) a [P2 (f43 + Ft) f y]/ar - a [P2 if - G))/de =
= (l//2p2) [(pJ (p2X* - Aa/2) 4- (p*J (p2^ + Aa*/2)]. A37)
Исключая из уравнений A34) и A35) величину {F\ -\-F\—U),
а из A36) и A37) величину [р2(^4 Ч-Ft) + V], находим (после
некоторых преобразований с помощью уравнений A31) и A32))
Л1/2 * П2 J+H д Д1/2 д , У-Я
5г ^
д1/2 «56 Q dr ^ д1/2
= A/2р2) [(А/2) (р*х* f- рх) - Bр4/А) (p*v + pv*)] -
Ж {W[1/2 Л (р*х* " и ~BpVA) №*v ~ pv*}]} ' A38)
= - A//2р2) [(рJ (р^* 4- Да/2) 4- (Р*J (Р2^ + Аа*/2)] 4-
Уравнения A38) и A39) можно преобразовать к более удоб-
удобному виду, воспользовавшись уравнениями A31) и A32). Перепи-
Перепишем с этой целью левую часть уравнения A38) в виде
tbiQ)±?{J
Я) - -^- р2 (/ - Я; + (Q,e/Q) Р2 (^ - Н)}
A40)

178 Глава 9. Гравитационные возмущения черной дыры
и рассмотрим выражение в квадратных скобках в правой части.
Можно с помощью уравнения A32) сделать следующие преобразо-
преобразования:
+ 2а2 (J - Н) sin Э cos 8 + (Q,e/Q) p2 (/ - Н) - 2iar (F + G) sin 6 =
= A/Q) (Q.e + Q ctg 9) p2 (/ - H) + 2a2 (/ - Я) sin 9 cos 9 -
- 2lar(F + G) sin 9 =
= Bao cos 0/Q) p2 (J—H) +2а2 (У—Я) sin 9 cos 8—2шг (F+G) sin 9 =
= Ba/Q) (p2cr + Qa sin 9) (/ — #) cos 9 - 2iar (F + G) sin Q =
= Ba/Q) [/C (/-Я) cos 9-trQ(F + G) sin 9]. A41)
Полагая теперь
iF = /((/- Я) cos 9 - trQ (F + G) sin 9, A42)
находим, что уравнение A38) может быть приведено к виду
/а А <р*х*+и - B
- Q-A- |(l/2p2Q) [V, А (Р*х* - рх) - Bр4/А) (p*v - pv*)]}. A43)
Действуя аналогичным образом, находим, что уравнение A39)
может быть приведено к виду
KP)S (Р2Я* + А°Ю + (Р*J (Р2^ + Ло*/2)] +
+ Ж-А {—'— [(рJ (р2Х* - Ао/2) + (р*J (р2Х - Аа*/2)]}. A44)
Заменяя дифференциальные операторы в правой части уравнений
A43) и A44) операторами 2? и ?Dy определенными в гл. 8 (§ 68),
получаем следующую пару уравнений:
- 2а A1/2-|r (?/А1/2) = - VaQ2 (^о+ (V* Ах7р - 2p2p2v/A)/Q -
- 2>0 (V2 Ax/p* - 2p3pv*/A)/Q), A45)
= (iK2//2) \®\ [V2 А (ар/р* + а*р*/р)]//( -
) A46)
Очевидно, что уравнения A45) и A46) требуют выполнения ус-
условия интегрируемости: действие операторов
и
дв дг

87. Решение условия интегрируемости 179
на правые части, соответственно уравнений A45) и A46) должно
приводить к одинаковым выражениям. Это условие является од-
одним из важнейших соотношений в теории: как будет показано
ниже в § 87, оно определяет относительную нормировку функций
R+2 и R-2 и аргумент постоянной Старобинского Ф.
87. Решение условия интегрируемости
Заметим прежде всего, что в правой части уравнения A45)
появляются как спиновый коэффициент х, так и спиновый коэффи-
коэффициент v. Но как следует из решений B5) и B8) для этих спиновых
коэффициентов, коэффициент х выражается через функции /?+2 и
5+2, тогда как v — через функции R-2 и 5-2, а мы неоднократно
подчеркивали, что относительная нормировка функций R+2 и R_2
(при нормировке угловых функций 5+2 и 5-2 на единицу) пока
еще неизвестна. Как следствие выражение в правой части урав-
уравнения A45) не полностью определено. То же самое можно сказать
и о правой части уравнения A46).
Обсуждение тождеств Тьюкольского — Старобинского, прове-
проведенное в § 81, показало, что задача определения относительной
нормировки функций R+2 и R-2 тесно связана с проблемой раздель-
раздельного определения действительной и мнимой частей гюстоянной
Старобинского 9 = <ё>1 + №2. Действительно, если бы Мы норми-
нормировали функции Д2#+2 (= Р+2) и R-2 (= Р-2) в соответствии
с уравнениями D1) и D2), то нам оставалось бы определить лишь
численный коэффициент в решении для ?4 (или Ч^). Но при этом
еще не будет решена проблема раздельного определения с&1 и ^
Существо поднимаемой здесь проблемы станет яснее, если
вспомнить этапы исследования уравнений Максвелла, проведен-
проведенного в гл. 8 (§§ 70 и 71). Там было найдено, что при выборе функ-
функций A/?+i и R-\, согласно уравнениям C3) и C4) гл. 8, требуется
учесть дополнительный множитель 1/2 в решении для ф2 (см.
уравнение G0) гл. 8) и этот множитель определялся одновременно
с доказательством действительности соответствующей Постоянной
Старобинского.
Вернемся теперь к условию интегрируемости. Мы вскоре уви-
увидим, что если в качестве базисных решений для радиальных функ-
функций выбрать Р+2 и Р_2, то решения для вейлевских скаляров %
и ?4 будут иметь вид
А2^о - Я+25+2, ?4 = [1/4 (р*L ] Я.25_2, A48)
т. е. появляется множитель 1/4 вместо 1/2 в случае спина 1. Удобно
предположить справедливость решений A48) с самого начала,
хотя это и не является строго необходимым: можно включить до-
дополнительный множитель, скажем q, в выражение для Т4 (тогда
последующий анализ покажет, что q = 1). Опуская множитель q,
мы ничего существенного не теряем: восстановление этого множи-

180 Глава 9. Гравитационные возмущения черной дыры
теля на каждом шаге вычислений очевидно, но он нарушит сим-
симметрию последующих формул.
Предположим поэтому, что решения для То и Т4 даются фор-
формулами A48) и что Р+2 = A2i?+2 и Р_2 = R-2 в согласии с D1) и
D2) и удовлетворяют G4). Полагая (ср. с уравнениями (80))
X = Р+2 + Р_2 = [Р ]+, IY = Р+2 - Р-2 = [Р ]", A49)
перепишем уравнения G4) в более удобной для последующего
анализа форме
- Л2) X + (ДУх + А - fii/Г/Д) У, A50)
- Л + В1К/А)Х- (Д«?2 + Л2) Г, A51)
где величины Лх, Л2 и Вх имеют тот же смысл, что и в уравнениях
G6).
При введении дополнительного множителя 1/4 в решение для
Т4 решения для спиновых коэффициентов х, сг, % и v принимают
следующий вид:
_1_
6М
A52)
1 /2 р / ^+ 3ш?ш9
р2 ^
Вернемся к уравнениям A45) и A46) и подставим вышеприве-
вышеприведенные решения для х, а, X и v в их правые части. После громозд-
громоздких преобразований с использованием уравнений (87) и (88) нахо-
находим
Р — ( ^ + баа cos 8
r L \ '
я2<7sin Э cos 9
тт^
+ 2 (ctg 6 + Q — ш sin 9/р* - аа cos 9/Q) ^S+a
+ р [— (А, — баа cos 9 + 6ш2а sin 9 cos 9/Qp) 5_2 +
+ 2 (ctg 9 - Q + ia sin 9/p - ao cos 9/Q) ^S_2] ^+2 +
+ P* [— (^ - баа cos 9 - 6ш2а sin 9 cos 9/Qp*) 5_2 +
+ 2 (ctg 9 -r-Q-ia sin 9/p* - аа cos 9/Q) 3?tS-2] P-2 -

87. Решение условия интегрируемости 181
- Р [— (*¦ + бает cos 0 + 6ш2а sin 6 cos 8/Qp) S+2 -(-
-f- 2 (ctg 0 + Q + w sin e/p — a(T cos 0/Q) ,S?2S+2] P_21 =
A53)
'-* Г /л i с- i 6га ^ \ r, ,
^Р (
+ 2(r-M- LK - го Д//С - Л/р") 2>1Р+2] 5+2 +
+ p [(A, + бгаг + 6га А/Щ Р+2 +
+ 2 (г - M - iK - га А/К - Д/р) ^о^+г] S_2 -
- р* [(К - 6ior + 6га А//Ср*) Р_2 +
+ 2 (г - М + t/C - га А/К - Д/р*) a>o^_a] S_2 -
— р [(А, — бгаг + 6га А/Щ Р.2 +
+ 2 (л - Af -f iK - го А/К - Д/р) 5>вЯ_а] 5+2! = 2adW/dQ.
A54)
Дальнейшее преобразование этих выражений приводит к урав-
уравнениям
A/12 /2М А) [ш
- Bаа cos 0) &2S+2] cos 8 - 2 [(Зав cos 8) St2 — Q^S^] sin 0 +
+ [Q2\2tS-2 - Bao cos 8) StS^ cos 0 -
- 2 [Cflo cos 0) S_2 - QS'JS^] sin 9) (P+2 - P-2) -
- {[Q2\#aS+a - Baacos0) ^2S+2] -
- [Q^J-^S-s - Baa cos 0) ^2+S_2]) r (P+2 + Я-2I =
= 2aAl'2d(W/A^2)/dr, A55)
0712 /2/И) {[r
+ 2 CraP+2 -
- 2 Cra/>_2 - /С^о/'-г)] (S+s
- ш [(/C^oo+2 t+i)
- S_2) cos 0} = 2aa?/50. A56)

182 Глава 9. Гравитационные возмущения черной дыры
В сокращенной «скобочной» записи (§ 81, б) эти уравнения при-
принимают вид
+ a{Q \seaest cos e + 2(Q sm e — ao cos2 в) [S?s\* -
- 6o0 (sin 0 cos 0) [S]+\ Y}, A57)
+ Gra [P]-} [S]+ - ia {K [?>?>P]+ - 2ra [2>P]+] [S]~ cos в]. A58)
Теперь мы должны потребовать, чтобы результат действия опе-
оператора <?е на выражение в левой части уравнения A55) совпадал
с результатом действия оператора Д1/2дгА-1/2 на выражение в ле-
левой части уравнения A56). На первый взгляд непонятно, как дей-
действовать дальше, поскольку приравниваемые выражения содержат
производные от радиальных и угловых функций вплоть до третьего
порядка, а функции определяются только уравнениями Тьюколь-
ского. Однако вскоре становится понятно, что требуемое условие
может быть получено, только если на каждом этапе производные
от функций Р±2 (г) и S±2 @) заменять подходящими комбинациями
функций, используя при этом уравнения G9), A50) и A51). В ре-
результате таких замен получаем из уравнений A55) и A56)
— A/12М Др1>/2)[{2 (Qctg 0 — аа cos 0) (D — 1\) +
+ 8aoXQ2 cos 0}E+2 + 5_2) +
+ { — 2Q2 (D —1\) — 8ааХ (Q cosec 0 — ao cos 20)} (S+2 — S.,)J rX —
— (а/12М Ар! /2) [BQ2 (D + 1\) — 8ааХ (Q cosec 0 —
— аа cos2 0)} (S+2 + S_2) cos 0 + {— 2 (Q ctg 0 - ao cos 0) (D + Гх) +
+ 8aaXQ2 cos 0} (S+2 — 5_2) cos 0 — 2 {[(Заа cos 0) px +
+ <*tQ] (S+2 + S_2) + Q (a! + D) E+2 - S_2)} sin 8] У =
= 2a Al<'2d (?/A> 2)/^r, A59)
«?2 — Г2
2
— 2[/((r — Af) — (!\)} +
{2/C2 («?! — Гх) +2 [/( (r — ЛГ) — ar A ] («•, - Г2 —
+ 2/C (A«\ — Л1) X — 2 [ЗгаЙ! + /С (А^2 + Л2) ] F] X
X E+2 +5_2) +(a/12MB1/2)[{2iB(^1 +Tt) +
+ 2 IK (r — М) — аг А ] (92 + Г2 + 4А,ог) — 8Ха/С А) X +

87. Решение условия интегрируемости 183
+ { — 2К2 (V2 + Г2 + 4Ястг) +2 [К (г — М) — or A] x
X («\ + 1\)} 7] (S+2 — S_2) cos 0 - 2adW/dQ. A60)
Напомним, что (ср. с уравнениями D3), G1) и G5))
у= <g?x + №29 Гх = Я. (Я + 2) — 12ст2а2, Г2 = 12аМ,
D2 - Я2 (Я + 2J — 8а3Я [а2 EХ + 6) — 12а2] + 144а4а4,
|У|а = D2 + 144а2 УИ2, а2 = а2 + шл/а, A61)
а остальные величины Лх, Л2, Вь аь а2 и |3Х имеют тот же смысл, что
и в уравнениях G6) и G8). Отметим, также, что преобразования,
которые привели к уравнениям A59) и A60), были выполнены с по-
помощью уравнений D7), D8), F4) и F5) (и с помощью комплексно-
сопряженных и присоединенных уравнений).
Действуя теперь операторами <9е и А1/2 дг А~1/2 на выражения
в левых частях соответственно уравнений A59) и A60) и проводя
те же самые замены производных на комбинации функций, нахо-
находим после громоздких преобразований и ряда сокращений
+ Da/a) (ba2 - 6a2) (S+2 + S_t)} У +{-(?>- Г,) (S+2 + S_2) +
+ 4aoft (S+, - S_j) cos 6} rX], A62)
' J_Ja_av__
дг Д 39 "~
= A/48 /2 MA) [a {[(У, + Г2) + 4W] X + (^ + Гх) Y) x
X (S+2 - S_2) cos 0 + f- (^ - Г,) rX + [r (Va + Г2) +
+ 4aacc2-6a2)]r}(S+2 + S_2)l. A63)
Сравнение выражений в правых частях уравнений A62) и A63)
показывает, что их равенство требует только лишь (!), чтобы
«?! = ?, 3?2= -Г2= -12оМ. A64)
Это замечательно простой результат после столь долгого и утоми-
утомительного пути.
Определим теперь функции
<?+ = f (S+2 + S_2) de, 9>_ = f (S+2 + S_2) cos Э d0,
r r A65)
Я+ = Д'/2 J (гХ/Дз/2) dr, Ж. - Д'/2 J (У/Д3/2) dr.
Интеграл уравнений A62) и A63) через введенные функции можно
записать в следующем виде:
W = A/96/2 М) [(«?! + ГО Й_^_ + Da/a) (Яяя - 6а2) й!_^+ +
_ - (I/a) (#x - ГО 52+^+]. A66)

184 Глава 9. Гравитационные возмущения черной дыры
Напомним, что
цг = # (/ _ Н) cos 0 — irQ (F + G) sin 0. A67)
Уравнение A66) представляет собой решение условия интегри-
интегрируемости уравнений A45) и A46). При выводе этого решения мы
попутно решили задачу определения действительной и мнимой
частей постоянной Старобинского и задачу определения относи-
относительной нормировки радиальных функций Тьюкольского.
В заключение параграфа отметим, что определение функции
A67) позволяет записать уравнения A31) и A32) в альтернатив-
альтернативной форме
d4J 1Я1 д о2 J~H
Р W t П) р
d4J 1Я1- д о2 J~H Г
Р W -t" П) — т р Q h Q
. oF — G д oF + G 2iaV naQ,
88. Разделение переменных в функциях W и Ж и &
Замечательным фактом является возможность разделения пере-
переменных в функции W и явное вычисление интегралов, через ко-
которые выражается эта функция.
Заметим прежде всего, что конечность функции W в пределе
а -> 0 требует, чтобы (&1 равнялась положительному квадрат-
квадратному корню из D2 (ср. с уравнениями F1) и A64)), потому что
только тогда сё>1 — 1\ -> 0 при а -> 0. Фактически мы имеем тож-
тождество
«Р? — Г? = — 16сЛ (tat2 - 6а2). A69)
Следовательно, можно написать
A/я) («?! - ГО = ffi - Т\Iа (Яг + Г,) =
- - 16а2Я (Act2 - 6а2)/а («?! + Га). A70)
С помощью вышеприведенных соотношений запишем решение
A66) для функции W в виде
? = A/96 /2 М) {[(«?! + Гх) Я. + 4Я(Т^+] ^ +
+ Dа/а) (^а2 - 6а2) [Я_ + 4ХогЯ+/(«?х + Гх)] ^+}, A71)
или иначе
? = [(«?! + Гх)/96 /2 М] [^!_ + 4А,аЯ+/(«?1 + Г^] X
X [9>_ + 4а (Яа2 - 6а2) 9>+/а (Ъх + Га)]. A72)
Возможность разделения переменных теперь очевидна:
V = [(«?! + Г0/96М /2] <Й (г) 9> (в), A73)
где
Я (г) = $_ + [4bor/(*i + Гх)] Я+,
4 Г)]^ ( }

S. Разделение переменных 185
Из определений функций 3t и 9* следует, что
Д1/2
Д НГД1/2- Д l + /
d5? rct-^ofl i 4а (Яа2 — 6а2) гС1+ П7ЙЧ
-ae-=[S] cos0 + д;У1 + Гх) [S]+. A76)
а. Запись функций R и 9" через функции Тьюкольского. Из урав-
уравнений A58), A73) и A76) следует, что
] J-
4 [{г/( [?>?>РГ - 2
- га {/([2J>Р]+ - 2ra \2DP]+) [5]" cos e]. A77)
Приравнивая коэффициенты при [S ]~ cos 0 и IS ]+ в двух выраже-
выражениях в правой части этого уравнения, получаем два альтернатив-
альтернативных выражения для функции 31
XU (&1 JrVlKt = K [2>2>Р}+ - 2га [2>Р\+, A78)
а (Яа2 - 6а2) 9l = i{rK [3>S>P\~ - 2 (r2a + К) [3>Р\- + bra [P]~\.
A79)
Из сравнения уравнений A58) и A60) теперь можно получить
явные выражения для правых частей уравнений A78) и A79) через
функции X и Y:
V4 (Vt +Т1)Я
+ 8Хаг [К (г — М) — аг А ] — 8Л.О/С А} X +
+ {-8/t2U/- + 2 («?! + 1\) [/С (/¦ — М) — or А]) Г], A80)
а (А,а2 — 6а2) 31 = A/Bj) [{ —8/Bа FМ + Яг) —
— 2 [/С (г — М) — от- Д ](«?! — rj} гХ +
+ {2К2 (&! - Tt) — 8а FМ + Яг) [К (г — М) — аг А ] +
+ 8Яа/(А) гГ + 2/( (А^ — Ах) X —
- 2 [ЗгаВг + К (А^2 + Л2) ] Г]. A81)
Из уравнений A73), A75) и A57) далее следует
2.Д./2
i + Ti У
^ А1'2 48]Л2МД
- (l/12/2/WA)[(Q[5'57Sr - Ba(TCOS0)[575]-} rX +
+ a |Q [2?&SY cos 0 + 2 (Q sin 0 - aa cos2 0) [S'S]* -
-6aa(sin0cose)[5]+jr]. A82)

186 Глава 9. Гравитационные возмущения черной дыры
Приравнивая коэффициенты при функциях гХ и У в двух выра-
выражениях в правой части, находим следующие альтернативные вы-
выражения для функции ЯР\
- Хао9> = Q \ggS\- - 2аа [2S\- cos 0, A83)
— V4 («\ + Гх) 9> = Q [S?2S\+ cos 0 +
+ 2 (Q sin 0 - aa cos2 0) [&S]+ - бает [5]+ sin 0 cos 0. A84)
Из сравнения уравнений A57) и A59) можем теперь получить яв-
явные выражения для правых частей уравнений A83) и A84) через
функции [S]+ и [S]~
— Хао9> = A/рх) [{2 (Q ctg 0 — яа cos 0) (^ — Гх) +
+ 8aoXQ2 cos 9} [S]+ +{ — 2Q2 (сё>1 — Гх) —
— 8aofc (Q cosec 0 — aa cos2 0)} [S ]-], A85)
-V4 (^i + Гх) ^ = A/Px) [{2Q2 (Vt + T±) -
— 8aoX (Q cosec 0 — ao cos2 0)} [5 ]+ cos 0 +
+ {— 2 (Qctg 0 — ao1 cos 0) (^ +I\) +8aoXQ2 cos0} [S]"cos0 —
— 2{ [ (Заа cos 9) px + a2Q ] [5 ]+ + Q (ax + ^х) [5 ]"} sin 0].
A86)
Читателю не нужно объяснять, что соотношения A78), A79),
A83) и A84) удивительны не только сами по себе, но и тем, что они
дают явные выражения для неопределенных интегралов, через
которые функция W была первоначально определена. Мы еще вер-
вернемся в § 94 к этим аспектам решения условия интегрируемости.
89. Завершение редукции системы II
и дифференциальные уравнения для функций 31 и ЯР
В § 86—88 мы ограничились исследованием четырех уравне-
уравнений A34)—A37), выведенных из восьми уравнений A33), которые
в свою очередь эквивалентны системе II. После того как мы удо-
удовлетворим условию интегрируемости, следующему из этих урав-
уравнений, остаются два уравнения, именно уравнения A34) и A36),
и, кроме того, решение для функции ?, которое мы нашли. Необ-
Необходимо рассмотреть остальные четыре уравнения, независимо от
уже рассмотренных.
Вычитая второе уравнение из первого в каждой из четырех
пар уравнений, входящих в A33), получаем
2шр2 (F - G) cos 0 = V2A (Р*и* - ри) + Bр4/А) (p*v - pv*), A87)

89. Завершение редукции системы II 187
/2 р2
39 ^ * '
+ 2mp?C2 cos Э = V«A (P*x* + P*) + Bp4/A) (p*v + pv*), A88)
- iSp* (Fl - Ft) - A//2) (-1- - ctg 0) p4d -
- (Q//2) p4 (F + G) - /2 шгр2 (У + Я) sin в = (pJ (p2^* - Aa/2) -
— (p*J (p2X -f- Aa*/2), A89)
— P2A -|r P2 (^4 - ^з) - A//2) (-^- — ctg e] p4C2 -
- (Q//2) p4 (F - G) + /2 tarp2Bj sin в =
= - (pJ (p2X* + Aa/2) + (p*J (p2X + Aa*/2). A90)
Исключая величину {Fl— Fi) из уравнений A87) и A88),
имеем
-ж- ~ш ^^ (р*3** "" рх) + Bр4/д) (p*v — pv*)J -
С/О l^JJ
- (А/2р2) (р*х* + Р>с) - Bр2/А) (p*v + pv*) =
__ 2ia cos 9 д Г д _0 ^ , г ггч , 4a2 cos2 0
2ш sin 8 л 3 2F — G 2iKa
Аналогично, исключая р2(/ч — ^з) из уравнений A89) и A90),
находим
А 4г ^w~[№J (р2Я* -Л0/2) - (р*J (р2^ - А<т*/2)]+
4г w
+ -^ [-(РJ (Р2^* + Аа/2) + (Р*J (Р2А + Ла*/2)] =
2/arAsin0r д о / д . i. л\/с i ^>\ i 4a2/-2sin2 0/г?
2аА sin 0 д cos2 0 / т . „. , 2aAQ
2аД
Отметим, что в преобразованиях, приводящих к окончатель-
окончательному результату в уравнениях A91) и A92), важную роль играет
уравнение A68).

188 Глава 9. Гравитационные возмущения черной дыры
Уравнения A91) и A92) могут быть записаны в альтернативной
форме
ш^( д / к д V \ / 4а*а* К*
{ V.A *L + ^v) - ^ ?(ViA JSr 4-2? v*)},
A93)
a { д (oJJL\ / 4a2(j2
A94)
Подставляя известные решения для спиновых коэффициентов
х и v в правую часть уравнения A93), находим в результате преоб-
преобразований, аналогичных преобразованиям A53), что
l2]/-2MA l\Q[22Sr- 2ao[2STcos6} rY -
— a{Q \S2SSY cos 0 + 2 (Q sin 0 - a a cos2 0) [S\S]+ -
где на последнем шаге были использованы соотношения A83) и
A84). С другой стороны, факт разделения переменных функции
W (уравнение A73)) позволяет записать правую часть уравнения
A93) в виде
К 96/2Af I d/4A &г К )
Мы приходим, таким образом, к следующему дифференциальному
уравнению для радиальной функции 2&\
А2 Г d / у d 0 \ , / 4а%^ ^2\л1 о /у
A97)
Рассматривая затем уравнение A94), аналогичным образом
находим, что правая часть его может быть записана в виде
- 2 (г*о + к) [фру + era [P]-} [sr +
to {/С [00Р]+ - 2/-О [S)P]+} [5]+ cos Э] =
ia (Ка2 - 6а2) Я [S]~ + V4to (^i +1\) ^ [5]+ cos 9} =
12 1^2 М [
^ a((Fl + Г\)
[SI-}, A98)

90. Четыре тождества Риччи 189
где на последнем шаге были использованы уравнения A78) и
A79). Левая же часть этого уравнения дает
V d0 Q
Мы приходим, таким образом, к следующему дифференциальному
уравнению для угловой функции 91:
.L\J-(nJ-^-\ Da2g2 оЛ<р]-
q [ de Vy de q ) \ q« y j^J -
4^2^)} B00)
Уравнения A97) и B00) можно записать в альтернативной
форме
_^_ __
/С ^ d/-2 ~ /С йг
- cosec2 9 - ^- cosec б) ^] =
= -2 {[SI*cose + 4^1^[5]-}. B02)
Таким образом, условия интегрируемости уравнений A87)—
A90) приводят к замечательным тождествам — уравнениям B01) и
B02). Помимо этих тождеств, у нас есть еще уравнения A87) и
A89), которые можно рассматривать как уравнения для определе-
определения (Fl — F2\) и р2(/^4 — ^з) через остальные величины.
90. Четыре линеаризованных тождества Риччи
Прежде чем продолжать далее, уточним, какие задачи нам
еще нужно решить.
Мы видели, что уравнения системы I позволяют выразить
функции Въ В2, Съ С2, F — G и / + Я через функции F + G,
J — Я, U и V.
Из уравнений системы II, помимо определения относительной
нормировки радиальных функций R+2 и R_2 и действительной и
мнимой частей постоянной Старобинского ®\ получается решение
с разделяющимися переменными для функции Y
хр = К (J — Я) cos 9 — irQ (F + G) sin 0 B03)
и четыре уравнения A34), A36), A87) и A89), позволяющие выра-
выразить комбинации (f2± F2\) и р2 (Fl ± F*) через другие функции,
которые мы перечислили ранее.

190 Глава Р. Гравитационные возмущения черной дыры
Уравнения системы III служат только для определения возму-
возмущений спиновых коэффициентов а, р, у и е, если известно пол-
полностью решение для матрицы А. Кроме того, мы покажем, что
функции U и V остаются неопределенными до самого конца, так
что можно использовать две из оставшихся четырех степеней кали-
калибровочной свободы и положить их равными нулю.
Таким образом, для завершения нашей программы осталось
определить функции F -f- G и / — Н.
Поскольку 16 тождеств Бианки и 24 коммутационных соотно-
соотношения уже были использованы, мы должны в силу необходимости
вернуться к тождествам Риччи. Изучение этих тождеств, пере-
перечисленных в гл. 1 (уравнения C10)), дает возможность предполо-
предположить, что нам следует обратить внимание на уравнения C10а),
(ЗЮо), (ЗЮж) и C10р) из гл 1. Линеаризация этих четырех урав-
уравнений дает
+ 2p<1Vp* — DA) (p*)-1 -j- (e + 8*)A>/р* -
= 6*х — к (За + р* — я) — х*т,
+B,х +у +7*)(х<1> +ДA)(х +(V +Y*)(I)H =
= 8V — v (т — ЗР — а*) + v*Jt,
B04)
+ Bя + а - р*
— Bт + р — а*) тЯ + б^)! + (а* - Р)О> - -
= д а + ст(х — Х*/р* — а (Зу — 7*).
Подставляя в вышеприведенные уравнения решения для и а, Я и v
(уравнения A52)), решения для рП), т^1), (хA) и яA) (уравнения
A05)) и решения для а*1*, р<!>, 7A) и еA) (уравнения A19) из си-
системы III), находим после громоздких преобразований
—iKF\ + (A/2) S>JU + A /V 2)(iasin0)?>-lP2F +
+ l/2"(a2sin0cos0)F- |/ 2" (tor sin 0) (F* - Ft) =
= - (A/2 ^ 2) [(p*J ^ix/(p*)a + to sin 9x*/p], B05)
+ (A/2) ^o^ - (l/(/ 2") (to sin0) ^1!р2О -
- V 2 {a sin 0 cos 0) G - V 2 (iar sin 0) (F? - F}) =
B06)
(iaQ sin 0) F3 + (to sin 0/2p2) ^oV + (l/1/ 2") [^_i/ — Bto sin 0/p) /] +
+ V 2V (sin 0 cos 0/p2) {F\ + F32) = (pVp) 12>o (р*Я,) + Aa*/2p2],
B07)

91. Решение уравнений B09) и B10) 191
(iaQ sinQ)Fl~(ia sin в/2р2) &tV - (\I^2)[SUH —Bга sin 0/p) #] +
+ V 2 (a2 sin 0 cos 0/p2) (F\ + Fl) = - [4f Sb\ Jjfo + -f Г ].
B08)
Вычитая уравнение B06) из B05) и складывая уравнения B07)
и B08), получаем следующую пару уравнений:
iK (Fi + F\ - U) - V 2 (a sin 0 cos 8) (F + G) -f
+ 1/2" (far sin 6) (J-H)- (lit/ 2) (tosm 6) @-ip2/7 + 0tip2G) =
= (|/ 2" p4p7A) [(l/p2p) <?Г (p2v) + ia sin 0У'/(р*J) +
+ (A/2 V 2) [(p*J ^!X/(p*J + ш sin0x*/p], B09)
(faQ sin e/p2) [p2 (F\ + F^) + V] + V 2 (a2 sin 0 cos 0/p2) (F + G) +
-4- A/K 2") \S-\1 - &UH - Bic sin e/p) (/ - Я)] =
= (p7p) № (p*X) + (A/2P2) a'] - [-^- Й>\ ^r + ^ X-] . B10)
Аналогично, складывая уравнения B05) и B06) и вычитая уравне-
уравнение B08) из B07), имеем дополнительную пару уравнений
-iK (Fl2 - F\) + (А/2) @>о + ®t)U + A//2") ia sin 0 (?>-ip2F -
— ?>-\p2G) + /2" (a2 sin 9 cos 0) (F - G) - /2~ (mr sin 0) 52 =
K P4P*
2
(iaQ sin 0) (Fl ~ Fi) + (ш sin 0/2p2) (SQ + S'J) К +
+ /2~ (a2 sin 0 cos 0/p2) C, + (l/K 2") [S7.,/ + ^1,Я -
- Bia sin 0/p) J - Bia sin 0/p) H] = -С- [^0(Р*Я) + -^- a*] +
91. Решение уравнений B09) и B10)
Покажем теперь, что, исключая функции (Fl -\- F\ — U) и
[р2(/74 + /;з) + ^/] из уравнений B09) и B10) (с помощью урав-
уравнений A34) и A36), можно получить удивительно простую систему
уравнений B42)—B45) для функций К (J — Н) cos Э (= ZJ
и —irQ(F +G) sin 0 (= Z2).

192 Глава 9. Гравитационные возмущения черной дыры
Рассмотрим сначала мнимые части уравнений B09) и B10).
Имеем
(ia sin в) { Л-^ (р2 "У#) -lr(F + G) + (ia cos0) (У - Я)]} =
= [к, v] - [к, v]*, B13)
os 9) (У - Я)] =
= [X, а] - [К, о]*, B14)
-щ- р2 (У - Я) - (ш sin 9) [г (F + G) h («a cos 9) (У - Я)] =
где
B15)
^^Ра +^Г1 B16)
2^2 L 2p (p*J ' p* J v 7
Мы видим, что в уравнениях B13) и B14) появляется комбина-
комбинация [г (F -{- G) -(- ia (J — Н) cos 9 ]. Заменим ее комбинацией
функций F + G и ? в уравнении B13) и комбинацией функций
J — Я и ? в уравнении B14), используя для этого одно из следую-
следующих двух соотношений:
г (F + G) + (ia cos 9) (J — Н) = (га/К) р2 (F + G) + iaW/K -
= — (ia/Q sin 9) р2 (J — Н) cos 9 + iW/Q sin 9. B17)
После такой операции уравнения B13) и B14) принимают вид
[){, v]_[x, v]% B18)
= [X) a)-[X, oy. B19)
Вернемся снова к уравнениям B09) и B10) и рассмотрим их
действительные части
A//2) IK (Fl + F\ - U) + (a sin 6) [/г (У - Я) - a (F + G) cos 9] =
= [х, v] + [х, v]*, B20)
A//2") iQ (a sin 6) [р2 (F\ + Fj) + V) -
— (a sin 9) [|>(У - Я) - fl(F + G)cos9] = [A,, a] + [A,, a]*. B21)
Проделывая с этими уравнениями аналогичную операцию, но
теперь с помощью других соотношений
ir (У — Я) —a(F +G) cos 9 =
= (ioc^a/arQ sin 9) p2 (У — Я) — (ia cos Q/rQ sin 9) ? =
= — (a2a/a/( cos 9) p2 (F + G) + (tr//C cos 9) W, B22)

91. Решение уравнений B09) и B10) 193
приведем уравнения B20) и B21) к виду
(\IVr2)iK{F\ + F\-U) + (iaopVrQ) (J - Н) - (ia cosQ/rQ) ? =
= [x, v] + [и, v]*, B23)
A1/2) iQ {a sin9)[p2{F\ + F\) + V} + (a2osin Wcos9) p2(F + G)-
- (iar sin в/К cos 9) W = [ky o] + [A,, a]*. B24)
Теперь можно исключить комбинации (F\ + F\ — U) и
[p2 (F\ + ^з) + V] из уравнений B23) и B24), воспользовав-
воспользовавшись уравнениями A34) и A36). Эти последние можно записать
в следующем виде:
A//2) Q {Fl + F\ - U) + А1/2 4" [р2 (^- ^)/А1/21 = (*> v), B25)
где
(х, v) - A/2р2) [(А/2) (р*х* - рх) - Bр4/А) (p*v - pv*)], B27)
(К a) = A//2" р2) [(рJ (Р2Х* - Да/2) + (р*J (р2^ - Да*/2)]. B28)
Исключая указанные комбинации, получаем пару уравнений
= /Q {[к, v] + [х, v]*} + /С (х, v), B29)
\,9 а). B30)
Левые части этих уравнений можно записать и в другом виде
-^2- р2 (J - Я) 1 + fl22cQs61/2 ? ) , B31)
(a cos 9) (Q sin 9I/2 -^г —^б— р2 (F + G) on^'" Qu/2 ^ I •
v /v 7 аэ L cos9 J cos2e(Qsin6)I/2 j
B32)
Выпишем полностью полученную систему уравнений для ком-
комбинаций функций F + G и / — Я:
B33)
<? [ (Q sin 6I/2 , ,v i r^\ /r sin в
"STL cose ^(F + r
cos2 8 (Q sin 9)l/2
7 Чандрасекар С, т. 2

194 Глава 9. Гравитационные возмущения черной дыры
о] +lK of] +(Qasine)<*" °* B34)
= A/г) (A/C)-'/2[iQ j[x, v] + [х, v]*} + Я(х, v)|, B35)
-w^"*'01*'^- B36)
а. Редукция уравнений B33)—B36). Положим
Zx = К (J — H) cos 9, Z2 - —irQ (F + G) sin 9, B37)
так что
XV = Z1 + Z2. B38)
Будем искать такое преобразование уравнений B33)—B36), чтобы
в окончательных уравнениях / — Н и F + G появлялись в ком-
комбинациях Zx и Z2. Этого можно достичь, если умножить уравнения
B33)—B36) соответственно на множители —/ (Q sin 9I/2/cos 9,
—i/(AK)l/2, 1/(Q sin 9I/2 и Kl/2/r Л1/2. Действительно, вводя опре-
определения
Е = рУг cos 9 (Л/CQ sin 9I/2, B39)
Аг = (r/pJ sin 9/cos 9, Вг = (aK/p2Q) cos 9,
А2 - (arQ/Kp2) sin 9, B2 = (a2/rp2) cos2 9,
X, - (rQ/яр2) |[х, v] - [х, v]*|,
Гх = (/(/р2) cos 9 {[^, а]- [%, а]*},
Х2 - (cos 9/p2)[tQ {[х, v] + [х, v]*l + К (х, v)], ( }
Y2 - A>/ар2)[/С{[Л,, а] + [X, а\*\ + Qa sin 9 (К, а)],
находим, что после умножения на указанные множители уравне-
уравнения приобретают удивительно простой вид
-J- ?Z2 -А2ЕУ = ~ЕХи B42)
-^- EZ2 - A,EW = -?Уа, B43)
-^r EZ1 + В2?? = +?Х2) B44)
^ B45)
Для дальнейшего отметим, что различные выражения со скоб-
скобками, в которые заключены спиновые коэффициенты, появляю-

91. Решение уравнений B09) и B10) 195
Щиеся в определениях величин Хг, Х2, Y1 и Y2, расшифровываются
следующим образом:
(х, v) = A2/2~МД)~' \гХ [&S)- + aY ([S'Sj+cose + 3[S]+sin 6}],
[х, v] - [х, v]* = B4 /2~ MA) [X {(г2 - a2cos20) [S^S]" -
— 2а2 [S'Sj-sin 6 cos 61 + 2агУ {[##SJ+ cos 6 -f [2?S]+ sin 6}J,
[x, v] + [x, v]* = (»/241/2"ЛГД)[2агХ {[S'^SJ-cos6+
+ 2 [2\S]-sin 0} + 7 I— (r2 - a2 cos2 ©H^^Sf 4-
4- 4a2 [&S]+ sin 0 cos 0 f 6a2 [S]+ sin2 6}]; B46)
(X, a) = A2/2 M)-1 [{-r [?>/>]- 4- 3 [РП [5]+ +
[К, а]-[%, а]*
4¦ 2r [2)Р}+) [S)~ 4- 2ia jr [3>S>P]~ - [3>P)-\ [S]+ cos в],
[X, о] 4 [A,, a]* = B4 /2" тИ) [2ta {r [^^P]+ - 2 [?>P]+\ x
X [S]~cos 0 4-1 - (r2 - a2cos20) [2>@P]- + 4r [й>/>]' - 6 [Py\ [S)+J.
B47)
Существуют довольно неожиданные соотношения, связывающие
коэффициенты Е, А1у А2, Вх и В2- Эти соотношения играют решаю-
решающую роль в \становлении разрешимости уравнений B42)—B45).
Мы перечислим их в следующей лемме.
ЛЕММА:
1) ЛХВ2 - Л2В1; (А, + Вг) (Л2 - В2) - (Аг - В,) (А2 + В2);
2) Лг + Вх = a2a/aQ cos 9 (функция только 9);
3) Л2 + В2 = а2а/гК (функция только г);
4) дЛх/дг = дЛ2/д9; dBJdr = дВ21дв;
5) д In ?/дл - Л2 — В2 — (г — М)/А\ д In E/dQ = Аг — В±;
6) Ах д In ?/аг — Л2 5 In ?/^9 - —Аг (г — МIА\
7) Вх д In Е/дг ~ В2д\п E/dQ = —Вх (л — М)/А. B48)
Поскольку ? = Zx + Z2, то по существу смысл уравнений
B42)—B45) в том, что производные функций Zx и Z2 no r и 9 можно
выразить в виде линейных комбинаций самих функций Zx и Z2. Дей-
Действительно, используя соотношения, перечисленные в лемме, по-
получаем из уравнений B42)—B45)
B50)

196 Глава 9. Гравитационные возмущения черной дыры
= + A2ZX + (в2 + l^L) Z2 - Хъ B51)
i + B1Z2-Y2. B52)
б. Условия интегрируемости. Уравнения B42)—B45), или, что
эквивалентно, уравнения B49)—B52), приводят к условиям ин-
интегрируемости, представляющим некоторый интерес. Действи-
Действительно, складывая уравнения B49) и. B51) и уравнения B50) и
B52) и вспоминая, что ? = Zx -f Z2, получаем следующую пару
уравнений:
Вследствие известных свойств функции XV (см. уравнения A73),
A75) и A76)) из этих уравнений вытекает, что
B54)
B55)
Если учесть сложность уравнений, которые определяли функции
Хъ ..., Y2, вышеприведенные соотношения удивительны — их
трудно было предвидеть. Однако в рассматриваемом случае их
можно непосредственно проверить, правильно использовав соот-
соотношения A78), A79), A83) и A84).
Уравнения B42) и B43) и B44) и B45) также приводят к паре
уеловий интегрируемости
±r (A.EW) - ± (А2ЕУ) = ^ (EY2) - -^ (EXJ, B56)
± (BtEW) - JL {B2EW) = ± (EYJ - А (ЕХ2). B57)
С помощью соотношений, перечисленных в лемме, можно приве-
привести эти уравнения к виду
в
Подставляя для величин в правых частях уравнений B58) и B59)
выражения B53), получаем следующую пару уравнений:
Д1/2 W ($)
А'/2 w ({&) ~^щ- = ~в^ + ЛЛ - A*Yi + ВЛ- B61>

92. Явные решения для функций ZL и Z2 197
Разность этих уравнений дает
Но это соотношение как раз и следует из уравнений B53) как ус-
условие интегрируемости. Однако сумма уравнений B60) и B61)
(после некоторых преобразований, в которых существенным обра-
образом используются соотношения, перечисленные в лемме) приводит
к новому соотношению
-Jr Е [(Yг + Y2) - (А, + Вг) У] = -Цр Е [(X, + Х2) - (А2 + Вг)
B63)
Это соотношение должно быть тождеством, поскольку все входя-
входящие в него величины известны. Ниже в § 94 мы рассмотрим след-
следствия, вытекающие из этого тождества.
Вернемся опять к уравнениям B42)—B45). Вычитая уравне-
уравнение B44) из B42) и B45) из B43), получаем следующую пару
уравнений:
j-EiZ,- Z2) = Е КХ, + Ха) - (Л2 + Б2) П
-^ Е (Z, - Z2) - Е [(Y, + У,) - (Аг + Вх) Y].
Уравнение B63) гарантирует интегрируемость этих уравнений,
и решение для функции Е (Zx — Z2) имеет вид
г
Е (Zx - Za) = J Е [(Хг + Х2) - (А2 + В2) У) дг, B65)
или
в
Е (Z, - Z2) = J E [(Y, + У8) - (Лх + Вг) W) d0. B66)
Это решение является лишь формальным, поскольку в подынтег-
подынтегральное выражение входит много функций. Ниже, в § 92, мы по-
покажем, как из оставшейся пары уравнений B11) и B12) с помощью
B49)—B52) можно найти явное решение для функций Zx и Z2.
92. Явные решения для функций Zx и Z2
Основным результатом исследования пары уравнений B09) и
B10) (которые были выведены из четырех линеаризованных тож-
тождеств Риччи B04)) является получение уравнений B49)—B52),
позволяющих выразить производные функций Zx и Z2 в виде ли-
линейных комбинаций самих этих функций. Покажем теперь, что ис-
используя оставшуюся пару уравнений B11) и B12), можно найти
решения для функций Zx и Z2.

198 Глава 9. Гравитационные возмущения черной дыры
Но прежде заметим, что с помощью уравнений B49)—B52)
можно в любом уравнении, в котором встречаются производные
функций Zx и Z2 (независимо от порядка этого уравнения), заме-
заменить производные любого порядка на сами эти функции. Рассмо-
Рассмотрим в качестве примера уравнения A31) и A32). Переписывая
правые части этих уравнений через функции Zx и Z2, получаем
(r/CQ/Д) sin 9 (F — G) = 0Z2/dr - ZJr - BarQ/Kp2) sin 9Zb B67)
KQ (J + H) cos 9 - dZJdQ + Z^cos 6 sin 9) + BaK/Qp2) cos 9Z2.
B68)
Подставляя вместо производных функций Zx и Z2 выражения B50)
и B51), имеем
(r/CQ/Д) sin 9 (F — G) = — (arQ/Kp2) sin %ZX +
+ [{г - М)/А - r/p2] Z2 - Хь B69)
KQ (J + Н) cos 0 = [(г2 + а2)/р2] ctg 0Zi + (a/(/Qp2) cos 6Zo + YV
B70)
Для дальнейшего анализа нам понадобятся мнимая часть урав-
уравнения B11) и действительная часть уравнения B12). Эти уравне-
уравнения могут быть записаны в следующем виде:
x, v} - {и, v)*], B71)
B72)
где
, , А
|x, v) = —
' al =
IrtTF^]' B73)
4r]. B74)
P* J v ;
Переписывая уравнение B71) в виде
^+ Р 2(^ + G)
р2 rr/ ffl
rKQ sin 6 L Д ^ U;J ~ rAQsinQ
^H«. v)-{x,vr] B75)

92. $вные решения для функций Z1 и Z2
и используя уравнение B69), получаем
д рз г arQsine 7 / r — М г
L +
= —2* (r/CQ/fif) [{x, v) - {х, v)*]. B76)
Аналогичным образом, переписывая уравнение B72) в виде
tf +Qp4J-H) = 2[{'k, o\ + {K 0)*] B77)
и используя уравнение B70), имеем
.,„ й д Р2 r(r» + a*)ctg8 7 , аК cose 7 .
sin6e" /(Qcosesine L p1 zi + QP2 Z2 + i
+ TOT2! = 2 [{X, o\ + [K oj*]. B78)
Расписывая теперь левые части уравнений B76) и B78) и снова
подставляя вместо производных функций Zx и Z2 выражения
B49)—B52), получаем после довольно громоздких преобразований
следующую пару уравнений:
[(р2/А) (а2 - М2 - К2) - (а/К) |Aa2cos26 + 2rp2 (г~М)~2гЩ] Z2 +
+ (Зао/К2) (г2 AQ sin G) Zx = (arQ/K) sin 6 AX2 +
> (г - M) - гЛ] X, + (rKQ/a) | А -^ l*' VJ ~l*' VJ -
-2/[{х, v}-{k, v}*]], B79)
[p2 (Q2 __
— Ca2a/Q2) (K cos2 9) Z2 = - [(r2 + a2) ctg 9] Yx + (a/C/Q) cos 9 Y2 +
^a^Q]*+2[{^ o} + {%, a}*] j, B80)
где
{x, v} — {x, v}* =
= (t/24 /2 MJS){Y \(r2-~a2co
— 2arX{[2?5?5]+cos9 + [S?5]+sin9}l, B81)
= A/24 /2" Af) [|(r2 - a2 cos2 9) [^5^5P]+ - 2г [2)Р}+\ [S]+ -
- 2ш {г [3>3>P\- - [2>P]-) [S]~ cos 9]. B82)
Теперь очевидно, что достаточно любого из уравнений B79) и
B80) для определения функций Z3 и Z2, поскольку их сумма равна
Чг. Удобнее, однако, анализировать оба уравнения, используя
присущую им симметрию, что мы и сделаем.

200 Глава 9. Гравитационные возмущения черной дыры
а. Преобразование решений для Zx и Z2. Заменим в левой части
уравнения B79) функцию Zx на W — Z2, а в уравнении B80) сде-
сделаем аналогичную замену Z2 -> W — Zx. Кроме того, в правых
частях этих уравнений заменим функции Х2 и Y2 выражениями
B54) и B55), содержащими только функции Хг и Ух. Уравнения
B79) и B80) при этом принимают следующий вид:
р2 [A/Л) (я2 - М* - К2) - (оА/К) \ 1 + 2г (г - М)/А - ЗгаЩ\] Z2 =
_ arQsine д UU2± JV_ Зга „
~ К [ дг д!/2 К
д . г — М Зг
+
-2i[{x, v)-\x, v}*]J, B83)
p2 [(Q2 _ cosec2 0) + (QQjQ sin 0) C sln2 0 _ 2 + (Заа/Q) cos2 0 sin 0)] X
aKсоз8 / ЗУ Зшхсове
7 _
x zi0 (,аё о )
(^ ) ^] , a] - [X, a]*\ +
B84)
Подставляя теперь сюда выражения для спиновых коэффи-
коэффициентов B46), B47), B81) и B82), получаем следующие решения
для функций Zx и Z2 (мы опустили общий множитель 1/24 Y2M):
р2 [(Q2 - cosec2 0) + -q^- C sin2 Q - 2 + -|^-cos2 0 sin в)] Zx =
j rcos 0
+ /C cos 0 {{[&S]- - [ctg 0 + Cao/Q) cos 0] [S]~ +
i(/-2 - a2 cos2 0) [^)^)P]+ - 2r
— 2ia U^S]+ - A/sin 0 cos 0 + 3a0cos 0/Q) [S]+ + Q [S]"} X
X \r \SbSbP\~ - [3>P\~\ cos 0 + 2a2 [?>@P]+ [S)~ sin 0 cos в|, B85)
p2 [(a2 - M2 - /B)/A - (oA!K) \l + 2r(r- M)/A - 3r2a//C}]Z2 =
X |(r2 - a2 cos2 0) [SSST - 2a2 [S'S]" sin 0 cos 0[

92. Явные решения для функций Zx и Z2 201
х \{gg?sr cose + [gs)+ sin e| + 2/- [s^sr *]. B86)
Разумеется, необходимо, чтобы функции Zx и Z2, определенные
уравнениями B85) и B86), удовлетворяли требованию
Zi + Z.^Mffi + rOtf^. B87)
б. Дальнейшие следствия из уравнений B11) и B12). Мы рас-
рассмотрели мнимую часть уравнения B11) и действительную часть
уравнения B12). Остается исследовать действительную часть
уравнения B11) и мнимую часть уравнения B12), которые имеют
следующий вид:
—iK{F\ - F\) 4- А Щг - /2 (tar sin 9) В2 +
+ /2" (a2 sin 9 cos 9) (F - G) = - /2" [{и, v| 4" К v}*], B88)
— (iaQ sin 9) p2 (Fl - F3) + ia sin 9 -|^- 4- /2" (a2 sin 9 cos 9) d -
a) - \K o\*]. B89)
На первый взгляд кажется, что уравнения B88) и B89) задают
функции U и V, которые до сих пор не были определены: с самого
начала нашего исследования в § 86 функции U и V всегда появля-
появлялись в комбинациях (F\ + F* — О) и [р2 (F% -f Fl) 4- V], не-
несмотря на то что в выражения A27)—A30) для Въ В2, Сг и С2 они
входили явно. Однако, как мы сейчас удостоверимся, члены с U
и К в уравнениях B88) и B89) тождественно сокращаются. Дейст-
Действительно, в уравнении B88), кроме члена Л?/,г, функция О появ-
появляется в решении для В2 и (F\ — F\) (уравнения A28) и A87)).
Выпишем эти члены и найдем, что
т=- А -з- -г* -^i? ^— U \~ V 2 (tar sin 9) -rr? -^— U 4-
рр2 j/2 ar |_ A i/C p2 J x 7 iK p2
.-^- = 0. B90)
Аналогично в уравнении B89) пом iMO члена (ia sin 9; V,q функ-
функция V появляется в решениях для CL и (Fl — FI) (уравнения A29)
и A89)). Выписывая эти члены, получаем
+ (iaQ sin 0) [-^ ^ D- " ctg 0) (р* -^L W) j +
+ >' 2" (a2 sin 0 cos 0) ~^ iKV + ia sin 0 -^- =
^ _ igW. y ^ _ ctg e) -g- - 2'a2 УcoseKV = 0. B91)

202 Глава 9. Гравитационные возмущения черной дыры
Заключаем отсюда, что в выбранной нами калибровке
^ = 4^3= ^2° -0 B92)
функции
U = A\ + Al и V = Al + At B93)
остаются неопределенными. Этот результат согласуется с тем, что
после выбора калибровки B92) у нас еще остаются четыре кали-
калибровочные степени свободы. Мы можем использовать этот произ-
произвол и положить
U = V = 0. B94)
Другими словами, можно положить все четыре диагональных
элемента матрицы А равными нулю.
93. Завершение решения
Имея явные выражения для функций Zx и Z2
Zx ^ K(J — Н) cos 9, Z2 - —irQ (F + G) sin 9, B95)
можно выразить через эти решения все другие функции, необхо-
необходимые для определения возмущений метрики. Действительно,
уравнения B69) и B70), т. е.
(rKQ sin б/А) (F — G) =
= — (arQ sin 9ДО) Z1 + [(г — М)/А — r/p2] Z2 — Хъ B96)
KQ (J + Н) cos 9 - [(г2 + a2) ctg е/р2] Zx + (аК cos 9/p2Q) Z2 + Yl9
B97)
дают решения для функций F — G и / -f H-
Уравнения A28) и A29), записанные через функции Zx и Z2,
дают решения для функций В2 и Сх. В калибровке U = V = 0
находим
']' <298>
nr ir (p2a — aQ sin 6) 7
УС>1 "" p2/(Qcose Zl "
^ Г v i / flacose (r2 + a2j ctg 6 \
"" rQsinG L 2 + \~Q P /
Явные выражения для функций Хх -f- X2 и Y± -\- Y2 будут
даны в § 94 (уравнения C19) и C20)); эти уравнения вместе с B54)
и B55) для функций Хх — Х2 и Yx — Y% явным образом опреде-
определяют функции Xv ..., К2.

93. Завершение решения 203
Решения для функций В2 и Сх определяются уравнениями
B98) и B99), а решения для функций Вг и С> следуют из уравнений
A27) и A30):
A/С/Д) Bi = Bш cos e/p2) d — д (J + Н)/дг, C00)
QC2 = - Bшг sin e/p2) Я2 + -j^ -^-(F-G) sin 9. C01)
И наконец, уравнения A34) и A36) (или уравнения B20) и B21) и
A87) и A89)) завершают решение. Выраженные через функции
Zx и Z2 эти уравнения принимают следующий вид:
= - (ia/rKQ cos 0) [(r2Q sin 0) Zt - (aK cos2 0) Z2] + [к, v] -j- [%, v]*,
C02)
= + (ia/rKQ cos 0) [(r2Q sin 0) Zj - (aK cos2 0) Z2] + [k, a] + [K, a]*,
C03)
ОЛ/ТИР1 p2\ i ; /C2P4-2a2 A2 cos26 7 L
Q/l/ 2 ) (F2 - F0 + i 2A/CVcose ^i +
+ 7XQitae[(— T^-^J + ^IFX^Hk.v), C04)
^ 2/P3 Р4ч . QV + 2aV» sin2 0 7
2rp2Q2sin6
C05)
Функции спиновых коэффициентов, которые появляются в пра-
правых частях C02) и C03), были уже выписаны явно в уравнениях
B46) и B47), а дополнительные функции, появляющиеся в уравне-
уравнениях C04) и C05), имеют вид
(х, v> = A/2р2)[(А/2) (р*х* - рк) + Bр*/Д) (P*v - pv*)] =
= (j/12/2" МД) [гК [SSY—aX \[&S}+ cos 0 + 3 [S]+sin вЦ, C06)
<*,, о) = A//Тр2)[р2 (Р2Х* - Да/2) - (р*J (р2Х - Да*/2)] =
= A/12 /2 УИ)[{—г [^)РГ + 3 [Р]-} [S]-+ w [^Pj+[5]+ cos 0| C07)
Решения для метрических функций в калибровке U = V = 0
удовлетворяют следующим тождествам:
UKIV2) {F[2 - F?) + (mr sin0) В2 - (a2sin0cos в) (F - G) =
= [{x, v} + {x, vl*j, C08)

204 Глава 9. Гравитационные возмущения черной дыры
(Qp7/2) (Fl - Ft) + (to cos 9) Cx -b r (J + H) =
= (i/asin9)[{A,, a} - {X, a}*]. C09)
Эти тождества следуют из уравнений B88) и B89) вследствие
сокращения в них членов с U и V.
94. Интегральные тождества
Увлекшись решениями уравнения Ньюмена—Пенроуза мы
пропустили несколько интересных вещей. Прежде всего функции
31 и 9* дают явные выражения для неопределенных интегралов
г
Ж = Д1/2 J [Y + 4Ха (Ух + T^rX] A~3/2 dr,
C10)
g> = J {[S]~cos 9 -f- [4a (Яа2 - 6a2;/a (^i + Гх)] [S]+} d9.
Можно ли было догадаться, глядя на эти интегралы, что они
могут быть вычислены в явном виде?
Другой особенностью является существование уравнений B01)
и B02), связывающих функции Й?и^с функциями Тьюкольского.
Нетривиальность этих уравнений становится очевидной, если по-
поставить вопрос о том, как удостовериться в их справедливости.
Члены в левых частях этих уравнений могут быть выражены
через функции X (= Р+2 + Я_2) и Y (= —iP+2 -f iP^) или
через функции [S]+ (= S+2 + S_2) и [S]~ (= S+2 — S.2) с по-
помощью уравнений
di% _ ! (у i 4^a ry\ i r —м
d2^ _ 1 / dF 4Xa dX 4A,a y\
+"^Г+ТГ / + A1 ' ( ^
d^ rci- n i 4a(tax2 — 6a2) rCl.
w = [S] cos 9+ fl(V1 + ri) tgi>
a2 —6a2) d
C14)
поскольку нам известны выражения функций 31 и ^ через X, К,
[S]+ и [5]- (уравнения A80) или A81) и A85) или A86)), а произ-
производные функций X, Y, [SY и [S]~ выражаются через сами эти
функции в силу уравнений G4) и G9). Сложность этих соотноше-
соотношений, которые необходимо подставить в уравнения B01) и B02) для
сведения их к тождествам, и является мерой их нетривиальности.
И обратно, можно написать для функций 31 и 9 такие диффе-
дифференциальные уравнения, в которых нет и намека на функции Тью-

94. Интегральные тождества 205
Кольского. Действительно, выражая производные функций Хи Y
в уравнении C12) через сами эти функции с помощью A50) и A51),
получим второе уравнение, связывающее X и Y с производными
функции 01, и это второе уравнение вместе с уравнением C11) поз-
позволяет выразить функции ХиКпо отдельности через31 и ее пер-
первую и вторую производные. Подстановка этих последних соотно-
соотношений в правую часть уравнения A97) даст дифференциальное
уравнение второго порядка для функции 3ty в которое не входят
X или Y. Выпишем результат перечисленных операций
- (А2 + 1Lг- + г(р*а* - 1I Гд.2* (г - М)Я]|, C15)
где
[det],. = A [(fr* - 1LJ" + (/.V + (?) ^
C16)
Аналогичным образом получаем уравнение для функции 9*
L\±(q±^\ ( 4«2q2 0А yl _
Q LdO ^ d0 Q У V Q2 V / J ~
? i №> + 2^ ct§ 0) (92 - cos2 0) -
Aqp Л
2^17 cos e — Pi cos e sin 9] -^-j, C17)
где
[det]e == (I/Pi) [pi^ sin 6 + (ax + ptQ) (^2 - cos28) + <g\ (^ + COs29)],
C18)
я ¦= 4a (A,a2 - 6a2)/a (^ + I\).
a. Другие тождества, получаемые из условия интегрируемости
B53). Нелишне напомнить, что явные выражения для 31 и 9* через
функции Тьюкольского удалось получить с помощью тождеств,
вытекающих из условия интегрируемости, рассмотренного в § 87.
Кажется поэтому, что условие интегрируемости B63) уравнений
B65) и B66) должно приводить к аналогичным тождествам. Для по-
получения этих тождеств необходимы явные выражения для функций
Хг + Хо и Yx + Y2. Найдем их исходя из определений B41) и

206 Глава 9. Гравитационные возмущения черной дыры
выражений для различных «скобок» B46) и B47). После громозд-
громоздких преобразований получаем следующий результат:
Xi + Х2 = (rX/a A) [GL (в) - Da2Q cos 0/p2) G2 (9) ] +
+ (Г/А) [G3 (в) — Da2Q cos 6/p2) G4 (в) ], C19)
Yx + Y2 - [SI- (cos в) [F, (r) - DrK/p2) F2 (r)] +
+ (ild) [SY \F3 (r) — Drtf/p2) F, (r)]. C20)
Здесь опущен общий множитель 1/24 У2М. и, кроме того,
Fx (г) = К {2>?>Р)+ + 2га [^Р]+,
F2 (г) = г [^5^)Я]+ - [ФРТ,
F3 (г) = ЗКг [&&Р]- - 2а2о \®Р\~ - 6га [Я]",
F4 (г) = г2 \&2)Р\- - г
2ao[S?S)-cosQ, C21)
G2 @) = [SSPSy cos 0 + [^5]- sin 0,
G3@) = 3Q [SSS}+ cos0 + Ba2o/a) [S75]+ + 6«o [5]+ cos 0 sin 0,
G4 @) = [22?S}+ cos2 0 + [gS]+ cos 0 sin 0.
Несложно проверить, что функции Fit ..., G4 удовлетворяют
следующим соотношениям:
Fi - 2/С [^^>Р]+ = - V4 («*1 + Гх) Л,
F3 - 4KFjr = iff (Xa2 - 6а2) 5Z
G3 - 4QG4/cos 0 = V4 (*i + Гх) ^.
Обратите внимание на появление в этих соотношениях функций
31 и ?\
Возвращаясь к условию интегрируемости B63), заметим, что
оно требует равенства двух выражений
1 д Г д р ,7 7 \\ —
Y2) + (Л2 + В2) 4*
в,) ^ -If (w) + ^ + в)
If (w) + ^ + в>) ж +
} C23)
(А - 5,) (*! + х2)

94. Интегральные тождества 207
+ (А + Si) Д JrOF/A'/*) - {(А + fix) A! ()
-f Ma + В2) -§f- + (А - Вх) (А + В2) У]. C24)
Заметим, что выражения в фигурных скобках в обоих уравнениях
совпадают, следовательно, достаточно рассмотреть только осталь-
остальные члены.
Подставляя вместо Хх + Х2 и У\ + Y2 выражения C19) и
C20), находим, что эти оставшиеся члены в уравнениях C23) и
C24) можно привести к следующему виду (если надлежащим об-
образом использовать различные соотношения B48) и C22), а также
тождества для функций Я и 9>):
Д1/2 i (-$г) - 2Fi/r + B
ii^M]^'(з25)
2а% ]
f
[d 1 \\ rX
-je~ (QG2) — aoG2 cos 9 4- l/2Gi sin 9 м —- -j-
au j)\ а д
% , n sin 0 „
r ]
^(QG4) - aaG4cos 9 + V,G8sine]}] L. C26)
Нашей целью является приведение уравнений C25) и C26)
к такому виду, чтобы, помимо простых множителец типа г2 или
cos2 9, в них входили только функции X, К, IS]+ и IS]-, а их
производные отсутствовали. Необходимые для этого преобразо-
преобразования, хотя и не столь громоздкие, как при исследовании условий
интегрируемости в § 87, тем не менее не являются простыми. В ре-
результате получаем
+ 2or (a2 + a2 cos2 9) (XX -
-I- -Щ- [a (^a2 - 6a2) (— r2 -f 3a2 cos2 6) (Y + -=^
- 2a2o {6or (r2 - a2) X -(- \{Ы1 - 6a2) + 3 (X -f 2) г2] Г) cos2б], C27)

208 Глава 9. Гравитационные возмущения черной дыры
{Хаа (-,• + Мcos»в) {[5Г cos9 + ffff
- 2ао (г2 - а2) {А, [5]" + бас [5]+ cos 6} cos в] +
^ + г>) (-3rS +а2 cos2 0) {isrcos 0
cos2
- [(Xa2 - 6a2) - 3a2 (X + 2) cos2 9] [5]+} J. C28)
Сравнение этих выражений показывает, что они совпадают.
После некоторой перегруппировки членов в уравнениях C27)
и C28) мы можем теперь записать вместо C23) и C24) одно-един-
одно-единственное уравнение
-1 = э5ё ^ Bi - Z2) = ко [- 3 (r2~a2 cos2 в) + 2а2] r*ff
+ {V* («\ + 1\) (— Зг2 + a2 cos2 в) - 12oV2 (а2 + a2 cos2 9)} х
X
- 12а2о2 (г2 - a2) cos2 е}r^ f2S|+ + (о (Act2 - 6a2) (— r2 + a2 cos2 0) —
{ ^ ^ (Л2 + B2) ^- + (Лх + Bt) (A, - B2) ?}.
C29)
Полагая
fi = Ala/^ + I\),
9 = 4a (Aa2 — 6a2)/a (^ + I\), C30)
можно переписать уравнение C29) в более удобной форме
4^ ^ C0S 9 +
V,y [S]+l -!- 74a2 (9t + Гх) (У + 3^rX) {[S]" cos 0 + 9 [5]+) cos2 0 -
12oV2r (a3 j- a2 cos2 0) [S]~ cos 0 - 12acr2 (r2 - a2) rX [S]+ cos2 0 -|-
+ 2a?XerX \S]- cos 0 - 6ao (X + 2) f-Y [S]+ cos2 0 -
или
+-^-л US]-cose + у [S]+}},
a2a ^? 5

94. Интегральные тождества 209
Альтернативные формы для членов в последних двух строках этого
уравнения следуют из соотношений B48).
Решение для функции (Zx — Z2) может быть теперь сразу же
выписано, если проинтегрировать по г и 0 выражение в правой
части уравнения C31), умноженного предварительно на
Е/р2 Д - (г2 A*K)-]/2(Q cos2 9 sin 9)-1/2. C32)
Поскольку ?Ур2Д является произведением функции от г и функции
от 9, ясно, что решение для (Zx — Z2) получаемое интегрированием
по /* и 9, является суммой произведений интеграла по г и интеграла
по 9. При этом появляются радиальные интегралы шести типов:
интегралы от функций rX, r3X, У и r2Y с весовой функцией
(г2К Д3)~1/2 C33)
и интегралы от функций 01 и г201 с весовой функцией
(г*К3 А)/2. C34)
Аналогичным образом мы встретимся с шестью типами угловых
интегралов:
от функций IS ]+, [S ]+ cos2 9, [S ]~ cos 9 и [S ]- cos3 9 с весовой
функцией
(Q cos2 9 sin 9)-1/2 C35)
и от функций 9* и ЗР cos2 9 с весовой функцией
(a2Q3 cos4 9 sin 9)-1/2. C36)
Будем обозначать различные интегралы (с указанными весовыми
функциями) символами подынтегральных функций, заключен-
заключенными в угловые скобки. Так, например,
= | rsX (r2K A3)'2 dr,
е
{9> cos2 0 ) = J 9> cos2G (a2Q3 cos* 0 sin б)-'/2 dG. C37)
В этих обозначениях решение для функции (Zx — Z2) имеет вид
Е (Zt - Z2) = - V4 («\ + I\) {{r*Y) + p (r*X)} {([S]- cos 6} +-
+ Ve? ([5j+)} + V4a2 («-i + ГО {(Г) + 3^ (rX)} {([ST cos'' в) +
+ ?([S]+cos29)) - 12a2(r2K){a2([S]-cos0)
- 12aa2 ([S]+ cos2 0) {(/-3X) - a2
+ 2a2Xo (rX) ([S]- cos 0} - 6aa (X + 2) (r2Y) ([S]+ cos2 0)
- 74а2<т (^ + ГО {{[Я/г (ДКI/2] {r2 E^) + a2 (^ cos2 0}}
-h (r2^!) {([S]- sin 0 f y ([S]+)} + tf (Я) {({S}- cos-^ 0) +
4- y<[Sl+ cos20)}], или

210 Глава 9. Гравитационные возмущения черной дыры
s29} \-
f p(rX)\}\. C38)
Интегральные тождества получаются из уравнения C38) для
функции (Zx — Z2) точно так же, как получаются интегральные
тождества из уравнения A66) для функции Т. Чтобы найти эти
интегральные тождества, продифференцируем решение C38) по г
и по 0 и приравняем результирующие выражения тем выражениям,
которым, как мы знаем, они должны быть равны, т. е. уравне-
уравнениям B64). Таким путем приходим к следующим уравнениям:
= (p2G1-№QG2cosQ)-%3
+ (РЮ3 - ia*QG4 cos 0) -^ -
= 1-74 (?i + ГО г2 (У + frX) \{[S)~ cos 0} + Vs?
+ Via2 (^i + Гх) (У + 3/ггХ) {{[5]- cos3 0) + y ([S]+ cos2 0)} -
- 12о2/-2У {a2([S]-cos0) + a2([S]-cos30)} -
"- 12ao2 (r2 - a2) rX ([S}+ cos2 0) + 2Xa2orX ([S]~ cos0) -
- 6aa (K + 2) г2У ([5]+ cos2 0) - 4ta*o (Vt + Ty) (Y + ^rX) x
X {/-2 (^) + a2 (^ cos2 0)}] (Q sin 0)'/2 cos 0/Ap2 -
- [a2o (W1 + ri)/4r/C] ЛР', C39)
ap2
+ Г,) {(г2У) + /г (r'X)} {[5]-cos 0 + W/ [S]+l ^-
- 12o2 (г2У) (a2 + a2 cos2 0) [S]~ cos 0 -
- 12aa2 {(r3X) - a2 (/-X)} [S]+ cos2 0 +
+ 2?ux20 (rX) [S]~ cos 0 - 6ao а + 2) (r2Y) \S]+ cos2 0 -
os20; {[5j"cosO ь-
-h у 15Г)] [/-(А/О'^/р2] - [a^^! + rj)/4aQ cos 0] Й^. C40)

94. Интегральные тождества 211
Члены, пропорциональные Я91', сокращаются как в уравнении
C39), так и в уравнении C40). Оставшиеся члены в уравнении
C39) представляют собой функции 9, умноженные на r3X, rX,Y
и r2Y. Следовательно, можно приравнять функции 0, имеющие те
или другие радиальные множители. Подобным же образом можно
приравнять в уравнении C40) функции г, появляющиеся с угло-
угловыми множителями [Sl+, \S]+ cos2 Э, [S]-cos0 и [Sbcos3 0.
Получаем следующие восемь тождеств:
cos 0) + 7.,? ([S]+) +
+ V3a2o (^}} - 12а3о2 ([S)+ cos2 0), C41)
Ев (Gx cos2 0 - 4QG2 cos 0) = ЗХаа \([S)- cos3 0) -f
4- 9 ([S]+ cos2 0) - 7«а2а (9> cos2 0)} 4-
+ 12а2а2 ([S]+ cos2 0) 4- 2% (a2a/a) ([S]" cosO), C42)
E<>G3 =-. - % (Vi + Ti) {([Sj- cos 0) -\- %9 {[S]+) 4-
-|- '/Уо (9>)\ - бао (A, + 2) ([5]+ cos2 0) -
- 12o2 [a2 ([S]- cos 0) + a2 ([S]" cos^)}, C43)
?e (G3 cos2 0 - 4QG4 cos 0) = l/tE9 (&i -f Г,) ^ cos2 0 =
- V4 (^i + Г,) (([5]- cos18 0) f 9 ([S]+ cos2 0) - а2а <5? cos2 0», C44)
E,,FL = V4 (^i H - Г,) |(F) + 3/г</-Х) - а2о (Я)} - 12o2 <r2F), C45)
% (*i -h Гх) |(г2Г) +
^ 4- VscAr (r2^)} - 12а2о2 (rW) + 2Ха2о <гХ>, C46)
iErF3 = V,a («?x + I\) у {(У) 4- 3^ (rX) - a2o (Я)} -
- 12o2 |(/-3X) - a2 <rX)} - 6a (Я 4- 2) (r2F), C47)
IE,. (r*F3 - 4rKF4) = - V4?ra («"г + Гх) ,уг2^ =
= - 7,a («'i + Г,) y \{rW) -f Л (r3X> 4- a2a (/-2Й)}, C48)
где
Er = (г2 А/С)-»/2, ?е -"- (Q cos? 0 sin 0)-'/2, ? = ?r?6p2. C49)
Заметим, что в соотношениях C44) и C48) использованы два
из соотношений C22).
Другие тождества получаются в результате интегрирования
уравнений
(o/p2aQ cos 0) (r2a2 - a2a2 cos2 0 - 2aV2 cos2 0) 9>\, C50)

212 Глава 9. Гравитационные возмущения черной дыры
= Е [(I/A) (Y + ргХ)) + (a/pV/C) {r-a? - с?о? cos2 9-2aV2 cos2 9) #].
C51)
Находим, что
Еъ9> = <[SJ- cos 9) + ^ ([S]+> + a [a2 (У) - 2a2 (У cos2 9)], C52)
Еъ9> cos2 9 = <[S]- cos3 9) + 9 <[S]+ cos2 9) - a2a (^ cos2 9), C53)
ЕГЖ = (Y) + p (rX) - a [a2 Щ + 2 <r2^)], C54)
га?гЯ = (r2Y) + ^ (r3X) + a2a (r2^). C55)
Но два из этих тождеств C53) и C55) совпадают с полученными ра-
ранее тождествами C44) и C48).
Отметим, наконец, что с помощью восьми вышеприведенных
тождеств решение для функции (Zx — Z2) (уравнение C88)) может
быть переписано следующими двумя альтернативными способами
(мы здесь восстанавливаем множитель (l/24 j/r2M)i который был
опущен в уравнениях C19) и C20)):
(г2 ЛКI/2
a (d cos2 9 - 4QG2 cos 9) (rX) + G3 (rW) +
- 74a2a (W, + Гг) 9> [(гЩ + a2 (Я) cos2 9]} =
QS39)
1 1V J 7
+ (r2F, - 4rKF2) ([S]- cos 9) + iaF3 ([S]+ cos2 9) -
- V^i + rx) 9([S]+)rW-
- V4a2a (Уx + Гх) Я [г2 (У) + a2 (^ cos2 9)] j. C56)
Для шести интегралов, которые появляются в каждом из двух
альтернативных выражений для решения (Zx — Z2), у нас есть
только пять уравнений, связывающих их с известными функциями.
Ситуация, следовательно, отлична от ситуации, получившейся
при исследовании решения для функции W: тогда решение опре-
определялось однозначно. К счастью, явные решения для функций Zx
и Z2 были найдены независимыми способами. Тем не менее появле-
появление различных интегральных тождеств — это проявление соотно-
соотношений, природа которых скрыта во мраке.

95. Ретроспектива 213
95. Ретроспектива
Исследование, которое мы только что закончили, было на-
настолько сложным и запутанным, что нелишне будет распутать
основные нити.
Анализировалась задача о гравитационных возмущениях чер-
черной дыры Керра, описываемых уравнениями формализма Нью-
Ньюмена — Пенроуза. Основной проблемой является определение
изменений компонент метрики, вызванных возмущением. В фор-
формализме Ньюмена — Пенроуза возмущения метрики прямо
связаны с изменениями 11A) базисных векторов 1' (= 1, n, m, т).
Изменения базисных векторов описываются матрицей А пре-
преобразования
l'A) = A\V. C57)
Кроме элементов матрицы А, нужно найти возмущения пяти
вейлевских скаляров и 12 спиновых коэффициентов — всего
50 действительных величин. Для нахождения этих величин у нас
есть 8 тождеств Бианки, 12 коммутационных соотношений и
18 тождеств Риччи — всего 76 действительных уравнений. Иско-
Искомые решения должны быть совместны с десятью калибровочными
степенями свободы — шесть из них соответствуют возможности
бесконечно малых преобразований Лоренца для тетрадного ба-
базиса, а четыре степени свободы соответствуют возможности бес-
бесконечно малых координатных преобразований.
Исследование показывает, что наиболее естественной для рас-
рассматриваемой задачи калибровкой является калибровка, в ко-
которой
W{ = Ъ = Ч#} = 0, Л} = А\ = Al = At = 0. C58)
Этот выбор исчерпывает весь допустимый калибровочный произ-
вол и полностью фиксирует калибровку. Следующее ниже опи-
описание основных этапов исследования опирается на этот выбор
калибровочных условий.
Четыре из тождеств Бианки и два из тождеств Риччи допу-
допускают явные решения для вейлевских скаляров ?0 и 4я4 и спино-
спиновых коэффициентов х, аД и v; т. е. решения для тех величин,
которые равны нулю в фоновой геометрии Керра в силу при-
принадлежности последней к типу D по классификации Петрова.
Разделение переменных в уравнениях для вейлевских скаля-
скаляров Wo и ?4 и выражение решений для них через радиальные и
угловые функции Тьюкольского R±2 и 5±2 соответственно сде-
сделало возможным изучение решений для остальных величин.
Для последующего анализа почти столь же важными оказались
замечательные тождества Тьюкольского и Старобинского. Но
этот анализ не позволяет определить относительную нормировку
решений для функций R+2 и /?_2, и аргумент комплексной

214 Глава 9. Гравитационные возмущения черной дыры
постоянной Старобинского — серьезный пробел в информации,
которая нам необходима.
Четыре оставшихся тождества Бианки позволяют выразить
спиновые коэффициенты р, т, fx и я прямо через элементы ма-
матрицы А.
Основные уравнения для определения элементов матрицы А
получаются в результате линеаризации 12 коммутационных
соотношений. Это линейные неоднородные уравнения, причем
неоднородные члены являются линейными комбинациями воз-
возмущенных спиновых коэффициентов. Последний факт позволяет
сгруппировать 24 получающихся уравнения в три системы (си-
(системы I, II и III) по восемь уравнений в каждой. Действительно,
если решения для возмущений спиновых коэффициентов р, т,
ft и я выразить через элементы матрицы А, а решения для спи-
спиновых коэффициентов х, а, X и v выразить через функции Тью-
кольского, то две из трех систем уравнений — однородная си-
система I и неоднородная система II — становятся уравнениями
для 12 линейных комбинаций элементов матрицы А, которые были
обозначены следующим образом:
F + G, J — Я, F — G, / + Я,
Въ Въ Съ С2, C59)
Остальные восемь уравнений системы III служат для определе-
определения возмущений спиновых коэффициентов а, р, у и е после того
как найдено решение для матрицы А.
Только шесть из восьми уравнений системы I независимы.
Но они позволяют выразить шесть линейных комбинаций C59),
именно комбинации
F — G, J + Н, В1з 52, С19 С2, C60)
через функции F + G к J — Я.
Восемь уравнений системы II (записанных в альтернативной
форме A33)) разбиваются на две системы по четыре уравнения
в каждой (уравнения A34)—A37) и A87)—A90)). Первая система
приводит к важнейшему в теории условию интегрируемости,
решением которого является функция
? - К (J — Я) cos 9 — irQ (F + G) sin 9. C61)
Решение условия интегрируемости является, наиболее трудоем-
трудоемкой частью всего исследования и приводит к значительному
упрощению формул. Это решение является также архимедовой
точкой опоры для теории: удается ликвидировать две основные
неопределенности — найти относительную нормировку решений
для вейлевских скаляров Wo и 4% и вычислить аргумент постоян-
постоянной Старобинского. Наконец, наиболее важно то, что решение

95. Ретроспектива 215
условия интегрируемости открывает путь к установлению новых
неожиданных соотношений: разделению переменных для функ-
функции W и представлению ее в виде произведения радиальной функ-
функции 31 и угловой функции 9>\ выводу двух систем уравнений,
связывающих функции 31 и 9* с функциями Тьюкольского,
и, что удивительнее всего, получению с помощью функций 31
и 9> явных выражений для некоторых неопределенных интегра-
интегралов от функций Тьюкольского.
Условия интегрируемости для других четырех уравнений из
системы II являются дифференциальными уравнениями для
функций 31 и 9, связывающими их с функциями Тьюкольского.
Используя эти уравнения, можно получить такие дифференциаль-
дифференциальные уравнения для 31 и &, в которых нет и намека на функции
Тьюкольского и с помощью которых можно в принципе исключить
функции Тьюкольского из теории. Оставшиеся уравнения из
этой системы вместе с подобной же парой уравнений первой си-
системы из четырех уравнений позволяют выразить последние че-
четыре функции
Fl±Fl Fl±F\ , C62)
через функции F + G и / — Я.
После завершения редукции системы II остается только один
пробел: для полного задания всех функций, перечисленных
в C59), необходимо определить F-f G и / — Я по отдельности.
Удобнее ввести новые функции
Zx = К (/ — Я) cos 9, Z2 - -irQ (F + G) sin 0. C63)
Проблема теперь состоит в том, что известна сумма функций
Z± + Z2 (=ЧГ), но не известна другая линейная комбинация Zx
и Z2.
На этой стадии мы уже полностью использовали тождества
Бианки и коммутационные соотношения, поэтому необходимо
рассмотреть тождества Риччи.
Четыре тождества Риччи, выбранные нами для исследования,
разбиваются на две пары уравнений. Первая пара позволяет
выразить производные функций Zx и Z2 по г и по 0 через линей-
линейные комбинации самих этих функций и вдобавок дает еще одно
условие интегрируемости. Вторая пара совместно с соотноше-
соотношениями, найденными при исследовании первой пары уравнений,
позволяет завершить решение получением явных выражений для
функций J?! и Z2 по отдельности. В то же время условие инте-
интегрируемости приводит к восьми очень сложным интегральным
тождествам.
Итак, для нахождения решений для 40 различных величин
и получения 10 интегральных тождеств пришлось использовать
26-комплексных уравнений (8 тождеств Бианки, 12 коммутацион-
коммутационных соотношений ц 6 тождеств Риччи). Два из вышеупомянутых

216 Глава 9. Гравитационные возмущения черной дыры
интегральных тождеств, в которые входят функции 31 и &,
чрезвычайно существенны для анализа: без них решение нельзя
было бы довести до конца.
Наше исследование наталкивает на важный вопрос (особенно
в § 94): может ли избыточность уравнений Ньюмена — Пен-
роуза — 60 уравнений для 50 величин, допускающих еще 10 ка-
калибровочных степеней свободы, — привести к открытию новых
классов интегральных тождеств между функциями математиче-
математической физики, которые являются решениями уравнений Эйн-
Эйнштейна?
Оставляя в стороне детали, отметим в заключение замеча-
замечательный факт, что систему 60 уравнений, описывающих суще-
существенные свойства пространства-времени Керра, удается решить
во всей полноте.
96. Вид решения в шварцшильдовом пределе а -> 0
Представляет интерес шварцшильдов предел а -> 0 получен-
полученных выше решений: помимо всего прочего, это позволит предста-
представить основные тождества в наиболее простом и в некоторых слу-
случаях наиболее легко проверяемом виде. Заметим, что, как видно
из некоторых уравнений, появляющихся в теории (например,
уравнений A79) и A85)), переход к пределу а -> 0 требует неко-
некоторых предосторожностей.
Отметим прежде всего, что в пределе а -> 0
Q = т cosec 0, К = г2о, р = р* = г, р2 = г2,
А = г2 — 2Мг, V1 = T1 = X(X + 2). C64)
Из уравнения A70) следует, что
+ О(а2). C65)
Далее, коэффициенты, перечисленные в уравнениях G6) и G8),
в рассматриваемом пределе равны
Ах = X (X + 2) А — 4XaV4 — 24MaV3,
Л2 - —12Мо& — 4W2 Bг — ЗУИ) + 24а?\ C66)
BL = 4аг2 [ЬД + 2М (г — ЗМ) - 2gV4];
а1 = К (I + 2) ~ 4lm2 cosec2 9,
а2 = 4A,m cos 0 cosec2 0, C67)
Pi - 4m [2 (m2 — 1) - X sin2 0 ] cosec3 0.
Наибольший интерес, разумеется, представляют предельные
выражения для функций $2, 9*, Zx и Z2. С помощью уравнений

96. Вид решения в шварцшильдовском пределе 217
C66) и C67) находим, что уравнения A80) и A81) и аналогично
уравнения A85) и A86) дают (в согласии друг с другом) следу-
следующие предельные выражения для функций 31 и 9*:
V2 [ЯЛ + 2М (г — ЗМ) — 2aV4 Я =
= {г — [2/(А, + 2)] (г — ЗМ)}агХ + [УИ — 2aV3/(X + 2)] Y,
C68)
V2 [A, sin8 9 — 2 (m2— 1)] S? =
= [тЩХ + 2) ] [S ]+ cos 9 sin 0 + *{ [2m2/(X + 2) ] —
— 1} [S]-sin 9. C69)
Эти выражения для М и 91 равны следующим неопределенным
интегралам:
9. C71)
Как уже говорилось в § 95, доказательство новых интегральных
соотношений для функций из классического анализа является
одним из удивительных следствий применения метода Ньюмена —
Пенроуза к исследованию возмущений пространства-времени.
Что касается решений для функций Zx и Z2, то тщательное
изучение предельного перехода а -> 0 в уравнениях B85) и B86)
приводит к следующему результату (мы снова опускаем общий
множитель 1/24 >/ М):
^ (я.+2) я XSin*es—2(m«—о (m [5]+ - [SJ"cos
8-2(^-1) l
+ (m2 - V»(A. + 2) A + cos2 9)] [5]}. C73)
При выводе этих формул были использованы следующие соот-
соотношения, справедливые в пределе а -*¦ 0:
т [Z&ST cosec 9 = - о (Х9> - 2 [^S]~ cos 0) a + О (a2), C74)
m \[SeSSY cos 9 + 2 [S'S]* sin 9) cosec 9 = - 1/i% (K + 2) #\ C75)
ra {/• [2>3>PY - 2 [S)P]+} = Vu*. (Я, + 2) Я, C76)
+ 2) 9> + m [&S]+ = - V« (X + 2) {- № + 2 [^S]~ cos 9} =
- XM (Я. + 2) A + cos2 9) [5]"}. C77)

218 Глава 9. Гравитационные возмущения черной дыры
Если функции Zx и Z2 заданы уравнениями C72) и C73), то
можно прямым вычислением проверить, что выполняется тре-
требуемое равенство
Z1 + Z2 = V2A, (X + 2) 919>. C78)
Решения для остальных функций, определяющих метрику,
могут быть получены, если в выражениях, приведенных в § 93,
перейти надлежащим образом к пределу а -> 0.
97. Теория преобразований и потенциальные барьеры
для падающих гравитационных волн
Обратимся теперь к задаче об отражении и поглощении пада-
падающих гравитационных волн черной дырой Керра. Как и в случае
электромагнитных волн, рассмотренном в гл. 8, сведем прежде
всего эту задачу к задаче отражения и прохождения волн через
одномерный потенциальный барьер, следуя процедуре, описан-
описанной в § 72 и 73.
Напомним (ср. с уравнениями A00) и A05) гл. 8), что в резуль-
результате замены переменных
йа = г2 + а2 = г2 + а2 + ат/а C79)
уравнение Тьюкольского B4) для функции Р+2 принимает вид
(ср. с уравнениями A08)—A10) гл. 8)
Л2 К + PA_Y — QY = 0, C80)
где
р = ^г1п4-> <381)
(О8
Зш2 (г2 - а2) - Зг2А]. C82)
Будем искать преобразование уравнения C80) к одномерному
волновому уравнению вида
Л22 - VZ. C83)
Теория преобразований, развитая в § 73, применима также
и к исследуемой задаче: нужно только в соответствующих урав-
уравнениях положить s = 2. Действительно, делая подстановки, рас-
рассмотренные в гл. 8, (уравнения A20) и A22)) и положив s = 2,

97. Падающие гравитационные волны 219
приходим к следующим уравнениям (ср. с уравнениями A30)—
A33) гл. 8):
k C84)
л \ -л2~ ^) = ~тг (QT — 2iaR) -f p, C85)
-f -^- PT = —- К, C86)
~^7) = ^Г-Н77- C87)
а. Явный вид решений. Будем искать решения уравнений C85) —
C87), имеющих вид
Т - Тг Ы + 2ш, р - рх (г*) + 2итр2, C88)
/( == Xl + 2/ах2, C89)
где р2, хх и х2 — постоянные, требующие определения, а функ
ции R и 1/ не зависят явно от частоты а в том смысле, что они
не содержат членов, линейных по ш (в отличие от функций Т
и Р). Предположим далее, что если решения такого вида подста-
подставить в уравнения C85)—C87), то можно приравнять по отдель-
отдельности члены, содержащие частоту а, и члены, не содержащие
частоту. Делая такие предположения, мы накладываем больше
ограничений, чем допустимо. Тем не менее мы увидим, что реше-
решения такого вида действительно существуют, если функция Q
(вернее, F = 58Q/A2) удовлетворяет определенному нелинейному
дифференциальному уравнению (уравнение D04) ниже). (Для
сравнения см. уравнение C11) гл. 4 и уравнение B67) гл. 5.)
Подставим теперь функции Тир C88) в уравнение C85)
и приравняем члены с множителем ia и члены, не содержащие
этого множителя. Получаем при этом пару уравнений
R - Q + (А2/й8) р2, C90)
dr*
Подобным же образом из уравнения C86) получаем другую пару
уравнений
Pi + Р27\ = х2, C92)
ar* (О8
где
4a2p2. C94)

220 Глава 9. Гравитационные возмущения черной дыры
В силу последнего соотношения можем записать (ср. с уравне-
уравнением C89))
К = (К — 4а2р2) + 2/ах2. C95)
Подставляя вместо функций R и рх выражения C90) и C92),
имеем
a^(^)-^-Q7'i-P27'1 + xa. C96)
Положим
F = (й8 /A2) Q - A/Д) [Хй4 + Зй2 (г2 — а2) — Зг2Л ]. C97)
Тогда
R = (Л2/со8) (F + ра), C98)
и уравнение C96) принимает вид
dF/dr, = 71! (f — р2) + х2, C99)
или иначе
Г! = (Г - K2)/(f - р2), где Г - /v,. D00)
Вернемся к уравнению C93) и перепишем его для функции F:
-^ (/¦ + Р2J - (F + Ра) ^ + rx(x2 - Р.Г0 = х. D01)
со8 аг*
Исключим теперь 7\ из этого уравнения, воспользовавшись
формулой D00) и соотношением
T[ = (F- рзГ2 [(F - р2) F" - (F' - х2) F']. D02)
Находим
41 (F2 - plf - (F2 - р2) F" + (F'2 - ^) F = х (F - p2f. D03)
(О8
Расписывая последнее уравнение, получаем
-'%+^fs - м - »м)+(»+2-^-
причем следует помнить, что F — известная функция. Уравне-
Уравнение D04), следовательно, налагает условие на функцию F, если
решения в предполагаемом нами виде существуют. Уравнение D04)
обобщает уравнение C11) гл. 4 и сводится к нему в случае |32 = 0.
Замечательным фактом является то, что функция F, опреде-
определяемая уравнением C97), действительно удовлетворяет урав-
уравнению D04), если выбрать
* = %(% +2), ра = ±3а2, - D05)
*а = ± {36М2 - 2Х [а* E% + 6) - 12а2] + 2р2^ (^ + 2)}1/2, D06)

97. Падающие гравитационные волны 221
причем знаки C2 и х2 можно выбирать независимо, но для про-
проверки этих утверждений требуются громоздкие вычисления.
Решение для функции V может быть найдено из уравнения
C87). Переписывая его в виде
^ ^^- D07)
(О8
и воспользовавшись уравнениями C90) и C92), получаем
*<y-Q) = -(Q + -g-b)%r- = -*%7- D08)
Таким образом,
V = Q — dTi/dr*, D09)
где можно вместо Т[ подставить выражение D02). Удобно, однако,
исключить F" из уравнения D02), воспользовавшись дифферен-
дифференциальным уравнением D03), которому удовлетворяет функция F.
В результате получаем
Vt^w')- <4I0)
Для функции V теперь находим
V— Д2 а | х
б. Функции Z(+a) w Z(~a). Как и в п. 74, а, будем различать
функцию К и функцию, удовлетворяющую комплексно-сопря-
комплексно-сопряженному уравнению, с помощью верхних индексов уч+д) и УЧ~а),
а функции, удовлетворяющие соответствующим одномерным вол-
волновым уравнениям, будем обозначать Z(+a) и Z(~a).' И снова, как
и в п. 74, ау найдем, что функции Z(+o) и Z<-a) удовлетворяют
волновым уравнениям с одним и тем же потенциалом D11).
Выпишем различные выражения функций Y^±o) через функ-
функции Z(±a) и обратные соотношения
D12)
= (р, ± 2шр2)
где (ср. с уравнениями C95) и D05))
= [X (А, + 2) — 4о2р2] ± 2tox,. D13)

222 Глава 9. Гравитационные возмущения черной дыры
Важные соотношения связывают постоянные К{+0) и К(~о)
с постоянной Старобинского ^:
К(+0)К{~0) = [X (I + 2) - 4а2р2]2 + 4а^ =
= X2 (X + 2J - 8а2Х [а2 EА, + 6) - 12а2] + 144а2 (М2 + а4а2) = |«? |2,
D14)
это соотношение свободно от произвола в выборе знаков р2 и Х2-
Существования подобного соотношения между постоянными Ста-
Старобинского & и ^* и /((+а) и /С<~~а), возможно, и следовало бы
ожидать: обе пары постоянных связывают, хотя и различным
образом, функции с s = +2 и частотой +а с функциями с s = —2
и частотой —а. Необходимость соотношения D14) для совмест-
совместности полной теории станет более ясной в § 98.
в. Структура потенциалов. Поскольку знаки р2 и х2 могут
быть выбраны произвольными и независимыми друг от друга,
уравнение D11) в общем случае дает четыре возможных потен-
потенциала для уравнения C83). Ясно также, что в зависимости от
знака величины, стоящей в фигурных скобках в определении
х2 D06), у нас будет пара комплексно-сопряженных потенциалов
(точно так же, как при исследовании падающих электромагнит-
электромагнитных волн в гл. 8).
Выпишем явный вид потенциала, заданного уравнением D11):
[х'ю'А - (д'А - Д'<?)] [к^д - р2 (<?Л - &q)]) lg
где
q = Аи4 + Зй2 (г2 — а2) — 3r2A = AF, D16)
' f й2 (Х5>2 + 6Мг - 6а2) при р2 = + За2,
Я ~ р2 ~ ( Ал4 + 6г2 (а2 - а2) + 6Мг (г2 - а2) при ря = - За2,
D17)
^'А — A'q = — 2 (г — М) ?1Й4 +
+ 2й2 BХгА — ЗМг2 — ЗМа2 + 6га2) +
+ 12гД (Mr — а2). D18)
На рис. 43 и 44 вычерчены графики потенциалов D15) для
типичных случаев.
Заметим прежде всего, что в шварцшильдовом пределе (а = 0)
р2 = 0, х2 = ±6М, X = (I — 1) (/ + 2) = ц2 = 2п,
^2 (^2 + 2) ± 12/аМ D19)

97. Падающие гравитационные волны
223
-q,qi -
Рис. 43. Потенциальные барьеры вокруг черной дыры Керра для падающих
гравитационных волн. Из четырех потенциалов, соответствующих параметрам
1=2, т = О, а = 0,9 и а2 = 0,13, два действительных (длц них х2 = ±7,848
и Р2 = +2,43) и два комплексно-сопряженных (для них х2 = ±13,288i и Р2 =
= —2,43). а — действительный потенциал с х2 = +7,848 и Р2 = +2,43, дру-
другой же действительный потенциал, которому соответствуют х2 = —7,848 и |32 =
— +2,43 в масштабе графика невозможно отличить от предыдущего, бив —
действительная и мнимая части потенциала с х2 = +13,288t и Р2 = — 2,43.

224
Глава 9. Гравитационные возмущения черной дыры
0,2
ОД
г
—0,2
Рис. 44. Семейство потенциалов для падающих гравитационных волн с параме-
параметрами а = 0,95, / = —т = 2 и частоты о в интервале 0<G^as. а — о =
= ас = 2,11, х2 = 12,311, а2 = О, |32 = 0 и к = —8,66; потенциал (кривые,
помеченные индексами / и /') комплексный и имеет как действительную, так и
мнимую часть, б — для значений о между частотой синхронного вращения и as;
о = 1,41, а2 = —0,4406 и X = —4,608; два потенциала (кривые 2 и 4) действи-
действительны и для них Р2 = 1,322 и соответственно х2 = ±6,096, а два других ком-
комплексно-сопряжены и для них х2 = ±5,137/ и Р2 = —1,322; кривая 3 изобра-
изображает один из них. в — о — os; о = 0,72, а2 = —1,722 и X = —0,478; два по-

97. Падающие гравитационные волны 225
в согласии с равенством C27) гл. 4. Четыре потенциала, таким
образом, в этом пределе вырождаются в два, и эта пара суть
потенциал Редже — Уилера и потенциал Церилли соответственно
для аксиальных и полярных возмущений шварцшильдовой чер-
черной дыры. Поэтому возникает вопрос, не может ли существова-
существование в общем случае четырех потенциалов для черной дыры Керра
указывать на некоторую внутреннюю симметрию (помимо чет-
четности).
Отметим далее, что все потенциалы имеют общее свойство,
убывают обратно пропорционально квадрату радиуса при г -> оо
и экспоненциально стремятся к нулю при г% ->—оо (в случае
а > gs) и г* -> + оо (в случае а < as) по мере приближения
к горизонту г+ + 0. Заключаем отсюда, что во всех случаях
решения одномерных волновых уравнений имеют следующие
асимптотики:
Z -> ехр [±1ог+] при г -> оо и г -> г+ + 0. D20)
Когда a > as и зависимость г* от г однозначна, все четыре
потенциала непрерывны, ограниченны и короткодействующи.
Более того, из уравнения D09) следует, что интегралы от всех
четырех потенциалов по всей области изменения г* (— оо, +оо)
равны между собой.
-{-оо -{-оо
J Vdrt= J Qdr, + (Ti)a=o при a>os, D21)
—оо —оо
где
(Г1)д=0 - -2(г+ - М)/(й2+) = ~(М2 - а2У/2/Мг+ A - es/o). D22)
В частности, интегралы действительны даже тогда, когда потен-
потенциалы комплексны. Равенство интегралов от потенциалов напо-
напоминает подобное равенство, которое было получено для потенциа-
потенциалов около черных дыр Шварцшильда и Рейсснера — Нордстрема.
Действительно, при р2 = 0 выражение для V принадлежит к спе-
специальному классу (уравнение A33) гл. 4), что гарантирует ра-
равенство коэффициентов отражения и прохождения для всех
значений /, х и р, а не только для их частных значений, характе-
тенциала (для кривой 5 х2 — —3,4941 и Р2 = 5,166, а для кривой 6 к2 = —5,217
и р2 = —5,166) регулярны всюду, кроме горизонта, где они становятся беско-
бесконечными; два других потенциала (им соответствуют значения х2 = 5,217 и р2 =
= —5,166 и х2 = 3,491 и Р2 = 5,166) имеют сингулярности в точке, где q —
— Р2Д = 0. г — значение о лежит в интервале суперрадиации; о == 0,36, а2 =
= —4,3465 и X = 1,736; кривая 9 соответствует значениям параметров х2 ==
== 11,226 и р2 = —13,039, а кривая 10 — параметрам х2 = 21,551 и р2 = 13,039;
оба этих потенциала имеют сингулярность при г = | a | == 2,085. (Для кривой 9
ось ординат находится справа.) Два других потенциала имеют сингулярности,
связанные с нулями функции q — Р2А.
8 Чандрасекар С, т. 2

226 Глава 9. Гравитационные возмущения черной дыры
ризующих^ рассматриваемую задачу. Ниже^в § 98 мы увидим,
что все четыре потенциала, задаваемых уравнением D15), также
приводят к одинаковым коэффициентам отражения и прохожде-
прохождения. Уместен поэтому вопрос, не выделяет ли уравнение D11)
подобный же (но больший) класс потенциалов, гарантирующий
равенство между собой коэффициентов отражения и прохождения?
Случай аксиальной симметрии, когда т = О и а2 = а2, оче-
очевидно, является простейшим. В этом случае все четыре потен-
потенциала (ограниченные и короткодействующие) могут быть дей-
действительными (как мы сейчас увидим, для достаточно малых
значений а/М) или пара потенциалов могут быть действительными,
а другая пара — комплексно-сопряженными, или же могут быть
две пары комплексно-сопряженных потенциалов. Условием су-
существования комплексно-сопряженной пары потенциалов явля-
является выполнение неравенства (ср. с уравнением D06))
2а2к Eк — 6) — 2р2А, (X + 2) > 36Л12. D23)
Для двух разрешенных значений E2, именно —За2 и +3а2, усло-
условие D23) дает
к > 3 + 3 A + М2/а2I'2, I > ЗМ/2а. D24)
Поскольку наименьшее значение к равно (/ — 1) (/ + 2), отсюда
следует, что все четыре потенциала будут действительными,
если
а/М <3/[2 (/ — 1) (I + 2I D25)
т. е. только для достаточно малых значений отношения а/М.
Из рис. 43 и 44 следует, что в общем случае действительные
части потенциалов доминируют и почти равны, а небольшая раз-
разность между ними «компенсируется» различающимися малыми
мнимыми частями. Во всяком случае, как было показано, инте-
интегралы от мнимых частей должны быть равны нулю, а интегралы
от действительных частей должны быть равными между собой.
Потенциалы в случае отсутствия аксиальной симметрии,
когда а > ас = —а/т, имеют практически такой же вид, как
и в случае аксиальной симметрии.
В предельном случае g = gc и а2 = 0 (и, следовательно,
Р2 = 4:3а2 = 0) имеются только два потенциала
-*» {*»+*>+- ??+ff,-?g}¦<«*»
где
ха = ± C6Л42 + 24а2^I/2, q = г2 (кг + 6Мг — 6а2), D27)
и в зависимости от того, действительно или мнимо х2, потен-
потенциалы будут действительными или комплексными. При as <
<о<ас потенциалы остаются почти одинаковыми. Однако
при а -> as + 0 они становятся сингулярными точно на гори-

97. Падающие гравитационные волны 227
зонте и приводят к единичному значению коэффициентов отра-
отражения, что предвещает появление суперрадиации (см. § 98).
В случае а < as потенциалы имеют характерную сингуляр-
сингулярность при г = | а | > г+. Несложно проверить, что вблизи точки
г = | а | поведение потенциалов таково:
и оно совпадает с поведением потенциалов для электромагнитных
возмущений (ср. с уравнением A93) гл. 8). Следует отметить,
что помимо сингулярности при г — | a | в некоторых случаях,
как следует из рис. 44, в, тот или другой потенциал имеет и дру-
другую сингулярность, эти добавочные сингулярности появляются,
когда знаменатель q — C2A в выражении D15) для V становится
равным нулю.
г. Соотношения между решениями, относящимися к различ-
различным потенциалам. Обозначим V1 (у = 1, ..., 4) различные потен-
потенциалы, и пусть Z/ — соответствующие им решения. Можно пока-
показать (как и выше), сделав подходящее преобразование уравне-
уравнений D12), как, зная решение Z', соответствующее потенциалу 1/',
построить решение Z', соответствующее потенциалу V1. Действи-
Действительно, подставляя в выражение для KlZl вместо функций Y
и A_Y их выражения через функции Z> и A+Z>, получаем
К111 = (с58/Л2) R'Y - (с58/А2) (Tt + 2fa) Л_Г =
= [(S8/A2) R*f Vj + (Ti + 2ia) (p{ + 2ta^)] Zj +
+ (ш8/А2) [R( (T{ + 2ia) - R1' (T{ + 2ia)] A+Z*. D29)
Выражение в правой части можно упростить, если воспользо-
воспользоваться уравнениями C98), D00) и C84) и C87). Действительно,
поскольку
(Й8/Д2) [R1 (П + 2/с) - & (Т{ + 2*с)] =
- 2/a (f^ - ) W О ^ 1'
-p- -?T'w rrl + (Ti + 2ia) (Pf + 2wpO =
= -?- [/(' - (Pf + 2/apO G{ + 2/a)] + (Ti + 2ia) (pf + 2/ap0 =
^ ^1
^JSL^L^ D3i)

228 Глава 9. Гравитационные возмущения черной дыры
то уравнение D29) принимает вид
'QP? Д / + D'/A+Z/. D32)
Воспользовавшись снова уравнениями C92) и D00), находим
- (F2 - Pi) CM + 2/apO F - &F' - 2*арП- D33)
Подставляя это выражение в уравнение D32), получаем окон-
окончательное соотношение
j
dr.
D34)
Очевидно, что это соотношение позволяет получить решение Z1,
соответствующее потенциалу Vе, если известно решение Zfy соот-
соответствующее потенциалу VL
Поскольку функция F стремится к бесконечности как при
г -> оо, так и при г -> г+ + 0, из уравнения D34) следует, что
/C'Z' -> (/С7 + faD'O Z7' + DijZ[ r*. D35)
Это соотношение можно использовать для нахождения связи
между асимптотиками решений, принадлежащих разным потен-
потенциалам. При выводе упомянутых соотношений полезна другая
формула для Dlf, которую мы сейчас получим. Поскольку
К1 -Kf = - 4a2 (р? - рО + 2/а Ы - 4) =
- 2/а [2/а (pi - рО + (х| - х01 D36)
и (Р2J = pi( = 9a4), можно записать (ср. с уравнением D30))
D" = (/с' - /cO/2to + (^ - 4) (Р2 + РО Д/7 - Р0. D37)
Из этого уравнения следует, что
D'i-+(К1 - W)/2io при r->oo, r->r+ + 0. D38)
Мы уже видели, что решения одномерных волновых уравне-
уравнений имеют асимптотики exp (±'ior#) как при г-> оо, так и при
г -> г+ + 0. Следовательно, если Z'' имеет асимптотики
+/a/g, D39)
то из уравнений D35) и D38) следует, что соответствующие реше-
решения для Z1', построенных из решений для Z'*, имеют асимптотики
Z/-*(/C'7/@exp[—/arj, Z,-^exp[+/arj. D40)

98. Задача об отражении и прохождении волн
229
д. Асимптотическое поведение решений. Вернемся теперь
к уравнениям D12), связывающим решения Г<±а) и решения Z(±o).
Как и выше, можно получить асимптотики решений для Г<±а),
зная асимптотики решений для Z<±a). Имеем
Z(+°) -> exp [+iau] при г -> оо; г -> г+ + 0:
D41)
'.—4a2exp[+ ior%] при г-^оо,
- [4а2/(а - а,)] [(а - as) + 2/е0] exp [+ mr,]
при г->г+ +
exp [—t'crr*] при г -> оо; г -> г+ + 0:
(/(<+а>/4а2) exp [— tarj/r1 при г ->- оо,
-2
где
D42)
4 (сДУ а2 [(а - а8) + 2ieQ][(o - os) + 4ie0]
;<-о) _^ еХр [-f/(TA\J при г -> оо; г -> г+ + 0:
— (/С(~а)/4а2) ехр [ + lar^J/r4 при г -> оо,
,~9 чл о * при r->r+-f-O;
4(co2.La2[(a-as)-2te0][(a-as)-4/e0] H +^
D43)
Z(-o) .+ ехр [-tarj при г -> оо; г — г+ + 0: D44)
— 4а2ехр[—ior*] при г—>-оо,.
7iT) -> - - [4а2/(а - as)] [(а - а8) - 2fe0] ехр [- /агJ
при г->г+ + 0;
е0 - (г+ - Л1)/2 D + а2) = (М2 - а2I/2/4М/-+. D45)
98. Задача об отражении и прохождении волн
Преобразовав радиальные уравнения Тьюкольского к одно-
одномерным волновым уравнениям, мы можем теперь завершить
решение задачи об отражении и прохождении падающих грави-
гравитационных волн точно так же, как в § 75 и 76 для электромагнит-
электромагнитных волн. Основное различие состоит в том, что в рассматри-
рассматриваемом здесь случае мы имеем четыре потенциала вместо двух.
Однако это различие не приводит к новым следствиям, поскольку,
как мы увидим ниже, все четыре потенциала дают одинаковые
коэффициенты отражения и прохождения.
Потенциалы могут быть и комплексными, поэтому удобно
так сформулировать задачу об отражении и прохождении волн,
чтобы рассуждения были применимы как к действительным,
так и к комплексным потенциалам.

230 Глава 9. Гравитационные возмущения черной дыры
Пусть Z<±a) — решения одномерного волнового уравнения
с ограниченным короткодействующим потенциалом V (действи-
(действительным или комплексным), имеющие следующие асимптотики:
Z(±Q)->< * * * D46)
[ 5(±or>exp[± ior] при г*-> — оо. '
Если потенциал V действительный, то коэффициенты Л<+а) и
?(+?) будут комплексно-сопряженными Л(~а) и В^~°\ что не
выполняется если потенциал V комплексный. Однако во всех
случаях, если ввести определения
R = Л(+а>Л<-а>, Т = В<+а>В<-а>, D47)
мы придем к закону сохранения
R + T=l. D48)
При этом вещественность величин R и Т не гарантируется.
Ниже мы докажем две теоремы для конкретного вида потен-
потенциалов рассматриваемой задачи.
Удобства ради ограничимся случаем а > а89 когда зависи-
зависимость г% от г монотонна и однозначна, а потенциалы являются
ограниченными и короткодействующими. Обобщение на случай
а < а3 требует лишь некоторых дополнительных уточнений
о происхождении сингулярности потенциала V (которые возни-
возникают в этом случае, см. п. 75, в гл. 8).
ТЕОРЕМА 1. Все потенциалы приводят к одинаковым коэф-
коэффициентам отражения и прохождения.
Доказательство. Рассмотрим решения Z(/> ±a), отвечающие
потенциалу V{j) и имеющие асимптотики
;(/. ±о) ехр [4. iGr^ _|_ ди. ±о) ехр [=F ior*)
приг*-> + оо,
В</. ±а> ехр [± tor*] { }
при г*-+-оо.
В соответствии с соотношениями D39) и D40), установленными
в п. 97, г, решения Z<*» ±a), отвечающие потенциалу V и полу-
получающиеся из соответствующих решений, отвечающих потенциа-
потенциалу V1 с вышеприведенными асимптотиками, будут иметь такие же
асимптотики с коэффициентами, равными
D50)

58. Задана об отражении и йрохождении волн 251
Следовательно,
i, —а) q(/, -fa)?(/, —а)
. -<*) о(/. +o)n(h —о)
D51)
D52)
СA"'+а)СA''
что и доказывает теорему.
ТЕОРЕМА 2. Если Z^' ±0) есть решения, соответствующие
комплексному потенциалу V1 и имеющие асимптотики
. ехр [4- iarJ + Л('- *а> exp [=F iarJ при
iziar^] при /•„,->—оо,
D53)
то коэффициенты отражения и прохождения равны
12 __ I Л(/, -а) 12 г/^(
= /((/.+<*)/((/.-<*) — квадрат модуля постоянной Ста-
робинского.
Доказательство. Заметим прежде всего, что потенциал V'
может быть комплексным тогда и только тогда, когда величина х2,
определяемая уравнением D06), чисто мнимая, и в этом случае
можно написать
и2 = ±ik2, D55)
где k2 — действительная величина. Пусть для потенциалов V'
и V* величина х2 равна соответственно — ik2 и +ik2, а р2 одина-
одинаковы. Тогда потенциалы V* и V1 являются комплексно-сопря-
комплексно-сопряженными функциями, а постоянные К1 и К1 равны
Ки> 0) = [X (X + 2) - 4а2р2] + 2а?2,
/(С а) = [я, (А, + 2) - 4а2р2] - 2а^2 = 7((/' "а) D56)
и действительны.
Поскольку функции V1 и V7 являются комплексно-сопря-
комплексно-сопряженными, уравнения, которым удовлетворяют функция Z1 и
комплексно-сопряженная к ней функция Z!\ совпадают. Соответ-
Соответственно этому решение для потенциала V\ имеющее асимптотики
ехр [-юг*] + Л(/' 'а) {К11К}) exp l+iorj
7(l.-a, ПРИГ*->+ОО,
fl(/'-0)exp[-iarJ
при Л. —> — оо,

§32 Глава 9. Гравитационные возмущения черной дыры
будет комплексно-сопряженным решению Z(y'+G), асимптотики
которого заданы уравнением D53). (Этот факт можно проверить,
рассматривая решение с асимптотиками Z{}'~0) и выводя из
него решение Z(I'"a) в соответствии с соотношениями D50), а
затем умножая это решение на множитель Kl/KJ\ чтобы коэф-
коэффициент при ехр (—j'orj в асимптотике г% —> оо стал равным
единице.) Следовательно (ср. с уравнением D56)):
[Л(/'+а)]* = Л(/> -О)КС/К} = Аи' ~о)Ки' -а)/Ки' +а), D58)
[Ви- +0)Т = В(У' 'о). D59)
Вследствие этих соотношений имеем
R = Л(у> +О)А{}'~О) = I Л(/' +а)|2/((/' +а)//((/'-а) -.
= | Л(/' +а)|2 [Ки' +а)]2/| У |2 = | Л<'• "а)|2 [/((/' "а)]2/| У |2; D60)
Т = |В(Л+О)|2 = |В(Л-О)|2. D61)
На этом доказательство теоремы завершается.
СЛЕДСТВИЕ. В общш случае можно записать
" D62)
Это соотношение очевидно, поскольку когда потенциал V1 дей-
действительный, то К1 комплексная величина, а когда потенциал V]
комплексный, то
lKu'*a)]' = KUt+a)- D63)
Теперь ясно, что различные случаи а > ас, ас > а > as
и a < о',, могут быть исследованы в точности так же, как в гл. 8
(§ 75), в частности возникает явление суперрадиации.
В табл. 10 приведены коэффициенты отражения и прохожде-
прохождения для гравитационных волн различной частоты, падающих на
керровскую черную дыру с а = 0,95.
а. Выражения для R и Т через решения уравнений Тьюколь-
Тьюкольского с заданными граничными условиями. Сначала напомним, что
Wo - Фо - R+2S+2 ехр [/ (at + тФ) ], .
(р*L?4 = Ф4 = R_2S_2 ехр [/ (at + ту) ], ( '
где мы восстановили зависимости от / и ф (ср. с уравнением F)).
Функции Тьюкольского R+2 и R_2 в свою очередь связаны с функ-
функциями К+2а) и Y(L2°) соотношениями (ср. с уравнением C79))
+2 = [(й2K/2/А2] Yi?\ R-2 = F2K/2П-2О). D65)

98. Задача об отражении и прохождении волн
233
Таблица 10
Коэффициенты отражения для гравитационных волн, падающих на керровскую
черную дыру с а = 0,95 (I = 2, т = —2)
а
0,50
0,55
0,60
0,65
0,70
0,73
0,74
0,75
0,76
g/gs
0,6907
0,7597
0,8288
0,8979
0,9669
1,0084
1,0222
1,0360
1,0498
R
1,04422
1,07031
1,10693
1,15358
1,15101
0,92530
0,76882
0,58828
0,41376
а
0,77
0,78
0,79
0,80
0,81
0,82
0,83
0,84
0,85
g/gs
,0636
,0774
,0912
,1051
,1189
,1327
,1465
1,1603
1,1741
R
0,27057
0,16754
0,10007
0,05844
0,03372
0,01932
0,01103
0,00628
0,00357
Поскольку все четыре потенциала приводят к одинаковым
коэффициентам отражения и прохождения, мы не будем поме-
помечать решения какими-либо индексами. Для определенности
ограничимся рассмотрением случая, когда потенциал комплекс-
комплексный и а > as. Эти ограничения не приводят к сколько-нибудь
существенной потере общности: для включения в рассмотрение
случая а2 < 0 и действительных потенциалов достаточно сделать
незначительные и в основном формальные модификации. Кроме
того, нетрудно проверить, что окончательные результаты при
этом не затрагиваются.
С помощью соотношений D41)—D44), выписанных в п. 97, д,
мы можем написать асимптотики решений R+2 и R_2y следующих
из уравнений D12) теории преобразований, если решения Z(±a)
имеют асимптотики D46). Находим
exp [+iorj/r
exp
при
D66)
при r-vr+-f0;
R-2
Я1'2ПС) exp l + iorj/r + tfir2ef)r3exp [-for,]
при
oo,
D67)
при
где
A
i+0\
D68)

234
Глава 9. Гравитационные возмущения черной дыры
ns) =-4 [(й2K/7(сх - os)W[(o - os) + 2/ео
n(trans)
/С(-а) (а -
4 («»)«« о» [(а - а.) - 2/е0] [(а - <,,)-««.] "
Из предыдущих соотношений следует, что
TТ = [/С(+а>]2| Л(+(Т)|2/256а8,
#!ГТ = 256а81 Л(-
D69)
Если воспользоваться соотношением D58) между А('+о) и Л( а\
то получим
| R%ei)/R{:2nc)\2 = \V? Л(+0)Л(-а7256а8,
?[!2пс)|2 = 256оМ<+а)Л(-а7к12. D?0)
Из уравнения D47) следует, что выражение для коэффициента
отражения может быть записано в одной из двух форм:
D71)
Аналогично, для коэффициента прохождения получаются сле-
следующие две формулы:
т=
Т
г+)*(о-о.)Цо-оя)*+гЦ]
= {2М1+>Ь (о - о,) [(а - asf + Аг\] х
R^c)
, D72)
n(trans)
. D73)
Закон сохранения D48) требует, чтобы
+ {aVBMr+f (а - as) [(о - of + 4е02]) \RTns) Р, D74)
|
D75)
+ BMrJcf (а - as) [(а - of + 4e21J [(а - of + 16$ | R
Хотя мы ограничились рассмотрением случая а2 > 0 и ком-
комплексных потенциалов, нетрудно убедиться, что уравнения D71)—
D73) справедливы без всяких ограничений. Мы видим, что в со-

98. Задача об отражении и прохождении волн
235
ответствии с результатами, полученными из исследования одно-
одномерных волновых уравнений,
Т < 0 при о < о8, D76)
т. е. имеет место, как и было предсказано, суперрадиация.
Как и в п. 76, а, мы можем найти альтернативные выражения
для коэффициентов отражения и прохождения, используя усло-
условие унитарности, которое справедливо и в рассматриваемом здесь
случае. Рассматривая решения уравнений Тьюкольского, имею-
имеющие асимптотики
exp [-
° exp [
при г
exp
г+ -f- О,
при г -»• оо;
f) Д2 exp [ + iarji
при г ->¦ г+ + 0,
D77)
D78)
при г -> оо,
находим
R =
256 BMr+f (о —
256
)8 [(a -
4eg]* [(a - а,)^ + 16ei]
D79)
(a - ae) [(a -
[(a -
16eg]
+2
а —
n(inc)
+2
n(trans)
4-2
D80)
В шварцшильдовом пределе (а = 0) выражения для R и Т
D71)—D73), D79) и D80) сводятся к выражениям C71), C72),
C77) и C78) гл. 4.
б. Прямое вычисление потока излучения на бесконечности.
Нам осталось убедиться в том, что коэффициенты отражения
и прохождения, полученные в предыдущем разделе, имеют тот

236 Глава 9. Гравитационные возмущения чёрной Ьырь1
физический смысл, который им обычно приписывается. Проблема,
с которой мы здесь сталкиваемся, немного тоньше, чем задача,
которую пришлось решать в гл. 8 (п. 76, б): в данном случае
у нас нет однозначного и общего определения тензора энергии-
импульса гравитационного поля в отличие от случая электромаг-
электромагнитного поля. Однако если фоновое пространство-время стацио-
стационарное и асимптотически плоское, то для возмущенного простран-
пространства-времени можно несколькими способами выделить величины,
обладающие требуемыми физическими свойствами, которые можно
интерпретировать как падающие и отраженные потоки гравита-
гравитационной энергии. Строгое исследование вопроса со всеми необ-
необходимыми подробностями уведет нас далеко в сторону. Удовле-
Удовлетворимся поэтому тем, что приведем только некоторые общие ар-
аргументы, которые могут быть подкреплены результатами более
тщательного исследования.
Можно показать, что при подходящем выборе калибровки —
калибровки де Дондера, или гармонических координат, — урав-
уравнения Эйнштейна в пустоте, линеаризованные над фоновым пло-
плоским пространством-временем Минковского, допускают решения
в виде плоских волн, линейный элемент которых равен
ds2 - (dx0J — (dx2J — A — Au) (dx1J —
- A + An) (dx3J + 2Й31 dx3 dx\ D81)
где по предположению hn и A31 — малые величины первого по-
порядка, являющиеся функциями аргумента (х° ± х2):
Аи = йп (*° ± *2), А81 = А31 (х* ± х2). D82)
Другими словами, решения представляют плоские волны, ухо-
уходящие (знак «—») или входящие (знак «+»). Действительно, в этой
метрике единственными ненулевыми компонентами тензора Ри-
мана, которые вычисляются по формуле
дх1 дхг
являются следующие компоненты:
б^?0303 — 6^2323 = tWo
6^0301 = 6^2321 = A3i/2, (AQA\
6^0323 = —6/?oi21 = ±Йц/2,
где точки обозначают дифференцирование по аргументу (х° ± х2);
а свертыванием компонент тензора Римана получаем, что все
компоненты тензора Риччи равны нулю. Это подтверждает, что
метрика, заданная уравнениями D81) и D82), действительно удо-
удовлетворяет уравнениям Эйнштейна в пустоте.

98. Задача об отражении и прохождении волн 237
Теперь можно вычислить вейлевские скаляры ?0 и Ч^, соот-
соответствующие метрике D81), относительно изотропного базиса
(ср. с уравнением C33) гл. 4)
1' = A, 0, 1, 0), n'=V.(l, О, -lf 0),
, i\ 0, 1).
В этом базисе (ср. с уравнением C34) гл. 4)
%) = —I F^0301 + б/?2321 + $#2301 + 6i?o32l) —
— /2 (^Аозоз г 2ок0з2з "г
+ б^2з2з — б^ою1 — 26#0121 — 6#2Ш). D86)
Если подставить сюда значения для компонент тензора Римана
из уравнений D84), то получим
0 для уходящих волн,
о/Ь -ь ч D87)
—2(пп — ih3i) для входящих волн.
Подобным же образом находим
I -"V2 (йп + I'M для УХ°ДЯ1ДИХ волн>
т4 = i л D88)
I 0 для входящих волн. '
Итак, вейлевский скаляр % не равен нулю только для при-
приходящих волн, а Ч;4 — только для уходящих волн.
Поток энергии через единицу площади, связанный с плоской
волной
exp [ia(x° ± x2)], D89)
равен
^ = V4a8(|Aii|a + IM2)- D9°)
Выражения для потоков энергии в приходящих и уходящих
волнах, записанные через вейлевские скаляры, имеют следующий
вид:
<F(in) = A/16а2) | 4filn)|2, ^(out) == A/а2) | Y{out)|2. D91)
Предыдущий анализ был выполнен для плоских волн. Однако
в асимптотически плоских областях пространства-времени резуль-
результаты будут справедливы (локально) и для сферических волн,
распространяющихся внутрь (в направлении падающей волны)
или наружу (в направлении отраженной волны). Вместо уравне-
уравнения D90) теперь нужно писать следующее выражение:
d2? ^2 + |M2). D92)

238 Глава 9. Гравитационные возмущения черной дыры
Соответствующие выражения для энергии в падающей и отражен-
отраженной гравитационных волнах через вейлевские скаляры имеют
следующий вид:
d/dQ \J
1 ^l^f D94)
Для вейлевских скаляров ?о и 'ф У нас есть следующие реше-
решения (ср. с уравнением A48)):
% = R+2S+2 ехр [/ (Ы + тер)],
4 (р*)* ?4 = /?_2S_2 ехр [f (at + /шр)], ( }
где угловые функции 5+2 и S_2 нормированы на единицу, а ра-
радиальные функции R+2 и /?_2 нормированы так, чтобы удовлетво-
удовлетворять уравнениям D1) и D2), т. е. мы знаем все необходимое для
использования уравнений D95).
Подставляя решения D95) для вейлевских скаляров Wo и ?4
в уравнения D93) и D94), получаем
dtdQ
D97)
Из уравнений D66) и D67) следует, что уравнения Тьюкольского
действительно допускают решения, для которых существуют пре-
пределы D96) и D97). Действительно, подставляя коэффициенты
R+2C) и R-2f\ определенные формулами D66) и D67), имеем
D99)
Подставляя вместо коэффициентов R+?c+o) и т. д. выраже-
выражения D68) и интегрируя по углам, находим, что коэффициент
отражения равен
R = А(+О)А{-О) E00)
в полном согласии с выражением D47), полученным при иссле-
исследовании одномерных волновых уравнений, которым удовлетво-
удовлетворяют функции Z{±o).
в. Поток энергии через горизонт событий. В общем случае
можно построить, по существу, однозначно сохраняющийся тен-

98. Задача об отражении и прохождении волн 239
зор энергии-импульса гравитационного поля, соответствующего
возмущению пространства-времени над стационарным фоновым
многообразием. Следовательно, из того что выражение для коэф-
коэффициента отражения R действительно представляет часть пада-
падающего потока гравитационной энергии, отраженной потенциаль-
потенциальным барьером, мы можем заключить, что коэффициент прохожде-
прохождения Т, который удовлетворяет требованию D48) для закона со-
сохранения энергии, с необходимостью представляет собой долю
падающей энергии, пересекающей горизонт событий и поглощае-
поглощаемой черной дырой. Интересно тем не менее проверить, что выра-
выражение, полученное нами для потока энергии через горизонт
событий, совместно с утверждением теоремы Хокинга (ср. с § 65, г)
о том, что поток энергии через горизонт событий прямо связан
со скоростью возрастания площади поверхности горизонта.
Площадь поверхности горизонта керровской черной дыры 2
следующим образом связана с массой М и моментом количества
движения Lz (=aM) относительно оси вращения:
2 = 4я (г9; + а2) = 8л [М2 + (М4 - Ll)l/2]. E01)
Следовательно, изменение массы dM и момента количества дви-
движения ALZ вызывает изменение площади d2, равное
dS = 8я (М4 - LlYU2 {2 [М2 + (МА - LlY/2] MdM-Lz dZj, E02)
или иначе
dS - (8я/М) (М2 — a2)'42 BM2r+ dM — Lz dLz). E03)
Поскольку в рассматриваемом случае (ср. с уравнением B53)
гл.8) ^
dLz = — т dM/a E04)
(минус появляется вследствие того, что теперь dLz — изменение
момента количества движения черной дыры, а не поля), из урав-
уравнения E03) следует, что
d2 - Dя/е0) A — (Ts/cr) dM, E05)
где (ср. с уравнением D45))
80 - (М2 — a2)U2/4Mr+. E06)
Ниже в разделе г мы выведем формулу
dS = BMrJeoy\ a™ |? d/ dQ, E07)
где стг+ — возмущение первого порядка для спинового коэф-
коэффициента а на горизонте в базисе Хартля — Хокинга (уравне-
(уравнение B43) гл. 8). Объединяя уравнения E05) и E07), получаем,
что в соответствии с теоремой Хокинга

240 Глава 9. Гравитационные возмущения черной дыры
мгг
Вычислим <тг+ с помощью тождества Риччи (уравнение C106)
гл. 1, а также уравнение C) настоящей главы):
Da — 6х = а (р + р* + Зе — е*) — х (т — я* + а* + ЗР) + "?0
E09)
в базисе Хартля — Хокинга, поскольку именно этот базис регу-
регулярен на горизонте. Поскольку базис Хартля — Хокинга полу-
получается из нашего стандартного базиса (уравнение A70) гл. 6)
вращением из класса III (гл. 1, п. 8, ж) с параметром А = 2 (г2 +
+ а2)/А, то из формулы C47) гл. 1 следует, что
(поскольку 6 = 0 в первоначальном базисе). Следовательно, на
горизонте
е™ = (г+ - М)/2 (г* + а) = (М2 - а2)ш/4Мг+ = е0. E11)
Кроме того, рНИ равно нулю на горизонте, а х = 0 по определе-
определению. Мы получаем, таким образом, следующее уравнение:
D?l*o?^ = 2в0а?// + (х?оИ)г+- E12)
С другой стороны, на горизонте (уравнения B50) и B52) гл. 8)
имеем
D?+H = ia + iam/2Mr+ = i(a — as). E13)
Следовательно,
Имеем также
(ФоН)г+ = [A24fo/4 {г1 + а2J]г+ = (А2Чг0)г+/4 BМг+J. E15)
Подставляя выражения E14) и E15) в уравнение E08), получаем
^(trans) ._ 1 а .A2V ,2 ,-1б.
d/dQ ~ 64я BМг+)^ [(а — ааJ + 4е§] (а — а8) ' ° |г+< w;
Подставляя решение для 4V приходим к следующему резуль-
результату:
2
dt dQ ~ 64я BМг+)*' [(а — asJ + 4e^] (a — os) '
Наконец, используя асимптотическое выражение для решения
R+2 на горизонте (аналогично тому, как это было сделано в урав-
уравнении D66)), получаем
64я BМг+K [(а — asJ + 4е§] (а — os)
2. E18)
Если поток энергии в падающей волне дается выражением D98),
то уравнение E18) приводит к значению коэффициента прохожде-
прохождения, которое согласуется с выражением D72).

98. Задача об отражении и прохождении волн 241
Итак, мы удостоверились в том, что коэффициенты отражения
и прохождения, выведенные в п. 98, я, имеют как раз тот физи-
физический смысл, какой мы им приписали интуитивно.
г. Формула Хартля — Хокинга. Формула Хартля — Хо-
кинга E07) следует из уравнений для оптических скаляров,
рассмотренных в п. 9, а гл. 1.
Напомним, что спиновые коэффициенты р и а измеряют соот-
соответственно сходимость и сдвиг изотропной конгруэнции 1. Если
конгруэнция является геодезической, то х = 0 и тождество
Риччи (уравнение C10а) гл. 1) дает
Dp = (р2 + | а |2) + (е + е*) р. E19)
Рассмотрим это уравнение в базисе Хартля — Хокинга на го-
горизонте. Поскольку в настоящем разделе мы будем пользоваться
исключительно этим базисом, опустим индекс НН> описывающий
принадлежность величин к рассматриваемому базису.
На горизонте е = е0 = const (значение постоянной дается
уравнением E11) для керровской черной дыры) и уравнение E19)
принимает вид
Dp = (p2 + |a|2) + 280p, E20)
где D = dl&v (как и в гл. 8, уравнение B42)).
Поскольку в стационарном состоянии и р, и а равны нулю
на горизонте, уравнение E20) можно линеаризовать по возму-
возмущениям
Dp(]> - 2гор^К E21)
Единственное допустимое решение этого уравнения следующее:
р<!> - 0, E22)
поскольку р(]) (и а*1*) должны быть периодичны по v для вра-
вращающейся черной дыры, а уравнение E21) не допускает таких
решений. Следовательно, нужно разложить уравнение E20)
до второго порядка, и в результате получаем
Dp<2> =|a<1>|2 + 2eopB>. E23)
Запишем решение этого уравнения в виде
оо
рB) = _ j exp [2e0 (v - v')} \ a<'> (v'f do', E24)
V
совместимом с требованием, чтобы р<2) было равно нулю на верх-
верхнем пределе. С другой стороны, если d2 — элемент поверхности
горизонта, то скорость его изменения определяется сходимостью
изотропной конгруэнции, выходящей из-под горизонта, поэтому
-^с12 = — 2p<2>dl, E25)

242 Глава 9. Гравитационные возмущения черной дыры
ИЛИ
[^f]jB)(y)dy. E26)
О
Подставляя сюда решение E24) для рB), получаем
In [^щ-] = 2 J dv } dv' | a") (v'f exp [2e0 @ - v% E27)
О и
Изменим порядок интегрирования:
v'
In [4|§f ] = 2 J du' | a<» (y')l2exp [-2eoy'] j duexp [2e0y] +
0 0
oo vx
+ 2 f ck/ | a(^ (yr)|2exp [—2e0?/] j d^exp [2eou]. E28)
После интегрирования по v имеем
In [-^-] = A/eo) j {1 - exp [-
0
oo
+ (l/e0) exp [280^ - 1] J | a<n (u)|2exp [-280f] du. E29)
Как указал Картер, второй член в правой части этой формулы
«имеет дальнодействующий (в противоположность причинному)
характер: поведение горизонта во временном интервале от 0
до v± зависит от того, что происходит после момента времени i^».
Объяснение Картера следующее: «Это странное свойство является
следствием способа определения черной дыры (основанного на
представлении о дальнодействии) как области, из которой свет
не может попасть на бесконечность». Исключим дальнодейству-
дальнодействующий член, предположив, что
|a(l> (v)\2 - 0, если v > vx и vx > 1/2е0. E30)
Тогда уравнение E29) упрощается:
y)|2dt;- E31)
о
Если еще предположить, что изменение 2 (v) мало в интервале
@, Vi), то в таком пределе можем записать
=^- fla(') (ufdy. E32)

99. Квазинормальные моды керровской дыры
243
Для керровской черной дыры получаем отсюда
^)|2. E33)
Это и есть искомая формула. Интересно заметить, что формула,
потребовавшая для своего доказательства столь тонких рассу-
рассуждений, неявно содержится в анализе в п. 98, я, приводящем
прямо к выражениям для коэффициентов отражения и прохо-
прохождения.
99. Квазинормальные моды керровской черной дыры
В гл. 4 (§ 35) и 5 (§ 48) были исследованы квазинормальные
моды черных дыр Шварцшильда и Рейсснера — Нордстрема.
Как уже объяснялось, эти моды определяют замирающие тоны
возмущенной черной дыры. Ясно, что такие моды существуют
1,0
0,6
0,4
0,2-
= ч
1=1
- Re (б)-
/я=-2^^^ч>А
/77 — 2 ^^\\
/77=2
0,2 0,4 0,6 0,8
а/М
а
1,0
0,2
0,4 0,6 0,8
п/М
б
Рис. 45. Зависимость от параметра а действительной и мнимой частей резонансной
частоты черной дыры Керра для различных значений / и m. a — 1=2 для всех
значений т между —2 и 2. б — / = 3; мнимые части показаны только для зна-
значений т = —3, 0 и 3. в — / = 4; действительная часть показана для всех чет-
четных значений т, мнимая часть — только для т = —4, 0 и 4.

244 Глава 9. Гравитационные возмущения черной дыры
и в общем случае черной дыры Керра. Они были определены
Детвейлером. На рис. 45 показаны зависимости действительной
и мнимой частей характеристических частот квазинормальных
мод от параметров черной дыры Керра.
100. Последние замечания
Проведенное в настоящей главе исследование возмущений
пространства-времени Керра оказалось исключительным по своей
сложности. Возможно, со временем удастся распутать этот клу-
клубок и сделать предмет более доступным для понимания. А пока
анализ завел нас в царство рококо — пышное, вычурное и пол-
полное неожиданных находок.
Библиографические замечания
Задача об исследовании возмущений керровской черной дыры стала раз-
разрешимой только после открытия Тьюкольским возможности получения расцеп-
расцепленных уравнений для вейлевских скаляров из системы уравнений Ньюмена—
Пенроуза и разделения переменных в них:
1. Teukolsky S. A. Phys. Rev. Lett., 29, 1114—1118, 1972.
2. Teukolsky S. Л. Astrophys. J., 185, 635—649, 1973.
3. Press W. #., Teukolsky S. A. Astrophys. J., 185, 649—673, 1973.
4. Teukolsky S. A., Press W. H. Astrophys. J., 193, 443—461, 1974.
Тождества Тьюкольского—Старобинского были доказаны в работе [4] и в работе
5. Старобинский А. А., Чурилов С. М. ЖЭТФ, 65, 3—8, 1973.
§ 79—96. Изложение в этих параграфах целиком основано на работах
6. Chandrasekhar S. Proc. Roy. Soc. (London), A358, 421—439, 1978.
7. Chandrasekhar S. Proc. Roy. Soc. (London), A358, 441—465, 1978.
8. Chandrasekhar S. Proc. Roy. Soc. (London), A365, 425—451, 1979.
9. Chandrasekhar S. Proc. Roy. Soc. (London), A372, 475—484, 1980.
В книге дано более последовательное изложение теории, чем в оригинальных
статьях, что естественно, поскольку во время написания первых статей оконча-
окончательный результат еще не был известен: Однако громоздкость анализа так и
не удалось сколько-нибудь существенно уменьшить — сама задача оказалась
сложной. $|
§ 97. Изложение теории преобразований следует в основном работам
10. Chandrasekhar S., Detweiler S. Proc. Roy. Soc. (London), A345, 145—167,
1975.
11. Chandrasekhar S., Detweiler S. Proc. Roy. Soc. (London), A350, 166—174,
1976.
См. также
12. Chandrasekhar S. In: General Relativity — An Einstein Centenary Survey,
eds. S. W. Hawking, W. Israel, Cambridge, England, 1979, ch. 7, pp. 371—391.
n. 98, б. Решение уравнений Эйнштейна в пустоте, линеаризованных над
плоским пространством-временем Минковского, рассматривается в любой моно-
монографии по общей теории относительности. Автор считает наиболее привлекатель-
привлекательным изложение Г. П. Робертсона в книге
13. Robertson Н. P., Noonan Т. W. Relativity and Cosmology, W. В. Saunders
and Co., Philadelphia, 1968, pp. 255—262.
Более подробное обсуждение тонких вопросов теории см. в работах
14. Trautman A. Lectures on General Relativity, mimeographed notes, Kings
College, London, 1958.
15. Trautman A. Bulletin de L'Academie Polonaise des Sciences, 6, 407—412,
1958.

Ёиблиографические замечания 245
См. также
16. Cornish F. Н. J. Ргос. Roy. Soc. (London), A282, 372—379, 1964.
17. Cornish F. G. J. Proc. Roy. Soc. (London), A282, 358—371, 1964.
n. 98, в. В этом разделе мы следовали в основном работе [4].
п. 98, г. Основные работы, в которых доказывается теорема Хартля и Хо-
кинга, следующие:
18. Hawking S. W., Hartle J. В. Commun. Math. Phys., 27, 283—290, 1972.
19. Hartle J. B. Phys. Rev. D8, 1010—1024, 1973.
20. Hartle J. B. Phys. Rev. D9, 2749—2759, 1974.
Изложение в тексте следует работе
21. Carter В. In: General Relativity — An Einstein Centenary Survey, eds.
S. W. Hawking, W. Israel, Cambridge, England, 1979, pp. 310—312.
§ 99. Комплексные характеристические частоты для квазинормальных мод
керровской черной дыры были определены Детвейлером:
22. Detweiler S. Astrophys. J., 239, 292—295, 1980.
См. также
23. Detweiler S. Proc. Roy. Soc. (London), A352, 381—395, 1977.
24. Detweiler S. Astrophys. J., 225, 687—693, 1978.
25. Detweiler S., Szedenits ?., Jr. Astrophys. J., 231, 211—218, 1979.
26. Detweiler S., Szedenits ?., Jr. In: Sources of Gravitational Radiation, ed.
L. Smarr, Cambridge, England, 1979, pp. 211—230.
Сделано все возможное, чтсбы изложение в настоящей главе было логи-
логически последовательным. Однако сам материал просто не дает такой возмож-
возможности: необходимые преобразования часто очень длинны и требуют десяти, два-
двадцати и даже пятидесяти страниц выкладок. Если читатель пожелает скру-
скрупулезно проследить весь ход выкладок, к его услугам выкладки автора, депо-
депонированные в библиотеке им. Джозефа Редженстейна Чикагского университета
(примерно 600 страниц обычного формата и шесть блокнотов).

Глава 10
ЧАСТИЦЫ СПИНА 1/2 В ГЕОМЕТРИИ КЕРРА
101. Введение
До сих пор наше исследование распространения волн в геоме-
геометрии Керра было ограничено рассмотрением электромагнитных
и гравитационных волн — и те, и другие являются волнами
безмассовых полей с целочисленным спином (один и два). Теперь
же мы обращаемся к полям спина 1/2 как массивным, так и без-
безмассовым, описывающим электроны и двухкомпонентные ней-
нейтрино. С математической точки зрения интерес к этим полям
вызван главным образом возможностью разделения переменных
в уравнении Дирака в геометрии Керра. С точки зрения физики
интерес вызывает отсутствие суперрадиации для волн поля
спина 1/2.
Поскольку наиболее удовлетворительным способом записи
уравнения Дирака является аппарат спиноров, изложение начи-
начинается с краткого обзора спинорного анализа и описания спи-
норного базиса в формализме Ньюмена — Пенроуза в объеме,
необходимом для дальнейшего.
102. Спинорный анализ и спинорный базис
в формализме Ньюмена—Пенроуза
4-вектор в пространстве Минковского может быть также
представлен эрмитовой матрицей, а унимодулярное преобразова-
преобразование в комплексном двумерном пространстве (см. уравнения A0)
и A1)) индуцирует преобразование Лоренца в пространстве Мин-
Минковского. Так возникает понятие спинора.
Рассмотрим точку х1 (I = 0, 1, 2, 3) в пространстве Минков-
Минковского, и пусть
(х0J — (х1J — (х2J — (х3J = 0. A)
Запишем теперь координаты точки х* через два комплексных
числа 1° и I1 и и два комплексно-сопряженных к ним числа |°
и I1' следующим образом:
х° = + A//2) (IV + ?|), х + A//2) (IV + Е!),
*« = - 07/2) (go|i' - gi|o'), хз = + A//2) (IV - I1!1')-

102. Спинорный анализ в формализме Ньюмена—Пенроуза 247
Обратное преобразование имеет вид
ЪФ = A //2) (*> + д8}> gof i' = (XIу 2) (*i + /х2),
Б1!0' = A//2) A /2) |i|i' (l//2) (о 3)
В силу этих уравнений получаем
(хУ — (х1J — (х2J- (х3J -
= (л:0 + Xs) (х° — х3) — (х1 + ix2) (х1 — ix2) =
- 2 (Е0!0^1!1' - Е0!1^1!0') = о. D)
Таким образом, представление B) гарантирует, что точка лежит
на световом луче в пространстве Минковского, исходящем из
начала координат и направленном в будущее, поскольку х° с не-
необходимостью положительно.
Пусть теперь
^=0^*, i*' = aA'BiB'(A, В, А\ В'=0, 1) E)
есть линейные преобразования комплексных двумерных про-
пространств (g°, ll) и (|0', I1'), где (аАв) и {аЛ'в')—две комплексно-
сопряженные матрицы. Если х[ записать через величины ?*
и |^' аналогично представлению B), то линейное преобразова-
преобразование E) будет индуцировать линейное преобразование
*1 = Р'У F)
в пространстве Минковского, коэффициенты ft. которого являются
линейными комбинациями матриц а и а. Нужно найти такие
условия на преобразования E), при которых индуцированное
преобразование F) в пространстве Минковского было бы пре-
преобразованием Лоренца.
Из соотношений E) следует, в частности, что
х°, = A//2) (а°0|° + а0,!1) (а^Г + о°,Т) +
= V, (а°оа°о' + «'„«'„.) (х° + /) + V, (а°,а°;. + aSo'i.) (/ - х3) +
+ V» (aW + aWiO (хх + ix2) -f V2 (a°ia°0- + a\al0.) (x1 - ix2).G)
Следовательно,
, P°o - Р°з = a°
( )

248 Глава 10. Частицы спина 1/2 в геометрии Керра
Требование, чтобы преобразование F) было лоренцевым, приво-
приводит (в частности) к тому, что
(Э°о)9 - 0°iJ - (Р°2)я - О0»J = 1 - О)
Вследствие соотношений (8) отсюда вытекает
о i||
'-г _,J=AA = 1, A0)
|| \\
I
o-o' , i-i' o-o' , i -I-
a ia0' +a ia0- a i<x P +a ia P||
где А и Д —детерминанты преобразований E). Следовательно,
необходимым условием того, что преобразования E) представляют
преобразования Лоренца, является равенство единице модуля
детерминантов этих преобразований, другими словами, эти пре-
преобразования должны быть унимодулярными. Очевидно, что это
условие является достаточным. В дальнейшем мы будем пред-
предполагать, что
Д = Д=Г1, A1)
т. е. мы ограничиваемся преобразованиями с единичными детер-
детерминантами. Ясно, что эти преобразования (сохраняющие напра-
направление времени) включают в себя все лоренцевы преобразования
без отражений. Если же вдобавок рассматривать преобразования,
отличающиеся знаком от преобразований, подчиняющихся усло-
условию A1), то мы восстановим всю совокупность преобразований
Лоренца.
Определим теперь спиноры ?л и г]Л' ранга 1 как комплексные
векторы в двумерном пространстве (А, А' = 0, 1), имеющие
следующие законы преобразований:
5? = аАБ5*, 1\*' = аАв.1\В'(А, А\ В, В' = 0, 1), A2)
где (аАв) и (аАВ')—комплексно-сопряженные матрицы с единич-
единичными детерминантами
||сЛ! = |йЛв-|=1. A3)
Важно различать спиноры двух классов: нештрихованные
и штрихованные — последние преобразуются с помощью комплекс-
комплексно-сопряженной матрицы. Для спинорных индексов мы будем
использовать только прописные буквы латинского алфавита.
Если два спинора 1А и г\А принадлежат к одному и тому же
классу, то детерминант
инвариантен относительно унимодулярных преобразований. Сле-
Следовательно, можно определить кососимметричную метрику гАВ
в пространстве спиноров, такую, что
в = inv, A5)

10%. Спинорный анализ в формализме Ньюмена—Пенроуза 249
Из сравнения с уравнением A4) следует, что
?оо = 8и = 0, 8Oi = —ею = 1, A6)
т. е. гАВ — двумерный символ Леви-Чивиты. Подобным же
образом можно определить метрику гл'В' для штрихованных
спиноров, она также будет задаваться символом Леви-Чивиты.
Как и в тензорном анализе, метрики глв и гА>В' могут исполь-
использоваться для опускания спинорных индексов
1а = 1с*са, A7)
или в явном виде
10 = -g\ I, = 1°. - A8)
Индексы могут подниматься символом Леви-Чивиты гАВ:
Вследствие антисимметричности символов гАС и гСА в уравне-
уравнениях A7) и A9) важно сохранять порядок индексов по отноше-
отношению к свертываемому индексу. Поскольку
1а = Ъс*са = &св1в*са> B0)
имеем
6л = гсвгсл = г/ = -еБл. B1)
Очевидно, что рассматривая штрихованные спиноры, мы полу-
получим снова формулы A7)—B1), но со штрихованными индексами.
Так же как в тензорном анализе, можно построить спиноры
более высокого ранга
1ЛВ, Ъав'с, Iabc>D'Ef>g и т. д. B2)
с соответствующими трансформационными свойствами. Например,
Ь* — ОС С ^* ?)'ъ * Кг'д)
Важно отметить, что порядок индексов каждого типа является
существенным и должен сохраняться, но относительный порядок
штрихованных и нештрихованных индексов может быть произ-
произвольным.
И снова, как и в тензорном анализе, с помощью метрики гАВ
или гА'В' можно произвести свертку пары нештрихованных
или пары штрихованных индексов, однако свертка штрихован-
штрихованного индекса с нештрихованным, разумеется, запрещена. Имеем
ЬА' —6 5Л'Б'- \^V
С другой стороны,
с л' = е 5В'Л'1 1^;

250
Глава 10. Частицы спина 1/2 в геометрии Керрй
следовательно,
в частности.
t А' t'4'
6А' = —S Л'>
Ъа>1а' = 0.
Формула B6) — пример «правила пилы» Пенроуза
B6)
B7)
B8)
а. Спинорное представление векторов и тензоров. Уравне-
Уравнения B) и C) дают представление радиуса:вектора х1 через пару
комплексно-сопряженных спиноров 1А и 1А\ Это представление
можно записать в виде
ГЛ"... а.. .
х1
ix2
\ _ ix
_ хз
B9)
В общем случае мы свяжем произвольный 4-вектор X1 со спино-
спинором второго ранга 1АВ' следующим образом:
toe tor
i10' 6»'
Х° +
X1 + tX2
X1 - iX2 X° - X3
= ХАВ' C0)
Таким образом, 4-вектор связан с эрмитовой матрицей.
С 4-вектором связан следующий инвариант:
(X0J - (X1J - (X2J - (X3J = (Х° + *3) (Х° - V3) -
- (X1 + ;х2)(Х! - tX2) = г^00'!11' - ^х ') =
= AооЪо> + bi'g"' + gio-g10' + 101Ъу) = ХАВ.ХА*\ C1)
Этот инвариант можно записать с помощью метрики gu простран-
пространства Минковского и метрик гАв и &А'В' спинорного пространства:
C2)
C3)
Соотношение
X1 — ХАВ'
теперь принимает следующий вид:
X' = аА1
Обратное соотношение имеет вид
ХАВ' = <
AB'
C4)
C5)
где о1Лв' и ofB' — эрмитовы матрицы для каждого значения
индекса i. Следствием этих определений являются соотношения
АВ' i
AB
= 0/.
C6)

102. Спинорный анализ в формализме Ньюмена—Пенроуза
251
И наконец, из соотношений C2) и C5) получаем
AB'CD'
gij =
C7)
C8)
Матрицы (Тля- и о?в\ определяемые представлением B9),
имеют следующий вид:
1 О
0 1
О i
—i О
1 О
О 1
ТЛЯ' _
1
1
1
о?° =
1
V2
1
V2
0 1
1 О
1 О
О —1
C9)
V2
О
0
1
1
0
1
0
0
—1
D0)
Итак, с точностью до нормировочного множителя 1/-/2 ма-
матрицы (Тля-, Оав' и Оав- совпадают со спиновыми матрицами
Паули.
С помощью матриц а можно сопоставить тензорам произволь-
произвольного ранга их спинорные эквиваленты:
л/Ц i '] EF'yrAB'CD' \/AB'CD' AB' CD' k \rij ,Ллк
У k = GAB'VCD'Gk У EF'> У EF' = &i Gf &ЕР'У k • V^V
В силу этих соотношений имеем правило соответствия
УАВ'СВ'ЕР,~УЧ. D2)
В этом смысле формула C8) представляет собой правило соот-
соответствия
&AC&B'D' *-* gij- D3)
б. Наглядное представление спинора \Аввиде «флага». Рассмо-
Рассмотрим изотропный вектор их и его спинорное представление (Jab-
!через спинор |л и комплексно-сопряженный ему спинор ?в'«
иАВ> = ЫВ-
D4)
ректор иг изотропный, поэтому вследствие соотношения B7)
имеем
\ = Ыв>1Л1в' =0. D5)
D6)
русть г\Л — другой спинор, определяемый равенством

252 Глава 10. Частицы спина 1/2 в геометрии Керра
и пусть
Wi ^ WAB> = 1аЧв> + Ца1в>. D7)
Рассмотрим антисимметричный тензор
ри = UtWj - UjWi. D8)
Спинорное представление тензора ptj имеет вид
Pab-cd- = IaIb> (Ic4d- + ticId-) - ScId- (БаЛв- + Ла1в') =
= Ыс (Ib'TJd- - Id-Ля') + Ib-Id' Fдт|с - 1сЦа). D9)
С другой стороны,
1аЧс - Ча1с = ?>ас> E0)
поскольку левая часть антисимметрична по индексам Л и С,
в силу определения D6) она может принимать значения +1 или
— 1 в зависимости от значения парного индекса {АС), равного
@, 1) или A, 0). Поэтому Рab'cd' можно записать в альтерна-
альтернативной форме
Р* ab'cd' = IaIcZb-d- + uacIb'Id'- E1)
Теперь ясно, что тензор ри также определяется спинором 1а-
Вектор wt по определению действителен, и он ортогонален
вектору ии поскольку
utw. = |л|в- {1Лв, + Пл| в,} = о. E2)
Кроме того, вектор wt пространственноподобен, поскольку
WiW1 = fotjB. + х\Ав-) (W + г\Чв') = Чв'1в' - 1в'Чв' = -2.
E3)
При выводе этого соотношения нужно несколько раз исполь-
использовать уравнение D6). Таким образом, спинор 1А определяет не
только изотропный вектор и*, но и действительный простран-
ственноподобный вектор w\ ортогональный вектору и1 (разуме-
(разумеется, вектор w( определен с точностью до слагаемого, пропорцио-
пропорционального вектору и1). Следовательно, спинор ?л определяет изо-
изотропный вектор и1 — «флагшток» — и ортогональную двумер-
двумерную поверхность wl + аи1 — «флаг», и обратно, флаг задает
спинор с точностью до знака.
в. Диадный формализм. Поскольку пространство-время об-
общей теории относительности локально является пространством
Минковского, в каждой его точке можно построить ортонорми-
рованный диадный базис tfa), ?>&) (#» о!', Л, А' =0, 1) для спино-
спиноров так же, как мы строили тетрадный базис с1{а) (a, i = 0, 1,
2, 3) для тензоров в тетрадном формализме (см. гл. 1,§ 7). И так же
как в тетрадном формализме, диадные индексы — строчные буквы

102. Спинорный анализ в формализме Ньюмена—Пенроуза 253
начала латинского алфавита — будем заключать в скобки.
Удобно, однако, иметь специальные символы для двух базисных
спиноров ?А0) и ?а)- Будем писать
ГА — ОЛ ?А — ,Л (КЛ\
Ь@) — U > fell) — 1 ' \°*)
Условие ортонормированности имеет следующий вид:
гАвоЧв = ohx - оЧ° = oBiB = — oAiA = 1. E5)
Элементарными следствиями этих определений являются соот-
соотношения
E6)
о(а)F)*Д *В «.Д -В с.Л ^.В Л Б А В ОАВ /г>~,
в fe(a)bF) = wo)S(i) — &(i)&@) =0 i —to =8 . E7)
Ясно также, что можно поднимать и опускать диадные индексы
с помощью матриц е<а)^ и б(а)(&). Действительно,
Г(с) А —ГА c(a)(c)rA rW A (КЯ\
Ъ г(с) (а) — С,(а)» Б С,(С) = С, . (OOj
Кроме того, имеем
= —?{)?А = б() С() Л^F) = —S(a)CF) Л = 6(а) F)- E9)
Как и в тетрадном формализме, можно спроектировать любой
спинор ?д на диадный базис
Ьа) - Ы(а)> F0)
t@)=lAO\ БA)=ЕлИ. F1)
Обратные соотношения имеют вид
F2)
Имеется соответствие между изотропными векторами 1, п,
и m у
норами
m и m и спинорами оА и И и комплексно-сопряженными им спи-
V *+ олоБ', т{ « ол1Б', т1' «- Иов', п1' « Иьв'. F3)
Изотропные векторы удовлетворяют условиям ортогональности
11П\ = ОАОВ\а1>В' = 1, nCnti = О^1ВЧлОВ' = —1» F4)
а остальные скалярные произведения равны нулю. Таким образом,
диадный базис определяет четыре изотропных вектора, которые
могут быть использованы в качестве базиса в формализме Нью-
Ньюмена — Пенроуза (гл. 1, § 8).
Представление F3) вводит в рассмотрение эрмитовы матрицы
Оав'9 <?; > F5)

254
Глава 10. Частицы спина 1/2 в геометрии Керра
такие, что
Л i Л
i ^А'В' i
= <*ав'О о , т =
п =
I A~n
Поэтому можно написать
°AB-= YT
i'
т1
т1
1/2
Tli —t
h
F6)
F7)
Сравнение с формулами C9) и D0) показывает, что вышеприве-
вышеприведенные определения позволяют естественным образом обобщить
спиновые матрицы Паули.
И наконец, производные по направлению в формализме Нью-
Ньюмена—Пенроуза (определения B85) гл. 1)
D = Vdb А = п*ди б = т*ди S* = rh^i F8)
имеют свой спинорный эквивалент
д00, = D, 3ip = A, doi- = в, die = S*. F9)
г. Ковариантная производная спинорных полей и спиновые
коэффициенты. В настоящем разделе мы определим ковариантное
дифференцирование спинорных полей. Самосогласованное опре-
определение должно основываться на следующих соответствиях:
V; — Vab>, G0)
ViXj = Xi; i <-+ Vab-Xcd- = XCD'\ ab>. G1)
В соответствии с соотношением D1) это последнее соотношение
требует, чтобы
XCD'\ AB' = OCD'G1AB'XJ: ,-. G2)
Кроме того, потребуем, чтобы ковариантное дифференцирование
спинорных полей удовлетворяло правилу Лейбница, т. е. чтобы
Улв- (S-... X Г"...) - T~\..Vab>(S'~...) + S-/..Vab>(T-...),
G3)
где S' ' и Т"\ —два произвольных спинорных поля. Потре-
Потребуем также, чтобы оператор Vab' был действительным:
Улв- = Va>b. G4)
Покажем теперь, что предыдущих постулатов достаточно для од-
однозначного определения операции ковариантного дифференциро-
дифференцирования. Но прежде заметим, что как и в тетрадном формализме
мы можем определить внутреннее дифференцирование. Действи-
Действительно, определим внутреннюю производную диадной компоненты
|(а) спинора вдоль «направления» (а) (Ьг) равенством
В'?(а)?(Ь')> G5)

102. Спинорный анализ в формализме Ньюмена—ftенроуза 255
ИЛИ
\{с)\АВ* = ?(с)?с;ЛВ'« G6)
Докажем два элементарных следствия вышеприведенных оп-
определений и постулатов.
ЛЕММА 1.
оЬ>;ав>=0, о^Рав* = 0. G7)
Доказательство. Лемма следует из соотношения G2), левая
часть которого может быть записана в виде
AB' = (Oco-Xj)- АВ'у G8)
а правая — в следующей альтернативной форме:
Ъ1св- (°Ав>Хг, {) = o'cd.Xj; ab>. G9)
Из требуемого равенства правых частей соотношений G8) и G9)
следует первое из двух утверждений леммы. Второе же утвержде-
утверждение следует из соотношений ортогональности C6) и правила
Лейбница.
ЛЕММА 2.
ZCD',AB> =0. (80)
Доказательство. Вследствие правила соответствия G1) и пра-
правила Лейбница, справедливого как для тензорных, так и для спи-
норных полей, из уравнения C7) вытекает, что
0 = gjk; i = ОГ* (*>CDbE'F'OCjE ^ ); AB', (81)
Из леммы 1 получаем
OfB' (eCD6?'F'); AB' = 0, (82)
откуда и вытекает доказываемое утверждение (80).
ОПРЕДЕЛЕНИЕ. Спиновые коэффициенты Г(а) {Ь) {с) (^)
в диадном формализме определяются следующим образом:
Г(а) (Ь) (с) (</') = ll(a) f]\ CD'l(b)Uc)Ud')- (83)
Удобно краткости ради использовать другую формулу (несмотря
на менее симметричный вид)
Г(а) (b) CD' = [?(а) f]; CD'Ub)' (84)
Определенные таким образом спиновые коэффициенты симмет-
симметричны по первой паре индексов. Эта симметрия следует из соот-
соотношения (ср. с уравнением E9))
(85)

256 Глава 10. Частицы спина 1/2 в геометрии Керра
потому что в силу этого соотношения и леммы 2 имеем
Г(а) (b) CD' = — UF)J; CD'^>(a) F = + [?(&) f]; CD'^(a) = ^(b) (a) CD'- (86)
Мы получим альтернативную запись уравнения (84), если свернем
его со спинором ?<?> и используем соотношения E9):
[?>(а) e];CD' = —?>Е F(b)(a)CD' = ?F) еГ (a) CD" (87)
Покажем, что внутренние производные диадных компонент
спиноров первого и второго ранга могут быть выражены через спи-
спиновые коэффициенты, а в силу правила Лейбница этого достаточно
для получения ковариантных производных спиноров произволь-
произвольного ранга. Действительно,
Ъ(а)\ВС = 1>{п)Ьа\ ВС = [5л?(а)]; ВС ~ %А [S(fl)J; ВС- ' (88)
Величина в первой квадратной скобке в правой части уравнения
является скаляром и равна ?(а). Поэтому в силу соотношения
(87) имеем
1(а)\ВС = 1(а), ВС ~~ ?лГ (a) BC'?>(d)> (89)
ИЛИ
lia)\BC' = l(a).BC> + T(d){a)BC'lid). (90)
Подобным же образом находим
о(а) с.(<2) , р(<3) ?(rf) /Q1\
SI ВС =|. ВС + 1 (rf)BC'S ' (У1)
В силу симметрии спиновых коэффициентов по первой паре ди-
диадных индексов нужно задать только 12 коэффициентов. В фор-
формализме Ньюмена—Пенроуза за этими коэффициентами закреп-
закреплены специальные обозначения Г(а) (b) (с) (<*>:
(с) {df)
00'
10'
or
11'
00
X
P
a
T
(a) (b)
01
или
10
8
a
P
У
11
Jt
A,
|Я
V
(92)
Остается убедиться, что эти определения спиновых коэффициентов
согласуются с определениями, введенными выше через коэффи-
коэффициенты вращения Риччи yijk (определения B86) гл. 1).
t Докажем прежде всего следующую лемму, сформулированную
Дж. Фридманом.
ЛЕММА 3.
Г(а, (b) CD' - ll^kf) {П1В{пIи>) [?<*) El(k>) H; CD- (93)

102. Спинорный анализ в формализме Ньюмена—Пенроуза 257
(Заметим, что в силу правила соответствия F3) комбинации
?fa)?ff-) и ?F) ?&(*') F' представляют базисные изотропные век-
векторы.)
Доказательство. Расписывая правую часть соотношения (93)
по правилу Лейбница и преобразуя ее с помощью соотношений E9),
получаем последовательно
V28 f?(a)?(/')?F)?[?(fe') F'],CD' + ?(a)?</')?<*') F'[?F) e\\ CD'\ =
1/ ЛЬ') (f) { o fF' r(rf') «. ,
+ 8(?') (/')b(a)l F) CD'Q(d) E\ =
= V2e(* ) (/ ) {— 8(a) (Ь)б^ )(/')Г(^) (k') CD' + ?(/г') (f')^d\a)^(d) (b) CD'} ==
== 1/2е(*') (//) |— 8(e) (б)Г(й') (/-) CD' + 8(fe') (/')Г(а) (b) CD') =
= Vae<*') </'>e(*,, (/,,Г(в) F) со- = Г(в) F) CD- (94)
Лемма доказана.
С помощью леммы Фридмана можно выразить различные спи-
спиновые коэффициенты Г@) <&) <с> <^> через ковариантные (тен-
(тензорные) производные базисных изотропных векторов 1, n, m
и m и проверить, что определения, введенные в настоящем разделе,
находятся в согласии с определениями спиновых коэффициентов
через коэффициенты вращения yijh. Действительно, с помощью
определений E4), F3) и F9) находим (опуская скобки при диад-
ных индексах, когда они принимают конкретные значения О
или 1)
Г1/ Лк') (f')rE ZF' г* "Z -,
0000' = 72е ?@)?(/') l?0E?(ife') F']; 00' =
= 1/2е(Л')(По?СГп[о?С(„Н;оо' =
- Va [оЕ~1Р'1*(о&Р.); i - oV/'(o?7F,); Л =
- V2 [тП% i - Wmv% i] = V2 [7зп - Tiai] = Тзи = к (95)
в полном согласии с определением спинового коэффициента х
в гл. 1 (определения B86)). Аналогично этому
Hoi- = /28
= V2 [i?i
= V2 [т'т*тг, t - т1т1п}; t] = V2 (Y243 — 7423) = 7243 = Ц> (96)
что снова находится в полном согласии с определением спинового
коэффициента \i в гл. ^(определение B86)). Точно так же могут
быть вычислены и остальные спиновые коэффициенты.
На этом мы заканчиваем изложение спинорного анализа и
построение спинорного базиса в формализме Ньюмена—Пенроуза.
9 Чандрасекар С, т. 2

258 Глава 10. Частицы спина ll2 в геометрии Керра
103. Уравнение Дирака в формализме Ньюмена—Пенроуза
Хорошо известно, что в релятивистской теории частицы спина
1/2 описываются парой спинорных волновых функций РА и QA\
В пространстве Минковского уравнение Дирака для этих спино-
спиноров имеет следующий вид:
oiAB-diPA + i|i.Qfl- = 0, (97)
OAB>diQA + wJPb- = 0, (98)
где о1Ав' — матрицы Паули, a (i^f/2 — масса частицы (равная
в подходящей системе единиц обратной компотоновской длине
волны). Множитель У 2 в определение массы входит потому,
что определение матриц Паули D0) отличается от обычного опре-
определения множителем 1/V.
В формализме Ньюмена—Пенроуза в искривленном простран-
пространстве-времени уравнения (97) и (98) останутся справедливыми, если
обычные производные заменить ковариантными производными,
а матрицы Паули заменить матрицами а, определенными форму-
формулами F7). Искомые уравнения, таким образом, имеют вид
где
Выпишем теперь в явной форме эти уравнения через введенные
спиновые коэффициенты.
Рассмотрим уравнение (99) для В' = 0. Имеем
аоо'Р? t + aiV/>! i ~ W*Q1' = 0. A02)
В силу определений F8), F9), (91) и A01) получаем
(доо-Р0 + Поо-Я6) + (дю>Р1 + Т\ х*Рь) ~ щЛ1' = 0, A03)
или более подробно
(D + Гюоо- - Гоою-) Ро + (б* + Гпоо- - ГоиоО^1 - М1' = °- (Ю4)
Заменим теперь различные спиновые коэффициенты в уравнении
A04) специальными обозначениями, перечисленными в (92). По-
Получаем
(D + е - р) Р° + (б* + я - а) Р1 - iiijQ1' - 0. A05)
Аналогично уравнение (99) для В' = 1 дает
(Л + |х - 7) Р{ + F + Р ~ *) Р° + М0' = 0. A06)
Из уравнения A00) получаются уравнения A05) и A06), но с пе-
переставленными Р и Q. Удобно, однако, рассмотреть уравнение,
l
C'ec
/'
в- =
В' =
m'
0,
0,
•
(99)
A00)

104. Уравнение Дирака в геометрии Керра 259
комплексно-сопряженное уравнению A00), и, кроме того, ввести
обозначения
Fx = po, F2 = P\ Gt = Q1', G2 = -Q0'. A07)
Выпишем результирующие уравнения
(D + е — р) F! + (б* + я - a) F2 = ipjQ^
(A+ix~y)F2 + (8 + $-T)F1 = ;>,G2;
(D + e* - p*) G2 - (б + я* - a*) d - i|x#f2; ( }
(Л + fx* — Y*) Oi - (s* + P* — т*) G2 - /ji^.
Это и есть запись уравнения Дирака в формализме Ньюмена—¦
Пенроуза.
104. Уравнение Дирака в геометрии Керра;
разделение переменных
Предполагая, что четыре компоненты волновой функции —
в наших обозначениях Flt F2y Gx и G2 — имеют обычную зависи-
зависимость exp [I (ot + mcp)] от t и ф, и подставляя вместо спиновых
коэффициентов и производных по направлению выражения, полу-
полученные в гл. 6 (уравнения A70)—A73) и A75)) и в гл. 8 (уравне-
(уравнения B)—E)), находим, что система A08) сводится к следующей:
j-) G2 - -^ ^Г/2С,
г2? ш sin 0
/2 Г~
Форма уравнений A09) подсказывает, что вместо функций
и G2 удобно ввести функции
fx = p*FL = (г — ш cos 0) Z7! ( = р*Я°),
g = pG2 = (r + ia cos 9) G2 (= — pQ0').
Если теперь вместо F2 (= Pl) и Gi (= Q1') писать f2 и g (чтобы
результирующие уравнения имели симметричную форму), то
уравнения A09) примут вид
^o/i + 2-xi29?\pf2 = + (t>*r + а(х# cos9)gb
- 2+1/22^/2/i = ^2 (ф,г -f (цх, cos 9) ^2,
,,. . (Ill)
= + (i\ij — a\x^ cos 9) /2,
= —2 (iji^r — а(ы# cos 9) /1.

260 Глава JO. Частицы спина 1/2 в геометрии Керра
Теперь очевидно, что переменные могут быть разделены следую-
следующими подстановками:
/, (г, 0) = #_,/2 (г) S-i/2 (9), /2 (г, 0) = R+l/2 (r) S+i/2 (9),
?, (Г/0) = #+1/2 (Г) S-,/2 (9), ?2 (Г, 6) = /?_1/2 (Г) S+,/2 @), ( }
где /?±i/2 (/") и 5±i/2 @) — функции соответственно только г и 0.
В результате уравнения A11). принимают следующий вид:
B5o#-i/2 - i\i,rR+U2) 5_i/2 +
+ [2-l!2&i/2S+U2 - (afi. cos0) S_i/2)] #+i/2 = 0,
_1/2) 5+i/2 -
^,V-i/2 - 2 (вA. cos 0) S+i/г] Л—1/2 = 0, A13)
B>oR-\/2 - ф.Г/?+1/2) S+l/2 —
- [2-1/2^i/2S_,/2 - (ацф cos0) S+,/2] /?+I/2 = 0,
- 2 (ацф cos0) S_i/2] /?-i/2 = 0.
Из этих уравнений следует, что
&0R-\/2 - l
2+1/22'l/2S_,/2 - 2 (ац. cos 0) S+i/2 = +X2S+1/2, A14)
St)uR-\,2 - ty.rR+\/2
2-1/2^f/2S_i/2 - (ац, cos0)
, cos 0) S_i/2 = —^S_i/2,
где Xb ..., A,4 — постоянные разделения. Ясно, однако, что для
совместности вышеприведенных уравнений требуется
А-! = Хв = VA, = XUK = Я-. A15)
Мы получили, таким образом, две пары уравнений
&oR-i/2 = (А, + 1>.г)
= -21/2 (х _ а^ cos 0) S-i/2,
cos0)S
Здесь удобно сделать изменения в обозначениях
-^ те, 2'/2/?_1/2 -> /?_1/2. A18)

105. Нейтринные волны в геометрии Керра 261
Тогда уравнения A16) и A17) принимают следующий вид:
imer) AV2R+l/2, A19)
intef) Д-1/2, A20)
os0)S_1/2, A21)
cos е) s+i/2» A22)
где me — масса частицы, записанная через обратную комптонов-
скую длину волны (т. е. вместо тес/й написано тв).
Из уравнений A19) и A20) можно исключить функцию Al/2R+{/2
и получить уравнение для функции R-\/2
] _1/2 = 0. A23)
Функция A 1/2/?_^_i/2 удовлетворяет комплексно-сопряженному урав-
уравнению.
Исключив функцию S+i/2 из уравнений A21) и A22), полу-
получим уравнение для функции S_i/2
22 2л\1о л
flm^cos e)J s-v2 = о.
A24)
Функция S_i/2 удовлетворяет «присоединенному» уравнению (по-
(получаемому заменой 0 на я — 0). Величина % теперь выступает
в качестве собственного значения, определяемого из граничных
условий, которые требуют, чтобы функция S_i/2 (а следовательно,
и функция S+1/2) была регулярной в точках 0 = 0 и 0 = я.
Мы вернемся к этим уравнениям с разделенными переменными
в § 106, после того как рассмотрим более простой случай безмас-
безмассовых двухкомпонентных нейтрино в § 105.
105. Нейтринные волны в геометрии Керра
Уравнения для двухкомпонентных нейтрино (для которых
в пространстве Минковского справедливы уравнения Вейля)
можно получить, положив те = 0 в уравнениях A19)—A24).
Полагая также (ср. с уравнением F5) гл. 8 и уравнением G2)
гл. 9)
?—1/2 = Я-1/2, A25)
имеем две пары уравнений
1/2? 1/2 A26)

262
Глава 10. Частицы спина 1/2 в геометрии Керра
Им соответствуют следующие расцепленные уравнения второго
порядка:
= 0, (Д0?/2Фо - >?) Р-\/2 = 0; A28)
? СР Ср3? С \ 2 о /1OQ\
>_j_]/2, °? 1/2«^ 1/2^ 1/2 == —™ *^ 1/2* V*^^/
Итак, уравнения A28) действительно принадлежат к специ-
специальному классу, рассмотренному в гл. 8 (уравнения (96) и (97)
гл. 8), если в последних положить | s | = 1/2. Общая теория пре-
преобразований, развитая в § 72 и 73, применима и здесь и позволяет
преобразовать уравнения A28) к одномерным волновым уравне-
уравнениям. Однако в данном случае проще исходить прямо из уравне-
уравнений A28) и кратко повторить теорию преобразований.
Как было показано в § 72, введение функции г^ в качестве не-
независимой переменной (уравнения A00) и A01) гл. 8) придает
операторам 3H и 3)\ простой вид
550 = -5L /._ у ia\ 9 0j = J^__ /._ tcr4), A30)
где
со2 = г2 + а2 = г2 + а2 + ami о. A31)
Вместо уравнений A26) теперь получаем
Д1/2
со*
-1/2,
A32)
A33)
Полагая
Z± = P+l/2 ± Р_1/2, A34)
получаем вместо уравнений A32) и A33) следующую систему:
Д1/2
52
(О
Z_ = iaZ+.
A35)
A36)
Эти уравнения сразу же дают пару одномерных волновых
уравнений
/ ^2 . 2\ 7 — v z П37)
где
д1/2
со
A38)
а. Задача об отражении и прохождении в случае а >
сг,(= —am/2Mr+). Ясно, что при a > os существует однознач-

HS. Нейтринные волны в геометрии Керра 263
ное соответствие между решениями одномерного волнового урав-
уравнения A37) с любым из двух потенциалов A38) и решениями ис-
исходных уравнений, поскольку в этом случае зависимость г^ от г
однозначна, а сами потенциалы являются ограниченными и корот-
короткодействующими. Кроме того, поскольку потенциалы 1/±, опре-
определяемые уравнениями A38), принадлежат к общему классу по-
потенциалов
^- + P2f + x/. A39)
рассмотренных в § 26 гл. 4, с параметрами
р/ = ^А1/2/©2, х - 0, A40)
уравнения для Z+ и Z_ дадут одинаковые коэффициенты отраже-
отражения и прохождения. Равенство коэффициентов отражения и коэф-
коэффициентов прохождения прямо следует из уравнений A35) и
A36), согласно которым
Будем искать, как обычно, решение волнового уравнения A37),
скажем с потенциалом У+, имеющее следующие асимптотики:
+ ~Ч fi(or)exp[ + iarj (Гф -> -оо).
С помощью уравнения A35) мы можем получить из этих решений
для Z+ решения волнового уравнения с потенциалом 1/_ — реше-
решения Z_, которые (в силу уравнения A41)) имеют следующие
асимптотики:
jexp Жал,] - А (а) ехр [—iar#] (г* -> +оо),
"~Ч B(o)exp[+iarJ (г, ^-оо).
Следовательно, потенциалы V± приводят к одинаковым коэффи-
коэффициентам отражения и прохождения, которые определяются равен-
равенствами
R = | А(о)\\ Т = | ^ (а) |2 A44)
и удовлетворяют условию
R + T= 1. A45)
Ниже в § 106 и 107 мы проверим в более общем случае урав-
уравнения Дирака, что определенные таким образом через решения
волновых уравнений Z± коэффициенты отражения и прохождения
согласуются с физическим определением потока нейтрино через
горизонт событий.
На рис. 46 показано семейство потенциалов V± в интервале
частот os < о ^. ос (= —т/а). В этом ш.терЕале а2 < 0, но

264
Глава 10. Частицы спина ll2 в геометрии Керрй
О < | а | < г+ и | а | -> г+ + О при а -> as + 0. Вследствие по-
последнего факта потенциальный барьер для падающих нейтрино
неограниченно возрастает при a -> as + 0. Однако сингулярность
потенциала на горизонте в этом пределе слабее, чем соответству-
соответствующая сингулярность для фотонов и гравитонов. Действительно,
рассмотрим интеграл от 1/, который является мерой величины
о,зг
Рис. 46. Потенциальные барьеры К(+) (сплошные кривые) и ]/( > (штриховые
кривые) вокруг черной дыры Керра (а = 0,95) для падающих нейтринных волн
с / = 2,5, т = —2,5 и частот в интервале ос < a < as. У кривых указаны
соответствующие значения частоты а.
барьера. Находим, что для обоих потенциалов A38) этот интеграл
равен
у dr -
c, 0<|a|<r+). A46)
Он расходится логарифмически в пределе a -> os + 0 в отличие от
расходимости типа A — os/o)-2 в случае электромагнитных и
гравитационных волн. Оказывается, эта более слабая сингуляр-
сингулярность потенциала для нейтрино приводит к конечному коэффи-
коэффициенту прохождения нейтрино в пределе а -> as + 0. Численные
результаты, приведенные в табл. 11, подтверждают наше подо-
подозрение, однако это нужно еще строго доказать.
б. Отсутствие супер радиации @ < a < as). В интервале ча-
частот 0 < a < gs зависимость г* от г становится двузначной и,
кроме того, потенциалы V± становятся сингулярными в точке

105. Нейтринные волны в геометрии Керра
265
г = | а | (>г+ при а < os). Действительно, из явного выражения
для потенциалов V±
A47)
находим, что в окрестности г = \а\ они имеют следующее по-
поведение:
^'L 1
У*~=»*4|'«р (г- | , У A48)
Это поведение отличается от соответствующего поведения (см.
уравнение A93) гл. 8 и уравнение D28) гл. 9) потенциалов для
| 5 | = 1 и 2 в важном отношении — теперь мы имеем полюс треть-
третьего, а не четвертого порядка.
Вернемся к задаче об отражении и прохождении. Как уже объ-
объяснилось в п. 75, в и 76, в гл. 8, мы должны искать решения урав-
уравнений для Z, удовлетворяющие следующим граничным условиям:
{exp [+ior#] -f A exp [—iorj вдоль ветви г ~*ос и /•*->+«>>
A49)
Вехр [+1аг#] вдоль ветви г-> г++ 0 и г#-* + оо. A50)
Кроме того, вследствие уравнения A40) гл. 8 для случая | s \ = 1/2,
который мы рассматриваем, вронскиан решений Z и Z* должен
оставаться одинаковым по обе стороны от сингулярности при
г = | а | в противоположность изменению знака вронскиана
в случае целого спина. По этой причине закон сохранения для
падающих нейтринных волн остается неизменным и в интервале
0 < а < а8:
R + T = 1 @<g<os). A51)
Таблица 11
Коэффициенты отражения для нейтрино, падающих на керровскую черную дыру
с а = 0,95 (I = 0,5, т = —0,5)
а
0,181987
0,182987
0,183987
0,184987
0,185987
0,186987
0,187987
0,188987
0,189987
0,200987
0,210987
o/os
1,0055
1,0111
1,0166
1,0221
1,0276
1,0332
1,0387
1,0442
1,0497
1,1105
1,1658
R
0,97627
0,97556
0,97479
0,97398
0,97313
0,97223
0,97129
0,97012
0,96925
0,95353
0,92971
а
0,220987
0,230987
0,240987
0,250000
0,250987
0,260987
0,300000
0,350000
0,400000
0,450000
ojos
1,2210
1,2763
1,3315
1,3813
1,3868
1,4420
1,6576
1,9338
2,2101
2,4864
0,89187
0,83457
0,75356
0,66005
0,64885
0,52777
0,14125
0,01622
0,00197
0,00027

266 Глава 10. Частицы спина 1/2 в геометрии Керра
Другими словами, супер радиации не будет — это следует также
из численных результатов, представленных в табл. И.
Ниже мы кратко опишем поведение решений Z± в окрестности
точки г = | а |.
Полагая
х = г — |а|, A52)
находим, что в окрестности точки г = \ а \ уравнение для Z±
принимает вид
"^-^±^^ = 0. 053)
Решением этого уравнения являются функции
( }
) Для V_,
где
у - 4ta/A}?,, A55)
а ^а — общее решение уравнения Бесселя второго порядка. Зная
это поведение решений Z+ в сингулярности, нетрудно проинтегри-
проинтегрировать уравнение в интервале, включающем точку г — \ а |,
и завершить решение, как в п. 75, в гл. 8 для электромагнитных
волн.
Основной физический результат нашего исследования —
это отсутствие суперрадиации для частиц спина 1/2. (В § 107
мы подтвердим это и для массивных частиц.) С аналитической
точки зрения причина этого кроется в том, что, во-первых, потен-
потенциальные барьеры имеют полюс третьего порядка (а не четвертого
порядка, как в случае частиц целого спина) и, во-вторых,
вронскиан [Z, Z*] не меняется при прохождении сингулярности
потенциала V (в отличие от случая частиц с целым спином, где
происходило изменение знака вронскиана).
106. Сохраняющийся ток и сведение уравнений Дирака
к одномерным волновым уравнениям
В § 104 было показано, что решения для базисных спиноров
РА и QA' в геометрии Керра, описывающих частицу спина 1/2,
представимы в виде
-i/2 (г) S+i/2 (9), A56)
Р[ = Я+1/2 (г) 5+i/2 (9), Q1' - Я+1/2 (г) S-,/2 (9),
где в выражениях для Р° и Q0' восстановлен множитель
который мы опустили при переходе от уравнений A16) и A17)
к уравнениям A19)—A22).

166. Сохраняющийся moti
Уравнения для радиальных функций имеют следующий вид:
д1/2 (J_ _ /Il+al ^
где
Р+1/2 = Д1/2Я+1/2, Р_1/2=Я_,/2. A59)
Из уравнений A57) и A58) сразу же находим, что
-?-A/>+,„] *-|Я_,/2|*) = Р A60)
Эквивалентное соотношение, но в которое входит вронскиан
[Р_1/2, Р+1/21, имеет вид
[А1/2/(^ + ш,0] [P-i/2, Р+Г/2] = const. A61)
Величина (| P+i/2 Г2 ~ I Р-\/212), постоянство которой гаранти-
гарантируется уравнением A60), равна сохраняющемуся суммарному
току частиц, который определяется следующим образом:
^(/=i)d0d9, A62)
A63)
A64)
есть радиальная компонента дираковского тока /'.
Для выбранных базисных изотропных векторов 1, n, m и m
имеем
где
а величина
V=i =
A//2)
Р2
Г
0
sin
0
е =
GAB'
(РА
\- a2 cos
2в) sin
QAQB'
в,
)
1Г тг
1
1 0
1^2 mr nr i^« л л/о„2 • A65)
0 —А'2о2
Вычисляя Jr с помощью соотношений A56), A64) и A65), на-
находим
f =A/2р2) (| Я_1/2|2-Л | Я+1/2|2) (S2_1/2 + S2+1/2). A66)
Предполагая, что угловые функции S+i/2 (9) нормированы на
единицу, получаем из уравнений A62), A63) и A66), что
Щ- = 2я (| Р+т р - | Р_1/2 Г) = const. A67)
а. Приведение уравнений Дирака к одномерным волновым урав-
уравнениям. Если, как обычно, ввести в качестве неазависимой пере-

268 Глава 1б. Частицы спина i\2 в геометрии Керрй
менной функцию г*, то уравнения A19) и A20) примут следующий
вид (ср. с уравнениями A32) и A33)):
л1/2
Р+1/2 = "V
CD*
4j- (A, + t'mer) P-f-i/2. A69)
Пусть
* = arctg (т^/Я,). A70)
Тогда
cos « = Х/(А,2 + тУ)и\ sin d = тег/(к2 + т2/I/2, A71)
X ± ШеГ = ехр [ ± 1Щ (к2 + тУУ'2 A72)
и можно переписать уравнения A68) и A69) в альтернативной
форме
A73)
+iarctg/jvAj: ,
A74)
Можно исключить экспоненциальные множители в правых частях
уравнений A73) и A74), сделав подстановки
-г|)+1/2ехр[—V2^arct . . ..
P_1/2 = гр i/2 ехр [ + V2^' arctg merfk]. * '
В результате получаем
A76)!
A77).
Можно привести эти уравнения к более простому виду, сделав,
замену независимой переменной:
К = г* + (Vaa) arctg mer/k, A78)»
^^^W A79»

106. Сохраняющийся ток 269
В результате двух замен A75) и A78) получаем следующие
уравнения:
)
d
где
W = —
Полагая теперь
Z± = lp-|-i/2 ± "Ф—1/2, A83)
получаем следующую систему уравнений:
A84)
Эти последние уравнения сразу же дают пару одномерных волно-
волновых уравнений
^ + a2)z± = V±Z±i A85)
где
V± = W2± dW/dr* =
— \ -ТГП/ ) г д 1 /2 /л 1 /2 , 2 2\3/2
/л 1 /2 , 2 2\3/2 ,
± {(л - М) (X2 + пгУ) + Зт'гД)] =F
+ 2т^ш2/- + Хте (г - М)/а]. A86)
Уравнения A84) и A85) имеют в точности такой же вид, как и
уравнения A37) и A38) для безмассовых нейтрино.
б. Разделение переменных в уравнениях Дирака в сплюснутых
сфероидальных координатах в плоском пространстве. Ясно, что,
полагая
М = О, А - г2 + а2 A87)
в уравнениях A57) и A58) и в последующих вариантах этих урав-
уравнений, мы получим уравнения Дирака с разделенными пере-
переменными в сплюснутых сфероидальных координатах в плоском
пространстве, потому что при М = 0 метрика Керра принимает
вид
ds2 = Ctf2 - I 7г _l,,2 dr2 + (r2 + fl2cos2 9) d02 +
+ (r2 + a2) sin2 0 d(f>2] , A88)

270 Глава 10. Частицы спина 1/2 в геометрии Керра
и если вдобавок положить
г = ash 7], A89)
то метрика принимает стандартный вид плоской метрики в сплюс-
сплюснутых сфероидальных координатах
ds2 - At2 — a2 [(ch21\ — sin2 9) (drf + d92) +
+ ch2ri sin2 9 dcp2]. A90)
Поскольку возможность разделения переменных в уравнении
Дирака в сплюснутых сфероидальных координатах, вероятно,
не является широко известным фактом, выпишем явный вид
уравнений для этого случая.
В результате подстановок A56) радиальные уравнения прини-
принимают вид
>. — i
)ipi== p+l/2 A92)
где
P+1/2 = (/-2 + a2)#+1/2, P_,/2 = /?-i/2. A93)
Если сделать дальнейшие замены зависимой и независимой пере-
переменных
Z± = Р+12 exp [t^/2] ± Р-1/2 ехр [—i»i/2], A94)
Г^г + а^^ + тЪ,), A95)
где
*! = arctg (m/A), fl2 = arctg (л/а). A96)
то уравнения примут простой вид
^г + a2) Z± = V±Z±, A97)
где
V± = W2 ± dr/dr^, A98)
(r2 + а2) (^ + m^r2) + [am (tf + m^r2) + i/,^ (r2 + a2)] a
'
l ^
И наконец, заметим, что уравнения A21), A22) и A24) для угло-
угловых функций S.j-i/2 остаются неизменными при переходе к плоскому
пространству.
107. Задача об отражении и прохождении волн
Наиболее важным различием взаимодействия массивных ча-
частиц с черными дырами от взаимодействия безмассовых частиц
является поведение потенциалов V+ при г->оо. В отличие от

107. Задача об отражении и прохождении волн 271
потенциалов, с которыми мы сталкивались до сих пор, изучая
безмассовые частицы, потенциалы V±} задаваемые уравнением
A86), не убывают пропорционально г~2 при г->оо:
V± -> т\ - 2Mm2e/r + О (r~2). B00)
В результате асимптотики решений Z± волнового уравнения A85)
при г -> оо имеют вид
^ ]}B01)
Z± ^ exp {± i [(а2 - т1Г2г + (g2^)l/2 In (r/2M)]
Вследствие такого поведения решений для реальных волн (падаю-
(падающих или отраженных) на бесконечности частота о должна превы-
превышать те (напомним, что мы приняли соглашение считать а всегда
положительным), ^то ограничение на о согласуется с требованием,
чтобы свободные частицы на бесконечности имели энергию, пре-
превышающую их энергию покоя.
а. Постоянство вронскиана [Z+, Z*±] в интервале г+ <г<оо.
Потенциалы 1/+, определяемые уравнениями A86), становятся
бесконечными на горизонте при г = г+, когда а = as, A = 0 и
щ. = г\ + а2 + ат/о = 2Мг+ + ат/о = 0. B02)
Потенциалы могут иметь и дополнительные сингулярности, если
К принимает отрицательные значения (что и происходит при
т = —1/2 иаа^ 1,8, см. приложение, табл. VII). Хотя не воз-
возникает никаких принципиальных трудностей при интегрировании
уравнений для Z+ в интервале, содержащем такие сингулярности
(как уже объяснялось в п. 75, в и 76, в и § 105), нужно знать
еще, как ведет себя вронскиан [Z+, Z1] при пересечении сингу-
лярностей. Покажем, что вронскиан [Z+, Z*±] принимает одно
и то же значение во всей допустимой области изменения г, т. е.
в интервале г+ < г < оо. Действительно, из уравнений A67),
A75), A83) и A84) находим последовательно
¦ij- Щ- = | Р+1/2 |2 - | Р-,/2 |2 =
= v41 z+ + z_ |2 - v» 12+ - z_ |2 = z^e
геа|) / d \V/\ 7<im)
|2 =
1 Г 7<геа|) / d \V/\ 7<im
(im) d y(realI

272 Глава 10. Частицы спина 1/2 в геометрии Керра
Поскольку величина dNIdt остается неизменной во всем интер-
интервале r_j_ < г < оо, отсюда следует постоянство вронскиана в том
же интервале изменения г. Аналогично доказывается постоянство
вронскиана [Z_, Z1].
Вернемся снова к задаче об отражении и прохождении волн,
связанной с решением уравнения A85). Мы должны искать такие
решения, например, для Z_j_, которые имеют следующие асимпто-
асимптотики:
B04)
B05)
Для решений с такими асимптотиками имеем
= - 21 [I - | /?+(a) |2] (a2 - m2)I/2. B07)
Вследствие постоянства вронскиана (доказанного во всех случаях)
получаем
1 - | R+ (а) |2 = о(а2- m2)-1/21 Т+ (а) \\ B08)
Коэффициент отражения, таким образом, всегда меньше единицы,
и супер радиации быть не может. Кроме того, из сравнения урав-
уравнений B03) и B06) заключаем, что
Г1Т+^>0- B°9)
Суммарный ток частиц, пересекающих горизонт событий, таким
образом, всегда положителен.
б. Положительность потока энергии через горизонт событий.
Поиски причин отсутствия суперрадиации для частиц спина 1/2,
которое мы продемонстрировали с помощью уравнений движения,
побуждает обратиться к спинору энергии-импульса для этих
частиц, вид которого задается соотношением
Таа>вв> = 072) [РаРа>- вв> - Ра-Ра; вв> -У РвРв>; аа> -
— Рв-Рв; АА' — QaQ.A'; BB' + QaQa; BB
-ЦвЯв>; AA' + Qb'Qb, AA'l B10)

107. Задача об отражении и прохождении волн 273
Тогда для изменения энергии и момента количества движения
будем иметь (ср. с уравнениями B47) и B53) гл. 8)
2я я
О О
2я я
О О
в той же системе координат, в которой мы записывали метрику
Керра (уравнения A34) и A35) гл. 6). Поскольку
г; = - (д/р2) тги К = - (д/р2) ггф, B13)
V—1 = Р2 sin 9, B14)
можно объединить уравнения B11) и B12):
я
= 2я j [Д (г2 + a3) Гг* + а Д^гф] sin 9 dQ. B15)
о
С другой стороны, легко проверить, используя выражения для
базисных изотропных векторов 1 и п (уравнение A70) гл. 6),
справедливость соотношения
Д (г2 + a2) Trt + а АТщ = (Д2/4) Г,//у - p4r,/tV. B16)
Имеем поэтому
й2 ^)f = 2л j (y^Ttjl'l1 - р*Тцп'п1) sin 0 d9. B17)
о
Используя формулу для спинора энергии-импульса B10),
находим с помощью уравнений A59), что по мере приближения
к горизонту
= шV'oV [РАРА>; вв' - Ра-Ра, вв- - QaQa>, ев- + Qa'Qa; ввЛ =
= i [PUDPO- ~ Po-DPo - QqDQo- + Qo-DQo] =
= / JP'AP1' - Я»'/)?1 - Q'DQ1' -b C?'DQX] —
|2E+1,2 Ь 52_1/2). B18;

274 Глава 10. Частицы спина 1/2 в геометрии Керра
Подобным же образом получаем
Тцп'п} = iVWYh^bb' -> V2a D/p4) I Я-1/212 E+,/2 + SLi/2).
B19)
Подставляя выражения B18) и B19) в уравнение B17) и вспоми-
вспоминая, что угловые функции S+i/2 @) и S_i/2 @) нормированы на еди-
единицу, получаем следующую формулу:
(^)г+ =2яа[|Р+1/2|2-|Р_1/2|2]. B20)
Суммарный поток энергии через поверхность радиуса г в единицу
времени и в единице телесного угла, следовательно, равен
-|/'-1/2|2] = ^(^+. B21)
В силу уравнения B09) этот поток через горизонт событий всегда
положителен.
в. Квантовая природа отсутствия суперрадицаии. Отсутст-
Отсутствие суперрадиации для частиц спина 1/2, находящееся в явном
противоречии с теоремой Хокинга о площади поверхности черной
дыры, связано с тем, что тензор энергии-импульса, соответству-
соответствующий спинору B10), нарушает слабое условие энергодоминант-
энергодоминантности:
Тчк*к!>0, B22)
где к — произвольный времениподобный вектор, при а < а8. Дей-
Действительно, выбирая
?' = (l/r?)(A/72 + pV) при Л% = Др2/г4>0, /->/-+, B23)
получаем
Tuklk' = (I//4) [(А2/4) Г,//' + Р47>У + р2 ДТу V). B24)
Комбинации Ttjlllj и ТцП1п* мы нашли выше — уравнения B18)
и B19). Подобным же образом находим, что
-> a (S2+/P2A) (I P+U212 -f I P-i/212) (S2+U2 + S-1/2). B25)
Объединяя теперь результаты B18), B19), B24) и B25), имеем
Ttjk'k1 - 2 (gco2+/>-4+) (I P+i/212 + I P-M212) E2+1/2 -f SL1/2), B26)
а эта величина отрицательна, когда а < aSi и условие энерго-
энергодоминантности нарушается.
Хотя проведенное обсуждение и проясняет многие аспекты
процессов отражения и прохождения дираковских волн в гравита-
гравитационном поле керровской черной дыры, остается еще ряд нерешен-
нерешенных вопросов, имеющих самостоятельное значение. Так, правоме-
правомерен вопрос: действительно ли потенциалы V± имеют сингуляр-

Библиографические замечания 275
ности вне горизонта событий для значений частот сг > те, возни-
возникающие из-за присутствия члена КтеА/2о в знаменателе W, ко-
когда % отрицательно? Это невозможно в геометрии Шварцшильда.
Если бы это имело место в геометрии Керра (скажем, при некото-
некоторых значениях а > as), то можно было бы ожидать, что коэффи-
коэффициент отражения достигает на этой частоте максимального зна-
значения, равного единице, а затем убывает. В таком случае мы бы
заключили, что в явлении отражения частиц спина 1/2 керровской
черной дырой проявляется парадокс Клейна. Это привело бы
к интересным физическим следствиям, однако этот вопрос нельзя
решить, если не известна зависимость собственных значений А,
от параметров те, т и а. (Впоследствии было показано, что
парадокс Клейна не возникает.) /
Библиографические замечания
Разделение переменных для уравнения Дирака в геометрии Керра было
выполнено в работе
1. Chandrasekhar S. Proc. Roy. Soc. (London), A349, 571—575, 1976.
Как указано в этой статье, положив в полученных уравнениях М = О, мы при-
приходим к уравнению Дирака с разделенными переменными в сплюснутых сферо-
сфероидальных координатах в плоском пространстве (см. § 106, б).
Метод, примененный в работе [1 ], просто и естественно обобщается на произ-
произвольное пространство-время типа D по классификации Петрова:
2. Guven R. Proc. Roy. Soc. (London), A356, 465—470, 1977.
Разделение переменных в уравнении Вейля, описывающем безмассовые двух-
компонентные нейтрино, было проведено ранее в работах
3. Unruh W. G. Phys. Rev. Lett., 31, 1265—1267, 1973.
4. Teukolsky S. Astrophys. J., 185, 635—647, 1973 (Appendix B, p. 646).
§ 102. Спинорный формализм для исследования структуры пространства-
времени был предложен и развит Пенроузом:
5. Penrose R. Ann. Phys., 10, 171—201, 1960.
6. Penrose R. An Analysis of the Structure of Space-Time, Cambridge University
Adams Prize Essay, Cambridge, England, 1966.
7. Penrose R. In: Batelle Recontres A967 Lectures in Mathematical Physics), eds.
С M. DeWitt, J. A. Wheeler, W. A. Benjamin Inc., New York, 1968, pp. 121 —
135.
Основной работой о спинорном базисе для формализма Ньюмена—Пенроуза,
разумеется, является работа
8. Newman Е. Т., Penrose R. J. Math. Phys., 3, 566—579, 1962.
п. 102, а и б. Изложение спинорного анализа в настоящей главе основы-
основывается почти целиком на моих конспектах лекций Дирака, прочитанных им
весной 1932 г., в которых развивался спинорный анализ и релятивистская теория
электрона. Стиль и содержание лекций совсем не устарели, несмотря на то что
с тех пор прошло пятьдесят лет.
п. 102, в и г. Изложение этих разделов было отработано в дискуссиях автора
с Дж. Фридманом. В частности, автор следовал фридмановскому представлению
ковариантного дифференцирования (раздел 102, г).
§ 103. Очевидно, нет необходимости давать ссылки на литературу, содер-
содержащую уравнение Дирака в плоском пространстве. Автор считает, однако, 'что
изложение в курсе Л. Д. Ландау и Е. М. Лифшица лучше всего подходит для
перевода на язык формализма Ньюмена—Пенроуза:
9. Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Релятивистская кван-
квантовая теория.—М.: «Наука», 1968, §20, с. 91.

276 Глава 10. Частицы спина 1/2 в геометрии Керра
§ 104. В этом параграфе в основном излагается работа [1]. Альтернативный
вывод тех же уравнений см. в работе
10. Carter В. у McLenaghan R. G. In: Proc. 2d Marcel Grossman Meeting on General
Relativity, ed. R. Ruffini, North-Holland Publishing Co., Amsterdam, 1980.
§ 105. Анализ, проведенный в этом параграфе, является упрощенным ва-
вариантом исследования, изложенного в работе
И. Chandrasekhar S., Detweiler S. Proc. Roy. Soc. (London), A352, 325—328,
1977.
См. также
12. Unruh W. G. Phys. Rev. D10, 3194—3205, 1974.
Подобная же задача для геометрии Шварцшильда рассматривалась в работах
13. Brill D. R.% Wheeler J. A. Rev. Mod. Phys., 465-479, 1957.
14. Hartle J. B. In: Magic without Magic: John Archibald Wheeler, ed. J. R. Klau-
der, W. H. Freeman and Co., San Francisco, 1972, pp. 259—275.
§ 106. Изложение настоящего параграфа основано почти целиком на не-
неопубликованной работе автора. Эквивалентные результаты были представлены
в работе
15. Guven R. Phys. Rev. D16, 1706—1711, 1977.
См. также [12].
§ 107. Отсутствие суперрадиации при отражении дираковских волн кер-
ровской черной дырой было в явном виде продемонстрировано в [15] и рядом
другим авторов вскоре после доказательства возможности разделения перемен-
переменных в уравнении Дирака:
16. Martellini M., Treues A. Phys. Rev. D15, 3060—3064, 1977.
17. Lee С. Н. Phys. Lett., 68B, 152—156», 1977.
18. Iyer В. R., Kumar A. Phys. Rev., D18, 4799—4801, 1978.
О парадоксе Клейна, упомянутом в заключительном параграфе, см.
19. Klein О. Z. f. Physik, 53, 157—165, 1931.
20. Sauter F. Z. f. Physik, 69, 742—764, 1931.
Исследование других вопросов, касающихся уравнения Дирака в геометрии
Керра и разделения переменных, не рассматривавшихся в данной книге, см.
в работах
21. Carter В., McLenaghan R. G. Phys. Rev., D19, 1093—1097, 1979.
22. Iyer В. R., Kumar A. Pramana, 8, 500—511, 1977.
23. Iyer B. R., Kumar A. Pramana, 11, 171 — 185, 1978.
24. Iyer B. R.y Kumar A. Pramana, 12, 103—120, 1979.

Глава 11
ДРУГИЕ РЕШЕНИЯ, АЛЬТЕРНАТИВНЫЕ МЕТОДЫ
108. Введение
Исследованием частиц спина 1/2 в главе 10 завершилось изуче-
изучение решений Шварцшильда и Керра. Гл. 5, в которой рас-
рассматривалось решение Рейсснера—Нордстрема, — это своего рода
отступление, которое диктовалось в основном тем соображением,
что оно способствует более глубокому пониманию решения Шварц-
Шварцшильда и служит мостом для перехода к изучению решения Керра.
Это наводит на мысль, что исследование решения Керра—Нью-
Керра—Ньюмена, которое находится в таком же отношении к решению Керра,
как решение Рейсснера—Нордстрема к решению Шварцшильда,
позволит лучше понять решение Керра. Хотя вывод метрики
Керра — Ньюмена (§ 110), при котором мы будем следовать тем же
путем, что при выводе метрики Керра (§ 54), приводит к некоторым
полезным обобщениям основных понятий, оказывается, что ме-
методы, развитые в гл. 9 для исследования гравитационных возму-
возмущений керровской черной дыры, не удается естественным образом
распространить и использовать при изучении возмущений вза-
взаимодействующих электромагнитных и гравитационных полей
черной дыры Керра—Ньюмена. Причины этого, без сомнения,
важного различия в структуре подвергшихся возмущениям
многообразий Керра и Керра—Ньюмена, по-видимому, лежат
глубоко и связаны с нерасцепляемостью взаимодействующих
полей спина 1 и 2 в возмущенном пространстве-времени Керра—
Ньюмена — связь, которую удалось расцепить только в силу
специальных причин в возмущенном пространстве-времени Рейс-
Рейсснера—Нордстрема.
Помимо решения Керра—Ньюмена будут рассмотрены еще два
класса решений: аксиально-симметричные решения для черных
дыр, которые являются статическими, но не асимптотически пло-
плоскими, и решения, описывающие произвольное число изолирован-
изолированных черных дыр и представляющие релятивистский аналог стати-
статической равновесной конфигурации (возможной в ньютоновской
теории) из произвольного числа заряженных точечных масс,
для которых взаимное гравитационное притяжение в точности
компенсируется кулоновским отталкиванием.
Эта глава и вся книга заканчивается длинным параграфом,
посвященным все еще нерешенной проблеме устойчивости кер-

2/S Глава 11. Другие решения, альтернативные методы
ровской черной дыры и предварительному рассмотрению альтер-
альтернативного метода исследования возмущений пространственно-
временных многообразий.
109. Уравнения Эйнштейна—Максвелла
для стационарных аксиально-симметричных
пространственно-временных многообразий
Как и в гл. 5, начнем с метрики стандартного вида
ds2 - (?2v (d/J - е2^ (d<p - со d/J - е2^ (dx2J - е2^ (dx3J, A)
где v, \|), со, [А2 и [х3 - функции только координат х2 и х3 и, кроме
того, можно наложить одно координатное условие на функции \i2
и (г8.
Поскольку нас теперь интересуют уравнения Эйнштейна—
Максвелла, рассмотрим сначала уравнения Максвелла в простран-
пространстве-времени с метрикой данного вида. Эти уравнения нетрудно
сразу же выписать, поскольку они представляют собой специаль-
специальный случай уравнений из § 15 гл. 2. Из уравнений (95а)—(95з)
гл. 2 находим, что в стационарном аксиально-симметричном про-
пространстве-времени
FOi = F23 = 0, B)
а остальные уравнения имеют следующий вид:
= 0, C)
), з = 0, D)
, 2 + ^+^_F03co, 8, E)
), 2 = e*+^F,a©, 3 - е*+**Р1Яр, 2. F)
Из уравнений C) и D) следует, что две пары компонент тен-
тензора Максвелла (F12, FJ3) и (F02, F03) могут быть записаны через
потенциалы А и В:
12 = A, 2; e*+»*Fls = А, 8;
03 = -В,2; ёЬ+ъРъ = + В,,. ( }
Уравнения E) и F) теперь принимают следующий вид:
), 2 + (е^+^-ч*А, 8),, = ©, 2S, 3 - ©, 3В, 2; (8)
)_ з _|_ (е_ф+г+цг-д3S, 3), 3 = со, 3Л, 2 - со, 2Л, 3. (9)
Поскольку тензор энергии-импульса максвелловского поля
имеет вид
Tab = VfFacFbd - VtoAFefF1*, A0)

109. Уравнения Эйнштейна—Максвелла 279
можно записать уравнения Эйнштейна следующим образом:
Rab = -2ГаЬ = -2^FacFbd - цаЬ [(F02J + (F03J-(Fl2J - (F«)8].
(И)
Вычисляя компоненты тензора #а& с помощью уравнений G),
находим
Ron = Да - ^-2Ф-2м2 [(Л, 2J + (В, а)*] + е~^~^ [(Л, 3)8 + (В, »J].
A2)
#22 = -Rs3 = е-2*-2"*' [(Л, 2J + (В, 2J] - е-2*-2м., [(А, 3J + (В, 3J],
A3)
R10 = 2е-2*-^-Мз (Л, 2В, з - Л, 3В, 2), A4)
R23 = 2e-2*-i*.-»*- (Л, 2Л, з + В, 2В, 3). A5)
Искомые уравнения поля получаются приравниванием выражений
в правых частях предыдущих уравнений соответствующим выра-
выражениям для тензора Риччи (или тензора Эйнштейна), записанным
через компоненты метрики. Выражения для последних мы нахо-
находим в гл. 6 (уравнения E)—A3)). Уравнения A2), A3), G)—A0)
гл. 6 теперь заменяются соответственно на
2 Vf a)) 2 + (еР+м2-Из у, з), з =
{«*-¦*, [(Л, 2J + (В, 2J] + &*-*> [(Л,зJ + (В.зJ]}, A6)
, 2 + (eP+^'ib). з =
= — V2en*-V [е^з-^» (со, 2J + е^~^ (со, 3J] —
аJ] + е1»,-ц, [(Л) зJ + {В> зJ]1) A7)
д1й)> з);3 = 4 (Л, 2В, з - Л, 3В, 2), A8)
, 23 — (^ + V), 2 hj, з - (Ф + V), з fl3, 2 + \JJ, al|3, з + V 2V, 3 =
=V/*-2X 2co, 3 - 2e~W (А, 2Л, з + В, 2В,3), A9)
ф ^ v)( 33 + (^ + V), з (V - Щ),з + Ч>, зФ, з] +
+ в-2"' [V, 2 (* + (*«), 8 + *,^»,»] =
= — V^2*-^ [г-2^ (со, 2J - е~2^ (со, 3J] +
+ е-w \е~^ [(Л, 2J + (В, 2J] - е~^ {(А, 3J + (В, 3J]}, B0)
^ V), 22 + A|5 + V), 2 (V - |1Я), 2 + 1», 2^, 2] +
+ е-2мз [v, з (v|5 + ца), з + У, 3f4 з] =
= +V4e2*-2v [е-^^ (со, 2J - е~2»> (со, 3J] -
_Г-2# |е-2ц2 [(Л> гJ + (fi> гJ] + с-^. [(Л) зJ 4- (В, зJ]}, B1)
где, как и в гл. 6,
р = t + v. B2)

280 Глава 11. Другие решения, альтернативные методы
Запишем сумму и разность уравнений A6) и A7)
[<*.-*. (бЭ)> 2]( 2 + [би,-и, (е% з]. з = 0, B3)
1*. (ф _ v), 2],2 + [еЭ+д.-и. (ф - v), 3], з =
^-д2 [(Л, 2J + (В, ?J] + е*.-* [(Л, 3J + (В, зJ]Ь B4)
Уравнение B3) совпадает с уравнением A4) гл. 6, полученным для
пустого пространства-времени.
Кроме того, сложение уравнений B0) и B1) снова приво-
приводит к уравнению B3), тогда как их разность дает
4e*w (pf а|А8,2 + ф, 2v, 2) - 4е^~^ (Р, 3^2, з + Ч>, 3v 8) =
+ 4в^ {е*-»*. [(Л,2J + (В,2J] - е^~^ [(Л, 3J + (В,3J]}. B5)
а. Выбор калибровки и приведение уравнений к стандартному
виду. Как и в § 53 гл. 6, мы можем использовать калибровочный
произвол, чтобы наложить координатное условие на функции ^2
и [i3 и, воспользовавшись далее уравнением B3), добиться того,
чтобы там, где рассматриваемое пространство-время имеет гладкий
горизонт событий, некоторая квадратичная функция переменной г,
а именно функция (ср. с уравнениями D5) и D6) гл. 6)
Д (г) = г2 - 2Мг + Л18, B6)
обращалась в нуль и, кроме того,
е2 {^-м = Д(г), е* = Д1/2 sin 9. B7)
В уравнении B6) М и Мо — постоянные, смысл которых станет
ясен ниже.
Вернемся к уравнениям (8) -и (9). Можно объединить их в одно
уравнение для комплексного потенциала
Н = А + 1В B8)
и записать в виде
(e-*+V-U2+H3#, 2),2 + (g-i'+V+li.-li.tf, з), з - / (СО, 3# 2 - СО,2Я,3). B9)
Записывая далее уравнение A8) в виде
(^^ + 2 BAt3)t2 +
^co,3 + 2 ЛВ,2-2ВЛ,2),3 -0, C0)
получаем
- 2 Im НН^), 3 = 0. C1)

109. Уравнения Эйнштейна—Максвелла 281
Если ввести новую переменную
(х - cos 9 C2)
вместо переменной 9, обозначенной индексом «3», и подставить
в уравнения B9) и C1) выражения B7) для е$ и exp (\i3 — \i2),
то в результате получим
^^ (зз)
= О, C4)
где введены обозначения (такие же, как и гл. 6)
% = exp (-у + v), C5)
б = 1 — ц2 = sin2 0. C6)
Аналогично можно записать через % и Я уравнение B4):
- A/Х2) [А К / + б (со, 3J] + Bх/А1/2б1/2) [А | Я,, |2 + б | Я,, |2].
C7)
Уравнения C3), C4) и C7) — основные уравнения теории;
если они решены, то окончательное решение получается в квад-
квадратурах из уравнений A9) и B5) (см. § ПО).
б. Дальнейшее преобразование уравнений. Уравнение C4) поз-
позволяет определить потенциал Ф посредством следующих урав-
уравнений (ср. с уравнением (87) гл. 6):
- Ф, 2 - (S/x2) со, з + 2 Im HHU\ +Ф , 3 = (А/%2) со, 2 - 2 Im Я#%,
C8)
потому что уравнение C4) есть не что иное, как условие интегри-
интегрируемости для этих уравнений. Решая эти уравнения относительно
со,2 и со,3, имеем
со, 2 - (х2/А) (Ф, з + 2 Im HHU\ ю. 3 = — (х2/б) (Ф. 2 + 2 Im HH*^),
C9)
а условие интегрируемости для этих уравнений имеет следующий
вид:
[(Х2/б)(Ф.2 + 2 1тЯЯ:2)]12 + [(х2/А)(Ф,з+2 1тЯЯ:з)|,з = 0. D0)
Удобно ввести функцию (ср. с уравнением (98) гл. 6)
W = (ЛбI/2/х. D1)
Переписанное через W, уравнение D0) принимает вид
*'2) (Ф. 2 + 2 Im HHU)\, 2 + [F7«F2) (Ф, 3 + 2Im HHU)] 3 = 0.
D2)

282 Тлйба 11. Jtpi/гиё решения, пльтернйШйёныё методы
Расписывая его подробно, получаем
Y {[А (Ф, 2 + 2 Im Я/Г 2)], 2 + [б (Ф, з + 2 Im HHU)], 3\ =
= 2А (Ф, 2 + 2 Im HHU) ^.2 + 26 (Ф, 3 + 2Im ЯЯГ3) Y, 3- D3)
Аналогичным образом можно переписать уравнение C7) че-
через функции f иФ:
= Д (?, 2J + б (?. 3J - 2<F [А | Я, 212 + б | Я, з |2] -
— Д (Ф, 2 + 2 Im HHUJ — б (Ф, з + 2Im ЯЯГзJ, D4)
а вместо уравнения C3) получаем
V [(ЛЯ. 2), 2 + FЯ, з), з] = ЛЯ, 2 [V, 2 + i (Ф, 2 + 2 Im ЯЯ;2)] +
+ бЯ,3[^.з + t (Ф.з + 2 1тЯЯГз)]. D5)
Выпишем теперь мнимую и действительную части уравнения
C3):
[(A/-V) Л.2],2 + [(б/Я Л,з],з = со.зВ.2- со>2В,з,
() В,2],2 + [F/40 5;з].з = «>2Л,з — со.зЛ.2. ( }
Наконец, приведем в виде лемм два следствия предыдущих
уравнений:
ЛЕММА 1.
= 2? [Л | Я. 212 + б | Я, з |2] + Л [| Я |22Т 2 +
+ 2 Im ЯЯГг (Ф, г -f 2 Im HH^)] +
+ б [| Я |2з Y. з + 2 Im ЯЯ;3 (Ф.з + 2 Im HHU)}. D7)
ЛЕММА 2.
2Ч [(Aim HHU),2 + (б Im HHU),3] = 2Д Im
+ 2б1тЯЯ:8Т,з- [А|Я|22(Ф>2 + 21т
+ б|Я|2з(Ф,з + 21т ЯЯ:8I. D8)
в. Уравнения Эрнста. Заметим прежде всего, что в силу тож-
тождества
B/ Im ЯЯ:2) АЯ,2 = (HHU + Н*Н, 2 — 2Я*Я>2) ДЯ,2 =
= Д!Я|%-2Я*Д (Я,2J D9)
уравнение D5) может быть переписано в виде
? [(ДЯ.2).2 + (бЯ,з).з] = -2Я* [А (Я,2J + б (Я,зJ1 +
+ /Ф)>3. E0)

109. Уравнения Эйнштейна—Максвелла 283
Далее, исключая члены с Im HH*2 и Im НН*г из левой части
уравнения D3) с помощью леммы 2 (уравнение D8)), получаем
J + (бФ.з).з1 -A №,2BF + |Я|2),2 +
6 [Ф,зBЧг + |Я|2),3 + 21тЯЯ:3(Т + |Я|2),3]. E1)
нируя уравне
|Я|2),3],з1 =
Подобным же образом, комбинируя уравнения D4) и D7),
находим
- А
+ 6 [(?,3J + |Я|%Т.з - (Ф,зJ - 21т ЯЯГзФ.з]. E2)
Теперь ясно, что левые части уравнений E1) и E2) могут быть
объединены в выражение, зависящее от одной комплексной функ-
функции
Z = Т + |Я|2 + 1Ф. E3)
Чтобы показать, что правые части этих двух уравнений могут
быть также объединены в одно комплексное выражение, включа-
включающее только функции Z и Я, рассмотрим комбинацию
+ *Ф, 21Я |% + 2i ImНЩ2 (W + | ЯI2 + /Ф), 2, E4)
которая появляется в правой части с коэффициентом А. Члены
с Im НН*2 могут быть преобразованы следующим образом:
+ Н*Н, 2 - 2Я*Я, 2)Z. 2 =
E5)
и выражение E4) принимает вид
- 2Я*Я, 2Z, 2 = (Z. 2J - 2Н*Н, 2Z, 2. E6)
Члены с коэффициентом б могут быть объединены аналогичным
образом, и в результате получим
(Z,3J — 2H*H,3Z,3. E7)
Следовательно, уравнения E1) и E2) эквивалентны одному комп
лексному уравнению
= Д (Z, 2J + б (Z. 3J - 2#* (AZ, 2Я, 2 + 8Z, зЯ. 8). E8)

284
Глава 11. Другие решения, альтернативные методы
а уравнение E0) можно переписать следующим образом:
где
= ДЯ, 2Z, 2 + 6Я, 3Z, 3 - 2Я* [А
W = ReZ — \H\\
J]> E9)
F0)
Уравнения E8) и E9) и есть уравнения Эрнста; они очень
удобным и симметричным образом объединяют четыре уравнения
для функций х, ы, А и В в два комплексных уравнения, заменя-
заменяющие одно уравнение Эрнста которое мы рассматривали в гл. 6
(уравнение (94)) для вакуумного пространства-времени.
г. Трансформационные свойства уравнений Эрнста. Пусть
пара (Z, Я) есть решение уравнений E8) и E3). Тогда следующие
пары также являются их решениями:
1) (Z + ia', Я), где а — любое действительное число,
2) (P2Z, $eiaH), где аир —два действительных числа,
3) (Z + 2а*Н + аа*у Н + а), где а — любое комплексное
число,
4) (Z-\ HZ-1). F1)
Инвариантность относительно преобразований 1 и 2 тривиальна
и ясна без доказательства, преобразование 3 легко проверяется,
а для доказательства преобразования 4 требуется произвести
кое-какие выкладки.
Последовательно применяя то или другое из преобразований
1—4, мы можем получить новые решения. Действительно,
(Z, Я) =ф- A/Z, HIZ) => (A/Z) + ia, HIZ) =>
=> (Z/(l + foZ), Я/A + taZ)), F2)
(Z, Я) => A/Z, Я/Z) => (A/Z) + 2a* (Я/Z) + aa*,{HlZ) + a) =*
=>(Z/A + 2а*Я + aa*Z), (Я + aZ)/(l + 2а*Я + aa*Z)). F3)
Эти преобразования называются соответственно преобразованиями
Элерса и Гаррисона. Гюрши и Ксантопулос открыли замечательный
способ записи уравнений Эрнста, который выявляет их транс-
трансформационные свойства. Определим эрмитову матрицу
Р =
4 44- 0
' \jr 1 "Т" z —1^~
h*z
F4)

109. Уравнения Эйнштейна—Максвелла 285
Обратная матрица имеет вид
У 2 хр 1 ~г 2 ^ i у 2 -^— ^ F5)
Гюрши и Ксантопулос показали, что уравнения Эрнста можно
представить в виде одного матричного уравнения
Р.з),з = 0, F6)
которое, будучи записано поэлементно, дает девять уравнений,
причем все они являются различными комбинациями уравнений
Эрнста. Немедленным следствием уравнения F6) является тот
факт,, что если матрица Р представляет решение, то решением яв-
является и матрица АРА-1, где А — произвольная постоянная
обратимая матрица. Выбирая различные матрицы А, мы можем
получить все преобразования, которые допускают уравнения
Эрнста.
д. Операция сопряжения. В гл. 6 (п. 52, а) было показано, что,
имея заданную метрику вида A), мы можем построить сопряжен-
сопряженную метрику того же вида путем преобразования
t -> icp, ф -> —it F7)
и замены % и со на величины
% = -Х/(Х2 - со2), й = со/(х2 - со2). F8)*
Чтобы установить, как преобразуется потенциал Я при такой
операции сопряжения, заметим, что, переписывая уравнение C3)
в виде
(X (Д/б^Я, 2 - iaH. 3). 2 + (X (б/АI/2Я, з + коЯ, 2), 3 = 0, F9)
мы можем определить потенциал Я уравнениями
_ Я 3 = х (А/бI/^, 2 - шН, 3; + Я 2 = ноЯ. 2 + ХГ(8/ДI/2Я 3. G0)
Разрешая эти уравнения относительно ЯJ и Я( 3> получаем
Я, 2 = X (б/АI/2 Я. з + 1'5Я. 2, Я, 3 = - х (А/бI/2 Я 2 + ЙЯ. 3, G1)
где х и й определены соотношениями F8); условие интегриру-
интегрируемости этих уравнений имеет вид
H, 2 - &Я. з). 2 + (X (б/АI/2 Я, з + ЛоЯ. 2). з = 0. G2)
* В случае пустого пространства, расмотренном в гл. 6, величина % мо-
может быть выбрана с любым знаком, но теперь, как станет ясно ниже, пра-
правильным является отрицательный знак.

286 Глава //. Другие решения, альтернативные методы
Это уравнение почти совпадает с уравнением F9), различие лишь
в том, что оно записано в переменных с тильдой, а уравнение F9)
зависит от переменных без тильды, т. е. операция сопряжения
приводит к замене Я на Я. Этот результат может быть подтвер-
подтвержден прямой проверкой: функции %, со и Я действительно удов-
удовлетворяют уравнениям точно того же вида, что и функции %, со
и Я (уравнения C0) и C7)), но проверка эта довольно утоми-
утомительна.
Из сказанного выше следует, что если ввести функции ЧС и Ф
такие, что
/х, G3)
_ ф, 2 = (б/х2) <о, з + 2 Im ЯЯГ2, + Ф, з = (А/?) ю. 2 - 2 Im
G4)
то функции
Z - ? + | Я |2 + /Ф и Я G5)
будут удовлетворять уравнениям Эрнста E8) и E9).
110. Решение Керра—Ньюмена: вывод решения
и описание его в формализме Ньюмена—Пенроуза
Как и решение Керра (гл. 6, § 54), решение Керра—Ньюмена
получается, если выбрать простейшее решение уравнений Эрнста
для сопряженной метрики.
Поскольку мы теперь имеем дело с парой уравнений, поиск
«простейшего решения» делится на два этапа. Во-первых, сущест-
существует ли какое-нибудь простое предположение, позволяющее све-
свести пару уравнений E8) и E9) к одному уравнению? И, во-вто-
во-вторых, если такое уравнение существует, каково его простейшее ре-
решение?
Что касается первого вопроса, то ответ таков: линейное соот-
соотношение вида
Я = Q (Z + 1), G6)
где Q — комплексная постоянная, совместно с парой уравнений
E8) и E9), потому что при этом предположении
4? = 1/2(Z + Z*)-\Q(Z + 1)|2 = .
= V2 [(I -2jQ|2) (Z + Z*)-2|Q|2(|2|2+ l)], G7)
- и оба уравнения E8) и E9) сводятся к одному и тому же уравне-
уравнению
V2 [(I -2|Q|2) {Z + Z*) -
= [1 — 21 Q |3 (Z* + 1)] [Д (Z>2J + 8(Z.3J]. G8)

1Ю. Решение Керра—Мьюмёнй 28?
Задача, таким образом, эффективно свелась к решению уравнения
Эрнста в пустоте. Поэтому при поиске решения уравнения G8)
сделаем то же преобразование, что и в гл. 6 (уравнение (95)):
Z = A + ?)/A —Е). G9)
При этом
У = |1 -Е\-2(\ -4|Q|2-|?|2), (80)
Ф = Im Z = —i (? — Е*)/\ 1 — Е\\ (81)
а уравнение для Е имеет следующий вид (ср. с уравнением (96)
гл. 6):
A -4|Q|2-|?|2) [(Д? 2),2 + (б?.3).з1 ^
= -2?* [Д (?, 2J + б (Е, зJ1. (82),
Замена переменной г на г|
т, - (г - М)/(М* - М%I/\ (83)
когда
А = (м2-М02)(т12-1), (84)
позволяет записать уравнение (82) в более симметричной форме
iVin (85)
Дальнейший вывод решения Керра—Ньюмена можно продол-
продолжать теперь так же, как и в § 54. Рассмотрим уравнение (85) для
сопряженной функции Ё. Можно проверить, что оно допускает
простое решение
Е = —рц — fyji, (86)
где р и q — две действительные постоянные, связанные соотно-
соотношением
рг + <? = 1-4|Q|2. (87)
Если функция Е задана уравнением (86), то
Гз|= (i+J« + «v [-Ра(ча-1) + ?'A-и>) +
+ 4|QP-2/W]. (88)
Следовательно,
Рр7 - _ Р2(т12-1)^2Aц2L|<3[2

288 Глава 11. Другие решения, альтернативные методы
В силу формулы (80) имеем также
~ Р2№-1)-</2A-^2)
и из уравнения F0) теперь следует, что
B Y = (TTiHL. (92)
Если теперь вернуться к переменной г, то предыдущие решения
значительно упрощаются при определенном выборе постоянных
р и q, совместном с соотношением (87). Действительно, выраже-
выражение
-ReZ= [а-^(М2 - Ml)b-4\Q\2(M2 - Ml)/p2] х
X {[(г - М) + (М2 - Ml)mlpf + {qlpf (M2 - Ml) и2) (93)
значительно упрощается, если выбрать
р = (М2 - М2оI/2/М, q = a/M, (94)
где а — постоянная, потому что при таком выборе
[(г -М) + (М2 - M^'Vpf + (q/pf (M2 - Ml) v? = г2 + а2^2 - р2,
(95)
А - (qlpf (М2 - Жо) б = А - а28. (96)
Однако условие совместности с соотношением (87) требует, чтобы
(M2~Ml) + a2 = M2A-4|Q|2), (97)
М20 = а2 + 41 Q \2М2 = а2 + Q2, (98)
или
где
Ql = 4|Q|2M2. (99)
Выражение для А теперь принимает вид
А = г2 — 2Мг + а2 + QJ. A00)
Таким образом, выбор (94) и (99) приводит уравнения (89)—
(92) к очень простому виду
ReZ - - (А - аЧ - Ql)/p2y ImZ = ф = - 2aMfx/p2, A01)
Ф = (АбI/2/^ = - (А - я2б)/р2, Я2 - Q,2/P2. (Ю2)
В силу соотношения G6) имеем также
Я = Q (Z + 1) = Q, (' - '«^)/р2. (ЮЗ)
и поэтому
Л = QV/p2, В = -aQ^/p2- (Ю4)

110. Решение Керра—Ньюмена 289
Из решений A04) находим
Л,2 = (Q./р4) (-г2 + aV), A,3 = (QJP*) (-2а2Ф),
В,3 = (aQM) (-г2 + «У), В,2 = (Q*/p4) (Ч^Ф)- A05)
С помощью этих уравнений получаем
2 Im НЩ 2 = 2 (Ы,, - Д,) = - 2 @2»/р4) fl|i, :
2 Im ИHU = 2 (ВЛ, з - ЛД 3) = + 2 (Q2Jp4) ar.
Теперь из уравнений C9), A01) и A06) следует, что
5.2 = Ф, з + 2 Im НЩ з = - 2aMj(r2 - aV2)/P4 +
— (S/X2) ©, з = Ф, а + 2Im ЯЯГ2 = 4aMrfi/p4 - 2 (QJ/p4) ац. A07)
С другой стороны, в соответствии с решением для У, задаваемым
соотношением A02), имеем
Д/22 = (Д - й2бJ/р4б, 8/%2 = (А — о2бJ/р4А. A08)
Поэтому для определения функции б получаем следующие урав-
уравнения:
Из этих уравнений сразу же находим
ю = ab BMr — Q2)/(A _ Q2S)> A щ
что можно записать в альтернативной форме (ср. с уравнениями
F8) и A00))
б = w/(x2 — со2) = а8 [(г2 + а2) — А ]/(А — а2б). A11)
Аналогично из соотношений F8) и A02) получаем
X = -Х/(Х2 — со2) = -р2 (Аб)'/2/(Д _ а*8). A12)
С помощью решений A11) и A12) для функций й и % мы можем
получить решения для метрических функций e7v, e2* и со точно
так же, как в § 54 (уравнения A15)—A22) гл. 6):
в2* = в2а/Ра. e2v = p2A/22, е2» = е2 <*+v> = Дб, A13)
со = (а/22) (г2 + а2 — А), х = ^~'*'+v = P2AU2/Z2№, A14)
где
22 = (г2 + а2J-а2бД. A15)
х/г Ю Чандрасекар С, т. 2

290 Глава 11. Другие решения, альтернативные методы
Эти решения отличаются от соответствующих решений для мет-
метрики Керра (уравнения A21)—A25) гл. 6, и в уравнении A23)
для функции со нужно предварительно заменить 2Мг на г2 + а2—
— А) только определением функции А.
Вернемся к уравнениям A05). Воспользовавшись уравнениями
A11) и A12), мы можем теперь получить решения для величин
без тильды, исходя при этом из уравнений G1):
Л,г = + (Q*/p4) 2а2г sin2 Э cos Э,
Л, е ^ ~(Q*/p4) (г2 + а2) (-г2 + a2 cos2 Э) sin 9,
Btr = — (Q*/p4)a (—r2 + a2 cos2 Э) sin2 Э,
В,е = — (Q*V) 2ar (r2 + a2) sin 9 cos 9, A16)
где во избежание недоразумений явно указаны переменные, по
которым производится дифференцирование. Выпишем здесь также
следующие соотношения, которые понадобятся нам в дальнейшем:
Л,Де + ?,гВ,е = 0; A17)
(Л, гJ + (В, г? = (Q^/p4) я2 sin4 9,
(А 9J + (В, еJ = (Q2*/P4) (г* + a2J sin2 9.
И наконец, чтобы определить функцию (|ы2 + ^з) и завершить
определение метрических функций, обратимся снова к уравнениям
A9) и B5). Сравнение с соответствующими уравнениями из
гл. 6 (уравнения (8) иAб)), которые были получены для пустого
пространства-времени, показывает, что в силу соотношения A17)
уравнение A9) совпадает с уравнением (8) гл. 6, тогда как урав-
уравнение B5) имеет дополнительный член
4е-^ {«"•-¦»• [{A,r? + {B,Tf\ - 0ыъ [(Л>9J + (В,вП =
= 4е-*» {А1/2 (Q2»/p4) a2 sin4 6 - (Q|/p4AI/2) (r2 + а2J sin2 8} =
где в процессе упрощения было использовано соотношение A18).
Таким образом, вместо уравнений E9) и F0) из гл. 6 теперь
имеем следующие уравнения:
= 2 (X,tY,, + Y,2X,3)/(X + Y)\ A20)
2(r — M) (|i, + |i,)f, + 2ц (щ + ц,),, -
= 4 (АХ>2Г,2 - 6X,,Y,9)/(X + Y? ~
— C/A) [(r - M2) — A1 + (Ц2 + б)/б — 4Q2/p2, A21)
где
X = x + «. Г = х-со. A22)

ПО, Решение Керра—Ньюмена 291
Вследствие формальной идентичности решений для функций х
и со (уравнения A14)) с соответствующими решениями для мет-
метрики Керра преобразование правой части уравнения A20) при-
приведет к такому же уравнению, как и уравнение A29) гл. 6. Но
наличие дополнительного члена — 4Q2/p2 в правой части уравне-
уравнения A21) требует тщательного рассмотрения. Имеем
i2Y,2 = (г - М)УА - 4Мг/р2 + Ы\1*гМ№ + 4Q2r2/p4, A23)
(А/Х2) Xi2Yi2 - (б/х2) Х,37,з = (г - МJ/Л. - 4Мф2 +
+ 8аУгМ/р4 + 4Q2r2/p4 - (ц2/Р46) [(г2 + а2 + а2бJ - 4а2Дб] =
= (г - Л1J/А - 4Мг/р2 - ^/б + 4Q2/p2. A24)
Объединяя уравнения A21) и A24), снова приходим к такому же
уравнению, что и в гл. 6 (уравнение A30)). Следовательно, реше-
решение для функции (fx2 + |^з) имеет тот же вид, что и в случае мет-
метрики Керра (ср. с уравнением A31) гл. 6):
en2+Mi = р2/Д1/2. A25)
Решение полной системы уравнений закончено: оказывается,
метрика Керра—Ньюмена отличается от метрики Керра только
видом функции А. Отсюда следует, что постоянная М действи-
действительно обозначает инертную массу черной дыры, а параметр а
снова интерпретируется как момент количества движения на
единицу массы черной дыры.
а. Описание пространства-времени Керра—Ньюмена в форма-
формализме Ньюмена—Пенроуза. Из формальной идентичности метрик
Керра и Керра — Ньюмена с точностью до определения функ-
функции А следует, что для описания метрики Керра — Ньюмена в
формализме Ньюмена — Пенроуза мы можем определить изотроп-
изотропный тетрадный базис, как в § 56 гл. 6 для пространства-времени
Керра. В частности, требуемый базис по-прежнему задается соот-
соотношениями A70) и A73) гл. 6, а спиновые коэффициенты относи-
относительно выбранного базиса по-прежнему определяются соотноше-
соотношениями A75) гл. 6. И теперь из равенства нулю спиновых коэффи-
коэффициентов х, а, А, и v можно заключить, что пространство-время
Керра-Ньюмена, подобно пространству-времени Керра, является
пространством типа D по классификации Петрова и, кроме того,
в выбранном нами базисе
?0 - Уг = ?3 = Ъ = 0. A26)
Следовательно, чтобы закончить описание, остается определить
вейлевский скаляр V2 и максвелловские скаляры ф0, ф1 и ф2.

292 Глава 11. Другие решения, альтернативные методы
Максвелловские скаляры можно определить, свертывая тен-
зор Ру с базисными векторами, заданными соотношением A77)
гл. 6. Вспоминая, что F01 и /^равны нулю, получаем
2фг = Ftj A*п[ + т{№) =
— * 02 V ^ L tX J ~у~ * 12 1* ^ — I tl ) ~у~ * 03 \Х^Ь fft — 171 tTl ) ~\~~
+Fi3 (mlm* - fh?rn>) = - A/р2) (г2 -f a2) ev+^F02 — (аА/22) ^+^^12 —
- (i/p2) gv+i*. (a sin 9) F03 - (t/Sism 0) &+*ш (r2 + a2) F18. A27)
Воспользовавшись далее соотношениями G) и A16), находим после
некоторых преобразований, что
Фг = -IQJ2 (р*J. A28)
Действуя аналогичным образом, находим также
^о = Ф* = 0, A29)
так что единственным не равным нулю максвелловским скаляром
является скаляр ф1. | %
Для определения вейлевского скаляра ?2 поступим несколько
иначе и рассмотрим тождества Бианки (уравнения C216) и C21 в)
гл. 1, в которых члены Риччи заданы формулами C396) и C39в)
гл. 1). Вспоминая,что в нашем случае единственным не равным
нулю вейлевским скаляром является ^2, а единственным не рав-
равным нулю максвелловским скаляром — фх и что спиновые коэф-
коэффициенты х, сг, К и v равны нулю, получаем из тождеств Бианки
Г = 0,
¦Г= 0. A30)
Воспользовавшись теперь списком спиновых коэффициентов из
гл, 6.(формула A75)) и определениями операторов D и б* в гл. 8
(соотношения C) — E)), получаем следующие уравнения:
дЧ2/дг = - C/р*) Т2 - Q2,/4p4p*,
ffV2/dQ = — (Зш sin e/p*)^1 + Q2m sin 9/p4p*, A31)
в которые подставлено решение A28) для скаляра фг.
Легко убедиться, что частное решение уравнений A31) равно
Тг = Q2Jp (р*K, A32)
тогда как общее решение однородных уравнений имеет вид
Y2 = const/(p*K. A33)
Из сравнения с формулой A80) гл. 6 заключаем, что постоянная
в решении. A33) равна —М, поскольку она должна быть такой
же, как для решения Керра (в пределе Q* = 0). Таким образом,
искомое решение для Т2 имеет вид
+ Q>/p(p*K. A34)

Ill. Возмущения пространства-времени Керра — Ньюмена 293
111. Уравнения для взаимодействующих
электромагнитно-гравитационных возмущений
пространства-времени Керра—Ньюмена
Как уже говорилось во введении (§ 108), методы, которые ока-
оказались столь успешными для исследования гравитационных воз-
возмущений пространства-времени Керра, неприменимы (и не допу-
допускают простых обобщений) при исследовании взаимодействующих
электромагнитно-гравитационных возмущений пространства-вре-
пространства-времени Керра — Ньюмена. Основным препятствием являются за-
затруднения при расцеплении уравнений. В этом параграфе мы
кратко рассмотрим причину нерасцепляемости уравнений для
взаимодействующих полей спинов 1 и 2, описывающих возмуще-
возмущения пространства-времени.
Основными уравнениями, описывающими возмущения про-
пространства-времени Керра — Ньюмена, как и прежде, являются:
четыре «уже линеаризованных» тождества Бианки (уравнения
C21а), C21 г), C21д) и C21з) гл. 1), два тождества Риччи (уравне-
(уравнения C106) и (ЗЮк) гл. 1) и уравнения Максвелла в приведенном
виде (уравнения B07) и B08) гл. 5). Эти последние уравнения под-
подсказывают, что, как и при исследовании возмущений пространства-
времени Рейсснера — Нордстрема, удобно выбрать калибровку,
в которой максвелловскиескаляры ф0 и Достаются равными нулю:
Фо = <f>2 = 0. A35)
Как уже объяснялось в п. 44, б гл. 5, этот выбор калибровки
вполне допустим *. В такой калибровке уравнения Максвелла за-
заменяются парой уравнений
(Л - 3y - 7* - 2fx + fx*) х -
— (б* — За + р* — т* — 2я) а + 2W, = 0, A36)
(б + я* + 2т — а* + ЗР) X —
— (D + Зе + 8* + 2р - р*) v + 2Ч*з = 0 A37)
для спиновых коэффициентов. (Заметим, что в выбранной калиб-
калибровке нельзя предполагать равными нулю вейлевские скаляры
^i и 4V)
Обратимся теперь к тождествам Бианки (уравнения C21а),
C21 г), C21д) и C21з) гл. 1) и заменим выражения в правых ча-
частях первых двух уравнений из систем C) и D) гл. 9 на выра-
выражения (ср. с формулами B20) гл. 5)
* Он несомненно является и наиболее простым: любой другой выбор при-
приводит к более сложной системе уравнений, чем A39)—A42).
10 Чандрасекар С, т. 2

294 Глава 11. Другие решения, альтернативные методы
-|- аC?2 + Wf) = - -^s- Гз (/И - Ж) - Q2 _?1] ,
A38)
— v CW2 — 4*i*f) = + —^-r- \S ( М %*- ) + Q2 -?-
(p K I. \ p / * p2
Таким образом, оставляя без изменений определения, данные
в гл. 9 (соотношения F)), мы должны теперь рассматривать вместо
уравнений G) — (9) гл. 9 четыре уравнения, последнее из которых
суть преобразованное уравнение A36):
A39)
= +2s [3(M-4L)-<2*.-!?-], A40)
A41)
А (ф% --pr)k + (g. - З'а-?9 )s = 2pO,/(pV- A42)
Уравнение A42) совпадает с уравнением B9) гл. 9, которое мы
добавили там (ad hod) для восстановления симметрии уравнений
G) - (9).
Теперь мы можем проделать над уравнениями A38) — A42) те
же операции, что привели в гл. 9 к уравнениям A7) и C1). Дей-
Действительно, с помощью тождеств "~Л
>j + 3/р*) {Щ - 3/р*) + B% + 3ifl sin 9/р*) Bг - Ыа sin в/р*) =
= АЮ.Щ + 27+1272 - 6iap + (бр/р**) (М - Q2/p), A43)
5+ - 3/р*) C90 + 3/р*) + (^2 - 3»a sin 9/р*) (S_x + 3m sin 9/р*) =
+ ^2^+, - бктр + A2р/р*г) (М - Q2,/p) A44)
вместо расцепленных уравнений с разделенными переменными
B0), B1), C3) и C4) гл. 9 получаем пару связанных уравнений
- 6iap) Фо = - 2QI (S'+.fep'/P2 + ^oSP*/P2), A45)
p2 - S'jSpVp2),
A46)

112. Решения для статических черных дыр 295
и все усилия расцепить их (или разделить переменные) не увенча-
увенчались успехом. Все многочисленные манипуляции с системой урав-
уравнений A39) — A42), отличные от указанных выше преобразова-
преобразований, также оказались безуспешными.
Возникает вопрос, почему система уравнений A39) — A42)
не поддается исследованию в противоположность аналогичным
системам уравнений, с которыми мы сталкивались при исследо-
исследовании возмущений пространственно-временных многообразий
Рейсснера — Нордстрема и Керра. Опыт работы с уравнениями
B22) — B25) гл. 5 при исследовании пространства-времени Рейс-
Рейсснера — Нордстрема, вероятно, поможет нам в этом отношении.
Прежде всего угловые функции S±\ и S+2 связаны между собой
очень простыми соотношениями (уравнения B34) гл. 5), а соб-
собственные значения А,, соответствующие этим функциям, равны.
Кроме того, сферическая симметрия фонового пространства гаран-
гарантирует разделение переменных. Но расцепление системы уравне-
уравнений на пару уравнений второго порядка было неожиданностью:
оно оказалось возможным только благодаря выбору весьма специ-
специальных комбинаций радиальных функций, описывающих вейлев-
вейлевские скаляры и спиновые коэффициенты (уравнения B39) гл. 5),
комбинаций, в которые собственное значение К (общее для угло-
угловых функций S±\ и S±2) входит существенно нелинейно. В общем
аксиально-симметричном случае нет a priori никаких причин ожи-
ожидать, что угловые функции для полей спинов 1 и 2 будут связаны
простыми соотношениями: это не так даже для фоновой метрики
Керра. Далее, сравнивая уравнения A39) и A40) с соответствую-
соответствующими уравнениями гл. 9 (уравнения G) и (8)), мы видим, что в про-
противоположность простым членам в правых частях уравнений гл. 9
теперь имеем комбинацию членов (М — QV?) и Q*P*/p2-
Это наводит на мысль, что если расцепление системы уравне-
уравнений A39) — A42) и разделение переменных и будут возможны (если
это вообще возможно), то только в уравнениях четвертого или
более высокого порядков.
112. Решения, описывающие статические черные дыры
Мы видели в § 55 гл. 6, что решение Шварцшильда является
единственным статическим решением уравнений Эйнштейна в пу-
пустоте, имеющим гладкий горизонт событий и совместимым с тре-
требованием асимптотически плоского характера метрики на беско-
бесконечности. Это требование эквивалентно тому, что мы ограничи-
ограничиваемся только черными дырами, которые изолированы в простран-
пространстве. Хотя естественно ограничиться на первых порах исследова-
исследованием изолированных черных дыр, тем не менее представляет не-
который'интерес вопрос, как эти черные дыры могут деформиро-
деформироваться под влиянием внешних распределений массы. До тех пор
пока мы рассматриваем лишь окрестность таких деформированных
10*

296 Глава 11. Другие решения, альтернативные методы
черных дыр, предположение о существовании внешних распреде-
распределений массы эквивалентно ослаблению предположения об асимп-
асимптотически плоском характере метрики. В этом параграфе мы
покажем, как можно построить статическое аксиально-симметрич-
аксиально-симметричное решение уравнений Эйнштейна в пустоте, которое можно рас-
рассматривать в качестве деформированной шварцшильдовой черной
дыры.
Построение статических аксиально-симметричных решений
уравнений Эйнштейна начнем с метрики вида
ds2 = е2* (dtJ — е2^ (dcpJ — е2^ (dx2J — е2^ (dx3J, A47)
т. е. того же самого вида, который рассматривался в гл. 6 (и в
§ 109 настоящей главы), только член с со (описывающий увлече-
увлечение инерциальной системы отсчета в стационарных пространст-
пространственно-временных многообразиях) здесь опущен. Исследование
получающихся при этом полевых уравнений не представляет
трудностей.
Не теряя общности, мы можем в рассматриваемом случае
предположить, что (ср. с уравнениями B6) и B7))
в2(Цз-ц2) = д (г) = г2 - 2Мг, е$ = еФ+v = Д1/2 sin 9, A48)
что согласуется с существованием горизонта событий при г = 2М.
Основная задача затем сводится к исследованию линейного урав-
уравнения (ср. с уравнением D9) гл. 6)
[A(^-v)J],2+ [6(a|>-v),3],3 = 0, A49)
где
б = 1 — ц2 = sin20, A50)
а индекс 3 относится к переменной ц, (= cos 0). Полагая теперь
т, = (г— МIМ, A51)
когда
д = м2 (л2 — 1), A52)
мы можем записать уравнение A49) в более симметричной форме
[(Л2 - 1) (In Х),л]л + [A - Ц2) (In х)Дц = 0, A53)
где, как обычно,
X = e-^+v. - A54)
При исследовании решений Керра и Керра — Ньюмена мы
нашли, что функции, относящиеся к сопряженной метрике, в не-
некотором смысле более фундаментальны, чем функции первона-
первоначальной метрики. Поэтому рассмотрим вместо функции % функ-
функцию W:
= X КЛ2 - 1) A - f*2)l1/2 A55)

112. Решения для статических черных дыр 297
(ср. с уравнениями (97) и (98) гл. 6). Поскольку функция % =
= (т]2 — 1) A — \i2) является решением уравнения A53), этому
уравнению удовлетворяет и функция W:
[(тJ - 1) (In ЧЧД, + [A - ц2) (In ЧОДц = 0. A56)
Можно теперь проверить, что решение
W = Wsc = (r]~ 1)/(т| + 1) A57)
дает метрику Шварцшильда. Соответствующее решение для %
имеет следующий вид:
• A58)
Помимо «сингулярного» решения A57), уравнение A56) до-
допускает решения с разделяющимися переменными. Действитель-
Действительно, если
1пЧ' = R (ц) Р (fx), A59)
то для Р (\i) мы должны выбрать функцию Лежандра* Рп ([i).
Тогда радиальная функция R (ц) удовлетворяет уравнению Ле-
Лежандра
-sr [(ТJ - 1) igH ~ п {п + Х) R = °- A60)
Решением для R (ц), соответствующим Рп ((.i), будет, таким обра-
образом, линейная комбинация функций Лежандра первого и второго
рода Рп (т]) и Qn (ц):
Rn (Ц) = АпРп (ц) + BnQn (л), A61)
где Лп и Вп — постоянные. Общее решение для Y, полученное
таким способом, следовательно, имеет вид
In Т = S Rn (л) Рп (ц) = 5 (л, и)- A62)
п=0
Для шварцильдовой черной дыры, деформированной внешним
распределением массы, предположим решение вида
W = Wsces = е*(ч- 1)/(т| + 1), A63)
где S — общее решение A62). Этому соответствует следующее
решение для %:
[ j ]'/2^- 064)
* В действительности выбор функции Рп (ju), регулярной на оси, дикту-
диктуется требованием (которое мы рассмотрим ниже в п. а) локально плоского
характера метрики при р,2 = 1 и т)^1. Это же требование приводит к тому,
что функции Лежандра второго рода Qn (ц) также не должны входить в ре-
решение для R (т]) уравнений A61) и A62).

298 Глава 11. Другие решения у альтернативные методы
Из уравнения A64) и соотношения
е$ = e^v = [(т12 _!)(!_ ^2) ]i/2 A65)
находим
g2v = eS (т| _ 1)/(т1 + ^ ^ = A ___ ^2) (Л + lJe-S#
В результате получаем следующую метрику:
^ - A - ц*) (г, + 1Jе-^(с1фJ - {ц?^у/2 X
A67)
Для завершения решения нужно рассмотреть уравнения, кото-
которые определяют функцию (fx2 + \i3). Поскольку в нашей задаче
X = Y = %, получаем следующие уравнения (ср. с уравнениями
F4) и F5) гл. 6):
1п X)*,
= № - 1) [AпХ),л]2 - A - li2) [(lnxU2 - 3/(л« - 1) + 1/A - fx2).
A69)
Разрешая уравнения A68) и A69) относительно (\i2 + |13),л и
0*2 + |х3),ц» получаем
« 2(л2-^) г 2-л
^~" (т]2 — 1)A-jli2) L Л2— 1
+ [4т|/(т|* - 1)] S,, - [4|А/(т|» - l)]SfIi - 2|*S|T|Sf|1 + г! (S)T1J -
-[т1A-^)/(т12-1)]E,цJ, A70)
2 (т|2 — Ц,2) ^
2_1)A_JLl2) ^,|i-h 1_JLl2 ^,Т1"|- Т]2_
ylif. A71)
Интегрируемость этих уравнений гарантирована.
а. Условие равновесия черной дыры. Нетрудно понять, что рав-
равновесие черной дыры во внешнем поле требует, чтобы пространство
вдоль оси 0 было локально плоским при всех т| ^ 1, потому что
в противном случае на черную дыру будет действовать прилив-
приливные силы, которые будут толкать ее в ту или другую сторону.
Это требование локально плоского характера метрики, если его
иначе сформулировать, требует, чтобы отношение длины окруж-
окружности к радиусу для бесконечно малой окружности, проведенной

112. Решения для статических черных дыр 299
ортогонально оси, было равно 2jt для всех ц ^ 1. Для метрики,
записанной в форме A67), это требование сводится к тому, что
y^ A72)
или я L v ' l '
ИЛИ
ea = [(Ti—l)/(ri + lK]1/2^2+|l3+s= 1 при |Л2=1, т]^1. A73)
Уравнения A70) и A71), переписанные через а, упрощаются:
^ *^ ~~ 2MSS+Ti (о) — ц 2_ 1
A74)
A75)
Необходимым (но не достаточным) условием для выполнения
уравнения A73) является условие
а>л = 0 при 1 — [г2 - 0. A76)
Уравнение A'74) будет совместным с этим требованием, только если
5 (т), [г) регулярно при |х = ±1. Именно это требование застав-
заставляет ограничиться функцией Рп (\i) при написании решения A62)
для функции In Ч?.
Поскольку на оси а,л = 0, всегда можно устроить так, чтобы
a = 0 при 9 = 0 и т] 5> 1. Но чтобы а также имело значение 0
и при 0 = я, мы должны вдобавок потребовать
сЮ = 0. A77)
Из уравнения A75) следует, что первым требованием является ре-
регулярность S при г) = 1. Поэтому мы не можем включить функ-
функции Лежандра второго рода в решение A61) для Rn (т|), и реше-
решение для S сводится к следующей сумме:
оо
S (л, |л) = 5] АпРп (\\) Рп (\i). A78)
Для этого регулярного при т] = 1 решения уравнение A75) дает
at|1 - 2SfPl (л - 1), A79)
а из условия A77) получаем
S (л = 1, fi = +1) = S (л = 1, fi = -1). A80)

300 Глава 11. Другие решения, альтернативные методы
Если решение для S дается уравнением A78), то условие ло-
локально плоского характера метрики на оси требует, чтобы нечет-
нечетные коэффициенты Л2п+1 подчинялись условию
оо
2л«»Л+1A) = о, A81)
п=0
а на четные коэффициенты А2п никаких ограничений нет.
Наконец, отметим, что метрика, описывающая статическую
деформированную черную дыру, представима также в виде
X [e° (d9J + sin2 6 (с!фJ], A82)
где a может быть получено в квадратурах из уравнений A74)
и A75), а решение для S определяется уравнением A78), причем
на нечетные коэффициенты наложено условие A81).
113. Решение уравнений Эйнштейна—Максвелла,
описывающее семейство черных дыр
В настоящем параграфе мы рассмотрим решение уравнений Эйн-
Эйнштейна— Максвелла, являющееся аналогом ньютоновского рас-
распределения массивных точечных зарядов, взаимное гравитацион-
гравитационное притяжение которых точно компенсируется кулоновским от-
отталкиванием. Решение это было найдено Мажумдаром и Папа-
петру, однако правильная интерпретация его как решения, опи-
описывающего семейство экстремальных черных дыр Рейсснера —
Нордстрема (с Q% = ±М), принадлежит Хартлю и Хокингу.
Решение Мажумдара — Папапетру можно получить, если
рассмотреть статические решения уравнений Эйнштейна — Мак-
Максвелла для пространства-времени с метрикой
ds2 - е2* (d/J — e^ [(dx1J + (dx2J + (dx3J], A83)
где v и a|) — функции только пространственных координат х1, х2
и х3. Уравнения поля для этой метрики можно выписать сразу,
воспользовавшись уравнениями гл. 2. Действительно, из уравне-
уравнений (95а) — (95з) гл. 2 получаем уравнения Максвелла
)A = 0; A84)
),i = 0,
(e*+vF01\3 - (e^F03)tl = 0, A85)
(e^F12\2 - (e^F31)>3 = 0;
)tl = 0; A86)
31)tl = 0,
=0, A87)
= 0.

113. Решение уравнений Эйнштейна—Максвелла 301
Из двух систем уравнений A85) и A87) следует, что компо-
компоненты (F01, F02, F03) и (F12, F23, F31) тензора Максвелла можно по-
получить из потенциалов А и В:
e^Fap = Byy A88)
(причем во втором уравнении значения индексов а, C и у состав-
составляют циклическую перестановку индексов 1, 2 и 3). Здесь и ниже
греческими буквами обозначаются пространственные координаты,
а суммирование по а означает суммирование по а = 1, 2 и 3.
Уравнения A84) и A85) дают уравнения для потенциалов А
и В
2>*-МДа = 0, Е(^Я.а),а - 0. A89)
а а
Тензор энергии-импульса для максвелловского поля задан
уравнением A1), поэтому
[|Aa|2 + |S,a|2], A90)
| В>а р - 2 (Л,,J - 2 (ЯдJ], A91)
з - В,И,з), A92)
/?м = - 2e~2<*+v> (Л"гЛ,2 + ВЛВЛ), A93)
где принято обозначение
Ka|S= S(^Ja. A94)
а
Выражения для компонент R22 и т. д., не перечисленные здесь,
могут быть получены циклической перестановкой индексов 1, 2
и 3.
Уравнения G5а) — G5х) из гл. 2 дают следующие выраже-
выражения для ненулевых компонент тензора Римана в метрике A83):
#1212 = е-2** (Ф,и + ^,22 + ФЛз), A95)
#Ш4 = е~п (v,n + vava - v,1i|),l + v,2i|),2 + v 3\|),з), A96)
#1442 - - e~^ (v,12 + vflv>2 - *flv 2 - ^v,!), A97)
а также уравнения, которые получаются из приведенных выше
циклической перестановкой индексов 1, 2 и 3. Остальные компо-
компоненты равны нулю:
#2114 — #3114 ~ #1224 — #3224 = #1334 =
= Я2зз4 = 0, A99)
#1234 = #1423 -~ #1342 ~ 0-
(Напомним, что в соответствии с соглашением, принятым в гл. 2,
индекс 4 обозначает it.)

302 Глава 11. Другие решения, альтернативные методы
а. Преобразование уравнений поля. Из уравнений A99) заклю-
заключаем, что
#н = #т4 + #1334 = 0, т. е. R10 = 0. B00)
Следовательно, в силу уравнения A92)
Л,2В,3 — В,2Л,з = 0. B01)
Из этого уравнения и аналогичного ему, которое получается
вследствие равенства нулю R20 и R30i имеем
4*-=4*-=4*- B02)
"л В& #з
Поэтому мы можем с помощью преобразования дуальности, при-
применив его к антисимметричному тензору Fy и дуальному к нему
тензору *Ftj (=&ijkiFkl), добиться, чтобы или Л, или В стало
равным нулю. Поскольку А соответствует электростатическому
потенциалу, удобно положить
В = 0. B03)
Ясно, что это предположение не приводит к потере общности.
Поскольку след тензора энергии-импульса максвелловского
поля равен нулю, скалярная кривизна R также должна быть рав-
равной нулю, т. е.
# = #1212 + #2323 + #3131 + #1414 +
+ #2424 + #3434 = 0. B04)
Подставляя для компонент тензора Римана выражения из урав-
уравнений A95) и A96), находим
v),ae + S v,a (г|) + v),a = 0. B05)
a
ЩИз равенства нулю скалярной кривизны R следует, в частно-
частности, что Roo = Goo- Полезно выписать в явном виде соответствую-
соответствующие компоненты уравнений поля. Поскольку
+ #00 ~ #44 == #1414 ~Ь #2424 ~f~ #3434> B06)
Goo = +G44 == #1212 Ч~ #2323 Ч~ #3131» B07)
из уравнений A90), A95) и A96) находим
S v,aa + 2 v,a (г|) + v),a = + <r2v I ^4,a I2, B08)
t,a = - e-^\A>a\\ B09)
a a
потому что мы положили В = 0.

113. Решение уравнений Эйнштейна—Максвелла 303
Сложение уравнений B08) и B09) приводит к уравнению B05).
В качестве другой линейно независимой комбинации этих урав-
уравнений удобно выбрать следующую:
2 М,* + 2 Е (ф + vU + 2 2] v>a (ф + v),a = e-2v | Л,а р. B10)
Наконец, рассматривая компоненту /?12 тензора Риччи
Riz = ^?1зз2 + ^?i442> B11)
получаем из уравнений A93), A97) и A98)
2vflvl2 + (ф + v),12 - (г|) + v)fl (ф + v),2 = 2e-*>AtlAa2, B12)
или в более общем виде
2v,av,p + (г|) + v)M - (г|) + v),a (ф + v),3 = 2<г2М,аЛ э. B13)
Уравнения A89), B05), B10) и B13)—основные уравнения
теории.
б. Решение Мажумдара — Папапетру. Из уравнений B05),
B10) и B13) с очевидностью следует, что случай
1> + v = 0 B14)
особый, так как уравнения чрезвычайно упрощаются, и мы полу-
получаем:
? Е>,а = 0, B15)
аА, з (а^р). B16)
Уравнение B15) можно записать в альтернативной форме
Е(**).««=-0. B17)
a
Из уравнений B16) следует, что (ср. с уравнением A88))
Л a = =F <НЧ, a = ± (в-*), a (= ^Oa)- B18)
Это решение для Ауа совместно с уравнением A89) в силу B17),
которому удовлетворяет функция Л Отсюда получаем решение
для электростатического потенциала А
А = ±е-*, B19)
причем выбор знака—это вопрос соглашения.
Далее удобнее писать (х, у> г) вместо (л:1, л:2, х3) и U вместо Л
При этом метрика принимает следующий вид:
' ds2 - U-2 (dtJ — U2 (dx2 + dy2 + dz2), B20)
а функция U удовлетворяет трехмерному уравнению Лапласа
в декартовых координатах
$ S)/-0. B2.)

304 Глава 1L Другие решения, альтернативные методы
Электростатический потенциал равен
А = U-1. B22)
Это и есть решение Мажумдара — Папапетру.
в. Решение, описывающее семейство черных дыр. Разумеется,
любое решение уравнения Лапласа B21) может быть использовано
в сочетании с метрикой B20). Но нас особенно интересует решение,
описывающее семейство черных дыр, которое получается из
ньютоновского потенциала для ряда точечных масс М-ъ (i = 1, ...
.... N):
N
U = 1 + 2 Mt/rh B23)
где
г г = [(х - xty + (у- У1У + (z- zW, B24)
а аддитивная постоянная 1 в решении для U гарантирует, что
в отсутствие источников мы имеем метрику Минковского.
Два факта требуют прояснения.
Во-первых, исходя из вида метрики B20), когда различные
точки (хь yt, zt) достаточно далеко удалены друг от друга, мы
можем отождествить постоянные Mt с инертными массами внутри
сфер достаточно большого радиуса, окружающих различные точ-
точки. Следовательно, мы должны потребовать, чтобы все постоян-
постоянные Mt были положительными:
Mt >0 (i = 1, ..., N). B25)
Таким образом, в той части многообразия, которую покрывает
карта (х, у, г), — а мы увидим, что она покрывает только часть
максимально расширенного многообразия, — величина U (х, у, г)
положительна и не равна нулю, а метрика регулярна всюду, за
исключением точек гг.
Во-вторых, заряд Qt точечной массы Мг можно определить,
вычислив интеграл от дивергенции вектора Fa0 (—g)~]/2 по сфе-
сферическому объему Vt, окружающему точку (xiy yiy zt) *:
= J
a =
dVi
B26)
Таким образом, в принятых нами единицах заряд и масса источ-
источника, расположенного в точке (xt, yt, zt), равны. Поскольку мы
Это утверждение следует из одного из уравнений Максвелла:

113. Решение уравнений Эйнштейна—Максвелла 305
выбрали А положительным (уравнение B22)), все заряды Qt ( = Mt)
положительны. Если бы мы выбрали для А противоположный знак
в уравнении B22) (а у нас было право выбора; см. уравнение B19)),
то получили бы, что все заряды отрицательны. Во всяком случае,
все заряды должны быть одного знака.
Возвращаясь к уравнению B23), заметим, что в случае только
одной точечной массы
U = 1 + Mir, B27)
и мы получим решение Рейсснера — Нордстрема в стандартном
виде, записав метрику в сферических координатах и заменив г
на (г — М).
Случай двух точечных масс, когда
G=1 + Мг/гг + М2/г2, B28)
хорошо иллюстрирует общий случай, поэтому рассмотрим его
подробнее. В принятой нами системе координат (х, у, г) решение
для U и метрика B20) не являются регулярными в точках г =
= гг и г = г2. Однако сингулярности в этих точках являются ко-
координатными, а геометрия в них регулярна. Чтобы показать
это, преобразуем сначала метрику к полярным координатам с цен-
центром в точке Мг и осью 0Х вдоль линии, соединяющей точечные мас-
массы Мх и М2 (рис. 47, а). Тогда
U = 1 -f Mj/n + АГ2/(г? + а2 - 2arx cos в^172, B29)
где а — расстояние между массами Мх и М2, и метрика принимает
следующий вид:
ds2 - (dt)VU2 — U2 [(dr,J + r\ (dexJ +
+ (r?sin2e,)(d<pJ]. B30)
Теперь очевидно, что площадь поверхности небольшой сферы ра-
радиуса гъ окружающей начало координат, при стремлении гх
к нулю (гг -> 0) стремится не к нулю, а к конечному значению
4лMl (которому равна и площадь поверхности горизонта событий
экстремальной черной дыры Рейсснера — Нордстрема массы Мг).
Следовательно, г± = 0 не точка, а поверхность, площадь которой
равна конечному значению 4пМ\.
Чтобы показать, что геометрия при гг = 0 регулярна и что
поверхность г± = 0 изотропна, сделаем, следуя Хартлю и Хокин-
гу, еще одно преобразование координат
t = и + F^), B31)
где
^ (^ ^J = V2(M. B32)

306
Глава 11. Другие решения, альтернативные методы
Метрика в этих координатах имеет вид
- r\U2 [(d9tJ -Ь sin2 0, (dcpJ]. B33)
Карта (л', 0i,0)
Рис. 47. Аналитическое продолжение многообразия* через координатную сингу-
сингулярность при Мх для случая двух заряженных точечных масс (Мх = Qv M2 =
= Фг)- Q- — начало координат в точечной массе Мъ координатная сингуляр-
сингулярность при /-х = 0 не является точкой, а представляет собой изотропную поверх-
поверхность, геометрия на которой регулярна, б — расширение многообразия через
точку гг — 0 в область отрицательных значений гг в карте (/•{, 0J, ф). В этой рас-
расширенной области Мх отрицательно; масса заключена внутри сингулярной
поверхности, которая является истинной точечной сингулярностью. Времени-
подобная траектория, приходящая в Мг в карте а, будет продолжаться в том же
направлении в области карты б. У нее есть две возможности: или продолжать
следовать тем же курсом и в конце концов оборваться в сингулярности, или
снова пересечь изотропную поверхность гх = 0 и попасть в другой мир.
В окрестности гх = 0
U (ri) ~ V (г,) = М2 cos 9^/а2 + О (г?), B34)
ds2 -> {r\lM-J (duJ -f 2d;/dr1 — DMiM2 cos 9x/a2) (d^J —
—Ml [(d9xJ + sin2 0J (dcpJ] (rx -+ 0). B35)
Регулярность метрики при rx = 0 теперь очевидна, ясно также,
что поверхность гг = 0 является стационарной и изотропной.

113. Решение уравнений Эйнштейна—Максвелла 307
Поскольку на поверхности гг = 0 геометрия регулярна, мно-
многообразие может быть расширено на область отрицательных зна-
значений гх\ времениподобная траектория, приходящая к поверх-
поверхности гх = 0 вдоль некоторого направления 9Х, будет продол-
продолжаться вдоль того же направления в область отрицательных зна-
значений гг. Если ввести определения (рис. 47, б)
г[ = - rv К = (г[2 + а + 2< cose,I73, B36)
то метрика (в области отрицательных гх) сохранит свой вид B30),
но при этом функцию U (r1, 0Х) нужно будет заменить на
U' (г,\ 9,) = 1 - Mx/ri + М2Г2. B37)
Ясно, что функция V (п, 9i) обратится в нуль на
поверхности. Простое исследование «эквипотенциальных» по-
поверхностей функции U' показывает, что поверхность, на которой
U' равно нулю, полностью охватывает начало координат г[ = 0.
И на поверхности V = 0 метрика сингулярна. Эта сингуляр-
сингулярность — истинная, что может быть подтверждено вычислением,
например, инварианта FefFef, который расходится на поверхно-
поверхности V == 0. Действительно (см. уравнение A88)),
FefF*t =-2|Л,а|2=-2 (grad (У'Д/'2J, B38)
и этот инвариант явно расходится, когда U' = 0. Более того,
хотя в карте (г{, 0ь ф) U' = 0 представляется поверхностью,
в действительности это точка, потому что, вычисляя площадь
поверхности, примыкающей изнутри к поверхности V = 0, и
переходя к пределу, когда эта поверхность стремится к поверх-
поверхности U' = 0, находим
J J [(/' (г;, в,)]2 г;2 sin вх d0x d9 -> 0. B39)
Таким образом, область внутри поверхности г\ = 0 очень похожа
на область внутри горизонта событий экстремальной черной дыры
Рейсснера — Нордстрема. В частности, времениподобная траек-
траектория, пересекающая изотропную поверхность гх = 0, может за-
затем следовать двумя путями: или она попадет на поверхность
(/' - 0 и там оборвется, или она обогнет эту поверхность и по-
попадет в совершенно новый мир, снова пересекая поверхность тх —
= 0 (рис. 47).
Все предыдущие замечания, которые относились к массе Ми
расположенной в точке ги равно применимы и к массе М2
в точке г2. И в общем случае, когда U определяется уравне-
уравнением B23), каждая точка rt представляет собой изотропную по-
поверхность площадью 4яУИ?, а карта (х, у, z) может быть расширена
так, чтобы описывать область внутри этих изотропных поверхно-
поверхностей, которые окружают истинные сингулярности. Во всех слу-
случаях можно построить максимальное аналитическое продолже-
продолжение многообразия. Мы не будем более вдаваться в этот вопрос,

308 Глава П. Другие решения, альтернативные методы
но уже и сейчас ясно, что нам удалось построить максимально
аналитически расширенное многообразие, описываемое решением
B20) с функцией (У, задаваемой уравнением B23), и представля-
представляющее семейство N экстремальных черных дыр Рейсснера — Норд-
стрема.
До сих пор наше исследование метрики B20) ограничивалось
рассмотрением простейшего решения B23) уравнения Лапласа.
Возможно, на данном этапе изложения у читателя возникает же-
желание рассмотреть подобные суперпозиции других более общих
решений уравнения Лапласа. Однако, Хартль и Хокинг показали,
что во всех других случаях пространство-время обладает голыми
сингулярностями. Именно поэтому другие решения не представ-
представляют столь большого интереса, как рассмотренные выше. Те же
замечания относятся и к стационарному обобщению статического
решения Мажумдара — Папапетру, найденному Перешем и Из-
раэлем и Уилсоном.
114. Вариационный метод и устойчивость решений
для черных дыр
При исследовании решений Шварцшильда и Керра, описыва-
описывающих черные дыры, широко использовался алгебраически спе-
специальный характер этих метрик, что особенно просто учитывается
в формализме Ньюмена — Пенроуза. Но успех, достигнутый бла-
благодаря использованию формализма Ньюмена — Пенроуза, — раз-
разделение переменных в основных уравнениях математической фи-
физики, описывающих возмущения рассмотренных нами решений,
раскрытие аналитического богатства математической теории чер-
черных дыр — несколько затемняет их физическую сущность, ко-
которая скрывается под покровом геометрии. Физическая природа
черных дыр существенно связана с наличием гладкого горизонта
событий в асимптотически плоском пространстве-времени, скры-
скрывающего сингулярность. И следует помнить, что единственность
решения Керра не есть следствие его алгебраически специального
характера, а скорее следствие этой физической природы, потому
что алгебраически специальный характер решения Керра не имеет
никакого отношения к аргументации, на которой основаны тео-
теоремы Картера — Робинсона. Кроме того, уравнения формализма
Ньюмена — Пенроуза оказались чрезвычайно неподходящими
для решения важной физической задачи об устойчивости простран-
пространства-времени Керра. В этом последнем параграфе книги мы опи-
опишем подход к решению подобных физических задач, который в
некоторых существенных аспектах отличается от методов, описан-
описанных в книге.
Метод решения, который мы собираемся описать здесь, состоит
в исследовании возмущений путем непосредственной линеариза-
линеаризации уравнений Эйнштейна около стационарного решения и форму-

114. Вариационный метод и устойчивость решений 309
лировки вариационного принципа, из которого вытекают решения
уравнений, описывающих возмущения. Этот достаточно распро-
распространенный в других областях математической физики метод
должен включать в себя некоторые черты, присущие только об-
общей теории относительности. Сюда входят выбор калибровки,
роль уравнений, задающих начальные условия, и тождеств Биан-
ки. Мы познакомим читателя с этими проблемами. Мы ограни-
ограничимся, однако, лишь возмущениями аксиально-симметричных ре-
решений уравнений Эйнштейна в пустоте, сохраняющими аксиаль-
аксиальную симметрию (хотя метод имеет более широкое применение).
Рассмотрим стационарное аксиально-симметричное решение
уравнений Эйнштейна, метрика которого имеет стандартный вид:
ds2 = e2v (dtJ — е2* (dcp — cod^J —
— e2^ (dx2J — e2^ (dx3J, B40)
причем в этой метрике по условию уже использован калибровоч-
калибровочный произвол в выборе функций |12,и jli3. Как было показано в
§ 12 гл. 2, нестационарная метрика, достаточная для описания
аксиально-симметричных возмущений пространства-времени с ме-
метрикой B40), имеет следующий вид (уравнение C8) гл. 2):
ds2 - e2v (dtJ — е2^ (dcp — q2dx2 — q3dx3 — cod/J —
— e2^ (dx2J — e2»* (dx3J, B41)
где уже нельзя наложить координатное условие на функции ji2
и ji3. Другими словами, возмущение метрики B40), сохраняющее
аксиальную симметрию, приводит к появлению у всех функций v,
ар, со, |i2 и |i3 приращений первого порядка, так что эти функции
становятся равными:
v + 8v, «ф + бар, со + бсо, |i2 + 6|i2, |i3 + 6|i3. B42)
Вдобавок могут быть не равными нулю в первом порядке по тео-
теории возмущений функции q2 и q3t причем они должны подчиняться
ограничениям, указанным в гл. 2 (уравнение D2)). Однако, как
было показано Фридманом и Шутцем, из соображений устойчи-
устойчивости важно, чтобы приращение первого порядка функции (|i2 +
+ [1з) было равно нулю, т. е. мы должны гарантировать равен-
равенство
б (|ха + fx3) = 0. B43)
Очевидно, для достижения этой цели нужно рассмотреть более
общую, чем B41), метрику. Поэтому обобщим метрику B41)
таким образом, чтобы можно было наложить ограничения B43):
ds2 = e2v (dtJ - е2^ (dcp - со dt - q2 dx2 - q3 dx3J —
- e2»* (dx2 -|- x dx3J - e2^ (dx3J, B44)
где x — еще одна функция переменных t, х2 и Xs. Эта метрика бо-
более общего вида, чем рассматривавшаяся в § 13 гл. 2, потому что

310 Глава 11. Другие решения, альтернативные методы
есть добавочная функция %, но она менее общая в том смысле,
что теперь метрические функции не зависят от координаты ср.
При вычислении компонент тензора Римана для метрики вида
B44) в исчислении Картана мы примем (как в § 13 гл. 2) комп-
комплексные обозначения (уравнение D4) гл. 2)
cU = —i dx4, dt = /d4, v = ji4, со = iq± B45)
и будем использовать вместо базисных форм D6) гл. 2 следующие
базисные 1-формы:
dcp— 2] qAdxA = со1^,
A
со2 = е»* (dx2 + х dx3), dx2 = в"^^2 — х^^^оK, B46)
со3 = в*1* dx3, dx3 = ?-^чо3,
со4 = е*1* dx4, dx4 = ^-^4(о4,
где (как и в § 13 гл. 2) заглавные латинские индексы пробегают
значения 2, 3 и 4.
Большая часть результатов анализа, проведенного в § 13 гл. 2,
может быть использована и в рассматриваемом случае, если опре-
определить производные /:3 и /:3- функции / (х2, х3, х4) по индексу 3
следующими равенствами:
Ь=Ь-ХА». f:>'=f,»-W),*=f:*-X,ff- B47)
(Заметим, что производная /: 3 удовлетворяет правилу Лейбница,
а производная /: 3- — нет.) Таким образом, вместо уравнений
F0) гл. 2 имеем теперь
I 1/ Z?M'2~M'3"M'4'Y (VI
! / 2 /Vj 4 '
4 _ 1/ Ф-М-2-Й4/) 1 _|_ -1*« 4 e"^*!! CO2
- iLe^-^-^% m\ B48)
где (ср. с уравнением E8) гл. 2)
Яав = Ча,в-Яв,а, B49)
Q34 = Q34 - XQ24 = - Q43- B50)

114. Вариационный метод и устойчивость решений 311
Вместо уравнений F2) и F3) гл. 2 получаем
d (/чо1) = e-w* (Fe*), 2 со2 Д со1 -f <г*-^» (Fe% 3 со3 Д со1 +
+ е-*-»* (Fe^>), 4 со4 Д со1 + /^ [e-^-^Q23<o2 Доо3 +
4- <г^-^0з4«3 Л <°4 + e-^-v-'Qva* Д со2],
d (FoJ) = е-мч-и. (Fe^): з- со3 Д со2 4 ^-1*»-»*. (Fe»')t 4 со4 Д со2 +
4- е^-^ -^«Fyv> 4со4 Д (о3,
d (f(o3) = e-ns-n» {Fe^)t 2 со2 Д (о3 4- е-»*»-»*' (f^1), 4 «4 Л w3.
d (fco4) = ег»-*-»-* (Fe^\ 2 со2 Д со4 4 e"^-»1* (Fe»*). 3 со3 Д со4. B51)
Компоненты тензора Римана мы можем теперь вычислить
с помощью второго картанова уравнения структуры. Находим
- #Ш2 = - е-^»> (е*ч»п|>, ,\ 2 -
~ #1313 —
- #1414 =
— #23i3 =
— #2421 =
_ e-i*,-2n
— #3434 =
— <
— #1213 =
~ #1214 =
— #1314 =
— #1223 =
~" #1224 =
— e 2M"'h?, 4t
- e'2^, 4h
_e-i*.-i*. {[<n*»(
r2|ij!*2. 4^3,4 - f
'(в1*'):3.И4:з-8
2|iV3. 2^4, 2 - =
_ g-*-n, (e*-i*.^
I 1/ ^2ф-
/ 2 L^23|
+ V«e
1 / /)lt-2Uo-Ui Г Л
/ л^ LX.^4»
f 4 -f V^2* ^2 (^"M"Q23 + * '
: з): 3 — е-2»*\р, 2|13, 2 —
,4 + 1/4^^И^32 + ^4
4/1 4 ii 2r^4i 2
(:34i//№(<r2^Q224e-^
У1*'): 3']: 3' + {<Р'-»г\1а, 2), 2} -
V ^Зф-ЗДг-ЗДзОЗ 1 1/ /^!Ы2—Jblj—1^4^
/4g2,Ml*.-2|*4Q|4 4 l/4 (gl*^.-!*^
4|^3, 4), 4 ~Ь (бЙ4"й»Ц4: з): з] —
/4 Vc34 /4 V /
' 2)' Я —— ^ ^з\р- qJLLq 2 ——
-21Л.4/'") ^) W z?!^2—М'З — M'Aili л/
Sc42^l43 /2е Т) 4л* 4
'j 4/j 2 1" ^ ^'4lpj 2^2, 4 1~
'.^з+е^Ч 3(^3,4 +
2 ~Г У2З W Y — (^2 — М^з), 2J Г
*-I*.-2l*.Q4etla> 4 _ l/4e*-H,-2|i.Q4
а + Q*4 (Зф — Ца — Ц4>, с] +
Q24), B52а)
(&), B526)
V43/) ^OZBj
;4J' B52г)
:,4J, B52д)
СмJ, B52е)
B52ж)
:ЗХ,4 B523)
2Х.4. B52и)
2Х,4, B52к)
I2X.4- B52л)

312 Глава 11. Другие решения, альтернативные методы
- Rnu = 'fa*-3»-». [Qn: з + Q34Cij) - ц, - ц4): 3] +
_|_ V,e*-2"*«-^Qa4(i8> 2 + 'Л^^'&зХ, 4- B52м)
- #1332 = Ч**-**-»* [<?32:3 + <Э32 (Зф - Ц8 - Ц8):,] +
+ Vs^-^-^QaHs. 4 - V4e*+|i>-2tl'-2|i'Q«X. 4, B52н)
- /?Ш2 = V2^-^-2^ [Qn, 4 + Q42 (Зф ~ |i8 - Ц4), 4] -b
+ V^^'-^'QsjH*^ - V4e*+tl'-2|1'-2ll'Q48X, 4. B52o)
- -R1443 = Vs**'11'-211' [Q43, 4 + Q43 (Зф - Us - Hi), 4] +
+ V^^'-^Qas^, 2 + Vi^'^-^'Q^X, 4. B52n)
- ^2334 = er»*-^ []l3< 24 + ЦЗ, 2 (|*8 - И2), 4 - H«, 4^4, 2] -
- 3Ле21;^2-2(Хз-^4C2з9з4 - V2e-(i2-»l= (е2м-2-^-^4Х_ 4):8. _
_. i/2e-2^-^ (en,):s. x> 4, B52p)
- /?3224 = e-v-rih (ef.-^|ia> 4):3- - e-»».-^-^ (en.):S. |is> 4 -
- %e2*-2»^-»>QS2Qu - Vje-»1'-»1' (^«-^X, 4), 2 - V*^'""'!^, 2X, 4.
B52c)
- Ram = e-"'"»1' (e-^'14 2):S - е-^-^|х4:8ц8,2 -
- »/4e2*-|it-tl'-2tl'QsiQ48 + l/2e-^-^ {&*-*,-»tXi 4) 4 +
+ V2e^-^-^^2) 4ЗС 4, B52т)
- /?1234 = 1/ae*-|i'-|1'-tl' !Q24 №:S - в1' (^!): 3'] ~ <?23 (^ - Иг), 4} +
+ l/,e-^^ (е2*-'1'-^^), 2, B52y)
- #UM = '/г^-^^1"^ [Q43 (Ф - (l4), 2 - Q42 (Ф - H4):s] +
+ 1/2e-1!-(i< (^-•'•-^Qje), 4. B52ф)
- #1324 = Vtf*-»'-*,-»* [Q34 (^ _ цз), 2 _ Q32 (^ - цз), 4] -f
-i».-»'.Q24).3. B52x)
Нелишне будет заметить, что для отдельных компонент тензора
Римана получаются разумные выражения, которые на первый
взгляд не совпадают. Действительно,
R '14 = _е-*-^ (g*-^: з), 4 + в-^'-"^. 4ц4: з +
+ 1/4е2*~2^-A»-^24<Э23 - lUe-^~^, 2X 4, B53)
R 1,з = -г-*"*' (е*-»'Ъ 4): з + е-1*'1^: 3Цз. 4 -
_ V4^-2^-^-^Q23Q42 + Ч^-»*-»^, 2Х, 4- B54)

114. Вариационный метод и устойчивость решений 313
Эти выражения получаются, если воспользоваться соответственно
следующими уравнениями структуры:
Q3 = d©3 + «г Л »з + e>i Д ©з. B55)
п\ = deal + соз Д »4 + «2 Д ©4- B56)
Тем не менее если использовать тождества, которым удовлетворяют
производные B47), то можно показать, что выражения B53)
и B54) одинаковы (хотя установление подобных равенств не всегда
простая задача).
Комбинируя соответствующим образом перечисленные компо-
компоненты тензора Римана, получим компоненты тензора Риччи и
тензора Эйнштейна
N>. M + t.W- Иг), 4 - Ф, #4, 2 + Из, 24 + ИЗ, 2 (ИЗ — И2), 4 ~ Из, #4, si ~
— 1/2e2*~2(i3Q23Q34 = 1/,?»*-2»' [ifc з + е-**2 (ef«): з-] X, 4 +
+ Va^-*' (в2»*--!»»-»*^. 4):3' №в), B57)
№, 4 : 3 + Ф: 3 0l> ~ Из), 4 - ^, 4.1U : 3 + ^~^ (<?^->*«Ц2, 4): 3' ~
- ей. (е^):з-Из, 4] - У^^
= V. A> + Из), 2 X, 4 + 1/«в-^+"« (е^-^Х, 4), 2 (#43), B58)
_ 4 =
B59)
-^-^Q43)) 4 = о (#18), B66)
, 2
[^ 22 + \jj, 2v|5,2 + (ф + цз), 2 (fx3 - ц2), 2 + |л3, п] +
вД.-й. {ф. зз + 1р: 3^. 3 + ^.3 [е^2 (в"*'): 3' ~ Из : з] +
i*. [i|>, 4 (ца + цз), 4 + Ms,,Из, J = 0 (G44), B62)
[V) 22 + v, 2v, 2 + (v + цз), 2 (Из — Иг), г + Из, гг] +
+ е*'-»* {V; зз + v: 3v: з + v: 3 [е~^ (e"*«): з- - Из: з] +
H, [Из, 44 + И2.44 + И2, 4 (И2 ~ ЦД 4 +
+ Из, 4 (Из - И4), 4 + Из, 4Иг, 4] = О (GU), B63)
р, 44 + ^, 4 (^ - И4 + Из), 4 + ИЗ, 44 + Из, 4 (Из ~ Ы, i\ +

314 Глава 11. Другие решения, альтернативные методы
+ е~2^ [1E:з3 + ^: з№ ~ Из + N: 3 + И4 : 33 4" И4 : 3 (Н-4 - Из) з] +
+ e~2il2 №. 2Ц4. 2 + ЦЗ. 2 (* + |*4). 2] + 7/*~2(г3~2^34 -
-V/*-2t"(e-2|1'Ql2 + e-^Q22) + 3Д(е^-^-^х, 4J = 0 (G22), B64)
e-2|i< №,44 + t 4№ - 1*4 + На), 4 + Иг, 44 + Иг, 4 (М"Я ~ »*«), J +
_|_ е-2д2 [г|5( 22 -f. ^ a (vE _ ц2 + М-4), 22 + М-4. г + Ц4,2 (Нч — Иг), г] +
+ е-^ \% 3R : з 4" ^ (в*'): 3- № + Щ): з] + ^A^^'^^L -
- V/*^ (е~*'(& + e-2^Q23) - V4 (e^-^'x, 4f = 0 (G33), B65)
№ + N. 2:3- № -Ь И-4). 2 М.2 : 3 — (^ -h N: 3 ^3. 2 + Ф. 2^: 3 +
+ Ц4. 2Ц4 : 3 4" Vae2*-2|1*Q43Q42 + W»'-*»* № 4" Иг), 4Х. 4 +
4- У2е^~^ (е^-^-^%, 4), 4 = 0 (/?„), B66)
еи»-й2 [v|5) 22 4- г|5,2 № 4- И4 4- Из - 14), г] 4-
4- е^-»° {1C:33 4" *: 3 [(* + 1*4 — Из): 3 + «"^ (^): 3']} 4"
4- &*»'-*»* №, 44 +14 № - И4 4- и2 4- Из)] -
-^-^(e^Qh + e^-^-^-^Ql^O (/?u). B67)
а. Линеаризация уравнений поля около стационарных решений;
уравнения начальных условий. Предположим теперь, что в резуль-
результате возмущения, сохраняющего аксиальную симметрию, ста-
стационарное аксиально-симметричное пространство-время с метри-
метрикой B40) не является более стационарным и метрика его прини-
принимает более общий вид B44). В этом случае уравнениям B57) —
B67) удовлетворяют функции
v + 6v, -ф + бгр, (о + бсо, \i2 + б[х2, \i3 + 8[i3t q2, q3, x, B68)
где 6v, 6ip, бсо, б[х2, б|Ыз, 92> Яг и X — величины первого порядка
малости, зависящие от времени, тогда как v, ip, со, \л2 и [is — функ-
функции, не зависящие от времени и удовлетворяющие уравнениям,
соответствующим стационарному аксиально-симметричному про-
пространству-времени, именно уравнениям E) — A6) гл. 6.
Поскольку величины q2 и q3 не равны нулю только с учетом
возмущения, оказывается удобно заменить их производными по
времени от других функций, которые мы также обозначим q2
и q3, т. е. будем писать
?2,о и <7з, о вместо q2 и q3. B69)
Кроме того, поскольку х по предположению величина первого
порядка малости, мы не будем различать производные B47) и
комбинации функций, в которые х входит в виде множителя, и
обычные производные (обозначаемые запятой). Мы также не будем
делать различие между <?4з и Q43> если Q43 умножается на величину
первого порядка малости например Q23.

114. Вариационный метод и устойчивость решений 315
Уравнения для возмущений могут быть теперь получены лине-
линеаризацией уравнений B57) — B67) около стационарного решения.
Результирующие уравнения делятся на два класса: уравнения
начальных условий и динамические уравнения. Уравнения началь-
начальных условий линейны и однородны относительно производных по
времени, а динамические уравнения — это уравнения второго
порядка относительно производных по времени и неоднородные.
Уравнения начальных условий могут быть, следовательно, проин-
проинтегрированы (по времени) и в результате дают простые соотноше-
соотношения, линейные и не зависящие от времени, между различными
возмущениями. В сущности соотношения, которые следуют из
этих уравнений, можно считать определяющими начальные усло-
условия для возмущений. Динамические уравнения определяют эво-
эволюцию этих начальных условий во времени.
Рассмотрим сначала уравнения начальных условий, потому
что они играют основную роль во всей теории. Уравнения началь-
начальных условий — это компоненты D,2), D,3), A,2) и A,3) уравнений
поля.
Рассмотрим компоненту D,2) (уравнение B57)). Помня, что
в соответствии с условием B69)
Q23 = <72,34 — ?3,24> B70)
мы можем проинтегрировать уравнение B57) по л;4 и в резуль
тате получим
Н 2 + *, 2 (в* - 6|га) - бфУ, 2 + 6^3, 2 +
h) - v, 2 б^з + г/2е^-2^ (ft, з - <7з, 2) о), з =
-2^ (ф + Nb X + *№-*• (^-^х). з. B71)
Вводя определение
Q = вЗф+У-Д,-!*, (^ 3 _ д3у 2), B72)
мы можем переписать уравнение B71) следующим образом:
^,-и,+Р [бг|), 2 + ft - v), 2 6ф + б^з, 2 - (v - |х8), 2 б[х3 -
- (* + И-з), 2 S^2] + V2Qo), з - V2e2v-2^ (^-v+3^2-^x)j з = 0, B73)
где р = яр + v (ср. с уравнением A1) гл. 6). Аналогично компо-
компонента D,3) уравнения дает
+ 6^2, з - (v - [Х2),3 б^2 -
). з SM - V2Qo),2 - V2e2v-2^ (^-v+^+ii,x)> 2 = o. B74)
Альтернативные формы записи уравнений B73) и B74), которые
окажутся полезными, следующие:
, 2 - (еР), 2 б^з + е* 8\i3j 2 - 2efiv, 2 бг|) +
|х3), з в (|i3 - |i8)] + V2Qco,3 - V^2v^ (^-v+3^I-n,x)f з = о,
B75)

316 Глава 11. Другие решения, альтернативные методы
*> [(е* бф), з - И, з Sfx2 + е* б|х2>3 - 2ePv, 3 6ф + *Р (ф + |ia), 3 X
X8(h- Цз)] ~ V2Q0),2 - V2^2v-2^3 (еФ-v+^+^x),2 = 0. B76)
- Рассмотрим далее компоненту A, 2) (уравнение B59)) и пре-
пренебрежем членами, явно имеющими второй порядок малости.
Получим в результате
'1'-vQa3X,<b B77)
где мы снова вернулись к переменной х° (см. определения B45)).
Уравнение B77) интегрируется, и мы получаем в силу уравнений
B70) и B72)
Qf з + gSD-li.+Ji.-v [F@, 2 - </2, оо) + 0), 2 C Ц - бц2 + 6^3 - 6V)] =
= ^+M..-M..-v(Ojj|jc> B78)
или иначе
бо), 2 — q2i 00 = — <*>, 2 C бф — 6v — б[х2 -f б[х3) —
_ e-W+v+iL2-ix3Q^ з _)_ е2ц2-2м,в(О> 3^. B79)
Аналогично рассматривается и компонента A,3) уравнения поля.
Имеем
— 8v + б|ха-б|х3) +
B80)
Уравнения B79) и B80) дают начальные условия для функ-
функции со, но они служат и динамическим уравнением для функ-
функции Q. Действительно, условие интегрируемости для функции (о
дает для функции Q неоднородное волновое уравнение
s)f 3 + (eW+v^+»>Q, 2), 2 =
nI+n,Q> 00 + (е2ц,-2ц,(о1 зх), з - (со, 2Х), а -
— [(О, 2 C б\|3 - 6V — б|12 + б[Х3I, 3 + [©, 3 C б\|5 - 6V + 8\i2 - б(Х8)], 2-
B81)
Это уравнение описывает гравитационное излучение.
Докажем два соотношения, которые следуют из уравнений
B79) и B80). и которые окажутся важными для линеаризации
оставшихся уравнений поля.
ЛЕММА.
+ Y8 ([х3—|i2)] + 2S + 4^-2v-^3+^2@) 2&щ зХ, B82)
- ^2"^3Qo3)] =
2D, B83)

114. Вариационный метод и устойчивость решений 317
где
X = ецл-ц, (соэ 2J + ^2-^з (ш> зJ, B84)
У = ^2-^з ((Oj 2J - ^«-м-. (со, 3J, B85)
, 2(о,з - Q, зЧ 2), О = -^"р (Q, яю, з + Q, 8©, 2). B86)
Доказательство. Очевидно, что
v* [2@,2 (So, 2 - ?2, оо) + (ю, 2J б Bф - 2v + [х3 -
B87)
и, воспользовавшись уравнением B79), получаем
g (^-2v+i*.-^Qg2) = __ [4 вф + б Gi3 - \i2)] e4~2v+^-^ (со, 2J -
— 2e-^-vQ, Зсо, 2 + 2^-2v~^3+^2(Oj 2@> зХ. B88)
Аналогично
S (e2^2^^Ql,) = - [4 в* - б (^ - М ^*-^^-^ (со, зJ +
+ 2^-^-^Q, 2со, з + 2^-2v-^3+^2@> 2(o, зх- B89)
Складывая и вычитая эти два уравнения, получаем требуемые
соотношения.
Наконец, отметим еще одно соотношение, которое следует из
уравнений B79) и B80):
Ч з (б(о, 2 — <72j 00) + (о, 2 (б(о, з - <7з, оо) = —2о), 2(о,з C б\|з - 6v) +
_l_ e_3^+v (^из-^2C? 2(Oj 2 — e^^-M'3Qj 3(o, 3) + е^-^ХХ. B90)
б. Тождества Бианки. Нужно заметить, что если пренебречь
величинами второго порядка малости, то выражения для /?4i
и G44, которые задаются уравнениями B61) и B62), не будут со-
содержать производные по времени. Они напоминают уравнения
начальных условий, однако их статус другой. Чтобы убедиться в
этом, вернемся к переменной х° в компоненте @,1) уравнения поля:
(^-nd-^-vQ^ 2 + ^+li1-li,-vQ03): з = e34)+H.-H,-vQ03Xf 2. B91)
С точностью до первого порядка по % имеем:
~^-Чи 2), з + О (х2). B92)
Следовательно, линеаризованное уравнение B91) имеет вид
б [(*3*-»4+ib-vQoa)f 2 + (^+^2-^3-vQ03);3] =
^3-^ 3),2 + (^+^2-^3-vX@>2)j3. B93)

318 Глава 11. Другие решения, альтернативные методы
Вычисляя правую часть этого уравнения, находим
еЧЛ-^-^-v |2Хо), 23 + X, 2со, з + X, зсо, 2 +
+ X К 2 Ci|) - v + \i2 - |Л3), з + о), з Ci|) + \i2 - ^з - v), 2]}, B94)
тогда как левая часть дает:
LX3-V [F(Oj 2 _ q^ oo) + ^ 2 C 6l|) - б^2 + б^з - 6v)]}, 2 +
*-*>-*[(б(о,з -ft,oo) + o),3C 6^ + 6tx2-6pi3-6v)]},3. B95)
Подставляя теперь вместо величин в квадратных скобках в урав-
уравнении B95) выражения B79) и B80), получаем
(—Q, з + tfW-v+n.-ii.©, зх), 2 + (Q, 2 + ^-^-^со, 2Х), 3; B96)
а это выражение, очевидно, сводится к уравнению B94). Таким
образом, компонента @,1) уравнения не дает нам новой информа-
информации и выражает тождество Бианки для линеаризованных уравне-
уравнений.
Рассмотрим далее компоненту @,0) уравнения поля (уравнение
B62))
еш-ц2 [^ 22 _|_ ф( 2^ 2 _(.. |Хз> 22 _[- (^, _(_ цз), 2 (цз - Ц2), 2] -f
+ вИ.-Д. {^зз + lf: зЧ>: з + Ч>: 3 [е^2 (^):3- - ^3 : з] +
ix.^ >ш> зХ + о (х2). B97)
С помощью уравнения B82) находим, что линеаризация правой
части дает следующее выражение:
i/4e2i,-2v [4X бг|; + У б (Цз-Иг)]-1^-1^-^'"^^^*- B98)
Линеаризуя левую часть, мы должны прежде всего заменить опре-
определенную формулой B47) производную эквивалентной частной
производной. В результате получаем
, 22 + 2^ 2 бф,2 + fys, 22 +
(бф + 6ц-з), 2 (Из - Н-а), 2 + (\|з + Цз), г б (Из — Иг), г] +
4- еи.-д. |2 ** 3} - V4e2*-2v [4X бф + Y6 (ц8 - Иг)] =
= — V2S - Vs®, 2«, 3е2*-2^+^^-^зХ 4- е^=-^» |х, аз +
4- Х,2 (^ + 2Иг - Из),з 4- Х.з (У + ИгХг 4" X t2 (^ + Иг),гз 4"
+ 2*, 2^, з + (Ч> + Иг), 2 (Иг - Из), з + (* + Иг), з (Иг - Из), г] I • B99)
Уравнение B99) в сочетании с уравнениями начальных условий
B73) и B74) приводит к новому важному соотношению. Действи-
Действительно, из этих последних уравнений имеем
>, з + e2v^ И
4- V2 [+Q<», г 4-

114. Вариационный метод и устойчивость решений 319
,), 2 + Aр - v), , бф + ц8> 2б (ц, - (ia) -
-v>26ji3-^26^]},2 + {^-^+P[2-3]}. C00)
Левая часть этого уравнения приводится к виду
— VsSeP + V2 [e2v~2^ (^-v+3^-^x)>3], 2 +
+ V« [e2v-2^ (e^-v+^+^%),,], 3. C01)
Вычисляя правую часть уравнения C00), после некоторых зна-
значительных упрощений с точностью до общего множителя е$ по-
получаем члены левой части уравнения B99). Приходим, таким
образом, к следующему равенству:
gp+ii,-ii, [_ 72e2*-2v<o, 2co, зх + 1х, 23 + X, 2 (ф + 2^2 - Из), з +
+ Х,з (Ф + Иг), 2 + X [2 (^ + Иг), 23 + 2ф, 2^,з + № + Иг), 2 (Иг — Ия),з +
+ (ф + Иг),з (На ~ Из), 8]}] = V2 [e2v-2^ (e+^+^'-^x)^]. 2 +
+ V2 [e2v-2^3 (e*-v+^2+^x), i], з. C02)
Это важное уравнение для функции %: оно выражает тождество
Бианки, но на этот раз дает нетривиальную информацию.
в. Линеаризация остальных уравнений поля. Ниже мы выпи-
выпишем результат линеаризации оставшихся уравнений поля
еИз-М.2 |[6V> 22 + 2V, 2 6V, 2 + 6U3, 22 + FV + 6Ц,3), г (М-З - Иг), 2 +
+ (v + Из),2 S (Из - Иг),2] + б (Из — Иг) [v,22 + v, 2v,2 + Из,2 +
+ (v + Из), 2 (Из - Иг), г\\ + ^«-^ { 2 -> 3 } =
= в-^+и,+и.б (ц, + Иг), оо + 72S - 74 [4Х б* + 2F6 (Из - Из)] +
+ е»г-»> [[3/2С0, 2« ,C2*-2VX + {%, 23 + X, 2 (V + 2^2 ~ Из), 3 +
+ Х,з (v + Иг), г + X [2 (v + Иг), гз + 2v, 2v, 3 + (v+ Иг), 2 (Иг — Из),з +
+ ^4-Иг),з(Иг-Из),2]Ц FGU = 0), C03)
е»--»> [бр, 22 + 2р, 2бр,2 + (Из - Иг), г 60,8] + ^~^ [2 ¦* 3] =
= e-2v+n2+n3 [2 845,00 + 6 (Из + Иг), оо] - е^~^у 28 (ц3 - Иг), 2 +
+ ед.-^.р, 36 (из - Иг), з - Be-VW -f Vafi2*^) 6 (Из - Иг) +
+ ^-^{Р,гХ.з + Р,зХ,г + Х[2р,23+2р,2р,з + Р,г(Иг-Из),з h
+ Р,з(Иг - Из),2]1 [6(G33 + G22) = 0], C04)
ецл-И2 х
X [бр, 22 + 2i|>, 2 6i|3,2 + 2v, 2 6v, 2 - 6P, 2 (Из 4" Иг), г—Р, 2б (Из Ь Иг), г] —
- е^~^ [2 «. 3] = 2e-Pt/6 (из - Иг) - e~2v+^+^6 (ц, - ц,), 00 -
- Vae2*-2v [4У 8г|5 + ХЬ (из - ИгI + D-
_ ед,-н, [_ со, 2со, Зе2*-2- х + р, 2х, з - Р, зХ, а 4- X [2fc » 4- 2ф, 9ф, 3 4"

320 Глава //. Другие решения, альтернативные методы
+ 2v, av, з - Р, 2 (ца + И-з), з - Р, з (И2 + Из). 2] [б (Сзз - G22) = 0],
C05)
6Р, 23 — 6Э, 2И2 , 3 — бр,3^3,2 — Р, 2^2,3 ~
— Р, з б|И3 ,2 + ^,2 6ф, 3 + *|\3 6Ф, 2 + ^, 2 6V, з "f V, 3 8v, 2 =
^соу 2(о, з 6ф + Vae-2V f 2^2Х, оо +
e^-^Q, 2со, 2 - e^-H'Q, 3(о, 3) + V2^-2v+^2-2^3 (со, 3J X +
2-Ы^2 + Из),2 + М,2 + ^,2] (б/?23 = 0), C06)
где в уравнениях C04) и C05) мы использовали следующие сокра-
сокращения:
U = e* [е*>-** (Pt 2Из, 2 + 12v 2) + е**-*> (B,3u2,3 + ^.av, 3)],
W = e* [&>-** (P, 2(i8 ,2 + t av, 3) - &*-»* (P. 3Ц2,3 + ^,3v,,)]. ( }
Отметим также, что при выводе уравнений C04) и C05) были ис-
использованы следующие два уравнения, которые справедливы в
стационарном случае (ср. с уравнениями A4) и A6) гл. 6):
[еч,-и, (eP)f a]j 2 + [^,-и, (^)$ з], з = 0,
И*^ И, а], а - №**' И>8]>8
На этом формальные выкладки заканчиваются.
г. Уравнения, описывающие квазистационарные деформации;
теорема Картера. Для иллюстрации того, каким целям послужат
выведенные нами линеаризованные уравнения, рассмотрим пре-
предельный случай бесконечно медленных деформаций, когда система
(подвергаемая деформации) находится всечвремя в состоянии рав-
равновесия. Такие деформации называются квазистационарными или
адиабатическими. Квазистационарные деформации полезны при
определении возможности (или невозможности) появления точки
бифуркации при переходе от одной стационарной системы к дру-
другой (последовательность таких стационарных систем задается не-
некоторым параметром). Теорема Картера гарантирует, что в се-
семействе Керра (с параметром а) такие бифуркации не появляются.
Мы сейчас покажем, как строится доказательство теоремы Кар-
Картера, рассмотрев квазистационарные деформации стационарных
аксиально-симметричных пространственно-временных многооб-
многообразий, внешние по отношению к горизонту событий черной дыры.
Квазистационарная деформация аксиально-симметричного про-
пространства-времени с метрикой B40) приведет к появлению беско-
бесконечно малых приращений функций v, <ф, со, [i2 и |i3, сохранив
при этом координатное условие, которое могло быть наложено
на функции [х2ги ^3- Вследствие этого последнего свойства удобно
начинать с метрики, которая первоначально имеет вид
ds2 = e2v (d/J - e*b (dq> - со dtJ - e^ [(dr2J + (d*3)a]f ^309)

114. Вариационный метод и устойчивость решений 321
т. е. положив \х2 = \х3. Квазистационарная деформация про-
пространства-времени приведет к бесконечно медленному изменению
функций v, \|), со и |х на величину соответственно 8v, б\|), бсо и б[х.
Уравнения, которые описывают эти изменения, могут быть полу-
получены прямо из уравнений, выведенных выше в п. 114, б и 114, в,
если положить равными нулю производные по времени во всех
динамических уравнениях и во всех уравнениях начальных усло-
условий, записанных в интегральной форме. Кроме того, для квази-
квазистационарных деформаций пространства-времени с метрикой C09)
имеем
X = 0, 6 0г3 - |х2) = 0. C10)
Прежде всего мы видим, что уравнение C04) теперь упро-
упрощается и для квазистационарных деформаций принимает следу-
следующий вид:
FР, 22 - h 2Р, 2 6Р, 2) + («Р, 33 -h 2P, з 6Р, 3) = 0. C11)
записанное через двумерные декартовы тензоры (которые мы
будем использовать и в дальнейшем), оно имеет вид
(еЩ),аа = 0 (а -2,3), C12)
поскольку уравнение, описывающее состояние равновесия, га-
гарантирует равенство
И, аа = 0. C13)
Из уравнения C12) следует, что
бр = 0, C14)
поскольку, умножая уравнение C12) на е$ бр и интегрируя по
всему трехмерному пространству (х1, х2, Xs) вне горизонта событий,
получаем после интегрирования по частям
dx = 0, C15)
Jj
а проинтегрированная часть равна нулю вследствие граничных
условий (ср. с §§ 53 и 55 гл. 6):
0 на горизонте,
(г), вр = О(г1) при г->оо. C16)
Равенство нулю бр следует из положительной определенности
подынтегрального выражения в C15). Отсюда заключаем, что
в случае квазистационарных деформаций к условию C10) следует
добавить
6ф = — 6v. C17)
В силу требований C10) и C17) уравнения начальных условий
B75, B76), B79) и B80) теперь принимают следующий вид:
(еЩ\ 2 - И, 2 б[х -f е$8\1 %2 - 2еНу 2 бф = - V2Qo), 8,
(еЩ\ з - И, з б^ + ^б[х, з - - 2ePv, 3 бф - + V2Qo),2, ( }
бо),2 = —4(о,26^-^-3^+vQ3) бо),з = — 4(о,з6^ + ^-^+vQ,2, C19)

322 Глава 11. Другие решения, альтернативные методы
где
Q = ^^(ft,8-?8,2), C20)
а уравнения B81) и B82) дают
coJ6^3), C21)
ip + 2S, C22)
где
X = со, aco, a, SeP - Q, 2co, з - Q, 3(o, 2. C23)
Рассмотрим теперь линеаризацию уравнения Rn (ср. с уравне-
уравнением F) гл. 6)
H,a),a + V2^-^ = 0. C24)
С помощью уравнений C14) и C22) получаем
(е$ Sip, a), a = 2e3^-vX Sip - SeP. C25)
Это уравнение также следует прямо из линеаризованного уравне-
уравнения B67).
Умножая затем уравнение C25) на 8\р и интегрируя по всему
трехмерному пространству вне горизонта, находим после интегри-
интегрирования по частям
J j j [eP Sip, a Sip, a + 2^~VX Fi|;J - Se$ Sip] dx - 0, C26)
причем подстановка обращается в нуль вследствие условий C16
и требования (которое следует из уравнения C25)), чтобы
Ц = О (г1) при г -> оо. C27)
Можно записать уравнение C26) в более симметричном виде,
заметив, что
\\\ SePSipdx = + J jj (Q,2co,3 - Q, з<о>2)
= ~" JJ [
C28)
где при переходе от первой строчки ко второй было выполнено ин-
интегрирование по частям, при переходе от второй строчки к третьей
было использовано уравнение C21), а при переходе от третьей
строчки к четвертой было выполнено интегрирование по частям.
В обоих случаях подстановки обращались в нуль вследствие усло-
условий C16) и C27), в силу убывания функции со на бесконечности
как г3 и требования гладкости функции Qe~2^ на горизонте (по-
(последнее следует из уравнений C16) и C18)). Используя оконча-

114. Вариационный метод и устойчивость решений 323
тельный результат преобразования C28), мы можем переписать
уравнение C26) в виде
J J
, «Q, a] dx - 0. C29)
Для доказательства невозможности квазистационарной дефор-
деформации и справедливости теоремы Картера подынтегральное вы-
выражение в уравнении C29) нужно преобразовать к положительно
определенной форме. Нам понадобятся следующие две леммы.
ЛЕММА 1.
2 со, з - (е~2Щ, Зсо, 2] f 2Q (i|), 2со, 3 - ф, 8<о, 2)> C30)
ЛЕММА 2.
x = 0. C31)
Лемма 1 доказывается непосредственной проверкой. Для доказа-
доказательства же леммы 2 умножим уравнение C24) на функцию
1/2О2е~4^ и проинтегрируем по всему трехмерному пространству
вне горизонта. После интегрирования по частям первого члена
в подынтегральном выражении получаем
] dx = 0,
C32)
где подстановки обращаются в нуль в силу граничных условий
на бесконечности и на горизонте. Перегруппировав члены в по-
подынтегральном выражении C32), получаем уравнение C31).
Для доказательства теоремы Картера проверим, воспользовав-
воспользовавшись соотношениями C28), что справедливы следующие равенства:
= J J |
\ j j
, 2 + 1/2<HJ«<o, зJ + (Ч з - l/2e-pQ<o, 2J] -
dx. C33)
Исключая затем член —1/^XQ2 из уравнения C33) с помощью
леммы 2, перепишем уравнение C29) в виде
, 2 + VaepQ<o, зJ + Fip, з ~ Xke-VQ^ 2f] -f
o, a (8i|)J| dx = 0. C34)

324 Глава 11. Другие решения, альтернативные методы
С другой стороны, в силу уравнений C28) и C30)
74 j j j e-^+vQi aQf a dx = j j j evS ц dx =
= J J J (Q, 2®, з — Q, зЧ 2) бф dx =
<?** [(^Q), 2 0). з - (^Q), 3 03, 2] +
|- 2Q (\|), 2(o, з - i|), 3(o, 2)} dx. C35)
Подставляя это последнее соотношение в уравнение C34) и пере-
перегруппировав члены, получаем
J J j p {Ga*-pQ<o, з + бф>2J + G2*-pQ<o, 2 - бф, sJ +
= [ j j
), 2 - **Ч 3 вф]2 + [Gae2*Q), 3 -h e*v<o, 2 ^]21 +
_ ^-v^ 3 Щ2 _|_ (Ql|)j з + ^-vtt) 2 6^J]| dx = 0.
C36)
Мы свели, таким образом, подынтегральное выражение C29)
к сумме квадратов. Равенство интеграла нулю возможно только
в том случае, если каждое из слагаемых тождественно равно нулю,
и сразу же видно, что это выполняется тогда и только тогда, когда
бф = Q = 0. C37)
Нетривиальная квазистационарная деформация, следовательно,
невозможна, и теорема Картера доказана.
д. Вариационная формулировка задачи о возмущениях. Начнем
с того, что заново сформулируем задачу. Мы рассматриваем ста-
стационарное решение уравнений Эйнштейна в пустоте, удовлетво-
удовлетворяющее определенным граничным условиям, которые обычно тре-
требуются для решений вне горизонта событий черных дыр. Затем
рассматриваем вариацию этого решения, описываемую прираще-
приращениями первого порядка малости 6v, 6\|), бсо, Q, б|л2, б|л3 и % в раз-
различных метрических функциях. Эти вариации удовлетворяют урав-
уравнениям двух типов: уравнениям начальных условий и динамиче-
динамическим уравнениям. Мы также требуем, чтобы вариации подчиня-
подчинялись определенным граничным условиям на горизонте и на бес-
бесконечности. Если теперь предположить, что зависимость вариа-
вариаций от времени имеет вид exp (lot), где а может принимать ком-
комплексные значения, то динамические уравнения, которым удов-
удовлетворяют вариации, в сочетании с наложенными на них гранич-
граничными^ условиями составляют задачу на собственные значения
для а. ,
При вариационной формулировке задачи на собственные зна-
значения мы сопоставляем собственным вариациям (которые удовлет-
удовлетворяют и уравнениям начальных условий, и динамическим урав-
уравнениям) пробные вариации 6v, б\|), бсо, Q, бр,2, 8\х3 и %, которые

114. Вариационный метод и устойчивость решений 325
должны быть совместны с уравнениями начальных условий и удов-
удовлетворять тем же граничным условиям, что и собственные вариа-
вариации, но в остальном произвольные. Другими словами, пробные
вариации отличаются от собственных вариаций лишь те**, что
последние должны удовлетворять динамическим уравнениям,
тогда как первые — нет. В частности, пробные величины будут
иметь ту же зависимость от времени exp (iot), что и собственные.
Первым шагом при вариационной формулировке задачи на
собственные значения является получение формулы для а2 по-
посредством умножения уравнения начальных условий, которому
удовлетворяет пробная величина, на ту или иную- собственную
величину (или умножением динамического уравнения, которому
удовлетворяет собственная величина, на. пробную величину).
Затем интегрированием по всему трехмерному пространству вне
горизонта событий надо попытаться, если возможно, с помощью
интегрирования нужное число раз по частям (как в предыдущем
разделе при доказательстве теоремы Картера) и использования
уравнений начальных условий и динамических уравнений, кото-
которым удовлетворяют собственные величины, и уравнений началь-
начальных условий, которым удовлетворяют пробные величины, сделать
так, чтобы в интегралы в формуле для а2 собственные и пробные
величины входили полностью симметрично. Если такие преобра-
преобразования окажутся возможными, то будем говорить, что дифферен-
дифференциальные операторы, определяющие задачу на собственные зна-
значения, являются самосопряженными и в этом случае вариационная
формулировка становится возможной. Но прежде всего укажем,
как такая формула для а2 может быть получена для рассматривае-
рассматриваемой нами задачи.
Запишем уравнения B75) и B76) для пробных величин (мы
уверены, что они удовлетворяют этим уравнениям, поскольку
это уравнения начальных условий) и умножим их на 8\|)|2 и 8\|з, 3
соответственно, затем сложим и проинтегрируем по трехмерному
объему, заключенному между двумерными поверхностями Sx и S2.
В конце концов устремим поверхность Sx к горизонту," а поверх-
поверхность S2 — к бесконечности, но пока оставим их произвольными.
Проинтегрировав несколько раз по частям, получим, воспользо-
воспользовавшись (только лишь!) компонентой @,0) линеаризованных урав-
уравнений поля и соотношением C02), которое следует из него, что
0 = Ш [—2еР (е^2 б^. « *Ь + е>1г^ 6t з Н з) +
<«!*.—•»» бц3B) 6ф -
p, 25 (ц, - pi,) + бф,2б (|i, - ц2))\ +

326 Глава 11. Другие решения, альтернативные методы
], 2
(tp + fx3),2« (Из ~
+ V.Q®.
збф-1^-2
'.-*+*№, a
;),36i|;6(i2-
2б1|; + 1/2е-2
6l|) -j- (l|) + (Лз), з
б\|> б(х2,3] ¦-)-
Hs+2V tgyf:—V-M2+M
), 2 Sip]^.] Aф d^. C38)^
Символ
в подынтегральных выражениях C38) поверхностных интегралов
(которые получаются после различных интегрирований по частям)8
имеет следующий смысл. Пусть при фиксированном х$ ф Ф а)
соответствующие пределы для ха равны ха A) и ха B), причем
^B) >д;аA); тогда символ означает разнссть значений выра-
выражения, заключенного в двойные скобки, при ха B) и ха A).
Уравнение C38) было получено с помощью только уравнений
начальных условий: это видно хотя бы из того, что в него не
входит о2. Объемный интеграл в уравнении C38) симметричен по
входящим в него собственным и пробным величинам.
Умножим теперь уравнения B75) и B76) на 8v, 2 и 8v, 3- Кроме
того, умножим на % компоненту B,3) линеаризсванного уравнения
поля (ср. с уравнением C06))
, оо + 1/2e3*-v+3'A2-3jA3 (со, 3J X -
^^ко, 2о), з Sip + 1/2^2-Дз (e^-^Q, 2co, 2 -
- *n.-ii.Qf Зсо, 3) + е^з+fy fр> 22 _ ^ 2 (ц8 + |хя), 2 +
+ ^, 2^, 2 + V, 2V, 2] - в^«—»*•+» [6V, 23 + 6V 2 (V - [Л2), 3 +
+ 6V, з (V - Из), 2 - Р, 2 б|Л2, з +
+ «1рэ аз + б\р, 2 (ip - |ia), з + бг|), з (ip - Из), 2 - Р, з в|хя, 2] = 0. C39>
(Поскольку уравнение C39) в отличие от B75) и B76) является
динамическим, мы рассматриваем его как уравнение для собствен-
собственной вариации % и умножаем его на пробную вариацию %.) Про-
Проинтегрируем теперь сумму получившихся трех уравнений по трех-
трехмерному пространству, заключенному между поверхностями Sb

114. Вариационный метод и устойчивость решений 327
S2. После многочисленных интегрирований по частям и пере-
уппировок членов получаем в конце концов
xUb (цз - 14) б (И» - Иг)] +
+ У^-^Y - W) [6t|>6 (Цз - И.) + б# (из
- {/б (Из - Иг) б (Из - Иг) - «¦*•-¦*«+» {[р,, + биз, 2 +
+ (v + Из), г б\|\ 2] б (Из - Иг) + Ш, г бИз, г +
v + Из),2б>,2 б (Из - Иг)} - е^-и*+е {2^3} +
2 б> + (**•-¦*• бИи, г) Ц] + еЭ [2 « 3] +
_gr)l/2 [i/46 (из + Иг) б (Из + И.) + Vi бфб (ц,
Й з + Иг) — V«6 (Из — Иг) б (Из - Иг)] —
- Иг) + 5в (Из - Иг]
, г
, 2@,
^Q, 24, - e»'~»> Q, 3@,3)X +
^.Q, 2to, 2 - e^-^Q, 3(o,,) % -
6ip,2 (Ц» +_Иг), з +_бф,з (t - Из), г -
г.з - Р, збИз,21 X - [бф.гз + б>>2 (¦ - Иг),з +
- ИзЬ - Р.2бИг, з - Р,збИз,г]X-
- tP, 22 - Р,г (Из + Иг),2 + М, 2 + vJv, 2] XX -
- 1/^-^+^-^' (©, 3J XxlJ dф dx2 dx3 +
Н- J1 Кз-и.+Р [6v, 2 Ц + (v + Из), г б (Из - Иг) Ц - ЬМр 5и3, % +
+ 0I3 + v), 2 бфбиз + б (t|> + v)>2 биз + Р,2б (Из - Иг)бИз] +
+ V.Qffl,3 [3 «Я» - б (из - Иг)] - V2e-3*+v+^-^QQ,, -
- V2Q<», гХ - 1he-2^+2v (e*-v+^'-»>x), з 6v +
+ efi+ъ-и, [($ + 2и2 - Из), з X 6v - (v + 2и2 - Из), з X б> -
- Р. з бИзХ + X. з 6v - х. з Ц]\хЧ йф dx3 +
+ J I p'-^+|3 [6v, з б> + (v + Щ), з 6 (Иг - Из) б> - 6i|) 6И2, з +
+ (^ + Ч з Ц би2 + б (ф + v), з биг 4" Р, зб (Иг — Из) б"иг] —
- Vi$a», г [3 6i|) 4- б (Из - (*г)] - l/^-^+v+^~^QQ, 3 4"

328 Глава 11. Другие решения, альтернативные методы
-v+^+^x), 2 6v -f
. 2 X 6v - (v + ц,),, X H - P, 2 *HaXl -
-n. 6v), 2 x - (e*+i»«-i«« dip), ,xli*i] d(P d*2- C40>
В процессе преобразований, которые привели к уравнению
C40), были использованы другие динамические уравнения C03)—
C05) и снова только для собственных величин.
Объемный интеграл в уравнении C40) симметричен, относи-
относительно входящих в него собственных и пробных величин. Вычи-
Вычитая уравнение C38) из C40), получаем несколько более простое
уравнение
о2 J J J e~2v [2бтбт + 2 6i|>dt|> - 26 (ф + ц)б (tp + ц) +
+ Vitr-^QQ + 1/2<?2^-2м'ХХ] (—g)~1/2 d<f> dx2 dx3 =
- Ш lx^~v D S^ ** + бт ^t) + 2Fe3*~v Fv|) бт + 6i|> бт) -
- W бт бт + 2eP (e».-i«. бф, a 6\|), 2 + e-^» бг|), 3 бф, 8) -
- 2e^-^«+P UP, 2 6fi3) 2 - (Ф - v), 2 бф, j бт + [р,, бц3( 2 -
- (* - v), 2 4 2] бт} + 2е^-М-е цр1 з б[г2,, - (ф - v),, fiip, 3] бт +
+•№. з «На, з - № - v), з 6i|), ,1 бт} -
- еР BS б> - 2S бг|з + D бт + # бт)
+ e^.-i».Q, ,Q, 3) -f V2 {[e-a
Va {[e-2
»> (e^-^Q, ,©, 2 - e^-^Q, Зсо, 3) X +
l3 (e«*»-M2,2(о, 2 - e^^-^'Q, 3<й, з) X -
— 2e3*-v+»*'-'1»ci), 2о), з (X 6\f
|з, 2 (tp - ц2), 3 + бф, з (Ч> - Из), 2
- Р, 2 бц2, з - Р, з б^з, г] X + [«*, 23 + бф, г (^ - Цг). з
-}-б\|),з№- ^з),2- Р,« *|*а, 8 - Р, в в|*8. il X-
- [Р,22 - P,2(^3 + ИгЬ + ^,2^,2 + V,2V,3]XX -
4- Поверхностные интегралы, C41)

114. Вариационный метсд и устойчивость решений 329
где ради краткости мы не выписали явно поверхностные интегра-
интегралы и введены следующие сокращенные обозначения:
б^ = V2S (Уз + N. бт = V2S (Уз - N- C42)
/) Вариационный принцип. При выводе уравнения C41) пред-
предполагалось, что пробные вариации, представленные величинами
с чертой, удовлетворяют только уравнениям начальных условий.
Вследствие симметрии подынтегрального выражения в объемном
интеграле относительно собственных и пробных величин мы можем
формально отождествить их и в результате получаем
-2v j2 (бт)* + 2 (б*)* - 2 [6 (ф + ix)f +
= J J J [
[4 (SipJ + (бтJ] + 4F^~V Sip бт ~ 4(/ (бтJ +
»* (б\р, 2J + ^2~^ Fipf 3J] -
¦*• [p, 2 6fi3i2 - (Ф - v), 2 Sip, 2] -
§ 36^2,3 - (Ф - v), збгр, 3]1 бт - 2e$ BS6\p + D бт) -f
v [ei*.—1*. (Qt 2J + ^.-1*. (Q, 3J] +
2v(eiJ)-v+3n2-^3X)) 3] 2 _j_ [e-2M,3+2v(^D-v+|i2+|iajt)f 2]f 3} 6lp +
lia-|i2Qi 2@f 2 _ el*2-|iaQf 3©f 3) X ~
0) 2@ 2X g^ _|_
{[P. 22 - P, 2 (|i3 + N. 2 + Ф. 2^, 2 + V, 2V, 2] X' +
2^3 (^^ 3J X2| _ 2eP+*A2-|i. [6lpf 23 + 6lpf 2 (^ - N. 3 +
+ бгр, з (гр — N. 2 - P, 2 6fx2,3 — P. 3 б[г3, г] %} dq> dx2 dx3 +
, + Поверхностные интегралы. C43)
Будем теперь рассматривать соотношение C43) как формулу,
определяющую а2, предполагая, что вариации удовлетворяют
только уравнениям начальных условий и надлежащим граничным
условиям. Предположим теперь, что мы вычисляем последователь-
последовательно а2 для двух множеств пробных вариаций: бгр, 6v, Q, % и т. д.
и бгр + б2гр/2, 6v + 62v/2, Q + 6Q/2, % + 8%/2 и т. д., где б2гр/2,
6V2, 6Q/2, б%/2 и т. д. — бесконечно малые приращения. Другими
словами, будем рассматривать влияние на а2, задаваемую уравне-
уравнением C43), произвольных бесконечно малых приращений проб-
пробных вариаций, совместных только с уравнениями начальных ус-
условий и надлежащими граничными условиями. Если подвергнуть
подынтегральное выражение в уравнении C43) указанным вариа-
вариациям, то мы сразу же получим явное выражение для ба2. Возьмем
это выражение для ба2 и проделаем в обратном порядке все пре-
преобразования, которые привели нас к уравнению C41), т. е. прой-
11 Чандрасекар С, т. 2

330 Глава 11. Другие решения, альтернативные методы
дем последовательно через уравнения C39), B76) и B75), но толь-
только с одним существенным отличием: мы не имеем теперь права ис-
использовать динамические уравнения. Находим в результате
6а2 J J j е~^ \2 (8тJ + 2 (бфJ - 2 [б (ф + [г)]2 +
+ 1/2е'~4Щ2 + 1/2^2-2ДзХ21 (—gI/2 dq> ck2 ck3 =
= - J J J [* UG<3) C) +
+ б |[G<3> <3> - G<2> <2>] (—gI'2} б2т
+ б {#<2> (з)^8-м.з (_g)W2j бх + б j
+ V2 {a^-^-^^+^^+^sQ _j_ (e-3i|L-v-M.2+M.?Qf 2), 2
- (^2-2^3@ 3X) 3 4- [@} 2 C бф - 6V + 6^3 - 6^2)], 3 -
- [со, 3 C бф - 6v -f- 6(^2 - 6^3)], ?1 6Q] Aф djc2 dx3. C44)
Отсюда, если подвергнуть пробную вариацию произвольным
бесконечно малым изменениям, подчиняющимся только урав-
уравнениям начальных условий и надлежащим граничным условиям,
и потребовать, чтобы ба2- равнялась нулю для всех таких прираще-
приращений, то должны удовлетворяться динамические уравнения рассма-
рассматриваемой задачи. Другими словами, пробная вариация должна
представлять истинное решение задачи. Это и есть вариационный
принцип, приводящий к решению линеаризованных уравнений.
2) Устойчивость решения Керра относительно аксиально-сим-
аксиально-симметричных возмущений. Покажем, как из вариационного выраже-
выражения C43) для а2 может быть выведена устойчивость решения Керра
относительно аксиально-симметричных возмущений. В этой связи,
как было впервые показано Фридманом и Шутцем, решающее зна-
значение приобретает следующий выбор калибровки:
вц - V26 (|х3 + |i2) = 0, C45)
потому что в случае метрики вида B41) коэффициент при а2 в ле-
левой части уравнения был бы равен
2v {2 (8тJ + 2(бг|)J - 2
dx2 dx\ C46)
а это выражение не является положительно определенным. С дру-
другой стороны, в случае более общей метрики B44), мы можем поло-
положить 8]ы = 0, допуская появление функции % Ф 0. При выборе
калибровки
8ц = 0, х ф 0 C47)

114. Вариационный метод и устойчивость решений 331
коэффициент при о2 в вариационном выражении становится рав-
равным
j j j e~^ [2 (8тJ + y2e-^Q2 + y2e^~^tf] (-g^2 dcp dx2 dx*, C48)
а это выражение является положительно определенным. В даль-
дальнейшем будем предполагать, что выбрана калибровка C47).
Устойчивость решения Керра относительно аксиально-сим-
аксиально-симметричных возмущений следует из трех основных фактов:
1) последовательность решений Керра не допускает нулевых
мод;
2) неустойчивость могла бы наступить (если вообще наступит)
только в результате наличия чисто мнимой моды о = —ik, при-
причем k > О,
3) мнимые частоты неустойчивых мод (если они существуют)
должны непрерывно зависеть от параметра а последовательности
Керра.
Недопустимость нулевых мод, очевидно, гарантируется теоре-
теоремой Картера. И как мы видели в п. 114, г, вариационный подход
к задаче о возмущениях дает независимое доказательство этого
факта.
Чтобы доказать вещественность а2, исходя из вариационного
выражения (даже в калибровке C47)), мы должны прежде всего
удостовериться в том, что поверхностные интегралы при стрем-
стремлении поверхности Sx к горизонту, a S2 к бесконечности (см.
замечание в абзаце, предшествующем уравнению C38)), не вно-
вносят никакого вклада в выражение в правой части C43). Это, од-
однако, следует из общего исследования, проведенного в гл. 9,
где показано через переменную г* (в случае т = О и г > г+ пре-
преобразование к этой переменной является однозначным), что реше-
решения имеют структуру уходящих и входящих волн. Этот факт и
расходимость коэффициента C48) (вследствие появления множи-
множителя e~2v в подынтегральном выражении) гарантирует, что для
неустойчивых мод с комплексной частотой а поверхностные ин-
интегралы не вносят никакого вклада. (Заметим, что отношение ин-
интегральных выражений в правой и в левой частях уравнения C43)
постоянно для всех значений г.) Таким образом, положительная
определенность коэффициента" C48) гарантирует, что если неу-
неустойчивость и возникает, то она может быть вызвана только ко-
конечной чисто мнимой модой (так как величина а2 действительна).
Поскольку а = 0 запрещено, спектр о должен лежать целиком
на положительной или целиком на отрицательной мнимой полу-
полуоси. Но мы знаем, что для решения Шварцшильда с а = 0 не су-
существует неустойчивых экспоненциально растущих мод. Следо-
Следовательно, если удастся показать, что а зависит от параметра а
непрерывным образом, то возможность появления неустойчивости
для любого значения а исключена.
11*

332 Глава 11. Другие решения, альтернативные методы
Оказывается, есть теоремы, с помощью которых можно уста-
установить непрерывность функции а (а). Условия этих теорем в на-
нашем случае выполнены, потому что рассматриваемые дифферен-
дифференциальные операторы являются самосопряженными и плотно оп-
определенными на пространстве функций, интегрируемых с квад-
квадратом, и, кроме того, эти операторы аналитичны по параметру а.
Этого достаточно, чтобы гарантировать требуемую непрерывность
функции о (а).
Заключаем отсюда, что решение Керра устойчиво относительно
аксиально-симметричных возмущений.
Воникает вопрос, нельзя ли изложенный в этом разделе фор-
формализм распространить и использовать для решения других
проблем математической теории черных дыр. «Это могло бы соста-
составить тему нового рассказа, но теперешний рассказ наш окончен.»*
Библиографические замечания
§ 109, 110. Решение, которое теперь называется решением Керра—Ньюмена,
было впервые опубликовано в работе
1. Newman E. Т., Couch ?., Chindapared К. et at. J. Math. Phys., 6, 918—919,
1965.
Оно было получено этими авторами путем комплексного преобразования реше-
решения Рейсснера—Нордстрема аналогично тому, как ранее Ньюмен и Джанис в [2]
вывели решение Керра, подвергнув комплексному координатному преобразо-
преобразованию решение Шварцшильда.
2. Newman Е. Г., Janis A. J. J. Math. Phys., 6, 915—917, 1965.
Смысл такой процедуры, которая воспринималась поначалу как «любопытный
трюк», был выяснен в работе
3. Newman E. Т. J. Math. Phys., 14, 774—776, 1972.
Вывод метрики Керра—Ньюмена в тексте повторяет вывод решения Керра
в гл. 6 (§§ 52—54), а также работу
4. Chandrasekhar S. Proc. Roy. Soc. (London), A358, 405—420, 1978.
Выкладки § 109 в основном посвящены выводу уравнений Эрнста прямо из урав-
уравнений Эйнштейна—Максвелла, явно выписанных для стационарного аксиально-
симметричного пространства-времени. Оригинальный вывод Эрнста для других
целей содержится в работе
5. Ernst F. J. Phys. Rev., 168, 1415—1417, 1968.
Трансформационные свойства уравнений Эрнста, рассмотренные в п. 109, г,
см. в работах
6. Xanthopoulos В. С. Phys. Lett., 98B, 377—380, 1981.
7. Gurses M., Xanthopoulos В. С. J. Phys. A (in press).
8. Harrison В. К. J. Math. Phys., 9, 1744—1752, 1968.
Влияние операции сопряжения на потенциал Н (п. 109, д) исследовалось в со-
сотрудничестве с Б. С. Ксантопулосом, которому автор благодарен за многочислен-
многочисленные обсуждения, касающиеся изложения этих вопросов.
Из формального совпадения метрик Керра и Керра—Ньюмена, отличаю-
отличающихся лишь определением «функции горизонта» А, очевидно, конечно, что изо-
изотропный тетрадный базис, принятый нами в § 56 гл. 6 для описания простран-
пространства-времени Керра в формализме Ньюмена—Пенроуза, и различные выраже-
выражения для спиновых коэффициентов, выведенные в гл. 6 (уравнения A75)), можно
без всяких изменений использовать и для описания пространства-времени
Керра—Ньюмена. См. по этому вопросу работу
9. Bose S. К. J. Math. Phys., 16, 772--775, 1975.
* Ф. М. Достоевский. Преступление и наказание,—Прим. ред.

Библиографические замечания 333
§ 111. Возмущения пространства-времени Керра—Ньюмена широко иссле-
исследовались в литературе, например в работах
10. Lee С. Я. J. Math. Phys., 17, 1226—1235, 1976.
11. ChitreD. M. Phys. Rev., D13, 2713—2719, 1976.
Изложение в тексте следует работе
12. Chandrasekhar S. Proc. Roy. Soc. (London), 358A, 421—439 (Appendix B,
pp. 437-439), 1978.
Можно утверждать, что в этих вопросах не было продвижения вперед, но только
в той степени, в какой это касается вопроса о расцеплении основных уравнений
и разделения переменных в этих уравнениях.
Однако те задачи, в которых не требуется подвергать возмущениям про-
пространство-время, могут быть исследованы точно так же, как и в пространстве-
времени Керра. Это относится, в частности, к обсуждению поведения геодезиче-
геодезических (нужно рассмотреть дополнительно несколько случаев вследствие другого
определения функции А) и к разделению переменных в уравнении Дирака (при
этом не требуется никаких изменений по сравнению с гл. 10). Эти вопросы осве-
освещены в работах
13. Catvani M., Felice de, F.t Nobili L. J. Phys., A13, 3213—3219, 1980.
14. Felice de, /\, Nobili L., Calvani M. J. Phys., A13, 3635—3641, 1980.
15. PageD. N. Phys. Rev., D14, 1509—1510, 1976.
§ 112. Преобразование уравнений Эйнштейна в пустоте для стационарных
аксиально-симметричных пространственно-временных многообразий к уравне-
уравнению Лапласа в евклидовом трехмерном пространстве было впервые выполнено
в работе
16. Weyt Я. Ann. Phys., 54, 117—145, 1917.
По этому вопросу см.
17. Synge J. L. Relativity: General Theory, North-Holland Publishing Co., Amster-
Amsterdam, 1964, pp. 309—317.
Получающиеся решения в литературе обычно называют решениями Вейля. Ясно,
что сведение к уравнению Лапласа может быть выполнено различными путями
при различных выборах калибровки и системы координат. В оригинальном вы-
выводе, принадлежащем Вейлю (он обычно и используется), возникает решение
Шварцшильда, горизонт событий которого представляет координатную сингу-
сингулярность в виде линии вдоль оси. Для исследования искаженных шварцшильдо-
вых черных дыр хотелось бы иметь такой вывод, в котором решение Шварц-
Шварцшильда появлялось бы в привычном виде. Именно такая калибровка и такая
система координат и использовались в тексте.
Искаженные статические черные дыры, следующие из общего решения
Вейля, рассматривались несколькими авторами, среди них
18. Israel W., Khan К. Я. Nuovo Cim., 33, 331—344, 1964.
19. Peters Р. С. J. Math. Phys., 20, 1481—1485, 1979.
Но наиболее полное обсуждение вопроса содержится в работе
20. Geroch R., Hartle J. В. J. Math. Phys., 23, 680—692, 1982.
Эта статья прояснила многие аспекты теории искаженных черных дыр, в том
числе и в связи с излучением Хокинга. Автор благодарен Дж. Хартлю за об-
обсуждение многих из этих вопросов, и в особенности за указание на важность
условия локально плоского характера метрики вдоль оси.
§ 113. Решение, рассмотренное в данном параграфе, было открыто неза-
независимо двумя авторами
21. Majumdar S. D. Phys. Rev., 72, 390—398, 1947.
22. Papapetrou A. Proc. Roy. Irish Acad., 51, 191—205, 1947.
Правильная интерпретация этих решений была дана в работе
23. Hartle J. B\, Hawking S. W. Commun. Math. Phys., 26, 87—101, 1972.
Обсуждение в п. 113, в в основном следует работе [23].
Обобщение метрики Маджумдара—Папапетру на стационарный случай
было независимо выполнено в работах
24. Israel W., Wilson G. A. J. Math. Phys., 13, 865—867, 1972.
25. Perjes Z. Phys. Rev. Lett., 27, 1668—1670, 1971.
Эти решения обсуждаются в работе Хартля и Хокинга [23].

334 Глава П. Другие решения, альтернативные методы
§ 114. Основные элементы теории, изложенной в настоящем параграфе,
были развиты Чандрасекаром и Фридманом в серии статей в более широком
контексте устойчивости однородно вращающихся звезд в рамках общей теории
относительности:
26. Chandrasekhar S., Friedman J. L. Astrophys. J., 175, 379—405, 1972.
27. Chandrasekhar S., Friedman J. L. Astrophys. J., 176, 745—768, 1972.
28. Chandrasekhar S., Friedman J. L. Astrophys. J., 177, 745—756, 1972.
29. Chandrasekhar S., Friedman J. L. Astrophys. J., 181, 481—495, 1973.
Одна из этих статей статья [28] была посвящена решениям в пустоте и теореме
Картера. Но все статьи основывались на нестационарной метрике вида B41).
Решающее значение включения коэффициента #2з в метрику для доказатель-
доказательства вещественности величины а2 для неустойчивых мод аксиально-симметрич-
аксиально-симметричных возмущений было впервые понято Фридманом и Шутцем. И это послужило
основой их доказательства устойчивости решения Керра относительно аксиально-
симметричных возмущений:
30. Friedman J. L., Schutz В. F., Jr. Phys. Rev. Lett., 32, 243—245, 1973.
Поскольку Фридман и Шутц не опубликовали подробностей своего исследова-
исследования, вся теория была развита с самого начала, как изложено в тексте. В основ-
основном автор следовал работам [26, 27], но для более общего вида метрики B44).
Доказательство теоремы Картера в п. 114, г совпадает с приведенным в [28],
а основные аргументы в п. 114, д, касающиеся устойчивости решения Керра
относительно аксиально-симметричных возмущений (пункт 2), взяты из статьи
[30]. Однако Фридман и Шутц доказывали непрерывность функции а от пара-
параметра Керра а, опираясь на теорию рассеяния, примененную к уравнениям
Тьюкольского, и на менее общие теоремы (но достаточные для их целей), чем
теоремы, доказанные Хартлем и Уилкинсом:
31. Hartle J. ?., WilkinsD. С. Commun. Math. Phys., 38, 47—63, 1974.
Как указывалось в тексте, можно избежать обращения к теоремам из теории
рассеяния, а опираться прямо на теоремы, которые утверждают, что собственные
значения самосопряженного дифференциального оператора, аналитически зави-
зависящего от параметра и всюду плотного на пространстве функций, интегрируемых
с квадратом, непрерывно зависят от этого параметра. См. по этому вопросу
работу
32. Riesz F., Sz.-Nagy В. Functional Analysis, Blackie and Son Limited, London,
1956, § 136, pp. 373—379.
Автор благодарен Джону Л. Фридману за советы и полезные обсуждения всех
вопросов, рассматривавшихся в этом параграфе.

* Приложение
ТАБЛИЦЫ ФУНКЦИЙ ТЬЮКОЛЬСКОГО
И СВЯЗАННЫХ С НИМИ ФУНКЦИЙ
В гл. 7, 9 и 10 было показано, как можно полностью описать
с помощью радиальных и угловых функций Тьюкольского для
различных значений спина реакцию керровской черной дыры на
падающее электромагнитное и гравитационное излучение и поток
безмассовых нейтрино. Кроме Брейера, Райяна-мл. и Уоллера
[2], Фэкерелла и Кроссмана [3] никто не предпринимал серьез-
серьезных попыток изучить эти функции так, как того требует место,
занимаемое ими среди специальных функций математической
физики. Функции, которые возникают при разделении переменных
в уравнении Дирака и обладают дополнительным свойством —
явной зависимостью собственного значения от массы частицы, —
вообще не изучались.
Можно надеяться, что удастся понять истоки замечательных
тождеств и свойств, которые были обнаружены при решении лине-
линеаризованных уравнений Ньюмена — Пенроуза в гл. 9. Но до
сих пор не удается подобрать ключ к этой задаче.
Поскольку большинство тождеств и соотношений в гл. 9 были
выведены после трудоемких преобразований, казалось полезным
проверить их непосредственными численными расчетами, чтобы
убедиться в отсутствии случайных алгебраических и других оши-
ошибок. С этой, а также с другими целями д-р С. Детвейлер любезно
согласился взять на себя труд составить таблицы для радиальных
и угловых функций для 5 = ±2 и 5 = ±1 для двух характерных
случаев а = 0,95 и 0 и а = 0,5 и 0,25. Эти таблицы включены в
приложение, ибо они могут оказаться полезными и для других
специалистов, заинтересовавшихся этой областью анализа.
Радиальные и угловые функции для спина 2 (табл. I и II)
нормированы, как указано в тексте: радиальные функции, при-
принадлежащие s = +2 и —2, удовлетворяют комлексно-сопряжен-
ным соотношениям Старобинского (уравнения D1) и D2) гл. 9),
а угловые функции нормированы на единицу. Функции 31
и 9 определены в гл. 9 уравнениями A78), A79), A83) и A84),
а различные «скобочные» выражения — в п. 81, б. Различные по-
постоянные (уравнение A61) гл. 9), связанные с табулированными
функциями, равны
а = 0,95 / = — т = 2
а = 0,5 0,25

336 Приложение
I = 0,88693 2,4308
а2 = _2,8975 —6,6975
о (Ха2 — 6а2) = —3,99244 —5,42382
Гх= 11,2530 15,7935
<вх = 12,4482 17,3831
^2(=-Г2)=—6 -3
В табл. III и IV затабулированы функции в шварцшильдовом
пределе а = 0.
Табл. V и VI дают радиальные и угловые функции (в стан-
стандартной нормировке) для спина 1. С этими решениями связаны
постоянные
a
a
=
—
=
a2
D
0,95 / =
0,5
=3,9317
= —2,8975
= 4,2844
—/72= 2
0,25
4,9294
—6,6925
5,0964
Наконец, в таблице VII перечислены собственные значения к,
принадлежащие угловым функциям для различных значений
спина, I и т\ данные для вычислений в случае 5 = 2 и 1 взяты из
работ Пресса и Тьюкольского [4, 5], а данные для 5 = 1/2 были
предоставлены Пейджем.
Библиографические замечания
В цитируемых статьях авторы работали со спиновыми сплюснутыми сферо-
сфероидальными гармониками:
1. Goldberg J. N.t Macfarlane A. J., Newman E. Г., et al. J. Math. Phys., 8,
2155—2161, 1967,
2. Breuer R. A., Ryan M. P., Jr., Waller S. Proc. Roy. Soc. (London) A, 71—86,
1977.
3. Fackerell E. D., Crossman R. G. J. Math. Phys., 18, 1849—1854, 1977.
Пресс и Тьюкольский составили таблицы коэффициентов разложения собствен-
собственных значений X в ряд по степеням ао как для s = 2 [4], так и для s = \ [5]:
4. Press W. Я., Teukolsky S. A. Astrophys. J., 185, Appendix С, 668, 1973.
5. Teukolsky S. Л., Press W. H. Astrophys. J., 193, Table 2, 454, 1974.
Коэффициенты разложения собственных значений X в степенной ряд при s = 1/2
были любезно предоставлены автору Д. Н. Пейджем.
Примечание при корректуре. В табл. I и II величины [Р]~, [DP]' и
[DDP]~ чисто мнимые, и числа в соответствующих столбцах следует умно-
умножить на мнимую единицу /.

Таблица I
Радиальные функции для s = ±2(а = 0,95; а = 0,5; I т — 2)
г/М
2,00
2,10
2,20
2,30-
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,10
3,20
3,30
3,40
3,50
3,60
3,70
3,80
3;90
4,00
4,10 *
4,20
4,30
4,40
4,50
4;60
4,70
4,80
4,90
5,00
5,10
5,20
5,30
5,40
5,50
5,60
5,70
5,80
5,90
6,00
6,10
6,20
6,30
6,40
6;5О
6,60
6770
6,80
6,90
[Р] +
2,00000
1,87877
1,70012
174155О
0,973712
0,321416
-0,596200
- 1,83470
- 3,44959
- 5,49545
- 8,02499
-11,0882
-14,7313
-18,9959
-23,9181
- 29;5276
-35,8469
-42,8904
- 5О76637
-59,1632
-68,3750
-78,2751
-88,8282
-99,9879
-111,697
-123,884
-136,470
-149,362
-162,455
-175,634
-188,773
-201,737
-214,379.
-226,545
-238,072
-248,791
-258,525
- 267,094
-274,312
-279,992
-283,945
- 285,982
-285,917
-283,564
-278,745
-271,285
-261,018
-247,788
-231,449
-211,867
- 1,07940
-0,926641
-0,990398
- 1,30720
-1,91092
-2,83272
-4,10067
-5,73938
- 7,76962
-10,2079
-13,0665
-16,3526
-20,0688
-24,2125
- 28,7763
- 33,7473
-39,1078
-44,8347
- 50,9003
-57,2717
-63,9116
-70,7783
-77,8255
-85,0035
-92,2585
-99,5336
- 106,769
-113,902
-120,869
-127,602
-134,035
- 140,099
-145,725
-150,844
-155,388
-159,289
-162,482
-164,904
-166,491
-167,188
-166,937
- 165,687
-163,392
-160,008
-155,498
-149,830
- 142,976
-134,917
-125,637
-115,128
\_DDP] +
5,38789
5,46889
5,40319
5,15534
4,70475
4,04018
3,15689
2,05492
0,738136
-0/786504
- 2,50942
-4,41878
-6,50082
-8,74010
-11,1197
-13,6215
-16,2264
-18,9142
-21,6643
-24,4554
-27,2658
-30,0737
-32,8571
-35,5943
-38,2636
-40,8436
-43,3135
-45,6531
-47,8427
-49,8635
-51,6977
-53,3283
- 54,7395
-55,9167
- 56,8463
-57,5163
-57,9157
-58,0353
-57,8670
-57,4045
-56,6427
-55,5784
-54,2096
-52,5362
-50,5593
-48,2820
-45,7085
-42,8450
- 39,6987
-36,2788
[Т
0,000000
0,727147
1,71762
2,97871
4,51446
6,32375
8,39906
10,7257
13,2813
16,0357
18,9503
21,9788
25,0668
28,1522
31,1658
34,0314
36,6664
38,9830
40,8882
42,2851
43,0735
43,1511
42,4146
. 40,7602
38,0854
34,2896
29,2756
22,9506
15,2274
6,02563
-4,72704
-17,0940
-31,1282
-46,8715
-64,3534
-83,5902
-104,584
-127,321
-151,774
-177,897
- 205,629
- 234,890
-265,583
-297;593
- 330,788
-365,016
-400,109
-435,880
-472,126
- 508,626
[DP]'
4,75963
7,29748
10,0176
12,9180
15,9838
19,1910
22,5081
25,8982
29,3198
32,7278
36,0743
39,3091
42,3805
45,2362
47,8229
50,0880
51,9795
53,4463
54,4393
54,9116
54,8187
54,1192
52,7752
50,7526
48,0216
44,5567
40,3373
35,3479
29,5783
. 23,0237
15,6853
7,56960
-1,31055
-10,9365;
-21,2837*
-32,3215
-44,0132
-56,3166
-69,1834
-82,5601
-96,3875
-110,601
-125,133
-139,907
-154,848
-169,872
-184,895
-199,827
-214,577
-229;052
[DDPy
25,1627
26,9098
28,8345
30,8465
32,8803
34,8845
36,8177
38,6449
4О;3359
41,8645
43,2076
44,3451
45,2592
45,9345
46,3580
46,5186
46,4074
46,0175
45,3439
44,3837
43,1359
41,6011
39,7819
37,6828
35}ЗО97
32,6704
29,7742
26,6320
23,2561
19,6602
15,8593
11,8797
7,70867
3,39469
-1,05287
-5,61379
-10,2671
-14,9912
- 19,7639
-24,5625
- 29,3643
-34,1459
-38;8841
-43,5556
-48,1373
-52,6061
-56,9393
-61,1148
-65,1107
-68,9059
О;865586
1,02641
1,25339
1,54821
1,91043
2,33813
2,82829
3,37695
3,97938
4,63018
5,32336
6,05242
6,81043
7,59012
8,38391
9,18399
9,98243
10,7712
11,5421
12,2873
12,9987
13;6686
14,2894
14,8537
15,3545
15,7852
16,1394
16,4114
16,5958
16,6878
16,6831
16,5780
16,3695
16,0551
15,6329
15,1018
14,4613
13,7117
12,8537
11,8891
10,8199
9,64910
8,38033
7,01777
5,56628
4;03132
2,41895
0,735764
-1,01110
-2,81401

(a = 0,95; a = 0,25; / = —m = 2)
Таблица I (продолжение)
r/M ,
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,10
3,20
3,30
3,40
3,50
3,60
3,70
3,80
3,90
4,00
4,10
4,20
4,30
4,40.
4,50
4,60
4,70
4,80
4,90
5,00
5,10
5,20
5,30
5,40
5,50
5,60
5,70
5,86
5,90
6,00
6,10
6,20
6,30
6,40
6,50
6,60
6,70 *
6,80
6,90
[Ч+
2,00000
3,809,31
6,11835
9,02331
12,6134
16,9716
22,1750
28,2943
35,3937
43,5302
52,7529
63,1025
74,6100
87,2969
101,173
116,239
132,480
149,872
168,374
187,934
208,485
229,943
252,210
275,174
298,702
322,650
346,852
371,129
395,282
419,095
442,336
464,753
486,079
506,028
524,296
540,563
554,493
565,731
573,907
578,635
579,513
576,125
568,038
554,809
535,979
511,077
479,622
441,119
;)95,066
340,951
15,9355
20,6317
26,1438
32,4815
39,6531
47,6631
56,5116
66,1930
76,6962
88,0043
100,094
112,938
126,500
140,740
155,613
171,067
187,044
203,483
220,317,
237,47 Г
254,871
272,433
290,071
307,695
325,209
342,517
359,515
376,097
392,155
407,577
422,249
436,053
448,870
460,578
471,055
480,175
487,814
493,843
498,135
500,563
500,997
499,311
495,375
489,063
480,248
468,806
454,612
437,545
417,486
394,316
45,1217
51,7891
59,0316
66,7997
75,0438
83,7152
92,7676
102,156
111,838
121,770
131,913
142,226
152,670
163,206
173,797
184,406
194^996
205,531
215,976
226,297
236,458
246,428
256,172
265,660
274,859
283,738
292,269
300,422
308,168
315,479
322,330
328,693
334,545
339,860
344,616
348,789
352,360
355,307
357,610
359,252
360,215
360,483
360,039
358,871
356,964
354,307
350,887
346,697
341,726
335,967
[РГ ^
0,000000
-0,402230
-0,658754
-0,676982
-0,356858
0,411260
1,74745
3,78248
6,65774
10,5250
15,5461
21,8926
29,7451
39,2928
50,7332
64;2710
80,1179
98,4917
119,615
143,717
171,027
201,782
236,217
274,571
317,081
363,987
415,523
471,925
533,421
600,239
672,597
750,710
834,784
925,017
1021,59
1124,70
1234,48
1351,11
1474,72
1605,43
1743,35
1888,57
2041,15
2201,17
2368,64
2543,51
2725,99
2915,82
3113,02
3317,52
[ШРГ
-2,95809
-1,48548
0,583079
3,32893
6,83718
11,1946
16,4885
22,8062
30,2342
38,8584
48,7633
60,0320
72,7458
86,9840
102,824 '
120,340
139,604
160,685
183,648
208,557
235,469
264,440
295,521
328,757
364,193
401,863
441,803
484,040
528,597
575,491
624,735
676,336
730,294
786,606
845,261
906,243
969,529
1035,09
1102,90
1172,90
1245,06
1319,33
1395,63
1473,91
1554,16
1636,11
1719,87
1805,28
1892,24
1980,66
23,9078
28,1807
32,9755
38,3038
44,1730
50,5885
57;5543
65,0734
73,1480
81,7790
90,9666
100,710
111,007
121,855
133,250
145,186
157,659
17O,66g
184,181
198,214
212,748
227,772
243,274
259,240
275,657
292,510
309,783
327,458
345,519
363,947
382,722
401,825
421,235
440,930
460,888
481,085
501,500
522,107
542,881
563,797
584,830
605,954
627,140
648,363
669,595
696,861
711,973
733,062
754,047
774,898
-5,59002
-6,18269
-6,77236
-7,33757
-7,85760
-8,31243
-8,68270
-8,94952
-9,09449
-9,09959
-8,94717
-8,61998
-8,10110
-7,37402
-6,42263
-5,23120
-3,78450
-2,06771
-0,0665556
2,23276
4,84347
7,77822
11,0491
14,6675
18,6443
22,9895
27,7126
32,8223
38,3264
44,2323
50,5462
57,2738
64,4199
71,9883
79,9822
88,4037
97,2543
106,534
116,243
126,379
136,941
147,925
159,326
171,141
183,361
195,982
208,994
222,389
236,157
250,288

Таблицы функций Тьюкольского
339
Нормированные угловые функции для s = ±2
(а = 0,95; а = 0,5; / = — tn — 2)
Таблица II
co$0
0,96
0,92
0,88
0,84
0,80
0,76
0,72
0,68
0,64
0,60
0,56
0,52
0,48
0,44
0,40
0,36
0,32
0,28
0,24
0,20
0,16
0,12
0,08
0,04
s+2
1,66329
3,57437
3,48894
1,40690
3,32816
3,25261
1,18017
3,11074
1,04423
0,98056
0,91965
0,86140
0,80574
0,75260
0,70190
0,65356
0,60751
0,56368
0,52200
0,58242
0,44485
0,40925
0,37554
0,34368
я-,
0,00037
0,00149
0,00340
0,00612
0,00970
0,01414
0,01949
0,02578
0,03304
0,04132
0,05064
0,06104
0,07256
0,08524
0,09912
0,11424
0,13064
0,14837
0,16747
0,18799
0,20998
0,23348
0,25855
0,28524
ra+
1,66366
1,57586
3,49234
1,41303
1,33785
1,26675
1,19966
1,13652
1,07728
1,02188
0,97028
0,92244
0,87830
0,83784
0,80101
0,76779
0,73$ 15
0,71205
0,68948
0,67041
0,65483
0,64273
0,63410
0,62892
-0,87863
-1,17445
-1,35688
-1,47481
-1,54843
-1,58874
-1,60267
-1,59501
-1,56926
-3,52815
-1,47384
-1,40809
-1,33241
-1,24806
-1,15615
-1,05767
-0,95350
-0,84443
-0,73120
-0,61449
-0,49493
-0,37313
-0,24968
-0,12513
0,55703
1,08767
1,59237
2,07158
2,52573
2,95522
3,36043
3,74172
4,09942
4,43387
4,74535
5,03415
5,30053
5,54472
5,76695
5,96741
6,14629
6,30375
6,43992
6,55494
6,64890
6,72189
6,77398
6,80522
[ST
lf66292
1,57287
1,48553
1,40077
3,31846
1,23847
1,16068
1,08496
3,01119
0,93924
0,86901
0,80036
0,73319
0,66737
0,60278
0,53932
0,47687
0,41531
0,35453
0,29442
0,23487
0,17577
0,11699
0,05844
isesr
-0,89925
-1,23281
- 1,46413
-1,63997
-1,77926
-1,89212
-1,98481
-2,06159
-2,12551
-2,17890
- 2,22354
- 2,26086
- 2,29204
-2,31801
- 2,33959
- 2,35743
-.2,37209'
- 2,38405
-2,39369
-2,40134
-2,40725
-2,41164
-2,41466
-2,41643
[OT
0,12516
0,23460
0,32906
0,40925
0,47591
0,52974
0,57143
0,60167
0,62116
0,63056
0,63053
0,62173
0,60483
0,58046
0,54927
0,51189
0,46895
0,42108
0,36891
0,31306
0,25414
0,19277
0,12956
0,06513
Sf
0,13581
0,18038
0,20711
0,22376
0,23358
O;23833
0,23915
0,23680
'0,23185
0,22475
0,21583
0,20538
0,19360
0,18072
0,16687
0,15222
0,13687
0,12093
0,10450
0,08767
0,07051
0,05310
0,03550
0,01778

340
Приложение
(а = 0,95; а = 025; / = — т =2)
Таблица II (продолжение)
COS0
0,96
0,92
0,88
0,84
0,80
0,76
0,72
0,68*
0,64
0,60
0,56
0,52
0,48
0,44
0,40
0,36
0,32
0,28
0,24
0,20
0,16
0,12
0,08
0,04
1,59016
1,51587
1,44380
1,37393
1,30621*
. 1,24061
1,17709
1,11563
1,05618
0,99872
0,94321
0,88962
0,83792
0,78808
0,74006
0,69384
0,64939
0,60667
0,56566
0,52633
0,48865
0,45259
0,41813
0,38523
S-,
0,00049
0,00196
0,00443
0,00792
0,01246
0,01805
0,02473
0,03250
0,04140
0,05144
0,06263
0,07502
0,08860
0,10341
0,11947
0,13681
0,15543
0,17538
0,19666
0,21931
0,24335
0,26880
0,29568
0,32404
1,59064
1,51782
1,44823
1,38185
1,31867
1,25866
1,20182
1,14813
1,09758
1,05016
1,00585
0,96464
0,92653
0,89^49
0,85954
0,83065
0,80482
0,78205
0,76232
0r74564
0,73199
0,72138
0,71381
0,70927
-0,86289
-1,15641
- 1,33936
-1,45925
-1,53558
- 1,57897
-1,59610
-1,59156
- 1,56876
-1,53031
- 1,47832
-1,41451
- 1,34036
-1,25712
-1,16592
-1,06775
-0,96350
-0,85400
-0,74002
-0,62227
-0,50144
-0,37818
-0,25310
-0,12683
0,63892
1,25074
1,83560
2,39362
2,92490
3,42958
3,90774
4,35949
4,78492
5,18413 (
5,55719 '
5,90419
6,22519
6,52026
6,78947
7,03287
7,25052
7,44245
7,60871
7,74933
7,86435
7,95378
8,01765
8,05596
1,58967
1,51391
1,43937
1,36601
1,29375
1,22256
1,15237
1,08313
1,01478
0,94729
' 0,88058
0,81461
0,74932
0,68467
0,62059
0,55704
0,49396
0,43129
0,36900
0,30702
0,24530
0,18379
0,12244
0,06119
l*si-
-0,89008
- 1,23295
- 1,47926
-1,67351
- 1,83339
- 1,96822
- 2,08370
-2,18360
- 2,27064
-2,34681
-2,41365
- 2,47239
- 2,52400
- 2,56927
- 2,60887
- 2,64333
-2,67313
- 2,69863
-2,72015
- 2,73795
-2,75224
-2,76319
- 2,77092
-2,77553
l**sr
0?06868
0,12890
0,18102
0,22539
0,26239
O,2923S
0,31570
0,33272
0,34380
0,34929
0,34954
0,34491
0,33575
0,32241
0,30525
0,28460
0,26083
0,23428
0,20530
0,17424
0,У145
0,10726
0,07204
0,03612
V
0,13895
0,18550
0;21407
0,23241
0,24375
0,24983
0,25177
0,25032
0,24606
0,23941
0,23072
0,22015
0,20827
0,19496
0,18049
0,16503
0,14870
O;13163
0,11394
0,09572
0,07708
0,05781
0,03887
0,01948

Радиальные функции для а — О, s = ±2
(а = 0,5; / = — т = 2)
Таблица III
г/М
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,10
3,20
3,30
3,40
3,50
3,60
3,70
3,80
3,90
4,00
4,10
4;20
4,30
4,40
4,50
4760
4;70
4,80
4,90
5,00
5,10
5,20
5,30
5,40
5,50
5,60
5,70
5;80
5,90
6;00
6,10
6,20
6,30
6,40
6,50
6760
6/7G
6,80
6,90
7,00
[Р} +
1,66046
0,691547
-0,0598288
-0,672384
-1,22137
-1,75141
-2,28981
-2,85426
-3,45673
-4,10555
-4,80645
-5,56319
-6,37787
-7,25114
-8,18227
-9,16922
-10,2087
-11,2960
-12,4253
-13,5895
-14,7801
-15,9876
-17,2009
-18,4082
-19,5962
-20,7507
-21,8564
-22,8971
-23,8558
-24,7147
-25,4554
-26,0588
'-26,5058
-26,7766
—26,8516
-26,7112
-26,3358
-25,7065
-24,8047
-23,6124
-22,1129
-20,2901
-18,1295
-15,6177
-12,7430
-9,49563
-3,86740
-1,85241
2,55311
7,35054
[DP]+
3,05695
3,23681
2,72551
2,09362
1,43940
0,779221
0,111032
-0,570955
-1,27231
-1,99734
-2,74888
-3,52837
-4,33594
-5,17060
-6,03031
-6,91210
-7,81218
-8,72601
- 9,64835
-10,5734
-11,4948
-12,4057
-13,2990
-.14,1670
-15,0019
-15,7958
-16,5404
-17,2276
-17,8490
-18,3965
-18,8619
-19,2375
-19,5154
-19,6885
-19,7496
-19,6923
-19,5104
-19,1983
-'18,7512
-18,1645
-17,4348
-16,5589
-15,5346
-14,3606
-13,0363
-11,5617
-9,93821
-8,16761
-6,25284
-4,19766
\_DPP] +
- 1,64363
1,12446
2,51969
3,23429
3,56968
3,67008
3,61248
3,44184
3,18648
2,86547
2,49250
2,07795
1;63012
1,15600
0,661616
0,152402
-0,366673
-0,890978
-1,41615
-1,93804
-2,45271
- 2,95639
- 3,44548
.-3,91656
-4,36636
-4/79182
-5,19003
-5^55829
- 5,89407
-6,19508
-6,45920
-6,68454
-6,86944
-7,01245
-7,11234
-7,16814
-7,17908
-7,14466
-7,06459
-6,93883
-6,76755
-6,55119
-6,29038
-5,98600
-5,63914
-5,25110
-4,82339
-4,35771
-3,85597
-3,32025
[/>]-
1,25666
2,14365
2,44870
2,60223
2,71122
2,80879
2,90446
2,99841
3,08650
3,16232
3,21803
3,24485
3,23337
3,17363
3,05535
2,86801
2,60095
2,24353
1,78522
1,21572
0,525111
-0,296069
- 1,25666
-2,36476
-3,62761
-5,05148
-6,64151
— 8-40164
-10,3345
-12,4411
-14,7213
-17,1729
-19,7923
-22,5740
-25,5107
-287593О
-31,8100
-35,1485
-38,5935
-42,1279
-45,7328
-49;3874
-53,0689
-56,7528.'
-60,4128
-64,0211
- 67,5483
-70,9635
-74,2347
-77,3286
-1,31413
0,848822
2,22828
3,24104
4,05816
4,75533
5,36838
5,91439
6,40083
6,82987
7,20064
7,51049
7,75577
7,93227
8,03553
8,06112
. 8;00472
7,86229
7,63019
7,30517
6,88455
6,36618
5,74853
5,03072
4,21255
3,29452
2,27787
1,16455
-0,0427275
-1,34051
-2,72459
-4,19003
-5,73117
-7,34165
-9,01439
-10,7417
-12,5151
-14,3259
-16,1643
-18,0205
-19,8839
— 21,7436
-23,5884
-25,4066
-27,1864
-28,9157
-30,5824
-32,1743
-33,6790
-35,0845
[DDPJ-
-4,21285
-1,11410
1,09792
2,69108
3,89029
4,82288
5,56265
6,15443
6,62671
6;99828
7,28197
7,48683
7,61947
7,68486
7,68697
7,62902
7,51381
7,34388
7,12160
6,84927
6,52920
6,16373
5,75525
5,30626
4,81933
4;29717
3/74255
3,15838
2,54766
1,91347
1,25898
0,587458
-О;О977922
-0,793399
-1,49595
-2,20202
.-2,90813
— 3,61086
-4,30674
-4,99236
-5;66436
-6,3194
-6,95425
-7;56572
-8,15074
- 8,70633
-9,22965
-9,71797
-10,1687
-10,5795
Я v
-0,836984
-0,366649
0,0329922
0,357504
0,629729
0,864907
1,07231
1,25756
1,42407
1,57389
# J/7O817
1,82749
1,93205
2,02181
2,09654
2,15593
2,19960
2,22716
2,23823
2,23244
2,20947
2,16905
2,11101
2,03520
1,94161
1,83027
1,70135
1,55508
1,39181
1,21198
1,01616
0,804980
0,579209
0,339700
0,0874053
-0,176624
-0,451246
-0,735232
-1,02727
-1,32596
-1,62985
-1,93741
-2,24704
-2,55711
-2,86593
-3,17179
-3,47291
-3/76755
-4,05390
-4,33020

Радиальные функции для а = 0, s = ±2
(а = 0,25; I = ~т = 2)
Таблица III (продолжение)
г/М
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,10
3,20
3,30
3,40
3,50
3,60
3,70-
3,80
3,90
4,00
4,10
4,20
4,30
4,40
4,50
4,60
4,70
4,80
4,90
5,00
5,10
5,20
5,30
5,40
5,50
5,60
5,70
5,80
5,90
6,00
6,10
6,20
6,30
6,40
6,50
6,60
6,70
6,80
6,90
7,00
1,89407
1,67027
1,49950
1,33458
1,14265
0,902794
0,600980
О7227683
-0,223299
-0,755401
- 1,36955
-2,06426
-2,83565
-3,67742
-4,58076
-5,53435
-6,52418
-7,53358
-8,54306
-9,53028
-10,4700
-11,3339
-12,0907
-12,7061
-13,1425
-13,3592
-13,3126
-12,9555
-12,2378
-11,1062
-9,50427
-7,37234
-4,64781
-1,26502
2,84462
• 7,75260
13,5332
20,2634
28,0227
36,8932
46,9594
58,3077
71,0270
85,2079
100,943
118,325
137,451
158,417
181,320
206,258 '
[D>] +
0,0254419
-0,0627552
-0,796229
- 1,85072
-3,13445
-4,61037
-6,25930
- 8,06876
-10,0287
-12,1299
-14,3627
-16,7171
-19,1821
-21,7459
-24,3957
-27,1177
-29,8972
-32,7185
-35,5649
-38,4188
-41,2619
-44,0748
-46,8376
-49;5295
-52,1289
-54,6137
-56,9612
-59,1480
— 61,1504
-62,9441
-64,5043
-65,8060
-66,8240
-67,5326
-67,9060
-67,9184
-67,5437
-66,7560
-65,5292
-63,8376
-61,6553
-58,9569
-55,7171
-51,9109
-47,5138
-42,5016
-36,8508
-30,5382
-23,5414
-15,8384
[DDP]+
- 17,8501
-20,0000
-21,9234
-23,9919
-26,2211
-28,5881
-31,0684
- 33,6404
- 36,2856
-38,988
-41,7339
-44,5102
-47,3055
.-50,1090
-52,9104
-55,7002
-58,4690
-61,2081
-63,9088
-66,5630
-69,1627
-71,7002
-74,1679
-76,5587
- 78,8654
-81,0813
-83,1998
-85,2144
-87,1191
-8&.9079
-90,5751
-92,1151
-93,5228
-94,7930
-95,9210
-96,9021
-97,7320
-98,4066
-98,9220
-99,2746
-99,4610
-99,4781
-99;3229
-98,9928
-98,4854
-97,7986
-96,9304
-95,8793
-94,6439
-93,2231
[РГ
0,492948
0,664771
0,424666
-0,0727141
-0,802836
-1,7733
- 3,00389
-4,52032 .
-6,35201
-8,53087
-11,0908
-14,0671
-17,4968
-21,4176
-25,8685
-30,8891
-36,5196
-42,8008
-49,7736
-57,4793
-65,9590
-75,2535
-85,4033
-96,4484
-108,428
-121,380
-135,342
-150,350
-166,437
-183,636
-201,979 •
-221,493
-242,204
-264,137
-287,312
-311,747
-337,458
-364,456
-392,749
-422,342
-453,236
-485,427 '
-518,908
- 553,667
-589,687
-626,949
-665,425
-705,085
-745,893
-787,808
[ОРГ
-4,45715
- 5,42842
-6,65023
-8,14248
-9,90537
-11,9442
- 14,2681
-16,8885
-19,8179
-23,0693
- 26,6562
-30,5917
-34,8888
-39,5603
-44,6184
-50,0747
-55,9404
-62,2257
-68,9404
-76,0933
-.83,6925
-91,7452
-100,258
-109,235
-118,682
-128,601
-138,995
-149,866-
-161,212
-173,033
-185,327
-198,090
-211,318
-225,004
-239,142
-253,724
-268,739
-284,176
-300,025
-316,271
-332,899
-349,894
-367,238
-384,914
-402,900
-421,177
-439,722
-458,512
-477,521
-496,725
\_DDP]-
-9,16049
- 10,6939
-12,0473
-13,4951
-15,0779
-16,8018
-18,6657
-20,6670
-22,8033
-25,0719
- 27,4706
-29,9971
-32,6494
-35,4252
-38,3222
-41,3381
-44,4704
-47,7165
-51,0735
-54,5385
-58,1085
-61,7799
-65,5495
-69,4135
-73,3681
-77,4093
-81,5328
-85,7345
-90,0097
-94,3538
-98,7620
- 103,229
-107,751
-112,321
-116,934
-121,586
-126,269
-130,980
-135,711
•-140,457
-145,211
-149,969
-154,723
-159,467
-164,196
-168,902
-173,580
-178,223
-182,824
-187,377
-1,64221
-2,01092
-233983
- 2,69396
- 3,08770
-3,52670
-4,01435
-4,55324
-5,14573
- 5,79403
-6,50029
-7,26657
-8,09491
-8,98725
-9,94548
-10,9714
-12,0667
-13,2330
-14,4718
-15,7846
-17,1725
-18,6368
-20,1783
-21,7982
-23,4972
-25,2757
-27,1343
-29,0733
-31,0928
-33,1929
-35,3732
-37,6335
-39,9733
-42,3919
-44,8884
-47,4617
-50,1107
-52,8539
-55,6298
-58,4966
-61,4323'
-64,4348
-67,5019
-70,6309
-73,8193
-77,0642
-803626
-83,7113
-87,1068
-90,5457

Таблицы функций Тьюкольского
343
Угловые
(I = ~т
cos в
0,96
0,92
0,88
0,84
0,80
0,76
0,72
0,68
0,64
0,60
0,56
0,52
0,48
0,44
0,40
0,36
0,32
0,28
0,24
0,20
0,16
0712
0,08
0,04
функции
,51853
,45718
,39709
,33828
,28072
,22443
,16941
1,11565
1,06316
1,01193
3,96196
3,91327
3,86583
3,81966
3,77476
3,73112
3,68874
3,64763
0,60779
0,56921
0,53189
0,49584
0,46106
0,42754
для а =
S-2 [
0,00063
0,00253
0,00569
0,01012
0,01581
0,02277
0,03099
0,04048
0,05123
0,06325
0,07653
0,09107
0,10688 (
0,12396 (
0,14230 (
0,16191 (
0,18278 (
0,20492
0,22832
0,25298
0,27891
0,30611
0,33457
0,36429
0, s
,51916
,45971
,40279
,34840
,29653
,24720
,20040
,15613
,11439
,07517
,03849
,00434
3,97272
3,94362
3;917О6
3,89303
3,87152
3,85255
3,83611
3,82219
3,81081
3,80195
3,79563
3,79183
*
= ±2
- 0,85002
-
-1
- 1
- 1
-
-
-
-
-
-
-
-
-
,14021
,32176
,44128
,51789
,56198
,58007
,57666
,55508
,51789
,46716
,40458
,33160
,24948
,15931
- 1,06209
-0,95872
-0,85002
-0,73676
-0,61968
- 0,49945
-0,37673
-0,25217
-0,12639
1</'#'S]+ [
0,74377
1,45718
2,14023
2,79292
3,41526
4,00724
4,56886
5,10012
5,60102
6,07157 (
6,51176 (
6,92159 (
7,30106
7,65018 (
7,96893
8,25733
8,51538
8,74306
8,94039
9,10735
9,24396
9,35022
9,42611
9,47165
S]~
,51789
,45465
,39140
,32816
,26491
,20167
,13842
,07517
,01193
3,94868
3,88544
3,82219
3,75895
3,69570
3,63246
3,56921
3,50596
3,44272
3,37947
3,31623
3,25298
3,18974
3,12649
3,06325
Таблица IV
tsesr
-0,88544
-1,23935
- 1,50200
- 1,71581
- 1,89737
-2,05524
-2,19454
-2,31862
-2,42981
- 2,52982
-2,61992
-2,70111
-2,77417
- 2,83972
-2,89827
-2,95025
-2,99600
-3,03579
-3,06985
- 3,09839
-3,12154
-3,13943
-3,15214
-3,15975
У
0,14166
0,19003
0,22029
0,24021
0,25298
0,26033
0,26334
0,26277
0,25918
0,25298
0,24453
0,23410
0,22193 .
0,20825
0,19322
0,17701
0,15979
0,14167
0,12279
0,10328
0,08324
0,06279
0,04203
0,02106

Радиальные функции для s = ±1
(а = 0,95; о = 0,5; I = —т = 2)
Таблица V
г/М
2,10
2.20
2.30
2,40
2,50
2.60
2,70
2,80
2,90
3,00
3,Ю
з;о
3,30
3,40
3,50
3,60
3,70
3,80
3,90
4,00
4,10
4,20
4,30
4,40
4,50
Re
Р±х
1.2003
1.4350
1,6992
1,9887
2,2994
2,6272
2,9679
3,3173
3.6711
4,0251
4,3748
4,7160
5.0442
5,3551
5,6447
5,9086
6,1430
6,3439
6,5077
6,6310
6.7105
6,7432
6,7264
6,6576
6;5346
dP-^/dr
2,1833
2;5О17
2,7757
3;0079
3,1991
33492
3,4575
3,5234
3,5463
3,5258
3,4617
3,3540
3,2031
3,0095
2/7741
2,4980
2,1827
1,8298
1.4412
1,0191
О;56571
0,83637
- 0,042439
-0,095550
- 1,5066
Im
Р±1
-0,10873
- 0;24999
- 0,42574
-0,63781
-0,88783
- 1,1771
- 1,5066
- 1,8770
- 2,2884
- 2,7407
-3,2336
- 3,7660
-4,3368
- 4,9445
-5,5871
- 6,2625
-6,9681
-7,7012
- 8,4586
-9,2371
- 10,033
- 10,843
- 11,662
-12,487
-13,313
dP-t./dr
- 1.2*68
-1,5818
- 1,9361
- 2,3080
- 2,6946
- 3,0926
- 3,4985
- 3,9087
-4,3194
-4,7270
-5,1279
-5,5185
-5,8953
- 6,2549
- 6,5940
-6,9095
-7,1984
- 7,4579
-7,6853
-7,8781
-8,0341
-8,1510
- 8,2272
- 8,2608
-8,2505
г/М
4,60
4,70
4,80
4,90
5,00
5,10
5,20
5,30
5,40
5,50
5,60
5,70
5,80
5,90
6,00
6,10
6,20
6,30
6,40
6,50
6,60
6,70
6,80
6,90
7,00
Re
6,3557
6,1192
5:8241
5.4694
5,0547
4,5797
4,0448
3,4505
2,7977
2,0876
1,3220
0,50282
-0,36768
-1,2868
-2,2516
- 3,2589
- 4,3049
- 5,3860
- 6,4980
-7,6365
- 8,7970
- 9,9747
-11,165
- 12,362
-13,561
dP+1/dr
- 2,0746
- 2,6562
- 3,2480
- 3,8466
- 4,4484
- 5,0499
- 5,6475
- 6,2376
-6,8167
-7,3812
- 7,9277
- 8,4527
- 8,9528
-9,4250
- 9,8659
- 10,273
- 10,642
- 10,972
- 11,260
- 11,503
- 11,699
- 11,847
- 11,944
- 11,989
- 11,980
Im
Р±1
- 14,135
- 14,950
- 15,752
- 16,538
-17,301
- 18,037
-18,743
- 19,412
- 20,040
-20,623
-21,157
-21,636
- 22,058
-22,417
-22,711
-22,935
-23,087
- 23,163
-23,161
- 23,078
-22,9*3
- 22,662
-22,326
~21,9OZ
-21,390
d/J±1/dr
-8,1951
-8,0937
-7,9455
-7,7500
-7,5071
-7,2168
- 6,8793
- 6,4952
-6,0653
- 5,5906
- 5,0722
-4,5118
-3,9110
-3,2716
- 2,5960
- 1;8863
-1,1451
-0,37505
0,42089
1,2397
2,0784
2,9334
3,8015
4,6791
5,5627

Радиальные функции для s — +1
(а = 0,95; а = 0,25; I = ~т = 2)
Таблица V (продолжение)
г/М
2.10
2.20
2,30
2.40
:,5о
2,60
2,70
2,80
2,90
3,00
3,10
3,20
3,30
3,40
3,50
3,60
3,70
3,80
3,90
4,00
4,10
4,20
4,30
4,40
4,50
Re
P*i
0,94906
0,93987
0,96682
1,0259
1,1144
1;23О5
1,3728
1;5406
1,7334
1,9507
2,1925
2,4585
277488
3,0631
3,4015
3,7639
4,1501
4,5600
4,9935
5,4504
5,9303
6,4330
6,9582,
7,5053
8,0739
d/\,/dr
- 0,28975
0?096678
0,43572
0.74175
1,0253
1,2936
1,5518
1,8035
2,0510
2,2959
2,5392
2,7814
3,0229
3,2638
3,5039
3,7431
3,9812
4,2177
4,4522
4,6844
4,9137
5,1397
5,3619
5,5797
5,7927
р±1
0.070474
0,11579
0,14371
0,15841
0,16201
0,15552
0,13922
0,11295
0,076319
0^028707
- 0,030602
-0,10241
-0,18758
-0,28701
-0,40163
-0,53238
- 0,68020
- 0;84606
- 1,0309
-1,2357
- 1,4614
- 1,7089
-1,9792
-2,2731
- 2,5916
dP+1/dr
0,56174
0,35698
0,20822
0,089098
-0,015377
-0,11405
-0,21232
-0,31361
-0,42012
-0,53332
- 0,65420
-0,78344
-0,92149
- 1,0687
- 1,2252
-1,3913
- 175668
- 1,7520
- 1,9467
-2,1509
- 2;3645
- 2,5874
-2,8195
-3,0606
-3,3105
г/Ч
4,60
4,70
4,80
4,90
5,00
5,10
5,20
5,30
5,40
5,50
5,60
5,70
5,80
5,90
6,00
6,10
6,20
6,30
6,40
6,50
6,60
6,70
6,80
6,90
7,00
Re
^м
8,6636
9,2738
9,9038
10,553
11,221
11,906
12,609
13,327
14;060
14,808
15,569
16,342
17,126
17,920
18;722
19,532
20,349
21,170
21,995
22,823
23,651
24,480
25,306
26,129
26,947
dP»,/dr
6,0004
6,2021
6,3975
6,5859
6,7670
6,9401
7,1049
7,2607
7,4073
7,5441
7,6706
777864
7,8912
7,9845
8,0659
8,1351
8,1916
8,2353
8,2656
8,2824
8,2853
8,2741
8,2485
8,2082
8,1532
1т
р±1
-2,9355
-3,3057
- 3,7030
-4,1282
-4,5821
- 5,0655
- 5,5790
-6,1234
- 6,6993
-7,3073
-7?9481
-8,6221
- 9,3299
- 10,072
- 10,849
- 11,661
-12,508
- 13,391
- 14,310
- 15,265
-16,256
- 17?284
-18,349
-19,450
-20,587
dPi./dr
- 3,5691
-3,8361
-4,1113
- 4,3944
-4?6851
- 479832
- 5,2884
- 5 ?6ООЗ
-5,9186
- 6,2430
-6,5731
- 6,9084
- 7,2487
-7,05935
- 7,9424
- 8,2949
- 8,6507
- 9,0093
-9;3701
-9,7329
- 10,097
- 10,462
- 10,827
- 11,192
-11,557

346
Приложение
Радиальные функции для $ — ±1
(а = 0,95; а = 0,5)
Таблица VI
(а = 0,95; а = 0,25)
COS0
0,96
0792
0,88
0,84
0,80
0,76
0,72
0,68
0,64
0,60
0,56
0,52
0г48
0,44
0,40
0,36
0,32
0,28
0,24
0,20
0,16
0,12
0,08
0,04
0,00
0?484864
0,659681
0,776809,
0,861868
0,925258
0,972562
1,007246
1,031673
1,047558
1,056202
1,058631
1,055674
1,048019
1,036245
1,020847
1,002255
0,980847
0,956955
0,930879
0,902887
0,873222
0,842106
0,809744
0,776324
0,742020
1,566731
1,363899
1,171990
0,990669
0,819615
0,658514
0,507061
. 0,364960
0,231925
0,107677
-0,008053
-0,115529
-0,215005
- 0,306726
- 07390932
-0,467355
-0,537719
- 0,600743
-0,657136
-0,707103
-0,750843
-0,788545
-0,820397
- 0,846577
-0,867258
0,007161
0,020161
0,036860
0,056467
0,078507
0,102647
0,128628
0,156242
0,185310
0,215674
0,247191
0,279731
0,313168
0,347384
0,382264
0,417693
0,453558
0,489747
0,526143
0,562631
0,599087
0,635389
0,671403
0,706995
0,742020
dS_,/d0
0,074963
0,147218
0,216699
0,283339
0,347065
0,407804
0,465477
0,520003
0,571297
0,619269
0,663826
0,704873
0,742307
0,776025
0,805917
0,831871
0,853768
0,871487
0,884900
0,893877
0,898280
0,897970
0,892799
0,882617
0,867266
COS0
0,96 (
0;92 (
0,88 (
0,84 (
0,80 (
0,76 (
0,72 (
0,68
0,64
0,60
0,56
0,52
0,48
0,44
0,40
0,36
0,32 (
0,28 (
0,24 (
0,20 (
0,16 (
0,12 (
0,08 (
0,04 (
0,00 (
s+l
3,457337
);624867
),7389О9
),823242
),887456
3,936665
3,974032
1,001698
1,021213
1,033749
1,040229
1,041399
1,037877
1,030183
1,018765
1,004013
3,986270
3,965842
3,943003
3,918004
3,891073
3,862419
3,832239
3,800714
3,768015
dS+Jdd
1,491370
1,317715
1,151512
0,992645
0,841005
0,696481
0,558966
0,428355
0,304541
0,187424
0,076902
-0,027125
-0,124754
-0,216082
-0,301203
-0,380210
-0;453195
- 0,520248
-0,581457
-0,636910
-0,686692
-0,730888
-0,769579
-0,802849
-0,830776
0,007979
0,022405
0,040852
0,062411
0,086531
0,112820
0,140974
0,170746
0,201921
0,234314
0,267754
0,302086
0,337162
0,372844
0,408999
0,445494
0,482202
0,518996
0,555748
0,592331
0,628612
0;664460 •
0,699739
0,734306
0,768015
dS^/dfl
0,083382
0,163014
0,238847
0,310830
0,378909
0,443033
0;503147
0.559195
0,611121
0,658866
0,702373
0,741582
0,776430
0,806858
0,832799
0,854192
0,870968
0,883063
0,890406
0,892930
0,890563
0,883233
0,870867
0^53390
0,830727

Таблицы функций Тьюкольского
347
Собственные значения К для s = 2
Таблица VII
I = 2
m = 2
1= 2
m = 1
/ = 2
m = О
/ =:
-1
/ = 2
О
0,2
0,4
0,6
0,8
1)°
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3,8
4,0
4,0000
5,3446
6;7137
8,1108
9,5395
11,004
12,508
14,056
15,654
17,305
19,014
20,787
22,630
24,546
26,542
28,623
30,794
33,059
35,425
37,896
40,476
4,0000
4,6839
5,4035
6,1600
6,9542
7,7856
8,6528
9,5528
10,481
11,432
12,397
13,364
14,321
15,252
16,136
16,949
17,665
18,252
18,673
18,885
18,842
4,0000
4,0186
4,0740
4,1645
4,2873
4,4387
4;6136
4,8056
5,0071
5,2089
5,4000
5,5682
5,6990
5,7764
5,7821
5,6960
5,4954
5,1558
4,6500
3,9484
3,0187
+ 4,0000
+ 3,3503
+ 2,7330
+ 2,1463
+ 1,5889
+ 1,0601
+ 0,56000
+ 0,08978
- 0,34779
-0,74819
-
-
-
-
-
-
-
-
,1047
,4081
,6460
,8028
,85X8
,7899
,5673
,1563
-0,5166
+ 0,3992
f 1,6454
+ 4,0000
.+ 2,6767
'+ 1,3717
+ 0,08242
-1,1935
-2,4580
-3,7124
-4,9576
-6,1937
-7,4199
- 8,6344
- 9,8344
- 11,016
-12,173
- 13,298
- 14,383
- 15,417
- 16,387
-17,278
-18,072
- 18,750

348
Приложение
Собственные значения X для s = 1 и 1/2
Таблица VII (продолжение)
0*
°,2
0;4 •
0,6
0,8
1,0
1.2
1,4
1,6
1,8
2,0
2,2
2,6
2,8
3,0
3,2
3,4
3,6
3,8
4,0
/-1,0
т = \,0
2,0000
2,6189
'3,2775
3,9787
4,7243
5,5150
6,3497
7,2255
8,1368
9,0754
10,029
10,984
11,919
12,809
13,624
14,327
14,874
15,216
15,291
15;О32
14,360
/= 1
т = 0
2,0000
2,0227
2,0905
2,2003
2,3477
2,5266
2,7294
2,9470
3,1685
3,3816
3,5724
3,7253
3,8232
3,8478
3,7791
3,5960
3,2762
2,7961
2,1316
1,2574
0,1478
/=1,6
т = - 1,0
+ 2,0000
+ 1,4173
+ 0,86643
+ 0,3428
-0,15866
-0,64375
-1,1187
- 1,5904
- 2,0664
- 2,5547
-3,0641
-3,6040
-4,1844
-4,8163
-5,5110
-6,2811
-7,1397
-8,1007
-9,1791
-10,390
-11,752
1 = 2
т= -2
+ 6,0000
+ 5,0934
+ 4,2389
+ 3,4341
+ 2,6762
+ 1,9618
+ 1,2872
+ 0,6480
+ 0,0392
-0,5451
-1,1114
-1,6671
-2,2206
-2,7814
-3,3602
- 3,9688
- 4,6205
- 5,3300
-6,1138
- 6,9900
- 7,9785
/ = 0,5
т = 0,5
1,0000
1,2908
1,6311
2,0228
2,4671
2,9658
3,5210
4,1362
4,8170
5,5713
6,4113
7,3535
8,4204
9,6416
,11,0553
12,709
14,663
16,990
19,776
23,127
27,165
/ = 0,5
т= -0,5
1,0000
+ 0,75658
+ 0,55754
+ 0,39903
+ 0,27622
+ 0,18321
+ 0,11286
+ 0,056690
+ 0,0047234
-0,054695
-0,13508
-0,25199
-0,42325
-0,66921
-1,01293
-1,4805
-2,1012
- 2,9080
-3,9377
-5,2311
-6;8339

эпилог
Не существует красоты
без некоторого нарушения пропорций.
Фрэнсис Бэкон
Красота — это гармония
частей между собой и с целым.
Вернер Гейзенберг
Автору этих строк однажды представилась возможность спро-
спросить Генри Мура: как нужно смотреть скульптуру — на рас-
расстоянии или вблизи? Мур ответил, что работы величайших скуль-
скульпторов можно и даже должно смотреть с разных расстояний, ибо
из любого положения зрителю будут открываться новые грани
прекрасного. Мур привел в качестве примера скульптуры Микел-
анджело: от превосходных общих пропорций до тончайшей неж-
нежности ногтей. Так и в математическом совершенстве черных дыр,
изваянных ее величеством Природой, на всех уровнях обнаружи-
обнаруживается некоторое нарушение пропорций при полной гармонии
частей между собой и с целым.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатические деформации См. Ква-
Квазистационарные деформации
Бардина—Пресса—Тьюкольского не-
неравенство 98
Вариации пробные 324
— собственные 324
Гаррисона преобразования 284
Геодезические в метрике Керра 49
в экваториальной плоско-
плоскости 56
времениподобные 61, 88
изотропные 75
Гипотеза космической цензуры 100
Главные изотропные конгруэнции 78
Голая сингулярность 100
Горизонт Коши 43, 58
— событий 10, 43, 58
площадь поверхности 47
Групповая скорость 149
Диадный базис 252
Динамические уравнения 315
Дирака уравнения 259
Дифференцирование спиноров кова-
риантное 254
• внутреннее 254
Дуальности преобразования 302
Закон сохранения 134, 138
Израэля теорема 29
Интегралы движения 54, 71
Калибровочные степени свободы 157
Картера теорема 28, 320
Квазистационарные деформации 320
Керра—Шилда форма 32
Киллита вектор 10, 147
аксиальный 147
— конформный тензор 51
Клейна парадокс 275
Кольцевая сингулярность 37
Комплексные потенциалы 280
Конгруэнция изотропных геодезиче-
геодезических 35
Кососимметричная метрика 248
Коэффициент отражения 134, 230
— прохождения 134, 230
Лагранжиан 71
Леви-Чивиты символ 249
Лоренца преобразование 247
Мажумдара—Папапетру решение 304
Максвелловский скаляр 148, 292
Метрика в пространстве спиноров 248
— деформированной черной дыры 298
— Керра—Шилда 32
— Мажумдара—Папапетру 303
— сопряженная 8, 285
Начальных условий уравнения 315
Неприводимая масса 95, 99, 100
Несвязанные орбиты 67, 89
Обратимые процессы 100
Операция сопряжения 8, 285
Опускание спинорных индексов 249
Орбиты второго рода 59
— неустойчивые фотонные 68
— обратные 57
— первого рода 59
— переходные 68У 89
— последние устойчивые временипо-
времениподобные 68
— прямые 57

Предметный указатель
351
Папапетру форма 9
Паули спиновые матрицы 251
Пенроуза «правило пилы» 250
— процесс 46, 94, 100
Переходные орбиты 68, 89, 92
Поверхность стационарного предела 45
Поляризация 85
Правило соответствия 251
Преобразование сопряжения 9, 14
Призрачная калибровка 157
Принцип причинности 103
Пробные вариации 324
Робинсона леммы 24
— теорема 23
— тождество 28
Световой луч 85
Связанные орбиты 67, 89
«Скобочные» обозначения 165
Собственные вариации 324
Спиновые коэффициенты в диадном
формализме 255
Спинор 246, 248, 250 ^
— энергии-импульса 272
Старобинского постоянные 117, 161,
179
Суперрадиация 125, 137, 139, 143,
150, 227, 235, 272
Тетрадный базис 252
Точка бифуркации 320
Тьюкольского уравнения 112, 156
Тьюкольского—Старобинского тожде-
тождества 113, 159
Унимодуляр-ность 248
Уолда неравенство 96
Фазовая скорость 150
«Флаг» 252
Фотонная орбита 59
Хартля—Хокинга базис 240
формула 241
Хокинга теорема 100, 239
Эйлера преобразование 16
Эйнштейна уравнения 279, 236, 279
Элерса преобразования 284
Энергии-импульса тензор 145
спинор 272
Энергодоминангности условие 274
Эргосфера 45
Эрнста уравнение 16; 282, 284
матричное 285

ОГЛАВЛЕНИЕ
Глава 6. Метрика Керра
§ 51. Введение 5
§ 52. Уравнения для стационарного и аксиально-симметричного вакуум-
вакуумного пространства-времени 5
а. Сопряженные метрики 8
б. Преобразование Папапетру 9
§ 53. Выбор калибровки и приведение уравнений к стандартному виду 10
а. Некоторые свойства уравнений для X и Y 13
б. Альтернативные формы уравнений 14
в. Уравнение Эрнста 15
§ 54. Вывод метрики Керра 17
а. Тетрадные компоненты тензора Римана 20
§ 55. Единственность метрики Керра; теоремы Робинсона и Картера . . 22
§ 56. Описание пространства-времени Керра в формализме Ньюмена—
Пенроуза 29
§ 57. Метрика в форме Керра—Шилда 32
а. Приведение метрики Керра к форме Керра—Шилда 36
§ 58. Структура пространства-времени Керра 38
а. Эргосфера 45
Библиографические замечания 47
Глава 7. Геодезические в пространстве-времени Керра
§ 59. Введение 49
§ 60. Теоремы об интегралах геодезического движения в пространстве-
времени типа D по классификации Петрова 49
§ 61. Геодезические в экваториальной плоскости 56
а. Изотропные геодезические 58
б. Времениподобные геодезические 61
§ 62. Общее уравнение геодезических и разделение переменных в урав-
уравнении Гамильтона—Якоби 70
а. Разделение переменных в уравнении Гамильтона—Якоби и аль-
альтернативный вывод основных уравнений 72
§ 63. Изотропные геодезические 75
а. Движение по координате 9 76
б. Главные изотропные конгруэнции 78
в. Движение по координате г 78
г. Случай а— М 83
д. Изменение направления поляризации при движении вдоль изо-
изотропной геодезической 85
§ 64. Времениподобные геодезические 88
а. Движение по координате 9 88
б. Движение по координате г 90
§ 65. Процесс Пенроуза 92
а. Процесс, предложенный Пенроузом 94

Оглавление 353
б. Неравенство Уолда 96
в. Неравенство Бардина—Пресса—Тьюкольского 97
г. Обратимое извлечение энергии 99
§ 66. Геодезические в пространстве-времени Керра с а2 ;> М2 100
а. Изотропные геодезические 101
б. Времениподобные геодезические 102
в. Нарушение принципа причинности 103
Библиографические замечания 105
Глава 8. Электромагнитные волны в геометрии Керра
§ 67. Введение 108
§ 68. Определения и леммы 109
§ 69. Уравнения Максвелла: редукция и разделение переменных ... ПО
а. Редукция уравнений для Фо и Ф2 и разделение переменных 111
§ 70. Тождества Тьюкольского—Старобинского 112
§ 71. Завершение построения решения 118
а. Решение для функции </>А 118
б. Проверка тождества (80) 120
в. Решение для векторного потенциала 120
§ 72. Преобразование уравнения Тьюкольского к стандартному виду . . 122
а. Зависимость г* от г 124
§ 73. Общая теория преобразований и редукция к одномерному волно-
волновому уравнению 125
§ 74. Потенциальные барьеры для падающих электромагнитных волн . . 128
а. Связь между решениями Z(+a) и Z(~a) 130
б. Асимптотическое поведение решений 132
§ 75. Задача об отражении и прохождении волн 134
а. Случай о > ас (= — т/а) при а2 > 0 {34
б. Случай as<a<(Jc \ЗЬ
в. Случай 0 < a <as 13»
§ 76. Дальнейшее развитие теории и физическая интерпретация .... 141
а. Следствия условия унитарности 143
б. Прямое вычисление потока излучения на бесконечности и на
горизонте событий 144
в. Дальнейшее развитие теории 149
§ 77. Общие замечания 150
Библиографические замечания 151
Глава 9. Гравитационные возмущения керровской черной дыры
§ 78. Введение 153
§ 79. Редукция и расцепление уравнений для вейлевских скаляров 4V
fь fз и f4 154
§ 80. Выбор калибровки и решения для спиновых коэффициентов
х, а, X и v ' 157
а. Призрачная калибровка 157
§ 81. Тождества Тьюкольского—Старобинского 157
а. Сводка полезных формул 169
б. «Скобочные» обозначения 164
§ 82. Возмущения метрики; постановка задачи 165
а. Матричное представление возмущений базисных векторов . . . 166
б. Возмущения метрических коэффициентов 168
в. Сводка подлежащих определению величин, имеющихся для
этого уравнений и допустимого калибровочного произвола . . 169
§ 83. Линеаризация остальных тождеств Бианки 169
§ 84. Линеаризация коммутационных соотношений. Три системы урав-
уравнений 171

354 Оглавление
§ 85. Редукция системы I 174
§ 86. Редукция системы II; условия интегрируемости 176
§ 87. Решение условия интегрируемости 179
§ 88. Разделение переменных в функциях ? и 32 и ^ 184
а. Запись функций 31 и 9> через функции Тьюкольского .... 185
§ 89. Завершение редукции системы II и дифференциальные уравнения
для функций 31 и 9> 186
§ 90. Четыре линеаризованных тождества Риччи 189
§ 91. Решение уравнений B09) и B10) 191
а. Редукция уравнений B33)—B36) 194
б. Условия интегрируемости 196
§ 92. Явные решения для функций Zt и Z2 197
а. Преобразование решений для Zt и Z2 200
б. Дальнейшие следствия из уравнений B11) и B12) 201
§ 93. Завершение решения 202
§ 94. Интегральные тождества 204
а-. Другие тождества, получаемые из условия интегрируемости
B63) 205
§ 95. Ретроспектива 213
§ 96. Вид решения в шварцшильдовом пределе а ->¦ 0 216
§ 97. Теория преобразований и потенциальные барьеры для падающих
гравитационных волн 218
а. Явный вид решений 219
б. Функции Z(+CT) и Z(~a) 221
в. Структура потенциалов 222
г. Соотношения между решениями, относящимися к различным
потенциалам 227
д. Асимптотическое поведение решений 229
§ 98. Задача об отражении и прохождении волн 229
а. Выражения для R и Т через решения уравнений Тьюколь-
Тьюкольского с заданными граничными условиями 232
б. Прямое вычисление потока излучения на бесконечности . . . 235
в. Поток энергии через горизонт событий 238
г. Формула Хартля—Хокинга 241
§ 99. Квазинормальные моды керровской черной дыры 243
§ 100. Последние замечания 244
Библиографические замечания 244
Глава 10. Частицы спина 1/2 в геометрии Керра
§ 101. Введение 246
§ 102. Спинорный анализ и спинорный базис в формализме Ньюмена—
Пенроуза 246
а. Спинорное представление векторов и тензоров ........ 250
б. Наглядное представление спинора ? в виде «флага» .... 251
в. Диадный формализм 252
г. Ковариантная производная спинорных полей и спиновые коэф-
коэффициенты 254
§ 103. Уравнение Дирака в формализме Ньюмена—Пенроуза 258
§ 104. Уравнение Дирака в геометрии Керра; разделение переменных 259
§ 105. Нейтринные волны в геометрии Керра 261
а. Задача об отражении и прохождении в случае о > os
(= _ aml2Mr+) 262
б. Отсутствие суперрадиации @ < а < о$) 264
§ 106. Сохраняющийся ток и сведение уравнений Дирака к одномерным
волновым уравнениям 266
а. Приведение уравнений Дирака к одномерным волновым урав-
уравнениям 267

Оглавление 355
б. Разделение переменных в уравнениях Дирака в сплюснутых
сфероидальных координатах в плоском пространстве 269
§ 107. Задача об отражении и прохождении волн 270
а. Постоянство вронскиана [Z±, Z*±] в интервале г+ < г < оо 271
б. Положительность потока энергии через горизонт событий . . . 272
в. Квантовая природа отсутствия суперрадиации 274
Библиографические замечания 275
Глава 11. Другие решения, альтернативные методы
§ 108. Введение 277
§ 109. Уравнения Эйнштейна—Максвелла для стационарных аксиально-
симметричных пространственно-временных многообразий 278
а. Выбор калибровки и приведение уравнений к стандартному
виду 280
б. Дальнейшее преобразование уравнений 281
в. Уравнения- Эрнста 282
г. Трансформационные свойства уравнений Эрнста 284
д. Операция сопряжения 285
§ ПО. Решение Керра—Ньюмена: вывод решения и описание его в фор-
формализме Ньюмена—Пенроуза 286
а. Описание пространства-времени Керра—Ньюмена в формализме
Ньюмена—Пенроуза 291
§ 111. Уравнения для взаимодействующих электромагнитно-гравитацион-
электромагнитно-гравитационных возмущений пространства-времени Керра—Ньюмена .... 293
§ 112. Решения, описывающие статические черные дыры 295
а. Условие равновесия черной дыры 298
§ 113. Решение уравнений Эйнштейна—Максвелла, описывающее семей-
семейство черных дыр 300
а. Преобразование уравнений поля 302
б. Решение Мажумдара—Папапетру 303
в. Решение, описывающее семейство черных дыр 304
§ 114. Вариационный метод и устойчивость решений для черных дыр . . 308
а. Линеаризация уравнений поля около стационарных решений;
уравнения начальных условий 314
б. Тождества Бианки 317
в. Линеаризация остальных уравнений поля 319
г. Уравнения, описывающие квазистационарные деформации;
теорема Картера 320
д. Вариационная формулировка задачи о возмущениях 324
Библиографические замечания 332
Приложение. Таблицы функций Тьюкольского и связанных с ними
функций 335
Библиографические замечания 336
Эпилог 349
Предметный указатель 350