Линейное программирование, его применения и обобщения - Данциг Дж.

Автор: Данциг Дж.

Теги: программирование линейное программирование

Год: 1966

Похожие

Математическое программирование и электрические цепи

Прикладные задачи динамического программирования

Неравенства

Нелинейное и динамическое программирование

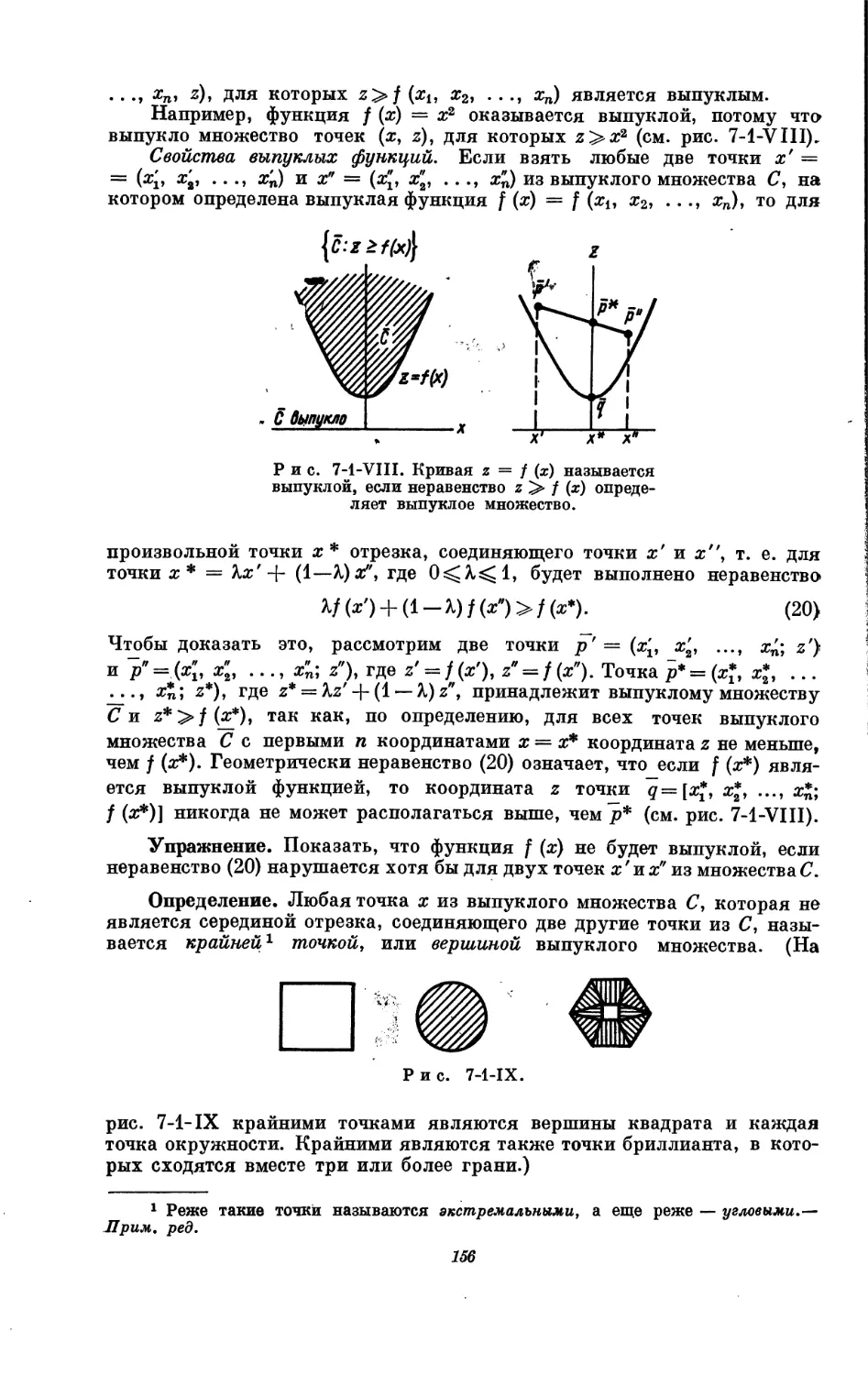
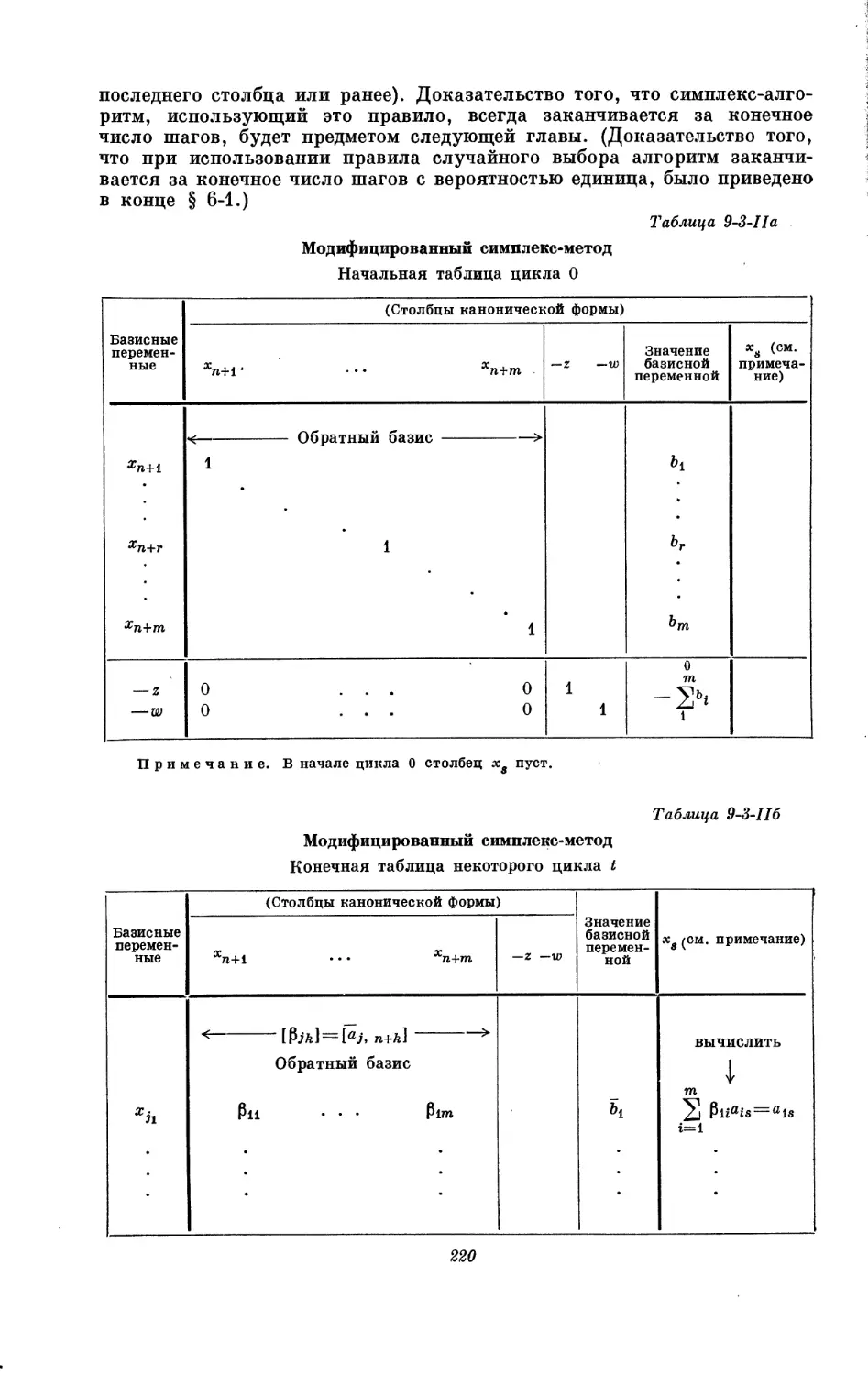
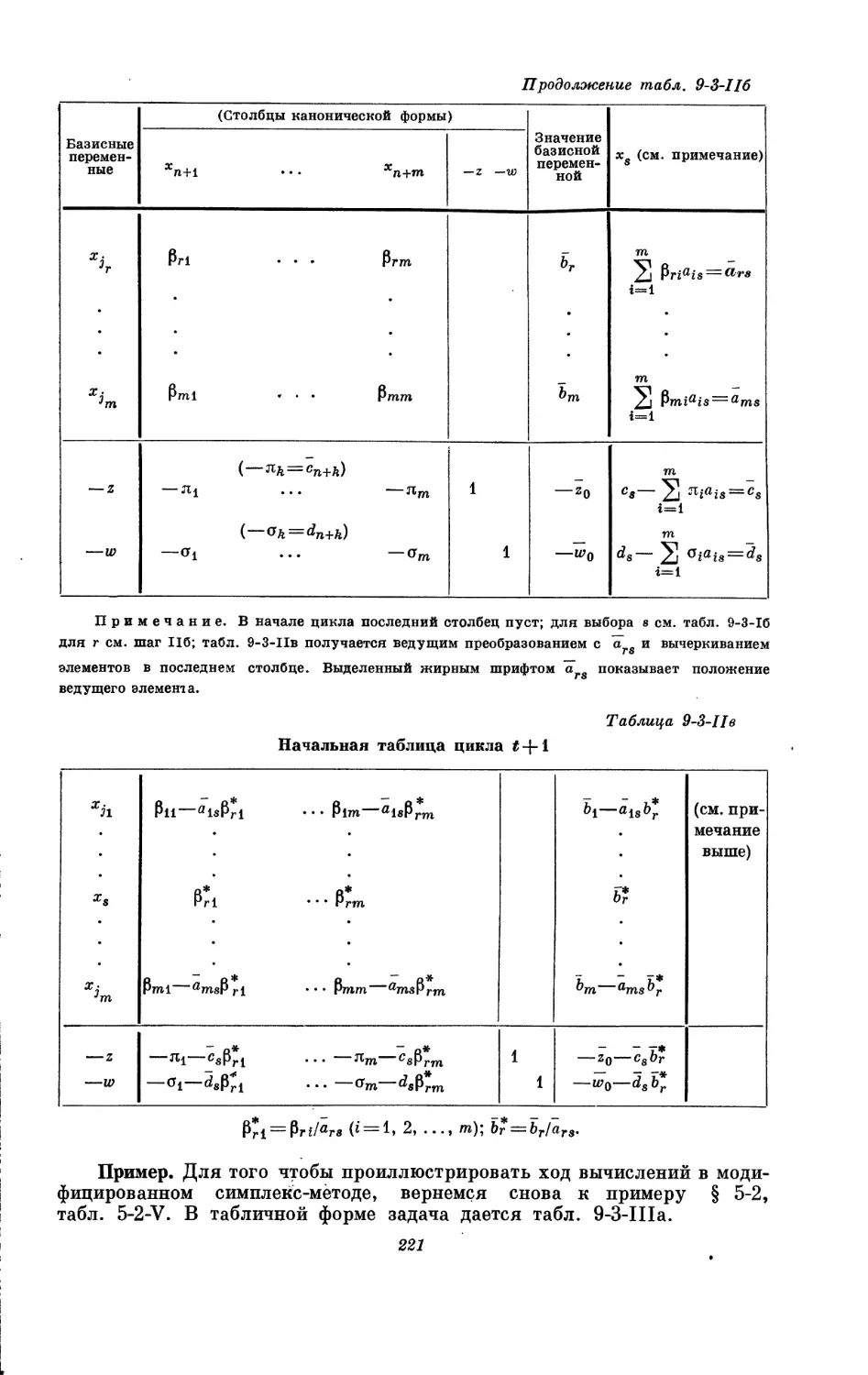
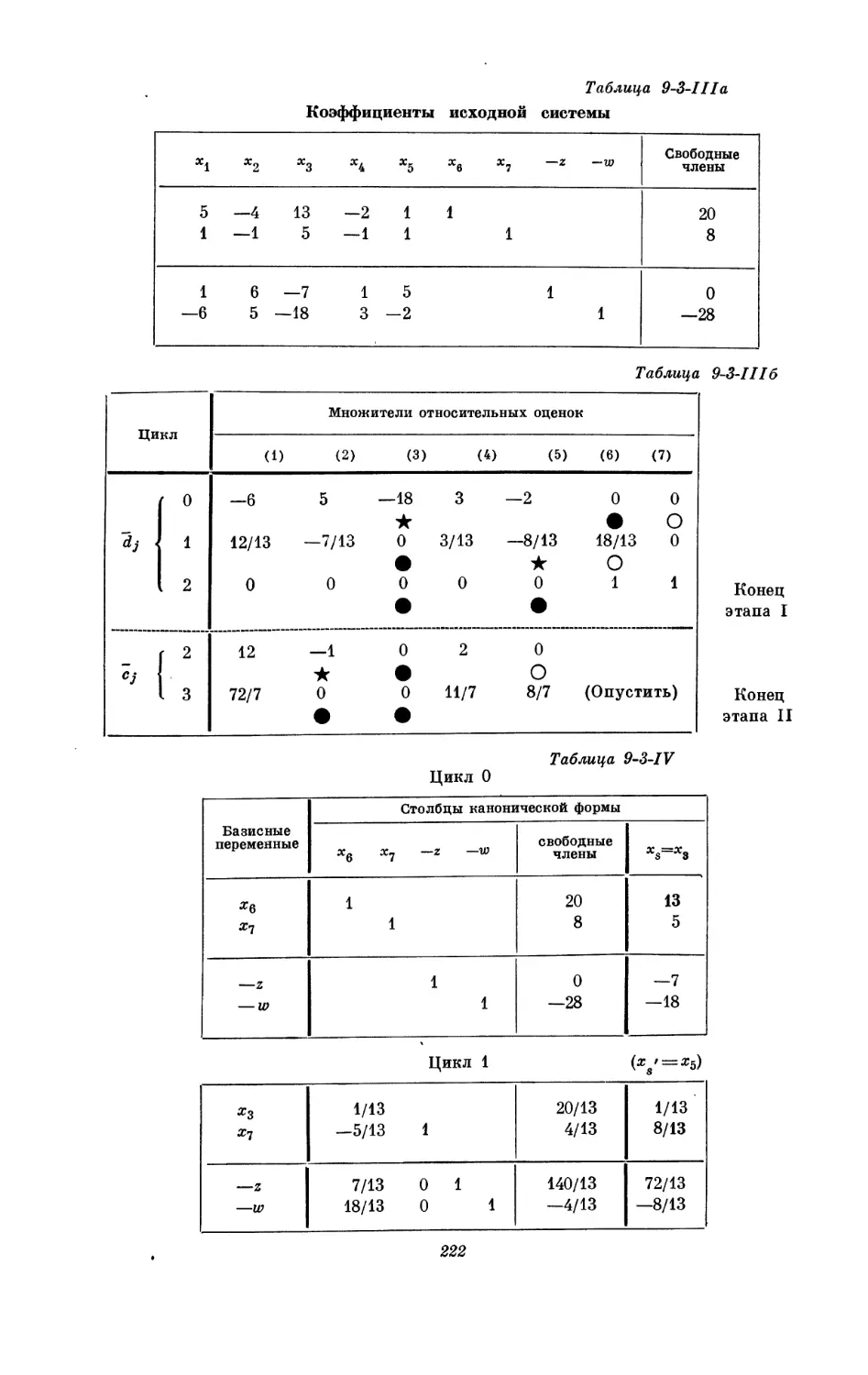
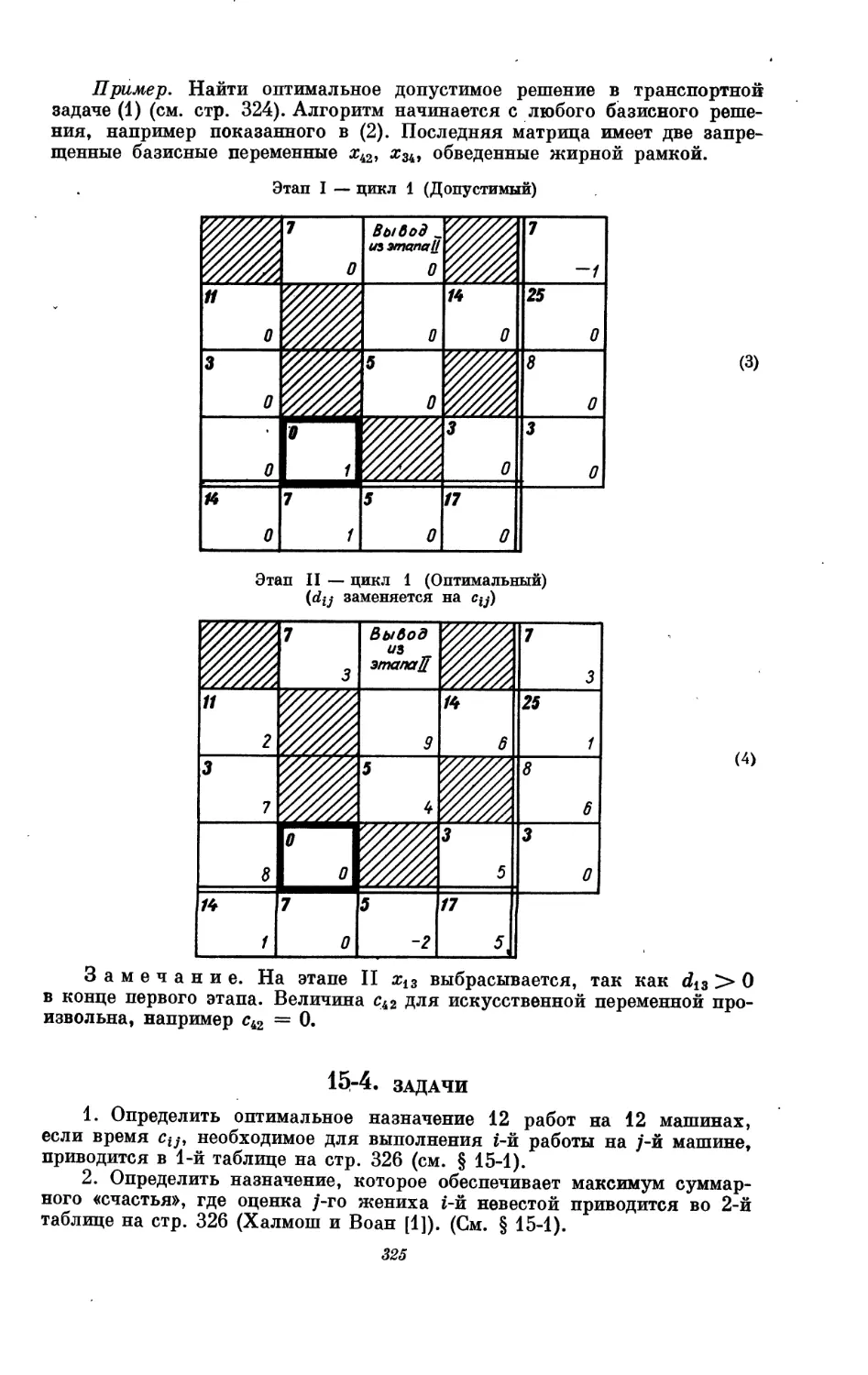
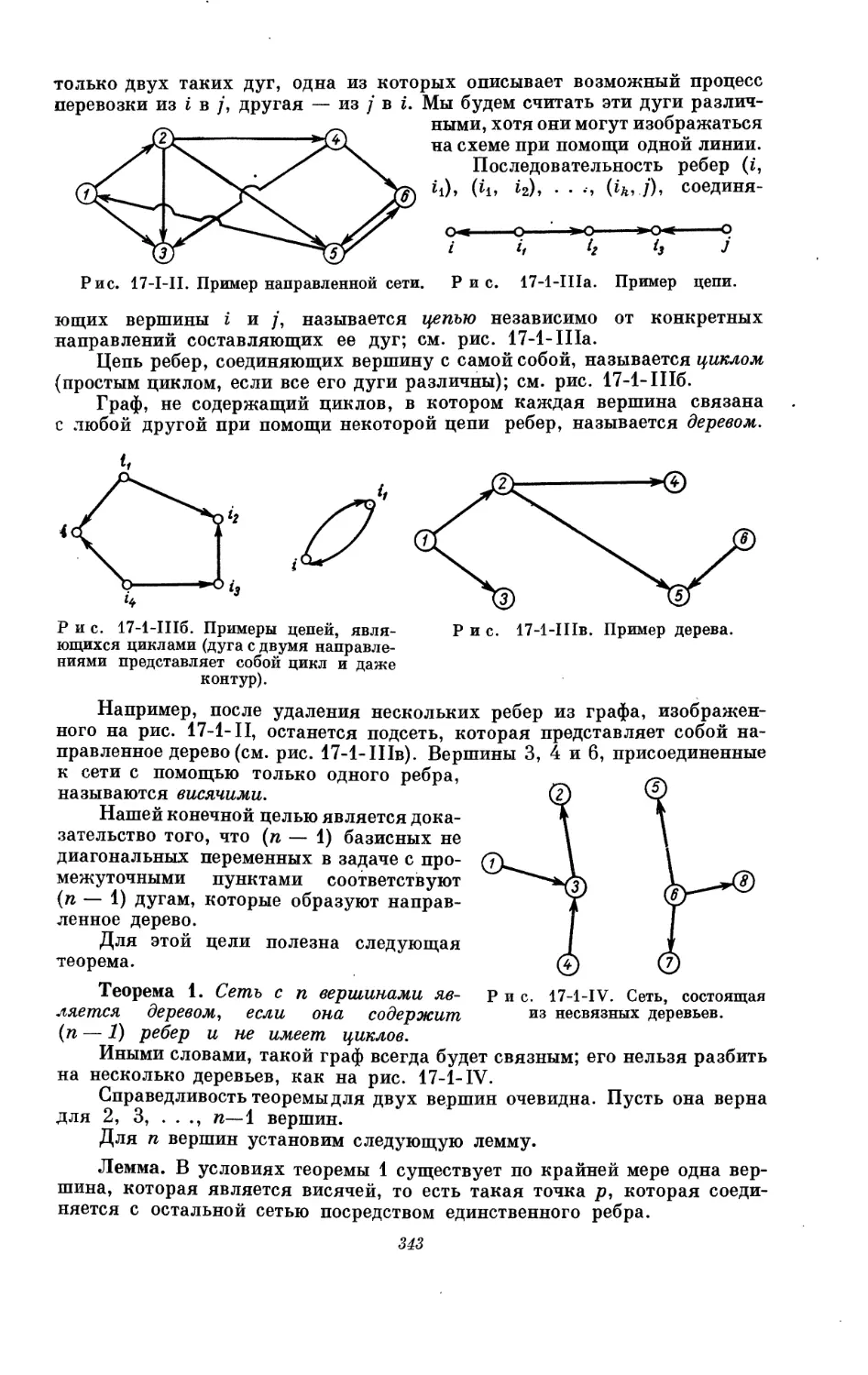
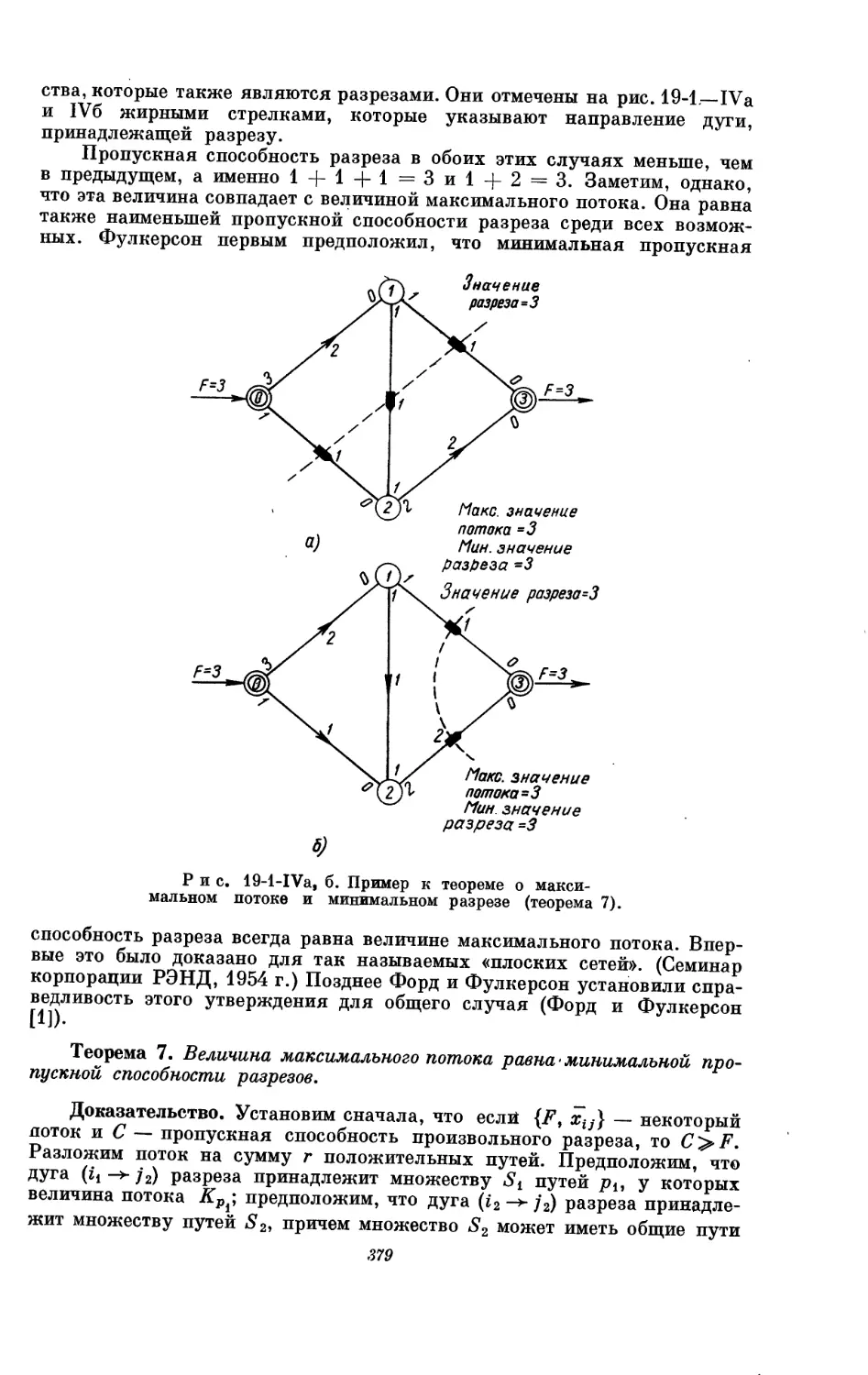
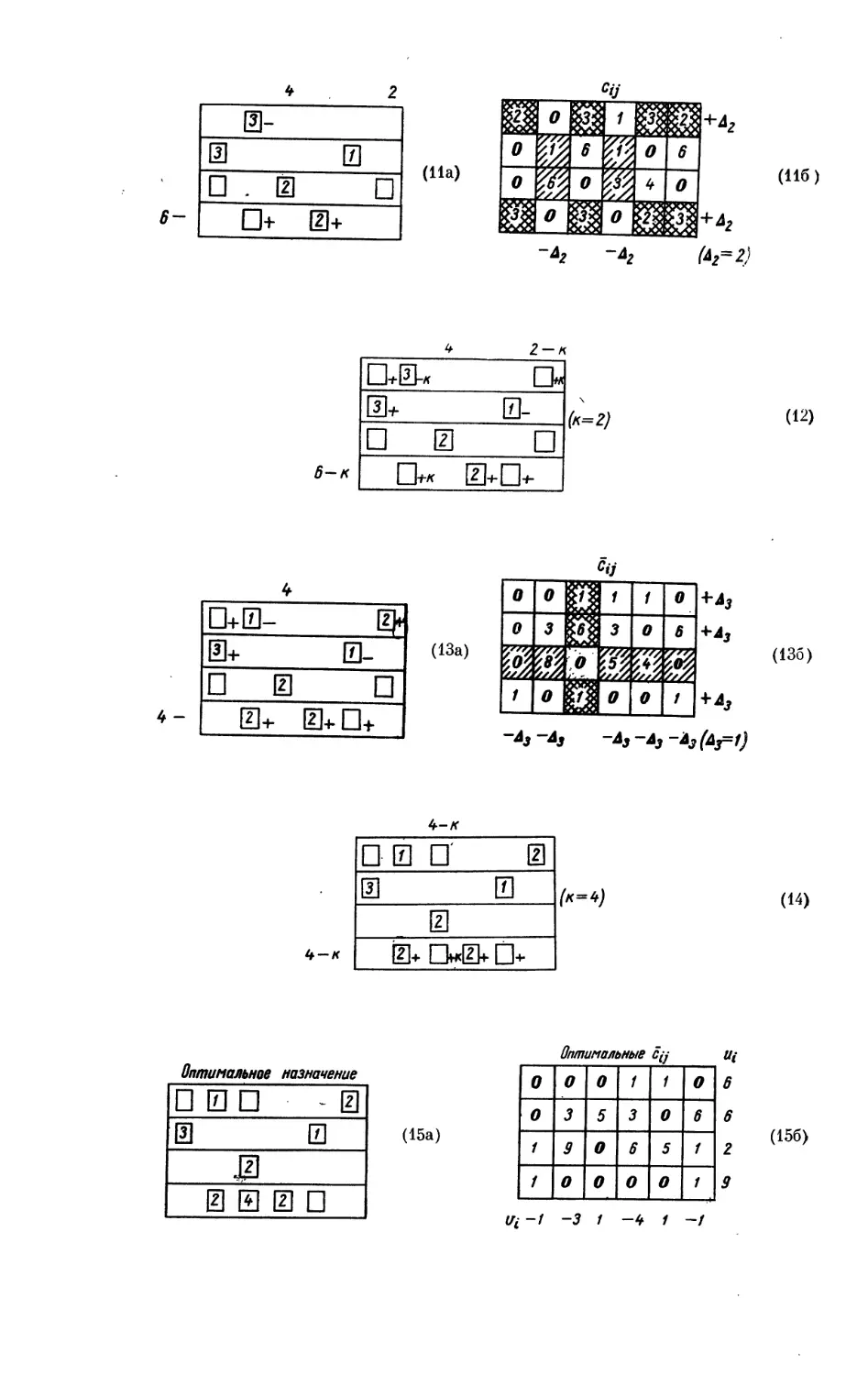
Текст

Линейное
программирование
его обобщения
и применения

□ш
LINEAR
PROGRAMMING AND
EXTENSIONS
ВУ GEORGE B. DANTZIG
The Rand Corporation
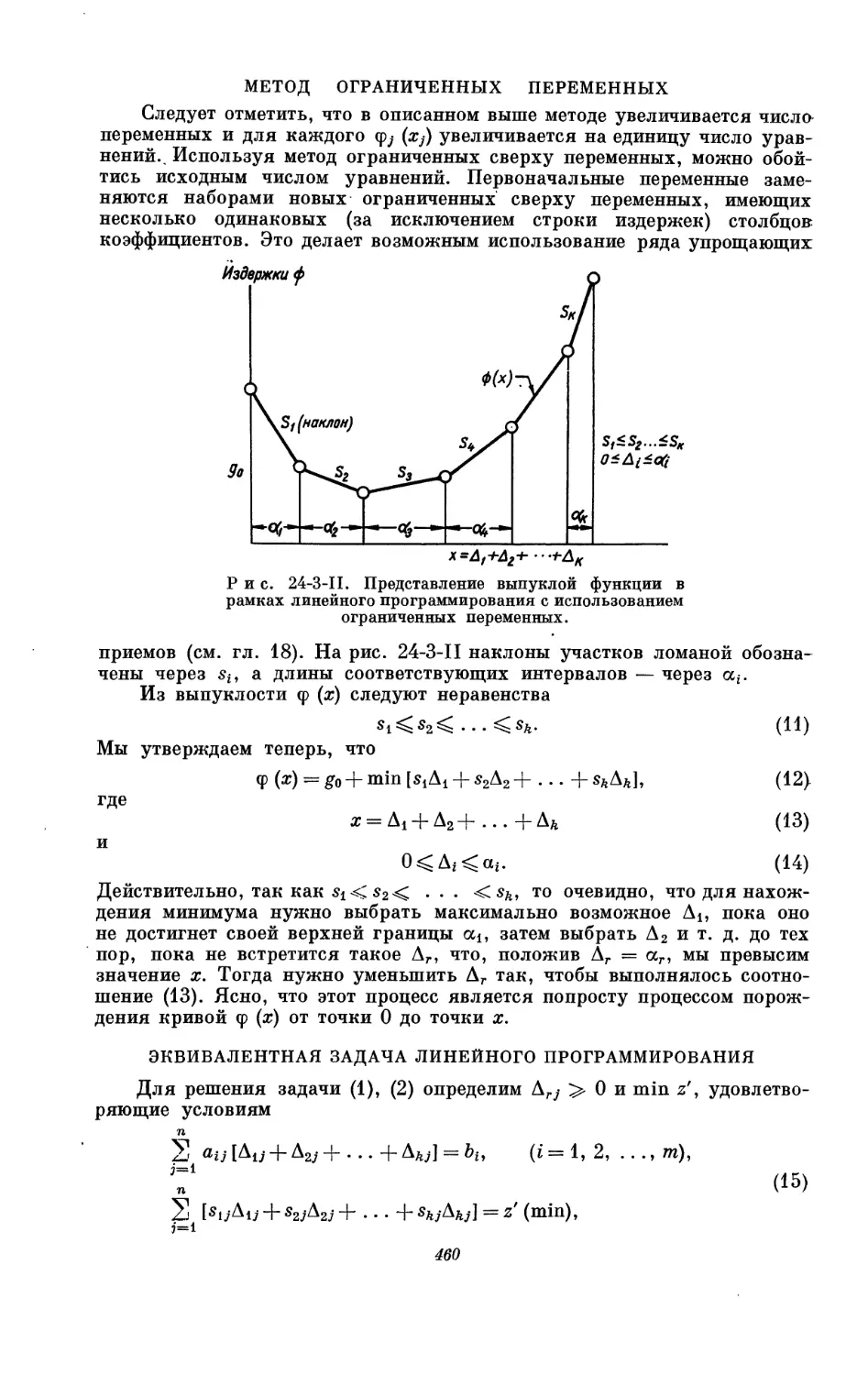
and
University of California, Berkeley
1963
PRINCETON UNIVERSITY PRESS
PRINCETON, NEW JERSEY
ДЖ. ДАНЦИГ
ЛИНЕЙНОЕ
ПРОГРАММИРОВАНИЕ
ЕГО ПРИМЕНЕНИЯ
И ОБОБЩЕНИЯ
ПЕРЕВОД С АНГЛИЙСКОГО
Г. Н. АНДРИАНОВА, Л. И. ГОРЬКОВА,
А. А. КОРБУТА, А. Н. ЛЯПУНОВА
ОБЩАЯ РЕДАКЦИЯ И ПРЕДИСЛОВИЕ
Н. Н. ВОРОБЬЕВА
ИЗДАТЕЛЬСТВО «ПРОГРЕСС»
МОСКВА 1966
Дж. Данциг
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ, ЕГО ПРИМЕНЕНИЯ И ОБОБЩЕНИЯ
Редактор Ф. Окунева
Художник М. Шлосберг Художественный редактор Л. Шканов
Технический редактор Л. Харьковская
Сдано в производство 11/VIII 1965 г. Подписано к печати 29/III 1966 г. Бумага № 1-70 х
Х1081/1б=19 бум. л. 52,5 печ. л. Уч.-изд. л. 42,12. Изд. № 8/4872. Цена 2 р. 78 к. Зак. 1258
Издательство «Прогресс» Комитета по печати
при Совете Министров СССР
Москва Г-21, Зубовский бульвар, 21
Московская типография № 16 Главполиграфпрома Комитета по печати
при Совете Министров СССР
Москва, Трехпрудный пер., 9
1-8-3, 2-2-3
568—65
Редакция литературы по экономике
П реди словие
Работавший над переводом книги коллектив
посвящает свой труд светлой памяти
Василия Сергеевича Немчинова
В январе 1964 г. на заседании одной из многочисленных ныне кон-
ференций по применениям математики в экономике пишущему эти строки
была передана записка: «В Ленинграде не предпринято ли издание пере-
вода новой книги Данцига, вышедшей в 1963 г.? Очень хорошая книга,
и ее следовало бы перевести. В. Немчинов». В дальнейшем Василий Серге-
евич решительно поддержал предложение об издании русского перевода
этой монографии и даже согласился написать к нему предисловие, в ко-
тором предполагал сказать, какой «хорошей, нужной и полезной» является
эта книга. Еще в середине октября Василий Сергеевич обсуждал вопросы,
относящиеся к книге Данцига, а 5 ноября его не стало. Перевод остался
без задуманного предисловия.
С данной В. С. Немчиновым общей оценкой предлагаемой советскому
читателю книги Дж. Данцига нельзя не согласиться. К этой оценке оста-
ется добавить лишь некоторые фактические сведения об авторе книги и об
ее содержании.
Дж. Б. Данциг является видным американским математиком. На
Западе Данцига считают основоположником линейного программирова-
ния, так как развитие этой дисциплины в США фактически началось с раз-
работки им в конце 40-х годов знаменитого симплекс-метода для числен-
ного решения основной задачи линейного программирования.
Монография Данцига удачно сочетает в себе предельно элементарное
изложение основных, исходных вопросов линейного программирования,
которое .будет доступно даже совсем неискушенному в математике чита-
телю, с главами, посвященными таким глубоким и математически тонким
теориям, как принцип разложения или дискретное (целочисленное) про-
граммирование. Эту книгу можно, с известным основанием, считать своего
рода энциклопедией линейного программирования, в которой содержится
в той или иной форме описание большинства основных вопросов, относя-
щихся к этой дисциплине. Разумеется, как и в любой другой энциклопе-
дии, изложение каждого из вопросов неизбежно оказывается недостаточно
полным. Поэтому читатель, желающий получить более исчерпывающую
информацию о каком-нибудь конкретном вопросе, должен будет обра-
титься к библиографии, составленной автором очень обстоятельно. К сожа-
лению, приведенные автором источники относятся самое позднее к 1960 г.
В связи с этим из его указателя не могли не выпасть все последние иссле-
дования, и, в частности, большое число работ советских математиков. Для
того чтобы хотя бы отчасти восполнить этот пробел, библиография, при-
веденная в книге Данцига, дополнена перечнем важнейших работ, появив-
шихся за последние годы в области линейного программирования. При
этом особое внимание было уделено работам отечественных авторов.
Кроме того, отдельные ссылки Данцига на труднодоступные ведомствен-
ные издания заменены ссылками на более распространенные издания этих
5
же работ. Но, разумеется, и в таком виде библиография не может пре-
тендовать на абсолютную полноту.
Книга Данцига весьма убедительно рассеивает разделяемые еще
отдельными математиками предрассудки об узости линейного программи-
рования как математической дисциплины (в крайнем своем проявлении
эта точка зрения отождествляет все линейное программирование с симплекс-
методом решения стандартной задачи!).
Проблемы линейного программирования (как и вообще большинство
проблем исследования операций) неотделимы от своих вычислительных
аспектов. Поэтому автор снабжает книгу большим количеством примеров,
которые иногда носят иллюстративный характер, а часто являются даже
формой изложения материала. Правда, здесь необходимо отметить, что
автор совершенно не касается вопросов использования современной вычис-
лительной техники для решения задач линейного программирования,
хотя решение многих из этих задач стало практически осуществимо только
в результате огромных достижений в области электронных вычислитель-
ных машин. Однако в его оправдание можно сказать, что достаточно под-
робное освещение еще и этой стороны вопроса потребовало бы сущест-
венного увеличения и без того немалого объема книги.
Монография может быть использована как учебник или как учебное
пособие. С этой точки зрения большую ценность представляют задачи,
приводимые автором в конце каждой главы. Эти задачи отличаются весьма
различной степенью сложности: начиная от методических «вопросов для
повторения» и кончая весьма трудными и даже вообще еще пока нерешен-
ными задачами.
Изучая изложенный в книге материал и решая помещенные в ней зада-
чи, читатель сможет квалифицированно и даже в известной мере творчески
овладеть методикой рассуждений и расчетов, применяемых при линейном
программировании. Важная особенность монографии, выгодно отличаю-
щая ее от. других изданий подобного рода и состоящая в широте охвата
научного материала, позволит использовать ее в качестве основы для
обучения по программам, весьма отличающимся друг от друга как по
объему, так и по профилю.
В частности, в этой монографии собраны математические модели,
которые могут оказаться полезными при применении математики к тех-
нико-экономическим проблемам. Однако ни это обстоятельство, ни нали-
чие в ней глав более конкретного экономического содержания не дают еще
основания рассматривать ее в целом как книгу по приложениям матема-
тики к экономике. Те «конкретные» примеры, которые в книге встречают-
ся, носят большей частью условный, «заданный» характер.
Перевод книги выполнили Г. Н. Андрианов (главы 1, 2, 4 и 27),
Л. И. Горьков (главы 5—7 и 18—23), А. А. Корбут (предисловие автора,
главы 14—17 и 24—26) и А. Н. Ляпунов (главы 3, 8—13 и 28). Работа по
составлению указателя и библиографии выполнена В. В. Вишняковой х.
Н. Н. Воробьев
1 Основой для библиографических справок в пределах монографии является
общий указатель литературы, помещенный в конце книги, в котором библиографи-
ческие перечни расположены в алфавитном порядке авторов, а для статей каждо-
го автора или авторского коллектива — хронологически, со сквозной нумерацией по
всем годам опубликования. В отдельный список выделены все сборники статей.
Приводимые автором в конце каждой главы библиографические списки для удоб-
ства пользования ими собраны все вместе и помещены непосредственно после об-
щего алфавитного указателя.
От автора1
Решающим критерием при оценке той или иной теории является
ее способность решать те проблемы, которые послужили исходным толчком
для ее развития.
Эта книга посвящена теории систем линейных неравенств и их реше-
нию. На первый взгляд эта область должна была бы представлять такой
же интерес для математиков, как и ее частный случай — системы линейных
уравнений. Странным является, однако, тот факт, что до 1947 г. теории
линейных неравенств было посвящено лишь несколько не связанных
друг с другом статей, в то время как по линейным уравнениям, а также
близким к ним вопросам линейной алгебры и теории приближений была
выпущена обширнейшая литература. По-видимому, этот несоразмерный
интерес к теории линейных уравнений вызывался (в большей степени,
чем это могли бы признать сами математики) той большой ролью, которую
она играет в теориях, занимающихся познанием физического мира.
Однако начиная с 1947 г. появились тысячи работ, посвященных
проблемам выбора одного из возможных образов действий. Вряд ли можно
сомневаться в том, что использование математических моделей в принятии
решений стало привлекать к себе такое внимание именно благодаря проис-
ходившему одновременно развитию электронных вычислительных машин.
Не удивительно поэтому, что область принятия решений стала — подобно
тому, как это уже произошло с физикой, — важным источником математи-
ческих проблем.
Если задача принятия решения требует минимизации линейной формы
при наличии ограничений в виде линейных неравенств, то она называется
задачей линейного программирования. Ее анализ путем естественного
обобщения делает возможным исследование задачи минимизации выпуклой
функции, переменные которой должны удовлетворять некоторой системе
выпуклых ограничений в виде неравенств. Эту модель можно использо-
вать для изучения топологических и комбинаторных задач, которые могут
быть сформулированы в виде системы линейных неравенств относительно
1 Предисловие автора приведено в сокращенном виде.
7
переменных, принимающих дискретные значения. Она создает основу для
обобщения многих задач математической статистики. Таков вкратце
круг математических вопросов, охватываемых этой книгой.
В целях детального обоснования первые три главы посвящены основ-
ным понятиям, происхождению и постановке задач линейного програм-
мирования. Для освещения вопросов применений теории к реальным ситу-
ациям книга завершается двумя главами, посвященными применениям
линейного программирования.
Эта книга основана на конструктивном рассмотрении исследуемых
проблем. Она отражает начальную стадию развития теории, достаточно
могущественной для того, чтобы справиться с теми трудностями, которые
возникают при решении задач, лежащих в основе этой теории.
Настоящее исследование было предпринято Корпорацией РЭНД1 как
часть программы исследований для Военно-воздушных сил США.
Джордж Б. Данциг
Корпорация РЭНД
1 Корпорация РЭНД (RAND — Research and Development) — одна из крупней-
ших научных корпораций США, занимающаяся разработкой математических проб-
лем исследования операций для нужд военного дела, экономики и других при-
кладных областей. — Прим. ред.
Глава 1
ПОНЯТИЕ О ЛИНЕЙНОМ
ПРОГРАММИРОВАНИИ
1-1. ВВЕДЕНИЕ
Летом 1949 г. в Чикагском университете состоялась конференция,
организованная комиссией Коулса по экономическим исследованиям; мате-
матики, экономисты и статистики из научных институтов и различных
правительственных учреждений представили исследования по использо-
ванию аппарата линейного программирования. Диапазон рассмотренных
вопросов простирался от планирования севооборота до планирования круп-
ных военных операций, от составления маршрутов кораблей между
портами до оценки потока товаров между отраслями экономики. Самым
удивительным было то, что исследования, о которых сообщалось на конфе-
ренции, были выполнены в течение двух предшествовавших конференции
лет. (См. библиографию, Купманс [2].)
В годы второй мировой войны и в послевоенный период работа над
этими и аналогичными задачами проводилась разобщенно до тех пор, пока
в 1947 г. линейное программирование не объединило внешне разнообраз-
ные явления, обеспечив их, для более точной формулировки задач и опре-
деления более эффективных путей их решения, математической базой
и вычислительным методом, симплекс-алгоритмом. Эти разработки совпа-
ли по времени с созданием электронных вычислительных машин, которые
быстро стали необходимым инструментом для применения линейного про-
граммирования в тех областях, где вычисления вручную оказывались
невозможными.
Наша непосредственная цель состоит в определении математического
программирования вообще и линейного программирования в частности,
в рассмотрении нескольких типичных задач и тех их характеристических
черт, которые позволяют осуществлять решение этих задач с использова-
нием моделей линейного программирования. Далее, в этой же главе мы
рассмотрим отношение линейного программирования к математическому
программированию вообще, а также место математического програм-
мирования в тот век автоматизации, к которому мы приближаемся.
1-2. ЗАДАЧА ПРОГРАММИРОВАНИЯ
Промышленное производство, поток ресурсов в экономике, напряже-
ние сил на театре военных действий — все это комплексы многочисленных
взаимосвязанных процессов. Различия здесь могут иметь место лишь в це-
лях, которые должны быть осуществлены в природе рассматриваемых про-
цессов и в объеме необходимых усилий. Тем не менее в управлении этими
совершенно различными явлениями, или, как далее будет говориться,
системами, можно выделить существенные черты сходства. Для этого необ-
ходимо уяснить структуру и состояние системы, а также цель, которая
9
должна быть достигнута; это нужно для перечисления действий, которые
необходимо выполнить, их распределения во времени и их количественных
характеристик (то, что называется «программой», или «графиком»), что
позволит системе перейти от заданного состояния к определенной цели.
Если в исследуемой системе обнаруживается структура, которая
может быть математически описана (это описание называется математи-
ческой моделью) и если цель может быть также количественно выражена,
то в этом случае можно использовать тот или иной вычислительный метод
для выбора из всех возможных альтернатив лучшего плана действий.
Такое использование математических моделей и называется математи-
ческим программированием. Установление того, что многие военные, эконо-
мические и производственные задачи могут быть математически описаны
(хотя бы приближенно) системами линейных неравенств и уравнений \
содействовало интенсивному развитию линейного программирования.
Следующие три примера являются типичными задачами программи-
рования, поддающимися линейной формулировке; они аналогичны зада-
чам, решенным в ранних исследованиях в данной области (Вуд и Данциг
[1]; Данциг [1], [2]).
Представляется полезным освоить эти примеры, прежде чем перейти
к рассмотрению общих задач линейного программирования.
В системах, рассматриваемых в каждом из трех примеров, цель со-
стоит в минимизации полных затрат, выраженных в денежных единицах.
Однако в других приложениях целью может быть или минимизация тру-
довых затрат, или максимизация числа собранных деталей, или максими-
зация количества обученных студентов при заданном распределении их по
квалификациям и т. д.
1. Пример из области консервного производства. Предположим,
что в Портленде (штат Мэн), Сиэтле и Сан-Диего находятся три консерв-
ных завода. Эти консервные заводы могут производить соответственно 250,
500 и 750 ящиков консервов за день. Для реализации продукции в стране
имеется пять складов оптовой торговли: в Нью-Йорке, Чикаго, Канзас-
Сити, Далласе и Сан-Франциско. Каждый склад может продать 300 ящи-
ков за день. Специалист, занятый распределением продукции, хочет
определить число ящиков, которое должно быть доставлено от трех кон-
сервных заводов к пяти сбытовым складам так, чтобы каждый склад смог
бы получить столько ящиков, сколько может продать ежедневно, а полные
транспортные издержки были бы минимальными.
В задаче имеется 15 возможных процессов по доставке ящиков от каж-
дого завода к каждому складу (рис. 1-2-1). Тем самым имеется 15 неиз-
вестных интенсивностей процессов (которые подлежат определению),
выражающих количества грузов, которые должны быть перевезены по этим
15 путям. Такое распределение перевозок обычно называется программой.
Имеется ряд ограничений, которым должен удовлетворить допустимый
план перевозок, а именно: согласно плану, каждый склад оптовой торговли
получит требуемое количество ящиков и каждый завод отправит ящиков
не больше того, что он может произвести за день. (Заметим, что имеется
одно ограничение для каждого склада и одно — для каждого консервного
завода.) Может существовать несколько допустимых планов перевозок,
1 Читателю следует обратить внимание на то, что мы пользуемся словом нера-
венство. Системы линейных неравенств являются весьма общими; выражаемые линей-
ными неравенствами связи вида а; > 0, х + у <7 могут быть использованы для опи-
сания различных общих ограничений, таких, например, как то, что количество
закупок х не должно быть отрицательным, или то, что полное количество закупок
х + у не должно превосходить 7, и т. д.
10
которые будут удовлетворять этим ограничениям, но некоторые из них
будут требовать больших транспортных расходов, чем другие. Наша
задача состоит поэтому в определении такого плана перевозок, называемо-
го оптимальным, который связан с наименьшими расходами. Транспорт-
Р и с. 1-2-1. Задача: найти план доставки консервных ящиков к скла-
дам с минимальными издержками (стоимость транспортировки каждого
ящика, наличие и потребность в продукции указаны на схеме).
ная задача такого типа сформулирована математически в § 3-3, а свойства
ее решения описаны в главах 14—20.
2. Задача домашней хозяйки. Семья из пяти человек живет на скром-
ную заработную плату главы семьи. Постоянной задачей является опре-
деление еженедельного меню после надлежащего рассмотрения потребно-
стей и вкусов семьи и цен на продукты. Муж должен получать 3000 кало-
рий в день, жена — 1500 калорий (диета для похудания), а детям требуется
соответственно 3000, 2700 и 2500 калорий в день. Согласно предписанию
домашнего врача, эти калории должны быть получены каждым членом
семьи в результате употребления ограниченного сверху количества жиров
и углеводов и ограниченного снизу количества белков. В указанной диете
особое значение имеют белки. Помимо этого, каждый член семьи должен
удовлетворять свои ежедневные потребности в витаминах. Задача заклю-
чается в том, чтобы, исходя из цен на продукты в четверг, составить недель-
ное меню, минимизирующее издержки.
Эта задача является типичной задачей линейного программирования:
допустимые процессы состоят в покупке продуктов различных видов;
программой является количество различных продуктов, которые могут
быть куплены; ограничениями в задаче являются потребности членов
семьи в калориях и витаминах, а также предписанные врачом верхние
и нижние пределы количеств углеводов, белков и жиров, которые могут
потребляться каждым из членов семьи. Количество пищевых комбинаций,
удовлетворяющих этим ограничениям, велико. Однако некоторые из этих
допустимых планов связаны с более высокими затратами, чем другие.
Задача состоит в нахождении комбинации, имеющей минимальную полную
стоимость1 (Штиглер [1]). Задачи на смешения такого типа, как эта,
сформулированы в § 3-4.
1 В гл. 27 дается подробное объяснение типичной задачи питания. Читатель
может быть удивлен, почему эта задача по существу является единой, а не состо-
11
Рис. 1-2-11. Задача: определить про-
грамму найма, производства и обучения,
удовлетворяющую требуемым условиям и
минимизирующую издержки.
3. Обучение в процессе работы. Промышленное предприятие заключает
договор на выпуск некоторой продукции. Предприятие располагает суще-
ственно меньшим количеством рабочей силы, чем это необходимо для
выпуска некоторого товара в пределах, предусмотренных выработанным
планом на несколько недель вперед. В связи с этим требуется нанять
дополнительное количество рабочих, обучить их и использовать на работе.
Имеющаяся на предприятии рабочая сила может быть использована либо
для производства определенного объема продукции, либо для обучения
на рабочих местах определенного количества новых рабочих, либо для
выполнения одновременно обоих этих видов работ в условиях заданного
соотношения между выработкой
одного рабочего и числом обучае-
мых им новичков. Даже при назна-
чении всей бригады на обучение
новых рабочих в течение полной
недели она не была бы в состоянии
обучить требуемое количество. На
следующей неделе данная бригада
вместе с вновь обученными рабо-
чими может или работать, или обу-
чать вновь принятых рабочих, или
одновременно работать и обучать
и т. д. Продукция относится к раз-
ряду скоропортящихся; поэтому
при хранении ранее произведенной
продукции придется нести опре-
деленные затраты. Задача заклю-
чается в определении программы
найма рабочих, выпуска продук-
ции и хранения, которая обеспечи-
вает минимум полных издержек.
Это также задача линейного
программирования, хотя и отли-
чающаяся от двух ранее приведен-
ных примеров. Ее можно назвать
задачей на планирование работы
во времени. Процессами в этой задаче является использование имею-
щихся квалифицированных рабочих в двух направлениях: для выпуска
продукции или для обучения новых рабочих, а также прием новых
рабочих каждую неделю. Интенсивности этих процессов ограничены
числом рабочих, имеющихся в начале каждой недели, и отношением числа
инструкторов к числу обучаемых. Суммарный выпуск продукции, произ-
веденной всеми рабочими за договорный период, должен быть не меньше,
чем требуемый объем. Одна из возможных программ производства и обуче-
ния изображена на рис. 1-2-П. Теперь задача может быть сформулирована
более точно: определить соотношение между числом нанятых и обучаемых
рабочих, между числом инструкторов и числом рабочих, занятых на произ-
водстве, между размерами пере- и недопроизводства продукции, с тем
чтобы минимизировать полные затраты.
Математическая формулировка этой задачи может быть найдена
в § 3-7.
ит из пяти отдельных задач для каждого члена семьи. Дело здесь в том, что некоторые
продукты (такие, как яйца, молоко, мясо) могут быть подразделены на части, отличные
по содержанию жира и выдаваемые различным членам семьи.
12
1-3. ОПРЕДЕЛЕНИЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Мы будем пользоваться термином построение модели, чтобы описать
процессы объединения по определенным правилам символов, обозначающих
те или иные объекты, и создания структуры, или модели, которая соответ-
ствовала бы реальной изучаемой системе. Такими символами могут быть
маленькие квадратики, или палочки, или, как в нашем случае, ими могут
быть алгебраические символы.
Линейное программирование обладает известной методологией, под-
ходом к построению модели, которая применима к широкому классу задач
по принятию решений, встречающихся в административных органах,
в промышленности, экономике и технике. По-видимому, эта методика имеет
наиболее простую математическую структуру, которая может быть исполь-
зована в этих сферах деятельности при практическом решении задач пла-
нирования. Так как этот метод предназначен для изучения поведения тех
или иных систем, он обобщает различные черты науки управления или
теории исследования операций, или, говоря иначе: «Операции рассмат-
риваются как единое целое. Предметом изучения не является ни исполь-
зование оборудования, ни моральное состояние участников, ни физичес-
кие свойства выпускаемой продукции, а комбинация всех этих фак-
торов, вместе взятых, понимаемая как экономический процесс» (Герман
и Мэджи [1]).
Линейное программирование 1 связано с описанием взаимосвязей
составных частей системы. Как мы увидим, на первом этапе проекти-
руемая система считается состоящей из ряда элементарных функ-
ций, которые называются «процессами» 2. Как следствие, Т. Купманс
[2] ввел термин анализ технологических процессов, чтобы описать этот
подход. Различные процесс^, которые могут быть реализованы в систе-
ме, составляют ее технологию. Они представляют собой строительные
блоки, которые можно комбинировать в различных количествах, для созда-
ния саморегулируемой структуры, удовлетворяющей определенным огра-
ничениям и по возможности обеспечивающей достижение поставленной
цели. Математическое представление этой структуры (как мы увидим
в гл. 3) часто приводит к системе линейных неравенств и уравнений;
в тех случаях, когда это имеет место, она называется моделью линейного
программирования. Специалисты, использующие модели линейного про-
граммирования, манипулируют, подобно архитектору, «на бумаге»
символическими изображениями строительных блоков (процессов) до
тех пор, пока не будет получена удовлетворительная конструкция. Теория
линейного программирования занимается научными методами для полу-
чения лучшего варианта конструкции при заданной технологии и ограни-
чениях и при сформулированных целевых установках.
Чтобы стать моделью линейного программирования, система должна
удовлетворять определенным условиям линейности {пропорциональности),
неотрицательности и аддитивности. Как это фактически получается,
показано в гл. 3, где также будут сформулированы модели линейного
программирования на примерах, подобных тем, которые уже рассматри-
вались. Приступая к рассмотрению моделей реально существующих
1 Термин «линейное программирование» был предложен автору Т. Купмансом
в 1951 г. в противоположность ранее использовавшейся формулировке «программиро-
вание в линейной структуре» (Данциг [1]).
2 Термин «процесс» (activity) в этой связи имеет военное происхождение. Он был
использован вместо термина «процесс» (process), которым пользуется фон Нейман
в статье «Модель общего экономич*еского равновесия» и который по своему смыслу более
ограничен (фон Нейман [2]).
13
систем, важно помнить, что сама действительность очень редко (если вообще
это когда-нибудь имеет место) представляет собой ясно выраженную
задачу линейного программирования и что упрощение и игнорирование
некоторых реальных фактов является при использовании линейного
программирования столь же необходимым, как и в любом научном методе
решения каких бы то ни было задач.
Возьмем за правило пренебрегать пренебрежимым. Так, в примере
с консервными заводами число отправляемых и число получаемых ящиков
может быть различным, потому что возможны случайные потери при их
доставке. Это различие неизвестно заранее и может оказаться незначитель-
ным. В примере оптимальной диеты истинная питательная ценность про-
дуктов изменяется от одного сорта к другому, от сезона к сезону, от одного
поставщика к другому. Точно так же выработка и качество обучения
будут неодинаковыми для разных рабочих и для разных периодов. Воз-
можно, для некоторых приложений окажется необходимым уделить серь-
езное внимание различию между действительностью и ее представлением
в математической модели для того, чтобы быть уверенным, что эти различия
сравнительно невелики, и обеспечить себе операционную полезность полу-
ченных результатов.
Какие именно упрощения допускаются, является предметом конкрет-
ного суждения и опыта. Люди часто не сходятся в оценке адекватности
той или иной модели с описываемыми ею явлениями действительности.
1-4. КЛАССИФИКАЦИЯ ЗАДАЧ ПРОГРАММИРОВАНИЯ
Задачи программирования, рассматриваемые в этой книге (за исклю-
чением задач, описанных в гл. 25), относятся к классу детерминированных.
Это означает, что если предпринимаются те или иные действия, то с досто-
верностью можно заранее описать: а) необходимые условия осуществления
действий и б) исходы этих действий. Если и существуют в объективном мире
процессы, обладающие этим свойством, то таких процессов немного. Быть
может, процесс сжигания двух частей водорода в одной части кислорода
для получения воды может служить примером задач детерминированного
класса. На практике, однако, из-за загрязнения, утечки в резервуарах
и т. д. эта принимаемая зависимость является лишь идеальной. Тем не ме-
нее для многих целей может быть использована именно идеальная форму-
ла, ибо отклонения от нее настолько незначительны, что лишь время от
времени окажется необходимым вносить небольшие корректировки.
Детерминированная ситуация может быть создана преднамеренно.
Например, никогда не удается точно определить количество бензина и масла,
необходимое для осуществления некоторых автомобильных перевозок.
Однако если в планах фигурируют запасы бензина и масла, намного пре-
восходящие их ожидаемый расход, то можно предположить, что перевозки
будут выполнены успешно, а излишек запасов можно будет использовать
позднее. Обычно время для выполнения операции является частью вре-
мени, допускаемого в плане. Так, рассмотрим производство детали само-
лета: время от начала первой операции резки металлического листа до
момента готовности детали к сборке может быть равно трем месяцам и бо-
лее; между тем всего лишь несколько часов могут понадобиться для опе-
раций обработки, сверления отверстий и монтажа. Все остальное время
предусматривается для хранения деталей на складах, во время которого
единственной операцией, по-видимому, является накапливание нарядов,
позволяющее перераспределять их с учетом более эффективного исполь-
зования рабочей силы.
14
Задачи, включающие неопределенность, относятся к другому основ-
ному классу, который мы будем называть вероятностным. Неопределен-
ность может возникать во многих случаях. Результаты данного действия
могут зависеть от ряда случайных факторов, таких, как погода, задержки
транспорта, политика правительства, уровень занятости, повышение или
падение покупательского спроса.
Распределение случайных факторов в некоторых случаях известно
заранее, а в других оно неизвестно или известно лишь частично. В ряде
случаев неопределенность возникает в связи с действиями конкурента
или противника.
Как показано на приведенной ниже схеме, двумя основными клас-
сами задач математического программирования являются детерминирован-
ный и стохастический (вероятностный). Первый из них подразделен на
два основных, часто выделяемых математических подкласса линейных и
нелинейных моделей, которые часто оказываются объектами исследова-
ния. Второй из указанных классов в свою очередь подразделяется по
области применения на два подкласса, первый из которых касается без-
различных (непредсказуемых) явлений, а второй предполагает наличие
противников с иными целями. На схеме показано, каким образом эти
классы подразделяются на дальнейшие подклассы, и указываются извест-
ные частные случаи
Классификация задач программирования
Дискретные и непрерывные. Многошаговые и одношаговые.
(Динамические и нединамические)
Детерминированные
Стохастические
Линейные
Нелинейные
Без противников
С противниками
Общие Частные
задачи задачи
Выпук- Невы-
лые пуклые
Известное
вероятност-
ное распре-
деление
Неизвест-
ное вероят-
ностное
распреде-
ление
Игры Игры
двух лиц многих
лиц
Частные случаи описанных выше задач
Теория линей- ных не- равенств Динами- ческие системы; модели Леонтье- ва; сети Убывающая доходность; химическое равновесие; выпуклые программы Возрастаю- щий доход; множест- венность локальных максимумов Управ- ление запаса- ми; цепи Маркова Секвен- циаль- ный ста- тисти- ческий анализ Антаго- нисти- ческие игры Коопе- ратив- ная] теория
Рис. 1—4—1.
1 Автор относит стохастические модели с неизвестными вероятностями к под-
классу «без противников». Естественнее отнести эти модели к теоретико-игровым,
рассматривая в качестве противника природу, выбирающую решения с неизвестными
вероятностями. — Прим. ред.
15
В этой книге мы будем обращать внимание как на общие, так и на
частные задачи линейного программирования, на те задачи нелинейного
выпуклого программирования, которые могут быть приведены к задачам
линейного программирования, на некоторые вероятностные задачи, кото-
рые также можно привести к задачам линейного программирования (на-
пример, матричные игры, а также задачи планирования, содержащие
неопределенный спрос).
Один из важнейших способов классификации задач программирования
состоит в делении их на многошаговые и одношаговые. Многошаговые
модели охватывают динамические модели, в которых основную роль играет
планирование во времени, как в примере 3. Примеры 1 и 2 относятся
к одношаговым задачам в той же мере, как и к стационарным экономичес-
ким моделям (в которых объем выпуска продукции остается постоянным
в течение определенного отрезка времени).
Другой путь классификации моделей основан на различении тех
моделей, в которых некоторые из определяемых значений затрат, выпусков,
распределений работ и уровней производства должны выражаться в виде
дискретных величин вида 0, 1, 2, 3... (промежуточные значения недопу-
стимы) и тех, в которых эти величины могут принимать произвольные
значения в непрерывном диапазоне. Многие комбинаторные задачи отно-
сятся к дискретному классу, как, например, задачи распределения ряда
рабочих по соответствующему числу рабочих мест, или задачи определе-
ния порядка, в котором коммивояжер должен посетить ряд городов. Строго
говоря, дискретные задачи относятся к классу задач нелинейного програм-
мирования (см. гл. 26).
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Многие многошаговые, и в частности динамические, задачи имеют
структуру, которая позволяет получить решение на основе принципа
индукции. В начале каждого этапа, как и при поиске кладов, даются
указания на дальнейший поиск, а также указывается конечный результат
действий, если кто-либо должен продолжать поиск в соответствии с дан-
ными указаниями. Допускается (и это основное допущение в структуре),
что оптимальный порядок действий и их результат зависят только от
положения исследователя на первоначальном этапе, но не от каких-то
его предыдущих действий. В конце последнего этапа все возможные конеч-
ные состояния обычно легко оценить. Это позволяет построить без большого
усилия для каждого из возможных состояний то направление, в котором
находится максимальный результат на конец предпоследнего этапа; исхо-
дя из этого, можно указать направление, в котором находится максималь-
ный результат для всех возможных состояний на конец третьего от конца
этапа, ит. д., индуктивно возвращаясь назад во времени до начала перво-
го этапа, где первоначальное состояние считается уже известным. Чтобы
выполнить этот обратный ход, необходимо знать для каждой комбинации
состояний в начале и в конце любого этапа доходы и затраты на этом этапе.
Ответ на вопрос о целесообразности использования метода зависит от того,
насколько поддается обработке анализ возможных комбинаций. Метод
индукции был известен еще в древней Греции, а в связи с ранними исполь-
зованиями этого метода применительно к задачам принятия решений сле-
дует упомянуть работы, А. Вальда [3], П. Массе [1], К. Эрроу, Т. Гар-
риса и Д. Маршака [1], А. Дворецкого, Д. Кифера и Д. Вольфовица
[1]. Однако только в 1952 г. Ричард Веллман первым обратил внима-
ние на важность для программирования индуктивного метода, кото-
рый он назвал принципом оптимальности, и раскрыл его потен-
16
циальные возможности (Веллман [1], [2]; Веллман, Гликсберг и Гросс
[1]). Вся область исследований, использующая данный метод, называется
«динамическим программированием», поскольку большинство случаев
применения имеет многошаговый характер.
1-5. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
И АВТОМАТИЗАЦИЯ
Период, наступивший после второй мировой войны, характеризуется
ускоренными темпами автоматизации и высших форм механизации. Внед-
рение механизации освобождает человека от физического труда и заменяет
его машиной; внедрение автоматизации освобождает человека в известной
степени и от умственного труда и связанной с ним физической работы.
Многие считают, что электронные вычислительные машины, которые
сами являются примерами автоматизации, будут играть важную роль
в механизации управления массовыми процессами.
Некоторые полагают, что «решения на высшем уровне будут подго-
тавливаться главным образом человеком, ибо только он в силу своего
умственного развития обладает способностью объединения и согласования
информации, для которой пока еще невозможно или очень сложно дать
точную формулировку» (Белтер [1]). Однако автор считает, что даже
в области более высоких ступеней управления, и в частности в той области
умственной деятельности, которая связана с вариантами выбора среди
альтернативных решений, механизация уже осуществляется. Это отно-
сится к умственной деятельности, известной как программирование (или
планирование), и к ее физическому воплощению, известному как управле-
ние производством.
Эти два послевоенных достижения, автоматизация и программирова-
ние, часто связываются друг с другом ввиду использования ими элект-
ронных вычислительных машин. Насколько же тесна связь между
ними?
Чтобы ответить на этот вопрос, рассмотрим некоторые достижения
в той отрасли промышленности, которая была одной из первых в вопросах
автоматизации производства и внедрения программирования в производ-
ственный процесс. Современный нефтеочистительный процесс является
комплексом взаимосвязанных операций. Число возможных комбинаций
подачи запасов, последовательности и условий выполнения операций,
методов смешивания и отбора окончательных продуктов очень велико;
как следствие этого, методы математического программирования исполь-
зуются здесь в оценке экономичности схем технологических процессов
с большим эффектом. Как только конкретный производственный план
определен, достаточно набрать нужный номер на диске и нажать кнопку
в диспетчерской, чтобы очистительный завод стал выпускать нужную
продукцию в предписанных количествах.
Этот пример показывает, что каждый из двух процессов, выработки
решения и управления производством, может быть полностью автомати-
зирован и даже может быть связан с операторами, которые передают
инструкции от одной системы к другой, от системы, принимающей реше-
ния, к системе производства. Следует отметить, что хотя программиро-
вание и является составной частью управления на более высоком уровне,
однако оно не эквивалентно той обратной связи, которая поддерживает
постоянную температуру в котле. Оно скорее является методом определе-
ния того, какая это будет температура и как долго она должна поддержи-
ваться для того, чтобы обеспечить цели производственного процесса.
2 Дж. Данциг 17
Хотя механизация процессов принятия решений на более высоком
уровне не всегда требует механизации физических связующих звеньев,
с помощью которых решения реализуются, все же возможно, что в опре-
деленных областях будет экономично объединить эти два автоматических
процесса в один. Такая «сверхавтоматизация» процессов является необ-
ходимой в сверхскоростных ракетах, которые требуют жесткого управле-
ния и использования гибких методов программирования. Некоторые
отрасли, такие, как авиационная промышленность, высказываются за
внедрение универсальных станков, на которых можно производить раз-
нообразную продукцию в зависимости от устройств управления. В свою
очередь эти станки могут быть заменены на станки с управлением на еще
более высоком уровне, с автоматическим управлением. В таких системах
поломки станка, брак в заготовках и поступление новых заказов могут
потребовать быстро перепрограммировать загрузку станков. И здесь
снова жесткие методы управления производством могут быть механиче-
ски связаны с гибкими методами автоматического программирования.
Глава 2
ИСТОКИ и связи
За десятилетие, прошедшее с момента зарождения в 1947 г. линейного
программирования в связи с работами по планированию деятельности
вооруженных сил США, эта отрасль науки получила широкое распро-
странение в промышленности. В научных кругах математиками и эконо-
мистами на эту тему написаны целые книги. Цель данной главы состоит
в том, чтобы сжато описать истоки этой науки и те факторы, которые обус-
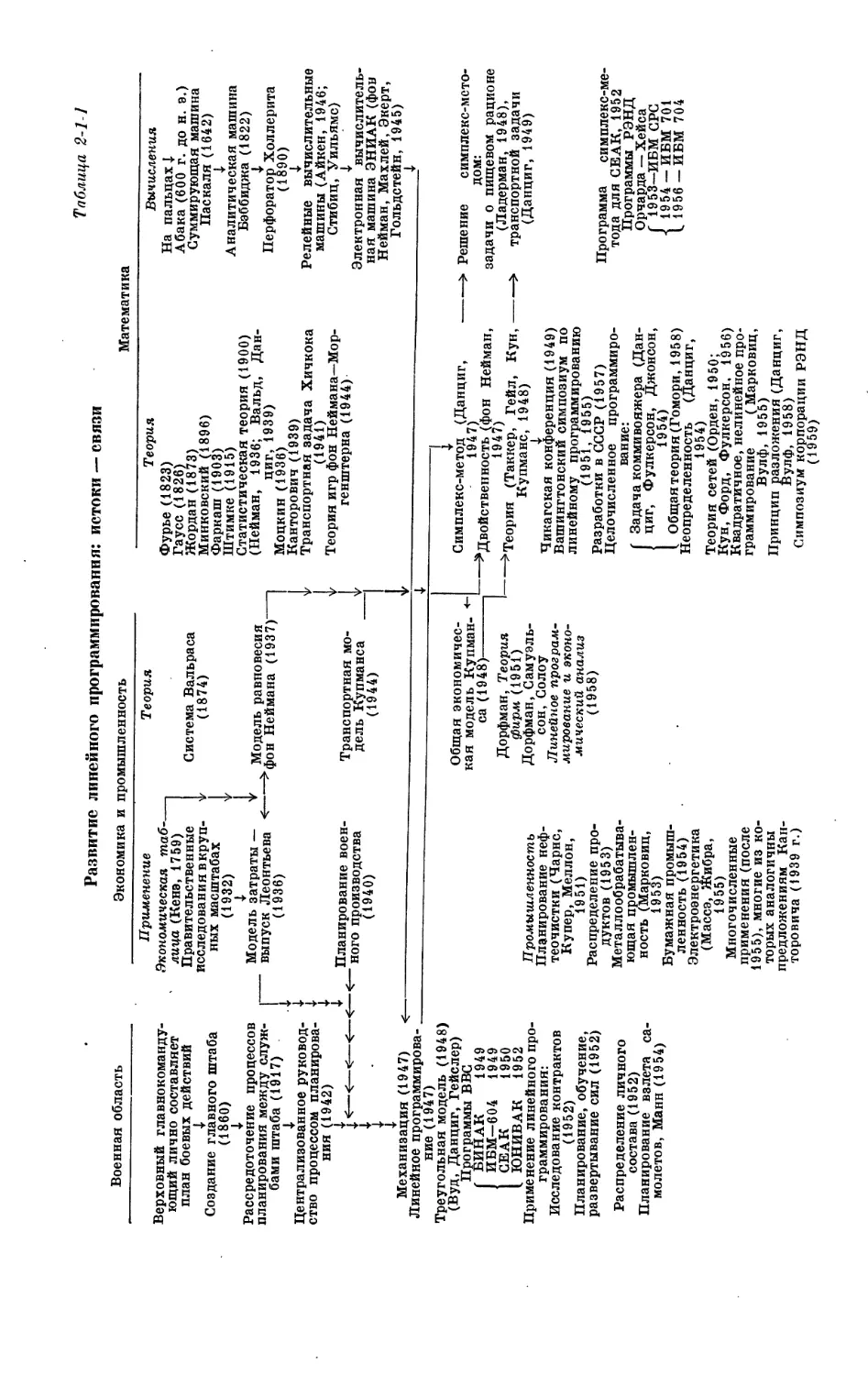
ловили ее бурное развитие. В табл. 2-1-1 показано развитие линейного
программирования от его истоков до более поздних разработок. Напра-
вление стрелок указывает непосредственное влияние одних работ на дру-
гие. Интересно отметить, что, несмотря на возможность широкого приме-
нения линейного программирования к повседневным задачам, до 1947 г.
о нем ничего не было известно. Фурье мог знать о его потенциальных воз-
можностях еще в 1823 г. В СССР в 1939 г. Канторовичем были высказаны
идеи линейного программирования, преданные забвению на те два деся-
тилетия, которые ознаменовались открытием теории линейного програм-
мирования и решительным и повсеместным ее внедрением.
2-1. ВЛИЯНИЕ ВТОРОЙ МИРОВОЙ ВОЙНЫ
ХАРАКТЕР ШТАБНОГО ПЛАНИРОВАНИЯ
Военная организация страны как в военное, так и в мирное время
объединяет экономическую и военную деятельности, требует самой совер-
шенной, тщательно продуманной координации работ по осуществлению
планов, разрабатываемых различными ведомствами. Если один из таких
планов направлен на проектирование и изготовление некоторого оборудо-
вания, то в этом случае количество заказываемого оборудования должно
быть согласовано с экономическими возможностями перевода рабочей
силы, материалов и производственных мощностей из гражданского сектора
хозяйства в военный. Эти преобразования, а также вспомогательные рабо-
ты должны непосредственно вписываться в военную программу. Чтобы
дать некоторое представление о характере взаимозависимости различных
видов важнейших работ, можно отметить, что каждый отдельный вид
работы, связанный с планированием рабочей силы, включает в себя сотни
подвидов, а в области материально-технического снабжения количество
подвидов может доходить до нескольких тысяч. Всегда ли задачи были
столь сложными? Здесь уместно привести следующее заявление М. К. Вуда
и М. А. Гейслера [1]:
«Некогда главнокомандующему удавалось составлять план боевых
операций лично. Но поскольку подлежащие планированию действия
разрослись как в пространстве и времени, так и по общей сложности^
19
2*
Развитие линейного программирования: истоки — связи
Таблица 2-11
Военная область
Экономика и промышленность
Математика
Верховный главнокоманду-
ющий лично составляет
план боевых действий
I
Создание главного штаба
(1860)
Ф
Рассредоточение процессов
планирования между служ-
бами штаба (1917) .
Централизованное руковод-
ство процессом планирова-
ния (1942)
;<-< <—«—
1
I
Механизация (1947) <
Линейное программирова- _
ние (1947)
Треугольная модель (1948)
(Вуд, Данциг, Гейслер)
Программы ВВС
1949
1949
1950
1952
БИНАК
ИБМ-604
GEAK
ЮНИВАК
Применение линейного про-
граммирования:
Исследование контрактов
(1952)
Планирование, обучение,
развертывание сил (1952)
Распределение личного
состава (1952)
Планирование взлета са-
молетов, Манн (1954)
Применение
Экономическая таб----
лица (Кенэ, 1759)
Правительственные
исследования в круп- v
ных масштабах
(1932)
____ Модель затраты — '
I выпуск Леонтьева <—
(1936)
• *
г
I
______Планирование воен-
* ного производства
(1940)
Промышленность
Планирование неф-
теочистки (Чарнс,
Купер, Меллон,
1951)
Распределение про-
дуктов (1953)
Металлообрабатыва-
ющая промышлен-
ность (Марковиц,
1953)
Бумажная промыш-
ленность (1954)
Электроэнергетика
(Массэ, Жибра,
1955)
Многочисленные
применения (после
1955), многие из ко-
торых аналогичны
предложениям Кан-
торовича (1939 г.)
Теория
Система Вальраса
(1874)
. Модель равновесия
"^фон Неймана (1937)"
Транспортная мо-
дель Купманса
(1944)
Теория
Фурье (1823)
Гаусс (1826)
Жордан (1873)
Минковский (1896)
Фаркаш (1903)
Штимке (1915)
Статистическая теория (1900)
(Нейман, 1936; Вальд, Дан-
циг, 1939)
Моцкин (1936)
Канторович (1939)
Транспортная задача Хичкока
(1941)
Теория игр фон Неймана—Мор-
генштерна (1944)
Общая экономичес-
кая модель Купман-
са (1948)----------
Дорфман, Теория
фирм (1951)
Дорфман, Самуэль-
сон, Солоу
Линейное програм-
мирование и эконо-
мический анализ
(1958)
-------------1
I
Симплекс-метод (Данциг,
.. 1947)
^Двойственность (фон Нейман,
1947)
^Теория (Таккер, Гейл, Кун,
Купманс, 1948)
Чикагская конференция (1949)
Вашингтонский симпозиум по
линейному программированию
(1951, 1955)
Разработки в СССР (1957)
Целочисленное программиро-
вание:
Задача коммивояжера (Дан-
, циг, Фулкерсон, Джонсон,
1954)
Общая теория (Гомори, 1958)
Неопределенность (Данциг,
1954)
Теория сетей (Орден, 1950;
Кун, Форд, Фулкерсон, 1956)
Квадратичное, нелинейное про-
граммирование (Марковиц,
Вулф, 1955)
Принцип разложения (Данциг,
Вулф, 1958)
Симпозиум корпорации РЭНД
(1959)
Вычисления
На пальцах ф
Абака (600 г. до н. э.)
Суммирующая машина
Паскаля (1642)
4
Аналитическая машина
Бэббиджа (1822)
Перфоратор^Холлерита
Релейные вычислительные
машины (Айкен, 1946;
Стибиц, Уильямс)
Электронная вычислитель-
ная машина ЭНИАК (фон
Нейман, Махлей, Экерт,
Гольдстейн, 1945)
____________I
—> Решение симплекс-мето-
дом:
задачи о пищевом рационе
(Ладерман, 1948),
—> транспортной задачи
(Данциг, 1949)
Программа симплекс-ме-
тода для СЕАК, 1952
Программы РЭНД
Орчарда — Хейса
f 1953-ИБМ СРС
1954 -ИБМ 701
I 1956 -ИБМ 704
появились ограничивающие факторы, связанные с человеческими способ-
ностями. Военная история полна случаев, когда командующие терпели
поражения из-за того, что они запутывались в деталях; не потому, что они
не смогли бы в конечном счете эти детали охватить, но из-за того, что им не
удавалось охватить все существенные детали за то время, которым они
располагали для принятия решения. По мере того как задачи планирова-
ния усложнялись, верховный главнокомандующий окружал себя главным
штабом из специалистов, которые дополняли командующего при выработ-
ке решения. Наличие главного штаба позволило расчленять процесс
планирования и назначать ответственных специалистов по каждому
вопросу. Обязанности командующего ограничивались выбором целей опе-
раций, а также координированием, планированием и разрешением конф-
ликтов между службами штаба».
Крупные войны велись на протяжении всей истории цивилизации.
Однако главный штаб при верховном главнокомандующем вооруженных
сил появляется лишь около середины прошлого века (Пруссия, 1860)
вследствие возросших сложностей ведения военных действий. Расчлене-
ние планирования военных действий между службами штаба зарождается
в труднейшие периоды первой мировой войны (1917).
РАЗВИТИЕ В ГОДЫ ВТОРОЙ МИРОВОЙ ВОЙНЫ
В годы второй мировой войны вопросы штабного планирования
разрабатываются в гигантских масштабах во всех военных организациях
США и связанных с ними гражданских учреждениях, таких, как Мини-
стерство военной продукции. В этот период авиация становится основным
родом вооруженных сил США. Отказавшись от традиционных приемов,
ВВС развили ряд методов, облегчающих планирование \ что в конечном
счете привело в послевоенные годы к рассмотрению научных методов
планирования.
Во время войны процесс планирования сам по себе намного услож-
нился, стал настолько растянутым по времени и многоцелевым, что в одно
и то же время (как показало выборочное обследование штаба авиации)
велись работы над различными планами, причем некоторые из разработок,
находясь в ранних фазах, базировались на самых последних инструк-
циях и оперативных сводках армейского командования, в то время как
другие, проходя свои завершающие этапы, базировались на более старых
инструкциях и сводках. Для сокращения времени планирования отдель-
ные части таких планов часто сводились воедино на базе противоречащих
друг другу фактов и инструкций. Для совершенствования координации
этой работы штаб авиации приблизительно в 1943 г. учредил службу
контроля планов во главе с профессором Гарвардского университета
Э. П. Лерндом. Окончательный план исходил из военного плана, который
содержал задачи военного времени. На основе этого общего плана путем
последовательных вычислений составлялся детализированный военный
план, характеризующий развертывание боевых частей по театрам воен-
ных действий, требования по подготовке летного и технического персо-
нала, снабжение и обслуживание и т. д. Для обеспечения согласованности
1 Наибольшее значение имели разработки под руководством К. Б. Торнтона из
группы статистического контроля. Эта группа обеспечивала непрерывный поток под-
робной информации о положении многих подразделений ВВС, включая сведения
о личном составе, снабжении, боевых действиях и основные данные, использовавшиеся
для определения норм износа, норм самолетовылетов, норм чередования экипажей,
потребности в обслуживании, норм снабжения и т. д.
21
планов очередность разработки этапов плана была такова, что поток
информации от эшелона к эшелону шел лишь в одном направлении,
а согласованность информации во времени обеспечивалась тем, что часть
плана, подготовленная на каждом этапе, не зависела от последующих
этапов. Даже при очень тщательном планировании для выполнения этой
работы потребовалось около семи месяцев.
РАЗРАБОТКИ ПОСЛЕВОЕННЫХ ЛЕТ
После второй мировой войны ВВС США объединили функции ста-
тистического контроля, финансирования и проверки планов в штабе глав-
ного инспектора ВВС генерала Е. У. Роулингса, являющегося ныне пре-
зидентом корпорации «Дженерал миллз». Членам этой организации стало
ясно, что эффективная координация усилий всей страны в случае тоталь-
ной войны потребует научных методов планирования. Несомненно, что
и в прошлом неоднократно возникала необходимость в этом, но в то время
велись разработки одновременно в двух направлениях, оказавших боль-
шое влияние: а) разработка быстродействующих электронных вычисли-
тельных машин и б) разработка модели межотраслевого баланса. Послед-
няя представляет собой метод описания межотраслевых взаимосвязей
в экономике. Этот метод впервые предложил Василий Леонтьев [1]х.
О нем будет сказано в следующем параграфе.
Интенсивные работы начались в июне 1947 г. в группе, которой позд-
нее (в октябре 1948 г.) был присвоен официальный титул «Проект СКООП»
(научный расчет оптимальных планов). В этой группе ведущую роль
играли Маршалл Вуд и автор настоящей книги, а несколько позднее —
Джон Нортон и Мэррей Гейслер.
Потенциальные возможности межотраслевого баланса будут рас-
смотрены в следующем параграфе. Простота его структуры, и в частно-
сти использование в нем линейных производственных функций при описа-
нии всей экономической деятельности в масштабе отрасли промышленно-
сти, оказали значительное влияние на сотрудников исследовательской
группы ВВС. Однако нединамический характер модели и упрощающее
предположение о том, что любая отрасль промышленности располагает
всего одним технологическим процессом, производящим только один
продукт, ограничивали практическую применимость модели. Другим
ограничением модели являлось то, что в ней не допускалось существова-
ние других допустимых планов. Отсюда возникла необходимость обобще-
ния межотраслевого метода, в результате чего к июлю 1947 г. была разра-
ботана модель линейного программирования.
Вычислительный симплекс-метод для выбора оптимально допустимого
плана появился в конце лета 1947 г. (см. гл. 5). Интерес к линейному про-
граммированию начал быстро расти. В это же время ВВС опекали работу
Бюро стандартов США по применению электронных вычислительных
машин и математических методов для решения таких моделей. Сотруд-
ники Бюро стандартов Джон Куртис и Альберт Кан играли активную
роль в пробуждении интереса к этой работе среди математиков и эконо-
мистов.
В результате контактов с Т. Купмансом, в то время сотрудником
комиссии Коулса, впоследствии — Чикагского университета, а в настоящее
время — Йельского университета, и Робертом Дорфманом, который в то
1 Впервые этот метод был использован при составлении баланса народного хозяй-
ства СССР за 1923—1924 гг. (см. «Труды ЦСУ СССР», т. XXIX, М., 1926).— Прим. ред.
22
время сотрудничал в ВВС (теперь работает в Гарварде), а также интереса,
проявленного со стороны такого экономиста, как Пауль Самуэльсон из
Массачусетского технологического института, началась эра интенсив-
ного пересмотра классической экономической теории на основе идей
и результатов линейного программирования.
Контакты с сотрудником института перспективных исследований
Джоном фон Нейманом помогли выявить основные понятия математиче-
ской теории линейного программирования и заинтересовали группу сотруд-
ников и студентов Принстонского университета во главе с А. У. Таккером,
которые взялись за разработку задач в области теории линейных неравенств
и теории игр. Начиная с тех пор этой группе принадлежит ведущая
роль в разработке указанных областей.
На основании наблюдений над размерами задач линейного програм-
мирования ВВС США, с которыми имели дело сотрудники группы СКООП
еще на самых первых этапах своей работы, стало понятно, что даже самые
мощные вычислительные средства в будущем будут не в состоянии решить
подробную общую модель линейного программирования ВВС. Поэтому
группа СКООП модифицировала свою методику и весной 1948 г. предло-
жила создавать частные модели линейного программирования, названные
треугольными, структура и метод численной обработки которых были
бы аналогичны методу пошагового решения, описанному выше (Вуд
и Гейслер [1], стр. 189).
С 1948 г. штаб ВВС при решении задач линейного программирования
все более активно использует программы для электронных вычислитель-
ных машин. Треугольные модели постоянно применяются для вычисления
детальных планов, в то время как общие модели линейного программиро-
вания используются лишь в таких областях, как а) исследование контрак-
тов, б) составление графиков полетов самолетов, подготовки экипажей
и развертывания авиационных соединений, в) планирование циклов
ремонта и обслуживания, г) распределение персонала, д) задачи плани-
рования маршрутов самолетов (Джейкобс [1]; Натрелла [1]).
2-2. ЭКОНОМИЧЕСКИЕ МОДЕЛИ И ЛИНЕЙНОЕ
ПРОГРАММИРОВАНИЕ
ВЛИЯНИЕ ТЕОРЕТИЧЕСКИХ МОДЕЛЕЙ
То, что линейное программирование внедряется в экономику только
сейчас, представляется анахронизмом; было бы логичнее, если бы оно
началось где-нибудь около 1758 г., когда экономисты впервые начали
математически описывать экономические системы. Действительно, про-
стейшие примеры моделей линейного программирования можно найти
в Экономической таблице Кенэ, который пытался определить взаимосвязи
между землевладельцами, крестьянами и ремесленниками (см. Монро [1]).
Мы находим также, что Л. Вальрас предложил в 1874 г. сложную мате-
матическую модель, частью которой являлись постоянные технологиче-
ские коэффициенты. Однако до 1930 г. все эти работы носили разрозненный
характер, и в области использования моделей линейного типа было сде-
лано очень мало.
Подавляющее большинство специалистов в области математической
экономики занималось анализом теоретических проблем, связанных с воз-
можностью экономического равновесия и его эффективности в условиях
конкуренции или монополии. При этом было обнаружено, что для иллю-
страции условий равновесия удобнее использовать классические выпук-
23
лые функции с непрерывными производными, а не функции, связанные
с линейными неравенствами. Среди этих направлений особого внимания
заслуживает работа, проведенная в 30-х годах группой австрийских
и немецких экономистов, которые занимались обобщением линейной
технологической модели Вальраса. В этой работе поставлено несколько
вопросов, которые, возможно, стимулировали появление работы мате-
матика фон Неймана (1932) «Модель общего экономического равновесия»
(фон Нейман [2]), в которой сформулирована динамическая модель
линейного программирования, введены различные процессы выпуска
рассматриваемых продуктов не только каждого в отдельности, но и неко-
торой их совокупности. Фон Нейман исходил из а) постоянного темпа
роста экономики и б) полностью замкнутой системы. Хотя сама модель
и не содержала явно сформулированной цели, фон Нейман показал, что
рыночные силы максимизируют темп роста экономики, и доказал, что
в точке максимума он равен процентной ставке на капитал, инвестирован-
ный в производство.
Что касается влияния работы фон Неймана, как, между прочим,
и многих других теоретических работ, то все они доказывают определенную
интересную математическую теорему. Экономистов с математическим
уклоном, вероятно, больше заинтересовали бы аналогичные результаты
для более общей модели, поскольку «для многих экономистов термин
линейность ассоциируется с понятием узости, ограниченности и негибкости
гипотез» (Купманс [2], стр. 6). Иными словами, эти усилия, как и боль-
шинство усилий того времени, относятся к качественной стороне эконо-
мики, в которой цель математической модели заключалась в описании
предполагаемых взаимосвязей внутри системы скорее с качественной,
чем с количественной, стороны; манипулирование уравнениями являлось
удобным способом получения ценных логических выводов из предполо-
жений.
ВЛИЯНИЕ ЭМПИРИЧЕСКИХ МОДЕЛЕЙ
Работы над общей моделью линейного программирования велись
совершенно независимо от упомянутых выше разработок и преследовали
другие цели. Эти работы возникли из практических потребностей плани-
рования для ВВС и возможности обобщения простой практической струк-
туры модели Леонтьева. С чисто формальной точки зрения леонтьевскую
модель можно рассматривать как упрощение модели Вальраса. Но именно
на этом и кончается формальное сходство.
«Сто пятьдесят лет назад, когда Кенэ впервые опубликовал свою зна-
менитую экономическую таблицу, современники и последователи назвали
ее величайшим открытием после законов Ньютона. Идея о всеобщей
взаимозависимости между различными частями экономической системы
к настоящему времени легла в основу экономического анализа. Однако,
когда дело доходит до практического применения этого теоретического
инструмента, современные экономисты должны полагаться, точно так же
как это делал Кенэ, на условные численные примеры» (Леонтьев [1],
стр. 9).
По мнению автора, большой заслугой Леонтьева является то, что
он создал количественную модель американской экономики для того,
чтобы можно было проследить влияние правительственной политики
и тенденций в области закупок на целый ряд промышленных отраслей,
находящихся в исключительно сложно переплетенных связях. Чтобы
оценить разницу между чисто формальной и эмпирической моделями, сле-
дует напомнить, что сбор данных, необходимых для реальной модели,
потребует многие месяцы, а иногда и годы работы целой организации.
24
После того как собрана вся информация о модели, появляется другая
трудность — решение очень большой системы линейных уравнений.
В 1936—1940 гг. электронных вычислительных машин еще не было;
самое большее, на что можно было рассчитывать,— это на решение двад-
цати уравнений с двадцатью неизвестными. И, наконец, существовали
трудности «сбыта» результатов таких • исследований. Следовательно,
инициатива Леонтьева с самого начала была связана с тройным
риском.
Чтобы лучше оценить значение перехода от теоретической модели
к эмпирической, необходимо вспомнить, что начиная с 30-х годов в рас-
поряжение исследователей поступало все больше информации о доходах,
количестве выпускаемой продукции, капиталовложениях, прибылях
и структуре потребления. К тому же начиная с 1900 г. разработанный
статистиками выборочный метод получал все более широкое применение
как средство оценки взаимосвязей между данными наблюдений. При изме-
рении экономических явлений начинают пользоваться регрессивным ана-
лизом. К 1940 г. работы таких статистиков, как Карл Пирсон, Р. А. Фи-
шер, а также современной школы, берущей начало от Дж. Неймана, пре-
вратились в науку о проверке гипотез и оценках параметров генераль-
ной совокупности.
После кризиса 1929—1933 гг. и провозглашения «нового курса»
отдельными членами правительства были предприняты серьезные попытки
выявить и финансировать некоторые виды работ, которые могли бы быстро
окупить себя. Это привело к интенсификации сбора статистических сведе-
ний о стоимости жизни, заработной плате, национальных ресурсах,
производительности труда и т. д. Возникла необходимость сбора и обра-
ботки этих данных для того, чтобы использовать их при создании мате-
матической модели, описывающей экономику в количественных пока-
зателях.
С 1936 г. масштабы, точность и сфера применения моделей леонтьев-
ского типа были значительно расширены благодаря работам Бюро стати-
стики труда (под руководством Дуана Эванса, Джерома Корнфилда,
Мартина Хоффенберга и др.) (Корнфилд, Эванс, Хоффенберг [1]).
Именно эти работы стимулировали поиски математического обобщения,
пригодного для динамических задач ВВС США. Таким образом, впервые
интерес к математической структуре был проявлен со стороны ВВС США
за несколько лет до того, как Министерство обороны начало финанси-
ровать разработку межотраслевых моделей Леонтьева для оценки согла-
сованности своих планов с гражданской экономикой.
Теперь несколько слов о самой модели Леонтьева. Основу анализа
«затраты — выпуск» составляет таблица коэффициентов, которая назы-
вается либо матрицей «затраты — выпуск», либо «экономической табли-
цей». Столбец в этой матрице соответствует затратам различных това-
ров, приходящихся на один доллар стоимости определенного выпускае-
мого товара. Каждому товару, производимому в стране, соответствует
один столбец. Отсюда понятие выпуска товара соответствует понятию тех-
нологического процесса в модели линейного программирования. Если
коэффициенты затрат, помещаемые в строке матрицы, умножить на соот-
ветствующие полные выпуски закупающей отрасли, то получится распре-
деление закупок среди продающих отраслей, выраженное в долларах.
Следовательно, модель дает возможность не только определять объемы
выпуска каждой отрасли для удовлетворения определенных прямых гра-
жданских и военных потребностей, но по ней можно также проследить
косвенное влияние, оказываемое на каждую отрасль правительственными
затратами, например, по военным программам.
25
ПОСЛЕВОЕННЫЕ РАЗРАБОТКИ
В 1947 г. Т; Купманс первым обратил внимание экономистов на
потенциальные возможности моделей линейного программирования. Быст-
рое создание экономической теории таких моделей Купмансом объясняется
опытом, который он получил в годы войны при разработке некоторого
частного класса моделей линейного программирования, называемых
транспортными моделями. Он был организатором получившей историче-
скую известность конференции комиссии Коулса по «линейному про-
граммированию», о которой говорилось в гл. I. На конференции присут-
ствовали такие известные экономисты, как К. Эрроу, Р. Дорфман, Н. Геор-
геску-Реген, Л. Гурвиц, А. Лернер, Д. Маршак, О. Моргенштерн,
С. Рейтер, П. Самуэльсон и Г. Симон; такие математики, как Г. У. Браун,
М. М. Флад, Д. Гейл, Г. У. Кун, Ч. Б. Томпкинс, А. У. Таккер, а также
автор настоящей книги. На ней присутствовали также статистики госу-
дарственных учреждений, среди которых были У. Д. Эванс, М. А. Гейслер,
М. Хоффенберг и М. К. Вуд. Представленные на конференцию материалы
позднее были собраны в сборнике «Анализ технологических процессов
производства и распределения» (сборник [18]). Этот сборник отражает те
интересы, которыми жили эти специалисты в течение двух предшествую-
щих лет. Ниже приводится одна интересная цитата из предисловия
к сборнику, в котором Купманс призывает экономистов-теоретиков отка-
заться от некоторых традиционных понятий.
«Прилагательное в термине «линейная модель» относится лишь:
а) к предположению о пропорциональности затрат и выпуска в каждом
элементарном технологическом процессе и б) к предположению, что
результатом совместного использования двух или более технологических
процессов будет сумма результатов отдельных технологических про-
цессов. В более близких для экономиста терминах это соответствует
прямой пропорциональной зависимости во всех частях технологии.
Из этих предположений не вытекает линейность производственной функ-
ции... Криволинейные производственные функции... можно получить
из исследуемых здесь моделей путем введения бесконечного множества
элементарных технологических способов...»
«Никакое предположение о пропорциональности... не следует счи-
тать существенным для иллюстрируемого метода подхода, хотя при попыт-
ке выйти за пределы этих допущений могут возникнуть новые матема-
тические задачи. Более важным для современного подхода является
введение... элементарного технологического процесса — первичного поня-
тия производства — в основные постулаты анализа. После этого задача
об эффективном производстве сводится к нахождению конкретных правил
комбинирования этих «строительных блоков» х. Понятие «анализ техно-
логических процессов»... предназначено для выражения этого подхода»
(сборник [18], стр. 6).
Купманс был первым, кто отметил, что многие из теорем по эконо-
мике жизненного уровня и исследованию принципов эффективного рас-
пределения ресурсов в экономике можно переформулировать, введя
допущение о линейности технологии для фирм. Решения, которые должны
приниматься людьми, стоящими у пульта управления по распределению
ресурсов, не вступают в конфликт с более ранними результатами тради-
ционной экономической теории; по существу, они носят более общий
характер и рассматривают совокупные продукты и побочные продукты
фирм (Купманс [2]).
1 Т. е. элементарных технологических процессов.— Прим. ред.
26
Примерно в то же самое время ряд других экономистов заинтере-
совался анализом технологических процессов и линейным программиро-
ванием. Дорфман (1951) сформулировал в терминах линейного програм-
мирования экономическую теорию фирмы в условиях конкуренции и моно-
полии и сопоставил область применимости этой теории с традиционным
маржинальным анализом (Дорфман [1]). Самуэльсон в 1955 г. написал
работу о «Рыночных механизмах и максимизации» и сформулировал свою
теорему о замещении для обобщенной модели леонтьевского типа (Самуэль-
сон [1]; сборник [18]). Различные классические экономические задачи,
такие, как торговля между двумя странами и парадокс Гиффена \
могут быть переформулированы как задачи линейного программирования
(Бекман [1]; Дорфман, Самуэльсон и Солоу [1]; сборник [18]).
Практические применения линейного программирования в эконо-
мике непрерывно растут. Линейное программирование используется эко-
номистами для детального исследования экономики отдельных отраслей
промышленности, например металлообрабатывающей (Марковиц [2]),
нефтеперерабатывающей1 2, металлургической (Фейбиан [1] — [3]), а также
для составления долгосрочных планов по энергетике в масштабе всей
экономики (Массэ и Жибра [1]). Некоторые из этих применений будут
приведены в примерах и упражнениях в последующих главах.
Для более полного ознакомления с экономическими приложениями
читатель отсылается к книге Дорфмана, Самуэльсона и Солоу «Линейное
программирование и экономический анализ» [1] и книге У. Г. Баумоля
«Экономическая теория и исследование операций» [2].
2-3. МАТЕМАТИЧЕСКИЕ ИСТОКИ И РАЗВИТИЕ
ИСТОРИЯ ДО 1947 г.
Модель линейного программирования, сформулированная в чисто
математических терминах (так, как это будет сделано в следующей главе)
требует метода нахождения решений системы линейных уравнений
и линейных неравенств, минимизирующих некоторую линейную форму.
До появления в 1947 г. линейного программирования эту основную мате-
матическую задачу линейного программирования не относили к числу
важнейших, имеющих множество практических приложений. Именно
этим можно частично объяснить тот факт, что математики уделяли не-
достаточно внимания нахождению эффективных путей решения таких задач.
Все знакомы с методами решения систем линейных уравнений,
с которых начинается наш первый курс алгебры (Гаусс [1]). В математи-
ческой литературе имеются тысячи работ, в которых рассматриваются
методы решения систем линейных уравнений: матричная алгебра
(примыкающая дисциплина), методы линейной аппроксимации и т. д.
С другой стороны, изучению систем линейных неравенств практически
не уделялось никакого внимания до появления теории игр в 1944 г. и ли-
нейного программирования в 1947 г. Так, Т. Моцкин в своей докторской
диссертации по линейным неравенствам, написанной в 1936 г., смог при-
вести в результате тщательных поисков всего 42 работы в том числе около
30 работ, относящихся к периоду 1900—1936 гг. (Моцкин [1]). В 30-х годах
были опубликованы четыре статьи, в которых создавалась исчерпывающая
теория линейных неравенств и содержался анализ предыдущих работ.
1 Сущность парадокса Гиффена состоит в возможности одновременного повыше-
ния цены на товар и спроса на него.— Прим. ред.
2 (Чарнс, Купер и Меллон [1]; Саймондс [1]; Манн [1], [2]; Гарвин, Крандалл,
Джон и Спеллман [1].)
27
Это были статьи Р. У. Стокса [1], Дайнса и Мак-Коя [1], Г. Вейля
[1] и Т. Моцкина [1]. Для подтверждения того, что математики
не отдавали себе отчета о важности задачи нахождения решений систем
неравенств, минимизирующих некоторую линейную форму, можно заме-
тить, что ни в одной из перечисленных работ не упоминалось об этой
задаче, хотя раньше в математической литературе такие примеры и встре-
чались.
Известный математик Фурье, по-видимому, впервые всесторонне
исследовал линейные неравенства и подчеркнул их большое значение
в механике и теории вероятностей, хотя и не дал глубокого анализа
проблемы (Фурье [1]). Его интересовала задача определения наи-
меньшего максимального отклонения в системах линейных уравнений.
Эту задачу он свел к задаче нахождения самой нижней точки многогран-
ного множества. Предложенный Фурье метод определения этого мини-
мума состоит в последовательном перемещении от одной вершины к дру-
гой. Подход Фурье лежит в основе симплекс-метода, который применяется
в настоящее время. Этот пример является, по-видимому, самым ранним
из известных примеров задач линейного программирования. Позднее
другой известный математик Валле Пуссен [1] рассмотрел ту же задачу
и предложил аналогичное решение.
Значительная часть ранних математических работ была посвящена
определению условий, при которых можно решать системы однородных
линейных неравенств. Все полученные результаты выражают в той или
иной форме взаимосвязь между исходной (прямой) системой и другой
системой (называемой двойственной), использующей столбцы исходной
матрицы коэффициентов, с помощью которых по определенным правилам
образуются новые линейные уравнения или неравенства. Типичной
является теорема П. Гордана [1], где говорится, что однородная
система уравнений с неотрицательными переменными имеет решение,
в котором по крайней мере одна переменная положительна, если в двой-
ственной системе нет решения со строгими неравенствами. Штимке [1]
добавил теорему о наличии решения со всеми положительными перемен-
ными. Эти результаты нашли более ясное выражение в теореме Моцкина
[1] о транспозиции и в теоремах Таккера [5] о двойственных системах.
Вопросу алгебраического доказательства теоремы минимакса посвящены
специальные работы Билля [1], фон Неймана и Моргенштерна [1].
Существенно, что эти теоремы утверждают, что либо исходная (прямая)
t система имеет нетривиальное решение, либо в двойственной системе
содержится решение со строгими неравенствами. Ввиду наличия этого
«либо-либо» фон Нейман и Моргенштерн назвали свой результат теоре-
мой об альтернативах для матриц (см. § 6-4).
Сопоставим две следующие теоремы:
Во-первых, известная теорема для систем уравнений: если любое
решение системы линейных уравнений удовлетворяет также и данному
линейному уравнению, то это уравнение может быть получено в виде
линейной комбинации уравнений системы. Во-вторых, неожиданная
и важная теорема Д. Фаркаша [1] о неравенствах формулируется так:
если любое решение системы линейных однородных неравенств удов-
летворяет также некоторому заданному линейному неравенству (где
все неравенства имеют вид > 0), то это неравенство может быть получено
в виде неотрицательной линейной комбинации неравенств системы.
В теоремах, аналогичных теоремам для систем уравнений, рассмат-
риваются вопросы построения общего решения системы неравенств в виде
линейной комбинации частных решений. Основной результат, полученный
Минковским [1], состоит в том, что для однородной системы общее реше-
28
ние может быть образовано в виде неотрицательной линейной комби-
нации из конечного числа существенных решений, называемых или
экстремальными, или угловыми, или базисными (последний термин при-
меняется в данной книге).
РАБОТЫ КАНТОРОВИЧА
Советский математик Л. В. Канторович на протяжении ряда лет
интересовался применением математики к задачам планирования.
В 1939 году он опубликовал обстоятельную монографию под названием
«Математические методы организации и планирования производства [1]».
Во введении Канторович пишет: «Существуют два пути повыше-
ния эффективности работы цеха, предприятия и целой отрасли промыш-
ленности. Один путь — это различные улучшения в технике, т. е. новые
приспособления в отдельном станке, изменение технологического про-
цесса, нахождение новых, лучших видов сырья. Другой путь, пока гораздо
меньше используемый,— это улучшения в организации производства
и планировании. Сюда относятся, например, такие вопросы, как распре-
деление работ между отдельными станками предприятия или механизмами,
правильное распределение заказов по предприятиям, правильное распре-
деление различных видов сырья, топлива и пр.» (Канторович [1]).
Канторовича следует признать первым, кто обнаружил, что широкий
класс важнейших производственных задач поддается четкой математиче-
ской формулировке, которая, по его убеждению, дает возможность под-
ходить к задачам с количественной стороны и решать их численными
методами.
В первой части своей работы Канторович рассматривает задачи,
известные в настоящее время как задачи двухиндексного взвешенного
распределения. Эти задачи были обобщены сначала до включения задачи
с условием в виде одной линейной формы, а затем и класса задач с про-
цессами, имеющими несколько одновременных выходов (последние
математически эквивалентны общей задаче линейного программиро-
вания). Канторович описал метод решения, основанный на имеющемся
первоначально допустимом решении двойственной задачи (применительно
к исследуемым конкретным проблемам решение этой второй задачи
не составляет труда). Хотя двойственные переменные и не назывались
«ценами», в целом идея метода состоит в том, что выбранные значения
этих «разрешающих множителей» для недостающих ресурсов можно дове-
сти до уровня, когда становится целесообразной переброска ресурсов,
являющихся избыточными. На простейших примерах Канторович пока-
зал, каким образом можно осуществить переброску излишних ресурсов.
Однако в общем виде задача о переброске ресурсов сама превращается
в задачу линейного программирования, для которой не было дано вычис-
лительного метода. В работе содержится интересный обзор возможных
применений описанных методов.
Статья «О перемещении масс» (Канторович [3]), опубликованная
в 1942 г., явилась этапом подготовки его следующей работы «Применение
математических методов в вопросах анализа грузопотоков», написанной
вместе с М. К. Гавуриным (Канторович и Гавурин [1]). В ней можно
найти в завершенном виде теорию задачи о перевозках, связь между
основной и двойственной (оценочной) системами, использование линейных
графов сети, а также важное обобщение для задач с ограниченными про-
пускными способностями. Кроме того, не вызывает сомнений, что авторы
разработали интересный метод для регулирования моделей грузопотоков
от неоптимальных к оптимальным применительно к сложным системам,
29
которые часто встречаются на практике. Однако и в этом случае дается
лишь неполный вычислительный алгоритм. Как успех авторов можно
отметить то, что работа написана на доступном языке, чтобы действи-
тельно дать возможность лицам, ответственным за перевозки, воспользо-
ваться предлагаемыми процедурами.
В 1959 г., спустя 20 лет после публикации первой работы, Канторо-
вич опубликовал свою вторую работу под названием «Экономический
расчет наилучшего использования ресурсов», предназначенную преиму-
щественно для экономистов [5]1.
Если бы первые работы Канторовича были бы в должной мере оце-
нены в момент их первой публикации, то возможно, что в настоящее
время линейное программирование продвинулось бы значительно дальше.
Однако его первая работа в этой области на протяжении почти двух деся-
тилетий оставалась неизвестной как в Советском Союзе, так и в других
странах, а за это время линейное программирование стало настоящим
искусством.
НЕПОСРЕДСТВЕННЫЕ ВЛИЯНИЯ
Все перечисленные выше работы, за исключением теоретико-игровых
результатов, полученных Нейманом и Виллем, не оказали, по-видимому,
непосредственного влияния на послевоенное развитие линейного про-
граммирования. Рассмотрим теперь те работы, которые, как известно,
оказали непосредственное влияние на развитие этой дисциплины.
В 1936 г. Д. Нейман и Е. С. Пирсон уточнили основные понятия
обоснования статистических проверок и оценок основных параметров
распределения по данным наблюдений (Нейман и Пирсон [1]). Ими
была использована ныне хорошо известная лемма Неймана — Пирсона
для построения наилучшего критерия проверки простой гипотезы, имею-
щей единственную альтернативу. Для более общего класса гипотез авторы
показали, что если существует критерий, удовлетворяющий их лемме
в обобщенной форме, то он будет оптимальным. В 1939 г. (и в своей док-
торской диссертации в 1946 г.) автор настоящей книги впервые доказал,
что для весьма общих условий такой критерий всегда существует. Эта
работа позднее была опубликована совместно с А. Вальдом, который
совершенно самостоятельно получил те же результаты в 1950 г. (Данциг
и Вальд [1]). Она явилась первым доказательством не только важной
теоремы двойственности линейного программирования, но также доказа-
тельством аналогичной теоремы для бесконечного (счетного) множества
переменных или (при использовании интегралов) для несчетного множе-
ства переменных. Но это уже относится к тем вопросам, которые
у Даффина называются бесконечными программами (см. Даффин [1]).
Интересно отметить, что условия обобщенной леммы Неймана — Пирсона
в действительности являются условиями, при которых решение задачи
линейного программирования с ограниченными переменными оказывается
оптимальным. Исследования автора по данной проблеме явились основой
его последующих работ по линейному программированию.
Заслуги в разработке математических основ линейного программи-
рования более чем кому-либо другому принадлежат Дж. фон Нейману
(см. Кун и Таккер [4]), который еще при своей жизни стал всемирно
известным математиком. Нейман играл ведущую роль во многих областях
1 Необходимо указать, что в 1951 г. Л. В. Канторович вместе с В. А. Залгаллером
опубликовал книгу «Расчет рационального раскроя промышленных материалов»,
также тесно связанную с описываемым циклом его работ.— Прим. ред.
30
науки; атомная энергия и электронно-вычислительная техника являются
теми двумя отраслями науки, где его влияние было огромно. В 1944 г.
Дж. фон Нейман и О. Моргенштерн опубликовали свою монументаль-
ную работу по теории игр, которая является отраслью математики, анали-
зирующей конфликтные ситуации с помощью моделей, называемых «игра-
ми» (Нейман и Моргенштерн [1]). Теория игр впервые появилась в 1921 г.
в работе Эмиля Бореля, а развил ее фон Нейман в 1928 г. в своей
известной теореме минимакса (Билль [1]; Борель [1]). Значение этих
работ заключается в том, что теория игр, как и линейное программи-
рование, имеет математической основой теорию линейных неравенств
(Кун и Таккер [4]).
РАБОТЫ ПОСЛЕВОЕННОГО ПЕРИОДА (1947—1956 гг.)
Летом 1947 г. известный эконометрик Леонид Гурвиц, связанный
с комиссией Коулса, работал вместе с автором настоящей книги над мето-
дами решения задач линейного программирования. Результаты этой
работы, а также некоторые рекомендации Т. Купманса легли в основу
симплекс-метода. Простая идея движения по ребрам выпуклого много-
гранника от одной вершины к другой (чем и характеризуется симплекс-
метод) ранее была интуитивно отвергнута как неэффективная. Однако
в другой геометрии она оказалась полезной и по счастливой случайности
была проверена и принята.
Фон Нейман во время первой встречи с автором в октябре 1947 г.
сумел переформулировать основные теоремы теории игр применительно
к системам линейных неравенств (Голдман и Таккер [2]). Он ввел
понятие двойственности х, подчеркнул важность этого понятия и выска-
зал предположение об эквивалентности задач теории игр и линейного
программирования (Данциг [3]; Гейл, Кун и Таккер [3]). Позднее фон
Нейман предложил ряд приемов численного решения задач линейного
программирования и теории игр (фон Нейман [4], [6]).
А. У. Таккер начал интересоваться теорией игр и линейным програм-
мированием в 1948 г. С этого времени Таккер и его бывшие студенты
(в особенности Дэвид Гейл и Гарольд У. Кун) работали над развитием
и систематизацией основополагающей математической теории линейных
неравенств. Их основная работа, так же как деятельность группы корпо-
рации РЭНД (в особенности Н. К. Дэлки, М. Дрешера, О. Хелмера,
Д. К. К. Мак-Кинси, Л. С. Шепли и Д. Д. Вильямса), была связана с обла-
стями, смежными с теорией игр (фон Нейман [4])^
Важную роль в развитии теории линейного программирования
сыграло Национальное бюро стандартов США (НБС). Оно не только через
своих сотрудников Джона X. Кэртиса и Альберта Кана установило важ-
ные контакты с работающими в данной области специалистами, но и пре-
доставило возможность проверки численных методов в своих лаборато-
риях. В конце 1947 г. в Нью-Йорке сотрудник группы («проекта») «Мате-
матические таблицы» Ладерман нашел оптимальное решение задачи
о диете Штиглера (Штиглер [1]) во время проверки только что пред-
ложенного симплекс-метода. В Институте численного анализа проф. Тео-
дор Моцкин, чьи работы по теории линейных неравенств были упомя-
нуты выше, предложил несколько вычислительных схем для решения
задач линейного программирования: «метод релаксации» (Моцкин и Шён-
1 Д. Рей Фулкерсон в беседе с С. Карлином, желая отметить заслуги фон
Неймана в теории двойственности, случайно приписал ему симплекс-метод. Позднее
эта ошибка была допущена в работе Карлина [1] и была повторена Чарнсом
и Купером [5].
31
берг [1]) и «метод двойного описания» (Моцкин, Райфа, Томпсон
и Тролл [1]). Чарльз Б. Томпкинс предложил свой метод проекций
(Томпкинс [1]). В контакте с группой Национального бюро стандар-
тов (НБС) работал Алекс Орден из Военно-воздушных сил. Эта группа
подготовила для СЕАК (автоматической электронно-вычислительной
машины НБС по обслуживанию восточных штатов страны) программы обще-
го симплекс-метода, а также программы для решения транспортной зада-
чи. Аллан Д. Гофман вместе с группой НБС оказал помощь в проведении
экспериментов по ряду возможных вычислительных методов (Гофман,
Манное, Соколовский и Вигман [1]). Гофман впервые установил, что
в симплекс-алгоритме можно получить «цикл», если не принять мер по
предотвращению вырождения (Гофман [1]).
В июне 1951 г. в Вашингтоне Управлением ВВС США и Националь-
ным бюро стандартов был проведен первый симпозиум по линейному
программированию. К тому времени линейным программированием стали
широко интересоваться правительственные и научные круги. А. Чарнс
и У. У. Купер только что приступили к своим первым работам в области
промышленного применения линейного программирования. Помимо этой
работы, о которой будет сказано в следующем параграфе, ими было опуб-
ликовано много статей по теории линейного программирования. Были
изданы их лекции «Введение в линейное программирование» (Чарнс,
Купер и Хендерсон [1]). В 1961 г. Чарнс и Купер издали свой двух-
томный труд [5].
РАЗРАБОТКА ВЫЧИСЛИТЕЛЬНЫХ МЕТОДОВ (1947-1956 гг.)
Как в США, так и за рубежом постоянно разрабатываются новые
вычислительные методы и новые варианты существующих методов. Кроме
того, что уже было перечислено выше, имелись ранние предложения
Г. У. Брауна и Т. С. Купманса (Браун и Купманс [1]), а также метод
решения игровых задач, принадлежащий Г. У. Брауну [1]. Позднее
известным специалистом по эконометрике Р. Фришем из университета
г. Осло была проведена большая исследовательская работа над своим
«мультиплекс-методом» (Фриш [2]). Исследования в Великобритании
велись под руководством С. Вайды [2]. Имеется несколько важных
вариантов симплекс-метода, разработанных К. Лемке [1], В. Орчард-
Хейсом [2], Е. М. Л. Билом [1] и др. (см. гл. 11).
ПРОГРАММЫ ДЛЯ ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
(1947-1956 гг.)
Программа симплекс-метода, разработанного для случая транспорт-
ной задачи (Данциг [4]), была впервые составлена в 1950 г. для машины
СЕАК, а программа для общего симплекс-метода была составлена в 1951 г.
под руководством А. Ордена из ВВС США и А. Д. Гофмана из Бюро стандар-
тов. В 1952 г. сотрудник корпорации РЭНД В. Орчард-Хейс разработал
программу симплекс-метода для вычислительной машины ИБМ — С. Р. С.
и для машин ИБМ 701 и 704 соответственно в 1954 и 1956 гг. Последняя
программа отличалась большой гибкостью и позволяла с высокой точно-
стью решать задачи с двумя сотнями уравнений и тысячей и более пере-
менных в течение примерно пяти часов (Орчард-Хейс [4]).
Частный прием для решения треугольной модели ВВС США был впер-
вые разработан в 1949 г. Весной 1949 г. М. Монталбано из Националь-
ного бюро стандартов создал предварительную программу для вычисли-
тельной машины ИБМ-602-А; позднее более разработанная программа
32
была создана для машины ИБМ-604. В начале 1950 г. он же совместно
с С. Димом подготовил программу симплекс-метода для машины СЕАК,
которая была продемонстрирована во время пуска вычислительной маши-
ны. После получения в 1952 г. ВВС США вычислительной машины
ЮНИВАК эти вычислительные программы были перекодированы.
Использование электронных вычислительных машин в промыш-
ленной и деловой сферах росло исключительно быстро. Много цифровых
вычислительных машин, которые имелись в продаже, были снабжены
программами симплекс-метода. Наряду с этим был проявлен интерес
к созданию аналоговых вычислительных машин для отдельных случаев ре-
шения задач линейного программирования (Эблоу и Бригам [1];
Пайн [1]). Возможно, что такие вычислительные машины окажутся эффек-
тивным средством оценки параметрических изменений в системе, представ-
ленной моделью линейного программирования; они также могут быть
полезными в тех случаях, когда постоянно существует необходимость
быстро решать задачи линейного программирования, как, например, при
производственном планировании. Указанные вычислительные машины
работают хорошо при решении небольших задач (например, в задачах
с двадцатью переменными и десятью уравнениями). Ввиду искажения
электрических сигналов представляется непрактичным конструировать
аналоговые вычислительные машины для решения в общем случае боль-
ших задач линейного программирования. Тем не менее представляется
весьма целесообразным пытаться исследовать вопросы использования
таких вычислительных машин для решения больших систем специфиче-
ской структуры.
РАЗВИТИЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Если мы фиксируем различие, а в действительности мы именно так
и должны поступать, между теми видами обобщений в математике, кото-
рые ведут к доказательствам существования, и обобщениями, дающими
конструктивное решение практических задач, то можно сказать, что
период, следующий за первым десятилетием, положил начало ряду важ-
ных конструктивных обобщений понятий линейного программирования,
затрагивающих смежные разделы математики. Сюда относятся:
1. Теория сетей. Замечательное свойство частного класса задач
линейного программирования транспортной или эквивалентной задачи
о потоке в сети состоит в том, что крайние точки их решений являют-
ся целочисленными, если свободные члены в задачах суть целые числа
(Г. Биркгоф [1]; Данциг, [4]). На этом строится одна из интересней-
ших теорий, связывающая некоторые комбинаторные задачи тополо-
гии с непрерывными процессами теории сетей. В этой области имеется
много разработок. Особого внимания заслуживает работа Куна [1],
в которой подход Эгервари применяется к задаче нахождения перестанов-
ки единиц в матрице, состоящей из нулей и единиц, а также работа Форда
и Фулкерсона [1] о потоке в сети. Эти вопросы освещены в гл. 19 и 20
(Гофман [3]; Берж [1]; Форд и Фулкерсон [8]).
2. Выпуклое программирование. Заменяя в ограничениях, если они
даны в виде неравенств, линейные функции выпуклыми и проделывая
то же с целевой функцией, мы получаем естественное обобщение линей-
ного программирования. В ранних работах этой области рассматрива-
лась квадратичная целевая функция (Дорфман [1]; Баранкин и Дорф-
ман |1]; Марковиц [4]); работы по выпуклому программированию
3 Дж. Данциг
достигли своей вершины в изящном методе, разработанном одновременно
Билом [3], Хаутэккером [2] и Вулфом [2], который показал, как можно
использовать некоторый вариант симплекс-метода для решения задач
этого класса. К более раннему этапу относится также исследование слу-
чая, в котором выпуклая целевая функция может быть представлена
в виде суммы слагаемых, каждое из которых является выпуклой функцией
от одной переменной (Данциг [12], Чарнс и Лемке [1]). Общий случай
рассматривался в фундаментальных трудах Куна и Таккера [1], Эрроу,
Гурвица и Удзавы [1]. (См. библиографию к гл. 24.) В данной книге
упомянутая задача решается с использованием принципа разложения для
задач линейного программирования (гл. 22, 23, 24). В математической
литературе можно найти много других интересных подходов (Розен [1]).
3. Целочисленное программирование. Можно показать, что важные
классы нелинейных, невыпуклых, дискретных, комбинаторных задач
формально можно привести к задачам типа линейного программирования,
однако при этом переменные в этих задачах (или некоторая их часть)
могут принимать лишь целые значения. Введение понятия секущих пло-
скостей позволило методами линейного программирования найти опти-
мальный маршрут следования коммивояжера, посещающего Вашингтон
и центры всех 48 штатов США (Данциг, Фулкерсон и Джонсон [1]).
Эта теория не была закончена. Основы точной теории впервые были созда-
ны Гомори [1] — [4] (см. гл. 26).
4. Программирование в условиях неопределенности Ч Маданский
[2] установил, что область программирования при неопределенности
не может быть естественным образом сформулирована в виде некоторой
единой задачи. В данной книге рассматривается один из важнейших
классов — класс многошаговых задач, в которых технологическая матри-
ца коэффициентов затраты — выпуск считается известной, значения
постоянных членов неопределенны, но совместное вероятностное распре-
деление их возможных значений считается известным. О некоторых мето-
дах решения данного класса задач можно прочитать в гл. 25 и 28. Много-
обещающий подход, основанный на принципе разложения, был рассмот-
рен Данцигом и Маданским [1].
2-4. ПРИМЕНЕНИЕ линейного программирования
В ПРОМЫШЛЕННОСТИ
История первых лет линейного программирования была бы непол-
ной без краткого обзора его использования в промышленности и деловой
жизни. Применение линейного программирования в этих областях начи-
нается с 1951 г., но значительный размах оно получило в 1955—1960 гг.,
и именно этот период по своему охвату имеет большую значимость, неже-
ли весь предыдущий опыт использования линейного программирования
в военной области.
В промышленности линейное программирование применяется при
решении различных вопросов. Во-первых, оно обеспечивает новую точку
зрения на все технологические процессы; во-вторых, оно стимулирует иссле-
дования по математическому анализу структуры промышленных систем;
1 Здесь речь идет о так называемой стохастической неопределенности, при кото-
рой вместо известных значений параметров задачи рассматриваются известные веро-
ятностные распределения значений.— Прим. ред.
34
и, в-третьих, оно стало важным инструментом коммерческого и промыш-
ленного руководства в деле повышения его эффективности. Поэтому
применение линейного программирования к деловым и промышлен-
ным задачам потребовало математической формулировки задач и точного
описания поставленных целей. Во многих случаях количественное осмыс-
ливание экономических задач дает возможность лучше понять вопросы
принятия административных решений (раньше эти решения оставались
скрытыми в тумане словесных доводов). Следствием этого, в частности,
явилось то, что некоторые промышленные фирмы уже приступили к обу-
чению руководящего персонала по программам, в которых делается упор
на важность определения целей и ограничивающих условий в коммерче-
ской политике. К тому же планирование производства в промышленно-
сти, как и в сфере военной деятельности, по традиции основывалось на
интуиции и опыте, на нескольких правилах и на использовании непосред-
ственных средств. Линейное программирование стимулировало обширные
исследования в деле разработки количественных моделей промышленных
систем для производственного планирования. Конечно, многие из слож-
ных систем к настоящему времени еще не нашли количественного выраже-
ния, но даже проекты таких моделей вызывают широкий интерес. В ка-
честве примера можно указать на проблему календарного планирования
производства, где исследования по разработке опытной модели типа линей-
ного программирования были начаты М. Салвесоном [1]. В настоя-
щее время исследования по этой проблеме ведутся несколькими научными
и промышленными исследовательскими группами (Джэксон [1]).
Время от времени появляются сообщения о прибылях, получаемых тор-
говыми и промышленными фирмами благодаря использованию линейного
программирования в работах по планированию и составлению графиков
(Данциг [13]).
Первый из наиболее эффективных случаев использования линейного
программирования в промышленности относится к планированию нефте-
перерабатывающего производства. Как было указано ранее, Чарнс,
Купер и Меллон начали свою работу в этой области в 1951 г. (Чарнс,
Купер и Меллон [1]). По данному вопросу написано две книги: одна
Гиффордом Саймондсом (Саймондс [1]), а другая Алланом Манном (Манн
[1]). В обзоре, составленном Гарвином, Крандаллом, Джоном и Спел-
лманом [1], отмечено, что нефтяная промышленность использует ли-
нейное программирование в работах по разведке, добыче, распреде-
лению и очистке нефтепродуктов, что само по себе говорит об интенсив-
ности исследований. К этому перечню вскоре можно будет добавить работу
по составлению методами линейного программирования маршрутов сле-
дования танкеров.
На втором месте по внедрению линейного программирования стоит
пищевая промышленность. В 1953 г. одна из крупнейших пищевых фирм
впервые использовала линейное программирование для определения
плана перевозки томатного соуса от 6 заводов к 7 складам (Хендерсон
и Шлейфер [1]), а один из поставщиков молочных продуктов приме-
нил этот метод к такой же задаче, с той лишь разницей, что в данном слу-
чае число складов составляло несколько сотен. Один из крупнейших
поставщиков мясных продуктов определяет с помощью линейного про-
граммирования наиболее экономичные рационы кормления животных
(Фишер и Шрубен [1]).
В металлургической промышленности линейное программирование
используется для оценки качества различных видов железных руд,
а также обогащения низкосортных руд (Фейбиан [1]). Кроме того, его
применяют для определения состава шихты в печах и загрузки прокатных
35
3*
станов (Фейбиан [2]); в настоящее время составляется модель линей-
ного программирования для описания комплексного сталеплавильного
завода (Фейбиан [3]). Сообщалось, что в английской металлургиче-
ской промышленности линейное программирование используется при
определении ассортимента продукции прокатных станов на основе макси-
мизации прибыли.
Металлообрабатывающая промышленность применяет линейное про-
граммирование для расчета загрузки цехов (Морин [1]), а также при
определении соотношения между производством и закупкой каких-либо
деталей (Льюис [1]; Мейнард [1]). На бумажных фабриках линей-
ное программирование используют для уменьшения потерь при обрезке
(Эйземанн [1]; Полл и Уолтер [1]; Дойг и Белз [1]).
Определение оптимальных потоков сообщений в сетях связи (Калаба
и Хункоса [1]), арбитражные задачи по контрактам (Голдстейн [1];
Гойнен [1]), составление маршрутов следования самолетов и кораб-
лей (Данциг и Фулкерсон [1]; Фергюсон и Данциг [1], [2]) — все это
проблемы, которые уже рассматривались военными специалистами
и которые обсуждаются в настоящее время промышленными кругами.
Во Франции с помощью методов линейного программирования иссле-
дуют оптимальные программы капиталовложений в энергетику (Массэ
и Жибра ЦП-
Области применения линейного программирования начиная с 1957 г.
настолько расширились, что невозможно перечислить все из них в пре-
делах этой работы.
ФО РМУЛИРОВЕА МОДЕЛИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ1
3-1. ОСНОВНЫЕ понятия
Предположим, что изучаемая система (которая может либо сущест-
вовать в действительности, либо лишь в проекте) представляет собой
комплекс машин, людей, вспомогательного оборудования и сырья. Для
существования этой системы имеются те или иные причины: она должна
обеспечивать эффективные действия войск или же в промышленности
производить определенные виды продуктов.
Основанный на линейном программировании подход состоит в том,
чтобы рассматривать систему в виде совокупности нескольких элемен-
тарных функций, называемых технологическими процессами. Технологи-
ческий процесс мыслится здесь как своего рода «черный ящик» 2, для кото-
рого на вход подаются материальные ресурсы (люди, сырье, оборудова-
ние), а выходом оказываются продукты промышленного производства
или обученные военные подразделения. Что происходит с ресурсами вну-
три «ящика»— дело инженера или соответственно лица, производящего
обучение; что же касается лица, формулирующего задачу, то его интере-
суют в этом технологическом процессе только величины затрат и выпуска.
Различные виды затрат и выпуска называются ингредиентами.
Количественный показатель использования каждого технологиче-
ского процесса называется его интенсивностью. Для того чтобы изме-
нить интенсивность технологического процесса необходимо изменить
его затраты и выпуск.
ПРЕДПОЛОЖЕНИЕ 1: ПРОПОРЦИОНАЛЬНОСТЬ
В модели линейного программирования величины затрат и выпуска
различных ингредиентов технологического процесса всегда пропорцио-
нальны его интенсивности. Если мы хотим осуществить процесс с двой-
ной интенсивностью, то мы просто удваиваем все затраты, соответствую-
щие единичной интенсивости. Так, в примере 3 § 1-2, если бы мы хотели
удвоить число рабочих, обученных в течение периода обучения, то мы долж-
ны были бы удвоить на этот период число инструкторов и соответственно
число нанятых рабочих. Это характеристическое свойство модели линей-
ного программирования называется условием пропорциональности.
ПРЕДПОЛОЖЕНИЕ 2: НЕОТРИЦАТЕЛЬНОСТЬ
В то время как допускаются любые положительные кратные некото-
рого технологического процесса, отрицательные их интенсивности невоз-
1 Эта глава, написанная Филиппом Вулфом, основана на более ранних набро-
сках автора.
2 «Черным ящиком» называется любая система, процессы, происходящие внутри
которой, намеренно игнорируются.
37
можны. Так, в примере 1 1-2 нельзя погрузить отрицательное число
ящиков. Другой пример имеется в хорошо известной классической лите-
ратуре: Безумный Шляпочник, как вы можете вспомнить, в «Приклю-
чениях Алисы в стране чудес» убеждал Алису выпить еще немного чаю,
а Алиса возражала, что ей не ясно, как, собственно, она могла бы выпить
еще, если она не пила вообще. «Вы имеете в виду, что вам не ясно, как
вы можете выпить еще меньше чаю,— сказал Шляпочник,— но ведь
совсем не трудно выпить больше, чем ничего». Эта тонкость Льюиса Ка-
ролла была, вероятно, оставлена без внимания его читателями, не имев-
шими представления о линейном программировании, ибо с какой стати
нужно подчеркивать тот очевидный факт, что технологический процесс «чае-
питие» не может осуществляться в отрицательном количестве? Возможно,
этим Кэррол хотел сказать, что математики в течение столетий были так
заняты обобщением числовой системы с целых чисел на дроби, отрица-
тельные числа, мнимые числа, что они мало думали о том, как удерживать
участвующие в задачах переменные в их первоначальной области неотри-
цательных чисел. Это характеристическое свойство переменных модели
линейного программирования известно как условие неотрицательности.
ПРЕДПОЛОЖЕНИЕ 3: АДДИТИВНОСТЬ
Следующий шаг в построении модели состоит в том, чтобы опреде-
лить, какая совокупность технологических процессов является полной
в том смысле, что полный расчет технологического процесса может быть
сделан по каждому ингредиенту. Говоря точно, требуется, чтобы общее
количество каждого ингредиента, определенное системой как целым, было
равно сумме количеств, поступающих в различные технологические про-
цессы, минус сумма количеств, выходящих из них. Таким образом, в на-
шей абстрактной системе каждый ингредиент характеризуется уравне-
нием материального баланса, различные члены которого представляют
собой затраты или выпуск различных технологических процессов. В при-
мере, связанном с консервным заводом, число ящиков, отправленных
на склад, должно быть полностью сбалансировано с количествами, посту-
пающими от различных* заводов (включая, возможно, хранение или
использование каких-либо излишков).
ПРЕДПОЛОЖЕНИЕ 4: ЛИНЕЙНАЯ ЦЕЛЕВАЯ ФУНКЦИЯ
Один из ингредиентов нашей системы рассматривается как «ценност-
ный» в том смысле, что общее его количество, произведенное системой,
измеряет выигрыш системы. Этим ингредиентом может оказаться квали-
фицированный труд, завершенные агрегаты, используемые ресурсы,
запасы которых дефицитны, подобно ограниченному денежному бюджету.
Вклад каждого технологического процесса в общий выигрыш есть коли-
чество ценностного ингредиента, которое потребляется или выпускается
в этом технологическом процессе. Таким образом, если цель состоит
в том, чтобы максимизировать доход, технологические процессы, которые
требуют денег, вносят в общий доход отрицательную величину, а те тех-
нологические процессы, которые производят деньги, вносят в общий
доход положительную величину. Расходы домашней хозяйки на каждый
из видов пищи в примере 2 § 1-2 представляют собой отрицательный
вклад в общий «доход» семьи; в этом примере нет технологических про-
цессов, которые бы вносили положительную величину. Эта черта модели
линейного программирования называется условием линейной целевой
функции.
38
СТАНДАРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Определение таких неотрицательных интенсивностей технологиче-
ских процессов, при которых количества каждого ингредиента (для этих
интенсивностей технологических процессов) удовлетворяют уравнениям
материального баланса, а величина выигрыша максимальна, называется
стандартной задачей линейного программирования. Представление реаль-
ной системы, как в любом из трех примеров § 1-2, в виде математической
системы, обладающей перечисленными выше характеристиками, назы-
вается моделью линейного программирования. Задача планирования тех-
нологических процессов реальной системы преобразована, таким обра-
зом, в задачу нахождения решения для модели линейного программи-
рования.
3-2. ПОСТРОЕНИЕ МОДЕЛИ
Ввиду того что построение модели представляет собой существенный
аспект планирования, теперь будут систематизированы отдельные шаги,
которые должны быть предприняты при построении модели линейного
программирования. После этого мы покажем, как построенная модель
определяет задачу линейного программирования. Симплекс-метод как
средство решения общей задачи линейного программирования будет
рассматриваться в гл. 5. В настоящей же главе мы применим к двум типич-
ным примерам менее общий графический метод.
Математическая модель системы представляет собой совокупность
соотношений, которые определяют допустимые в системе планы. Под
допустимыми планами далее понимаются такие планы, которые могут быть
осуществлены при соблюдении ограничений системы. Построение мате-
матической модели часто дает возможность столь глубокого проникнове-
ния в систему и получения сведений о ней, что его можно рассматривать
как более важную задачу, чем та задача математического программиро-
вания, которой оно предшествует. Построение модели часто оказывается
затруднительным ввиду богатства, разнообразия и неопределенности
реального мира. Тем не менее можно сформулировать некоторые прин-
ципы, выделяющие последовательные шаги в процессе построения модели.
Излагаемая далее схема этого процесса основана на основных пред-
положениях а) пропорциональности, б) неотрицательности, в) адди-
тивности и г) линейности целевой функции, которые положены в основу
модели линейного программирования. Читателю рекомендуется просмот-
реть эти понятия и в дальнейших примерах выявлять эти характеристики
моделей.
Шаг 7. Определить множество технологических процессов. Разложить
всю изучаемую систему на все ее элементарные функции, технологические
процессы, и для каждого технологического процесса выбрать единицу,
которой можно измерить его объем или интенсивность.
Шаг 2. Определить систему ингредиентов. Определить классы объек-
тов, ингредиентов, которые потребляются или производятся технологи-
ческими процессами, и выбрать единицу для измерения каждого из них.
Выбрать один ингредиент так, чтобы чистое количество его, произведен-
ное всей системой, измеряло «затраты» (или так, чтобы это количество
со знаком минус измеряло «доход») всей системы Ч
1 В следующем примере оказалось, что «стоимости» являются деньгами; однако
в экономических примерах они могли бы измеряться трудом или любым другим дефи-
цитным ресурсом, затраты которого должны экономиться, или же любым ингредиентом,
общий, выпуск которого из системы нужно максимизировать.
39
Шаг 3. Определить коэффициенты затрат — выпуска. Определить
количество каждого ингредиента, потребленное или произведенное при
использовании каждого технологического процесса в условиях его еди-
ничной интенсивности. Эти числа, коэффициенты затрат—выпуска,
представляют собой коэффициенты пропорциональности, связывающие
интенсивности производственных способов и потоки ингредиентов.
Шаг 4. Определить экзогенные потоки. Определить чистые затраты
или выпуски ингредиентов между системой, рассматриваемой как целое,
и внешним миром.
Шаг 5. Составить уравнения материального баланса. Всем техноло-
гическим процессам приписать неизвестные неотрицательные интен-
сивности Xi, х2, . . затем для каждого ингредиента выписать уравне-
ние материального баланса, которое утверждает, что алгебраическая сум-
ма расходов этого ингредиента в каждом технологическом процессе (выра-
женных в виде произведения его интенсивности на соответствующий
коэффициент затрат — выпуска) равна экзогенному потоку этого ингре-
диента.
Таким образом, в результате построения модели получается сово-
купность математических соотношений, описывающих все допустимые
планы системы. Эта совокупность и есть модель линейного программиро-
вания.
После того как модель построена, задача линейного программирова-
ния может быть сформулирована в математических терминах. Решение
этой задачи можно интерпретировать как план для системы — расписа-
ние времени и объема действий, которые должны быть выполнены нахо-
дящейся в заданном начальном состоянии системой для осуществления
заданной цели.
ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Определить интенсивности всех технологических процессов системы,
которые а) неотрицательны, б) удовлетворяют уравнениям материального
баланса и в) минимизируют общую стоимость.
Разработка методов решения задачи линейного программирования
составляет основную математическую задачу линейного программиро-
вания, которой посвящены многие из последующих глав.
В приведенных ниже примерах при выполнении нами шагов построе-
ния модели необходимо отметить одно обстоятельство: мы не всегда будем
завершать модель за одну последовательность шагов. Часто случается,
что на некоторые технологические процессы, обычно связанные с управ-
лением используемыми ресурсами или перевыполнением требований,
не обращают внимания до тех пор, пока уравнения материального баланса
не потребуют их включения. Таким образом, возвращение от шага 5
к шагу 1 иногда будет необходимо, прежде чем будет завершено построение
модели.
3-3. ТРАНСПОРТНАЯ ЗАДАЧА
В примере § 1-2 с консервными заводами мы потребовали, чтобы план
перевозок ящиков минимизировал общую стоимость перевозок от заводов
к складам. Для того чтобы упростить эту задачу, мы предположим, что
имеется два завода, завод I и завод II, и три склада, обозначенные через
А, В и С. Наличие ящиков с консервами на заводах и их потребности на
склад ах следующие:
40
Наличие ящиков
350 на заводе I
650 на заводе II
1000 общее наличие
Потребности в ящиках
300 на складе А
300 на складе В
300 на складе С
900 общая потребность
Излишки производства (100 ящиков) должны не перевозиться, а оставать-
ся на месте. Стоимости перевозки каждого ящика от любого завода до
каждого склада приведены в таблице стоимостей перевозок (1). Задача
состоит в том, чтобы определить число ящиков, которое нужно перевезти
с каждого завода на каждый склад для минимизации общих транспортных
расходов
Таблица стоимостей перевозок
(в долл, за ящик)
Консервные заводы Склады
Нью-Йорк (А) Чикаго (В) Канзас-Сити (С)
Сиэтл (I) 2,5 1,7 1,8
Сан-Диего (II) 2,5 1,8 1,4
Для того чтобы построить модель, которая описывает взаимоотно-
шения между наличиями ящиков на заводах и потребностями на складах,
мы начнем с анализа одной из элементарных функций, а именно с техно-
логического процесса, состоящего в перевозке с одного завода на один склад.
Перевозка ящика с завода I на склад А (т. е. из Сиэтла в Нью-Йорк)
показана на диаграмме (2). В качестве затрат она требует двух ингреди-
ентов: один ящик в Сиэтле и 2,5 долл, расходов. В качестве выпуска она
производит один игредиент: один ящик в Нью-Йорке. Основное предпо-
ложение состоит в том, что х ящиков, которые должны быть отправлены
из I в Л, потребуют в качестве затрат 1-х ящиков и 2,5-я долл, расходов;
в качестве выпуска будет произведено 1-х ящиков в А.
Каким образом этот технологический процесс осуществляется и что
именно происходит с ящиком между его пунктами отправления и назна-
чения, не входит в задачу программирования. В этом смысле технологи-
ческий процесс действительно становится «черным ящиком», в который
некоторые ингредиенты поступают, а другие выходят; в нашем случае
выпуск есть аналогичный ингредиент, но в другом месте.
Схема «черного ящика» транспортного технологического
процесса
(2)
Пример с консервными заводами содержит шесть технологических про-
цессов, которые представляют собой шесть возможных способов перевозки
ящиков от двух заводов к трем складам. Можно также хранить продукцию
на заводах, что приводит к другого рода возможной элементарной функ-
41
ции, технологическому процессу, состоящему в хранении. Хранение
потребляет ингредиент и стоимость (измеренные в этом примере в долла-
рах; см. § 3-2, сноску на стр. 39) в некоторый момент t и производит этот
ингредиент в некоторый более поздний момент t + 1.
Схема «черного ящика» типичного процесса хранения
(3)
Сходство технологических процессов, описанных на схемах (2) и (3),
состоит в том, что перевозка есть преобразование в пространстве, а хране-
ние — преобразование во времени. Ввиду того что в нашей конкретной
задаче мы не будем рассматривать ни выпуски в более поздние моменты
времени, ни приписывание каких-либо стоимостей хранению, эти два про-
цесса хранения примут упрощенную форму (4).
(4)
Шаг 1. Рассмотрим теперь первый шаг построения модели. Мы нач-
нем с составления (5) списка восьми возможных процессов перевозки
и хранения. Для удобства слева от этих способов выписаны номера для
ссылок; так, технологический процесс «4» есть «перевозка из II в Л».
В качестве единицы для измерения объема перевозки или хранения есте-
ственно выбрать один ящик; однако для каждого технологического про-
цесса можно было бы выбрать свою единицу измерения. Например, еди-
ницей первого технологического процесса могли бы быть десятки переве-
зенных ящиков, а второй мог бы измеряться в долларах транспортных
расходов и т. д.
Перечень технологических процессов
1. Перевозка от I до Л 5. Перевозка от II до В
2. » » I до в 6. » » II до С
3. » » I до С 7. Хранение излишков в I
4. » » II До А 8. » » в II
(5)
Шаг 2. Можно было бы полагать, что, кроме стоимостей, имеется еще
только один вид ингредиента, а именно ящик. Однако экономисты ука-
зывают, что аналогичные ингредиенты в разных местах 1 или же в разные
1 Птица в руках стоит двух в кустах. (A bird in the hand is worth two in the
bush.) (Лучше синица в руках, чем журавль в небе.— Прим, перев.)
42
моменты времени1 являются в сущности различными ингредиентами.
В соответствии с нашими целями мы игнорируем изменение времени
и сосредоточимся только на перемещениях из одних мест в другие. Соглас-
но этому, получится список из шести ингредиентов, отражающих два заво-
да, три склада и ингредиент стоимости (деньги). Слева к ингредиентам,
выписанным в (6), приписаны номера для ссылок; так, ингредиент 4
представляет собой «ящики в В». Для каждого из ингредиентов 1—5
в качестве единицы измерения будет использоваться один ящик, а для
ингредиента 6, т. е. стоимости — один доллар.
Перечень ингредиентов
1. Ящики в I 4. Ящики в В (6)
2. » » II 5. » » С
3. » » А 6. Стоимости (долл.)
Шаг 3. При выписывании коэффициентов затрат — выпуска в модели
будет использоваться следующее соглашение об алгебраическом знаке
коэффициента: затраты будут считаться положительными, а выпуск —
отрицательным. Символически:
Технологичес-
кий процесс
Мы не будем, однако, записывать значения коэффициентов в таком виде,
а расположим их в форме таблицы (см. табл. 3-3-1).
Таблица 3-3-1
Таблица коэффициентов — транспортная модель
Ингредиенты Технологические процессы
1—1 to м 1 00 О 4 5 6 1Г*А Ц->В II-+C 7 8 хра- хра- нить нить в А в В
1. Ящики в I +1 +1 +1 +1
2. Ящики в II +1 +1 +1 +1
3. Ящики в А —1 —1
4. Ящики в В —1 —1
5. Ящики в С -1 —1
6. Стоимости (долл.) 4-2,5 4-1,7 4-1,8 4-2,5 4-1,8 4-1,4
Каждому технологическому процессу в этой таблице соответствует верти-
кальный столбец^ а каждому ингредиенту — горизонтальная строка;
на пересечении каждой строки и каждого столбца мы помещаем коэффи-
1 Один стежок, сделанный вовремя, стоит девяти. (A stitch in time sakes nine.)
(Дорога ложка к обеду.— Прим, перев.)
43
циент затрат — выпуска со знаком для того ингредиента, который тре-
буется единичной интенсивностью технологического процесса.
Таким образом, технологический процесс 4, примененный с единич-
ной интенсивностью для перевозки (одного ящика) из II в Л, имеет в ка-
честве затрат один ящик в II (коэффициент +1 в строке 2, столбце 4)
и 2,5 долл, (коэффициент +2,5 в строке 6, столбце 4); в качестве выпуска
он имеет один ящик в А (коэффициент —1 в строке 3, столбце 4). Состав-
ление этой таблицы легко контролируется путем рассмотрения каждой
строки для того, чтобы выяснить, произведен или нет полный расчет по каж-
дому ингредиенту; так, в строке 1 ингредиент 1 (ящики в I) входит только
в качестве затрат, и эти затраты потребляются технологическими процес-
сами 1, 2, 3 и 7; а в строке 3 ингредиент 3 (ящики в А) выступает только
как выпуск технологических процессов 1 и 4.
Шаг 4. Экзогенные (внешние) потоки, поступающие в систему и тре-
буемые от системы как целого, показаны на схеме (8) в виде «черного ящи-
ка». Затраты суть ящики, имеющиеся в распоряжении системы в I и II,
а выпуски суть потоки, требуемые от системы. Заметим, что пока еще
не были определены денежные затраты. Они должны быть как можно
меньше. До тех пор, пока они не определены, они будут обозначаться
через z.
’/МЮ//////,
' Экзогенные Z
^технологические/
' процессы <
7///////////,
Система
/ как
' целое
Z долларов
300 ящиков в А
300 ящиков в В
300 ящиков в С
(8)
Полезно выписать эти экзогенные потоки в столбец, упорядоченный
по ингредиентам, аналогично столбцу для каждого технологического про-
цесса в табл. 3-3-1. Это сделано в табл. (9), где должно использоваться
то же самое соглашение относительно алгебраического знака экзогенных
потоков, которое принято относительно потоков в каждый технологиче-
ский процесс внутри системы, потому что алгебраическая сумма потока
по всем технологическим процессам будет приравнена к экзогенным пото-
кам. Следовательно, экзогенные затраты будут положительны, а экзо-
генные выпуски отрицательны. Таким образом:
Ингредиент
Экзогенные потоки
1. Ящики в I
2. Ящики в II
3. Ящики в А
4. Ящики в В
5. Ящики в С
6. Стоимости (долл.)
350 ]
650 I затРаты» поступающие в систему
—300 ।
—300 I выпуски, требуемые от системы
—300 J
1 минимальные затраты, поступающие
J в систему
___________________________________________I
(9)
44
Шаг 5. Сопоставим каждому из технологических процессов 1,2, . . . ,
. . . , 8 неизвестную и подлежащую определению величину, которая
представляет собой интенсивность этого технологического процесса.
Обычно мы обозначаем интенсивность технологического процесса 1 через
хь технологического процесса 2 через х2, . . . , технологического про-
цесса 8 через х8.
Используя таблицу коэффициентов, полученную на шаге 3, теперь
легко записать уравнения материального баланса для системы, по каж-
дому ингредиенту.
Для ингредиента 1 (ящики в I) технологические процессы, потреб-
ляющие его, суть 1, 2, 3 и 7 (перевозки, хранение в I). Ввиду того, что
коэффициенты затрат — выпуска, связанные с ингредиентом 1, все рав-
ны +1, чистый поток ингредиента 1 в точности равен
+ + 1-ж7.
Этот поток должен быть равен экзогенному потоку в систему ингредиента
1, который равен 350. Это дает нам первое уравнение материального
баланса
х^ “I- *%2 Ч~ Ъ Ч~ ==: 350.
Точно так же уравнение материального баланса для ингредиента 2 (ящи-
ки в II) есть
#4 + %5 + ^6 + #8 — 650.
Для ингредиента 3 (ящики в А) уравнение приобретает иной вид.
Здесь технологические процессы 1 и 4, представляющие собой перевозки
в А, имеют коэффициенты —1 и никакие другие технологические процес-
сы не включают ингредиент 3. Чистый поток равен
— 1-Xi—1-х4,
и ввиду того, что экзогенный поток есть выпуск —300, уравнение будет
таким:
—Xi—х± = —300.
Остальные уравнения, соответствующие ингредиентам 4 и 5, дают анало-
гичный расчет ящиков в В и С, т. е. соответственно:
— х2—хъ = —300,
—х3—xQ = —300.
Эти уравнения различными способами записаны в виде табл. 3-3-11 и в фор-
ме системы уравнений (11).
Наконец, поток в систему ингредиента 6, очевидно, описывается
выражением
2,5х^ 1,7x2 Ч- 1,8x3 Ч~ 2,5х4 Ч- 1,8x5 Ч~ 1 ,4xg.
Мы приведем это выражение к виду уравнения материального баланса,
приравнивая это выражение к неопределенным денежным затратам z.
(Напомним при этом, что мы еще не знаем, какое численное значение долж-
но иметь z.)
2,5xj 4“ 1,7х2 Ч~ 1,8x3 Ч~ 2,5x4 Ч~ 1,8x5 Ч~ 1,4хе ~
Теперь шаг 5 завершен.
45
МОДЕЛЬ В ФОРМЕ УРАВНЕНИЙ
Система уравнений материального баланса, полученная здесь, вместе
с условиями неотрицательности интенсивностей х19 . . . , х8 всех техно-
логических процессов составляет модель линейного программирования
для этой транспортной задачи. Эти уравнения выражены неравенствами
(10) и равенствами (11), которые вместе и составляют то, что называется
моделью в форме уравнений.
ТАБЛИЦА
Таблица линейного программирования дает как компактную форму
для записи данных модели линейного программирования, так и метод
получения из этих данных уравнений материального баланса, минуя
подробные рассуждения, аналогичные тем, которые мы проводили на ша-
ге 5.
Таблицей для этой задачи является табл. 3-3-IL
Таблица 3-3-11
Модель линейного программирования для транспортной задачи
Табличная форма
Технологические процессы 1->А 1->В 1->С II -* А II -» В II— С Хра- Хра- нить нить в I в II Экзоген- ные потоки
Интенсивности Ингредиенты XI Х2 Хз х4 X# хе Ху Х8
1. Ящики в I 1 1 1 1 350
2. Ящики в II 1 1 1 1 650
3. Ящики в А -1 —1 —300
4. Ящики в В -1 —1 -300 ,
5. Ящики в С —1 —1 —300
6. Стоимости (долл.) 2,5 1,7 1,8 2,5 1,8 1,4 z (min)
Модель в форме уравнений
*2>0, я3>0, я4>0, я5>0, я6>0, я7>0, х8>0. (10>
Г х^
Уравне-
ния ма-
териала- -
ного
баланса
+ ^2 + ^3 + ^7 — 350
х4 4- х$ 4“ Ж6 4" ~ 350
—я4 =—300
—х2 — х5 =—300 (Н>
— х3 —xQ = — 300
2,5^ 4- 1,7ж2 4- 1,8ж3 4- 2,5ж4 + 1,&г5 4-1,4r6 = z (min)
Модель состоит из следующих частей:
46
а) Список технологических процессов системы и их неизвестных
интенсивностей.
б) Список ингредиентов системы.
Коэффициенты затрат — выпуска системы расположены в столб-
цах по технологическим процессам и в строках по ингредиентам, как
в «таблице коэффициентов» 3-3-1 и затем в «табличной форме» 3-3-11.
в) Экзогенные потоки в систему, в столбце, как в (9).
Соотношение в табл. З-З-П между моделью в форме уравнений и ее
табличной формой должно быть внимательно изучено. Таблица может
быть получена из уравнений выписыванием коэффициентов при интенсив-
ностях технологических процессов , х8, т. е. отбрасыванием
букв, обозначающих входящие в уравнения неизвестные. Если модель
представлена в табличной форме, то подразумевается, что условия неотри-
цательности (10) выполнены в табл. З-З-П; с другой стороны, уравнения
(11) могут быть сразу восстановлены из таблицы образованием в каждой
строке, соответствующей ингредиенту, произведений коэффициентов за-
трат — выпуска на соответствующие неизвестные интенсивности техно-
логических процессов, суммированием вдоль всей строки и приравнива-
нием этого выражения для чистого потока экзогенному потоку ингре-
диента.
ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Наконец, мы можем сформулировать задачу для нашего конкретного
примера. Она состоит в том, чтобы определить интенсивности техноло-
гических процессов #1, я2, • • • , #8, которые а) неотрицательны (соот-
ношения (10), табл. З-З-П), б) удовлетворяют уравнениям материального
баланса (11) и в) минимизируют z.
3-4. ПРИМЕРЫ СМЕШИВАНИЯ
Часто встречается один тип задачи линейного программирования,
в который входит смешивание. Типичным является пример, связанный
с закупкой различных товаров, каждый из которых имеет известные харак-
теристики и цены. Задача состоит в том, чтобы дать рецепт, указывающий,
какое количество каждого товара следует закупить с тем, чтобы после
смешивания всех купленных товаров характеристики смеси лежали
в пределах заданных границ, а общая закупочная цена была минимальна.
В примере, который мы здесь приводим, характеристики смеси опре-
делены точно. Как будет видно позже, в случае, когда характеристики
смеси должны лежать между некоторыми нижней и верхней границами,
достаточны лишь небольшие изменения модели.
ЗАДАЧА О СМЕСЯХ I
Предприниматель собирается производить сплав, содержащий 30%
свинца, 30% цинка и 40% олова. Предположим, что на рынке имеются
сплавы Л, В, С, ... , составы и цены которых приведены в табл. (1).
Какое количество сплава каждого типа следует закупить на каждый
фунт производимой смеси для минимизации затрат?
Очевидно, предприниматель может ограничиться покупкой только
сплава Е, но он стоит 7,60 долл, за фунт. Если он купит по х/4 фунта каж-
дого из сплавов Л, В. С и D, то он также получит один фунт смеси в 30
—30—40%, но уже за 5,05 долл.; х/4 фунта Л, х/4 фунта В и х/2 фунта Н
снова дадут один фунт смеси с нужной пропорцией, но за 5,55 долл. После
небольшого числа подобных проб предприниматель вполне может найти
более общий подход к этой задаче.
47
Данные для задачи о смесях I
Сплав А в С D Е F G н I Требуе- мая смесь
% свинца 10 10 40 60 30 30 30 50 20 30
% цинка 10 30 50 30 30 40 20 40 30 30
% олова 80 60 10 10 40 30 50 10 50 40
Стоимости за фунт в долл. 4,1 4,3 5,8 6,0 7,6 7,5 7,3 6,9 7,3 min
При формулировке модели линейного программирования для этого
примера мы должны прежде всего заметить, что задача о смесях не была
поставлена в столь же исчерпывающем виде, как, скажем, транспортная
задача из предыдущего параграфа. Здесь не были определены количества
свинца, цинка и олова в окончательной смеси, а были указаны лишь их
доли и требовалось минимизировать стоимость каждого фунта выпуска.
Ввиду того что нам необходимы определенные данные относительно экзо-
генных потоков, мы потребуем, чтобы было произведено некоторое опре-
деленное количество сплава. Ясно, что рецепт, дающий наиболее эконо-
мичный план закупки на один фунт выпуска сплава, может быть сразу
превращен в рецепт, дающий самый экономичный план закупки на п фун-
тов выпуска путем умножения на п всех интенсивностей, участвующих
в модели технологических процессов; таким образом, мы ограничим
объемы технологических процессов теми комбинациями, которые произ-
водят один фунт сплава. Это ограничение выражено позже неявно при
составлении экзогенных потоков (6), а затем явно в уравнениях материаль-
ного баланса (8).
Это соглашение имеет еще одно полезное следствие, состоящее в том,
что требование процентного состава в исходной постановке задачи теперь
становится более конкретным: смесь должна содержать 0,3 фунта свинца,
0,3 фунта цинка и 0,4 фунта олова. (Часто начинающий пытается форму-
лировать задачу, не ограничивая общее произведенное количество, и в этом
случае становится трудно интерпретировать уравнения материального
баланса, когда они записываются в терминах процентного состава, а не
в абсолютных количествах.)
Шаг 1. Определение технологических процессов. Единственные тех-
нологические процессы, которые нам необходимо рассмотреть, суть за-
купки каждого из девяти сплавов, так как мы предполагаем, что весь
закупленный металл подвергнется смешиванию. Единичной интенсивно-
стью для каждого технологического процесса будет закупка одного фунта
сплава.
Перечень технологических процессов
1. Закупка сплава А\ интенсивность Х1
2. » » В; » #2
3. » » С; » х3
4. » » D; » х± (2)
5. » » Е; » х5
6. » » F; » Х6
7. » » G; » X'l
8. » » Н; » х8
9. » » I; 48 » х9
Шаг 2. Определение ингредиентов. Теперь можно выписать рассмат-
риваемые в системе ингредиенты:
Перечень ингредиентов
1. Общее количество металла в фунтах
2. Количество свинца » »
3. » цинка » » (3)
4. » олова » »
5. Стоимость (долл.)
Шаг 3. Коэффициенты затрат — выпуска. В последующем изло-
жении мы примем первую из трех точек зрения, перечисленных в сноске х.
Типичный технологический процесс — скажем, способ 1, закупка спла-
ва А, если использовать данные табл. (1), имеет вид
4,7 доллара
[др. металла
0,1 дэ.свинца
0,1 др. цинка
0,8 ср. олова
(4)
Аналогично каждый из девяти технологических процессов имеет один
вход и четыре выхода. Каждый технологический процесс имеет, конечно,
в качестве выпуска один фунт металла; остальные элементы табл. 3-4-1,
коэффициенты затрат — выпуска, получены непосредственно из данных
табл. (1).
Таблица, 3-4-1
Таблица коэффициентов: задача о смесях I
Технологические процессы Ингредиенты 1 А 2 в 3 с 4 D 5 Е- 6 F 7 G 8 9 Н I
1. Металл —1 —1 —1 —1 —1 — 1 —1 —1 —1
2. Свинец —0,1 —0,1 —0,4 —0,6 —0,3 —0,3 —0,3 -0,5-0,2
3. Цинк —0,1 —0,3 -0,5 —0,3 —0,3 -0,4 -0,2 —0,4— 0,3
4. Олово —0,8 —0,6 —0,1 —0,1 —0,4 —0,3 -0,5 —0,1—0,5
5. Стоимости (долл.) 4,1 4,3 5,8 6,0 7,6 7,5 7,3 6,9 7,3
1 Имеются три точки зрения, которые можно принять при формулировке этой
модели: 1) точка зрения покупателя сплава, которая состоит в том, что он получает
доллары и выпускает вклады в фунты готовой смеси и в характеристики свинца, олова,
цинка; 2) точка зрения производящего смесь, которая состоит в том, что он получает
вклады в характеристики свинца, олова, цинка и выпускает доллары и фунты готовой
смеси; 3) точка зрения получателя готовой смеси, которая состоит в том, что он полу-
чает готовый металл и вклады в характеристики свинца, олова, цинка и выпускает
деньги.
4 Дж. Данциг 49
Шаг 4. Экзогенные потоки. Они показаны в форме «черного ящика»
на диаграмме (5) и в виде списка в (6):
Экзогенные потоки — задача о смесях I
1 ф. металла
0,3 ф, свинца
0,3 ф. цинка
0,4 ф. олова
(5>
Ингредиенты
1. Металл
2. Свинец
3. Цинк
4. Олово
5. Стоимости (долл.)
Экзогенные потоки
—1,0
—0,3
—0,3
—0,4
(&)
z (min)
Шаг 5. Уравнения материального баланса. Как отмечалось в § 3-3,
модель в форме уравнений может быть собрана непосредственно из ре-
зультатов шагов 3 и 4. Комбинируя таблицу коэффициентов (табл. 3-4-1)
и список экзогенных потоков (6), мы приходим к табличной форме нашей
модели, показанной в табл. 3-4-П.
Задача линейного программирования для модели смешивания I. Опре-
делить интенсивности технологических процессов xi9 х2, . . . , х9, кото-
рые а) неотрицательны (соотношения (7), табл. 3-4-П), б) удовлетворяют
уравнениям материального баланса (8) и в) минимизируют z.
Таблица 3-4-П
Модель линейного программирования для задачи о смесях I
Табличная форма
Технологические процессы А В с D Е F G н I
Покупать ч. в коли- честве Ингреди- енты ч. XI Х2 х3 1 х4 Х6 х6 х7 Х8 Х9 Экзо-^ генные пото- ки
1. Металл (об- щее количе- ство) —1 —1 —1 —1 —1 —1 —1 — 1 —1 —1
2. Свинец —0,1 —0,1 —0,4 —0,6 —0,3 —0,3 —0,3 —0,5 —0,2 —0,3
3. Цинк —0,1 —0,3 —0,5 —0,3 —0,3 —0,4 —0,2 —0,4 -0,3 -0,3
4. Олово —0,8 —0,6 —0,1 —0,1 —0,4 —0,3 —0,5 —0,1 —0,5 —0,4
5. Стоимости (долл.) 4,1 4,3 5,8 6,0 7,6 7,5 7,3 6,9 7,з| Z (min)
50
Уравне-
ния ма-
териаль-
ного
баланса
Модель в форме уравнений
Неотри- Г 1
цатель- { х4>0, х2>0, х3>0, х4>0, х5>0, хв>0, #7>0, х8>0, х9>0
ность [
(7)
— Х4 а?2 ^3 ^4 *^5 *^6 *^7 *^8 —1
—0,1^1—0,1х2—0,4ггз—0,6х4—0,Зх5—0,3rre—0,3x7—0,5х8—0,2х9=—0,3
— 0,1 — 0,Зх2—0,5х3—0, Зх4 — 0,Зх5 — 0,4х6 — 0,2х7 — 0,4х8—0,Зх9 = — 0,3
— 0,8xj — 0,6^2 — 0» — О Л ^4——0,Зх8—0,5x7—0,1х8—0,5х9= —0,4
4,lXj-|- 4,3х2 + 5,8x34~ 6,0х4+7,6x5“I- 7,5х6-|- 7,3x7 4- 6,9x8-J- 7,3x9=z (min)
(8)
ЗАДАЧА О СМЕСЯХ' II
Рассмотренная выше частная задача линейного программирования
несколько трудна для непосредственного решения до тех пор, пока не
будут изложены в гл. 5 соответствующие методы. (Эта задача предложена
в виде примера 2 этой главы.) Оказывается, что ее решение есть х4 = О,
3 2
я2 = у, я4 = -у, а все остальные технологические процессы применяются
с нулевой интенсивностью.. Минимальная стоимость одного фунта металла
равна 4,98 долл. Рассмотрим, однако, вместо этой задачи другую, более
легкую.
Для того чтобы упростить задачу о смесях до такой степени, чтобы
ее можно было решить графически, попытаемся найти самую дешевую
смесь сплавов, которая будет иметь 0,4 фунта олова в каждом фунте метал-
ла (остальные 0,6 фунта металла могут состоять из свинца и цинка в любом
соотношении). Это, конечно, не та задача, которую мы сформулировали
раньше, но для ее формулировки совсем не обязательно осуществлять
заново весь процесс построения модели. Все, что мы должны сделать,—
это опустить требования, наложенные в (6) на ингредиенты 2 (свинец)
и 3 (цинк); остальные требования, технологические процессы и коэффи-
циенты затрат — выпуска не должны изменяться при построении этой
более простой модели. Таким образом, мы можем получить упрощенную
модель в форме уравнений, просто вычеркивая второе и третье уравнения
(8), которые относятся к свинцу и цинку. Нам остаются первое, четвертое
и пятое уравнения (8).
Рассуждение станет еще проще, если мы изменим знаки при всех
членах уравнений, относящихся к «металлу» и «олову».
Задача линейного программирования для модели смешивания II.
Определить интенсивности технологических процессов xi9 х2г - • • » х9,
которые а) неотрицательны, б) удовлетворяют уравнениям
#1+ ^2 + ^з+ Я4+ #в+ xi 4“ #8 + ж9 = 1, (9)
0,814 + 0,6х2 + 0,1я3 + 0,1х44~ 0,4х5 + 0,Зя6 + 0,5я7 + 0,1х84- 0,5х9 = 0,4 (10)
4,1^14~4,3х24“ 5,8х36,0х44~ 7,6x54- 7,5х84“ 7,3x7 4~ 6,9х84- 7,3х9 — z (11)
и в) минимизируют z.
Графическое представление. Условия задачи о смесях поддаются
теперь графическому представлению, которое приведено на рис. 3-4-1.
Для каждого из девяти технологических процессов мы берем соответ-
ствующие два коэффициента из уравнений (10) и (И) и представляем
технологический процесс точкой, имеющей эти два числа своими коорди-
натами. Таким образом, точка Л, представляющая сплав А, имеет коорди-
наты (0,8, 4,1), которые изображают количество олова в сплаве А и стои-
мость каждого его фунта; аналогично точка В имеет координаты (0,6, 4,3),
51
4*
количество олова и стоимость каждого фунта для сплава В и т. д. Пусть
(u, и) — координаты произвольной точки.
Это графическое представление ценно не столько тем, что коэффи-
циенты затрат — выпуска любого технологического процесса могут быть
представлены точкой, сколько тем, что чистый экзогенный поток в систему
также можно представить точкой для любого плана с неотрицательными
интенсивностями х19 . . . , ж9, сумма которых равна единице. Рассмотрим,
например, план Xi = х2 = , х3 = х^ = ...= О, который заключается
А
3
8
7
6
5
4!"
3
1
D
С
Прямая ________ »
ограничения П
GtI R *есть наинизшая точка R
на прямой ограниченияt
лежащая д зааиприхован-
'.\ной области
.теорема
двойственности
нин.к=максЗ=5
0,5 0,6 0,7 OjB 0,9
фунт сплава, и (0 фунтах)
6(0,5,7,3)
Н(О,Г, 6,9)
Г (0,5; 7,3)
2 - Чтобы полечить R*nado j
смешать В и С с бесами ।
и х3=0,4 или |
провести прямую ।
L через точки б и С
п-------1----1------1----L_
О 0J 0,2 0,3 0/+
Количество олова на <
Координаты. А'(0,8;4-,1)
0(0,6; 4,3)
&(0,1; 5,8)
0(0,1; 6,0)
Е(о,4; 7,6)
F(0,3; 7,5)
1
I
I
В
г>* 1 а
к есть наивысшая точка S
на прямой ограничения, лежащая
на прямой L ниже заштрихованной
области
Я=(Ц4;5,5)
R*-(0,4>4,9)
Рис. 3-4-1. Иллюстрация теоремы двойственности на модели
смешивания II.
в использовании каждого из сплавов А и В в количестве полуфунта. Этот
план дает 0,8-1/2 + 0,6-1/2 = 0,7 фунта олова, а стоимость его 4,1-1/2 +
+ 4,31-х/2 = 4,2. Таким образом, этот план может быть представлен на
рис. 3-4-1 точкой расположенной посредине между точками Л и В. Дру-
1 1
гой план, xt = у, х2 = х^ = , использующий полфунта А и по четверти
фунта каждого из сплавов В и I, имеет координаты 0,8-V2 + 0,6-х/4 +
+ 0,5-Vi = 0,675 для олова и 4,1-х/2 + 4,3-х/4 + 7,3-1/4 = 4,95 для
стоимости и может быть представлен точкой Р2.
В любом случае координаты точки, представляющей смесь, суть
взвешенные средние соответствующих координат точек, представляющих
чистые сплавы; так, мы говорим, что точка Pi есть взвешенное среднее
точек А и В с весами соответственно 1/2 и 1/2, а Р2 есть взвешенное сред-
нее точек Л, В и I с весами соответственно х/2, х/4 и х/4. (В физике Pi
называется центром тяжести системы, состоящей из веса в х/2 единицы
52
в точке А и х/2 единицы в точке В; аналогично Р2 есть центр тяжести
системы, состоящей из весов х/2, расположенных соответственно
в точках Л, В и /.)
Теперь становится ясно, что множество всех неотрицательных планов,
удовлетворяющих соотношению (9), представлено на рис. 3-4-1 заштрихо-
ванной областью, которая является совокупностью всех возможных взве-
шенных средних девяти точек Л, ..., I. Допустимыми планами, однако,
являются те планы, которые дают в точности 0,4 фунта олова; они пред-
ставлены теми точками заштрихованной области, которые лежат на верти-
кальной прямой с абсциссой 0,4. Точка Е дает именно такой план, точно
так же как и точка R = (0,4, 5,55), которая есть взвешенное среднее
точек Л, В и Н соответственно с весами х/4, х/4 и х/2. Очевидно, однако,
ни одна из этих точек не дает решения задачи с наименьшим г; точка,
которая дает такое решение, есть наинизшая точка на вертикальной пря-
мой, находящаяся в заштрихованной области. Таким образом, задача ли-
нейного программирования может быть графически интерпретирована
как задача приписывания вершинам фигуры неотрицательных весов таким
образом, чтобы взвешенное среднее вершин лежало на вертикальной пря-
мой с абсциссой 0,4 и имело как можно меньшую ординату 2. Из чертежа
мы можем усмотреть, что требуемое взвешенное среднее R* расположено
на прямой ВС, т. е. оно есть среднее, полученное приписыванием некото-
рых весов х2 и х3 точкам В и С и нулевых весов всем остальным точкам.
Для того чтобы определить х2 и х2, положим в (9) и (10) все Xj, кроме
х2 и х3, равными нулю. Это значит, что мы ограничиваемся рассмотрением
смесей, в которые входят только В и С; тогда мы должны иметь
•^2 + *3 := >
0,6я24-0,1я3 = 0,4,
что дает
#2 = 0,6, #3 = 0,4
и
min z — 4,3я2 + 5,&г3 = 4,9.
Отсюда мы заключаем, что наилучшей является смесь, при которой берут-
ся 0,6 фунта сплава В и 0,4 фунта сплава С. Это приводит к получению
самого дешевого сплава, содержащего 40% олова. Эта смесь будет стоить
4,9 долл, за фунт.
Алгебраическая проверка — двойственная задача линейного програм-
мирования. Мы можем проверить алгебраически, правилен ли наш выбор
точек В и С на рис. 3-4-1, определяя сначала прямую, соединяющую
В и С, и затем исследуя, имеет ли каждая точка заштрихованной области
ординату v, большую, чем точка на этой прямой с той же самой абсцис-
сой и. Если это так, то мы скажем, что заштрихованная область лежит
«над» прямой, соединяющей В и С.
Далее, уравнение произвольной прямой в плоскости и, v есть
V = Jtj л2и,
где лх — длина отрезка, отсекаемого на оси v, а зт2 — наклон прямой
к оси и. Для того чтобы заштрихованная область лежала выше этой пря-
мой, каждая из точек А, В, С, . . . , I (которые порождают заштрихо-
ванную область) должна лежать выше этой прямой или на ней. Подстав-
ляя в это уравнение значение координаты и = 0,8 точки А, мы получаем,
что значение v — + л2-0,8 не должно превосходить координаты v
точки А. Таким образом, наша проверка для точки А сводится к неравен-
53
ству Л1 + тг2-0,8 < 4,1, так что для всей системы точек А, В, С, . . .
мы должны иметь
^ + ^2* 0,8 <4,1,
*4-|-:rt2-0,6 <4,3,
Ttj —|—Л2 • 0,1 5,8,
Лх + Лг’О,! <6,0,
7Ц +л2*0,4< 7,6, (12)
л1 + л2-0,3< 7,5,
Jti "4~ *^2 *0,5 < 7,3,
л14-л2*0,1<6,9,
Tti 4- 7(2 • 0,5 < 7,3.
Пусть S = (0,4; v) — точка пересечения вертикальной прямой и —
= 0,4 с прямой v = Tti 4- л2и; тогда прямая, которую мы ищем (и кото-
рая, как мы надеемся, будет прямой, соединяющей В и С), есть прямая,
лежащая ниже заштрихованной области, для которой координата v—v
точки S максимальна, т. е.
7t4 4- л2 • 0,4 = v (max). (13)
Задача нахождения л4, тг2 и max v, удовлетворяющих (12) и (13), известна
под названием двойственной задачи по отношению к нашей исходной
{прямой) задаче (9), (10) и (11). Тот факт, что для этих двух задач max v =
= min z, есть частный случай важной теоремы двойственности для задач
линейного программирования (см. гл. 6). Если мы догадались, что неко-
торая смесь пары точек, подобно В, С (полученная визуальным изучением
чертежа или как-нибудь иначе), дает, оптимальный выбор, то это легко
проверить, выяснив, во-первых, расположено ли пересечение S между
выбранными двумя точками и, во-вторых, расположены ли все точки
А, В, С, ... на прямой, соединяющей выбранные две точки, или выше
нее. Для того чтобы проверить первый факт, мы решаем систему
х2 + ?
0,6я2 + 0,1я3==0,4, (14)
получая х2 = 0,6, — 0,4, которые положительны, так что S лежит
между В и С. Таким образом, эти значения с остальными хь равными
нулю, удовлетворяют прямой системе (9), (10) и (11). Для того чтобы про-
верить второй факт, мы находим уравнение прямой, формулируя усло-
вия прохождения этой прямой через точки й и С:
я1 + я2*0,6 = 4,3,
тг14-л2-0,1 = 5,8. (15)
Это дает значения Tti = 6,1, тс2 = —3, которые удовлетворяют двойствен-
ной системе (12).
3-5. ЗАДАЧА О СМЕСИ ПРОДУКЦИИ
Мебельная компания производит четыре модели письменных столов.
Каждый стол сначала изготовляется в столярном цехе, а затем отправ-
ляется в отделочный цех, где он лакируется, покрывается воском и поли-
руется. Количество рабочих часов, требуемое в каждом цехе, описывается
следующей таблицей:
54
Столярный цех
Отделочный цех
Стол 1 Стол 2
4 9
1 1
Стол 3
Стол 4
10
40
(1)
7
Из-за ограничений, налагаемых на мощность завода, в течение ближай-
ших шести месяцев можно рассчитывать не более чем на 6000 рабочих
часов в столярном цехе и на 4000 рабочих часов в отделочном цехе.
Прибыль (т. е. доход минус производственные расходы) от продажи
каждого стола следующая:
Столы 1 2 3 4
Прибыль (долл.) 12 20 18 40
(2)
В предположении, что сырье и оборудование имеются в достаточных коли-
чествах и что все изготовленные столы можно продать, компания по про-
изводству столов хочет определить оптимальную смесь продукции, т. е.
объемы продукции каждого типа, которые в совокупности максимизируют
прибыль.
Шаг 1. Технологические процессы. Четыре технологических процесса
суть
1. Производство столов 1 (измеренное в произведенных столах)
2. » » 2 » » » »
3. » » 3 » » » »
4. » » 4 » » » »
Шаг 2. Ингредиенты.
1. Объем столярных работ (измеренный в человеко-часах).
2. Объем отделочных работ (измеренный в человеко-часах).
3. Стоимость (измеренная в долл.).
Шаг 3. Коэффициенты. Технологический процесс 1, например, может
быть изображен на диаграмме следующим образом:
4 часа столярных работ
1 час отделочных работ
(3)
Таблица коэффициентов затрат — выпуска, составленная из (1) и (2),
показана на табл. 3-5-1.
Шаг 4. Экзогенные потоки. Так как объемы столярных и отделочных
работ являются затратами для каждого из этих технологических процес-
сов, они должны быть затратами для системы как целого. Однако мы долж-
ны учесть еще и тот факт, что допустимый план не обязательно должен
использовать эти объемы полностью. Известно, что общие затраты не
должны превышать 6000 часов столярных работ и 4000 часов отделочных
работ, но меньше этих предельных объемов они могут быть и поэтому
не обязательно должны выражаться точно в виде уравнений материаль”
ного баланса.
55
Таблица 3-5-1
Таблица коэффициентов: задача о смеси продукции
Технологические процессы Ингредиенты Производство столов
(1) (2) (3) (4)
1. Объем столярных работ (в часах) 4 9 7 10
2. Объем отделочных работ (в часах) 1 1 3 40
3. Стоимость (долл.) —12 —20 —18 —40
Шаг 5. Материальный баланс. Если мы хотим продвинуться как-то
в формулировке задачи, используя для экзогенных потоков перечис-
ленные цифры, то для сохранения реальности в математической формули-
ровке мы должны для материального баланса вместо уравнений написать
неравенства, выражающие, например, ограничения, налагаемые на объем
столярных работ, в виде неравенства
4- 9ж2 + 7х3 4-10^4 6000,
а отнюдь не в виде уравнения, которое не вполне соответствует нашим
условиям.
Мы видим, что модель не может быть завершена построением приве-
денных выше списков технологических процессов и ингредиентов, и мы
имеем дело со случаем, упомянутым в первом параграфе, когда необхо-
дим повторный переход к началу построения модели.
Все, что нам остается теперь сделать,— это добавить к модели тех-
нологические процессы, которые учтут столярные и отделочные мощности,
неиспользованные в остальной части плана.
Если мы определим в качестве технологического процесса «не ис-
пользовать мощность», то получим два дополнительных технологических
процесса к тем, которые уже были выписаны на шаге 1.
5. Не использовать мощность столярного цеха (измеренную в человеко-часах).
6. Не использовать мощность отделочного цеха (измеренную в человеко-часах).
Процесс 5 может быть абстрактно изображен следующим образом:
/час столярным работ
(4)
Полная таблица коэффициентов затрат — выпуска и экзогенных возмож-
ностей системы как целого показана в табл. 3-5-П.
56
Таблица 3-5-11
Задача линейного программирования для модели смешивания продукции
Технологические х. процессы Ингредиенты х. Производство Столов Не использовать мощность цехов Экзоген- ные по- токи: затраты (+) выпуск (-)
столяр- ного отделоч- ного
(1) XI (2) Х2 (3) хз (4) *4 (5) хб (6) *6
1. Объем столярных ра- бот (в часах) 4 9 7 10 1 6000
2. Объем отделочных ра- бот (в часах) 1 1 3 40 1 4000
3. Стоимости (долл.) —12 —20 —18 —40 z (min)
Таким образом, задача составления плана состоит в нахождении
чисел
^>0, ж2>0, ж3>0, я4>0, я5>0, я6>0 (5)
и нахождении минимума величины 2, которые бы удовлетворяли уравне-
ниям
4xt + 9я2 + 7я3 + 10я4 + хь = 6000,
х2 -J- Зх3 -f- 40^4 -f- Xq = 4000, (6)
— 12х х — 20ж2—18я3—40х4 = z.
Заметим, что те же самые значения х, которые минимизируют функцию
стоимости, также максимизируют противоположную ей по знаку вели-
чину, именно функцию прибыли, заданную выражением *
+12#! + 20ж2 + 18х3 + 40ж4 = р.
Таким образом, задача максимизации прибыли может быть сформулиро-
вана в виде задачи, эквивалентной задаче минимизации стоимости.
Графическое решение. Для того чтобы применить метод, изложенный
в предыдущем параграфе, к модели смешивания продукции, необходимо
так изменить определения ингредиентов и интенсивностей технологиче-
ских процессов, чтобы сумма всех интенсивностей технологических про-
цессов была равна единице. Это достигается простым введением в качестве
ингредиента общей мощности, которая равна сумме мощностей столяр-
ного и отделочного цехов, и новых единиц измерения интенсивностей
технологических процессов, так что одна новая единица каждого техноло-
гического процесса требует всего 6000 + 4000 — 10 000 часов общей мощ-
ности. Для того чтобы изменить единицы, заметим, что одна единица пер-
вого технологического процесса в табл. 3-5-11 требует 5 часов общей мощ-
ности; следовательно, 2000 единиц первого технологического процесса
потребовали бы 10 000 часов мощности и эквивалентны одной новой еди-
нице первого технологического процесса. Вообще, если у^ — количества
новых единиц первого технологического процесса, то 2000^ = xt. Соот-
57
ношения между старой и новой интенсивностями технологических про-
цессов после такой замены единиц для каждого технологического про-
цесса таковы:
2000^ = 10001/2 = ^2, 1000^з = ж3,
200j/4 = x4, 10000у5 = я5, 10000у6 = я6.
Удобно также изменить единицы измерения мощности и стоимости. Пусть
40 000 часов = 1 новой единице мощности, 10 000 долл.= 1 новой единице
Таблица 3-5-1II
Модель о смешивании продукции (после изменения единиц)
Технологические процессы Производство столов (1=10 000 часов) Не использовать мощность столяр- отделоч- ного ного Экзо- генные потоки
Ингредиенты (1) (2) (3) (4) У1 2/2 УЗ У4 (5) (6) уъ уз
0. Общий объем работ (1 = 10 000 часов) 1,0 1,0 1,0 1,0 1,0 1,0 1,0
1. Объем столярных работ 0,8 0,9 0,7 0,2 1,0 0,6
I 2. Объем отделочных работ 0,2 0,1 0,3 0,8 1,0 0,4
3. Стоимости (1 = 10 000 долл.) —2,4 —2,0 —1,8 —0,8 z' (min)
Требуемая мощность отделочного цеха на
единицу технологического процесса
Координаты: (ОА-г.Ь), (0,1;-2,0), (0,3;-1,0)
(0fi;-0,8), (0;0), (1,0; 0)
Рис. 3-5-1. Графическое решение за-
дачи о смеси продукции.
стоимости. Тогда легко видеть (и это
оставляется в качестве упражнения),
что табл. 3-5-11 модели смешивания
продукции перейдет в табл. 3-5-III
после указанных выше изменений
единиц технологических процессов,
замены z на 10 000 z' = z в уравне-
нии стоимости и сложения этих двух"
уравнений для того, чтобы получить
уравнение общей мощности.
Теперь мы можем найти графиче-
ское решение. Ввиду того что неиз-
вестные ^;>0 в сумме дают едини-
цу, мы будем интерпретировать этот
факт как приписывание неотрицатель-
ных весов точкам Alt А2, . . . , А6
на рис. 3-5-1. Как и в задаче о смесях
предыдущего параграфа, мы будем
игнорировать одно из уравнений ма-
териального баланса, а именно урав-
нение для ингредиента 1, мощности
«столярного цеха; однако мы обнаружим, что это не повлияет на
минимальное решение, потому что это уравнение избыточно.
58
На рис. 3-5-1 каждая точка Aj соответствует столбцу, или техноло-
гическому процессу, табл. 3-5-1II; ее координаты суть коэффициенты мощ-
ности отделочного цеха и стоимости процесса. Так, координаты суть
(0,2; —2,4); А2 — (0,1; -2,0), . . . , А - (0,0) и А6 - (1,0; 0).
Мы ищем такие составляющие в сумме единицу неотрицательные веса
yj для каждой из этих шести точек, чтобы их взвешенное среднее имело
координаты (0,4; z'), где z' минимально. Такой точкой является, очевидно,
точка 7?*, полученная приписыванием нулевых весов всем точкам, кроме
точек Ai и Л4, причем последние взвешиваются так, чтобы центр тяжести
точек Ai и Л4 имел абсциссу, равную 0,4. Для того чтобы определить
и у4, положим все у^ = 0, кроме иу4в табл. 3-5-III, что дает уравнения
0,2у4 + 0,8у4 = 0,4,
У1+ =
— 2,4^—0,8j/4==z',
откуда
2 1 , 5,6
3/1 — 3 , Уь — з , 2 — 3 -.
Таким образом, оптимальное решение состоит в том, чтобы производить
Xi — 2/з* 2000 столов типа 1, я4 = 1/3-200 типа 4, что полностью исполь-
зует мощность завода и будет стоить z ~ 10 000- (—5,6/3) долл., или дает
18 666,66 долл, прибыли.
Мощность столярного цеха использована при этом решении полно-
стью, несмотря на то что соответствующее ей уравнение материального
баланса в приведенных выше выкладках не фигурировало. Как уже отме-
чалось ранее, это произошло потому, что добавление к системе уравнения
общей мощности дает нам возможность опустить любое из оставшихся
уравнений, сохраняя при этом модель, которая учитывает все мощности;
уравнение мощности столярного цеха оказывается избыточным и может
быть отброшено.
3-6. ПРОСТАЯ ЗАДАЧА О СКЛАДЕ
Рассмотрим задачу создания запасов некоторого товара на складе
с целью продажи в будущем. Склад может вместить только 100 единиц
товара. Затраты на хранение каждой единицы товара в течение квартала
равны 1,00 долл. В каждом квартале закупочная цена равна продажной.
Эта цена меняется от квартала к кварталу согласно табл. (1):
Квартал (t) Цена единицы товара (долл.)
1 10
2 12
3 8
4 9
Отсюда следует, что можно извлечь прибыль, покупая товар по низкой
цене и продавая его по высокой. Задача состоит в том, чтобы определить
оптимальный план продажи, хранения и покупки по кварталам в течение
59
одного года, предполагая, что начальный запас на складе составляет
50 единиц.
В течение каждого периода (квартала) t мы различаем четыре типа
технологических процессов:
Количество
1. Продажа запаса xti
2. Хранение запаса xt2
3. Покупка запаса xt3
4. Не использовать возмож-
ности (свободные перемен-
ные)
и три типа ингредиентов:
1. Запасы
2. Объем склада
3. Затраты
Эти технологические процессы имеют характеристики затрат — выпу-
ска, схематически изображенные в (2).
В течение четырех периодов времени каждый ингредиент и каждый
технологический процесс повторяются четыре раза, что приводит к табл.
3-6-1, которая и является таблицей задачи о складировании. Задача состо-
Наличные запасы X Продажа 1 единицы доходы
в момент t запаса
1 единица наличных запасов в момент t 1 единица объема . X Хранение 1 единица наличных
1 единицы
склада в течение £-го запасов в момент
квартала Затраты на хранение 1 единицы запаса <+1 (2>
ит здесь в том, чтобы наити значения xti 0, которые удовлетворяют урав-
нениям, вытекающим из таблицы^ и которые минимизируют общую стои-
мость.
60
Таблица 3-6-1
Простая модель складирования
Технологические процессы Ингредиенты 1-й квартал 2-й квартал 3-й квартал 4-й квартал Экзогенные потоки
И л « К g Н _ л ей И rt £ £ Д д Я й £ ЕС® rt Й И oS « ® «О ® О св К О & Рч Рч О д ф и и и 3 и *11 Х12 *13 *14 № д я w S И _ £ се и rt £ Й И М 03 Е"< Сб и-г rt S И ЕС й Ю ф о се И о рч Рч Рч О Д Ф й И й О й *21 *22 *23 *24 и £ n W « ь _ £ rt И rt £ £ д д m Й 2 ЕС® св S й д SS ЕС И ю ф о rt х о & Рч Рч О Д ф и и и о и *31 *32 *33 *34 W fl « к 2 Ен - ей И rt л Ен д д и н rt ££ S. § Р о S Рч. Д Р* о Ф о « X о Рч Рч Рч О Д ф И И И О и *41 *42 *43 *44
t==0 запасы Объем склада 1 1 —1 1 1 50 100
t = i запасы Объем склада — 1 1 1 —1 1 1 0 100
t = 2 запасы Объем склада —1 1 1 —1 1 1 0 100
t = 3 запасы Объем склада —1 1 1 —1 1 1 0 100
Стоимость —10 1 10 —12 1 12 —8 1 8 —9 1 9 z(min)
3-7. ОБУЧЕНИЕ НА РАБОТЕ
Цель этого примера состоит в разъяснении того, что модель линей-
ного программирования может охватывать много разнообразных условий,
которые так характерны для практических применений.
Задача. Согласно контракту, завод должен произвести 1200 единиц
некоторого товара С, причем расписание поставок rt указано в табл. (1).
Конец недели 1 2 3 4 5
Количество единиц 74 = 100 г 2=200 7*з—300 74 = 400 7-5=200
Какой план найма, увольнения, производства и хранения должен при-
нять фабрикант для того, чтобы минимизировать затраты выполнения
контракта при следующих условиях:
а) Каждая единица продукции, не поставленная в срок, влечет штраф
р = 30 долл, за каждую неделю до тех пор, пока поставка не будет выпол-
нена.
б) Любая единица продукции, произведенная раньше срока, тре-
бует хранения, расходы по которому составляют 5 — 10 долл, в неделю.
в) Все требуемые поставки должны быть выполнены в конце пятой
недели.
г) Вначале имеется g = 20 рабочих и h = 10 единиц товара С в на-
личии.
61
д) Каждый рабочий, использованный на производстве в течение*
недели, может выпустить к = 8 единиц товара С.
е) Каждый рабочий, использованный для обучения учеников в тече-
ние недели, может обучить I — 1 = 5 новых рабочих (т. е. произвести
I обученных рабочих, включая себя).
ж) Зарплата рабочего составляет т — 100 долл, в неделю незави-
симо от его занятости.
з) Зарплата рабочего и I — 1 его учеников в процессе обучения в тече-
ние одной недели составляет п = 600 долл.
и) Стоимость увольнения одного рабочего составляет / = 100 долл.
Мы выберем в качестве единицы времени период, равный одной неде-
ле. В начале каждой недели мы определяем число рабочих и единиц това-
ра С, необходимые для того, чтобы осуществить технологический процесс
в течение этой недели. В соответствии с этим в каждый из шести моментов
времени t = 0, 1, . . . , 5 должны быть составлены уравнения мате-
риального баланса для следующих двух ингредиентов.
Обозначение
Рабочие Wt
Товар Ct
К этим уравнениям добавится уравнение стоимости для стоимостного*
ингредиента. В течение каждого из пяти недельных периодов будут осу-
ществляться следующие технологические процессы, перечисленные в (2)^
Обозначение
1. Обучение Tt
2. Производство Pt
3. Простой
4. Увольнение Ft (2)
5. Хранение St
6. Выплата штра- фа (за нехватку) Dt
Характеристики затрат — выпуска для каждого из этих технологи-
ческих процессов, за исключением, возможно, штрафа, получаются непо-
средственно. Каждое невыполнение поставки одной единицы заставляет
уменьшить на одну единицу спрос на товар в настоящий период и увели-
чить на одну единицу спрос в следующий период по цене р долл. Другое
понимание этого технологического процесса состоит в том, чтобы предста-
вить, что дефицит временно покрывается заимствованием на открытом
рынке 1 единицы товара, которая должна быть возвращена на следующей
неделе по цене р долл.
Эти технологические процессы описаны в обозримой форме в табл.
3-7-1. Штраф на пятой неделе опускается ввиду условия (в), которое
62
Модель обучения на работе
Таблица 3-7-I
Ингре- диент 1-я неделя 2-я неделя 3-я неделя 4-я неделя 5-я неделя Рб *64 Экзоген- ные потоки
T1 Pi Ii Fi Si Di *11 X12 X13 X14 X15 X16 Тг Рг 1% 82 #2 *21 X22 *23 *24 *25 *26 Т3 Рз 1з Рз S3 D$ *31 *32 *33 *34 *35 *36 Т4 Р4 I4 Р4 84 1>4 *41 *42 *43 *44 *45 *46 Тъ Рб 1ъ F& S& *51 *52 *53 *54 *55
Wo Со 1111 1-1 5-
Wi Ci 1 <4-4 1 1 1 7 1111 1 -1 0 -ri
w2 Сг -I -1 -1 -к -11 1111 1-1 0 -'2
w3 С3 1 1 1 1 »-*> 1111 1 -1 0 -г3
w4 Ci > 1 1 U 1 1 Н-Ь. н* 111 1 1 0 -г4
w5 C6 ь 1 1 1 1 1 * 1 0 ~г5
Сто- имость n m m f s p п т т j s р п т т f s р п т т f s р п т т f s .: —Г— / z (min)
утверждает, что все поставки должны быть выполнены к концу пятой
недели. На шестой неделе должно быть применено увольнение F6 для того,
чтобы избавиться от всех рабочих и завершить программу. (Почему это
необходимо?)
3-8. ОСНОВНАЯ МАТЕМАТИЧЕСКАЯ ЗАДАЧА
В предыдущих параграфах для нескольких примеров были построены
модели линейного программирования. В каждой из этих моделей задача
состояла в том, чтобы найти решение системы линейных уравнений или
неравенств, которое минимизирует или максимизирует линейную форму.
Эта оптимизация линейной формы при линейных ограничениях называется
основной математической задачей линейного программирования.
Всякий раз, когда в примерах ограничения устанавливались в форме
неравенств, было возможно добавлением свободной переменной превратить
каждое неравенство в уравнение. Кроме того, задача, в которой линейная
функция должна была максимизироваться, могла бы быть превращена
в задачу минимизации формы, противоположной этой по знаку.
Таким образом, все задачи линейного программирования можно
сформулировать одним и тем же общим способом; именно найти в неотрица-
тельных числах решение системы линейных уравнений, которое миними
зирует линейную форму. Так как эта алгебраическая постановка задачи
возникает естественным образом во многих приложениях, она называется
«стандартной формой» задачи линейного программирования. В этом пара-
графе формулировка стандартной формы основной математической задачи
линейного программирования будет пересмотрена и формализована.
Если индекс / = 1, 2, . . . , N обозначает /-й тип технологического
процесса, a Xj — его объем (или интенсивность), то обычно Если,
например, Xj представляет собой объем запасов, предназначенных для
/-го процесса, то, как правило, отрицательные количества здесь вообще
не имеют смысла. В некоторых случаях, однако, естественно интерпрети-
ровать отрицательное количество как изъятие запаса из /-го процесса.
Но здесь должна быть проявлена некоторая осторожность; например,
могут быть такие стоимости, как транспортные расходы, которые поло-
жительны независимо от направления потока запасов. Нужно также
заботиться о том, чтобы не превысить запасы для используемого процесса.
По этим причинам лучше при формулировке моделей различать два вида
технологических процессов, каждый с неотрицательной областью изме-
нения соответствующей переменной Xj, а не пытаться объединить их в еди-
ный список.
Взаимозависимости между различными технологическими процес-
сами возникают потому, что все практические задачи программирования
описываются ограничениями на ресурсы того или иного рода. Ограни-
ченными ресурсами могут быть сырье, рабочая сила или деньги; все они
обозначаются общим термином ингредиент. В задачах химического равно-
весия смесей роль технологических процессов играют молекулы различ-
ных типов, а ингредиентами являются атомы различных элементов.
Различные ингредиенты обозначаются индексом i (i = 1, 2, . . . , М).
В работах по линейному программированию количество ингредиен-
та, потребляемого технологическим процессом, предполагается пропор-
циональным его интенсивности; если ингредиент не потребляется, но про-
изводится, то снова предполагается, что он пропорционален интенсивно-
сти этого процесса. Коэффициент пропорциональности обозначается через
aij. Знак при а^ зависит от того, потребляется ингредиент или произво-
64
дится. Как мы уже видели в § 3-3 (7), соглашение о знаке будет состоять
в том, что коэффициент имеет знак (+), если ингредиент потребляется,
и знак (—), если он производится. Наконец, параметр &$, если он положите-
лен, обозначает количество г-го ингредиента, поступающего в систему
из внешних (экзогенных) источников; если эта величина отрицательна,
то она означает количество, которое должно быть произведено системой.
Зависимости между величинами Xj выражаются в виде системы М линей-
ных уравнений, причем i-e уравнение полностью учитывает i-й ингредиент.
В общем случае эта система М линейных уравнений записывается в виде
+ ^12^2 + • • • +
Л21^1 4" ^22^2 4~ • • • 4“ a2NXN “ ^2>
‘ + aAf2^2 4“ • • • 4” aMNXN ~
где ху>0 (/ = 1, 2, ..., N). (2)
Мы будем употреблять прописные буквы М и N всякий раз, когда будем
иметь дело со стандартной формой задачи линейного программирования,
и будем употреблять строчные буквы т и п для произвольной т X п —
системы линейных уравнений. Любая система значений х^, удовлетворяю-
щих соотношениям (1) и (2), называется допустимым решением, потому что
соответствующий план возможен, или допустим. j
Такое описание цели плана часто труднее всего поддается на прак-
тике выражению в математических терминах. На это имеется много исто-
рических причин, обсуждение которых, выходит за пределы этой книги.
Во многих задачах, однако, цель состоит просто в том, чтобы выполнить
требования (выраженные теми из bi, которые отрицательны) так, чтобы
общая стоимость была минимальна. Стоимость может измеряться долла-
рами, числом вовлеченных в процесс людей или количеством использо-
ванного дефицитного ресурса. В линейном программировании предпо-
лагается, что общая стоимость, обозначаемая через z, есть линейная
функция интенсивностей технологических процессов:
+ С2Х2 4“ • • * 4" CNXN = (3)
Определение. Линейная форма z называется целевой функцией (или
формой).
Для решения мы, как правило, будем записывать (3) в виде несколько
иного уравнения (4), где z есть переменная, значение которой должно
минимизироваться:
(—z) + CjXi + с2х2 + .*• + cnxn — 0. (4)
В некоторых задачах линейная целевая форма должна не минимизи-
роваться, а максимизироваться. Например, задача может состоять в том,
чтобы получить максимальную ценность продуктов в долларах при фик-
сированном бюджете, фиксированной машинной мощности и фиксирован-
ных ресурсах рабочей силы. Предположим, что линейная форма, выра-
жающая общую прибыль, которая должна максимизироваться, есть
Г PiXi 4" Р2Х2 + • • • + PnXN-
Тогда наша задача математически эквивалентна минимизации формы
----------- Р2Х2— • • • PnxN = С1Х1 4~ С2Х2 4“ • • • =
где
С1=—р±, с2-=—р2, ..., cN=—pN.
5 Дж. Данциг 65
Таким образом, в качестве стандартной формы задачи линейного
программирования принимается определение решения системы линей-
ных уравнений в неотрицательных числах, которая минимизирует линей-
ную форму.
Двойственная задача линейного программирования. С каждой задачей
линейного программирования (которую можно назвать прямой задачей)
связана другая задача, называемая двойственной. Если цель прямой зада-
чи состоит в минимизации, то целью двойственной задачи является неко-
торая максимизация. В § 3-4 мы уже видели, что двойственная задача
возникает совершенно естественно как алгебраическая проверка пред-
положенного оптимального решения прямой задачи. Далее будет видног
что таблица коэффициентов и параметров двойственной задачи получается
транспозицией коэффициентов и параметров прямой задачи. Переменные
Яг двойственной задачи соответствуют уравнению i прямой задачи, ног
однако, не ограничены по знаку. Неотрицательные переменные Xj прямой
задачи соответствуют неравенствам типа «меньше или равно» в двойст-
венной задаче. Для общей прямой задачи в стандартной форме двойствен-
ная задача состоит в нахождении значений л4, л2, . . . , лм и max
удовлетворяющих соотношениям:
^11^1 + <^2V^2 + • • • + <?li
U31'! + #22^2 4“ • • • + аМ2^М с2>
4- a2N3t2 4-*.. + ам^м
Mi + М2 4- • • • 4- Ъмям = V (max).
В гл. 4 излагается метод преобразования двойственной задачи в обыч-
ную стандартную задачу линейного программирования. Если допустимое
решение прямой задачи оптимально, то этот метод проверки оптималь-
ности автоматически приводит к оптимальному решению двойственной
задачи. Так как задача, двойственная к двойственной задаче, есть в|свою
очередь некоторая прямая задача, решать ли прямую задачу или двойст-
венную представляет собою вопрос удобства.
3-9. ЗАДАЧИ
ОБЩИЕ ВОПРОСЫ
1. а) Что понимается под целевой функцией основной задачи линей-
ного программирования; под допустимым решением?
б) Во многих приложениях каждая из переменных и каждое из урав-
нений имеют типичную интерпретацию. Какова она? Где появляются
соотношения в виде неравенств; где — целевая функция?
в) Предполагая, что увольнение противоположно найму, указать
причины, почему лучше рассматривать их как два неотрицательных тех-
нологических процесса, нежели как один технологический процесс с поло-
жительной и отрицательной интенсивностями?
2. Если такой технологический процесс, как производство стали,
требует затраты кирпича и цемента для того, чтобы построить доменные
печи, то что повлекло бы изменение знака у этих технологических про-
цессов, если бы они использовались как допустимые технологические
процессы?
3. Предполагая, что разность между производством и потреблением
интерпретируется как излишек или дефицит (в зависимости от знака),
66
показать, каким образом можно интерпретировать излишек как хранение
и дефицит как закупку, в которых все коэффициенты при соответствующих
переменных могут быть совершенно различны.
ТРАНСПОРТНАЯ ЗАДАЧА
(см. § 3-3. объяснение двойственности см. § 3-4)
4. Два склада имеют в своем распоряжении консервированные поми-
доры, и три магазина желают пополнить свои запасы.
Склад На личные ящики Магазин Требуемые ящики-
, I 100 А 75
II 200 В 125
С 100
Стоимость (в центах) перевозки каждого ящика от складов к магазинам
приведена в следующей таблице:
АВС
I
II
10 14 30
12 20 17
а) Построить модель, описывающую перевозку помидоров из складов
в магазины, если целью является минимизация общей стоимости перево-
зок.
б) Переформулировать эту задачу, предполагая, что в В требуется
только 60 ящиков, и вводя технологический процесс, состоящий в ликви-
дации ящиков на складах с убытком в 5 центов за каждый ликвидирован-
ный ящик.
в) Показать, что оптимальное решение задачи а) не изменится, если
стоимость перевозки каждого ящика из склада I возрастет на 3 цента;
на 10 центов.
г) Переформулировать задачу а), предполагая, что на складе I имеет-
ся 90 ящиков. Ввести технологический процесс, состоящий в закупке ящи-
ков из внешних источников по цене с надбавкой 20 центов за ящик сверх
стоимостей на складах I и II.
д) Как бы вы сформулировали модель, учитывающую как возмож-
ность закупок ящиков извне в пунктах назначения, так и ликвидацию
ящиков на складах?
е) Сформулировать задачи, двойственные задачам б) и г). Как задача,
двойственная в), связана с задачей, двойственной а)?
5. Обобщить задачу 4 (а) на случай т складов и п пунктов назначе-
ния. Предположить, что производство в г-м пункте производства равно
аг-, а потребность в /-м пункте назначения равна бу. Для части а) предпо-
ложить, что
m п
2 ai— 3
<= 1 j==l
Сделать необходимые изменения для частей б), в) иг). Стоимость перевоз-
67 5*
ки из пункта производства i в пункт назначения / равна сг-7-. Показать,
что в задаче а) имеется одно избыточное уравнение. Как повлияет на двой-
ственную задачу отбрасывание одного избыточного уравнения?
ЗАДАЧА СМЕШИВАНИЯ (см. § 3-4)
6. Домохозяйка просит мясника размолоть несколько кусков мяса,
чтобы получить смесь, состоящую из равных частей белков и жиров.
Будучи добросовестным, мясник хочет сделать это с наименьшей стоимо-
стью каждого фунта продаваемого мяса, исключая содержание воды.
Толстый край ^Пашина Вырез- ка Гру- динка Ссек Огузок Филей
% белка 19 20 16 17 19 16 17
% жира 16 18 25 23 11 28 20
Стоимость за фунт 69 98 1,39 1,29 1,19 1,50 1,65
а) Сколько мяса каждого типа должен он использовать и сколько он
должен запросить?
б) Обычно в его распоряжении имеется избыточный бесплатный
жир. Как это изменит решение?
в) Решить эту задачу графически.
г) Найти решение двойственной задачи.
7. (Тролл.)
а) Предположим, что кусок мяса содержит в каждой своей единице
1 единицу углеводов, 3 единицы витаминов, 3 единицы белков и стоит
50 денежных единиц. Предположим, что каждая единица картофеля соот-
ветственно содержит 3, 4, 1, а стоит 25 единиц этих ингредиентов. Обозна-
чая через Xi количество мяса и через х2 количество картофеля, выразить
математические соотношения, которые должны быть выполнены, чтобы
удовлетворить минимальные потребности в 8 единицах углеводов, 19 еди-
ницах витаминов и 7 единицах белков. Если хг и х2 должны быть выбраны
так, чтобы стоимость диеты была минимальна, то какова целевая функ-
ция?
б) Свести систему неравенств задачи (а) к системе уравнений в неотри-
цательных переменных.
8. а) Сформулировать задачу домохозяйки из § 1-2.
б) Имеется ли какая-нибудь разница между технологическим про-
цессом, состоящим во введении в диету отца пищи i и технологическим про-
цессом, состоящим во введении той же самой пищи в диету ребенка?
в) Могла ли бы предположительно домашняя хозяйка справиться
с задачей приготовления пяти различных обедов в один день, по одному
для каждого члена семьи?
ЗАДАЧА О СМЕСИ ПРОДУКЦИИ (см. § 3-5)
9. Решить задачи, двойственные трем прямым задачам о смеси про-
дукции. Как связаны между собой эти двойственные задачи?
10. а) Предположим, что с различными поставщиками уже подписаны
контракты на изготовление следующих количеств столов:
68
Стол 12 3 4
Проданное количе- ство 60 30 10 50
Как это повлияет на модель?
б) Как интерпретировать оптимальное решение, если получено дроб-
ное число столов? Одна возможная интерпретация состоит в том, что они
исчисляются для шестимесячного периода. Предположим, что дробное
решение округляется до ближайшего целого числа; выяснить, как сле-
дует изменить производственные коэффициенты или мощности цеха для
того, чтобы подогнанное решение было оптимально. Действительно ли
коэффициенты и постоянные члены известны точно в любой реальной
ситуации?
11. Субподрядчик заключил соглашение поставить некоторой ком-
пании 150 агрегатов в январе и 225 в феврале. При восьмичасовом рабочем
дне субподрядчик может производить только 160 агрегатов в месяц. При
работе ежедневно два часа сверхурочно можно произвести дополнительно
30 агрегатов, с оплатой за сверхурочные по 20 долл, за каждый агрегат.
Агрегаты могут храниться; стоимость хранения составляет 3 долл, в ме-
сяц. Сформулировать модель для нахождения плана производства, кото-
рый минимизирует стоимость.
12. Строитель домов массового производства планирует строить дома
на 100 участках в новом районе. Он выбрал 5 основных типов домов:
A, Bt С, D, и Е. Для того чтобы построить дома, строитель имеет двух
главных подрядчиков: каменщики для заложения фундамента и плотники
для остальной части строительства. Количество дней, требуемое для
работы, следующее:
А В С D Е
Фундамент 1 2 2 1 1
Каркас 4 7 6 5 3
Доход 2000 3000 2500 1700 2000
Строитель занял деньги под очень низкий процент на три года. Ввиду
того что обычно продажа дома занимает два месяца, строитель хочет,
чтобы все дома были закончены за 34 месяца, или приблизительно за
610 рабочих дней.
а) Сколько нужно построить домов каждого типа, для того чтобы
максимизировать доход?
б) Если строитель хочет построить по крайней мере 10 домов каждого
стиля, то какова должна быть его строительная программа для того, чтобы
гарантировать максимальный доход?
в) Решить эту задачу методом, примененным при решении задачи
о смеси продукции, § 3-5.
13. Задача Канторовича [1] о станках.
Сформулировать, но не решать. Собранное устройство состоит из двух
металлических деталей. Фрезерная работа может быть выполнена на
69
различных станках: фрезерных станках, револьверных станках или на
автоматических револьверных станках. Основные данные приведены в таб-
лице. Исходя из этой таблицы,
а) распределить время работы каждого станка так, чтобы получать
в час максимальное число полных устройств;
б) доказать, что оптимальное решение обладает тем свойством, что
ни один станок не будет простаивать и что обе детали будут сделаны в рав-
ных количествах;
в) сформулировать двойственную задачу.
Производительность станков для двух деталей
Тип станка Число станков Максимальный выпуск 1 1 станка в час
первая деталь вторая деталь
^Фрезерные станки 3 10 20
Револьверные стан- ки 3 20 30
Автоматические ре- вольверные станки 1 30 80
1 Если он отведен для обработки только одной из деталей.
14. а) Обобщить задачу 13 на т станков, п деталей, если цель состоит
в том, чтобы выпустить наибольшее число полных устройств#
б) Показать в общем виде, что если каждый станок пригоден для
обработки каждой детали и если неиспользуемая (избыточная) производи-
тельность станков, а также некомплектные детали имеют цену, равную
нулю, то любое оптимальное решение будет иметь только комплектные
детали и все станки будут полностью загружены. Что произойдет, если
некоторые станки непригодны для обработки некоторых деталей?
в) Сформулировать двойственную задачу.
15. Предположим, что вместо одного имеется два типа устройств
и каждому можно придать его «ценность». Максимизировать взвешен-
ный выпуск.
16. Обобщить формулировку задач 14 и 15 так, чтобы охватить сле-
дующие случаи:
а) Предположим, что имеется ограничение на использованную элек-
троэнергию, которая зависит от комбинации деталь — станок.
б) Предположим, что возможно, применяя г-й технологический про-
цесс, обработать единиц fc-й детали на Z-м станке.
в) Предположим, что возможно придать значение избыточным дета-
лям; неиспользованной производительности станка.
17. Каждая из трех деталей може? быть обработана на 2 станках.
Предположим, что подготовительное время отсутствует и что это непре-
рывный тип производства, т. е, деталь сначала обрабатывается на станке 1,
а затем сразу переводится на станок 2, причем практически между опера-
циями не проходит никакого времени. Единица времени на деталь на
каждом станке и прибыль от каждой обработанной детали дается в таб-
лице.
70 '
Станок Деталь
А В С
1 0,02 0,03 0,05
2 0,05 0,02 0,04
Прибыль 0,05 0,04 0,03
а) Сформулировать модель для оптимальной смеси продукции. Выра-
зить ее в виде модели с линейными неравенствами при условии, что на каж-
дой машине можно работать не более 40 часов. Преобразовать эту систему
в систему уравнений.
б) Обобщить эту задачу на п различных видов деталей и т машин.
в) Сформулировать задачи, двойственные задачам а) и б).
ПРОСТАЯ ЗАДАЧА О СКЛАДЕ (см. § 3-6) *
18. а) Переформулировать простую задачу о складе из § 3-6,
если требуется, чтобы продаваемые, хранимые и покупаемые количества
были одними и теми же для соответствующего квартала каждого года.
Сформулировать модель с наименьшей стоимостью за год, предполагая,
что начальный уровень запасов такой же, как запасы, хранящиеся на
складе в конце года.
б) Обсудить специфические свойства матрицы коффициентов в дина-
мической задаче этого типа.
ЗАДАЧА ОБУЧЕНИЯ НА РАБОТЕ (см. § 3-7)
19. Переформулировать задачу обучения на работе из § 3-7, предпо-
лагая, что стоимость увеличения интенсивности производства по срав-
нению с интенсивностью последней недели составляет q = 4 долл, на каж-
дую единицу увеличения. Для уменьшения интенсивности стоимость не
вводится. Вся продукция хранится с расходами 5=1 долл, за единицу
в неделю до последней недели. Если начальная интенсивность производ-
ства равна Р о — 5 и конечное требуемое состояние запасов составляет
= 200 рабочих, то каков оптимальнй план производства?
20. Фермер может продать часть своего урожая и посеять остаток,
причем его урожай составит к бушелей на каждый посеянный бушель. Он
надеется получить pt долл, дохода на бушель за урожай, который он
посеял, р2 и р3 долл, на бушель за два следующих урожая. Его первый
урожай составит А бушелей.
Задача. Составить основные уравнения и линейную форму, которая
представляет его общий доход за три периода. Показать, что ему всегда
выгодно продать третий урожай. Показать, что если 2l2p3 >Pi, А,р3
то ему выгодно сеять весь первый и весь второй урожаи. Показать, что
если pi — р2 >0, р2 — рз >0, то ему выгодно продать весь первый
урожай. Когда ему выгодно продать весь второй урожай?
21. (Кемени). Задача о курице и яйцах.
Сформулировать. Предположим, что курице нужно две недели для
того, чтобы снести 12 яиц на продажу или чтобы высидеть 4 яйца. Какова
наилучшая программа несения и высиживания, если в конце четвертого
периода все куры и цыплята, полученные в течение периода, продаются
по 60 центов за штуку, а яйца — по 10 центов за штуку. Предполо-
жим, что начальный запас составляют:
а) 100 кур и 100 яиц,
б) 100 кур и ноль яиц,
71
в) 100 кур и ноль яиц, а кроме того, конечный запас составляет
100 кур и ноль яиц.
22. (Орчард-Хейс). Предприниматель покупает предмет А и произ-
водит предмет В. Каждый предмет В требует один предмет Л, и фабрика
имеет производственную мощность в 3000 предметов В в каждый квартал.
Однако в каждый квартал предметы А доступны. в различных количествах
и предметы В требуются в различных количествах. Кроме того, хранение
предмета В дорого, и общие остатки этого предмета, сохраняющиеся от одно-
го квартала до следующего, должны минимизироваться. В начале года
имеется в наличии 3000 предметов Л и по крайней мере столько же должно
быть отложено в конце года. Доступность предметов А и потребность
в предметах В поквартально следующие:
1-й квартал 5000 А
2-й квартал 3000 А
3-й квартал 1000 А
4-й квартал 2000 А
доступно, 1000 В
» 4000 В
» 3000 В
» 1500 В
требуется
»
»
»
Имеется склад, пригодный для хранения 10 000 предметов А или 2000 пред-
метов В или любой их комбинации в этом отношении. Предположим, что
для каждого квартала q уравнение
sq:Aq + 5Bq + Sq^ 10000 (g = l, 2, 3, 4)
достаточно для того, чтобы описать ограничение на вместимость склада
(оно не учитывает узкие места в течение квартала). Переменные опреде-
лены ниже.
Построить модель линейного программирования для задачи
минимизации общих остатков предмета В, сохраняющихся после
каждого квартала при поставленных ограничениях. Для каждого квартала
использовать следующие 7 переменных.
Mq: количество предметов В, произведенное в квартале q.
pq: количество предметов А, закупленное в квартале q для использо-
вания в квартале q (или позже).
Aq: количество предметов Л, не использованное в конце квартала q.
Bq: количество предметов В, имеющееся в наличии (после удовлетво-
рения потребностей) в конце квартала q.
Cq. излишек производственной мощности в течение квартала q.
Sq: излишек вместимости склада в течение квартала q.
Uq: излишек доступности предмета А в течение квартала q.
Это дает 28 переменных; одна особая переменная, выражающая потреб-
ность в предмете А в конце года, есть
v: излишек запасов предмета Ав конце года.
Эти 29 переменных будут иметь коэффициенты в следующих 21 урав-
нении ограничений:
aq: уравнение баланса по предмету А для квартала q.
bq: уравнение баланса по предмету В, произведенному в квартале q.
cq. уравнение ограничения производственной мощности в квартале q.
pq: уравнение ограничения доступности предмета А в квартале q.
sq: уравнение баланса для вместимости склада в квартале q (см. выше),
г: уравнение потребности для остатка предмета А в конце года.
Найти некоторое допустимое решение. Является ли ваше решение опти-
мальным? Что произойдет, если доступность предмета А изменится да
3000 в каждый квартал? Можете ливы увидеть, как другие изменения в кон-
стантах доступности и потребности могли бы сделать задачу труднее?
Невозможной? Избыточной? Несовместной?
Глава 4
СИСТЕМЫ. ЛИНЕЙНЫХ УРАВНЕНИЙ
Й НЕРАВЕНСТВ
4-1. СИСТЕМЫ УРАВНЕНИЙ С ОДИНАКОВЫМИ МНОЖЕСТВАМИ РЕШЕНИЙ
СОВМЕСТНЫЕ УРАВНЕНИЯ И ЛИНЕЙНЫЕ КОМБИНАЦИИ
Так как методы, используемые для решения задач линейного про-
граммирования, основаны на известных методах решения систем линей-
ных уравнений, целесообразно в данном случае рассмотреть некоторые
элементарные положения. Для этого мы рассмотрим следующий пример
системы двух уравнений с неизвестными значениями трех переменных:
—Х2-\-Х3 = 2 (^1),
2^14" ^2 хз ~ (^2)* (1)
Упорядоченный набор значений = 3, х2 = 2, х3 = 1 называется
решением уравнения El9 так как подстановка величин xt, x2l х3
в первое уравнение дает тождество 2 = 2. Говорят также, что решение
(3, 2, 1) удовлетворяет уравнению Ei.
В общем случае пусть мы имеем систему т уравнений с п неизвест-
ными:
а11ж14" ^12^2+ • • • + =
^21^1 4“ ^22^2'4“ • • • 4“ ^2пхп — ^2,
............................................. (2}
^7711*^1 + «7П2^2 4- • • • 4“ ^тпхп ~ Ьщ*
(Это произвольная т X и-система линейных уравнений. Мы будем
использовать прописные буквы М, N для обозначения системы линейных
уравнений в стандартной задаче линейного программирования, приве-
денной в § 3-8 (I).) Решение z-го уравнения есть такой упорядоченный
набор чисел (я{, я', . . ., хп), что
^11^1 4" ai2xz 4- • • • 4- ttinXn — Ь/.
Упорядоченный набор чисел будет называться решением системы
уравнений, если он удовлетворяет каждому уравнению системы. Напри-
мер, поскольку подстановка (3, 2, 1) в уравнение Е2 приводит к тождеству
7 = 7, мы получаем, что (3, 2, 1) является решением обоих уравнений
Е^ и Е2, а поэтому и всей системы.
Часто мы говорим о некотором решении, но не о данном конкретном
решении, с тем чтобы не касаться вопросов единственности. Совершенно
ясно, что система уравнений не обязана обладать единственным решением
и, более того, она может не иметь решений вообще. Так, кроме значений
(3, 2, 1), рассмотренная выше система удовлетворяется любым набором
чисел вида (3, + 1» «,), где число я' может быть выбрано произвольно.
Система, которая имеет одно или несколько решений, называется совмест-
ной, или разрешимой. В противном случае мы называем ее несовместной^
или неразрешимой.
73
Совокупность решений системы составляет множество ее решений.
Если система несовместна, то говорят, что множество ее решений пусто.
Если дана система уравнений вида (1), то на ее основе легко составить
новые уравнения, которые обладают тем свойством, что каждое решение
системы (1) является также решением нового уравнения. В следующей
системе уравнений (3) новое уравнение выписано под чертой; оно обра-
зуется путем умножения первого уравнения на 2, второго на —3 и сло-
жения.
2: х। —--* х2 4” х$ = 2
— 3: 2#i х2— = 7 (3)
—4#! — 5т2 + 5т3= —17 ’
Отметим, что решение (3, 2, 1) системы уравнений (1) является также
решением нового уравнения.
Схема формирования новых уравнений, множество решений которых
включает все решения общей линейной системы уравнений (2), показана
на примере системы (4). Для каждого f-ro уравнения берется произволь-
ное число kiх, показанное слева; новое уравнение, записанное под чертой,
-образуется путем умножения г-го уравнения на ki и суммирования:
ftf. a^Xi 4- а12я2 + • • • + = 61,
к2: ^21^1 + «22^2 + • • • + ^2тЛ1 — 62,
кщ*. Ч~ ^тп2^2 4~ ♦ ♦ ^тпп^тг — fyn
<21#1 4“ ^2Ж2 4“ •• • 4“ &п%п = (5)
Коэффициенты суммы легко найти; они имеют следующий вид:
di — kiUii + &2a21 + • • • + &татпь
d2 — kiai2 + k2a22 4- ... +
.................................................... (6)
dn — kiUin + к2а2л + . . . + ^mamni
< d = kibi + k2b2 -J- ... + kmbm.
Уравнение типа (5), полученное этим способом, называется линейной ком-
бинацией исходных уравнений. Числа ki в этой линейной комбинации
называются множителями, или весами.
Записав систему уравнений (4) и (5) в виде таблицы коэффициентов
(7) и (8), мы видим, что способ образования линейной комбинации урав-
нений аналогичен способу образования линейной комбинации строк
таблицы (7). Под этим мы подразумеваем, что любой элемент строки (8)
можно получить суммированием произведений kt на соответствующие
элементы i-й строки матрицы (7).
Множитель
(йи ^22 • • • ат 61 \ • fyi
#21 а22 • • • #2тг 62 I : к2
&т1 ат2 • • • атп бт / : кт
(di d2... dn d) (8)
1 Постоянные могут быть и нулями.
74
Упражнение. Пусть некоторая линейная комбинация столбцов мат-
рицы (7) равна какому-то другому ее столбцу. Показать, что это останется
в силе, если строку (8) присоединить к строкам матрицы (7).
Если множество чисел fa, х2, . . ., хп) составляет решение системы
уравнений (4), то уравнение (5) превращается путем подстановки во взве-
шенную сумму тождеств и поэтому само становится тождеством. Поэтому
любое решение линейной системы является также решением любой линей-
ной комбинации уравнений этой системы. Следовательно, такое уравне-
ние можно ввести в систему уравнений, не влияя при этом на множество
решений.
Определения. Если в какой-либо системе уравнений одно из уравне-
ний является линейной комбинацией других, то оно называется зависимым
от них; зависимое уравнение называется иногда избыточным. Нулевое
уравнение^ т. е. уравнение типа
О#! + 0ж2 + ... + 0жп — 0,
также называется избыточным, когда оно встречается в системе, состоя-
щей из одного уравнения. Система, не содержащая избыточных уравне-
ний, называется независимой.
Линейная система, очевидно, является неразрешимой или несовмест-
ной, если можно найти линейную комбинацию ее уравнений вида
0^ + 0^+ ... 4-0ял = о?, где d^Q. (9)
В самом деле, любое решение системы должно удовлетворять уравнению
(9); но это невозможно ни при каких значениях переменных. Уравнение
(9) будем называть несовместным. (См. упражнение ниже.) Например,
система w
1: х± 4- х2 + х2 = 5
— 1- #i 4~ #2 4~ #з —
9#i 4- 9#2 + 9#з
является неразрешимой, потому что первое уравнение утверждает, что
сумма трех чисел равна 5, в то время как из второго уравнения следует,
что та же сумма равна 4. Однако если мы возьмем множители ki = 1,
k2 = —1, то путем исключения, скажем х^ мы автоматически придем
к противоречию, которое и выявлено в написанном снизу уравнении. Вооб-
ще, как мы покажем в следующем разделе, метод исключения примени-
тельно к несовместной системе приведет в конце концов к несовместному
уравнению.
Упражнение. Показать, что несовместная линейная система, состоя-
щая из одного уравнения, имеет вид (9).
Упражнение. Показать, что если система содержит нулевое уравне-
ние, то она является зависимой.
КАК РЕШАЮТСЯ СИСТЕМЫ?
Обычный метод «исключения» для нахождения решения системы
уравнений состоит в расширении системы путем формирования новых
уравнений; при этом линейные комбинации будут подбираться таким
образом, что определенные коэффициенты будут обращаться в нуль. (Затем
можно исключить определенные избыточные уравнения.)
Так, например, в приведенной далее системе уравнений (10) уравне-
ние Ei умножается на к± = —2, а Е2 — на к2 = 1, так что после сложе-
75
ния коэффициент при Xi становится равным нулю. Это дает уравне-
ние Е3. Эти действия могут быть записаны символически Е3 = (—2) Ei +
+ (1) Е2. Таким же образом мы можем получить уравнение 7?4, умножин
Е3 на Va, а также получить /?5, сложив Ei и Ек.
Расширенная система {Дь Е2, . . . , Е*} имеет то же множества
решений, что и исходная система уравнений (1), потому что все уравнения
типа #4 и Еъ могут быть вновь представлены как прямые линейные ком-
бинации Ei и Е2.
—^2 4” #з = 2 (^i)
4-#2 #3 — 7 (Е2)
Зж2 — 3^з = 3 (Е3 =—2Ei~}~E2) (10)
х2— #3=1 (Е^ — 1/3Е3)
— 3 (1?5 = Ei 4- Е^).
Интересно отметить, что подсистема {Е^, Е5} может быть использо-
вана для выяснения того, любое ли уравнение является линейно зависи-
мым от нее. Заметим, что х2 появляется в уравнении Е^ с коэффициентом,
равным единице, и с коэффициентом, равным нулю в уравнении Е$, а для
Xi имеет место обратное положение. Это позволяет легко исключить xt
и х2 из любого другого уравнения. Например, совершенно ясно, что если
Ei должно быть линейной комбинацией Е^ и Е5, то коэффициент при Е&
должен быть равен 1, а коэффициент при Е^ должен быть равен (—1).
Легко проверить, что Ei = Е3 — Е±, Е2 — 2Е5 + Е^ Е3 = ЗЕ±. Таким
образом, все решения {£4, Е5} также являются решениями {£\, Е2}
и, как отмечалось ранее, все решения {Ei, Е2} являются решениями {£4г
Е5}; следовательно, решения этих двух подсистем совпадают.
Вторым преимуществом подсистемы {Е±, Е3} является то, что она
позволяет легко выявить множество всех возможны! решений. Действи-
тельно, выберем любое произвольное значение для х3 = х3 и выразим
х2 и Xi через х3. В этом случае (xi = 3, х21 + #з, #3 = #з) описывает
множество всех решений. Например, х3 = 0 дает частное решение (xt — 3,
х2 = 1, х3 = 0).
Вообще метод решения систем (более подробно мы опишем это в § 4-2)
заключается в расширении системы путем присоединения к ней линей-
ных комбинаций до тех пор, пока в расширенной системе не появится
такая подсистема, множество решений которой можно легко найти, и та-
кая, что каждое уравнение полной системы является линейно зависимым
от нее, кроме, быть может, свободного члена. Полученная подсистема
относится к классу, называемому каноническим.
Определение. Канонической системой с упорядоченным подмножест-
вом переменных, называемых базисными, является такая система, где
для каждого i i-я базисная переменная имеет коэффициент единицу в i-м
уравнении и нулевые коэффициенты в других уравнениях.
Например, подсистема {Е^, Е5} в системе (10) является канонической,
причем х2 связано с Е^ и xt — с Е5. Приводимая далее система (И) Является
канонической, поскольку для каждого i, хг имеет коэффициент единицу
в z-м уравнении и нуль в остальных уравнениях.
+ ai, r+i^r+i 4" • • ‘ 4“ fli, пхп — bi,
х2 + а2, г+1хг+1 4" • • • 4“ а2, пхп = Ь2,
(И)
ХТ 4" ат, г+1^г+1 4- ••• Л~ат, пхп — Ъг.
76
Упражнение. Показать, как путем произвольного выбора значений
для яг+1, .. . , хп можно породить класс всех решений. Каким образом
можно использовать систему уравнений (11), чтобы легко проверить, зави-
симо ли от нее другое уравнение?
Другая операция, которая не влияет на множество решений системы,
состоит в исключении уравнения, являющегося линейной комбинацией
других. Если после расширения одно из исходных уравнений в системе
окажется линейной комбинацией других, то оно может быть исключено.
В результате новое уравнение становится как бы «заменителем» одного из
исходных уравнений. При использовании электронных вычислительных
машин, имеющих ограниченную память для хранения информации, воз-
можность исключения уравнений приобретает особую важность.
Определение Ч Две системы называются эквивалентными, если одна
система может быть получена из другой путем приписывания или исклю-
чения избыточного уравнения или если одна система может быть полу-
чена из другой через цепочку систем, каждая из которых получается
из предшествующей путем такого же приписывания или исключения.
Теорема 1. Эквивалентные системы имеют одно и то же множество
решений.
ЭЛЕМЕНТАРНЫЕ ОПЕРАЦИИ
Имеются два простых, но важных типа линейных комбинаций, кото-
рые можно использовать для получения эквивалентных систем.
1. Замена любого уравнения Et уравнением [kEt], где к =?^= 0.
2. Замена любого уравнения Et уравнением [Е* + кЕг], где Ег —
любое другое уравнение системы.
Чтобы показать, что элементарная операция первого типа приводит
к эквивалентной системе, напишем kEt в качестве нового уравнения после
Et, а затем вычеркнем Et. Заметим, что Et является избыточным уравне-
нием, так как оно может быть получено из kEt как 1 lk{kEt], если к 0.
Аналогично для второго типа элементарных операций напишем Et + kEt
после Et и затем исключим Et. Заметим, что Et является здесь избыточ-
ным уравнением, поскольку оно выражается как [Et + kEi \ — кЕг.
Один из способов преобразования системы нашего примера (1) в экви-
валентную ей систему (10) путем последовательных элементарных опе-
раций состоит в следующем:
Элементарная операция
—^гЧ-^з — 2 (Ei)
2xi -f-x2—х3 = 7 (Е2)
Заменить Е2 на Е' —^2 + ^1
—#2-l_^3:=2 (^1)
$Х1 =9 (^)
1 1
Заменить Et на E[ = Ei—Е'2
—х2-}-х3 ——1 (EJ
3^ =9 (Е'2)
Заменить Е[ на Е[ = —Е[
х2—х3 — 1 (Е^)
3^ =9 (Е'2)
1 Это определение эквивалентности принадлежит А. У. Таккеру (сообщено в лич-
ной беседе).
77
Вообще каждой элементарной операции соответствует обратная
операция, которая также является элементарной операцией и притом
того же типа. Например, начиная с последней пары уравнений, можно-
получить предпоследнюю пару путем замены Е[ на Е[ = — 2?"; пред-
шествующую пару можно получить в свою очередь путем замены Е[ на
= Е[ + ЧзЕ' и, наконец, первую пару — путем замены Е' на Е* =
= Е'2- Е,.
Теорема 2. Последовательности элементарных операций соответ-
ствует обратная последовательность элементарных операций, с помощью'
которой данная система может быть получена из преобразованной
системы.
Легко видеть, что если система может быть получена из данной систе-
мы путем последовательных элементарных операций, то каждую строку
преобразованной системы в виде таблицы коэффициентов можно получить
непосредственно как линейную комбинацию строк данной системы. Наобо-
рот, по теореме 2, каждая строка данной системы является некоторой
линейной комбинацией строк преобразованной системы.
Теорема 3. Строки одной из двух эквивалентных систем в виде таблиц
коэффициентов можно получить в виде линейных комбинаций строк другой
системы.
Теорема 4. Если t-e уравнение данной системы заменить линейной
комбинацией с множителями где kt=£Q, то получается эквивалентная
система.
Упражнение. Доказать теоремы 2, 3, 4.
Наиболее важным свойством систем, получаемых из данной путем
применения элементарных операций, является, по теореме 1, то, что они
имеют одно и то же множество решений.
Здесь возникает интересный вопрос. Все ли системы линейных урав-
нений с одним и тем же множеством решений можно получить путем
последовательных приписываний и исключений избыточных уравнений?
Мы покажем (это составит содержание теоремы 1 в § 4-2, и теоремы 4
в §18-1), что если две системы разрешимы и имеют одно и то же множество
решений, то они эквивалентны. Вместе с тем если системы неразрешимы,
то это может и не иметь места. Действительно, рассмотрим две системы
ГОх= 11
{ta-1} и
Обе эти системы имеют пустое, а отсюда одно и то же множество решений.
Ясно, однако, что если бы эти две системы были эквивалентными, то неко-
торое кратное (линейная комбинация) уравнение 0# = 1 первой системы
оказалось бы уравнением ix = 1 второй системы, что, очевидно, невоз-
можно.
4-2. КАНОНИЧЕСКИЕ СИСТЕМЫ
РЕШЕНИЕ КВАДРАТНЫХ СИСТЕМ
Системы линейных уравнений, о которых говорится в элементарных
курсах алгебры, обычно содержат столько же уравнений, сколько пере-
менных в общей системе уравнений (2), которая была рассмотрена в пре-
дыдущем разделе; это будет соответствовать случаю т = п. Такую систе-
му уравнений часто называют квадратной системой.
Предполагая, что квадратная система из т уравнений с т неизвест-
ными имеет единственное решение, можно применить обычный процесс.
78
решения таких систем, состоящий в исключении одного из неизвестных,
отбрасывании одного из уравнений и решения полученной системы урав-
нений, в которой на одно уравнение и на одно неизвестное меньше. Этот
процесс повторяется т — 1 раз, что дает в результате одно уравнение
с неизвестным значением одной переменной. Затем найденное значение
подставляется в предыдущее уравнение, чтобы определить значение дру-
гой переменной. Этот процесс, называемый «обратным решением», прово-
дится до тех пор, пока не будут найдены значения всех переменных (Гаусс
[1]). Наша непосредственная задача — проследить этот процесс во
всех деталях, чтобы показать, что он действительно представляет не что
иное, как последовательность элементарных операций, которые приводят за-
данную систему к эквивалентной системе в простой диагональной форме (1).
Здесь множество решений очевидно.
*1 = Ьр
#2 =
Рассмотрим систему из трех уравнений с тремя неизвестными:
alixi + ^12^2 4" а13х3 ~
^21Ж1 4" а22Х2 4“ ^23^3 ~ ^2, (2}
«31*1 4- Л32Ж2 4“ #33^3 ~ &3-
Если ait 0, то первое уравнение может быть использовано для исклю-
чения Xi из второго уравнения с помощью элементарной операции Е2 =
= Е2 — (a2i/an) Ei и исключения Xi из третьего уравнения с помощью
элементарной операции над полученной системой Е3 — Е3—
Таким образом, мы получаем эквивалентную систему:
а11Ж1 4“ ^12Ж2 4~ «13^3 ~ (а11=7^0)
^22*^2 4~ ^28*^3 ~ ^2> (3)
^32*^2 4“ «33^3 “
Первое из этих уравнений обычно не рассматривается, и процесс вычис-
лений повторяется над системой, состоящей из оставшихся уравнений.
Если «22 0, то второе уравнение может быть использовано для исклю-
чения х2 из третьего уравнения, что дает в результате эквивалентную
треугольную систему:
+ «12ж2 + «13я3 = («и 0, а22 #= 0)
^22*^2 4" ^23*^3 = ^21 (^)
<з^з =-ь;.
Если «з3 =# 0, то обратное решение начинается с определения х3 из
последнего уравнения. Затем х3 подставляется во второе уравнение, что дает
значение х2. Наконец, оба значения подставляются в первое уравнение.
Эти две подстановки совершенно равноценны использованию третьего
уравнения при исключении х3 из второго и первого уравнений с помощью
последовательных элементарных операций Е2 = Е2 — (а23/а33)Е3 ~
= Ei -— («1з/«33) Е3, дающих в результате
O'iiXi -J- «12Ж2 = &п (Яд1 =7^= 0, «22 =7^ 0, «33 =4= 0)
^22*^2 “ ^2> (5)
аЗЗХ3 — ^8*
79
Подстановка значения х2, полученного из второго уравнения, в первое
для определения имеет такой же результат, что и элементарная опера-
ция Е"г — E[ — (ai2/a2^E2 и дает
(^11 0, #22=7^=0, #33=7^0)
^22*^2 = ^2» (6)
^Х3 = Ь''.
Наконец, деление на диагональные коэффициенты, которое является
последовательностью из трех элементарных операций, приводит
к диагональной системе вида (1).
Если система имеет единственное решение, то описанный процесс
вычисления всегда выполним, хотя не обязательно в указанном порядке.
Так, например, если als = 0, то можно перейти к любому другому члену,
коэффициент при котором не равен нулю, например atsxs, который назы-
вается ведущим элементом, для исключения xs.
В этом случае t-e уравнение можно использовать для исключения xs
из уравнений путем последовательных элементарных операций, заменяю-
щих i-e уравнение суммой i-ro уравнений и £-го уравнения, умноженного
на (—aislat&). Если такой процесс повторяется в каждой системе, полу-
ченной путем отбрасывания уравнений, используемых для исключения,
то это даст систему, соответствующую системам (1) и (4), которая может
быть приведена к диагональному или треугольному видам путем соответ-
ствующей перестановки уравнений.
Вообще квадратную систему мы будем называть треугольной, если
после соответствующей перестановки ее строк и ее переменных все коэф-
фициенты ниже диагонали окажутся нулями, а все коэффициенты на диа-
гонали не нули; если, кроме того, отличны от нуля только диагональные
коэффициенты, то система называется диагональной.
В качестве примера приведения к треугольному и диагональному
виду рассмотрим 3 X 3-систему:
1о*. х^ 4“ х2 + х3 = 1,
По: х^—я2 + я3 = 3,
Шо: х^-\-2х2—я3 = 4.
Она может быть приведена к треугольному виду следующим образом:
Операция
11 =
П1:
III*:
ж1 + а:2 + а:3=1
—2х2 —2
д?2 — 2^^ — 3
11 = Io
П1 = П0—Io
IHt-IIIo-Io
Операция
80
Эта последняя система (12, П2, П12) является треугольной и может быть
легко приведена к диагональному виду,
Операция
13: xi — 4-4 13=12—П2—Ш2
П3: х2 ~ 1 п3=п2
1П3: а:3= —2 ш3 = ш2
уже выписано в явном виде.
в котором решение
ВЕДУЩИЕ ОПЕРАЦИИ ДЛЯ ОБЩЕЙ СИСТЕМЫ
Предположим для общности, что мы вместо квадратной системы имеем
дело с системой из т уравнений с п переменными, где т^п.
анх14- ^12*^2 4~ • • • 4~
Л21Ж1 4~ ^22^2 4“ • • • 4-«271^71 = Ь2, (У)
Omixl + ат2Х2 4" • • • 4“ атпхп = &т-
Мы ищем возможный путь замены этой системы некоторой эквивалентной
канонической системой (определение см. § 4-1). Для канонической системы
множество решений является очевидным, и легко определить, имеется .
или нет какая-либо другая эквивалентная ей система.
Каноническая система с базисными переменными xi, х2, ...» хт
Х1 ~Ьа1т+1хт+1 • • • 4- а 1^7’4- ••• 4*а 1пхп = &1 Х2 4- а2771+1^771+1- • • 4" a2jXj + • • • 4'Л27ГГ71 =62 хт ~hamm+lxm+l- • • 4" fl77iJxj4" • • • атпхп — ^тп
Базисные переменные Небазисные (независимые) переменные Правые части
Диагональная система (1) для квадратных систем является, очевидно,
частным случаем канонической системы (8) при т = п. Далее мы рассмот-
рим обычный метод приведения (если это возможно) общей системы (7)
к эквивалентному каноническому виду.
Принципы этого приведения лучше всего вначале проиллюстрировать
на примере, а затем обобщить. Рассмотрим 2 X 4-систему
4-3^2 4~ я3 4- #4 = 5,
—2х2 — х3+ я4 = 2.
Выберем в качестве «ведущего элемента» любой член с ненулевым коэф-
фициентом (например, тот, который выделен жирным шрифтом в пер-
вом уравнении) и исключим при помощи элементарных операций соот-
6 Дж. Данциг &Z
ветствующую переменную х2 из других уравнений:
^гЧ’^зЧ" я4 = 5,
Ч~ 1 Ч” "4” 3^4 = 12.
Возьмем далее в качестве ведущего элемента любой член из оставшихся
уравнений (скажем, тот, который выделен жирным шрифтом во вто-
ром уравнении). Исключаем соответствующую переменную, в данном
случае xt, из всех остальных уравнений. (Так как х^ в первом уравнении
имеет нулевой коэффициент, никаких дальнейших исключений факти-
чески не требуется.) Отсюда, переставляя уравнения, мы получаем систему
Ч” *з 4“ 3^4== 12,
•^гЧ^^зЧ- #4 = 3.
Из этой канонической системы с базисными переменными х2 при под-
становке х3 = я4 = 0 становится ясным, что одним из решений явится
Xi = 12, х2 = 5, я3 = я4 = 0.
ВЕДУЩИЕ ОПЕРАЦИИ
Определение. Ведущая операция состоит из т элементарных опе-
раций, заменяющих систему уравнений эквивалентной ей системой,
в которой некоторая переменная имеет коэффициент единицу в одном
уравнении и нуль во всех остальных. Отдельные шаги состоят в сле-
дующем:
а) выбираем член arsxs, называемый ведущим элементом в системе
уравнений (7), так, чтобы ars #= 0;
б) заменяем r-е уравнение системы на ее r-е уравнение, умноженное
на (1 /ars);
в) для каждого z = l, 2, . . ., т, кроме i = г, заменяем z-e уравнение
суммой z-ro уравнения и измененного г-го уравнения, умноженного на
( ais)'
Вообще приведение к какому-то каноническому виду может быть
выполнено при помощи ряда последовательных ведущих операций. В ка-
честве первого ведущего элемента выбираем любой член arsxs так, чтобы
ars =/= 0. После первого исключения в качестве второго ведущего эле-
мента выбирается ненулевой член из любого уравнения, за исключени-
ем г, скажем из уравнения г'. После этого исключения выбирается третий
ведущий элемент из любого уравнения полученной системы т уравне-
ний, кроме уравнений гиг', допустим из уравнения г". Вообще мы
повторяем операцию исключения, всегда выбирая ведущий элемент из
уравнений, которые не входят в число ранее выбранных. Продолжаем
выполнять эти действия до тех пор, пока либо будут использованы т
ведущих элементов, либо когда после выбора г переменных окажется
уже невозможным найти ненулевой член в каком-либо уравнении,
отличном от тех уравнений, которые соответствуют ранее выбранным
ведущим элементам.
Например, если ряд ведущих операций был выполнен над перемен-
ными Xi, х2, . . ., хг в уравнениях 1 = 1, 2, . . ., г, то первоначальная
система (7) будет приведена к эквивалентной системе вида (9), которую
будем называть приведенной системой с исключенными переменными
х2, . . ., хг. Будем также называть систему приведенной относительно г
ведущих переменных, если при изменении порядка переменных и урав-
нений она может быть приведена к виду (9).
Так как система (9) была получена из системы уравнений (7) в резуль-
тате некоторой последовательности ведущих операций, каждая из кото-
82
рых состоит из т элементарных операций, из этого следует, что приведен-
ная система: а) состоит из линейных комбинаций уравнений исходной
системы и б) эквивалентна исходной системе.
Исходная система уравнений (7) разрешима тогда и только тогда,
когда соответствующая ей приведенная система (9) является разрешимой,
а система уравнений (9) является разрешимой тогда и только тогда, когда
br+i — Ьг+2 — • • • Ът = 0. (10)
Если выполнено условие (10), то множество решений станет очевид-
ным, поскольку любые значения (независимых) переменных яг+1, . . .,
определяют соответствующие значения (зависимых) переменных ...
. . ., xr. С другой стороны, если &г+/ =/= 0 для некоторого i, то множество
решений является пустым, так как (г + i)-e уравнение несовместно
с остальными, ибо оно утверждает, что 0 = br+i. В этом случае исходная
система уравнений (7) и приведенная система уравнений (9) обе несовме-
стны (т. е. неразрешимы).
КАНОНИЧЕСКАЯ СИСТЕМА
Если исходная система совместна, то система, полученная путем
исключения нулевых уравнений из приведенной системы, называется ее
каноническим эквивалентом с ведущими переменными в качестве базисных.
Каноническая система с базисными переменными хь х%, ...» хг
Х1 +fll, Г+1ХГ+1 + а1, r+2^r+2+ • • • +<2171^71 = &! x2 +й2, r+lxr+l + fl2, r+2rcr+2 4“ • • • +G2na:n==^2 xr-\-aTi r+l^r+i 4“ flr, r+2xr+2~b • • • 4“amxn=^bT
Зависимые (базис- ные) переменные Независимые переменные Правые части
83
6*
ЕДИНСТВЕННОСТЬ КАНОНИЧЕСКОГО ЭКВИВАЛЕНТА
Основным свойством канонической системы, полученной в процессе
приведения, является то, что для любой другой системы с тем же множе-
ством решений приведение может быть выполнено путем использования
тех же ведущих переменных; при этом получается та же каноническая
система^ если перегруппировать уравнения так, что их соответствие
с базисными переменными в обеих системах будет одинаковым.
Теорема 1. Существует не более одной эквивалентной канонической
системы с фиксированным множеством базисных переменных.
Доказательство. Пусть даны две эквивалентные канонические систе-
мы относительно х^ х2, .... хг. Подставляя xr+i — хг+2 — ... =
= хп = 0 в первую систему, получаем = Ь4, х2 = Ь2, ..., хг = Ъг.
В случае эквивалентности подстановка во вторую систему должна дать
те же значения; это будет достигаться только в том случае, если их соот-
ветствующие свободные члены одинаковы. Точно так же подстановка
значений независимых переменных хг+^ — жг+2 = ... = = О, за исклю-
чением х& — 1, покажет (после приравнивания свободных членов),
что их соответствующие коэффициенты при xs одинаковы для любого
4? = Г + 1, Г + 2, ..., п.
Эту теорему можно также доказать с помощью следующей леммы.
Лемма 1. Любое уравнение либо может быть получено как единствен-
ная линейная комбинация уравнений канонической системы (при этом
веса будут коэффициентами базисных переменных в этом уравнении),
либо такой линейной комбинации вообще не существует.
Упражнение. С помощью леммы проверить, является ли некоторая
система уравнений эквивалентной канонической системе.
БАЗИСНЫЕ РЕШЕНИЯ
Частное решение, полученное путем приравнивания независимых
переменных нулю и нахождения зависимых переменных, называется
базисным решением. Так, если система уравнений (8) является канони-
ческой системой (7) с базисными переменными х^ х2, ..., хт, то соответ-
ствующее базисное решение имеет вид
•^1 ==- ^1, *^2 ==: ^2» • • • , *^771 == ^7714-1 == *^771+2 == • • • =: == 0. (12)
ВЫРОЖДЕННОЕ РЕШЕНИЕ
Базисное решение называется вырожденным, если значения одной
или нескольких зависимых (базисных) переменных равны нулю. В частно-
сти, базисное решение (12) является вырожденным, если Ъг = 0 хотя бы
для одного i.
БАЗИС
В соответствии с общепринятым пониманием этого термина в линей-
ном программировании под базисом будет пониматься упорядоченное
множество столбцов первоначальной независимой системы (в виде табли-
цы коэффициентов), соответствующее упорядоченному множеству базис-
ных переменных канонического эквивалента. Столбцы базиса будем
{называть базисными столбцами (или базисными процессами).
84
В примере, следующем за уравнением (8), базис, соответствующий
канонической системе с базисными переменными х2, х19 имеет вид
/ 1 0\
\— 2 1) •
Читателю следует обратиться к § 8-1 «Метод ведущих элементов»,
который обобщает результаты данного параграфа. Там доказывается, что
разрешимые системы с одним и тем же множеством решений эквивалентны.
4-3. ЛИНЕЙНЫЕ НЕРАВЕНСТВА
В дальнейших параграфах данной главы мы обратимся к системам
линейных неравенств, которые также играют важную роль в решении
задач линейного программирования.
Как и в том частном случае, когда мы имеем дело с решением линей-
ных уравнений, может оказаться, что система линейных неравенств не
имеет решений вовсе или имеет более одного решения. Чтобы представит^
это геометрически, запишем задачу линейного программирования не в стан-
дартной форме, а в виде системы линейных неравенств. Рассмотрим систему
“F" ^2 2,
Xi >0,
х2 >0,
(1)
Xi--#2>3.
Пусть (ж1? ж2)—декартовы координаты точки на плоскости. Все точки
(#i, я2), которые удовлетворяют условию хх + я2>2, лежат по одну
сторону прямой Xi + х2 = 2. По какую именно сторону — это может
быть определено путем подстановки значения координат какой-нибудь
выбранной точки (например, начала координат) в линейное неравенство.
Если линейное неравенство удовлетворяется, то все такие точки лежат
по ту же сторону, что и выбранная точка; в противном случае точки лежат
по другую сторону прямой. Чтобы обозначить сторону прямой, представ-
ленной неравенством, мы будем пользоваться маленькими стрелками,
как это показано на рис. 4-3-1. В заштрихованной области находятся
точки, одновременно удовлетворяющие всем четырем неравенствам.
В данном случае область неограничена. Если добавить к системе
неравенство
Xi 4-2ж2< 6, (2)
85
то общая область становится ограниченной (см. рис. 4-3-1II без 2-урав-
нения). Если теперь присоединить еще ограничение
4я2—*i>0, (3)
то область сжимается до единственной точки (4,1), как это показано
на рис. 4-3-П. Наконец, если к системе присоединить условие
— 2^14“^2^2, (4)
то уже ни одна точка не будет одновременно удовлетворять всем ограни-
чениям и, следовательно, решения существовать не будет.
• Если требуется найти решение, которое минимизирует форму
-5^— Х2 = 2,
(5)
Где точка (#i,
прямая 5#i +
ж2) лежит в заштрихованной области на рис. 4-3-Ш, то
х2 = const
перемещается параллельно самой себе до тех
пор, пока не коснется заштрихованной
области в крайней точке (6,0). Оптималь-
ное (единственное) решение получается
при Xt=6, я2=0 и 2 = —5(6)—(0) = —30.
С другой стороны, если бы стояла задача
минимизировать форму того же вида, на-
пример на рис. 4-3-1, то было бы возможно
переместить прямую 5Xi + х2 = —z не-
ограниченно вправо, все еще оставаясь в
пределах неограниченной области решений.
В последнем случае можно построить ре-
шения, в которых 2 будет меньше любой
наперед заданной величины.
Заметим, что для любой линейной
формы 2 минимальное решение единст-
и 4-3-Ш). С другой стороны, если линия z —
венно (см. рис. 4-3-1
=const параллельна одной из сторон заштрихованной области, то, воз-
можно, имеются различные решения. Вообще для систем линейных нера-
венств, содержащих много переменных, оптимальное решение единственно,
за исключением тех случаев, когда гиперплоскость, представленная
уравнением в виде целевой функции, равной z (где значение 2 является
неизвестным свободным членом), параллельна одной из граничных гипер-
плоскостей, определяющих область решений. В последнем случае решение
может и не быть единственным.
Если решение неединственно, то незначительное изменение (или, как
его называют, возмущение) коэффициентов целевой функции может при-
вести к однозначности (см. гл. 10). Парадоксально, что на практике
неоднозначность оптимума является скорее правилом, чем исключением.
Причины этого несовсем ясны. Математические модели экономических,
военных и промышленных систем имеют сугубо специфическую структуру,
которая позволяет определить более одной оптимальной программы,
и в этом, несомненно, одна из причин (Данциг [4], [5]). Вторая из причин
состоит в том, что коэффициенты а^ и С; практически учитываются лишь
с точностью до немногих значащих цифр.
Упражнение. Показать, что если линия z = const на рис. 4-3-Ш
параллельна одной из сторон заштрихованной области, то из этого не
всегда следует неединственность решения. При каких условиях будет
иметь место единственность? Неединственность?
Там, где единственность является скорее правилом, чем исключением,
желательно иметь иной критерий, например другую целевую функцию.
86
После минимизации первой формы z уравнение z = z0, где z0 = minz,
присоединяется к системе уравнений; вторая форма в свою очередь также
минимизируется. С другой стороны, вместо присоединения уравнения
можно исключить определенные переменные; дальнейшее рассмотрение
дано в § 5-2 (9).
4-4. МЕТОД ИСКЛЮЧЕНИЯ ФУРЬЕ — МОЦКИНА 1
Для решения небольших задач линейного программирования можно
использовать метод исключения. Этот метод сокращает число переменных
на единицу за каждый цикл, но при нем может значительно увеличиться
число неравенств относительно оставшихся переменных. Принцип при-
менения метода проиллюстрирован на примере (1а), который подобен одно-
му ранее рассмотренному примеру, показанному на рис. 4-3-Ш. Мы опре-
деляем наименьшее значение и, для которого система имеет решения.
Перепишем систему (1а), как это показано в (16).
Г >0, Xi —2х2 6,
(1а) xt + х2 2, Q или (16) Я2>3,
я2>0, — 2X1— Я2<2.
6—2я2,
2 — х2^хх,
3 -|- х2 х^,
1 1 .
— у 2—
и я2>0.
Шесть неравенств относительно (первая переменная, подлежащая
исключению) можно разделить на три класса: во-первых, неравенства
(здесь их будет четыре), в которых Xi может быть больше определенных
линейных форм, во-вторых, неравенства (в данном случае — одно), где х^
меньше других линейных форм. Наконец, остаются неравенства, которые
не содержат х^.
Это означает, что каждая форма первого класса меньше или равна
любой форме второго класса, т. е.
(2а)
0^6—2я2,
2—ж2^6— 2х2,
3 + х2 < 6 — 2я2,
— 4- 2 — ^-х2 < 6 — 2х2,
или (26) <
я2^3,
х2<4,
я2<1,
^2 4 + у
и я2>0
0<я2,
где мы включаем неравенство я2>0 из третьего класса. Наоборот, любое
х2, удовлетворяющее этим пяти неравенствам, может быть использовано
для определения значения х^ удовлетворяющего системам неравенств (1а)
или (16). Если можно найти значения х2 и 2, удовлетворяющие системе
неравенств (2а), то наибольшее выражение в левой части первых пяти
неравенств (2а) меньше или равно наименьшему выражению в их правой
части; отсюда следует, что значение х^ может быть выбрано произвольно
между этими двумя величинами и будет вместе с заданными х2, z состав-
лять решение систем неравенств (1а) и (16).
1 Фурье первым предложил этот метод (Фурье [1]). Метод был усовершенство-
ван Т. Моцкином и часто называется методом исключения Моцкином (Моцкин [1]).
87
Следующий этап состоит в повторении действий над системой нера-
венств (26) путем исключения х2. Имеется одно неравенство, в котором х2
больше или равно некоторой постоянной (именно нулю), имеется также
четыре неравенства, в которых х2 меньше или равно постоянной или
линейной форме z (из которых два заменяются другими и могут быть опу-
щены). Это означает, что каждая форма первого класса меньше или равна
любой форме второго класса. Три результирующих отношения 0^3,
0<4, 0^1 позволяют найти 0^4 + rl3z или z>—12. Следовательно,
z — —12 является наименьшей величиной z, для которой система имеет
решения. Подставляя z = —12 в систему неравенств (26), можно выбрать
любое значение х2 в пределах или (в данном случае) х2 = 0.
Подставляя z = —12 и х2 = 0 в систему неравенств (16), получаем х^
в пределах б^я^б или х^ = 6.
Таким образом, для этой сравнительно небольшой задачи довольно
легко найти решение: х± = 6 и х2 = 0. Для больших задач необходимы
более формальные методы. Вообще, если половина из т коэффициентов
при Xi имеет противоположный знак, то исключение приводит к увели-
чению числа неравенств с т до (лг/2)2. Но это означает, что после
нескольких исключений число оставшихся неравенств может стать слиш-
ком большим.
4-5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
В ВИДЕ НЕРАВЕНСТВ
Покажем теперь, что задача линейного программирования в стан-
дартной форме, как она сформулирована в § 3-8, эквивалентна задаче
нахождения решения системы линейных неравенств. По этой причине
очень часто основная задача формулируется еще как минимизация линей-
ной формы, подчиненной системе линейных неравенств.
ПРИВЕДЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ К СТАНДАРТНОЙ
ФОРМЕ
Под линейным неравенством понимается соотношение
+ а2Х2 4" • • • + апхп
а не строгое линейное неравенство
^ixi + &2Х2 + • • • + апхп <
(1)
(2)
Следует заметить, что если система содержит строгие неравенства, то не
всегда возможно найти значения переменных, которые удовлетворяют
неравенствам и в то же время минимизируют линейную форму. Например,
не существует значения Xi > 1, которое минимизирует форму z = xt.
Любая задача, включающая систему линейных неравенств, может быть
при помощи одного из нескольких методов преобразована в другую
систему нормального вида, т. е. в систему уравнений с неотрицательны-
ми переменными. Шаги (Л) и (В), приведенные ниже, составляют один из
этих методов; шаги (А) и (В') составляют другой. В гл. 6 изложен двой-
ственный метод для системы линейных неравенств; заметим, что двой-
ственная система дается в стандартной форме. Это будет третьим методом.
Первым и, по-видимому, наиболее удобным является следующий.
Шаг (Л). Заменим произвольное линейное неравенство вида (^урав-
нением, присоединив свободную переменную zn+1>0, и получим
alxi + а2х2 + • • • 4" апхп + ХП+! — Ь.
88
(3)
Шаг (В). Замечая, что любое число может быть записано как разность
двух положительных чисел, заменим любую переменную х^ не имеющую
ограничений на знак, разностью двух неотрицательных переменных
Xj=Xj — Xj, (Я;>0, Xj>0). (4)
Пример. (Таккер). Доказать, что в уравнении (4), в котором каждое Xj
не имеет ограничений на знак, можно заменить Xj на х]— х0, где х] О,
а я0>0, — одно и то же для всех таких /.
Шаг (В'). Как альтернатива шага (5), пусть Xj будет любой перемен-
ной, не имеющей ограничения на знак, которая оказывается в Zc-м урав-
нении с ненулевым коэффициентом. Решим уравнение относительно х^
и подставим его значение в оставшиеся уравнения, если их несколько,
а также и в целевую линейную функцию z. Если отбросить это уравнение,
то оставшиеся видоизмененные уравнения (если, конечно, такие еще
останутся) составляют приведенную систему ограничений. Описанный
процесс повторяется применительно к новой задаче линейного програм-
мирования до тех пор, пока либо 1) будет получена приведенная система
ограничений, в которой все оставшиеся переменные неотрицательны,
либо 2) в приведенной системе не останется ни одного уравнения.
Как только решение приведенной задачи получено, первоначальная
задача решается с помощью последовательных обратных подстановок
в исключённые уравнения.
Чтрбы обосновать этот метод, заметим прежде всего, что минимум
для приведенной системы не превосходит минимума для исходной систе-
мы, потому что первая охватывает только часть условий задачи. С дру-
гой стороны, решение, полученное для исходной системы (путем обрат-
ной подстановки), имеет то же значение для z и является поэтому
минимумом.
Пример 1. Приведем систему к стандартной форме.
Я1+ Z2>6,
а?1 + 2х2 = и.
Шаг (А). Введем свободную переменную я3.
Я1+ я2—я3 = 6, (я3>0)
xi-\-2x2
Шаг (В). Подставив xt = я' — я2 = я' — я", получаем
(х[ — z") + (;r' — я")—я3 = 6, (я3>0, Я;>0, £j>0)
(5)
(6).
(7),
(Л~х"1) + 2(х’2 — х"2) = z.
Шаг (В'). Решаем уравнение х^ + х2 — х3 = 6 относительно xlf.
которое не имеет ограничений на знак, получаем
xt = 6—х2 + х3 (жз>0) (8)
и подставляем в целевую функцию z, чтобы получить
x2 + x3 + 6 = z. (хз>0) (9)
Теперь нужно решить уравнение относительно х2, но для подстановки
не остается уравнений; это случай (2). Общее решение первоначальной
системы (5) может быть получено путем выбора любого значения для
я3>0, любого значения для z и подстановки этих величин в (9) и затем
в (8), чтобы определить х2 и xt. Заметим, что для z не существует конечной
нижней границы, так как z может быть выбрано произвольно.
89
Пример 2. Преобразовать систему
-Хх— х2^ — 6,
— я2>5,
Xi + 2х2 — z
к стандартной форме.
Шаг (Л). Введем свободные переменные х3 и х±
— Xi— Х2 + х3 = — 6, (гг3>0, я4>0)
— Xi -{“ -#4 = 5,
Xi-}-2x2 = z.
(10)
(И)
Шаг (В). Подставляем х[ — х'2 — х2 вместо xt и х2, где я;>0,
xJ>0; и далее переходим к шагу (В').
Шаг (В'). Решаем первое уравнение относительно Xi и подставляем
во второе уравнение и в линейную целевую функцию z. Далее решаем
видоизмененное уравнение для х2 и подставляем в видоизмененную линей-
ную функцию z. Это исключает ограничения-равенства, и у нас остается
приведенная система, состоящая только из одного ограничения с неотри-
цательными переменными х3, х^:
z = (23 4-3#з + х4)/2 (я3, я4>0)
(12)
и из исключенных уравнений
— 6 — х2 4~ х3,
х2=^(11+х3 + х^)/2.
(13)
Общее решение первоначальной системы ограничений получается путем
выбора любого я3>0, х4>0 и определения х2 и xt из уравнений (13). Если
целевая функция минимизирует величину z, то тогда из уравнения (12)
находится оптимальное решение путем подстановки х3 = 0, 0;
23 11 1
в результате получаем z = , я2 = т , = •
Zi л л
Вообще предположим, что мы имеем п неравенств с к^п перемен-
ными (ui, и2, ..., ufe), которые не имеют ограничений на знак и нужно
минимизировать форму z от этих переменных
+0,2^2+ • • • +^jkUk — а,о>О,
Yi^i + Y2W2 + .. • + ykUk = 2,
где а л и yi константы. Если мы положим
Xj = (LjiUi + a/2u2 + ... + ajkuk — a/0,
то ясно, что
Xj > 0.
(7 = 1,2, ..., n)
(7 = 1,2, ...,n)
(7 = 1,2, ..., n)
Если предположить, что возможно решение по крайней мере одной систе-
мы к уравнений относительно и2, . .., Uk через Xj, тогда подстановка
этих значений щ в оставшиеся уравнения и в форму z дает п — к урав-
нений и линейную форму z с неотрицательными переменными. Следо-
вательно, при данном предположении п неравенств ск^п перемен-
ными эквивалентны т = п — к уравнениям с п неотрицательными
переменными.
90
ПРИВЕДЕНИЕ СИСТЕМЫ УРАВНЕНИЙ К СИСТЕМЕ НЕРАВЕНСТВ
Наоборот, любую задачу, содержащую уравнения, можно заменить
эквивалентной системой, содержащей ограничения в форме линейных
неравенств. Один из способов состоит в замене каждого уравнения
+ а2я2 + ... + апхп ~Ь (14)
парой неравенств
aixi + а2х2 + . .. + ипхп
aixi + a2x2+ . .. +anxn^b.
Другой путь состоит в том, чтобы заменить каждое уравнение нера-
венством со знаком (>), а сумму уравнений записать с противополож-
ным знаком (^). Таким образом, можно заменить систему уравнений,
приведенную в § 4-1-(2), на
4" а12^2 + •. . + атхп &i,
^21^1 4" ^22^2 4” • • • Л~^2пхп ^2,
4“ &т2х2 4" • • • 4“ ^тпхп
(16)
(3 аи) Xi 4" • • • 4~ (2 ^zn) хп 3 &z •
4-6. ЗАДАЧИ
СИСТЕМЫ УРАВНЕНИЙ С ОДИНАКОВЫМИ МНОЖЕСТВАМИ РЕШЕНИЙ
(См. § 4-1)
1. Вопрос для повторения. Что такое элементарные операции?
Почему они приводят к эквивалентной системе уравнений?
2. Показать, что в транспортной задаче без свободных переменных
система уравнений в § 3-3 является избыточной. Интерпретировать это
как отношение избыточности среди данных задачи. Показать, что любое
уравнение является избыточным. Возможна ли избыточность в уравнении
со свободными переменными? Выписать уравнения в виде таблицы для
каждого из случаев.
3. Привести уравнения
3xj —2х2 -х$ := 4,
xi 4~ ж2 4" = 3
к виду
2xt -j— х2 = 1,
xi ~ х3 = — 2
с помощью элементарных операций. Какое решение является очевидным
из приведенной системы? Проверить это решение путем подстановки
в первоначальную систему.
4. Доказать, что невозможно с помощью элементарных операций
преобразовать систему уравнений § 4-1-(1) в эквивалентную форму
{Е^, Е5} § 4-1-(10) без использования по крайней мере одной элементарной
операции первого типа.
КАНОНИЧЕСКИЕ СИСТЕМЫ (См. § 4-2)
5. Доказать, что (возможно, с точностью до знака) произведение
ведущих элементов равно определителю базиса, где базис является квад-
ратной матрицей коэффициентов базисного множества переменных.
91
6. Вопрос для повторения. Что такое каноническая форма? Можно
ли любую систему уравнений привести к каноническому виду?
7. Вопрос для повторения. Что составляет базисное множество
переменных? Что такое базисное решение, связанное с базисным множе-
ством? Что такое вырожденное базисное решение?
8. Что такое независимые или небазисные переменные?
9. Должно ли базисное решение быть допустимым, т. е. являются ли
значения переменных, связанных с базисным решением, необходимо
неотрицательными?
10. Какие элементарные операции могут быть использованы, чтобы
преобразовать систему
2х± 4~ х2 4“ х3 = 6, Xi = 2,
I Xi+ ж2 + х3 = 4, в 1 х2 =1,
( 2хх + Зя2 + х3 = 8 [ xt + Зх2 + х3 = 6.
Можно ли найти решение этой системы? Привести эту систему к кано-
ническому виду.
11. Представить следующую систему в каноническом виде с и х4
в качестве базисных переменных.
х^ — 2ж2 + х3 = 1,
#14" Х2 4 #4 ”4.
12. Привести систему
5xi — 4ж2 —j- 13я3 *— 2х± —х§ = 20,
x2~h 5^з— я4 + я5 = 8
к каноническому виду, используя х2 и в качестве базисных переменных.
13. Привести систему к каноническому виду относительно перемен-
ных х2 и я4, если это возможно, и найти соответствующее базисное решение.
2#i 4~ Зж2 4х3 4~ 5#4 = —-1,
2^ —3z2 — х3— х4=—7.
14. Рассмотреть систему
3#! + 2я2 4~ 11#з 4~ 5я4 •— Зя5 = 5,
xi 4~ #2 4~ 4#3 4~ Зя4 4~ #5 — 2.
а) Привести эту систему к каноническому виду, используя Xi и х2
в качестве базисных переменных. Какое решение подсказывается этим
каноническим видом, когда переменные х3, х^ х5 нулевые?
б) Привести исходную систему к каноническому виду с х^ и х3 в каче-
стве базисных переменных. На какое решение указывает эта канони-
ческая форма?
в) Используя результаты пункта а), найти каноническую форму для
пункта в), не обращаясь к исходной системе уравнений.
15. Рассмотреть систему
2я?| 4~ Зя2 — 2гг3 -—• 1х^ = 1,
Xi 4- я24" #34“2#4=6,
Xi— #2 4~ х3 4~ ^#4 = 4.
а) Привести ее к каноническому виду с х2 и х3 в качестве базисных
переменных. На какое решение указывает эта каноническая форма?
Проверить путем подстановки в первоначальную систему.
92
б) Из канонической формы, полученной в пуйкте а), найти другую
каноническую форму с хь х2, #4 в качестве базисных переменных. Какое
будет решение, когда х3 = О?
в) Из канонической формы пункта б) найти каноническую форму
с xi9 х3 и х^ в качестве базисных переменных. Какое будет решение, ког-
да х2 = О?
г) Из канонической формы пункта (в) найти каноническую форму
с х2, х3 и Xi в качестве базисных переменных. Какое будет решение,
когда xt = О?
16. В приведенной далее системе переменные yi9 у2, Уз выражены
через xt, х2, х3. Определить значение х19 х2, х3 через у19 у2, у3 и показать,
что получающаяся система эквивалентна первоначальной. Показать, что
первоначальная система по существу является канонической формой
относительно переменных yi9 у2, у3, в то время как окончательная систе-
ма находится в канонической форме относительно xi9 х2, х3.
2^1 + Зх2 + 4х3 — yi,
^1— Я2+ ^3=^2,
iXi + Зх2 + 2х3 ~ у3.
17. Система, выражающая yi9 у2, у3 через х19 х2, х3, называется
обратной системой. Почему обратная система является единственной?
Показать, что если имеется т уравнений, в которых yi9 у2, ..., ут
выражаются через xl9 х2, . . ., хт, то существует обратная система, выра-
жающая х^, х2 . . ., хтчерез у2, . . ., ут, если хи х2, . . ., хт являются
базисным множеством переменных.
18. Вопрос для повторения. Почему две эквивалентные канониче-
ские системы относительно одних и тех же базисных переменных сов-
падают?
19. Почему невозможно иметь два или более различных базисных
решения при одном и том же множестве базисных переменных?
ЛИНЕЙНЫЕ НЕРАВЕНСТВА (См. § 4-3)
20. Привести каждую из систем неравенств а), б) и в) к эквивалент-
ной системе уравнений с неотрицательными переменными с помощью
двух различных способов.
a) Xi —{— 2х2 3,
Xi — 2х2> — 4,
+ 7я2 <16.
б) Х1 + ^2>2, в)
Xi —х2<4,
Xi х2 <1 7.
+ #2 2,
xt —х2^4,
+ ^2 ~Ь хз 7.
Показать, что системы б) и в) соответствуют случаям 1) и 2) в шаге
(В'). Показать, как можно определить класс всех решений для в).
21. Преобразовать систему уравнений с неотрицательными пере-
менными в систему неравенств:
2Х| -{- Зх2 4~ 4х3 — 5,
4xi — 7х2 4- Зх3 = 4.
(xi>0, х2>0, х3>0)
22. Показать, что не существует нижней границы
а) для системы Xi>0, —— z;
б) для системы
Ж1 —х2=1, (^i>0, х2>0)
— Xi — х2 —z.
93
в) Показать, что нижняя граница для z существует для системы
xt > 0, Xi — z, но, несмотря на существование допустимых решений,
оптимального допустимого решения не будет.
23. Пусть (aij, bt, Cj) — коэффициенты и параметры задачи до ее
приведения к каноническому виду относительно xlf х2, . . ., хт, а
6$, cj) —соответствующие коэффициенты и параметры после приведения.
В системе, двойственной к исходной
2 (/ — 1, 2, . . . , 70
1
т
2 biiii = v (max),
1
введем свободные переменные yj>0 и исключим не имеющие ограничений
на знак переменные jq, используя ведущие элементы в первых т из п урав-
нений. Показать, что в результате получается обычная задача линейного
программирования с п неотрицательными переменными и п — т урав-
нениями в виде
2 iVt + У) = Cj, (i = m+l, п)
1
т т
^1biyi = v — ^bici.
I 1
24. Использовать «метод центра тяжести» из гл. 3, чтобы найти
Xj 0 и min z, удовлетворяющие
Z = iXi 4~ 2^2 4~ 4~ 4^4,
4 = Xi + ^2 + Х3 +
— 2 = lxt — 2х2 + Зх3 — 4я4.
25. Привести систему
4~ ^2 4~ ^з~5, (#1^0, я3>0)
Х1— Х2~Ь х3~7,
Xi -j— 2х2 4“ 4я3 = 2
к эквивалентной системе неравенств.
26. Решить графически систему с неотрицательными переменными
xi 4~ ^2^1»
4xi4-8x2<32,
Xi 4~ Х2^4:,
• Xi — 2з?2 2.
Какие неравенства являются следствиями других?
МЕТОД ИСКЛЮЧЕНИЯ ФУРЬЕ — МОЦКИНА (См. § 4-4)
27. Используя метод исключения Фурье — Моцкина, найти значения
xi9 х2 и z, удовлетворяющие системе неравенств задачи 29, случай в),
и дающие min z — х2.
94
28. Использовать метод исключения, чтобы определить положи-
тельные Xi и min z, удовлетворяющие системе
xi Х2 1»
Х2 2,
—X2<J 1,
Xj —Х2> —1,
— x2 = z.
Вычертить график и показать выпуклое множество допустимых
решений. Видоизменять форму z с помощью четырех различных способов
так, чтобы решение не было единственным.
ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ОГРАНИЧЕНИЯМИ
В ФОРМЕ НЕРАВЕНСТВ (См. § 4-5)
29. Выяснить графически, существует ли только одно решение, мно-
жество решений или ни одного решения системы неравенств в следующих
случаях.
Случай (а) Случай (б) Случай (в) Случай (г)
х4 >0 Xi>0 xt>0 Xi>0
х2>0 х2>0 х2>0 х2>0
4* 2 Xi -|- х2 2 Х| 4“ х2 2 xt 4- х2 > 2
Xi 2х2 6 4- 2х2 < 6 Х| 2х2 6
— Х\ + ^х2 0 — Xi 4- 4х2 > 0 —Xf 4- х2 > 2 — Х1 "4“ 4:Х2 0 — Xi -|- х2 2
Xi х2 3
Глава 5
•СИМПЛЕКС-МЕТОД
Краткое содержание. Стандартная форма основной задачи линейного
программирования, как показано в § 3-8 (1), представляет собой задачу
-отыскания значений некоторого множества неотрицательных переменных,
которые удовлетворяли бы системе линейных уравнений и минимизирова-
ли бы линейную форму z.
Мы различаем симплекс-метод, используемый. для решения ли-
шейной задачи в стандартной форме, и симплекс-алгоритм, который
применяется к канонической форме. Симплекс-алгоритм состоит из
последовательности основных операций и является основой симплекс-
метода.
На первом шаге симплекс-метода в стандартную форму вводятся
некоторые искусственные переменные. Получающаяся вспомогательная
задача является задачей в канонической форме. С этого момента приме-
няется симплекс-алгоритм. Он состоит из ряда ведущих операций, объе-
диненных в этап I, которые производятся с последовательностью различ-
ных канонических форм. Целью этих действий является нахождение
допустимого решения, если оно существует. Если последняя каноническая
форма имеет допустимое решение, то вторично применяется симплекс-
алгоритм и эта группа операций объединяется в этап II. Цель этого этапа
состоит в нахождении оптимального допустимого решения, если оно
существует.
Симплекс-алгоритм будет описан в следующем ниже § 5-1; использо-
вание симплекс-алгоритма как части симплекс-метода рассматривает-
ся в § 5-2.
5-1. СИМПЛЕКС-АЛГОРИТМ
Симплекс-алгоритм всегда применяется к задаче с уравнениями
в канонической форме* пусть, например, мы имеем каноническую систему
{1), (2) с базисными переменными xi9 х2,..., хт, (—z)1. Связь этой
канонической системы т уравнений с п неизвестными с системой М
уравнений с N неизвестными в стандартной форме будет выяснена
в § 5-2.
1 То есть —z рассматривается как базисная переменная. В литературе читатель
может встретиться с обозначением этой переменной через xq и расположением уравне-
ния (2) перед уравнениями (1).
96
Задача. Найти значения xt>0, х2>0, . . хп>0 й min z, УДО-
влетворяющие соотношениям xi 4" <4, m+ixm+i + • • х2 + а2, т+1хт+1 + • • • 4" a2jxj 4“' • • + ainxn = bv 4- ау^ = Ъ2, • » (1)
хт 4~ О'т, т+1хт+1 4“ • (—z) 4- ст+1хт+1 4~ • • + amjxj 4“ • • • . • + Cjxj + • • • 4“ ^mnxn ~ 6m, 4~ Cnxn = *“ Zq, (2)
где Cj, bt и z 0 суть постоянные. Для этой канонической формы базис-
ным решением является
2 — Zq, Xi — Хг — &2> • • •» #тп+1 — ^т+2 — • • • — — 0. (3)
Так как предполагается, что это базисное решение является также
и допустимым, величины Xj в (3) должны быть неотрицательными и
Ь1>0, Ь2>0, ..., bm>0. (4)
Определение. Будем говорить, что линейная задача представлена
в допустимой канонической форме, если выполнено условие (4).
КРИТЕРИЙ ОПТИМАЛЬНОСТИ
Мы видели, что каноническая форма позволяет сразу же найти
соответствующее базисное решение. Ее можно использовать также для
выяснения, будет ли базисное решение (если оно допустимое) минималь-
ным. Для этого исследуются коэффициенты «модифицированного» целе-
вого уравнения (2).
Определение. Коэффициенты Cj в стоимостном или целевом уравне-
нии канонической системы (2) называются относительными оценками.
«Относительными» они называются потому, что их значения будут зави-
сеть от выбора базисного множества переменных.
Теорема 1. Базисное допустимое решение является минимальным
допустимым решением с общими затратами z0, если все относительные
оценки неотрицательны*.
с7>0 (7 = 1, 2, ..., п).
Доказательство. Для канонической формы очевидно, что если все
коэффициенты модифицированного целевого уравнения неотрица-
тельны, то наименьшая величина суммы ^jCjXj есть нуль при любом выбо-
ре неотрицательных Xj. Следовательно, наименьшая величина разности
2—20 равна нулю и min 2 > 20. В частности, для допустимого базисного
решения z = z0; поэтому min 2 = z0 и решение оптимально. Очевид-
на также
Теорема 2. Дано минимальное базисное допустимое решение с отно-
сительными оценками Cj^Q; тогда любое другое допустимое реше-
ние (не обязательно базисное), обладающее тем свойством, что Xj = 0
для всех Cj >0, также является минимальным решением; если, кроме того.
7 Дж. Данциг 97
решение обладает тем свойством, что для некоторого j как Xj >0,
так и Cj >0, то оно не может быть минимальным решением.
Следствие* Базисное допустимое решение является единственным
минимальным допустимым решением, если cj >0 для всех небазисных
переменных.
УЛУЧШЕНИЕ НЕ ОПТИМАЛЬНОГО БАЗИСНОГО ДОПУСТИМОГО
РЕШЕНИЯ. ПРИМЕР
Для иллюстрации рассмотрим задачу минимизации z, где
5#i—4г2+13я3—2ж4+ я5 = 20 (ху>0)
— + 5ж3— я4+ я5 = 8 (5)
+ 6х2— 7х3 + 5x5 — z.
Пусть нам известно, что х19 х5 и (—z) можно использовать как базис-
ные переменные и что это базисное решение будет допустимым. Тогда
мы можем привести систему (5) к эквивалентной канонической форме
относительно переменных х19 х5, (—z):
1 3
— у ®2+-Зх3—4 ®4+®6 =5
«1—Ja:2+2a?8—4 ж4 =3 (6)
&г2—24г3 + 5я4 —z— —28,
сохраняя при этом порядок, переменных и уравнений. Роль выделенных
жирным шрифтом символов будет объяснена позднее. Базисное допусти-
мое решение системы (6) получается немедленно:
х^~3, ^5 = 5, я2 = я3 = я4=0, z = 28. (7)
Заметим, что произвольная пара переменных не обязательно даст
допустимое базисное решение задачи (5). Например, если бы в качестве
базисных выбрать переменные х^ и ж2, то базисным было бы решение
= —12, я2 =—20, ж3 = ж4 = х5 = 0, z ——132,
которое не является допустимым, так как х^ и я2 отрицательны.
В численном примере (4) одна из относительных оценок в кано-
нической форме (6) отрицательна, а именно коэффициент при х3 равен
—24. Критерий оптимальности, сформулированный в теореме 1, не выпол-
нен. Если я3 увеличится на некоторую положительную величину (осталь-
ные небазисные переменные останутся нулями), то, очевидно, значение z
уменьшится, потому что соответствующее значение z получается по
формуле
z = 28—24х3. (8)
Поэтому естественно попытаться сделать х3 как можно больше, так как
большему значению х3 будет отвечать меньшая величина z. Но значение х3
не может увеличиваться неограниченно, если другие небазисные пере-
менные остаются нулями, потому что соответствующие значения базис-
ных переменных из (6) суть
и мы видим, что если я3 превысит 3/2, то х^ станет отрицательным, а если х3
будет больше чем 5/3, то окажется отрицательным и хъ. Очевидно, наи-
98
большим допустимым значением для х3 является наименьшая из указан-
ных дробей, а именно х3 = 3/2. После подстановки этого значения х3
в (8) и (9) мы получаем новое допустимое решение с меньшим значением
целевой функции
3 1
хх = х2 = х4 = 0, z= — 8. (10)
Это решение уменьшило z с 28 до —8; наша ближайшая задача состоит
в том, чтобы выяснить, будет ли это решение минимальным. Теперь можно
несколько задержаться. Новая каноническая форма с новыми базисными
переменными х3 и х$ может быть получена непосредственно из старой
канонической формы с базисными переменными х^ и хь. Выберем в качест-
ве ведущего элемента элемент х3. Его максимальное значение ограйичи-
валось неотрицательностью базисных переменных хх и хь, а именно эле-
ментом 2х3, выделенным в (6) жирным шрифтом. После соответствующего
преобразования, выделяющего ж3, новая каноническая форма относительно
х3, хъ и (—z) примет вид
3 7 3 1
2* Х1 Ч g" Х5 ” у
1 3 I 1 3 /..К
уXt — у х2 + х3—gX4 = у (11)
12xi— х2 +2я4 —2 = 8.
Она дает допустимое базисное решение (10). Хотя величина z и уменьше-
на, коэффициент с2 = —1 показывает, что решение еще не является
минимальным и что можно получить лучшее решение, если увеличить х2,
положить для небазисных переменных xt = х4= 0 и выразить новые
значения х5 и х3 через х2
1 7
— 2 8 ^2’
3 3
жз = т + (12)
2= —8 — х2.
Заметим, что второе уравнение не накладывает ограничений на х2,
а первое уравнение ограничивает х2 максимальной величиной х/2 : 7/8,
при которой ж5 обращается в нуль. Поэтому для дальнейших исключений
7
используется ведущий элемент у-х2 из первого уравнения (11). Новые
базисные переменные суть х2 и х3. Переписывая систему (11) в канони-
ческой форме относительно х2, ; г3, (—z), получаем системы
12 у + #2 3.8 7"Я4-|-у х5 7 ’
1 , jXi + Х3 2 , 3 7 хк 7 хъ = (13)
72 7 Х1 , 11 ,8 + 7 + 7 хъ 60 Z = 7
и базисным допустимым решением будет
4 12 л 60
= ж3 = у , х1 = х4 = х5 = 0, 2=—у. (14)
Поскольку все относительные оценки при небазисных переменных
положительная, по следствию из теоремы 2 это решение является един-
ственным минимальным. Это оптимальное решение получено из перво-
начального базисного решения (7) за две итерации.
7*
99
УЛУЧШЕНИЕ НЕОПТИМАЛЬНОГО БАЗИСНОГО ДОПУСТИМОГО
РЕШЕНИЯ В ОБЩЕМ СЛУЧАЕ
Как мы видели на численном примере, каноническая форма сразу же
дает критерий для выяснения, является ли базисное допустимое решение
оптимальным. Более того, если критерий не удовлетворяется, то получает-
ся другое решение, которое уменьшает величину стоимостной, или целе-
вой, функции (за исключением некоторых случаев вырождения).
Опишем теперь формально этот процесс улучшения неоптимального
базисного допустимого решения. Если хотя бы одна из относительных
оценок в канонической форме (2) отрицательна, то можно (если предпо-
ложить невырожденность, т. е. что все bi >0) построить новое базисное
допустимое решение с меньшей стоимостью, чем z = z0. Это решение
с меньшими затратами может быть получено путем увеличения значения
одной из небазисных переменных х8 и соответствующего изменения базис-
ных переменных; в качестве х8 выбирается любая переменная, для которой
относительная оценка отрицательна. В частности, индекс 5 можно
выбрать так, что
с8 = min Cj < 0. (15)
В практической вычислительной работе значение s выбирают имен-
но по этому правилу, поскольку оно удобно; кроме того, замечено, что
обычно оно ведет к меньшему числу итераций в алгоритме, чем произволь-
ный выбор 5 среди тех /, для которых Cj < 0.
Используя каноническую форму (1) и (2), построим решение, в кото-
ром х8 принимает некоторое положительное значение, значения всех
других небазисных переменных остаются по-прежнему нулями, а базис-
ные переменные, включая и z, преобразуются в зависимости от увеличе-
ния х8 по формулам
Xi-bi—ai8x8,
г - (16)
3*2 — ^2
— Ьт — ат8Х8 >
z = zo + c8xs (c8<0).
(17)
Поскольку cs было выбрано отрицательным, понятно, что значение х8
нужно сделать как можно большим, чтобы значение z стало как можно
меньше. Единственное, что помешает нам сделать х8 бесконечно боль-
шим,— это то, что одна из базисных переменных может стать отрицатель-
ной. Однако если все то х8 можно брать сколь угодно большим.
Тем самым установлена
Теорема X Если в канонической системе для некоторого s все коэф-
фициенты diS неположительны и с8 отрицательно, то можно построить
класс допустимых решений, для которого множество значений z не будет
ограничено снизу.
С другой стороны, если хоть одно из dis положительно, то невозмож-
но бесконечно увеличивать значение х8, потому что как только будет
х8 > bi fais, так Xi станет отрицательным. Если di8 положительно более
чем для одного i, то наименьшее из таких отношений, номер строки кото-
рого будем обозначать через г, определит наибольшее возможное значение
х, и при этом базисные переменные будут неотрицательны. Наибольшим
- 100
значением х8, допустимым при этом предположении, будет
X* = А- = min -А > 0 (aTS > 0). (18)
ars ais>Q й'8
Здесь следует особо отметить, что рассматриваются только те i и г, для
которых diS >0, dr8 >0. В случае, когда минимум достигается для
нескольких г, выбор г является произвольным, если среди соответствующий
отношений нет Ьг — 0; в последнем, вырожденном, случае г можно выби-
рать случайно (с равными вероятностями) среди них. Например, если
dls >0 и а28 >0, a bi = b2 = 0, то можно бросить монету, чтобы выб-
рать: г = 1 или г = 2 Ч
Базисное решение является вырожденным, если значение хотя бы одной
базисной переменной равно нулю (см. § 4-2). В этом случае из (16) выте-
кает, что если для некоторого dis > 0 соответствующее значение bi для
базисной переменной окажется нулевым, то нельзя увеличить х8 так,
чтобы базисные переменные остались неотрицательными, и поэтому z не
будет уменьшаться. Однако если базисное решение является невырож-
денным, то справедлива
Теорема 4. Если в канонической системе для некоторого s относитель-
ная оценка с8 отрицательна и по крайней мере один коэффициент dis по-
ложителен, то из невырожденного базисного допустимого решения можно
построить новое базисное допустимое решение с меньшей общей стои-
мостью z.
Точнее, мы покажем, что в результате замены хТ на х8 в множестве
базисных переменных х2, .. ., хт, получается новое множество, которое
является базисным, а соответствующее базисное решение является
допустимым.
Докажем сначала допустимость. Подставив значение ^>0, опре-
деленное в (18), в соотношения (16) и (17), мы получим допустимое решение
Xi = bi — ai8x* > 0, (i=l, 2, ..., т; i=/=r)
x8 = xt, где xf = (19)
аТ8
Xj = 0, (j — Г, ^+1, . .., П9 }=/=$)
с общей стоимостью
z = z0 + c8x8^z0 (c8<0). (20)
Это допустимое решение отличается от предыдущего, так как по пред-
положенному Ьг =# 0, х* >* 0 и z < z 0.
Остается показать, что новое допустимое решение является базисным.
Из того, как определен в (18) индекс г, ясно, что
хт = Ът — аТ8х* = 0. (21)
Мы хотим доказать, что х8 и х±, х2, ..,, хт (исключая хг) образуют новое
базисное множество переменных. Чтобы убедиться в этом, заметим лишь,
1 Выбор г в случае, когда минимум достигается для нескольких I, явился объек-
том многих исследований, так как теоретически возможно, что непродуманный выбор
может после нескольких итераций привести к повторению уже встречавшегося базис-
ного решения. В практической работе можно использовать произвольный выбор.
Так, У. Орчард-Хейс [3], который экспериментировал с различными процедурами,
сообщает, что в практических задачах часто давало хорошие результаты (см. § 6-1
и гл. 10) следующее правило: среди отношений, для которых достигается минимум,
выбираем отношение с максимальным знаменателем и соответственно полагаем i = г.
101
что, поскольку drs >0, мы можем использовать r-е уравнение системы (1)
и коэффициент drs как ведущий элемент для исключения переменной х8
из остальных уравнений и минимизируемой формы. Для того чтобы преоб-
разовать систему в каноническую форму относительно нового множества
переменных, необходимо только одно это исключение. Этот факт дает
ключ к эффективным вычислениям по симплекс-методу. В силу теоремы 1,
§ 4-2, новое базисное решение единственно; следовательно, это решение
дается формулами (19).
ИТЕРАТИВНЫЙ ПРОЦЕСС
Новое базисное допустимое решение можно снова испытать на опти-
мальность, проверив выполнение неравенства cs — min Cj > 0. Если это
решение не оптимально, то на основе критерия (15) можно выбрать новую
переменную ввести ее в базис и получить либо а) множество решений,
для которых z не ограничено снизу (если все dis<Z 0) или б) новое базис-
ное допустимое решение, в котором значение z меньше, чем предыдущее
(при условии, что значения базисных переменных для последнего шага
строго положительны; в противном случае новое значение z может быть
равно предыдущему значению).
Симплекс-алгоритм состоит в повторении этого цикла снова ненова.
Этот процесс заканчивается только в том случае, когда получим либо:
а) множество допустимых решений, для которых z ->—оо, либо
б) оптимальное базисное допустимое решение (все с7->0).
Теорема 5. В предположении, что ни на одной итерации нет выро-
жденности, симплекс-алгоритм закончится за конечное число итераций.
Доказательство. Существует лишь конечное число возможностей
выбрать из п переменных т базисных. Если бы алгоритм продолжался
бесконечно, то это могло бы быть только при повторении некоторого базис-
ного множества переменных и, следовательно, некоторой канонической
системы и некоторого значения z (см. теорему единственности, § 4-2,
теорема 1). Такое повторение невозможно, так как значение z убывает
с каждой итерацией.
Когда же появляются вырожденные решения, мы не можем больше
утверждать, что процесс обязательно закончится за конечное число ите-
раций, потому что при вырождении, а это возможно, если 6Г= 0 в (19),
значение z в (20) уменьшается на 0, а это значит, что это базисное множе-
ство переменных может повториться. Если процесс продолжить, выбрав
те же самые $ и г для каждой итерации, которые выбирались раньше, то
это же базисное множество появится вновь, скажем, через к итераций
и снова через 2к итераций и т. д., бесконечно. В сймплекс-алгоритме
существует, следовательно, возможность движения по кругу (зациклива-
ния) х. Примеры, показывающие, что это действительно случается, были
фактически построены (см. гл. 10).
Мы установили сходимость симплекс-метода к оптимальному решению
за конечное число итераций только для случая невырожденных базисных
решений. В § 6-1 будет обосновано правило случайного выбора, а в гл. 10
мы покажем простой способ незначительного изменения («возмущения»)
коэфф циентов, обеспечивающий невырожденность. Мы докажем, что
описанный там процесс годится даже для вырожденных задач.
1 В литературе используется именно термин «зацикливание», Гофман [1];
Бил [1].
102
5-2. ДВА ЭТАПА СИМПЛЕКС-МЕТОДА
ЗАДАЧА
Стандартная форма, введенная в гл. 3, для основной математической
задачи линейного программирования, состоит в нахождении значений
переменных xlf х2, ..., xN, удовлетворяющих системе уравнений
^11^1 4" #12^2 4" • •» + UiNXN — ^1»
#21^1 + &22Х2 + • • • + a2NxN ~ &2,
(1)
(2)
(3)
О'М Iх! + aM2#2 + • • • + aMNxN — Ъм
и минимизирующих целевую форму
^1Х1 4“ С2Х2 4“ • • • 4“ CNXN —
где на значения Xj наложены ограничения
Xj>0. (j = l,2, N)
Симплекс-метод в основном и применяется для решения этой задачи»
Этот метод использует представленный в двух этапах в § 5-1 симплекс-алго-
ритм, как это будет описано в этом параграфе.
Многие задачи, возникающие на практике, часто позволяют сразу
найти начальную допустимую каноническую форму. Например, можно
немедленно построить много различных начальных базисных допустимых
решений для важного класса задач, называемых «транспортными» (см.
гл. 14). Экономические модели часто содержат запасы сырья и вспомо-
гательные технологические процессы; это позволяет указать очевидное
начальное решение, в котором ничего нет, кроме этих вспомогательных
технологических процессов. Такое решение может быть очень далеко от
оптимального, но по крайней мере с него легко начать решение. В этих
случаях обычно приходится затратить немного труда (или даже никакого
труда не приходится затрачивать), чтобы привести эту задачу к канони-
ческому виду. В таких случаях этап I упомянутого выше процесса не нужен.
На практике встречаются и другие задачи, не имеющие такого оче-
видного начального допустимого канонического вида. Это имеет, напри-
мер, место для модели, которая не содержит свободных переменных или
в которой эти переменные имеют отрицательные коэффициенты. О такой
задаче, говоря математически, может быть ничего неизвестно. Такая
задача может иметь:
а) избыточность; она возникает, например, если уравнение балан-
са денежного потока получается из уравнений баланса материальных
потоков умножением цены на количество и суммированием. Классическая
транспортная задача является вторым примером (см. § 3-3; см. также зада-
чу о смесях, § 3-4, как третий пример);
б) несовместность; это могло бы случиться из-за простых описок,
из-за использования противоречивых данных или в силу набора требо-
ваний, которые не могут быть выполнены при имеющихся ресурсах.
Например, можно предложить задачу, в которой известно, что ресурсы
имеются в малых количествах; основным здесь является вопрос, сущест-
вует ли допустимое решение.
Ясно, что общий математический метод должен быть разработан так,
чтобы решать задачи линейного программирования независимо от апри-
орных знаний и предположений о системах, с которыми приходится иметь
дело. Действительно, если имеет место несовместность или избыточность,
-го в процессе решения эти важные факты должны быть обнаружены.
103
Этап I процесса использует симплекс-алгоритм для получения началь-
ной допустимой канонической формы (если она существует) для этапа II.
Этап I имеет некоторые важные особенности.
а) Никаких предположений о начальной системе не делается; она
может быть избыточной, несовместной или не иметь решений в неотрица-
тельных числах.
б) Для получения начального решения в канонической форме для
этапа I никаких преобразований не требуется.
в) Конечным результатом этапа I является базисное допустимое
решение (если оно существует) в канонической форме, пригодное для
начала этапа II.
ОПИСАНИЕ ПРОЦЕССА
А. Преобразуем исходную систему уравнений так, чтобы все свобод-
ные члены bi были неотрицательными, изменив для этого, если необходи-
мо, знаки обеих частей некоторых из уравнений.
Б. Увеличим число неизвестных в системе, введя базисное множе-
ство искусственных переменных xN+i > 0,xN+2 > 0, ...» xn+m>®> в резуль-
тате мы получим расширенную систему уравнений
а11Х1 4“ а12Ж2 4" • • • 4“ xiNxN 4~ XN+1 — &1,
^21^1 4" а22Х2 4- • • • 4” a2NXN 4" xN+2 — ^2
. (bi>0) (4)
аМ Iх 1 4" аМ2Х2 + • • • + aMNXN 4“ XN+M =
с1ж14"^2^2 4“ • • • + CNXN +(— Z) = 0
И
Xj>0 (7 = 1, 2, ..., A, N + i.....N + M) (5)
В. (Этап I.) Используем симплекс-алгоритм (без ограничения на
знак z) для получения решения систем (4) и (5), которое минимизирует
сумму искусственных переменных, обозначенную через w:
XN+1 + XN+2 4“ • • • 4“ XN+M=Wt (6)
Уравнение (6) называется искусственной формой. Начальную допусти-
мую каноническую систему для этапа I мы получим, если выберем в каче-
стве базисных переменных arN+1, xN+2, ...» (—z)» (~^) и исключим
эти переменные (кроме w) из формы w, вычитая сумму первых М уравне-
ний (4) из (6). Это дает нам
Естественные переменные Искусственные переменные
anxi 4'ai2*2 4-.. . 4-«in*n + *N+1 =Ь1
а21х1 4- а22х2 4- • • . + a2NxN + zW+2 = b2
аМ1х1 + аМ2х2 + • .. + aMp;xN + XN+M =bM
+ с2*2 +• .. +cNxN —z —0
^1*^1 4“ • .. +dNxN —w =—w о
104
где fy>0 и
dj — — (ay + a2j + ... + (j — 2, •.., N) (8)
— Wq = — (&1 + Й2+ • • • +&m)*
Оставляя в (7) только коэффициенты, получаем начальную таблицу
для этапа I (см. табл. 5-2-1).
Г. Если min w >0, то допустимого решения нет, и процесс окончен.
С другой стороны, если min w = 0, то этап II симплекс-алгоритма мы
начинаем следующим образом: (1) исключаем из дальнейшего рассмотре-
ния все небазисные переменные Xj, которым в последнем измененном
и?-уравнении соответствуют положительные (не нулевые) коэффициенты dj;
(II) заменяем линейную форму w (измененную различными исключения-
ми) линейной формой 2, которая получается после первого исключения
из 2-формы всех базисных переменных. (На практике при вычислениях
исключение базисных переменных из 2-формы обычно делается в каждой
итерации этапа I, см. табл. 5-2-1, 5-2-II и 5-2-III. И если это уже сделано,,
то измененную 2-форму можно сразу же использовать для этапа II.)
Д. (Этап II.) Применим симплекс-алгоритм к полученной в конце-
этапа I допустимой канонической форме для того, чтобы либо получить
решение, минимизирующее величину 2, либо обнаружить такое множество*
решений, что 2 оо.
Приведенное выше описание этапа I заслуживает некоторого обсу-
ждения. Ясно, что если существует допустимое решение исходной систе-
мы (1), то это же решение удовлетворяет также (4) и (5) с равными нулю
искусственными переменными; таким образом, в этом случае w = 0. Иа
(6) следует, что наименьшее возможное значение для w есть нуль, посколь-
ку w — сумма неотрицательных переменных. Следовательно, если допу-
стимое решение существует, то минимальным значением w будет w = 0;
наоборот, если из (4) и (5) получено решение с w = 0, то, очевидно, все
xN+i = 0, а значения Xj для образуют допустимое решение систе-
мы (1). Отсюда следует также, что если min w >0, то у системы (1) не
существует допустимых решений.
Всякий раз, когда исходная система содержит избыточные уравнения,
и часто, когда появляются вырожденные решения, искусственные пере-
менные будут оставаться как часть базисного множества переменных
в этапе II. Поэтому необходимо, чтобы их значения в этапе II никогда
не превышали нуля. Это достигается в (Г) тем, что все те небазисные пере-
менные, у которых относительные оценки в форме w положительны,
не рассматриваются. Для того чтобы убедиться в этом, заметим, что фор-
ма w в конце этапа I удовлетворяет уравнению
d\X^ d2x2 + •. • + w — 20о, (9)
где и w0 — 0, если допустимое решение существует. Для допу-
стимости решения w должно быть нулем; это означает, что каждое х?
должно быть нулем, если соответствующее dj >0; так что все такие xf
можно считать нулями и исключить из дальнейшего рассмотрения в эта-
пе II. Если мы их исключим, все наше внимание будет сосредоточено на
переменных, которым соответствуют dj = 0. Из (9) следует, что для реше-
ния, состоящего только из таких переменных, w = 0, и, следовательно,
оно является допустимым для исходной задачи. Итак,
Теорема 6. Если искусственные переменные образуют часть базисного-
множества переменных на различных шагах этапа II, то их величины,
никогда не превысят нуля.
105
Одна из возможностей исключения из рассмотрения переменных
«соответствующих неравенствам dj >0 в конце этапа I, состоит в следу-
ющем. Мы можем сохранять базисные искусственные переменные с нуле-
выми значениями в течение этапа II, исключая сначала (если это вообще
возможно) все искусственные переменные из базисного множества. Это
делается с помощью ведущего элемента, выбранного в строке г, соответ-
ствующей этой искусственной переменной, и в некотором столбце s, для
Рис. 5-2-1. Блок-схема симплекс-метода.
которого drs 0. Если все коэффициенты в такой строке для j = 1, . . ., N
равны 0, то строка вычеркивается, потому что соответствующее урав-
нение в исходной системе является избыточным (см. § 8-1).
Вторая возможность состоит в том, что мы сохраняем де-уравнение
в течение этапа II и рассматриваем переменную (—де) как еще одну неот-
рицательную естественную переменную. Затем система увеличивается
введением z-уравнения после исключения из него базисных перемен-
ных. Поскольку всегда справедливо неравенство де>0, дополнительное
условие (—де)>0 на этапе II приводит к де = 0.
Вычислительный процесс этапа I с искусственными переменными
и переход к этапу II схематически изображен на блок-схеме (см. рис. 5-2-1).
106
ПОДРОБНОЕ ОПИСАНИЕ ИТЕРАТИВНОГО ПРОЦЕССА
Как выглядит симплекс-метод на различных шагах, показано
в табл. 5-2-1, II и III. К началу некоторого /с-го шага все элементы таб-
лицы, связанной с этим шагом, известны (см. табл. 5-2-II). Под каждым
столбцом из числа соответствующих базисным переменным (включая (—и)
и (-— w)) помещены значки® или Q. Поскольку рассматривается система
в канонической форме (за исключением того, что изменен порядок пере-
менных по сравнению с исходным), все величины в столбцах, отмеченных
знаками® или О, будут нулями, кроме одного, который равен единице.
Если единица появляется в f-й строке (кроме двух последних), то мы будем f
говорить о соответствующей базисной переменной как об г-й базисной
переменной и обозначать ее через Xj . Например, если единица встречается
в первой, второй и третьей строках, соответственно для базисных пере-
менных я3, хъ и х2, то Xjr — я3, Xj2 — х5 и Xj3 — х2 являются теми симво-
лами, которые вводятся в левый столбец таблицы; их значения в соот-
ветствующем базисном решении равны числам которые выпи-
саны в последнем столбце таблицы, как и значения базисных переменных
(—z) и (—и?). Эти величины обозначены через — z0 и — wQ. Столбец,
который соответствует переменной, вводимой в базисное множество на
следующей итерации, отмечен значком он заменит базисную перемен-
ную со значком Q.
Следующие правила применимы ко всем итерациям с незначительны-
ми изменениями в зависимости от того, на каком этапе (I или II) ведутся
вычисления.
Шаг Г.
(I) Если все dj 0 (этап I) или с7>0 (этап II), то для
а) этапа I с wQ >0: конец — допустимого решения не существует
б) этапа I с w0 = 0: перейти к этапу II следующим образом:
1) исключить все переменные Xj, для которых dj >0х,
2) вычеркнуть из таблицы строку w и
3) снова начать итерацию (шаг I), используя правила для
этапа II. _
в) Этап II: конец — оптимальным решением является Xj. — biy
Xj = 0, z = z0 (/ ji, i = 1, 2, •, M). _
(II) Если некоторое значение dj <Z 0 (этап I) или Cj <Z 0 (этап II),
то выбрать переменную xs, которая будет введена в базисное множество
на следующей итерации вместо r-й базисной переменной (г будет опре-
делено на следующем шаге), так чтобы
этап I: d& = min dj < 0,
этап II: cs = mincj<;0.
Шаг II:
(I) Если все afs^O, то конец1 2; множество решений есть:
произвольно
Xj. = bi—aisxs (xj. — базисные переменные)
Xj = 0 (Xj—небазисные переменные: ;=#5)
1 Возможен и другой путь решения, в котором этот шаг можно опустить, а в эта-
пе II изменить щаг П-(П) следующим образом: если для соответствующей искусствен-
ной базисной переменной x^+i найдется ais ф 0 при s N, то с помощью ведущего
элемента ars вывести первую такую переменную, что i == г; в противном случае приме-
нить шдг П-(П), как он описан.
2 В этапе I этот случай не может встретиться, так как из него вытекало бы, что w
не ограничено снизу.
107
Таблица 5-2-1
Таблица симплекс-метода
Начальная таблица, нулевая итерация
Базисные переменные Естественные переменные Искусственные переменные Целевые перемен- ные Свобод- ные члены
*1 • ’ • х8 • • • XN xN+lxN+2'-xN+M —z — w
xN+i «11 • . .«is . . . aiN 1 bi
xN+2 «21 . • • «2s • • . а2м 1 b2
XN+M аМ1 • • • «Ms • • . aMN 1 Ьм
—z С1 • ’ . С8 * • • CN 1 0
—w 1 м & см. м Со’ 5 Q* И 1 1
Базисные1 переменные ★ • • • • •
*- (Эти столбцы можно опустить)2 ->
1 Знаки > и О выделяют столбцы, соответствующие базисным переменным. Все
величины в этих столбцах являются нулями, кроме одного, который равен 1. Знак ★
отмечает положение наибольшего отрицательного d), этап I (или су < 0, этап II), т. е.
столбец, соответствующий той переменной, которая войдет в базис на следующей ите-
рации вместо столбца, отмеченного знаком Q.
2 Столбцы — z и —w обычно опускают, потому что они не изменяются во всех табли-
цах; опускаются также столбцы искусственных переменных, так как эти переменные,
однажды выведенные из базиса, можно из дальнейшего рассмотрения исключить.
Напротив, в симплекс-метод е, использующем множители (гл. 9), рассматриваются
только те элементы таблицы, которые соответствуют столбцам с искусственными пере-
менными.
удовлетворяет исходной системе и обладает свойством
Z = Zq-\-CsXs—> —со при х3—
(II) Если какое-то Ujs>0, то выбираем r-ю базисную переменную,
чтобы вывести ее в следующей итерации, следующим образом:
brlar8 = min Ъг1аш
a i иг берутся из тех г, для которых а/8 >0. В случае совпадения1 выбор г
производится случайно (с равными вероятностями) из тех г, для которых
получились равные отношения.
Шаг III:
Чтобы получить из предшествующей таблицы начальные данные
таблицы, описывающей следующую итерацию, умножим каждый элемент
выбранной строки г на число, обратное ведущему элементу drs, и поместим
1 См. обсуждение вырожденности гл. 10; см. также § 6-1.
108
Таблица, 5-2-11
Исходная таблица для итерации к
xh Лц .. . «is ... a1N 1 - ^2
xh «21 •• . «2s • • • a2N 1
• • •
аг1 • • . Cbrs1 1 «r2V Ьг
X- аМ1 1 flMs • • • aMN Ъм
—z c8 Cft 1 —£о
—w di dg djy 1 —щ0
Базисные пере- менные • ★ о • • (опустить) • •
1 Жирным шрифтом выделен ведущий следующей итерации; см. табл. 5-2-III. элемент, используемый для вычислений на
Таблица 5-2-1II
Таблица перехода к следующей итерации 7с+ 1
Базисные переменные Естественные переменные Искусствен- ные перемен- ные Перемен- ные Свободные члены
«1 .. .х8 XN XN+lxN+2- • •XN+M — z — w
хн ail — «1«Я*1 — - ♦ «21—a2sari - ♦ «12V—«is«HV «22V—«2sa*W 1 1 c-l C-| ьэ 1 1 R| Й1 в £ о- сг^
х8 а*4 1 rl arN ъ*
Зм — - * аМ1 —аМ8аГ1 — — * aMN—aMsarN Ьм— амзЬ*
т । - - * Cj св«п —ds«*i - - * —csarN dN—dsa*N 1 1 Zq c8br —Wq—d8br
' Базисные переменные • • • (опустить)
(Ъ*Г = ЬГ/
(«г!—a,TJaT^, ...» (arN — arNlars)
109
Где
эти произведения в r-ю строку таблицы для следующей итерации; см~
отмеченные звездочкой элементы в r-й строке табл. 5-2-III. Вводим г-н>
базисную переменную х8 на место переменной xjr в предыдущей итерации.
Чтобы получить элемент, стоящий в г-й строке и /-м столбце в новой табли-
це, вычтем из соответствующего элемента предыдущей таблицы произведе-
ние числа, стоящего в i-й строке и 5-м столбце предыдущей таблицы на
число, стоящее в r-й строке и у-м столбце следующей таблицы.
ИЛЛЮСТРАТИВНЫЙ ПРИМЕР 1
Мы выполним все шаги симплекс-метода на простом числовом примере^
5ж^—4:^2 -]-1 Зж3—2х4 -j— х^ = 20
Xt-- х2~\- 5х3- Я4+ #5 = 8
xi “Н -- 7х3-}- Х± -}- = 2.
Поскольку свободные члены системы неотрицательны, мы начинаем
этап I симплекс-метода с расширенной системы
Естественные переменные Искусственные переменные
5х|—4х2 -j- 13ж3—2х4х$
х1— хг + 5я3— я4+ хь
^ + 6^2— 7я3+ я4 + 5я5
+ ж6 — 20,
4“ xi = 8,
— z =0,
—w =0.
Для того чтобы эту систему привести к каноническому виду, вычи-
таем суммы первых двух уравнений из последнего. Это приводит нас
к начальной таблице этапа I. Чтобы показать связь между обычным реше-
нием системы уравнений методом исключений и симплекс-алгоритмом,
вычисления ведутся параллельно в форме уравнений (10) и в табличной,,
чисто коэффициентной форме (табл. 5-2-IV).
Шаги этапа I, состоящего в минимизации гр, подобны шагам мини-
мизации z. Детальные объяснения к этому примеру читатель найдет
в § 5-1, (4)—(14). На первой итерации величина w уменьшается с 28 до
4/13, на второй — до нуля, и получается базисное допустимое решение
х3 — 3/2, хъ = 1/2, z = —8 для исходной нерасширенной системы. Пере-
менные Xq и я7 имеют положительные относительные оценки в форме гр
и потому на этапе II могут не рассматриваться. На третьей итерации зна-
чение z уменьшается с z0 — —8 (шаг 2) до z0 = —е0/7, которое и являет-
ся минимальным. Оптимальное решение х2 — 4/7, х3 = 12/7, все другие'
Xj = 0, z = — 60/7.
Симплекс-метод в форме уравнений
Итерация 0 (этап I)
5ж4—4^2 —Ь13^з — 2ж4 —|— х$ —|— х^ = 20,
хх— £г+ 5я3— я4+ хь +ж7 =8,
-j-6ж2— 7ж3-|- ж4 -j- 5^5 'Z = 0,
— Qxt + 5ж2— 18я3 + Зя4—2^5 —w = — 28.
★ О • • •
по
Таблица 5-2-IV
Симплекс-метод: табличная форма
Итерация 0 (этап I)
Базисные переменные Естественные переменные Искусствен- ные пере- менные —Z — W Свободные члены
Х1 х2 *3 х4 *5 *6 х7
•^6 5 -4 13 -2 +1 1 20
X*] 1 -1 +5 -1 +1 1 8
— Z 1 6 —7 1 5 1 0
—W -6 +5 -18 +3 —2 1 -28
★ о • • •
Итерация 1 (этап I)
5 4 А 2 1 1 20
а?3 13 13 1 13 13 13 13
12 J.2 3 8 5 А 4
X*] 13 +13 13 13 13 1 13
48 50 1 72 7 А 140
— Z 13 13 13 13 13 1 13
. 12 7 , 3 8 18 4
— W + 13 13 +13 13 13 1 13
• ★ (опустить) ООО
Итерация 2 (этап I—II)
*5 £ 2 12 8 _ 3 8 7 8 Iе0 CQ |оО 4-1 1 |°О ю Joo + 1 __ 1 8 13 8 со |см чг [оо
— Z 12 — 1 2 4 -9 1 -8
— W 1 1 1 0
★ • о (опустить) Ф ф
111
Продолжение табл. 5-2-1V
Итерация 3 (этап II—решение оптимально)
1 3 , 4 12
*3 7 1 7 7 7 + Т 7
12 3 8 5 13 4
х<> ~ 1 - - -
7 7 7 7 7 7
72 11 8 23 50 Л 60
— Z - - - - — - 1
7 7 7 7 7 7
• • (опустить) ф
Итерация I (этап I)
5 13 Xl 4 , #2 + X3 2 .1 .1 13*4 + 13a:5 + 20 — 13
12 “13 Xl +ix2 3 I 8_ 5 . 13Ж4'^13аС® is^e + z? _ 4 — 13 (11)
48 13 Xl , 50 + 13 1 i 72 .7 —13 *4 +13 *5+ 13*6 z _ 140 — 13
12 13 Xl 7 13*2 ,3 8 .18 +13*4 13^5 + 13^e W _ 4 13
• it (опустить) О • •
Итерация 2 (этап I — II)
13. 1 у Xi —g- x2 + x3 —g xt , 1 1 + у^6—“g“^7 3 “ 2
12 , 7 3 , 5 , 13 4
--3-^1+8’«2 + x5 g" x6 + g" X1 = 8' (12)
12xi— x2 + 2 x^ + 4 x6— 9 x7—z = 8
Xq x7 —w = 0
★ • О (опустить) • •
Итерация 3 (этап II — решение оптимально)
1 — yXi . 2.3 1 ,4 + X3—-7Я4 + -7 *5 — yX6 + yX7 __12 “ 7
12 . — уЛ + «2 3 .8 5 .13 — Tx4 + yX5 — уЯб + у X1 4 ~ 7 (13)
72 .11 .8 .23 50 _60
7 Xl + у + у x5 + у x6 ^fxl — Z 7
(опустить)
Оптимальное решение:
60
Z 7 .
=у» я2=у i все остальные xj = 0;
112
00
Дж. Данциг
Иллюстративный пример 2
Симплекс-метод в табличной форме для задачи о смесях, § 3-4
Таблица 5-2-V
Итерация 0 (этап I)
Базисные перемен- ные Естественные переменные Искусственные переменные — Z — W Свобод- ные члены
*1 х2 Хз *4 хз *6 *7 *8 *9 *10 *11 *12 *13
*10 1 1 1 1 1 1 1 1 1 1 1
*11 0,1 0,1 0,4 0,6 0,3 0,3 0,3 0,5 0,2 1 0,3
*12 0,1 0,3 0,5 0,3 0,3 0,4 0,2 0,4 0,3 1 0,3
*13 +0,8 0,6 0,1 о,1 0,4 0,3 0,5 0,1 0,5 1 0,4
— Z 4,1 4,3 5,8 6,0 7,6 7,5 7,3 6,9 7,3 1 0
— W -2,0 -2,0 -2,0 -2,0 -2,0 -2,0 - -2,0 -2,0 -2,0 1 -2,0
★ • • • о • • 1
Итерация 1 (этап I)
Базисные перемен- ные Естественные переменные Искусственные переменные — Z — W Свобод- ные члены
*1 *2 *3 *4 *б *в *7 *8 *9 *10 *11 *12 *13
*10 0,250 0,875 0,875 0,500 0,625 0,375 0,875 0,375 1 0,50
*11 0,025 0,388 0,588 0,250 0,262 0,238 0,488 0,138 1 0,25
*12 0,225 +0,488 0,288 0,250 0,362 0,138 0,388 0,238 1 0,25
*1 1 0,750 0,125 0,125 0,500 0,375 0,625 0,125 0,625 0,50
— Z 1,22 5,29 5,49 5,55 5,96 4,74 6,39 4,74 1 -2,05
— W 0,50 -1,75 -1,75 -1,00 -1,25 -0,75 -1,75 -0,75 1 -1
• ★ • • О (опустить) ф •
Итерация 2 (этап I)
Продолжение табл. б-2-V
Базисные перемен- ные Естественные переменные Искусственные переменные —Z —w Свобод- ные члены
XI Х2 *3 х4 *5 *6 х7 Х8 х9 хю XII Х12 *13
*10 -0,154 0,359 0,051 -0,026 0,128 0,179 -0,051 1 0,05
*11 -0,154 +0,359 0,051 -0,026 0,128 0,179 -0,051 1 0,05
*3 0,462 1 0,590 0,513 0,744 0,282 0,795 0,487 0,51
Xi 1 0,692 0,051 0,436 0,282 0,590 0,026 0,564 0,44
— Z -1,22 2,37 2,84 2,03 3,25 2,18 2,16 1 -4,76
— W 0,31 -0,72 -0,10 0,05 -0,26 -0,36 0,10 1 -0,10
• • ★ • о (опустить) • •
Итерация 3 (этап I—II)
Базисные перемен- ные Естественные переменные Искусственные переменные —Z — W Свобод- ные члены
Х1 х2 Хз х4 *5 х7 Х8 Х9 хю ХЦ Х12 Х13
*10 *4 *3 *1 1 -0,428 +0,714 0,714 1 1 0,142 0,428 0,428 -0,071 0,786 0,286 0,357 0,071 0,571 0,500 0,500 0 -0,143 0,571 0,571 1 0 0,14 0,43 0,43
n S 1 1 -0,20 2,50 2,20 2,40 1,00 2,50 1 1 -5,10 0
• ★ о • • (опустить) • •
Опустить уравнение w после исключения всех переменных с dj>0 (в этом случае только w).
Продолжение табл, 5-2-V
Итерация 4 (этап II — решение оптимально)
Базисные перемен- ные Естественные переменные Искусственные переменные —Z — w Свобод- ные члены
XI Х2 *3 Х4 *5 хе х7 Х8 *9 Х10 Хц Х12 Х1з
•Чо *4 *1 1 1 0,6 1,4 1 0,4 0,6 0,4 1,1 0,4 0,1 0,8 0,7 0,2 0,8 1 0 0,4 0,6 0
— Z 0,28 2,62 2,42 2,42 1,14 2,66 1 -4,98
• • • ф (опустить) • (опус- тить)
5-3. ЗАДАЧИ
1. Какие должны быть выполнены условия, чтобы некоторое множе-
ство переменных было базисным? В чем различия между допустимым реше-
нием, базисным допустимым решением, оптимальным решением и опти-
мальным базисным решением? Почему говорится «некоторое оптимальное
решение» вместо «оптимальное решение»?
СИМПЛЕКС-АЛГОРИТМ (к § 5-1 и § 5-2)
2. Коротко описать словами симплекс-алгоритм. Составить блок-схему
последовательности шагов, итераций и т. д. Что такое вырожденность?
3. Для системы с избыточностью
+ #12^2 “F а13Х3 =
^22*^2 а33х3 ~ О,
--а22Х2-а33х3 ~ О,
где 0 < Н12 < 1, 0 < а13 < 1, >0, показать, что введение искус-
ственных переменных и применение этапа I симплекс-метода приводит
к тому, что после исключения искусственных переменных в базисе оста-
ются две искусственные переменные и из двух уравнений, связанных
с искусственными переменными в системе в канонической форме, при
отбрасывании искусственных переменных одно оказывается избыточным,
но ни одно не исчезает.
4. Показать в общем случае, что если имеется исходная система ранга г,
т. е. система ст — г избыточными уравнениями, то к концу этапа I
остается по крайней мере т' > т — г искусственных переменных. Если
эти искусственные переменные опустить, то подсистема уравнений, свя-
занных с этими искусственными переменными, будет иметь ранг
т'— (т — г), т. е. тоже будет содержать т — г избыточных уравнений.
Если т' = т — г, то соответствующая подсистема вообще не содержит
уравнений.
5. Обсудить недостатки и возможные пути улучшения последнего
решения этапа I симплекс-метода, с тем чтобы уменьшить в этапе II чис-
ло итераций.
6. Показать, что изменение единицы измерения некоторого техно-
логического процесса к, для которого ch < 0, позволит определять «канди-
дата» на введение в следующее базисное множество по правилу cs = min Cj.
Можете ли вы предложить другое правило выбора, которое было бы лучше;
не увеличит ли оно работу?
7. Какое условие является достаточным, чтобы оптимальный план
был единственным? Если это условие не выполнено, то как можно постро-
ить другой оптимальный план, если он существует?
8. Показать, что если (х4, #2, • • •, хт) являются базисными перемен-
ными, то переменная xs может заменить хг в роли базисной переменной
только в том случае, когда коэффициент ars У= 0 в канонической форме.
9. Используя метод искусственных переменных этапа I симплекс-
метода, доказать, что если существует некоторое допустимое решение
системы т линейных уравнений, состоящее из неотрицательных пере-
менных, то существует и такое допустимое решение, в котором не более
чем т переменных положительны.
^10. (Т. Робакер). В ряде приложений часто оказывается, что многие
переменные, вошедшие однажды в базисное множество для некоторой
начальной канонической формы, остаются там до последней канонической
116
формы, причем соответствующие этим переменным столбцы в таблицах
симплекс-метода никогда не используются как ведущие, хотя сами табли-
цы все время изменяются.
Придумать способ преобразования только тех столбцов, которые
фактически используются как ведущие, и тем самым сократить ненужную
работу.
11. Предположим, что к концу этапа Ic w = 0 в канонической форме
осталась некоторая искусственная переменная в базисном множестве
с единичным коэффициентом в к-й строке. Показать, что любая естествен-
ная переменная Xj может заменить эту искусственную, если d^j ¥= 0.
Если все dkj = 0 для допустимых /, то к-ю строку можно исключить из
дальнейшего рассмотрения и это означает, что в исходной системе к-е
уравнение было избыточным.
12. Доказать: если после исключения избыточных уравнений нет
вырожденных решений, то число искусственных переменных в конце
этапа I, до исключения этих уравнений, равно числу избыточных уравне-
ний, а уравнений, связанных с искусственными переменными в ка-
нонической форме (после исключения искусственных переменных), не
будет.
13. Найти избыточное уравнение в случае, когда искусственным
переменным не разрешается вновь появляться, если они однажды были
выведены из базиса. В каком случае множество решений, каждое из
которых содержит т положительных переменных (т = числу уравнений),
может иметь нижнюю границу, равную минус бесконечности?
14. Показать, что если ранг (см. задачу 4) системы уравнений равен
числу уравнений и существует допустимое решение, то существует и базис-
ное допустимое решение. Если, кроме того, z имеет конечную нижнюю
границу, то существует минимальное базисное допустимое решение.
15. Продумать, как можно использовать симплекс-метод, чтобы отли-
чить совместную систему, которая не имеет решения в неотрицательной
области переменных, от несовместной системы.
16. Как устанавливается избыточность при помощи симплекс-метода?
17. Дано базисное недопустимое решение (т. е. по крайней мере
одно bi < 0), для которого все относительные оценки > 0; доказать,
что и о является нижней границей для возможных значений z в § 5-1-(2).
18. Показать, что единственность канонической формы означает,
что существует одна и только одна линейная форма, в которой базисные
переменные могут быть выражены через небазисные. Используя это,
доказать, что для формы недопустимости относительные оценки dj = 0
для неискусственных переменных и dj = 1 для искусственных перемен-
ных, если базисное множество переменных не содержит никаких искус-
ственных переменных.
19. Показать, что условие с7->0 для всех / является необходимым,
чтобы невырожденное базисное допустимое решение было минимальным.
20. Показать, что вырожденное базисное допустимое решение может
быть минимальным, хотя условие Cj 0 выполнено не для всех /.
21. Показать, что не существует нижней границы формы z для системы
xi—^2=1, (^i>0, я2>0)
— Xi — x2 = z
и, таким образом, можно добиться удовлетворения условий теоремы 3
из § 5-1.
117
22. Одним из решений системы
Л+ х2—2я3 + я4 = 2 (я;>0)
х । — 2j^2 —— х3 ~j~ 2х4 z= 3
Xi + Зя4 = 9
является ж4 = 3, х2 = 1, ж3==2, я4 = 2.
а) Преобразовать эту систему в каноническую форму по отношению
к х^ х2, х3; рассмотреть х4 как независимую переменную и показать, как
уменьшить значение я4 от я4= 2 до нуля и в то же самое время преобразо-
вать значения базисных переменных так, чтобы получить решение,
в котором не больше 3 переменных положительны.
б) Найти все решения, в которых не больше 3 переменных поло-
жительны.
23. а) Используя прием, описанный в задаче 22, найти вариант
симплекс-алгоритма, который бы уменьшал число положительных пере-
менных по крайней мере на единицу, если ранг (см. задачу 4) их подсисте-
мы меньше, чем их число.
Можно ли в этом случае изменить более чем одну переменную от
положительного значения до нуля?
б) При тех же условиях, что и выше, найти вариант симплекс-алгорит-
ма, который, начав с некоторого допустимого решения (базисного или
нет), будет путем увеличения значения небазисных переменных или
уменьшения их (если они не равны нулю) успешно улучшать решение до
получения оптимального.
в) Доказать, используя полученный выше вариант симплекс-алгорит-
ма, что:
I) если существует допустимое решение, то существует и базисное
решение;
II) если существует какое-то оптимальное допустимое решение, то
существует базисное допустимое решение, которое является оптимальным;
III) если существуют допустимые решения и значения z, связанные
с этим множеством решений, ограничены снизу, то существует оптималь-
ное базисное допустимое решение.
24. Пусть существует допустимое решение, содержащее к перемен-
ных, и ранг (см. задачу 4) подсистемы, образованной отбрасыванием
остальных переменных, равен г. Показать, что в этом случае существует
допустимое решение, содержащее не более г переменных, где г^к.
25. Если система т уравнений с п неотрицательными переменными
имеет допустимое решение, то существует решение, в котором к перемен-
ных положительны и п — к равны нулю, где (m, п).
26. Показать, что в задаче о диете со свободными переменными,
в которой рассматривается один продукт F, содержащий понемногу каж-
дого питательного вещества, существует начальное базисное допустимое
решение, состоящее из т — 1 избыточных переменных и переменной, свя-
занной с продуктом F. Какие избыточные переменные опущены?
ДВА ЭТАПА СИМПЛЕКС-МЕТОДА (см. § 5-2)
27. Используя симплекс-метод, решить систему
Х1 4" х2 1
Х1 + х2 2
Х1 — x2^i 1
Xi — Я2> 1
— X2 = Z
118
в неотрицательных Xj и найти min z. Изобразить графически область,
определенную неравенствами, используя Xi и х2 как координаты; просле-
дить графически этапы решения и интерпретировать переход от одного
решения к другому на графике (см. рис. 7-2-1).
28. (Уо [1]): для питания молочных коров и получения молока
необходима некоторая минимальная комбинация питательных веществ.
Часть из них должна быть закуплена. Ниже приведены данные для того,
чтобы ответить на вопрос, сколько каждого корма должен приобрести
фермер для того, чтобы иметь все необходимые питательные вещества
по минимальной цене? (Указание: найти пропорции требующихся веществ
на 1 долл, стоимости каждого корма.)
А. Оптовые цены и содержание питательных веществ в кормах
Виды кормов Оптовые цены, Канзасси- ти, долл, за 100 фунтов Содержание питательных веществ в кормах (фунты каждого вещества в 100 фунтах корма)
общее количе- ство усваи- ваемых питатель- ных веществ усваивае- мый белок кальций фосфор
Кукуруза (зерно) Овес Сорговый силос Отруби Мучные отходы Льняная мука Хлопковая мука Соевая мука Сушеная клейковина Очищенная вареная кукуруза 2,40 2,52 2,18 2,14 2,44 3,82 3,55 3,70 2,60 2,54 78,6 70,1 80,1 67,2 78,9 77,0 70,6 78,5 76,3 84,5 6,5 9,4 8,8 13,7 16,1 30,4 32,8 37,1 21,3 8,0 0,02 0,09 0,03 0,14 0,09 0,41 0,20 0,26 0,48 0,22 0,27 0,34 0,30 1,29 0,71 0,86 1,22 0,59 0,82 0,71
Б. Требования 74,2 19,9 0,21 0,67
29. Показать, что допустимое решение = 1, х2 — 0, х3 = 1, z = 6
системы
si 4- 4“ — 2 (xj 0)
%i — х2 4- #з ~ 2
2хг + Зя2 4- 4х3 = z (min)
не является базисным.
30. В приведенной ниже системе форма z имеет все положительные
коэффициенты и = х2 — х3 = я4 = х5 = 1; z = 5 является допусти-
мым решением системы. Без каких-либо вычислений показать, что долж-
но существовать оптимальное базисное допустимое решение. Исполь-
зуя этапы I и II симплекс-метода, построить оптимальное решение
Z = ^14-^2 4" жз+ £4 + ^5 (я7 >0, minz)
2 — 2^r4- х2— я3+ ^4—#5
2 = •— х^ -f- х2 -}- Зх3—2х^ -}- х§.
119
31. Рассмотрим систему
2^ — я2 + яз = 2 (я1>0, я2>0, я3>0)
4ж1 + х2 + ^3 = 6
+ х2 + хз — z (min).
а) Каково максимальное число решений, в которых не более двух
положительных переменных?
б) Найти все решения, в которых не более двух положительных
переменных. Какое решение дает наименьшее значение z?
в) Привести задачу к канонической форме относительно Xi и х2-
Является ли это решение оптимальным? Если нет, то, используя итератив-
ный процесс симплекс-алгоритма, найти оптимальное решение. Как это
согласуется с результатом пункта б)?
32. Найти и цпп z для каждой из следующих систем
(а) 2хг—Зх2 #з 4“ За?4 — х§ — 3
#14~ х2—2я34-9я4 = 4
2^4 — Зя2 4-6я3 4~ хь—2x5 = z
(б) Зх^ 4~ х2 4~ 2ж3 4~ х^ + #5 — 2
2xi — х2 + х3 4- х^ 4~ 4^5 = 3
xi— я24-Зя3—2я4 4- x5 = z
(в) Xi 4~ 2х2 4“ Зя3 4~ 2ж4— х$ — 6
2^2 4~ ^хз—4х^ 4~ 2^5 — 6
я24“ жз4~ xi~h х5= 5
— ^4-2^2+ Яз4-Зя4— z5 = z.
33. Решить задачу о смеси продуктов § 3-5 с помощью симплекс-
метода. Заметим, что модель с добавленными свободными переменными
уже находится в канонической форме.
34. Используя симплекс-метод, решить задачу 12, гл. 3.
35. Следующие задачи решить симплекс-методом. Проверьте свои
ответы графически (за исключением (в)).
Найти min z при условиях я7>0 и
(а) ж44~^2—хз —2 xi 4- х2 4- х^ = 4 — 2xi—х2 =z
(б) X\.~Y х2~\~хз — 2 Xi—Зя2 —я4 = 3 —~2xi—х2 =— z
(в) 2xi 4~ х2"~~ хз 4~ х& ’==z2 2xi— х2 4~ 5х3 4-ж5 = 6 4xi 4~ х2 4~ ж3 4~ х^ = 6 — Xi—2х2— х3 =z
(г) —4xi 4~ х2 -}- х% —4 2xi—3#2 4-ж4 = 6 — Xi — 2х2 =z.
120
36. Является ли решение иллюстративного примера 1 § 5-2 единствен-
ным? Дайте правило для определения, является ли решение единствен-
ным или нет.
37. Найти оптимальные решения для каждой системы задачи 32,
используя искусственные переменные.
38. Задачу минимизации формы 4ж4 + 8я2 + Зх3 при пяти огра-
ничениях
2,
2*^2 ,
^•>0 (j=l, 2, 3)
можно привести, применив непосредственно симплекс-метод, к следую-
щему виду:
минимизировать + 8я2 + Зх3 + Wx§ + Жг7 при девяти ограничениях
&1 “F “*^4 “1“ =: 2,
2ж24~ж3 —х$ —}~х7 = 5,
х^>0, (/=1, 2,..., 7)
где W — произвольное большое положительное число.
а) Объяснить, какую роль играют я4 и х5.
б) Объяснить, какую роль играют xQ и х7.
в) Почему необходимо вводить х6 и х7, если уже введены х± и х^'
г) Какую роль играет W? Показать, что если W достаточно велико,,
то последовательность шагов решения совпадает с этапами I и II.
д) Решить, используя симплекс-метод.
39. Минимизировать —2^!—5^2 при ограничениях
У1 + Уз =4,
У1 +2^2 +^4 =8,
У2 + У5 = 3,
U yj > 0.
40. Сформулировать и решить задачу, двойственную следующей:
максимизировать щ + и2 + Vi +
при ограничениях щ + — ij (произведение i и /; г, J = 1, 2).
ЗАДАЧА О ДИЕТЕ
41. Сформулировать как задачу линейного программирования сле-
дующий вопрос: предположим, что шесть продуктов, приведенных ниже-
в таблице, обладают калорийностью и содержат белок, кальций и вита-
мин А в указанных количествах, а также известна их цена за фунт.
В каких количествах должны быть куплены эти продукты, чтобы точно
обеспечивать суточную потребность человека в питательных веществах,
указанную в последнем столбце, при минимальной стоимости? Как изме-
нится модель, если суточные потребности можно превысить или если
можно превысить все потребности, кроме калорий?
а) Переформулировать модель с точными ограничениями, если еди-
ницей измерения каждого продукта будет не фунт, а 3000 калорий хлеба,
мяса и т. д. Получить графически оптимальное решение для упрощенной
задачи, в которой рассматриваются только уравнения для калорий,
белка и стоимости (т. е. опускаются уравнения для кальция и витами-
на А). Решить полную задачу, используя симплекс-метод.
121
Содержание и закупочная цена на 1 фунт Дневная потребность
хлеб мясо карто- фель капуста молоко жела- тин
Калории 1254 1457 318 46 309 1725 3000
Белки 39 73 8 4 16 43 70(a)
Кальций 418 41 42 141 536 — 800 (мг)
Витамин’А — — 70 860 720 — 500 (и. е.)
Цена в долл. 0,30 1,00 0,05 0,08 0,23 0,48 минимум
42. (Грин, Чатто, Хикс и Кокс (1]). Найти оптимальный план
для мясоперерабатывающего предприятия, которое хочет определить,
какова должна быть та доля корейки, грудинки и ветчины, которую сле-
дует произвести для продажи в копченом виде, и какую долю следует
продавать свежей.
Не прибегая к сверхурочной работе, предприятие за день может
закоптить корейки 106 (на 100 единиц веса), а грудинки и ветчины — 315.
В случае необходимости может быть применена и сверхурочная работа.
Количество свежих продуктов,
поступающих для переработки
корейка 480 грудинка 400 ветчина 230
Себестоимость продуктов в долларах
корейка грудинка ветчина
Копченый продукт (без 5,18 4,76 5,62
сверхурочных работ)
Копченый продукт (сверх- 6,58 5,54 6,92
урочные работы)
Свежий продукт 0,50 0,48 0,51
Копченые продукты продаются по более высокой цене, чем свежие:
разность продажных цен на копченую и свежую корейку = 6,00 долл.;
на копченую и свежую грудинку = 5,00 долл.; на копченую и свежую
ветчину — 6,00 долл.
Глава 6
ОБОСНОВАНИЕ СИМПЛЕКС-АЛГОРИТМА
И ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
ДВОЙСТВЕННОСТИ
6-1. ИНДУКТИВНОЕ ОБОСНОВАНИЕ СИМПЛЕКС-АЛГОРИТМА
При доказательстве в § 5-1 конечности симплекс-алгоритма предпола-
галось, что все базисные решения, получающиеся в итеративном процессе,
оказываются невырожденными. Для вырожденного случая имеются два
типа доказательств. Преимущество первого, индуктивного, заключается
в том, что оно непосредственно дает строгое и элементарное доказатель-
ство основной теоремы двойственности (Данциг [18]).
С конструктивной точки зрения преимущества второго, основанного
на изменении («возмущении») или лексиграфической модификации коэф-
фициентов, заключаются в том, что на его основе мы получаем простое
правило для определения того, какую базисную переменную следует
исключить в случае неопределенности (Данциг, Орден и Вулф [1]).
Однако это доказательство требует более глубоких знаний, и поэтому оно
откладывается до гл. 10. Любое из этих двух доказательств может быть
использовано для получения простого правила случайного выбора, кото-
рое требует наименьших затрат труда и «с вероятностью единица» гаран-
тирует, что симплекс-алгоритм закончится через конечное число шагов.
Доказательство конечности симплекс-алгоритма можно найти в конце
этого параграфа. Сейчас нами будет доказана
Теорема L Пусть дана задача линейного программирования, представ-
ленная в допустимой канонической форме. Тогда существует такая конеч-
ная последовательность ведущих операций, дающих базисное допустимое
решение, что последняя каноническая форма либо дает оптимальное базис-
ное решение, либо указывает бесконечное множество допустимых решений,
для которых значения z не ограничены снизу.
Обсуждение. Для задачи линейного программирования, записанной
в допустимой канонической форме, например, с базисными переменными
х^, . . ., хГ, . . ., хт, мы должны иметь
4" ai, m+i xm+i + • • • + 0>isxs + • • • + ainxn = &i,
xr + ar, m+ixm+i 4" • • • 4" ttrsxs 4“ • • • 4“ ^rnxn —
xm + ^m,m+lxm+l 4“ • • • 4“ ^msxs 4-... 4" amnxn — bm,
( — z)+ ст+1ж7П+14“ • • • 4“ csxs + • • • ~\~cnxn — —2(b
где z0, atj суть постоянные (см. § 5-1). Базисное допустимое реше-
ние получается приписыванием каждой небазисной переменной нулевого
значения и соответствующих значений базисным переменным (включая z).
123
Симплекс-алгоритм, изложенный в гл. 5, можно описать следующим
образом: каждая итерация начинается с допустимой канонической формы
и некоторого множества базисных переменных. Соответствующее базисное
решение является к тому же допустимым, т. е. свободные члены ~Ъг (после
модификации) не отрицательны. Процесс заканчивается получением
канонической формы, для которой либо q > О для всех j (в этом случае
последнее базисное допустимое решение является оптимальным), либа
в некотором столбце с с8 < 0 все коэффициенты не положительны, т. е.
ai8 < 0 (в этом случае существует класс допустимых решений, для кото-
рых z -> — оо). Во всех других случаях в столбце $ и строке г выбирает-
ся ведущий элемент. Номера s и г определяются из условий с8 = min cj <
<0и brlaT8 = min (bilai8) для положительных ars и ai8. Переменная
x8 становится новой базисной переменной, заменив собой некоторую
переменную в базисном множестве, именно уравнение с ведущим эле-
ментом используется для исключения переменной х8 из других уравнений.
После того как коэффициент при ведущей переменной станет равным еди-
нице, модифицированная система окажется в канонической форме и мы
получим новое базисное допустимое решение, в котором величина z =
уменьшилась, если Ьг > 0. В невырожденном случае все Ьг- положитель-
ны. Если от итерации к итерации это остается справедливым, то процесс
должен закончиться за конечное число шагов, поскольку 1) каждая
каноническая форма единственным образом определяется выбором т
базисных переменных; 2) убывание величины z0 обеспечивается тем, что
все базисные множества не совпадают; 3) число базисных множеств конеч-
но, поскольку их не больше, чем число сочетаний из п элементов по mt
т. е. С™.
В вырожденном случае может оказаться, что Ъг = 0; это приводит
к тому, что zQ принимает одно и то же значение до и после изменения
базиса. Гофман и Бил (см. § 10-1) показали, что в этой процедуре может
повторяться некоторая каноническая форма и, следовательно, возможно
бесконечное движение по кругу х. Такое может случиться, как это будет
видно из дальнейшего, если выбор ведущего элемента по описанному
выше правилу будет неоднозначным. Некоторое несложное правило выбо-
ра в таких случаях позволит всегда избежать трудностей. Для того чтобы
показать это, докажем сначала следующую полезную лемму.
Лемма 1. Если теорема 1 справедлива для системы, у которой п&
крайней мере один из свободных членов не равен нулю, то она справедлива
и для системы, полученной в результате замены всех свободных членов
нулями.
Доказательство. Пусть все свободные члены системы в канонической
форме равны нулю. Заменим одно (или несколько) равных нулю на
Ъ\ = 1 (или любое другое положительное число). Тогда в силу предполо-
жения существует такая последовательность базисных допустимых реше-
ний, получающихся в результате изменения базиса, что последняя кано-
ническая форма обладает требуемыми свойствами. Если в полностью
вырожденной задаче использовать ту же самую последовательность
ведущих выборов, то каждое базисное решение по-прежнему будет допу-
стимым, именно нулем. Поскольку требуемое свойство последней канони-
ческой формы зависит только от выбора базисных переменных и не зави-
сит от правых частей, лемма доказана.
1 Это называется зацикливанием.—Прим, перев.
124
Доказательство теоремы 1. Для доказательства основной теоремы
в вырожденном случае, так же как и для невырожденного случая, мы
сделаем следующее:
Индуктивное предположение. Пусть для 1,2, . . ., т— 1 уравнений
справедливо утверждение: при помощи конечного числа изменений допу-
стимого базисного множества можно получить каноническую форму,
с которой либо все коэффициенты z-уравнения не отрицательны (сj 0),
либо же для некоторого столбца s будет с8<0, а все коэффициенты
не положительны (ai8 < 0).
Проверим прежде всего справедливость индуктивного предположения
для одного уравнения. Если начальное базисное решение невырождено
{bi > 0), то, как нетрудно заметить, и каждое последующее базисное
решение должно быть невырожденным (это замечание справедливо только
для системы, состоящей из одного уравнения). Отсюда вытекает справед-
ливость утверждения о конечности описанного выше симплекс-алгоритма,
ибо последняя каноническая форма удовлетворяет индуктивному пред-
положению. Вырожденный случай = 0 установлен в силу леммы 1.
Осуществим индуктивный переход. Именно предположим, что наше
индуктивное предположение справедливо для 1, 2, . . ., т — 1 уравнений
и по крайней мере для одного i в системе т уравнений (1) мы имеем
bi 0. Если итеративный процесс не законечен, то он продолжается до
тех пор, пока на некоторой итерации вследствие вырожденности дальней-
шее уменьшение zQ будет уже невозможно. Перенумеруем уравнения так,
чтобы было bi = b2 = . . . = Ъг = 0 и bi =/= 0 для i = г + 1,. .., т.
Заметим, что для любой итерации справедливо неравенство г < т,
поскольку полная вырожденность на последующей итерации невозможна,
€сли предполагалось, что в начале хотя бы одно bt =И= 0. Оставим пока без
внимания уравнения г + 1, . . ., т. В силу индуктивного предположения
существует конечная последовательность изменений базисного множества,
при которых используются ведущие элементы из первых г уравнений.
В результате этих изменений в подсистеме либо все Cj > 0, либо для неко-
торого s все ai8 <Z 0, 1 i < г и с8 <Z 0. Выполним те же самые веду-
щие операции, но теперь уже над полной системой. Поскольку свободные
члены первых г уравнений равны нулю, их значения при выполнении
•ведущих операций для подсистемы не изменятся; это означает, что
мы можем использовать те же самые ведущие элементы и для полной
системы т уравнений, не заменяя xr+i, . . ., хт, используемых в ка-
честве базисных переменных, и не изменяя''их значений в базисном
решении.
Отсюда вытекает, что если для подсистемы в последнем базисе все
0, то это же свойство сохранится и для всей системы в целом. Если
в подсистеме для некоторого s выполняются неравенства с8 < 0 и 0
для i = 1, 2, ..., г, то либо ai8 < 0 для всех оставшихся i = г + 1, . . ., т
(в этом случае индуктивное предположение справедливо для т уравне-
ний), либо ais > 0 по крайней мере для одного i > г; в последнем случае
в базисное множество уже для всей системы можно ввести переменную
х8, что приведет к строгому убыванию z0, поскольку bi > 0 для i = r+1, ...
..., т. Мы уже видели, что значение z можно уменьшать только конеч-
ное число раз. Следовательно, итеративный процесс должен закончиться,
но это возможно Только в том случае, когда индуктивное предположение
справедливо для системы т уравнений.
125
Это завершает доказательство для т уравнений, исключая полностью
вырожденный случай, когда = 0 для всех i = 1, 2, . . ., т. Однако
доказательство последнего случая вытекает теперь непосредственно из
леммы, что и требовалось доказать.
Как следствие из теоремы 1 мы получаем следующую теорему.
Теорема 2. Если в условиях вырожденности переменная, которая долж-
на быть опущена, определяется единственным образом, то симплекс-
алгоритм закончится в конечное число шагов.
Доказательство правила случайного выбора. Это правило выбирает
переменную, которую следует опустить из базисного множества, с равной
вероятностью среди тех г, для которых
Ь^~ = min (ars > 0, ai8 > 0) (2)
ars ais
Начиная с произвольного базисного множества Т, мы знаем, что
в силу теоремы 1 существует конечное число итераций, приводящих
к последней канонической форме. Обозначим через кт наименьшее число
итераций, начинающихся с Т. Поскольку начальных базисов имеется
только конечное число, существует к = max кт, которое является наи-
большим среди этих кратчайших цепочек шагов.
Лемма 2. Правило случайного выбора позволит заканчивать симплекс-
алгоритм за к итераций с вероятностью
?>(J^ (3)
где т — число уравнений, а к — наибольшее из кратчайших цепочек
шагов, приводящих к оптимальной канонической форме.
Доказательство. На каждой итерации имеется не более т выборов.
Таким образом, при к итерациях существует не более mk последователь-
ностей («путей»), из которых по крайней мере одна приводит к оптимуму;
вероятность каждого выбора на каждом шаге не меньше 1/тп, поскольку
мы предполагаем, что все выборы имеют одинаковые вероятности. Следо-
вательно, для к шагов справедливо (3). Кроме того, вероятность неполу-
чения оптимума за к итераций меньше, чем [1 — (1/т)к]. Отсюда выте-
кает, что вероятность неполучения оптимума за 2к итераций меньше,
чем [1—(l/m)kl2, а неполучения оптимума за N = tk итераций меньше, чем
Это выражение, однако, при t оо стремится к нулю. Этим установлена
Теорема 3. Если в случае неоднозначности выбора переменной, подле-
жащей выведению из базисного множества, применяется правило случай-
ного выбора, то вероятность того, что оптимум не будет достигнут за N
итераций, стремится к нулю при N —оо.
6-2. ЭКВИВАЛЕНТНЫЕ ДВОЙСТВЕННЫЕ ФОРМЫ
Как было указано в § 3-8, с каждой задачей линейного программиро-
вания связывается другая задача линейного программирования, которая
называется двойственной. Это основное понятие ввел Джон фон Нейман
(в беседе с автором в октябре 1947 г.), а неявно оно появилось в рабочих
заметках, которые он написал спустя несколько недель (фон Нейман
126
[3]). Впоследствии Гейл, Кун и Таккер [3] сформулировали в явном
виде теорему двойственности, которую они доказали с помощью класси-
ческой леммы Фаркаша [1]. Лемма Фаркаша рассматривается в § 6-4,
теорема 6. Систематическое изложение теории двойственных задач линей-
ного программирования было дано Голдманом и Таккером [4], а также
Гейлом [4]. Освещение роли фон Неймана можно найти у Куна и Так-
кера [4].
Исходная задача по отношению к двойственной называется прямой.
Допустимые решения прямой и двойственной задач, вообще говоря, мало
связаны друг с другом, однако их оптимальные базисные допустимые
решения таковы, что, используя одно из них, можно сразу же получить
и другое. Часто оказывается более удобным использовать для решения
задачи линейного программирования именно двойственную задачу, а не
прямую. В связи с этим следует заметить, что, решая двойственную
задачу к двойственной, выиграть ничего нельзя, поскольку она экви-
валентна прямой задаче.
ДВОЙСТВЕННАЯ ЗАДАЧА
Если рассмотреть следующие системы линейных неравенств с неотри-
цательными переменными (а не уравнений), то мы получим почти симме-
тричное соотношение между прямой задачей и задачей, двойственной к ней.
Прямая задача: найти > 0 и min z, удовлетворяющие
^11^1 + tt12‘r2 + • • • + d\nxn
а21ж1 + а22Х2 + • • • + а2пхп t>2
........................... (1)
amixl + ^7712*^2 + • • • + ^тпхп
+ С2Х2 + ... + спхп = z (min)1.
При такой записи двойственная задача получится, если транспониро-
вать матрицу коэффициентов и поменять ролями свободные члены и коэф-
фициенты целевой формы, изменив при этом направление неравенств
и подставив max вместо min.
Двойственная задача: найти > 0 и max г?, удовлетворяющие
аиУ1 + а21Уг + • • • + ат1Ут <4
а12У1 + а22У2 + • • • + аШ2Ут с2
............................................. (2)
а1пУ1 + а2пУ2 + • • • + атпУт сп
Ь1У1 + ь2у2 bmym = v (max).
Такая форма двойственной задачи, предложенная фон Нейманом,
обладает особенностью, позволяющей легко увидеть, что задача, двой-
ственная к двойственной, есть прямая задача (см. задачу 5).
Для того чтобы более отчетливо представить себе связь между пря-
мой и двойственной задачами, воспользуемся таблицей коэффициентов,
предложенной Таккером, табл. 6-2-1.
Прямая задача читается по строкам, а двойственная по столбцам.
Простое правило запоминания направления неравенств состоит в том,
чтобы выписать прямые неравенства > соответствующие z-форме,
1 «z (min)» означает «переменная z подлежит минимизации»; не путать с величи-
ной min z, которая является минимальным значением z.
127
полагая всегда > min z, и выписать двойственные неравенства < , соот-
ветствующие г?-форме, полагая всегда < max v.
Схема Танкера
Таблица 6-2-1
Прямая
Переменные xi 0 х2^0 Неравенства Свободные члены
У 2 5 >0 >0 аи «21 «12 «22 • а1п . «271 АЛ • гО Л
Двой- ствен- ная Ут < >0 ат& «m2 • атп > Ъщ
Неравенства max v
Свободные члены «2 •• • сп > min z
В теореме двойственности высказывается утверждение относительно
возможных областей изменения как значений z япя. прямой задачи, так
и значений v для двойственной задачи. Это схематично изображено в (3)
для случая, когда прямая и двойственная задачи являются допустимыми.
Двойственная
— оо------ область v--------->
или конечно max v —>
Прямая
область z------1- оо
или конечно
(3)
<-------
ч— min z
Теорема двойственности. Если существуют решения прямой и двой-
ственной систем, то значение целевой формы z, соответствующее любому
допустимому решению прямой, не меньше значения целевой формы v,
соответствующего любому допустимому решению двойственной*, кроме
того, для обеих систем существуют оптимальные допустимые решения
и max v = min z.
СИСТЕМА, ДВОЙСТВЕННАЯ К СМЕШАННОЙ
Двойственную систему для системы уравнений и неравенств (любого
знака), в которую, кроме неотрицательных переменных, могут входить
переменные без ограничений, всегда можно получить, приведя эту
•систему к эквивалентной системе неравенств вида (1). Этот подход
можно фактически использовать для установления того, что задача,
двойственная для задачи линейного программирования в стандартной
форме, как это описано в § 3-8, совпадает с тем, что приведено в данной
главе. Как прямую, так и двойственную системы можно рассматривать
как множество переменных со своими ограничениями на знаки и множе-
ство линейных уравнений и неравенств; при этом переменные прямой
системы находятся во взаимно однозначном соответствии с уравнениями
и неравенствами двойственной системы, а уравнения и неравенства пря-
мой системы находятся во взаимно однозначном соответствии с перемен-
ными двойственной системы. Если ограничением прямой системы является
128
линейное неравенство (>), то соответствующая переменная двойственной
системы не отрицательна; если ограничением является равенство, то на
знак соответствующей переменной ограничение не накладывается. Имеют
место следующие правила соответствия:
Прямая задача
Целевая форма (>min z)
Свободные члены
Матрица коэффициентов
Ограничение:
i-e неравенство: >>
i-е уравнение: =
Переменная:
для xj ограничения на знак нет
Двойственная задача
Свободные члены
Целевая форма «max v)
Транспонированная матрица
коэффициентов
Переменная:
для yi ограничения на знак нет
Ограничение:
;-е неравенство:
7-е уравнение: =
Для иллюстрации рассмотрим смешанную прямую систему
xt—Зя2 + 4я3 = 5, (Xi>0, я2>0, ограничения на знак х3 нет)
Xi — 2х2 ^3,
2х2 —х3 >4, (4)
Xi + х2 + = 2 (min).
Применяя перечисленные выше правила, мы можем прочитать в таблице
коэффициентов (табл. 6-2-П) по строкам прямую задачу, а по столбцам—
двойственную.
Таблица 6-2-П
Прямая
Двой- ствен- ная Переменные Х1 > 0 Х2 > 0 Хз Ограничения Свободные члены
о о АЛ th N М 1 1 -3 4 1 —2 2 -1 VA и 5 3 4
Ограничения — max v min z
Свободные члены 1 1 1
Для того чтобы убедиться, что это то же самое, перепишем систему (4)
в эквивалентной форме в виде неравенств (см. § 4-5)
Xi—Зя2 + 4 (Яд — я") >5, «>0, я2>0, я'>0, Хд>0),
—-[Я! —Зя:2 + 4 («;—«:)]> —5,
— (Xt—2ж2) > —3, (5)
2ж2— (ха—жр>4,
Xi + х2 + (я'—£g)>minz.
Здесь мы записали х3 = х3 — я", т. е. представили х3 в виде разности двух
неотрицательных переменных, а вместо первого уравнения из (4) запи-
сали два эквивалентных ему неравенства Xi — 3±2 + 4я3 > 5 и xt —
9 Дж. Данциг 129
— 3^2 + 4&3 < 5. Связь между прямой и двойственной формами 1 в соот-
ветствии с (1) и (2) представлена в табл. 6-2-1II.
Таблица 6-2-1II
Прямая
Переменные Xi > 0 Х2 0 х' 0 х" > 0 Ограничения Свободные члены
о о ЛА 1-3 4-4 -1 +3 —4 +4 ЛЛ 5 -5
Двой- ствен- «С СО СО ¥ V О о -1 +2 2 +1 +1 л л -3 4
ная Ограничения max v
Свободные члены 1 11-1 >min z
Здесь удобно обозначить через О и 0 двойственные пере-
менные, соответствующие первым двум неравенствам. Поскольку в наших
неравенствах коэффициенты при у[ и у[ отличаются только знаком, можно
положить у'г — = У1, где величина yi может иметь уже любой знак.
Заметив, далее, что коэффициенты в неравенствах двойственной формы,
соответствующих х3 и х"3, также отличаются только знаком, мы получаем
уравнение
У1)—Уз — 1 или 4^—^з=1.
Теперь уже ясно, что табл. 6-2-II дает то же самое, что и табл. 6-2-Ш.
ЗАДАЧА, ДВОЙСТВЕННАЯ К СТАНДАРТНОЙ
Мы можем применить сформулированные выше правила получения
двойственной формы для стандартной формы; см. табл. 6-2-IV. Удобно
Таблица 6-2-IV
Прямая
Двой- ствен- ная Переменные xi 0 Х2 0... xN 0 Ограничения Свободные члены
+ л2 + а11 а12 ... aiN а21 а22 • • • a2N = (коэффициенты Ь2 двойственной целевой формы) ьм
аМ1 аМ2 • • • aMN
Ограничения < < ... max v min z
Свободные члены С1 с2 ... cN (коэффициенты прямой целевой формы)
1 Автор часто вместо прямой и двойственной задач говорит соответственно о пря-
мой и двойственной формах или о прямой и двойственной системах.— Прим. ред.
130
будет обозначать двойственные переменные (на знак которых в этом случае
не налагается ограничений) через +л^ (вместо в (2), где были ограни-
чения на знак).
6-3. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ДВОЙСТВЕННОСТИ
Для стандартной задачи линейного программирования, приведенной
в табл. 6-2-IV, прямая задача состоит в нахождении переменных Xj > О
и min z, удовлетворяющих
Л11Ж1 + а12^2 + • • • + aiNXN —
#21^1 4“ ^22*^2 4“ • • • 4“ ^2N^N = ^2
........................... (1)
1^1 4" аМ2Ж2 4“ • • • 4” aMNxN ~ Ъм
cixi + с2х2 4- • • • 4- cnxn = z (min).
Двойственная задача для этой стандартной задачи линейного програм-
мирования заключается в нахождении переменных л2, . . ., Ям и max г?,
удовлетворяющих
#11211 + #21^2 4" • • • 4" аМ1 ЛМ С1
а12^1 4- ^22^2 4" • • • + С2
4" a2N^2 4“ • • • 4" aMN^M CN
Mi4- Ъ2п24- ... 4- ьмлм = V (max),
где ограничений на знак не наложено.
Возможны все четыре комбинации допустимости и недопустимости
в прямой и двойственной системах. Эти четыре случая можно свести
в следующую таблицу:
Прямая имеет допу- стимые решения Прямая не имеет допустимых решений
Двойственная имеет допу- стимые решения min z = max v max v —> + оо
Двойственная не имеет допустимых решений min z —> — oo возможно
Следующие примеры показывают, что каждый случай возможен
а) Прямая допустима Прямая Двойственная
Двойственная допустима #1 >0 д?1 = 5 #1 = z (min) [min z = jti i 5jq = v (max) max i> = 5]
131
9*
Продолжение табл.
б) Прямая допустима Двойственная недопустима — а?2 = 5 - Jtj - 1 — xl — х2 = z (min) 5л4 = v (max) [z —> — оо]
в) Прямая недопустима Двойственная допустима н н ч II II V N [ О Б* 04 । — 5 = v (max) -^ч-со]
г) Прямая недопустима Двойственная недопустима #1>0, х2>0 Х^ — х2 = ”Ь -|- ^2 — ! Х^ Д?2 ~~ — 5 — Jtj Л 2 1 — х± — х2 = z (min) 5jIi — 5^2 = + v (шах)
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ДВОЙСТВЕННОСТИ
И СВЯЗАННЫХ С НЕЙ ТЕОРЕМ
Для доказательства ряда основных теорем, связанных с теоремой
двойственности, мы будем использовать симплекс-метод.
Теорема}! (Теорема двойственности). Если существуют допустимые
решения как в прямой, так и в двойственной системах, то для обеих систем
существует оптимальное решение и
min 2 = max и.
Теорема 2 (Теорема о неограниченности).
а) Если допустимое решение существует для прямой системы, но не
существует для двойственной, то существует такой класс решений пря-
мой системы, что z-^ — оо.
б) Если допустимое решение существует для двойственной системы,
но не существует для прямой, то существует такой класс решений двой-
ственной системы, что + оо.
Теорема 3 (Теорема о недопустимости).
а) Если система линейных уравнений с неотрицательными перемен-
ными недопустима, то существует линейная комбинация этих уравнений,
которая является недопустимым уравнением.
б) Если система линейных неравенств недопустима, то существует
неотрицательная линейная комбинация, которая является недопустимым
неравенством.
Поскольку система уравнений с неотрицательными переменными
эквивалентна системе линейных неравенств и наоборот, теорема 3(6)
оказывается переформулировкой теоремы 3(a) для эквивалентной системы.
Тем не менее, используя симплекс-метод, мы дадим независимые
доказательства всех частей этих теорем. Прежде чем перейти к доказа-
тельству, сделаем несколько предварительных замечаний, имеющих
отношение к доказательству теоремы двойственности. *
32
Если для прямой и двойственной задач существуют допустимые реше-
ния, то значения о и z связаны интересным соотношением, именно значе-
ние v всегда меньше (или равно) значения z. Это обстоятельство было
отмечено еще в 6-2 (3). Для доказательства^ обозначим через (хи я2, . ..
..., xN и z) и (л4, л2, .. ., лм и о) какие-нибудь решения соответственно
прямой (1) и двойственной (2) систем. Через cj 0 обозначим разность
между правой и левой частями системы (2), т. е. положим
м
Cj—2 аия1 = ci (j = i, 2, (3)
Если мы теперь умножим первое уравнение прямой системы (1) на
Л1, второе на л2, . . ., и вычтем сумму полученных уравнений из z-урав-
нения, то сразу получим
ciXi + С2Х2 4“ • • • ~Ь CNXN ~z-V- (4)
Поскольку > 0, Xj 0, отсюда вытекает, что все члены, стоящие слева,
неотрицательны; следовательно, для любого решения двойственной систе-
мы мы имеем 0 < z — г?, или
z> v. (5)
Таким образом, если существуют решения как прямой, так и двой-
ственной систем, то значение z для любого решения прямой задачи являет-
ся верхней границей значений г?, а значение о является нижней границей
значений z; следовательно, в этом случае невозможно ни z->— оо,
ни + оо. Поэтому, если в прямой и двойственной задачах сущест-
вуют 1 оптимальные решения, то для этих решений имеем
min z> max о. (6)
Это утверждение известно как слабая форма теоремы двойственности.
Для доказательства теоремы 1 рассмотрим вспомогательную задачу,
полученную из задачи (1), во-впервых, изменением свободных членов
каждого уравнения i (если это необходимо) так, чтобы 6^ > 0 и, во-вто-
рых, введением «лишних» или «искусственных» переменных ^N+f>0.
Переменные и и/>0 определим следующим образом:
м
^ = ^ХН+Ь w + w' = W, (7)
г=1
где w является суммой искусственных переменных. Через W обозначена
некоторая известная верхняя граница сумм ю, а и/ равно разности меж-
ду W и w. Например, в качестве верхней границы для w можно исполь-
м
зовать W =2^’ что соответствУет начальному базисному решению
этапа I (см. § 5-2).
Вспомогательная задача. Найти такие xj 0, и/, z, что z = minz,
w' — max w' и
а11Ж1 + • • • + aiNxN + XN+i — ^i,
aMixl + • . . + aMNxN XN+M ~ Ъмч (8)
XN+1 + • • • + XN+M + K) = W,
clxl~l- • • • ~\~CNXN (--2) — 0.
1 Заметим, что мы ничего еще не знаем о существовании минимизирующего реше-
ния в прямой задаче и максимизирующего в двойственной.
133
Отметим, что форма (8) точно совпадает со стандартной формой этапа I
симплекс-метода, если wf заменить на W — w. Она будет канонической
формой относительно переменных x^v+i, .. ., Ял+м» w', — zпосле исключе-
ния этих переменных из гр'-формы. Мы можем теперь перейти к макси-
мизации w', что соответствует минимизации w = W — w'. Поскольку
нижняя граница для w существует (именно нуль) в силу теоремы 1 из
§ 6-1, существует и такая оптимальная каноническая форма в конце
этапа I, что все коэффициенты и свободные члены в гр'-уравнении (9) не-
отрицательны.
JV-f-M _ __ _ _
2 djXj+w' = + w'o (dj> О, w’o> 0). (9)
7=1
G другой стороны, это уравнение можно получить с помощью последова-
тельности ведущих операций из вспомогательной системы (8); отсюда
вытекает существование некоторой линейной комбинации уравнений
i — 1,2, . . ., М из системы (8) с весами nJ, п®,..., сгм, которая, будучи при-
бавлена к гр'-уравнению из (8), дает (9). Следовательно, веса = п®
удовлетворяют соотношениям
м _
2 = для 7 = 1, 2, ...,7V,
г=1
о“ 4-1 = с^-н > 0 для i = 1, 2, ..., М, (10)
м _
2 авЛ+И^ = г₽;>0.
1=1
Беря эти же линейные комбинации уравнений прямой системы (1) и пола-
гая wQ = W — гр' > 0, мы получаем
N __ _ _ _
№>0, w0>0).
7=1
(И)
В частности, если система (1) имеет допустимое решение, то
min w = гр0 = 0. С другой стороны, если прямая задача допустимых реше-
ний не имеет, так что гро>О, то уравнение (11) становится несовместным
для неотрицательных переменных Xj. Это доказывает теорему 3(a).
Предположим теперь, что существует решение (Л1 = rcj, ..., Лм =
двойственной системы, удовлетворяющее
м
2 < с}, (j = 1, 2, ..., N)
i=i
(12)
м
2 Л*6г=1>°,
г=1
тогда двойственным соотношениям (12) удовлетворяет также и класс
решений Я1 = (nJ — 0oJ), лм = (лм — (Mr), v — v° + 0гго при любом
134
0 > О, поскольку из (12) и (10) получаем
м м _
2 (л? —0а?)аг> = 2
i=l i=l
(13)
м _
2 (л? — 0о°) bi = v° + 6w0 = v.
i=l
Предположим еще, что прямая задача недопустима, т. е. min w = гг0 > 0.
Тогда этот класс решений двойственной задачи обладает тем свойством,
что v — г° + 0гго -> оо при 0 -> оо, что и устанавливает теорему 2(6).
Наша задача теперь состоит в том, чтобы найти решение системы (8),
которое минимизирует z для некоторого специально выбранного значе-
ния РИ, начиная с последней канонической формы (конец этапа I). В каче-
стве такого значения W на этом шаге можно взять значение, использован-
ное нами вначале, либо любое другое PK>min w. Например, мы могли
бы переопределить Ж, положив его равным min w, как это обычно делается
на этапе II процедуры, и тогда значение гг' в канонической форме в конце
этапа I становится гг' = 0. Любой выбор W > min гг мы будем называть
этапом II задачи.
Если мы начинаем с этой канонической формы, то в силу теоремы 1 из
§ 6-1 существует последовательность ведущих операций, приводящих
эту форму к окончательной канонической форме, которая дает либо
решение, минимизирующее z, либо класс решений, для которых z -> — оо.
Рассмотрим сначала последний случай.
Во вспомогательной задаче случай z -> — оо может появиться только
тогда, когда некоторый столбец j = s в окончательной канонической
форме (полученной в конце этапа II) состоит из ai8 < 0 и с8 < 0. Заметим
теперь, что если искусственная переменная xn+i входит в последнее базис-
ное множество, то соответствующий коэффициент ai8 = 0, поскольку
в противном случае увеличение переменной х8 -> + оо, привело бы
к классу решений, для которых ->-|-со, что противоречило бы
нашему предположению гг = < W. В силу тех же причин
х8 не может совпадать ни с одной из искусственных переменных xN+^
следовательно, 1 < s < N. Заметим далее, что в окончательной канони-
ческой форме коэффициенты столбца s можно, очевидно, получить как
линейную комбинацию коэффициентов 1 в столбцах, соответствующих
базисным переменным х$ , х$ , ..., XjM; —w, —z с весами -\-ai8^ +a2s, • • •
. .. , +aMs; ds, c8 (потому что матрица из коэффициентов этих столбцов
состоит сплошь из нулей, за исключением диагонали). Представление
же в виде этой линейной комбинации должно выполняться не только
для соответствующих столбцов вспомогательной системы (8), но также
и для соответствующих столбцов исходной системы (1), потому что
веса ai8, соответствующие дополнительным столбцам системы (8), если
таковые имеются, равны нулю2. Это изображено в виде соотноше-
ния (14), являющегося удобной матричной записью. Матричная запись
1 Под линейной комбинацией столбцов мы понимаем столбец чисел, полученных
суммированием произведений соответствующих элементов столбцов на веса этих столб-
цов. См. гл. 8, где рассматриваются такие операции над вектор-столбцами.
2 Упражнение. Показать, что если некоторая линейная комбинация столбцов
линейной системы обращается в нуль до проведения ведущей операции, то она обратит-
ся в нуль и после ее проведения, и наоборот.
Упражнение. При каких условиях можно составлять линейные комбинации нера-
венств для получения нового нееравнства?
135
будет рассмотрена в гл. 8.
аи2 • • • «ьм 0 (а18 / «18 \
a2jl «2j<> • • • а2эм 0 0 «28 «28
. • — • (14)
ам12... aMjM 0 0 aMs аМз
0 0 ... 0 +1 0 &S 0
( Cjj сз2 • • сзм 0 + 1/ \с« / ( Св /
Применительно к коэффициентам 2-уравнения это дает, в частности,
соотношение + .. . + CjM«Ms + cs = cs. Поскольку
столбцы прямой системы находятся во взаимно однозначном соот-
ветствии с линейными неравенствами двойственной системы, из этого
и других соотношений вытекает, что если мы умножим неравенство ц
двойственной системы (2) на — «и>0, неравенство j2 на — a2s^ 0, . . .
. .неравенство jM на —aMs>0, неравенство j = s на +1 и затем про-
суммируем, то получим недопустимое неравенство
О-л1 + 0*л2+ ... + 0-лмcs (cs<0). (15)
Отсюда следует, что если для вспомогательной задачи z — оо, то двой-
ственная система недопустима.
Случай, когда нижняя граница z для вспомогательной задачи конеч-
на, возможен только тогда, когда в канонической форме, полученной для
*(8) в конце этапа II, коэффициенты 2-уравнения неотрицательны
2 + n^w'^z — z0 (cJ*>0, z0 — minz). (16)
j=i
С другой стороны, это уравнение можно получить непосредственно из (8),
если взять некоторую линейную комбинацию уравнений i = 1, 2, . . ., М
с весами — л*, w-yравнение с весом +л™ и z-y равнение с весом 1.
Поскольку в де-уравнении коэффициенты при Xj для / = 1, 2, . . ., N все
равны нулю, мы получили допустимое решение двойственной системы лг- =
= л*.
м
'%rfaij^ch (j = l, 2, ...,7V)
i=l
(17)
м
3 ^=2,+ ^ = »’.
i=l
Отсюда следует, что двойственная система допустима, если нижняя гра-
ница z конечна для любой вспомогательной задачи, каков бы ни был выбор
РИ>0. Таким образом, допустимость прямой системы зависит от резуль-
татов этапа I, а допустимость двойственной системы — от результатов
этапа II (и не зависит от результатов этапа I).
Если мы предположим, что двойственная система неравенств недо-
пустима, и поэтому z -> — оо для любого ТУ > О, то мы получим несовме-
стное неравенство (15). Таким образом, теорема 2 (б) доказана. Если
прямая задача также допустима и в начале этапа II мы положим W = О,
то в конце этапа II будет построен такой класс допустимых решений
136
прямой задачи, что значение 2 будет стремиться к — оо. Это доказывает
теорему 2 (а).
Пусть для прямой задачи существует допустимое решение, а на этапе
II взято W = 0. Предположим также, что для двойственной системы суще-
ствует допустимое решение, так что на этапе II достигается конечная
нижняя граница. Тогда, положив в (17) W = 0, мы убедимся в существо-
вании для обеих задач допустимых решений, для которых min z = z0 =
= г?*. Но любое, 2, связаное с допустимым решением прямой системы,
является верхней границей для v; следовательно,
max и = min z, (18)
что и доказывает теорему двойственности (теорема 1).
6-4. ОСНОВНЫЕ ТЕОРЕМЫ О ДВОЙСТВЕННОСТИ
Рассмотрим систему в стандартной форме. Сейчас мы сформулируем
и докажем следующие важные теоремы.
Теорема 1. Если (я*, . . ., х^, z*) — допустимое решение прямой зада-
чи, а (л*, . . ., Ям, v *) — допустимое решение двойственной задачи, для
которых
__ м м
с* = с}- 3 ntatj>0, ^ntbi = v*, (j = l, 2, (1)
1=1 1=1
то условие
c* = 0 для я*>0 (2)
является необходимым и достаточным для оптимальности обоих решений.
Теорема 2. Если для прямой задачи существует допустимое решение
и нижняя граница z конечна, то существует оптимальное допустимое
решение^
Теорема 3. Если для прямой задачи существует оптимальное допусти-
мое решение, то для двойственной задачи также существует оптимальное
допустимое решение.
Доказательство теоремы 1. Пусть Xj >0 —некоторое допустимое
решение, удовлетворяющее § 6-3 (1), а — любые значения перемен-
ных, для которых (см. § 6-3 (3)). Если первое уравнение из §6-3 (1)
умножить на второе на л2 и т. д. и взвешенную сумму первых М ура7
внений вычесть из 2-уравнения, то мы получим
+ С2^2 “Ь • • • + ~ Z — V. (3)
Поскольку мы предположили, что с7>0 и £/>0, левая часть равенст-
ва (3) неотрицательна и поэтому всегда
м
р= (4)
1=1
т. е. v является нижней границей z. Из условий теоремы 1 вытекает
существование некоторого допустимого решения х7 = ж*>0, 2 = 2*,
некоторых л^ = л* и таких величин с*, что с*= 0, если х* > 0.
Если подставить эти значения в (3), то произведения в левой части обра-
тятся в нуль и v * = 2 *. В силу § 6-3 (6) мы заключаем, что max v = v* =
— 2*= min 2.
137
Для доказательства необходимости условий теоремы 1 предположим,
что v * = z *. Подставляя это в (3), мы заключаем, что все члены в левой
части должны обратиться в нуль-, это означает, что с* =* 0, для х* > 0.
Доказательство теоремы 2. Доказательство этой теоремы было дано
в § 6-2. Оно непосредственно вытекает из применения симплекс-алгоритма
к введенной там вспомогательной задаче. Мы показали, что процесс закон-
чится за конечное число итераций, поскольку либо а) не существует
допустимого решения, либо б) можно построить класс допустимых реше-
ний, для которых z -> — оо, либо в) будет получено базисное оптималь-
ное допустимое решение Xj = х*. Поскольку в силу предположения
случаи а) и б) исключены, теорема доказана.
Доказательство теоремы 3. Воспользуемся вспомогательной задачей
§ 6-3 (8). Предположения теоремы 3 соответствуют тому случаю, когда
существует допустимое решение прямой задачи и минимум z конечен.
Следовательно, для двойственной задачи существуют оптимальные мно-
жители, именно л*, г?*, определяемые соотношениями § 6-3 (17), 6-3 (18).
ДОПОЛНЯЮЩАЯ НЕЖЕСТКОСТЬ В ПРЯМОЙ И ДВОЙСТВЕННОЙ
СИСТЕМАХ
Если прямая и двойственная системы записаны в виде систем нера-
венств, то теорема 1 приобретает более симметричный вид.
Пусть > 0произвольное допустимое решение, удовлетворяю-
щее § 6-2 (1), а г/г>0 — некоторое допустимое решение, удовлетворяю-
щее § 6-2 (2), а первую из упомянутых систем запишем в стандартной
форме: найти Xj 0, min z, удовлетворяющие системе
#11#! 4“ ^12^2 4“ • • • 4“ а1пхп — хп±1 = ^1»
^21^1 4“ а22Х2 4~ • • • 4- а2пХп — хп+2 = ^2>
...................................................... (5)
^mlxi 4~ &т2х2 4" • • • 4“ Ятпхп хп^т =
4- С2Х2 4- • • • 4- Спхп = Z (min),
где xn+i 0 суть переменные, характеризующие степень выполнения
неравенства или отрицательную нежесткость, между левой и правой
частями i-го неравенства.
Удобно будет также обозначить через ут+; переменную, измеряющую
положительную нежесткость в у-м неравенстве, у — 1, 2, . . ., п, двойствен-
ной системы. При этом система § 6-2 (2) в стандартной форме запишется
так: найти yt > 0, max г?, удовлетворяющие системе
а11У1 4" а21£/2 4“ • • • 4“ атпдУт + Ут+1 =
а 12У1 + а22У2 4- • • • 4- ат2Ут 4“ Ут+2 = с2»
........................................................ (6)
атУ1 4" а2пУ2 + • • • 4“ атпУт ^1У1 + 4- • •• + Ътут Умножая у-е уравнение системы (5) на yi4 i = 4- Ут±п — = v (max). = 1, 2, . .., т и вычитая их
138
сумму из z-формы, мы получаем
(т \ / т \ / т \
С1 — 3 ааУ1 + с2 — S ai2Vi «2+ • • • + I Сп — S а1пУ1 хп +
г=1 / \ г=1 / \ i=l /
+ Vl^n+l 4" У2^п+2 + • • • + Утхп+т — Z — 3 (7)
г=1
или на основании определения ym+j и г в (6), мы имеем
(Уш+1^1 + Ут+2Х2 + • • • + Ут+пхп) + (У1хп+1 + У2хп+2 + • • • + Упхп+т) = Z~V. (8)
Левая часть равенства (8) является суммой произведений неотрицательных
чисел, следовательно, 0<z — г?, или z?<z.
Поскольку мы предположили, что существуют решения прямой и двой-
ственной задач, условия теоремы двойственности выполнены и для обеих
систем существуют оптимальные решения. Докажем теперь следующую
теорему.
Теорема 4. Для оптимальных допустимых решений прямой и двой-
ственной систем всякий раз, когда в k-м соотношении одной из систем
свободная переменная отлична от нуля, к-я переменная в двойственной
к ней системе равна нулю', если к-я переменная в одной из систем поло-
жительна, то к-е соотношение в двойственной к ней системе является
равенством.
Доказательство. Пусть Xj = z*> 0 (/ = 1, 2, . . . , п), z — z *
и Уг — У*1 > 0 (i = 1, 2, .. ., т), v — v* — значения переменных в некото-
рых оптимальных решениях прямой и двойственной задач, a я£+г>0
и Ут+1> 0 — соответствующие значения свободных переменных, полу-
ченных из (5) и (6); тогда в силу основной теоремы z* — г?* =minz —
—max v — 0; поэтому правая часть равенства (8) обращается в нуль. Однако,
как было отмечено выше, каждый член в (8) неотрицателен и, следова-
тельно, все они должны быть равны нулю, т. е. y™+j х% = ® к yt xn+i = 0.
Далее, член y^+jX* является призведением значения свободной перемен-
ной /-го соотношения двойственной системы на значение соответствую-
щей ей переменной из прямой системы; аналогично член y*Xn+i является
произведением значения свободной переменной Z-го соотношения прямой
системы на значение соответствующей переменной двойственной системы.
Следовательно, если Ут+j >0, то х* = 0; аналогично, если х*+г >0,
то У* = 0. Это является переформулировкой теоремы 1 о соответствии
между оптимальным решением прямой системы и соответствующими
соотношениями между свободными переменными оптимального решения
двойственной системы.
ОДНОРОДНЫЕ СИСТЕМЫ
Имеется несколько важных теорем типа теоремы двойственности,
которые предвосхитили эру линейного программирования (Таккер [5]).
Самый ранний из известных результатов связан с допустимостью в одно-
родных системах (системы с нулевыми свободными членами).
Теорема 5 (Гордан [1]). Либо однородная система линейных урав-
нений имеет нетривиальное решение с неотрицательными значениями
переменных, либо существует уравнение, являющееся некоторой линейной
комбинацией остальных уравнений системы, причем все его коэффициенты
положительны.
139
Доказательство. Рассмотрим однородную систему для г = 1,2,... ,яг—1
2 = (^у^О). (9)
j=i
Если эта система имеет нетривиальное решение (т. е. не все Xj = 0), то
найдется и решение, удовлетворяющее условию
п
S^=i- (Ю)
;=1
Присоединим это уравнение в качестве иг-го к системе (9). В силу теоремы
о недопустимости (§6-3 теорема 3 (а)) либо существует допустимое решение,
либо существуют такие множители л4, л2, ..., что линейная
комбинация с этими множителями оказывается несовместным уравне-
нием с неотрицательными переменными:
2 djXj = — w0, где dj > 0, w0 > 0. (11>
j=i
Если имеет место вторая возможность, то лт = —w0 < 0 и
2 ЯцЛ$= dj 0. (у = 1, 2, . . ., м). (12}
1^1
Следовательно, если множители (ль л2, . . ., ят) используются для образо-
вания линейной комбинации уравнений, то все приведенные в (11) коэф-
фициенты полученного уравнения положительны.
Упражнение. Доказать утверждение, обратное теореме Гордана.
Именно если существует линейная комбинация, все коэффициенты кото-
рой положительны, то однородная система с неотрицательными перемен-
ными имеет только тривиальное решение.
Теорема 6 (лемма Фаркаша [1]). Если линейное однородное нера-
венство
3 (13)
г=1
выполняется для всех систем значений Kt, удовлетворяющих системе одно-
родных неравенств
т
(/ = 1, п), (14)
г—1
то неравенство (13) является неотрицательной линейной комбинацией
неравенств системы (14).
Доказательство. Предположим, что не существует неотрицательной
комбинации неравенств системы (14), которая дает (13). Тогда система
2 = (^7 0) (15}
j=l
несовместна. На основании теоремы 3(a) из § 6-3 существуют значения
Лг = л?, с помощью которых из (15) получается несовместное уравнение.
140
Коэффициентами этого уравнения будут
3 (j — 1, 2, ...,п)
1=1
(16)
2 btn.i=wo>o,
2=1
что противоречит (13).
Упражнение. Что является аналогом этой теоремы для систем линей-
ных уравнений?
Теорема 7 (Штимке [1]). Либо линейная однородная система имеет
решение, в котором все неизвестные имеют положительные значения, либо
существует линейная комбинация, все коэффициенты которой неотрица-
тельны, причем хотя бы один коэффициент положителен.
Доказательство. Если однородная система имеет строго положи-
тельное решение, то система
п
2 aijXj = Q, (i = l, 2,...,т)
3—1
(17)
1 (] = 1, 2, . . П)
также имеет решение. Заменяя на xj = x'j + 1, где x'j > 0, мы
получим систему
2 ai3Xj = — 2 «о- (хз > °) (18)
7=1 7=1
Согласно теореме 3 (а) из § 6-3, либо эта система имеет допустимое реше-
ние (первая возможность), либо существуют такие множители л2, . . .,
лт, что результирующая линейная комбинация
2 djXj— — w0 (dj>Q, +^о>О) (19)
7=1
является несовместным уравнением с неотрицательными переменными.
п
В последнем случае >0. Легко видеть также, что 2 = потому
7=1
что неотрицательная сумма коэффициентов каждого уравнения систе-
мы (18), из которых она получена, равна соответствующему свободному
члену. Отсюда вытекает, что по крайней мере один из коэффициентов dj
этого уравнения должен быть положительным (что является второй воз-
можностью).
ТЕОРЕМА МОЦКИНА О ТРАНСПОЗИЦИИ [1]
Рассмотрим двойственные задачи линейного программирования, укла-
дывающиеся в схему Таккера (20). Мы предполагаем, что все столбцы
ненулевые. Рассмотрим Произвольное подмножество, состоящее из к столб-
цов; пусть это будут, например, первые к столбцов, расположенных
в (20) слева от вертикальной пунктирной линии.
141
Прямая
Переменные xi 0, ... жА+1>°- .. x_ 0 71 Свободные члены
ап aik alk+l ain = 0
и2 а21 a2k a2k+l a2n = 0
Двой- ствен- ит атп1 amk amk+i > • °mn = 0
ная Соотношения < ...
Свободные 0 . 0 0 . 0
члены
(20)
Теорема 8. Либо для двойственной системы существует такое реше-
ние, что все неравенства, соответствующие выбранному подмножеству,
будут строгими, либо же прямая система имеет такое решение, что по
крайней мере одна соответствующая переменная положительна.
Доказательство. Если существует решение прямой системы с тре-
буемым свойством, то существует и такое решение, что
Х1 + х2 + • • • + xk == 11
(21)
где / — 1, 2, . . ., й определяет заданное подмножество. Оставшаяся часть
доказательства аналогична доказательству теоремы 5.
ТЕОРЕМА ОБ АЛЬТЕРНАТИВАХ ДЛЯ МАТРИЦ (БИЛЛЬ [1])
Рассмотрим двойственные однородные задачи линейного програм-
мирования без целевых форм г.
%аих}>0, Xj>0 (i=l,2, .. .,т) (22)
j=i
и
т
yt>0. (7 = 1,2, .. .,п) (23)
i=l
Одну из этих систем будем считать прямой, а другую двойственной.
Теорема 9. Либо существует решение прямой системы, где все нера-
венства строгие, либо существует нетривиальное решение двойствен-
ной системы.
Упражнение. Показать, что эта теорема является частным случаем
теоремы о транспозиции, если в прямую систему ввести свободные пере-
менные.
Упражнение. Даны два решения однородной системы (22); показать,
что сумма соответствующих их значений также является решением.
1 Здесь уместнее говорить не о задачах линейного программирования, а о двой-
ственных системах линейных неравенств.— Прим. ред.
142
Упражнение. Предположим, что однородная система неравенств име-
ет решение, обращающее все неравенства в точные равенства. Показать,
что тогда будет существовать решение системы неравенств, у которой все
нулевые свободные члены заменены единицами.
ТЕОРЕМА ТАККЕРА О ДОПОЛНЯЮЩЕЙ НЕЖЕСТКОСТИ [5]
Продуманное применение теоремы о транспозиции позволяет полу-
чить более тонкую форму теоремы об альтернативах.
Теорема 10. Существуют такие решения однородных двойственных
задач линейного программирования (22) и (23), что каждая переменная
и дополняющая ее свободная переменная принимают одно положитель-
ное и одно нулевое значение.
Доказательство. Расширим системы введением свободных пере-
менных так, как это было сделано с системами (5) и (6). Выделим в пря-
мой системе подмножество, содержащее только одну свободную пере-
менную яп+р. В, силу теоремы 8 можно найти такое решение, что либо для
прямой системы хп+р >0, либо для двойственной системы ур >0.
Пусть решение прямой системы таково, что хп+р >0 и Xj ~ х% для
j = 1, 2, ..., п, . . ., n-j-m суть это решение, a yt = у? = 0 для
i — 1, 2, ..., тп,..., т + п — соответствующее (тривиальное) решение двой-
ственной системы. С другой стороны, пусть существует решение двойствен-
ной системы с ур >0; значениями yi для этого решения оказываются
уг = у®, а соответствующее (тривиальное) решение прямой задачи
есть Xj = х? = 0. Если мы теперь сложим соответствующие значения
и у® для различных р, то мы получим пару «составных» решений пря-
мой и двойственной систем, причем для таких решений каждая свобод-
ная переменная прямой системы или соответствующая переменная двой-
ственной системы положительна.
Если поменять ролями прямую и двойственную системы, то можно
получить и другую пару составных решений, обладающих тем свойством,
что каждая переменная (исходной) прямой системы или соответствующая
ей переменная двойственной системы положительна. Это дает решения,
обладающие тем свойством, что по крайней мере один член из каждой
пары соответствующих друг другу чисел положителен. Для завершения
доказательства теоремы 10 остается выполнить следующее.
Упражнение. Пользуясь равенством (8), показать, что в случае
однородности (все Ъг = 0, Cj = 0) каждое решение прямой и двойствен-
ной систем является оптимальным, а произведения всех дополняющих
пар равны нулю.
6-5. МНОЖИТЕЛИ ЛАГРАНЖА
Двойственные системы могут возникнуть и на другом пути. Если мы
хотим, пользуясь дифференциальным исчислением, минимизировать функ-
цию z двух переменных
F(Xi, x2) = z (1)
при условии
G(xb х2) = 0, (2)
наложенном на переменные Xi и х2, то стандартная процедура математи-
ческого анализа состоит в нахождении абсолютного минимума функции Z,
143
которая определяется как разность
Z = F(^b — ж2), (3)
где л — параметр, называемый множителем Лагранжа. Смысл этого
параметра будет определен далее. Если абсолютный минимум функции Z
достигается при некотором значении л = л° и тех rq — zj, х2 —
которые удовлетворяют уравнению (2), то ясно, что эти же значения мини-
мизируют функцию (1) при условии (2), поскольку для всех (xl9 х2), удо-
влетворяющих (2) Z = z. Предположим, что можно найти такое значение л,
которое минимизирует Z, и что частные производные по хи и х2 функции Z
в точке абсолютного минимума обращаются в нуль. Это дает для неизвест-
ных Xi и х2 два уравнения, из которых можно найти xt и х2, выраженные
через л. Значение л получается после подстановки найденных значений
Xi и х2 в (2); иными словами, значение л выбирается так, чтобы решение,
доставляющее абсолютный минимум, удовлетворяло условию (2).
Найдем, например, на единичной окружности точку (xi, я2), сумма
координат которой минимальна:
Х1 +Ж2= 1,
(4)
Я1 + *2 = *-
Рассмотрим абсолютный минимум функции
Z = (Xi-|-a:2) —л(^ + ж| —1). (5)
В точке абсолютного минимума частные производные Z по xt и х2 обра-
щаются в нуль:
Д = 0: 1- 2ж1л = 0,
(6)
^ = 0: l-2z2it = 0.
1 1
Отсюда мы получаем минимизирующее решение: xt = —, х2 = — .
Определим теперь значение л так, чтобы это решение удовлетворяло
уравнению окружности; подстановка дает нам

(7)
или л = ±]Л2/2, откуда (1:1 = 1/]/'2, ж2 = 1/|Л2),
или (#1 = — 1/]/"2, х2 — — 1/1/~2). Первое решение максимизирует сум-
му координат, а второе (искомое решение) минимизирует ее.
Такой же процесс используется и в общем случае, если задача состо-
ит в отыскании значений х^ я2, .. ., которые минимизируют
х2,..., xn)~z и удовлетворяют к уравнениям связи
х2, .. .,Яд) = 0,
G2 (xj, ж2, ..., жп) = 0,
(8)
G& (#i, х2, ..., — 0.
В этом случае надлежит находить абсолютный минимум функции
Z = F (хь я2, ..., [л^С^ (xj, х2, ..., жп) -f- л2С2 (хи х2. .. -, Хп) +
+ •. - + ЛдСд (х4,\ ж2, ..., Жд)], (9)
144
где множители Лагранжа л$ суть неопределенные постоянные, которые
будут определены ниже. Предполагается, что можно найти такие значе-
ния ль что решение, доставляющее абсолютный минимум, удовлетворяет
уравнениям связи. Решая п уравнений, полученных в результате при-
равнивания пчастных производных функции (9) нулю, выразим xlf х2,.. .
..хп через Л1, л2, ..., Лд. Эти значения подставляются в к выражений
Gi (Xi, я2, ..., хп) = 0, и полученные к уравнений решаются относитель-
но Л^, Л2, • • • Лд.
В качестве примера рассмотрим задачу линейного программирования
х±2#2 + = 6, О, х2^0, x^^Q) (19)
xi + х2 + хз = 2 (min).
Эта задача эквивалентна системе с произвольными вещественными
переменными я2, я3 и с квадратами вещественных переменных щ, и2, и3г.
Множители Лагранжа
X1 = 0 : с^
ж2 — = 0 *• с2,
хз — и! = 0 О • С3> (11)
+ 2х2 + Зя3 = 6 : л,
+ я2 + я3 = z(min),
где первые три уравнения заменяют ограничения на знак переменных.
Найдем теперь абсолютный минимум выражения
Z = (хг + Х2 + Я3) — Ci (Xi — и[) — с2 (х2 — ul) —
— Сз(х3 —ttj) —л(Ж1 + 2ж2 + Зж3 —6), (12)
или _ __
Z = 6л 4~ (1—л—^i) xi 4“ (1 ““ 2л —- с2) х2 “Н (1 — Зл сз) х% 4“
+ 4-^2^2 ^змз- (13)
Приравнивая шесть частных производных нулю, мы после несложных
преобразований получаем
Ci = 1 — л, clul = Q,
’ е2=1— 2л, с2и2 = 0, (14)
с3 = 1 —Зл, с3и3 = 0.
К этим соотношениям можно при желании добавить условия, гарантирую-
щие существование минимума
с2 0, £3^0, (13)
поскольку очевидно, что функция Z не имеет абсолютного минимума,
если коэффициенты Cj при и} в (13) отрицательны.
В этом случае, если мы попытаемся выразить явно Xj и Uj через множи-
тели Лагранжа, мы столкнемся с неприятностями — членов, содержащих
Xj, нет; кроме того, для каждого / имеются две возможности: либо Cj = О,
либо Uj = 0. Вспоминая, что Xj = и], мы можем заменить условие
Cj Uj = 0 на Cj Xj — 0, откуда либо Cj — 0, либо xj = 0. Поскольку j = 1,
1 Квадраты выражают здесь неотрицательность.— Прим. ред.
10 Дж. Данциг 145
2, 3, нам потребуется рассмотреть 23 различных вариантов; в общем слу
чае для задачи линейного программирования потребуются, как мы уви-
дим, рассмотреть 2п различных вариантов. В силу (15) условия существо-
вания минимума, которым должны удовлетворить множители Лагранжа,
можно переписать так: найти такие Xi, Cj, i = 1, 2, 3, что
(а) х4>0, я2>0, удовлетворяют Xi~\-2x2-\-3x3 = &,
' Ci= 1— л,
(б) с4>0, с2>0, с3>0, удовлетворяют с2 = 1 —2л, (16)
1 с3 = 1—Зя,
(в) ctXi = 0, с2х2 — 0, с3х3 = 0.
Для общей задачи линейного программирования, заключающейся
в отыскании Xj > 0 и min z, удовлетворяющих уравнениям
а11х1 + а12ж2 4“ • • • 4“ а1пхп — ^1,
#21^1 4" &22Х2 + • • • 4~ = ^2i
............................................ (17)
атп1х1 + ат2х2 4" • • • 4“ атпхп = Ьт,
0^ + 0^+ . . . +cnXn = Z,
заменим условия неотрицательности на равенства
Xj — Uj = Q (/ = 1, 2, ...,п) (18)
и попытаемся найти абсолютный минимум выражения
n г / П \ I п
Z = 2 Cjxj I ^1 | 2 ^ljxj ^1)4“ • • • 4" I 2 ^тп]Х] Ьт
7=1 L \7=1] / \ 7=1
— [С1(Х1 — *4)4- ... +cn(xn — ul)], (19)
или
Z = I 2 / 4- I Cl 2 Ci j Xf 4~ • • • 4- I Cn 2 ^i^in Cn I Xn 4“
\i=l / \ i=l / \ i=l J
4“ ^iKi 4“ c2u^ 4"... 4~ cnUn. (20)
Функция Z не имеет абсолютного минимума, если а) коэффициенты при
xj равны нулю и б) коэффициенты при и} неотрицательны; следовательно,
мы можем к тому же при желании потребовать, чтобы множители и е7
для /=1, 2, . . ., п удовлетворяли соотношению
Cj Cj 4“ ^2^27 4“ • • • 4“ ^m^mjl 0. (21)
Кроме того, в точке абсолютного минимума частные производные по Uj
должны также обращаться в нуль; поэтому
c-Uj = 0, или CjXj = 0 (7 = 1, 2, ... п). (22)
Если для фиксированных л, = л* существуют Cj, удовлетворяющие (21),
и Uj или Xj = и], удовлетворяющие (22), то в (20), очевидно, мы получим
7П
2 я*bt- Тем самым нами будет получен истинный (глобальный) минимум
1
(исключая возможность локального минимума, см. рис. 7-1-VII). Посколь-
146
ку Z = z для любых Xj — и] из, удовлетворяющих системе (17), нами
установлена
Теорема L Если существуют множители (я< = л*) и (cj = с*),
удовлетворяющие (21), и значения переменных (Xj = я*>0, и z = z*),
удовлетворяющие (17), причем с*х* = 0 для всех j, то (х*, х£, х%, z*)
является минимизирующим решением.
ЗАКЛЮЧЕНИЕ
Если к задаче линейного программирования применить метод мно-
жителей Лагранжа, то мы найдем, что эти множители, если они существу-
ют, должны удовлетворять «двойственной» системе — именно они должны
удовлетворять системе линейных неравенств (21) и максимизировать
форму v — 5 be, при этом должны выполняться условия (22) (см. § 6-4,
теорема 1). Множители Cj (или относительные оценки) обладают также тем
свойством, что CjXj = 0 для j — 1, 2, . . ., п. Последнее дает нам 2П воз-
можных случаев: либо Cj — 0, либо Xj = 0. Именно, поэтому метод мно-
жителей Лагранжа оказывается несостоятельным, поскольку для боль-
ших п рассмотрение всех 2П случаев практически неосуществимо.
В некотором смысле симплекс-метод можно рассматривать как метод
систематического исключения большинства таких случаев и рассмотре-
ния лишь немногих. Действительно, число рассматриваемых случаев
ограничивается сразу же теми, для которых количество Xj = 0 всегда
равно п — т, определитель из оставшихся т переменных отличен от
нуля, а единственные значения этих переменных положительны (в усло-
виях невырожденности). Условия CjXj = 0 означают, что Cj = 0 для
Xj >0, и это единственным образом определяет как Л/, так и оставшиеся Cj.
Если не все Cj 0, то этот случай опускается и на следующей итерации
проверяется новый, специальным образом построенный случай и т. д.
6-6. ЗАДАЧИ
1. Доказать, что оптимальное решение двойственной системы не будет
единственным, если оптимальное базисное решение в прямой задаче выро-
ждено, а в двойственной — нет.
2. Показать, что о? = 0 для i = 1, 2, . . ., М, если в конце этапа I
все искусственные переменные исключены (см. § 6-3 (10)).
3. Доказать, что если невырожденное оптимальное базисное допу-
стимое решение единственно, то единственны и оптимальные множители л,-
в двойственной задаче (см. § 6-3).
4. Доказать, что если в конце этапа I в базисном решении нет иных
искусственных переменных, кроме w' (см. § 6-3 (И)), то все dj = 0.
5. Показать, что задача, двойственная к двойственной, совпадает
с прямой, если предварительно изменить все знаки в (§ 6-2 (2)) на проти-
воположные, с тем чтобы для нахождения двойственной записать систе-
му (§ 6-2 (2)) в стандартной форме неравенств.
6. Определим «двойственную» систему так: транспонируем матрицу
и изменим знак ее элементов, поменяв (и изменив их знаки) ролями сво-
бодные члены и коэффициенты целевой формы. При этом сохраним знаки
неравенства и условие минимизации. Показать, что при таком определе-
нии доказательство утверждения «двойственная двойственной системы
совпадает с прямой системой» получается сразу. Показать, что это опре-
деление двойственной системы эквивалентно определению из § 6-2.
147
10*
1. Показать, что ни прямая система, ни двойственная ей не имеют
допустимого решения.
— х2>2 (^>0, я2>0),
— Ж1 + ^2> —1,
xi — 2x2 = z (min).
8. Построить другие примеры, иллюстрирующие все четыре случая
допустимости и недопустимости в прямой и двойственной системах.
9. Могут ли иметь решения прямая и двойственная задачи (§ 6-3(1)),
(§6-3(2)), если отбросить ограничения Я;>0, ^>0и если известно, что
не существует решений, когда эти ограничения имеются?
10. Доказать в общем случае, что уравнение из прямой системы
соответствует в двойственной системе переменной, для которой нет огра-
ничений на знак, а переменная, для которой нет ограничения на знак,
соответствует уравнению.
И. Предположим, что 2°, я£>*0, х\ >0, ..., >0 и xk+i = ...==
= х^п = 0 является допустимым решением задачи линейного програм-
мирования. Пусть каноническая форма для подсистемы, полученной
в результате вычеркивания переменных xk+i, .. ., хп, имеет менее к урав-
нений; показать, что можно образовать новое решение, содержащее
меньшее количество переменных с положительными значениями, для
которого значение z будет не больше 2°. Показать, что этот процесс можно
повторять до получения подсистемы, в которой будет столько же перемен-
ных с положительными значениями, как и в ее канонической форме.
Показать, что это решение единственно, если все другие переменные
равны нулю.
12. Применить результаты задачи 11 для прямого доказательства
следующего утверждения: если существует допустимое решение задачи
линейного программирования и значения величины z ограничены снизу,
то существует также и оптимальное допустимое решение.
13. Предположив, что лемма Фаркаша справедлива, получить теорему
двойственности.
14. а) Рассмотрим следующую «игровую» задачу: найти у7>0 и
minAf, удовлетворяющие условиям:
п
%yj = i (i = l, 2, ...,тп),
* 2 аиУ1 М.
;=1
Показать, что двойственная задача состоит в отыскании таких > 0
и maxTV, которые удовлетворяют соотношениям:
т
3 xt = i,
г=1
т
г=1
т п
б) Доказать, что #<2 2 х1аиУ1^М и maxTV = minМ.
г=1 j=l
в) Доказать, что в прямой и двойственной системах всегда существу-
ют допустимые решения.
148
г) Почему положителен max7V=minM, если все >0? Примене-
ние систем этого типа см. в гл. 13.
15. Сформулировать задачу, двойственную к задаче линейного про-
граммирования с ограниченными переменными.
(/ = 1, 2, ...,п)
п
2 a^Xj — bi (i = 1, 2, ..., тп),
;=i
п
2 CjXj = z (min).
j=i
16. Метод исключения Фурье — Моцкина позволяет выводить пере-
менную, увеличивая при этом количество неравенств.
Построить двойственную процедуру для уменьшения числа неравенств
за счет увеличения числа переменных.
17. Предположим, что для данной целевой формы z оптимальное
решение не единственно и желательно ввести еще одну целевую форму z *,
которую надо минимизировать при заданном минимальном значении 2.
Показать, что существует оптимальное решение, которое является базис-
ным для системы ограничений, включающей формы z и z *. Доказать,
что это решение можно получить, опуская сначала все такие перемен-
ные ж;, что Cj >0 в конце этапа II, и подставляя затем форму z * вме-
сто формы 2.
18. Обобщить обычные этапы I и II, во-первых, для нахождения
решения, являющегося наиболее «допустимым» (min w) (при этом решение
может быть как единственным, так и не единственным), и, во-вторых, для
нахождения решения, минимизирующего z при условии, что w = min w.
19. Показать, что z не может стремиться к — оо, если никакая поло-
жительная комбинация технологических процессов не обращается в нуль.
Обсудить, что практически означает обращение в нуль положительной
комбинации при условии, что стоимость положительна, отрицательна или
равна нулю. Показать, что существует однородное допустимое решение
системы, если z —— оо. Показать, что для одной и той же системы воз-
можно, ЧТО 2 —>+ оо и 2 —* ОО.
20. Обобщить этап I процедуры так, чтобы можно было использовать
искусственные переменные любого знака. Ввести в рассмотрение перемен-
ную, которая увеличивается, пока сумма абсолютных значений искус-
ственных переменных убывает.
21. Пусть существует оптимальное решение ^>0, 2 = 2°= min 2.
Доказать избыточность системы уравнений, которая получится, если
опустить все те х^ для которых = 0, и положить z 2°.
22. Верно ли, что из существования в исходной таблице столбца
с отрицательными элементами вытекает (если существуют допустимые
решения) существование класса решений, для которого z ->— оо?
Глава 7
ГЕОМЕТРИЯ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
7-1. ВЫПУКЛЫЕ ОБЛАСТИ
ВЫПУКЛЫЕ ДВУМЕРНЫЕ ОБЛАСТИ
Множество точек я2)> удовлетворяющих неравенству
£i + x2^2, (1)
образует в двумерном пространстве область, расположенную по одну
сторону от прямой (см. рис. 7-1-1а)
X|-f-X2 = 2. (2)
Эта область является примером выпуклой области, или, что то же самое,
выпуклого множества точек. Область внутри угла между двумя прямыми,
рис. 7-1-16, также является выпуклым множеством.
Рис. 7-1-16.
Другие примеры выпуклых множеств в двумерном пространстве —
это области, заключенные внутри прямоугольника, рис. 7-1-Па, внутри
круга, рис. 7-1-Пб, или многоугольника, рис. 7-1-Пв.
Рис. 7-1-Па. Рис. 7-1-Пб. Рис. 7-1-Пв.
В трехмерном случае часть пространства, заключенная внутри куба
или сферы, также представляет собой выпуклое множество. Выпуклые
области могут как включать, так и не включать свою границу. Они могут
быть ограниченными или неограниченными.
150
Напротив, заштрихованные области на рис. 7-1-Ша, Шб, Шв, не
являются выпуклыми множествами. .
Р и с. 7-1-Ша. Рис. 7-1-Шб, Рис. 7-1-Шв.
Определение. Множество называется выпуклым, если все точки отрез-
ка, соединяющего две произвольные точки множества, принадлежат
этому множеству.
Определение. Множество называется замкнутым, если оно содержит
свою границу. (Например, выпуклым замкнутым множеством оказывается
множество, состоящее из окружности и области внутри нее, внутренность
круга является выпуклым, но не замкнутым множеством.)
Таким образом, L-образная область на рис. 7-1-Ша не является
выпуклым множеством, потому что в этом множестве можно найти такие
две точки, например р и q, что не все точки соединяющего их отрезка
принадлежат этому множеству.
Теорема 1. Множество точек, принадлежащих одновременно двум
или более выпуклым множествам, выпукло.
Например, выпуклым множеством будет общая часть двух кругов,
рис. 7-I-IVa, а также множество точек, лежащих в пересечении двух или
Рис. 7-1-IV6.
Рис. 7-1-IVa.
более областей, определяемых линейными неравенствами, рис. 7-1-IV6,
IVb и рис. 7-1-16, Ив. ,В § 4-3 выпуклыми являются множества допусти-
мых решений, которые образованы с помощью последовательно добавля-
емых ограничений (§ 4-3—(1), рис. 4-3-1 и следующие).
Доказательство. Пусть С и С" —два выпуклых множества, a R —
множество точек, общих для С и С" (см. рис. 7-1-УЬ Возьмем произволь-
151
ные точки р и q из R. Поскольку точки р и q принадлежат множеству (7,
а С — выпукло, отрезок, соединяющий р и д, должен принадлежать мно-
жеству С; в силу тех же причин этот отрезок должен принадлежать и мно-
жеству С". Но отрезок, лежащий и в (7, и в С', принадлежит R.
Упражнение. Распространить доказательство на случай более чем
двух выпуклых множеств.
ВЫПУКЛЫЕ ОБЛАСТИ (ОБЩИЙ СЛУЧАЙ)
Поскольку в линейном программировании мы будем рассматривать
линейные неравенства со многими переменными, наглядно представить
себе решение как точку в многомерном пространстве невозможно. Поэто-
му мы должны уметь узнавать, является ли то или иное множество выпук-
лым, алгебраически. По определению, для выпуклости множества тре-
буется, чтобы все точки отрезка, соединяющего две произвольные точки
множества, принадлежали этому множеству. Необходимо определить, что
такое в общем случае «точка» и «отрезок».
Определение. Точкой х в n-мерном пространстве называется упоря-
доченное множество 1 * п чисел или координат (жь я2, Координаты
точки х мы будем называть также компонентами х.
Определение. Отрезком, соединяющим две точки р и q в п-мерном
пространстве, имеющие соответственно координаты (рь р2, ..., рп)
и (<7i, #2, •••, называется множество точек с координатами
+ —X) qu
^2 = ^Р2 + (1 — #2» (3)
= + K)qn,
где % — параметр, Рассмотрим, например, в двумерном про-
странстве две точки: р = (6,2) и q = (1,4). Они изображены геометрически
на рис. 7-1-VI. Теперь рассмотрим точку х с ко-
ординатами (xi, я2). По определению, если х при-
q=(1A) надлежит отрезку, соединяющему р и q, то
- Х1 ==\Р1 + (1 — Qi = 6Х +1 (1—Х) = 5Х + 1,
^^•Р=(6,2) , ж2 = Хр2+(1 —Х)д2 = 2% + 4(1-Х)=-2% + 4. 1 7
...............Например, пусть X = 1, тогда xt = 6 и х2 = 2 и
точка х совпадает с точкой р. Аналогично при
Рис. 7-1-VI....% = 0 мы имеем х — q. Для других значений
% (0 < % < 1) мы получаем все точки между р и q.
Например, при % = */2 точка х имеет координаты = 7 /2, х2 = 3, которые
являются координатами середины отрезка, соединяющего р и q.
Упражнение. Получить линейное уравнение, связывающее Xi и х2,
исключив А из системы (4).
Пользуясь определением отрезка, можно выяснить, является ли
данное множество выпуклым. Рассмотрим, например, область R, коор-
1 Лучше было бы сказать «система чисел», потому что некоторые координаты од-
ной и той же точки могут быть численно равны друг другу.— Прим. ред.
динаты точек которой удовлетворяют неравенству
х, >2
Чтобы доказать выпуклость этой области, рассмотрим две произвольные
точки р = (рп р2) и q = (gt, g2) из R. Поскольку р и q взяты из области Rr
их координаты должны удовлетворять неравенству (5); следовательно,
Pi + Рг > 2,
<7i + <?2>2. (6}»
Тогда координаты^, х2) произвольной точки х отрезка, соединяющего точ-
ки р и д, находятся как взвешенная комбинация координат этих двух
точек, как это видно из (7) и (8).
• Р=(Р1, р2),
• ® = —A.)g1? Хр2 + (1— 92L (7)*
" Q = (?ь 9г),
где X равно отношению расстояний xq и pq. Используя векторное обозна-
чение (более подробно оно будет изучено в § 8-2), одновременное «взве-
шивание» соответствующих координат точек р и q можно переписать,
компактно х = Кр + (1 — X) д, что означает
Я1 = Ар1 + (1 — Х)£1, (0<А<1)
(8).
ж2 — Кр2 -f- (1 — X) q2.
Чтобы доказать выпуклость множества, определяемого неравенством (5)„.
нам необходимо показать, что точка х принадлежит этому множеству R.
А это означает, что координаты х должны удовлетворять неравенству
Xi + я2 >2. Иными словами, нужно показать, что
kPi + (1 —“ Qi + ^р2 + (1 ~ 2. (9)л
Для доказательства этого утверждения умножим первое неравенство из (6)>
на А>0, а второе на 1—Х>0 и получим неравенства
-f- Кр2 2Х,
(10>
(1-Х)£1 + (1-Х) g2>2(l—X).
Сложив эти два неравенства, мы получим неравенство (9), которое и уста-
навливает выпуклость множества R.
ВЫПУКЛОСТЬ ОБЛАСТЕЙ, ОПРЕДЕЛЯЕМЫХ ЛИНЕЙНЫМИ
НЕРАВЕНСТВАМИ И УРАВНЕНИЯМИ
Множество всех точек в n-мерном пространстве, координаты которых
удовлетворяют линейному уравнению
«1^1 + «2^2 + . • • + ап^п = b9 (Ну
153
называется гиперплоскостью, а множество всех точек, координаты которых
удовлетворяют линейному неравенству
+ а2х2 + .., + апхп < Ь, (12)
называется полупространством, или, точнее, замкнутым полупростран-
ством, поскольку оно содержит собственную границу. (В двумерном
пространстве такое множество называется полуплоскостью.)
Чтобы доказать выпуклость полупространства, определяемого линей-
ным неравенством, возьмем две точки р и q из этого множества; для
них будем иметь:
а1Р1 + а2Р2 4" ’ • • 4" апРп !(13а)
alQl + a2#2~b • • • 4" (136)
Пусть 0X 1 — значение параметра, связанного с некоторой точкой х
на отрезке, соединяющем точки р и q.
Умножая неравенство (13а) на А>0, а неравенство (136) на (1—Х)>0
и складывая, получаем
+ (1 — Л) #1] + а2 [Хр2 + (1 — £2] + • • • + ап [A/Pn + (1 — ^) Ь,
(14)
или, подставляя из (3) xt = kpt + (1 — X)gf, мы имеем
«1^1 + а2х2 + ... + апхп < Ь. (15)
Следовательно, произвольная точка отрезка, соединяющего любые две
точки полупространства, лежит в этом же полупространстве, что и дока-
зывает его выпуклость.
Чтобы доказать выпуклость гиперплоскости, перепишем уравне-
ние (11) следующим образом:
+ ^2Х2 + • » t 4“ апхп
(16)
«й + «2^2 + ’•••+ ^пхп > Ь.
Каждое из этих неравенств определяет полупространство, а их пересечение
определяет гиперплоскость. Поскольку полупространства выпуклы, по
теореме 1 гиперплоскость также является выпуклым множеством. В п-мер-
ном пространстве может быть много таких выпуклых множеств. По теоре-
ме 1 их пересечение является выпуклым множеством.
Определение. Выпуклым многогранником называется пересечение
одного или более полупространств. В частности, выпуклым многоуголь-
ником называется пересечение одной или более полуплоскостей.
ВЫПУКЛОСТЬ МНОЖЕСТВА ДОПУСТИМЫХ И ОПТИМАЛЬНЫХ
ДОПУСТИМЫХ РЕШЕНИЙ
Рассмотрим теперь общую задачу линейного программирования,
описываемую системой
^12^2 4" • • • + ainxn —^i, (Xj^O)
^21^1 4“ ^22^2 4“ • • • 4" a2nxn = Ъ2, (17)
amixl + Um2x2 4” * • • 4" ^mnxn — (18)
clxl 4“ C2X2 4“ • • • 4" cnxn z — Q,
причем z подлежит минимизации. Нами только что установлена
154
Теорема 2. Множество точек, соответствующих допустимым (или
оптимальным допустимым) решениям общей задачи линейного програм-
мирования, является выпуклым множеством.
Следовательно, если р = (pi9 р2, ..., рп, zp) — какое-то допустимое
решение, a q — (gb q2, ..., gn, zg) — другое допустимое решение, то их
взвешенная линейная комбинация
+ %Рп + (1 — A,)gn; %zP + (l— k)zq], (19)
где X фиксировано, также является допустимым решением.
(Кратко это решение можно^црисать так: + — X) q.) Более того,
при фиксированном значении z, скажем z =' zQ, множество точек, удо-
влетворяющих системе (17), (18) и z = z0, тоже оказывается выпуклым.
В частности, при z0 = min z, очевидно, выпуклым множеством будет
также и множество минимальных допустимых решений.
ЛОКАЛЬНОЕ МИНИМАЛЬНОЕ РЕШЕНИЕ ЯВЛЯЕТСЯ ГЛОБАЛЬНЫМ
Как известно из математического анализа, минимум (или максимум)
непрерывно дифференцируемой функции достигается при том значении
переменной х, при котором обращается в нуль производная. Это может
быть точка типа х = х^ на рис. 7-1-VII, в которой значение функции f(x)
является минимальным в окрестности точки х^, такой минимум называется
локальным. Заметим, однако, что в данном случае имеется и другой локаль-
ный минимум в точке х = х2, где f (х) достигает своего наименьшего зна-
чения; этот минимум называется глобальным. Для задач линейного про-
граммирования любое локальное минимальное решение является также
и истинным (или глобальным) минимальным решением. Чтобы убедиться
в этом, рассмотрим локальное минимальное решение р = (pi, Pz, •••
..., рп, zp) и предположим, что оно не является истинным минимальным
решением, т. е. что существует другое решение q = (qi9 q2, . . ., qn, zq),
для которого zp >zq. Тогда любая точка х~ (xi9 х2. . . ., Хп, z) на отрезке,
соединяющем эти две точки, является допустимым решением и z = Xzp 4-
+ (1—K)zq. В этом случае значения z непрерывно убывают от zp до zq
и поэтому все точки отрезка, соединяющего р и q (включая точки окрест-
ности р), соответствующие допустимым решениям, имеют значения z
меньше zp. Следовательно, нельзя одновременно иметь локальные мини-
мумы в точках р и q, с тем чтобы при этом было zp Z>zq. Это означает, что
zp^.zq для всех q; поэтому zp является истинным (глобальным) мини-
мальным значением.
Определение. Функция / (а?±, х2, . . ., хп) называется выпуклой функци-
ей, если 1) она определена на выпуклом множестве С точек р = (х19 х2, . . .
..., хп) и 2) множество С точек п-\- 1-мерного пространства р = (xi9 х2, . . .
155
. . Xn, z), ДЛЯ которых Z>f (Xi, Х2> • • *j яп) является выпуклым.
Например, функция / (х) = х2 оказывается выпуклой, потому что
выпукло множество точек (я, z), для которых z>£2 (см. рис. 7-1-VIII).
Свойства выпуклых функций. Если взять любые две точки х' =
= (х[, х*, ..., Жп) и х" = (а£, х*, ..., Хп) из выпуклого множества (7, на
котором определена выпуклая функция f (x) = f (rq, х2, ...» хп), то для
Рис. 7-1-VIII. Кривая z — f (z) называется
выпуклой, если неравенство z > / (z) опреде-
ляет выпуклое множество.
произвольной точки х* отрезка, соединяющего точки х’ и я", т. е. для
точки х * = Kxf + (1—А) я", где O^A^l, будет выполнено неравенство
X/(ж') + (1 — X) / (ж") >/(ж*). (20)
Чтобы доказать это, рассмотрим две точки р'— (xv x'v ..., х^, z')
и рп = (х", я", ..., х"п*, z"), где z' = / (ж'), z' — f (х"). Точка р* = (я*, х*, ...
..., Хп\ z*), где z* = Xz'+ (1 — X) z", принадлежит выпуклому множеству
Си z*>f (я*), так как, по определению, для всех точек выпуклого
множества С с первыми п координатами х = х* координата z не меньше,
чем / (гг*). Геометрически неравенство (20) означает, что если f (х*) явля-
ется выпуклой функцией, то координата z точки q=[x*, х*, ..., х*;
f (ж*)] никогда не может располагаться выше, чем р* (см. рис. 7-1-VIII).
Упражнение. Показать, что функция f (х) не будет выпуклой, если
неравенство (20) нарушается хотя бы для двух точек х'и х" из множества С.
Определение. Любая точка х из выпуклого множества С, которая не
является серединой отрезка, соединяющего две другие точки из (7, назы-
вается крайней1 точкой, или вершиной выпуклого множества. (На
Рис. 7-1-IX.
рис. 7-1-IX крайними точками являются вершины квадрата и каждая
точка окружности. Крайними являются также точки бриллианта, в кото-
рых сходятся вместе три или более грани.)
1 Реже такие точки называются экстремальными, а еще реже — угловыми.—
Лрим, ред.
156
Теорема 3. Базисное допустимое решение соответствует крайней точке
выпуклого множества допустимых решений.
Легко показать, что базисное допустимое решение соответствует край-
ней точке. Предположим, например, что решение х° = (&ь Ь2, ..., Ьт9
О, ..., 0) является базисным допустимым решением системы (17) с базис-
ными переменными х2, •.., хт, и это решение представимо как среднее
двух других допустимых решений р = (р4, р2, . ..,рт, .. ., рп) и q = (gn
...» 9/n, • • м 9»)- Тогда
у (Pj + = 0
для всех /, отвечающих небазисным (или независимым) переменным. Но
и qj^O, так как р и q — допустимые решения системы (17). Это
возможно только в том случае, если pj = qj — 0 для j = т + 1, ..., п.
Следовательно, в векторах р, q и зР небазисные переменные имеют одно
и то же значение (а именно нуль). Но значения базисных переменных опре-
деляется через значения небазисных единственным образом, и поэтому
значения базисных переменных также будут совпадать. Тем самым пока-
зано, что р = q = я0, и доказано, что ж0 не может быть средним двух
решений р и q, отличных от аР.
Определение. Отрезок, соединяющий две крайние точки множества С
и обладающий тем свойством, что никакая его точка не является сред-
ней для двух других точек из этого множества, не принадлежащих рас-
сматриваемому отрезку, называется ребром выпуклого множества С;
в этом случае говорят, что эти две крайние точки являются соседними,
или смежными.
Теорема 4. Класс допустимых решений, которые образуются при
возрастании значений некоторой небазисной переменной и пересчете зна-
чений базисных переменных при переходе от одного базисного решения
к следующему, соответствует перемещению вдоль ребра выпуклого мно-
жества.
Доказательство. Предположим, чтор == (bi9 Ь2, . . ., Ьт*, 0, 0, ..., 0)—
некоторое базисное допустимое решение, a q = (0; Ъ*, ..., Ь^, b^+i;
О, 0, ..., 0),то базисное допустимое решение, которое получается, если за-
менить xi9 скажем, на жт+1. Ясно, что для любой точки и = kp + (1—K)q
отрезка, соединяющего р и q, имеет место ит+2 = ит+3 = ... — ип — 0.
Поэтому, если и является серединой отрезка, соединяющего точки р' и q'
из выпуклого множества допустимых решений, то соответствующие коор-
динаты точек р' и д' также должны быть равны нулю. Это позволяет
выразить каждую из первых т координат точек р' и д' в виде линейной
функции от значения (т-}~ 1)-й координаты соответственно точек р' и д'.
Действительно, для любой точки х из выпуклого множества С, у которой
хт+2 = хт+3 = ... — хп = 0, a xm+i произвольно, мы имеем
= bi (^ = 1, 2, . . ., т) (21)
и, в частности, для g = (0; &*, 6*, ..., %, Ь^; 0, ..., 0) выполнено
равенство
Ъ% = bi (i — 1, 2, ..., т). (22)
Умножив равенство (22) на = з:т+1/Ь^+1 и вычитая из равенства (21),
157
мы получаем
Xi = KbX +(1-х)бг
^тп+1 = + (1 — О
z7 = X0 +(1-Х)0.
(г-1, 2, . .., т) (23)
(у = щ + 2, ..., п)
Этим доказано, что любые две точкир' и q' из множества С, для кото-
рых точка и является серединой отрезка, соединяющего точки р и q,
лежат на прямой, проходящей через точки р и q. Из предположения о том,
что точки р и q являются крайними, следует, что 1; поэтому точ-
ки р' и q' лежат на отрезке, соединяющем точки р и q, а тем самым дока-
зано, что отрезок, соединяющий точки р и д, является ребром.
В качестве дополнительной литературы к этому параграфу рекомен-
дуется (Таккер [3]).
7-2. СИМПЛЕКС-МЕТОД КАК МЕТОД НАИСКОРЕЙШЕГО
СПУСКА ВДОЛЬ РЕБЕР
ИСПОЛЬЗОВАНИЕ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ КАК КООРДИНАТ
ТОЧКИ В п — m-МЕРНОМ ПРОСТРАНСТВЕ
Рассмотрим задачу линейного программирования с п = т + 2, кото-
рая имеет базисное допустимое решение с базисными переменными,
например, я3, ж4, . . ., хт+2. Каноническая форма по отношению к этим;
переменным запишется так
^11^1 4~ ^12*^2 4~ ^3 = ^1, (Ь, 0)
#21^1 4" а22Х2 4-^4 — ^2,
_ • • ...................._....................... (О
4- ^т2*^2 4" ^тп+2 =
-|-^2*^2 =Z Z0>
и задача состоит в нахождении > 0 и min z, удовлетворяющих систе-
ме (1). Это эквивалентно нахождению значений xt и х2 и наименьшего зна-
чения постоянной cq=z—z0, удовлетворяющих линейным неравенствам:
Xi >0,
х2 > 0,
4"а12Ж2
^21*^1 4“ а'22^2 ^2» (2)*
Я/пЛ + ^тп2^2 ^/п,
+ с2х2 — с0*
Эти т + 2 соотношения можно изобразить в двумерном пространстве
небазисных, или независимых, переменных xt и х2, как показано на
рис. 7-2-1.
На рис. 7-2-1 жирными линиями выделена выпуклая область Кг
образованная полупространствами (в данном случае это полуплоскости)*
158
«иЛ + di2x2^ bi. Мы найдем оптимальное решение, перемещая пунк-
тирную линию с^х\ + с2X2 = с0 параллельно самой себе до тех пор, пока
эта прямая не коснется выпуклого мно-
жества, и тогда с0 станет минимальным.
(Если ct и с2 оба меньше нуля, то дви-
жение нужно производить в направле-
нии от начала координат.) С каждой
точкой из множества К связано одно
допустимое решение системы (1). Дей-
ствительно, эта точка Р должна удов-
летворять всем неравенствам (2), а не-
отрицательные разности между правыми
и левыми частями неравенств (2) дают
единственные значения базисных пере-
менных системы (1), когда небазисные
переменные и принимают значе-
ния (х^, я°). Значение г-й базисной пе-
ременной Xi +2 = x°i+2 пропорционально
расстоянию точки р = м, от гра-
ницы множества, отвечающей i-му огра-
Р и с. 7-2-L Геометрический смысл
симплекс-метода заключается в дви-
жении по граням выпуклого мно-
жества.
ничению, потому что из аналитической _ __ __
геометрии известно, что расстояние точки Р от прямой а^х^ + а12х2 = bt
(i == 1, 2, . .., т) определяется по формуле
расстояние = ——• (3)
1^ + ^/
Если точка (х[, х°2) удовлетворяет строгому неравенству, то геометрически
это выглядит так:
где ki = (а\ + а^)"1/*.
Если произведена замена переменных yt = ktXi+2 для i = 1, 2, . . ., ти,
а координатами точки Р являются значения независимых переменных, та
значение i-й базисной переменной в точности равно расстоянию от точки Р
до множества, соответствующего i-му ограничению.
В каждом базисном решении системы (1) есть по крайней мере два
х^ = 0, следовательно, соответствующая точка, являясь точкой множест-
ва К, находится на нулевом расстоянии от двух различных граничных
прямых этого множества. Интуитивно ясно (а строго мы это покажем ниже),
что такая точка будет вершиной множества К. В частности, базисному
допустимому решению канонической системы (1) отвечает точка (х* = О,
^2 ~ 0) на Рис- 7-2-1; поэтому начало координат всегда принадлежит
выпуклому множеству К.
Покажем теперь более строго, что каждой крайней точке выпуклого
множества допустимых решений системы (7) сопоставляется крайняя.
159
точка множества К, и наоборот. Рассмотрим для этого две точки:
Р = (я£, х°) и Q = (#', Xg) из множества К и соответствующие им допусти-
мые решения системы (1) р = (я£, я®, . .., я®) и д = (я', я', ..., х'п), кото-
рые, как показано в теореме 2 §7-1, принадлежат выпуклому множест-
ву С. Очевидно, что любой точке КР + (1—tyQ на прямой, соединяющей Р
и Q, отвечает точка Кр + (1—tyq, которая удовлетворяет системе (1),
и обратно. Поэтому отрезку из выпуклого множества С решений системы (1)
соответствует отрезок из множества К, и в частности середина отрезка из С
соответствует середине отрезка из К, и наоборот. Отсюда следует, что
некрайние точки должны соответствовать друг другу, а тогда, естествен-
но, и крайние точки (т. е. базисные допустимые решения) для системы (1)
►соответствуют крайним точкам множества К, и обратно.
Более того, перемещению вдоль ребра, соответствующего классу
допустимых решений, возникающих при возрастании небазисной пере-
менной и пересчете базисных переменных при переходе от одного базисного
решения к другому, должно отвечать движение вдоль границы множе-
ства К от одной вершины к соседней. Чтобы убедиться в этом, рассмотрим
две различные точки р и q, соответствующие базисным допустимым реше-
ниям, полученным с помощью симплекс-метода для невырожденной задачи.
Тогда отрезок, соединяющий точки р и q, является ребром множества С.
Если бы теперь соответствующие вершины Р и Q множества К не были
•соседними, то на отрезке PQ нашлась бы точка X, которая была бы сере-
диной отрезка, соединяющего точки Р' и Q' из К, не лежащие на отрез-
ке PQ. Мы покажем, что точки Р'и должны лежать на отрезке, соеди-
няющем Р и Q. Мы показали, что точка х, соответствующая точке X,
должна делить пополам отрезок, соединяющий точки р'и д', которые
♦соответствуют точкам Р' и Q'. Однако точка х должна лежать также на
прямой, соединяющей точки р и д, так как точка X была взята на прямой,
соединяющей Р и Q. А поскольку отрезок pq является ребром (§ 7-1,
теорема 4), точки р' и д'должны обе находиться на этом ребре, и поэтому
соответствующие им точки Р'и должны находиться на прямой, проходя-
щей через Р и Q. Этим показано, что ребра выпуклого множества допу-
стимых решений системы (1) соответствуют ребрам на рис. 7-2-1.
Таким образом, симплекс-метод осуществляет переход от одной
вершины к следующей в пространстве фиксированного множества небазис-
ных переменных. Если начать с вершины, находящейся в начале коорди-
нат, и двигаться последовательно от одной вершины к другой, соседней
с ней, то каждый шаг уменьшает значение с0 до минимального значения с0;
этот процесс показан стрелками на рис. 7-2-1.
ОБЩИЙ СЛУЧАЙ
Несмотря на то что наши замечания касались ради простоты только
случая п = т + 2, они вполне применимы также и в общем случае,
когда п = т + к. В этом случае координатами точки в ^-мерном про-
странстве становятся значения к — п — т переменных из некоторого
множества небазисных переменных. В этой геометрии выпуклое множе-
ство К допустимых решений определяется системой т неравенств, которые
получаются после исключения базисных переменных в канонической
форме и добавления к неравенств х7>0 для небазисных переменных.
Каждое базисное допустимое решение соответствует вершине множества К.
В общем (невырожденном) случае из каждой вершины выходит п — т
ребер, ведущих к п — т соседним вершинам; они соответствуют п — т
базисным решениям, которые получаются при введении одной из п — т
небазисных переменных вместо одной из базисных переменных. В симплекс-
160
методе правило выбора cs = min Cj <Z 0, позволяющее указать то xs,
которое следует увеличить, соответствует движению вдоль того ребра
выпуклого множества, которое указывает путь наискорейшего убыва-
ния z на единицу изменения вводимой переменной.
Например, при п = пг+ 2 [см. схему (5)], если < с2, то перемеще-
ние на расстояние Д вдоль оси Xi дает большее уменьшение величины z,
чем такое же перемещение вдоль оси х2.
(5)
Вообще можно показать, что симплекс-метод является «градиент-
ным» методом наискорейшего спуска, в котором «градиентное направле-
ние» определяется в пространстве небазисных переменных, например,
xm+i, хт+2, . . . , хп. Перенесем начало координат в некоторую точку,
соответствующую рассматриваемому промежуточному решению. Тогда
обычное градиентное направление наискорейшего спуска мы получим,
как предельное при Д -> О направление от этого начала координат к точке
на сферической поверхности
Хт+1 + Хт+2 + • • • + *п = Д2, (Xj>0)
(6)
где функция z минимизируется. Напротив, градиентное направление
наискорейшего спуска в симплекс-алгоритме находится с помощью плоской,
а не сферической поверхности
хт+1 + хт+2 + • • • + хп — Д • {xj 0) (7)
Другими словами, при нахождении градиента обычное (эвклидово) рас-
стояние (6) от начала координат (перенесенного в некоторую точку,
отвечающую рассматриваемому решению) заменяется на расстояние (7),
являющееся суммой абсолютных величин координат.
Упражнение. Рассмотрим задачу минимизации ст^хт^ + ст+2 X
X хт +2 + ,.. + спхп при ограничении (7) для фиксированного Д , где
Xj > 0. Показать, что решение состоит в выборе xs = Д , где cs = min Cj
и Xj = 0 для всех других /. Каково градиентное направление наиско-
рейшего спуска при Д -->0?
Упражнение. Рассмотрим задачу минимизации cm+1^m+i + c?n+2 X
X ят+2 + • • • + спхп при ограничении (6) для фиксированного Д, когда
нет ограничения на знак Xj. Показать, что решением является Xj — — CjQ,
где 9 = Д2/2с*. Каково градиентное направление наискорейшего спуска
при Д —> 0?
И Дж. Данциг 161
7-3. СИМПЛЕКСНАЯ ИНТЕРПРЕТАЦИЯ СИМПЛЕКС-МЕТОДА
Хотя использование симплекс-метода в n-мерном пространстве пред-
ставляется естественным, все же можно a priori ожидать, что он окажется
неэффективным, так как он может привести к длительному блужданию
по ребрам выпуклого множества решений, прежде чем будет достигнута
оптимальная крайняя точка. Это представляется справедливым, когда
мала разность п — т ~ к, как, например, на рис. 7-2-1, где к = 2. Однако
непосредственное решение большого количества практических задач
показывает, что число итераций обычно близко к числу базисных пере-
менных из последнего базисного множества, которые не входили в началь-
ное множество. Если в задаче с т уравнениями в последнее базисное множе-
ство входит т различных переменных, то число итераций может колебать-
ся от минимального, равного т, до 2т и реже до Зтп. Если в системе меньше
50 уравнений и 200 переменных, то, судя по не вполне обоснованным
эмпирическим наблюдениям, число итераций обычно бывает меньше Зап/2.
Некоторые полагают, что для случайно выбранной задачи с фиксированным
числом уравнений т число итераций растет пропорционально п.
Было высказано предположение, что при правильном выборе пере-
менных, которые вводятся в базисное множество, можно перейти от неко-
торого базисного решения к любому другому не более чем за т шагов,
причем каждое базисное решение должно быть допустимым. Известно,
что при тп^4 это предположение справедливо (У. М. Гирш, 1957, устное
сообщение).
Кроме того, если рассматривать симплекс-метод в тп-мерном про-
странстве столбцов коэффициентов при переменных, как это будет сдела-
но в данном параграфе, то метод оказывается вполне эффективным. Изло-
женный в такой геометрии метод и был впервые предложен, хотя до этого
он был отвергнут как малоперспективный.
В гл. 3 была графически проанализирована модель смешивания II
и задача о смесях, причем в качестве координат использовались коэффи-
циенты при неизвестном в одном из уравнений и в стоимостной форме.
Для этого предположили, что одно из уравнений этой модели можно запи-
сать в виде
“И “Ь* • • • 4" хп — 1 0 • ло) (1)
и для случая т — 2 можно оставить еще одно уравнение и стоимостную
форму
а^хх + а2х2+ ... +апхп = Ъ, (:яч) (2)
CiXi + с2х2 + ... + спхп == z (min). (3)
Переменные Xj интерпретировались как неотрицательные веса, которые
приписываются системе точек Aj = (dj, Cj) из двумерного простран-
ства (и, г?), при этом точка R — (&, min z) является их взвешенным средним
(центром тяжести); т. е. значения выбираются так, что центр
тяжести лежит на «линии требований» и — Ъ (постоянная), и так, чтобы
координата v была минимальной (см. рис. 7-3-1).
ВЫПУКЛАЯ ОБОЛОЧКА
Заштрихованная область С на рис. 7-3-1 представляет собой множе-
ство всех возможных центров тяжести G, которые получаются, если точ-
кам Aj приписывать различные веса Xj. Легко показать, что эти центры
тяжести образуют выпуклую область С, называемую выпуклой оболочкой
множества точек Aj. Чтобы убедиться в этом, рассмотрим некоторую
162
точку G' из множества С, полученную с помощью неотрицательных весов
wv w'2, . . . , w'n, и другую точку G", соответствующую неотрицательным
весам ip*, гг", . . . , ш”п. Любая точка отрезка, соединяющего точки G'
и G", имеет вид G* = ХС?' + (1 — X) G", где O^X^Cl. Точка G* также
должна принадлежать множеству С, поскольку ее можно получить с помо-
щью весов w* = + (1 — X) w] для j ~ 1, 2, . . . , п; кроме того.
если гг-> 0,1 2 wi = 1»
2 wj = 1 и O^X^l, то гг*>0,
2 гг* =1- Этим установлена выпуклость множества С.
Легко видеть, что любой столбец (технологический процесс), соответ^
ствующий некоторой точке А?«, которая не является крайней точкой
выпуклой оболочки, можно в задаче линейного программирования не
рассматривать. Так, можно опустить
точки А3, А4, А6, которые находятся
внутри множества С на рис. 7-3-1, и
Рис. 7-3-1. Геометрически задача ли- Рис. 7-3-П. Симплекс, связанный с
нейного программирования является за- итерацией симплекс-алгоритма 2).
дачей о центре тяжести.
Если Cj отрицательное, то оно ра&но
расстоянию по Вертикали
до точки Aj\ лежащей
точку А7, лежащую на ребре, т. е. можно положить х3 = х4 = xQ = х1 = 0
и в се-таки найти допустимое решение с минимальным z.
Базисное допустимое решение соответствует паре точек, скажем
Ai и А6, на рис. 7-3-1; при этом прямая, проходящая через точки А4 и А6,
пересекает прямую и = Ъ в некоторой точке G, принадлежащей отрез-
ку AiA6. Чтобы это было так, должно быть выполнено соотношение
Хл^ (1 — X) а§ = (0 X 1).
А это соответствует базисному решению задачи (1), (2), в котором х^ = X,
х& = (1 — X) и Xj- = 0 для остальных /.
Для улучшения этого решения симплекс-метод предписывает сначала
вычислить относительные оценки Cj с помощью исключения базисных
переменных из стоимостного уравнения. Теперь мы хотим показать, что
это то же самое, что сначала найти прямую, проходящую через точки
и А6 (эту прямую мы будем называть прямой решения) и затем подставить
координаты точек А; в уравнение прямой, чтобы определить, сколько из
них (если такие есть) расположено выше или ниже прямой в направлении v;
см. рис. 7-3-П. Для исключения базисных переменных Xi и xQ из формы (3)
вычтем из (3) уравнение (1), умноженное на л:0, и уравнение (2), умножен-
ное на лР Тогда л0 и должны быть выбраны так, чтобы было
Ci — (л0 + ^1«1) = 0, (4)
cQ — (л0 + л^е) = 0, (5)
причем относительные оценки Cj вычисляются по формулам
= (ло + л^). (6)
11*^
163
Сравним это с тем, что потребовалось бы проделать для того, чтобы найти
уравнение прямой
v = л0 + (7)
где коэффициенты л0 и выбираются из условия прохождения этой
прямой через точки Аг = (аь с4) и А6 = (а6, с6). Условие прохождения
прямой через точку получается, если в (7) подставить и = at и v — с19
а подстановка и = aQ и v = с6 дает условие того, что на этой же прямой
лежит и точка А6. Но эти условия совпадают с условиями (4) и (5). Чтобы
определить, сколько точек с координатами и = aj, v — Cj лежит выше
или ниже прямой решения в направлении г?, мы сначала вычисляем орди-
нату точки, в которой прямая и = aj пересекает прямую v = л0 + щи,
и
Рис. 7-3-Ш. Геометрическая иллюстрация ре-
шения задачи о смеси продуктов с помощью сим-
плекс-алгоритма.
т. е. ординату точки v = л0 + ЩОф а затем вычитаем это значение из
ординаты cj точки Л7-; эта величина в соотношении (6) обозначена через Cj.
Итак, точка Aj лежит выше, на или ниже прямой, если соответственно
Cj >0, Cj = 0 или Cj <Z 0.
Условие минимальности базисного допустимого решения состоит
в том, что для всех небазисных переменных Xj. Геометрически
это означает, что базисное допустимое решение будет оптимальным,
если все точки Aj лежат на соответствующей прямой решения или выше
нее. Например, на рис. 7-3-1 линия требований и = b пересекает отрезок,
соединяющий точки А5 и А6, а все другие точки Aj лежат выше прямой,
проходящей через точки А5 и А6; следовательно, если в качестве базисных
переменных взять х5 и х6, то получится минимальное решение.
С другой стороны, если имеется точка Aj, как на рис. 7-3-II, лежащая
ниже прямой решений, то мы соединяем эту точку Aj с точками и А6
и рассматриваем выпуклое множество S с вершинами А19 А6, Aj. Это мно-
жество является выпуклой оболочкой трех точек в двумерном пространстве
и называется двумерным симплексом. Если точка Aj лежит ниже линии
решения, то ниже лежит и каждая точка симплекса 5. Если точка G
не совпадает с вершиной, то на линии требований существует отрезок G*G,
принадлежащий симплексу S, который лежит под прямой решения;
164
при этом G* — самая нижняя точка отрезка. Следовательно, существует
прямая нового решения, проходящая через G*. Это либо прямая А19
либо прямая А6, Aj в зависимости от того, лежит ли точка A j правее или
левее прямой и = Ь.
На рис. 7-3-III геометрически проиллюстрированы шаги симплекс-
метода для задачи (8) о смеси продуктов из § 3-5.
У1+ Уг+ Уз 4- У 4 4- Уб 4- Уе = 1> (У/>0)
0,+ 0,1у2 + 0, Зуз + 0,8^4+ 0у5 4- 1у6 = 0,4, (8)
— 2,4г/4— 2,0у2 — 1,8у3 — 0,81/4 4- 0у5 4- 0у6 = z (min).
Пусть координатами точек Aj на рис. 7-3-III будут коэффициенты при
неизвестных yj во втором и третьем уравнениях:
A=(0,2; —2,4), Л2 = (0,1; —2,0), А3 = (0,3; -1,8),
А4 = (0,8; -0,8), А5=(0;0), Л=(1; 0).
Симплекс-итерации можно свести в одну таблицу
Итерация Базисные переменные Прямая решения Симплекс
0 Уб» Уб А&Ав / A&AqAi
1 У1, Ув
2 Уи Уь Л1А4
ОПРЕДЕЛЕНИЕ СИМПЛЕКСА
Выпуклая оболочка тп-\-1 находящихся в общем положении (см.
определение ниже) точек в m-мерном пространстве называется т-мерным
симплексом; итак,
0-мерным симплексом является точка,
1 » » » отрезок,
2 » » » треугольник
3 » » » тетраэдр.
Определение. Рассмотрим точки Я у = (aij, a2j, . . ., amj) в m-мерном
пространстве. Говорят, что точки (Alf А2, . . ., Ат+1) находятся в общем
положении, если определитель, составленный из координат этих точек,
и строки из единиц, как в (9), неравен нулю
1 1
а12
(9)
ат2 • • • &т, т+1
165
Рассмотрим в трехмерном пространстве задачу нахождения
Л min z, удовлетворяющих условиям
Множители
И
xi 4" х2 4~ • • • + хп — 1 {xj >0) • л0
4“ #12^2 4~ • • • 4" а\.пхп = bi : Л1
Л21^1 4- а22Х2 4" • • • 4” а2пхп = Ъ2 ‘ л2
С1Х1 4“ С2Х2 + • • • 4” спхп — Z
(10)
(И)
В качестве координат u2, v) точки возьмем коэффициенты при пере-
менной Xj в системе (11), т. е. Aj = (а^, a2j, Cj). Линия требований опре-
,. Линия требований —а»
' (и,=Ь„ а2*Ьг). J
Плоскость началь-
ного решения
А1
Чч.Ъг.О)
А3
Рис. 7-3-IV. Симплекс, связанный
итерацией симплекс-алгоритма (яг=3).
Плоскость нового
решения
“1
деляется уравнениями щ и2 =
= Ь2. Базисное допустимое решение
соответствует трем точкам, скажем А ь
А2, А3, при этом линия требований
пересекает «плоскость решения»,
образованную точками Aif А2, А3,
в точке двумерного симплекса Я ь Л 2,
А3, см. рис. 7-3-IV. Если точка Aj
лежит ниже плоскости решения
г? = л0 4- 4- л2гг2, проходящей че-
рез точки Ль Л2, Л3, то Cj = Cj —
Л Q ^i&lj ^>2^,2j 0. В ЭТОМ
случае можно рассмотреть трехмер-
ный симплекс AjA^A^A 3 и найти ниж-
нюю точку G*, в которой линия тре-
бований протыкает этот симплекс.
В зависимости от расположения точ-
ки Aj точка G* будет находиться на
одной из трех граней AxA2Aj, A2A3Aj, A^A3Aj. На рис. 7-3-JV точка G*
попала на грань AtA3Aj, и эти три точки используются для нахождения
плоскости нового решения.
По правилам симплекс-метода в качестве новой базисной перемен-
ной xs выбирается не произвольная переменная Xj, соответствующая точ-
ке Aj, лежащей под плоскостью решения, а именно та переменная xs,
которая соответствует точке As = Aj, лежащей на максимальном расстоя-
нии^ = min Cj ниже плоскости. Рис. 7-3-1 и 7-3-П позволяют убедиться
в том, что такая точка дает возможность существенно приблизиться
к оптимальному плану. Это подтверждают тысячи решенных задач, и имен-
но в этом причина эффективности симплекс-метода на практике.
с
Упражнение. Изучить рис. 7-2-1 и § 7-2 (5); построить пример, пока-
зывающий, что при п — т 4- 2 правило выбора cs — min Cj может при-
вести к максимальному числу итераций в симплекс-методе.
7-4. ЗАДАЧИ
ВЫПУКЛЫЕ’ОБЛАСТИ (См. § 7-1)
1. Рассмотреть еще раз связь между выпуклыми множествами и линей-
ным программированием.
2. Определить, какие из приведенных ниже множеств являются
выпуклыми.
(a) Xi + x2+ х3>6,
Xi—z2 + 3z3>4,
Xj > 0,
166
(б) + Я2>5-
(в) +
(г) х* — 2Х1 <2,
(д) — 2^ >3,
^ + 23:2^4,
2х£ + 3#2
3. а) Решить графически и с помощью метода исключения Фурье —
Моцкина из § 4-4 следующую задачу: максимизировать х^ — х2 при
ограничениях
Xi — Зя2 > О»
Xi > О,
я2>0,
2^! + 3^2 > 6.
б) Записать эту задачу в стандартной форме.
в) Указать выпуклое множество допустимых решений. Почему опти-
мальное решение соответствует крайней точке?
г) Опустив условия rq > О и я2 > 0, привести к стандартной форме
двумя методами.
4. Приведенные ниже системы неравенств (Л) и (В) преобразовать,
изменив переменные, в систему уравнении с неотрицательными пере-
менными; изобразить графически область, определяемую системой (5),
в терминах исходных переменных. Изобразить графически область,
соответствующую системе, двойственной к (Л).
(А)
2хг —р 3^2 4* 4я3 5,
4Х|—7ж2 -f- З^з 4.
(В)
Х1+
4хх + &г2 32,
*1+
Xi — 2я2>2.
5. В симплекс-методе процесс возрастания переменной xs, в то время
как другие независимые переменные остаются равными нулю, порождает
класс решений, соответствующих ребру выпуклого многогранника допу-
стимых решений, если вершина соответствует невырожденному базисному
допустимому решению. Что будет в случае вырождения?
6. Если базисное решение невырожденное, то у соответствующей
ему крайней точки существует ровно п — т соседних крайних точек
и эти точки получаются при возрастании одной из п — т независимых
переменных, в то время как остальные остаются равными нулю. Что будет
происходить в случае вырождения?
7. Показать, что если нет ограничения на знак переменной xk, то
можно получить оптимальное решение, исключая xk из всех уравнений,
кроме одного, отбрасывая это уравнение и оптимизируя оставшуюся
систему, а затем определяя xk путем обратной подстановки.
8. Предположим, что в одном уравнении задачи линейного программи-
рования в стандартной форме есть один положительный коэффициент,
скажем, при переменной xk, и все остальные коэффициенты этого уравне-
ния не положительны, а свободный член положителен. Отсюда следует,
что для любого решения будет xk >0, какими бы ни были значения осталь-
167
ных переменных Xj > 0. Используя в качестве ведущего любой ненулевой
коэффициент при исключим xk из остальных уравнений и отбросим
одно уравнение, содержащее xh. Доказать, что можно найти оптимальное
решение первоначальной задачи, если решить получившуюся задачу,
в которой меньше на одно уравнение и на одну переменную.
9. Показать, что если заранее известно, что решение не будет опти-
мальным, пока переменная xk не станет положительной, то эту переменную
можно исключить и решать вместо исходной задачи, задачу, в которой
на одно уравнение и одну переменную меньше.
10. Придумать метод нахождения второго наилучшего базисного
допустимого решения. Обобщить метод для третьего наилучшего, четвер-
того и т. д. Обсудить возможные усложнения.
11. Показать, что допустимому решению отвечает крайняя точка,
если г переменных имеют единственным образом определенные неотрица-
тельные значения, а остальные переменные равны нулю.
12. Взяв решение (г?ь г?2, • • •» г?п), отвечающее крайней точке,
показать, что если переменные соответствующие Vj = 0, равны нулю,
то остальные переменные определяются единственным образом и Xj —
= Vj >0.
13. (У. М. Гирш; задача нерешенная). Существует ли последователь-
ность из т (т — число уравнений) или менее ведущих операций, каждая
из которых порождает новое базисное допустимое решение (б. д. р.),
причем первое б. д. р. и последнее б. д. р. заданы? Геометрически:
Для выпуклой области п — тп-мерного пространства, определенной
п полуплоскостями, будет ли число т верхней границей для числа вершин
в самой короткой цепочке, соединяющей две заданные вершины?
14. Доказать, что однородная система т уравнений с т неизвестными
всегда имеет нетривиальное решение (решение, в котором хотя бы одна
неизвестная не равна нулю), если в системе есть избыточное уравнение
(т. е. если ранг системы меньше тп).
15. (Гейл) Доказать, что однородная система т неравенств с т неиз-
вестными всегда имеет нетривиальное решение.
16. Показать, что в задаче линейного программирования множество
допустимых значений любой переменной xk является выпуклым множе-
ством, т. е. является отрезком a^Zxh^.b.
17. Показать, что множество допустимых значений двух перемен-
ных, скажем (яь я2) или (а^, z), удовлетворяющих условиям задачи
линейного программирования, является двумерным выпуклым множе-
ством.
18. Как следствие задачи 17, показать, что если xk рассматривать
как параметр, определенный на области допустимых значений, то зна-
чение min z становится выпуклой функцией.
19. Показать, что min z является выпуклой функцией параметра 0,
если свободные члены в системе соответствующей задачи линейного
программирования являются линейными функциями параметра 0. Пока-
зать, однако, что значение некоторой другой переменной, например,
в приведенном ниже примере, может оказаться ни выпуклой, ни вогнутой
(выпуклой с противоположным знаком) функцией параметра 0
—хъ + х^ =0, (я? 0)
^1 + ^2 =0,
-f- х§ = 1,
4~ ж2 4- #6= 1 >
4я t + 2х2 + = z (min) •
168
20. Показать, что, если Р — (аъ а2, . . ., ат) — точка в тп-мерном
пространстве, то множество точек С с координатами ахХ, а2Л, . . .,
где О^СХ<оо, является выпуклым. Это множество называется лучом.
Изобразить графически луч, проходящий через точку Р = (1, 1, 1).
21. Множество точек называется конусом, если для любой точки Р
этого множества все точки луча, проходящего через точку Р, также
принадлежат этому множеству. Построить пример, показывающий, что
конус, вообще говоря, может быть и невыпуклым.
22. Показать, что если Р = (а19 а2, . . ., ат) и Q = (а',
. . ., а’пй — две точки тп-мерного пространства, то множество точек С
с координатами X = (ХбцН- Ха2 + ра2, . . . , + ра™) для про-
извольных К и р из областей < оо, 0^р< оо, является выпуклым
конусом. В векторных обозначениях (см. § 8-2) точка X записывается так:
X — КР + р@. Это множество называется конусом, порожденным луча-
ми ЛР и р(). Изобразить графически конус, порожденный лучами, про-
ходящими через точки Р = (1,1, 1) и Q = (1,1,0).
23. В общем случае конусом называется множество неотрицательных
линейных комбинаций точек Д, Р2, . . ., Р*. Таким образом, С — это
множество всех точек X = %±Р± + Х2Р2 + .. . + Л^Р* с произвольными
из области 0^Xf<oo. Доказать, что конус С является выпуклым
конусом.
24. Показать, что множество С точек Р = (Ьи Ъ2, . . ., Ьт), коорди-
наты которых получаются из соотношений
^^ + ^2X2+...+ainxn^=bi (г = 1, 2, ..., т)
при произвольном выборе «4>0, «2>0, . . ., яп>0, является выпук-
лым конусом.
25. Рассмотрим в тп-мерном пространстве бесконечный набор точек
Pi9 Р2, . . ., Рд, . . . Обозначим через С множество конечных неотрица-
тельных линейных комбинаций рассматриваемых точек. Через С' обозна-
чим множество неотрицательных линейных комбинаций не более т точек.
Показать, что выпуклые конусы С и С' совпадают.
ИНТЕРПРЕТАЦИИСИМПЛЕКС-МЕТОДА (См. § 7-2, 7-3)
26. Проделать все шаги симплекс-метода алгебраически и геометри-
чески для а) задачи о смеси продуктов и б) задачи о смешивании II и пока-
зать, как они связаны между собой. (По этим задачам см. § 3-4 и § 3-5.)
27. Задачу о складах (§ 3-6) решить алгебраически и геометрически»
используя симплекс-метод в трехмерном пространстве.
28. С помощью метода исключения Фурье — Моцкина решить задачу:
2yi+ ^2 <2,
— З3/1 + у2^—3,
Уг~ 2у2<6,
— У1 —2,
3^! + 4i/2 = v (max).
29. Решить приведенную выше задачу с помощью следующего вариан-
та симплекс-метода: для неравенств с положительными правыми частями
ввести свободные переменные у7>0; для неравенств с неположительными
правыми частями ввести искусственные переменные избытка yj 0.
169
Применить обычный симплекс-метод для минимизации суммы искусствен-
ных переменных, в данном случае у^ + у1 = w. Показать, однако, что
переменные уг и у2 могут быть любого знака (см. следующую задачу).
30. Изменить симплекс-метод так, чтобы можно было решать задачи
без ограничения на знак для некоторых переменных. Применить этот ме-
тод к задаче 28.
31. Используя симплекс-метод, решить задачу
2^1+ (У1>0, у2>0)
3*/1 + 9у2<1,
3*/i + 4#2 = i; (max).
Интерпретировать геометрически . шаги симплекс-метода в двумерном
пространстве с координатами у± и у2.
32. Дана система
Х1 + х2 + • • • + хп — 1 > (#? 0)
(^ixl 4“ &2Х2 + • • • + ==
<4*1 + С2Х2 + • • • + Спхп = 2 (min).
Показать, что коэффициенты прямой решения г? = л* + л*п, соответ-
ствующей минимальному базисному решению, должны удовлетворять
соотношениям
(а) .с7~(л* + л*а1/)>0,
(б) + jt*& = minz.
33. Для поставленной выше задачи показать, что выпуклая оболочка
точек Aj = (aj, Cj) лежит выше произвольной прямой г? = Ло + Jtiw, если
с~ (ло + *40;) >0.
Воспользовавшись этим, показать, что такая прямая пересекает линию
требований и = bi в точке с ординатой r<^min z.
34. Используя результаты двух предыдущих задач, показать, что
значения До» *4 и max v, удовлетворяющие (двойственной) системе
щ + niaj^Cj, (/ = 1, 2, ...,п)
л0 +л4Ь = г (max),
даются прямой решений v = л* + л*и, связанной с минимальным базис-
ным решением, и
max v = min z.
Рассмотреть эту частную геометрическую интерпретацию теоремы
двойственности, сформулированной в § 3-4 и показанной на рис. 3-4-1.
35. Заметим, что двойственной к стандартной задаче линейного про-
граммирования является система неравенств без ограничений на знак
переменных. Предположим, что нам дана система в этой последней форме;
рассмотреть вопрос о том, как можно использовать двойственную к ней
систему, чтобы найти третий путь получения стандартной формы задачи
линейного программирования из системы неравенств. Найти стандартную
форму задачи линейного программирования, двойственной к которой
170
является задача
л0+ 0,214^ —2,4,
Ло + ОДя:^ —2,0,
л0 +0,3:1!^ —1,8,
Ло + О,8л!^ —0,8,
л0 О,
Ло + Л| О,
л0 <5 и (max).
Решить двойственную задачу, используя симплекс-метод и метод исключе-
ния, и доказать, что max v — min z, где min z является решением системы
двойственной для исходной.
36. Если v — л0+ JtiUi + л2и2 — уравнение плоскости решения,
проходящей через точки А19 А2 и А3 (см. рис. 7-3-III), то интерпретировать
алгебраически, используя симплекс-метод и геометрические условия
Vj — (ЛО + ntav + л2а27) = 0 (/ = 1,2,3)
и величины
Vj — (Л0 + ^l^ij + ^2a2j) — Cj*
37. Третью геометрическую интерпретацию симплекс-метода можно
получить, если рассматривать /-й столбец как прямую л0+ а^ = Cj
в пространстве (л0, Л1). Следовательно, симплекс-метод можно интер-
претировать в том же самом пространстве независимых переменных лои л4
двойственной задачи линейного программирования л0 + а^ л0 +
+ Ьщ = г? (max) для / = 1, 2, . . ., п. Показать, что в этой геометрии
симплексная процедура решения двойственной задачи отличается от интер-
претации симплекс-метода для решения исходной задачи. (На этой гео-
метрии основан принадлежащий Келли метод решения нелинейных задач.)
См. (Вулф [3]).
38. В тексте подчеркивалась связь между классическим градиент-
ным методом и симплекс-методом. Показать, что каждая итерация сим-
плекс-метода выражает минимизируемую функцию с помощью различных
множеств независимых переменных. Показать, что направление макси-
мального убывания функции при ограничениях 2^ = А, гг7->0, совпа-
дает с направлением, выбираемым по симплекс-методу. Что получилось
бы, если бы использовалось ограничение 5 = Д2?
39. а) Используя «метод центра тяжести», найти Zj > 0 и min z,
удовлетворяющие системе
+ 2я2 + Зя3 + 4^4 = z (min),
•^1 “Н *С2 ~^4 == 4,
я?! — 2д^2 —|— Зя3—4^4=— 2.
б) Написать и изобразить графически двойственную задачу.
в) Решить двойственную задачу методом исключения Фурье — Моц-
кина (§ 4-4).
г) Решить прямую задачу симплекс-методом. Проследить шаги этой
процедуры на рисунках, построенных для а) и б).
40. Минковский [1]. Теорема. Допустимое решение ограниченной
задачи линейного программирования можно представить в виде линейной
неотрицательной комбинации базисных допустимых решений. Геометри-
чески это означает, что точка ограниченного выпуклого многогранника С,
171
определяемого конечным множеством полуплоскостей, может быть пред-
ставлена как линейная неотрицательная комбинация крайних точек
многогранника С.
Показать, что если многогранник С неограничен, то теорема неверна.
ЗАДАЧИ ПОВЫШЕННОЙ ТРУДНОСТИ
41. Теорема. Пусть М — множество точек (т — 1)-мерного эвклидо-
ва пространства, a Q — выпуклая оболочка множества М. Тогда можно-
найти т точек Pf, Р2, Рз, • • •» Рт (не обязательно различных) из множе-
ства Мит вещественных чисел xif . . ., для которых ^>0^
2 — 1 и 2 zfPf = Q (Е. Steinitz, Reine Angew. Math., vol. 143, 1913,
i=l 2=1
p. 128-275).
42. Теорема. Пусть M — бесконечное множество точек тп-мерного-
эвклидова пространства, a Q — выпуклый конус, натянутый на М. Тогда
можно найти т точек Рь Р2, . . ., Рт (не обязательно различных)
т
и т вещественных чисел ж4>0, . . ., zm>0, для которых 2 xiPi ~ Q*
2 = 1
Указание: Установить справедливость этой теоремы для любой точки
Q, которая может быть представлена в виде конечной линейной комби-
нации точек Pi £ М. Показать, что все такие точки и определяют выпуклый
конус, натянутый на множество М.
Глава 8
МЕТОД ВЕДУЩИХ ЭЛЕМЕНТОВ.
ВЕКТОРНЫЕ ПРОСТРАНСТВА.
МАТРИЦЫ И ОБРАТНЫЕ МАТРИЦЫ
8-1. ТЕОРИЯ ВЕДУЩИХ ОПЕРАЦИЙ 1
Наша цель состоит в том, чтобы продолжить начатые в § 4-2 исследо-
вания свойств, инвариантных относительно ведущих операций, и харак-
теристики самих этих операций. Первое из пяти важных свойств касается
избыточности и несовместности.
Теорема 1. Если существует линейная комбинация уравнений системы
с ненулевыми весами, дающая или тождественный нуль (избыточность),
или несовместное 1 2 уравнение, то это же имеет место для системы, полу-
ченной из исходной путем применения к ней некоторой последовательно-
сти элементарных (или ведущих) операций.
Доказательство. Пусть Eq обозначает либо тождество, либо несовмест-
ное уравнение, а £\, Е2, • • •, ^—уравнения системы, которые, по пред-
положению, удовлетворяют условию
4- ^2^2 + • • •*+ ^kEh — Eq, где (1)
Если первая из последовательностей элементарных операций не затраги-
вает этих уравнений Ег, то для новой системы это соотношение оче-
видно, не нарушится. Это справедливо, также и для того случая, когда
элементарная операция заменяет, например, Ei на kEi, где к У= 0. Если
Ei заменяется на Ei + кЕ2 = Е[, то Ei = E't — кЕ2, и для новой системы
будет выполнено соотношение
^i^i +(^2 — ^к)Е2-\- ... = Ео. (2)
Так как в этом случае #= 0, ненулевая линейная комбинация уравне-
ний полученной системы дает Ео. Наконец, если Et заменяется, напри-
мер, на 2?1 + kEt = E'v где t У= 1, 2, ..., к, то оказывается выполненным
соотношение
+ ^2^2 + • • • + "kkEk — kikEt = Eq, (3)
откуда получаем требуемый результат, так как Х4 =# 0. Теорема может
быть распространена по индукции на любое число элементарных операций.
Так как ведущие операции являются частными случаями элементарных,
доказательство закончено.
Вторым важным свойством ведущей операции является ее необрати-
мость, за исключением некоторых случаев.
1 Автор признателен А. У. Таккеру за предложение разработать этот параграф
на основе необратимости ведущих операций, за исключением того случая, когда они
применяются к канонической форме.
2 Применительно к единственному уравнению лучше было бы сказать «невоз-
можное».— Прим. ред.
173
Теорема 2. Если система имела каноническую форму до применения,
ведущей операции, то она сохраняет каноническую форму и после ее при-
менения.
Доказательство. Предположим, что система записана в канонической
форме с базисными переменными . . ., Xjm. Пусть ведущий эле-
мент выбирается в уравнении г с использованием переменной xs. Тогда,
как мы видели в § 5-1, полученная система будет системой в канонической
форме, причем xs заменяет XjT в роли базисной переменной. Если ведущий
элемент в новой системе выбирается в уравнении г с использованием
переменной Xjr, то вторая ведущая операция восстанавливает первона-
чальную систему. Из этой теоремы вытекают следствия.
Следствие 1. Если система представлена в канонической форме, то
обращение ведущей операции является ведущей операцией.
Следствие 2. Если подсистема S была в канонической форме до приме-
нения ведущей операции и если ведущий элемент выбирается в уравнении
из S, то после применения ведущей операции соответствующая подсистема
будет оставаться в канонической форме-, обращение ведущей операции
является ведущей операцией (в предположении, что коэффициенты при
базисных переменных в неканонических уравнениях равны нулю).
Следствие 3. Если подсистема S была в канонической форме до при-
менения ведущей операции и если ведущий элемент выбирается в уравне-
нии Е, не принадлежащем S, то после применения ведущей операции
подсистема, соответствующая {5, £*}, будет в канонической форме-, если
{5, Е} не была первоначально в канонической форме, то обращение ведущей
операции ведущей операцией не является. *
Третье важное свойство ведущей операции состоит в том, что между
уравнениями имеется взаимно-однозначное соответствие и что легко опре-
деляемые подмножества уравнений исходной и вновь полученной систем
эквивалентны.
Определение. Ведущей подсистемой называется множество уравне-
ний Р исходной системы, соответствующих уравнениям, выбранным для
ведущих элементов в последовательности ведущих операций.
Ясно, что число уравнений ведущей подсистемы в процессе приме-
нения ведущих операций возрастает или остается без изменения в зави-
симости от того, выбираются ли последовательные ведущие элементы
из уравнений, соответствующих ведущей системе, или из остальных урав-
нений. Пусть 5 — любое подмножество исходных уравнений, которое
включает ведущее множество Р и пусть S' и Р' — соответствующие под-
множества, полученные после применения последовательности ведущих
операций.
Теорема 3. Система S' эквивалентна системе S; в частности Р' экви-
валентна Р и, кроме того, Р' будет в канонической форме.
Доказательство. Тот факт, что Р' является канонической, вытекает
из следствий 2 и 3. Для доказательства эквивалентности систем S и S'
заметим, что, если вычеркнуты уравнения, не принадлежащие S, та же
самая последовательность ведущих операций может быть применена
к уравнениям, соответствующим S, и, следовательно, последние экви-
валентны 5.
Теорема 4. Ведущая подсистема Р независима и разрешима.
174
Доказательство. По теореме 3 система Р' имеет каноническую форму
и, следовательно, разрешима и независима. Так как система Р эквивалент-
на Р', она также разрешима. Эта система не может содержать избыточ-
ных уравнений, потому что в противном случае, по теореме 1, то же была
бы верно и для системы Р'.
Теорема 5. (Условие избыточности и несовместности.) Если уравне-
ние Е\ преобразованной системы является нулевым (или несовместным),
то либо в исходной системе уравнение Et является избыточным по отноше-
нию к ведущей системе Р, либо линейная комбинация уравнений из Р
и Et может дать несовместное уравнение.
Доказательство. Заметим, что система {Р, Et} может быть получена
из системы {Р', Е\} путем применения обратной последовательности
элементарных операций и, следовательно, по теореме 1, существуют такио
коэффициенты А^>0, не все равные нулю, что
+ X2Z?2 + • • • + ^kEk + 'htEt — Eq, (kt > 0) (4)
где (Et, . . ., Ek) — ведущие уравнения (которые не обязательно должны
быть первыми к уравнениями), a Eq — либо нулевое, либо несовместной
уравнение. В любом из этих случаев X* =/= 0 по теоремам 3 и 4; следова-
тельно, если Eq является нулевым уравнением, то Et зависит от других
уравнений.
ИССЛЕДОВАНИЕ СИСТЕМ НА ЭКВИВАЛЕНТНОСТЬ
Четвертое важное свойство ведущей операции состоит в том, что
путем применения одновременно к двум системам шаг за шагом ведущих
операций, использующих одни и те же ведущие элементы, можно выяс-
нить, имеют или нет эти системы одно и то же множество решений. Этот же
процесс будет проверять две системы на эквивалентность.
Теорема 6. Две разрешимые системы имеют одни и те же множества
решений тогда и только тогда, когда они эквивалентны.
Теорема 7. Две системы эквивалентны тогда и только тогда, когда
возможно применять к ним ведущие операции над одной и той же упорядо-
ченной последовательностью переменных и а) если обе системы совместны*
то канонические части этих систем тождественны, а остальные уравне-
ния являются нулевыми; б) если обе системы несовместны, то канонические
части тождественны, кроме, может быть, свободных членов, а остальные
части каждой системы имеют не менее одного несовместного уравнения.
Доказательство теорем. Предположим сначала, что эти две системы
можно привести к канонической форме, используя одну и ту же систему
ведущих переменных. Мы предполагаем, что уравнения канонических
частей упорядочены так, что обе подсистемы являются каноническими
с одним и тем же множеством базисных переменных. Если эти две системы
должны быть эквивалентны, то необходимо, чтобы их канонические части
были тождественными, потому что имеется только один способ представить
левую часть уравнения канонической части одной системы в виде линейной
комбинации уравнений системы, полученной из другой. Свободные члены
этих систем могут не совпадать, если в неканонической части имеются
несовместные уравнения (но прибавлением подходящего кратного какого-
либо из них свободные члены можно уравнять). Если эти две системы
разрешимы и при этом имеют одно и то же множество решений, то их кано-
нические части совпадают (см. доказательство теоремы 1 из § 4-2). Вообщё
175
неканонические части либо обе должны содержать несовместное уравне-
ние, либо обе должны состоять из нулевых уравнений, потому что един-
ственный способ получить несовместное уравнение одной системы из урав-
нений другой состоит в образовании линейной комбинации несовместных
уравнений последней.
Предположим теперь, что хотя две системы привести к канонической
форме с использованием одного и того же множества ведущих элементов
невозможно, но это можно сделать, применяя ведущие операции с одним
и тем же множеством ведущих элементов в ходе первых t шагов; пусть
это будут переменные Xi, х2, . . ., xt в первых t уравнениях. Пусть на
шаге (t + 1) переменную xt+t в уравнении t + 1 в системе I можно выбрать
в качестве ведущей, но выбрать эту переменную в качестве ведущей
в системе II невозможно, потому что коэффициенты при xt+i во всех
оставшихся т — t уравнениях системы II равны нулю. Заметим, что
получить (t + 1) — е уравнение системы I из уравнений системы II
невозможно, потому что коэффициенты при первых t уравнениях должны
быть равны нулю, и, значит, автоматически должен быть равен нулю
коэффициент при xt+i, каковы бы ни были коэффициенты при оставшихся
уравнениях. Следовательно, эти две системы не могут быть эквивалентны.
В этом случае рассматриваемые нами системы не могут быть также
и разрешимы с одним и тем же множеством решений. Чтобы убедиться
в этом, обозначим через ж®, . . ., ж?, я?-и, ...,#„ любое решение систе-
мы I. Это решение либо не удовлетворяет системе II, либо удовлетворяет
ей; в последнем случае существует решение системы II, которое не удо-
влетворяет системе!, а именно, решение х*, . . ., я*; х?-н,#г+2, • • • , хп,
полученное заменой x?+i на я*+1 У= и соответствующим изменением
значений переменных хг в канонической части из первых г урав-
нений системы II. Заметим, что это решение удовлетворяет остальным
уравнениям системы II (которые не содержат xl9 . . ., хг, xr+i), но не
может удовлетворять системе I, потому что оно не удовлетворяет уравне-
нию г + 1 этой системы. Следовательно, в любом случае эти две системы
не имеют одного и того же множества решений.
Пятое важное свойство ведущей операции состоит в том, что она дает
возможность доказать ряд интересных теорем относительно числа незави-
симых и зависимых уравнений системы.
Теорема 8. Две эквивалентные, независимые, совместные системы
имеют одинаковое число уравнений.
Доказательство. На основании теоремы 4 эти две системы можно
одновременно привести к каноническому виду, и при этом канонические
части новых систем будут тождественны. Нулевых уравнений при этом
получиться не может, потому что приведение системы к каноническому
виду состоит из последовательности элементарных операций, так что,
по теореме I, появление таких уравнений означало бы наличие в исходных
системах избыточных уравнений. Следовательно, тождественные канони-
ческие формы, которые эквивалентны, имеют то же число уравнений,
что и соответственные исходные системы.
Следующие три теоремы являются следствием только что доказанной.
Теорема 9. Две эквивалентные канонические системы имеют одно
и то же число уравнений.
Теорема 10. Если система имеет канонический эквивалент с г уравне-
ниями, то при любом разбиении системы на систему независимых уравне-
ний и на систему уравнений, зависимых от первых, число уравнений в неза-
висимой системе будет в точности равно г.
176
Теорема И. Если система имеет канонический эквивалент с г уравне-
ниями, то с помощью линейных комбинаций любых г независимых уравне-
ний можно получить все остальные уравнения.
Определение. Наибольшее число независимых уравнений разрешимой
системы называется ее рангом.
Упражнение. Доказать теоремы 9, 10 и 11. Показать, что число г
из теоремы 10 является рангом системы.
8-2. ВЕКТОРНЫЕ ПРОСТРАНСТВА
ОПЕРАЦИИ НАД ВЕКТОРАМИ
Многие операции, которые применяются к системе уравнений, могут
рассматриваться как несколько операций, выполняющихся параллельно.
Например, систему
2х* —j— Зя2—-- 4хз = 5
(1)
— 4#! — 2х2 + Зя3 = 7
можно переписать в виде
эта запись означает следующее: если умножить соответствующие элементы
(компоненты) в столбце на неизвестные и сложить по строкам, то их суммы
дадут соответствующие элементы столбца в правой части. Столбцы здесь
называются также вектор-столбцами. Операции, называемые «сложением»
и «умножением векторов на скаляр» выполняются над ними так же, как
и операции над обычными числами. Коэффициенты (2, 3, —4), которые
входят в первое уравнение (или (—4, —2, 3) во втором уравнении), точно
так же могут рассматриваться как объекты, называемые векторами-стро-
ками. Векторы, элементы которых взяты из строки, записываются обычно
в квадратных или круглых скобках. Часто векторы, элементы которых
взяты из столбца, для экономии места в тексте записываются как векторы-
строки: в этом случае вместо квадратных или круглых будут использовать-
ся угловые скобки { ). Таким образом, <2, —4) есть обозначение векто-
ра-столбца
/ 2\
\ — 4/ *
Определение, тп-вектором называется упорядоченный набор т чисел,
называемых его компонентами (элементами).
Мы начнем с определения двух основных операций над векторами,
которые представляют собой естественное распространение сложения
и умножения чисел на соответствующие действия над системами чисел.
Определение. Произведением пг-вектора на число (скаляр) х назы-
вается тп-вектор, полученный умножением каждой его компоненты на х.
Таким образом, для вектора-столбца
12 Дж. Данциг
177
Определение. Суммой двух m-векторов называется вектор, состав-
ленный из сумм соответствующих компонент. Таким образом,
(4)
Определение. Два zn-вектора равны, если равны их соответствующие
компоненты. Таким образом,
б?2
&2
означает, что = для г==1, 2, ...,тп.
(5)
\amJ \Ьт/
При такой интерпретации операций над векторами ясно, что (2) означает
то же самое, что и (1), потому что по определению умножения вектора
на скаляр равенство (2) равнозначно
/ 2жа \ / Зя2 \ / — 4гг3\ /5\
\ — / ~\ — 2х2 / "\ + Зхз/ \7 / ’
а по определению сложения векторов (скажем, прибавления третьего
вектора к сумме первых двух)
3^2—4ж3 \ /5
— 4#| — 2х2 3#з / \ 7
(7)
но по определению равенства векторов (7) совпадает с (1).
Мы теперь в состоянии сделать важное замечание, состоящее в том,
что так называемые элементарные операции над уравнениями представ-
ляют собой в сущности умножение на скаляр векторов-строк, образованных
выписыванием коэффициентов и свободных членов уравнений, и их сложение.
Переменные всюду играют пассивную роль. Например, если первое
уравнение системы (1) умножить на 2 и прибавить ко второму, то мы полу-
чим 0-#i + 4ж2 — 5я3 =17. Это соответствует операциям 2 (2, 3, —4, 5) +
+ (-4, —2, 3, 7) = (0, 4, -5,17).
ЛИНЕЙНО ЗАВИСИМЫЕ ВЕКТОРЫ
Вектор, каждая компонента которого равна нулю, называется нуле-
вым вектором. Таким образом, равенство нулю вектора V означает, что
178
/0\
о
(8).
ко/
неравенство V Ф 0 означает, что по крайней мере одна компонента векто-
ра V отлична от нуля.
Говорят, что век’гор {yi, у2, . . ., ут) линейно зависит от п других
векторов Pj~ а2у, • • •> amj), если можно найти такие числа (ска-
Хп —
У2
\Ут/
(9>
Упражнение. Выбрать такие частные значения и yi9 чтобы не суще-
ствовало чисел Xj, удовлетворяющих равенству (9); выбрать такие значе-
ния atj и yi, чтобы числа Xj, удовлетворяющие (9), определялись един-
ственным образом; выбрать такие значения и уг, чтобы существовало
много наборов Xj, удовлетворяющих (9).
Определение. Система г векторов Pt называется линейно независимой,
если из равенства
Рixi + Р4“ • • • РТ%Т = 0 (10)
следует, что хг = х2 = • . . = хт = 0. Если система векторов не является
линейно независимой, то в равенстве (10) по крайней мере одно =/= 0;
в таком случае говорят, что эта система линейно зависима. Легко видеть,
что этот вектор Р^ линейно зависит от остальных.
Упражнение. Показать, что система, состоящая из одного вектора,
линейно независима, если только этот вектор не является нулевым. Пока-
зать, что нулевой вектор линейно зависит от любой системы векторов.
тп-вектор, f-й элемент которого равен единице, а все остальные эле-
менты равны нулю, называется единичным вектором 1 2.
тп различных единичных векторов обозначаются через
W \oj
Упражнение. Показать, что векторы С7г- линейно независимы. Пока-
зать, что любой другой zn-вектор можно представить в виде линейной
комбинации единичных векторов t7f.
1 Т. е. вектор Рг-, для которого = 0.— Прим, перев.
2 Чаще такие векторы называют ортами, а название единичного сохраняют для
вектора, все компоненты которого равны единице.— Прим, перев.
179 12*
ВЕКТОРНЫЕ УРАВНЕНИЯ
Если, как и выше, для обозначения векторов мы будем использовать
буквы, то т линейных уравнений мы сможем представить в виде одного
векторного уравнения. Например, пусть
(7 = 1,2---п).
(12)
Тогда равенство (9) превращается в задачу определения (если это возмож-
но) весов Xj, которые выражают линейную зависимость между вектора-
ми Pj и Q,
Р ixl~\~ ^2X2~V • ' • Рпхп= Q • (13)
ВЕКТОРНОЕ ПРОСТРАНСТВО
Вместо того чтобы искать числа Xj, удовлетворяющие равенству (13),
мы можем обратить этот процесс и порождать векторы-столбцы Q =
₽ J/2, • • •, Ут)> изменяя значения х^ х2, . . ., хп. Множество
векторов {yi, у2, . . порожденное при всех возможных выборах
векторов (xi, х2, . . ., хп), называется векторным пространством. Напри-
мер, если мы рассмотрим в двумерном пространстве точки с координата-
ми (yi, у2), полученные, выбором в равенстве (14) различных значений Xi
и х2, то очевидно, что эти точки в совокупности составят всю плоскость
(У1, У г)
2 ) + (-I / ж2 — I и I •
z/ Х1/ \У2/
(14)
С другой стороны, точки (уи у2), определяемые равенством (15), лежат
на прямой 2yi = у 2.
(15)
Векторы (уи у2, уз), определяемые равенством
скость уз = yi + у2 в трехмерном пространстве,
1\ /2\ /уЛ
2 I Х1 ~Ь I 1 I = I У% I •
3 / \ 3 / \Уз/
(16), заполняют пло-
(16)
Легко видеть, что точки (yi, у2, уз) из равенства (17) также лежат в пло-
скости уз = у± + у 2, потому что векторы-столбцы, соответствующие
Хз и х^, линейно зависят от векторов-столбцов, соответствующих х± и х2
1\ /2\ /3\ /“Л (У\
2 I xl + I 1 I х2 +1 3 I Хз +1 + 1 I ^4 = | У2 | •
з/ \з/ \б/ \ о/ w
(17)
180
Действительно, преобразуя (17) с помощью равенств
3\ /1\ /2\ /—1\ /1\ /2\
3 | = | 2 ] + ( 1 I, I + 1 | = ( 2 1-1 1 I (18)
6/ \3/ \3/ \ 0/ \3/ \3/
мы получаем
! \ /2\
I (#1 + + #4) +1 1 I
3/ \3/
(УЛ
У 2 I ,
yj
(19)
и ясно, что класс векторов {у1у у2, Уз), порожденных равенством (19),
не меньше класса векторов, порожденных равенством (16).
Определение. Базисом векторного пространства называется любая
такая система линейно независимых векторов этого пространства, что все
другие векторы пространства могут быть представлены в виде линейных
комбинаций векторов этой системы.
Легко видеть, что может существовать много систем линейно незави-
симых векторов, которые порождают одно и то же векторное пространство.
Так, например, совпадают векторные пространства, порожденные равен-
ствами (14) и (20):
/ 1 \ / 0 \ [уЛ
( 0 ) Xi + (1 ) Х* = \уг] <2°)
РАНГ, ИЛИ РАЗМЕРНОСТЬ, ВЕКТОРНОГО ПРОСТРАНСТВА
Рангом векторного пространства называется наибольшее число линей-
но независимых векторов пространства. Мы покажем, что если векторное
пространство может быть порождено г линейно независимыми векторами,
то любая другая система г линейно независимых векторов этого про-
странства также может служить в качестве базиса. Более того, ни поро-
дить это пространство числом векторов, меньшим г, ни найти в нем более г
линейно независимых векторов невозможно. Это число г называется
рангом, или размерностью, векторного пространства.
Теорема 1. Пусть Q — любой вектор из векторного пространства;
порожденного системой линейно независимых векторов (Р±, Р2, . . Рг);
тогда числа xi9 х2, . . ., хг, удовлетворяющие равенству
PtXi + РгХ2 + ... + PrXr = Q, (21)
единственны.
Доказательство. Если бы эти числа были не единственны, то суще-
ствовал бы другой такой набор чисел x'i, х2, что
Pix'i~\~ Р2х* + • • • + Рrxr == Q- (22)
Вычитание равенства (22) из равенства (21) дает
ж;)4-Р2(^2—^2)+ • • • +Рт(хт — хг)=^0, (23)
и мы заключаем, что если не все (xi — xi) = 0, то векторы Pi9 Р2, . . Рг
не являются линейно независимыми, что противоречит предположению.
Определение. Выражение (21) называется представлением вектора Q
в базисе (Рп Р2, . . ., Рг), а числа (жх, х2, . . ., хг) называются коорди-
натами Q в этом базисе.
181
Упражнение. Показать, что система единичных векторов (11) состав-
ляет базис в пространстве Ет всех векторов с т компонентами, и коорди-
наты вектора в этом базисе совпадают с его компонентами.
Теорема 2. Если в векторном пространстве даны базис и вектор У? у= О,
то хотя бы один из векторов базиса можно заменить на R и получить
при этом новый базис.
Доказательство. Пусть представление вектора R в нашем базисе
имеет вид
Р ivl + Р2V2 + ... + РtVt = R- (24)
Так как /? =# 0, в представлении (24) по крайней мере одно у= 0. Пред-
положим, что =И= 0; покажем, что . новый базис может быть образован
заменой Pi на R. Прежде всего, векторы Р2, Рз, . . Рг, R линейно
независимы, так как в противном случае, ввиду того что коэффициент при
R отличен от нуля, представление R в базисе отличалось бы от представле-
ния (24), которое, однако, единственно (теорема 1).
Теперь если нам удастся показать, что произвольный вектор Q (опре-
деляемый, скажем, равенством (21)) может быть представлен в виде линей-
ной комбинации линейно независимых векторов Р2, Рз, • • Pr, R,
то мы покажем, что эти векторы образуют базис. Но умножение (24)
на произвольную константу 0 и почленное вычитание из (21) дает
Р1 (Ж1—4- Лг (^2—®у2) 4” • • • 4~Рг (хг~^т) 4~7?0 ~ Q, (25)
положив в этом равенстве
Q^xJVi, (^i¥=0) (26)
мы получим, что Q линейно зависит от остальных векторов, так как
Xi — 0г?1 = 0. Следовательно, наши независимые векторы могут поро-
дить любой другой вектор Q пространства.
Теорема 3. Если даны базис и к линейно независимых ненулевых векто-
ров R±, R2, . . . , Rk в векторном пространстве, порожденном этим
базисом, то найду/пся такие к векторов базиса, которые можно заменить
на Ri, R2, ...» Rk-
Доказательство проводится по индукции. Случай к = 1 был рас-
смотрен в предыдущей теореме. Предположим, что новый базис может
быть образован подстановкой к — 1 векторов Ri4 R2, . . ., Rk-i,
вместо к—1 векторов из базиса, например векторов Pi,P2, . . ., Рд-i,
так что новый базис есть Ri9 R2, - - Rk-i, Pk, • • •, Рг- Пусть пред-
ставление Rk в этом базисе имеет вид
+R2Vz + • • • + P-k-ivk-i 4~ Рkvk 4- • • • 4" Рrvr — Rk- (27)
По крайней мере одно =И= 0 для i к, так как в противном случае
вектор Rk линейно зависел бы от векторов Ri, R2, . . ., Rk-t, что про-
тиворечит предположению. Пусть для некоторого t к, vt 0. Тогда,
повторяя рассуждения предыдущей теоремы, в этом базисе Pt можно заме-
нить на Rk и получить новый базис, состоящий из векторов R2, . . .
, . Rk-i, Rk, Pk+i, - - Pt (исключая Pt). Следующие теоремы пред-
лагаются в качестве упражнений.
Теорема 4. Если существует базис, состоящий из г векторов, то любые г
линейно независимых векторов в векторном пространстве образуют базис.
182
Теорема 5. Если существует базис, состоящий из г векторов, то в век-
торном пространстве не существует более чем г линейно независимых
векторов.
Теорема 6. Если существует базис, состоящий из г векторов, то
в векторном пространстве не существует базиса с числом векторов, мень-
шим г.
Упражнение. Показать, что символические операции над уравне-
ниями Ei в § 8-1 могут также рассматриваться как векторные соотноше-
ния. Пусть Ei — (ан, ai2, . . ., ain; — вектор-строка, составленный
из коэффициентов и свободного члена Ef, тогда формулу (1) из § 8-1 можно
понимать как
М-^1 + ^2^2 + М?3 + • • • + — Eq.
Интерпретировать другие символические соотношения из § 8-1.
Упражнение. Показать, что ранг совместной системы уравнений
Ei, Е2, . . .-— равен рангу системы векторов-строк Е±, Е2, . . ., свя-
занных с этими уравнениями. Определение ранга системы уравнений
дано в конце § 8-1.
8-3. МАТРИЦЫ
ОПЕРАЦИИ НАД МАТРИЦАМИ
Прямоугольная таблица чисел называется матрицей. Таким образом,
коэффициенты из § 8-2 (1)
/ 2 3,— 4\
(-4 -2 3/ (1)
образуют 2 X 3-матрицу, т. е. матрицу с двумя строками и тремя
столбцами.
Вообще т X п-матрицей называется
(аи а12 ... ain \
а21 а22 ... а2п 1 = л = (а</)> (2)
^тп2 • • • Orrin/
что можно обозначить одной буквой А, или (ац), где — символ величи-
ны, стоящей на пересечении строки i и столбца /. Матрица, транспониро-
ванная к матрице А и обозначаемая через А' или через Ат, получается
взаимной перестановкой * 1 строк и столбцов. Если А = (а^) и Ат = (6^),
то bji = ai}.
Определение. Две m X «-матрицы называются равными, если равны
все их соответствующие элементы. Таким образом, равенство (яц) =
= (Ь„) означает, что
an = bij (i = l, 2, .,., m; / = 1, 2, ..., га). (3)
Определение. Суммой двух m X га-матриц называется матрица,
полученная сложением соответствующих элементов. Таким образом,
равенство
= + (4)
1 Как бы переменой ролями.— Прим, ред.
183
означает, что для любых i = 1, 2, . . т и j = 1, 2, . . п
сц = ац + Ьц. (5)
Например,
/2 3 4\ /11 0\ /3 4 4\
U 6 7/ + \1 0 1/ = \6 6 8/ ’
Понятие умножения двух векторов получается в результате суще-
ственного обобщения операций над числами. Основная идея состоит
в том, чтобы выражение
2х^ —|— 3^2 — 4я3 (7)
рассматривать как произведение двух векторов (2, 3, —4) и fo, х2, х3).
Удобно считать один из них вектор-строкой, а другой — вектор-столбцом
и притом так, чтобы вектор-строка предшествовал вектор-столбцу.
Определение. (Скалярным) произведением вектора-строки на вектор-
столбец, содержащих п компонейт каждый, называется число (скаляр),
равное сумме произведений соответствующих компонент, т. е.
Если п = 1, то равенство (8) сводится к обычному умножению двух
чисел
Определение. Произведением т X n-матрицы А на n-вектор X назы-
вается
Xt + #12 х2 + • • • + а1п хп
а21 Х1 + а22 х2 + • • • + а2п Хп
amlxi + ат2х2 + • • • + атпхп
Это определение обобщает введенные выше определения § 8-2 (3) и (8),
поскольку первое из них получается при п = 1, а последнее получается
при т = 1. Согласно определению (9), произведение АХ является век-
тором, г-я компонента которого равна произведению г-й строки матри-
цы А (рассматриваемой как вектор-строка) на вектор-столбец X. Действи-
тельно, если через At обозначить i-ю строку матрицы (2), т. е.
А = (flfi, • • • > ^in) (^== 1» 2, ..., т) (Ю)
то матрицу А можно рассматривать как столбец из векторов-строк
(11)
Теперь, если обозначить через X п-вектор
(12)
184
то понятно, что аналогично умножению вектора-столбца на скаляр,.
§ 8-2 (3), можно определить умножение матрицы на вектор (9) как
(13).
Матрицу можно также рассматривать и как строку, состоящую из векто-
ров-столбцов. Таким образом, если через Pj обозначить у-й столбец
матрицы (2), т. е.
(aij \
у 1
: I, (; = 1, 2, .п), (14).
/
ТО
(15}
Поэтому аналогично умножению вектора-строки на вектор-столбец (8)
произведение матрицы на вектор описывается формулой
\
. I = 4- Р2Х2 • • • + Pnxn, (16)*
xn /
поскольку
P lxl + P2x2 4~ • • • + Pnxn —
(ail X1 + a12 x2 + • • • + ain xn
fl21 X1 + a22 x2 4“ • • • + a2Jb xn
amtxi + am2^2 + • • • + amnxn
(17>
Мы можем по аналогии с векторами [см. § 8-2 (3)] определить также
и произведение вектора-строки л = (ль л2, . . ., лт) с т компонентами
на т X n-матрицу. Здесь следует положить
лА = л (Рн Р2, ..., Рп) = (лРь лР2, ..., лРп). (18)
Определение. Произведением вектора-строки л с т компонентами
на т X n-матрицу называется вектор-строка, /-я компонента которого
равна произведению л на у-й столбец матрицы А (рассматриваемый как
155
вектор-столбец). Таким образом,
где
(а11 а12
а21 а22
«ml ат2
&1п \
^2п I
= (лРь лР2, ...,яРЛ), (19)
^пт
ЭТР1 — Л1а11 + ^С2«21 4~ • • • 4" ^тат19
ЛР2 = Я1#12 + л2^22 4“ • • • + ^т«т2>
JtPп — Л^щ Л2&2п 4" • • • 4“ V^nn-
Это определение обобщает определение § 8-2 (3), которое получается при
т = 1; при п = 1 оно совпадает с определением (8), являющимся частным
случаем определения (9). Однако можно еще шире обобщить определение
произведения и сделать как определение (9), так и определение (19) частным
случаем следующего.
Определение умножения матриц. Произведением т X А-матрицы А
на А X n-матрицу А называется т X n-матрица АА, в которой эле-
мент, стоящий на пересечении строки i и столбца j, равен произведению
г-й строки матрицы А (рассматриваемой как вектор-строка) на у-й столбец
матрицы А (рассматриваемый как вектор-столбец).
Для того чтобы проиллюстрировать это, положим
(а11 «12 • • • «1Л \ / -^1 \
«2. —22 «2» 1 _ I Л 1 (20)
«ml «m2 • • • /
(«И а12 • • • «1п \
«21 «22 • • • «2/1 j (рь р2> . _ Рп), (21)
«Д1 «Й2 • • • «Лтг '
где через Pj обозначены столбцы матрицы А. Тогда, по определению,
где элементом матрицы А А, стоящим в строке i и столбце у, является
AtPj = «zi«ij 4- «z2«2j 4- • • • 4" «za«aj- (23)
Это определение является естественным обобщением умножения скаляра
на вектор-строку,’1 ибо, рассматривая А А как произведение матрицы
на строку из векторов-столбцов, мы должны положить
ЛА = А(Л,Р2, ...,РЛ) = (ЛЛ,^2, ...МРП), (24)
что совершенно понятно, поскольку у-й столбец матрицы АА из (22)
равен APj. С другой стороны, по аналогии с умножением вектора-столбца
Ж
на скаляр можно рассматривать АА как произведение столбца из векто-
ров-строк на матрицу
что снова совершенно естественно, поскольку i-я строка матрицы АА
>есть AjA.
ЗАКОНЫ МАТРИЧНОЙ АЛГЕБРЫ
Подобно обычным числам (скалярам), матрицы удовлетворяют ассо-
циативному и дистрибутивному законам для матричного сложения и умно-
жения. Сложение матриц подчиняется также и коммутативному закону.
Однако в общем случае коммутативный закон для умножения не имеет
места даже для квадратных матриц.
Пусть А — (ajk), В = (bj-fe), С = (cjk), три J X A-матрицы, D =
= / X /-матрица, а Е = (ем) — К X /-матрица.
1. Ассоциативный закон для сложения:.
(А + В) + С^А + (В + С).
Доказательство.
(ауй 4- bjk) 4- (cjk) = (ajh 4- bjk 4- cjk) = (ajk) + (bjk + Cjk).
2. Коммутативный закон для сложения:
А 4- В — В 4- А.
Доказательство.
(ajk + bjk) = (bjk + ajk).
3. Дистрибутивный закон для умножения суммы имеет вид
D (А + В) = DA 4- DB\ (А + В)Е = АЕ + BE.
Доказательство. Для доказательства первого равенства обозначим
через ( ) операцию составления матрицы из чисел и вычислим элемент
{i, к) матрицы — произведения
/ j \ / j
(dzj) (ajk 4- bjk) = I 3 dtj (ajk 4- bjk) 1 = 1(2 dijttjk) 4"
U=1 / \ 1
J \ J J
+ ( 2 dijbjk}j = ( 2 dijUjk) + ( 2 dijbjk} = DA 4- DB.
j=i / j=i j=i
4. Ассоциативный закон для умножения'.
D (АЕ) = (DA) Е.
Доказательство. Пусть АЕ = F = (/jZ) и DA = G = (gth), тогда
Z) (АЕ) = (dtj) (fji) = ( S dtjfji) = ( S dtj ( 3
\ j=l k=l
К (KJ
(DA) E = (gik) (eki) = ( 2 gik^ki) = 12(2 dijUjk) eki
fe==l \k=l j=l
Следует отметить, что можно изменить порядок суммирования в послед-
нем выражении для (DA) Е, тогда значение каждого (г, I) элемента будет
187
равно значению того же самого элемента матрицы D (АЕ), который полу-
чен в написанном выше уравнении.
Определение. Рангом матрицы называется ранг векторного простран-
ства, образованного ее столбцами.
Теорема 1. Ранг столбцов матрицы совпадает с рангом ее строк.
Доказательство. Рассмотрим однородную систему уравнений, коэф-
фициенты которой образуют исследуемую матрицу. Эквивалентная ей
каноническая система имеет столько же уравнений, что и ранг матрицы
по строкам. Поскольку всякое отношение зависимости или независимости
между столбцами является инвариантным относительно ведущих опера-
ций, ранг формы по столбцам совпадает с рангом исходной системы.
Но ранг формы по столбцам совпадает с рангом формы по строкам, т. е.
с числом базисных переменных, поскольку соответствующие этим пере-
менным столбцы, будучи единичными векторами, являются линейно
независимыми и могут быть использованы для получения столбцов с помо-
щью линейных комбинаций.
8-4. ОБРАТНАЯ МАТРИЦА
Квадратная т X zn-матрица называется невырожденной, если ее
столбцы независимы. В силу теоремы 4 из § 8-2 эти столбцы должны
составлять базис в пространстве m-векторов, поскольку т единичных
векторов образуют базис. Если можно привести систему т уравнений
к каноническому виду с базисными переменными х$х, Xj2, . . ., Xjmr
то коэффициенты при этих переменных в исходной системе, рассматривае-
мые как векторы, образуют базис. Для того чтобы убедиться в этом, заме-
тим, что если множество столбцов является линейно независимым (зави-
симым) до выполнения какой-нибудь ведущей операции, то это утвержде-
ние будет, справедливо для соответствующих столбцов и после ее выпол-
нения, и обратно. Отсюда, поскольку единичные векторы-столбцы из
коэффициентов при х^, Xj2, . . ., Xjm в каноническом виде являются,
очевидно, линейно независимыми, это же утверждение остается в силе
и для соответствующих им векторов в исходной системе.
Рассмотрим произвольное множество из т независимых столбцов^
являющихся коэффициентами при переменных х^, Xj2, . . ., Xjm в систе-
ме т уравнений; тогда эту систему всегда можно привести к каноническому
виду, причем эти переменные будут базисными. Для того чтобы убедиться
в этом, попытаемся привести систему к каноническому виду, используя
х^, хз& • • •> хзг- Предположим противное, т. е. что на r-м шаге (г < т)
невозможно преобразовать систему, используя переменное xjr+1 (потому
что все его коэффициенты в уравнениях, соответствующих небазисному
множеству, равны нулю). Очевидно, что в этой частично преобразованной
системе столбец /г+1 может быть получен как линейная комбинация из
г единичных векторов в столбцах /1, • • •, 7г- Но тогда это же спра-
ведливо и для соответствующих столбцов исходной системы, что противо-
речит предположению о независимости. Тем самым доказана
Теорема 1. Множество т т-векторов тогда и только тогда линейна
независимо, когда систему из т уравнений, коэффициентами которой
являются рассматриваемые т-векторы, можно привести к каноническому
виду с т базисными переменными.
Сформулированная теорема указывает конструктивный путь выяс-
нения того, является ли данная матрица невырожденной или нет. Свяжем
188
с невырожденной матрицей (или базисом) другую матрицу, называемую
обратной к ней. Далее мы проиллюстрируем это понятие и несколько
позднее определим его. В частности, использование обратной матрицы
базиса, связанного с /с-й итерацией симплекс-метода, дает удобный метод
приведения стандартной задачи линейного программирования к канони-
ческому виду и делает возможным проводить вычисления в симплекс-
методе, что будет рассмотрено в следующей главе.
ИЛЛЮСТРАЦИЯ
В системе (1) Xi и х2 можно исйользовать в качестве базисных пере-
менных, поскольку эта система может быть приведена к каноническо-
му виду с помощью этих переменных:
5^—4ж2 + 13ж3 — 2х4 + х5 = 20, (Е^
Xi— я24" 5xs— xk -|- x$ = 8. (E2) (
Матрица коэффициентов при этих переменных есть
и, в соответствии с введенным выше определением, образует базис, связан-
ный с переменными (xl9 х2).
Для обозначения базиса удобно пользоваться одним символом,
например В. Будем использовать и символ (аг/), где индексы показывают,
что элемент матрицы В, стоящий на пересечении i-й строки и /-го столбца,
^сть аи. Таким образом, для рассмотренного только что примера мы можем
написать
/5 — 4
В = (ац) = । ।
(3)
где ап = + 5, а12 = — 4, a2i = + 1, «22 = — !•
Для того чтобы найти обратную матрицу к матрице (базису) В (3),
рассмотрим каноническую систему уравнений с базисными переменны-
ми у19 у2.
5xi — 4х2 + у! =0,
^1“ ^2 +*/2 = 0,
где коэффициенты при Xi и х2 образуют базис В. Выразим из (4) Xi и х2
через yi и у29 исключая, получим
Xi +2/1 — 4у2 = 0;
^2 + У1“ 5^2 = 0. '
Ясно, что система (5) эквивалентна системе (4) и записана в канониче-
ском виде с базисными переменными и х2.
Таблица коэффициентов при yi и у2 в системе (5) называется обратной
матрицей матрицы (3) и обозначается через В"1. Таким образом,
Обратно, если коэффициенты при yt и у2 в системе (5) рассматриваются
как матрица, то, поскольку система (4) эквивалентна системе (5), коэффи-
циенты при Xi и х2 составляют матрицу, обратную этой, и мы сразу заклю-
189
чаем, что обратная матрица к обратной матрице есть сама исходная
матрица. Этот факт для квадратной таблицы чисел аналогичен известному
факту, состоящему в том, что обратное число обратного числа есть само
число.
Обратный базис 1 может использоваться для того, чтобы привести
систему линейного программирования, подобную системе (1), к канониче-
ской форме относительно соответствующих базисных переменных. Будем
считать, что первое уравнение системы (5), именно + yi — 4у2 — О,
означает, что если первое уравнение системы (4) умножить на 1, второе —
на 4 и затем их сложить, то все базисные переменные, за исключением
будут исключены. (Если бы это было не так, то приравнивание друг другу
этих двух различных выражений привело бы к линейному соотношению
между Xi и х2, что противоречит системе (4), в которой эти переменные
линейно независимы.) Аналогично из уравнения х2 + У\ — 5г/2 = О
следует, что если первое уравнение системы (4) умножить на 1, второе —
на —5 и затем их сложить, то все базисные переменные, за исключением х2г
будут исключены. Посмотрим теперь, каков будет результат применения
тех же самых операций к исходной системе (1). Так как коэффициенты
при Xi и х2 те же самые, что и в системе (4), то те же самые операции,
примененные к системе (1) вместо системы (4), приведут систему (1)
к канонической форме с базисными переменными и х2.
Xi — 7я3 + 2я4 — Зя5 = —12, {JEj-^ = Ei—^Е^
х2—12я3 + Зя4—4я5 = — 20. (Е' = — 5Е2)
Справа в (7) указаны операции, необходимые для того, чтобы из системы (1}
получить систему (2)'; заметим, что таблица из коэффициентов в уравне-
ниях Е[ и Е'2 есть обратный базис для базиса (6).
ОБЩИЕ СВОЙСТВА МАТРИЦЫ И ОБРАТНОЙ К НЕЙ МАТРИЦЫ
Наша цель состоит в том, чтобы формализовать и доказать в общем
виде утверждения, сформулированные в предыдущем пункте на основе
рассмотрения иллюстративного примера.
По теореме 1 квадратная матрица чисел
является невырожденной и ее столбцы образуют базис, если система
уравнений
а11 Х1 + а12 х2 + • • • + а1т хт + У1 = 0»
а21 х1~\~а22х2^~ • • • а2т хт ~УУ2
amixl + «тп2ж2 + • • • + ^mmxm ~^гУт~0
эквивалентна некоторой системе (10) в канонической форме с базисными
переменными (а^, х2, . . ., хт); иначе говоря, В является базисом, если
мы можем разрешить систему (9) относительно х2, . . ., хт, выражая
1 Термин автора, широко используемый и в дальнейшем. Удобнее было бы
говорить о матрице, обратной к матрице данного базиса.— Прим, ред.
190
их через уи у2, .
*1
х2
. ут, так что
+ 011 У1 + 012^2 + • • • + 01m Ут = О,
+ 021 У1 + 022^2 + • • • + 02m Ут = О,
хт + 0т12/1 + РтгУг + • • • + РттУт = 0.
(10)
Ясно, что если (8) является матрицей, образованной коэффициентами при
некотором подмножестве из т переменных в задаче линейного программи-
рования размерами т X п, то эту задачу можно привести к канонической
форме, используя соответствующие переменные в качестве базисных.
Определение. Матрица из коэффициентов при уг в системе (10) назы-
вается обратной матрицей к матрице В из коэффициентов при Xj в систе-
ме (9). Мы обозначим через В"1 обратную матрицу к матрице В. По опре-
делению,
(011 012 •••01m \
₽21 ₽22 • • • Ргт j Щ)
Pml Рп»2 • • • Ртт /
Теорема 1 § 4.2 устанавливает единственность канонической формыг
а значит, и единственность обратной матрицы. Наоборот, так как систе-
ма (9) эквивалентна системе (10) и находится в канонической форме отно-
сительно переменных р4, р2, • • •, Ут, нами установлены две следующие
теоремы.
Теорема 2. Обратный базис единственен.
Теорема 3. Обратная матрица к обратной матрице есть сама
матрица.
Если в системе (10) значения всех независимых переменных yi поло-
жить равными нулю, за исключением уь = — 1, то мы получим для базис-
ных переменных очевидное решение Xi = 01А, х2 = 02ь, . . ., хт = ртй.
Так как система (9) имеет то же множество решений, то эти значения х,
и yi также должны удовлетворять ей. Подстановка в i-е уравнение систе-
мы (9) дает соотношение между г-й строкой базиса В и А-м столбцом обрат-
ного ему базиса В-1, именно:
Теорема 4. Сумма произведений соответствующих элементов i-й
строки матрицы В и k-го столбца матрицы В1 равна нулю или единице
в зависимости от того, будет i=£ к или i = к:
+ аг202Л + • . • + —
Например, для базиса (2) мы видим, что
0, если &=/=&,
1, если i = к.
а110и + а12021 — (5) (1) + (— 4) (1) = 1,
а11012 + а12022 " (5) ( 4) + ( 4) ( 5) = 0,
а21011 + а22021 = (!)(!) + ( — 1) (1) = 0,
а21012 + а22022 — (1) ( 4) + ( 1) ( 5) — 1.
(г = 1, * = 1)
(i = l, к = 2)
(1 = 2, * = 1)
(i==2, к = 2)
(12)
(13)
После того как теорема 4 установлена, мы
ролями В и Б-1 и получить следующую теорему.
можем далее поменять
Теорема 5. Сумма произведений соответствующих элементов i-й стро-
ки матрицы В'1 и к-го столбца матрицы В равна нулю или единице в зави-
191
симости от того, будет к или i = к.
10, если к =^i,
л ОРТТТЛ л _ j (14)
В нашем примере мы видим, что
₽ue« + ₽A= (1)(5) + (-4) (1) = 1, (i = i, k = i)
611^12 + Pi2a22 — (1) ( 4) + ( — 4)( 1) = 0, (i = l, к = 2)
Р2Л1 + М21- (1)(5) + (-5) (1) = 0, (i = 2, Л = 1)
Р 21а12 + 022^22 = (1) ( — 4) + ( — 5) (— 1) = 1. (* = 2, к = 2)
Теорема 6. Если каноническая система (10) может быть получена
из канонической системы (9) с помощью линейных комбинаций, то она
эквивалентна системе (9) и матрица, составленная из коэффициентов
при yt в системе (10) является обратной для базиса, и наоборот.
Доказательство. Рассмотрим совместно системы 9 и 10. По теоре-
мам 8, 9, 10 § 8-1 ранг этой системы равен т, потому что первые т уравне-
ний независимы и по предположению о том, что остальные т уравнений
от них зависят. Однако последние т уравнений независимы и, так как
максимальное число независимых уравнений равно т, первые т уравне-
ний (9) зависят от уравнений (10). Следовательно, из уравнений (10) сле-
дуют уравнения (9), и эти две системы эквивалентны. Оставшаяся часть
теоремы следует из определения обратной матрицы.
Рассмотрим теперь другую теорему, обратную теореме 4 (или тео-
реме 5). Предположим, что нам даны система (10) с матрицей коэффициен-
тов (Рц) и другая матрица коэффициентов (а^), строки и столбцы которых
удовлетворяют соотношениям (12). Мы хотим доказать, что система (9)
эквивалентна системе (10) и, следовательно, матрица (а^) является обрат-
ной для матрицы (Pij).
Чтобы убедиться в этом, умножим первое уравнение системы (10)
на ан, второе — на ai2 и т. д., т-е уравнение — на aim и сложим; мы
получим г-е уравнение системы (9). Таким образом, из соотношений (12)
и (10) следуют уравнения (9). Отсюда, по теореме 6, следует:
Теорема 7. Для того чтобы матрица (0 ц) была обратной к матрице
(аи), необходимо и достаточно, чтобы между их строками и столбцами
имели место соотношения (12) или (14).
Вспомним, что транспонированная матрица для матрицы В есть
т X w-матрица, элементы которой получены переменой ролями строк
и столбцов матрицы В\ в качестве упражнения предлагается доказать,
что из соотношений (12) и (14) следует.
Теорема 8. Обратная матрица к транспонированной матрице есть
.транспонированная матрица' к обратной матрице.
Матрица В, все элементы главной диагонали которой равны единице,
а все остальные элементы равны нулю, называется единичной матрицей
и обозначается символом I или 1т; она называется единичной потому, что
для любой т X n-матрицы М имеет место Im М = М. Например, еди-
ничная матрица для т = 4 есть
(1 0 00\
0 1 00 ]
0 0 10 Г
0 0 0 1 /
192
(m = i)
(16)
Легко Проверить, что В-1 — В, потому что соответствующая ей систе-
ма (9) находится в этом случае в канонической форме как по отношению
к xi9 х2, х3, х^ так и по отношению к уи у2, Уз, Уь
ПРИВЕДЕНИЕ М х ^СИСТЕМЫ К КАНОНИЧЕСКОЙ ФОРМЕ
Для того чтобы привести систему
а11 Х1 + а12 х2 4" • • • 4" ат Хп — Ь{,
а21 Xi + а22 Х2 4" • • • 4" а2п хп — ^2> (
amixi + ат2х2 4" • • • 4" атпхп — Ьт
к канонической форме с базисными переменными я2, • • •» хт, пред-
положим, что квадратная матрица В = (ai?) есть базис и известна обрат-
ная матрица В-1 — ($ц). Если первое уравнение (17) умножить на 0ц,
второе — на pi2 пт. д., тп-е — на 01?п, а затем полученные произведения
сложить, то сумма будет равна
( 2 PlA^Al) Х1 4“ ( 2 Р1&ЯЛ2) х2 4- • • • 4“ ( 2 хп — 2 Plfe^A’ (18)
fe=l fe=l fe=l Ь=1
Вообще r-e уравнение системы (19) может быть получено умножением
первого уравнения (17) на pri, второго — на 0г2 и т. д., тп-го — на рг7П
и образованием их взвешенной суммы; в результате этого получится кано-
ническая система:
Х1 4“ ^1, m+1 хт+1 4- • • • 4- хп — ^1,
хг 4~ т+1 хт+1 4~ • • • 4" ^гп хп — Ьг,
хт 4- т+1 #т+1 + • • • 4- &тпхп —
где для 7 = 1, 2, . . . , п мы положили
а17 — Р11 alj 4- Р12 a2j 4- • • • 4- Р17П amj,
a2j = P21 alj 4" P22 a2j 4“ • • • 4“ Ргтп G/nj,
amj — Pmi^ij 4“ Pm2a2j 4~ • • • 4“
&1 — PH 4- P12 b2 4" • • • 4“ Pirn bm,
^2 = P21 4- P22 b2 4~ • • • 4“ Ргт bm,
bm = pmi&i 4“ Pm2^2 + • • • 4" Pr^mm-
Заметим, что система (19) находится в канонической форме по отношению
к переменным х1у х2, ... , хт в силу соотношения между строками
и столбцами матриц В-1 и В; именно из (14) следует, что для j = 1, 2, . . .
. . . , т.
О для i = l,2,..., т и г #= /,
1 для i = j.
(22)
13 Дж. Данциг
193
8-5. СИМПЛЕКС-АЛГОРИТМ В МАТРИЧНОЙ ФОРМЕ
Основная задача в векторном обозначении состоит в том, чтобы
найти значения rq > 0, я2 > О, . . . , хл > 0 и min 2, удовлетворяющие
условиям
Р 1^1 + Р 2Х2 + • • • + Р пхп — Qt (1)
С1Х1 4- С2Я2 + • • • + спхп — Z, (2)
где
и afj, biy Cj постоянные.
Для симплекс-алгоритма требуется, чтобы тп-векторов из числа Р/
были линейно независимы Пусть Pj1? . . . , Pjm — такая система
линейно независимых векторов. Эти векторы образуют базис В в век-
торном пространстве, порожденном векторами Piy Р2, . . . , Рп:
Р—(Рз^ Pjtf •••’Pjm)* (4)
Каноническая форма получается умножением уравнения (1) на 5-1, т. е.
(5-^1) xi + (^2) Х2 + .. • + (В-'Рп) хп = В-Ч}, (5)
или
Р Iх! + Р2Х2 + • • • + Р пхп = Q, (6}
где (см. § 8-2)
B-4>j = Pj>, B-'Q = Q (7)
суть представления в базисе соответственно Pj и Q. Заметим, что из равен-
ства B^B — l (единичная матрица) следует, что
P^B-'Pj^lh, (8>
где Ut есть единичный вектор, у которого i-я компонента равна единице,
а все остальные компоненты равны нулю. Но последнее, по определению,
означает, что система (6) находится в канонической форме с базисными
переменными . . . , xjm (см. § 4-2).
Базисное решение получается, если положить небазисные перемен-
ные Xj — 0; таким образом, значения базисных переменных даются урав-
нением
иiXji + U2Xj2 4-... + Umxjm = Q (9)
ИЛИ
Упражнение. Показать, на что влияет изменение порядка базисных
переменных и базисных векторов.
Базисное решение допустимо, если
(?>0. (И)
1 В случае, когда это условие не выполнено, применяется этап I симплекс-
алгоритма.
194
Определение. Q 0 означает, что каждая компонента вектора Q
удовлетворяет неравенству Ъг 0.
Относительные оценки Cj получаются в результате исключения
из уравнения для z. Если мы определим вектор-строку
N = с}2, (12)
и умножим равенство (6) на у, то мы получим
(тЛ) «I + (тЛ) х2+ ... + (уРп) хп = (y<2), (13)
где (yPj) — постоянные (так как каждая из них представляет собой про-
изведение вектора-строки на вектор-столбец). В частности, yPj. = yUi =
= Cj.i так что базисные переменные в уравнении (13) имеют те же коэф-
фициенты, что и в уравнении (2). Поэтому, вычитая равенство (13) из
равенства (2), мы исключаем базисные переменные, получая равенство
(ci — yP1)xi+(c2—yP2)x2+... + (cn — yPn)xn==z — yQ. (14)
Следовательно, относительные оценки выражаются формулами
С} = с} — уР} =
= с}-у(В~Ч>}) = (15)
= (уВ-^Р,
или
Cj = Cj — ftPj, (16)
где мы положили для вектора-строки
л-уВ'1. (17)
В словесной формулировке равенство (16) утверждает, что относитель-
ные оценки Cj получаются вычитанием из Cj взвешенной суммы коэффи-
циентов «и, a2j, . . . , amj, причем весами (одними и теми же для всех /)
являются т компонент л4, л2, ...» лт вектора л. Эти компоненты лг
называются симплекс-множителями (более подробно они будут рассмотре-
ны в следующей главе). Умножая соотношение (17) на В, мы получаем
лВ = у (18)
или
Л • ’ ’ ’ = %* • • • ’ СЬп)' (19)
В частности,
= для г = 1, 2, ..., т. (20)
Таким образом, веса л$ суть именно те числа, на которые нужно умножить
исходные уравнения (1) и затем сложить их, для того чтобы исключить
из уравнения (2) коэффициенты при базисных переменных.
Базисное решение оптимально, если все с7>0. Если не все
то ищется улучшенное решение; для этого сначала выбирается такое $, что
cs = mine7, (21)
и затем значение xs увеличивается как можно больше, причем остальные
небазисные переменные оставляются равными нулю. Для того чтобы быть
неотрицательным, вектор значений базисных переменных должен удо-
влетворять неравенству
(<?—Psz8)>0. (22)
195 13*
При некотором критическом значении xs = я* значение некоторой компо-
ненты г этого вектора изменит знак, в то время как все другие его компо-
ненты останутся неотрицательными (в противном случае z -> — оо при
xs -> + оо). Компоненты векторов Q, Ps и число г, которые определены
ранее, суть
О| II . <3*1 О'4! ьэ со II Со Со 4 = A- = min3-- (ars>0) (23)
Ьтп ars ais>Q ais
Следовательно, для того чтобы получить базис В* следующего цикла,
вектор базиса Pj заменяется на вектор Ps. Это завершает описание симп-
лекс-процесса в матричном обозначении. Теперь мы углубимся в сущность
перехода от цикла к циклу.
ПЕРЕХОД ОТ ЦИКЛА К К ЦИКЛУ К+1
Последний шаг симплекс-процесса состоит в преобразовании таблицы
с использованием ведущего элемента ars. Вместо этого мы будем исполь-
зовать базис, обратный новому базису, для того чтобы, слегка видоизме-
нив представления (7) векторов Pj и Q в старом базисе 5, получить их
представления в новом базисе В*. Прежде всего заметим, что Pj — B~4>j
или Pj = BPj. так что
(«Is \
а\s = • • • +Pi+ + • • • + Pi+s, (24)
fyns'
где (ais, a2s, • • • > ams) есть представление вектора Ps в базисе В.
Мы можем использовать равенство (24), для того чтобы выразить век-
тор Pjr в новом базисе В*; таким образом,
Pir = P^i ++ РЛ +...+ Pimkm = В*К, (25)
где мы положили К = {fc1? k2, . . . , km}, В* = (Pj^ • • • > Ps, • • •
• • • ’ и
^•=-4^-, (i#=r) (26)
ars
kr = J-. (27)
ars
Для других i У= г мы можем тривиальным образом представить вектор Ру
в базисе 5*
Pit = Рй-0+ .. .я+ Ps-0 + ... + Р;. 1 + .. , + Pjm-0 = B*Ult (28)
так что соотношение между старым и новым базисом дается равенством
В = (Р^ ...» Pjm) = B*(Ub U2, ..., К, ..., Um). (29)
Умножая это равенство справа на В'1 и слева на (5*)"1, мы получаем
соотношение между базисами, обратными новому и старому.
(Б*)-^(^ь U2, ..., К, ..., Um)B~\ (30)
196
Матрица (31) почти совпадает с единичной матрицей, за исключением
столбца г, в котором расположены значения kt. Матрица, которая отли-
чается от единичной только одной строкой (или столбцом), называется
элементарной матрицей.
/1 к, \
1
(Uit и2, К, ..., ит) =
кТ
1
fym
Таким образом, согласно равенству (30), базис, обратный новому, пред-
ставляет собой произведение элементарной матрицы на базис, обратный
старому. Если теперь мы умножим обе части равенства (30) справа на любой
вектор Pj, то мы сможем из представления вектора Pj в старом базисе
Pj = B~rPj получить его представление в новом базисе:
Ку Um)pja (32)
Удобно записать матрицу (31) в виде суммы единичной матрицы и матри-
цы, отличающейся от нулевой только одним столбцом:
(С7Ь U2, ..., К, ..., ит) = (иь U2, ..., Ur, ..., Е7™) +
+ (0, 0, ... , К — иг, .... 0) (33)
и ввести вектор к = к-иг / йЛ = кТ = ( ki у kr — l (34)
Теперь мы имеем \&т / \ km /

+ (0, 0, ...,K-Ur, 0, ..., OjB-^^-HO, 0, ...,0)В-х. (35)
Если мы теперь обозначим через строки матрицы В"1, т. е., если мы
положим
\Ртп /
(36)
197
и произведем подстановку в предыдущее равенство, то мы получим
или
(37)

(38)
Заметим, что матрица (В*) 1 отличается от матрицы В~г на матрицу К$г,
которая представляет собой произведение вектора-столбца К на вектор-
строку рг. Таким образом,
(Prl, • • •, prj) • • • > рттп),
(39)
^ = (₽о).
\kmJ
Элемент (i, /) матрицы К$г есть просто k$rj. Следовательно, чтобы полу-
чить элемент (i, /) матрицы (В*)"1, мы к прибавляем т. е.
(40)
Наконец, новое представление из старого мы получаем, пользуясь равен-
ством (38):
(В*)-1 Р; = (В-1 + Арг) Р; = В-1Р; + (Apr) Pj = Pj + Karj, (41)
где мы заменили постоянную РгРу на значение arj r-й компоненты в пред-
ставлении вектора Pj в базисе В. Таким образом, новый вектор Pj отли-
чается от старого на вектор, пропорциональный К, причем множитель
пропорциональности есть r-я компонента вектора Pj.
ПРЕДСТАВЛЕНИЕ ОБРАТНОГО БАЗИСА В ФОРМЕ ПРОИЗВЕДЕНИЯ
Соотношения (30) и (40) дают два способа выразить базис, обратный
новому, через старый базис. Нужно заметить, что, вообще говоря, пред-
ставление (40) требует т2 изменений компонент матрицы В-1, в то время
как соотношение (30) показывает, что процесс получения (В*)"1 из В-1,
состоящий в умножении на элементарную матрицу (31), требует только
знания т компонент вектора к и его положение г в матрице.
А. Орден еще на заре линейного программирования отметил, что
с вычислительной точки зрения может оказаться удобным представ-
лять обратный базис в виде произведения элементарных матриц. Напри-
мер, базис, обратный исходному, путем использования искусственных
переменных можно сделать единичным. Обратный базис для цикла 1
представлял бы собой тогда одну элементарную матрицу, которую легко
можно было бы записать на магнитной ленте электронной вычислительной
машины в виде одного вектора-столбца К (и его положения г). Обратный
базис для цикла 2 был бы тогда произведением новой элементарной матри-
цы и предыдущей для цикла 1. Это произведение могло бы храниться
198
просто путем записи нового столбца К после первого столбца К на той
же самой магнитной ленте и т. д. Это предложение Ордена по записи
обратного базиса было использовано как в программе РЭНД Орчард-Хейса
[1], так и в программе РЭНД Филиппа Вулфа (использующей гибкий
язык-посредник для вычислительной машины ИБМ-704).
Упражнение. Рассмотреть связь между вектором К в (31) и представ-
лением нового вектора Ps, входящего в базис.
Упражнение. Предположим, что обратный базис дан в форме про-
изведения; определить детальный вычислительный процесс представле-
ния вектора Ps в базисе путем умножения его слева на последовательные
элементарные матрицы, порожденные циклом 1, циклом 2 и т. д.
БЛОЧНЫЕ ВЕДУЩИЕ ЭЛЕМЕНТЫ
Таккер ]9] обобщает понятие ведущего элемента путем введения одно-
временно нескольких столбцов в базисное множество. Пусть в таблице
коэффициентов (42) xm+i, хт+2, • • • , xm+k заменяют хи х2, . . . , xh
в качестве базисных переменных
• • • aim+k
&in
(42)
^km+i • • • ^km^k
\ 1 • • • ^mm+k • • • ^mn
, базис .^вводятся Другие свободные
в базис столбцы члены
Заметим, что новый базис имеет структуру
в* = (р 0 V
\ Q I т-k /
где Р обозначает квадратный блок, отмеченный в (42) и называемый
ведущим блоком. Так как значение определителя матрицы В* совпадает
со значением определителя матрицы Р, то отсюда следует, что, для того
чтобы матрица В* была базисом, необходимо, чтобы определитель матри-
цы Р был отличен от нуля. Для того чтобы перейти от одного базиса
к другому, обозначим через Р“х матрицу, обратную Р. Аналогично перво-
му шагу обычного перехода (делению на ненулевой ведущий коэффициент)
первые к строк матрицы (42) умножаются на Р"1. Пусть первоначальная,
структура в матричной форме такова:
Л о
О Im-k
Р R е\
Q S /г
(43)
Тогда умножение на Р"1 дает
Л,_/Р“1 0 h
“ \ о Im_h Q S f Г
199
(Щ
Следующий шаг состоит в «исключении» системы переменных
, ят+д из оставшихся уравнений. Для этого первые к строк
умножаются на — Q слева и прибавляются к нижним строкам, что дает
новую матрицу
А*( Р1 0 Ik P1R Р ±е
\-QP~1 Im k o S-QP-'R f-QP-'e
Заметим, что столбцы, соответствующие новому базису, если их должным
образом упорядочить, образуют единичную матрицу, так что А* имеет
требуемую каноническую форму.
8-6. ЗАДАЧИ
ПОВТОРЕНИЕ
1. Доказать, что значения в канонической форме не зависят,
вообще говоря, от порядка исключения, если только единичный коэффи-
циент при каждой базисной переменной в канонической системе находится
в одной и той же строке. Если это условие не выполнено, то после соответ-
ствующей перестановки строк канонические формы будут одинаковы.
2. В следующих примерах определить для каждой системы, совместна
она или несовместна и содержит ли она избыточные уравнения. Если систе-
ма совместна, определить ее ранг.
2х| — 2#2 4~ #з 3,
(a) 2#i -j— х2 — 2#з = 2,
4" #2 4" #3 — 3,
#2 — #3=1-
(б) 2&1 — х2 -j- За?з = 1,
— 4^4 4~ 3^2 + #з—3,
— 5^14- 4^2 4“ 3#з — 3,
#14~2х24“ #з = 2.
(в) #i 4~ #2 4" Зх3 4~ #4 4" #5 4~ ^#6 — 1»
2^ — х2 — я34~ #4 — 2х5— 2я6 = 3,
4*С| 4“ #2 4~ 3#з 4~ 3#4 4~ 10xg '== 5,
6ж4 — х2 — 9х3 + 2я4 — 7я5 + 12я6 = 5.
3. Классическая транспортная задача Хичкока — Купманса состоит
в нахождении неотрицательного решения системы
п
2 = (г = 1, 2, .т; аг>0).
j=i
* т
= (/=1, 2, .... п; ^>0).
г=1
2=1 ;=1
т п
Показать, что равенство 2 at = 2 bj является необходимым условием
г—1 j=i
для совместности уравнений.
200
4. Каков ранг транспортной задачи без свободных переменных?
Со свободными переменными? Дать доказательство (см. гл. 3, задачи 4 и 5).
5. Даны две линейные системы; как бы вы выяснили, одно и то же
у них множество решений или нет? Эквивалентны они или нет? Доказать*
что системы (А) и (В) эквивалентны.
(А) 2#! + 3#2 + 4я3 = 9 (В) я2+ ^3 = 3
х1'— хг+ #3=1 7я1--2;г2 + 5я3= 11
4xj. —}— Зх2 -j- 2х3з= 9 5х^ ~ 2з?2 7^с3 === 1(
7xt — 2я2 + 5я3 = 10
5ж4 — 2х2 + 7х3 = 10.
6. Показать, что в разрешимой системе ранга г представить зависи-
мое (г + 1)-е уравнение в виде линейной комбинации г независимых
уравнений можно только одним способом.
7. Пусть даны система г независимых уравнений и система тп — г
уравнений, зависимых от первых уравнений. Доказать, что любое уравне-
ние первой системы и любое уравнение второй системы можно поменять
ролями при условии, что в линейную комбинацию уравнений первой
системы, дающую зависимое уравнение, рассматриваемое уравнение
первой системы входит с ненулевым весом.
СВОЙСТВА, ИНВАРИАНТНЫЕ ОТНОСИТЕЛЬНО ВЕДУЩИХ ОПЕРАЦИЙ
(См. § 8-1)
8. Построить пример, показывающий, что последовательность эле-
ментарных операций в отличие от ведущих не сохраняет взаимнооднознач-
ное соответствие между разрешимыми независимыми уравнениями и между
оставшимися зависимыми или противоречивыми уравнениями.
9. Найти ранг г системы, приведенной ниже, определяя число уравне-
ний в ее каноническом эквиваленте. Найти наибольшее число независимых
уравнений исходной системы и проверить, равно ли это число рангу.
Показать, что это число равно рангу матрицы, составленной из коэффи-
циентов и свободных членов.
2xt + Зя2 + 4я3 = 9,
х2+ х3 — 19
3#i 2х2 —j— 5х3 = 10,
4#i х2 —j— 6х3 = 11,
6#! + 4я2 + 10я3 = 20.
Показать, каким образом можно получить все решения этой системы
уравнений.
10. Каково наибольшее число независимых уравнений полученной
системы? Как определить, совместна или несовместна система? Имеет
ли несовместная система ранг? Показать, что если ранг матрицы коэффи-
циентов и свободных членов не меняется после вычеркивания свободных
членов, то система разрешима.
11. Почему, еслц некоторая система независимых уравнений экви-
валентна данной разрешимой системе, то число уравнений первой системы
равно рангу второй системы?
12. Показать, что если система имеет к независимых уравнений,
а остальные уравнения зависят от них, то максимальное число независи-
мых уравнений системы равно к.
13. Показать, что системы, полученные из данной последовательными
элементарными преобразованиями, имеют тот же самый ранг.
201
14. Пусть Xi = . . . , xk = x°k и xk+i = . . . = xn = 0 — реше-
ние некоторой системы уравнений, где ж? 0 для i — 1, 2, . . . , к.
9 Пусть г — ранг подсистемы, полученной отбрасыванием членов, содержа-
щих Xk+i, . . . , хп. Показать, что существует решение, содержащее
не более г отличных от нуля переменных.
15. Предположим, что целевая функция z для системы линейных
уравнений с неотрицательными переменными неограничена сверху; пусть
к — минимальное число положительных переменных, необходимое для
того, чтобы получить класс решений, для которого z -> + оо. Показать,
что к = г + 1, где г — ранг подсистемы, образованной отбрасыванием
всех нулевых переменных в указанном выше решении.
16. Предположим, что
2 ~ ajhi 2 xijk — ^iht 2 = Cib
i j k
i=l, 2, ..., m; /=1, 2, ..., n; Zc = 1, 2, ..., p.
Каким соотношениям должны удовлетворять для того чтобы
система была совместна? Сколько уравнений независимы?
ВЕКТОРНЫЕ ПРОСТРАНСТВА (См. § 8-2)
17. Повторить определение независимой системы векторов; пока-
зать, что любой отдельный вектор независим, за исключением нулевого
вектора. Показать также, что нулевой вектор не содержится ни в какой
•системе независимых векторов.
а) Показать, что если Рь Р2, • . . , Рп и Q -— векторы-столбцы из
тп-компонент и
Р iXi + Р2#2 + • • • + Рпхп '= Qi
где Xj — скаляры, то для любого скаляра к
Pi (kXi) + Р2 (кх2) + ... + Рп (**п) = Qk-
б) Показать, что если, кроме того, имеет место равенство
Р1У1 + Р2У2 + • • • + Р пУп = Р,
то
Р1 (У1 + kxi) 4- Р2 (у2 + кх<^ 4“ • • • + Рп (Уп 4~ кхп) — Qk 4~ R*
18. Показать, что если система линейных уравнений записана в век-
торной форме
а) РiXi 4- Р2х2 4- ... 4~ Рпхп — Qi
где Pj и Q суть соответственно у-й вектор-столбец коэффициентов и сво-
бодных членов, то
б) Р }Xi 4- Р2х2 4- ... 4~ Рпхп — Q »
где P'j и Q' суть соответствующие векторы-столбцы после элементарного
преобразования.
19. В задаче 18 показать, что если векторы Рь Р2, . . . , Pk линейно
независимы, то векторы Р[, Р'2, . . . , Р'ь также линейно независимы,
я если между векторами Р1? Р2, . . . , Pk имеется линейная зависимость,
что такая же зависимость имеется и между векторами Р', Р^, . . . , Р&.
202
МАТРИЦЫ (См. § 8-3)
Пусть
Л = (4, 4, 2), Л = (1, — 2, 3).
Л2=(6, 3, -1),
20. Показать, что AtPt = 2 и A2Pi = 3.
21. Найти ЗЛ2; Ai + Л2; Ai + ЗЛ2.
22. Если Ai + Л3 = А21 то чему равны компоненты Л3?
23. Предположим, что Ai = (2, 1), А2 = (1, — 1) и Pi = (х19 х2).
Если AiPi = 1 и A2Pi = 3, то чему равны компоненты Р^
24. Покупатель купил в универмаге 10 платьев по 12 долл, каждое,
15 свитеров по 6 долл., 3 костюма по 40 долл, и 20 блуз по 4 долл. Пусть
вектор А = (10, 15, 3, 20) представляет купленные количества, а Р =
— (12, 6, 40, 4) — вектор цен. С помощью скалярного умножения векто-
ров показать, что общая стоимость покупок равна 370 долл.
25. Фабрикант пластмасс обнаружил, что машина для отливки неко-
торой детали требует для своей наладки двух рабочих в течение 3 часов.
Плата каждому из этих наладчиков составляет 20 долл, в час. Предположим,
что отливка каждой детали требует 20 секунд. Эксплуатационные издерж-
ки, включая накладные расходы, составляют 2,5 долл, в час. Кроме того,
каждая деталь требует 2 унции материала, стоимость которого равна
0,16 долл, за фунт. Написать вектор-строку из четырех компонент, кото-
рый представлял бы издержки производства одной детали, каждой из
двух деталей, каждой из трех деталей и т. д. Используя скалярное умноже-
ние векторов, найти издержки производства одной детали. С помощью
операций над векторами найти общую стоимость производства 300 деталей.
26. Найти компоненты вектора X = (ж1? х2), где
/2 1\ 1хЛ /1\
\1 —1/ \я2/ \ 3 /
27. Показать, что если А — вектор-строка и Р — вектор-столбец,
то A (kP) = к (АР), где к — константа.
28. Выполнить указанные действия:
ч /2 3\ II -1\
а) ,
\1 3/ \1 1/
ч /1 -1\ /2 3\
В \1 1) (1 3/ ’
г) (2 -1) (2 3) ,
\1 3/
/2 3\ /4 1 3 -1 \
Д U 3/ \2 0 2 2/ ’
29. Пусть I — единичная 3 X 3-матрица, а М — любая 3 X 3-матри-
ца. Показать, что MI — IM = М.
30. Пусть 0 — квадратная нулевая матрица (все ее элементы равны
нулю). Показать, что МО = ОМ = 0.
203
31. Пусть
/ 3 1 2\
М ==( —10 2),
\ 12 1/’
а 1 и 0 определены, как в задачах 29 и 30. Найти
а), М2, 7И3, М4,
б) Z2, Z3, Z4,
в) О2, О3, О4.
ОБРАТНАЯ МАТРИЦА (См. § 8-4)
32. Для каждой из следующих матриц найти обратную:
33. Каковы обратные матрицы для каждого из базисов примеров 1 и 2Г
§ 5-2? Для каждой обратной матрицы показать, что выполнены соотно-
шения (12) и (14) § 8-4.
34. Показать, что каждый элемент Bij матрицы В”1, обратной матри-
це В, может быть представлен как (— l)i+j'/B, где D — определитель
матрицы В, a Dji — определитель матрицы, полученной из матрицы В
вычеркиванием строки i и столбца /.
35. Известные уравнения поворота системы координат имеют вид
У1 = xt cos 0—х2 sin 0,
у2 = Xi sin 0 + ^2 cos 0*
Выразить Xi и x2 через yi и у2. Каков обратный базис? Показать, что
соотношения (12) и (14) § 8-4 выполнены.
36. а) Найти обратную матрицу для матрицы, составленной из коэф-
фициентов при Xi и х2 в системе:
3&1 — 2#2 “I- 4^з -j— 2rr4 — х§ Xq = 4,
xi 4" ^2~Ь ^з 4~ 3^4 4~ х§ 4~ ^7 — 3.
б) Привести эту систему к канонической форме относительно Xi и х2.
Каковы коэффициенты при xQ и х7 в сравнении с элементами обратной
матрицы?
37. Показать в общем виде, что элементами обратной матрицы для
любой системы базисных переменных в т X w-системе (т п) с неотри-
цательными переменными
а11ж14" ^12^24~ • • • 4" атхпЛ~ xn+i —
Л21^1 + а22Х2 4- • • • 4" а2пхп 4" хп±2 — ^2>
4“ ^7712*^2 4“ • • • 4“ &тпхп 4" хт+п — Ьт
будут коэффициенты при яп+1, . . . , хт+п после того, как система
приведена к канонической форме.
204
38. Показать, что если х19 ж2, . . . , хт — базисная система пере-
менных (так что систему из задачи 17 можно привести к канонической
форме относительно этих переменных с помощью ряда элементарных
преобразований), то векторы Pi9 Р29 ... 9 Рт линейно независимы
и образуют базис в тп-мерном векторном пространстве.
39. Показать, что ранг матрицы совпадает с рангом векторного
пространства, порожденного ее строками. Сравнить этот факт с опреде-
лением § 8-2.
40. Показать, что определитель т X тп-матрицы равен нулюу если
ее ранг г меньше т и отличен от нуля, если ее ранг равен т.
п *
41. а) Пусть даны уравнения 2 atjxj ~ Уг Для * = 1» 2, . . . , т
i=i
(см. § 8-2 (2)); показать, что можно так выбрать значения и yi9 что
1) не существует значений xj9 которые удовлетворяют системе;
2) существует единственная система значений Xj9 удовлетворяющая
системе;
3) существует много систем значений xj9 удовлетворяющих системе.
б) Доказать, что если при любом выборе yi9 у29 . . . , ут всегда
существует единственная система значений xj9 удовлетворяющая системе,
то п = т и матрица (а^) является базисом.
СИМПЛЕКС-МЕТОД В МАТРИЧНОЙ ФОРМЕ (См. § 8-5)
42. Показать, что если векторы Pi9 Р2, . . . , Рт образуют базис, то
CbisP 1 4" a2sP 2 4“ • • • + amsP m~Ps,
alsc\ 4~ #2sc2 4“ * • • 4~ amscm ~ cs — cs9
ais и cs — коэффициенты соответствующей канонической формы.
43. Дать определения линейного пространства, векторного простран-
ства, размерности, аффинной векторной геометрии, базиса в векторном
пространстве, абсолютных координат, координат относительно базиса,
выпуклости, выпуклой оболочки, выпуклого конуса, луча, полупро-
странства, опорного полупространства, гиперплоскости (некоторые из этих
терминов в этой книге определены не были).
44. Пусть v 0 означает, что все компоненты вектора неотрица-
тельны; доказать, что
а) уравнение Ах = а не имеет решения х 0 тогда и только тогда,
когда существует такой вектор л, что nA 0, па > 0;
б) система неравенств Ах < « не имеет решения тогда и только
тогда, когда существует такой вектор л 0, что nA = 0 и па < 0;
в) система неравенств Ах g; а, не имеет решения х 0 тогда и только
тогда, когда для некоторого вектора л, nA 2^ 0 и па < 0.
45. Теорема. Предположим, что имеется 4 множества базисных
m-j-2
допустимых решений системы 2 Рjxj — Q, г®е Pj векторы с т компо-
j=i
нентами
Р 1а1 4“ Р2а2 4" РЗаЗ 4~ РGa6 4" • • • + Рт+2ат+2 = Q,
Р2^2 4“ Р3^3 4“ Р4^4 4“ Р6^6 4” • • • 4" Рт^т+2 ~Q> /4 \
р3С3 4“ Рьск 4- Рьс5 4- PqcG 4" • • • 4“ Рт+2ст+2 = Q,
Р1<1Г A-P^d^~[-P5d5-^ Р&^в+ • . • A-Pm+2^m+2 = Q*
Тогда базисное решение
Рlei 4“ Р2е2 4- Р4- РGeG + • • • 4" Ртет = Q (2)
205

допустимо, если
сз—аз —а3 Q
И
(к = 6, .... т + 2) (4)
и недопустимо, если не выполнены неравенство (3) или неравенство (4}
для некоторого к и выбранной области значений bh.
46. Пусть
2 “ bi 0? i — 1, 2, ..., т)
j=i
бесконечная задача линейного программирования, которая имеет допу-
стимое решение. Доказать, что существует допустимое решение, содержа-
щее не более т переменных Xj > 0.
47. Теорема. Пусть (Рь Р2, . . . , Рт) — т линейно независимых^
векторов в т-мерном пространстве и Ро — любой другой вектор. Если
мы положим
(8 \
82 |
I ’
8т/
то существует такое 80, что для всех 0 < 8 < 80
Xi =/= 0 (i = l, 2, ..., т).
48. а) Рассмотрим систему уравнений марковского типа
( 1+Р11)ж1+ Р 12^2 + ••• + 0,
, РгЛ + ( — 1 + Р22)х2 + • • • + Р2ПХП — 0»
РпЛ+ ZW2+ . . . +( — l+Pnn)*n = 0,
*1+ Х2+...+ Жд = 1,
п
где р^ >0 и 2 Ра — 1 Для j = 1, 2, . . . , в. Доказать, что первые
г=1
п уравнений с п неизвестными избыточны; но если каждое уравнение i
видоизменить вычитанием из него последнего уравнения, умноженного-
на Ki > 0, где Ki выбрано так, что ри — Ki > 0, то новая система п урав-
нений избыточной не будет и имеет единственное решение, которое в дей-
ствительности ДОПУСТИМО C Xj > 0.
п
б) Система (1), где 2 Ра < 1 для 7 = 1, 2, . . . , п и свободные*
i=i
члены (столбец из нулей) заменены на bt < 0, называется системой
Леонтьева. Показать, что такая система всегда имеет единственное допу-
стимое решение и что указанный выше процесс можно использовать для
того, чтобы свести марковскую систему к системе Леонтьева.
49. Для системы из трех уравнений доказать или опровергнуть пред-
положение о том, что если х^ х2 находятся в оптимальном базисном множе-
стве, когда третье уравнение опущено, х2, х3 — когда первое уравнение
опущено и rq, х3 — когда второе уравнение опущено, то если art, х2, х^
образуют допустимое базисное множество, то оно оптимально.
Глава 9
симплекс-мвтол, использующий
МНОЖИТЕЛИ (МОДИФИЦИРОВАННЫЙ
СИМПЛЕКС-МЕТОД)
В то время как на каждой итерации симплекс-метода необходимо
вычислять и записывать новую таблицу целиком, можно заметить, что
в процессе решения играют роль только измененные строка цен и стол-
бец, соответствующий переменной, которая вводится в базисное множество.
Идея симплекс-метода, пользующегося множителями, состоит в использо-
вании системы чисел, называемых симплекс-множителями (ценами), и
обратного базиса, чтобы получить необходимую для принятия этих реше-
ний информацию непосредственно из исходных уравнений. В литературе
этот метод называется также модифицированным симплекс-метод ом (Дан-
циг и Орчард-Хейс [1]).
Модифицированное уравнение стоимости, полученное исключением
базисных переменных из целевой функции, может быть получено непо-
средственно из начальной системы умножением исходных уравнений
на некоторые веса, сложением и последующим вычитанием из целевого
уравнения. Именно эти веса называются симплекс-множителями, а в не-
сколько более широком смысле (см. гл. 12) — ценами. С теоретической
точки зрения они наиболее важны, так как они связаны с переменными
двойственной системы и играют роль, аналогичную множителям Лагран-
жа в математическом анализе (гл. 6). Они наиболее полезны, как мы уви-
дим в гл. 12, для определения узких мест программы, эффекта от увели-
чения запасов некоторых ресурсов, результатов роста производственной
мощности, либо ценности вновь предложенного технологического процесса.
Вычислительные выгоды этого подхода состоят в следующем:
а) От одной итерации до следующей хранится меньшее количество
данных, что позволяет запоминать большее число значащих цифр или
решать задачи больших размеров в условиях ограниченной памяти эле-
ктронных вычислительных машин.
б) В случае, когда исходные данные имеют большой процент нуле-
вых коэффициентов (90 или больше процентов — обычное явление),
требуется меньше умножений (см. замечания по поводу вычислительной
стороны дела в конце следующего параграфа).
в) Существует простой способ избежать вырожденности и, следова-
тельно, возможности «зацикливания» в симплекс-алгоритме (см. лекси-
кографическое правило в конце § 9-3). (Ввиду того что обратный базис
составляет часть всей таблицы, этот способ также приложим и к перво-
начальному методу.)
Модифицированный симплекс-метод основан на теории, уже раз-
витой в § 8-5. Поэтому наша цель состоит в том, чтобы описать его вычис-
лительные черты. Ввиду того что некоторые читатели могли бы подумать,
что матричные обозначения затемняют вычислительные аспекты, мы
будем стремиться избегать их использования здесь.
207
9-1. ПРИМЕР ИСПОЛЬЗОВАНИЯ МНОЖИТЕЛЕЙ
Для того чтобы проиллюстрировать этот метод, рассмотрим задачу (1),
(1)
которая представлена в канонической форме относительно переменных
(я7, ж8, я9, я10, —z). После нескольких итераций симплекс-алгоритма она
может быть записана в эквивалентной канонической форме (2) относи-
тельно, скажем, переменных (xi9 х2, х3, —z).
Цикл к
(2)
Базис В для цикла к (см. (3)) представляет собой квадратную матрицу
коэффициентов, связанных с базисными переменными в исходной систе-
ме (1). В нашем примере мы исключаем z и z-уравнение.
Первый столбец матрицы В соответствует базисной переменной
в (2) с коэффициентом единица в первой строке, . . ., к-й столбец матрицы
В соответствует переменной с единичным коэффициентом в к-й строке
и т. д. (Другими словами, столбцы матрицы В должны быть упорядочены
в соответствии с базисными переменными, которые выписаны в первом
208
столбце (2); см. § 4-2.) Для рассматриваемого случая (см. (11) § 8-4 по опре-
делению обратной матрицы).
/1 0 1 0\ В101011 110 0 1 /0 1; 5-1= (М = |? ' 11 -1 0 1 1 0 -1 1\ 1 1 -1 1 (3)
\0 1 0 0/ \о 1 0 -1/
Обратный базис, обозначаемый через В'1 или (PfJ, представляет собой
квадратную матрицу коэффициентов в (2) (исключая 2-уравнение), соот-
ветствующих переменным (я7, х8, х9, х10), где последние образуют перво-
начальную систему базисных переменных в (1). Для того чтобы доказать
это утверждение, заметим, что, согласно § 8-4(20), обратный базис можно
использовать для вычисления коэффициентов в любом столбце (2), исходя
из соответствующего столбца первоначальной системы (1) по формулам*.
alj = Риа1 j + P12a2j + Р13а3 j + P14a4j,
a2j = p21^1J + ?22a2j + Ргз^зу + P24a4j>
a3j = Рз1а1 j + Рз2а2? + Рз3а3? + Рз4а47»
= p41aij + P42a2j + P43^3J + P44a4J-
Так как столбец (a17, a27, «37, a47) = (l,0,0,0>, то подстановка в (4) дает
(ai7, a27, a37, a47> = (PH, p21, p31, P4i>, т. e. столбец коэффициентов при
x7 в (2) совпадает с первым столбцом матрицы В"1. Вообще, если Xj —
любая переменная в (1), коэффициенты которой образуют единичный
вектор с единицей в i-м уравнении, то подстановка в (4) показывает, что
соответствующий столбец коэффициентов в (2) совпадает с i-м столбцом
матрицы Б"1. Следовательно, обратный базис для цикла к представляет
собой совокупность коэффициентов в таблице цикла к при переменных,
которые были базисными в цикле 0.
Симплекс-множители, или цены, определяются как такие числа
л4, л2, л3, л4, что взвешенная сумма, полученная умножением первого
уравнения (1) на ль второго — на л2 и т. д. и сложением, будучи вычтена
из 2-уравнения, исключает базисные переменные и дает новое 2-уравне-
ние (2). В частности, очевидно, что так как единственный ненулевой
коэффициент при х7 в (1) равен единице (из первого уравнения), то полу-
чающийся коэффициент при х7 в 2-уравнении (2) равен — Аналогично
коэффициентами при х8, xQ, xi0 в (2) должны быть —я2, —л3, —л4. Поэтому
П1 = —7, л2 = —5, л3 = —1, л4 = —4. Тот факт, что эти значения
найдены правильно, может быть непосредственно проверен умножением
на них соответствующих уравнений (1), сложением и вычитанием из z-
уравнения для того, чтобы получить 2-уравнение (2). Таким образом,
симплекс-множители л^, л2, л3, л4 могут быть использованы для того,
чтобы вычислить относительные оценки Cj в (2), исходя из соответствую-
щего столбца начальной системы по формуле (см. (16) § 8-5).
Cj = Cj — (л^и 4- л2а2 j + л3а37- 4- ft4tf4j). (5)
До сих пор в наших рассуждениях мы исключали —2 из системы
базисных переменных и 2-уравнение из базиса и обратного ему базиса.
Если, наоборот, мы включим их, то базис В*, связанный с базисными
переменными Xi, х2, х3, х^, и —2 для некоторого цикла к будет составлен
14 Дж. Данциг
209
из коэффи в* = циентов при этих пере»! / 1 0 1 0 ! 0\ 0 1 0 1 | 0 . 1 0 0 1 | 0 0 _ 1 0 0 | 0 генных в в [сходной системе i /0-1 1 1 0 0 0 1 1 1-1-1 0 10-1 (!)• °\ 0 0 0
\ —8 —9 —7 -6 1/ V 5 1 4 1/
(6)
Обратная матрица для В* будет тогда состоять из коэффициентов
при исходных базисных переменных я7, я8, я9, я10 и — z в канонической
форме для цикла к. Согласно § 8-4(20), если элементы, которые содер-
жатся в к-й строке матрицы (В*)~г, используются для умножения на них
соответственно пяти уравнений (1), то их сумма также воспроизведет
к-е уравнение (2). С этой точки зрения уравнения (4) должны получиться
путем использования первых т строк матрицы (Б*)"1, а равенство (5) —
путем использования последней строки матрицы (В*)"1. Это действительно
так, потому что В* отличается от £ в (6) граничным столбцом из нулей,
граничной строкой стоимостей и +1 в правом нижнем углу; аналогично
(В*)-1 отличается от В"1 граничным столбцом из нулей, граничной стро-
кой отрицательных цен и +1 в правом нижнем углу.
В модифицированном симплекс-методе предполагаются известными
только некоторые ключевые столбцы симплекс-таблицы в начале цикла к
именно:
а) Обратный базис для базиса В* в цикле к, который численно сов-
падает со столбцами цикла k, соответствующими базисным переменным
цикла 0.
б) Базисное допустимое решение для цикла к, которое выражается
через константы 6^, —z0, и базисные переменные, которым они соответ-
ствуют, причем значения всех остальных переменных равны нулю. Все
остальные данные, необходимые для проведения шагов стандартного
симплекс-метод а, вычисляются по мере необходимости из начальной таб-
лицы.
Все сказанное иллюстрируется табл. (7), незаштрихованная часть
которой показывает запоминаемую часть в начале цикла к.
Начало цикла к
Обратный
— оазис, [В*]
(7)
Следующий шаг состоит в вычислении относительных оценок Cj, которые
являются значениями, находящимися в нижней строке (2), исходя из дан-
ных, находящихся в таблице цикла 0, и известных множителей (kj = —7,
л2 = “5, л3 = —1, л4 = —4). Из равенства (5) мы, например, имеем
210
с I — Cj jTjttj j — ^2^21 — л3а31 — 3X46144 — — 8 -J- 7 • 1 4~ 5 • 0 -{-1 • 1 4~ 4-0 = 0
_.....................................................(8)
Cg = Cq jt jtz 16 — ^2^26—л^зе *“ ЗТ4Л46 = — 9 -j- 7 • 0 4~ 5 • 1 1 • 0 4 • 0 = — 4*
Для проверки укажем, что значения Cj для базисных переменных, вычис-
ленные этим способом, должны быть равны нулю, а для /, соответствую-
щих базисным переменным цикла 0, значения Cj должны быть равны
ценам, взятым с обратным знаком, —соответствующим i-й базисной
переменной. Если вычисленные cj вводятся в таблицу и определяется
такое значение $, что cs — min cj (это отмечено звездочкой под столбцом
s = 6), то мы имеем ситуацию, изображенную табл. (9).
Шаг I цикла к
Правые
части
базисные
перемен-
ные
Xr Х2 Х3 X* *5 *6 *7 *8 *9 *10-Z
0 0 0 0 3 -1 7 5 111
1
1
2
1
(9)
Теперь мы знаем, что ж6 является кандидатом на роль новой базисной
переменной. Для того чтобы определить, какую базисную переменную
надо исключить, для каждого i вычисляются значения и вводятся
в столбец 6, используя коэффициенты а16, а2б, «зв» «46, находящиеся
в столбце 6 начальной таблицы цикла 0, и г-ю строку обратного базиса.
Согласно (4),
«16 = Р11«16 + Р12«26 + Р13«36 4" Р14«46 = 0- 0 — 1-1 + 1,0+1*0== — 1
«26 = Рг1«1б + Рг2а2б + Ргз«зв + Рз4а4б = б- 0 + 0*14-0-04-1*0 = 0
«36 = Рз1«16 + Рз2«26 4“ Рз3«36 4- Рз4«46 = 1 • 0 4" 1 ‘ 1 — 1*0 — 1-0 = 1
«46 = р41« 16 + ?42«26 4“ Р43«3б 4“ ?44«46 = 0- 04-1*14“0-0 — 1*0=1
Если вычисленные значения ai6 поместить в таблицу и определить такое г,
что bTlaT8 = min /ais для ais > 0, то мы окажемся в ситуации, пока-
занной на табл. (11), где г — 4, так что аГ8 = й46 становится ведущей
позицией.
211
14*
Следующий шаг стандартного симплекс-метода состоял бы в том,
чтобы заменить я4 на х6 в качестве базисной переменной приведением (2)
к канонической форме с помощью ведущего элемента а46. В (11) мы это
и делаем, за исключением того, что здесь мы ограничиваемся полными
столбцами, именно столбцами, соответствующими ведущему элементу,
базису, обратному В*, и свободным членам. После исключения х6 в (11),
с использованием d46 в качестве ведущего элемента, мы приходим к ситуа-
ции, показанной в табл. (12). Опуская вычисленные относительные
оценки последнего цикла и коэффициенты при х6, мы можем начать
цикл к + 1.
Начало цикла А +1
базисные перемен- ные х, Хг х3 Xi, х5 xg х7 х8 xg x„-z Л pa bbi е ласти
X, Xz Х3 шш 1 1 1 -f 1 2 1 1 1
-z ШШ 0 1 —49

• /Нодый обратный базис
/Новые множители тг=(-7-9,-1,0)
ВЫЧИСЛИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В стандартном симплекс-методе каждый цикл требует хранения
не меньше (т + !)(» + 1) величин (или больше, если имеются искус-
ственные переменные). В рассматриваемом методе путем использования
скалярных произведений1 число хранимых данных уменьшается до
(т + 1) (т + 2) величин, а фактически до (тп-f-l)2, если игнорировать
столбец (—z).
Например, значения {—л4, —л2, —л3, —л4, 1} можно записать
по вертикали на полоске бумаги и двигать ее вдоль /-го столбца, как это
показано на схеме (13а), после чего удобно вычислять Cj перемножением
соответствующих величин и сложением произведений.
Определение. Операция (13а) умножения симплекс-множителей базиса
на вектор коэффициентов при Xj для определения коэффициента при этой
переменной в новой целевой форме называется оцениванием2, /-го техно-
логического процесса через базисную систему технологических процессов
/—Л1 \ aij
— ^2 a2j ^16 Й26 Л36 й4б
*^3 a3J (13а) — (136)
~л4 fl4j Pfei 0А2 Раз Ра4
к 1J Cj
1 Настольные и электронные вычислительные машины имеют специальные регист-
ры с двойным числом разрядов, которые дают возможность удобно вычислять с накоп-
лением скалярные произведения
а1^1Ч~а2^2» (а1&1 а2^2) 4"а3^3> •••»
что позволяет удвоить число знаков обычного регистра памяти машин.
2 Причиной введения этого термина является тот факт, что симплекс-множители
могут интерпретироваться как цены (см. гл. 12); умножение этих цен на коэффициенты
затрат — выпуска технологического процесса и сложение «оценивает» технологиче-
ский процесс через заменяющие процессы, базисные технологические процессы. Срав-
нение этой суммы с исходной стоимостью cj указывает нам. выгодно или нет введение
небазисного технологического процесса j в базисное множество.
212
Аналогично значения ai6, а2е, «зв, а4б, находящиеся в столбце s = 6,
можно расположить горизонтально на полоске бумаги и двигать ее вдоль
/с-й строки базиса, обратного В. Тогда удобно вычислять а^ умножением
соответствующих величин и вычислением их суммы, как показано
на схеме (136).
Определение. Операция умножения строк обратного базиса на вектор
коэффициентов при Xj называется представлением j-го технологического
процесса через базисное множество технологических процессов.
Так как исходные коэффициенты часто бывают заданы в виде деся-
тичных дробей с числом знаков от трех до пяти, то при использовании
метода множителей для хранения информации требуется меньший объем
машинной памяти. Это число знаков значительно меньше, чем необходимо
Рис. 9-1-1. Условия для выбора метода с мно-
жителями или стандартного метода (начиная
с канонической формы без искусственных пере-
менных).
для а^ при использовании стандартного симплекс-метода, так как моди-
фицированный метод позволяет избежать трудностей, связанных с ошиб-
ками округления при переходе от итерации к итерации. Кроме того, при
использовании метода множителей удобно проводить накопление пол-
ных произведений без их округления в машине при операциях оценива-
ния и представления и лишь затем округлять получающуюся сумму.
Этот способ приводит обычно к значительно меньшим ошибкам округле-
ния, чем стандартный метод, где каждое произведение должно округляться
до его запоминания.
Для дальнейшего уменьшения хранимых данных большинство про-
грамм для электронных машин вычисляет последовательные значения
Cj по (13а), но хранит только значение и местоположение наименьшего
Cj, полученного к любому моменту вычисления.
Если вычисления начинаются с т х n-системы в допустимой канони-
ческой форме, то общее число умножений на каждой итерации равно
t (п — m)(m-\-\.)-\-tm(m 4-1) 4- (т 4-1)2 = tn (т 4-1) 4- (т 4-1)2» (14)
где предполагается, что в среднем доля ненулевых коэффициентов как
в исходной таблице, так и в столбце, который вводится в базис, равна t.
Три члена слева представляют собой число умножений (или делений),
необходимых (а) при «оценивании» (б) для представления нового столбца
и (в) для выполнения ведущей операции. С другой стороны, стандартный
213
симплекс-метод требует
{(п — т) +1} (т +1) = (п — 2т) (т +1) + (т +1)2 (15)
операций на каждом цикле. Следовательно, если доля ненулевых коэф-
фициентов
£<1 — 2т/п, (16)
то симплекс-метод, использующий множители, потребует меньше работы.
Например, если п > Зтп, то требуемая доля ненулевых коэффициентов
равна t Рис. 9-1-1 может использоваться для того, чтобы решить,
применять ли стандартный симплекс-метод или метод множителей.
9-2. ОБЩЕЕ ОПИСАНИЕ МОДИФИЦИРОВАННОГО
СИМПЛЕКС-МЕТОДА
Рассмотрим систему уравнений (7) из § 5-2 в канонической форме
для этапа I симплекс-метода, где вместо букв М, N мы будем употреблять
буквы тп, п
Цикл О
Допустимые переменные
Искусственные
переменные
аПх1~\-а12х2~\~ * • • ~\~а\.пхп +^n+l
а21ж1 + а22х2~\~ • • • + ^271^71 + ^п+2
(1)
ат1х1 + «7712^2 + • • • + атпхп
61^1 + 62^2+••• + ^71
dlxi + ^2х2 + • • • + ^пхп
~\~хп+т —
—z =0
-w=--Wq
Свободные члены Ь2, . . ., Ът сделаны неотрицательными путем
изменения, если это необходимо, знаков при всех членах исходных
уравнений еще до введения искусственных переменных, и
7П 771
dj— 2 ^Ро = S (2)
i—1 i—1
Таким образом, если сложить первые т уравнений и форму для гр, то
в результате получится равенство
Ятг+1 + жтг+2 + • • • + жтг+тп — ™ = 0- (3)
Задача состоит в том, чтобы найти такие числа гр, z и неотрицатель-
ные Xj. удовлетворяющие системе (1), что w = 0 и z минимально. Табл. (4)
представляет собой каноническую форму с базисными переменными
Xj^. Xj^. . . ., Xjm. —z, —w при обычном симплекс-методе для цикла к.
Базисное допустимое решение получается, если положить Я;* = . . .
. . ., Xjm — bm; z = z0; w = wQ, а все остальные Xj = 0.
В начале любого цикла при использовании модифицированного
симплекс-метода хранится только информация, получаемая из таблицы
обычного симплекс-метода и состоящая из коэффициентов при искус-
214
ственных переменных, свободных членов и номеров соответствующих
базисных переменных. В течение цикла часть недостающих данных
в симплекс-таблице получается по мере необходимости; эти данные пред-
ставляют собой значения Cj или dj для j = 1, 2, . . ., п и значения коэффи-
циентов в столбце / = $. Цель этого параграфа состоит в том, чтобы иссле-
довать в общем виде, какие части симплекс-таблицы в цикле к могут
быть получены непосредственно из таблицы цикла 0 с использованием
обратного базиса. В следующем параграфе мы используем эти результаты
для того, чтобы сформулировать правила вычисления модифицированного
симплекс-метода. Так как первые тп-уравнений системы (1) находятся
Таблица обычного симплекс-метода — цикл к
Базисные переменные Допустимые переменные Искусственные переменные —z —w Свободные члены
Х1 .. . Xs • • • xn xn+i • xn+m
хп а11 • • • als ... aln n+i • - • al, n+m bi
• • • • • >
• х3г Лг1 • • • ars • • • arn ar, n+1 • • • йг, n+m
• • . • • • bm
X- jm ат\ • • • ams • • • amn am, n+1 • • • am, n+m
Z ... cs • • • cn cn+l • • • cn+m 1 —Zq
W di... ds • • • dn dn+l.. • dn+m 1 —n?0
В 1—(ai, п+у)> я— (сп+1> •••» сп+т)
О = (dn+i, ..., dn+m)
в канонической форме относительно переменных xn+l, xn+2i . . ., хп+т
и эквивалентная ей система (4) находится в канонической форме относи-
тельно переменных Xj^ х^ . . ., то из формул (9) и (10) § 8-4
следует:
а) Если базис В представляет собой систему коэффициентов при
Xj2, . . ., Xjm в системе (1), то обратный ему базис Б"1 представляет
собой систему коэффициентов при яп+1, хп+2, . . ., хп+т в (4), за исклю-
чением z- и ^-уравнений. Более того, так как вся система (2) находится
в канонической форме относительно переменных xn+i, хп+2, . . ., хп+т,
—z, —ip и вся система (4) находится в канонической форме относительно
переменных х^, Xj2, ...» xjm, —z, — w, то отсюда также следует, что:
б) Если базис 5* образован системой коэффициентов при перемен-
ных Я;2, . . ., xjm-> ~~w в системе (1), то обратный ему базис (Б*)-1
образован системой коэффициентов при xn+i, ял+2, . . ., хп+т, —z, —w
в системе (4).
215
Согласно формуле (20) § 8-4, любой элемент в данных строке й столбце
табл. (4) может быть получен из таблицы (1) образованием скалярного
произведения соответствующей строки в обратном базисе и соответствую-
щего столбца табл. (1). Таким образом, а^, например, для / = $, может
быть получен образованием скалярного произведения i-й строки базиса,
обратного В, и /-го столбца табл. (1), исключая z- и де-уравнения, т. е.
aij = Pi ia lj + Pi2a2j + • • • + PinAnj» (5)
где через 0^ мы обозначили элементы матрицы Б"1 и показали, что,
согласно сформулированным выше утверждениям а) и б),
РгЛ “ ^z, n+k Л = 1, 2, . . ., 771). (6)
Аналогично коэффициенты Cj или dj могут быть получены как ска-
лярные произведения z- или де-строк обратной матрицы (5*)”1 и /-го
столбца табл. (1), включая z- и де-строки. После перестановки членов
мы имеем
с/ — cj — (л1^и* + л2а2 j + • • • + > ( 7)
“ dj— (alalj + &2a2j + • • • + (8)
где через —(nb л2, . . ., лт) и —(<т4, о2, . . ., от) мы обозначили коэф-
фициенты при искусственных переменных в z- и де-уравнениях системы
(4); следовательно,
Яд — Сд+ft, Од — dn+д (к = 1, 2, ..., ти). (9)
Наконец, свободные члены z0, wQ могут быть получены образо-
ванием скалярного произведения соответствующей строки обратного
базиса и столбца свободных членов табл. (1):
bi = Pz 1^1 + Pz2^2 + • • • + Pzm^m>
Ио = Л^ + Л2Ь2 + • • • + ttrnbin, (10)
w0 — aibi + O2&2 + • • • + Om^m + W
Так как в процессе выполнения ведущих операций в модифициро-
ванном симплекс-методе базисные переменные получают новые значения,
формулы (10) используются только для проверки.
Определение. Множители л = (ль л2, . . ., лт) называются симп-
лекс-множителями относительно z-yравнения, если умножение первого
уравнения системы (1) на л4, второго уравнения на л2 и т. д., тп-го урав-
нения на и вычитание их суммы из 2-уравнения исключает базисные
переменные. Система симплекс-множителей относительно w-yравнения
обозначается через о = (Oi, о2, . . ., от).
Теорема 1. Симплекс-множители единственны и равны коэффициен-
там при искусственных переменных в z- и w-уравнениях канонической
формы (4).
Доказательство. Если использовать частные значения лд = —сл+д,
Од = —dn+k для k = 1, 2, . . ., т, то коэффициенты Cj и dj при Xj,
определенные правыми частями равенств (7) и (8), для столбцов j, соответ-
ствующих базисным переменным, обращаются в нуль. Следовательно, эти
значения удовлетворяют определению симплекс-множителей.
216
Чтобы показать единственность, предположим для удобства, что
базисными являются переменные аг4, ж2, ...» хт\ тогда множители
должны быть выбраны так, что
л1а11 4" ^2^21 4~ • • • 4" ^тат1 = е1>
л1а12 4" ^2а22 + • • • + ^т^т2 = с2»
(11)
^1®1т + • • • Н“ — Ст-
Эта система т уравнений с т неизвестными должна быть сопоставлена
с системой т уравнений с т неизвестными, которой должны удовле-
творять базисные переменные
Ж1Й11 4“ #2а12 4" • • • 4" Xmaim —
^1^21 4“ х2а22 4“ • • • 4“ хт^2т = ^2»
4“ х2^т2 4“ • • • 4" Хтатт ^тп-
В системе (11) строки и столбцы являются соответственно столбцами
и строками системы (12), а свободные члены системы (12) заменены
на коэффициенты стоимостей при базисных переменных. Коэффициенты
при xj в (12) образуют в нашем случае базис В и, следовательно, коэффи-
циенты при л/ в (11) образуют транспонированный базис. По теореме 7
§ 8-4 базис, обратный к транспонированному, существует и равен транс-
понированному обратного базиса В"1. Отсюда следует, что множители
ль л2, . . ., пт могут быть выражены единственным образом через
Ci, с2, ...» ст по формулам
Л1 — Р11с1 4- р21с2 4- • • • + р7П1с7П>
Я2 = Р 12С1 4" ₽22С2 4“ • • • 4" Ртп2С7П, . . о.
(13)
• ••«•«••••ft»**#
лтп ~ Pim^i 4" р2?п^2 4" • • • 4“ $ттстп,
где xi9 х2, . . ., хт — базисные переменные; или, в более общем виде,
если базисными являются переменные Xj , Xj^, . . ., то в приведен-
ных выше формулах ct нужно заменить на коэффициенты стоимости при
i-й базисной переменной Cj. = yf (см. (17) § 8-5).
9-3. ВЫЧИСЛИТЕЛЬНЫЕ ПРАВИЛА ИСПОЛЬЗОВАНИЯ
множителей
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Выпишем систему уравнений в канонической форме для этапа I
симплекс-метода, как показано табл. (1) § 9-2. Вся система записывается
в виде табл. 9-3-1а коэффициентов, приведенной в конце этого параграфа.
Таблица модифицированного симплекс-метода, табл. 9-3-Пб, меняет-
ся от цикла к циклу. (Величины для начального цикла 0 показаны
в табл. 9-3-11а.) Элементы этой таблицы, за исключением стоящих в по-
следнем столбце, представляют собой коэффициенты при искусственных
переменных хп+1, хп+2, . . ., хп+т, при — z и —w и свободные члены таб-
лицы обычного симплекс-метода для этого цикла. Ее можно также рас-
сматривать как состоящую из «обратного базиса» (Реj), двух строк из «сим*
плекс-множителей» л,- и взятых со знаком минус, столбца из значений
217
базисных переменных в базисном решении и столбца для переменной xs.
В начале цикла все элементы таблицы, за исключением последнего столбца,
«х8» известны.
В течение некоторого цикла, например цикла t, вычисляются значе-
ния относительных оценок dj для этапа I или Cj для этапа II и записы-
ваются в табл. 9-3-16. После этого (за исключением конца этапов I или II)
вычисляется каждое ais, которое записывается в последний столбец
табл. 9-3-Пб. В конце цикла элементы этой таблицы используются для
вычисления соответствующей начальной таблицы следующего цикла t + 1.
Табл. 9-3-Пв показывает, каким образом начальная таблица цикла t + 1
связана с окончательной таблицей цикла t.
ПРАВИЛА ВЫЧИСЛЕНИЙ
Эти правила применимы ко всем циклам, но несколько различаются
в зависимости от того, находятся ли вычисления в этапе I или в этапе II.
Они отличаются от правил стандартного метода, изложенных в § 5-2,
лишь следующими модификациями:
Шаг 1а. Использовать значения (в этапе I) или jq (этап II) из
табл. 9-3-Пб для вычисления относительных оценок (этап I) илису
(этап II) для / = 1, 2, . . ., п, . . п + тп по формулам (7), (8), (9) и за-
писать в табл. 9-3-16 в строке, соответствующей циклу.
Шаг 16. Совпадает с шагом I стандартного метода.
Шаг Па. Для i = 1, 2, . . ., т вычислить коэффициенты ais при xs
в канонической форме по формулам (5) и (6) и записать их в последний
столбец табл. 9-3-Пб.
Шаг Пб. Совпадает с шагом II стандартного метода. Вместо правила
случайного выбора в случае неоднозначности можно в качестве альтер-
нативы использовать лексикографическое правило, приведенное после
шага III.
Шаг III. Совпадает с шагом III стандартного метода, за исключением
следующего: использовать ведущий элемент аг& в табл. 9-3-Пб (вместо
табл. 5-2-П) и записывать величины в табл. 9-3-Пв. Оставить столбец xs
пустым. В списке базисных переменных в левом столбце табл. 9-3-Пб
меняется только jT на значение s, определенное на шаге I. Вернуться
к шагу 1а, чтобы начать цикл t + 1.
ЛЕКСИКОГРАФИЧЕСКОЕ ПРАВИЛО ПРЕОДОЛЕНИЯ ВЫРОЖДЕННОСТИ
Если минимум достигается для двух или более индексов г2, . . .,
то следует образовать отношения соответствующих величин, взятых
из первого столбца обратного базиса, к числам ar s, ar s...;
1 2
v
Рг2, 1
<zr2s
• • •
и выбрать индекс строки с минимальным отношением по г. Если все еще
остались равные числа, то следует повторить этот процесс для тех индек-
сов, которые все еще равны, используя теперь отношения соответствую-
218
щих величин, взятых из второго столбца обратного базиса, к соответ-
ствующим им dr^s. В этом методе отношения образуются из последова-
тельных столбцов обратного базиса до тех пор, пока все «конкуренции»
не будут разрешены однозначно (это всегда произойдет при достижении
Таблица 9-3-1а
Модифицированный симплекс-метод.
Коэффициенты исходной системы
Уравнение i Допустимые переменные Искусственные переменные —z — w Свободные члены
Х1 х2 XJ • xn эсп+i Xn+2 . xn+m
1 2 ali а21 «12 • • • «22 • • • aij • a2j • • • aln •. a2n 1 1 1 &2
m ami ат2 • • • amj • • • amn 1 bm
z-форма ci с2 ... Cj .. • • cn 0 0 0 1 0
ш-форма di d2 ... dj . .. dn 0 0 0 1 m — 3 bi i
т
dj — 2 aif> bi О, •••> Ът
г=1
Таблица 9-3-16
Относительные оценки dj или Cj
Переменная j
п, п+1»
Цикл
0
1
Этап I х
Этап II
I к
к '
& + 1 ’•
С?2 • • •
Используя
Of, если этап I
или
jif, если этап II
из табл.
9-3-116 того же цикла
вычислить
{dj = dj—(aijei -[- «27^2+ • • • + amJam)
1 или
Cj — Cj—(atj + a2j n2 + • • • +
Записать dj или cj в строку, соответствующую циклу, и вы-
(ds — min dj (этап I) 1
- - I
ce = mincj (этап II)J
219
последнего столбца или ранее). Доказательство того, что симплекс-алго-
ритм, использующий это правило, всегда заканчивается за конечное
число шагов, будет предметом следующей главы. (Доказательство того,
что при использовании правила случайного выбора алгоритм заканчи-
вается за конечное число шагов с вероятностью единица, было приведено
в конце § 6-1.)
Таблица 9-3-Па,
Модифицированный симплекс-метод
Начальная таблица цикла О
Базисные перемен- ные (Столбцы канонической формы)
хп+г хп+/п — Z —W Значение базисной переменной xs (см. примеча- ние)
Л'ЬЛ'ПЯ 'ТИК.ТТГ
хп+1 1 VyUjJa. 1HJtuИ UadHL bi
хп+т 1 br
хп+т 1 bjn
1 1 0 0 . . . 0 0 1 1 1
Примечание. В начале цикла 0 столбец х8 пуст.
Таблица 9-3-Пб
Модифицированный симплекс-метод
Конечная таблица некоторого цикла t
(Столбцы канонической формы)
Базисные перемен- ные хп+1 ••• хп+т —Z —W Значение базисной перемен- ной xg (см. примечание)
xh < [PjZtl — [aj, n+ft] Обратный базис ₽ц ... pirn bi вычислить т 2 Р1гЛг8 = я18 г=1
220
Продолжение табл. 9-3-116
Базисные перемен- ные (Столбцы канонической формы) Значение базисной перемен- ной xs (см. примечание)
хп+1 хп+т — Z —W
\ Рм . . . Przn Ьг т 2 ftrflis — ars г=1
xim Pml * . . Pmm Ьщ т 2 ^miais==ams г=1
— Z — Л! ( ^k = cn+k) лт 1 —zo о to w 1 а to* II с 1 to
— W — (Т1 ( ^k = ^n+k) 1 —Wq to IMS 'а to* II aj to
Примечание. В начале цикла последний столбец пуст; для выбора s см. табл. 9-3-16
для г см. шаг 116; табл. 9-3-Пв получается ведущим преобразованием с ars и вычеркиванием
элементов в последнем столбце. Выделенный жирным шрифтом ars показывает положение
ведущего элемента.
Таблица 9-3-Пв
Начальная таблица цикла £ + 1
xii Pll—fllsPri • • • Plm alsPrrn &1—aisb* (см. при- мечание выше)
xs a* Prl • • • Prm к* br
xi Pml ^msP ri • • • Pmm amsPrm Ьщ amsbr
N S 1 1 Л1 csPrl ^1 ^sPrl £ В 'T 7 g £ к ъ 1 1 1 1 § 1 I о о л 1 to to с-1 o-l -s * -s*
Рг£ — Ргг/аг8 (1— 2, ...» т)\ Ьг—br/ars.
Пример. Для того чтобы проиллюстрировать ход вычислений в моди-
фицированном симплекс-мётоде, вернемся снова к примеру § 5-2,
табл. 5-2-V. В табличной форме задача дается табл. 9-3-Ша.
221
L
Таблица 9-3-IIIa
Коэффициенты исходной системы
Х1 Х2 хз х4 Ж5 хв *7 —Z —W Свободные члены
5 —4 13 —2 1 1 20
1 —1 5 —1 1 1 8
1 6 —7 1 5 1 0
—6 5 —18 3 -2 1 —28
Таблица 9-3-Шб
Цикл Множители относительных оценок
(1) (2) (3) (4) (5) (6) (7)
' 0 —6 5 —18 3 —2 0 0
★ • О
4?; 1 12/13 —7/13 0 3/13 —8/13 18/13 0
• ★ О
. 2 0 0 0 0 0 1 1 Конец
• • этапа I
2 12 —1 0 2 0
CJ ★ • О
. 3 72/7 0 0 11/7 8/7 (Опустить) Конец
• • этапа II
Таблица 9-3-IV
Цикл О
Базисные переменные Столбцы канонической формы
х6 Х7 —Z —w свободные члены Х8=Х3
*6 1 20 13
Xq 1 8 5
2 1 0 —7
— W 1 —28 —18
Цикл 1 (Xg'=X5)
*7 1/13 —5/13 1 20/13 4/13 1/13 8/13
Z —W 7/13 0 1 18/13 0 1 140/13 —4/13 72/13 —8/13
222
Продолжение табл. 9-3-IV
Цикл 2
(xs=x2)
х3 хь 1/8 —5/8 -1/8 13/8 3/2 1/2 —3/8 7/8
Z +4 —9 1 8 —1
—W 1 1 1 0 0
Конец этапа I, djOO, «7 = 0.
Опустить х6 и з>7, так как
(S6,d7)=(l, 1) > 0;
Опустить ^-строку.
Цикл 3
хз *2 —1/7 4/7 —5/7 13/7 12/7 4/7
м $ 1 1 23/7 —50/7 1 (^-строка опу- щена) 60/7
Конец этапа П,
9-4. ЗАДАЧИ
1. Решить с помощью модифицированного симплекс-метода задачу:
Зж। — 3^2 4” 4Жз —J- 2^4-----Х§ Xq = О,
4~ 4“ 3^4 х5 -|-^7 = 2,
2^ 4-Зх2 + 2я3—х^ 4-я5 ~z,
«в 4- х1 = w
и минимизировать z, где £;>0 и w = 0.
2. Решить с помощью модифицированного симплекс-метода:
Xi +2ж3— х4 >3, (ж>0)
2^£-4*^2 4-2ж4—2я5<1,
4-я2— Хз >0,
—4~ 3#5 2,
—Xi—х2— х3 4- z5 = niinz.
3. Обсудить взаимоотношение между обычным и модифицированным
симплекс-методами.
4. Сформулировать двойственную задачу для задачи нахождения
чисел Xj, которые минимизируют форму 4~ #2 = 2 при условиях
4~ 2я^2 3,
Xi—2х2> —4,
4- 7^2 6,
где х^О, а х2 произвольно по знаку. Определить симплекс-множители
оптимального решения прямой задачи и проверить, что они удовлетво-
ряют ограничениям двойственной задачи и дают то же самое значение
целевой форме.
223
5. Решить II задачу о смесях из § 3-4 модифицированным симплекс-
методом.
6. Решить задачу Уо, используя симплекс-множители (см. зада-
чу 28, гл. 5).
7. Доказать, что
+ c2a2j + • • • + cmamj — + ^2a2j + • • • +
где ль л2, . . — симплекс-множители, связанные с базисной систе-
мой переменных xi9 х2, ...» хт. См. гл. 12 относительно экономической
интерпретации этого соотношения.
8. Доказать, что если вектор Ps заменяет r-й столбец базиса Pjr
и если л* — новый вектор симплекс-множителей, то
л* = n k = cslars,
где рг — строка матрицы соответствующая Pjr.
9. В § 8-5 рассматривалось представление обратного базиса в форме
произведения. Пересмотреть это обсуждение и переделать упражнения.
Обсудить, как бы вы вычислили симплекс-множители л*, если бы обрат-
ный базис был дан в форме произведения.
Глава 10
(
K()IIE4IIO(TI> СИМПЛЕКС-МЕТОДА
С ВОЗМУЩЕНИЯМИ
10-1. ВОЗМОЖНОСТЬ ЗАЦИКЛИВАНИЯ В СИМПЛЕКС-АЛГОРИТМЕ
Мы видели, что если имеет место вырождение, то может случиться,
что последовательность итераций не будет приводить к уменьшению
значений z. Может ли в этом случае базисное множество повторяться,
давая в результате нескончаемые циклы таких повторений? Если да, то
можем ли мы предложить эффективный метод, предотвращающий воз-
можность зацикливания? В начальный период развития линейного
программирования эта проблема оставалась нерешенной.
В 1951 г. Гофман построил пример, приведенный в табл. 10-1-1,
содержащий три уравнения и одиннадцать переменных. Он показал, что
если бы неоднозначность выбора переменной, которую надо вывести
из базиса, разрешалась путем выбора первой из них, то таблица цикла 9
совпала бы с таблицей цикла 0. Отсюда следует, что в этом случае
одно и то же базисное множество повторялось бы через каждые девять
итераций и симплекс-метод никогда не привел бы к решению. Это явле-
ние в симплекс-алгоритме называется обычно зацикливанием 2.
Позднее Бил [2] построил другой пример, вариант которого, заме-
чательный своей простотой, приведен в табл. 10-1-II. Он также содержит
три уравнения, но уже только семь переменных. Если использовать
то же самое правило для разрешения неоднозначности, то таблица цикла 6
совпадет с таблицей цикла 0. Предполагается, что это простейший при-
мер; говоря более точно, предполагается, что независимо от числа урав-
нений нельзя построить других примеров зацикливания с меньшим чис-
лом переменных.
Так как зацикливание в симплекс-алгоритме возможно только в слу-
чае вырождения, уместно спросить, каким образом вырождение может
возникнуть, как часто оно встречается в практике и как часто оно влечет
зацикливание. Вырожденные решения возможны только тогда, когда
свободные члены исходной правой части связаны специальным соот-
ношением с коэффициентами при базисных переменных. Это ясно, так
как процесс приведения к одной из конечного числа канонических форм
зависит только от коэффициентов, а не от правой части; окончательные
значения представляют собой взвешенные суммы исходных свободных
членов bi, в которых веса зависят только от коэффициентов. Если бы все
свободные члены bt были выбраны случайно, было бы довольно удиви-
тельно, если бы одна или более из правых частей bt канонической системы
обратились в нуль. Тем не менее опыт, основанный на решении симплекс-
методом тысяч практических задач линейного программирования, пока-
1 В оригинале «circling», а слово «cycle» обозначает одну итерацию симплекс-
алгоритма. В тех случаях, когда это не приводит к недоразумению, мы не будем прово-
дить такого терминологического различия.— Прим, перев.
15 Дж. Данциг 225
Пример зацикливания в си мп леке-алгоритме, принадлежащий Гофману
[0 = 2л/5, w > (1 — cos 0)/(1 — 2cos 0)]
Цикл О
Таблица 10-1-1
Х1 х2 хз Х< X5 xq X7 Xg Xg «10 хи Сво- бодные члены
1 1
1 | COS 0| —w (cos 0) cos 20 -2u?cos20 cos 20 2 w cos2 0 cos 0 w cos 0 0
1 sin 0 tg Q/w cos 0 tg 0 sin 20/ip cos 20 —2 sin2 0/w cos 20 —tg 0sin0/w cos 0 0
—(1—COS0)/COS0 +2^ +4 sin2 0 —2w cos 20 +4 sin2 0 ip (1—2 cos 0) z(min)
О • ★
Цикл 1
1 sec 0 —tg2 0/ip 1 1 —w | sec 0| 4 cos2 0 — 3 tg26/u> —2tpcos0 1 4 cos2 0—3 2 sin 0 tg 0/ip 2w; cos 0 4 cos2 0—3 1 —2 sin0tg 0/u; w 4 cos2 0—3 1 0 0
(1—cos 0)/cos20 h?(2cos0—l)/cos0 —2 sin 0 tg 0 2w cos 0 (cos 0—1)/COS0 3ip 2 sin 0 tg 0 -ip(4cos2 0-3) z
Цикл 2
1 cos 0 —tg 0 sin 0/zp w cos 0 cos 0 1 1 I cos 0| sin 0 tg 0/ip —w cos 0 COS0 cos 20 tg 0 sin 20/ w —2w cos2 0 cos 20 cos 20 —2 sin2 0/ip 2u?cos 0 cos 20 1 0 0
| 4 sin2 0 w (1—2 cos 0) -(1—COS0)/COS0 +w 2w 4 sin2 0 —2u? cos 20 z
• О • . ★
Заметим, что столбцы (2, 3, 4, ...» 11) цикла 0 совпадают соответственно со столбцами (4, 5, 6, , . И; 2, 3) цикла 2; следовательно, еще через 8
итераций повторится цикл Q. Знак О показывает положение ведущего элемента
зывает, что почти каждая задача на некотором этапе решения оказы-
вается вырожденной. Можно было бы думать, что так как вырождение
происходит все время, то должно было бы наблюдаться много случаев
зацикливания. Однако, согласно данным, не было ни одного случая
зацикливания, за исключением специально сконструированных примеров
Гофмана и Била. По-видимому, зацикливание — очень редкое явление
на практике. Поэтому большинство программ для электронных вычисли-
тельных машин не предусматривает специальных блоков для видоизме-
нения задачи с целью избежать вырождения и возможности зациклива-
ния. Ячейки оперативной памяти вычислительной машины, если они
не заняты целиком данными большой задачи, отводятся для подпрограмм,
предназначенных для повышения точности посредством арифметического
контроля и просчета с большим числом разрядов.
Явление зацикливания представляет интерес с математической точки
зрения. Задолго до того, как Гофман построил свой пример, для избе-
жания вырождения были предложены простые рецепты. Главная задача
состояла в том, чтобы разработать метод, позволяющий избежать вырож-
Таблица 10-1-II
Пример зацикливания в симплекс-алгоритме, принадлежащий Билу
Свободные
*1 Х2 х3 Х4 х5 *6 х7 — 2 члены
Цикл О
1/4 1/2 —60 —90 —1/25 —1/50 1 9 3 1 1 1 0 0 1
—3/4 ★ 150 —1/50 6 • • 1 • 0
Цикл 1
1 —240 30 —4/25 3/50 1 36 —15 1 1 1 0 0 1
—30 -7/50 33 3 1 0
• ★ • •
Цикл 2
1 1 8/25 1/500 1 —84 —1/2 —12 —1/15 8 1/30 1 0 0 1
• • —2/25 ★ 18 1 1 0 1 • 0
227
15*
Цикл 3
Продолжение табл. 10-1-11
25/8 1 —525/2 —75/2 25 0
X—1/160 1 1/40 1/120 —1/60 0
—25/8 525/2 75/2 —25 1 1
1/4 —3 —2 3 1 0
• • ★ •
Цикл 4
—125/2 10,500 1 50 —150 . 0
—1/4 40 1 1/3 —2/3 0
125/2 —10,500 —50 150 1 1
-1/2 120 —1 1 1 0
• • ★ •
Цикл 5
—5/4 1/6 210 —30 1/150 —1/150 1 1 1 —3 1/3 1 0 0 1
-7/4 330 1/50 • • —2 ★ 1 • 0
Примечание. Цикл 6 должен совпадать с циклом 0, так как он имеет те же самые
•базисные переменные в том же порядке.
дения и требующий как можно меньше дополнительной работы. Первое
достижение в этом направлении было изложено автором настоящей книги
осенью 1950 г. в своем курсе линейного программирования в высшей
школе Департамента сельского хозяйства США. Студентам были пред-
ложены упражнения, содержащие доказательства метода в направлении,
указанном в этом параграфе (Эдмонсон [1]; Данциг [4]). Впоследствии
Орден, Вулф и автор настоящей книги опубликовали доказательство
этого метода, основанного на понятии лексикографического упорядо-
чения векторов (Данциг, Орден и Вулф [1]). Чарнс [1] независимо
от них разработал метод возмущения, который описан в одной из задач
в конце этой главы.
В противоположность правилу случайного выбора, описанному
в § 6-1, в следующем параграфе мы покажем, что можно несколько изме-
нить свободные члены так, что
а) базисные допустимые решения станут невырожденными, и
б) кроме того, соответствующие базисные решения невозмущенной
задачи останутся допустимыми. По существу, возмущение просто указы-
вает подходящий выбор переменных, которые нужно вывести из базиса
в случае неопределенности.
228
10-2. ВОЗМУЩАЮЩИЕ ПАРАМЕТРЫ
ДЛЯ ИЗБЕЖАНИЯ ВЫРОЖДЕНИЯ 1
Начнем с этапа I симплекс-метода и предположим, как и в § 9-2,
что все Ьг > О и что система переменных дополнена искусственными
переменными xn+it Хп+г, • • , жп+пг, так что основная задача этапа I
состоит в нахождении таких ж7>0 и min w, что
2 aijxj + xn+i = bi, (bi>0; i = l, 2,
(1)
2 Xn+i = w.
i=l
Пусть начальное базисное множество переменных будет жп+1, хп + 2^ • • •
. . хп+т- Если один или более из свободных членов bt равен нулю, то
соответствующее решение будет вырожденным. Мы избежим этого, рас-
сматривая возмущенную задачу
S aiixi + xn+i = bi + s* (6i>0; 8>0; i = l, 2, ..., m),
(2)
2 zn+i = w (min).
2—1
Очевидно, что начальное базисное решение невырожденно, потому что
для всех i
жп+г = ^ + е‘>0 (6г>0; е>0). (3)
Ясно также, что при 8 = 0 базисное решение допустимо для невозму-
щенной задачи.
На последующих итерациях значения базисных переменных станут,
вообще говоря, полиномами от 8. Действительно, предположим, что для
цикла t (яд, я>2, . . ., Xjm) есть некоторое базисное множество перемен-
ных; тогда, согласно формуле (21) § 8-4, значения базисных переменных,
которые мы обозначим через (е), суть
Мв)=3 + G = 2, ..., т) (4)
k=i
= bi + Рн* 8 + Pi2g2 + • • • + Pim8™»
где [Piy ] — обратный базис и — значения x^ при 8 = 0.
Упражнение. Показать, что для каждого i существует pift =/= 0.
Упражнение. Показать, что никакие две строки обратной матрицы
не могут быть пропорциональны.
В выражении (4) теперь уже нельзя гарантировать, что значения
базисных переменных останутся положительными для всех положитель-
ных 8 и неотрицательными для 8 = 0. Докажем следующую лемму.
Лемма 1. Пусть дан полином
/ (8) = а0 + «I8 + • • • + V™ (5)
1 Изложенный в этом параграфе метод основан на возмущении свободных членов.
В работе Данциг, Орден и Вулф [1] приведено иное доказательство, основанное на
лексикографическом упорядочении, которое тесно связано с данным здесь. Для
дальнейшего обсуждения см. задачи И, 12 и 13 в конце этой главы и § 13-4.
229
тогда / (е) > 0 для всех О <Z 8 < Ло, где hQ — некоторое положительное
число, тогда и только тогда, когда этот полином имеет хотя бы один
ненулевой член и первый (младший) из таких ненулевых членов имеет поло-
жительный коэффициент.
Доказательство. Пусть номер первого члена / (е) с ненулевым коэф-
фициентом (мы будем далее называть его главным членом) будет fc; тогда
в наших условиях
«о = . = ak_t = 0 и ak > 0. (6)
Пусть для / = к + 1, . . т
Af = max(0, max( —а,)). (7)
Тогда для 0 < 8 < 1 и р > 1,
а?-8р>—М8р>—Мь = ..., т)
и, следовательно,
/ (е) = efe (aft + aft+1e + ... + amem-ft) >
>eft(afi—Мг—Me—...—Ме)> (8)
> 8fc (ад—М (т—к) е).
Если мы положим
A0 = min(l, аь/М (т—к)), (9)
где h0 = 1, если М = 0 или М = к, то из (8) следует, что / (s) > 0 для
всех 8 в интервале 0 < 8 < Ло.
Упражнение. Доказать необходимость в лемме 1: см. задачу 4.
Лемма 2. Пусть даны такие два полинома f (г) и g (е):
т т
/(е)=3««е\ Я(е)=3&ге\ (10)
г=0 г—0
что
ai = bi для i = l, 2, ..., к — 1,
ak<-bk (11)
йг, bt произвольные для i=^k.
Тогда для некоторого hQ> 0 будет / (е) < g (е) при всех 0 < 8 < Ао.
Доказательство. Лемма 2 следует из леммы 1, так как условия (11)
означают, что для полинома g (е) — / (е) выполнены условия (6). Сле-
довательно, должно существовать такое h0, что для всех 0 < 8 < hQ
т
(12)
г=0
Теорема 1. Для цикла t каждый полином от 8 (4) имеет по крайней
мере один ненулевой член; если первый такой член положителен для каж-
дого i, то имеется такая область значений 8 : 0 < 8 < ht, что для любого
фиксированного 8 из этой области значения всех базисных переменных
положительны.
Первая часть теоремы справедлива, потому что для фиксированного i
не все = 0. Вторая часть теоремы следует из леммы 1 и того факта,
что если имеются различные области значений 8, в которых значения
230
различных базисных переменных как функций 8 остаются положитель-
ными, то для наименьшей из этих областей положительны все х^.
Для наших целей важно только, что для цикла t существует такая
область значений 0 < 8 < ht. для которой все базисные переменные
как функции 8 остаются положительными. Точное значение ht нас не инте-
ресует, так что при проведении вычислений ht никогда не оценивается.
Теорема 2. Существует такая общая область 0 <; 8 < Л*, что для
любого конечного числа итераций симплекс-метода, примененного к любой
возмущенной задаче в пределах этой области, значения всех базисных пере-
менных остаются положительными и выбор переменной, которая вводится
и выводится из базисного множества, единствен и не зависит от конкрет-
ного значения 8 из этой области*
Доказательство. Применим симплекс-алгоритм на некотором цикле
t для улучшения базисного решения возмущенной задачи (1), в которой
для доказательства по индукции мы предполагаем, что полином Ъ} (е)
положителен в некоторой области 0 < 8 < ht (и, следовательно, его
главный член имеет положительный коэффициент). Ясно, что, согласно
(3), это предположение выполнено для цикла 0. Выбор новой переменной
xs. которая вводится в базисное множество, зависит только от коэффи-
циентов при переменных из базисного множества и не зависит от Ь} и 8.
С другой стороны, выбор r-й базисной переменной, которая должна быть
выведена из базиса, зависит от bi и 8. Однако мы теперь покажем, что
для класса возмущенных задач, для которых 8 находится внутри доста-
точно малой области, из базисного множества будет выводиться одна и та
же переменная хг. Действительно, согласно формуле (21) § 5-1, макси-
мальное значение я* переменной xs. которая вводится в базис, и выбор
r-й базисной переменной, которая выводится из него, определяется соот-
ношениями
4 = W- = min {(bt + ₽ие + рг-2е2 + ... + (13)
ars ai8>0
где х% положительно для любого 8 в некоторой области 0 < 8 < ht
по предположению о том, что bi (е) > 0 в этой области.
ЛЕКСИКОГРАФИЧЕСКОЕ ПРАВИЛО
На основании леммы 2 минимум нескольких полиномов (для доста-
точно малой области значений 8) находится сначала путем сравнения их
свободных членов, т. е. выбором такого г. что
= (аГ5>0; azs>0). (14)
ars к ais
Если, однако, имеется несколько i = г2. . . ., удовлетворяющих (14),
то из этих i выбираем такое i = г. что
для i = rt. г2. ... (15)
ars ais
Иначе говоря, для тех i. которые входят в (15), сравниваются коэффи-
циенты при 81 в этих различных полиномах. Если снова г не единственно,
то для оставшихся i. из которых выбирается минимум, сравниваются
соответствующие коэффициенты при 82, затем — при 83 и т. д.; таким
образом сравнивается по очереди столько степеней, сколько необходимо,
231
пока не определится единственное г. Это всегда произойдет при сравне-
нии коэффициентов при 8W или ранее, потому что, если бы два (или более)
полинома имели бы равные коэффициенты при всех степенях, то это озна-
чало бы, что две (или более) строки обратного базиса отличаются друг
от друга на постоянный множитель, что невозможно; см. приведенное
выше упражнение и задачу 2. Этим способом можно выбрать единствен-
ное г, соответствующее единственному наименьшему отношению (13),
где один и тот же выбор г может быть сделан для всех 8 > 0 в некоторой
области. Это означает также, что значения всех базисных переменных
на следующей итерации, выраженные- полиномами по 8, должны оста-
ваться положительными (т. е. нулевые значения исключаются) в некото-
рой области 0< 8 С ht+i, что завершает индукцию. Теорема 2 будет
доказана, если мы через Л* обозначим наименьшее hp для всех 0
Теорема 3. Симплекс-алгоритм, примененный к возмущенной задаче,
заканчивается за конечное число итераций.
Доказательство. Для любого фиксированного числа итераций N все
значения базисных переменных для любого фиксированного 8 в некоторой
области 0 < 8 < положительны. Отсюда следует, что значение целе-
вой формы строго убывает. Следовательно, никакое базисное множество
переменных не могло бы совпасть ни с каким множеством, полученным
на предыдущих итерациях. Так как имеется лишь конечное число базис-
ных множеств переменных ^не превосходящее числа сочетаний из п по т,
С™ = з невозможно, чтобы было N > С™. Легко также видеть,
что справедлива
Теорема 4. Минимальное базисное допустимое решение возмущенной
задачи дает соответствующее решение невозмущенной задачи, если поло-
жить в (4) 8 = 0.
ЭТАП I — ЭТАП II. ОБСУЖДЕНИЕ
Возмущенная задача для этапа II должна быть выбрана подходящим
образом, так чтобы быть естественным продолжением этапа I. В то же
время ее структура должна быть такова, чтобы любые искусственные
переменные, остающиеся в базисе, имели нулевые значения в базисных
решениях в последующих итерациях при 8 = 0. Пусть dj > 0 — отно-
сительные коэффициенты формы недопустимости в конце этапа I; тогда
возмущенная задача для этапа II для i = 1, 2, . . ., т такова:
>=1
^djXj +(—w) = +em+1, (16)
j=l
n
2 cjXj =z(min),
где для i = 1, 2, . . ., m d; = 1 или 0 в соответствии с тем, содержится
ли в базисном множестве в конце этапа I переменная или нет. Нужно
заметить, что если В — базис, связанный с первыми тп-уравнениями,
и мы теперь присоединяем ^-уравнение системы (16) и (—w) в качестве
базисной переменной, то расширенный базис и обратный к нему для
232
первых т + 1 уравнений будут соответственно равны
IB 0\ /в-1 0\
I I И I I
\0 1/ \0 1/
(17)
Значения базисных переменных в начальном решении для этапа II теперь
равны
ХН ~ 4" Pil8 + Pi2e2 + • • • + Pirn8™ + 08m+1 > 0,
( — w) = 8w+1, '
где, на основании теоремы 2, главные члены положительны. В течение
этапа II все переменные z7>0, яп-н>0 и (—ip)>0 рассматриваются
как допустимые переменные и минимизируется z. Это, конечно, в точ-
ности соответствует процедуре этапа I. Остается только показать, что
если положить 8 равным нулю, то значение любой искусственной базис-
ной переменной будет равно нулю в любом допустимом решении. Пусть
Ui — симплекс-множители, связанные с конечным базисом этапа I. Тогда,
вспоминая, что dj = — ^а^, мы получаем
г
т т
dj — dj—2 ai— — 3 flzj(az + l)- (19)
i=l i=l
Следовательно, если г-е уравнение (16) умножить на (Oi + 1) и их сумму
для i = 1, 2, . . ., т сложить с ip-уравнением (16), то, используя (19)
и тот факт, что О/ = — dn+i, мы получим
т т т
3 ^n+i + (-W) = 3 (пг +1) bi + 2 (*« +1) е1 + Sm+1. (20)
i=l z=l i=l
Теперь постоянный член в полиноме относительно 8 в правой части равен-
ства (20) равен нулю, и главный член положителен.
Доказательство. Уравнение (20) должно иметь место для каждого
решения этапа II, в частности оно должно быть выполнено для значений,
приданных искусственным переменным в начальном решении для этапа II,
заданным формулой (18); но эти значения обладают тем свойством, что
все их свободные члены равны нулю, а главные члены положительны.
Следовательно, если подставить их выражения в виде полиномов в левую
часть (20) и учесть, что б^ > 0, то получим, что этим же свойством должны
обладать и полиномы справа. Обратно, если выражение справа имеет
нулевой свободный член, то это же имеет место для xn+i и (—w) в любом
последующем решении, потому что их ведущие члены сохраняются поло-
жительными. Отсюда следует, что если 8 = 0, то xn+i = 0.
Теорема 5. Если существует минимальное допустимое решение
Xj = х*, z — z*, то в конце этапа II получается система множителей,
обладающая следующими свойствами:
e* = Cj—2 ^*а^>0, (/=1,2, ..., п),
1=1
с*>о=»4=о, ж*>о=^с*=о, (21)
т
minz = z* = 2 ^ibi.
1=1
Замечание. Символ =Ф~ означает «влечет».
233
Доказательство. Симплекс-множители ль полученные в конце этапа II
для расширенной задачи, удовлетворяют указанным выше условиям
в случае, когда для де-уравнения (16) включен множитель к. Однако
если опустить искусственные переменные и возмущение, то де-уравнение
2 djXj может быть получено из первых тп-уравнений с помощью множите-
з
лей Оь определенных в конце этапа I; учитывая формулу (19), мы полу-
чаем, что требуемые множители равны
n* = :rq — &(oz + l). (22)
10-3. ЗАДАЧИ
1. Доказать (упражнение из § 10-2), что хотя бы один элемент в каж-
дой строке и в каждом столбце обратного базиса отличен от нуля.
2. Доказать (упражение из § 10-2), что элементы ни одной из строк
обратного базиса не могут быть пропорциональны элементам другой
строки. (Используя транспозицию матрицы, доказать, что то же самое
верно и для столбцов.)
3. Доказать, что если (е)>0 для 0 < е < /г, то существует такое
h' < h, что bi (е) положительно для 0 < 8 < Л', где bt (в) = bt +
+ W и В-? = (₽о).
з
4. Доказать, что если ak < 0 и а0 — = . . . = = 0, то суще-
ствует такое h >0, что многочлен
/ (е) — aQ 4- + a2g2 + • • • +
отрицателен для всех 0 < 8 < Л.
5. Доказать, что если все базисные переменные в возмущенных реше-
ниях для каждого цикла t остаются положительными в области 0 < 8 <
<С то существует общая область для всех циклов вплоть до £-го, в кото-
рой все базисные переменные для первых ^-итераций остаются положи-
тельными.
6. Решить пример Гофмана, используя метод возмущений (см. § 10-1,
табл. 10-1-1).
7. Решить пример Била, используя метод возмущений (см. § 10-1,
табл. 10-1-П).
8. а) Можно ли построить класс возмущенных задач, которые недо-
пустимы, в то время как соответствующий класс невозмущенных задач
допустим?
б) Может ли класс возмущенных задач быть допустим, в то время
как невозмущенные задачи недопустимы?
в) Может ли класс возмущенных задач иметь конечную нижнюю гра-
ницу для и, а невозмущенных — не иметь ее?
г) Может ли класс возмущенных задач иметь нижнюю границу оо
для и, а невозмущенных не иметь ее?
9. (Чарнс). Разработать иной метод возмущения, связанный с заме-
ной Ъг на bi (е) = bi + Для * = 1, 2, . . ., т. Выразить пра-
з
вила выбора в терминах полной таблицы обычного симплекс-метода.
10. (Не решена). Предполагается, что пример Била имеет наимень-
шее число переменных среди всех примеров, в которых может возникнуть
зацикливание в симплекс-алгоритме. Так ли это? Если нет, построить
пример с наименьшим числом переменных.
234
ЗАДАЧИ, ОСНОВАННЫЕ НА ЛЕКСИКОГРАФИЧЕСКОМ МЕТОДЕ
(ДАНЦИГ, ОРДЕН И ВУЛФ [1])
И. Говорят, что вектор А с m-компонентами лексикоположителен,
что обозначают через А > 0 (см. § 13-3), если по крайней мере одна его
компонента отлична от нуля и первая такая компонента положительна.
Термин «лексико» является сокращением слова «лексикографически».
Говорят, что вектор А «лексико-больше» вектора В и пишут А > В, если
А — В > 0. Наименьший из нескольких векторов будет обозначаться
lexico-min. Доказать, что это лексикографическое упорядочение век-
торов транзитивно, другими словами, что
А > В и В > С^А > С.
12. Предположим, что свободные члены в (1) из § 9-2 не изменены
добавлением возмущающих членов, а заменены векторами
(Ь1, 1, о, .... 0), (&z>0).
Ъ^ = (Ъ2, 0, 1, ..., 0),
Ь^(Ьт, О, О, 1),
где верхний индекс v обозначает «вектор».
а) Аналогично (4) из § 9-2 показать, что в этом случае значения
базисных переменных на некоторой последующей итерации заменяются на
Ьг— (Ьц Pit, •••» Pim)» (* “ 1» 2, 7П)
Z — (zt, Л2, . . ., Л?п).
б) Аналогично (10) из § 9-2 показать, что переменная, которая
должна быть выведена из базиса, выбирается так, что
br/drs = lexico-min {blldis} > 0, (ai8 > 0)
где bl /diS — вектор, полученный делением компонент векторов bl
на скаляр агз.
Доказать, что bl > 0 для всех итераций и z” > z” > z% >. . .
13. Определим отношение частичного упорядочения для и-компо-
нентных векторов следующим образом:
Если х = (£х, • •, In) и у = (Т]!, . . ., цп), то х у и у х,
если для i = 1, 2, . . ., п.
Пусть х, у, xi9 yi, а обозначают n-компонентные векторы, доказать:
Если х у и у z, то х z.
Если х^ у^ и х2 у2, то xi + Х2 1/1 + у2.
Если х у, то Кх Ху, где Х> 0 — скаляр, и Кх Ху, если X < 0.
Если х у и а 0, то аТ х^> ат у, где ат — транспонированный
вектор d.
Глава 11
ВАРИАНТЫ СИМПЛЕКС-АЛГОРИТМА
ВВЕДЕНИЕ
Под вариантом симплекс-метода (в этой главе) понимается алгоритм,
состоящий из последовательности ведущих преобразований в прямой
системе, но использующий иные правила выбора ведущего элемента.
Исторически эти варианты были разработаны для использования ситуа-
ции, когда известно некоторое недопустимое базисное решение прямой
задачи. Например, в приложениях часто встречаются классы задач,
отличающихся друг от друга только свободными членами и коэффициен-
тами стоимости. В таких случаях удобно опустить этап I и использовать
оптимальный базис одной из задач в качестве начального базиса для
следующей.
Для такой модификации симплекс-алгоритма, имеющей целью умень-
шение числа итераций, было предложено несколько методов. Уменьшение
числа итераций особенно необходимо для задач, содержащих много урав-
нений, ибо тогда снижаются затраты на проведение вычислений. Это
также необходимо для задач с большим числом п переменных, так как
число итераций, по-видимому, растет пропорционально п.
В качестве альтернативы для использования правила выбора cs =
— min Cj можно было бы выбирать такое j = s, при котором введение
в базис переменной xs в следующем базисном решении дает наибольшее
уменьшение значения z. Это правило, очевидно, невыгодно в симплекс-
методе, использующем множители, см. гл. 9. Даже при использовании
стандартной канонической формы на каждую итерацию потребовалось бы
в таком случае значительно больше вычислений. Однако можно разра-
ботать такую модификацию канонической формы, в которой коэффициент
при i-й базисной переменной может отличаться от единицы в i-м уравне-
нии, но bt = 1. В этой форме выбора согласно критерию наибольшего
убывания, потребовал бы немного усилий; более того (если воспользо-
ваться специальным приемом), для поддержания таблицы в соответ-
ствующей форме от цикла к циклу требуется не больше усилий, чем
в стандартном симплекс-алгоритме.
Начиная с 1960—1961 гг. много исследований было посвящено систе-
матическому сбору эмпирических данных о сравнительной эффективности
различных предложений, подобных описанным выше. Гарольд Кун
в Принстоне и Филипп Вулф в корпорации РЭНД сделали особенно много.
Представляется, что критерии, основанные на их предварительных наблю-
дениях и не зависящие от числа переменных и ограничений, оправдывают
затрачиваемые на них дополнительные усилия.
Важный частный случай возникает, когда новая задача отличается
от исходной только свободными членами. Оптимальный базис первой
задачи будет все еще оптимальным «по стоимости» для второй (т. е.
236
>0), но соответствующее решение может не быть допустимым. Заметим,
однако, что из оптимальности вытекает допустимость соответствующего
решения двойственной задачи. Для этого случая Лемке [1] разра-
ботал двойственный симплекс-алгоритм как вариант стандартного пря-
мого симплекс-алгоритма; см. § 11-2. Были разработаны аналогичные
в вычислительном отношении варианты, «метод ведущих переменных»
Била [1] и ПЛП (параметрическое линейное программирование) Ор-
чард-Хейса [3], (Орчард-Хейс, Кутлер и Джадд [1]). Эти вариан-
ты изложены в методе одновременного решения прямой и двой-
ственной задачи в § 11-4, разработанном впервые для транспортной
задачи Фордом и Фулкерсоном (см. гл. 20) и позднее распространенном
на общую задачу линейного программирования (Данциг, Форд и Фул-
керсон [1]). Эти варианты алгоритма применяются в том случае,
когда старый базис является все еще оптимальным по стоимости в новой
системе и, следовательно, составляет допустимое начальное решение
для новой двойственной задачи. Напротив, Гасс и Саати [1] в своей
статье по параметрическому программированию изучили случай фикси-
рованных свободных членов и переменных коэффициентов целевой
функции.
Однако, когда задачи отличаются друг от друга не только свободными
членами, старый базис может уже не быть оптимальным в новой задаче
и следует искать другие методы. Если ни базисное решение, ни двойствен-
ное решение, порожденное его симплекс-множителями, не остаются допу-
стимыми, то соответствующий алгоритм называется составным (Орчард-
Хейс [1] и [3]). Примером такого алгоритма является самосопряженный
(двойственный себе) алгоритм § 11-3.
11-1. ДОПОЛНИТЕЛЬНЫЕ ПРЯМОЙ
И ДВОЙСТВЕННЫЙ БАЗИСЫ
Лемке [1] обнаружил некоторую дополнительность между бази-
сами прямой и двойственной систем, которая дает возможность интер-
претировать симплекс-алгоритм в применении к двойственной задаче как
последовательность базисных изменений в прямой задаче; однако в этом
случае соответствующие базисные решения прямой задачи не являются
допустимыми, но симплекс-множители продолжают оставаться по стои-
мости оптимальными (и, следовательно, дают допустимое решение двой-
ственной задачи). Эта дополнительность заслуживает исследования, так
как она дает возможность легко строить двойственную задачу, фактически
не формулируя ее заново.
В качестве базисных переменных в прямой задаче будет удобно
выбрать переменные х2, . . ., хт и показать, что (jq, л2, . . ., л^)
H(cTO+i, cm+2 . . ., сп) составляют базисное допустимое решение в двой-
ственной задаче. Этот факт может быть пояснен с помощью диаграммы
Таккера на табл. 11-1-1. Меньший квадрат, обведенный жирной линией,
содержит базис В прямой системы, в то время как больший, обведенный
двойной линией, дает транспонированный базис В двойственной системы.
Нетрудно показать (это предлагается в качестве упражнения), что опре-
делитель В по абсолютной величине равен определителю В, так что если
существует В"1, то существует и В"1. С помощью табл. 11-1-1 легко убе-
диться, что имеет место соответствие, показанное в табл. 11-1-II.
237
Таблица 11-1-1
Диаграмма Таккера прямой и двойственной систем
Прямая система
переменные Х1 Х2 . . . хт xm+i • . хп Отно- шение Свобод- ные члены
V 'V о о 1 1 . W V 0 0
• • 1 •
Двой- ствен- ная систе- ма ст+1 0 сп 0 1 1 1 0 0
Л j Л2 ап «21 «12 • • «22 • • • aim . ам «17П+1 • • «2тп+1 ♦ • • а1п • а2п . II II — Ъ1 Ь2
Луп ат1 ат2 • • • атт amm+i • • • атп — bjn
Отношение 1 = . = = . . . — ^max v
Свободные члены 1 j С1 с2 • • • ст cm+i • • • сп > min z
Таблица 11-1-II
Соответствие между прямой и двойственной задачами
Прямая задача Двойственная задача
Базис Базисные переменные Небазисные переменные Условие допустимости В #2> • • •» хт хт+1,> • • хп х^Щ 0 для всех i В cm+h • • •» сп> *4, ^2» • • •» с1» с2> •••» ст cj 0 для всех /
Прямой симплекс-метод Двойственный симплекс-метод
Критерий оптимальности Правило введения пере- менной (выбор новой базисной переменной) для всех / Если cs = min ^<0, то выбрать xs (веду- щий столбец s) dj > 0 для всех i Если &r=min bt < 0, то вы- брать сг (ведущая строка г)
Продолжение табл. 11-1-11
Прямой симплекс-метод Двойственный симплекс-метод
Представление нового вектора в базисе Правило выведения пере- менной (выбор перемен- ной, которую нужно вывести из базиса) ais-> a2s> • • • > ams Если br/ars=min ajg>0 >0, то вывести xr (ведущая строка г) аг, /п+1» • • •» аг, п Рг1» Рг2» • • •» Рг/п Если cs/(—ars) = = — min CjK—arj) 0, то —arj вывести cs (ведущий стол- бец $)
Ведущий элемент ars ars
Поведение целевой функции z убывает v возрастает
11-2. ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД
Двойственный симплекс-метод имеет дело с той же таблицей, что
и прямой метод. Однако относительные оценки неотрицательны от ите-
рации к итерации (е;>0 вместо 6/>0). Если случится также, что и все
bi неотрицательны, то соответствующее решение будет не только допу-
стимым, но и оптимальным. Если же не все bi неотрицательны, то веду-
щая строка г выбирается так, что br — min bi <Z 0; а ведущий столбец $
так, что csl(— ars) = min cj/(— arj) для отрицательных—arj. Если все arj
неотрицательны, то легко видеть, что прямая задача не имеет допустимого
решения. Таким образом, в двойственном симплекс-методе, если его рас-
сматривать в терминах переменных прямой задачи, определяется сначала,
какую базисную переменную следует вывести из базиса, а затем — какую
небазисную переменную ввести.
Пример. Предположим, что система была преобразована к виду:
Цикл 0
Х± -j- 4ж4-5^5 —j— 7Xq := 8
х2 — 2i0c^ -f- 4#5—2я6 = — 2
жз4" ^4—3&52^6 — 2 (1)
х^ -j- 3#5 2#б — —4
•ое ★
Так как все Cj неотрицательны, но свободные члены этим свойством
не обладают, выводим базисную переменную х2, соответствующую Ь2 =
= min bi = —2, и вводим я4 в следующее базисное множество, так как
/ = 4 определяется согласно критерию min Cj /(—a2j) = с4 /(—а24) = -у
для а2; < 0. После преобразования с выбранным ведущим элементом
система принимает вид (2). Так как все bt и Cj неотрицательны, базисное
решение теперь оптимально.
239
Цикл 1
2я2 “F 3#5 -j- 3#6 == 4
— +^4 — 2я5+ ^6 = 1
+ у ^2 + ^3 — ХЬ + #6 — 1
(2)
j
“h"2"^2 ~ЬЗХ5 4~ xq~z— 5
ИСКУССТВЕННЫЕ ПЕРЕМЕННЫЕ В ДВОЙСТВЕННОМ
СИМПЛЕКС-МЕТОДЕ
Предположим, что в предыдущем примере х2 и х3 — искусственные
переменные; в таком случае мы будем действовать, как и раньше, однако
мы не будем обращать внимания на все искусственные переменные, как
только они выводятся из базисного множества. Так, х2 будет выведена
из системы (2). Базисное решение все еще не допустимо, потому что х3—
искусственная переменная. Вообще говоря, любая искусственная базис-
ная переменная Xj, значение которой в базисном решении положительно,
может быть заменена на — х$ — х^ так что базисное решение становится
«недопустимым», и оказывается возможным применение правил двойст-
венного симплекс-метода.
Ясно, что алгоритм не может закончиться до тех пор, пока искус-
ственные переменные с ненулевыми значениями остаются в базисном
решении. Он должен закончиться либо доказательством недопустимости
в прямой задаче, либо нахождением допустимого решения прямой задачи,
искусственные переменные которого равны нулю или выведены.
На практике, вероятно, лучше для искусственных переменных с поло-
жительным значением не делать формальной подстановки Xj = —х$, но
так модифицировать правила метода, чтобы получить тот же самый резуль-
тат. Возвратимся к примеру. Здесь получаем мы, выводя из системы х2
и заменяя х3 на —я':
Цикл 1 (х2 выведена, х3 = —х3 — искусственная переменная)
Xi -f- 3#5 + 3Xq = 4
4" ^4-%х5 + Х6 — 1
+ ^3 + х5~ 1^6 =— 1 (3)
5^5 4~ х&== z—б
• О • ★
Цикл 2 (оптимальный)
Xi -j- Зз?з -|- = 1
+ ^з + ^4— х5 =0
— х3 — х5 + ^6 = 1 (4)
Х3 +6#5 = Z—6
• • •
Как мы указывали, во многих случаях допустимое решение двой-
ственной задачи находится без труда. Например, если уравнения умно-
жаются на множители ранее оптимизированной системы с той же матрицей
коэффициентов сщ и если их взвешенная сумма вычитается из я-урав-
нения, то коэффициенты c'j преобразованного z-уравнения будут неотри-
цательными. После пополнения новой системы искусственными перемен-
ными система (а) оказывается в канонической форме по отношению к искус-
ственному базису и (б) ее относительные оценки с$ становятся неотри-
цательными. Следовательно, оптимизация двойственным алгоритмом дает
оптимальное решение прямой системы, минуя обычный этап I.
Даже в тех случаях, когда минимизируемая форма имеет немного
отрицательных коэффициентов, по-видимому, было бы выгодно заменить
каждое отрицательное Cj на c'j = 0 и затем оптимизировать. Это даст
базисное допустимое решение исходной системы (не обязательно опти-
мальное), которое затем может быть использовано с истинными значе-
ниями Cj для того, чтобы начать обычный этап II симплекс-метода.
Упражнение. Рассмотреть, как найти истинные значения в этом
случае.
Упражнение. Доказать, что требуется не более к итераций для устра-
нения из базисного множества к искусственных переменных, сохраняя
в то же время допустимость в двойственной задаче.
11-3. САМОСОПРЯЖЕННЫЙ (ДВОЙСТВЕННЫЙ СЕБЕ)
ПАРАМЕТРИЧЕСКИЙ АЛГОРИТМ
Предположим, что ни базисное решение, ни его дополнительное
двойственное решение не являются допустимыми. Существует простой
способ увеличить все отрицательные bi и Cj до неотрицательных значений
путем добавления ко всем из них некоторой константы 0.
Модифицированная задача теперь оптимальна. Мы рассмотрим далее
способы, сохраняющие допустимость в прямой и двойственной системах,
по мере того как свободные члены и коэффициенты стоимости постепенно
меняются в направлении своих исходных значений. В зависимости от того,
становится ли недопустимым базисное решение двойственной или прямой
задачи, будет использоваться либо прямой, либо двойственный критерий
выбора.
Например, в приводимой далее канонической системе исходная задача
получается, если положить 0 = 0; соответствующие базисные решения
недопустимы как для прямой, так и для двойственной задач.
+ 2я4 + 2^5 = 10
Х% -- Х^ -р 1^5 ~ --l-j-0
Х3 -р — 2^5 =---1-f-0 (1)
Зя4 + (—3 + 0) Х5 = Z
*** ★
С другой стороны, если 0 > 3, то соответствующие решения допу-
стимы в обеих задачах. Если мы начнем, например, с 0 = 4 и затем устре-
мим 0 к нулю, то соответствующие решения будут оставаться допусти-
мыми вплоть до критического значения 0 = 3. Для значений 0, чуть
меньших 0 = 3, решение прямой задачи все еще остается допустимым,
но решение двойственной становится недопустимым, так как с3 = — 3 + 0
отрицательно. Поэтому для 0, меньших, чем 3, но «очень близких» к этому
числу, мы используем прямой симплекс-алгоритм, вводя х5 и в то же
16 Дж. Данциг 241
время сохраняя допустимость в обеих системах. Переменная, которая
должна быть выведена, определяется из условия минимума отношений
bilats для положительных azs. Так как
61/^15 = 5, £>2/^25 = —1 + 0,
в окрестности 0 =’3, второе отношение минимально; следовательно,
на следующем цикле из базисного множества должна быть выведена
переменная х2. Новая каноническая система имеет вид
xi — 2х2 + 4я4 = 12—20 (1<0<3)
х2 — я4 + я5 = — 1 + 0
2я2 + яз—1^4 —— 3 + 30 (2)
(3— 0)я2 + 0я4 =z + (3 — 0)(0 — 1)
• О ★ •
Решения для этой системы остаются допустимыми в области 1 0 3.
Для значений 0, меньших критического 0 = 1, базисное решение пря-
мой задачи становится недопустимым. Следовательно, для 0, меньших
единицы, но близких к ней, мы используем двойственный симплекс-
алгоритм, для того чтобы вывести х3 как базисную переменную и сохра-
няя допустимость в обеих системах . Переменная, которая должна быть
введена, определяется из условия минимума отношений су/(—av) для
отрицательных а17-; в нашем случае единственная переменная с отрица-
тельным коэффициентом есть я4. Преобразуя систему, мы получаем:
Xi + 6гг2 + 4#з = 0 +100
— х2— х$ +^5 = 2 — 20
— 2х2— £з + #4 =3—30
(О<0<1)
(3)
(0 + 3)^2 + 0^3 =z + (3 —0) (0 — 1)+ 0(30—3)
Решение при 0 = 0 допустимо как для прямой, так и для двойственной
систем. Следовательно, оптимальное решение получается при 0 = 0.
Вообще говоря, не обязательно прибавлять один и тот же параметр 0
ко всем отрицательным членам bi и cj, как это было сделано в системе (1).
Можно было бы добавить несколько различных параметров и устремить
к нулю каждый из них в отдельности. Во всяком случае, окончательный
результат получается последовательным применением правил изменения
базиса либо прямого, либо двойственного симплекс-метода.
Как удостовериться, что такой процесс закончится за конечное число
шагов? Чтобы ответить на этот вопрос, докажем две теоремы для случая
одного параметра. Заметим предварительно, что значения любой базис-
ной переменной представляют собой линейные функции 0. Поэтому, если
переменная неотрицательна как для 0 = 0Ь так и для 0 = 02, то она
неотрицательна во всем интервале 01^0^02; следовательно, имеет
место
Теорема 1. Невозможно, чтобы один и тот же базис был допустим
в прямой и двойственной задачах для двух значений 0, где 0Х < 02, если
только он не является также допустимым для всех значений 0 в области
0i<0<02.
Заметим далее, что если переход к базису В допускает при некотором
критическом значении 0 = 04 положительное (ненулевое) убывание 0,
242
то этот базис В не совпадает ни с каким предыдущим базисом, связанным
с некоторым 02 >01, потому что при этом критическом значении 0Ь
где возникает изменение базиса, В дал бы недопустимое базисное реше-
ние при 0, чуть больших, чем 04. Следовательно, справедлива также
Теорема 2. Если каждое изменение базиса сопровождается положи-
тельным убыванием 0, то число итераций может быть только конечным.
Теорема 3. Если имеется только одно вырождение в прямом и двой-
ственном решениях до и после преобразования при критическом значении
0, то 0 строго убывает.
Последняя теорема принадлежит Гассу и Саати [1] для случая
вырождения в двойственном базисном решении и Орчард-Хейсу [3]
для случая вырождения в прямом базисном решении. Если мы докажем
теорему для одного из этих случаев, то справедливость ее в оставшемся
случае будет следовать из доказанного в силу двойственности. Предполо-
жим, что с8, соответствующее х8 при критическом значении 0 = 0О, выра-
жается в виде с8 — к (0 — 0 о) = в; однако для всех других небазисных
переменных Xj, Cj выражаются линейно по 8 : Cj = «у + 80;, где, по пред-
положению, aj положительно для / #= 5. Кроме того, предположим, что
для 8 — 0 решение прямой задачи невырождено до и после того, как xs
заменяет некоторую переменную Xjr в базисном множестве (в действи-
тельности нам нужно только потребовать, чтобы базисное решение пря-
мой задачи оставалось допустимым при некотором строгом уменьшении
в). В этих условиях новые значения множителей относительных оценок
с* будут равны
Су = Cj (^rj/ars) 6 = ® j “F [Pj «rj7
c?r=-(l/ars)8.
Так как числа at положительны для всех небазисных переменных Xj,
за исключением х8, имеется область значений 80 < 8 < 0, где 80 < 0,
для которой с* остается положительной. В этой области с*г>0, откуда
следует
Теорема 4. Если существует допустимое решение прямой и двойствен-
ной систем для 0 = 0О и 0 == 0, то допустимые решения существуют
для всех 0 в интервале О^0^0о.
Упражнение. Доказать теорему 4. Из этой теоремы также следует,
что множество решений, порожденное всеми векторами свободных членов
bi и коэффициентов стоимости с7-, для которых как прямая, так и двой-
ственная задачи одновременно остаются допустимыми, есть выпуклый
многогранник. Доказать также этот факт.
11-4. АЛГОРИТМ ОДНОВРЕМЕННОГО РЕШЕНИЯ ПРЯМОЙ
И ДВОЙСТВЕННОЙ ЗАДАЧ
Практика показывает, что метод одновременного решения прямой
и двойственной задач, разработанный Фулкерсоном и Фордом (гл. 20)г
весьма эффективен при решении задач распределения. Он тесно связан
с работой Куна, который предложил специальный метод для решения
задач о назначении, называемый «венгерским методом»; эта работа
основана на исследованиях венгерского математика Эгервари [1]; см.
243 16*
(Кун, [!])• Наша цель состоит в обобщении этого метода для решения
общих задач линейного программирования. Как здесь устанавливается,
этот метод представляет собой вариант симплекс-метода, число итераций
которого очень часто оказывается меньше, чем это требуется в двойствен-
ном симплекс-методе (Данциг, Форд и Фулкерсон [1]).
Для начала предлагаемого метода может использоваться любое допу-
стимое решение двойственной системы. С решением двойственной системы
связывается ограниченная прямая система, требующая оптимизации.
Когда найдено решение ограниченной прямой задачи, может быть полу-
чено улучшенное решение двойственной системы. Последнее в свою оче-
редь дает новую ограниченную прямую систему, которую нужно оптими-
зировать. После конечного числа улучшений получается оптимальное
решение исходной неограниченной задачи.
Алгоритм Форда — Фулкерсона для задач распределения заметно
отличается от более общего рассмотренного здесь случая тем, что первый
использует метод оптимизации ограниченной прямой системы, который,
по-видимому, более эффективен, чем симплекс-метод, в то время как его
обобщение использует симплекс-метод, потому что он представляется
наиболее эффективным из пригодных методов. [Согласно Гомори, пер-
вый метод фактически представляет собой спиральную последователь-
ность симплексных ведущих шагов. ]
Как и в предыдущих параграфах, можно считать, что весь процесс
начинается с недопустимого базисного решения и использует уже полу-
ченное базисное решение двойственной задачи, чтобы уменьшить значе-
ние формы недопустимости прямой задачи таким образом, что когда
достигается допустимое базисное решение, оно уже является оптимальным.
Начальная каноническая форма для алгоритма одновременного реше-
ния прямой и двойственной задач та же, что и для этапа I обычного
симплекс-метода, см. (7) § 5-2. Пусть
^HXi + • • • + ainXn + ^71+1 =
am\.xi + . • • + ^тпхп “Н хп+т — (1)
+ • • • + dnxn = w—w0,
C{xl 4“ • • • + cnxn = %0i
где bi сделаны неотрицательными до введения искусственных переменных и
d} - — 3 ai} и w0 = 2 bt, (2)
i г
так что сумма первых т + 1 уравнений дает
хп+1 + хп+2 + • • • + хп+т = (3)
Как и раньше, мы предполагаем, что допустимое решение двойственной
задачи известно и что после умножения на соответствующие множители
и суммирования с$ приведены к нужному виду до введения искусственных
переменных, так что теперь
с7>0 для /=1» 2, ..., и. (4)
Задача состоит в том, чтобы найти w = 0 и min z, удовлетворяю-
щие системе (1).
Предположим, что на цикле t таблица после переименования и изме-
нения расположения переменных имеет вид (табл. 11-4-1). Искусственные
переменные, не содержащиеся в базисном множестве выведены из систе-
мы. Заметим, что:
244
Таблица 11-4-1
Таблица алгоритма одновременного решения прямой и двойственной задач
Цикл t
Базис
Искусственные cj=O с7->0
переменные
i _ - _ >
Ограниченная прямая задача
а) Соответствующее решение прямой системы, включая искусствен-
ные переменные, допустимо; 6$>0.
б) Множители а являются симплекс-множителями базиса относи-
тельно формы недопустимости и порождают dj.
в) Множители л не являются симплекс-множителями базиса.
г) Множители л составляют допустимое решение двойственной
системы, исключая искусственные переменные Xj, и, следовательно,
порождают
д) Значения Cj, соответствующие искусственным базисным перемен-
ным Xj, могут иметь любой знак и могут быть выведены; в остальных слу-
чаях для базисных переменных Xj Cj = 0.
Теорема L Если w0 — 0, то базисное решение оптимально.
Если ш0 = 0, то в базисном решении все искусственные переменные
имеют нулевые значения. После выведения этих переменных в допусти-
мом решении Cj, соответствующие положительным Xj, равны нулю; таким
образом, выполнено условие оптимальности.
Шаг 1. Минимизация формы недопустимости ограниченной прямой
задачи. Предполагается, что в начале цикла t имеется одна или более
небазисных переменных Xj, которой соответствует Cj = 0. Эти перемен-
ные Xj вместе с базисными переменными образуют ограниченную прямую
задачу. С учетом только этих переменных при выборе ведущего элемента
для минимизации w применяется симплекс-алгоритм. Обычно искусствен-
ные переменные, когда они становятся небазисными, выводятся из систе-
245
мы. На этом шаге значения множителей rtf не меняются. Симплекс-мно-
жители а/, конечно, меняются на каждой итерации до тех пор, пока
не «минимизируется» ш, т. е. до тех пор, пока числа dj не станут неотри-
цательными для каждой переменной Xj ограниченной прямой задачи.
Шаг 2. а) Если w0 = 0, процесс закончен; в этом случае базисное
решение допустимо и минимально; б) если w0 >0 и все (/ =
= 1, 2, . . п), процесс закончен; в этом случае допустимого решения
прямой задачи не существует. В противном случае перейти к шагу 3.
Шаг 3. Улучшение двойственного решения (нахождение новой огра-
ниченной прямой задачи). Улучшенное решение двойственной задачи
и новая ограниченная прямая задача ищутся с использованием новых
множителей
= (f = l, 2, ..., т), (5)
которые порождают неотрицательные коэффициенты стоимости
= cj-\~kdj> (6)
где к — положительное число, определенное равенством
А- = c8l(—d&) = min Cj/( — dj) > 0. (7)
dy<0
Новая ограниченная прямая задача получается в результате исполь-
зования всех базисных переменных и тех небазисных переменных, для
которых коэффициенты стоимости с* равны нулю. Этим завершаются
шаги алгоритма.
Нужно заметить, что на шаге 3 по крайней мере одна новая перемен-
ная вводится в ограниченную прямую задачу, именно переменная х8,
определенная формулой (7). Заметим также, что ds < 0, так что должна
быть сделана по крайней мере одна итерация, прежде чем минимизи-
руется w в новой ограниченной прямой задаче. В предположении невы-
рожденности каждая итерация уменьшает недопустимость; следовательно,
ни один базис не может повториться и оптимальное решение будет полу-
чено за конечное число итераций.
Нужно также заметить, что в случае шага 2Ь, если все множители
недопустимости dj неотрицательны, но wQ все еще положительно, то
переменные (5) и (6) составляют класс допустимых решений двойственной
задачи, целевая функция которой
v = z0 + kw0 (8)
стремится к+оо при возрастании к. В то же время, из неотрицательно-
стивсех dj и > 0 следует, что min ш положителен, так что допустимых
решений прямой задачи не существует.
ИСХОДНАЯ ОГРАНИЧЕННАЯ ПРЯМАЯ ЗАДАЧА
На первый взгляд может показаться, что (1) не подходящая форма
системы для того, чтобы начать осуществление алгоритма, если все Cj
положительны. Если, однако, Cj >0 для / = 1, 2, . . ., п, то положим
л = 0 и будем рассматривать базисное множество искусственных пере-
менных как полную систему переменных ограниченной прямой задачи
с множителями о = (1, 1, . . ., 1). Алгоритм в этом случае начинается
с нахождения улучшенного решения двойственной задачи посредством
шага 3.
246
Чтобы проиллюстрировать этот метод, рассмотрим задачу нахожде-
ния > О, х2 > 0, . . ., > 0, min z и искусственных переменных
х§ = х7 = х8 = w = 0, удовлетворяющих ограничениям
xt 4- 4я2 — 5х3 4- 7я4— 4я5 4-^6 =8,
— 4х2 4-4я3 — 4я4 4~ 4х5 4-я7 = 2,
^2—Зж3 4~ 4я4 — 2^5 4" = 2, (Q)
—Xi— х2 4~ 4#3—7ж4 4~ 2xg —12,
Xi 4~ 4^2 4- 8ж3 4- Sx& 4~ 23х5 = z.
^-уравнение порождается таким образом, чтобы сумма первых четырех
уравнений была равна
х8 + х7 + Х8 = W.
(10)
Первый шаг состоит в таком определении наибольшего числа к,
чтобы все коэффициенты выражения z 4- kw были неотрицательны.
В нашем случае, согласно (7), к = 1, так что, просто складывая z- и w-
уравнения, мы получаем (11); для удобства мы опустили букву w, так
как все, что мы в действительности делаем, это прибавление к z-уравне-
нию линейной комбинации исходных уравнений без искусственных
переменных.
3&2 4“ 12^з 4“ 4- 25я5 ® z —12.
(11)
Первая ограниченная прямая задача получается выбором наших пере-
менных только среди переменных х6, х7, х3 и xt (так как первые три уже
являются базисными и так как только xt имеет в (11) множитель относи-
тельной оценки, равный нулю); теперь мы переходим к минимизации w.
Цикл 0 (Первая ограниченная прямая задача (xQ, х7, х3, хх)).
+ 4#2 — 5^3 + 7я4 — 4^5 4“ х3 — 8,
— 4^2+ 4^з — 4х4 + 4ж5 +^7 =2,
я2 — Зя3 + 4я4 — 2я5 +я8 = 2, (12)
— Xi— х2-\-4х3— 7rr44-2x5 =w—12.
* О • •
Преобразуя с помощью ведущей переменной Xi и опуская xQ из дальней-
шего рассмотрения (так как это искусственная переменная), мы получаем
следующий цикл (13). Значение w минимизировалось в ограниченной
прямой задаче с переменными (я6, хъ х8, ж4), так как все соответствующие
числа dj неотрицательны. На этом наше рассмотрение первой ограничен-
ной прямой задачи заканчивается.
Цикл 1 (Первая ограниченная прямая задача (я6, х7, я8; х^ закончена;
вторая ограниченная прямая задача (жь я7, х8\ х3) начинается).
Xi + 4х2 — 5я3 + 7я4 — 4#5 = 8,
— 4я2 + 4х3 —4ж4 + 4гг5 + ^7 = 2,
х2 ~- Зя3 -j~ 4#4 — 2#5 4~ 2, (13)
4-Зж2— х3 —2^5 — w—4.
• ★ О •
247
Чтобы определить новую ограниченную прямую задачу, мы снова
преобразуем z-уравнение, определяя такое наибольшее значение А,
чтобы коэффициенты выражения z — kw z и w, определенных (11)
и (13), были неотрицательны. Мы найдем, что таким значением является
к = 12, так что новое уравнение стоимости (после опускания искусствен-
ных переменных, как это объяснялось выше) таково:
О#! + 39^2 + 0#з + + Х5 = Z — 60. (14)
Так как в этом уравнении с3 — 0, переменными новой ограниченной пря-
мой задачи являются х^ х8 и ж3. Вводя в базисное множество х3 и вы-
водя из него я7 (тем самым я7 выводится из системы, потому что эта пере-
менная — искусственная), мы имеем (15). Мы теперь минимизировали w
в ограниченной прямой задаче с переменными (жь я7, я8, я3).
Цикл 2 (Вторая ограниченная прямая задача (хь х^ х8; х3) закончена;
третья ограниченная прямая задача (х^ х3, х8; х^хъ) начинается)
х2 + 2^4+ ^5 = 10 у,
- -- #4 + #5 ==’2~ ’
-2х2 + 1^4 +^5+^8 = 3 у , (
j
+ 2х2 — х4 — х5 =w-3j.
• • ★ О
Мы можем еще раз преобразовать z-уравнение, чтобы определить новую
ограниченную прямую задачу, определяя одновременно такое наиболь-
шее значение к, что выражение z + kw для z и w, определенных (14)
и (15), имеет неотрицательные коэффициенты. Это значение оказывается
равным к = 1, давая (после вывода искусственных переменных) уравнение
® 0#! + 41^2 + 0#3 + 0^4 + 0^5 = Z — 63 4 • (16)
Соответствующая ограниченная прямая задача имеет переменные (^,
я3, х8\ х^ х5), так как и я4 и х5 имеют нулевые коэффициенты стоимости.
Между прочим, мы видим, что все исходные переменные, за исключением
х2, снова вошли в задачу.
Чтобы минимизировать w в новой ограниченной прямой задаче,
мы теперь вводим х4 в базисное множество, получая систему
Цикл 3 (Оптимальный)
^4-3^2 — ^5 = 34 ,
•— 3&2 + Х3 -j- 2^5 = 4,
-----2^2 + ^4 ~Ь ^5 ~ 3 ~2 ,
0х । —j— 0з/2 4~ 0ж3 4~ 0х4 4- 9^5 = w—0.
(17)
Соответствующее решение этой системы ^Зу> 0, 4, 3^-, 0^ и w — 0 допусти-
мо для исходной неограниченной задачи. Так как коэффициенты z-уравне-
248
ния в процессе решения сохранялись неотрицательными, это решение,
очевидно, минимально.
Заметим, что если бы в (15) вместо переменной была бы введена
переменная х5, то потребовались бы две итерации, чтобы минимизировать
ш, так как вместо х8 была бы выведена х3.
Минимальное значение z, 63-~, получается из (16).
11-5. ДРУГОЙ КРИТЕРИЙ ДЛЯ ЭТАПА I
Этот критерий, впервые предложенный в описательной форме Марко-
вицем, имеет много общего с алгоритмом одновременного решения пря-
мой и двойственной задач (Данциг, Форд и Фулкерсон, [1]), изложен-
ного в предыдущем параграфе, и с двойственным алгоритмом (Лемке [1]).
Подобно стандартному симплекс-методу, этот метод использует базис-
ные допустимые решения, но основан на ином критерии выбора новой
базисной переменной на этапе I. Стандартный критерий выбирает xs
таким образом, чтобы величина ш, которая измеряет недопустимость
в прямой задаче, убывала с максимальной скоростью при возрастании
xs. Так как на этот критерий не влияет целевая форма и, допустимое
решение, полученное на этапе I, может сильно отличаться от того, кото-
рое минимизирует z. Чтобы исправить этот недостаток, предлагается X;
выбирать так, чтобы имело место максимальное убывание (наименьшее
возрастание) целевой формы на каждую единицу убывания формы недопу-
стимости.
Пусть для некоторой итерации каноническая таблица имеет вид (3).
Предполагается, что переменные расположены и обозначены так, что
базисное множество составляют переменные х^, я2, . . ., хт, часть кото-
рых может быть и искусственными. По стандартному критерию для эта-
па I s выбирается так, чтобы
ds = mind^<0. (1)
Вместо этого в настоящем методе предлагается выбирать j = s, так что
csl( —ds) = mincj/( — dj), (ds<0), (2)
dj<0
а в остальном алгоритм не меняется. В случае, когда несколько j мини-
мизируют это отношение, то выбор среди них производится по стандарт-
ному критерию (1). Для этапа II s выбирается обычным способом (т. е.
так, что cs = min Cj < 0).
Ж1 х2 • • • хт х/п+1 • • • п • • • хп+пг Свободные члены
1 а1, т+1 • > • «1, п • • • fll, п+т &1
1 а2, /п+1 • • • rt2, п • • • а2, п—т ^2
1 аШз 7П+1‘ • • ат, п • • > • п+т &т
cm+i • • • сп • • • сп+т Z — Zq
dm+1 • • • dn ... &п+т W Wq
249
11-6. ЗАДАЧИ
1. Рассмотреть следующие результаты из § 6-3:
а) Показать, что если задача линейного программирования имеет
конечную нижнюю границу для некоторой данной совокупности свобод-
ных членов, то она имеет конечную нижнюю границу и для любой сово-
купности свободных членов при условии, что допустимое решение суще-
ствует.
б) Предположим, что задача линейного программирования дополнена
искусственными переменными, сумма которых ограничена некоторой
постоянной (не обязательно равной нулю). Доказать, что если минимизи-
руется z при условии, что искусственные переменные могут входить
в базисное множество с неотрицательными значениями, то минимум
конечен или бесконечен в зависимости от того, конечен или бесконечен
min 2 в исходной задаче.
2. Показать, что никакой базис не может появиться снова в методе
параметрического линейного программирования. Какое предположение
делается о вырожденности?
3. Разработать лексикографические приемы (приемы возмущения)
для двойственного симплекс-метода; для самосопряженного (двойствен-
ного себе) параметрического метода. Каков лексикографический прием
для алгоритма одновременного решения прямой и двойственной задач
и для этапа I алгоритма Марковица?
4. Решить заново задачу о смесях, приведенную в § 5-2 (см.
табл. 5-2-V), используя различные варианты симплекс-метода, рассмотрен-
ные в этой главе.
5. Показать, что если в алгоритме одновременного решения прямой
и двойственной задач в базисном множестве не осталось никаких искус-
ственных переменных, то решение оптимально.
Глава 12
ПОНЯТИЕ ЦЕНЫ
В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
В предыдущих главах мы часто называли симплекс-множители
«ценами». В этой главе мы рассмотрим экономические примеры, которые
покажут, что такая точка зрения на множители не только естественным
образом возникает, но и допускает также экономическую интерпретацию
самого симплекс-метода. Как мы видели, эти множители являются реше-
нием второй задачи линейного программирования, которая называется
двойственной к первоначальной. Первый пример показывает, как может
возникнуть цена в случае, в котором вначале никаких цен не было; вто-
рой и третий пример в § 12-2 показывают, каким образом «естественно»
появляется двойственная система конкурирующих цен на новые ингре-
диенты в ситуации, в которой уже существуют цены на старые продукты
и процессы. Более полное изложение связи линейного программирования
с экономической теорией можно найти в ряде превосходных книг (см.
литературу, приведенную в конце этой главы).
12-1. МЕХАНИЗМ ЦЕН СИМПЛЕКС-МЕТОДА
УПРАВЛЯЮЩИЙ ИНСТРУМЕНТАЛЬНЫМ ЗАВОДОМ М
Рассмотрим задачу управляющего инструментальным заводом, вхо-
дящим, скажем, в только что национализированную отрасль промышлен-
ности. Предположим, что центральный планирующий орган выделил
этому управляющему ресурсы материалов, виды которого мы занумеруем
числами от 1 до А: в количествах +&i, . . +Ьд, и поручил управляющему
произвести выпуск инструментов, занумерованных числами от k + 1
до т соответственно в количествах —Ьд+ь • • •> —Ьт (числа Ьд+j, . . .
. . ., Ьто, обозначая объемы выпускаемой продукции, отрицательны в си-
лу принятого нами условия). Планирующий орган указывает далее
управляющему, что для осуществления поставленных перед ним произ-
водственных целей он должен свести к минимуму затраты труда и что он
должен оплачивать рабочих трудовыми сертификатами, по одному серти-
фикату за каждый час работы. Центральный планирующий орган объя-
вил, что старые цены на ингредиенты не должны применяться, и вместе
с тем не дал управляющему никаких новых цен, которыми он мог бы
руководствоваться.
Управляющий имеет в своем распоряжении несколько технологиче-
ских процессов, скажем п, каждый из которых он может описать векто-
1 Этот раздел написан Алмоном.
2 Разумеется, приводимые в этом разделе рассуждения являются не более чем
педагогическим приемом при описании задачи и наглядном разъяснении сущности
понятий.— Прим, ред.
251
ром-столбцом amj). Если у-й процесс потребляет единиц
г-го ингредиента на каждую единицу интенсивности операции, то число
aij положительно. Если, с другой стороны, у-й процесс выпускает
единиц ингредиента i на каждую единицу интенсивности операции, то
atj отрицательно. Кроме того, у-й процесс потребляет на каждую единицу
интенсивности операции cj единиц труда. Задача управляющего состоит
тогда в том, чтобы найти для всех процессов интенсивности операции
х1у . . ., хп, которые удовлетворяют системе уравнений
^11^1 4“ #12^2 • • • + ^171^71 = bi,
^21Xi + а22Х2 4“ • • • 4“ а2пхп =Ь2,
^mixl 4“ &т2х2 + • • • 4~ ^7)171*^71 — Ьт
и минимизируют общее количество затраченного труда
Cixi + С2Х2 + • • • + Спхп = 2 (min).
Числа х^, конечно, должны быть неотрицательными. В матричном обозна-
чении мы можем записать эти соотношения как
Ах — b, cx — z.
Управляющему известны т старых надежных процессов, имение
1, . . ., т, с которыми, как он уверен, он сможет произвести требуемые
выпуски с заданными затратами, хотя потребности в затратах труда
могут оказаться значительными. Таким образом, он знает, что может
найти такие неотрицательные х±, . . ., хт, что
а11#1 + Л12^2 4" • • • 4" а1тхт = bi
а21х1 4" а22х2 + • • • + а2тхт = Ь2
ат1х1 4“ ат2х2 4“ • • • + аттхт — Ьт
или в матричных обозначениях Вх = Ь. Мы будем предполагать, что В
является допустимым базисом для системы (1).
Однако управляющий узнал, что его рабочие склонны к расточи-
тельству материалов, затрачивая их гораздо больше, чем это предусматри-
вается системой (1). Он знает, что если он не будет сдерживать эту тен-
денцию, то ему не удастся осуществить свои цели. Раньше он вычитал
стоимость сверхнормативных материалов из зарплаты рабочих; теперь
же, когда все цены аннулированы, он уже не располагает какой-либо
общей мерой для материалов и зарплаты. Внезапно, в момент вдохнове-
ния, его осеняет, что он может назначить свои собственные цены в виде
трудовых сертификатов, удерживать у участвующих в каждом из про-
цессов рабочих стоимость материалов, которые они используют, кредито-
вать их за продукцию и выплачивать им разность в виде зарплаты. Будучи
справедливым человеком, он предполагает назначить цены так, чтобы
квалифицированный рабочий фактически мог принести домой сертификат
за каждый проработанный час. Иными словами, он хочет так назначить
цены яь . . ., лт на продукцию и сырье, чтобы чистый доход при еди-
ничной интенсивности каждого базисного процесса / был равен количе-
252
ству затрат труда которого он требует.
^1^11 + ^2а21 + • • • + ^тат1 = с1>
^1^12 + ^2а22 + • • • + лтат2 = e2f
^1а1т + ^2а2т + • • * + ^татт = ст->
или, используя матричные обозначения,
лВ = с,
где лис суть векторы-строки.
Теперь управляющий решает систему (2) относительно х, находя
Б-1 и полагая
x==B^b = b.
Возвращаясь к (3), он замечает, что решение почти готово, именно
л = сВ"1.
Здравый смысл подсказывает управляющему, что, используя этот
механизм цен, он должен был бы выплатить ровно столько трудовых серти-
фикатов, сколько он выплачивал бы, если бы он оплачивал труд по часам
и вся работа выполнялась бы эффективно. Действительно, это легко дока-
зывается, так как общие издержки, учитывающие вычисленные им цены
для всех процессов, равны лЪ = сВ^Ъ — сх, где сх — зарплата, выпла-
ченная непосредственно. Однако у управляющего * возникло сомнение
относительно своего механизма цен. Он помнит, что, помимо тех т про-
цессов, которые он намерен использовать, имеются и другие процессы;
он предполагает даже, что среди оставшихся процессов могут быть такие,
для которых его механизм цен потребовал бы уплатить
Cj = л^ j + n:2fl2j + • • • + (4)
что больше, чем непосредственные затраты Cj. Если один из таких про-
цессов привлечет внимание рабочих, то рабочие увидят, что, используя
его, они могут, получить более одного трудового сертификата за час
работы. Умные людй будут тогда пытаться осуществлять эти процессы
так, чтобы, не увеличивая расхода материалов, выпускать те же
объемы продукции. Если они смогут так сделать, то они присвоят боль-
шую зарплату до тех пор, пока не будет раскрыт секрет, что управ-
ляющий платит за невыполненную работу. Просматривая список про-
цессов в (1), управляющий найдет несколько процессов, для которых
имеет место неравенство c'j > Cj. Обозначая излишек зарплаты для /-го
процесса через Cj
cj = С3 — 4" ^2а2У + • • • +
управляющий отбирает процесс s, дающий наибольший излишек зар-
платы:
с8 = min cj < 0. (5)
Прежде чем принимать административные меры, которые удержат
рабочих от использования процессов, дающих им дополнительную зар-
плату, управляющий, склонный к трезвому размышлению человек, сделает
перерыв, чтобы обдумать смысл этой дополнительной зарплаты. Имея
склонность к математике, он вскоре обнаруживает зависимость, которую
мы выражаем математически, говоря, что вектор коэффициентов для
253
любого процесса j в канонической форме может быть использован в каче-
стве весов для образования линейной комбинации исходных векторов:
базисных процессов, которая имеет те же коэффициенты затрат и вы-
пуска, что и процесс / для всех ингредиентов, за исключением, возможно,
ингредиента издержек. В частности, он найдет, что он может представить
процесс $, дающий наибольшую дополнительную зарплату, в виде линей-
ной комбинации своих «старых надежных» процессов следующим образом:
вами соотношение (6) утверждает, что х& единиц процесса s можно заме-
нить комбинацией aisxs. O2Sxs, . . ., amsxs единиц базисного множества
процессов (1, 2, . . ., т). Таким образом, если рабочие используют xs
единиц процесса s, то интенсивности базисных процессов должны быть
приведены в соответствие с этими величинами (увеличением или умень-
шением в зависимости от знака), если ограничения на материалы и доли
выпуска должны по-прежнему удовлетворяться. Теперь затраты на рабо-
чую силу при замене одной единицы процесса s т старыми надежными
процессами равны
+ c2a2s + • • • + стаms-
Эта величина и есть в точности та сумма, которую уплатил бы управляю-
щий за различные затраты и выпуски, потребляемые одной единицей
фактического процесса 5, если бы он использовал цены jq. Действительно,
рассматривая векторное уравнение (6) как т уравнений, связывающих
числа, и умножая первое уравнение на второе на л2 и т. д., а затем
складывая их, из (3) сразу получаем, что
+ C2a2s + • • • + + ^2a2s 4~ • • • + nmams- (7)
Теперь легко показать, что тот факт, что процесс $ дает излишек зарплаты,
означает для управляющего, что этот процесс, когда он фактически при-
меняется, потребляет меньше труда, чем в том случае, когда он заменяется
т старыми технологическими процессами. Это ясно из соотношений (4),
(5) и (7), откуда следует, что
ciais + • • • + Г8 + • • • + стаms >С8. (8}
Следовательно, как он рассуждает, процесс s должен быть в некотором
смысле более эффективным, чем по крайней мере один из рассматривав-
шихся старых процессов. Вспоминая, что планирующий орган предложил
ему свести затраты труда к минимуму, управляющий решает исполь-
зовать вместо одного из исходных т процессов процесс s. Вскоре он
обнаруживает, что если он хочет избежать бессмысленной с точки зре-
ния планирования ситуации, состоящей в использовании некоторого
процесса с отрицательной интенсивностью, то процесс г, который дол-
жен быть заменен процессом $, должен быть выбран так, как мы видели
в § 5-1 (18), т. е. так, чтобы
Ьг/аГ8 =*ш1п Ъ}1а}8
254
Ввиду неравенства ars > 0 из (8) следует, что
+ • • • + cr-i^r-i,s + ^r+l,sar+l,s + • • • + WWCs)/(— ars)}<Cr. (9)
Коэффициенты при с4, с2, • • •> cs, . . ., ст в (9) суть в точности те веса,
которые необходимы для замены процесса г процессами нового базиса,
что можно увидеть, выражая на основании равенства (6) столбец г через
другие столбцы. Но, например, Cidis!(—drs) представляет собой затраты
на рабочую силу первого технологического процесса при замене про-
цесса г, так что левая часть (9) представляет собой общую сумму затрат
на рабочую силу при замене единичной интенсивности процесса г про-
цессами нового базиса, в то время как сг, конечно, представляет собой
затраты на рабочую силу одной единицы реального процесса г. Следова-
тельно, неравенство (9) показывает, что действительно процесс г менее
эффективен по своему использованию рабочей силы, чем процессы нового
базиса.
Короче говоря, управляющий теперь знает, что если существуют
процессы, при которых его механизм цен дает больше трудовых серти-
фикатов, чем это требуется в действительности, то он может подставить
один из этих процессов вместо некоторого процесса в исходной системе
и тем самым осуществить более эффективное использование труда. Так
как планирующий орган предложил ему свести затраты труда к минимуму,
то, очевидно, он должен планировать производство, используя процесс $
вместо одного из тех т процессов, которые он первоначально намеревался
использовать, заново привести в соответствие интенсивности использо-
вания остальных процессов и изменить цены, так чтобы ни один из про-
цессов, которые будут затем использоваться, не требовал бы дополнитель-
ной зарплаты.
Усвоив этот урок, управляющий снова начинает искать процессы,
дающие дополнительную зарплату, использовать наихудший из них,
заново приспосабливать цены, искать дополнительную зарплату и т. д.
до тех пор, пока он не найдет такую систему цен л°, при которой ни один
из процессов не дает дополнительной зарплаты. К счастью для него,
оказывается (как мы уже знаем), что такую систему цен он за конечное
число шагов найдет.
Прервемся на некоторое время, чтобы рассмотреть смысл одной
из этих цен, например цены jq. Предположим, что мы вводим в матричное
уравнение (1) управляющего фиктивный процесс, который состоит просто
в увеличении его доли ингредиента £, если > 0, или в уменьшении
его доли г, если Ъг < 0. Такой процесс будет представлен столбцом, состоя-
щим из нулей, за исключением единицы в f-й строке. Таким образом,
затраты на рабочую силу при замене этого процесса процессами конечного
базиса равны, согласно (4), в точности л^. Таким образом, есть «цена
труда», который может быть заменен одной добавочной единицей ингре-
диента I.
Теперь управляющий достиг своей цели. Он нашел такую систему
цен на сырье и готовую продукцию, которая будет удерживать его рабо-
чих от чрезмерного расхода материалов и вместе с тем сделает невозмож-
ным перерасход зарплаты. Но теперь он начинает интересоваться, дей-
ствительно ли он гарантирован от критики со стороны планирующего
органа за те расходы на рабочую силу, которые он намеревается про-
извести. Используемый им план состоит из системы интенсивностей
процессов х° — (xj, ж®, . . ., Хп), удовлетворяющих условиям системы цен
Ах° = Ь, (х? > 0)
гт0 ’ (10)
СХи =
25d
л° = (л л®, . . л?п) и, для каждого процесса, излишка затрат на
рабочую силу
С* = Cj— 3 > О, (11)
1=1
которые обладают следующим свойством:
_ m
если Су = С;— 3 ^iaij > 0, TO X® == 0. (12)
2—1
Докажем теперь, что составленный управляющим план минимизирует
его затраты на рабочую силу. Представляя с° в виде с° = с — л° А =
= (cj, Сп), мы из (10) находим, что
с°я° = (с°—л°А) х° = 2°—л°Ь, (13)
где, согласно (10), 2° есть общая потребность в затратах труда в условиях
действующего плана. Но ввиду (12) с° ж0 = 0 и, следовательно,
20 = л°6. (14)
Пусть теперь х =- (жь х2, ...» хп) — любой другой допустимый дей-
ствующий план, и пусть z — потребность в затратах труда при этом
плане; тогда
Ах = Ь, (х,->0)
(15)
СХ = 2. v '
Умножая равенство Ах — Ъ на л°, вычитая полученное из равенства
сх = 2 и учитывая (14), мы имеем
(с — Л°Л) X = Z— Я°Ь = 2 — 2°
ИЛИ
Ус°Х} = 2—Zf>. (16)
j
Но левая часть есть сумма неотрицательных слагаемых, и, следо-
вательно, 2 >2°. Поэтому не существует никакого другого допустимого
плана, для которого потребность в затратах труда меньше, чем у плана,
найденного управляющим. В этот момент мы можем представить себе
восхищение управляющего своей гениальностью, так как в качесте побоч-
ного результата поиска цен, которые заставят его рабочих работать
эффективно, он попутно обнаружил те процессы, которые минимизируют
его потребность в затратах труда. Не пытаясь делать это явно, он тем
не менее решил поставленную перед ним задачу сведения затрат труда
к минимуму}
ДВОЙСТВЕННАЯ ЗАДАЧА
Рассмотрим снова требования, которым удовлетворяет система цен,
найденная управляющим. Во-первых, ни по одному из процессов не долж-
но быть перерасхода зарплаты, т. е. должно выполняться неравенство
(17)
Во-вторых, общая сумма заработной платы, которая должна быть упла-
чена по всем процессам, должна оставаться неизменной независимо
от того, уплачивается ли она прямо или через использование механизма
256
цен, т. ё.
z° = сж° = лй, (18)
где я0 — оптимальное решение задачи (1).
Покажем теперь, что сами эти цены л представляют собой оптималь-
ное решение другой задачи линейного программирования — именно
задачи, двойственной для исходной задачи управляющего о производ-
стве. Умножая J-e неравенство (17) на х° и суммируя, мы получаем, что
«1 3 аиХ^ + п2 3 + • • • +пт 3 2 cix°i- (19)
j=l }=1 j=i j=l
Подстановка из (1)
bi = 2 aux] (i = 1, 2, ..., т) (20)
j=i
дает нам
+ Л2&2 + • • . + Mmbm С1Х1 4“ 4" • • • 4" спхп-
Таким образом, неравенство справедливо для любого вектора л,
который удовлетворяет условиям (17). Цены л°, найденные управляющим,
дают равенство л°Ь = сх® и, таким образом, л° максимизирует nb при
ограничениях (17). Следовательно, л = л° может рассматриваться как
оптимальное решение двойственной задачи линейного программирования,
именно
лА<с,
д / ч (21)
ло = р (max). v '
Соотношение л°6 = ся°, где л° — оптимальное решение задачи (21),
а ж0 — оптимальное решение задачи (1), согласуется с теоремой двой-
ственности. установленной в § 6-3 (теорема 1). Читатель может сам
проинтерпретировать экономический смысл максимизации л Ъ в случае
задачи управляющего инструментальным заводом.
Рассмотрим теперь два других примера, показывающих, как двой-
ственная задача возникает в других областях и как она может быть
интерпретирована.
12-2. ПРИМЕРЫ ДВОЙСТВЕННЫХ ЗАДАЧ
СХЕМА ЧЕСТОЛЮБИВОГО ПРЕДПРИНИМАТЕЛЯ
В этом параграфе мы сформулируем задачу, в которой двойственная
задача возникает «естественным образом». Рассмотрим оборонный завод,
который только что был построен правительством. Заводу запланировано
производить определенные количества —Ъи i — к 4- 1, . . ., т неко-
торой оборонной продукции и использовать только определенные коли-
чества + bt. z = l, 2, . . ., к некоторых дефицитных материалов, которые
поставляются бесплатно другими государственными заводами. Инже-
неры-консультанты, которые проектировали завод, обеспечили прави-
тельство списком различных процессов, которые можно осуществить
на заводе, и их коэффициенты затрат — выпуска. Несколько смущенные
этой массой данных, государственные служащие, которым было предло-
жено управлять заводом, решили обратиться к частному предпринимателю,
чтобы проконсультироваться о том, как они должны планировать свое
производство. Предприниматель сознает, что это было бы не только
хорошей школой для его людей, но и большим подспорьем в управлении
17 дж. Данциг 257
заводом. В соответствии с этим, получив информацию и изучив данные,
он вносит предложение о непосредственном вознаграждении, за которое
он будет управлять заводом, поставлять правительству требуемые коли-
чества продукции и использовать дефицитные материалы в количествах,
не превышающих заданные. Служащие заявляют, что, при прочих рав-
ных условиях, лучше всего было бы доверить управление заводом самому
правительству. Однако если он сможет убедить их, что его предложение
достаточно хорошо (подразумевая при этом, что если бы заводом управ-
ляло правительство, то маловероятно, чтобы оно могло бы сделать это
с меньшими расходами), то они примут его предложение.
Предприниматель берет данные к себе в контору, достает свою книгу
по линейному программированию и использует данные о коэффициентах
затрат — выпуска для составления матрицы А, аналогичной матрице
управляющего станкостроительным заводом, однако со следующим отли-
чием: он включает стоимость приобретенных материалов, потребляемых
каждой единицей процесса /, в расходы процесса Cj.
Для того чтобы определить тот минимальный гонорар, за который
он может согласиться управлять оборонным заводом, предприниматель
должен только решить следующую задачу линейного программирования:
найти такой вектор х 0, что
Ах = Ь,
cx = z (min).
(1)
Он приглашает своего математика, дает ему эту задачу, и на следующее
утро у него на столе лежат результаты: минимальная стоимость 2° и век-
тор оптимальных интенсивностей использования процесса ж0. Первое
его побуждение — объяснить своим коллегам по государственной службе
метод линейного программирования, показать им окончательную таб-
лицу и посредством этого убедить их в том, что им не остается ничего
лучшего, чем принять его предложение и платить ему сумму 2°. Но затем
он понимает, что этот план выдает его секрет; государственные служащие
не будут больше в нем нуждаться; они возьмут его вектор х° и станут
управлять заводом сами. Поэтому он должен убедить их в минималь-
ности 2° не выдавая, однако, своего плана xQ.
С этой целью он решает ввести систему цен, которые он предложит
платить за материалы при условии, что ему будут выплачивать некото-
рую сумму за производимую продукцию. Он хочет, чтобы{эти цены были
таковы, чтобы никакой отдельный процесс не приносил прибыли, так как
если бы прибыли появились, то правительство зафиксировало бы их
и захотело бы само использовать этот конкретный процесс. С другой
стороны, при этих ограничениях он хочет получить как можно больше
денег. Иными словами, он хочет, чтобы его вектор-строка цен л удовлетво-
рял условиям
лА< с
лЬ = v (max).
(2)
Он снова приглашает математика, который узнает в этой задаче двой-
ственную той, которую он решал прошлой ночью, и выдает решение
немедленно: оптимальным является л = л°, т. е. симплекс-множители,
полученные на последнем шаге решения предыдущей задачи, а максимум
есть v = гА К счастью, они с облегчением замечают, что г?° = 2°.
С этими результатами в руках предприниматель возвращается к слу-
жащим и выдвигает свое предложение о ценах. Служащие занимаются
258
бюрократической проверкой, чтобы быть уверенными в соблюдении каж-
дого из неравенства (2) и, конечно, вычисляют общие затраты при исполь-
зовании этих цен: л°Ь = г?°. Затем предприниматель предлагает им рас-
смотреть любой план х, удовлетворяющий условиям (1). Затраты при
этом плане для них, если бы они сами управляли заводом, были бы равны
сх. Но замена в (2) л на л° с последующим умножением обеих частей этого
неравенства на любой допустимый план х дает ;
л°Ах сх, (3)
или, согласно (1),
(4)
Следовательно,
р° < сх, (5)
так что стоимость этого плана будет не меньше чем г?°. Это рассуждение
убеждает чиновников в том, что им не остается ничего лучшего, чем при-
нять предложение предпринимателя о непосредственном вознаграждении,
равном г?°. С последней надеждой управлять заводом самим они пытаются
выпытать у него, с какой именно интенсивностью он намерен использо-
вать каждый процесс; но он прикидывается незнающим такие подроб-
ности и вскоре идет счастливый с подписанным контрактом.
ФАБРИКАНТ ПИТАТЕЛЬНЫХ ТАБЛЕТОК1
Домашняя хозяйка может покупать в бакалейном магазине различ-
ные по стоимости и по содержанию питательных элементов продукты.
Для простоты предположим, что имеется только пять видов продуктов
и два питательных элемента, калории и витамины. Задача домашней
хозяйки состоит в том, чтобы определить диету с минимальной стоимо-
стью, содержащую не менее 21 X 100 калорий и 12 X 100 единиц вита-
минов на человека в день. Данные простой модели линейного програм-
мирования для этой задачи приведены в табл. 12-2-1.
Таблица 12-2-1
Основная задача о питательных таблетках
Ингредиенты Технологические процессы Постоянные
Покупаемые продукты Имеющиеся излишки
XI х2 хз Х4 Хб калории витамины хе х7
Калории Витамины -1 -1 -1 — 2 -1 -1 1 1 н* ЬЭ 1 1 -21X100 -12X100
Затраты 20 20 31 И 12 2 (min)
Фабрикант питательных таблеток хочет выполнить все требования
диеты, продавая аптекам чисто калорийные и чисто витаминные таблетки
1 Этот пример представляет собой вариант примера, приведенного в книге Дорф-
мана, Самуэльсона и Солоу «Линейное программирование и экономический анализ»
[1]. Наше рассмотрение может рассматриваться как дополнение к приведенным
в этой книге исследованиям.
259
17*
по ценам, которые не только конкурируют с аналогичными ценами про-
дуктов 1 и 2, имеющихся в бакалейном магазине, но будут более дешевым
источником удовлетворения потребностей в пище, чем любой продукт
на рынке. Какие цены должен он назначать, чтобы максимизировать
свой доход?
Пусть Л1 — цена, которую он назначает на каждую калорийную
таблетку, а л2 — цена одной витаминной таблетки (каждая таблетка
содержит 100 единиц соответствующего элемента). Тогда двойственная
задача принимает вид (6а). Подстановка
придает ей более удобный для графического представления вид (66) (см.
рис. 12-2-1).
Двойственная задача о таблетках
— Jti
— —
— JTj —-
— 2nt—
«1
s$20
л2< 20
2л2<31
л2< 11
я2< 12
<0
л2< 0
(6а)
У1
У1 +
У1 +
2yi +
Vi
<20
У2^ 20
2у2<31
*/2<12
>0
(66)
— 21^i—12л2 = v (шах)
21^ + 12^2^ (шах).
В (66) сумма членов, стоящих в левой части каждого неравенства (напри-
мер, + 2у2 в третьем ограничении) представляет собой расходы домаш-
ней хозяйки, если она заменяет рассматриваемый вид продукта покупкой
питательных таблеток с теми же количествами питательных элементов;
число в правой части неравенства представляет собой ее расходы, если
она, напротив, покупает продукт. В каждом случае требуется, чтобы
покупка замененного продукта обходилась не дороже.
Неравенства (66) изображены графически на рис. 12-2-1, и очевидно,
что оптимальный выбор цен состоит в назначении единицы стоимости
за калорийную таблетку и 10 единиц стоимости за витаминную.
Оптимальные цены: л* ——1, л*=—10. (7)
Максимальный доход: v* = л*&1 + я*Ъ2 =—(—21) —10(—12) = 141.
Необходимо заметить, что нами было сделано предположение о том,
что фабрикант таблеток удовлетворяет все потребности в пище. При этом
условии очевидно, что его цены должны быть конкурентоспособными
по сравнению с ценами на каждый из видов продуктов, так как в про-
тивном случае часть продуктов домохозяйка будет покупать в бакалейном
магазине и только часть — в аптеке. Другой факт, заслуживающий
упоминания, состоит в том, что продукты 4 и 5 все еще конкурентоспо-
собны по сравнению с таблетками, иначе говоря, они не дороже, чем
таблетки, и это можно увидеть, подставляя соответствующие значения
л* в (6а). Поэтому цены на таблетки должны быть несколько ниже опти-
мальных, для того чтобы вызвать некоторое разностное смещение в сто-
рону таблеток и таким образом обеспечить им рынок сбыта. В случае
260
задачи о питании из рис. 12-2-1 ясно (и это верно всегда, когда все
^0), что небольшое уменьшение всех yt (или увеличение л^) по сравнению»
Рис. 12-2-1. Двойственная,задача о таблетках.
с оптимальным решением достаточно, чтобы обеспечить весь рынок при
том условии, что решения всех домохозяек определяются только мини-
мумом затрат. Будем надеяться, что на самом деле это не так.
12-3. СОГЛАШЕНИЕ О ЗНАКАХ ЦЕН
Определение. Цена ингредиента есть его меновое отношение по срав-
нению с некоторым стандартным ингредиентом. Если ингредиент, изме-
ряемый целевой функцией, выбирается в качестве стандарта, то цена лг
ингредиента i есть то изменение, которое вызывается в целевой функции z
единицей изменения bt в случае малых изменений bt. Дефицитные ингре-
диенты будут иметь для цен отрицательные значения, потому что увели-
чение их количества должно вызвать уменьшение целевой функции, так
как мы занимаемся минимизацией.
Оптимальные двойственные «цены» jq удовлетворяют соотношению
Zo = П^Ь^ + Л2&2 + • • • +
гдеппп£ = £0. Это же самое соотношение дает значение z в любом базис-
ном решении, если л4 — соответствующие симплекс-множители. Если
базисное решение невырождено^ то для малых изменений любого
базис, а следовательно, и симплекс-множители останутся неизменными.
Таким образом, очевидно, что Л/ есть изменение значения z на каждую
единицу изменения bt для малых изменений следовательно, согласно
приведенному выше определению, могут быть интерпретированы как
цены.
Введем в план фиктивный процесс «закупки» — «увеличение ресур-
сов ингредиента г», коэффициенты которого равны нулю, за исключением
минус единицы в строке i и pt в строке стоимости. Вопрос: сколь низкой
должна быть стоимость рг с тем, чтобы увеличение ресурсов ингредиента i
было оправданным? Вычисляя оценку для этого процесса, мы видим, что
это целесообразно, если
Pi + Яг < 0 ИЛИ Рг<, —
261
Следовательно, —есть в точности критическая покупная стоимость
ингредиента L
Теперь, согласно нашей интерпретации схемы цен, изложенной
в § 12-1 и § 12-2, для каждой единицы процесса / затраты а^ > 0 повлекли
бы для управляющего издержки, равные Если ингредиент дефици-
тен, то щ < 0 и ща^ <2 0. Другими словами, поток денег направлен
из системы (отрицателен). Аналогично если а^ < 0, то поток денег
направлен к процессу > 0.
Общий поток денег в процесс благодаря механизму цен дается вычис-
лением его оценки, т. е. равен
г
Если это значение больше Cjf количества, которое могло бы быть получено
иначе, прямым платежом, то этот способ (или любой другой с тем же
самым свойством) будет использован, как мы видели в примере § 12-1,
вместо базисного способа, который используется теперь. Это в свою оче-
редь породит новую систему цен и т. д.
12-4. ИЛЛЮСТРАЦИЯ АНАЛИЗА УСТОЙЧИВОСТИ1
Термин анализ устойчивости (чувствительности) означает исследова-
ние влияния изменений коэффициентов затрат — выпуска, коэффициентов
целевой функции и правых частей на оптимальное решение задачи
линейного программирования. Мы рассмотрим эти влияния на примере.
Читатель не встретит трудностей при распространении результатов на
общий случай.
Рассмотрим задачу о смеси продукции, сформулированную в § 3-5 (6).
4я' + 9х' + 7я' 4-10^ + хъ -6000 Столярный цех.
#1+ ^2+ Зхз + 40^ + #'=4000 Отделочный цех. (1)
— 12х[—20^2 — 18^з—40я* — z (min).
Для удобства вычислений определим масштаб измерений в задаче
так, чтобы единицы технологических процессов составляли тысячи сто-
лов, единицы мощностей — тысячи часов и единицы издержек — тысячи
долларов. После замены х\ = 1000 Xjf zf = 1000 z система (1) в форме
симплекс-таблицы принимает вид (2).
Базисные переменные Допустимые переменные (включая свободные переменные) 1 ^Постоянные
Х1 Х2 Хз х< Х5 Хв — Z
4 9 7 10 1 0 0 6
хб 1 1 3 40 0 1 0 4
— Z — 12 -20 -18 -40 0 6 0
1 Этот параграф написан У. Б латтнером.

262
Так как она уже находится в канонической форме, добавление искус-
ственных переменных не обязательно и мы можем начинать прямо с эта-
па II симплекс-метода. После нескольких циклов мы приходим к опти-
мальному решению (3).
Базисные переменные Допустимые переменные (включая свободные переменные) Постоянные
XI х2 Х3 Х4 Хб Х6 — 2
1 7/3 5/3 0 4/15 -1/15 0 4/3
0 -1/30 1/30 1 -1/150 2/75 0 1/15
— Z 0 20/3 10/3 0 44/15 4/15 1 56/3
• • •
Из данных, содержащихся в этой таблице (3), мы заключаем, что
оптимальная смесь продукции для задачи, сформулированной таким
1 2
образом, состоит из 1333у столов типа 1 и 66у столов типа 4 в каждый
период времени с общей прибылью и' = 18667 дол. за период.
Помимо того что оптимальная таблица дает нам наиболее выгодный
план, из нее можно получить богатую информацию, касающуюся широ-
кой области планов в окрестности этого оптимума, проведя анализ устой-
чивости. Во многих приложениях полученная таким образом информа-
ция ценна как средство определения оптимального решения.
Анализ устойчивости важен по нескольким причинам:
а) Устойчивость оптимального решения при изменениях параметров
может быть критической. Например, при использовании точки, соответ-
ствующей старому оптимальному решению, небольшое изменение пара-
метра в одном направлении может вызвать значительное неблагоприятное
изменение целевой функции при переходе к новому минимуму, в то время
как существенное изменение параметра в другом направлении может
вызывать лишь небольшое ее изменение. В промышленности, где имеются
некоторые не учитываемые моделью флуктуации, присущие процессам
и материалам, может оказаться желательным отклониться от оптималь-
ного решения, для того чтобы получить решение, которое с меньшей
вероятностью потребует существенных изменений.
б) Значения коэффициентов затрат — выпуска, коэффициентов целе-
вой функции и (или) правых частей ограничений могут до некоторой сте-
пени управляться, и в этом случае мы хотим выяснить влияния, которые
могли бы быть вызваны изменением этих значений.
в) Даже если коэффициенты затрат — выпуска и целевой функции
и правые части ограничений не управляемы, то оценки их значений могут
быть лишь приближенными, что делает важным знание тех областей
этих значений, в которых решение остается оптимальным. Если окажется,
что оптимальное решение крайне чувствительно к значениям параметров,
то может оказаться необходимым получить более точные оценки.
263
ОБЛАСТЬ ОПТИМАЛЬНОСТИ КОЭФФИЦИЕНТОВ ЗАТРАТ:
НЕБАЗИСНЫЕ ПРОЦЕССЫ
Задача 1. Спроектирован новый стол типа 7, изготовление которого
требует 6 человеко-часов работы в столярном цехе и 2 человеко-часа
работы в отделочном цехе. Исходя из ожидаемой прибыли в 18 долларов
за стол, выяснить, целесообразно ли производить стол этого типа?
Заметим, что значения симплекс-множителей, взятых с противополож-
44 4
ным знаком, на последней итерации, равные J5, 45, 1, МОГУТ быть полу-
чены из нижнего вектора-строки базиса, обратного конечному, и оче-
видно, что они представляют собой просто преобразованные множители
относительных оценок, соответствующие начальным базисным пере-
— - • 44 л 4
менным х5, xQ, (—2). После вычисления цен это дает с7 = —6 +
1<Э Ю
2 — •
•2— 18 Так как с7 > 0, этот стол производить не имеет смысла.
Задача 2. На сколько следовало бы изменить прибыль от стола типа 7Г
для того чтобы его производство стало выгодным?
Для того чтобы небазисный процесс стал кандидатом на введение
в базис, его множитель относительной оценки должен быть неположи-
тельным. Если любой небазисный процесс имеет множитель относительной
оценки, в точности равный нулю, то он может быть введен в базис без
изменения значения целевой функции. Следовательно, если коэффициент
затрат Cj для любого небазисного процесса уменьшается на величину
своего множителя относительной оценки Cj в оптимальном решении,
то он становится кандидатом на введение в базис. В нашем случае стол
типа 7 становится кандидатом для производства, если прибыль от каж-
дого стола может быть увеличена на с7 =
Упражнение. На сколько должна быть увеличена прибыль от стола типа
2, чтобы ввести его производство в оптимальное решение? На сколько бы
вы увеличили продажную цену стола типа 3 для того, чтобы сделать era
производство выгодным, в предположении, что все произведенные столы
типа 3 могут быть проданы по новой цене? Как бы вы модифицировали
модель, если бы количество столов, которое можно продать, было функцией
продажной цены? См. гл. 18, а также гл. 24.
ВЛИЯНИЕ ИЗМЕНЕНИЯ КОЭФФИЦИЕНТОВ ЗАТРАТ - ВЫПУСКА:
НЕБАЗИСНЫЕ ПРОЦЕССЫ
Задача 3. На сколько следовало бы изменить затраты труда в сто-
лярном цехе при изготовлении стола типа 7, чтобы его производство
стало выгодным?
Для небазисных процессов влияние изменения коэффициентов
затрат — выпуска а^ в исходной таблице легко можно вычислить, исполь-
зуя симплекс-множители с обратным знаком. Заменяя при вычислении Cj
исходное значение aj7 = 6 параметром ai7, мы получаем
(Я17 \
о I 44 262 //ч
2 1-15й1>7—Тб’
— 18/
Для того чтобы процесс j = 7 стал кандидатом на введение в реше-
ние, с7 должно быть не больше нуля, или ai7^~-^.
264
Упражнение. До какого значения следует уменьшить количество»
часов, необходимых для изготовления стола типа 2 в столярном цехе^
чтобы сделать его конкурентоспособным?
Задача 4. Предположим, что мы не вполне уверены в значениях
затрат труда или в прибыли для стола типа 2. Вывести для этих парамет-
ров формулу, которую можно использовать для определения, выгодна
ли производить стол типа 2.
Для того чтобы процесс j — 2 стал кандидатом на введение, необхо-
димо выполнение неравенства
(^12 \
| 44 ,4 (
а22 I —^12 +J5 а2г + ^2^0.
С2 /
Если, например, окажется, что а12 = 8, а22 — 2, с2 = —25, то под-
становка в приведенную выше формулу дает с2 = —1, так что стол типа 2
производить выгодно.
ВЛИЯНИЕ ЗАМЕЩЕНИЯ НЕБАЗИСНЫХ ПРОЦЕССОВ
НА БАЗИСНЫЕ ПРОЦЕССЫ
Задача 5. Сколько единиц процесса 7 =,s можно включить в решение
и какое влияние это окажет на интенсивность других базисных процес-
сов? Здесь снова ответ дается симплекс-методом:
max xs— min (. (5)
ais>Q ttis
Рассмотрим информацию, получаемую непосредственно из оптимизи-
рующей таблицы (3). Строки этой таблицы выражают базисные перемен-
ные через небазисные переменные, а ее столбцы выражают небазисныа
процессы через базисные процессы. Для каждой переменной Xj вектор-
столбец элементов матрицы может интерпретироваться как система
коэффициентов «замены». Например, на каждую единицу процесса / = 2,.
которую мы вводим в решение, мы для получения чистого увеличения
целевой функции на 20/3 единиц должны отнять 7/3 единиц базисного про-
цесса / = 1 и добавить 1/30 единицы базисного процесса 7 = 4.
Из формулы (5) следует, что если в решение вводится max х2 единиц,
процесса j = 2, то соответствующий f-й базисный процесс выводится.
Заметим, что для каждой переменной множитель относительной
оценки Cj может быть вычислен на основании коэффициентов «замены»
аи и исходных коэффициентов затрат Cj. Именно
= 'ZatjCj, (6)
г 1
где ji — индекс i-ro базисного процесса. Это другой способ проводить
вычисления «оценок». Для каждой добавляемой единицы процесса / = 2
получаются следующие изменения базисных переменных:
Переменная Величина
изменения
*1 (-7/3)
(+1/30)
*з (+1)
Затраты Затраты на
на единицу изменения
(-12) = +28
(-40) == -4/3
(-20) = -20
(7>
Коэффициент относительной оценки
с2
20
3
на каждую введенную единицу х2.
265
Упражнение. Показать, что если прибыль от каждого стола типа 2
- 20
увеличивается ровно на с2 — за каждый стол, то за один период может
о
3
быть произведено до 571у столов типа 2 без уменьшения общей прибыли.
.Какова полученная смесь продукции?
ВЛИЯНИЕ ИЗМЕНЕНИЯ СВОБОДНЫХ ЧЛЕНОВ ОГРАНИЧЕНИЙ
Задача 6. Каково влияние увеличения мощности отделочного цеха?
Увеличение значения правой части ограничения можно считать
эквивалентным введению фиктивного процесса закупки с коэффициен-
тами, равными по абсолютной величине соответствующим свободным
переменным в исходной формулировке (2), но противоположными им
по знаку. Отсюда следует, что влияние увеличения мощности отделоч-
ного цеха сказывается в увеличении чистой прибыли на 4/15 долл, на каж-
дый дополнительный час, до 20 тыс. дополнительных часов в период,
потому что для соответствующей свободной переменной с6 = .
10
Упражнение. Если мощность отделочного цеха увеличивается
на 20 тыс. часов в каждый период, то какой будет оптимальная смесь
продукции? Какой базисный процесс выводится из решения?
Упражнение. Оборудование, необходимое для увеличения мощности
•столярного цеха на 10%, может быть арендовано за 5 тыс. долл. Кроме
того, сверхурочные часы в размере до 20% установленной мощности
любого цеха могут быть получены при условии оплаты в 1,50 долл, в час.
<3верх этой величины (20%) устанавливается оплата, около 3,00 долл,
в час из-за снижения эффективности производства. Что бы вы сделали?
Упражнение. Показать, что если свободная переменная входит в ба-
зисное множество и в оптимальном решении имеет значение то соот-
ветствующая правая часть ограничения в начальной таблице может
принимать любые значения Ъг > bi — Xj, где 6? — ее исходное значение,
причем значения целевой функции и других базисных переменных в опти-
мальном решении не изменятся. Действительно ли bt ограничивает
решение в этой области?
ОБЛАСТЬ ОПТИМАЛЬНОСТИ КОЭФФИЦИЕНТОВ СТОИМОСТИ:
БАЗИСНЫЕ ПРОЦЕССЫ
Задача 7. Для какой области изменения коэффициентов стоимости
базисных процессов имеющееся оптимальное решение все еще остается
таковым?
Рассмотрим, в частности, базисный процесс j = 1. Имеющееся опти-
мальное решение будет оставаться оптимальным до тех пор, пока коэф-
фициент стоимости Ci не увеличится или не уменьшится настолько, что
множитель относительной оценки для одного из небазисных процессов
обратится в нуль, и этот небазисный процесс станет кандидатом на вве-
дение в решение.
Учитывая (6), мы имеем
;^-20-[+|(C1)-±(-40)] = -lc1-f. (8)
Мы видим, что коэффициенту стоимости необходимо придать зна-
чение — (64/3)/(7/3) для того, чтобы множитель относительной
266
оценки с2 обратился в нуль. Мы должны исследовать также влияние изме-
нения Ci на все другие небазисные процессы; в общем случае мы найдем,
что изменение необходимое для того, чтобы обратить Cj в нуль, дается
формулой .
с1 = с; = Д. (q°=-12) (9)
aij
Следовательно,
20
- Л 3 20
с2 = 0, если увеличивается на -у- = у ;
“3
10
— 3
г3 = 0, если увеличивается на -=- = 2;
о
Т
44
15
с5 = 0, если Ci увеличивается на -у = 11;
15
4
— 15
с6 = 0, если Ci увеличивается на ---j- = — 4.
“15
Таким образом, имеющееся решение (3) все еще оптимально для —12—4^
^Ci^ — 12 + 2, где cj = —12 — исходное значение
Правило вычисления в общем виде может быть сформулировано следую-
щим образом:
max Cj = Cj. + min f j , j — небазисный,
min Cj. = Cj. 4-max () , j— небазисный.
1 1 “ij<Q aij
(10)
Упражнение. В каком интервале прибыли от стола типа 4 имеющееся
решение (3) сохраняет оптимальность? Определить, какой процесс входит
в решение, если ct уменьшается до —20? Увеличивается до —19/2? Какой
процесс выводится из решения в каждом из этих случаев?
Упражнение. Изменяя /ц в исходной задаче (2), построить пример,
показывающий, что если ct возрастает до —19/2, то не обязательно про-
изводство стола типа 1 есть процесс, который выводится из решения.
Упражнение. Доказать, что если расходы по базисному процессу
уменьшаются, то он не будет выводиться из оптимального решения.
Упражнение. Причина ирландского восстания. Средний ирландец
тратит 27 пенсов на питание в день и потребляет пищу, содержащую
2000 калорий. Ирландский картофель стоит 3 пенса за каждые 1000 кало-
рий, а мясо стоит 24 пенса за каждые 1000 калорий. Так как ирландец
питает отвращение к картофелю, он съедает в день 1000 калорий мяса
и 1000 калорий картофеля. Показать, что если цена картофеля поднимется
до 10 пенсов за 1000 калорий (в чем, конечно, будут виноваты англичане),
то средний ирландец должен будет увеличить свое ежедневное потребление
картофеля на 50%.
267
ВЛИЯНИЕ ИЗМЕНЕНИЯ КОЭФФИЦИЕНТОВ ЗАТРАТ — ВЫПУСКА:
БАЗИСНЫЕ ПРОЦЕССЫ
Задача 8. Что произойдет, если изменить условия производства стола
типа 1 в столярном цехе? Изменение коэффициента затрат — выпуска
для базисного процесса вызовет изменения симплекс-множителей, взятых
с обратным знаком, и других элементов нового базиса, обратного исход-
ному. Для того чтобы оценить влияние изменения аи, мы должны найти
/ аи 10 0V1
1 40 0 ,
\—12 —40 1/
уже зная, что
{ ±
4 10 0V1 15
1 40 ° =
-12 -40 1/
' 15
Мы можем записать В в виде А -В где
4 0
4 0
4 1
(4лц —1 4 — а1А
15 15 V
0 1 о
О 0 1,
(11).
(12)
(13)
Так как А — элементарная матрица (см. § 8-5), мы можем легко найти
обратную ей. Пусть у — обратная величина диагонального элемента первой
строки, так что
(14)
Тогда
15
Y~ 4au—1
И
ап —
15 + Y
4у
Покажем, что Л 1 и, следовательно/ В'1 линейны относительно у.
(15)

/ 4у
15
~ V
150
44у
\15"
=4 0\
15 и
Y±15 о
600 v
15-Иу 4
15 1/
(16)
где, согласно (14), у0 = 1 соответствует = 4. Заметим, что, для того
чтобы матрица В была базисом, должна существовать обратная ей матрица
В"1. Это означает, что должна существовать Л"1, что в свою очередь тре-
бует выполнения неравенств 1 /у =И= 0, у У= 0. Далее мы покажем, что для
допустимости должно выполняться неравенство у > 0. Вместе с двумя
предыдущими условиями это дает у > 0. Теперь вопрос состоит в, нахо-
ждении такой области изменения у, в которой имеющиеся базисные про-
268
цессы остаются оптимальными. Определим для этого, во-первых, те зна-
чения у, которые обеспечивают неравенство > 0 для каждого из небазис-
ных процессов.
/ 9\
\—20/
= -~—15 о, если -гг ,
О 11
/1\ (17)
С5==С^1^1Г^ 0l ° J ^“>0, если Y>°>
\ 1U Ю у I I Ю
\°/
/0\
< 44у 15—Ну , \ / Л I 11у . л Л ^.15
Св=(л5 ~15 1 Л 1 =----1^ + 1>0’ еСЛИ ?<1Г-
\0/
Для сохранения допустимости мы должны определить также,
в какой области значений у каждый из элементов bt остается неотрица-
тельным:
4у
"3"
3-—у
30
12 + 44у
3
(18)
Из этого равенства мы видим, что &i>0, если у>0, и 62>0, если у^З.
Замечая, что первая строка матрицы В"1 есть просто первая строка мат-
рицы В"1, умноженная на у, мы видим, что = yb[. Если имеет место
невырожденность, то >* 0. Таким образом, из условия Ь4>0 вытекает,
что у>0. Так как у #= 0, должно быть у> 0 и > 0. Выбирая из при-
веденных выше условий (17) и (18), которым должно удовлетворять у,
наиболее ограничительное, мы находим, что целевая функция z и все зна-
чения bi базисных переменных линейны по у, а установленное базисное
решение допустимо и оптимально в области — у , или у > аи > 3.
Упражнение. Каково влияние увеличения времени, расходуемого
в столярном цехе на каждый стол типа 1, до 4 у часов? До 5 часов?
Упражнение. При каких условиях значение коэффициента затрат —
выпуска для базисного процесса может быть изменено без какого-либо
влияния на стоимость?
Задача 9. Каково влияние одновременных изменений затрат труда
в столярном и отделочном цехах и прибыли для столов типа 1? Здесь
-задача состоит в том, чтобы найти
/ап 10 0\ 1
(В')-1 = 1а21 40 0 .
Vi —40 1/
(19)
269
Записывая на этот раз В' в виде В-А', мы имеем
(А') = (В)~1-(5/) =
4йц+ «21
15
4«21— аи
150
44вц+4«2i 4~
\ 15
о о\
1 о
0 ъ
(20)
Полагая 4а‘1— 0,21 — п iazi — aM_a и 44ан4-4а21 + 15ci _
полагая 15 - р, 15Q -q и -г,
получим
(Л'И =
0 0\
1 0
0 V
(21)
(В'г=(Л')-цвг =
4
15р
— р —40g
150р
44р— 4г
15р
2р + 5<? п
75р и
4р + г л
i5P1 У
(22)
где, как и раньше, ведущий элемент р 0 и 1/р #= 0.
Заметим, что значения р° = 1, qQ = г° = 0 соответствуют значениям
а?п = 4, а®21 = 1, = —12. Определим теперь, какие значения р, q и г
гарантируют неравенство cj > 0 для каждого из небазисных процессовг
с2 —
а также сохраняют каждый из элементов Ъг неотрицательным.
44р —4г
15р
44р —4г 4р + г
15р ’ 15р
— 1
15р
2р-|-5д
75р
4р + г
15р
( \
4
15р
—р—40g
150р
44р — 4г
15р
4 . г . г ,
ге + тё— >0, если — >—4.
15 1 15р ’ р
(24)
270
— 1 --- Q 1
Откуда следует, что bi 0, если — >0; Ь2 > 0, если ~ ^26» а значение*
целевой функции z равно —+ Заметим, что предположение невы-
о ор
рожденности, как и раньше, обеспечивает соблюдение неравенств ==
= -bi >0 и—>0.
р 1 р
Выбирая наиболее ограничительные из границ, найденных выше,,
мы видим, что z и bi линейны относительно —, — и — в области — > 0,
Р Р Р Р
и —4. Эти ограничения эквивалентны неравенствам
р > 0, р > 20# и 2р > г >- —4 р. После подстановки в них выражений
для р, q и г мы получим условия, которым должны удовлетворять коэф-
фициенты затрат — выпуска и коэффициенты затрат для базисного про-
цесса 7 = 1, при которых базисные переменные, указанные в (3), остаются
в оптимальном решении:
2ац—3a2i^0, (25)
12ац + 2а21^ ,
------g---> Ci > —
Влияние изменения ац и ct в этих пределах на bt и и из оптимального реше-
ния выражается формулой (24).
Упражнение. Показать, что если ац и a2i изменяются в области, опре-
деляемой первыми двумя неравенствами (25), и если Ci изменяется соот-
44«11 + 4«21 « X
ветственно так, что Ci=----то значение целевой функции изме-
няться не будет.
Упражнение. Доказать следующую теорему:
Теорема. Если дана произвольная задача линейного программированияг
то область всех возможных изменений столбца Р в оптимальном допусти-
мом базисе является выпуклой в пространстве компонент вектора Р.
12-5. ЗАДАЧИ
1. Показать (см. § 12-1), что если в оптимальном решении некоторые
ингредиенты имеются в избытке, то их цены равны нулю. Показать, что*
если стоимость, связанная с процессом хранения некоторого ингредиента,
равна нулю и если этот ингредиент имеется в избытке, то его цена равна
нулю.
2. Показать, что описанный выше случай мог бы привести к излишним
затратам сырья, если только центральный планирующий орган не назна-
чит некоторую цену излишкам сырья, выраженную в единицах труда.
3. Показать, что было бы лучше ввести также процессы для закупки
дополнительных ресурсов и назначить на них также цену в единицах
труда.
4. (Повторение.) Показать, что цена представляет собой изменение
общей стоимости z на каждую единицу бесконечно малого изменения ре-
сурса ингредиента г.
5. Какое из различных свойств, связанных с теоремами двойствен-
ности гл. 6, объясняет, почему управляющий инструментальным заводом
271
«открыл процесс, минимизирующий его потребности в рабочей силе при
разработке системы цен?
6. Пусть даны оптимальное базисное допустимое решение и соот-
ветствующая система в канонической форме; показать, что Cj представляет
юобой величину, на которую нужно изменить единичную стоимость /-го
небазисного процесса для того, чтобы он стал кандидатом на введение
в базис. Показать, что если другие коэффициенты, так же как коэф-
фициенты стоимости, могут изменяться, то
Cj- = Cj 2
г
есть величина изменения, где суть цены, связанные с базисной системой
переменных.
7. Вывести формулу для пределов изменения стоимости Cj базисного
процесса до того, как он станет кандидатом на выведение из базиса. Какой
процесс должен будет войти вместо него?
Глава 13
ИГРЫ И ЛИНЕЙНОЕ
ПРОГРАММИРОВАНИЕ
13-1. МАТРИЧНЫЕ ИГРЫ
ВВЕДЕНИЕ 1
Согласно Гейлу [1], стр. 272, «одним из самых удивительных со-
бытий, связанных с появлением современной теории линейных экономи-
ческих моделей, явилось одновременное, но независимое развитие
линейного программирования, с одной стороны, и теории игр—с дру-
гой, и выявившаяся затем тесная связь между этими двумя пред-
метами».
На эту связь между линейным программированием и теорией игр
впервые указал Дж. фон Нейман осенью 1947 г. в частных беседах с авто-
ром настоящей книги. Он отметил, что центральная математическая задача,
связанная с матричной игрой, могла бы быть сформулирована как задача
линейного программирования. Он высказал также предположение о том,
что верно и обратное. Таккер и его группа в Принстоне в начале 1948 г.
предприняли систематическое изучение взаимосвязей между этими двумя
областями, для того чтобы дать строгое обоснование всей теории (Гейл,
Кун и Таккер [1]). Цель настоящей главы состоит в выявлении этих
связей.
Теория игр имеет дело с нахождением наилучших «стратегий» для
разрешения конфликтных ситуаций. Абстрактно эти ситуации могут быть
охарактеризованы как ситуации, в которых каждый из соперничающих
участников может контролировать некоторые, но не все действия, которые
могут предприниматься. Этот факт, вместе со случайными событиями
(если таковые допускаются условиями), определяет исход, которому участ-
ники могут придавать весьма различные значения. Математические осно-
вы теории игр были заложены в некоторых статьях Дж. фон Нейманом
в 1928 и 1937 гг. и в менее далеко идущих работах Борелем в начале
20-х годов (фон Нейман [1], [2]; Борель [1], [2] и [3]). Фактически до
1944 г. статей по теории игр почти не было; они появились только после
опубликования фон Нейманом и Моргенштерном [1] их знаменитой
книги «Теория игр и экономическое поведение».
1 Популярное изложение теории игр читатель найдет в «Совершенном стратеге»
Джона Вильямса (Вильямс [1]) * *; более формальное введение можно найти в книгах
Льюса и Райфа «Игры и решения» (Льюс и Райф fl]) и Дрешера «Стратегические
игры: теория и приложения» (Дрешер fl]). Глубокие статьи по этому предмету
можно найти в сборниках «Annals of Mathematics Studies» № 24 (1950) и № 28
(1953), озаглавленных «Contributions to the Theory of Games» под редакцией Куна
и Таккера (Кун и Таккер, сб. [15] и [16]) **.
* См. также популярные книги Е. С. Вентцель, «Элементы теории игр», М.,
Физматгиз, 1959, и Н. Н. Воробьева, «Математическая теория игр», Л., „Знание44,
1963.— Прим, ред.
** Значительная часть статей, составляющих эти сборники, переведена на рус-
ский язык и опубликована в сборниках: «Матричные игры» сб. [2]* и «Бесконечные
антагонистические игры», М., Физматгиз, 1963.— Прим. ред.
18 дж. Данциг 273
ОПРЕДЕЛЕНИЕ МАТРИЧНЫХ ИГР
В матричной игре участвуют два игрока, которых мы будем назы-
вать I и II1. Предполагается, что каждый из них производит один выбор
из множества возможных для него выборов, не зная о выборе другого
игрока. Для каждого такого совместного выбора этих двух игроков, ска-
жем i для I и у для II, имеется исход, который может быть определен одним
числом выигрышем, получаемым I, выигрышем, который будет поло-
жительным, отрицательным или нулевым в соответствии с тем, выигры-
вает ли I у II, проигрывает ему или имеет место ничья; в то же время II
находится в противоположном положении к I и должен получить то, что
I теряет, а именно — аи. Если выборы i для I изменяются в области i=
= 1,2, . . ., тп, а выборы J для II — в области 7 = 1, 2, . . ., п, то воз-
можный выигрыш I может быть изображен в виде матрицы:
Выигрыш I
если I выбирает строку i, а II выбирает столбец j
^#11 #12 • • •
#21 &22 • • • #2п
\ #7П2 • • • #77171J
Задача каждого игрока состоит в следующем: какой выбор должен
он сделать для того, чтобы его частичное влияние на исход принесло ему
наибольшую выгоду?
Наша непосредственная цель состоит в том, чтобы показать, что мно-
жество конкурентных ситуаций может быть представлено в виде матрич-
ной игры, если мы интерпретируем «выбор» игрока в этих случаях как
выбор среди «чистых стратегий», доступных для него.
Определение. Чистая стратегия есть некоторый план, настолько
исчерпывающий, что он не может быть нарушен действиями противника
или природы (Вильямс [1]). Это есть полное множество заранее соста-
вленных предписаний, которые указывают определенный выбор в каждой
возможной ситуации, в которой игроку, может быть, придется действовать
(Кун и Таккер [2]).
Пример 1. Игра в отгадывание. Игрок I имеет две карты — черную
и красную. Он выбирает одну из них. Не показывая ее своему противнику,
он кладет ее на стол. Затем игрок II называет ее. Карта переворачивается.
Если карта отгадана, то игрок I платит игроку II один пенс, в противном
случае игрок II проигрывает один пенс. Чистые стратегии игрока I выпи-
саны в левых частях строк таблицы (1); по этой причине игрока I можно
назвать игроком, выбирающим строки. Аналогично стратегии игрока II
выписаны в верхних частях столбцов и игрока II можно назвать игро-
ком, выбирающим столбцы. Числа в таблице представляют собой выигры-
ши игрока I, если игрок II отгадал карту или не отгадал ее.
1 В оригинале В (row player — т. е. «выбирающий строки») и С (column player —
«выбирающий столбцы»). Мы в переводе придерживаемся терминологии, распростра-
ненной в отечественной и в зарубежной литературе.— Прим. ред.
274
Чистые стратегии игрока I Чистые стратегии игрока II
Назвать черную карту Назвать красную карту
Выбрать черную карту Выбрать красную карту -1 +1 +1 -1
Эта матричная игра показывает, насколько важно как для игрока 1,
так и для игрока II, чтобы их планы не были известны заранее. Резуль-
тат мог бы быть плачевным. Какой бы выбор игрок I ни производил, era
наивысший «нижний предел», максимальный выигрыш, который он может
себе гарантировать, если его выбор отгадан, равен —1. Аналогично наи-
низший «верхний предел» игрока II, минимальный убыток, который игрок
II может себе гарантировать, если его выбор отгадан, равен +1. Мы,
однако, покажем, что имеется способ играть в эту игру так, что игрок I
может иметь ожидаемый выигрыш, равный 0, а игрок II может иметь
ожидаемый убыток, равный 0.
Пример 2. Морра (Вильямс [1]). Два игрока одновременно пока-
зывают один или два пальца и высказывают свои предположения относи-
тельно того, каково будет общее число показанных пальцев. Если один
игрок угадал, а его противник не угадал, то угадавший получает выигрыш,
равный сумме показанных пальцев. Во всех остальных случаях выигрыш
обоих игроков равен нулю.
Чистые стратегии у каждого игрока следующие: показать 1, назвать
2; показать 1, назвать 3; показать 2, назвать 3; показать 2, назвать 4.
Если мы обозначим для краткости эти комбинации как (1,2), (1,3) и т. д.,
то матрица игры примет (кососимметричную) форму.
и
(1,2) (1,3) (2,3) (2,4)
(1,2) 0 2 -3 0
(1,3) — 2 0 0 3
(2,3) 3 0 0 — 4
(2,4) 0 -3 4 - 0
Максимальный нижний предел игрока I, если его чистая стратегия
известна, равен — 2, аналогично минимальный верхний предел игрока II
равен +2. Снова мы видим, насколько важно не открывать чистую стра-
тегию заранее.
Пример 3. Туристы. Джон Вильямс [1] в своем юмористи-
ческом элементарном введении в теорию игр, «Совершенном стратеге»,
приводит следующий прокомментированный пример, который мы цити-
руем с небольшими изменениями.
«Для усвоения этих идей нам может помочь некоторая физическая
модель. Если все выигрыши положительны, то мы можем рассматривать
их как высоты отдельных точек в гористой местности. Различные страте-
гии игроков I и II будут тогда соответствовать значениям географической
широты и долготы этих точек.
«Для того чтобы в игре имелись действующие лица и мотивировки,
предположим, что муж и жена — Рэй и Кэрол — задумали совершить
275
18*
туристический поход и что Рэй любит, лазить по вершинам, а Кэрол пред-
почитает низменности* 1. Интересующая их область пересечена крест-
накрест сетью маршрутов, по четыре в каждом направлении. Туристы
договорились разбить лагерь на перекрестке дорог. Далее они догово-
рились, что Рэй выбирает дорогу с востока на запад, а Кэрол — дорогу
с севера на юг, что совместно определяет перекресток.
«Предположим, что перекрестки на дорогах г, доступных Рэю, и доро-
гах у, доступных Кэрол, имеют следующие высоты (в тыс. футов):
Кэрол (/)
(1) (2) (3) (4)
(1) 7 2 5 1
(2) 2 2 3 4
(3) 5 3 4 4
(4) 3 2 1 6
Будучи разумным человеком, желающим просто получить как можно
больше, Рэй, естественно, предпочитает дорогу Рэй 1, имеющую пересе-
чения на отметках 7, 2, 5 и 1, так как только на ней есть пик высотой
7 тыс. футов. Но он не смеет принять этот план, который сулит ему многое
в случае успеха, но который может привести к неудаче, если Кэрол про-
явит должное искусство при своем выборе. Не надеясь на то, что она сде-
лает выбор, не подумав, он в своих собственных интересах вынужден
игнорировать пики; вместо этого он должен обратить особое внимание
на спуски и низины, которые, с его точки зрения, портят местность. Это
изучение приводит его наконец к выбору дороги Рэй 3, на которой имеется
низина, наиболее привлекательная в данном районе, а именно на высоте
3 тыс. футов. Выбирая дорогу Рэй 3, он может гарантировать, что лагерь
будет разбит на высоте не ниже 3 тыс. футов; он будет еще выше, если
Кэрол окажется менее осмотрительной.
«Его жена, как он сам догадывается, настолько же сильна в этих
вопросах, как и он сам. После изучения таблицы она сразу поняла, что
не стоит тратить времени на мечты о дорогах Кэрол 3 и Кэрол 4, на кото-
рых имеются глубокие долины и которые ей нравятся больше всего. Буду-
чи реалистом, она изучает вершины, которые встречаются на ее дорогах,
решив выбрать такую дорогу, на которой расположены наиболее низкие
вершины. Это приводит ее наконец к дороге Кэрол 2, где ночевка на высоте
3 тыс. футов — самое худшее для нее, что может случиться.
«Теперь мы замечаем, что произошло нечто вроде совпадения. Рэй
выбрал стратегию (Рэй 3), которая гарантирует ему расположение лагеря
на высоте 3 тыс. футов или более, а Кэрол выбрала стратегию (Кэрол 2),
которая обеспечивает ей отдых на высоте 3 тыс. футов или менее. Иными
словами, каждый игрок может получить стоянку на высоте 3 тыс. футов,
1 Вильямс неявно предполагает, что интересы мужа и жены в той степени, в кото-
рой они касаются высоты местности, диаметрально противоположны, и что «выигрыш»
I может быть измерен в футах высоты.
27 6
имея перед собой умного противника. Он может добиться лучшего резуль-
тата, если его противник будет менее осмотрительным».
Определение. Если гарантированный максимальный нижний предел
игрока I и минимальный верхний предел игрока II в точности равны
(как это случилось в предыдущем примере), то говорят, что игра имеет
седловую точку, а сама игра называется вполне определенной, потому что
игроки должны выбирать стратегии, соответствующие этим выигрышам.
Если только один из игроков отклонится от стратегии, соответствующей
седловой точке, то он потерпит неоправданный убыток. Если оба игрока
отклоняются от этой стратегии, то ситуация становится полностью неопре-
деленной и кто-то проиграет. Отметим также одно следствие наличия сед-
ловой точки: меры секретности совершенно не обязательны. Любой из игро-
ков может открыто объявить о своем выборе (если этот выбор является для
него подходящим), него противник не сможет воспользоваться этой инфор-
мацией и навязать первому игроку выигрыш, отличный от гарантирован-
ного максимального нижнего предела или минимального верхнего предела.
Упражнение. Показать, что для произвольной матричной игры мак-
симальный нижний предел для игрока I меньше или равен минимальному
верхнему пределу для игрока II.
Пример 4. Случай и блеф. Колода карт, состоящая из туза, короля
и дамы, тасуется, после чего каждому игроку дается по одной карте,
а последняя кладется на середину стола рубашкой вверх. Игрок I , посмот-
рев свою карту, может либо поставить величину Ъ (включая начальную
ставку), утверждая, что у него более крупная карта, либо может «спа-
совать». В последнем случае он теряет величину а, начальную ставку,
в пользу своего противника и игра заканчивается. Если игра продол-
жается, то II может посмотреть карту, лежащую на столе, и либо урав-
нять ставку, либо спасовать; в последнем случае он теряет величину а.
Если же игрок II уравнивает ставку, то игрок с более высокой картой
получает величину Ъ от своего противника.
Игрок I имеет четыре чистые стратегии (если мы предположим, что,
получив туза, он всегда ставит). Например, два из своих четырех полных
взаимно исключающих плана он мог бы сформулировать (для себя) сле-
дующим образом: Сокращение]
г Если я получаю туза, то я ставлю л
Чистая стратегия (1) 1 » » » короля » » » | 1(6, Ь, Ь)
1 » » » даму » » » J
Если я получаю туза, то я ставлю ч
Чистая стратегия (2) » » » короля » » » 1 (*. Ь, /)
» » » даму » » пасую J
Чистые стратегии игрока II зависят от того, спасовал ли I, или если
он не спасовал, то от того, какова третья карта. У него восемь чистых
стратегий, две из которых он мог бы сформулировать (для себя) следую-
щим образом: Сокра-
щение
" Если I спасует, то я получу начальную ставку \
Если I ставит и третья карта есть туз, то я уравняю I
’ » I » » » » » король » » » I (Ь, Ь, Ь)
» I » » » » » дама » » » J
Если I спасует, то я получу начальную ставку \
Если I ставит и третья карта есть туз, то я уравняю !
№ » I » » » » » король » » » { b* f)
k » I » » » » » дама, то я пасую J
277
Рассмотрим теперь выигрыш в случае, когда как I, так и II приме-
няют чистую стратегию (Ь, Ь, Ь). Мы исследуем выигрыши в шести слу-
чаях, соответствующих, случайным раскладам карт.
Карта I Третья карта Вероятность Партия Выигрыш
Туз король 1 6 I ставит » II ставит » b
Туз дама 1 6 » » b
Король туз 1 6 » » b
Король дама 1 6 » » —Ъ
Дама туз 1 6 » —Ь
Дама король 1 6 » » —b
Ожидаемый выигрыш равен -^ = 0.
о
В этой задаче для данных чистых стратегий I и II выигрыш не может
быть достоверно определен ввиду элемента случайности, которым не мо-
жет управлять ни один из игроков. В подобной ситуации элементы матри-
цы игры определяются как ожидаемые выигрыши.
Вычисленная по этому определению матрица игры (умноженная на 6,
чтобы избавиться от дробей) равна
II
(bbb) (bbf) (bfb) (bff) (fbb) (fbf) (ffb) (fff)
(ЪЬЬ) 0 2a 2a 4a 2a 4a 4a 6a
(№/) 2b—2a 2b b—a & + a b—a b-\-a 0 2a
(bfb) —2a — b—a 0 —b-j-a b—a 0 a + b 2a
(bff) 2b—^a b—3a b—3a —2a 2b—4a b—3a b—3a —2a
Упражнение. Проверить элементы этой матрицы игры. Который
из игроков имеет преимущество?
Упражнение. Ввести в матричную игру полное множество чистых
стратегий игрока I, т. е. включить стратегии (fbb) (fbf), (ffb), (///). Счи-
таете ли вы разумным решение игрока I не рассматривать эти возможности?
СМЕШАННЫЕ СТРАТЕГИИ
По мере того как игрок I оценивает последствия различных способов
действия, доступных ему в матричной игре, он все больше убеждается
в необходимости держать в тайне свой выбор чистой стратегии. В слу-
чаях, когда одна и та же игра будет повторяться много раз, любой очевид-
ный способ выбора мог бы привести к плачевным последствиям.
Если игрок I является законченным пессимистом, т. е. если он пред-
полагает, что игрок II знает его план и будет стремиться свести к мини-
278
муму его выигрыш, то I выберет свою «максиминную» чистую стратегию,
т. е. такую строку г, в которой минимум максимален.
Как мы видели в матричной игре
(/ = 1) (7 = 2)
(i = l) / —1 +1\
(i = 2) 1 + 1 -1/
(5)
этот максимальный нижний предел равен —1 и достигается он, когда I
выбирает либо (i — 1), либо (i = 2). Если игрок II такой же пессимист,
то он использует свою «минимаксную» чистую стратегию, т. е. выбирает
столбец $, максимум в котором минимален; в нашем случае он равен +1-
Выигрыш в матричной игре между двумя законченными пессимистами
равен ars и находится где-то между наивысшим нижним пределом игрока I
и наинизшим верхним пределом игрока II, т. е.
max (min atj) aTS min (max ац). (6)
i j 3 г
В случае, когда имеется седловая точка, так что max min = min max,
выборы г, $, согласно соответствующей чистой стратегии, дают полное
решение игры, потому что, является ли I пессимистом и предполагает,
что его противник знает его выбор, или I является пессимистом и окажется,
что его противник также пессимист, все равно лучшего выбора I сделать
не сможет. В любом случае II может вынудить I принять максимальный
выигрыш ars, и если I отклонится от этой стратегии, то, вообще говоря,
он может только потерять, а если II отклоняется от нее, может только
выиграть.
Если же седловой точки не существует, то противоречивые предполо-
жения о поведении игроков приведут к неустойчивой ситуации. В случае
повторения одной и той же игры с одними и теми же игроками мы можем
ожидать, что раньше или позже один из игроков осмелеет и изменит свои
предположения о знаниях своего противника и о том, как он находит свой
план и извлекает из него выгоду. В зависимости от того, какие предпо-
ложения делаются игроками о знании противником их планов, могут
получаться, вообще говоря, различные решения игры.
Если I не является полным пессимистом (в этом случае мы будем назы-
вать его консервативным), т. е. если он предполагает, что II не может
знать точно его планы, но может угадать вероятности, с которыми I будет
применять ту или иную чистую стратегию, то I будет выбирать вероят-
ности строк так, чтобы наименьший «средний» выигрыш в столбце был
максимален. (Например, в повторяющихся партиях одной и той же игры I
может пытаться защитить свой план, изменяя выбор строки и предпола-
гая, что его противник не может узнать его отдельный выбор, но в лучшем
случае может лишь определить частоту выбора различных строк.)
Если в матричной игре, приведенной выше, игрок I выбирает строку I
о вероятностью хг и строку 2 с вероятностью 1—и если его противник
выбирает стратегию /, то ожидаемые выигрыши равны
(/-1) (/-2)
— 1ж1Ч-1(1 — Zj), Lq—1(1 — Xi)
I
или, после упрощения, 1 — 2xt и —1 + 2xlt Для 0 < у второе
1
выражение меньше и достигает максимума, равного 0, при = у. Для
279
1 первое выражение меньше и достигает максимума, равного
нулю, также при = у . Следовательно, в этом случае если бы I выбирал
свои чистые стратегии с равными вероятностями и если бы II узнал эти
вероятности, то I мог бы гарантировать себе ожидаемый выигрыш, по край-
ней мере равный 0.
Ввиду симметрии игры ясно, что если II сделает аналогичные пред-
положения относительно своего противника, то эн может гарантировать
себе ожидаемый выигрыш, не больший 0, если он рандомизирует свои
чистые стратегии, выбирая столбцы / = 1 и J = 2 с равными вероятностя-
ми. Так как максимальный ожидаемый нижний предел для I равен мини-
мальному ожидаемому верхнему пределу для II, то ясно, что даже если
он изменит свою точку зрения и предположит, что I играет против него
консервативно, то он не сможет извлечь из этого выгоду и проиграть
меньше нуля, но может проиграть и больше, если отклонится от этой
стратегии. С другой стороны, II замечает также, что он может проиграть
меньше, если он будет придерживаться своей оптимальной консервативной
смеси чистых стратегий, а I отклонится от нее.
Определение. Смешанная стратегия есть выбор чистых стратегий
с фиксированными вероятностями.
Определение. Консервативным игроком называется игрок, который
предполагает, что его смешанная стратегия известна противнику.
В качестве второго примера оптимального выбора вероятностей в сме-
шанной стратегии мы изменим в примере Вильямса (3) значение а42 = 2
на а42 = 6, чтобы ликвидировать решение, соответствующее седловой
точке. Рассмотрим теперь более простую задачу определения оптимальной
смеси двух стратегий I = 3 и i — 4 для матрицы
(i=D 0=2) 0=3) 0=4) Вероятности
(i = 3) 5 3 4 4 *3
(i = 4) 3 6 1 6 1— X3
Ясно, что любой выбор чистой стратегии со стороны I, который стано-
вится известным II (например, в результате многих повторений одной
и той же игры, в которых каждый раз используется одна и та же чистая
стратегия), в лучшем случае мог бы дать 3 единицы (стратегия i = 3),
потому что его противник, несомненно, выберет j = 2. С другой стороны,
если I выбирает i = 3 с вероятностью х3 и i = 4 с вероятностью 1 — я3 =
= я4, то его ожидаемый выигрыш для различных стратегий j его про-
тивника будет представлять собой взвешенное среднее выигрышей I:
(/ = 1) (7 = 2) (/ = 3) 0=4)
5х34-3(1—х3), Зх34-6(1— х3), 4ж3 + 1 (1—ж3), 4«3 + 6(1—х3).
Если х3 = 1, то его противник выберет дорогу / = 2 и его выигрыш будет
равен 3; если х3 = 0, то его противник выберет дорогу j = 3 и его выигрыш
2
будет равен 1. Если, однако, у < х3 < 1, то ожидаемый выигрыш для
любого у будет больше 3. Для того чтобы определить наилучшее значение,
280
мы вычертим для различных стратегий j эти математические ожидания
как функции х3. Ясно, что II будет выбирать j = 3 для 0 <
5 5
и будет выбирать у = 2 для у < х3 1. Для х3 = у он может выбрать
у
как / = 2, так и j = 3; ожидаемый выигрыш I будет равен , и этот
а
выбор является наилучшим, который он может сделать, если II знает
его смешанную стратегию (см. рис. 13-1-1).
Рис. 13-1-1. Графическое ре-
шение 2х4-матричной игры.
С другой стороны, если II рандомизирует свои чистые стратегии, выби-
рая j с вероятностью yj9 где у2 = Уз = у и У1 = Уь = 0, то все альтер-
нативы, которыми располагает I, сведутся к одной пунктирной линии
на постоянном уровне у. Другими словами, II может ограничить
7
максимальный выигрыш I числом у, не зная его смешанной стратегии,
и может уменьшить его выигрыш, если I отклонится от своей оптимальной
смешанной стратегии.
МАТЕМАТИЧЕСКАЯ ЗАДАЧА
Таким образом, представляется, что консервативный игрок может
увеличить свой ожидаемый выигрыш перед лицом противника, который
(по его мнению) знает, что он консервативен, случайным выбором своих
чистых стратегий с некоторыми вероятностями хи х2, ...» хт. Любой
конкретный выбор значений хг называется смешанной стратегией игрока I.
Таким образом, математически задача для него состоит в выборе таких
я^>0, 2^ = 1, чтобы его ожидаемый выигрыш был максимален. Этот
выбор называется оптимальной смешанной стратегией I. Как именно выби-
рать эти в общем случае, будет рассматриваться в следующем пара-
графе. Мы будем также рассматривать смешанные стратегии II, которые
будут обозначаться через (у^ у2, . . ., уп), где 0 и 2г/; = 1.
Замечательная теорема фон Неймана утверждает, что игрок I всегда
может гарантировать себе выигрыш г?, называемый значением игры, если
он придерживается своей оптимальной стратегии, и не может надеяться
получить больше этой величины, даже если он играет так, чтобы извлечь
выгоду из консерватизма своего противника. Более того, любое отклоне-
ние I от своей оптимальной стратегии повышает риск убытка. То же самое
утверждение относится, конечно, и к игроку II, так что мы можем
ожидать, что оба игрока будут играть свои оптимальные смешанные
стратегии.
281
13-2. ЭКВИВАЛЕНТНОСТЬ МАТРИЧНЫХ ИГР
И ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ;
ТЕОРЕМА О МИНИМАКСЕ
Пусть х19 х2 . . хт обозначают вероятности, с которыми игрок I
выбирает свои чистые стратегии i = 1, 2, . . т. Мы предполагаем, что
игрок I консервативен, т. е. что I рассчитывает на то, что игрок II знает
только вероятности, с которыми I производит выбор (но не его конкретный
выбор), и что II будет играть так, чтобы извлечь всю выгоду из этой инфор-
мации. Если II выбирает чистые стратегии / = 1, 2, . . ., п, то для любо-
го.
го частного выбора ожидаемый выигрыш I равен где, по опре-
i—1
делению, есть выигрыш I, если он выбирает чистую стратегию i и II
выбирает чистую стратегию /. Таким образом, I ожидает, что II выберет
такую чистую стратегию /, которая соответствует минимуму из этих
выражений. Иначе говоря, если мы обозначим через L любую нижнюю
т
границу для этих выражений, так что ^a^Xf L, то II (для фиксирован-
г=1
, т
ных Xi) будет так выбирать свою чистую стратегию / = /0, что =
— max L. Так как I заинтересован в том, чтобы L было как можно больше,
он будет пытаться так выбрать свои xi9 чтобы этот max L был как можно
больше. Таким образом, max L есть наибольший нижний предел, кото-
рый I может себе гарантировать.
Задача игрока I. Выбрать > 0 и max Z, удовлетворяющие усло-
виям:
+ #21#2 + • • • 4“ amixm > L,
(xi > 0)
а12ж1 4“ a22x2 4" • • • 4" am2xm L,
(1)
alnxi + a2nx2 + • • • + amnxm L,
xl 4" x2 4" • • • + xm — 1 •
Очевидно, мы свели решение матричной игры для консервативного иг-
рока I к задаче линейного программирования. Предположим теперь, что
его противник II также играет консервативно. Аналогично этому II
заинтересован в выборе возможно меньшего числа М в приведенной ниже
задаче. Таким образом, min М есть наименьший верхний предел, кото-
рый II может себе гарантировать.
Задача игрока II. Выбрать > 0 и min Af, удовлетворяющие усло-
виям:
аи У\. 4- ai2 У24- • • • 4~ Уп^М, (yj 0)
^21 У1 4" а22 У2 4" • • ’ 4- а2п Уп^М,
.............................................. (2)
ат1У1 4- ат2У2 4- • • • 4- атпУп М,
У14- у 2 4“ • • • 4- Уп — 1 •
Теорема 1. Если каждый из игроков играет консервативно, то каждый
решает задачу линейного программирования, двойственную задаче другого
игрока; отсюда следует, что наибольший нижний предел для I равен
наименьшему верхнему пределу для II.
Доказательство. Для того чтобы убедиться, что задачи (1) и (2) двой-
ственны друг другу, перенесем L и М налево и обозначим через М = z
282
целевое уравнение в задаче (2), где z должно минимизироваться, а через
L — z — целевое уравнение в задаче (1), где z должно максимизироваться.
Ввиду того что любые значения xL 0, = 1; > О, = 1 дают
допустимые решения в прямой и двойственной задачах, теорема двой-
ственности гарантирует существование оптимальных решений и равенство
max L = min М (§ 6-3, теорема 1).
В сущности теорема 1 утверждает, что если игрок II играет консер-
вативно, то он всегда может получить от I максимальный гарантирован-
ный выигрыш независимо от того, играет I свою оптимальную смешанную
стратегию или нет. Любое отклонение I от оптимальной стратегии повы-
шает риск убытка, если II придерживается своей оптимальной смешан-
ной стратегии, и существует возможность для I выиграть, если II откло-
няется от своей оптимальной стратегии»
Определения. Пара оптимальных смешанных стратегий, если оба
игрока играют консервативно, называется решением матричной игры;
получающийся в результате гарантированный ожидаемый выигрыш игро-
ка I называется значением игры.
Теорема 2 (Теорема о минимаксе фон Неймана).
Если 2жг = 2Уг = :1> *;>0, ^>0, ТО
max min 3 2 aij^yj = min max 3 2 аих1У; (3)
x у \ x i j у x\y г 3
Символ y\x означает «у при данном х». Левая часть (3) означает сле-
дующее: для фиксированного (данного) х требуется минимизировать
по у сумму; результат есть функция х; теперь надо так выбрать х, чтобы
это значение достигало максимума. Выражение, стоящее под знаком
min в правой части (3), может быть переписано (ввиду того, что ^xt = 1,
у
>0) следующим образом:
max 3^2 сьцУ] = max 2 ^аУр
х I у г 3 г 3
Это выражение представляет собой выигрыш I, если I знает смешанную
стратегию II и использует этот факт. Если II играет консервативно, то
он минимизирует выражение справа. Следовательно, правая часть пред-
ставляет собой новую формулировку задачи II и значение правой части
есть min М. Аналогично левая часть есть новая формулировка задачи I
и значение левой части равно max L. Короче говоря, теорема 2 есть сокра-
щенная формулировка теоремы 1, так как она охватывает (1) и (2).
Следствие 1. Если оптимальная стратегия II дает строгое неравен-
ство в i-м соотношении (2), то в оптимальной стратегии I должно быть
Xi = 0; если оптимальная стратегия I дает строгое неравенство в /-м
соотношении (Г), то в оптимальной стратегии II должно быть yj = 0.
(Доказательство см. теорему 4 § 6-4).
ЭКВИВАЛЕНТНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Рассмотрим теперь различные задачи линейного программирования,
эквивалентные игровой задаче (Данциг [3]; Гейл, Кун и Таккер
[1]). Вводя в (2) свободные переменные, мы имеем
аи Vi + ai2 Уъ + • • • + ат Уп + Уп+1 = М,
ат1У1 + ат2У2 + • • • + атпУп + Уп+т = М,
У1 + У2 + • • • + Уп — 1
283
(4)
Если первое уравнение вычесть из всех остальных, кроме последнего,
то полученная система будет эквивалентна задаче линейного программи-
рования в стандартной форме. Найти у}- 0 и min М, удовлетворяющие
условиям:
а11У1~\~ #12^+ • • • + а1пУп-[- Уп+1 — М9
(«21 — #11) У1 + (#22 #12) У 2 + • • • + (#2п #1п) Уп + {У п+2 Уп+1) = О,
.............................................................. (5)
(#znl— #11) У1 + (#7П2 — а12) У2~\~ • • • + (#ттг— #1п) Уп + {Уп+т—Уп+1) = О
У1+ &+•••+ Уп = !•
Упражнение. Показать, что решения прямой и двойственной систем
(1) и (2), а следовательно, и системы (5) всегда существуют.
Упражнение. Показать, что если к каждому элементу матрицы выигры-
шей прибавить некоторое постоянное к, то оптимальные смешанные стра-
тегии не изменятся ни у одного из игроков.
Другой более симметричный способ сведения к стандартной форме
заключается в подстановке в (2) y'j М — yj, в результате чего получается
система:
#и У1 + #12 У2 + • • * + #ш Уп 1, {Уз 0)
ат1У1 + ат2У2 + • • • + атпУп 1 >
У1+ Уь+--- + ^n = -^-(max).
Заметим, что у'з >0. Эта подстановка выполнима только в том случае,
когда известно, что значение игры М положительно. Однако, так как
ко всем элементам матрицы выигрышей можно прибавить произвольную
постоянную К, не влияя на оптимальную смешанную стратегию, то огра-
ничение М > 0 не представляет трудностей.
Упражнение. Как велико должно быть К9 чтобы гарантировать
неравенство М > 0?
СВЕДЕНИЕ ПРОИЗВОЛЬНОЙ ИГРЫ К СИММЕТРИЧНОЙ
Игра двух лиц называется симметричной, если оба игрока имеют
одно и то же число чистых стратегий и выигрыш игрока I, если он выби-
рает стратегию i, а его противник выбирает /, равен выигрышу игрока II,
если последний выбирает Z, а его противник выбирает /; другими словами,
если для всех г, j = —а^. Матрица, обладающая этим свойством, назы-
вается кососимметр ичной.
Упражнение. Доказать, что значение симметричной игры рав-
но нулю.
Фон Нейман и Моргенштерн [1] впервые показали, как можно
построить симметричную матричную игру, эквивалентную произвольно
заданной матричной игреЧ Позже Гейл, Кун и Таккер [1] указали
более простой способ симметризации игры, основанный на том же приеме,
с помощью которого задача линейного программирования сводится
к игре (см. (11)). Для того чтобы свести игру с матрицей А к симметрич-
1 Здесь термин «эквивалентный» употребляется в неформальном значении: одна
игра эквивалентна другой, если по решению первой игры можно «легко» построить
решение второй.— Прим, ред.
284
ной игре, предположим, что все > 0 (если необходимо, мы добавим
ко всем элементам матрицы достаточно большую постоянную), и рассмот-
рим двойственные друг другу задачи линейного программирования, кото-
рые дают оптимальные смешанные стратегии х и у двух игроков:
uTz = l, pyTi/ = l, (я>0, у>0)
Ау^Ми (7)
L=z (max), М — z (min),
где Т, как и в главе 8, обозначает транспонирование и ит — (1, 1, . . 1),
vT = (1, 1, . . ., 1) суть векторы-строки из m и п компонент; таким обра-
зом, итх = Szj = 1, vTy = Sz/; = 1.
Рассмотрим теперь новую матричную игру с кососимметричной мат-
рицей (8), имеющей m + п + 1 столбцов и строк, и с новой парой игроков:
х у t
х / О' А —гЛ
У ( —Ат 0 v I, (8)
t \ ит —vT 0 /
где (ж, у, 0 = («1, • • Уь • ••, Уп1 0 обозначает оптимальную сме-
шанную стратегию любого из игроков и + t = 1.
Упражнение. Доказать, что если стратегия ж, i/, t оптимальна для
игрока I, то она также оптимальна для игрока II.
Теорема 3. Если все элементы матрицы А игры положительны, то
любая оптимальная смешанная стратегия (х, у, t) любого из игроков сим-
метричной игры (8) даст оптимальные смешанные стратегии х,уи выигрыш
М игроков исходной игры, именно
У-У^У3, x^xl^x,, М = 2t/(i—t) (9а)
или, обратно,
у = у/(М + 2), х = х/(М + 2), t = M/(M + 2). (96)
Доказательство. Так как значение симметричной игры должно быть
равно нулю, оптимальные смешанные стратегии игроков должны удовлет-
ворять условиям
Ау—ut ^0, (я>0, у>0, £>0)
— ATx~\~vt <0,
2 xi 2 У} С o,
Соотношения (10) представляют собой тот частный случай соотношений
(2), в котором кососимметричная матрица S заменяет матрицу А задачи
(2), а значение игры заменяется нулем. Заметим теперь, что если все эле-
менты матрицы А положительны, то t > 0, потому что из t = 0, согласно
первому неравенству, следует, что у = 0, а тогда из предпоследнего нера-
венства следует, что ^хг — 0, что противоречит последнему уравнению.
Теперь заметим, что из следствия 1 вытекает равенство = 5^-, потому
что из t > 0 следует, что игрок I симметричной игры выбирает последнюю
285
строку с положительной вероятностью. Это означает, что ожидаемый
выигрыш Zxi — 2 yj максимален, т. е. равен нулю. Наконец, заметим
что х у= 0, так как предположение о том, что х = 0 противоречило бы
второму неравенству; из равенства 2^ = следует, что у =£= 0 и, сле-
довательно, согласно последнему уравнению, t < 1. Следовательно, можно
определить смешанные стратегии х и у и число М = L по формулам (9);
заметим, что (10) сводится к (7), где М = L; следовательно, х и у — опти-
мальные решения двойственных задач линейного программирования
и, значит, х и у — оптимальные смешанные стратегии в игре с матрицей Л.
СВЕДЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
К СИММЕТРИЧНОЙ ИГРЕ
Аналогично сказанному выше рассмотрим двойственные задачи линей-
ного программирования
А?х с,
bTx = z (max),
Ау>Ь. ,
сту = z (min),
(я>0, у>0)
(И)
где Ь и с — векторы-столбцы, и рассмотрим их связь с кососимметричной
игровой матрицей
х / 0
F +лт
t \—ът
—А
0
ст
(12)
Теорема 4. Для того чтобы задачи линейного программирования (11)
имели решения, необходимо и достаточно, чтобы в симметричной игре
с матрицей (12) существовала оптимальная смешанная стратегия (х. у. t).
в которой t > 0. Оптимальные решения этих задач даются равенствами
х — x/t и у = у It.
Впервые задача линейного программирования была сведена к игре
в 1948 г. на основе бесед между автором настоящей книги и Дж. Брауном.
Несколько позже Браун и Таккер заметили, что соответствующая матрица
игры кососимметрична (Данциг [3]).
Доказательство. Оптимальная смешанная стратегия удовлетворяет
неравенствам
— Ау
А7х —ct^.Q.
— ЪТх-\-сТу ^0.
(x>Q. y>Q)
(13)
Полагая у = yt. х = xt и замечая, что t > 0, мы получаем
Ау >Ъ (х>0. у>0)
Атх^.с.
сту Ъ? х.
(14)
Однако если первое неравенство (14) умножить слева на хт. а второе —
на ут. то получим Ът х^хтАу < ст у. Вместе с последним неравенством
х у t
286
(14) это дает
г = сту = Ътх = z. (15)
Следовательно, по теореме двойственности (§ 6-3, теорема 1) х и у являются
оптимальными решениями двойственных задач.
Обратно, если двойственные задачи имеют оптимальные решения
х, у, то мы можем обратить наши рассуждения, определяя t > 0 равен-
ством
<(S®/ + 3^+i) = i (16)
и полагая tx = х и ty = у.
Сведение задачи линейного программирования к игре основано
на нахождении решения игры, для которого t > 0. Если в решении t = 0,
то это не обязательно означает, что оптимальное допустимое решение зада-
чи линейного программирования не существует. См. задачи 3—7 в конце
главы.
13-3. КОНСТРУКТИВНОЕ РЕШЕНИЕ МАТРИЧНОЙ ИГРЫ
(ДРУГОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О МИНИМАКСЕ)
Матричная игра решается путем применения последовательности ве-
дущих операций к задаче линейного программирования, представляющей
задачу либо игрока I, либо игрока II. Правила выбора ведущего элемента
будут изложены заново, так что читатель познакомится с конструктивным
доказательством теоремы о минимаксе, не использующим результаты пре-
дыдущих глав х.
Коэффициенты линейной системы (4) § 13-2 образуют таблицу (1)
со свободными членами в первом столбце; затем следуют столбцы уп+1,
соответствующие свободным переменным, столбец (—М), соответствую- ,
щий переменной, которая максимизируется, и, наконец, столбцы главных
переменных yj.
Свободные члены ^71+1 ’ ’ * 1 Уп+m (-М) yi У2, Уп
1 0 1 1 1
0 1 1 аи «12 • я1п
• i 0 1 1 Лт- i, j ат— 1, 2 ат—1, п
0 1 1 Gm^ ат2 атп
Предположим для удобства, что строки и столбцы табл. (1) располо-
жены так, что
aml — min (max ао-).
3 i
После умножения последней строки на —1, первой строки на (а/п1 — akl)
и сложения их суммы с каждой строкой к = 2, 3, . . ., тп, — 1 получается
эквивалентная табл. (2), где a'kj = — amj — Последняя
1 Результаты этого параграфа взяты из работ Данцига [И], Таккера [9]
и Дорфмана [2].
287
строка получается умножением верхней строки на —ami и сложением
е последней строкой. Жирные точки поставлены под единичными векто-
рами-столбцами уп+1, . . уп+т-ъ (-М), уъ
Цикл О
Свободные члены УП+1 • ‘ • Уп+т— 1 уп+т -М У! У2 уп
1 0 1 1 1
Я7П1 flll 1 — 1 0 а12 а\п
. • -
• . • • •
aml атп—11 I 1 — 1 0 ат—1, 2 ат— 1,п
ат1 1 1 0 ат2—ami а7ПП а7П1
(2)
Каждый цикл дает улучшение смешанной стратегии игрока II. Вероят-
ность выбора столбца у в матричной игре равна нулю, за исключением
столбца, соответствующего yj, который на некотором цикле оказывается
единичным вектором-столбцом, отмеченным точкой внизу. Значение yj
для такого столбца с единичным коэффициентом в строке i равно i-й ком-
поненте вектора-столбца свободных членов. Таким образом, для цикла
О yi — 1. Предположим, что эквивалентная система в табличной форме для
цикла р дается табл. (3), которая всегда включает некоторые т + 1
единичных векторов (обычно указываемые точками ниже этих столбцов).
Цикл р
Свободные члены уп+1 Уп+2 • • Уп+т -М У1 '• У8 ... vn
bi Р11 Р12 * * • Pirn 0 «18 ain
Ъг Prl Рг2 ‘ * ’ Ргтп 0 аг1 • ars arn
bm Pn»l Ртп2 ’ • • Рттн 0 «7П1 > • ams amn
—Мо cn+i сп+2‘ • * сп+т 1 С! cs cn
Теорема 1. Если для всех j Cj 0 и для всех i Ъ$ 0, то оптимальная
смешанная стратегия игрока I определяется равенствами хг — сп+г
для i = 1, 2, . . ., т, а оптимальная смешанная стратегия II состоит
в выборе столбцов j матрицы с вероятностью 0, за исключением столбца j,
соответствующего в таблице (3) отмеченному точкой i-му единичному
столбцу] = jt, и в этом случае укроме того, MQ есть значение мат-
ричной игры.
288
Доказательство. Заметим, что линейная комбинация строк таблицы
(1) с весами М, х2, . . ., хт, которая образует последнее уравнение (3),
представляется набором чисел — Мо, сп+1, . . ., сп+т. Умножение коэф-
фициентов столбца —М на эти веса и сложение дает равенство S xt = 1,
а те же операции с любым другим столбцом / дают неравенство S хга^ =
= Cj + Мо MQ. Так как выбор yj. = bi9 очевидно, решает задачу игро-
ка II и выигрыш также равен Мо, то решения оптимальны.
ПРАВИЛА ВЫБОРА ВЕДУЩЕГО ЭЛЕМЕНТА
Шаг 1. Выбрать ведущий столбец 5 (и отметить его точкой) по формуле
cs = minc/ (7 = 1, 2, ..., п + тп). (4)
Если с8 0, то перейти к шагу 4.
Шаг 2. Выбрать ведущую строку г (и убрать точку у столбца с еди-
ницей в строке г) среди тех строк Z, для которых ais > 0, так, чтобы на
векторе-строке
(Ьг, рг1, рг2, . . Prm)/^rs (5)
достигался лексикографический минимум средв векторов-строк
Pib Pz2, •••> Pim)/^zs* (6)
Этот выбор производится сравнением в первую очередь ведущих ком-
понент этих векторов, так что
br/ars = min bja^ (ars, а^>0),
где ais — ргд, если 5 = п + к.
Правило выбора в случае неоднозначности
Если выбор г не единственен, так что минимум в написанном выше отно-
шении достигается при г = ri,r2 . ’ то перейти к столбцу уп+1 и выбрать
ведущую строку г по формуле
= min -В^-, (г, i = r19 r2, • • •)
ars ais
Если выбор г все еще не единственен, так что минимум в написанном выше
отношении достигается при г = г', г' . . ., то перейти к столбцу yn+z
и выбрать г по формуле
Ы = тш-1^-, (г, г = г;, г;, ...)
ars ais
Продолжать таким образом, переходя к столбцам • • • Д° тех
пор, пока г не определится единственным образом.
Шаг 3. Применить ведущую операцию; цикл р завершен. Вернуться
к шагу 1
Шаг 4. Закончить вычислением оптимальной смешанной стратегии
игрока I:
1» ^2 “ сп+2> • • • > %тп = cn+mt (7)
и оптимальной смешанной стратегии игрока II: выбирать столбец / мат-
рицы игры с вероятностью 0 для 7 = 1, 2, . . ., п, за исключением столбца,
19 Дж. Данциг
289
соответствующего такому у в цикле р, который является отмеченным точ-
кой Z-м единичным вектором-столбцом, и в этом случае для каждого
такого I
Vjt = bt.
(8)
ЗАМЕЧАНИЕ О ЛЕКСИКОГРАФИЧЕСКОМ УПОРЯДОЧЕНИИ
Отвлечемся теперь на время и рассмотрим способ расположения или
упорядочения системы векторов (с одинаковым числом компонент) в после-
довательность так же, как упорядочиваются слова в словаре; мы будем
поэтому называть этот способ упорядочения векторов «лексикографиче-
ским». Мы будем говорить, что вектор R больше нуля в лексикографиче-
ском смысле, или, проще, лексико-положителен1, и обозначать это как
R >*• 0, если он имеет по крайней мере одну ненулевую компоненту, первая
из которых положительна. Мы будем говорить, что вектор R больше век-
тора 5 в лексикографическом смысле, и обозначать это символом R > 5,
если R — S > 0.
Упражнение.
1) Показать, что отношение лексикографического порядка транзи-
тивно, т. е. что из R > S, S > Т следует R > Т.
2) Показать, что любые два вектора R и 5 с одним и тем же числом
компонент удовлетворяют одному йз трех соотношений R > S, S > R
или R = S; показать также, что из R > 5 следует, что R S.
3) Пусть R >2 5 означает, что либо R > 5, либо R = S; показать,
что если R >2 S и 5 > R, то R = S.
4) Если Я > 0 и 5 > 0, то R + 5 > 0. Если к > 0 — скаляр и
R > 0, то kR > 0.
Пример. Таккер [9] в своей статье «Решение матричной игры
с помощью линейного программирования» приводит следующую матрич-
ную игру:
/1—1 0\
(—6 3 —2). (9)
\ 8 -5 2/
Коэффициенты задачи игрока II образуют таблицу
Свободные члены 1/4 Уъ 1/6 -м У1 1/2 УЗ
1 0 1 1 1
0 1 1 1 — 1 0
0 1 1 —6 3 —2
’ 1 0 1 1 8 —5 2*
По аналогии с (2) отмеченный звездочкой элемент а33—2 равен min (max а^)
3 i
и, следовательно, табл. (11) цикла 0 получается из табл. (10) дцумя про-
стыми ведущими операциями, так что столбцы у4, у5, —М, у3 являются
единичными векторами.
1 Это сокращенное название принадлежит Таккеру.
290
Цикл О
Свободные члены 1/4 УЪ 1/6 -м VI 1/2 1/3
1 1 1 1
2 1 —1 —5 6 (11)
4 1 —1 —10 12
—2 1 1 6 — 7
• • • ★ •
Заметим, что г = 2 и г = 3 годятся для ведущей операции, так как
2 4 11
— = —. Однако лексикографически вектор -g- (2, 1, 0, — 1, 0) > (4, 0,
1,-1, 0). Следовательно, г = 3 выбирается как ведущая строка.
Применение ведущей операции с элементом 12 дает таблицу
Так как все элементы в нижней строке неотрицательны, цикл закончен.
Оптимальное решение для I берется в нижней строке в столбцах у^ у5,
7 5
у6; оно таково: xt = 0; х2 = тъ, х3 = Оптимальное решение для II
берется из столбца свободных членов; оно таково: у3 = , у2 = Л, а все
остальные несвободные у; равны нулю. Значение игры равно Мо =
ДОКАЗАТЕЛЬСТВб КОНЕЧНОСТИ АЛГОРИТМА
В табл. (2) цикла 0 элементы в столбцах у19 уп+1, yn + 2f . . ., yn+m_lf
—М образуют единичную матрицу. Ведущая операция с ведущим эле-
ментом в столбце $, строке г преобразует столбец s в единичный вектор
с единицей в r-й строке. После нескольких циклов единичная матрица
перемещается в столбцы у^, у^, • • yjm и — М (столбец —М от цикла
к циклу не меняется). Система столбцов таблицы цикла 0, соответствующая
этим единичным столбцам в таблице цикла р, называется базисом для
цикла р. Мы будем обозначать его через В. Легко видеть, что матрица В
невырожденна и, ввиду того, что ведущие операции преобразуют В в еди-
291
19*
яичную матрицу (см, (9), (10) и далее, § 8-4), единичная матрица с ©стоя-
щая из первых т ф 1 столбцов цикла 0, преобразуется в матрицу В~г
цикла р.
Покажем теперь, что правило шага 2 всегда дает единственное значе-
ние г для выбора ведущей строки. Так как г должно выбираться среди
таких г, для которых ais > 0, мы сначала покажем, что по крайней мере
одно из ais положительно (так как этот класс i не пуст). Заметим, что в табли-
це цикла р столбцы, соответствующие yJV . . ., —Л/, образуют
единичную матрицу; следовательно, линейная комбинация этих столб-
цов с весами ais дает столбец s и, значит, то же самое соотношение между
столбцами должно иметь место и для исходной таблицы (1) (так как веду-
щая операция не изменяет отношения линейной зависимости между столб-
цами). Однако из предположения о том, что все ais 0, следовало бы,
что неположительная линейная комбинация некоторых столбцов (1)
смогла бы дать столбец $. Но это, очевидно, невозможно, так как каждый
столбец у* = 1, 2, . . ., п имеет единицу в верхней строке и линейная ком-
бинация должна включать по крайней мере одно такое /.
Покажем теперь, что правило для определения строки, в которой
надо выбрать ведущий элемент, приводит к однозначному выбору, потому
что из неединственности следовало бы, что по крайней мере два вектора-
строки (5) и (6) были бы равны покомпонентно; но тогда квадратная под-
матрица таблицы (3), состоящая из. первых т + 1 строк и столбцов (начи-
ная со столбца свободных членов), была бы вырожденной, что невозможно,
так как эта подматрица получается из таблицы (1) с помощью последо-
вательности ведущих операций и соответствующая подматрица таблицы
(1) является единичной и, следовательно, невырожденной.
Правило выбора г делает также невозможным повторение базиса,
полученного на одном из предыдущих циклов. Чтобы показать это, обо-
значим через 7?i, • • •, Rm\ Rm+i строки таблицы цикла р, а через
7?*, 7?*, . . ., 7?™; Rm+i — строки таблицы цикла р + 1. Докажем сле-
дующие утверждения.
Лемма 1. Ri >- 0 для всех I и любого цикла р.
Лемма 2» 7?тд_}_1 х*- Rm-^-i*
Доказательство индуктивное. Соотношение между Rt и 7?* дается
формулами
Rl = Rt -RT^-,
ars
R* = RTJ~,
ars
P* ____ p T> C8
1 — -iim+i ~ >
ars

(13)
где cs < 0,
где r — ведущая строка и ar8 > 0. Если Rr > 0, то отсюда сразу следует,
что R* > 0; кроме того, если а^<0, то 7?* > 0, так как каждый из век-
торов Ri и —Rr (ais/drs) лексико-положителен по индуктивному пред-
положению (те же рассуждения применимы к 7?^+1, так как cs < 0, и это
доказывает лемму 2). С другой стороны, если аг8>0, то мы имеем
Ri —(Ri/dis'— Rrlars)
Заметим теперь, что правило шага 2 для выбора ведущей строки означает
292
выбор лексико-наименьшего вектора Ri!dis для таких г, для которых
dis > 0* Следовательно, R* > 0.
Как было отмечено раньше, квадратная подматрица из первых т + 1
строк и столбцов табл. (3) невырожденна, так что для каждого вектора Rt
среди его первых т + 1 компонент имеется ненулевая и, значит, на сле-
дующей итерации также R* У= 0. Так как мы уже показали, что R* >- 0,
то R* > 0.
Для того.чтобы показать конечность алгоритма, заметим, что послед-
няя строка в лексикографическом смысле строго возрастает; следова-
тельно, никакая таблица не может совпасть с полученной ранее. Предпо-
ложение о бесконечности числа итераций приведет нас к противоречию,
потому что число различных базисов конечно и, следовательно, на неко-
торой итерации базис совпал бы с полученным ранее. Но в этом случае
также была бы повторена вся таблица, потому что элемент таблицы
представляет собой просто комбинацию столбцов базиса, которая обра-
зует столбец /, и эта линейная комбинация единственна и инвариантна
относительно ведущей операции.
13-4. ЗАДАЧИ
1. Предположим, что каждый из двух игроков имеет монеты в пенни,
пять пенсов и десять пенсов, выбор из которых представляет его чистые
стратегии. Если оба игрока выбирают монеты одинакового достоинства,
то игрок I выигрывает монету игрока II; если эти две монеты разного
достоинства, то игрок II выигрывает монету игрока I. Сколько игрок II
должен был бы дать игроку I до игры, для того чтобы сделать эту игру
справедливой?
2. Что является аналогом решения игры, определяемого седловой
точкой (если она существует) для задачи линейного программирования?
3. а) Показать, что если в теореме 4 § 13-2 t = 0, то отсюда
еще не следует, что задача линейного программирования не имеет
решения.
б) Показать, что если t — 0 и если оптимальное решение имеет поло-
жительные свободные переменные в дополнительном соотношении двой-
ственной системы, использующей решение симметричной игры, то реше-
ния задачи линейного программирования не существует.
в) Показать, что если t = 0 и в дополнительном соотношении имеются
нулевые свободные переменные, то отсюда не следует, что задача линей-
ного программирования не имеет решения.
г) Показать, что t > 0, если коэффициенты > 0.
д) (Шепли). Показать, что в прямой задаче, приведенной ниже, не
существует допустимого решения, но что t = 0 и ее дополнительные сво-
бодные переменные равны нулю в эквивалентной игре.
Прямая Г >4-1,
задача [ Oy4=z (min).
Решение —>
Эквивалентная
игра
0 1 0
О О 1\ °
ООО1
— 10 0/°
решение
е) (Шепли). Показать, что допустимое решение существует и что
не существует нижней границы для v в задаче, двойственной приведенной
выше (которая приведена ниже), но что t = 0 и ее дополнительные сво-
бодные переменные равны нулю в эквивалентной игре.
293
Двойственная
задача
г 0 О,
t 4- 1 x4 = r(max),
Решение —>
Эквивалентная
игра
1 О
О О
О О
О 1
О
О\ 1
—1 j О
О/ о
t
решение
где xi > О, у4 > О.
4. Построить пример, показывающий, что допустимые решения как
прямой, так и двойственной систем могут существовать, но что решение
эквивалентной игры может иметь t = 0.
5. Показать: если решение игры единственно, когда переменные,
соответствующие положительным значениям дополнительных свободных
переменных, опущены, то остальные переменные имеют положительные
значения.
6. (Вулф). Доказать следующую теорему: все решения соответствую-
щей игры имеют t > 0 тогда и только тогда, когда существуют такие
и, х > 0, что иА > с и Ах < Ь.
7. (Вулф). Доказать следующую теорему: если множество х 0,
Ах 5g Ъ не пусто, ограничено и имеет внутренние точки и А не имеет
нулевой строки, то для любого решения [ж, и, £] соответствующей игры
t>0.
Глава 14
КЛАССИЧЕСКАЯ ТРАНСПОРТНАЯ ЗАДАЧА
14-1. ИСТОРИЧЕСКИЙ ОБЗОР
Важный класс задач экономического и физического происхождения
можно описать в терминах сети, состоящей из точек (узлов), соединенных
путями (дугами), по которым осуществляются различные виды перевозок
(потоки) (см. гл. 19).
Классическая транспортная задача возникает при определении опти-
мального плана перевозок, которые
а) производятся из источников (пунктов производства) с фиксиро-
ванными запасами грузов;
б) направляются непосредственно в конечные пункты назначения
(пункты потребления), в которых имеется потребность в различных фик-
сированных количествах грузов;
в) исчерпывают запасы и удовлетворяют потребности; следовательно,
суммарный спрос равняется суммарным запасам;
и, наконец, затраты должны
г) удовлетворять линейной целевой функции; иными словами, затраты
по каждой перевозке должны быть прямо пропорциональны перевозимому
количеству, а суммарные затраты должны слагаться из суммы отдельных
затрат.
В этой главе мы рассмотрим эту задачу и покажем, как она решается
симплекс-методом. (В последующих главах будут рассмотрены некоторые
разновидности транспортной задачи.)
Л. В. Канторович [1] показал, что класс задач, близких к клас-
сической транспортной задаче, имеет удивительно многообразные при-
ложения, в частности, в задачах распределения работ по станкам, когда
затраты и нормы производительности зависят от вида работ и типа станка.
Он дал полезный, но неполный алгоритм для решения таких задач
(см. гл. 21). Правда, в то время эта работа не привлекла достаточного вни-
мания. Затем в 1942 г. он написал математическую статью, касающуюся
непрерывного варианта транспортной задачи, а в 1948 г. опубликовал сов-
местно с М. К. Гавуриным прикладную работу [1], посвященную транспорт-
ной задаче с ограничениями на пропускные способности (см. гл. 18).
Транспортная задача в той формулировке, которая сейчас стала уже
стандартной, была впервые сформулирована Ф. Хичкоком [1]. В его
статье «Распределение продукта из нескольких источников к много-
численным пунктам» были сделаны наброски теории метода, предвосхи-
щающего симплекс-метод; при этом, однако, он не использовал индиви-
дуальных особенностей транспортной задачи, за исключением построения
начального решения. Эта статья также не привлекла большого внимания.
Однако другой исследователь, Т. Купманс, являясь членом Объеди-
ненного комитета перевозок во время второй мировой войны, использовал
решение транспортной задачи для снижения суммарных затрат времени
295
на перевозку, так как недостаток грузовых судов представлял собой кри-
тическое узкое место.
В 1947 г. Купманс возглавил исследования возможностей применения
линейного программирования для изучения экономических задач. Его
имеющая историческое значение статья «Оптимальное использование
транспортной системы» [1] основывалась на его опыте военного времени.
Эта работа и цитированная выше работа Хичкока объясняет, почему
классический вариант задачи часто называют задачей Хичкока — Купманса.
Следующим ученым, чья работа предвосхитила современный этап
в развитии линейного программирования, был венгерский математик
Эгервари. В его работе [1] рассматривалась задача о нахождении неко-
торой перестановки единиц в матрице, составленной из нулей и единиц.
Основываясь на этом исследовании, Кун [1] разработал эффективный
алгоритмический метод решения задач о назначении (см. § 15-1). Подход
Куна в свою очередь лежит в основе метода Форда — Фулкерсона для
решения классической транспортной задачи (гл. 20).
Метод, который будет описан в этой главе, разработан независимо
от этих работ, путем конкретизации общего симплекс-метода (Данциг [4]).
14-2. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ТРАНСПОРТИРОВКИ
Пусть на т складах (источниках) имеются различные количества
некоторого товара, которые должны доставляться в п городов (пунктов
назначения). Точнее, f-й склад должен располагать количеством товара,
в точности равным а J-й город должен получить в точности bj единиц
товара. При этом предполагается, что суммарный спрос равен суммарно-
му предложению, т. е.
т п
(1)
1=1 5=1
Кроме неотрицательных величин и Ь7-, нам дан также набор чисел
Си, которые могут и не иметь ограничений на знак (хотя в данной интер-
претации они обычно неотрицательны). Величина представляет собой
затраты (или прибыль, если она отрицательна) на перевозку единицы груза
от пункта производства i до пункта потребления у. Наша задача заклю-
чается в определении количеств единиц груза, подлежащих транспорти-
ровке из i до у таким образом, чтобы при этом все запасы были исчерпаны,
потребности удовлетворены и был достигнут минимум суммарных затрат.
Специфическая структура матрицы станет очевидной, если записать
уравнения в стандартной форме (2).
^11+^12+ • • • +^171 --а1
+ ^21 + ^22+ ••• +^2/1 =а2
+ хт1~\~хт2 "Ь • • • А~хтп —ат
xli +Х21 +^7711 --^1
+ ^12 ~ЬХ22 ~Ьхт2 ~^2
+ хтп —
с11х11 + • • • + cinxin + c2ix21 + • • • + с2пх2п + • • • + cmlxmi + • • • + стпхтп — z
296
Упражнение. Условие (1) делает систему зависимой, так как при его
соблюдении сумма первых т уравнений становится равной сумме послед-
них п. Доказать, что ранг этой системы в точности равняется т + п — 1.
Показать также, что любое уравнение является линейной комбина-
цией других т + п — 1, так что любое из уравнений можно считать
избыточным и отбросить его.
СТАНДАРТНАЯ ТРАНСПОРТНАЯ МАТРИЦА
Характерной особенностью этой модели является то, что ее можно
привести к форме прямоугольной таблицы, в которой величины xtj и
размещаются в строке i и в столбце у, значения правых частей и соответ-
ствующих множителей для первых т уравнений — в последнем столбце,
а для остальных уравнений — в последней строке.
Суммы по строкам
Суммы по
столбцам
хи СП *12 с12 *13 с13 *14 С14 *15 с15
*21 С21 *22 с22 *23 с23 *24 с24 *25 с25
*31 С31 *32 с32 *33 с33 *34 с34 *35 с35
”1 Ь2 v2 &3 ”3 *4 ”4 Ъ5 vt>
(3)
На любом шаге алгоритма в правом нижнем углу клетки (г, у), рас-
положенной на пересечении f-й строки и у-го столбца, находятся значения
Cij, а в ее левом верхнем углу — величины — текущие числовые зна-
чения переменной х^. Отсутствие какого-либо х^ говорит о том, что данное
Хи является небазисным и, следовательно, равно нулю. Базисные пере-
менные, имеющие нулевое значение, отмечаются нулем (вырождение).
Любая клетка крайнего справа столбца или крайней снизу строки
отличается тем, что в ней слева сверху стоят суммы по строкам (столбцам),
ai (или ЬД а справа снизу — соответствующие текущее значение и* или
v] симплекс-множителей. Каждая строка и столбец матрицы представляют
некоторое уравнение. Именно
уравнение по строкам: ^х^ = а^ (4)
j=i
(i — 1, 2, ..., т)
т
уравнение по столбцам: (5)
i=l
(7 = 1, 2, ...,n)
Чтобы эти уравнения удовлетворялись на протяжении всего алгоритма,
надо соблюдать равенство сумм по строке и столбцу соответственно вели-
чинам «j и bj, которые проставляются в крайних столбце и строке.
297
ПОСТРОЕНИЕ ДОПУСТИМОГО БАЗИСНОГО РЕШЕНИЯ
В качестве кандидата на роль первой базисной переменной выбираем
любую переменную xpq и придаем ей максимально возможное значение
в соответствии с суммами по строке и по столбцу, т. е. полагаем
Zpg = min(ap, bq).
Случай 1. Если ар меньше bq, то все остальные переменные в р-й
строке полагаются равными нулю и считаются небазисными. Затем вычер-
киваем р-ю строку, заменяем величину bq на (bq — ар) и осуществляем
тот же самый процесс вычисления переменных в уменьшенной матрице,
состоящей из оставшихся т — 1 строк и п столбцов.
Случай 2. Если ар больше bq, то аналогично вычеркивается g-й стол-
бец, а ар заменяется на (ар — bq) и т. д.
Случай 3. Если ар равно 6Q, то вычеркиваем либо строку, либо стол-
бец, но не оба сразу. При этом если в уменьшенной матрице остается
несколько столбцов и только одна строка, то выбрасывается g-й столбец,
и наоборот, если остается несколько строк и один столбец, то выбрасы-
вается p-я строка.
В результате этого правила в качестве базисных отбирается столько
переменных, сколько имеется строк плюс столбцов минус один, т. е.
т + п — 1, так как на последнем шаге, когда остается только одна стро-
ка и один столбец, после того, как последняя переменная получила свое
значение, выбрасываются сразу оба. Важным обстоятельством является
то, что, как мы это покажем далее, все базисные решения имеют такой вид.
• Поэтому при определении алгоритма для достижения оптимума нет
необходимости рассматривать другие виды решений.
Упражнение. Предположим, что
т п
i=l j=l
Доказать, что каждая уменьшенная матрица сохраняет это свойство,
так что последней оставшейся переменной можно присвоить значение,
совместное с итогом по единственной строке и единственному столбцу,
остающимся в последней уменьшенной матрице.
Упражнение. Пусть В — квадратная матрица.
Доказать, что В невырожденная тогда и только тогда, когда урав-
нение Вх = Ъ имеет единственное решение при любом Ъ.
Теорема 1. Переменные, выбранные по изложенному правилу в каче-
стве^ исходного решения, образуют базис.
Доказательство. Так как ранг системы равен т + п — 1, набор
переменных xpq образует базис, если их значения, удовлетворяющие
всем т + п уравнениям, однозначно выражаются в виде линейной комби-
нации любых тп + п — 1изтп + гс величин а2, ...» Ъи Ь2, • . Ьп,
а значения остальных переменных равны нулю. Далее, значение, при-
данное каждой базисной цеременной по исходному правилу, совпадает
с суммой по строке или столбцу для некоторой уменьшенной матрицы;
но последняя величина в силу самого своего построения равна разнице
между частичными суммами исходной строки и общими итогами по столб-
цам. Это показывает, что величины однозначно определяются некоторым
конкретным набором т + п — 1 строчных и столбцовых сумм.
298
Однако в силу условия (1) любую из этих величин можно выразить
в виде линейной комбинации остальных, например
т п—1
Ьд = 2 S
г=1 ;=i
Следствие 1. Суммы по строкам каждой уменьшенной матрицы равны
разности частных сумм at и bj, а каждая сумма по столбцам выражается
в виде этой же разности с противоположным знаком.
Упражнение. Доказать это утверждение методом математической
индукции.
СВОЙСТВО ТРЕУГОЛЬНОСТИ БАЗИСА
Если система обладает тем свойством, что любой ее базис является
треугольным (см. § 4-2), то базисные решения получаются очень легко.
Пусть в качестве значений всех небазисных переменных поставлены
некоторые числа, скажем нули. Получающаяся система уравнений будет,
конечно, содержать только базисные переменные. По определению,
если подсистема является треугольной, то она будет содержать хотя бы
одно уравнение, имеющее в точности’ одну переменную. Тогда значение
этой переменной можно сразу же вычислить посредством одного действия
деления. Если определенное таким образом значение подставить в остав-
шиеся уравнения, то в уменьшенной системе мы снова будем иметь хотя бы
одно уравнение в точности с одной переменной и так далее. Таким обра-
зом, можно вычислить все базисные переменные. В частности, так как
каждое уравнение соответствует некоторой строке или столбцу, это
равносильно тому, что все базисные множества переменных можно образо-
вать с помощью исходного правила решения (Данциг [4]).
Теорема 2. (Основная теорема для транспортной задачи.) Все базисы
треугольны.
Доказательство. Пусть имеется стандартная транспортная матрица,
подобная (3), с т строками и п столбцами и с произвольными постоянными
аг и bj. Рассмотрим любой конкретный набор базисных переменных и при-
дадим нулевое значение всем небазисным переменным.
Будем рассуждать от противного. Предположим, что строк или
столбцов, содержащих в точности по одной базисной переменной, не
имеется. Мы не принимаем в расчет того случая, когда в некоторой строке
или в некотором столбце вообще нет базисных переменных, так как это
означало бы, что левая часть соответствующего уравнения равна нулю,
в то время как сумма по строке (столбцу), которую мы считаем произ-
вольной, может нулю и не равняться. Следовательно, при наших предпо-
ложениях все столбцы должны иметь не менее двух базисных переменных.
Если общее количество базисных переменных в таблице равно /с, то,
поскольку в каждом столбце имеется по меньшей мере две такие перемен-
ные, мы должны иметь
2л.
Аналогично
2m,
так как в каждой строке имеется по крайней мере две базисные переменные.
Суммируя, мы получим
(6)
299
Теперь мы имеем т + п уравнений, но так как условие (1) делает одно
из них избыточным, то число базисных переменных к должно удовлетво-
рять также неравенству
А<тп4-п, (7)
что противоречит условию (6).
Таким образом, нами доказана
Лемма 1. Некоторая строка или столбец имеет в точности одну
базисную переменную.
Для того чтобы установить треугольность базиса, мы должны дока-
зать следующее утверждение.
Лемма 2. Подсистема, полученная в результате исключения любого
избыточного уравнения из исходной системы, все еще содержит некоторое
уравнение ровно с одной базисной переменной.
Предположим, что мы исключили некоторое избыточное уравнение
(скажем, уравнение последней строки), и снова будем рассуждать от про-
тивного.
Тогда
&>2п, (8)
2 (т—1),
где к' — общее число базисных переменных во всех строках, за исключе-
нием последней. Однако так как в последней строке имеется хотя бы одно
значение базисной переменной, то мы должны иметь
к к' +1. (9)
Следовательно, складывая оба неравенства (8) и (9), мы имеем
или
2&> 2m2п—1,
к^т-}-п—у ,
(Ю)
что противоречит тому факту, что имеется по крайней мере одно избыточ-
ное уравнение. Тем самым лемма доказана.
Теперь, начиная с исходной матрицы, мы вычеркнем строку или стол-
бец, содержащие единственное базисное значение, и повторим наши рас-
суждения для оставшейся матрицы и т. д., устанавливая тем самым нуж-
ную нам теорему.
Теорема 3. Если все суммы по строкам и по столбцам целочисленны, то
значения всех базисных переменных также будут целочисленными.
Доказательство. Значение каждой базисной переменной равняется
строчной или столбцовой сумме некоторой уменьшенной матрицы, кото-
рая выражается в виде разности между частными суммами исходных
at и bj (см. следствие 1).
СИМПЛЕКС-МНОЖИТЕЛИ
Вместо того чтобы использовать символ щ, будем обозначать множи-
тель для уравнения г-й строки через иг, а для уравнения /-го столбца —
через Vj. Так как любое уравнение можно рассматривать как избыточное,
мы можем задать произвольно значение для одного из симплекс-множи-
телей, а затем вычислять остальные уже однозначно. Это приведет к обраще-
нию в нуль всех относительных оценок, соответствующих базисным пере-
300
менным. В рассматриваемом случае мы предположим, что
Vn = 0. (11)
После умножения уравнения г-й строки (2) на а уравнения у-го
столбца на Vj вычтем эту взвешенную сумму из целевой функции, чтобы
получить видоизмененное 2-уравнение:
2 — 2 Zq, i, i (12)
где [ i — 1, 2, ..m Cij = Ctj— (Ui + Vj) при | n (13)
и z0 = 2 aiui + S bivi- i=l (14)
Значения щ и Vj выбираются так, чтобы обратить в нуль коэффициенты
при базисных переменных, т. е.
Cij^Ui + Vj (15)
для Хи, входящего в базис.
Заметим, что (15) определяет систему уравнений, в которой симплекс-
множители играют роль переменных. Матрица этой системы уравнений
является транспонированной к матрице того базиса, для которого желатель-
но получить симплекс-множители (напомним, что под базисом понимает-
ся матрица коэффициентов при переменных, входящих в базисное мно-
жество (см. § 4-2 и § 8-2)).
Упражнение. Доказать, что щ и Vj можно заменить на (щ + Л)
и (Vj — к), не изменяя значений и z0 в (13) и (14); следовательно, любо-
му из т + п множителей можно при определении остальных придать
произвольное значение.
Теорема 4. Если единичные затраты Сц являются целыми и одному
из множителей придается произвольное целочисленное значение, то все
симплекс-множители также будут целочисленными.
Доказательство. Так как базис треугольный, треугольным будет
и транспонированный к нему базис. Кроме того, транспонированный базис
также имеет ранг т + п — 1. Поэтому значения щ и г?у, удовлетворяю-
щие (15), могут быть получены единственным образом после придания
одному из них произвольного значения, точно таким же образом, как
и значения базисных переменных, т. е. путем обнаружения сначала одного
уравнения с одним неизвестным и т. д. Так как коэффициенты в базисе
равны либо нулю, либо единице, то значениями для щ и Vj будут суммы
и разности Си, соответствующие базисным переменным.
НАХОЖДЕНИЕ УЛУЧШЕННОГО БАЗИСНОГО РЕШЕНИЯ
_ Симплекс-критерий оптимальности сводится к выполнению условия
си 0 для всех (г, /), т. е.
cu>Ui + Vj i = l, 2, ..., т; 7 = 1, 2, ..., п (16)
С другой стороны, если для некоторых s и t
Cst<Us + vt, (17)
301
то новое базисное решение получается путем увеличения значения небазис-
ной переменной xst, если это возможно, и пересчета значений базисных
переменных с тем, чтобы сбалансировать это изменение.
Для определения влияния увеличения xst члены, содержащие xst,
переносятся в правую часть (2), а значения базисных переменных опре-
деляются заново.
Теорема 5. Если значение небазисной переменной xst следует увеличить,
а остальные небазисные переменные остаются нулевыми, то значение любой
базисной переменной xtj изменится от xlj до
хи = Xij ± 8xst, где 6 = 0 или 1. (18)
Доказательство. Если в общем симплекс-алгоритме значение небазис-
ной переменной xs следует увеличить, в то время как другие независимые
переменные остаются нулевыми, то значение г-й базисной переменной
определяется равенством
Xj. = bi UieXs,
где bi получается в результате решения базисной системы уравнений,
когда правая часть f-го уравнения равна bi. Величина ais получается
в результате решения той же системы, когда правая часть равна ais.
В этом случае коэффициент при xst., как указано в (2), равен 1 для $-го
уравнения по строке и для /-го уравнения по столбцу и равен 0 во всех
остальных случаях. Следовательно, коэффициент при xst в канонической
форме получается в результате нахождения значений базисных перемен-
ных, если положить as = l и bt = 1, а все остальные аг- и bj оставить
нулевыми.
В силу следствия 1 значение базисной переменной представляет собой
разность (положительную или отрицательную) между некоторой частич-
ной суммой (которая в этом случае может быть только нулем или еди-
ницей) и некоторой частичной суммой bj (также единичной или нулевой).
Эта разность может быть, очевидно, равной +1,0 либо —1; (18) таким
образом установлено.
ВЫРОЖДЕНИЕ
Если все числа at положительны, то вырожденности в транспортной
задаче можно избежать, рассматривая следующий класс задач с возму-
щениями:
«1
\ (19)
ат-1
«ш + ^е
6f + 8, ^2 + ^? •••» Ьп~\~&
Для конкретности предположим, что уравнение последней строки
было исключено как избыточное. Произвольное базисное решение выби-
рается с помощью процесса, описанного в теореме 1, за исключением того,
что базисные переменные не выбираются в последней строке до тех пор,
пока все другие строки не будут исключены. Если на каком-либо шаге
при 8 = 0 имеется возможность выбора между строчной и столбцовой сум-
мой в уменьшенной матрице, то в качестве минимума выбирается сумма
с меньшим коэффициентом при 8.
2ц *12 • • % in
*21 *22 . . Ж2д
%m-l, 1 %т-1,2 • • • ^т-1, п
%т1 *7712 • • хтп
302
Теорема 6. Наличие неоднозначности при нахождениии минимума,
а следовательно, и вырожденности в базисном решении для последующей
возмущенной задачи невозможно.
Доказательство. Коэффициент при 8 в любой строчной сумме умень-
шенной матрицы равняется нулю или отрицательному числу, так как
он составляется из непустой частичной суммы аг (за исключением ат +
+ пь), из которой вычитается (возможно, нулевая) частичная сумма
bj + 8. Точно так же коэффициент при 8 в любой столбцовой сумме умень-
шенной матрицы является всегда .положительным, так как он составляется
из (непустой) частичной суммы bj + 8 за вычетом (возможно, нулевой)
частичной суммы аг (за исключением ат + пг).
Пересчитанные строчные суммы в каждой уменьшенной матрице
будут всегда оставаться строго положительными при 8 = 0, тогда как столб-
цовые суммы будут неотрицательными. Это легко установить по индукции.
Предположим, что все at положительны, а все bj неотрицательны. Пусть
это справедливо для некоторой уменьшенной матрицы, так что a't =
= а — рг (где а — положительная, ар- неотрицательная величина),
a b'j = р + де (где Р — неотрицательная, a q — положительная величи-
на). Теперь, если становится базисной переменной, то ее значение
равно min [(а — ре), (Р + ^е)]. При а^Р сумма по строке удовлетво-
ряется, а новая сумма по столбцу становится равной (Р — а) + (р + q) 8,
где (Р — а) является величиной неотрицательной, а (р + q) — положи-
тельной. С другой стороны, если р < а, то для 8 из некоторого промежут-
ка 0 С 8 С 80 сумма по столбцу удовлетворяется, а новая сумма по стро-
ке станет равной (а — Р) — (р + Я) где (а Р) и (Р + я) поло-
жительны.
Тем самым устанавливается, что начальное базисное решение являет-
ся невырожденным в некотором положительном интервале изменения 8
в окрестности 8 = 0. Если мы теперь выполним одну итерацию симплекс-
метода, то новое базисное решение будет допустимым в некотором поло-
жительном интервале изменения 8. Так как базис (образованный исклю-
чением последнего уравнения по строке) треугольный, мы получаем путем
повторения такого же рассуждения, как и выше, в качестве значений новых
базисных переменных величины а + 8р, где а либо положительно,
либо равно нулю, а Р - положительное число. Следовательно, новое
базисное решение должно быть невырожденным для некоторого интерва-
ла изменения 8, 0 < 8 < 8Ь а первые два базисных решения остаются
допустимыми и невырожденными при любом 0 С 8 С min (80, 84).
Вообще для любого достаточно малого 8 после каждого цикла будет
иметь место строгое (положительное) уменьшение значения z. Орден [3]
доказал, что ни одно допустимое базисное решение не будет вырожденным,
если 0< 8 С 1/и (см. задачи . 14 и 15). Таким образом, ни один базис
не может повториться и алгоритм завершается через конечное число
шагов.
14-3. ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ ДЛЯ ТРАНСПОРТНОЙ
ЗАДАЧИ
Примечательной чертой рассматриваемой задачи является следующее.
В то время как для решения общих задач линейного программирования
требуются настольные вычислительные машины, а для задач большого
размера — быстродействующая электронная техника, наилучшим сред-
ством решения транспортных задач часто являются такие нехитрые орудия,
303
как карандаш и бумага. Это связано с тем, что единственными необходи-
мыми действиями в данном случае являются сложение и вычитание.
Воспроизведем еще раз для удобства табл. § 14-2-(3). Изображенная
здесь матрица, однако, несколько отличается от первой тем, что в ней
содержатся символы 9. Они входят в вычислительный процесс; их смысл
будет пояснен несколько ниже.
си 9 с12 с13 * с14 + 0* (ввод) с15 <4 Ui
С21 ^22 “Ь 9 с22 с23 ^24—9 с24 с25 а2 w2
С31 с32 хзз с33 а?34 + 0 с34 ж35 — 9 с35 а3 из
V1 &2 ”2 *3 »3 bi Vi Неявные ч- цены t
ПОСТРОЕНИЕ ДОСТАТОЧНО ХОРОШЕГО ИСХОДНОГО РЕШЕНИЯ
С вычислительной точки зрения метод исходного построения, приве-
денный в последнем параграфе, не всегда практически оправдывается,
так как обычно число итераций, необходимых для получения оптимума,
можно значительно сократить, если выбрать базисное решение с учетом
значений коэффициентов целевой функции. Некоторые правила для пост-
роения достаточно хорошего базиса можно найти в литературе. Одно из
них заключается в следующем.
Правило минимальных затрат. В матрице транспортных затрат
(2)
находится наименьшее значение а в качестве первой базисной перемен-
ной выбирается такое xpq, для которого
cpg = mincZj. (3)
з
В качестве xpq выбирается минимум из соответствующих сумм по
строке и по столбцу, а строка или столбец, для которых достигается этот
минимум, уже не используются для дальнейшего увеличения значений
соответствующих переменных; если обе суммы, по строке и по столбцу,
равняются минимуму одновременно, то исключается либо строка, либо
столбец, но не оба одновременно. Для определения последующих значе-
ний находят среди оставшихся «недогруженных» клеток наименьший эле-
мент Си и ставят соответствующее значение Хц9 которое также согласуется
с суммами по строке и по столбцу (и с уже введенными значениями).
М Всего будет заполнено т + п — 1 клеток. Если какая-либо из этих
тп + п — 1 перевозок нулевая, то существенно ввести символ 0, отличая
304
этот нуль, являющийся символом базисной переменной, от нулевого зна-
чения небазисной переменной (которое обозначается отсутствием какого-
либо числового значения). Описанные далее шаги выполняются над началь-
ным решением или над любым последующим базисным решением.
ПРОЦЕСС ВЫЧИСЛЕНИЯ НЕЯВНЫХ ЦЕН (СИМПЛЕКС-МНОЖИТЕЛЕЙ)
Прежде всего, так как одно уравнение является избыточным, можно
придать одной из цен произвольное значение. Достаточно хорошее пра-
вило состоит в нахождении строки или столбца, имеющих максимально
возможное число базисных переменных, и в обозначении соответствующей
ей цены через 0. Остальные иг и Vj затем выбираются из условия
cij — ui — Vj = 0, (4)
если Хи входит в базис. Мы можем определять такие цены, просматривая
клетки, соответствующие базисным переменным, до тех пор, пока не встре-
тится клетка, для которой либо цена строки ui9 либо цена столбца Vj
уже была найдена; вычитая одну из этих цен из мы определяем сле-
дующую цену. Основная теорема о треугольности базиса гарантирует,
что повторение этого процесса приведет к нахождению всех щ и Vj.
Критерий оптимальности. Каждое значение единичных затрат
сравнивается с суммой неявных цен по соответствующим строке и столбцу.
Если все их разности, представляющие собой относительные оценки,
неотрицательны, т. е. если мы имеем для каждой клетки матрицы
Сц = сц— (ui + Vj)>Q, (5)
то данное базисное решение оптимально и задача решена.
УЛУЧШЕНИЕ БАЗИСНОГО РЕШЕНИЯ
Если какая-то из величин отрицательна, то следует ввести в базис
некоторую небазисную переменную xst, заменяя одну из т + п — 1
базисных переменных, которая выводится из базиса и становится небазис-
ной переменной.
Выберем в качестве новой базисной переменной x$t, для которой
c8t — us—vt = min [(см—щ—Vj) < 0]. (6)
г, 3
Символ +0 вводится в клетку (s, t), чтобы показать, какое значение 0
надо придать небазисной переменной xst. Затем, полагая xst = 0, базисные
клетки символически пересчитывают для сохранения баланса; при
этом некоторым клеткам приписывают символ (+0), а некоторым (—0),
оставляя остальные без изменения. В силу треугольности базиса каковы бы
ни были значения небазисных переменных, всегда возможно оценить значе-
ния базисных переменных путем повторного обследования строк и столбцов
в поисках таких, где только одна базисная клетка еще не является опре-
деленной. Эта клетка символически пересчитывается (если это необходимо),
и рассмотрение продолжается до тех пор, пока не будут просмотрены все
клетки.
Символ 0 заменяется наибольшим возможным значением, при кото-
ром все базисные переменные остаются неотрицательными; иначе говоря,
в качестве 0 выбирается наименьшее значение xpq по всем клеткам, снаб-
женным символом (—0), так что — 0 обращается в нуль. Таким обра-
зом, xpq — это именно та переменная, которая выводится из базиса.
20 Дж. Данциг 305
(Если минимум достигается на нескольких переменных х, то для отбра-
сывания выбирается только одна из них; надлежащий выбор может быть
сделан либо случайным образом (см. § 6-1), либо с помощью специальной
процедуры возмущения, описанной в § 14-2-(19).)
Используя определенное таким образом значение 0, снова пересчи-
тываем все базисные клетки и образуем новое базисное решение. После
этого, если есть необходимость, цикл повторяется.
Рассмотрим три примера. Первый из них принадлежит Хичкоку,
второй является примером задачи о назначениях (транспортная задача,
в которой каждое равняется либо нулю, либо единице, в то время, как
все и bj равны 1 (см. гл. 15); третий пример иллюстрирует метод воз-
мущений для предотвращения вырождения.
Таблица 14-3-1
Пример 1 (Хичкок)
Цикл О
Суммы по строкам
10 5 6 25 7 25 —1
8 20—0 2 7 5+0 6 25 —2
15 9 4-0* (ввод) 3 30 4 5—0 (ввод) 8 50 0
15 9 20 4 30 4 35 8 неявные цены t
Суммы по
столбцам
Цикл 1
(оптимальный)
10 5 6 25 7 25 0
8 15 2 7 10 6 25 —1
15 9 5 3 30 4 8 50 0
15 9 20 3 30 4 35 7 неявные цены t
1 Это и есть случай вырождения. Не известно *, возможно ли зацикливание
в транспортной задаче. Простая процедура для преодоления вырожденности иллю-
стрируется в примере 3, она требует лишь ничтожного увеличения необходимого
объема работы.
* См. сноску на стр. 309.— Прим, перев.
306
Таблица 14-3-П
Пример 2 (Задача о назначении 4x4)
Цикл О
Суммы по строкам
Суммы по
столбцам
14 0+0 5 0-0 (вывод) 8 1 5 1 1 1 0
1 2 12 6 7 1 1 1 —1
7 8 1 3 9 1 1 1 —5
0 2 1-0 4 0* (ввод) 6 10 1 1 1
1 3 1 5 1 8 1 5 неявные цены t
Цикл 1 (оптимальный)
14 0 5 8 1 5 1 0
1 2 12 6 7 1 —1
7 8 1 3 9 1 —4
0 2 1 4 0 6 10 1 —1
1 3 1 5 1 7 1 5 неявные цены t
Таблица 14-3-III
Пример 3 (задача с возмущениями)
Цикл О
14 5 8 1 5 1 —5
1—0 2 12 6 +0* (ввод) 7 । 1 1 0
7 8 1 3 9 1 1 —3
е+0 2 1+е 4 8 6 8—0 (вывод) 10 | । 1+4е 0
1+8 2 1+8 4 1+8 6 1+8 10 1 неявные цены t
307
20*
Цикл 1 (оптимальный)
14 5 8 1 5 1 —2
1—8 2 12 6 8 7 1 0
7 8 1 3 9 1 —3
28 2 14-8 4 8 6 10 1+4е 0
‘ +5 2 14-8 4 1+8 6 1+е 7 неявные <- цены t
14-4. ЗАДАЧИ
г п
1. (Повторение.) Доказать, что 2 ai = 2 является необходимым
т=! >=1
и достаточным условием существования допустимого решения в транс-
портной задаче.
2. (Повторение.) Доказать, что в классической транспортной задаче
имеется т + п — 1 независимых уравнений и что любое из исходных
уравнений можно отбросить как избыточное.
3. (Повторение.) Какова двойственная задача к транспортной задаче?
4. (Повторение.) Доказать, что любой базис двойственной транспорт-
ной задачи треугольный.
5. (Повторение.) Доказать, что симплексные цены щ и являются
целочисленными, если целочисленные и взято целочисленным.
6. Доказать, что в регулярной транспортной задаче (ит = 0) зна-
чения неявных цен всегда равны +1, 0 или —1, если все си = 0, за исклю-
чением Сц = 1.
7. Доказать для классической транспортной задачи, что единичные
затраты Сц для любого столбца I можно заменить на сц + сг1 не изме-
няя оптимального решения; точно так же для любой строки k, Ckj можно
заменить на ckj + rk.
8. Доказать, что классическую транспортную задачу, в которой
некоторые (или все) < 0, можно заменить эквивалентной задачей,
в которой все Си > 0.
9. Пусть соответствующие значения в двух строках отличаются
на постоянную; доказать, что эти две строки можно объединить в одну
строку.
10. а) Решить пример 1 (табл. 14-3-1), используя метод возмущений.
б) Решить транспортную задачу, приведенную на рис. 16-1-1.
11. Доказать, что любой минор, составленный из коэффициентов
матрицы транспортной задачи, равен +1, 0 или —1.
12. Решить транспортную задачу из гл. 1.
13. Решить транспортную задачу из гл. 3.
308
14. (Орден [3].) Доказать, что если и bj целочисленные
(i = 1, 2, . . ., т; j = 1, 2, . . ., п) и если заменить на ъ3 + е/„),
а ат на ат + 1, то новая задача никогда не будет вырожденной относи-
тельно базисного допустимого решения и соответствующее решение
исходной задачи всегда допустимо. Как можно использовать это обстоя-
тельство для того, чтобы избежать возможность зацикливания?
15. (Орден [3].) Опираясь на результат задачи 14, доказать, что,
применяя симплекс-алгоритм, можно избежать дробей, если начальное
bj заменить на nbj + 1, а — на nai4 кроме ат, которое заменяется
на пат + п.
16. (Нерешенная.) Может ли вырожденная транспортная задача иметь
цикл?1 * 3 (См. гл. 10.) Если нет, то требуется ли некоторая схема с возму-
щениями, подобная описанной в гл. 10, или же более простая, приведен-
ная в § 14-2-(19) и в задачах 14 и 15?
1 Утвердительный ответ на этот вопрос (применительно к задаче о назначениях)
дан в работе Бетти Гасснер [1], показавшей, что зацикливание невозможно в задачах
3 X 3 и возможно в задачах 4 X 4 и более высоких порядков.— Прим, перее.
Глава 15
ОПТИМАЛЬНОЕ НАЗНАЧЕНИЕ
И ДРУГИЕ РАСПРЕДЕЛИТЕЛЬНЫЕ
ЗАДАЧИ
На первый взгляд может показаться, что транспортная задача, рас-
смотренная в предыдущей главе, решает довольно узкую проблему.
Однако разработанный для нее метод решения можно распространить
на некоторые ситуации, которые на первый взгляд являются различными,
но могут быть представлены в форме, эквивалентной классическому
случаю.
1. Оптимальное назначение
Мы приведем задачу об оптимальном назначении операторов на
работы.
2. Задачи с нарушенным балансом (избытком или недостатком) про-
изводства и потребления
Мы укажем способ решения транспортной задачи, когда предполо-
жение о равенстве балансов по строкам и столбцам нарушено.
3. Фиксированные значения
Мы рассмотрим задачи, которые возникают, когда некоторые пере-
менные должны принимать заранее предписанные значения (например, 0).
15-1. ЗАДАЧА ОБ ОПТИМАЛЬНОМ НАЗНАЧЕНИИ
Слово «назначение» описывает задачу, касающуюся, в частности,
нахождения наилучшего способа назначения п лиц на п работ в предполо-
жении, что эти лица различаются по своим способностям выполнять ту
или иную работу. Предполагается также, что с помощью определенных
тестов можно определить в некотором смысле «ценность» от назначения
i-ro лица на J-ю работу. Значение этой величины, взятое с обратным знаком
(т. е. единичные затраты), будет обозначаться через с^. Предполагается,
что для каждого i г-е лицо будет назначаться на работу мы предпола-
гаем, что общие затраты z при таком назначении персонала будут рав-
няться сумме индивидуальных затрат, т. е.
п
Z — 2 С|р..
Числа pt, р2, . . Рп, образуют перестановку чисел 1,2,.. п; следо-
вательно, задача об оптимальном назначении заключается в нахождении
минимизирующей перестановки.
Поставленная в такой форме задача, очевидно, является комбинатор-
ной. Имеется п способов выбора р4, (п — 1) остается для выбора Р2» • • • ;
таким образом, всего имеется
п! = (тг) (тг—1) (п—2) ... (2) (1)
310
различных возможностей. При п = 6, п\ = 720 и после вычисления зат-
рат по всем 720 допустимым назначениям можно найти наименьшее z.
Но это число возможных перестановок растет чрезвычайно быстро. Напри-
мер, 12! 4,79 X 108. Решать задачу о назначениях даже 12 X 12
путем непосредственного отыскания всех перестановок вряд ли разумно
даже на современных вычислительных машинах. Однако эту задачу
можно преобразовать в транспортную размером 12 X 12, которую с помо-
щью описанного ранее алгоритма можно решить вручную за несколько
минут.
С этой целью положим
(1, если г-е лицо назначается на у-ю работу,
0—в противном случае.
Так как (по предположению) каждое лицо можно назначать только
на одну работу, мы имеем
п
2Жу = 1, (j = l, 2, ri) (2)
j=l
и так как каждая работа предназначается только для одного лица, должно
быть
2^ = 1. (7 = 1, 2, .... п) (3)
г=1
Квадратные матрицы с неотрицательными элементами обладающими
тем свойством, что сумма элементов по всем строкам и столбцам равна 1,
часто встречаются в статистической теории. Они называются бистохасти-
ческими матрицами, а х^ интерпретируются как вероятности (не обя-
зательно нулевые или равные единице). Если в таких матрицах все х^
равны 0 или 1, то они называются перестановочными матрицами.
Цель в задаче о назначениях заключается в выборе х^, удовлетво-
ряющих (1), (2) и (3), с тем чтобы общие затраты
п п п
2=2 = 2 2 (4)
i=l 1=1
были минимальными.
Условие (1), однако, препятствует непосредственному применению
методов линейного программирования к этой формулировке. Условия
такого типа сами по себе могут сделать задачу очень трудной для решения.
Условие типа х^ = 0 или 1 приписывает х^ несвязный промежуток, соста-
вленный из дискретных значений, как это изображено в (5):
В качестве другого примера несвязного промежутка, который может
вывести задачу из области, непосредственно подвластной методам линей-
ного программирования, можно привести условие „х^ = 0 или 1 < xtj 2”
изображенное в (6).
0
ХЧ
(6)
В гл. 26 мы изложим общие методы подхода к подобным условиям,
которые порождают переменные с несвязными или дискретными областями
изменения.
311
Вместо сформулированной выше задачи о назначениях мы покажем,
что можно получить эквивалентную транспортную задачу простой заме-
ной условия (1) на условие
0<х... (7)
Г. Биркгоф [1] доказал, что множество матриц перестановок описы-
вается крайними точками выпуклой оболочки множества неотрицательных
бистохастических матриц. Иначе говоря, имеет место следующий ре-
зультат.
Теорема 1. Оптимальное решение задачи о назначениях (1), (2), (3)
и (4) совпадает с оптимальным решением задачи линейного программиро-
вания (2), (3), (4) и (7).
Доказательство. Любое допустимое базисное решение обладает тем
свойством, что значения х^ равны нулю или единице. В самом деле, тео-
рема 3 § 14-2 утверждает, что если все суммы по строкам или по столбцам
целые, то целочисленными будут и значения базисных переменных,
а из (7) и (2) или (7) и (3) следует, что единственными допустимыми целы-
ми значениями для х^ могут быть нуль или единица. Отсюда вытекает,
что оптимальное базисное допустимое решение будет перестановкой. Так
как все решения-перестановки удовлетворяют условиям (2), (3), (4) и (7)
и так как минимальное решение также является некоторой перестановкой,
оно должно также быть минимальным решением для исходной задачи
о назначениях. Фон Нейман [5] доказал теорему Биркгофа путем све-
дения задачи о назначениях к одной интересной матричной игре. См. также
работу Маркуса [1].
ВЫРОЖДЕНИЕ
Вырождение, определенное нами выше, наступает всякий раз, когда
одна или более базисных переменных равны нулю. Задача линейного
программирования, эквивалентная задаче о назначении, имеет ту осо-
бенность, что любое ее базисное решение является вырожденным, так как
только п базисных переменных могут быть равны единице, а значения
всех остальных п — 1 базисных переменных должны быть равными нулю.
Если число базисных переменных с нулевым значением взять в качестве
мерила для «степени» вырожденности, то эквивалёнтная задача линей-
ного программирования оказывается сильно вырожденной. Как указыва-
лось раньше, не известно, может ли случиться зацикливание 1 в транс-
портных задачах (см. гл. 10).
Когда вследствие вырожденности на практике имеется неясность,
какую базисную переменную надо выбросить, Применяются различные
процедуры. Наиболее простое правило состоит в том, чтобы выбрать пере-
менную xrs, для которой соответствующее crs является максимальным.
Специальный 8-метод, приведенный в § 14-2-(19) для борьбы с вырождени-
ем в транспортных задачах, требует лишь ничтожного объема допол-
нительной работы и может использоваться всякий раз, когда необходимо
застраховаться от возможности зацикливания. Другим методом, гаранти-
рующим успех с вероятностью единица, является преодоление вырожден-
ности с помощью случайного выбора (см. § 6-1).
1 См. сноску на стр. 309.— Прим, перев.
312
ЭКВИВАЛЕНТНОСТЬ ТРАНСПОРТНОЙ ЗАДАЧИ И ЗАДАЧИ
О НАЗНАЧЕНИЯХ
Мы уже видели, что задача о назначениях является лишь частным
случаем транспортной задачи. Сейчас мы покажем, что с надлежащими
изменениями и транспортная задача в свою очередь является частным слу-
чаем задачи о назначениях, так что обе задачи вполне эквивалентны друг
ДРУГУ- Предположим, что at и bj являются целыми числами; если они
являются рациональными, то путем соответствующего изменения масшта-
ба их можно сразу заменить на целые. Если же они иррациональны, то
их можно аппроксимировать рациональными числами, а затем заменить
целыми.
Конструктивное доказательство будет проведено на примере. Рас-
смотрим транспортную задачу, заданную матрицей (8).
«11 cu=10 *12 с12=5 *13 С13 —6 *14 С14=7 2=at
*21 c2i —8 *22 с22==2 *23 с23= 7 *24 С24 = 6 Зт=а2
*31 с31 = 9 *32 с32 = ^ *33 с3з —4 «34 с34=8 1=а3
2 = 1=62 1=г»3 2 —&4
(8>
Уравнение по первой строке
Х11 + #12 + ж13 + ж14 — 2
заменяется двумя уравнениями (так как а± = 2).
*Гц 4“ *^12 + ^13 4“ •Гц = 1 >
^14-^24~^з4-^4 = 1-
Уравнение по второй строке
^21 4“ Х22 4- ^23 4- *^24 — 3
точно так же заменяется тремя уравнениями (так как а2 = 3)
*^21 4“ Х22 4~ *^23 4“ *^24 = ’
#21 4" #22 4“ ж23 4" #24 ~ 1 ’
#21 + Ж22 4“ #23 4" #24 = 1 *
Так как а3 = 1, третье уравнение по строкам остается неизменным.
В результате получается эквивалентная транспортная задача, в которой
все суммы по строкам равны единице (см. (9)).
313
#11 С11 —19 #Ь 5 #13 6 #14 7 1 = а[
#11 c;'1=io #12 5 #1з 6 #14 7
#21 8 #22 2 #23 7 #24 6 i=«2
#21 8 #22 2 #23 7 #24 6 1=4
#21 8 #22 2 #28 7 #24 6 1=а"
#31 9 #32 3 #33 4 #34 8 i = a3
2 1 1 2
(9)
В этой таблице = 10 заменяется на (с'ц = 10 и — 10) и т. д. Любое
решение задачи (9) порождает решение задачи (8) после замены:
#н4~#и = #11 #21 4- #21 4- #21 = *21
#12 4“ #12 = #12 #22 4“ #22 4“ #22 = *22
#13 4“ #13 = #13 #23 4“ #23 4" #23 — *23
#14 4- #14 = #14 •Г24 4- #24 4- #24 = *24
Вследствие линейности этих зависимостей и равенства соответствую-
щих коэффициентов затрат в (9) ясно, что точно такие же значения z
получаются для (8). Кроме того, если исходная задача имеет решение,
то решение (9) можно получить распределением хц между строками произ-
вольным способом при условии, что суммы по строкам будут равняться
единице. Например, значение xtj в первой строке в (8) можно поделить
поровну между двумя соответствующими строками в (9); значения для
второй строки можно разделить на три равные части. Получается одно
и то же значение z. Из этих соображений следует, что минимизирующее
решение первой задачи соответствует минимизирующему решению второй,
и наоборот.
Следовательно, эти две задачи эквивалентны.
Однако до сих пор видоизменялись только уравнения по строкам
в (9). Чтобы получить соответствующую задачу о назначениях, необходимо
точно таким же образом видоизменить и уравнения по столбцам. В резуль-
314
тате получается приведенная ниже матрица назначений, где через уц
обозначены новые переменные.
Уи 10 2/12 10 2/13 5 2/14 6 2/15 7 2/16 7 1
2/21 10 У 22 10 2/23 5 2/24 6 2/25 7 2/26 7 1
Уз1 8 У32 8 2/зз 2 2/34 7 2/35 6 2/36 6 1
Уы 8 УЬ2 8 2/43 2 2/44 7 2/45 6 2/46 6 1
Уб1 8 УЬ2 8 2/53 2 2/54 7 2/55 6 2/56 6 1
У 61 9 Уб2 9 2/бз 3 2/64 4 2/65 8 2/бб 8 1
1 1 1 1 1 1
(Ю)
НЕКОТОРЫЕ ТИПИЧНЫЕ ПРИМЕНЕНИЯ МОДЕЛИ О НАЗНАЧЕНИИ
Переналадка машин (см. задачу 1). Имеется п работ, которые пред-
назначаются для выполнения на п различных машинах. Каждая машина,
прежде чем приступить К выполнению конкретной работы, должна под-
вергнуться переналадке.
В качестве затрат рассматривается время на выполнение работ,
а общие затраты равны сумме затраченных человеко-часов. Время, потреб-
ное для переналадки машины, зависит от той работы, которую машина
выполняла перед этим; если выполнялся один и тот же вид работы,
то нет необходимости переналаживать машину, или если исполь-
зуется одно и то же сырье, то нет необходимости удалять остатки
сырья и т. д.
Игра бракосочетания (см. задачу 2). Колония поселенцев, состоящая
из 10 холостяков, пополняется десятью потенциальными невестами.
После короткого периода ухаживания молодые люди решают немедленно
сочетаться браком. Каждая невеста получает список из 10 имен, в кото-
ром она должна оценить свои предпочтения по десятибалльной системе,
т. е. она может обозначить свой первый выбор числом 10, свой второй
выбор числом 9 и т. д. Она может также вычеркивать неприемлемые для
нее имена.
Предположим, что сумма всех проставленных чисел представляет
адекватную меру предвкушаемого «счастья» всей колонии (Халмош
и Воан [1]).
Оставляя этот пример читателю, позабавим его следующей историей.
315
Летом 1955 г. на конференции Общества исследования операций
в Лос-Анжелесе я давал интервью прессе. Репортер оказался братом
учителя музыки моей младшей дочери, так что, установив это, мы быстро
нашли общий язык. Я объяснил ему, что модели линейного программи-
рования впервые возникли в военно-воздушных силах, а затем описал
их проникновение в задачи из области промышленности. Мне сразу стало
ясно, что этот старый голливудский газетный волк тщетно пытается облечь
весь материал в приемлемую для прессы увлекательную форму. «Может
быть, что-нибудь насчет секса?»— в отчаянии предложил я. «Ну-ну,
давайте»,— оживился он. «Так вот,— продолжал я, — интересным резуль-
татом нашей работы над моделями линейного программирования является
математическое доказательство того, что из всех допустимых форм брака
(моногамия, бигамия, полигамия и т. д.) наилучшей является монога-
мия». «Вы утверждаете, что моногамия является самой совершенной фор-
мой отношений?»— переспросил он. «Да»,— подтвердил я. «Эх, парень,—
сказал он, укоризненно качая головой,— вы работаете не над теми моде-
лями».
15-2. ЗАДАЧИ С НАРУШЕННЫМ БАЛАНСОМ
Часто оказывается возможным отождествлять одну систему итогов,
скажем с объемами производства, a bj — с ’объемами потребления.
Однако в некоторых приложениях удовлетворение всех потребностей
или исчерпание всех запасов может оказаться невозможным (или невыгод-
ным). В этих случаях таблица принимает вид (1), где > 2
г з
Пункты производства i Пункты потребления з 1 2 ... п Суммы по строкам
1 2 т Х11 xi2 • • • х1п Х21 х22 • • • х2п xmi хт2 • • • хтп А- АА & • & &
Суммарные потребности по столбцам । bj ь2 ... ьп
(1)
где знаки неравенства показывают, что строчные и столбцовые суммы не
превосходят соответствующих значений и bj.
Пусть xi0 обозначает избыток f-ro пункта производства, xOj —
недостаток у-г о пункта потребления, а я00 — общий объем перевозок
из всех пунктов производства во все пункты потребления
т п
^00 = 3 S &11* (2)
i=l j=l
Избыток по столбцу и недостаток по строке компенсируется введе-
нием свободных переменных xiQ и xQj так, что матрица (1) принимает
вид (3).
316
Излишек по столбцу Пункты потребления Суммы по строкам
Недостаток по строке *00 *01 • • • хоп п 1
Пункты про- изводства *10 хто *11 • • • х1п Хт1 • • • хтп =«1 ~ат
Сумма по столбцам т ^ai 1 • bi ...
(3)
Это стандартная транспортная матрица, так как из самого способа опре-
деления переменных ясно, что
т т п п т п
3 “ S bj ^Oj = S 2 3'ij — 3'00> (4)
i=l i=l j=l j=l i=l j=l
Таким образом, мы привели (1) к стандартной форме; однако следует
отметить, что при отсутствии штрафа, связанного с отказом от поставки
необходимых количеств грузов, задачи фактически нет: просто не следует
ничего перевозить. Содержательная задача возникает тогда, когда отказ
от перевозки приводит к потере доходов или расположения клиента,
т. е. когда избытку или недостатку приписаны положительные затраты
CjO ИЛИ ‘Cqj*
Случай избытка. В случае, когда производство превышает спрос
(т. е. 2 at > 2 ЬД но спрос должен быть в точности удовлетворен,
i 3
матрица принимает форму (5).
Избыток по столбцу Пункты потребления Суммы по строкам
Пункты про- изводства *10 *20 *7П0 *11 *12 • • • *171 *21 *22 • • • *2тг Хт1 *тп2 • • • хтп II II . II
Общие по- требности по столбцу м 1 II м о Й II II II
(5)
Случай недостатка. В случае, когда спрос превышает производство
(т. е. 2 bj > 2 at), но весь имеющийся запас должен быть распределен,
транспортная матрица принимает вид (6).
317
Пункты потребления Суммы по строкам
Недостаток по строке *01 *02 • ♦ • x0n II M e?
Пункты произ- водства *11 xml *12 • - *m2 • • - • xin • xmn = «i — am
Суммы потреб- ностей по столбцам ' bl d2 • II
(6>
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
После введения свободных переменных xiQ и задачу с нарушенным
балансом можно представить в виде (7).
*01 *02 • • • *0n
*10 *11 *12 • • • *ln I = «1
*ml xm2 xmn — am

• 1
bl &2 • • • 1
(7>
Всё т + п уравнений здесь являются независимыми в противополож-
ность классической транспортной задаче, в которой независимыми являют-
ся только т + п — 1 уравнений. Например, легко видеть, что свободные
переменные образуют базисное множество из т + п переменных.
Кроме того, каждый базис является треугольным. Поступая, как
в ранее приведенном доказательстве треугольности базиса в транспортных
задачах, обозначим через / число базисных переменных среди переменных
«избытка» xiQ, через g — среди переменных «недостатка» xQj и через h —
среди основных переменных, так что

(8)
Теорема 1. Всякий базис содержит хотя бы одну свободную перемен-
ную, т.%е.
Доказательство. Если какой-то базис не содержит свободной пере-
менной, то он будет служить базисом и для аналогичной транспортной
задачи без свободных переменных. Это может случиться только в случае
2 аг- = 2 bj; известно, однако, что в этом случае число базисных пере-
менных не может превосходить т + п — 1.
Отсюда мы заключаем, что

(9>
Теорема 2. Любой базис является треугольным.
318
Доказательство. Если это не так, то каждая строка (за исключением
строки недостатков) и каждый столбец (за исключением столбца избытков}
имеют по две или более базисных переменных. Таким образом,
2m^h + f,
2п < h + g,
так что
n + zn<* + y(/ + g).
(10)-
(11)
Так как в силу (9), сумма / + g положительна, из (11) следует строгое
неравенство
n + m<.h + f + g, (12)
противоречащее (8).
Таким образом, предположение о том, что все основные строки и столб-
цы содержат по крайней мере по две базисные переменные, неверно;
поэтому хотя бы один из них должен содержать в точности одну перемен-
ную. Вычеркивая такую строку или столбец и пересчитывая надлежащим
образом суммы, мы можем повторить предыдущие рассуждения для полу-
ченной таким путем уменьшенной системы. Доказательство теоремы 2
завершается по индукции.
ОЦЕНКИ
Если щ и Vj являются симплекс-множителями (или «ценами») для
соответствующей строки i и столбца у, то соответствующие относитель-
ные оценки равны
= — (Ui+Vj)
c0j — c0j Vj
CiO = CiO Ui
при г #= 0, у #= 0,
при у 0,
при i 0.
(13)
Надо заметить, что нет необходимости определять оценки для свобод-
ных переменных и0 и г?0, так как уравнений, относящихся к нулевой
строке или к нулевому столбцу, нет. Для единообразия, однако, удобно
положить фиктивные цены
Uq = v0 = Q. (14)
Теперь можно охарактеризовать выбор цен как выбор таких ut и Vj,
что если Хц является базисной переменной, то
Ui + Vj = Cij. (15)
ОПТИМАЛЬНОЕ ПРИКРЕПЛЕНИЕ ПРИЕМНЫХ УСТРОЙСТВ
К ПЕРЕДАЮЩИМ
(Пример распределения с нарушением баланса)
$ Некоторое контрольно-испытательное устройство использует четыре
вида приборов: 200 термопар, 50 манометров, 50 акселерометров и 40 из-
мерителей тяги Каждый из них измеряет один тип характеристики
и передает данные о них по отдельному каналу связи. Имеется, далее,
4 типа приемных устройств, каждый из которых может регистрировать
один канал информации: 200 фотоаппаратов, 150 осциллоскопов, 256 само-
1 Например, реактивного двигателя.— Прим. ред.
319
писцев и 50 индикаторов. Время на монтаж канала зависит от типа прибо-
ров, а также от характера регистрируемых данных. Предполагается, что
все данные должны быть зарегистрированы. Задача состоит в том, чтобы
найти такое прикрепление приемных устройств к передающим, при кото-
ром достигается минимум общих затрат времени на монтаж.
Измерительные инструменты 1 J II Наличие общих регистри- рующих каналов
Регистрирующий инструмент г темпе- ратура 1 давление 2 ускоре- ние 3 тяга 4
Фотоаппараты 1 1 *12 3 *13 оо *14 1 <200
Осциллоскопы 2 *21 0,5 *22 0,5 *23 0,5 *24 0,5 <150
Самописцы 3 *31 2 *32 2 *33 10 *34 2 <256
Индикаторы 4 *41 1,5 *42 1,5 *43 1,5 *44 1,5 <50
Наличие кана- лов, подлежа- щих регистра- ции 200 50 50 40 1
Число Си, стоящее внизу справа в клетке (г, /), представляет собой
затраты, или время на монтаж при прикреплении f-ro канала для регист-
рации к у-му измерительному каналу.
Условие с13 = оо означает, что фотоаппарат не используется для
регистрации ускорений. С точки зрения вычислительного процесса клетка
(1, 3) при построении исходного решения по возможности избегается;
если она не использовалась в исходном решении, то в дальнейшем она
не может служить кандидатом в базисное множество (по поводу дальней-
ших деталей, связанных с запрещенными клетками, смотри § 15-3). Цель
заключается в выборе неотрицательных минимизирующих
т п
2 3 (17)
г=1 j—1
Если ввести свободные переменные, указывающие число неисполь-
зуемых регистрирующих каналов, то мы получим транспортную матри-
цу (18).
Сумма по столбцу избытков равна разности между числом имеющихся
каналов и числом необходимых каналов, т. е.
(200 +150 + 256 + 50) - (200 + 50 + 50 + 40) - 316.
Все затраты в этом столбце с10 равны нулю, так как неиспользование
канала не связано с затратами на монтаж.
. 320
Измерительные инструменты
Регистри-
рующий
инструмент
Избыток
О
темпера-
тура
1
давление
2
ускоре-
ние
3
тяга
4
ui
190
1
200
0,5
10
0,5
50 50 40
0,5 0,5 0,5
150
О
(18)
256
0,5
50
О
50
0,5
Приведенное в таблице базисное решение построено с помощью рас-
смотренного ранее в этом параграфе правила построения достаточно хоро-
шего исходного решения. Если минимум достигается одновременно на не-
скольких Си, то выбираются клетки, которые приводят к вычеркиванию
строк или столбцов, имеющих большие значения Например, так как
затраты на монтаж при регистрации большинства сообщений выше всего
для приборов третьей и четвертой строк, избыток распределяется сначала
в этих строках. Остаются строки 1 и 2 и столбцы 1, 2, 3 и 4. Так как для
этих столбцов затраты во второй строке выше соответствующих затрат
в первой строке, следующий избыток распределяется в строку 1. Осталь-
ные распределения осуществляются по приведенному ранее правилу.
Вычислив неявные цены, можно легко установить, что это базисное
решение является оптимальным.
Когда имеет место нехватка регистрирующих приборов (или имеются
приборы, малопригодные для этой цели), следует принять решение о том,
какое количество данных каждого типа не регистрировать. Рассмотрим
следующие единичные затраты, которые из технических соображений
установлены для строки недостатков и столбца избытков:
Coi=lO, Со2=1О, Соз = 4, С04=Ю0,
Сю = 0, с2о ——1, с зо — 0, С40 — 0, cqo = O.
Например, пренебрежение данными о тяге (с04=100) обходится в 25 раз до-
роже, чем пренебрежение данными об ускорении (с03=4). В общем, однако,
регистрация данных приводит к меньшим затратам, чем пренебрежение ими.
Отрицательное значение с2о свидетельствует о том, что неиспользуе-
мые осциллоскопы можно с выгодой использовать на стороне; насколько
это выгодно, определить часто бывает трудно. Как отмечалось в § 14-4
(задача 7), оптимальное решение не изменится, если все в некоторой
строке или в некотором столбце эквивалентной транспортной задачи уве-
личить на постоянную. Таким образом, при экспериментальном выяснении
21 Дж. Данциг 321
влияния изменений целесообразно фиксировать хотя бы один показа-
тель затрат в одной из строк и в Некотором столбце.
Эту задачу можно превратить в стандартную транспортную матрицу
(19) со строкой недостатков и столбцом избытков. С другой стороны, ее
Регистри- рующий инструмент г Избыток 0 Измерительные инструменты ai ui
темпера- тура 1 давление 2 ускорение 3 тяга 4
Недостаток 0 340 0 10 10 4 100 340 0,5
1 10 0 190 1 3 сю 1 200 0,5
2 —1 10 0,5 50 0,5 50 0,5 40 0,5 150 0
3 256 0 2 2 10 2 256 0,5
4 50 0 1,5 1,5 1,5 1,5 50 0,5 »
656 —0,5 200 0,5 50 0,5 50 0,5 40 0,5
(19)
Этап II —цикл О
10 10 4 100
10—0 0 190+0 1 3 сю 1 200 ^0
0* —1 10—0 0,5 50 0,5 50 0,5 40 0,5 150 +-0,5
256 0 2 2 10 2 256 & 0
50 0 1,5 1,5 1,5 1,5 50 0
200 1 50 1 50 1 40 1
322
можно представить в виде (7). С вычислительной точки зрения оба метода
являются почти тождественными; в этом легко убедиться при вниматель-
ном анализе (20) и (21).
Этап II —цикл 1
(оптимальный)
10 10 100
200 1 3 оо 1
0 0,5 50 0,5 50 0,5 40 0,5
2 2 10 2
1,5 1,5 1,5 1,5
200 1,5 50 1,5 50 1,5 40 1,5
15-3. ФИКСИРОВАННЫЕ ЗНАЧЕНИЯ И ЗАПРЕЩЕННЫЕ
КЛЕТКИ
(21)
При решении транспортных задач довольно часто случается, что неко-
торые переменные должны принимать заранее предписанные значения.
В предыдущем параграфе, например, было невозможно назначить фото-
аппараты для регистрации данных об ускорениях, так что я13 должен
был равняться нулю. Точно так же, если не существует пути от некоторого
пункта производства i до пункта потребления / на сети, то переменная
Хи должна быть равна нулю. В задаче о распределении специалистов
по видам работ некоторые назначения не могут быть произведены (напри-
мер, назначение физика на медицинскую должность). Заметим при этом,
что фиксированную переменную всегда можно заменить переменной
с заранее предписанным нулевым значением путем вычитания ее пред-
писанного значения из соответствующих сумм по строке и по столбцу.
Будем называть клетки, связанные с нулевыми переменными, запрещен-
ными, и заштриховывать такие клетки, когда они появляются в таблице.
Если заштриховано лишь несколько клеток, то наилучший практи-
ческий прием будет заключаться в построении исходного допустимого
базисного решения с помощью правила наименьших затрат, описанного
ранее в § 14-3-(3); однако во многих задачах запрещенных клеток можно
избежать лишь ценой выбора таких базисных переменных, которые имеют
большие значения единичных затрат, чем предписывается этим правилом.
Кроме того, если заштриховано очень много клеток, то задача может либо
вообще не иметь решения, либо не иметь видимого с первого взгляда базис-
ного допустимого решения, использующего только разрешенные клетки.
Если избежание запрещенных клеток оказывается невозможным,
то их можно использовать в качестве искусственных переменных первого
этапа симплекс-метода, в котором строится — если это вообще возможно —
базисное допустимое решение. Для этой цели используется так называе-
ма
21*
мая форма недопустимости.
, т п
w =2 2 в которой элементы матрицы си заменены на
i=i j=i
г 1, если клетка (г, /) запрещена,
lJ I 0, если клетка (/, /) допустима.
Если допустимое решение существует, то min w = 0, но если min w —
положительный, то задача недопустима.
Даже если задача имеет допустимое решение, то может случиться,
что в конце первого этапа некоторые запрещенные клетки останутся в бази-
се. Если это так, то их значения будут нулевыми и останутся таковыми
в дальнейших вычислениях. Перед началом этапа II любое небазисное
выбрасывается из дальнейшего рассмотрения, если его относительная
оценка недопустимости положительна, т. е. если
df j щ v j 0,
где Ut и — оценки, соответствующие форме недопустимости в койце
первого этапа.
7 = Ьг 5=Ь3 17=Ь4
Этап I — цикл 0
Начальное решение
(сц заменяется на dy)
(2)
324
Пример. Найти оптимальное допустимое решение в транспортной
задаче (1) (см. стр. 324). Алгоритм начинается с любого базисного реше-
ния, например показанного в (2). Последняя матрица имеет две запре-
щенные базисные переменные я42, х34, обведенные жирной рамкой.
(3)
Этап II — цикл 1 (Оптимальный)
(dy заменяется на су)
Замечание. На этапе II я13 выбрасывается, так как d13 > О
в конце первого этапа. Величина с42 для искусственной переменной про-
извольна, например с42 = 0.
15-4. ЗАДАЧИ
1. Определить оптимальное назначение 12 работ на 12 машинах,
если время необходимое для выполнения i-й работы на у-й машине,
приводится в 1-й таблице на стр. 326 (см. § 15-1).
2. Определить назначение, которое обеспечивает максимум суммар-
ного «счастья», где оценка у-го жениха i-й невестой приводится во 2-й
таблице на стр. 326 (Халмош и Воан [1]). (См. § 15-1).
325
Задача о распределении работ по машиной
Маши- ны Работы
(1) (2) (3) (4) (5) (6) (7) (8) (9) (Ю) (И) (12)
1 79 24 13 53 47 66 85 17 92 47 46 13
2 43 59 33 95 55 97 34 55 84 94 26 56
3 29 52 26 27 13 33 70 11 71 86 6 76
4 88 83 64 72 90 67 27 47 83 62 35 38
5 65 90 56 62 53 91 48 23 6 89 49 33
6 44 79 86 93 71 7 86 59 17 56 45 59
7 35 51 9 91 39 32 3 12 79 25 79 81
8 50 12 59 32 23 64 20 94 97 14 И 97
9 25 17 39 0 38 63 87 14 4 18 И 45
10 68 45 99 0 94 44 99 59 37 18 38 74
И 93 36 91 30 44 69 68 67 81 62 66 37
12 19 36 5 50 49 94 95 17 63 41 84 1
Задача о бракосочетании
Билл Джон Эгберт Катберт о й ч Гастон Чэнси Клайд Ньют 1 Уолдо
Джейн 9 6 3 X 2 8 7 4 1 5
Мэри 3 7 8 2 1 X 5 4 X 6
Клу 4 2 1 6 X 8 3 9 7 5
Бьюла 6 3 5 7 9 X 1 4 2 8
Фиби 7 5 6 9 1 8 3 X 2 4
Октавия 1 10 8 4 5 3 6 9 2 7
Джулия 6 8 10 9 4 3 5 1 7 2
Миртл 7 8 4 3 2 6 1 9 5 X
Ольга 3 9 4 2 5 6 7 X 8 1
Мэйбл 9 3 1 8 X 4 2 7 6 5
Замечание. В соответствии с описанием в тексте каждой невесте
дается список из 10 имен, в котором она должна оценить свои пред-
почтения по десятибалльной системе, т. е. своему первому избраннику она
может приписать 10, второму — 9 и т. д. Она может также вычеркивать
имена, неприемлемые для нее. Таким образом, закономерно предполо-
жить, что все невесты своему первому избраннику припишут число (10),
хотя в приведенной задаче это не так. Если невеста вычеркивает одно
имя, то своему первому избраннику она приписывает уже не 10, а 9,
если она вычеркивает два имени, то первому избраннику приписывается
число 8 и т. д. Будет ли это та же задача?
3. Доказать, что во втором методе из § 15-2 т + п множителей иг
и Vj определяются единственным образом т + п уравнениями (14) и (15).
4. (Повторение.) Показать, что система уравнений (14), (15) из § 15-2
имеет треугольную форму.
5. В § 15-2 показать, что щ и Vj являются целыми числами, если
сц — целые.
6. В транспортной задаче, где одна из оценок положена равной нулю,
скажем ит = 0, или в задаче с нарушенным балансом, приведенной
326
в § 15-2, доказать, что если все затраты равны нулю, за исключением
одной, которая равна 1, то оценки всегда равны +1, 0 или —1.
7. Почему выбрасывается я13 из первого цикла II этапа в примере
из § 15-3 (см. правила перехода от этапа I к этапу II в симплекс-методе
в § 15-2)?
8. а) Показать, что дополнительная строка (или столбец) свободных
переменных с произвольными единичными затратами могут вводиться
в классическую транспортную задачу без изменения оптимального решения.
б) Показать также, что решение не изменится, если вводятся как
дополнительная строка избытков, так и дополнительный столбец свободных
переменных с произвольными затратами.
в) Показать, что при такой форме в системе нет лишних уравнений или
оценок с произвольными значениями, относящихся к базисному решению.
Глава 16
ЗАДАЧА О ПЕРЕВОЗЕ АХ
С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ
16-1. ФОРМУЛИРОВКА МОДЕЛИ
В транспортной задаче Хичкока перевозки осуществляются из пунк-
тов, производящих товары (пунктов производства), только к пунктам,
потребляющим эти товары (пунктам потребления): перевозки между пунк-
тами производства или между пунктами потребления, а также от пунктов
потребления к пунктам производства в ней не рассматриваются. Однако
в то время, как в модели Хичкока фигурируют только перевозки от пунк-
та производства к конечному пункту потребления, на практике перевозки
могут фактически осуществляться и через несколько промежуточных
пунктов.
При этом молчаливо предполагается, что перевозки между любыми
двумя пунктами всегда осуществляются по самым дешевым маршрутам,
где величина затрат может выражать время, расстояние или затраты.
Но это молчаливое предположение о кратчайшем пути не всегда вы-
полнимо, так как в некоторых случаях объем допустимой перевозки
на участке между двумя пунктами должен быть ограниченным. Другое
обстоятельство заключается в том, что определение кратчайших путей
от каждого из пунктов производства к каждому пункту потребления,
как того требует формулировка Хичкока, может само по себе оказаться
весьма утомительным делом. Желательно найти такой алгоритм, который
будет вырабатывать эту информацию автоматически.
А. Орден [3] предложил обобщенную транспортную модель,
в которой допускаются перевозки через промежуточные пункты. В этой
модели для каждого пункта составляется уравнение материального балан-
са, выражающее, что объем вывезенного груза минус количество завезенно-
го груза равен чистому объему груза, произведенного в этом пункте
(если разность положительна), или чистому объему потребляемого в нем
груза (если разность отрицательна).
Перейдем поэтому к рассмотрению обобщенной транспортной модели,
в которой допускаются перевозки через промежуточные пункты. Для
каждого пункта мы будем иметь уравнение материального баланса сле-
дующего вида:
Суммарный объем перевозок =
= ввозу + производству =
= вывозу + потреблению,
или, в виде уравнения:
= + = (j = l, 2, .... п), (1>
где
xij — общий объем перевозки из I в j для i
х*зз — суммарный объем поставки в /,
328
a* — производство в пункте J,
Ь* — потребление в пункте у\
Если местное производство для внутреннего потребления исключено
из модели, так что либо а*, либо Ь* обращается в нуль, то мы будем
использовать символы а7- и bj без звездочек. В общем случае чистое про-
изводство aj и потребление bj выражаются через а* и Ь* следующим
образом:
а7 = а*—min(a*, #),
bj = b*—min (а*, Ь*)
Мы будем называть aj и bj чистыми объемами производства и потреб-
ления.
Задача о перевозках с промежуточными пунктами заключается
в нахождении > 0 и min z, удовлетворяющих уравнениям (1) и целе-
вому уравнению
п п
3 3 CiyVij ~
i=l j=l
G =И= /)
(3)
После приравнивания выражений для суммарного объема поставок,
приведенного в (1), мы получим полную модель перевозок с промежуточ-
ными пунктами для п пунктов. Матрица коэффициентов этой задачи выпи-
сана явно в табл. 16-1-1. За исключением стоимостного фактора, каждый
столбец содержит только по два ненулевых коэффициента +1 и —1;
в общем случае, если мы учитываем избыток или недостаток, то строки
содержат свободные переменные, а соответствующие столбцы содержат
только один ненулевой коэффициент +1 или —1 (в гл. 21 рассматривают-
1 ся системы, в которых имеется не более двух ненулевых коэффициентов
в каждом столбце, не обязательно равных по величине и противополож-
ных по знаку).
Таблица 16-1-1
* Модель с промежуточными пунктами—сетевая постановка задачи
(Матрица коэффициентов)
*12 *13 • • . *1п *21 *23 • • • *2п • • • Хп1 хп2 • • • Хп, П-1
Чистое
производство
или потреб-
ление
Пункт 11 1
Пункт 2 —1
—1
... 1 —1
1 1---1
— 1
Пункт п
Затраты
1 1 ... 1
с12 с13 • • • с1п С21 с23 • • • с2п • • • Сп1 сп2 • • ’ cn, п— 1
Таким образом, общая модель с промежуточными пунктами характе-
ризуется целевой функцией и системой уравнений с неотрицательными
переменными, каждый столбец которой содержит не более двух ненулевых
329
коэффициентов (+1 или —1, или как тот, так и другой). Стандартная
транспортная модель является, очевидно, частным случаем этой форму-
лировки. Однако мы покажем, что при некоторых не очень ограничитель-
ных предположениях, которые будут рассмотрены в § 16-2, общая задача
о перевозках с промежуточными пунктами оказывается эквивалентной
классической транспортной задаче.
СЕТЕВОЕ ПРЕДСТАВЛЕНИЕ
Матрица в табл. 16-1-1 содержит п (п — 1) столбцов, соответствую-
щих числу столбцов перевозок от каждого пункта до любого другого.
Однако если все перевозки от одного пункта до другого осуществляются
посредством цепи, состоящей из звеньев между соседними пунктами, то
достаточно рассматривать только сеть, составленную из таких локаль-
ных звеньев. Все переменные, связанные с перевозками к пунктам, не
являющимся соседними, можно игнорировать.
На сети, изображенной на рис. 16-1-1, затраты на перевозку одной
тонны груза от пункта i до соседнего пункта j проставлены на соответ-
ствующем ребре: так, е36 — затраты на перевозку от 3 до 6 равны 13.
Рис. 16-1-1. Пример задачи с промежуточными пунктами.
Нами не выписано с63 (затраты на перевозку от пункта 6 до 3), так как
в данном случае каждое оказывается равным Сц. Однако развиваемая
нами теория справедлива и в случае, когда ctj У= сл.
В самом деле, хотя чаще всего транспортные тарифы между двумя
пунктами одинаковы в обоих направлениях, можно, однако, привести эконо-
мическую мотивировку их различия. Ситуация, когда не равно
может возникнуть, например, в системе нефтепровода, если i находится
на возвышенности а / — в долине, так как дешевле качать нефть под гору,
чем в гору. В качестве стабилизирующего фактора в некоторых экономи-
ческих приложениях Купманс [1] и Купманс и Рейтер [1] предложи-
ли, что с общегосударственной точки зрения может оказаться выгодным
иметь различные тарифы для стимулирования перевозок по менее загру-
женному из направлений между двумя пунктами.
Далее, мы покажем, что вариант симплекс-метода, развитый для
решения классической транспортной задачи, можно с небольшими видо-
изменениями использовать и для решения задачи с промежуточными
пунктами.
В гл. 17 мы приведем удобный с вычислительной точки зрения про-
цесс, непосредственно используя для этой цели сетевой график, чтобы
выявить геометрическое существо задачи.
330
СВЕДЕНИЕ К КЛАССИЧЕСКОМУ СЛУЧАЮ МЕТОДОМ
НЕПОСРЕДСТВЕННЫХ ПЕРЕВОЗОК
При формулировке модели с промежуточными пунктами мы предпо-
лагали известными только затраты на перевозки между соседними пунк-
тами; однако здесь мы предположим, что транспортные затраты для любой
пары несоседних пунктов могут быть получены путем нахождения мини-
мальных сумм затрат вдоль отдельных звеньев цепи, соединяющих два
пункта через все допустимые промежуточные точки (фактические транспорт-
ные тарифы часто не удовлетворяют этому предположению аддитивности).
Для небольших задач можно довольно легко определить все минимальные
затраты путем простого обследования сети.
Наиболее дешевые маршруты перевозок от пунктов производства 1
и 5 до трех пунктов потребления 2, 6 и 8 в сети, изображенной на
рис. 16-1-1, даны в классической транспортной матрице (табл. 16-1-П).
Таблица 16-1-11
— Пункты потребления Пункты про- изводства Объем произ- водства (ар
II 2 6 8
1 ^12 с12— 9 *16 с1б — 21 *18 618 = 29 7 .
СП £ Ci м Сл м II со *56 ^56 — 6 *58 с58“ 13 3
Потреб- 4 НОСТЬ (bj) 4 2 10
Например, наиболее экономичный маршрут для перевозки из 1 в 6
проходит по ребрам от 1 до 2 и затем к 6. Следовательно, должно быть
£16 = ci2 + с2б — 9 + 12 = 21.
Хотя таким путем можно решать задачу с промежуточными пунктами
и обычными методами, разработанными для классической транспортной
задачи, но нашей целью будет разработка другого подхода, который имеет
определенные преимущества.
а) В нем отсутствует необходимость определения самого экономного
маршрута для каждой пары «пункт производства — пункт потребления».
б) Он позволяет рассматривать задачи, в которых для некоторых дуг
сети заданы фиксированные пропускные способности, ограничивающие
потоки по этим дугам.
в) Он обычно приводит к меньшему числу переменных, так как коли-
чество дуг в сети часто оказывается меньшим, чем количество пар:
«пункт производства — пункт потребления».
СВЕДЕНИЕ к классическому случаю путем использования
ПРОМЕЖУТОЧНЫХ ПУНКТОВ
В табл. 16-I-III для сети с промежуточными пунктами, изображенной
на рис. 16-1-1, выписана матрица, аналогичная классической транспортной
матрице. Используя уравнения (1), уравнение по строкам можно полу-
чить путем приравнивания суммарного объема поставок, с одной стороны,
331
и потребления плюс вывоз — с другой, а уравнение по столбцам — путем
приравнивания суммарного объема поставок и ввоза плюс производство.
Таблица 16-1-1 II
Модель с промежуточными пунктами с диагональными
переменными поставок
СТАНДАРТНАЯ МАТРИЦА ДЛЯ МОДЕЛИ С ПРОМЕЖУТОЧНЫМИ
ПУНКТАМИ
Для определенности нашего анализа будет удобно заменить перемен-
ные для суммарного объема поставок x*j новым набором «диагональных»
переменных ху7, представляющих собой чистый объем транзитного груза,
перевозимого через пункт /. Эти переменные связаны с суммарными объ-
емами поставок следующими соотношениями:
х*,- = х;> + (а* + ^ —min(a*, 6*)). (4)
Для оправдания термина «транзитные переменные» применительно к
перепишем (4) в виде
хМ = (х*э—min (а*, — —min (а*, &*))—(6*—min(a*, &*)) (5)
Вычитанием min (а*, 6*) из каждого члена мы исключаем из рас-
смотрения местное производство для внутреннего потребления. Если
а* > Ь*, то последний член выпадает и Xjj = — а* представляет
собой ту часть суммарного объема поставок, которая производится в дру-
332
гих местах и подлежит транзитной перевозке через данный пункт. Если
a* < bj, то выпадает второй член и Xjj = x*j — b* оказывается той
частью суммарного объема поставок, которая не потребляется в данном
пункте и, следовательно, подлежит транзитной перевозке через этот
пункт. Из (1) следует также, что x*j — а* > 0, x*j — b* > 0 и поэтому
xjj
Если x*j заменено согласно (4) и если dj и bj представляют собой чистое
производство и потребление, определенные в (2), то задачу с промежуточ-
ными пунктами можно поставить в следующей стандартной диагональной
форме.
Задача о перевозках с промежуточными пунктами. Определить неотри-
цательные числа х^ и min z, удовлетворяющие следующим условиям (6),
(7) и (8):
Уравнения по столбцам: 2хг— bj* (j = l, 2, ..., n) (6)
(Общее количество направляемого в пункт j груза минус объем транзит-
ного груза равно чистому потреблению.)
Уравнения по строкам: 2 xjk—xjj~aj- (& = 1, 2, ..., п) (7)
(Общее количество вывезенного из j груза минус объем транзитного
груза равно чистому производству.)
п п
Целевая функция: 3 = (8)
i=l j=l
где Cjj = 0 для всех /. Общая матрица для этой стандартной формы выпи-
сана в табл. 16-1-IV.
Теорема 1» Любой базис задачи с промежуточными пунктами является
треугольным.
Доказательство. Если переменные х^ при i Ф / заменить на х^ =
= —хи, то уравнения (1) и (3) становятся такими же, как в стандартной
транспортной задаче. Так как доказательство треугольности для этой
задачи, приведенное в § 14-2, не зависело от знака переменных, оно остает-
ся в силе и для задачи с промежуточными пунктами. Аналогичное рас-
суждение можно применить к системе (6), (7) и (8), если Xjj заменить
на —«я-
Теорема 2. Диагональные переменные Xj$ или x*j могут быть взяты
в качестве части любого допустимого базисного множества.
Доказательство. Рассмотрим некоторую новую задачу с промежуточ-
ными пунктами, в которой в уравнении (1) и bj заменены соответствен-
но на at + 8 и bj + 8, где 8 — произвольное положительное число,
а х”ц — новые переменные. Очевидно, в любом допустимом решении мы
будем иметь х^ 8, так что диагональные переменные будут положи-
тельными и, следовательно, должны составлять часть любого базисного
множества. Любое допустимое решение исходной задачи определяет
допустимое решение новой задачи, и наоборот. Действительно, если поло-
жить
% 33 — %jj “F 6, = %iji {l f) (9)
то оптимальные решения обеих задач должны соответствовать друг другу,
так как значение z инвариантно относительно этого преобразования.
333
Таблица 16-1-1V
Стандартная матрица для задачи с промежуточными пунктами
. Пункт
производ-
ства
Пункт потребления j
(2)
(3)
(1)
-*11
_____£
*21
Си
*31
С31
*41
С41
(2)
х1г
0/2
-хгг
_____0_
хзг
O32
(3)
х13
С/З
хгз
с23
~х33
_____0_
Хоз
(<>)
*74
с»
(5)
(6)
(?)
(8)
извод-
ст во.,
оценка
(*)
(S)
(S)
(»
fy: потреб-
ность.
Оценка:
*34
с«з
х53
с53
+Л3
+3TS
х85
____с25
Х56
_____0_56
~ХМ
_____0_
х76
Ото
ХМ
— cff
4
х50
___
ХО8
____fte
хм
___to.
~Х&
____о
Z
+7Г^
х67
с67
-Х77
_____0
Х«7
OS7
О
с34
~XW
х25
с25
х35
с35
Х2В
____&
хзо
-JTl
О
Сзв
*У7
Ст
-JT3
о
х52
____с52
~х55
_____0_
х65
О05
О
-”б
О
О
~^з
(D
т

7
О
3
С вычислительной точки зрения нежелательно выполнять это пре-
образование задачи в явном виде, так как тех же результатов можно добить-
ся, допуская для переменных неограниченную область изменения.
Тогда эти переменные, войдя один раз в базисное множество, будут в нем
оставаться, даже если их значения будут нулевыми (см. гл. 18).
Это справедливо и для транзитных переменных, они находятся во
взаимно-однозначном соответствии, и мы показали, что из 0 для
г / следует > 0 (см. рассуждения, следующие за (4)).
Теорема 3. Неявные цены щ и Vj для задачи с промежуточными пунк-
тами можно выбрать так, чтобы они удовлетворяли соотношениям
— Uj = Vj, 7 = 1, 2, ш. ♦, тп» (10)
Доказательство. Так как для всех базисных переменных х^ должно
быть Си = Ui + а по теореме 2 можно предположить, что Xjj входит
в любое допустимое базисное множество, налагая условие Cjj — 0, мы при-
ходим к нужному соотношению.
Обозначим общее значение Vj и — Uj через Купманс и Рейтер [1]
называют «потенциалом» точки i в сети по аналогии с электростатиче-
ским потенциалом в электрической сети. В частности, как тот, так и дру-
гой потенциалы таковы, что в состоянии равновесия
еСЛИ Жг;>0, ТО dj = 7tj — Лг, (11)
если Cfjttj—~tt[, то Xij —10
334
Иными словами, положительный поток от i к ; реализуется тогда
и только тогда, когда падение напряжения равно по величине и проти-
воположно по знаку разности потенциалов между i и /.
16-2. ЭКВИВАЛЕНТНОСТЬ ТРАНСПОРТНОЙ ЗАДАЧИ
И ЗАДАЧИ С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ
Между транспортной задачей и задачей с промежуточными пунктами
имеется существенное различие: в транспортной задаче любая переменная
ограничена сверху минимумом сумм по строке и по столбцу, в то время
как задача о перевозках с промежуточными пунктами допускает увеличе-
ние значений в диагональной 2 х 2-подматрице (хц, х^, xiif х^) на лю-
бую произвольную постоянную &, так как суммы по строке и по столбцу
в получающейся подматрице остаются неизменными, именно
(xij “Ь ^) \
хи\ 1—(хп + к)
— Xjjl\ (Xji + ty
(1)
В случае, когда все затраты положительны, транзитная перевозка
большего количества, чем сумма производительностей всех источников,
очевидно, всегда будет невыгодной. Однако если некоторые из чисел с и
будут отрицательными, то нижней границы для z может не существовать.
Например, если + Сц < 0, то для класса решений, получающихся
из (1) при к -> + оо, должно быть z -> — оо. Более общо, на сети было бы
выгодно иметь кругообороты потока, если сумма с^ по некоторому циклу
отрицательна Ч
По поводу формального доказательства этих интуитивно ясных
утверждений см. теорему 2 о разложении цепи в § 19-1. (См. также задачу
7 в настоящей главе.) Из последней теоремы вытекает
Теорема 1. Если сумма с^ по любому циклу в сети положительна, та
в любом оптимальном решении, если оно существует, величина транзитной
перевозки Xjj ограничена и
xjj S — S
г 3
(2>
Обозначив свободные переменцые для транзитных переменных через
%з) — L
(3>
мы можем свести задачу с промежуточными пунктами к стандартной
транспортной задаче. В нашем примере L = S at = S bj = 10, так что
* 3
задачу с промежуточными пунктами, описанную в табл. 16-1-IV, можно
свести к задаче, которая описана в табл. 16-2-1.
Наоборот, классическую транспортную задачу легко свести к задаче
с промежуточными пунктами. Рассмотрим транспортную задачу 3x4
1 Возможны ситуаций, когда курсы обмена валюты на мировом рынке таковы,
что в результате обмена между A, С, D ... и возврата снова к А получается чистый
выигрыш. Теоретически можно было бы накопить состояние, повторяя такой цикл
снова и снова. Практически некоторые люди накопили значительные прибыли, прежде
чем курсы обмена изменились.
335
Таблица 16-2-1
Транспортная задача, эквивалентная задаче с
промежуточными пунктами
(табл. 16-2-П), в которой пункты потребления отличаются от пунктов
производства обозначением их большими индексами.
Таблица 16-2-11
Пункты производ- ства Пункты потребления Произ- водство
(4) (5) (7)
(1) *14 с14 *15 с15 *16 с16 *17 с17 «1
(2) *24 с24 *25 с25 *26 с26 *27 с27 а2
(3) *34 с34 *35 с35 *36 с36 *37 с37 ^3
Потреб- ность ь4 ^5 &6 Всего
336
Исходную таблицу можно привести к стандартному строчно-столбцо-
вому виду
7
= (i = 1,2,3), (4)
j=4
3
= (/ — 4, 5, 6, 7) (5)
i=l
и затем уже интерпретировать ее, как в (1) и (6) из § 16-1; более удобно
представить ее в виде матрицы задачи с промежуточными пунктами, при-
веденной в таблице 16-2-Ш, где возможности осуществления перевозок
вдоль ребер между пунктами производства или между пунктами потреб-
ления должны быть исключены.
Таблица 16-2-1II
Пункты производства Пункты потребления Производ- ство
| (1) (2) (3) || (4) (5) (6) (7)
(1) (2) (3) — *11 *22 — *33 *14 *15 *16 *17 *24 *25 *26 *27 *34 *35 *36 *37 а2 а3
(4) (5) (6) (7) 1 — *44 — *55 — *66 —*77 j 0 0 0 0
Потребность j ООО &4 &5 &6 &7 Всего
16-3. РЕШЕНИЕ ЗАДАЧИ С ПРОМЕЖУТОЧНЫМИ
ПУНКТАМИ СИМПЛЕКС-МЕТОДОМ
НАХОЖДЕНИЕ НАЧАЛЬНОГО БАЗИСНОГО ДОПУСТИМОГО РЕШЕНИЯ
В любой связной сети х, такой, как изображенная на рис. 16-1-1,
можно найти начальное решение путем непосредственного обследования.
Следует начать с выбора пути по сети от любого пункта производства
до любого пункта потребления и определить максимальный поток, кото-
рый не превосходит суммарных объемов производства или потребления.
Далее либо прямым путем, либо ответвлением от предыдущего пути
соединяют любой пункт производства, если его суммарная производи-
тельность еще не исчерпана, с теми пунктами потребления, чьи суммар-
ные потребности еще не удовлетворены, и увеличивают поток по пути
до максимально допустимого. (Если два пути пересекаются, как на
рис. 16-3-1, то по их общей дуге иногда могут возникнуть встречные
потоки.) Эта процедура повторяется до тех пор, пока все потребности не
будут удовлетворены.
1 Сеть называется связной, если для любой пары ее узлов i и / можно найти
цепочку ребер, соединяющих i с j\ с /2, /2 с /3, . . fh с /. Когда сеть состоит
из нескольких отдельных частей и каждая часть является связной подсетью, то,
очевидно, задачу можно разложить на независимые подзадачи, которые можно
решать одним и тем же способом.
22 Дж. Данциг 557
При построении базисного решения важно осуществлять ответвления
без образования циклов и соединять каждую точку с любой другой точкой
вдоль построенных путей. Для осуществления последней цели может
Рис. 16-3-1. Рис. 16-3-II. Граф базисного допустимого решения
(см. табл. 16-3-1, цикл 0).
понадобиться включение некоторых дополнительных путей с нулевыми
потоками. (Доказательство того, что выполнение этих шагов всегда воз-
можно, и более точное разъяснение таких сетевых терминов, как «цикл»,
будут составлять предмет обсуждения следующей главы и поэтому здесь
опускаются.) Например, один допустимый путь для осуществления тре-
буемых перевозок для сети на рис. 16-1-1 показан на приводимом далее
рис. 16-3-II. Другой допустимый путь приведен на рис. 16-3-III, но нельзя
его считать базисным решением, так как он содержит цикл, соответствую-
щий ребрам и узлам, изображенным на рис. 16-3-1V.
ИТЕРАТИВНЫЙ МЕТОД
Базисное решение, изображенное на рис. 16-3-П, используется
в табл. 16-3-1 в качестве начального решения (цикл 0). Шаги решения
симплекс-методом приводятся в таблицах для последующих циклов.
Так как метод практически остается точно таким же, как в лгоритме для
транспортной задачи, приведенном в гл. 14, подробное рассмотрение всех
итераций здесь приводиться не будет.
338
Цикл О
Таблица 16-3-1
Матрица задачи с промежуточными пунктами
Цикл 1
Пункты производ- ства Пункты потребления а, -п.
(1) (2) (3) (9) (5) (6) (7) (8)
(1) 0 0 1 9 0 9 О 12 %6ууу6 7 0
(?) 9 -3 0 8 9 д* (Обод) 12 у/у/У/ 0 -9
. (з) 9 8 О 0 8 9 (быббд) 13 О -9
(9) 12 8 О 0 'Ш ж 8 10 в -12
(5) 9 9 W 0 0 1 6 2 13 3 -16
(6) 12 13 УУЛ7 6 8 0 5 8 8 -22
(7) 10 5 8 0 9 8 -22
(8) уУУ/Л v/T/ss 8 9 8 О 8 -29
S О 0 4 9 о 9 8 ' 12 8 16 8 22 8 22 2 29
В базис вводится переменная х^, так как min cij — ci7 = r47 — (л7 — =
= — 5, Из базиса выводится переменная «67, так как тах 0 = 0 для
«67 = 0 — О,
В базис вводится переменная «2в> так как m^n cij “ С26 = с2в —*
— (лб — л2) = — 1. Из базиса выводится переменная «зв, так ” как
max 0 = 3 для «зв = 3 — 0.
Таблица 16-3-1 (продолжение)
Цикл 2 (Оптимальный)
16-4. ЗАДАЧИ
1. Доказать, что если в модели с промежуточными пунктами, при-
веденной в табл. 16-1-1, суммарный объем производства 'отличен от сум-
марного объема потребления, то допустимых решений не существует.
2. Обобщить модель, описываемую уравнениями, на случай, когда
в некотором пункте допускается хранение избытка, если суммарный объем
ввезенного и произведенного груза превысит суммарный объем вывезен-
ного и потребленного груза.
3. Показать, что в такой обобщенной модели не существует допусти-
мого решения, если 2 л* < 2 Ь*, и интерпретировать этот результат.
4. Сформулировать модель с промежуточными пунктами в сетевой
постановке (табл. 16-1-1) для примера, приведенного на рис. 16-1-1,
опуская все те переменные xtj, для которых сеть не содержит ребра, свя-
зывающего пункт i с пунктом /.
5. Допуская, что пункты могут производить и потреблять одновре-
менно (так что оба числа а* и Ь* могут быть положительными), пересмот-
реть доказательство того, что объем транзитной перевозки равен
Хц := %ii bi»
Доказать, что стандартная модель с промежуточными пунктами
^(табл. 16-1-IV) получается из исходной, если определить новые правые
340
части и переменные следующим образом:
^==аГ-пнп(яГ, Ы),
bi = bt — min (а*, ^),
Хц =x*i — min (а*, Ь*).
6. Почему в стандартной задаче с промежуточными пунктами (см.
табл. 16-1-IV) мы имеем хц > О?
7. Доказать, что для любой задачи с промежуточными пунктами,
если Xjj превышает У то в потоке будет иметь место кругооборот,
а если все c-L j положительны, то такое решение не может быть оптимальным.
8. Решить задачу, представленную на рис. 16-1-1, путем сведения ее
к эквивалентной транспортной задаче (табл. 16-2-1) и применения методов,
изложенных в гл. 14 и 15.
9. Почтовое отделение хочет отправить посылку из Лос-Анжелеса
в Бостон самым выгодным путем. Затраты на перевозку между соседними
точками транспортной сети пропорциональны числам, проставленным на
соединительных дугах карты, изображенной на рис. 17-3-1. Найти
этот путь.
Глава 1/
СЕТИ И ЗАДАЧА
С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ
17-1. ГРАФЫ И ДЕРЕВЬЯ
Т. Купманс в своей основополагающей работе по транспортным зада-
чам [1] впервые. изложил свойства оптимальных и неоптимальных
решений по отношению к линейному графу, соответствующему сети маги-
стралей.
Линейный граф, или сеть, состоит из вершин (узловых точек), соеди-
ненных между собой при помощи ребер (дуг)1 Изображенные на схеме
кружки с проставленными внутри цифрами 1, 2 ... 6 (см. рис. 17-1-1)
представляют собой вершины графа. Ребра изображаются прямыми или
Рис. 17-1-1. Пример линейного графа
(сети).
лишь перекрещиванием, мы
кривыми линиями, каждая из ко-
торых соединяет ровно две верши-
ны, а именно (1,2), (1, 3), (1, 5),
(2, 3), (2, 4), (2, 5), (3,4), (4, 6), (5, 6).
Пересечение двух таких линий вовсе
не означает фактического пересече-
ния соответствующих ребер; послед-
нее имеет место только в вершинах.
Иногда, желая подчеркнуть, что
пересечение ребер на рис. 17-1-1
не образует узла, а является
будем употреблять символ , иногда
применяемый в электрических схемах.
В транспортных задачах вершины графа часто интерпретируются
как пункты производства или потребления, а ребра — как магистрали
между ними. Односторонний характер транспортных или товарных пото-
ков по магистралям приводит к рассмотрению направленного графа (то
есть сети, составленной из направленных ребер, называемых дугами).
Для обозначения дуги обычно применяется символ i -> /, который изобра-
жает допустимое предшествование между i и /.
Предположим, к примеру, что в данной нам ситуации мы можем
из пункта 1 перемещаться только в пункты 2 или 3; из пункта 2 — только
в пункты 3, 4 или 5; из пункта 4 — в пункты 3 или 6; из пункта 5 —
в пункты 1 или 6 и из пункта 6 — только в пункт 5. Этот процесс можно
изобразить при помощи дуг следующим образом: 1 ->2, 1 ->3, 2 ->3,
2 ->4, 2 ->5, 4 ->3, 4 ->6, 5 ->1, 5 ->6 и 6 ->5, что и представлено
на рис. 17-1-II.
Две вершины i и / могут соединяться несколькими различными дуга-
ми; для наших целей, однако, мы можем ограничиться рассмотрением
1 Мы рекомендуем читателю следующую терминологию, принятую в отечествен-
ной литературе по теории графов: к направленным (ориентированным) графам отно-
сятся понятия дуги, пути, контура; в неориентированных графах им соответствуют реб-
ро, цепь и цикл.— Прим, перев.
342
только Двух таких дуг, одна из которых описывает возможный процесс
перевозки из i в /, другая — из j в i. Мы будем считать эти дуги различ-
ными, хотя они могут изображаться
на схеме при помощи одной линии.
Последовательность ребер (г,
ч), (ч, ч), • • (Ч, /), соединя-
о-
4
с. 17-1-Ша.
(X о
i h
Р и
—хх-----о
6 J
Пример цепи.
ющих вершины i и /, называется цепью независимо от конкретных
направлений составляющих ее дуг; см. рис. 17-1-Ша.
Цепь ребер, соединяющих вершину с самой собой, называется циклом
(простым циклом, если все его дуги различны); см. рис. 17-1-Шб.
Граф, не содержащий циклов, в котором каждая вершина связана
с любой другой при помощи некоторой цепи ребер, называется деревом.
Рис. 17-1-Шв. Пример дерева.
Сеть, состоящая
Рис. 17-1-IV.
из несвязных деревьев.
Рис. 17-1-Шб. Примеры цепей, явля-
ющихся циклами (дуга с двумя направле-
ниями представляет собой цикл и даже
контур).
Например, после удаления нескольких ребер из графа, изображен-
ного на рис. 17-1-II, останется подсеть, которая представляет собой на-
правленное дерево (см. рис. 17-1-Шв). Вершины 3, 4 и 6, присоединенные
к сети с помощью только одного ребра,
называются висячими.
Нашей конечной целью является дока-
зательство того, что (п — 1) базисных не
диагональных переменных в задаче с про-
межуточными пунктами соответствуют
(п — 1) дугам, которые образуют направ-
ленное дерево.
Для этой цели полезна следующая
теорема.
Теорема 1. Сеть с п вершинами яв-
ляется деревом, если она содержит
(п — 1) ребер и не имеет циклов.
Иными словами, такой граф всегда будет связным; его нельзя разбить
на несколько деревьев, как на рис. 17-1-IV.
Справедливость теоремы для двух вершин очевидна. Пусть она верна
для 2, 3, . . ., п—1 вершин.
Для п вершин установим следующую лемму.
Лемма. В условиях теоремы 1 существует по крайней мере одна вер-
шина, которая является висячей, то есть такая точка р, которая соеди-
няется с остальной сетью посредством единственного ребра.
343
Доказательство. Чтобы найти вершину, которая является висячей,
выберем произвольную вершину, скажем р^, она соединена некоторыми
ребрами хотя бы с одной другой вершиной, скажем с р2- (Если это было
бы не так, то, вычеркнув любое ребро (Z, /), соединяющее некоторую пару
вершин из оставшихся (п—1) вершин, мы получили бы (п — 2) ребра, не
содержащих цикла. По нашему индуктивному предположению, они обра-
зуют дерево, и существует цепь ребер, соединяющих pi с Pj. Присоединяя
к этойцепиребро (рг-,Р;), мы получили бы цикл, что противоречит нашему
предположению.) Так как из р^ ведет ребро к некоторой вершине р2,
будем двигаться к р2 по ребру (рь р2). От р2 по другому ребру (если это
возможно) пойдем к р3. Так как число точек конечно, а циклов нет, то,
продолжая аналогичным образом, мы придем к вершине р, которая
является висячей, соединяясь с остальной сетью при помощи одного ребра
(р, я)-
Доказательство теоремы!. Если висячую вершину и ее единственное
ребро вычеркнуть, то оставшаяся сеть будет содержать (п — 1) вершину,
(п — 2) ребра, а так как в ней нет циклов, она будет связной в силу индук-
тивного предположения. Если вычеркнутую вершину р и ее ребро (р, q)
вновь восстановить, то появится возможность соединять р с любой другой
вершиной через д; это доказывает, что сеть с п вершинами, (п — 1) ребром
и без циклов является связной и, следовательно, образует дерево.
Мы доказали, что дерево содержит по крайней мере одну висячую
вершину. В качестве упражнения предлагаем доказать следующую теорему.
Теорема 2. Любое дерево содержит по крайней мере две висячие вер-
шины.
ГРАФ, СООТВЕТСТВУЮЩИЙ ЗАДАЧЕ С ПРОМЕЖУТОЧНЫМИ
ПУНКТАМИ
Рассмотрим задачу с промежуточными пунктами в следующем виде:
S (Лт= 1, 2, ...у ft), (1)
i j
где первая сумма распространяется на индексы (i, к), соответствующие
допустимым дугам (г, к), а вторая сумма — на индексы, соответствующие
допустимым дугам (к, j). Требуется определить > 0 и min и, удовлет-
воряющие условиям (1) и условию
= (2)
i j
Мы установим взаимно-однозначное соответствие (<—>) с сетью следующим
образом:
Каждое к-е уравнение » к-й вершине графа.
Любое допустимое хц <—> дуге, соединяющей i-ю вершину с / -й.
В сети, изображенной на рис. 17-1-V, наличные ресурсы а^ и а5
в пунктах производства 1 и 5 для удобства выписаны рядом со стрелками,
направленными в эти точки. По определению, эти стрелки не являются
дугами сети, так как они не соединяют пар вершин. Аналогично и размеры
спроса в пунктах потребления 2, 6 и 8 указаны рядом со стрелками,
направленными из них. Такие стрелки пропущены в тех пунктах, для
которых at = bi = 0. Дуги (i, /), сети, соответствующие базисным пере-
менным Хи, изображены жирными линиями.
344
Выписанные конкретные значения хц являются значениями из исход-
ного базисного решения, приведенного выше в табл. 16-3-1 для сетевой
задачи, изображенной на рис. 16-1-1.
Все решения системы уравнений для этой задачи, как допустимые,
так и недопустимые, можно изобразить на соответствующих направленных
дугах сети. Следовательно, необходимо, чтобы для каждой вершины к
Рис. 17-1-V. Дерево, образованное жирными
дугами, соответствует базисному множеству пе-
ременных.
сумма значений xih и ak на стрелках, направленных в эту вершину, рав-
нялась бы сумме значений xkJ- и bk на стрелках, направленных из этой
вершины (как в табл. 16-1- IV, в которой общее значение этих двух сумм
приписывается диагональным переменным хц). И наоборот, любое мно-
жество значений, проставленных на дугах сети и обладающих указанным
свойством, можно дополнить до решения (допустимого или недопустимого)
уравнений, определяя пропущенные диагональные переменные, как общие
значения описанных выше сумм.
СООТНОШЕНИЯ МЕЖДУ БАЗИСАМИ И ДЕРЕВЬЯМИ
Теорема 3. Подсеть, соответствующая базисным переменным, пред-
ставляет собой дерево.
Если подсеть из (п — 1) дуг, соответствующих (п — 1) базисным не-
диагональным переменным, не содержит контуров, то она является деревом
о)

Рис. 17-1-Via, б. Почему контуры не могут
отвечать крайним точкам.
в силу теоремы 1. Остается доказать, что ни один базис не может породить
контура. Предположим, к примеру, что ж35 и я53 входят в базисное множе-
ство, как это имеет место на рис. 17-1-VIa, или я35, я56 и #3б, как это имеет
место на рис. 17-1-VI6. Если бы это было так, то значения базисных пере-
менных вдоль контура можно было бы изменить, как показано на
рис. 17-1-IVa, в то время как значения всех остальных переменных сохрани-
345
лись бы. Тем самым мы получили бы второе решение уравнений задачи
с промежуточными пунктами, что противоречит единственности базисных
решений. Следовательно, базис не может содержать контуров.
Упражнение. Провести это доказательство формальным образом
для контура общего вида.
Теорема 4. Любая подсеть графа, являющаяся деревом, соответствует
некоторому базисному множеству переменных.
Для доказательства того, что дерево соответствует некоторому базис-
ному множеству переменных, достаточно показать, что (п — 1) перемен-
ных, отвечающих дугам дерева, которые мы будем называть переменными,
относящимися к дереву, можно однозначно вычислить при любом выборе
Hi и bj, если только = 3 Чтобы найти эти величины, положим
все переменные, не относящиеся к дереву, равными нулю. Начиная с любой
висячей вершины к и с единственной вершины i, с которой она соединяется,
мы видим, что в уравнении к имеется только одна нулевая переменная,
относящаяся к дереву, а именно Xik или xki.
Следовательно, ее значение равно xth — (at — bt), iwixki = (bt — а^.
Таким образом, свойство треугольности, которое делает возможным
нахождение некоторого уравнения (скажем, к ) только с одним неизвест-
ным, вычисление этой переменной и отбрасывание /с-го уравнения анало-
гично свойству дерева, с помощью которого можно найти висячую вер-
шину (скажем, вершину к) и его ребро, вычислить переменную, связанную
<с этим ребром, а затем вычеркнуть к-ю вершину и ее ребро. То, что остается
после вычеркивания, также является деревом, поэтому процесс может
повторяться до тех пор, пока останутся (на последнем шаге) две вершины
и связывающая их дуга, соответствующие одной переменной и двум урав-
нениям. Так как 2 ai = 2 то сумма постоянных в (1) обращается
в нуль с самого начала и после каждого вычеркивания; это позволяет осу-
ществить непротиворечивое вычисление на последнем шаге. Из этих
рассуждений ясно, что переменные, относящиеся к дереву, образу-
ют базис.
17-2. ИНТЕРПРЕТАЦИЯ СИМПЛЕКС-МЕТОДА НА СЕТИ
ЭТАП I. ПОСТРОЕНИЕ ИСХОДНОГО БАЗИСНОГО
ДОПУСТИМОГО РЕШЕНИЯ
В этом разделе мы рассмотрим процедуру симплекс-метода для пост-
роения исходного решения, если не удастся его выявить путем непосред-
ственного обследования графа.
Шаг 1. Соединить каждый пункт производства с другими вершинами /
на сети, используя только допустимые дуги, выходящие из пунктов I.
Аналогично соединить различные пункты потребления г' с другими вер-
шинами /' на сети, используя только допустимые направленные дуги,
входящие в конечные пункты потребления Повторить этот процесс
итеративно, используя вершины / и /' вместо вершин i и Z', не допуская
на всех итерациях образования циклов.
Когда цепь дуг, исходящих из некоторого пункта производства, сое-
диняется с цепью дуг из некоторого пункта потребления, вершины вдоль
цепи можно соединять с вершинами вне цепи, используя дуги любого
направления. Если при этом еще остаются не связанные друг с другом
вершины, то для установления таких связей используют дуги любого
направления. Если в конце концов в графе остаются изолированные друг
346

ют друга множества точек, то это означает, что исходная задача распадается
на две или более самостоятельные задачи.
Упражнение. Доказать, что если исходная сеть является связной,
то описанный процесс всегда дает дерево.
Шаг 2. Вычислить базисные переменные, соответствующие дугам
дерева. Так как дерево необязательно соответствует некоторому допу-
стимому множеству, то некоторые переменные Xij могут быть отрицатель-
ными. Надо изменить направление стрелки на дуге и заменить хц на Xjt
для. каждой отрицательной переменной; при этом она станет положитель-
ной. Некоторые переменные х^ могут теперь соответствовать недопу-
стимым дугам.
Шаг 3. Если все направленные дуги (i, 7) дерева являются допусти-
мыми, то дерево соответствует базисному допустимому решению.
Если это не так, то стараются исключить недопустимые дуги (i, 7)
с помощью итераций этапа 1, заключающегося в этом случае в решении
вспомогательной задачи с промежуточными пунктами, в которой «форма
недопустимости» имеет вид
w=^di}xi}. (1)
1,3
Суммирование производится как по допустимым, так и по недопустимым
дугам, где:
О, если (i, 7) является допустимой дугой,
1, если (i, 7) является недопустимой дугой.
Теперь мы получили в чистом виде запись, необходимую для при-
менения метода деревьев, который будет рассматриваться в сле-
дующем разделе.
Шаг 4. Если оказывается, что min w >0, то, разумеется, допусти-
мого решения не существует. Если, с другой стороны, допустимость дости-
гается на любом шаге и недопустимых переменных Хц не останется, то
допустимое базисное решение и соответствующее ему дерево построены.
Наконец, если w — 0, но недопустимые х^ еще остаются, то имеются две
возможности:
а) либо исключить все дуги (г, /), для которых соответствующие стои-
мостные параметры d^ в форме недопустимости положительны, и перейти
к этапу II на подсети дуг, для которых = 0;
б) либо изменить направление недопустимой дуги (г, /), делая ее
допустимой, и заменить соответствующую базисную переменную x^j
на Xji, значение которой в' базисном решении равно нулю.
В том и другом случае переходят к этапу II, используя исходные си
вместо dij. Таким образом, нами доказана
Теорема 1. Если связная сеть имеет допустимое решение, то суще-
ствует дерево, соответствующее базисному допустимому решению.
Рассмотрим в качестве примера задачу с промежуточными пунктами
из гл. 16. Исходное решение (например, приведенное на рис. 17-1-V) можно
использовать для того, чтобы начать этап II. Мы могли бы построить
и другое такое решение, используя метод, описанный в предыдущем разде-
ле. Из пунктов производства 1 и 5 мы можем направиться непосредственно
только к вершинам 2, 3, 4, 6, 8. Из (2, 3, 4, 6, 8) можно добраться только
до одной точки — именно до точки 7. Следовательно, дерево сразу же
принимает вид, указанный на рис. 17-2-1. Значения переменных на дугах
дерева таковы, что их алгебраическая сумма в каждой точке равна нулю
347
(знак определяется направлением стрелок). Так, значение х12 = 4 опре-
деляется с помощью уравнения, связанного с висячей вершиной 2 на дере-
ве. Висячие вершины 6, 7, 8 определяют соответствующие переменные
Рис. 17-2-1. Исходное дерево и недопустимое
базисное решение, полученное отправлением из пунк-
тов производства.
я56, и я58. Это в свою очередь позволяет определить значение перемен-
ных, связанных с дугами, ведущими в висячие вершины поддерева, для
которого хи нельзя вычислить. В данном случае такими переменными
Рис. 17-2-11. Графическое улучшение допустимого
базисного решения (цикл 0).
являются гг5з и я14. Наконец, вычисляется х13. Решение не является допу-
стимым, так как х53 = —3. Изменяя направление стрелки и заменяя
ж53 на я35, мы приходим к искомому допустимому базисному решению,
которое изображено на рис. 17-2-II.
ЭТАП II. НАХОЖДЕНИЕ ОПТИМАЛЬНОГО РЕШЕНИЯ
Вычисляем неявные цены удовлетворяющие в сети рис. 17-1-V
условию Ttj — щ ~ Cij для всех дуг (£, /) дерева. С этой целью выбираем
любую вершину i и приписываем ей произвольную цену лг*. Например,
на рис. 17-2-II выбираем вершину 1, из которой расходится больше всего
дуг, и полагаем для нее nt = 0. Затем на основе рис. 17-1-V мы можем
вычислить все те для которых (1, i) или (г, 1) являются дугами дерева.
Этими дугами в нашем случае являются (1,2), (1, 3) и (1, 4); тем самым
348
мы получаем л2, л3, л4. С помощью дуг (3, 5) и (4, 7) можно вычислить
л5 и л7. Наконец, с помощью дуг (5, 6) и (5, 8) можно вычислить л6 и л8.
Чтобы определить, является ли базисное решение на рис. 17-2-II
оптимальным, надо сравнить разности л7- — с с^. Такое сравнение легко
Рис. 17-2-1V. Граф улучшенного базисного
допустимого решения (цикл 1, оптимальный).
Цикл (1,2,6>5,3,1)
Рис. 17-2-1II. Пересчет значений
базисных переменных по циклу.
провести на графе (рис. 17-1-V) с помощью систематического просмотра
каждой дуги (i, /) и вычисления
— Сц (Лу (3)
Если эти величины неотрицательны для всех дуг, то решение опти-
мально. На рис. 17-2-II это условие нарушено, так как
С26 — ^26 (-^6 л2) = 12 (24 — 9) — 3.
Следовательно, имеет смысл увеличить поток по дуге (2, 6), изображенной
пунктирной линией на рис. 17-2-II.
При наличии дуги (2, 6) подсеть уже не будет деревом, так как она
содержит цикл, показанный на рис. 17-2-III. Увеличение значения х2§
до 0 >0 влияет только на значения переменных в цикле. Из рис. 17-2-III
ясно, что наибольшим значением, при котором сохраняется допустимость,
будет 0 — 3. При этом значении одна из дуг (1,3) или (3, 5) удаляется из
дерева и заменяется дугой (2, 6). На рис. 17-2-IV вычеркнута дуга (3, 5).
Значения л$ заново пересчитываются; после этого мы получаем, что все
Cij > 0, поэтому решение является оптимальным. Это оптимальное реше-
ние совпадает с решением, приведенным в табл. 16-3-1 (цикл 2).
17-3. ЗАДАЧА О КРАТЧАЙШЕМ пути
А. Итеративное решение. Пусть некоторый груз надо доставить из
Лос-Анжелеса в Бостон по любому из нескольких различных маршрутов,
показанных на рис. 17-3-1. Нас интересует перевозка груза по кратчай-
шему пути.
* В настоящем изложении = 1 означает, что груз перевозится из
города i в город /; Xij — 0 означает, что такой перевозки нет (где i =/= j).
Пусть x*i (i = 1, 2, . . ., 8) обозначает общее количество груза, перево-
зимое транзитом через город i. Числа, стоящие в кружочках, являются
расстояниями от Лос-Анжелеса по путям, изображенным жирными стрел-
ками. Это приводит нас к следующей системе ограничений.
349
Для вывоза:
#12 + #13 + #14
#21 — #22 4“ #23 + #25
#31 4~ #32 — #33 4“ ^34 + #35 4~ #36
= 1,
-о,
-о, (1>
#85 + #86 4“ #87 — Х*й 4" #89 — О,
Для ввоза:
#12---#22 + #32 4“ #52
#13 4" #23--#33 4" #43 4~ #53 4“ #63
#14 + #34 — #« #64 4- #74
-О,
-о,
-О, (2>
#59 4~ #89 — 1 •
Нужно минимизировать:
9 9
3 3 ^ijxij ~ 2> (3)
i—l ;=1
где dij в этом случае представляет собой расстояние между городом i
и городом /.
Первое уравнение фиксирует, что количество груза, вывозимого
из Лос-Анжелеса, равно единице. Последнее уравнение показывает, что
Портленд
Рис. 17-3-1. Исходное дерево начального приближе-
ния к кратчайшему пути из Лос-Анжелеса в Бостон.
количество груза, ввезенного в Бостон, равно единице. Приравнивая
Хц в Z-м уравнении (1) и Хц в (г — 1)-м уравнении (2), мы балансируем
объемы ввоза и вывоза для каждого города.
Если мы заменим условие (хц — 0 или 1) на (х^ 0) (см. теорему 1
в гл. 15-1), то задачу по-прежнему можно решать как задачу с проме-
жуточными пунктами, используя либо матричный метод, либо теорию гра-
фов, которая разъяснялась в последнем разделе. Однако имеется близкий
к ним, но еще более простой графический метод. Отправляясь из Лос-Ан-
желеса, мы выбираем некоторый маршрут, который, по нашему мнению,
является оптимальным. Например, можно перевозить груз сначала по
южной дороге \ а затем по восточному побережью до Бостона, помечая
этот маршрут стрелками. Подобным же образом выбирают предполагае-
мые кратчайшие пути и направления из Лос-Анжелеса до всех остальных
1 То есть, на Даллас и Мемфис. — Прим, перев.
350
городов^ следя за тем, чтобы стрелки не образовывали циклов. Заметим,,
что в результате получается дерево, так как начальный пункт соединяется
с любой другой вершиной. Заметим также, что цепь из начального пункта
к любой вершине состоит только из направленных дуг вида
начальный пункт (4)>
1 /
Пример такого дерева изображен с помощью жирных стрелок на
рис.17-3-1. Каждое такое дерево соответствует некоторому базису, и легко»
убедиться, что соответствующее базисное решение является допустимым.
На основе (4) ясно, что оценки щ вычисляются следующим образом.
Полагают для начального пункта = 0. Для каждого города в кружочке
помещают число, соответствующее расстоянию от начального пункта
по единственному пути по дереву. Например, расстояние по дереву от
Лос-Анжелеса до Мемфиса равно 85 4- 28 = 113. Следующий шаг заклю-
чается в проверке того, является ли это дерево решением задачи о крат-
чайшем пути. Для этого выясняют, являются ли числа в кружках действи-
тельно кратчайшими расстояниями из Лос-Анжелеса по сравнению с дру-
гими допустимыми маршрутами. Если нет, то решение можно улучшить
в том смысле, что можно найти более короткий путь из начального пункта
до конечного. Проверка минимальности этих расстояний делается следую-
щим образом. Заметим, что общее расстояние до Бостона равно 191;
однако, если наш путь будет идти через Чикаго, а затем уже в Бостон,
то расстояние будет равно 1284-58 = 186 (уменьшение составит 5 еди-
ниц), так что это конкретное дерево не является оптимальным решением.
Можно улучшить решение, если провести стрелку между Чикаго и Босто-
ном, записав 186 в Бостоне и убрав стрелку между Вашингтоном и Босто-
ном. Снова проверяем, нельзя ли получить более короткий путь, скажем,
через Портленд — Чикаго. Однако 58 4- 130 > 128, так что пробуем
проехать через Канзас-Сити — Чикаго. Здесь снова 109 4- 29 > 128.
Продолжая поступать таким образом, мы в конце концов придем к такому
положению, когда нельзя будет улучшить расстояние, обозначенное
в каком-либо из кружков. В результате получается оптимальное решение.
Например, для рассматриваемой задачи приведенное дерево будет опти-
мальным, если убрать стрелку Вашингтон — Бостон и ввести стрелку
Чикаго — Бостон, изменяя число 191 в Бостоне на 186. Значения
равны единице по всему пути в последнем дереве из Лос-Анжелеса в Бостон
и нулю во всех других местах. Следовательно, оптимальный маршрут
таков: Лос-Анжелес — Солт-Лейк-Сити — Чикаго — Бостон. Доказа-
тельство этих утверждений основано на следующих соображениях:
1) Метод просмотра других городов в поисках более короткого пути
совпадает с критерием оптимальности л,-— Л/Cd^.
2) Дерево, в котором все дуги направлены вдоль цепей, соединяющих
начальный пункт с любой вершиной, обладает следующими свойствами:
а) соответствующее базисное решение всегда допустимо и б) только одна
из дуг, имеющих данную вершину своим концом, направлена к этой вер-
шине; другие направлены из нее (рис. 17-3-П).
Отметим, что если дуга (г, /) вводится в дерево для его улучшения,
то выводимая дуга (в предположении невырожденности) должна быть дугой
старого дерева, направленной в /. Каждое новое дерево обладает теми же
свойствами.
Б. Непосредственное решение. Наша цель состоит в изложении наи-
более компактного, на наш взгляд, метода для отыскания кратчайшего
пути из данного начального пункта до всех остальных вершин сети или
до конкретного пункта потребления. Этот метод (Данциг, [19]) можно
351
интерпретировать как незначительное усовершенствование методов, опи-
санных выше в пункте А, которые были предложены Веллманом [3],
Муром [1], Данцигом [14], а также методов, описанных автору лично
Д. Гейлом и Д. Фулкерсоном. Этот метод сходен с методом Мура —
«развертывания» из начального пункта. Однако его особенность заклю-
чается в том, что развертывание производится каждый раз по одной точке
и что приписанное расстояние является окончательным.
Предполагается, что а) можно без труда выписать для каждой вер-
шины все дуги, ведущие к другим вершинам, в порядке возрастания их
Рис. 17-3-IL Пересчет особого вида по
циклу в задаче о кратчайшем пути.
длин и б) легко исключить из списка
Рис. 17-3-Ш. Отыскание
кратчайшего пути не более,
чем за п (п—1)/2 сравнений;
все дуги, выбранные в на-
рисованном поддереве, яв-
Дугу, если она ведет к вершине, расстоя- ляются окончательными,
ние до которой было проставлено раньше.
Мы покажем, что для нахождения кратчайших путей от начального
пункта до всех остальных вершин для графа, состоящего из п вершин,
требуется не более п (п — 1) /2 сравнений.
Предположим, что на некотором шаге к вычислительного процесса
кратчайшие пути до к вершин из некоторого начального пункта известны.
Обозначим это множество к точек через 5 (рис. 17-3-Ш).
Пусть
a) i — некоторая вершина из 5,
б) бг — ее наименьшее расстояние до начального пункта;
в) ji — ближайшая к i вершина, не принадлежащая S (если таковые
имеются), и
г) di — ее расстояние от i.
Выберем в качестве (к + 1)-й точки то /3, для которого
6S + ds — min (6Z + di). (i = 1, 2, . .., k) (5)
(В случае неоднозначности минимума процесс можно сделать более эффек-
тивным путем одновременного определения нескольких новых вершин j.)
Такой выбор означает, что'минимальный путь к js из начального пункта,
имеющий отстояние 6S + ds, проходит через s. Чтобы в этом убедиться,
проанализируем любой другой путь из js в начальный пункт. В конце кон-
цов путь должен дойти до некоторой вершины i из S от некоторой вер-
шины /, не принадлежащей S (где / может совпадать с Д). Предположим
теперь, что расстояния вдоль пути от js до j являются неотрицательными
(см. задачу 5), так что общее расстояние от начального пункта вдоль пути
не меньше, чем бг- + cfo в силу (5) имеем, однако, б^ + di > 6S + ds.
Заметим, ► что минимум требует только к сравнений для выбора
(к + 1)-й точки; следовательно, для сети с п вершинами требуется не
«больше, чем 14-2+ . . . + (п — 1) = п (п — 1) /2 сравнений.
352
Практически число сравнений может оказаться значительно мень-
шим, так как после нескольких шагов одна или более вершин из S могут
иметь дуги, ведущие только к точкам, которые уже входят в S. Граф
с восемью вершинами, изображенный на рис. 17-3-IV, например, требует
только 16 сравнений вместо (8 X 7) /2 = 28 сравнейий.
Если задача состоит в нахождении кратчайшего пути из данного
начального пункта к данному конечному, то число сравнений практически
можно еще сократить, проводя одновременное «развертывание» из началь-
ного и конечного пунктов, добавляя каждый раз к множествам у началь-
ного и конечного пунктов по одной точке, как если бы мы имели дело
с двумя отдельными независимыми задачами.
Однако как только кратчайший путь между некоторой вершиной
и начальным или конечным пунктом найден в одной задаче, то сразу же
в другой задаче этот путь схематически заменяется одной дугой. Алгоритм
заканчивается всякий раз, когда «веер» одной из задач достигает своего
конца в другой.
Пример. Расстояние на дугах сети проставлены на рис. 17-3-IV.
Для каждой вершины выпишем выходящие из нее дуги в порядке воз-
растания их длин:
(О) (А) (В) (С) (D) (Е) (Е) (G)
ОА — 1 АВ-3 ВС-2 СВ —2 DC —2 EF — 1 FE—1 GF—1
ОВ—2 АС-3 ВА — 3 CD —2 DA — 3 ЕС-3 FG—1 GC — 3
AD — 3 BG—4 со со со 1 1 1 DE — 3 ED — 3 GB-4
Шаг 0. В начале процесса множество S состоит из 0.
Шаг 7. Выберем дугу 0А; записываем ее длину 1 над столбцом А,
вычеркивая все дуги, ведущие в А. (Вычеркиваем О A, BA, СА, DA;
Рис. 17-3-IV. Пример задачи о кратчайшем пути
(оптимальное решение показано жирными дугами).
присоединяем А к множеству 5.) Под «длиной» понимается наименьшее
расстояние от 0.
Шаг 2. Сравниваем ОВ-2 и АВ (1 + 3); выбираем путь через ОВ
и записываем его длину 2 над столбцом Б, вычеркивая все дуги, ведущие
в В. (Вычеркиваем OB, АВ, СВ, GB; присоединяем В к множеству S.)
Шаг 3. Сравниваем АС (1 + 3), AD (1+3) и ВС (2 + 2); из-за
наличия неоднозначностей выбираем пути через АС (или ВС) и AD и запи-
сываем их длину 4 над столбцами С и О, вычеркивая все дуги, ведущие
в С и О. (Вычеркиваем АС, АО, ВС, ОС, ЕС, ED, GC; присоединяем С и D
к множеству S.) .
Шаг 4. Сравниваем BG (2 + 4), CG (4+3) и DE (4 + 3); выбираем
путь через BG и записываем его длину 6 над столбцом G, вычеркивая все
23 Дж. Данциг
353
дуги, ведущие в G. (Вычеркиваем BG, CG, FG; присоединяем G к мно-
жеству S.)
Шаг 5. Сравниваем СЕ (4 + 3), DE (4 4- 3) и GF (6 + 1); выбираем
путь через СЕ (или DE) и GF и записываем его длину 7 над столбцами
Е и F, вычеркивая*все дуги, ведущие в Е и F. (Вычеркиваем СЕ, DE, FE,
GE; присоединяем Е и F к множеству S.)
Из-за наличия неоднозначностей некоторые шаги осуществляются
одновременно.
Кратчайшие пути из начального пункта к остальным вершинам про-
ходят вдоль пути ОА, OB, AC, AD, BG, СЕ, GF. (См. жирные дуги на
рис. 17-3- IV) с альтернативой ВС вместо Л С, DE вместо СЕ и EF вместо GF.)
17-4. ЗАДАЧИ
1. Рассмотреть задачу с промежуточными пунктами, состоящую из к
независимых сетей, каждая из которых является допустимой. Соединить
эти к сетей вместе путем введения (к — 1) новых дуг (is, js), где is есть точка
в 5-й сети, a js — точка в ($ + 1)-й сети (s = 1, 2, . . ., к — 1).
Доказать, что в любом допустимом решении для расширенной сети будет
XisJs О*
2. Показать, каким образом задачу о кратчайшем пути (рис. 17-3-1)
можно решить при помощи методов для задачи с промежуточными пунк-
тами. Показать, что в соответствующем базису дереве не обязательно
все стрелки направлены от начала (то есть от Лос-Анжелеса).
3. Доказать, что этот способ одновременно решает задачи о кратчай-
ших путях из Лос-Анжелеса до каждого из городов. Каковы эти кратчай-
шие пути?
4. Каковы наилучшие пути для распределения груза в количестве
из начального пункта до (п — 1) городов с потребностями 62, Ъг, . . ., Ьпу
где 3” bi = at-
5. Доказать, что если в задаче о кратчайшем пути (§ 17-3) допу-
скаются не только положительные, но и отрицательные значения dij
и если сумма значений dtj по любому циклу положительна, то итеративный
метод и метод непосредственного решения применимы; однако если послед-
нее условие не выполняется, то оба они теряют силу.
6. Решить пример из § 17-3 об отыскании кратчайшего пути, который
был использован для иллюстрации непосредственного метода, с помощью
итеративного метода и метода, описанного в главе 16.
7. Задача о поставщике (Джейкобс [1]). Поставщик принимает заказы
на обслуживание на ближайшие Т дней. Ему требуется rt свежих
салфеток в t-й день, £=1,2, . . ., Т. Он отправляет грязные салфетки
в прачечную, которая имеет три срока обслуживания / = 1, 2 или 3 дня.
Чем быстрее осуществляется обслуживание, тем выше затраты с? на
стирку и глажение салфеток. Он может покупать также новые салфетки
по цене с0 за штуку. Он имеет начальный запас из 5 салфеток. Поставщик
желает минимизировать свои суммарные затраты.
Сформулировать эту задачу в сетевой постановке, рассматривая
поставщика в момент t как «источник» в некоторой абстрактной сети для
загрязненных салфеток, которые соединяются с «прачечными» £ + 1,
£ + 2, £ + 3. Обратное направление дуги недопустимо. Прачечная £
соединяется с чистой салфеткой «пунктом назначения» £, который в свою
очередь соединяется с точкой такого же типа £ + 1.
Приписать числовые значения различным параметрам и решить задачу
численно.
Глава 18
ОГРАНИЧЕННЫЕ СВЕРХУ ПЕРЕМЕННЫЕ
18-1. ОБЩИЙ СЛУЧАЙ
Нашей целью является изложение упрощенных вычислительных
методов решения важного класса задач, в которых переменные ограничены
сверху.
В связи с этим следует заметить, что при использовании моделей
линейного программирования для решения динамических и статических
задач основным препятствием для их применения становится то, что совре-
менные вычислительные методы не могут справиться с размерами матриц
даже для простейших технологических ситуаций. Однако в некоторых
случаях, таких, как уже ставшая теперь классической транспортная
модель Хичкока — Купманса (см. гл. 14), оказывается возможным из-за
простой структуры системы решить соответствующую задачу линейного
программирования независимо от ее размера. Это наводит на мысль, что
для обеспечения быстрого решения больших систем следует использовать
различные специфические свойства структуры матриц.
Метод, описанный в этой главе (Данциг, [8]), был впервые приме-
нен в корпорации РЭНД при разработке упрощенного вычислительного
процесса решения следующей задачи: персонал, занятый на проектных
работах, недоволен большим несоответствием, с которым обычно прихо-
дится сталкиваться, между сроками проведения вычислений и сроками
завершения всей работы. Главная причина недовольства совершенно
ясна, ибо бывают и очень срочные и очень большие по объему проекты,
которые полностью занимают все вычислительные средства на много
недель. Исследователи, по вполне понятным причинам перестают интере-
соваться ответами вычислителей на их задачи, если вычислительная рабо-
та продолжается дольше их собственной . Этот пример показывает, что
метод приоритетного расписания является, вообще говоря, не наилучшим1.
Чтобы предложить более гибкий метод решения, чем метод приори-
тетного расписания, была придумана модель, в которой значимость рабо-
ты уменьшалась, как только отодвигались сроки ее выполнения. Опре-
деление оптимального расписания зависело от решения описываемой
далее распределительной задачи.
Переменная Xij — число часов, которое отводится для i-й работы в у-й
неделе. Следовательно, нужно так выбрать неотрицательные Xij и min z,
чтобы 1) суммарное число часов, отведенных на г-ю работу, равнялось
требуемому количеству; 2) все занятое время в у-й неделе не превосходило
1 «Модель оптимального расписания проектных работ на перфорационной маши-
не» была предложена К. Шоу из корпорации РЭНД и автором настоящей книги и была
доложена ими на семинаре по промышленным задачам о расписаниях зимой 1952 г.
(этот семинар случайно оказался одним из предшественников Института управления
(Institute of Management Science)).
355 23*
Виды работы 1-Я неде- ля 2-я неде- ля 3-я неде- ля п-я ... педе- ля Требуемое число часов
Работа 1 *11 *12 *13 ... х^п = Г1
Работа 2 *21 *22 *23 - .- *2п = г2
• •
Работа т Хт1 хт2 *7ПЗ • • • хтп ==rm
Имеющееся число ча- сов. hi \ » А I Л3 hn
________________________________________________________________________________________________________________________________________________________________________________________________.______________________________________________________________________________________________________________________________________________________________
имеющегося в распоряжении; и 3) суммарная стоимость была бы мини-
мальной:
п
2^м=гь (1)
j=i
т
2 (^)
i=l
ТП п
2 2 = (3)
i=l ;=1 ‘
где (—Cij) суть оценки (с точки зрения заказчика) одного часа, затрачен-
ного на его проект в /-й неделе. Эти оценки удовлетворяют неравенствам
( * C/t) ‘ ^12) ( ^in)« (За)
Помимо этих ограничений; в задаче для некоторых i и / имеются еще
ограничения
(36)
или, что то же самое,
+ (Уи>®)- (Зв)
Другими словами, время, отведенное для i-й работы в /-й неделе,
не Должно превосходить а^-. Если бы мы, как обычно, ввели дополнитель-
ные уравнения и свободные переменные в ограничения (36), то это зна-
чительно увеличило бы объем задачи. В качестве иллюстрации рассмот-
рим задачу расписания для *18 работ на 10 недель, которая имеет 28
уравнений с 180 неизвестными, не ограниченными сверху; если включить
в нее ограничения сверху, то это потребовало бы введения дополни-
тельно 180 уравнений типа (Зв) и 180 свободных переменных.
Общий случай. Найти Xj и min 2, удовлетворяющие условиям
п
2 aijXj = bi (х^>0; г = 1, 2, т),
’=‘„ (4)
2 CjXj — z (min),
j=i
356
и, если переменные Xj также должны удовлетворять неравенствам Xj
то использовать свободные переменные и новые уравнения
Xj + yj = a} (xj>0; yj>0) (5>
для каждого такого ограничения. Мы будем называть (4) и (5) системой
с ограничениями на интенсивности.
ИЛЛЮСТРАЦИЯ МЕТОДА.
Метод, позволяющий найти решение системы с ограничениями на
интенсивности, основан на незначительном обобщении симплекс-метода.
Дополнительные вычисления, связанные с реализацией этого метода,
невелики. Хотя в симплекс-алгоритме небазисные переменные обычно
полагают равными нулю, легко видеть, что им можно приписать любое
фиксированное значение. Критерий для симплекс-метода показывает, что
выгодно увеличить переменную xs, если соответствующая относительная
оценка cs отрицательна, и выгодно уменьшить xs. если соответствую-
щая относительная оценка cs положительна. Если введены ограничения
на xs сверху или снизу, то будет выгодно увеличивать ее значение
только тогда, когда cs < 0 и переменная xs еще не достигла своей верхней
границы, либо уменьшать значение xs, если cs>0 и переменная xs не до-
стигла своей нижней границы.
Следующий пример показывает, как можно решить расширенную сис-
тему, применяя к исходной системе без ограничений на интенсивности
симплекс-алгоритм с очень простыми дополнениями. Эти дополнения будут
гарантировать, что значения, принимаемые переменными, останутся
между их нижними и верхними границами.
Пример 1. Найти числа
0<Xi^4, 0^ж2<5, 0<я3^1,
0<^2, <6>
и min и, удовлетворяющие системе уравнений
х^ х3— 2ос^ z= 3,
х2— 2^5 —4, * (7)
— 2я3 — я4+ я5 — z = 0.
• • ★ •
Используя xif х2 и (—z) как базисные переменные, мы получаем базис-
ное допустимое решение
(3, 4, 0, 0, 0, 0). (8)
• • •
Значения этих базисных переменных отмечены жирными точками.
Заметим, что ни одна из переменных не достигает своей верхней границы.
Поскольку с3 отрицательно, выгодно увеличить значение х3. Фикси-
руя остальные небазисные переменные, мы получаем решение
(3 — х3, 4 + х3, х3, 0, 0, — 2х3), (9)
• • ★ *
которое показывает, что значение х3 может возрасти до 3. Однако ввиду
третьего из ограничений (6) переменная х3 не может быть больше 1. Поэто-
му мы увеличим переменную х3 только до ее верхней границы и прирав-
няем ее этому значению, сохранив то же самое базисное множество.
357
Новое решение таково:
(2, 5, 1, 0, 0, —2). (10)
• • ★ •
Поскольку базисное множество не изменилось, значения Cj в z-урав-
нении системы (7) остались прежними. Ввиду того что с4= — 1, будем сна-
чала увеличивать я4. Это дает решение
(2 + 2я4, 5—-я4, 1, я4, 0, —-2 —я4.) (И)
• • ★ О
В данном случае переменная z4 не может возрасти до 5, так как ее
верхняя граница равна 2, но она не может быть равна и своей верхней
границе, поскольку тогда было быxt — 2 + 2-2 = 6, что больше верхней
границы для Xi 4. Следовательно, наибольшее значение, допустимое
для я4, есть я4 = 1. Поскольку при этом значении гг4 базисная переменная
Xi достигает своей верхней границы, мы выводим xt из базисного множества,
заменяя ее переменной я4. Каноническая форма, связанная с новым бази-
сом, получается с помощью ведущего элемента — 2я4, выделенного жирным
шрифтом в системе (7). Итак, мы получаем систему:
11, 3
2 2 — 2 ’
у Xi 4- х2 — у #3 +2#5 = у, (12)
15. 3
— “Т^з + *5 —у,
с которой связано решение:
(4, 4, 1, 1, 0, -3). (13)
• • •
Переменная Xi входит в небазисное множество со значением, равным
ее верхней границе, xt = 4. Отметим, что базисные переменные х2 и я4
находятся строго между верхней и нижней границами, в то время как
небазисные переменные хи х3, х5 находятся точно на своих верхних или
нижних границах. Заметим, что для переменной я5, находящейся на
своей нижней границе (нуль), относительная оценка положительна, а для
всех переменных, находящихся на своих верхних границах, относитель-
— 1 — 5
ные оценки отрицательны: — — % ис3 =— у Как мы сейчас покажем,
для задач с ограничениями на интенсивности это удовлетворяет критерию
оптимальности и никакие дальнейшие исправления не нужны.
Чтобы доказать оптимальность полученного решения, подставим
в систему (12) вместо небазисных переменных, которые находятся на своих
верхних границах, выражения
^ = 4 — х'19 х3=1—х^. (14)
Получим систему
2 ^1 4“ 2 *^з + *^4 — 1,
1 1
—2" xi ^2 + ~2 хз 4“2я5 = 4, (15)
1 5
у Х1 +-2^3 + —2 = 3.
358
с базисным решением
(О, 4, О, 1, О, -3),
(16)
которое, очевидно, оптимально, если не рассматривать ограничения
на интенсивности х{ ^4, х2 ^5, х% ^1, х^ ^2, x$ ^3. Далее, подставив
х{ = 0, х'3 — 0 в (14), мы получим множество неотрицательных величин,
удовлетворяющих всем ограничениям (14) и (15). Поскольку дополни-
тельные ограничения типа (14) могут разве лишь увеличить минимальное
значение и, значение z = —3 является минимальным для полной системы
(14) и (15), которая эквивалентна системе (6) и (7).
ТЕОРИЯ ЗАДАЧ С ОГРАНИЧЕНИЯМИ СВЕРХУ
В предыдущих главах базисное решение системы без ограничений
на интенсивности (4) определялось как решение, которое получается,
если положить п — т небазисных переменных равными нулю и решить
систему для оставшихся базисных переменных хц , . . ., Xjm- Говорят,
что решение является допустимым, если в этом решении значения всех
переменных не отрицательны. На каждой итерации симплекс-метода полу-
чается новое базисное решение, в котором одна из базисных переменных
Xj? (1 г ^т) полагается равной нулю и заменяется в базисном множе-
стве небазисной переменной xs.
В этой главе эти же термины мы будем использовать в несколько ином
смысле. Допустимым решением будем называть решение, в котором каж-
дая переменная Xj не отрицательна и не превосходит своей верхней гра-
ницы Под базисным допустимым решением будем понимать решение,
в котором небазисные переменные принимают значения либо нуль, либо а7-.
Заметим теперь, что исходную систему (4) и (5) можно заменить экви-
валентной ей системой без ограничений на интенсивности, в которой все
небазисные переменные равны нулю. Это достигается подстановкой —
х] для любой небазисной переменной Xj, находящейся на своей верхней
границе. После преобразования каноническая форма относительно
некоторого множества базисных переменных, скажем х2, . . хП1
примет вид
+«1,7п+1[^тп+1 ИЛИ (otm+1 ^m+1)] 4" •••4“
+ ain[xn или (ап — ж;)]='б1,
*2 + «2,тп+1кпг+1 ИЛИ («т+1 — Х^+1)] + . . . +
+ а2п[хп или (ап — Хп)] = Ь2,
............................................................................. (17)
“F fyn, тп+i [%т+1 ИЛИ ((%т+1 #m+l)] 4” • • • 4”
+ атп[хп или (ап — х'п)] = Ьт,
4- cm+i [хт+1 или (ат+1 —ж^+1)]4-... 4-
+ сп[хп или (ап — ^)] = z — z0.
359
Перенося постоянные (а^- а>) и CjUj в правую часть, мы получим
+«1, m+l ИЛИ -4н)+--‘+й1'Л^ ИЛИ — £s)+--«
• . • . + d\n (^п ИЛИ Xn) =
’.................................................... (18)
+ ^/n, m+l (%m+l ИЛИ ^m+1) “F • • • 4~ ^ms (% 8 ИЛИ Xs)
... —j— dmn (%n ИЛИ ' Xn) = bm,
Cm+l (^m+i ИЛИ — x'm+l) + . . . + Cs (xs ИЛИ — x's) + . . .
...+cn(xn ИЛИ — Xn)~Z~—
где
I) aij ~ коэффициенты исходной канонической формы;
II) х^, i — 1, 2, . . m — базисные переменные = i для при-
веденной выше системы);
III) в системе (17) небазисные переменные появляются либо как Xj,
либо как (— Xj) в зависимости от того, были ли соответствующие значе-
ния небазисных переменных в исходном решении равны 0 или а7-.
IV) 0 и (—zQ) суть значения, соответственно, базисных перемен-
ных и (—z) в базисном допустимом решении, которое получается
в результате проделанного преобразования.
Базисные переменные и их коэффициенты не участвовали в этом
преобразовании; поэтому симплекс-множители не изменились.
КРИТЕРИЙ ОПТИМАЛЬНОСТИ
Базисное допустимое решение для эквивалентной задачи (18) является
оптимальным, если
Г ’ _ ™
для Xj = 0 имеет место Cj = Cj— >,
и ’ 1 (19)
т
для Xj — O имеет место Cj = Cj— 3
2=1 \
где переменные со штрихами должны удовлетворять обратным неравен-
ствам, так как их коэффициенты противоположны по знаку коэффициен-
там при переменных без штрихов.
Теорема 1. Базисное допустимое решение системы (18), удовлетворяю-
щее условиям (19), эквивалентно некоторому оптимальному решению систе-
мы (4) и (5).
Доказательство очевидно.
УЛУЧШЕНИЕ БАЗИСНОГО ДОПУСТИМОГО РЕШЕНИЯ
Если решение не оптимально, то переменная, которую мы будем уве-
личивать, выбирается среди тех небазисных переменных xs (или xs) , для
которых:
- . — I с, для небазисной Xj,
cs = minq<Q, где Cj= - „ ,
J 4 [ —cj для небазиснои 'Xj.
(20)
360
Пусть 0 равно изменению величины xs (положительному или отрица-
тельному).
Случай /. Кандидатом в базисное множество является небазисная
переменная без штриха. Тогда новое значение переменной xs равно 0,
где 0 < 0 as.
Случай II. Пусть x's — небазисная переменная, значение которой
нужно увеличивать; новым значением xs будет as+0, где — as ^0^0
(поскольку в этом случае значение переменной xs должно стать меньше
своей верхней границы as).
В любом случае, если мы фиксируем значения всех остальных небазис-
ных переменных, то измененные значения базисных переменных Xj 9
z и xs выражаются через 0 следующим образом:
= ь;—а180 (0Xj. < а3-.),
Х32=Ь2 — «гД
Х3т — ,
Z = z0 + Cs0,
где
Случай I. xs = 0 и cs<0
Случай II. xs — а34-0 и cs>0
(21)
(O<0<as).
( —as<0<O).
Случай I. Наибольшее неотрицательное значение 0*, при
решение остается допустимым, определяется по формуле

котором
0* = min
&is
< (pi aj.'j/ais
(ats > 0)
(afS<0).
(22)
Случай II. Максимальное неотрицательное значение 0*, при котором
решение остается допустимым, равно
рз
— 0* = minW(—ais) __ (—ai8>0) (23)
(. (^i ®4.)/( ^is) ( ^is 0).
а) Если 0* = as в (22), то на следующей итерации небазисная пере-
менная xs фигурирует как х8; если —0* = as в (23), то небазисная пере-
менная x's на следующей итерации выступает как xs. И в том и в другом
случае базисное множество не изменяется, но переменные принимают
новые значения, которые вычисляются по формулам (21) при 0 = 0*.
б) Если, с другой стороны, минимум в (22) или (23) отличен от as,
то некоторая базисная переменная xjr заменяется на xs. В случае I новым
значением xs становится 0*, а переменная Xjr становится равной нулю или
as в зависимости от того, какое из неравенств ars > 0 или ars < 0 имеет
место. В случае II новое значение xs равно (as + 0*), а переменная Xj
становится небазисной и принимает значение соответственно нуля или
as при — ais > 0 или — ais<Z 0. Новые значения остальных базисных пере-
менных при ц jr получаются по формулам (21) при 0 = 0*.
361
Пример 2. Найти числа
0<*t<l, 0<*2<2, 0^*3<3, 0<*4^4 (24)
и min 2, удовлетворяющие системе уравнений
*1 -j— Х2 + *3 + = 6,
2xi + *2—4*3—5*4 + (— 2) = 0. ^5)
Начиная с допустимого решения *4 = 1, х2 = 2, х3 = 3, *4= 0
и (—z) = 8 и используя Xi как базисную переменную, получаем началь-
ную каноническую форму.
Итерация 0:
*1 + ^2 + ж3 + ^4==6,
— х2 —6*3—7*4 +(—z)=—12. (2®)
(1-0о, 2, 3, О + 0о, 8 + 70о)
• ★
шах 0О = 1; гг4 заменит в базисном множестве переменную *4.
Итерация 1:
+ ^2 + ^з + ^4 = 6,
1X1 + 6*2+*3 + ( —2) = 30 (27)
(0, 2—0П 3, 1 + 0ь 15 + 60J
* •
max 0! — 2; *4 все еще остается базисной переменной, а небазисная пере-
менная *2, будучи равна своей верхней границе, становится равной своей
нижней границе.
Итерация 2:
*1 4^2 4*^3 + #4 —6,
Ixi + 6*2 +^з +(— 2) = 30. (28)
(0, 0, 3-02, 3 + 02, 27 + 02)
max 02 = 1; *3 заменяет в базисном множестве переменную *4, которая
выходит на свою верхнюю границу.
Итерация 3: (решение оптимально)
+^2 + ^3 +^4 =6,
6*!+ 5*2 — *4 + (—2) = 24. (29)
(0, 0, 2, 4, 28)
МОДИФИЦИРОВАННЫЕ СИМПЛЕКС-ТАБЛИЦЫ
Чтобы учесть ограничения на интенсивности, необходимо произвести
незначительные изменения в симплекс-методе, использующем множители
(см. гл. 9). Эти изменения перечислены в следующих пунктах:
1) В табл. 9-3-1а ввести дополнительную строку и в ней записать
величины верхних границ для переменных.
2) В табл. 18-1-1 можно отмечать не только относительные оценки
dj или но и указывать также, какие небазисные переменные находятся
на своих верхних границах. В приведенных ниже таблицах используются
следующие обозначения:
362
а) Черточка над значением относительной оценки указывает, что
соответствующая переменная находится на своей верхней границе.
б) Скобки [] используются, чтобы отметить, что соответствующие
переменные являются базисными.
в) Значок * показывает, что соответствующая переменная Xj войдет
в базисное множество на следующей итерации. Так, для примера 1 (см.
(6), (7)) имеем:
Таблица 18-1-1
Относительные оценки: Cj или dj
3= (1) (2) (3) (4) (5)
Итерация 0 [0] [0] —2* —1 1
1 [0] [0] —2 — 1* 1
2 -Х/2 [0] -^2 [0] 1
3) В составлении табл. 9-3-На из § 9-3 изменений нет. Но выбор веду-
щего элемента производится в соответствии с формулами (22) или (23)
и последующими замечаниями. Если переменная xs вводится вместо
базисной переменной то табл. 9-3-Пб заменяется на табл. 18-1-П,
где 0* или as + 0* являются новыми значениями переменной xs в зави-
симости от того, xs = 0 или xs = as на этой итерации. Если при этом
базисное множество не изменяется, то все р^, и of также не изменяются;
новые значения базисных переменных, z и w приведены в последнем столб-
це табл. 18-1-П; в r-й строке этой таблицы стоит х^ = Ь'г — ars 0*.
Таблица 18-1-П
Начало 14-1-ой итерации (если заменяет базисную переменную
Базисные перемен- ные Столбцы канонической формы Значения базисных переменных XS
жП+1”--- хп+т ~z ~w
х8 хз Jm Матрица, обратная к базисной —> Pit aisP*i •••• Pirn aisP*w ₽r*l ₽rm Pml amsP*l • • • • Pmm a7nsP*m ь;—als0* 0* или as4"9* bm — a?ns0*
n в 1 1 — Л1 — csP?l •••• —лтп csP*m 1 — Ol — ^sP*i •••• ^sP*m 1 * * 1 1 'Y Гэ । 1 1
Ргг— Pri/ars G— 1, ...» 7И-)
0* определяется по формуле (22) или (23).
В начале итерации столбец я8пуст.
363
18-2. ТРАНСПОРТНАЯ ЗАДАЧА С ОГРАНИЧЕННЫМИ
ПРОПУСКНЫМИ СПОСОБНОСТЯМИ
И ЕЕ ОБОБЩЕНИЯ
РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ С ОГРАНИЧЕННЫМИ
ПРОПУСКНЫМИ СПОСОБНОСТЯМИ
Применим теперь теорию задач с ограниченными сверху переменными
к транспортной задаче с ограниченными пропускными способностями.
В общем случае задача состоит в нахождении неотрицательных xtj и ми-
нимального z, удовлетворяющих условиям:
Равенства по строкам:
(г = 1, 2, ..., т)
Равенства по столбцам:
(7 = 1,2, ...,п)
Ограничения сверху:
(для всех i и у)
Целевая функция:
п
S = (1)
j=l
т п
S 3 cijxtj ~ z* (4)
2=1 j—1
Рассматривая табл. (5) как стандартную транспортную таблицу
3 X 4 с ограниченными пропускными способностями, заметим, что, сфор-
мулированная далее теорема 1 является лишь перефразировкой критерия
оптимальности, приведенного в предыдущем параграфе.
*11 «и С11 1 *12 «12 с12 *13 а13 с13 *14 а14 с14
*21 а21 С21 *22 «22 с22 *23 «23 с23 *24 «24 с24
*31 «31 С31 *32 «32 с32 *33 «33 с33 *34 «34 с34
61 ^2 »2 Ь3 v3 64
(5)
Теорема 1. Допустимое решение xtj — xlj транспортной задачи с ограни-
ченными пропускными способностями является оптимальным, если
существует множество неявных цен иг и Vj и относительных оценок
Сц — Cij — Щ — Vj, для которых
О Xij CLij ~~т> Cfj = О,
Xij = O =фС^->0, (6)
~ 0.
Покажем теперь на простом численном примере (7), как можно эффек-
тивно к этому классу задач применить методы из § 18-1. В этом параграфе
мы покажем, что класс транспортных задач с ограниченными пропускны-
364
ми способностями в действительности эквивалентен классу обычных транс-
портных задач. Будут рассмотрены также различные обобщения понятия
«пропускная способность».
*14 <
25
*22 20
2
25
(7)
лг21<14
8
*31 < 18
9
*34 < 7
8
50
15 20 30 35
НАХОЖДЕНИЕ ИСХОДНОГО БАЗИСНОГО ДОПУСТИМОГО РЕШЕНИЯ
Хотя для нахождения исходного решения транспортной задачи без
ограничений на пропускные способности и было предложено простое
правило, для задачи с ограниченными пропускными способностями такое
правило указать невозможно. Если бы это удалось сделать, то это позво-
лило бы легко найти решение и такой задачи: найти распределение т
человек по т работам, когда некоторых из них на определенные работы
назначать не разрешается. Математически задача формулируется так:
дана произвольная матрица размера т X т (элементами ее являются 0
и 1), требуется выбрать из нее некоторую перестановку1 из единиц или
показать, что такой не существует. До сих пор еще не удалось найти
неитеративный метод решения этой задачи.
При отыскании исходного решения для задачи (7) в большинстве слу-
чаев целесообразно выбрать клетку с минимальным значением (в табл.
(7) это <?22, равное 2) и присвоить соответствующей переменной наиболь-
шее возможное значение, но так, чтобы эта переменная не превысила
своей верхней границы. В нашей задаче мы полагаем ж22 = 20. Если
выбранное значение переменной удовлетворяет уравнению по строке или
столбцу, то эту переменную будем рассматривать как базисную и в соот-
ветствующем столбце или строке больше выбирать переменные не будем.
С другой стороны, если значение выбранной переменной определяется
величиной верхней границы, то эту переменную рассмотрим как небазис-
ную переменную, находящуюся на своей верхней границе, и отметим ее
чертой сверху. Если имеют место оба случая, то обычно считают строку
или столбец лимитирующими, а переменную — базисной. Процесс повто-
ряют для оставшихся клеток.
Для табл. (7) это правило дает такие значения: я22 = 20 (базисная),
х33 == 25 (на ограничении), я13 = 5 (базисная), я24 — 5 (базисная), я14 =
= 20 (базисная), я34 = 7 (на ограничении), я31 = 15 (базисная). Поскольку
третья строка и четвертый столбец имеют по 3 нераспределенные единицы,
решение не является допустимым. Добавим к таблице «короткие» клетки:
строку с номером i = 0 и столбец с номером / = 0; заменим затем исход-
1 То есть множество элементов матрицы, взятых по одному из каждой строки
и каждого столбца.— Прим. ред.
365
ные си на dtj = 0, положив для коротких клеток dy = 1. Все это све-
дено в табл. (8).
(8)
Заметим, что d30 = d^ = 1 должны быть равны соответственно и3
и г?4, поскольку в § 15-2-(14) было показано, что неявные цены и0 и г?0
для свободных столбцов и строк можно считать равными нулю.
Применив теперь этап I симплекс-метода для минимизации суммы
искусственных переменных, мы получим в данном случае, проделав одну
итерацию, допустимое решение, представленное в табл. (9). В этой таблице
вновь записаны исходные стоимости.
12 10 13 5 5 5 6 20 20 7 25 0
14 8 17—е 20 2 10 7 84-0 9 6 25 — 1
15 18 9 34-0 4 3 25 25 4 7 — 0*7 8 50 0
15 9 20 3 30 6 35 7 vj
Однако это решение не является оптимальным, потому что я34 является
небазисной переменной, находящейся на верхней границе, и с34 = с34 —
—и3—г?4 = 8— 0 — 7 — +1, в то время как относительная оценка
такой переменной должна быть неположительной. Следовательно, выгод-
но уменьшить я34 по сравнению с величиной верхней границы, не изменив
при этом небазисные переменные, но преобразовав базисные переменные.
Наибольшее значение 0, при котором решение остается допустимым, есть
0 = 1, и это значение определяется ограничением сверху на переменную
ж24 = 8 + 0 < 9.
Новая табл. (10) дает оптимальное решение
366
12 10 13 5 5 5 6 20 20 7 25 —1
14 8 16 20 2 10 7 9 9 6 25 — 1
15 18 9 4 4 3 25 25 4 6 7 8 50 0
15 9 20 3 30 7 35 8 Vj
(10)
Из описанного метода вытекает следующая теорема, доказательство
которой в общем случае для транспортных задач с ограниченными про-
пускными способностями оставлено в качестве упражнения.
Теорема 2. Если в транспортной задаче с ограниченными пропускными
способностями верхние границы, производимые количества и требуемые
количества суть целые числа, то каждое базисное решение будет целочис-
ленным.
ЭКВИВАЛЕНТНОСТЬ ТРАНСПОРТНОЙ ЗАДАЧИ
С ОГРАНИЧЕННЫМИ ПРОПУСКНЫМИ СПОСОБНОСТЯМИ
И КЛАССИЧЕСКОЙ ТРАНСПОРТНОЙ ЗАДАЧИ
Заметим, что каждая переменная появляется с ненулевыми коэф-
фициентами в трех уравнениях; не только в условиях (1) и (2), то есть
равенствах по строкам и столбцам, которые используются и в классиче-
ской задаче, но также и в ограничениях (3), которые можно переписать
Хц + Уи = ац, (уи>0) (11)
где У а — свободные переменные. Эту систему, однако, можно заменить
эквивалентной ей, где каждая переменная входит только в два уравнения,
точно так же как в классической транспортной задаче. Рассмотрим задачу
нахождения xtj > 0 и min z, удовлетворяющих условиям:
Строка:
(i = 1, ..., т)
Столбец;
(все i, j)
Строка:
(все i, j)
п
2 xij ~
Vij “Ь
(12)
' xij Уц—
Столбец:
(7 = 1, n)
m
2 xij “
i=l
m n
2 2 CijXtj = z (min).
i=i ;=i
Поясним этот результат в терминах сетей. Транспортную задачу с огра-
ниченными пропускными способностями можно представить в виде графа,
приведенного на рис. 18-2-1. Числа на направленных дугах, соединяю-
щих начальный пункт i и пункт назначения j, являются пропускными
способностями дуг. Схема, использованная в (12), позволяет заменить
367
каждую дугу с ограниченной пропускной способностью (рис. 18-2-11а)
на множество дуг без ограничений (рис. 18-2-Пб).
Рис. 18-2-1. Двухсторонний граф транспортной зада-
чи с ограниченными пропускными способностями.
б)
Рис. 18-2-Па, б. Замена дуги с ограни-
ченной пропускной способностью дугами
без ограничений.
ТРАНСПОРТНАЯ ЗАДАЧА С ОГРАНИЧЕНИЯМИ НА ЧАСТИЧНЫЕ
СУММЫ ПЕРЕМЕННЫХ
Идея, которую формализовал Манн, связана с задачами, в которых,
помимо уже рассмотренных ограничений на переменные, введены также
ограничения на частичные суммы переменных. Ради простоты рассмотрим
случай, когда имеется только одна такая частичная сумма. В рассмотрен-
ной выше задаче составления расписания работ для вычислительной
машины условие хИ 40 можно интерпретировать так: в течение первой
недели 1 можно выделить не более одного человека для выполнения первой
работы. В некоторых задачах может потребоваться более сложное условие,
например, условие xlt + ж31 + я61 40, выражающее тот факт, что на
работы 1, 3 и 6 должен быть назначен любой, но один и тот же исполни-
1 Имеется в виду сорокачасовая рабочая неделя.— Прим, перев.
368
тель. Аналогично условие типа + я12 + #13 > & может означать,
что на работе 1 за первые три недели должно быть отработано по крайней
мере к часов. Так же, как и задачу с ограничениями на интенсивности,
транспортную задачу с ограничениями на частичные суммы переменных
по строкам или столбцам можно свести к стандартной транспортной задаче.
Чтобы убедиться в этом, рассмотрим систему (1), (2) и дополнительное
условие:
^11 + ^12+ • • • + #tfe^a« (13)
Это можно записать в виде табл. 18-2-1.
Таблица 18-2-1
(Недопустимые клетки заштрихованы.) Понятно, что к системе можно доба-
вить любое количество ограничений вида (13), последовательно интерпре-
тируя каждое из них так, как было показано. Например, дополнительное
ограничение на второй столбец
#12 + Х32 + #62 Р (14)
можно учесть, раздваивая второй столбец и используя вторую свободную
переменную. Более того, для второго столбца может быть еще и такое
ограничение, как
#22+ #42 +#52^ Y? (15)
которое не содержит переменных, входящих в ограничение (14). На одни
и те же переменные одного столбца может быть наложено несколько огра-
ничений. Например, можно учесть условие (14) и
#12 + #62 3, (13)
для этого надо еще раз раздвоить столбец, содержащий переменные #i2
#32? #62*
Теорема 3. Транспортную задачу с дополнительными ограничениями
на частичные суммы по строкам и столбцам можно свести к стандартной
транспортной задаче, если любые два ограничения по столбцу (или строке)
либо не имеют общих переменных, либо переменные, входящие в одно из огра-
ничений, образуют подмножество множества переменных, входящих
в другое ограничение.
Теорема 4. Если в частичную сумму, на которую наложено ограниче-
ние, входят переменные из различных столбцов или строк, то базис не
обязательно будет треугольным; поэтому могут получаться и нецело-
численные базисные решения.
Упражнение. Доказать эти последние две теоремы.
24 Дж. Данциг 369
18-3. ЗАДАЧИ
ОБЩИЙ СЛУЧАЙ (см. § 18-1)
1. а) Рассмотреть еще раз правила определения «кандидата», который
будет введен в базисное множество или покинет базисное множество,
достигнув своей верхней или нижней границы.
б) Модифицировать процесс улучшения допустимого решения в общем
случае.
в) Модифицировать метод так, чтобы он охватывал задачи, в которых
нижние границы для переменных отличны от нуля.
г) Применима ли к методу решения задач с ограниченными интенсив-
ностями лексикографическая схема, позволяющая избежать вырожден-
ности? Если не применима, то какие изменения необходимо сделать?
ТРАНСПОРТНАЯ ЗАДАЧА С ОГРАНИЧЕНИЯМИ НА ПРОПУСКНЫЕ
СПОСОБНОСТИ И ЕЕ ОБОБЩЕНИЯ (см. § 18-2)
2. Дать прямое доказательство теоремы 1 из § 18-2.
3. Показать, что для транспортной задачи с ограниченными пропуск-
ными способностями § 18-2-(1), (2), (3) и (4) не существует допустимого реше-
п
ния, если существует такая строка р, что у ар или такой столбец д,
7=1
что 2 aiq < bg.
1=1
4. Построить пример, показывающий, что допустимое решение,
удовлетворяющее условиям (1), (2) и (3), может и не существовать, даже
если для всех i = 1, 2, . . ., т и j = 1, 2, . . ., п
п т
7=1 1=1
5. Рассмотрим пример, приведенный в § 18-2-(7); переформулировать
его в виде условий § 18-2-(1), (2), (3) и (4).
6. В приведенной ниже таблице 5x5 заштрихованные клетки показы-
вают, какой рабочий и на каких работах не может использоваться. Пока-
зать, почему эта задача является задачей с ограниченными интенсивностя-
ми. Использовать метод § 18-2 для нахождения допустимого решения.
7. Построить пример, в котором искусственные переменные xi0
и xOj являются частью каждого базиса на протяжении этапа II. Распро-
странить на этот случай приведенные в тексте рассуждения, касающиеся
случая, когда искусственные переменные образуют часть базиса в тече-
ние этапа II.
370
8. Доказать, что приведенное в § 18-2-(10) решение является опти-
мальным. Является ли оно единственным? Если нет, то построить все
другие оптимальные решения.
9. Дана транспортная задача с ограниченными пропускными спо-
собностями с т = 5 строками и п = 7 столбцами и дополнительным усло-
вием на частичную сумму по строке ^32 + ж35 + ж37^а. Сформулиро-
вать эквивалентную ей транспортную задачу с ограниченными пропускны-
ми способностями без дополнительного условия.
10. Построить примеры, показывающие, что если множества пере-
менных, входящих в частичные суммы, для некоторой строки (столбца)
пересекаются и ни одно из этих множеств не является частью другого,
то базис может оказаться и не треугольным.
11. Показать, что если ограниченные частичные суммы переменных
включают переменные из разных строк или столбцов, то базис не обязан
быть треугольным; другими словами, показать, что такая задача не экви-
валентна транспортной задаче.
\
24*
Глава 19
МАКСИМАЛЬНЫЕ ПОТОКИ В СЕТЯХ
19-1. ТЕОРИЯ ФОРДА — ФУЛКЕРСОНА
Рассмотрим сеть, связывающую два пункта, источник и сток, путями,
проходящими через некоторые промежуточные пункты. Каждому ребру
сети сопоставляются два числа, характеризующие пропускную способность
ребра в каждом направлении. Предполагая потоки установившимися,
найти максимальный поток от источника к стоку. В этом параграфе мы
будем придерживаться теории, предложенной Фордом и Фулкерсоном
(1,8].
На сети, представленной на рис. 19-1-1, источник и сток выделены
из остальных пунктов двойными кружками. Пропускные способности
Рис. 19-1-1. Задача о максимальном потоке с пропускными
способностями направленных дуг.
в каждом направлении на каждом ребре равны числам, написанным около
того пункта, в котором поток может начинаться.
Если О обозначает объем потока от пункта i к пункту /, то имеют
место следующие ограничения на пропускные способности:
(1)
(2)
Таким образом, на рис. 19-1-1, например, 0<я01<4, 0^я10<0,
0<х14<оо, 0<ж41<0 и т. д. Кроме того, имеются следующие урав-
нения неразрывности потока: за исключением источника, для которого
к = 0, и стока, для которого к = п, сумма потоков, приходящих в к-й
пункт, равна сумме потоков, выходящих из него, т. е.
= (А = 1, 2, п-1) (3)
г j
где в суммах учитываются только те члены и хду, которые соответ-
ствуют дугам1 сети. Обозначим через F поток, приходящий в источник сети
1 Напоминаем, что каждое ребро как бы состоит из двух дуг с противополож-
ными направлениями. — Прим. ред.
372
извне; тогда, по определению,
Р +3 Xio X0J = 0- (^)
i 3
Нетрудно показать, что в силу условия (3) поток, выходящий за сеть через
сток, тоже равен F, ибо если мы суммируем п — 1 соотношения (3) и усло-
вие (4), то каждая переменная входит в два уравнения с противополож-
ными знаками (поэтому они взаимно уничтожаются), за исключением тех,
которые представляют потоки из стока. Поменяв знаки, получаем
= (5)
г 3
Задача о максимальном потоке состоит в выборе ; > О и max F, удовле-
творяющих условиям (1), (2), (3), (4) и (5).
НАХОЖДЕНИЕ ДОПУСТИМЫХ РЕШЕНИЙ ДЛЯ ТРАНСПОРТНОЙ ЗАДАЧИ
С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ И КЛАССИЧЕСКОЙ
ТРАНСПОРТНОЙ ЗАДАЧИ
Интересно отметить, что задача нахождения допустимого решения
для задачи о назначениях или, в более общем случае, для транспортной
задачи, в которой не все xtj, допустимы, эквивалентна (как мы вскоре уви-
дим) решению задачи о максимальном потоке. Вспомним, что алгоритм
одновременного решения прямой и двойственной задачи (§ 11-4) отыски-
вает допустимые решения для последовательности суженных прямых
задач. Отсюда следует, что транспортные задачи можно решать с помощью
последовательности задач о максимальном потоке. В следующей главе
эта идея будет воплощена в эффективном алгоритме. Приведенную ниже
транспортную задачу (фактически неразрешимую) можно записать кац
задачу о потоке в сети типа представленной на рис. 19-1-1.
Ясно, что допустимое решение задачи (6), если оно существует, соот-
ветствует нахождению таких значений в таблице (7), что, сложив
неизвестные суммы по строкам xoi и суммы по столбцам Xj0, мы получим,
что сумма z этих последних сумм максимальна и равна сумме пропускных
способностей по столбцу или строке.
С другой стороны, если максимальное значение z меньше, чем соот-
ветствующие суммы пропускных способностей, как в рассматриваемом
случае, то для задачи (6) не существует допустимого решения. Теперь
понятно, что на рис. 19-1-1 представлена сеть для задачи (7).
373
Для транспортной задачи с промежуточными пунктами модифици-
рованная сеть строится следующим образом: все пункты, в которых имеют-
ся излишки, соединяются в один фиктивный начальный пункт (источник)
при помощи дуг с пропускными способностями, равными имеющимся
излишкам; все пункты, для которых не удовлетворены потребности, сое-
диняются в один фиктивный пункт назначения (сток) дугами с пропускны-
ми способностями, равными дефициту. Тогда допустимое решение рас-
сматриваемой задачи будет соответствовать решению для модифицирован-
ной сети задачи о максимальном потоке, который равен сумме пропуск-
ных способностей дуг, выходящих из начального пункта (или входящих
в пункт назначения).
СВОЙСТВА ЗАДАЧ О ПОТОКЕ В СЕТИ
Легко видеть, что справедлива следующая
Теорема 1. Множество величин zZj->0, удовлетворяющих ограниче-
ниям на пропускные способности и уравнениям неразрывности потока,
можно заменить, сохранив тот же самый общий поток F, на другое мно-
жество xij, в котором либо х'ц, либо х'# равно нулю, положив
x\j = Xij—min (х^, хл). (8)
Мы будем рассматривать только такие потоки, для которых всегда имеет
место последний случай. Например, если на направленной дуге, соединяю-
щей пункты i и j, появилось число 6, то это означает, что х^ = 6
и хл = 0.
(г) * (3). (xij7, Xjt 3)
о
Теперь можно заменить все переменные xif- и хп на их разности
Xij = Xij Xji* (9)
{Xij^Q соответствует «н = х«и жя = 0.
-' - , , „
Xtj^. 0 соответствует—х^ = хц и =
Ограничения на пропускные способности и уравнения неразрывности
потока принимают вид
Mji Xij (Х/j
= (Л = 1, 2, п—1)
г
^+S*io=°. (10)
i
—Xin~Q.
г
Теорема 2. Множество xtj и F > 0, удовлетворяющих ограничениям
на пропускные способности и уравнениям неразрывности потока, можно
представить в виде суммы положительных потоков вдоль пути от источни-
ка к стоку и множества циркулирующих потоков; при этом направление
положительных потоков на любой дуге, общей для всех путей, одно и то же.
Определение. Потоком К в пути называется постоянный поток вели-
чины ~Xij = К для всех дуг (г -> /) вдоль пути и = 0 в остальных слу-
чаях. Эта теорема интересна, поскольку она означает, что решение задачи
о потоке или транспортной задачи с промежуточными пунктами соответ-
374
ствует нашему интуитивному представлению о том, что поток начинается
в пункте с излишками и движется (течет) от одного пункта к другому,
не изменяясь, пока наконец не достигнет некоторого пункта с дефицитом.
Теорема доказывается непосредственно. Предположим, что F > 0.
Выберем путь, начинающийся в пункте 0 с начальной дугой (0 -> ц), где
xoil = max хщ > 0. (11)
То, что я0/1 > 0, вытекает из условия F > 0 и уравнения неразрывности
потока F = S xQi. Повторим теперь этот процесс для пункта выбрав
вторую дугу (fi -> f2) пути из условия
£ii,i2 =max#il}i >0. (12)
г
Снова из уравнения неразрывности потока для пункта ft и неравенства
> 0 следует, что xili2 > 0.
В результате повторения этого процесса мы либо а) построим путь,
который вернется в пункт, через который он уже проходил, образовав,
таким образом, контур, либо б) доведем путь до стока. Если образовался
контур, то вычтем постоянную К > 0 из тех для которых дуги (f, у)
принадлежат контуру, где
X = min#jj. ((м) € контуру) (13)
Знак £ означает «принадлежит». Понятно, что новые значения удов-
летворяют ограничениям на пропускные способности и уравнениям нераз-
рывности потока. Начиная снова с пункта, где путь впервые образовал
контур, продолжаем процесс построения пути. При решении задачи опи-
санным способом может образоваться лишь конечное число контуров,
так как каждое новое решение, получающееся в результате уничтожения
контура, имеет число равных нулю, больше хотя бы на единицу, чем
предыдущее.
Следовательно, через конечное число шагов можно построить путь
с положительными потоками вдоль него от источника до стока. Наконец,
пути приписывается значение К
K = minxij>^ для всех (f, у) £ пути. (14)
Затем для задачи о потоке строится новое решение с новым значением
потока F — К, вычитая К из всех соответствующих дугам (f, у) вдоль
пути. Если/1 — К > 0, то весь этот процесс можно повторить снова. Заме-
тим еще раз, что можно построить только конечное число путей, так как
каждое новое решение имеет по крайней мере на одно #£;, равное нулю,
больше.
Наконец, если F = 0 и некоторое #г-у > 0, то, начав с пункта i и дуги
(f у), можно воспользоваться описанным выше процессом, чтобы
построить контур, который можно устранить. Все оставшиеся контуры
можно устранить за конечное число шагов. Это завершает конструктивное
доказательство теоремы.
Теорема 3. Если не существует пути из дуг с положительными' про-
пускными способностями, соединяющего источник со стоком, то макси-
мальный поток равен нулю.
Доказательство. Предположим противное, т. е. что максимальный
поток положителен. По предыдущей теореме этот поток можно разложить
на пути с положительными потоками. Вдоль любого такого пути с вели-
375
чиной потока К >0 должны быть выполнена неравенства 0<ZK^xtj^
так как метод разложения таков, что каждое > 0 представляет-
ся как сумма неотрицательных потоков в путях вдоль направленных дуг,
соединяющих пункты i и /. Отсюда следует, что выбранный путь имеет
дуги с положительными пропускными способностями.
Наоборот, можно утверждать, что если существует путь из дуг с поло-
жительными пропускными способностями, то можно выбрать К =
= mintx/j >0 для дуг вдоль этого пути и получить поток F = К > 0
вдоль пути; следовательно, справедлива
Теорема 4. Максимальный поток положителен, если существует путь
из дуг с положительными пропускными способностями, соединяющий источ-
ник и сток.
Следующая теорема позволяет нам конструктивно находить мак-
симальный поток в сети, отыскивая в сетях, связанных с исходной сетью,
пути из дуг с положительными пропускными способностями, соединяющие
источник и сток.
Теорема 5. Решение F = FQ, х^ = х°у является максимальным тогда
и только тогда, когда максимальный поток F' равен нулю во второй сети,
полученной из исходной заменой на — Xij.
Доказательство. Предположим противное, т. е. что существует реше-
ние F' = F'o > 0, —узадачи, связанной с исходной. Тогда
( Mji “F ^ij) ytj (15)
— «Я +
Отсюда следует, что xtj = является допустимым решением для
исходной сети, причем для этой сети поток F = (F' + Fo) > Fo, что
противоречит предположению о максимальности потока Fo. Следователь-
но, если поток F = Fo не является максимальным, то можно построить
улучшенное решение для исходной сети.
рация 0). (итерация 1).
Упражнение. Показать, что условие теоремы 5 является необходимым
и достаточным.
Проиллюстрируем описанный процесс простым примером, составляю-
щим содержание рис. 19-1-Па. Чтобы начать вычисления, найдем путь
с положительными пропускными способностями от пункта 0 к пункту 3.
(Далее мы опишем, как это делать систематически.) Таким путем является,
например, путь (0->2), (2 —> 1), (1 -> 3) с пропускными способностями
376
(1, 1, 1); вдоль этого пути первоначальный поток К'ь — 1. Поток обозна-
чен на сети числом, стоящим в середине дуги, стрелки показывают напра-
вления потока вдоль пути. Изменим пропускную способность каждой
дуги, вычтя Kq = 1 из пропускной способности, написанной у основа-
ния стрелки, и прибавив KQ — 1 к пропускной способности, написанной
у острия стрелки. Результаты этих действий приведены на рис. 19-1-Нб.
Рис. 19-1-Пв. Последние значения
пропускных способностей дуг; нет пути
с положительным потоком (итера-
ция 2).
Рис. 19-1-11г. Этот максимальный поток
является алгебраической суммой потоков
для предыдущих путей.
В новой сети есть только один путь из дуг с положительными про-
пускными способностями, а именно (0-^-1), (1-> 2), (2-^-3) соответ-
ственно с пропускными способностями (3, 2, 2). Следовательно, по этому
пути можно пропустить поток Ki = 2. Снова изменяя пропускные спо-
собности сети, получим сеть, приведенную на рис. 19-1-Пв.
Нет ни одного пути с положительными пропускными способностями,
который соединил бы пункты 0 и 3. Теперь мы образуем максимальный
поток как алгебраическую сумму потоков для путей, приведенных на
рис. 19-1-Па и Пб, что показано на рис. 19-1-Пг.
ПОСТРОЕНИЕ ПУТИ ИЗ ДУГ С ПОЛОЖИТЕЛЬНЫМИ ПРОПУСКНЫМИ
СПОСОБНОСТЯМИ, СОЕДИНЯЮЩЕГО источник И сток
Такой путь можно построить с помощью дерева всех пунктов, через
которые могут пройти пути, выходящие из источника. Следовательно,
первыми должны быть определены все те пункты, в которые из источни-
ка ведут дуги с положительными пропускными способностями. На
рис. 19-1-III это пункты 1 и 5; дуги (0->1) и (0—>5) образуют часть дерева.
Процесс повторяется по очереди для каждого нового пункта, причем
встречавшиеся ранее пункты, опускаются. Легко показать, что если вооб-
ще существует путь из дуг с положительными пропускными способностя-
ми, соединяющий источник и сток, то этот процесс позволит построить
по крайней мере один такой путь.
Упражнение. Показать, что описанный выше процесс всегда построит
путь с положительными пропускными способностями, соединяющий источ-
ник и сток, если такой путь вообще существует.
Теорема 6. Если существует максимальный поток и пропускные спо-
собности являются целыми числами, то описанный процесс построит
только конечное число положительных путей-потоков, алгебраическая
сумма которых дает максимальный поток.
377
Доказательство. Заметим, что если а17- являются целыми числами,
то поток пути К тъяне будет целым, и это же справедливо для соответ-
ствующим образом преобразованных пропускных способностей alj. Но
Рис. 19-1-Ш. Веерообразный процесс нахождения
пути с положительным потоком.
поскольку каждый поток положителен, величина F на каждой итерации
должна возрастать по крайней мере на единицу. Поэтому возможно только
конечное число итераций, так как F конечно.
СВОЙСТВА РАЗРЕЗОВ СЕТИ
Когда поток F = FQ является максимальным для х^ = х^, как бу-
дет выяснено, пропускные способности некоторых из дуг сети исполь-
зуются полностью, т. е. эти дуги используются с полным насыщением:
ха — Легко заметить, что если множество всех насыщенных дуг
исключить из сети, или, точнее, для этих дуг положить ац равными нулю,
то поток становится невозможным. Действительно, если существует поло-
жительный поток вдоль некоторого пути из ненасыщенных дуг, то этот
путь должен иметь дуги с положительной пропускной способностью для
измененной сети а'ц = аг; — x\j и по теореме 5, Хц = х\^ не должно быть
решением задачи о максимальном потоке.
Определение. Разрезом называется множество дуг, содержащее по
крайней мере по одной дуге из каждого пути с положительными пропуск-
ными способностями, соединяющего источник и сток.
Определение. Пропускной способностью разреза называется сумма
пропускных способностей принадлежащих ему дуг.
Из наших замечаний следует, что набор насыщенных дуг в максималь-
ном решении образует разрез. Так, на рис. 19-1-Пг множество дуг (1->2),
(1 -> 3), (0->2), (2 -> 3) с пропускными способностями (1, 1, 1, 2) является
разрезом. В этом случае пропускная способность разреза равна 1 + 1 +
+ 1 + 2 = 5. Следует отметить, что этот разрез содержит два подмноже-
378
ства, которые также являются разрезами. Они отмечены на рис. 19-1—IVa
и 1V6 жирными стрелками, которые указывают направление дуги,
принадлежащей разрезу.
Пропускная способность разреза в обоих этих случаях меньше, чем
в предыдущем, а именно 14-1+1=Зи1 + 2 = 3. Заметим, однако,
что эта величина совпадает с величиной максимального потока. Она равна
также наименьшей пропускной способности разреза среди всех возмож-
ных. Фулкерсон первым предположил, что минимальная пропускная
6)
Рис. 19-1-1 Va, б. Пример к теореме о макси-
мальном потоке и минимальном разрезе (теорема 7).
способность разреза всегда равна величине максимального потока. Впер-
вые это было доказано для так называемых «плоских сетей». (Семинар
корпорации РЭНД, 1954 г.) Позднее Форд и Фулкерсон установили спра-
ведливость этого утверждения для общего случая (Форд и Фулкерсон
[!])•
Теорема 7. Величина максимального потока равна минимальной про-
пускной способности разрезов.
Доказательство. Установим сначала, что еслй {F, х^} — некоторый
поток и С — пропускная способность произвольного разреза, то C^F.
Разложим поток на сумму г положительных путей. Предположим, что
дуга (ц -> /2) разреза принадлежит множеству путей pi, у которых
величина потока Кр^ предположим, что дуга (г2 7г) разреза принадле-
жит множеству путей S2, причем множество S2 может иметь общие пути
379
с множеством 5Ь и т. д, Мы можем написать
Cil, 31 xii, 31 = ^Pi>
PieSi
C$2, 32 X432 ~ S ^P2*
P26S2
(16)
Поскольку каждый путь p = 1, 2, . . ., г разложения должен иметь
хотя бы одну дугу, принадлежащую разрезу, величина Кр должна хотя
бы один раз войти в написанные выше суммы. Поэтому, суммируя все
неравенства, мы получаем
С = cilt + Ci2f j2-|- ... Ki 4- K2 + ... + Kr = F. (17)
Покажем теперь, что если F = Fo является максимальным потоком
для Xij = xlj, то подмножество насыщенных дуг образует разрез с про-
пускной способностью Со = Fo. Отсюда будет следовать утверждение
теоремы, так как в общем случае C>F. Разделим все пункты сети на два
класса. К первому классу отнесем все пункты, в которые можно попасть
из источника по крайней мере по одному пути, составленному из нена-
сыщенных дуг. Ко второму классу отнесем все остальные пункты (если
такие есть). Все направленные дуги (I -> у), соединяющие пункт i из пер-
вого класса с пунктом j из второго класса, должны быть насыщены. (В про-
тивном случае в пункт у можно было бы попасть из источника по некото-
рым ненасыщенным путям, проходящим через пункт i.) Мы покажем,
во-первых, что множество таких дуг образует разрез и, во-вторых, что
пропускная способность этого разреза является минимальной.
Обозначим множество этих насыщенных дуг через 5 и предположим,
что существует некоторый путь, соединяющий источник и сток, но не содер-
жащий ни одной насыщенной дуги из множества 5. Поскольку все мно-
жество насыщенных дуг 5* образует разрез, пусть путь р выбран так,
что он имеет наименьшее число дуг, общих с S*, и не имеет ни одной дуги,
общей с S. Пусть дуга (i -> у) является первой такой насыщенной дугой
в пути р. Отсюда следует, что пункт i принадлежит первому классу. Сле-
довательно, пункт у тоже должен быть из первого класса. (Иначе дуга
(i -> у) принадлежала бы множеству S.) Но в таком случае из источника
можно попасть в пункт у по пути из ненасыщенных дуг. Этот путь можно
затем присоединить к оставшемуся пути от пункта у до стока; новый путь
имеет по крайней мере, на одну насыщенную дугу из S* меньше, чем
путь р, что противоречит предположению о наименьшем числе общих дуг
у пути р и множества 5*.
Теперь мы хотим показать, что пропускная способность разреза S
равна Со ~ Fo. Просуммируем уравнения неразрывности потока (3) по всем
пунктам первого класса. Если пункты i и у принадлежат первому классу,
то переменные х^ и Хц взаимно уничтожаются. Остается только сумма
= для (i—(18)
где пункт i принадлежит первому классу, а пункт у второму. Поскольку
все дуги (I -> у) принадлежат разрезу S и поскольку все эти дуги являются
насыщенными, мы имеем
= = = l(i->/)G5] (19)
и теорема доказана. Теперь легко может быть доказана
Теорема 8. Возьмем некоторое разбиение пунктов на два класса,
первый из которых содержит источник, а второй — сток. Тогда допусти-
380
мое решение (F — Fo, xtj = xlj) является максимальным, если каждая дуга
(i -> у) является насыщенной дугой, соединяющей пункт из первого класса
с пунктом из второго класса.
Заметим, что если мы просуммируем уравнения неразрывности потока,
соответствующие первому классу, то мы получим для любого допустимого
решения
F = ^xtj, (20)
где суммирование распространяется на все такие дуги (i->y), для которых
пункт i взят из первого класса, а пункт j — из второго. В силу допусти-
мости решения выполняется неравенство Хц^ац. Однако рассматриваемое
решение обладает свойством х^ = Отсюда следует, что
F = 2 Xij^ S == S Xi3 ~ ^о- (21)
Упражнение. Показать, что множество дуг (i -> /), определенных
выше, образует разрез и пропускная способность этого разреза мини-
мальна.
Рис. 19-1-V. Второй пример использования алгоритма
Форда—Фулкерсона для нахождения максимального потока.
Чтобы проиллюстрировать этот метод, рассмотрим второй пример,
приведенный на рис. 19-1-Vai, на котором указаны пропускные
способности ребер в каждом направлении. Так, пропускная способность
дуги (0 -> 1) равна 1, а дуги (1->0) равна нулю и т. д. Предположим, что
для начального потока = 0; тогда рис. 19-1-Va2 представляет
собой дерево дуг с положительными пропускными способностями, выхо-
дящих из источника. Вдоль пути (0, 1, 3, 5) поток может возрасти до Ki =
= 1; в этом пути дуги (0, 1) и (1, 3) являются насыщенными. Измененная
сеть, представленная на рис. 19-1-V6i, преобразована с помощью
замены — Kt и = ал + Ki для дуг (i -> у), принадлежащих
рассматриваемому пути. На рис. 19-1-V62 изображено новое дерево
дуг с положительными пропускными способностями, выходящих из цунк-
та (0). Это дерево приводит к пути (0, 2, 4, 5). На рис. 19-1-V61?
и Уг4 показаны последовательные решения, а на рис. 19-1-V62, Vb2
и Vr2 — различные деревья. Поскольку, как следует из последнего
рис. 19-1-Vr2, невозможно достичь стока, процесс закончен. Сумма
потоков путей, представленных на рис. 19-1-Va2, V62 и Vb2 образует
максимальный поток. Это показано на сети рис. 19-1-VI. Насыщен-
ные дуги отмечены жирными стрелками, указывающими направление
насыщения. Чтобы найти разрез с минимальной пропускной способностью,
выберем насыщенные дуги, ведущие из пунктов первого класса в пункты
второго. Все пункты первого класса могут быть достигнуты, если от источ-
ника двигаться вдоль ненасыщенных путей. Это множество составляет
пункты поддерева дуг с положительными пропускными способностями
на рис. 19-1-Vr2. Следовательно, первому классу принадлежат пунк-
ты 0, 2, 3, 1, 4 и разрез образуют дуги (3 -> 5) и (4 -> 5), что и показано
на рис. 19-1-VI.
19-2. РЕШЕНИЕ ЗАДАЧИ О МАКСИМАЛЬНОМ ПОТОКЕ
МЕТОДОМ ДЕРЕВЬЕВ
Этот метод (Данциг и Фулкерсон [2]; Фулкерсон и Данциг [9])
совпадает в основном с методом, который раньше применялся для
решения транспортных задач с ограничениями на пропускные способ-
ности. Однако мы приведем различные модификации этого метода, давая
вновь задаче о максимальном потоке сетевую интерпретацию. Предполо-
жим, что имеется сеть, представленная на рис. 19-2-1а, с источником А
и стоком В; пропускные способности ребер указаны на рисунке, причем
здесь предполагается, что они равны в обоих направлениях. Чтобы начать
382
процесс, выберем два поддерева1 дуг: одно ТА содержит дуги, выходя-
щие из источника А. другое Тв содержит дуги, выходящие из стока 5,
причем каждый промежуточный пункт относится только к одному из этих
деревьев. Например, поддерево Тв вообще может не содержать ни одной
дуги, а поддерево ТА может содержать дуги AC. CD. DE. EF (см.
рис. 19-2-16). Заметим, что такие два поддерева всегда можно выбрать,
Пропускная
способность
Рис. 19-2-1а. Пример задачи
о максимальном потоке: поток
в начале итерации 0 равен нулю.
Рис. 19-2-16. Жирные дуги обра-
зуют базис для итерации 0: при-
ращение потока равно = 10.
так как рассматривается связная сеть. Далее, введем в рассмотрение
любую дугу, ведущую от ТА к Тв- Тогда будет ровно один путь от пунк-
та А к пункту В*, поток выбираем настолько большим, насколько это воз-
можно для данного пути. В нашем примере такой дугой является дуга ЕВ
и мы имеем тогда поток, изображенный на рис. 19-2-Па, с насыщен-
ными дугами AC. CD и DE. Выберем любую из этих насыщенных дуг,
скажем АС. и отметим ее каким-нибудь знаком. На рис. 19-2-Па
Рис. 19-2-Па. Начальное до-
пустимое решение для итера-
ции 1.
Рис. 19-2-Пб. Базис для ите-
рации 1: приращение потока
равно 02 = 10*
используется знак (|). Этим знаком мы будем всюду отмечать насыщен-
ные дуги. Заметим теперь, если мы выбросим перечеркнутую дугу (т. е.
отмеченную знаком |), то мы вновь получим два дерева; это дерево ТА.
не содержащее дуг вовсе, и Тв = {ЕВ. ED. DC. EF}. Если бы исходное
базисное решение было невырожденным, то ТАи Тв всегда состояли бы из
ненасыщенных дуг, т. е. мы всегда , имели бы — Снова
вводим в рассмотрение любую неотмеченную дугу, ведущую из ТА в Тв,
например AF. Это дает поток в 10 единиц вдоль пути AF. FE. ЕВ и насы-
щает все дуги этого пути. Выберем одну из них, скажем AF. и отметим ее;
тогда мы приходим к рис. 19-2-Ш, для которого поток равен 20 еди
1 Ясно, что в связной сети с равными пропускными способностями ребер в обоих
направлениях дуги можно исключать до тех пор, пока мы не выйдем из дерева. Тогда
останется только один путь, соединяющий пункты А и В. Выбросив любую дугу из это-
го пути, мы получим два дерева, обладающие нужным свойством.
383
ницам. Выбросив отмеченные дуги, мы получаем то же самое дерево, что
и на рис. 19-2-116. Введем дугу АЕ от дерева ТА к дереву Тв. Это
приводит к ситуации, ранее не встречавшейся: в построенном таким обра-
зом пути, а именно пути АЕ, ЕВ, нельзя получить большего потока, пото-
му что дуга ЕВ насыщена, хотя она и не отмечена (вырожденный случай).
Рис. 19-2-1II. Начальное до-
пустимое решение для итера-
ции 2.
Рис. 19-2-IVa. Начальное до-
пустимое решение для итера-
ции 3.
Отметим ЕВ и оставим на дуге АЕ поток, равный нулю, тогда получим
рис. 19-2-IVa и новые деревья, показанные на рис. 19-2-IV6. Вве-
дем дугу DB, чтобы получить путь АЕ, ED, DB. Теперь мы можем
Рис. 19-2-IV6. Базис для ите-
рации 3: приращение потока
равно 04 = 10.
Рис. 19-2-Va. Начальное до-
пустимое решение для итера-
t ции 4.
увеличить поток, хотя DE и является насыщенной дугой, поскольку поток
на " ”
от
рис. 19-2-IVa направлен от D к Е. Следовательно, если поток
L к Е увеличится на ~ ”
0.
0, то поток от D к Е должен уменьшиться
на 04, а поток от D к В возрасти на 04, что-
бы оставались выполненными уравнения
неразрывности потока для пунктов Е и D
(см. рис. 19-2-IV). Наибольшее возможное
значение 04 равно 10, так как пропускная
способность дуги ДБ (и дуги АЕ) равна 10.
В результате поток от D к Е аннулируется.
Отметим дугу DB и продолжим процесс.
Вновь применяя описанный процесс, мы
Рис. 19-2-V6. Начальное до-
пустимое решение для итера-
ции 5.
больше дуг, идущих от
получим последовательность потоков, изо-
браженную на рис. 19-2-Va, б и 19-2-VIa, б.
На рис. 19-2-VI6 деревьями теперь являют-
ся ТА~ {AD, DC}, Тв = {FB, EF} и нет
ТА к Тв, которые можно было бы ввести
в путь. Далее исследуем отмеченные дуги, связывающие пункты дерева
ТА с пунктами дерева Тв. Как будет показано, оптимальное решение найде-
но, если поток на каждой из этих дуг идет в прямом направлении, т. е. от
ТА к Тв. Если, с другой стороны, поток на одной из отмеченных дуг, сое-
384
диняющих Та и Гр, идет в противоположном направлении, то можно
увеличить общий поток за счет уменьшения потока на этой дуге. Чтобы
убедиться в этом, заметим, что рассматриваемая дуга вместе с дугами
Рис. 19-2-VIa. Начальное до- Рис. 19-2-VI6. Начальное до-
пустимое решение для итера- пустимое решение для итера-
ции 6. ции 7.
деревьев ТА и Тв образует (единственный) путь, соединяющий пунк-
ты А и В, который может выглядеть, например, так, как это показано на
рис. 19-2-VII. В этом случае итеративный процесс окончен.
Рис. 19-2-VII.
Обоснование метода деревьев. Предположим, что итеративный процесс
конечен для сети общего вида, а полученные в последней итерации под-
деревья То и Тп такие, как показаны на рис. 19-2-VIII. Соединим
сток п с источником дугой (п, 0) с фиктивным обратным потоком, так что
теперь поддеревья Тои Тп и дуга (и, 0) образуют в сети простое дерево.
Рис. 19-2-VIII. Граф, соответствующий ба-
зису, вместе с дугой обратного потока обра-
зуют простое дерево.
Направления стрелок на всех дугах соответствуют направлениям поло-
жительных потоков. Если поток равен нулю, то направление не определе-
но и может быть выбрано произвольно. Транспортная задача с проме-
жуточными пунктами и ограниченными пропускными способностями состо-
ит в максимизации потока F вдоль дуги (п, 0). Условия этой задачи сле-
дующие: __
2«о' = °, ($ = 1,2, ..re)
i
—zra,0 = — F (min).
Следовательно, в этом случае cnQ = —1, а все остальные Cjj равны нулю.
25 Дж. Данциг 385
Как показано в § 17-1, переменные соответствующие дугам
(г, /) дерева, образуют базисное множество. Для дуг, отвечающих базис-
ным переменным, симплекс-множители удовлетворяют уравнению —
— ni = Ctj. Поскольку один множитель можно выбрать произвольным,
полагаем л0 = 0. Тогда каждый пункт i поддерева То будет иметь мно-
житель Л/, равный нулю, а каждый пункт поддерева Тп будет иметь мно-
житель, равный единице. Теперь легко убедиться в том, что решение,
полученное в последней итерации х^ = x\j, является оптимальным. Дей-
ствительно, все дуги (г, /), связывающие поддеревья То и Тп, насыщены,
т. е. все соответствующие небазисные переменные находятся на своих
верхних границах (х^ = ац) и имеют неположительные относительные
стоимости (си —(tcj — Jtj) = —1), в то время как для всех остальных
базисных переменных —(л7- — л^) = 0. Условия оптимальности для
задачи с ограниченными сверху переменными выполнены (см. § 18-2-(6)).
Мы предполагали конечность числа итераций. Следует отметить, что
каждая итерация порождает два поддерева, которые после проведения
дуги (п, 0) образуют простое дерево. Следовательно, каждое последователь-
ное решение соответствует базисному решению. Если предположить невы-
рожденность задачи, то поток действительно увеличивался бы на каждой
итерации, следовательно, повторение базиса было бы невозможно. В слу-
чае вырождения (который в примерах встречается часто) правило слу-
чайного выбора вектора, выводимого из базиса, позволяет с вероятностью
единицы избежать зацикливания в алгоритме (см. гл. 10; см. также зада-
чу 1 и § 6-1).
19-3. ЗАДАЧИ
1. Как следует изменить описанный процесс, чтобы избежать выро-
ждения? Используя подход Ордена (§ 14-4, задачи 14, 15), найти зара-
нее некоторое фиксированное значение е. Заметим, что необходимо будет
использовать эквивалентность задачи о максимальном потеке с ограни-
ченными пропускными способностями и обычной транспортной задачи.
2. Решить задачу, приведенную на рис. 19-1-Ш, методом Форда —
Фулкерсона и симплекс-методом. Сравнить их эффективность.
Глава 20
ПРИМЕНЕНИЕ МЕТОДА
ОДНОВРЕМЕННОГО РЕШЕНИЯ
ПРЯМОЙ И ДВОЙСТВЕННОЙ ЗАДАЧ
К ТРАНСПОРТНОЙ ЗАДАЧЕ
20-1. ВВЕДЕНИЕ
Симплекс-метод, изложенный в гл. 14 применительно к транспортной
задаче, успешно используется для решения задач, содержащих сотни
уравнений и тысячи неизвестных; тем не менее некоторыми преимущества-
ми, по-видимому, обладает метод одновременного решения прямой и двой-
ственной задач, описываемый в этой главе. На примерах ряда небольших
задач Форд, Фулкерсон и автор настоящей книги сравнивали этот метод
с симплекс-методом. Оказалось, что для его реализации затрачивается
вдвое меньше усилий. Например, для решения вручную симплекс-методом
задачи о назначениях 20 X 20 потребовалось свыше часа, в то время как
описываемым далее методом задача была решена примерно за полчаса.
В больших задачах преимущества этого метода могут быть еще большими.
Однако проведенные эксперименты не позволяют еще сделать окончатель-
ного вывода.
В процессе получения допустимого решения по этому методу мы все
время, как указывалось в § 11-4, имеем дело с неотрицательными относи-
тельными оценками. Как только допустимое решение будет получено,
оно будет уже оптимальным. Исторически этот метод, использованный
Куном [1] для решения одной частной задачи о назначениях, возник
из комбинаторного метода, называемого «венгерским методом». Он основан
на доказательстве венгерского математика Эгервари [1] и теоремы Кенига
о линейных графах.
Впоследствии Форд и Фулкерсон [2] предложили простой метод
решения задач о максимальном потоке в сетях (см. гл. 19). Приме-
нение этого алгоритма к транспортной сети Хичкока может заменить
часть процедуры Куна и дает возможность находить решение не только
классической транспортной задачи, но и транспортной задачи с проме-
жуточными пунктами. Для решения таких задач были предложены также
и другие методы, основанные на алгоритме Куна, например, алгоритмы
Манкреса [1] и Флада [1].
«Метод беспорядков», предложенный Фулкерсоном [4] для ре-
шения задач о потоке с минимальными затратами, обобщает метод
одновременного решения прямой и двойственной задач и позволяет начи-
нать решение задачи с недопустимого решения не только прямой, но и
двойственной задачи. Для решения задач на вычислительных машинах
на основе этого алгоритма были составлены (Дж. Д. Литл и Р. Дж. Клазен
из корпорации РЭНД) программы, которые успешно используются
в некоторых отраслях промышленности.
387
25*
20-2. АЛГОРИТМ ФОРДА — ФУЛКЕРСОНА
Задача Хичкока состоит в нахождении т X п матрицы, х = (хц)
с неотрицательными элементами х^, которые минимизируют целевую
т п
функцию 2 3 Cij Xii ПРИ 0ГРаНИЧеНИЯХ
г=1 j=l
п
Зжг> = аг, (t = l, 2, ..т)
3=i (1)
т ' '
= (/=1,2, ...,«)
г=1
где bj — неотрицательные целые числа, удовлетворяющие условию
m п
2 ai ~ 3 (если т ~п и все ai и fy равны единице, то эта задача сводится
i=l j=l
к задаче об оптимальном назначении).
Для описания процесса будем использовать пример Форда и Фулкер-
сона [3].
Избытки Нехватки
«1=3 Ь1=3
«2=4 &2=з
«з=2 &з=6
«4=8 64=2
«>5=1
&в=2
Стоимость перевозки единицы ctj
(1) (2) (0 (6)
(3) (4) (5)
(1) 5 3 7 3 8 5 (2)
(2) 5 6 12 5 7 11
(0 (3) 2 8 3 4 8 2
(4) 9 6 10 5 10 9
В ходе вычислений используются исходная матрица стоимостей (с^)
и вспомогательная матрица того же размера, которая называется преобра-
зованной матрицей прямой задачи. С каждым элементом связываются
такие цены щ и Vj, что щ — Vj не отрицательно.
На каждом шаге этого процесса с каждой строкой и каждым столбцом
преобразованной матрицы прямой задачи связываются соответственно
«избыток» и «нехватка», которые являются нераспределенными частями
«г ,И Ь}.
ОПРЕДЕЛЕНИЕ НЕОТРИЦАТЕЛЬНЫХ ЗНАЧЕНИЙ
ОТНОСИТЕЛЬНЫХ ОЦЕНОК сц ДЛЯ НАЧАЛЬНОГО ВЫБОРА
ПРЕОБРАЗОВАННОЙ МАТРИЦЫ ПРЯМОЙ ЗАДАЧИ
Припишем каждой строке i значение щ = min Сц. Вычитая это зна-
3
чение из каждого элемента f-й строки, мы получим i-ю строку матрицы
(си — щ). Далее, каждому столбцу ; припишем значение Vj = min (с^ —
— нг). Вычитая это значение из элементов Cij— щ соответствующего столб-
ца, получим J-й столбец матрицы относительных оценок (си) (элементы ее
равные,- — Ui —Vj). Для нашего примера это последовательно дает (3),
(4) и (5).
Для преобразованной матрицы прямой задачи мы попытаемся умень-
шить нехватки, приписав положительные значения только тем х^, для
которых = 0. Таким образом, в нашем примере ненулевые элементы
388
cij
5 3 7 3 8 5
5 6 12 5 7 И
2 8 3 4 8 2
9 6 10 5 10 9
uz-=min
I /
3
5
2
5
(3)
= ui
2 0 4 0 5 2
0 1 7 0 2 6
0 6 1 2 6 0
4 1 5 0 5 4
min c^=vj -> О О 1 0 2 0
i
cij — cii ui vj
2 0 3 0 3 2
0 1 6 0 0 6
0 6 0 2 4 0
4 1 4 0 3 4
(5)
должны быть поставлены в (6) только в тех местах, в которых нарисованы
квадраты, поскольку эти квадраты соответствуют нулевым в (5).
Шаг 0. Предварительная разметка
Сначала отметим каждую строку, у которой имеется избыток, запи-
сывая знак минус (метка) после величины избытка.
Исходная матрица прямых ограничений
Шаг 1. Поиски путей
В каждой строке, содержащей метку минус, возле каждого неотме-
ченного квадрата проставляем метку плюс. Если в строке имеется не менее
389
двух минусовых меток, то заменяем все метки, кроме одной, на плюсовую
метку, сохраняя минусовую метку при квадрате с наибольшим элемен-
том. В каждом столбце, содержащем плюсовую метку, приписываем мину-
совую метку каждому квадрату с ненулевым элементом. Продолжаем этот
процесс до тех пор, пока либо а) плюсовая метка попадает в столбец
с «нехваткой» (в этом случае переходим к шагу 2), либо б) окажется, что,
пользуясь описанными выше правилами, расставлять метки уже нельзя;
в этом случае переходим к шагу 3.
Шаг 2. Распределение нехватки вдоль пути
Обозначим через к некоторую величину, которую определим далее
и отметим, что эту величину надо вычесть из нехватки в столбце, содержа-
щем плюсовую метку, определенную на шаге 1 в соответствии с правилом
1 (а). Далее, процесс заключается в том, что либо а) выбирается столбец,
в котором величина к вычиталась из некоторого элемента или текущей
нехватки, и в этом столбце величина к добавляется к одному из элемен-
тов, отмеченных знаком плюс (всегда существует по крайней мере один
такой элемент), либо б) выбирается строка, в которой величина к была
прибавлена к некоторому элементу, и величина к вычитается либо из эле-
мента, отмеченного знаком минус, либо из избытка, отмеченного знаком
минус (в отмеченной строке существует только один элемент, отмеченный
знаком минус).
Этот процесс продолжается до тех пор, пока величина к не будет
вычтена из некоторого элемента в строке с избытком. Затем, положив
к равным значению наименьшего элемента, который должен быть умень-
шен на й, подставим это значение в последнюю матрицу. Если в какой-
нибудь строке остался избыток, стираем все плюсовые и минусовые метки
и возвращаемся к шагу 0. Если избытков нет, то процесс закончен, ибо по-
лучен допустимый план и множество элементов образует оптимальное реше-
ние, поскольку все относительные стоимости остались неотрицательными.
Шаг 3. Определение новой преобразованной матрицы прямой задачи
Пусть (i, j) g S означает, что квадрат (г, /) принадлежит отмеченной
строке и неотмеченному столбцу, а (г, /) С S' означает, что квадрат при-
надлежит неотмеченной строке и отмеченному столбцу. (Заметим, что
ни S ни S' не содержат отмеченных квадратов.)
Найдем Д и квадрат (г, s) £S, где
A = crs= min Cij (7)
(г, i)gS
и вычислим новые величины сц\
f Cij—если (i, j)£S (отмеченная строка и неотмеченный
| _ столбец),
с*>=={ Czj + A, если (i, /)£5/ (неотмеченная строка и отмеченный
j столбец),
си в остальных случаях.
Эти преобразования можно выполнить и иначе, именно можно сначала
заменить значения щ на и* = щ + Д для отмеченной строки i и значения
Vj на v*j — Д для отмеченного столбца. После этого величины c*j можно
определить по формуле
= Cij Ui Vj.
В преобразованной матрице прямой задачи исправляем положение
квадратов, соответствующих c*j = 0. В S появится по крайней мере один
390
новый квадрат, ибо А = cTs. Все клетки в S' опустим (их элементы равны
нулю), а другие оставим без изменения. Сохраняя метки, мы переходим
к шагу 1 и продолжаем процесс разметки, выявляя те строки, где появи-
лись новые квадраты.
Пример. В нашем примере, расставив минусовые метки у избытков,
мы начинаем со строки 1, в которой у первого квадрата £i2 из (6) ставим
плюсовую метку. Поскольку во втором столбце имеется нехватка, правило
1 (а) отсылает нас к шагу 2. В результате получаем (8).
(8)
Полагаем к = 3 и завершаем шаг 2 уменьшением нехватки на 3 единицы.
Теперь повторяем шаг 1, поскольку допустимое решение еще не получено.
После нескольких повторений цикла шаг 1— шаг 2 мы получим (9), а за-
тем и (10а)
(9)
Поскольку плюсовых и минусовых меток больше ввести нельзя в соот-
ветствии с правилом 1 (б), мы переходим теперь к шагу 3, снова используя
таблицу (5) (которая повторена в виде (10в)). Единственный отмеченный
элемент находится в четвертой строке и четвертом столбце, множество
S состоит из клеток с двойной штриховкой, а множество S' — из клеток
с одинарной штриховкой. Далее, поскольку наименьший элемент в клетках
из S равен 1, вычитаем А = 1 из значений принадлежащих 5, и при-
бавляем А = 1 к значениям из множества S'. Это преобразование не
изменяет нулевого значения с44 и уменьшает относительную стоимость
с42 до нуля, что и показано в (116).
Новая преобразованная матрица прямой задачи показана в (На),
а оставшаяся часть процесса систематически изложена далее.
391
(116)
(12)
(136)
(14)
Оптимальное назначение
□ ИР - в
0 и
□ ВИП
(15а)
(156)
Vi -1 -31-41 -1
Оптимальное множество цен, указанных в (156), получается последова-
тельным изменением исходных значений иг и г^, приведенных в (3) и (4),
на соответствующие величины ± Д (если это требовалось), что и показано
в (106), (116), (136) и (156)
КОНЕЧНОСТЬ МЕТОДА ОДНОВРЕМЕННОГО РЕШЕНИЯ ПРЯМОЙ
И ДВОЙСТВЕННОЙ ТРАНСПОРТНЫХ ЗАДАЧ
Каждый раз шаг 1 должен привести либо к шагу 2, либо к шагу 3.
Преобразования на шаге 2 можно проделать не более, чем N = =
= 2 bj раз, если и bj являются целыми числами, ибо в этом случае
все последовательные значения параметра к положительны и поэтому
избытки и нехватки на каждом шаге 2 уменьшаются хотя бы на единицу.
Теорема L Описанный алгоритм не может привести к шагу 5, если
столбцы с нехватками (а, быть может, и другие столбцы) не снабжены
метками.
Это заведомо справедливо, если в некотором столбце имеется нехват-
ка, поскольку если бы такой столбец был отмечен плюсом, то за шагом
1, согласно правилу 1 (а), выполнялся бы шаг 2 (а не шаг 3), а если бы та-
кой столбец был помечен знаком минус, то процесс замены минусовой мет-
ки на плюсовую продолжился бы в том же самом столбце.
Теорема 2. Между двумя последовательными выполнениями шага
2 возможно не более п —2 выполнений шага 3 (где п — количество столб-
цов).
Для того чтобы убедиться в этом, заметим, что элементы, помещенные
в квадраты и отмеченные к концу шага 1 , остаются в квадратах и после
шага 3, поскольку изменяются только те которые находятся в неотме-
ченных строках или столбцах. Кроме того, в неотмеченном на предыдущем
шаге столбце s, где (г, s) £ S, crs = Д, появится по крайней мере один новый
отмеченный элемент. Поскольку строки множества S отмечены (по опре-
делению) и каждая отмеченная строка содержит одну минусовую метку,
последовательное применение шага 1 приводит к шагу 3. Следовательно,
у всех квадратов xrs по этим правилам будут расставлены плюсовые метки.
Таким образом, после шага 1 не более чем через п —2 выполнений шага
3 в столбце с нехваткой окажется метка (включая использование шага 2).
Теорема 3. Метод одновременного решения прямой и двойственной
задач позволяет получить решение транспортной задачи не более, чем
за N (п —2) итераций, где N = = Sbj, an — число столбцов.
20-3. ЗАДАЧИ
1. Закончить доказательство теоремы 3.
2. Модифицировать метод одновременного решения прямой и двой-
ственной задач для решения транспортных задач, в которых некоторые
Xjj недопустимы.
3. Как связан метод одновременного решения прямой и двойственной
транспортных задач с более общим методом решения прямой и двойствен-
ной задач из § 11-4?
4. Показать, что шаги 1 и 2 являются частным случаем метода Форда —
Фулкерсона для нахождения максимального потока в сети (см. гл. 19).
5. Объяснить графически метод одновременного решения прямой
и двойственной транспортных задач с помощью блок-схемы шагов 1,2 и 3.
393
6. Как влияет величина Д на изменение значения двойственной целевой
функции на итерации?
7. Показать, что, вместо того чтобы начинать наш процесс разметки
с расстановки минусовых меток у строк с избытками, мы могли бы начать
с расстановки минусовых меток у столбцов с нехватками и т. д.
8. Показать, что эффективность алгоритма можно увеличить путем
двойной разметки, используя на шаге 1 оба упомянутых в последней зада-
че метода для последовательной расстановки меток.
9. Задача о складе. Предположим, что в начале периода t ряд товаров
i можно купить (или продать) по ценам pit* затраты на хранение в течение
одного периода равны sit. Если емкость S склада фиксирована, то какова
оптимальная программа покупки, хранения и продажи? Показать, что
в оптимальной программе либо, как правило, склад используется полно-
стью, либо если склад заполнен, то это состояние склада сохраняется, либо
все распродается. Библиография: Данциг [2,15], Кан [1], Прагер [2],
Чарнс и Купер [1].
Глава 21
ПАДЛ ЧА О ВЗВЕШЕННОМ
РАСПРЕДЕЛЕНИИ
21-1. ПОЧТИ ТРЕУГОЛЬНЫЙ БАЗИС
Матрица ограничений обычной транспортной задачи такова, что каж-
дой переменной соответствуют не более двух ненулевых коэффициентов
со значениями +1 или —1. Мы хотим рассмотреть модели, похожие по фор-
ме на транспортную, именно модели, в которых каждой переменной раз-
решается иметь не более двух ненулевых коэффициентов.
ЗАДАЧА I. ЗАДАЧА О РАСПРЕДЕЛЕНИИ, ВЗВЕШЕННОМ
ПО СТРОКАМ И СТОЛБЦАМ
Найти неотрицательные и min z, удовлетворяющие условиям
п
Равенства по строкам: (i = 1, 2, .. .,т) 3=1 (1)
Равенства по столбцам: (/=1,2, ...,п) 2 fyjyij = bj. 1=1 m n (2)
Целевая функция: 2 2 СгзУ ij = (3)
1=1 3=1
где числа at и bj — не отрицательны, а — положительны. Прежде
чем приступить к изучению этой задачи, сделаем такое преобразование
переменных, чтобы все коэффициенты в равенствах по строкам стали равны
единице. Так, если мы вместо переменных у^ введем новые у^,
то в равенствах по строкам вместо коэффициентов atj появятся единицы,
в то время как коэффициентами в равенствах по столбцам будут ptj —
= Ъ*j/a^j, а коэффициентами целевой функции станут = c'ijlaij. Итак,
нами получена
СТАНДАРТНАЯ ФОРМА ЗАДАЧИ О ВЗВЕШЕННОМ^ РАСПРЕДЕЛЕНИИ
п
2 Xij = ai, (равенства по строкам i = 1, 2, ..т) (4)
j=i
т
2 Puxij — bj, (равенства по столбцам /=1, 2, ...,п) (5)
i=l
m п
2 S cijxij — (6)
1=1 ;=1
где и величину z нужно минимизировать.
395
f Очень часто в приложениях числа ai представляют собой имеющиеся
ресурсы, расход которых нельзя превысить (как в примере о загрузке
станков, который будет рассматриваться ниже). В этом случае условие
(4) заменяется на условие (7).
S xij
;=1
для i = , 2, ..., т.
7)
Теория и техника решения систем {(5), (6) и (7)} и {(4), (5) и (6)} одна
и та же.
Задача, двойственная к задаче о взвешенном распределений, форму-
лируется так: найти щ, Vj и max q, удовлетворяющие условиям
где
для i = 1, 2, ..., т
и у = 1, 2, ..., п,
т п
2 + 3 vjb} = Ч (max).
г=1 j=l
(8)
(9)
Щ + PijVj^Cij
Критерий оптимальности: множество значений удовлетворяю-
щих условиям прямой задачи, является оптимальным решением, если
существуют такие числа ut и г?;, удовлетворяющие условиям двойствен-
ной задачи, что
j > 0 ==> щ + pi jVj =
Щ + PijVj < Ci J => Xij = 0.
(10)
НАГЛЯДНЫЕ ПРИМЕНЕНИЯ
1. Несколько различных работ можно выполнить на станках одного
из имеющихся типов, различных по эффективности. Требуется распреде-
лить работы по станкам так, чтобы все они были выполнены за имеющееся
в распоряжении рабочее время станков, а общая сумма затрат была бы
минимальной.
Чтобы получить математическую модель, введем обозначения:
Ui — фонд рабочего времени станка i-го типа,
bj — объем работ у-го вида, которые должны быть выполнены,
Cij — стоимость выполнения единицы работы г-го вида на станке
у-го типа,
Ри — производительность (часовая) у-го станка при выполнении рабо-
ты i-го вида,
хц — время работы (в часах) станка у-го типа, которое отводится для
выполнения работ i-ro вида.
2. Воздушный флот, состоящий из самолетов различных типов, должен
быть так распределен по воздушным трассам, чтобы при минимальных
эксплуатационных расходах были удовлетворены потребности пассажи-
ров. Пусть для некоторого периода
at — число самолетов i-го типа,
bj — количество пассажиров, которым нужно пролететь по у-й трассег
Cij — эксплуатационные расходы на один самолет i-го типа на у-й
трассе в течение данного периода,
Ри — общее количество пассажиров, которых может обслужить один
самолет г-го типа на у-й трассе за данный период,
Хи — число самолетов i-ro типа, выделенных на у-ю трассу.
396
ТАБЛИЦА И НЕЯВНЫЕ ЦЕНЫ ДЛЯ ЗАДАЧИ О ВЗВЕШЕННОМ
РАСПРЕДЕЛЕНИИ
Эта таблица для задачи 2x3 имеет вид (11)
*.и РЙ си *12 Р12 с12 *13 Р13 с13
*21 Р21 С21 *22 Р22 с22 *23 Р23 с23
”1 Ь2 у2 Ь3 ”3
Практическое замечание: поскольку величины xtj, щ и Vj являются
числами, которые должны изменяться от итерации к итерации, при руч-
ном счете важно, чтобы таблица была составлена достаточно удобно,
например, как указано выше.
НАХОЖДЕНИЕ ИСХОДНОГО БАЗИСНОГО РЕШЕНИЯ
Задача о взвешенном распределении отличается от обычной транспорт-
ной задачи, в частности, тем, что до сих пор еще не найдено простых пра-
вил, позволяющих непосредственно получить исходное базисное допу-
стимое решение. Однако для случая, когда все числа ptj не отрицательны,
мы опишем и проиллюстрируем примером метод, аналогичный приведен-
ному в § 15-3; для этого мы воспользуемся следующим простым численным
примером
*11 Р11=1 сц=4 £ to to 'll 11 'l* to 00 *13 P13=l £13=3 ^4=4
*21 />21=2 c2i=6 *22 Р22=1 c22~ *23 7’23=1 С 23=7 аг=5
ca- ll сл b2=2 63=3
(12)
Шаг 1. Выбираем базисную переменную; беря произвольную клетку
(хорошим был бы выбор клетки с наименьшим полагаем соответствую-
щее Хи равным наибольшему значению, совместимому с величинами' at
и bj. Вычеркнем насыщенную строку (столбец), т. е. ту строку (столбец),
для которой достигнуто ограничение (если насыщенными оказываются
одновременно и строка и столбец, то вычеркивается либо строка, либо стол-
бец, одновременно и то и другое не вычеркивается). Повторяем эту ите-
397
рацию столько раз, сколько нужно. В примере (12) клетки выбирались
следующим образом:
Клетка Значение переменной Насыщенные строка и столбец
(1,3) яг13 = 3 столбец 3
(1,1) *11 = 1 строка 1
(2,2) *22 = 2 столбец 2
(2,1) *21 столбец 1
Шаг 2. Вообще говоря, один столбец (строка) останется ненасыщен-
ным. Введем в этом случае искусственную переменную, добавляя недо-
стающую клетку «дефицита» (г, s) либо (г, 0), либо (0, s) в соответствующую
ненасыщенную строку или столбец. Минимизируем далее искусственную
форму SdijXij, в которой du = 0 для всех i и у, кроме добавленной клет-
ки, для которой drs = 1. Если дефицит оказался в столбце, то полагаем
prs = 1, в то время как для строки нам вообще не нужно определять prs
(поскольку нет ограничения, соответствующего приписанному столбцу).
Упражнение. Изменить это правило так, чтобы оно было применимо
к задачам, в которых некоторые ptj отрицательны.
На этапе I множители щ и Vj должны быть найдены так, чтобы щ +
+ Ptjvj — 0, если является базисной переменной, кроме случая иг =
— 1, если ненасыщенной оказалась r-я строка, или случая Vj = 1, если
ненасыщенным оказался у-й столбец. В нашем примере оказалась нена-
сыщенной вторая строка, и поэтому исходная таблица для этапа I имеет
Точка в клетке (2,0) показывает, что здесь ptj не определено (т. е. для
столбца 0 нет ограничения). В силу нехватки цена и2 — 1, а остальные
цены Ui и Vj вычисляются по формулам (10), в которых c^j заменено на dtj.
Поскольку d23 —(^2 + Ргз^з) = 0— [1 + 1-(—V2)] = -—С/г)» форму не-
допустимости можно уменьшить, если увеличить я2з и соответственно пе-
ресчитать базисные переменные для компенсации этого увеличения, см. (14).
Понятно, что max 0 = 2 и при таком выборе 0 форма недопустимости обра-
щается в нуль. Следовательно, я23 становится новой базисной переменной,
заменяя переменную дефицита гг20; этап I завершен, мы вычеркиваем
дополнительную клетку. Табл. (15) является исходной для этапа П;
в ней немедленно находятся величины щ и Vj и 0.
398
Дефицит 1 + 0 1 0 2 0 3—0 1 0 4
1—(1/2)0 2—(1/2)9 2 0* 5
• 2 1 1
1 0 0 0
5 2 3
(14)
(15)
ВЫЧИСЛЕНИЕ НЕЯВНЫХ ЦЕН (СИМПЛЕКС-МНОЖИТЕЛЕЙ)
Величины щ и Vj в силу условий (10) должны удовлетворять системе
пяти уравнении с пятью неизвестными U1 +Vi Ui и2 -|- 2i^i = 4, + v3 = 3, = 6, (16)
W2 +l>2 = 4,
U2 + v3 = 7.
В отличие от стандартной транспортной задачи здесь нет избыточности
в системе уравнений {(1), (2)}. Поэтому в общем случае нельзя произволь-
но выбирать одну из цен. Аналогично базисы системы {(1), (2)} не обязаны
быть треугольными. Тем не менее эта система является почти треугольной
в следующем смысле: выберем некоторую переменную, скажем и2, и будем
рассматривать ее как параметр, через который можно выразить все осталь-
ные переменные. Это приводит к уравнениям с одним неизвестным, кото-
рое можно выразить через параметр. Из (16) мы имеем
1^1 = 3-2*^2» ==: ^3 “
Z 1 \ 1
и^ = 4— 3—^2 J ~ 1 ~2 ^2, и^ = 3 — (7 — U2) — — 4 -|- u2.
399
Мы получили два выражения для щ через параметр и2. Приравнивая эти
выражения, находим и2 и затем определяем остальные переменные. Пос-
кольку 1 + г/2 и2 = —4+^2, мы имеем и2 = 10, откуда Vi = —2, z?2 =
=—6, v3 = —3 и щ = 6.
Итак, в нашем примере найдены вручную все цены. Однако могут
встретиться случаи, когда в результате таких действий некоторые из неяв-
ных цен могут оказаться и невычисленными. Тогда одну из невычислен-
ных цен можно, как и раньше, рассматривать в качестве параметра и выра-
зить через этот параметр остальные невычисленные цены. Этот процесс
продолжается до тех пор, пока не получатся два уравнения с двумя
неизвестными, из которых определится значение параметров. Обобщим
теперь эти замечания.
Теорема 1. Если ранг базиса равен п + тп, то неявные цены можно
вычислить, рассматривая любую из цен как параметр и решая последова-
тельно уравнения с одним неизвестным; если еще остаются невычисленные
цены, то этот процесс повторяется.
Доказательство. В каждое из уравнений (10) входят две цены. Если
одну из них выбрать в качестве параметра, то через нее можно выразить
некоторые другие цены. В результате последовательной подстановки
мы получим множество переменных, выраженных через этот параметр.
Это множество не содержит переменных, входящих в те уравнения, в кото-
рых имеются переменные, не выраженные через параметр (ибо в противном
случае эти переменные сразу же можно было бы выразить через параметр
и присоединить к рассматриваемому множеству). Мы покажем, что в этом
множестве только для одной из переменных имеются два различных линей-
ных представления через параметр. Приравнивая эти выражения, мы мо-
жем определить значение параметра. Если бы в рассматриваемом множе-
стве для двух или более цен нашлись два выражения (т. е. если одна
переменная могла бы быть выражена более чем двумя путями), то это
означало бы, что система уравнений является либо избыточной, либо
несовместной. С другой стороны, если бы никакая переменная не выра-
жалась через параметр дважды, то значение этого параметра можно было
бы выбрать произвольно. Однако если ранг базиса равен п + т, то ни
один из этих случаев не может встретиться, ибо система уравнений, матри-
ца которой является транспонированной к базисной, должна всегда иметь
единственное решение.
УЛУЧШЕНИЕ БАЗИСНОГО РЕШЕНИЯ
Вычисленные выше неявные цены используются для выяснения с помо-
щью условий (10), является ли рассматриваемый план оптимальным;
если план не оптимален, то неявные цены используются для нахождения
улучшенного решения. Решение, полученное для нашего примера, не
является оптимальным, поскольку
с12—Щ—Р12Р2 ~ —8 — 6—2 (—6) = — 2.
Положим поэтому х12 = 0 и преобразуем базисные переменные. В нашем
примере мы вычисляем значения базисных переменных, изменив свобод-
ные члены следующим образом:
«1 = 4—0, а2 = 5, Ъ'г = 5, Ь'2 = 2 — 20, и Ь'3 = 3.
Новые значения базисных переменных находятся как линейная комбина-
ция а + Р0, где а — старое значение переменной, а Р0 — величина,
компенсирующая увеличение на 0 значения небазисной переменной, вво-
400
димой в базисное множество. Старые значения а известны, и поэтому
нужно вычислить только величины Дх^, на которые изменяются значения
базисных переменных. Они должны удовлетворять системе пяти уравнений
с пятью неизвестными.
(18)
ДЯ13
+ 2A#2i
________+ ^22 )
-f- Д#23 —0
Л*13 •
+
+ ^22 +
> = -0
= 0
= -29
Эта система, очевидно, является транспонированной по отношению к систе-
ме, которая ранее использовалась для нахождения неявных цен. Взяв
Дя22 из четвертого уравнения и подставив найденное значение в другие
уравнения, мы получим, что каждое из этих уравнений содержит по две
неизвестные величины. Кроме того, ясно, что если одно из неизвестных
выбрать в качестве параметра, то остальные можно выразить через этот
параметр. Поэтому, выбрав в качестве параметра A#n, можно выразить
через него Дж13, Дя23 и Дя21, а затем снова вернуться к Дян. Это дает нам
уравнение с одним неизвестным Дяи, из которого это неизвестное и нахо-
дится. Порядок вычислений для случая системы (18) указан пунктирными
линиями со стрелками. Подробнее:
Ах22 — — 20,
Д^13 = — 0 —Д#ц,
Д*23 = — А^13 = 0 + Д^и, (19)
Дя21 = — Дя22 —- Дя2з = + 0 — Дяц,
Д^и— — 2Дя21= — 204-2Аяи или Дя11 = 20.
Подставляя значение Джи = 20 в остальные уравнения, мы получаем
ЛЯ1з = —30, Дя23 = 30 и Дя21 = —0.
Описанный метод нахождения изменений базисных переменных являет-
ся достаточно общим методом. В самом деле, процесс, примененный здесь
к почти треугольным базисам, аналогичен процессу, в котором использо-
валась треугольность базисов, имеющая место для транспортных задач.
Теорема 2. Пусть в задаче о взвешенном распределении задан некоторый
базис ранга п + т, Тогда либо а) существует строка или столбец лишь
с одной базисной переменной, либо б) каждая строка и каждый столбец
содержат ровно две базисные переменные ит — п. Если имеет место случай
а), то теми же свойствами обладает подбазис, получающийся вычеркиванием
той строки или того столбца, где имеется только одна базисная переменная.
Доказательство. Каждая строка и каждый столбец содержит не менее
одной базисной переменной. Если среди строк и столбцов нет таких, кото-
рые содержали бы только одну базисную переменную, то в каждой строке
и каждом столбце имеется не менее двух базисных переменных. В таком
случае число базисных переменных п + гп не может быть меньше удвоенно-
го числа строк или удвоенного числа столбцов; поэтому
п-\-т^2т и п-^т^-2п, (20)
26 дж. Данциг
401
или, складывая,
2 (га + гаг) > 2m + 2га.
Равенство имеет здесь место только тогда, когда равенствами являются оба
соотношения (20), т. е. если каждая строка и каждый столбец содержат
ровно две базисные переменные, а т = га. Но последнее соотношение
должно быть равенством. Это рассуждение можно повторить для подбази-
са, если есть одно уравнение с одной переменной и соответствующая стро-
ка (или столбец) вычеркнуты.
21-2. СТРУКТУРА БАЗИСА С ТОЧКИ ЗРЕНИЯ ГРАФОВ
Если задача о взвешенном распределении интерпретируется в терми-
нах линейной сети, то граф, дуги которого соответствуют переменным
базисного множества, имеет характерную структуру.
Изучение этого вопроса упростится, если мы будем рассматривать
модель просто как множество уравнений, обладающее некоторыми вполне
определенными свойствами. В этом случае удобно в обозначениях вводи-
мых переменных использовать только один индекс. Напомним, что систе-
ма ограничений в классической транспортной модели § 14-2 состоит
из двух подсистем, одна из которых (уравнения по строкам) относится
к вывозу из каждого источника в различные пункты назначения, а другая
подсистема (уравнения по столбцам) относится к ввозу в каждый пункт
назначения из различных источников. В транспортной модели с проме-
жуточными пунктами, § 16-1, каждая переменная имела не более двух
ненулевых коэффициентов, равных ±1. В моделях со взвешенным рас-
пределением ненулевые коэффициенты уже не обязательно должны рав-
няться ±1; мы рассматриваем класс задач, в которых не более двух коэф-
фициентов при каждой переменной xj отличны от нуля; пусть из них
один находится в уравнении с номером i = g (/), а другой — в уравнении
с номером i = h (/). Если у переменной Xj есть только один ненулевой
коэффициент, то g (/) = h (7).
ЗАДАЧА 2. ОБЩАЯ ЗАДАЧА О ВЗВЕШЕННОМ РАСПРЕДЕЛЕНИИ
Найти множество неотрицательных Xj и min 2, удовлетворяющих
условиям
п
S aijxJ ^=bi (i = 1, 2, ..., гаг),
j==n (1)
2 CjXj = z (min),
j=i
где aij = 0, если i Ф g (j) или i (7). Если для некоторой переменной
Xj одно из чисел agj или ahj равно нулю (но не оба одновременно), то эту
переменную мы будем называть свободной.
Каждое уравнение системы (1) соответствует определенной вершине
графа, построенного для данной модели, а каждая переменная х^ не являю-
щаяся свободной, отвечает ребру, соединяющему g (7) с вершиной h (j).
Свободные ребра можно рассматривать (как указывает Ф. Харари) как
ребра, которые связывают две совпадающие вершины.
При вычерчивании графа вершины можно размещать так, как это
удобно. Например, на рис. 21-2-1 и 21-2-П изображен один и тот
402
же граф, но на рис. 21-2-П вершины размещены так, чтобы видна
была лучше структура графа. Если в рассматриваемой модели встречают-
ся свободные переменные, то в сеть должны быть включены свободные
Рис. 21-2-1. Граф задачи о взвешенном
распределении.
Рис. 21-2-П. Преобразованный граф
задачи о взвешенном распределении.
(или «слабые») ребра, или дуги, соответствующие тем переменным, каж-
дая из которых связана только с одной вершиной.
На рис. 21-2-III показан граф, ребра которого соответствуют
базисным переменным. Этот граф состоит из четырех изолированных связ-
ных подграфов.
Теорема 1. Каждый связной подграф базисного графа для системы
(1) содержит ровно один цикл.
Доказательство. Ясно, что каждая связная часть графа содержит
равное число вершин и ребер, ибо переменные, сопоставленные ребрам,
Рис. 21-2-Ш. Базисный граф содержит одну (или более)
связную часть; каждая из частей состоит из дерева и
одного дополнительного ребра.
появляются только в уравнениях, соответствующих вершинам подграфа,
а эти уравнения в общем случае не могут содержать меньше переменных,
чем число уравнений. С другой стороны, общее число базисных перемен-
ных равно общему числу уравнений, и поэтому равенство должно иметь
место для каждого изолированного подграфа рассматриваемой сети.
Далее, связный подграф, не имеющий свободных ребер, должен
содержать по крайней мере один цикл, так как в противном случае он имел
бы ребер меньше, чем вершин. Если бы мы вычеркнули некоторое ребро,
принадлежащее циклу этого подграфа, то остался бы связный подграф,
в котором число ребер было бы на единицу меньше, чем число вершин;
следовательно, этот подграф был бы деревом (теорема 1, § 17—1). Но дере-
во не содержит циклов; поэтому первоначально подграф должен иметь
точно один цикл.
С другой стороны, если связный подграф содержит одно или более
свободное ребро, то граф, образующийся после вычеркивания ребер,
403
26*
имеет ребер меньше, чем вершин, на число вычеркнутых ребер. Но посколь-
ку были вычеркнуты только свободные ребра (т. е. ребра, связывающие
одну вершину), то полуденный подграф остается связным, а это возможно
только в том случае, когда число свободных ребер равно единице и остав-
шийся подграф является деревом. Доказательство завершено, если рас-
сматривать подобное ребро как цикл, состоящий из одного ребра.
ВЫЧИСЛЕНИЕ РЕШЕНИЯ, СООТВЕТСТВУЮЩЕГО ГРАФУ
Нахождение базисных переменных можно начать с вершин, через
которые проходит ровно одно ребро. Так, для рис. 21-2-П мы имеем
л1,6^6 —
«8, 7^7 = /94
«Ю, 8^8 ^1о>
«5, 10^10 ==: ^5*
Если к вершине подходят несколько ребер, для которых все переменные,
кроме одной, вычислены, то можно немедленно определить и оставшуюся
переменную. Например, после того как из (2) найдено значение перемен-
ной #io, можно из уравнения для вершины 6 вычислить значение х9:
9^9 + «6, 10^10 “ ^6- (3)
Таким образом, последовательно можно найти значения всех пере-
менных, кроме тех, которые принадлежат циклу. Вычисление же этих
переменных можно осуществить методом, который мы сейчас проиллю-
стрируем.
«31^1 4“ «32^2 — ^3»
«42^2 + «43^3 = &4>
, Т (4)
«73^3 “Г «74^4 — «7,
«94*^4 + «95*^5 — ^9,
«21*^1 ”Ь* «25*^5 == ^2*
ЧислоП^ равно разности значений bi и тех элементов исходной матрицы,
которые не входят в систему (4). Эти не входящие в систему (4) величины
соответствуют тем ребрам, для которых значения переменных уже были
определены раньше. Ввиду почти треугольной структуры системы (4)
мы можем рассматривать одну из переменных, принадлежащих циклу,
как параметр и затем, двигаясь по соответствующему циклу, выразить
остальные переменные через этот параметр. Завершив это движение,
мы получим второе выражение для параметра и, приравнивая эти выра-
жения друг другу, вычислим значение параметра.
Так, двигаясь по циклу в графе на рис. 21-2-П в направлении
часовой стрелки, мы находим следующую формулу для х^.
(ъ* —&4-^-ь3х)'Ш
X = V 095 \ а74 \ <*43 \ 032 7 77/ /5ч
1 1 _ ~~^25 . ~~g94 . —fl73 е —042 , —031 * '
095 074 043 032 Й21
Упражнение. Получить аналогичное выражение для х^ если дви-
жение по циклу производится против часовой стрелки. Показать алге-
браически, что эти две формулы совпадают.
404
НАХОЖДЕНИЕ НЕЯВНЫХ ЦЕН, СВЯЗАННЫХ С БАЗИСОМ
Если среди базисных переменных есть свободные, то сразу же можно
найти неявную цену для некоторого уравнения, соответствующего един-
ственной вершине со свободным ребром, а затем и все цены для соответ-
ствующего подграфа.
С другой стороны, если некоторый изолированный подграф содержит
цикл, то сначала можно определить цены для вершин, принадлежащих
циклу. Оставшиеся цены мы получим, переходя последовательно к верши-
нам, имеющим одно общее ребро с теми вершинами, для которых цены
уже определены. Если Xj является базисной переменной, а — ценой,
соответствующей г-му уравнению, то имеет место равенство
^gj^g 4“ ^hj^h == Cj, (6)
где g = g (/) и h = h (7) — номера пунктов назначения в уравнениях,
соответствующих ненулевым коэффициентам при переменной
Ребрам, образующим цикл на рис. 21-2-П, соответствует система
уравнений
«31^3 + #21^2 — Ci,
Л32Л3 4“ ^42Л4 — с2,
Я43Л4 + а73Л7 = С3, (7)
Я74ЗТ7 6Z943T9 = С4,
#95^9 + ^25^2 ~ с5«
Кроме того, поскольку матрица этой системы является транспонированной
по отношению к матрице системы (4), эти системы имеют одинаковую
структуру и для вычисления неявных цен можно воспользоваться теми
же приемами, что и для нахождения базисного решения.
21-3. ПОДКЛАСС ЗАДАЧ С ТРЕУГОЛЬНЫМИ ОПТИМАЛЬНЫМИ БАЗИСАМИ
Методы решения, которые мы описали, опирались на почти треуголь-
ность базисов и были несколько сложнее, чем методы решения стандарт'
ной транспортной задачи. В частности, это связано с тем, что уравнения
взвешенного распределения могут иметь нетреугольные базисы.
Однако даже среди тех задач, для которых неоптимальные базисы
не обязательно должны быть треугольными, существует, как обнаружил
Марковиц [3], важный класс задач, у которых любой базис, соот-
ветствующий оптимальному решению, является треугольным, независи-
мо от величин свободных членов. К сожалению, при применении обычного
симплекс-метода из факта треугольности окончательного базиса не удается
извлечь вычислительных выгод. Идея Марковица состояла в таком изме-
нении процесса решения, чтобы сделать треугольным каждый базис,
встречающийся по ходу решения. Он заметил, что при некоторых значе-
ниях свободных членов оптимальное базисное решение получается немед-
ленно, а выбрав эти свободные члены в качестве параметров, можно после-
довательно придавать им любые нужные значения. При таких действиях
базисы остаются и допустимыми, и оптимальными в течение всего процес-
са, поэтому они должны оставаться треугольными. Эта идея и будет разви-
та в настоящем параграфе.
Марковиц рассматривал два типа задач; задача первого типа приве-
дена ниже, а задача второго типа будет изучена позднее под номером (5).
405
Определить неотрицательные числа и минимальное значение z, удо-
влетворяющие условиям
п
S ацХц + ъ = at для г = 1,2, ..., т,
' (1)
ДЛЯ 7 = 7П + 1, m-f-2,
i=l
— %CtXt=z (2)
1=1
где коэффициенты и не отрицательны, a at й bj положительны.
Уравнениям, соответствующим п столбцам, приписаны номера j = т +
4- 1, т + 2, . . т + п, чтобы установить взаимно-однозначное соответ-
ствие между т + п пунктами и т + и уравнениями. Задачи этого типа
впервые встретились при попытке так загрузить станки заданным объемом
работ, чтобы минимизировать время работы станков или, что то же самое,
максимизировать общую величину времени, которое остается у станков
свободным после выполнения всех работ. Последнее означает введение
некоторых свободных переменных (см. иллюстративный пример
в § 21-1).
Теорема 1. Каждый оптимальный базис для задачи {(1), (2)} является
треугольным.
Доказательство. Если предположить противное, т. е. что некоторый
базис не является треугольным, то существует такое подмножество уравне-
ний, что соответствующий этому подмножеству связный линейный под-
граф содержит один цикл и по теореме 1 из § 21-2 не имеет ребер, отве-
чающих свободным переменным. Цены, соответствующие вершинам, при-
надлежащим циклу, можно вычислить с помощью системы уравнений
вида 21-2-(7). Но, поскольку свободных переменных нет, для подмно-
жества базисных переменных, входящих в эти уравнения, коэффициенты
целевой функции равны нулю. Поэтому и все неявные цены для этого
подмножества уравнений должны быть равны нулю. В частности, если
xrs — одна из базисных переменных, входящих в рассматриваемое под-
множество, то иГ — 0. Однако условия оптимальности базиса таковы:
(tijUi + bijVj^Q.
— ut^Ci>0 для i = 1, 2, ..., т (3)
и /=7п-]-1, т 4-2, ...,тп+тг,
а это противоречит тому, что иг = 0. Следовательно, существование циклов
невозможно (кроме циклов, состоящих из единственного свободного реб-
ра) и базис должен быть треугольным.
НАХОЖДЕНИЕ ИСХОДНОГО ДОПУСТИМОГО РЕШЕНИЯ
ДВОЙСТВЕННОЙ ЗАДАЧИ
Если все at заменить достаточно большими величинами аД то началь-
ное решение для треугольного базиса немедленно становится допустимым.
В качестве базисных переменных выберем свободные переменные и по
одной переменной из каждого столбца так, чтобы
min^f7 = ^7 = v> (bi}, &Г7#=0). (4)
406
Тогда (предполагая, что все числа не отрицательны) легко проверить,
что цены щ = Ci и только что определенные Vj удовлетворяют условиям
(3); поэтому базисное решение является и допустимым, и оптимальным.
Упражнение. Определить в явном виде, насколько большим нужно
взять а*, чтобы обеспечить допустимость.
Следующий шаг состоит в том, что постоянные at заменяются на +
+ X (а* — аг) и значения базисных переменных рассматриваются как
функция от Л. ЕслиХ = 1, то решение является допустимым и оптималь-
ным. А тогда, чтобы уменьшить X до нуля, можно применить алгоритм
параметрического линейного программирования (§ 11-3). В конце это-
го параграфа будет описан вариант указанного алгоритма, приспособлен-
ный для решения рассматриваемой задачи.
Второй тип задачи, рассмотренный Марковицем, состоит в следующем.
Определить числа и максимальное X, удовлетворяющие
условиям:
G'ijXij Xi = Cbi (J, === 1,2, • . , 772-),
2. (5)
Л bijXij = X67- (j =тп+ 1, m-\- 2, ..., m + тг).
г
В предыдущей постановке задачи мы хотели максимизировать время
станков, которое остается неиспользованным после выполнения всех
заданных работ. В данном же случае мы отыскиваем такое распределение
работ по станкам, при котором заданы числа bj, определяющие доли
различных видов работ, и максимизируется объем выполняемых работ.
Задачи этого типа, естественно, возникают в тех случаях, когда для изго-
товления полных комплектов нужны различные виды работ в заданном
отношении (например, детали арифмометров, необходимые для сборки
полных машин).
Теорема 2. Для любого фиксированного X можно найти базис, который
будет треугольным.
Доказательство. Пусть X — некоторое фиксированное значение, удо-
влетворяющее системе (5). Максимизируем По теореме 1 базис,
получающийся в результате решения этой подзадачи, будет треугольным,
и это завершает доказательство теоремы. Чтобы решить задачу (5) можно
поступить следующим образом: дляХ = 0 используем то же самое базис-
ное множество, которое было найдено с помощью соотношений (4). Соот-
ветствующее базисное решение xtj = 0, хг = at для всех i и / является
допустимым и оптимальным решением задачи (5). Для максимизации
X применим алгоритм параметрического программирования. Все последо-
вательно получающиеся базисы будут треугольными.
Итеративный процесс. Чтобы упростить вычисления, предположим,
что aij > 0; кроме того, нам будет удобно записывать задачу {(1), (2)}
в следующей форме:
Найти Хц>0, шах 2', удовлетворяющие условиям
Г п
x^j * j хг — а%,
j=i
т
=-ЬУ, (₽М>0) (6)
I 1=1
I т
2 x'i =z'(max).
L i=l
407
Здесь задача на минимум заменена задачей на максимум. Такую форму
можно получить, произведя преобразование переменных х^= с^х^ (х^=
= х'иу если = 0) и = х\ и положив = /с^а^ =
= btj9 если = 0) и = а\. Мы предположим, что для системы (5)
все а,ц 0.
Упражнение. Объяснить, почему на практике из а^ = 0 обычно
следует Ъи = 0.
Задача, двойственная к задаче (6), такова: найти щ Vj, min z', удовлет-
воряющие условиям
Щ —
ut>i (7)
2 a'iUt — 2 bjVj — z' (min),
i 3
где i = 1,2, .. ., m* j = 1,2, . . ., n.
Замена a'i на Qa'i. Предположим, что числа > 0 заменены на
для i == 1,2, . . т и что для достаточно большого 0 у нас есть оптимальное
базисное решение задачи (6). Тогда базис является треугольным и состоит
из ряда деревьев, каждое из которых связано с свободным ребром, как это
показано на рис. 21-3-1. Такую часть базиса будем называть ребро +
+ дерево, всегда имея в виду здесь свободное ребро. Однако если величи-
на 0 уменьшится, то значение некоторой базисной переменной, связанной
с ребром из некоторого графа ребро + дерево, может стать отрицатель-
ным. Правила алгоритма параметрического программирования (§ 11-3)
предписывают на следующей итерации вывести из базиса ту переменную,
которая первой изменит знак, если 0 станет меньше критического значе-
ния 0 = 0*. Если переменная, которая выводится, не является свободной,
например, xpq на рис. 21-3-1, то после удаления ребра (р, q) граф
ребро + дерево распадается на две части (F) и (G). Для удобства предпо-
ложим, что вершина p£F, а вершины к, q£G. Тогда часть (F), не содер-
жащая свободной переменной в графе нового базиса, должна соединить-
ся либо с (G), либо с некоторым другим графом ребро + дерево при
помощи ребра (г, $), соответствующего новой базисной переменной. Если
из базиса выводится свободная переменная хь, то, конечно, (G) являет-
ся пустым множеством, a (F) должно соединиться с некоторым другим
графом ребро + дерево.
Теперь мы будем определять, какую новую переменную нужно ввести
в базисное множество. Заметим, что в результате изменения базиса для
всех вершин, принадлежащих всем другим графам ребро + дерево, цены
не изменились; не изменились цены и для вершин из (G). Следовательно,
цены изменились только для вершин из (F). Однако до изменения базиса
цены для вершин из (F) определялись из следующих соотношений:
“г — = 0 (г, / 6 F), (8)
408
где (j, 7) — ребро из (F), а ир — цена для вершины р, которая была опре-
делена из аналогичных соотношений для (G) и = 1. Соотношения (8)
остаются в силе и после изменения базиса, но цена ир для вершины р мо-
жет оказаться равной, скажем, р,^р. Поскольку соотношения (8) являются
однородными, то цены для всех пунктов i из (F) будут изменяться пропор-
ционально ut и станут равными р,и?. Мы предполагали, что p£F и q. k£G;
аналогичные замечания имеют место и тогда, когда q£F, а р, k£G.
Упражнение. Показать, что все неявные цены неотрицательны.
Пользуясь этими замечаниями, легко получить следующие правила
определения коэффициента пропорциональности р, и той переменной,
xrs или хг, которую нужно ввести в базисное множество:
Случай I. Если из базиса выводится xpq. где р из F. a q не принадле-
жит F. или если выводится свободная переменная хк. то р > 1. Выбе-
рем, если это возможно, переменную xrs, которую нужно вводить в базисное
множество, где г не принадлежит F. а s из F. причем
(9)
Если такого ребра (г, s) не существует, то процесс окончен.
Случай II. Если из базиса выводится xpq. где р не принадлежит F.
a q принадлежит, то р < 1. Выберем, если это возможно, в качестве пере-
менной, которую нужно ввести в базис, xrs. где г принадлежит F. а 5 не при-
надлежит F. причем
и' = ₽гзЕз.==тахРу£1< 1 (i£F, j$F), (10)
ur ui
или для введения в базис выберем свободную переменную хг, где г из F и
fA’ = r = maxir< 1 (и)
в зависимости от того, какое из отношений, р = р' или р — р" больше.
Если такого ребра (г, s) нет, то процесс окончен. Выполнение следующих
упражнений не должно представить труда.
Упражнение. Пусть в базисное множество вместо xpq или хр вводятся
xrs или хг, выбранные, как описано выше. Показать, что новое решение
(если задача невырожденная) будет допустимым для некоторой области
значений 0 < 0*.
Упражнение. Показать, что не существует допустимых решений для
0 < 0*, если нельзя найти z, не принадлежащие F. / из F для случая
I или i из F, / не из F для случая II.
Пример: Рассмотрим матрицу
(/ = 3) (7 = 4) (/=5) Свободная
переменная а1
*13 Р13 = 1 *14 ₽и=2 *15 Р15 = 3 *1 8
*23 *24 Р24=3 *25 ₽25 —6 *2 2
8 6 12
которая соответствует условиям:
409
Равенства по строкам:
ж1з + #14 + #15 + = 8, (= 80, если правая часть зависит от параметра)
^гз + ^24+^25 + ^2 — 2, (== 20, если правая часть зависит от параметра)
Равенства по столбцам:
ж1з + 4#2з ~ 8,
2Х|4 4“ 8^24 == 8,
3^15 4“ 6^25 =12,
xi + х2 =2 (max).
(14)
Для построения начального решения выберем в качестве базисных
переменных свободные переменные и из каждого столбца / по одной пере-
менной, соответствующей max 0г;. В рассматриваемом примере базисными

х,*88
/
a.
Рис. 21-3-П.
г&хг=2в-6
«г'Лз Ь’О
Выдавится
И*'
J4i3fi№Ui
)4.£2
21-3-П. Граф базиса
для итерации 0.
Рис. 21-3-IIL Граф базиса для итерации 1.

'W/e (s,
переменными являются ж23, х24, ж23, xlt х2. На рис. 21-3-П приведен
граф для этого базиса, цены и значения базисных переменных.
Легко проверить, что для j = 3, 4, 5 справедливы неравенства щ —
Pi;Vj>0; следовательно, это решение является оптимальным и допу-
стимым для 0>3. Если взять 0 меньше критического значения 0* = 3,
Ъ=3/8
иг=3/2 ъ=1/2 ф=/
^4=20-4 ® x1lt=9-3ff^xt=1ie-9
*5=3/,2
Рис. 21-3-IV. Граф базиса для итерации
2 (начало).
то х2 изменит знак; следовательно, х2 нужно вывести из базисного множе-
ства. Чтобы сделать это, изменим цены, как это показано на рис. 21-3-III.
Из приведенных справа от чертежа вычислений вытекает, что пере-
менная я14 становится новой базисной переменной, заменяя переменную
х2. Граф нового базиса, цены и значения базисных переменных приве-
дены на рис. 21-3-IV.
410
Когда 0 станет меньше критического значения 0* = 2, изменит знак
переменная я24 и, в соответствии с правилом, она не войдет в базисное мно-
жество на следующей итерации. Поэтому цены изменятся так, как пока-
Р и с. 21-3-V. Граф базиса для итерации 2 (конец).
зано на рис. 21-3-V, а из приведенных справа вычислений следует,
что переменная я15 станет новой базисной переменной.
Граф нового базиса приведен на рис. 21-3-VI. При уменьшении
величины 0 до 1 решение остается допустимым. Рассматриваемые как функ-
Р и с. 21-3-VI. Граф базиса для итерации 3 (опти-
мальное решение).
ции от параметра правые части системы (1) при 0 = 1 обращаются в нуж-
ные нам следовательно, при 0 = 1 оптимальным является решение
(15). Это решение приведено ниже (клетками обведены базисные пере-
менные).
#13= 0, Я14 = 3
«15 = 4
#23— , *^24— О,
1
х2= 0.
(15)
«25 = 0 ,
21-4. ЗАДАЧИ
1. (Повторение.) В чем состоит изменение переменных, на которое
мы ссылались во втором разделе § 21-1? Почему это не удается, если
•в каком-нибудь равенстве по строке есть отрицательный коэффициент?
Как бы вы стали применять симплекс-метод, если бы некоторые перемен-
ные могли быть отрицательны? Как связаны с предыдущими коэффи-
циентами?
2. Как написать систему, двойственную к системе уравнений (4),
(5) и (6) из § 21-1?
3. В примере из § 21-1 изменить свободные члены ai и Ь7 так, чтобы
в этапе I требовалось более одной итерации.
411
4. (Повторение.) Показать, как выбрать а* достаточно большим, чтобы
базисное решение было также допустимым (§ 21-3). Объяснить, какой
смысл в этом случае имеет оптимальное решение.
5. Как нужно производить выбор, если некоторые отрицательны?
6. Применить рассмотренный процесс для решения какого-нибудь
примера 3x4. Для вычисления цен и изменений значений базисных пере-
менных использовать линейные графы.
7. Решить какой-нибудь пример 3x4, подобный примеру 1 из § 21-1,
в котором Ъг заменены на Xbj. Вначале выбрать X достаточно малым,
чтобы решение было допустимым, а затем, рассматривая X как параметр,
увеличить его до 1.
8. Рассмотрим задачу о загрузке станков в стандартной форме задачи
о взвешенном распределении (§ 21-1 (4), (5), (6)). Предположим, что
стоимость си часовой работы в течение часа на г-м станке не зависит от вида
работ; таким образом, — прибыль (за час работы), которую можно полу-
чить от использования оставшегося свободным рабочего времени j-ro
станка на других работах. Показать, что если нужно минимизировать
чистую стоимость работ, то для такой модели систему (6) из § 21-3 мож-
но получить из системы {(1), (2)} из § 21-3.
9. Показать, что если щ и Vj — цены, связанные соответственно с i-м
уравнением по строке и /-м уравнением по столбцу, то для оптимального
решения щ > 0, Vj > 0.
10. Начав с решения (15) из § 21-3, продолжить уменьшение 0
и найти такое число, что если 0 станет меньше него, то решение перестанет
быть допустимым. Показать, что в этом случае нельзя определить, какая
переменная должна войти в базисное множество.
11. Еще раз рассмотреть задачи и иллюстративные примеры из
глав 3, 4, 5 и определить, какие из них являются задачами о взвешенном
распределении. Решить те из них, в которых имеются числовые данные.
12. (Нерешенная.) Существует ли такое преобразование переменных
и свободных членов, которое позволило бы свести задачу первого типа,
рассмотренную Марковицем (§ 21-3 (1), (2)), к его же задаче второго
типа § 21-3-(5)?
Глава 22
ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
€ ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ
22-1. ОБОБЩЕННАЯ ЗАДАЧА ВУЛФА1
В этой главе мы будем рассматривать задачи, в которых допускается
некоторая свобода выбора коэффициентов технологического процесса.
Такие задачи возникают при проектировании какой-нибудь системы или
когда характеристики затрат и выпуска продукции в некотором процессе
зависят от одного или нескольких поддающихся регулированию пара-
метров (например, температуры).
Прежде всего об обозначениях; нам будет удобно рассматривать зада-
чу линейного программирования в векторной форме: найти для
j #= 0 и max х0, удовлетворяющие условию
+ + ^2^2+ ••• ~\~Рпхп = Q- (1)
Например, если мы хотим найти > 0 и min z, удовлетворяющие условиям
-J- ^2-^Х3 + 2^4 = 5,
— ^£-1-^2 — ^зЧ“ 3^4=1, (2)
6xt + 4е2 + хз— 2xi = z,
то следует положить z = — я0 и получить
/0\ ( Ц (~^\ f 2 * *\ /5\
I О I я0 + | —1 I л + | 1 I Яг + 1 —1 I я3 + ( 3 1^4 = 1 1 I • (3)
\1 / ' 6/ \4/ \+1/ 2 7 \0/
Нам будет также удобно переопределить симплекс-множители л =
(*^i, *^2, • • •, л^, •^TTi+i) так, что
nPj = 0, если Xj х0 является базисной переменной,
(4)
Последний из этих множителей nm+i всегда равен единице, потому что
Ро = Um+i является единичным вектором и нет ограничений на знак
переменной х$. Следовательно, эти множители будут порождать модифи-
цированное стоимостное уравнение S CjXj, где (имея в виду стандартную
задачу линейного программирования)
Cy = nPj=2 лгаг>+1-су.
i=l
1 Подход к этому классу задач был впервые намечен в совместной работе Ф. Вул-
фа и автора настоящей книги о принципе разложения для задач большого объема (кото-
рый рассматривается в гл. 23). Именно Вулф предположил, что предложенный нами
процесс можно рассматривать как особый случай «Обобщенной задачи линейного
программирования», поэтому здесь эта задача связывается с его именем (Данциг и Вулф
[1]; Гомори и Ху [1]).
413
Поскольку мы сумму прибавляем к Cj, вместо того чтобы ее вычитать,
очевидно, что множители л2, . . ., лт будут иметь противоположные-
знаки по сравнению с определенными в § 9-2. Как обычно, для опти-
мальности базисного допустимого решения условие Cj = л Р0 должно*
выполняться для всех /.
Определение. Обобщенной задачей линейного программирования назы-
вается задача линейного программирования с переменными коэффициента-
ми следующего вида: найти я7 >0 для ]=£0и шах я0, удовлетворяющие
условию
Р о%о + Р 1%1 + • • • + Р п^п = Qf (5)
где каждый вектор Pj для / =/= 0 можно выбрать произвольно из выпуклого
множества Cj.
Для дальнейшего обобщения задачи векторы Ро и Q, фиксирован-
ные в системе (5), можно заменить на любые векторы Ро, Q из выпук-
лых множеств CQ и Cq. Это будет сделано в конце параграфа в пункте
«Эквивалентные формулировки». Рассматриваемые здесь выпуклые мно-
жества определяются системой линейных неравенств. Однако с помощью*
метода, изложенного в главе 24, все получаемые результаты можно рас-
пространить и на любые выпуклые множества.
Например, задача (3) становится задачей линейного программирования
с переменными коэффициентами, если мы рассмотрим такое обобщение:
найти Xj^Q для /У=0 и max х0, удовлетворяющие условию
0\ ( i\ [Г\ (У1\ /5\
О I хо + ( —1 I Zi + I 1 I Я2 + ( —1 ) ^3 +1 У2 ) ^4 = 1 1 j , (6>
1/ \ 6/ \4/ \ 1/ W W
где на значения yi накладывается одно ограничение
У1 + 2г/2 + Зу3 = 2 (2/i>0). (7}
Может вызвать удивление, что система вида (6), (7) формально является
задачей линейного программирования. Однако если мы положим У1Х^=
= Wi, ^2^4= ^2, = и3 и умножим условие (7) на я4, то, как легко
убедиться, эту систему можно переписать так, что она станет линейной
относительно Xj и ut (см. задачу 2). В общем случае справедливо
Утверждение. Если в системе (5) один из столбцов Pt = (у±, у2,..ут)
удовлетворяет системе линейных неравенств St относительно пере-
менных у^ £ = 1,2, . . . , т и вспомогательных переменных ym+i, . . .,
Ут+h, не зависящих от остальной системы, то эту систему можно перепи-
сать в виде системы линейных неравенств, если умножить соотношения
St на xt 0 и перейти к новым переменным uit = ytxt.
Хотя это высказывание позволяет нам формально преобразовать систе-
му так, чтобы она стала линейной, но описанное преобразование не обя-
зательно приводит к задаче линейного программирования, эквивалентной
исходной системе, поскольку возможно, что существует решение задачи
линейного программирования, для которого одновременно xt = 0 и uit 0.
Дальнейшее обсуждение этого вопроса предлагается в задаче 2 (§ 22-3).
Большой успех выпал на долю тех методов, в которых использовался
другой подход, при котором не используется идея переменного коэффи-
циента, и обобщенная задача решается с помощью ряда преобразований
значений уг, которые получаются при решении вспомогательных задач,
или подзадач, относительно упомянутых yt. В результате большая задача
линейного программирования распадается на несколько задач меньшего
размера.
414
ИЛЛЮСТРАЦИЯ МЕТОДА
Общий процесс будет достаточно ясно продемонстрирован на решении
примера {(6), (7)}. Предположим, что вычисления начинаются с базисного
множества переменных х0, xlf х2. Мы хотим установить, является ли
базисное допустимое решение х0 = —24, Xi = 2, х2 = 3, я3 = я4 = О
оптимальным для задачи (6), называемой далее главной задачей. Симплекс-
множители
л = (—5, 1, 1) (8)
определяются из условий лР0 = 1, = 0, лР2 = 0- Умножая соотно-
шение (6) слева на вектор л, мы получим
я0 + (лР3) х3 + (лР4) х4 = (л0, (9)
где
лР3 —20 л(?=—24, (10)
лР4= — 5z/i + ^2 + i/3. (11)
Ясно, что критерием максимальности xQ является выполнение для всех /
неравенств лР; > 0. С другой стороны, если лР4< 0, то решение можно
улучшить, увеличивая значение переменной х4. Положим поэтому z4 =
= лР4 и рассмотрим вспомогательную задачу линейного программирова-
ния, которая состоит в нахождении ^>0 и minz4, удовлетворяющих
условиям
J/i + 2у2 + Зу3 = 2 (*Ц>0), (12)
— 5^i + y2 + V3 = 24(min) (24 = лР4). (13)
Теперь с помощью обычного симплекс-метода в базис вводится столбец
с наименьшей ценой. Решение, дающее минимальное лР4, получается
немедленно, именно yi = 2, у2 = 0, у3 = 0, лР4 = —10.
Теперь мы можем получить улучшенное решение главной задачи, введя
в базис столбец (у[ = 2, у2 = 0, у' = 0). Однако нам следует учесть воз-
можность последующего изменения значений у}. Мы можем это сделать,
переписав задачу в следующей форме:
/0\ ( Ц (l\ fy*\ /5\
I 0 I яо + l — 1 ) Я1 + 1 1 I я2 + | — 1 I Яз + | 0 1 я; + [ у2 I х* = \ 1 |, (14)
\1/ \ 6/ \4/ \ 1/ \0/ \y"J \0/
(опустить)
• • • ★
где величины yl удовлетворяют тому же условию, что и yt
у[ + 2у; + 3у;=2 (у<>0). (15)
Столбец < у'{, у2, у"9 > мы будем называть сопутствующим столбцом.
Оказывается, что хотя мы изменили нашу первоначальную задачу, но полу-
ченная задача эквивалентна старой. Чтобы убедиться в этом, перепишем
произвольное решение задачи (14) в виде решения задачи (6), положив
xi — + и взяв в качестве коэффициента при я4 вектор
/У1\ /2\ /уУ
(^+^>о). (16)
\Уз/ \0/ \у"3/
Правая часть в (16), очевидно, является выпуклой комбинацией двух
точек, принадлежащих выпуклому множеству, которое определено условием
415
(12). Но тогда точка (уь у2, Уз) также должна принадлежать этому выпукло-
му множеству. Наоборот, любому решению уравнения (12) мы можем
сопоставить решение уравнения (16), полагая, например, х4 = 0; в этом
случае х± = х4, уг = у1.
Если в базисное множество главной задачи вводится переменная
х'„ то, как оказывается, выйти из него должна переменная Новым
базисным решением является решение х0 = — 4, х2 = 1, х'4 — 2, xt = х3 —
= z" = 0. Соответствующие симплекс-множители запишем в виде вектора
л-(0, —4, 1), (17)
где л определено из условий (4), т. е. лР0 = 1> яр2 = 0, лР* = 0. Чтобы
проверить, не является ли это решение максимальным, рассмотрим
лР4 = 10,
лР3 = 5, (18)
Единственная возможность увеличить значение х0 состоит в том, чтобы
найти такие значения переменных у'\, при которых лР"< 0. В соответ-
ствии с этим рассмотрим новую подзадачу
^' + 2j/'' + 3^ = 2 (tf>0),
-4^ + ^ = «P;(min). (19)
Отсюда мы получаем у" = 0, у”2 = 1, у” = 0 и пР'[ = —4.
Теперь наша расширенная главная задача примет вид
/0\ / 1\ /1\ /—4\ /2\
I 0 j £о 4“ I — 1 I 4" I 1 *2 + -1 I З'З -ЬI 0 I xi -1-
\1/ \ 6/ \4/ \ 1/ \о/
опустить
• • •
/°\ (У*\ f5\
+ 1 1 I х;+| у2" U"=j 1 I, (20)
\0/ \Уз/ \0/
где мы снова учли возможность изменения значений у;, введя «сопутствую-
щий» столбец и переменную х4".
Вводя в базисное множество переменную х'4", выводим из него пере-
5 п
менную х2. Получаем новое базисное решение хй = 0, , ж" = 1,
Xj = х2 = х3 = 0 и новые симплекс-множители
л = (0, 0, 1), (21)
которые определены из условий пР0 = 1, nP't — 0, лР" = 0. Теперь
мы имеем
nPt = 6,
лР2 = 4, (22)
лР3 = 1,
яРГ = Уз"-
Вспомогательная задача линейного программирования такова: найти
y'i" и minnP4", удовлетворяющие условиям
+2у2 + 3Уз =2 (yt >0),
у'" = пР4' (min)- (23)
416
Но эта задача имеет единственное оптимальное решение ^'"—2, у %' = 0
и у*' = min лР'" =0. Следовательно, на этом шаге мы не можем улучшить
решение задачи (20), изменяя значения переменных у^ Поскольку все
другие nPj > 0, базисное решение оптимально.
Упражнение. Из оптимального решения задачи (20), (23) получить
оптимальное решение задачи (6), (7).
Может показаться, что при многократном повторении этого процесса
получается задача с бесконечным числом столбцов. Однако в действи-
тельности это не имеет места, поскольку добавочных столбцов, которые
приходится вводить, не может появиться больше, чем было столбцов
в исходном базисе. Мы покажем, что любой столбец, который выводится
из базиса, можно «опустить», так как он содержится в выпуклых множе-
ствах, определяемых сопутствующими столбцами, связанными с главной
задачей, и каждое из этих выпуклых множеств определяется системой
линейных неравенств. Формализуем теперь некоторые понятия и термины,
которыми мы пользовались до сих пор.
Определение. Ограниченная главная задача (на Zc-м шаге алгоритма)
состоит из переменных с соответствующими столбцами коэффициентов
Р^\ взятыми из выпуклых множеств Су. Оптимальному решению этой
задачи сопоставляются значения симплекс-множителей л — л°, которые
используются в подзадаче.
Определение. Подзадача } состоит в следующем. Найти вектор Pj £ Су,
который минимизировал бы линейную форму л°Ру (с неизвестными
координатами вектора Ру), где значения л = л° известны. Оптимальное
решение Ру = Р* порождает дополнительный полностью определенный
столбец коэффициентов Р* для следующей ограниченной главной задачи.
Теорема 1. Если члены S^PyXy добавляются к ограниченной главной
задаче, причем «сопутствующие столбцы» являются произвольными эле-
ментами выпуклых множеств Cj, то получаемая задача эквивалентна
исходной обобщенной задаче линейного программирования.
ОБЩАЯ ТЕОРИЯ ДЛЯ МНОГОГРАННЫХ МНОЖЕСТВ Су
Мы предполагаем здесь, что каждое выпуклое множество Су является
многогранным, т. е. определяется системой линейных неравенств. В этом
случае произвольный элемент Ру множества может быть представлен как
выпуклая линейная комбинация конечного множества точек множества
Cj плюс неотрицательная линейная комбинация конечного множества
однородных решений (если множество Су является неограниченным).
Определение. Однородным решением Pj будем называть решение,
обладающее следующим свойством: если Pj^Cj, то Ру + kPj^Cj при всех
к > 0.
Теорема 2. Решение (х*, Р*) для / = 0,1,2, . . ., п является оптималь-
ным, если существует такой вектор л, что тьР$ = 1, л Ру > 0 для всех
Pj 6 Сj и = 0 для всех тех i’ для которых х* > 0, / 5^ 0.
Теорема 3. Если каждое базисное допустимое решение улучшать либо
введением в базис крайней точки Р* g Су, выбранной так, что
nP* = min лРу<0 (/ = 1, 2, ..и), (24)
pjtcj
27 Дж. Данциг
417
где л — вектор симплекс-множителей, либо введением в базис любого
однородного решения Р* из конечного множества, для которого лР* < Ог
то потребуется лишь конечное число итераций симплекс-алгоритма.
Доказательство. В силу наших предыдущих замечаний теорема 2 оче-
видна. Что касается теоремы 3, то конечность алгоритма тоже станет оче-
видной, если мы сможем доказать, что столбцы любого базиса должны
выбираться из конечного множества. Поскольку Cj — выпуклое множество,
определенное с помощью неравенств, каждое решение Р* получается
при решении некоторой задачи линейного программирования. В этой
задаче минимизируется линейная форма лРу, где л — фиксированный
вектор, а компоненты вектора Pj являются неизвестными.
Если множество Сj ограничено, то решение Р* совпадает с одним из
базисных решений, которых конечное число. Если множество Cj не ограни-
чено, то может случиться, что лР; не будет ограничено снизу. В этом
случае на некоторой итерации симплекс-метода будет получено однородное
решение (см. гл. 6, задача 19). В. обозначениях стандартного симплекс-
метода, примененного к канонической форме подзадачи для множества Cj
на некоторой итерации, будет получен столбец, для которого все коэффи-
циенты, скажем, ais, будут не положительны, а относительная J оценка
< 0. Обозначим г-ю базисную переменную подзадачи через у^, тогда
множество значений yj = — ais > 0, & = 1 и все другие уг = 0 является
для множества Cj однородным решением Pj, обладающим нужными свой-
ствами, а именно cs = ztPj^O, где л — вектор симплекс-множителей для
базиса главной задачи. Поскольку число канонических форм для различ-
ных подзадач (если опустить целевое уравнение) конечно, конечно и число
столбцов, обладающих свойством ais 0 для всех i. Следовательно, мно-
жество решений Pj тоже конечно.
ЭКВИВАЛЕНТНЫЕ ФОРМУЛИРОВКИ
Предполагалось, что векторы Ро и Q в задаче (5) фиксированы.
Однако при желании вектор Q можно выбирать произвольно из выпуклого
множества Cq; это можно сделать, рассмотрев систему
Рохо + Р+ ... + Рпхп— Qxn+i — 0, (25)
Яд+1 — 1 •
Упражнение. Обобщить результаты так, чтобы и вектор Ро можно
было выбирать из выпуклого множества Со.
Упражнение. Следующую задачу свести к обобщенной задаче линейно-
го программирования: найти такие векторы Pj £ Cj, Q fz Сq, чтобы
p1 + p2+...+^ = <?. (26)
Упражнение. Предположим, что вместо условия (7) мы имеем условие
У1 + У1 + Показать, что эта задача является обобщенной зада-
чей линейного программирования. Применить методы этого параграфа
и сопоставить со случаем многогранного множества.
ЗАДАЧИ ВЫПУКЛОГО ПРОГРАММИРОВАНИЯ (см. гл. 24)
Кун и Таккер [1] рассмотрели широкий класс задач следующего
вида: найти х = (Xf, х2, . . ., хп) и min z, удовлетворяющие условиям
Gi (х) 0, (г = 1, 2, ..., т)
'Gq (х) = z (min),
418
где Gi (х) — выпуклые функции, а вектор х принадлежит выпуклому
множеству R.
Заменим сформулированную задачу на эквивалентную; найти X, Хь
yi удовлетворяющие условиям
X = 1, (Xj > О, А,2 О, ..., А,т 0)
=0,
i/2X +а2 — о,
(28)
Утк +^тп = О,
=2 (min),
где yi > Gi (х) для некоторого х С R.
Чтобы показать, что множество допустимых у = (у0, yiy . . ут)
образует выпуклое множество Су, предположим, что у[ Gt (xf), yl
> Gi (ж"), и пусть Л, + р, = 1, А > 0, р, > 0, тогда
Уг = tyi + > ^Gi СИ + СИ > Gi № + рУ'), (29)
где (АУ + рУ) € R, так как R — выпуклое множество. Методы главы 24
можно использовать для распространения результатов на решение этой
задачи линейного программирования, содержащей, по существу, одну
переменную и коэффициенты которой порождены множеством произволь-
ных выпуклых функций n-мерной точки.
Упражнение. Доказать, что если у* Gt (х°) является решением
задачи линейного программирования с X = АД Xf = A?, то y* = Gi(xQ)
также является решением этой задачи, причем Go (x°)<yj.
Упражнение. Предположим, что допустимое решение системы (28)
существует для некоторого у — у0, где yQ — выпуклая комбинация таких
yk, что yi Gi (xk) для каждого к, и предположим, что не известно, суще-
ствуют ли допустимые решения для этих yk. Доказать, что существует
такое У, что у\ > Gt (У), где у° = (1, у", . . ., у°т, у°).
Упражнение. Доказать, что симплекс-множители л?, соответствую-
щие оптимальному решению каждой главной задачи для системы (28),
не отрицательны. Показать, что подзадачу можно сформулировать следую-
щим образом: найти х £ R так, чтобы было минимальным F (ж), где
F (ж) = 3 л?Сг (ж).
Доказать, что F (х) является выпуклой функцией. Связать эти< рассуж-
дения с методом множителей Лагранжа, § 6-5.
22-2. ЗАМЕЧАНИЯ О ЧАСТНЫХ СЛУЧАЯХ
СЛУЧАЙ ОДНОГО КОНТРОЛИРУЕМОГО ПАРАМЕТРА Т
Во многих промышленных процессах рассматривается непрерывный
спектр технологических процессов, зависящих от значения некоторых
контролируемых параметров, таких, как температура (Г), давление (Р),
отношение показателей в циклах (7?) и т. д. В частности, это справедливо
для задач, возникающих в нефтеперегонной промышленности, где часто
27*
419
ради простоты в любой задаче предполагается, что имеется один-единствен-
ный стандартный способ управления оборудованием, или иногда выби-
рается несколько типичных значений параметров, на которые и «натяги-
вается» область возможностей.
Предположим, что имеется один контролируемый параметр Т,
область изменения которого 7\^.Т^Т2\ пусть / = 1 соответствует
единственному технологическому процессу, технологические коэффициенты
которого зависят от Т.
Технологические коэффициенты этого процесса при Т = Т\, Т = Т
и произвольном Т суть
Т2 Т
а'Г Vi
а<Г У2
(1)
здесь для i = 1, 2, . . ., тп, т + 1 величины уг = yt (Т) являются функция-
ми от Т.
Во многих приложениях достаточно хорошее приближение для yt (Т)
дает линейная интерполяция по первым двум столбцам матрицы коэффи-
циентов (1). В этом случае возникает эквивалентная задача линейного
программирования:
4" + Я12^2 4“ • • • 4" ainxn =
а^Хц “И a<21X2i + а22х2 4“ • • • + а2пхп = ^2»
................................................... (2)
4“ ttmi*^21 4" а/»2^2 4" • • • 4~ атпхп —
4- 4- С2Х2+.. .4- CnXn=Z,
Где Xl = Хц 4- #21 — это интенсивность первого технологического про-
цесса. Конечно, мы предполагаем, что переменные коэффициенты yt выбра-
ны с помощью линейной интерполяции (3), где Xi = Хц/xi соответствует
некоторой температуре Т.
Xj 4~ ^2 »
4“ ^2^П = yii —2, . . . , 77l),
МС1° 4“ ^2С12> = Ут+1* (3)
В частности, если температура Т тоже определяется с помощью линейной
интерполяции, то
1^1 4~ ^21^2 _ р / Z \
*11+ *21 ‘ V 7
Множество соотношений (3) определяет выпуклое множество допу-
стимых значений (уь у2, . . ., Ут)- Поэтому можно применить метод из
§ 22-1. Если л — вектор симплекс-множителей, связанных с базисом,
и = и С1У = с™ — 2 fya™, то соответствующая подзадача
имеет вид
Х14~^2“1> (^*1^0)
4- с!2)%2 = (min).
420
Крайними решениями (%4, X 2) будут либо точка (1, 0), либо точка (0, 1).»
Следовательно, в базис следует ввести либо первый столбец, либо второй.
Поскольку число допустимых крайних точек для этой подзадачи мало
(всего две), то не имеет смысла использовать метод из § 22-1.
Чтобы интерполировать по нескольким возможным значениям Т,,
например Г = рассмотрим следующую задачу линейного
программирования:
«и *и + aJTar2t + ... + a^xhi + 2 a^Xj = bif
2
а21>:Г11 + a21>a;21 + • • • + + 3 a2iXj — ^2>
2
........................•.......................... (5)
“F • • • “F 4" 2 amjXj —
2
ci^u + C™XU + . . . + C<V>Xki + 2 CjXj = z,
2
где — значения yt = yt (T) для T = Tr, r = 1, 2, . . ., к. В общем
случае, если мы полагаем
= xix 4~ #21 + • • • + xkli (6)
то, конечно, предполагается линейная интерполяция
£H.a<i, + ^2ia<2>+...+^La(fe) = „ (7)
xt 11 1 г1 1 1 х^ г! '
и аналогично для
Однако в некоторых приложениях можно ограничиться линейной
интерполяцией между двумя столбцами, если область изменения значений
Т достаточно мала. Если это не так, то необходимо разбить эту область,
на несколько частей . -^Tr* . с тем чтобы линейная
интерполяция между векторами (yi (Z), у2 (Г), . . ., ym+i (Т)) для сосед-
них пар Т = Tt и Т = Tt+t давала бы достаточно хорошее приближение.
В этом случае оптимальное решение системы (5) является приемлемым
только тогда, когда положительные xTi появляются в смежных парах,
как это приведено в (8):
или (а) хи 0, л?21 > 0, я31 = 0, я41 = 0, ...
или (б) хп = 0, #21 >0, я31>0, ^41 = 0, ... (8)
или (в) хи = 0, я21 = 0, гг31 >0, #41>0, ...
Можно установить следующее:
а) если коэффициенты уь кроме ym+i, являются линейными функция-
ми от Т, а ym+i является строго выпуклой функцией от Т, то условия
(8) выполняются;
б) пусть Т' — некоторая строго монотонная функция от контролируе-
мого параметра Т\ если коэффициенты уг, i m + 1 являются линейны-
ми функциями от 7', а ут+^ является строго выпуклой функцией от Т',
то должны выполняться условия (8);
в) если ут+1 является просто выпуклой (но не обязательно строго
выпуклой) функцией от Т', то условия (8) могут и не выполняться, и в
этом случае средние значения ац и сц, соответствующие минимальному
значению целевой функции, являются коэффициентами уь отвечающими
421
йекоторому фиксированному Т', и оптимальное решение задачи (5) являет-
ся точным, а не приближенным решением исходной нелинейной задачи;
г) предположим, что рассматриваемая система обладает тем свойством,
что оптимальные цены для некоторого подмножества индексов
(где определены таким образом, что для базисных хг);
предположим, что только для этих индексов зависят от Т' и являются
выпуклыми функциями от Т'\ тогда либо оптимальное решение обладает
свойством (8), либо среднее решение является точным решением для
некоторого фиксированного Т'.
ИНТЕРПРЕТАЦИЯ СМЕШАННОГО РЕШЕНИЯ
Интересный вопрос возникает в случае, когда не выполняется (8)
и, кроме того, любое изменение решения, для которого выполняется (8),
приводит лишь к увеличению значения z. В этом случае мы не можем при-
вести физическую интерпретацию полученного решения, обладающего
тем свойством, что существуют xi9 определяемые по формуле (6), и
определяемые по формуле (7), которые соответствуют некоторому зна-
чению Т. Такой результат не всегда может быть приемлемым. Если техно-
логический процесс таков, что Т не является регулируемым параметром,
а одно из его значений, которое не может изменяться, является некоторой
запроектированной характеристикой рассматриваемого процесса, то этот
ответ, конечно, не будет приемлемым. (Несколько позднее мы обсудим,
что делать в этом случае.)
Если Т регулируется легко, то может быть только один исход. Предпо-
ложим, что в оптимальном решении Хц > 0, х12 = ж13 = 0, я14> 0.
Мы можем это интерпретировать так: выгодно использовать более чем
одно состояние Г. Следовательно, если технологический процесс действи-
тельно связан с несколькими видами оборудования, то для некоторых видов
можно взять Т = Ti9 а для других Т = Р4. Если же используется только
один вид оборудования, то можно положить для некоторого периода вре-
мени Т = Т7!, а для оставшегося времени Т = Т4.
ЕСЛИ ПРИЕМЛЕМО ТОЛЬКО ОДНО ЗНАЧЕНИЕ Т
Если число возможных значений Т ограничено, то может представить-
ся такой случай. Предположим, например, что в имеющемся базисном
решении используется фиксированное значение Т — Тг и не существует
альтернативных столбцов для других значений Т. Теперь мы хотим видеть,
можно ли улучшить решение, изменяя значение Т. Для этого вводятся
новые столбцы, соответствующие соседним значениям Т, скажем Tr-i и TT+i,
которые выбираются настолько близкими к ТГ9 чтобы линейная интерполя-
ция соответствующих им ац была бы приемлемой. Затем эти столбцы оце-
ниваются, и если это выгодно, то один из них вводится. Если в результате
этих действий Тт заменяется в базисе, скажем, на Tr+i9 то Тг+2 становится
возможным альтернативным столбцом, а Tr-i исключается из рассмотрения
на следующей итерации. Затем с помощью нового решения оценивается
добавленный столбец и все Р;, 7 = 2, . . ., п, поскольку в результате
изменения Т может оказаться выгодным изменить базисные переменные.
С другой стороны, если введение альтернативного столбца Tr+i приводит
к тому, что выводится из базиса не Тг, а какой-нибудь другой столбец,
то Тг+2 становится ^возможным альтернативным столбцом и таким же
остается Tr-i. Оба эти столбца оцениваются наряду с другими столбцами.
Если после оценки кандидатом становится Рг+2, то он может войти в ба-
зис, если только он^заменит ТГ9 если же нет, то Тг+2 остается кандидатом
422
на следующей итерации*, аналогично Tr_i может быть кандидатом
только в том случае, если он заменяет Tr+i* #
В конце концов процесс может привести к такому значению Т = Т*,
что альтернативы и Т*+1 не дают допустимого улучшения, или
к интерполяции между двумя значениями Т, Тт и Гг+р Это не означает,
что полученное Т является наилучшим, а лишь что Т является локально
наилучшим. Если есть подозрение, что существует другой локальный
оптимум, который лучше уже полученного, то необходимо так изменить
процесс, чтобы Т пробегало по очереди все значения Т = Т2, . . .
Tk- Если существуют другие локальные оптимумы, лучшие, чем
в т = то их значения z должны лежать между значением z для Т =
— Тг и значением z, полученным в результате свободного выбора среди
всех альтернативных столбцов Тг. Практически лучше всего было бы
решить первоначально задачу при неограниченном выборе. Если решение
удовлетворяет условию (8), то его, конечно, можно интерпретировать
«физически и оно является оптимальным. Если условие (8) не выполнено,
то часто в качестве исходного значения для описанного процесса можно
использовать среднее значение Т.
Т = 3 xr±rrlxi. (9)
г
Например, в задачах о смесях сортов бензина имеется нелинейный член,
соответствующий «октановому числу», который является функцией коли-
чества Т тетраэтила, добавляемого к смеси компонент, пропорцию которых
тоже нужно определить. Поскольку структура такой задачи сложнее
описанной здесь, решение, полученное рассмотренными методами линейно-
го программирования, не имеет прямой физической интерпретации. Это
связано с потерей выпуклости некоторой поверхности, соответствующей
«октановому числу». Однако эта нелинейность незначительна, и решение
(9) дает настолько хорошие результаты, что последующие итерации прак-
тически не нужны (Каваратани, Улман и Данциг [1]).
СЛУЧАЙ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ ПАРАМЕТРОВ,
КОТОРЫЕ ВЛИЯЮТ НА РАЗЛИЧНЫЕ ТЕХНОЛОГИЧЕСКИЕ ПРОЦЕССЫ
Хотя до сих пор обсуждался случай одного параметра Т и одного
технологического процесса j = 1, следует заметить, что если бы имелось
несколько независимых контролируемых параметров, которые влияют
на различные технологические процессы, то значения всех параметров
можно было бы определять одновременно, разбивая каждый столбец техно-
логического процесса на части, соответствующие разным контролируемым
параметрам.
СЛУЧАЙ НЕСКОЛЬКИХ КОНТРОЛИРУЕМЫХ ПАРАМЕТРОВ,
Г" ВЛИЯЮЩИХ НА ОДИН И ТОТ ЖЕ ТЕХНОЛОГИЧЕСКИЙ ПРОЦЕСС
Для случая "только двух контролируемых параметров, у которых
области изменения ТТ2 и 51 5 5 2, имеются четыре край-
них («экстрамальных») варианта (Л, 5t), (7\, S2), (Т2, и (Z2, S2)
и четыре альтернативных столбца. Поэтому в (5) коэффициенты при
можно интерпретировать как результат, полученный при (Т, 5) = (7\,
51) и т. д. С другой стороны, если полученная линейная интерполяция
(6) и (7) является приемлемой, то эту задачу можно решить этим путем.
Ничего не изменит при получении более точного приближения введение
любого числа альтернативных столбцов, соответствующих узлам решетки
423
(Tj, Sj). Может опять возникнуть только одна трудность — трудность физи-
ческой интерпретации, если в оптимальное решение с положительными
весами попали не соседние точки решетки.
(10>
Если с одним технологическим процессом связано более двух парамет-
ров, то рекомендуется использовать переменные, измеряющие изменения
значения параметров. Пусть, например, координаты вектора первого
технологического процесса являются функцией трех контролируемых пара-
метров Я, 5, Т (для каждой координаты вектора Pi), которую мы обозна-
чим Pi = Pi (Я, 5, Т). Предположим, что для (Я, S, Т) = (Яо, So, То)
известно решение соответствующей задачи линейного программирования
и линейное приближение
Р^Яо + ДЯ, ^о + А5, Го + А7т) = Р? + ДД.Ео + Д5.Ро + Д7т.Со, (И)
где PJ, Е°, F°, GQ фиксированы, является допустимым в областях
— —а'<Д5^а2, —а'<ДГ^а3. (12)
Эта формулировка позволяет непосредственно и без труда получить реше-
ние, используя методы § 22-1 и методы решения задач с ограниченными
сверху переменными из § 18-1.
Пусть компонентами вектора являются л — симплекс-множители,
связанные с известным базисом главной задачи. Используя теорему 3,
§ 22-1, построим подзадачу: минимизировать лР± = nPJ + ДЯл/?° +
+ Д5лР° + ДГлб?0 при ограничениях (12). Эта подзадача распадается
на три независимые задачи линейного программирования:
— а^ДЯ^сц (jiEq)AR==zr (min),
— а'^СД5^а2 (nF°)AS — zs (min),
— а'<ДТ^а3 (лС0)ДЗр = 2т (min).
Задачи эти легко решаются; например, полагая е = лЯ0, мы получаем
для ДЯ решение ДЯ = — а', 0 или в зависимости от того, е > 0, е =
= 0 или е < 0. Подстановка этих значений в (11) дает новый столбец
Р', который следует ввести в базис на следующей итерации. После этой
итерации выражение (11) можно либо оставить для последующих итера-
ций, либо заменить на новое линейное приближение от новых значений
Я, S и Г, полученных на этой итерации. Однако, если выражение (И)
изменилось, поскольку вектор Р\ еще остается в базисе, мы можем встре-
титься с трудностями физической интерпретации полученных результатов.
В качестве возможной подзадачи из § 22-1 может быть получена
эквивалентная задача, если умножить все выражения (11) и (12) на Xi
и ввести новые переменные ^ДЯ = Хц, Х1Д5 = rr2i ^1ДЯ = я31. Если
положить Pi = (ац, ai2, . . ., alm, Ci) , то получаем
ацХ1 = a^Xi -f- ецХц + /и^21 + (1^)
— а'#! Хц ар?!, — a'xt я21 a2xt, — a^i х31 < а3ж1в
424
Поэтому последняя задача линейного программирования, которую нужно»
решить, имеет вид
ailXl е11Х11 +/11^21 + £11Х31 + (#12^2 + • • • ~Ьа1пхп) ==
а21Х1 е21Х11 +/21^21 +^21^31 + (^22^2 + • • • ~Ьа2пхп) = ^2»
................................................ (14}
arniXl + emlxil + fmix21 + gm 1х 31 + (ат2х2 + • • • + ^тпхп) —
c^i + ехц + fx2i+ gx3l+ (c2x2cnzn) = z(min),
где Xj>0 и xri и Xi удовлетворяют ограничениям (13).
22-3. ЗАДАЧИ
1. Повторение. Распространить теорию § 22-1 на случай, когда С&
и Cq являются выпуклыми множествами общего вида, а не выпуклыми
множествами, состоящими из одного фиксированного вектора каждое.
2. а) В системах § 22-1 (6) и (7) заменить у^х^ на преобразовать
эти системы в линейные системы с неравенствами и решить их численно.
Можно ли полученное решение использовать для решения исходной
системы?
б) Повторить § 22-1, замечание, общий случай. Предположим, что
для новой системы получено решение с xt — 0; показать, что может ока-
заться ytxt 0. Построить пример, соответствующий этому случаю.
в) Показать, что задача линейного программирования эквивалентна
исходной обобщенной задаче для систем (6) и (7).
г) Показать в общем случае, что задача линейного программирования
эквивалентна исходной обобщенной задаче, если в линейную задачу
входит соотношение aoxt с положительными где щ yiXt.
д) Рассмотрим общую задачу о существовании таких аг > 0, что»
Для всех ^>0и > 0, удовлетворяющих системе нера-
венств (х, и) D > d. Сформулировать задачу линейного программирова-
ния для нахождения таких а^ если они существуют.
Указание. Учитывая однородность, положить аг = 2^ + 1, где 2Д >
> 0. Тогда эта задача эквивалентна нахождению таких Mj, Xj и что
х>0, и>0
(х, u) > d
s Ut — xt = xt
vt = 1.
0 = min max (2 — vQxt 4- vtxt).
V xfv
Если 0<O, то существуют at > 0. Чтобы полностью провести это рас-
суждение, использовать задачу 2 из гл. 13.
3. Выполнить упражнения, сформулированные в § 22-1.
4. Упростить ограничения (13) из § 22-2, произведя замену пере-
менных
ХТ\ — ХП + Urxi
(г — 1, 2, 3).
5. (Нерешенная.) Создать теорию для случая одного контролируемого
параметра, влияющего одновременно на несколько технологических про-
цессов.
425
6. (Нерешенная.) Эта задача относится к пункту (г), вытекающему
из § 22-2-(8). Найти процесс преобразования k данных функций Ft (Т)
в выпуклые функции параметра 7", где 7" — монотонная функция пара-
метра Т, при условии, что такое преобразование возможно (см. задачу 7).
7. Сформулировать задачу 6 как задачу линейного программирования,
если к заданных функций определены для дискретных и мы хотим най-
ти такие возрастающие T'i, соответствующие возрастающим Ti4 что лома-
ная линия, проходящая через дискретные точки (7^, F (Тг) ), является
выпуклой функцией от Т'.
8. Установить справедливость утверждений а), б), в), г), вытекаю-
щих из § 22-2-(8).
Глава 23
ПРИНЦИП РАЗЛОЖЕНИЯ ДЛЯ ЗАДАЧ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
23-1. ОБЩИЙ ПРИНЦИП
Для того чтобы дать представление о типичных случаях, в которых
можно применить принцип разложения, рассмотрим задачу, возникаю-
щую перед директором завода. Завод состоит из двух мало зависящих
друг от друга цехов. В каждом цехе имеется много ограничений, которые
не зависят от технологических процессов другого цеха, но оба эти цеха
«вязаны общностью цели и несколькими общими ограничениями. В терми-
нах линейного программирования задача директора завода формулирует-
ся следующим образом. Найти X > О, У > 0 и max я0, удовлетворяю-
щие условиям
(1)
2^ о^о 4“ А^Х -j— A2Y = b.
Здесь мы используем запись, введенную в начале гл. 22 X, У — векторы
интенсивностей технологических процессов соответственно в первом и вто-
ром цехах. Первая строка в (1) соответствует ограничениям, имеющимся
только в первом цехе, вторая строка в (1) дает то же самое для второго
цеха; наконец, в последней строке записана целевая функция и те огра-
ничения, которые связывают оба цеха.
Просматривая условия (1), директор чувствует, что размер задачи
не позволит справиться с ней вручную. Как матрица Ai9 так и Л2 имеют
умеренные размеры, однако совместное рассмотрение их делает задачу
недоступной для имеющихся в распоряжении директора вычислитель-
ных машин. «Но ведь фактически то, что я имею,-—размышляет директор,—
не является одной большой задачей. Это на самом деле две задачи умеренно-
го объема для каждого цеха. Мне необходимо лишь расчленить задачу
на две части и учесть при этом их взаимосвязь».
В этой главе, встав Па точку зрения нашего директора, мы опишем,
как разложить задачи линейного программирования типа (1) на
а) подзадачи, соответствующие почти независимым частям, и
б) главную задачу, которая связывает эти подзадачи воедино.
Получаемый от такого разложения выигрыш заключается в возмож-
ности разновременного решения главной задачи и подзадач. Сначала
решается главная задача, и на основе полученного решения строятся
целевые функции для каждой подзадачи. Затем решаются эти подзадачи
и на основе их решения составляется новый вектор-столбец, который
добавляется к главной задаче. Это процесс повторяется до тех пор, пока
не будут выполнены условия критерия оптимальности1. (Это произойдет
1 Исторически это было тем первым частным случаем, который привел к более
общему понятию обобщенной задачи линейного программирования, рассмотренной
в § 22-1 (Данциг и Вулф [1]). Идея принципа разложения возникла из предложен-
ного Фордом и Фулкерсоном [6] метода решения многопродуктовых задач для сети.
Необходимо отметить также и влияние У. С. Джуэла [2], использовавшего анало-
гичный подход.
427
после конечного числа итераций.) В следующем параграфе мы покажем,,
как этот метод можно использовать для решения некоторых задач, воз-
никающих в динамических системах, а в последнем параграфе этот
аппарат будет использован для того, чтобы показать, как можно осу-
ществлять централизованное планирование, не располагая полной инфор-
мацией в центре.
Для наших целей задачу (1) удобнее представлять в следующем виде.
Решить задачу линейного программирования
Р о^о + АхХ + A2Y = Ъ (2)
при дополнительных ограничениях
ХС-А1Х = Ъ1 (Х>0),
Z2-.A2Y=b2 (У>0). (3)
Здесь Ai, Ai — матрицы, а Ро, Ъ и — векторы.
Для того чтобы упростить рассуждения, предположим, что допусти-
мые множества ограничений Xi и Хг ограничены и выпуклы, а далее мы
укажем, какие небольшие изменения необходимо сделать в формулах,
чтобы учесть и случай неограниченности допустимых множеств. При
таком предположении любой вектор X > 0, удовлетворяющий уравнению
Ai X = bi, можно представить в виде выпуклой линейной комбинации
крайних точек множества допустимых решений уравнения Х\. Поскольку
множество различных базисных допустимых решений X = Х19 X = Х2,
. . ., X = Хк определяет конечное множество крайних точек, любой вектор
X мы можем представить в виде
х = (4>
1 1
Наоборот, любой вектор X, представленный в виде (4), является допусти-
мым для Xi- Аналогично любой вектор У > 0, удовлетворяющий уравне-
нию A2Y = b2, можно представить в виде
L L
У=2|Ь’Ъ (5)
1 1
где Yi, Y2, . . ., Yl — конечное множество базисных допустимых реше-
ний Хг- Следовательно, любое решение X и У, являющееся решением
задачи (1), можно выразить через р7-; таким образом,
Г к _ L _ _
Р о%о + 3 (AiXz) + 3 И; (^2^?) — b > 0; р>>0),
i i
=1, (6>
1
Sp-j =1,
1
и, наоборот, любые А и р, удовлетворяющие уравнениям (6), позволяют
по формулам (4) и (5) определить векторы X и У, которые будут допусти-
мым решением задачи (1). Обозначим в общем случае линейные преобра-
зования X и У через
S^AiX, T = A2Y (7)
428
и, в частности
= = = 2, ...,Х; / = 1, 2, ..., L), (8)
тогда исходная задача линейного программирования будет эквивалентна
следующей задаче:
Найти Xi > 0, . . ., > 0; щ > 0, . . ., > О и max xQ, удовлетво-
ряющие условиям
К L _
P0XQ + 2 4“ 2 ~ (^i 0; [Xf > 0),
1 1
К
'Zbi =1, (9)
1
2 и j ~ i •
i
• Определение. Задача линейного программирования (9), полученная
по формулам (8) из крайних («экстремальных») точек множества решений
Хь называется эквивалентной экстремальной задачей, или полной главной
задачей.
Для нас базисные решения уравнений Xi и X2, по-видимому, всегда
слишком многочисленны для того, чтобы в явном виде выписать эту
экстремальную задачу; поэтому для решения этой задачи мы будем полу-
чать только те столбцы St и Т j, которые появляются в последовательных
базисах симплекс-метода.
Предположим, что для экстремальной задачи у нас имеется исходное
базисное допустимое решение Xi = X? и = р,°. Если вектор Ъ имеет т
компонент, то в соответствующем базисе будет т + 2 столбца, напри-
мер Si, S2, • • Ski Ti, Ть где & + I = m + 2. Соответствую-
щее этому базису допустимое решение экстремальной задачи есть решение
X = Х°, Y = У0, Xq = х^ задачи (1), получающееся по формулам
X» = XpG+r8x2+...+№ (SM = 1; Л?>о),
/ (Ю)
7»=^+^+...+^ (2м? = 1; н?>о).
В конце этого параграфа мы опишем первый этап процедуры, который
позволяет получить такое исходное решение и соответствующее предста-
вление.
Для проверки оптимальности базисного решения или для получения
улучшенного решения экстремальной задачи обозначим через (л°,— $°,—
t°) вектор-строку симплекс-множителей, связанных с исходным базисом
Множители
/Ро Si S2...Sk Ti Т2... ТЛ : (л°)
В = | 0 1 1 1 0 0 0 ):( —$°) (И)
\0 0 0 0 1 1 1 /:( —Z0),
где s°, tQ соответствуют двум последним строкам базиса В. Как было
показано в § 22-1, вектор (л°;— s°,— Z°) определяется из условий
л0Р0 = 1, ^St = sQ, rt>Tj = t° (12)
для i = 1,2, . . ., к; j = 1,2, . . ., Z.
Далее, стандартный симплекс-метод требует обнаружения того столб-
ца из системы (9), который имеет наименьшую относительную стоимость
л°5г- — $° < 0 или nPTj — <Z 0, и, если такой найдется, введения
429
его в базис. Иными словами, мы должны найти такие 5* и Т7*, что
л°5* = min
i
л0?7# = min я?Тj.
з
Но
min ft°Si — min (jtMJ Xi = min y?X
AtX=blf
(13>
(14>
где yj = лМр Иными словами, мы определяем 5* с помощью вектора
X*, который является решением следующей задачи.
Подзадача Xi-
А,Х^Ъи (Х>0)
yJX = Zi(min). (у^зт0^)
(15)
Если для решения этой подзадачи применяется симплекс-метод, то вектор
X* всегда будет совпадать с одним из векторов Хь . . ., Хк. Затем мы мо-
жем построить вектор S* = AiX* и ввести его в базис. Если
min = у?Х*<$°, (16)
то относительная оценка для 5*, равная л°5# — s° = yJX# — 5°, будет
отрицательная и введение в базис вектора 5* позволит (предполагая
невырожденность) увеличить х0.
Аналогично с помощью вектора Т7*, являющегося решением сформу-
лированной ниже задачи, мы можем построить У*.
Подзадача <^2-
л2у = г>2, (у>0)_
y’y = z2(min). (^ = зг°Л2). ’
Если min z2 <Z t°, то введение в базис вектора Т* = A2Y* (предполагая
невырожденность) увеличит х$ на конечную величину. Мы вводим тот
из векторов 5* или Т*, у которого относительная оценка меньше.
С другой стороны, если min z^ = s° и min z2 — t°, то для системы
(9) все относительные оценки не отрицательны. Следовательно, полу-
чено оптимальное решение эквивалентной экстремальной задачи и тем
самым вычисленные по формулам (10) векторы Х° и У0 являются опти-
мальным решением задачи (1).
Определение. Ограниченной главной задачей1 называется задача, полу-
чающаяся из экстремальной задачи (9) отбрасыванием всех столбцовг
не вошедших в базис, кроме нового столбца 5* (или Т7*), который будет
введен в базис:
Найти Xi > 0, > 0 и max я0, удовлетворяющие условиям
Pq£q + 5i^i + ... + + 5*Х# + T’lPi + ... + T/рг = fe,
Xi +... 4~ Хд 4- X, =1» (18)
Hi+ • • • ==
ИТЕРАТИВНЫЙ ПРОЦЕСС И ОКОНЧАТЕЛЬНОЕ РЕШЕНИЕ
Приступим теперь к решению ограниченной главной задачи. Полу-
ченное оптимальное решение дает вектор (л, s, t), который в свою очередь
1 См. также определение на стр. 417. — Прим. ред.
430
определяет новые yi и у2. Эти числа задают новые целевые формы для
задач # 4 и £ 2. Затем эти подзадачи решаются с новыми целевыми формами
и проверяется выполнение условий критерия оптимальности, сформули-
рованного выше. Если условия критерия оптимальности не выполнены,
то в ограниченную главную задачу вводится новый столбец в соответствии
с подзадачей, для которой нарушены условия критерия. Затем весь про-
цесс повторяется до тех пор, пока не будут выполнены условия критерия
оптимальности. Далее, оптимальное решение получается по формулам
X = иУ=3 р7У7, где А, г, - решение последней ограниченной
г j
главной задачи, a Xt и Yj — решения задач и £2, соответствующие
столбцам окончательного базиса в последней ограниченной главной задаче.
Если ограниченная главная задача невырожденна (или е-измененна), то
каждое введение столбца или как мы отмечали, увеличивает xQ
на конечную величину. Следовательно, ни один из базисов (9), которых
конечное число, не может повториться и, таким образом, итеративный про-
цесс конечен. Итак, установлена
Теорема 1. Решение X = Х°, У — У0, соответствующее базисному
решению главной задачи, оптимально, если не существует решений для
подзадач, у которых значения z± и z2 меньше соответствующих величин
для решений, использованных для построения базиса главной задачи, т. е.
решение X = Х°, У = У0 оптимально, если
minzj^s*0, minz2 = Z°. (19)
Если ограниченные главные задачи невырожденны (или г-измененны), то за
конечное число итераций будет получено оптимальное решение.
Теорема 2. Верхняя граница значений xQ такова:
max х0 arj + (s°—min %1) + (*°—min z2)
<^ + (S0-jt0<SJ + (Z0-n°7’J. (20)
Доказательство. Умножим равенства (9) соответственно на числа (л°;
— $°,— t°) и просуммируем их. Свободный член равен х*, что является
значением переменной xQ для базисного решения. Следовательно, мы име-
ем соотношения
Хо + 3 (л% - s°) 1, + S («°^-1°) И} = х0°, (21 >
1 1
К L
£o + S (minzi — s°) Ki + 3 (minz2 —(22)
i i
из которых вытекает требуемый результат.
ЗАМЕЧАНИЯ О ВЫЧИСЛЕНИЯХ
Изменение базиса в ограниченной задаче осуществляется, конечно,
с помощью симплекс-метода, использующего множители (гл. 9). В такой
постановке для борьбы с вырожденностью можно использовать правило
лексикографического упорядочения. Это же правило может быть использо-
вано для обеспечения невозможности повторения одного и того же базиса
(гл. 10). По ходу появления в итеративном процессе различных столбцов
главной задачи, обычно используется один из следующих трех вариантов.
1) Каждый новый столбец пополняет ограниченную главную задачу,
но каждый столбец, выпадающий из базиса, исключается из рассматривае-
мой главной задачи.
431
2) Ограниченная главная задача пополняется все время новыми столб-
цами, а также столбцами, выпадающими из базиса, но остающимися
в задаче.
3) Ограниченная главная задача все время пополняется новыми столб-
цами, а столбцы, выпадающие из базиса остаются, пока это возможно,
в памяти электронной вычислительной машины; с этой точки зрения
целесообразно опускать те столбцы, которым соответствует наибольшая
положительная относительная оценка.
Заметим также, что на каждой итерации после первой мы можем
начинать решение подзадачи или главной задачи с базисного решения,
которое было оптимальным на предыдущей итерации. Таким образом,
этап I описанного процесса необходим только для первой итерации и впол-
не возможно, что потребуется всего лишь несколько ведущих операций
для получения решений подзадач и главной задачи.
НЕОБХОДИМЫЕ МОДИФИКАЦИИ ДЛЯ СЛУЧАЯ НЕОГРАНИЧЕННОСТИ
МНОЖЕСТВ Xi
Хотя множество допустимых решений всей задачи (1) ограничено,
но вполне возможно, что множества решений для некоторых Xi не огра-
ничены. В этом случае нижняя граница для может и не существовать,
и минимизация симплекс-методом приведет к однородному решению
X*, Y*, удовлетворяющему условиям
А{Х* = 0 или Л2У. — О,
•Y1X»<O или у2^*<0. (23)
Эти векторы X*, У*, как указывалось в конце § 22-1 при рассмотрении
аналогичных вопросов, составляют конечное множество (крайние лучи,
гл. 7). В этом случае мы можем построить весь класс решений для Xi.
рассматривая те решения, которые являются выпуклыми комбинациями
неоднородных решений и неотрицательными комбинациями однородных
решений. Таким образом, вместо (4) и (5) мы имеем
X' = ХД1+ X2I2+ • • • + ХКХК,
— - - (24)
У' = У1Р/1 + У2Н2 + . •. + УъНь»
где Хг > 0, р,7- > О удовлетворяют следующему условию: если i и / соот-
ветствуют неоднородным решениям, то каждое из чисел Xj и
суммироваться с коэффициентом единица, т. е.
дД1 + 62^2 + • • • + = 1»
SiPi + 62р2 + • • • +
где
Si = l, если Xi — базисное допустимое решение,
Sj = 0, если Xi — однородное решение,
| 6{ = 1, если Yi — базисное допустимое решение,
| 6- = 0, если Yi — однородное решение.
Это означает, что базис В переопределяется следующим образом:
/Ро ... Sk ... Т\
в= 0 Si ... SA 0 ... О (27)
\о о ... о s;... s;/
должно
(25)
(26)
432
Если или = 0, или Ъ2 = О, то представляют интерес только однород-
ные решения. В этом случае из главной задачи можно опустить соответ-
ствующие ограничения (25).
Поскольку симплекс-метод дает лишь конечное число однородных
решений, доказательство конечности итеративного процесса остается
в силе.
НАЧАЛО АЛГОРИТМА
Мы предполагали, что исходное решение Х°, У0 в (10) выражено
через базисные решения У7- и — теперь можно добавить — однород-
ные решения соответственно уравнений Xi и jC2. Такое исходное решение
можно получить с помощью этапа I процесса решения.
Обозначим через и У4 произвольные решения уравнений Xi
и <^2, а через Si и Ti — их преобразования по формулам (7). Пусть
начальный базис главной задачи на этапе I имеет вид
•Ро#о4“ + Hi^i ± Ufti i U2^2 zb... zb Um&m = &,
М =1,
Hi (28)
81 + е2 + • • • + -2Р =0,
где Ut есть т + 1-я компонента орта с единицей в строке г, а т + 1 равно
числу строк в матрице (Л4, Л2). Переменные 8Ь 82, . . ., 8т; я0, Xi, Hi
и w образуют базисное множество. Знаки перед Ut выбираются так, чтобы
искусственные переменные 8^ в базисном решении были бы неотрица-
тельны. Этап I состоит в минимизации w. Поэтому симплекс-множители
определяются так, чтобы цены всех столбцов были равны нулю, кроме
цены, соответствующей столбцу (—ш). Эта цена равна единице. Из эта-
пов I — II процесса вытекает
Теорема 3. Оптимальное базисное решение исходной системы можно
представить в виде суммы не более, чем т + 2 базисных допустимых
решений подзадач, где т — число уравнений в связующей части уравне-
ния (2), исключая целевую форму.
23-2. ПРИНЦИП РАЗЛОЖЕНИЯ,
БЕЛЛЕТРИЗОВАННОЕ ИЗЛОЖЕНИЕ
ПРОЛОГ
Координатор Центрального агентства Зав должен выделить в распоряжение
своего диспетчера Зама1 танкеры для перевозки .продукции двух своих заводов
в четыре пункта назначения. Зав ненавидит подробности и просит Зама сообщить
ему только два числа: с—затраты в предложенном плане перевозок и t—количе-
ство танкеров, необходимое для реализации этого плана.
У диспетчера Зама есть две матрицы: матрица удельных затрат [с^-] и матрица
необходимых количеств танкеров (количество танкеров, требующихся для пере-
возки единицы груза):
r 1 < 3 6 6 5 \ r , <0020 \
kul—8 13 6/ ’ 1^1 —0 2 0 0 /
(Нули в матрице Rij] указывают на то, что транспортировка производится по
нефтепроводам, а не танкерами.) Поскольку основная цель состоит в минимизации
затрат, Зам намерен решить приведенную ниже транспортную задачу, в которой
числа ai — известные количества продукции на заводах, a — известные количе-
ства, требующиеся в пунктах назначения.
1 Зав и Зам — имена собственные.— Прим, пер ев.
28 дж. Данциг 433
Имеется:
Требуется: 2=Ь4, 7 = &2» 3=Ь3, 5=&4.
Прослушав десятидневный курс лекций по исследованию операций, Зам на-
учился решать небольшие транспортные задачи. Это позволяет ему вскоре найти
для сформулированной задачи следующее решение с минимальными затратами
г Л _<2 0 2
kvh Qo 7 4 07 •
В этом случае c='^i^1cijXij=b3i * * = 32 = 13. Поэтому Зам сообщает Заву
два числа, получающиеся по его плану:
где компонентами вектора являются числа первого плана.
Однако Зав внезапно обнаруживает нехватку танкеров, и поэтому он не сможет
выделить Заму более 9 танкеров. Замечая, что из восьми вариантов использования
танкеров Зам воспользовался только двумя, Зав требует, чтобы Зам нашел реше-
ние, «облегчающее использование танкеров». Зам, будучи буквоедом, забывает
о затратах и сразу же приходит с новым решением, в котором минимизируется
использование танкеров:
Г .1 _<° 7 0
[жгЛ2 0 3 ЗУ '
В этом случае 23 95== с2, 32 Следовательно, для нового-
плана, предложенного Замом,
АКТ I
Зав: Хорошо, что бы ни говорили о новом плане Зама, но в этом плане, безусловно,
«облегчается» использование танкеров; фактически ни один из них не исполь-
зуется. Но взгляните, что произошло с затратами — они почти удвоились!
Я просто не могу сказать Заму, чтобы он использовал только 9 танкеров
и нашел свое собственное решение с минимальными затратами.
Я удручен тем, что в последнее время ощущается нехватка танкеров и за-
траты возросли. Как мне хотелось бы, чтобы Зам был послан на шестине-
дельный курс исследования операций вместо десятидневного. В конца
концов, это обошлось бы, по-видимому, дешевле.
Ввиду этого Зав решил пригласить в качестве консультанта своего друга эко-
номиста Ф. М. Далкса х.
Далке: Насколько я разбираюсь в экономических теориях, Вам следовало бы сказать
Заму, что использование танкеров вызовет, возможно, дополнительные рас-
ходы. Это заставит Зама сохранить низкие затраты и в то же время не лозво-
1 Ф. М. Далке, как указывают буквы его имени ♦, является собирательным
образом ведущих математических экономистов, применявших линейное программиро-
вание в экономической теории.
* По-видимому, имеются в виду Фейбиан Т., Моргенштерн О., Дорфман Р.,
Аллен Р., Леонтьев В., Купманс Т., Самуэльсон П.— Прим, перев.
434
лит слишком интенсивно использовать танкеры, потому что они являются
частью затрат в общей сумме.
Зав: (Восторженный и не откладывающий в долгий ящик дело, если оно выгодно.)
Давайте именно так и сделаем. (Ф. М. пал духом; теория теорией, но приме-
нение ее на практике — совсем другое дело.)
Далке: Не будем спешить. Не всегда легко вычислить, каковы должны быть цены
на дефицитные товары. Это зависит от многих факторов. Но предположим,
я убедил вас в том, что такие цены можно определить, нисколько не сомневаясь
в их существовании. (Глядя в глаза Зава, у которого закрадывается недоверие,
Ф. М. ощущает желание сбежать в башню из слоновой кости.) В этом случае,
однако, у нас имеется только один дефицитный товар, танкеры, и мы могли
бы попытаться задавать различные цены за использование танкеров и посмо-
треть, как Зам будет их использовать. Это в конце концов мы могли бы сооб-
щить Заму. Он будет приходить с планами, которые не только допустимы,
но и имеют минимальные затраты.
Зав: Может быть, это и не так плохо.
Далке: В соответствии с теорией, если имеется избыток танкеров, цена на танкеры
должна быть равна нулю. Поскольку в последнем плане Зама Р2 танкеры
совсем не используются, мы имеем именно этот случай. Сначала мы можем
сообщить Заму, что цена на танкеры равна нулю, л = 0. Ну, как?
Зав: (саркастически) Ужасно! С этим сплошные неприятности. Мы уже пытались
назначать нулевую оценку танкерам, и Зам приходил с тем или иным планом,
который мы не могли использовать. Я не воспользовался этими планами,
но, может быть, Мардж сохранила копию... О! Смотри, насколько ценным
может быть секретарь; копия здесь. Вот старый план Зама: = <53,18>.
Он недопустим, так что же в нем хорошего?
Далке: У меня другая идея. Я на днях читал один журнал по исследованию операций.
Правда, обычно я не читаю журналы такого рода, но, прочитав его, я обна-
ружил, что исследование операций не так далеко от эконометрики, как это
представляется некоторым. Во всяком случае, один мой знакомый захотел
узнать мое мнение о статье, в которой изложен «принцип разложения». Ему
показалось, что эта статья могла бы пролить свет на решение задач о ценах
в тех случаях, когда отсутствует согласование из-за разрывности про-
изводных основных технологических функций. Но мы отвлеклись. Эта
статья наводит на мысль, что следовало бы взять среднее взвешенное двух
планов (подходит к доске) такого вида
Р1Х1 + -Р2^2= 18^ ^1+ q ^2>
где Xi + Х2 = 1, и» конечно, 0 1. Например, мы могли бы взять
= х/2, Х2 = х/2. Это дает
-1(53 + 95)=74,
1
А(18+0)=9,
*
что значительно дешевле, чем 95, и при этом используются имеющиеся танке-
ры. Ну, как?
Зав: Замечательно, просто великолепно! Но как мы узнаем, как нужно нам усред-
нять планы Зама? Как Зам определит, что ему делать! Я не хочу вдаваться
в детали плана перевозок, предложенного Замом. Вы это знаете.
Далке: О! Не стоит об этом беспокоиться. Попросим Зама лишь усреднить подробные
расписания, которые он использовал для получения планов и Р2; это даст
ему ответ.
Зав: Это изящный способ — усреднение старого и нового планов, и, наверно,
я оказался недостаточно проницательным, отбросив старый план. Босс будет
очень доволен, когда я расскажу ему, как мы это получили. Сначала сделаем
так: проанализируем немного ваш средний план для того, чтобы быть уверен-
ными, что с ним все в порядке. Смотрите, 9 танкеров и все затраты на транс-
портировку равны 74. Это достаточно много по сравнению с минимальными
затратами, которые были бы равны 53, если бы танкеров было достаточно.
Не так ли?
Далке: Ну, разумеется, это решение не обязательно будет наилучшйм. Теперь нам
предстоит сформулировать небольшую задачу линейного программирования,
435 28*
которая укажет нам, как наилучшим образом «смешать» старый и новый
планы. Вот эта задача:
53ХА + 95Х2 + (—z) =0 (ki > 0),
% о-j-18X14“ 0^2 = 9,
Xi4“ Х2 = 1»
• • •
где Хо — неиспользуемые (если таковые есть) танкеры. В этом случае совер-
шенно очевидно, что значения Хо = 0, = 1/2, Х2 = х/2 дают затраты z1 = 74.
При этом мы ничего еще не анализировали и ничего не знаем. Существенно
здесь то, что эта задача позволит нам сообщить Заму цену танкеров. Это мы
сможем сделать, решив двойственную задачу линейного программирования.
Зав: Я боюсь, что вы заморочите мне голову. Что это за решение?
Далке: Хорошо, двойственное решение очень интересно. Это делается так. Смотрите,
базисные переменные, связанные с оптимальным решением прямой задачи,
отмечены тремя точками под столбцами Х4, Х2 и (— z). Это означает,
что мы должны так выбрать множители (1, л1, — s1) для трех уравнений,
чтобы после умножения и суммирования исчезли бы члены с Х1 и Х2. Легко
видеть, что должны быть выполнены следующие условия:
534-18л1—5г=0 (коэффициент при XJ,
95 4“ 0л1—$1=0 (коэффициент при Хг)
42 1
или $1=4-95 и л1—4~тб = 2—-.
io о
Зав: Я не понимаю, почему л1 == 2г/3 положительно. Насколько я понимаю согла-
шение о ценах в линейном программировании, это означает, что Заму платят
за использование танкеров, вместо того чтобы брать с него за это деньги (§ 12-3).
Далке: Да, но не в этом случае. В данном случае, для такого типа задач, специалисты
по линейному программированию сознательно ввели такое соглашение о зна-
ках; именно так выбираем знаки мы, экономисты. Поэтому в данном случае
смысл л именно таков. Другими словами, мы сообщим Заму, что плата за один
танкер равна 21/3. Сделаем так и посмотрим, что из этого получится.
Зав: Довольно интересную игру мы разыгрываем с Замом. Что означает, что
si = 4-95?
Далке: О, это для того, чтобы знать, целесообразно ли пытаться смешивать третье
предложение Зама (когда оно появится) с и Р2. Но об этом мы сможем рас-
сказать подробнее потом (§ 23-1, теорема 1).
Зав: Но я не понимаю. Означает ли это, что Зам принесет нам другой «недопусти-
мый» план и мы должны будем комбинировать все эти предложения?
Далке: Да, я боюсь, что это может случиться, но будем надеяться, что нам повезет!
В соответствующее время Зам получает новую матрицу удельных затрат
1 /3
kd+2TI«i/l=
\ 8
6 6+44 (5
О
[2
14-44 3 6
О
благодаря которой он находит следующее оптимальное решение своей транс-
портной задачи:
г 1 < 2 2 0 5 \
[*и]з 0 5 з о J •
В этом случае 22 ~ §7 и 22 Ю» Следовательно, третий
план, который представляет Зам, таков:
МЧСЧ
АКТ II
Зав: Теперь я начинаю понимать. Наша цель состоит в том, чтобы сформулировать
новую небольшую задачу линейного программирования. Имеется ли какое-
нибудь специальное название, которое можно использовать для этих задач?
436
Далке: Она называется «ограниченная главная» задача. Прежде всего мы хотим убе-
диться в том, что план Р3 стоит рассматривать. Вы помните, что s1 = 95?
Наша задача состоит в «оценивании» нового предложения и сравнении его
с 95, «начальным значением». Поскольку в новом плане транспортные затраты
равны 57, а издержки на каждом из 10 используемых танкеров равны 21/3,
имеем 57 + 23х/3 = 80х/3. Это меньше, чем s1 = 95, и поэтому теперь мы
смело можем приступить к ограниченной главной задаче. Вот она:
53% < + 95%2 + 57%3 + (—z)=0,
%о-Ь 18%i-Ь 0%24~Ю%3 ==:9,
%i + %2~Ь =1.
• • •
Зав: А не много ли потребуется времени на ее решение? Мне любопытно увидеть,
каков ответ.
Далке: Хорошо, в этом случае много времени не потребуется.В соответствии с теорией
линейного программирования из трех предложенных Замом планов будут
использоваться только два. Поскольку никакое среднее из планов 1 и 3 не даст
меньше 10 танкеров, остается единственная новая возможность, комбинация Р2
и Р3. Новое решение легко получить. Очевидно, %2 = г/10, %3 = 9/10. Это
соответствует затратам z2 = 95 (х/10) + 57 (9/10) = 60,8.
Зав: Это существенное улучшение! Мы уже уменьшили затраты с z° = 95 до z1 = 74,
а теперь до z2 — 60,8. Как вы думаете, намного ли еще мы сможем уменьшить
затраты, если будем продолжать этот процесс?
Далке: Думаю, что ненамного. Они не могут опуститься ниже 53, поскольку нам
известно, что значение z для решения с наименьшими затратами равно 53
и это соответствует случаю, когда нет ограничений на танкеры. Но еще немнож-
ко снизить затраты мы, по-видимому, сможем. В соответствии с теорией раз-
ложения с помощью предыдущего базисного решения мы всегда можем дать
оценку нижней границы. Вот эта формула (§ 23-1, теорема 2):
minz>zi—si + c3 + ni<3 = 74— 954-57 + 2з4 = 594- .
О о
Зав: Фантастика! Если мы правы, то затраты можно опустить ниже, чем z2 — 60,8.
Мне хотелось бы увидеть, каков истинный минимум и насколько хороши
ваши предположения в действительности.
Далке: Хорошо, но угадать этот минимум нельзя. Определим новую оценку танкеров.
Поскольку %2 и %3 — новые базисные переменные, мы имеем
95 + 0л2—$2=0,
57 4-Юл2—$2—0,
38
или з2 = 95 и л2 = уф = 3,8. Это показывает, что мы должны увеличить .
оценку танкеров с л1 = 21/3 до л2 = 3,8.
Зав: Я надеюсь, что Зам не слишком опечалится, узнав, что наши предложения
так часто меняются. Иначе он может начать жаловаться большому боссу до
окончания этого великолепного эксперимента.
В надлежащее время Зам строит свою новую матрицу'.
1+’,в “Т о
и получает новое оптимальное решение
г , /2 7 0 0\
[*«>14 о 0 з 5 j •
Здесь 23 ~ 8? и 23 ^JXU == 0* Таким образом, четвертый план
Зама имеет вид
-(<:)=( о7)-
АКТ III
Зав: Дела идут все лучше и лучше. Очевидно, мы можем подставить 1/10Р4 вместо
1/ю^>2» которое было использовано раньше и дало улучшенное решение. Итак,
437
рассмотрим ограниченную главную задачу. Вот она:
53Х4 -j- 95Л»2 4" 57Х3 -J- 87Х4 -J- (—z) =0,
Xq4“18X|4- 0А<2 4- IOX3 4" 0X4 =9,
М4~ ^2 4~ Х34- Х4 =1.
• • •
Найдем теперь новое значение z. Улучшение невелико, Ъ = 57 (*/10) 4-
4- 87 р/ю) = 60. В конце концов, может быть, ваша нижняя граница
не так уж и плоха. Воспользуемся еще раз вашей формулой для нижней гра-
ницы. Для этого возьмем предыдущее базисное решение. Не так ли? Странно!
Что же мы получим в этот раз
min z > z2—52_|_С4_|_ Л2;4=6О,8—954-87,0=52,8?
Далке: По-видимому, наша предыдущая оценка 591/3 была очень удачной. Я думаю,
что нам следовало бы находить оценку нижней границы на каждой итерации,
• потому что одни из них лучше других.
Зав: Теперь, я полагаю, мы должны найти новую оценку
57 4-10л3—$3=0,
874-Ол3—$3=0,
или 53 = 87 и л3 = 3. На этот раз мы сообщим Заму, что новая оценка танкеров
упала до 3.
Новая задача Зама принимает вид
Г„ .О, .1-< 3 6 64-6 5 \
[co + 3t,j]—(^8 3 6J.
Эту задачу он быстро решает, поскольку последнее его решение [%ij]4 все еще
оптимально. Он находит также, что оптимально и его предыдущее реше-
ние [Ягу]3.
АКТ IV
Зав: Что это означает? Зам пришел с тем же самым решением, что и в прошлый раз.
Далке: Это означает, что улучшения нет. Попытаемся найти оценку нижней границы
и посмотрим, что из нее вытекает. Если мы подставим с4= 87, = 0 в фор-
мулу, то получим
min z z3—$34~с44" л3^4—60—874-87-]-0=60.
Если вместо с4 и f 4 мы возьмем с3 = 57 и t3 = 10, что соответствует другому
оптимальному решению Зама, то получим
z > 60-874-574-3 (10) = 60.
Поскольку наша нижняя граница 60 совпадает с полученным значением z,
это доказывает, что мы закончили работу.
Зав: Я должен рассказать боссу о нашем новом децентрализованном процессе
принятия решения и отдать распоряжение Заму, чтобы он построил среднее
взвешенное своих планов, именно 0,9Р3 + 0,1Р4.
После выполнения распоряжения Зам нашел, что оптимальный план имеет вид
(1 1 \
2 2- ° 4у\
1 1 I *
0 Ц 3 2/
Далке: Строго говоря, это не совсем то, что имеем в виду мы, экономисты, когда гово-
рим о «децентрализованном планировании». По-видимому, более правильным
термином будет «централизованное планирование без наличия полной инфор-
мации в центре». Очень интересный эксперимент! Пожалуй, я напишу статью
о том, как впервые в реальной жизненной ситуации цены использовались для
контроля совершенно четким и определенным путем.
Конец
438
23-3. ЦЕНТРАЛИЗОВАННОЕ ПЛАНИРОВАНИЕ
БЕЗ ПОЛНОЙ ИНФОРМАЦИИ В ЦЕНТРЕ 1
Развитая в § 23-1 теория позволяет укрупненно планировать
работу всей организации даже в том случае, когда центральное руковод-
ство не располагает полной информацией о технологии каждой части орга-
низации. Мы будем рассматривать случай, когда технологическая матри-
ца не изменяется в течение планируемого периода и капитал увели-
чивается разве лишь для удовлетворения текущих потребностей.
Рассмотрим, далее, экономику промышленного комплекса с Т заво-
дами, производящими ш видов продукции, которой они торгуют между
собой. Технологическая матрица Ар завода р имеет тпр строк. Эта матрица
включает ограничения на промежуточные продукты, мощность завода
и внутренние потребности. Кроме матрицы Лр, каждый завод имеет тор-
говую матрицу Ар, т строкам которой соответствуют тп видов продукции.
Зта продукция продается и покупается заводами либо идет в потреби-
тельский сектор экономики. Завод р имеет также вектор постоянных
затрат Ър. Тогда ограничения для завода р имеют вид
АРХР = ЪР, Хр>0 (р = 1,2, (1)
где Хр — вектор интенсивностей завода р.
Ограничения Центрального торгового агентства характеризуются
тем, что суммарное количество продукта /, произведенного всеми заво-
дами, за вычетом поставленной им продукции, не меньше количества
продукции в окончательном минимальном основном спросе (потребление,
оборона, экспорт и т. п.). Обозначив через I единичную матрицу, эти
ограничения можно записать в виде
4Л + А2Х2 + ... + ATXT + IY = b (У >0). (2)
Y — вектор превышения окончательного спроса над минимальным основ-
ным спросом Ъ. (В силу наших соглашений о знаках все компоненты век-
тора b отрицательны.)
Превышению спроса плановики приписывают некоторое множество
чисел, характеризующихся вектор-строкой — с, при этом величина
— cY является для них оценкой плана. Тогда стоящую перед экономикой
основную задачу можно сформулировать следующим образом:
AiXi =
А2Х2 — Ь2,
(3)
• •
АТХТ == Ър,
А^Х^ 4“ А2Х2 -j- ... -}- АТХТ 4“ IY = Ъ,
cY — z (min).
Это — блочная система, которую теория из § 23-1 разлагает на Т под-
задач и одну главную задачу. Если бы были доступны все матрицы Ар,
1 Написанию этого параграфа содействовал К. Алмон, который выявил некото-
рые потенциальные возможности использования принципа разложения для децентра-
лизованного планирования.
439
то их можно было бы направить в Центральное планирующее агентство,
где имеется большая вычислительная машина, которая по запрограмми-
рованному принципу разложения вскоре выдала бы оптимальное ре-
шение.
Однако практически получить матрицы Ар весьма затруднительно.
Это может потребовать больших затрат времени инженеров для полу-
чения характеристик каждого нового технологического процесса, даже
если не вводятся принципиальные нововведения и не изменяется суще-
ствующая технология. Многое можно было бы, несомненно, сделать, но
это потребовало бы слишком больших затрат времени для подробного
описания. Например, ни один инженер не будет ради добавления одного
технологического процесса в матрицу Ар тратить неделю на кропотли-
вое получение характеристик трансформатора, использующего медную
проволоку вместо алюминиевой, если несколько приближенных вычисле-
ний покажут, что затраты на изготовление нового изделия увеличатся
примерно вдвое по сравнению с существующими, а ощутимых преимуществ
не получится.
По тем же причинам все матрицы Ар, по-видимому, полностью неиз-
вестны; скорее мы можем рассматривать их как потенциальную инфор-
мацию о заводах, а для их явного получения необходимо затратить неко-
торые усилия. Поскольку потенциальную информацию едва ли можно
передать в Центральное планирующее агентство, это агентство не рас-
полагает полной информацией. Это не означает, однако, полного отсут-
ствия информации, ибо в распоряжении агентства имеются материалы
Центрального торгового агентства. Из этих материалов видно, сколько
и какой продукции использовал и произвел каждый завод в течение
нескольких предыдущих лет, например, двух лет. Таким образом, извест-
ны значения Sp = АРХР, определяемые двумя допустимыми решениями
главной задачи и тем самым каждой подзадачей:
ApXp = bp; SP = APXP
(р=1, ...,Т). (4)
ApXp = bp; Si^ApX*.
(Если не происходило увеличение капитала, то числа Ър в течение двух
лет не изменялись. Если бы капитал увеличился, то первый годовой план
можно было бы преобразовать в допустимый план второго года и исполь-
зовать в (4).)
Центральное планирующее агентство использует эти данные для
составления следующей главной задачи с т + Т ограничениями
S^t + + ЭД + + ... + SWt + SWt + IY=b,
%?+ =1,
X“+ Ц =1
(5)
At At
= 1,
cY = z (min).
440
Затем плановики решают эту главную задачу и получают симплекс-
множители (л; —s), где векторы л, s имеют соответственно т и Т элемен-
тов. С экономической точки зрения л является, конечно, вектором цен.
Далее для каждого завода можем найти целевую форму:
минимизировать ър = л5р = (лЛр) Хр.
Иными словами, это означает: минимизировать превышение затрат
на покупки над выручкой от продаж, т. е. минимизировать потери, или,
что то же самое, максимизировать прибыль.
Затем плановики объявляют эти цены л и доводят до сведения всех
директоров заводов разработанные планы работы их заводов в течение
будущего года. В частности, каждому заводу указывается в плане объем
покупок и продаж Центральному торговому агентству. Проанализиро-
вав эти предложения, они должны решить, что они могут купить, при
объявленных ценах, из тех т продуктов, которые им требуются, и подоб-
ным же образом определить, что они получат от продажи произведенной
продукции. Наконец, директорам разъясняются планы, которые макси-
мизируют их прибыль.
Получив эти указания, директора вызывают своих инженеров, сооб-
щают им цены и предлагают приложить максимум усилий при отыскании
путей уменьшения затрат и увеличения прибыли при этих ценах. Инже-
неры, получив инструкции, приступают к разработке конкретных пла-
нов производства. Через месяц или как только они убедятся в оптималь-
ности своих планов, директора сообщают эти планы в Центральное пла-
нирующее агентств о.
Было бы очень хорошо, если бы эти планы удовлетворяли условию
(2) и образовывали допустимую программу для всей экономики, но обычно
Центральному планирующему агентству приходится корректировать их.
Каждому заводу р, прибыль которого sp превзошла предполагаемую,
агентство добавляет технологический процесс Sp в главную задачу (5).
Затем агентство пересматривает эту задачу, получая новый вектор цен
(л; —5), например (л'; —s'), а также новое Х-решение. Обычно А-решение*
является комбинацией новых и старых предложений и позволяет ука-
зать оптимальный допустимый план на основе информации, имеющейся
в Центральном планирующем агентстве.
В принципе плановики могли бы затем сообщить новые цены л'
и новые предложения и повторяли бы этот процесс до тех пор, пока
не было бы найдено оптимальное решение. Практически же планирова-
ние требует времени и продукция должна производиться непрерывно,
а плановики убеждены в том, что последовательные планы, которые ста-
новятся все лучше и лучше, должны быть предпочтительнее любых дру-
гих планов. Поэтому они сообщают количественные показатели своега
допустимого плана. Директору каждого завода указывается, сколько он
должен произвести продукции для продажи и сколько продукции ему
разрешается купить; вся эта информация для завода р сводится в вектор-
столбец Sp = 2 где взяты из оптимального решения главной
i
задачи. Они сообщают также новые цены (л'; —s') и указывают, что тор-
говля должна производиться по этим ценам. Они могут также подска-
зать директорам, что, оставаясь в пределах количественных показателей
плана Sp, они могли бы также максимизировать прибыль. Такое правила
предназначается для того, чтобы избежать «ножниц» в производства
в случае, когда по тем или иным причинам объем производства откло-
няется от S. Важно отметить, что нельзя дать указание директору проста
максимизировать прибыль (опуская при этом цели производства Sp), иба
441
в этом случае Центральное торговое агентство почти наверняка столкнется
о трудностями при рассмотрении ограничений (2).
К концу периода, на который планировалось производство, повто-
ряется тот же процесс составления планов для следующего периода,
используя теперь цены л'. Директора, зная, что этот процесс повторится,
в течение всего года изыскивают пути максимизации прибыли, и вскоре
они вырабатывают свои собственные предложения. На основе этих пред-
ложений Центральное планирующее агентство находит новые технологи-
ческие процессы, которые надо включить в главную программу, и, как
выше, процесс повторяется. Качество планов всегда улучшается. Важно
понять, что главная задача сохраняет все предыдущие предложения,
кроме тех, которые в дальнейшем совсем не используются.
Мы оставляем читателю решить важный экономический вопрос
о конечности процесса § 23-1. Читателю следует также рассмотреть
связанный, но несовпадающий с ним вопрос, всегда ли плановики могут
отказаться от нормирования и разделения системы, заменив это непосред-
ственным указанием директорам на максимизацию их прибыли.
ЗАКЛЮЧИТЕЛЬНОЕ ЗАМЕЧАНИЕ
Наше обсуждение предназначалось лишь для того, чтобы показать,
как можно использовать принцип разложения в качестве орудия пла-
нирования, но оно не объясняет фактические методы, используемые
современными промышленными комплексами или социалистической эко-
номикой. Мы показали, что у центральных органов имеется специальный
метод распределения и специальным образом выбранная система цен,
которые могут убедить разрозненные заводы принять суммированные
предложения. Затем эти предложения можно объединять во все лучшие
и лучшие планы. Используется ли этот метод распределения, цены и пред-
ложения какой-нибудь экономикой или комплексом или хотя бы под-
ходят ли к решению этих задач нашим методом, мы не можем сказать.
Наш итеративный процесс можно графически изобразить следующим
образом:
Рис. 23-3-1. Децентрализованное планирование, использующее принцип
разложения.
Большинство людей, знакомых с планированием в крупных орга-
низациях, представляют себе поток информации подобно только что
описанному. Различие состоит в том, что принцип разложения заме-
няет не слишком хорошо осознаваемый процесс на строгий и хорошо опре-
деленный процесс.
442
23-4. РАЗЛОЖЕНИЕ МНОГОШАГОВЫХ ЗАДАЧ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Описанный в § 23-1 метод непосредственно обобщается на задачи,
в которых имеется более двух подзадач,— на так называемые «блочные»
задачи следующего вида:
= b19
AtXt
= bt

A^Xf — b'fj
AjXj + ... 4~ AfXf -|- .4~ AjXt = b,
CiXi -j— ... -f- (JtXf • • • ~|“ CtXt (min),
где At, Ai — матрицы, Xi9 Ct — векторы.
Рассмотрим теперь другой важный класс задач: найти Xt и max xQ,
удовлетворяющие условиям
.Ар?! = &1, (Xt>0)
AiXi -f- А2Х2 = е2, (2)
А2Х2 + А3Х3 — е3,
А3Х3 -|- А4Х4 4- Р qXq = е4,
где Xt — векторы, Af — матрицы, et и Ро — векторы. Такие задачи
называются многошаговыми (так называемая ступенчатая система). Они
часто возникают при изучении процессов, протекающих во времени.
Для таких процессов технологические процессы одного периода непо-
средственно связаны только между собой и с технологическими процес-
сами предыдущего и последующего периодов и не связаны ни с какими
другими процессами, более удаленными по времени. В таких случаях
некоторые At, так же как и At, могут совпадать. Хотя наши результаты,
относящиеся к вычислительным схемам, при этом предположении можно
было бы улучшить, тем не менее сейчас мы не будем этого делать.
В соответствии с общими принципами, рассмотренными в § 23-1,
мы начинаем с построения подзадач, образующихся на каждом шаге,
переписывая (2) следующим образом.
Решить задачу линейного программирования: найти > 0 и max х$,
удовлетворяющие условиям
AiX4 4- А2Х2 = е2,
А3Х3 4" А4Х4 4" Р о#о — еь,
при ограничениях
<24: AfXf = • А2Х2 -f- А3Х3 = е3. (4)
Таким образом, уравнения (4) выбраны так, чтобы они играли роль неза-
висимых частей, в то время как уравнения (3) связывают ограничения.
443
Читатель, конечно, понимает, что роли уравнений (3) и (4) можно было-
поменять местами и что построение этих подзадач можно было бы осуще-
ствить различными путями.
Обозначим крайние точки Х± и Хг соответственно через Xi = Хц
для i = 1, 2, . . . , К и через IX2;, X3j] для / = 1, 2, . . ., L, а их
образы — через
Si = AiXa, [Т j == A2X2jf Т j — A3X3j]. (4a)
В этом случае главная задача принимает вид:
Mv > 0> удовлетворяющие условиям
I---------------------
! К L
! S + 2
j i=l ;=1
i к
। 2
• i=i
найти max xOi Aj > 0r
L _
5=1
2w
5=1
= *2
= 1
= ^4
= 1.
(5>
Начиная с некоторого базисного для главной задачи множества
переменных Ai, и компонент Х4р вектора Х4, мы можем найти симплекс-
множители, получить целевые формы для <£1 и #2, решить получившиеся
задачи, использовать преобразование решений этих задач для добавления
столбцов к ограниченной главной задаче, вновь решить ее и повторять
этот процесс до тех пор, пока не будут выполнены условия критерия
оптимальности.
Когда мы приступаем к решению задачи (5), мы прежде всего заме-
чаем, что сама по себе главная задача оказывается ступенчатой системой
типа (2), но количество шагов уменьшено в два раза. Естественно, сле-
довательно, разложить эту главную задачу. Систему (5) назовем поэтому
первым уровнем главной задачи и продолжим ее разложение. Перепишем
систему (5) следующим образом.
Найти такой max я0, что
2 ^4^4 + ^0 = е4 Х4>0) (6)
=1
и выполнены условия
к L
2^«М+2 T№j—e2 (А$>о),
1=1 5=1
2 и =1. (7>
г=1
S н> = 1-
5=1
Обозначим крайние точки X 3 через А г = А?, ц,- = p-J для q = 1, 2, . . .
L __
. . ., Q, а преобразование последних через 2 = Rq* Подстановка
3=1
444
В (6) дает нам второй уровень главной задачи.
Q
2 PqXq= е^, Х4 0)
Т L _ <8)
3 Vg =1, где Яд = 2
q=l j=i
Мы разложили одну четырехшаговую задачу на четыре задачи Хи
_jg2, и (8), суммарное количество уравнений в которых на три больше
соответствующего числа уравнений в исходной четырехшаговой задаче.
Опишем теперь итеративный процесс решения этих задач. Сначала
мы решаем ограниченную главную задачу второго уровня (8) и находим,
кроме vg, такие симплекс-множители (л®, —и®), что л£Р0 = 1, оценка
базисных столбцов Rq не превосходит uj и оценка базисных столбцов Л4
неотрицательна. (Ср. с § 23-1-(12).) Затем мы определяем целевую форму
для X з, а именно:
минимизировать Z4=3 (Л4Уj) Ь- (9)
Предполагается, что некоторое допустимое решение для Хз У нас
уже есть. Значения симплекс-множителей (л®; и3, г?®) можно теперь полу-
чить, используя значения (л4, Tj), соответствующие базисным столбцам.
Далее проверяем оптимальность X 3, оценивая (с помощью этих множителей)
асе столбцы i = 1, 2, . . ., К и / = 1, 2, ...,£. Однако, поскольку К
и L могут быть достаточно велики, мы находим столбцы i = i0 и / = /0,
оценка которых минимальна, не выписывая фактически всех столбцов
заранее. В силу (4а) имеем
л^о—= min [л£7\- =
з
= min[(—л3Л2) Х2 + (л4А3) XJpj ((Х2, Х3)£Х2), (10)
и
— л°5г0 = min [ — = min [ — (л°А7) Xt] < и°3 (Xt С Xi). (И)
i
Следовательно, задача сводится к минимизации двух линейных целевых
форм; во-первых, формы (10) с переменными (Х2, Х3), где (Х2, х3) ех 2,
и, во-вторых, формы (И) линейной по Хь где Х± £ Если решения
этих двух подзадач удовлетворяют соответствующим уравнениям, то под-
задача Хз оптимальна и задача решена. Если это не так, то присоединим
к ограниченной задаче Хз преобразование экстремальной точки реше-
ния Xi = Xj* или (Х2, Х3) = (Х2*, Х3*), соответствующего наиболь-
шему отрицательному значению, и опять используем его для получения
нового экстремального решения для главной задачи второго уровня.
Заметим, как и в § 23-1, что нет необходимости сохранять от итера-
ции к итерации небазисные столбцы систем (7) или (8). Небазисные
-столбцы в этих задачах можно опустить и забыть; в случае необходи-
мости их вновь можно получить.
Несмотря на то что мы решали четырехшаговую задачу, наш про-
цесс имеет общий характер. Обозначая через [р] наибольшее целое число,
не превосходящее р, сформулируем следующую теорему.
Теорема L Каждую К-шаговую задачу можно разложить на К под-
задач, соответствующих каждому шагу. Суммарное количество уравнений
з этих подзадачах на К — 1 больше числа уравнений в исходной задаче;
445
эти подзадачи образуют «лестницу» с [К/2] или [К/21 + 1 элементами
для наименьшего ранга, {К/4] или [К/4] + 1 для следующего и т. д.
Следует отметить, что описанный процесс дает оптимальные множи-
тели, а для получения оптимальных значений исходных переменных
необходимо проделать некоторые дополнительные вычисления. Может
оказаться полезным рассмотрение задачи, двойственной к многошаговой,
ибо двойственная задача имеет ту же самую структуру. Вычисления,
связанные с двойственной задачей, позволяют непосредственно оценить
переменные прямой задачи и косвенным образом оценить множители.
23-5. ЗАДАЧИ
1. Рассмотреть метод, использующий разложение многошагово й сис-
темы § 23-4-(2); построить аналогичный метод децентрализованного пла-
нирования в таких структурах. Обобщить.
2. Опираясь на задачу 1, построить возможные методы, соответствую-
щие другим способам разложения такой системы.
3. Используя результаты § 23-4 (теорема 1), построить двойственную*
систему для § 23-4-(2) и описать метод, опирающийся на принцип разло-
жения, который позволяет непосредственно вычислять значения пере-
менных прямой задачи.
4. Доказать в общем случае утверждение § 23-4 (теорема 1), именно
что существуют подзадачи, имеющие на К —1 уравнений больше, чем
исходная система.
5. По аналогии с § 23-1 (20) получить с помощью симплекс-метода
нижнюю границу z для случая, когда одно из уравнений имеет вид
3 xj == 1-
1
п
6. Пусть aj — верхняя граница для Xj и х0 + 2 cjxj = xq- В общем
случае показать, что другая верхняя граница xQ равна sj[ —
суммирование идет только по тем индексам /, для которых Cj < 0.
Глава 24
ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ
24-1. ОБЩАЯ ТЕОРИЯ
Кун и Таккер в своей статье о нелинейном программировании [1J
(см. также Таккер [6]) рассмотрели задачу минимизации выпуклой
функции переменных я2, • • •, хп при условии, что значения, прини-
маемые некоторой системой вогнутых функций от этих же переменных,
были бы неотрицательными. Они показали, что если эти вогнутые функ-
ции дифференцируемы, то метод множителей Лагранжа можно соответ-
ствующим образом распространить на случай ограничений в виде нера-
венств для вогнутых функций (см. § 6-5). Вместо вогнутых функций мы
будем рассматривать выпуклые функции (т. е. вогнутые функции с про-
тивоположным знаком; по поводу определения см. § 7-1 и рис. 7-1-VIII);
их значения должны быть в этом случае неположительными. Следуя
Слэйтеру [1] и Удзаве [1], мы покажем, что эти результаты Куна
и Таккера остаются справедливыми даже в случае недифференци-
руемости этих функций, если только: а) область изменения переменных
представляет собой замкнутое ограниченное выпуклое множество R,
б) существует по крайней мере одна точка, в которой все рассматривае-
мые выпуклые функции отрицательны, и в) выпуклые функции непре-
рывны1 в R. Мы изложим также конструктивный метод решения подоб-
ных задач, основанный на обобщенных алгоритмах линейного программи-
рования. Впервые эта идея была высказана Ф. Вулфом на симпозиуме
корпорации РЭНД по математическому программированию в 1959 г.;
на том же симпозиуме Г. Хартли рассмотрел случай переменных коэф-
фициентов в столбце некоторого специального вида.
Первое доказательство сходимости можно найти в статье Дан-
цига [21]; см. также работу А. Вильямса [1].
Задача А. Найти точку х = (xlf х2, . . ., хп) замкнутого ограничен-
ного выпуклого множества R и минимальное значение 2, удовлетворяю-
щие условиям
<Pi(*)<0 (i = l,2, ..т),
Фо (ж)—2 (min), ' '
где фг (х) — непрерывные выпуклые функции.
Теорема 1. Если существует точка х° g /?, в которой ф^ (х°) < О,
i = 1, 2, . . ., т, то существуют множители > О, л2> 0, . . .
• • •, Л/п>0 и точка х £R, являющаяся решением (1) и удовлетворяющая
1 Поскольку выпуклая функция всегда непрерывна внутри области своего опре-
деления R, здесь мы по существу предполагаем, что непрерывность имеет место на гра-
нице области.
447
условию
т
F (х) = min F (х) = min (<р0 (х) + 3 «гфг («)) (2а)
x£R i=l
или, в случае дифференцируемости фг (ж), условию Куна—Танкера
п
2 (2«)
5=1
где F (х) представляет собой величину, стоящую в скобках в (2а).
Упражнение. Показать, что выпуклая дифференцируемая функция
F (х), определенная на замкнутом ограниченном выпуклом множестве R,
достигает минимума в точке х = х в том и только в том случае, когда
выполняется условие (26).
Упражнение. Показать, что обычное свойство дополняющей нежестко-
♦сти оптимальных решений для прямой и двойственной задач является
частным случаем (26).
Мы будем рассматривать задачу А в несколько более общем виде.
Задача Б. Найти точку х ~ (xt, х2, . . ., хп) замкнутого ограничен-
ного выпуклого множества R и min z, удовлетворяющие условиям
= 0 (i = l,2, ...,г),
<Pi(z)<0 (f = г + 1, ..., тп), (3)
фо (ж) = z (min),
где фг (х) = Lt (х) при t = 1, 2, . . ., г линейны, а ф^ (х) при i = О
и i = г 1, ..., т — непрерывные выпуклые функции.
Как указывалось в § 22-1, систему (3) можно переписать в виде
%о =1,
j/iXq == О,
J/r+Ао + Рт+1
Ут^Ъ + Цт — О,
1/0^0 =2 (min),
где yi — переменные коэффициенты, которые можно свободно выбирать
из условий, что yi = Li (х) при j = 1, . . ., г и > фг (я) при i =
= г + 1, . . ., т для некоторого х £ R.
Упражнение. Показать, что множество возможных Р = (1, z/i,
У 2> • • • , Ут> У о) выпукло и что (4) представляет собой обобщенную задачу
линейного программирования; см. § 22-1-(27), (28).
Предположение о невырожденности. Существует хотя бы одно невы-
рожденное базисное допустимое решение ограниченной главной задачи
448
(5), порожденное некоторым выбором р допустимых векторов Р
МЛ + • • • + крРр + Иг+1<7г+1 + ... +p-m^m + ( — z) Um+l = UQ (5)
(kj > О, Рч 0),
где Ui обозначает единичный вектор, единичная компонента ’ которого
соответствует г-му уравнению (4); i может изменяться от i = 0 до i —
~ т + 1. Эта ограниченная главная задача (для удобства мы предполо-
жим, что она представляет собой исходную ограниченную задачу), столбцы
которой образуют базис, подробно расписана в явном виде в (6). Так как
базисное решение является невырожденным, значения ki и p,r+z поло-
жительны.
Исходная ограниченная главная задача для задачи Б, цикл h
(для исходного базиса положить fe=0, р=г-{-1)
S+^° • <-2> ’ Правые части Множители
1 . 1 .. 1 0 ... 0 1 (л0)
J/1 .. У1 •• • yf+k 0 ... 0 0 (Л1)
у\ • .. у? .. y»+h 0 .. 0 0
Уг+i •• у?+1 „р+fe Fr+1 1 .. 0 0
• 1 0 0 (пт)
Уо .. У? • У^к 0 0 1 0 (1)
(6)
Упражнение. Показать, что из предположения о невырожденности
следует существование такой точки ж0, что (ж0) = 0 для i = 1, 2, ...
. . ., г и (ж0) < 0 для Z = г + 1, . . ., т.
Упражнение. Показать, что если существует точка ж0, удовлетворяю-
щая указанным выше условиям, и невырожденный базис для системы г
линейных уравнений Ьг (х) = 0, то существует невырожденный базис
для системы в целом.
Так как мы показали, что (4) представляет собой обобщенную задачу
линейного программирования, то для получения ее решения мы можем
использовать методы, развитые в § 22-1. Было показано, что этот итера-
тивный процесс сходится за конечное число шагов, если только пере-
менные коэффициенты, соответствующие каждому из столбцов, выби-
раются из некоторого выпуклого многогранника. Однако в задачах А
и Б мы имеем дело с выпуклыми множествами общего вида. Поэтому нам
нужно показать, что этот процесс хотя может быть и бесконечным, но
должен сходиться к решению.
Упражнение. Предполагая сходимость итеративного процесса, сфор-
мулировать задачу типа «этапа I», которая в конечное число итераций
даст невырожденное базисное допустимое решение, удовлетворяющее (5),
если таковое существует. Указание. Использовать результаты двух пре-
дыдущих упражнений.
29 Дж. Данциг
449
НАХОЖДЕНИЕ ИСХОДНОГО НЕВЫРОЖДЕННОГО БАЗИСНОГО
ДОПУСТИМОГО РЕШЕНИЯ ОГРАНИЧЕННОЙ ГЛАВНОЙ ЗАДАЧИ
В условиях теоремы 1, если линейных уравнений (х) — 0, подле-
жащих удовлетворению, не имеется, существует точка х = ж0, в которой
фг (я0) < 0 при i = l,2, . . ., тп. Тогда условие невырожденности удо-
влетворяется базисным решением, образованным т свободными перемен-
ными и переменной хi — 1, где коэффициенты при Ki равны у\ = (я0),
см. (7). Следовательно, в задаче А всегда существует хотя бы одно невы-
рожденное базисное допустимое решение.
Исходная ограниченная главная задача (и базис) для задачи А
Ki щ . . . цт (—z) Правые части
1 Ф1(®°) 1 Фт И) 1 Фо И) 1 1 0 0 0
(7)
Для задачи Б мы будем предполагать, что невырожденное базисное
допустимое решение некоторой ограниченной главной задачи, с которого
начинается алгоритм, уже имеется.
ИТЕРАТИВНЫЙ ПРОЦЕСС
Пересмотрим теперь итеративный процесс решения обобщенной задачи
линейного программирования, описанный в гл. 22. На некотором цикле к
оптимизируется ограниченная главная задача (5), давая новое базисное
допустимое решение и новый набор симплекс-множителей лА Эти
множители используются для формирования нового столбца Рр+д+t
ограниченной главной задачи цикла А 4-1, причем все столбцы главной
задачи цикла к сохраняются и используются на цикле к + 1. Отметим,
что сохранение столбцов было в гл. 22 необязательным; здесь же оно
необходимо для доказательства сходимости.
Компоненты й-го базисного допустимого решения будут обозна-
чаться через
^1» • • • , РН-1 ’ • • • > О*
Пусть
p+fe
j=l
Для того чтобы иметь возможность удобно выразить к-е приближение хк
к минимизирующему решению задачи Б, предположим, что мы опреде-
ляем каждый столбец Pj главной задачи, выбирая некоторое значение
х = х? и полагая
Р> = (1, <p2(*J), • • •» фт(^3); <Ро (*’)>, (/ = 1,2, р + к).
450
Л%Р;>0, I
(10)
(11)
В этом случае fc-e приближение к минимизирующему решению задачи (3)
записывается как
р+Ь
2 z* = <po (8)
Симплекс-множители для цикла к удовлетворяют следующим
условиям:
nftC7m+1 = l,
nkPj = 0, I
— n I если или jxf базисная переменная.
если X7- или рг небазисная переменная.
Следовательно, компоненты вектора л^ = (л&, л&, . . ., л&; 1) с номе-
рами I = г+1, . . ., т неотрицательны, так как для этих i мы имеем
л? = akUi > 0.
Для проверки на оптимальность А-го приближенного решения (8)
следует минимизировать функцию
Д (х I лк) = фо (я) + 2 л? Ф» (*) + л*
г=1
по всем х £ R.
Теорема 2. Если min Д (х | > 0, то xh оптимально.
Доказательство. Пусть х 6 R удовлетворяет условиям:
Li(z) = 0, (i = l ,2, ..., г),
фг(ж)<0, (f = r+l, ...,7П).
Умножая i-e соотношение на л?, где л* > 0 при i — г + 1, . . ., тп,
и складывая, мы получаем
2^(pi(^)<0. (12)
i
Прибавим фо (х) + л* к обеим частям этого неравенства:
Д (х | л^) < фо (х) + л£. (13)
Полагая в главной задаче (6) X = Xfe, умножая ее строки на соответствую^
щие компоненты вектора nk и суммируя, получаем в силу условий допол-
нительной нежесткости (9) оптимальных решений прямой и двойственной
систем
— Zk = Лд . (14)
Таким образом,
Д (х I л£) + < ф0 (я). (15)
С другой стороны, из выпуклости функции ф0 (х) следует, что для при-
ближенного решения xk = 2 ^jX*
р-4-k p+fe
фо < 2 ^Фо (*’) = 2 = zk. (16)
j=l j=l
Выбирая сначала х, которое минимизирует ф0(я) в (15), а затем х, кото-
рое минимизирует Д (ж|л^), мы видим, что справедлива
451 29*
Теорема 3. Верхняя и нижняя границы для min <р0 (х) суть
min Д (х|ль) + zk < min <p0 (x) < <p0 (xh) < zh. (17)
Вернемся к доказательству теоремы 2. Полагая в (13) х = х и учитывая
(16), мы получаем
min A (rr|< А (£|пь) ф0 (xk) + nJ = ф0 (xk) — zk < 0. (18)
Если воспользоваться теперь предположением о том, что min А (я|л?) >
> 0, то отсюда будет следовать
minA(z|nJ) = 0 (19)
и, согласно теореме 3,
—nJ = zk = фо (я&) = min ф0 (ж). (20)
Тем самым теорема 2 доказана.
Упражнения.
а) Дать подробное доказательство теоремы 3.
б) Показать, что сумма выпуклых функций с неотрицательными
весами есть выпуклая функция.
в) Показать, что А (х | nfe) — непрерывная выпуклая функция на R.
г) Показать, что существует х £ R, для которого
A (z|nfe) = min A (#|nfe).
ФОРМИРОВАНИЕ НОВОГО СТОЛБЦА ДЛЯ ГЛАВНОЙ ЗАДАЧИ
Если min A (#|nfe) < 0, определим £ R и
A (#/J+1|nk) == min A (z|nh) < 0, (21)
x£R
Рр+А+1 = (1, Ф1(^+1), ...,Фго(^+1); ф0(^+1)>. (22)
Из определений (10), (21) и (22) следует, что
xkPp+k+l = А (хк+1\лк) < 0. (23)
Если бы мы смогли теперь показать, что min А (х | п&) —> 0 при
fc->oo, то из теоремы 3 легко устанавливалась бы сходимость после-
довательности фо (хк), так как zk образует монотонно убывающую после-
довательность, ограниченную снизу (см. упражнение (г)). Отметим,
однако, что эту сходимость можно установить и в том случае, когда
min А стремится к нулю для некоторой подпоследовательности индек-
сов к; в действительности нам удастся доказать лишь последний факт.
С этой целью докажем сначала следующую теорему.
Теорема 4. Если для некоторой главной задачи существует невырож-
денное базисное допустимое решение, то имеется такое бесконечное под-
множество К значений к, что lim nfe существует для к £ К.
fc~>oo
Доказательство. Пусть В — базис некоторой главной задачи, соот-
ветствующий невырожденному базисному допустимому решению. Пред-
положим для удобства, что это есть решение исходной главной задачи (6),
отвечающей к = 0. Пусть
B=^Pi,P2, ...,Pm^Um+i), (24)
где некоторые из векторов Pj могут быть ортами Ц}, соответствующими
свободным переменным. Таким образом, вектор%° = • • •, Xm+i, —z°)
452
удовлетворяет соотношению
ВМ = UQ (25)
и в силу невырожденности компоненты X? положительны. Поэтому
ХО = В"1С7О = [Л1°, Х2°, ...,Хт+1, ~z°]T, где Х?>0. (26)
С другой стороны, любое являющееся решением двойственной
основной задачи на цикле й, удовлетворяет в силу (9) условиям nkPj 0г
sihUm+i = 1, и поэтому компоненты вектора ук = (yf, у£, . . уД, 1),
определяемого в (27), неотрицательны:
лкВ = ук>0 (у*>0). (27)
Отметим, что лк = yhB~1 и, в частности,
Л* — nhU0 = ук (В-Юо) = уЧо = уЭД + + • • • + Yrn+1^+1 - 2».
Следовательно, учитывая неравенства л* = — zh < — ф (хк) — тшф0(я),
мы имеем
zO-min фо (*) > (уЭД + Уг^2 + • • • + Ym+^m+l)- Щ > 0) (28)
Теперь легко видеть, что, уменьшая правую часть (28) отбрасыванием
всех произведений, кроме Z-ro, мы имеем в силу неравенств ук 0,
М>о.
. (29)
Поэтому компоненты вектора ук имеют конечные верхние и нижние гра-
ницы, и теорема 4 вытекает из результатов приводимых ниже упраж-
нений.
Упражнение. Если компоненты вектора ук имеют конечные верхние
и нижние границы, то это же самое справедливо и для любого линейного
преобразования этого вектора, в частности для компонент вектора як =
= укВ~1.
Упражнение. Если компоненты лк имеют конечные верхние и ниж-
ние границы, то существует бесконечное подмножество К значений к,
такое, что Ит лк существует для к £ К при к—»оо.
fe->oo
Теорема 5. Если х удовлетворяют условиям задачи Б, то
Ит фо (хк) = min ф0 (х).
k—>оо
Доказательство. Либо процесс конечен и достигнуто оптимальное
решение, либо для всех к мы имеем
min Д (rr| jtfe) = nkPk+l < 0. (30)
Тогда, поскольку главная задача на любом цикле I > к содержит стол-
бец Р*+1, мы имеем также для всех к и для всех I > к
rfPk+l>0. (1>к) (31)
Для к g К и I g К разность лй — л/ -> 0 при к -> оо и I > к, сог-
ласно теореме 4. Так как область В ограничена, а фг (х) непрерывна в /?,
то фг (х) в R ограничена и Z-я компонента ф^ (х^ вектора Rj также огра-
ничена в R при всех у. В силу ограниченности компонент РА+1 сверху
и снизу разность (пк—лг) P^+i также должна стремиться к нулю. Но если
разность между левыми частями (30) и (31) стремится к нулю и JtkPk+t
453
отрицательно, a неотрицательно, то л?Рд+1 должно подходить
к нулю сколь угодно близко; иначе говоря, по любому е > 0 можно найти
такое йе, что для всех к £ К, к> к&
— 8 < min Д Офт*) < 0. (&>Л8, к£К) (32)
x£R
Теперь из теоремы 3 и (32) следует сходимость zk к min ф0 (х) на множе-
стве к £ К. Но zk монотонно убывают при всех к. Мы заключаем, что zh
стремится к min ф0 (ж), для любого множества к -> оо (а не только для
к С К). Так как zh представляет собой верхнюю границу для <р0 (хк), то
эта последовательность также должна сходиться к указанному пределу.
Теорема 5 доказана.
Теорема 6. Пусть л = lim л? для к £ К, и пусть х — любое опти-
fc->oo
мольное решение задачи Б. Тогда
F (х) = min F (х) = min (<р0 (х) + 2 зт.фг (ж)), (33)
x£R г=1
где вектор л имеет неотрицательные компоненты при i =. г + 1» . . т.
Доказательство. Из (32) мы имеем для к> ке и к £ К
—е<Д (х^Х <р0 (х) + л*, (34)
где неравенство в правой части взято из (13). В пределе при А-> + оо,
8 -> 0 получаем lim л* = л и
0< Д (х| л) = F (х) + л0<фо (я) + л0, (35)
где Д(я|л) определено согласно (10).
С другой стороны, согласно (20),
л0 = lim л£ = lim (—zk) = —min ф0 (х) = — ф0 (ж). (36)
x£R
Поэтому, подставляя х = х в (35) и учитывая последнее соотношение,
мы имеем
0 = F (х) + л0 F (х) + л0, (37)
устанавливая тем самым как теорему 6, так и ее частный случай—теорему 1.
24-2. ОДНОРОДНЫЕ ЦЕЛЕВЫЕ функции
И ЗАДАЧА ХИМИЧЕСКОГО РАВНОВЕСИЯ
ОДНОРОДНЫЕ ЦЕЛЕВЫЕ ФУНКЦИИ ПЕРВОЙ СТЕПЕНИ
В некоторых приложениях, подобных рассматриваемой ниже задаче
химического равновесия, нужно минимизировать выпуклую функцию
G(z) = xG , (1)
\ X X X У
где
x = xt + x2+ ... +хп (2)
при ограничениях в форме системы линейных неравенств с неотрицатель-
ными переменными
3 ацХ] = Ъь Xj>Q (i = 1, 2, ..., т). (3)
3=1
454
Отметим, что если каждую компоненту х умножить на t, то значение
G (х) также умножится на t:
G(tx) — tG(x). (4)
Иначе говоря, G представляет собой однородную функцию первой степени.
Мы будем предполагать, что G (и) > 0 — непрерывная выпуклая
функция на множестве допустимых и, удовлетворяющих условию
и1 + и2 + • • • + ип = 1» (Uj>0). (5)
В ходе итеративного процесса мы образуем решения ж1, я2, . . ., удовлет-
воряющие (3), и такие, что G (xk) составляет монотонно убывающую
последовательность. Обозначая через z0 верхнюю границу для G (х) при
А ь
х = х , мы имеем для таких х
G (х) = xG (и) <ZzQ (х = xk)
(6)
min G (и)
Отсюда следует ограниченность комйонент такого вектора сверху и снизу.
Рассмотрим эквивалентную обобщенную задачу с одной переменной
_ п
x(2J = (х>0, Uj>o, =
.’=1 j
п
* (2 a2j«>) = Ь2, (7)
j=l
.................
п
3=1
xG(u) = z(min),
где x > 0 — переменная, коэффициенты при которой линейны относи-
тельно Uj, подчиненных условию (5). Это порождает некоторую главную
задачу, в которой общее решение образуется из неотрицательной линей-
ной комбинации столбцов коэффициентов, порожденных различными
решениями подзадач ик. В противоположность этому, в обычном случае
требуются выпуклые комбинации. Такая большая гибкость оказывается
в этом случае возможной потому, что коэффициенты являются однород-
ными функциями и. Осуществим это в явном виде. Начнем с некоторого
набора т векторов и = ир, удовлетворяющих (5), и, полагая А — (ац),
образуем
Sp — Aup, (р = 1, 2, ..т),
cp = G(up). ()
Предполагая, что эти т столбцов образуют допустимый базис, мы можем
записать первую ограниченную главную задачу в виде
2 spk1p=b (U>0),
p=l (9)
т
2 СрХр = z1 (min).
p=i
Отсюда определяются симплекс-множители л1, удовлетворяющие условию
л1|$р4-Ср = 0 (р=1» 2, (10)
455
Для проверки решения на оптимальность нужно минимизировать выра-
жение
Д (ф1) = С(и) + (лМ)и (И)
по всем и, удовлетворяющим (5). Если min Д > 0, то решение
х = 2 Цир (12)
Р=1
оптимально. Если это не так, то выберем u™+1, для которого
G (uw+1) + (лМ) u?n+1 = min Д (ф1). (13)
Расширим основную систему (9) посредством Sm+l = Aum+1 и ст+1 =
= G (uw+1), оптимизируем новую ограниченную главную задачу с X =
= X2 и повторим весь цикл с множителями л = л2 и т. д.
Небольшое видоизменение нашего прежнего доказательства, при-
веденного в § 24-1 (учитывающее тот факт, что в этом случае мы уже
не имеем ни ограничения = 1, ни соответствующего ему множителя
i
$), подводит нас к следующей теореме.
Теорема 1. Если существует хотя бы одно невырожденное базисное
допустимое решение главной задачи, то модифицированный алгоритм
сходится к оптимальному решению.
Упражнение. Показать, что если целевая функция G (х) линейна, то
она является выпуклой и однородной первой степени и описанный только
что процесс сводится к стандартному симплекс-методу.
Упражнение. Доказать теорему 1. Какую роль играют в доказатель-
стве соотношения (6)?
ЗАДАЧА ХИМИЧЕСКОГО РАВНОВЕСИЯ
В качестве приложения описанной теории рассмотрим задачу опре-
деления молекулярного состава некоторой газообразной смеси в состоя-
нии равновесия, содержащей т различных типов атомов (Уайт, Джонсон
и Данциг [1]). Хотя теоретически эти атомы будут объединяться
во все химически возможные молекулярные соединения, на практике
рассматриваются лишь стандартные их типы, присутствующие в измери-
мых количествах.
Пусть
bt — количество грамм-атомов атомов типов i, имеющихся в смеси,
х7- — количество грамм-молекул молекулярного соединения /, имеющегося
в смеси, где
я;>0, (/=1, 2, ..., п), (14)
х — общее число грамм-молекул газа в смеси, т. е.
x=^Xj, (15)
j=i
atj — количество атомов типа i в молекуле соединения /.
Тогда уравнения сохранения массы примут вид
^aijXj^bi, (i = 1,2, ..., т). (16)
5=1
Определение равновесного состава газообразной смеси эквивалентно
определению значений количеств грамм-молекул Xj, удовлетворяющих
456
ограничениям (16) и минимизирующих полную свободную энергию смеси,,
задаваемую выражением
С(х„ ...,,:п)=2сл+за:)1„г5-_^(2^т+2т1<>гт>
3=1 3=1 j=i j=l
n
= X 2 (ciui + ui log mj)• = - J- > o) (17}
;=1
Можно показать, что это выражение определяет выпуклую функцию.
Коэффициенты cj представляют собой значения функций свободной энер-
гии Гиббса FQ/RT атомных соединений при данной температуре плюс
натуральный логарифм давления в атмосферах.
Наша задача заключается в минимизации выражения G, описывае-
мого соотношением (17) и представляющего собой однородную форму
первого порядка при ограничениях (14), (15) и (16), имеющих вид линей-
ных равенств и неравенств. Функция
G (и) = 2 (C/U; + Uj log Uj), (Uj > 0) (18)
j=l
очевидно, выпукла.
Тогда в этой интерпретации
Д = G (и) + 2 2 a4ui = 3 i°g «7 + 4“?), (19)
i 3 3
ь «
где Лг — симплекс-множители некоторой итерации, которые определяются
соотношениями, аналогичными (10). Положим
С5=С;+2 (20)
Для нахождения min Д при условии
2u/ = l (Uj>0) (21)
3
мы игнорируем соотношения и7>0 и найдем безусловный минимум функции
Д = 2 (»/ log Uj + сjUj)—0 (2 Uj— 1), (22)
3
где 0 — множитель Лагранжа (см. § 6-5). Приравняем нулю частные
производные Д по ufi тогда
^- = l + logu7 + c|-0 = O. (23).
Следовательно, Uj можно представить в виде
-k
Uj = Ae~c^ (24)
где А = > 0. Подставляя эти значения в (21), мы определяем А
и находим
-k
= (25)
2
i=l
так что в точке минимума условия Uj (^выполняются. Тогда эти зна-
fe+i
чения как раз и являются значениями Uj = Uj , с которых начинается
следующая итерация.
457
24-3. ВЫРОЖДЕННЫЕ 1 ВЫПУКЛЫЕ ЦЕЛЕВЫЕ ФУНКЦИИ
Определение. Если подлежащая минимизации целевая функция,
не являясь линейной, имеет вид
п
3 <py(xj) = z(min), (1)
где каждая функция фу (х;) выпукла, то она называется выпуклой вырож-
денной целевой функцией. Этот термин был использован для описания
данного класса целевых функций Чарнсом (см. Чарнс и Лемке [1];
Данциг [12]). Мы будем предполагать, что hj есть известная верхняя
граница для и что переменные х^ подчинены ограничениям
2 = (i — 1,2, ...,тп). (2)
j=i
Проиллюстрируем сказанное. Предположим, что первые 100 единиц
интенсивности некоторого технологического процесса могут быть осу-
ществлены с издержками 1 долл, за единицу, дальнейшие 50 единиц —
о издержками 1,25 долл, за единицу и следующие 50 единиц — с издерж-
ками 1,5 долл, за единицу. Тогда функция суммарных издержек ф (х)
будет выпуклой в интервале 0<я<200. Вообще, если первые еди-
ниц стоят за единицу, вторые а2 единиц стоят s2 за единицу, последние
единиц стоят sk за единицу, то суммарные издержки ф (х) будут выпук-
лыми, если и не будут выпуклыми, если sr> $г+1
хотя бы для одного г.
Упражнение. Определение выпуклой функции было дано в § 7-1.
Показать, что оно эквивалентно следующему определению: функция
Ф (х) называется выпуклой, если
ф (2 ^r^r) 2 м (#?•) (3)
г г
для любых > 0, таких, что = 1*
г
Упражнение. Показать, что если издержки, связанные с J-м процес-
сом, пропорциональны квадрату его интенсивности, т. е. фу (яу) = Cjx],
то функция ф (х^ выпукла при Cj 0, но не является таковой при
Су < 0.
В качестве третьего примера рассмотрим случай, когда суммарные
издержки ф (ж) складываются из некоторой фиксированной доплаты /,
а в остальном издержки пропорциональны уровню интенсивности. Тогда
функция ф (х) выпукла. С другой стороны, если фиксированная доплата /
присутствует только при х > 0, то мы можем записать
В этом случае ф (х) не будет выпуклой, если / > 0.
Упражнение. Показать, что при /<0 написанная выше функция
ф (х) выпукла.
Для того чтобы заменить уравнения (1) и (2) стандартной задачей
линейного программирования, мы предположим, что функция фу (х)
кусочно-линейна. Впоследствии мы снимем это ограничение. (Если фу (х)
1 В оригинале separable — сепарабельные.— Прим, персе.
458
имеет непрерывную производную, то на кривой можно выбрать к + 1
точку таким образом, чтобы проведенная через них ломаная давала
достаточно хорошее приближение к этой кривой.)
ЭКВИВАЛЕНТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Пусть (/rj, grj), г = 0, 1, 2 . . ., к — координаты точек перелома
{х^ фДя,)) функции ф7- (х) (см. рис. 24-3-1). Любое Xj из промежутка
можно представить в виде
xi = + • • • + (Кj > 0), (5)
где
1 = Aoj + %ij + ... + (6)
В силу выпуклости фу мы имеем, согласно (3),
Ф; (xj) ^goj 4- + ... + ^hjgkr (^)
Для решения (1) и (2) определим Ц- > 0 и min 2', удовлетворяющие
условиям
(i = l, 2, ...,m), (8)
^0/ + + •.. + = 1, (/=1,2,..., тг), (9)
2 14-goj + Kjgxj + • • • + W/d = z' (min) (10)
j=i
и подставим получающиеся А в (5) для определения Xj. Для доказатель-
ства эквивалентности задач (8) — (10) и (1), (2) нужно только показать,
/

к
----
л и
п К
Заданный xj-EArjfrj
Рис. 24-3-1. Представление выпуклой функции в рам-
ках линейного программирования.
что min 2 > min 2'. Из (7) мы имеем min 2<min 2'. Для доказательства
неравенства min 2 > min 2' возьмем х^ дающие минимум (1) при усло-
виях (2), и представим их в виде комбинаций абсцисс двух точек пере-
лома, лежащих непосредственно слева и справа. Получающиеся А удовлет>
воряют условиям (8) и (9) и удовлетворяют условию (7) как равенству,
так что получающийся в (10) 2' равен min 2.. Следовательно, min 2 >
>min2', что и требовалось.
459
МЕТОД ОГРАНИЧЕННЫХ ПЕРЕМЕННЫХ
Следует отметить, что в описанном выше методе увеличивается число
переменных и для каждого ф; (xj) увеличивается на единицу число урав-
нений., Используя метод ограниченных сверху переменных, можно обой-
тись исходным числом уравнений. Первоначальные переменные заме-
няются наборами новых ограниченных сверху переменных, имеющих
несколько одинаковых (за исключением строки издержек) столбцов
коэффициентов. Это делает возможным использование ряда упрощающих
Рис. 24-3-11. Представление выпуклой функции в
рамках линейного программирования с использованием
ограниченных переменных.
приемов (см. гл. 18). На рис. 24-3-П наклоны участков ломаной обозна-
чены через St, а длины соответствующих интервалов — через аг.
Из выпуклости ф (х) следуют неравенства
(И)
Мы утверждаем теперь, что
ф (*) = go + min [А± + s2A2 + ... + ^ДА], (12>
где
x = Д1 + Аг + • • • + А& (13)
0<Af<af. (14)
Действительно, так как $i<s2< • • • <sh, то очевидно, что для нахож-
дения минимума нужно выбрать максимально возможное Дь пока оно
не достигнет своей верхней границы затем выбрать Д2 и т. д. до тех
пор, пока не встретится такое Дг, что, положив Дг = аг, мы превысим
значение х. Тогда нужно уменьшить Дг так, чтобы выполнялось соотно-
шение (13). Ясно, что этот процесс является попросту процессом порож-
дения кривой ф (х) от точки 0 до точки х.
ЭКВИВАЛЕНТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Для решения задачи (1), (2) определим Агу- > 0 и min z', удовлетво-
ряющие условиям
аи [Д17- + Д2; 4-... + АдЛ = bi, (£ = 1,2,..., т),
j=n (15)
S [«оА1 j + «27^2/ + • • • + = z (min),
3=1
460
где
0^ Дгу ^ary,
и определим Xj посредством соотношений
xj — Ди + Дг? + • • • + Да;-
(16)
(17)
МЕТОД ПЕРЕМЕННЫХ КОЭФФИЦИЕНТОВ
Этот метод имеет то преимущество, что в нем используются исходные
выпуклые функции, а не их аппроксимации посредством ломаных. Так
как этот процесс представляется непрерывным аналогом описанного
нами ранее процесса, то мы привлекаем для его обоснования данное
в § 24-1 доказательство сходимости. Обращаясь к уравнениям (5), (6)
и (7), мы можем записать чисто формальным образом
Х1 ~ hjfj’
1 = (18)
фу (*/) < М7,
где (/у, gj) — пара переменных коэффициентов. Множество Cj допусти-
мых значений этих коэффициентов состоит из точек (/у, gy), для которых
gy > фу (/у). Из выпуклости функции фу следует выпуклость этого мно-
жества; поэтому уместно применить метод переменных коэффициентов,
изложенный в гл. 22. В указанной главе мы предполагали, однако, что
множества Су определялись конечным числом линейных уравнений. В этом
случае итеративный процесс конечен. Процесс оказывается бесконечным,
если производная фу непрерывна и отлична от постоянной. По поводу дока-
зательства сходимости см. § 24-1.
Формально полная система с переменными коэффициентами при-
нимает следующий вид. Найти Xj 0, /у, gy > фу (/у) и min z, удовлет-
воряющие условиям
Множители
&1 1X1 + ^12^2 + • • • -}~а1пхп =ъ,
«21^1 + а22Х2 + • ' • • “F ^2пхп = Ь2 зт2
(1тпЛх\. “Ь &т2х2 4“ •• • “Ь ^тпхп —
Х1 — ^1/1 = 0 — $1
Xi = 1 h (19)
х2 ^2/2 = 0 S2
Х2 = 1 ^2
ХП ^nfn 0» ---$П
“ 1» tn
^igi + ^2#2 + • • • + Kign = z (min).
Связанные с этой системой множители выписаны справа. Всего здесь
2п + т ограничений.
461
Упражнение. Показать, что множество возможных коэффициентов
(Л, gi) в (19) выпукло.
В соответствии с теорией переменных коэффициентов (гл. 22) базис
образуется путем взятия конкретных значений и g7, причем для дан-
ного J допускается образование столбцов, использующих более одного
набора значений (/7, gj). Некоторым из индексов j будет соответствовать,
ровно один столбец значений (/я, g71) в базисе, а другим — два значения
(Ль ёп) и (fJ2, gJ2).
Упражнение. Показать, что в базисе число различных (/j7, gJf)^
i = 1, 2, 3 ... не может быть ни нулем, ни большим двух.
Переменные, соответствующие gji), мы будем обозначать через
Можно обеспечить, чтобы все Xj вошли в базисное множество. Напри-
мер, этап I можно начать, взяв в качестве базисного множества перемен-
ные Xj, Kj и набор т искусственных переменных. Поскольку можно пред-
положить, что Xj не имеют ограничения на знак, они будут оставаться
во всех последующих базисных множествах. Предполагая, что в конце*
этапа I искусственных переменных не остается, мы видим, что из общего
числах 2п + т базисных переменных будет п штук Xj, п — т одиночек
Хл и т пар и KJ2.
Если интерпретировать это иным образом, то т из переменных xjr
скажем Xj , Xj2, . . ., Xj^, удовлетворяют соотношениям
fji^xJ^fj2> (j — 7 г) (20)
а остальные подчинены ограничениям
* xj~fjb (21)
Упражнение. Рассмотреть случай, когда на этапе II могут присут-
ствовать искусственные переменные.
Теорема 1. Симплекс-множители определяются соотношениями
(/ = 7ь 72, ...,7m)- (22)
'J2 s * 7 Ji
т
= /2, • • •, 7m), (23)
i=l
m
sj = JS ^ij^i 1 ]b (2^)'
г= 1
= — Sjtii- (25)
Доказательство. Из (19) мы имеем
sjfji~\-tj — Sjb (/ —7i, 7г, ••Jm) (26)
Sjtj2~\~ij = Sj2-
Вычитая первое равенство из второго и разрешая относительно Sj, мы
приходим к (22). Уравнения (23) — (25) непосредственно следуют из (19).
Отметим, что в (23) известны Sj, а определяются fy, в то время как в (24)*
л- известны и определяются Sj. В (25) неизвестными являются только tj.
Для оптимальности решения Xj — х} мы требуем, чтобы
^—(^Л + Л)>0- (7 = 1, 2, ...,«) (27)
при всех возможных выборах (/7, g7).
Упражнение. Почему эти условия являются достаточными?
Так как Sj и tj фиксированы, мы решаем подзадачу минимизации
z. == (^f^-^Sjfj. Если ф; имеет непрерывную производную ф/ (/7), мы
462
ищем fj > 0, такие, что
<Pi
(28>
На рис. 24-3-Ш изображен график функции gj = фу (fj). Для каждой
точки (/J, gj) на этой кривой рассмотрим проходящую через нее прямую
gj — sjfj — — SW Мы ищем прямую с минимальным gj. Обозначим
ее через Zj. В силу (28) соответствующей точкой, если она вообще суще-
ствует, будет точка касания.
Нахождение такой точки касания (/у, gj) может оказаться невозмож-
ным, так как наклон при fj — 0 может быть больше Sj\ тогда наилучшим
выбором будет fj = 0, gj — фу (0), так как из выпуклости фу (х) следуег
Рис. 24-3-Ш. Решение задачи с вырожденной целе-
вой функцией с использованием обобщенного програм-
мирования.
монотонное возрастание наклона. Если ф^ (/у) < Sj для всех /у > 0, то>
лучшим выбором будет /у = Лу. Если индекс j соответствует переменной,
имеющей два связанных с ней значения X в базисе, то наклон прямой,
соединяющей точки (/у1? gyi) и (/у2, gj-г), равен в силу (22) Sy. В этом случае
между этими точками всегда имеется точка, удовлетворяющая (28), если
только наклон представляет собой непрерывную функцию от /у. Тем самым
мы приходим к следующей теореме.
Теорема 2. Решение (х[, х^, . . ., Хп) оптимально, если для любого j
симплекс-множители, определяемые согласно теореме 2, удовлетворяют,
условиям:
sj — если 0<ж$<Лу.
sy < ф j (0), если 0 = х J,
Sy > ф} (йу), если х] = Лу,
или, более общо, условиям

где производные слева и справа соответственно в точках 0 и hj не обозна-
чаются.
АЛГОРИТМ
Проведенные выше рассуждения наводят на мысль о некотором
варианте симплекс-метода, в котором т переменных Xj считаются базис-
ными с границами /yi<#y</y2> а п — т переменных Xj с фиксирован-
ия
ными значениями /д являются небазисными. Предполагается, что нам
известно некоторое базисное допустимое решение Xj = х} указанного
типа. Оно используется для того, чтобы начать алгоритм, состоящий из
следующих шагов.
Шаг 1. Вычислить наклоны Sj = ф} (я°)- Для базисных переменных Xj
либо уменьшить верхнюю границу fj2, либо увеличить нижнюю границу
fji с тем, чтобы измененные границы сблизились и удовлетворяли соот-
ношению
= (29)
ВГслучае разрывности <р, (Xj) в предыдущих рассуждениях ф; (xj) заме-
няется на производную слева cpf (Xj).
Шаг 2. Вычислить симплекс-множители согласно (23).
Шаг 3. Вычислить Sj и tj для небазисных переменных согласно (24)
и (25).
Шаг 4. Для небазисных / определить /* следующим образом:
а) /* = 0, если Sj < (0),
б) f* = hj, если Sj > ф| {hj),
в) (/*) < Sj < ф* (/*) в остальных случаях.
Шаг 5. Вычислить g* — ф; (/*) и z* = g* — Sjf*.
Шаг 6. Определить индекс р той небазисной переменной, для которой
z* —= т*п (z*i — 0,
где минимум берется по индексам небазисных переменных /. Если
min (Zj — tj) = 0 — процесс окончен. Данное базисное решение опти-
мально.
Шаг 7. Сохраняя значения всех остальных небазисных переменных
равными /л, изменить значения хр и базисных переменных следующим
образом. Уменьшить или увеличить хр, имевшее фиксированное значе-
ние /Р1, в зависимости от того, будет ли fp меньше или больше, чем fpl.
Удалить базисную переменную, которая достигает своей верхней или
нижней границы первой, или остановиться, если хр достигает первым
значения fp. В последнем случае fp будет новым фиксированным значе-
нием переменной хр, которая все еще будет оставаться небазисной.
В предыдущем же случае хр становится новой базисной переменной,
a fp и /Р1 — ее новыми границами; базисная переменная, которая дости-
гает своей границы, удаляется в этом случае из базиса и фиксируется
на значении этой границы.
Сходимость. Неизвестно, сходится ли описанный выше алгоритм
к min z. Для того чтобы применить изложенное в § 24-1 доказательство
сходимости, в алгоритме следует предусмотреть, что первым повторно
вводится в базис любой из ранее порожденных столбцов, для которого
gj — sifj - tj < °-
Упражнение. Обобщить этот алгоритм, допуская повторное введение
ранее порожденных столбцов. Пересмотреть доказательство сходимости
и показать, почему оно не проходит, если этого не сделать.
Упражнение. Построить более простую форму алгоритма, заменяя
определенные выше верхнюю и нижнюю границы и fj2 на = 0
и fj2 = hj и полагая Sj = ф} (х°) для базисных Xj.
464
2АЛ. КВАДРАТИЧНОЕ ПРОГРАММИРОВАНИЕ
Хотя выпуклую квадратичную целевую функцию можно рассматри-
вать посредством развитых в § 24-1 методов или же свести к выпуклому
вырожденному случаю, рассмотренному в § 24-3, линейный характер ее
частных производных послужил источником изящной теории, имеющей
самостоятельную ценность. Сомнительно, чтобы к настоящему времени
мы могли осознать все многообразные возможности этой теорий.
Задачи квадратичного программирования могут возникать различ-
ными путями. Вулф в своей статье [2] перечисляет следующие четыре.
Регрессия. Найти наилучшее квадратичное приближение к имею-
щемуся набору данных, если заранее известно, что некоторые параметры
удовлетворяют ограничениям в форме линейных неравенств.
Эффективное производство. Максимизация прибыли в предположе-
нии линейности производственных функций и линейного изменения мар-
гинальных издержек (Дорфман [1]).
Минимальная дисперсия. Найти решение задачи линейного програм-
мирования с переменными коэффициентами издержек, которое приведет
к данной величине математического ожидания издержек и к минимальной
их дисперсии (Марковиц [4], [5]).
Выпуклое программирование. Найти минимум выпуклой функции
общего вида при линейных ограничениях, используя квадратичную
аппроксимацию (Уайт, Джонсон и Данциг [1]).
Баранкин и Дорфман [1] были первыми, кто отметил, что при
сочетании линейных лагранжевых условий оптимальности с исходными
условиями задачи оптимальное решение является одним из базисных
решений расширенной системы и обладает тем свойством, что только
одна из некоторых пар переменных присутствует в базисном множестве.
С другой стороны, Марковиц [4], [5] показал, что можно видоизменить
расширенную систему и затем параметрически породить некоторый
класс базисных решений, обладающих указанным выше свойством, кото-
рый даст сходимость к оптимуму за конечное число итераций. Нако-
нец, Вулф [2] показал, что это легко осуществить при помощи
небольшого видоизменения симплекс-алгоритма, не допуская вхождения
переменной в базисное множество, если «дополнительная» к ней перемен-
ная уже находится в базисном множестве. Таким образом, заменяя
несколько команд в программе симплекс-метода для задач линейного
программирования, оказывается возможным решить задачу выпуклого
квадратичного программирования! Мы изложим здесь один вариант
изящного метода Вулфа. Основное отличие заключается в том, что наш
вариант является более точным аналогом симплекс-метода; он характе-
ризуется более строгим правилом выбора и монотонным убыванием целе-
вой функции.
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Прежде чем перейти к постановке задачи, отметим, что любую квад-
ратичную форму можно удобным образом записать посредством симмет-
ричной матрицы, связанной с ее коэффициентами. Например, при п — 3
переменных
Q (*) = + с22х* + Сзз^з + + 2с23х2Жз + =
(СИ С12
£12 ^22 ^23 II *^2 I== (1)
С13 С23 С 33/ \Х3/
где индекс Т обозначает транспонирование.
30 Дж. Данциг 465
Определение. Квадратичная форма называется положительно, опре-
деленной, если хТСх > 0 для всех х У= 0; она называется положительно
полу определенной, если жтС'х>0 для всех х.
Задача. Найти х = (жь х2, . . ., яп)>0 и min Q (ж), удовлетво-
ряющие условиям
Ах — Ь, А = (аи), (i = 1, 2, ..., т) (9.
xTCx = Q(x), С = (с^ '
где Q (x) — выпуклая квадратичная функция.
Лемма 1. Квадратичная форма хТСх выпукла тогда и только тогда,
когда она положительно по л у определенна.
Доказательство. Пусть хт Сх — выпуклая функция. Для доказа-
тельства неравенства хт Сх^О предположим, рассуждая от противного,
что (xQ)TCx° < 0 для некоторого х = х°. Тогда для х' = —также спра-
ведливо неравенство (х')тСх' < 0. В силу выпуклости хт Сх для любой
выпуклой комбинации ж* векторов xQ и х' мы также должны иметь
11 <11 Л7,
(х*)т Ся*<0. В частности, для ж* == —ж°+— х' мы имеем ( -^х^-^х' ] х
х <0, или (0)т С (0)<0. Получено противоречие, так как
Выпуклость положительно полуопределенной формы следует из при-
водимой ниже леммы 2, так как линейное преобразование х переменных х
сводит Q (х) к сумме выпуклых, относительно х функций.
Лемма 2. Если квадратичная форма хтСх положительно полуопреде-
ленна, то существует такая невырожденная матрица Е, что замена пере-
менных х = Ех дает
хтСх=^Ь}х‘, (^>0) (3)
;=1
где A,j>0 — J-й диагональный элемент диагональной матрицы Ет СЕ.
Доказательство. Выберем любую переменную, скажем для кото-
рой Сц > 0 (см. первое из приводимых ниже упражнений). Представим
Q (х) как квадратичный полином относительно х^ и дополним его до квад-
рата. Получаем
п п п
xTCx = clix21 + 2x1 2 CijX} + ^\ 2 cHxixi (сц>0)
3— 2 i= 2 j— 2
= [ 2 cHxi ] — TH" [ 2 cVxi ] + 2 2 ciJxixi =
j = l j=2 i—2j—2
n n
= -^-«1 + 2 2 c'uxixj’ (V
i=2 3=2
n
где Xi = 3 cijxj и c'ij — (cuCij — Сцс^/сц. Теперь этот процесс можно
3=1
повторить, используя стоящую справа квадратичную форму относи-
тельно переменных (х2, . . ., хп). Процесс заканчивается за к^п шагов.
Полагаем xj — Xj и А; = 0 для / = к + 1, . . ., тг.
466
Упражнение. Показать, что для положительно полуопределенной
квадратичной формы либо Сц > 0, либо Сц = с12 = • • • = ctn = 0.
Упражнение. Показать, что если форма Q (х) положительно опре-
деленная, то определители всех главных миноров матрицы С положи-
тельны (в частности, ctl >0).
Упражнение. Показать, что при к = п форма Q (х) положительно
определенная, а при к < п она является полуопределенной.
Упражнение. Применив лемму 2, показать, что если форма хтСх
положительно полу определенна и (я°)т CxQ = 0 для х — ж0, тоСгг0 = 0,
Упражнение. Завершить доказательство леммы 1.
УСЛОВИЯ ОПТИМАЛЬНОСТИ
Пусть Aj и Cj обозначают соответственно /-е столбцы матриц А и С
и пусть
У]~С^х ztAj, л = (Л|, л2, • ••, зТуп). (5)
Теорема 1. Решение х = xQ минимально, если существуют такие
л = л° и у = г/°, что
AxQ = b, х°>0, (6)
y^Cjxo—noAj^O, (/ = 1, 2, (7)
y°j = Q, если (8)
Доказательство. Перепишем Q (х) в виде
Q (?)—Q (х°) = 23(3 с^хХ) {Xj -х?) + 3 S (xi—x?) (x3— x?) =
1 $= 1 1 i = l
= 23 (CjxO) (Xj-X?) + (x-x°)T C (x-XO). (9)
i= 1
Пусть я>0 — любое решение, удовлетворяющее условию Ax=b. Тогда
A (x—xQ) =. 3 Aj (xj — x'j) =f 0. (10)
i=i ' •
Умножая слева на 2л0 и вычитая из (9), получаем
Q(x)—Q(x°) = 2 S (Cjx°—rt>Aj) (Xj—x") + (x—-x°)T C (x—x°) =
(11)
= 2 S y°j(xj—£j) + (x — xQ)T C (x—ж°).
3=1
Для класса решений, обладающих тем свойством, что у] = 0 при х] > 0,
(11) упрощается следующим образом:
Q(x) — Q (жо) = 2 2 У*зхз + (х — Х°)Т С (х — я°). (12)
Отметим, что (12) выполняется в силу (8), а неравенства г/J > 0 — в силу
(7). Таким образом, все члены в (12) неотрицательны и поэтому О (х) >
467
30*
УЛУЧШЕНИЕ НЕОПТИМАЛЬНОГО РЕШЕНИЯ
Рассмотрим систему
Ах =Ь, (х^ 0)
Сх—Атлт — 1пу=0, (13)
где форма хтСх предполагается положительно полуопределенной.
Пусть х?. л°, у0 — базисное решение, соответствующее некоторому базис-
ному множеству и обладающее свойством дополнительности. Последнее
означает, что для любого j в базисное множество входит либо либо i/y,
но не обе эти переменные. Далее мы будем предполагать, что правые
части подвергнуты возмущениям, чтобы обеспечить невырожденность
всех базисных решений. Отметим, что на знак л и у ограничений не накла-
дывается; для допустимости решения (13) требуется лишь, чтобы я>0.
Оптимальное решение будет получено, если у7->0 и x^j = 0 для всех /.
Теорема 2. Если базис является дополнительным и yl < 0, то любое
увеличение небазисной переменной xs. сопровождаемое пересчетом только
базисных переменных, порождает такой класс решений х'. п', уг. что хТСх
убывает, пока y's < 0.
Доказательство. Пусть х — любое решение из указанного класса
(т. е. порожденное увеличением xs). Пусть, в частности, xf порождено
х8 = х&. По аналогии с (И) мы имеем Q (х) — Q (х') = 2y's (xs — x's) +
4- (х — х’)ТС (х — х’). так как для всех j ф s либо Xj = х$ = 0, если
Xj — небазисная переменная, либо yj = y'j = 0. если Xj — базисная
переменная (в силу предположения о дополнительности). Измененные
значения базисных переменных являются линейными функциями от xs.
так что (х — х') — (xs — x's) v. где v — постоянный вектор. Следова-
тельно, Q (х) — Q (х') = (xs — x's) \2y's + (xs — xs) (vTCv) ], откуда ясно,
что при у'8 <Z 0 правая часть при достаточно малых (х& — х'^ > 0 отри-
цательна.
Кроме того, убывание Q (х) при увеличении xs>0, скажем, от х'8
до xi возможно лишь при y's < yl. В самом деле,
Q (х*)—Q (х') = 2 (а£ — x's) y's + (x's — Яз)2 vTCv.
Меняя ролями х' и хп. получаем
Q (#') — Q (х") = 2 (x's—x's) yl + (x's — x's)2 vTCv.
2 (yl — y's) = 2 (x"s — x's) vTCv^Q. Ho vTCv^= 0, так как для
положительно полуопределенных форм из vT Cv = 0 следует, что Cv = 0
(см. последнее упражнение, следующее за доказательством леммы 2),
а при Cv = 0 мы получаем из (9) Q (х") — Q (xf) = 2 (x's — x's) (x')TCv +
_|_ — xs)2vTCv = 0, что противоречит неравенству Q (xn) — Q (x') <Z
< 0. Следовательно, y's > y's-
Как и в симплекс-методе, мы требуем, чтобы все решения, порожден-
ные увеличением xs и пересчетом базисных переменных, оставались допу-
стимыми, т. е. Xj>0 для всех J. В этом процессе либо ys первым дости-
гает нулевого значения и, таким образом, может быть удален из базис-
ного множества, либо значение некоторого базисного хг достигает нуля
и удаляется.
Теорема 3. Если хт удаляется из базиса, то введение уг либо умень-
шает хТСх и выводит из базиса некоторое хГ1 или ys. либо сохраняет фик-
468
сированное значение хт Сх и выводит у8. Если из базиса удаляется хГ1*
можно применить повторно настоящую теорему; если же удаляется у8—
либо вначале, либо после увеличения уг, можно применить повторно пгео-
рему 2.
Доказательство. Для удобства мы будем проводить доказательство
применительно к системе (14); однако оно полностью приложимо и к об-
щему случаю.
Xl Х2 Xg Х4 Х5 —Л1 —Л2 У1 1/2 УЗ У4 УЪ Правые части
«11 «12 «13 «14 «15 «21 «22 «23 «24 «25
«11 «12 «13 «14 «15 «12 «22 «23 «24 «25 «13 «23 «33 «34 «35 «14 «24 «34 «44 «45 «15 «25 «35 «45 «55 & & & & & W W N & & & & & £ £ « £ £ -1 — 1 -1 — 1 — 1 0 0 0 0 0
• • • • * • • •
• • • • • • ★ •
Пусть запись системы (14) в векторной форме есть
Р+ Ргх2 + Рфз + Рьхь + Р$х$ + (Pe^i + РчЩ) +
+ Р1У1 + Р2У2 + РзУз + Р&ь + РьУь = Л). (15)
Предположим, что на некотором цикле мы имеем базис В и базисное допу-
стимое дополнительное решение (я0, я0, у0) с базисными переменными
х4, х2у хз> х^ л1> л2, причем значение у5 = у* < 0. В этом случае х5
будет новой базисной переменной, и мы предположим, что х^ будет выво-
диться. Это даст новый базис В'. Жирные точки ф в (14) указывают, что
данный столбец входит в базис В, а звездочки отмечают, что столбец Р5,
соответствующий х5, при образовании базиса В' заменяет вектор Р4 из В;
см. вторую строку из точек. Выведение я4 из базиса автоматически тре-
бует, чтобы у4 стало новой базисной переменной в базисе, следующем
за В'; см. ★ в строке В' схемы (14).
Пусть представления векторов Р5 и Р4 через базис В имеют вид
Р§ = Р 1^1 + Р 2а2 + Р ЗаЗ + Р 4а4 + (Р 6а6 + Р 7а?) + Р 5а5, (16)
Р4 = Р-|- Р2А2 + РзА3 -|- Р4^4 + (Р6^6 + Р7^?) + Р5^5* (17)
Покажем сначала, что в (17) А4<0. Полагая А = (Ai, Аг» Аз, А4), полу-
469
чаем из первых шести строк (17) соотношения (18) и (19)
1аи ^12 а1з = О
[^21 ^22 ^23 ^24] = О
(18)
(19)
Умножая (19) слева на X и обозначая квадратную матрицу через С4, мы
получаем в силу (18) ХС4ХТ = — Х4. Так как матрица ХС4ХТ является
положительно полуопределенной, (С4 представляет собой главный минор
положительно полуопределенной матрицы С*), то должно бытьХС^Х7 >0,
откуда Х4<0.
Случай Х4 < 0. Наша цель состоит в доказательстве того, что если
х± выводится из базисного множества после введения в него я5 и если
небазисная дополнительная к переменная, именно z/4, в дальнейшем
Увеличивается (при надлежащем пересчете значений новых базисных
переменных), то хь и у5 будут продолжать увеличиваться, а хтСх —
уменьшаться, пока у5 остается отрицательным. Здесь предполагается,
что Х4 < 0. (Для случая Х4 = 0 мы далее покажем, что хь и хтСх будут
оставаться неизменными, а у5 — убывать до нуля при увеличении i/4.)
Пусть представление Р4 через базис В' есть
Р4 = Р1^1 4- Р2^2 + Р3^3 + Р5^5 + (Р6^6 4" Р7^7) 4" Р5^5» (20)
а базисное решение, соответствующее базису 5', записывается в виде
Р о = Pi^ + Р 2Х2 4~ Р зхз 4“ Р ьхъ 4- {Р ел14" Р 7^2) 4- Р ьУь- (21)
Отметим, что в представлении (16) вектора Р5 через базис В коэффи-
циент а4 при Р4 положителен, поскольку х4 убывает с увеличением х5.
Так как (20) получено .исключением Р4 из (16) и (17) и так как Х4 < 0,
а а4 > 0, то Xg < 0. Если в решение вводится вектор Р4 с интенсивностью
у4 = 9 > 0, а значения базисных переменных соответствующим образом
пересчитываются, то мы получаем из (20) и (21)
Ро = Pi (xi — 9Хх) 4~ • • •-4~ Рз (хз—9Х3) 4~ Р5 (х5 — 9Х5) + • • •
...+р49+р5(У;-ох;). (22)
Таким образом, х5 = хь — 0Х б при возрастании ук = 0 > 0 также будет
возрастать, так какХб < 0. Кроме того, для целей нашего доказательства
мы можем считать, что возрастание z/4 вызывается, возрастанием х5,
а не наоборот, так что фактически мы воспроизводим только что рас-
смотренную ситуацию, в которой увеличивался х5 и пересчитывались
другие базисные переменные, с той только разницей, что здесь в базисное
множество входит у^ вместо ж4. Следовательно, увеличение х5, как и выше,
вызывает уменьшение хтСх, пока значение у5 при пересчете базисного
решения с увеличением х5 остается отрицательным.
Случай Х4 = 0. С другой стороны, если в (17) Х4 = 0, то мы должны
положить в (20) Xj = XJ, так как представление Р4 будет одним и тем же
и в В и в В'; следовательно, Х5 = 0. В этом случае ХС4ХТ = — Х4 = 0,
й поэтому в силу положительной определенности матрицы С мы имеем
С4Х = 0. Кроме того, должно иметь место X = 0, так как из X ф 0 сле-
довала бы зависимость первых четырех столбцов в (18) и (19), что невоз-
470
можно, так как в этом случае квадратные матрицы коэффициентов в (18)
и (19), а также В были бы вырожденными. Полагая в (20) и (21) Ai = . . .
... = А5 = 0, мы видим (это имеет место и в общем случае), что Р4 зави-
сит только от столбцов и yi и поэтому значения х$ — OAj в (21) остаются
при возрастании у4 = 0 неизменными.
Поскольку на знак у^ ограничений не накладывается, у± можно уве-
личивать, пока Уь не выйдет из базисного множества с нулевым значе-
нием (так как все значения остаются неизменными). Следовательно,
при таком изменении базиса значение хтСх не меняется; однако введение у4
в базисное^, множество и удаление из него у5 порождают новое базисное
множество, удовлетворяющее свойству дополнительности. Таким обра-
зом, мы можем еще раз применить теорему 2, уменьшая хтСх.
АЛГОРИТМ КВАДРАТИЧНОГО ПРОГРАММИРОВАНИЯ
Шаг 1. (Начало алгоритма.) Пусть ж0 — базисное допустимое реше-
ние системы Ах = Ъ, ж>0 с базисными переменными х^, Xj2, . . ., Xj^',
выбираем в качестве исходного множества базисных переменных Xj рас-
ширенной задачи эти дополнения небазисных Xj и набор Л/.
Рис. 24-4-1. Блок-схема алгоритма для квадра-
тичного программирования.
Шаг II. Для значений из базисного решения определим min у] =
Если у?>0, то процесс окончен — решение оптимально. Если y°s < 0,
введем в базисное множество xs; если ys выводится из базисного множе-
ства, повторить шаг II. Перейти к шагу III, если я, выводится из базиса.
Шаг III. Вводим уг в базисное множество. Если ys выводится из ба-
зиса, возвратиться к шагу II; в противном случае, если из базиса выво-
дится некоторое хГ2, повторить inar III с г2 в роли г.
471
Теорема 4. Итеративный процесс конечен.
Упражнение. Доказать теорему 4.
Упражнение. Распространить результаты этого параграфа на случай
выпуклой целевой функции, содержащей как квадратичные, так и линей-
ные члены.
24-5» задачи
1. Показать, что задача с ограниченными переменными 24-3-(12),
(13), (14) эквивалентна исходной выпуклой вырожденной задаче.
2. Показать, что если в условиях 24-3-(15), (16), (17) ДРд принад-
лежит базису, то где t^p, ему не принадлежит. Показать, что если
Ард принадлежит базисному множеству, то, согласно симплексному кри-
терию, Д^д не является кандидатом на включение в базисное множество.
3. Решить приведенную ниже задачу распределения обоими изло-
женными в § 24-3 методами. Который из них оказывается легче?
Сумма
*11 *12 *13 *14 9
*21 *22 *23 *24 9
*31 *32 *33 *34 9
Сумма 5 10 4 8
Здесь издержки на транспортировку единицы из i в ] являются возра-
стающими функциями транспортируемого количества:
Издержки на единицу
1-я единица 1
2-я единица 2
3-я единица 3
4-я единица 4
9-я единица 9
4. Показать, что в задаче 3 суммарные издержки ф (х) на транспор-
тировку х = Xij единиц из i в j равны ф (х) = х (х + 1) /2, если х — целое
число. Показать, что если мы положим ф (х) = х (х + 1) /2 для дробных
значений ж, то значения х^ в оптимальном решении будут дробными.
5. Показать, как найти решение задачи распределения с целочислен-
ными переменными, если целевая функция является выпуклой и вырож-
денной. Говоря более точно, найти целочисленные xtj 0, min z, удовлет-
воряющие условиям
S Xij = ai, (i = l, 2, т)
j=l
т
2 Xij — bj, (j = 1, 2, ..., n)r
i=i
3 S 4>u(*ij) = z(min),
i=l j=l
где at и bj — целые, a (xi}) — выпуклые функции (например,
Фи (хи) = или Фг/ (xu) = xij (xtj + l)/2).
Глава 25
НЕОПРЕДЕЛЕНН ОСТЬ
Большинство прикладных задач программирования в конечном счете-
содержат неопределенность либо в технологической матрице, либо в пра-
вых частях. Однако рассмотренные до сих пор методы не учитывают неоп-
ределенную природу коэффициентов задачи. В период 1955—1960 гг.
различные авторы пытались распространить методы линейного програм-
мирования на задачи оптимизации тех или иных целевых функций при
ограничениях, коэффициенты которых подвержены случайным изме-
нениям (Данциг [9], Фергюсон и Данциг [2]). Одна из основных трудно-
стей заключается в том, что эта проблема допускает много формулировок,
для каждой из которых получены лишь разрозненные результаты (см.
Маданский [1], [3], [4]). В настоящей главе мы изучим некоторые
из задач, решенных в этой области, предупреждая читателя, что наше
изложение является неполным и что необходимы обширные дальнейшие
исследования.
По поводу вероятностных понятий и статистической теории, исполь-
зуемых в этой главе, мы отсылаем читателя к книге Феллера [1].
25-1. СОСТАВЛЕНИЕ ПЛАНОВ В СЛУЧАЕ ПЕРЕМЕННЫХ
ИЗДЕРЖЕК
Напомним сначала, что в практике планирования употребительны
два существенно различных подхода — краткосрочное и долгосрочное
планирование. В последнем случае влияние случайных факторов сво-
дится к минимуму при.помощи обычного в таких задачах приема — введе-
ния в систему значительной свободы. Например, уровни потребления,
скорости истощения ресурсов или износа оборудования всегда плани-
руются с некоторым завышением; нормы времени на перевозку или
на производство назначаются с большим превышением против реальных
потребностей. В действительности система в целом обеспечивается зна-
чительной свободой в надежде на то, что последняя будет служить своеоб-
разным амортизатором, позволяющим обеспечить осуществление общих
целей плана и его выполнение во времени, несмотря на непредвиденные
события. Говоря точнее, свобода, запас, вводится в систему таким обра-
зом, чтобы при любом случайном непредвиденном событии выбираемые
нами процессы оставались бы допустимыми. Процессы, удовлетворяющие
этому требованию, мы будем называть перманентно допустимыми.
Влияние случайных событий сводится к минимуму также путем
введения в систему значительной вялости. Под этим мы понимаем, напри-
мер, следующее. Затраты экзогенных ограниченных факторов в системе
оцениваются с большим занижением, так что представляется весьма мало-
4П
вероятным, что выбранное нами множество процессов окажется недопус-
тимым из-за нехватки ресурсов.
На практике долгосрочные планы приходится часто подвергать пере-
смотру в силу назойливого вторжения случайных элементов задачи.
По этой причине главное достоинство — если таковые вообще имеются —
долгосрочного плана заключается в возможности принятия немедленного
решения — скажем, о распределении фондов или о разработке более
совершенной технологии.
При краткосрочном планировании применяются многие из приемов
введения свободы и вялости, используемых в долгосрочном случае. Основ-
ные различия состоят в большем внимании к деталям и в краткости пла-
нового периода. Пока возможности значительно превышают требования
или уровни спроса либо же удовлетворение спроса можно сдвинуть во вре-
мени, этот подход не выдвигает никаких проблем, так как в этом случае
оказывается возможным осуществить план во всех его деталях. Однако
при наличии дефицита план, составленный на основе подобных приемов,
может привести к действиям, весьма далеким от оптимальных, в то время
как излагаемые здесь новые методы в случае своей применимости могут
дать значительную экономию..
МИНИМАЛЬНЫЕ ОЖИДАЕМЫЕ ЗАТРАТЫ
Эксперт по питанию хочет посоветовать своим приверженцам при-
держиваться диеты с минимальными затратами, не зная наперед цен
(Штиглер [1]). Так как цены на пищевые продукты проявляют —
за исключением тенденций типа инфляции — известную склонность
к колебаниям в зависимости от условий погоды, от предложения и т. п.,
он предполагает, что на каждый продукт имеется не фиксированная цена,
а некоторое распределение возможных цен, и пытается определить диету,
удовлетворяющую определенным требованиям по питательности и мини-
мизирующую ожидаемые суммарные издержки. Пусть Xj — количество
фунтов /-го пищевого продукта, подлежащее закупке, a pj — его цена.
Пусть atj — количество z-го питательного вещества (например, витамина
Л), содержащееся в весовой единице /-го продукта, а bt — минимальное
количество этого питательного вещества, необходимое индивидууму для
поддержания сил и здоровья. Тогда значения должны быть выбраны
так, чтобы
S auXj > Ъг, Xj > 0. (z = 1, 2, ..., тп) (1)
Затраты на эту диету составят
С=^Р}х}. (2)
j—i
Однако Xj выбираются до того, как станут известными цены, так что при
фиксированных значениях Xj суммарные затраты С оказываются случай-
ной величиной, представляющей собой взвешенную сумму случайных
величин Pj. Мы будем обозначать математическое ожидание случайной
величины и через Ми или М(и). В соответствии с этим математическое
ожидание затрат при такой диете составит, очевидно,
Е=МС = ^Р)Х1, (3)
j
где Pj — ожидаемая цена продукта /. Поскольку pj предполагаются
Ш
заранее известными, наилучшим выбором для Xj будет тот,, при котором
•Я; удовлетворяют (1) и минимизируют Е. Поэтому мы получаем следую-
щую общую теорему.
Теорема 1. Если цены за единицу pj в (2) представляют собой случай-
ные величины,, распределение которых не зависит от Xj, то решение,
дающее минимальные ожидаемые затраты, получается путем нахожде-
ния ж7>0, удовлетворяющих (1) и минимизирующих С, в котором Pj
заменены на pj = М (р^.
С другой стороны, если каждое pj зависит от Xj, мы можем записать
Pjxj — Фу (xjyPj)- Вспоминая, что математическое ожидание суммы равно
сумме математических ожиданий, получаем
Е = МС= 2 Pj)= 2 <pj(xj), (4)
3=1 3=1
где ф (Xj) — некоторые (не обязательно линейные) функции от Xj. Спе-
циальные методы минимизации Е в случае, когда ф (Xj), выпуклы отно-
сительно Xj, были изложены в § 24-3.
Следующий пример иллюстрирует случай, когда ожидаемые издержки
не являются линейными по Xj. Пусть Xj — объем производства /-го товара,
а ограничения представляют ограниченность производственных возмож-
ностей. Предположим, что имеются издержки трех видов: детерминиро-
ванные издержки на производство cQj, детерминированные издержки
на хранение товаров, не востребованных в результате случайного спроса,
и детерминированные издержки от нехватки возникающие, когда
случайный спрос превышает предложение. Тогда
Е = 3 CojXj 4- 2 (Xj — dj | Xj > d}) +
i з
+ 2 (°G‘ X3 I xj <
3
где символ M (A | В) понимается как условное математическое ожидание А
при условии В. Хотя эта задача сформулирована как одношаговая и содер-
жит неопределенность только в целевой функции, ее можно поставить
и как двухшаговую задачу, в которой неопределенность будет фигури-
ровать уже в ограничениях. В этом случае она становится задачей того
класса, который описан в § 25-2 и исследован более полно в § 25-3,
а также в работе Эль-Маграби [2].
МИНИМАЛЬНАЯ ДИСПЕРСИЯ ПРИ ФИКСИРОВАННЫХ ОЖИДАЕМЫХ
ЗАТРАТАХ
Возвращаясь снова к нашей проблеме питания, отметим, что может
оказаться желательным управлять дисперсией V ожидаемых затрат. Таким
образом, решение задачи (1)у (3), дающее низкие ожидаемые затраты,
но проявляющее значительную неустойчивость, может оказаться не столь
желательным, как решение,, проявляющее большую степень устойчивости.
Именно такой случай был рассмотрен Г. Марковицем в его исследованиях
по выбору портфеля ценных бумаг (Марковиц [1]).' Биржевые макле-
ры часто предлагают своим покупателям большой выбор акций, одни
из которых расцениваются ими как весьма надежные, но приносящие
относительно низкие доходы, тогда как другие могут давать высокий
средний доход, обладая в то же время большой дисперсией. Таковы,
например, акции на разведку нефти, в которых колебания зависят,, ска-
жем, от того, будет ли вообще обнаружена нефть. Целью подобного иссле-
дования является указание для каждого из множества уровней ожидаемых
475
прибылей того набора ценных бумаг, который минимизирует дисперсию*
дохода (рис. 25-1-1).
Теперь покупателю предоставляется решить, какую комбинации*
«уровня дохода» и «уровня риска» (min У) он предпочитает.
Предположим, что цена не зависит от Xj и что нам известны дисперсия
а* цены конкретного товара pj и ковариация Ojk между двумя ценами р;
и pk. Положим = оjakQjk, где коэффициент корреляции между двумя
ценами удовлетворяет условию —1 < +1. Так как все Xj единиц,
товара покупаются по одной и той же цене дисперсия величины x^pj,
Ожидаемая прибыль (Е)
Ожидаемая приЬыльЬЕ)
Рис. 25-1-1. Минимальная дисперсия является выпуклой
функцией математического ожидания прибыли.
равна zjoj, а ковариация между Xjp^ и xhpk равна x^xh<oiK. Отсюда следует,
что дисперсия V случайной величины Е определяется квадратичной формой
К = Я[С-£]!= 2 2 (<Ъ> = <>*) (5)
7=1 Й=1
Если, в частности, цены на пищевые продукты сильно коррелировав
ны, так что для всех практических целей можно считать = 1 и =
= то в этом случае было бы целесообразно заменить У1/2 ограничи-
вающим его линейным выражением, указанным в (6)
1
V2 < x1ai + х2а2 + ... + жп<тп. (6>
Знак равенства здесь имеет место в том случае, когда все коэффициенты
корреляции Qjk = 1. С другой стороны, если все цены независимы, так
ЧТО Qjk = 0, то
У = ф1 + ф22+...+^. (6л = 0) (7)
Обратимся теперь к общей задаче определения решения (1), (3),
(5), минимизирующего У при фиксированном Е.
Случай Г. Ух/2 линейно. Если имеет место неравенство (6), то мы решаем
задачу определения min У1/2 при условии £’<£'*, где Е* — некоторая
верхняя граница, которую мы хотим наложить на математическое ожи-
дание затрат. Так как это ограничение линейно, мы можем проанализи-
ровать влияние на У изменения Е*, рассматриваемого как параметр.
В этом случае мы имеем стандартную задачу параметрического програм-
мирования (см. § 11-3).
Случай 11\ У представляет собой сумму квадратов. Если справедливо
равенство (7), то функция У оказывается выпуклой и вырожденной и вы-
пуклые функции х] можно аппроксимировать ломаными линиями. При
этом задача снова сводится к стандартной задаче параметрического про-
граммирования. При желании этот метод можно сочетать с методом, учи-
тывающим ограничения сверху на переменные. Здесь мы варьируем один
из свободных членов. См. § 11-3 и 24-3. Можно; однако, рекомендо-
476
вать и следующий прием. Заменим V на
V =^ + Ф22+ • • • +4<& + ЛЯ*. (Е^Е*) (8)
Снова используя аппроксимацию х* посредством ломаной, решим сначала
задачу для значения к = 0. Легко видеть, что это соответствует случаю
оо. Если теперь постепенно увеличивать /с, то определится кри-
тическое значение к = при котором решение уже не будет оптималь-
ным. Это приведет к одной или нескольким переменам базиса, после чего
решение снова станет оптимальным. После этого к снова можно увеличи-
вать до достижения нового критического значения к = к2 и т. д.
Упражнение. Показать, что описанный процесс представляет собой
в скрытом виде не что иное, как первый метод параметрического линейно-
го программирования. Развить другие возможности, основанные на § 24-3.
Почему выше вместо Е используется Е*1
По-видимому, целесообразно, однако, вместо постепенного увеличе-
ния к выбрать заранее некоторое множество его дискретных значений.
Решение даст нам ряд различных пар значений Е* и V, которые можно
использовать для нанесения точек на кривой. Если желательно иметь
лучшее распределение значений Е*, то для определения того, какие новые
значения к надлежит выбрать, можно использовать график зависимости
Е* от к.
Случай III: V имеет общий вид. Так как квадратичная форма V
является положительно полуопределенной, ее можно привести к сумме
квадратов при помощи подходящим образом выбранного линейного преобра-
зования (случай II); следовательно, описанный метод может быть применен
для решения задачи и в общем случае. С другой стороны, можно исполь-
зовать и какой-нибудь общий алгоритм для квадратичного программиро-
вания, скажем метод Марковица [4] или Вулфа [2], сочетая его с
методом параметрического программирования для правых частей (см.
§ 11-3). Однако и здесь рекомендуется использовать аналог (8) с чле-
ном, содержащим Е*, взвешенное посредством параметра к.
Упражнение. Объединить методы решения задач квадратичного про-
граммирования и параметрического программирования, изложенные в па-
раграфах 24-4 и 11-3, для решения задачи о минимальной дисперсии.
25-2. ПЛАНИРОВАНИЕ ПРИ НЕОПРЕДЕЛЕННОМ СПРОСЕ
Рассмотрим следующий простой случай. Предприятие имеет в нали-
чии 100 объектов, которые можно транспортировать по цене 1 долл, за
штуку на внешний рынок для удовлетворения неопределенного спроса
d. В случае, если спрос превзойдет предложение, необходимо удовлетво-
рить избыточный спрос путем закупок на внутреннем рынке по цене 2 долл,
за штуку. Уравнения, которым должна удовлетворять система, имеют
следующий вид:
100 = я-|- у (ж, у, v, $>0)
d = x +i? — s, (1)
С = х + 2v
где Гх — число объектов, транспортируемых с предприятия,
\у — число объектов, сохраняемых на предприятии,
fv — число объектов, закупленных на внутреннем рынке,
I s — превышение спроса над предложением,
477
d — неизвестный спрос, равномерно распределенный между 70 и 80г
С — суммарные издержки.
Мы рассматриваем транспортировку и зайуйку как этапы двухшагового
процесса. На первом шаге принимается решение о количестве транспорти-
руемых объектов, совместимое с имеющимся запасом. На втором шаге
возникает неизвестный спрос.
Описанный выше простой пример принадлежит к общему классу
двухшаговых задач, имеющих следующую структуру. На первом шаге
определяются величины я7>0, 0, удовлетворяющие условиям
п
2 atjXj = bt, (i = 1, 2, ..., т)
jZ1 _ . • (2>
2 = (к = 1, 2, ..., р)
где начальные запасы bt, i = 1, 2, . . ., т заданы. Здесь Xj 0 представ-
ляют решения первого шага, имеющие своим результатом определенные
величины uh, поступающие в наше распоряжение для второго шага.
На втором шаге определению подлежат величины vh и Sk, для которых
dk = Uk + vk — Sk- (Л = 1, 2, ..., р) (3)
Здесь dk — неизвестный спрос с заданным распределением вероятностей,
Vh — нехватка предложения и sk — превышение предложения над спро-
сом. Предполагая для удобства, что в случае нехватки никаких закупок
на внутреннем рынке не производится, мы можем записать суммарные
издержки в виде
п р
С — 3 cjxj fk(&k (4)
i=i h=i
где vk = 0, если > d&. Здесь Cj представляют собой издержки от осу-
ществления процесса /, &fk^ 0 — Доход от удовлетворения одной единицы
спроса. Таким образом, всегда выгодно продавать столько из предложен-
ного количества ид, сколько это возможно, так что (dk — Vk) —
min (uk, dk) и
n p
C — 3 3 Amines, dft). (5)
1 fe= 1
Ясно, что для любого выбора Xj и uh, совместного с уравнениями перво-
го шага, значение С зависит от этого выбора и от неизвестного спроса.
Следовательно, при фиксированном выборе Xj и иь математическое ожида-
ние С определяется как
МС = 2 СЛ — S min (uk, dk), (6)
i fe=i
так как математическое ожидание min (u^, d*) зависит от Uh- Обозначим эту
функцию от Uh через
(pft (uk) = М min (uk, dh). (7)
Если известно распределение спроса d&, то функция фд (и^ легко вычи-
сляется. Пусть dk принимает значения 1,2 с вероятностями 1/2, 1/2. Тогда
нетрудно найти фд (uk).
478
Объем поставок <иЛ> Объем продажи dA”vft=min dk) Математическое - ожидание дохода 1 Vk <uk> (3)
при dj=i (1) при db—2 (2)
“а = 0 0 0 0
0<«й<1 uk Uk Uk
Uft = l 1 1 1
1<“й<2 1 Uk
“Л = 2 1 2 3/2
2 uk 1 2 3/2
1 Здесь величины в столбце (3) получаются путем ум-
ножения величин столбца (1) на “р1 = 1/2, величин столбца (2)
на р2=1/2-и сложения.
(8)
В общем случае для вычисления ф (и) = М min (и, d), когда d может
принимать последовательные значения ei < е2, с вероятностями
t ;
Pi, Рг, • • •» Pt, 3 Pi = 1> отметим, что
1=1
min (u, d) = и, d> и,
min (и, d) = d, d и.
Пусть ег^<и<ег. Тогда
ф (и) = и | Р (d > и) + Р '(d и) М (d | dи).
Поэтому
ф (и) = и (рг + Рг+1 + • • . + pi) 4- (eiPi + е2?2 + • • • + er-lpr-l) —
= и (1 — pi — р2— ... —pr-i) + (etfi + е2р2 + ... + ег-1Рг-1), (10)
где при г = 1 мы полагаем е0 = 0 и р0 = 0. Таким образом, ф (и) представ-
ляет собой ломаную, исходящую из начала координат и имеющую началь-
ный наклон $! = 1; в точке и — Cf на-
клон убывает до s2 = 1-— pi и т. д.
(см. рис. 25-2-1).
Обращаясь к § 24-3, посвящен-
ному вырожденным выпуклым функ-
циям, отметим, что функция ф (и) выпукла,
так как наклоны отдельных участков на
рис. 25-2-1 убывают. Действительно,
st — $f+i = Pi > 0. Тем самым мы уста-
новили следующий результат, сообщен-
ный автору настоящей книги Г. Скарфом.
Ожидаемый
доход
Р и с. 25-2-1. Максимальный ожи-
даемый доход есть вогнутая функ-
ция от поставленного количества^
Теорема 1. Суммарные ожидаемые
издержки при неопределенном спросе яв-
479
.ляются выпуклой вырожденной функцией
п р
МС = s CjXj— 2 /лфл (Uft), (И)
1 л==1
где <pk (uk) представляет собой ломаную, наклон участка которой между
двумя последовательными значениями спроса = ег ь и dk = er+1k равен
вероятности превышения спроса erk-
Теорема 2. Для минимизации ожидаемых издержек следует найти
> О, ид > 0, удовлетворяющие (2) и минимизирующие выпуклую
вырожденную функцию (11).
НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ СПРОСА
Для того чтобы проиллюстрировать случай непрерывного распределе-
ния, рассмотрим небольшой двухшаговый пример, описанный выше в (1).
Издержки даются формулой.
С = Xi + 2max (0, d—х4), (12)
где d непрерывно распределено между 70 и 80. Определение математическо-
го ожидания издержек требует вычисления М max (0, d — xt) как функции
ЮТ Xi'.
< 70
70<^ < 80
(13)
Xi > 80
Следовательно, из (12) мы имеем
МС =
' 150—Xi
а?1 + (80—Д1)2
Xi 10
OOiCTO
70<Ж!<80
Xi >80
(14)
Отсюда следует, что minX1 МС = 77,5 достигается при Xi = 75, т. е. что
в этом случае наилучшим решением является транспортировка количе-
ства, равного математическому ожиданию спроса.
Упражнение. Видоизменить описанную выше задачу таким образом,
чтобы транспортировка количества, равного математическому ожиданию
опроса, не всегда была оптимальной.
Когда транспортировка ожидаемого спроса является оптимальной?
Следующий результат, принадлежащий Маданскому [2], представляет
собой обобщение более ранних результатов Тейла [1] и Саймона [1].
Он дает достаточное условие того, чтобы решение задачи линейного
программирования, в которой спрос заменен величиной его математи-
ческого ожидания, служило бы также решением задачи планирования
при неопределенном спросе. Если С можно представить в виде Ci (d, х) +
С2 (d), где Ci (d, х) есть линейная функция от d при любом х, а С2 (d)
зависит только от d, но не от х, то х, являющееся решением] задачи
линейного программирования, в которой d заменено на М (d), служит
также решением задачи с неопределенностью.
Упражнение. Доказать этот результат. Удовлетворяет ли приведен-
ный выше пример сформулированному условию достаточности?
480
25-3. о МНОГОШАГОВЫХ ЗАДАЧАХ 1
ДВУХШАГОВАЯ ЗАДАЧА С ОБЩЕЙ ЛИНЕЙНОЙ СТРУКТУРОЙ
Сейчас мы установим одну общую теорему о выпуклости для двух-
шаговой задачи, представляющей собой своеобразную базу индук-
ции для многошаговой задачи. О значении этой выпуклости мы скажем
несколько слов ниже. Предположим, что общая двухшаговая модель,
частным случаем которой является 25-2-(2), имеет следующий вид:
&1 = ^4цХ1, (Xi, Х2 0)
Ь2 = A21Xt + Л22Х2, (1)
f = ф (Хь Х21 е2),
где Ац — заданные матрицы, — заданный вектор исходных запасов,
Ъ2 — неизвестный вектор, компоненты которого зависят от некоторого
множества параметров Е2, а С — издержки, зависящие от Хь Х2 и Е2.
Мы предположим, что события развиваются следующим образом.
1. Выбирается вектор Xt > 0, удовлетворяющий условию Ь± — АцХ^
Обозначим через Qi множество возможных векторов Х4. Предполагается,
что Qi не пусто.
2) Случайно выбирается Е2, как точка из многомерного простран-
ства выборок 5 2 с известным распределением вероятностей. Е2 опреде-
ляет Ъ2.
3) Выбирается вектор Х2 > 0, удовлетворяющий условию Ъ2 =
= А21X1 + А22Х2. Обозначим через Q2= (Х41 Е2) множество возможных
векторов Х2. Предполагается, что Q2 не пусто; иначе говоря, для любых
выборов Xi и Х2, сделанных ранее, существует хотя бы один такой вектор 1 2.
Задача состоит в выборе Xi, затемХ2 таким образом, чтобы матема-
тическое ожидание С было минимальным.
Замечая, что сумма выпуклых функций, взятых с неотрицательными
весами, выпукла и что математическое ожидание представляет собой имен-
но такую сумму (или в общем случае — интеграл Стилтьеса), мы прихо-
дим к следующей полезной лемме.
Лемма 1. Если функция <р (X | Е) выпукла по X £ Q при любом выборе
Е из пространства выборок S с известным распределением вероятностей,
то функция ф (X) = ЛГф (X | Е) выпукла.
Е
Теорема 1. Если ф(Х1, X 21Е^ — выпуклая функция относительно
Xi £ Qi, Х2 С Q2 (Xi | Е^, то функция
фо (Xi) — Af [inf ф (Xj, Х2|Е2)1 (2)
Е2 Х2
выпукла и обладает тем свойством, что Xi = X* является решением
задачи с неопределенностью, если
Фо (X*) —min фо (Xi).
1 Материал этого параграфа основан на статье Данцига [9].
2 Это предположение можйо интерпретировать как обеспечивающее либо доста-
точное количество свободы в системе, либо достаточное количество «вялых» перемен-
ных, так что множество перманентно допустимых способов (+, JT2) не пусто.
31 Дж. Данциг 481
Математическое ожидание здесь берется по распределению Е2, наиболь-
шая нижняя грань1 (inf)— по всем Х2С й2 (Xi\E2).
Доказательство2. Ясно, что для минимизации Л£ф (Хь Х2|Е2), если
Xi выбрано, а Е2 определено случайным образом, Х2 следует выбирать
так, чтобы минимизировать ф (Х£, Х21 Е2) при фиксированных Xi и Е2.
Таким образом, издержки при’данных Xi и Е2 определяются как
^(Х,\Е2) = inf ф(Хь Х2|Я2). (3)
Х2 6 ^2
Тогда математическое ожидание издержек при данном Xi будет попросту
условным математическим ожиданием ф± (Х± | Е^\ обозначим эту величи-
ну через фо (Х^. Таким образом, оптимальный выбор Х^ минимизирую-
щий математическое ожидание издержек, сводится к выбору Хр мини-
мизирующего фо (Х^. Остается установить только свойство выпуклости.
Покажем сначала, что функция ф! (Xi | Е2) при ограниченных ф4 выпукла
по Xi g Если это так, то заключение о выпуклости фоРн) немедленно
следует из леммы. Предположим, что ф4 (Xi | Е2) не выпукла; тогда сущест-
вуют три точки X', Х[, X"', g £24, Х[" = КХ[ + [iX[, (X + р = 1,0<
для которых условие выпуклости нарушается, т. е.
хФ1 (х; IЕ2) + ИФ1 (Х'11 е2) < ф! (х;1 е2) (4)
или
Лф1(х;|^2) = Иф1(х;|^2) = ф1(х;'|£2)-80. (е0>0) (5)
Однако для любого е0 > 0 существуют такие X' и X", что
Ф1 (Хх1Е2) = Ф (Хр Х2\Е2) — (О^е1<ео) (6)
Ф1(х;|е2) = ф(х;, х''\е2)-*2.
Полагая X’" = XX' + рХ", отметим, что в силу предположенной нами
линейности модели (1) мы будем иметь (ХХ' + рХ") С Q2(X/' | Е2). Следова-
тельно, по выпуклости ф
Хф (х;, х21 е2) + рф (х;, х; | е2) > Ф (х;\ х-1 е2) . (7)
Отсюда, согласно (6),
хФ1 (X;IЕ2) + рФ1 (X'i। е2) >Ф (х;, х;| е2)-(8)
а по (5)
ф1(Х7|£2)>ф(Х7, x;z|£2)-Z81-p82+80, (9)
где 0 <X8i + рг2 < 80. Но это противоречит предположению
Ф1(х; |я2)= inf ф(х;', х2|е2).
X2f ^2
Доказательство для случая неограниченной функции ф! мы опускаем;
см. работу Данцига [9]. Иллюстрация использования этой теоремы при
решении конкретной задачи с неопределенностью дана в гл. 28.
1 Наибольшая нижняя грань вместо минимума используется здесь во избежание
случая, когда минимальное значение не достигается ни для одной допустимой точки
Х2 6 Q2 или С &р В последнем случае подразумевается, что не существует Xit
на которых достигался бы минимум, но зато существуют на которых достигаются
значения, сколько угодно близкие к минимуму.
2 Идея этого доказательства принадлежит И. Гликсбергу.
482
МНОГОШАГОВАЯ ЗАДАЧА С ОБЩЕЙ ЛИНЕЙНОЙ СТРУКТУРОЙ
Предположим, что задача имеет следующую структуру
Й4 = АцХи
Ь2 = A21Xi + А22Х2,
Ь3 = ЛЛ + ^32^2 + ззХ3,
^4== ^4-41-Xi А&ХъЛ" А^Хз^ A^Xfr (Ю)
= Am\Xi + Ат2Х2 + АтзХ3 + • • • + АттХт,
С = ц> (Х19 Х2, ..., Хт | Е2, Е3, ..., Ет).
Здесь bi — заданный вектор, bt (i = 2, . . ., т)— случайный вектор,
компоненты которого являются функциями точки Ei9 подчиненной извест-
ному многомерному распределению, Ац — известные матрицы. Реше-
ния принимаются в такой последовательности: сначала выбирается неотри-
цательный вектор Xi уровней интенсивности процессов на первом шаге,
удовлетворяющий ограничениям первого шага bi — АнХ^ Выбираются
случайным образом значения компонент вектора Ь2 путем определения
точки Е2. Выбирается вектор Х2, удовлетворяющий ограничениям второ-
го шага Ь2 = Л21Х4 + А22Х2 и т. д. по индукции для третьего и дальней-
ших шагов. Далее предполагается, что
а) компоненты векторов Xj неотрицательны;
б) существует хотя бы один вектор Xj, удовлетворяющий ограниче-
ниям j-ro шага при любых выборах Х4, Х2, . . ., Xj_i9 удовлетворяющих
предыдущим ограничениям или при любых исходных bi9 Ъ2, . . ., Ьт\
в) суммарные издержки С представляют собой выпуклую функцию
от Х^ . . ., Хт, зависящую от значений выбранных точек Е2, Е3, . . ., Ет.
Теорема 2. Эквивалентную (т — 1)-шаговую задачу с выпуклой целевой
функцией можно получить, опуская ограничения т-го шага и заменяя
выпуклую функцию издержек ф на
фтп-i(Xi, Х2, . • Xm~i | Е2, ..., Em~i) —
= М inf ф (Xj, Х2, ...,Хт\Е2, ...,Ет), (11)
Ет Хт € Q т
где Qm — множество допустимых векторов Хт, удовлетворяющих огра-
ничениям тп-го шага.
Поскольку доказательство сформулированной теоремы аналогично
доказательству для двухшагового случая, мы не будем останавливаться
на деталях. Возможность получения функции издержек для (т —1)-го
шага из тп-го шага является простым следствием полной определенности
оптимального поведения для zn-го шага. Иначе говоря, при любом состоя-
нии (Xt, Х2, . . ., Xm~i) в начале этого шага можно определить оптималь-
ный образ действий и вычислить минимальные ожидаемые издержки.
По сути дела это есть стандартный подход динамического программирова-
ния. Читателя, интересующегося методами, основанными на этом подхо-
де, мы отсылаем к книге Р. Веллмана [1] по динамическому програм-
мированию.
Хотя мы установили существование выпуклых функций, позволяю-
щих свести тп-шаговую задачу к эквивалентным ей (тп —1)-шаговой,
(тп —2)-шаговой, . . ., одношаговой задачам, фактическое вычисление этих
функций — за исключением разве лишь простейших случаев — предста-
вляется маловероятным. Мы установили теорему о выпуклости не в каче-
483
31*
стве решения тп-шаговой задачи, а лишь в надежде, что она наведет на след
эффективной вычислительной теории для таких моделей. Не следует
забывать, что любой процесс, дающий локальный оптимум, приведет
к истинному (глобальному) оптимуму только в случае выпуклости целевой
функции. Это представляется весьма важным, так как многомерные задачи
с невыпуклыми функциями, заданными на невыпуклых областях, при-
водят, как правило, к локальным оптимумам, и задача обследования дру-
гих частей области в поисках других экстремумов представляется, вообще
говоря, почти безнадежной (Данциг и Маданский [1]). По этому поводу
см. также § 26-3.
ОБЩИЙ ДВУХШАГОВЫЙ СЛУЧАЙ
Если множество возможных реализаций случайного вектора Ь2 есть
Ъ™, Ь<2>, . . с вероятностями рьр2, • • .,Ра, (2pf = 1), то для неболь-
ших к (скажем, &=3) решение нетрудно получить непосредственно методами
линейного программирования. Поскольку эта конкретная структура яв-
ляется весьма специальной, представляется правдоподобным, что для боль-
ших к можно развить специализированные методы, которые могут быть
использованы для приближенного решения в случае общего распределения
вектора Ь2. При к = 3 задача эквивалентна определению вектора
и векторов X™, Xf\ Х(23>, для которых
&i = АцХ1,
b^A^ + A^X™,
Ь^ = А21Х, +Л22х® (12)
6<’> = Л21Х1 + А22Х™
МС = YiXi + P1Y2X2 ’ + Pz^iXf+р2у2Х*> = z (min),
где мы для простоты предположили целевую функцию линейной. Таким
образом, общая двухшаговая задача линейного программирования с неопре-
деленным вектором правых частей сводится к задаче линейного програм-
мирования специального вида (12).
Упражнение. Разработать алгоритм для решения систем типа (12)
при больших /с, переходя к двойственной задаче и используя затем прин-
цип разложения (гл. 23). Воспользоваться многократным появлением
А22 и у2.
25-4« задачи
1. Доказать, что квадратичная форма 25-1-(5) является положи-
тельно полуопределенной, т. е. F > 0.
2. (Повторение.) Доказать, что любую квадратичную форму Q при
помощи линейного преобразования можно привести к сумме и разности
квадратов новых переменных. Показать, что если Q содержит разности
квадратов, то она не может быть положительно определенной.
3. Показать, что если Q положительно полу определенна, то она пред-
ставляет собой выпуклую функцию.
4. Показать, что когда V и х удовлетворяют 25-1-(1,3,5) и
где Е* — параметр, то min V есть монотонно убывающая функция
ют Е*, если допустить, что Е* может принимать возрастающие значения.
484
5. Показать, что если Q — произвольная выпуклая функция от х,
то min Q есть выпуклая функция от Е, где Е и х удовлетворяют
25-1-(1,3).
6. Решить задачу 25-2-(1), используя дискретное распределение d =
= 70, 71, 72, . . ., 80 с вероятностью 1/11.
7. а) Решить транспортную задачу
di d2 d3 d^
*11 2 *12 3 *13 4 *14 1
*21 7 *22 2 *23 5 *24 1
*31 4 *32 3 *33 2 *34 2
если потребности равны
d1 = 3 с вероятностью 1,
d2 = 3 с вероятностью 1,
d3 — 2 с вероятностью 1,
d4 = 2 с вероятностью 1.
б) Решить ту же задачу в случае, когда каждое из значений для
di^ d2^ d3] d£
di = 2, 3, 4,
d2 = 2, 3, 4,
d3-l, 2, 3,
d4 = l, 2, 3
принимается с вероятностью x/3.
Сравнить это решение с решением для случая 7а, в котором вместо
переменных значений 76 использованы их математические ожидания.
8. Рассмотрим задачу линейного программирования, в которой все
коэффициенты подвержены неопределенности. Пусть требуется выполне-
ние соотношений (i = 1, 2, . . ., т)
п
ег(ж)= 2 + (х3>0)
3=1
п
80 (х) = 2 aQjxj = 2 (min),
;=1
но, к сожалению, все X; должны быть выбраны до случайного выбора коэф-
фициентов распределения которых, однако, известны. Обозначим через
(х) стандартную ошибку 8^ (х). Показать, что
(^) = ( -2 XjXhM (Oij 0,1 j) (fl Ik •
j=l fc=i
485
Предположим, что мы решаем задачу (i =1, 2, . . ., т)
(я) + ttOi (х) <0, (х> 0)
е0 (х) + IqGq (х) = z (min),
где, скажем, значение = 3 означает, что мы включили в задачу некото-
рый «коэффициент безопасности», так что 8Z (х) (математическое ожида-
ние (х)) меньше нуля на величину трех стандартных ошибок. Пока-
зать, что эта задача представляет собой задачу выпуклого программиро-
вания. Применить для ее решения результаты § 24-1. Показать, что
в силу неравенства Чебышева
Р(ег(х)>0)<А.
Чему равна написанная вероятность, если (х) распределено прибли-
женно нормально? Показать, что если — независимые одинаково рас-
пределенные случайные величины, то 8^ (х) распределены нормально.
Глава 26
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ
С ДИСКРЕТНЫМИ ПЕРЕМЕННЫМИ
Теперь нашей целью будет решение задач линейного программиро-
вания, в которых переменные принимают целочисленные значения. Пер-
вый параграф посвящен общему обзору предмета; во втором параграфе
описывается метод целочисленных форм Гомори, который в настоящее
время вытеснил более ранние несовершенные разработки в этой области.
Наконец, в третьем параграфе мы подчеркиваем важность этих результа-
тов, описывая широкий класс трудных математических задач, которые
можно свести к целочисленным задачам линейного программирования.
В § 26-3-(14) указан простой прием, позволяющий свести переменную
с дискретными значениями к переменной с целочисленными значениями.
26-1. ОБЗОР МЕТОДОВ
Целый ряд важных задач составления графиков, например распреде-
ление полетов на авиалинии или размещение рабочих мест на сборочной
линии, требует анализа астрономического числа размещений для выявле-
ния «наилучшего» из них. С математической точки зрения проблема здесь
заключается в нахождении наилучшего размещения некоторым более
прямым путем, при котором не нужно прибегать к перебору всех возмож-
ных комбинаций. Допуская непрерывное изменение искомых размеще-
ний в некоторой области, мы можем получить псевдорешения, в которых
одно или более размещений будут характеризоваться не целыми, а дроб-
ными числами. Общепринятым приемом является округление таких зна-
чений до целых чисел. Поскольку математические модели часто являются
лишь весьма несовершенными отражениями действительности, такой под-
ход можно рекомендовать для большинства практических задач. Но так
как такие методы вполне могут дать ответ, далекий от наилучшего,
математики немало работают над созданием более совершенной ме-
тодики.
Целью настоящего параграфа является обзор некоторых недавних
успехов, достигнутых в результате применения в этой сложной области
методов линейного программирования. Мы скажем также несколько слов
о подходе с точки зрения функциональных уравнений динамического про-
граммирования и приведем один пример, в котором этот метод дает эффек-
тивный алгоритм.
Выскажемся более определенно. Некоторые классы задач являются
по своей природе комбинаторными. Они легко формулируются, но в их
решении математики добились лишь отдельных частных успехов. Эти
задачи часто возникают в форме задач программирования с дискретными
переменными. Примерами последних могут служить:
487
1. Задача о пустых контейнерах. Транспортная компания должна
отправить большое количество объектов, которые она помещает в контей-
неры фиксированного размера. Каково минимальное число необходимых
контейнеров?
2. Задача теории расписаний. Цех должен выполнить большое число
различных работ. Каждая работа должна производиться сначала на маши-
не Л, затем на машине Б и т. д.; затрачиваемое при этом время зависит
от вида работы. В каком порядке должны выполняться работы, если тре-
буется закончить их за минимальное время? (Джонсон [1]).
3. Задача составления графика полетов. Задано несколько источни-
ков, из которых следует перевезти определенные количества грузов в ряд
пунктов назначения. Требуется составить наиболее эффективный график
полетов (Марковиц и Манн [1]).
4. Задача об отходах. Газетная бумага поступает в виде рулонов раз-
личной ширины, которые в свою очередь нарезаются из рулонов гораздо
большей ширины. Как следует разрезать последние, чтобы минимизиро-
вать отходы? (Полл и Уолтер [1]; Эйземан [1]; Лэнд и Дойг [1]; Дойг
и Белз [1].)
5. Задача с фиксированными доплатами. См. § 26-3.
6. Задача о бродячем торговце. См. § 26-3.
Примерами задач, которые поддаются исследованию, как мы это
видели в предшествующих главах, являются:
7. Задача о назначениях. См. гл. 15.
8. Задача о кратчайшем пути в сети. См. гл. 17.
На первый взгляд человеческий разум обладает замечательной
способностью исследовать множество комбинаций и находить ту из них,,
которая нам представляется наилучшей или хотя бы очень хорошей.
Однако число возможных комбинаций может оказаться чрезвычайно
большим, и это затруднит нам проверку того, что сделанный выбор дей-
ствительно является хорошим. Поэтому любые идеи, которые облегчают
проверку оптимальности выбранного нами решения, представляют инте-
рес. Мы рассмотрим следующий класс задач.
Найти Xj, удовлетворяющие условиям
п
2 aijXj = bi, (i = 1, 2, ..., т) (1}
(О
Xi ~ | j (2)
и минимизирующие линейную форму
2 cjXj = z. (3)
Для того чтобы задача линейного программирования была дискрет-
ной, вовсе не обязательно, чтобы переменные принимали только значения
О или 1. В задаче составления графика полетов, например, требуется,,
чтобы переменные, представляющие число полетов, были целыми неотри-
цательными числами. Однако существует очень простой прием, позволяю-
щий свести такие задачи к задачам с переменными, принимающими только
значения 0 и 1, если рассматриваемые переменные имеют известные верхние
границы. В самом деле, пусть х — переменная, которая может принимать
только целые, неотрицательные значения, а целое к — верхняя граница
х (т. е. я<&); тогда х можно заменить суммой
х = У1 + Уг+ ••• +Уь
488
где все щ равны 0 или 1. По этой причине представление задачи дискретно-
го программирования в форме (1) — (3) часто называется стандартной
дискретной формой.
Важное свойство любого множества точек, координаты которых удо-
влетворяют уравнению (2), состоит в том, что эти точки являются верши-
нами выпуклого многогранника в n-мерном пространстве. Это, по-види-
мому, интуитивно ясно, так как точка вида (0, 1, 0, . . ., 1) является одной
из вершин единичного n-мерного куба (который, разумеется, является
выпуклым). Как известно, если в задаче линейного программирования
существует оптимальное решение, то среди оптимальных точек имеется
хотя бы одна, являющаяся крайней точкой множества допустимых реше-
ний. Это подсказывает нам, что при
поиске решения стандартной дис-
кретной задачи мы прежде всего
можем ослабить наши предположе-
ния следующим образом:
дискретная область я7=0
ИЛИ Xi—i
„ (4)
заменяется непрерывной
областью
Так как определенные посред-
ством (4) условия являются менее
ограничительными, чем условие (2),
то множество допустимых решений
задачи линейного программирова-
ния (1), (4) образует многогранное
выпуклое множество 67, которое со-
держит выпуклое многогранное мно-
жество (7*, являющееся выпуклой
оболочкой решений систем (1) и (2).
Однако легко видеть, что все край-
ние точки (вершины) множества 67*
z=MLn
Рис. 26-1-1. Схематическое изображе-
ние многогранного множества С*, верши-
ны которого представляют собой решения
дискретной задачи, и выпуклого много-
гранного множества С решений соответ-
ствующей непрерывной задачи (двумер-
ный случай).
являются крайними точками мно-
жества С (см. незачерненные точки на рис. 26-1-1), но у множества С мо-
гут иметься крайние точки, лежащие и вне С* (зачерненные точки на
рис. 26-1-1). Параллельные прямые на рис. 26 -1-1 представляют раз-
личные положения гиперплоскости.
Ci#i 4- с2я2 + •. • + спхп = z = const.
Отсюда ясно, что в зависимости от значений Cj крайняя точка, отвечаю-
щая минимальному значению z, может либо принадлежать 67* (как на
рис. 26-1-1), либо принадлежать С, но не принадлежать С* (Гофман
и Краскал [1]).
Замечательным свойством задачи о назначениях и задачи о кратчай-
шем пути является то, что для них
67* - С. (5>
В действительности этот результат справедлив для общего класса транс-
портных задач, частными представителями которого являются назван-
ные задачи. Таким образом, если мы заменяем условие х^ = 0 или 1 на
условие 0 < xtj 1, то в условиях задачи о браках (гл. 15) мы тем самым
допускаем расширение класса решений с моногамных браков на полигам-
489
ные, в которых можно делить между собой спутниц жизни. Тот факт, что
С* = С устанавливает, что моногамия все же оказывается наилучшим
выходом из положения!
ЗАДАЧА О РЮКЗАКЕ
В некоторых классах задач мы можем получить в качестве решений
крайние точки, в которых не все значения Xj равны нулю или единице.
Если некоторые из Xj имеют дробные значения, то мы будем называть
соответствующие крайние точки дробными крайними точками. Типичным
примером является задача о рюкзаке, которую можно сформулировать
следующим образом. Некто, планируя загородную вылазку, решил взять
с собой не более 70 фунтов поклажи, которая может состоять, к примеру,
из постельных принадлежностей, банок с консервами, а в наши дни —
также и из счетчиков Гейгера.
Попытаемся дать математическую формулировку этой задачи. Пусть
«У — вес у-го объекта, a bj — его относительная ценность, определенная
нашим туристом по сравнению с ценностями других объектов, которые
он хотел бы взять с собой в поход. Пусть Xj — 1 означает, что у-й объект
выбирается, a Xj = 0 означает, что он не выбирается. Ограничение по весу
можно выразить в виде
3 (6)
5=1
Я; = 0 ИЛИ 1. (7)
Мы хотим выбрать Xj таким образом, чтобы суммарная ценность
п
2 — % (8)
5=1
была максимальной.
Теперь мы можем изобразить это геометрически на плоскости
(рис. 26-1-II), если по одной из осей координат будем откладывать вес а,
а по другой — ценность Ъ. Тогда каждый объект представится точкой с коор-
динатами (а7-, bj). Говоря геометрически, задача заключается в выборе
некоторого подмножества этих точек, представляющего тот набор объектов,
который следует взять с собой; остальные объекты приходится оставить.
Посмотрим, какое геометрическое решение мы получим, если заменим
условие Xj — 0 или 1 на условие, допускающее произвольное изменение
переменных в интервале от 0 до 1. Последнюю задачу можно легко решить
обычными методами линейного программирования. Однако в силу своей
простой структуры она допускает и непосредственное решение, заклю-
чающееся в следующем. Нужно вращать луч, начальное положение кото-
рого совпадает с осью 6, вокруг начала координат по часовой стрелке.
При этом последовательно выбираются объекты, которые отвечают точ-
кам, заметаемым этим лучом, пока сумма их весов не превзойдет весового
ограничения. Если при выборе объекта у весовое ограничение будет пре-
вышено, то в качестве соответствующего значения Xj берется такая дроб-
ная часть его веса о,, которая доведет общую сумму ровно до 70 фунтов.
За исключением этого единственного объекта, все заметенные лучом
объекты будут иметь значение Xj = 1, в то время как для остальных объек-
тов будет Xj = 0. Отметим, что это дает нам решение, близкое к требуемо-
му: все Xj равны 0 или 1, за исключением одного, имеющего дробное зна-
чение.
В этом месте естественно поставить вопрос — что произойдет, если
решение округлить? Следствием округления вверх или вниз будет, разу-
490
меется, изменение общего веса до числа, отличного от 70 фунтов. Если
наша модель не является вполне точной (иными словами, если наш турист
связан ограничением примерно в 70 фунтов), то округление может ока-
заться вполне удовлетворительным способом избавиться от дробного реше-
ния. Это, в частности, будет справедливо, если вес отдельных объектов
невелик по сравнению с 70 фунтами. Для большинства практических
задач иного, вероятно, и не потребуется. Однако здесь нашей целью будет
исследование путей получения точного математического решения.
Метод функциональных уравнений динамического программирования
(см. § 1-4) является пока наилучшим из имеющихся методов для слу-
чая, когда число объектов невелико и имеется только одно ограничение.
Рис. 26-1-IL Графическое решение задачи о рюкзаке
(непрерывный случай).
Можно дать его обобщение на случай двух или более ограничений, ска-
жем на общий вес и на общий объем, но это уже приведет к значительному
увеличению вычислительной работы. Этот метод заключается в упорядо-
чении объектов произвольным образом и выяснении того, какие объекты
следует выбрать, если а) при выборе мы ограничивались бы только первы-
ми к объектами и б) весовые ограничения составляли бы w = 1, 2, . . ., 70.
Например, если к = 1 и w < где а^ есть вес первого объекта, то этот
объект выбирать не следует; если же w то его нужно выбрать. Отсюда
легко решить, какие выборы следует произвести для первых двух объек-
тов (к = 2) при любом общем весе w = 1, 2, . . ., 70, а затем по индукции
сделать то же для к = 3, 4, . . ., п.
В самом деле, предположим, что мы хо^им определить, следует ли
выбирать (&Ц-1)-й объект, если наше весовое ограничение составляет
iz;, причем нам известно, как производить выбор для первых к объектов
при любом весе w = 1, 2, . . ., 70.
Пусть Fh (w) означает наибольшую суммарную ценность, которую
мы можем получить выбором среди первых к объектов при весовом огра-
491
ничении w. Тогда при том же весовом ограничении w наибольшая сум-
марная ценность, которую можно получить из первых к-|-1 объектов,,
равна Fh (де), если (&-|-1)-й объект не выбирается, и bk+i-\-Fk(w—
— а&+1), если он выбирается. Следовательно, (/с-|-1)-й объект выбирается
или не выбирается в зависимости от того, какая из этих величин больше.
Таким образом, мы не только получаем выбор для первых к + 1 объектов,,
но и выясняем, что Fh+i (w) определяется формулой
Fk+i (w) =
max [2?* (де), bk+i +Fk{w—ak+i)] для w>ak+1
Fk(w) для w<ak+i.
(9>
Эта процедура итерируется для каждого w и повторяется для к =
= 1,2, . . ., п. Хотя в методе функциональных уравнений члены были
расположены произвольным образом, при практическом его осуществле-
нии рекомендуется вначале упорядочить их в порядке убывания bjlaj
(см. рис. 26-1-П).
Метод линейного программирования заключается в добавлении к си-
стеме новых линейных ограничений-неравенств таким образом, чтобы дроб-
ные крайние точки множества С в окрестности max z были бы исключены,
но множество крайних точек выпуклой оболочки С* допустимых решений
содержалось бы в новом С. Эта процедура может считаться полной; един-
ственное исключение состоит в том, что правила систематического форми-
рования дополнительных ограничений требуют использования методов,
рассматриваемых в следующем параграфе.
Определение. Отсекающей плоскостью называется гиперплоскость,,
являющаяся границей дополнительного линейного ограничения-неравен-
ства. Можно считать, что она «срезает» часть выпуклой оболочки допусти-
мых решений, образуя новую выпуклую оболочку.
Предположим в соответствии с рис. 26-1-П, что наш луч замел
объекты 5, 3,12, 11, 8 и 9, прежде чем весовое ограничение было нарушено,
но включил объект 6 сразу после его нарушения; тогда
а5 4" йз4“ а12~Р я114“ as4“ Я9 <70,
Я5 4“ а3 4" а12 4“ аИ 4" а8 4" 4” а6 >70.
Мы хотим исключить дробную крайнюю точку, для которой
Я5 = Яз==Я12 = Я11 =х8 = х9= 1, x6 = f (0</<1) (10>
и Xj = 0 для всех других у.
Ясно, что для того, чтобы семь точек, отвечающих у = 5, 3, 12, 11,
8, 9, 6, могли войти в допустимое решение, мы не можем положить все
соответствующие Xj равными единице, так как в этом случае нарушилось
бы весовое ограничение. Это означает, что сумма этих переменных не мо-
жет превзойти 6, то есть
#5 + ^3 4“ ж12 + 4" 4“ #9 4“ #6 6. (11)
Так как дробная крайняя точка (10) не удовлетворяет этому ограничению,
ясно, что в результате добавления конкретного ограничения (И) эта
дробная крайняя точка будет исключена. Форма (8) максимизируется
при условиях (6) и 0<^-<1, но с добавлением ограничения (И). Новая
492
крайняя точка для новой выпуклой оболочки снова может оказаться
дробной, и нам понадобится снова искать условие, которое ее исключило
бы. Добавляемые условия будут большей частью другими частичными
суммами Xj, аналогичными (11). Однако иногда могут потребоваться и более
тонкие условия, пока мы наконец не придем к допустимой крайней точке.
Метод, рассматриваемый в следующем параграфе, дает непосредственный
способ определения этих ограничений.
Многие эксперименты, проведенные автором и другими исследовате-
лями, показывают, что очень часто практическую задачу можно решить,
используя только очевидные дополнительные условия типа (И). В одном
эксперименте с рядом случайно выбранных задач о бродячем торговце,
включавших девять городов, для получения требуемого дискретного реше-
ния часто оказывалось достаточно простых верхних границ и так называе-
мых «условий петель» на переменные (Данциг, Фулкерсон и Джонсон,
11], [2]). Чтобы оценить эффективность этого метода, отметим, что для
каждой решавшейся задачи с девятью городами маршрут, минимизирую-
щий суммарное пройденное расстояние, являющийся одним из 362 880 спо-
собов объезда девяти городов, удавалось находить примерно за два часа
вычислений вручную.
26-2. МЕТОД ЦЕЛОЧИСЛЕННЫХ ФОРМ ГОМОРИ
В этом параграфе мы изложим принадлежащий Р. Гомори [1], [2]
метод автоматического формирования отсекающих плоскостей, или цело-
численных форм, дающий надежду на получение эффективного решения
целочисленных задач линейного программирования в конечное число
шагов. Этот подход был распространен на случай, когда некоторые из
переменных изменяются непрерывно, а на другие наложено ограниче-
ние целочисленности. Это обобщение было впервые проделано Э. М. Л. Би-
лом [4] и Р. Гомори ]4]. Здесь мы будем следовать изложению Гомори.
Мы начнем с точного изложения метода, а затем обсудим различные
способы его упрощения на практике. Мы будем заниматься задачами
линейного программирования, в которых некоторые из переменных долж-
ны принимать целочисленные значения, а другие могут принимать дроб-
ные значения. Первые мы будем называть целочисленными переменными,
последние — дробными переменными.
Задача. Определить min > 0, J = l, 2, . . ., п таким образом,
чтобы v и yj для некоторого подмножества J множества индексов / были
целыми и
а11У1 + а12У2 + • • • + а1пУп — bi,
а21У1 + а22У2 + • • • + а2пУп — ^2»

(1)
ат1У1 + Ят2У2 + • • • + атпУп —
CiVi + с2у2 + .. • + Спуп = V (min).
Отметим, что требование целочисленности накладывается на v и yj
для j £ J, в то время как для остальных переменных допускаются дроб-
ные значения.
493
ИСХОДНЫЕ ПРЯМАЯ И ДВОЙСТВЕННАЯ СИСТЕМЫ
Алгоритм начинается с решения задачи без учета ограничений цело-
численности. Предположим, что канонической формой, полученной на
последней итерации, будет
а11У1 + Л12^2 + • • • + а1, п-тУп-т + Уп -т+1 — &1,
я21^1 + а22У2 + • • • + а2, п-тУп-т + Уп-т+2 = ^2,
(2)
ат1У1 ат2У2 п-тУп-т Уп — Ьтч
С1У1~\~С2У2 ••• ^п-тУп-т = V—
где мы для удобства приняли в качестве базисных переменных yn^m+i, .. .г
. . ., уп. В силу оптимальности нашего решения мы имеем для i = 1, 2, . . .
. . . т и у = 1, 2, . . п
6,>0, ?у>0. (3)
Если теперь положить для всех небазисных переменных
yi — fti (* = 1, 2, . ..,п — т) (4)
и выразить базисные переменные через лг-
Уп-т+л = &л— S aki^i (к = 1, ..., т)
t п-~. <5>
v = v0+ 2
г=1
то все переменные yir у2, • • уп окажутся выраженными параметрически.
через
Обозначим теперь в выражении для у^ через +aij коэффициенты
при через а0~ свободные члены; через о^о обозначим коэффициенты
в выражении для v. Полагая
т — п — т, (6)
мы можем придать исходной задаче следующий вид.
Найти min v, yj 0, ль где г?, у^ целочисленны для j С J так, чтобы
У1 “ «01 + ац/Ч + . .. + а— *11—,
У 2 — а02 + а12Я 1 + • • • + ат2Ят,
... . (7)
Уп = «0п+ сНтЛ + ... + а-пя-,
и = а00 + а 10л1 + . • . + атОЛт‘
Если отбросить ограничения целочисленности, то (7) можно заменить на
“Oj + S aijni >°> (/= 1, 2, ..п)
♦ i
а00 + S a;o«i = v (min).
г
Теперь ясно, что двойственной к (7) задачей будет
494
Двойственная задача. Найти max х0 и^>0 для j =/= О, удовлетворяю-
щие условиям
%0 4“ «01*1 + «02*2 4" • • • 4" «0п*п = «00,
«и*14- «12*2 4“ • • • 4“ атхп = «ю,
’ : <8>
«т1Ж1 + “т2*2 + • • • + = “тО ’
Поскольку система (7), по определению, совпадает с (4), (5), то система
(8) совпадает с выписанной ниже системой (9):
Х0 + Ь1Хт±1 + ’ * * ~^ ЬтХп =V0,
*1 ^llXm-j-i * * * ^mlX п ~ ^1,
(9)
х— — at—х— , . — ... — а --Хп — с—,
т Im m-j-l тт п т
Эта система находится в канонической форме, и ее базисное решение допу-
стимо и оптимально (Ь$ > 0, Су > 0). Фактический порядок переменных
Xj может быть тем же, что и в прямой задаче, а порядок уравнений может
соответствовать порядку небазисных переменных прямой задачи. Мы
будем предполагать, что это в действительности имеет место. Кроме того,
мы предположим, что переменные прямой задачи заранее упорядочены
таким образом, что все целочисленные переменные предшествуют осталь-
ным. Это предположение делается не просто для удобства изложения;
в действительности именно от его соблюдения зависит конечность алго-
ритма Гомори.
В качестве иллюстрации рассмотрим задачу нахождения min г?, > 0,
где v, у2 — целые числа, удовлетворяющие уравнениям
о . 4 13
4-^24~Уз —"у ,
1 , з 9
-2-У1 I 4 Уз 1 Z/4 4” > (10)
1 , 4 ,7
т?* +-3~Уз =”+12-
Если ПОЛОЖИТЬ yt = у3 = л3, то
У1 = Л|,
У 2 = 13 о 4 3 2Л1 з л3,
Уз = л3, (11)
9 1 3
Уь~ 4 2 Л1 4 Лз’
7,1 ,4
V — 12 + 4 Л1+ 3 Яз>
где параметр jq целочислен. Игнорируя ограничение целочисленностиг
495
двойственную к (11) задачу можно записать в вйде
. 13 ^0 1 *^2 , 9 7 + 4 Xi~ 12 ’
хг — 2 х2 1 1 2 4 ’ (12)
4 3 4
--3-ж2 + ж3-у-ж4 = -у- .
ФОРМИРОВАНИЕ НОВЫХ ОГРАНИЧЕНИЙ
Если окажется, что минимизирующее решение прямой задачи удо-
влетворяет условиям целочисленности, то оно будет являться решением
исходной задачи. Таким образом, если значения v = а00 и yj = а0; для
целочисленных переменных будут целыми, то базисное решение будет
целочисленным и оптимальным. Если это не так, то хотя бы в одном выра-
жении для целочисленной переменной или в выражении для v в (7) будет
иметься дробный свободный член. В нашем примере их будет два:
7 1 4
р== ““"п + т л1+“з~
13 п 4
Уг— й"Лз.
(13)
Любое такое выражение можно использовать для формирования линейно-
го неравенства (в действительности — целого класса неравенств), которому
текущее базисное решение, получающееся при л^ = 0, не удовлетворяет.
Нам будет удобно ввести1 символ [а7]* для обозначения наибольшего
целого числа, не превосходящего а7-. Определим положительную собствен-
ную дробную часть числа а7- как
y. = a._[a.j*>0. (14)
Например, если а,- = у , то [а,]* = 1 и/у = -у; если = —у , то [а;]*=—2
2 ‘-
и fj = у. Определим также дополнение fj положительной дробной части
a.j как положительную собственную дробную часть числа — ay. Легко
видеть, что
Теорема L Если у — целочисленная переменная, а л^ > 0— парамет-
ры, связанные соотношением
y = aQ + ainl +... 4-а-л- ([а0]*<а0), (16)
где > 0 для i =/= 0, то линейное неравенство
. 1 /о + «1^! + • • • + атоЛт (17)
выполняется для всех л^, порождающих целочисленное у, но не удовлетво-
ряется базисным решением, порождаемым значениями Hi = 0,i = 1,. . .,т.
1 Обычным символом для наибольшей целой части числа являются скобки без
звездочки; однако снабжение их звездочкой уменьшает опасность смешения их со
скобками в обычном смысле.
496
Доказательство. Так как а^>0 и Jif > 0, должно быть min# > а0;
однако возможные значения у целочисленны, так что
#>[а0]* + 1. (18)
Вычитая это из (16), мы получаем (17). Кроме того, записывая у — #* =
= [а0]*+ 1, где #* > 0— целое, и, вычитая это равенство из (16), мы при-
ходим к соотношению
У* = —/о + + • • • + а-л- (у* > 0), (19)
которое представляет собой более сильную форму неравенства (17), так как
новая свободная переменная #* должна быть целым неотрицательным
числом.
В нашем иллюстративном примере
7 1 4
*> = --12+-4-л1 + -3-л3, (20)
где v — целочисленная переменная, не имеющая ограничений на знак,
а Ли > 0, л3 > 0. (В действительности требуется, чтобы Л1 > 0 также было
целым.) Применяя нашу теорему, мы имеем, обозначая #*, скажем, через #5,
7 4 4
1/5= — ^2 я1+тяз> (г/5>0) (21)
где у5 > 0— новая целочисленная переменная.
Теперь систему (11) можно расширить, присоединяя к ней выражение
для этой новой базисной переменной через ль л3. Следует отметить, что
базисное решение, порождаемое значениями л4 = л3 = 0, уже не будет
7
допустимым, так как #5 = — .
Отметим также, что двойственная к расширенной системе образуется
7
путем добавления новой переменной, скажем с коэффициентами — ,
1^
1 4
; см. (57)1. Двойственная задача все еще находится в канонической
форме; ее базисное решение допустимо, но уже неоптимально. Далее
будет показано, что последовательность перемен базиса, требующихся
для его оптимизации, отвечает изменению параметров ль используемых
в представлении уг.
Мы можем сформировать также и другие неравенства, умножая
выражение (20) на произвольное целое число к, так как если v целое,
то таковым же будет nkv. Таким образом,
ь= —<*>°)
у*=1+^кУ-^к+4-П1+-£Пз’ (у*>У
где #* — целое.
Информацию о том, что одно или несколько значений лг — целые,
можно использовать для формирования новых, притом еще более силь-
ных неравенств.
Теорема 2. Если у и л^ > 0— целочисленные переменные, связанные
соотношением
г/ = а0 + а1л1+ ... +а-л-, ([«о1*<«о) (23)
1 В (57) мы использовали более сильное условие, чем (21), применив теорему 2.
32 Дж. Данциг 497
то линейное неравенство
1 /о + /1^1 + • • • + (24)
выполняется для всех ль порождающих целочисленное у. но не удовлетво-
ряется базисным решением, получаемым при = О.
Доказательство. Отметим, что в этой теореме могут иметь любой
знак, а лг- — неотрицательные числа. Подставляя а7 = /7- + [а7]* в (23),
получаем
О — [<А>]* — 21^1*ЯО = /о + /Л+ • • • +/тЯт‘ (25)
г
Левая часть этого выражения представляет собой целое число, а /7- > 0;
следовательно, можно применить теорему 1, получая (24) или его более
сильную форму
i/**=-/0 + /1л14-/2л2+...+/-л-) (26)
где у**> 0— целочисленная переменная.
Упражнение. Интерпретировать (24) в случае= f2— . . . =Ап = 0*
Пусть, например, у > 0 и у > 0—* целочисленные переменные,
связанные соотношением
5,7 8 ,1
У — ~у + ~4 — з" я2 + 2 Яз’
Тогда новое условие имеет вид
* 1 , 3 ,1 .1
У* = —-у + у я‘ + т Я2+ у Яз
0— целое).
Другое новое условие можно сформировать, используя 2г/. Таким
образом, из
о 10 , 14 16 , 2
Я1--з — Л3
следует
** 2 । 1 . 2
У**= — -3- + у «1 + у л2
(у** >0 — целое).
Несложное обобщение этих двух теорем можно получить в случае,
когда некоторые oq относятся к целочисленным параметрам лг (г =
= 1,2, ...,&), а остальные параметры могут принимать дробные значе-
ния, причем для этих параметров все > 0 (или все 0) при i > к;
тогда смешанное выражение
У * ~ —/о + /1л1 + • • • + fk^k + (aft+l^/i+l + • • • + атЛт) (27)
справедливо в случае, когда > 0 для всех i > к, а выражение
У * — —/о+ /1^1 + • • • Л-fk^k-(«*+1^+1+ • • • +атЯт)
имеет место для случая aj<:0, i > к при всех лг, порождающих цело-
численное у. Здесь у* 0— целое число. (Это у* не совпадает с г/*, исполь-
зованным выше.)
В нашем иллюстративном примере
г/2=4-2я1—(28)
О о
где у2 >0, Л1 > 0— целые и л3 > 0. Применяя второй случай, поло-
498
жим у* — yQ; тогда
ув=—г+4яз’ <29>
где у& > 0— новая целочисленная переменная; ее выражение через
также можно использовать для расширения системы (11), (21).
Пусть все параметры jq целочисленны. Интересно отметить, что
в этом случае существует особенно простое соотношение, представляющее
собой некоторую частичную сумму л^ Это условие не является таким
сильным, как предыдущие, поскольку его можно вывести, комбинируя
два известных неравенства. При к = т из (27) вытекают два равенства
У *== —/0 + /1Л1+• • .+/-Л-, (г/*>0)
(3°)
,/**= + ...+/-л-, (у**>0)
где у* и г/** —целые. Складывая их и полагая у’ = у* + г/**, мы полу-
чаем
У' = ~ 1Н-б1Я1+...+6_Я-, (/>0) (31)
где dj = 1, если > 0, и = 0, если = 0. Например, если в (28) пере-
менные jq и л3 были целочисленными, то новое соотношение имело бы вид
/ = — 1 + я3. (32)
Интересно также отметить, что иногда можно сформировать сильное
ограничение из целочисленной переменной у, которая принимает целое
значение в решении, в котором все л^ = 0. Пусть, например,
у = 2 + -| iti —у л2, (33)
где jq и л2 образуют множество всех параметров. Представляя (33) в виде
1 1
у—2—Л1 + л2 = ^ jq + y л2, (34)
мы замечаем, что левая часть целочисленна. Поскольку правая часть
неотрицательна, мы заключаем, что
г/* = 4Я1 + ТЯ2’ (35)
где у* 0— целое. Однако равенство у* — 0 невозможно, так как в этом
случае мы имели бы л, = л2 = 0 и другие целочисленные у} должны
были бы принимать дробные значения из текущего базисного решения.
Поэтому у* = у** +1 > 1 и новым ограничением будет
/*= —1+4 я1 + уЛ2- (36)
Вообще, если а0; = [aOj]* Для некоторого / и /г = аг; — 0 для
всех i #= 0, то новое ограничение будет иметь вид
У** = — 1+(Л=/=0) (37)
ФОРМИРОВАНИЕ НОВЫХ ОГРАНИЧЕНИЙ ДЛЯ ОБЩЕГО
СМЕШАННОГО ЦЕЛОЧИСЛЕННОГО СЛУЧАЯ
Для задач со смешанными, т. е. целочисленными и «дробными» пере-
менными (переменными, которые могут принимать дробные значения),
мы должны уметь формировать новые неравенства в случае, когда коэф-
499 32*
фициенты при дробных переменных имеют любой знак. Положим
У = «о+ S = ао + ^—N, ([«о]* < «о) (38)
г=1
где Р йТУ — частичные суммы положительных и отрицательных членов,
d0 — не целое, а у — целочисленная переменная.
Если для определенных значений ttf мы будем иметь Р — N О,
to, поскольку у = а04--Р — N должно быть целым числом, таковым
же должно быть и /0 4- Р —,N\ но последнее выражение строго положи-
тельно, так как мы предполагаем, что а0 нецелочисленно. Следовательно,
мы должны иметь
, 1</о + Р-ЛГ,
; (39)
: —L- n^-Lp+2-n.
fo /о /о fo
;• Если для других значений tit будет N — Р > О, то —у = —а0 +
+ N — Р есть целое число; поэтому
i^fo + N-P,
f0^N-P, (40)
: 1 —J- P^4~N + ~^P-
fo fo fo f0
Следовательно, для любого набора значений at справедливо неравенство
l^-X-P + 4-W. (41)
. ... /о fo 7
Теорема 8. Если у — целочисленная переменная и л^>0 удовлетворяют
соотношению
J/ = a0+Sa«^i, (42)
г=1
где :ao>[ao]*, то неравенство
1с-у-С2 ^Яг+2 агЯ0+т"(2^Яг—3 агЯ0 (43)
'° Л /г ° /з h
выполняется для всехщ, порождающих целочисленное у, но не удовлетво-
ряется базисным решением, получаемым при л$ = 0. Здесь
если ЙС tn и Лг целочисленное,
1 6-^2» если at^ >0 и tti дробное,
если h< ”/o и tti целочисленное, (44)
i С если at < :o и tti дробное.
Доказательство . Если — целое, положим в (42) = lad*+/i
или = [aj*4-l— ft в зависимости от того, будет ли /г- < /0 или /г- <
< /0. Перенося все целочисленные члены в левую часть и обозначая
«ее через у', мы получаем
р'= а0+{2 Мг+ 2 аглг) — {57<лг — 2а;Л||, (45)
21 2г 2g 2<
500
где у'— целочисленная переменная. Если отождествить (45) с (38) , то*
соотношение (43) будет соответствовать (41), откуда и следует утвержде-
ние теоремы.
Если рассматривать у* > 0 как свободную переменную для неравен-
ства (43), то можно записать новое соотношение
у* = —1 + -=- + — Sai3t*} •
° 11 Тз ^4
Здесь, однако, добавленная новая переменная уже не обязательно будет
целочисленной, как это было в случае всех предыдущих аналогичных
соотношений. (Это обстоятельство весьма досадно, ибо, как мы уже виде-
ли, целочисленность у* можно с выгодой использовать для формирования
на одном из последующих шагов новых, более сильных неравенств.)
Рассмотрим для иллюстрации соотношение
г/ = у+-|я1 + 4 я*~Тяз—4я4’ (я>>°) (47)
где у, и л3 — целые. Перепишем его в виде
(У— 1 + л3) = у+ у ni + y л2—у л3—(48)-
Группируя положительные и отрицательные члены, мы приходим к нера-
венству
л 1 < 3 ,4 \ , 1 / 2 .5 \ //ос
1 + 2" Л2у+“2~ Лз+у Л4 J • (49)
У ~з
3 2
С другой стороны, мы можем положить в (48) у = л* — у л4. Тогда
группировка целочисленных членов
у 1 + л3 л4 = у + л^ — ^уЛ1 + уЛ3 + у л4^ (50)
приводит к неравенству
+ j (4я1 + тяз + 4 я4^ • (51>
¥ У
Это неравенство сильнее, чем (49), так как в нем коэффициент при л>
меньше.
В действительности мы можем, вообще говоря, свести дело к слу-
чаю, когда коэффициенты при всех целочисленных переменных не пре-
восходят единицы, если свободные члены новых ограничений равны еди-
нице. Чтобы в этом убедиться, предположим, что лг > 0— целое. Заме-
ним ai либо на [ail*+A, либо на [aj*+ 1 — /г — в зависимости от того,
будет лиили fi < /0. В первом случае коэффициентом при л*
будет filfQ<,i, а во втором Д//о < 1.
Для общего случая можно образовать также второй тип неравенств.
При этом образуются более сильные неравенства, но размер системы
увеличивается. Пусть индексы i = 1, . . ., к относятся к целочисленным
переменным, а I > к — к дробным переменным. Положим
J/ = .S аглг—л*, (0<л*<1) (52)
где у — новая целочисленная переменная, не имеющая ограничения на
501
знак, ал*— положительная собственная дробная часть суммы членов,
отвечающих дробным переменным. Тогда новое ограничение принимает вид
_ k
г/* = -7о+2Мг+л*. (0^л*<1) (53)
где у*— целое. Так как новые ограничения содержат теперь ограничен-
ную переменную л*, то, вероятно, выгоднее остаться в рамках прямой
системы, чем переходить к двойственной.
ИТЕРАТИВНЫЙ ПРОЦЕСС
Любое новое ограничение
yt = dot + а^Л! + • • • + a-tn~, (54)
используемое для расширения исходной системы, приведет в двойствен-
ной системе к новой переменной xt с коэффициентами ait. Разумеется,
двойственная система останется при этом в канонической форме, но ее
базисное решение уже не будет оптимальным, так как а0^ < 0. Следова-
тельно, переменная xt будет введена в базис путем выполнения ведущей
операции над некоторым элементом art двойственной системы. Матрица
двойственной системы [ац] при этом преобразуется в [оцД
С другой стороны, если мы перейдем обратно к прямой системе и вве-
дем вместо лг новый параметр yt (выразив из уравнения (54) лг через
другие и yt) и подставим его в выражения для yj и v, то легко видеть,
что матрица [<хгу] также преобразуется в [а^].
Таким образом, новая двойственная задача соответствует представле-
нию прямой задачи набором таких параметров, что свободная переменная
нового ограничения становится новым параметром вместо одного из ста-
рых параметров. Вообще, каждый двойственный цикл соответствует
использованию одной из переменных у^ в качестве нового параметра вместо
одного из предыдущих.
Если после ведущей операции двойственная система все еще не будет
оптимальной из-за того, что некоторое а0#<0, то следует применять
симплекс-метод до тех пор, пока оптимизация не будет выполнена. Фор-
мально это соответствует последовательному применению в качестве но-
вых ограничений для прямой задачи любого из имеющихся соотношений
(54) с а0г<0.
Пример. Найти целые числа min v, yj 0, удовлетворяющие системе
+ Уг + уУз — у »
у У1 + у Уз + S/4 — у »
14 7
~^У1 + у^/з =г; + 12-
(55)
К счастью, эта система уже находится в оптимальной канонической фор-
ме, если не учитывать ограничений целочисленности. Далее, положим
небазисные переменные yj равными и выразим все переменные через
Uj. (В приводимых ниже итерациях каждое уь используемое в качестве
параметра, мы для удобства отмечаем, полагая Л; = yj.)
502
Прямой цикл 0.
У1 = Л!
Уг = 13 о 4 ЛЯ} $ л3,
Уз — Vi = ^3» 9 1 3 4 ~~ 2 Я1 4 Яз’
V = 7 1 4 — й + т я1 + улз,
Уь-~ 12 + ТЯ 1+-3 Яз
(56)
Здесь новое ограничение выведено из v. Теперь перейдем к двойственной
задаче и проведем оптимизацию:
Двойственный цикл 0. 7 12
.13 ,9 ^0 + “з" 4~ 7 12*5
' 2(^2 2“ + т*5 __ 1 4
4 , 3 — — х2 + ж3 — + 4*5 II Оо| os
• О • ★
(57)
Двойственный цикл 1.
.7 1 .13 п
Яо + у*1— 3-^2 +j2*4 = 0’
—3^2 '—2^4 -|~Х5 = 1, (58)
4 , 4 1 Л
-у ^ + -3-^2+^ —J2 =1‘
• ★ О •
Это соответствует исключению л4 из прямой задачи с использованием
соотношения
7 . «П1 . ЗТ3
Л5 = J/5= —12 + -4- + -3- ’
где мы приняли уь = л5 в качестве нового параметра. На практике это
осуществляется путем выполнения ведущей операции над элементом
Л1 табл. (56) после перенесения члена л5 в правую часть и затем — на
место Лр После выполнения ведущей операции ведущее уравнение опу-
скается. После исключения все члены с Л1 становятся равными нулю и не
входят в таблицу. Таким образом, имеем
Прямой цикл 1.
7 , , 4
У1 = -з- + 4л:5—з л3,
1 Q , 4
У2~----з~ — 0Л5 + -3- Л3,
Уз — Л3,
Уь — 12 — —12 Лз’
У 5 = я5
У = Л5 + л3.
(59)
503
Так как -базисное решение не является оптимальным, мы, возвращаясь
к (58), выполняем указанную ведущую операцию. Это дает нам, за исклю-
чением обведенного рамкой столбца,
Двойственный цикл 2.
1 о 1 1 1 17
Xq + 2xt + -4-Я3
— 4“6ж3 2* *^4 + X5
1 . 3 1
•—^1 + ^2 +"4 X3 ”"Jg^4
• О • ★
з i
4 Хб “ 4 ’
= 7,
. 3 3
+ -^-Хб
(60)
Это соответствует исключению л3 из прямой системы путем формального
присоединения одного из имеющихся соотношений, именно
1 о 4
Я2 — ^2 —----з~ — 8л5 Л3
и принятия У2 = я2 за новый параметр. Это можно выполнить, совершив
над табл. (59) ведущие преобразования по элементу ~ л3, перенеся сначала
л2 = У2 в правую часть. В результате л3 будет исключено из других
уравнений, и мы получим
Прямой цикл 2.
Уг — 2 — 4л5 — л2,
У2 = л2,
1 3
Уз = 4" + 6л5 + л2,
17 5 _ 1
Уь “ 16 2 16 ЗТ2>
Уъ = Л5,
1 . „ .3
v = + 7я:5 + «г,
(61)
3 3
I/б = — -4- + -4- П2
Новый столбец (60) выводится из коэффициентов при я3, соответствующих
у а — -|- + 6л5-|-|л2; именно новый столбец отвечает новому ограничению
3 3
Уь = — -4- +"4 л2 > 0, указанному в (61). Итерируя, получаем
Двойственный цикл 3 (оптимальное целочисленное решение)
£o + ^i+ Х3 + ^4 =1,
— 6ж3—7, (62)
—3 + з + хз 12 + жв = 1 •
• • •
504
Прямой цикл 3
2/1 = 1— 4л5 -|л6,
2/2—1 +у Л6,
Уз = 1 + 6Л5 4“ Jig,
5 1
2/4 — 1 2~ 12 *^6’
р = 14-7^5 + Л6*
(63>
Оптимальное решение находим отсюда, полагая л5 = л6 = 0.
ДОКАЗАТЕЛЬСТВО КОНЕЧНОСТИ АЛГОРИТМА (ГОМОРИ, [2], [3])
Для того чтобы провести доказательство конечности алгоритма, бу-
дем считать, что правые части исходной двойственной системы (8) полу-
чили возмущения, порожденные столбцами, стоящими слева для j =/= 0..
(См. гл. 10.)
п п
Хо + 2 aOJXJ = 3 = «о (8),
п 1 П 0 _ (64>
2 UijXj = 2 aij8? = ai (8)* (* = 1, . . ., 7П)
f 0
Таким образом, значения базисных переменных становятся полиномами
от 8. Мы будем предполагать, что главный член (т. е. ненулевой член
наименьшей степени) каждого о^(е) положителен, исключая, возможно,.
i = 0.
Если базисные переменные можно расположить перед небазисными
переменными, как это сделано в (9), то это предположение будет с самого
начала выполнено. Однако, как было отмечено в абзаце, следующем за (9),
для доказательства сходимости требуется, чтобы соответствующие
целочисленным переменным предшествовали дробным переменным.
Упражнение. Использовать искусственные переменные и симплекс-
метод с возмущениями для получения в последнем случае начальной
канонической системы с требуемыми свойствами, если таковая вообще
существует. Что произойдет, если такой системы нет?
После каждого расширения системы путем добавления новой пере-
менной, соответствующей новому ограничению, мы требуем применения
к (64) симплекс-метода с возмущениями до тех пор, пока система не станет
оптимальной. Мы будем называть такой процесс оптимальным шагом.
На каждом таком шаге коэффициенты полинома а0 (е) равны в точности
значениям v и в допустимом решении прямой системы, т. е. а0/ > О
для / = 1, 2, . . ., и. Так как мы предполагаем ограниченность выпуклого
множества допустимых решений прямой задачи, то на каждом таком
оптимальном шаге значения aOj- будут иметь конечную верхнюю границу.
Если к4-1 главных коэффициентов a00, aOi, . . ., a0& полинома a0 (s}
все будут целыми, то неотрицательные коэффициенты будут давать реше-
ние прямой задачи и процесс заканчивается. Если, однако, среди первых
к 4-1 коэффициентов имеются дробные, обозначим номер первого из них
через / = /0. Пусть / = п-|-1 — индекс нового столбца, образованного
из 7 = 7о5 тогда, поскольку а0) л+1 < 0, новый ведущий элемент (г,
505
выбирается в столбце s = 1 и строке г = i, где > 0, и
0<_M£L = min М-0. (б5)
аг, п+1 е_>0 аг, п+1
Так как (64) находится в канонической форме, нетрудно показать, что
ведущий элемент определяется единственным образом (см. гл. 10). В резуль-
тате преобразования новое значение а0 (е) будет равно
«О (е) = «о (8) — аг (е) ~—+i- > а0 (е). (66)
wr» п+1
Для ясности изложения приведем снова определение j = j0 и определим
также / = J*.
а) Пусть 7 = /о — индекс первого члена полинома а0 (е) с нецело-
численным коэффициентом.
б) Пусть / = J*— индекс первого члена полинома а* (е) — а0 (е)
с ненулевым коэффициентом.
Теорема 4. Либо j* <2 jo, либо j* — j0 и а*7- > [ао>о1* + 1-
Доказательство. 70-й коэффициент полинома а* (е) равен
aU = ao;o-a^0-^-. (67)
и ur, п+1
Первый ненулевой член полинома а* (е) — а0 (е), согласно (66), положи-
телен. Если он не встретится раньше, чем при j*=jo, то arjo 0 (так
как a0,n+i <0и ведущий элемент ar?n+i > 0, то неравенство arjo < 0
противоречило бы неравенству (66)). Остальная часть заключения теоремы
выводится путем рассмотрения связи между
Wo = «0}o + ljaiio«J (68)
г
и новым ограничением на i/*. Если все параметры целочисленны, то
У* = — /o + S/i^i, (69)
где аг>0 = [агл]*+/г, так что
«*50 = aoio - {[«гу0Г + fr} ( - > (ао,0 + /о) = [a0iol* +1. (70)
Тем самым теорема для этого случая доказана. Если некоторые параметры
дробные, то в качестве нового соотношения для у* мы будем иметь (46).
В этом случае сс0, n+i = —1- Если — целое, то
= А]<1. (71)
Последнее соотношение было установлено в рассуждениях, следовавших
за (51). Доказательство завершается, как и в (70), если аг>п+1 — /г//о-
С другой стороны, если 0 < ar^n+1 = fr/f0 <2 1, то
«U = - {[<Мо] + 1 —7г} ( - fo/fr) > (72)
> aOjo+ (/o/fr) — fo > aOJo+ 1 —fo = IaOJol*+ 1-
Если, наконец, лг — дробный параметр, то, поскольку arJ^ > 0,
а, л
ar,n+1 = ^p->0, (73)
JO
506
так что (67) сводится попросту к равенству
ctojo = aoj + /о = [ао; ]* +1- (74)
Теорема 5. Если выпуклая оболочка дробных решений ограничена,
то алгоритм конечен.
Доказательство. Предположим, напротив, что алгоритм бесконечен;
тогда а0 (е) образует монотонно возрастающую последовательность. Одна-
ко ее первый член должен после конечного числа итераций принять неко-
торое конечное целочисленное значение и оставаться затем неизменным.
В противном случае в силу предположения об ограниченности выпуклой
оболочки для некоторой бесконечной последовательности оптимальных
шагов он принимал бы множество значений, стремящихся к некоторой
верхней границе или достигающих ее, т. е. бесконечную последователь-
ность неубывающих дробных значений, разность между которыми стре-
мится к нулю. В силу предыдущей теоремы на каждом оптимальном шаге
получается такое решение, в котором первый член полинома а0 (е), кото-
рый принимает дробное значение, должен на следующем цикле быть
по меньшей мере равным следующему большему целочисленному значе-
нию. Здесь /о — 7* = 0- Следовательно, дробное значение одного опти-
мального шага должно отличаться от значения шага, следующего за ним
через один, не меньше, чем на единицу. Получено противоречие.
Установив, что первый член принимает постоянное целочисленное
значение после pi итераций, отметим, что второй должен вести себя анало-
гичным образом после pi + р2 итераций. Рассуждение здесь то же самое:
так как а0 (в) монотонно возрастает при достаточно малых 8, то после
первых pi итераций второй член должен быть неубывающим. В силу
ограниченности выпуклой оболочки значения в конце последовательных
оптимальных шагов должны приближаться к некоторой конечной верхней
границе или достигать ее. Второй член не может принимать бесконечное
множество дробных значений, так как, согласно предыдущей теореме,
он ввиду фиксированности первой компоненты на каждом следующем шаге
принимал бы значения, по меньшей мере равные следующим большим
целочисленным значениям и т. д. Это рассуждение можно повторять
до тех пор, пока первые к компонент, отвечающих целочисленным пере-
менным, не окажутся целыми.
ВИДОИЗМЕНЕНИЯ
На практике выбор нового ограничения не всегда делается по правилу
наименьшего индекса (т. е. ограничение порождается целочисленной пере-
менной yj с наименьшим индексом, значение которой в базисном решении
оказывается дробным). Вместо этого j часто выбирают таким, чтобы
— foj было минимальным. В ряде пробных расчетов это иногда снижало
число итераций. Если это правило периодически чередовать с правилом
наименьшего индекса, сходимость можно по-прежнему гарантировать.
Другим приемом является добавление не одного, а нескольких ограниче-
ний одновременно. Если бы мы проделали это в нашем примере, то одно-
временное добавление всех ограничений, порожденных целочисленными
переменными и их кратными, сразу привело бы к искомому целочислен-
ному решению. Если бы, однако, этого не произошло, то следовало бы
наложить новые системы условий и повторить процесс. Используя возму-
щения и замечая, что aj (е) имеет по меньшей мере ту же величину, что
и перед этим, мы видим, что такое видоизменение процесса также даст схо-
димость к решению в конечное число шагов.
507
Другой слабой стороной правила наименьшего индекса является
требование целочисленности г?, отвечающего наименьшему индексу. Поло-
жение было бы гораздо более удовлетворительным, если бы v могло при-
нимать также и дробные значения. Чтобы гарантировать сходимость в слу-
чае, когда v есть дробная переменная, а все остальные переменные
целочисленны, Гомори предложил специальные правила. Его доказатель-
ство, однако, не проходит в смешанном случае, если используются усло-
вия (46). Неизвестно, что произойдет, если-вместо них использовать
условия (53). Разумеется, на практике описанные выше видоизменения
часто используются даже в тех случаях, когда v не целое.
Упражнение. Пусть v — дробная переменная, а все остальные пере-
менные целочисленны. Показать, что в случае рациональных коэффи-
циентов можно заменить форму для v другой максимизируемой формой,
значение которой будет целочисленным.
26-3. о ЗНАЧЕНИИ РЕШЕНИЯ ЗАДАЧ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ, В КОТОРЫХ
НЕКОТОРЫЕ ПЕРЕМЕННЫЕ ЦЕЛОЧИСЛЕННЫ
Наша цель состоит в систематическом обзоре и классификации задач*
сводящихся к задачам линейного программирования, в которых все или
некоторые переменные принимают целочисленные значения (Данциг
[20]). Мы покажем, что множество трудных и на первый взгляд даже
недоступных задач поддается теперь непосредственному анализу. Настоя-
щий параграф имеет следующее строение:
I. Общие принципы.
а) Обсуждение.
б) Дихотомии.
в) Л-кратные альтернативы.
г) Выбор из многих пар областей.
д) Задачи с дискретными переменными.
е) Задачи с нелинейными целевыми функциями.
ж) Условные ограничения.
з) Нахождение глобального минимума вогнутой функции.
II. Задача с фиксированными доплатами.
III. Задача о бродячем торговце.
IV. Задача об ортогональных латинских квадратах.
V. Задача о четырех красках.
I. ОБЩИЕ ПРИНЦИПЫ
а) Обсуждение. Обратимся к нашему основному предмету — рас-
смотрению классов задач, которые сводятся к задачам линейного про-
граммирования, в которых все или некоторые переменные целочисленны.
Довольно часто появляются статьи, в которых формулируются зада-
чи, целиком находящиеся в рамках линейного программирования, если
не считать определенных граничных условий вида • х2 = 0. Могут появ-
ляться и суммы произведений такого типа, например х^-х2 + я3-я4= 0.
Подобные условия для неотрицательных переменных означают, что по
крайней мере одна переменная из каждой пары должна равняться нулю.
При поверхностном рассмотрении можно подумать, что такая задача
относится к области квадратичного программирования. Однако наличие
подобных условий может, как мы сейчас увидим, в корне изменить харак-
тер задачи, и поэтому оно должно служить предостережением тем, кто
508
захотел бы бездумно применить к ней общие методы нелинейного програм-
мирования. Если мы нанесем на график условия х^х2 — 0, > 0, х2 >
> 0, #1 + #2 > 1, то область допустимых решений будет изображаться
жирными линиями (см. рис. 26-3-1). Отметим, что эта область рас-
падается на две несвязные части. Если в более крупной задаче имеется
много подобных дихотомий, то в результате может появиться область
-с многими несвязными частями или связными, но невыпуклыми подобла-
стями. Например, к пар переменных, произведения которых равны нулю,
могут привести к 2fe несвязным частям. Традиционные математические
область, возникающая из ли-
нейных неравенств и условий
типа х±х2 = 0.
подходы к таким задачам могут дать в лучшем случае лишь локально
оптимальное решение, т. е. решение, оптимальное лишь на некоторой
связной выпуклой части.
Хорошо известно, что во многих случаях локально оптимальных
решений можно избежать путем введения целочисленных переменных.
Однако этот факт представлял весьма относительную ценность до тех пор,
пока последние разработки не сделали его
практически применимым. Нашей целью здесь
будет систематизация этих приемов.
б) Дихотомии. Начнем с важного класса
задач, содержащих условия типа «либо —
либо». Для того чтобы такая задача была
трудной в вычислительном отношении, в ней
должно присутствовать много наборов по-
добных условий. Сосредоточим наше внима-
ние на одном из них. Пусть, скажем, условия
(1)
(2)
либо G (xi9 х2, . . ., хп) 0,
либо Н (хи х2, ..., хп) > 0
должны выполняться для векторов
л?2 • • хп) из некоторого множества S. Мы
не исключаем случая, когда оба эти условия
но, если только это возможно. Пусть, например, аукционист обусловил
размеры ставок следующим образом: либо xt 10000 либо = 0. Если
все ставки неотрицательны, так что Xi 0, то мы можем написать
выполняются одновремен-
либо —10 000 > 0,
либо —Xi
>0.
(3)
Из других соображений может быть известно, что предельный размер ста-
вок составляет 1 млн. долл., так что рассматриваемое нами множество
S есть 0 xt 1 000 000.
Предположим теперь, что известны нижние границы функций G и Н
на множестве всех векторов (жь я2, . . ., хп) из S. Если LG есть нижняя
граница для G, a LH — для Н, то при 6 = 1 условие
G(xn х2, ... xn) — 8LG>Q
выполняется для всех (ж4, я2, . . ., хп) из S. Аналогично при 6 = 0 условие
Н (Ж|, х2, ..., хп} — (1 —- б) Ln0
выполняется для всех (жь х2, . . ., хп) из S. Для нашего примера мы
имели бы
Xi—10 000- б (—10 000) > 0,
-^-(1 — 6) (-1000000) >0. (4)
509
Альтернативное условие (1), (2) можно теперь заменить условиями
G(x19 х29 ..., хп) —6Ло>0, (6 = 0, 1) (5}
Н (х19 х2, ..., хп)~ (1 —6)LH>0, (6)
O^d^l, (7)
где 6 — целочисленная переменная. Воздействие значения 6 = 1 заклю-
чается в снятии ограничения G, когда Н выполняется, а значения 6 = 0—
в снятии Н9 когда выполняется G. Если функции GwH линейны, то мы тем
самым свели условие типа «либо — либо» к системе трех линейных нера-
венств, в которой переменная 6 должна принимать значения 0 или 1.
Дихотомию можно использовать для описания L-образной невыпуклой
области. Пусть, например, >0, х2 0, 2, х2 2 и либо 1,
либо ж2<1. Мы можем заменить эти условия следующими:
0<xf<1 + §
0<хг<2 - d
0<$<1

Если задача содержит не одну, а несколько пар дихотомий (1) и (2)г
то каждую из них следует заменить системой (5), (6), (7) с целочисленны-
ми переменными 6f.
в) к-кратные альтернативы. Предположим, что у нас имеется более
общая система условий
^2^, х2, . . . , Хп)>09
(9)
^р (*Ц> • • • » *^п) 0.
Пусть требуется получить решение, в котором должны выполняться одно-
временно по меньшей мере к из этих условий. Заменим (9) на
Gi (х) — 6А>0,
С2 (#) — 627у2 0
(10}
Gp (х) — dpLp 0,
где Li есть нижняя граница для Gt (х) при х = (х±9 х2, . . ., хп) g S, a 6Z —
целочисленные переменные, удовлетворяющие условию
6i + 62+...+6p<p^/i:, (И)
причем
0 <6^1. (6/ = 0 или 1) (12)
Приведем пример. Пусть нужно найти минимум по заштрихованным
областям (рис. 26-3-П), описываемым неравенствами Gt > 0, G2 >
> 0, G3 > 0 и по меньшей мере двумя из условий <?4>0, G5 0, <?6>0.
510
г) Выбор из многих пар областей. Шестиконечную «звезду Давида»,
изображенную на нижней части рис. 26-3-11, проще всего описать
посредством дихотомии, в которой точка должна принадлежать одному
из двух треугольников. Задача становится содержательной только тогда,
когда одновременно должно бцггь выбрано много таких пар. Вообще
мы можем иметь несколько пар областей (R^ R[), (Д2, Я2), • • •» (fin*
R'n), причем точка решения х должна лежать либо в Ri9 либо в R[ для
всех i. Для каждой пары R, R' мы поступаем следующим образом. Пусть
Рис. 26-3-11. Примеры невыпуклых областей, представляемых
смешанными целочисленными условиями.
область R описывается системой неравенств Gi (х) 0,? G2 (я) > О, . . ..
. . ., Gm (х) > 0, а область R'— системой (х) > О, Н2 (я) > О, . . .
. . ., Яп (я) > 0. Условие того, что точка должна быть выбрана либо
из первой, либо из второй области, можно записать в виде
{x) — 6Li>0.
G2(x)-8L2>0,
Gm (%) $Lm 0?
0 < 6< 1
Hi (я)_(i-б) l;>o,
н2 (х)—(1 — 6) ь;>о,
(13)
ЯЛ(^)-(1-б)Лп>0,
(6 = 0 или 1),
где Li9 Li — нижние границы для Gt 11 1Ц. Более общий случай выбора
из нескольких областей исследуется путем введения нескольких 6Н как
в (11) и (12).
д) Задачи с дискретными переменными. Пусть некоторая переменная
может принимать только одно из нескольких значений: или
Xi = а2» • • • , или Xi = а*; в то же время аналогичные ограничения нало-
жены на некоторые другие переменные. Исследование всех возможных
511
комбинаций было бы непосильной задачей. Вместо этого мы заменим
каждую А-кратную дихотомию на
+ a2S2 + • • • +^/А, (14)
l = 6i+ 62 + ... + 6д. (6^ = 0 или 1) (15)
Аналогично пусть х = (аг4, х2, . . ., хп) — вектор, который может при-
нимать только определенные векторные значения х = а1 или х = а2,
или х = а3, ... . Это можно заменить на
х = + а262 + ... + akbk, (16)
1 = 61 + б2+...+6А. (6; = 0или1) (17)
«Этот прием позволяет произвести замену нелинейной функции =
п
= Fij (х^ в системе (xj) = О, i = 1, 2, . . ., т на значения этой
j=i
•функции, соответствующие некоторому определенному набору значений
-Xj, скажем Xj = Xj, г = 1, 2, . . ., к. В этом случае вектор пробегает мно-
-жество значений F^, F 2j-, ...» Fmj для каждого значения Xj = xrj.
Рис. 26-3-1II. Преобразование невыпуклой функции
в рамках частично целочисленного программирования.
е) Задачи с нелинейными целевыми функциями. Пусть целевая функ-
ция (см. рис. 26-3-Ш) может быть представлена в виде
п
2 Фу («у) =2 (min), (18)
J=1
где функции <pf нелинейны и невыпуклы. Пусть каждое ф (х) аппроксими-
ровано кусочно-линейной функцией. Тем самым определяется множество
интервалов i = 1, 2, . . ., к ширины hi, в которых наклоны аппроксими-
рующих хорд равны Si. Определим теперь yt как длину пересечения интер-
вала [0, ж] с интервалом i.
Тогда
я = У1 + у2+ • •• +Уа (19)
и ф(я) можно приближенно представить в виде
ф (х) = bo + Sij/i + s2y2 + ... + skyk, (20)
512
где
(г = 1, 2, ...,*). (21)
В случае выпуклой функции <р процедура заключается в замене х и гр (х),
согласно (19) и (20), при условиях (21). Здесь наклоны образуют монотонно
возрастающую последовательность, так что
s2 . (22)
Для фиксированного (р (х) будет минимальным, если уг выбрано
максимальным и если при максимальном yt у2 выбрано максимальным
и т. д. Иными словами, уг в минимизирующем решении представляют со-
бой пересечения i-ro интервала с интервалом [0, х], так что все обстоит
благополучно. См. § 24-3.
Если однако функция ср (х) невыпукла, как на рис. 26-3-Ш,
то простая замена х и <р (х) привела бы к тому, что первыми максимизиро-
вались бы у} с меньшими наклонами. В этом случае сегменты, содержа-
щие ж, были бы несвязными и наше приближение для ср (х) перестало
бы быть пригодным. Чтобы избежать этого, наложим следующее условие:
либо hi‘—yi = O, либо yf+1 = 0, (23)
из которого следует, что если уг не максимально, то yi+i = 0, а если yt
максимально, то возможно неравенство yi+i > 0. Перепишем это условие
в виде
либо yi — либо — Уг+1>0, (24)
а затем заменим его формально на
— У1 + о,
Уг —/^ —( —А*) 6г1>0, (г = 1, 2, ...,&-!)
> (25)
0<6j<1. (6f = 0 или 1)
Подстановкой 61 = 1— 6; (25) можно упростить:
yi^hif
yi>ht6i (Z-l, 2, ..., к-1) (26)
Уг+i
0<6i^l. (6'i = 0 или 1)
X.
Эти условия вместе с (19) и (20) и дают постановку задачи (отметим, что
выполнения условия (21) здесь не требуется). Описанная процедура для
невыпуклого случая рассматривается в статье Марковица и Манна
[1]. Анализ выпуклого случая можно найти в работах Данцига [12]
и Чарнса и Лемке [1].
Заслуживает упоминания и второй метод, основанный на (16). Любую
точку кривой <р (х) можно представить как взвешенное среднее двух
последовательных точек перелома. Следовательно, х и ср (х) можно заме-
нить на
х = Хо«о + ^iai + • • • +
<р (х) = А/о^о + • • • +
1 = Хо + М + • • • + (28)
наложив затем условия, чтобы всеХг равнялись нулю, кроме одной пары
33 Дж. Данциг
Xi>0 (27)
Ki иХж- Для к = 4 это условие можно записать в виде
Хо^ 6о
Х4^ 60 + 6i
Х2< 6i + 62 (29)
Хз 62 4" 63
Х4 63 + 64
Х5 64, ,
где 6j — целочисленные переменные, связанные соотношением
бо + 61 + 62 4“ 63 4- 64 4- 65 = 1. (6j = 0, 1) (30)
Отметим, что если 6г*о — 1 для некоторого i — i0, то неравенства, содержа-
щие Xf0 и % < 4-1, ослабляются, а остальные удовлетворяют условию
X, < 0, так как в силу (30) для них будет 6$ = 0.
ж) Условные ограничения. Пусть х и у — функции нескольких пере-
менных. Предположим, что для х известна верхняя граница С7Х, а для
х и у — нижние границы Lx и Ly. Мы хотим наложить условия типа
если х>®, то у>0. (31)
Мы можем записать (31) в виде
либо #>*0, у>0, либо х^.0, (32)
а последнее условие переписать как
х
y>bLy, (33)
я<(1- 6)С7Х. (6 = 0, 1)
Здесь первое неравенство записано со знаком > вместо знака >, так
как при х = 0 условие у > 0 автоматически выполняется, если взять
6 = 1.
Теперь мы можем развить этот метод для случая, когда наложены
условия
если х > 0, то и > 0,
(34)
если x<zO, то w^>0. ' '
Эти условия можно записать в виде
я (1 63) L х,
я<(1 —63) С7Х,
^>6tLx,
u>^Lu, (35)
62£^х>
w > 82Lw,
61 + 62 = 1 + б3. (6j = 0, 1)
Пусть, например, в некоторой задаче с Т периодами мы хотим закон-
чить какую-то определенную работу в максимально ранний из возмож-
ных периодов. Пусть xt — накопленная сумма уровней интенсивности
процесса от периода t до последнего периода Т. Мы хотим, чтобы xt =
= 0 для наименьшего t. Отметим, что в этом случае из xh > 0 следует,
что х8 > 0 при s < к. Положим для t = 1, 2, . . ., Г,
если 6* = 0, то xt = 0. (36)
514
Утверждение (36) можно переписать в виде
0<^<6^, (6< = 0, 1), (37)
где Ut есть верхняя граница для xt, и определить затем min z, где
z = 6i 4- 62 $т* (38)
з) Нахождение глобального минимума вогнутой функции1. Пусть нам
нужно минимизировать вогнутую функцию Z — Z (хи х2. . . ., Хп) по
некоторой области R. Если область R выпукла, то задача становится
по существу весьма трудной, так как вогнутая функция может иметь
локальные минимумы во многих — более того, даже во всех крайних
точках области R. Мы будем предполагать, что область R выпукла, так
как рассмотренные выше приемы позволяют нам использовать выпуклость
области в сочетании с целочисленными переменными для решения широ-
кого класса задач, содержащих условия типа «либо — либо». Пусть
область R задана — после подходящей замены переменных — в стан-
дартной для линейного программирования форме
Ех — е, я>0, (39)
где Е — данная т X n-матрица, а е — данный тп-мерный вектор.
Вогнутая функция Z может быть задана явным или неявным образом.
В качестве примера неявного задания предположим, что вектор у и вели-
чина Z для фиксированного х определяется условиями
Fy = f + Ex, у>0
max $у = Z (min), (^0)
где Е и F — данные матрицы, а / и ₽ - данные векторы.
Упражнение. Доказать, что max $у есть вогнутая функция от х.
У\%
Доказать, что функция ф (х) = min{(pi (ж), <р2 (ж), . . .} вогнута, если
функции ^t(x) вогнуты при всех I.
Можно привести следующую интерпретацию этой модели, имеющую
яркие аналогии в реальных ситуациях. Рассмотрим двухходовую игру,
в которой первый игрок, выбирая свою стратегию я, подчиненную усло-
виям (39), изменяет уровень ресурсов / своего оппонента на величину
Ех. Второй игрок, выбирая свою стратегию у в соответствии с условиями
(40), получает выигрыш $у. Задача первого игрока заключается в выборе
стратегии х, минимизирующей максимальный выигрыш второго игрока.
Мы будем предполагать, что Z во всех точках х можно разумным
образом аппроксимировать минимумом Z на некотором конечном множе-
стве к касательных к поверхности Z = Z (х) гиперплоскостей
Z = tfii£i +012^2+ - • • + bi. G’ = l, 2, ...,&) (41)
Задача сводится к выбору х и min Z, удовлетворяющих условиям
(39), и таких, что пара (х, Z) удовлетворяет хотя бы одному из условий
Z — [йц^14“ ^12^2 Ч” • • • + ^in^n— ^11 0,
Z — [^21^1 4" а22х2 4- • • • 4“ а2пхп — Ъ2} 0,
......................... • •• • г (42)
% — + flfe2^2 4" • • • "h aknxn — bk] 0.
1 Этот вопрос был разработан совместно с Ф. Вулфом,
515 33*
Мы можем переписать (42) в виде
Z— [ail^1 + ai2x2+ ... + ainxn]>M (1 — 6t), (i = l,2,
61 + б24-...+6й = 1, (6, = 0, 1) (43)
где M — некоторая нижняя граница для написанных разностей. Этот
способ решения зависит от аппроксимации функции Z = Z (х) гиперпло-
скостями. Решение задачи, данное в работе Данцига [17] для слу-
чая, когда Z задается неявно посредством (40), требует нахождения х, у,
min z и вспомогательных переменных л =(ль . . и т]7- > 0, j =
= 1, 2, . . ., п', удовлетворяющих условиям
Ех = е, Fy — f-}-Ex, z = $y,
jiF + t] —р = 0 (44)
либо > 0, либо У;>0,
где л =(Л1, ...» лт')— вектор-строка, у; — J-я компонента вектора у,
Ц; — J-я компонента вектора ц.
Упражнение. Проверить (44).
II. ЗАДАЧА С ФИКСИРОВАННЫМИ ДОПЛАТАМИ
Выше мы описали задачу, в которой аукционист требовал, чтобы
размер ставок был подчинен следующему условию: либо х = 0, либо
я > а. В основе этой и многих других задач лежит понятие фиксирован-
ной доплаты, не зависящей от размера заказа. В этом случае х = а пред-
ставляет собой своеобразную точку перелома для аукциониста. В общем
случае издержки С характеризуются формулой
кх-[-Ь, если х>0,
С = n п (45)
0, если х = 0, '
где b — фиксированная доплата. Мы можем записать это в виде
С = кх-\-дЬ. (6 = 0, 1) (46)
При 6 = 0 здесь х также должен равняться нулю. Чтобы обеспечить это,
мы наложим условия
я<6?7 (47)
и
0<6<1, (6 = 0, 1) (48)
Где U — некоторая верхняя граница для х. Рассмотрение задачи с фикси-
рованной доплатой, основанное на этом приеме, можно найти в работе
Данцига и Гирша [1].
III. ЗАДАЧА О БРОДЯЧЕМ ТОРГОВЦЕ
Постановка задачи. В каком порядке бродячий торговец должен
объезжать п городов, чтобы минимизировать суммарное расстояние, прой-
денное при объезде всех городов? Мы приведем три формулировки этой
широко известной задачи.
516
Пусть xijt — 1 или 0 в зависимости от того, идет ли t-я дуга
пути от вершины i к вершине j или нет. Положим Хип+1 = х^.
Тогда условия
= (+1, (/, Z = l, ...,n) (49) i k 2^ = 1, (i = l,...,n) (50) j, t 2 dijxtjt = z (min) (51) i, j, t
выражают, что а) если мы прибываем в город у на шаге t, то на шаге t + 1
этот город покидаем, б) существует только одна дуга, выходящая из верши-
ны г, и в) длина контура минимальна. Нетрудно показать, что целочислен-
ное решение этой системы представляет собой контур (Флад [2]).
В двух статьях Данцига, Фулкерсона и Джонсона [1], [2] слу-
чай симметричных расстояний
нением только двух индексов. Здесь
Хц = xij ~ 1 ИЛИ О в зависимости от
того, был ли в контуре в какой-то мо-
мент пройден путь от I к у или от j к I
или нет. В этом случае соотношения
2^ = 2 (/ = 1, 2, ...,«) (52)
был
сформулирован с приме-
Рис. 26-3-1V. Для устранения под-
контуров в задаче о бродячем торгов-
це добавляются условия петель.*
(53)
И
2 dijXij = z (min)
i, j
выражают условие, что сумма коли-
честв въездов и выездов для каждой
вершины равна двум. Отметим, что в этом случае не делается различия
между двумя возможными направлениями обхода дуги между двумя
городами. Однако, хотяная^ наложены условия целочисленности в интер-
вале
1,
(54)
этцх условий оказывается все же недостаточно для характеризации конту-
ра, так как подконтуры, подобные изображенным на рис. 26-3-1V,
также удовлетворяют им. Однако если в качестве дополнительных огра-
ничений наложить так называемые условия петель типа
#12 + #23 + #31 2,
(55)
то непригодные целочисленные решения будут исключены..
Упражнение. Построить дробное решение системы (49), (50), (51),
являющееся минимальным. Показать, что любое целочисленное решение
без подциклов представляет собой полный контур.
Третий способ сведения задачи о бродячем торговце к целочислен-
ной задаче линейного программирования принадлежит А. У. Таккеру
(см. Миллер, Таккер, Землин [1]). Он связан с меньшим числом ограни-
чений и переменных, чем описанные выше постановки. Пусть = 1 или
0 в зависимости от того, переезжает ли торговец из города i в город у
или нет, где I = 0, 1, . . ., п. Тогда оптимальное решение можно опреде-
лить, найдя целые числа Хц, произвольные вещественные числа щ и min 2,
517
удовлетворяющие условиям
2 = (/=1, 2, П)
г=0
У Xij — 1, (i = l, 2,
3=0
(56)
Ui—Uj + nxtjt^n — 1, (1 г =/=/^ «)
п п
3 S dya;v = z(min).
г—0 j=0
Если мы получим целочисленное решение, удовлетворяющее первым
двум группам ограничений, но не являющееся контуром, то нарушится
третья группа ограничений. В самом деле, в этом случае решение содер-
жит не менее двух петель с к < п дугами. Если сложить все неравенства,
отвечающие = 1, вдоль такой петли, не проходящей через город О,
то все разности щ — uj сократятся и мы получим пк (п —1) к —
противоречие. Нам осталось только показать, что для любого контура,
начинающегося из i = 0, можно найти числа ut, удовлетворяющие треть-
ей группе условий. Положим ut = t, если город i посещается на t-м шаге,
где t = 1, 2, . . ., п. Ясно, что ut — Uj п —1 для всех i и /. Следова-
тельно, эти условия выполняются для всех Хи = 0; для хи = 1 мы полу-
чаем Ui — Uj + nXij = t — (t + 1)+ n = n —1.
IV. ЗАДАЧА ОБ ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТАХ
Латинский квадрат состоит из п множеств п объектов, расположен-
ных в Квадратной таблице размером п X п таким образом, что ни один
объект не повторяется ни в одной строке и ни в одном столбце. Два латин-
ских квадрата называются ортогональными, если все п2 упорядоченных
пар объектов, стоящих в клетках с одинаковыми номерами, различны.
Таковы, например, квадраты
(1) (2) (3) (2) (3) (1)
(2) (3) (1) (1) (2) (3) (57)
(3) (1) (2) (3) (1) (2)
Эйлер высказал гипотезу, что для некоторых п не существует ортогональ-
ных латинских квадратов. После большой работы случай п = 10, напри-
мер, был проанализирован в 1959 году1. Дэвид Гейл предложил испробо-
вать в этом вопросе целочисленное программирование.
Формулировка является непосредственной и следует уже знакомым
образцам. Пусть х^н — 0 или 1 в зависимости от того, помещается ли пара
(г, /) в строку к и столбец I или нет. Условие, что каждая пара (i, j) поме-
щается в одну клетку, записывается в виде
2 xijla = i. (г, / = 1, 2, ...,п) (58)
fe, I
1 Р. Бозе и С. Шуканде доказали, что знаменитая гипотеза Эйлера о несуще-
ствовании ортогональных латинских квадратов некоторых четных порядков была
неверной. Э. Паркер построил пару ортогональных латинских квадратов порядка 10.
Для дальнейшей информации отсылаем читателя к резюме 558-27 в августовском
номере журнала «Notices of the American Math. Society». Популярный отчет об их ре-
зультатах был опубликован в журнале «Scientific American», Vol. 201, No 5, 1959,
pp. 181—188.
518
Условие, что в каждую клетку А, I помещается одна пара (f, 7), есть
3«ум = 1. (к, 1 = 1, 2, п) (59)
i, j
Условие, что в Z-м столбце первого латинского квадрата i появляется
только один раз, дается формулой (60). Формула (61) представляет
условие, что во втором латинском квадрате в столбце к индекс j также
появляется только один раз.
%xi)kl = i, (i, 1 = 1, 2, ...,п) (60)
j, k
= (/, Z = l, 2, ...,n) (61)
i, k
Аналогично условие, что в /с-й строке первого и второго латинского квад-
ратов индексы i (соответственно у) появляются только один раз, имеет вид
= (i, к = 1, 2 ..п)
(62)
^xijkl = l. (j, к = 1, 2 ...n)
i, I
Интересно отметить, что суммирование в этих условиях ведется по всем
возможным парам индексов из четырех; при этом получаются шесть сис-
тем из п2 уравнений каждая. При п — 10 мы имеем 600 уравнений, что
пока недоступно для машинных программ по целочисленному программи-
рованию, созданных к 1962 г. Однако введение специальных сокращенных
приемов вполне может сделать эту задачу разрешимой.
V. ЗАДАЧА О ЧЕТЫРЕХ КРАСКАХ (ЕСЛИ ОНА РЕШАЕТСЯ)
Одна из знаменитых нерешенных математических проблем заклю-
чается в следующем. Доказать или опровергнуть, что любую карту на
плоскости можно раскрасить, используя не более четырех красок. При
этом области, имеющие общую границу, отличную от точки, должны
иметь разные цвета. Мы укажем два пути конструктивной раскраски
Рис. 26-3-V. Задача о четырех крас-
ках эквивалентна нахождению мно-
жества подциклов четного порядка.
конкретной карты — если такая раскраска вообще возможна. Хотя это
и не содействует доказательству или [опровержению самой гипотезы, тем
не менее эффективный способ решения конкретных задач на электронной
вычислительной машине может помочь найти опровергающий пример.
Нетрудно свести дело к случаю, когда, как это показано ниже, три
области имеют не более одной общей точки, которую мы будем называть
вершиной. При этом соответственно будут иметься три дуги, ведущие
из любой вершины i к другим узлам /. Известно, что если возможно рас-
красить карту в четыре цвета, то (верно также и обратное) возможно,
рассматривая вершины как города, а дуги — как дороги между ними,
либо обойти все узлы, либо построить несколько взаимно непересекаю-
щихся четных подконтуров, подобных изображенным на рис. 26-3-V.
519
Упражнение. Показать, что число дуг кратно трем, а число узлов
четно.
Теперь мы можем сопоставить каждому такому объезду по четному
циклу дуги, которые изменяют свое направление, когда мы переходим
от вершины к вершине. Это означает, что вершины i можно разбить на два
класса: вершины, имеющие две выходящие дуги, и вершины, имеющие
две входящие («заходящие») дуги. Положим x-Lj.= 1, если дуга (i /)
входит в подобный подконтур; в противном случае полагаем xi} = 0. Следо-
вательно,
(63)
Подразумевается, что рассматриваются только дуги (г, /) и переменные
Хи, соответствующие областям, имеющим общий участок границы. Все
дуги (/, /), не отвечающие границам, в ограничениях опускаются.
Условия
.S^j = 2Si (Sf = 0; 1) (64)
выражают тот факт, что при 6^ — 1 в некотором подконтуре, ведущем из
вершины г, должно быть две дуги; в противном случае таких дуг нет
вовсе. Условия
2хм = 2-26г (65)
г
устанавливают, что при 6f = 0 в некотором подконтуре, ведущем в верши-
ну i, должно быть две дуги, а в противном случае — ни одной. Три набора
условий (63), (64), (65) представляют собой условия транспортной задачи
с дополнительными ограничениями на переменные. Если — целые
числа, то крайняя точка, определенная из этих условий, будет целочислен-
ной. Отсюда, казалось бы, следует, что стоит только предположить бг- цело-
численными, как в экстремальном решении все х^ без всяких дальнейших
предположений окажутся целочисленными. Однако ошибочный выбор сис-
темы целых чисел б* может привести к пустому множеству допустимых
решений. В качестве другой возможности при использовании методов
целочисленного линейного программирования для решения этой задачи
может оказаться полезным допустить изменение б^ в интервале Ос 6f < 1
и выбирать случайным образом различные целевые функции — поскольку
их выбор находится в нашей власти — до получения оптимальной край-
ней точки с целочисленными х^.
Второй подход, предложенный Гомори, является более непосредствен-
ным. Пусть области занумерованы индексом г = 1, 2, . . ., Я, a tr—
целочисленная переменная, для которой
0</г<3.
Здесь четыре значения переменной tr= 0, 1, 2, 3 соответствуют четырем
краскам. Если области г и s имеют общую границу, их окраска должна
быть различной. Следовательно, для каждой такой пары
tr-t8^O. (66)
Это соотношение можно записать в форме условия типа «либо — либо»:
либо tT — ZS>1, либо ts—£г>1. (67)
Последнее мощно переписать, как
tr — 46rs, (6rs = 0; 1)
Глава 27
МОДЕЛЬ ДИЕТЫ ШТИГЛЕРА:
ПРИМЕР ФОРМУЛИРОВКИ И РЕШЕНИЕ
Одно из первых применений симплекс-алгоритма было связано с опре-
делением соответствующей требованиям диеты при минимальных затра-
тах1. Осенью 1947 г. сотрудником проекта «Математические таблицы»
Национального бюро стандартов США Д. Лэдерманом впервые в данной
области были проведены обширные вычисления с целью проверки только
что предложенного симплекс-метода. Рассматриваемая система состояла
из 9 уравнений с семьюдесятью семью неизвестными. Для решения этой
задачи с использованием ручной настольной счетной машины понадоби-
лось около 120 человеко-дней.
Эта частная решенная задача исследовалась ранее Д. Д. Штигле-
ром [1], который предложил решение, основанное на замене одних
пищевых продуктов другими, содержавшими на каждый затраченный
доллар большее количество питательных веществ. Штиглер рассмотрел
510 возможных вариантов сочетаний выбранных продуктов. Он не ставил
целью получить решение на минимум затрат; тем не менее им были при-
ведены веские доводы, говорящие о том, что годовые затраты нельзя
сократить более чем на несколько долларов. Действительно, мы увидим,
что решение Штиглера после пересчета затрат из ежедневных в годовые
было только на 24 цента выше истинного годового минимума, равного
39,69 долл. (10,9 цента в день).
27-1. ЗАДАЧИ ПРИ ФОРМУЛИРОВАНИИ МОДЕЛИ
Прежде чем начать математическое описание задачи о диете, полезно
уяснить, каким образом создаются «математические модели». Будет пока-
зано, что это далеко не точная операция, так что естественно поставить
под сомнение обоснованность усовершенствованных методов решения
такой приближенной модели. Такое положение является типичным
почти для всех случаев, где применяются методы программирования.
Однако следует помнить, что одна из причин того, что в настоящее время
рассматриваются только приближенные модели, состоит в исторической
неспособности исследователя решить какую-либо большую сложную
модель. По мере создания средств вычислительной техники для решения
таких систем росло и желание исследователей усовершенствовать модели,
с тем чтобы использовать все преимущества новых методов. В течение
нескольких ближайших лет, по-видимому, будет положен конец этому
порочному кругу прошлого, при котором создание неудовлетворительных
моделей оправдывало быстрые грубые «решения», и, наоборот, отсутствие
1 Д. Корнфилд, сотрудник правительственного аппарата США, сформулировал
подобную математическую задачу еще в 1940 г.
521
методов точного решения оправдывало создание неудовлетворительных
моделей. По всей вероятности, как методы построения моделей, так и мето-
ды их решения начнут, несомненно, подкреплять друг друга.
В статье Штиглера приводится весьма подробное обсуждение пред-
посылок модели пищевой диеты; большая часть последующего изложе-
ния основана на этом источнике и очень близко его придерживается.
С тех пор как была опубликована статья Штиглера, в модель было
внесено много усовершенствований. Тем не менее интересно рассмотреть
некоторые типичные случаи, с которыми лицо, формулирующее модель,
сталкивается на ранних этапах. Штиглер начинает с некоторых сведений
об исследовании питания.
1) Если удовлетворен определенный минимум в питательных веще-
ствах, то дополнительные количества этих веществ ведут к уменьшению
полезного воздействия (а в некоторых случаях оказывают и отрицательное
воздействие) на здоровье человека.
2) Оптимальное количество какого-либо питательного вещества зави-
сит от наличия в диете других питательных веществ.
Убывание полезности иллюстрируется тем фактом, что количество
усваиваемого организмом кальция растет значительно медленнее, чем
он вводится в организм, и что увеличение продолжительности жизни
непропорционально вводу кальция в организм. В некоторых случаях
можно заменять один вид питательного вещества другим.Штиглер приводит
пример, в котором рекомендуется 30 микрограммов тиамина заменять
на 100 калорий, получаемых не от жиров, а от других источников питания,
кроме жиров. Другой пример состоит в том, что потеря рибофлавина сопро-
вождается недостатком тиамина.
Далее Штиглер ставит другой вопрос. Сколько требуется различных
питательных веществ? В какой степени потребности одного человека
отличаются от потребностей другого? Решая эти вопросы, он заметил, что
оптимальное количество калорий известно достаточно точно, но потребно-
сти в других компонентах питания выявлены лишь приближенно или
совсем неизвестны. Многие минимумы, которые обычно из-за предосто-
рожности увеличивают на 50%, находят путем определения наименьшего
уровня потребления питательных веществ, сравнимого с устойчивой нор-
мой потерь этих веществ через выделение.
Взаимосвязи между различными питательными веществами еще менее
ясны и в диетических рекомендациях фактически игнорируются. Очень
сложным является даже простое перечисление веществ, необходимых для
здоровья человека. Так, например, кроме кальция, организму требуется
около 13 видов минеральных веществ (некоторые из них в незначитель-
ных количествах), много видов витаминов, около десятка разных типов
аминокислот и, возможно, еще больше веществ, пока еще не установленных.
Составленная Штиглером диета требовала значительно меньших зат-
рат по сравнению с диетами, рекомендуемыми другими. Одна из причин
этого заключается в том, что другие диеты предусматривали большее
разнообразие пищи для «страховки» от того, что могут быть пропущены
какие-либо неизвестные питательные элементы. Другая причина состояла
в том, что специалисты по диете придавали некоторое значение социаль-
ному и политическому давлению, и в особенности в тех случаях, когда
они не имели доводов для обоснования своих предложений. С другой сто-
роны, Штиглер обосновывает свою диету в этом отношении, ссылаясь
на мнение Национального исследовательского совета о том, что если
определенная группа известных питательных веществ потребляется орга-
низмом с обычными продуктами питания, то все другие минеральные
вещества и витамины будут в соответствующих количествах автомати-
522
чески введены в организм. Если принять это положение, то первым шагом
в составлении математической модели должно быть принятие утверждения
Совета о ежедневных нормах потребления питательных веществ, которые
приведены в табл. 27-1-1. Заметим, что в перечень вошло всего
Таблица 27-1-1
Ежедневные нормы потребления веществ для умеренно
работающего человека
(При весе около 70 кг)1
Элемент питания Ежедневная норма
Калории Белки Кальций Железо Витамин А Тиамин (В4) Рибофлавин (В2 или G) Ниацин (никотиновая кислота) Аскорбиновая кислота (С) 1 Национальный исследовательс щевые нормы», Печатная и циркуля 3000= bi (кал.) 70 = Ь2 (а) 0,8 = Ь3 (г) 12 = 64 (мг) 5000 = 65 (междунар. ед.) 1,8 = &б (мг) 2,7=&7 (мг) 18 = 68 (мг) (мг) кий совет, «Рекомендуемые пи- рная серия № 115, январь 1943.
лишь девять наиболее известных питательных веществ; при этом предпо-
лагается, что все остальные питательные вещества включаются в диету
автоматически. Следует также отметить, что нормы потребления (о кото-
рых говорилось выше) являются приближенными и, возможно, за исклю-
чением калорийности, почти любое их числовое значение в довольно
широком диапазоне, могло бы быть хорошо обосновано.'i
Рассматривая питательные ценности пищевых продуктов, мы снова
наблюдаем аналогичную ситуацию, так как питательные ценности обыч-
ных продуктов известны лишь приблизительно, и это все, что можно
узнать о них. Широкая полоса неопределенности возникает цо несколь-
ким причинам. Так, например, содержание аскорбиновой кислоты в мг
на каждые 100 г яблок колеблется в зависимости от их сорта:
Джонэтэн 4,4
Макинтош 2,0
Нозерн Спай 11,0
Онтарио 20,8
Вайнсэп 5,8
Зимний банан 6,6
Содержание аскорбиновой кислоты в молоке имеет сезонные коле-
бания. При этом существенное значение имеют такие условия хранения
продуктов, как температура и продолжительность.
В более зрелом плоде содержится большее количество витамина А, но
меньшее количество аскорбиновой кислоты. Длительное приготовление
пищи уменьшает ее питательную ценность; в хорошо приготовленном
ростбифе содержится около 70% тиамина, рибофлавина и ниацина по срав-
нению с сырым мясом. Помимо того что существует значительное непосто-
янство содержания питательных веществ в самих продуктах, которое,
по-видимому, можно учитывать при формулировке модели, привлекая
вероятностный подход (как это сделано в гл. 25, посвященной задачам
в условиях неопределенности) согласно Штиглеру, питательная ценность,
523
Таблица 27-1-11
Питательные свойства известных продуктов на каждый затраченный доллар.
15 августа 1939 г.
(Перечень 20 продуктов, являющийся сокращенным вариантом перечня из 77 продуктов)
Питательные единицы (i)
Продукты 1 (j) Калории (1000) Белки (2) Кальций (г) Железо (Л€2) Витамин А (1000 между- нар. ед.) Тиамин (мг) Рибо- флавин (мг) Ниацин (.иг) Аскорби- новая кислота (мг)
1 2 3 4 5 6 7 8 9 10
*♦ 1. Пшеничная мука (обогащенная) 44,7 1411 2,0 365 55,4 33,3 441 —
5. Кукурузная мука 36,0 897 1,7 99 30,9 17,4 '7,9 106 —
*♦ 15. Сгущеное молоко (банки) 8,4 422 15,1 9 26,0 3,0 23,5 И 60
* 17. Маргарин 20,6 17 0,6 6 55,8 0,2 — — —
** 19. Сыр (Чеддер) 7,4 448 16,4 19 28,1 0,8 10,3 4 —
21. Арахисовое масло 15,7 661 1 48 — 9,6 8,1 471 —
24. Лярд 41,7 — — —. 0,2 — 0,5 5 —
** 30. Печень (говяжья) 2,2 , 333 0,2 139 169,2 6,4 50,8 316 525
34. Мясо свиное (филейное) 4,4 249 0,3 37 — 18,2 3,6 79 —
40. Молодой лосось (банки) 5,8 705 6,8 45 3,5 1,0 4,9 209 —
* 45. Зеленая фасоль 2,4 138 3,7 80 69,0 4,3 5,8 37 862
** 46. Капуста 2,6 125 4,0 36 7,2 9,0 4,5 26 5369
* 50. Лук репчатый 5,8 166 3,8 59 16,6 4,7 5,9 21 1184
* 51. Картофель 14,3 336 1,8 118 6,7 29,4 7,1 198 2522
** 52. Шпинат 1,1 106 — 138 918,4 5,7 13,8 33 2755
53. Сладкий картофель 9,6 138 2,7 54 290,7 8,4 5,4 83 1912
* 64. Персики сушеные 8,5 87 1,7 173 86,8 1,2 4,3 55 57
* 65. Чернослив сушеный 12,8 99 2,5 154 85,7 3,9 4,3 65 257
** 68. Лимская фасоль (сушеная) 17,4 1055 3,7 459 5,1 26,9 38,2 93 —
** 69. Морские бобы (сушеные) 26,9 1691 11,4 792 — 38,4 24,6 217 —
1 Номера продуктов взяты из первоначального списка Штиглера. Строки со звездочкой относятся в § 27-2. г к сокращенному перечню, объяснения которому даны
установленная в 1944 г. для многих пищевых продуктов, определялась
при помощи устаревших и неточных методов или могла быть явно оши-
бочной по другим причинам.
В процессе отвлечения от всех этих деталей, была создана модель,
в которой приводится нечто вроде среднего значения питательности весовой
единицы для каждого вида закупаемых продуктов. Если было закуплено
Xj единиц /-го продукта, а в каждой единице продукта содержится
единиц i-го вещества, то предполагается, что человек получит
п
j=i
единиц Z-ro вещества, считая, что не было никаких потерь, связанных
с приготовлением пищи. Имеется также неявное предположение, состоя-
щее в том, что между различными продуктами не происходит взаимодей-
ствия, т. е. что на общее количество единиц того или иного питательного
вещества, содержащегося в каком-то продукте, наличие в диете других
продуктов не влияет.
Наконец, был составлен перечень потенциальных продуктов, розничные
цены на которые сообщило Бюро статистики труда. Перечень этот не был
полным, поскольку в него не вошли почти все виды свежих фруктов,
многие из недорогих сортов овощей, богатых питательными веществами,
и свежая рыба. Если бы все это можно было включить в перечень, то диету
с минимальными затратами, по-видимому, можно было бы значительно
удешевить. Однако другие исследователи нашли, что оптимальный вариант
очень мало зависит от этих конкретных цен, ввиду наличия в оптимальной
диете определенных видов основных продуктов.
В табл. 27-1-11 коэффициенты ац на каждый доллар затрат
даны для сокращенного перечня некоторых из 77 типов продуктов, рас-
смотренных Штиглером. В тех случаях, когда цены из-за местных и сезон-
ных условий подвержены изменениям и когда необходимо решить не одну,
а несколько таких задач, Штиглер рекомендует пользоваться для измерения
количества продуктов такими физическими единицами, как вес или —
в случае жидкостей — объем. Если это будет сделано, то данные по це-
нам и данные по питательным свойствам могут составляться независимо
друг от друга.
МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА
Модель питания может быть теперь сформулирована как задача линей-
ного программирования. Пусть множество возможных процессов (/) и их
интенсивностей Xj имеет вид:
Интенсивности
процессов
Процессы (единица=1 долл, ежед-
невных затрат)
1. Закупка 1-го типа
продукта (пшенич-
ная мука)
2. Закупка 2-го типа #2
продукта (макаро-
ны)
п. Закупка п=77-го типа ^77
продукта (земля-
ничные консервы)
525
Пусть множество ингредиентов (i) будет состоять в данном случае
из девяти типов питательных веществ, которые перечислены в табл. 27-1-1.
Остается единственный вопрос, который следует выяснить для построе-
ния математической модели, а именно, ставим ли мы цель, чтобы
потребности в питательных веществах удовлетворялись бы точно, или же
они могут превышаться. В первом случае мы рассматриваем задачу типа
п
2 aijXj^bi, (Xj>0) (1)
j=l
а во втором — задачу типа
2 ^ijXj^bi, (Xj^O) (2)
где Xj следует выбрать так, чтобы минимизировать суммарные затраты
п
z = 2 (3)
Может показаться, что наложить условие строгого удовлетворения
потребностей лучше, чем допускать возможность их превышения, посколь-
ку для получения пищевого рациона сверх фактической потребности
необходимо произвести большие затраты. Однако это рассуждение обман-
чиво, так как любая система значений Xj, которая удовлетворяет системе
(1), автоматически удовлетворяет и неравенствам (2), и, следовательно,
минимальное значение z, полученное при условиях (2), конечно, не боль-
ше, чем при условиях (1). Другими словами, всегда дешевле (или в крайнем
случае не дороже) допустить избыточное удовлетворение потребностей,
чем требовать их точного удовлетворения.
Люди часто критикуют план, поскольку им кажется, что в нем имеют-
ся «излишества». Они подмечают, что не каждый человек занят в течение
всего рабочего времени или какая-то установка или машина простаивает
часть рабочего времени. По их мнению, хороший план должен поставить
дело так, чтобы все эти люди и машины все время работали производи-
тельно. Однако один из первых выводов, которому учит программирова-
ние, состоит в том, что не всегда целесообразно пытаться устранить все эти
«недостатки». Например, чтобы привлечь к работе незанятых людей,
необходимо обеспечить их инструментом и материалами, которые могут
быть крайне нужны где-то в другом месте. Если обратиться к ссылке
под табл. 27-2-1, то в случае задачи о диете можно увидеть, что
требование о недопущении излишков питательных веществ увеличивает
минимальные затраты с 10,9 цента до 13,8 цента ежедневно, т. е. более
чем на 25%.
Мы сформулируем задачу о пищевой диете, в которой допускается
превышение по всем питательным веществам. При таком подходе имеется
опасность того, что в решении может быть получена диета, которая содер-
жит излишек калорий или других питательных веществ, вредных для
здоровья человека.
Во-первых, расширим систему, введя в нее свободные переменные
яп+1, . . хп+т, что дает
п
2 xn+t~ = 2, ..., т) (4)
j==l
п
2 Xj = z (min). (5)
1
526
Далее расширим систему, введя в нее искусственные переменные xn+m+1,...
• • М ^п + 2т» так ЧТО ТвПврЬ ДЛЯ 1 = 1, 2, . . ., ТП
п
2 %n+i Ч- ^n+m+i — Ь}. (6)
j=i
27-2. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ О ДИЕТЕ
РЕШЕНИЕ С ПОМОЩЬЮ ЭЛЕКТРОННОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
Задача о диете, для решения которой в 1948 г. (с использованием
настольной вычислительной машины) требовалось 120 человеко-дней, мо-
жет быть обработана на современной электронной вычислительной маши-
не в течение нескольких минут. Продолжительность этой обработки зави-
сит от того, какой объем информации требуется получить в отпечатанном
виде, учитывая особенности задачи. Так, для решения подобной задачи
в 1953 г. с использованием вычислительной машины ИБМ-701 и про-
граммы симплекс-метода корпорации РЭНД с выводом на печать результа-
тов по всем итерациям, потребовалось 12 минут; без печати промежуточных
Рис. 27-2-1. Уменьшение значения формы
недопустимости и целевой функции как функция
итерации в задаче о диете.
результатов необходимое время можно было бы уменьшить до одной чет-
верти. Если ту же задачу решать на вычислительной машине, выпущен-
ной после 1960 г., то необходимое время исчислялось бы долями минуты.
Так как предполагалось сравнение решения, минимизирующего затра-
ты в случае, описанном в § 27-1-(1), когда имеет место строгое удовлетво-
рение потребностей, и в случае, описанном в § 27-1-(2), когда допу-
скаются превышения над потребностями, то программа не предусматрива-
ла введение первоначально в базисное множество какой-либо свободной
переменной. Этап I был закончен на 12-й итерации, и в результате было
получено базисное допустимое решение. Этап II был закончен на 16-й ите-
рации, и в результате было получено оптимальное допустимое решение
для задачи § 27-1-(1). На данном этапе было предусмотрено ввести
в базисное множество избыточные переменные, после чего для получения
оптимального решения в задаче § 27-1-(2) потребовалось дополнительно
8 итераций. В целях выяснения возможности сокращения количества итера-
ций для последней задачи была решена вторая задача, в которой
допускалось включение избыточных переменных в базисное множество на
любом этапе решения. По случайному совпадению потребовалось то же
количество в 24 итерации. Возможное объяснение см. в задаче 15. Резуль-
таты этих вычислений сведены в табл. 27-2-1 и представлены на рис.27-2-1.
527
Таблица 27-2-1
Изменения в базисных процессах: значения для w и £
Ите- рация Базисные процессы Форма недо- пустимо- сти (w) Целевая форма z (центы)
Этап I °| 1 2 недоста- ток калорий то же » » недостаток белков то же » » недоста- ток кальция то же » » недостаток железа то же морские бобы недостаток витамина А то же » » недоста- ток тиа- мина то же » » недостаток рибофлави- на то же » » недостаток ниацина то же » » недостаток аскорбино- вой кислоты капуста то же । 191,3 110,3 69,6 0 1,4 2,8
3 4 5 » » » » » » » » » » » » » » » » » » то же лосось то же » » » » » » мука то же » » » » » » » » » » » » свинина » » » » » » ' 38,2 27,8 19,5 4,4 5,6 7,0
6 7 8 » » » » » » » » » » кУкУРУзная мука » » » » » » » » » » » » » » шпинат То же фасоль то же » » » » » » » » То же » » » » » » » » » » 11,0 7,3 4,2 14,3 14,6 14,5
9 10 11 » » лярд то же то же >> » » » » » » » сгущен- ное мо- локо » » » » » » говяжья печень то же » » » » » » » » » » » » » >> » » » » • » » » » » » » » 2,6 1,5 0,2 13,0 15,6 19,9
12 13 14 » » » » » » » » » » » » » » » » » » » » » » » » » » » » » шпинат лимская фасоль мука » » » » » » » » » » — 1 20,5 16,9 14,8
Продолжение табл. 27-2-1
34 Дж. Данциг
Ите- рация Базисные процессы Форма недо- пустимо- сти (ub) Целевая форма z (центы)
15 лярд кукурузная сгущен- арахисовое говяжья шпинат мука свинина капуста — 14,0
мука ное масло печень
молоко
16 то же то же то же то же то же то же то же картофель то же Min - = 13,81
17 » » » » » » » » » » » » » » избыток » » — 13,5
J—< ►—f железа
и
св 18 » » морские » » » » » » » » » » то же » » — 13,4
л бобы
19 » » то же » » избыток » » » » » » » » » » — 12,8
тиамина
20 » » лимская » » то же » » » » » » » » » » — 12,7
фасоль
21 » » избыток » » » » » » » » » » » » » » — 12,7
ниацина
22 » » то же » » » » избыток » » » » » » » » — 11,8
белков
23 морские » » » » » » то же » » » » » » » » — 10,9
бобы
24 то же » » говяжья » » » » » » » » » » » » Min z2 = = 10,9 2
печень
1 Min zi, полученный в итерации (16), есть решение на минимальную стоимость без избытка питательных веществ.
2 Minz2, полученный в итерации (24), есть решение на минимальную стоимость при избытке питательных веществ.
Симплексное
сокращенного вида
Цикл
Наименование Базисное решение Пше- нич- ная мука (обо- гащен- ная) Сгущен- ное мо- локо Сыр чеддер Говяжья печень Ка- пуста Шпинат
пере- мен- ная значение bi О«1) (15) (19) (30) (46) (52)
Калории *111 3,0 44,7 8,4 7,4 2,2 2,6 1,1
Кальций *113 0,8 2,0 15,1 16,4 0,2 4,0
Витамин А *115 5,0 26,0 28,1 169,2 7,2 918,4
Рибофлавин Аскорбиновая кислота ^117 *119 2,7 75,0 33,3 23,5 60,0 10,3 50,8 525,0 4,5 |5369,0| 13,8 2755,0
Целевая форма (-2) 1,0 1,0 1,0 1,0 1,0 1,0
Форма недопу- стимости (—») —86,5 —80,0 —133,0 —62,2 —747,4 —5387,3 —3688,3
★
Цикл
Калории Кальций *ш *113 2,9637 0,7441 44,7 2,0 8,3709 15,0553 7,4 16,4 1,9458 —0,1911 —0,2341 . —2,0525
Витамин А *115 4,8994 25,9195 28,1 168,4960 |914,7055|
Рибофлавин *117 2,6371 33,3 23,4497 10,3 50,3600 11,4909
Аскорбиновая кислота *46 0,0140 0,0112 W 0,0978 1,0 0,5131
Целевая форма (-*) —0,0140 1,0 0,9888 1,0 0,9022 0,4869
Форма недопу- стимости (—1₽) —11,2444 —80,0 —72,7955 —62,2 —220,6106 —923,9097
★
Цикл
Калории Кальций Витамин А *111 *113 *52 2,9649 0,7551 0,0054 1^,7| 2,0 8,3776 15,1135 0,0283 7,4072 16,4631 0,0307 1,9889 0,1870 0,1842 1,0
Рибофлавин *117 2,5756 33,3 23,1241 9,9470 48,2433
Аскорбиновая кислота *46 0,0112 —0,0034 —0,0158 0,0033 1,0
Целевая форма (-2) —0,0166 1,0 0,9750 0,9850 0,8125
Форма недопу- стимости (—W) —6,2956 —80,0 —46,6151 —33,817 —50,4191
★
530
Таблица 27-2-11
решение
штиглеровской задачи о диете
О
Сладкий картофель Лимская фасоль (сушеная) Мор- ские бобы (суше- ные) Избыточные переменные Искусственные переменные
(53) (68) (69) (101) (ЮЗ) (105) (107) (109) (111) (ИЗ) <115) (117) (119)
9,6 2,7 290,7 5,4 1912,0 17,4 3,7 5,1 38,2 26,9 11,4 24,6 —1,0 —1,0 —1,0 —1,0 —1,0 1,0 1,0 1,0 1,0 1,0
1,0 —2220,4 1,0 -64,4 1,0 —62,9 1,0 1,0 1,0 1,0 1,0
• • • • О ' —f ’
1
8,6741 1,2755 288,1359 3,7975 0,3561 17,4 3,7 5,1 38,2 26,9 11,4 24,6 —1,0 -1,0 —1,0 —1,0 0,0005 0,0007 0,0013 0,0008 —0,0002 1,0 1.0 1,0 1,0 —0,0005 —0,0007 —0,0013 —0,0008 0,0002
0,6439 1,0 1,0 0,0002 —0,0002
—301,8830 —64,4 —62,9 1,0 1,0 1,0 1,0 —0,0034 1,0034
О • опустить
2
8,7478 1,9221 0,3150 0,1778 0,1945 17,4013 3,7114 0,0056 38,1359 —0,0029 26,9 11,4 24,6 —1,0 —1,0 —0,0003 —0,0022 —0,0011 0,0126 0,0006 —1,0 0,0005 0,0007 0,0008 —0,0002 1,0 1,0 0,0003 0,0022 0,0011 —0,0126 —0,0006 1,0 -0,0005 —0,0007 —0,0008 0,0002
0,4905 —10,8477 0,9973 -59,2487 1,0 —62,9 1,0 1,0 0,0005 —0,0101 1,0 0,0002 —0,0021 —0,0005 1,0101 —0,0002 1,0021
О Ф опустить • опустить
531
34*
Симплексное
сокращенного вида штигле
Цикл
Наименование Базисное решение Пше- нич- ная мука (обо- га- щен- ная) Сгущен- ное мо- локо Сыр чеддер Говяжья печень Ка- пу- ста Шпи- нат Сладкий карто- фель Лимская фасоль (суше- ная)
пере- менная Значение ь/ О‘=1) (15) (19) (30) (46) (52) (53) (68)
Калории Кальций Витамин А Рибофлавин Аскорбиновая кислота Целевая фор- ма Форма недо- пустимости Х1 *113 *52 *117 ХЫ (-Z) (-W) 0,0663 0,6225 0,0054 0,3668 0,0112 —0,0829 —0,9893 1,0 0,1874 14,7386 0,0283 16,8831 —0,0034 0,7876 —31,6217 0,1657 16,1316 0,0307 4,4289 —0,0158 0,8193 —20,5605 0,0445 0,0980 0,1842 |46,761б] 0,0033 0,7680 —46,8596 1,0 1,0 0,1957 1,5307 0,3150 —6,3391 0,1945 0,2948 4,8084 0,3893 2,9329 0,0056 25,1725 —0,0029 0,6080 —28,1054
• 'Аг • •
Цикл
Калории Кальций Витамин А Рибофлавин Аскорбиновая кислота Целевая фор- ма Форма недо- пустимости Х1 *из *52 *30 *46 (-Z) 0,0660 0,6217 0,0039 0,0078 0,0112 -0,0889 -0,6217 1,0 0,1714 14,7033 —0,0382 0,3610 —0,0045 0,5103 -14,7033 0,1615 |16,1224| 0,0133 0,0947 —0,0161 0,7466 —16,1224 1,0 1,0 1,0 0,2017 1,5440 0,3400 —0,1356 < 0,1949 0,3989 -1,5440 0,3653 2,8801 —0,0936 0,5383 —0,0046 0,1945 -2,8801
• ★ • • •
Цикл
;Калории Кальций Витамин А Рибофлавин Аскорбиновая кислота Целевая фор- ма Форма недо- пустимости *1 *19 *52 х30 (-2) (—W) 0,0598 0,0386 0,0034 0,0042 0,0118 —0,1177 1,0 0,0241 0,9120 —0,0503 |0,2747| 0,0101 —0,1706 1,0 1,0 1,0 1,0 0,1863 0,0958 0,3387 -0,1446 0,1965 0,3274 0,3365 0,1786 —0,0960 0,5214 —0,0017 0,0612
• ★ • о • •
532
Продолжение табл, 27-2-II
решение
ровскои задачи о диете
3
Морские бобы (сушеные) Избыточные переменные Искусственные переменные
(69) (101) (ЮЗ) (105) (107) (109) (111) (ИЗ) (И5) (И7) (И9)
0,6018 0,0224 —0,0224
10,1964 0,0447 —1,0 • —0,0022 0,0007 —0,0447 1,0 0,0022 —0,0007
—0,0011 0,0011
4,5604 0,7450 0,0128 —1.0 0,0005 —0,7450 —0,0128 1,0 —0,0005
0,0006 —0,0002 —0,0006 0,0002
0,3982 0,0224 0,0005 0,0002 —0,0224 —0,0005 —0,0002
—14,7568 —0,7897 1,0 —0,0105 1,0 —0,0012 1,7897 1,0105 1,0012
опустить • опустить Q опустить
4
0,5975 10,1869 —0,0231 0,0432 —1,0 —0,0023 0,0010 0,0021 0,0007 0,0231 —0,0432 1,0 0,0023 —0,0010 —0,0021 —0,0007
—0,0180 -0,0975 —0,0003 —0,0029 0,0159 —0,0001 —0,0011 0,0003 0,0006 0,0039 —0,0214 0,0001 —0,0002 0,0029 —0,0159 0,0001 0,0011 —0,0003 —0,0006 —0,0039 0,0214 —0,0001 0,0002
0,3233 0,0101 0,0003 0,0164 0,0002 —0,0101 —0,0003 —0,0164 —0,0002
—10,1869 —0,0432 1,0 0,0023 —0,0021 —0,0007 1,0432 0,9977 1,0021 1,0007
опустить О опустить опустить опустить
5 (допустимый)
0,4954 0,6318 —0,0264 0,0377 0,0098 -0,0235 0,0027 —0,0030 0,0157 0,0100 —0,0620 0,0008 0,0059 -0,0010 —0,0001 —0,0011 0,0003 0,0006 0,0009 0,0001 0,0039 —0,0214 0,0001 —0,0002 0,0235 —0,0027 0,0030 —0,0157 —0,0100 0,0620 -0,0008 —0,0059 0,0010 0,0001 0,0011 —0,0003 —0,0006 0,0009 —0,0001 —0,0039 0,0214 -0,0001 0,0002
—0,1484 0,0081 0,0463 0,0004 0,0163 0,0001 —0,0081 —0,0463 —0,0004 —0,0163 —0,0001
1,0000 1,0000 1,0000 1,0000 1,0000
опустить опустить опустить опустить
533
Симплексное
сокращенного вида
Цикл
Наименование Базисное решение Пше- нич- ная мука (обо- га- щен- ная) Сгущен- ное молоко Сыр чеддер Говяжья печень Ка- пу- ста Шпи- нат Сладкий карто- фель Лимская фасоль (суше- ная)
пере- менная значение О‘=1) (15) (19) (30) (46) (52) (53) (68)
Калории Кальций Витамин А Рибофлавин Аскорбиновая кислота Целевая фор- ма Форма недо- пустимости *1 *19 *52 *15 *46 (-г) (—ю) 0,0594 0,0246 0,0042 0,0153 0,0117 —0,1151 1,0 1,0 1,0 —0,0876 —3,3203 0,1830 3,6407 —0,0368 0,6210 1,0 1,0 0,1989 0,5760 0,3122 —0,5266 0,2018 0,2376 0,2908 —1,5525 —0,0005 1,8983 —0,0209 0,3849
• • о • •
Цикл
Калории Кальций Витамин А Рибофлавин Аскорбиновая кислота Целевая фор- ма Форма недо- пустимости *1 *69 *52 *15 *46 (-*) (—W) 0,0355 0,0486 0,0051 0,0086 0,0112 —0,1090 1,0 1,0 —0,9711 11,9734 0,0384 —0,2707 —0,0167 0,2467 3,1368 —6,5523 0,0556 |4,539б| 1,о 1,0 -0,3604 1,1366 0,3343 —0,6825 0,1922 0,3797 1,7985 —3,0638 —0,0601 2,3186 0,0049 0,0019
0,0185 —0,1982
• о ★ • •
Цикл
Калории Кальций Витамин А Рибофлавин Аскорбиновая кислота Целевая фор- ма Форма недо- пустимости *1 *69 *52 *30 *46 (-) (—“0 0,0295 0,0610 0,0050 0,0019 0,0112 —0,1087 1,0 —0,6910 1,4434 —0,0122 0,2203 —0,0041 0,0437 —0,7841 1,5827 0,0417 —0,0596 —0,0156 0,2349 1,0 1,0 1,0 0,1112 0,1516 0,3427 —0,1503 0,1950 0,3499 0,1964 0,2827 -0,0885 0,5107 —0,0045 0,1031
• • • •
534
Продолжение табл. 27-2-11
решение
штиглеровской задачи о диете
6
Морские бобы (суше- ные) Избыточные переменные Искусственные переменные
(69) (101) (ЮЗ) (105) (107) (109) (111) (ИЗ) (115) (117) (119)
0,4921 |0,5067| —0,0195 0,1372 0,0084 —0,1250 —0,0249 —0,0494 —0,0001 0,0571 —0,0006 0,0179 0,0095 —0,0815 0,0019 0,0214 —0,0012 0,0500 —0,0011 —0,0011 0,0010 0,0005 0,0006 0,0028 0,0712 —0,0779 0,0009 0,0030 —0,0002 0,0001 0,0249 0,0494 0,0001 —0,0571 0,0006 —0,0179 1,0000 -0,0095 0,0815 —0,0019 —0,0214 0,0012 —0,0500 1,0000 0,0011 0,0011 —0,0010 —0,0005 —0,0006 1,0000 0,0028 —0,0712 0,0779 —0,0009 —0,0030 1,0000 0,0002 —0,0001 1,0000
* опустить опустить опустить опустить
7
1,0 0,0231 —0,0974 —0,0020 0,0887 —0,1609 —0,0012 0,0010 —0,0022 —0,0011 —0,0663 0,1405 0,0028 0,0001 —0,0231 0,0974 0,0020 —0,0887 0,1609 0,0012 —0,0010 0,0022 0,0011 0,0663 —0,1405 —0,0028 —0,0001
0,0704 0,0435 0,0013 —0,0972 -0,0704 —0,0435 —0,0013 0,0972
0,0002 0,0001 0,0006 —0,0003 —0,0002 —0,0002 —0,0001 -0,0006 0,0003 0,0002
0,0057 0,0298 0,0003 0,0206 0,0001 —0,0057 —0,0298 —0,0003 —0,0206 -0,0001
1,0000 1,0000 1,0000 1,0000 1,0000
опустить опустить опустить опустить
8 (оптимальный)
1,0 —0,0256 0,0042 —0,0029 0,0155 —0,0001 0,0586 —0,0982 —0,0018 0,0096 0,0001 —0,0002 —0,0011 0,0003 0,0006 0,0008 0,0002 0,0039 —0,0214 0,0001 0,0001 —0,0002 0,0256 —0,0042 0,0029 —0,0155 0,0001 —0,0586 0,0982 0,0018 —0,0096 —0,0001 0,0002 0,0011 —0,0003 —0,0006 —0,0008 —0,0002 -0,0039 0,0214 —0,0001 —0,0001 0,0002
0,0088 0,0317 0,0004 0,0164 0,0001 —0,0088 —0,0317 —0,0004 —0,0164 —0,0001
1,0000 1,0000 1,0000 1,0000 1,0000
опустить опустить опустить опустить
535
РЕШЕНИЕ ВРУЧНУЮ
Штиглер сократил перечень из 77 продуктов до 15 продуктов (на табл.
27-1-П они обозначены звездочками), изъяв из него все те продукты,
в которых на каждый доллар затрат содержится не больше питательных
веществ, чем в каком-то другом продукте. Он произвел дальнейшее сокра-
щение перечня до 9 продуктов (обозначенных двумя звездочками), изъяв
из него все те продукты, в которых на каждый доллар затрат содержится
любого питательного вещества не больше, чем в смеси других продуктов
в расчете на один доллар. Однако такой метод можно применять лишь
в том случае, когда пищевые потребности могут удовлетворяться с избыт-
ком. Там, где потребности в питательных веществах должны точно удо-
влетворяться, это сокращение становится необоснованным. В задачах
1—5 доказательства этих утверждений предлагаются в виде упражнений.
В окончательном решении для случая, когда допускается избыток
питательных веществ, количества таких веществ, как белки, железо,
тиамин и ниацин, превышают потребности. Зная это заранее, можно
представить теперь полностью численное решение сокращенной задачи
о диете. Для этого возьмем, как это сделал Штиглер, сокращенное мно-
жество из 9 продуктов вместо 77 и используем всего 5 уравнений из 9,
приведенных в § 27-1-(2). Уравнения i = 2, 4, 6, 8 (соответствующие
избыточным свободным переменным для ниацина, тиамина, белков и желе-
за) были опущены. В полном виде вычислительный процесс показан
в табл. 27-2-П.
Вполне естественно усомниться в любом методе, который не учиты-
вает некоторые из ограничений задачи и при котором решение данной
задачи сводится к решению меньшей задачи с меньшим количеством огра-
ничений. Однако в ряде случаев такой подход можно положить в основу
весьма эффективного алгоритма. Предположим, что при решении задачи
линейного программирования игнорируется к уравнений, в каждом из кото-
рых имеется свободная переменная. После решения мы можем, подставив
значения переменных сокращенной системы в эти к уравнений, определить
значения опущенных свободных переменных. Если по счастливой слу-
чайности значения этих свободных переменных окажутся неотрицатель-
ными, то нетрудно заметить, что решение ограниченной системы вместе
со значениями, полученными для свободных переменных, дает оптималь-
ное решение для всей системы в целом.
В задаче о диете потребуются незначительные модификации в струк-
туре, если симплекс-множители должны интерпретироваться как неяв-
ные затраты на одну калорию, на грамм кальция и т. д. Cj представляют
собой затраты в модели, в то время как > 0 означает выпуск f-го типа
питательного вещества в единице у-го продукта. В этом случае нам неудобно
придерживаться нашего соглашения о знаках, в соответствии с которым
затраты должны быть положительными, а выпуски отрицательными. В дан-
ном случае знаки цен о которых говорилось в гл. 9 и 12, не соответ-
ствуют нашему соглашению.
27-3. ЗАДАЧИ
1. Решить задачу о диете, используя модифицированный симплекс-
алгоритм.
2. Что представляют собой неявные цены на питательные вещества?
Объяснить знак при л^.
3. На сколько должна быть понижена цена на сгущенное молоко, чтобы
это сказалось на решении? Какой продукт должен быть изъят из базиса?
536
4. Каким должно быть соотношение между стоимостью сгущенного*
молока и стоимостью продукта, выведенного из базисного множества,
чтобы один из них входил в решение, если стоимость всех остальных про-
дуктов стабильна?
5. Доказать, что в задаче типа задачи о диете, где все потребности
могут удовлетворяться с избытком, количество любого продукта s в опти-
мальном решении может быть заменено другим продуктом J, закупаемым
на равное количество долларов, при условии, что для всех I.
6. Доказать в общем виде, что закупка любого продукта $ в оптималь-
ном решении может быть заменена, из расчета на каждый доллар затрат,
закупкой на Xi долл, продукта 1, А 2 долл, продукта 2, . . . , Хг долл, про-
дукта г, при условии, что
Xjttfj 4" X2flf2 “И • • • 4“ ^rair > G = 1, 2, . . ., 7Tl)
^1 + ^2 + • • • + ,
Xj О, Х2 0» • • •, Ху 0.
7. Доказать для общей задачи линейного программирования:
(xjOO; f = l, 2,
2 CjXj = z (min),
что если после перемены обозначений для к = 1, 2,..., г и f = 1, 2, . . ., т
Х^Лц 4” ^2^/2 + • • • 4“ Xyfljy
XjCj 4~ X2c2 4- • • • 4- Xrcr cs,
то существует оптимальное допустимое решение, у которого xs = 0.
8. Доказать, что в задаче о диете, где потребности могут удовлетво-
ряться с избытком, в оптимальном решении по меньшей мере одна из
потребностей должна удовлетворяться точно.
9. Доказать, как следствие из задачи 8, что в оптимальном решении
не будет xs> 0, если существует у, удовлетворяющее неравенствам >
> ais для всех i или, в более общем виде, если имеется множество / =
= 1, 2, . . ., г после перемены обозначений, удовлетворяющее соотношени-
ям задачи 6 со строгими неравенствами.
10. Доказать для общей системы линейного программирования в
§ 27-1-(2) с общей линейной целевой функцией, что строгие неравенства
не могут выполняться для всех i в оптимальном допустимом решении,
если min z #= 0.
Показать на примере, что эта теорема не верна, если min z = 0.
11. Построить пример, показывающий, что если потребности должны
точно удовлетворяться, то может существовать оптимальное решение
с xs> 0, несмотря на существование /, удовлетворяющего условиям
приведенных выше задач 5 и 6.
12. При решении задачи о диете сделаем предположение, в соответ-
ствии с которым свободные переменные положительны. Допустим, что
соответствующие уравнения были опущены и получено оптимальное реше-
ние для результирующей системы. Допустим, наконец, что подстановка
этого оптимального решения в опущенные уравнения дает положитель-
ные значения для их свободных переменных. Показать путем исключения
базисных переменных ограниченной системы из ранее опущенных урав-
нений, что а) система в целом приведена к каноническому виду, б) предпо-
лагаемое решение для всей системы является базисным решением и в)
оно будет оптимальным решением.
537
13. Допустим, что в задаче 12 при подстановке в опущенные уравне-
ния одна из соответствующих свободных переменных окажется отри-
цательной. Показать, что один из способов устранения недопустимости
заключается во введении искусственной переменной, коэффициентами
при которой являются отрицательные свободные переменные, а затем —
в минимизации этой переменной. Обобщить этот метод.
14. Показать, что путем достаточно большого увеличения количества
сгущенного молока (/ — 15) можно получить сразу допустимое решение
для сокращенных задач о диете, приведенных в § 27-2 (см. табл. 27-2-П).
15. Показать, изменяя единицы измерения переменной, что, поль-
зуясь правилом выбора max Cj > 0, можно выбрать любое /, при котором
Cj > 0. Показать в табл. 27-2-П, каким образом изменение единиц
какой-либо переменной будет менять ход вычислений. Используя этот
факт, объяснить, почему введение свободных переменных в самом начале
вычисления могло бы дать ту же последовательность итераций, что и при
введении их после того, как был получен минимум без допущения свобод-
ных переменных.
Глава 28
РАСПРЕДЕЛЕНИЕ САМОЛЕТОВ
ПО ЛИНИЯМ В УСЛОВИЯХ
НЕОПРЕДЕЛЕННОГО СПРОСА
28-1. ПОСТАНОВКА ЗАДАЧИ
И МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА
Цель этой главы состоит в иллюстрации применения линейного
программирования к задаче такого распределения самолетов по линиям,
которое максимизирует ожидаемую прибыль в условиях неопределенного
спроса со стороны потребителей. Вычислительный процесс отличается
от случая фиксированного спроса только несколько большим объемом
необходимых вычислений. Решение численного примера мы сравним с рас-
пределениями, полученными обычным методом, основанным на предполо-
жении, что спрос фиксирован и равен своему математическому ожиданию.
Материал этой главы был взят с незначительными изменениями из сов-
местных статей Аллана Фергюсона и автора настоящей книги (Фергюсон
и Данциг [1], [2]).
Многие деловые, экономические и военные задачи имеют следующие
общие характеристики: ограниченные ресурсы основного оборудования
или конечного продукта должны быть распределены между несколькими
процессами использования конечного продукта, причем уровень спроса
для каждого из этих процессов, а следовательно, и доход является неопре-
деленным; далее, после того, как это распределение осуществлено, эконо-
мически недопустимо производить перераспределение либо ввиду геогра-
фической разобщенности процессов, либо из-за различия форм конечных
продуктов, либо, наконец, из-за недостатка времени между решением и его
осуществлением. Примерами таких задач являются (1) составление распи-
сания транспортных средств по нескольким маршрутам с целью удовлетво-
рения спроса в течение некоторого периода времени в будущем и (2) рас-
пределение ресурсов некоторого товара в дискретные интервалы времени
среди нескольких складов или распределительных пунктов, когда спрос
на товар в будущем неизвестен. Предполагается, однако, что спрос можно
предсказать или оценить в виде распределения значений, каждое из кото-
рых принимается с определенной вероятностью.
Общая область приложения методов этой главы схематически может
быть описана задачами, в которых
а) возможные множества интенсивностей процессов можно выбрать так,
чтобы они были совместимы с данными ресурсами;
б) каждое множество выбранных интенсивностей процессов обеспечи-
вает средства или запасы для удовлетворения неопределенного спроса,
распределение которого предполагается известным;
в) прибыли зависят от стоимостей средств, запасов и от спроса.
В этих задачах общей целью является определение тех интенсивностей
процессов, которые максимизируют прибыль.
Гл. 25, основанная на статье «Линейное программирование в усло-
виях неопределенности» (Данциг, [9]), является теоретической осно-
539
вой данной главы. Здесь мы проиллюстрируем шаги метода на примере
(Фергюсон и Данциг [2]), который фактически положил начало
теоретической работе в этой области. Поэтому здесь будет предложена
некоторое строгое теоретическое обоснование, хотя интуитивно каждый
шаг представляется достаточно естественным.
Предлагаемый метод объясняется на модели распределения самоле-
тов по линиям. Несколько типов самолетов распределяется по несколь-
ким маршрутам; предполагается, что известно только распределение воз-
можных значений месячного спроса по каждому маршруту. Самолеты
должны быть распределены так, чтобы минимизировать сумму стоимости
перевозок и ожидаемого значения убытка из-за невозможности обслужить
все нужные перевозки.
Для составления месячного расписания диспетчер воздушного флота,
вероятно, скорее захочет оценить область и распределение будущих путе-
шествий (или перевозок) по маршрутам, чем ограничиться одним матема-
тическим ожиданием. Действительно, он мог бы почувствовать, что опти-
мальное назначение было бы нечувствительно к распределениям спроса
в довольно широкой области и что назначение, основанное на математи-
ческих ожиданиях (как если бы они представляли собой известные фикси-
рованные величины спроса), было бы ошибочным. Чтобы убедиться в этом,
читателю предлагается провести испытания устойчивости путем измене-
ния распределений спроса, приведенных в примере. Анализ устойчивости
рассматривается в § 12-4.
Конечно, пассажирский спрос меняется день ото дня, или, точнее,
от рейса к рейсу. Предполагаемое число пассажиров каждого типа самоле-
та для каждого данного типа рейса может рассматриваться как некоторое
идеальное число, которое можно несколько увеличить, уменьшая стои-
мость проезда и «сглаживая» спрос поощрением пассажиров подавать
предварительные заказы на другие рейсы взамен не являющегося абсо-
лютно надежным получения билетов на требуемый рейс. Несмотря на все
эти возможные мероприятия, предпочтения путешественников и неизбеж-
ные отказы от билетов в последний момент должны вызывать потери
возможных мест. Однако наилучший способ отразить эти влияния ежеднев-
ных колебаний спроса находится вне предмета этой главы. Для наших
целей здесь можно считать, что либо пассажировместимость, либо спрос
несколько занижены, для того чтобы учесть убыток, происходящий из-за
ежедневных колебаний спроса. Мы будем интересоваться исключительно
только месячными колебаниями спроса.
Используемый далее метод прост, и приведенный пример можно ре-
шить вручную за час или два. Задачи больших размеров можно решить
с помощью вычислительных машин.
После формулировки задачи мы кратко опишем природу решения,
основанного на предположении о фиксированном спросе (Фергюсон и Дан-
циг [1]), а затем продемонстрируем метод решения задачи, исполь-
зующий стохастические значения спроса, и наконец сравним эти два реше-
ния. Заметим, что пример построен так, что величина фиксированного
спроса равна математическому ожиданию случайного спроса.
ПРИМЕР С ФИКСИРОВАННЫМ СПРОСОМ
В примере с фиксированным спросом, приведенном для иллюстрации
метода, предполагается, что в воздушном флоте имеются самолеты четы-
рех типов, перечисленных в табл. 28-1-1. Эти самолеты отличаются
друг от друга по скорости, дальности полета, грузоподъемности, а также
по экономическим характеристикам. Предполагаемые маршруты и ожи-
540
.даемые размеры перевозок (распределение спроса будет рассматриваться
ниже) приведены в табл. 28-1-IL
Таблица 28-1-1
Предполагаемый воздушный флот
Тип само- лета Характеристика самолета Число самоле- тов
А Послевоенный четырехмотор- ный самолет 10
В Послевоенный двухмоторный самолет 19
С Довоенный двухмоторный са- молет 25
D Довоенный четырехмоторный самолет 15
Таблица 28-1-11
Загрузки маршрутов
Маршрут Расстоя- ние в милях 1 Ожидаемое число пассажиров 2 Цена би- лета в од- ном на- правле- нии (долл.)
1. Нью-Йорк—Лос-Ан- желес (с одной по- садкой) 2475 25 000 130
2. Нью-Йорк—Лос-Ан- желес (с двумя по- садками) 2475 12 000 130
3. Нью-Йорк—Даллас (без посадки) 1381 18 000 70
4. Нью-Йорк—Даллас (с одной посадкой) 1439 9000 70
5. Нью-Йорк—Бостон (без посадки) 185 60 000 10
1 По официальному справочнику авиалиний («Official Airline
Guide», july, 1954, p. 276) маршруты Нью-Йорк — Лос-Анже-
лес проходят через Чикаго и через Чикаго — Денвер; на
маршруте Нью-Йорк — Даллас производится посадка в Мем- фисе.
2 Это ожидаемое число пассажиров в одном направлении, кото-
рые перевозятся по каждому маршруту ежемесячно. Если пас-
сажир сходит в середине маршрута и заменяется другим, то они считаются как один пассажир.
Так как в этой главе предполагается проиллюстрировать примени-
мость метода решения задач, содержащих некоторые черты, отражающие
реальность, предполагается, что не все самолеты могут быть полностью
541
загружены по всем маршрутам и что достижимый уровень использования
самолетов меняется от маршрута к маршруту. В частности, предполагает-
ся, что на маршруте 3 самолет типа В может быть загружен только
на 75%, а на маршруте 1 самолет типа D — только на 80%; самолет типа
С не может использоваться ни на маршруте 1, ни на маршруте 3, а самолет
типа В не может использоваться на маршруте 1. Использование самолета
определяется здесь как среднее число часов полезной работы, выполняе-
мой ежемесячно каждым самолетом, приписанным к определенному мар-
шруту- Предполагается, что на маршрутах 1 и 2 использование составля-
ет 300 часов в месяц, на маршрутах 3 и 4 оно составляет 285 часов и на
маршруте 5—240 часов.
Предполагаемые расходы в долларах на каждые 100 пассажиро-миль
приведены в табл. 28-1-III. В эти расходы не включаются капиталь-
ные затраты, как, например, стоимость самолета и наземного оборудова-
ния; они учитывают лишь текущие расходы, как, например, стоимость
бензина, жалованье экипажа и расходы по обслуживанию самолета.
Таблица 28-1-1II
Расходы в долларах
Маршрут
Тип само- лета (1) Нью- Йорк — Лос- -Анжелес с одной посадкой (2) Нью- Йорк — Лос- Анжелес с двумя по- садками (3) Нью- Йорк — Дал- лас без посадки (4) Нью- Йорк — Дал- лас с одной посадкой (5) Нью- Йорк — Бос- тон без посадки
1-А 2-В 3-С 4-D Pacxi 5-Е 1 Цифр! паевая ров из Расходы в д 0,45 0,74 эды в доллар 130 (13) л в скобках ук; киров, не полу’; меряется сотня долларах на 0,57 0,64 0,92 0,61 ах на каждо 130 (13) азывают у быт [ивших билета ми.) каждые 100 0,45 0,83 0,59 го неудовлел 70 (?) ки в тысячах .. (Во всем это пассажиро-м 0,47 0,63 0,93 0.62 ’воренного п 70 (7) : долларов на *м анализе чис иль 0,64 0.88 1,13 0,81 ассажира1 10 (1) каждые 100 ло пассажи-
Существует, однако, другой вид «стоимости». Это убыток, возникаю-
щий в случае, когда назначенных на маршрут самолетов недостаточно,
чтобы удовлетворить пассажирский спрос. Мы будем предполагать, что
этот убыток равен цене билета в одном направлении, приведенной в строке
Е табл. 28-1-III.
На основании данных о скорости, дальности, грузоподъёмности и об-
щего времени от вылета до возвращения были определены возможности
пассажирских перевозок. Полученные числа Ри сотен пассажиров, кото-
рые могут быть перевезены ежемесячно каждым самолетом типа i по мар-
шруту /, приведены в табл. 28-1-IV, в верхнем правом углу каждой
клетки. Умножая эти числа на соответствующие расходы на каждые 100
пассажиро-миль, приведенные в табл. 28-1-Ш, а затем на расстоя-
ния, указанные в табл. 28-1-П, можно также получить ежемесяч-
ные расходы на каждый самолет. Эти расходы указаны в левом нижнем
углу каждой клетки; очевидно, представляют собой ежемесячные
542
расходы в тысячах долларов по каждому самолету типа i на маршруте /.
Убытки в тысячах долларов на каждые 100 неперевезенных пассажиров
приведены в строке Е таблицы 28-1-IV; наконец, мы полагаем p5j =
= I1 *. Разбивка этой таблицы на клетки была выбрана так, чтобы устано-
вить соответствие с данными, найденными в табл. 28-2-П; последняя
является рабочей таблицей, на которой основано решение всей задачи.
Основная задача состоит в определении количества самолетов каждо-
го типа, которые нужно приписать каждому маршруту, совместимого
с наличием самолетов, а также в определении убытка, возникающего
из-за невозможности удовлетворить размещенными самолетами пасса-
жирский спрос по различным маршрутам. Так как возможны различные
способы размещения, наша конкретная цель будет состоять в нахожде-
нии такого размещения, которое минимизирует общие затраты, в которые
включаются как эксплуатационные расходы, так и убытки, основанные
на данных табл. 28-1-III.
Таблица 28-1-IV
Возможности пассажирских перевозов и расходы
Тип само- лета Маршрут
(1) Нью-Йорк — Лос-Анжелес с одной посад- кой (2) Нью-Йорк — Лос-Анжелес с двумя посадками (3) Нью-Йорк — Даллас без посадки (4) Нью-Йорк — Даллас с одной посадкой (5) Нью- Йорк — Бос- тон без по- садки
1-А м Рн=16 сц=18 [есячные расход Р12=1б с 12=21 (ы на каждый ( Р13=28 С1з=18 замолет Р14=23 с14=16 Р15=81 С15=10
2-В * Р22~Ю С22= 15 Ргз=14 С 23= 16 Р24=15 С24=14 Р25 —^7 с25=9
3-G * Рз2=5 с32 —1^ * Рз4=? с34=9 Р35 29 с35 = 6
4-D 5-Е р« = 9 с41=17 Убытки Pai = l c5i=13 Р42=П с42=16 на каждые 100 Рб2—1 с52 = 13 Р43—22 с43=17 неперевезенны: Рбз=1 С53 — 7 р44= 17 С44=15 к пассажиров Р54=1 С54=7 Р45=55 С45 = 10 Р55 = 1 055 = 1
Математически эту задачу можно сформулировать как задачу линей-
ного программирования. Пусть обозначает пока неизвестное количе-
ство самолетов t-го типа, назначенных на маршрут /, где i — 1, 2, . . .
. . ., т —1 и J = 1, 2, . . ., п —1. Если xin обозначает излишек самолетов
(т. е. количество неразмещенных самолетов), то уравнение (1) выражает
тот факт, что сумма размещенных и неразмещенных самолетов каждого
типа равна общему количеству самолетов at. Далее, если xmj обозначает
число сотен пассажиров, которым было отказано, то уравнение (2) выра-
жает тот факт, что сумма провозных способностей самолетов каждого
1 Это облегчит формулировку баланса пассажиров или вывод «столбцовых»
уравнений (2).
543
типа, назначенных на маршрут /, xtj, плюс неудовлетворенный спрос
равна общему спросу dj. Неравенства (3) утверждают, что все неизвестные
величины Xij должны быть неотрицательными. Наконец, общие расходы
z представляют собой сумму всех отдельных эксплуатационных расходов
по каждому размещению xtj и убытков, вызванных неудовлетворенным
спросом cmj xmj (см. уравнение (4)).
Модель с фиксированным спросом
Найти такие числа и минимальное значение z, чтобы для Z=l,
2, ..., тп; / = 1, 2, ..., п выполнялись равенства:
Суммы по строкам: #и + хг2+ • • • ~^xin — ai (1)
Суммы по столбцам: Рцх1)+рцхг] + ... +Pmjxmj=dj (2)
xij 0 (3)
т п
2 2 ««*«/=* (4)
1=1 j==i
Оптимальное распределение самолетов по маршрутам, основанное
на предположении о фиксированном спросе, представляет собой взвешен-
ную задачу распределения. Численное решение, приведенное в табл.
28-2-П, было получено методами, изложенными в гл. 21. Полученные
значения неизвестных если они отличны от нуля, отмечены жирным
шрифтом в левом верхнем углу каждой клетки; значения xtj, равные ну-
лю, не выписаны. Структура клетки имеет вид
PiJ
Cij
Суммы по строкам элементов xtj табл. 28-2-П после приравнивания
количествам самолетов дают уравнения (1). Суммы по столбцам величин
xtj, умноженных на соответствующие значения ptj, после приравнивания
спросу дают уравнения (2); сумма по всей таблице величин xtj, умножен-
ных на соответствующие значения ctj, дает уравнение (4). Как упомина*
лось ранее, табл . 28-2-П действительно является рабочей таблицей,
на которой основано решение всей задачи. Позже мы рассмотрим модифи-
кацию этой таблицы, необходимую для решения задач с переменным
спросом. Все числа таблицы, за исключением величин xtj в левом верхнем
углу каждой клетки и значений так называемых «неявных цен» щ и Vj,
указанных по краям таблицы, являются постоянными, которые не меняют-
ся в процессе вычисления. Однако значения переменных xtj, и Vj будут
меняться в ходе последовательных итераций симплекс-метода, приспо-
собленного для этой задачи. Поэтому обычно рабочую таблицу покрывают
прозрачной ацетатной пленкой и информацию, меняющуюся от цикла
к циклу, записывают жирным карандашом, который легко можно сте-
реть; можно также использовать грифельную доску или накладку из полу-
прозрачной папиросной бумаги. Подробные правила получения приведен-
ного оптимального решения описаны в гл. 21 и здесь повторяться не бу-
дут. Вместо этого для случая неопределенного спроса будет дана более
общая система правил, которая, конечно, могла бы быть использована
для случая фиксированного спроса.
Ш
В табл. 28-1-V мы приводим удобную сводку для нахождения
и определения численных данных табл. 28-2-11 и даем способ про-
верки оптимальности решения.
Таблица 28- 1-V
Сводка обозначений и правил для случая фиксированного спроса
(приведенных в табл. 28-2-II)
Индексы: i* = l, 2,... i = m, если 7 = 1, 2,... f = если ,тп — 1 относятся к типу самолета, к которому припи- саны пассажиры. пассажиры не приписаны. , п— 1 относятся к типу маршрута, к которому припи- саны самолеты. самолеты не приписаны (излишек).
Постоянные: а—наличное число самолетов типа i, dj—ожидаемый ежемесячный пассажирский спрос на маршруте / в сотнях, Pij—ежемесячная провозная способность в сотнях пассажиров каждого самолета типа i, назначен- ного на маршрут / = 1 по определению), сц—ежемесячные расходы в тысячах долларов на каждый самолет типа i на маршруте / (cmj— убыток на каждую сотню неудовлетворенных пассажиров).
Элементы хц : Опущенные эле- менты хц: хц—число самолетов типа i, назначенных на мар- шрут j (xmj — число сотен неудовлетворенных пассажиров). хц—0, если верхний левый угол клетки пуст.
Неявные цены: числа ui и vj определяются так, что ui-^-ptjVj— — сц для тех клеток (i, /), которые соответству- ют положительным т, е. неопущенным эле- ментам хц (по определению, um—vn=0).
Проверка оптимальности: Решение оптимально, если для всех пар (i, у) выполнено соотношение ut-^-PijUj сц.
РАСПРОСТРАНЕНИЕ ПРИМЕРА НА СЛУЧАЙ НЕОПРЕДЕЛЕННОГО
СПРОСА
Для того чтобы ввести в спрос элемент неопределенности, мы предпо-
ложим, что на каждом маршруте спрос не является известной величиной,
но известно его распределение. Предполагаемые распределения приведены
в табл. 28-1-VI. Так, по маршруту 2 (Нью-Йорк — Лос-Анжелес
с двумя посадками) в течение месяца захотят проехать либо 5 тыс., либо
15 тыс. пассажиров, соответственно с вероятностями 30% и 70%. Конеч-
но, предлагаемые распределения перевозок являются гипотетическими
и приведены только для иллюстрации метода. Распределения спроса
на пяти маршрутах изменяются в широких пределах и имеют различные
характеристики: так, распределение для маршрута 1 — приблизительно
равномерное, для маршрута 2— U-образное, для маршрутов 3, 4 и 5 —
унимодальное, но с различными степенями концентрации около вершины.
545
35 дж. Данциг
Маршрут 4 имеет распределение с очень длинным «хвостом», что отражает
вполне реальную транспортную ситуацию.
Для иллюстрации существа характера задачи линейного программи-
рования в случае неопределенного спроса сосредоточим внимание на одном
маршруте — например на маршруте 1 с вероятностным распределением
спроса, приведенным в табл. 28-1-VI. Предположим, что самолеты,
назначенные на маршрут 1, могут взять 100 Yi пассажиров, где У^ должно
быть определено. Эта провозная способность, если она не превосходит 200
единиц (в сотнях пассажиров), наверняка будет использована, и доход
от этого источника (отрицательные затраты) составит 13 = к^ единиц
(в тысячах долларов) на единицу провозной способности. Если 100 У4 >
> 200, то с вероятностью y2i = 0,8 будет использовано еще 20 дополни-
тельных единиц провозной способности. Действительно, 80% времени
спрос будет не меньше, чем 220 единиц, а 20% времени он будет равен
200 единицам; следовательно, ожидаемая прибыль на единицу этого
приращения провозной способности равна 0,8-13 = 10,4, или 10,4 =
= &1Y21 единиц. При третьем увеличении на 30 единиц (с 22 001 до 25 тыс.
мест) ожидаемая прибыль составит 0,75-13 — 9,8, или kry3i единиц на
Таблица 28-1-VI
Предполагаемое распределение пассажирского спроса
—вероятность спроса dnj)
Маршрут Пассажирский спрос (в сотнях) Приближен- ное среднее (в сотнях пассажиров) Вероятность пасса- жирского спроса Вероятность того, что спрос больше или равен
1 Z! оа со 5 43 II II II II II 88888 СМ СМ СМ СМ со 250 0,2=%ц 0,05=%21 0,35=%з1 0,2=%41 0,2=^51 N S 5 « ?-?->-?-?- II II II II II О 00 LO см тч о - О О о
2 2 а 43 43 II II т-4 120 р р •О 00 II II to со а й II II <р р Т-7 О
3 ЬЗ М Н» Н» н- 080S0 II II II II II а. Сл i> СО tO н» со со со со со 180 р р р О О N? tJS II II II II II >*>*>*>*>* СП CONO- CO со со со со рр о р w м со о II II II II || gf Z? со со со со со
4 -4 *4< т. cq со ю 43 43 43 43 43 II II II II II 8888^ 90 3< -3* чч (М ОО Ю II II II II II СМ СМ СО СМ чгн Ф О Ф о о -S' -S' н и оо Ю II II II II II О р СО 00 р т-7 о о о о
5 Ю UO 1Q тч со 43 43 43 II II II 888 НО со со 600 р р р оо II II II >>>>>* со to ьь сл сл сл Ю 1ГЭ ю «н N М II И II О 03 тн чн" О Ф
546
каждую единицу провозной способности, так как в 25% случаев ни одна
из этих единиц провозной способности не будет использоваться, а в 75%
случаев будут использоваться все. При четвертом увеличении провозной
способности на 20 единиц (с 25 001 до 27 тыс. мест) ожидаемая прибыль
составит 0,4-13 = 5,2, или/qy41 единиц на каждую единицу провозной
способности, а при пятом увеличении на 30 единиц (с 27 001 до 30 тыс.
мест) она будет равна 0,2-13 = 2,6, или kty5l единиц на каждую единицу
провозной способности. При шестом увеличении, которое представляет
собой число единиц сверх уровня в 30 тыс. мест, ожидаемая прибыль рав-
на 0,0-13 = 0 на каждую единицу, так как наверняка ни одна из этих
единиц провозной способности не сможет быть использована. Ясно, что
никакие назначения сверх 30 тыс. мест не оправданы, и, следовательно,
последнее увеличение можно не рассматривать. Индекс h = 1, 2, 3, 4, 5
будет использоваться для обозначения 1-го, 2-го, . . ., 5-го увеличений
спроса.
Число приписанных единиц при каждом увеличении можно, однако,
рассматривать как неизвестное, которое зависит от общей провозной спо-
собности, приписанной маршруту ; = 1. Так, если всего приписано Yt ==
= 210 единиц провозной способности, то ее часть, относящаяся к первому
увеличению и обозначаемая через уи, равна уп = 200, а часть, относя-
щаяся ко второму увеличению и обозначаемая через y2i, равна 1/21 = Ю.
Величины для больших увеличений суть ум = 0 для i = 3, 4, 5.
Мы знаем, что провозная способность У; определяется числом самолетов,
назначенных на маршрут /, так что
У; = pijXij + p2jx2j + p3jx3j + р^хц. (5)
С другой стороны, само У7- разлагается на сумму пяти приращений
У; — У1 j + У2} + Уз j + Ум + Ум (6)
для маршрутов j = 1, 3, 4 и соответственно на сумму меньшего числа
приращений для маршрутов / = 2,5. Независимо от общего количества
каждая величина z/aj , представляющая собой приращение, ограничена
общим объемом bhj этого увеличения; последний, однако, есть просто
изменение уровня спроса, так что
Полагая
0 У и drj = blj9
9 y%j d2j d^j = b2j,
0 Ум d3j—d2j = b3j,
Ум d^j d3j = &4j-,
Ум^^м—dy = b5j.
Khj = вероятности спроса dhj.
(7)
(8)
мы получим, что общая ожидаемая прибыль от маршрута у, следовательно,
равна
(Yijyij + УмУ2} + - - - + ЧмУм)> (9)
где kj — прибыль (в тысячах) на каждые 100 провезенных по маршруту
7 пассажиров, и, как видно из табл. 28-1-IV, вероятности yhJ того,
что спрос не меньше dhj, связаны с Хл;, вероятностями спроса d^, соотно-г
547 35*
шениями:
1 = Nij = ^17 + X2J +
Y2J = ^27 + k3j + k^j + Xsy,
Уз> = ^37 + ^47 + ^57>
Yv = X47 + k$j,
Ys/ = X57.
(10)
Численные значения Хл/ и yhj приведены в табл. 28-I-IV. Согласно
(9), общий ожидаемый доход от маршрута 1 равен 13 (1,0 уц + 0,8 y2i +
+ 0,75 у31 + 0,4 у41 + 0,2 у51). Следует заметить, что самой важной чер-
той этой линейной формы является убывание последовательных значений
коэффициентов yhj. Более того, это всегда должно быть так для любого
распределения спроса, так как вероятность того, что спрос будет не мень-
ше данного уровня убывает с возрастанием значений уровня.
Предположим теперь, что yily y2i,... рассматриваются как неизвестные
значения переменных в задаче линейного программирования, подчинен-
ные только условиям (6) и (7), где цель состоит в максимизации прибыли.
Предположим далее, что Yy фиксировано. Так как в подлежащей макси-
мизации форме (9) коэффициент при уп наибольший, то ясно, что пере-
менная уц будет выбираться первой и возможно большей при условиях
(6) и (7); для выбранного значения у и следующее приращение у21 будет
выбираться максимальным при условиях (6) и (7) и т. д.; в результате,
когда достигнут максимум, значения переменных ун, У21» • • • будут в точно-
сти значениями приращений, связанных сУь которые мы рассматривали
раньше (6). Даже если провозная способность У4 не фиксирована, как
в случае, который будет рассматриваться далее, то нужно заметить, что
для любого значения У1 значения у а, у21, . . ., которые минимизируют
форму общей стоимости (14), приведенную ниже, должны максимизиро-
вать (9) для / = 1 и, следовательно, значения приращений У4 будут порож-
даться числами ун, у2н ....
Задача линейного программирования в случае неопределенного спро-
са задается условиями (11), (12), (13) и (14).
Модель в случае неопределенного спроса
Найти такие числа хц и yhj и минимальное значение z, что для i = l, 2,..., т;
/ = 1, 2,..., n; h = l, 2,..., г выполняются условия:
Суммы ПО строкам #ii + a:i2+ • • • -\~* * * * xin=ai (И)
Суммы по столбцам Рихи+Р2}хг}+-.. +pnjXnj=ylj+y2j+ . .. + yrj (12)
xij 0> 0 yhj bhj (13)
т п п г
Ожидаемая стоимость z=2 2 cUxij+lRo — S kJ 3 4hjyhj\ (14)
1=1 ;=1 7=1 й=1
Таким образом, ожидаемые затраты определяются как общие расходы
(первый член) плюс ожидаемый убыток из-за недостатка мест (последние
два члена), где Ro (постоянная) есть ожидаемая прибыль в случае, если
бы было достаточно мест для всех пассажиров.
Для рассматриваемой задачи границы bhj и ожидаемые прибыли
kjyhj на каждую единицу «переменных приращений» yhj могут быть вычи-
548
сиены из табл. 28-1-VI вероятностных распределений по формулам
(7) и (10).
Численные значения постоянных для стохастического случая приве-
дены в табл. 28-1-VII.
Таблица 28-1-VII
Границы приращении Ъщ и ожидаемая прибыль kj^hj на единицу
назначенной провозной способности
При- раще- ния h Маршрут 1 Маршрут 2 Маршрут 3 Маршрут 4 Маршрут 5
bhi bh2 ft2Yh2 bh3 ft8Vh3 "Л4 bh5
1 200 ^ = 13 50 fc2=13 140 *з=7 10 A:4=7 580 *5=1
2 20 0,8Zq = = 10,4 100 0,7 к2 = = 9,1 20 0,9&з = = 6,3 40 0,8 &4= = 5,6 20 0,9 &5 = = 0,9
3 30 0,75 kl = = 9,8 * 20 0,7fc3= =4,9 30 0,6 Ar4= = 4,2 20 0,1*5 = =0,1
4 20 0,4 Ач = = 5,2 * 20 0,3 k3 = = 2,1 20 0,3fc4= = 2,1 *
5 30 0,2^= = 2,6 * 20 0,1 *3= =0,7 240 0,1 Л4= = 0,7 *
* Для того чтобы описать распределение спроса, необходимо только два увеличения на маршруте 2 и три увеличения на маршруте 5.
ПРАВИЛА ВЫЧИСЛЕНИЙ
Для определения оптимального назначения в условиях неопределен-
ного спроса используется рабочая табл. 28-2-1II.
Заполнения клеток с х^ и yhj имеют вид
%ij
Pij
Cij
yhj
— 1
— kiVh]
Для получения уравнений по строкам (11) элементы xtJ суммируются
и приравниваются значениям at, указанным в столбце наличия самолетов.
Для получения уравнений по столбцам (12) величины х-^ умножаются
на Pij, Uhj умножаются на —1 и затем их сумма приравнивается нулю.
Шаг 1. Для начала вычислений неизвестным х^ и yhj можно придать
любые неотрицательные значения, удовлетворяющие уравнениям и, сле-
довательно, составляющие некоторое допустимое решение.
Шаг 2. Заключить в клетку любые (т + п —2) элементов Хц и yh^
где та + п — сумма числа уравнений по строкам и по столбцам. Эти
заключенные в клетки элементы могут быть выбраны произвольно, за
549
исключением того, что они должны обладать следующим свойством: если
произвольно изменять значения других (не заключенных в клетки) пере-
менных и свободных членов, то переменные, заключенные в клетки, дол-
жны определяться через них единственным образом. Такая система заклю-
ченных в клетки переменных составляет, очевидно, базисную систему;
матрица коэффициентов, связанных с этой системой переменных в уравне-
ниях (11) и (12), образует базис (гл. 8).
Замечание. Простой способ выбора базисной системы показан в табл.
28-2-IV. В каждой строке, соответствующей уравнению по строкам,
произвольно выбирается один элемент и заключается в клетку (предпо-
лагается, что заключаются в клетку те элементы, которые, по-видимому,
в оптимальном решении будут иметь положительные значения). Затем
каждому yhj по очереди для h = 1, 2, ... в столбце придается его верхнее
граничное значение bhj до тех пор, пока для некоторого h — hQ столбец
«чистые неявные цены» не станет отрицателен, и в этом случае для h =
= Ло значение y^j < выбирается так, чтобы чистая неявная цена обра-
тилась в нуль; тогда заключается в клетку элемент (Ло, /).
Шаг 3. Для комбинаций пар (г, /) и (Л, /), соответствующих базисным
переменным, вычислить связанные с уравнениями неявные цены ut и г?;,
определяя значения иг и г?7-, удовлетворяющие уравнениям:
Щ + PijVj~ cij (для базисных Xij), (15)
О + (— 1) vj — kflhj (для базисных yhJ)(16)
Эта система т + п —2 уравнений (15) и (16) относительно т + п —2
неизвестных щ и г^, как легко можно показать, всегда имеет единственное
решение (см. § 21-1). Эти уравнения можно решить непосредственно,
так как можно показать, что эта система либо вся треугольна, либо в худ-
шем случае распадается на подсистемы, часть которых треугольна, а осталь-
ные превращаются в треугольные после определения значения одного
неизвестного1.
Шаг 4. Для всех (i, /) и (й, J) вычислить
Ci}= +с0— (iii + PijVj), (17)
с’м = + (—kflhj) — (O—Vj). (18)
В § 5-2 было показано, что если значения Xij или у^, связанные с неко-
торыми небазисными переменными, изменяются на
х^ ± 0 или yhj ±0, (0 > 0) (19)
а другие небазисные переменные остаются фиксированными, в то время
как базисные переменные изменяются соответственным образом, то ожи-
даемая стоимость z изменится на z', где
z' = z ± §cij или соответственно z' = z ± 0с^-. (20)
Предполагая в общем случае, что также могут быть ограничены, мы ви-
дим, что Xij или y^j должны быть увеличены, если Cij < 0 или c^j < 0,
если любая из этих переменных не достигла своей верхней границы;
в противном случае увеличение не допускается. Аналогично, если > 0
или c'hj > 0, то Xij или yhj должны быть уменьшены, если Xij 0 или
yh. 0; если Xij — 0 или yhj — 0, то уменьшение невозможно.
1 Этот факт является для взвешенной задачи распределения (И), (12), (13),
(14) аналогом хорошо известной теоремы для стандартной транспортной задачи, состоя-
щей в том, что все базисы треугольны. Доказательство аналогичное (см. гл. 14 и 21).
550 •
ПРОВЕРКА НА ОПТИМАЛЬНОСТЬ
Согласно теории симплекс-метода с ограниченными переменными
(см. гл. 18), из того, что небазисные переменные удовлетворяют следующим
условиям:
а) каждое из них равно либо своей верхней, либо нижней границе,
б) если они равны своим нижним границам, то соответствующие
си > 0 и ckj > 0, и
в) если они равны своим верхним границам, то соответствующие
0 и cij < О
следует оптимальность решения и окончание алгоритма. В против-
ном случае имеются такие ctj или для которых не выполнено б) или в).
В этом случае возможно увеличение или уменьшение (в зависимости от
знака) соответствующей переменной; мы будем называть эти комбинации
(i, 7) или (Л, 7) беспорядочными; пусть наибольшее по абсолютной величине
среди этих Cij или c^j обозначается через сГ8 или соответственно c'rs.
Шаг 5. Фиксируя все небазисные переменные, за исключением пере-
менной, соответствующей определенной на шаге 4 паре (г, $), изменить
значение xrs (или yrs), если только она не равна своей верхней границе, на
^гв4“0(или 1/г«4“9)> если crs < 0 (или crs <0) (21)
или, если она не равна своей нижней границе, на
хГ8—0 (или уТ8—9), если crs>0 (или Crs>0), (22)
где 9 > О — пока неизвестная величина, и вычислить заново значения
базисных переменных в виде линейных функций 9. Выбрать наибольшее
значение 9 = 9*, при котором все базисные переменные (значения кото-
рых теперь зависят от 9), находятся между своими верхней и нижней гра-
ницами; в следующем цикле исправить значения базисных переменных,
исходя из предположения, что 9 = 9*.
Кроме того, если при значении 9 = 9* одна (или более) из базисных
переменных достигает своей верхней или нижней границы, то в следующем
цикле вывести любую из этих переменных (но не больше одной) из базисно-
го множества и вместо нее заключить в клетку переменную хг8, Если слу-
чится, что хГ8 или уГ8 достигают своей верхней или нижней границы при
9 = 9*, то система базисных переменных не меняется; однако меняются
их значения, так чтобы хГ8 или уГ8 стали равными своей новой границе.
Начать следующий цикл итеративного процесса, возвращаясь к шагу 3.
28-2. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ
РАСПРЕДЕЛЕНИЯ САМОЛЕТОВ ПО ЛИНИЯМ
В качестве начального решения в табл. 28-2-1V (цикл 0) мы
использовали значения Xij в оптимальном решении, полученном в предпо-
ложении, что спрос фиксирован и равен своему математическому ожида-
нию, вычисленному в соответствии с распределениемх, приведенным
в табл. 28-2-П. Эти значения xtj удовлетворяют ожидаемый спрос,
так что Yj = dj, за исключением маршрута 5, на котором имеется дефицит,
1 В юмористической пародии Пола Гантера [1], озаглавленной «Применение
линейного программирования к финансированию» упоминалось, что миссис Эффек-
тивность удивлялась, почему мистер Исследование операций не начинал с хороших
догадок. В этой главе вы заметите, что мы следуем предложению миссис Эффектив-
ности и в качестве начального приближения выбираем окончательное решение, а не
проходим через случайное использование искусственных переменных и фазу I сим-
плекс-процесса.
551
равный 100, и У5 = 500 (см. § 28-1-(5)). Эти числа Y j представляются
в виде суммы приращений, приведенных ниже черной линии в табл.
28-2-IV, цикл 0.
Затем одна из переменных в каждой строке заключается в клетку.
Выбранные переменные суть Хц, #23, #35, #43; каждая из них, по-видимому,
войдет в оптимальное решение; однако в клетку была заключена пере-
менная я4з, а не #4i, которая, может быть, представляет собой лучший
выбор. Затем заключается в клетку последний положительный элемент
в каждом столбце, т. е. переменные p3i, у22, Узг, Уш У15- Всего имеется
т + п —2 = 9 переменных, заключенных в клетки. Неявные значения
Ui и Vj, приведенные в таблице, определяются путем решения девяти
уравнений:
щ + РнЩ = Сц, (Ри = 16; сп = 18)
и2 4“ P22V2 = с229 (P22 = 10; c22 = 15)
и3 4" Рз5^5 = ^35, (p35 = 29; c35= 6)
й4 + Аз^З = с43> (Р4з = 22; c43 = 17) (1)
0 + (— 1) Vi = — (&iY3i = 9,8)
0 + ( —l)v2== —&2Y22, (&2Y22 — 9,1)
0 + (—1) v3 = —к3у33, (^3Y33 = 4,9)
° + ( —1) А = —*4Y44 (&4Y44 = 2,1)
0 + (— 1) v5 — —k5yi5. (Mis = 1,0)
Это позволяет вычислить величины и chi (см. § 28-1 (17), (18)).
Равенства Сц — 0 и c'hj — 0 для (i, j) и (Л, /), соответствующих базисным
переменным, служат в качестве проверки. Наибольшее по абсолютной
величине из cLj или Chj для тех (г, /) или (h, j), которые не упорядочены,
равно
с24 == 14—[—76 +15-2,1] = +58,5.
Следовательно, уменьшение переменной #24 с соответствующими изме-
нениями базисных переменных уменьшит ожидаемую стоимость на 58,5
единиц на каждую единицу уменьшения #24. Если #24 = 6 изменяется
до #24 =6— 0, то, для того чтобы удовлетворить уравнение по столбцу 4,
базисная переменная у44 = 10 должна быть изменена на у44 = 10—150
(а все остальные переменные в столбце 4 фиксированы). Кроме того, для
того чтобы удовлетворить уравнение по строке 2, #22 = 8 должно быть
заменено на #22 =8 + 0; это в свою очередь заставляет изменить у22 =
= 70 на у22 = 70 + 10 0, для того чтобы удовлетворить уравнение по столб-
цу 2. Наибольшее значение 0 равно 0* = ||, и при этом значении 0,
г/44 = 0. Численные значения переменных в табл. 28-2-IV, цикл 1,
получаются из значений этих переменных в табл. 28-2-IV, цикл 0,
10
если положить 0 = 0* = j^. Переменная #24 становится новой базисной
переменной вместо переменной у44, которая достигла своей нижней гра-
ницы, равной нулю. Вычисление новой системы неявных цен показывает,
что наибольшее по абсолютному значению ctj, которое может увеличить
или уменьшить хи (в зависимости от знака сц), равно с23 =—23,4. Изме-
нение #23 на 5 — 0 требует, чтобы переменные #22, р22, у33 были изменены,
как это показано в табл. 28-2-IV, цикл 1. Максимальное значение
20
0 равно 0 = 0*= и при этом значении у33 = 0. Новое решение, в кото-
552
ром #2з заменяет у33 в качестве базисной переменной, приведено в табл.
28-2-IV, цикл 2. В табд. 28-2-IV, цикл 2, уменьшение незаклю-
ченной в клетку переменной я41 вызывает изменения переменных я43,
9
я22, я23, Узь Угг- Наибольшее значение 0 = jg и при этом значении у22
достигает своей верхней границы Ъ22 — 100.
При переходе от табл. 28-2-IV, цикл 3, к табл. 28-2-IV,
цикл 4, мы начинаем несколько увлекаться и берем «двойной» шаг.
80
Максимальное приращение равно 0 = ^д, и в этой точке у15 достигает своей
верхней границы &i5 = 580. Легко видеть, что если затем переменная при-
ращения у25 возрастает, то с32, связанная с ж32, должна быть заменена
на с32 —29 (у15— у25) к5 = + 4,5—29 (1,0—0,9) = + 1,6; следовательно,
экономично увеличивать, как у15, так и у25. Одцако можно показать, что
с32 станет отрицательным, если рассматривать следующее приращение
у35. Максимальное 0=0*= .
Нужно заметить, что при переходе от цикла 4 к циклу 5 табл.
28-2-IV переменная у33 снова вводится в решение, после того как рань-
22
ше она была выведена из него. Максимальное значение 0 равно и при
этом значении у33 достигает своей верхней границы, так что решение, табл.
28-2-IV, цикл 5, имеет ту же самую систему базисных переменных
и, следовательно, те же самые неявные цены, что и в цикле 4 табл.
28-2-IV. Более того, это решение оптимально, так как все небазисные
переменные достигли своей верхней или нижней границы; переменным,
достигшим верхних границ, соответствуют 0, а переменным, достиг-
шим нижних границ, соответствуют 0.
При сравнении этого решения (табл. 28-2-IV, цикл 5) с опти-
мальным решением для случая фиксированного спроса (табл. 28-2-
-II) интересно отметить, что, как кажется, главное различие состоит
в общей тенденции сдвинуть для распределений с острыми пиками общее
число мест, имеющихся на маршруте, к моде1 распределения, а не к его
математическому ожиданию. Общее число мест на маршруте с равномер-
ными распределениями спроса, по-видимому, находится на наивысшем
уровне, достижимом с оставшимися возможностями провозной способности.2
Таблица 28-2-1
Сравнительные затраты для различных решений
См. табл. 28-2-IV Ожидаемая прибыль от имеющихся мест (1) Ожидаемые убытки 1 (2) Эксплуатаци- онные расходы (3) Чистые ожида- емые затраты (в тыс. единиц) (2)+(3)
Цикл 0 —6,534 766 900 1,666
Цикл 1 —6,574 726 901 1,627
Цикл 2 —6,607 693 901 1,594
Цикл 3 —6,638 662 899 1,561
Цикл 4 —6,641 659 883 1,542
Цикл 5 —6,659 641 883 1,524
1 Данные в столбце (2) получены вычитанием ожидаемых прибылей от
имеющихся мест (столбец (1)), из Во=7300, ожидаемой прибыли в случае,
если бы в наличии имелось неограниченное число мест.
1 Модой в распределении случайной величины называется наиболее вероятное
ее значение. — Прим. ред.
2 Продолжение текста см. на стр. 563 — Прим. ред.
553
Таблица 28-2-П
Оптимальное размещение самолетов при фиксированном спросе
(эксплуатационные расходы и убыток составляют 1000000 долл.)
Тип самолета Маршрут Наличные самолеты Неявные цены ui
Йорк— Лос-Ан- желес с одной посадкой (2) Нью- Йорк— Лос-Ан- желес с двумя посадка- ми Йорк- Даллас без по- садки Йорк- Даллас с одной посадкой (5) Нью- Йорк— Бостон без по- садки (6) Избы- ток само- летов
1-А 10 16 18 15 21 28 18 23 16 81 . 10 0 0 10 — а1 —171
2-В * 8 10 15 5 14 16 6 15 14 57 9 0 0 19 = а2 —51
3-С * 7,8 5 10 * 7 9 17,2 29 6 0 0 25 = аз —23
4-D 10 9 17 И 16 5 22 17 17 15 55 10 0 0 15 = а4 , —89
5-Е Дефицит 1 13 1 13 1 7 1 7 100 1 1 0 0 ** 0
Спрос dj Неявные цены Vj 250 11,8 120 6,6 180 4,8 90 4,33 600 1 ** 0
♦ Клетка не используется; самолет не может летать по этой линии.
** Строка или столбец не имеют уравнения.
Таблица 28-2-III
Рабочая таблица для определения оптимального назначения
в условиях неопределенного спроса
Тип . самолета Маршрут Наличные самолеты Неявные цены ui
(1) Нью-Йорк— Лос-Анже- лес с одной посадкой Йорк— Лос-Ан- желес с двумя посадка- ми (3) Нью- Йорк— Даллас без по- садки (4) Нью- Йорк— Даллас с одной посадкой Йорк- Бостон без по- садки „ («6> Избыток самоле- тов
1-А 2 ОО II II S 3 а *12 15 21 *13 28 18 *14 23 16 *15 81 10 *16 0 0 10 W1
2-В * *22 10 15 *23 14 16 *24 15 14 *25 57 9 *26 0 0 . 19 п2

Продолжение табл, 28-2-1II
Тип самолета Маршрут Наличные самолеты Неявные цены иг
<12 Нью-Йорк— Лос-Анже- лес с одной посадкой Йорк— Лос-Ан- желес с двумя посадка- ми (3) Нью- Йорк— Даллас без по- садки (4) Нью- Йорк— Даллас с одной посадкой (5) Нью- Йорк— Бостон без по- садки (6) Избыток самоле- тов
3-С * *32 5 10 * *34 7 9 *35 29 6 *36 0 0 25 w3
4-Р *41 9 17 *42 11 16 *43 22 17 *44 17 15 *45 55 10 *46 0 0 15 м4
Прираще- ние 1 Уи<200 —1 —13 У12<50 — 1 —13 {/13<140 —1 —7 У14<Ю —1 —7 1/15<580 —1 —1 * ** 0
2 s/2i<20 —1 —10,4 1/22^309 —1 —9,1 2/23^ 20 — 1 —6,3 1/24<40 —1 —5,6 У 25<J20 —1 —0,9 * ** 0
3 Уз1<30 —1 —9,8 * 2/33^20 —1 —4,9 У34<30 —1 —4,2 1/35^20 — 1 —0,1 * ** 0
4 ?/41<20 —1 —5,2 * У43"С20 —1 —2,1 У44<20 —1 —2,1 * * ** 0
5 —1 -2,6 * 1/53^20 —1 —0,7 У54<240 —1 —0,7 * * *♦ 0
Чистые не- явные цены Vj 0 0 *2 0 *3 0 *4 0 ^5 ** 0
♦ Клетка не используется, потому что самолет этого типа не может летать по рас- сматриваемой линии или же потому, что для описания распределения спроса на мар- шруте необходимо меньшее число приращений. ♦* Соответствующие строки или столбцы не имеют уравнения.
555
Таблица 28-2-IV
Цикл О
Рабочая таблица для определения оптимального назначения
в условиях неопределенного спроса
10
(с24—4-58,4, 9*=*ТЁ"> ожидаемые расходы равны 1666 000 долл.)
Маршрут Наличные
Тип самолета (1) Нью- Йорк— Лос-Ан- желес с одной посадкой Нью-Йорк— Лос-Анжелес с двумя посадками Йорк— Лос-Ан- желес без по- садки Йорк- Даллас с одной посадкой (5) Нью- Йорк— Бостон без по- садки (6) Избыток самоле- тов само лоты Неявные цены ui
i-A 10 1 16 8 15 21 28 18 23 16 81 10 0 0 10 —139
2-В 4 84-0 10 15 5 14 16 6—0* 15 14 57 9 0 0 19 —76
3-С 4 t 7,8 5 10 4 7 9 17,2 29 6 0 0 25 —23
4-D 10 9 17 11 16 5 Г 22 7 17 15 55 10 0 0 15 —91
Прираще- ние 1 200 —1 13 50 — 1 —13 140 —1 7 10 —1 —7 500 —1 —1 * 4:4с 0
2 20 —1 —10,4 70+100 —1 —9,1 20 —1 —6,3 40 — 1 —5,6 —1 —0,9 45 4с 4: 0
3 30 —S — 1 1,8 * 20 —4 —1 :,9 30 —1 —4,2 —1 —0,1 4s 4:4с 0
4 —1 —5,2 * —2 — 1 И 10—150 —1 —2,1 * 4s 4с 4с 0
5-56
Продолжение табл. 28-2-IV
Цикл О
Тип самолета Маршрут Наличные самолеты Неявные цены ui
(1) Нью- Йорк— Лос-Ан- желес с одной посадкой (2) Нью-Йорк— Лос-Анжелес с двумя посадками (3) Нью- Йорк— Лос-Ан- желес без по- садки Йорк- Даллас с одной посадкой (5) Нью- Йорк— Бостон без по- садки (6) Избыток самоле- тов
5 —1 —2,6 * —1 0,7 —1 —0,7 * * ** 0
Чистые не- явные цены *7 0 9,8 0 9,1 0 4,9 0 2,1 0 1 ** 0
Таблица 28-2-IV
Цикл 1
Рабочая таблица для определения оптимального назначения
в условиях неопределенного спроса
20 \
4-23,4» 0*=—, ожидаемые расходы равны 1627000 долл. \
Тип самолета Маршрут Наличные самолеты Неявные цены ui
(1) Нью- Йорк— Лос-Ан- желес с одной посадкой Нью-й!орк— Лос-Анжелес с двумя посадками (3) Нью- Йорк— Даллас без по- садки (4) Нью- Йорк— Даллас с одной посадкой Йорк- Бостон без по- садки Избыток самоле- тов
1-А 10 16 18 15 21 28 18 23 16 81 10 0 0 10 —139
2-В * 8,7+0 10 15 5—0* 14 16 5,3 15 14 57 9 0 0 19 —76
3-С * 5 10 * 7 9 17,2 6 29 0 0 25 —23
k-D 10 9 17 И 16 в 22 17 17 15 55 10 0 0 15 —91
Прираще- ние 1 200 —1 —13 50 —1 —13 140 —1 —7 10 —1 —7 500 —1 -1 * ** 0
557
Продолжение табл. 28-2-IV
Цикл 1
Тип самолета Маршрут Наличные самолеты Неявные цены и1
Йорк— Лос-Ан- желес с одной посадкой (2) Нью-Йорк— Лос-Анжелес с двумя посадками Йорк- Даллас без по- садки Йорк- Даллас с одной посадкой (5). Нью- Йорк— Бостон без по- садки (6) Избыток самоле- тов
2 20 — 1 —10,4 20 —1 —6,3 40 —1 —5,6 —1 —0,9 * ** 0
77+100
—1 —9,1
3 S —1 —9,8 * 30 —1 —4,2 —1 —0,1 * ** 0
20—140
—1 —4,9
4 —1 —5,2 * —1 —2,1 —1 —2,1 * * ** 0
5 —1 —2,6 * —1 —0,7 —1 —0,7 ♦ * ** 0
Чистые не- явные цены vj 0 9,8 0 9,1 0 4,9 0 6 0 1 ** 0
Таблица 28-2-IV
Цикл 2
Рабочая таблица для определения оптимального назначения
в условиях неопределенного спроса
с41 = + 56,8, 0 * = - jg- , ожидаемые расходы равны 1 594 000 долл.
Тип самолета Маршрут Наличные самолеты Неявные цены ui
411. Йорк— Лос-Ан- желес с одной посадкой (2) Нью-Йорк— Лос-Анжелес с двумя посадками (3) Нью-Йорк— Даллас без посадки 4‘i. Йорк- Даллас с одной посадкой (5) Нью- Йорк— Бостон без по- садки (6) Избыток самоле- тов
1-А 10 16 18 15 21 28 18 23 16 81 10 0 0 10 —139
2-В * 57 9 0 0 19 —76
10,1+1,60 3,6+1,60 5,3
10 15 14 16 15 14
558
Продолжение табл. 28-2-IV
Цикл 2
Тип самолета Маршрут Наличные самолеты Неявные цены ui
(1) Нью- Йорк— Лос-Ан- желес с одной посадкой (2) Нью-Йорк— Лос-Анжелес с двумя посадками Ныо-11орк— Даллас без посадки Йорк- Даллас с одной посадкой (5) Нью- Йорк— Бостон без по- садки (6) Избыток самоле- тов
3-С * 7,8 5 10 * 7 9 0 0 25 —23
17,2
29 6
4-Z) 10—0* 9 17 11 16 17 15 55 10 0 0 15 —128
5+0
22 17
Прираще- ние 1 200 —1 —13 50 —1 -13 140 —1 —7 10 —1 —7 * *♦ 0
500
—1 -1
2 20 —1 —10,4 20 —1 —6,3 40 —1 —5,6 —1 —0,9 * ** 0
91 + 160
—1 —9,1
3 ♦ —1 —4,9 30 —1 —4,2 —1 -0,1 * ** 0
30—90
—1 -9,8
4 —1 —5,2 ♦ —1 —2,1 —1 —2,1 « * ♦♦ 0
5 —1 —2,6 * —1 —0,7 —1 —0,7 ♦ * ** 0
Чистые неявные цены vj 0 9,8 0 9,1 0 6,6 0 6 0 1 ** 0
559
Таблица 28-2-IV
Цикл 3
Рабочая таблица для определения оптимального назначения
в условиях неопределенного спроса
(^32“+5,5; 0* = -^-, ожидаемые расходы равны 1561000 долл.
Тип самолета Маршрут Наличные самолеты Неявные цены ui
Нью-11орк— Лос-Анжелес с одной посадкой Нью-^орк— Лос-Анжелес с двумя посадками (3) Нью-Йорк— Даллас без посадки Йорк- Даллас с одной посадкой (5) Нью-Йорк— Бостон без посадки (6) Избыток самоле- тов
1-А 10 16 18 15 21 28 18 23 16 81 10 0 0 10 —139
2-В * 57 9 0 0 19 —40
11+0,50 2,7-0,50 5,3
10 15 14 16 15 14
3-С * 7,8—0* 5 10 7 9 0 0 25 —23
17,2+0
29 6
4-D И 16 17 15 55 10 0 0 15 —71
9,4—0,30 5,6+0,30^
9 17 22 17
Прира- щение 1 200 —1 —13 50 —1 —13 140 —1 —7 10 —1 —1 * ** 0
500+290
—1 —1
2 20 —1 —10,4 100 —1 —9,1 20 —1 —6,3 40 —1 —5,6 —1 —0,9 * ** 0
3 * —1 —4,9 30 —1 —4,2 —1 —0,1 * ** 0
| 25—2,70
—1 —9,8
4 —1 —5,2 * —1 —2,1 —1 —2,1 * * ** 0
5 —1 —2,6 * —1 —7 —1 —7 * * ** 0
Чистые неявные цены Vj 0 9,8 0 5,5 0 4 0 3,6 0 1 *♦ 0
660
Таблица 28-2-IV
Цикл 4
Рабочая таблица для определения оптимального назначения
в условиях неопределенного спроса
20 х
?зз=—0,9; 0*=-^-, ожидаемые расходы равны 1 542 000 долл. )
Тип самолета Маршрут Наличные самолеты Неявные цены ui
(D Нью-Йорк— Лос-Анжелес с одной посадкой (2) Нью- Йорк— Лос-Ан- желес с двумя посадка- ми (3) Нью- Йорк— Даллас без по- садки (4) Нью-Йорк— Даллас с одной посадкой (5) Нью- Йорк— Бостон без по- садки (6) Избыток самоле- тов
1-А 10 16 18 15 21 28 18 23 16 81 10 0 0 10 -139
2-В * 57 9 0 0 19 —40
12,8 0,9 5,3
15 10 16 14 14 15
3-С * * 7 9 0 0 25 —18
4,3 20,7
10 5 2 6 !9
4-Я 11 16 17 15 55 10 0 0 15 —71
8,3—0 6,7+0
9 17 22 17
Прира- щение 1 200 —1 —13 50 —1 —13 140 —1 —7 10 —1 —7 580 —1 —1 * 0
2 20 —1 —10,4 100 —1 —9,1 20 —1 —6,3 40 —1 —5,6 20 —1 —0,9 * ** 0
3 15-90 —9,8 1 * +220* —1 —4,9 30 —1 —4,2 —1 —0,1 * ** 0
4 —1 —5,2 * —1 —2,1 —1 —2,1 * * ** 0
36 Дж. Данциг
561
Продолжение табл. 28-2-IV
Цикл 4
Тип самолета Маршрут Наличные самолеты Неявные цены ui
(1) Нью-Йорк— Лос-Анжелес с одной посадкой Йорк— Лос-Ан- желес с двумя посадка- ми (3) Нью- Йорк— Даллас без по- садки (4) Нью-Йорк— Даллас с одной посадкой (5) Нью- Йорк— Бостон без по- садки (6) Избыток самоле- тов
5 —1 —2,6 * — 1 —0,7 —1 —0,7 * * ** 0
Чистые неявные цены Vj 0 9,8 0 5,5 0 4 0 3,6 0 0,8 *♦ 0
Таблица 28-2-IV
Цикл 5 (оптимальный)
Рабочая таблица для определения оптимального назначения
в условиях неопределенного спроса
(минимальные ожидаемые расходы равны 1 542 000 долл.)
Тип самолета Маршрут Наличные самолеты Неявные цены . ui
Нью-Йорк— Лос-Анжелес с одной посадкой (2) Нью-Йорк— Лос-Анжелес с двумя посадками (3) Нью- Йорк— Даллас без по- садки Йорк- Даллас с одной посадкой (5) Нью- Йорк— Бостон без по- садки (6) Избыток самоле- тов
10 10
1-А 16 15 28 23 81 0
18 21 18 16 10 0 —139
2-В 12,8 | 0,9 5,3 19
* 10 14 15 57 0
15 16 14 9 0 -40
4,3 20,7 25
3-С 5 Ис 7 29 0
10 9 6 0 —18
7,4 7,6] 15
4-D 9 И 22 17 55 0
17 16 17 15 10 0 —71
Прира- 200 50 140 10 580 ♦*
щение —1 —1 —1 —1 —1 *
1 —13 —13 —7 — 7 —1 0
562
Продолжение табл. 28-2-IV
Цикл 5 (оптимальный)
Тип самолета Маршрут Наличные самолеты Неявные цены и1
(О Нью-Йорк— Лос-Анжелес с одной посадкой Нью-Йорк— Лос-Анжелес с двумя посадками (3) Нью- Йорк— Даллас без по- садки Йорк- Даллас с одной посадкой Йорк- Бостон без по- садки (6) Избыток самоле- тов
2 20 —1 —10,4 100 —1 —9,1 20 —1 —6,3 40 —1 —5,6 20 —1 —0,9 * ♦* 0
3 н —1 —9,8 * 20 —1 -4,9 30 —1 —4,2 —1 —0,1 * ** 0
4 —1 —5,2 * —1 —2,1 — 1 —2,1 * * *♦ 0
5 —1 —2,6 * —1 —0,7 —1 —0,7 * * ** 0
Чистые неявные цены Vj 0 9,8 , 0 5,5 0 4 0 3,6 0 0,8 0
* Клетка не используется; самолет не может летать по этой линии. * * Строка или столбец не имеют уравнения.
Для вычисления ожидаемых расходов различных решений первый
шаг (см. § 28-1-(14)) должен состоять в определении ожидаемой при-
были 7?0, которая была бы получена, если бы во все моменты времени было
достаточное количество мест, чтобы удовлетворить всех пассажиров, кото-
рые появляются. Из табл. 28-1-II легко видеть, что Ro = 13-250 +
+ 13-120 + 13-120 + 7-180+ 7-90 + 1-600 = 7300, или 7 300 000долл.
Сразу видно, что решение, приведенное в табл. 28-2-П (совпа-
дающее с исходным решением, табл. 28-2-IV, цикл 0, которое предпола-
гает, что спрос в точности равен ожидаемому спросу), имеет чистые ожи-
даемые расходы, равные 1666 тыс. долл. (Интересно отметить, что если бы
спрос не был переменным, а был фиксирован и равен ожидаемому спросу,
то расходы составили бы только 1 млн. долл. (см. табл. 28-2-П). Увеличе-
ние чистых расходов на 67% произошло из-за 13 400 пассажиров (в среднем),
которым не хватило мест из-за предположенного распределения спроса.)
Последовательные улучшения решения (табл. 28-2-IV, циклы
0—5), уменьшают чистые ожидаемые расходы с 1666 тыс. долл, до 1524
тыс. долл, в оптимальном решении.
Таким образом, оптимальное решение, полученное в предположении
о том, что спрос фиксирован и равен своему ожидаемому значению, имеет
ожидаемые расходы на 9% выше ожидаемых расходов оптимального
решения, полученного при предположенном распределении спроса. Видно
также, что потребовалось очень мало вычислительных усилий, чтобы
учесть эту неопределенность спроса.
563
36*
БИБЛИОГРАФИЯ
ОБЩИЙ УКАЗАТЕЛЬ1
А г м о н (A g m о n S.)
[1] The relaxation method for linear inequalities, Canad. J. Math. 6, № 3 (1954),
382-392.
Аллен (Allen R. G. D.)
[1] Математическая экономия, M., ИЛ, 1963, 667 стр.
Аллендорфер, Окли (Allendoerfer С. В., Oakley С. О.)
[1] Principles of mathematics, New York, McGraw-Hill, 1955, 448 pp.
Баббар (Babbar M. M.)
[1J Distribution of solutions of a set of linear equations (with applications to linear
programming), J. Amer. Statist. Assoc. 50, № 271 (1955), 854—869.
Баранкин, Дорфман (Barankin E. W., D о r f m a n R.)
[1] On quadratic programming, Berkeley, Univ. California Pubis, in Statistics 2,
№ 13 (1958), 285—318.
Баумоль (Baumol W. J.)
[1] Economic dynamics— an introduction, 2nd ed., New York, Macmillan, 1959,
396 pp.
[2] Economic theory and operations analysis, New Jersey, Prentice — Hall, Inc.,
Englewood Cliffs, 1961, 438 pp.
Бекенбах (Beckenbach E. F.)
[1] Convex functions, Bull. Amer. Math. Soc. 54, (1948), 439—460.
Бекман (Beckmann M. J.)
[1] Comparative studies in linear programming and the Giffen paradox, Rev. Econ.
Studies 23, № 3 (1955—1956), 232—235.
Б e к м а н, M а к - Г а й p, В и н с т e н (McGuire С. B., WinstenC.)
[1] Studies in the economics of transportation, The RAND Corporation, Research
Memorandum RM-1488,1955, 347 pp.; New Haven, Yale Univ. Press, 1956, 232 pp.
Беллман (Bellman R.)
[1] Динамическое программирование, M., ИЛ., 1960, 400 стр.
[2] Dynamic programming of continuous processes, The RAND Corparotion, Report
R—271, 1954, 141 pp.
[3] On a routing problem, Quart. Appl. Math. 16, № 1 (1958), 87—90.
Беллман, Блэкуэлл (Blackwell D.)
[Ц Red dog, blackjack, poker, Scient. Amer. 184, № 1 (1951), 44—47.
Беллман, Гликсберг, Гросс (Glicksberg I., Gross O. A.)
[1] Некоторые вопросы математической теории процессов управления, М., ИЛ,
1962, 336 стр.
Белтер (Boelter L. М. К.)
[1] Some reflections on automation. Symposium on electronics and automatic produ-
ction, San Francisco, California, 1955.
Б e p ж (Berge C.)
[1] Теория графов и ее применения, М., ИЛ, 1962, 319 стр.
Бил (Beale Е. М. L.)
[1 ] Linear programming by the method of leading variables. Report of the Conference
linear programming. May, 1954. London, arranged by Ferranti Ltd., 56—71.
[2] Cycling in the dual simplex algorithm, Naval Res. Logist. Quart. 2, № 4 (1955),
269—276.
1 Звездочкой отмечены работы, дополнительно включенные в русский пере-
вод. Прим. ред.
564
[3] On minimizing a convex function subject to linear inequalities, J. Roy. Statist*
Soc., Ser. В 17, № 2 (1955), 173-184.
[4] A method of solving linear programming problems when some but not all of the
variables must take integral values, Statistical Techniques Research Group, Prince-
ton, Princeton Univ., 1958.
[5] An algorithm for solving the transportation problem when the shipping cost
over each route is convex, Naval. Res. Legist. Quart. 6, № 1 (1959), 43—56.
[6] On quadratic programming, Naval Res. Logist. Quart. 6, № 3 (1959), 227—243.
[7]* Two transportation problems. Сборник [14]*, 780—788.
Биркгоф (Birkhoff G.)
[1] Three observations on linear algebra, Rev. Univ. пае. Tucuman, Ser. A, Vol. 5,
(1946), 147—151.
Биркгоф, Мак-Лейн (MacLane S.)
[1] A survey of modern algebra, New York, Macmillan, 1953, 276 pp.
Блекуэлл, Гиршик (Blackwell D., Girshick M. A.)
[1] Теория игр и статистических решений, М., ИЛ, 1958, 374 стр.
Бодевиг (Bodewig Е.)
[1] Matrix calculus, Amsterdam, North—Holland PubL, 1959.
Болдырев (Boldyreff A. W.)
[1] Determination of the maximal steady state flow of traffic through a railrood
network, J. Operat. Res. Soc. Amer. 3, № 4 (1955), 443—465.
Боненбласт, Карлин, Ш еп л и (В oh n en b 1 u s t H. F., Karlin S.,
S h a p 1 e у L. S.)
[1] Решения дискретных игр двух лиц. Сборник [2]*, 17—44.
Борель (Borel Е.)
[1] La theorie du jeu et les equations integrates a noyau symetrique, Compt.aRend.
Acad. sei. 173, 1921 (dec. 19), 1304—1308. Английский перевод: Econometrica 21,
№ 1 (1953), 97—100.
[2] Sur les jeux ou interviennent le hasard et I’habilete des joueurs, Librairie scien-
tifique, Paris, Hermann, 1924, 204—224. Английский перевод: Econometrica
21, № 1 (1953), 101—115.
[3] Sur les systemes de formes lineaires a determinant symetrique gauche et la theorie
generale du jeu, Compt. Rend. Acad. sci. 184, 1927, 52—53. Английский пере-
вод: Econometrica 21, № 1 (1953), 116—117.
Боулдин г, Спиви (Boulding К. Е., Spivey W. А.)
[1] Linear programming and the theory of the firm, New York, Macmillan, 1960,
227 pp.
Браун (Brown G. W.)
[1] Iterative solution of games by fictitious play. Сборник [18], 374—376.
Браун, Купманс (Koopmans T. С.)
[1] Computational suggestions for maximizing a linear function subject to linear
inequalities. Сборник [18], 377—380.
Браун, фон Нейман (von Neumann J.)
[1] Solutions of games by differential equations. Сборник [16], 73—79.
Булавский В. A.
[1]* Итеративный метод решения общей задачи линейного программирования,
Сиб. машем. ж. 3, № 3 (1962), 313—332.
Булавский В. А., Рубинштейн Г. Ш.
[1]* О решении задач выпуклого программирования с линейными ограничениями
методом последовательного улучшения допустимого вектора, Докл. АН СССР
150, № 2 (1963), 231—234.
Бэтчелор (Batchelor J. Н.)
[1] Operations research. An annotated bibliography. 2nd. ed. St. Louis(Mo), Univ.
Press, 1959, 866 pp.
[2]* Operations research. An annotated bibliography, Vol. 2, St. Louis (Mo), Univ.
Press, 1962, 628 pp.
[3]* Operations research. An annotated bibliography, Vol. 3, St. Louis (Mo), Univ.
Press, 1963, 384 pp.
[4]* Operations research. An annotated bibliography, Vol. 4, St. Louis (Mo), Univ.
Press, 1964, 477 pp.
565
Вагнер (Wagner Н. М.)
[1] A comparison of the original and revised simplex methods, Operat. Res. 5,
№ 3 (1957), 361—369.
[2] A linear programming solution to dynamic Leontief type models, Manag. Sci.
3, № 3 (1957), 234-254.
[3] The dual simplex algorithm for bounded variables, Naval Res. Logist. Quart. 5,
№ 3 (1958), 257—261.
[4] On the distribution of solutions in linear programming problems, J. Amer. Sta-
tist. Assoc. 53 (1958), 161—163.
[5]^On a^class °* capacitated transportation problems, Manag. Sci. 5, № 3 (1959),
Важоньи (Vazsonyi A.)
[1] Научное программирование в промышленности и торговле, М., ИЛ, 1963,
387 стр.
[2] Optimizing a function of additively separated variables subject to a simple restri-
ction. Сборник [9], 453—469.
Вайда (V a j d a S.)
[1] Теория игр и линейное программирование. Сборник [1], 11—106.
[2] Readings in linear programming, New York, Wiley, 1958, 99 pp.
[3] Inequalities in stochastic linear programming, Bull. Internal. Statist. Inst. 36,
№ 3 (1958), 357—363.
[4] Mathematical programming, Reading, Mass.— London, Addison—Wesley Publ.
Co. 1961, 310 pp.
Валле-Пуссен (Poussin M. Ch. J. de Vallee)
[1] Sur la methode de Г approximation minimum, Ann. Soc. sci. de Bruxelles 35,
(1911), 1-16.
Вальд (Wald A.)
[1} Ober die eindeutige positive Losbarkeit der neuen Produktionsgleichungen,
Ergebnisse eines M athematischen Kolloquiums, № 6 (1935), 12—18.
[2] Ober die Produktionsgleichungen der okonomischen Wertlehre, Ergebnisse eines
Mathematischen Kolloquiums, № 7, (1936), 1—6.
[3] Statistical decision functions, New York, Wiley, 1950, 17 pp.
Вальрас (Walras L.)
[1] Elements d’economie politique pure on theorie de la richesse sociale, 1st fasc,
Vol. 8, Lausanne, Paris et Basel, 1874, 208 pp.
Вейль (W e у 1 H.)
[1] Элементарная теория выпуклых многогранников. Сборник [2]*, 254—273.
Билль (Ville J. А.)
[1] Sur la theorie generale des jeux ой intervient I’habilete des joueurs, Applications
aux jeux de hasard par Emile Borel et Jean Ville, Tome 4, Fasc. 2, dans le Traite
du calcul des probability et de ses applications, par Emile Borel, 1938, 105—113.
Вильямс (Williams A. C.)
[1] The method of continuous coefficients, Socony Mobile Oil Co., Part I, Report
№ ECC 60.3, 1960; Part II, Report № ECC, 60.4, 1960.
Вильямс (Wiliams J. D.)
[1] Совершенный стратег, или букварь по теории игр., М., Советское Радио, 1960,
269 стр.
Воробьев Н. Н.
[1]* Конечные бескоалиционные игры, Успехи матем. наук 14, вып. 4 (1959), 21—56.
12]* Матричные игры. Сборник [2]*, 7—16.
В ото (V о t a w D. F., 1г.)
[1] Methods of solving some personnel classification problems, Psychometrika 17, № 3
(1952), 255—266.
[2] Programming under conditions of uncertainty. Сборник [9], 187—195.
Вото, Орден (Orden A.)
[1] Personnel assignment problem. Сборник [20], 155—163.
Вулф (Wolfe Ph.)
[1] Computational techniques for non-linear programs, Princeton, Princeton Univ.
Conference, 1957.
[2] The simplex method for quadratic programming, Econometrica 27, № 3 (1959),
382—398.
566
[3] Accelerating the cutting plane method for non-linear programming, J. Soc.
Industr. Appl. Math. 9, № 3 (1961), 481—488.
[4]* Methods of non-linear programming. Сборник [13]*, 67—86.
[5]* Experiments in linear programming. Сборник [13]*, 177—200.
[6]* The present status of nonlinear programming. Сборник [10]*, 233—249.
[7] * A technique for resolving degeneracy in linear programming, J. Soc. Industr.
and. Appl. Math. 11, № 2 (1963), 205—211.
[8]* The composite simplex algorithm, SIAM Rev. 7, № 1 (1965), 42—54.
Вуд (Wood M. K.)
[1] Scientific planning techniques, Project SCOOP, Discussion Paper Number 1-DU,
Planning Research Division, Directorate of Program Standards and Cost Control,
Comproller, USAF, Washington, D. C. 1948, p. 6A.
Вуд, Гейслер (Geisler M. A.)
[1] Development of dynamic models for program planning. Сборник [18], 189—192.
Вуд, Данциг (D antzig G. B.)
[1] The programming of interdependent activities: general discussion, Econometrica
17, №№ 3 и 4 (1949), 193—199. (В переработанном виде опубликована в качестве
гл. I сборника [18].)
Гаддум (Gaddum J. W.)
[1] A theorem on convex cones with applications to linear inequalities, Proc. Amer.
Math. Soc., 3, (1952), 957—960.
Гаддум, Гофман, Соколовский (Hoffman A. J.,S okolowsky D.)
[1] On the solution of the caterer problem, Naval Res. Logist. Quart. 1, № 3 (1954),
223-229.
Гантер (Gunther P.)
[1] Use of linear programming in capital budgeting, J. Operat. Res. Soc. Amer. 3,
№ 2 (1955), 219-224.
Гарвин (Garvin W. W.)
[1] Introduction to linear programming, New York, McGraw-Hill, 1960, 281 pp.
Гарвин, К p а н д а л л, Д ж о н, C n e л м а н (Crandall H.W.,John J.B.,
Spellman R. A.)
[1] Applications of linear programming in the oil industry, Manag. Sci. 3, № 4 (1957),
407—430.
Г a с c (G a s s S. I.)
[1] Линейное программирование (методы и приложения), М., Физматгиз, 1961,
303 стр.
[2]* Первое допустимое решение в задачах линейного программирования. Сбор-
ник [4]*, 47—54.
Г а с с, С а а т и (S a a t у Т. L.)
[1] The computational algorithm for the parametric objective function, Naval Res.
Logist. Quart. 2, № 1 (1955), 39—45.
Гаусс (Gauss K. F.)
[1] Theoria combinationis observationum erroribus minimus obuoxiae, Supplemen-
turn Vol. 4, Werke, Gottingen, 1826, 55—93.
Гейл (Gale D.)
[1] Теория линейных экономических моделей, М., ИЛ, 1963, 418 стр.
[2] Convex polyhedral cones and linear inequalities. Сборник [18], гл. XVII, 287—297.
[3] Соседние вершины на выпуклом многограннике. Сборник [1], 355—362.
[4] The basic theorems of real linear equations, inequalities, linear programming and
game theory, Naval Res. Logist. Quart. 3, № 3 (1956), 193—200.
[5] A theorem on flows in networks, Pacif. J. Math. 7, № 2 (1957), 1073—1082.
[6] Transient flows in networks, Michigan Math. J. 6, № 1 (1959), 59—63.
Гейл, Кун, Таккер (Kuhn H.W., Tucker A. W.)
[1] О симметричных играх. Сборник [2]*, .62—71.
[2] Редукция игровых матриц. Сборник [2]*, 72—80.
[3] Linear programming and the theory of games. Сборник [18].
Гейнен (Gainen L.)
[1] Linear programming in bid evaluations. Сборник [9], 29—38.
Герман, Мэджи (Herrmann С. C., Magee J. F.)
[1] Operations research for management, Harvard Business Rev. 31, № 4 (1953),
100—112.
567
Г ер стенх абер (Gerstenhaber М.)
[1] Theory of convex polyhedral cones. Сборник [18], гл. XVIII, 298—316.
[2] A solution method for the transportation problem, J. Soc. Industr. Appl. Math,
6, № 4 (1958), 312—316.
Гирш, Данциг (Hirsch W. M., D a n t z i g G. B.)
[1] The fixed charge problem, The RAND Corporation, Paper P-648, 1954.
Голдман (Goldman A. J.)
[1] Теоремы разложения и отделимости для многогранных выпуклых множеств.
Сборник [1], 162—171.
Голдман, Таккер (Tucker A. W.)
[1] Многогранные выпуклые конусы. Сборник [1], 142—161.
[2] Теория линейного программирования, Сборник [1], 172—213.
Голдстейн (Goldstein L.)
[1] Problem of contract awards. Сборник [20], 147—154.
Гомори (Gomory R. E.)
[1] Outline of an algorithm for integer solutions to linear programs, Bull, Amer. Math.
Soc. 64, № 5 (1958), 275—278.
[2] An algorithm for integer solutions to linear programs. Сборник [13]*,
269—302.
[3] Extension of an algorithm for integer solutions to linear programs, Amer. Math.
Soc. Notices 6, № 1 (1959), 52 (abstract 553—190).
[4] An algorithm for the mixed integer problem, The RAND Corporation, Paper P-1885,
1960.
Г о м о p и, X у (Hu T. C.)
[1] Multi-terminal network flows. J. Soc. Industr. and Appl. Math. 9, № 4 (1961),
551-570
[2] An application of generalized linear programming to network flows, J. Soc.
Industr. and Appl. Math. 10, № 2 (1962), 260—283.
Гордан (Gordan P.)
[1] Ober die Auflosung linearer Gleichungen mit reellen Coefficienten, Math. Ann.
6, (1873), 23—28.
Гофман (Hoffman A. J.)
[1] Cycling in the simplex algorithm, National Bureau of Standards Report, № 2974
(1953), 7 pp.
[2] Systems of distinct representativesand linear programming, Amer. Math. Monthly
63, № 7 (1956), 455—460.
[3] Some recent applications of the theory of linear inequalities to extremal combi-
natorial analysis. Сборник [11], 113—127.
Гофман, Краскал (Kruskal J. G.)
[1] Целочисленные граничные точки выпуклых многогранников. Сборник [1],
325—347.
Гофман, Кун (Kuhn Н. W.)
[1] О системах различных представителей. Сборник [1], 302—310.
Гофман, Манное, Соколовский, Вигман (Mannos М., S о к о-
lowsky D.,Wiegmann N.)
Д1] Computational experience in solving linear programs, J. Soc. Industr. Appl. Math.
1, № 1 (1953), 17-33.
Гольштейн E. Г.
[1]* Транспортная задача и ее обобщения. Сборник [3]*, 3—34.
Грин, Чатто, Хикс, Кокс (Greene J. Н., С h a 11 о К., Hicks С. R.,
С ох С. В.)
[1] Linear programming in the packing industry, J. Industr. Eng. 10, № 5 (1959),
364—372.
Гросс (Gross O.)
[1] The bottleneck assignmen tfproblem. The RAND Corporation,"Paper P-1630, 1959.
Гуд (Good R. A.)
[1] Systems of linear relations, J. Soc. Industr. and Appl. Math. 1, № 1 (1959),
1—31.
Дайне, Мак-Кой (Dines L. L., McCoy N. H.)
[1] On linear inequalities, Trans. Roy. Soc. Canada. Sect. Ill (1933), 37—70.
568
Данциг (D а n t z i g G. B.)
[1] Programming in a linear structure, Washington, Comptroller, USAF, 1948.
[2] Programming of interdependent activities, II, Mathematical model, Econometrica
17, № 3, 4 (1949), 200—201. В переработанном виде статья помещена в сборнике
[18], 19—32.
[3] A proof of the equivalence of the programming problem and the game problem.
Сборник [18], гл. XX, 330—335.
[4] Application of the simplex method to a transportation problem. Сборник [18],
359—373.
[5] Максимизация линейной функции переменных, подчиненных линейным нера-
венствам. Сборник [4]*, 26—34.
[6] Notes on linear programming: Part XI, Composite simplex dual simplex algo-
rithm — I, The RAND Corporation, Research Memorandum RM-1274, 1954, 15 p.
[7] Notes on linear programming: Part VII — The dual simplex algorithm, The
RAND Corporation, Research Memorandum RM-1270, 1954, 10 pp.
[8] Notes on linear programming: Parts VIII, IX, X — Upper bounds, secondary
constraints and block triangularity in linear programming, Econometrica 23, № 2
(1955), 174—183.
[9] Linear programming under uncertainty, Manag, Sci. 1, № 2, (1955),197—206.
[10] Notes on linear programming: Part XIII — Optimal solution of a dynamic
Leontief model with substitution, Econometrica, 23, № 3 (1955), 295—302.
[11] Constructive proof of the min-max theorem, Pacif. J. Math. 6, № 1 (1956),
25-33.
[12] Recent advances in linear programming. Manag. Sci. 2, № 2 (1956), 131—144.
[13] Thoughts on linear programming and automation, Manag. Sci. 3, № 2 (1957),
131—139.
[14] Discrete variable extremum problems, Operat. Res. 5. № 2 (1957), 266—277.
[15] On the status of multistage linear programs, Manag. Sci. 6, № 1 (1959), 53—72.
[16] On integer and partial integer linear programming problems, The RAND Corpora-
tion, Paper P-1410, 1958.
[17] Solving two-move games with perfect information, The RAND Corporation,
Paper P-1459, 1958.
[18] Inductive proof of the simplex method, IBM J. Res. and Develop. 4, № 5 (1960),
505—506.
[19] On the shortest route through a network, Manag. Sci. 6, № 2 (1960), 187—190.
[20] On the significance of solving linear programming problems with some integer
variables, Econometrica 28, № 1 (1960), 30—44.
[21] General convex objective forms. Сборник [21], 151—158.
Данциг, Вальд (Wald A.)
[1] On the fundamental lemma of Neyman and Pearson, Ann. Math. Statist. 22, № 1
(1951), 87—93.
Данциг, Вулф (W о 1 f e Ph.)
[1] Decomposition principle for linear programs. Operat. Res. 8, № 1 (1960), 101—111.
[2]* The decomposition algorithm for linear programs, Econometrica 29, № 4 (1961),
767—778.
Данциг, Mаданский (Madansky A.)
[1] On the solution of two-stage linear programs under uncertainty. Сборник [23],
165—173.
Данциг, Орден (Orden A.)
[1] Notes on linear programming: Part II — Duality theorems. The RAND Corpo-
ration, Research Memorandum RM-1265, 1953.
Данциг, Орден, Вулф (Wolfe Ph.)
[1] Обобщенный симплексный метод минимизации линейной формы при ограниче-
ниях в виде линейных неравенств. Сборник [4]*, 33—46.
Данциг, Орчард-Хейс (Orchard-Hays W.)
[1] Notes on linear programming: Part V — Alternate algorithm for the revised sim-
plex method using product form for the inverse, The RAND Corporation, Research
Memorandum RM-1268, 1953.
Данциг, Форд, Фулкерсон (Ford L. R., Fulkerson D. R.)
[1] Алгоритм для одновременного решения прямой и двойственной задач линей-
ного программирования. Сборник [1], 277—286.
Данциг, Фулкерсон (Fylkerson D. R.)
[1] Minimizing the number of tankers to meet a fixed schedule, Naval Res. Logist.
Quart. 1, № 3 (1954), 217—222.
569
[2] Теорема о максимальном потоке и минимальном разрезе в сетях. Сборник [1],
318—324.
Данциг, Фулкерсон, Джонсон (Johnson S.).
[1] Solution of a large-scale traveling-salesman problem, J. Operat. Res. Soc. Amer.
2, № 4 (1954), 393—410.
[2] On a linear programming combinatorial approach to the traveling-salesman pro-
blem, Operat. Res. 7, № 1 (1959), 58—66.
Дафф ин (Duffin R. J.)
[1] Бесконечные программы. Сборник [1], 263—276.
Дворецкий, Кифер, Вольфовиц (D v о г е t z к у A., Kiefer J..
Wolfowitz, J.)
[1] The inventory problem: I, Case of known distributions of demand; II, Case of
unknown distributions of demand, Econometrica 20, № 2, 3 (1952), 187—222, 450—
466.
Деннис (Dennis J. B.)
[1] Математическое программирование и электрические цепи. М., ИЛ, 1961,215 стр.
Джейкобс (Jacobs W. W.)
[1] The caterer problem. Naval. Res. Logist. Quart. 1, № 2 (1954), 154—165.
[2] Military applications of linear programming. Сборник [9], 1—27.
Джон (John F.)
[1] Extremum problems with inequalities as subsidiary conditions, Studies and Essays,
New York, Interscience Publ., 1948, 187—204.
Джонсон (Johnson S.)
[1] Оптимальные расписания для двух- и трехступенчатых процессов с учетом
времени наладки. Кибернетический сборник (новая серия), вып. 1, М.,
Мир, 1966, 78—86.
[2] Discussion: sequencing п jobs on two machines with arbitrary time lags: alternate
proof and discussion of general case, Manag. Sci. 5, № 3 (1959), 299—303.
Д ж у э л (J e w e 11 W. S.)
[1] Warehousing and distribution of a seasonal product. Naval Res. Logist. Quart.
№ 1 (1957), 29—34.
[2] Optimal flow through networks, Interim Technical Report № 8 on Fundumental
Investigations in Methods of Operations Research, Mass. Institute of Technology,
Cambridge, Massachusetts, 1958.
[3] Optimal flow through network with gains, Operat. Res. 10, № 4, (1962), 476—499.
Джэксон (Jackson J. R.)
[1] Simulation research on job shop production, Naval Res. Logist. Quart. 1, № 4
(1957), 287—294.
Дилворт (Dilworth R. P.)
[11 A decomposition theorem for partially ordered sets, Ann. Math, 51, № 1 (1950),
161-166.
Дойг, Белз (Doig A. G., В e 1 z M. H.)
[1] Report in trim problems for May, 1956, Australia, Univ, of Melbourn, Department
of Statistics, 1956.
Д о p н (D о r n W. S.)
[1] On Lagrange multipliers and inequalities, Operat. Res. 9, № 1 (1961), 95—104.
Дорн, Гринберг (Greenberg H. J.)
[1] Linear programming and plastic limit analysis of structures, Technical Report
№ 7, Carnegie Institute of Technology, Pittsburgh, Pennsylvania, 1955, 30 pp.
Дорфман (Dorfman R.)
[1] Application of linear programming to the theory of the firm, Berkeley and Los
Angeles, Univ, of California Press, 1951, 98 pp.
[2] Application of the simplex method to a game theory problem. Сборник [18],
348—358.
Д орфман, Самуэльсон (Samuelson, P. A., Solow R. M.)
[1] Linear programming and economic analysis, New York, McGraw-Hill, 1958, 527 pp.
Дрешер (D resher M.)
[1] Стратегические игры. Теория и приложения, Сов. Радио, 1964, 352*стр.
Дуаер, Галлер (Dwyer Р. S., Galler В.)
[1]* Применение метода приведенных матриц к решению общей транспортной
задачи. Сборник [3]*, 115—121.
570
Егер (Jaeger А.)
[1] Introduction to analytic geometry and linear algebra, New York, Holt, Rinehart
and Winston, 1961, 299 pp.
Зойтендейк (Zoutendijk G.)
[1] Методы возможных направлений, M., ИЛ, 1963, 128 стр.
[2] Maximizing a function in a convex region, J. Roy, Statist, Soc, Ser, B. 21, № 2
(1959), 338—355.
И p и (I r i M.)
[1] A new method of solving transportation network problems, J, Operat. Res> Soc.
Japan, 3, № 1, 2 (1960), 27—87.
Истерфилд (E asterfield T. E.)
[1] A combinatorial algorithm, J. London Math. Soc. 21, № 83 Part 3 (1946), 219—
226.
Йордан (Jordan W.)
[1] Handbuch der Vermessungskunde, Vol. 1, Stuttgart, J. B. Metclersche Buchhan-
dlung, 7-ое изд., 1920, 36 pp.; также в 5-ом изд., 1904, Vol. 1, 81—83, 100—
105.
Каваратани, Улман, Данциг (Kawar atani Т. К.,Ullman R.J.
D a n t z i g G. В.)
[1] Computing tetraethyllead requirements in the linear programming format, Ope-
rat. Res, 8, № 1 (1960), 24—29.
Калаб а, Хункоса (Kalaba R. E., Juncos a).
[1] Optimal design and utilization of communication networks, Manag. Sci. 3, № 1
(1956), 33—44.
К а н (Cahn A. S.)
[1] The warehouse problem, Bull. Amer. Math, Soc. 54, (1948), 1073 (abstract).
Канторович Л. В.
[1] Математические методы организации и планирования производства. Сборник
[6]*, 251—309.
12]* Об одном эффективном методе решения некоторых классов экстремальных
проблем, Докл. АН СССР 28, № 3 (1940), 212—215.
[3] О перемещении масс, Докл. АН СССР 37, № 3 (1942), 227—229.
[4]* О методах анализа некоторых экстремальных планово-производственных
задач, Докл. АН СССР 115, № 3 (1957), 441—444.
[5] Экономический расчет наилучшего использованья ресурсов, М., АН СССР,
1959, 343 стр.
Канторович Л. В., Г авур ин М. К.
[1] Применение математических методов в вопросах анализа грузопотоков. Сбор-
ник: «Проблемы повышения эффективности работы транспорта», М., Изд.
АН СССР, 1949, 110—138.
Канторович Л. В., г3 а л г а л л е р В. А.
[1]* Расчет рационального раскроя промышленных материалов, Лениздат 1951.
198 стр.
Капланский (Kaplansky I.)
[1] A contribution to von Neumann’s theory of games, Ann, Math, 46, № 3 (1945),
474—479.
К a p л и н (К a r 1 i n S.)
[1] Математические методы в теории игр, программировании и экономике, М.,
«Мир», 1964, 838 стр.
Келли (Kelley J. Е.)
[1] The cutting plane method for solving convex programs, J. Soc. Industr, Appl.
Math. 8, № 4 (1960), 703—712.
[2] Critical-path planning and scheluling; mathematical basis, Operat. Res. 9, № 3
(1961), 296—320.
Кемени, Мирки л, Снелл, Томпсон (Kemeny J. G., Mirkil H.,
Snell J. С., T h omp.s on G. L.)
[1] Finite mathematical structures, New Jersey, Prentice-Hall, 1959, 487 pp.
Кемени, Снелл, Томпсон
[1] Введение в конечную математику, М., ИЛ, 1963, 486 стр.
Кендалл (Kendall D.)
[1] On definite doubly-stochastic matrices and Birkhoff’s problem III, J. London
Math, Soc. 35, Part 1, № 137 (1960) 81-84.
571
Кёниг (К 6ni g D.)
[1] Theorie der endlichen und unendlichen Graphen, Leipzig, Akad. Verl., 1936;
перепечатка: New York, Chelsea Publ. Co. 1950, 258 pp.
Кларк, Симпсон (Clarke G. В., Simpson LG.)
[1] A theoretical approach to the profit maximization problems in farm management,
J. Agric. Econ., Univ, of Leeds, England 13, № 3 (1959), 150—164.
Корнфилд, Эванс, Хоффенберг (Cornfield J., E v an s W. D.,
Hoffenberg M.)
[1] Full employment pattern, 1950. Parts I and II, Monthly Labor Rev. 64, Feb-
ruary and March (1947), 163—190, 420—432.
Корбут A. A.
[1]* Целочисленные задачи линейного программирования. Сборник «Экономико-
математические методы» вып. II (Методы оптимального планирования — транс-
портные задачи). М., «Наука», 1965 г. 141—186.
Крамер (Cramer Н.)
. [1] The elements of probability theory and some of its applications, New York,
Wiley, 1955, 281 pp.
Краскал (Kruskal J. B., Jr.)
[1] On the shortest spanning subtree of a graph and the traveling salesman problem,
Proc. Amer. Math. Soc. 7, № 1 (1956), 48—50.
Кун (Kuhn H. W.)
[1] Венгерский метод решения задачи о назначениях. Сборник [3]*, 35—52.
[2] Solvability and consistensy for linear equations and inequalities, Amer. Math.
Monthly 63, № 4 (1956), 217—232.
[3] A note on Prager’s transportation problem. J. Math. Phys. 36, № 2 (1957), 107—111.
Кун, Таккер (Tucker A. W.)
L [1] Non-linear programming. Сборник [22]*, 481—492; Econometrica 19, № 1 (1951),
50—51 (abstract).
[2] Games, theory of. Encyclopaedia Britannica 10, 1958, 5—10.
[3] Библиография по линейным неравенствам и смежным вопросам. Сборник [1],
421—458.
[4] John von Neumann’s work in the theory of games and mathematical economics,
Bull. Amer. Math. Soc. 64, № 3, Part 2, (1958), 100—122.
Кунц (Kunz K. S.)
[1] Numerical analysis, New York, McGraw-Hill, 1957.
Купманс (К о о p m a n s T. C.)
[1] Optimum utilization of the transportation system, Econometrica 17, (1949).
[2] Analysis of production as an efficient combination of activities. Сборник [18],
33—97.
[3] Uses of prices. Proceedings of the conference on operations research in production
and inventory control, Cleveland, Ohio, Case Institute of Technology, 1954, 90—96.
Купманс, Рейтер (Reiter S.)
[1] A model of transportation. Сборник [18], 222—259.
Курант, Гильберт (Curant R., Hilbert D.).
[1] Методы математической физики, T. 1, М.— Л., Гос. изд. техн.- теорет. лит.,
1951.
Ла Валле (La Vallee R. S.)
[1] The application of linear programming to the problem of scheduling traffic sig-
nals, J. Operat. Res. Soc. Amer. 3, № 4 (1955), 562 (abstract).
Ламбер (Lambert F.)
[1] Programmes en nombres entiers et programmes mixtes, Metra 1, № 1 (1962),
93—112.
Ле Гарф, Мальгранж (Le Garff, Mai grange)
[1]* Resolution des programmes lineaires a valeurs entieres par une methode booleien-
ne «compacte». Сборник [14]*, 695— 704.
Лезурн (Lesourne J.)
[1] Technique economique gestion industrielle, 2nd. ed. Paris, Dunod, 1960, 408—476.
Лемке (Lemke С. E.)
[1] Двойственный метод решения задачи линейного программирования. Сборник
[3]*, 55—70.
572
Леонтьев (Leontief W. W.)
[1] The structure of american economy, 1919—1939, New York, Oxford Univ.
Press, 1951.
[2] Исследования структуры американской экономики, Теоретический и эмпири-
ческий анализ по схеме затраты — выпуск, М., Госстатиздат, 1958, 640 стр.
Лурье А. Л.
[1]* Алгоритм решения распределительной задачи. Сборник [6]*, 200—224.
[2]* Применение метода условно-оптимальных планов к сетевой транспортной
задаче. Сборник [7]*, 439—456.
Льюис (Lewis R. Е.)
[1] Top managenwnMooks at linear programming and inventory management. Сбор-
Льюис, Райфа (Luce R. D., R a i f f a H.)
[1] Игры и решения, M., ИЛ, 1961, 642 стр.
Лэнд, Дойг (Land А. Н., D о i g A. G.)
[1] An automatic method of solving discrete programming problems, Econometrica
28, № 3 (1960), 497—520.
Маданский (Madansky A.)
[1] Some results and problems in stochastic linear programming, The RAND Corpora-
tion, Paper P-1596, 1959.
[2] Inequalities for stochastic linear programming problems, Manag. Sci. 6, № 2
(I960), 197—204.
[3] Methods of solution of linear programs under uncertainty, Operat. Res. 10, № 4
(1962), 463-471.
[4]* Linear programming under uncertainty. Сборник [13]*, 103—110.
Мак-Доналд (McDonald J.)
[1] Strategy in poker, business and war, New York, Norton, 1950.
Мак-Кинси (McKinsey J. С. C.)
[1] Введение в теорию игр, М., Физматгиз, 1960, 420 стр.
Манн (М a n n е A. S.)
[1] Scheduling of petroleum refinery operations, Cambridge (Mass.), Harvard Univ.
Press, 1956, 185 pp.
[2] An application of linear programming to the procurement of transport aircraft,
Manag. Sci. 2, № 2 (1956), 190—191 (abstract).
Манкрес (Munkres J.)
[1] Алгоритмы решения задачи выбора и транспортной задачи. Сборник [3]*,
73—79.
Марковиц (Markowitz Н. М.)
[1] Portfolio selection, J. of Finance 7, № 1 (1952), 77—91..
[2] The nature and applications of process analysis, The RAND Corporation, Research
Memorandum RM-1254, 1954.
[3] Concepts and computing procedures for certain Хц programming problems.
Сборник [9], 509-565. •
[4] The optimization of a quadratic function subject to linear constraints, Naval
Res. Logist. Quart. 3, № 2 (1956), 111-—113.
[5] Portfolio selection: efficient diversification of investments, New York, Wiley,
1959, 344 pp.
Марковиц, Манн (Manne A. S.)
[1] On the solution of discrete programming problems, Econometrica 25, № 1 (1957),
84—110.
Маркус (Marcus M.)
[1] Some properties of doubly stochastic matrices, Amer. Math. Monthly 67, № 3
(1960), 215-221.
Мартин (Martin G.)
[1]* An accelerated Euclidean algorithm for integer linear programming. Сборник
[13]*, 311-318.
Массе (Masse P.)
[1] Les reserves et la regulation de 1’avenir dans la vie economique, Vol. I, Avenir
determine, Vol. II, Avenir aleatoire, Paris, Librairie scientifique, Hermann, 1946.
Массе, Жибра (Gibrat R.)
[1] Applications of linear programming to investments in the electric power industry,
Manag. Sci. 3, № 1 (1957), 149—166.
573
Мейнард (Maynard Н. В.)
[1] Putting new management tools to work. Сборник [24]*.
Миллер (Miller С. E.)
[1] The simplex method for local separable programming. Сборник [13]*, 89—100.
Миллер, Таккер, Землин (Tucker A. W., Ze ml in R. A.)
[1] Integer programming formulation of traveling salesman problems, J. Assoc.
Comput. Machinery 7, № 4 (1960), 326—329.
Миле (Mills H. D.)
[1] Маргинальные значения матричных игр и задач линейного программирования.
Сборник [1], 287-297.
Минковский (Minkowski Н.)
[1] Geometric der Zahlen, Leipzig, Berlin, В. G. Teubner, 1910, 256 p.; New York,
Chelsea Publ. Co, 1953.
Монро (Monro A. E.)
[1] Early economic thought; selections from economic literature prior to Adam Smith,.
Cambridge (Mass.), Harvard Univ. Press, 1924, 400 pp.
Моргенштерн (Morgenstern O.)
[1] The theory of games, Sci. American 180, № 5 (1949), 22—25.
Морин (Morin G.)
[1] More effective production planning with linear programming. Сборник [24]*, F.
M о ц к и н (M о t z k i n T. S.)
[1] Beitrage zur Theorie der linearen Ungleichungen, Jerusalem, Inaugural Dis-
sertation, 1936.
[2] The multi-index transportation problem, Bull. Amer. Math. Soc. 58, № 4 (1952),
494 (abstract.)
[3] The assigument problem, Proceedings of the Sixth Symposium in Applied Mathe-
matics, New York, McGraw Hill Book, 1956, 109—125.
Моцкин, Райфа, Томпсон, Тролл (Raiffa Н., Thompson G. L.
Thrall R. M.)
[1] Метод двойного описания. Сборник [2]*, 81—109.
Моцкин, Шёнберг (Schoenberg I. J.)
[1] The relaxation method for linear inequalities, Canad. J. Math. 6, № 3 (1954),
393-404.
M у p (Moore E. F.)
[1] The shortest path through a maze. Proceedings of International Symposium on
Theory Switch. (April 1957). Part 2, Cambridge, Mass., Harvard Univ. Press,
1959, 285—292..
Натрелла (Natrella J. V.)
[1] New applications of linear programming. Computers and Automat, № 11 (1955),
22.
Нелсон (Nelson R. R.)
[1] Degeneracy in linear programming: a simple geometric interpretation, Rev.
Econ. and Statist. 39, № 4 (1957), 402—407.
Ньюман (Newman P.)
[1] Some calculations on least-cost diets using the simplex-method, Bulletin, Oxford
Univ. Institute of Statistics, Oxford, England 17, (1955), 303—320.
Нейман (Neyman J.)
[1] First course in probability and statistics, Vol. I, New York, Holt, 1950, 350 pp.
Нейман, Пирсон (Pearson E. S.)
[1] Contributions to the theory of testing statistical hypothesis, Statist. Res. Mem.,.
Parts I—II, 1936, 1938.
Норман (Norman R. Z.)
[1 ] On the convex polyhedra of the symmetric traveling salesman problem, Bull. Amer.
Math. Soc. 61, № 6 (1955), 559 (abstract).
Орден (Orden A.)
[1] Application of the simplex method to a variety of matrix problems. Сборник [20].
[2] Survey of research on mathematical solutions of programming problems, Manag.
Sci. 1, № 2 (1955), 170—172.
[3] The transshipment problem, Manag. Sci. 2, № 3 (1956), 276—285.
574
Орчард-Хейс (Orchard-Hays W.)
[1] A composite simplex algorithm — II, The RAND Corporation, Research Memo-
randum RM-1275, 1954.
[2] RAND code for the simplex, The RAND Corporation,1! Research Memorandum
RM-1440, 1955.
[3] Evolution of linear programming computing techniques, Manag, Set, 4, № 2
(1958), j 183—190.
Орчард— Хейс, Кутлер, Джадд (Cutler L.,Judd H.)
[1] Manual for the RAND IBM code for linear programming on the 704, The RAND
Corporation, Paper P-842, 1956, 24—26.
Пайн (Pyne I. B.)
[1] Linear programming on an electronic analogue computer, AIEE Transaction
Annual 1956, также Reeves Instrument Corporation, Technical Article Reprint
№ 110.
П о л л, У о л т e p (Pauli A. E., W a 11 e r J. R.)
[1] The trim problem: an application of linear programming to the manufacture of
newsprint paper, Econometrica 23, № 3 (1955), 336 (abstract).
Прагер (Prager W.)
[1] On the caterer problem. Manag. Sci. 3, № 1 (1956), 15—23.
[2] A generalization of Hitchcock’s transportation problem, J. Math. Phys. 36, № 2
(1957), 99-106.
Раднер (Radner R.)
[11 The linear team: an example of linear programming under uncertainty. Сборник
[9], 381—396.
Райзер (Ryser H. J.)
[1] Matrices of zeros and ones, Bull. Amer. Math. Soc. 66, № 6 (1960), 442—464.
Райли, Гасс (Riley V., Gass S. I.)
[1] Linear programming and associated techniques, a comprehensive bibliography
on linear, nonlinear and dynamic programming. Baltimore, Johns Hopkins
* Press, 1958, 613 pp.
Райфа, Томпсон, Тролл (Raiffa H., Thompson G. L., Thrall
R. M.)
[1] An algorithm for the determination of all solutions of a two-person zero-sum game
with a finite number of strategies (Double description method). Сборник [2]*,
81—109, [20], 100-114.
Рейнфельд, Фогель (Reinfeld N. V., Vogel W.)
[1]* Математическое программирование. Методы решения производственных
и транспортных задач, М., ИЛ, 1960, 303 стр.
Рейтер (Reiter S.)
[1] Surrogates for uncertain decision problems: minimal information for decision
making, Econometrica 25, № 2 (1957), 339—345.
Рейш, Эйсгрубер (Reisch E., Eisgruber L.)
[1] Bibliography of linear programming and its application to agricultural economic
problems, mimeographed report. (Purdue Univ.), 1960, 30 pp.
Ричардсон (Richardson M.)
[1] jFundamentals of mathematics, New York, Macmillan, 1958.
Робинсон (Robinson J.)
[1] Итеративный метод решения игр. Сборник [2]*, 110—117.
Розен (Rosen J. В.)
[1] Gradient projection method for non-linear programming, Part I, Linear constraints,
J. Soc. Industr. Appl. Math. 8, № 1 (1960), 181—217. Part. II, Non-linear con-
straints. J. Soc. Industr. Appl. Math. 9, № 4 (1961), 514—532.
С а а т и (S a a t у T. L.)
[1] Математические методы исследования операций, М., Воениздат, 1963, 420 стр.
[2] The number of vertices of a polyhedron, Amer. Math. Monthly 65, № 5 (1955),
327-331.
Сазьени, Ясная, Фридман (SasieniM. W., Yaspan A., Friedman L.)
[1] Operations research: methods and problems, New York, Wiley, 1959, 316 pp.
Саймон (Simon H. A.)
[1] Dynamic programming under uncertainty with a quadratic criterion function,
Econometrica 24, № 1 (1956), 74—81.
575
Саймондс (Symonds G. H.)
[1] Linear programming: the solution of refinery problems, New York, Esso Standard
Oil Company, 1955.
[2] Mathematical programming as an aid to decision making, Advanced Manas. 20,
№ 5 (1955), 11-17.
Салвесон (Salveson M. E.)
[1] A computational technique for the fabrication scheduling problem, J. Industr.
Engng 13, № 1 (1962), 30—41.
Самуэлсон (Samuelson P. A.)
[1] Linear programming and economic theory. Сборник [9], 251—272.
Слэйтер (Slater M.)
[1] Lagrange multipliers revisited, The RAND Corporation, Research Memoran-
dum RM-676, 1951.
Смит (Smith L. W., Jr).
[1] Current status of the industrial use of linear programming, Manag. Sci. 2, № 2
(1956), 156—158.
Смит (Smith V. E.)
[1] Linear programming models for the determination of palatable human diets,
J. of Farm. Econ. 41, № 2 (1959), 272—283.
Солоу (Solow R. M.)
[1] On the structure of linear models, Econometrica 20, № 1 (1952), 29—46.
Стокс (Stokes R. M.)
[1] A geometric theory of solution of linear inequalities, Trans. Amer. Math. Soc.
33 (1931), 782—805.
Суонсон (Swanson E. R.)
[1] Integrating crop and livestock activities in farm management activity analysis,
J. of Farm. Econ. 37, № 5 (1955), 1249—1258.
[2] Solving minimum-cost feed mix problems, J. of Farm. Econ.Wl,№ 1 (1955),
135—139.
Таккер (Tucker A. W.)
[1] Linear programming and theory of games, Econometrica 18, № 2 (1950), 189.
[2] Analogues of Kirchoff’s laws, George Washington Univ. Logistics Papers 3, (1950), 4.
[3] Linear inequalities and convex polyhedral sets. Сборник [9], 569—602.
[4] Game theory and programming. Oklahoma, National Science Foundation, Summer
mathematics Institute Notes, Department of Mathematics. Stillwater, 1955.
[5] Двойственные системы однородных линейных соотношений. Сборник [1],
127—141.
[6] Linear and nonlinear programming, Operat. Res. 5, № 2 (1957), 244—257.
[7] On directed graphs and integer programs, IBM Mathematical Research Project,
Technical Report, Princeton, Princeton Univ. Press, 1960.
[8] A combinatorial equivalence of matrices. Сборник [11], 129—140.
[9] Solving a matrix game by linear programming, IBM J. Res. Develop. 4, № 5
(1960), 507-517.
[10]* Simplex method and theory. Сборник [10]*, 213—231.
[11]* Combinatorial theory underlying linear programs. Сборник [13]*, 1—16.
Талакко (Talacko J. V.)
[1] On stochastic linear inequalities, Trabajos estadist. 10, № 2 (1959), 89—112.
Тейл (Theil H.)
[1] A note on certainty equivalence in dynamic planning, Econometrica, 25, № 2
(1957), 346—349.
Тинтнер (Tintner G.)
[1] Stochastic linear programming with applications to agricultural economics.
Сборник [9], 197—228.
Томпкинс (Tompkins С. B.)
[1] Projection methods in calculation. Сборник [9], 425—448.
[2] Some methods of computational attack on programming problems, other than
the simplex method, Naval Res. Logist. Quart. № 1 (1957), 95—96.
Тролл (Thrall R. M.)
[1] Some results in non-linear programming. Сборник [9], 471—493.
Тролл, Торнхейм (Tornheim L.)
; [1] Vector spaces and matrices, New York, Wiley, 1957, 318 pp.
T у т т e (T u t t e W. T.)
[1] On Hamiltonian circuits, J. London Math. Soc. 21, Part 2, № 82 (1946), 98—101.
576
Уайт, Джонсон, Данциг (White W. В.,Johnson S. М., Danzig G. В.)
[1] Chemical equilibrium in complex mixtures, J. Chem. Phys. 28, № 5 (1958),
751—755. См. также Данциг, Джонсон, Уайт, A linear programming
approach to the chemical equilibrium problem. Manag. Sci. 5, № 1 (1958), 38—43.
Уд зав a (Uzawa H.) .
[1] Теорема Куна — Таккера о вогнутом программировании. Сборник [21], 57—64.
[2] Market mechanisms and mathematical programming, Econometrica 28, № 4 (1960),
872—881.
У о (W a u g h F. V.)
[1] The minimum-cost dairy feed, J. of Farm. Econ, 33, № 3 (1951), 299—310.
[2] Alligations, forerunner of linear programming, J. of Farm. Econ. 40. № 1
(1958), 89-101.
Фаркаш (Farkas J.)
[1] Ober die Theorie der einfachen Ungleichungen, J. Reineund angew. Math. 124,
№ 1 (1902), 1-24.
Фаулкс (Foulkes J.)
[1] Linear programming and structural design. Сборник [9J, 177—184.
Фейбиан (Fabian T.)
[1] Process type analysis of the iron and steel industry, Part IV — Programming open
hearth steel production. Discussion Paper № 46, Management Sciences Research
Project, California, Univ, of California, 1954, 12 pp.
[2] Process analysis of the iron and steel industry: a model, Econometrica 23, № 3 (1955),
347—348 (abstract).
[3] A linear programming model of integrated iron and steel production, Manag. Sci,
b, № 4 (1958), 415-449.
Феллер (Feller W.)
[1] Введение в теорию вероятностей и ее приложения. М., Мир, 1964, 498 стр.
Фенхель (Fenchel W.)
[1] Convex cones, sets and functions, Lecture notes, Dept, of Math., Princeton Univ.
1953, 74 p.
Фергюсон, Данциг (Ferguson A. R., Dantzig G. B.)
[1] Notes on linear pro^amming. Part XVI — The problem of routing aircraft —
a mathematical solution, Aeronaut. Engng. Rev. f4, № 4 (1955), 51—55.
[2] The allocation of aircraft to routes — an example of linear programming under
uncertain demand, Manag. Sci. 3, № 1 (1956), 45—73.
Фергюсон, Сарджент (Sargent L. F.)
[1]* Линейное программирование, методы и применение, М., Госстатиздат, 1962,
361, стр.
Фипс (Phipps С. G.)
[1] Maxima and minima under restraint, Amer. Math. Monthly 59, № 4 (1952), 230—
235.
Фишер, Шрубен (Fisher W. D., Schruben L. W.)
[1] Linear programming applied to feed-mixing under different price conditions,
J. Farm. Econ. 35, № 4 (1953), 471—483.
Флад (Flood M. M.)
[1] Проблема распределения Хичкока. Сборник [3]*, 80—94.
[2] 4The traveling salesman problem, Operat. Res. 4, Xs 1 (1956), 61—75.
[3] An alternative proof of a theorem of Konig as an algorithm for the Hitchcock
distribution problem. Сборник [11], 299—307.
Ф о к c (F о x L.)
[1] Practical solution of linear equations and inversion of matrices, in Olga
Taussky (ed.). Contributions to the solution of systems of linear equations and the
determination of eigenvalues, National Bureau of Standards. Appl. Math. Series
39, Washington, 1954, 1—54.
Фон Нейман (von Neumann J.)
[1] К теории стратегических игр. Сборник [2]*, 173—204.
[2] Ober un okonomisches Gleichungsystem und ein Verallgemeinerung des Brouwer-
schen Fixpunktsatzes, Ergebnisse eines Mathematischen Kolloquiums № 8 (1937),
73—83. Английский перевод: A model of general economic equilibrium, Rev.
Econ. Studies 13, № 1 (1945-1946), 1—9.
[3] On a maximization problem (manuscript), Institute for Advanced Study, Prince-
ton, 1947.
т/г 37 Дж. Данциг
[4] A numerical method for determination of the value and best strategies of a zero*
zum, two-person game. Institute for Advanced Study, Princeton, 1948.
[5] Об одной нулевой игре двух лиц, эквивалентной задаче оптимального назначе-
ния. Сборник [2]*, 145—155.
[6] A numerical method to determine optimum strategy, Naval Res. Legist. Quart.
1, № 2 (1954), 109-115.
Фон Нейман, Моргенштерн (Morgenstern О.)
[1J Theory of games and economic behavior, 3d ed., Princeton, Princeton Univ.
Press, 1953.
Ф о p д, Ф у л к e p с о н (Ford L. R., Fulkerson D. R.)
[1] Maximal flow through a network, Canad. J. Math. 8, № 3 (1956), 399—404.
[2] A simple algorithm for finding maximal network flows and an application to the
Hitchcock problem, Canad. J. Math. 9, № 2 (1957), 210—218.
[3] Решение транспортной задачи. Сборник [3]*, 61—72.
[4] Dynamic network flow, The RAND Corporation, Paper P-967, 1956, 29 p.
[5] Алгоритм одновременного решения прямой и двойственной задачи для пробле-
мы Хичкока с ограниченными пропускными способностями. Сборник [3]*,
95—102.
[6] Constructing maximal dynamic flows from static flows, Operat. Res. 6, № 3
(1958), 419—433.
[7] Suggested computation for maximal multi-commodity network flows, Manag. Sci.
5, № 1 (1958), 97—101.
[8] Flows in networks, Princeton, Princeton Univ. Press, 1962, 208 pp. Готовится
русский перевод.
Форсайт (Forsythe G. Е.)
[1] Solving linear algebraic equations can be interesting, Bull. Amer. Math. Soc.
59, № 4 (1953), 229—329.
[2] Computing constrained minima with Lagrange multipliers, J. Soc. Industr.
Appl. Math. 3, № 4 (1955), 173—178.
Фреййд (Freund R. J.)
[1] The introduction of risk into a programming model, Econometrica 24, № 3 (1956),
253—263.
Фриш (Frisch R.)
[1] Principles of linear programming with particular reference to the double gra-
dient form of the logarithmic potential method. Memorandum, Univ. Socialoko-
nomiske Institut, Oslo, Univ. Institute of Economics, 1954, 219 pp.
[2] Linear dependencies and a mechanized form of the multiplex method for linear
programming. Memorandum, Univ. Socialokonomiske Institut, Oslo, Univ.
Institute of Economics, 1957.
Фулкерсон (Fulkerson D. R.)
[1] Note on Dilworth’s decomposition theorem for partially ordered sets, Proc.
Amer. Math. Soc. 7, № 4 (1956), 701 — 702.
[2] A network-flow feasibility theorem and combinatorial applications, Canad. J.
Math. 11, № 3 (1959), 440—451.
[3] Increasing the capacity of a network: the parametric budget problem, Manag.
Sci. 5, № 4 (1959), 472—483.
[4] An out-of-kilter method for minimal cost flow problems, J. Soc. Industr. Appl.
Math. 9, № 1 (1961), 18—27.
[5] Zero-one matrices with zero trace, Pacij. J. Math. 10, № 3 (1960),
831—836.
[6] A network flow computation for project cost curves, Manag. Sci. 7, № 2 (1961),
167—178.
Фулкерсон, Данциг (D antzig G. B.)
[1] Computations of maximal flows in networks, Naval Res. Logist. Quart. 2, № 4
(1955), 277—283.
ф у p ь e (Fourier J. B. J.)
[1] Solution d’une question particuliere du calcul des inegalites, 1826, см. также
«Histoire de Г Academies, 1823, 1824, Oeuvres II, 317—328.
X а л м о ш, Воан (H a 1 m о s P. R., Vaughon H.)
[1J The marriage problem, Amer. J. Math. 72, № 1 (1950), 214—215.
Хартли, Лофтсгард (Hartley Й. О., Loftsgard L. D.)
[1] Linear programming with variable restraints, J. Sci, Iowa, State Collego, Ames,
Iowa 33, № 2 (1958), 161—172.
578
Хаутэккер (Houthakker Н. S.)
[1] On the numerical solution of the transportation problem, J. Operat. Res. Soc.
Amer. 3, № 2 (1955), 210—214.
[2] The capacity method of quadratic programming, Econometrica 28, № 1 (1960),
62-87.
Хейман (Heyman J.)
[1] Plastic design of beams and plane frames for minimum material consumption,
Quart. Appl. Math. 8, № 4 (1951), 373—381.
Хеллер (Heller I.)
[1] On the traveling salesman problem. Сборник [9], 643—665.
[2] Constraint matrices of transportation type problems, Naval Res. Logist. Quart.
№ 1 (1957), 73—76.
[3]* On unimodular sets of vectors. Сборник [13]*, 39—54.
Хеллер, Томпкинс (Tompkins С. В.)
[1] Обобщение одной теоремы Данцига. Сборник [1], 348—354.
Хендерсон, Шлейфер (Н end enson A., Schlaifer R.)
[1] Mathematical programming, Harvard Business Rev. 32, (1954), 73—100.
Хендерсон (Henderson J. M.)
[1] A short-run model for the coal industry. Rev. Econ. and Statist. 37, № 4 (1955),
336—346.
Хиди, К эндл ep (Heady E. О., Candler W.)
[1] Linear programming methods, Iowa, Iowa State College Press, Ames, 1958,
597 pp.
Хикс (Hicks J. R.)
[1] Linear theory, Econ. J. 70, № 280 (1960), 671-709.
Хилдрет (Hildreth C. G.)
[1] Economic implications of some cotton fertilizer experiments, Econometrica 23, № 1
(1955), 88-98.
Хилдрет, Рейтер (Reiter S.)
[1] On the choice of crop rotation plan. Сборник [18], 177—188.
Хичкок (Hitchcock F.L.)
[1] The distribution of a product from several sources to numerous localities, J. Math.
Phys. 20, № 2 (1941), 224—230.
Хэдли (Hadley G.)
[1] Linear algebra, London, Reading (Mass.) Addison Wesley, 1961, 269 pp.
[2] Linear programming, London, Reading (Mass.), Addison Wesley, 1961, 517 pp.
Ху, Прагер (Hu T. C., Prager W.)
[1] Network analysis of production smoothing, Division of Applied Mathematics,
Brown Univ., Providence, Rhode Island, 1958.
Циммерн (Zimmern B.)
[1] Resolution des programmes lineaires de transport par la methode de separation
en etoile, Rev. rech. operat. 1, № 3 (1957), 117—132.
Чарнс (Charnes A.)
[1 ^Optimality and degeneracy in linear programming. Econometrica 20, № 2 (1952),
Чарнс, Гринберг (Greenberg H. J.)
[1] Plastic collapse and linear programming—preliminary report, Bull. Amer. Math.
Soc. 57, № 6 (1951), 480 (abstract).
Чарнс, Купер (Cooper W. W.)
[1]iGeneralizations of the warehousing model, Operat. Res. Quart. 6, № 2 (1955),
[2] Management models and industrial applications in linear programming, Manag.
Sci. 4, № 1 (1957), 38-91.
[3] Chance-constrained programming, Manag. Sci. 6, № 1 (1959), 73—79.
[4] Some uses of model prototypes in an operations research study, Graduate school
of industrial administration, Reprint № 35, Carnegie Institute of Technology,
Pittsburgh. Pennsylvania, 1959.
[5] Management models and industrial applications of linear programming, Vol.
I—II, New York, Wiley, 1961.
Чарнс, Купер, Меллон (Mellon В.)
[1] Blending aviation gasolines—a study in programming of interdependent activities
in an integrated oil company, Econometrica 20, № 2 (1952), 135—159.
579 07*
Ч а р н с, Купер, Хендерсон (Henderson А.)
[1] Введение в линейное программирование, М., Изд. МГЭИ (1960).
Чарнс, Лемке (Lemke С. Е.)
[1] Minimization of non-linear separable convex functionals, Naval Res, Logist.
Quart. 1, № 4 (1954), 301—312.
Черчман, Аккофф, A p н о ф ф (Churchman C. W., A с k о f f R. L.,
A r n о f f E. L.)
[1] Introduction to operations research, New York, Wiley, 1957, 645 pp.
Щепли (S h a p 1 e у L. S.)
[1] On network flow functions. Naval Res. Logist. Quart. 8, № 2 (1961), 151—158.
Шепли, Сноу (Snow R. N.)
[1] Basic solutions of discrete games. Сборник [15], 27—35. См. также
сборник [2]*.
Шерман, Кемпбел, Л энфорд (Sherman Н. С., Campbell H.L.,
Lanford С. S.)
[1] Experiments on the relation of nutrition to the composition of the body and the
length of life, Proc. Nat. Acad, of Sci. U.S.A. 25 (1939), 16—20.
Шетти (Shetty С. M.)
[1] A solution to the transportation problem with non-linear costs, Operat. Res.
7, № 5 (1959), 571—580.
Шт игл ep (Stigler G. J.)
[1] The cost of subsistence, J. Farm. Econ. 27, № 2 (1945), 303—314.
Штимке (Stiemke E.)
[1] Ober positive Losungen homogener linearer Gleichungen, Math. Ann. 76 (1915),
340-342.
Штиф ель (Stiefel E.)
[1] Note on Jordan elimination, linear programming and Tchebycheff approximation,
Numer. Math. 2 и 4, № 1 (1960), 1—17.
Шубик (Shubik M.)
[1] Strategy and market structure; competition, oligopoly, and the theory of games,
New York, Wiley, 1959.
Эблоу, Брайгэм (A blow C.M., Brigham G.)
[1] An analog solution of programming problems, Operat. Res. 4, № 3 (1955), 388—
392.
Эгервари (Egervary E.)
[1] Matrixok kombinatorius tulajfonsagairol, Mat. es. Fiz. Lapok, № 38 (1931), 16—28.
Эдмондсон (Edmondson J. H.)
[1] Proof of the existence theorem of an epsilon transformation, Class exercise dated
March 28, 1951, for Department of Agriculture Graduate School course in linear
programming given by G. B. Dantzig.
Эйземан (Eisemann K.)
[1] The trim problem, Manag. Sci. 3, Ks 3 (1957), 279—284.
Эйземан, Лурье (Lourie J. R.)
[1] The machine loading problem. IBM 704 Program, IBML. 1, International Business
Machines Corporation, IBM Applications Library, Vew York, 1959.
Эль-Маграби (El-Maghraby S. E.)
[1] An approach to linear programming under uncertainty, Operat. Res. 7, № 2 (1959),
208—216.
[2] Allocation under uncertainty when the demand has continuous d. f., Manag.
Sci. 6, № 3 (1961), 270.
Эрроу (Arrow K. J.)
[1] Alternative proof of the substitution theorem for Leontief models in the general
case. Сборник [18], гл. IX.
Эрроу, Гаррис, Маршак (Harris Т. Е., Mars ch a k J.)
[1] Optimal inventory policy, Econometrica 19, № 3 (1951), 250—272.
Эрроу, Гурвиц, Удзава (Hurwicz L., Uzawa H.)
[1] Исследования по линейному и нелинейному программированию, М., ИЛ,
1962, 334 стр.
580
Эрроу, Карлин, Скарф (Karlin S., Scarf Н.)
[1] Studies in the mathematical theory of inventory and production, Stanford, Cali-
fornia, Stanford Univ. Press, 1958, 340 pp.
Сборники
11] Линейные неравенства и смежные вопросы. Перевод сборника статей под ред.
Куна, Таккера (Kuhn Н. W., Tucker A. W., eds). Linear Inequalities and Related
Systems, Annals of Mathematics study № 38 Princeton, Princeton Univ. Press,
1956, 322 pp. С приложением книги С. Вайда, Теория игр и линейное програм-
мирование, М., ИЛ, 1959, 470 стр.
[2]* Матричные игры (под ред. Н. Н. Воробьева), М., Физматгиз, 1961, 280 стр1
[3]* Методы и алгоритмы решения транспортной задачи (Сборник статей под ред.
В. С. Немчинова, Л. Е. Минца, Л. А. Серебровского). Вып. 1, М., Госстатиздат,
1963, 151 стр. J
[4]* Методы решения общей задачи линейного программирования (Сборник статей
под ред. В. С.Немчинова, Л. Е. Минца, Л. А. Серебровского). Вып. 2, М., Госстат-
издат, 1963, 86 стр.
[5]* Применение математики в экономических исследованиях (под ред. В. С. Немчи-
нова), М., Соцэкгиз, 1959, 486 стр.
[6]* Применение математики в экономических исследованиях, том 2 (под ред.
В. С. Немчинова), М., Соцэкгиз, 1961, 535 стр.
[7]* Проблемы оптимального планирования, проектирования и управления произ-
водством, М., Моск, ун-т, 1963, 547 стр.
[8] Вулф, ред. (Wolfe Ph., е d.)
The Rand Symposium on Mathematical Programming. The Rand Corporation,
Report R-351, March 16 — 20, 1959.
[9] Антосевич, ред. (Antociewicz H. A., e d.)
Linear programming, Proceedings of the Second Symposium (Vol. I—II). National
Bureau of Standards, U. S. Dept, of Commerce, Washington, January 27—29,1955.
[10]* Веллман, ред. (Bellman R., ed.)
Mathematical optimization techniques, The Univ, of California, Press, 1963.
[11] Веллман, Маршалл, ред. (Marshall H., eds.)
Proceedings of Simposia in Applied Mathematics, Vol. X, Combinatorial Analysis.
Amer. Math. Soc., Providence, Rhode Island, 1960.
[12] Боуман, Феттер, ред. (Bowman E. H., Fetter R. B., eds)
Analysis of industrial operations. Homewood (Ill.), Irwin, 1959, 485 pp.
[13]* Г p e й в з, В у л ф, ре д. (Graves R. L., W о 1 f е Ph., eds)
Recent advances in mathematical programming, New York, McGraw Hill, 1963,
347 pp.
[14]* Кревера, Морла, ред. (Kreweras G., Morl at G., eds)
Actes de la 36me conference internationale de recherche operationnelle, Oslo, 1963,
Paris, Dunod, 1964, 952 pp.
[15] К у н, T а к к e p, p e д. (K u h n H. W., Tucker A. W., eds)
Contributions to the theory of games, vol. I (Ann. of Math. Studies, №24), Princeton,
Princeton Univ. Press, 1950.
[16] Кун, Таккер, ред.
Contributions to the theory of games, vol. II (Ann. of Math.Studies, № 28), Prince-
ton, Princeton Univ. Press, 1953.
[17]Дрешер, Таккер, В у л ф, p e д. (Dresher М., Tucker A. W.,
Wol fe Ph., eds).
Contributions to the theory of games, vol. Ill (Ann. Math. Study № 39) Princeton,
Princeton UniV. Press, 1957, 448 pp. ‘
[18] К у п м а н с, p e д. (К о о p m a n s T. C., e d). *
Activity analysis of production and allocation. (Cowles Commission Monograph
№ 13), New York, Wiley, 1951, 404 pp.
[19] M оргенштерн, ред. (M orgenstern O., ed.)
Economic activity analysis, New York, Wiley, 1954, 554 pp.
552
(20] О р д е н, Голдстейн, ред. (Orden A., Goldstein L., eds)
Symposium on Linear Inequalities and Programming. Project SCOOP, № 10,
Planning Research Division, Director of Management Analysis Cervice, Comptrol-
ler, USAF, Washington, D.C., 1952.
(21] Э p p о у, К a p л и н, Сапе, ред. (Arrow K. J., Karlin S., S u p-
p e s P., e d s)
Mathematical methods in the social sciences. Proceedings of the First Stanford
Symposium, Stanford Univ. Press, 1960, 365 pp.
[22]* Нейман, ред. (Neyman J. e d.)
Proceedings of the Second Berkeley Symposium on Mathematical Statistics and
Probability, Berkeley and Los Angeles, Univ, of California Press, 1951.
[23]* H ейман, ред. (Neyman J., e d.)
Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and
Probability, vol. I, Berkeley, Univ, of California Press, 1961.
[24]* Proceedings of the Linear Programming and Inventory Management Seminar,
Methods Engineering council, Pittsburgh, Pennsylvania, 1955.
ЛИТЕРАТУРА К ОТДЕЛЬНЫМ ГЛАВАМ
ЛИТЕРАТУРА К ГЛ. 1
Динамическое программирование, управление запасами
Беллман [1], [2] Массе [1]
Беллман, Гликсберг, Гросс [1] Эрроу, Гаррис, Маршак [1]
Вальд [3] Эрроу, Карлин, Скарф [1]
Дворецкий, Кифер, Вольфовиц [1]
Автоматизация
Белтер [1] Данциг [13]
Линейное программирование
Вуд, Данциг (Ц Герман, Мэджи [1] Данциг [1], [2] фон Нейман [2] Штиглер [1] Сборник [18]
ЛИТЕРАТУРА К ГЛ. 2
Экономические модели
Аллен [1] Купманс [2] Баумоль [1], [2] Леонтьев [1], [2] Бекман [1] Самуэльсон [1] Вальд [1], [2] фон Нейман [2] Вальрас [1] Фриш [1] Гейл [1] Хикс [1] Дорфман [1] Эрроу [1] Дорфман, Самуэльсон, Солоу [1] Эрроу, Гурвиц, Удзава [1] Корнфилд, Эванс, Хоффенберг [1] Сборники [18], [21]
Деловые и промышленные применения
Гарвин, Крандалл, Джон, Спелман Голдстейн [1]
II] Данциг [131
Гейнен [1] Джэксон [1]
582
Дойг, Белз [1] Саймондс [1]
Канторович [1] Салвесон [1]
Лезурн [1] Смит [1]
Льюис [1] Фейбиан [1]—[3]
Лэнд, Дойг [1] Фергюсон, Данциг [1], [2]
Манн [1], [2] Фишер, Шрубен [1]
Марковиц [2] Хендерсон [1]
Массе, Жибра [1] Хендерсон, Шлейфер [1]
Мейнард [1] Чарнс, Купер [2], [5]
Морин [1] Чарнс, Купер, Меллон [1]
Полл, Уолтер [1] Эйземан [1]
Вуд, Гейслер [1] Джейкобс [1] Военные приложения Натрелла [1]
Линейное программирование, теория игр, анализ производственных
процессов
Борель [1], [2] Вайда [1], [2] Билль [1] Гарвин [1] Гейл [11 Гофман [3] Данциг [1], [2] Данциг, Вальд [1] Йордан [1] Карлин [1] Кун, Таккер [4] Льюс, Райфа [1] Моцкин [1] Орден [2] Таккер [Ц, [4] фон Нейман, Моргенштерн [1] Хэдли [21 Чарнс, Купер [5] Чарнс, Купер, Хендерсон [11 Штифель [1] Сборники [8а], [9], [18], [20] Бесконечные программы
Данциг, Вальд [1] Даффин [1] Нейман, Пирсон [1] Исследование операций
Важоньи [1] Саати [1 ] Чарнс, Купер [4] Черчман, Аккофф, Арнофф [1]
Сазьени, Яспан, Фридман [11 Сборник [12]
Инженерное проектирование, физическая химия
Дорн, Гринберг [1] Кал аба, Хункоса [11 Ла Валле [1] Уайт, Джонсон, Данциг Фаулкс [1] Хейман [11 Чарнс, Гринберг [1] [11 Сельское хозяйство
Кларк, Симпсон [1] Рейш, Эйсгрубер [1] Суонсон [ 1 ] Тинтнер [1] Уо [1] Хиди, Кэндлер [1] Хилдрет [1] Хилдрет, Рейтер [1] Теория транспортных сетей
Берж [1] Биркгоф [1] Гофман [3] Данциг [4] Кун [1], [3] Форд, Фулкерсон [8]
583
Выпуклое программирование
Баранкин, Дорфман [1] Бил [3], [5], [6] Вулф [2]-[4], Гб] Данциг [21] Дорфман [1] Кун, Таккер [1] Марковиц [1], [4] Розен [1] Хаутэккер [2] Чар нс, Лемке [1] Сборник [8]
Целочисленное программирование
Гомори [1] —[4] Данциг [14], [16], [20] Данциг, Фулкерсон, Джонсон [1], [2]
Программирование в условиях неопределенности
Данциг, Маданский [1] Маданский [1] — [4]
Математические истоки и дальнейшие разработки
Бил [1], [2] Бодевиг [1] Браун [1] Браун, Купманс [1] Вайда [1], [2] Валле-Пуссен [1] Вейль [1] Билль [1] Гаусс [1] Гейл, Кун, Таккер [2] Голдман, Таккер [2] Гордая [1] Гофман [1], [3] Кун, Таккер [1] —[4] Кунц [1] Лемке [1] Минковский [1] Моцкин [1] Моцкин, Райфа, Томпсон, Тролл [1] Моцкин, Шенберг [1] Нейман, Пирсон [1] Орчард-Хейс [1]—[3] Пайн [1] Стокс [1] Таккер [1], [3], [5], [6] Томпкинс [1], [2]
Гофман, Манное, Соколовский, Виг- Фаркаш [1]
ман [1] Дайне, Мак-Кой [1] Данциг [3] — [5] Данциг, Вальд [1] Даффин [1] Йордан [1] Канторович [1]—[5] Канторович, Гавурин [1] фон Нейман [4], [6] фон Нейман, Моргенштерн [1] Фриш [1], [2] Фурье [1] Штиглер [1] Штимке [1] Эблоу, Брайгэм [1] ЛИТЕРАТУРА К ГЛ. 4 Общие сведения
Аллендорфер, Окли [1] Биркгоф, Мак-Лейн [1] Егер [1] Кемени, Снелл,, Томпсон [1] Тролл, Торнхейм [1] Хэдли [1]
Кемени, Мирки л, Снелл, Томпсон [1] Штифель [1]
(Гаусс [1] Гейл [11 Гуд [1] Йордан [1] Системы уравнений Кун [2] Таккер [5], [8], [10], [И] Фокс [1] Форсайт [1]
Гейл [11, [2], [4] Кун [2] Системы неравенств Моцкин [1] Фурье [1] 584
ЛИТЕРАТУРА К ГЛ. 5
Бил [1]
Важоньи [2]
Вайда [1], [21, [4]
Гарвин [1]
Гасс [11
Гофман [1]
Симплекс-метод
Данциг [51
Орден [2]
Орчард-Хейс [3]
Орчард-Хейс, Кутлер, Джадд [1]
Таккер [41
Хэдли [2]
Решение задач линейного программирования методами,
отличными от симплекс-метода
Агмон [1] Орден [21
Браун, Купманс [1] Пайн [11
Гофман, Манное, Соколовский, Вигман Розен [1]
[1] Томпкинс [1], [2]
Канторович [1] Фриш [2]
Моцкин, Райфа, Томпсон, Тролл [1] Штифель [1]
Моцкин, Шёнберг [1] Эблоу, Брайгэм [11
ЛИТЕРАТУРА К ГЛ. 6
Обоснование симплекс-метода
Данциг [18]
Данциг, Орден, Вулф [1]
Доказательство теоремы двойственности и теорем типа
теоремы двойственности
Вайда [4]
Гейл [1], [41
Гейл, Кун, Таккер [31
Голдман [1]
Голдман, Таккер [1], [2]
Кун, Таккер [4]
Минковский [1]
Моцкиц [1]
Таккер [2], [4]—[61
Гуд [1]
Данциг, Вальд [1]
Данциг, Орден [1]
Жордан [1]
Карлин [1]
Фаркаш [1]
фон Нейман [3]
Штимке [1]
Штифель [1]
Множители Лагранжа
Джон [11
Дорн [1]
Кун, Таккер [1]
Курант, Гильберт [1]
Слейтер [Ц
Таккер [6]
Фипс [1]
Форсайт [2]
Сборник [1]
ЛИТЕРАТУРА К ГЛ. 7
Выпуклые множества и функции
Бекенбах [1]
Вейль [1]
Вулф [3]
Гаддум [1]
Гейл [2]
Герстенхабер [11
Голдман, Таккер [1]
Минковский [1]
Моцкин [1]
Саати [2]
Стокс [1]
Таккер [3]
Фенхель [1]
(См. также гл. 4)
38 Дж Данциг
585
ЛИТЕРАТУРА К ГЛ. 8
Биркгоф, Маклейн [1]
Бодевиг [1]
Гейл [4]
Кемени, Миркил, Снелл, Томпсон
Кемени, Снелл, Томпсон [1]
Кунц [1]
Орден [1]
Таккер [1], [8], [9]
[1] Тролл, Торнхейм [1]
Фокс [1]
ЛИТЕРАТУРА К ГЛ. 9
Гарвин [1] Гасс [1] Данциг, Орден, Вулф [1] Данциг, Орчард-Хейс [1] Орден [1], [2] Орчард-Хейс [2], [3] Хэдли [1] ЛИТЕРАТУРА К ГЛ. 10
Бил [2] Гофман [1] Данциг [4], [5], [18] Данциг, Орден, Вулф [1] Нелсон [1] Хэдли [2] Чарнс [1] Эдмондсон [ 1 ] ЛИТЕРАТУРА К ГЛ. 11
Бил [1] Гантер [1] Гасс, Саати [1] Данциг [6], [7] Данциг, Форд, Фулкерсон Кун [11 Лемке [1] Орден [1], [2] Орчард-Хейс [1], [3] Орчард-Хейс, Кутлер, Джадд [1] [1] Эгервари [1] ЛИТЕРАТУРА К ГЛ. 12
Аллен [1] Баумоль [1], [2] Бекман [1] Боулдинг, Спиви [ 1] Вагнер [2] Вальд [1] Вальрас [1] Гейл [1] Купманс [2], [3] Леонтьев [1] Массе [1] Массе, Жибра [1] Миле [1] Солоу [1] Удзава [2] Фишер, Шрубен [1]
Гейл, Кун, Таккер [1]— [3] фон Нейман [2]
Данциг [16] Дорфман [1] Фриш [ 1 ] Хикс [1]
Дорфман, Самуэльсон, Солоу [1] Эрроу [1]
Карлин [1] Сборники [18], [19], [21]
ЛИТЕРАТУРА К ГЛ. 13
Беллман, Блекуэлл [1]
Б леку элл, Гиршик [1]
Боненбласт, Карлин, Шепли [1]
Борель [1]—[3]
Браун [1]
Браун, фон Нейман [1]
Вайда [1]
Билль [1]
Вильямс [1]
Гасс [1]
Гейл [1], [4]
Гейл, Кун, Таккер [1]
Данциг [3], [И], [17]
Дорфман [2]
Дрешер [1]
Капланский [1]
Карлин [1]
Кемени, Снелл, Томсон [1]
Кун, Таккер [2], [4]
Льюс, Райфа [1]
Мак-Доналд [1]
Мак-Кинси [1]
Миле [1]
Моргенштерн [1]
Райфа, Томсон, Тролл [1]
Ричардсон [1]
Робинсон [1]
Таккер [1], [4], [9]
фон Нейман [1], [2]
фон Нейман, Моргенштерн [1]
Шепли, Сноу [1]
Шубик [1]
Сборники [15]—[17]
586
ЛИТЕРАТУРА К ГЛ. 14
Бекман, Мак-Гайр, Уинстон [1]
Берж [11
Гарвин [1]
Гасс [1]
Гейл [1]
Герстенхабер [2]
Данциг [4]
Данциг, Фулкерсон [1]
Деннис [1]
Дуаер, Галлер [11
Ири [1]
Канторович [1], [3]
Канторович, Гавурин [Ц
Кун [11, [3]
Купманс [1J
Купманс, Рейтер [1]
Манкрес [1]
Моцкин [2]
Прагер [2J
Таккер [1]
Флад [1], [3]
Форд, Фулкерсон [21, [3], J5]
Хаутэккер [1]
Хеллер [21
Хеллер, Томпкинс [1]
Хичкок [1]
Хэдли [2]
Чарнс, Купер [3]
Шетти [11
ЛИТЕРАТУРА К ГЛ. 15
Берж [1]
Биркгоф [1]
Вайда [4]
Вото [1]
Вото, Орден [1]
Гасс [1]
Гейл [Ц
Гофман [2], [3]
Гофман, Кун [Ц
Гросс [1]
Деннис [Ц
Истерфилд [1]
Кендалл [ 1 ]
Кун [1]
Кун, Таккер [4]
Манкрес [1]
Маркус [1]
Моцкин [3]
фон Нейман [5]
Форд, Фулкерсон [8]
Халмош, Воан [1]
Хэдли [2]
Эгервари [1]
ЛИТЕРАТУРА К ГЛ. 16
Берж [1]
Гейл [11
Деннис [1]
Дилворт [Ц
Канторович, ГавуринЗ[1]
Купманс [1]
Купманс, Рейтер [1]
Орден [3]
Форд, Фулкерсон [8]
ЛИТЕРАТУРА К ГЛ. 17
Веллман [3]
Берж [11
Вайда [4]
Гейл [11
Гофман [3]
Данциг [19]
Деннис [1]
Ири [Ц
Келли [2]
Кениг [Ц
Краскал [ 1 ]
Купманс [1]
Купманс, Рейтер [1]
Мур [1]
Орден [3]
Таккер [1]
Форд, Фулкерсон [8]
Хэдли [2]
Задача о поставщике
Гаддум, Гофман, Соколовский [1] Джейкобс [Ц
Гарвин [1] Гасс [1] Прагер [11 Хэдли [1] ЛИТЕРАТУРА К ГЛ. 18
Берж [1] Вагнер [31, [5] Вайда [2], [4] Данциг [21, [8], Кан [1] Прагер [2] Форд, Фулкерсон [5], [81 Ху, Прагер [1] [12], [151 Чарнс, Купер [1], [3]
587
38*
ЛИТЕРАТУРА К ГЛ. 19
Берж [1] Болдырев [1] Гейл [1], [5], [6] Гомори, Ху [11, [2] Гофман [3] Данциг, Фулкерсон [2] Фулкерсон, [Ц, [2], [5], Фулкерсон, Данциг [1] Хэдли [21 Ири [1] Кун [3] Манкрес [1] Райзер [1] Флад [1] Форд, Фулкерсон [1]—[6], [8] [6] Шепли [1] Эгервари [1] ЛИТЕРАТУРА К ГЛ. 20
Гарвин [11 Гоффман [131 Данциг [2], [15] Джуэл [11 Кан [1] Кун [1] Манкрес [1] Прагер [2] Флад [1] Форд, Фулкерсон [2], [3], 18] Фулкерсон [3], [4] Хэдли [2] Чарнс, Купер [1] Эгервари [1] ЛИТЕРАТУРА К ГЛ. 21
Джуэл [3] Канторович [1] Марковиц [31 Фергюсон, Данциг [1], [2] Хэдли [2] Эйземан, Лурье [1] ЛИТЕРАТУРА К ГЛ. 22
Гомори, Ху [1], [2] Данциг [15] Данциг, Вулф [1] Каваратани, Улман, Данциг [1] Кун, Таккер [1] Форд, Фулкерсон [6] ЛИТЕРАТУРА К ГЛ. 23
Гомори, Ху [2] Данциг [15] Данциг, Вулф [1] Джуэл [2] Каваратани, Улман, Данциг [Ц Кун, Таккер [1] Форд, Фулкерсон [6] ЛИТЕРАТУРА К ГЛ. 24
Баранкин, Дорфман [1] Беккенбах [1] Бил [3], [6] Важоньи [2] Вильямс [1] Вулф [1] — [6] Данциг [121, [21] Даффин [1] Дорн [1] Дорфман [1] 3 ойтенд ейк [ 1 ], [ 2 ] Карлин [1] Келли [1] Кун, Таккер [1] Марковиц [1], [4], [5] Миллер [1] Розен [1] Саймон [1] Слейтер [1] Таккер [6] Тролл [1] Уайт, Джонсон, Данциг [1] Удзава [1] Форсайт [2] Хартли, Лофтсгард [1] Чарнс, Лемке [1] Шетти [1] Эрроу, Гурвиц, Удзава [1] ЛИТЕРАТУРА К ГЛ. 25
Баббар [1] Беллман [1] Вагнер [4] Важоньи [2] Вайда [3] Вальд [3] Вулф [2] Данциг [91, [12]
588
Данциг, Маданский [1] Тейл [1]
Крамер [1] Тинтнер [1]
Кун, Таккер [1] Феллер [1]
Маданский [ 1 ] — [4=1 Фергюсон, Данциг [2]
Марковиц [1], [5] Фрейнд [1]
Нейман [1] Чарнс, Купер [3]
Раднер [1] Чарнс, Лемке [1]
Рейтер [1] Штиглер [1]
Саймон [ 1 ] Эль-Маграби [1], [2]
Талакко [1] Бил [4] ЛИТЕРАТУРА К ГЛ. 26 Марковиц, Манн [1]
Гейл [3] Миллер, Таккер, Землин [1]
Гирш, Данциг [1] Норман [1]
Гомори [1]—[4] Полл, Уолтер [1]
Гофман [3] Райзер [1]
Гофман, Краскал [1] Саати [2]
Данциг [14], [16], [17], [20] Таккер [7]
Д анциг, Фулкерсон [ 1 ] Тутте [1]
Джонсон [1], [2] Дойг, Белз [1] Краскал [1] Ла Валле [1] Ламбер [1] Лэнд, Дойг [1] Ньюман [1] Смит [1] Суонсон [1] Гантер [1] Данциг [9] Манн [1] Флад [2] Форд, Фулкерсон [8] Фулкерсон [1], [5] Хеллер [1]— [3] Чарнс, Лемке [1] Эйземан [1] ЛИТЕРАТУРА К ГЛ. 27 Уо [1] Фишер, Шрубен [1] Штиглер [1] ЛИТЕРАТУРА К ГЛ. 28 Фергюсон, Данциг [1], [2] Циммерн [1]
ПРЕДМЕТНЫЙ
Альтернативы
К-кратные 510
теорема об альтернативах для мат-
рицы 28, 142
(См. также Дихотомии)
Анализ технологических процессов 13,26
Анализ устойчивости (чувствительно-
сти) 262—272
Базис
в задаче линейного программиро-
вания 84, 97—101
векторного пространства 181—183
дополнительный в квадратичном
программировании 468
дополнительный прямой и двойст-
венный 237—239
обратный 198, 207
представление в виде произ-
ведения 198
соотношение между деревом и бази-
сом 345—346
треугольный 299, 318, 333
(См. также Вектор; Матрицы;
Системы линейных уравнений)
Базисное решение 29, 84
вырожденное 84,101
допустимое, оптимальное 97
в задаче о перевозках через
промежуточные пункты
337, 373, 374
в транспортной задаче 298,
299, 373, 374
исходное допустимое в транспорт-
ной задаче с ограничениями
365—366
во взвешенной транспортной
задаче 397—399
определение 84
(См. также Допустимые решения)
Блочные ведущие элементы 199, 200
Ведущие операции 82, 173
Ведущий элемент 82, 83, 173—176, 199,
200
УКАЗАТЕЛЬ
Вектор
единичный 179
лексико-положительный 235, 290
линейно независимый 179, 188
операции 177, 178
определение 177
представление через базис 183
произведение матрицы на вектор
185
Векторное пространство 180, 181, 202
Венгерский метод 243, 387
(См. также Задача о назначениях)
Вершина 28, 156
решение 28
(См. также Крайние точки)
Вес 74, 207
(См. также Множители; Цены)
Вогнутая функция 447
глобальный минимум 515, 516
Выигрыш 274
ожидаемый 278
Выпуклая оболочка 162
Выпуклая функция 155—156
определение 155
Выпуклое программирование 16, 447 —
472
задача Куна—Таккера 418, 419, 447
сведение к задаче обобщенного
программирования 418, 419
общая теория 447—454
сходимость итеративного процес-
са 450—454
условия Куна—Таккера 447, 448
(См. также Задача химического
равновесия; Квадратичное про-
граммирование; Куна—Так-
кера условия)
Выпуклые множества 151—155
замкнутые 151
многогранные 417, 418, 428
неограниченные многогранные 432
пересечение 151, 152
Выпуклые области 150—158, 166—169
590
Выпуклый многогранник 154, 171
ребро 154, 157, 162
Вырождение 32, 102, 124, 218, 225,
229—234
в задаче о назначениях 312
в транспортной задаче 302, 303
(См. также Зацикливание; Лек-
сикографическое правило;
Правило случайного выбора)
Вырожденные выпуклые целевые функ-
ции 458—464
Вырожденные решения (См. Базисное
решение) 157
Вычислительные машины 32—33
использование для решения задачи
о диете 527, 528
программы 20, 32, 199, 212, 229,465
Вычислительные методы 32, 33
Гирша гипотеза 162, 168
Градиент 161, 171
Граф
линейный 29, 342
(См. также Сети)
Двойного описания метод 32
Двойственная задача линейного про-
граммирования 53, 54, 66
126, 131
диаграмма Таккера 127, 141, 237,
238
для смешанной задачи 128—131
для стандартной задачи 66, 130
дополнительные прямые и двойст-
венные базисы 237
допустимость 131
метод множителей Лагранжа 147
пример «честолюбивого предпри-
нимателя» 257—259
Двойственная система 28
Двойственный симплекс-метод 237, 239,
240
Двойственность 28, 29
основные теоремы 137—143
Дерево 343
(См. также Базис)
Динамическое программирование 16, 17,
483
подход к задаче о ранце 491
принцип оптимальности 16
Дискретное программирование 487—520
задачи, разрешимые с его помощью
509—520
итеративной процесс 502—505
Дискретные задачи 16
(См. также Нелинейное програм-
мирование)
Дихотомии 509, 510
Дополнительная нежесткость 138—139
Дополнительные прямые и двойственные
базисы 237, 238
Допустимая задача 39
Допустимые решения 158
выпуклые множества 154—158
(См. также Крайние точки)
для прямой и двойственной задач
131
исходный базис 29, 97, 103
(См. также Этап I симплекс-
метода)
определение 65
(См. также Базисное решение)
Дуга графа 342
Задача о бродячем торговце 516—518
(различные формулировки) 516—518
Задача о кратчайшем пути 328, 349—
354, 488—490
итеративное решение 349—351
непосредственное решение 351—354
(См. также Задача о перевозках
через промежуточные пункты)
Задача о назначениях 243, 305, 310—
313, 488—490
вырождение 313, 314
сведение к задаче линейного про-
граммирования 313
эквивалентность транспортной зада-
че 314, 315
(См. также Задачи распределения;
Распределение самолетов по
линиям)
Задача о перевозках с промежуточными
пунктами 29, 328—341
граф 344
допустимые решения (см. Базисное
решение)
решение, использующее граф 346 —
349
решение с помощью симплекс-мето-
да 337, 338
стандартная форма 332, 333
треугольность базиса 332
формулировка 328, 329
эквивалентная транспортная зада-
ча 335—337
(См. также Задача о кратчайшем
пути)
591
Задача о поставщике 354
Задача о рюкзаке 490—493
Задача о складе 59, 71, 394
(См. также Многошаговые модели)
Задача о четырех красках (две фор-
мулировки) 519—520
Задачи о смесях 47—54, 66—68, 119—122
Задачи программирования 9, 10
вероятностные 15—16
(См. также Программирование
в условиях неопределенности)
детерминированные 14
классификация 14—16
линейные 37—39, 64
(См. также Выпуклые области;
Симплекс-метод; Линейное
программирование; Матема-
тическое программирование)
Задачи распределения 310—327, 355,
356
взвешенные 28, 395—412
исходное базисное решение
397—399
подкласс с треугольным опти-
мальным базисом 405—411
почти треугольность базиса
401, 402
пример 544, 545
структура графа базиса 402—
405
метод решения прямой и двойствен-
ной задач 243
с заранее предписанными значе-
ниями 323—325
(См. также Задача о назначениях)
Задача с возмущениями 229, 231—234
для транспортной задачи 307, 309
для этапа II 231—234
(См. также Лексикографическое
правило; Лексикографическое
упорядочение)
Задача химического равновесия 456, 457
Зацикливание 32, 102, 207, 225, 229
примеры 225—235
в транспортной задаче 303, 304,
309
(См. также Вырождение)
Игра
антагонистическая 15
вполне определенная 277
задача линейного программирова-
ния 273—294
матричная, конструктивное решение
287—293
значение 281, 283
определение 274, 275
Морра 275
определение 274
решение 283
эквивалентная задача линей-
ного программирования
283, 284
сведение к задаче линейного про-
граммирования 286, 287
сведение матричной игры 284—286
симметричная матричная 284
теория 27, 31
См. также Игрок; Теорема мини-
макса
«Игра» бракосочетания 315, 325, 489
Игрок
второй 274
первый 274
консервативный 280
Изменения правых частей ограничений
Изменения коэффициентов стоимости
для базисных процессов 266
Итерации
число 101, 162, 244, 355
Каноническая форма (См. Системы линей-
ных уравнений)
Квадратичное программирование 33 г
465-471
алгоритм 471
дополнительность базисов 468
приложения 465
условия оптимальности 467
Квадратичная форма 466
выпуклость 466
положительно определенная 466
положительно полуопределенная
466
Комбинаторные задачи 310, 487
примеры 488
Комбинации
взвешенные 153
линейные 28
векторов 179
уравнений 74
(См. также Крайние точки)
Консервативный игрок 280 (см. Игрок)
Конус 169
Коэффициенты затрат—выпуска 40
Крайние решения 28
(См. также Крайние точки)
692
Крайние точки 28, 156
дробные 489
линейные комбинации 172
определение 156
(См. также Выпуклые множества)
Куна — Таккера условия 447, 448
(См. также Выпуклое програм-
мирование)
Лагранжа множители 143—147, 207, 447
определение 144
Латинские квадраты 518, 519
Лексикографическое правило
доказательство 231—234
в симплекс-методе, использующем
множители 217, 218
Лексикографическое упорядочение 228,
290, 291
(См. также Вектор; Задача с воз-
мущениями)
Леонтьева модели 25
Линейное программирование
алгоритмы 96, 194, 241—243
геометрия 150—172
(См. также Выпуклые области)
графические методы 39
задача в форме неравенств 21—91,
95
истоки 19
метод множителей Лагранжа 147
методы, отличные от симплекс-
метода 32
параметрическое 241
понятие 9
приложение к теории матричных
игр 273—294
примеры, задачи 10—12
с ограниченными сверху перемен-
ными 355—371
эквивалентность с матричными иг-
рами 282—287
экономические модели 23—28
(См. также Симплекс-метод)
Линейные неравенства 10
системы 27, 28, 85—91, 93, 94
(См. также Выпуклые области;
Линейные уравнения)
Линейные уравнения 10
избыточные, зависимые 75, 103
материального баланса 38, 40, 56
несовместные 73 — 75, 103
(См. также Системы линейных
уравнений)
Луч 169
5Р5
Математическое ожидание 474
Математическое программирование
определение 10
(См. также Задачи программиро-
вания)
Матричная алгебра 187—189
Матричные операции 183—187
Матрица
бистохастическая 311
единичная 192, 203
затрат — выпуска 25
игры 273, 274
(См. также Игра)
косо-симметричная 284
невырожденная 188
обратная 188—193
определение 183
перестановочная 311—312
теорема об альтернативах 28, 142’
технологическая 34
транспонированная 183, 192
транспортной задачи 397
элементарная 197
(См. также Вектор)
Метод Гомори 493 — 508
Метод исключения для решения систем
неравенств 87, 88, 95, 251
Метод исключения Фурье—Моцкина (См.
Метод исключения для решения сис-
тем неравенств)
Метод одновременного решения прямой
и двойственной задач 237, 243—249
для транспортных задач 387—
394
Метод релаксации 31
Многогранник (См. Выпуклый много-
гранник)
Многошаговые задачи
двушаговый случай 481, 482
применение принципа разложения
443—446
Множители 74
(См. также Лагранжа множители;
Симплекс-множители)
Модель
Вальраса 24
Леонтьева 25
линейного программирования 13, 14
табличная форма 46
формулировка 37—72
математическая 10
определение 39
многошаговая 16
построение 13
экономическая 23
Модель линейного программирования
13, 27
формулировка 37—72, 521—526
Мультиплекс-метод 32
Нелинейное программирование 15
(См. также Выпуклое програм-
мирование; Дискретное про-
граммирование)
Неопределенность 15, 473—486
(См. также Программирование
в условиях неопределенности)
Неравенства (См. Линейные неравенст-
ва)
Обобщенная задача Вулфа 413—419
использование для решения задачи
Куна—Таккера 448, 449
определение 414
Ограниченная главная задача 417,
418, 449
частные случаи 419—425
с точки зрения линейного програм-
мирования 414, 415
эквивалентная формулировка 418,
419
Ограничения сверху на переменные
355—371
Однородные системы (См. Системы ли-
нейных уравнений)
Относительные оценки 97
Отсекающая плоскость 492, 493
(См. также Дискретное програм-
мирование; Целочисленные
формы)
Параметрическое линейное программи-
рование 241 — 243, 250
(См. Линейное программирование)
Переменные
дискретные 487—520
дробные 493
искусственные 96, 104—106, 133,
214, 232
в двойственном симплекс-мето-
де 239—240
(См. также Этап I симплекс-мето-
да)
метод ведущих переменных 237
свободные 64
с ограничениями сверху 355—371
транзитные 332
(См. также Ограничения сверху
на переменные)
Питания модель 118, 121, 122
применение к задаче домашней
хозяйки 11
Планирование 19
организация 29
централизованное, без полной ин-
формации в центре 439—442
Полупространство 154
Поток в сети 33, 372 — 386
Правило случайного выбора 101—102,
126, 218, 228
доказательство 126
(См. также Зацикливание)
Программа бесконечная 30
Программирование в условиях неопре-
деленности 34, 473—486
минимизация ожидаемых издер-
жек 474, 475
дисперсии издержек 475—477
Пропускная способность 372
Пространство (см. Векторное простран-
ство)
Путь в графе 342
Разложения принцип 34, 413, 427—446
итеративный процесс 430, 431
популярное изложение 433—438
(См. также Обобщенная задача
Вулфа)
Разрез в сети 378—382
значение 378
определение 378
равенство максимального значения
потока минимальному разрезу 379
Ранг
векторного пространства 181—182
матрицы 188, 189
системы 176, 177
Распределение с избытками и недостат-
ками 316—323
постановка в виде транспортной
задачи 317
пример 319—323
Распределение самолетов по линиям
539—563
случай неопределенного спроса
численное решение 551 —563
случай фиксированного спроса 540—
545
формулировка задачи 539—549
Седловая точка 277, 279
Сеть 33, 295
594
задача максимального потока 372—
386
алгоритм Форда — Фулкерсона
388—393
кратчайший путь (См. Задача о
кратчайшем пути)
метод деревьев 382—386
определение 342
плоская 379
разрез (См. Разрез в сети)
связная 337
с ограничениями 29
(См. также Транспортная задача;
Задача о перевозках с про-
межуточными пунктами)
Симплекс 162, 164
определение 165
Симплекс-алгоритм 9, 96—102, 116—118
варианты 236—250
в матричной форме 194—200
индуктивное доказательство 123—
126
конечность 102, 123—126, 232
(См. также Симплекс-метод)
Симплекс-метод 22, 28, 31, 32, 96—122
блок-схема 106
геометрическая интерпретация
158—161
двойственный 237, 239—241
метод множителей Лагранжа 147
механизм цен 251—272
модифицированный 214—222
применение к доказательству тео-
ремы двойственности 131—138
принцип разложения 430
решение задачи о перевозках с про-
межуточными пунктами 337—
340
решение транспортной задачи 297,
298
(См. также Симплекс-алгоритм;
Этап I симплекс-метода; Этап
II симплекс-метода)
Симплекс-множители 195, 207, 209, 212,
233
интерпретация как цен 251
использование в задаче распре-
деления 325
в задаче взвешенного распреде-
ления 399—400
в задаче о перевозках с про-
межуточными пунктами 335
в транспортной задаче 300
•определение 216, 413
(См. также Цены)
Система линейных неравенств 85—91,
154
Системы линейных уравнений И, 27,
73-95
диагональные 80
зависимые 75
канонические 78, 85, 91—93, 96,
174—189, 214
определение 76
эквивалентные 174—176
квадратные 78—80
независимые 75
однородные 29, 189
определение 139
треугольные 80
тривиальное решение 139
эквивалентные 77, 174
(См. также Линейные уравнения)
Среднее взвешенное 52
Стандартная форма задачи линейного
программирования 64, 88—90
Стохастическое программирование
(См. Программирование в усло-
виях неопределенности)
Стратегия
оптимальная смешанная 281
смешанная 280
чистая 274
(См. также Игра)
Таккера диаграмма 126—128, 141, 237
(См. также Двойственная задача
линейного программирова-
ния)
Теорема двойственности 30, 123, 128
доказательство 131—138
матричные игры 283
слабая форма 133
(См. также Дополнительная не-
жесткость; Симплекс-метод)
Теорема о минимаксе 28, 31
доказательство, использующее тео-
рему двойственности 284
использующее симплекс-алго-
ритм 287—293
Теорема о транспозиции 28, 141—143
Технологический процесс 10, 13, 413
интенсивность 10, 37
определение 37
с несколькими контролируемы-
ми параметрами 423—425
с одним контролируемым пара-
метром 419—423
595
с переменными коэффициентами
413
Точка (л-мерного пространства) 152
Транспортная задача 26, 32, 33, 67,
103, 295—309
вырождение 302, 303
вычислительный алгоритм 303—308
допустимые решения (См. Базисное
решение)
исторический очерк 295, 296
метод одновременного решения пря-
мой и двойственной задач 387—
394
определение 295, 296
правило минимального элемента
304, 323
решение симплекс-методом 296—
303
с ограничениями 364—367
треугольность базиса 299
целочисленность базисных пере-
менных 300
(См. также Задача о назначе-
ниях; Задача о потоках в
сети; Задача о перевозках
с промежуточными пунктами)
Узел 342
Управление запасами 14
пример 477—480
Уравнение векторное 180
материального баланса 40
(См. также Линейные уравнения)
Фаркаша лемма 28, 127, 140, 148
Форма недопустимости 104, 232, 324
Целевая функция 65
вырожденная выпуклая 458—464
линейная 37, 65
определение 65
нелинейное и дискретное програм-
мирование 512—514
неограниченная 123, 131
однородная первой степени 454 —
456
параметрическая 237
Целочисленное программирование 34
(См. также Дискретное програм-
мирование)
Целочисленные формы
метод Гомори 493—509
формирование в целочисленном
программировании 496—499
(См. также Дискретное програм-
мирование)
Центр тяжести 52, 94, 162
Цены 29, 207
механизм цен в симплекс-методе
251—272
неявные (См. Симплекс-множители)
соглашение о знаках 261—262
(См. также Симплекс-множители)
Цепь 342, 343
Цикл в графе 343
Эквивалентные системы (См. Системы
линейных уравнений)
Экономические модели и их связь с ли-
нейным программированием 23—
27, 251
Элементарные операции 77—78
(См. также Ведущие операции;
Системы линейных уравне-
ний)
Этап I симплекс-метода 96, 103—106
другой критерий 249
Этай II симплекс-метода 96, 105
возмущенная задача 232
ОГЛАВЛЕНИЕ
Предисловие............................................................ 5
От автора ............................................................. 7
Глава 1
ПОНЯТИЕ О ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
1-1. Введение...................................................... 9
1-2. Задача программирования ..................................... 9
1-3. Определение линейного программирования ..................... 13
1-4. Классификация задач программирования ....................... 14
1-5. Математическое программирование и автоматизация............. 17
Глава 2
ИСТОКИ И СВЯЗИ
2-1. Влияние второй мировой войны................................ 19
2-2. Экономические модели и линейное программирование............ 23
2-3. Математические истоки и развитие............................ 27
2-4. Применение линейного программирования в промышленности ... 34
Глава 3
ФОРМУЛИРОВКА МОДЕЛИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
3-1. Основные понятия............................................. 37
3-2. Построение модели........................................... 39
3-3. Транспортная задача......................................... 40
3-4. Примеры смешивания.......................................... 47
3-5. Задача о смеси продукции.................................... 54
3-6. Простая задача о складе..................................... 59
3-7. Обучение на работе ......................................... 61
3-8. Основная математическая задача ............................. 64
3-9. Задачи...................................................... 66
Глава 4
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
4-1. Системы уравнений с одинаковыми множествами решений........ 73
4-2. Канонические системы ....................................... 78
4-3. Линейные неравенства ....................................... 85
4-4. Метод исключения Фурье — Моцкина............................ 87
4-5. Задачи линейного программирования в виде неравенств......... 88
4-6. Задачи...................................................... 91
Глава 5
СИМПЛЕКС-МЕТОД
5-1. Симплекс-алгоритм............................................ 96
5-2. Два этапа симплекс-метода................................... ЮЗ
5-3. Задачи..................................................... 116
597
Глава 6
ОБОСНОВАНИЕ СИМПЛЕКС-АЛГОРИТМА И ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ДВОЙ-
СТВЕННОСТИ
6-1. Индуктивное обоснование симплекс-алгоритма .................. 123
6-2. Эквивалентные двойственные формы............................. 126
6-3. Доказательство теоремы двойственности........................ 131
6-4. Основные теоремы о двойственности............................ 137
6-5. Множители Лагранжа .......................................... 143
6-6. Задачи....................................................... 147
Глава 7
ГЕОМЕТРИЯ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
7-1. Выпуклые области............................................. 150
7-2. Симплекс-метод как метод наискорейшего спуска вдоль ребер ... 158
7-3. Симплексная интерпретация симплекс-метода ................... 162
7-4. Задачи....................................................... 166
Глава 8
МЕТОД ВЕДУЩИХ ЭЛЕМЕНТОВ. ВЕКТОРНЫЕ ПРОСТРАНСТВА, МАТРИЦЫ И
ОБРАТНЫЕ МАТРИЦЫ
8-1. Теория ведущих операций ..................................... 173
8-2. Векторные пространства ...................................... 177
8-3. Матрицы . .................................................. 183
8-4. Обратная матрица............................................ 188
8-5. Симплекс-алгоритм в матричной форме.......................... 194
8-6. Задачи....................................................... 200
Глава 9
СИМПЛЕКС-МЕТОД, ИСПОЛЬЗУЮЩИЙ МНОЖИТЕЛИ. (МОДИФИЦИРОВАННЫЙ
СИМПЛЕКС-МЕТОД)
9-1. Пример использования множителей.............................. 208
9-2. Общее описание модифицированного симплекс-метода............. 214
9-3. Вычислительные правила использования множителей.............. 217
9-4. Задачи.................................................... 223
Глава Ю
КОНЕЧНОСТЬ СИМПЛЕКС-МЕТОДА С ВОЗМУЩЕНИЯМИ
10-1. Возможность зацикливания в симплекс-алгоритме............... 225
10-2. Возмущающие параметры для избежания вырождения.............. 229
10-3. Задачи...................................................... 234
Глава 11
ВАРИАНТЫ СИМПЛЕКС-АЛГОРИТМА
11-1. Дополнительные прямой и двойственный базисы................. 237
11-2. Двойственный симплекс-метод................................. 239
11-3. Самосопряженный (двойственный себе) параметрический алгоритм 241
11-4. Алгоритм одновременного решения прямой и двойственной задач 243
11-5. Другой критерий для этапа I................................. 249
11-6. Задачи...................................................... 250
Глава 12
ПОНЯТИЕ ЦЕНЫ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
12-1. Механизм цен симплекс-метода................................ 251
12-2. Примеры двойственных задач.................................. 257
12-3. Соглашение о знаках цен.............♦....................... 261
12-4. Иллюстрация анализа устойчивости........................... 262
12-5. Задачи...................................................... 271
598
Глава 13
ИГРЫ И ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
13-1. Матричные игры.......................................... 273
13-2. Эквивалентность матричных игр и задач линейного программирова-
ния; теорема о минимаксе .................................. 282
13-3. Конструктивное решение матричной игры (другое доказательство
теоремы о минимаксе)....................................... 287
13-4. Задачи.................................................. 293
Глава 14
КЛАССИЧЕСКАЯ ТРАНСПОРТНАЯ ЗАДАЧА
14-1. Исторический обзор.................................... 295
14-2. Элементарная теория транспортировки .................... 296
14-3. Вычислительный алгоритм для транспортной задачи......... 303
14-4. Задачи.................................................. 308
Глава 15
ОПТИМАЛЬНОЕ НАЗНАЧЕНИЕ И ДРУГИЕ РАСПРЕДЕЛИТЕЛЬНЫЕ ЗАДАЧИ
15-1. Задача об оптимальном назначении......................... 310
15-2. Задачи с нарушенным балансом ........................... 316
15-3. Фиксированные значения и запрещенные клетки............. 323
15-4. Задачи.................................................. 325
Глава 16
ЗАДАЧА О ПЕРЕВОЗКАХ С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ
16-1. Формулировка модели .................................... 328
16-2. Эквивалентность транспортной задачи и задачи с промежуточными
пунктами .................................................. 335
16-3. Решение задачи с промежуточными пунктами симплекс-методом . . 337
16-4. Задачи................................................. 340
Глава 17
СЕТИ И ЗАДАЧА С ПРОМЕЖУТОЧНЫМИ ПУНКТАМИ
17-1. Графы и деревья ..................................... 342
17-2. Интерпретация симплекс-метода на сети................... 346
17-3. Задача о кратчайшем пути.......................... 349
17-4. Задачи.................................................. 354
Глава 18
ОГРАНИЧЕННЫЕ СВЕРХУ ПЕРЕМЕННЫЕ
18-1. Общий случай............................................ 355
18-2. Транспортная задача с ограниченными пропускными способностями
и ее обобщения ............................................ 364
18-3. Задачи...............................................• . 370
Глава 19
МАКСИМАЛЬНЫЕ ПОТОКИ В СЕТЯХ
19-1. Теория Форда — Фулкерсона............................... 372
19-2. Решение задачи о максимальном потоке методом деревьев... 382
19-3. Задачи.................................................. 386
Глава 20
ПРИМЕНЕНИЕ МЕТОДА ОДНОВРЕМЕННОГО РЕШЕНИЯ ПРЯМОЙ И ДВОЙСТВЕН-
НОЙ ЗАДАЧ К ТРАНСПОРТНОЙ ЗАДАЧЕ
20-1. Введение ................................................... 387
20-2. Алгоритм Форда — Фулкерсона............................. 388
20-3. Задачи.................................................. 393
599
Глава 21
ЗАЛАЧ.А О ВЗВЕШЕННОМ РАСПРЕДЕЛЕНИИ
21-1. Почти треугольный базис ............................... 395
21-2. Структура базиса с точки зрения графов.................... 402
21-3. Подкласс задач с треугольными оптимальными базисами.... 405
21-4. Задачи ........................................................ 411
Глава 22
-ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕН-
ТАМИ
22-1. Обобщенная задача Вулфа........................................ 413
22-2. Замечания о частных случаях.................................... 419
22-3. Задачи........................................................ 425
Глава 23
ПРИНЦИП РАЗЛОЖЕНИЯ ДЛЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
23-1. Общий принцип.......................................... 427
23-2. Принцип разложения, беллетризованное изложение......... 433
23-3. Централизованное планирование без полной информации в центре 439
23-4. Разложение многошаговых задач линейного программирования . . 443
23-5. Задачи................................................. 446
Глава 24
ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ
24-1. Общая теория............................................ 447
24-2. Однородные целевые функции и задача химического равновесия . . 454
24-3. Вырожденные выпуклые целевые функции................... 458
24-4. Квадратичное программирование ....................... 465
24-5. Задачи.......................................................... 472
«Г лав а 25
НЕОПРЕДЕЛЕННОСТЬ
25-1. Составление планов в случае переменных издержек....... 473
25-2. Планирование при неопределенном спросе.................... 477
25-3. О многошаговых задачах.......................................... 481
25-4. Задачи.......................................................... 484
Глава 26
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ С ДИСКРЕТНЫМИ ПЕРЕМЕННЫМИ .........
26-1. Обзор методов *.......................................... 487
26-2. Метод целочисленных форм Гомори . ...................... 493
26-3. О значении решения задач линейного программирования, в которых
некоторые переменные целочисленные *.................... 508
Глава 27
МОДЕЛЬ ДИЕТЫ ШТИГЛЕРА: ПРИМЕР ФОРМУЛИРОВКИ И РЕШЕНИЕ.............
27-1. Задачи при формулировании модели........................ 521
27-2. Численное решение задачи о диете........................ 527
27-3. Задачи.................................................. 536
Глава 28
РАСПРЕДЕЛЕНИЕ САМОЛЕТОВ ПО ЛИНИЯМ В УСЛОВИЯХ НЕОПРЕДЕЛЕННО-
ГО СПРОСА
28-1. Постановка задачи и математическая формулировка......... 539
28-2. Численное решение задачи распределения самолетов по линиям . . 551
БИБЛИОГРАФИЯ
Общий указатель................................................... 564
Литература к отдельным главам .................................. 582
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ..........,................................... 590