Текст
ИЗДАТЕЛЬСТВО
<МИР»
NONLINEAR
AND DYNAMIC PROGRAMMING
BY
G. HADLEY
University of Chicago
and
Universidad de Los Andes
Bogota, Colombia
ADDISON-WESLEY PUBLISHING COMPANY, INC.
READING, MASSACHUSETTS • PALO ALTO • LONDON
1964
Дж. Хедли
НЕЛИНЕЙНОЕ
и
ДИНАМИЧЕСКОЕ
П РО ГРАМ М ИРОВ АНИЕ
Перевод с английского
Ю. И. ВОЛКОВА, А. Б. ГОРСТКО.
А. А. КАПЛАНА. Э. О. РАПОПОРТА
Под редакцией
Г. П. АКИЛОВА
ИЗДАТЕЛЬСТВО ,МИР« МОСКВА 1967
УДК 519.9
Монография содержит подробное исследование теоретических
и вычислительных аспектов нелинейного и динамического про-
граммирования. Автор систематически рассматривает вопросы
практической реализуемости предлагаемых вычислительных мето-
дов. В книге имеется большое количество примеров. Предпола-
гается, что читатель знаком с математическим анализом, линей-
ной алгеброй и линейным программированием, однако для удоб-
ства в книгу включена глава, содержащая необходимый минимум
сведений.
Книга рассчитана на научных работников, инженеров, эконо-
мистов и лиц других специальностей, интересующихся матема-
тическими методами планирования, а также на математиков,
занимающихся приложениями к экономике. Она доступна сту-
дентам и аспирантам соответствующих специальностей.
Редакция литературы по математическим наукам
Ивд. 2-2-3
ОТ РЕДАКТОРА ПЕРЕВОДА
Предлагаемая вниманию читателя книга Дж. Хедли «Нели-
нейное и динамическое программирование» имеет целью позна-
комить неискушенного в математике читателя с задачами, ре-
шение которых сводится к отысканию наибольшего или наи-
меньшего значения некоторой функции, зависящей, как правило,
от большого числа переменных. Такие задачи возникают в
самых разнообразных областях человеческой деятельности
и в первую очередь — это и обусловило повышенный инте-
рес к ним — в практике планирования и организации производ-
ства.
Имея в виду указанный выше круг читателей, автор не стре-
мится углубляться в дебри теоретических исследований. Его
интересует, во-первых, математическое описание различных си-
туаций, типичных для оптимального планирования, и, во-вторых,
численное решение возникающих при этом математических за-
дач. Надо сказать, что эти стороны вопроса совершенно недо-
статочно освещены в советской литературе. Поэтому столь по-
дробное их изложение, которое мы находим в книге Дж. Хедли,
следует расценивать как явление весьма положительное.
Все это дает основания надеяться, что книга окажется
полезной для обширного круга специалистов, так или иначе свя-
занных с оптимальным планированием: от сотрудников научных
учреждений до практических работников предприятий и плано-
вых органов, занимающихся организацией и планированием
производства.
Книга не обращена непосредственно к математикам, но те
из них, кто работает по реализации на ЭВМ задач математиче-
ской экономики или им подобных, также прочтут ее с пользой
для себя.
6 От редактора перевода
При переводе мы сочли нужным сделать некоторые, впрочем
совсем небольшие, сокращения. В ряде случаев оказались не-
обходимыми и другие отступления от текста, главным образом
уточнения отдельных формулировок. Указанные изменения в
оригинале ввиду их незначительности, как правило, не оговари-
ваются.
Список литературы дополнен важнейшими советскими изда-
ниями, имеющими прямое отношение к затронутым в книге во-
просам.
Главы 1, 10, И переведены А. Б. Горстко, главы 2, 8 —
Ю. И. Волковым, главы 3, 4, 6. 7 — А. А. Капланом, главы 5,
9 — Э. О. Рапопортом.
Г. П. Акилов
ПРЕДИСЛОВИЕ
Эта книга задумана как продолжение книги автора «Линей-
ное программирование» и посвящена изучению теоретических и
вычислительных аспектов нелинейного программирования.
Первая глава посвящена обсуждению тех трудностей, ко-
торые возникают при переходе от линейных задач к нелинейным.
Во второй главе делается попытка дать необходимые для
дальнейшего чтения сведения по математике/а также вводятся
принятые обозначения. Благодаря включению этой главы на-
стоящую книгу можно читать независимо от книг автора «Ли-
нейное программирование» и «Линейная алгебра».
Глава 3 содержит описание классических методов оптимиза-
ции, основанных на использовании дифференциального исчисле-
ния. Особенно подробно обсуждается метод множителей Ла-
гранжа. Здесь же определяются основные свойства выпуклых и
вогнутых функций, которые используются в дальнейшем. В этой
главе не делается попытки изучить вариационное исчисление,
так как для этого понадобилось бы слишком много места. О нем
лишь коротко упоминается в главах, посвященных динамиче-
скому программированию.
В гл. 4 изучаются приближенные методы для отыскания ло-
кальных или глобальных экстремумов в задачах нелинейного
программирования.
Пятая глава посвящена задачам стохастического программи-
рования, а шестая — теории Куна—Таккера.
Задачи квадратичного и целочисленного программирования
обсуждаются соответственно в седьмой и восьмой главах.
Глава 9 посвящена градиентным методам решения нелиней-
ных задач, а две последние главы — динамическому программи-
рованию.
Проблемы нелинейного программирования гораздо шире и
разнообразнее, чем проблемы линейного программирования. От-
части это и послужило причиной того, что отдельные главы
иногда содержат описания никак не связанных между собой
методов решения специальных типов задач. Другая причина
состоит в том, что в настоящее время не существует теории»
8
Предисловие
объединяющей все относящееся к нелинейному программирова-
нию, да и вычислительные алгоритмы разработаны лишь для
очень специальных классов задач. Схемы этих алгоритмов
весьма существенно зависят от особенностей решаемых задач.
Для решения рассматриваемых в книге задач было предло-
жено множество вычислительных методов. Так как не предста-
влялось возможным изложить все методы, автор был вынужден
отобрать лишь наиболее интересные. Конечно, в ряде случаев
этот выбор был довольно субъективным, так как не имелось
данных, позволяющих сравнить эффективность различных вы-
числительных схем. Некоторые интересные методы могли ока-
заться неупомянутыми просто потому, что автор не знал об их
существовании.
Нелинейное программирование в настоящее время бурно
развивается. При выборе материала для этой книги автор ста-
рался включать то, что более или менее уже выдержало испы-
тание временем. Однако вполне возможно, что в недалеком бу-
дущем многие из обсуждаемых алгоритмов будут вытеснены но-
выми, которые окажутся лучше существующих.
Математическая подготовка, необходимая для изучения этой
книги, неодинакова для разных глав. В большинстве случаев не-
обходимы первоначальные сведения из линейной алгебры и ли-
нейного программирования (например, в пределах первых вось-
ми-девяти глав книги автора «Линейное программирование»).
Большая часть материала, относящегося к динамическому про-
граммированию, может быть изучена и без этих сведений. При
чтении третьей и шестой глав необходимо знание, хотя и не
слишком основательное, дифференциального исчисления.
Как уже говорилось, в гл 2 сделана попытка собрать все не-
обходимые для дальнейшего изложения сведения из матема-
тики. Исключение составила лишь элементарная теория вероят-
ностей, даже не упоминающаяся в этой главе, но используемая
далее в гл. 3, 5, 10 и 11.
Автор очень обязан Д. Е. Моррису, который подобрал вели-
колепные эпиграфы к каждой главе.
Рецензенты Р. Дорфман и С. Дрейфус внесли много полез-
ных предложений, за которые автор им очень благодарен. По-
мощь при перепечатывании рукописи и издании книги была
любезно оказана аспирантурой Школы бизнеса Чикагского уни-
верситета.
Дж. Хедли
Богота, Колумбия
июнь 1964 г.
ГЛАВА
ВВЕДЕНИЕ
Каждое дерзание —
Это новый риск, новый шаг в темноту
непознанного
Со старым и все более устаревающим
оснащением.
Т. С. Элиот. Восточный Колос
1.1. Задачи математического программирования. Всякая задача,
в которой отыскивается максимум или минимум числовой функ-
ции (или функционала), может быть отнесена к задачам опти-
мизации. Эти задачи уже давно интересуют математиков,
физиков и инженеров. Возможность использования методов
дифференциального и вариационного исчислений для решения
некоторых типов таких задач, возникающих в геометрии и фи-
зике, была известна с середины XVIII в.
В последние пятнадцать лет значительно возрос интерес к
новому классу задач оптимизации, которые, как правило, не
поддаются решению классическими методами. Это так называе-
мые задачи математического программирования.
Задачи математического программирования в отличие от
классических задач, возникающих в геометрии и физике, часто
относятся к вопросам математической экономики. Как правило,
они возникают в тех случаях, когда заданные дефицитные ре-
сурсы— людей, машины и сырье — следует распределить таким
образом, чтобы произвести необходимое количество продуктов
и в то же время максимизировать или минимизировать некото-
рую целевую функцию (прибыль, затраты). Большой интерес
к этим задачам объясняется именно тем, что они встречаются
не только в теоретической экономике, но и в практике производ-
ства, торговли, управления и в военном деле.
Общая задача математического программирования может
быть сформулирована следующим образом: требуется найти
значения п переменных х2, ..., хп, которые удовлетворяют m
уравнениям или неравенствам
gi(xv х2, *„)(<, =, >}fy. 1=1, 2,..., т, (1.1)
10
Гл. 1. Введение
и максимизируют или минимизируют функцию
z = f(xv х2, .. ., х„). (1.2)
Условия (1.1) называются ограничениями, а функция (1.2) —
целевой функцией. Предполагается, что функции gi(x\,x2, ..., хп)
известны, a bi — заданные константы. Кроме того, в каждом из
ограничений (1.1) сохраняется только один из знаков =
или однако разные, ограничения могут, конечно, иметь раз-
ные знаки. Величины т и п между собой не связаны, так что
т может быть больше, меньше или равно п. В частности, т мо-
жет быть и нулем, так что в рассмотрение включается и случай,
когда ограничения (1.1) отсутствуют. Обычно некоторые или
все переменные удовлетворяют условию неотрицательности.
Кроме того, в качестве ограничений может фигурировать усло-
вие, по которому часть или все переменные могут принимать
лишь некоторые дискретные, например равные целым числам,
значения.
В некоторых случаях переменные Xj сами оказываются функ-
циями одного или нескольких параметров. Задача состоит тогда
в определении функций xh х2,..., хп, оптимизирующих выраже-
ние (1.2) при условиях (1.1) и, возможно, некоторых добавоч-
ных ограничениях на функции хр
Интерес к практическому использованию- математического
программирования возрос с 1947 г., когда Дж. Данциг разрабо-
тал симплекс-метод для решения общей задачи линейного про-
граммирования *). Если в (1.1) и (1.2)
п
gi(xlt 1=1, 2, .... т, (1.3)
7=1 J J
и
п
f (Xj, х2, ..., х„) = S CjXj, (1.4)
где ац и Cj—известные константы, то задача называется линей-
ной при условии, что нет других ограничений, исключая разве
требование неотрицательности всех или части переменных.
Обычно в формулировке общей задачи линейного программиро-
0 Нелишне напомнить, что первая обстоятельная работа по линейному
программированию была выполнена еще в 1939 г. в Советском Союзе. Мы
имеем в виду «Математические методы организации и планирования произ-
водства» Л. В. Канторовича [27*]. Правда, господствовавшие тогда и в после-
дующее время взгляды на экономическую пауку надолго задержали попу-
ляризацию,' развитие и практическое использование идей Л. В. Канторовича,
в связи с чем линейное программирование и было переоткрыго в 1947 г. в
США. — Прим. ред.
1.2. Типы задач
11
вания требуется, чтобы все переменные были неотрицатель-
ными, т. е.
Xj >0, 7=1, 2, /х, (1,5)
так как такая форма задачи более удобна для численного реше-
ния. Задача, в которой некоторые переменные могут быть произ-
вольного знака, легко преобразуется в задачу с ограниче-
ниями (1.5).
Таким образом, задача линейного программирования состоит
в отыскании неотрицательных значений п переменных удо-
влетворяющих пг ограничениям
=. >\bt
J
и максимизирующих или минимизирующих линейную функцию
z = 2 cjxj
Всякую другую задачу математического программирования,
в том числе и такую, где ограничения и целевая функция имеют
вид (1.3) и (1.4), но предполагается, например, целочисленность
переменных, мы будем считать нелинейной.
В этой книге мы будем иметь дело почти исключительно с
решением задач нелинейного программирования. Методы реше-
ния нелинейных задач так или иначе включают в себя алго-
ритмы, аналогичные используемым в симплекс-методе. Поэтому
предполагается, что читатель знаком с линейным программиро-
ванием, достаточно полно изложенным в первых девяти главах
книги автора «Линейное программирование» [13]1). К сожале-
нию, задачи нелинейного программирования почти всегда ре-
шаются значительно труднее, чем задачи линейного программи-
рования,— вычислительные приемы разработаны для решения
лишь немногих типов таких задач, изучением которых мы и бу-
дем заниматься. Что касается огромного разнообразия практи-
ческих ситуаций, исследование которых приводит к задачам не-
линейного программирования (следует заметить, что в большин-
стве случаев, когда дело сводится к линейной задаче, более
детальное рассмотрение все же позволяет обнаружить нелиней-
ность), то некоторые из них будут предметом обсуждения в при-
мерах и упражнениях,
1.2. Типы задач. Большинство последующих глав посвящено
либо изучению методов решения очень специальных типов задач
нелинейного программирования, либо исследованию тех типов
’) Это примерно соответствует книге Д. Б. Юдина и Е. Г. Гольштейна
[29*]. — Прим. ред.
Г2
Гл. 1. Введение
нелинейных задач; которые могут быть решены каким-то опре-
деленным методом. Представляется желательным вначале крат-
ко рассмотреть специальные классы задач нелинейного програм-
мирования, которым будет уделено наибольшее внимание, и
общие типы вычислительных методов, полезных для решения
задач этих классов. В этом параграфе мы остановимся на клас-
сах задач, а следующий параграф будет посвящен вычислитель-
ным методам. В дальнейшем, если только это не оговорено осо-
бо, предполагается, что на переменные не наложено условие
дискретности.
К классу задач нелинейного программирования, изученному
наиболее основательно, относятся задачи с линейными ограни-
чениями и нелинейной целевой функцией. В общем виде такая
задача записывается следующим образом:
п
/=1, 2......т, (1.6)
ху>0, /==1, 2.....я; (1.7)
найти max или min z —f (хп х2, ..хл), (1.8)
что читается так: найти неотрицательные значения п перемен-
ных Xj, удовлетворяющих ограничениям (1.6) и максимизирую*
щих или минимизирующих целевую функцию z=f(xbx2, хп).
Для удобства в этой формулировке на переменные наложены
условия неотрицательности. Задачи, в которых эти условия от-
сутствуют, сводятся к такой формулировке с помощью простого
преобразования, рассмотренного далее.
Даже для задач с линейными ограничениями вычислитель-
ные методы разработаны лишь в тех случаях, когда целевая
функция имеет определенные свойства. Два из них будут пред-
ставлять для нас особый интерес. В первом случае целевая
функция может быть записана как сумма п функций, каждая из
которых является функцией только одной переменной,, т. е.
Z=f (хи х2, . . ., Х„) = fi (Xj) + f2(X2)± • • + f „(*„) (1.9)
Чтобы гарантировать возможность отыскания оптимального ре-
шения, на fj(Xj) должны быть наложены добавочные ограниче-
ния. Какие—мы обсудим позднее. Если целевая функция мо-
жет быть записана в форме (1.9), она называется сепарабель-
ной. Иногда при изучении задач с сепарабельными целевыми
функциями и очень малым числом линейных ограничений мы
будем также рассматривать случай, когда переменные могут
принимать только целочисленные значения.
1,2. Типы задач
13
Во втором случае целевая функция может быть записана как
сумма линейной и квадратичной форм, так что
Z == / (Хь Х2...Хп) == Д CjXj -I- Д 2 citjxixj ==
==CjX1 С%Х% • • н~ СЯХЛ 4“ <1\\Х\ 4-4/12X1X2 4- ...
• • • (1\пХ\хя 4- ... 4- dnnXif (1.10)
Такие нелинейные задачи называются задачами квадратичного
программирования. Чтобы быть уверенным, что оптимальное
решение и в этом случае может быть найдено, на величины (1ц
следует наложить некоторые ограничения, которые мы не будем
сейчас рассматривать. Теории и методам решения задач квадра-
тичного программирования целиком посвящена гл. 7.
В силу многих причин, которые станут ясными в дальней-
шем, задачи с нелинейными ограничениями значительно более
трудны, чем с линейными. В дальнейшем эти задачи рассматри-
ваются, однако основное внимание здесь уделяется случаям,
в которых ограничения сепарабельны. Это означает, что функ-
ции gi(xi, х2, ..., хп) в (1.1) могут быть записаны в виде
gi(xx, х2, ..., x„) = gn(x1) 4- М + •• • + guM- (1.11)
Для того чтобы в задачах с ограничениями вида (1.11) было
возможно получение оптимального решения, на функции gtf(Xj)
и на целевую функцию должны быть наложены весьма жесткие
условия.
Имеется еще один класс задач с нелинейными ограниче-
ниями, на изучении которого мы остановимся. Задачи этого
класса относятся к классическим задачам оптимизации. Чтобы
получить о них представление, вернемся к общей задаче нели-
нейного программирования (1.1), (1.2) и допустим, что среди
ограничений нет неравенств, нет условий неотрицательности или
дискретности переменных, пг<п и функции g<(x\, х2, ..., хп) и
f(xi, х2, ..., хп) непрерывны и имеют частные производные по
крайней мере второго порядка. В этом случае задача приво-
дится к виду
^(хь х2,..x„) = djt i— 1, 2, .... m; (1.12)
найти max или min z = f(xi, x2,.... хя).
Задачи такого типа называются классическими задачами опти-
мизации. Особенность их состоит в том, что по крайней мере
в принципе эти задачи могут быть решены средствами класси-
ческих методов, основанных на использовании дифференциаль-
14
Гл. 1. Введение
ного исчисления. Однако обычно на этом пути встречаются
такие вычислительные трудности, которые делают необходимым
поиск других методов решения. В связи с этим будем рассма-
тривать классические методы не в качестве вычислительного
средства, а как теоретический аппарат, о котором важно иметь
представление, так как во многих областях он составляет основу
проводимого теоретического анализа. Например, значительная
часть экономической теории производства и поведения потреби-
теля основана на классических методах. Выделение задач
вида (1.12) в специальный класс и его изучение имеет своей
целью развитие теории классических методов оптимизации, а не
развитие вычислительных приемов для их решения. Классиче-
ские методы оптимизации изучаются в гл. 3.
Классические методы могут быть обобщены также на случаи,
когда переменные неотрицательны, а ограничения имеют вид
неравенств, однако эти обобщения имеют преимущественно
теоретическое значение и не дают конкретных вычислительных
приемов. Тем не менее мы увидим, что эти теоретические ре-
зультаты очень полезны. В случае квадратичного программиро-
вания они позволяют даже построить вычислительный метод.
Этим теоретическим обобщениям классических методов оптими-
зации будет посвящена гл. 6.
Другой класс задач нелинейного программирования, кото-
рым мы будем интересоваться, составляют задачи линейного
программирования с дополнительным требованием, чтобы пере-
менные принимали только целочисленные значения. Часто такие
задачи называют задачами целочисленного линейного програм-
мирования. Математическая формулировка их такова:
п
У аих, {<, —, >) bt, i = 1, 2, ..., tn,
Xj^O, /=1, 2, п, некоторые или все Xj — целые; (1.13)
п
найти max или min z—^CjXj.
j=i
Если все Xj должны быть целыми, то задача называется пол-
ностью целочисленной, а в противном случае — частично цело-
численной. Задачам целочисленного программирования целиком
посвящена гл. 8. Здесь изложены методы их решения и пока-
зано, что к такой постановке сводится большое число интерес-
ных задач.
Еще один класс нелинейных задач будет рассмотрен весьма
подробно. Это стохастические многошаговые задачи принятия
решений, часто встречающиеся в планировании производства,
1.3. Вычислительные методы
15
при управлении запасами и т. д. Сейчас мы не будем пытаться
привести их математическую формулировку. Скажем лишь, что
это пример того случая, когда переменные Xj являются функ-
циями других параметров.
1,3. Вычислительные методы. Симплексный алгоритм для ре-
шения общей задачи линейного программирования представляет
собой итеративную процедуру, с помощью которой точное опти-
мальное решение может быть получено за конечное число ша-
гов. Для задач нелинейного программирования вычислительный
метод, дающий точное оптимальное решение в конечное число
шагов, удается построить не всегда. Здесь часто приходится
соглашаться на использование методов, дающих только прибли-
женное решение или требующих для сходимости бесконечного
числа шагов.
Один из наиболее мощных методов решения задач, нелиней-
ного программирования состоит в преобразовании задачи ка-
ким-либо образом к виду, допускающему применение симплекс-
ного алгоритма (или одного из алгоритмов типа симплексного).
Таким образом, оказывается, что симплексный алгоритм служит
хорошим средством для решения не только линейных, но и не-
линейных задач. Природа «преобразования», с помощью кото-
рого нелинейная задача может быть приведена к форме, до-
пускающей применение симплексного метода, очень сильно
зависит от типа задачи. В некоторых случаях не требуется ни-
какой предварительной аппроксимации, в других аппроксима-
ция нужна. Однако эта аппроксимация может быть сделана
сколь угодно точной (ценой увеличения объема вычислений).
Другим полезным вычислительным методом для решения не-
которых типов задач нелинейного программирования является
динамическое программирование. Название настоящей книги
может вызвать мысль, что динамическое программирование от-
носится к специальному классу задач, отличных от задач нели-
нейного программирования. Некоторые оправдания у такого
предположения есть, так как термин «динамическое программи-
рование» часто применяется к таким задачам оптимизации,
в которых учитываются временные изменения и, следовательно,
время должно рассматриваться явно.
Здесь термин «динамическое программирование» не будет
использоваться в таком смысле. Вместо этого мы будем пони-
мать под ним вычислительный метод, использующий аппарат
рекуррентных соотношений, развитый в значительной степени
в работах Р. Веллмана. Сам термин «динамическое программи-
рование» возник в результате изучения задач математического
программирования, в которых были существенны изменения bq
16
Гл. 1. Введение
времени. Однако этот метод может быть использован и в таких
задачах, где время вообще не фигурирует, в связи с чем было
бы целесообразно ввести для него другое название. Однако тер-
мин «динамическое программирование» уже так прочно укре-
пился, что всякое его изменение трудно осуществимо.
Следует отметить, что мы используем этот термин в довольно
узком смысле: обычно мы встречаемся с ним при описании спе-
циального типа вычислительной процедуры; Впрочем, анализ
широкого класса функциональных уравнений также уклады-
вается в схему метода динамического программирования, при-
чем в этом случае он выступает не только как вычислительный,
но и как аналитический инструмент.
Последним вычислительным методом, который будет исполь-
зован, является градиентный метод. Как и симплексный метод,
он представляет собой итеративную процедуру, в которой мы
переходим шаг за шагом от одного допустимого решения к дру-
гому так, что значение целевой функции улучшается. Однако
в отличие от симплексного метода в нем не используется пере-
ход от одной вершины к другой. Вообще говоря, для сходимости
к решению здесь требуется бесконечное, число итераций.
1.4. Трудности, порождаемые нелинейностями. Прежде чем
приступить к детальному изучению специальных типов задач
нелинейного программирования, мы рассмотрим некоторые
черты нелинейных явлений, делающие эти задачи значительно
более трудными, чем линейные. Напомним, что для задач линей-
ного программирования характерно следующее:
а) Множество допустимых решений (т. е. множество всех то-
чек [хь х2, ..., хп] п-мерного пространства, удовлетворяющих
условиям (1.6) и условиям неотрицательности (1.7)) выпукло.
Это выпуклое множество имеет конечное число вершин, назы-
ваемых обычно крайними точками.
Ь) Множество всех точек [xi, х2, ..., хп] n-мерного простран-
ства, в которых целевая функция принимает заданное значение,
есть гиперплоскость. Кроме того, гиперплоскости, соответствую-
щие разным значениям целевой функции, параллельны.
с) Локальный максимум или минимум является также гло-
бальным максимумом или минимумом целевой функции на мно-
жестве допустимых решений, т. е. не существует локального
оптимума целевой функции, отличного от глобального оптимума.
(Допустимое решение доставляет глобальный (или абсолютный)
максимум целевой функции, если величина z для этого решения
по крайней мере не меньше, чем для любого другого допусти-
мого решения; допустимое решение доставляет целевой функ-
ции локальный максимум, если, грубо говоря, значение ? для
1.4. Трудности, порождаемые нелинейностями
17
этого допустимого решения больше, чем значение z для близких
допустимых решений.)
d) Если оптимальное значение целевой функции ограничено,
то по крайней мере одна крайняя точка множества допустимых
решений является оптимальным решением. Кроме того, начав
с произвольной вершины множества допустимых решений, мож-
но достичь оптимальной крайней точки в конечное число шагов,
причем на каждом шаге' совершается переход только в сосед-
нюю вершину. Окончательно, данная вершина является опти-
мальной тогда и только тогда, когда значение целевой функции
в ней по крайней мере не меньше, чем значения целевой функ-
ции во всех примыкающих вершинах.
У произвольной задачи нелинейного программирования неко-
торые или все эти свойства, характеризующие линейные задачи,
отсутствуют.
Задачи, содержащие только две переменные, легко могут
быть решены графически. Мы приведем сейчас несколько таких
графических примеров, чюбы проиллюстрировать более на-
глядно разницу между линейными и нелинейными задачами.
Рассмотрим сначала следующую задачу линейного программи-
рования:
*1 + х2 'С 6,
*1 — х2 < 1,
2х1 + х2>6, <1Л4>
0,5%! — х2 > — 4,
Xi > 1, х2 > 0;
найти max z = CUJxj + 2х2.
Графическое решение показано на рис. 1.1. Область допусти-
мых решений заштрихована. Оптимум достигается в вершине.
Значения переменных, доставляющих максимум целевой функ-
ции, единственны и являются координатами точки пересечения
линий Xi+X2 = 6, 0,5*1—х2 = —4. Оптимальные значения пере-
менных есть х* = 4/3, х* = 14/3. Максимальное значение целе-
вой функции г* =10.
Рассмотрим теперь задачу нелинейного программирования,
которая отличается от предыдущей только тем, что целевая
функция имеет вид
г=10(х1 — 3,5)2 + 20(х2 — 4)2. (1.15)
Пусть решается задача на минимум. Заметим, что здесь мы
имеем сепарабельную целевую функцию и решаемая задача
имеет вид (1.6) — (1.9). Графическое решение задачи дано на
2 Зц«. 735
18
Гл. 1. Введение
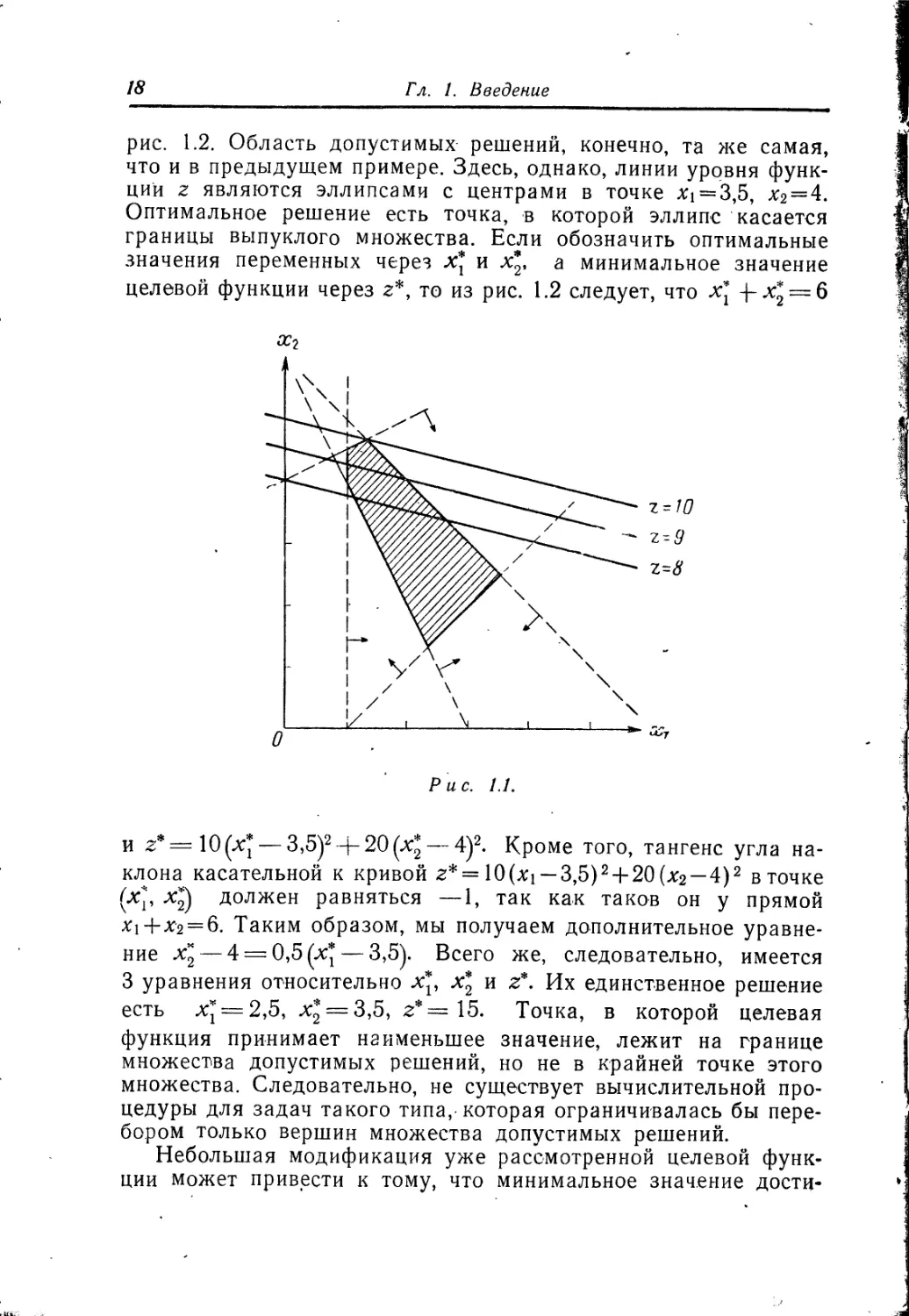
рис. 1.2. Область допустимых решений, конечно, та же самая,
что и в предыдущем примере. Здесь, однако, линии уровня функ-
ций z являются эллипсами с центрами в точке %i = 3,5, х2=4.
Оптимальное решение есть точка, в которой эллипс касается
границы выпуклого множества. Если обозначить оптимальные
значения переменных через х* и х*. а минимальное значение
целевой функции через г*, то из рис. 1.2 следует, что х* -рх* = 6
и г*=10(х*— 3,5)2-|-20(х* — 4)2. Кроме того, тангенс угла на-
клона касательной к кривой z* = 10(xi~3,5)2 + 20(х2—4)2 в точке
(х*, х*) должен равняться —1, так как таков он у прямой
Х1 + Х'2 = 6. Таким образом, мы получаем дополнительное уравне-
ние х* — 4 = 0,5(х*— 3,5). Всего же, следовательно, имеется
3 уравнения относительно х*, х* и z*. Их единственное решение
есть х* = 2,5, х* = 3,5, z*= 15. Точка, в которой целевая
функция принимает наименьшее значение, лежит на границе
множества допустимых решений, но не в крайней точке этого
множества. Следовательно, не существует вычислительной про-
цедуры для задач такого типа, которая ограничивалась бы пере-
бором только вершин множества допустимых решений.
Небольшая модификация уже рассмотренной целевой функ-
ции может привести к тому, что минимальное значение дости-
1.4. Трудности, порождаемые нелинейностями
19
гается во внутренней точке этого, множества. Пусть, например,
целевая функция имеет вид
г == 10 (Xj — 2)2 + 20 (х2 — З)2, (1.16)
а множество допустимых решений то же, что и раньше (см.
рис. 1.3). Оптимальные значения xi9 х2 и z есть х* = 2, х* = 3,
z* = 0. Таким образом, оптимизирующая точка не обязательно
лежит на границе. Отметим, что в рассмотренном случае мини-
мум целевой функции при наличии ограничении и условий не-
отрицательности тот же, что и без них. В таких случаях мы бу-
дем говорить, что ограничения несущественны.
В каждом из рассмотренных примеров локальный оптимум
совпадал с глобальным. Легко, однако, привести примеры, где
это будет не так. Рассмотрим следующую задачу с линейными
ограничениями и сепарабельной'целевой функцией (рис. 1.4):
Xi -|- х2 2,
Xj — х2 —2,
%1 4~Х2 6,
— Зх2 < 2,
хп х2 > 0;
найти max z — 25 (Xj — 2)2 -|- (х2 — 2)2.
20
Гл. 1. Введение
Нетрудно понять, что в вершине 4 достигается глобальный
максимум целевой функции. Вместе с тем в вершине 2 дости-
гается относительный максимум целевой функции, отличный от
глобального (значение целевой функции в точке 2 больше, чем
значения ее в соседних вершинах 1 и 3).
Здесь мы имеем случай, когда глобальный экстремум цеЛе-
вин функции достигается в вершине выпуклого множества до-
IА. Трудности, порождаемые нелинейностями
21
пустимых решений. Кроме того, существует другая вершина,
в которой достигается относительный экстремум (по отношению
к соседним вершинам), отличный ог глобального. Следует отме-
тить, что в задачах такого типа глобальный экстремум дости-
гается в вершине, однако нет возможности использовать вы-
числительную процедуру симплексного типа (основанную на
переходе от одной вершины к соседней, которая оканчивалась
бы при достижении вершины, доставляющей относительный экс-
тремум целевой функции по сравнению со всеми соседними вер-
шинами. Такая процедура может привести к относительному, но
не обязательно к глобальному оптимуму.
Если задача содержит нелинейные ограничения, то не сохра-
няет силу утверждение о выпуклости области допустимых реше-
ний. Более того, она может даже состоять из нескольких несвя-
занных областей. Пусть, например, ограничения имеют вид
(Xj —1)Х2<1,
(1-18)
X] —1~ х2 3,5,
и переменные должны быть неотрицательны. Множество до-
пустимых решений в этом случае состоит из двух отдельных
частей, ни одна из которых не выпукла (рис. 1.5). Если мно-
жество допустимых решений не выпукло, то может существовать
отличный от глобального локальный оптимум даже при линей-
ной целевой функции.
22
Гл. Введение
Для- задач нелинейного программирования, имеющих отлич-
ные от глобального локальные оптимумы, большинство вычисли-
тельных методов, которые мы будем рассматривать, позволяет
найти точку именно локального оптимума. В общем случае они
не позволяют установить, совпадает л.и она с точкой глобаль-
ного оптимума. Тем не менее эти методы отыскания локального
оптимума часто оказываются очень полезными на практике.
Единственный вычислительный метод, приводящий к глобаль-
ному оптимуму независимо от числа локальных экстремумов,—
это метод динамического программирования. Следовательно,
если задача может быть решена с помощью динамического про-
граммирования, мы всегда получаем возможность отыскать гло-
бальный оптимум.
Последней мы рассмотрим следующую задачу целочислен-
ного программирования (рис. 1.6):
ОДлх-г х2< 1,75,
^ + 0,30X2 <1,50, (1Л9)
хн аг2:>0, Хр х2— целые;
найти max z = 0,25%! 4-х2.
Заштрихованная область была бы выпуклым множеством допу-
стимых решений при отсутствии целочисленных ограничений.
1.5. Краткий исторический обзор
23
При учете требования целочисленности переменных Xj имеется
лишь четыре допустимых решения, изображенных кружочками
на рис. 1.6. Если игнорировать требования целочис/Лшости, то
решение соответствующей задачи линейного программирова-
ния есть х* = 0, х*=1,75, г*—1,75. Однако при учете цело-
численности оптимальным решением будет •х*=1, х*=1,
1,25. Отметим, что это решение не совпадает с тем, которое
было бы получено путем решения задачи линейного программи-
рования с последующим округлением результатов до ближай-
ших целых, удовлетворяющих ограничениям (таким путем мы
получили бы Xi = 0, л'2=1 иг=1).
1.5. Краткий исторический обзор. Уже было отмечено, что
искрой для феноменального роста интереса к теории и практике
математического программирования послужило открытие в
1947 г. вычислительного метода для решения задач линейного
программирования. Этот численный метод, названный симплекс-
методом, был разработан Данцигом, когда он был членом груп-
пы 15уда, работавшей над некоторыми типами задач математи-
ческого программирования для ВВС США. Хотя метод и был
разработан в 1947 г., широко известен он стал лишь со времени
опубликования в 1951 г. книги [16].
Интерес к нелинейным задачам рос одновременно с интере-
сом к линейному программированию. В 1951 г. Кун и Таккер
опубликовали работу [17], в которой приведены необходимые и
достаточные условия оптимальности для решений нелинейных
задач. Эта важная работа послужила основой для многих по-
следующих работ в нелинейном программировании. Некоторые
обобщения их теоретических исследований, сделанные другими
авторами, появились позднее в книге, изданной в 1958 г. под
редакцией Эрроу, Гурвица и Удзавы (см. [1]).
В 1954 г. Чарнс и Лемке опубликовали приближенный метод
решения задач с сепарабельной выпуклой целевой функцией и
линейными ограничениями [6]. Альтернативная формулировка
этой задачи была дана Данцигом [7]. Позднее этот метод был
обобщен Миллером [21] на случай сепарабельных ограничений.
Начиная с 1955 г. начало появляться большое число работ раз-
личных авторов, посвященных квадратичному пограммированию.
Сюда относятся работы Баранкина и Дорфмана [2] (1955).
Била [3] (1955), Франк и Вольфа [10] (1956), Марковица [19]
(1956), Хилдрета [14] (1957), Хаутеккера [15] (1957) и Вольфа
[23] (1959). Еще ряд работ появился после 1959 г. Все перечис-
ленные работы, за исключением статьи Баранкина и Дорфмана,
содержали мало отличающиеся между собой вычислительные
методы для решения задач квадратичного программирования.
24
Гл. 1. Введение
Наиболее известным среди них является метод, предложенный
Вольфом. Его преимущество состоит в том, что он приводит за-
дачу к форме, допускающей применение симплекс-метода. По-
дробно этот метод будет рассмотрен в гл. 7.
Интерес к целочисленным решениям задач линейного про-
граммирования появился в начале раз-Ьития математического
программирования. Одна из первых работ, посвященных этому
вопросу, было опубликована Данцигом, Фалкерсоном и Джонсо-
ном [8] в 1954 г. В более поздней работе Марковица и Манне [20)
обсуждались вычислительные методы и, кроме того, были приве-
дены некоторые типы нелинейных задач, сводящихся к целочис-
ленному программированию. Хотя эти работы и содержат вы-
числительные приемы для решения задач целочисленного про-
граммирования, первым по сути дела оказался Гомори [11, 12],
так как им был разработан вычислительный метод, приводивший
к оптимальному решению за конечное число итераций. Это было
сделано в 1958 г. для полностью целочисленной задачи и в
1960 г. — для частично целочисленной.
История динамического 'программирования тесно связана с
именем Р. Веллмана, сделавшего самый большой вклад в раз-
витие этого метода и опубликовавшего свои результаты за
50-е годы более чем в 100 статьях. Итоги его работы содержатся
в книге «Динамическое программирование» [4] и в написанной
им вместе с Дрейфусом книге «Прикладные задачи динамиче-
ского программирования» [5].
Градиентные методы уже давно интересуют математиков и
физиков. Внимание на возможность их использования для реше-
ния задач нелинейного программирования было обращено в уже
упоминавшейся книге [1]. Деннис [9], по-видимому, одним из
первых предложил вычислительный алгоритм, хотя и не разра-
ботанный в деталях. Позднее несколько различных алгоритмов
были развиты Зойтендейком [24] и Розеном [22]. Большое коли-
чество работ, посвященных этому вопросу, появилось в послед-
нее время.
Этот краткий исторический обзор доводит нас до 1962 г. Мы
не делаем попытки проследить развитие классических методов
оптимизации, берущих свое начало в XVIII в. Свой вклад сюда
г несли такие великие математики, как Ньютон, Лагранж, Бер-
нулли, Гамильтон и Вейерштрасс.
В этом очень кратком историческом обзоре мы перечислили
лишь те работы, которые представляются наиболее важными
сегодня. Следует сказать, однако, что нелинейное программиро-
вание находится еще в состоянии непрерывного развития, и
история, написанная несколькими годами позже, возможно, от-
метит совсем другие факты. Точно так же некоторые или даже
1.6. Обзор дальнейшего содержания
25
все вычислительные методы, рассматриваемые в этой книге, мо-
гут быть вытеснены более эффективными в не очень далеком
будущем.
1.6. Обзор дальнейшего содержания. В следующей главе мы
рассмотрим некоторые вопросы линейной алгебры, линейного
программирования и анализа, которые нам понадобятся в даль-
нейшем. Главная цель этой главы — ввести обозначения и слу-
жить кратким справочником. В большинстве случаев доказа-
тельства не приведены, так как предполагается, что читатель
более или менее знаком с материалом.
В гл. 3 рассматриваются классические методы оптимизации.
Здесь же рассмотрены свойства выпуклых и вогнутых функций.
Глава 4 посвящена изучению задач нелинейного программи-
рования с сепарабельными целевыми функциями и ограниче-
ниями.
В гл. 5 изучаются задачи стохастического программирования,
т. е. такие, в которых некоторые параметры являются случай-
ными.
В гл. 6 обсуждается работа Куна и Таккера, посвященная
обобщению классических условий оптимальности на задачи с
ограничениями типа неравенств и условиями неотрицательности
переменных.
В гл. 7 эти результаты применяются для изучения задач
квадратичного программирования. С их помощью здесь обосно-
вывается метод Вольфа. Другие вычислительные методы рас-
сматриваются весьма кратко. Обсуждаются также вопросы
двойственности в применении к задачам квадратичного програм-
мирования.
В гл. 8 рассматривается целочисленное линейное программи-
рование и алгоритмы Гомори обобщаются на случай полностью
и частично целочисленных задач. Здесь также показано, что
многие интересные задачи нелинейного программирования мо-
гут быть сведены к целочисленным.
В гл. 9 изучается несколько типов градиентных методов для
решения задач нелинейного программирования.
Главы 10 и 11 посвящены динамическому программирова-
нию. Так как этот термин относится скорее к вычислительной
методике, чем к специальному типу задач, в этих главах рас-
сматриваются довольно разнообразные задачи. Показано, что
динамическое программирование можно, по крайней мере теоре-
тически, использовать для решения многих задач нелинейного
программирования. Мы увидим, однако, что имеются строгие
ограничения на типы задач, которые могут быть решены чис-
ленно.
26
Гл. 1. Введение
ЛИТЕРАТУРА')
1. Э р р о у К. Дж., Гурвиц Л., У д з а в а X., Исследования по линейному
и нелинейному программированию, ИЛ, М., 1962.
2. В а г а п к i n Е. W., Dorfman R., Towards Quadratic Programming,
Office of Naval Research Logistics Projects at Columbia University and
University of California, Berkeley, 1955.
3. Beale E. M. L., On Minimizing a Convex Function. Subject to Linear
Inequalities, J. Roy. Statist. Soc. (B), 17 (1955), 173—184.
4. Веллман P., Динамическое программирование, ИЛ, M., 1960.
5. Веллман Р., Дрейфус С., Прикладные задачи динамического про-
граммирования, изд-во «Наука», М., 1964.
6. С h а г n е s A., L е m k е С., Minimization of Nonlinear Separable Convex
Functionals, Nav. Res. Logist. Quart., 1 (1954), 301—312.
7. D a n t z i g G. B., Recent Advances in Linear Programming, Manag. Sci.,
2 (1956), 131 — 144.
8. D a n t z i g G. B., Fulkerson D. R., Johnson S., Solution of a Large-
Scale Traveling-Salesman Problem, J. Operat. Res. Soc. Amer., 2 (1954),
393—410.
9. Деннис Дж. Б., Математическое программирование и электрические
цепи, ИЛ, М., 1961.
10. Frank М., Wolfe Р., An Algorithm for Quadratic Programming, Nav.
Res. Logist. Quart., 3 (1956), 95—110.
11. G о m о г у R., Essentials of an Algorithm for Integer Solutions to Linear
Programs, Bull. Amer. Math. Soc., 64 (1958), 275—278.
12. Go mor у R., An Algorithm for the Mixed Integer Problem, RM-2597,
RAND Corp., 1960.
13. Had Ге у G., Linear Programming, Reading, Addison-Wesley, 1962.
14. Hildreth C., A Quadratic Programming Procedure, Nav. Res. Logist.
Quart., 14 (1957), 79—85.
15. Houthakker H., The Capacity Method of Quadratic. Programming,
Econometrica, 28 (1960), 62—87.
16. Koop mans T. (ed.), Activity Analysis of Production and Allocation,
New York, Wiley, 1951.
17. Kuhn H. W., Tucker A. W., Nonlinear Programming, Proc. Second
Berkeley Symp. on Math. Statistics and Probability, 1951, 481—492.
18. Lemke C., The Constrained Gradient Method of Linear Programming,
J. Soc. Indust, and Appl. Math., 9 (1961), 1—17.
19. Markowitz H., The Optimization of a Quadratic Function Subject to
Linear Constraints, Nav. Res. Logist. Quart., 3 (1956), 111 —133.
20. Ma rkowitz H., Manns A. S., On the Solution to Discrete Programm-
ing Problems, Econometrica, 25 (1957), 84—110.
21. Miller С. E., The Simplex Method for Local Separable Programming,
in Graves R., Wolfe P. (ed.), Recent Advances in Mathematical Pro-
gramming, New York, McGraw-Hill, 1963.
22. Rosen J., The Gradient Projection Method for Nonlinear Programming.
Part I. Linear Constraints, J. Soc. Indust, and Appl. Math., 9 (1960), 181—217.
23. Wolfe P., The Simplex Method for Quadratic Programming, Econometri-
ca, 27 (1959), 382—398.
24. Z о u t e n d i j k G., Maximizing a Function in a Convex Region, J. Roy.
Statist. Soc. (B), 21 (1959), 338—355.
25* . Гол ьштейн E. Г., Юдин Д. Б., Новые направления в линейном про-
граммировании, изд-во «Советское радио», М., 1966.
J) Звездочкой отмечены названия, включенные переводчиками и редак-
тором перевода. — Прим. ред.
Упражнения
27
26*. 3 о й т е н д е й к Г., Методы возможных направлений, ИЛ, М., 1963.
27*. Канторович Л. В., Математические методы организации и .планиро-
вания производства, Л., 1939.
28*. Канторович Л. В., Об одном эффективном методе решения некото-
рых классов экстремальных проблем, ДАН СССР, 28 (1940), № 3, 212—
215.
29*. Юлин Д. Б., Гольштейн Е. Г., Задачи и методы линейного про-
граммирования. изд-во «Советское радио», М., 1961.
30*. Graves R., Wolfe Р. (ed.), Recent Advances in Mathematical Pro-
gramming, New York, McGraw-Hill, 1963.
Упражнения
РенЙгть следующие задачи нелинейного программирования и проиллю-
стрировать их с помощью геометрических построений:
1.1. 0,5%) -|~х2 < 4,
3х । х 2 4$^ 15,
Х| -j— Л" 2 1,
хн х2 > 0;
найти min z — 4 (хх — 6)2 6 (х2 — 2)2.
1.2. 0,5х, 4-х2 4,
Зх] —|— х2 15,
хи х2 >> 0;
найти max z — 3 (хх — 1,5)2 4- 6 (х2 — 1,5)2.
1.3. xt — х2 > 0,
Xj + *2 < 4,
Xj < 3; х-
найти max и min г = 2хг -f- Зх2 + 4х? -|- 2хгх2 +
1.4. (Xi— 2)2 + (х2—1)2<9,
Xi , х2 >> 0;
найти max z — 3xi -ф- 2х2.
1.5. х{х2 1,
Х14“ Л2 9;
найти min z — 7 (xj — 6)2 -}- 3 (х2 — 4)2.
28
Гл, 1. Введение
1.6. ххх2 1,
*14--«2<9,
*i<2,
х(, х2>0;
найти max z «* 8л^ 4* 2*1
1.7.
4“ *2 3,
хь х2>0;
найти min г ~ 6 (X) — 5)2 4“ (*г — 4)*.
1 -8. Зх । 4" 2х2 9,
** 0.5х । 4- *2 < 4,
Х|, х2 >0;
найти max-г = х,х2.
1.9. (лг, — 3) (л;2 — 3) » 1
Х|. *2>0;
найти max и min^»^—2,5)24-С*г— 3,5)*.
1.10. (Х, _ 3)(х2 —3)< 1,
хь х2>0;
найти min z ® (*, — 6)2 4* (*г — 8)2.
111. Х| 4~*2<5’
0,Зх} 4* 3>
Х|. х2 >0;
найти max и min z » 5х\ 4"3х1 — 4л2.
1.12. 2л( — х2>0,
0,5*! — х2 < 0,
*1 4- *2 < 5,
х{, х2>0, х{ и х2—-целые;
найти max z » 4xj 4~ Зх2.
1.13. 2Х| — х2 > О,
0,5Х|—х2<0.
х} + х2 < 5,
*2 > 9, х} — целое. х2 — непрерывно;
найти max z 4х} 4е
ГЛАВА 2
НЕОБХОДИМЫЙ МАТЕМАТИЧЕСКИЙ АППАРАТ
Все, что случилось с нами, лишь пролог
К тому, что мы с тобой должны свершить.
Шекспир. Буря
2.1. Матрицы и векторы. Справочный материал, излагаемый
в этой главе, касается линейной алгебры и линейного програм-
мирования. Подробное изложение этих вопросов читатель най-
дет в работах автора «Линейная алгебра» [3] и «Линейное про-
граммирование» [4] *). В дальнейшем мы будем часто ссылаться
на эти работы. Для удобства ссылок примем сокращенные обо-
значения: так, {ЛА 3.6} будет означать ссылку на § 6 3-й главы
книги «Линейная алгебра»; при ссылке на книгу «Линейное
программирование» вместо ЛА будем писать ЛП.
Под матрицей мы будем понимать прямоугольную таблицу
действительных чисел. Эти числа называются элементами мат-
рицы. Для обозначения матриц обычно используют заглавные
буквы, например А, В и т. д. Элементы матрицы мы будем обо-
значать малыми буквами, имеющими двойной индекс, напри-
мер atj, bij. Таким образом, мы можем записать
а12 • •. а1л
#21 #22 • • * #2л
А-|1М“ • » •
_#/и1 #т2 • • • ^тп
(2,1)
Матрицу можно задать, указав ее общий элемент. В этом слу-
чае мы используем обозначение ||а<>||. Матрица А в (2.1) назы-
вается матрицей с размерами тХп — она имеет т строк и
п столбцов. Первый индекс элемента а^ означает номер строки,
') Необходимые сведения по линейному программированию советский чи-
татель может найти в упоминавшейся в гл. 1 книге Д. В. Юдина и
Е. Г. Гольштейна. — Прим. ред.
30
Гл. 2. Необходимый математический аппарат
а второй — номер столбца, в которых находится этот элемент.
Если т = п, то говорят, что матрица квадратная и имеет поря-
док п.
Две матрицы А и В считаются равными (А=В) тогда и
только тогда, когда все их соответствующие элементы равны,
т. е. a^ = bij для всех i и /. Чт.обы сложить две матрицы с раз-
мерами mXn, необходимо сложить их соответствующие эле-
менты; сумма матриц А и В обозначается через А + В. Сложе-
ние матриц подчиняется ассоциативному и коммутативному
законам
АЧ-В4-С = (А4-В) + С = А + (В4-С) и А4-В = В4-А.
В дальнейшем мы часто будем называть действительные
числа скалярами. Произведение матрицы А на скаляр X (пи-
шется ЛА или АЛ) получается умножением каждого элемента
матрицы А на Л:
XA = ||U0||.
Заметим, что А + А = 2А и если А = В, то ЛА = ЛВ. Вычитание
матриц можно определить, пользуясь уже введенными поня-
тиями:
А —В = А-Н—1)В.
Произведение АВ матриц А и В может быть определено
лишь тогда, когда число столбцов матрицы А равно числу строк
матрицы'В. Если А — матрица с размерами тХг, а В — с раз-
г
мерами гХп, то С==АВ имеет размеры тХп и S aikbkj.
k^i 7
Умножение матриц ассоциативно,
АВС = (АВ) С == А (ВС),
но в общем случае не коммутативно, так что АВ не всегда рав-.
но ВА.
Матрица называется нулевой, если все ее элементы равны
нулю. Нулевая матрица обозначается символом 0. Если соот-
ветствующие операции выполнимы, то
А + О = А = О+А и А0 = 0А = 0.
В общем случае из равенства АВ = 0 не следует, что либо
А = 0, либо В = 0. Существуют ненулевые матрицы, произведе-
ние которых равно нулевой матрице.
Квадратная матрица называется диагональной, если < 0^ = 0
при i=/=j; говорят, что элементы ац лежат на главной диагонали
матрицы (идущей из левого верхнего угла в правый нижний
2.1. Матрицы и векторы
31
угол). Диагональная матрица, для которой все ац равны между
собой, ац = к, называется скалярной матрицей. Если воспользо-
ваться символом Кронекера который равен 0, если /=£/, и
единице, если i~j, то диагональная и скалярная матрицы могут
быть записаны в виде Наиб^Н и Между множеством всех
скалярных матриц ||Хб^|1 порядка п и множеством всех действи-
тельных чисел л имеется полная аналогия. Квадратная матрица
1 = ||6^|| называется единичной матрицей. Иногда, чтобы указать
порядок единичной матрицы, мы будем символ I снабжать ниж-
ним индексом, например 1п. В единичной матрице единствен-
ными элементами, отличными от нуля, являются элементы глав-
ной диагонали; эти элементы равны единице. Таким образом,
например,
Г1 О
1з= 0 1
~0 О
О’
о
1 _
Если А —матрица с размерами тХм, то IwA = AIn = A. Кроме
того, 11 = 1.
Матрицей, транспонированной для матрицы А с размерами
тХп, называется матрица с размерами пХ/п, получающаяся
из А заменой строк на столбцы. Таким образом, первая строка
матрицы А становится первым столбцом транспонированной
матрицы и т. д. Матрица, транспонированная для матрицы А,
обозначается через Az. Если Az = || а'.. ||, то = ajr .Нам бу-
дут полезны следующие свойства:
(A + B)Z = AZ + BZ,
• (AZ)Z = A, (AB)Z = B AZ. .
Отметим, что матрица, транспонированная для произведения
матриц, равна произведению транспонированных матриц-сомно-
жителей, взятых в обратном порядке {ЛА 3.7}. Квадратная
матрица А называется симметрической, если A = AZ, т. е. ац—ац.
Квадратная матрица А называется кососимметрической, если
А = —Az, т. е. ао = —ац~0.
Если мы в матрице А с размерами mXn вычеркнем все
строки и столбцы, кроме выбранных t строк и и столбцов, то в
результате мы получим матрицу с размерами tXu, которая на-
зывается подматрицей матрицы А. В некоторых случаях, напри-
мер для иллюстрации особенностей структуры матрицы или для
упрощения умножения матриц, удобно разбивать матрицу на
подматрицы .(блоки). Такое разбиение можно осуществить, про-
ведя разбивающие прямые между выбранными строками и
32
Гл. 2. Необходимый математический аппарат
столбцами. Так, например, выглядит одно из возможных раз-
биений матрицы с размерами 4X4:
#12 #13 i #14
А — #21 #22 #23 • #24 ГАп
л — #31 #32 #33 : #34 LA21
— #41 #42 #43 i #44-
Л12
^22
Получившиеся в результате разбиения блоки мы обозначили
через Aij. Если существует произведение АВ матриц А и В, то
это произведение может быть вычислено с помощью блочного
умножения при условии, что столбцы матрицы А и строки
матрицы В разбиты одинаковым образом. При этом сам способ
разбиения не имеет значения. Например, если произведение АВ
существует и столбцы матрицы А разбиты тем же способом, что
и строки йатрицы В, так что
Вп
и В = В21
-В31 -
Ап А12 А13
-A2i А22 А23
А =
то
АВ АцВц + А12В214- А13В31
L А21ВП+а22в21+а23в31 j
Более подробно разбиение матриц рассматривается в {ЛА 3.9}.
Матрицы, состоящие из одной строки или одного столбца,
часто называют векторами. Матрица, состоящая из одной стро-
ки, называется вектором-строкой, а матрица, состоящая из од-
ного столбца, — вектором-столбцом. Вектор-строку мы будем
записывать в виде а= (#ь ..., #п), а вектор-столбец — в виде
а=[#ь ..., ап]. Вектор (#ь ..., ап) или [#ь ..., ап} называется
n-мерным, а число #; — его i-й компонентой или координатой. ,
В дальнейшем нам придется иметь дело в основном с векто- I
рами-столбцами. Поэтому ниже, если не оговорено противное, j
мы будем считать всякий вектор вектором-столбцом. Часто мы
будем рассматривать такое разбиение матрицы А с размерами
/иХп, что каждая ее подматрица совпадает с одним из ее столб-
цов, т. е. матрица А в этом случае представляет собой строку I
векторов-столбцов. Если столбцы матрицы А обозначить через j
а> = [#и, ...» ОтпД то A=(ai, ..., ап). Аналогично матрицу A ।
можно представить в виде столбца из векторов-строк. Если
строки матрицы А обозначить через а^=(#гь ain), тО’ |
А = [а!, ат]. I
2.1. Матрицы и векторы
3$
Часто удобно n-мерный вектор понимать как точку в ц-мер-
ном пространстве. Таким образом, геометрической интерпрета-
цией вектора является точка. В этом смысле вектор-строка и
вектор-столбец не различаются. Используя геометрический язык,
мы будем поэтому часто векторы называть точками. В двумерт
ном и трехмерном пространствах вектор удобно представлять
в виде направленного отрезка, идущего из начала координат
в точку, характеризующую вектор. В этом случае легко могут
быть проиллюстрированы такие операции над векторами, как
умножение на скаляр (рис. 2.1) и сложение (рис. 2.2).
Чтобы показать, что n-мерное пространство, являющееся
совокупностью всех n-мерных векторов, обладает свойствами,
аналогичными свойствам обычных двумерных и трехмерных
пространств, введем для этого пространства понятия системы
координат и расстояния. Для этого рассмотрим п п-мерных
векторов
в1 =-[1, 0, 0], е2 = [0, 1, 0,0], ...» ей = [0, 0, 0, 1],
называемых единичными векторами. Тогда любой n-мерный век-
тор может быть записан в виде
а == [ап ..., ап\ — -]-•••+ cint}V (2.2)
Говорят, что вектор а является линейной комбинацией дан-
ных векторов аь ..., а&, если существуют такие скаляры Х;-, что
k
a-^S^Ar Из равенства (2.2) видно, что любой n-мерный векг
тор может быть представлен как линейная комбинация единич-
ных векторов. Единичные векторы могут быть использованы для
определения системы координат: оси координат в этой системе
3 Зак. 735
34
Гл. 2. Необходимый математический аппарат
определяются началом координат 0 = [0, 0, 0] и каждой из
точек е,.
Скалярным произведением двух n-мерных векторов а и Ь
п
называется число S afi^ Если а и b — векторы-столбцы, то это
число можно записать как произведение матриц а'Ь (мы не бу-
дем отличать матрицу, состоящую из одного элемента, от соот-
ветствующего действительного числа). Если а — вектор-строка,
а b — вектор-столбец, то их скалярное произведение может быть
записано в виде ab. Отметим, что для векторов-столбцов а'Ь = Ь'а
и для любого скаляра Л (Ла')Ь = а'(ЛЬ) =Х(а'Ь). Расстояние
|а—Ь| между двумя точками (векторами) а и b определяется
следующим образом:
| а — Ь | = [(а — Ь)' (а — Ь)]1/2 =
п
(2.3)
Это определение расстояния является прямым обобщением опре-
деления расстояния в двумерных и трехмерных пространствах.
Длиной или абсолютной величиной |а| вектора а называется
расстояние от начала координат до точки а: |а| = |а — 0j. Сово-
купность всех n-мерных векторов ..., ап] вместе с расстоя-
нием, определенным выражением (2.3), будем называть п-мер-
ным евклидовым пространством и обозначать символом Еп.
Символы Е2 и Е3 означают обычные двумерные и трехмерные
пространства, рассматриваемые в аналитической геометрии.
Для любых двух n-мерных векторов а и b справедливо нера-
венство |а'Ь|<Ца| |Ь|, где |а'Ь( —абсолютная величина скаляр-
ного произведения. Это неравенство известно под названием не-
равенства Шварца1). Если а, Ь¥=0, то угол 0 между векто-
рами а и Ь определяется соотношением
cos0==T^TbT’ (2-4)
Вследствие неравенства Шварца |cos0|-<l, и мы всегда можем
определить угол 0 так, что О^0^л. В Е2 и Е3 это угол между
направленными отрезками, соответствующими векторам а и Ь
{ЛА 2.3}. Два вектора называются ортогональными, если а'Ь = 0.
Таким образом, если а, Ь=#0, то они ортогональны тогда, когда
угол между ними равен л/2. Единичные векторы ортогональны:
е<еу. = 0, /=£ / Система координат, определяемая единичными
векторами, называется ортогональной.
9 В советской математической литературе указанное соотношение обыч-
но называется неравенством Буняковского. — Прим. ред.
2.1. Матрицы и векторы
35
Примем обозначения: а>Ь означает, что /=1, ..., п
и а>Ь — что aj>bh /=1, .... п.
Векторы аь ..., afe называются линейно зависимыми, если
существуют числа Xj, не все равные нулю, такие, что
*
2М/ = 0; (2.5)
в противном случае векторы называются линейно независимыми.
Если векторы линейно независимы, то соотношение (2.5) выпол-
няется лишь тогда, когда BceXj=0, /=1, ..., k. Конечное мно-
жество векторов является линейно зависимым тогда и только
тогда, когда один из векторов может быть представлен в виде
линейной комбинации остальных {ЛА 2.7}. Если множество, со-
стоящее из k векторов, линейно независимо, то любое •подмно-
жество этого множества также линейно независимо. Говорят,
что число г является максимальным числом линейно независи-
мых векторов для некоторого множества, если в этом множестве
имеется по крайней мере одно подмножество, состоящее из г ли-
нейно независимых векторов, и нет ни одного подмножества, со-
держащего г+1 линейно независимых векторов. Нулевой вектор
линейно зависим по отношению ко всем остальным векторам, и
множеств линейно независимых векторов, содержащих его, не
существует. Единичные векторы линейно независимы, так как
п
из равенства •••> ^л]=0 следует, что Х? = 0,
/-1
/ = 1, ..., п.
Говорят, что множество векторов а1э..., аг из Еп порождает
пространство Еп, если любой вектор, принадлежащий Еп, мо-
жет быть представлен в виде линейной комбинации векторов
ai, ..., аг. Базисом Е” называется линейно независимое под-
множество векторов из Еп, порождающее все пространство. Из
предыдущего ясно, что единичные векторы представляют собой
базис Еп. Любое множество векторов, образующих базис в про-
странстве Еп, может быть использовано для введения в нем си-
стемы координат. Представление любого вектора в виде линей-
ной комбинации базисных векторов единственно {ЛА 2.8}.
В линейном программировании часто рассматривается опера-
ция изменения базиса путем замены в нем одного вектора.
Пусть имеется множество базисных векторов аь ..., аг для Еп
г
и какой-нибудь другой вектор d=£0. Тогда d=2a.a/. Если
/==1 7
один из векторов а7, для которого aj=A0, удалить из базиса и
вместо него ввести вектор d, то новое множество из г векторов
также будет базисом для Еп {ЛА 2.9}. Если х — произвольный
3*
36 Гл. 2. Необходимый математический аппарат
вектор из £п, х = 2 ^уау» то после замены а& на d мы, разрешив
Г / = 1
уравнение d=2aJaJ относительно и подставив результат в
г ;=i
*Х= 2 получим
а/
«Л
— d.
(2.6)
Если d замещает вектор а;, для которого aj = 0, то новое множе-
ство векторов оказывается линейно зависимым и, следовательно,
не может быть базисом.
Любой базис пространства Еп содержит в точности п векто-
ров; любые п линейно независимых векторов из Еп составляют
базис Еп. Отсюда следует, что любые п+1 векторов из Еп ли-
нейно зависимы. При т<п любые m линейно независимых век-
торов образуют часть базиса пространства Еп. Таким образом,
существует бесконечное число базисов для Еп. Доказательство
всех этих фактов можно найти в {ЛА 2.10}.
Подпространством S пространства Еп называется множество
векторов из Еп', замкнутое относительно операций сложения и
умножения на скаляр. Размерность подпространства опреде-
ляется как максимальное число линейно независимых векторов
в этом подпространстве. Любое подпространство должно содер-
жать начало координат, так как подпространство замкнуто от-
носительно умножения на скаляр. Таким образом, подпростран-
ство пространства Еп представляет собой евклидово простран-
ство, размерность которого меньше или равна п. Подпростран-
ствами пространства £3, например, являются начало координат
(размерность 0), прямые, проходящие через начало координат,
плоскости, проходящие через начало координат, и само Е3. Мно-
жество всех линейных комбинаций из пг векторов простран-
ства Еп является подпространством пространства Еп {ЛА 2.13}.
Если даны два подпространства Si и S2 пространства Еп, то
совокупность всех векторов вида u + v, где и принадлежит Sb
a v — S2, называется суммой этих подпространств и обозна-
чается Si + S2. Множество St + S2 также является подпростран-
ством, и если 0 — единственный вектор, принадлежащий одно-
временно как Si, так и S2, то размерность Si + S2 равна сумме
размерностей Si и S2. Если S является подпространством Еп,
то ортогональным дополнением к S называется подпростран-
ство O(S), каждый из векторов которого ортогонален всем век-
торам из S. Размерность суммы S + O(S) равна п, т. е.
S + O(S)=En. Любой вектор х из Еп единственным образом
2.1. Матрицы и векторы
37
может быть представлен в виде x = u + v, где и принадлежит S,
av-O(S).
Максимальное число линейно независимых столбцов в матри-
це А называется рангом матрицы А. Максимальное число ли-
нейно независимых строк в А равно максимальному числу ли-
нейно независимых столбцов, и поэтому ранг матрицы А может
быть также определен как максимальное число линейно неза-
висимых строк матрицы А. Ранг матрицы А мы будем обозна-
чать через г (А). Ранг произведения АВ не определяется един-
ственным образом рангами сомножителей А и В, однако
r(AB)<min[r(A), г(В)], {ЛА 4.3}.
Говорят, что квадратная матрица А имеет обратную матрицу,
если существует такая матрица В, что ВА = АВ = 1. Для того
чтобы матрица А порядка п имела обратную матрицу, необхо-
димо и достаточно, чтобы г (А) =п. Если г (А) то матрица А
называется неособенной. Для того чтобы квадратная матрица
была неособенной, необходимо и достаточно, чтобы ее опреде-
литель |А| был отличен от 0. Столбцы неособенной матрицы
образуют базис пространства Еп. То же верно и для строк не-
особенной матрицы. Если для матрицы А не существует обрат-
ной, то она называется особенной. Матрица, обратная для
матрицы А, обычно обозначается через А-1. Обратная матрица
единственна {ЛА 3.18}. Если А и В — неособенные матрицы по-
рядка п, то матрица АВ также неособенная и (АВ)-1 = В_1А-1
{ЛА 3.19}. Верны также соотношения (А-1)-1 = А и (А')-1= (А-1)'.
Если А — неособенная матрица, то г(АВ) =г(В).
Пусть B=(bi, ..., Ьп)—неособенная матрица. Рассмотрим
матрицу Ва, которая получается из матрицы В заменой столб-
ца Ьг на вектор а. Если существует матрица В« \ то она может
быть найдена с помощью матрицы В-1 следующим образом.
Обозначим у = В-1а и
_ Г __У г-i 1 Уг+i __ Уп. 1
1 L У Г. 1 ’ Уг ' Уг' Уг ' " ' ' Ут J *
Затем, построим матрицу Е, заменив в 1л г-й столбец на я.
Тогда Вд1 —ЕВ’1. Для того чтобы матрица В^1 существовала,
необходимо и достаточно, чтобы //г=#0 {ЛА 3.21}.
Если неособенная матрица М может быть представлена
в виде
₽
6 ’
а
V
где 6—неособенная матрица, то
ГА
С
м =
м-1 =
в
D ’
38 Гл. 2. Необходимый математический аппарат
причем {ЛА 3.20}
А = (а —р6~‘у)Л В = —А06"1,
. I, (2.7)
С = — 6-1уА, D = 6-1 —6"\В.
2.2. Системы линейных уравнений. Система m линейных
уравнений с п неизвестными Xj, j=\, п, может быть
п
записана в виде Ах = Ь или —* = 1, •••, w- Такая
7 = 1
система может: а) не иметь решения, Ь) иметь единственное
решение либо с) иметь бесконечное множество решений.
Рассмотрим матрицу АЬ = (А, Ь), называемую расширенной
матрицей данной системы. Возможны два случая: либо г(А&)—
= г(А), либо г(А^)>г(А). Если г(А^) = г(А) = Л, то суще-
ствует k линейно независимых столбцов матрицы А, таких,
что каждый столбец матрицы А*, в частности столбец Ь,
может быть представлен как линейная комбинация этих k
столбцов. Поэтому в этом случае система Ах = Ь имеет по
крайней мере одно решение. С другой стороны, если г(А*)>
>г(А) и r(Aft) = &, то любое множество, состоящее из k
линейно независимых столбцов матрицы Aft, должно содержать
столбец b и, следовательно, столбец b не может быть пред-
ставлен в виде линейной комбинации столбцов матрицы А.
В этом случае система Ах = Ь не имеет решения.
Если для системы Ах=Ь пг уравнений с п неизвестными мы
имеем г(А) =г(А&) =6<п, то существует бесконечное число ре-
шений системы, таких, что n — k переменных могут принимать
произвольные значения. Если г(А) =г(Аь) =п, то система имеет
единственное решение. Если r(A) =r(A&) = k<m, то m — k урав-
нений системы является следствием остальных. Это означает,
что любой вектор х, удовлетворяющий k уравнениям, которым
соответствуют линейно независимые строки в матрице А, удо-
влетворяет всем m уравнениям системы. Для того чтобы полу-
чить все возможные решения, выберем из А неособенную под-
матрицу порядка k. Если k<m, то в исходной системе отбросим
все уравнения, которым в матрице А соответствуют строки, не
вошедшие в выбранную подматрицу. Если n — k переменным,
которые соответствуют столбцам матрицы А, не вошедшим в
подматрицу £-го порядка, придать произвольные значения, то
значения тех k переменных, которые соответствуют столбцам
матрицы А, вошедшим в подматрицу й-го порядка, могут быть
найдены единственным образом, так как эта подматрица неосо-
% бенная. Так мы получим решение системы Ах = Ь. Если указан-
2.2. Системы линейных уравнений
39
ным выше п — k переменным 'позволить пробегать -все возможные
значения, то тогда можно получить все решения системы.
Система уравнений называется однородной, если Ь = 0. Мно-
жество решений системы Ах = 0 представляет собой подпро-
странство пространства Еп размерности п— k, где &==г(А).
(Доказательства, относящиеся к материалу этого параграфа,
даны в {ЛА 5.5} и {ЛА 5.6}.) Заметим, что х=0 всегда является
решением системы Ах=0; х = 0 называется тривиальным реше-
нием. Для того чтобы существовали нетривиальные решения,
необходимо и достаточно, чтобы г(А)<и, где п— число пере-
менных в системе.
Рассмотрим систему m уравнений с п неизвестными, для ко-
торой г(А) =г(А&) = т. Из матрицы А выберем подматрицу по-
рядка т; обозначим ее через В. Пусть хв— вектор, содержащий
переменные, соответствующие столбцам матрицы В. Через' xR
обозначим вектор, содержащий остальные переменные, а че-
рез R — матрицу, состоящую из соответствующих этим перемен-
ным столбцов матрицы А. Для произвольного хв решение си-
стемы можно получить, если положить хв = В-1Ь — В-1 RxB.- Реше-
ние хв = 0, хв = В~1Ь называется базисным решением. Базисное ре-
шение содержит не более чем т отличных от нуля переменных.
Переменные, вошедшие в хв, называются базисными перемен-
ными; остальные переменные называются небазисными. По
определению небазисные переменные равны нулю. Базисное ре-
шение называется вырожденным, если одна или более базисных
переменных равны нулю. Максимальное число возможных ба-
зисных решений для системы Ах = Ь равно n!/m!(n —т)! Это со-
ответствует числу различных комбинаций из т столбцов мат-
рицы А, которые могут быть выбраны для получения подмат-
рицы В. Однако для некоторых таких комбинаций базисное
решение может не существовать, так как входящие в нее век-
торы могут оказаться линейно зависимыми.
Если А — матрица с размерами тХп и х — некоторая точка
из Еп, то у = Ах можно рассматривать как точку из Ет. Для
каждой точки из Еп таким образом определяется единственная
точка у = Ах из Ет. Точка у называется образом х. Говорят, что
матрица А отображает Еп в Ет (или в часть Ет). Совокупность
точек у, которые можно получить, когда х пробегает все Еп,
представляет собой подпространство пространства Ет {ЛА 4.2}.
Таким образом, матрица А отображает (или переводит) Еп в
подпространство Ет.
Отображение, определяемое матрицей, часто называют ли-
нейным преобразованием. Оно сохраняет сложение и умножение
на скаляр, т. е. если yi = Axi и у2 = Ах2, то y = A(xi+x2) =yi+y2.
Аналогично если у=Ах, то Ау является образом Хх.
40
Гл. 2. Необходимый математический аппарат
2.3. Линейное программирование. Общая задача линейного
программирования состоит в том, чтобы найти неотрицательные
значения п переменных xj, удовлетворяющие m линейным огра-
п
ничениям dijXj =, ^}bi> i=\, ..., m, и максимизирую-
щие или минимизирующие линейную целевую функцию
z = 2 с]хг
В этом параграфе мы рассмотрим симплекс-метод для чис-
ленного решения задач линейного программирования. В этом
методе требуется, чтобы все Ь^О. Можно считать, что это усло-
вие выполняется, поскольку если в исходной формулировке за-
дачи какое-либо 6г<0, то мы умножим соответствующее огра-
ничение на —1 (если ограничение было неравенством, то при
этом знак неравенства изменится на противоположный). Если
все то первый шаг состоит в том, чтобы от заданных огра-
ничений перейти к системе линейных уравнений. Это легко мо-
жет быть сделано путем введения дополнительных переменных
{ЛП 3.2}. Предположим, что все ограничения занумерованы та-
ким образом, что первыми оказались ограничения со знаком
неравенства вторыми — ограничения со знаком неравен-
ства <и третьими — равенства. Если ограничение i имеет вид
У а^Х] < bi, то мы введем новую вспомогательную перемен-
i
ную x-n+i, полагая
п п
Xn+i = bi — ^ai)xj, т. е. ^ачх}-\-хп+1 = Ь1. (2.8)
н 7 /=1
Для любых значений переменных Xj, / = 1, .и, удовлетворяю-
щих исходному ограничению, xn+i>0. Если ограничение i имеет
вид ^aijX^bi, то мы введем новую вспомогательную пере-
j
менную %п+г следующим образом:
п п
хп+1=Ъачх} — Ь1, т. е. ^ачх) — хп+1 = Ь1. (2.9)
И здесь при любых xj, удовлетворяющих исходному ограниче-
нию, xn+i>0. Таким образом, от данных ограничений мы пере-
шли к системе m линейных уравнений с N неизвестными: Ах = Ь;
при этом n^N^n + m. Число вновь введенных переменных
равно N—n. Столбцы матрицы А называются производствен-
ными векторами. Производственный вектор, соответствующий
вспомогательной переменной, равен либо единичному вектору,
либо единичному вектору, умноженному на (—1). Между не-
отрицательными векторами, удовлетворяющими исходным огра-
2.3. Линейное программирование
4J
ничениям, и неотрицательными решениями системы Ах = Ь суще-
ствует взаимно однозначное соответствие. Таким образом,
добавлением вспомогательных переменных любую задачу линей-
ного программирования можно свести к следующей эквивалент-
ной задаче: найти max или minz=cx, где с= (сь . ..,Су),при
условиях Ах=Ь и хХ). Это стандартная форма задачи, исполь-
зуемая в симплекс-методе. В дальнейшем число переменных в
задаче линейного программирования мы всегда будем обозна-
чать через п независимо от того, содержат ограничения задачи
неравенства или нет. Любой вектор х, удовлетворяющий усло-
виям Ах = Ь, хХ), будем называть допустимым решением.
Понятно, что описанный только что прием применим и в слу-
чае нелинейной целевой функции, так что задача вида (1.6) —
(1.9) с линейными ограничениями и нелинейной целевой функ-
цией равносильна следующей:
Ах = Ь, х>^0; найти шах или min z — f (хр ..хп\ (2.10)
Вспомогательные переменные могут быть введены и в ограниче-
ния целочисленных задач программирования. При этом но-
вые переменные, определяемые формулами (2.8) и (2.9), даже
при целочисленных значениях исходных переменных могут ока-
заться нецелочисленными, если ац и bi нецелые. Таким образом,
в общем случае введение вспомогательных переменных преобра-
зует полностью целочисленную задачу в смешанную целочис-
ленно-непрерывную. Следует отметить, что во многих случаях
изменение размерности физических величин задачи и времени
позволяет сделать ее полностью целочисленной.
Но вернемся к симплекс-методу. Будем считать, что за-
дача приведена уже к стандартному виду: Ах = Ь, хХ): найти
maxz = cx (мы рассмотрим лишь задачу максимизации, так как
задача минимизации может быть сведена к ней изменением
знака целевой функции). Тогда (см. {ЛП3.6) — {ЛП3.8}):
а) если задача имеет оптимальное решение, то существует
по крайней мере одно базисное оптимальное решение;
Ь) если имеется допустимое базисное, но не оптимальное ре-
шение, то через конечное число шагов от этого решения, можно
перейти к базисному оптимальному решению или же установить,
что целевая функция неограничена на множестве всех допусти-
мых решений, т. е. что существуют допустимые решения, кото-
рым соответствуют сколь угодно большие значения целевой
функции; при этом на каждом шаге осуществляется замена
только одной базисной переменной.
Предположим, что г(А) =г(Аь) =т. (Мы увидим, что это
предположение не исключает вырожденности.) В этом случае
любое базисное допустимое решение содержит не более чем m
42 Г л. 2. Необходимый математический аппарат
положительных переменных. Пусть В — матрица, состоящая из
m линейно независимых столбцов матрицы А. Соответствующее
базисное (не обязательно допустимое) решение может быть за-
писано в виде хв = в-»ь, где все небазисные переменные равны
нулю. Значение целевой функции для этого решения равнб
г = свхв, где св=(свь ..., сВт) содержит коэффициенты целе-
вой функции, соответствующие базисным переменным. Пусть
aj — какой-либо производственный вектор (т. е. какой-либо
столбец матрицы А). Найдем У; = [Уи, ..., В и Zj=cByj.
Теперь предположим, что мы имеем базисное допустимое решение
хв=В“1Ь и yj, Zj, вычисленные для всех а;. Имеются следующие
возможности:
a) Zj — fjX), /=1, ..., п. В этом случае базисное допусти-
мое решение оптимально;
b) Zj —cj<0 для некоторого / и Z=l, ..., т. В этом
случае целевая функция неограничена;
с) z~c7<0 для одного или нескольких / и для каждого та-
кого / по крайней мере одно уцХК /=1,... ,т. В этом
случае существует другое базисное допустимое решение,
которому соответствует значение целевой функции не
меньшее, чем значение целевой функции для исходного
решения. Если же исходное базисное решение невыро-
жденное, то значение целевой функции можно увеличить,
заменив в матрице В один вектор, т. е. заменив одну из
базисных переменных. Эти результаты доказаны в
{ЛП3.6}—{ЛП3.8}.
Симплекс-метод исходит из допустимого базисного решения
и на каждой итерации производит замену одного вектора в ба-
зисе. Правила замены векторов в базисе следующие:
1) Определение вектора, вводимого в базис. Вычисляем
zk — c* = min(zy — Cj), Zj — c}<Q.
Вектор а,< на следующей итерации вводится в базис. Если вы-
численный минимум достигается при нескольких векторах, то
в базис вводится вектор с наименьшим индексом /.
2) Определение вектора, исключаемого из базиса. Вычис-
ляем
xBrlyrk = min для yik > О
(если все Угл-^О, то имеем случай неограниченности целевой
функции). Из базиса исключается r-й столбец матрицы В и за-
меняется вектором а&. В случае неоднозначности выбираем век-
тор, для которого ут наименьшее; если этим неоднозначность не
2.3. Линейное программирование
43
исключается, то среди оставшихся векторов выбираем вектор с
наименьшим индексом I.
Новые значения yj, Zj — хв и z, которые мы обозначим че-
рез у;, Zy — Ср хв и z, могут быть вычислены следующим обра-
зом. Пусть Хв=Уо, Zj — Cj=ym+1, j, z=ym+i,o. Тогда
Уц = Уи-^Угр i = .... т + \, yr) = j^ (2-11)
j = 0, 1, ...» n.
Эти формулы выведены в {ЛП 4.1}—{ЛП 4.4}.
Рассмотрим задачу нахождения исходного базисного реше-
ния. Если матрица А содержит в качестве подматрицы единич-
ную матрицу (так может быть, например, в случае, когда пере-
менные типа (2.8) были введены в каждое ограничение), то
базисное допустимое решение получается легко: В=1, хв = Ь,
у; = а;-, Zj — Cj = cBaj — tj, z = cBb. Если единичная матрица не со-
держится в А, то присоединим к А необходимое число единичных
векторов с тем, чтобы получить в А такую подматрицу. Допол-
нительные векторы мы назовем искусственными векторами, а
соответствующие переменные — искусственными переменными
(обозначим их через хаг). Исходные переменные в отличие от
искусственных мы будем называть истинными переменными.
Для получения допустимого решения исходной задачи значения
искусственных переменных нужно уменьшить до нуля. Для этой
цели коэффициенты целевой функции, соответствующие искус-
ственным переменным, положим равными —М, где М — доста-
точно большое положительное число. При ручном счете нет
необходимости придавать числу М какое-либо конкретное значе-
ние. Если исходная задача имеет допустимое решение, то значе-
ния искусственных переменных могут быть сделаны равными
нулю. Если матрица А не содержит ни одного единичного век-
тора, то вводят искусственные переменные и решают следую-
щую задачу линейного программирования:
Ах4-1ха = Ь, х>0, ха>0; найти maxz = cx — ЛПха, (2.12)
где ха = [хаь ..., Xaml 1 = (L L • • •» 0- Начальное базисное до-
пустимое решение для задачи (2.12) равно хв=Ь, y> = aj,
z=—Aflb и Zj — Cj = —Mlaj — Cj. Если матрица А содержит еди-
ничный вектор е&, то искусственный вектор вводить не нужно.
Методы с искусственными переменными подробно описаны в
{ЛП4.5} и {ЛП4.6}.
При ручных вычислениях с помощью симплекс-метода удоб-
но пользоваться табл. 2.1. На каждой итерации такая таблица
преобразуется в новую таблицу в соответствии с формулами
44
Гл. 2. Необходимый математический аппарат
Таблица 2.1
Образец таблицы для симплекс-метода
CJ Ч сп
СВ Базисные перемен- ные ь а1
СВ1 хв\ xbi ~ Ую Уп У1П
• •
с Вт хВт хВт — УтО У ml У тп
z ~ У ztz ч-1,0 zl С1 — У/и + 1,1 - • • Zn Сп~ Ут + 1,п
(2.11). Таблица не содержит столбцов для искусственных век-
торов, так как вытесненный из базиса искусственный вектор уже
никогда не может быть включен в базис.
2.4. Модифицированный симплекс-метод. При решении задач
линейного программирования с использованием электронных
вычислительных машин удобнее вместо описанного вышедгим-
плекс-метода применять так называемый модифицированный
симплекс-метод. В этом методе на каждой итерации преобра-
зуются не все yj, а только лишь В-1, свВ-1, хв и г. Величины
Zj — Cj и уь вычисляются по формулам Zj~ c-j = (свВ-^а, — Cj,
У^В"1 а&. В изложении модифицированного симплекс-метода
мы выделим два случая в зависимости от того, вводятся или нет
в задачу искусственные переменные.
Рассмотрим сначала случай, когда искусственные перемен-
ные в задачу не вводятся. Как обычно, мы будем предполагать,
что решается задача определения maxz = cx при Ах —Ь, х>0.
Пусть базисное допустимое решение определяется матрицей В.
Если мы запишем равенство z = cBxB в виде г — свхв = 0, то
базисное допустимое решение может быть, представлено в виде
1 —Св
О В
"О
ь
или
Z
*в.
свВ
В”
О'
ь
. (2.13)
хф =
О
1
О
2.4. Модифицированный симплекс-метод
45
Отметим также, что
(2-14)
Столбцы
СдВ1'
В-1
матрицы с размерами (т+1)Х/и обозначим через ...,
Данные, необходимые для вычислений, удобно располагать
в виде табл. 2.2.
Таблица 2.2
Образец таблицы для модифицированного симплекс-метода
Базисные перемен- ные 01 Р/72 ХВ
Z ₽01 Роуп • Z 2k
хв\ Р11 Pirn ХВ1 Угк
хВт Pml х Вт У ink
Вычислительный процесс состоит в следующем: предполо-
жим, что в табл. 2.2 внесены все данные, относящиеся к базис-
ному допустимому решению, за исключением столбца у£}. Мы
должны определить, является ли это решение оптимальным или
нет, и если нет, то найти вектор, который будет введен в базис
на следующей итерации. Для этого, вычислив скалярное произ-
ведение первой строки таблицы и вектора а?, а затем вычитая
из результата q, для всех небазисных переменных найдем вели-
чины Zj — Cj. Если все z~ то решение оптимально. Если
нет, то, согласно правилу, используемому в симплекс-методе, на-
ходим вектор a/t, который должен быть введен в базис. Для
определения вектора, исключаемого из базиса, нам необходим
вектор yft. Находим его координаты у^, *=1, . w, равные
скалярному произведению (i+ 1)-й строки таблицы и вектора а&.
Эти величины вносим в столбец у^Р. Исключаемый из базиса
г-й вектор определяется теперь так же, как и в симплекс-методе.
46
Гл. 2. Необходимый математический аппарат
Затем табл. 2.2 преобразуется в новую аналогичную таблицу,
соответствующую новому базисному допустимому решению.
Если ввести обозначения zk—ck—y$h\ [г, Хв] = Рт+ь то формулы
преобразования можно записать в следующем виде (галочкой
отмечены новые значения): 4
Pry = 7=1. •••. /и-4-1. (2.15)
Рассмотрим теперь случай, когда в задачу необходимо вве-
сти искусственные переменные. В этом случае решение прово-
дится в два этапа. На первом этапе значения искусственных
переменных уменьшаются до нуля. Для этого коэффициенты це-
левой функции, соответствующие истинным переменным, пола-
гаются равными нулю (независимо от их действительных
значений), а коэффициенты, соответствующие искусственным пе-
ременным, — равными — 1. Оптимальное базисное допустимое
решение мы находим на втором этапе. Здесь коэффициенты це-
левой функции, соответствующие истинным переменным, пола-
гаются равными своим действительным значениям, а коэффи-
циенты, соответствующие искусственным переменным, остав-
шимся в базисе (с нулевыми значениями), — нулю. Предполо-
жим, что в задачу было введено m искусственных переменных.
В этом случае на первом этапе мы максимизируем функцию
za = —Xai — ха2— ... —Хат, а на втором этапе — функцию z = cx.
На втором этапе коэффициенты целевой функции, соответствую-
щие искусственным переменным, равны нулю; поэтому если
после завершения первого этапа в базисе остались какие-либо
искусственные переменные со значением 0, то в задачу необхо-
димо ввести дополнительное ограничение, закрепляющее эти
переменные на их нулевых значениях. Это дополнительное огра-
ничение имеет вид za+xai + ... +хаш=0; если исходная задача
имеет допустимое решение, то по окончании первого этапа za = 0
и в дальнейшем не меняется, если рассматривать za как новую
искусственную переменную (с нулевым коэффициентом в целе-
вой функции). Поэтому она может быть включена в дополни-
тельное ограничение, вводимое в задачу перед началом второго
этапа. Для некоторой базисной подматрицы В матрицы расши-
ренной системы ограничений, включающих искусственные пере-
менные, обозначим через св вектор коэффициентов целевой
функции, используемых на втором этапе, а через cBi — на пер-
вом этапе (здесь эти коэффициенты равны либо 0, либо —1).
На первом этапе желательно преобразовать как сВ1В-1, так и
cBB“!. Для этого базисное допустимое решение с соответствую-
2.4. Модифицированный симплекс-метод
47
щими значениями z и удобно представить в виде
1 0—св -
О 1 —СД1
00 В _
“0“
О
-Ь_
или
z
Если через z^ — обозначить величины
щие первому этапу, то
Zj — Cj, соответствую-
ZJ ci
cji
L У/
О свВ 1 ’ — Су
1 Св В Cji
О В4 J
(2.17)
1
О
О
Если а; является истинным вектором, то cji=O, если искусствен-
ным, то Q = 0, Qi=—1.
Здесь также удобно пользоваться табл. 2.2, в которую нужно
будет ввести одну дополнительную строку и один дополнитель-
ный столбец 0о, соответствующий za на первом этапе. Столбец 0о
на первом этапе всегда остается равным ег, но может, как мы
увидим, изменяться на втором, этапе. Для того чтобы опре-
делить вектор, вводимый в базис на первом этапе, нужно сна-
чала вычислить скалярные произведения второй строки таблицы
и векторов [0, aj, где а^ — истинные векторы, и тем самым полу-
чить величины Zji — Cji; затем следует применить критерий обыч-
ного симплекс-метода. Вектор, исключаемый из базиса, опреде-
ляется также в соответствии с критерием симплекс-метода. Пер-
вый этап заканчивается, когда za = 0 (или, если нет допустимого
решения, когда все z^ — Сд>0, а га<0). На втором этапе у нас
ш+\ ограничение, и мы имеем дело с базисом размерности
т + 1. Интересно отметить, что оказалось возможным так орга-
низовать вычисления, что конечная для первого этапа таблица
является исходной таблицей для второго этапа. В начале вто-
рого этапа мы находим Zj — Cj для каждого истинного вектора,
не вошедшего в базис. Для этого нужно из скалярного произве-
дения первой строки таблицы и вектора [0, aj вычесть Cj. Затем
обычным путем находится вектор, вводимый в базис. Вектор,
исключаемый из базиса, также находится по обычному правилу.
Однако теперь мы должны учитывать возможность того, что
первый столбец таблицы, т. е. столбец, соответствующий на пер-
вом этапе переменной za, также может быть замещен. Преобра-
зование таблицы осуществляется по формулам (2.15). Модифи-
цированный симплекс-метод подробно изложен в {ЛП7.1}—
{ЛП 7.9}.
48 , Гл. 2. Необходимый математический аппарат
2.5. Двойственность. Если дана задача линейного програм-
мирования: Ах = Ь, х>0; найти maxz = cx, то существует другая
задача линейного программирования: A'w>c'; найти minZ = b'w,
которая называется двойственной задачей по отношению к ис-
ходной. Исходную задачу будем называть прямой задачей. Пря-
мая и двойственная задачи обладают следующими свойствами:
1) если какая-либо из задач имеет ограниченное оптимальное
решение, то это верно и для другой задачи, причем maxz =
= minZ, т. е. оптимальные значения целевых функций для этих
задач равны; 2) если Хв — В-1Ь—оптимальное базисное реше-
ние прямой задачи со значением целевой функции, равным
z ~свхв’ то w*, = cBB"1 является оптимальным решением двой-
ственной задачи. Наоборот, если Wb==^d1c/ есть оптимальное
базисное решение двойственной задачи со значением целевой
функции Z* —bBwB, то х^^ЬвВБ1 является оптимальным ре-
шением прямой задачи. Отметим, что в двойственной задаче не
требуется неотрицательности переменных. Если х — произволь-
ное допустимое решение прямой задачи, a w — двойственной, то
cx<b'w. Доказательство всех этих результатов можно найти в
{ЛП 8.1}—{ЛП 8.7}.
Число переменных в прямой задаче равно числу ограничений
в двойственной. Таким образом, если нам необходимо решить
задачу линейного программирования с большим числом ограни-
чений и малым числом переменных (в такой задаче базисная
матрица будет иметь высокий порядок)., то удобно перейти к ре-,
шению двойственной задачи. Из предыдущего параграфа сле-
дует, что если прямая задача решается модифицированным сим-
плекс-методом, то первая строка таблицы, соответствующей ее
оптимальному решению, дает оптимальное решение двойствен-
ной задачи. Обратно, если с помощью модифицированного сим-
плекс-метода решается двойственная задача, то в первой строке
таблицы, дающей оптимальное решение двойственной задачи,
получается оптимальное решение прямой задачи. Оптимальное
решение двойственной задачи в случае, когда прямая задача
решается симплекс-методом (или оптимальное решение прямой
задачи, когда симплекс-методом решается двойственная за-
дача), может быть получено из конечной симплексной таблицы.
Рассмотрим те столбцы в таблице, которые соответствовали
столбцам, образующим единичную матрицу исходного базиса.
Допустим, что симплекс-методом была решена прямая задача.
Тогда, если вектор а^ = вг в исходном базисе был вектором, соот-
ветствующим вспомогательной переменной, то число, находя-
щееся в конечной таблице на месте, предназначенном для
— равно Если вектор ег- соответствовал искусственной
2.6. Выпуклые множества
49
переменной, то z. — — M = ‘W* (для того чтобы определить
значения двойственных переменных, величины Zj — Cj для векто-
ров, соответствующих искусственным переменным, нужно ввести
в таблицу и преобразовывать на каждой итерации). Точно та-
ким же образом можно найти оптимальное решение прямой за-
дачи в случае, если симплекс-методом была решена двойствен-
ная задача.
Отметим, что каждому ограничению прямой задачи соответ-
ствует переменная двойственной задачи. Если в i-e ограничение
прямой задачи, была введена вспомогательная переменная вида
(28), то если же вида (2.9), то w^O. Если не наклады-
вается ограничений на знак переменной х7, то /-е ограничение
двойственной задачи превращается в равенство. Если х — ка-
кое-либо оптимальное решение прямой задачи, а вектор ws со-
стоит из вспомогательных переменных типа (2.9), вошедших в
какое-либо оптимальное решение двойственной задачи, то
должно выполняться равенство x'ws = 0 {ЛП 8.5}.
Применяя симплекс-метод к двойственной задаче, для реше-
ния прямой задачи можно получить новый алгоритм, называе-
мый двойственным симплекс-методом. Предположим, что у нас
имеется базисное, но недопустимое решение для прямой задачи,
для которого Zj — Cj^Q при всех /. От этого решения заменой
одной переменной в базисе можно перейти к другому базисному
решению, для которого также все Zj — c^O и т. д. Любое до-
пустимое базисное решение, полученное таким путем, будет
оптимальным решением. Правила изменения базиса здесь та-
кие: 1) из базиса исключается наибольшая отрицательная пере-
менная хВг (обозначим ее через хВг); 2) в базис вводится пере-
менная Xk, где k определяется из соотношения
Zk — Ck Zj — C}
-------= max —------, yTi< 0.
Утк j Уг]
Если среди чисел ут$ нет отрицательных, то задача не имеет
допустимых решений. С помощью двойственного симплекс-ме-
тода удобно учитывать различные изменения, вводимые в усло-
вия задачи после получения оптимального решения. Непо-
средственно для решения задач линейного программирования
двойственный симплекс-метод редко используется, так как не
являющееся допустимым базисное решение, для которого все
z?—с7>0, обычно трудно найти. О двойственном симплекс-ме-
тоде см. в {ЛП 8.7, 8.8}.
2.6. Выпуклые множества. Произвольную совокупность точек
из Еп мы будем называть точечным множеством. Для обозначе-
ния точечных множеств мы будем использовать большие бук-
4 Зак. 735
50
Гл. 2. Необходимый математический аппарат
вы, например X, S и т. д. Если х есть элемент множества X, то
пишут х€Х. Пересечением двух множеств X и У называется
множество X П У, состоящее из точек, принадлежащих как X,
так и У. Объединением множеств X и У называется множество
всех точек, принадлежащих либо X, либо У (или обоим этим
множествам). Объединение множеств X и У обозначается Х1)У.
Множество, не содержащее ни одного элемента, называется
пустым множеством. Множество можно задать, указав свойство,
которым обладают элементы только этого множества. Если
X является множеством всех точек х, обладающих свойством
р(х), то мы записываем Х={х1р(х)}. Для данной точки а и е>0
множество точек Х = {х| |х — a|=s} называется гиперсферой в
Еп радиуса 8 с центром в точке а. Множество Х = {х| [х — а| < е}
называется внутренностью гиперсферы. Внутренность гипер-
сферы радиуса 8 с центром в точке а называется 8-окрестностью
точки а. Точка а называется внутренней точкой множества, если
существует 8-окрестность точки а, содержащая лишь точки дан-
ного множества. Точка а называется граничной точкой множе-
ства, если любая ее 8-окрестность содержит как точки данного
множества, так и точки, не принадлежащие этому множеству.
Множество, содержащее все свои граничные точки, называется
замкнутым. Множество, которое не содержит ни одной своей
граничной точки1), называется открытым. Так, 8-окрестность
точки а — открытое множество.
Прямая, проходящая через две различные точки Xi и х2 в Еп,
может быть определена как множество точек
X = (х|х = Хх2 + (1 — ^)х1? —оо<Х<-|-оо}. (2.18)
Если X таково, что то множество (2.18) представляет
собой прямолинейный отрезок, соединяющий точки Xi и х2.
Если Л удовлетворяет условию 0<Х<Т, то точка x = Zx2 + (1—X)xi
называется выпуклой комбинацией точек Xj и х2. Гиперплоскость
в Еп определяется как множество точек X = {x|cx = z}, где с=#0 —
заданный вектор-строка, а г — заданное число. Вектор с назы-
вается нормалью к гиперплоскости; при Х=#0 вектор Хс также
является нормалью к гиперплоскости. Две гиперплоскости
CiX = Zi и c2x = z2 называются параллельными, если Ci = Xc2. Мно-
жества X = {x|cx<z} и X = {x|cx>z} называются открытыми
полупространствами. Аналогично множества X={x|cx<^z} и
X = {x|cx>z} называются замкнутыми полупространствами. Ги-
перплоскости и замкнутые полупространства являются замкну-
тыми множествами. Множество X называется ограниченным,
если существует такое число г, г>0, что для любой точки х£Х
’) То есть такое, что все его точки внутренние. — Прим. ред.
2.6. Выпуклые множества
51
выполняется неравенство |х| <г (в этом случае множество X
оказывается внутри сферы радиуса г с центром в начале коор-
динат). Множество X называется ограниченным снизу, если
существует вектор а, такой, что для каждого х£Х выполняется
неравенство а41х. Аналогично X ограничено сверху, если суще-
ствует вектор а, такой, что х<^а для каждого х€ X {ЛА 6.3}.
Множество называется выпуклым, если оно содержит любую
выпуклую комбинацию любых двух точек xt и х2 из этого мно-
жества. Таким образом, выпуклое множество содержит отрезок,
соединяющий любые две точки из этого множества. Множество,
состоящее из одной точки, полагают выпуклым. Точка х, при-
надлежащая выпуклому множеству, называется его крайней точ-
кой, если в данном множестве не существует двух различных
точек Xi и х2, таких, что х = %х2+(1 —Z)xb 0<Х<1. Крайняя точ-
ка обязательно должна быть граничной точкой. Однако не все
граничные точки являются крайними, так как некоторые гра-
ничные точки могут принадлежать отрезку, соединяющему две
крайние точки. Множество точек х^О — неотрицательный ок-
тант— является замкнутым выпуклым множеством. Гиперпло-
скости и замкнутые полупространства тоже представляют собой
замкнутые выпуклые множества. Пересечение двух и более выпук-
лых множеств выпукло. Пересечение замнутых множеств замк-
нуто. Множество точек х, удовлетворяющих условиям Ах=Ь,
х>0, можно рассматривать как пересечение m гиперплоскостей и
п замкнутых полупространств. Поэтому если существуют точки,
удовлетворяющие этим условиям, то множество таких точек
замкнуто и выпукло. Следовательно, если задача линейного про-
граммирования имеет допустимые решения, то множество всех
допустимых решений является замкнутым и выпуклым. Базис-
ному допустимому решению системы Ах=Ь соответствует край-
няя точка в выпуклом множестве допустимых решений, и на-
оборот, каждая крайняя точка соответствует базисному допу-
стимому решению. Поэтому оптимальному решению будет
соответствовать по крайней мере одна крайняя точка выпуклого
множества допустимых решений. Линейное преобразование
у = Ах с матрицей А размеров mXn переводит выпуклое множе-
ство из Еп в выпуклое множество из Ет. Более того, неособен-
ное линейное преобразование (преобразование с неособенной
матрицей А) переводит крайние точки в крайние. Доказатель-
ства, относящиеся к материалу этого параграфа, см. в {ЛА 6.4}
и {ЛП 3.10}.
Если имеется замкнутое выпуклое множество X, то точка v
или является элементом X, или существует гиперплоскость, со-
держащая v и такая, что множество X целиком содержится в
одном из открытых полупространств, порождаемых этой гипер’
' 4*
52
Гл. 2. Необходимый математический аппарат
плоскостью (теорема об отделяющей гиперплоскости). Пусть
w — граничная точка выпуклого множества X. Гиперплоскость
сх = 2 называется его опорной гиперплоскостью в точке w, если
cw — z и множество X целиком лежит в замкнутом полупро-
странстве, порождаемом этой гиперплоскостью. Для любой гра-
ничной точки w множества X всегда существует по крайней
мере одна опорная гиперплоскость. Если замкнутое выпуклое
множество ограничено или ограничено сверху (снизу), то пере-
сечение любой опорной гиперплоскости с множеством X содер-
жит по крайней мере одну его крайнюю точку. Прямая, соеди-
няющая две различные крайние точки выпуклого множества,
называется его ребром, если она является пересечением множе-
ства с его опорной гиперплоскостью. Две точки называются
смежными, если соединяющий их отрезок является ребром
выпуклого множества. В симплекс-методе на каждой итерации
совершается переход от одной крайней точки к смежной ей край-
ней точке. Доказательства сформулированных выше теорем
можно найти в {ЛА 6.6}—{ЛА 6.8}.
Замкнутое ограниченное выпуклое множество, имеющее ко-
нечное число крайних точек, называется выпуклым многогранни-
ком. Любая точка выпуклого многогранника может быть пред-
ставлена в виде выпуклой комбинации его крайних точек
{ЛА 6.8}. Если пересечение конечного числа полупространств и
гиперплоскостей не пусто и ограничено, то оно представляет со-
бой выпуклый многогранник.
2.7. Характеристические числа и квадратичные формы. За-
дача нахождения векторов х=#0 и чисел Л, таких, что для данной
квадратной матрицы А выполняется равенство
Ах = Хх> (2.19)
называется задачей о характеристических (собственных) числах.
Очевидно, что х = 0 удовлетворяет уравнению (2.19) при лю-
бом %. Если этому уравнению удовлетворяет вектор х=#0, то
(А—Х1)х = 0. Это возможно лишь тогда, когда матрица А —XI
особенная, так что |А — XI| =0. Таким образом, для того чтобы
существовал отличный от нуля вектор х, удовлетворяющий
уравнению (2.19), необходимо и достаточно, чтобы число X удо-
летворяло уравнению f(X) = |A— XIj =0. f(X) является полино-
мом степени п относительно X. Следовательно, уравнение f(X) =0
имеет п корней (действительных или комплексных), если ка-
ждый корень считать столько раз, какова его кратность. По-
этому имеется не более п различных значений X, для которых
существуют отличные от нуля векторы х, удовлетворяющие
(2.19). Корни уравнения f(X) =0 называются характеристически-
2.7. Характеристические числа и квадратичные формы 53
ми или собственными числами матрицы А. Если X — характери-
стическое число, то существует по крайней мере один вектор
х=#0, удовлетворяющий уравнению (2.19); такой вектор х назы-
вается характеристическим или собственным вектором матри-
цы А. Число линейно независимых векторов х, удовлетворяющих
"уравнению (2.19) при некотором значении А, равно/г—r(A—XI),.
где п— порядок матрицы А, а Аг—рассматриваемое собственное
число. Полином / (А) называется характеристическим полиномом*
а уравнение/(А) =0— характеристическим уравнением матрицы
А. Если S — неособенная матрица, то матрица S-1AS имеет те
же самые характеристические числа, что и матрица А. В этом
случае матрицы S^AS и А называются подобными.
Далее мы ограничимся рассмотрением случая, когда А — сим-
метрическая матрица. В этом случае все ее характеристические
числа действительны, а характеристические векторы, соответ-
ствующие различным характеристическим числам, ортогональ-
ны. Если характеристическое число имеет кратность т, то мож-
но найти m соответствующих ему взаимно ортогональных харак-
теристических векторов. Поэтому для симметрической матрицы
порядка п всегда существует п взаимно ортогональных характе-
ристических векторов. Поскольку длина характеристических век-
торов не имеет никакого значения, мы будем предполагать, что
характеристические векторы нормированы, т. е. что их длина
равна единице; такие характеристические векторы мы будем
обозначать через и;, /=1, ..., п. Очевидно, u(uy. = д/у.. Отлич-
ные от нуля взаимно ортогональные векторы линейно незави-
симы. Поэтому п взаимно ортогональных собственных векторов
матрицы А образуют базис пространства Еп. Такой базис, назы-
вается ортонормированным.
Рассмотрим матрицу Q=(ui, ..., un), столбцами которой
являются ортонормированные собственные векторы матрицы А.
Тогда Q'Q=I, или Q-1 = Q'. Матрица Q называется ортогональ-
ной матрицей. Легко видеть, что
Q-1AQ = Q'AQ = Q'(Au1, .... Au„)=Q'(Mi, • • •, M„)=ll Wl-
(2.20)
Таким образом, симметрическая матрица А подобна диагональ-
ной матрице, элементами главной диагонали которой являются
характеристические числа матрицы А. Если Q—произвольная
неособенная матрица, то матрица Q'AQ называется конгруэнт-
ной по отношению к матрице А. Таким образом, любая симме-
трическая матрица А конгруэнтна диагональной матрице, диаго-
нальные элементы которой равны ее характеристическим числам.
54 Гл. 2. Необходимый математический аппарат
Квадратичной формой относительно п переменных хь ...» хп
называется числовая функция этих переменных, имеющая вид
п п
z=^^aijXiXj. Если обозначить A=||aijll, х=[хь хп], то
;=1Z = 1
z = x'Ax. Заметим, что если i=£=j, то коэффициент при XtXj равен
aij + aji. Отсюда сразу следует, что матрицу А коэффициентов
квадратичной формы всегда . можно считать симметрической.
Действительно, определяя новые коэффициенты равенством
, , alj~\raji . .
bij = bjt — —2— для всех У»
получаем, что &о + Ьц==Яъ- + йя и матрица B=||&ij||—симметри-
ческая. Очевидно, что при таком переопределении коэффициен-
тов значение z для любых значений х остается прежним. По-
этому в дальнейшем мы всегда будем предполагать, что мат-
рица коэффициентов квадратичной формы симметрическая.
Квадратичная форма х'Ах называется положительно опреде-
ленной, если х'Ах>0 для любого х, кроме х = 0; форма х'Ах
называется неотрицательной, если х'Ах>0 для любого х и суще-
ствует х=£0, для которого х'Ах=0. Квадратичная форма х'Ах
называется отрицательно определенной (неположительной), если
квадратичная форма —х'Ах — положительно определенная (не-
отрицательная). Форма х'Ах называется неопределенной, если
она положительна \для одних значений х и отрицательна для
других. Рассмотрим несколько квадратичных форм от двух пере-
менных. Очевидно, г = х2_|_2х1х2 + х2 = (х1+^,2)2 положитель-
но определена; z = x\ — 2хгх2 + х2 = (хг — х2)2 неотрицательна,
так как она нигде не принимает отрицательных значений, но при
_х1==х2 обращается в нуль; квадратичная форма г = х2—
— 2хгх2— х2 — неопределенная, так как z>0 при %i = 5, Х2 = 0 и
z<0 при Х1 = 0, х2 = 5.
Иногда квадратичную форму z = x'Ax удается упростить, при-
меняя преобразование переменных x = Sy, где S — неособенная
матрица. В новых переменных квадратичная форма имеет вид
z = y'S'ASy = y'By, где матрица В конгруэнтна А. Если х пробе-
гает все Еп, то z пробегает множество, называемое множеством
значений квадратичной формы. При преобразовании перемен-
ных x=Sy с неособенной матрицей S множество значений ква-
дратичной формы остается прежним. При таком преобразовании
переменных положительно (отрицательно) определенная форма
остается положительно (отрицательно) определенной. Если в ка-
честве матрицы преобразования переменных взять матрицу Q,
столбцами которой являются ортонормированные собственные
2.8. Функция п переменных
55
векторы матрицы А, то в новых переменных t/j квадратичная
п
форма будет иметь вид z = S^yf/^где Xj — характеристические
числа матрицы А. Если квадратичная форма содержит лишь
квадраты переменных, то говорят, что она имеет канонический
вид. С помощью ортогонального преобразования любая квадра-
тичная форма может быть приведена к каноническому виду с
коэффициентами, равными характеристическим числам мат-
рицы А. Отсюда следует, что для того, чтобы квадратичная фор-
ма х'Ах была положительно (отрицательно) определенной, необ-
ходимо и достаточно, чтобы все характеристические числа мат-
рицы А были положительными (отрицательными). Аналогично*
для того, чтобы квадратичная форма была неотрицательной (не-
положительной), (необходимо и достаточно, чтобы все собствен-
ные числа матрицы А были бы неотрицательными (неположи-
тельными) и по крайней мере одно ее собственное число обра-
щалось в нуль. Квадратичная форма является неопределенной
тогда и только тогда, когда матрица А имеет как положитель-
ные, так и отрицательные собственные числа. См. {ЛА 7.1} —
{ЛА 7.10}.
2.8. Функция ппеременных. Любое правило, сопоставляющее
каждой точке x = [xi,x2] из Е2 или каждой точке из некоторога
подмножества X пространства Е2 единственное число z, мы бу-
дем называть функцией двух (переменных. Для записи такой
функции обычно используют обозначение z=f(xi,x2). Геометри-
чески функция двух переменных может быть описана некоторой
поверхностью в трехмерном пространстве. Однако более нагляд-
ное представление о функции двух переменных можно получить,
если найти ее линии уровня в пространстве Е2. При фиксиро-
ванном z соотношение z=f(xi,*2) между х{ и х2 соответствует
некоторой кривой в плоскости (хь х2). Эта кривая называется
линией уровня. Она характеризует профиль поверхности при
фиксированном значении z. Например z = x2-\-x2 представляет
собой параболоид вращения; линиями уровня этой поверхности
являются окружности с центром в начале координат радиуса z1/2.
Аналогично функцией п переменных мы будем называть пра-
вило, которое каждой точке х из Еп или каждой точке из неко-
торого подмножества X пространства Еп ставит в соответствие
единственное число z. Для записи функции п переменных
обычно используется обозначение z=f(xi, ..., хп) или z=f(x)._
Иногда, если это не вызывает недоразумений, для обозначения
функции п переменных мы будем использовать просто сим-
волы f или z. По аналогии с предыдущим случаем можно счи-
L
•56 Г л. 2. Необходимый математический аппарат
тать, что функции z = /(x) соответствует некоторая поверхность
в En+1. Такую поверхность мы будем называть n-мерной поверх-
ностью или гиперповерхностью, так как здесь каждая из и пере-
менных (компонент вектора х) может изменяться независимо от
других (т. е. имеется п степеней свободы). При каждом фикси-
рованном /Zзначении z соотношению z=f(x) соответствует неко-
торая поверхность (размерности и—1) в Еп, называемая поверх-
ностью УРОВНЯ ДЛЯ фуНКЦИИ Z = f(X').
В дальнейшем нас будут интересовать, как правило, непре-
рывные функции п переменных. Функция z = f(x) непрерывна
в точке х0, если f(x0) существует и для каждого х из 6-окрест-
ности (6>0) х0 значение f(x) может быть сделано как угодно
близким к f(x0), если 6 выбрано достаточно малым. Более точно:
функция z=?f(x) называется непрерывной в точке Хо, если для
любого сколь угодно малого е>0 найдется такое 6>0 (завися-
щее от е), что для всех х, удовлетворяющих неравенству
|х—х0| <6, справедливо неравенство (х) — f (х0) | <8. Линейная
функция z = сх и квадратичная форма г = х'Ах непрерывны в ка-
ждой точке Еп.
Сумма и произведение непрерывных функций непрерывны.
Частное двух непрерывных функций непрерывно во всех точках,
где делитель не обращается в нуль. Если f(x) непрерывна в х0
и если f (х0) >0, то существует б>0, такое, что f (х) >0 для всех х,
для которых |х — х01 <6. Это непосредственно следует из опреде-
ления непрерывности, так как если f(xo)=y>O, то по определе-
нию непрерывности найдется такое 6, что для всех х, таких, что
|х —х0|<6, справедливо неравенство (х) — f (х0) |<^у/2 и, сле-
довательно, f(x)>0.
2.9. Частные производные. Производная функции от одной
переменной в точке х0, обозначаемая df(xv)ldx или f'(xQ), опре-
деляется выражением
f' (х0) = lim = lim (2.21)
x->x0 x n
при условии, что указанный предел существует. Число а назы-
вается пределом функции g(x) при х->х0, если для произволь-
ного сколь угодно малого 8>0 найдется такое 6, что
|g(x) —а\<8, как только 0< |х— Хо| <6. Геометрически f'(xo)
представляет собой наклон кривой z=f(x) в точке xQ. Таким
образом, производная характеризует скорость изменения функ-
ции в точке х0.
Для функции п переменных можно определить частные про-
изводные, характеризующие в данной точке скорость измене-
ния функции в направлении каждой из п координатных осей.
2.9. Частные производные
57
Частная производная функции f по переменной Xj в точке
х0 — [*?, ..., определяется как предел
f he;) — f (x0)
= lim /2.22)
h-+0 n
Частную производную функции f по переменной в точке х0 мы
будем обозначать через df(x0)/dxj. Часто употребляются и дру-
гие обозначения: (df/dxj)o, (dz/dXj)Q или Djf(xQ). Когда нас не
интересует точка, в которой вычисляется частная производная,
мы будем пользоваться обозначениями df/dxj или dz/dxj. Каждую
из п частных производных можно рассматривать как функцию п
переменных. Чтобы получить частную производную функции f
по переменной xj, нужно определить обычную производную, счи-
тая все переменные, кроме Xj, постоянными. Как правило, в даль-
нейшем мы будем предполагать, что в каждой точке Епу где
определена функция f, существуют и непрерывны все п частных
производных f по переменным Xj. Обозначим через С множество
функций, непрерывных на некотором подмножестве простран-
ства Еп, а через С1 — множество функций, непрерывных вместе
со своими первыми частными производными. Функцию f(x) мы
будем называть дифференцируемой в точке х0, если JCC1 при
х=х0. Если f С С1 для некоторого подмножества пространства Еп,
то в каждой точке х этого подмножества мы можем определить
n-мерный вектор
Вектор Vf называется градиентом функции f; символ Vf чи-
тается «набла f». При необходимости отметить, что каждая ком-
понента Vf вычислена в некоторой фиксированной точке хо, мы
будем писать Vf(x0).
Так как каждая из частных производных функции f по пере-
менным Xj, /=1, ..., п, является функцией п переменных, то*
можно найти п частных производных для каждой из этих функ-
ций. Эти производные называются вторыми частными производ-
ными функции f и обозначаются d2f/dxidxjt d2z/dxidxj или zftjf •
Всего имеется п2 вторых частных производных. Если вторые
частные производные функции f существуют и непрерывны, то
говорят, что f € С2. Если f € С2, то
<2 24\
( dxidxj dxjdxi ’ \ /
58
Гл. 2. Необходимый математический аппарат
т. е. порядок дифференцирования не имеет значения, п2 вторых
частных производных функции f можно рассматривать как эле-
менты матрицы = порядка п. Ну называется гес-
сианом, функции f; из (2.24) следует, что Н/ — симметрическая
матрица. Если каждый элемент Ну вычислен в точке х0, то мы
будем использовать обозначение Н/(х0).
Взяв частные производные от вторых частных производных
функции f, мы получим частные производные более высокого
порядка.
Предположим, что каждая переменная Xj функции f сама яв-
ляется некоторой функцией от m переменных yi9 т. е.
^• = ф5(х/1, ..., ут). Функция f в этом случае называется слож-
ной функцией. Функция z = f(xb ..., хп) оказывается функцией
от переменных r/i, ..., ут, и мы можем записать
...» Ут), ym)] = g(yi, Ут)- (2.25)
Если f^C1 и € С1, /=1, ..п, то dz/dyt, i=l, т, суще-
ствуют и могут быть найдены по формуле
дг df дх} .
-з—=7.-5—> i—т, (2.26)
dyt Д дх> dyt ’ v '
i-i
где при вычислении df/dxj мы рассматриваем f как функцию от
%1, . . . , Хп-
Частные производные функции f характеризуют скорость из-
менения функции в направлении координатных осей. Можно,
однако, определить производную f в любом направлении. На-
правление в пространстве определяется ненулевым вектором г.
Выберем какое-либо направление, предположив для удобства,
что для характеризующего его вектора г |г| = 1. Производная
функции f в направлении г, вычисленная в точке х0, опреде-
ляется пределом
Dtf (х0) = lim , (2.27)
Л->0 п
если этот предел существует. Позднее мы увидим, что если
f { С1, то производная Drf(x0) может быть представлена как ли-
нейная комбинация частных производных функции f, вычислен-
ных в точке х0.
Примеры. 1. Пусть задана квадратичная форма
f (х) == х'Ах =22 aijxixj • '
2.10. Теорема Тейлора
59
Тогда
= 7=1...................(2'28)
1 i-i
и
Vf = 2x'A. (2.29)
Далее,
= «•’" Н/ = 2А- <230>
2. Предположим, что f = x®x^’/2ln-x3. Тогда
Йг = ЗХ1Х2-1/2 1П Хз! = - Т ХГ*2"3/2 1П Х&
&=х?х2-1/2хз-1;
д Г 1 A v-2v-3/2 1П г . Г df 1 А у2у-3/21пЛ.
~5xi I дх, ] — 2 X1X2 ln хз’ dxt L дх2 J —’ 2 Л 1п хз
и, следовательно,
d2f _ d2f
дх2 dxL дх1 дх2
2.10. Теорема Тейлора. В этой теореме утверждается, что
если f(x)^Cl на открытом выпуклом множестве X из Еп, то
для любых двух точек Xi и x2 = Xi + y, принадлежащих X,
существует такое число 0, 0 < 0< 1, что
f(x2) = f(x1)+Vf[0x1+(l-0)x2]y. (2.31)
Далее, если на множестве X f(x)£C2, то существует 0,
О-<0-<1> такое, что
f (х2) = f (Х1) + Vf (Х1) у 4-1 у'Н; [0Х1 + (1 - 0) х2] у. (2.32>
В этих формулах Vf[0xi+(1—0)х2] является градиентом функ-
ции f, вычисленным в точке 0xj+(l—0)х2, a H/[0Xi+ (1—0)х2] —
гессианом функции Д вычисленным в точке 0Xi+ (1—0)х2. Тео-
рема Тейлора может быть распространена на случай, когда
f € С\ k>2, но этот результат нам не понадобится.
Если f(x) СС1, то мы можем с помощью теоремы Тейлора
производную по направлению от функции /, определяемую вы-
ражением (2.27), выразить через частные производные этой
функции. В силу (2.31)
f(xB + fer)-f(Xo) vq0Xo + (1 _ 0) (Хо + Аг)] г.
во
Гл. 2. Необходимый математический аппарат
Таким образом,
п
W = W = jWry, - (2-33)
так что если частные производные функции f непрерывны, то
производная по направлению от этой функции равна линейной
комбинации частных производных.
Пусть f С С1 в точке х0. Обозначим *f(x0) через г0. Гиперпло-
скость
Z — Z;j = Vf(x0)(x — х0) или Vf(х0)х — z = Vf(х0)х0 — z0 (2.34)
называется касательной гиперплоскостью к поверхности z = f(x)
в точке х0. Вектор (V f(x0),— 1) является нормалью к гиперпло-
скости (2.34); этот вектор называют также нормалью к поверх-
ности (х) в точке х0.
Гиперплоскость (2.34) является касательной гиперплоскостью
в точке х0 к n-мерной поверхности z = f(x) в пространстве En+1.
Выберем произвольное значение г, например 2Ь и рассмотрим в
Еп (п— 1)-мерную поверхность уровня, определяемую соотноше-
нием Zi=/(x). Пусть Xi — точка из Еп, такая, что Zi=f(xi).
Тогда гиперплоскость
Vf(xj)(x —Х!) = 0 или V* (х^х = Vf (xjxj (2.35)
в Еп называется касательной к (п—1)-мерной поверхности
уровня в точке хь Вектор Vf(xi), являющийся нормалью к ги-
перплоскости (2.35), называется также нормалью к поверхности
уровня в точке хь Заметим, что исходная n-мерная гиперповерх-
ность может рассматриваться как поверхность уровня для
(п+1)-мерной поверхности.z = f(x)—z при z = 0. Поэтому каса-
тельная гиперплоскость к этой гиперповерхности в точке [х0, z0]
может быть определена как
(Vf (Хо), -1) [х, z] = (ff (х0), -1) [х0, z0], (2.36)
что в точности совпадает с (2.34).
2.11. Теорема о неявных функциях. Предположим, что имеет-
ся система m линейных уравнений с п неизвестными Ах=Ь, при-
чем r(A)=m. Тогда, если из матрицы А выбрать какую-либо
неособенную подматрицу В порядка т, то m переменных, соот-
ветствующих столбцам матрицы В, можно однозначно выразить
через остальные п—m переменных. Например, если подматрица
-порядка т, образованная первыми пг столбцами матрицы А,
2.11. Теорема о неявных функциях 61
неособенная, то, разрешая систему уравнений относительно пер-
вых т неизвестных, получаем
= 3 (2.37)
j-m+l
где и Vij — некоторые постоянные. Если теперь переменным
Xj, / = т+1, ..., п, придавать произвольные значения, а значе-
ния z = l, . .., т, вычислять в соответствии с (2.37), то в ре-
зультате мы получим вектор х, являющийся решением системы
Ах=Ь. Равенства (2.37) выражают переменные xb i=l,...,m,
как функции переменных Xj, j — m+1, ..., п.
Предположим теперь, что вместо системы линейных уравне-
ний мы имеем систему т уравнений с п неизвестными
g,(x) = 0, У = 1, ..., т, (2.38)
которая в общем случае может быть нелинейной. Нас интере-
сует вопрос, можно ли, выбрав произвольным образом т пере-
менных, например ..., хт, выразить их как функции осталь-
ных переменных. Другими словами, нас интересует вопрос о су-
ществовании функций
Xi = 4>i(xm+1, ..хп), г = 1.......т, (2.39)
таких, что если переменным xw+b ..., хп придать произвольные
значения, а значения ^переменных xb 1 = 1, ..., т, вычислить в
соответствии с (2.39), то полученный в результате вектор х будет
удовлетворять уравнениям (2.38). Если функции существуют,
то говорят, что переменные xb Z=l, ..., т, могут быть-выраже-
ны через переменные хт+1, ..., хп. Однако решение вопроса о
существовании функций <рг- не всегда позволяет найти представ-
ление переменных xb /=1, ..., т, через хт+1, ..., хп. В общем
случае эта задача может быть не только очень трудной, но и
неразрешимой в элементарных функциях.
Ответ на вопрос, когда функции ср^ существуют, дает теорема
о неявных функциях. Прежде чем сформулировать эту теорему,
введем несколько понятий. Рассмотрим для каждой функции
gi в (2.38) п ее первых частных производных dgildxj, j=l,... ,п.
Для т функций gi мы получим тп частных производных пер-
вого порядка. Эти производные могут рассматриваться как эле-
менты матрицы G = Ildgi/dxjH с размерами mXn. Из этой матри-
цы можно выделить n!/m!(n—т)\ различных подматриц поряд-
ка т. Типичная матрица такого вида может быть записана
62
Гл. 2. Необходимый математический аппарат
следующим образом:
Jx(/b • •
dgi dgi
Jm) — dxJt ‘ dXf Jm •
dgm dxf _ J\ dgm dX ; Jm —
(2.40)
Матрица (2.40) называется якобианом функций по перемен-
ным л:., ..., х. . Индекс х у символа J указывает точку из Епу
в которой вычислены элементы якобиана. Пусть k\, ..., —
множество индексов из числа 1,...,п, не принадлежащих мно-
жеству /1, ..., jm. Теорема о неявных функциях формулируется
следующим образом.
Пусть х0=[Хр ...» х^]— точка из Еп, обладающая свой-
ствами:
1) В некоторой 6-окрестности точки х0 функции g2(x) €С\
/=1, ...» т.
2) (х0) =0, i=l, ..., т.
3) Матрица JXo (/ь ..., jm) неособенная.
Тогда существует 8-окрестность (е>0) точки х0==
из Еп~т, такая, что для любой точки
Х = [Хь , . . ., Хь 1
L 1 л-mJ
из этой е-окрестности существуют однозначные и непрерывные в
точке х^ функции <Pi(xj, <р2(Д •••, Фт(х), обладающие свой-
ствами:
а) Z=l, ..., nv,
Ь) при любом х из 8-окрестности х0 значения i = 1,..., m,
вычисленные в соответствии с (2.39), вместе с компонен-
тами вектора х образуют вектор х, удовлетворяющий
уравнениям (2.38);
с) в 8-окрестности х0 функции срДх) дифференцируемы, и при
данных kr, г=1, ... ,п—т, производные dq^/dx^ являются
единственным решением системы линейных уравнений
т
у dgi__d1u_ = _dgL_> (2.41)
JU дх I dxk dxk v 7
Упражнения
63
Приведенная теорема о неявных функциях решает вопрос о
существовании функций <рг- лишь «в малом», т. е. в е-окрестно-
сти х0. Ее доказательство можно найти в [1] и [2]1).
ЛИТЕРА ТУРА
1. Ар о slot Т. М., Mathematical Analysis, Reading, Addison-Wesley, 1957.
2. К у р а и т Р., Курс дифференциального и интегрального исчисления, т. 2,
ГТТИ, М., 1931.
3. Хедли Дж., Линейная алгебра, «Высшая школа», М., 1966.
4. Hadley G., Linear Programming, Reading, Addison-Wesley, 1962.
5*. Ф их тенгол ьц Г. М., Курс дифференциального и интегрального исчис-
ления, т. 1, 2, Физматгиз, М., 1962.
Упражнения
2.1. Вычислить АВ и ВА (если они
существуют) в следующих случаях:
а)
Ь) А = (2, 1, 3], в = (—2, 4, 5);
с) А-[_6 “4 1- 1 В= 0 7
_2 9_
d) А = -зоо- 0 2 0 0 0 1 _ , в = 1 6 9 2 0 3
11 “
5
7_
2.2. Для каждой из матриц в упражнении 2.1 найти транспонированную.
В случае а) показать, что (АВ)'=В'А'.
2.3. Пусть А и В — матрицы, для которых существует АВ. Записать ма-
трицу В в виде строки векторов-столбцов, В=(ЬЬ..., Ьп), и показать, что
АВ = (АЬь АЬ2, ..., АЬЛ).
2.4. Дана неособенная матрица
где А — матрица с размерами kxk, a D — с размерами гХг. Предполагая,
что А-1 существует, найти М-1, выразив ее через А, В, С и D. [Указание: 1YT1
представима в том же виде, что и М.]
2.5. Показать, что п—1 линейно независимых векторов из Еп однозначно
определяют гиперплоскость, проходящую через начало координат, и что лю-
бая гиперплоскость, проходящая через начало координат, является подпро-
странством размерности п—1.
9 См. также [5*]. — Прим. ред.
64
Гл. 2. Необходимый математический аппарат
2.6. Найти все базисные решения системы уравнений
3xj -|- 2х2 — 9х3 х4 = 16,
7х^ — Зх2 4~* 5х3 — 9х4 = 8.
2.7. Решить графически и с помощью симплекс-метода следующую задачу
линейного программирования:
3xj 4“ 2х2 <. 6,
Xj + 4х2 4,
хь х2 0;
найти max z = х^ *2-
Указать крайние точки выпуклого множества решений, соответствующие каж-
дой итерации симплекс-метода.
2.8. Задачу упражнения 2.7 решить с помощью модифицированного сим-
плекс-метода.
2.9. Задачу, двойственную к задаче упражнения 2.7, решить симплекс-
методом и таким образом найти оптимальное решение задачи 2.7.
2.10. Задачу, двойственную к задаче упражнения 2.7, решить модифициро-
ванным симплекс-методом и таким путем получить оптимальное решение
прямой задачи упражнения 2.7.
2.11. Показать, что множество Х={х||х—а|=е} замкнуто.
2.12. Дать графическое изображение опорной гиперплоскости.
2.13. Найти характеристические числа и ортогональные характеристиче-
ские векторы для матрицы
2.14. Изобразить следующие квадратичные формы в Е3 и нарисовать их
линии уровня в Е2:
a) z — 3X14- 4x2; b) z = XjX2;
с) z = 4xi-—x%; d) г = Xj + 3x^2 + 4^2-
2.15. Найти преобразование переменных, приводящее квадратичную форму
z = 2xi — 3xjX2 + х2
к каноническому виду, и дать этому преобразованию геометрическую интер-
претацию.
2.16. Вычислить первые частные производные для функций
a) z = 3x^2 + 4г*1*2; b) z == xf2 4- In XjX2.
2.17. Найти гессиан для каждой из функций в упражнении 2.16.
2.18. Найти уравнение плоскости, касательной к поверхности
г — 4х^ — 5xjX2 + 6х2 + 8хх 2х2.
ГЛАВА $
КЛАССИЧЕСКИЕ МЕТОДЫ ОПТИМИЗАЦИИ
И СВОЙСТВА ВЫПУКЛЫХ ФУНКЦИЙ
Что-то скрыто, — иди, найди!
В путь! И ищи там, за Г ранью.
Что-то скрытое там, за Гранью,
Втуне тебя ожидает. Иди...
Р. Киплинг
3.1. Введение. В этой главе мы будем рассматривать классиче-
кие методы решения задач оптимизации некоторых типов.
В гл. 1 было указано, что эти методы используются для ре-
шения задач, названных там классическими задачами оптими-
зации. Мы отметили также, что классический подход исполь-
зуется главным образом при теоретическом анализе и лишь
ограниченно применим для получения численных результатов.
Однако в некоторых особенно простых ситуациях становится
возможным использование классической теории для нахождения
оптимального решения задачи в аналитическом виде, через раз-
личные параметры, встречающиеся в задаче. В таком случае
классический подход оказывается весьма удобным.
3.2. Максимум и минимум при отсутствии ограничений. При
изучении классической теории максимума и минимума следует
ясно представлять себе различие между абсолютным и относи-
тельным максимумом и минимумом.
абсолютный максимум. Говорят, что функция f (х), определенная
на замкнутом4 множестве ХаЕп, достигает на нем абсо-
лютного максимума в точке х*, если f(x)^f(x*) для лю-
бой точки х С X.
Часто вместо термина абсолютный используют термин глобаль-
ный максимум.
Если замкнутое множество X ограничено, а функция f непре-
рывна на этом множестве, то абсолютный максимум функции
. f на X обязательно достигается в одной или более точках X.
Если множество X не является ограниченным, абсолютный мак-
симум функции f может и не достигаться ни в одной точке X;
5 Зак. 735
66
Г л. 3. Классические методы оптимизации
однако он может оказаться равным предельному значению функ-
ции f, которое достигается, когда х стремится к бесконечности
каким-либо определенным образом.
сильный относительный максимум. Пусть функция f(x) определена
во всех точках некоторой б-окрестности точки х0 в Еп, Го-
ворят, что f(x) имеет в х0 сильный относительный макси-
мум, если найдется число е, 0<8<б, такое, что для всехх,
0< |х—х0|<8, выполнено неравенство f(x)<f(x0).
Иными словами, функция имеет сильный относительный макси-
мум в точке х0, если существует её 8-окрестность (хотя бы и с
очень малым 8), такая, что для всех х из этой 8-окрестности,
отличных от х0, f(x) строго меньше, чем f(x0).
слабый относительный максимум. Пусть функция f (х) определена
во всех точках некоторой б-окрестности точки Хо в Еп.
Говорят, что f(x) имеет в х0 слабый относительный мак-
симум, если она не имеет в этой точке сильного относи-
тельного максимума, но существует число 8, 0<8<б, та-
кое, что f(x)<7(x0) для всех х из 8-окрестности точки х0.
Часто нет необходимости различать сильный и слабый отно-
сительные максимумы. В таких ситуациях мы будем просто ука-
зывать: относительный (или локальный) максимум.
Определения абсолютного минимума, сильного относитель-
ного минимума и слабого относительного минимума получаются
из соответствующих определений максимума заменой на обрат-
ные знаков неравенства в соотношениях f(x)<f(x*), или
/(х)<7(х0), или f(x)<7(xo). Отметим, что если функция f имеет
абсолютный максимум в точке х* либо относительный максимум
в точке х0, то функция —f имеет абсолютный минимум в х*
либо относительный минимум в Хо.
На рис. 3.1 функция Цх) =f(%i, х2) имеет сильный относи-
тельный максимум в точках хь х2.
На рис. 3.2 любая точка, над которой лежит гребень волны,
является точкой слабого относительного максимума, а точка,
соответствующая впадине волны, — точкой слабого относитель-
ного минимума.
Классический подход теории максимума и минимума не ука-
зывает конкретных способов отыскания абсолютного максимума
или минимума функции. Он дает только признаки относитель-
ного максимума и минимума. В признаках используются част-
ные производные функции f, в связи с чем нам придется пред-*
полагать, что f € С1 на всем Еп или на той части Еп, которая нас
интересует.
2
Рис. 3.2
5*
68
Гл. 3. Классические методы оптимизации
Если Пх) имеет в точке х0 относительный максимум, то су-
ществует число 8>0, такое, что для всех х из 8-окрестности х0
(х0). Возьмем точку х этой 8-окрестности и представим ее
в виде x = x0 + /iej, где 0<\h\<8. Тогда
f (х0 + йеу) — Цх0)<0,
j= 1, 2, ..., га,
для всех h, 0< \h\ <е, или
f(xo+Лер —f(x0)
---------------< 0 при п > О
и
f (х0+ fiej) — f (х0) о
при А < 0.
(3-1)
h
Переходя в этих неравенствах к пределу при А-> + 0 и
h->—0, мы получим, что df(хо)/дх/^О и 5f(xo)/d.Xj^-O. Отсюда
^(Хо).. = О, /=1, 2, .... п.
dr, ’ J ’
(3.2)
Аналогичные рассуждения показывают, что соотношение (3.2)
имеет место и в точках относительного минимума. Равенство
(3.2) означает, что в точке х0, где f имеет относительный макси-
мум или минимум, все п частных производных функции /(х)
должны обращаться в нуль. Это эквивалентно утверждениям,
что а) градиент функции f в точке х0 есть нулевой вектор; Ь) ка-
сательная плоскость к поверхности г=/(х) в точке х0 имеет
уравнение г=г0=/(х0) (иначе говоря, касательная плоскость
горизонтальна).
Мы показали выше, что если fCC1 и f(x) имеет относитель-
ный максимум или минимум в точке х0, то х0 является решением
системы п (вообще говоря, нелинейных) уравнений
= z —1, 2, ...,га. (3.3)
дх; ’ v 7
Отметим, что решением этой системы уравнений должна быть
каждая точка, в которой f(x) достигает относительного экстре-
мума. Однако f(x) не обязательно имеет относительный макси-
мум или минимум в каждой точке, которая является решением
системы (3.3). Читатель помнит, что для функции одной пере-
менной решение уравнения dfldx — Q может давать точку пере-
гиба, в которой f не имеет относительного максимума или мини-
3.2 Максимум и минимум при отсутствии ограничений
69
мума. Подобно этому соотношения df/dXi = df/dx2 = 0 имеют ме-
сто в седловой точке функции двух переменных, однако в
такой точке f не имеет относительного максимума или мини-
мума.
Решения системы (3.3) называются стационарными точками
функции f. Точка, в которой f достигает своего относительного
максимума или минимума, является стационарной точкой f, но/
не обязательно достигает относительного максимума или мини-
мума в каждой стационарной точке.
Если определенная на всем Еп функция f имеет абсолютный
максимум (минимум) в некоторой точке х*, то, очевидно, f имеет
в точке х* также и относительный максимум (или минимум).
Следовательно, точка х* должна быть решением системы (3.3).
Поэтому для нахождения точки, в которой f имеет абсолютный
максимум (в предположении, что такая точка существует), тре-
буется лишь вычислить f во всех точках х, являющихся решением
системы (3.3), и наибольшее из полученных значений будет
абсолютным максимумом /.
К сожалению, решение системы (3.3) может оказаться весь-
ма трудной задачей, особенно в случае большого числа пере-
менных. Трудности еще более возрастают, если система имеет не
единственное решение. Для отыскания решений произвольных
систем вида (3.3) не существует какой-либо надежной вычисли-
тельной схемы. Даже если решение единственно, трудности его
фактического отыскания могут быть очень велики. Иногда для
нахождения численного решения системы (3.3) можно исполь-
зовать так называемый метод Ньютона. Для его применения
нужно предположить, что f € С2. Допустим, что известно началь-
ное приближение Xi для решения системы (3.3). Если х является
решением, то по известной теореме Тейлора
4^==0==^+v
J— 1, 2, .... п.
Заменим эту систему уравнений более простой
0= х,), /=1, 2, .п,
дх) 1 dXj v j
ИЛИ
(х- Х1)'Н/(Х1) = - Vf (х,). '(3.4)
Эта система п линейных уравнений с п неизвестными имеет
единственное решение, если только матрица Н/(хд) неособенная.
70
Гл. 3. Классические методы оптимизации
Допустим, что мы нашли некоторое решение системы (3.4), ска-
жем х2. Мы можем использовать х2 в качестве приближения к х
и повторить процесс. На n-м шаге получаем xn+i=xn+yn, где
уп — решение системы y'Hz(xn) = — Vf (хД К сожалению, мы не
можем гарантировать в общем случае, что этот итеративный
процесс будет сходиться к решению системы (3.3), даже если
известно, что эта система имеет единственное решение.
Предположим теперь, что вместо задачи нахождения абсо-
лютного максимума f на всем Еп требуется отыскать абсолют-
ный максимум f в неотрицательном октанте. В этом случае если
абсолютный максимум f достигается в точке х*, то х* не обяза-
тельно должна удовлетворять системе (3.3), потому что эта точка
может оказаться лежащей на границе октанта, т. е. одна или
несколько ее координат могут обратиться в нуль. Для отыска-
ния абсолютного максимума нужно применять теперь следующую
процедуру. Сначала находятся решения уравнения (3.3), лежащие
в неотрицательном октанте. Затем мы должны рассмотреть п
функций fj от п—1 переменных, которые получаются из f(x)
подстановкой Xj = 0, и для каждой fj найти решения системы
dfj/dXi = O, i^j, лежащие в неотрицательном октанте простран-
ства Еп~\ После этого рассматриваются п(п— 1)/2 функций fij
от п — 2 переменных, которые получаются из f при Х; = Х; = 0
и т. д. Абсолютный максимум функции f будет совпадать с наи-
большим из абсолютных максимумов всех рассмотренных
функций.
Из этих рассуждений ясно: если замкнутая область, в кото-
рой ищется абсолютный максимум f, не совпадает с £п, необхо-
димо учитывать, что максимум может достигаться на границе
области; задача определения абсолютного максимума f в этом
случае, вообще говоря, сильно усложняется.
3.3. Пример. Мы сейчас рассмотрим задачу, для решения
которой применим классический подход, рассмотренный в преды-
дущем параграфе. Этот пример иллюстрирует черты, общие для
большого числа экономических задач, таких, где затраты или
прибыль не являются детермированными, а зависят от значения
случайных параметров.
Прием, обычно используемый в этом случае, состоит в мак-
симизации математического ожидания прибыли или минимиза-
ции математического ожидания затрат на определенном интер-
вале-времени. В ситуациях, в которых одни и те же условия бу-
дут повторяться снова и снова и ожидаемая прибыль или затра-
ты могут быть интерпретированы как средняя прибыль или
затраты за долгий срок, представляется абсолютно логичным
максимизировать ожидаемую прибыль или минимизировать
3.3, Пример
71
ожидаемые затраты. Однако этот же самый критерий исполь-
зуется и тогда, когда некоторые обстоятельства имеют место
только однажды и никогда не повторяются в дальнейшем, так
что нет возможности интерпретировать математическое ожида-
ште как долгосрочное среднее.
Перейдем непосредственно к примеру. Деталь машины произ-
водится на токарном станке в механической мастерской. Диа-
метр выпускаемых деталей не всегда одинаков и изменяется
случайным образом, в связи с чем диаметр х детали может рас-
сматриваться как случайная переменная. Математическое ожи-
дание ц этой случайной величины может изменяться при изме-
нении режима токарного станка. Предполагается, однако, что
среднее квадратичное отклонение о постоянно и не зависит от
режима станка, т. е. от математического ожидания ц. Плотность
распределения задается функцией f(x; ц); вероятность того, что
диаметр детали лежит между х и x+dx, есть f (х; ц)йх. Диа-
метр х не должен выходить из допустимого интервала xi<x<ix2.
Если х<хь деталь должна быть выброшена. Если х>х2, деталь
может быть передана для вторичной обработки. Предполагается,
что мастерская, о которой идет речь, не будет вторично обраба-
тывать деталь, а вместо этого продаст деталь с диаметром х>х2
другой мастерской по цене рх за штуку. Деталь, пропущенная
контролем, продается по цене р>рь Суммарная стоимость
сырья, труда и рабочего времени машины при обработке каждой
заготовки равна k.
Требуется определить значение ц, при котором недельная
прибыль достигает максимума.
Если W — число заготовок, обрабатываемых в неделю, сле-
дует ожидать, что будет выброшено
W j f(x; ii)dx
О
деталей, где значение интеграла есть просто вероятность того,
что диаметр детали окажется меньше хь Точно так же следует
ожидать, что число деталей, продаваемых для доработки, будет
равно
хт
W fix', \L)dx,
Х2
где хт есть диаметр наибольшей из деталей.
72
Гл. 3. Классические методы оптимизации
Таким образом, ожидаемый недельный доход есть
Р(ц) = р№
1 — J f (х; ц) dx — j f (х; ц) dx
tn
A-PxW J f(x; n)dx— Wk =
X2
•*1 m v
= (p — k)W —W pf f (x; ii) dx + (p — Pi) j f(x;p)dx . (3.5)
L 0 X2 .
Ясно, что абсолютный максимум функции Р(ц) не будет дости-
гаться на границе при ц=0 или ц=хт. Следовательно, значе-
ние ц, доставляющее максимум Р, должно быть решением урав-
нения
р$ ^(х; Mdx + tp — Pi) J ii)dx
-° X2
(3-6)
Рассмотрим случай, когда величина х распределена по нор-
мальному закону. Тогда
/ (х; ц) =--e-(x-nF/2o»; £L =---------1 р—ВЛ r(x-nW. (3J)
а]/2л ф, а2}^2л \ а / '
Обозначим
Если предположить, что площадь под кривой нормального рас-
пределения на интервалах — oo<jc<X) и хт-^х^оо пренебрежи-
мо мала, так что нижний предел первого интеграла в (3.6)
может быть заменен на — оо, а верхний предел второго инте-
грала в (3.6) —на оо, то мы получим
X, Vi
f — f(x; \i)dx = —f e~vdv =-------------
J ф ' V 7 а/2л J а/2л
0 oo
xm oo
f — f (x; p.) dx = —[ e~v dv — —
J ф ' 1 а/2л J аК2л
34. Условный максимум и минимум
73
Таким образом, условие (3.6) принимает вид
ре - {х. - ц)2/2а2 = (р — Pj) е- (лг2 “ H)72ff2
или
202 ln ( \ = (Х1 _ и)2 _ (х2 _ И)2
\ г г\. /
Отсюда получается единственное решение
и = л+а+^,„(^). (з,8)
Так как решение единственное, ясно, что это значение ц должно
обеспечивать абсолютный максимум ожидаемой недельной при-
были.
3.4. Условный максимум и минимум. Множители Лагранжа.
Мы рассмотрим сейчас классический подход к решению класси-
ческих задач оптимизации. Будем разыскивать точку х*, кото-
рая доставляет абсолютный максимум или минимум функции
f(x) на множестве тех х£Еп, которые удовлетворяют условиям
g\-(x) — b^ /=1,..., m, m<n. Предполагаем, что f€C' и gi£C\
i= 1,..., m, на En. Пусть У — множество точек х, удовлетворяю-
щих условиям gi(x) =bi, f= 1,..., m.
Подобно тому как это сделано в § 3.2, удобно начать с опре-
деления абсолютного и относительного максимума.
абсолютный максимум. Говорят, что функция f(x) достигает в
точке х* С X П У абсолютного максимума на замкнутом
множестве XczEn при условиях gi (х) = b^ если
f (x)<^f (х*) для всех х П У.
сильный относительный максимум. Говорят,что функция f(x) име-
ет сильный относительный максимум при ограничениях
gi(x) =bi, /=1, ..., m, в точке х0, если х0 С У и существует
число 8>0, такое, что в 8-окрестности х0 для любой точки
х С У, х=#х0, выполняется неравенство f(x)<f(x0).
СЛАБЫЙ относительный максимум. Говорят, что функция/(х) имеет
слабый относительный максимум при ограничениях
g. (х) = bi = 1, ..., m, в точке х0 С У, если она не имеет в
этой точке сильного относительного максимума, однако
существует 8 > 0, такое, что для каждой точки х € У из
8-окрестности х0 справедливо неравенство /(х) <7(хо).
Когда нет необходимости различать сильный и слабый отно-
сительные максимумы, мы будем говорить просто об относитель-
ном максимуме. Необходимые изменения при формулировке
определений абсолютного минимума, сильного и слабого относи-
74
Г л. 3. Классические методы оптимизации
тельного минимума являются очевидными. Мы будем называть
иногда максимум и минимум, определенные выше, условным
максимумом и условным минимумом и использовать название
безусловный максимум и безусловный минимум для ситуации,
рассмотренной в § 3.2. Максимум и минимум функции назы-
ваются также ее экстремумами.
Как будет показано, классический подход к решению задач
вида (1.12) дает систему уравнений (необходимые условия),
которым должна удовлетворять точка хо, доставляющая f(x)
относительный максимум или минимум на множестве точек х,
удовлетворяющих условиям g,(x) =6,, t«=l,..., tn. Классический
подход не дает способов для непосредственного получения точ-
ки или точек, доставляющих f абсолютный максимум или ми-
нимум при х € У. Однако если абсолютный максимум или мини-
мум достигается в точке х*, которая входит в область определения
функции f вместе с некоторой своей окрестностью, то точ-
ка х* должна также доставлять функции f относительный мак-
симум (минимум). Отсюда, если fCC1 и z=l,...,m,
получаем, что точка х* должна быть решением упомянутой выше
системы. В том случае, когда все решения системы уравнений
могут быть найдены, для определения абсолютного максимума
(минимума) и точки, в которых он достигается, остается только
вычислить f в каждой из найденных точек.
Мы установим сейчас наиболее удобную, но не самую общую
форму небходимых условий, о которых шла речь выше. Начнем
с изучения задачи с двумя переменными и одним ограничением.
Таким образом, мы хотим установить необходимые условия, ко-
торым должна удовлетворять точка xo=[xj, х®], если функция
z=f(x\, х2) достигает в ней относительного максимума или ми-
нимума при ограничении g(xlt х2) = Ь. Напомним, что мы пред-
полагали f,g€ С1. Допустим, что производная dg/dx^ или dg/dx2
не равна 0 в х0. Для определенности пусть dg(xo)/dx2=#O. Тогда
по теореме о неявных функциях существует е-окрестность х®,’
в которой мы можем решить уравнение g(xi, х2)—Ь=0 относи-
тельно х2, так что х2=ф(Х1), где <р —непрерывно дифференци-
руемая функция, заданная на указанной окрестности х®, и
х° = ф(х^). Каждая точка [хь ф(хО] принадлежит У. Следова-
тельно, мы можем исключить х2 в f(xi, х2). Имеем
z = h. (хО = f [Xj, ф (xO] (3.9) '
для |Xj — x®|<e. Но если f имеет в точке Хо относительный
максимум при условии g(x) = b, должно существовать такое чис-
ло ео, О<ео<8, что для всех х4 в 8о-окрестности справедливо
3.4. Условный максимум и минимум
75
(3.10)
A(Xj)й(xj). Следовательно, h имеет безусловный максимум в
xj. Точно так же если f имеет относительный минимум в х0 при
условии g(x)=6, то h имеет безусловный относительный мини-
мум в xj. Сложная функция h дифференцируема в окрестности
xj. Так как h имеет в точке xj безусловный относительный
максимум или минимум, то dh(x^dxx = 0. Дифференцируя h
как сложную функцию, получим
dh __ df df б/ср _ df_____df dgjdxx
dxx dxx ' dx2 dxx dxx dx2 dgjdx2 ’
так как по теореме о неявных функциях
dq dg!dxx
dxx dgfdx2
Следовательно, должно выполняться соотношение
df (ХО) df (х0) dg (x0)/dxi _ 0
dxx dx2 dg (xQ)/dx2
Обозначим
1— df (xQ)/dx2
dg(x0)/dx2
Таким образом, необходимо, чтобы точка х0* удовлетворяла
уравнениям
— = X-^21=0; g(x0) = b. (3.11)
dxx dxi dx2 dx2 * s \ и/ \ /
Мы имеем три соотношения, которым должна удовлетворять ч
точка х0, если она доставляет относительный максимум или ми-
нимум функции f(x) при g(x)=b в предположении, что
dg(xo)/dX2=/=O. Соотношения (3.11) представляют систему трех
уравнений с тремя неизвестными х°, х° и Л. Функция f не обя-
зательно достигает относительного максимума или минимума
при х€ Y в каждой точке, являющейся решением системы (3.11).
Однако если мы предположим, что обе частные производные
функции g не равны 0 в каждой точке, где f(x) достигает отно-
сительного максимума или минимума при х£ У, то каждая
точка, в которой f(x) достигает относительного максимума или
минимума при условии g(x)=6, будет решением этой системы;
значит, находя все решения системы (3.11), мы определим все
точки, в которых f(x) имеет относительный максимум или мини-
мум при условии g(x)=b.
Необходимые условия (3.11) удобнее получать следующим
образом. Составим функцию
F(x. X) = f(x) + MZ>-g(x)J (3.12)
76
Гл. 3. Классические методы оптимизации
и приравняем нулю ее частные производные относительно хь
х2, Считая все переменные независимыми и дифференцируя
F(xy К) по каждой переменной, получаем
= = -^ = 4-«(х) = 0. (3.13)
Функция F называется функцией Лагранжа, а % — множителем
Лагранжа.
Легко дать геометрическую интерпретацию задачи с двумя
переменными и одним ограничением. На плоскости Xi.r2 прове-
дем кривую g(xlt x2)=b и линии уровня функции Z=f(Xt, х2).
Геометрическая иллюстрация этой задачи дана на рис. 3.3.
Функция f(xi, х2) при условии, что х удовлетворяет соотноше-
нию g(x)=b, имеет сильный относительный максимум в точках
Xi и х2 и сильный относительный минимум в точке х3. Абсолют-
ный максимум f(x) при условии g(x)=b достигается в точке х2.
Каждая из точек хь х2 и х3 будет решением системы (3.13).
Возвратимся к общему случаю с п переменными и /n(zn<n)
ограничениями. Предположим, что в точке х0 функция /(х)
имеет относительный максимум или минимум для х € У. Предпо-
ложим также, что в точке х0 ранг r(G) матрицы G= lldgi/dxjl
равен ш. Для простоты обозначений будем считать, что матрица
JXo (1, ..., m) является неособенной. Тогда по теореме о неявных
функциях существует е-окрестность точки х0 = р-тн» •••»
ЗА. Условный максимум и минимум
77
такая, что для каждой точки х из этой е-окрестности мы можем раз-
решить уравнения
gk(xlt xn) = bk, k = \, 2, ..т,
относительно хь ... , хт:
xz = <pz(x), Z= 1, т,
причем функции фг, i=l, непрерывно дифференцируемы
в указанной окрестности точки х0 h<pz(x0) = xz, / = 1, ..., т-
Функция
Л (х) = f [<Р1 (х), .... фт (х), х] (3.14)
имеет безусловный относительный максимум или минимум в х0,
и, поскольку h дифференцируема в е-окрестности точки х0,
^1=0, у=/п+1, .... п. (3.15)
По правилу дифференцирования сложной функции
dh у, df d<p df , .
-д— —У. -Т-- . /=/«-)- 1, .... й. (3.16)
dxi dxi дх,- 1 dxi J 1 ' '
Z = 1
По теореме о неявных функциях производные dqi/dXj, f = 1,..., m,
для каждого номера / представляют собой решение (единствен-
ное) системы уравнений
<•=.....-
Z? = l J
Мы имеем п—т систем уравнений вида (3.17), по числу номе-
ров /. Вместо того чтобы решать системы уравнений (3.17) отно-
сительно dqi/dxj и подставлять в (3.16), мы поступим следую-
щим образом. Рассмотрим набор чисел z=l, ... , m, являю-
щийся решением системы т линейных уравнений
= k=\,...,m. (3.18)
1 dxk dxk ' v f
z=i
Заметим, что решение системы существует и единственно, ибо
ее матрица коэффициентов Ао (1, ..., /я) по предположению не-
особенная.
78
Гл. 3. Классические методы оптимизации
Умножим Z-e уравнение из (3.17) на X* и просуммируем по Z.
Для каждого /, / = т+1, ... , п, получаем
m л
х д%1 \
1 dxfi I dxj
(3.19)
Из (3.15) и (3.16) следует
V ^(х0) d<pft(x0) ff(x0)
21 дх^ dxj ’ dxj
y = /n 4-1, ..., n. (3.20)
Вычислив (3.19) в точке x0, после вычитания из (3.20) по-
лучим
j — 1, ...» п. (3.21)
Отсюда, используя (3.18), имеем
Объединяя эти уравнения с уравнениями (3.18) и ограниче-
ниями, мы заключаем, что точка х0, в которой f(x) достигает
относительного максимума или минимума при х€У, должна
удовлетворять следующей системе т + п уравнений:
dxj
JhJ $XJ
gi^ = bi, i=\,
/=1. ••
..., т.
п\
(3.23)
Не обязательно, чтобы любое решение системы уравнений
(3.23) доставляло относительный максимум или минимум функ-
ции /(х) при х£У. Однако каждая точка х0, в которой f(x) до-
стигает относительного максимума или минимума при х € У,
должна быть решением системы (3.23) при условии, что G(x0)
имеет ранг т.
Необходимые условия (3.23) могут быть более просто полу-
чены следующим образом. Составим функцию
т
F(*,k) = f (х) + 2 k( [1>г - gl (х)] (3.24)
Z-1
и приравняем нулю ее частные производные по каждой из т + п
переменных xh /=1, ... , п, и Z=l, ... , т. При вычислении
3.5. Общий случай
79
частных производных все переменные считаем независимыми.
Имеем
dxj dxj /=1, ..., п; (3.25)
z==l, ,,,, т. (3.26)
Функция F(x, X), определенная выражением (3.24), назы-
вается функцией Лагранжа, а числа Лг- называются множителя*
ми Лагранжа. Если при х=х0 система (3.25), (3.26) имеет реше-
ние, множители Лагранжа единственным образом определены,
если г (G) «т в точке хо.
Метод получения необходимых условий, заключающийся
в построении функции F и приравнивании нулю ее производных,
получил название метода множителей Лагранжа. Его большое
преимущество с практической точки зрения состоит в том, что
нет необходимости выражать одни переменные через другие или
учитывать, что не все переменные независимы. Так же как для
недбходимых условий § 3.2, и здесь не существует какого-нибудь
вычислительного процесса для получения всех решений системы
(3.25), (3.26), в связи с чем эти условия оказываются полезными
лишь в случае, когда система имеет единственное решение и оно
может быть получено аналитически или с помощью достаточно
простого алгоритма.
Мы сейчас показали, что если f(x) имеет в точке х0 относи-
тельный максимум или минимум при х( У и притом r(G)=m
в х0, то в х0 должны выполняться условия (3.25) и (3.26). Если
r(G)=#m в точке х0, х0 может и не удовлетворять системе (3.25),
(3.26). В следующем параграфе мы укажем более общие необ-
ходимые условия, имеющие место и в случае, когда в точке'х0
ранг матрицы G не равен т.
3.5. Общий случай. Как и в предыдущем параграфе, мы бу-
дем предполагать, что fZC1, gi^C1, f=l, ... , tn. Рассмотрим
матрицу
~ dgi
dxi ' * * дхп
JL
_ dxt ‘ ’ дхп
80
Гл. 3. Классические методы оптимизации
с размерами (m+l)Xn. Ранг матрицы G/ не превосходит т + 1.
Покажем сначала, что если r(G/) в точке х0 равен т+1, то
f(x) не может иметь в этой точке относительного максимума или
минимума при х С У.
Итак, пусть в точке х0 r(G/)=m+l. Для определенности
предположим, что неособенной в точке х0 является подматрица,
составленная из т+1 первых столбцов матрицы G/. Тогда из
теоремы о неявных функциях следует, что для системы т+1
уравнений
f(x) —z = 0; gz(x) = 6z, / = 1, ...» т, (3.28)
относительно п+1 переменных ... , хп и z существует такая
е-окрестность (е>0) точки [х^ч 2, ..., х?п, г0], zG=f(x0), в кото-
рой мы можем выразить ... , xw+i через остальные пере-
менные:
^ = ф/(хт+2, хл, z\ /==1, ..., т + 1. (3.29)
Важно отметить, что z является здесь просто одним из аргумен-
тов функций фг-. Следовательно, если мы положим хт^~
= х^+2, •• •, хп~х^ то для любого z,\z—г0|<8, существует
такая точка х€ У, что z=f(x). Так как функции фг- непрерывны,
мы, выбрав некоторую б-окрестность (6>0) точки х0 в Е\ смо-
жем найти в ней такие точки х€У, что ^m+2 —хт+2’ •••»
—и в некоторых из них f(x)>z0, в других f(x)<z0.
Таким образом, f(x) не может иметь относительного максимума
или минимума в точке х0 при х 6 У.
Из доказанного выше следует, что если f(x) имеет в точке х0
относительный максимум или минимум при х С У, то в точке х0
r(G/)<m+l. Пусть Хо — точка, в которой f(x) достигает относи-
тельного максимума или минимума при х € У. Рассмотрим одно-
родную систему п линейных уравнений с т+1 неизвестными %z:
^о-Л—— т—= 0, 7=1, (3.30)
и dxj 1 дх] m dxj J v 7
Так как r(G/)<m+l в точке х0, существует нетривиальное ре-
шение системы (3.30). Мы изучим сейчас различные случаи,
которые могут здесь иметь место.
Сначала предположим, что r(G)=m в точке х0. Мы можем
выбрать любые m уравнений с матрицей ранга m и выразить из
них единственным образом ... , Кт через Хо. Значение Хо мо-
жет быть выбрано произвольно. Оно не может, однако, равняться
нулю, если речь идет о нетривиальном решении. В нашем случае
удобно положить Хо=1. Остальные при этом определятся
3.5. Общий случай 81
единственным образом. Допустим далее,чтов точке х0 r(Gy)—т,
но r(G)=m—1. Выберем из (3.30) т уравнений так, чтобы ма-
трица их коэффициентов содержала неособенную подматрицу
порядка т. Ясно, что эта система уравнений не имеет решения
при Хо=#О. В противном случае мы имели бы систему уравнений
для определения Кг, у которой ранг расширенной матрицы был
бы больше ранга матрицы коэффициентов, т. е. несовместную
систему. Если, однако, Хо = О, то существуют удовлетворяющие
(3.30) числа Кг. f=l,..., m, не все равные нулю. В этом случае
К-t, i= 1, ... , т, определяются не единственным образом, реше-
ния заполняют одномерное подпространство пространства Ет.
Перейдем к случаю, когда в точке х0 r(Gy) = r(G) =г<т. Вы-
берем г уравнений из системы (3.30) таким образом, чтобы мат-
рица их коэффициентов содержала неособенную подматрицу
порядка г матрицы G. Тогда мы можем выразить г перемен-
ных Кг через Хо и остальные т — г переменные Кг. И в этом слу-
чае Хо может быть выбрано произвольно. Удобно положить Хо = 1.
Остальные Кг, /=1, ...» т, не определяются единственным обра-
зом. и т — г переменным можно придавать любые значения.
Остается рассмотреть случай, когда в точке xft r(G/)==r<m и.
r(G/)>r(G). Точно так же выберем из системы (3.30) г уравне-
ний, матрица коэффициентов которых имеет ранг г. Рассуждая,
как раньше, можем заключить, что не существует решения си-
стемы с Хо¥=О. Если мы положим Хо = 0, найдутся удовлетворяю-
щие системе (3.30) Хг-, г=1, ..., m, не все равные нулю. Множе-
ство наборов таких Кг заполняет подпространство размерности
т — г + 1 в пространстве Ет.
Приведенными выше рассуждениями мы показали, что если
f(x) имеет в точке х0 относительный максимум или минимум
при хС У, то точка х0 должна удовлетворять системе уравнений
..................................- (331)
7 м 7
хотя бы для одного набора Хг-, £=0, 1, ..., т, где не все Хг = О, и
системе уравнений
^(Хо) = ^, (3.32)
Эти необходимые условия могут быть получены приравниванием
нулю частных производных по Xj и (7=А0) от функции Лаг-
ранжа
т
F(x Л) = W (X) + 2 [bt - gi (x)].
б Зак. 735
82
Гл. 3. Классические методы оптимизаиии
Мы показали, что, не умаляя общности, в (3.31) можно
положить равным 0 или 1. Если r(G/)=r(G) в точке х0, то мы
полагаем Хо—1. Если r(G/)>r(G), то для того, чтобы среди Хг-,
f— 1, ..., п, удовлетворяющих системе (3.31), были ненулевые,
необходимо положить %о = О. Хг- определены однозначно, если в
точке Хо r(G/)=r(G)=m и определяются не единственным об*
разом, если в х0 r(G/)>r(G) либо r(Gy) —r(G) <m.
Это завершает формулировку необходимых условий в общем
случае. Большинство работ рассматривают только случай Хо=1.
Обобщения, приведенные в настоящем параграфе, рассмотрены
В работе [2].
Существуют также и достаточные условия, при выполнении
которых решение системы уравнений (3.31), (3.32) определяет
точку, в которой f(x) имеет сильный относительный максимум
или минимум при х£У. Одну из форм этих условий читателю
предлагается получить в упражнениях к настоящей главе. Как
и при отсутствии ограничений, эти условия представляют глав-
ным образом теоретический интерес. Тем не менее они имеют
фундаментальное значение в некоторых теоретических исследо-
ваниях.
3.6. Случай неотрицательных переменных и ограничений
в форме неравенств. Ценой введения больших вычислительных
трудностей можно обобщить метод множителей Лагранжа на
случай, когда переменные неотрицательны и некоторые ограни-
чения заданы в форме неравенств. Начнем с задачи отыскания
глобального максимума или минимума функции г = /(х) при
условиях х^>0, gi(x)—bi, i=l, ..., m, m<n. Мы будем по-
прежнему предполагать, что fCC1 и g^CC1, t=l, ... , m.
Допустим, что глобальный экстремум функции f(x) достав-
ляет точка х*. Экстремум может достигаться либо во внутренней
точке неотрицательного октанта, где все компоненты х* положи-
тельны, либо в граничной точке, когда хотя бы одна из компо-
нент х* равна нулю. Если х* — внутренняя точка, она должна
удовлетворять системе (3.31), (3.32). Поэтому первый шаг со-
стоит в отыскании всех решений системы (3.31), (3.32), лежа-
щих внутри неотрицательного октанта, и вычислении z для ка-
ждого из этих решений. Далее должна быть исследована граница
неотрицательного октанта. Чтобы это сделать, мы сначала рас-
смотрим случай, когда лишь одна из переменных обращается
в нуль, т. е. мы приравняем одну из переменных нулю и рас-
смотрим получающуюся в результате этого задачу с п—1 пере-
менными и пг ограничениями. Составив уравнения вида (3.31),
(3.32) для этой задачи, мы найдем все решения, лежащие внутри
неотрицательного октанта пространства Еп~1. После этого вы-
3.6. Случай неотрицательных переменных 83
числим z для каждого из этих решений. Заметим, что, поскольку
каждая из переменных может быть приравнена нулю, мы дол-
жны решить п таких задач с п—1 переменными и m ограниче-
ниями. Затем мы приравняем нулю две переменные и рассмот-
рим получающуюся^ в результате задачу с п—2 переменными и
m ограничениями. Число такого рода задач будет п!/2!(п— 2)!
После этого мы рассмотрим задачу, получающуюся в результате
фиксирования трех нулевых значений переменных и т. д. Вслед-
ствие наличия ограничений мы не можем, вообще говоря, сво-
бодно фиксировать более п—m переменных одновременно. Когда
п-m переменных приравнены нулю, ограничения определяют
(обычно единственным образом) остальные т переменных. По-
этому на последнем этапе мы вычисляем z в каждой точке ре-
шения с п—т нулевыми компонентами. Абсолютным максиму-
мом является наибольшее из всех величин z, получаемых выше,
а абсолютным минимумом — наименьшее.
Очевидно, что если не все переменные подчинены требованию
неотрицательности, мы должны приравнивать нулю лишь те из
них, которые подчинены этому требованию. Ясно, что из-за тре-
бований неотрицательности переменных может сильно возрасти
объем вычислений. Если переменных достаточно много, вычис-
лительные трудности могут оказаться непреодолимыми.
Легко дать геометрическую интерпретацию описанного выше
процесса для случая двух переменных и одного ограничения.
Допустим, что задача имеет структуру, представленную на
рис. 3.3. Здесь единственной точкой неотрицательного октанта,
которая является решением системы (3.31), (3.32), будет х2. Да-
лее, когда одна из переменных приравнена нулю, другая опре-
деляется единственным образом и мы получаем точки, в кото-
рых кривая g(x)=& пересекает оси Xi и х2. Абсолютный макси-
мум функции f(x) в неотрицательном октанте достигается в
точке х2, абсолютный минимум — на границе, в точке, где кри-
вая g,(x)=& пересекает ось х2.
Рассмотрим теперь случай, когда нет ограничений неотрица-
тельности, но некоторые из ограничений имеют форму нера-
венств. Пусть ограничения с номерами 1, ..., и имеют вид
gi(x)^bi, ограничения с номерами и+1, ...., и— вид g'i(x)>&i
и при /=у+1, ... , т должны выполняться строгие равенства
g\(x) =bi. Мы можем превратить ограничения первого вида в ра-
венства, если добавить вспомогательные переменные xsi, полагая
gi(x) +xsi = bi, z=l, ..., и. Теперь условие gi(x)^bi равно-
сильно неравенству xsl->0. Подобным же образом введением
вспомогательных переменных ограничения с номерами 1, ...,
v могут быть превращены в равенства gjx)—xsi = bi. Здесь
условие gi(*)^bj эквивалентно ограничению xsi^0.
6*
84 Гл. 3. Классические методы оптимизации
z = 1, ..., я,
i = it —f-1, ..., т), (3.33)
i — v 4- 1, ..., tn,
i = 1, ...,
или min z = f (x).
глобальный экстремум функции f,
Таким образом, мы сводим исходную задачу к задаче, рас-
смотренной в начале этого параграфа:
g/(x)4-x5/ = Z>z,
gi(x) — xsl = bt,
gi (x) = bt,
xsi о»
найти max
Для того чтобы определить
мы должны рассмотреть внутренность неотрицательного октанта
пространства Е\ где все х5г>0, и его границу, где некоторые из
xsz=0. Рассмотрим сначала тот случай, когда все xsi>0. Функ-
ция Лагранжа имеет вид
F(x, х5, Х) = М(х)4- 2 K[bt— xsl — g/(x)]4-
Z = 1
v m
+ S ^\bi + xsl-g,.(x)]+ s ^{bi-gz(x)J. (3.34)
Z = zz-|-1 Z=^--l
Из условия (3.31) следует, что частные производные F по
всем переменным, включая xsi, должны быть равны нулю. При-
равнивая нулю производные по xsi, получаем
bxsi 1
дР , л . , .
-т— — К: — 0, i — и -Т-1, ..., т).
dxsi 1 ' 1
Отсюда ясно, что если в точке экстремума %Ai>0, f=l, ... , и,
то соответствующие обращаются в нуль, т. е. ограничения
в форме неравенств при поиске этой точки мы можем отбросить.
Другими словами, если в точке, где f(x) достигает своего абсо-
лютного минимума либо максимума, ограничения в форме не-
равенств выполняются со знаком строгого неравенства, мы можем
при определении глобального экстремума функции f(x) эти ог-
раничения не принимать во внимание. Это обстоятельство пред-
ставляется ясным и интуитивно. Когда же мы движемся по гра-
нице октанта, где некоторые xSi = 0, ограничения с соответствую-
щими номерами следует учитывать, т. е. соответствующие
могут отличаться от нуля.
Для того чтобы найти глобальный экстремум функции /(х)
при наличии ограничений, мы будем поступать следующим об-
разом. Сначала найдем все решения системы уравнений (3.31),
(3.32) для случая, когда отброшены ограничения в форме нера-
венств, и для каждого из них вычислим значение z. Затем по-
37. Интерпретация множителей Лагранжа
85
вторим процедуру, подключая одно неравенство и рассматривая
его как существенное. Проделаем это с каждым из неравенств.
Далее проделаем то же, подключая по два неравенства во все-
возможных комбинациях и рассматривая их как существенные
и т. д. Процесс будем продолжать до тех пор, пока не будут
подключены все неравенства. Оптимальное значение г равно
наибольшему или наименьшему из полученных значений г, если
рассматривать лишь те решения, которые удовлетворяют всем
ограничениям.
Интересно отметить следующее: из приведенного выше вид-
но, что если х* является точкой глобального экстремума/, —
соответствующие х* значения вспомогательных переменных и
V=[Xp — набор множителей Лагранжа, соответствую-
щих х*, то или х* = 0, или Z* = 0, i = 1, ..., v, т. е. /Лх*. = 0.
3.7. Интерпретация множителей Лагранжа.. Возвратимся к
задаче нахождения глобального экстремума функции z = /(x)
при m ограничениях gi(x)=bh Z=l, ... , m. Предположим, что
х* — точка, в которой f достигает глобального экстремума и
r(G)=m в точке х*, так что, не умаляя общности, мы можем
положить Хо=1. Пусть АЛ=[Х*, ..., Z/Ц—набор множителей
Лагранжа, соответствующий х*. Вообще говоря х*. и будут
зависеть от значений bit которые участвуют в задаче. Допустим,
что все х* и Z* являются непрерывно дифференцируемыми
функциями вектора Ь=[&ь bm] в некоторой 8-окрестности
точки Ьо. В упражнении 3.12 от читателя требуется найти доста-
точные условия, которые гарантируют существование таких
функций.
Мы вычислим частные производные глобального экстремума
z*=/(x*) по bi в точке Ь, лежащей в е-окрестности точки Ьо:
= (3.35)
дь1 ^дх/ дь1
Из условия gfc(x*)=6ft мы имеем
й ik
или
= (3-36)
“ дх . db,
j-i ) 1
86
Гл. 3. Классические методы оптимизации
где 6ik — символ Кронекера. Домножим (3.36) на к*, просум-
мируем по k и добавим к (3.35). Это даст
±- = 2*,.+S %- (3.37)
dbi £ jZjxi £ dXj_db,
Так как х* и X* должны удовлетворять условиям (3.23), мы за-
ключаем, что
<=^ (з.з8)
Следовательно, производные глобального экстремума по bi про-
сто равны соответствующим множителям Лагранжа X/, вычис-
ленным при данном Ь.
Нередко г будет интерпретироваться, как доход или стои-
мость, bi — как затраты некоторых ресурсов. В этом случае раз-
мерностью kz будет единица стоимости на единицу /-го вида
ресурсов. Грубо говоря, числа kz показывают, как изменится
максимальный доход (или минимальная стоимость), если коли-
чество z-го вида ресурсов увеличится на единицу. Приведенная
здесь интерпретация множителей Лагранжа может быть рас-
пространена также на случай ограничений в виде неравенств и
на случай, когда переменные подчинены требованиям неотри-
цательности. Мы предлагаем читателю сделать это в упражне-
нии 3.13.
3.8. Интерпретация функции Лагранжа; двойственность.
Предположим, что /(х) имеет в точке х0 относительный макси-
мум при условиях £г (х) = 6Z, /=1, ..., т, и в х0 r(G) =гп. Пусть
= к^]— вектор, компонентами, которого являются
множители Лагранжа, соответствующие х0. В реальных задачах
часто оказывается, что в точке х0 функция Лагранжа F (х, ко)
имеет безусловный относительный максимум, т. е. F(x, ко)4^
<Т(х0, ко) Для всех х из некоторой 8-окрестности точки х0.
Предположим теперь, что существует такая 6-окрестность точ-
ки ко в Еш, что при любом к из этой 6-окрестности F(x, к) имеет
безусловный относительный максимум по х в точке, удовлетво-
ряющей условиям
= /•='......"• (3-39)
В реальных задачах это предположение часто выполняется.
3,8. Интерпретация функции Лагранжа; двойственность
87
Представим себе, что система уравнений (3.39) имеет един-
ственное решение при любом X из S-окрестности Хо и точка мак-
симума х может рассматриваться как функция от X. В зада-
че 3.14 мы предлагаем читателю проверить, при каких условиях
это предположение выполняется. Тогда в 6-окрестности Хо мы
можем записать
тахЛ(х, Х) = Л(х, Х) = й(Х), (3.40)
X
т. е максимум по х будет функцией от %, которую мы обозна-
чили й(Х). Отметим, что
h^^F^.
Интересно установить, будет ли й(Х) иметь относительный
максимум или минимум в точке Хо. Рассмотрим F(x, X) при
фиксированном X. Заметим, что при х, удовлетворяющем усло-
виям gf(x) =й,, i = l, ,.., m,
F(x, b) = f(x).
Отсюда
тах/Дх, X) = maxf (x) = f(x0) = A(X0). (3.41)
xer . x£K
Так как в (3.41) x подчинен требованию х(У, ав (3.40) ника-
ких ограничений на х нет, то справедливо неравенство
А(Х)>Л(Х0),
т. е. А(Х) имеет относительный минимум в точке Хо. Поскольку
“когда х и X связаны условиями (3.39) Л(Х)=^(х, X), отсюда
следует, что F(x, X) имеет относительный минимум по,Х в точ-
ке Хо при выполнении ограничений (3.39), которые определяют х
при каждом X. Задача минимизации F(x, X) по X при ограниче-
ниях (3.39) называется двойственной к задаче отыскания мак-
симума f(x) при ограничениях ^(х)=&й z = l, ... , m. Двой-
ственные задачи обладают тем свойством, что в окрестности х0
при соответствующих ограничениях
min F (х, X) = max f (х) = f (х0) = h (Хо). (3.42)
X X
В силу (3.40) тах/7(х, 1) = й(А.) и min й (1) — й (10); отсюда
X X
мы можем написать
f (х0) — min max F (х, X), (3.43)
1 X
и f(xo) есть решение задачи на минимакс.
88
Гл. 3. Классические методы оптимизации
Это же самое может быть записано и в другой форме. Рассмо-
трим окрестность точки [х0, Хо] в En+m. В силу сделанного пред-
положения о том, что F(x, X) имеет относительный максимум
по х при любом X в S-окрестности Хо, должно выполняться соот-
ношение
F (х, Хо) F (х0, Хо) — f (х0).
Отметим также, что F(x0, X)=f(x0), так как х0 С Y. Отсюда
F(xo, Xo)=F(xo, X). Поэтому мы можем написать
F (х, Хо) < F (х0, Хо) = F (х0, X). (3.44)
Говорят, что функция F(x, X) имеет седловую точку в точке
[х0, Хо], если существует е>0, такое, что для всех х и X, удовле-
творяющих условиям |х—х0|<е, |Х—Х0|<е,
F (х, Хо) F (х0, Хо) F (х0, X).
Мы только что показали, что при сделанных выше предполо-
жениях функция Лагранжа имеет в [х0, Хо] седловую точку, кото-
рая является, однако, вырожденной, поскольку справа имеет
место равенство. Затронутые здесь вопросы будут значительно
более подробно изучены и обобщены в гл. 6. В этом параграфе
мы следовали Куранту и Гильберту [3].
3.9. Примеры. Рассмотрим три примера. Два из них будут
иллюстрировать те типы задач, которые можно решать с исполь-
зованием множителей Лагранжа. Третий покажет, почему метод
множителей Лагранжа не облегчает решение задач линейного
программирования.
1. Владелец магазина одежды может израсходовать
3000 долл, на закупку одежды трех моделей, которая будет про-
даваться магазином в течение наступающего сезона. Эта одежда
должна быть им заказана к началу сезона, и заказ не может
быть впоследствии изменен. Одежда первой модели стоит при
закупке 35 долл., а продаваться в розницу будет по цене 66 долл.,
одежда второй модели — соответственно 20 и 37 долл., одежда
третьей модели — 50 и 105 долл. Одежда, не проданная до кон-
ца сезона, будет продаваться на 20% ниже закупочной цены.
Если в магазине не окажется достаточного количества одежды
нужной модели, владелец теряет в расчете на 1 комплект
70 долл, по одежде первой модели, 40 долл, по одежде второй
модели и 220 долл, по одежде третьей модели. Предполагается,
что спрос на одежду каждой модели подчинен закону нормаль-
ного распределения с математическим ожиданием 30, 60 и
15 единиц и стандартным отклонением 8, 12 и 3 единицы для
первой, второй и третьей моделей соответственно,
3.9. Примеры
89
Сколько и какой одежды следует закупить, чтобы суммарная
ожидаемая прибыль была максимальной?
При решении задачи мы будем считать, что все переменные
непрерывны. Пусть Xj — количество закупленной одежды /*-й мо-
дели. Если спрос на одежду /-й модели равен vjf то магазин
продаст одежды /-й модели на сумму
PjVj, если
vj
pjXji если Vj Хр
где pj — розничная цена.
При продаже одежды /-й модели теряется прибыль
О, если Vj < Xj,
лj (Vj ~ х7), если Vj Хр
где jtj — потеря при нехватке одного комплекта одежды /-й мо-
дели.
Одежда, оставшаяся на конец сезона, продается на сумму
0,8f; (Xj — Vj), если Vj < Ху,
О, если Vj Xj,
где Cj есть стоимость одежды /-й модели. Ожидаемая прибыль
от продажи одежды /-й модели равна ожидаемому доходу (вы-
ручке) минус стоимость товара, минус ожидаемая потеря, плюс
ожидаемый доход от продажи остатка по сниженным ценам.
Обозначим через п(и; ц, о) плотность нормального распре-
деления с математическим ожиданием ц и стандартным откло-
нением о. Мы будем предполагать, что нет зависимости между
спросом на одежду различных моделей, т. е. покупатель не ста-
нет покупать одежду другой модели, если запас одежды инте-
ресующей его модели распродан, так что Vj— независимые слу-
чайные величины. Тогда ожидаемая прибыль Pj от продажи
одежды /-й модели есть
00 / х J
pj = Pjxi j J vjn(vf, —
xi
оо
— CjXj — л J j (Vj — Xj)n(vj; M.y, <Jj)dVj +
xj
xj
+ 0,8c7 J {х} — vj)n(vf, iij, a^dVj.
90
Гл. 3. Классические методы оптимизации
Мы предполагаем при этом, что площадь под кривой нормаль-
ного распределения на интервале от —оо до 0 пренебрежимо
мала, и поэтому в приведенном выше выражении мы можем
нижним пределом интегрирования взять —оо вместо 0.
Преобразуем выражение для Pj следующим образом:
Pj = Ну (Pj — 0,8с у) — 0,2сух у —
ОО
— (/>уЧ-Лу—0,8су) / (©у— Ху)п.(d/ Иу, ay)dDy.
xj
Для того чтобы выполнить это преобразование, мы воспользова-
лись соотношениями
xj оо
J Dy/г(Dy; Цу, Оу)rfDy = gy—J Dy«(®у; gy, Gy)t/Dy
-ОО Xj
И
г
J (^/-®у)л(г»у; Ну, Oj)dvj = Xj-Hj+ J (Dy-Xy)n(Dy;
-ОО Xj
Ожидаемая прибыль от продажи одежды трех моделей по-
лучается суммированием Pf, Р2 и Р2:
Р = 1140 — 7xi — 108 ^(D! — xj п (Dp 30, 8) d^ +
Xi
-]-1260 —4х2 —61 J (d2—x2)/z(d2; 60, 12)c?d2+
Хг
-|-975 — 10x3 — 285 J (d3—x3)zz(d3; 15, 3)</d3. (3.45)
X»
Мы должны найти неотрицательные величины хь х2 и Хз, кото-
рые минимизируют Р при ограничении
35х1-Ь20х2-4-50х3<3000, (3.46)
поскольку для того, чтобы доставить максимум прибыли, не 'обя-
зательно истратить всю располагаемую сумму.
Сначала мы будем искать абсолютный максимум Р, не обра-
щая внимания на это ограничение. Ясно, что максимум будет
достигаться в точке, где все Ху будут конечны. Значит, экстре-
3.9. Примеры
91
мальная точка, если предположить, что ее компоненты положи-
тельны, должна удовлетворять системе уравнений
<=<>’ /=1,2,3.
Вычисляя эти производные, заметим сначала, что
d
dxj
X
-x)
~ 00
-X)
co
= — Xjn(Xj; njt ay) — j n(vf, ц,. Gj)dVj + х}п(х/, |iy, <jy) =
7 J Oj)dvj =
где
oo
= - j n{Vj, Ну, Ру)^у = -ф(Х-7-~Цу
xj
Значения функции Ф(/) (или функции, с помощью которой
Ф(/) легко вычисляется) приводятся в таблицах закона нор-
мального распределения. Мы имеем:
^-==0 = -74 Ю8Ф(^^) или Ф(^‘7--) =0,0648,
^-=0= — 4Н-61ф(-г-760) или Ф = 0,0656.
<=0 = - 10Н-285ф(--3-~15) или ф(Хз~7—) = 0,0351.
С помощью таблиц мы можем найти единственное решение этих
уравнений:
xt —30__
8
1,515,
хг — 60
12
1,51,
х3 —15
3~~
= 1,81,
откуда
откуда
откуда
хх 42,
х2^78,
х9 «%= 20,
7
92
Тл. 3. Классические методы оптимизации
При этих значениях Xj общая сумма, равная 35-42 + 20’78 +
+ 50’20=4030, превышает располагаемую сумму в 3000 долл.
Таким образом, ограничение задачи оказывается существенным.
У нас £(х) =35Х1 + 20х2 + 50х3, r(G) = l при любом х=#0, и,
следовательно, не умаляя общности, в функции Лагранжа мы
можем положить Хо=1. Тогда
з
F (х, 1) = 2 Pj — Ь [3000 - 35%! - 20х2 — 50х3].
Если каждая компонента экстремального вектора х положи-
тельна, то х должен удовлетворять соотношениям
= о = - (7 + 35%) + 108Ф (-7—°-).
откуда
8 108 ’
= о = - (4 + 20%) 4- 61Ф (^^-).
откуда
/л2-60\ 4 + 20% .
\ 12 61 ’
^. = 0 = -(Ю4 5ОХ) + 285Ф(Хз~ 15),
откуда
Ю + 50А
\ 3 285 ‘
Мы должны решить эти три уравнения совместно с уравне-
нием £(х)=3000. Удобный способ решения состоит в следую-
щем. Выберем некоторое Х>0, определим из трех уравнений
единственное решение Xj и вычислим значение £(х). Если
g“(x)=3000, мы имеем решение. Если g,(x)>3000, мы возьмем
большее значение X и повторим вычисления. Если g(x)<3000,
мы повторим вычисления с меньшим положительным значе-
нием X. Мы непременно придем к единственному решению, так
как для данного X все xj определяются единственным образом
и их величины монотонно убывают с возрастанием X. Это озна-
чает, что найдется только одно значение X, для которого
g(x)=3000. Результаты итеративного процесса, начатого с
Х = 0,50, приведены в табл. 3.1. Подходящее значение X можно
быстро получить с помощью интерполяции.
3.9. Примеры
93
Таблица 3,1
Вычисления для первого примера
X Хх х2 •Г3 «(х)
0,50 36 69 18,5 3565
1,00 32 63,2 17,4 3254
1,50 29 58,3 16,6 ЗОН
1,52 28,8 58,0 16,55 2996
Поскольку очевидно, что владелец должен закупить положи-
тельное число единиц одежды каждой модели, нет необходи-
мости проверять значения Р на границе, где одно или более
xj = O, Оптимальное решение будет х* = 29, х* —58 и х*=17
(илих*=16, в зависимости от того, будет ли отпущенная сумма
незначительно перерасходована или недорасходована). Эти ре-
шения получаются округлением до ближайших целых значений.
Следует заметить, что полученное таким путем решение не обя-
зательно является оптимальным значением задачи с условием
целочисленности Однако практически часто это оказывается
так. В гл. 10 мы покажем, как находить точное решение задачи
с требованием целочисленности.
2. Напомним, что Drf(x0) (производная от z=f(x) в направ-
лении вектора г в точке х0) означает скорость изменения z в
точке х0 в направлении г. Для в § 2.10 мы показали, что
при |г | = 1
= (3.47)
н 1
Определим теперь направление г, по которому скорость измене-
ния z в точке х0 максимальна. Это означает, что мы хотим найти
максимум выражения
V <У(х0) ,
Ь дХ) ’
при ограничении |г| —1, или
/г
?(г)=2Д = 1. (3.48)
Заметим, что dgldrj=2rj. Значит, r(G) = l в любой точке,
удовлетворяющей условию |г| = 1, и, следовательно, не умаляя
94
Гл. 3. Классические методы оптимизации
общности, мы можем в (3.31) положить Zo=l. Поэтому опти-
мальный вектор г* должен быть решением системы
= дНх0)____2Хг — 0 7 — 1 П' — =1_______У г2 — О
dr, dxf ~ 1 > • • • ’ ", 1 гу — и,
7=1
где
п
F (г, X) = г у - V2] + X (3.49)
— функция Лагранжа. Отсюда
_ 1 <У(х0)
'7 2Х dxj
и с учетом ограничения
X2 = |lW0)P или Х = ± 1| Vf(x0)|.
Здесь мы имеем два решения:
г/_ + Wo)
" Р/(х0)Г
Одно из них дает направление, в котором максимальна ско-
рость возрастания z, другое — направление, в котором макси-
мальна скорость убывания z. Подставляя (3.50) в (3.47), мы
сможем выделить интересующее нас решение.
Выбирая решение со знаком ( + ), мы получим, что
ЛИХо)==| Vf(Xo)|>O, (3.51
т. е. z не убывает. Следовательно, решение со знаком ( + ) дает
направление, в котором максимальна скорость возрастания z,
решение со знаком (—) —направление, в котором максимальна
скорость убывания z. Таким образом, мы получили важный ре-
зультат: направление скорейшего возрастания z совпадает с на-
правлением градиента, а направление скорейшего убывания z
противоположно направлению градиента. Из (3.47) следует, что
DJ(x0) = Vf(x0)r = |Vf(x0)|cos9,
где 0 есть угол между г и V/(x0). Таким образом, мы факти-
чески должны были найти значение 0, которое максимизирует
cos0. Ясно, что это 0 = 0, и мы приходим к полученному выше
результату.
3. В последнем примере мы покажем, почему метод множи-
телей Лагранжа не облегчает решения задач линейного про-
граммирования.
(3.50)
3.9. Примеры
95
Допустим, мы должны решить задачу
Ах —Ь, х>0; найти maxz = cx.
Пусть А — матрица с размерами mXn, r(A)=m. Отметим, что
ограничения и целевая функция везде дифференцируемы. Следо-
вательно, можно попытаться здесь применить метод множителей
Лагранжа Мы будем действовать, как предлагается в § 3.6, на-
чиная с определения относительных максимумов внутри неотри-
цательного октанта, где все п переменных положительны. Затем
мы будем исследовать границу, где одно или несколько Xj = 0.
Для точек внутри неотрицательного октанта r(G)=m, так
как G = A. Следовательно, мы положим Хо=1 и соответствую-
щая функция Лагранжа есть
Любая экстремальная точка внутри неотрицательного октан-
та должна удовлетворять уравнениям
dxj ~ 0 — ci
'дЦ = 0 = bt aijXj,
/=i
j — 1, ..., n,
Z=l, (3.52)
или, в матричной форме,
А'1 = с', Ах —Ь.
На первый взгляд может показаться, что любое допустимое
решение должно удовлетворять необходимым условиям (3.52).
Однако это не так. Рассмотрим систему п уравнений с т неиз-
вестными A'Z = cz. Оказывается, что эта система уравнений в об-
щем случае несовместна, т. е. r(A', с') =т+1, так что в дей-
ствительности точек внутри неотрицательного октанта, удовлет-
воряющих необходимым условиям, нет, и, следовательно,
относительный максимум здесь достигаться не может. Это ста-
новится более ясным, если мы введем матрицу
Так как г{А', с') — т+1, то r(G/)=m+l во всех точках внутри
неотрицательного октанта, и, как показано в § 3.5, отсюда сле-
дует, что ни в одной из этих точек z не достигает относительного
максимума или минимума. В случае когда г(Az, с') =т, система
96
Гл. 3. Классические методы оптимизации
= имеет единственное решение, z = const в допустимой об-
ласти и любое допустимое решение является оптимальным.
В задаче 3.52 предлагается доказать приведенное здесь утвер-
ждение.
В общем случае, когда r(G/)=m+l, мы далее изучаем гра-
ницу неотрицательного октанта, где лишь одна переменная, ска-
жем %], равна нулю. В результате получаем задачу с новой со-
вокупностью необходимых условий Ajl = Cj и А4Х1=Ь1, где Аь Ci
и Xi получаются из А, с и х вычеркиванием первого столбца.
Снова, как правило, г(А', с[) = яг +1, и мы заключаем, что
стационарной точки, у которой только компонента Xi = 0, нет.
В случае когда г (A', с^) = г (А') = т, система A'X = Cj имеет
единственное решение, z=const для любого допустимого реше-
ния с Х1 = 0 и любое допустимое решение с Xi = 0 доставляет
максимум или минимум целевой функции. При xi = 0 возможно
также, что г(А[) = т— 1 и, если есть допустимое решение, одно
ограничение является лишним. Отбросив это лишнее ограниче-
ние, мы видим, что если г (A', Cj) = m, то стационарной точки,
у которой лишь компонента Xi = 0, нет. С другой стороны, если
r(A[, = —1, любое допустимое решение с Xi = 0 является
стационарной точкой и оно будет доставлять максимум или мини-
мум целевой функции. В задаче 3.52 предлагается детально рас-
смотреть утверждения, сделанные относительно двух последних
случаев.
Мы получили, что среди точек с Xi = 0 либо нет стационар-
ных, либо любая допустимая точка доставляет максимум или
минимум целевой функции. Если в нашем случае нет стационар-
ных точек с Xi = 0, мы переходим к рассмотрению точек, у ко-
торых лишь х2 = 0, и повторяем анализ.
Возможно, придется продолжать этот процесс для всех слу-
чаев, когда лишь одна переменная равна нулю. Если при этом
не получена стационарная точка, мы рассматриваем точки, у ко-
торых две переменные равны нулю. В неблагоприятном
случае процесс будет продолжаться, пока мы не дойдем до
п—пг нулевых переменных. Оставшиеся m переменных опреде-
ляются единственным образом, если матрица коэффициентов не-
особенная, т. е. здесь мы имеем экстремальную точку. Таким
образом, метод множителей Лагранжа показывает, что, вообще
говоря, оптимальное решение задачи линейного программирова-
ния (если экстремум единственный) имеет не более m положи-
тельных переменных, т. е. в общем случае оптимальное решение
будет крайней точкой выпуклого множества допустимых реше-
ний. Однако метод це решает практически задачу линейного
3.10. Выпуклые и вогнутые функции
97
программирования, так как он не дает способа определить, ка-
кая именно крайняя точка является оптимальной. В то же время
при использовании метода множителей Лагранжа остается от-
крытым вопрос о наличии неограниченных решений.
3. 10. Выпуклые и вогнутые функции. В дальнейшем мы бу-
дем часто иметь дело с так называемыми выпуклыми и вогну-
тыми функциями.
выпуклая функция. Функция /(х), заданная на выпуклом
множестве Хс.Еп, называется выпуклой, если для любых
двух точек Xi и х2 из X и любого %, 0<ОХ1,
f[%x2 + (l -МХ1]<Ч(х2) + (1-%)Г(Х1). (3.53>
Часто интересующим нас множеством X будет все Еп или неот-
рицательный октант.
вогнутая функция. Функция f(x), заданная на выпуклом
множестве X<z.En, называется вогнутой, если для любых
двух точек Xi и х2 из X и любого X, (К^ХЛ,
f [Лх2 + (1 - X) Х1] > Kf (х2) + (1 - X) f (Х1). (3.54)
Заметим, что если f(x) —выпуклая функция, то —f(x) —вогну-
тая, и наоборот.
Мы говорим, что гиперповерхность z = f(x) выпуклая, если
отрезок, соединяющий любые две ее точки [хь zj, [х2, z2] лежит
на поверхности или выше ее. Выпуклая функция одной перемен-
ной изображена на рис. 3.4. Аналогично гиперповерхность
z=f(x) вогнутая, если отрезок, соединяющий любые две точки
поверхности, лежит на поверхности или ниже ее. Функция одной
переменной, изображенная на рис. 3.5, является вогнутой при
7 ♦Зак. 735
98
Гл. 3. Классические методы оптимизации
xi>0. Функция, показанная на рис. 3.6, не является ни вогнутой,
ни выпуклой, так как отрезок с концами [xb f(x4)] и [х3, f(х3)]
лежит выше f(x) на участке между Xi и х2 и ниже f(x) на уча-
стке между х2 и х3. Отметим, однако, что функция эта выпукла
на интервале 0-Сх-Сх4 и вогнута при х>х4. Следует заметить,
что мы определяем выпуклость и вогнутость только относитель-
но выпуклых множеств в Еп, так как определение предполагает,
что вместе с любыми X) и х2 множеству принадлежат точки
Хх2+(1—X)Xi при всех %, 0<Х<1. Последнее справедливо лишь
в том случае, если множество выпуклое.
строго выпуклая функция. Функция f(x), заданная на вы-
пуклом множестве называется строго выпуклой, если
для любых двух точек х4 и х2 из X, Хц=#х2, и любого X,
0<Х<1,
f [Хх2 + (1 -1) х,] < Kf (х2) + (1 - X) f (Х1). (3.55)
Подчеркнем, что в (3.55) имеет место строгое неравенство.
Функция f(x) строго вогнута на X, если —f(x) строго выпук-
ла. Геометрически функция z=f(x) строго выпуклая, если отре-
зок, соединяющий любые точки поверхности, лежит выше этой
поверхности при всех х=Хх2+(1—X)xlt 0<Х<1. Функция на
рис.^3.4 строго выпуклая для х>х, но не строго выпуклая для
х<х.
Линейная функция z=cx является выпуклой (и вогнутой) на
всем Еп, так как для любых двух точек Xi и х2 и любого X
. С [Хх2 -ф- (1 — X) Xj] Хсх2 (1 — X) СХГ
3.10. Выпуклые и вогнутые функции
99
Однако линейная функция не является ни строго выпуклой, ни
строго вогнутой.
Н еотрицательная. квадратичная форма z=x'Ax является вы-
пуклой функцией на всем Еп. Чтобы доказать это, рассмотрим
любые две точки Xj и х2 и любое X, 0<Х<1. При х—Хх2+
+ (1—Х)х1 имеем
х'А£ = [Хх2 + (1 - X) xj' А [Хх2+(1 -1) xj =
= [Xi + X (х2 — х,)]' А [Х1 + X (х2 — Х1)] =
= x'AXj + 2Х (х2 — х,)' AXj + X2 (х2 — х^' А (х2 — х,). (3.56)
Так как по предположению х'Ах>0 при любом х, имеем
Хх'Ах^>Х2х'Ах при 0-=CX4U. Используя это неравенство в выра-
жении (3.56), получаем
х'Ах < Xj'AXj + 2А (х2 — х^' AXj + А, (х2 — х^' А (х2 — х^ (3.57)
или
х'Ах < Xj'AXj + А, (х2 — х^' AXj + А, (х2 —- х^' Ах2 <
< Хх'Ах2 + (1 — А.) Х1'Ахг (3.58)
Неравенство (3.58) и означает, что функция 2 = х'Ах выпук-
лая. Отсюда непосредственно следует, что неположительная
квадратичная форма является вогнутой функцией на всем Еп.
Аналогичные рассуждения показывают, что положительно опре-
деленная квадратичная форма является строго выпуклой функ-
цией на всем Еп, так как в этом случае
% (х2 — хО' А (х2 — X!) > А,2 (х2 — хО' А (х2 — Xj) (3.59)
при 0<Х<1, x2’=#xi и, следовательно, знак в (3.57) может
быть заменен знаком <. Подобно этому, отрицательно опреде-
ленная квадратичная форма является строго вогнутой функцией
на всем Еп.
Предположим, что функции fj(x), ... , k, являются вы-
пуклыми на некотором выпуклом множестве Х£Еп. Тогда
функция
k
f(x)=2fj(x) (3.60)
7-1
также выпукла на X. Для доказательства этого утверждения
достаточно отметить, что для любых точек Х1ИХ2изХи любого X,
7*
100
Гл. 3. Классические методы оптимизации
k
f l^X2 + (1 — X)xJ — Jj f;[^x2 +(1 Xil <
k
<SRf;(x2)+(l-^)fy(x1)] =
y-i
=* i fj (x2)+a - x) i fj (X1)=у (x2)+a - %) f (X1)
Таким образом, сумма выпуклых функций есть выпуклая функ-
ция. Конечно, также справедливо, что сумма вогнутых функций
есть вогнутая функция.
В определении выпуклости и вогнутости мы не требуем, что-
бы /(х) была непрерывной или дифференцируемой. Можно по-
казать, что если f(x) —выпуклая или вогнутая функция, задан-
ная на замкнутом множестве X, то f(x) будет непрерывна в
каждой внутренней точке множества. Однако на границе множе-
ства X функция f(x) может не быть непрерывной. Доказатель-
ство этих свойств приведено в работе [4]. Выпуклая или вогнутая
функция f(x) не обязательно будет везде дифференцируемой.
Например, у функции, изображенной на рис. 3.4, не существует
производной в точке х=х.
Если f^C1 во внутренних точках множества X и выпукла
на X, мы можем получить следующий полезный результат. Из
определения (3.53) имеем при всех X, 0<X4U,
z [х, 4- Л (х2 - х,)] - f (х,) f (Хг) _ {(xj. (3 б1)
По формуле Тейлора
f [xj + X (х2 - х,)] = f (х,)+W [X! + (x2 - x,)] (x2 - X1). (3.62)
O<0< 1,
так что (3.61) можно переписать в виде
Vf [х, 4-10 (х2 — х,)] (х2 — Х1) < f (х2) — f (Х1). (3.63)
Переходя к пределу при Л ->0, мы получим, что
V/(X1)(x2 —X1)Cf(x2) —f(X1) (3.64)
для любой внутренней точки Xj€ X и любой точки х2€ X. Анало-
гично, если /€ С* и вогнута на X, тем же путем получаем
Vf (*l) (Х2 - Xj) > f (x2) - f (Xj). (3.65)
3.10. Выпуклые и вогнутые функции
101
Если f — функция одной переменной, (3.64) можно пере-
писать (для x2¥=Xi) в виде
Л-2 Л-]
(3.66)
Геометрически это означает, что если функция f(x) выпукла, то
наклон касательной к графику функции f(x) в точке [х1( /(xj]
меньше или равен наклону секущей, проведенной через точки
[х1( f (xj] и [х2, f (х2)] (см. рис. 3.7).
Рис. 37. Здесь .
Х2 — Xi
наклон секущей, f'(xi) — наклон
касательной в точке
Если f(x)—выпуклая функция, заданная на неотрицатель-
ном октанте пространства Еп, то множество V всех точек, удо-
влетворяющих условиям f(x)<s£b и х>0, выпукло (если оно не
пусто).
Чтобы доказать это утверждение, мы покажем, что множе-
ство V вместе с точками xi и х2 при любом 0^<Х-<1, содержит
также точку х=Хх2+(1 —Х)хь Ясно, что х^>0. Остается пока-
зать, что f(x)<C&. Это следует из выпуклости f(x). Мы имеем
f (X) = f [Хх2 + (1 - X) xj < If (х2) + (1 - X) f (Х1).
Далее, так как f(xi)-C6 и f(x2)<O, то для любого X, О^СХ-^1,
справедливо Xf (х2) 4^Х&, (1—X)f(xi)<C(l—Х)6. Следовательно,
Xf(x2) + (1— Х)/(Х1)<Хд + (1— Х)6 = & и f(x)<b,
что и завершает доказательство.
Следует заметить, что множество точек, удовлетворяющих
соотношениями f(x)=b, х>0, в общем случае не выпукло.
Тем же путем доказывается, что если )(х) —вогнутая функ-
ция, заданная на неотрицательном октанте пространства Еп, то
множество V всех точек, удовлетворяющих условиям f(x}^b,
х>0, является вогнутым (если оно не пусто),
102
Гл. 3. Классические методы оптимизации
Наконец, поскольку пересечение выпуклых множеств вы-
пукло, множество W всех точек (в предположении, что W не
пусто), удовлетворяющих условиям
fz(x){<, >}&z, Z = l, x>0,
выпукло, если в неравенствах со знаком fi — выпуклые
функции, а в неравенствах со знаком f г — вогнутые функции
для х>0.
Пусть f(x)—выпуклая функция в неотрицательном октанте
пространства Еп. Предположим также, что С1. Тогда каса-
тельная гиперплоскость размерности (n—1) к поверхности
f(x)=b в точке х0<>0 является опорной к выпуклому множеству
/<={x|f (х)<О, х>0) в точке х0.
Для доказательства этого утверждения напомним, что урав-
нение гиперплоскости, касающейся поверхности в точке х0, есть
V/ (х0)х= Vf (хо)хо. Мы хотим показать, что для любой точки
wCX справедливо Vf(x0)w<lVf(хо)хо. Это следует немедленно
из выпуклости f(x), если мы используем (3.64) с w = x2, xo = xi.
Так KaKf(w)<&, a f(x0)=6, получаем V f(х0) (w — хо)^О, что и
требовалось доказать.
Аналогично если f(x) —вогнутая функция в неотрицательном
октанте и f(x) С С1, то касательная гиперплоскость к поверхно-
сти f(x)=b в точке хо^О является опорной гиперплоскостью
к выпуклому множеству Х={х|/(х)>&, х>0} в точке х0.
3. 11. Примеры. 1. Положительно определенная квадратичная
форма одной переменной f1(x1) = 3x2 является выпуклой функ-
цией на Е1. Аналогично/2(х2) = 4х^— выпуклая функция на Е1.
Отметим, что fi(xi) и ^(хг) могут рассматриваться как функции
от x=[xi, х2], такие, что f\ зависит лишь от первой компоненты х,
a /2— только от второй компоненты. Таким образом, fi(xi) и
f2(x2) —выпуклые функции на Е2. Следовательно, f(x) = 3x2 +
+ 4х^— также выпуклая функция на Е2.
2. Так как f (х) — Зх2-|-4х^ — выпуклая функция, множе-
ство X={х | f (х) 12, х>0} должно быть выпуклым (см. рис. 3.8).
Точка [1, 3/2] лежит на кривой Зх2 + 4х2=12. В этой точке
Г/ = (6x1, 8х2) = (6, 12), так что уравнение касательной есть
6(xi — 1) + 12(х2 —3/2) =0. Эта прямая проведена на рис. 3.8.
Видно, что она действительно является опорной к выпуклому
множеству.
3. Функция , .
{0, х С а,
а (х —а), х > а, а > 0,
3.11. Примеры
ЮЗ
график которой изображен на рис. 3.9, является выпуклой функ-
цией. Чтобы доказать это, изучим функцию Л[Лхг+ (1 — A)xi].
Надо рассмотреть три случая:
а) хп х2<а. Тогда
f 11“ О 4 Л-1] — (Х2) (1 — Л.) fj (Xj) = 0.
Отсюда /Дх)— выпуклая функция для х<а.
Ь) Хр х2Д-а. Тогда
fi 1Мг + (1 — 4 -*1] ~ аК (х2 — а) 4* а (1 — %) (Xj — а) =
= ^fi(x2) + (l —^-) fi (по-
следовательно, fi(x) — выпуклая функция и для х>-а.
с) х2<^а, X] > «• Тогда
fi[U2-b(l-X)Xi] =
| ак (х2 — а) 4 - а, (1 — %) (xt — а), если Хх2 4- (1 — 4 xi > а«
I 0, если А,х24~(1—1)Х1<а,
a
41(*2) + (1 ~ 4 fl (Xjj = а (1 - X) (Xj - а).
Поэтому и при х = Хх24-(1 — 4xi > а. и при х<а
fi(x)<Xfi(x2)4-(l-4fi(^i)-
Таким образом, /Дх) является выпуклой функцией при всех х.-~
Аналогично функция
( Ь(х— а), х<4,
h(x) | q( х > а, b < 0,
выпукла для всех х.
104
Гл. 3. Классические методы оптимизации
4. Функция
. . ( а(х — а),
^) = Ь(х-а),
х> а,
х <а,
а > О,
6<О,
выпукла при всех х, так как представляет собой сумму двух
выпуклых функций Л(х) и f2(x).
f(x) График f(x) приведен на рис. 3.10.
5. Предположим, что f (х) не-
прерывна и f(x)>0, —оо <х < ОО.
Тогда функция
Ш)= f (У — x)f(y)dy
Рис. З.'.о. выпукла при условии, что инте-
грал сходится. Для доказательства
положим х = Хх2 + (1—Х)х1( 0< X< 1, предполагая для опре-
деленности х2 > хР Тогда
ф(х) = J [t/ — Хх2 — (1 — X)Xj]f(y)rfy =
X
= х j (у — x2)f(y)<Zy + (l —X) j (у — х^ f (у) dy =
X X
= х J (у — X2) f (у) dy + X J (y — x2) f (y) dy +
X2 X
+(\—K)J(y—xi)f(y)dy~O—X)j(y — x1)f(y) dy.
Xt ' Xi
Поскольку f(y)>0 и у — Xj>0 для значений у, лежащих
между Xj и х, и у —х2<0 для значений у, лежащих между х
и х2, мы заключаем, что
J {У — x2)f(y)dy^0 и J (у —Xi)f(y)iZy>0.
х х<
Таким образом, непосредственно из выражения для ф(х) полу-
чаем, что
ф (х) < Хф (х2)+(1 — X) ф (Xi).
3.12. Максимум и минимум выпуклых и вогнутых функций 105
Следовательно, функция ф выпуклая. Более того, если f(x)>0
при всех х, рассуждения, аналогичные проведенным выше, по-
казывают, что функция ф строго выпуклая. Отсюда следует, что
функции Pj в примере 1 § 3.9 являются строго вогнутыми. Сле-
довательно, функция Р также строго вогнутая и, ввиду вы-
пуклости £(х), функция Лагранжа является строго вогнутой
по х. Почему функция Лагранжа строго вогнутая?
3.12. Максимум и минимум выпуклых и вогнутых функций.
Ниже будут получены результаты, которые поясняют, почему
выпуклые и вогнутые функции представляют особый интерес в
теории нелинейного программирования.
Пусть f(x) — выпуклая функция, заданная на замкнутом вы-
пуклом множестве ХаЕп. Тогда любой относительный мини-
мум f(x) на X является абсолютным (глобальным) минимумом
f(x) на X.
Будем доказывать это утверждение от противного. Допустим,
что цх) достигает относительного минимума в точке х0 в то
время как абсолютный минимум достигается в точке х*, при-
чем f(x0)>f(x*). Так как f(x) —выпуклая функция, то для лю-
бого X, 0 X 1.
f (Хх*+(1 - X) х0] < и (х*)+(1 - X) f (х0).
Однако, поскольку f (х*) <f (х0), для всех X, 0<Х<1, должно
быть справедливо строгое неравенство
f [Хх*+(1 - М х0] < Xf (х0) + (1 - X) f (х0) = f (х0). (3.67)
Рассмотрим любую 8-окрестность точки х0 с 8<|х*— х0|. Если
0<Х<в/|х* — х0|, то точка х=Хх*+(1—Х)х0 лежит в 8-окрест-
ности точки х0 и f (х) </(х0). Это невозможно, ибо f(x) дости-
гает в точке х0 относительногоминимума. Таким образом, мы
показали, что любой относительный минимум функции f(x) яв-
ляется одновременно ее глобальным минимумом. Здесь мы пред-
полагали, что значение |х*| конечно. В упражнении 3.15 мы
предлагаем читателю провести обобщение доказанного утвер-
ждения на тот случай, когда абсолютный минимум функции f(x)
достигается при |х|->оо.
Покажем, что подмножество точек из X, в которых /(х) до-
стигает глобального, минимума, есть выпуклое множество.
Если глобальный минимум достигается в единственной точке,
это утверждение, очевидно, справедливо. Допустим теперь, что
глобальный минимум достигается в двух различных точках Xi
и х2. Убедимся, что абсолютный минимум должен достигаться
в каждой точке х=Хх2 + (1 —Х)хь 0<Л<Л. Это следует сразу из
106
Гл. 3. Классические методы оптимизации
выпуклости f(x) и того факта, что f(xi) = f(x2) есть глобальный
минимум f(x). В силу выпуклости
f (хW Rx2 + (1 - X) xj < kf (x2) + (1 - X) f (X1) = f (x2). (3.68)
Но так как f(x) не может быть меньше f(x2), мы имеем
f(х) =f(х2) =f(xi). Таким образом, множество точек, в которых
f(x) достигает глобального минимума, является выпуклым.
Отметим два следствия из полученного результата. Во-пер-
вых, если абсолютный минимум достигается в двух различных
точках, то он достигается в бесконечном числе точек. Во-вторых,
не может быть двух или более точек, в которых функция f(x)
достигала бы сильного относительного минимума (и глобаль-
ного минимума тоже), так как функция f(x) принимает одно и
то же значение в каждой точке на отрезке, соединяющем две
точки с равными значениями f(x), а это противоречит предпо-
ложению, что f(x) достигает в этих точках сильного относитель-
ного минимума. Если f(x)—строго выпуклая функция, оче-
видно, что абсолютный минимум ее на выпуклом множестве X
достигается в единственной точке, т. е. не существует двух раз-
личных точек из X, в которых достигался бы глобальный мини-
мум f(x). Действительно, если f(x) принимает равные значения
в двух различных точках, то на середине отрезка, соединяю-
щего эти точки, она будет иметь меньшее значение.
Предположим, что f(x) — выпуклая функция, заданная на
выпуклом множестве Х€ЕП, и, кроме того, f(z.Cx во всех вну-
тренних точках множества X. Пусть Хо—чгочка, в которой
df(xo)/dXj = O, j==l, и, т. е. Vf(xo)=O. Тогда f(x) имеет от-
носительный минимум в точке х0 и f достигает в этой точке гло-
бального минимума на X. Действительно, пусть х — произволь-
ная точка множества X. Из {3.64), полагая xo = xi и х = х2, полу-
чим f(x)>/(x0), что и следовало доказать. Таким образом, вы-
пуклая функция f(x) достигает своего глобального минимума на
множестве X в каждой точке, где V f (х) =0.
Допустим, что мы хотим определить глобальный максимум
(а не минимум) выпуклой функции f(x) на замкнутом выпук-
лом множестве X, ограниченном снизу. Мы докажем следующее
утверждение:
Пусть X — замкнутое выпуклое множество, ограниченное
снизу. Если абсолютный максимум выпуклой функции f(x) на X
конечен, он будет достигаться в одной или более крайних точках
множества X.
Отметим для начала, что f(x) не может иметь строгого отно-
сительного максимума во внутренней точке х0 множества X. Дей-
ствительно, так как х0 — внутренняя точка, существует ее
^-окрестность, которая содержит лишь точки из X. Пусть xt —
3.12. Максимум и минимум выпуклых и вогнутых функций 107
любая точка в этой е-окрестности, отличная от х0. Точка
х2 = 2х0 — Xi также лежит в указанной е-окрестности и отлична
от х0. Имеем х0= (xi+x2)/2, поэтому из выпуклости /(х) сле-
дует, что (Х= 1/2)
f (Хо) f (Xi) + f (х2),
так что значение f(x0) не превосходит большего из значений
f(xi), f(x2), т. е. в точке х0 функция f(x) не может достигать
строгого относительного максимума. Отсюда следует, что если
глобальный максимум достигается во внутренней точке х0€Х,
он достигается в каждой точке любой е-окрестности х0, содер-
жащей только точки из X.
Докажем, что если глобальный максимум /(х) достигается
во внутренней точке х0, он будет достигаться в любой точке мно-
жества X. Рассмотрим любую внутреннюю точку х£Х, отлич-
ную от х0. Если х находится в е-окрестности точки х0, содержа-
щей только точки из X, из приведенных выше рассуждений сле-
дует, что в точке х также достигается глобальный максимум
f(x). Предположим, что х не лежит ни в какой такой е-окрест-
ности. Точка х принадлежит множеству X с некоторой е*-окрест-
ностью. Пусть ео-окрестность точки х0 содержит лишь точки
из X. Очевидно, что 81-окрестность точки х0, где ei<min (ео, е*),
также содержит лишь точки из X. Если 81-окрестность точки х0
и е-окрестность точки х не содержат общих точек, то возьмем
x1==x0 + ei(x — х0)/|х — х0| и рассмотрим 81-окрестность точки хь
Очевидно, что Xi принадлежит ерокрестности точки х0, а ерокре-
стность точки Xt содержит лишь точки из X.
Если ерокрестности точек х4 и х не имеют общих точек, возь-
мем x2 = xi + ei(x — Xi)/|x — Xi| и рассмотрим ei-окрестностьточ-
ки х2. Продолжая этот процесс, легко видеть, что найдется
число k, при котором ерокрестности точек xft и х пересекутся.
По цепочке построенных ерокрестностей при этом можно легко
проследить, что в точке х также будет достигаться глобальный
максимум f(x). Для граничных точек X указанное свойство бу-
дет следовать по непрерывности.
Так как мнол^ртво X ограничено снизу, оно имеет по мень-
шей мере одну крайнюю точку и отсюда в этом случае теорема
справедлива;
Допустим теперь, что глобальный максимум достигается в
граничной точке хоСХ и не достигается ни в одной внутренней
точке X. Если х0 — крайняя точка, теорема справедлива. Если х0
не является крайней точкой, рассмотрим пересечение множе-
108
Гл. 3. Классические методы оптимизации
ства X с гиперплоскостью, опорной к X в точке х0. Это пересече-
ние является замкнутым выпуклым множеством (обозначим
его Т) и содержит по меньшей мере одну крайнюю точку мно«
жества X, если X ограничено снизу. Можно считать, что Т лежит
в (п—1)-мерном пространстве. Если х0 — внутренняя точка мно-
жества Т в этом пространстве, приведенные выше рассуждения
показывают, что глобальный максимум f(x) должен достигаться
в любой точке Т, следовательно, и в той крайней точке множе-
ства X, которая принадлежит Т.
Если хо — граничная точка Г, мы рассмотрим множество 7\,
являющееся пересечением множества Т с опорной в точке х0
гиперплоскостью к Т. Множество Ti лежит в пространстве раз-
мерности п—2.
Этот процесс можно повторить не более п — 1 раз, так
как множество Tn-i будет лежать в пространстве размерности О,
т. е. будет представлять единственную точку х0, являющуюся
в этом случае крайней точкой множества X (почему?). Это за-
вершает доказательство теоремы. Если X — выпуклый много-
гранник, доказательство теоремы намного проще. Его предла-
гается выполнить в упражнении 3.26.
Мы показали, что глобальный максимум функции f(x) до-
стигается в крайней точке. Однако использование этого факта
при построении вычислительных схем может оказаться затруд-
нительным, поскольку наряду с глобальным в крайних точках
могут достигаться и отличные от него относительные максимумы
(этот случай иллюстрируется на рис. 1.4). Поэтому обычная для
симплексного метода процедура «отыскания соседней крайней
точки» не обязательно будет приводить к глобальному макси-
муму.
Доказанные выше результаты применительно к вогнутым
функциям могут быть сформулированы следующим образом.
Пусть f(x) —вогнутая функция, заданная на замкнутом вы-
пуклом множестве ХаЕп. Тогда любой относительный макси-
мум f(x) на X является одновременно глобальным максиму-
мом f(x) на X. Кроме того, множество точек из X, в которых
f(x) достигает глобального максимума, является выпуклым. От-
сюда, если глобальный максимум достигается в двух различных
точках, он достигается в бесконечном множестве точек. Не
может быть двух или более различных относительных макси-
мумов.
Если f(x) —строго вогнутая функция, ее глобальный макси-
мум достигается в единственной точке. Если f(x)—вогнутая
функция на выпуклом множестве X и то f(x) достигает
глобального максимума в точке, где Vf(x)=O. Если X — замкну-
тое ограниченное снизу множество и глобальный минимум во-
Упражнения 109
гнутой функции f(x) конечен, глобальный минимум Дх) дол-
жен достигаться в одной или более крайних точках множе-
ства X.
ЛИТЕРАТУРА
1. Allen R. G. D., Mathematical Analysis for Economists, New York, St
Martin’s Press, 1938.
2. CaratheodoryC., Variationsrechnung und partielle Differentialgleichun-
gen erster Ordnung, Leipzig, Teubner, 1935.
3. Курант P., Гильберт Д., Методы математической физики, т. I,
ГИТТЛ, М., 1951.
4. Курант Р., Курс дифференциального и интегрального исчисления, т. 2,
ГТТИ, М., 1931.
5. Hancock Н., Theory of Maxima and Minima, New York, Dover, 1960.
6. Samuelson P., Foundations of Economic Analysis, Cambridge, Harvard
Univ. Press., 1947.
7. von Neumann J., Morgenstern O., Theory of Games and Economic
Behavior, Princeton, Princeton Univ. Press, 1953; готовится к печати рус-
ский перевод: фон Нейман Дж., Моргенштерн О., Теория игр и
экономическое поведение (изд-во «Наука»).
Упражнения
3.1. Некоторые кристаллы, например хлористого натрия (NaCl), представ-
ляют собой определенным образом построенную из ионов решетку. В NaCl
каждый ион Na+ или С1" окружен шестью ближайшими соседями — ионами
противоположного знака и двенадцатью несколько более удаленными сосе-
дями-ионами одноименного знака. Имеются две группы сил, действующих
в противоположных направлениях: силы кулоновского притяжения, изменяю-
щиеся обратно пропорционально расстоянию между ионами, и силы оттал-
кивания, изменяющиеся как (п+1)-я степень расстояния между ионами,п>2.
После суммирования по всем ионам мы можем записать потенциальную энер-
гию кристалла следующим образом:
тт G с2
Rn Я ’
где ci, с2 — положительные константы, R — расстояние между двумя бли-
жайшими ионами. Учитывая, что природа стремится к минимуму потенциаль-
ной энергии, найти значение R и потенциальной энергии в состоянии равно-
весия. Найти количество энергии, требуемой для разрыва (распада) кристалла
(т. е. приводящее к R= ос)«
3.2. Монополист производит q единиц продукта за данный период вре-
мени. Он может продать все количество, если установит цену р=ф(<?) или
ниже. Нет смысла устанавливать более низкую цену, поэтому следует счи-
тать р=ф((7). Известны общие затраты c(q) на производство q единиц, Тре-
буется определить количество продукции, которое следует производить, чтобы
общий доход л за весь период времени был максимальным. Найти dcfdq и
Дать экономическую интерпретацию результата. В частности, объяснить смысл
выражения qdpldq. Что происходит в случае свободной конкуренции, когда
Данный предприниматель может продать все, что он производит, по фикси-
рованной рыночной цене?
ItO
Гл. 3. Классические методы оптимизации
' 3.3. Монополист за данный период времени производит одновременно
два вида товара в количествах соответственно и Х2. Функция суммарных
затрат есть
с (х^ х2) = Xj + 2х2 +1300.
Зависимость спроса от цены задается условиями
Xj «в 600р2 — 400/?j, х2 = 1800 — 100/?j — 300/>2,
Определить, в каких количествах следует производить товары и по ка-
кой цене продавать, чтобы доход был максимальным.
3.4. Значение некоторой физической величины у зависит от п других
физических величин х\, .. ., хп. Предположим, что сделано пг наблюдений.
Каждое наблюдение представляется точкой в пространстве En+i. Требуется
найти гиперплоскость
п
У = ^ajxj + b,
J-i
наименее удаленную от m точек Еп+\ Термин «наименее удаленная» здесь
понимается в следующем смысле: величины aj, /==1, ...» п, и b‘должны
быть определены так, чтобы сумма
m m
'21е21 = '%(У1-у1)г
Z = 1 i=l
была минимальной. Это классическая задача наименьших квадратов. Найти
уравнения, определяющие оптимальные значения и Ь, Показать, что со-
отношения, определяемые необходимыми условиями, всегда совместны.
3.5. Допустим, что задана функция f(x), х£Еп, и предположим, что х0
является точкой относительного минимума f(x). Мы хотим проверить это
предположение путем вычислений.. Есть ли какой-либо непосредственный путь,
чтобы это сделать? Достаточно ли для этой цели вычислить значения
f(xo±eej), /=1, ... , п, при достаточно малом е?
3.6. Найти кратчайшее расстояние от точки (1,0) до параболы у2=4х
с помощью: а) исключения переменной у, Ь) множителей Лагранжа. Отметим,
что способ а) не всегда позволяет получить корректный ответ, в то время
как способ Ь) универсален. Объяснить причины этого.
3.7. Установить формулу для определения кратчайшего расстояния d от
точки хо £ Еп до гиперплоскости г=сх. Предполагается, что |с| = 1. Показать,
что с?2= (г — схо)2.
3.8. Рассмотрим квадратичную форму f(x)=X]X2. Найти максимум и
минимум этой квадратичной формы на единичной окружности xf-j-x^ — 1
Дать геометрическую иллюстрацию. Какие точки соответствуют максимуму
и какие минимуму?
3.9. Допустим, что абсолютный максимум функции f(x) в неотрицатель-
ном октанте достигается в лежащей на границе октанта точке х* (х*«»0).
Показать, что если f £ С1, то df (x*)/dxj<0.
3.10. Компания производит некоторый продукт, используя п видов сырья
в количествах ..., хп. Производственная функция (которая связывает
количество продукции с израсходованными количествами сырья) есть
q = f(xi....хп),
общие затраты на производство —
Упражнения
lit
где Рз, цена единицы /-го сырья, предполагается постоянной. Определить, ка-
кое количество каждого сырья следует израсходовать, чтобы произвести q
единиц продукта при минимальных затратах. Когда мы сможем получить
функции спроса *j=cpj(pi, ...» Рп, q)?
3.11. Пусть мы хотим максимизировать функцию /(х) при ограничениях
gi(*)=bit i=l, ..., т. Предположим, что /(х) имеет относительный максимум
в точке хо, удовлетворяющей ограничениям, и что в этой точке r(G)=m.
Найти значения множителей Лагранжа, если ~~ = 0, /=1, ..., п, в точ-
ке хо. Пояснить физический смысл ситуации.
3.12. Установить достаточные условия того, чтобы все Xj и рассма-
триваемые в § 3.7, были непрерывно дифференцируемыми функциями век-
тора b в некоторой 8-окрестности Ьо-
3.13. Рассмотрим задачу максимизации г=/(х) при ограничениях
^г(х)<^г, *=1, . . k\ gi(x)^bi, i=k+\, ..., т. Пусть в точке х* функция
f(x) достигает абсолютного максимума для х, удовлетворяющих ограниче-
ниям. Показать, что если ограничения в точке х* не существенны, то
dz*/dbi—O. Дать физическую интерпретацию этого случая. В экономике ре-
сурсы bi при этом следует называть свободными. Почему? Показать, что
если в точке х* существенны ограничения с номерами i—\, ... , k для рас-
сматриваемых значений 6/, 1=1, ... , k, и их окрестностей, то dz*/dbi могут
быть вычислены по способу, рассмотренному в § 3.7. Допустим далее, что
ограничения существенны в точке х*, но при любом увеличении bi перестают
быть таковыми. Показать, что в этом случае dz*ldbi должны рассматри-
ваться как односторонние производные. Привести геометрическую иллю-
страцию.
Рассмотреть случай, когда переменные должны быть неотрицательными.
3.14. Установить условия, гарантирующие, что система (3.39) дает един-
ственное решение х, как функцию , в некоторой окрестности 1о<
3.15. Обобщить приведенное в § З.Г2 доказательство того, что любой
относительный минимум выпуклой функции является глобальным минимумом
на случай, когда глобальный минимум достигается при |х|->оо. [Указание.
Если /(хо) не является глобальным минимумом, то существует точка х с до-
статочно большим | х |, такая, что f(x) <f (х0).] •
3.16. Доказать, что функция 1/х является строго выпуклой при х>0 и
строго вогнутой при х<0.
3.17. Пусть fi(x) и /г(х)—выпуклые функции. Показать, что, вообще
говоря, /1(х)/г(х) не является выпуклой функцией. Сделать это с помощью
контрпримера.
Имеются ли специальные условия, при которых (х)^2(х) будет выпуклой
функцией?
3.18. Пусть х* — точка, в которой z=f(x) достигает абсолютного мини-
мума при ограничениях g<(x)=h, i=l, ..., т. Предположим, что r(G)=m
в точке х*. Предположим также, что функцию Лагранжа мы определили
следующим образом:
т
F(x, 1) = /(х)+2Ш(х)-Ч-
Показать, что dz*ldbi=—Ki.
3.19. Рассмотрим задачу отыскания абсолютного минимума z=f(x) при
w линейных ограничениях Ах=Ь в предположении, что г(А)—т. Пусть
/(х)—выпуклая функция. Показать, что функция Лагранжа F(x, X) также
выпуклая и что Е(х, ) достигает относительного и глобального минимума
при фиксированном 1 в любой точке, удовлетворяющей условиям dF/dXj=0,
/*1, ...» п. Показать та^же, что /(х) достигает своего глобального минимума
112
Гл. 3. Классические методы оптимизации
для точек, удовлетворяющих ограничениям, в любой точке, удовлетворяющей
ограничениям и условиям dFldxj=0, /=1, ..., п. Отсюда можно будет за-
ключить, что F(x, Z) достигает относительного минимума по х в той точке,
где f(x) достигает глобального минимума для точек, удовлетворяющих огра-
ничениям.
3.20. Рассмотреть задачу отыскания максимума и минимума квадратичной
формы z=x'Ax для х, лежащих на единичной гиперсфере |х|=1. Найти урав-
нения, определяющие точки, в которых z принимает максимальное или мини-
мальное значение. Обобщить рассмотренный вариант для случая отыскания
точек максимума и минимума z=x'Ax при |х| = 1 и дополнительном пред-
положении, что х удовлетворяет условиям Dx=0. Здесь D — матрица с раз-
мерами /пХп, т<п и r(D)=m.
3.21. Пусть f(x)—выпуклая функция, заданная на выпуклом множе-
стве X, и пусть Xi, ..., xft — любые k точек из X. Доказать, что при всех
р,/>0, S справедливо неравенство
i
k k
f (X)< 2 Ji/(x,). где x = 2 Нгхг
i-i f-i
Дать геометрическую интерпретацию этого результата.
3.22. Совокупность п функций g;(x), i==l, ..., и, называют функциональ-
но зависимой, если существует нетривиальная функция F(g\, . . ., gn), тож-
дественно равная нулю при всех х. Показать, что если функции gz(x) функ-
ционально зависимы, то соответствующая им матрица Якоби будет особенной
для всех х. [Указание. Показать, что VF(x)=0.]
3.23. В экономике в теории потребления часто предполагают, что каждый
индивидуум имеет функцию полезности U(x) и что он осуществляет потреб-
ление таким образом, чтобы его функция полезности принимала максимальное
значение при бюджетных ограничениях рх I. Определить уравнения, ко-
торым должны удовлетворять оптимальные значения Xj. Считать, что
U(х) £ С1. Когда решение этих уравнений будет единственным? При каких
условиях можно точно выразить спрос Xj как функцию цен pi и величины /?
Дать экономическую интерпретацию множителей Лагранжа. Сформулировать
двойственную задачу.
3.24. Определить стороны прямоугольника с максимальной площадью,
если его диагональ равна Ь.
3.25. Используя материал § 3.8, получить двойственную задачу к общей
задаче линейного программирования, приведенной в примере 3 § 3.9. Каково
оптимальное решение двойственной задачи, если х^ = В-1Ь — оптимальное
базисное решение прямой?
3.26. Пусть X — выпуклый многогранник, так что каждая точка X может
быть представлена линейной комбинацией вершин X. Используя простое до-
казательство, приведенное в .§ 3.12, показать, что абсолютный максимум
выпуклой функции на X будет достигаться в крайней точке X. [Указание.
См. задачу 3.21.]
3.27. Покупатель имеет доход 7 и может купить товары трех. видов по
цене pi, р2 и р3 за единицу. Его функция полезности х^х^Хд, где с —
положительные константы, хь х% и х3— количества товаров трех видов, ко-
торые он покупает. Определить, какое количество каждого товара он купит
(как функции от 7, рь р2, р3). См. задачу 3.23.
3.28. Рассмотреть возможность применения способа множителей Лаг-
ранжа для решения задачи
Xj + х2 = 0; найти max z ~ х1 + х2.
Упражнения
113
3.29. Дать детальное доказательство того, что способ, описанный в § 3.2
для нахождения абсолютного максимума функции f(x) в неотрицательном
октанте, дает абсолютный максимум, если |х*| конечен.
3.30. Решить уравнение ех — 2=0 методом Ньютона.
3.31. Рассмотреть пример § 3.3. Пусть деталь, прошедшая контроль, стоит
25 долл., для доработки заготовка продается за 15 долл. Стоимость заготов-
ки, поступающей в производство, 12,5 долл. Размер диаметра х не должен
выходить за пределы 2,500 2,505 дюйма. Пусть о, стандартное отклоне-
ние случайной величины х, равно 0,0015 дюйма. Определить ц — математиче-
ское ожидание х (иначе говоря, режим станка), при котором прибыль макси-
мальна. При условии, что в неделю в производство поступает 500 заготовок,
выразить ожидаемую недельную прибыль как функцию от и.
3.32. Доказать, что S (Ю — выпуклая функция, если отрицательные
I
коэффициенты аг- соответствуют вогнутым функциям а положительные —
выпуклым.
3.33. Доказать, что ех — выпуклая функция.
3.34. Пусть Xi — случайная переменная, обозначающая потребность в не-
котором товаре в момент времени /, х2 — случайная переменная, обозначаю-
щая потребность в момент времени /+т, т>0. Пусть fi(xi) и /2(^2)—плот-
ности распределения соответственно величин Х[ и х2. Пусть у — количество
товара в начальный нулевой момент времени. Вычислить ожидаемый спрос
в интервале времени между t и Z+т, когда товара нет*в продаже. Пусть
ожидаемый спрос F(y). Является ли F(y) выпуклой функцией?
3.35. Пусть
оо
j F (х, у) —— f (и — х) f (и) du, у > 0; f (w) > 0, — 00 > и < оо.
У J
Является ли F(x, у) выпуклой функцией от х и у?
3.36. Доказать, что |х| — выпуклая функция.
3.37. Пусть f(x;a)—выпуклая функция на выпуклом множестве X при
каждом a, d^a^b. Доказать, что если ф(а)^>0, то
ь
J f (х, а) Ф (а) da
а
является выпуклой функцией на X.
3.38. Найти кратчайшее расстояние от эллипса 2х% 4"3^2 = 12 до прямой
Х1 +Хг = 6.
3.39. Рассмотрим функцию f(x), f £С2. Пусть х0 — точка, в которой
W(xo)=O. Показать, что f(x) имеет в х0 сильный относительный максимум,
если квадратичная форма h'H/(x0)h отрицательно определенная, и f(x) имеет
в х0 сильный относительный минимум, если квадратичная форма h'H/(x0)h
положительно определенная. [Указание, Представить f(x) в окрестности точ-
ки х0 с помощью формулы Тейлора. Следует использовать то, что h'H/(x)h —
непрерывная функция от х.]
3.40. Пусть х0 — точка, удовлетворяющая условиям gi (х0) =Ьг-, 1,..., /и,
и такая, что существуют Z?, при которых выполняются
<^(хо) v,o^(xo) _
dxj JU i dx, ~
i=l
0,
n.
8 Зак. 735
114
Гл. 3. Классические методы оптимизации
Предположим, что f£C2, gi£C2, f=l, ..m. Пусть F(x,X) — функция Ла-
гранжа. Доказать, что f(x) имеет сильный относительный максимум для
х£У в точке Хо, если квадратичная форма h'HF(x0, lo)h отрицательно опре-
делена для h, удовлетворяющих условиям Vgi(Xo)h=O, t=l, ... , m, и f(x)
имеет сильный относительный минимум в хо, если форма h'HF(xoAo)h поло-
жительно определена для h, удовлетворяющих условиям Vgi(xo)h=O,
/=1, ..., т. Символом HF мы обозначаем гессиан функции F. [Указание. Фик-
сируя Хо, разложить F в ряд Тейлора в окрестности хо. Отметим, что для
хY F(x, Хо)~f(x). Также следует разложить gi(x) в ряд Тейлора в
окрестности хо. Выяснить, какой вид имеет это разложение при х £ У.]
3.41. Показать на примере функции одной переменной, что выпуклая
функция, заданная на замкнутом выпуклом множестве, может оказаться не
непрерывной на границе множества.
3.42. Показать, что если g(x)—выпуклая функция и множество значе-
ний х, удовлетворяющих условию g(x)=&, выпукло, то g(x) непременно
является линейной функцией.
3.43. Доказать непосредственно (из определения), что если fj(Xj),
/ = 1. , л, — выпуклые функции xj, то
п
f (х) = 2 fj (xj)
j-i
является выпуклой функцией х==[хь ..., хп]>
3.44. Доказать, что если f(x) —выпуклая функция для х $ Еп, то f(x+b)
является выпуклой функцией х при любом Ь.
3.45. Рассмотрим задачу линейного программирования: Ах=Ь; найти
max z—cx. Отметим, что при фиксированных А и с г* (максимальная вели-
чина z) будет функцией Ь. Показать, что г*(Ь) является вогнутой функцией Ь.
3.46. Доказать, что fi (х) —х2 является выпуклой функцией при—оо<х<оо
и использовать этот факт для доказательства утверждения, что f2(x)=3.(x—2)2
является выпуклой функцией. Дать графики этих функций и функции fi+fz
и показать для этого частного случая геометрически, что сумма двух выпук-
лых функций также является выпуклой функцией.
3.47. Пусть f(x)—дифференцируемая выпуклая функция на некотором
промежутке а<х<Ь. Доказать, что для произвольных значений xt и х2 из
этого промежутка f'Ua) >f'(xi) при х2>хь Отсюда следует, что f'(x)—мо-
нотонно неубывающая функция х. Сформулировать соответствующий резуль-
тат для вогнутых функций. [Указание. Вспомнить, что соотношение 3.64 имеет
место для любых х\ и х2.]
3.48. Пусть f(x)—дифференцируемая выпуклая функция от х на неко-.
тором открытом выпуклом множестве X пространства Еп. Пусть Xi и х2 —
любые две точки из X, а у — любая точка на отрезке, соединяющем Xi и х2.
Доказать, что
V/ (у) (Х2 — Xj) > Vf (Xj) (Х2 — Xj).
3.49. Рассмотрим дифференцируемую функцию f(x), которая обладает
следующим свойством: для любых Х] и х2 из промежутка а<х<Ь
f (*г) > I (xi) + Г Ui) (*2 — *1)-
Доказать, что f(x)—выпуклая функция на промежутке а<х<Ь.
3.50. Рассмотрим дифференцируемую функцию f(x), для которой
f (Х2) > f (Xj) 4- Vf(Xj) (х2 — Xj)
при всех Xi и х2 из открытого выпуклого множеству X. Доказать, что f(x) —
выпуклая функция на X.
Упражнения
Н5
3.51. Пусть f £С2 на открытом выпуклом множестве X. Доказать, что
f (х) является выпуклой функцией на X тогда и только тогда, когда квадра-
тичная -форма-h'Hf(x)h является неотрицательной для всех х £ X. Каковы
условия строгой выпуклости /(х)?
3.52. Для примера 3 § 3.9 показать, что если г (А', с')=т, то каждое
допустимое решение является оптимальным. Расширить анализ, распростра-
нив его на случай, когда k переменных равны нулю. Убедиться, что в этом
случае одно или более ограничений могут быть излишними.
3.53. Может показаться, что мы можем избежать трудностей, связанных
с применением метода множителей Лагранжа к задачам линейного програм-
мирования, с помощью замены переменных вида ху = £/у. Тогда нет необхо-
димости накладывать требования неотрицательности на yj, Показать, что это
преобразование действительно может быть сделано и что подход с примене-
нием множителей Лагранжа может быть применен к задаче с переменными yj.
Показать далее, что и при этом преобразовании мы сталкиваемся с теми же
трудностями, которые были до замены переменных.
Проиллюстрировать эти положения на примере задачи:
*1 + *2 < 2, jq, х2>0; найти max z = 2xt Зх2.
Дать графическое изображение этой задачи как в пространстве Xi, xs,
так и в пространстве yi, ys. Показать, что с теми же трудностями мы сталки-
ваемся при любом преобразовании Xj-fj(yj), где Х; = 0 соответствует
i/j = yQj и f j (4/у) симметрична относительно */у. Почему мы налагаем эти
специальные условия на fj(yj)?
8*
ГЛАВА
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
С СЕПАРАБЕЛЬНЫМИ ФУНКЦИЯМИ
Хотя это может показаться парадок-
сом — вся наука подчинена идее аппро-
ксимации.
Бертран Рассел
4.1. Введение. В этой главе мы будем иметь дело с приближен-
ными методами для решения задач нелинейного программиро-
вания следующего вида:
ij gij (Xj) {<> =, >} bi, i = 1.....m,
xy>0, J=1.........n-, (4.1)
n
найти max z= 2f/(x.«).
J
Здесь предполагается, что все функции в ограничениях и целе-
вая функция являются сепарабельными.
В основу излагаемых приближенных методов будет поло-
жена кусочно-линейная аппроксимация функций gij(Xj) и fj(xj),
в результате чего получается приближенная задача, которая
может быть решена симплексным методом. Вообще говоря, мы
сможем определить только локальный максимум в приближен-
ной задаче и, следовательно, приближенный локальный макси-
мум для задачи (4.1). Только в случае когда функции gij(Xj),
fj(Xj) обладают соответствующими свойствами выпуклости или
вогнутости и, следовательно, локальный максимум является
одновременно глобальным, мы сможем находить глобальный
максимум в приближенной задаче и таким образом аппроксими-
ровать искомое решение задачи (4.1). Вначале мы покажем, как
строится приближенная задача и как определяется локальный
максимум в этой задаче.
4.2. Построение приближенной задачи и определение локаль-
ного максимума. Рассмотрим произвольную непрерывную функ-
4.2. Построение приближенной задачи
117
цию h(x) одной переменной, определенную для всех х из интер-
вала Функция h(x) может, например, иметь вид, пока-
занный на рис. 4.1. Выберем в интервале г+1 точек Xk
так, что Хо = О, Xi<x2<.. .<хг=а. Вычислим для каждой точки xk
величину hk — h(Xk). Соединим попарно точки (xft, hk) и
(л*+1, ^м-1), & = 0, ..., г—1, отрезками прямых. Мы получим та-
ким образом кусочно-линейную функцию, которая аппроксими-
рует функцию h(x) на интервале Эту кусочно-линей-
ную функцию мы обозначим через А(х). Такая аппроксимация
может быть сделана с любой точностью за счет выбора точек xh.
Предположим теперь, что в задаче (4.1) непрерывны все функ<
ции fj и gij. Разобьем интервал, который может пробегать пере*
менная Xj, / = 1, ..., п, точками xkj и, используя только что опи-
санный способ, построим кусочно-линейную аппроксимацию
Sij(xd) и Функций gij(Xj) и fj(xj) соответственно. Мы за-
меним таким образом задачу (4.1) следующей:
п
ху>0, /=1, (4.2)
п
найти max г=2Г/(х/)-
Последнюю мы будем называть приближенной задачей для за-
дачи (4.1).
Займемся определением локального максимума приближен-
ной задачи (4.2). Для этого сначала найдем аналитическую
118 Гл. 4. Методы решения задач с сепарабельными функциями
запись кусочно-линейных функций gtj(Xj) и fj(Xj). Возвратимся
к рис. 4.1. Если х лежит в интервале Xk-^x^Xh+i, мы аппрокси-
мируем h(x) следующей функцией Л(х):
Л W = + v + IE-77 (4-3>
+ 1 Л,Л
Отметим, что любое значение х в интервале хА<х-<хА+1 мы
можем представить в виде x=Xxfe+i + (1—%)х^ за счет выбора
некоторого А, 0<Х<1. Отсюда х—xfe==X(xft+1—xk)t так что вы-
ражение (4.3) может быть переписано в виде h(x) = XAft+i +
+ (1 —Если обозначить %=Xa-i-i, (1 —X)=Z&, можно утвер-
ждать, что при фиксированном х, xfe<x-<Xfe+i, существуют един-
ственные значения Kk и Z^-i, такие, что
х = Kkxk 4~ Ч+Л+i»
/г (х) = hkhk + Kk+lhk+1, (4.4)
Ч + Ч+i^o.
На самом деле для любого х, 0<х<а, мы можем написать
(4-5)
Л(х)=2М*. (4.6)
k =0
24 = 1. **>0, Л = 0, 1, ...» г, (4.7)
л=о
условившись, что положительным может быть одно Kk или два
(соседних) — не более. При этих условиях определены
единственным образом, и для х, выраженного с помощью (4.5),
функция А(х), имеющая вид (4.6), является аналитическим вы-
ражением ломаной, изображенной на рис. 4.1. Требуя, чтобы
лишь одно либо два соседних значений были положительны-
ми, мы получаем, что точки, определяемые выражениями (4.5)
и (4.6), лежат на нашей ломаной. Если это требование не на-
кладывать, точки, определяемые (4.5) и (4.6), не обязательно
будут лежать на ломаной.
Мы показали сейчас, как любая непрерывная функция может
быть приближена ломаной, и получили для нее аналитическое
представление (4.5) — (4.7). Возвратимся к задаче (4.2). Допу-
стим, что из физических соображений определено а,— макси-
мальное значение» которое ^может принимать переменная Xj.
4.2. Построение приближенной задачи
119
Разобьем интервал O^x^aj на /у- подинтервалов с помощью
rj+1 точек xftJ, так что х0;=0, хгу> у = aj. Тогда все функции
fj(xj), Sij(xj) можно записать в виде
Г1
1 j (х>) 4“ 2 fkj — fj (хД (4.8)
Л—О
rJ
Sij (xj) = 2j hjgkij, gkij = gij M / = 1, ..., m, (4.9)
где
rj
xi~ 'kkjXkj, (4-10)
k = o
ri
^>0 при BCex k, j, (4'11)
^=0
помня, что для данного Xj не более двух в (4.10) могут быть
положительными, причем эти (если их два) должны быть
соседними. Отметим, что в выражении каждой из функций fj(Xj)
и gij(Xj), Z=l, ..., m, мы используем одно и то же разбиение
интервала О^х^ау. Точки х&у должны быть выбраны так, чтобы
все функции fj(Xj) и ga(Xj) могли быть аппроксимированы с до-
статочной точностью.
Используем (4.8) и (4.9) для исключения функций fj(Xj) и
gij(Xj) из (4.2). Это приведет к следующей форме приближен-
ной задачи с переменными Kkj вместо Xjt
п Ч
2 =, >\bh /=1, m, (4.12)
ч
/=1, • ••> я, ПРИ всех (4.13)
ЬО
п Ч
найти max z = 2 2X4,- (4.14)
/ = 1 * = 0 J
Эта задача была бы линейной, если бы не условие, что для
каждого / не более двух Kkj положительны и эти положительные
Xkj являются соседними.
Мы можем искать локальный максимум задачи (4.12) — (4.14)
с использованием симплекс-метода в обычной схеме, но при
построении базиса следует учитывать, что не допускается, чтобы
при каждом / более двух были положительными, причем эти
два Zfey должны быть соседними. Отметим, что мы не включаем
120 Гл. 4. Методы решения задач с сепарабельными функциями
соотношения (4.10) в приведенные выше ограничения задачи.
Уже после решения задачи (4.12) — (4.14) равенства (4.10) мо-
гут быть использованы для определения приближенных значе-
ний Xj.
После введения вспомогательных переменных в (4.12) мы
можем переписать задачу (4.12) — (4.14) в следующей сокращен-
ной форме:
GX —Ь, Х>0; найти max z~ fl, (4.15)
Матрица G состоит из m + n строк и + 5 + n столбцов (s —
число введенных вспомогательных переменных).
Мы докажем далее, что если симплексный метод с ограни-
чениями на выбор базиса, о которых сказано выше, приводит
к тому, что Zbj—fkj^O для всех Х^-, входящих в базис, то мы
получаем относительный максимум приближенной задачи, запи-
санной в переменных Xj. Другими словами, если х0 — значение х,
соответствующее в силу (4,10) последнему базисному решению
Хо задачи (4.15), то существует е>0, такое, что при всех х>0,
|х — хо| <е, для которых X, определенное через х, удовлетворяет
ограничениям (4.15), справедливо fX<TX0, т. е. f;(ху)
Здесь х®. есть у-я компонента х0.
Обратимся теперь к ситуации, когда симплекс-метод, приме-
ненный к задаче (4.15) с учетом ограничений на выбор базиса,
описанных выше, привел нас к стадии, в которой следующая
итерация не может быть сделана. Пусть В — матрица послед-
него базиса, Хв содержит базисные переменные и Хл — небазис-
ные переменные. Тогда каждое решение уравнения GX = b
должно удовлетворять уравнению
Хв=-В_1Ь-В_,КХЛ) (4.16)
где R — матрица, составленная из столбцов матрицы G, не во-
шедших в В. Для любого решения уравнения GX = b мы можем,
используя (4.16), исключить базисные переменные и выразить z
только через небазисные. Тогда
z = fBXB + f^X# = fBB b —(f— f]R) =
= Ж*-^)^ + ^В-’Ь. (4.17)
V
Для окончательного решения уравнения (4.15), полученного
с применением симплекс-метода с ограничением на выбор бази-
са, мы имеем Хд = 0, Хв=В1Ь, г^ТдВ^Ь. Пусть х0 —значение х,
соответствующее этому решению. Мы хотим показать, что х0 до-
ставляет относительный максимум для приближенной задачи.
4.2. Построение приближенной задачи
121
Чтобы сделать это, докажем существование такого 8>0, что при
всех удрвлетворяющих ограничениям' (4.15), для которых
|х(Х)—х0|<е, выполняется При обозначениях, при-
мененных в (4.12) — (4.14), окончательное решение Хо = [В~1Ь, 0]
задачи (4.15) будет при Каждом / обладать одним из следующих
свойств: a) и ta+i, j положительны; b) только одно поло-
жительно. Очевидно, что по крайней мере одно должно быть
положительно (при каждом /), так как сумма Kkj по всем k
должна равняться 1.
Допустим, что для некоторого фиксированного / имеет место
(а). Тогда х/ лежит между xfej и х/ж, j- Для достаточно малого 8
/-я компонента каждого х, лежащего в 8-окрестности х0, должна
находиться между xfej- и xft+i) j, так что и j должны оста-
ваться положительными, т. е. все другие должны оставаться
равными нулю. Если для некоторого/ имеет место (Ь),тоА^= 1 и
х9. = xk].. Тогда, если х лежит в 8-окрестности х0 при достаточно
малом 8, Xj не может лежать левее xft_i, j или правее xfe+1> j.
Отсюда в любой такой е-окрестности только hk-i, j или Xfe+i, j
могут становиться положительными, все остальные должны
оставаться нулевыми. Кроме того, fa-t, j может становиться по-
ложительным, только если £>1. Однако для каждого из тех
которые могут становиться положительными, условия окончания
при решении задачи (4.15) гарантируют, что zkj—и поэто-
му из (4.17) для любого х в 8-окрестности х0 имеет место
B~Jb, так что мы действительно получаем локальный мак-
симум в приближенной задаче.
Мы рассмотрели метод для нахождения относительного мак-
симума в приближенной задаче. Ограничительные условия на
выбор базиса могут быть учтены в программе симплекс-метода.
Следует, впрочем, отметить, что задача (4.1) даже и небольшой
размерности может превратиться в задачу (4.15) очень большой
размерности. Однако если некоторая переменная Xj входит в
задачу линейно, т. е. gij(Xj) — а^х^ f=l, ..., m, и fj(xj) =CjXj,
то нет необходимости выражать Х; через Кц. Мы можем просто
использовать Xj как переменную. Так как нередко значительное
число переменных будет входить в задачу линейно, это замеча-
ние позволяет значительно уменьшить размерность приближен-
ной задачи.
К сожалению, описанный способ приводит в общем случае
только к локальному максимуму приближенной задачи. При
этом часто нет никаких соображений, позволяющих определить,
насколько мы приблизились к глобальному максимуму.
При решении задачи (4.15) с ограничительными условиями
на выбор базиса первый этап симплекс-метода обычно будет
122 Гл. 4. Методы решения задач с сепарабельными функциями
использоваться. Может даже случиться, что локальный макси-
мум встретится на первом этапе (это может быть истолковано
как признак того, что нет допустимого решения) и, следова-
тельно, мы можем не найти допустимого решения задачи (4.1),
даже если оно имеется. Кроме того, в некоторых случаях при-
ближенная задача может иметь максимум, который не близок
ни к одному локальному максимуму задачи (4.1), — в резуль-
тате аппроксимации могут возникнуть посторонние локальные
максимумы. В общем случае трудно определить, будут ли реше-
ния приближенных задач сходиться к локальному максимуму
задачи (4.1), если разбиение интервалов для Xj делать все бо-
лее мелким.
Можно заметить, что, вообще говоря, точка, доставляющая
относительный максимум в приближенной задаче, не обязательно
будет допустимым решением в задаче (4.1). На практике тот
факт, что решение задачи (4.2) может не быть допустимым ре-
шением задачи (4.1), не вызывает сколько-нибудь больших
осложнений1). Читателю предлагается показать, что если мно-
жество допустимых решений задачи (4.1) выпукло, то любое до-
пустимое решение приближенной задачи (4.2) будет также до-
пустимым решением задачи (4.1).
* Несмотря на трудности, о которых шла речц выше, способ,
развитый в этом параграфе для нахождения приближенного
локального максимума в задаче (4.1), является весьма полез-
ным, поскольку он не чувствителен к аналитическим свойствам
функций, входящих в условия задачи. Кстати сказать, в настоя-
щее время созданы вычислительные схемы, которые позволяют
применять симплекс-метод при ограничительных условиях на
выбор базиса к задаче (4.15). Вместе, с тем метод можно при-
менять лишь с большой осторожностью: мы покажем- позднее на
примере, что имеются реальные задачи с локальным экстрему-
мом, сильно отличающимся (по значению целевой функции) от
глобального экстремума.
Отметим, наконец, некоторые интересные соображения, осно-
ванные на вычислительном опыте в применении этого метода.
Прежде всего, хотя при использовании все более мелких разбие-
ний промежутка число ограничений не возрастает, может значи-
тельно возрасти количество требующихся итераций (так же как
и вычислительные трудности при проведении итераций). Причи-
ной возрастания числа итераций является то, что в начальном
допустимом решении х, может значительно отличаться от его
окончательного значения, а обычно за одну итерацию удается
!) Поскольку нарушения ограничений, как правило, незначительны.—
Прим, ред.
4.3. Пример
123
перевести значение Xj лишь в соседний интервал. В определен-
ных случаях, однако, можно делать большие скачки по х^
В упражнении (4.44) читателю предлагается установить, когда
это допускается.
Чтобы исследовать, является ли локальный максимум при-
ближенной задачи достаточно хорошей аппроксимацией локаль-
ного максимума задачи (4.1), т. е. проверить точность прибли-
женного метода, использовался способ дробления интервала
пополам. Этот способ заключается в решении двух или более
приближенных задач* соответствующих некоторой задаче (4.1),
причем в («+1)-й задаче разбиение вдвое мельче, чем в зада-
че и. К сожалению, недостаток этого способа заключается в
невозможности гарантировать, что решение задачи и будет
базисным или хотя бы допустимым решением задачи и+1. Таким
образом, (и-М)-я задача, вообще говоря, также должна ре-
шаться с самого начала, включая первый этап. Замечено, что
если проводить дробление интервала пополам везде (не только
в окрестности решения задачи и), то решение (и+1)-й задачи
может приводить к локальному экстремуму, существенно отлич-
ному от локального экстремума, найденного в задаче и. Кроме
того, локальный экстремум в (и+1)-й задаче может доставлять
меньшее, нежели в задаче и, значение х. Для некоторых клас-
сов задач окрестность наилучшего локального экстремума может
быть легче достигнута при более крупном разбиении, нежели
при более мелком.
Приведенные выше соображения показывают, что по крайней
мере для некоторых классов задач может оказаться выгодным
решать задачу вначале при довольно грубом разбиении, а затем
уточнять результат, используя мелкое разбиение в окрестности
полученного ранее решения. Это может быть сделано довольно
просто. Полезно также попытаться использовать одно из допу-
стимых базисных решений предыдущей задачи в качестве
базисного допустимого решения в новой задаче; при этом исче-
зает необходимость проводить вычисления в новой задаче, начи-
ная с первого этапа. Однако осуществление этой процедуры
представляется нелегким.
4.3. Пример. Чтобы продемонстрировать использование ме-
тода аппроксимации, изложенного в предыдущем параграфе,
найдем относительный максимум в следующей задаче:
2x2+ 3x2 <6,
Х1, х2>0; (4.18)
z — 2х} — xj + хг.
124 Гл, 4. Методы решения задач с сепарабельными функциями
Отметим, что эта задача является задачей типа (4.1), в обо-
значениях которой gx (х:) = 2x2, g2 (х2) — 3x2, fj (х^ = 2Xj — x*,
f2(x2) = x2. Множество допустимых решений является выпук-
лым. Кроме того, fi и f2— вогнутые функции. Следовательно, как
покааано в § 3.12, любой локальный максимум в задаче (4.18)
будет глобальным максимумом. Поэтому метод, изложенный в
предыдущем параграфе, будет давать приближение к глобаль-
ному экстремуму этой задачи.
Глобальный максимум задачи (4.18) легко найти графически.
Он достигается в единственной точке х* = 0,7906, х2= 1,258.
Как видно из рис. 4.2, х* может быть определена как точка,
в которой ограничение выпол-
няется со знаком равенства
и касательная к кривой
2x2 Зх| = 6 совпадает с каса-
тельной к целевой функции,
т. е. как точка, являющаяся ре-
шением системы
2x24-3x2 = 6, 37-= 2(1 — Xj).
(4.19)
Из второго уравнения системы
(4.19) x2=Xi/3(l—Xi), и после
подстановки х2 в первое урав-
нение получаем
Г? I 1 1 1 — 6
L з (1 —Х1)2
Отсюда легко может быть най-
дено приведенное выше реше-
ние.
Максимальное значение z есть z*=2,213. Зная точку, в ко-
торой z достигает глобального максимума в точной задаче, мы
можем установить, насколько хорошо работает метод аппро-
ксимации. Перейдем к приближенной задаче. Заметим, что Xi и
х2 должны быть не больше 2. Допустим, что точки Xkj мы вы-
брали равноотстоящими с интервалом 0,25. Отсюда для каждого
/=1, 2 будет девять Функции gi(Xi) и fi(xi) показаны на
рис. 4.3, функции g2(x2) и f2(x2) —на рис. 4.4. Аппроксимирую-
щие ломаные на рисунках не отмечены, так как они почти совпа-
дают с кривыми и были бы трудно отличимы от них при столь
малых размерах рисунка. Значения функций в соответствующих
4.3. Пример
125
точках разбиения приведены в табл. 4.1. Выписывать прибли-
женную задачу (4.12) — (4.14) с 19 переменными подробно
весьма долго. В сокращенной форме задача принимает следую-
щий вид:
2 * 8
2 26,
/ = 1 /?=0
8 8
2 ~ 1 Чг — 1 >
А> = 0 /?=0
(4.20)
Ч2^>0 при всех k, х3>0;
28
найти max z —
J=l А_о J J
Значения gkj й fkj берутся из табл. 4.1, х3 — вспомогательная
переменная (ее нет необходимости выражать через Z,). Мы будем
решать задачу (4.20), используя модифицированный симплекс-
метод. Отметим, что goi=go2=O. Следовательно, мы можем
сразу получить исходное базисное решение для (4.20), исполь-
зуя в качестве начальных базисных переменных х3, ZOi, %ог.
Коэффициенты целевой функции каждой из этих переменных
равны нулю, поэтому для этого базисного решения ТвВ-1=О.
125 Гл. 4. Методы решения задач с сепарабельными функциями
Таблица 4,1
Данные для примера
Xi или х2 gi Л g? Л
0 0 0 0 0
0,25 0,1250 0,4375 0,1875 0,2500
0,50 0,5000 0,7500 0,7500 0,5000
0,75 1,1250 0,9375 1,6875 0,7500
1,00 2,0000 1,0000 3,0000 1,0000
1.25 3,1250 0,9375 4,6875 1,2500
1,50 4,5000 0,7500 6,7500 1,5000
1,75 6,1250 0,4375 9,1875 1,7500
2,00 8,0000 0 12,0000 2,0000
Данные для начала процесса приведены в табл. 4.2. Век-
торы §У)(с —fkJB качестве первой компоненты), которые нам
потребуются, равны:
ga) = [0, 0, 1, 0]; g$ = [0, 0, 0, 1];
= 0,4375, 0,1250, 1, 0]; g$ = [—0,2500, 0,1875, 0, 1[;
g$ = [—0,7500, 0,5000, 1, 0J; g$ = [—0,5000, 0,7500, 0, 1];
g$ = [—0,9375, 1,1250, 1, 0]; g$ = [—0,7500, 1,6875, 0, 1[;
g$ = [-l, 2, 1, 0]; g$-[~ 1, 3, 0, 1J;
gW = [—0,9375, 3,1250, 1, 0]; g$ = [—1,2500, 4,6875, 0, 1];
g$ = [—0,7500, 4,5000, 1, 0]; g$ = [—1,5000, 6,7500, 0, 1];
g$ = [—0,4375, 6,1250, 1, 0]; g$ = [—1,7500, 9,1875, 0, Ij;
g$ = [0, 8, 1, 0]; g$ = [-2, 12, 0, 1];
g$ —[0, 1, 0, 0J.
Проверка первых компонент векторов показывает, что
min (zkj — fv) = z82 — f 82 = —2.
Отметим, что вектор g$ принадлежит базису. Поэтому g$
может быть введен в базис, только если g$ выводится из ба-
зиса. Мы видим, однако, что из базиса должен быть выведен
вектор g$. Следовательно, g$ нельзя ввести в базис. Наимень-
шей среди остальных разностей является разность z72—f72.
Однако g$ не может быть введен в базис по той же причине,
4.3. Поимев
127
Таблицы для решения примера
Таблица 4.Z
Базисные переменные Д1 02 0з х(1) у11)
Z 0 0 0 0 -1,2500
хз 1 0 0 6 4,6875
Хо1 0 1 0 1 0
Х()2 0 0 1 1 о
Таблица 4.3
Z 0 0 1,2500 1,2500 -0,9375
ХЗ 1 0 -4,6875 1,3125 1,1250
Xoi 0 1 0 1 о
Х.52 0 0 1 1 0
Таблица 4.4
Z 0 0,9375 1,2500 2,1875 -0,2500
Хз 1 — 1,1250 -4,6875 0,1875 <2^062^)
Хз1 0 1 0 1 0
Х52 0 0 1 1 1
Таблица 4.5
Z 0,1212 0,8013 0,6819 2,2102
Хб2 0,4848 -0,5454 -2,2725 0,0909
Хз 1 0 1 0 1
Х52 -0,4848 0,5454 3,2724 0,9091
то и g.,®2 .Далее мы должны будем проверить g^n придем к тому
же выводу.. Однако, когда мы дойдем до g^, мы увидим, что
положение изменилось и g$ должен быть выведен. Следова’
тельно, g^ вводится в базис и Х52 становится положительным.
128 Гл. 4. Методы решения задач с сепарабельными функциями
Получаем данные для следующего шага, приведенные в табл 4.3.
Отметим, что
Zk\ fkl~ — Zk2 fk2 = L25 fk2.
Далее, min(z/u-—fkj) =Zu—fu. Однако g^ нельзя ввести в базис,
так как отсюда следует, что х3 должно обращаться в нуль, что
влечет за собой положительность и Z4i и ZOi. Наименьшей среди
остальных разностей является z3i—/зь Теперь значение Xoi может
быть сделано нулевым и, следовательно, g$ можно ввести в
базис. Таким образом, при следующей итерации %oi обращается
в нуль и Лз1 становится единицей. Новые данные приведены в
табл. 4.4.
Теперь только разности z4i—f4i, Зег—fs2, Z72—/72 и z62—fez
являются отрицательными, причем только i4i и Лб2 могут стано-
виться положительными. Так как z62—fe2<^4i—/и, то g^ вво-
дится в базис на следующей итерации. Теперь х3 обращается
в нуль. Полученные результаты показаны в табл. 4.5. Сейчас все
Zkj—fkj^O- Следовательно, табл. 4.5 содержит оптимальное ба-
зисное решение приближенной задачи. Это решение есть
Х31 = 1, Х52 = 0,9091, Х62 = 0,0909, 2 = 2,2102
или
Xj — ^31^31 — 0,7500,
*^2 ==z \s2*^52 “4“ ^62 "^62 === 112726»
4.4. Другая формулировка
Ш
Ранее мы получили решение х* = 0,7906, х*— 1,258, z* = 2,213.
Видно, что решение приближенной задачи оказалось весьма
близким к точному. Аппроксимация могла быть сделана, ко-
нечно, еще более точной за счет более мелкого дробления интер-
валов для %! и %2. Отметим, что значение z значительно ближе
к г*, чем Xi и х2 к х* и х*2.
На рис. 4.5 показано выпуклое множество допустимых реше-
ний приближенной задачи (4.20) и последовательность ее реше-
ния при использовании симплексного метода с ограничительными
условиями на выбор базиса. Точки соответствуют данным, при-
веденным в таблицах. Отметим необычную последовательность
точек. Решая задачу (4.20) симплексным методом с ограничи-
тельными условиями на выбор базиса, мы переходим на каждой
итерации к соседней экстремальной точке только в Х-простран-
стве; это не означает движения по соседним экстремальным точ-
кам в х-пространстве.
4.4. Другая формулировка. Приближенная задача для за-
дачи (4.1) может быть записана в другой форме, если иначе
ввести новые переменные. В (4.8), (4.9) и (4.10) положим
&fkj — fkJ — fk-l, p ^Skij — Skij Sk-l, ip
&xkJ = xkJ — £ = 1, ..., ry. (4.21)
Тогда, если Xj лежит в интервале Xk-i, j'^CxpCxkj, мы можем на-
писать
— xk-i> j~)r<Axkj)(>kp (4.22)
где
(4.23)
причем
(4.24)
Из (4.3) мы видим, что если X] лежит в интервале Xk-i.j-^
^Xj^.Xkj, то gn(Xj) и fj(Xj)—кусочно-линейные приближения
для gij(xj) и fj(xj) — могут быть записаны следующим образом:
gij(xj) —gk-i.ij-^-^gkij^kf, f (4.25)
Предположим сейчас дополнительно, что если б^>0, то
6Uj=l при и=1, .... k— 1. Для рассматриваемого случая мы
9 Зак. 735
130 Гл. 4. Методы решения задач с сепарабельными функциями
можем тогда написать
k-\
j~ 2
и ~ 1
Л-1
g’s-i, ij = 2 bUj + gotp (4.26)
Л-1
Приведенное выше предположение обеспечивает, что если
0<6лу<1, то duj==0, u>k. Следовательно, если мы потребуем,
чтобы при Sftj>0 выполнялось 6uj=l, —1, то мы мо-
жем написать
rj
Xj = (Д-^лу^лу»
ri
= 2 (^^*л/у)^лу 4~ £o/y, (4-27)
Л=»1
rJ
Л — 1
и бу единственным образом определяются, если выполнены
условия (4.24). Приближенная задача (4.2) может быть запи-
сана с помощью переменных блУ. В этих переменных она прини-
мает следующий вид:
п rJ п
2j 21 (,^gkij)\j=> bt 2^goip * — i, • • •»
0-С^уС1 ПРИ всех k и /; (4.28)
п г]
найти max z — jS 2 (Л/лу) j*
Здесь мы накладываем дополнительное требование, что если
бу>0, то биj = 1, и=1, ..., Л — 1. В целевой функции мы опу-
п
стили постоянное слагаемое 2 for
Задача (4.28) могла бы рассматриваться как линейная,
если бы не приходилось учитывать приведенные выше дополни-
тельные требования на бу. Мы можем решать эту задачу с ис-
пользованием симплекс-метода с указанными выше ограничи-
тельными условиями на выбор базиса подобно тому, как это
4.4. Другая формулировка
131
делалось в § 4.3. Мы не должны позволять переменной bkj ста-
новиться положительной, пока не выполняется условие 6UJ=1,
u=l, k— 1. На этапе, когда достигается неравенство
Zkj — Afkj^O для всех разностей, соответствующих перемен-
ным которые могут войти в базис, последнее базисное реше-
ние доставляет относительный максимум в приближенной за-
даче (4.28) (в терминах переменных х^ а не 6^). Доказатель-
ство этого утверждения почти аналогично приведенному в § 4.3.
В упражнении 4.12 читателю предлагается провести это дока-
зательство. В дальнейшем мы будем называть задачу (4.28)
приближенной задачей в 6-форме, а задачу (4.12) — (4.14) —
задачей в Х-форме.
Можно применить симплекс-метод к задаче (4.28), не рас-
сматривая верхние границы как ограничения, т. е. работая
только с базисными матрицами порядка т. Специальный алго-
ритм описан в {ЛП 11.7}. В нем учитываются ограничительные
условия на включение 6kj в базис. Если не использовать такой
алгоритм, число векторов базиса будет чрезвычайно большим
даже для весьма простых задач (порядок базисной матрицы бу-
дет тЦ-2г/) и переход к переменным dkj будет вряд ли по-
1
лезным. Следует и здесь отметить, что если переменная х$ вхо-
дит в задачу линейно, нет необходимости выражать ее через
переменные dfej. Это обстоятельство часто помогает значительно
уменьшить порядок решаемой задачи.
Интересно сравнить приближенную задачу в Z-форме с зада-
чей в 6-форме. Это будет сделано для случая, когда все пере-
менные входят в задачу не линейно. Задача в Х-форме содержит
2 rf переменных (включая вспомогательные переменные) и
J
т + п ограничений. Окончательное решение будет содержать не
более т + п положительных (при этом для каждого / не бо-
лее, чем два положительны). Задача в 6-форме содержит
2 г, переменных (также включая вспомогательные переменные)
и т ограничений. Кроме того, имеются 2yrj верхних границ, ко-
J
торые нет необходимости рассматривать как ограничения об-
щего вида. Окончательное решение задачи в 6-форме содержит
не более т + 2г/ положительных Преимущество 6-формы
j
в том, что мы имеем дело с малым базисом; недостаток состоит
в необходимости использовать специальный симплексный алго-
ритм, особым образом учитывающий верхние границы перемен-
ных. Обе формы должны учитывать ограничительные условия на
базис, хотя и несколько различные. Алгоритмы для решения
9*
132 Гл. 4. Методы решения задач с сепарабельными функциями
приближенной задачи в обеих формах запрограммированы для
быстродействующей вычислительной машины. Задачи решались
в той и другой форме и имеющийся небольшой опыт показал,
что реализация алгоритма решения задачи в 6-форме в силу
меньшей размерности базиса требовала меньше машинного вре-
мени, даже если число итераций было несколько больше, чем при
решении задачи в Х-форме. Опыт также наводит на мысль,
что по крайней мере в некоторых случаях каждая из форм мо-
жет потребовать значительно большего числа итераций, чем
строго линейная задача такого же размера. Например, для за-
дачи в h-форме с 120 ограничениями требовалось в среднем
1200 итераций, в то время как для решения строго линейной за-
дачи обычно бывает достаточно 400 итераций.
4.5. Замена переменных для получения сепарабельности.
Хотя задача в первоначальной постановке может не иметь
форму (4.1), часто ее удается привести к такому виду введением
новых переменных. В этом параграфе мы покажем некоторые из
наиболее употребительных для этого приемов.
В качестве первого простого примера рассмотрим случай,
когда пройзведение XiXj содержится (в качестве слагаемого)
в одном из ограничений или в целевой функции. Чтобы исклю-
чить такое произведение и получить сепарабельную форму, вве-
дем две новые переменные Уг и уг
+ yj = ^(xi-х^. (4.29)
Тогда
х.х}=у2 — у2, (4.30)
и мы имеем сепарабельную форму относительно новых перемен-
ных yi, У1. В результате замены в исходной задаче вместо X{Xj
появляется y2t—yl. Кроме того, мы включаем в задачу два до-
полнительных ограничения (4.29). Так как в выражение для у$
входит разность Xi и xj, то уз может принимать значения любого
знака, даже если хг- и Xj должны быть неотрицательными. Это
не вызывает никаких трудностей в постановке приближенной
задачи в 6- или h-форме, так как h&j и 6^ будут всегда неотри-
цательными. В упражнении 4.35 читателю предлагается иссле-
довать, как следует поступать с неограниченными переменными.
Если интервалы изменения Xi и Xj есть 0-<хг<Х- и O^Xj^aj
соответственно, интервалом изменения уз будет —аз^Уз^йг.
Если ХгХз — единственная несепарабельная функция в исходной
задаче, мы будем после указанной замены иметь задачу в фор-
ме (4.1) и сможем перейти от нее к приближенной задаче в X-
4.5. Замена переменных для получения сепарабельности
733
или 6-форме. Отметим, что для того, чтобы привести задачу
к сепарабельной форме, мы расширили задачу включением двух
дополнительных ограничений.
Произведение XiXj может быть преобразовано и другим пу-
тем, который можно обобщить в применении к задачам, содер-
жащим произведение трех или более переменных, при условии,
что все переменные положительны. Введем новую переменную
y=XiXj. (4.31)
Логарифмируя, получаем
In у = In xt + In Xj. . (4.32)
Везде, где в задаче встречается выражение x^xj, мы заменяем
его на //, а равенство (4.32) вводим в задачу как дополнитель-
ное ограничение. Этот прием может быть использован, только
если известно, что Xi и Xj должны быть положительными. Если
одна или обе переменные могут принимать нулевые значения,
возникают трудности, так как In 0 =—оо, и ограничение (4.32)
не может быть представлено в X- или 6-форме.
Можно, однако, модифицировать изложенный выше прием
так, чтобы он был пригоден при любых неотрицательных Xi и Xj.
Введем новые переменные и Wjt
®7 = */ + ez> = + (4.33)
где ez и e,j — фиксированные положительные числа. Тогда
wz^>ez> 0 и е;-> 0. Кроме того,
XtXj = (щ — ez) (wj — ey) = WfWj — ez®y — eywz 4- еге/- (4.34)
Далее мы запишем
t/ = ‘a>lWj (4.35)
и
In у — In wz-f-In (4.36)
Прием заключается в замене xtXj на
у —ezT0y —eywz4-eze; (4.37)
и добавлении трех новых ограничений (4.33) и (4.36). Отметим,
что этот подход требует введения трех новых переменных и трех
дополнительных ограничений. Этот метод может быть обобщен
в применении к произведению любого числа переменных. В уп-
ражнении 4.16 читателю предлагается указать преобразования
для случая трех переменных.
134 Гл. 4. Методы решения задач с сепарабельными функциями
Легко преобразовать к сепарабельным
е(ах1+Ьх 1), где х. о, Xj 0, записывая
(ах2,+Ьх ,)
у — е^ 1 1!,
In у — ах2. -I- bXj.
Подобным образом для выражения хр при
имеем
!/=<>.
Wj — Xj-j-e.j, £j>0,
v = Wjlnxl,
In у — v — e,j lnxz,
1П V = 1П Wj + In In xt.
выражения вида
(4.38)
(4.39)
x{ > 1, Xj >0 мы
(4.40)
(4.41)
(4.42)
(4.43)
(4.44)
Другие приемы могут быть использованы для представления
в сепарабельной форме функций несколько необычной струк-
туры. Допустим, что Xi, х2^> 0 и
т. е.
и — min [х1? х2],
(4.45)
%1 > х2.
(4.46)
График функции и(хь х2) показан на рис. 4.6. Он состоит из
двух плоских частей. Функция может быть представлена в сепа-
рабельной форме следующим образом. Рассмотрим три век-
тора: Vi = eb v2 = [l, 1, 1], v3 = e2. При %i>x2 имеем и=х2. Этому
случаю соответствует часть плоскости, являющаяся выпуклым
конусом, порождаемым векторами Vi и v2, т. е. любая точка
[%1, х2, и] соответствующей части графика имеет вид
[Хр х2, й] = AqVj-|_Z2v2, Zj, Z2>0. (4.47)
Аналогично при x2>Xi имеем и=Х\, и соответствующая часть
графика есть выпуклый конус,, порожденный векторами v2 и v3,
т. е. любая точка этой части графика представима в виде
[Хр х2, и\ = A2v2 —|- A3V3, 12, А3 0. (4.48)
Следовательно, любая точка [%i, х2, и] поверхности может быть
представлена следующим образом:
[xb х2, и\ = XjVj + A2v2 Ч—A3v3, М, А2, А3^>0, (4.49)
или -
Xj = Xj А2, х2 = А2-А3, it=== А2, (4.50)
4.5. Замена переменных для получения сепарабельности 135
если поставить условие, что не более чем два из чисел Хг- поло-
жительны и положительными могут быть лишь два соседних чис-
ла Хг-. Отметим, что здесь не требуется, чтобы сумма равня-
лась единице. Для того чтобы удобным образом использовать
это представление, следует рассматривать приближенную задачу
в Х-форме, так как в этой форме подходящим образом исполь-
зуются ограничения на ввод вектора в базис.
Рис. 4.6.
Только что рассмотренный прием может быть использован
также для представления поверхности, состоящей из нескольких
плоских частей, например показанной на рис. 4.7. Векторы vb v2,
v3, v4 и v5 должны быть выбраны так, как показано на рисунке,
и тогда любая точка [хь х2, и] поверхности представима в виде
[Xi, х2, == XjVi 4~ X2v2 4" X3v3 4~ X4v4-|~X5v5, (4.51)
где все Хг- > 0, причем не более чем два Х< положительны и поло-
жительными два числа Хг могут быть, лишь если они соседние.
Приемы приведения задачи к сепарабельной форме (4.1),
изложенные в этом параграфе, достаточно хорошо иллюстри-
руют способы, с помощью которых такое приведение может
быть осуществлено. Нам кажется, что лишь немногие из возни-
кающих на практике задач не могут быть приведены к форме
(4.1) введением новых переменных и ограничений. Однако, если
136 Гл. 4. Методы решения задач с сепарабельными функциями
в задаче много функций в несепарабельной форме, размерность
приближенной задачи может становиться очень большой из-за
Рис. 4.7.
большого количества новых ограничений, которые должны быть
добавлены к исходным.
4.6. Случаи, когда локальный экстремум одновременно яв-
ляется глобальным. Мы показали в § 3.12, что если множество
допустимых решений в задаче нелинейного программирования
выпукло и целевая функция является вогнутой, то любой отно-
сительный максимум целевой функции на множестве допустимых
решений является одновременно ее глобальным максиму-
мом. Когда задача имеет вид (4.1), целевая функция будет вог-
нутой, если все функции fj(Xj) —вогнутые. Кроме того, множе-
ство допустимых решений при условии, что допустимое решение
существует, будет выпуклым, если: a) gij(Xj) —вогнутые функ-
ции при всех /, когда номера i соответствуют ограничениям, вхо-
дящим со знаком «>»; b) gij(Xj)—выпуклые функции при всех/,
когда номера i соответствуют ограничениям, входящим со зна-
ком «<»; с) gij(Xj) —линейные функции при всех /, когда но-
мера i соответствуют ограничениям, входящим со зна-
ком « = ».
4.6. Случаи, когда экстремум является глобальным
137
При изложенном способе аппроксимации функции fj, gij яв-
ляются, очевидно, выпуклыми (вогнутыми), если fj, gij— выпук-
лые (вогнутые) функции. Следовательно, если функции fj, gij
обладают подходящими свойствами выпуклости либо вогну-
тости, так что любой относительный максимум в задаче (4.1) яв-
ляется глобальным, то любой локальный максимум в приближен-
ной задаче (4.2) также является глобальным. Кроме того, в та-
ких случаях множество точек, в которых достигается глобальный
максимум в приближенной задаче, является выпуклым, так что
не может быть двух или более изолированных относительных
максимумов приближенной задачи. В условиях, когда локаль-
ный максимум является также и глобальным, решение прибли-
женной задачи дает приближение к глобальному максимуму
задачи (4.1). Далее, делая разбиение интервалов для Xj все
более мелким, мы получаем последовательность максимальных
значений целевых функций приближенных задач, сходящуюся к
абсолютному максимуму целевой функции для задачи (4.1) (см.
упражнение 4.32). Однако нельзя сделать вывод, что последователь-
ность решений приближенных задач будет сходиться к пределу,
если не известно, что задача (4.1) имеет единственное оптималь-
ное решение. Отметим, что даже если целевая функция в задаче
(4.1) строго вогнутая и множество допустимых решений выпукло
(а значит, глобальный максимум достигается в единственной
точке), отсюда не следует, что приближенная задача имеет един-
ственный глобальный максимум, так как целевая функция при-
ближенной задачи не строго вогнутая. Однако при дроблении ин-
тервала все точки, доставляющие оптимальное решение в при-
ближенных задачах, будут сходиться к точке глобального макси-
мума в задаче (4.1) и в пределе оптимальное решение прибли-
женной задачи будет достигаться в единственной точке.
Мы докажем сейчас, что если функции fj(Xj) —вогнутые и
функции gij(Xj) обладают соответствующими свойствами выпук-
лости или вогнутости, так что множество допустимых решений
выпукло, то, решая приближенную задачу как задачу линей-
ного программирования (без учета ограничительных условий на
выбор базиса), мы получим тем не менее оптимальное решение
приближенной задачи. Иными словами, мы получим оптималь-
ное решение как при учете ограничительных условий на выбор
базиса, так и не учитывая этих ограничений. Это важный ре-
зультат, потому что, как будет показано в следующем пара-
графе, для решения приближенной задачи можно применить
более эффективный численный метод, если нет необходимости
учитывать ограничительные условия на выбор базиса.
Мы дадим доказательство этого утверждения для прибли-
женной задачи в б-форме. Читателю предлагается провести до-
138 Гл. 4. Методы решения задач с сепарабельными функциями
казательство для приближенной задачи в Х-форме. Введем но-
вые переменные = так что задача запишется в виде
=>z==1>
i k j
0 < ф*; -C ^xkj при всех k, J; (4.52)
найти max г = 2i fcj
j k
Заметим, что Xj через ф^- выражается следующим образом:
Xj = 2Фл/, /==1,..., п. (4.53)
.А
Проведем доказательство от противного. Предположим, что
задача (4.52) решается просто как задача линейного програм-
мирования, без учета ограничительных условий на выбор ба-
зиса. Как мы покажем, предположение, что не существует опти-
мального решения этой задачи линейного программирования,
обладающего свойством, что фи^ = Дхи?-, и—\у ..., k—1, если
ф^>0, приводит к противоречию. Чтобы показать это, предпо-
ложим, что мы решили задачу (4.52) как задачу линейного
программирования и в решении, найденном таким образом, при
некотором / получили фг;,->0, но ф^<Дх^-, где v<r. Покажем,
что, не изменяя всех х$ и не нарушая соотношения
мы можем определить либо новую совокупность допустимых ф^-,
которая доставляет лучшее значение целевой функции, либо но-
вую совокупность допустимых xpfej, доставляющую то же самое
значение целевой функции. Причем в обоих случаях новая сово-
купность будет обладать тем свойством, что фи7- = Ахю-,
и—\, ... , k— 1, если ф^-Х). Каждая из этих альтернатив про-
тиворечит нашему предположению.
Мы просто уменьшим фп- и одновременно на ту же вели-
чину увеличим ф^-, пока не будет выполнено одно из равенств:
фг<7 = 0 или ф^==Дх^. Это не изменит значений х7. Пусть рве-
личина, на которую мы уменьшили фп- и увеличили фг;-. Значе-
ние целевой функции изменится на величину
Mfw У г Л
у &Xrj/
и левая часть Лго ограничения изменится на
I bgvlj _ ^grij \
\ &Xvj &xrj / Р*
(4.54)
(4.55)
4.6. Случаи, когда экстремум является глобальным /39
Так как fj(Xj)—вогнутая функция, fj(Xj) также является
вогнутой функцией. Поэтому
kfvj > &frj
&Х ^Х
и, следовательно, целевая функция или возрастает, или оста-
нется без изменения. Для ограничений со знаком «<» каждая
функция gij(Xj), а значит, и gij(Xj) является выпуклой. Но для
выпуклых функций
kgrtj
\х&х f j
Следовательно, поскольку исходная совокупность ф^ удовлетво-
ряет всем ограничениям, новая совокупность ф^ будет, очевид-
но, удовлетворять ограничениям, имеющим знак «^», ибо левая
часть этих ограничений остается неизменной или уменьшается.
Подобным образом для ограничений, имеющих знак «>», каж-
дая функция g’ij(xj) будет вогнутой. Для вогнутых функций
&£vij &grij Q
^Xyj \Xj.j
и отсюда новая совокупность ф^- будет удовлетворять ограниче-
ниям, имеющим знак «^>». Наконец, для ограничений в форме
равенств gtj(xj) являются линейными функциями, откуда
kgvij kgrlj____q
^Ху j &Х fj
т. е. новая совокупность ф/?,?- тоже удовлетворяет этим ограниче-
ниям. Окончательно новая совокупность ф^ удовлетворяет
условиям 0 ф&; Axhj и всем-остальным ограничениям. Таким
образом, она представляет допустимое решение, при котором
значение целевой функции увеличивается или остается неизмен-
ным, что противоречит исходному предположению.
Таким образом, решая задачу (4.52) как задачу линейного
программирования, мы с помощью полученного оптимального
решения находим значения Xj, дающие оптимальное решение
приближенной задачи. Отметим, что мыслима возможность, ког-
да, рассматривая (4.52) как чистую задачу линейного програм-
мирования, мы можем получить решение, которое не обладает
тем свойством, что фи} = ЛХи;, и=1, ..., k— 1, если ф^>0. Тем
не менее из предыдущих рассуждений следует, что Xj, опреде-
ленные по найденным фго-, доставляют оптимальное решение
приближенной задачи.
140 Гл. 4. Методы решения задач с сепарабельными функциями
В случаях когда оптимальное решение приближенной задачи
может быть получено в результате решения чистой задачи ли-
нейного программирования, принцип декомпозиции (ЛП 11.10)
позволяет существенно упростить вычислительный процесс.
В следующем параграфе мы объясним, как он используется для
решения приближенной задачи в 6-форме.
Использование кусочно-линейной аппроксимации для полу-
чения приближенных решений задач с сепарабельными функ-
циями первоначально ограничивалось задачами в форме (4.52),
в которых только целевая функция была нелинейной и притом
вогнутой.
Первыми рассмотрели эту задачу Чарнс и Лемке [4]. Они
пользовались постановкой, похожей на Х-форму приближенной
задачи. Вскоре после них Данциг [5] ввел б-форму в том виде,
как она изложена здесь. Позднее он изложил ее в более подроб-
ном виде [6]. Совсем недавно Миллер [14] сделал обобщение на
случай нелинейных ограничений, позволяющее получить локаль-
ный максимум.
4.7. Использование принципа декомпозиции при наличии
ограничений сверху. Метод, учитывающий верхние границы на
переменные без включения их в число ограничений общего вида,
приведен в {ЛП 11.7}. По-видимому, значительно более эффек-
тивный метод может быть получен при использовании принципа
декомпозиции {ЛП 11.10}. Однако нет необходимости в знаком-
стве с этим принципом для того, чтобы понять приводимые ниже
доводы, так как все особенности проявляются непосредственно
и при обычном подходе.
Рассмотрим задачу линейного программирования следую-
щего вида:
А1х1 + А2х2 = Ь,
IxjCh, хп х2>0; (4.56)
найти max z = -ф с2х2.
Здесь мы имеем дело с ситуацией, когда имеются ограниче-
ния сверху на переменные, входящие в Xi, а на переменные, вхо-
дящие в х2, таких ограничений нет.
Предположим, что размеры матрицы At — mXnb матрицы
А2— пгХп2. Обозначим через /2 множество значений индекса /
при / = П1 + 1, ..., П1+и2. Множество X точек хь удовлетворяю-
щих условиям 1х1<Ъ, Xi>0, есть замкнутое ограниченное вы-
пуклое множество с конечным числом крайних точек х*г Таких
крайних точек 2"‘ и каждая может быть представлена в форме
x>[AA- ..., АД], (4.57)
4.7. Использование принципа декомпозиции 141
где 6j=l или 0. Все крайние точки получаются при рассмотре-
нии всех возможных комбинаций Si, ..., 6П из нулей и еди-
ниц. В упражнении 4.20 мы предлагаем читателю показать, что
крайние точки действительно представимы в такой форме.
Так как X — замкнутое ограниченное выпуклое множество
с конечным числом крайних точек, то каждая точка этого мно-
жества, как известно, может быть представлена как выпуклая
комбинация крайних точек, т. е. если XiCX, то существует на-
бор чисел pv (не обязательно единственный), такой, что
2«1
Xi=3pXi> гДе Pv>° ПРИ всех Sp„=l- (4-58)
V
Справедливо и обратное: любой набор чисел > 0 при усло-
вии, что 2р® — 1» определяет по формуле (4.58) точку Xi€X.
V
Следовательно, исходная задача эквивалентна задаче, в кото-
рой мы отбрасываем верхние ограничения на переменные и вво-
дим переменные рг, т. е. эквивалентна следующей задаче:
2(а1х;1)ро-+-а2х2=ь,
Sp„=1. (4-59)
V
Рр^-0 при всех v, х2>0;
найти max z — 2 (CX1) Pr + C2X2‘
V J
Использование равенств (4.58) дает возможность получить оп-
тимальное решение задачи (4.56) с помощью оптимального ре-
шения задачи (4.59).
Таким образом, можно было бы прямо выписать экстремаль-
ные точки х*! и, вычисляя AjX*j и CjX*,, непосредственно ре-
шить задачу (4.59). Однако число экстремальных точек может
оказаться очень большим, так что проведение этих вычислений
будет весьма трудоемким. В то же время следует иметь в виду,
что- многие из чисел pv могут оставаться нулевыми и соответ-
ствующие величины AjX*! и CjX^ нет надобности вычислять.
Мы покажем сейчас, что нет необходимости в использовании
этой процедуры. Вместо этого можно выделить те экстремаль-
ные точки, которые необходимы для решения задачи. Запишем
d,=AX. (4.60)
Предположим, что мы имеем базисное допустимое решение за-
дачи (4.59), и пусть В — базисная матрица порядка т+1, а св—
142 Гл. 4. Методы решения задач с сепарабельными функциями
вектор оценок базисных переменных. Пусть
<*т+1] = СдВ1' (4-61)
удобно для дальнейшего.
Такое выделение последней компоненты внутри вектора-строки а
Допустим, что мы хотим определить переменную, которая
становится базисной на следующей итерации. Для всех индек-
сов j соответствующих небазисным переменным, вычислим
Zj — Cj = — с J, (4.62)
где a.j есть /-й столбец матрицы А2. Для индексов о, соответ-
ствующих переменным рг,
~ ev = + om+1 - ev - (аД - с,) +о,в+г (4.63)
Если мы не имеем значений х*р мы не можем вычислить zv — ev
непосредственно. Отметим, однако, что нам не нужны все
zv— ev и х*Р Нам нужно только то значение х*Р которое соот-
ветствует наименьшей разности zv — ev. Другими словами, нам
нужно только то х*Р которое минимизирует (<т1А1 — с^х^.
Важно заметить, что эта крайняя точка будет получаться
автоматически, если мы решим следующую задачу линейного
программирования:
Ix<h, х>0; найти min Z —— с^х, (4.64)
так как ее оптимальное решение будет крайней точкой множе-
ства X. Но решение задачи (4.64) не вызывает вычислительных
трудностей, поскольку она распадается на щ независимых задач
линейного программирования
О < Xj < hj,
найти min Zj = (eiA.l — c1)jXj, /=1, nP (4.65)
Решением /-й задачи является
Г 0, если (tfiAi — Ci)/ > О,
, / А п (4.66)
J { hp если (a^i — Cj)y < О, ' • 7
а при (giAi — Ci)j = O решением является любое значение Xj из
интервала В этом последнем случае мы можем по-
ложить Xj равным 0 или hj, получая крайнюю точку.
Обозначим через х^ крайнюю точку, полученную в резуль-
тате решения задачи (4.64). Тогда
min " ^) = zt “ et = (G1A1 - С1) Х?1 + °т+1 • (4-67)
4.8. Пример
143
Далее мы вычисляем
min{zz — et\ min (гу — гу), j£J2}- (4.68)
Если это число неотрицательное, соответствующее базисное до-
пустимое решение является оптимальным. Если оно отрицатель-
ное, вектор (или один из векторов), соответствующий наимень-
шей из разностей Zt — et или г$ — с^ /С/2, включается в базис
на следующей итерации.
Если переменная, которая становится базисной, есть xj, / € J2,
мы вычисляем 0] и обычным путем определяем пере-
менную, которая исключается из числа базисных. Если базисной
становится переменная рь мы сначала вычисляем
определяем 1] и затем обычным путем узнаем, какой
вектор покидает базис. Затем делаем соответствующее преоб-
разование таблицы. Это дает.новый вектор а, который опреде-
ляет новый набор коэффициентов для Z в* (4.64). Описанная
выше процедура повторяется, и либо мы получим оптимальное
решение, либо найдем вектор, который должен быть включен в
базис на следующем шаге.
Описанный алгоритм имеет то преимущество перед алгорит-
мом, приведенным в {ЛП 11.7},. что большое число переменных
может выходить на верхнюю границу за одну итерацию, в то
время как в {ЛП 11.7} за одну итерацию на свою верхнюю гра-
ницу выходит лишь одна переменная.
Вычислительный эксперимент (проведенный, впрочем, на ма-
лом количестве задач) наводит на мысль, что изложенный метод
позволяет уменьшить вычислительные трудности чуть ли не на-
половину. К сожалению, этот метод не может быть рационально
использован в случае, когда ограничительные условия на выбор
базиса должны быть учтены с целью обеспечить равенства
би;=1, «=1, k— 1, если 6/г?>0. Причина в том, что мы не
работаем непосредственно с переменными 6kj.
4.8. Пример. Мы покажем на примере, как определяется при-
ближенный глобальный максимум в задаче с линейными огра-
ничениями и вогнутой сепарабельной целевой функцией в ре-
зультате решения приближенной задачи в 6-форме. Рассмотрим
задачу
2Xj + Зх2 < 6,
2X1 —|— х2 4,
хр х2>0; (4.69)
НЗЙти max z — 2х* — х] + х^
144 Гл. 4. Методы решения задач с сепарабельными функциями
Отметим, что целевая функция в этой задаче та же, что и в
примере § 4.3. Ограничения здесь, однако, линейные. Задача мо-
жет быть легко решена графически, как это и показано на
рис. 4.8. Сразу ясно, что единственное оптимальное решение
получается в точке, где 2xi + 3x2=6 и наклон касательной к ли-
нии уровня целевой функции равен —2/3: 2(xi—1)=—2/3. Из
Рис. 4.8.
этих двух уравнений получаем х* = 2/3, 14/9 — 1,5555. Сле-
довательно, z* = 2,4444.
Целевая функция может быть представлена в виде z=
=fi(Xi) +Ых>), где fJ(Xj) = 2xl — x* и f2(x2)=x2. Так как fz —
линейная функция, нам не надо вводить для нее кусочно-линей-
ную аппроксимацию, т. е. не надо выражать х2 через перемен-
ные 6. Отметим, что х4 не может быть больше 2. Разобьем ин-
тервал 0-^X1^ 2, как и в примере § 4.3, на части Дхм = 0,25.
Тогда хг = 0,25 2 и, используя табл. 4.1 для получения
k
мы можем перейти к следующей приближенной задаче:
8 8
0,5 2 Ч- Зх2 -1- х3= 6, 0,5 2 Ч~ х2 -1- х4 = 4, (4.70)
Й = 1 Л-1
0 <; 6Й 1, k — 1, ..., 8; х2, х3, х4 0;
найти max £=0,43756! 4-0,312562 4-0,187563Ч-0,062564 —
— 0,062565 - 0,187566 - - 0,312567 — 0,437568 + х2.
4.8. Пример
145
Как было ранее отмечено, ограничительные условия на выбор
базиса здесь могут не учитываться, т. е. мы имеем дело с обыч-
ной задачей линейного программирования. Автоматически сле-
дует, что бь=О, если 6и=1 не при всех и=\, ..., k — 1. Верхние
границы будут учитываться с помощью метода декомпозиции,
O-^dfe-Cl, k = \, ..., 8, — нули или единицы.
Для данной задачи матрица Ai (в обозначениях предыду-
щего параграфа) имеет размеры 2X8, все ее элементы равны 0,5.
Далее
q = (0,4375; 0,3125; 0,1875; 0,0625;
—0,0625; —0,1875; —0,3125; —0,4375), (4.71)
а все компоненты любой крайней точки б® выпуклого множества
0 "Сбй 1, k= 1, ..., 8 — нули или единицы.
Любой вектор 6^>0, удовлетворяющий верхним ограниче-
ниям, может быть записан в виде 6 = где Sp® = 1 и
V V
pD>0 при всех и. Введением pv мы получаем задачу вида (4.59)
с тремя ограничениями. Отметим, что решение 61 = 0 является
крайней точкой параллелепипеда двухсторонних ограничений на
переменные и для него = А^* = 0, ех — сх6* = 0. Отсюда, если
положить pi=l, х3 = 6, х4=4, мы получим начальное базисное
допустимое решение с базисной матрицей В = 13. Необходимость
в первом этапе отпадает. Табл. 4.6 является исходной симплекс-
ной таблицей. Для выбранного базисного решения ав = 0, так что
min (zv — ev) = min (— c^) = — max сД
Максимизирующая c46 крайняя точка выпуклого множества, по-
рожденного верхними ограничениями, будет найдена, если счи-
тать 6^ = 1 при Cfei>0 и 6k = 0 при сы<0. Поэтому из (4.71) полу-
чаем, что крайняя точка (обозначим ее 6*) есть
62 = [1, 1, 1, 1, 0, 0, 0, 0]
и
min (zv — ev) = —0,4375 — 0,3125 — 0,1875 - 0,0625 = —1.
Единственной небазисной переменной является х2 и для нее
г2— с2 =—с2 = — 1. Поэтому мы можем позволить либо х2,либор2
стать положительным. Для определенности пусть р2 становится
положительным. Тогда d2 = Aj6* = [2,2], е2 = с^* = 1. Столбец
yW вычислен и приведен в табл. 4.6. Видно, что pi должно
обращаться в нуль, когда р2 становится положительным. Дан-
ные следующей итерации приведены в табл. 4.7,
10 Зак. 735
Таблицы для решения примера
Таблица 4.6
Базисные переменные 31 02 0з Хв" У?’
Z 0 0 0 0 -1
Х.З 1 0 0 6
Х4 0 1 0 4 I i' 1 2
Pi 0 0 1
Таблица 4.7
2 0 0 1 1 -1
ХЗ 1 0 — 2 4
Х4 ~ 0 1 — 2 2 1
Р2 0 0 1 1 1 0
Таблица 6.8
Z 0,3333 0 0,3333 2,3333 -0,1041
Х2 0,3333 0 -0,6667 1,3333 —0,1667
Х4 -0,3333 1 -1,3333 0,6667 -0,3333
Р2 0 0 1 1 (7)
Таблица 4.9
Z 0,3333 0 0,4374 2,4374
Х2 0,3333 0 —0,5000 1,5000
Х4 -0,3333 1 -1 1
РЗ _ 0 0 1 1
4.8. Пример
147
Теперь о¥=0, но 03=1; таким образом,
—^) = min[—С16 + о3] = (— max с16)+о3 = 0>
так как из вышесказанного следует, что maxci6=l и ог3=1. Та-
ким образом, никакое новое pv не может становиться положи-
тельным. Из остальных переменных лишь х2 является неба-
зисной. Мы видим, что z2— с2 =— 1. Поэтому переменная х2 дол-
жна становиться положительной на следующей итерации. Значе-
ния следующего столбца приведены в табл. 4.7. Легко видеть,
что %з обращается в нуль, когда переменная х2 становится базис-
ной.
Данные для следующей итерации приведены в табл. 4.8.
Здесь ог1= (0,3333; 0), о3=0,3333,
а /1 1 1 1 1 1 1 1 \
б , б» б> б> б, 6, б, 6 J
и
OjAt — Ci = (—0,2708; —0,1458; —0,0208; 0,1042;
0,2292; 0,3542; 0,4792; 0,6042)
Вектор 6, который минимизирует (oriAj. — Cj)S (обозначим его
через 6*), есть 6* = [1, 1, 1, 0, 0, 0, 0, 0]. Отсюда
min (zv — ev) = Ах - q) 6* + о3 =
= —0,2708 — 0,1458 — 0,0208 + 0,3333 = —0,1041.
Из переменных, не подчиненных верхним ограничениям, только
х3 является небазисной, но х3 не может войти в базис, так как
она была выведена из базиса на предыдущем шаге. Таким об-
разом, на следующем шаге положительной становится перемен-
ная р3. Мы находим, что d3=[l,5; 1,5]. Очередной столбец
вычислен и приведен в табл. 4.8. Легко видеть, что р2 обра-
щается на следующем шаге в нуль.
Данные для следующей итерации приводятся в табл. 4.9. Мы
видим, что <У1= (0,3333; 0) —то же, что и на предыдущей итера-
ции,— и о3 = 0,4374. Следовательно, д* доставляет минимум
(oiAi — Ct) 6 и
min (zv — ev) = (аД — q) 6^ + а3 = — 0,4374 + 0,4374 = 0,
так что zv — > 0 для любого небазисного pv. Из остальных
переменных небазисной является х3, и мы отметим, что z3— х3=
= z3=0,3333. Следовательно, оптимальное решение приближен-
ной задачи получено. Это решение есть х2=1,5, х4=1, р3=1 (т. е.
Xi = 0,75), 2 = 2,4374. Мы нашли раньше, что оптимальное реше-
ние исходной задачи (4.69) есть х* = 0,6667, х* = 1,5555,
10*
148 Гл. 4. Методы решения задач с сепарабельными функциями
z*= 2,4444. Таким образом, мы видим, что полученное оптималь-
ное решение приближенной задачи является достаточно хорошей
аппроксимацией для оптимального решения исходной задачи,
причем значения целевых функций более близки, чем значения
соответствующих переменных.
Читателю предлагается отметить по рис. 4.8 последователь-
ность решений, представленных в табл. 4Г6—4.9.
4.9. Метод Хартли для максимизации функции на выпуклом
множестве при сепарабельных ограничениях. Рассмотрим задачу
нелинейного программирования следующего вида:
ху>0, /=1, (4.72)
11
найти
j~i 1
где gij(Xj) —выпуклые функции в ограничениях со знаком «<О>,
gij(xj) в ограничениях со знаком « = » и gij(Xj)—вогнутые
функции в ограничениях со знаком «>». При этих условиях,
если допустимое решение существует, множество допустимых
решений является выпуклым и, так как целевая функция ли-
нейна, локальный максимум является глобальным.
Приближенный глобальный максимум в этой задаче может
быть найден с помощью решения приближенной задачи в X- или
d-форме. Хартли [10] предложил для нахождения приближен-
ного глобального максимума по существу двойственный подход.
Как и в § 4.2, заменим функции gij(Xj) их кусочно-линей-
ными приближениями gtj(Xj). Тогда из (4.3) имеем
gij = gkij sklj (xj xkj)< xkj xj Xk + \, j>
где
____ Sk+1, ij— Ski J
^4__Xk+i, j Xkj
Когда Xj лежит в интервале
Xkj, j^x j^xkj+i, p n>
функция gz(x) = Sio-(^) имеет ВИД
n n
i/(x) U~Sbj, ijXHj. 4Xi'
(4-73)
(4.74)
(4-75)
4.9. Метод Хартли
149
Рассмотрим те из ограничений задачи (4.72), которые имеют
форму gi(x)^.bi. По предположению g,(x) должна быть вы-
пуклой функцией х. Функция g,(x) также должна быть выпук-
лой. Рассмотрим поверхность gi(x) — хп+1=0 в En+i. Для каж-
дого хСД”, при котором функция gi(x) определена, найдется
точка^х, хп+1], лежащая на поверхности gi(x) —хп+1 = 0. Кроме
того, множество точек в £п+1, удовлетворяющих неравенству
gi(x) —xn+i<<0, должно быть выпуклым, так как g,(x) — xn+i—
выпуклая функция от [х, xn+i]. Для любого х, компоненты ко-
торого удовлетворяют условиям (4.74), соотношениеgi(x)—xn+i =
=0 можно переписать в виде
п п
2~ xn+i==~^i1(.Skj,u~skjt ijxkjt j)> (4-76)
поскольку gi(x) имеет вид (4.75). Следовательно, (4.76) опре-
деляет уравнение касательной плоскости к поверхности
gi(x) —xn+i=0 при любом х, удовлетворяющем условиям (4.74).
Но любая касательная плоскость к gi(x)—xn+i=0 является
опорной гиперплоскостью к выпуклому множеству gi(x)—хп+1-С
40и любая точка [х, xn+i] этого выпуклого множества должна
удовлетворять условию
п п
2 skijxj ~ x«+i < ~ 2 (£kj.ij — sk., tjxkp /)•
J 1 J J * J J J
В частности, для любого х, удовлетворяющего условию gi(x)
должно выполняться
п п
2 skuxj < bt — 2 (gkj, I,—skj< tjXk}, jy
Проводя аналогичные рассуждения относительно ограниче-
ний в форме gi(x) bt и линейных ограничений, мы заключаем,
что для любого х£Х (где X— выпуклое множество допустимых
решений приближенной задачи) должны выполняться все огра-
ничения вида
п »
2 sk,, 11хj {~ 2 ~ ., ijxkr j)> (4-77)
где знак «<^», «~» или «^'» совпадает со знаком соответствую-
щего ограничения в (4.72).
150 Гл. 4. Методы решения задач с сепарабельными функциями
Имеется лишь конечное число ограничений (4.77). Если ин-
тервал изменения переменной Xj разбит на rj интервалов, то их
п
будет 7? = JI(здесь JJ—символ произведения), так как
может находиться в любом из п возможных интервалов, х2 — в
любом из г2 возможных интервалов и т. д. Эти ограничения мо-
гут быть получены из общей формы (4.77) рассмотрением всех
возможных комбинаций значений sk.tij и gkpij- Каждая точка
множества X должна удовлетворять R ограничениям (4.77). Бо-
лее того, не существует точек вне X, которые удовлетворяют
ограничениям (4-77) и требованию неотрицательности х. Чтобы
показать это, предположим, что существует у О, у(£ X, для
которой выполнены все ограничения (4.77). Пусть w — точка X,
ближайшая к у. Тогда имеется по крайней мере одна опорная
к X в точке w гиперплоскость, такая, что у лежит в одном от-
крытом полупространстве, порожденном этой гиперплоскостью,
а X — в другом замкнутом полупространстве (см. {ЛА 6.6}). Но
это означает, что существует новая опорная гиперплоскость,
отличная от всех ранее рассмотренных гиперплоскостей вида
(4.77) со знаком равенства, что невозможно, так как мы рас-
смотрели все опорные к X гиперплоскости.
Таким образом, X есть пересечение R полупространств и ги-
перплоскостей (4.77) и неотрицательного октанта х > 0. По-
этому приближенная задача для задачи (4.72) эквивалентна
задаче линейного программирования с R ограничениями (4.77)
и целевой функцией задачи (4.72). Здесь мы имеем задачу с п
переменными и более чем п ограничениями (обычно с очень
большим числом ограничений). Для нахождения решения этой
задачи решается двойственная задача, которая имеет R + n пере-
менных и п ограничений. Решение будет доставлять приближен-
ный глобальный максимум для задачи (4.72), как и при реше-
нии приближенной задачи в X- или б-форме.
Стоит сравнить размеры указанной выше двойственной за-
дачи и приближенных задач в X- и б-форме. Задача в Л-форме
будет иметь Srj + n + s переменных (s — число вспомогательных
переменных) и т + п ограничений, так что здесь на т ограниче-
ний больше, чем в двойственной задаче, но переменных суще-
ственно меньше. Задача в б-форме будет иметь Srj-Fs перемен-
ных и т ограничений плюс ограничения сверху на переменные.
Надо полагать, что, если мы будем решать задачу с верхними
ограничениями, применяя метод декомпозиции, вычислительные
трудности будут существенно меньше, чем при решении указан-
ной выше двойственной задачи. Кроме того, метод Хартли не
4.10. Задача с фиксированными затратами
151
может быть использован, если не обеспечены необходимые свой-
ства выпуклости и вогнутости ограничений и линейности целевой
функции. Последнее ограничение, впрочем, не является важным
(см. упражнение 4.22).
Таким образом, есть основания считать, что. метод Хартли
не имеет заметных преимуществ по сравнению с другими прие-
мами, но он является иллюстрацией иного подхода к задаче.
4.10. Задача с фиксированными затратами. Рассмотрим за-
дачу нелинейного программирования следующего вида:
Ах = Ь,
х>0; (4.78)
п
найти min z — ^fAxA,
где
fj^x^CjXj + A^ AjX). (4.79)
и
( 0, если xt—=0,
6/= 1 А
7 (1, если Xi > 0.
(4.80)
Пример функции fj(Xj) показан на рис. 4.9. Числа Aj назы-
ваются фиксированными затратами; Aj включаются целиком в
том и только в том случае, когда
%j>0. На практике такие задачи
встречаются, например, на тран-
спорте, когда некоторые затра-
ты включаются независимо от
объема перевозок при условии,
что перевозится положительное
количество груза. При отсут-
ствии фиксированных затрат за-
дача (4.78) становится обычной
задачей линейного программиро-
вания.
Из рис. 4.9 ясно, что функции
fj(Xj) ЯВЛЯЮТСЯ вогнутыми ДЛЯ'
упражнении 4.33 предла-
fj(xj)
гается доказать это аналити-
чески. Поскольку в задаче (4.78) целевую функцию требуется
минимизировать, то, согласно сказанному в § 3.12, оптимальное
решение этой задачи будет достигаться в крайней точке выпук-
лого множества допустимых решений. К сожалению, могут су-
ществовать локальные минимумы, отличные от глобального,
152 Гл. 4. Методы решения задач с сепарабельными функциями
Действительно, если, например, фиксированные затраты имеются
по каждой переменной, любая крайняя точка выпуклого мно-
жества допустимых решений доставляет локальный минимум.
Причина этого явления заключается в том, что если сдвинуться
немного из любой крайней точки, оставаясь при этом в множе-
стве допустимых решений, многие переменные станут положи-
тельными. Это означает, что по многим переменным включатся
фиксированные затраты. В то же время, если оставаться доста-
точно близко к крайней точке, переменные затраты настолько
малы, что не могут компенсировать возникших фиксированных
затрат и, следовательно, в крайней точке будет достигаться ло-
кальный минимум.
Наличие локальных экстремумов осложняет решение задач
линейного программирования с фиксированными затратами.
В гл. 8 будет показано, что задачи этого типа могут быть сфор-
мулированы как смешанные целочисленно-непрерывные задачи
линейного программирования. К сожалению, мы увидим, что
хотя и существуют алгоритмы для решения таких задач цело-
численного программирования, они не являются достаточно эф-
фективными, чтобы решение могло быть получено за приемле-
мое время счета даже при мощных вычислительных средствах.
Приближенные методы, приведенные в этой главе, могут
быть использованы для нахождения локального экстремума в
задаче с фиксированными затратами, однако, как ясно из ска-
занного выше, они не обязательно будут давать лучшие резуль-
таты, чем решение соответствующей задачи линейного програм-
мирования, полученной отбрасыванием фиксированных затрат,
которое также доставляет локальный экстремум для рассматри-
ваемой задачи. Мы тем не менее покажем, как приближенная
задача в Х-форме может быть использована для нахождения
локального экстремума в задаче с фиксированными затратами.
Как обычно, мы начнем с нахождения наибольшего значения aj,
которое может принимать переменная х$. Затем мы записываем
1 j (xj) = j + (Л j -|- c fk j) X2 j, (4.81)
Xj = K2jap (4.82)
X0 j + + ^2/ = 1 > (4.83)
где не более двух при каждом / могут быть положитель-
ными, причем положительными два khj могут быть лишь в том
случае, если они соседние. Отметим, что когда Xj = O, т. е. Z2;=0,
значение fj(xj) не определено. Вместо (4.81) и (4.83) мы полу-
4.10. Задача с фиксированными затратами
153
чаем fj(O) %o3+2iij= 1, так что за счет подбора соответ-
ствующего значения Ло, ?Д0) может принимать любое значе-
ние между 0 и Aj. Геометрически мы можем представить себе
в этом случае f3(0) в виде вертикального отрезка. Приближен-
ная задача принимает вид
11
S aijO-jK.j = t>i, i=\, ..m,
+ /=1> •••> К,
при всех k, /; (4.84''
п
найти min z— 5 + ( Д/ + С/а/) ^2 j] ‘
В упражнении 4.34 читателю предлагается показать, что когда
приведенная здесь задача решается с учетом ограничительных
условий на выбор базиса, решение обладает тем свойством, что
если X2j = 0, то Xoj = l, т. е. /ДО) =0. Итак, решение задачи (4.84)
доставляет локальный минимум для задачи с фиксированными
затратами (точный, а не приближенный).
Одной из первых работ, посвященных задаче с фиксирован-
ными затратами, была работа Гирша и Данцига [11}. В этой
статье они обратили внимание (см. выше) на тот простой факт,
что оптимальным решением должна быть крайняя точка выпук-
лого множества допустимых решений. Они сделали и другое до-
статочно очевидное замечание, именно что если все фиксиро-
ванные затраты Aj равны между собой и если нет вырождения,
то точка х, которая доставляет оптимальное решение в задаче
линейного программирования, получающейся при отбрасывании
фиксированных затрат, доставляет и оптимальное решение в
задаче с фиксированными затратами. Требование невырожден-
ности здесь существенно, потому что может существовать опти-
мальное вырожденное базисное решение, в которое входят ме-
нее чем m фиксированных затрат, и оно может не быть реше-
нием, полученным из задачи линейного программирования.
За последние годы появилось очень немного работ теорети-
ческого и вычислительного плана, освещающих рассматривае-
мую проблему. Исключение составляют задачи целочисленного
программирования, которые мы рассмотрим ниже. Некоторое
внимание было уделено отысканию приближенных решений
транспортных задач с фиксированными затратами. Две работы,
посвященные этому вопросу, принадлежат Балинскому [1] и
Куну и Бомолу [13]. Мы вкратце рассмотрим подход Балин-
ского. Работу Куна и Бомола мы обсуждать не будем, по-
скольку эти авторы занимались главным образом разработкой
154 Гл. 4. Методы решения задач с сепарабельными функциями
очень простых способов для получения приближенных решений
при весьма малом объеме вычислений.
Транспортная задача с фиксированными затратами имеет вид
п
'^хп = а1, аг > О, i=\....................m,
i-г
m
= bj>0, J=i. .... n,
лгу>0 при всех i, у;
(4.85)
найти
где = O при Хц = 0 и дг?— 1 при хг;>0. В типичных транспорт-
ных задачах, встречающихся на практике, много пунктов по-
требления (и велико) и сравнительно немного пунктов произ-
водства (т мало). Так как оптимальное решение задачи (4.85)
достигается в крайней точке выпуклого множества допустимых
решений, оптимальное решение должно иметь не более п + т— 1
положительных Хц (только п + т— 1 ограничений являются не-
зависимыми). Если п велико по сравнению с т, оптимальное
решение обычно будет обладать тем свойством, что имеется, как
правило,' лишь немного пунктов потребления, которые будут
обеспечиваться более чем из одного пункта производства, так
что количество, которое перевозится из пункта производства i
в пункт потребления /, часто будет определяться условием
= (bj, а^). Приближенный метод Балинского для реше-
ния задач с фиксированными затратами заключается лишь в
замене задачи с фиксированными затратами обычной транспорт-
ной задачей с теми же самыми запасами в пунктах производ-
ства, с теми же объемами потребления и затратами на пере-
возку единицы груза
ЛЧ-=^ + ^- (4.86)
Таким образом, Балинский решает транспортную задачу
с теми же ограничениями, что и в задаче (4.85), и целевой
функцией 2 = т- е- заДачУ
п
^Xfj^dt, i=\, .... т,
Ч h -1 (4>87)
Z-l J
при всех i, J;
найти min z — T d^x^.
4.10. Задача с фиксированными затратами
155
Он использует оптимальное решение, полученное для этой зада-
чи, в качестве приближенного решения для транспортной задачи
с фиксированными затратами. Это, конечно, позволительно, ибо
совокупность полученных при решении задачи (4.87), дает
допустимое решение задачи с фиксированными затратами,
так как обе задачи имеют одни и те же множества ограни-
чений.
Если 2* — минимальное значение целевой функции в задаче
с фиксированными затратами и z+ — значение целевой функции
задачи (4.85) в точке, являющейся решением приближенной за-
дачи (4.87), то, очевидно, z* 4 Допустим теперь, что мы
решили задачу (4.85), рассматривая 6ц как переменные и до-
бавляя ограничения 0 46ij4 1, 0 ^хц гпцбц, не требуя,
чтобы были целыми. Пусть z__ — полученное при этом мини-
мальное значение целевой функции. Тогда z_4z*, так как
оптимальное решение задачи (4.85) является допустимым
в задаче, в которой 6ц не подчинены требованиям целочис-
ленности, но не обязательно является оптимальным реше-
нием задачи (4.87). Таким путем мы можем получить границы
для z*.
Оказывается, что z_ легко получить, поскольку оптимальное
решение задачи, где не должны быть целыми, обладает тем
свойством, что Хц = тц6ц. Чтобы доказать это, заметим, что
если в оптимальном решении 6ij = 0, то х^ = 0 и Пред-
положим теперь, что 6г;>0. Если Хц<тц6ц> можно уменьшать
6ij до тех пор, пока не получим Хц = тц6ц, сохраняя при этом
допустимость решения. Таким образом, получим меньшее зна-
чение целевой функции. Это противоречит тому, что мы имели
оптимальное решение. Следовательно, мы должны получить
одно и то же оптимальное решение как в задаче с ограниче-
ниями Хц = тцдц, так и с ограничениями Xij4mi?-6ij. Но огра-
ничения Хц — Шцдц могут быть использованы для исключения
переменных Sij. Ограничения 0 4 6ц 4 1 становятся излишними
и могут не включаться, так как они учитываются в ограниче-
ниях 04х^-4^г;> которые будут всегда удовлетворены. В це-
левой функции вместо слагаемых Ацбц получаем Л^х^/т^.
Окончательно задача, которая будет, решаться, не отличается
от задачи (4.87), т. е. z_ = minz. Следовательно, решая задачу
(4.87), мы получаем непосредственно z_, a z+ получается под-
становкой оптимального решения задачи (4.87) в целевую функ-
цию задачи (4.85), так что, решая задачу (4.87), мы находим
приближенное решение в задаче с фиксированными затратами
и границы для z*. Хотя изложенный метод в некоторых случаях
дает очень хорошие результаты, имеются случаи, когда он ока-
зывается малопригодным, так что нельзя заранее рассчитывать
156 Гл. 4. Методы решения задач с сепарабельными функциями
на получение удовлетворительного ответа. Исключение состав-
ляет случай, когда значения г_ и оказываются очень близ-
кими.
Мы отметили в этом параграфе, что метод, приведенный в
§ 4.2, может быть использован для получения локального эк-
стремума в задаче линейного программирования с фиксирован-
ными затратами. Этот метод, конечно, применим и к транспорт-
ным задачам с фиксированными затратами. К сожалению, од-
нако, в общем случае затруднительно учитывать специальную
структуру транспортной задачи. Исключение составляет случай,
когда затраты являются выпуклыми функциями. Это позволяет
использовать специальный прием, который обеспечивает эффек-
тивность вычислений. Этот случай будет рассмотрен в § 4.12.
4.11. Пример задачи с фиксированными затратами. Мы пока-
жем на примере, что методы, изложенные в этой главе, далеко
не всегда позволяют найти хорошее решение задачи с фикси-
рованными затратами. Рассмотрим следующую задачу.
Предприниматель заключил контракт на поставку продукции
в течение семи месяцев в следующих объемах (по месяцам): 90,
125, 140, 100, 45, 60, 130. Отметим, что количество продукции
от месяца к месяцу меняется. Предприниматель должен постав-
лять каждый месяц заданное количество продукции. Однако он
не обязан производить ее именно в течение этого месяца. Он
может, если желает, несколько месяцев производить продукцию -
про запас и хранить ее до тех пор, пока она не потребуется.
Стоимость хранения единицы продукции 2 долл, в месяц. Пред-
положим для простоты, что это стоимость хранения до конца
данного месяца, даже если продукция хранится не полный ме-
сяц. Стоимость наладки оборудования на один производствен-
ный цикл равна 300 долл. Наладка осуществляется только в на-
чале каждого месяца (если в этот месяц мы будем производить
хоть какое-нибудь количество). Мы пренебрегаем временем, ко-
торое затрачивается на производство, так что продукция, кото-
рая производится в месяц /, может быть реализована в том же
месяце. Мы хотим определить, в какие месяцы следует произво-
дить наладку и какое количество продукции производить в ка-
ждый из производственных циклов, чтобы комплексные затраты
на наладку оборудования и хранение продукции были бы мини-
мальными. Допустим, что на начало первого месяца мы не
имели никакого запаса и не стремимся иметь запас на конец
седьмого месяца.
Сформулируем задачу математически. Пусть xj > 0 — коли-
чество продукции, произведенное в месяц /, У) 0 — запас на
конец месяца / — 1 (начало месяца /) и dj — спрос в месяц /.
4.11. Пример задачи с фиксированными затратами 157
Тогда должны выполняться следующие соотношения:
— Уч ~ = 90,
yj + Xj — yj+l = dj, J==2, ..., 6, (4.88)
У 7 + %7 = = 130.
Эти соотношения являются ограничениями в задаче. Мы хотим
минимизировать значение величины
7 7
z = 300Sd/ + 2S щ
/“1
при дополнительном условии, что 6j=l, если Xj>0, и dj=O, если
Xj = O. Здесь мы имеем задачу линейного программирования
с фиксированными затратами и семью ограничениями (4.88).
Мы можем найти локальный минимум в этой задаче, используя
метод, приведенный в предыдущем параграфе.
Отметим, что верхней границей для любой переменной яв-
ляется суммарный спрос за семь месяцев, т. е. 690. На самом
деле Xj не может быть больше суммарного вопроса за месяцы
начиная с /-го, но можно использовать 690 в качестве верхней
границы для всех Xj. Тогда, используя метод, приведенный в
предыдущем параграфе, мы можем написать
Xj = 690X2},
так что условия (4.88) принимают вид
690Х21 — у2 = 90, уу + 690Х2у — yJ+1 =dp J = 2, ...» 6;
у7 + 690%27 = 130; (4.89)
+ — 1» /=1» •••» 7.
Далее, fj(Xj) =300 6j = 300(Xij+X2j), так что целевая функция за-
писывается в виде
z = 300jS (Мj + ^2/) + 2 1&У1' (4.90)
Мы должны потребовать, чтобы для каждого / было не более
двух положительных значений Kkj и чтобы положительными
два Kkj могли быть только в том случае, если они соседние.
В переменных kkj мы имеем задачу с 14 ограничениями. Она
была решена на вычислительной машине IBM-7090 с использо-
ванием модифицированного симплекс-метода по алгоритму, учи-
тывающему необходимые ограничительные условия на выбор
базиса.
158 Гл. 4. Методы решения задач с сепарабельными функциями
Прежде чем обсуждать полученные при этом результаты,
следует отметить, что задача легко может быть решена с по-
мощью динамического программирования (с использованием
метода, изложенного в гл. 10). Это дает абсолютный минимум
z=1770 и следующие единственные оптимальные значения Xf.
х^ = 215, х* = 0, х* = 240, х* = 0, х*=105, х* = 0,
х7 =130.
Рассмотрим теперь результаты, полученные при нахождении
локального экстремума при решении задачи в Л-форме на вы-
числительной машине. Непосредственное решение задачи дало
следующий результат:
z = 2100, Xi =-90, х2=125, х3=140,
х4 = 100, х5 =— 45, х6 = 60, х7 —= 130.
В этом варианте наладка производится каждый месяц. Решение
действительно дает локальный минимум, но значение г, полу-
ченное при этом, намного больше, чем глобальный минимум.
В базисном решении из переменных у$ только ут входило в ба-
зис. Вычислительный процесс оказался достаточно гибким и мог
указать, что определенную совокупность векторов следует ввести
в базис в первую очередь. Задача была повторно решена с усло-
вием, что У) должны входить в базис в первую очередь. При
этом был получен другой локальный минимум, именно
z = 2180, Xj = 90, х2 = 365, х3 = х4 = 0, х5 = 45,
х6 = 60, х7=130.
Здесь значение z больше, чем в предыдущем случае.
Из оптимального решения, приведенного выше, видно, что не
выгодно производить наладку во втором месяце. С учетом
этого задача была заново решена при условии %02=1, так что хъ
равнялось 0. В этом случае был получен третий локальный ми-
нимум
z = 2050, Xj = 215, х2 = 0, х3=140, х4=100,
х5 = 45, х6 = 60, х7 = 130,
который все еще не является глобальным минимумом.
Здесь мы встретились с примером достаточно простой задачи
с большим числом локальных минимумов, значения которых
больше глобального минимума. Кроме того, изложенный подход
для определения локальных минимумов при прямом использо-
вании не дает глобального минимума.
4.12, Транспортные задачи
159
4t12. Транспортные задачи с выпуклыми сепарабельными
целевыми функциями. Рассмотрим транспортную задачу
2tXo = az, «г > 0, 4 = 1,
^х^Ь,. bj>0, (4.91)
хгу>0 при всех i, J;
найти min z = 2 fij (Kj),
t. i
где все —выпуклые функции. В этом случае любой ло-
кальный минимум является одновременно и глобальным. При-
ближенный глобальный минимум может быть найден при реше-
нии приближенной задачи в б-форме с использованием метода,
описанного в § 4.7 для случая с верхними ограничениями на
переменные. Однако на этом пути могут встретиться определен-
ные трудности. Обычно транспортная задача имеет относитель-
но малое число пунктов производства (от 2 до 50) и большое
число пунктов потребления — порядка 1000, 2000 или более.
Способ, описанный выше, будет приводить к задаче с m+n+]l
ограничениями (не считая верхних границ). В настоящее время
нет возможности решать задачи, содержащие по нескольку ты-
сяч ограничений. И даже когда такая возможность имеется, та-
кой подход требует огромных затрат времени.
Интересно заметить, однако, что, применяя принцип деком-
позиции в несколько ином, чем обычно, варианте, мы можем
получить задачу, содержащую только т+1 ограничение. Такая
задача может быть легко решена, и, более того, вычислитель-
ный метод оказывается весьма эффективным.
Вместо того чтобы пользоваться переменными дьи, нам будет
удобнее иметь дело с переменными
%// = <Axkij) (4.92)
причем ограничения сверху на фед имеют вид
(4.93)
Тогда
= (4.94)
k
где фи/у-= Ахи/;., z/ = l, k—\, если фы/>0. В перемен-
ных функция (кусочно-линейная аппроксимация
160 Гл. 4. Методы решения задач с сепарабельными функциями
функции может быть записана следующим образом:
hj (xij) — 2 akijtykij ~Ь fij (0)> (4.95)
где aw/ = Afwy/Axwy.
Приближенная задача имеет вид
п гч
2 = «= 1, •т,
/ = 1 ы
m rij
2 2^=^. /=1, (4.96)
z-i й=1 J
О <^xkij при всех k, i, J;
найти min z= 2 akij^kij-
lt j, k
Она может быть решена ка-к чистая задача линейного програм-
мирования (без учета ограничительных условий на выбор ба-
зиса), и полученное таким образом оптимальное решение дает
приближение к оптимальному решению задачи (4.91).
Общее число переменных в задаче (4.96) есть Обо-
значим через tp вектор из этих переменных. Множество векто-
ров г|), удовлетворяющих ограничениям
m rU
2 2ФмУ = ^. Л=1. .... «. (4-97)
Z = 1 k-l
ПРИ всех k, i, J,
является выпуклым, с конечным числом крайних точек. Обозна-
чим крайние точки через ф*. Тогда любой вектор ф, удовлетво-
ряющий (4.97), может быть записан в виде выпуклой комби-
нации крайних точек
Ф = 2рЖ’ Ро>° при всех v, 2ро=1.
V V
Следовательно, мы можем заменить задачу (4.96) эквивалент-
ной задачей с т+1 ограничениями
2(2О, = а(> 1 = 1,
V \k, j /
2р©=1. Р»>0 при всех »; (4.98)
найти min ^ZQ^a^/^Pv’
где ф^/уг, — компоненты вектора ф*.
4.12. Транспортные задачи
161
Обозначим через dv m-мерный вектор, Z-я компонента кото-
рого равна
Пусть далее
ev 2
К, lt J
Допустим, что мы имеем базисное допустимое решение задачи
(4.98), и обозначим базисную матрицу порядка т+1 через В.
Пусть вектор ев содержит элементы ev, соответствующие базис-
ным переменным р„. Запишем
° = о2, om+i) = eBB-1. (4.99)
Тогда
zv-ev=a[dv, \]-ev=^k^^-aki^*t/v-}-Om+v (4.100)
Как и в § 4.7, мы не обязаны знать с самого начала ф* и dv.
Они могут вырабатываться в процессе решения. Чтобы опреде-
лить, является ли текущее решение оптимальным и, если нет,
какой именно вектор следует ввести . в базис на следующей
итерации, мы должны вычислить max (zv — ev). Если
max(zp—ev) текущее решение является оптимальным. В про-
тивном случае потребуются дальнейшие итерации. Отметим, что,
как и в § 4.7,
max(з^ — e„) = maxZ+0OT+i, . (4.101)
где max Z определяется решением следующей задачи линей-
ного программирования:
m rtj
м k=\ J
ПРИ всех Л
найти шах 7 = ^2 (ау —
Эта задача распадается на п подзадач (по у)
m riJ
2 2Фл0 = ^
£-1 Л-1
0<фИу<Дх4гу при всех k, I;
найти max Z/= 2 (°£ —
k, I
Для решения каждой из подзадач (4.103) не
(4.102)
(4.103)
потребуется
симплексных итераций. Они могут быть решены с помощью про-
11 Зак. 735
162 Гл. 4. Методы решения задач с сепарабельными функциями
стого анализа. Мы выбираем наибольшую из разностей сч—
и определяем соответствующую переменную из условия
= Если значение переменной равно bh пола-
гаем все остальные переменные равными нулю и полученное
допустимое решение является оптимальным. Если значение пе-
ременной равно &xhij<bj, мы обозначаем через bf. разность ме-
жду bj и &Xkij- Среди остальных переменных, не находящихся на
верхней границе (на рассматриваемом этапе на верхней границе
лежит только одна переменная), выбирается та, которая соот-
ветствует наибольшей из остальных разностей Мы по-
лагаем эту переменную равной меньшему из значений b'j и со-
ответствующей этой переменной \xkij. Если меньшее значение
равно Ьр приравниваем оставшиеся переменные нулю, и полу-
чающееся таким образом допустимое решение является опти-
мальным. В противном случае следует повторить описанную
выше процедуру. Последовательно исчерпывая таким образом bj,
мы получим оптимальное решение.
Каждая из п задач (4.103) решается отдельно. В результате
max Z = 2 max Z}.
i
Объединяя компоненты оптимальных решений всех задач (4.103),
мы получим оптимальное решение ф* задачи (4.102). Далее вы-
числяется /п-мерный вектор du, f-й компонентой которого слу-
жит 2 tykiiu- Вектор, входящий в базис задачи (4.98) на следую-
л *
щей итерации, есть [dw, I]. После определения вектора, который
должен быть выведен из базиса, и преобразования соответст-
вующей таблицы для (4.98) мы получаем новое значение векто-
ра а, и процесс повторяется.
Преимуществом приведенного метода является то, что хотя
при большом .числе пунктов потребления в исходной задаче при-
ходится иметь дело с большим числом переменных, обычно
удается работать с малым числом ограничений. Вектор, который
должен быть введен в базис, легко находится, ибо при решении
подзадач нет необходимости в симплексных итерациях.
В работе [2] Бил предложил другой метод для решения транс-
портных задач с выпуклыми сепарабельными функциями за-
трат. Его алгоритм не использует симплексный метод. Поскольку
проверка алгоритмов на больших задачах не проводилась, нет
возможности сделать определенное заключение о сравнительной
эффективности этих методов. Алгоритм Била мы здесь рассма-
тривать не будем.
Вероятно, весьма редко реальные транспортные затраты
представляются выпуклыми функциями (если они не являются
Литература
163
линейными), и поэтому может показаться, что материал этого
параграфа не представляет практического интереса. Однако
практические задачи с выпуклыми сепарабельными целевыми
функциями могут возникнуть в других вопросах, например, как
это будет показано в следующей главе, при изучении задач сто-
хастического программирования.
ЛИТЕРА ТУРА
1. В а 1 i n s k i М. L., Fixed Cost Transportation Problems, Nav. Res. Logist.
Quart., 8 (1961), 41—54.
2. Beale E. M. L., An Algorithm for Solving the Transportation Problem
when the Shipping Cost over each Route is Convex, Nav. Res. Logist.
Quart., 6 (1959), 43—56.
3. Charnes A., Cooper W. W., Management Models and Industrial Appli-
cations of Linear Programming, vol. I, II, New York, Wiley, 1961.
4. Charnes A., Lemke C., Minimization of Nonlinear Separable Convex
Functionals, Nav. Res. Logist. Quart., 1 (1954), 301—312.
5. D a n t z i g G. B., Recent Advances in Linear Programming, Manag. Sci.,
2 (1956), 131—144.
6. D a n t z i g G. B., On the Status, of Multistage Linear Programming Pro-
blems, Manag. Sci., 6 (1959), 53—72.
7. Dantzig G. B.. Johnson S., White W., A Linear Programming
Approach to the Chemical Equilibrium Problem, Manag. Sci., 5 (1958),
38—43. В этой статье приводится пример из области химии, где могут
быть использованы изложенные в данной главе методы.
8. Griffith R. Е., Stewart R. A., A Nonlinear Programming Technique
for the Optimization’ of Continuous Processing Systems, Manag. Sci., 7
(1961), 379—392.
9. H a d 1 e у G., How Practical is Nonlinear Programming? Product Engineer.,
31 (1960), April 18. 78—80.
10. Hartley H. O., Nonlinear Programming by the Simplex Method, Econo-
metrica, 29 (1961). 223—237.
11. H i r s c h W. M., D a n t z i g G. B., The Fixed Charge Problem, RM-1383,
RAND Corp., 1954.
12. Kelley J. E., The Cutting-Plane Method for Solving Convex Programs,
J. Soc. Indust, and Appl. Math., 8 (1960), 703—712. В этой статье обсу-
ждается метод минимизации некоторой линейной формы на выпуклом
множестве. Для сходимости итеративного метода, которым решается эта
задача, может потребоваться бесконечное число шагов: на каждом шаге
решается задача линейного программирования. Этот метод, по-видимому,
не имеет никаких преимуществ по сравнению с теми методами решения
таких задач, которые излагаются в данной главе.
13. К u h n Н., В a u m о 1 W.. Ап Approximative Algorithm for the Fixed Charge
Transportation Problem. Nav. Res. Logist. Quart., 9 (1962), 1—15.
14. Miller C., The Simplex Method for Local Separable Programming, in
Graves R., Wolfe P. (ed.), Recent Advances in Mathematical Pro-
gramming, New York, McGraw-Hill, 1963.
15, Vajda S., Mathematical Programming, Reading, Addison-Weslev, 1961.
16. Wolfe P., Computational Techniques for Nonlinear Programs, Princeton
Univ. Conference on Linear Programming, March 13—15, 1957.
17. Wolfe P. (ed.), The RAND Symposium on Mathematical Programming,
R-351, RAND Corp., I960.
11*
164 Гл. 4. Методы решения задач с сепарабельными функциями
Упражнения
4.1. Использовать приближенную задачу в Х-форме для нахождения при-
ближенного оптимального решения в следующей задаче:
4*1 -|-х2< 16, хр х2>0; найти max z = 3xj -[- 2х2.
Решить задачу графически.
4.2. Используя приближенную задачу в Х-форме, найти приближенный
локальный максимум в следующей задаче:
4xi + < 16, хр х2 > 0; найти max z = XjX2.
Решить задачу графически. Можно ли гарантировать, что вычислительный
метод дает в этом случае приближенный глобальный максимум?
4.3. Используя приближенную задачу в Х-форме, найти приближенное
оптимальное решение следующей задачи:
Xi-|-x|<6, **1>
найти min z—{xx — 5)2 + (х2 — 8)2.
Решить задачу графически.
4.4. Используя приближенную задачу в Х-форме, найти приближенное
оптимальное решение следующей задачи:
+ <2, Хр х2>0;
найти т1пг = 4(х! — 1)2-]-16(х2— 5)2.
Решить задачу графически.
4.5. Решить предыдущую задачу, используя приближенную задачу в
6-форме и мотод, изложенный в § 4.7 (с учетом ограничений сверху на пе-
ременные).
4.6. Используя приближенную задачу в 6-форме, определить приближен-
ное оптимальное решение следующей задачи:
3xj + 2х2 <6, хр х2 > 0;
найти max z = 8xj -|- 10 r2 — Xj — x2.
4.7. Используя приближенную задачу в 6-форме, определить приближен-
ное оптимальное решение следующей задачи:
Х] + 4х2<4, Xj 4~*2<2, ХрХ2>0;
найти max г = 2xj -|- Зх2 — 2х2.
4.8. Используя приближенную задачу в 6-форме, найти приближенный
локальный максимум для следующей задачи:
3xi + 2^2 <6, Хр х2> 0;
найти max 2- == х^ + х2.
Упражнения
165
Близок ли локальный максимум приближенной задачи к глобальному макси-
муму исходной?
4.9. Используя приближенную задачу в б-форме, определить приближен-
ное оптимальное решение следующей задачи:
х ] Зх2 5,
0,5xj + 2х2 >2, хъ х2 > 0;
найти min z = -|- Зх2.
4.10. Используя приближенную задачу в б-форме, попытаться определить
приближенное оптимальное решение следующей задачи:
xt — х2 > 0, — xt + 2х2 <2, Aj, х2 0;
найти max z = 2х^ -|“ Зх2 — х^
4.11. Определить приближенное решение в примере § 4.3, используя при-
ближенную задачу в б-форме. Для учета ограничений сверху на переменные
использовать алгоритм, рассмотренный в {ЛП 11.7}.
4.12. Показать непосредственно, что если на данном шаге из-за ограни:
чительных условий на выбор базиса не может быть осуществлена симплекс-
ная итерация, то текущее решение доставляет локальный экстремум при;
ближенной задачи в б-форме.
4.13. Показать, как перейти от приближенной задачи в б-форме к при-
ближенной задаче в Х-форме и наоборот, т. е. показать, что имеет место
взаимно однозначное соответствие между допустимыми решениями в этих
задачах и что значение целевой функции при соответствующих решениях
пп.но и то же. Указание:
k k
= + (х2?. — хх]) + • • • + (XrJ, } — Xrf- 1, j) j =
= xlj (51/ ~ S2/) + x2f (б2/ — 63/) + • • • + xrp f'tj, j
Можем ли мы написать
? £ = 1, ...» Гу —1; / = ?
4.14. В задаче
<16, xlt х2 0;
найти max z Зя*1 + х2
сделать замену переменных, приводящую ее к сепарабельной форме. Опре-
делить приближенный локальный максимум, используя приближенную задачу
в Х-форме. Проиллюстрировать графически.
166 Гл. 4. Методы решения задач с сепарабельными функциями
4.15. Сделать замену переменных, приводящую к сепарабельной форме,
и записать приближенную задачу в Х-форме для следующей задачи:
х} sin х2 + 41п х4 > 17’
Sin [х2 cos х4] > 8,
xit х2, х3, х4>0;
найти max z = 2xt -|- *2 ~НП хзх4-
4.16. Показать, как с помощью замены переменных функция
х1х2хз» а> с > 0, xlf х2, х3>0,
может быть представлена в сепарабельной форме.
4.17. Решить заново пример § 4.3, раздробив пополам интервалы преж-
него. разбиения. Сравнить результаты. Решить задачу, изменяя интервалы
только в окрестности оптимального решения.
4.18. Решить заново пример § 4.8, раздробив пополам интервалы преж-
него разбиения. Затем изменять интервалы только в окрестности оптималь-
ного решения. Сравнить результаты.
4.19. Для примера, решенного в § 4.3, показать, что базисное решение
с 152=1 (т. е. *2=1,25) и I31, l4i, определяемыми ограничениями, дает сово-
купность Xj, более близкую к оптимальному решению исходной задачи, но
значение целевой функции при этом оказывается меньшим, чем для решения,
полученного в § 4.3.
4.20. Показать, что крайняя точка множества Ix< h, х >0 представима
в форме (4.57).
4.21. Используя метод § 4.9, найти приближенное оптимальное решение
задачи
2xj-|-3*2 < 6, xlf х2>.0; найти maxz = хх х2.
4.22. Рассмотреть задачу максимизации вогнутой функции f (х) на выпук-
лом множестве. Показать, что можно перейти от нее к задаче максимизации
линейной функции на выпуклом множестве, если добавить ограничение
f(x) — t/>>0 и максимизировать у.
4.23. Используя результат предыдущей задачи, найти приближенное опти-
мальное решение примера из § 4.3 методом, описанным в § 4.9.
4.24. Найти приближенное решение транспортной задачи с фиксирован-
ными затратами, описанной ниже. Кроме того, определить нижнюю границу
действительного минимума.
Упражнения
167
В приведенной таблице верхние числа в клетках обозначают затраты на
транспортировку единицы продукции, нижние числа — фиксированные за-
траты. Заметим, что количество продукции в пунктах производства превышает
суммарную потребность, так что в системе имеется определенная свобода.
4.25. Показать, что за счет соответствующего выбора фиксированных
затрат любая крайняя точка выпуклого множества допустимых решений в
задаче с фиксированными затратами может быть сделана оптимальной, ка-
кими бы ни были коэффициенты при переменных в целевой функции.
4.26. Пусть f(xbx2)—однородная функция первой степени, т. е.
f(Xxb lx2)«lf(XbX2). Тогда ч
f(*i- x2) = xj (1, Х!=#0.
Каким образом это соотношение может быть использовано для преобразова-
ния однородной функции первой степени в сепарабельную? Применить най-
денный способ к функции (xix2)ly<2 и сравнить число дополнительных связей,
возникающих при этом, с числом дополнительных связей, возникающих при
замене по способу p=xix2. Считать везде Xi>0.
4.27. Можно ли определить начальное базисное решение в задаче (4.98),
не используя первого этапа вычислений?
4.28. Обобщить подход, развитый в § 4.12, на случай, когда имеются огра-
ничения сверху на переменные Хц.
4.29. Пусть множество X допустимых решений в задаче (4.1) выпукло.
Показать, что в этом случае каждая точка выпуклого множества допустимых
решений для приближенной задачи (4.2) принадлежит X.
4.30. Предположим, что целевая функция в задаче (4.1) выпуклая. Пока-
зать, что если z(x) —значение целевой функции в задаче (4.1) при некотором
х и Z\ (х) — значение целевой функции приближенной задачи (4.2) при
том же х, то Zi(x) <z(x). Затем, используя результаты упражнения 4.29,
показать, что если в задаче (4.1) множество допустимых решений выпукло и
целевая функция вогнутая, то абсолютный максимум целевой функции за-
дачи (4.2) не может быть больше абсолютного максимума целевой функции
задачи (4.1).
4.31. Показать, что при применении вычислительного метода, описанного
в § 49, существует последовательность задач ри со все более и более мелким
дроблением промежутка, такая, что последовательность zu максимальных
значений целевых функций для этих задач сходится к максимальному зна-
чению z* целевой функции для исходной задачи. Показать также, что, если
оптимальное решение исходной задачи единственно, последовательность ре-
шений задач ри должна сходиться к этому решению.
[Указание. Сделать разбиения так, чтобы точки сетки для задачи ри вклю-
чали все точки сетки для задачи при этом любое базисное допустимое
решение задачи, двойственной к ри-ъ будет базисным допустимым решением
задачи, двойственной ри. Отсюда zu_\^zu. Последовательность должна
сходиться к пределу, если целевая функция исходной задачи имеет конечный
максимум.]
4.32. Рассмотреть предыдущее упражнение с точки зрения вычислитель-
ного метода, описанного в § 4.2, при условии, что множество допустимых
решений выпуклое, а целевая функция вогнутая.
4.33. Доказать, что функции fj (хД вида (4.79) — (4.80) являются вогну-
тыми при Xj 0.
4.34. Показать, что если в решении задачи (4.84) Х2/=0, то Xoj = l. Иначе,
показать, что решение задачи (4.84) доставляет относительный минимум для
задачи с фиксированными затратами (4.78).
4.35. Показать, что если нет ограничений на знак переменной xj, но даны
верхняя и нижняя границы ее изменения, то это может быть учтено в при-
168 Гл. 4. Методы решения задач с сепарабельными функциями
ближенной задаче в X- или б-форме так же, как требование неотрицатель-
ности Xj. [Указание. Для приближенной задачи в б-форме удобно сделать
замену переменных Xj—yj—pj, где pj — нижняя граница Xj.]
4.36. Доказать, что если fj, gij — выпуклые (вогнутые) функции, то
f., g.f также являются выпуклыми (вогнутыми) функциями.
4.37. Показать, что если fj(Xj) — вогнутые функции и функции gij(x})
обладают соответствующими свойствами выпуклости и вогнутости, так что
множество допустимых решений выпукло, то, решая приближенную задачу
в Х-форме как чистую задачу линейного программирования, мы получим
оптимальное решение приближенной задачи.
4.38. Проиллюстрировать выводы предыдущего упражнения, решив за-
дачу (4.20) без ограничительных условий на выбор базиса.
4.39. Выполнить упражнение 4.1, используя метод, изложенный в § 4.7, и
выводы упражнения 4.37.
4.40. Приближенную задачу в б- или Х-форме можно использовать, если
интервал изменения Xj не ограничен,—oo<Xj<oo. Это можно сделать, пред-
ставляя fj(Xj) на некотором интервале — pj<JCj<aj так, как это предла-
галось в этой главе, и полагая = Yy^y+ /у (ay), ПРИ xj> ay
и f j (Xy) == — PyXy + fy (— Pу), Ху > 0, при Xj < — Pyj других ограничений
на Ху и Ху нет. Таким образом, fj вне интервала —Pj-^xj^^j рассматри-
вается как линейная функция. Показать это графически. Ясно, что представ-
ление fj не будет сколько-нибудь точным, если Xj находится далеко от ин-
тервала — Ру <^ху <iay. Выяснить, почему такой подход в некоторых случаях
тем не менее может оказаться полезным. Как этот подход может быть ис-
пользован в приближенной задаче в X- и б-форме?
4.41. Рассмотреть задачу нелинейного программирования следующего вида:
Ах = Ь, х > 0;
найти шах z = »
dx + d0
предполагая, что dx+rfo>O при всех х>4). Заменой переменных эта задача
может быть преобразована в задачу линейного программирования. Действи-
тельно, пусть i? = dx+do>O. Обозначив f/jsXj/u>0, /=1, ..., т, и г/0=1/и>0,
получаем в новых переменных задачу линейного программирования:
2а/у-ьуо=о,
найти max z = 2 + c0J/0.
Рассмотреть ее оптимальное решение, полученное при условии у>0
у0>0. Показать, что, если yQ =# 0, мы можем получить из решения линей-
ной задачи оптимальное решение исходной задачи. Что получается, если
г/0=0? Показать, что, когда #о>,О, имеется соответствие между каждым до-
пустимым решением исходной задачи и задачи линейного программирования
в переменных yj.
4.42. Допустим, что мы используем приближенную задачу в б-форме для
решения некоторой задачи, в которой нет ограничений на знак Xj. Предста-
вим Xj в виде
Xj = 2 kxkjbbj — 2 bx_kjb_kj,
k k
kxkj, &X-kj > 0.
Упражнения
169
Какие дополнительные трудности могут здесь возникнуть? Показать, что если,
однако, множество допустимых значений Xj выпуклое и целевая функция,
которую мы максимизируем, вогнутая, то в окончательном решении оба зна-
чения б к j и д-kj никогда не будут положительными.
4.43. Мы отмечали, что когда множество допустимых решений выпуклое
и функции fj(Xj) вогнутые, то приближенная задача в X- или б-форме может
решаться как чистая задача линейного программирования и, таким образом,
получается оптимальное решение приближенной задачи. Можно ли, если
множество допустимых решений не выпукло или не все функции fj(Xj) во-
гнутые, получить полезную информацию о том, насколько может отличаться
полученный нами локальный оптимум от глобального, решая наряду с при-
ближенной задачей (с ограничительными условиями на выбор базиса) чисто
линейную задачу?
4.44. В каких условиях при использовании приближенной задачи в
Х-форме возникает возможность вместо перехода по Xj из одного интервала
в соседний сделать более крупный скачок? Показать, что при использовании
стандартного алгоритма для решения задачи с ограничениями на переменные
сверху (а не специального алгоритма, основанного на принципе декомпози-
ции) следует ожидать, что для решения задачи в Х-форме потребуется мень-
ше итераций/ чем для решения задачи в б-форме. [Указание. Рассмотреть
пример § 4.3.]
ГЛАВА 5
СТОХАСТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
Начиная с незыблемого, человек всегда
кончит сомнениями, но если он сможет
начать с сомнений, то придет к незыб-
лемому.
Фр. Бекон, Успехи Познания
5.1. Введение. Неизвестные в задачах математического програм-
мирования обычно называют управляющими переменными, пе-
ременными регулирования или решающими переменными. Это
реальные физические величины, которые можно произвольно
выбирать в пределах, определяемых ограничениями. Задача
принятия решения состоит в выборе значений управляющих пе-
ременных, оптимизирующих заданную целевую функцию. Цель
решения задач математического программирования и состоит в
определении оптимального набора управляющих переменных.
Оптимальные значения этих переменных являются функциями
различных параметров, встречающихся в задачах математиче-
ского программирования (например, запасов ресурсов, стоимо-
стных и технологических характеристик, таких, как время, тре-
буемое для производства единицы данного продукта на обору-
довании данного типа). Обычно при изменении одного или
нескольких параметров изменяются также и оптимальные зна-
чения некоторых или всех управляющих переменных. Стандарт-
ные методы решения таких задач, базирующиеся на симплекс-
методе, дают оптимальное решение только для определенного
набора значений параметров. Используя эти методы, нельзя по-
лучить точное представление набора оптимальных значений
управляющих переменных как функций от всех параметров.
Действительно, изучение зависимости изменений управляющих
переменных от изменений различных параметров потребовало
бы значительного объема вычислений.
Оказывается, что во многих практически важных случаях
некоторые из встречающихся в задаче параметров следует счи-
тать не детерминированными, а случайными. Два примера, рас-
смотренных в гл. 3, иллюстрируют задачи такого типа. В гл. 3
5.1. Введение
171
было также указано, что если процесс принятия решения удов-
летворяет определенным аксиомам, то существует такая функ-
ция полезности, определенная на множестве всевозможных ис-
ходов, что следует выбирать управление, максимизирующее
ожидаемую полезность. Следовательно, когда некоторые из па-
раметров исходной задачи математического программирования
являются случайными величинами, принятая методика состоит
в оптимизации математического ожидания целевой функции.
Обычно в качестве функции полезности берется либо прибыль,
либо затраты. Оправданием для максимизации ожидаемой при-
были или минимизации ожидаемых расходов является предполо-
жение, что имеется соответствующая функция полезности и что
она достаточно точно может быть выражена для любого исхода
либо через соответствующую прибыль, либо через затраты.
В этой главе мы всегда будем предполагать, что если некоторые
параметры задачи математического программирования являются
случайными величинами, то следует определять набор опти-
мальных значений управляющих переменных, оптимизируя ма-
тематическое ожидание целевой функции.
Задачи, в которых нельзя предположить, что имеется функ-
ция полезности нужного типа, или где вероятностные распреде-
ления для случайных величин неизвестны, изучены гораздо хуже.
Здесь они рассматриваться не будут. ’
При исследовании задач математического программирования,
в которых некоторые параметры могут быть случайными вели-
чинами, удобно разбить их на два основных класса. Первый
включает те задачи, в которых принимаются два или более ре-
шений в различные моменты времени и которые обладают тем
свойством, что на последующие решения могут влиять не только
решения, принятые ранее, но и некоторые стохастические пара-
метры, реализации которых можно наблюдать, прежде чем ре-
шения будут приняты. Такие задачи мы будем называть много-
шаговыми. Другой класс задач естественно назвать одношаго-
выми. Для задач этого класса характерно, что можно принимать
голько одно решение, или если принимается несколько решений,
то реализации случайных параметров не наблюдаются и не
влияют на последующие решения. Естественно, что для прак-
тики наиболее интересные задачи — это многошаговые, хотя их
исследование, вообще говоря, более сложно, чем одношаговых.
Мы будем называть задачи математического программиро-
вания, в которых некоторые из параметров являются случай-
ными величинами, стохастическими задачами математического
программирования.
В этой главе мы изучим несколько различных типов возни-
кающих на практике стохастических задач.
172
Гл. 5. Стохастическое программирование
5.2. Одношаговые стохастические задачи со случайностями,
появляющимися только в спросе. Простой пример такой задачи
можно получить, воспользовавшись первым примером § 3.9. Бу-
дем считать, что владелец магазина собирается потратить не-
которую сумму на приобретение одежды трех различных моде-
лей так, чтобы максимизировать всю ожидаемую от реализации
прибыль. Задача сводится к максимизации функции (3.45) при
ограничениях (3.46). Очевидно, что целевая функция нелиней-
на. Однако целевая функция является вогнутой и сепарабельной
(пример 5 § 3.11), и, следовательно, приближенное значение аб-
солютного экстремума может быть найдено методами предше-
ствующей главы. Читателю предлагается сделать это в упраж-
нении 5.1. Для рассматриваемой задачи случайные параметры —
это спрос на одежду. Когда владелец решает, сколько и какой
одежды купить, он не знает, каков будет спрос на одежду каж-
дой модели.
^Цля любого данного распределения средств между моде-
лями, т. е. для любого данного набора величин управляющих
переменных, максимальная прибыль, полученная магазином, бу-
дет зависеть только от значений случайных величин, определяе-
мых спросом на различные модели одежды. При определенных
значениях спроса и переменных Xj легко получить выражение
для прибыли. Если усреднить этот результат по всем возмож-
ным значениям спроса, используя для этого в качестве весовой
функции функцию плотности вероятности спроса, мы получим
ожидаемую прибыль для данного набора Xj. Задача владельца
и состоит как раз в определении набора xjt который максимизи-
рует его ожидаемую прибыль.
Интересно сравнить рассмотренную задачу с той, в которой
владелец должен принять решение, если ему заранее известно,
каков будет спрос на одежду каждой модели. В этой ситуации
случайные параметры отсутствуют.
Предположим, что спрос на одежду /-й модели будет vj.
Тогда Xj = Vj + wj, где Wj— свободная переменная, характеризую-
щая величину, на которую закупленное количество отличается
от истинного спроса Vj. Положим далее Wj = Uj — где и^у^О.
Тогда ограничения запишутся в следующем виде:
35 их — 35^ + 20я2 — 20г/2 + 50я3 — 50у3 <
< 3000 — 35^ — 20г>2 — 50^3, (5.1)
а прибыль будет иметь вид
Р = 31^1 — 31 у^ — 7 —|— 1 7tj2 — 171/2 — 4^2 4-
+ 55^з - 55t/3 —Ю^з — 70ух - 40//2 - 220у3. (5.2)
5.2. Задачи со случайностями в спросе
173
Это весьма простая задача линейного программирования. Ясно,
что владелец никогда не купит одежду сверх спроса. Однако
ему придется, может быть, купить меньшее количество, так как
для полного удовлетворения спроса может не хватить денег.
Один из приемов решения нелинейной задачи (3.45) — (3.46) за-
ключается в замене случайных величин их средними значениями
с тем, чтобы потом решить задачу линейного программирования
(5.1) — (5.2). Такой способ приближенного нахождения опти-
мальных Xj, фактически игнорирующий стохастический характер
задачи, может оказаться очень ненадежным: полученные Xj мо-
гут сильно отличаться от их оптимальных значений. Это будет
подробно обсуждено в следующем параграфе.
Разберем еще одну ситуацию, в которой возникает задача
того же типа. Представим себе патрулирующую ядерную под-
водную лодку. Для хранения запасных частей и ракет необхо-
дим некоторый объем. Пусть b — допустимый объем, а п — чис-
ло различных запасных частей, которые необходимо иметь.
Объем одной части типа / есть aj. Предположим, что отсутствие
запасной части типа / в случае, когда в ней возникнет потреб-
ность, влечет за собой потери, характеризуемые величиной л;.
Вероятность того что при патрулировании понадобится Vj еди-
ниц детали /, обозначим через pj(^). Требуется определить х$—
число запасных деталей, которое минимизирует ожидаемые по-
тери, причем объем деталей не превышает допустимого. Ясно,
что оптимальные х$ являются решением следующей экстремаль-
ной задачи:
п
"S а,х,</>,
/-1
ху > О, j' = 1, ..., «;
оо
найти min г = щ 2 (^i — *i)Pi (^1) + • • • +
”l=xl+1
з (®л — xn)pn(vn), (5.3)
%=-v«+1
прцчем требуется, чтобы все Xj были целыми (требование цело-
численности здесь игнорировать нельзя, так как обычно х$— ма-
лые целые числа). В гл. 10 будет показано, что такая задача
с требованием целочисленности может быть решена методом
динамического программирования.
174
Гл. 5. Стохастическое программирование
Рассмотрим теперь несколько иной тип задач стохастиче-
ского программирования, в которых случайные переменные по-
являются только в спросе. Такая задача была довольно под-
робно исследована Данцигом [5]. Представим себе, что имеется
однородный товар, размещенный на m складах. Допустимое ко-
личество товара на складе i есть сц. В рассматриваемый период
товар будет требоваться на п розничных рынках. Однако спрос
каждого рынка не может быть заранее точно определен. По- .
требности рынков следует считать непрерывными случайными
величинами с плотностью вероятности срД^) для рынка /. Счи-
таем, что Vj — независимые случайные величины, т. е. спрос
одного рынка не влияет на спрос другого.
Пусть Cjj — стоимость перевозки единицы товара со склада i
на рынок /. Стоимость перевозки будем считать пропорциональ-
ной количеству перевезенного товара. Обозначим через yj коли-
чество товара, привезенного на рынок /. Тогда если yj<Vj, то
имеются потери —z/j) • Если же yj>Vj, то убыток составит
kjtjjj—Vj). Это может быть интерпретировано следующим обра-
зом: если количество привезенного товара превышает спрос, то
товар продается в убыток (это оказывается выгоднее перевозки
излишков обратно на склад). Требуется определить, сколько то-
вара с каждого склада следует привезти на рынок / для того,
чтобы минимизировать сумму транспортных издержек и ожи-
даемых убытков. Ожидаемые потери от нехватки товара на
рынке / составят величину
со
ni J (.vj — »№№№)' (5-4).
у}
а ожидаемые потери от избытка
у)
(yj-v№Wdvi = k№j — Vi> + ki\ ('°j-yj)4j(‘vJd'oj' (5-5)
о yj
где pj — ожидаемый спрос рынка /. Ожидаемые потери от из-
бытка и недостатка товаров
п п [оо
2 ki (yj — + 2 {kj + лу) J (vj — yj) <ру {vj) dvj (5.6)
/-1 J-i Uj
5.2. Задачи со случайностями в спросе
17Ъ
есть выпуклая сепарабельная функция от z/j. Задача, которую
нужно решить, имеет вид
- п
"^Хц^о-ц 1=1,
^х1}-У/ = 0, /=1.......п, (5.7)
хг?>0 для всех I, J; у} >0, /=1, ..., п;
найти min z = с1}хч + к)У) +
I. i i
ОО
+ 2 (fy+я>) / — Уу) Фу (®у)
j yi
Сумму —необязательно включать в целевую функцию,
так как она постоянна. Она может быть прибавлена, когда за-
дача уже решена. При желании можно рассматривать вторые п
ограничений как определяющие у$ через Хц и использовать эти
ограничения для исключения z/j из целевой функции. Однако
если сделать это, целевая функция перестанет быть сепарабель-
ной. Поэтому форма (5.7) предпочтительнее.
Приближенное оптимальное решение этой задачи может быть
непосредственно получено с помощью методов гл. 4. Однако
структура этой задачи достаточно близка к структуре транс-
портной задачи, так что следует применить в слегка модифици-
рованной форме упрощенную схему § 4.12. Запишем
оо
fj (У)) = М/ + (ki -+ J “ У if Ф/ (vif dvi (5-8)
yi
У] = 2 Фа/ fj{yj) — l£iakjtykj~%~fjWh (5-9)
k k
где
(5.10)
Задача принимает следующий вид:
п
2 хи < at, tn,
/-i
m
— = . (5-11)
0<фйу<Д1/й? для всех k, J,
Хц^-О для всех I, J',
найти min z = 2 CtjXij+ 2.
Ь / Л, /
176
Гл. 5. Стохастическое программирование
Обозначим через [х*, ф*] крайние точки выпуклого множества
решений системы
2 xij— — О» J— h * •
х=1 J k J
0<ф^у<Д1/^ для всех k, j, (5.12)
х/у>0 для всех Z, у.
Тогда любое допустимое решение [х, ф] задачи ^$5.12) может
быть записано как выпуклая комбинация крайних точек
IX, 14=2р„К, t;]. Р^о,
(5.13)
2рв=1.
и задача (5.11) эквивалентна следующей:
2dt,p1)<a, = Ро>0; (5-14)
найти пипг = 2^®Рг»
где
»,= 2/Л+2"А' <2 * * 5-IS>
ч„ = А,х;+м;. Л1=о,
и Ai таково, что f-я компонента cU есть
, IJV
Поступая так,
как в § 4.12, получим п подзадач, которые при фиксированном /
имеют вид
2 Xtj — 2 Фйу — О»
i-l k
0<ф^<Дг/й/- дЛя всех k,
хг;>0 для всех г,
(5.16)
найти max Z, = 2(a/ —fy)*// —
Эти задачи также могут быть решены без преобразований ка-
кими-либо симплексными алгоритмами. В упражнении 5.2 мы
предлагаем читателю показать, как это делается.
Если бы спрос рынка на продукт, который предстоит пере-
везти с различных складов, был детерминирован и равен bj на
рынке /, то отпала бы необходимость в учете избытка и надо-
5.2. Задачи со случайностями в спросе
177
статка (если 2#z>2^/) и задача свелась бы к обычной
транспортной задаче
п
/-1
пг
^х1} = Ь}, (5.17)
для всех /, у;
найти min z— 2 СцХ1}.*
Если считать спрос случайным, то мы избавляемся от ограниче-
ний 2 xtj = bj, так как общее количество продукта, завозимого
i
на каждый рынок, также детерминировано и создается впечатле-
ние, что задача имеет меньше ограничений. Однако мы можем
сформулировать обычную транспортную задачу таким образом,
что количество продукта, привезенного на каждый рынок, не
регламентируется, а вместо этого имеются штрафы за нехватку
и избыток. Это является обобщением' обычной транспортной
задачи, поскольку оно имеет смысл для любой 2#/ (не обяза-
тельно, чтобы 2 ai S bj, поскольку bj не определены). В та-
кой формулировке между детерминированной и стохастической
задачами имеется полная аналогия. Однако решить стохастиче-
скую задачу гораздо труднее, поскольку, в отличие от детерми-
нированной, она является нелинейной.
Задача, в которой спрос является случайной величиной, рас-
сматривалась Билом [2] и Данцигом [5] как задача, в которой
некоторые компоненты вектора спроса, а именно bj, случайны,
т. е. как задача со случайными величинами в ограничениях.
Другими словами, предполагается, что ограничения 2х/7==^
из задачи (5.17) имеют измененную форму
m
S Xij = Vj, (5.18)
rug 8j — свободная случайная переменная, определенная так,
что (5.18) выполняется как точное равенство. В наших старых
обозначениях bj = Vj — yj и, когда оно положительно, предста-
вляет собой нехватку, когда отрицательно, — избыток; кроме
того, имеется стоимость, связанная с (стоимость будет разной
в зависимости от того, положительно или отрицательно Sj).
Хотя такая интерпретация совершенно законна, она, по-види-
мому, делает недостаточно ясным тот факт, что если считать
12 Зак. 735
178
Гл. 5. Стохастическое программирование
спрос случайной величиной, то общее количество продукта, по-
сылаемого на каждый рынок, также является переменной, кото-
рую предстоит определить. К тому же ограничения вида (5.18)
никогда непосредственно не используются.
Другая практически интересная задача со структурой, по-
добной структурам уже рассмотренных задач, исследовалась
Фергюсоном и Данцигом [6]. Эта задача имеет дело с распреде-
лением самолетов по маршрутам. Поскольку полная и точная
формулировка задачи достаточно трудна, рассмотрим следую-
щую упрощенную постановку: аэрофлот имеет m различных ти-
пов самолетов и п маршрутов, и требуется распределить само-
леты по маршрутам на некоторый будущий период. Может быть
использовано щ самолетов типа i. Если самолет типа i рабо-
тает на маршруте /, то он может перевести пассажиров за
некоторый промежуток времени (предполагается, что сюда
включены путешествия в оба конца). Представим, что спрос
одинаков на любом направлении и, если пассажир выходит на
промежуточной остановке, кто-то сразу же занимает его место.
Спрос Vj на маршруте / нельзя точно предсказать, так что его
следует рассматривать как случайную величину с плотностью
q)j(ttj). Пусть yj — общий спрос, который можно удовлетворить
на маршруте /, если на нем размещено самолетов типа L
Тогда
m
yj=^idijXij, j=\...........га. (5.19)
i =»1
Затем, как и в предыдущих задачах, nj — убыток на каждого
пассажира, который не может быть перевезен из-за недостатка
места на маршруте Z, и kj — убыток за каждое место, на кото-
рое нет спроса. Требуется найти такие Хц, которые минимизиро-
вали бы ожидаемые убытки за рассматриваемый период, если
дано, что Cij — стоимость эксплуатации самолета типа i на ли-
нии /. Математически задача сводится к следующей задаче нели-
нейного программирования:
п
2 / = 1, ..., m,
j=i
2 dijxij — z/y = 0, y=l,..., n, (5.20)
хг,>-0 для всех Z,/; fZy>0, /=1
oo
найти min z = У CijX4-\- (fy + яу) J — У?)Ф,
i, i i Vj
Эта задача может быть решена так же, как и задача (5.7),
5.2. Задачи со случайностями в спросе
179
Рассмотрим последний пример стохастической задачи, где
случайные величины появляются только в спросе. Предположим,
что фермер производит п различных продуктов, используя m ре-
сурсов (томаты, бобы и т. д.). Производство единицы продукта /
требует единиц ресурса i. Предположим, что в наличии
имеются bi единиц ресурса I. Фермер не может предсказать точ-
но, каков будет спрос на каждый продукт. Спрос Vj на продукт j
должен рассматриваться как случайная величина с плотностью
Ф; (у>). Если спрос на продукт j за год превысит предложение, то
убыток составляет jtj за каждую единицу неудовлетворенного
спроса. С другой стороны, если произведено слишком большое
количество продукта /, стоимость хранения и обложение нало-
гом дают убыток kj за каждую единицу. Пусть Pj — продажная
цена за единицу продукта /, a Cj— стоимость производства. Фер-
меру требуется определить количество Xj каждого продукта, ко-
торое ему следует произвести, чтобы максимизировать ожидае-
мую прибыль за текущий год. Предположим, что перед произ-
водством новых продуктов у него есть запас у$ продукта /. Ясно,
что задача, которая должна быть решена, такова:
п
ai}x} < bh i — \, ..., tn,
xy>0, (5.21)
найти max z = — Cj)Xj—
i
co
— ^Pi+ni + ki) J (Vj — У J —
J yj+xi
где константы и — У;)» связанные с ожидае-
мым спросом pj на продукт /, не включены в прибыль, посколь-
ку они могут быть добавлены после решения задачи.
Мы опять имеем дело с нелинейной задачей при линейных
ограничениях и сепарабельной вогнутой целевой функцией.
Приближенный глобальный экстремум может быть найден с по-
мощью методов, описанных в гл. 4.
Мы рассмотрели несколько не связанных друг с другом
стохастических задач, которые являются задачами с сепарабель-
ной целевой функцией, обладающей свойствами выпуклости или
вогнутости, так что для поисков глобального экстремума могут
12*
180
Гл. 5. Стохастическое программирование
быть использованы методы гл. 4. Каждая из рассмотренных
задач была бы линейной, если бы все параметры были детерми-
нированными, а не случайными. Учет случайного изменения
параметров сводит задачу к задаче с линейными ограничениями
и нелинейной целевой функцией. Следовательно, введение слу-
чайных параметров осложняет нахождение множества опти-
мальных значений* управляющих переменных. Если задача нели-
нейна, когда все пара-метры считаются детерминированными, то
соответствующая ей стохастическая задача формулируется ана-
логично тому, как это делалось выше. В этом случае возмож-
ность решения полученной задачи будет зависеть от того, можно
ли решить детерминированную задачу.
5.3. Одношаговые стохастические задачи со случайными ве-
личинами в технологических коэффициентах. Рассмотрим группу
стохастических задач, которые отличаются от изученных выше.
Начнем с примера. Допустим, что на небольшом предприятии,
имеющем несколько высококвалифицированных мастеров, из-
готавливаются вручную небольшие точные детали. Предприятие
выполняет только специальные заказы, и большинство из них
по контрактам министерства обороны. За текущий месяц пред-
приятию предоставлена возможность сделать такое количество
каждой из п точных деталей, какое оно пожелает. Предприятие
должно решить заранее, какое количество каждой из деталей
оно желает произвести, и затем гарантировать доставку за-
явленного количества к концу месяца. Факторами, ограничиваю-
щими число деталей каждого типа, являются следующие: 1) на-
личие рабочего времени; 2) наличие сырья. Будем предполагать,
что мастеров можно подразделить на группы согласно типу
деталей, которые они могут вырабатывать. Все члены группы
делают одинаковую работу. Вообще говоря, рабочие данной
группы могут производить несколько различных деталей, но
данная деталь может вырабатываться только рабочими одной
группы.
Рассмотрим сначала стандартный подход к поставленной за-
даче с точки зрения линейного программирования. Пусть —
количество ресурса f, требуемого для изготовления одной детали
типа /, где i относится ко времени, требуемому рабочему, или
к количеству некоторого сырья. Пусть bi — количество ре-
сурса /, имеющегося в текущем месяце. Обозначим *через pj
доход на одну деталь j после вычета стоимости сырья. Предпо-
ложим, что жалованье рабочих, накладные расходы и т. п. не
зависят от решения, которое предстоит принять, и, следователь-
но, могут быть исключены. Пусть Xj— количество деталей /, из-
готовление которых предприятие будет гарантировать. Тогда
5.3. Задачи со случайными величинами в коэффициентах 181
получаем задачу линейного программирования
/ = 1,
м
(5.22)
найти max z = 2 Pjxj-
На самом деле время, требуемое мастеру*на изготовление
детали типа /, будет изменяться от человека к человеку и, для
данного рабочего, от детали к детали. Следовательно, более есте-
ственно рассматривать это время как случайную величину. По-
добным же образом количество данного сырья, требуемого для
детали /, не абсолютно постоянно, а меняется от детали к де-
тали. Таким образом, количество сырья, используемого при из-
готовлении одной детали, также может быть описано случай-
ной величиной, т. е. можно сказать, что технологические коэф-
фициенты aij — действительно случайные величины. Для многих
практических задач дисперсия этих случайных величин так
мала, что их можно считать детерминированными. Однако
можно себе представить ситуацию, когда эффект от учета слу-
чайных явлений настолько велик, что с ним следует считаться.
Если aij — случайные величины, то может оказаться, что для
данного набора Xj общее количество требуемого ресурса i
больше чем bi. Например, рабочие не могут сделать всю работу
за необходимое время. Можно представить себе два выхода в
этой ситуации: либо вводить сверхурочные работы, либо сдавать
заказ с опозданием. И в том и в другом случае это приводит
к некоторым дополнительным затратам. Мы будем предпола-
гать, что если действительное количество ресурса i на Wi мень-
ше запланированного, то это влечет за собой убытки в раз-
мере TtiWi.
Пусть требуется определить набор переменных Xj, который
максимизирует минус средний убыток от недостатка ре-
сурсов. Для любого набора случайных величин aij определим
случайные величины по формуле
У1 = 2 Л/jXj, i = 1, .... tn. (5.23)
Плотность распределения случайной величины а^ есть 'Ф/;(#/;),
а и — ее среднее значение и дисперсия соответственно.
Мы хотим определить плотность распределения случайной ве-
личины tji. Рассмотрим сначала yij = aijXj— количество ре-
сурса /, требуемого для изготовления Xj деталей типа /. При
182
Гл. 5. Стохастическое программирование
естественном предположении о независимости расхода ресурса i
на одну деталь / от числа изготовляемых деталей функция
— плотность распределения величины z/^- — есть повто-
ренная Xj раз свертка плотности распределения ф^а^). При
этом среднее значение случайной величины у^ есть
а дисперсия случайной величины есть Так
как уц предполагаются независимыми при различных /, то yi —
сумма п независимых случайных величин. Плотность фг(г/О мо-
жет быть получена как свертка ф^Р(у/у.) для фиксированного L
Тогда среднее значение gi и дисперсия а] для у. равны
И/ = 2 И/о? = 2 °? jXf (5.24)
Сложность вычисления фДуО зависит от плотностей ф^-(а^).
Поскольку плотность фг(г/г) определена, задача сводится к
максимизации выражения
оо
z = 2 PiXj — 2 я/ / (У1 ~ bi) Ф/ (&) dyt (5.25)
i i
при ограничениях x3>0. Других ограничений нет (при условии,
что все ац считаются случайными величинами), так как они
включены в стоимостные слагаемые, учитывающие г/,-. Следует
заметить, что Xj появляется в фДг/»), так как в силу (5.24) сред-
нее значение и дисперсия <f>i(f/i) зависят от Xj. Это делает за-
дачу максимизации выражения (5.25) при ограничениях
крайне трудной. Функция z не обязательно вогнута по Xj и не
обязательно сепарабельна. В настоящее время нет никаких об-
щих методов для получения глобального максимума выраже-
ния (5.25), хотя иногда можно найти локальный максимум.
Для того чтобы лучше уяснить приведенные выше рассужде-
ния, полезно рассмотреть специальный пример. Представим, что
имеются только два ограничения. Первое, 2avx/<C^i, пред-
ставляет ограничение на сырье. Предположим, что количество
сырья, нужного для производства единицы j, детерминировано,
так что ац не считаются случайными. Тогда ограничение на
сырье останется. Второе Ограничение связано с допустимым ра-
бочим временем. Пусть 6г—наличное время при нормальных
условиях. Время а2з-, требуемое рабочему для создания одной
детали типа /, будет предполагаться нормально распределенным
со средним значением и дисперсией Тогда у2, есть сумма
нормально распределенных случайных величин и поэтому яв-
5.3. Задачи со случайными величинами в коэффициентах
183
ляется нормально распределенной величиной со средним р,2Л* и
дисперсией aljXj- Тем самым «/ = 2^2; также есть нормально
распределенная величина со средним значением р, и диспер-
сией о2, где
Н = = (5-26)
Следовательно, чтобы найти оптимальные значения перемен-
ных Xj, нужно решить задачу
найти maxz =
/= 1, ..п,
(5.27)
S pjXj — л j (у — Ь2) п (у, i^jXj, i / У о2у.х J dy,
ь, \ j V j I
где п(у;р, о)—плотность нормального распределения со сред-
ним р и стандартным отклонением о. Нам неизвестен какой-
либо прямой метод для определения глобального экстремума z.
Однако в упражнении 5.10 читателю предлагается показать, что
для этой задачи можно получить локальный экстремум.
Если yi можно рассматривать как сумму большого числа
случайных величин, то по центральной предельной теореме ее
распределение будет приблизительно нормальным, даже если
этим свойством не обладает.
В этом параграфе мы увидели на примере, как может воз-
никнуть задача, в которой некоторые технологические коэффи-
циенты являются случайными величинами. Было показано, что
если технологические коэффициенты в ограничении i— случай-
ные величины, то от этого ограничения можно избавиться, а
связь между Xj и количеством ресурса i учитывается при на-
хождении плотности распределения величины уг по плотностям
распределения технологических коэффициентов. При этом убы-
ток при нехватке некоторого ресурса учитывается в целевой
функции. Таким образом, как и в предыдущем параграфе, на
первый взгляд кажется, что рассмотрение некоторых пара-
метров как случайных величин уменьшает число ограничений
задачи. Это верно, но лишь отчасти, поскольку и в случае детер-
минированных параметров можно сформулировать задачу так,
чтобы на переменные не накладывалось никаких ограничений
(кроме положительности). Вместо этих ограничений можно
ввести некоторый штраф за превышение имеющегося количества
ресурсов. Мы предлагаем читателю сделать это в упражне-
184
Гл. 5. Стохастическое программирование
нии 5.3. Когда некоторые из технологических коэффициентов
случайны, задача становится нелинейной, причем такой, что в
настоящее время не существует эффективных методов нахожде-
ния ее оптимального решения.
5.4. Многошаговые стохастические задачи. G практической
точки зрения многошаговые стохастические задачи, по-види-
мому, наиболее интересны. Как мы увидим далее, решать их
крайне трудно. Чтобы показать, что мы понимаем под многоша-
говой стохастической задачей, рассмотрим следующую задачу
о запасах. Требуется составить план для регулирования запасов
некоторого товара, поступающего в течение п периодов времени.
Допустим, что заказ на пополнение запасов может быть сделан
только в начале каждого периода и поступает раньше, чем пе-
риод кончится. Спрос Vj на продукт за период / будет считаться
случайной величиной с плотностью фДо,). Предположим, что
для различных периодов эти случайные величины независимы.
Однако плотность распределения спроса может меняться для
различных периодов. Если требования поступают, когда в си-
стеме нет запаса, они выполняются в первую очередь, когда при-
будет пополнение. Предположим, что стоимость доставки Xj еди-
ниц заказанного в начале периода / товара имеет следующий
вид:
{О, если Xj — О,
1, если ху>0,
так что имеется фиксированная цена плюс линейная функция от
величины заказа. Кроме того, существует стоимость хранения
запаса и штраф за отсутствие в системе запаса товаров в мо-
мент появления спроса. Для того чтобы ради простоты избежать
точного вычисления стоимости хранения и стоимости отказа, до-
пустим, что стоимость хранения за период / есть k^hj, где /г,Х)—
имеющийся запас к концу периода /, и штраф за /-й период есть
jtjSj, где — число отказов к концу периода /.
Обозначим через у\ запас в начале первого периода. Тогда
запас к концу периода /, если Vi— спрос, а Хг — заказанное ко-
личество товаров в период г, есть
j j
hi = yx-\-^xi—У vh если й/>0, (5.28)
и число отказов к концу периода / равно
/ 1
$/ = 2 — 2 ~ f/i> если
I — I 4^1
Sj > 0.
(5.29)
5.4. Многошаговые стохастические задачи
185
Заметим, что если приходится платить за хранение в период /,
то штрафов за отказ в этот период не будет, и наоборот. Опре-
делим функции
\ t=i г—1 / I
если
если
Ау>0,
Sj > О,
(5.30)
где hj, Sj задаются формулами (5.28) и (5.29) соответственно.
Для данного набора Xj и данного множества случайных вели-
чин Vj стоимость функционирования системы за п периодов со-
ставляет
л п / j J \
2 а> I+ 2 j (//1+2^—2^J* (5.3i)
j=l 7 = 1 J \ Z = 1 i = l /
Если длительность периода времени, на который составляется
план, достаточно велика, обычно употребляют приведенную
стоимость, причем коэффициент aj в (5.31) может быть интер-
претирован как норма прибыли. Если норма прибыли не учиты-
вается, то aj=l. Плотность вероятности для данного множе-
ства Vj есть
п
П Фу (®у) = Ф1 (^1) • • • Ф« (^«)- (5-32)
/=1
Соотношение (5.32) следует из предположения о статистической
независимости спроса в различные периоды. Для любого дан-
ного набора ожидаемая стоимость за п периодов нахо-
дится усреднением по всем возможным значениям vif..., vn,
так что эта (приведенная) стоимость есть
ОО ОО п ( Ь
О 0 _ j~l /-1
« / j
+ djFj I yx 4~
\ м
xt
dv1 ... dvn. (5.33)
В (5.33) мы имеем среднюю стоимость функционирования си-
стемы за п периодов для любого набора Нам нужно найти
набор Xj, минимизирующий это выражение. Здесь мы подходим
к основному различию между одношаговыми и многошаговыми
задачами. Было бы заманчиво поступить так, как раньше, и
попытаться найти набор п чисел Х;>0, которые минимизи-
руют г. Мы действительно могли бы действовать так. Однако
на практике решение о том, какое количество товара следует
заказать в начале второго периода, не следует принимать
186
Гл. 5. Стохастическое программирование
до начала этого периода, когда станет известно о состоянии Си-
стемы к началу периода. Для конкретности предположим, что
в начале периода k известно, какое количество товара было за-
везено и каков был действительный спрос в предшествующие
периоды. Ясно, что знание тех значений, которые принимали
случайные величины Vj в периоды от 1 до k, должно влиять на
выбор Xk- Посмотрим, как используется эта информация. Из
(5.33) видно, что убытки за период k зависят только от
!/* + ** —
где
/г-1 й-1
Уч = У1 + 2 — S 'Vi (5.34)
i = 1 i = 1
и ук известно к началу периода k, прежде чем выбирается xh.
Единственная случайная величина, влияющая на стоимость в
период k, — это Vh- Таким образом, вся предшествующая ин-
формация, заключающаяся в хь ..., Xk-\, vlf ..., Vk-ъ содер-
жится в переменной у^ Эта переменная, называемая чистым за-
пасом, представляет собой запас, имеющийся к началу пе-
риода k, если у/г>0, и неудовлетворенный спрос к началу перио-
да k, если №<0.
Очевидно, что в начале периода k, когда принимается реше-
ние о величине заказа на этот период, оптимальное значение хд
будет зависеть только от уъ. Если yk велико, так что в наличии
имеется достаточный запас, целесообразно сделать Xk малым,
но если yk отрицательно, приходится делать Xk большим. Следо-
вательно, оптимальное значение Хь представляет собой функцию
хЦУа), которая дает оптимальную величину заказа, когда из-
вестно у^
Здесь мы подошли к той особенности, которая отличает мно-
гошаговые стохастические задачи от одношаговых. В многоша-
говых задачах решение k не будет сделано прежде, чем станут
известными один *или более случайных параметров системы.
Чтобы принять наилучшее возможное решение, нужно использо-
вать наблюдаемые значения случайных параметров. Это означает,
что будет функцией одного или большего числа переменных,
которые связаны со случайными величинами, наблюдаемыми до
принятия решения k. Методы решения, которые обсуждались
до сих пор, давали его в виде ряда чисел, а не функций, как это
требуется в приведенном выше примере. Таким образом, реше-
ние многошаговых задач имеет значительно более высокий по-
рядок трудности по сравнению с одношаговыми. Задача о запа-
сах может быть сведена к задаче линейного программирования,
5 4. Многошаговые стохастические задачи
187
если только все переменные считать дискретными (это будет
показано в гл. 11). Однако в общем случае это не приводит
к эффективной вычислительной процедуре, так как получаю-
щаяся при этом задача линейного программирования может
иметь 1000 или^даже более ограничений.
В гл. 10 мы увидим, что задача о запасах может быть ре-
шена методом динамического программирования, причем в этом
случае становится возможным вычислить функции х*(//Д Од-
нако задача о запасах — всего лишь простейшая из многошаго-
вых стохастических задач, и не следует думать, что динамиче-
ское программирование может быть использовано для решения
более общих типов таких задач. Этот метод годится только для
задач специального класса.
Как правило, при решении многошаговых стохастических за-
дач интересуются лишь начальным решением. Когда приходит
время принимать второе решение, ситуация может настолько
измениться, что становится желательным пересмотреть исполь-
зуемые в задаче данные и решить ее заново. Это будет происхо-
дить каждый раз, когда принимается решение. Так, в сформули-
рованной выше задаче о запасах только х* представляет инте-
рес, когда задача решена. Заметим, что оптимальное значение
х*—только число, а не функция, так как в тот момент, когда
выбиралось ни одна из случайных переменных не наблюда-
лась, и поэтому х* не является функцией от них. Однако для
того чтобы вычислить х*. обычно приходится определять функ-
ции x*j(y^ так что один лишь факт, что эти функции не
представляют интереса, не устраняет необходимости их вы-
числения.
Выше мы рассмотрели два возможных пути определения на-
бора управляющих переменных Xj. В первом предполагалось,
что все Xj должны быть определены без использования какой-
либо информации о состоянии системы в момент, когда решение
должно быть принято, т. е. без использования наблюденных ве-
личин Vj. Нужно просто определить набор чисел, которые мини-
мизируют (5.33). При этом политика Ху, />-2 не должна зави-
сеть от имеющегося запаса у$. На практике эту политику ис-
пользовать нецелесообразно, потому что, учитывая значение z/j,
можно принять лучшее решение. Другими словами, если счи-
тать х*, функциями z/j, то ожидаемую стоимость можно
сделать ниже, чем в том случае, когда Xj не зависит от yj. Во
втором рассмотренном случае использовалась вся доступная ин-
формация, т. е. предполагалось, что yj известно к моменту при-
нятия решения, В реальной обстановке может, впрочем, слу-
188
Гл. 5. Стохастическое программирование
читься и так, что z/j неизвестно в момент, когда должно быть
выбрано Xj, но известна, например, величина yj-i+Xj^. Это мо-
жет произойти из-за задержки отчета о спросе uj-i за предше-
ствующий период. При этом приходится решать задачу, считая
Xj функцией z/j-i+Xj-i, а не z/j. Понятно, что процесс решения
становится еще более сложным. Рассуждения, приведенные
выше, указывают, как получить разные (й, возможно, сильно
отличающиеся) решения и оптимальные средние убытки для
многошаговой задачи в зависимости от того, какая информация
предполагается известной в момент принятия ^решения. Для
того чтобы полученные результаты достаточно точно отражали
действительность, необходимо решать задачу, считая Xj функ-
цией всех тех параметров, которые действительно известны к мо-
менту принятия решения.
В задаче о запасах мы предполагали, что спрос в различные
периоды — независимые случайные величины. Естественно, что
в действительности это предположение может не выполняться.
Например, значения спроса могут быть коррелированы так, что
высокий уровень спроса в один период влечет за собой столь же
высокий уровень и в следующий. Другими словами, плотность
спроса в различные периоды есть условная плотность
, Vj-i) спроса Vj, если известен спрос в первые / —1
периодов. Введение этих условных плотностей может суще-
ственно осложнить процесс решения.
В задачах о запасах иногда трудно определить численную
величину штрафа за нехватку товара, или, вообще говоря,
штраф за нехватку товара как функцию числа невыполненных
заказов/ Однако можно избежать определения этого штрафа.
Пусть вероятность истощения запасов в период j будет меньше
либо равна некоторому числу т. е.
оо
/ ...,«. (5.35)
xi+yi
В этом случае характер функции плотности <pj(vj) определяет
число yj, такое, что если pj>Yj> то
оо
J Фу
так что ограничения (5.35) эквивалентны неравенствам
(5.36)
5.4. Многошаговые стохастические задачи
189
Если предположить, что в момент принятия решения / извест-
но Уз , то задача сводится к минимизации выражения
СО ОО р п -1 п
z = I • • • J II ф/ (®/) S + CjXj) +
о о L/-1 - I/-1
(5.37)
при условиях и ограничениях (5.36), где
kjhj, если
О, если
О,
0.
(5.38)
Эта задача также может быть решена методами динамического
программирования.
От ограничений типа (5.35), требующих, чтобы вероятность
некоторого события была меньше или равна некоторому числу,
почти всегда можно избавиться, включив в целевую функцию
соответствующую стоимость появления события. Кроме того,
вероятностные ограничения типа (5.35) не всегда легко сво-
дятся к простым ограничениям типа (5.36). Поэтому, по-види-
мому, целесообразнее исключать вероятностные ограничения и
вводить в целевую функцию соответствующую стоимость.
Ограничениям вида (5.35) соответствует некоторая мини-
мальная стоимость появления события. Эта стоимость может
быть определена решением задачи для различных предполагае-
мых стоимостей и нахождением наименьшей из них, для которой
выполняются вероятностные ограничения типа (5.35). Знать
этот сопоставленный штраф полезно, так как произвольно взя-
тым величинам в (5.35) могут соответствовать слишком высо-
кая или слишком низкая стоимости.
В этом параграфе мы на простом примере показали сущ-
ность многошаговых стохастических задач. Как оказалось, ре-
шение таких задач более трудно, чем решение детерминирован-
ных или одношаговых. Дополнительные трудности возникают
из-за того, что в многошаговых задачах можно пользоваться
знанием реализации случайных величин, которые наблюдаются
прежде, чем выносится очередное решение. Оптимальная поли-
тика здесь становится функцией случайных величин, а не просто
числами. Ни один из методов, рассмотренных до сих пор, не в
состоянии дать непосредственно эти функции. Следует, впрочем,
обратить внимание на то, что имеются некоторые специальные
190
Гл. 5. Стохастическое программирование
классы многошаговых стохастических задач, решать которые
относительно легко. Пример таких задач — задача о запасах, в
которой предполагается, что система функционирует бесконеч-
но долго и распределение спроса не меняется со временем. За-
дачи такого рода были подробно исследованы Хедли и Уайти-
ном [8]. Более подробный анализ таких задач приведен в гл. 10
и 11.
Мы закончим этот параграф рассмотрением в общих чертах
одной весьма сложной многошаговой стохастической задачи.
Нефтяная компания каждый год должна принимать решения
о вложении капитала. Например, насколько следует увеличить
мощность существующих очистительных заводов; предпринять
ли строительство новых заводов, где и каких размеров; следует
ли увеличить число танкеров и насколько; какая часть вложе-
ний должна быть направлена на увеличение добычи сырой неф-
ти и где; каковы должны быть ассигнования на исследования,
на поиски, на рекламу и т. д.?
Решения об инвестициях должны быть сделаны с учетом
имеющихся фондов и возможных кредитов. Отдельные решения,
принимаемые компанией, само собой разумеется, взаимосвя-
заны: при постройке заводов на Дальнем Востоке нужна мень-
шая мощность танкеров, а если строится много танкеров, заводы
не нужны. Если на Дальнем Востоке строится завод, то жела-
тельно увеличить там добычу или использование сырья, и т. д.
Чтобы принять правильное решение сегодня, компания должна
учитывать его последствия, которые могут сказаться через не-
сколько лет.
Требования на продукты, перерабатываемые и продаваемые
в разных районах, естественно считать случайными величинами,
параметры которых меняются со временем. Если решения о ка-
питаловложениях принимаются на годичный период, то описан-
ная ситуация приводит к многошаговой стохастической задаче.
Хотя интерес представляет определение политики только на те-
кущий год, все же необходимо учитывать большой планируемый
период и все решения, которые могут быть приняты в последую-
щие годы.
В настоящее время еще не существует методов, позволяю-
щих решить задачу такого масштаба. Если даже считать все
параметры детерминированными и с достаточной точностью
свести задачу к задаче линейного программирования, получен-
ная задача будет настолько сложной, что решить ее современ-
ными средствами невозможно.
В этом параграфе мы не пытались сформулировать много-
шаговую стохастическую задачу, технологические коэффициенты
которой являются случайными величинами, Постановка задач
5.5. Средняя стоимость из-за неопределенности 191
такого вида является достаточно сложной, и, как правило, ре-
шить их численно не представляется возможным.
5.5. Средняя стоимость из-за неопределенности. В стохасти-
ческих задачах большую роль играет величина, которая назы-
вается средней стоимостью из-за неопределенности. Чтобы дать
определение этого понятия, введем сначала так называемую де-
терминированную среднюю стоимость. Предположим, что ре-
шаемая задача содержит случайные параметры ..., Пред-
ставим себе, что заранее известно, какие значения будут иметь
эти параметры. Тогда, решая детерминированную задачу, мо-
жно будет найти соответствующие оптимальные значения пере-
менных, приводящие к значению z*(£i, ... , £<) целевой функ-
ции, которое зависит от реализованных значений случайных па-
раметров. Предположим, что мы решаем задачу многократно,
каждый раз заранее зная значение случайных величин. Если
теперь усреднить оптимальное значение целевой функции по
всем результатам, т. е. образовать интеграл
U<p(£i, .... (5.39)
где <p(£i, ... , tt)—совместная плотность распределения для
рассматриваемых случайных параметров, то число zc называется
детерминированной средней стоимостью, которая (в задачах,
где минимизируются убытки) представляет собой средний мини-
мальный убыток при определенности.
Если z* — оптимальное значение целевой функции, опреде-
ленное из условия минимизации ожидаемых убытков, то ясно,
что z*>zc, так как при вычислении zc мы предполагали, что зна-
чения случайных величин известны до решения задачи. Раз-
ность z*—zc называется средней стоимостью из-за неопределен-
ности. Она показывает, какой средний выигрыш мог бы быть
получен, если бы при принятии решения имелась полная инфор-
мация о значениях случайных параметров. Если средняя стои-
мость из-за неопределенности высока, имеет смысл пытаться
получить больше информации о значениях, которые могут при-
нимать случайные величины. Если же она мала, то не имеет
смысла предпринимать усилия для более подробного изучения
этих величин. К сожалению, вычислять zc довольно трудно, так
как для этого нужно решать много детерминированных задач и
далее определять zc по формуле (5.39), хотя найти z* много
легче. Таким образом, очевидно, что вычисление средней стои-
мости из-за неопределенности представляет собой достаточно
сложную задачу.
192 Гл. 5. стохастическое программирование
5.6. Замена случайных параметров их средними значениями.
Для приближенного решения задач стохастического программи-
рования часто используется метод, который состоит в замене
всех случайных величин их средними значениями и в последую-
щем решении полученной детерминированной задачи. Средняя
стоимость при использовании управляющих переменных, полу-
чаемых при решении этой детерминированной задачи, может
быть найдена посредством вычисления целевой функции (сред-
ней стоимости) при этих значениях управляющих переменных.
Обозначим через Zd среднюю стоимость, соответствующую тем
управляющим переменным, которые найдены при решении де-
терминированной задачи. Так как эти параметры образуют до-
пустимое, но не обязательно оптимальное решение, то
Представляет интерес величина (Zd—z*)/z*, которая показывает,
на какую часть z* может быть уменьшен средний убыток, если
использовать управляющие переменные, найденные решением
стохастической задачи, а не детерминированной. Ответ на этот
вопрос может быть различен и зависит от характера распреде-
ления случайных величин. В некоторых случаях Zd — z* очень
мало по сравнению с z*, и тогда вполне приемлемо заменить
случайные величины их средними. В других случаях (Zd—z*)/z*
велико, и описанный прием дает плохие результаты. Оба эти
случая будут проиллюстрированы на простых примерах в уп-
ражнениях. Часто характер самой задачи определяет, будут или
нет управляющие переменные, полученные решением детермини-
рованной задачи, достаточно хороши для использования. Неред-
ко оказывается известным направление, в котором следует ме-
нять управляющие переменные, чтобы подойти ближе к опти-
мальному решению стохастической задачи.
ЛИТЕРА ТУРА
1. Bab bar М. М., Distributions of Solutions of a Set of Linear Equations
(With an Application to Linear Programming), J. Amer. Statist. Ass., 50
(1955), 854—869.
2. В e a 1 e E. M., On Minimizing a Convex Function Subject to Linear Ine-
qualities, J. Roy. Statist. Soc. (B), 17 (1955), 173—184.
3. Charnes A., Cooper W. W., Chance-Constrained Programming, Ma-
nag. Sci., 6 (1959), 73—79.
4. Charnes A., Cooper W. W., Symonds G. H., Cost Horizons and
Certainty Equivalents: An Approach to Stochastic Programming of Heating
Oil, Manag. Sci., 4 (1958).
5. D a n t z i g G. B., Linear Programming Under Uncertainty, Manag. Sci,,
.1 (1955), 197—206.
6. Ferguson A. R., D a n t z i g G. B., TJie Allocation of Aircraft to Rou-
tes — An Example of Linear Programming Under Uncertain Demand, Ma-
nag. Set., 3 (1956), 45—73.
7. Freund R. J., The Introduction of Risk into a Programming Model, Eco-
nometrica, 24 (1956), 253—263.
Упражнения
193
8. Hadley G., W h i t i n T. M., Analysis of Inventory Systems, Englewood
Cliffs, Prentice-Hall, 1963.
9. H a n s о n M. A., Errors and Stochastic Variations in Linear Programming,
Austral. J, Statistics, 2 (1960), 41—46.
10. Madansky A., Inequalities for Stochastic Linear Programming Pro-
blems, Manag. Sci., 6 (1960), 197—204.
11. Manne A. S., Linear Programming and Sequential Decisions, Manag,
Sci., 6 (1960), 259—267.
12. Tin ter G., Stochastic Linear Programming with Applications to Agri-
cultural Economics, in Second Symposium in Linear Programming, 1955,
197—228.
13. V a j d a S., Inequalities in Stochastic Linear Programming, Bull. Internal.
Statist. Inst., 36 (1958) , 357—363.
14. Vajda S., Mathematical Programming, Reading, Addison-Wesley, 1961.
15. Wagner H., On the Distribution of Solutions in Linear Programming
Problems; J. Amer’. Statist. Ass., 53 (1958), 161—163.
16. Wagner H., On the Optimality of Pure Strategies, Manag. Sci., 6 (1960),
268—269.
17*. Солдатов В. E., О задачах линейного программирования со стохасти-
ческими данными, сб. Математические модели и методы оптимального
планирования, изд-во «Наука», Новосибирск, 1966.
18*. Солдатов В. Е., О некоторых задачах стохастического программиро-
вания, сб. Математическое программирование, изд-во «Наука», 1966.
19*. Хеди и Кандлер, Методы линейного программирования, 1965, 415—
444.
20*.Charnes A., Cooper W. W., Deterministic Equivalents for Optimizing
and Satisfying under Chance Constraints. Operat. Res., 11 (1963), 18—39.
21*. D antzig G. B., Madansky A., On the Solution of Two-stage Linear
Programming Problems under Uncertainty, Pros. Fourth Berkeley Sympo-
sium on Math. Statistics and Probability, 1961.
22*.Madansky A., Methods of Solution of Linear Programs under Uncer-
tainty, Operat. Res., 10 (1962), № 4.
23*. Miller C., Wagner H., Chance Constrained Programming with Joint
Constraints, Operat. Res., 13 (1965), № 6, 930—945.
24*. Shinji К a t a oka, A Stochastic Programming Model, Econometrica, 31
(1963), № 1—2, 181—196.
25*. Williams A. C., On Stochastic Linear Programming, Soc. Industr. and
Appl. Math., 13 (1965).
Упражнения
5.1. Найти приближенное оптимальное решение задачи первого примера
§ 3.9, используя методы гл. 4.
5.2. Указать способ решения задачи, описываемый уравнениями (5.16),
не использующий симплексные итерации.
5.3. Сформулировать детерминированную задачу (в которой нет ограни-
чений), соответствующую стохастической задаче, рассмотренной в § 5.3.
5.4. Написать уравнение (5.33) для случая, когда имеется только два
периода.
5.5. Торговец хлебом должен решить, сколько хлеба покупать в опре-
деленный день недели, скажем во вторник. Опыт показал, что для вторни-
ков спрос можно считать нормально распределенным со средним значением
300 и стандартным отклонением 50. Хлеб продается по цене 25 центов за
буханку, а стоимость хранения — 19 центов. Хлеб, не проданный в конце дня,
13 Зак. 735
194
Гл. 5. Стахастическое программирование
выкладывается на специальный прилавок и продается в среду по 15 центов
за буханку. Весь хлеб на этом прилавке может быть продан по этой цене.
Определить число буханок, которые следует купить, чтобы максимизировать
среднюю прибыль. Найти среднюю прибыль, детерминированную среднюю
стоимость, среднюю стоимость из-за неопределенности и среднюю прибыль
при запасании хлеба только в размере ожидаемого спроса. Использовать эти
результаты для определения гс, z* и Zd, рассмотренных в §§ 5.5 и 5.6.
5.6. Проделать заново упражнение 5.5, предполагая, что при закупках
следует учитывать убыток в 50 центов на каждую требуемую буханку в том
случае, когда запас иссяк.
5.7. Рассмотреть стохастическую задачу, в которой случайные величины
присутствуют только в функциях стоимости, входящих в целевую функцию.
Показать, что для получения среднего значения целевой функции каждое
стоимостное слагаемое следует заменить его средним значением. Каково
среднее значение целевой функции, имеющей вид ScjXj, где Cj — случайные
величины, не зависящие от xft Какого вида будет среднее значение целевой
функции, если плотность распределения Cj зависит от Xj?
5.8. Показать, что задачи, описываемые уравнениями (5.11), могут быть
приведены к одному из видов транспортной задачи с ограничениями на про-
пускные способности введением новых переменных Д^;==—и добавочных
ограничений вида
j
Обратить внимание на то, что 0 и ограничены снизу.
5.9. Рассмотреть следующую задачу производственного планирования.
В начале каждого месяца фирма планирует, сколько единиц товара будет
произведено. В месяц j можно произвести aj единиц в обычное время и
дополнительно bj единиц в сверхурочное время. Производственная стоимость
единицы товара в обычное время — Cj, а в сверхурочное — d,. Для периода /
стоимость хранения единицы товара, полностью оплачиваемая в начале
периода, будет fj. Спрос Vj в период / можно считать случайной величиной
с плотностью (pj(Vj). Все заказы на товар, которые поступают, когда запасов
нет, не удовлетворяются. За каждый невыполненный заказ к концу месяца j
платится штраф nj. Начальный запас равен уо. Поставить задачу производ-
ственного планирования на 12 месяцев, в которой требуется минимизировать
средние убытки. Обсудить вопросы, возникающие при нахождении решения.
5.10. Показать, что введением достаточного числа новых переменных
можно представить задачу, описываемую уравнениями (5.27), в сепарабель-
ной форме. Обратить внимание на то, что только после этого можно полу-
чить локальный максимум.. [Указание. Ввести новую случайную переменную
*=(//—И)/<ь]
5.11. Доказать, что z*—zc>0, где г* и zc определены в § 5.5. Сделать
это, показав, что как г*, так и zc являются интегралами по всем возмож-
ным значениям случайных величин от их функции, умноженной на плотность
распределения. Вычесть один интеграл из другого и обратить внимание на
знак по’интегрального выражения.
3.12. Рассмотреть стохастическую задачу, в которой случайный харак?
тер имеет как спрос, так и технологические коэффициенты. Показать, как
ставятся эти задачи, и выяснить, какие трудности возникают при решении.
Станет ли задача сложнее, если случайные технологические коэффициенты
зависят от случайного спроса?
ГЛАВА
ТЕОРИЯ КУНА — ТАККЕРА
Ловя фортуны взор златой,
Жди терпеливо, смирно;
И хитрость невредна порой,
Коль чести не противна.
Р. Бёрнс. Послание юному другу.
6.1. Введение. В гл. 3 отмечалось, что ценой значительного уве-
личения вычислительных трудностей метод множителей Лагран-
жа может быть обобщен на задачи, которые содержат ограни-
чения в форме неравенств и условия неотрицательности пере-
менных. Эта глава й посвящена указанному вопросу. Основное
внимание здесь обращено не на вычислительные методы, а на
теорию.
Идея обобщения была уже изложена в § 3.8, где показано,
что в определенных условиях компоненты точки, в которой f(x)
достигает относительного максимума при ограничениях gjx)
1 = 1, т, являются компонентами седловой точки функции
Лагранжа F(х, X).
Основные результаты настоящей главы получены Куном и
Таккс^ом [7]. Хотя рассматриваемая теория не связана прямо
с вычислительной процедурой, она является (как мы увидим в
следующей главе) фундаментально важной для построения
вычислительного метода решения задач квадратичного програм-
мирования.
6.2. Необходимые и достаточные условия для седловой точки.
Напомним данное в § 3.8 определение седловой точки для функ-
ции F(x, X), где х есть n-мерный вектор и X есть /п-мерный
вектор. Говорят, что функция F(x, 1) имеет в точке [х0, Хо] седло-
вую точку, если
F(x, X0)<F(x0, X0)<F(x0, X) (6.1)
для всех х из е-окрестности х0 и всех X из 8-окрестности Хо.
Если неравенства (6.1) выполняются для всех х и X, говорят, что
13*
196 Гл. б. Теория Куна-—Танкера
функция F(x, X) имеет седловую точку в большом или глобаль-
ную седловую точку в точке [х0,Хо].
В этой главе мы обобщим определение седловой точки на
случаи, когда некоторые компоненты векторов х и X должны
быть неотрицательными, другие — неположительными, третьи не
имеют ограничений на знак. Согласно этому разделению, запи-
шем х —[х<4 х<2), х<3)] и X—[XX1), Х(2), Х<3)]. Пусть х(’> — вектор с s
компонентами, х<2> — с t—s компонентами, х<® — с п—t компо-
нентами, Х(1)— с и компонентами, Х<2)— с v—и, Х(3)— с m~v
компонентами. Пусть требуется, чтобы х^^О, х<2)^0 и
Х(2)4^0; х<3) и Х(3) не имеют ограничений на знак.
Обозначим через Wi множество точек х, а через IF2— мно-
жество точек X, удовлетворяющих указанным выше ограничени-
ям. Под W будем понимать множество точек [х, X], таких, что
х € Wi, W2. Будем говорить, что функция F(x, X) имеет седло-
вую точку в точке [х0, Хо] для [х, X] С W, если [х0, Хо] € W и суще-
ствует е>0, такое, что условия (6.1) имеют место для всех х €
из е-окрестности х0 и всех X € IF2 из е-окрестности Хо.
Допустим, что F£CX. Если F(x, X) имеет седловую точку в
[хо, Хо] для [х, X] € то, как следует из рассуждений, приведен-
ных, в § 3.2, точка [х0, Хо] должна удовлетворять уравнениям
^-F(Xo, М = 0, / = / + 1,
7 (6-2)
^-F(x0, Хо) = О, / = пг,
ибо компоненты вектора х с номерами f+1, ..., п и компоненты
вектора X с номерами v + 1, tn не имеют ограничений на знак.
Иными словами, если мы рассмотрим зависимость F от xh,
где индекс k принимает значения /4-1, ...» п, и положим
Xj — х^., j =/= k, и 1 —Хо, то в окрестности х^ график функции F
должен иметь вид, показанный на рис. 6.1. При аналогичных
условиях F как функция лг, r=v + l, ..., ш, будет иметь отно-
сительный минимум. Отметим также, что еслил^¥=0 для какой-
либо из первых t компонент вектора х, то также должно выпол-
няться равенство
dF(xa, A,o)/dxft = O,
и аналогично если X” =£ 0 при г=1, 2, ..., v, то
<?F(Xo, Хо)Ж = О.
Пусть х^ — 0, где k принимает одно из значений 1, .... t.
Что можно сказать о значении dF(хо, Хо)/0А в этом случае?
6.2. Условия для седловой точки
197
Допустим сначала, что k принимает одно из значений
1, $, так что Xk должно быть неотрицательным. Тогда из
того, что /7(хАо)</7(хоДо) при [хД0]€№, должно следовать
^^(Хо, Ч<0. (6.3)
Чтобы доказать это, предположим противное: пусть в точке
[хо, Хо] dFldxh>^. Так как производная dFjdXh непрерывна, из
теоремы, доказанной в § 2.8, следует существование 8о>О, та-
кого, что для всех [хД] из ео-окрестности точки [х0Д0] dF!dxk>Q.
Выберем любое 8 из интервала О<8<8о и рассмотрим точки из
е-окрестности [х0, Хо], представив их в виде [хо+Ае^Др], 0<А<8.
По формуле Тейлора
F (х0 Х0) = /?(х0, М Д--hF(хрД-0АеЛ, 10), 0^0 ^1.
Но поскольку точка [хо + 0Ле&, 10] лежит в 8-окрестности [х0, Ко]
и, значит,
-£_F(x0 + Qhek, 10)>0,
то при любом Л, 0<Л<8,
^(хо + йе*. Х0)>/7(х0, М- (6-4)
Следовательно, любая е-окрестность [х0, Хо] содержит точки
[х, Хо] С W, для которых справедливо неравенство (6.4), что не-
возможно, так как [х0, Ко] является седловой точкой F(x, X) при
[х, 1]€ W. Отсюда мы заключаем, что справедливо неравенство
(6.3). Другими словами, график F, как функции от хк при
= j =£ k и Х = Х0 должен иметь вид, показанный на
рис. 6.2. Из аналогичных соображений следует, что если k
198
Гл. б. Теория Куна — Таккера
принимает одно из значений sи х° = 0, то
df(x0, 1о)/дХй^>О. Точно так же при Х° = 0 должно быть
^-F(x0, Х0)>0, г-
t (6.5)
^F(x0, Х0)<0, г = « + 1, v.
Из приведенных выше рассуждений ясно, что в точке [х0, Хо]
dF(x0, ko)/dXj — O либо х°=0 и, аналогично, dF(x0, Xo)/5Xf = O
либо Х° = 0. Таким образом, если [х0, Хо] является седловой
точкой функции F(x, X]. для [х, Х]€ W, и если С1, то точка
[х0, Хо] должна удовлетворять соотношениям
/=1, s,
^7Л(х0. Ч>0. / = $4-1, (6.6)
^(4 ч=о. j — t 4-1, ..., n\
х}>0, /=1, ..., s,
х»<0, / = $4-1, (6-7)
xj свободны, j — 14~ 1 > ... /z;
/=1, .... (6-8)
Ч>0, i — 1, ..., u,
Ч<0. t=== и 4~ 1, • • •» (6-9)
^(х,. 4 = 0, i = v 4-1, ..., m\
Х°>0, Z = 1, ..., a.
Х?<0, i=== и 4** 1, (6.10)
Х° свободны, i — v 4-1, ..., m\
X?-^7F(Xo, Хо) = О, i — 1, ..., m. (6.11)
Соотношения (6.6) — (6.11) дают совокупность необходимых
условий, которым должна удовлетворять точка [х0, Хо], если
она является седловой точкой функции F(x, X) для [х, Х]€ W в
предположении, что F€ С1.
6.2. Условия для седловой точки
199
Определим градиент функции F(x, X) относительно х в точке
[х0, М
VxF(xo,M = (^r/7(Xo> М. .... 10)) (6.12)
и градиент F(x, X) относительно 1 в той же точке
VxF(xo, Xq) = ^^щ-/г(Хо, Ч» F (Xq, Хо) j. (6.13)
Суммируя равенства (6.8) по / и равенства (6.11) по i, получаем
VxF(Xq, Хо)хо = О, V^(Xo, Хо)Хо = О. (6.14-)
к Сформулируем теперь достаточные условия того, что точка
[х0, Ко], удовлетворяющая соотношениям (6.6) — (6.11), является
седловой точкой F(x, 1) для [х, k](F.
Пусть существует такая е-окрестность точки [х0, Ло], что для
точек [х, Хо]€ W этой е-окрестности
F (х, Xo)-^F(Xo, Хо) ~Ь ^xF(Xq, М(х—Хо) (6.15)
и для точек [Хо, 1] £ W этой е-окрестности
F (Хо, 1) > F (Хо, Ч + VxF (Хо, Ч (X - Ч- (6.16)
Тогда [х0, Хо] является седловой точкой функции F(x, X) для
[х, Х]€ W. Если соотношения (6.15) и (6.16) справедливы для
всех х£ Wi и Х€ 1^2, то [хо, Хо] является глобальной седловой
точкой F(x, 1) для [х, Х]Е W.
Чтобы доказать это утверждение, заметим, что так как в
точке [хо, Хо] выполняются условия (6.14), то
VxF(xo, Х0)(х —Xo) = VxF(xo, Х0)х.
Однако если х£ lFb то Xj> 0, /= 1,..., $, и Xj-CO, j=s+1,..., t.
Кроме того, справедливы неравенства (6.6). Отсюда
VxF(x0, Хо)х^О. Следовательно, при выполнении соотношения
(6.15) для x^lFi справедливо неравенство F(x, Xo)^F(xo, Хо).
Подобным же образом для любого Х€ IF2, удовлетворяющего
соотношению (6.16), F(x0, Xo)-<F(xo, X), т. е. для х € Wlt
для которых справедливы соотношения (6.15) и (6.16),
F(x, ko)-<F(xo, X0)<F(x0, X). Таким образом, F(x, 1) действи-
тельно имеет в [хо, Хо] седловую точку. Если соотношения
(6.15) — (6.16) справедливы для всех [х, Х]€ W, функция
F(x, X) имеет в [хо, Хо] глобальную седловую точку.
В § 3.10 было показано, что если F(x, Хо) является вогнутой
функцией х, то имеет место соотношение (6.15), и аналогично
если F(xo, X)—выпуклая функция X, то выполняется соотно-
шение (6.16). Таким образом, если точка [х0, Хо] удовлетворяет
200
Гл. 6. Теория Куна — Таккера
условиям (6.6) — (6.11) и функция Г(х, Хо) является вогнутой
для хС Wi из е-окрестности х0, а функция F(x0, 1) является вы-
пуклой для X С W2 из е-ркрестности Хо, то [хо, Хо] является седло-
вой точкой F (х, X). Если /’(х, Хо) —вогнутая функция при всех
х£ Wt и Г(х0, X)—выпуклая функция при всех Х€ !F2, то
F(x, X) имеет глобальную седловую точку в точке [х0, Хо] для
[х, Х]€ №..
6.3. Теорема Куна—Таккера. Мы приведем сейчас фундамен-
тальные результаты, полученные Куном и Таккером. Рассмот-
рим задачу нелинейного программирования:
«Дх)<^, i=l, «,
g/(x)>^, i = u+l, V,
. ^(х)=^, / = 1, .... Ш,
х>0;
найти max z~f(x).
Будем предполагать, что С1, g& С1, z = 1, ..., m, во всем
неотрицательном октанте. После введения вспомогательных
переменных мы получаем эквивалентную задачу:
gi(*) + xsi = bh / —1, и,
gi^) — xsl = bh / = «4-1,...,^,
gt (х) = bh i — v 4-1, ...m,
[x, xJ>0;
найти max z —
Обозначим через Y множество точек x>0, удовлетворяю-
щих ограничениям. Предположим, что в точке х* функция f(x)
достигает абсолютного максимума для х£ У. Предположим да-
лее, что r(G) =r(G/) в точке х*, причем матрица G состоит лишь
из столбцов, соответствующих положительным х*, лЛ, так что,
не умаляя общности, мы можем построить функцию Лагранжа,
полагая Хо=1. Пусть J — множество индексов / из /=1,...,п,
для которых х*. >0, а 1 — множество индексов /, для которых
х* = 0. Аналогично пусть I — множество индексов i из i=
= 1, ..., v, для которых gt(x*) = 0, а I — множество, содержа-
щее индексы z, для которых ограничения gi(x) в точке х* вы-
полняются со знаком строгого неравенства1).
х) Отметим, чт.о некоторые из множеств J, J, / и I могут быть пустыми.
6.3. Теорема Куна — Такиера '
291
Мы доказали в гл. 3, что существует совокупность т мно-
жителей Лагранжа Ху,—единственная, если r(G)=m в точке
х*, и не единственная в противном случае, такая, что
т
= t = К'- <6-19)
В гл. 3 мы не исследовали выражение
<V(X*) пр„ }г I /й ООЧ
----ПРИ <6-20'
f wl
Сделаем это здесь. Простейший путь исследования знака этого
выражения — предположить, что мы рассматриваем условие
х>0 как совокупность п добавочных обычных ограничений.
После введения вспомогательных переменных xs, г+р) условия
принимают вид Xj— xs>v+j = 0, /=1, ..., п. Мы получаем
задачу с т + п ограничениями и + переменными. Вспомога-
тельные переменные подчинены требованиям неотрицательности,
но-на знак Xj ограничений уже не накладывается. Отметим, что
если при исходной системе т ограничений r(G)=r(G7) в тсртке
х*, то это же соотношение должно иметь место для системы
m + n ограничений, включающих условия Таким обра-
зом, используя сказанное в гл. 3, получаем, что существует
т+п множителей Лагранжа %*, z — l,...,m+n, таких, что
в точке х*
, т
dxj dxj 7 7
tel /€/•
Так как^т+; = 0 при /£7, отсюда снова'получаем (6.19).
Рассмотрим соотношения
<V(x*) i* о /- г /коп
-a*—---------------------X,„ty = 0, (6.21)
Можно показать (см. § 3.7 и упражнение 3.13), что в терминах
§ 3.7
л
- = /=1, т-рл*
]) Отметим, что в (6.18) мы уже имели V вспомогательных переменных,
202
Гл. 6. Теория Куна — Таккера
В упражнении 6.14 читателю предлагается получить условия, до-
статочные для существования производных dz*ldbi. Здесь пред-
полагается, что эти производные существуют. Рассмотрим огра-
ничения где для нашей задачи 6w+j = 0. Предполо-
жим, что мы меняем Ьт+з от нуля до некоторой отрицательной
величины. При этом z* не может уменьшиться, так как любое
допустимое решение с &m+j = 0 является также допустимым при
6m+j<0. Поэтому dz*/d&m+j^0, и отсюда заключаем, что
< 0. Это приводит непосредственно к следующему резуль-
тату:
<У(х*) у »<^(х*)
dxj 1 dxj
(6/2
Такой анализ дает нам некоторую дополнительную инфор-
мацию: если мы увеличиваем bi при i=l, ..., и, то z* может
лишь возрастать или оставаться неизменным. Следовательно,
dz*jdbi 0, т. е. /=1, ..., и. Подобным же образом
при f=u+l, ..., v, если bi убывает, то z* может только воз-
растать, и, следовательно, ^/<^0, i = и,-|-1, v. Для
/ = г> + 1, ..tn Ki может иметь любой знак. В том крайнем
случае, когда существенное ограничение становится несуще-
ственным при бесконечном малом изменении bi в определен-
ном направлении, может оказаться необходимым интерпретиро-
вать dz*)dbi как одностороннюю производную. Однако учет
этого случая не меняет приведенных выше рассуждений.
Мы можем записать полученные выше результаты в следую-
щей форме. Если х* — точка абсолютного* максимума f(x) при
х € У, то существует такой вектор X*, что
tn
^F (х\ I*) = Vf (х‘) - 3 (х*) < 0, (6.23)
причем для / € J справа стоит знак строгого равенства. Здесь
F(x, 1) —функция Лагранжа
F(x, l) = f(x)+Sx/[^-gi(x)]. (6.24)
Далее
W’ V)x- = £x;!^-£>.:^^p4 = 0. (6.25)
/-1 ( Z-l
Аналогично первые и компонент вектора
V.F (х*, Г) = (6, - g. (х*), ..., bm - gm (х*)) (6.26)
6.3. Теорема Куна — Таккера
203
неотрицательны, компоненты с номерами и+1, v неполо-
жительны и компоненты с номерами я+1, т нулевые. Кро-
ме того,
V>F (х*, X*) X* = Д X* р, - gt (х*)] = 0. (6.27)
Сравнивая соотношения (6.19), (6.22), (6.25) и (6.27) с усло-
виями (6.6) — (6.11), мы видим, что точка [х*, X*] удовлетворяет
необходимым условиям существования седловой точки функции
F(x, 1) при х>0, XEIVV
Теперь мы докажем, что если [х*, X*] удовлетворяет приве-
денным. выше условиям и f(x)—вогнутая на неотрицательном
октанте функция, a gi(x)—выпуклая функция, если X/ > 0,
и вогнутая, если <0, i= т, то /(х*) является абсо-
лютным максимумом f(x) при х£ Y.
Для доказательства отметим, что при сделанных предполо-
жениях F(x, X*) является вогнутой функцией х при х>0.
Функция F(x*, X) является линейной и, следовательно, выпук-
лой функцией вектора X. Ввиду этого, как показано в § 6.2,
[х*, X*] является глобальной седловой точкой функции F(x, X)
при х^>0, ХЕ W2, т. е.
F(x, X*)<F(x*, X*)<F(x*, X) (6.28)
при всех х>0, ХЕ W2. Вследствие равенства (6.27) имеем
F(x*,X*) =/(х*). Однако
m
F (х, X*) = f (х) + S ** \Jh - gi (х)]. •
Z = 1
Рассмотрим любое значение х>0, удовлетворяющее огра-
ничениям. Имеем 6г=£г(х), f==v+l, ..., m, и X* [6Z—^(х)] = 0.
Для z = l, ..., исправедливо bi^g^x). Для этих же значений
i мы показали, что X* 0. Следовательно, X* [6. -- gt (х)] i>0, i —
~ 1, ..., и. Когда / = «+1, ..., у, имеем бг^йДх). Однако в
этом случае и, следовательно, опять, Ч [bi - ^(х)]>0.
Поэтому для всех х£ У
m
£x;pz-gz(x)]>o,
/=1
т. е. при всех х£ У справедливо f(x)<F(x, 1*), откуда
f(x)<f(x*).
Таким образом, в точке х* функция f(x) действительно дости-
гает абсолютного максимума для х£У.
204
Гл. 6. Теория Куна —Танкера
Резюмируем полученные результаты. Мы установили необ-
ходимые условия, которым должна удовлетворять точка х*,
если она доставляет глобальный или относительный максимум
f(x) для хСУ. Затем было показано, что если f(x)—вогну-
тая функция на неотрицательном октанте, а функция gi(x) при
каждом i выпуклая или вогнутая (в соответствии со знаком Xf)
то в удовлетворяющей необходимым условиям точке х* /(х)
будет достигать глобального максимума для х£ У. Иными сло-
вами, при этих ограничениях на f(x) и g\-(x) необходимые усло-
вия являются также и достаточными.
Наконец, мы доказали, что если /(х)—вогнутая функция,
а функция gi(x) при каждом Л—выпуклая или вогнутая (как
требуется), то удовлетворяющая необходимым условиям точка
[х*,Х*] является седловой точкой функции Лагранжа F(x, 1)
при х^>0 и Х€ 1^2-
В заключение отметим следующий интересный факт. Допу-
стим, что f(x)—вогнутая функция, а §Дх)—выпуклая, если
ki > 0, и вогнутая, если X/< О (при любом z). Тогда если
точка [х*, V] удовлетворяет необходимым условиям максимума
функции /(х) для х£ У, то соотношение (6.28) должно выпол-
няться при всех х>0 и всех Х€ W2, т. е.
F(x*, X*) = f(x*)<F(x*, X).
Значит, X* должно доставлять минимум функции F(x*, 1) для
значений X, удовлетворяющих условиям
1г .... cf дн\ ' ' (6.29) . df (х*) . с 7. dxj ' J '
> 0, 1 — 1, ..., it, 0, i — и 1, .... v,
Xz свободны для i — ...,
Здесь мы имеем задачу линейного программирования, причем
X* служит оптимальным решением этой задачи.
6.4. Установление необходимых условий методом Куна—Так-
кера. Необходимые условия, рассмотренные в предыдущем пара-
графе, были получены Куном и Таккером другим способом. Они
рассматривали задачу нелинейного программирования вида
gi (х) > 0, I — 1, ..., М\ х > 0;
найти шах z=±=f(x). (6.30)
6.4. Установление необходимых условий
205
Мы можем преобразовать задачу (6.17) к такому виду, вводя
обозначения
gz(x) = dz- gz(x),
gi (X) = gi (х)~Л>
(6.31)
z = w 4-1, ..., V, (6.32)
и заменяя каждое из равенств вида gi(x)=bi эквивалентной
ему парой неравенств gi(x)>fei, g,(x)•<.&,•. При этом m — v
равенств §Дх)=д4 заменяются на 2(пг — v) неравенств
in(x) = £7(x) — ^>0,
iz2(x) = ^ —§\(х)>0, Z = x>4-1, .... m. (6.33)
Следовательно, задача, изученная Куном и Танкером, эквива-
лентна задаче, рассмотренной в предыдущем параграфе.
Важным исходным пунктом у Куна и Таккера при получении
необходимых условий было введение требования регулярности
ограничений. Это требование является весьма серьезным огра*
ничением на структуру множества допустимых решений в ок-
рестности точки х*. Прежде чем ввести условие регулярности,
сделаем несколько замечаний.
Отметим прежде всего, что если в точке х* некоторые огра-
ничения являются несущественными или некоторые компоненты
х* являются положительными, то существует достаточно малая
окрестность точки х*, такая, что для всех x = x* + h в этой окре-
стности эти ограничения будут оставаться несущественными,
а переменные — положительными. Следовательно, рассматри-
вая малую окрестность точки х*, мы не должны учитывать огра-
ничения с номерами i£I и переменные с индексами /С J (мно-
жества /, /, /, J определены в предыдущем параграфе). Обра-
тим внимание лишь на ограничения с номерами /С / и перемен-
ные с индексами /€/. При J£J x*=0, так что, рассматривая
точки x = x*H-h>0, мы должны иметь в виду, что для
Напомним, что касательная гиперплоскость к поверхности
gJxJ^O, i£I в точке х* имеет уравнение
Vgz(x*)x== Vgz(x*)x*. (6.34)
Рассмотрим теперь множество точек у, принадлежащих пересе-
чению замкнутых полупространств
vgz(x*)y> v^(x*)x*, /£/, и ^>0, /е/.
206
Гл. 6. Теория Куна — Таккера
Если любую точку у из выпуклого множества (6.35) представить
в виде y = x* + h, то вектор h должен удовлетворять неравен-
ствам
Vgz(x*)h>0, и Лу>0, /С 7. (6.36)
Предположим, что мы выбрали некоторую точку у, удовлетво-
ряющую (6.35), и рассмотрим луч, начинающийся в х* и про-
ходящий через у. Этот луч лежит целиком в выпуклом множе-
стве (6.35) и любая его точка w представима в виде
w = x*+Th0 ct>0, где h0 = y— х*. Кроме того, h0 и h = Th0 удов-
летворяют условиям (6.36). Вектор h0 или h=xh0 при т>0 опре-
деляет направление движения по лучу из х* к у.
Условия регулярности, введенные Куном и Таккером, тре-
буют, чтобы для каждого луча, начинающегося в точке х* и
лежащего в выпуклом множестве (6.35), или, иными словами,
для каждого h, удовлетворяющего условиям (6.36), имелась бы
в некоторой ^-окрестности точки х* непрерывная гладкая кри-
вая, каждая точка х которой удовлетворяет условиям
gt(x) 0 при z'C I и 0 при j£J и такая, что указанный луч
касается ее в точке х*. Под непрерывной гладкой кривой мы по-
нимаем кривую, допускающую параметризацию х = ф(т), такую,
что существуют производные dxjfdx, /=1, ..., п. Мы будем счи-
тать, что параметризация выбрана таким образом, Дто х* = ф(0)
и т возрастает при движении вдоль кривой от точки х*. Условие
регулярности означает, что для каждого луча, лежащего в
(6.35), такая кривая существует в е-окрестности х*, все ее точки
лежат в допустимой области и кривая касается луча в точке х*.
То обстоятельство, что кривая касается луча, означает, что
если
= п, (6.37)
то уравнение луча записывается в виде w = x*+rho, т>0, где
вектор h0 имеет компоненты №.. Иными словами, если мы пред-
ставим некоторую точку луча в виде w = x* + h, где h удовлет-
воряет условиям (6.36), то должны выполняться соотношения
= Н>о, (6.38)
Геометрическая иллюстрация приведена на рис. 6.3. Произ-
водные й<р,(0)/о?т могут быть определены только при т—►+0 и
не определены для т<0 (так как кривая может начинаться в
х*). Заметим, что в приведенных выше рассуждениях предпо*
6.4. Установление необходимых условий
207
лагалось, что разным лучам, удовлетворяющим условиям (6.35),
соответствуют разные кривые. Условие регулярности может
быть задано и несколько иначе: для каждого h, удовлетворяю-
щего соотношению (6.36), в некоторой 8-окрестности точки х*
должна существовать по меньшей мере одна кривая х = ср(т),
такая, что х принадлежит до-
пустимой области при каждом
т и имеет место (6.38).
Мы докажем сейчас, что
если выполнено условие регу-
лярности и х* доставляет мак-
симум функции f(x) при х>0
и выполнении ограничений, то
для всех h, удовлетворяющих
(6.36), выполяется неравенство
Vf(x*)h<0.
Для доказательства пред-
положим противное. Пусть су- Рис- 6.3.
ществует некоторый вектор h,
скажем Ь1 = [Ац,..., Ani], удовлетворяющий условиям (6.36),
для которого Vf(x*)hi>0. Тогда Vf(x*)h>0 при всех h(p) =
= phi, р>0. Так как Vf(x)hi— непрерывная функция вектора х,
то для всех х в некоторой 6-окрестности х* также V/(x)hi>0
и, следовательно, Vf(x)h(p)>0.
Рассмотрим кривую в допустимой области, касающуюся лу-
ча, проведенного из точки х* в направлении hb Используя
(6.38), имеем
фу СО — X*J = л ч- TgYJ (тц),
где у^(тр) -*0 ПРИ ^“*0, или
х = х* + rphi + тцу (тр) = х* + phi 4- ру (р), р > 0, (6.39)
причем х принадлежит допустимой области. Обозначим h(p) =
= p[hi+y (р)]. Мы можем выбрать р0 столь малым, что для всех
р, О^р^ро, вектор х, определяемый условием (6.39), лежит
в указанной выше 6-окрестности, так что Vf[x* + h(p)]hi>0.
При фиксированном р из интервала О^р^Ро Vf[x* + h(p)]y
является непрерывной функцией вектора у и, следовательно,
существует ор-окрестность точки hi, такая, что для всех у из
этой окрестности V/[x* + h(p)]y>0. Заметим, что орзависит отр.
Пусть
а = min ор,
р
(6.40)
208
Гл. 6. Теория Куна — Таккера
Тогда для всех у из о-окрестности hi и всех х из р0-окрестности
х* мы должны иметь V/(х)у>0. Следовательно, мы можем вы-
брать р настолько малым, что hi+y(p) лежит в о-окрестности
hi и x* + 0h(p) лежит в ро-окрестности х* при любом 0, 0^0-44,
Для таких р
Vf[x* + 0h(p)][h1+v(p)] > 0
и, умножая на р, имеем
V/[x* + 0h(p)]h(p)>O.
Но тогда соотношение
Их) = f (Х*).+ v; [X*+Oh (р)1 h (Р) > f (X*) (6.41)
должно иметь место при некотором 0 и x = x* + h(p)>0, удов-
летворяющем ограничениям. Таким образом, мы пришли к про-
тиворечию. Отсюда для всех h, удовлетворяющих соотношениям
(6.36), должно выполняться V/(x*)h<CO.
Кун и Таккер не проводили изложенного выше анализа. Они
просто указали, что если условие регулярности имеет место, то
условие Vf(x*)h<C0 должно выполняться для всех h, удовлет-
воряющих соотношениям (6.36). Выше приведено доказатель-
ство этого утверждения.
Целью введения условия регулярности является исключение
случаев вырожденности (в определенном смысле) допустимого
множества. Пусть ограничения имеют вид
ii (х) = (3 — х,)3 — (х2 — 2) > 0,
g<> (X) — (3 — хО3 + (х2 — 2) > 0.
Множество допустимых решений показано на рис. 6.4 *). Допу-
стим, что х*=[3, 2]. Тогда условие Vg-i(x*)h>0 принимает вид
—/i2>0, а условие Vg2(x*)h>0— вид Л2>0. Из этих двух
условий Л2 = 0, в то время как hi может иметь любое значение.
Следовательно, точки у, удовлетворяющие соотношениям (6.35),
должны лежать на прямой, показанной на рис. 6.4, и, значит,
вектор h с началом в х* должен быть направлен вдоль этой
прямой. Однако для вектора h, у которого Ai>0, в допустимой
области не существует кривой, касающейся его в точке х*, так
как в допустимой области не существует точек > х*. Здесь мы
встретились со случаем, когда условие регулярности нарушено.
Более того, в этом случае неравенство V/(x*)h<^0 выполняется
не для всех h, удовлетворяющих (6.36); это можно видеть, если
]) Здесь и на некоторых других рисунках удобно вектор градиента стро-
ить в точке, в которой он вычислен, а не в начале координат,
6.4. Установление необходимых условий
209
взять f(x)=Xi, так что Vf(x*)h = &i. Ясно, что hi не обязано все-
гда удовлетворять условию Ai^O.
Этот пример показывает, что условие регулярности является
важным в том смысле, что если оно не выполнено, соотношение
Vf(x*)h<^0 не обязательно выполняется для всех h, удовлет-
воряющих (6.36). Существует весьма непосредственная связь
^2
Рис. 6.4.
х2
Рис. 6.5.
между условием регулярности и требованием, введенным в пре-
дыдущем параграфе, которое состоит в том, что должны суще-
ствовать dz*ldbi и выполняться равенство r(G/)=r(G). Однако
для установления строгих соотношений между этими условиями
необходим серьезный анализ; здесь мы его приводить не будем.
Рис. 6.5, 6.6 и 6.7 иллюстрируют различные случаи, в кото-
рых требование регулярности выполнено. Для рис. 6.5 множе-
ство / пусто, но два ограничения являются существенными.
Выпуклое множество, образованное пересечением двух полу-
пространств Vgi(x*)h > 0, на рисунке обозначено темной штри-
ховкой. Для каждой точки указанного множества Vf(x*)h<^0.
На рис. 6.6 У1 = 0 и темной штриховкой обозначено выпуклое
множество, образованное пересечением полупространств /ii>0
и Vg,1(x*)h>0. Снова для любой точки выпуклого множества
имеет место Vf(x*)h^0.
Для того чтобы перейти от условия «Vf(x*)h-<0 при всех h,
удовлетворяющих (6.36.)», к необходимым условиям, полученным
в предыдущем параграфе, следует воспользоваться леммой
Фаркаша, которая формулируется следующим образом:
И Зак. 73^
210
Гл. 6. Теория Куна — Таккера
Вектор b будет удовлетворять неравенству Ь'у>0 привсеху,
для которых выполняется Ау>0, в том и только в том случае,
если существует вектор w>0, такой, что A'w=b.
Для доказательства достаточности предположим, что суще-
ствует вектор w>0, такой, что A'w = b (или w'A = b'). Тогда для
любого у справедливо 'w'Ay = b'y. Следовательно, если Ау>0,
то w'Ay^O и Ь'у^О, что и требовалось доказать.
Рис. 6.6.
Рис. 6.7.
Чтобы доказать необходимость, используем теорему двой-
ственности для линейного программирования. Если Ь'у>0 для
любого у, удовлетворяющего системе неравенств АуХ), то за-
дача линейного программирования
Ау>0; найти minZ = b'y
имеет оптимальное решение у = 0. Следовательно, двойственная
задача
Azw = b, w>0; найти maxz = 0w
также имеет оптимальное решение, т. е. существует по крайней
мере один вектор w>0, удовлетворяющий ограничениям
A'w=b. В ограничениях двойственной задачи имеет место стро-
гое равенство, так как переменные прямой задачи не имеют
ограничений на знак. Но это именно то, что мы и хотели дока-
зать.
Применим лемму Фаркаша к интересующему нас случаю.
Так как неравенство —V/(x*)h>0 должно выполняться для
6.4. Установление необходимых условий
211
всех h, удовлетворяющих (6.36), то существуют такие О,
i = 1, ..., М, и ц* > 0, j £ Л что
/ел («2)
>*J- <блз>
/€/
Отметим, что, применяя лемму Фаркаша, мы учли условия
/ij>0, / С/, как обычные ограничения. Из соотношений (6.42) и
(6.43) следует, что если х* — оптимальное решение задачи
(6.30), то вектор —Vf(x*) будет лежать в выпуклом много-
гранном конусе, образованном векторами V£г(х*), /С/, и ej,
/С/. Это обстоятельство иллюстрируется на рис. 6.5, 6.6 и 6.7.
Приведенные выше уравнения-могут быть объединены:
у л * dg. (х*) ~ df (х*)
дх; dxj
/=1,
п, (6.44)
где Л,* = 0 для 7 С/ и строгое равенство имеет место для /GZ.
Условие, что для /€/ имеет место строгое равенство, удобно
записать следующим образом:
VxF(x*, Г)х* = 0, (6.45)
где F(x, X) —функция Лагранжа,
м
FMHW+2W (6.46)
1=1
Условие, что ^*.= 0 для / удобно записать в виде
VxF(x*, Г)Г = 0. (6.47)
Для изучаемой здесь задачи условия (6.44), (6.45) и (6.47)
совпадают с необходимыми условиями, полученными в предыду-
щем параграфе.
Когда ограничения (6.30) линейны, условие регулярности
всегда выполнено. Действительно, в этом случае существует та-
кая окрестность точки х*, что любая точка, удовлетворяющая
(6.35), удовлетворяет также ограничениям. Таким образом, для
любого луча, начинающегося в х* и лежащего в множестве
(6.35), мы можем использовать сам луч в качестве кривой,
о которой идет речь в условии регулярности. Поэтому для ли-
нейных ограничений необходимые условия, полученные в этом
и предыдущем параграфах, должны иметь место при единствен-
ном предположении, что функция f дифференцируема.
14*
212
Гл. б. Теория Куна —Таккера
При выводе необходимых условий в этом и предыдущем па-
раграфах предполагалось, что все участвующие функции были
дифференцируемыми. В практических задачах эти условия, как
правило, выполняются. Однако в том случае, когда функции
/(х) и £г(х), /==1, ... , Л1, вогнутые, тот факт, что функция
F (х, 1) имеет седловую точку, может быть доказан и при более
общих предположениях.
6.5. Один частный случай и пример. Допустим, что рассмат-
риваемая ниже задача нелинейного программирования имеет
линейные ограничения и вогнутую (в неотрицательном октанте)
целевую функцию, т. е. задача имеет вид
п
X a; jXJ = bt,
i-i
i — и 41, ..., v,
i = v -j- 1, ..., m,
(6.48)
x>0;
найти max z=f(x).
Так как функция f(x) вогнутая, а ограничения линейные и,
следовательно, входящие в них функции можно рассматривать
и как выпуклые, и как вогнутые, мы можем сформулировать
необходимые и достаточные условия того, что f(x) достигает
глобального максимума в точке х*. Условия состоят в том, что
должен существовать вектор X* с компонентами X/ > 0 при
/=1,...,«, X* при Z = w+1, ... , v и X/произвольного знака
при / = и + 1, ... , т, такой, что
т
j
i» 1
dxj
/=1.........n, (6.49)
(6.50)
(6.51)
и
6.5. Один частный случай и пример
213
Более того, функция Лагранжа
m Г п
F (х, 1) = f (х) 4- 3 bt — ^ atjXj
i-i L j-i
(6.52)
имеет глобальную седловую точку [х*, 1*] для х>0,
Xz>0, / —1, и, и Xz0, i —
На первый взгляд кажется странным, что F(x*, 1) достигает
минимума в 1*. Причина этого в ограничениях на знаки компо-
нент вектора X. Из (6.51) мы видим, что F(x*, X) будет дости-
гать минимума п'ри Х=Х*, если
m Г п
3 М Ь[—
Z " 1 У =» 1
>о
для всех X € 1Г2. В справедливости последнего неравенства мо-
жно убедиться, если учесть, что х* удовлетворяет ограничениям
и Xz 0, / = 1, ..., и, и Xz 0, i = и -|- 1, ..., V. Следует отме-
тить, что вектор X, который минимизирует F(x*, X), не обязатель-
но единственный; Х=0 также минимизирует F(x*, X).
Соотношение (6.50) мы можем переписать в виде
(6.53)
Поскольку X* = 0, если j-e ограничение выполняется со знаком
строгого неравенства, то в (6.53), не нарушая его справедли-
вости, можно заменитьЗ atjx*j на Отсюда
m
V / —
Х/ дХ) ~
(6.54)
Пусть f(x)=cx, так что (6.48) превращается в задачу линей-
ного программирования. Выражения (6.49) и (6.54) принимают
при этом вид соответственно
и
2 Каи сг
/= 1, .... п,
3 tibi = 3 «’Ху
(6.55)
(6.56)
214
Гл. 6. Теория Куна — Таккера
Ввиду того что для любого к € №2, удовлетворяющего неравен-
ствам сг и любого х>0, удовлетворяющего ограни-
чениям, имеют место соотношения
п
К 2 at IхI ‘С i — 1, • • • >
K^aijx] = Klbl, Z = d + 1, ..m,
/=i
будем иметь
m m f n \ n / m
2 М/ 2 ^z( 2 aijXjj— 2 ( 2 ^i^ij
Z = 1 Z = 1 W=1 J 7 / = = l J
Поэтому
2Mz> 2c<- (6.58)
Z=1 7 7
Из (6.56) и (6.58) следует, что Л* должен быть оптимальным
решением задачи линейного программирования
jп,
/ = 1
Zz>0, /=l,...,zz, Xz<0, z = (6.59)
т
найти minZ = 2 Мр
Z = 1
Эта задача является двойственной к исходной задаче линейного
программирования. Соотношения (6.50) и (6.51) являются из-
вестными соотношениями для пары двойственных задач линей-
ного программирования. Таким образом, применяя теорию
Куна — Таккера, мы показали, что если прямая задача линей-
ного программирования имеет оптимальное решение, то двой-
ственная задача также должна иметь оптимальное решение и,
кроме того, имеет место равенство (6.56).
Пример. Рассмотрим приведенный в -гл. 1 пример с огра-
ничениями (1.14) и целевой функцией (1.15). Решение этого
примера иллюстрируется рис. 1.2. Чтобы представить задачу в
форме задачи максимизации, запишем
min z — — max (— г), — z = z.
Таким образом, задача, эквивалентная исходной, состоит в оты-
скании максимума выражения
z = —10 (Xi - 3,5)2 — 20 (х2 - 4)2
Литература
215
при ограничениях (1.14). Производные целевой функции есть
£- = _w,-3,5); ^=-40^-4).
Если х* — оптимальное решение, то должен существовать век-
тор 1* с компонентами Х|, Х2>0 и Л3, М, Z5<0, такой, что
4- _|_ 2%з 4- 0,5Z*4 + Xj > — 20 (х? — 3,5) = 20,
х; _ 15+х3- _ х; > - 40 и; - 4)=20, (6'60)
так как оптимальное решение, найденное в гл. 1, есть х* —2,5,
х* = 3,5. Кроме того, мы знаем, что для тех ограничений, кото-
. *
рые не существенны, Л/ = 0. Здесь существенным является толь-
ко первое ограничение. Таким образом, Л2 = Х3 = Х4 = ^5 = 0.
Далее, строгое равенство должно иметь место для каждого
ограничения из (6.60), для которого х* > 0. Так как х*, Х2>0,
строгое равенство имеет место в обоих ограничениях и поэтому
Xj = 20. Из (6.54) следует, что
= — 20х* (х* — 3,5) ~ 40X2 (х2 — 4)>
что и имеет место при проверке:
20- 6 = 20 • 2,5 + 20- 3,5.
Поскольку z — вогнутая функция для всех х и ограничения
линейны, необходимые условия, которым должна удовлетворять
точка х*, являются также и достаточными. Поэтому тот факт,
что мы нашли вектор 1*, такой, что [х*,Х*] удовлетворяет необ-
ходимым условиям, означает, что f(x) достигает в точке х* гло-
бального максимума.
ЛИТЕРА ТУРА
1. Arrow К. J., Hurwicz L., Reduction of Constrained Maxima to Saddle-
Point Problems, in Neyman J. (ed.), Proc. Third Berkeley Symp. on
Math. Statistics and Probability, v. V, Berkeley and Los Angeles, Univer-
sity of California Press, 1956, 1—20.
2. Э p p о у К. Дж., Гурвиц Л., У д з а в а X., Исследования по линейному
и нелинейному программированию, ИЛ, М., 1962.
3. Burger Е., On Extrema with Side Conditions, Econometrica, 23 (1955),
451—452.
4. Forsythe G., Computing Constrained Minima with Lagrange Multipliers.
J. Soc. Indust, and Appl. Math., 3 (1955), 173—178.
5. John F., Extremum Problems with Inequalities as Subsidiary Conditions,
in Studies and Essays, Courant Anniversary Volume, New York, Inter’
science, 1948.
216
Гл. 6. Теория Куна — Таккера
6. Карлин С., Математические методы в теории игр, программировании
и экономике, ИЛ, М., 1964.
7. К u h n Н. W., Т и с k е г A. W., Nonlinear Programming, in Neyman J.
(ed.), Proc. Second Berkeley Symp. on Math. Statistics and Probability,
Berkeley and Los Angeles, University of California Press, 1951, 481—492.
8. P h i p p s C. G., Maxima and Minima under Restraint, Amer. Math. Month-
ly, 59 (1952), 230—235.
9. S 1 a t e r M., Lagrange Multipliers Revisited: A Contribution to Nonlinear
Programming, Cowles Commission Discussion Paper, Math. 403, Nov. 1950.
10. Tucker A. W., Linear and Nonlinear Programming, Operat. Res., 5
(1957), 244—257. Эта статья содержит элементарное изложение (без до-
казательств) теории Куна — Таккера применительно к задачам с линей-
ными ограничениями.
11. Vajda S., Mathemathical Programming, Reading, Addison-Wesley, 1961.
12*. Веллман P., Дрейфус С., Прикладные задачи динамического про-
граммирования, М., изд-во «Наука», 1965.
У пражнения
6.1. Сформулировать необходимые условия Куна—Таккера, соответствую-
щие условиям (6.6)— (6.11), для задачи минимизации. Почему, если выполнены
условия выпуклости, необходимые условия являются также достаточными?
Какой будет в этом случае функция Лагранжа и ее седловая точка?
6.2. Обобщить изложенное в § 6.3 на случай, когда для /==1, s,
для /=$+1, ..., t и для /=/+1, ...» я Xj свободно.
6.3. Доказать следующие варианты леммы Фаркаша:
а) Для данного вектора b неравенство Ь'у>>0 справедливо при всех у>>0
удовлетворяющих условию Ау<0, в том и только в том случае, если
существует такой вектор w^>0, что A'w^b.
b) Вектор b будет удовлетворять неравенству Ь'у>0 для каждого у,
такого, что аг’у>0 при р=1, ..., v и аг’у=0 при i=k+l, ..., т, в том
и только в том случае, если существует вектор w, удовлетворяющий
условию A'w==b, у которого первые v компонент неотрицательны,
а остальные — любого знака.
6.4. Обобщить результаты § 6.4 на задачи вида
g/(x)>0, i~ 1, .... v; i/(x)=0, i — v + 1, ..,, M;
x > 0; найти max z — f (x).
Как будет выглядеть условие регулярности Куна—Таккера для этого слу-
чая? [Указание. Показать, что ограничениям вида £г(х)=0 в (6.36) соответ-
ствуют ограничения вида Vg?(x*)h = 0. Затем использовать результат преды-
дущего упражнения.]
6.5. Показать, каким образом в каждой из задач, приведенных в кон-
це гл. 1, в которых не требуется целочисленности переменных, могут быть
использованы условия Куна — Таккера. Для тех случаев когда имеют место
соответствующие свойства выпуклости или вогнутости, проверить на основа-
нии условий Куна—Таккера, что полученное графическим путем решение
действительно является оптимальным.
Упражнения
217
6.6. Решить задачу
(1—xj3 —х2>0, х>0;
найти тахг==Х1.
Решить ее геометрически и показать, что необходимые условия Куна—
Таккера в этом случае не выполнены. Показать, что нарушено требование
регулярности.
6.7. Рассмотреть задачу отыскания минимального расстояния от начала
координат до выпуклого множества
X] —|— 4“
Решить ее графически и показать, что необходимые условия Куна—Так-
кера в точке минимума выполнены.
6.8. Применить теорию Куна—Таккера к транспортной задаче линейного
программирования. Выписать функцию Лагранжа и получить двойственную
задачу.
6.9. Показать, что если V и 1Г — выпуклые множества, не имеющие об-
щих внутренних точек, то существует гиперплоскость cx=z, которая отделяет
У и 1F, так что cv z для всех v $ V и cw z для всех w £ W. Проиллю-
стрировать геометрически. [Указание. Рассмотреть множествоХ= {v—w|v£
w£IF}.] Показать, что X— выпуклое множество и что точка 0 либо
лежит на границе X, либо не принадлежит X. Тогда по теореме об отделяю-
щей или опорной гиперплоскости (§ 2.6) существует гиперплоскость, содер-
жащая 0, такая, что все множество X лежит в замкнутом полупространстве,
образованном этой гиперплоскостью, т. е. с (v — w)^>0 для всех (v — w)£X
Другими словами, cv >> cw для всех v £ V, w £ W. Если множества V и W
имеют общую граничную точку Y, полагаем z==cy. Как можно выбрать г,
если V и W не имеют общей точки?
6.10. Пусть W— выпуклое множество, которое не имеет общих точек
с неотрицательным октаном. Доказать, что существует вектор с^>0, с^=0,
такой, что cw < 0 для всех w Q W. [Указание. Использовать результат пре-
дыдущего упражнения.]
6.11. Решить задачу
g (х) = — х2>0; х>0; найти max z = f (х) = х-
Будут ли в точке оптимума выполняться условия Куна—Таккера? Пока-
зать, что F(x,X} не имеет седловой точки, х-компонента которой совпадала бы
с точкой оптимума.. Почему?
6.12. Решить задачу:
J(x) = — Xi +(х2 —1)2>0, х>0;
найти max z = (хг — З)2 4- х%.
Удовлетворяются ли в точке оптимума условия Куна—Таккера? Пока-
зать, что, хотя для всех h, при которых x*+h удовлетворяет ограничениям,
должно выполняться Vf(x*)h<0, неравенство Vf(x*)h<0 нарушается, если
рассматривать векторы h,, удовлетворяющие условию (6.36). Почему? Какая
из гипотез, принятых при выводе необходимых условий, нарушена?
6.13. Выполняется ли условия Куна—Таккера в точке оптимума для си-
туации, показанной на рис. 6.8?
6.14. Найти условия, гарантирующие существование производных dz*/dbi,
.о которых идет речь в § 6.3.
6.15. Пусть f(x)—вогнутая функция и глобальный экстремум f(x) для
х>0, Ах=Ь достигается в точке х*. Показать, что оптимальное решение
218
Гл. 6. Теория Куна —Таккера
задачи линейного программирования «Ау=?Ь,у>0; найти max z=*Vf(x*)y>
получается при у=х*. Установить связь этого утверждения с (6.29).
6.16. Рассмотрим задачу планирования производства некоторого продукта
на п периодов. Предполагается, что продукт может производиться в запас,
но размер запаса ограничен емкостью склада в А единиц продукта. Потреб-
ность в продукте считается детерминированной, но меняющейся от периода
к периоду. Весь спрос за данный период должен быть удовлетворен до кон-
ца этого периода. Он может быть удовлетворен частью из запасов, которые
имеются к началу периода, частью за счет продукта, произведенного в те-
чение периода. Стоимость хранения единицы продукта начинает исчисляться
сразу после окончания периода, в котором он был произведен, и рав-
няется D (за полный или неполный период). Предполагается, что стоимость
производства в период / является выпуклой дифференцируемой функцией
произведенного в этот период количества продукта. План предусматривает
наличие запаса в s единиц после окончания последнего периода. Ставится
задача так спланировать производство, чтобы минимизировать сумму затрат
на производство и хранение на п периодов. Используя теорию Куна—Таккера,
выписать соотношения, которым должен удовлетворять оптимальный план.
6.17. Дать пример функции двух переменных, имеющей седловую точку
в точке [х0, М- Построить в £3 график этой функции в окрестности точки
[хо, %о].
6.18. Показать, что целевая функция в первом примере § 3.9 является
строго выпуклой. Затем, используя теорию Куна — Таккера, доказать, что ре-
шение, полученное в § 3.9, действительно доставляет глобальный экстремум.
6.19. Рассмотреть допустимую область, изображенную на рис. 6.9, ко-
торая содержит только дискретное множество отмеченных точек. Показать,
что условие регулярности в этом случае не выполнено. Записать уравнения
ограничений, которые определяют такую допустимую область.
6.20. Показать, что необходимые условия Куна—Таккера выполняются
в экстремальных точках 2 и 4 на рис. 1.4,
6.21. Рассмотрим задачу линейного программирования:
Ах = Ь, х >0; найти max z — сх.
Обозначим через z*(b) оптимальное значение целевой функции для некото-
рого Ь, и пусть х* — оптимальное решение. Допустим, что мы заменили b на
Упражнения
219
b+eaj (а^ есть /-й столбец матрицы А). Заметим, что x* + eej есть допусти-
мое решение новой задачи, если Отсюда z*(b + eaj)>cx* + ecj.
Используем теорему Тейлора для того, чтобы выразить z*(b + eaj) через
z*(b) и е. Допустим, что функция z* везде дифференцируема. Показать, что
это приводит к следующему заключению:
V дг* * Л
если *>>0
и
V дг* » л
2^'дГаи>сР если xi = Q>
где dz*ldbi вычислены в соответствующей точке. Обозначим X* = дг*/дЬ{.
Используя этот подход, получить необходимые условия Куна—Таккера для
задачи с линейными ограничениями и нелинейной целевой функцией. Можно
ли подобным образом получить необходимые условия Куна—Таккера для
задачи с нелинейными ограничениями?
Такой подход предложен Дрейфусом и Фримером в приложении 2 кни-
ги [12*1.
ГЛАВА
КВАДРАТИЧНОЕ ПРОГРАММИРОВАНИЕ
Всякий дол да наполнится, и всякая
гора и холм да понизятся, кривизны вы-
прямятся, и неровные пути сделаются
гладкими.
Исаия
7.1. Введение. Как указывалось в § 1.2, задача квадратичного
программирования представляет собой частный случай задачи
нелинейного программирования, когда, ограничения линейные, а
целевая функция есть сумма линейной функции и квадратичной
формы. Целевая функция может быть записана в виде (1.10).
После введения вспомогательных переменных в ограничения
(так, как это сделано в § 2.3) мы можем записать общую за-
дачу квадратичного программирования в матричной форме, сле-
дующим образом:
Ах = Ь,
х>0; (7.1)
найти max z = ex-|-х'Dx.
Предполагается, что задача имеет m ограничений и п пере-
менных, так что матрица А имеет размеры mXn, D — размеры
nXn, Ь есть /n-мерный вектор, х и с суть n-мерные векторы. Как
указано в § 2.7, не умаляя общности, матрицу D можно считать
симметрической, что мы и будем делать в дальнейшем. Доста-
точно рассмотреть лишь задачу максимизации, ибо задача ми-
нимизации может быть к ней сведена простым изменением знака
целевой функции, поскольку
min f (х) — — max (— f (х)).
Так же как и в общем случае нелинейного программирова-
ния, не существует эффективного вычислительного метода для
нахождения глобального экстремума задачи квадратичного
программирования, если только не известно заранее, что любой
локальный экстремум является одновременно глобальным. Так
7.1. Введение
221
как в задаче (7.1) множество допустимых решений выпукло, то,
если целевая функция вогнутая, любой относительный макси-
мум является глобальным. Целевая функция есть сумма линей-
ной (и тем самым вогнутой) функции и квадратичной формы.
Она будет вогнутой, если x'Dx— вогнутая функция. Как пока-
зано в § 3.10, квадратичная форма x'Dx будет вогнутой функ-
цией, если она является неположительной или отрицательно
определенной (если форма отрицательно определенная, то она
является строго вогнутой функцией и глобальный максимум
является единственным). В дальнейшем мы будем рассматри-
вать только случаи, когда функция x'Dx вогнутая.
Поскольку ограничения задачи линейные, условия регуляр-
ности Куна —Таккера автоматически выполнены и поэтому вы-
воды гл. 6 могут быть использованы для получения необходи-
мых и достаточных условий оптимальности решения.
Для задач квадратичного программирования функции g?(x),
f(x), о которых идет речь в гл. 6, таковы:
^(x) = azx, f(x) = cx4-x'Dx, (7.2)
где а*— ья строка матрицы А. Тогда
^(x) = az, (7.3)
Д = + Vf(x) = c + 2x'D. (7.4)
' i-i
Мы знаем (см. гл. 6), что если х*>0 является оптимальным
решением задачи квадратичного программирования, то должен
существовать вектор X*, такой, что х*, X* удовлетворяют соот-
ношениям (6.23), (6.25), (6.26), (6.27). Рассмотрим сначала со-
отношения (6.23). Используя (7.3) и (7.4), получаем
с 4- (х*)'2 D — (X*)z А < 0. (7.5)
Транспонируем (7.5), замечая, что D'=D, и введем вектор
вспомогательных переменных
v* = А'Х* —с' —2Dx*>0.
Тогда (7.5) запишется в виде
с'4 2Dx*—А'Х* 4-v* = 0* (7.6)
Используя V*. мы можем (6.25) записать следующим образом:
(х)' V* — 0 или = 0, (7.7)
222
Гл. 7. Квадратичное программирование
Соотношение (6.26) в данном случае есть просто
Ах* = Ь, (7.8)
а условие (6.27) удовлетворяется автоматически при любом до-
пустимом решении и, следовательно, может быть опущено. Та-
ким образом, мы заключаем, что если х*>0 является оптималь-
ным решением задачи, то существуют такие v*>0 и V, что вы-
выполняются соотношения (7.6) — (7.8), которые являются
условиями Куна — Таккера применительно к задаче квадратич-
ного программирования.
Однако, поскольку функции £г(х) =а*х могут рассматриваться
и как выпуклые, и как вогнутые, а функция f(x) предполагается
вогнутой, необходимые условия являются также и достаточными.
Иными словами, если существуют х>0, v>0, X, которые удов-
летворяют условиям д
2 Dx — А'Х 4- v == — с', (7.9)
= у — 1, ..., /г,
то вектор х является оптимальным решением задачи квадратич-
ного программирования.
Суммируя сказанное выше, утверждаем: если задача квад-
ратичного программирования имеет оптимальное решение, то
существуют векторы х>0, v>0, X, удовлетворяющие условиям
(7.9); если же существуют х>0, v>0, X, удовлетворяющие ус-
ловиям (7.9), то х является оптимальным решением. Таким об-
разом, решение задачи квадратичного программирования сво-
дится к отысканию векторов х>0, v>0 и X, удовлетворяющих
условиям (7.9). В следующем параграфе мы увидим, как это
осуществляется.
7.2. Решение задачи квадратичного программирования с от-
рицательно определенной формой x'Dx. Мы рассмотрим сейчас
метод решения задачи (7.9), предложенный Вольфом [16]. Боль-
шим преимуществом этого метода перед другими является то,
что для получения решения здесь используется симплекс-метод.
Весьма существенно для дальнейшего, что решение системы
г х л
А 0 0 ] Г b
2D — А' 1я —с'
L у J L
(7.10)
удовлетворяющее требованиям х>0, v>0, x'v = 0, имеет не бо-
лее т + п ненулевых компонент. В самом деле, если k компонент
вектора х положительны, то ввиду условия xzv^=0 по меньшей
7.2. Задачи с отрицательно определенной формой x'Dx
223
мере k компонент вектора v равны нулю; следовательно, не бо-
лее чем п—k компонент вектора v положительны. Поэтому не
более п компонент 2п-мерного вектора [х, v] положительны и,
так как 1 есть m-мерный вектор, не более пг + п компонент век-
тора [х, X, v] отличны от нуля. Отсюда мы можем заключить,
что вектор, который удовлетворяет условиям (7.9) при х^>0,
v>0, должен быть базисным решением для (7.10). Поэтому для
нахождения решения системы (7.9) следует проверять только
базисные решения системы (7.10). Это свойство было отмечено
в работе [1].
В этом параграфе мы остановимся на случае, когда x'Dx —
отрицательно определенная квадратичная форма. В случае если
эта форма неположительная, при численном решении могут воз-
никнуть трудности, способы устранения которых будут рассмот-
рены позднее.
Если x'Dx — отрицательно определенная форма, легко пока-
зать, что решение задачи квадратичного программирования не
может быть неограниченным. Действительно, рассмотрим любую
точку х, лежащую на гиперсфере радиуса а с центром в начале
координат. Тогда х = от, где г — точка единичной гиперсферы
с тем же центром. При этом x'Dx = o2r'Dr. Пусть максимум вы-
ражения r'Dr на единичной гипосфере достигается в точке г0.
Тогда roDro = d<O и x'Dx<o2rf<0 для любой точки х на
гиперсфере радиуса о. Следовательно, x'Dx->—оо, когда |х|-> оо.
Если х#=0, мы можем написать
г«х'Ох[1+^].
Пусть максимум выражения [cr/r'Dr | на единичной гиперсфере
достигается в точке гь Значение максимума будет конечным,
ибо r'Drj #= 0. Тогда
СГ1
г; Dr!
и при |х|->оо имеем cx/x'Dx->0, z-+—оо. Таким образом, неза-
висимо от направления, в котором изменяется х, если 1х|,->оо,
то z—►—оо, следовательно максимальное значение z не может
быть сделано неограниченно большим. Когда форма неположи-
тельна, может случиться, что целевая функция неограничена.
Так будет, если, не покидая множества допустимых решений,
можно неограниченно двигаться из данной точки в направлении,
в котором значение x'Dx остается постоянным, а значение сх
возрастает.
Возвращаясь к случаю, когда x'Dx — отрицательно опреде-
ленная форма, получаем, что, поскольку здесь не может быть
сх I < 1
х' Dx | а
224
Гл. 7. Квадратичное программирование
неограниченного решения, в задаче либо не существует допусти-
мого решения, либо оптимальное решение единственно (един-
ственность также следует из того, что x'Dx — отрицательно
определенная форма). Следовательно, если существует допусти-
мое решение, то должно существовать по крайней мере одно ба-
зисное решение [хД, v] системы (7.10), удовлетворяющее усло-
виям х>0, v>0, x'v = 0. Первые п компонент вектора [х, X, v]
единственны и определяют оптимальное решение задачи квадра-
тичного программирования.
Вычислительная схема для нахождения такого базисного ре-
шения для (7.10) представляет собой незначительную модифи-
кацию способа искусственных переменных, используемого для
отыскания исходного базисного допустимого решения задачи
линейного программирования. На первом шаге определяется ба-
зисное допустимое решение системы Ах=Ь. Это обычный первый
этап симплекс-метода. Как только допустимое решение системы
Ах = Ь найдено, мы можем быть уверены в существовании базис-
ного решения для (7.10) с х>0, v>0 и x'v = 0 (если форма x'Dx
отрицательно определенная). Способ его нахождения также
весьма напоминает первый этап в задаче линейного программи-
рования. Система уравнений (7.10) преобразуется путем до-
бавления некоторых неотрицательных искусственных перемен-
ных. Затем максимизируется сумма искусственных переменных,
взятая с обратным знаком при дополнительном условии x'v = 0.
Когда на некотором шаге эта сумма обращается в нуль, мы
получаем искомое решение системы (7.10).
Для осуществления только что описанной процедуры весьма
удобно при решении системы, полученной после введения искус-
ственных переменных, использовать базисное допустимое реше-
ние системы Ах = Ь. Пусть В — базисная матрица и хв— вектор
соответствующих базисных переменных, так что Вхв = Ь. Отме-
тим, что это базисное решение удовлетворяет m первым ограни-
чениям системы (7.10). Поэтому, используя его, мы будем до-
бавлять искусственные переменные лишь в последние п ограни-
чений (7.10). Это может быть сделано следующим образом.
Вместо системы (7.10) рассмотрим систему
Ах = Ь,
2Dx — AZX —Н v-f-Eu — — с', (7-И)
где Е= ||ДД;|| —диагональная матрица с диагональными эле-
ментами Л5=±1, причем требуется, чтобы и>0.
Выясним, как определяется знак Aj. Пусть DB содержит
столбцы матрицы D, соответствующие тем столбцам матрицы А,
которые вошли в В. Обозначим /-ю строку матрицы DBчерез
7.2. Задачи с отрицательно определенной формой x'Dx
225
Тогда
1+1, если — Cj — 2dBxB>0,
Д, = { .
I — 1, если — Cj — 2dBxB < 0.
При таких Ду, если положить
= | — Cj-2dixsI>0, /=1,...,«, Х = 0, v = 0, (7.13)
мы получим допустимое решение для (7.11). Это решение
содержит не более п + /п положительных переменных. Мы
можем написать
(7-12)
В 01
2DS EJ
Хд
U
Ясно, что полученное решение является базисным для (7.11),
поскольку если
Г в О'
2DB EJ’
Bq =
ТО Bq’ =
В 0
—2EDBB-1 E
- (7.14)
b
- c
т. е. матрица коэффициентов В<? неособенная. Выражение для
Bq1 может быть получено с помощью способов, описанных в
§ 2.1 и {ЛА 3.20}.
Имея базисное решение для (7.11) с хв^0, и>0, мы исполь-
зуем симплекс-метод, чтобы свести выражение — макси-
j
мизируя его, к нулю. Отличие от стандартной схемы симплекс-
метода состоит только в том. что если х3>0, то запрещается
вводить в базис а3>0, и наоборот.
Остановимся более подробно на новой задаче нелинейного
программирования, решение которой является одновременно
оптимальным в задаче квадратичного программирования. Отме-
тим, что компоненты вектора 1 не имеют ограничений на знак.
Для того чтобы в новой задаче нелинейного программирования
сделать все переменные неотрицательными, введем новые пере-
менные, полагая X,=g — где g+О, g+0. Тогда, если обозначить
01
в]’ t=|b,-c'].
V, u|, (7.15)
собираемся решать, примет
A 0 0 0
2D —А' А' 1л
w = [x, g, g,
то нелинейная задача, которую мы
вид
Qw = f,
Q =
x'v = 0;
найти maxZ =— 2+-
' (7.16)
15 Зак. 735
226
Гл. 7. Квадратичное программирование
В этой задаче нелинейным является лишь ограничение x'v = 0.
Мы будем решать ее симплекс-методом с описанным выше видо-
изменением. Для решения удобно использовать модифицирован-
ный симплекс-метод. Уже было показано, как определять
начальное базисное решение для (7.16). Сначала, используя пер-
вый этап, находим базисное решение хв и матрицу В, рассма-
тривая лишь ограничения Ах = Ь. Если затем положить
u = Е (-с' — 2DBxB) >0, (7.17)
то qB = [xB, и] будет базисным решением для (7.16) с базисной
матрицей BQ, определяемой выражением (7.14). Далее, мы на-
ходим выражение матрицы через В-1, Е, DB и используем ее
в исходной таблице для реализации модифицированного сим-
плекс-метода.
Объем вычислений при решении задачи квадратичного про-
граммирования с m ограничениями и п переменными примерно
такой же, как при решении задачи линейного программирова-
ния с п + т ограничениями.
Идея последовательного определения базисного решения си-
стемы (7.10), удовлетворяющего требованиям х>0, v>0, x'v = 0,
принадлежит Марковицу [12]. Вольф первым осуществил эту
идею, используя схему симплекс-метода.
Один из важных вопросов, связанных с вычислительной про-
цедурой, долгое время оставался невыясненным. Не было пока-
зано, что если очередная итерация симплексного метода (учи-
тывающего требование XjVj — O) неосуществима, то на последней
итерации выполняется равенство Z = 0 и мы получаем желаемое
решение. Ответ на этот вопрос приводится в следующем пара-
графе.
7.3. Окончание процесса в случае отрицательной определен-
ности формы x'Dx. Мы докажем здесь, что если при решении
задачи (7.16) с условием x'v = 0 очередная симплексная итера-
ция не может быть осуществлена, то последнему базисному ре-
шению соответствует Z = 0. Мы, конечно, по-прежнему считаем,
что форма x'Dx — отрицательно определенная.
Рассмотрим положение, соответствующее случаю, когда про-
ведение очередной симплексной итерации невозможно. Пусть
вектор Xi содержит положительные компоненты вектора х, a Vi —
соответствующие компоненты вектора v. Тогда Vj=O, так как
x'v1 = 0. Пусть v2 содержит положительные компоненты век-
тора v, а Х2 — соответствующие компоненты вектора х. Оче-
видно, что Х2 = 0. В этих обозначениях оптимальное решение
7.3. Окончание процесса
227
задачи
Qw = f, Vi = 0, х2 — О, w > О;
(7.18)
найти max Z =— 2^/ = hw
j J
будет точно таким, как решение задачи (7.16), полученное с уче-
том ограничения xzv = 0 на выбор базиса, так как способ, кото-
рым была решена задача (7.16), обеспечивает, что Zj — hj^O для
всех переменных, не содержащихся в vj или х2 (hj принимает
значение —1 для Uj и 0 для остальных переменных).
В Xi и х2 не обязательно содержатся все компоненты век-
тора х. Пусть х3 содержит тс компоненты вектора х, которые не
вошли в Xi и х2, а v3— те компоненты вектора у, которые не
вошли в Vi и v2.
При таком разбиении мы можем переписать ограниче-
ния Qw=f следующим образом:
AiXj + А2х2 + А3х3 00 0 0 0 0 — Ь,
20цХ1 4“2DI2x2 4~2D13x3 — Ajg Aj§ 4“ Ivj 4" ~ — ci,
2D21xt 4~2D22x2 4-2D23x3 — A2^ Ц-* A2I5 4~lv2 -|-~E2ii=—c2,
2D31Xi 4“ 2D32x2 4“ 2D33x3 — A3£ 4“ A3| 4~ 1уз 4~ Ези = — c3.
(7.19)
Рассмотрим задачу, двойственную по отношению к за-
даче (7.18). Пусть вектор-строка (s, ti, t2, t3) есть оптимальное
решение двойственной задачи (принцип разбиения компонент
оптимального решения аналогичен использованному в (7.19)).
При последующем анализе не обязательно включать двойствен-
ные переменные, соответствующие ограничениям vi = 0 и х2 = 0
в (7.18). Можно просто считать, что из матрицы Q исключены
столбцы, соответствующие переменным из х2 и уь а сами пере-
менные не рассматриваются. Тогда решение двойственной за-
дачи должно удовлетворять соотношениям
sAi + StjDn -4“ 2t2D2i + 2t3D31 = О,
sA3 + 2tjD13 2t2D23 —h 2t3D33 0,
tiAi + t2A2 -j- t3A3 =0, ,7 20\
t2 =0, '
t3 >0,
+ t2E2 + t3E3 —1
15*
228
Гл. 7. Квадратичное программирование
и, так как оптимальные решения прямой и двойственной задач
совпадают, значения целевых функций этих задач должны со-
впадать, т. е.
max Z = sb — txc[ — — t3c'. (7.21)
В первой группе соотношений (7.20) знак равенства имеет
место на основании сказанного в § 2.5. Так как компоненты век-
тора Xi положительны, соответствующие ограничения двойствен-
ной задачи должны выполняться со знаком равенства; по ана-
логичной причине t2 = 0. В третьей группе ограничений строгие
равенства имеют место в результате объединения ограничений,
соответствующих g и или, проще, ввиду того, что компоненты
вектора X не имеют ограничений на знак.
Рассмотрим сейчас более детально соотношения (7.20) с
целью выяснить свойства оптимального решения двойственной
задачи. Умножая первую группу ограничений справа на
а вторую — на t3, мы получаем, с учетом того что t2 = 0 и t3>0,
sAiti 4" 2ti Dnt] + 2t3 D3iti = 0,
sA3t3 -4 2ti Dist3 + 2t3 D33t3 0.
После сложения этих соотношений будем иметь
s [Aiti 4- A3t3] 2 (ti, t3)
Dn,
D3i,
D13
D.j3
0,
(7.22)
но из третьей группы соотношений (7.20) следует, что первое
слагаемое в (7.22) обращается в нуль. Кроме того, второе сла-
гаемое представляет собой квадратичную форму вида 2x'Dx, ко-
торая вычисляется для конкретного значения вектора х, компо-
нентами которого служат компоненты векторов tb t2 и t3. Так
как эта форма отрицательно определенная, то из неравенства
(7.22) следует ti = 0, t3 = 0. Именно в этом месте нам требуется
отрицательная определенность квадратичной формы x'Dx.
Итак, установлено, что ti = 0, t2 = 0, t3 = 0. Следовательно, из
первой группы ограничений (7.20) имеем sAi = 0, откуда sAix2 = 0.
Но так как AiXi = b, то sb = O. Принимая это во внимание, из
(7.21) найдем, что maxZ=0, т. е. ^ = 0, / = 1,...,/г, и, следова-
тельно, решая задачу (7.16) с учетом ограничения x'v = 0, мы
действительно получаем искомое решение на последней возмож-
ной симплексной итерации.
Выше мы не учитывали возможности вырождения или за-
цикливания. Эти трудности можно обойти, используя извест-
ные алгоритмы линейного программирования (см., например,
{ЛП6.1}—{ЛП6.8}).
7.4. Способ Чарнса
229
7.4. Способ Чарнса для случая неположительности квадра-
тичной формы. В случае когда квадратичная форма x'Dx
является лишь неположительной, при попытке реализации при-
веденной выше вычислительной схемы могут возникнуть суще-
ственные осложнения. Во-первых, в этом случае может не суще-
ствовать ограниченного решения, так что задача (7.9) не будет
иметь решения при х>0 и v>0. Во-вторых, даже если задача
квадратичного программирования имеет оптимальное решение,
нет уверенности, что при окончании вычислительной процедуры
мы получаем именно его.
Следует отметить, что неположительная квадратичная форма
может быть превращена в отрицательно определенную путем
малого изменения диагональных элементов матрицы D. Точнее,
если x'Dx — неположительная форма, то x'(D+eI)x — уже отри-
цательно определенная форма при любом е<0. Действительно,
x'Dx<<0 при любом х, а ех'1х<0 при любом х=#0. Таким обра-
зом, x'(D + eI) х<0 при любом х=#0. Следовательно, если мы
имеем задачу квадратичного программирования с неположи-
тельной квадратичной формой, то после незначительного умень-
шения диагональных элементов матрицы D мы преобразуем
форму в отрицательно определенную. Ввиду малости изменений
можно рассчитывать, что решение преобразованной задачи бу-
дет близким к решению исходной. Изменение формы будет суще-
ственно влиять на результат лишь в том случае, когда в исход-
ной задаче форма x'Dx не знакопостоянна и задача имеет не-
ограниченное решение. Однако, как и в задачах линейного
программирования, при решении достаточно хорошо сформули-
рованных практических задач такой случай не возникает. Ука-
занное преобразование исходной задачи в случае неположитель-
ной формы предложено Чарнсом [4].
Вообще говоря, метод, рассмотренный в § 7.2, применим и
в случае, когда форма x'Dx неположительная. Поэтому можно
сначала попытаться использовать обычную процедуру, не пре-
образуя D.
Читателя может интересовать, как заранее определить, яв-
ляется ли квадратичная форма положительно определенной,
отрицательно определенной и т. д. В простых случаях это можно
сделать непосредственной проверкой. В общем случае, однако,
требуется найти характеристические числа матрицы D1). Эта
задача может оказаться весьма трудной, и поэтому вид квадра-
Ч Именно, если все характеристические числа матрицы D отрицательны,
то форма x'Dx — отрицательно определенная, если же наряду с отрицатель-
ными имеются нулевые характеристические числа, форма будет неположи-
тельной. — Прим. ред.
230
Гл. 7. Квадратичное программирование
тичной формы x'Dx обычно устанавливается из косвенных (эко-
номических или физических) соображений, связанных с природ
дой задачи.
7.5. Способ Вольфа, использующий параметризацию целевой
функции. Вольф [16] предложил значительно более сложную, чем;
приведенная выше, процедуру для решения задачи квадратич-
ного программирования. С практической точки зрения способ,,
рассмотренный в предыдущем параграфе, более удобен для ре-
шения задачи с неположительной формой. Подход Вольфа инте-
ресен не столько из-за способа, который он использует для:
случая неположительной формы, сколько из-за процедуры, ко-
торую он вводит для решения задачи квадратичного програм-
мирования с целевой функцией
z = 0cx + x'Dx (7.23)
при всех значениях 0>О. Такая задача была рассмотрена Мар-
ковицем в работе [13].
Мы будем рассматривать задачу с целевой функцией (7.23)
лишь для случая, когда форма x'Dx отрицательно определенная.
В случае когда x'Dx неположительная, метод также применим,
но гарантировать успех при его использовании мы можем, толь-
ко если преобразуем форму к отрицательно определенной. Так
как предполагается, что форма x'Dx — отрицательно определен-
ная, то при каждом фиксированном значении 0>О задача будет
иметь единственное решение. Решаем сначала задачу при 0 = 0.
Далее рассмотрим следующий способ изменения 0. Мы хотим
построить последовательность базисных решений для системы
х
А О О
2D —А' А'
О'
I
ь '
-0С'
О '
— с'
(7.24)
£
ь
о
+ 0
v
при условиях, что все переменные неотрицательны, x'v = 0 и
0 изменяется от 0 до оо. Предполагается, что мы знаем такое
базисное решение для 0 = 0. Эта задача очень похожа на за-
дачу параметрического программирования, когда вектор в пра-
вой части ограничений зависит от параметра (см. {ЛП 11.4}).
Обозначим г = [х, g, v], и пусть Bq1—матрица, обратная к
той базисной матрице, которую мы получили при решении за-
дачи с 0 = 0. Будем считать, что если некоторые Uj вошли в по-
следний базис и оказались равными нулю, то они исключаются
из рассмотрения. Это всегда можно сделать (почему?). Обозна-
7.5. Способ Вольфа
231
чим через гв базисное решение, так что гв—B^Jb, 0]. Пусть
далее
h —Bq^O, — с']. (7.25)
Через гв обозначим вектор базисных переменных, вычисленных
для рассмотренного выше базисного решения при 0>О. Тогда
гв = Bq1 {[b, 0] + 0 [0, - с']} = гв + 0h. (7.26)
Базисное решение будет допустимым, если
Гв/ = Гвг + 0А/>О, Z-1, ..., т^п. (7.27)
В случае когда при всех /, начальное базисное решение
оказывается допустимым для всех 0>О и оптимальный базис
задачи квадратичного программирования не зависит от 0.
Однако, если хотя бы одно из hi меньше нуля, исходное базис-
ное решение уже не будет допустимым при
0 > 01 = min ( — < 0. (7.28)
i I ni J
Чтобы обеспечить допустимость решения при переходе 0 че-
рез значение 0Ь необходимо изменить базис. Отметим, что, когда
0 — 01, по крайней мере одна из базисных переменных равна
нулю. Условимся всегда исключать из базиса такую перемен-
ную, которая обращается в нуль при 0 = 01 (пусть это xR \. Но-
и/
выи вектор включается в базис с нулевой интенсивностью.
Выясним, какой вектор следует включить в базис, имея в виду,
что после изменения базиса можно будет увеличивать 0, сохра-
няя новый базис. Если вектор qj вошел в базис и уу. —B^q^,
то новое значение w-й компоненты вектора h будет hnlyUj. Однако
и, следовательно, для того чтобы можно было увеличи-
вать 0, начиная с 0Ь yUj должно быть меньше нуля; в этом слу-
чае новое значение u-й компоненты вектора h будет положи^
тельным.
Действительно, при 0 = 0± значение //-й базисной переменной
в новом базисе равно нулю, поскольку новый вектор входит в
базис с нулевой интенсивностью. Следовательно, ее значение для
0>0i есть (6—§i)hulyUj, и оно будет отрицательным, еслиум^<0.
Любой вектор с r/Uj<0, если он при введении в базис с положи-
тельной интенсивностью не приводит к нарушению условия
x'v = 0, может быть использован в новом базисе. Новое базис-
ное решение годится до тех пор, пока при увеличении 0 хотя
бы одна из базисных переменных не обратится в нуль.
232
Гл. 7. Квадратичное программирование
Таким образом, мы получаем последовательность критиче-
ских значений 0о = О, 01, 02, ..., такую, что Qk<®k+i и для всех 0,
лежащих в интервале 0/^0^0/t+i, оптимальным будет один и
тот же базис. Так как существует лишь конечное число различ-
ных базисов, то описанная процедура может привести лишь к
одному из следующих двух случаев:
а) приходим в такую точку, что ни для одного из векторов,
которые можно было бы включить в базис, не выполняется
b) полученный базис остается оптимальным при неограни-
ченном возрастании 0. I
Мы покажем, что на самом деле имеет место лишь случай (Ь).
Для каждой критической величины 0л существует оптималь- i
ное решение x*k задачи квадратичного программирования. Легко
определить оптимальное решение х* для любого 0, 0/г<^0^0/н-1,
используя лишь х£ и х*+1. Как было установлено выше, если |
Bq — базисная матрица для 0 из интервала 0& <0<C0ft+i, rBft — J
соответствующее этой матрице базисное решение при fl = 0h и
rB> k+i — базисное решение при 0 = 0fe+i (определенное до пере-
хода к новому базису), то
TBk — Bq1 {[b, 0]—0# [о, — с]}, Гд £ + 1 = Bq1 {[Ь, О]4~0/?4-1 [о, — с]}» я
или #
Гв, *+1 = Гв* + (0А+1 —0ft)h, где —с']. ||
Аналогично, для любого 0, 0^0^С0ы-ь соответствующее базис- J
ное решение гв есть
= rBfe+(0 — 0ft)h= 1 - eft+1 _ Гд- И ' ,1
(7.29) Я
Отсюда я
х''=[(1-<ст)<+(ёг^к)х».]' <7-3°) I
так как х^+1 — одно и то же до и после изменения базиса при
0 = 0ь+ь Если после того, как при 0==0fe сделано изменение ба- |
зиса, новый базис остается оптимальным при всех 0>0fe, то для f
ЛЮбоГО 0>0fe |
«•в = ^ + (0-0л)Ь> x- = x; + (0-0,)t, (7.31) I
где /j = 0, если xj — небазисная переменная, и t^ht, если Xj~rBi. Ц
7.5. Способ Вольфа
233
Интересно отметить, что при изменении базиса системы (7.24)
в точках Ой мы как бы проводим решение задачи линейного про-
граммирования
~х~
А 0 0 0 0 '
2D - Az А' I с'
(7.32)
_е
[х, С, I, V, 0]>О;
найти max Ze = 0
при ограничении x'v = 0. Заметим, что здесь нет противоречия
с тем, что в этой задаче переменная 0 оказывается базисной,
так как при критических значениях 0 одна из базисных перемен-
ных в базисном решении системы (7.24) обращается в нуль.
Следовательно, при критических значениях 0 базисное решение
системы (7.24) содержит не более m + n—1 положительных пере-
менных. В (7.32) может быть т + п положительных переменных
и одна из них 0, а остальные есть не что иное, как базисные
переменные соответствующего решения системы (7.24).
Решение задачи (7.32), начатое с базисного допустимого ре-
шения, соответствующего 0 = 0, представляет собой удобный спо-
соб для определения совокупности критических значений 0.
Покажем, что задача (7.32) имеет неограниченное решение и
что приведенный выше процесс заканчивается случаем (Ь). Пред-
положим противное: пусть мы пришли в точку, где любой век-
тор, который может войти в базис при выполнении условия
x'v = 0, удовлетворяет критерию оптимальности. Тогда рассмо-
трим, как и в § 7.3, совместно соответствующие прямую и двой-
ственную задачи линейного программирования. Двойственная
задача имеет форму (7.20), лишь в последней группе ограниче-
ний будем иметь
tiCi + t2c2 + t3c3 1 (7.33)
вместо
t1E1+t2E2 + t3E3<-1. (7.34)
Анализ, проведенный в § 7.3, показывает, что в оптимальном
решении двойственной задачи t1 = t2 = t3 = 0. Но это решение
должно также удовлетворять и условию (7.33), что невозможно.
Таким образом, мы приходим к противоречию и, значит, реше-
ние действительно не ограничено.
234
Гл, 7. Квадратичное программирование
7.6. Пример. Чтобы проиллюстрировать вычислительный ме-
тод, развитый в § 7.2, мы снова решим задачу, рассмотренную
в § 4.8,
2%i -j— Зх2 —1~ х3 =:::: 6,
2%i —j- Ч” ^4==: 4, (7.35)
хр х2, х3, х4>0;
найти max z = 2х14 х2 — х2,
как задачу квадратичного программирования. В обозначениях
§ 7.2 x'Dx——x2v и эта квадратичная форма, очевидно, неполо-
жительная. Далее
1 0 0 0"
’2 3 10’ 0 0 0 0
А = , D =
.2101 0 0 0 0
0 0 0 0_
с = (2, 1, 0, 0), ’ Ь = [6, 4].
Приведенные ниже ограничения (7.36) представляют сово-
купность условий вида (7.16) (для данного примера), с кото-
рыми мы начинаем решение. Несмотря на то что форма x'Dx
не является отрицательно определенной, мы увидим, что приме-
нение приведенного в § 7.2 вычислительного метода без преобра-
зования квадратичной формы не вызовет осложнений.
В настоящем примере легко определить базисное допустимое
решение для ограничений Ах=Ь, не используя первый этап сим-
плекс-метода. Таким является решение Xi = 3/2, х2= 1, х2=х4 = 0.
Для него
“—2 О”
1 ’ о 0 •
2 Л Л
Далее необходимо определить значения Д,- и начальные значе-
ния ttj. Полагая ^=^=0, v = 0, мы найдем из третьего ограниче-
ния (7.36), используя %! = 3/2, что A1^i=l. Отсюда Ai = l, tti = l.
Из четвертого ограничения Д2^2 =—1, так что Д2 =—1,
Наконец, из пятого и шестого ограничений Д3и3 = Д4Щ = 0, так что
мы можем взять Д3—Д4=1 и rz3 = u4 = 0. Здесь следует.заметить,
что вместо и3 и и4 мы можем ввести в базис с нулевой интенсив-
ностью и v4. Поскольку вреда такая замена не принесет, а
7.6. Пример
235
число итераций при этом может сократиться, мы так и сделаем.
Переменные м3 и могут быть исключены из рассмотрения.
В исходной базисной матрице BQ первые два столбца будут
тогда соответствовать переменным Xj и х2, третий и четвертый
столбцы — переменным щ и а последние два столбца — пере-
менным у3 и у4. Имеем
2xt 4-Зх2 4 х3 ' =6,
^2^4 2^-2^4 2^4-^ 4-A^i = -2,
— 3£i-'-3£i— ^4-^2
— t>2 "I" §2
30 0 0 0“
10 0 0 0
0 1 0 0 0
00—100
0 0 0 1 0
0 0 0 0 1
4-^2 4-Д2«2 = -l,
4-#з 4- Л3Я3 =0#
4-^4 4А4Щ=0(
(7.36)
- 1 4 3 4 0 0 0 о-
1 2 1 2 0 0 0 0
JI 70- аз 1 2 3 2 1 0 0 0
0 0 0 —1 0 0
0 0 0 0 1 0
0 ‘ 0 0 0 0 1
(7.37)
Матрица Bq1 вычисляется по формулам (7.14). Начальное ба-
зисное допустимое решение системы (7.36) есть
О
Хх = 2“ ’ х2 = 1 ’ ^1 == h zr2 == 1, = v4 = 0
(остальные переменные нулевые). Мы хотим максимизировать
Z = —щ—и?. Значение Z, соответствующее начальному базис-
ному решению, есть —2. Для нахождения максимума Z исполь-
зуется модифицированный симплекс-метод, но при его реализа-
ции учитывается требование =
Векторы, соответствующие небазисным переменным, суть
=ер =е2; ч£,=1°> °> - 2’ ~3’ q5l;
q^ = [0, 0, —2, —1, 0, —1] = — q? ; qOi = e3; qOj = e4.
'Оценки небазисных переменных равны нулю, и, следовательно,
.для всех векторов, которые рассматриваются на предмет
236
Гл. 7. Квадратичное программирование
включения в базис, надо проверять только знак Zj. Для началь-
ного базисного решения
св = (0, 0, -1, -1, 0, 0), свВ5’ = (|. —-1, 1, 0, О)
и, так как Z^CbBq^,
Zx.^-4, Z£, = -l, Z61 = l,
Zb=l, = Zv=-\, Z.2=l.
Таблицы для решения примера
Таблица 7J
базисные переменные 31 02 03 04 05 06 Че У?’
Z 1 2 3 2 -1 1 0 0 — 2 3 2
। 1 ~4 ’ 3 4 0 0 0 0 3 2 3 4
J 2 1 2 0 0 0 0 1 __ 1 2
i'i — 1 3 2 1 0 0 0 1
U-2 0 0 0 -1 0 0 1 0
1'3 0 0 0 0 1 0 0 0
1’4 0 0 . 0 0 0 1 0 0
Таблица 7.Z
Z 0 0 0 1 0 0 — 1 -3
Л 0 0 -4 0 0 0 1 1
*2 4 0 4 0 0 0 4 3 2 “3
Z4 -4 1 2 3 0 0 0 2 3 4 ~3
U2 0 0 0 -1 0 0 1
V3 0 0 0 0 1 0 0 — 1
V4 0 0 0 0 0 1 0 0
7.6. Пример
237
Наименьшее значение Zj есть —3/2, минимум достигается
при векторе, соответствующем переменной х4. Переменная ц4
входит в число базисных с нулевой интенсивностью. Следова-
тельно, мы можем позволить х4 становиться положительной,
оставляя равным нулю. Поэтому на первой итерации qx вхо-
дит в базис. Данные для первой итерации приведены в табл. 7,1.
Вектор qM в результате итерации исключается из базиса (см.
табл. 7.2). Отметим, что v4 должно оставаться равным нулю.
Новые значения Zj суть
Zr3 = 0, ZSl = -3, Zgl = 3, Z^ = -l, Z?2 = l, Z^ = 0, ZF,= 1.
На следующей итерации в базис входит вектор q^. Из табл. 7.2
видно, что вектор qf/2 будет исключен из базиса. Следовательно,
все искусственные переменные будут обращены в нуль, и при
этом получается искомое максимальное значение Z. Поэтому не
требуется преобразовывать всю табл. 7.2, достаточно преобразо-
вать лишь столбец q$. Новые значения базисных переменных
после того, как и2 обращено в нуль, суть
2 14 10 . 1 1 Л
' g » Х4 -- g , Xj -- 3 , ^3 -- 3 , ^4 - 0»
Таким образом, мы получили решение для (7.9), причем требо-
вание х>0, v>0 удовлетворено. Отсюда единственное оптималь-
ное решение задачи квадратичного программирования есть
2 14 А 10 «. 1
, х2 — g > Хз — 0, х4 — g ♦ Aq — »
Х2 = 0, = v2 = 0, , v4 = 0.
Мы пришли, конечно, к тому же результату, который был по-
лучен графически в гл. 4.
Помимо демонстрации метода решения задачи квадратично-
го программирования, изложенного в § 7.2, этот пример застав-
ляет сделать вывод, что даже весьма простые задачи квадратич-
ного программирования приводят в процессе их решения к
линейным задачам значительного размера. При практическом
решении задач квадратичного программирования следует попы-
таться оценить с вычислительной точки зрения, целесообразно ли
пользоваться приведенным методом или лучше проводить ап-
проксимацию задачи, как это показано в гл. 4.
Чтобы проиллюстрировать приведенный в § 7.5 параметри-
ческий метод решения, мы решим задачу с теми же ограниче-
ниями и целевой функцией
z — 20X1 4- 0X2 — Xi
Решение для всех 0>0
Таблица 7.3
Базисные переменные fil fh fh fit Дз 06 rlB y(D
Z, 0 0 0 0 0 0 0 0
‘*2 J 0 0 0 0 0 2 0
*4 -J 1 0 0 0 0 2 0
0 0 1 0 0 0 0 -2
^2 0 0 0 1 0 0 0 CEO
V3 0 0 0 0 1 0 0 -1
М 0 0 0 0 0 1 0 0
Таблица 7.4
г» 0 0 0 0 0 0 0 0
Х2 0 0 0 0 0 2 0
*4 -h 1 0 0 0 0 0 0
0 0 1 ~ 3 0 0 0 4 “3
0 0 0 -A 0 0 0
1 V3 0 0 0 -A 1 0 0
«4 0 0 0 0 0 1 0 CEO
Таблица 7.5
г> 0 0 0 0 0 0 0 -1
2*2 3 0 . 0 0 0 0 2 0
*4 -a 1 0 0 0 0 2 0
»1 0 0 1 “3 0 _4 3 0
fl 0 0 0 1 3 0 1 3 0 1 3
V.3 0 0 0 1 3 I 1 0 1 ~ 3
Г2 0 0 0 0 0 -1 0 0
7.6. Пример
239
Таблица 7.6
базисные переменные 0! 02 03 01 05 06 r(l) y*n
Z, 0 0 3 -4 0 -1 0 -t
^2 4 0 0 0 0 0 2
•Г 4 -4 1 0 0 0 0 2~
е 0 0 i -4 0 -1 0 -i
Г1 0 0 i -4 0 0 0 -4
гз 0 0 4 -4 1 0 0 -4
<2 0 0 0 0 0 -1 0 0
Таблица 7.7
Z, 3 ~8 9 8 3 4 -4 0 -1 9 4 — J
Х2 1 2 1 2 0 0 0 0 1 0
*1 _ 1 4 3 А 0 0 0 0 3 2 0
0 . _ 3 8 9 8 з 4 I — 2 0 -1 9 A -1
_zA_ 3 8 1 4 I 2 0 0 t 0
из — 1 8 3 8 1 4 -4 1 0 t 0
<2 0 0 0 0 0 -1 0 -1
для всех 9>0. Ограничения приводятся к виду (7.36). Мы уви-
дим, что при 0=1 получается решение, совпадающее с приведен-
ным выше.
Процесс начинается с определения решения задачи при 0 = 0,
т. е. для целевой функции z——x2v Ясно, что оптимальным
Является решение %i = 0, х2 — любое из интервала 0<Lr2^2. Мы
можем сразу записать оптимальное базисное решение для (7.36).
Значения базисных переменных есть
х2 = х4 = 2, <ох = 0, — 0, = 0, = 0,
240
Гл. 7. Квадратичное программирование
Этому базисному решению соответствует табл. 7.3 модифициро-
ванного симплекс-метода. Прежде чем пытаться увеличивать 0,
мы должны исключить из базиса векторы, соответствующие п2 и
w4. Это делается весьма произвольно (см. табл. 7.4 и 7.5). Необ-
ходимо лишь, если Xj — базисная переменная, не позволять Uj
становиться базисной, и наоборот.
Получив табл. 7.5, мы начнем максимизировать 0. Отметим,
что оценки каждого вектора, за исключением [0, с'], равны нулю,
а оценка вектора [0, с'] равна 1. На первой итерации 0 вводится
в базис с нулевой интенсивностью (см. табл. 7.6). Далее Xi вхо-
дит в базис вместо х4. Значение 0 возрастает от 0 до 9/4. Пы-
таясь ввести в базис а4, мы видим, что решение оказывается
неограниченным. На этом процесс вычислений заканчивается.
Таким образом,
0=4+б> £2=б> *з=4’
есть решение для (7.32) при любом д>0. Кроме того, эти значе-
ния (исключая 0) представляют собой базисное допустимое ре-
шение для (7.24) при любом б>0, причем удовлетворяется усло-
вие x'v = 0.
з
Следовательно, X)--у, х2=1, х3 = х4 = 0 является опти-
мальным решением квадратичной задачи при любом 0>9/4. Это
крайняя точка выпуклого множества допустимых решений. На
7.7, Другие методы
241
рис. 7.1 проиллюстрирован случай, соответствующий 0 = 4. От-
метим, что х* = [0, 2, 0, 2]. Хотя при 0 = 0 существует не един-
ственное оптимальное решение, мы не можем увеличивать 0 до
тех пор, пока в базисном решении х2=х4=2, х3 = 0. Введем в
[3 *1
у» 1, 0, 0 .
Решение, соответствующее 0=1, определяется тогда выражением
х* — х*_1_Ах* — Г2 — 0 —1 '
\ 9/ 0 ' 9Х1-[3’ 9 ’ и’ 9J’
что совпадает с полученным выше.
7.7. Другие методы решения задач квадратичного програм-
мирования. В этом параграфе мы коротко изложим некоторые
другие методы решения задач квадратичного программирования.
Отмётим, что мы не делаем попытки рассмотреть все существую-
щие методы.
а) Метод Франк и Вольфа. Еще до появления метода, изло-
женного в § 7.2, Вольф совместно с Франк [8] разработал
несколько иную схему решения задач квадратичного програм-
мирования для случаев, когда форма x'Dx отрицательно опре-
деленная или неположительная. И здесь отправным пунктом
метода являются условия Куна — Таккера (7.9). Однако при
нахождении допустимого решения для (7.10) применяется обыч-
ный первый этап симплекс-метода и не требуется выполнения
условия x'v = 0. Если допустимое решение для (7.10) не найдено,
проверяется условие Ах=Ь. Если оказывается, что система
Ах=Ь имеет допустимое решение, не удовлетворяющее (7.10),
это означает, что задача не имеет ограниченного решения. Если
существует допустимое решение для (7.10) (хотя бы и не удо-
влетворяющее условию x'v = 0), то (7.1) будет иметь конечное
оптимальное решение.
Предположим, что базисное допустимое решение для (7.10)
найдено. Франк и Вольф осуществляют далее переход к базис-
ному допустимому решению, для которого x'v = 0. Покажем, как
это делается. Обозначим Ф = [х, v]>0, Ф+= (v', х')^>0. Тогда
~ф+ф = l-(v'x-|- x'v) = x'v >0.
Следовательно, допустимое решение, для которого значение
Z = —Ф+Ф максимально (т. е. нуль), является оптимальным.
Для нахождения максимума Z решается последовательность
задач линейного программирования.
Пусть Фо+ есть Ф+, соответствующее начальному базисному
решению, полученному на первом этапе симплекс-метода. Далее
16 Зак. 735
242
Гл. 7. Квадратичное программирование
с помощью симплекс-метода ищется максимум линейной функ-
ции Zi = — Фо Ф (Фо — фиксированный вектор). Применение
симплекс-метода дает (если нет вырождения) последователь-
ность базисных допустимых решений Ф(1), Ф(2), такую,
что — Ф^Ф (1) < - Фо'Ф (2) < — Фо+ Ф (3) < .... Мы остановим
процесс на первом Ф(й), таком, что либо а) Ф4 (А)Ф(й) =0, либо
Ь) —Ф^Ф(£)> — уФо'Фо. В случае (а) мы имеем оптимальное
решение. Если процесс остановлен по признаку (Ь), мы опреде-
ляем — ФГ, как описано ниже, и ищем максимум Z2 =
=— Ф1+Ф, используя в качестве исходного последнее базисное
решение, и т. д.
Опишем, как вычисляется вектор Фг+1, если мы искали мак-
симум формы—Ф^Ф и остановили процесс при выполнении
соотношения — Фг+Ф(&)>—|ф/ Фг. Вектор Фг+1 определяется
следующим образом: пусть
( Ф? [ф — ф(£)1 1
H = min -р-——тгг ------------г» 1 И (7.38)
( [ф 1 (k) — ф; ] [ф (k) — ф/] J 7
тогда
Фг+1 = цФ(£) + (1--н)Фг. (7.39)
Читателю в качестве упражнения предлагается показать,
что приведенный процесс дает решение за конечное число шагов.
Ь) Метод Гилдрета. Гилдрет [9] предложил интересный вы-
числительный метод для решения задач квадратичного програм-
мирования. Он первый свел задачу с ограничениями к задаче
минимизации квадратичной функции на неотрицательном ок-
танте. Здесь мы рассмотрим лишь, как осуществляется такой
переход.
Предположим, что ограничения неотрицательности перемен-
ных в исходной задаче рассматриваются как ограничения общего
вида. Допустим также, что мы сделали соответствующие пре-
образования ограничений, после чего исходная задача может
быть записана в форме
Hx<h; найти max z = cx-|-x, Dx. (7.40)
Из § 6.3 мы знаем, что х* будет оптимальным решением за-
дачи (7.40) тогда и только тогда, когда существует вектор 1*>0,
такой, что для функции
Л (х, 1) = сх + х' Dx + V [h — Нх] (7.41)
7.7, Другие методы
243
[х*, X*] является седловой точкой для 1>0. Мы остановимся на
случае, когда форма x'Dx отрицательно определенная (и, следо-
вательно, матрица D неособенная). При любом к функция
F(x, X) является строго вогнутой функцией вектора х и дости-
гает своего абсолютного максимума в единственной точке х(Х).
Так как дополнительных ограничений на знаки компонент век-
тора х не накладывается, то х(1) должно быть единственным
решением системы
VxF = 0 = c + 2x'D — ГН,
т. е.
x'W^lfk'H-cID-1 или x(X) = 4D’'[H'k-c'], (7.42)
поскольку матрица, обратная к симметрической, является сим-
метрической.
Условия . Куна—Таккера гарантируют, что х*, X* удовлетво-
ряют условиям (7.42). Подставляя х(Х) в выражение для функ-
ции F(x, X), получаем функцию F(1), зависящую только от X,
F(X) = dk + X'EX ~4cD ’с » (7.43)
где
Е = —4HD'1H/, d==ycD H' + h'. (7.44)
Отметим, что если форма x'Dx — отрицательно определенная, то
форма u'HD^H'u будет отрицательно определенной или неполо-
жительной. Действительно, положим Dx= H'u. Тогда u'HD-1H,u =
=x'Dx<C0. Следовательно, форма Х'ЕХ — положительно опреде-
ленная или неотрицательная и F(X) является выпуклой функ-
цией X. Отметим, что F(X*) =F(x*, X*) и, при всех Х>0,
F (х*, X*) < F (х*, X) < F (X). (7.45)
В самом деле, левое из неравенств (7.45) справедливо ввиду
того, что [х*, X*] является седловой точкой F, правое имеет
место, так как F(X) — maxF(x, X) при любом X. Таким обра-
X
зом, F(x*,X*) есть абсолютный минимум ?(Х) при Х>0. Следо-
вательно, если мы определим абсолютный минимум выражения
Z = dX + X'EX (7.46)
при Х>0, мы тем самым найдем такое X*, что вектор х*, найден-
ный из (7.42) при Х = Х*, является оптимальным решением
исходной задачи.
46*
244
Гл. 7. Квадратичное программирование
Для определения минимума выражения (7.46) при Х>0 мо-
жет быть использован, например, какой-либо из рассмотренных
выше методов. Сам Гилдрет [9] предложил метод, приводящий
к решению лишь за бесконечное число шагов.
с) Метод Хаутеккера. Хаутеккер [10] построил оригинальный
метод решения задач квадратичного программирования на осно-
ве искусственной параметризации. Им разработаны два варианта
метода в зависимости от специфики задачи. Первый вариант
служит для решения задачи
х>0, найти max г = cx-+x'Dx. (7.47)
j J
Хаутеккер решает задачу параметрически, получая оптимальные
значения х для различных неотрицательных значений 0. Второй
вариант разработан для решения задачи (7.47) при дополни-
тельных линейных ограничениях в форме Ах<Ъ в предположе-
нии, что все а^-Х) и bi>0.
Мы рассмотрим лишь первый вариант. Он, кстати, приводит
к интересному алгоритму для минимизации функции (7.46) при
условии неотрицательности переменных. Имея в виду возмож-
ность малого изменения коэффициентов, мы будем предпола-
гать квадратичную форму x'Dx отрицательно определенной.
В процессе решения получается конечное число значений 0:
0о==О, Pi, р2, ...» ₽ь = оо, таких, что при всех 0, 0г<0<0г+1,
в оптимальном решении определенная совокупность переменных
будет принимать положительные значения, остальные перемен-
ные будут нулевыми, причем при переходе 0 через критическое
значение получается другая совокупность положительных значе-
ний переменных.
Рассмотрим более подробно, как определяется оптимальное
решение задач (7.47) для фиксированных значений 0. Мы начи-
наем с 0 = 0. Тогда очевидно, что оптимальное решение есть
х = 0. При х = 0 имеем dz/dx^Cj. Ясно, что если мы выберем
малое положительное 0, то в оптимальном решении положитель-
ной будет лишь та переменная хг, для которой сГ — max Cj > 0.
Следовательно, вначале мы положим хг = 0, а все остальные
переменные полагаем нулевыми. Мы пока останавливаемся на
случае, когда сr > maxty Случай, когда максимальное значение
j
не единственное, будет рассмотрен ниже. Когда хг возрастает,
значение dz/dXj, вообще говоря, изменяется. Частные производ-
ные dz)dxj имеют здесь вид
^ = с, + 2аггхт. (7.48)
7.7. Другие методы.
245
По мере возрастания
хотя бы для одного xs
хг=Р обычно найдется точка, в которой
dz____dz
dxs dxr
(7-49)
Наименьшее значение р, при котором (7.49) имеет место, яв-
ляется критическим (обозначим его Pi). Оно может быть опре-
делено непосредственно из (7.48). При p>Pi одно или более
значений xs могут становиться положительными. t
Может оказаться, что равенство (7.49) не будет достигнуто
и хг=р будет возрастать до тех пор, пока dz/dxr не обратится
в нуль. В этом случае через Pi обозначается значение хг, для
которого dz!dxr = Q, и полученное при этом решение будет опти-
мальным при всех ₽>Рь так как dzldx3^fd для всех осталь-
ных х3.
Рассмотрим случай, когда достигнуто равенство (7.49) и
две или более переменных становятся положительными. Этот
случай мог бы встретиться и на первом шаге, если максималь-
ное значение с? не единственное. Тогда мы с самого начала дей-
ствовали бы описываемым ниже способом. Пусть для определен-
ности лишь два значения, хг и х$1 становятся положительными.
Оптимальные значения этих переменных (как функций от р в
предположении, что остальные переменные остаются нулевыми)
определяются с помощью множителей Лагранжа так, как это
описано в гл. 3. Функция Лагранжа имеет вид
F = crxr -j- с*х, + d^x* + dssx2s 4- 2drsxTxs + X (р — xr — xs), (7.50)
где X —множитель Лагранжа. Необходимые условия, которым
должно удовлетворять оптимальное решение, есть
ст -j— <2с1ГГхГ = X,
cs + ^rsxr + = X,
^ = p.
Отсюда могут быть найдены xr, xs, X как функции от 0:
лг = аг + уг₽, *5 = a5 + yJ3, ^==ао+-уор. (7.51)
Мы попытаемся определить р2— наибольшее значение р, при
котором полученное решение остается оптимальным. Для его
определения мы сначала вычислим величины р2а, &2Ьг и p2cj.
Здесь р2а — такое значение р, что для всех р>р2а ограничение
^х^Ь становится несущественным, так что xr, х5, вычисленные
246
Гл. 7. Квадратичное программирование
при р=Р2а, дают абсолютный минимум определенной выраже-
нием (7.50) функции F\ р2а находится из последнего соотно-
шения (7 51), если положить Х = 0. Величина $2bi определяется
для каждого положительного значения xi9 которое убывает при
возрастании р, как значение р, при котором xt обращается в
нуль. Наконец, для каждой переменной xj, которая должна со-
хранять нулевое значение, мы определим значение производной
dzjdxj как функцию тех переменных хг-, которые могут прини-
мать положительные значения. Мы далее определим величину
р2с; как наибольшее значение, до которого может возрастать р,
пока не будет достигнуто равенство dz/dx^^. Это может быть
сделано с помощью соотношений (7.51), позволяющих выра-
зить X и dzjdXj через р. Значение 02 есть наименьшее из тех 02а,
Р2бл 02с}> значения которых превосходят 0Ь
Если 02 = 02(1, оптимальное решение для всех 0>02 полу-
чается при подстановке 0 = 02а. Если 02 = 02м, переменная хг вы-
водится из совокупности положительных переменных, когда 0
переходит через значение р2. Если 02= 02су, переменная Xj может
становиться положительной, когда 0 переходит через значе-
ние 02. После определения новой совокупности переменных, ко-
торые могут принимать положительные значения, мы повторяем
процедуру. При реализации процесса непременно должен встре-
титься случай, когда 0^ = 0^; при этом решение, полученное
с 0 = 0й, будет оптимальным и для 0>0&. Для доказательства
этого утверждения следует использовать условия Куна—Так-
кера. В упражнении 7.21 читателю предлагается провести это
доказательство. Отметим, что хотя число положительных пере-
менных может и увеличиваться и уменьшаться по мере перехода
от одной критической точки к следующей, число таких перемен-
ных будет, как правило, возрастать с увеличением 0, а следова-
тельно, будет возрастать и размерность задачи, которую мы
должны решать для получения соотношений (7.51).
Мы здесь не сравнивали различные методы решения задач
квадратичного программирования. Следует отметить, однако,
что метод, изложенный в § 7.2, представляется настолько же эф-
фективным, как и любой из других рассмотренных здесь ме-
тодов.
7.8. Двойственность в квадратичном программировании. Мы
изложим здесь принцип двойственности применительно к ква-
дратичному программированию. Исходным будет материал, при-
веденный в §§ 3.8 и 6.5. В § 3.8 было показано, что при выполне-
нии некоторых условий для задачи
gi(x) = bi9 Z=l, ..., m; найти max z — f(x)
7.8. Двойственность
247
двойственная задача имеет вид
dF
^7 = 0, /—1,...,/г; найти min Z — F(x, 1),
где
m
Fix, м = Г(х)+2ш - gz(x)b
Если мы рассмотрим задачу квадратичного программирова-
ния «Ах=Ь; найти max z=cx4-x'Dx», не требуя неотрицательно-
сти переменных, то приведенная выше двойственная задача при-
нимает вид
с + 2x'D — Х'А — 0;
найти min Z = сх4-х'Dx-}- X'b — Х'Ах, (7.52)
поскольку для этого случая F(x, X) =cx+x'Dx + X'[b —Ах]. Умно-
жив ограничение задачи (7.52) справа на х, мы получаем, что
Х'Ах — сх 4- 2х' Dx, (7.53)
и для любых х, X, удовлетворяющих ограничениям задачи (7.52),
Z= — x'Dx + X'b. (7.54)
Следовательно, двойственная задача принимает вид
— 2Dx4-A'X = c';
найти min Z = — х' Dx 4-X'b. (7.55)
В случае когда переменные подчинены условию х>0, для
формулировки двойственной задачи квадратичного программи-
рования могут быть использованы результаты § 6.3. Пусть
х*^>0 — оптимальное решение задачи
Ах = Ь, х>0; найти max a = cx4~x'Dx. (7.56)
Тогда по теореме Куна—Таккера существует такой вектор X*,
что
— 2Dx*4-A'X’>c'
и
max z = F (х*, X*) = сх*4- (х*)' Dx* + (X*)' [b - Ах*] =
= сх* 4-(х*)'Dx*, (7.57)
поскольку в силу (6.51) (Х*)'[Ь — Ах*]=0. Из (6.50) получаем
— 2 (х*)' Dx* 4- (X*)' Ах* = сх*. (7.58)
248
Гл. 7. Квадратичное программирование
Отметим теперь, что для любых х>0 и X, удовлетворяющих
соотношению — 2Dx-bA'X>c', мы получаем, после умножения
слева на х и транспонирования,
— Х'Ах < — сх — 2х' Dx;
поэтому
F (х, X) < — х' Dx + Xb = Z. z7.59)
С другой стороны, из (7.58) следует, что
F (х*, V) = — (х*)' Dx* + (V)' b max z.
Следовательно, [х*, X*] есть оптимальное решение задачи ква-
дратичного программирования
— 2Dx4-A/X>c/,
х>0; (7.60)
найти min Z= — x'Dx-j-X'b.
Кроме того, maxz = minZ. Задачу квадратичного программиро-
вания (7.60) мы и будем называть двойственной для за-
дачи (7.56).
Если задача (7.56) имеет оптимальное решение, то оптималь-
ное решение существует и для задачи (7.60). В самом деле,
оптимальное решейие х* задачи (7.56) есть часть оптимального
решения задачи (7.60). Для определения остальных компонент
решения мы должны решить задачу линейного программирова-
ния (6.29). Отметим, что если г— вогнутая функция от х, то
Z — выпуклая функция от [х, X]. Допустим теперь, что суще-
ствует оптимальное решение задачи (7.60). Можно показать, что
задача (7.56) тогда также имеет оптимальное решение. Мы про-
ведем доказательство для случая, когда x'Dx — отрицательно
определенная форма и, значит, матрица D неособенная. В этом
случае достаточно установить, что существует допустимое реше-
ние системы Ах=Ь.
Пусть [х*,Х*]— оптимальное решение задачи (7.60). Условия
Куна—Таккера применительно к этой задаче должны быть вы-
полнены. Следовательно, существует такой вектор 6* (почему?),
что
— 2Dx* + 2D6*>0, (7.61)
A6* = b. (7.62)
Из (7.61) следует, что 6*>х*>0, так что 6* — искомое допусти-
мое решение системы Ах=Ь.
Двойственная задача в той форме, как она приведена здесь,
сформулирована Дорном [6]. Он не показал, однако, непосред-
Упражнения
249
ственной связи двойственной постановки с условиями Куна—
Таккера. В несколько иной форме соотношения двойственности
рассмотрены Деннисом [5].
ЛИТЕРАТУРА
1. Barankin Е. W., Dorfman R., Towards Quadratic Programming,
Office of Naval Research Logistics Project at Columbia University and
University of California, Berkeley, 1955.
2. Beale E. M. L., On Minimizing a Convex Function Subject to Linear
Inequalities, /. Roy Statist. Soc. (B), 17 (1955), 173—184.
3. В e a 1 e E. M. L., On Quadratic Programming, Nav. Res. Logist. Quart., 6
(1959), 227—243.
4. Charnes A., Cooper W. W., Management Models and Industrial
Applications of Linear Programming, v. II, New York, Wiley, 1961, 682—
687.
5. Деннис Дж. Б., Математическое программирование и электрические
цепи, ИЛ, М., 1961.
6. Dorn W. S., Duality in Quadratic Programming, Quart. Appl. Math., 18
(1960), 155—162.
7. Dorn W. S., Self-Dual Quadratic Programs, J. Soc. Indust, and Appl.
Math., 9 (1961), 51—54.
8. Frank M., Wolfe P., An Algorithm for Quadratic Programming, Nav.
Res. Logist. Quart., 3 (1956), 95—110.
9. Hildreth C., A Quadratic Programming Procedure, Nav. Res. Logist.
Quart., 14 (1957), 79—85.
10. H о u t h a k k e r H. S., The Capacity Method of Quadratic Programming,
Econometrica, 28 (1960), 62—87.
11. Lemke С. E., A Method for Solution of Quadratic Programs, Manag.
Sci., 8 (1962), 442—453.
42. Markowitz H., The Optimization of a Quadratic Function Subject to
Linear Constraints, Nav. Res. Logist. Quart., 3 (1956), 111—133.
13. Markowitz H., Portfolio Selection, Cowles Foundation Monograph № 16,
New York, Wiley, 1959.
14. T h e i 1 H., van de 'P a n n e C., Quadratic Programming as an Extension
of Classical Quadratic Maximization, Manag. Sci., 1 (1960), 1—20.
15. Vajda S., Mathematical Programming, Reading, Addison-Wesley, 1961.
16. WT о 1 f e P., The Simplex Method for Quadratic Programming, Econometri-
ca, 27 (1959), 382—398.
Упражнения
7.1. Решить задачу квадратичного программирования
3xi -j- <16, х > 0;
найти max z = 8хт -|~ 10х2 — х? — х\
с помощью метода, изложенного в § 7.2 и графически.
7.2. Решить задачу упражнения 7.1 с помощью метода Франк и Вольфа.
7.3. Решить задачу упражнения 7.1 с помощью метода Хаутеккера.
250
Гл. 7. Квадратичное программирование
1А. При ограничениях задачи упражнения 7.1 решить при всех 0>0 за-
дачу максимизации целевой функции z = 80^ -f- Ю0х2 — х^ — х%.
7.5. Использовать метод, изложенный в § 7.2, для решения задачи ква-
дратичного программирования:
х^ —|— 4х2 4, Xi -j- Х2 2, х^, Х2 0;
найти max z — 2х} 4- Зх2 — 2%|.
7.6. Решить задачу упражнения 7.5 с помощью метода Франк и Вольфа.
7.7. Решить задачу упражнения 7.5, комбинируя методы Гилдрета и
Хаутеккера.
7.8. При ограничениях задачи упражнения 7.5 найти максимум при всех
0 0 целевой функции
z = 20jVj 30х2 — 2л|.
7.9. Решить задачу квадратичного программирования
3*! 4~ 2х2 6, х>0; найти max г = л2
с невогнутой целевой функцией графически и выяснить, какие могут быть
осложнения, если попытаться решать эту задачу одним из методов, приве-
денных в настоящей главе.
7.10. Получим ли мы оптимальное решение задачи упражнения 7.9, при-
меняя метод, изложенный в § 7.2?
7.11. Решить с помощью метода, изложенного в § 7.2, задачу квадратич-
ного программирования
х1~\-3х2'^3, 2х2 + 0,5-*j >2, хьх2>0;
найти min z — 4х? 4- Зх2.
7.12. Решить с помощью метода, изложенного в § 7.2, задачу квадратич-
ного программирования
-*1—-*2>0, —-*1 + 2-*2 < 2, хьх2 >0;
найти max г — 2х} 4~ Зх2 —
7.13. При ограничениях задачи упражнения 7.12 и целевой функции
z = 20XJ 30х2 — xj
найти оптимальное решение для 0>О.
7.14. Для каждого 0^>О решить задачу квадратичного программирования
—-*2^0» —а:14~2х2<;2, хьл2^0;
найти тах2' = 20л1 — х2.
7.15. Решить пример из § 7.6, используя способ Чарнса, учитывающий
малое изменение коэффициентов для получения отрицательно определенной
Квадратичной'формы. Положить е=0,001.
7.16. Допустим, что мы имеем задачу квадратичного программирования,
в которой требуется найти минимум выпуклой целевой функции. Записать
для этого случая условия Куна—Таккера и получить для задачи минймизации
условия типа (7.09). • 1
Упражнения
251
7.17. Доказать, что если функция x'Dx — строго вогнутая, то и функция
cx+x'Dx— также строго вогнутая.
7.18. В экономике часто считается, что предпочтение покупателя при вы-
боре из и видов товаров может быть представлено числовой функцией по-
лезности С/(х), где Xj — количество товара /, которое он может купить.
Если покупатель имеет сумму денег (3, а цена единицы /-го товара есть Pj,
то для того, чтобы определить, в каком количестве следует купить каждый
товар, покупателю надо решить следующую задачу:
х>0; найти max z — U (х).
Отметим, что если t/(x) = cx + x'Dx, причем U — вогнутая функция, мы имеем
задачу квадратичного программирования. Определить ее оптимальное ре-
шение в частном случае, когда имеется два вида товаров и
U (х) — 18*j -|- 16л2 — Зл2 — х1х2 — 5^2,
Pi = 1, А = 2, Р = 10.
Нарисовать линии уровня функции U в плоскости х2.
7.19. Рассмотрим функцию t/=Po+PiXi+...+рпхп. Коэффициенты р;
должны быть определены по данным М>п+1 экспериментов, в результате
которых мы получаем значения [yk, *ik, ..., *пь]. Мы будем искать значе-
ния pj, которые минимизируют значение функции
м
2 (У# -- ... — finxnkY*
k=l
Из физических соображений априорно известно, что некоторые Р, не могут
быть отрицательными. Показать, что получающаяся задача является зада-
чей квадратичного программирования. Будет ли функция z выпуклой?
7.20. Рассмотрим задачу квадратичного программирования
Ах = Ь, х>>0; найти maxz — Осх-[-x'Dx,
где x'Dx — неположительная форма. Запишем F(0) = max г. Доказать, что
множество значений х, при которых для некоторого 0 имеет место равенство
F(9) = Осх+x'Dx, выпукло и что значение сх на этом множестве постоянно.
[Указание. Показать, что если Xi и х2 — точки этого множества, то из вогну-
тости функции z следует, что точки %xi+(l—Х)х2, 0<Д<1, также принад-
лежат этому множеству. Пусть w=xi—х2. Показать, что
(0cw -j- 2х2 D w) Л -j- w D wA2 s 0
для всех %, 0<X<U.
Отсюда будет следовать, что w'Dw==0, т. е. Dw=0, и поэтому cw=0.]
7.21. Используя условия Куна—Таккера, показать, что при каждом Р >0
метод Хаутеккера, рассмотренный в § 7.7, доставляет оптимальное решение
задачи.
7.22. Показать, что если в задаче (7.1) решение не ограничено, то реше-
ния системы (7.10) при условиях x>0, v^>0 не существует. [Указание. За-
пишем z==f(x). Так как f — вогнутая функция, (3.65) имеет место для лю-
бых Xi, х2. Допустим, что X], X удовлетворяют (7.10), а х2 — любая точка,
удовлетворяющая условиям Ах = Ь, х^>0. Отсюда f(x2)—7(xi) <—F(xi.X),
но это невозможно, если значение /(х2) может быть как угодно большим.]
7.23. Показать, что вычислительная схема Франк и Вольфа, рассмотрен-
ная в § 7.7, приводит к решению за конечное число итераций.
252
Гл. 7. Квадратичное программирование
[Указание. Показать сначала, что всегда может быть получено неравен-
ство — Ф/Ф > — -g" Чтобы сделать это, отметим, что — ф+ф<0,
следовательно, максимум конечен. Кроме того, оптимальное решение Ф* до-
пустимо и Ф^Ф* == 0- Далее
фг+фг - 2ф;ф4 - (ф; - ф+) (фг - фф) > о,
так что максимум —ФГ Ф не меньше, чем —~ Фгч Фг Отсюда также
ф+ [Фг — Ф (й)] > у ф+фг > О
и, следовательно, 1. Показать далее, что
ф;+1фг+1<(1-|)ф;фг-
Так как коэффициенты линейной целевой функции изменяются от задачи
к задаче, базис может повторяться и доказательство сходимости не может
быть основано на свойстве конечности числа базисных решений.
Пусть W — выпуклый многогранник, образованный базисными допусти-
мыми решениями системы Qw—f. Пусть L = шах [(Ф^ — Ф*) (Ф2 — Ф])] Для
всех Ф1 и Ф2 из W. Тогда L>0 и, если ц<1,
у и > i- фг [фг - Ф (*)] > -ir Ф' Ф'
Отсюда в любом случае
i — у < max j 1 — ~ Фг+Фг, у | = у,
ИЛИ
А/ч-1 •С
где
Если Дг>1/2, то Дг+1< Дг/2. В силу сказанного существует такое /?, что
Дг<1/2 для всех R. Но тогда
+ 1 или r>R.
Следовательно, Дг стремится к нулю не медленнее, чем 1/г. Для доказатель-
ства конечности процесса следует учесть, что предельное значение Аоо=0, а
Фо, — выпуклая комбинация крайних точек решений Ф(&) (в этом противо-
речие) .]
7.24. Записать двойственную задачу для следующей задачи квадратич-
ного программирования
Ах<^Ь. х>0; найти max z = ex x'Dx,
предполагая, что функция z вогнутая.
Упражнения
253
7.25. В предположении, что функция z выпуклая, записать двойственную
задачу для следующей задачи квадратичного программирования:
Ах — Ь, х > 0; найти min z = сх -j- x'Dx.
7.26. Справедливо ли с точки зрения теории, изложенной в § 7.8, что
задача, двойственная к двойственной, совпадает с исходной?
7.27. Показать, что для критических значений 0 (см. § 7.5) вектор [0, с]
может быть заменен вектором, соответствующим переменным, которые в ба-
зисном решении для (7.24) обращаются в нуль, и таким образом получается
базисное решение для (7.32).
7.28. Пусть x'Dx — неположительная квадратичная форма. Показать, что
если существуют х > 0, v>0, являющиеся решением для (7.10), то суще-
ствует допустимое решение для (7.10), удовлетворяющее условию x'v=0. Это
означает, что, если (7.10) имеет допустимое решение, задача (7.1) должна
иметь оптимальное решение (ограниченное), так как если (7.10) имеет до-
пустимое решение, то и система Ах—Ь имеет допустимое решение.
[Указ ание. Использовать соотношение (3.65), где х2 есть векторная
х-компонента решения системы (7,10).]
ГЛАВА
ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ
ПРОГРАММИРОВАНИЕ
Семь лебедей на реке;
Шесть гусаков на песке;
Пять золотых петухов;
Четверо черных дроздов;
Трое французских цыпляток;
Два голубка, а на груше —
Одна куропатка.
Английская рождественская
песенка Двенадцать дней
Рождества
8.1. Введение. Эта глава посвящается изучению целочислен-
ных задач линейного программирования, т. е. таких нелинейных
задач, которые были бы линейными, если бы не требование цело-
численности некоторых переменных. Задача называется пол-
ностью целочисленной, если требуется целочисленность всех
переменных, и частично целочисленной, если ограничение цело-
численности касается только части переменных. Задача, рассма-
триваемая в этой главе, в самом общем виде может быть сфор-
мулирована следующим образом:
Ах = Ь, х>0, —целые числа, / СЛ; найти maxz = cx.
(8-1)
Если /1 содержит все /, мы имеем полностью целочисленную
задачу; если Л пусто, то (8.1) является обычной задачей линей-
ного программирования.
Поясним сначала, чем интересны задачи вида (8.1). Совер-
шенно очевидно, что во многих практических задачах необхо-
дима целочисленность переменных., Читателю показалось бы
естественным решить сначала задачу (8.1), не обращая внима-
ния на требования целочисленности, а затем округлить значения
переменных в полученном решении до ближайших целых чисел,
удовлетворяющих ограничениям задачи. Часто на практике
поступают именно так, и такой подход является обосно-
ванным, когда значения переменных достаточно велики, так что
8.2. Задача с фиксированными затратами
23д
влиянием округления можно пренебречь. Однако нередко встре-
чаются задачи, в которых целочисленные переменные должны
быть малыми целыми числами, часто 0 или I. Мы ниже увидим,
что многие нелинейные задачи программирования, которые на
первый взгляд кажутся никак не связанными с целочисленным
программированием, могут быть сформулированы как целочис-
ленные задачи программирования, в которых целочисленные
переменные принимают лишь значения 0 или 1.
Для решения задачи (8.1) Гомори [8—11] разработал алго-
ритмы, сходящиеся за конечное число итераций. Мы опишем
эти алгоритмы и докажем их сходимость за конечное число
шагов. К сожалению, опыт применения этих алгоритмов для
конкретных вычислений мало обнадеживает. Хотя алгоритмы
сходятся за конечное число шагов, число необходимых итераций
может быть очень большим даже для задач весьма скромного
размера. Таким образом, в настоящее время нельзя утверждать,
что для решения целочисленных задач существуют эффективные
численные методы.
В этой главе мы ограничимся решением задач вида (8.1).
Мы не будем рассматривать вопрос о том, как решать задачи,
имеющие ограничение целочисленности и остающиеся нелиней-
ными даже при отбрасывании этих ограничений. Однако в гл. 10
будет показано, что для решения некоторых задач такого типа
может быть использовано динамическое программирование.
8.2. Задача с фиксированными затратами. В § 4.10 мы изу-
чали следующую задачу с фиксированными затратами:
п
Ах = Ь, х>0; найти min z = + (8.2)
где
( 0, если Xj — 0,
I 1, если Xj > 0.
(8.3)
Для того чтобы свести эту задачу к целочисленной задаче
типа (8.1), очевидно, нам необходимо потребовать, чтобы пере-
менные принимали лишь целые значения. Чтобы каждая
переменная б; могла принимать лишь значения 0 или 1, доста-
точно ввести ограничения
0<б;<1, п. (8.4)
Однако у нас еще нет гарантии, что 6j будет принимать значе-
ния 0 или 1 в соответствии с (8.3). Предположим, что нам
256
Гл. 8. Целочисленное линейное программирование
известна верхняя граница dj для каждой переменной Xj. Введем
ограничения
или
Xj djbj < О, j = 1, ..., n. (8.5)
Из них ясно, что Xj не может быть положительным, если не
равно 1, так как если dj = O, то х^О, т. е. Xj = O. В то же время
если 6;=1, так что х$ действительно оказывается свобод-
ной переменной. Кроме того, если в оптимальном решении х; = 0,
то не может быть 6>=1, так как при этом затраты могут быть
уменьшены, если заменить 6j нулем.
Таким образом, задача (8.2) — (8.3) ‘эквивалентна следующей:
Ах = Ь,
— djbj <0, j = 1, ..., п,
0<6у<1, 7=1, ..., п, бу — целые, (8.6)
х>0;
п
найти min z— +
которая представляет собой частично целочисленную задачу
вида (8.1).
Заметим, что если А — матрица с размерами mXn, то число
ограничений задачи (8.6) равно m-f-2/г или т + п, если предпо-
ложить, что верхние границы 6; могут быть учтены каким-либо
специальным образом. Следовательно, (8.6) будет иметь очень
большое число ограничений, если тип велики и с каждой пере-
менной связаны фиксированные затраты. Как мы увидим позд-
нее, при применении целочисленных алгоритмов мы должны
будем решить сначала (8.6) как обычную задачу линейного
программирования, не обращая внимания на ограничения цело-
численности. При т=100 и /г=1000 (что при отсутствии фикси-
рованных затрат дало бы задачу линейного программирования,
которая может быть легко решена) было бы невозможно выпол-
нить первый этап целочисленного алгоритма и решить (8.6) как
обычную задачу линейного программирования, если фиксиро-.
ванные затраты связаны с каждой переменной.
8.3. Определение глобального экстремума для приближенной
задачи в 6-форме. Как следует из сказанного в § 4.4, прибли-
женная задача в 6-форме для задачи (4.1) может быть записана
8.3. Приближенная задача в б-форме
257
в виде
п г] п
=> >\bi — г=1, wz,
О bkj -< 1 для всех k, j, (8.7)
если bkj > О, то bUj = 1, а = 1, .... k — 1;
л rj
найти max
В гл. 4 было показано, что с помощью симплекс-метода с огра-
ниченной записью можно определить локальный максимум для
задачи (8.7). Однако, если задача не обладает соответствую-
щими свойствами выпуклости и вогнутости, нельзя гарантиро-
вать, что найденный таким образом локальный экстремум яв-
ляется глобальным. Здесь мы покажем, каким образом за-
дачу (8.7) можно свести к целочисленной задаче линейного
программирования. Решив эту задачу, мы получим глобальный
экстремум для задачи (8.7).
Для того чтобы свести задачу (8.7) к целочисленной задаче
линейного программирования, необходимо лишь представить
условия
если 6kJ > 0, то 6uj — 1, и = 1, ..., k — 1, (8.8)
в виде линейных ограничений. Заметим, что (8.8) эквивалентно
следующим условиям: 6^+1, j = 0, если не равно 1. Чтобы пре-
образовать эти ограничения, введем новые переменные ф^-, ко-
торые могут принимать целые значения 0 или 1. Для каждого k
и j рассмотрим ограничения
6*+1,7<’1’лл (8-9)
Если ф^=1, то из (8.9) следует, что бь/>1, т. е. 6^=1, а
бь+1, так что на бь+i, j никакого дополнительного ограниче-
ния не накладывается. С другой стороны, если ф^- = 0, то из
(8.9) следует, что бй^О, т. е. на 8kj не накладывается никакого
нового ограничения, а бл+1, j-^О, так что 6^+1, j = 0. Это в точности
то, что нам нужно. Отметим, что если ф^=1, то должно быть
выполнено условие: фи; = 1, и = 0, ..., fe—1. Действительно, если
и = то из (8.9) следует, что и 6uj>1, а это
невозможно. Для того чтобы значения целочисленных перемен-
ных ф^- исчерпывались значениями 0 или 1, необходимо лишь по-
требовать, чтобы фь/Х) для всех k и /. Ограничение 0^ф^-^1
вводить не нужно, так как из ограничений б^>ф^- и
следует, что ф^- не могут быть больше единицы. Таким образом,
17 Зак. 735
258
Гл. 8. Целочисленное линейное программирование
задача (8.7) может быть заменена частично целочисленной за-
дачей
nrj п
2 => bt — 2 gwr * = ь • • •,
J~l £ = 1 J J
bkj~ для всех k, J,
&k+i,j — для всех k, J, (8.10)
0 <C bkj 1 для всех k, j,
$kj 0, Ф*; — целые для всех k, j\
♦ n rj
найти max z — j*
Сведение задачи (8.7) к целочисленной задаче линейного про-
граммирования (8.10) неизбежно влечет за собой значительное
увеличение числа ограничений. Даже если тип крайне малы,
например 5 и 20 соответственно, и если для каждой исходной
переменной используется пять переменных 6^-, то задача (8.10)
будет иметь 305 ограничений, включая ограничения на верхние
границы, или 205, если последние не учитывать. Для значений т
и и, представляющих практический интерес, задача (8.10) имела
бы свыше 2000 ограничений. В том случае, когда некоторые пе-
ременные входят в задачу линейно, размеры целочисленной за-
дачи соответственно уменьшаются, так как для таких перемен-
ных Xj не нужно вводить переменные 6^.
8.4. Определение глобального экстремума для приближен-
ной задачи в Х-форме. Как и следует ожидать, приближенную за-
дачу в Х-форме для (4.1) можно также представить в виде це-
лочисленной задачи линейного программирования, и это, по
крайней мере в принципе, дает способ для определения гло-
бального экстремума в этой задаче. В § 4.2 было показано, что
приближенная задача в Х-форме для (4.1) имеет вид
п rj
5 5 gkijhj «.=,>} bt, I = 1,.. •, m,
j-l k-o
rj
24y=i, .....«’ (8-H)
ьо J
Xfty>0 для всех k, /;
n 4
найти max z = S S ЧЧ’
y=i
где, кроме того, требуется чтобы для каждого j положительными
могли быть не более чем две переменные Х^, причем две пере-
8.4. Приближенная задача в Х-форме
259
менные могут быть положительными лишь тогда, когда они
смежные.
Чтобы свести задачу (8.11) к целочисленной задаче линей-
ного программирования, необходимо лишь должным образом
записать ограничения, показывающие, какие могут быть по-
ложительными. Для этого опять введем новые переменные
принимающие лишь целочисленные значения 0 и 1. Потребуем,
чтобы
= /=1, (8.12)
k
Так как каждое равно или 0, или 1, то из (8 12) следует, что
для фиксированного / все окажутся равными 0, за исключе-
нием одного, которое будет равно 1. Далее, введя ограничения
^о/^Фо/ ^у^СФ^-i, j + Ф*у» А = 1, ...» Г; — 1;
7==1’ • ’ (8-13)
мы будем иметь нужное представление. Действительно, если
то из (8.12) следует, что фп;- = 0, u4=k, а из (8.13) —
т. е. Xwj = O, u=/=k, k+ 1. Далее ХА7<1, j^l, так что на
значение этих двух переменных не накладывается никаких до-
полнительных ограничений. Таким образом, из сказанного выше
следует, что для данного / положительными могут быть не более
чем две переменные» Xkj, причем две переменные положительны
лишь тогда, когда они смежные. Следовательно, задача (8.11)
эквивалентна следующей частично целочисленной задаче линей-
ного программирования:
п Г)
2 =. >}bt, Z=l,
. /.1 Й-О J
rJ
2^=1, /=1,
ГГХ
ЕфЛ/ = 1, /=1, (8.14)
6=0
^о/^Фоу» ^kj Фа-i, ;“НФлр k=\> ..., Гу 1,
Ч7,7<ФГг1, г
Фл/ 0» Ф^/ — целые для всех k, J,
Xkj 0» для всех /»
п rJ
найти max z = 2 2
17*
260
Гл. 8. Целочисленное линейное программирование
Здесь нет необходимости вводить ограничения на верхнюю гра-
ницу каждой переменной так как из (8.12) автоматически
следует, что не могут быть больше 1. Переменные фг у не
нужны. Однако их введение ничего не меняет. Действительно,
можно было бы ввести целочисленную переменную ф-i, j и запи-
сать (8.13) как
для всех & = 0, 1,..., rj. Отметим, что и в этом случае преобра-
зование задачи (8.11) в целочисленную задачу линейного про-
граммирования требует большого числа новых ограничений.
8.5. Представление некоторых поверхностей. В § 4.5 было
показано, что функция w = min [хь х2] может быть представлена
следующим образом:
Xj = %i—|—%2> Xg== А<2 ^3} и== ^2» 0, Z = 1» 2, 3, (8.15)
где дополнительно требуется, чтобы положительными могли быть
не более чем две переменные Хг-, причем две переменные поло-
жительные лишь в том случае, если они смежные. Эти ограни-
чения на могут быть записаны как ограничения целочислен-
ности, если ввести две новые переменные г|?1 и ^2, каждая из
которых принимает лишь значения 0 и 1. Предположим, что мы
можем определить число d, такое, что x^Cd, x2^d. Тогда если
мы запишем
Ф1 + Ф2 = 1 >
d$2, (8.16)
Ф1>^0, ф2>0, Ф1, ф2“—целые числа,.
то эти соотношения гарантируют, что положительными окажутся
не более чем две переменные и только тогда, когда они
смежные. Таким образом, функция w = min[xi, х2], а следова-
тельно, и поверхность, показанная на рис. 4.7, могут быть пред-
ставлены в терминах целочисленного линейного программирова-
ния соотношениями (8.15) и (8.16).
8.6. Конечные альтернативы. Рассмотрим задачу линейного
программирования, в которой решение х должно удовлетворять
одному из двух ограничений амх — Ьи^0 или avx —6^X0, но не
обоим одновременно. В задачу следует включить то ограничение,
которое позволит получить большее значение целевой функции.
В качестве практического примера предположим, что предприни-
мателю, который производит ряд продуктов, нужно определить
оптимальный набор продуктов и способы их производства. Для
8.6. Конечные альтернативы
261
одного из этих продуктов должно быть выполнено условие: если
он вообще производится, то в количестве, не меньшем чем Ь.
Предположим, что этот продукт может производиться несколь-
кими различными способами и пусть Xj — количество, произво-
димое j-м способом. Тогда либо ^х^Ь, либо 2х/ = 0-
/ j
Прямой способ решения задачи такого типа состоит в следую-
щем. Сначала, предполагая, что выделенный продукт произво-
дится, решаем задачу с ограничением ^х^Ь- Затем предпо-
лагаем, что этот продукт не производится, и решаем задачу с
ограничением = Из двух найденных решений в качестве
оптимального выбираем то, которому соответствует больший
ДОХОД.
Покажем теперь, что можно одновременно рассматривать две
альтернативы аих — Ьи^0 и а”х — 6^0, если ввести целочис-
ленную переменную. Мы это сделаем, предполагая, что для всех х,
относящихся к задаче, могут быть определены верхние границы
Lu и Lv функций аях — Ьи и а”х — bv соответственно. Введем те-
перь переменную 6, которая может принимать лишь значения 0
и L Тогда условие аих — Ьи^0 или а”х — bv^0 может быть за-
менено условиями
attx — bu^6Ztt; а^х — bv <(1 — б) Lv.
0<б<1, б —целое. (8.17)
Действительно, если 6 = 0, то awx—и поэтому должно вы-
полняться ограничение с индексом и, в то время как avx — bv^LVi
т. е. что касается ограничения с индексом v, то не требуется,
чтобы оно выполнялось. Когда 6=1, верно обратное. Таким
образом, вместо решения двух задач линейного программирова-
ния достаточно решить одну частично целочисленную задачу
с одной целочисленной переменной.
Описанный подход может быть обобщен на более сложные
случаи. Предположим, например, что имеется q ограничений
агх—6^0, f=l, ..., q, и требуется, чтобы по крайней мере k
из них, где k= 1,..., q— 1, были бы выполнены, но не обуслов-
лено, какие именно. Как и выше, эта задача может быть реше-
на, если решить q\lk\(q—k)\ различных задач линейного про-
граммирования и из полученных решений выбрать то, которому
соответствует наибольшее значение целевой функции. Однако,
если ввести целочисленные переменные, можно одновременно
оценить все имеющиеся здесь возможности.
Предположим, что для каждого i мы можем определить
верхнюю границу Ц функции агх—bt. Введем q целочисленных
262 Гл. 8. Целочисленное линейное программирование
переменных 6г, которые могут принимать лишь значения 0 и L
Тогда ясно, что условие, требующее, чтобы были выполнены по
крайней мере k из ограничений аг’х4+, может быть представлено
в виде
а'х — bt < 6zZz, i — 1, ...» q.
^6t = q-k, (8.18)
0<6z<l, 6Z —целые, z= 1, ..., q.
Здесь мы полагаем 2 б* ==?—так как q—k переменных бг’
должны равняться единице: если 6г=1, то f-е ограничение может
не выполняться.
Конечные альтернативы рассмотренного вида можно исполь-
зовать для описания различных невыпуклых областей. Рассмо-
трим, например, область, показанную на рис. 8.1.
Заметим, что любая точка х из этой невыпуклой области
принадлежит одному из двух выпуклых множеств: или множе-
ству
х1-|-х2<4, х2>2, Х)>0, (8.19)
или
Xi-hx2<4, *i>2, х2>0. (8.20)
Поэтому данную невыпуклую область мы можем представить
как
*1+*2 <4,
Хх>2 или х2>2, (8.21)
х>0
или, вводя целочисленную переменную, как
Х1+*2<4,
Х1_ 2 + 26>0,
х2 — 2^2(1— 6)>0, (8.22)
0<6<1, 6 — целое,
х>0.
Чтобы максимизировать линейную целевую функцию на
невыпуклой области рис. 8.1, можно было бы просто решить две
задачи линейного программирования: сначала максимизировать
целевую функцию на выпуклом множестве (8.19), а затем — на
выпуклом множестве (8.20), т. е. решить задачи
xi + х2 < 4, х2>2, %!>0; найти max z = cx (8.23)
и
xi + x2<4, %! >2, х2>0; найти maxz = cx. (8.24)
8.6. Конечные альтернативы
263
Оптимальным решением для невыпуклой области будет тогда
решение той задачи линейного программирования, которой со-
ответствует наибольшее значение целевой функции. Однако если
использовать (8.22), то для решения задачи достаточно найти
решение одной частично целочисленной задачи линейного про-
граммирования с одной целочисленной переменной.
В качестве примера, где должны учитываться по крайней
мере k из данных q ограничений, рассмотрим невыпуклое мно-
жество, показанное на рис. 8.2. Здесь даны ограничения
х2>2,5, %!<!, Xi >2, Xi — х2>0. (8.25)
Каждое из несвязанных множеств на рис. 8.2 может б’ыть опи-
сано ограничениями (8.25) совместно с ограничением х^>0 если
потребовать, чтобы а + %2^4 выполнялось всегда, а из остав-
шихся в (8.25) ограничений удовлетворялись бы одновременно
не менее двух ограничений (проверьте это, рассмотрев все воз-
можности). Введя целочисленные переменные 6^ мы можем опи-
сать несвязанные множества на рис. 8.2 соотношениями
Xj —j— х<2 4, х2 — 3 —Зд15 л*| — 1 Зд2,
4
хг — 2,5 > — 2,5д3, хг - z2 > —4б4, 3 б; = 2, (8.26)
О<б,< 1, б, —целые, / — 1, .... 4,
где, кроме того, требуется, чтобы х>0, и использован тот факт,
что верхняя граница для каждой переменной равна 4.
264
Гл. 8. Целочисленное линейное программирование
Аналогичная ситуация возникает тогда, когда требуется,
чтобы вектор х принадлежал по крайней мере одному из г вы-
пуклых множеств
Attx < Ьй, и = 1, ..., г. (8.27)
Чтобы оптимизировать линейную функцию f(x) при условии, что
вектор х принадлежит по крайней мере одному из множеств
(8.27), можно оптимизировать
f(x) на каждом из множеств в
отдельности, а затем из получен-
ных таким образом решений вы-
брать то, которому соответ-
ствует наибольшее значение це-
левой функции. Возможен и дру-
гой путь: нахождение оптималь-
ного решения данной задачи
можно свести к решению частич-
но целочисленной задачи линей-
ного программирования.
Чтобы сделать это, предполо-
жим, что мы нашли векторы аь
а2, такие, что, в какой бы из об-
ластей (8.27) ни находился век-
Рис. 8.3. тор х, выполняется неравенство
ai<JL<a2. Кроме того, будем
считать, что существуют векторы Lu, такие, что для всех х,
а1-<х^а2, справедливы неравенства Аих—bw<LM. Если мы вве-
дем г целочисленных переменных би, то условие, что вектор х
должен принадлежать по крайней мере одному из множеств
(8.27), может быть записано как
К* bu) Ltt, и — 1,
г,
и
(8.28)
целые, и = \, .г.
В качестве примера, иллюстрирующего сказанное, рассмот-
рим невыпуклую область (рис. 8.3). Очевидно, что любая точ-
ка х из этой области принадлежит или выпуклому множеству
X] —I- х% 4, х1-+-х2<>2, Xj О, х2 0, (8.29)
или выпуклому множеству
*1 + *2 <2, х2<1, ^1>0, х2>0. (8.30)
8.6. Конечные альтернативы
265
В соответствии с (8.28) область, показанная на рис. 8.3, может
быть представлена следующим образом:
Xi -J- х2 — 4 4-d], Xj + х2 — 2 — 2dj,
Xi —|— х2 — 2 662» х2 — 1 Зд2, (8.31)
61 + d2 = 1.
0< 61 <1, 0<62<1, 6п 62— целые,
х > 0.
В качестве другого примера^рассмотрим невыпуклую область,
показанную на рис. 8.4. Любая точка х из этой области при-
надлежит или выпуклому мно-
жеству
Xj — х2 > 0,
Xi+x2 <4, х>0. (8.32)
или выпуклому множеству
Xi < 4, х2 < 1, х > 0. (8.33)
Некоторые точки могут нахо-
диться в обоих множествах од-
новременно, однако этот факт
не вносит дополнительных
трудностей. В соответствии с
представлена как
Xj — Х2 — 461 > Х2 — 4 461,
Xi — 4<0, х2 — 1 <362,
61 + 62-1, . (8.34)
0 6i + 1, 0 + 62 + 1, 6р 62 — целые,
х>0.
В этом параграфе мы изучали ситуации, описываемые зада-
чами линейного программирования с конечным числом альтер-
натив. Мы видели, что решение задач такого типа может быть
получено либо решением ряда задач линейного программирова-
ния, либо решением некоторой частично целочисленной задачи
линейного программирования. Хотя тот факт, что рассмотренные
задачи могут быть сформулированы как целочисленные задачи
линейного программирования, и представляет большой интерес,
в настоящее время решение последовательности задач линейного
программирования по меньшей мере столь же эффективно, как
и решение целочисленной задачи.
266
Гл. 8. Целочисленное линейное программирование
8.7. Задачи с условиями очередности. Многие практические
задачи характеризуются тем, что некоторые операции или собы-
тия должны осуществляться в определенной последовательности
или по крайней мере удовлетворять некоторым ограничениям
порядка. Часто трудно или даже невозможно описать требова-
ния очередности в терминах линейного программирования.
Однако те задачи, которые были бы задачами линейного про-
граммирования, если бы не требования упорядоченности, обычно
могут быть сформулированы как целочисленные задачи линей-
ного программирования. В последующих двух параграфах
мы приведем два примера такого рода. Другие примеры будут
рассмотрены в упражнениях.
8.8. Реализация проектов и календарное планирование. Рас-
смотрим некоторый проект, например строительства здания, ре-
конструкции завода или очередного капитального ремонта пас-
сажирского самолета. Интересующие нас проекты включают
множество работ, которые требуют большого числа различных
видов квалифицированного труда, оборудования и должны вы-
полняться в определенном порядке. Требуется составить график
реализации проекта, минимизирующий общие затраты. Из этого
графика мы определим, в какой срок будут завершены все ра-
боты и какое количество квалифицированного труда каждого
вида, оборудования и т. д. потребуется ежедневно.
Рассматриваемую задачу мы будем считать детерминирован-
ной, исключив какую бы то ни было неопределенность. График
будем составлять, предполагая, что сутки являются наименьшим
периодом времени. Следуя терминологии, принятой в экономи-
ческих исследованиях, различные виды труда, материалов, обо-
рудования и т. п. мы будем называть факторами производства.
Предполагается, что количество факторов, которыми мы распо-
лагаем ежедневно, ограничено. Далее предположим, что еже-
дневный объем работ может выполняться либо в обыч-
ные рабочие часы, либо в сверхурочные. Соответственно этим
двум видам рабочего времени имеющееся у нас количество
каждого фактора мы разобьем на две части. Пусть akj и bkj —
количество фактора k, которое мы можем использовать в
день / в обычные рабочие часы и в сверхурочные соответ-
ственно. Предполагается, что всего имеется факторов произ-
водства.
Допустим, что проект может быть реализован максимум за
W и минимум за п дней. Всего должно быть выполнено I раз-
личных работ. Мы предполагаем, что имеется таблица, показы-
вающая, в каком порядке должны выполняться различные ра-
боты. Одновременно могут выполняться несколько работ, однако,
8.8. Реализация проектов и календарное планирование
267
прежде чем может быть начата работа Z, некоторая часть работ
.1(1) должна быть завершена.
Пусть ащ — количество фактора ky необходимое для выпол-
нения работы i в обычное время, a — количество фактора k,
необходимое для выполнения работы i в сверхурочное время.
Величина в общем случае может отличаться от величины р^.
Основными переменными, которые мы будем использовать при
формулировке задачи, являются переменные х^ и уц. Величина
Xij равна части работы Z, выполненной в день / в обычные ра-
бочие часы, а уц — в сверхурочные. Количество фактора k,
использованного при выполнении работы i в день /, равно
для обычного времени и РгкУц — для сверхурочного. Легко запи-
сать условия, требующие, чтобы все факторы расходовались в
количествах, не превышающих их запасы. Эти условия имеют вид
/
/ = 1, .... М (8.35)
4 = 1
/=1, (8.36)
Так как каждая работа в конечном счете должна быть пол-
ностью завершена, то должно выполняться ограничение
N
S(Xv+.^)=l, г = 1, ...,/. (8.37)
Далее работа i не может быть начата, пока не окажутся выпол-
ненными все работы из 1(1). Выясним, каким образом можно
записать это ограничение. Очевидно, что х^ = 0, если нарушено
условие
S^r«+M = 1’ <8-38>
и у^ = 0, если нарушено условие
! ге/(0. (8.39)
44=1 44 = 1
Здесь мы имеем условие типа «или-или». Аналогичные условия
изучались нами в § 8.6. Чтобы записать его в терминах цело-
численного линейного программирования, введем целочисленные
переменные дг/» принимающие лишь значения 0 и 1. Тогда
268
Гл. 8. Целочисленное линейное программирование
условие x;j = 0, если нарушено (8.38), может быть записано сле-
дующим образом:
/'£/(/), для всех /, у, (8.40)
/-1
+ для всех i',j, ' (8.41)
6/'/—целые, для всех у. (8.42)
Отметим, что если 6г/=1, то из (8.41) следует, что условие
(8.38) выполнено. При этом (8.40) лишь требует, чтобы
Однако если какое-нибудь д/'у = О, то из (8.40) следует, что
Xij^O, т. е. Xij — Q. Таким образом, хц не может быть положи-
тельным, если нарушено (8.38). Так как из (8.41) и (8.37) сле-
дует, что bi'j не могут быть больше единицы, то здесь нет не-
обходимости вводить ограничения на верхние границы этих
переменных.
Аналогично, вводя целочисленные переменные фГу., мы мо-
жем представить условие //г;=0, если нарушено (8.39), в сле-
дующем виде:
Уи<^гр для всех /, у, (8.43)
для всех I', j, (8.44)
а=1
Фг/>0, у—целые, для всех у. (8.45)
Теперь для завершения формулировки задачи осталось рас-
смотреть лишь структуру цен. Пусть ckj— стоимость единицы
ресурса k, используемого в обычное рабочее время /-го дня, а
dkj — в сверхурочное. Предполагается, что стоимость любого
ресурса, используемого в течение некоторого дня, прямо про-
порциональна его количеству, так что стоимость ресурса k,
использованного в день /, равна
/ I
ckj 2 aikxij + dkj (8.46)
В некоторых случаях желательно потребовать, чтобы каждый
рабочий выполнял полную норму независимо от количества
проработанного им времени. Это условие можно учесть, не-
сколько усложнив формулировку задачи.
Предположим, что ежедневное изменение в потреблении не-
которого ресурса, например рабочей силы, связано с определен-
ными затратами. Пусть и g^j — затраты, которые возникают,
если в /-й день фактор k используется в количестве, на единицу
8.8. Реализация проектов и календарное планирование
269
большем, чем в (/—1)-й день соответственно для обычного и
сверхурочного времени; fkj и hhj — аналогичные затраты, связан-
ные с уменьшением на единицу в потреблении &-го фактора. За-
метим, что потребление фактора k в /-й день отличается от по-
требления этого фактора в (/—1)-й день на величину (для
обычных рабочих часов)
I
i (Xij Xi, /-1)*
Z = 1
Аналогичное выражение имеет место для сверхурочного вре-
мени. Введем обозначения
/
vki 43Ы = aik х1, ;-1)>
v'kj, k=\, .... К, J — 2,...,N, (8.47)
и
/
^kj wkj = Hi, /-1)’
</>°> k=\,....K, j — 2,...,N. (8.48)
Затраты, связанные с изменением потребления фактора k в /-й
день по сравнению с предыдущим днем, теперь могут быть
представлены в следующем виде:
j + fk & j + Г <8-49)
В общих затратах необходимо учитывать убытки, которые
возникают ежедневно, пока не завершен проект. Эти убытки
характеризуются тем доходом, который можно было бы полу-
чить, если бы, например, завод не был остановлен на время ре-
конструкции, пассажирский самолет не был снят с линии и т. д.
Пусть D — теряемый ежедневно возможный доход. Ранее мы
предполагали, что проект может быть реализован минимум за
п и максимум за N дней. Потеря суммы nD, относящейся к пер-
вым п дням, неизбежна, и поэтому ее не следует включать в це-
левую функцию. Прибыль D теряется в /-й день, j>n, если в
этот или в последующие дни работа еще не. завершена, т. е. если
N I
2 (xiu + > О-
«=/ / = 1
Чтобы должным образом ввести эти потери в целевую функ-
цию, введем дополнительные целочисленные переменные pj,
270
Гл. 8. Целочисленное линейное программирование
принимающие лишь значения 0 и 1. Запишем
2 2 (*/в+ / = п-Н, .... N, (8.50)
U — j / = 1
0<pj<l, Pj — целые, / = /г-|-1, .... N, (8.51)
Если р3 = 0, то из (8.50) следует, что
л 1
2 2(х/и + ///и) = 0 (8.52)
U=j/ = 1
и, значит, в день j потери в доходе нет. Если pj=l, то на вели-
чину S (xiu-\~yiu) не накладывается никаких ограничений. Если
и, /
мы примем, что в день / потери в доходе равны
(8.53)
то они будут правильно учтены, если в /-й или в последующие
дни работы окажутся еще не завершенными. Однако приведен-
ные выше ограничения не гарантируют того, что теряемый в
день / доход D не будет вноситься даже тогда, когда уже все
работы по реализации проекта завершены. Но если значение
целевой функции минимизируется, это обстоятельство не будет
иметь места, так как в этом случае ее значение можно умень-
шить, положив соответствующую переменную pj равной нулю.
При этом не нарушается ни одно из приведенных выше ограни-
чений. Таким образом, потери в доходе в день j действительно
могут быть представлены формулой (8.53). Объединяя (8.46),
(8.49) и (8.53), мы получим целевую функцию, значение кото-
рой должно быть минимизировано,
к N 1
z = 2 2 2 (^Pikxij + dk j) Ч-
&=i /=1 i=i
KN N
+ 2 ^(ekj'v'kj + fkjvkj~y Skj'w'kj + llkj'w"kj)^ D % (8-54)
Значение (8.54) необходимо минимизировать при ограничениях
(8.35), (8.36), (8.37), (8.40), (8.41), (8.42), (8.43), (8.44), (8.45),
(8.47), (8.48), (8.50) и (8.51), где, разумеется, все перемен-
ные Хц и уц должны быть неотрицательными. Мы получили ча-
стично целочисленную задачу линейного программирования.
Для любой сколько-нибудь реальной задачи число ограничений
оказывается настолько большим, что в настоящее время ее ре-
шение совершенно невозможно. Однако возможность сформули-
ровать рассматриваемую задачу как целочисленную предста-
8.9. Задача о бродячем торговце
271
вляет определенный интерес. Число ограничений вида (8.41)
часто может быть значительно уменьшено. Действительно, если
требуется, чтобы работа i" была закончена раньше, чем будет
начата работа Г, которая должна предшествовать работе /, то
нет необходимости вводить ограничение, требующее, чтобы ра-
бота i" заканчивалась раньше начала работы L Это обстоятель-
ство будет автоматически учтено, если требуется, чтобы Г за-
канчивалась раньше, чем начинается г, а /" предшествовала
бы i'. Однако такого уменьшения размеров задачи недостаточно
для практического ее решения.
8.9. Задача о бродячем торговце. Предположим, что имеется
территория, на которой расположены п городов. Бродячему тор-
говцу необходимо выехать из своего дома, находящегося в од-
ном из городов (отметим этот город индексом 1), посетить ка-
ждый и$ остальных п—1 городов и вернуться домой. Он стре-
мится выбрать такую последовательность посещения городов,
чтобы суммарное расстояние, пройденное им, оказалось бы
минимальным. Расстояние от города i до города / обозначим че-
рез dij. В нашей формулировке задачи мы не будем требовать,
чтобы dij = dji. Очевидно, что всего имеется (п—1)! различных *
последовательностей посещения городов. Замкнутый путь бродя-
чего торговца можно представить себе в виде ломаной, состоя-
щей из п звеньев. Звену с номером k соответствует путь из горо-
да i в город /, с номером 1 —путь из города 1 в какой-то дру-
гой город, с номером п —путь из некоторого города в город 1.
Чтобы сформулировать задачу, решение которой дает после-
довательность посещения городов с минимальным пройденным
расстоянием, введем переменные &ijk, принимающие значение 1,
если торговец из города i в город / проезжает по &-му звену
пути, и 0 в противном случае. Так как звену k может соответ-
ствовать лишь одна пара городов, то должны выполняться соот-
ношения
ЕД* = 1, k = 2,...t п-1,
2б1Л = 1, . (8.55)
S == 1*
I
Кроме того, для любого города i существует лишь одно звено
пути, исходящее из i и оканчивающееся в некотором другом
городе. Таким образом,
2^ = 1, / = 2, ..., п, (8.56)
272
Гл. 8. Целочисленное линейное программирование
где требуется, чтобы & = п, если /=1, и наоборот. Ограничение
для /=1 содержится в (8.55). Аналогично в каждом городе j
оканчивается лишь одно звено пути. Следовательно,
= (8.57)
i, к
где требуется, чтобы й=1, если i’=l, и наоборот. Случай /=1
содержится в (8.55). Наконец, если й-е звено оканчивается в го-
роде /, то (& + 1)-е звено должно исходить из города /. Отсюда
следует, что
= 7=2, п, k = 2, га —1,
i i'
61/1 — 2 6//'2,
Г
2 6//, Л-1=б/1п.
(8.58)
Ограничения (8.58) исключают возможность несвязных путей,
один из которых показан на
Рис. 8.5.
рис. 8.5 для случая семи городов.
Отметим, что множество перемен-
ных Sijfe, соответствующих несвяз-
ному пути рис. 8.5, удовлетворяет
ограничениям (8.55) — (8.57).
Итак, сформулированы все
ограничения, относящиеся к рас-
сматриваемой задаче. Здесь нет
необходимости вводить ограни-
чения 6г-дг<3, так как из (8.55) —
(8.58) следует, что эти перемен-
ные не могут превосходить единицы. Таким образом, задача со-
стоит в том, чтобы найти неотрицательные целые б^ь, удов л е*
творяющйе (8.55) — (8.58) и минимизирующие
г— 2
(8.59)
Заметим, что ограничения задачи могут быть записаны в бо-
лее симметричной форме, где случаи г=1 и /=1 специальным
образом не выделяются. Именно -
2^ = 1, й=1,...,га; = i=l, ...,га;
I, i Л»
2^=1- J=l,..., п; (8.60)
i, k
^ijk=^jr,k+u Л = 1, ...» га—1. (8.61)
/ Г
8.10. Капитальные вложения фирмы 273
Однако при таком подходе вводится ряд переменных, относи-
тельно которых известно, что они равны нулю, а также некото-
рые лишние ограничения.
8.10. Капитальные вложения фирмы. Многие простые задачи,
касающиеся способа распределения имеющегося у фирмы капи-
тала среди различных проектов, могут быть сформулированы
как целочисленные задачи линейного программирования. Рас-
смотрим сначала простейший из возможных случаев. Пусть
фирма располагает свободным капиталом в размере D долла-
ров. Имеется п различных проектов, претендующих на эти
фонды. Капиталовложенйя, необходимые для проекта /, соста-
вляют dj долларов. Пусть pj— приведенная к настоящему мо-
менту оценка всего будущего дохода от реализации проекта /.
Необходимо определить, в какие проекты нужно вкладывать ка-
питал, чтобы максимизировать приведенный общий доход. Сум-
марные капиталовложения при этом не должны превышать
величины D. Каждый проект может либо выбираться как объект
для капиталовложений, либо отвергаться; если проект / выбран,
то капиталовложения в него не могут быть меньше dj. Анало-
гично каждому индексу j соответствует лишь один проект. Для
того чтобы сформулировать задачу как целочисленную задачу
линейного программирования, введем переменные б?-, принимаю-
щие лишь значения 0 и 1. Очевидно, что для выбора проектов,
максимизирующих суммарную приведенную оценку будущего
дохода, достаточно решить следующую целочисленную задачу
линейного программирования:
2‘'А-с °.
бу — целые, j = l, ..., п; (8.62)
п
найти max z =
;=i J
Здесь мы впервые получили полностью целочисленную задачу
линейного программирования. Но даже и в этом случае ее
можно рассматривать как частично целочисленную задачу, так
как отсутствует требование целочисленности вспомогательной
переменной, которую нужно будет ввести в ограничение на вели-
чину капиталовложений. Впрочем, величины di и D обычно
являются целыми, следовательно, и вспомогательная перемен-
ная также будет целочисленной. Как мы увидим в гл. 10, за-
дача (8.62) может быть решена с помощью динамического
программирования. Метод динамического программирования,
18 Зак. 735
274
Гл. 8. Целочисленное линейное программирование
по-видимому, здесь более эффективен, чем алгоритм целочис-
ленного программирования
Рассмотрим некоторые обобщения задачи (8.62). Пусть из
некоторой группы проектов, например для /СУ, следует выбрать
лишь один проект. Чтобы учесть это условие, необходимо доба-
вить лишь одно ограничение
(8-63) .
Для /С/ нет необходимости вводить ограничения 6^1, так как
они автоматически следуют из (8.63).
В качестве другой возможности предположим, что если вы-
бран проект /, то должен быть выбран и проект i; однако выбор
проекта i может быть осуществлен и без выбора проекта /. Для
описания такой ситуации достаточно ввести ограничение
dz-dy>0. (8.64)
Наконец, кроме ограничения на величину капиталовложений,
могут существовать и другие ограничения, например ограниче-
ние на использование рабочей силы. Обозначим через М всю
имеющуюся в наличии рабочую силу, а через mj — количество
рабочей силы, необходимое для реализации проекта /. В этом
случае к (8.62) присоединяется ограничение
(8.65)
/=1
Простая модель, описываемая формулами (8.62), совершенно
не учитывает динамики фондов при реализации имеющихся
проектов. Вполне возможно, что при реализации проектов по-
мимо начальных капиталовложений позднее могут потребо-
ваться дополнительные средства. Предположим, что имеются
ограничения’ Dk на капиталовложения в каждом из Д’ периодов,
и пусть dkj — капитал, необходимый для проекта / в период k.
Для того чтобы выбрать проекты, максимизирующие приведен-
ную оценку будущего дохода и не нарушающие ограничения
на капиталовложения для каждого периода, достаточно решить
следующую целочисленную задачу линейного программиро-
вания:
п
f>j — целые, у=1, ..., п; (8.66)
fl
найти max г= 2 Р/ц-
8.11. Решение целочисленных задач
276
Возможны и другие обобщения. Можно, например, считать,
что капитал, которым располагает фирма в период k, зависит от
фондов, полученных при эксплуатации проектов, реализованных
в предыдущие периоды. Можно также предусмотреть появление
со временем новых проектов. Подробное рассмотрение этих и
других возможных обобщений мы предоставляем читателю.
Применение целочисленного программирования к изучению ка-
питаловложений рассматривалось Вайнгартнером [20].
8.11. Решение целочисленных задач линейного программи-
рования. Обратимся теперь к способам решения целочисленных
задач вида (8.1). Основная идея решения таких задач, первона-
чально предложенная Данцигом, Фалкерсоном и Джонсоном [7],
заключается в том, что задача (8.1) сначала решается без огра-
ничений целочисленности. Если полученное таким образом
решение оказывается целочисленным, то оно должно быть опти-
мальным решением для задачи (8.1), так как ее любое допусти-
мое решение является допустимым решением задачи линейного
программирования, полученной из задачи (8.1) отбрасыванием
ограничений целочисленности. Задачу линейного программиро-
вания, полученную из задачи (8.1) отбрасыванием ограничений
целочисленности, обозначим через ЛП (8.1). Если оптимальное
решение задачи ЛП (8.1) не является допустимым решением
задачи (8.1), так как оказалось нарушенным какое-либо из тре-
бований целочисленности, то к задаче ЛП (8.1) присоединяют
новые ограничения, по одному на каждом шаге, и таким обра-
зом получают некоторую последовательность новых задач ли-
нейного программирования. Ограничение, присоединяемое к за-
даче ЛП (8.1) первым, обладает тем свойством, что множество
допустимых решений для новой задачи линейного программиро-
вания не содержит оптимального решения задачи ЛП (8.1) и
содержит все допустимые решения задачи (8.1). Затем решается
новая задача линейного программирования с учетом нового до-
полнительного ограничения. Если ее решение допустимо для
задачи (8.1), то оно и оптимально для этой задачи. Если полу-
ченное решение не допустимо для задачи (8.1), то вводится но-
вое ограничение, обладающее тем свойством, что множество
допустимых решений вновь полученной задачи содержит любое
допустимое решение задачи (8.1) и не содержит оптимального
решения предыдущей задачи линейного программирования. Эти
дополнительные ограничения, вводимые при переходе от одной
задачи линейного программирования к другой, в дальнейшем
мы будем называть сечениями. Каждое из вновь вводимых огра-
ничений отсекает некоторую часть множества допустимых ре-
шений задачи ЛП (8.1). Сечения, вводимые описанным выше
18*
276
Гл. 8. Целочисленное линейное программирование
способом, вообще говоря, не обязательно должны привести к оп-
тимальному решению задачи (8.1) за конечное число шагов. Од-
нако, как мы покажем ниже, эти сечения можно выбрать таким
образом, что гарантируется сходимость* к оптимальному реше-
нию задачи (8.1) за конечное число шагов, если только такое
решение существует. .
8.12. Алгоритм Гомори для решения полностью целочислен-
ной задачи. Сначала мы рассмотрим случай, когда множество Л
содержит все /, т. е. случай полностью целочисленной задачи.
Предположим, что задача ЛП (8.1) уже решена и пусть В —
матрица, соответствующая базису оптимального решения. Обо-
значим через R множество тех индексов /, которые соответст-
вуют небазисным переменным. Тогда если yj = B-1aj, /=1,..., п,
и у0 = В-1Ь, то хв=Уо представляет собой вектор, компоненты
которого равны значениям базисных переменных в оптимальном
решении задачи ЛП (8.1). Кроме того, как было показано в
§ 2.2, любое допустимое решение х должно удовлетворять соот-
ношению
= у0 — S VjXj. (8.67)
Существует единственное базисное решение хв = уо, хл==0, удо-
влетворяющее (8.67). Если это решение не обладает тем свой-
ством,. что все компоненты у0 — неотрицательные целые числа,
то, очевидно, в любом оптимальном решении задачи (8.1) по
крайней мере одна из переменных Xj, j€R, должна быть поло-
жительной. Так как все переменные в задаче должны быть це-
лыми, то необходимо; чтобы по крайней мере одна из перемен-
ных Xj, / была не меньше единицы. Рассмотрим ограничение
2х,>1. ’ (8.68)
Как мы только что показали, любое допустимое решение задачи
(8.1) должно удовлетворять (8.68). Наше решение, у которого
хя = 0, этому ограничению не удовлетворяет. Следовательно,
если мы рассмотрим новую задачу линейного программирова-
ния, присоединив ограничение (8.68) к ограничениям задачи ЛП
(8.1), то множество допустимых решений этой новой задачи
будет «меньше», чем соответствующее множество для задачи
ЛП (8.1), но тем не менее будет содержать все допустимые ре-
шения задачи (8.1). Предположим, что мы решаем новую за-
дачу линейного программирования, полученную присоединением
(8.68) к задаче ЛП (8.1). Если окажется, что оптимальное ре-
шение (которое будет содержать т+1 положительных значе-
ний), найденное для этой задачи линейного программирования,
8.12. Алгоритм Гомори
277
обладает тем свойством, что все его положительные перемен-
ные целые, то это решение оптимально для задачи (8.1). В про-
тивном случае для нового множества небазисных переменных
мы вводим новое ограничение вида (8.68) и повторяем процесс.
Метод решения полностью целочисленных задач, основанный на
введении сечений в виде (8.68), впервые был предложен Дан-
цигом [6]. Для небольшого числа задач, на которых этот метод
испытывался, он оказался сходящимся. Было, однако, доказано
[14], что существуют случаи, когда сходимости нет. Другие спо-
собы построения сечений рассматривали Марковиц и Манне [16];
однако они не нашли систематического метода — их приемы-
опираются на интуицию и изобретательность. С другой стороны,
Гомори [8, 9] разработал систематический способ построения ®
сечений, который, как можно показать, за конечное число шагов
приводит к оптимальному решению задачи (8.1).
Приступим к изложению метода Гомори. Как и выше, будем
предполагать, что мы уже решили задачу ЛП (8.1) и хв=Уо,
где уо определено ранее, — ее оптимальное решение. Допу-
стим, что не все компоненты у0 целые. Предположим, что уио
нецелое. Рассмотрим м-е равенство (8.67)
хви=Уиь- ^yUjxj (8-69)
и запишем
— +flip /€#’» УиО = ^иО + ((8.70)
где 6Uj — наибольшее целое число, не превышающее yUj, j£R
и / = 0. Так как по предположению уио не целое, то fuo>0. Кроме
того, Подставив (8.70) в (8.69), получим
ХВи~ &иО— 2 &ujxj~^~fuO S fujxj- (8-71)
/6Я j£R
Для любого целочисленного решения, удовлетворяющего (8.67),
величина
ХВи ^ujXj
j
должна быть целой (не обязательно неотрицательной). Следо-
вательно, как видно из (8.71), для любого целочисленного ре-
шения, удовлетворяющего (8.67), величина
Jujxi (8.72)
j£R
должна быть целой. Величина 2 fuifi не может быть отри-
цательной. Поэтому, так как О</ио<1, (8.72) не может быть
278
Гл. 8. Целочисленное линейное программирование
положительным целым числом. Следовательно, любое допусти-
мое решение задачи (8.1) должно удовлетворять неравенству
(8.73)
j£R
или
(8.74)
Очевидно, оптимальное решение, полученное для задачи ЛП
(8.1), не удовлетворяет неравенству (8.74), так как Xj = O, j£R.
Таким образом, если мы присоединим (8.74) к ограничениям
задачи ЛП (8.1), то новое множество допустимых решений ока-
жется уже соответствующего множества задачи ЛП (8.1), но
будет содержать все допустимые решения задачи (8.1). Соотно-
шение (8.74) и представляет собой сечение, введенное Гомори.
Присоединив (8.74) к задаче ЛП (8.1), решаем полученную
задачу, имеющую т+1 ограничение. В {ЛП 11.5} показано, что
для получения решения расширенной задачи нет необходимости
решать ее заново. Пусть $1 — вспомогательная переменная огра-
ничения (8.74) (индекс 1 означает, что эта переменная соответ-
ствует первому из ограничений, присоединяемых к задаче ЛП
(8.1)). Ограничение (8.74) принимает вид
Как было показано выше, для любого целочисленного решения,
удовлетворяющего (8.67), величина (8.72) должна быть целой.
Следовательно, переменная «1 также должна быть целочислен-
ной, так что мы опять имеем полностью целочисленную задачу.
Обозначив через Bi матрицу, соответствующую базису расши-
ренной задачи, получим
где em+i = [0, 1] — производственный вектор, соответствующий
переменной si. Таким образом, базисное решение расширенной
задачи равно
ВГЧь, -^о] = [Уо?~Ы (8.76)
Это базисное решение не допустимо, так как —/ио<О. Вектор
оценок, соответствующих базису Вь равен (св, 0). Далее, вели-
чины Zj—Cj для расширенной задачи в точности те же самые,
что и для оптимального решения задачи ЛП (8.1), так как ве-
8.12. Алгоритм Гомори
279
личины yj,/С 7?, для расширенной задачи (обозначим их через
у(Р) равны
(8-77)
Следовательно, мы имеем для расширенной задачи базисное, но
не допустимое решение, для которого все z,—Поэтому для
получения оптимального решения расширенной задачи можно
использовать двойственный симплекс-метод. В силу (8.77) мы
сразу можем записать исходную симплексную таблицу для рас-
ширенной задачи. Для этого нужно к таблице, соответствующей
оптимальному решению задачи ЛП (8.1), приписать одну
строку и один столбец. В новой строке на месте пересечения со
столбцом, соответствующим у0, мы записываем —/и0, а для
столбцов, соответствующих /, j €/?, записываем —fuj. В новом
столбце, соответствующем переменной $1, мы всюду записываем
нули, за исключением новой строки, где следует записать еди-
ницу. Оставшиеся в новой строке места заполняем нулями. По-
сле того как таблица полностью записана, применяем двой-
ственный симплекс-метод. Как правило, для получения опти-
мального решения расширенной задачи требуется сравнительно
небольшое число итераций, чаще всего одна. Если решение но-
вой задачи линейного программирования не обладает нужными
свойствами целочисленности, мы повторяем весь процесс, вводя
новые ограничения. Это продолжается до тех пор, пока не бу-
дет получено допустимое и, следовательно, оптимальное реше-
ние задачи (8.1).
Описывая метод, мы не указали никакого правила, которым
следует руководствоваться при выборе уравнения из (8.67) для
построения сечения (8.74) в том случае, когда несколько компо-
нент вектора у0 не являются целыми. Для обеспечения сходи^
мости за конечное число шагов необходимо следовать специ-
альному правилу выбора. Этот вопрос будет рассмотрен в сле-
дующем параграфе. Однако упомянутое правило не очень удоб-
но в практических вычислениях, поэтому встает вопрос о более
простом правиле. Интуитивно кажется разумным выбирать то
сечение, которое отсекает как можно большую часть множества
допустимых решений предыдущей задачи. Однако сформулиро-
вать точно, что это означает, затруднительно. По-видимому,
плоскость
2 ( f aj) xj~ fuO
j
нужно выбрать так, чтобы она пересекала оси Xj, j(zR, в точ-
ках, как можно более удаленных от начала координат. В этом
280
Гл. 8. Целочисленное линейное программирование
случае переменные Xj, удовлетворяющие (8.74), будут
принимать наибольшие из возможных значений. А это, по суще-
ству, соответствует наибольшему продвижению во множество
допустимых решений от точки х=[у0, 0]. Таким образом, жела-
тельно, чтобы все отношения fuo/fuj принимали как можно боль-
шие значения. К сожалению, часто при одном и том же и эти
отношения оказываются разными по величине. Поэтому при
практических вычислениях из соотношений (8.67) выбирают то,
для которого fuo наибольшее. Очевидно, можно сформулировать
множество других, относительно простых правил выбора. В ча-
стности, можно построить сечения, соответствующие всем неце-
лочисленным переменным, и рключить их в расширенную за-
дачу. В этом случае также нетрудно найти новое базисное ре-
шение, но число отрицательных переменных в этом решении
будет равно числу вновь введенных ограничений. Так как число
итераций по двойственному симплекс-методу быстро возрастает
с числом добавленных ограничений, то трудно что-либо сказать
о преимуществах этого подхода. .
Описанный нами метод представляет собой итеративный
процесс, на первом шаге которого мы решаем задачу ЛП (8.1).
Обозначим эту задачу через Pq. Если решение задачи PQ яв-
ляется допустимым для задачи (8.1), то оно оптимально для
нее. В противном случае мы определяем сечение (8.74) и полу-
чаем новую задачу линейного программирования которая
содержит на одно ограничение и одну переменную больше,
чем Ро. При решении Pi используется двойственный симплекс-
метод. Далее имеются две возможности: либо мы получаем до-
пустимое и оптимальное решение задачи (8.1), либо строим но-
вое сечение и новую задачу Р2. В процессе вычислений число
ограничений задачи с индексом v первоначально будет увеличи-
ваться с ростом v. Однако, как бы велико ни было v, число
новых ограничений в задаче Pv никогда не превзойдет п+1.
Чтобы убедиться в этом, заметим, что если какая-либо вспомо-
гательная переменная s$ является базисной переменной в опти-
мальном решении задачи то при построении задачи Pv
ограничение с вспомогательной переменной Sj может быть опу-
щено, так как нет необходимости в том, чтобы это ограничение
всегда выполнялось. Базисное решение полученной задачи мы
можем определить, используя те переменные xj, которые вхо-
дили в оптимальное решение задачи Pv-i. Чтобы отбросить лиш-
нее ограничение, достаточно в симплексной таблице, соответ-
ствующей оптимальному решению задачи Pv-i, вычеркнуть
строку, переменная Sj которой входит в базис, и вычеркнуть
столбец, соответствующий этой переменной. В упражнении 8.10
8.13. Доказательство конечности
281
мы предлагаем читателю доказать корректность этой проце-
дуры. Так как задача (8.1) содержит лишь п переменных, то
после исключения из задачи Pv_\ ограничений, переменные Sj
которых вошли в оптимальное базисное решение, мы получим
задачу, имеющую не более чем п дополнительных ограничений.
Обозначим эту задачу через Pv-i- Чтобы получить нужно
к Pv-i добавить одно сечение. Таким образом, число ограниче-
ний в задаче Pv может превосходить число ограничений в за-
даче Ро самое большее на п+1. Этот результат показывает, что
для расширения задач Pv имеется определенный предел.
Доказательство того, что для получения оптимального ре-
шения задачи (8.1) достаточно решить лишь конечное число
задач Рщ приведено в следующем параграфе. А пока отметим,
что для решения полностью целочисленной задачи имеются и
другие алгоритмы. Гомори [10] предложил алгоритм, при ис-
пользовании которого требуется, чтобы все элементы А и b в за-
даче (8.1) были целыми. В этом алгоритме не нужно решать
задачу ЛП (8.1). Исходным пунктом является базисное, не обя-
зательно допустимое, решение, для которого все Zj—q>0. За-
тем используется двойственный симплекс-метод. Сечения добав-
ляются при каждой итерации. Другой метод был предложен
Лэнд и Дойг [15]. На наш взгляд, ни один из указанных методов
не имеет каких-либо преимуществ по сравнению с методом, из-
ложенным выше.
8.13. Доказательство конечности. Чтобы получить процесс,
сходящийся после решения конечного числа задач Pv, необхо-
димо несколько модифицировать алгоритм, описанный в преды-
дущем параграфе. Во-первых, предположим, что Cj в (8.1) целые,
так что если Xj целые, то и г будет принимать целые значения.
Мы всегда можем добиться выполнения этого предположения,
если надлежащим образом выберем физические единицы, ъ ко-
торых измеряются величины Кроме этого, потребуем, чтобы z
имело верхнюю и нижнюю границы.
Присоединив к (8.67) уравнение для z, получим
г = Уоо— ЗуоЛр хв = у0— 2 УЛ, (8.78)
/ёЯ KR
где Уоо=СвУо равно значению z, соответствующему оптималь-
ному решению задачи ЛП (8.1), и yQj = Zj—Cj. Если обозначить
через хд вектор с компонентами Xj, j<zR, то можно записать
= £ (-е,-)ху, (8.79)
282 Гл. 8. Целочисленное линейное программирование
где е^ —единичный вектор размерности п—т с единицей на
надлежащем месте. Объединяя (8.78) и (8.79), получим
г = Уоо— 2 y.jXj,
Х8 = Уо-2у/р (8-80)
Х/? = 0— 2 (—еу)ху.
Для векторов, входящих в (8.80), введем обозначения
P/ = lf/oy-У/- -еД /€/?; Ро = [//оо, Уо» 01- (8-81)
Предположим, что первые п строк, следующие за г-строкой в
(8.80), упорядочены таким образом, что каждый вектор Pj, j(zR,
лексикографически положителен. Вектор-столбец Pj называется
лексикографически положительным, pj>*0, есЛи его первая от-
личная от нуля компонента, считая сверху вниз, положительна.
Далее pj)>pfe, если Pj— рл)>0. В общем случае не очевидно, что
строки (8.80) могут быть упорядочены так, что pj>* 0, j£R.
Но если предположить, что выпуклое множество допустимых
решений задачи ЛП (8.1) ограничено, то это всегда можно сде-
лать. Чтобы доказать это, введем вспомогательное ограничение
Jb Xj-{-xn+1 = М, (8.82)
яя
где М — настолько большое целое число, что для любого допу-
стимого решения задачи (8.1) ограничение (8.82) будет выпол-
няться при xn+i>0. Таким образом, хп+1 будет входить в каж-
дое базисное решение. Если предположить, что xn+i всегда яв-
ляется первой базисной переменной, и в (8.80) записать урав-
нение с Xn+i в виде хл+1 = Л4— 2 xi сразу за уравнением,
соответствующим z, то вторая компонента каждого вектора pj
будет равна единице. Так как в оптимальном решении задачи
ЛП (8.1) //0j>0, то pj > 0, j £R. В дальнейшем мы будем пред-
полагать, что ограничение (8.82) введено в (8.80), если это не-
обходимо для лексикографической положительности Pj,
Применим теперь к (8.80) описанный в § 8.12 метод, слегка
видоизменив его. Во-первых, если у00 нецелое, то для построе-
ния сечения привлечем уравнение, соответствующее z. Заметим,
что в § 8.12 мы этого не делали. Далее условимся приписывать
новые ограничения к (8.80) снизу. Уравнение, используемое для
построения нового сечения, мы будем выбирать в соответствии
со следующим правилом: просматривая уравнения в том по-
8.13. Доказательство конечности
283
рядке, в каком они записаны в (8.80), выбираем первое уравне-
ние, для которого /Ло, /=0, ... , т, «не является целым. Таким
образом, всегда, когда уОо дробное, для построения сечения бу-
дет использоваться соотношение, соответствующее г.
Теперь мы можем приступить к доказательству конечности.
Предположим, что р0 не является допустимым решением для^
задачи (8.1). Тогда, применяя описанное выше правило выбора,
мы определяем сечение и получаем задачу Задачу Р4 ре-
шаем двойственным симплекс-методом. При этом для определе-
ния вектора, вводимого в базис, мы будем использовать специ-
альное правило. Это правило заключается в следующем. Если
хВг — наибольшая по модулю отрицательная переменная, то она
должна быть выведена из базиса. Для определения перемен-
ной, вводимой в базис, мы сначала вычислим величину
= max —Уг1<$- (8.83)
Vrk Уг1 7
Если k единственное, то столбец k вводится в базис. Если не
единственное, то для тех /, для которых в (8.83) достигается
максимум, мы вычисляем величину
#1/
max —
y.rj
(8.84)
Если этот максимум достигается при единственном /, то мы тем
самым определим столбец, вводимый в базис. В противном слу-
чае для тех /, для которых в (8.84) достигается максимум, ну-
жно вычислить шах Уч^Угу В конце концов мы должны одно-
значно определить столбец, который следует ввести в базис, так
как в противном случае вектор pj оказался бы пропорциональ-
ным другому, что невозможно в силу (8.81). В результате выше-
описанных действий мы найдем вектор (—1/Угь)Ра)>0, такой,
что
(^)Р'“ЮР*>0' ^<0' <8-85’
Таким образом,
Р/ —для всех j^k^R. (8.86)
Vrk
В (8.86) содержатся все компоненты pj, за исключением г-й,
где pj—новый /-й столбец в симплексной таблице, которая по-
лучается после того, как переменная хВг исключена из базиса,
а переменная xk введена в него. Компонента г столбца pj равна
284
Гл. 8. Целочисленное линейное программирование
уГ]1утЬ' Вектор, соответствующий хВг, ставшей теперь небазис-
ной переменной, равен
77^- i^r, у-<0, i — r. (8.87)
lJrk vrk
Так как вектор pfe был лексикографически положительным, его
первая отличная от нуля компонента была положительна. Это
верно и для (8.87), так как величина //^<0, и поэтому она не
могла быть первой ненулевой компонентой pfe. Таким образом,
вектор, соответствующий хВг, будет лексикографически положи-
тельным. Из того факта, что yrk не является первой ненулевой
компонентой pk, и из (8.86) следует, что р; >0, j^k^R (про-
вести подробное доказательство). Следовательно, для всех /,
входящих в новое множество R, которое получается из R ис-
ключением ] = k и добавлением /, соответствующего хВг, имеем,
что р.; > 0.
Далее отметим, что
Ро = Ро—тгРй+-т^ег,
Угк УгЬ
так что
Ро —Ро>О. (8.88)
В каждой итерации двойственного симплекс-метода р0 будет
лексикографически уменьшаться. Это верно для каждой итера-
ции при решении фиксированной задачи Pv и остается верным
при переходе к задаче Pv+i, так как п+1 компонент исходного
вектора р0 в задаче Pv+i равны соответствующим компонентам
конечного вектора р0 в задаче Pv. Описанная нами лексикогра-
фическая схема исключает зацикливание при решении зада-
чи Р» (см. {ЛП6.7}). Эта же схема будет нами использована и
при доказательстве того, что допустимое и оптимальное решение
задачи (8.1), если такое существует, может быть получено после
решения конечного числа задач Pv,
По мере того как к (8.80) присоединяются дополнительные
ограничения, число компонент pj увеличивается. Однако отбра-
сывание сечений, вспомогательные переменные которых вошли
в базис, никак не влияет на тот факт, что все Pj>>0, j£R.
Чтобы убедиться в этом, заметим, что матрица в (8.80), столб-
цами которой являются п—m векторов pj, имеет ранг п—т.
После каждой итерации первые п+1 уравнений (или п + 2, если
было введено (8.82)) будут иметь в точности ту же форму, что
и в (8.80), так что невозможен случай, когда первые п+1 ком-
понент для некоторого вектора р^ в результате дальнейших ите-
раций оказались бы равными нулю. Следовательно, лексикогра-
8.13. Доказательство конечности
285
фические свойства векторов pj постоянно будут определяться
первыми п+1 компонентами, так что всегда pj)>0, j(zR. Это
показывает также, что при выборе вектора, вводимого в базис,
нам никогда не придется иметь дело с цепочкой, состоящей бо-
лее чем из п строк.
Если при решении задачи Pv окажется, что все #п->0, то это
будет означать, что двойственная задача имеет неограниченное
решение, а прямая задача решения не имеет. В этом случае для
задачи (8.1) не существует допустимого решения. Вполне воз-
можен случай, когда задача ЛП (8.1) имеет допустимые реше-
ния, а задача (8.1) их не имеет. В упражнении 8.11 мы предла-
гаем читателю построить пример такого рода.
В дальнейшем мы предполагаем, что случай, когда z/rj>0
для всех j£R, не имеет места. Применяя к задачам Pv двой-
ственный симплекс-метод, мы получим последовательность век-
торов ро, которую обозначим через ро(О- Мы будем предпола-
гать, что I увеличивается на единицу не только при переходе от
задачи Pv к задаче но и с каждой итерацией двойствен-
ного симплекс-метода. Нами было показано, что ро(/)5> Ро(/+1).
Докажем, что последовательность р0(/) конечна.
Предположим, что последовательность р0(/) не является ко-
нечной.. Однако первые компоненты последовательности р0(/)
должны удовлетворять условию #оо(/)>т/оо(/+1). Мы предпола-
гали ранее, что величина z ограничена снизу. Таким образом,
последовательность //оо(О монотонна и ограничена снизу. Сле-
довательно, она должна иметь предельную точку г*, такую, что
любая е-окрестность z* содержит бесконечное число точек z/oo(/)
и z*^//oo(/) для всех /. Пусть 6Оо — наибольшее целое число,
такое, что боо^//оо(О Для всех Мы покажем, что существует
такое /о, что Уоо(О=боо для всех />/0.
Из определения бОо следует, что, начиная с некоторого /, мы
можем записать z/oo(/) ==6oo + foo(/), O^C/ooG) <1. Предположим,
что это представление имеет место при решении задачи Pv, По-
сле решения задачи Ръ мы имеем
//оо (П = боо + foo (П> /оо (П К /оо (/). (8.89)
Если foo(/')=^O, то.в соответствии с нашим правилом выбора
для построения сечения следует использовать уравнение, соот-
ветствующее г. Это сечение имеет вид
2 -М(П^<-/оо(П- (8.90)
джп
Ограничение (8.90) вводится для получения задачи из
задачи Pv. В исходной форме задачи Рг+1 единственной
286
Гл. 8. Целочисленное линейное программирование
отрицательной переменной будет переменная sv+i. Таким обра-
зом, в результате применения первого шага двойственного сим-
плекс-метода к задаче Ръ^ переменная окажется равной
нулю, а величина //оо(/Л+1) будет вычислена по формуле
y^l'^r (8.91)
Так как t/ok(P)>O, то из (8.91) следует, что
Уо/г (t') fok (О>
или
У00 (I' + 1) {/оо (О — /оо (О ~ &00*
Отсюда для всех />7'+1 имеем, что уоо(/)=боо.
Первая компонента р0(/) постоянна для />/'+1. Когда z
достигло величины 6Оо, то лишь при крайне неблагоприятных
обстоятельствах не все переменные окажутся целыми Если z
не меняет своего значения в последующих итерациях, его дол-
жно выполняться следующее условие: если на следующем шаге
xh принимает положительное значение, то */оь(О =0. В против-
ном случае z будет меняться. Предположим, что когда г до-
стигло боо, базисная переменная в первом уравнении, следующем
за z-уравнением, имеет дробное значение. С помощью этого
уравнения строим сечение. Если переменная хк должна войти
в базис, то у^(/)=#0, а так как г/оИО=О и pfe>0, то £/1&(/) >0.
Следовательно, вторые компоненты векторов ро(/) образуют не-
возрастающую последовательность, ограниченную снизу нулем.
В точности повторяя те же самые рассуждения, что и выше, и
учитывая, что z/ife(/)>0, мы получим, что вторая компонента
вектора р0 (/) через конечное число итераций достигнет целого
значения. Затем мы перейдем к третьей компоненте. Заметим,
что если переменная xh должна войти в базис, то z/Ofe(/) =
=ylfe(/)=0 и z/2fe(/)>0, так что здесь могут быть повторены те
же самые рассуждения, и т. д. Но векторы pj(Z) имеют лишь
конечное число компонент. Таким образом, через конечное число
шагов все компоненты достигнут целочисленных значений, а это
противоречит предположению о бесконечности последователь-
ности. Следовательно, через конечное число шагов мы получим
оптимальное решение задачи (8.1) или придем к выводу, что
у этой задачи нет допустимых решений.
Метод, описанный в этом параграфе, обеспечивает сходи-
мость за конечное число шагов. Однако применение его на
практике так же неудобно, как и использование различных при-
емов, исключающих вырожденность в симплекс-методе. Для
практических целей более удобен метод, описанный в предыду-
8.14. Алгоритм, для решения частично целочисленных задач 287
щем параграфе. Для этого метода отсутствует какое-либо дока-
зательство сходимости за конечное число шагов. Однако если
предположить, что при применении двойственного симплекс-ме-
тода не будет зацикливания, то сходимость, по-видимому, будет
иметь место.
Как уже указывалось в начале главы, опыт вычислений на
основе метода Гомори оказался мало обнадеживающим. Хотя
с помощью надлежащих мер этот алгоритм может быть сделан
конечным, все же во многих случаях число необходимых итера-
ций оказывается настолько большим, что можно практически
говорить об отсутствии сходимости. В задачах вида (8.1), тре-
бующих менее 20 итераций для решения задач ЛП (8.1), было
безуспешно сделано 2000 и более итераций. Это обстоятельство,
а также тот факт, что при формулировке какой-либо задачи как
целочисленной задачи линейного программирования часто при-
ходится вводить большое число дополнительных ограничений,
делают в настоящее время невозможным практическое решение
многих интересных задач.
Отметим еще, что при составлении программ для решения
на цифровой вычислительной машине целочисленных задач воз-
никают затруднения, связанные с округлением. Истинное реше-
ние, если его вычислить точно, может оказаться оптимальным
решением задачи (8.1), но ввиду округления это же решение,
вычисленное машиной, не является целочисленным. Чтобы из-
бежать этих трудностей, необходимо модифицировать способ
выполнения арифметических операций.
8.14. Алгоритм для решения частично целочисленных задач.
Гомори [11] предложил алгоритм для решения частично целочис-
ленной задачи линейного программирования, т. е. такой задачи
(8.1), в которой Л не содержит всех /. В этом алгоритме, так же
как в случае полностью целочисленной задачи, сначала решает-
ся задача ЛП (8.1). Если ее решение оказывается допустимым
для задачи (8.1), то оно должно быть оптимальным и для этой
задачи. В противном случае мы поступаем так же, как и раньше,
т. е. вводим сечения. Различие между рассматриваемой и пол-
ностью целочисленной задачами заключается в способе постро-
ения сечений.
Чтобы определить сечения для частично целочисленного слу-
чая, рассмотрим решение задачи ЛП (8.1) и предположим, что
переменная хВи, которая в любом допустимом для задачи (8.1)
решении должна быть целой, имеет дробное значение. Рассмот-
рим выражение
ХВи — УиО 2 У uiXi*
288 Гл. 8. Целочисленное линейное программирование
Как и в § 8.12, запишем //uo = 6uo+fwo- Тогда для любого до-
пустимого решения задачи (8.1)
fuo~ 2 yUjXj = целое число = хВа — Ъий. (8.92)
KR
Пусть R+— подмножество R, для которого yuj^G, и R- — под-
"множество R, для которого г/«><0. Тогда
S yUjXj+ 2 yujXj — ftt0 — целое число.' (8.93)
J£R+ KR_
Далее-будем различать два случая в зависимости от того, будет
ли величина 2 Уи1Х1 неотрицательной или отрицательной. Рас-
KR
смотрим сначала случай, когда эта величина неотрицательна.
Тогда должно выполняться соотношение
2^Z; = 6 + U (8.94)
где 6 = 0, или 1, или 2, и т. д. Следовательно, любое допустимое
решение задачи (8.1) должно удовлетворять неравенству
2 yujXj fuO>
j£R
или, если вспомнить определение AL, неравенству
2 УиМ > fa0- (8.95)
jzr+
Теперь рассмотрим случай, когда величина 2 Уи)х) отрица-
KR
тельна. Из (8.93) следует, что
Hl yujxi = fuo — ь (8.96)
где 6=1, или 2, или 3, и т. д. Следовательно, для любого допу-
стимого решения задачи (8.1) должно выполняться неравенство
2 yujxj+ 2 yUjxj<fuo—^> (8-97)
KR+
или, так как 2 г/и,Х/>-0, неравенство
j£R+
2 yUjxj<fao — 1- (8-98)
KR_
Умножим теперь (8.98) на отрицательное число faOl(fuo — 1).
Это дает
2 (8-")
8.14. Алгоритм для решения частично целочисленных задач 289
Объединяя (8.95) и (8.99), мы получаем, что независимо от
того, какой случай имеет место, для каждого допустимого ре-
шения задачи (8.1) должно выполняться неравенство
2 УиМ + 2 tzzt- I У»11 xj > („р. (8.100)
Это следует из того, что левые части (8.95) и (8.99) положи-
тельны и по крайней мере одна из них должна быть больше или
равна fuo. Отметим, что оптимальное решение, полученное для
задачи ЛП (8.1), не удовлетворяет условию (8.100).
Следовательно, (8.100) можно использовать в качестве сече-
ния. Однако при выводе этого условия мы использовали требо-
вание целочисленности, касающееся лишь переменной хВи- Если
еще имеются переменные х3-, / € R, значения которых должны
быть целыми, то эту информацию можно использовать для по-
лучения другого сечения, которое, по-видимому, окажется «луч-
шим». Рассмотрим Xj, j Как и в § 8.12, будем пользо-
ваться представлением yuj — i>aj + faJ, < 1. Обозначим
через R* подмножество R, не содержащееся в R П Л. Соотноше-
ние (8.92) теперь может быть заменено соотношением
fuo— S fuixi~ 3 yujxi — целое число.
Так как то, вводя подмножества /?+ и R*_ множе-
ства R*, для которых и yUj<0 соответственно, и повторяя
те же рассуждения, что и выше, мы получим, что неравенство
2 fujxi+ 2 yujxj+ 2 (8-101)
/едЛл i£R+ /eZ.
выполняется для любого допустимого решения задачи (8.1) и
не выполняется для оптимального решения задачи ЛП (8.1).
Следовательно, (8.101) может быть использовано в качестве се-
чения.
Можно получить и другое сечение. Обозначим через 8В/ наи-
меньшее целое число, большее yuj, так что
= -/.,)• (8-102)
Тогда (8.92) может быть заменено соотношением
/ио+ 5 (1 — fUj)xj— S yUJxi — целое число. (8.103)
19 Зак. 735
290
Гл. 8. Целочисленное линейное программирование
Здесь —2(1 —Повторяя те же рассуждения, что и
выше, получаем, что неравенство
У fuo
1 (8-104)
*
также является сечением.
Можно получить еще более лучшее сечение. Гиперплоскость,
соответствующая такому сечению, должна пересекать оси xj в
точках, расположенных как можно дальше от начала коорди-
нат. Из (8.101) и (8.104) видно, что коэффициенты при Xj,
jCRfUi могут быть взяты равными
М «»
Мы будем выбирать наименьшее из этих чисел. Ясно,
является наименьшим числом, если
что fUj
0 f «о) fuj < f«0 futiftij ИЛИ fuj <C fuQ*
Наилучшее сечение может быть записано в виде
2 (—
(8.105)
где
УаГ
fuJ, fuj<fuO’
(8.106)
Теперь, зная способ построения сечений, мы можем получить
решение частично целочисленной задачи, применяя метод, опи-
санный в § 8.12 для полностью целочисленного случая. Сечение
(8.105) может применяться и при решении полностью целочис-
ленных задач.
Описанный нами алгоритм не является единственным мето-
дом для решения частично целочисленных задач линейного
программирования. Бил [3] предлагает другой алгоритм; кроме
того, можно использовать метод Лэнд и Дойг [15]. Впрочем,
8.16. Пример
291
эти методы не кажутся нам более эффективными, чем метод
Гомори.
8.15. Доказательство конечности для случая частично цело-
численной задачи. Гомори [11] доказал, что если при решении
частично целочисленной задачи использовать сечения (8.105),
то для получения оптимального решения задачи (8.1) доста^
точно решить лишь конечное число задач Pv. При этом предпо-
лагалось, что z имеет верхнюю и нижнюю границы и, кроме
того, величина z рассматривалась как одна из переменных, зна-
чение которой должно быть целым. При изложении доказатель-
ства мы примем все те предположения и допущения, которые
были использованы в § 8.13, и, кроме того, будем считать, что
уравнения в (8.80) записаны так, что уравнения, которые соот-
ветствуют целочисленным переменным, предшествуют осталь-
ным. Эти уравнения мы будем предполагать упорядоченными,
так чтобы векторы р7 в (8.80) удовлетворяли условию pj >> 0.
Этого всегда можно добиться, если сразу вслед за уравнением,
соответствующим z, записать дополнительное ограничение
2 вспомогательная переменная которого (цело-
численная) является базисной. Далее необходимо лишь повто-
рить каждый шаг доказательства, изложенного в § 8.13. В уп-
ражнении 8.12 мы предлагаем читателю вывести соотношение,
эквивалентное (8.91), для случая, когда вместо (8.90) исполь-
зуется (8.105).
Необходимо отметить, что доказательства, приведенные в
данном параграфе и в § 8.13, не являются общими, так как они
опираются на предположение о том, что z имеет нижнюю гра-
ницу и должно быть целым. Кроме того, дополнительные огра-
ничения должны выбираться специальным образом. По-види-
мому, конечность алгоритма имеет место и при более общих
предположениях, особенно в отношении выбора уравнений, ис-
пользуемых для построения сечений. Однако доказательства
этого еще нет.
8.16. Пример. В качестве примера численного решения цело-
численной задачи линейного программирования рассмотрим за-
дачу (1.19), проиллюстрированную на рис. 1.6. После введения
вспомогательных переменных задача (1.19)г примет вид
0,50xj —х% —х$ = 1,75,
Xj 0,30х2 -^4== 1 »50, (8.107)
ху>0, /=1, ..., 4, х19 х2—-целые;
найти max z = 0,25x!+x2.
19*
292
Гл. S. Целочисленное линейное программирование
Таблица 8.1
Оптимальное решение задачи ЛП (8.107)
CL 0,25 1 0 0
св Базисные перемен- ные b а2 Из а4
1 Xg 1,75 0,50 1 1 0
0 х4 0,975 0,85 0 —0,30 1
1,75 0,25 0 1 0
Здесь мы имеем частично целочисленную задачу: переменные Xi
их2 должны быть целыми, а вспомогательные переменные х3 и
х4 могут принимать и дробные значения. Решение задачи ЛП
(8.107) дано в табл. 8.1. В этом решении переменная х2 имеет
дробное значение, поэтому необходимы дополнительные вычис-
ления.
Первое сечение мы получим с помощью строки, соответ-
ствующей переменной xBi = х2 в табл. 8.1. Отметим, что
^01 = 1,75, z/u=0,50, i/i3=l, а из небазисных переменных xt и х3
только Xi по условию задачи имеет ограничение целочислен-
ности. Легко видеть, что fio=O,75, /и=0,50. Таким образом, ис-
пользуя (8.105) и (8.106), мы получаем сечение
— 0,50х! —х3< —0,75. (8.108)
Присоединяя (8.108) к задаче ЛП (8.107), получаем задачу Pi.
Исходная симплексная таблица для задачи Pi помещена в
табл. 8.2. Результаты применения двойственного симплекс-ме-
тода к этой задаче приведены в табл. 8.3 и 8.4. Для решения
потребовалось две итерации. В табл. 8.4 переменная х2 имеет
целое значение, a Xi — дробное. Следовательно, необходимо
ввести еще одно сечение.
Для построения,нового сечения используется строка, соот-
ветствующая хь Легко видеть, что fso=O,2O. Далее у34=1>0,
так что </34=1, но Узб=—0,30<0 (пятая позиция соответствуете),
поэтому
। Ж <°’30>= °’075
8.16. Пример
293
и новое сечение имеет вид
— х4 — 0,075$! < — 0,20. (8.109)
Решение задачи
Таблица 8.2
ci 0,25 1 0 0 0
св Базисные пере- . менные ь ai а2 аз а4 е3
1 1,75 0,50 1 1 0 0
0 х4 0,975 0,85 0 —0,30 1 0
0 51 —0,75 —0,50 0 -1 0 1
1,75 0,25 0 1 0 0
Таблица 8.3
1 х2 1 0 1 0 0 1
0 Xi —0,30 0 0 —2 1 1,70
0,25 Xi 1,50 1 0 2 0 —2
1,375 0 0 0,59 0 0,50
Таблица 8А
1 Х2 1 0 1 0 0 1
0 Хз 0,15 0 0 1 —0,50 —0,85
0,25 Xi 1,20 1 0 0 1 —0,30
1,30 0 0 б 6,25 6,925
294 Гл. 8. Целочисленное линейное программирование
Присоединяя (8.109) к задаче Рь получаем задачу Р2. Исход-
ная симплексная таблица для задачи Р2 помещена в табл. 8.5.
Решение задачи Р2
Таблица 8.5
св ci 0,25 1 0 0 0 0
Базисные перемен- ные b ai а2 аз а4 е3 е4
1 х2 1 0 1 0 0 1 0
0 *3 0,15 0 0 1 —0,50 —0,85 0
0,25 1,20 1 0 0 1 —0,30 0
0 S2 —0,20 0 0 0 —1 —0,075 1
1,30 0 0 0 0,25 0,925 0
Таблица 8.6
1 х2 1 0 1 0 0 1 0
0 *3 0,25 0 0 1 0 —0,8125 —0,50
0,25 Л1 1 1 0 0 0 . —0,375 1
0 х4 0,20 0 0 L 1 0,075 —1
1,25 0 0 0 0 0,90625 0,25
Оптимальное решение задачи Р2 получено в результате од-
ной итерации двойственного симплекс-метода. Это решение по-
мещено в табл. 8.6. Здесь Xi и х2 — целые, равные единице. Та-
ким образом, мы получили оптимальное решение задачи "(8.107);
х*—х* = 1, z*= 1,25. Это решение полностью-совладает с ре-
шением, которое мы раньше получили графически на рис. 1.6.
В этом примере—алгоритм сходится очень лбыстрр;, .ддя^олуче-
Литература
296
ния оптимального решения нам пришлось решить всего две за-
дачи Pv. Тем не менее это потребовало почти в четыре раза
большей вычислительной ра-
боты, чем для решения зада-
чи ЛП (8.107).
Геометрическая интерпре-
тация сечений дана на рис. 8.6.
Рассмотрим сначала сечение
(8.108). Если, используя
(8.107), мы исключим х3, то
получим
— 0,50*! —1,75 +
+ 0,50xj —х2 — 0,75,
или
х2<1. (8.110)
Таким образом, сечение (8.108)
эквивалентно ограничению
х2<С1. Первое сечение умень-
шает множество допустимых
решений задачи ЛП (8.107) до заштрихованной области на
рис. 8.6. Рассмотрим теперь второе сечение (8.109). В силу
(8.110) Si=l—х2, так что, исключая х4 с помощью (8.107), мы
получаем
^+0,30X2 — 1,50 — 0,075 + 0,075х2 < — 0,20,
или
хх + 0,375х2< 1,375.
ЛИТЕР АТУ РА
1. Bowman Е. Н., The Schedule Sequencing Problem, Operat. Res., 7
(1959), 621-624.
2. В о w m a n E. H., Assembly-Line Balancing by Linear Programming,
Operat. Res., 8 (1960), 385—389.
3. Beale E. M. L., A Method of Solving Linear Programming Problems
When Some but Not All of the Variables Must Take Integral Values, Sta-
tist. Techn. Res. Group Tech. Rep. № 19, Princeton, July 1958.
4. Charnes A., Cooper W. W., Management Models and Industrial Appli-
cations of Linear Programming, v. II, New York, 1961.
5. D a n t z i g G. B., On the Significance of Solving Linear Programming
Problems with Some Integer Variables, Econometrica, 28 (1960), 30—44.
6. D a n t z i g G. B., Note on Solving Linear Programs in Integers, Nav. Res.
Logist. Quart., 6 (1959), 75—76.
7. D antzig G. B., Fulkerson D. R., Johnson S., Solution of a Lar-
ge-Scale Traveling-Salesman Problem, J. Operat. Res. Soc. Amer., 2 (1954),
393-410.
296
Гл. 8. Целочисленное линейное программирование
8. G о тог у R. Е., Outline of an Algorithm for Integer Solutions to Linear
Programs, Bull. Amer. Math. Soc., 64 (1958), 275—278.
9. G omor у R. E., An Algorithm for Integer Solutions to Linear Programm-
ing, Princeton-IBM Mathematics Research Project, Tech., Rep. № T, Nov.
1958.
10. G о m о г у R. E., All-Integer Programming Algorithm, IBM Research Cen-
ter, Res. Rep. RC-189, 1960.
11. G omorу R. E., An Algorithm for the Mixed Integer Problem, P-1885,
RAND Corp,, June 1960.
12. G о in о г у R. E., В a u m о 1 W. J., Integer Programming and Pricing,
Econometrica, £8 (I960), 521—5150.
13. Go mor у R. E., An Algorithm for Integer Solutions to Linear Programs,
In Graves R., Wolfe P. (ed.), Recent Advances in Mathematical Pro-
gramming, New York, McGraw-Hill, 1963.
14. G от or у R. E., Hoffman A. J., On the Convergence of An Integer-
Programming Process, Nav. Res, Logist. Quart., 10 (1963), 121—123.
15. Land A. H., D о i g A., An Automatic Method of Solving Discrete Pro-
gramming Problems, Econometrica, 28 (1960), 497—520.
16. Markowitz H„ Manne A. S., On the Solution of Discrete Programm-
ing Problems, Econometrica, 25 (1957), 84—110.
17. S i rn о n n a r d M., Programmation Lineaire, Paris, Dunod, 1962.
18. V a j d a S., Mathematical Programming, Reading, Addison-Wesley, 1961.
19. Wagner H., An Integer Linear Programming Model for Machine Sche-
duling, Nav. Res. Logist. Quart., 6 (1959), 131—140.
20. W e i n g a r t n e r H. M., Mathematical Programming and the Analysis of
Capital Budgeting Problems, Ford. Thesis, Englewood Cliffs, Prentice-Hall,
1963.
21* . Волков Ю. И., Хохл юк В. И., Методы решения целочисленных задач
линейного программирования, сб. Математические модели и методы опти-
мального планирования, изд-во «Наука», 1966.
22* .Журавлев Ю. И., Финкельштейн Ю. Ю., Локальные алгоритмы
для задач линейного' целочисленного программирования, сб. Проблемы
кибернетики, вып. 14, изд-во «Наука», М., 1965.
23* . Корбут А. А., Целочисленные задачи линейного программирования,
сб. Экономико-математические модели, вып. 2, 1965.
24* . Финкельштейн Ю. Ю., Алгоритмы для решения задач целочислен-
ного программирования с булевыми переменными, Экономика и матем,
методы. 1 (1965), вып. 5.
Упражнения
8.1. Решить пример, рассматривавшийся в § 8.16, используя сечения в
виде (8.100).
8.2. Решить пример, рассматривавшийся в § 8.16, используя сечения в
виде (8.101).
8.3. Решить пример, рассматривавшийся в § 8.16, используя сечения в
виде (8.104).
8.4. Применяя алгоритм для полностью целочисленных задач, решить
следующую задачу;
3xj —j— 2x2 < 8»
? *i+4x2 <Ю,
лг2>0, -^2~целые;
найти max z » Зхг 4~ 4л-2.
Упражнения
297
8.5. Применяя алгоритм для полностью целочисленных задач, решить сле-
дующую задачу:
3xj “I- 2x2 5, х2 2,
хъ х2>0, xit х2— целые;
найти max z = Xj 4~ х2.
8.6. Решить следующую частично целочисленную задачу:
ЗХ| —5х2 11, 4Х[ -|~ х2 8,
Xj, х2 > 0, Xi — целое;
найти max z — 8xj -|- 6х2.
8.7. Решить следующую частично целочисленную задачу:
4,5xi -|~ 3x2 “F* 5хз 14,
2Х] —|— 6,3x2 х3 11,
х15 х2, х3>0, хь х3 —целые;
найти max г = 2,5х! 4х2 + Зх3.
8.8. Рассматривается ситуация, аналогичная исследованной в § 8.10.
Пусть фирма имеет возможность вкладывать свой капитал в п различных
проектов. Планируемый период разбит на К периодов. В период k фирма рас-
полагает капиталом Dh. Пусть dhj — капитал, который необходимо вложить
в Л-м периоде в проект /. Предполагается, что в /г-й период проект / может
дать доход гл;, который может быть использован для дальнейших капитало-
вложений (в (&4-1)-м или последующих периодах). Пусть pj — приведенная
к настоящему моменту оценка всего дохода, который может дать проект /.
Требуется сформулировать целочисленную задачу линейного программирова-
ния, решение которой показало бы, в какие проекты нужно вкладывать ка-
питал, чтобы максимизировать приведенную оценку всего дохода. При этом
должен быть учтен тот факт, что доходы, получаемые от эксплуатации
проектов, могут использоваться для дальнейших капиталовложений.
8.9. Обобщить упражнение 8.8 на случай, когда начало осуществления
проектов не обязательно связано с первым периодом.
8.10. Показать, что в двойственном симплекс-методе при построении но-
вой задачи отбрасывание неактивного сечения может быть осуществлено
простым вычеркиванием в симплексной таблице строки и Стблбца, содей-
ствующих вспомогательной переменной, вошедшей в базис.
8.11. Построить пример, в котором задача ЛП (8.1) имеет оптимальное
решение, а задача (8.1) не имеет допустимого решения. Отдельно рассмо-
треть случаи полностью и частично целочисленных задач.
8.12. Вывести соотношение, эквивалентное (8.91) для случая, когда вме-
сто (8.90) используется (8.105).
8.13. Показать, что с помощью алгоритма, описанного в § 8.13 можно
получить симплексную таблицу, все элементы кЪторой целые числа. [Указание.
После того как все компоненты вектора ро станут целыми, перейти к первому
из векторов pj. Если какая-либо компонента этого вектора нецелая, то с по-
мощью соответствующей строки образуем сечение. Так как fMo=O, то это
сечение не будет оказывать влияния на вектор ро. Применить лексикографи-
ческий метод § 8.13, поступая с pj так же, как ранее с ро. Воспроизвести все
детали доказательства.] Из этого результата следует, что можно ввести до-
статочное число новых переменных так, что, какие бы целочисленные значе-
ния Ни придавать небазисным переменным, базисные переменные также будут
> С?
298
Гл. 8. Целочисленное линейное программирование
целочисленными. Более того, любое допустимое решение задачи (8.1) в пол-
ностью целочисленном случае должно быть таковым и при некоторых цело-
численных значениях небазисных переменных.
8.14. Задача о раскрашивании карты. Раскрашивание должно быть осу-
ществлено таким образом, чтобы никакие две области с общей границей
(если эта граница не является точкой), не были окрашены в один цвет.
Предполагается, но никем не доказано, что для этого потребуются краски не
более чем четырех цветов. Сформулировать целочисленную задачу линейного
программирования, которая может быть использована для проверки этой
гипотезы в любом частном случае. [Указание. Пусть индекс j относится к /-й
области. Четыре краски обозначим через 0, 1, 2, 3. Тогда целочисленные
переменные ру, 0<Ру<3, будут указывать, какой цвет приписан области j.
Если области j и k имеют общую границу, то pj=#P&- Таким образом,
Pfe — pj > 1 или pj — рл>1. Выразить эти условия в терминах целочислен-
ного линейного программирования. Какая задача целочисленного линейного
программирования должна быть решена, чтобы выяснить, существует ли
допустимое решение для данной карты? Формулировка этой задачи" была
предложена Гомори и опубликована Данцигом [5].
8.15. Линия сборки состоит из некоторого числа рабочих мест. Чтобы
собрать какое-либо изделие, необходимо в определенной последовательности
выполнить некоторое число операций (работ). При заданном темпе произ-
водства требуется так распределить операции по рабочим местам, чтобы об-
щее число рабочих мест было минимальным и чтобы изделие двигалось по
линии сборки лишь в одном направлении, не возвращаясь на те рабочие
места, где оно уже было. .
Время, необходимое для выполнения каждой операции, задано. Пока-
зать, как эта задача, известная как задача о балансировке линии сборки,
может быть сформулирована в виде целочисленной задачи линейного про-
граммирования. Предположим, что имеется п операций и tj—. время, необ-
ходимое для выполнения операции /. Пусть R— заданный темп производства.
Очевидно, R не может быть больше чем величина, обратная наименьшему tj.
Если Т = О’ то число рабочих мест будет , равно по крайней мере наи-
/
меньшему целому числу, большему чем RT. Обозначим это число через т.
Предположим, что число рабочих мест не должно превышать М. Через /(/)
обозначим множество индексов t, таких, что операция i должна быть выпол-
нена до начала операций /. Предположим, что рабочие места на линии сбор-
ки располагаются последовательно одно за другим и на двух рабочих местах
одновременно не может обрабатываться одно и то же изделие. [Указание.
Пусть djfc = l, если операция / выполняется на k-м рабочем месте, и 6^=0
в противном случае.] Какое ограничение следует ввести, чтобы операция /
была выполнена на одном из рабочих мест? Заметим, что суммарное время,
затрачиваемое на каком-либо рабочем месте, не должно превышать 1/R и
k
это время равно Кроме того, если 6^ = 1, то 2 = €/(/).
J
Число операций, выполняемых на &-м рабочем месте, равно 2 &jk. Требуется
J
максимизировать число рабочих мест, для которых 2 ^jk = Если записать
J
% = ° или
то нужно максимизировать 2 Фл- Дать подробную формулировку задачи.
Упражнения
299
8.16. Бауман [2] предложил две другие формулировки задачи о баланси-
ровке линии сборки. Мы их рассмотрим в этом и следующем упражнениях.
Пусть tjk “ время, в течение которого операция / выполняется на k-м рабо-
чем месте. Запишите ограничения, требующие, чтобы ни одно рабочее место
не было перегружено и чтобы каждая операция выполнялась полностью. Рас-
смотрите соотношение tjk = tjbjh, где = O или 1. Покажите, что благодаря
этим ограничениям каждая операция будет выполняться только на одном
рабочем месте. Наконец, должны выполняться треббвания очередности. По-
кажите, что ограничения, приведенные ниже, гарантируют выполнение требо-
ваний очередности (при этом надо учесть, что из предыдущих ограничений
следует, что /л=0 или tj). Указанные ограничения имеют вид
V1 * Z- / / х
z г^/(Л
V = 1
Чтобы минимизировать число рабочих мест, рабочему времени, затрачивае-
мому на рабочих местах с номерами т+1, ..., М, поставим в соответствие
прогрессивно увеличивающиеся оценки и будем минимизировать величину
М Г "
z = 2 2
Л = /П4-1 L/ = l
(здесь стоимость в единицу времени на k-м рабочем месте (6>т + 1) при-
нята равной k — т). Привести подробную формулировку задачи.
8.17. Другая формулировка задачи упражнения" 8.15, предложенная
Бауманом, такова. Пусть т3- — время начала операции /. Тогда ограниче-
ние очередности имеет вид i £ I(/). Далее необходимо позабо-
титься о том, чтобы никакие две операции не выполнялись одновременно.
Пусть — время окончания /-й операции. Тогда для всех i и j
должно выполняться либо условие г» — > 0, либо Tj — gi > 0. Ограничения
этого типа не нужны для тех i и /, для которых из требований очередности
автоматически вытекает невозможность одновременного выполнения соответ-
ствующих операций. Теперь рассмотрим вопрос о рабочих местах. Все опера-
ции, для выполнения которых требуется время, не большее чем 1/7?, мы отне-
сем к первому рабочему месту; операции, для выполнения которых время
меняется от 1/7? до 2/7?,— ко второму рабочему месту и т. д. Пусть б; —
целочисленная переменная, принимающая значения 0, 1, ..., п—1. Если
dj=&, то операция / выполняется на &-м рабочем месте. Таким образом, мы
имеем ограничения < (1/7?) (д3 +1), Дать подробную постановку
задачи и определить целевую функцию.
8.18. В простейшем виде задача расписания состоит в следующем. Для
изготовления п деталей имеется т различных станков. Деталь I на станке /
должна обрабатываться в течение времени tn, и, кроме того, прежде чем
эта деталь попадает на станок /, она должна пройти обработку на стан-
ках Требуется определить такую последовательность обработки
деталей на станках, чтобы время, затрачиваемое на изготовление всех п де-
талей, было минимальным. Формулировка этой задачи как целочисленной
была предложена Бауманом [1]. Время предполагается дискретным, разби-
тым на достаточно малые периоды, так что все изменения совершаются лишь
в начале периодов. Таким образом, мы будем считать, что tn равно числу
периодов времени, в течение которых деталь i должна обрабатываться на
станке /. Пусть dijA — целочисленная переменная, принимающая значение 1,
если i-я деталь в k-н период обрабатывается на /-м станке; в противном
случае Запишите условие того, что деталь i в течение tn единиц
времени, должна обрабатываться на станке /. Запишите также условие того,
;00
Гл. 8. Целочисленное линейное программирование
что в каждый период времени на каждом станке может обрабатываться
лишь одна деталь. Далее необходимо учесть требования очередности. Пока*
жите, что это может быть сделано с помощью ограничений
Л-1
Из всех упомянутых условий не следует, однако, что обработка детали i на
станке / не будет совершаться с перерывами. Как можно избежать этого?
Какова при этом целевая функция? Дать подробную формулировку задачи.
8.19. Возможна другая формулировка задачи расписания, рассмотренной
в упражнении 8.18. Для каждого станка j требуется определить последова-
тельности деталей, обрабатываемых на нем. Пусть = если деталь i на-
ходится на k-м месте в последовательности деталей, обрабатываемых на /-м
станке; в противном случае 6/^=0. Пусть далее — время начала обра-
ботки &-й детали в последовательности, соответствующей /-му станку, a %jh —
время завершения обработки этой детали. Предположим, что обработка де-
тали i на станке j должна вестись непрерывно. Тогда должно выполняться
соотношение
Ijk — = S tlfoijk-
l
Кроме того, л + ь и если деталь i должна обрабатываться на стан-
ке /, то = 1. Рассмотрим далее ограничение очередности. Если /'£/(/)>
k
то время завершения обработки детали i на станке /' должно предшествовать
временихначала обработки этой детали на станке /. Это условие можно было
бы записать так: |у/й, Tyfe, если 6Zy,fe, = д^уй = 1,но мы поступим иначе.
Введем переменные ф/уу,^,, принимающие лишь значение 0 или 1. Запишем
следующие соотношения:
+ 1
Теперь ограничения очередности могут быть представлены в таком виде:
Ф/ jrw)’
где М — достаточно большое положительное число. Мы предлагаем читателю
самому построить другие необходимые ограничения, определить целевую
функцию и подробнее описать вышеприведенные рассуждения.
8.20. Заметим, что в задаче с фиксированными затратами, формулировка
которой дается соотношениями (8.6), допускается, чтобы и dj«l. По-
чему в этой задаче нет необходимости вводить следующее ограничение: если
то xj>0?
8.21. Решите пример из § 8.16 как полностью целочисленную задачу, пре-
образовав его к виду
2xi —4x2 7,
lOxi —J— 3x2 15,
Xi, х2>0, хь х2 — целые;
найти max z = Xj -|- 4х2.
8.22. При решении полностью целочисленной задачи может случиться, что
вводимая на некотором шаге секущая гиперплоскость оказывается параллель-
Упражнения
301
ной гиперплоскости, соответствующей целевой функции. Предположим, что
задача, полученная в результате введения такого ограничения, решена и
найден оптимум. В таких случаях часто оказывается, что введение дополни-
тельных секущих гиперплоскостей не меняет оптимального значения z на
протяжении некоторого числа итераций. Объясните это на основе доказа-
тельства сходимости, изложенного в § 8.13. Проиллюстрируйте этот факт гра-
фически. Каким образом можно выбрать секущие гиперплоскости, чтобы они
не были параллельными гиперплоскости, соответствующей целевой функции?
8.23. Фирма заключила контракт на изготовление небольших партий не-
которого числа высокоточных деталей, необходимых при производстве ракет.
Контракт заключен на два года, и ни одна деталь не должна быть изготовле-
на по истечении этого срока. Производство деталей требует специальных ма-
шин, которые фирма должна купить. Предположим, что в течение недели
должно производиться dj деталей /. Фирма располагает несколькими техно-
логическими процессами, позволяющими производить некоторую часть нуж-
ных деталей. При /-м технологическом способе потребляется единиц i-ro
фактора производства. Фирме нужно закупить т различных типов машин.
Если необходимо, на каждой из машин можно выполнять две различные
операции. Фирма рассчитывает на норму прибыли, равную 20%. Сформули-
ровать целочисленную задачу линейного программирования, решение которой
позволило бы определить, сколько нужно закупить машин каждого типа, ка-
кие из имеющихся технологических процессов следует использовать, потре-
буется ли для выполнения заказа работа в сверхурочное время и какова
максимальная величина дохода, На который фирма может рассчитывать по
истечении двухлетнего периода.
ГЛАВА
ГРАДИЕНТНЫЕ МЕТОДЫ
Мы, мы выбираем свой путь,
Путь к ясно намеченной цели,
Путь к Вершинам! Но он поведет
Длинной, крутой тропой, сквозь
Топи, теснины и горы в снегу
Мэтью Арнольд, Часовня в Регби
9.1. Введение. Каждый из рассмотренных до сих пор методов
численного решения нелинейных задач, за исключением класси-
ческих методов оптимизации, изученных в гл. 3, был в том или
ином смысле методом «ближайшей крайней точки», использую-
щим в качестве основного вычислительного средства симплекс-
ный алгоритм. К другому классу принадлежат различные ме-
тоды последовательного приближения, которые имеют в своей
основе тот доказанный в § 3.9 факт, что направление градиента
f(x) служит направлением максимальной скорости роста f(x).
Мы изучим в этой главе группу методов, в которых этот прин-
цип используется для решения задач оптимизации с ограниче-
ниями.
Градиентные методы, к которым относятся методы этой гла-
вы, в лучшем случае обычно сходятся лишь к локальному экс-
тремуму. Впрочем, бывает так, что и такого рода сходимость
отсутствует. Только в том случае, когда задача обладает под-
ходящими свойствами выпуклости или вогнутости, можно быть
уверенным, что процесс сходится к глобальному экстремуму.
Вообще говоря, для достижения решения требуется бесконечное
число итераций, и лишь в некоторых специальных случаях, та-
ких, как задачи линейного программирования, решение дости-
гается за конечное число шагов. В заключение отметим, что
хотя градиентные методы и не относятся к методам ближайших
крайних точек, симплексный алгоритм часто будет играть боль-
шую роль в их осуществлении, например при выборе направле-
ния движения, когда некоторые из ограничений мешают дви-
гаться в направлении градиента.
9.2. Случай линейных ограничений
303
9.2. Случай линейных ограничений. Рассмотрим сначала не-
линейную задачу с линейными ограничениями:
(9*1)
*/>0, j£J',
найти max z = f(x1, ..., хЛ),
где множества Л, /2 могут быть пустыми. Все неравенства будут
рассматриваться в форме, содержащей знак «^». Это можно
сделать, так как в описываемых методах bi могут иметь любой
знак. Здесь не очень удобно сводить неравенства к равенствам
добавлением вспомогательных переменных. Как обычно, будем
говорить, что точка х— допустимое решение задачи (9.1), если
она удовлетворяет ограничениям, и / С/. Предполагается,
что функция /(х) имеет непрерывные первые частные производ-
ные в каждой точке множества допустимых решений.
Пусть Хо — допустимое решение задачи (9.1). Одно из пре-
имуществ градиентного метода состоит в том, что итерационный
процесс может быть начат с любого допустимого решения, т. е.
нет необходимости в какой-либо специальной форме начального
допустимого решения, как, например, базисной. В связи с этим
вопрос о том, как получить начальное допустимое решение, мы
обсудим позднее, тем более что для многих практических задач
допустимое решение находится без затруднений. Предположим,
что градиент Vf(x0) функции f(x) в точке х0 отличен от нуля.
Мы построим итерационный процесс, приводящий к последова-
тельности допустимых решений xv, таких, что f(xv+1) >f (xr).
Чтобы построить хь рассмотрим две возможности:
1) существует такое е>0, что X! = x0 + Xd0, d' = Vf(x0) (на-
помним, что V /(х0) — вектор-строка), — допустимое решение
для всех X, В общем случае это означает, что множе-
ство /2 пусто, но это не является необходимым;
2) не существует Х>0, такого, что Xi=x0+Zd0 — допустимое
решение.
Сначала рассмотрим случай (1), поскольку он имеет непо-
средственное отношение к результатам § 3.9. Покажем, что су-
ществует Х>0, такое, что если
+ d^ = Vf(x0), (9.2)
то Xi — допустимое решение, и f(xl)>f(xQ). Заметим, во-первых,
что, согласно условию, x=x0-|-XdQ — допустимое решение для
304
Гл. 9. Градиентные методы
всех X, 0<Х<е. Во-вторых, по формуле Тейлора для любого Л
f (Хо + Xd0) = f (Хо) + XVf (&) d0, ,q „
£=xo+exdo, о<0<1. '
Но все df/dXj — непрерывные функции от х. Поэтому Vf(x)d0 —
также непрерывная функция от х и, так как dodo > О,
существует такое б>0, что Vf(x)do>O для всех х, |х—х0|<б.
Следовательно, если % удовлетворяет соотношению 0<Х<
<min(e, б), то x=Xo+Xdo является допустимым решением и
f(x)>f(x0).
Возникает вопрос, каким следует выбрать X в равенстве
x^Xo+Xdo? Естественно, желательно получить возможно боль-
шее значение f(x), но так, чтобы х оставалось допустимым ре-
шением. Имея это в виду, определим наибольшее значение X
(обозначим его через е), для которого x=xo+Xdo допустимо.
Для этого заметим, что при 0-<Х-<8 должны выполняться соот-
ношения
аг(Хо + Хс!оХбг, az(Xo-|-Xdo) = 6z, 1^,12,
hdyo 0, j£J,
где а’=(ап, ••> Обозначим через /1(0), /(0) подмноже-
ства множеств /i и /, для которых ограничения i€/i(0) суще-
ственны для Хо и для которых %jo=O, /€/(0), соответственно.
Так как некоторое время можно двигаться по направлению do,
не нарушая ограничений, то для некоторого Х>0
аг (x0+Xd0) bi, Z£/i(0); (Xo~|-^do) = J’CAa»
xjo+^ijo О,
Величину X лимитирует то, что когда она становится достаточно
большой, то некоторые ограничения, не существенные в точке Хо,
становятся существенными в точке x=xo+Xdo, или некоторые
компоненты Xj, j € /, которые были положительны для х0, стано-
вятся равными нулю. Таким образом, чтобы определить наи-
большее значение X, для которого x=xo+Xdo допустимо, вы-
числим
р=
^0<°’
оо, если нет dj0<0, J£J, 7^/(0),
(9-4)
и
min [I > а/(,о > 0, / € Л. Л (0),
I L a cio J
оо, если нет azd0>0, Z^/j(O).
9.2. Случай линейных ограничений
305
Если р конечно, некоторые компоненты x=Xo+Ado будут от-
рицательны при А>р, и если у конечно, то при А>у будут нару-
шаться некоторые ограничения.
Ясно, что в рассмотренном случае следует принять
8=min(p,y). Не надо, однако, думать, что лучше всего поло-
жить А=е. Действительно, Vf(x) изменяется в зависимости
от х, и хотя f(xo+Xdo)>f(хо), если к достаточно мало, из этого
не следует, что это неравенство выполняется при большом X, так
как Vf(g)d0 в (9.3) может стать отрицательным, когда % доста-
точно велико. Естественно было бы взять такое А, 0<А-Се, кото-
рое максимизирует f(Xo+Ado). Мы могли бы попытаться найти
это значение, положив dfld\=Q и решив это уравнение относи-
тельно Л. Хотя в простейших случаях это действительно приво-
дит к цели, в общем случае решение указанного уравнения мо-
жет оказаться очень трудным; кроме того, оно может не иметь
единственного решения. Поэтому, когда задача решается чис-
ленно, для определения значения А обычно используются раз-
личные специальные методы. Самый простой метод состоит в
делении интервала 0<А<е на равные части точками Аь=АДА и
вычислении f(xo4-Afedo) для каждого k. Понятно, что следует вы-
брать наибольшее f(xo+АмЬ), и Ай, дающее этот максимум, бе-
рется в качестве А. При этом необходимо сравнить наибольшее
f(xo+Aftdo) с f(x0), чтобы удостовериться в том, что f(x) воз-
растает. Если выбранное ДА слишком велико, f(xo+Afedo) может
быть меньше, чем f(x0), для каждого Ай. Мы не будем сейчас
говорить о деталях этого метода. Эта тема рассмотрена в следую-
щей главе. Обычно для этой задачи и не пытаются использовать
сложную процедуру поиска точного значения наилучшего А.
В большинстве случаев вполне достаточно грубо определить
наилучшее А, хотя, конечно, имеется связь между точностью
определения А в каждой итерации и общим числом итераций,
требующихся для решения задачи.
Следует заметить, что если Vf(x) не зависит от х, т. е.
если z — линейная функция от х, то А»е, так как из (9.3) видно,
что f(xo-+-Ado) линейно возрастает вместе с А. Иначе говоря,
когда целевая функция линейна, мы должны двигаться как
можно дальше. В этом случае поиск А не требуется.
Найдя Xi, мы оказываемся в той же ситуации, в которой мы
были, когда начинали процесс. Вычислим d{ = V/(Xi)- Если
опять Vf(xi)=O, то снова могут быть лишь два случая—(1)
или (2). Если по-прежнему имеет место случай (1), мы повто-
ряем описанную процедуру, меняя, разумеется, хо и d0 в (9.4) и
(9.5) на Xt и di. Затем определяются новые е, А и x2=x14-Ad1.
Займемся теперь случаем (2). Когда мы сталкиваемся с ним
(это может произойти как в самом начале процесса, так и на
20 Зак. 735
306
Гл. 9. Градиентные методы
последующих итерациях), полученное допустимое решение ле-
жит на границе множества допустимых решений. При этом
некоторые из неравенств или ограничений неотрицательности
переменных будут нарушаться, если пытаться двигаться в напра-
влении градиента, т. е. при таком движении мы выйдем из мно-
жества допустимых решений. Выясним, в каком направлении
нужно двигаться, чтобы ограничения не нарушались, а значения
целевой функции увеличивались.
Итак, будем считать, что после определения xv и Vf (х»)
мы сталкиваемся со случаем (2). Обозначим через J(v) подмно-
жество индексов /€/, для которых xJO = 0, и через I(v)—под-
множество индексов Z, для которых Z-e ограничение выпол-
няется как строгое равенство. Мы не будем рассматривать ин-
дексы /‘(£/(v) и Z(£/(t>), так как для всех х из некоторой
окрестности точки xv ограничения, соответствующие этим ин-
дексам, заведомо не будут нарушены. В § 2.10 было показано,
что если г — произвольный вектор единичной длины, то скорость
изменения функции f(x) при движении из х в направлении г
равна Vf(x)r. Предположим, что мы рассматриваем точки
х=хо+%г для любого г, |г | = 1, и любого Х>0. Если потребовать,
чтобы х было допустимым решением, то можно записать сле-
дующие соотношения: ;
ху = хуг,4-Хгу>0,
или
О>0, (9.6)
так как
xJV = 0, /€J(v), и Л>0.
Также
a'x = az(xl,-|-XrXZ>;, i£ 7 (г»), Z£/2,
alx = bi, i£I2,
или, если
/i(x») = {«|ZG/(t’)>
то
azr<0, Ze/jD); azr = 0, Z£/2, (9.7)
так как
azxo = Z>z,
Если г удовлетворяет (9.6) и (9.7), то мы знаем, что при доста-
точно малом Л>0 x = xv + Xr будет допустимым решением. Теперь
мы можем определить такое направление движения, чтобы по-
9.2. Случай линейных ограничений 307
лучить максимальную скорость роста f(x) без нарушения огра-
ничений. Оно является решением следующей нелинейной задачи:
а*г<0,
azr = 0, i £ /2,
О>0, (9.8)
г'г = Г,
найти max Drf (xj = Vf (xj г.
Решение задачи (9.8) будет называться локально наилучшим
направлением движения. Заметим, что Vf(xv)r/| Vf(xv) | есть
просто косинус угла между г и Vf(xv). Поэтому, решая за-
дачу (9.8), мы ищем такое г, удовлетворяющее ограничениям
(9.8), которое имеет наименьший угол с Vf(xv).
Эта задача может быть решена на каждой итерации (когда
имеет место случай (2)), и в § 9.5 будет показано, как это де-
лается. Вместо решения задачи (9.8) можно использовать более
простой способ, который заключается в нахождении такого г,
удовлетворяющего (9.6) и (9.7), что
ОЖ) = Шг>0. (9.9)
При этом Drf(xv) уже не будет, вообще говоря, максимальным
в силу того, что имеются разные способы построения г, удовле-
творяющего ограничениям (9.9). В связи с этим возникают и
различные градиентные алгоритмы. Все они различаются по спо-
собу определения направления движения в случае (2).
Предположим, что, решая задачу (9.8), мы нашли некото-
рое г (обозначим его через гг,), удовлетворяющее (9.9) и ограни-
чениям (9.6) и (9.7). Тогда мы полагаем xv+i = xv + %rv, где % —
некоторое положительное число, которое нам еще предстоит вы-
брать. Заметим, что xv+i будет удовлетворять неравенствам для
и ограничениям неотрицательности переменных для
]€Ци) при любом А->0 (доказать!). Это, однако, может быть
неверно для 1(£1(и), Тогда мы вычислим р и у по фор-
мулам, подобным (9.4) и (9.5). В результате получим величину
е>0, которая представляет собой наибольшее значение для та-
ких Z>0, что x=xv + Xrv является допустимым решением зада-
чи (9.1). Затем, как и раньше, мы определим X внутри интер-
вала 0<Х^8 так, чтобы f(xr + Zrv) принимало максимальное
значение. После определения xr+i мы снова приходим либо к слу-
чаю (1), либо к случаю (2).
Следует заметить, что если мы готовы на каждой итерации
решать задачу (9.8), можно и не различать случаи (1) и (2): оба
20*
308
Гл. 9. Градиентные методы
они включены в (9.8). Действительно, если реализуется слу-
чай (1), то, как нетрудно понять, do/|d„| будет допустимым ре-
шением задачи (9.8), а значит, в силу сказанного в § 3.9, и оп-
тимальным решением этой задачи. Таким образом, решение за-
дачи (9.8) даст нам направление dB, в котором мы двигались
в случае (1).
Итак, итерационный процесс может быть описан следующим
образом. Мы начинаем с начального допустимого решения хо,
такого, что Vf(xo)¥=O. Для определения направления гв, по ко-
торому нужно двигаться из хю для получения х^+ь мы на каждой
итерации сначала решаем задачу (9.8). Затем определяем
максимальное значение Л, обозначаемое через е, для которого
x = xv+Zr„ является допустимым решением. Чтобы определить е,
вычисляем
(9.10)
(9.И)
min — ’ г^<0’
р=| j L riv *
оо, если нет rjv < 0, j £ J, J(v)
m.in [~'7^XP'l’ a%>°-
у = l L « rv J
оо, если нет azr„ >0, i(£l (i>).
Тогда e=min (р*у). Определив X из условия, что на интер- i
вале 0<Х^е величина f (х^+Хг^) имеет локальный максимум, z
полагаем xv+i=xo+A.r„ и продолжаем процесс.
Если на некотором шаге итерационного процесса мы получим
допустимое решение х„=х, для которого оптимальное решение г ,
задачи (9.8) обладает тем свойством, что Vf(x)r-<0, процесс I
заканчивается, так как нет допустимого направления г, в кото-
ром можно двигаться, чтобы Drf(x)>0. Допустимое решение х ’
называется стационарной точкой функции f(x), если £)г/(х)<Х)
для любого направления г, которое не выводит решение из мно-
жества допустимых решений. Иначе говоря, точка х является
стационарной точкой функции f(x) тогда и только тогда, когда !
оптимальное решение задачи (9.8) таково, что целевая функция
неположительна. Когда относительно f(x) нет никаких специаль-
ных предположений, в стационарной точке функции f(x) может
и не быть глобального экстремума для задачи (9.1), В ней даже
может не достигаться локальный экстремум. Подробнее об этом
будет сказано в следующем параграфе. 1
Итерационный процесс окончится также, если мы получим
допустимое решение хс, для которого решение задачи (9.8) даст
такое направление гс, что х=х„-|-Лг„ является допустимым ре-
9.3. Сходимость итерационного процесса
309
шением для любого Х>0 и /(хс4-Лг„) >f(xv) для всех %>0.
Тогда естественно устремить Л к бесконечности, так что | х | -> оо.
Это обычно означает неограниченность решения, хотя возможно,
что f(xv+hrv) стремится к конечному пределу при Х->оо, Ите-
рационный процесс автоматически заканчивается только в двух
рассмотренных случаях. В противном случае из любого допу-
стимого xv мы сможем двигаться к допустимому Xt>+i, такому,
что f(xv+i)>f(xv). Совсем не обязательно, что какой-нибудь из
этих случаев встретится через конечное число шагов. Ниже мы
исследуем свойства такой последовательности xv, когда процесс
не заканчивается за конечное число шагов.
Мы считали, что итерационный процесс начинается из такой
точки хо, для которой 7/(хо)¥=О, иначе мы не смогли бы опреде-
лить направление движения. В этом случае процесс сразу бы
оборвался, так как Хо — стационарная точка. Поэтому, если все
же в качестве Хо было взято такое допустимое решение, следует
найти близкое допустимое решение с Vf(x)^=O и начинать про-
цесс из этой точки.
9.3. Сходимость итерационного процесса. Мы исследуем здесь
свойства последовательности допустимых решений, полученных
описанным выше итерационным процессом, для тех случаев,
когда процесс не обрывается через конечное число шагов, т. е.
когда xv — бесконечная последовательность. Если у нее нет точ-
ки сгущения, то |х„| ->оо, и обычно в этом случае f\xv) ->оо,
так что задача (9.1) имеет неограниченное решение. Однако мо-
жет случиться, что f(xv) стремится к конечному пределу.
Рассмотрим случай, когда х„ имеет по крайней мере одну
точку сгущения, которую обозначим через х. Докажем, что х —
стационарная точка функции f(x). Прежде всего ясно, что х —
допустимое решение. Предположим, что х не будет стационар-
ной точкой функции f(x)_, т. е. для оптимального решения г за-
дачи (9.8) в точке х Vf(x)r>0.
Обозначим через 71 подмножество индексов i C/i, для кото-
рых i-e ограничение при х=х несущественно. Аналогично, пусть
7—подмножество индексов / €/, для которых х>>0. Тогда суще-
ствует 6i>0, такое, что для всех х, |х — х| <бь ограничения i,
i€li, остаются несущественными и значения Xj, j — положи-
тельными. Итак, для любого допустимого решения х в ^-окрестно-
сти х могут быть существенными только те ограничения и могут
быть равными нулю только те компоненты вектора х с ин-
дексом /€/, которые соответствуют несущественным ограниче-
ниям и ненулевым компонентам, появляющимся в задаче (9.8)
310 Гл. 9. Градиентные методы
для х. Для данного х из этой ^-окрестности некоторые из огра^
ничений задачи (9.8) могут быть несущественными.
Так как первые частные производные функции f по предпо-
ложению непрерывны, то найдется такое б2, что Vf(x)r>g>0
для всех х, |х — х|<б2. Пусть d3==min(6i, б2). Рассмотрим
бз/2-окрестность точки х. Поскольку х — точка сгущения после-
довательности xv, эта окрестность содержит бесконечно много
точек xv. Рассмотрим задачу (9.8) для любого xv из бз/2-окрест-
ности х. Из сказанного следует, что г — допустимое решение за-
дачи для xv и f(Xv)r>|i>0. Кроме того, для любого х = хг+Лг
формула Тейлора дает
f(x) = f(xJ + ZV/(i)E § = 0x. + (l-0)x, О<0<1.
Следовательно, при движении из xv в xv+i f(x) увеличивается по
крайней мере на бз|ы/2. Но имеется бесконечно много таких хг;
если это так, то f(x) = +oo. Однако этого не может быть, так
как тогда не существовал бы Vf(x); таким образом, мы пришли
к противоречию. Стало быть,» х — стационарная точка функ-
ции /(х).
Обычно последовательность xv имеет только одну точку сгу-
щения, поэтому х будет предельной точкой последовательно-
сти х„: все точки xVi за исключением их конечного числа, лежат
в любой б-окрестности х. Однако последовательность xv может
иметь и несколько точек сгущения, хотя на практике это бывает
редко. В этом случае функция f(x) принимает одинаковые зна-
чения в каждой из упомянутых точек. В упражнении 9.22 мы
предлагаем читателю доказать этот факт.
С вычислительной точки зрения приведенное выше доказа-
тельство малоинтересно, так как для практического использова-
ния процесса важна не сама по себе сходимость итерационной
последовательности, а скорость сходимости. Определить ско-
рость сходимости в общем случае весьма трудно. Впрочем, опыт
вычислений показывает, что сходимость является достаточно
быстрой для того, чтобы процесс можно было использовать.
Ниже будет более подробно сказано о вычислительной эффек-
тивности градиентных методов.
Как уже отмечалось, стационарная точка может не быть точ-
кой глобального и даже локального максимума f(x). Любая
стационарная точка, полученная описанным выше итерационным
процессом, может не соответствовать относительному локаль-
ному минимуму f(x). Однако в ней может быть относительный
максимум по одним направлениям й относительный минимум
9.3. Сходимость итерационного процесса
311
по другим, как, например, в случае седловой точки. На практике
крайне трудно полностью охарактеризовать произвольную
стационарную точку или хотя бы выяснить, достигается ли
в ней относительный максимум. О возникающих здесь трудно-
стях уже шла речь в гл. 3. Лучшее, что можно сделать, это
попытаться найти несколько допустимых решений в окрест-
ности х, отличающихся от всех xv, и использовать каждое из них
в качестве начала итерационного процесса. Если в каждом слу-
чае итерационный процесс приведет к х, резонно предположить,
что в точке х достигается локальный максимум функции f(x).
Заметим, что если для стационарной точки х функции f(x)
вектор d (d'=Vf(x)) удовлетворяет ограничениям и условиям
неотрицательности задачи (9.8), соответствующей точке х, то,
поскольку Vf(x)r<CO, для любого допустимого решения г за-
дачи (9.8) должно быть V/(x)=0. Действительно, так как век-
тор r=d/|d| является оптимальным решением этой задачи, то
|Vf(x)|2<X). Это справедливо только тогда, когда Vf(x)=O.
Таким образом, в указанном случае х является абсолютной ста-
ционарной точкой функции f(x) !).
Следует также заметить, что если f(x) —вогнутая функция,
то на выпуклом множестве допустимых решений итерационный
процесс будет сходиться к глобальному максимуму или же по-
кажет, что существует неограниченное решение. В самом деле,
рассмотрим сначала случай, когда либо процесс приводит за ко-
нечное число шагов к стационарной точке х функции f(x), либо
последовательность xv имеет точку сгущения х. Как было пока-
зано выше, для любого г, удовлетворяющего ограничениям (9.6)
и (9.7) и соответствующего точке х, но для которого не обяза-
тельно гг'=1, должно выполняться неравенство Vf(x)r<0. На
основании (3.65) имеем, кроме того,
f(x + r)<f(x)H-Vf(x)r. (9.12)
Если хН-г— вектор, достаточно близкий к х, то он будет до-
пустимым решением, если удовлетворяет ограничениям (9.6) и
(9.7). Следовательно, учитывая _что V f(x)r<C0, можем на-
писать на основании (9.12), что f(x+rXf(x). Таким образом,
х служит точкой локального максимума. Но в рассматриваемых
1) Под абсолютной стационарной^ точкой автор подразумевает точку х,
удовлетворяющую соотношению V/(x)=0, или, что то же самое, Vf(x)r<jO
для любого г. — Прим. ред.
312
Гл. 9. Градиентные методы
условиях каждый локальный максимум является также и гло-
бальным максимумом, и, значит, х — точка глобального макси-
мума. Ясно, что если f(x) может быть сделано сколь угодно
большим на некоторой итерации или если последовательность
f(xv) неограничена, то задача имеет неограниченное решение.
Два оставшихся случая — это те, когда на некоторой итерации Л
может неограниченно возрастать и f(x) возрастает с X, но стре-
мится к конечному пределу, или когда |x^| -*оо и f(xv) стре-
мится к конечному пределу при v оо. В этих случаях предель-
ное значение f(x) есть глобальный экстремум /(х). В упражне-
нии 9.24 предлагается провести детальное доказательство для
этих случаев.
В этом параграфе мы предполагали, что задача (9.8) ре-,
шается на каждой итерации и расстояние, на которое нужно
двигаться по направлению гг, определяется нахождением X,
максимизирующего f(xv + krv), 0<Х-<8.
Если не стремиться к наибольшему возможному увеличе-
нию z на каждой итерации в том смысле, как это делалось
выше, а использовать какой-либо упрощенный метод определе-
ния rv и X, то приведенное доказательство не применимо. Сходи-
мость такого упрощенного процесса надо исследовать отдельно.
9.4. Геометрическая интерпретация. Прежде чем обсуждать
дальнейшие подробности метода, полезно на примере задачи с
двумя переменными показать геометрическую картину итера-
ционного процесса. Рассмотрим задачу, для которой выпуклое
множество допустимых решений показано на рис. 9.1. Там же
показаны линии уровня нелинейной целевой функции и напра-
вления возрастания г. Предположим, что мы начали с допусти-
мого решения х0. Градиент Vf(x0), или d0, является вектором,
нормальным к гиперплоскости, касающейся линии уровня
f (х) =z0 в точке хо, и направленным в сторону возрастания z.
В начале процесса существенных ограничений нет, поэтому
r0=d0/|d0|. Мы можем двигаться из х0 в направлении г0 до тех
пор, пока не достигнем границы множества допустимых реше-
ний. Вообще говоря, не рекомендуется двигаться до конца,
так как максимум f(x0 + Zr0) может достигаться раньше, чем гра-
ница. В нашем случае, однако, f(x0+Xr0) возрастает при воз-
растании Z. Точка Xi показана на рисунке. Мы не можем двигать-
ся в направлении db так как при этом мы выйдем из мно-
жества допустимых решений. Задача (9.8) для точки Xi имеет
только одно ограничение. Решением этой задачи является век-
тор и, составляющий с вектором di наименьший угол по срав-
нению с любым вектором, выходящим из точки х и лежащим
в множестве допустимых решений. Таким образом, на следую-
9;4. Геометрическая интерпретация
313
щей итерации мы двигаемся вдоль ограничения 1. Мы снова
должны двигаться как можно дальше, пока не придем в точку х2.
Выбор вектора г2 ясен из рисунка. На третьей итерации мы
снова как можно дальше двигаемся вдоль ограничения 2, полу-
чая точку Хз. В этой точке процесс заканчивается, так как, ре-
шая (9.8), мы обнаруживаем, что максимальное значение Drf(x3)
меньше нуля. Геометрически это выражается тем, что вектор da
X2t
Рис. 9.1.
составляет тупой угол с любым вектором в множестве допусти-
мых решений, выходящим из точки х3. В этом примере процесс
заканчивается за конечное число итераций. Заметим, что в точ-
ке Хз функция f(x) имеет относительный локальный максимум.
В точке хз функция f(x) достигает также и глобального опти-
мума на выпуклом множестве.
Предположим теперь, что, решая ту же задачу, в качестве
начального допустимого решения мы берем точку х0 (см.
рис. 9.2). В этом случае процесс заканчивается после первой же
итерации и приводит к точке хь Однако в точке Xi функция f(x)
не имеет относительного локального максимума; Xi представляет
собой относительную седловую точку, так как при движении
из Xj в любом направлении вдоль ограничения 4 f (х) будет воз-
растать, а при движении из Xi в х0 /(х) убывает.
Пусть теперь начальное приближение в той же задаче будет
таким, как показано на рис. 9.3. Ясно, что в этом случае про-
цесс заканчивается после двух итераций и приводит к локаль-
ному экстремуму в точке А.
В качестве последнего примера рассмотрим задачу, в кото-
рой нет ограничений, кроме требования неотрицательности
314
Гл. 9. Градиентные методы
переменных. Предположим, что линии уровня для z = f(x) имеют
вид, показанный на рис. 9.4. Если мы начнем из точки хоа, то
х2
Рис. 9.3.
получим указанную на рисунке
метим, что на первой итерации
последовательность точек. За-
мы не двигаемся как можно
дальше. Процесс заканчивается после трех итераций в точке х3а,
в которой достигается относительный локальный максимум
9.5. Численное определение г
313
функции f. Если мы начнем из точки хо&, то сразу придем к сед-
ловой точке х.ц>. Если начать из точки Хос, полученная последо-
вательность точек сходится к точке х, в которой достигается
абсолютный максимум функции f для х^>0. В этом случае число
требуемых итераций может и не быть конечным.
9.5. Численное определение г. Если на какой-нибудь итера-
ции ограничения не позволяют двигаться в направлении гра-
диента, то для определения направления движения г нужно ре-
шить задачу (9.8), которая сама является задачей нелинейного
программирования. В § 9.2 мы не рассматривали методы ее ре-
шения. Это будет сделано сейчас. Покажем сначала эквивалент-
ность задачи (9.8) некоторой задаче квадратичного программи-
рования.
Рассмотрим следующую задачу квадратичного программиро-
вания:
azu <0, I £ Л (-ц),
azu = 0,
и}>0, (9.13)
W(xju = l;
найти min Z— u'u.
Существует взаимно однозначное соответствие между допусти-
мыми решениями задачи (9.8), для которых Vf(x„)r>0, и до-
пустимыми решениями задачи (9.13). Если и —допустимое ре-
шение задачи (9.13), то r=u/|u| —допустимое решение задачи
(9.8). Наоборот, если г — допустимое решение задачи (9.8),
причем ц= Vf(x„)r > 0, то г/г) — допустимое решение задачи
(9.13). Покажем, что если г„— оптимальное решение задачи
(9.8), то ис=г„/'Г]1„ 1Ц>= vf(xi>)r«— оптимальное решение за-
дачи (9.13) при условии, что r)v>0, и обратно, если и„ — опти-
мальное решение задачи (9.13), то rt)=ul)/|uv|—оптимальное
решение задачи (9.8). Чтобы доказать это, положим
где Гр — оптимальное решение задачи (9.8) и т]„>0. Предполо-
жим далее, что существует допустимое решение и_ задачи
(9.13), такое, что u'_u_ < u'uv, откуда |u_|<|uv|. Если
r_=u_/|u-|, то г_ — допустимое решение задачи (9.8) и
Vf (хJ г_ = V/ (xj и_ = > V/ (xj rr = рЬ, (9.14)
поскольку
Vf(xv)u_ = Vf(x„)uo = l.
316
Гл. 9. Градиентные методы
Таким образом, получено противоречие, и и® = г®/т]в должно
быть оптимальным решением задачи (9.13). Пусть теперь и® —
оптимальное решение задачи (9.13). Тогда rB=u®/|uB|—опти-
мальное решение задачи (9.8). Действительно, если сущест-
вует г+, такое, что Vf (х®)г+=т]+>Vf(x®)r®=i]®, то и+=г+/т)+
является допустимым решением задачи (9.13). Так как г^г+ =
==гХ=1, то
'1+ '1®
что противоречит тому, что и® является оптимальным решением
задачи (9.13). Таким образом, мы можем использовать опти-
мальное решение и® задачи (9.13) для получения направления
движения на (о + 1)-й итерации, т. е. можно использовать и®
вместо г® (норми{Л>вать и®, разделив его на |и®|, необязатель-
но). В упражнении 9.2 предлагается дать геометрическую интер-
претацию эквивалентности задач (9.8) и (9.13).
Рассмотрим способы решения квадратичной задачи (9.13).
Заметим, что целевая функция выпуклая. Можно, следователь-
но, попытаться прямо использовать один из методов, изученных
в гл. 7, например метод Вольфа. Однако, чтобы сделать это, не-
обходимо применить симплекс-метод к задаче, содержащей от п
до 2/п+п ограничений. Если п велико, с работой не справится
даже самая большая вычислительная машина, особенно если
учесть, что эта задача должна решаться на каждом шаге гра-
диентного метода. Другие методы гл. 7 также могут привести
к недопустимо большим задачам.
Зойтендейк [8, 9] предложил другой подход, который часто
требует меньшего объема вычислений. Вернемся к первона-
чальной форме задачи (9.8) и заметим, что если условие 1^=1
заменить на r'r-^l, то множество оптимальных решений не из-
менится, если только оптимальное значение целевой функции
положительно, так как в случае г'г<1 целевая функция может
быть увеличена. С этим изменением множество допустимых ре-
шений становится выпуклым. Будем считать ограничения на не-
отрицательность переменных частью общих ограничений и
запишем задачу, эквивалентную задаче (9.8), в следующей
форме1):
Мвг<0,
(9.15)
найти max DTf (х®) = Vf (х®) г,
!) Заметим, что если в
требованию, есть —
(9.8) строки Mv, соответствующие этому
9.5. Численное определение г
317
где в ограничениях Мог<0 строгое равенство выполняется для
г€/2. Заметим, что в этой форме задачи не ограничены.
Тогда мы можем применить результаты гл. 6 и получить,
что необходимое и достаточное условие оптимальности реше-
ния г задачи (9.15) состоит в существовании векторов [<р, <рг] и
rs>0, таких, что
Mj,r + rf = 0, ф'г,=0, (9.16)
где все компоненты [<р, <рг] неотрицательны, за исключением та-
ких, i€/2, знак которых произволен. При i С/г также rsi=0.
Транспонируя второе соотношение в (9.16) и умножая его на
Мю, получаем
МЛ;ф + 2М„г<рг = МЛ- (9-17)
Но Мсг=—rs, и, так как <pr>0, мы можем переписать (9.17)
в виде
МкМ»ф — w = ЛМ», (9.18)
где w=2rs<pr>0. Условие <p'rg=O можно тогда заменить условием
<p'w=0, a>i=0, (С /а.
В гл. 7 было показано, что вектор [q>, w], такой, что <pi>0,
wz>0, -wf=0t f£Z2, удовлетворяющий (9.18) и условию
q/w=0, должен быть базисным решением системы (9.18). Базис-
ное решение при q>i>0, ич>0, i£I2, будем назы-
вать допустимым. Найдя базисное решение задачи (9.18) при
q/w=0, из (9.16) получаем, что г =(dp — Mp<p)/|cU — М®<р[ — оп-
тимальное решение задачи (9.15), если только dv— Лмр=£0.
Если же d®—Mt,<p=0,ToVf(xv) представляет собой линейную ком-
бинацию строк матрицы М„, причем каждое q>z>0, Следо-
вательно, ни для какого г, удовлетворяющего ограничениям, це-
левая функция не может быть положительной. Таким образом,
не существует допустимого направления, при перемещении вдоль
которого f(x) возрастает, т. е. стационарная точка достигнута.
Итерационный процесс при этом закончен. Заметим, что, когда
dv — М„<р =/= 0, нет надобности вычислять г; можно просто ис-
пользовать dp — Мрф как искомое направление перемещения.
Выясним, как можно получить такое базисное допустимое
решение задачи (9.18), что <p'w=0. Мы без труда можем полу-
чить это базисное (но не обязательно допустимое) решение, по-
лагая ф=0 и w=—Mpdp. Построим Новое базисное решение,
такое, что ®г=0, /С/г. Чтобы сделать это, просто заменим ач
на изменяя только одну базисную переменную за
318
Гл. 9. Градиентные методы
один раз посредством обычных преобразований симплекс-метода
(удобно одновременно преобразовывать ch, — ЛЦр). Сделав это,
мы получим, что условие <p'w = 0 выполнено. Если полученное
базисное решение допустимо, это нужное решение. Если нет,
процесс нужно продолжать. В упражнении 9.3 читателю пред-
лагается выяснить, что делать, если описанная замена окажется
безуспешной.
Рассмотрим любое базисное (не обязательно допустимое)
решение задачи (9.18), такое, что, во-первых, если ср?: — базис-
ная переменная, тогда Wi— небазисная, и наоборот, и, во-вто-
рых, Wi = 0, Тогда q/w = 0. Если это решение не то, кото-
рое мы ищем, то по крайней мере одна из базисных перемен-
ных, <р$ или wif должна быть отрицательна. Рассмотрим
любую отрицательную базисную переменную. Если базисная пе-
ременная— фг-, то в новом базисном решении, полученном ис-
ключением фг- и заменой ее на w^ w^O, Доказательство этого
утверждения является целью упражнения 9.3.
Конечно, в результате этой замены базисная переменная, ко-
торая первоначально была положительной, может стать отри-
цательной. Аналогично, если отрицательной базисной перемен-
ной является Wi и мы получаем новое базисное решение заме-
ной Wi на фг, то в новом решении фг>0. Зрйтендейк первым
доказал это. Заметим, что если изменять базис таким образом,
то равенство ф'^у=0 всегда сохраняется. Зойтендейк предложил
выбирать любую отрицательную базисную переменную
если эта переменная — фг-, мы получаем новое базисное решение
заменой фг на w^ если это w„ — заменой w{ на фг-.
Этот итерационный процесс продолжается до тех пор, пока
не получено допустимое базисное решение. Здесь мы не можем
гарантировать отсутствие зацикливания. Однако можно выби-
рать заменяемую переменную и так, что зацикливания не будет.
Зойтендейк [9] показал, как это можно сделать. На практике,
вероятно, самое лучшее — просто выбирать для замены самую
большую по абсолютной величине отрицательную базисную пе-
ременную (Z^/2). Заметим, что переменные фг, /€/2, в этом
процессе не используются, так как знак их произволен.
Порядок М^Мг, всегда меньше, чем т + п, но больше, чем
число ограничений в задаче (9.8), если должно быть включено
более чем одно ограничение на неотрицательность переменных.
Лемке [4] предложил несколько иной способ решения задач
(9.13) и (9.8). Однако его метод требует преобразования ба-
зисных матриц порядка п на каждом шаге, в то время как ме-
тод Зойтендейка имеет дело с базисными матрицами порядка
9.5. Численное определение т
319
существенно меньшего, чем п, на некоторых, или даже на всех,
итерациях градиентного метода.
Рассмотрим другой способ решения задачи (9.13). Заметим,
что целевая функция сепарабельна и выпукла. Далее, ограниче-
ния линейны, и, следовательно, любой локальный экстремум
является также глобальным. Можно, таким образом, для нахо-
ждения приближенного глобального экстремума использовать
методы гл. 4. В частности, можно использовать б-формулировку
и в особенности эффективный вычислительный алгоритм, осно-
ванный на принципе декомпозиции и описанный в § 4.7. При
использовании этого алгоритма нам не нужно будет иметь дело
с базисными матрицами порядка большего, чем т+1,.причем
базисная матрица такого размера появится только в том случае,
когда все ограничения исходной задачи присутствуют в задаче
(9.13). В использовании этого метода имеется, впрочем, одна
трудность, которая заключается в определении допустимого раз-
мера вариации для каждого Uj, Сначала следует попытаться
решить, какой шаг использовать для каждого В большинстве
случаев, вероятно, достаточно принять, что
Idf^/dxjl < < \dt(xv)/dxjl ’ j
2
Однако при этом предположении на каждом шаге процесса для
каждой переменной приходится рассматривать различные раз-
меры вариаций.
Было бы удобнее, если бы мы могли с достаточной уверен-
ностью ограничить размер вариации щ некоторым интервалом,
скажем —l^Uj^l, Это можно сде-
лать, так как если в (9.13) Vf(xv)u=l заменить на
Vf(xv)u=p при р>0, то оптимальное решение новой задачи
будет отличаться от соответствующего оптимального решения
задачи (9.13) лишь скалярным множителем и, следовательно,
может быть использовано в качестве искомого направления дви-
жения. Если выбрать
то естественно ожидать, что все |uj|-<I. Хотя обычно это под-
тверждается, у нас нет никакой гарантии, что так будет всегда.
Так, когда Uj может иметь любой знак, и2 можно приближенно
представить пунктирной кривой, показанной на рис. 9.5. Если
Uj>l или Uj< — 1, мы просто полагаем и2.^ 1 -|-е\«у|, где
320
Гл. 9. Градиентные методы
наклон е можно выбирать в пределах от 3 до 5. Этим методом
можно решить задачу, даже если Uj по модулю больше 1; од-
нако точность приближения быстро уменьшается, по мере того
как | tij | возрастает по сравнению с 1. Впрочем, при указанном
выше изменении масштаба щ не часто будет превышать 1. Для
приближенной задачи в 6-форме следует просто заменить нео-
граниченное щ выражением (см. упражнение (4.47)
t-i <-i
Uj— Zj + 2 b-tj.
где переменные bkh Ъ-kj неотрицательны и ограничены сверху
единицей, за исключением btj
и 6-о, которые сверху не ограни-
чены. Если щ должны быть не-
отрицательными, используется
то же самое представление, но
уже без переменных 6-hj.
Следует заметить, что опти-
мальное решение приближен-
ной задачи удовлетворяет огра-
ничениям (9.13) и действитель-
но дает допустимое направление
движения. Насколько близко
это решение к наилучшему, за-
висит от того, удачно ли сде-
лано дробление при переходе
к приближенной задаче. Опи-
санная выше процедура изме-
нения масштаба позволяет получить весьма хорошее приближе-
ние к решению задачи (9.13). Заметим, что при вычислении
нужна только одна положительная искусственная переменная.
Таким образом, не требуется длинных вычислений первой фазы.
Зойтендейк предложил вместо решения задачи (9.8), или, что
то же самое, (9.13), определяющего наилучшее направление дви-
жения, решать следующую задачу, дающую допустимое, но уже
не обязательно наилучшее направление:
azr < О,
azr = О,
(®),
/б Л®).
(®);
(9.19)
найти max Z1 — Vf(xv)r.
9.5. Численное определение г
321
Условие г'г = 1 заменено здесь более слабым ограничением,
требующим только, чтобы каждое не превосходило единицы.
Понятно, что каждое допустимое решение задачи (9.8) является
допустимым и для задачи (9.19). Таким образом, если имеется
такое направление, что в этом направлении f(x) может воз-
расти, то решение задачи (9.19) дает его. В частности, опти-
мальное решение задачи (9.8) является допустимым для задачи
(9.19), так что оптимальное значение целевой функции в задаче
(9.19) будет не меньше, чем для задачи (9.8). Однако решение
задачи (9.19) не дает, вообще говоря, наилучшего направления
движения, потому что после нормировки (так, чтобы |rl =1)
этого решения величина Vf(xv)r может оказаться меньше, чем
для оптимального решения задачи (9.8). Если использовать не-
который специальный алгоритм, учитывающий верхние границы
(нижние границы учитываются введением новых переменных
= 1), то для решения задачи (9.19) может потребоваться
меньше работы, чем для решения квадратичной задачи (9.13),
и почти столько же, сколько для решения приближенной задачи
в б-форме. Тем не менее нам представляется, что приближенная
задача в б-форме предпочтительнее, так как она определяет,
хотя и приближенно, наилучшее направление движения, в то
время как решение задачи (9.19) не обязательно близко к наи-
лучшему.
Ограничения 0-0^ 1, /€/(^); —l^r^l, j (£/(t>), в задаче
(9.19) можно заменить на
п
2|гу1<1- (9.20)
Уточняя это ограничение, запишем для j f£J(v)
r. = r'-r", r'rr';>0, r'/j = O.
Тогда
Следовательно, (9.20) можно записать в виде
s s б<=°’ <9-21)
/ел*) 3 33 33
Когда используется ’(9.21), мы вводим единственное дополни-
тельное ограничение вместо большого числа верхних и нижних
границ.'Заметим, что множество допустимых решений выпукло,
так как |г,|—выпуклая функция. Таким образом, задача
21 Зак. 735
322
Гл. 9. Градиентные методы
может быть решена как задача линейного программирования
без введения ограниченного базиса. Это предлагается доказать
в упражнении 9.44.
Использование (9.21) вместо ограничения г'г<1 или исполь-
зование верхних и нижних границ в задаче (9.19), вероятно, по-
требует меньших вычислений, чем при решении задачи (9.13)
с помощью приближенной задачи в 6-форме или задачи (9.19)
методом верхних границ. Решение задачи (9.13) с помощью
приближенного метода в б-форме тем не менее остается пред-
почтительным, так как нет гарантии, что введение ограничений
(9.21) даст наилучшее направление движения. Однако ниже мы
увидим, что ограничения (9.21) будут особенно полезны, когда
исследуется процесс при нелинейных ограничениях.
9.6. Градиентный проективный метод. В предшествующем
параграфе мы выяснили, как можно определить наилучшее на-
правление движения из допустимого решения xv задачи (9.1),
чтобы получить новое допустимое решение xv+1 с f(xv+i)>
>f(xv). Для этого нужно решать задачу квадратичного про-
граммирования. Была рассмотрена также задача линейного про-
граммирования с ограничениями (9.21), которая дает некото-
рое приближение к оптимальному направлению. Рассмотрим
теперь так называемый градиентный проективный метод, кото-
рый позволяет находить допустимое направление движения,
уже не являющееся, вообще говоря, наилучшим или близким к
нему. Этот метод был предложен Розеном [5] и обладает тем
достоинством, что он не требует решения экстремальной задачи
для определения направления движения.
Начнем с попытки найти такое г, чтобы Drf(xv)>0 и все не-
равенства (9.6) и (9.7) выполнялись как строгие равенства.
Если это удастся сделать, то г должно удовлетворять соотноше-
ниям
azr —О, (и), гу —О, (9.22)
Ограничения (9.22) можно записать в виде Mvr = 0, где — та
же матрица, что и в (9.15). Найдем проекцию вектора Vf(xr)
на подпространство пространства Еп, которое представляет со-
бой ортогональное дополнение подпространства, порожденного
строками матрицы Mv. Пусть ранг матрицы будет А, и пусть
матрица Qv=(qi, ... , q^) содержит h линейно независимых
столбцов матрицы М', Тогда подпространство S, порожденное
столбцами матрицы Qv, будет совпадать’ с подпространством,
порожденным строками MD. Имеем
E”=S + O(S),
9.6. Градиентный проективный метод
323
где 0(S)—ортогональное дополнение подпространства 5. Лю-
бой. вектор из Еп может быть единственным образом представ-
лен в виде суммы векторов из S и 0(5). Применяя это к век-
тору dr, можем написать
d^r^ + s,,; t\,£O(S), s^S. (9.23)
Но так как S порождено столбцами Qv, то
St, = 5 О/Л = Чл,- (9.24)
Итак,
dv = rv + Qt,ar (9.25)
Однако, так как rrCO(S), то q'r^ = O, /=1, ... , h. Следова-
тельно, умножая (9.25) слева на Q', получаем
0.26)
Матрица Q'Q^ невырожденная. Действительно, определитель
|Q'QJ равен сумме квадратов всех миноров порядка h матрицы
{ЛА 3.17}. -Поскольку ранг матрицы Qv равен А, существует
по крайней мере один минор порядка А, отличный от нуля, от-
куда |q;qj #= 0. Учитывая сказанное, получаем в силу (9.26),
что
(9.27)
а из (9.24)
' (9-28)
Наконец, на основании (9.23)
г, = d,, - s„ = [I - Q, (Q^Q,)-1 Qj do = PA’ (9.29)
где
p„=i-q,(q;q„) (9.30)
Вектор rr ортогонален всем векторам из 5, поскольку rvCO(S).
Следовательно, rv удовлетворяет соотношению Mrrv = 0. Ма-
трицу Pv иногда называют матрицей проектирования. Она «про-
ектирует» dt в ортогональное дополнение подпространства, по-
рожденного столбцами матрицы Mv.
Если rv=#0, вследствие равенства s'г^, = 0 и (9.23) имеем
W = d'r^ = r'vrv > 0. (9.31)
Следовательно, -если вектор rv, вычисленный по формуле
(9.29), отличен от нуля, мы нашли допустимое направление,
21*
324
Гл. 9. Градиентные методы
вдоль которого f(x) увеличивается. Заметим, что для опреде-
ления i\ нам не нужно было решать никакой экстремальной
задачи.
Предположим, что на каждой итерации мы определяем на-
правление движения, вычисляя гг по формуле (9.29). Как сле-
дует поступить, если rv = 0? В этом случае из (9.23) и (9.24) вы-
текает, что
= (9.32)
т. е. вектор dr лежит в подпространстве, порожденном столб-
цами матрицы Mv.
Рассмотрим две возможности. Сначала предположим, что а©
из (9.32) таково, что aw^>0, i^I2- Заметим, что из /^/2,
следует, что i’€/i(y), и для строк Mv, соответ-
ствующих ограничениям —г^О, /€/(у), в (9.8). Мы можем
тогда записать
h
Vf(xt,)=2a/X а/г>0, 102.
Напомним, что каждый вектор qz есть некоторая строка ма-
трицы М„. Вернемся к задаче (9.8). Для любого допустимого г
h
Vf(xv)r = 2м<г>
i = 1
Но q<r<0, /(£/2>и q^ = 0, i^I2. так как г —допустимое ре-
шение и q'— некоторая строка М^. Итак, учитывая, что ка-
ждое aZz,>0, мы должны заключить, что
АЖ)г<0
для любого допустимого решения г задачи (9.8) и, следова-
тельно, мы достигли стационарной точки функции f(x), т- е-
конца итерационного процесса. Таким образом, если на неко-
торой итерации оказывается, что rv = 0 и в (9.32)
то мы достигли стационарной точки функции f(x).
Рассмотрим случай, когда по-прежнему rv = 0 и по крайней
мере для одного i (fcl2 а™ < 0. Предположим пока, что в точке
xv ранг матрицы Мг равен числу ее строк, так что каждой
строке матрицы соответствует столбец матрицы Qv. Это
означает, что нормали к гиперплоскостям (9.22) линейно неза-
висимы. Покажем, что если требование того; чтобы каждое не-
равенство из (9.6) и (9.7) выполнялось как строгое равенство,
9.6, Градиентный проективный метод
323
ослабить в отношении одного из неравенств, соответствующего
отрицательному а^, то можно найти допустимое напра-
вление, в котором мы можем двигаться так, что f(x) увеличи-
вается. Пусть для определенности < О, причем Рас-
смотрим подпространство S', порожденное векторами qb...
..., Обозначим через О (S') ортогональное дополнение
подпространства S', и пусть pi, ..., рп-/н-1 — ортонормирован-
ный базис для О (S'). Тогда, так как векторы q2 и pj порождают
все пространство Еп, мы можем записать
л-Л+1 h—\
Я/г— jS Р7Р7 + 2 Yz4z- (9.33)
Далее, так как векторы qi, ..., q/г линейно независимы, то по
крайней мере одно р/=#0. Подставив (9.33) в (9.32), получим
2 Р/Рj + 2 (“/С, 4- а*Л) Ф = + S„,
j = 1 i = 1
где
л-Л+1
= 2 Р/Р/4 0.
Таким образом, dr имеет ненулевую проекцию на О (S'). Кроме
того, используя (9.33), имеем
n-h+1
ЧХ = “», 2 ₽? <0. (934)
7 = 1
Следовательно, rv удовлетворяет (9.6) и (9.7), так как, в силу
(9.34), q<r^ = O, Z==l, —1; Я^<0. Но благодаря
сделанному предположению это выполняется для всех ограни-
чений (9-6) и (9.7). Далее, из (9.31)
vf(x.)^=rZ>0’
так что, двигаясь в направлении rv, мы действительно увеличи-
ваем f(x).
Таким образом, установлено, что если Pt5dt, = O и по крайней
мере одно агг < 0, то, если ранг матрицы Мг равен числу
ее строк, мы можем найти такое допустимое направление, что
f(x) будет в этом направлении увеличиваться. Делается это
так: мы вычеркиваем из матрицы Qr любой столбец i, соответ-
ствующий aw < 0, в результате чего получаем новую ма-
трицу Qr порядка й—1. Затем, из (9.30) определяем матрицу
326
Гл. 9. Градиентные методы
проектирования Р„, соответствующую матрице Qv. Тогда
rv=Pvdv и является искомым направлением. В случае, когда бо-
лее чем одно aiv < 0, можно вычеркнуть любой из столб-
цов q,-, соответствующих < 0, На практике следует вы-
бирать i, соответствующее наибольшему по модулю отрицатель-
ному a,iV.
Когда ранг матрицы М„ меньше числа ее строк, возникает
небольшое осложнение. В этом случае не будет соответствия
между столбцами Qv и строками Mv, т. е. соответствия между
столбцами Qt, и ограничениями (9.6) и (9.7). Обозначим через
m\ АСК, строки М„, не входящие в Q,, как столбцы. Тогда
л
(т*)' = 2 Mz, k^K.
t-\
Предположим, что мы поступаем так же, как и раньше, т. е.
вычеркиваем такое qn из Q®, что qAr^CO. Выше было показано,
что 9^ = 0, I4=h. Однако
и не обязательно, чтобы
А £ КП ЛИ или k£K(\J (и)',
mftrt, = 0, АСКпЛг-
Это зависит от рл. Если все ограничения (9.6) и (9.7) выпол-
няются, тогда проблемы не возникает. Мы действуем, как и в
случае равенства ранга Мю числу ее строк. Если же ограниче-
ния не выполняются, можно прибегнуть к методу вариаций.
Для АСК заменим bk в (9.1) на Аа+6\ где б — малое положи-
тельное число. После этого ни одно из ограничений с номером
не является существенным в точке хю, и задача сведена
к изученному выше случаю. Можно показать, что существует
бо > 0, такое, что для всех б, О<б^бо, не более чем h
(h — число столбцов матрицы QB) ограничений из I(v) могут
быть существенными после того, как к Ь{ добавлена вариация б.
Это нужно доказать в упражнении 9.41. Действуя таким обра-
зом, мы никогда не встретимся с ситуацией, когда больше чем h
ограничений из 7(о) существенны (аналогично проблеме выро-
ждения в задачах линейного программирования). На практике
необязательно варьировать В упражнении 9.42 Мы просим
читателя обсудить этот вопрос.
9.6. Градиентный проективный метод
327
В этом параграфе мы рассмотрели метод выбора направле-
ния движения из точки xD, который не требует решения экстре-
мальной задачи. Было показано, что всегда можно найти такое
направление движения, что f(x) будет увеличиваться, кроме
того случая, когда Pvdv = O и из (9.27) удовлетворяет усло-
вию ocw>0, и что в этом слуйае хг,— стационарная точка
функции f(x), на которой итерационный процесс заканчивается.
Если r^P^d^O, то и определяет направление движения.
Когда rv=0, но по крайней мере одно < 0, iffch, мы вычер-
киваем из Qv столбец цг, соответствующий < О, iffch, полу-
чая Qp. Тогда можно найти матрицу Pv, соответствующую Qv,
и вектор rv = Pvd„ дает направление движения. В последнем
случае может потребоваться вариация, чтобы обеспечить ра-
венство ранга матрицы числу ее строк.
Заметим, что если r1) = Pvdu=#O, то x^+i =xv + Zrr и Mrrv = 0,
так что все ограничения, существенные в точке хР, останутся
существенными и в точке xv+i. Если Х = е, то хотя бы одно огра-
ничение, которое было несущественным в точке хр, станет су-
щественным в точке xu+i, и, чтобы получить Мг+Ь мы просто при-
писываем соответствующие строки к JAV. Если X < 8, то Mu+i =
==MV. Когда rv = 0, мы полагаем rw = Pvdv, и в этом случае одно
из ограничений, которые были существенными в точке хг, ста-
новится несущественным для xv+i. Если при этом % = 8, то, чтобы
получить Mv+b мы должны из Мг вычеркнуть одну строку и
одну (или, возможно, больше) добавить. Если же X < 8, ма-
трица Mr+i получается из вычеркиванием соответствующей
строки.
Выясним, как получить Qv+i, когда xu+i =xv + %rv. Прежде
всего, если Х<8, то Qv+i = Qv. Пусть теперь Z = 8. Обозначим
через m результат транспонирования новой строки, появившейся в
Mv+i. Тогда Qv+i= (Qv, m), если m линейно не зависит ют столб-
цов матрицы Qr, и в противном случае Qv+i = Qv. К счастью, до-
вольно легко определить, будет или нет m линейно зависеть от
столбцов Qr. Мы вычисляем Рьш, и, если этот вектор ненуле-
вой, tn имеет ненулевую проекцию на ортогональное дополнение
подпространства, порожденного столбцами и, следовательно,
(почему?) линейно не зависит от столбцов CL. Если Pvm = 0,
тогда m линейно зависит от столбцов Qv.
Когда xD+i=xv + Xrv и X < 8, то Qr+i = Qu, где Qr получается
из Qv вычеркиванием столбца, соответствующего ограничению,
которое становится несущественным. Если Z-8 и m определено
так же, как и раньше, то Qv+i=(Qv, m), если m линейно не за-
328
Гл. 9. Градиентные методы
висит от столбцов Qr, или Qr+i = Qr, если m линейно зависит от
них. Чтобы определить, будет или нет m линейно зависеть от
столбцов Qr, мы вычисляем Ргш, и если этот вектор ненуле-
вой, то m линейно не зависит от столбцов Qv Если становится
существенным более чем одно ограничение, когда Х = 8, то мы
действуем, как и раньше, добавляя каждый раз по одному огра-
ничению.
На каждой итерации нужно вычислять новые матрицы Рр и
векторы Это весьма трудоемкая операция, если (Q'Qp)"1
должно заново вычисляться на каждом шаге. Можно легко
получить способ вычисления новой обратной матрицы, ко-
гда к Qp добавляется или вычеркивается столбец, с помощью
формул, аналогичных приведенным в § 2.1 для блочной формы
обратной матрицы. В упражнениях 9.4 и 9.5 предлагается по-
лучить эффективный способ определения Pr+i и ar+i через Рр
и av.
При реализации градиентного проективного метода на циф-'
ровой вычислительной машине следует иметь в виду возмож-
ность появления дополнительных трудностей. Например, даже
если P„d1,=O, то из-за ошибок округления и тому подобных
причин вектор Pt,dp, вычисленный на машине, может отличаться
от нулевого. Нужно, следовательно, использовать другое пра-
вило перехода от употребления Ppdp как направления движе-
ния к вычеркиванию столбца из Qp и использованию направле-
ния Prdt. Одно из правил состоит в том, что всегда нужно
вычислять V/(xv)rr/|rv|, rr=P^dr, и Vf (xv)rv/\ гг|, rv=Prdv, где
получается из Qp вычеркиванием столбца, соответствующего
наибольшему по абсолютной величине отрицательному аг-р, если
есть по крайней мере одно отрицательное о^р. Затем следует
выбирать направление, соответствующее большему из этих двух
чисел. Хотя этот метод кажется приемлемым, он связан с не-
нужным увеличением объема вычислений. По-видимому, проще
вычислить Vf(xr)rj||, и, если результат оказывается слиш-
ком малым, можно также вычислить Vf (xv)rv/\rv\. После этого
следует выбрать направление, соответствующее наибольшему
из этих чисел, или, кроме того, следует также вычислять rv, если
было какое-то отрицательное аг-р, достаточно отличающееся от
нуля.
Что понимать под «слишком малый» или «отрицательное, до-
статочно отличающееся от нуля», будет зависеть от самой за-
дачи и, в частности, от выбора единиц измерения переменных
и данных задачи. Возможно, следует изменять эти критерии по
мере приближения к решению. С этими же вопросами мы стал-
97. Геометрические иллюстрации
329
киваемся, когда предстоит решить, можно ли уже оборвать ите-
рационный процесс; ведь машина может"'и не выдать равен-
ство PrcU = O, даже если на самом деле P2?d1) = 0. В связи со
сказанным следует ввести некоторый признак окончания про-
цесса, отличный от требования, чтобы Prdr = 0 и при
Имеется случай, когда можно быть уверенным, что Pvdv = O,
и, таким образом, нет надобности вычислять Prdv в явном виде.
Речь идет о той ситуации, когда Qr — матрица порядка п.
Столбцы Qv при этом порождают все пространство £п, и O(S)
содержит только 0, так что Prdr должно быть равно нулевому
вектору.
Так как в градиентном проективном методе мы не ищем наи-
лучшее направление движения, то сходимость последователь-
ности xv, когда процесс не заканчивается после конечного числа
шагов, к стационарной точке f(x) или же тот факт, что |xv | > оо,
нуждаются в доказательстве. Указанный факт можно доказать,
если процесс строится так, что на каждом шаге берется либо
fVi либо гР, в зависимости от того, какой из этих векторов дает
большую производную по направлению (см. упражнение 9.6).
9.7. Геометрические иллюстрации. Для лучшего представле-
ния о градиентном проективном методе полезно рассмотреть
геометрическую иллюстрацию (см. рис. 9.6). Предположим, что
получено допустимое решение хг. Мы не можем двигаться в
направлении градиента, не нарушая ограничения 1, Следова-
тельно, задача (9.8) имеет вид
а’г<0, г'г=1; найти max DTf (xv) = V/ (xv) г.
Матрица Qv, используемая в градиентном проективном методе
есть просто Q' = а1 и
гр = РЖ = |5-
Как показано на рисунке, вектор г7; представляет собой орто-
гональную проекцию вектора dv на границу множества допусти-
мых решений. Таким образом, на следующем шаге нужно дви-
гаться вдоль границы, пока не будет достигнута крайняя
точка А, в которой итерационный процесс заканчивается.
Рассмотрим теперь ситуацию, изображенную на рис. 9.7.
В этом примере будут нарушаться оба ограничения, если дви-
гаться в направлении градиента. Задача (9.8) имеет в этом слу-
чае вид
azr<0, Z=l, 2, г'г = 1; найти max D{f(xv) = Vf(Xv)r,
330
Гл. 9. Градиентные методы
а матрица Q' = [a1, а2]. Столбцы СК порождают Е2, так что
pvdv==rt = O. Ясно, что только точка 0 удовлетворяет соотноше-
ниям агг = 0, /=1,2, так что невозможно двигаться из xv в ка-
ком бы то ни было направлении, чтобы при этом оба ограниче-
ния выполнялись как строгие равенства. Заметим, что если
представить как линейную комбинацию векторов а1 и а2, то
Рис. 9.7.
cc2d < 0 и cciv > 0. Таким образом, мы можем найти направле-
ние движения, если допустим, что ограничение а2г<<0 выпол-
нялось бы как неравенство. Чтобы получить Qt„ вычеркиваем
(а2)' из Qv. Тем самым мы пришли к предыдущему случаю, ко-
торый уже рассмотрен, и rv==I\dv — изображенный на рисунке
вектор. На следующем шаге мы двигаемся по стороне / мно-
жества допустимых решений, пока не достигнем крайней
точки Л, в которой процесс заканчивается.
В обоих рассмотренных примерах утверждалось, что процесс
заканчивается, когда достигнута крайняя точка А. Это справед-
ливо при том условии, что Pr+idv+i=O и au+i > 0 в точке xv+b
Покажем это. Ситуация изображена на рис. 9.8. Задача (9.8) в
этом случае имеет вид
а!г<0, — Г1<0, г'г = 1; найти max Dtf(Xv+i) = Vf(Xv+\)r.
Qv+i содержит столбцы — е4 и (а1)'. Тогда Pv+idl+i = 0. Следова-
тельно, dy+i лежит в конусе, порожденном —ei и (а1)', и au+i>0.
Таким образом, условия окончания процесса выполняются.
В этом примере f(x) достигает в точке xu+i своего глобального
экстремума на множестве допустимых решений.
Предположим, что начальное приближение в задаче, пред-
9.7. Геометрические иллюстрации
331
ставленной рис. 9.9, взято в точке х0. Для х0 матрица Qq = [а1, а2]
и Podo = O. Однако аю < О и а2о < 0. Таким образом, чтобы
получить Qo, можно вычеркнуть любой столбец из Qo, т. е. d0
может быть спроектировано и на а2х = &ь и на а2х = 62, так что
можно двигаться вдоль любой из этих прямых. Если выбрать
наибольшее отрицательное аг0, мы будем двигаться вдоль сто-
роны 2.
хг
Рис. 9.8.
Рис. 9.9.
'Заметим, однако, что движение вдоль любой из этих сторон
потребует большего числа шагов, чем действительно необхо-
димо, так как можно было бы двигаться в направлении do и за
одну итерацию пересечь все множество допустимых решений.
Градиентный проективный метод, описанный в предыдущем па-
раграфе, не использует возможности движения вдоль напра-
вления dv (если вдоль него можно двигаться), так как в этом
методе на каждом шаге становится несущественным только одно
ограничение. Поэтому целесообразно модифицировать проек-
тивный метод, по крайней мере на первых итерациях, так, чтобы
после вычисления dv проверять, удовлетворяет лц d„ ограниче-
ниям (9.6) и (9.7), и, если удовлетворяет, двигаться в направле-
нии dv. Этот прием, однако, заключает в себе одну неприят-
ность: после движения в направлении dy мы, вообще говоря,
не сможем определить исходя из(О'Ог,)"1, так как
множество строк в может весьма существенно отличаться
от аналогичного множества в Мг. В связи с этим (Q' ^Q^)"1
нужно будет вычислять непосредственно, а это может потребо-
332
Гл. 9. Градиентные методы
вать больших вычислений, чем при применении градиентного
проективного метода на каждом шаге. Все зависит от того,
сколько итераций мы экономим, двигаясь в направлении dr. Та-
ким образом, хотя на первый взгляд кажется желательным по
возможности двигаться в направлении dr, более детальный ана-
лиз делает сомнительными преимущества этого пути. Полез-
ность этой модификации будет, несомненно, зависеть от типа за-
дачи и от выбора начального приближения.
9.8. Сравнение методов определения г. Нет численных ре-
зультатов, позволяющих сравнивать вычислительную эффектив-
ность рассмотренных в двух последних параграфах методов оп-
ределения направления движения на каждой итерации. По-
этому невозможно сделать окончательное утверждение о том,
какой метод предпочтительней. Тем не менее можно сравнить
количество вычислений для определения vV) требуемых различ-
ными методами. Точное решение задачи квадратичного про-
граммирования (9.13) связано с действиями над матрицами по-
рядка большего чем т, вплоть до порядка m + n. С другой сто-
роны, использование для решения задачи (9.13) приближенного
метода в б-форме должно быть достаточно эффективным, так
как при этом никогда не придется иметь дело более чем ст+1
ограничением. Однако этот прием требует решения на каждом
шаге задачи линейного программирования. Градиентный проек-
тивный метод не решает задачу оптимизации, но может потре-
бовать оперирования с матрицами порядка большего чем т,
так как необходимо включать ограничения на неотрицательность
переменных. Вероятно, приближенный метод в б-форме либо гра-
диентный проективный метод наиболее удобен для применения.
При использовании градиентного метода нужно стараться
начинать с такого допустимого решения, для которого суще-
ственно лишь небольшое число ограничений. Тогда в начальных
итерациях размер матриц, нужных для определения направле-
ний движения, будет относительно мал. Лишь к концу итера-
ционного процесса в (9.13) может появиться большое число
ограничений. В такой ситуации градиентный метод будет доста-
точно эффективен. Если же все m ограничений из (9.1) появ-
ляются в (9.13) на каждой итерации, то задача может оказаться
слишком трудоемкой.
Заканчивая, хочется сказать, что сравнивать различные ме-
тоды определения г трудно еще и потому, что наименьшее число
итераций совсем необязательно достигается при движении в
том направлении, в котором относительное приращение f(x)
максимально. Действительно, как и в задачах линейного про-
граммирования, иногда предпочтительней временно двигаться
9.9. Решение задач линейного программирования
333
даже в направлении убывания f(x). К сожалению, нет способов
выяснить это в процессе вычисления.
9.9. Решение задач линейного программирования с исполь-
зованием градиентных методов. Мы уже говорили о том, что
задачи линейного программирования могут быть решены гра-
диентными методами. Когда f(x)=cx, появляются некоторые
упрощения, так как Vf(x)=c и не зависит от х. Мы отмечали
также, что. в случае линейной целевой функции, когда мы дви-
гаемся из xv в направлении rv до получения хр+ь мы всегда дви-
гаемся как можно дальше, т. е. до тех пор, пока несуществен-
ное ограничение не становится существенным. Эта особенность
делает1 ненужным поиск X, для которого /(xv+%rv) максимально.
Далее, так как Vf не изменяется, при переходе от одной итера-
ции к другой мы только добавляем лишнее ограничение (или
в крайнем случае несколько ограничений) к старой задаче
(9.15), чтобы получить новую, и, возможно, вычеркиваем одно
или больше ограничений, которые были существенны в старой
задаче. Это дает нам возможность решать новую задачу с по-
мощью старого решения. В упражнении 9.7 мы предлагаем
детально разобрать эту процедуру. В некоторых случаях такие
упрощения могут существенно уменьшить объем вычислений,
когда для определения г на каждом шаге решается задача
(9.13). Градиентный проективный метод также немного упро-
щается благодаря тому, что V/ остается неизменным. Эти уп-
рощения предлагается рассмотреть в упражнении 9.8.
Для задач линейного программирования можно доказать,
что если для определения направления движения на каждохМ
шаге решается задача (9.8), то градиентный метод обеспечи-
вает сходимость к оптимальному решению за конечное число
шагов или же (также за конечное число шагов) выяснится, что
целевая функция неограничена. Действительно, рассмотрим за-
дачу (9.8), которую нужно решать на каждой итерации. Пусть
rv — ее оптимальное решение. Предположим, что а%<0, i €
£/< (у), и rjV>0, / С А (у)- Тогда точно то же решение rv было
бы получено для задачи (9.8), если бы ограничения /£/<(?>) и
ограничения неотрицательности с j £ J> (v) были бы отброшены.
Далее ограничения и ограничения неотрицательности
с будут опущены и одно (или, возможно, больше) но-
вое ограничение будет добавлено для получения новой задачи,
соответствующей xv+i. Заметим, что если ограничения
отброшены, то любое допустимое решение новой за-
дачи для xv+i должно быть допустимым и в предыдущей для
xv. Следовательно, так как решение задачи (9.8) единственно и
так как гг не удовлетворяет новому ограничению (или ограни-
334
Гл 9. Градиентные методы
чениям), добавленному для образования новой задачи, то оп-
тимальное решение rv+i новой задачи удовлетворяет неравен-
ству cru+i < сгр. Следовательно, мы *не можем на двух разных
итерациях прийти к решению одной и той же задачи (9.8). Так
как число таких задач конечно, итерационный процесс должен
кончиться за конечное число шагов.
Градиентный проективный метод также сходится за конеч-
ное число шагов, но доказывать это необходимо иначе, так как
в этом случае неверно, что производная по направлению убы-
вает на каждом шаге. Вместо этого устанавливается, что не
может быть бесконечного числа точек хг в какой бы то ни было
е-окрестности оптимального решения. Общее доказательство
сходимости к стационарной точке f(x) показывает, что за ко-
нечное число итераций будет получено решение, сколь угодно
близкое к оптимальному решению задачи линейного программи-
рования. Остается только доказать, что, начиная из любой
точки, достаточно близкой к оптимальной, мы придем к этому
оптимальному решению за конечное число шагов. Упражне-
ние 9.9 связано с деталями этого доказательства.
Расчеты, проделанные с различными модификациями гра-
диентйого метода, свидетельствуют о том, что они требуют боль-
ших вычислений на каждой итерации, но меньшего числа ите-
раций, чем при применении симплекс-метода. Число итераций
уменьшается, даже если отсутствует допустимое решение для
начала градиентного метода. Причина этого в том, что в гра-
диентных методах имеется возможность движения по внутрен-
ней части допустимого множества или по граням, что невоз-
можно при симплекс-методе, где перемещение всегда происхо-
дит по ребру от одной крайней точки к соседней. Когда не
имеется допустимого решения для начала градиентного метода,
тогда симплекс-метод, вероятно, приводит к оптимальному ре-
шению несколько быстрее, чем градиентный метод. Однако если
есть хорошее начальное решение, градиентный метод оказы-
вается значительно лучшим.
Как следовало ожидать, между способом выбора rv в гра-
диентном методе и соответствующими операциями в различных
типах симплекс-алгоритмов имеются интересные связи. В част-
ности, существует связь между градиентным проективным ме-
тодом и двойственным симплекс-методом в тех случаях, когда
начальное приближение градиентного проективного метода есть
базисное допустимое решение задачи (9.1). Мы исследуем эти
взаимосвязи для задач, в которых требуется, чтобы все пере-
менные были неотрицательными и все ограничения выполнялись
бы как строгие равенства (/2 содержит все i)t т. е. когда речь
9.9. Решение задач линейного программирования
335
идет об обычной форме задачи линейного программирования
Ах = Ь, х>0; найти max г —сх; г(А) = /?г. (9.35)
Двойственная к (9.35) задача имеет вид
A'w + Dw<s = c/, ws>0, D= — 1Я; найти min Z = b'w. (9.36)
Применим двойственный симплекс-метод к (9.36), т. е. не к ис-
ходной задаче (9.35), а к ее двойственной.
Пусть хо — начальное базисное допустимое решение задачи
(9.35). Предположим, что оно невырожденное. Заметим, что ка-
ждая матрица Qv, используемая в градиентном проективном
методе, состоит из линейно независимого подмножества столб-
цов из (A', D). Так как r(A)=m, каждая содержит А'.
Кроме того, так как мы начинаем с базисного решения задачи
(9.35), Qo содержит также п — т столбцов из D. Эти столбцы
вместе с т столбцами матрицы А' действительно линейно неза-
висимы, как и требуется ({ЛП8.8}). Итак, Qo порождает про-
странство Еп и Рос' = О. Следовательно, Qo— базисная матрица
для (9.36) и а0 — базисное, но не обязательно допустимое ре-
шение задачи (9.36).
Если aiV^0, f^/2»1), так что do — базисное допустимое ре-
шение задачи (9.36), тогда из результатов, изложенных в
{ЛП 8.8}, вытекает, если справедливо равенство xows = O, что
х0 — оптимальное решение задачи (9.35), а — оптимальное
решение задачи (9.36). Указанное равенство выполнено потому,
что столбец из D будет включен в Qo, если только соответствую-
щее Xj = O. Это, конечно, является также условием, которое об-
рывает итерационный процесс градиентного проективного ме-
тода.
Предположим теперь, что по крайней мере одно aiv < О,
Z(£/2. В градиентном проективном методе мы выбираем наи-
большее по абсолютной величине отрицательное а^, т. е. наи-
большую по абсолютной величине отрицательную базисную
переменную для базисного решения задачи (9.36), чтобы опре-
делить вектор, который нужно выбросить из Qo для образо-
вания Qo. Этот же критерий используется в двойственном
симплекс-методе для определения столбца, который нужно вычерк-
нуть из базиса. Пусть а^о — наибольшее по модулю отрицатель-
ное очо, iffch- Тогда как в одном, так и в другом методе стол-
бец s из Qo должен быть вычеркнут.
*) Заметим, что 1г содержит все ограничения в (9.35), так что только Z,
/(£/2, ОТНОСИТСЯ К условиям —G<;0, если Xjq = O.
336
Гл. 9. Градиентные методы
Обозначим оценки для задачи (9.36) через рг-. Тогда рг = &ь
если i соответствует и рг=0, если i соответствует wsi. Пред-
ставим, что Qo устроена так, что столбцы из А' стоят вначале,
перед столбцами из D. Рассмотрим столбец—ej из D, не вхо-
дящий в Qo. Для этого столбца
Z. - Ру = Zj = (Ь, 0) Q"1 (- е7) = - х)0 < 0, (9.37)
где Xj0 есть j-я компонента х0. Так как —е;- не входит в Qo, то
Xjo 6.
Применяя двойственный симплекс-метод к (9.36), мы опре-
делим вектор, входящий в базис, из условия
min ( , yi < 01, (9.38)
где yl равно минус /-й компоненте s-й строки матрицы Qo
Это следует из того, что yJ = Qo'1 (—е7). Обозначим /-ю компо-
ненту s-й строки Qo"1 через qJs. Тогда условие (9.38) эквива-
лентно следующему:
min , <7>>о). (9.39)
<ls J
Условие (9.39) очень похоже на условие нахождения е в гра-
диентном методе, т. е. на условие, определяющее, как далеко
можно двигаться из х0. Действительно, при использовании гра-
диентного проективного метода для определения направления
движения Го из Qo вычеркивается столбец s для получения Qo,
такого, что О (S') имеет размерность единицу (S' — подпро-
странство, порожденное столбцами Qo). Следовательно, при
движении из крайней точки (9.35) мы (используя градиентный
проективный метод) будем двигаться по ребру выпуклого мно-
жества к другой крайней точке. Когда новая крайняя точка
достигнута, для получения Qi к Qo будет добавлен один столбец.
Остается показать, что столбец будет именно тем, который
определяется из (9.39). Чтобы сделать это, рассмотрим матрицу
Qo"1- Ее s-я строка ортогональна каждому столбцу матрицы Qo,
за исключением s-ro. Таким образом, столбцы Qo и s-я строка
Qc?1 порождают Еп и s-я строка Qo"1 может быть использо-
вана при образовании подпространства О (S')- Следовательно,
проекция г0 из с на О (S') должна быть пропорциональна s-й
строке Qo1- Новое решение в градиентном методе будет иметь
вид х==хо+Хг‘о, где X выбирается так, чтобы xj0 + 0, j^J(O)-
9.10. Задачи с нелинейными ограничениями
337
При определении Л таким способом станет существенным по
крайней мере одно ограничение на неотрицательность перемен-
ных, связанное со столбцами, не входящими в Qo, когда мы дви-
гаемся как можно дальше. Вследствие пропорциональности ме-
жду г0 и s-й строкой Qo 1 это ограничение будет совпадать с ог-
раничением, определяемым из (9.39). Мы видим, следовательно,
что градиентный проективный метод дает точно то же множе-
ство базисных допустимых решений задачи (9.35), которое
можно получить, решая задачу (9.36) двойственным симплекс-
методом. Это и означает эквивалентность обоих методов.
9.10. Задачи с нелинейными ограничениями. Рассмотрим, ка-
ким образом изученные градиентные методы могут быть обоб-
щены применительно к задачам, включающим нелинейные огра-
ничения. Можно ожидать, что схема вычислений значительна
усложнится.
Мы будем изучать задачи вида
gz(x)<6z, /СЛ-
gz(x) = Z>z, ze4> (9-40)
Ху 0, J £
найти max z = f(x),
причем предполагается, что функция f(x) и все функции gt(x)
имеют непрерывные первые частные производные.
Сначала рассмотрим случай, когда функции g*i(x) выпуклы
•для а множество /2 пусто или, в крайнем случае, соответ-
ствующие ему ограничения линейны. При этих предположениях
множество допустимых решений, если оно непусто, выпукло.
Рассмотрим некоторое допустимое решение xv и обозначим че-
рез Ii(v) множество индексов существенных ограничений, а че-
рез J (и) — множество индексов переменных, равных нулю. Ка-
сательная плоскость к каждой поверхности £Дх)=6й f£/i(y),
в точке xv будет гиперплоскостью, опорной (в точке xv) к вы-
пуклому множеству допустимых решений. Уравнение для та-
кой опорной гиперплоскости имеет вид
Vgz(xt,)x = Vgz(xr)xt,.
Предположим, что мы хотим определить новое допустимое
решение х = хг + Хг, для которого f(x) >f(xv). Как следует из
(3.64), для того чтобы x = xr + Zr удовлетворяло ограничениям
i€/i(y), необходимо (но не достаточно), чтобы
Vgi(xv)r 0. Зойтендейк [8, 9] предложил следующий процесс
22 Зак. 735
338 Гл. 9. Градиентные методы |
определения г. Найдем вектор г и число о, являющиеся реше-
нием следующей задачи !):
Vgz(xt,)r + a<0, /6ЛМ
azr = 0,
-V/(xJr + a<0, (9.41)
r'r = 1;
найти max Z—в.
Эта процедура выбирает направление, которое возвращает нас
во внутренность множества (во всяком случае, по отношению
к нелинейным ограничениям), пока еще можно удовлетворить
неравенству Vf(xJr>0. Вектор г (обозначим его через rv),
являющийся решением этой задачи, изображён на рис. 9.10.
* После того как rv найдено, мы
определяем е, т. е. наибольшее
значение X, для которого £г(х» +
4“%г^)С Д, и Xjp4“
/€ J. Заметим, что нужно рассма-
тривать все i С Л, а не только
/^Л(и), так как, двигаясь в на-
правлении гг, мы можем нарушить
какое-нибудь из ограничений
i’C/i(u). Чтобы определить, как
далеко можно перемещаться, мы
находим X, 0<Х<е, которое мак-
симизирует величину f(xv + Xrr).
В упражнении 9.14 рассматри-
вается вопрос о численном реше-
нии задачи (9.41).
Розен [6] обобщил градиент-
ный проективный метод на за-
Рис. 9.10.
дачу максимизации вогнутых функций на выпуклом множестве.
По этому методу все сводится к задаче максимизации линей-
ной целевой функции z=xn+i добавлением еще одного ограни-
чения xn+i — f(x)^.Q. Новое множество допустимых решений
по-прежнему выпукло. Рассмотрим допустимое решение х-у, ле-
жащее на границе выпуклого множества. Для ограничений, су-
щественных в этой точке, найдем касательные гиперплоскости
к соответствующим поверхностям в точке xv. Градиентный про-
ективный метод состоит, как и раньше, в проектировании гра-
П В силу сделанных предположений, если функции gi—линейные.
Здесь принято £г(х)=а*х.— Прим. ред.
9.10. Задачи с нелинейными ограничениями
339
диента на ортогональное дополнение подпространства 5, поро-
жденного нормалями к касательным гиперплоскостям. Переме-
щение из точки xv осуществляется в направлении проекции
градиента. При этом мы двигаемся в пересечении касательных
гиперплоскостей и, следовательно, выходим за границы множе-
ства допустимых решений. В связи с этим, чтобы вернуться
к допустимому решению, необходимо корректирование. Все эти
операции совершаются так, чтобы новая допустимая точка xv+i
удовлетворяла соотношению f(xv+I) > f(xv). Мы не будем по-
дробно рассматривать это обобщение градиентного проектив-
ного метода, а изучим другой метод, который оказывается столь
же эффективным и более многообещающим.
Следует подчеркнуть, что при нелинейных ограничениях гра-
диентный проективный метод не столь эффективен, как при ли-
нейных. Это происходит из-за того, что при перемещении из xv
в xv+i градиенты функций gi(x) могут изменяться, несмотря на
то, что множество существенных ограничений в точке xv может
лишь единственным ограничением отличаться от множества су-
щественных ограничений в точке xv+i. Следовательно, в общем
случае невозможно вычислять (Q^+iQ^+i) , исходя из (Q^Q®) ,
и поэтому новая обратная матрица должна быть вычислена не-
посредственно. Так как матрица (Q^+iQ^+i) часто может иметь
порядок значительно больший, чем общее число ограничений
(появляются столбцы, соответствующие ограничениям неотри-
цательности), на каждой итерации потребуется производить
очень много вычислений. Вдобавок еще нужно возвращаться в
множество допустимых решений после движения в пересечении
касательных гиперплоскостей. Это осуществляется также с по-
мощью некоторого итерационного процесса, который к тому же
приводит не к допустимому решению, а только к точке, которая
лежит в 6-окрестности границы множества допустимых реше-
ний (6 > 0 может быть выбрано произвольно).
Рассмотрим случай, когда не требуется, чтобы множество До-
пустимых решений было выпуклым. Метод Зойтендейка не при-
меним, если среди ограничений имеются нелинейные равенства,
так как он не может обеспечить выполнение этих равенств.
В связи с этим метод может быть использован, если множе-
ство /2 пусто или индексам ZC /2 соответствуют только линейные
уравнения. Конечно, нельзя гарантировать что-либо большее,
чем сходимость последовательности решений к стационарной
точке функции f(x). Отсутствие сколько-нибудь значительного
опыта вычислений не позволяет сказать, насколько удобна за-
дача (*9.41) для определения направления движения. Возможно,
что будут выбираться только очень малые шаги.
22*
340
Гл. 9. Градиентные методы
Градиентный проективный метод может быть использован $
для невыпуклых областей, даже если /2 содержит нелинейные I
уравнения. Некоторые трудности его использования уже рас-
сматривались. Возникает также вопрос, не будут ли шаги по-
лучаться столь малыми, что потребуется нереализуемое число
итераций.
9.11. Градиентный метод для задач с сепарабельными огра-
ничениями. Нам хотелось бы рассмотреть сейчас различные
подходы для применения градиентного метода к задаче (9.40),
которые могут иметь некоторые преимущества перед двумя уже
упомянутыми методами. Мы предположим, что ограничения в
(9.40) сепарабельны, так что можно записать
gi ^)=iigij(xj).
Затем мы поступим так же, как в гл. 4, и заменим каждое
его кусочно линейной аппроксимацией gij(Xj). В частно-
сти, когда
(9.42)
мы можем представить gn(Xj) в виде
gij(*/) = gkj, ij + sk), и(Xj — xk.t j) (9.43)
или
gij^j) = gk)+i.ij.~skj.ij^kj+i,j-^j)’ (9-44)
где sk.'ij определено в (4.74). Пусть (x) = 2 gn С*/). Соглас-
но процедуре гл. 4, та область из Еп, в которой х может изме-
няться, разделяется на некоторое количество «прямоугольных»
клеток, описываемых (9.42). Функция g’i(x) для любой данной
клетки приближается линейной функцией gjx). Однако линей-
ное представление изменяется от клетки к клетке. Рассмотрим
фиксированную клетку, и пусть gi(x) есть представление gi(x)
для этой клетки. Тогда, если для любой точки в клетке удовле-
творяется условие gi(x)~bi, гиперплоскость gi(x)=bi есть при-
ближенное представление поверхности gi(x)=bi для рассматри-
ваемой клетки.
Заменим задачу (9.40) приближенной задачей
iz(x)<^, /ел,
iz(x) = &z, i 6 4. .(9.45)
xi ^0, J £ J;
найти max z = f(x).
9.11. Задачи с сепарабельными ограничениями 341
Заметим, что мы не аппроксимируем f(x), и нам не нужно пред-
полагать, что /(х) сепарабельна.
Решение задачи по обсуждаемому методу будет сходиться к
стационарной точке f(x), которая обычно соответствует относи-
тельному максимуму f(x). В общем случае нет метода, который
бы гарантировал, что процесс будет сходиться к точке, в кото-
рой f(x) достигает своего глобального экстремума на множе-
стве допустимых решений. Рассмотрим теперь итерационный
процесс построения допустимых решений хР для задачи (9.45),
таких, что f(xr+i)>f(xvj.
Пусть после v итераций мы получили допустимое решение
ху и Vf(xv). Нам нужно найти направление г, в котором нужно
двигаться на следующем шаге, такое, что V/(xv)r>0. Точка xv
может лежать внутри одной из упомянутых выше клеток или
может лежать на границе двух или более таких клеток. Пред-
положим, что для /€ Je(v) /-я компонента xv лежит на той или
иной концевой точке из (9.42). Мы не будем включать сюда слу-
чаи, в которых компонента хг равна нулю, т. е. Если
имеется р таких компонент, xv лежит на границах 2? клеток.
Мы ищем новое допустимое решение в виде x=xv + Ar. Обо-
значим через /(у) множество ограничений из (9.45), которые
существенны в точке xv. Нам нужно найти ограничения, кото-
рым должно удовлетворять г. Для U«/(^)/"я компонента
xv лежит внутри интервала (9.42), и, следовательно, будет ли
г?- положительным, отрицательным или равным нулю, для до-
статочно малых X Xj остается в том же интервале и ga(Xj) будет
представлено (9.43). Однако для j €Л?(и) представление ga(Xj)
будет зависеть от того, положительно или отрицательно rj. Что-
бы учесть это, запишем г,— г'.— г"., где г'., г^>0. Тогда =
= x^ + Zr'.— Vj. По предположению XjV~xkj, Если г'.>0,
= мы можем использовать (9.43), мы получаем
1ц а + ur'j- (9-46)
Если г'.— 0, г". >0, то, используя (9.44), чтобы написать
К (xj) = ек), и ~ 4y-i, иг"г <9-47)
Следовательно, для rj, имеющих произвольный знак,
(*,) = gkp ,-r'j - ./j (9.48)
при условии, что мы налагаем добавочное ограничение Г/Г/ = О.
Таким образом, у нас есть должное представление gtj(Xj)
342
Гл. 9. Градиентные методы
независимо от того, будет или нет х$ возрастать или убывать на |
следующем шаге. Т
Так как ограничения для /СI(v) существенны для хг, мы
заключаем, что г должно удовлетворять следующим ограниче- i
ниям: <
+ ,€/- (9-49)
О>0’
и, кроме того, ?
rfr г">о, г/;=о, ,
Было бы желательно задать еще ограничение г'г==1 или хотя
бы r'rCl, так чтобы можно было определить локально наилуч-
шее направление движения. Однако вследствие ограничений
г'.г". =0 мы не можем свести нашу задачу к задаче квадратичного
программирования и использовать для решения эффективный
алгоритм для приближенной задачи в б-форме. Вряд ли есть
простой способ включения требования r'r4U. Вместо этого мы
можем использовать подход, связанный с верхними границами,
подобно тому как это сделано в (9.19). Однако наиболее просто
здесь потребовать, чтобы так как мы уже имеем
условие, что г'г".— О для некоторых /. Следовательно, мы счи-
таем, что г удовлетворяет неравенству
1,
(9.50)
где
r^r'-r], r'r'' = 0, (9.51)
Условия (9.51) заменяют отмеченные выше условия
г;, г;>0, r'r"} = 0, I
Мы хотим определить г, удовлетворяющее (9.49) — (9.51), |
которое максимизирует выражение |
Z=V/(xJr. (9.52) J
Эта задача может быть решена посредством приема, описанно- i
го в гл. 4. Там же показано, что полученное таким образом ре- |
шение дает локальный максимум целевой функции, но нет га-
рантии, что это будет глобальный экстремум.
9.11. Задачи с сепарабельными ограничениями
343
Итерационный процесс закончится, когда решение, получен
ное в задаче (9.49) — (9.52), есть г = 0. Если мы знаем, что ему
соответствует глобальный экстремум, то полученное допустимое
решение есть стационарная точка функции f(x). Учитывая осо-
бый характер ограничений (9.49), можно показать, что если
г = 0 (заметим, что это всегда допустимое решение) —решение,
полученное применением симплекс-метода и соответствующее
локальному максимуму целевой функции, тогда это глобальный
экстремум. Мы предложим доказать это в упражнении 9.15. Та-
ким образом, здесь не может быть так, чтобы было получено
решение г = 0, когда имеется направление, двигаясь в котором,
можно увеличить f(x). Если ограничения, соответствующие
линейны, a gij(Xj) выпуклы, так что множество допусти-
мых решений выпукло, тогда и множество г, удовлетворяющих
(9.49), будет выпуклым. (В упражнении 9.16 это требуется до-
казать.) В этих условиях локальный экстремум является также
и глобальным, т. е. для таких задач не существует каких-либо
локальных экстремумов, отличающихся от глобального экстре-
мума целевой функции (9.52).
После того как получено rv, нам нужно узнать, как далеко
двигаться из хг в направлении rv. Здесь удобно отдельно рас-
смотреть те задачи, в которых некоторые ограничения, соответ-
ствующие /€/2, нелинейны, и те, в которых все такие ограниче-
ния линейны. Рассмотрим вначале случай, когда ограничения,
соответствующие /6/2, нелинейны. Если гг дано, то мы знаем
клетку, в которую собираемся двигаться из xv. Затем мы опре-
деляем полупространства, которые в этой клетке представляют
несущественные для xv ограничения. Обозначим эти представле-
ния ограничений через а*х4^. Определяем также пределы
(9.42) изменения xj в этой клетке. Затем вычисляем наибольшее
значение X (обозначим его через е), такое, что
(9.оо)
Xk., jj, /—1, П-
И, наконец, определяем значение X, 0<АЖе, которое макси-
мизирует Hx^ + Xr^). Новое допустимое решение есть xv+i =
=xv+%rv.
Во втором случае, когда все ограничения, соответствующие >
/С /2, линейны, мы начнем с подстановки в ограничения (9.49)
для i С /1 (v). Если rv удовлетворяет хотя бы одному из этих
ограничений как строгому равенству, мы поступаем точно так
же, как и в изученном выше случае. Предположим, что г?)
удовлетворяет каждому из этих ограничений как строгому
344
Гл. 9. Градиентные методы
неравенству. Тогда мы возвращаемся к исходным ограничениям
и определяем е — наибольшее значение X для которого .
^(х^ + Хг^Х^, г'еЛ- xjv-+-^rjv^Q, j£J. (9.54)
Чтобы определить Л, при котором ^(х^ + Х) =&;, в общем слу-
чае мы должны для решения этого уравнения использовать ка-
кие-либо численные методы, например метод Ньютона (см. уп-
ражнение 9.18). После того как 8 определено, ищется значение
X, 0<ZXs, которое максимизирует f(xv + krv). Если Х<8, мы
рассматриваем точку х = Ху + Хгг. Для клетки, содержащей х
(или для любой из клеток, содержащих х, если х лежит на гра-
нице двух или более клеток), определяем полупространства
f€/i, которые являются приближениями ограничений
gi(x)^.bi для этой клетки. Если х лежит во всех этих полупро-
странствах, мы полагаем xv+i=xv + Xrv и продолжаем процесс.
Если Л близко к 8, может оказаться, что хотя х — допустимое
решение задачи (9.40), оно не является допустимым решением
задачи (9.45). В этом случае мы должны уменьшать % до тех
пор, пока х не станет допустимым для задачи (9.45). Для этого
определим наибольшее значение X (обозначим его через X), та-
кое, что x==xv + Xrv удовлетворяет ограничениям а*х4&й /€/].
Если х находится в той же клетке, где было х, мы полагаем
xv+1=x. Может случиться, однако, что х находится в другой
клетке, так что ограничения агх<6г- уже не будут представлени-
ями неравенств gi(x)^bi для клетки, в которой расположена
точка х. В этом случае мы определяем клетку, в которую дви-
гаемся, когда значение X, дающее х, уменьшается. Затем нахо-
дим представления ограничений, соответствующие этой клетке,
и повторяем процесс. В итоге X все время уменьшается до тех
пор, пока не найдено допустимое решение задачи (9.45).
Если X, максимизирующее f(xv + Xrr), равно е, но должно
быть сделано меньше него, мы поступаем так же, как и выше.
Если, однако, х^ + ег^ удовлетворяет каждому из ограничений
tfx^bi, как строгому неравенству, X может быть сделано
больше 8, пока мы не достигнем границы множества допусти-
мых решений задачи (9.45). В этом случае мы можем по анало-
гии с описанной выше процедурой увеличивать X до тех пор,
пока не достигнем границы. Затем вычисляем f (x^ + XrJ. Если
оно больше или равно f(xP + erv), мы полагаем xy+1 = xv + Xrv,
если меньше, полагаем х^+^х^ + ег^.
Причина введения специальной операции, когда удовлет-
воряет всем ограничениям при как строгим неравен-
ствам в каждой итерации, состоит в том, что это позволяет дви-
гаться внутрь множества допустимых решений без выхода на
9.11. Задачи с сепарабельными ограничениями
345
границы клеток и без замены представления для ^(х). При
этом решается новая задача определения направления, даже ес-
ли все ограничения в форме неравенств несущественны. Моди-
фикация метода позволяет брать большой шаг, если это воз-
можно. Однако это полезно, вероятно,, лишь на ранних стадиях
процесса.
Для получения максимальной выгоды от возможности дви-
жения внутри множества допустимых решений полезно (если
Рис. 9.11.
множество h пусто), прежде чем пытаться вычислять гр, опре-
делять, будет ли dr удовлетворять ограничениям (9.49). Если
это так, мы сразу двигаемся в направлении dv.
Только что описанный метод может иметь некоторые допол-
нительные преимущества перед другими градиентными метода-
ми, помимо уже рассмотренных. Представленный выше метод
не требует, чтобы функции £;(х) обязательно имели частные
производные всюду на границе множества допустимых решений.
Действительно, если мы не используем специальный метод дви-
жения внутри множества допустимых решений, нам даже не
нужно аналитическое представление для Эти функции
могут быть, например, даны в виде кривых, полученных непо-
средственно из экспериментальных данных. Кроме того, при
желании легко таким же образом аппроксимировать f(x).
В заключение рассмотрим рис. 9.11. Проекция градиента на
346
Гл. 9. Градиентные методы
касательную гиперплоскость есть 0, и, действительно, V/(xv)
лишь положительным скалярным множителем отличается от
Vgjx^). Таким образом, процессы решения по методам Зойтен-
дейка и Розена закончатся в этой точке, которая является ста-
ционарной для функции f(x), но не будет точкой относительного
максимума. Однако, если ограничение аппроксимировано так,
как это показано на рисунке, процесс решения по аппроксима-
ционному методу в этой точке не останавливается.
При использовании описанного метода целесообразно снача-
ла пользоваться грубой аппроксимацией для gij(xj), так чтобы
можно было делать большие шаги и быстро достигнуть окрест-
ности стационарной точки. В этой окрестности следует ввести
более точную аппроксимацию, деля интервалы пополам, и та-
ким образом повысить точность вычисления. Заметим, что, хотя
окончательное решение будет допустимым решением прибли-
женной задачи (9.45), нет гарантии, что оно будет допустимым
решением задачи (9.40) (см. гл. 4). Однако, если множество до-
пустимых решений выпукло, тогда, как показано в гл. 4, любое
допустимое решение задачи (9.45) будет также допустимым и
для задачи (9.40).
Может возникнуть вопрос, разумно ли прибегать к градиент-
ному методу, согласно которому на каждой итерации должна
быть решена задача (9.49) — (9.52), вместо того чтобы исполь-
зовать методы гл. 4, которые позволяют решать тот же тип за-
дач только один раз, Чтобы ответить на этот вопрос, следует
иметь в виду, что объем вычислений, требующихся для решения
задачи линейного программирования симплекс-методом, возра-
стает приблизительно как куб числа ограничений. Но многие ог-
раничения часто несущественны для оптимального решения. По-
этому, если можно начать градиентный метод с такого допусти-
мого решения, для которого существенно лишь небольшое число
ограничений, и затем постепенно увеличивать число существен-
ных ограничений, так что все соответствующие ограничения бу-
дут существенны только в последних итерациях, может потребо-
ваться меньше вычислений, чем при прямом применении методов
гл. 4. Например, если исходная задача имеет 100 ограничений,
выгоднее сделать около 500 итераций, градиентного метода
с 10 существенными ограничениями на каждой итерации,
чем решать исходную задачу методами гл. 4. Кроме того, зада-
чи, слишком большие для того, чтобы решать их методами гл. 4,
все же могут быть решены градиентным методом, так как огра-
ничения вида 2^=1 при этом не нужны и потому может ока-
k
заться существенным только относительно небольшое число ог-
раничений.
9.12. Определение допустимого решения
347
9.12. Определение допустимого решения. Одним из основных
преимуществ градиентного метода является то, что любое допу-
стимое решение может служить в качестве начального' решения
итерационного процесса, так что не требуется находить базис-
ное решение. На первый взгляд может показаться, что при от-
сутствии начального допустимого решения градиентные методы
будут существенно менее полезными из-за добавочного труда,
нужного для его получения. Однако начальное решение можно
получить введением искусственных переменных, как и в сим-
плекс-методе. Допустим, что для задачи (9.40) неизвестно допу-
стимое решение. Предположим, что вектор х = 0 не допустим.
Пусть 1Г и /Г — подмножества i из Ц и /2 соответственно, для
которых gi(O)>bi. Тогда, чтобы найти начальное допустимое
решение, мы заменим задачу (9.40) следующей:
£-г(х)<&г, iQh.
g,(x)-5<61,
g,(x)-l, = b„ l^li-
S*z(x) + Sz = ^z, /£/2»
xy>0, B>0; az>0, /£Z2;
найти max z = — | —
/ел
Начальное допустимое решение этой задачи есть
х = 0, g=max(gz(0)-^), ^ = |gz(0)-^|, i$I2. (9.56)
Когда 2 = 0, допустимое решение задачи (9.40) найдено. Жела-
тельно вводить как можно меньше новых переменных, особенно
в случае применения градиентного проективного метода, по-
скольку благодаря им увеличиваются размеры матриц, с кото-
рыми приходится иметь дело. Вот почему в ограничениях, со-
держащих неравенства, была введена только одна переменная ~.
Заметим, что если множество допустимых решений задачи
(9.40) выпукло, то таким же будет и множество допустимых
решений задачи (9.55). Поэтому, если, применив к этой задаче
какой-либо из градиентных методов, мы придем к точке, для
которой выполнены условия окончания процесса, то вследствие
линейности целевой функции в указанной точке будет существо-
вать глобальный максимум. При отсутствии выпуклости множе-
ства допустимых решений, получив значение z<0, все-таки, мы
не можем утверждать, что исходная задача не имеет допустимых
348
Гл. 9. Градиентные методы
решений. Неясно, как обойти возникающие здесь затруднения.
В гл. 4 мы отметили, что подобная ситуация может возникнуть
и при использовании рассмотренных там методов.
9.13. Пример. Используем результаты § 9.11, чтобы получить
приближенный глобальный экстремум для примера, рассмот-
ренного в § 4.3. Мы будем аппроксимировать gi(xi) и £г(%2)
точно так же, как это было сделано там. Начало координат
х = 0 — допустимое решение, которое мы и возьмем в качестве
начального. Находим
Vf(x) = (2-2x15 1),
так что Vf(O) = (2; 1). Задача (9.49) — (9.52) при х = 0 имеет
вид
rj>0,
Г) + г2<1; (9.57)
найти max Z = 2r1-|-r2.
Ограничения, соответствующие (9.49), есть просто г>0. По-
скольку r'==Vf(0)>0, мы встретились здесь с тем случаем,
когда можно двигаться в направлении V/(0), и, следовательно,
нам не нужно решать задачу (9.57). Следует обратить внимание
на то, что в данном примере решение задачи (9.57) не дает наи-
лучшего направления движения. (Это решение есть Г\ = 1, г2 = 0«)
Условия неотрицательности переменных не нарушаются при
движении в направлении градиента. Таким образом, только
ограничение будет определять, как далеко можно двигаться.
Определим 8 — наибольшее значение Л, такое, что х = [2^Д]—
допустимое решение. Из сказанного ясно, что 8 должно удовле-
творять уравнению 2 (2s)2 + Зе2 = 6, что дает
8 ==0,739.
После этого определяем %, 0<Z<X),739, такое, что f(x), где
х = Х[2, 1] максимально, т. е. максимизируем выражение
4Z — 4V + % = 5Х — 4Х2.-
5
Это приводит к А, =-£- = 0,625, так что мы не проходим весь
возможный путь до границы. Итак,
Xi = 0,625[2; 1] = [1,250; 0,625].
Очевидно, что X! удовлетворяет неравенству g(xi)<6.
9.13. Пример
349
Вычисляем градиент в точке хр
WO = (-0,5; 1)'
Снова очевидно, что нам следует двигаться в направлении гра-
диента. Снова находим е — наибольшее значение Л, такое, что
x = Xi + X[—0,5; 1] — допустимое решение. На этот раз величина
возможного перемещения лимитируется двумя обстоятель-
ствами: может стать существенным ограничение, или может
стать отрицательным Ограничение становится существенным
раньше, и, следовательно, е должно удовлетворять уравнению
2(1,25 — 0,508)2 4- 3 (0,625 + г)2 = 6,
так что
8 = 0,542.
Для вычисления 8 мы не пользовались здесь рекомендациями
§ 9.11. Теперь можно определить %, 0<VC0,542, которое макси-
мизирует f (xi + Zdi), т. е. которое максимизирует выражение
2 (1,25 — 0,5^) - (1,25 — 0,5Х)2 + 0,625 + г.
Приравнивая производную нулю, получаем
— 1 4“ 1,25 — 0,5г 1 = 0, или г = 2,5 >8.
Таким образом, следует принять г = 8. Полагая x = Xi + edb бу-
дем иметь
х.= [1,25; 0,625]+ 0,542 [—0,5; 1] = [0,979; 1,167].
Определим подпространство, которое служит приближением
ограничения в клетке, содержащей х, т. е. в клетке 0,75^С+<С1,
1<+^1,25. Из табл. 4.1 следует, что это полупространство опи-
сывается неравенством
1,125 + ( 2’°725125 )(*i " 0,75) + 3,0+464^3-0 )(х2 — 1)<6,
или
3,5^ + 6,75х2 < 11,25. (9.58)
Теперь нужно определить точку пересечения границы полу-
пространства (9.58) и луча х = [1,25—0,5г; 0,625 + г]. Соответ-
ствующее г определяется из равенства-
3,5 (1,25 - 0,5г) + 6,75 (0,625 + г) = 11,25,
так что г-0,53. Таким образом, при движении в направле-
нии di мы пересекаем границу полупространства (9.58) прежде,
350
Гл. 9. Градиентные методы
чем границу фактически существующего ограничения. Оконча-
тельно получаем
х2 = [1,25; 0,625]-|-0,53 [—0,5; 1] = [0,985; 1,155],
так что эта точка действительно лежит в клетке, в которой
(9.58) является аппроксимацией ограничения. Заметим, что
г2=/(х2) =2,156.
Начиная новую итерацию, вычислим
V/(х2) = (0,03; 1).
Направление движения определяется решением следующей за-
дачи:
3,5 (г[ - <) + 6,75 (г'- г'') < 0,
4г2>0’ <г1=0’
найти max Z — 0,03 (г' — г'') + (г'2 ~ г'').
Рисунок 9.12 дает графическое изображение этой задачи. Реше-
ние получается, когда
г" + r'2 = 1, - 3,5г" + 6,75г' = 0,
так что г\ — — г'г= — 0,659 и г2 = г' = 0,341.
Если двигаться в направлении г2=[—0,659; 0,341], то ограни-
чение (9.58) всегда будет выполняться. Однако (9.58) служит
приближенным представлением исходного ограничения, только
когда 0,75<jci<C1,0 и 1,0-<X2<U ,25, в связи с чем мы не можем
пересекать границу этой клетки. Одно из этих ограничений за-
ставит прекратить движение раньше, чем ограничение на не-
9.13. Пример
351
отрицательность Xi. Найдем е, т. е. наибольшее %, такое, что
0,985 — 0,659% > 0,75, 1,155 + 0,341% < 1,25.
Это дает е = 0,279. Чтобы определить, как далеко следует дви-
гаться, нужно найти %, 0<%<Д279, которое максимизирует
f(x2+%r2). Приравняв нулю производную этой функции по %,
получим значение %=1,111, которое лежит вне допустимого ин-
тервала. Следовательно, % = е, и мы двигаемся, насколько это
возможно, так что х3=[0,801; 1,25] и г3=2,210.
Величина Vf(x3) есть
Vf(x3) = (0,398; 1).
Мы пришли к допустимому решению х3, которое лежит на гра-
нице Двух клеток (х2 = 1,25— концевая точка двух интервалов
1^х2^С1,25 и 1,25-Сх2<Л,5). Нам нужно вычислить наклон ли-
нии, приближающей g2(x2) в интервале 1,25<х2<1 ,5. Из
табл. 4.1 мы видим, что искомый наклон равен
6,75 — 4,6875 о о.
0,25 — 8,24.
Поэтому задача, которую нужно решить, чтобы определить
направление перемещения из точки х3, формулируется так:
3,5 - г'[) + 8,24г' - 6,75г; < 0,
rj+ri'+r^+r; < 1,
г' <, г' <>0, г.'г; = 0, гХ = 0;
найти max Z = 0,398(г{ — + — G-
Ее геометрическая иллюстрация дана на рис. 9.13. Оптимальное
решение есть г3=[—0,702; 0,298]. Новым допустимым решением
будет
х = [0,801; 1,25]+ Х[—0,702; 0,298],
так что первая координата убывает, а вторая — возрастает. Мы
двигаемся, таким образом, вдоль линии, аппроксимирующей
ограничение g(x)=6 в клетке 0,75<+^С1; 1,25<+<Л,5. Оче-
видно, что ограничение %i>0,75 определяет, как далеко можно
двигаться. Отсюда 8 = 0,0727. Чтобы определить, насколько сле-
дует двигаться, нужно найти значение X, 0<Х+е, максимизи-
рующее f(x3+Xr3). Приравняв нулю производную этой функции
по X, получим значение 0,733, которое опять лежит вне до-
пустимого интервала. Следовательно, надо взять Х=8. Тогда
х4=[0,75; 1,272] и г4 = 2,210.
С той точностью, с которой мы делали вычисления, вели-
чина z не увеличилась по сравнению с предшествующей
352
Гл. 9. Градиентные методы
итерацией, и, следовательно, мы должны закончить процесс. По-
лучено точно такое же решение, как и в § 4.3. Значение целевой
функции может здесь немного отличаться от полученного в
гл. 4, так как мы не использовали никаких приближенных пред-
ставлений целевой функции. Можно было бы продолжать ите-
рационный процесс, так как задача, определяющая направление
движения из х4, имеет решение. Тем не менее, если точность
вычислений оставить прежней, добавочные итерации ничего не
дадут. Чтобы убедиться в этом, в упражнении 9.17 мы предла-
гаем сделать еще несколько итераций.
Требующийся здесь объем вычислений приблизительно та-
ков, как и в § 4.3. Однако, если бы мы на каждой итерации
пользовались какими-нибудь численными методами для опреде-
ления наилучшего направления, объем вычислений возрос бы.
Последовательность решений, полученных градиентным мето-
дом, показана на рис. 9.14, на котором изображены и аппрокси-
мирующие гиперплоскости, которые встречались по ходу вычис-
лений.
9.14. Некоторые дополнительные замечания о сходимости.
Для каждого из рассмотренных вариантов градиентного метода
формулировались условия, при выполнении которых гаранти-
руется, что достигнута стационарная точка функции f(x). Од-
нако в общем случае может потребоваться бесконечное число
итераций, прежде чем эти условия будут выполнены. Следова-
тельно, требуется указать еще и другие условия окончания ите-
9.15. Градиентный метод Эрроу — Гурвица
353
рационного процесса, на случай, когда стационарная точка не
достигнута за конечное число шагов. Эти условия обычно осно-
вываются на характере изменений функции f(x) от одной ите-
рации к другой. Если относительное увеличение f(x) меньше,
чем некоторое заранее выбранное число, для некоторого за-
ранее выбранного числа итераций, тогда процесс следует закан-
чивать *)•
Часто при приближении к стационарной точке функции f(x)
размер шагов будет мал, вследствие чего сходимость окажется
очень медленной. Это выявится особенно резко, если процесс
сходится к внутренней точке множества допустимых решений,
так что df/dxj близко к нулю для всех /. Если в этом случае
значения производных df/dxj приходится определять приближен-
ными численными методами, процесс перестанет быть сходя-
щимся: последовательные приближения будут случайным обра-
зом распределяться около стационарной точки. Иногда можно
улучшить сходимость, привлекая вторые частные производные f
и приближая f суммой линейной и квадратичной форм, а не
только линейной формой. Пусть имеется допустимое решение
Xv и требуется определить стационарную точку, в которой
V f=0. Будем использовать приближение
f (х) = f (xv) + Vf (хг) х + у x'Hf (хг) х, (9.59)
где Ну(хг) = ||д* 2//дхгдх/| — гессиан функции f в точке х„. Поло-
жим в (9.59) Vf(x)=0 и решим полученную систему линейных
уравнений относительно х. Это дает 2)
х' = — Vf (Хг) Hf1 (Хг). (9.60)
Это соотношение и определяет (разумеется, приближенно) ста-
ционарную точку. Поскольку для вычисления х' нужно решить
систему п линейных уравнений, вряд ли целесообразно исполь-
зовать этот прием, разве что на последних одной-двух ите-
рациях.
9.15. Градиентный метод Эрроу — Гурвица для вогнутого
программирования. Методы, развитые в этой главе, иногда
!) Относительное изменение значения функции f(x) за счет добавления
к ней подходящей постоянной может быть сделано сколь угодно малым или,
наоборот, сколь угодно большим. Поэтому большего внимания заслуживает
критерий, заключающийся в том, что на нескольких итерациях подряд полу-
чаются одинаковые — в пределах принятой точности вычислений — значения
целевой функции. — Прим. ред.
2) Из приближенного равенства (9.59) получается также приближенное
равенство Vf(x) =57(xv)+х'Н/(Х1>), которое и приводит к (9.60).— Прим, ред,
23 Зак. 735
354
Г л. 9. Г радиентные методы
называют градиентными методами большого шага, потому что
на каждой итерации f(x) увеличивается на более или менее
большую величину. Эрроу и Гурвиц предложили другой метод,
который можно рассматривать как дифференциальный гра-
диентный метод решения класса задач, включающего, в част-
ности, задачу максимизации вогнутой функции f(x) на выпук-
лом множестве решений при gi(x)<I&i, f=l, ..., m, х>0, где
g’i(x) —выпуклые функции. Метод является дифференциальным
в том смысле, что на каждой итерации делается бесконечно ма-
лый шаг или, более точно, итерации заменяются интегрирова-
нием системы дифференциальных уравнений, решение которой
приводит к решению данной задачи.
Рассмотрим функцию Лагранжа, соответствующую исходной
задаче
с . . F(X, Х)==/(х)+2Ш-^(х)]-
В гл. 6 было показано, что если х* — оптимальное решение, то
существует Х*>0, такое, что [х*, 1*] служит глобальной седло-
вбй точкой функции Г(х, X) для [х*Д*]>0. Таким образом,
чтобы достичь [х*, X*], нужно двигаться «вверх» по отношению
к х и «вниз» по отношению к 1.
Авторы вводят параметр t и рассматривают систему обыкно-
венных дифференциальных уравнений
dxt гч д/7
> ' ' —± —о, если -г—<0 и х7- = 0,
at
dxj dF
fj = 7— в противном случае; (9.61)
^- = 0, если > 0 и Х/ = 0,
dt ’ d^i 1
. dfy dF
—в ПРОТИВНОМ случае.
Они показали, что если начинать с начального допустимого ре-
шения, достаточно близкого к [х*, Х*]>0, и если матрица
11 d^F/dxidXj|| — отрицательно определенная, то х(0 —решение
этой системы дифференциальных уравнений для данных началь-
ных условий — обладает тем свойством, что lim х(7) ==х*. Удзава
- , " /->оо
обобщил эти результаты, показав, что если функция F — строго
вогнутая и имеет непрерывные вторые производные, то для лю-
’бого’начального допустимого решения решение системы диффе-
ренциальных уравнений (9.61) обладает тем свойством, что
Иш х(/)=х*. ‘
J->oo
Упражнения
355
Мы не будем рассматривать детально этот метод, так как он
вряд ли дает удобный алгоритм для цифровых вычислительных
машин. Впрочем, следует отметить, что этот алгоритм можно
приспособить для аналоговых машин. Метод не очень хорош
еще и потому, что требует проверки некоторых условий, кото-
рым должна удовлетворять исходная задача для обеспечения
сходимости.
ЛИТЕР АТУ РА
1. Э р р о у К. Дж., Гурвиц Л., У д з а в а X., Исследования по линей-
ному и нелинейному программированию, ИЛ, М., 1962/
2. Деннис Дж. Б., Математическое программирование и электрические
цепи, ИЛ, М., 1961.
3. Dorn W. S., Non-Linear Programming — A Survey, Manag. ScL, 9 (1963);
’ 171—208.
4. Lemke С. E., The Constrained Gradient Method of Linear Programming,
J. Soc. Indust, and Appl. Math., 9 (1961), 1—17.
5. Rosen J. B., The Gradient Projection Method for Nonlinear Programming,
Part I, Linear Constraints, J. Soc. Indust, and Appl. Math., 8 (1960), 181—
217. v
6. Rosen J. B., The Gradient Projection Method for Nonlinear Programming,
Part II, Nonlinear Constraints, J. Soc. Indust, and Appl. Math., 9 (1961),
514—532.
7. S p a n g H. A., A Review of Minimization Techniques for Nonlinear Func-
tions, J. Soc. Indust, and Appl. Math., 4 (1962), 343—365.
8. Z о u t e n d i j k G.. Maximizing a Function in a Convex Region, /. Roy.
Statist. Soc. (B), 21 (1959), 338—355.
9. Зойтендейк Г., Методы возможных направлений, ИЛ, М., 1963.
Упражнения
9.1. Рассмотреть функцию
г = 36 —9 (Xi—6)2 —4 (х2 —6)2. , .
Использовать градиентный метод для нахождения точки, в которой z прини-
мает свое максимальное значение (начинать процесс из точки Xi=7,
а । -1/27 I и о ” \
х2 = 6 ф- у I • На последней итерации, применяя метод, описанный - в
§ 9.14, определить точку, дающую экстремум. ,
9.2. Для случая двух переменных дать геометрическую интерпретацию
эквивалентности задач, заданных уравнениями (9.8) и (9.13).
9.3. Рассмотреть задачу нахождения базисного допустимого решения
уравнений (9.18) при (pzw=0. Доказать сначала, что квадратичная форма
у'ММ'у неотрицательна, а если столбцы М' линейно независимы, то положи-
тельно определена. [Указание. Положить ц = М'у.] Если форма положительно
определена, то элементы главной диагонали ММ' положительны, есди форма
неотрицательна, то эти элементы неотрицательны. Рассмотрим сейчас любое
базисное решение уравнения (9.18), такое, что q)'w = 0. Обозначим базисную
матрицу через В и представим, что В построена так, что столбцы, содержа-
23*
356
Гл. 9. Градиентные методы
щие (pi, стоят вначале, а за ними следуют столбцы, содержащие Wi, т. е. что
В записана в виде
Определить матрицу, обратную В, и показать, что v'P~lv — положительно
определенная квадратичная форма. Пусть матрица коэффициентов уравнения
(9.18) имеет вид
гр Т —I от
LQ R 0 —I ]‘
Вычислить произведение В"1 на эту матрицу и показать, что форма
r'(-QPlT+R)r неотрицательна. Затем показать, что если для этого базисного
решения некоторые (рг<0, то новое базисное решение можно получить, за-
меняя на Wi, и в новом решении Wi>§. [Указание. Для вычисления новой
обратной матрицы при изменении только одного ее столбца использовать
процедуру, описанную в § 2.1.] При каких условиях невозможно сделать за-
мену? Как поступать в таких случаях?
9.4. Пусть в градиентном проективном методе, изученном в § 9.6, матрица
(Q^Qt,) 1 известна, а дребуется определить \ При этом пред-
полагается, что Q«+i отличается от Qv только тем, что для получения Qv-fi
в Qr вычеркнут или добавлен лишь один столбец. Описать эффективный
метод получения новой обратной матрицы из старой. [Указание. Рассмотреть
сначала случай, когда для получения Qv+i к нужно добавить столбец
так, что Qv+i=(Qv, q). Найти используя блочный вид матрицы
Qv+i- Затем, применяя метод вычисления матрицы, обратной для блочной,
определить (Qp+iQt,+i)~1- После этого рассмотреть случай, когда Qo =
•»(СЬ+ь q),’ так что из Qv вычеркнут столбец. Обобщить это на случай,
когда из Qv может быть вычеркнут любой столбец. См. § 2.1.]
9.5. Используя результаты, полученные в упражнении 9.4, показать, как
в градиентном проективном методе при переходе от одной итерации к другой
преобразуется матрица проектирования Pv. Показать также, как преобра-
зуется
9.6. Доказать, что решение по градиентному проективному методу будет
сходиться к стационарной точке функции f(x) или |xv|r> сопри у->оо, если
на каждом шаге используется rv, либо rv, в зависимости от того, какое из
этих направлений дает большее значение производной.
9.7. Показать, что для задач линейного программирования в градиентном
методе, в котором решается уравнение (9.13), при переходе от одной итера-
ции к другой на каждом шаге в качестве начального решения новой задачи
можно использовать предыдущее решение. [Указание. См. {ЛП 11.5}; имеется
в виду добавление нового ограничения после того, как задача решена.]
9.8. Для задач линейного программирования, в которых V f не изме-
няется, обобщить результаты упражнения 9.5 с тем, чтобы показать, как
можно непосредственно преобразовать Рс' при переходе от одной итерации
к другой.
9.9. Показать, что градиентный проективный метод решает задачу линей-
ного программирования за конечное число шагов. [Указание. Пусть х* —
оптимальная крайняя точка, и оптимальное решение единственно. Рассмотреть
е-окрестность точки х*, такую, что в ней нет других крайних точек. Показать,
что после попадания в эту окрестность для выхода на ребро выпуклого мно-
жества потребуется лишь конечное число шагов, а когда ребро достигнуто,
Упражнения
357
следующая итерация приводит к х*.] Что произойдет, если оптимальное ре-
шение не единственно?
9.10. Решить задачу линейного программирования, заданную уравнениями
(1.14), взяв в качестве начального допустимого решения Xi==3, х2=2 и решая
на каждом шаге задачу, описанную уравнениями (9.8) или (9.13).
9.11. С помощью градиентного проективного метода решить задачу, опи-
санную уравнениями (1.14), начиная с допустимого решения *1=3, х2=2.
9.12. Решить задачу (1.14) модифицированным градиентным проективным
методом, позволяющим двигаться в направлении градиента, если это воз-
можно. Взять за начальное допустимое решение Xj=3, х2==2.
9.13. Решить задачу (1.14), пользуясь каким-либо градиентным методом
и способом нахождения начального допустимого решения, описанным в §9.12.
9.14. Показать, как преобразовать уравнения (9.41) к форме, в которой
задача может легко решаться.
9.15. Показать, что если г=0 соответствует локальному максимуму за-
дачи, описанной уравнениями (9.49) — (9.52), то в этой точке достигается
также и глобальный максимум.
9.16. Доказать, что если gij(Xj) —выпуклые функции, множество /2 — пу-
стое или содержит только линейные уравнения, то множество г, удовлетво-
ряющих уравнениям (9.49), выпукло.
9.17. Выполнить еще несколько итераций в примере § 9.13.
9.18. Определить величину %, которая удовлетворяет уравнению
f(x+Zr)==O. Пусть %о — число, близкое к корню этого уравнения. Запишем,
что
f(x + Xr) = O«f(x + %or) + [
\/-1 7 /
Используя это соотношение, описать итерационный метод вычисления к.
(Этот метод называется методом Ньютона.)
9.19. Исследовать применение градиентных методов к решению задач ква*
дратичного программирования.
9.20. Решить пример § 9.13 градиентным проективным методом.
9.21. Решить задачу, представленную на рис. 1.2, одним из градиентных
методов.
9.22. Используя результаты § 9.3, доказать, что, если последовательность
xv имеет более чем одну точку сгущения, в каждой из этих точек функций
f (х) должна принимать одно и то же значение.
9.23. Дать простой графический пример, иллюстрирующий случай, когда
последовательность, рассмотренная в § 9.3 имеет более чем одну точку сгу*
щения.
9.24. Рассмотреть такую ситуацию в § 9.3, когда функция f(x) вогну*
тая и X может неограниченно возрастать на некоторой итерации, причем
либо f(x) возрастает и стремится к конечному пределу, либо |xv1*->ooh
f(xv) стремится к конечному пределу. Показать, что предельное значение f(x)
является ее глобальным экстремумом.
9.25. Решить пример § 9.13, предполагая, что сначала мы двигаемся в
направлении, задаваемом оптимальным решением уравнений (9.57), а на
каждом последующем шаге — в направлении решения уравнений (9.49)*
(9.51) и (9.52). -
9.26. Используя идеи § 9.11, рассмотреть случай, когда f(x) — сепара-
бельная функция и когда желательно также ее аппроксимировать,
9.27. Для случая двух переменных дать геометрическую иллюстрацию той
ситуации, когда при применении метода, изложенного в § 9.11, на некотором
шаге мы пересекаем внутренность множества допустимых решений, причем
358
Гл. 9. Градиентные методы
точки пересечения с приближенной и с истинной границей лежат в различных
клетках.
9.28. Решить пример § 9.13, не используя метода, позволяющего пересе-
кать внутренность множества допустимых решений без остановки на границах
клеток. Найти направление движения, когда достигается граница клетки.
9.29. Выяснить связь между условиями Куна — Таккера и условиями
окончания различных форм градиентного процесса.
9.30. Показать, что уравнение (9.18) с условиями q)'w=0, <р^>0, wJ>0
есть условия Куна — Таккера для следующей задачи квадратичного програм-
мирования:
найти max г = q/М^М'ф, <р>0.
9.31. Найти градиентным методом стационарную точку для упражне-
ния 1.1. Дать геометрическую иллюстрацию.
9.32. То же для упражнения 1.2.
9.33. То же для упражнения 1.3.
9.34. Используя метод Зойтендейка (§ 9.10), найти оптимальное решение
для упражнения 1.5.
9.35. Используя метод § 9.11, найти приближенное решение для упраж-
нения 1.5 и сравнить объемы вычислений в этом упражнении и в упражне-
нии 9.34.
9.36. Используя метод § 9.11, проделать упражнение 1.7 и дать геометри-
ческую иллюстрацию.
9.37. Решить пример § 9.13; используя метод Зойтендейка (§ 9.10).
9.38. Показать, что если множество допустимых решений задачи (9.1) со-
держит более чем одну точку, то ;всегда найдется допустимое решение за-
дачи (9.8).
9.39. В упражнении 9.4 при переходе от одной итерации к другой нужно
изменить матрицу (Q^Q^)"1. Как получить эту матрицу для начального до-
пустимого решения? Существуют ли случаи, в которых эта задача особенно
проста?
9.40. Как можно численно решить систему уравнений (9.60)?
, 9,41. Рассмотрим множество ограничений а*х{-<, =}&/, 1=1, ...» и. Пред-
положим, что ранг матрицы, строками которой являются векторы а*, есть h
и что векторы i=l, 2, ... , h, линейно независимы. Заменим bi на bi+6*
для, ..., и. Показать, что найдется бо>О, такое, что для всех д,
О<б<бо, не существует х, для которого более чем h ограничений существен-
ны. Показать, что это преобразование избавляет от трудностей, возникающих,
когда .ранг матрицы М„ меньше, чем число ее строк.
9.42. Что произойдет при реализации градиентного метода, если ранг
матрицы меньше, чем число ее строк?
9.43. Построить геометрический пример для случая, когда ранг матрицы
Мг,. в уравнениях (9.15) меньше числа ее строк и Prdr=0. Показать, как бу-
дет действовать метод § 9.6.
9.44. Пусть множество допустимых решений задачи (9.40) выпукло. По-
казать, что можно получить оптимальное решение задачи, описанной урав-
нениями, (9.49) —(9.52), решая задачу линейного программирования без доба-
вочных ограничений.
' 9.45. Решить задачу, которой соответствует рис. 9.12, симплекс-методом
с. добавочными ограничениями и без них. . .
ГЛАВА
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ 1
Повторяемость есть единственная форма ♦
постоянства, доступная природе.
Сантаяна. Английские монологи
10.1. Введение. Как уже было указано в гл. 1, термин «дина-
мическое программирование» относится скорее к вычислитель-
ному методу, чём к особому типу задач нелинейного программи-
рования. Однако возникновение динамического программирова-
ния связано с исследованием некоторых типов многошаговых
процессов управления, особенно многошаговых стохастических
процессов, возникающих в теории создания запасов. Название,
которое связывается теперь с вычислительным методом, ранее
относилось к тем типам задач,, где эти методы были впервые
использованы.
Основная идея, которая привела к созданию вычислитель-
ного метода, была развита Р. Веллманом в начале 50-х годов.
Он также ввел термин «динамическое программирование».
Очень большая часть работы, проведенная; с тех пор по совер-
шенствованию этих методов, была выполнена Беллманом и его
коллегами.
В этой и следующей главах мы хотим изучить вычислитель-
ный метод динамического программирования, рассмотреть типы
задач, которые могут быть решены, с его*помощью, а также ука-
зать границы применимости этого метода. Мы коротко рассмо-
трим также, как можно использовать этот подход в аналитиче-
ской форме для получения информации о структуре оптималь-
ного решения задачи без его численного решения.
10.2. Сущность вычислительного метода. Рассмотрим сле-
дующую задачу нелинейного программирования:
, п - . . ~ .
ajXj^b, а;>0, у = 1, 2, п,
Xj^-О, /==1, 2, п, все Xj целые; . (10.1)
найти, max z—fj(x'j).
360
Гл. 10. Динамическое программирование I
Отметим, что это целочисленная задача с сепарабельной целе-
вой функцией и только одним ограничением. Задачи такого рода
весьма часто встречаются на практике. Типичный пример —
задача об обеспечении запасными частями атомной подводной
лодки (см. § 5.2). В этой задаче
ОО
fj(xj) = — Я) 2 —
XJ
Появление знака «—» связано с тем, что в (10.1) целевая
функция максимизируется, в то время как в (5.3) она миними-
зируется. Если на Xj не наложены условия целочисленности, а
fj(xj)—вогнутые функции, то для получения приближенного
оптимального решения задачи могут быть использованы методы
гл. 4. Если к тому же функции fj(Xj) всюду дифференцируемы,
то решение может быть найдено и с помощью метода множи-
телей Лагранжа. Однако, если z имеет много локальных
максимумов, методы гл. 4 не могут дать большего, чем при-
ближенный локальный максимум. В этом случае становит-
ся также очень трудным использование и метода множителей
Лагранжа.
Если, кроме того, мы потребуем, чтобы Xj были целыми, то
ни один из методов, описанных ранее, не может быть использо-
ван для получения точного оптимального решения. Лучшее, что
можно сделать в таком случае, — это рассматривать вели-
чины Xj без требования целочисленности, а затем округлять
полученные значения до целых. Когда оптимальные значения Xj
велики, этот путь обычно вполне удовлетворителен. Однако,
вообще говоря, этот метод не может быть использован, если
fj(Xj) не вогнуты, поскольку в этом случае возможно наличие
локальных максимумов. Более того, если оптимальное значение ло-
мало, указанный способ округления обычно оказывается непри-
годным. Резюмируя, можно сказать, что изученные ранее ме-
тоды во многих случаях не обеспечивают получения оптималь-
ного решения задачи (10.1).
Рассмотрим теперь вычислительный метод, позволяющий
найти оптимальное решение задачи (10.1). Если это решение не
единственно, метод позволяет найти все оптимальные решения.
Будем считать все aj и Ь в (10.1) целыми. Это требование
не является ограничительным, так как его выполнение всегда
может быть достигнуто с любой степенью точности. По суще-
ству сделанное допущение ограничивает лишь выбор единиц
измерения величин aj и Ь. Например, если b есть объем, то для
того, чтобы все коэффициенты были целыми, может оказаться,
что его следует измерять в кубических сантиметрах, а не футах.
10.2. Сущность вычислительного метода
361
То же самое относится и к а,-. Причина введения этого допол-
нительного требования станет ясной ниже.
Будет полезно также сделать еще одно замечание относи-
тельно обозначений. Рассмотрим функцию h(x), зависящую от
компонент вектора х=[х1( х2, ..., хп]. Через
шах Л(х)
xl’ xj.хг
будем обозначать абсолютный максимум Л(х) по переменным
Xi, Xj, ..., xr при фиксированных значениях остальных перемен-
ных, не включенных в множество х;, Xj, ..., хг.
Обозначим через z* абсолютный максимум zb (10.1). Тогда
z* = max | 3 //(•*/)!, (10.2)
...ХП Ь-1 ' 1
где максимум берется по всем неотрицательным целым Xj, удо-
влетворяющим условию
п
/-1 7 7
(10.3)
Опишем схему вычислительной процедуры, позволяющей
определить z*. Выберем значение хп и, зафиксировав его,
максимизируем z по всем остальным переменным, т. е. по
Xi,х2, ..., хп-ь При этом величины хьх2, .... xn_i будут, ко-
нечно, зависеть от выбранного значения хп. Вообразим, что
максимизация выполнена для всех возможных значений хп.
Тогда z* будет наибольшим из всех полученных значений г, и
мы, таким образом, найдем множество х,, максимизирующее г.
Запишем теперь указанные операции в форме уравнений. Пер-
воначально выбирается величина хп и вычисляется
{п ) ( П-l 'I
Sf/*/) =М*Я)+ max 2 fj (•*/)[• (Ю.4)
.. . j-1 1 xx..xn-i Ь-j J
Член fn(Xn) может быть вынесен из-под знака максимума, так
как он не зависит от Xi, х2, .... хп_ь После того как хп вы-
брано, значения Xi, х2, .... xn-t, кроме условий целочисленно-
сти и неотрицательности, должны удовлетворять неравенству
(10.5)
362
Гл. 10. Динамическое программирование I
/2-1
В связи с тем что max У для неотрицательных це-
Л* • • хп-\
лых чисел, удовлетворяющих (10.5), зависит от о — апхп> можно
записать
л-1
max S fy(xy) = A„_i(f> — а„х„), (10.6)
х,...xn-l’-X
где максимум берется по неотрицательным целым числам
Xj, %2, удовлетворяющим (10.5).
Допустим, ЧТО МЫ ВЫЧИСЛИЛИ Ап-1(6—йпХп) для всех до-
пустимых значений хп. Тогда ясно, что
z* = max[f„(x„) + A„_1.(6 — апхп)], (10.7)
хп
где хп может принимать значения 0, 1, 2, ..., [Z>/an] ([^Мп] — це-
лая часть от Ь]ап). Для вычисления максимума в (10.7) вели-
чина
+ (10.8)
вычисляется для всех допустимых хп, а затем выбирается наи-
большее Qn. Одновременно определяется х* — оптимальное зна-
чение хп. Таким образом, если бы ням была известна функция
Лп-1 (Ь — апхп), можно было бы свести задачу отыскания г* к
максимизации функции одной переменной.
Выясним, как вычислить An-i(b — апхп). Напомним, что
функция Лп-1(6 — апхп) определена в (10.6), где максимум бе-
рется по неотрицательным целым числам, удовлетворяющим
условию (10.5). Для произвольного неотрицательного целого-
числа g получим
д-1
ЛЯ,1(Р= max 27/(•*,)> (Ю-9)
ХГ •••> хП-\ /-1
где максимум берется по неотрицательным целым числам, удо-
влетворяющим условию
/?-1
. . • (10.10)
Действуя как и выше, получаем равенство
Лл-1 (£) = max (/„_! (хя_1) + Ля_2 (£ — a„_iX„_1)]I (10.11)
хп—1
где
Л п-2
Л„_2(С) = max Sfy(x7), (10.12)
Хр ..., Хд_2 у-l
10.2. Сущность вычислительного меюда
363
а максимум берется по неотрицательным целым числам
%ь х2, ...» %п-2, удовлетворяющим условию
л—2 * '
(10.13)
В (10.11) величина xn-i может принимать значения
0, 1, 2, {Цап-J. Следовательно, если мы знаем функцию
Ап-2(?)> то можно вычислить Ап-1(|), взяв максимум по един-
ственной переменной xn-i. Отметим, что для различных значе-
ний £, для которых вычисляется An-i(|), должна быть повто-
рена операция взятия максимума в (10.11).
Тот же прием дает метод вычисления Дп_2(^). Этот процесс
продолжается до тех пор, пока на последнем шаге мы не при-
дем к вычислению
. ' A1(p) = maxf1(Xi), . (10.14)
где Х\ может принимать значения 0,1, ..., [p/aj.
Чтобы на самом деле решить задачу, следует начать с опре-
деления Д1 (р), а затем проделать весь путь в обратном напра-
w влении вплоть до определения An-i(5) иг*:
Вычисления могут быть систематизированы следующим об-
разом. Определим последовательность функций
k
Лл(&) = max 3fy(xy), k= 1, 2, ..., n, (10.15)
*1’ •••> Xk /-1
где максимум берется по неотрицательным целым числам, удо-
влетворяющим условию
k
(10.16)
Функция А] (£) определяется непосредственно, остальные Ай(£)
находятся с помощью рекуррентных соотношений. Действи-
тельно, поскольку
й-1
Ай(|) = тах max 2 f7(*,)
xk L xv •••• xk-i
(10.17)
и в фигурирующем в (10.17) выражении
Л-1
max (10.18)
Хр ...» xk_{ / = 1
364
Гл. 10. Динамическое программирование I
максимум берется по неотрицательным целым числам, удовле-
творяющим неравенству
jfe-i
то выражение (10.18) есть просто As-i(g—акхк). Таким образом,
Л*(|) = тах[/Л(х*)4-Лй_1^ — ал)], А = 2, 3,..., п, (10.19)
xk
где Xfe может принимать значения 0, 1, 2, ..., [g/fl/J- Оконча-
тельно
z* = A„(6). (10.20)
Мы дали схему5 вычислительной процедуры, позволяющей
найти г*. Осталось указать еще, как в результате этих вычисле-
ний может быть найдено множество оптимальных значений Xj.
Остановимся на этом вопросе более подробно. Вычисления на-
чинаются с определения
Л1(|)= max hiXt) (10.21)
0<х, < R/a.l
для всех 1=0, 1, ..., Ь. Обозначим через xi(g) значение (значе-
ния) Хь для которого
Л1а) = Л(х1(|)). (10.22)
Таким образом, xjg) есть то значение хь которое максимизи- рует fi(xj), когда X] может принимать значения 0,1, ..., [|/aj]. „ , .п, Это значение может быть Т аблииа 10.1 не единственным, т. е. соот-
£ л. £(£) ношение (10.22) может вы- полняться более чем для одного значения %i(£). По- строим теперь таблицу вида 10.1. Если Xi(g) не един- ственно и если нас интере- сует отыскание лишь какого- нибудь оптимального реше- ния, в нее можно включить только одно из этих значе-
0 1 • ь Л,(0) Л, (1) Л1 (6) х,(0) х> (О (6)
ний. Если же мы хотим найти все оптимальные решения, тогда для каждого £ следует выписы- вать все Xi, для которых выполняется (10.22). Получив Л1(£), с помощью соотношения
Л2(£) = max [f2(*2)4-Ai(| —ал)! (10.23)
0Xj
10.2. Сущность вычислительного метода
365
приступаем к вычислению Л2(|) для всех g = 0, 1, Ь. При
вычислении максимума в (10.23) х2 может принимать целочис-
ленные значения из указанного интервала. Для вычисления
Лг(|) при фиксированном £ последовательно отыскиваются ве-
личины
а2(о, ^)=/до)+л1а),
й2(1, ^)=;2(1)+л1а-а2),
(10.24)
й2 ([IM I) = h (feted) + Л! fe - а2 [Ца2]).
Наибольшее из них и есть Л2(|). Одновременно определяется ве-
личина или величины x2fe), для которых Л2(|) = Q2(x2,1). Отме-
тим, что для определения Л2(|) необходимо знать только
At (i — а2х2) для всех целых х2, 0<х2<С[£/а2]. Отметим также, что
для каждого такого х2 число § — а2х2 есть неотрицательное целое
в силу сделанного ранее предположения о целочисленности а2.
Так как мы вычислили Ai(g) для всех целых g=0, 1, b,
можно определить Aife—а2х2) из табл. 10.1. Нужно просто взять
число, стоящее на пересечении столбца Ai и строки, в которой
в столбце £ стоит число 1~а2х2.
Затем строится таблица, аналогичная табл. 10.1, для Л2(|)
и х2(|). Далее, используя (10.19) и таблицу A2(g), строим
таблицу Лз(£) и xsfe) для |=0, 1,..., Ь. Эта процедура повто-
ряется вплоть до вычисления An-ife). Функцию Лп(|) табули-
ровать не следует, так как достаточно знать An(b)—z*. Значе-
ние (значения) хп(Ь) = х*п, т. е. то хп, при котором достигается
ЛП(Ь), просто равно х*п> фигурировавшему в формуле (10.7).
Следовательно, значение хп> которое может быть и не един-
ственным, найдено. Для отыскания х*, х*2, ..., х* мы должны
использовать уже вычисленные таблицы значений х&(|). Коль
скоро известна величина х*. оставшиеся переменные должны
удовлетворять условию
п-1
aJxj < b — апх*п. (10.25)
л-1
Следовательно, выражение 2/;(Лу) должно достигать макси-
мума на множестве неотрицательных целых чисел, удовлетво-
ряющих (10.25). Но этот максимум есть просто Ля_, (Ь — аяхя).
366 Гл. 10. Динамическое программирование I
а значение (или значения) хп-и при котором этот максимум
достигается, есть хп1(Ь— анх:1). Следовательно,
= (10.26)
т. е. ^для вычисления х*п_х мы должны взять число в таблице
для xn_i(g), соответствующее I — b — апх*п. Таким же образом
мы найдем далее
Хя-2 ~ Хп-2 (? апХп ап-1Хп-1)
и вообще
(10-27)
\ и=0 /
Этим завершается вычислительная процедура, позволяющая
найти z* и множество оптимальных значений Xj. Ее использова-
ние делает возможным отыскание всех оптимальных решений.
Рис. 10.1.
При этом, начиная с выбранного х*, можно получить структуру
типа дерева . (рис. 10.1). Значения величин х*. на последних
ветвях будут соответствовать различным оптимальным реше-
ниям. Необходимо, конечно, повторить всю процедуру для всех
различных значений х*.
Объясним теперь более подробно, почему функции Ab(gj,
&=1,2, ..., и—1, табулировались для всех g = 0, 1, ..., b. Все,
что нужно в конечном счете, — это отыскать Лп(Ь). Однако,
чтобы вычислить ЛП(Ь), нужно найти An-i(b — anxn) для всех
хп = 0, 1, ..., [Ь/ап]. Значения g, для которых нам нужно знать
An-i(^), будут зависеть от а„. Если ап = 1, тогда нам понадо-
бится Лп-1(|) для всех g = 0, 1, ..., Ь. В других случаях может
потребоваться вычислить величину An-i (£) лишь при некоторых
‘значениях g. Для каждого g, при котором нужно знать значе-
ние An-i(g), необходимо вычислить An-2(£ — an-i*n-i) при всех
10.3. Эффективность метода
367
xn_i = 0, 1,..., [g/an_i], и т. д. Ясно, что при большом числе пере-
менных очень трудно проследить, для каких именно значений £
следует вычислять функции Лй(?). Проще вычислить Л&(|) при
всех £ = 0, 1, Ь. При этом можно быть уверенным, что будут,
вычислены все необходимые величины. При вычислениях в об-
ратном направлении очень часто оказывается, что хотя An-i(£)
может быть и не нужно для всех g = 0, 1, b, A*(g) должно
быть известно для всех значений g = 0, 1, .. ., Ь.
Причина введения требования целочисленности состоит в
е том, что оно гарантирует целочисленность аргументов функ-
ций Ад, т. е. позволяет упростить процесс вычисления этих
функций.
Для вычислений вручную описанная процедура очень утоми-
тельна и становится неосуществимой, если значения b и п ве-
лики. Однако она легко программируется для вычислений с по-
мощью цифровой машины. В этом случае желательно, чтобы
машина имела достаточно большую оперативную память, позво-
ляющую хранить одновременно функции Afe-i(g), Aft(g) и fk(Xk)
[функции fk(Xk) очень часто задаются в табличной форме].
Отметим, что после того как вычислено Л&(£), нет необхо-
димости хранить в памяти значения A^i(g). Величины х&(£),
которые определяются вместе с Afe(g), могут записываться на
ленту по мере их вычисления; Они не потребуются вплоть до вы-
числения х*. На современных быстродействующих цифровых
машинах, таких, как IBM 7090, при использовании только опе-
ративной памяти без труда могут решаться задачи, содержащие
до 10 000 значений в таблице Лй(|). Сравнительно большие за-
дачи, число переменных в которых превосходит 100, могут быть
решены в несколько минут.
Хотя иногда и может потребоваться таблица, содержащая
более 10 000 значений A*(g), эта необходимость возникает не
слишком часто, если позаботиться о выборе подходящих единиц
измерения для а$, b и иногда Xj. В действительности даже
таблицы с 20 000 значений Лй(£) не представляют серьезной
трудности для IBM 7090. Конечно, чем больше значений в та-
блице, тем больше времени требуется для ввода информации
в память машины и для решения задачи.
Вычислительный метод, изложенный в этом параграфе, пред-
ставляет собой иллюстрацию метода динамического программи-
рования. В § 10.4 мы постараемся охарактеризовать более точ-
но суть концепции динамического программирования.
10.3. Эффективность метода. Сравним теперь с точки зрения
вычислительной эффективности предложенную выше для решения
задачи (10.1) процедуру с полным перебором всех возможных
368
Гл. 10. Динамическое программирование 1
наборов значений удовлетворяющих ограничению неотрица-
тельных, целых чисел Xj, при котором целевая функция вы-
числяется для каждого из этих наборов и выбирается то (или
те) из них, которое доставляет целевой функции максимальное
значение. Весьма трудно провести точное сравнение числа не-
обходимых операций в общем случае. Для иллюстрации рас-
смотрим случай, когда все aj=l. Тогда ограничение принимает
вид В обоих методах необходимо вычислить fj(xj) для
каждого из 6 + 1 значений, которые может принимать X}. Суще-
ственная разница между двумя подходами состоит в числе раз-
личных комбинаций переменных, для которых должна вычис-
ляться целевая функция. Рассмотрим сначала прямой перебор.
Точное определение числа различных наборов целых значе-
ний Xj, удовлетворяющих ограничению, трудно осуществимо.
Однако здесь достаточно воспользоваться нижней границей этого
числа.
Найдем число различных комбинаций неотрицательных це-
лых чисел, обращающих наше ограничение в строгое равенство.
Оно равно числу способов, которыми можно разместить b оди-
наковых шаров в п урн. Это число равно
(п-\-Ь — 1 \ _ (п + Ь — 1)!
\ b Ь\(п — 1)! *
Для п=5 и 6=20 получаем
24'4233222'21 -10 626.
Таким образом, z в этом случае должно быть вычислено более
чем для 10626 различных наборов Xj.
Рассмотрим теперь описанный выше подход динамического
программирования. Чтобы вычислить Л/Д£) при данном g, мы
должны провести £+1 вычисление. Поэтому для построения
всей таблицы Л* (£) придется выполнить
ь
5-0
вычислений. Следовательно, чтобы вычислить первые п— 1 функ-
ций Aft(g), требуется провести число вычислений, в п—1 раз
большее. Для последней функции Ап необходимо лишь значе-
ние Дп(6), поэтому здесь потребуется вычислить только 6 + 1
ее значение. Таким образом, общее число вычислений равно
10.4. Основные свойства динамического программирования 369
что при п = 5 и Ь = 20 дает 945. Следовательно, общее число вы-
числений, которые должны быть сделаны при использовании
метода, описанного в предыдущем параграфе, меньше 10% от
числа вычислений, необходимых при непосредственном подсчете
значения целевой функции для всех возможных комбинаций
неотрицательных целых чисел xj, удовлетворяющих ограниче-
нию. Более того, использование вычислительной схемы преды-
дущего параграфа требует выполнения лишь одной операции
сложения для отыскания подлежащих сравнению чисел, в то
время как в методе перебора для вычисления z на заданном
множестве Xj требуется п таких операций.
Вычислительная эффективность подхода динамического про-
граммирования по сравнению с полным перебором становится
все более существенной с ростом п. Причина этого состоит в
том, что на каждом шаге для данного I все неблагоприятные
комбинации переменных исключаются из дальнейшего рассмо-
трения.
10.4. Основные свойства динамического программирования.
Задачу, изученную в § 10.2, можно понимать как задачу рас-
пределения, в которой имеется единственный ограниченный
источник сырья и Xj есть количество этого сырья, направляемое
на переработку по j-му способу. Тогда fj(Xj) может рассматри-
ваться как доход, получаемый при переработке j-м способом
Xj единиц сырья. Исходя из этой интерпретации, ясно, что Ль (|)
есть просто максимальный доход от первых k способов, когда
общее количество сырья, предназначенное для распределения
между ними, равно g. Подобным же образом xh(l) есть опти-
мальное значение х&, когда имеется только k способов, а коли-
чество сырья равно g.
Задача § 10.2 может рассматриваться как n-шаговый про-
цесс принятия решений, в котором на j-м шаге принимается ре-
шение о количестве сырья, направляемом на переработку по
J-му способу, т. е. выбирается Xj. Природа задачи не изменяется
с изменением количества шагов. Иными словами, форма задачи
инвариантна относительно п. В осйове метода динамического
программирования и лежит использование этого факта. Это
дает возможность решать последовательность задач так, что
сначала решается одношаговая, затем двухшаговая и т. д., пока
в конце концов не будут включены все п шагов.
Решение для ^-шаговой задачи-получается из решения для
(k—1)-шаговой задачи путем добавления &-го шага и исполь-
зования результата, полученного для (k—1) шагов. Когда рас-
сматривается только k шагов, оптимальные значения Xj,
24 Зак 735
370 Гл. 10. Динамическое программирование I
/=1, 2,..., k, зависят от g — общего количества сырья, распре-
деляемого между k шагами. После того как fj(Xj) и заданы,
величина g является единственным параметром, который влияет
на значения т. е. на количество сырья, распределяемое на
каждом шаге. Применение динамического программирования не
только позволяет решить задачу для 1,2, ..., п шагов, но и,
кроме того, дает для каждого k<n оптимальное решение при
всех значениях количества распределяемого сырья от 0 до Ь.
Вообще говоря, мы должны знать решение для k—1-шагового
процесса при g = 0, 1, ..., b для того, чтобы найти оптимальное
решение ^-шагового процесса, если количество сырья в этом
процессе равно g.
Сущность подхода динамического программирования со-
стоит, таким образом, в возможности заменить решение данной
n-шаговой задачи решением целой последовательности задач:
сначала одношаговой, потом двухшаговой и т. д., вплоть до
n-шаговой. Такой подход допустим потому, что шаги могут до-
бавляться по одному и решение для k шагов может быть полу-
чено относительно просто, если оно уже известно для k—1 ша-
гов при всех возможных значениях g.
Простая задача, изученная в § 10.2, иллюстрирует основные
особенности, которые будут встречаться в процессе решения за-
дач с помощью метода динамического программирования. По-
пытаемся обсудить в несколько более общих терминах, что
представляет собой этот подход к решению задач.
Чтобы сделать это, опишем сначала тип задач, к которым
может быть применена подобная методика. Прежде всего
должна быть возможной интерпретация задачи как п-шагового
процесса принятия решений, в котором решение, принимаемое
на /-м шаге, состоит в выборе одного или нескольких значений
управляющих переменных. Далее, задача должна быть опреде-
лена для любого числа шагов и иметь структуру, не зависящую
от числа шагов. При рассмотрении задачи, состоящей из k ша-
гов, должно быть задано некоторое множество параметров,-
описывающих состояние системы, т. е. параметров, от которых,
зависят оптимальные значения управляющих переменных. То
же самое множество параметров должно описывать состояние,
системы независимо от количества шагов. В задаче, рассмотрен-
ной в § 10.2, имелся единственный параметр g — количество
сырья для ^-шагового процесса. Выбор управления на &-м шаге
в й-шаговом процессе не должен влиять на предшествующие-
k— 1 шаги, если не говорить о преобразовании множества пара-
метров, описывающих состояние системы с k шагами, в мно-
жество параметров, описывающих состояние системы с k—1 ша-
гамш
10.4. Основные свойства динамического программирования
371
Если приведенные выше условия выполнены, то задача
обычно укладывается в схему динамического программирования
и, таким образом, ее решение может быть сведено к решению
последовательности задач, начиная с одношаговой и вплоть до
n-шаговой. Это делается следующим образом.
Пусть | обозначает вектор, компонентами которого служат
параметры состояния, т. е. параметры, описывающие состояние
системы при наличии k шагов. Тогда Л&(|) представляет собой
оптимальное значение целевой функции й-шагового процесса
при условии, что параметры состояния описываются вектором g.
В дальнейшем мы будем называть функции Л/Jg) функциями
состояния.
Через обозначим вектор, содержащий переменные, под-
лежащие выбору на k-м шаге. Допустим, что если выбраны х&
и g, то вектор параметров состояния для остальных k—1 шагов
есть Т (£, xft).
Существенной чертой подхода динамического программиро-
вания является построение ряда таких рекуррентных соотноше-
ний, что сравнительно просто может быть определена функ-
ция Afe(g), если при всех т известна функция Ль-Дт). Типичный
вид этих рекуррентных соотношений таков:
Л^) = тах[Ш + х*))]. (10.28)
Однако это не единственная форма, которую они могут прини-
мать. Возможны и многие другие формы. Некоторые из них бу-
дут упомянуты ниже. Определив Л^(|) при фиксированном g,
мы тем самым находим x&(g) — оптимальные значения управле-
ний на £-м шаге ^-шагового процесса, характеризуемого векто-
ром параметров состояния g. Мы будем называть Xfe(g)
стратегиями или управлениями. На n-м шаге мы получим
z* = Ля (g0) и х* = хп (g0), где go есть вектор параметров состоя-
ния, соответствующий данной задаче.
Отметим, что (10.19) есть частный случай соотношений
(10.28). В задаче § 10.2 имелся лишь один параметр состояния,
и на каждом шаге требовалось выбрать значения лишь одной
управляющей переменной. Именно такие задачи мы будем рас-
сматривать в этой главе. В следующей главе мы рассмотрим
случаи с большим числом параметров состояния и более чем
одной управляющей переменной.
Соотношениям (10.28) может быть дана интересная интер-
претация, которая лежит по существу в основе всех рекуррент-
ных соотношений, получаемых при решении задач с помощью
динамического программирования. Она состоит в том, что
24*
372
Гл. 10. Динамическое программирование 1
нельзя получить оптимальное значение целевой функции &-ша-
гового процесса, если для любого х&, выбранного на &-м шаге, |
значение целевой функции для оставшихся k—1 шагов не яв- г
ляется оптимальным при этом выбранном на &-м шаге значе- * ;
нии х*. Беллман [3] назвал это утверждение принципом опти- । j
мальности. Оно может быть использовано для непосредственного |
вывода рекуррентных соотношений, содержащих функции со-
стояния. Мы не будем получать рекуррентные соотношения та- i
ким образом, а будем выводить их из определения функций f
состояния.
Описание характеристик динамического программирования :
и типов задач, которые могут быть сформулированы.в его рам- 4
ках, по необходимости должно быть очень общим и несколько
неопределенным, так как существует необозримое множество \ j
различных задач, укладывающихся в схему динамического про-
граммирования. Только изучение большого числа примеров
дает отчетливое понимание структуры динамического програм- j
мирования. Мы проведем такое изучение в этой и следующих
главах.
При попытке сформулировать какую-либо задачу как задачу
динамического программирования, как правило, бывает легко
обнаружить ее n-шаговую структуру. Значительно труднее вы-
брать подходящие параметры состояния. Как только это еде- \
лано, обычно удается непосредственно получить рекуррентные i
соотношения.
10.5. Численный пример. Изучим очень упрощенный пример f
задачи о загрузке подводной лодки запасными деталями. Пусть
рассматривается лишь три типа запасных деталей, имеющих ?
объемы соответственно в 1,2 и 2 единицы. Общий объем склада I
равен 10 единицам. Штрафные затраты Jtj, возникающие при f
неудовлетворении потребности, равны соответственно 800, 600
и 1300. Будем предполагать, что спрос на каждую из запасных
деталей подчинен пуассоновскому распределению со средними
значениями 4, 2 и 1 соответственно. Требуется определить, ка-
ким должен быть запас деталей каждого типа, чтобы средние
штрафные издержки были наименьшими. В математических
терминах это приводит к следующей задаче:
о Г гл “I
о оо f.
найти min z=2 к 3 — цу)| (10.29) f
у-i L J ..
при условиях | j
Xj — неотрицательные целые числа, /—1, 2, 3, ?
Xi —|— 2х2 2х3 10.
10.5. Численный пример
373
Выражение
i
P&J’ =
(10.30)
в целевой функции представляет собой плотность вероятности
случайной величины, подчиненной закону Пуассона, a pj есть
ожидаемая потребность в деталях /-го типа.
Из (10.30) следует, что
VjP (Рр Ну) = Н/Р i.'Vj ~ 1 > Р7), > 1 •
Таким образом, можно записать
S (‘Оу—Xj)p(Vj, цу) =
vrxi
Нур(ху —t Ну) — XjPiXj, Цу),
Ну> Xj 0,
Xj>l,
(10.31)
где
P(Xj, Н/)= 2 p(vj, Н?
есть интегральная функция распределения. Соотношение (10.31)
дает возможность без труда вычислить средний спрос на /-ю де-
таль, возникающий в то время, когда запас их исчерпан, поль-
зуясь таблицами для распределения Пуассона.
Пусть
k
Лй (£) = min 3 (Xj — 1, р,;) — хjP (Xj, цу)], (10.32)
xi...Xki-x
где минимум берется по всем неотрицательным целым числам,
k
удовлетворяющим условию ЗауХу<<£ (а^ есть объем детали
/-го типа). Тогда z*=A3(10).
Если следовать рекомендациям § 10.2, мы должны табули-
ровать Л1 и Л2 для всех £ = 0,1, ..., 10. Для уменьшения коли-
чества вычислений мы построили пример, в котором Ai и Л2
нужно вычислить только для четных £. Чтобы пояснить это,
отметим, что х3 может принимать только значения 0, 1, ..., 5.
Таким образом, для вычисления Л3(10) потребуется знать Л2
для £=10 (х3=0), 8, 6, 4, 2, 0 (х3 = 5). В свою очередь, чтобы
вычислить Лг(£), нам потребуется Ai для всех £ — 2x2, где
х2 = 0, 1, ..., [£/2]. Следовательно, так как Л2(£) необходимо
только для четных значений £, Ai(£) также требуется вычислять
только для четных значений £.
374
Гл. 10. Динамическое программирование I
Вычисление Л1(|) осуществляется совсем просто: штрафные
затраты для деталей первого типа будут минимизированы, если
запасти их как можно больше. Итак,
Л, (£) = 800 [4Р (I -1; 4) - (|; 4)]; хх (У =
Значения ЛД^) и хДВ) приведены в табл. 10.2. Например,
Aj (6) = 800 [4Р (5; 4) - 6Р (6; 4)] =
= 800 [4 • 0,3712 - 6 • 0,2149] = 156,32.
Таблица 10.2
. £ Л^) . х,(У Л2 (£) . £(&)
0 3200 0 4400 0
2 1688 2 2888 0
4 625,3 4 1825,3 0
6 156,32 6 ' - 1306,5 1
8 26,91 8 837,5 1
10 3,30 10 481,1 2
Чтобы вычислить Л2 и Аз, используем рекуррентные соотно-
шения
ЛА(|)= min {«ИМЧ*! — 1, xkP(xk, ц*)] +
,+Лй_1(|-аЛ)], Л = 2,3. (10.33)
Разберем подробно определение, например, Л2(8). Для |=8
величина х2 может принимать значения 0, 1, 2, 3, 4. Для ка-
ждого из них вычислим
Й2 (х2; 8) = 600 [2Р (х2 — 1; 2) — х2Р (х2; 2)] + Л1 (8 — 2х2).
Л2 есть наименьшее из Йг(х2, 8). Прежде чем определить ка-
кое-либо значение Л2(£), следует вычислить выражение
600[2Р(х2 — 1; 2) — х2Р(х2; 2)] для х2 = 0, 1, 2, 3, 4, 5, так как все
они участвуют в определении различных Л2(|). Для рассматри-
ваемого случая находим, что Q2(0; 8) = 1226,9, й2(1; 8) =837,5,
Q2(2; 8) =950,1. Нет необходимости находить й2(3; 8) и Q2(4;8),
так как и без того очевидно, что они больше чем Q2(2;8). Отме-
тим, что
Q2 (1; 8) = 681,2 + Aj (6) = 681,2+156,3 = 837,5 = Л2 (8).
. Остается вычислить Аз(10). Для этого вычисляем Q3(0; 10)==
= 1781,1, Q3(l; 10) =1315,8; Q3 (2; 10) = 1441,3. Снова мож-
10.6. Несколько других практических примеров
373
но не вычислять Йз(4; 10) и Q3(5; 10), так как они больше
чем£23(2;10). Итак, z* = A3(10) = Q3(l; 10)=1315,8, а х^=1.
Чтобы вычислить х* и х*, заметим, что
х»=х2(Ю—2)=х2(8) = 1, 2 —2)=х,(6) = 6.
Следовательно, единственное оптимальное решение задачи есть
х* = 6, х*=1, х3=1. Соответствующие минимальные ожидае-
мые затраты составят 1315,8.
10.6. Несколько других практических примеров. В этом пара-
графе мы приведем три задачи,-которые могут встретиться на
практике и математическая формулировка которых сходна с
задачей (10.1).
1) Задача о загрузке корабля. Допустим, что для загрузки
судна ограниченного объема b имеется п различных типов гру-
за. Объем и стоимость единицы J-го груза будем обозначать
соответственно через а, и р^ Требуется определить величины
— количества груза каждого типа, которые должны быть по-
гружены на судно для того, чтобы максимизировать стоимость
груза. Математическая формулировка этой задачи такова: най-
ти неотрицательные целые числа xj, удовлетворяющие условию
у-1 7
и доставляющие максимум функции
п
Это простейший тип задачи вида (10.1), так как здесь
fj(Xj) —pjXj являются линейными функциями относительно xj.
Эта задача может также рассматриваться как целочисленная
задача линейного программирования.
2) Распределение поставок. Рассмотрим служащую для соз-
дания запасов систему, состоящую из большого числа складов. >
Периодически некоторые товары, которые должны быть в скла-
дах, заказываются у изготовителей, причем заказ делается цен-
трализованно для всех складов в одно время. Пусть заказанное
количество товара равно Q. Между моментами, когда произво-
дится заказ и когда он готов к отгрузке, проходит определенное
время. После выполнения заказа необходимо решить, как коли-
чество Q должно быть распределено между п складами. Для
простоты будем предполагать, что склады ниоткуда дополни-
тельно не получают рассматриваемого товара в течение
376
Гл. 10. Динамическое программирование I
времени Г, т. е. до реализации следующего заказа. Заказ дол-
жен быть так распределен между складами, чтобы минимизиро-
валась сумма затрат на перевозки и ожидаемых штрафных
затрат из-за неудовлетворенного спроса в течение периода до
следующей поставки.
Пусть Cj(xj) —транспортные затраты по перевозке Xj еди-
ниц продукта от изготовителя до /-го склада; у$— величина за-
паса этого продукта в /-м складе в момент, когда осуществляет-
ся распределение; nj — отнесенные к единице требуемого то-
вара штрафные затраты, когда запас в /-м складе равен нулю;
pj(Vj)—вероятность того, что возникает спрос в vj единицах
товара в /-м складе в течение времени Т. Тогда, пренебрегая
временем транспортировки, найдем, что функция затрат для
/-го склада имеет вид
fj (*j) = СJ(*р + Я] S — — (10.34)
vryj+Xj
Таким образом, предстоит найти неотрицательные целые чис-
ла Xj, удовлетворяющие условию
п
/=1
и минимизирующие функцию
• п
j-t
где/Дх^) определены в (10.34). %
При решении этой задачи иногда можно использовать раз-
личные приемы для сокращения вычислений. Например, может
быть известно заранее, что нецелесообразно отгружать более
чем Q/3 единиц товара в любой из складов. В этом случае нет
необходимости вычислять fj(Xj) при Xj>Q/3. Кроме того, если
£>Q/3, для вычисления Л^(|) не нужно просматривать значения
Qft(xft, g) при значениях xk>Q/3. Функции Ai(g) и Л2(?) должны
/ табулироваться только до значений g=Q/3 и g=2Q/3 соответ-
ственно. Более того, особенности упаковки и отгрузки могут
привести к дальнейшим упрощениям. Например, может суще-
ствовать некоторый минимальный размер (отличный от нуля)
отгружаемой партии и известно, что все большие размеры яв-
ляются его целыми кратными. Могут быть и другие правила
поставок, которые можно использовать для упрощения решения
задачи.
3) Распределение допусков. Рассмотрим некоторое изделие,
состоящее из п частей. Каждой из'этих частей сопоставлена не-
10.6. Несколько других практических примеров
377
которая измеряемая характеристика, которая может быть гео-
метрическим размером, электрическим сопротивлением и т. п.
Обозначим через xj значение этой характеристики для /-й части.
Имеется также измеряемая характеристика, которая сопостав-
ляется всему изделию. Ею может быть общий размер, напряже-
ние и т. п. Пусть у есть значение этой характеристики и связь
его с Xj определяется функцией z/ = g’(xi, ..., хп). При замене
экземпляров одной и той же части величина у несколько ме-
няется и ведет себя как случайная величина. Причина этого в
том, что сами Xj являются случайными величинами.
Пусть pj есть среднее значение Xj, а — среднее значение у.
Будем полагать, что отклонения xj от pj невелики. Пользуясь
формулой Тейлора, можно приближенно записать
п
У = ё(Хи ..., х„) g (Ц1, ..., ц„) + 2 (Xj — Ну). (10.35)
где (dg/dXj)o есть значение dgldXj, вычисленное в точке
pi, р2, ..., рп. Отсюда видно, что ру удовлетворяет приближен-
ному равенству
М2> •••> Нл)- (10.36)
Пусть теперь Xj— независимые'сйучайные величины. Из (10.35)
видно, что о2, дисперсия у, равна
п
°^2(Д)?г <10-37)
7-1
где o2j есть дисперсия Xj.
Допустим, что для того, чтобы изделие прошло контроль,
значение у должно лежать в интервале yi^y^yz. Допустим
также, что у подчинено нормальному закону со средним, опре-
деляемым выражением (10.36). Вероятность того, что у лежит
вне интервала у^-у^-уг, будет долей тех частей, которые не вы-
держивают контроля. Как только эта доля и определены,
находится о2у. С другой стороны, значение о2у определяется
значениями aj. Допустим теперь, что pj выбрано так, что
Ну—(У1+Уг)/2. Тогда при любом заданном о2 минимизируется
доля дефектных изделий. Однако доля дефектных изделий за-
висит от о2у и будет убывать при убывании о2у- Будем считать,
что в известных пределах мы можем уменьшить о2, но при этом
увеличивается стоимость /-й части. Пусть также о2 меняется
дискретно, и если Xj имеет дисперсию aj, стоимость /-й части
равна fj(o2^. Задача состоит в определении минимальной
378
Гл. tO. Динамическое программирование I
стоимости изделия, которая является функцией доли дефектных
изделий. Задание доли дефектных изделий определяетсй <Ту, а по
нему уже находятся ей. как решение задачи
п
<10-38>
а
найти min z=2f/(a^Y
iJ ' J'
Эта задача имеет форму (10.1) относительно переменных с^.
Здесь следует отметить, что вычислительная схема, введен-
ная в § 10.2, делает очень легким отыскание последовательности
оптимальных решений при изменении Ь, Все, что необходимо, —
это вычислить на последнем шаге Лп(£) при всех Ь, представ-
ляющих интерес, а не при одном его значении. Следовательно,
нужны совсем небольшие дополнительные усилия, чтобы изу-
чить, как z* и х* изменяются с изменением Ь. Конечно, проводя
вычисления, необходимо вычислять все Л&(£), Л=1, 2, ..., п—1,
при всех целых % вплоть до наибольшего ^интересующего нас
значения Ь. Использование этого приема позволяет легко по-
строить кривую, выражающую функциональную зависимость
между минимальной стоимостей) изделия и долей дефектных
изделий. Это именно то, что нам требуется.
10.7. Случай непрерывности переменных. В отличие от дру-
гих уже изученных нами вычислительных методов динамиче-
ское программирование больше подходит к задачам с дискрет-
ными переменными, чем с непрерывными. Для пояснения этого
рассмотрим решение задачи (10.1) беэ требования целочис-
ленности Xj, Отбросим также ограничения целочисленности, на-
ложенные на a,j и Ь,
.Формально мы можем приступить к решению точно так же,
как в §10.2. Определим последовательность функций состояния
k
. . ЛА(|) = . max SfM, k=\, 2............п, (10.39)
xi..
где максимум берется по всем неотрицательным Xj, удовлетво-
ряющим условию
(10.40)
. mi <
Тогда, как и раньше, „
Л1(^)=, max fM- (10.41)
‘0 < X, < b/ax
10.7. Случай непрерывности переменных
379
Отметим, что Xi меняется до Ь/а\, а не [fr/aj. Рекуррентные со-
отношения имеют тот же вид, что и при целочисленных Xj,
Л*(£) = max [М*л)+Л*_1(£-ал)]. k = 2, 3, .... п, (10.42)
°<xk<blak
И2*=Лп(Ь).
Разница между этой задачей и рассмотренной в § 10.2 воз-
никает в ходе вычисления максимума по % и в способе построе-
ния таблицы значений Аь(£). Прежде всего рассмотрим задачу
определения Л&(|) при фиксированном £. Здесь
Лй(|)= max (Ю.43)
°<^<6/вл
где
ЙИ^Л) = /И^) + ЛА_1(|-аЛ). (10.44)
Допустим, что функция Afe-i(g) известна. Тогда значения
g) определены для всех хк из интервала Если
нарисовать график ЙДх^, |), то он может иметь вид кривой,
изображенной на рис. 10.2. Нам нужно определить значение
Xft(g), при котором Qfe(Xfe, |) достигает своего максимального
значения. Для этого приходится искать все относительные
максимумы Йй, а затем выбирать то (или те) значение хк, ко-
торое доставляет йд абсолютный максимум.
Чтобы уменьшить насколько возможно вычислительные труд-
ности, можно сначала, воспользовавшись сеткой с большим ша-
гом, провести, начальный поиск. Это означает, что Йа(хл, £)
380
Гл. 10. Динамическое программирование 1
будет вычислено в достаточно широко разбросанных точках
(сплошные линии на рис. 10.2) и, таким образом, будет найдено
приближенное значение максимума. Затем в окрестности най-
денного приближения используется сетка с более мелким шагом
(пунктирные линии на рис. 10.2) для определения значения
x&(g) более точно. Процесс уменьшения шага сетки может быть
повторен несколько раз для получения желаемой точности опре-
деления Xfe(g)-
В ходе поиска вовсе не следует использовать сетку с мелким
шагом только в окрестности наибольшего из полученных значе-
ний. Ее желательно использовать и в окрестностях тех локаль-
ных максимумов, чьи значения достаточно близки к наиболь-
шему из полученных значений Qfc(Xfe, g). Это нужно для того,
чтобы быть уверенным, что действительный максимум не
пропущен. Хотелось бы иметь, конечно, критерии, указывающие
точно, какие из относительных максимумов должны быть иссле-
дованы с большой точностью. Вполне возможно, что исходный
шаг был настолько велик, что не дает никакой информации о
расположении абсолютного максимума Qfe(xfe, g). Теоретически
получение такой информации нельзя гарантировать при исполь-
зовании даже сколь угодно малого шага.
Мы предложили выше способ, с помощью которого x^(g) и
Afe(g) обычно могут быть найдены с любой желаемой точностью.
Конечно, чем выше необходимая точность, тем больше будет
объем вычислений. В следующем параграфе мы покажем, что
процедура определения A(g) и A*(g) может быть существенно
упрощена, если fj(Xj) являются выпуклыми или вогнутыми
функциями. В противном случае процедура поиска осуще-
ствляется по описанной выше схеме!
Рассмотрим теперь проблемы, которые возникают при табу-
лировании Afe(g). Трудности здесь связаны с тем, что функ-
ция A&(g) определена для любого g из интервала 0<Cg<!6. Бо-
лее того, анализ описанной выше процедуры поиска показы-
вает, что действительно может понадобиться вычислить A*(g)
при любом g из этого интервала. Объясняется это тем, что при
использовании сеток со все более мелким шагом для определе-
ния Afe(g) при фиксированном g функция Afe-i(g) может иона-,
добиться при очень многих различных значениях аргумента.
Обычно представляется невозможным табулировать A&(g) для
всех значений g, которые могут понадобиться при использовании
описанной выше схемы поиска. Очевидно, в этом случае следует
табулировать Afe(g) для небольшого числа различных g, а затем
находить Ak Для всех других значений аргумента с помощью
интерполяции. Однако интерполяцию нельзя применять с уве-
10.7. Случай непрерывности переменных
381
ренностью, если не известно, что функции Лд(|) хотя бы не-
прерывны. Между тем эти функции могут оказаться разрыв-
ными, если разрывными являются функции fj(Xj). К сожале-
нию, для некоторых приложений нам понадобится рассматривать
функции fj, имеющие конечное число скачков. Это существенно
затрудняет исследование в случае, когда переменные непре-
рывны.
Ниже мы скажем нисколько слов о случае разрывных функ-
ций fj(Xj). Сейчас же предположим, что каждая из них является
непрерывной. Докажем, что в этом случае все функции Ай(£)
также непрерывны. Доказательство проводится по индукции.
Рассмотрим сначала
Л!(|)= шах Ш).
0.<х, < V»!
Чтобы доказать, что ЛДВ) непрерывна, нужно показать, что
для всех | существует такое число б(е, |)>0, что как только
I? — 1|<б, неравенство |Ai(g) — Ai(£) |<е выполняется при лю-
бом е>0. Из определения А] (|) и Ai (£) следует, что оба они
определяются как наибольшие значения ft(xt) на некотором
интервале. Более того, интервалы, на которых осуществляется
этот выбор, отличаются только правыми концами, отстоящими
один от другого на |£—1|. Следовательно, величина |Ai(|) —
—Л1(£)| не превосходит разности между максимальным и ми-
нимальным значениями Л (xij на интервале длины —1|. В силу
непрерывности fi(xi) эта разность может быть сделана сколь
угодно малой за счет выбора достаточно малой величины |g—Jj|’.
Отсюда следует непрерывность Л](|).
Допустим теперь, что уже доказана непрерывность функ-
ции Лл-1(£). Покажем, что Лй(|) также непрерывна. Пусть
^k(xk> = + akxk). (10.45)
Ясно, что Qk(Xk, 5) — непрерывная функция хк и g. Следова-
тельно, разность между Ль (В) и Aft(£) не превосходит наиболь-
шего из двух чисел
У! = шах | (xk, £) — Q* (хк, I) |, 0 < хк < min (|, С) = е.
хь
и
у2 = max Q* (хй, ф) — min Q* (xk, Ф) +1 (e, S) — (e, £) |,
xk xk
eO*<e + |£ —1|, ф = тах(|, I).
В силу непрерывности Qfe(Xk, |) величины yi и у2, а тогда и
|Лл(£) —Лл(|) | могут быть сделаны сколь угодно малыми за
счет выбора достаточно малой величины ||—1|. Таким образом,
382
Гл. ГО. Динамическое программирование I
из непрерывности A^i(g) вытекает непрерывность Afe(g). Сле-.
довательно, из непрерывности fj(Xj) следует непрерывность
всех Aft (g).
Приведенные выше аргументы показывают, что если все
функции fj(Xj) непрерывны, то обычно можно применять интер-
поляцию в области значений Afe(g) 9- Вообще процедура вычис-
ления состоит в табулировании Afe(g) в точках gu/где gu = .
= gu-i + Ag, и применении линейной интерполяции для отыска-
ния Afe{g) при g, отличных от
gu. К счастью, Aft(g) часто
оказываются функциями, ко-
торые с изменением g меняют-
ся не очень быстро. Таким
образом, Ag может быть вы-
брано в этих случаях доста-
точно большим и таблица Ak (g)
не станет слишком обширной.
Окончательная погрешность
вычислений будет, конечно,
£ зависеть от выбранного зна-
чения Ag.
_ Даже в случае непрерывно-
сти функций Ak (g) вовсе не обя-
зательно, что Xfe(g) будут непрерывными. Тот факт, что функ-
ция Xfe(g) может быть разрывной, приводит к трудностям, если
мы попытаемся табулировать xft(g) только в тех же точках gu,
для которых вычислены Afe(g), а затем используем эти таблицы
для определения х*. Причина состоит в том, что для вычис-
ления
х* . = хп ДЬ~^ап х* „
П — l П — 1 I п — и п — и
\ w=0
необходимым ВЫЧИСЛИТЬ Xn-i(g) в точке I, от-
таким образом, может потребоваться интерпо-
если функция xn-i(g) окажется разрывной в
может оказаться
личной от gu, и,
ляция. Однако,
интервале интерполяции, полученная величина может оказаться
очень далекой от истинного значения x*_z. Это проиллюстриро-
вано на рис. 10.3, где истинный график xk(Q представлен
9 Хотя непрерывность функции и обеспечивает принципиальную воз-
можность сколь угодно точной интерполяции, из этого предположения нельзя
извлечь никакой информации о величине шага, гарантирующего заданную
точность. Чтобы это можно было сделать, нужно использовать информацию
о первой и старших производных функции. — Прим. ред.
10.8. Случай выпуклости или вогнутости функций fj(xj)
383
сплошной линией. Точками отмечены табулированные значения
функции. Если бы пришлось интерполировать между и £w+i,
для х* было бы получено значение В, в то время как его истин-
ное значение есть А. Всех этих трудностей легко избежать, за-
менив табулирование х&(£) вычислением значений этой функции
для необходимых значений аргумента.
Вообразим, что процедура вычислений аналогична предыду-
щей, но табулируются только значения Л&(£). На последнем
шаге определяются Лп(&) и х*. Чтобы найти х*}1_х = хп_х(Ь—
— апх*п)> НУЖНО вычислить Лл_1(6— алх*) непосредственно по
формуле
Лл_1 (* - йХ)=max [f«-i (*„-0+a„-2(* - ап< -
Та же самая процедура позволяет непосредственно вычислить
хл_2 и т. д. Этот метод является, пожалуй, единственным, гаран-
тирующим точность определения х*. Отметим, что все функции
Afe(g) должны сохраняться в памяти машины для того, чтобы
получить возможность выполнить эти вычисления.
Ранее было указано, что большие трудности встречаются
при рассмотрении случая непрерывности переменных и разрыв-
ных функций fj(xj). Если fj(Xj) разрывны, то лучше всего свести
задачу к задаче с дискретными переменными, принимающими
значения Xj = mAx, m = 0, 1, ..., Mj. Если ввести еще новые
переменные которые принимают только значения 0, 1,... , Mj,
так что = то задача приводится к виду
S (a, Ax)z/ <Z>,
/=1
У} 0, yj — целые;
п
найти max (10.46)
т. е. принимает вид задачи (10.1).
К счастью, во многих практических задачах переменные х$
оказываются дискретными или их можно считать дискретными.
По этой причине многие из упомянутых выше трудностей, кото-
рые возникают в случае непрерывных переменных, не вызы-
вают на практике так много затруднений, как это могло бы
показаться с первого взгляда.
10.8. Случай выпуклости или вогнутости функций
Рассмотрим снова задачу типа (ЮД) при условии, что
384
Гл. 10. Динамическое программирование 1
переменные Xj предполагаются непрерывными. Мы покажем
сейчас, какие упрощения могут быть внесены в вычислительную
процедуру, предложенную в предыдущем параграфе, если функ-
ции fj(Xj) выпуклы или вогнуты.
Сначала рассмотрим случай выпуклых функций. Прежде
всего установим, что тогда и Л&(|) являются выпуклыми функ-
циями
Доказательство проводится по индукции. Для простоты обо-
значений (и без потери общности) будем полагать все =
Очевидно, что
A,(Xg1+(l-X)g2) = max /,(*,). (10.47)
Введем обозначение = + — V)x". Изменение xt между
0 и Xgi4-(1—X)g2 эквивалентно независимому изменению х{ и х'2
соответственно между 0 и gi и между 0 и g^)- Таким образом,
(10.47) можно переписать так:
A,(4I + (l-X)g2)= max /ДЧ' + О -*)•<)• (Ю-48)
0 Xj
0 хj ^2
Однако, в силу выпуклости функции ^(х^,
A1(Xg1+(l-X)g2)< max [ХЛ(х() + (1 -1)AK)J<
<?2
max fi(^J)4-(l—ty max
<XA1(g1) + (l-X)A1(g2). (10.49)
Следовательно, Ai (g) есть выпуклая функция.
Допустим далее, что Afe-i(g) есть выпуклая функция. Дока-
жем тогда, что Afe(g) также выпукла.'Определим снова S2ft(xft,|)
соотношением (10.45). Так как Ац (g) выпукла по предположе-
нию, Afe-i(g — akxk) есть выпуклая функция от xk и g. Выпук-
лость fk(Xk) относительно Xk и g следует непосредственно из ее
выпуклости относительно Xk [добавление g не играет роли, так
) Сказанное здесь следует понимать так: для каждого xh 0-< х{ 4-
(1 — X) g2, существуют такие числа х{, х(, что 0<х, <|2,
Х!=ЛХ]4-(1 — К)х", и, обратно, если числа х{ и х" удовлетворяют соот-
ношениям 0 х\ gp 0 Xj < g2, то 0 X} = Хх[ -|- (1 — Л) х, Х|, 4-
-f- (1 — X) g2. — Прим. ред.
10.8. Случай выпуклости или вогнутости функций fj(Xj) ,?85
как fk(xh) от I не зависит]. Таким образом, £) есть вы-
пуклая функция от Xk и g. По определению
ЛДХ|1+(1 ~W== max Q^x*, X^-|-(l — Х)|2).
o<x4<^j+(i-W52
(10.50)
Используем теперь тот же прием, что и выше, и введем обозна-
чение xk = Хх'к 4- (1 — %) хк. Тогда
= max ЙДХх'+(1-Х)х;, X^l-X)^). (10.51)
- 0 ^2
Из выпуклости Qft(xft, £) следует
лй(Ч1+(1 - ад<
<% max Qfc(x',^) + (1-X) max &k(x"k, g2)<
<ХЛ,(|1) + (1-Х)Ла(|2). (Ю.52)
Итак, из выпуклости Aa-i(|) и fk(xk) следует выпуклость ЛД|).
Таким образом, по индукции получаем, что из выпуклости функ-
ций fj(Xj) следует выпуклость всех функций ЛД£).
Доказательство в точности такого же типа показывает, что
из вогнутости функций fj(Xj) следует вогнутость ЛД|).
В том случае когда все fj(Xj)—выпуклые функции, задача
исследования функции ПДх*, g) в области изменения xk, к кото-
рой сводится определение функции Aft(g), существенно упро-
щается. Выше уже показано, что Лй-iU) есть выпуклая функ-
ция от Поэтому Лй-1(| —flfcXft) есть выпуклая функция от Хн-
Следовательно, при фиксированном £ ЙДхд, £) есть выпуклая
функция от Хй, так как она представлена в виде суммы двух
выпуклых функций от хк. По определению
ЛД£) = max Q*(xt, £).
Максимум же выпуклой функции на замкнутом выпуклом мно-
жестве достигается в одной из крайних точек (§ 3.12). В нашем
случае выпуклым множеством является интервал Сле-
довательно,
ЛД&)==ЙД0, |) или ЛД|) = СШ у. (10.53)
Итак, единственное, что необходимо в данном случае, — это
вычислить при Xfe = 0 и xk = %. Наибольшая из этих двух вели-
чин есть Afe(g). В некоторых случаях и обе крайние точки могут
25 Зак. 735
386
Гл. 10. Динамическое программирование 1
дать Afe(g). Значение А&(£) может реализоваться в какой-либо
внутренней точке только в том случае, если g) не зависит
от Таким образом, приведенные выше результаты показы-
вают, что в случае выпуклости функций fj(Xj) решение постав-
ленной задачи существенно упрощается, так как для определе-
ния Afe(g) нет необходимости выполнять перебор по xk. Изуче-
нию подлежат лишь точки xk~0 и xfe==g.
В случае вогнутости функций fj(Xj) вычислительные трудно-
сти снижаются не так значительно, как в случае выпуклости, но
тем не менее иногда довольно существенно.
Если все fj(Xj) —вогнутые функции, то Qk(Xk, £) есть вогну-
тая функция от xk при фиксированном g, и, следовательно
(§ 3.12), всякий ее относительный максимум является также
глобальным максимумом. В этом случае снова представляется
возможным вначале использовать сетку с относительно боль-
шим шагом. Если значение ё) начинает убывать при из-
менении xk вправо от нуля, то сразу же ясно, что Afe(g) = Qfe(0, g)
и дальнейший поиск не нужен. Если же Qk(Xk,%) начинает воз-
растать, определяется изменение при изменении Xk до тех
пор, пока не будет пройден относительный максимум (измене-
ние Qfe становится отрицательным). Просмотр оставшейся части
интервала становится не нужным, в окрестности же относитель-
ного максимума дальнейший поиск осуществляется с помощью
сетки с более мелким шагом. При этом используется тот факт,
что двух изолированных строгих относительных максимумов в
рассматриваемом случае быть не может. В том случае когда
все Qfe — строго вогнутые функции или когда они вогнуты, но не
представляет интереса отыскание всех относительных экстрему-
мов, вычислительная процедура может быть сделана еще более
эффективной, чем только что описанная. В упражнении 10.30
рассматривается как раз такой, более эффективный подход.
Ранее мы уже отметили, что даже если все Л^(|) непре-
рывны, отсюда не следует непрерывность функций х&(|). Од-
нако если все fj(Xj) и, следовательно, g) вогнуты, то
Xk(l) непрерывны. Читателю будет предложено доказать это
в упражнении 10.13. Если все xh(%) непрерывны, то мы можем
табулировать эти функции с помощью той же сетки, что и
Afe(g). Чтобы вычислить xk(l) в промежуточных точках, исполь-
зуется интерполяция. Это означает, что нет необходимости вы-
числять х* непосредственно, как в случае разрывных функций,
а вычисления в обратном направлении для определения x*k мо-
гут быть осуществлены с помощью интерполяции по таблицам
х&(£). Есть и другое преимущество, обеспечиваемое непрерыв-
10,10. Простая задача об использовании рабочей силы
387
ностью функций Если Л&(£) и Л(^) уже определены, при
вычислении Л&(£ + Д£) мы можем воспользоваться тем свой-
ством, что при малых величина xk(l+&l) должна быть близ-
ка к Xfe(g). Таким образом, чтобы определить х1(£+Д|) и
Ль(£+Д£)> следует просматривать Qfe(xfe, £ + Д£) только в окрест-
ности точки Xfc(g). Это также часто позволяет снизить вычисли-
тельные трудности.
10.9. Детерминированные задачи последовательного приня-
тия решений. При обсуждении в этой главе различных форм за-
дач распределения не играло никакой роли название перемен-
ных. При решении задач мы могли рассматривать любой шаг в
качестве первого, т. е. отсутствовала специальная временная
последовательность, учитываемая при осуществлении распреде-
ления между различными способами производства. Все Xj
могли быть выбраны одновременно или в любой последователь-
ности, и это не оказывало никакого влияния на их оптимальные
значения.
Однако многие задачи имеют структуру, требующую, чтобы
решения принимались в определенной временной последова-
тельности. Такие задачи могут также рассматриваться как
многошаговые процессы принятия решений, и для них суще-
ственен определенный порядок, в котором должны приниматься
решения, т. е. х{ и Xj при i=£j, вообще говоря, нельзя менять
местами.
Для детерминированных задач последовательного принятия
решений имеется возможность выбора между двумя способами
решения, называемыми в дальнейшем решениями в прямом и
обратном направлениях. При решении в прямом направлении
первый шаг соответствует первому принимаемому решению, в то
время как при решении в обратном направлении первый шаг
схемы динамического программирования соответствует послед-
нему (во времени) принимаемому решению. Вопрос о выборе
первого или второго способа часто зависит от того, заданы ли
некоторые параметры задачи в начале или в конце процесса
(или и в начале, и В конце). В следующем параграфе мы
приведем пример, поясняющий специфику обоих типов решений.
10.10. Простая задача об использовании рабочей силы. Пред-
принимателю нужно определить оптимальное число работников
в каждый из п месяцев. Производственные задания для этих
месяцев известны. Допустим, что в /-й месяц идеальное
число рабочих, нужных для выполнения работ, равно mj. Если
предприниматель может увольнять и нанимать рабочих без вся-
ких затрат, тогда он должен просто использовать в этом
25*
388
Гл. 10. Динамическое программирование I
месяце человек. Однако на самом деле затраты по найму и
увольнению весьма осязаемы, и, следовательно, может ока-
заться невыгодным использовать в точности rrij человек в
/-й месяц. Мы будем предполагать, что работа /-го месяца мо-
жет быть выполнена и меньшим чем mj числом рабочих при
работе сверхурочно. Пусть Xj есть число рабочих, используемых
в j-й месяц. Затраты по изменению численности рабочей силы
при переходе от (/—1)-го к /-му месяцу есть /Дх,—Xj-i). В за-
висимости от знака разности эта функция определяет
затраты по найму или увольнению. Если число работников не
меняется, то эти затраты равны нулю, т. е. /ДО) =0.
Отклонение числа работников от идеального для данного
месяца приводит к затратам gj(Xj— т^). Если Xj>mj, то это за-
траты на содержание неработающих работников, в противном
случае — на сверхурочные работы. При Xj — rrij будем полагать
gj(O)=O. В начальный момент (нулевой месяц) число работни-
ков равно т0.
Оптимальные значения xj— это неотрицательные целые чис-
ла, минимизирующие выражение
п
2=3 — *j-i) + gj(Xj~m,)], (10.54)
где Хо = /Ио. Важно дтметить, что число работников задано толь-
ко для нулевого месяца, в то время как с (п+1)-м месяцем не
связаны никакие ограничения.
Приступим к выводу рекуррентных соотношений, которые
могут быть использованы для решения задачи. Можно записать
г= — mo)4~£i(*i —
п
+ х 3 [fj + Sj (*; — mj)]}
и
min S [/7(Xj - 4- gj (xj —m,)} =
хг..xn '“2
= min j f 2 (x2 — *i) 4- g2 (x2 — m2) 4-
n '
-b min 2 [f} (Xj — Xj-J + gj (Xj — my)| I.
x3,xn /-3 J
10.10. Простая задача об использовании рабочей силы 389
Этот процесс может быть продолжен очевидным образом. Он
указывает на целесообразность определения последовательно-
сти функций
Aft(|) = min 2 — х7._1) + ^.(лу — ntj)],
xk' •••’ xn i"*
Л—1, 2, ...,ra, (10.55)
где Xfe_i=g и минимум берется по неотрицательным целым чис-
лам. Тогда z* = Ai(m0) и
л« (0 == min [f„ (хп — l) + gn (хп — тя)], (10.56)
хп
(I) = min [/* (xk — |) + gk (xk — mk) + Aft+1 (x*)],
xk
A = l, 2, ..., n— 1. (10.57)
Проводя вычисления, мы будем одновременно табулировать
значения а(^), реализующие А&(£). На последнем шаге опре-
делится х*. Остальные х* находятся из соотношения
4 = ^(4-1)- . (10-58)
Для рассматриваемой задачи функция состояния Afe(g) пред-
ставляет собой минимальные затраты за месяцы от k-ro до
n-го включительно, если количество работников в (k— 1)-й ме-
сяц равно Отметим, что в этой задаче мы применяем решение
в обратном направлении. Оно начинается с отыскания опти-
мальной численности рабочих в n-й месяц при различных чис-
ленностях в (п—1)-й месяц. Затем выполняется то же самое
для (и—1)-го месяца. На последнем шаге определится опти-
мальное число работников в первый месяц при условии, что
перед этими численность их была равна т0. Здесь решение в
обратном направлении особенно удобно, так как ничего не из-
вестно о числе рабочих в (п+1)-й месяц, тогда как их число в
начале пррцесса задано и равно mQ.
Рассмотрим теперь случай, когда кроме задано число ра-
бочих mn+i в (п + 1)-й месяц (идеальное число рабочие в этот
месяц). На этот раз мы будем искать неотрицательные целые
числа Xj, доставляющие минимум выражению
г = s И, (Xj — Xj_i) + gj (Xj — nij)} + f„+1 (ma+1 — X,), (10.59)
390
Гл. 10. Динамическое программирование I
где х0 = W Здесь можно записать
z = min I f я+1 (/ип+1 — х„) +
Ж" *
+ min 2 [//(-«у — Xj-x) + gj(x}— (10.60)
Определим последовательность функций состояния
Aj(£)= min Ий+1(| — **) + g*+i(& ^»+i) +
xi...хь\
+ SIM*; — xi-J + gj(Xj — k=\, 2, .... n, (10.61)
где XQ — m^ и минимум берется по неотрицательным целым
числам хг, х2, ..., xk. Тогда
Л1 (£) = min (f2 (I — *i) + gi (1 — ^) + fi (*i — +- gi (*i - mi)}
(10.62)
И
л* (£) = min {fft+1 (I — xk) + gk+i (I — mk+1) 4- Aft_j (xft)},
xk
£ = 2, 3, n. (10.63)
Окончательно z* — Xn (тЛ+1).
Здесь приведено решение в прямом направлении. В этом
случае функция состояния Лй(£) есть минимальные затраты в
течение первых &+1 периодов при условии, что численность
рабочей силы в (&+1)-й период равна Таким образом, пара-
метр состояния | есть численность рабочей силы в период &+1.
Мы могли использовать решение в прямом направлении,
даже если бы не была задана численность рабочей силы в
(п+1)-й месяц. Следовало бы просто определить минимальные
затраты для каждого возможного в (п+1)-й период числа ра-
бочих. Оптимальной численностью окажется та, которой соот-'
ветствует наименьшая из всех минимальных затрат. Или, иначе
говоря, следует вычислить An-i(?) при всех а х* есть то зна-
чение которое минимизирует An-i (?).
Каждый из описанных двух способов решения имеет свои
достоинства и недостатки, определяющие всякий раз, какой из
них следует выбирать. Например, если желательно провести
исследование устойчивости решения относительно /п0, то, оче-
видно, предпочтительнее использовать решение в обратном на-
правлении, так как в этом случае на последнем шаге вычис-
ляется Ai(m0), что позволяет ценой небольших дополнительных
усилий решить задачу для целого набора значений т0. Это не
10.11. Детерминированные задачи создания запасов
391
может быть сделано с помощью решения в прямом направлении
(почему?). С другой стороны, при анализе устойчивости реше-
ния относительно mn+i решение в прямом направлении обладает
рядом преимуществ.
Возможно, что интерес представляет и длина планируемого
интервала, т. е. число п включенных в расчеты месяцев, влияю-
щее на решение о численности рабочей силы в первые несколь-
ко месяцев. В этом случае очень удобно использовать решение
в прямом направлении, так как добавочные месяцы в нем учи-
тываются аддитивно.
10.11. Детерминированные задачи создания запасов. Пусть
имеется предприятие, которое производит партиями некоторые
изделия. Оно является субподрядчиком крупной фирмы, произ-
водящей приборы, и обычно получает от нее месячные заказы
за 8—9 месяцев до срока их отгрузки. Предприятие всегда мо-
жет, если это ему удобно, выполнять заказ в тот месяц, когда
он должен быть отгружен. Однако, так как размеры заказов
значительно меняются от месяца к месяцу, это приведет к
сильной неравномерности загрузки предприятия. Иногда оказы-
вается лучше выполнить одной партией заказы нескольких ме-
сяцев, а затем хранить изделия, пока они не потребуются.
Предположим, что предприятие пытается спланировать раз-
меры производства на ближайшие п месяцев. Каждый месяц
может выпускаться не более одной партии изделий. Пусть dj есть
число изделий, которые должны быть отгружены в конце
месяца /, Xj — число изделий, произведенных в месяц /, и —
величина запаса в начале месяца / (это число не содержит из-
делий, произведенных в /-й месяц). Затраты в /-й месяц на
выпуск партии размером Xj определяются формулой Д^ + СДх;-),
где Aj — постоянные затраты на выпуск партии, а СД0)=0.
Затраты по хранению запаса в j-м месяце есть функция от
yj+Xj и равны gj(yj+Xj). Пока мы не будем останавливаться
на точном виде функций gj. Можно записать
f j (xj> У1) = aj [Д/ (xj) + SjiHj + </)], (10.64)
где aj может интерпретироваться как коэффициент эффектив-
ности капитальных вложений, a Sj = O, если = и 6j=l, если
Xj>0. Тогда для данных значений Xj суммарные затраты на
планируемый период равны
п
(Ю-65)
392 Гл. 10. Динамическое программирование I
Будем считать, что величина запаса ух задана. Значение yn+i
может быть либо заданным, либо свободным. Значения у$ и Xj
» связаны следующими уравнениями материального баланса:
У^ + Х; — (^ = У; + 1, /=1, 2, .... П. (10.66)
Будем предполагать, естественно, что заказы в каждый ме-
сяц должны быть удовлетворены. При этих условиях мы хотим
определить неотрицательные целые числа xj, которые удовле-
творяют условиям (10.66) и минимизируют выражение (10.65).
Эта задача может рассматриваться как n-шаговый процесс при-
нятия решений, где решение, принимаемое на /-м шаге, состоит
в выборе величины х^ Параметром состояния для каждого
шага может быть либо начальная, либо конечная величина за-
пасов.
Поставленная выше задача может быть решена средствами
динамического программирования. Сначала мы проиллюстри-
руем решение в обратном направлении. Для определенности
рассмотрим случай, когда конечный запас в n-й месяц не фик-
сирован.
Определим последовательность функций состояния
п
ЛА(|)== min s fjlXj, у}), k=\, 2, .... п, (10.67)
xk> --•> хп
где минимум берется по неотрицательным целым числам х$.
Параметры yj должны удовлетворять уравнениям (10.66) и
условию = Таким образом, функция состояния А&(£) выра-
жает минимальные затраты за месяцы k, ..., и, если имею-
щийся в начале &-го месяца запас равен £. Отметим, что
п
min .
k+V •••’ ХП + 1
Л* (В) = min fk(xk, в) 4-
xk _
2 у}) , k^n. (10.68)
Величина запаса в начале (£-|-1)-го периода равна dk.
Следовательно,
(I) — min [fs (х*> I) + Л*+i (В + xk — </*)],
xk '
k=l, 2, ..., га—1. 00.69)
Окончательно
Лл(£)= minf„(x„, В) (Ю.70) *
Х„
п
и г*=Л1(у1). Кроме табулирования Лл(В), табулируются также Й
значения х*(В)> доставляющие Л0|). На последнем шаге вы-
10.11. Детерминированные задачи создания запасов
393
числяется х*. Остальные х*к находятся из формулы
S-1
k — 2, 3, ..., п.
(10.71)
Аргумент Xk есть величина наличного запаса в начале
k-ro периода. При фактическом решении задач такого типа на
вычислительной машине следует заранее решить, для какой об-
ласти значений § должна вычисляться каждая функция Afc(i).
В качестве наибольшего £ можно было бы выбрать максималь-
ный разумный запас, который можно было бы иметь в начале
£-го месяца. Размеры таблиц функций A*(g) имеют тенденцию
уменьшаться или оставаться неизменными по мере приближе-
ния к концу планируемого периода.
Проиллюстрируем теперь решение в прямом направлении
при условии, что кроме у\ задана еще величина уп+\- Параметр
состояния в Ай(£) выражает в этом случае наличный запас
в конце k-ro месяца. Снова определим последовательность
функций
ЛА(|)= min у}), k = \, 2, .... п, (10.72)
...хк 7=1
где минимум берется по неотрицательным целым х$ при усло-
вии, что ^+1 = В (т. е. — = а остальные у$ связаны
соотношениями (10.66). Тогда
г < fe-i п
Afc(£) = min fk(xk, yft)4- min 5 fj(xj> У,) •
xk L xi...xk-i 7=1 J
Если величина запаса в конце k-ro месяца равна g, то в конце
(k—1)-го месяца она равна %+dk— Xk- Таким образом,
Лй(£)= min[fj(xk, B + — хЛ)],
xk
k = 2,...,n (10.73)
и
A1(|) = minf1(x1, z/O, f/i-t-Xj — =
Только одно значение Xf удовлетворяет ограничению, следова-
тельно,
Ml) = fdl + d1-y1,y1). (10.74)
На последнем шаге определяется х*; остальные х*к находятся
по формуле
Хк— Хк
п
Уа+1 + 2 (dj — X*)
* J "Г *
k = 1, 2, .... п—1. (10.75)
394
Гл. 10. Динамическое программирование I
Итак, оба способа решения могут быть применены к поста- |
вленной задаче. Если функции затрат, входящие в задачу, |
имеют особенно простой вид, можно использовать гораздо бо- ;
лее эффективную вычислительную схему, чем приведенная
выше. Мы обсудим этот вопрос в следующем параграфе.
*
10.12. Случай, когда/ДА^у/)--вогнутые функции. Рассмо-
трим упрощения, которые допускает вычислительная схема
предыдущего параграфа, если все fj(Xj,yj) являются вогнутыми
функциями непрерывных переменных Xj и yj. Вначале опреде-
лим более точно вид этих функций. По сделанному ранее пред-
положению fj может быть записана в виде (10.64), где СД0)=0.
Отметим, что Ajfy есть вогнутая функция от Xj. Допустим те-
перь, что и Cj(Xj) есть вогнутая функция от Xj, так что средние I
единичные затраты убывают или остаются неизменными с
ростом Xj. Рассмотрим затраты на хранение в j-и период, кото-
рые были обозначены в (10.64) через gj(yj + Xj). Чтобы полу- V
чить явное выражение этой функции, сделаем несколько до-
бавочных предположений. Прежде всего будем пренебрегать |
временем, необходимым для изготовления изделий. Будем пред* |,
полагать, иными словами, что если Xj единиц должны быть |:
произведены в j-м месяце, то они изготавливаются в его начале,
и вся партия попадает в запас в самом начале месяца.
Относительно заказов будем предполагать, что они подчи- |!
йены некоторому детерминированному закону.. При этом вели- |
чина спроса может меняться внутри периода. Предположим, что |
затраты на хранение в любой момент t /-го периода пропорцио- Д
нальны с коэффициентом пропорциональности Kj величине за-
паса, имеющегося в этот момент. Скорость изменения потока 1
заказов задается функцией Это означает, что величина
запаса в момент t j-va периода равна
t
х)^-Уг~ f W}dt.
V
где время отсчитывается от начала /-го периода, а заказы счи-
таются непрерывными. Затраты на хранение в /-й период, та-
-ки.м образом, выражаются формулой
(10.76)
где Tj есть длительность j-го периода. Чтобы упростить выра-
жение (10.76), удобно ввести обозначение yt+x^Xj+yj — dj для
10.12. Случай, когда fj(Xj, уj) — вогнутые функции 39S
величины запаса в конце /-го периода. Тогда (10.76) примет вид
Выражение
с
d}— $ %(t)dt dt,
(10.78)
о _ о
есть просто затраты на хранение в j-м периоде изделий, затре-
бованных в этом же периоде. Эти затраты не зависят от Xj, и,
следовательно, их можно не включать в целевую функцию. Та-
ким образом, оптимальные значения х,- могут быть найдены без
включения затрат (10.78). С другой стороны, величина K.jTjt/j+i
есть просто затраты в j-м периоде на хранение изделий, имею-
щихся к началу (/+1)-го периода. Только эти затраты на хра-
нение мы и должны рассматривать в /-й период. Общее выра-
жение для функции затрат /-го периода приобретает вид
(10.79)
где fj есть функция от xj и z/J+i. В дальнейшем будет показано,
что если Cj(Xj) —вогнутая функция и а^>0, то и fj будет во-
гнутой функцией от Xj и Прй этом
* = (10.80)
будет вогнутой функцией всех своих переменных. Мы хотим
найти неотрицательные Xj и которые минимизируют выраже-
ние (10.80) при ограничениях
t/y + xr-yy+1 = i//, /=1, .... п. (10.81)
Будем предполагать при этом, что у\ и yn+i заданы.
Прежде чем рассматривать упрощенную процедуру решения,
будет полезно отметить, что изучаемую модель можно истолко-
вать иначе, чем в предыдущем параграфе. Мы можем предста-
вить себе, что решается задача об отыскании оптимальной
политики в задаче создания запасов на ближайшие п периодов.
Предполагается, что закупки производятся лишь в начале перио-
дов. Допускается, что скорость изменения спроса есть известная
детерминированная функция времени Х(£). Все требования в
данный период должны быть удовлетворены. Желательно
396
Гл. 10. Динамическое программирование 1
определить время и размеры заказов так, чтобы минимизиро-
вать суммарные затраты по хранению и закупке изделий.
Теперь приступим к рассмотрению процедуры решения. Ми-
нимизируется вогнутая функция на выпуклом множестве. Мы
знаем, что в этом случае по крайней мере одна крайняя точка
множества допустимых решений будет оптимальной. Отметим
сразу же, что имеется п ограничений. Таким образом, известно,
что имеется оптимальное решение не более чем с п положитель-
ными переменными из множества xj, /= 1, 2,..., n; r/j, / = 2,... ,п.
Однако в каждый период либо Xj, либо должно быть поло-
жительным (если спрос в этот период не равен нулю), так как
по предположению все требования удовлетворяются из запаса.
Пусть теперь у\ = 0. Это означает, что, когда поступает пер-
вый заказ, величина запаса равна нулю. В этом случае не
существует периода, в котором бы одновременно выполнялись
неравенства х^>0 и z/j>0, ибо если бы это было не так, решение
содержало бы, вообще говоря, более п положительных перемен-
ных. Таким образом, существует оптимальное решение, удовле-
творяющее условию, что либо Xj>0, либо z/j>0, но не оба. Это
свойство можно выразить условием XjZ/j = O, /=1,2, ...,п.
Смысл этого свойства оптимального решения состоит в том, что
заказ никогда не поступает в начале периода, если имеется не-
который запас, и, наоборот, в начале периода никогда нет за-
паса, если в это время поступает заказ.
Читатель заметит, конечно, что эти аргументы оказываются
несостоятельными, если в некоторый период k спрос равен нулю,
так как тогда Х/г и у^ оба могут быть равны нулю, а это делает
возможным положительность и Xj, и yj в некоторый другой пе-
риод.
Если в k-м периоде оптимальным оказывается Хй = г/ь = 0, то
можно разбить задачу на две отдельные подзадачи, из которых
одна содержит периоды до &-го, а другая — после &-го. Приве-
денные выше аргументы можно применить к этим задачам и
заключить, что Х;^ = 0, j4=k. Следовательно, всегда справед-
ливо, что Xj//j = O. Отсюда немедленно следует, что если
Г1
j K(t)dt
О
есть спрос в /-й период, то
Ху = 0, или dj. или + или ••• или ••• + ^л + //л+ь
так что заказываемое количество будет равно спросу за целое
число периодов. Кроме того, если заказ, прибывающий в начале
10.12. Случай, когда f j(xjf уj)—вогнутые функции
397
/-го периода, удовлетворяет спрос от /-го периода до k-ro, сле-
дующий заказ не прибудет до начала ft-го периода.
Пусть теперь производится решение в прямом направлении,
и пусть Л&(|)—минимальные затраты в течение первых k пе-
риодов, если запас в конце ft-го равен g. Если величина запаса
в конце ft-го периода равна £, то оптимальная стратегия управ-
ления системой в первые k периодов обладает следующим свой-
ством: заказ, удовлетворяющий спрос ft-го периода, прибывает
в начале Лго периода (bCft) и удовлетворяет требования перио-
дов i, /4-1, ..., ft. Помимо этого, величина запаса уг в начале
i-го периода (перед прибытием заказа) равна нулю. Стратегия
обладает также тем свойством, что оптимальные значения
Xj, / = 1,2, ..., i — 1, будут теми же, что и в задаче, где имеется
только i—1 периодов и величина запаса в конце последнего из
них равна нулю. Это следует непосредственно из рекуррентных
соотношений. В силу (10.73)
ЛА G) = min [f* (xk, I) + ЛА_! (I + dk - xA)J. (10.82)
xk
Однако, так как xkyk = 0,
Л* (£) = min
fk(l + dk, D + A^CO),
(10.83)
Но
Л /.1,74 , J + l + rfft) + Aft_2(0),
Л.-.Й+ ".)=">">{ + + + + <I0'84>
и т. д. Таким образом, оптимальная стратегия имеет указанную
выше форму и
Лй(У = тШГй(0. (10.85)
где i принимает значения 1, 2, ..., k, и
А / & \
кй(/)= 2 fj о, 1+ 2 da +
(k k \
1+2^Л + 2 +А/-1(°) (10.86)
u^i u=i+l /
при условии, что Л0(0) = 0.
Отметим, что для вычисления Ла(?) нам требуется лишь
ЛД0), /=1, ..., ft—1. Следовательно, нам никогда не потре-
буется вычислять для %, отличных от нуля, исключая, воз-
можно, последний шаг, где потребуется An(//n+i). Таким обра-
зом, вместо целой таблицы на каждом шаге требуется лишь
одно значение Ла. Итак, решение задачи приведено к такой
398
Гл. 10. Динамическое программирование 1
форме, которая требует существенно меньших вычислений, чем
непосредственное применение метода динамического программи-
рования.
Особый интерес представляет частный случай, когда Cj(Xj) =
= Cxj, где С — постоянная, и а,= 1. Тогда общие затраты по
хранению равны
(п
Уп+1~^г 2
/=1
и не зависят от переменных Xj. Следовательно, в этом случае
задача упрощается и приводится к отысканию неотрицательных
чисел Xj, минимизирующих выражение
4
i
п
z = 2j ,у/+1)
(10.87)
при ограничениях (10.81) и #1=0. Здесь Hj=KjTj. Если £ = 0,
У*(0, определяемое выражением (10.86), принимает вид
к
А-1
= н, 2 dw +лг_1(0).
/=/L w===/+1
(10.88)
Оказывается, что в этом случае можно сделать еще одно
упрощение в вычислительной схеме. Можно показать, что если
при вычислении Л^ДО) оказалось, что заказ, с помощью кото-
рого удовлетворяется спрос в периоде k—1, должен поступить
в начале периода v, то при вычислении Л&(0) заказ, предназна-
ченный для удовлетворения спроса в периоде kt должен посту-
пить в начале периода v или позже. Упрощение состоит в том,
что при вычислении А&(0), определяя минимум в (10.85), нет
необходимости рассматривать Z<v. Докажем это методом от
противного. Допустим, что
л-i г k л
Лй(0) = ГИ«) = Л + 2 Hj 2 dw H-A^OXF^), (10.89)
j — U L
когда
лл_1(0)=к»_1
k—2 Г k-Л
(г>) = Л+2 Hj 2 dw +A,_1(0) (10.90)
L w=/+l
j-v
и v>u. Если затраты на хранение от и-го до k-ro периода из-
делий, предназначенных для удовлетворения спроса k-ro пе-
риода, вынести за скобки в Ал (0), то получим
к-1
ЛА (0)=dk 2 Hj+у„_, («)=ук («).
i-ч
(10.91)
10.13. Пример
399
Но
/г-1
+ (Ю.92)
j=v
Вычитая Yk(v) из Лй(0), находим
Aft(0)-rft(^)=^ 2 //7+r,_1(«)-rfe_1(^)>0,
/=«
так как по предположению
^-1(«)>Г,_1(г») = Лй_1(0)
0—1
и dk 2 #/>0. Мы приходим к противоречию.
j~u
Вычислительная схема для модели, в которой Cj(xJ =
= Cxj, aj=l, была впервые разработана Вагнером и Уити-
ном [17]. В табл. 10.3 показана форма вычислений, которую
удобно использовать в этом случае. В последней строке в скоб-
ки заключены номера тех периодов, для которых спрос удовле-
творяется заказом, поступающим в начале, первого из них. Эта
таблица содержит результаты, получаемые при решении типич-
ной задачи. Звездочки над Yk(i) указывают на то, что это
значение является минимальным по z, т. е. равно Ль(0). В лите-
ратуре эта модель часто упоминается как динамическая модель
выбора объема партии, так как ее можно рассматривать в ка-
честве динамического варианта простой модели выбора объема
партии в теории создания запасов.
10.13. Пример. В § 4.11 мы рассмотрели задачу линейного
программирования с фиксированными затратами, представляю-
щую собой пример задачи того типа, который изучался в преды-
дущем параграфе. Она заключалась в определении чисел х7>0,
минимизирующих выражение
7 7
г = 300 2б, + 2 2У/
/=1 №
при условии, что
x1 — y2==dl = 9Q; yj-Yxj — yj+^dj,
j = 2, 3, ..., 6; у~Ху=::= 130,
где d2=125, rf3=140, d4= 100, ds = 45 и d6=60. В гл. 4 мы уста-
новили, что эта задача имеет много локальных минимумов и
рассматривавшиеся там методы не позволяли найти абсолют-
ный минимум. Теперь мы решим эту задачу и покажем, как
было получено оптимальное решение, приведенное в гл. 4.
Таблица 10.3
Таблица для расчета динамической модели
Периоды 1 2 3 4 n — 1 n
Спрос ^3 dA . . . ’d n
Yk (?) i 1 r’(D ^(1) . . .
2 Г2(2) *1(2) Kj(2) . . .
3 Г3(3) Г4(3) . . .
4 Г4(4) . . .
• •
п —1 1 1
Aft (°) Moj-r.a) Л2(0)=Г2(1) Лз(0)=Г3(2) А4(0)=У4(2) Лл_1 (0) = K„_! («—1) Лл(0) = Гя(п-1)
* хк о) (1) (2) (1) (2, 3) (1) (2, 3, 4) (1)(2, 3, 4) (5...) (1) (2. 3, 4) (5...)... (n— 1, n)
10.14. Функциональные уравнения
401
Из соотношений (10.85) и (10.88) следует, что
Aj (0) = 300,
Л2 (0) — min
300 + + (0) =600)
300 + 2(125) = 550 J U'
Таким образом, при наличии только двух периодов и нулевом
запасе в конце второго периода выгодно иметь поставку в на-
чале первого периода, удовлетворяющую потребности обоих
периодов. Далее
Л3 (0) — min
300 + Л2(0) = 850
300 + 2 (140) + Л! (0) = 880
300 + 2 (140)+ 2 (140 +125) = 1110
= 850
Результаты остальных вычислений приведены в табл. 10.4.
Единственное оптимальное решение получается следующим:
z*=1770, х; = 215, х; = 0, х; = 240, х* = 0,
<=105, < = 0, <=130.
5 ’ о ’ 7
Это и есть то решение, которое фигурировало в гл. 4.
10.14. Функциональные уравнения для систем с бесконечным
числом шагов. В последних двух параграфах была рассмотрена
простая детерминированная задача о создании запасов, в кото-
рой уровень спроса на запасаемые предметы может меняться со
временем. Мы интересовались определением оптимальной поли-
тики поставок в течение п периодов при условии, что поставки
могли осуществляться только в начале периода. Изучим теперь
несколько иную детерминированную задачу о создании запасов.
Будем считать, что скорость изменения спроса не зависит от
времени и равна %. Мы также будем полагать, что не может
быть потребности в двух единицах продукта одновременно. Та-
ким образом, время между последующими требованиями есть
Д/=1Д. Пусть эта система может функционировать неограни-
ченно долго и после каждого очередного требования следует
решать, делать или не делать заказ. При этом налагается огра-
ничение, состоящее в том, что всякое требование должно удов-
летворяться. Это ограничение представляется разумным, по-
скольку моменты требований по предположению детерминиро-
ваны.
Обозначим через А фиксированные затраты на заказ, а че-
рез С — стоимость единицы продукта. Предполагается, что цена
не зависит от числа заказываемых единиц, так что стоимость
26- Зак. 735
402
Гл. 10. Динамическое программирование I
Таблица 10.4
Решение примера
Периоды 1 2 3 4 5 6 7
Спрос 90 125 140 100 45 60 130
У» (D i 300* 550* 1110 -
1
2 600 880
3 850* 1050* 1230* 1590
4 - 1150 1240 1480
5 1350 1470 * 1990
6 1530 1790
7 1770*
М (0) 300 550 850 1050 1230 1470 1770
4 (1) (1, 2) (1, 2) (3) (1, 2) (3, 4) (1, 2) (3, 4, 5,) (1, 2) (3, 4) (5, 6) (1, 2) (3, 4) (5, 6) (7)
х единиц составляет Сх. Затраты на хранение будем считать
пропорциональными величине запаса и коэффициент пропор-
циональности обозначим через К. Время между заказом и его
поставкой предполагается постоянным и равным т. Величины Д,
С, К и т по предположению не зависят от времени.
Пусть требование поступило в момент t. Сразу же после
этого следует решить, нужно ли делать заказ для пополнения
запаса, и если да, то какова величина этого заказа. Предполо-
жим, что моменты, в которые делаются заказы, и размеры за-
казов выбираются так, чтобы минимизировать затраты на заказ
и его хранение на все будущее время.
Прежде всего отметим, что все затраты на хранение за ин-
тервал времени между t и t+x не зависят от решения, прини-
маемого в момент t и всех будущих решений, так как заказ,
сделанный в момент /, не может быть выполнен до момента
t+X, Таким образом, эти затраты не должны включаться в об-
10,14. Функциональные уравнения
403
щее выражение затрат. Включать их следует лишь с момента
/+т. Далее заметим, что величину запаса в момент t+x можно
вычислить непосредственно, если известна его величина и объем
заказа в момент Л
Пусть g— имеющееся перед принятием решения количество
единиц продукта плюс величина заказа в момент /, после того,
как поступило требование. Через х>0 обозначим величину за-
каза. Таким образом, g+x есть величина имеющегося запаса
плюс заказанное количество после того, как решение принято.
Так как все без исключения требования удовлетворяются из
запаса и так как все заказанное в момент t и до него постав-
ляется к моменту /+т, можно заключить, что величина запаса
в момент /+т равна g+x —т, где т есть наибольшее целое
число, не превосходящее Лт. Иными словами, за время между
заказом и его получением потребуется т единиц продукта. Сле-
дующая единица продукта потребуется в момент (т+1)Д/, т. е.
через время (т+1)Д/ — т после того, как поступит заказанное
в момент времени А Таким образом, в интервале времени между
t+x и /+т+Д/ величина запаса равна g + x — m в течение про-
межутка времени длины (т+1)Д/—т и g + x — т— 1 в течение
т+Дт—(т+1)Д£=т—тДЛ Затраты на хранение, f(g+x), для
интервала времени между t+x и /+т+Д/ выражаются следую-
щим образом:
/ (I + X) = К {(g + х — т) {{т +1) Ы — т] +
-J-(g-(-x— т—1)(т— т№)} =
= — — — (10.93)
Так как мы хотим, чтобы величина запаса в момент, когда по-
ступает требование, была ненулевой, необходимо наложить
условие g+x>m+l. Чтобы оно выполнялось автоматически,
положим f (g+x) =оо при g+x</n+1.
Смысл других величин, введенных выше, проиллюстрирован
на рис. 10.4. Отметим, что затраты на хранение в интервале вре-
мени между моментами /+т и /+т+Д/ зависят только от g+x.
Пусть 0 есть коэффициент скидки, позволяющий пересчитать
затраты между моментами /+т и /+т + Д^ к моменту t, а а —
аналогичный коэффициент, приводящий затраты в момент t + &t
к моменту t. Обозначим через Az(g) приведенную к моменту t
суммарную величину всех будущих затрат, если оптимальная
политика заказов используется в момент t и все последующие
моменты времени (затраты на хранение за интервал времени
от t до /+тсюда не включены). Аналогично через A/+4/(g) обо-
значим приведенную к моменту / +Д/ величину всех последую-
щих затрат, если с момента / + Д/ принимаются оптимальные
26*
404 Гл. 10. Динамическое программирование I
решения и затраты на хранение в интервале времени от /+Д/
до / + Д/+т не учитываются. Если tjj есть величина запаса в мо-
мент t+j\t после поступления требования, но перед принятием
решения о размере заказа, Xj есть размер заказа, z/o = S> *о = х
Рис. 10.4. |
и f(yj+Xj)—затраты на хранение в интервале времени между У
/+/Д/+т и /+ (/+1)А/+х приведенные к моменту t, то
оо
min + + + (10.94) J
jf, Xj, ••• y=0
CO 4
A/+a/G) = min 2ay_I[Ady + Cxy + f(i/y+xy)]. (10.95) 4
X\t x2, ... J«=l
Следовательно,
A^) = min{Ad+Cx+f (£+*) +
+a min 2a^-I[Ad
x2, ... j-l
где Ц-х—1 есть величина запаса плюс заказанное до при-
нятия решения в момент времени /~|-Д/.
Используя теперь определение Лг+Дг(В), имеем
A/(^) = min{AdH-Cx + f(| +-х) + аЛ/+д/(£ + х—1)}. (10.96)
X
10.14. Функциональные уравнения 405
Отметим, однако, что если в (10.95) положить u=/—1, то полу-
чим выражение (10.94), т. е.
АД^^Л^-д.а) ' (10.97)
или, более общо,
A/a) = A/+MrQ), /=1, 2, .... (10.98)
Это попросту означает, что если наличный запас плюс заказ
равен § и в текущий момент t и все последующие моменты вре-
мени используется оптимальное управление, то величина всех
будущих затрат от t не зависит, Причина этого состоит, конеч-
но, в том, что рассматривается бесконечный промежуток вре-
мени. В силу (10.98) можно убрать индекс t в выражении для
Л/(|). Тогда соотношение (10.96) примет вид
Л(у = т1п{Лд + Сх + /а+^) + «Л(^+х —1)}. (10.99)
\ х
Заметим, что одна и та же функция, но вычисленная при раз-
ных значениях аргумента, фигурирует в (10.99) в двух местах,
так что выражение (10.99) можно рассматривать как уравне-
ние, решением которого является функция Л(£). Уравнения та-
кого типа, содержащие неизвестную функцию, называются
функциональными.
Уравнение (10.99) удается решить лишь в немногих спе-
циальных случаях, однако такие функциональные уравнения
часто полезны тем, что доставляют информацию о структуре
оптимального управления. Подробнее об этом вопросе будет
сказано далее.
Рассмотрим, каким образом такая информация может быть
получена для изучаемой нами простой задачи о создании за-
пасов. Прежде всего введем удобное для дальнейшего обозна-
чение
F(£+x) = C(x + £) + f(|+x) + aA(|H-x-l). (10.100)
Тогда формула (10.99) может быть записана в виде
Aa) = -C| + min[Ad4-7^ + x)] =
= — Q+min< л+minFd+x), (10-101)
где минимум берется по неотрицательным целым %. Пусть абсо-
лютный минимум функции F(y) достигается при y = R (если
этот минимум не единствен, то R будет обозначать наименьшее
из у, при которых он достигается). Пусть также г (r<R) есть
наибольшее целое число, для которого F(r)>/1 + F(R). Тогда
406 Гл. 10. Динамическое программирование 1
из соотношения (10.101) следует, что если g лежит между R и г,
то оптимальный способ управления состоит в следующем: ни-
чего не заказывать, пока сумма уже заказанного и имеющегося
в наличии не достигнет г. В этот момент заказывается количе-
ство R— г. Таким образом, величина наличного запаса вместе
с заказанным не превосходит R и не меньше чем г.
1Аъ\ не сказали еще, что делать, если в начальный момент
g — величина наличного запаса вместе с заказанным — меньше г
или больше R. Далее будет показано, что g не может быть
меньше г. Случай же g>/? требует более детального обсужде-
ния свойств функции F(y). Отметим, однако, что, как только
величина g попадает в интервал между г и R, она не выходит
больше из него, если управление системой оптимально. Кроме
того, g никогда не принимает значение г в случае конечного
промежутка времени, так как при уменьшении запаса до г не-
медленно делается новый заказ. Говорят, что система устойчиво
управляема, если величина наличного запаса вместе с заказан-
ным меняется между г+1 и R описанным выше образом. В тео-
рии создания запасов описанный здесь способ управления назы-
вается /?г-политикой. Мы доказали, что для рассматриваемой
модели такой способ оптимален. В то же время следует отме-
тить, что приведенный анализ не дает общего метода отыскания
величин R и г. Однако для рассматриваемой задачи можно не-
медленно определить г.
Напомним, что г не может быть меньше т, так как
f(g + x)=oo при g+x<m+l. Это следует из анализа случая
g = r+l. Если r<m, то f(r+l) = оо, так что А(г+1)=оо, или,
иначе говоря, если r<m, то, когда прибудет заказ, сделанный
в момент /, окажется одно или больше неудовлетворенных тре-
бований. С другой стороны, г не может быть больше чем т, так
как затраты можно было бы уменьшить, положив г = т. Объяс-
няется это тем, что если г>/п, то к прибытию заказа, сделан-
ного при g = r, величина наличного запаса равна г—т. Эти
г—т единиц никогда не будут использоваться, откуда следует,
что их хранение ведет к неоправданным расходам. Таким об-
разом, мы заключаем, что г = т. Заказ следует делать немед-
ленно после поступившего требования, снижающего суммар-
ное количество заказанного и наличного продукта до т.
Остается открытым вопрос о вычислении R или, что равносиль-
но, величины R — r, представляющей оптимальный размер
заказа. Ответ на этот вопрос мы дадим в следующем пара-
графе.
10.15. Явное решение функционального уравнения. Если чис-
ла г и R, введенные в предыдущем параграфе, известны, то
10.15. Явное решение функционального уравнения
407
можно в явном виде решить функциональнее уравнение (10.99)
относительно Л(|) при —1. Из определения чисел г и R
следует, что Л(Я-1) = /(Я-1) + аЛ(/?-2), A(/?-2) = f(/?-2)+aA(7?-3), (10.102) (10.103)
А(г) = Л + С(/?-г) + Н/?) + аЛ(/?-1). (10.104)
Таким образом,
Л(/?-1) = И^-1) + «Н^-2) + а2Л(/?-3) =
= f(/?-l) + af(/?-2) + aV(/?-3)4-a3A(/?-4) =
R-r-l
= 2 а7-7(/?-/) + аЛ'г"1И + С(^-/-) + Н^)1 +
+ a*-rA(7?-l), (10.105)
ИЛИ
л(^-1) = 77^{«^г’,М + С(^-'-)1 +
+ 2 а7"7(^-/)+а₽"г-7(/?)}. (10.106)
Начав с формулы (10.104) и двигаясь в обратном направле-
нии, можно получить выражения для Л(|) при |=г, R—2.
Читателю будет предложено сделать это в упражнении 10.18.
Выражению (10.106) может быть дана интересная интерпре-
тация. Отметим, что система приходит в прежнее состояние
через каждые (R — г) At единиц времени. Мы будем называть
период времени длиной (R — r)At циклом. Рассмотрим ситуа-
цию, в которой цикл начинается через время At после выполне-
ния заказа, т. е. немедленно после того, как поступит требование,
снижающее суммарный запас до R—1. Следующий заказ будет
сделан через время (R — г—1)Д/ после начала цикла, и цикл
закончится с суммарным запасом R на последние At единиц
времени. При таком определении цикла выражение в скобках
в (10.106) представляет собой просто затраты на цикл, приве-
денные к началу цикла, а Л(/?— 1) есть приведенная сумма за-
трат по всем таким циклам. Заметим, что если Н выражает за-
траты на цикл, приведенные к началу цикла, то приведенные
затраты за все время равны
fi+^-'H+a4R-r)H+ ... = И,
408
Гл. 10. Динамическое программирование I
что представляет собой в точности выражение для Л(7?~ 1).
Другие значения Л(£) отличаются от Л(/?— 1) лишь тем, что
точка, выбранная в качестве начала цикла, будет другой.
Имеется несколько способов, с помощью которых можно вы-
числить R — r. Например, можно аппроксимировать систему с
бесконечным числом шагов системой с конечным числом шагов
и по мере их добавления вычислять непосредственно минимум
в выражении (10.96). После того как взято достаточно большое
число шагов, х(£) при дальнейшем добавлении шагов переста-
нет изменяться. Тогда R — r есть величина скачка, когда x(g)
меняется от нуля до некоторого конечного значения. Другой
путь состоит в использовании формулы (10.106). Точный спо-
соб определения R — r заключается в подстановке соотношения
(10.106) в (10.100) при | = г и последующем отыскании мини-
мума по x = R — г в выражении (10.101) при g = r. Еще один
приближенный способ определения R — r состоит в минимиза-
ции не приведенных затрат за все будущее время, а средних
годовых затрат. В случаях, представляющих практический ин-
терес, найденная таким образом величина R — r будет очень
мало отличаться от значения, найденного точными методами,
при условии, что время между заказами не очень велико, ска-
жем не более года.
В самом деле, имеется тесная связь между Л(|) и средними
годовыми затратами. Приближенно средние годовые затраты
равны /Л(|), где i есть годовая норма процента. Эта прибли-
женная связь имеет место при f>0. Если же норма процента
равна нулю, средние годовые затраты равны
lim/A(/?—1).
z ->о
В упражнении 10.19 читателю предлагается проверить этот
результат. В упражнении 10.20 нужно показать, что 11ш/А(|)
z->o
имеет одно и то же значение при | = г, г+1, .R—1, так что
средние годовые затраты равны Иш/Л(|) для любого из этих
Z->0
значений g. Как утверждалось выше, средние годовые затраты
могут использоваться для определения величины R—г, даже
если i довольно значительно, и эта величина будет весьма близ-
ка к той, которая получена путем минимизации Л(|).
В упражнении 10.21 читателю предлагается определить вы-
ражение для средних годовых затрат при произвольном L Ис-
пользуя его, следует предложить метод отыскания величины
R—r-
10.16. Задачи о замене оборудования
409
10.16. Задачи о замене оборудования. Одна из важных проб-
лем, с которыми приходится встречаться в промышленности,
состоит в определении оптимальной политики замены оборудо-
вания, которое может быть самым различным, от станка до
ходовой части морского танкера. По мере того как части обо-
рудования стареют, производственные затраты и затраты на
содержание оборудования обычно возрастают, тогда как про-
изводительность и продажная цена убывают. Как правило, за-
тратив достаточно много средств на эксплуатацию, деталь мож-
но использовать неограниченно долго. Тем не менее при любой
непрерывной работе всегда наступает такой момент, когда вы-
годнее купить новую деталь, чем сохранять старую. Здесь мы
рассмотрим методы определения оптимальных сроков службы
оборудования.
Обычный критерий, используемый для определения опти-
мальной политики замены оборудования, состоит в максимиза-
ции приведенной ожидаемой прибыли или минимизации приве-
денных ожидаемых затрат за некоторый промежуток времени.
С практической точки зрения минимизация затрат представ-
ляется более удобной по целому ряду причин. Во-первых, если
изделие должно обрабатываться на нескольких машинах, труд-
но определить вклад отдельной машины в общую прибыль. Во-
вторых, план выпуска часто бывает задан, и, следовательно,
полученный доход постоянен, так что максимизация прибыли
эквивалентна минимизации затрат. Наконец, потеря прибыли
из-за низкой производительности может быть учтена в форме
определенных затрат.
Будем считать, что решения о замене оборудования прини-
маются периодически, например раз в год. Предположим так-
же, что оборудование может функционировать неограниченно
долго, если тратить достаточные суммы на его реставрацию. Ре-
шение о замене оборудования основывается только на его воз-
расте и затратах, являющихся функциями возраста. Здесь не
будет рассматриваться стохастическая модель, учитывающая,
что промежутки времени между поломками оборудования слу-
чайны и после каждой поломки принимается решение о починке
или замене оборудования. Такие модели часто очень удачно
описывают функционирование некоторых видов оборудования,
но мы будем полагать, что для рассматриваемого здесь типа
оборудования индивидуальные поломки играют очень незна-
чительную роль и сами по себе не< являются оправданием для
замены. Единственной случайной величиной будут тогда эксплу-
атационные затраты на период для оборудования заданного
возраста. Мы будем минимизировать приведённые ожидаемые
затраты, для чего нам понадобится лишь использовать средние
410
Гл. 10. Динамическое программирование I
значения функций затрат. Таким образом, задача сводится к
детерминированной, в которой затратами являются средние за-
траты, упомянутые выше.
Часто в задачах о замене оборудования важным фактором,
который должен учитываться, является технический прогресс.
К сожалению, очень трудно принять его в расчет, так как ре-
зультаты технического прогресса зачастую невозможно пред-
сказать. Начнем поэтому с рассмотрения случая, когда этот
фактор не учитывается. Мы будем предполагать, что машина
всегда заменяется машиной в точности того же типа (деталь
оборудования мы тоже называем машиной, хотя она может и
не быть машиной в обычном смысле слова).
Пусть / — затраты на установку машины (эти затраты сле-
дует учитывать, так как в некоторых случаях они составляют
существенную часть общих затрат), С(/)—ожидаемые эксплу-
атационные затраты в /-й период использования, £(/)—ожи-
даемая стоимость машины, проработавшей j периодов (под ней
понимается рыночная цена минус затраты на демонтаж). Пред-
полагается, что все эти затраты одинаковы для каждой новой
купленной машины. Пусть а есть коэффициент, позволяющий
привести затраты, произведенные в конце периода, к его на-
чалу. Коэффициент о^‘ приводит затраты, произведенные в конце
/-го периода, к началу первого. Для простоты будем считать
эксплуатационные затраты отнесенными к концу периодов.
Для рассматриваемого случая обычный подход к задаче при-
водит к выводу, что, поскольку нет технического прогресса,
оптимальная стратегия должна заключаться в использовании
машины в течение N периодов и последующей замене. Вели-
чина W определяется из условия минимума приведенных затрат,
подсчитанных в предположении, что машины рассматриваемого
типа будут использоваться неограниченно долго.
Затраты на одну машину в течение N периодов, приведен-
ные к моменту покупки, имеют вид
Н= I + 2 (J) - (N),
;=i
(10.107)
а для бесконечной последовательности таких машин —
K(N) = .H + aNH+a™H + ... = —1—Н=
1 — (X
— aNS(N) . (10.108)
10.16. Задачи о замене оборудования
411
Л (g) = min
Оптимальное значение А находится просто путем вычисления
K(N) при А=1,2,... и выбора того значения N, при котором
А (А) минимально.
Рассмотрим теперь подход к той же задаче с помощью ди-
намического программирования. Будем считать, что в начале
каждого периода принимается решение о замене или дальней-
шей эксплуатации машины, используемой в настоящее время.
Пусть g есть возраст (в периодах) используемой машины к на-
чалу текущего периода, a A(g) —затраты за все будущее время,
приведенные к началу текущего периода, при условии, что в те-
кущем и всех будущих периодах принимаются оптимальные
решения. Отметим, что, поскольку планируемый промежуток
времени бесконечен, A(g) имеет одно и то же значение незави-
симо от номера периода, если возраст используемой машины
равен g. Это следует из тех же соображений, которые уже ис-
пользовались в § 10.14.
Так как мы либо оставляем уже работающую машину, либо
покупаем новую, должно быть справедливо, что
/ — S(g)4-aC(l)4-aA(l): покупка новой машины,
aC(g+l)+aA(g+l)*- эксплуатация старой машины.
(10.109)
Уравнение (10.109) —это функциональное уравнение, опреде-
ляющее A(g).
В упражнении 10.22 читателю предлагается показать, что
существует число А, такое, что если g^A, то оптимальная стра-
тегия состоит в использовании машины в течение А периодов и
последующей покупке новой. Остается нерешенным, однако что
делать, если g>A. Можно найти также явное выражение для
A(g) при g=l, 2, А, как это было сделано в § 10.15 (см.
упражнение 10.23). При этом для Л (А) получаются соотноше-
ния типа (10.108) с той лишь разницей, что у S(A) не появ-
ляется множителя aN. Это объясняется тем, что при выводе этих
соотношений предполагалось, что процесс начинается с покупки
новой машины без продажи старой, тогда как для Л(А) при
покупке новой машины старая продается. Следует ожидать, что
использование функциональных уравнений даст тот же резуль-
тат, что и применение формулы (10.108), так как оба метода
решают одну и ту же задачу.
Рассмотрим теперь случай, в котором учитывается техниче-
ский прогресс. На этот раз в вычислениях должен использо-
ваться конечный планируемый промежуток времени. Будем счи-
тать, что общая продукция машины остается постоянной во вре-
мени, а любое увеличение производительности вследствие
412
Гл. 10. Динамическое программирование I
технического прогресса влечет снижение эксплуатационных за-
трат. Планируемый промежуток времени полагаем состоящим
из п одногодичных периодов. Решения принимаются только в на-
чале периодов, последние же занумеровайы от 1 до /г, так что
первый во времени период имеет номер 1.
Теперь затраты на монтаж машины могут зависеть от пе-
риода, в который она куплена. Аналогично и все остальные за-
траты могут зависеть не только от возраста машины, но и от
года покупки. Предполагается, что год покупки полностью опре-
деляет технические совершенства машины. Обозначим через Ц
величину затрат на монтаж машины, купленной в Лй период,
через Ci(j)—стоимость эксплуатации этой машины в течение
j-го периода и через Si (j) — ее стоимость после использования
в течение / лет.
Пусть теперь Afe(g) выражает затраты за период от 6-го до
n-го года, приведенные к началу 6-го года, при условии, что в
начале 6-го года и во все последующее время принимаются оп-
тимальные решения, а возраст используемой машины в начале
6-го года | лет. Тогда, так как мы должны либо продолжать
использовать имеющуюся машину, либо покупать новую, рекур-
рентные соотношения для Л&(|) имеют вид
AA(£) = min
купить новую машину,
+ + 1):
сохранить имеющуюся машину.
(10.110)
Допустим, что в конце n-го года используемая машина про-
дается. Тогда
4-5/г^а)+аСл(1) + а5/г(1),
аСл^а + 1) + а5л^а + 1)-
(10.111)
Решение задачи осуществляется в обратном направлении, в ре-
зультате чего находится оптимальная стратегия на каждый год.
При учете технического прогресса время эксплуатации по-
следующей машины может отличаться от времени эксплуатации
предыдущей.
Отметим, что задача динамического программирования, опи-
сываемая соотношениями (10.110) и (10.111), решается осо-
бенно легко, так как для вычисления А&(|) нужно рассматри-
вать только две альтернативы. Задачи такого типа относятся
к одному из немногих случаев, когда удается вручную находить
10.16. Задачи о замене оборудования
413
решение задач значительных размеров. Конечно, эти задачи
также очень легко программируются для вычислительных ма-
шин, использование которых и следует предпочесть при частом
решении таких задач.
Хотя приведенная выше весьма общая формулировка допу-
скает возможность учета любого влияния технического прогрес-
са на величину затрат, возникают трудности при попытке сде-
лать прогноз, относящийся к самой природе технического про-
гресса. В то же время задача о замене оборудования имеет,
к счастью, черту, общую, по-видимому, для многих экономиче-
ских задач — в окрестности минимума затраты слабо зависят от
изменения управления, что позволяет с помощью приближенно
найденных моментов замены оборудования получить стратегию,
близкую к оптимальной. Подход динамического программирова-
ния к таким задачам очень гибок и может быть использован и
в том случае, если в каждый год есть возможность закупать
несколько новых машин или допускается перестройка уже куп-
ленной машины. Формулировка задачи с этими двумя обобще-
ниями требует использования части материала следующей главы
и будет соответственно приведена ниже.
Читатель мог заметить, что в этом параграфе рекуррентные
соотношения (10.109) и (10.110) не выводились обычным путем,
а были написаны непосредственно. Здесь это было особенно
легко. В упражнении 10.24 предлагается вывести эти соотно-
шения с помощью обычной процедуры, приняв во внимание тот
факт, что переменные управления на каждом шаге принимают
только значения 0 и 1, соответствующие двум возможностям —
использованию имеющейся машины или покупке новой.
В приведенной выше постановке задачи можно было рассма-
тривать каждую машину независимо от остальных машин. Хотя
во многих случаях это допущение обосновано, тем не менее
имеются также важные случаи, когда все машины должны быть
рассмотрены одновременно. Допустим, что фирма в текущий мо-
мент имеет определенное число работающих машин (возможно,
разных возрастов). Имеется оценка того, как возрастает спрос
на изделия, производимые этими машинами, в последующие
несколько лет. Имеются также оценки эффекта, вызванного
дальнейшими техническими усовершенствованиями машин. За-
дача может состоять в определении оптимальной программы
замены машин и (или) увеличении их числа так, чтобы удо-
влетворить ожидаемый спрос с минимальными приведенными
затратами за планируемый период. Это очень сложная пробле-
ма, и мы не будем пытаться решить ее здесь. .
Вопросы применения динамического программирования к ре-
шению задач о замене оборудования были разработаны Р. Белл-
414
Гл. 10. Динамическое программирование I
маном и С. Дрейфусом [5, 8, 11]. Другие подходы к решению
этих задач изложены в работах [1, 15].
10.17. Стохастические задачи последовательного принятия ре-
шений. Природа стохастических задач последовательного приня-
тия решений обсуждалась в гл. 5. Там было отмечено, что стан-
дартные методы решения задач математического программиро-
вания, позволяющие определить лишь множество значений
переменных управления, не являются удовлетворительными при
решении этого класса задач. Причина та, что в этом случае пере-
менные управления оказываются функциями случайных пара-
метров, значения которых определяются перед принятием реше-
ний. В то же время метод динамического программирования
идеально подходит для решения некоторых типов таких задач,
так как на каждом шаге переменные управления автоматически
определяются как функции параметров состояния этого шага.
Тем не менее было бы заблуждением думать, что динамическое
программирование может быть использовано для решения всех
стохастических задач последовательного принятия решений.
Некоторые ограничения на класс задач будут указаны в следую-
щей главе. Сейчас же мы покажем, как задачи о создании запа-
сов, рассматривавшиеся в гл. 5, могут быть решены с помощью
динамического программирования. Напомним, что при решении
детерминированных задач последовательного принятия решений
можно было пользоваться как решением в прямом, так и в об-
ратном направлениях. В стохастическом же случае всегда необ-
ходимо использовать решение в обратном направлении, так как
стохастическая природа процесса не дает возможности задать
состояние системы в конце планируемого периода.
10.18. Стохастическая динамическая модель в теории созда-
ния запасов. Рассмотрим снова стохастическую задачу теории
создания запасов, поставленную в § 5.4. Покажем теперь, как
для ее решения может быть использован метод динамического
программирования. Но. сначала несколько обобщим прежнюю
формулировку.
Будем рассматривать некоторый продукт, запасаемый в си-
стеме. Состояние системы периодически проверяется, и в эти
моменты принимается решение, следует ли делать заказ, и если
делать, то какого размера. При принятии решения учитывается
срок планирования, состоящий из п периодов, и величина заказа
выбирается так, чтобы минимизировать ожидаемые затраты в
течение этого промежутка времени. Спрос в каждый период
планируемого промежутка времени будем считать случайной ве-
личиной. Для удобства этой случайной величине представ-
10.18. Стохастическая динамическая модель
415
ляющей спрос в /-й период, будем сопоставлять дискретную
функцию плотности вероятности pj(Vj). Спрос в различные пе-
риоды предполагается независимым, и средние значения спроса
в разные периоды могут быть неодинаковыми.
Будем предполагать, что если в /-й период заказано количе-
ство Xj, то это влечет за собой затраты двух типов — постоянные
затраты Aj и затраты, зависящие от размера партии, Cj(x3).
Функция С3(х3) может быть любой. Запаздывание между зака-
зом и его реализацией считается постоянным и равным т, так
что заказ, сделанный в момент /, прибывает к моменту t+x. Так
же как и в детерминированном случае, рассмотренном в § 10.14,
если решение принимается в момент t, то уже никак нельзя по-
влиять на транспортные или штрафные затраты в интервале вре-
мени между t и t + x, и эти затраты не зависят от решений, при-
нимаемых в момент t или любой другой более поздний. Следо-
вательно, эти затраты могут не включаться в целевую функцию.
Мы ограничим наше внимание случаем, когда все требова-
ния, поступающие при нулевом запасе, сохраняются, т. е. в ко-
нечном счете весь спрос должен быть удовлетворен.
Пусть yj обозначает величину имеющегося запаса плюс за-
казанное количество продукта и минус величина неудовлетво-
ренного спроса в начале /-го периода (если имеется неудовле-
творенный спрос, то наличный запас равен нулю, и наоборот).
В дальнейшем величину yj мы будем называть состоянием запа-
сов. Заметим, что она может, быть положительной, отрицатель-
ной или нулем. После того как сделан заказ, состояние запасов
становится равным y$+Xj, где Xj— величина сделанного заказа.
Если обозначить через dx спрос за время между заказом и его
поступлением, то немедленно после получения заказа, сделан-
ного в начале /-го периода, наличный запас будет равен yj+Xj—
—dx, если эта величина неотрицательна. В- противном случае
разность dx — yj — Xj равна неудовлетворенному спросу. Если
tj — начало /-го периода, а Д^- — длительность этого периода, то
ожидаемые затраты в промежутке времени между tj+x и ^+т+
+A/j обычно являются функцией только y$+Xj. Именно так
обстояло дело в случае, рассмотренном в § 5.4. Мы предпола-
гаем, что здесь рассматривается аналогичный случай и будем
записывать ожидаемые затраты (приведенные к моменту tj) как
+ Один частный вид этой функции был приведен в § 5.4,
но сейчас мы не будем делать никаких дополнительных пред-
положений относительно вида функции gj(yj + Xj).
Допустим, что в момент принятия решения в начале /-го пе-
риода известно состояние запасов yj, и мы интересуемся опти-
мальным размером заказа, который следует сделать в начале
первого периода. Так как принятое решение влияет на будущие
416
Гл. 10. Динамическое программирование 1
периоды, следует рассматривать планируемый промежуток
времени из п периодов и принимать во внимание решения, которые
будут приняты в будущем. Таким образом, задача каждый раз
при принятии решения будет решаться заново, с учетом плани-
руемого периода и последней имеющейся информации о спросе.
Оптимальное решение, принимаемое в начале первого периода,
находится из условия минимизации ожидаемых приведенных
затрат за весь планируемый промежуток времени. Однако, по-
скольку эти ожидаемые затраты зависят также от решений, при-
нимаемых в периоды от второго до n-го, нельзя определить х\
без оптимизации по х2, х3, ..., хп.
Как отмечалось уже в § 5.4, при выборе Xj, />2, следует учи-
тывать спрос за периоды от первого до (/—1)-го. Там же ука-
зывалось, что вся информация о прошлом содержится в у$. Та-
ким образом, следует рассматривать как функции от z/j,
т. е. как Xj(yj).
Используем теперь аппарат динамического программирова-
ния. Пусть
[п 1 [ п
J J
п / j у-1 \)
+ £’л(£+*л)+ 2 2 Xi—
\ i=k i~k /)
k=\. .... n. (10.112)
Величина Л^(^) есть минимум ожидаемых приведенных за-
трат за периоды от й-го до n-го, если состояние запасов в начале
fe-ro периода перед принятием решения о заказе было g. Так как
на этот раз из соотношений (10.112) мы определяем не числа Xj,
а функции xj(z/j), постараемся отчетливее понять точный смысл
этих соотношений.
Пусть выбраны некоторые стратегии Xj(z/j). Вообразим, что
нам заданы числа Vj, представляющие спрос в различные пе-
риоды. Тогда, начав с первого периода, мы можем последова-
тельно вычислить yj и, следовательно, значения xj. Зная Xj и Vj,
можно определить приведенные затраты на весь планируемый
промежуток времени для данных v$. Повторим теперь этот про-
цесс для всевозможных значений и$ и каждый раз будем вычис-
лять приведенные затраты. Далее взвесим все эти затраты с ве-
сами, равными вероятностям осуществления соответствующих
значений Vj. Наконец, сложим их, чтобы получить ожидаемые
затраты для данного набора стратегий. Представим себе, что
вся описанная процедура повторяется для любого мыслимого
набора стратегий. Оптимальным множеством стратегий будет
10.18. Стохастическая динамическая модель
417
тогда то, которому соответствует наименьшее значение ожидае-
мых затрат.
Отметим, что в приведенном выше выражении вполне законно
сначала перейти к средним затратам, а уж потом провести
усреднение по Vj. Читателю будет предложено доказать это в
упражнении 10.25.
Запишем теперь Л^(£) следующим образом:
ЛА(|)=пйп 2
( по всем Vj
1АА+Ck (х*) + gk (£+**)]
со
+ « 2 А (»*)
min У
Xk+v хп п0 всем V }
{п
У-Л + 1
л / j j-i \i 1)
+ 2 k 1 £/ £+xk — vk + 2 xi — 2 ) । г >
/-А+2 \ i-k + l l = k + l /)])
k=l, n—1, (10.113)
или
Л-k (|) = min ГА^ 4-СЛ(хй)4-£Л (£+**) “b
xk L
+a 2 А(^)Л*+1(^ + ^ —^ = 1. tl — 1. (10.114)
^=0
Чтобы получить4 выражение (10.113), было использовано ра-
венство
п
3 П/’Д®/) /(Ой, •••. *»«)==’
по всец L /=*&
{Г п
по всем Vj Ly-fe+l
= 3 Pk (®л)
vk-°
Уравнение (10.114) следует из определения ЛА+1(£), равенства
Г п 1
2 ПрД^) =1
по всем Vj[^j = k J
и независимости выражения Akf>k -f- Ck (xk) -|- gk (t, xk) or
..., -vn.
27 Зак. 735
418
Гл. 10. Динамическое программирование I
Для функции Лп(£) имеем выражение
Ап а) - min ИЛ + Сп (хл) + gn(l + *„)]. (10.115)
хп
При вычислении АД/л), где у\ есть начальное состояние за-
пасов, мы получаем х*—оптимальный размер заказа в первый
период. При вычислении для другого периода мы находим
Хь(|) —оптимальный размер заказа, если состояние запасов в
начале £-го периода есть g. Таким образом, для &>2 мы дей-
ствительно отыскиваем функции xk(%) необходимого типа (см.
§ 5.4). Следовательно, аппарат динамического программирова-
ния позволяет решать стохастическую задачу последовательного
принятия решений, сформулированную в § 5.4.
Рекуррентные соотношения (10.114) более сложны, чем ана-
логичные им соотношения (10.69), поскольку Ak+i(l + xi< — vk)
должно усредняться по всем возможным значениям спроса в
период k. При практическом решении задач такого типа верхний
бесконечный предел суммирования в формуле (10.114) заменяет-
ся таким конечным числом dk, при котором вероятность того, что
спрос в &-й период будет больше пренебрежимо мала. После
такой модификации задача может решаться с помощью вычис-
лительной машины в точности так же, как и рассматривавшиеся
ранее.
В некоторых случаях оптимальная политика заказов для
только что рассмотренной задачи может иметь особо простую
форму, так что, например, если в начале /-го периода состояние
запасов меньше или равно некоторому числу Г;, то следует зака-
зывать количество, достаточное, чтобы довести состояние запасов
до определенной величины если же уj>r^ то вообще не сле-
дует делать заказа. Рекуррентные соотношения (10.114) могут
использоваться для изучения условий, при выполнении которых
оптимальная политика имеет указанную форму. Необходймым
условием существования такой простой оптимальной политики
является независимость величины Cj(Xj) от %;. Остановимся не-
сколько подробнее на этом случае. Для последующего анализа
более удобно рассматривать все переменные как непрерывные.
Необходимые модификации в (10.114) состоят в замене дискрет-
ной плотности Pk(vk) непрерывной функцией ^k(vk) и знака
суммирования — интегралом. Соотношения (10.114) после этого
примут вид
Ak (у - Ckl + min |ДД + + хк)\, (10.116)
10.18. Стохастическая динамическая модель
419
где
Gk Q + xk) — U + xk) Gk + gk (g + xk) 4~
oo
•+« J Лл(| 4-xft — vb)(fk(vk)dvk.
0
(10.117)
Пусть, например, Gk{u) имеет график, изображенный на
рис. 10.5. В этом случае ясно, что если g>r^, заказ делать не
следует, если же g<A, тогда следует заказывать количество
Rk—g. Ясно, что в этом случае оптимальная стратегия в &-й пе-
риод имеет простую форму, о которой мы говорили выше.
' t J 'Ч - '4'5^2
Рис. 10.6.
Если же, например, Gh(u) имеет график, подобный изобра-
женному на рис. 10.6, оптимальная стратегия оказывается такой:
если g4>i, заказывать Ri — g; если n<g4>2, не делать заказа;
если r2<g<r3, заказывать /?1 — g; если не делать за-
каза; если г4<^/*5, заказывать R2— g; если g>r5, не делать за-
каза.
По-видимому, более вероятно, что график Gk(u) окажется
похожим на кривую рис. 10.5, а не на кривую рис. 10.6. Однако
исключительно трудно определить наиболее общие условия, при
выполнении которых простая структура стратегии, о которой го-
ворилось выше, оказывается оптимальной на каждом шаге. Наи-
более сильные результаты в этом направлении принадлежат
Скарфу [16]. Он показ-ал, что если стоимость единицы продукта
постоянна в каждый период и если все gk(u) — выпуклые функ-
27*
420
Гл. 10. Динамическое программирование I
ции, тогда для каждого k найдутся такие числа rk и Rk, что
оптимальная стратегия имеет следующий вид: если у^Гъ., сле-
дует заказывать Rk—уь, если же yk>rk, Т° заказа делать не сле-
дует. Доказательство приводится в работе [13].
В гл. 5 было указано, что при решении стохастических задач
последовательного принятия решений необходимо, чтобы пере-
менные управления являлись функциями информации, известной
в момент принятия решений. В приведенной выше формулировке
предполагалось, что состояние запасов известно в начале 6-го
периода перед принятием решения о размере заказа. Рассмотрим
теперь немного отличный случай, когда информация о спросе
запаздывает на один период, так что в начале 6-го периода
известно не yh, а только т. е. состояние запасов в на-
чале (k—1)-го периода, после того как сделан заказ.
Введем обозначение Wk-i—yk-i+Xk-i- При рассмотрении
этого случая будем понимать под приведенные к началу
6-го периода ожидаемые затраты от 6-го до n-гр периода, если
в начале 6-го периода и во все последующие принимаются опти-
мальные решения и Тогда
Лк (I) = min s
xk, хп п0 всем vj
{п
2 а7 \Aftj-\-Cgk (£— ,vk_-l +**) +
П ; и / 7 •/~1 \1
+ 2 «' 4+2^- 2 • k=l, 2...........п. (10.118)
/ = &+1 '\ i=k l=k-i /)
Снова используя те же соображения, которые привели
к (10.114) и (10.115), получаем
Л„ Q)=min
(£-<-i+*«)}•
Л*(£)—min I АкЪк + Ck (хк) + 2 A-i(^*-i)X
хь I
X [^*(1 — +^*) + aAft+1 (| — vk_i +xfc)]J,
£=1, 2, .... ft—1, (10.119)
АцЬп (x„)4~ 2 Pn-i^
(10.120)
Эти соотношения могут быть решены точно так же, как и
(10.114), (10.115).
Если информация о спросе запаздывает более чем на один
период,'ситуация представляется гораздо менее реалистичной, но
10.18. Стохастическая динамическая модель
421
тем не менее по-прежнему допускающей успешное применение
динамического программирования. Пусть, например, время за-
паздывания равно двум периодам. В этом случае в начале £-го
периода будут известны Wk-2 и, по-видимому, но не vk-z
и vk-i. Теперь Лд(5) выражает приведенные к началу А-го пе-
риода затраты от fe-ro до n-го периода, если в начале й-го пе-
риода и во все последующие принимаются оптимальные решения
и l = wk_2 + Xk-i. В упражнении 10.26 читателю будет предложе-
но показать, что рекуррентные соотношения в этом случае имеют
вид
(£) — In^n ] АЛ+(xk)+
xk
оо оо
+ 5 Pk-iiVk-i)Pk-^k-i)Sk (£ + •** '°k-2~ ^л-1) +
Рй-2“ ^-1=°
ОО
^-2=° J
A = l, 2, ..., п,— 1. (10.121)
Динамическое программирование не удается использовать
при рассмотрении одного частного случая, упоминавшегося в
гл. 5, где не делается даже попытки учесть информацию о на-
блюдавшихся значениях случайных переменных, а вместо этого
в начале первого периода определяются числа х2>. .. ухп —
размеры заказов на каждый период независимо от величины
спроса. В упражнении 10.27 предлагается объяснить, почему
метод динамического программирования в этом случае непри-
меним.
Как и в детерминированном случае, мы можем рассмотреть
еще одно видоизменение модели — пусть распределение спроса
и затраты не меняются от периода к периоду, а планируемый
промежуток времени считается бесконечным. Будем считать, что
величина Л(|) выражает затраты за все будущее время, приве-
денные к моменту принятия решения (с обычной оговоркой, что
затраты на хранение и затраты, возникающие из-за неудовлетво-
ренных потребностей, не включаются вплоть до момента прибы-
тия заказа) при условии, что всякий раз принимаются оптималь-
ные решения, а состояние запасов в момент принятия решения
равно Если все переменные считать непрерывными, то функ-
циональное уравнение для Л(|) имеет вид
(ОО 'I
464-C(x)-|-g(i+x) + a f Л(| + х —>»)<₽(»)cfo I.
* I о J
(10.122)
422
Гл. 10. Динамическое программирование I
В упражнении 10.28 требуется вывести это уравнение. Можно
доказать, что если g(u) —выпуклая функция и стоимость еди-
ницы продукта постоянна, то /?г-стратегия является оптималь-
ной. В этом случае есть также возможность найти явное реше-
ние функционального уравнения. Однако эта задача не так про-
ста, как в детерминированном случае. Метод ее решения изложен
в [13].
10.19. Динамическое программирование и вариационное исчи-
сление. Как уже отмечалось, для стохастических задач последо-
вательного принятия решений характерно, что в них требуется
отыскать не просто числа, представляющие оптимальные значе-
ния переменных, а множества функций случайных аргументов,
значения которых наблюдаются в моменты принятия решений.
Имеется, однако, и специальный класс детерминированных задач
оптимизации, требующих определения одной или более функций,
а не значений одной или более переменных. Эти задачи состав-
ляют предмет исследования вариационного исчисления.
Наверное, простейшая и наиболее известная задача вариа-
ционного исчисления состоит в отыскании кривой, лежащей в
плоскости ху, проходящей через две заданные точки а==(а, а) и
Ь=(р, Ь) и такой, что расстояние вдоль нее между этими точ-
ками минимально. Каждый знает, что кратчайшее расстояние
между двумя точками на плоскости дает прямая линия. Вариа-
ционное исчисление дает возможность доказать это обстоятель-
ство. Сформулируем упомянутую задачу точно.
Пусть у(х) —произвольная кривая, проходящая через точки
а и Ь. Всякую такую гладкую кривую будем называть допусти-
мой. Элемент длины кривой ds связан с dx и Ду соотношениями
ds2 = dx* 4- dy* или = [1 4- (-g V]1/2.
Общая длина D кривой между точками а и b выражается фор-
мулой
Р Р
<1а123>
а а
Требуется найти такую допустимую кривую у(х), которая ми-
нимизирует величину £), определяемую равенством (10.123).
Отыскание этой функции есть задача вариационного исчисления.
Другой элементарный пример. ПолЬжим, что кривая у(х)
проходит через точки а=(а, а) и Ь=(р, Ь) плоскости ху, причем
а, Ь>0, у(х)^0 и Пусть эта кривая вращается вокруг
оси х, образуя поверхность вращения. Требуется определить та-
10,19: Вариационное исчисление
423
кую кривую у(х), для которой площадь этой поверхности будет
минимальной.
Если ds есть элемент длины кривой, то элемент площади по-
верхности dA определяется равенством
dA = 2лу ds = 2лу ^1 + (-^“-)2]1/2 dx,
а общая площадь равна
Л = 2л j i/[l + (-g-j2]l/2rfx. (10.124)
а *
Определение функции у(х), минимизирующей интеграл (10.124),—
пример другой задачи вариационного исчисления.
Наконец, последний пример. Рассмотрим предприятие, про-
изводящее товар с сезонным характером спроса. Скорость про-
дажи товара q зависит не только от времени года /, но и от ско-
рости расходования средств на рекламу s(t) и определяется
некоторой функцией q = q(s, /). Товар предполагается скоропор-
тящимся и хранения не допускает. Поэтому скорость его произ-
водства следует поддерживать на уровне, равном предполагае-
мой скорости продажи. Кроме того, ставится условие, чтобы
весь спрос был удовлетворен. Если q есть скорость выпуска
товара, то скорость расходования средств на его производство
определяется функцией c(q, q), где q^dqjdt. Таким образом,
производственные затраты зависят от скорости выпуска и от ее
производной по времени. Так как q = q(s, /), скорость расходова-
ния средств на производство чиожно записать в виде c(s, s, t),
где s — ds/dt.
Требуется определить, какой должна быть скорость расходо-
вания средств на рекламу, s(/), в интервале времени между
и /1, чтобы получить максимальную прибыль от продажи товара.
Продажная цена единицы товара предполагается постоянной и
равной р. Таким образом, скорость изменения капитала равна
pq—с—s, а общая прибыль Р за время от /0 до Л равна
/)—-$] Л. (10.125)
Задача нахождения функции $(/), максимизирующей Р, также
является задачей вариационного исчисления.
Каждый из примеров, приведенных выше, является частным
случаем общей задачи поиска такой функции у(х). называемой
424
Гл. 10. Динамическое программирование I
экстремальной кривой, которая проходит через точки а=(а, а}
и Ь=(р, Ь) плоскости х, у и минимизирует интеграл
3
/ = ]>(//, у', x)dx, (10.126)
° 1
где y' = dyldx. Этот класс задач является простейшим из изу-
чаемых в вариационном исчислении. Классический подход к ре- -
шению такой задачи состоит в построении обыкновенного диф- *
ференциального уравнения второго порядка (уравнения Эйлера),
которому должна удовлетворять экстремальная кривая. Для ;
первых двух примеров, рассматриваемых выше, возможно ре-
шить это уравнение аналитически и получить аналитическое
выражение для у(х). Однако в общем случае для решения урав-
нения Эйлера приходится применять численные методы. /
Мы не будем ни выводить уравнения Эйлера для этих при-
меров, ни останавливаться на классических методах их реше-
ния. Вместо этого мы изучим, как для численного нахождения
функции у(х) можно использовать метод динамического про-
граммирования. Этот подход не позволяет найти аналитическое Ф
выражение для у(х), а дает лишь значения у(х) в конечном f
числе точек. . |
Прежде всего разобьем промежуток точками t
Xj — a + j\x, j = 1,...,п. Для любой допустимой кривой обо- J
значим Уз = у(Хэ). Если Ах мало, то y'(Xj) можно аппроксимиро-
вать по формуле .*
о0-127»
Тогда интеграл (10.126) может быть приближенно заменен ко-
нечной суммой
'л-1
<10-128)
/—0
Задача отыскания функции у(х), минимизирующей интеграл
(10.126), заменяется приближенной задачей нахождения п—1
значений у^ которые минимизируют выражение (10.128) при
условии, что уо и уп равны соответственно значениям а и Ь.
Пусть теперь
Л —1
Л*(£) = tnin J] F (у}, , х\\х, (10.129)
yk+V УП—\ J~k
10.19. Вариационное исчисление
425
i — У j
, Xj ) AX ,
где yk = l- Тогда
(|) = min I/? h , х 1 дх _|_
W к6’ лх Ч
п-1
+ min ?
yk+2> •••’ yn-i ;=й+1
ИЛИ
лл Ц) = min If (t, -k--'2x 1 , xj Ax + Л/г+1 (t/A+i)],
yk+1 L
£ = 0, 1, ...» n — 2, (10.130)
и
A„_1a)=F^, -^1, xn^x. (10.131)
Минимальное значение / будет тогда приближенно равно До (а).
В приведенной формулировке g и, следовательно,^являются
непрерывными переменными. Для получения численного реше-
ния можно действовать двумя способами. Первый из них состоит
в том, чтобы считать переменные g и yh дискретными. В этом
случае для каждого k определяется дискретное множество зна-
чений, которые могут принимать g и yk. Затем Afe(g) табули-
руется только для этих значений. При вычислении A&(g) предпо-
лагается, что уь+1 может принимать только дискретные значения,
соответствующие xh+b Как обычно, наряду с Afe(g) ведется так-
же табулирование z/fe+i(g). На последнем шаге определяется
Ло(п) и y*v Оптимальные значения остальных у^ находятся по
формуле
^+1 = ^+1(^). k=\, 2, .... п-2. (10.132)
При таком подходе не приходится сталкиваться с трудностями,
возникающими при отыскании минимума по непрерывным пере-
менным.
Другой подход состоит в том, что g и yh рассматриваются как
непрерывные переменные. Так как/7(yk, (Уь+i—Уь)/Ах, xh) обычно
является непрерывной функцией от //fe+i, yk и xk, то отсюда сле-
дует, что Afe(g) также есть непрерывная функция g. Кроме того,
для рассматриваемого типа задач отсюда следует, что непре-
рывны и функции (g). (Доказать эти утверждения предлагает-
ся в упражнении 10.29.) Это позволяет использовать интерпо-
ляцию при вычислении функций Afe(g) и f/fe(g). Далее можно
действовать как и в дискретном случае, вычисляя A^(g) и z/ft(g)
на дискретном множестве значений g. Однако, вычисляя мини-
мум по уь, следует считать эту переменную непрерывной и
428
Гл. 10. Динамическое программирование I
использовать методы, подобные обсуждавшемуся в § 10.7.
Задача нахождения минимума здесь несколько упрощается, так
как у(х) есть непрерывная функция от х. Имеет смысл начинать
поиск оптимального значения yk+t в окрестности //fe+1 = g. При
отыскании у*, вообще говоря, требуется проводить интерполя-
цию фуНКЦИЙ Z/fe(g).
При решении задачи вариационного исчисления только что
предложенным численным методом в действительности по мере
удаления от точки b определяется целое семейство экстремаль-
ных кривых. На последнем шаге определяется та кривая, кото-
рая проходит и через а, и через Ь. Геометрическая иллюстрация
сказанного приведена на рис. 10.7. Получая Aft(g), мы находим
определяющее ту экстремальную кривую, которая, окан-
чиваясь в xft+i, проходит через точку (xk,.%).
В этом параграфе мы рассмотрели только простейший класс
задач, возникающих в вариационном исчислении. Мы видим, что
численные решения этих задач могут быть получены средствами
динамического программирования. В следующей главе будут
рассмотрены несколько более трудные задачи и будет выяснена
эффективность динамического программирования при их ре-
шении.
10.20. Программы для решения задач методом динамического
программирования на вычислительных машинах. Рассматривая
рекуррентные соотношения, использованные для вычисления
Afe(g) в различных задачах этой главы, читатель без труда за-
метит, что эти соотношения для разных задач имеют различный
Литература
427
вид. Это одна из характерных особенностей динамического про-
граммирования. Как правило, вид этих соотношений существенно
зависит от структуры решаемой задачи. По этой причине, в част-
ности, нет возможности создать общую программу для решения
всех задач динамического программирования с помощью вы-
числительной машины, как это делается в линейном программи-
ровании.
В действительности часто оказывается трудным даже напи-
сать достаточно общую программу для решения хотя бы не-
большого подкласса задач динамического программирования.
Обычно для каждого типа задач, решаемых этим методом, при-
ходится создавать специальную программу. К счастью, в отли-
чие от линейного программирования создание программы, реа-
лизующей метод динамического программирования, представ-
ляется делом достаточно простым.
ЛИТЕРА ТУ РА
1. Alchian A., Economic Replacement Policy, R-224, RAND Corp., 1952.
2. Aris R., Bellman R., К a 1 a b a R., Some Optimization Problems in
Chemical Engineering, P-1798, RAND Corp., 1959.
3. Веллман P., Динамическое программирование, ИЛ, M., 1960.
4. Б е л л м а н Р., Процессы регулирования с адаптацией, изд-во «Наука»,
М., 1964.
5. Bellman R., Equipment Replacement Policy, J. Soc. Indust, and Appl.
Math., 3 (1955), 133—136.
6. В e 11 m a n R., Combinatorial Processes and Dynamic Programming,
P-1284, RAND Corp., 1958.
7. Bellman R., Dynamic Programming and the Smoothing Problem, Ma-
nag. Sci.,3 (1956), 111—113.
8. Б e л л м а н P., Дрейфус С., Прикладные задачи динамического про-
граммирования, изд-во «Наука», М., 1964.
9. Dreyfus S., Computational Aspects of Dynamic Programming, P-924,
RAND Corp., 1956.
10. Dreyfus S., Dynamic Programming Solution of Allocation Problems,
P-1083, RAND Corp., 1957.
11. Dreyfus S., A Generalized Equipment Study, J. Soc. Indust, and Appl.
Math., 8 (1960), 425—435.
12. Dreyfus S., Dynamic Programming and the Calqulus of Variations, J.
Math. Analysis and Applicat., 1 (1960), 228—239.
13. Hadley G., Whitin T. M., Analysis of Inventory Systems, Englewood
Cliffs, Prentice-Hall, 1963.
14. Molina E. C., Poisson’s Exponential Binomial Limit, Princeton, Van
Nostrand, 1942.
15. Terborgh G., Dynamic Equipment Policy, New York, McGraw-Hill, 1949.
16. Scarf H., The Optimality of (S, s) Policies in the Dynamic Inventory
Problem, in Arrow K. J., Karlin S., Suppes P. (ed.), Mathematical
Methods in the Social Sciences, Stanford, Stanford University Press, 1960,
196—202.
17. Wagner H. M., Whit in T. M., Dynamic Version of the Economic Lot
Size Model, Manag. Sci., 5 (1958), 89—96.
428 Гл. 10. Динамическое программирование 1
18*. Б у л а в с к и й В. А.,'Об одной простейшей динамической модели исполь-
зования машин, сб. Математическое программирование, изд-во «Наука»,
М., 1966.
19*. К а н т о р о в и ч Л. В., Романовский И. В., Амортизационные пла-
тежи при оптимальном использовании оборудования, ДАН СССР, 162
(1965), № 5.
20*. К^а u f m а n А., С г и о п В., Programmation dynamique, Paris, Dunod,
Упражнения
10.1. Рассмотреть задачу, обсуждавшуюся в § 10.2. Какие трудности воз-
никают, если одно или несколько а^ отрицательны? Как следует решать за-
дачу в этом случае?
10.2. Допустим, что в задаче 10.1 ограничение должно выполняться как
точное равенство. Какие изменения следует сделать в вычислительной схеме,
чтобы принять во внимание этот факт?
10.3. Рассмотрим задачу о загрузке корабля при наличии трех типов за-
пасных деталей. Общий используемый объем равен 13 единицам. Объем
одного предмета типа А равен 2, типа В— 3 и С — 2 единицам. Затраты
из-за неудовлетворенного спроса на предмет типа А равны 600, на предмет
В — 1200 и С — 800. Спрос на каждый предмет случаен и подчиняется пуас-
соновскому распределению со средними 3, 2 и 2 для типов А, В и С соот-
ветственно. Сколько предметов каждого типа следует запасти, чтобы мини-
мизировать средние затраты из-за неудовлетворенного спроса? Что дает
увеличение располагаемого объема на 1 единицу?
10.4. Какова оценка 1 единицы добавочного объема для примера, решен-
ного в § 10.5?
10.5. Удаленная морская база снабжается запасными частями один раз
в месяц. Обычно таким образом поставляются детали п типов, причем перед
отправкой известно имеющееся на базе количество у$ деталей /-го типа. Са-
молет, доставляющий детали, может транспортировать объем V, а объем де-
тали /-го типа равен Vj. Если возникает спрос на деталь /-го типа и ее нет
на базе, то это приводит к затратам jtj. Месячный спрос на детали /-го типа
есть случайная величина, подчиненная пуассоновскому распределению со
средним р,;. Показать, как с помощью динамического программирования мо-
жет быть найдено число деталей каждого типа Xj, которое следует отправить
на базу, чтобы минимизировать средние затраты из-за неудовлетворенных
потребностей в следующем месяце. Решить задачу для случая, когда имеется
только три типа деталей и соответствующие параметры равны: I/=14, 4,
02=3, Оз=2, t/i = l, {/2=0, 1/з=2, Л1 = 5000 долл., л2—3000 долл., л3=8000 долл.;
Ц1 = 1,5, Рг=3,4, р3=5,8.
10.6. Надежность — это одно из главных требований, предъявляемых к
электронным системам. Особенно важна она в системах, использующихся в
ракетах и спутниках. В то же время надежности в этих системах достичь
трудно, так как они содержат тысячи компонент, а поломка любой из них
может привести к выходу из строя всей системы.
Часто электронная система может рассматриваться как ряд «черных
ящиков» (рис. 10.8). Это могут быть усилители, трансформаторы или более
сложные подсистемы. Для того чтобы повысить надежность всей системы, в
некоторых (или всех) ее ступенях можно вводить дублирование, т. е. вместо
одного устройства устанавливать два или больше устройств, причем так,
что если одно из них ломается, то другое автоматически включается. Допу-
стим, что суммарные затраты на конструирование электронной системы не
Упражнения
429
должны превосходить М. В пределах этой суммы желательно сконструиро-
вать наиболее надежную систему. Затраты на конструирование /-й подсисте-
мы равны Cj. В качестве количественной меры надежности примем вероят-
ность того, что система не выйдет из строя, функционируя в течение задан-
ного промежутка времени. Будем считать, что повышение надежности воз-
можно только путем введения дублирующих элементов.
Ступень 1 Ступень 2 Ступень п
Рис. 10.8.
На /-й ступени мы должны использовать по крайней мере одну подси-
стему, т. е. число действительно используемых здесь подсистем можно запи-
сать в виде 1 +Xj, где неотрицательное целое число х$ есть мера дублиро-
вания, введенного на /-й ступени. Пусть fj(xj)—вероятность того, что /-я
подсистема функционирует успешно, если количество дублирующих элементов
равно Xj. Допустим также, что эта вероятность не зависит от того, как
функционируют другие ступени. Тогда надежность всей системы равна про-
изведению функций fj(xj), Показать, как с помощью метода динамического
программирования могут быть найдены оптимальные значения Xj. Определить
явный вид функции fj(Xj), если pj есть вероятность того, что /-я ступень
без дублирующих элементов не выходит из строя и если переключающий ме-
ханизм никогда не ломается. [Указание. Рекомендуемые соотношения имеют
вид
Л* (?) = max {fk (xk) Л*_( (£ — Ckxk)}. ]
xk
10.7. Рассмотрим сеть типа изображенной на рис. 10.9. В ней имеется
вершина с номером /, которую мы будем называть источником, и вершина с
430
Гл. 10. Динамическое программирование I
номером п, называемая стоком. Каждый отрезок, соединяющий вершины i
и /, характеризуется возможным направлением движения вдоль него (отме-
чено стрелкой) и временем tn, необходимым для достижения вершины /,
если двигаться из вершины i по указанному направлению. Требуется найти
наименьшее время перемещения от источника к стоку, если двигаться по сети
в направлениях, отмеченных стрелками. Для решения использовать методы
динамического программирования. [Указание. Ввести величину Aj, выражаю-
щую минимальное время, необходимое для прохождения от источника к вер-
шине /.] Какие вершины должны табулироваться вместе с Л;, чтобы можно
было найти этот путь? Показать, как можно определить наибольшее время
прохождения через сеть.
10.8. Предложить метод решения задачи 10.7, основанный на последова-
тельном маркировании вершин вплоть до n-й. [Указание. Использовать в ка-
честве маркера числа, определяющие минимальное время движения до /*-й
вершины и номер той вершины, по которой мы попадаем в /-ю.)
10.9. Рассмотрим некоторый комплекс работ, например большое строи-
тельство, для выполнения которого требуется завершить большое количество
различных операций. Некоторые из них не могут быть начаты, пока не за-
кончены другие. Чтобы оценить ход строительства, вообразим, что могут
быть определены некоторые характеристики выполненной работы, называемые
событиями. Каждое событие соответствует завершению одной или большего
числа операций.
Для наглядного представления комплексу работ можно сопоставить граф
(рис. 10.9), вершины которого соответствуют событиям, а дуги — выполняе-
мым операциям. Величина tn дает время завершения /-й операции, начатой
после f-й.
Показать, что задача определения наиболее раннего времени завершения
каждого события может быть решена по схеме динамического программиро-
вания. Определить наиболее раннее время завершения всего комплекса работ,
а также наиболее позднее время завершения каждого события, если весь
комплекс работ должен быть завершен в кратчайший срок. [Указание. Чтобы
решить последнюю задачу, начните с конца комплекса, взяв самое раннее
время его завершения, а затем последовательно определите позднейший до-
пустимый срок завершения каждого события.]
Разность между наиболее ранним и наиболее поздним моментами вре-
мени, в которые может завершиться событие, называется допустимым интер-
валом. Как можно интерпретировать допустимый интервал? На графе имеется
путь, называемый критическим, такой, что допустимый интервал в каждой
вершине этого пути равен нулю. Почему важен такой путь?
10.10. Для комплекса работ, изображенного в виде графа на рис. 10.10,
найти наиболее ранние моменты времени, когда может быть завершено каж-
дое событие и весь комплекс работ в целом. Определить также наиболее
поздние моменты завершения событий, допустимые интервалы для каждой
вершины и критический путь. [Указание. См. упражнение 10.9.]
10.11. Рассмотрим большую систему для создания запасов, в которой не-
который продукт запасен в различных складах. Возобновление запаса про-
исходит периодически в централизованном порядке, после чего полученное
количество продукта распределяется между складами. Однако из-за стохасти-
ческой природы спроса может случиться, что в период между возобновле-
ниями запаса в некоторых складах наблюдается нехватка продукта и жела-
тельно его перераспределение.
Пусть имеется п складов, и за время Т до следующего возобновления
запаса минимальный наличный запас продукта содержится в n-м складе и
равен уп (эта величина предполагается такой, что целесообразно рассмотреть
вопрос о перераспределении-продукта между складами). Затраты по транс-
портировке Xj единиц продукта из /-го склада в n-й будем обозначать через
Упражнения
431
Cg(Xj). Неудовлетворенный спрос в /-м складе ведет к затратам rtj на еди-
ницу продукта. Будем обозначать через Pj(vj) вероятность того, что за вре-
мя Т в /-м складе возникнет спрос на Vj единиц продукта. Требуется опре-
делить, какое количество продукта следует отправить из каждого склада в
n-й, чтобы минимизировать суммарные транспортные затраты и затраты, вы-
званные неудовлетворенными потребностями по всем складам за время Т.
Временем, необходимым для перераспределения, пренеб^чь. Показать воз-
можность применения динамического программирования. [Указание. Пусть
Ал (5) — ожидаемый минимум затрат для складов с номерами &,..., п, если
отгрузка в п-и склад производится только из складов k, &+1, ...., п—1, и
количество продукта в /г-м складе до перераспределения равно £.]
10.12. Найти
п
min z — 2 гЧ
/=1
при условиях
Г; >1, /== 1, 2, ..., п; г{г2 ... гп^=г.
Показать, как для решения задачи может быть применен аппарат динами-
ческого программирования.
10.13. Для задачи, обсуждавшейся в § 10.8, доказать, что если fj(Xj) —
вогнутые функции, то xk (g) — непрерывные функции от g. [Указание. Исполь-
зовать тот факт, что из вогнутости функций fj(Xj) следует также их непре-
рывность внутри любого интервалав]
10.14. Решить задачу, рассматривавшуюся в § 10.10, для конкретного
случая, когда имеется 4 периода и идеальное количество рабочей силы в
эти периоды равно соответственно 2, 5, 3 и 1, а в нулевой период равно 2.
Функции fj и gj определяются формулами
10(ху-ху_,), ху-ху_,>0,
1 1 I 7(%;_!— Xj), Xj_i—Xj>0;
„.ил=Г 7(ху-ту). Xj>mj,
-1 '1 Хи — mj > xj-
432 Гл. 10. Динамическое программирование I
10.15. Справедливо ли для модели, обсуждавшейся в § 10.12, следующее
утверждение: если C(%j) не зависит от / и вогнута, а а;=1, то при вычисле-
нии Aft(0) нет необходимости проводить вычисления в обратном направлении
дальше чем до начала периода, когда поступает заказ, удовлетворяющий
потребность (k— 1)-го периода при вычислении Аь-1(0)?
10.16. Предприятие, выпускающее радиоприемники, производит также и
конденсаторы. Фиксированные затраты на выпуск партии конденсаторов рав-
ны 250 долл. Кроме того, затраты на выпуск одного конденсатора составляют
0,85 долл. Хранение одного конденсатора в течение месяца обходится в
0,02 долл. График выпуска радиоприемников в наступающем году требует та-
ких количеств конденсаторов в каждый месяц: 15 000, 25 000, 20 000, 15 000,
11 000, 6000, 5000, 11 000, 13 000, 24 000, 30 000, 8000. Временем, необходимым
для выпуска конденсаторов, можно пренебречь. Допустим, что решение о вы-
пуске конденсаторов принимается только в начале месяца. Найти наилучшее
время для выпуска партий конденсаторов и размер этих партий, если в на-
стоящий момент уже имеется 1000 конденсаторов, а к концу года желательно
иметь их 5000.
10.17. Производитель насосов для ракетных двигателей заключил кон-
тракт на поставку в начале каждого месяца текущего года следующего ко-
личества насосов: 30, 60, 100, 200, 300, 325, 275, 125, 100, 75, 150, 200.
Стоимость переналадки оборудования при изменении числа производимых
насосов составляет 650 долл. Себестоимость каждого насоса — 150, а расходы
на хранение одного насоса в течение одного месяца — 2 долл. Пусть на-
ладка оборудования может производиться .лишь в начале месяца и продукция
предыдущего месяца отправляется потребителю в начале следующего месяца.
Определить месяцы, в которые следует проводить переналадку оборудования
и оптимальное число насосов для каждого месяца. Можно ли получить до-
полнительную выгоду, если производить переналадку оборудования чаще чем
один раз в месяц?
10.18. Использовать уравнение (10.106) для явного нахождения A(g),
£==г, г+1, ..., Я —2.
10.19. Для модели, изучавшейся в § 10.15, показать, что средние годовые
затраты при нулевой годовой норме процента определяются выражением
lim /А (R — 1),
i -> 0
где i — годовая норма процента. {Указание. Система завершает один цикл
своего функционирования за время между получениями двух последователь-
ных заказов. Определить среднегодовые затраты непосредственно, вычисляя
ожидаемые затраты за цикл и умножая их на среднее число циклов в год.]
10.20. Показать, что величина
limZA(g), g = г, ..., 7? — 2,
/->о
также выражает среднегодовые затраты для модели, описанной в § 10.15.
10.21. Показать, как с помощью минимизации среднегодовых затрат мож-
но найти величину R— г для модели, описанной в § 10.15. Будет ли эта
величина удовлетворять уравнениям (10.102) — (10.104) при всех значениях а?
[Указание. Чтобы получить среднегодовые затраты для произвольного а,
зная их для а=0, следует заменить К на K+i. Почему?]
10.22. Для процесса, описываемого уравнением (10.109), доказать, что
если он начинается с использования новой машины, то оптимальная страте-
гия состоит в использовании ее в течение N периодов и последующей по-
купке новой,
Упражнения
433
10.23. Решить функциональное уравнение (10.109) так, как это было
сделано в § 10.15.
10.24. Вывести рекуррентные соотношения (10.109) и (10.110) обычным
образом, определив последовательность функций ЛА (g) и установив для них
рекуррентные соотношения.
10.25. Объяснить, почему в уравнении (10.112) можно сначала вычислить
математическое ожидание gfe(g+Xfe), а потом провести усреднение по Vj.
В частности, показать, что если используется плотность распределения вре-
мён между требованиями, требования удовлетворяются немедленно и если
вместо gk(l,+xk) используются действительные затраты в интервале времени
между 7+т и /4-т+Д/, то после непосредственного вычисления ожидаемых
затрат и последующего усреднения их подходящим образом будет получено
уравнение (10.112).
10.26. Вывести рекуррентные соотношения (10.121).
10.27. Объяснить, почему при решении задач типа обсуждавшейся в
§ 10.18 использование динамического программирования не ведет к успеху,
если не используется информация о значениях, которые принимают случайные
параметры?
10.28. Вывести уравнение (10.122).
10.29. Для задач вариационного исчисления, рассмотренных в § 10.19,
доказать, что если F — непрерывная функция ук, Уь+\ и х^, то Afe(g) и
i/а (g) — непрерывные функции от g.
10.30. В § 10.7 отмечалось, что если переменная xh непрерывна, то могут
возникнуть трудности при определении
max (xk, g).
0<xk<b/ak
Рассмотрим, однако, случай, когда fife — строго вогнутая функция. Оказы-
вается, что тогда можно применить специальный прием для отыскания ее
максимума. Допустим, что выбраны два значения Хь, скажем ai и аг
(а1<аг), из интервала 0 х^^Ь^. Вычислим значения Qft(0, g), fife(ai,g),
fife(a2, g), Qfe(Z?/aft,g). Если наибольшим из этих значений является fife(0, g)
или fift (Ь/ah, g), то максимум находится соответственно в интервалах
или ^^Xk^b/a^. Если наибольшим является fife(ai,g), то аб-
солютный максимум находится в интервале 0 < xk < а2. Если, наконец, наи-
большим является fife (аг, g), то максимум заключен в интервале
On^Xk^bjafa Почему справедливы эти утверждения?
Если, например, исходный интервал на первом шаге сведен
к то мы можем выбрать из этого интервала значение р
(p =/= otj), вычислить fi/Др, g) и повторить процесс. Действуя таким образом,
можно очень -быстро сузить первоначальный интервал, причем на каждом
шаге требуется вычислять лишь одно новое значение fife. В начале процесса
целесообразно взять ai и а?, отстоящими от концов примерно на 1/5 длины
всего интервала 0 ^х^^.Ь/а^ В дальнейшем новую точку стоит выбирать
так, чтобы она была симметричной уже имеющейся внутренней точке относи-
тельно середины промежутка. Почему этот процесс представляется разум-
ным? Проиллюстрировать его графически.
10.31. Вывести функциональное уравнение для A(g, х), заменяющее урав-
нение (10.130) при Дх->0. [Указание. Разложить A(g + Ag, х + Дх) по формуле
Тейлора, удерживая члены с первыми производными, и получить уравнение
в частных производных
-4?=т;п W ]
28 Зак. 735
434
Гл. 10. Динамическое программирование I
10.32. Предприятие выпускает консервы — овощной суп с цыплятами —
в течение всего овощного сезона, т. е. в течение июля, августа и сентября.
Контракт на поставку цыплят заключается в марте, причем предполагается,
что цыплята поставляются разделанными. Цена цыпленка зависит от размера
покупаемой партии и даты поставки. Размер партии всегда есть число, крат-
ное 100. Цыплята могут поставляться на предприятие каждую неделю в те-
чение всего сезона работы. Если цыплята не используются в ту же неделю,
когда они доставлены,, их следует хранить в холодильнике, который арен-
дуется предприятием. Требуется определить количество цыплят, которое сле-
дует покупать каждую неделю, чтобы минимизировать суммарные затраты
на цыплят и хранение при условии, что недельная потребность в цыплятах
задана. Поставить задачу и показать как она решается с помощью динами-
ческого программирования. Провести решение для конкретного случая: период
работы длится 5 недель, запасы в начале и в конце отсутствуют, недельная
потребность составляет 300 цыплят и затраты на покупку не зависят от вре-
мени покупки.
Цены цыплят" и затраты на их хранение приведены ниже в таблицах.
Затраты на хранение указаны для количества цыплят, остающихся в холо-
дильнике полную неделю.
Цены цыплят Затраты на хранение
X цена запас цена
(в сотнях) (в долл.) (в сотнях) (в долл, за неделю)
1 150 1 10
2 280 2 20
3 410 3 30
4 540 4 50
5 660 5 70
6 780 6 100
7 890
8 1000
9 1100
10.33. Очень часто для задачи о загрузке судна удается найти близкое
к оптимальному решение следующим образом. Сначала загружается как
можно больше продукта с максимальной удельной ценой, затем грузится
продукт со следующей после максимума удельной ценой и т. д. Объяснить,
почему такой процесс не всегда приводит к оптимальному решению.
10.34. Можно ли использовать динамическое программирование для реше-
ния динамических задач теории создания запасов, если потребности в раз-
личные периоды не являются независимыми случайными величинами?
10.35. Рассмотрим систему создания запасов, состоящую из п складов.
Мы хотим перераспределить запасы некоторого продукта между складами
так, чтобы минимизировать суммарные транспортные затраты и ожидаемые
затраты из-за неудовлетворенного спроса в течение фиксированного периода
времени. Транспортировка продукта возможна между любыми двумя скла-
дами. Требуется определить оптимальный план перевозок. Можно ли сформу-
лировать эту задачу как задачу динамического программирования? Изменится
ли ситуация, если часть складов может служить только поставщиками, а
часть — только потребителями?
Упражнения
435
10.36. .Рассмотрим еще раз модель, обсуждавшуюся в § 10.18. Допустим,
что вместо задания затрат, вызванных неудовлетворенным спросом, поставле-
но условие, что вероятность появления неудовлетворенного спроса в интер-
вале времени между /,+ту и tj+ij + Atj должна быть меньше или равна
Показать, как можно решить эту задачу, пользуясь приемами динамического
программирования. [Указание. См. обсуждение этого вопроса в гл. 5.]
10.37. Вывести уравнение, аналогичное (10.107), для случая, когда Т —
время, в течение которого используется машина, — предполагается непрерыв-
ной переменной. Считать коэффициент приведения а непрерывной функцией
времени. Продифференцировать функцию затрат по Г и приравнять произ-
водную нулю. Дать экономическую интерпретацию результата.
28*
ГЛАВА
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ II
Мы действительно живем в эпоху при-
кладных наук.
А. Э й н ш т е й н. Обращение к студентам
Калифорнийского Тех-
нологического инсти-
тута.
ПЛ. Введение. В предыдущей главе мы изучили ряд задач
различного типа, которые могли быть сформулированы как за-
дачи динамического программирования. Все они характерны
тем, что на каждом шаге требуется только один параметр со-
стояния и выбору подлежит значение только одной управляю-
щей переменной. Перейдем теперь к исследованию более слож-
ных задач, в которых может быть несколько параметров состоя-
ния и несколько управлений. Здесь мы сразу же столкнем-
ся с одним из самых больших препятствий, возникающих при
использовании динамического программирования, а именно
с ограничением размерности. Оказывается, что объем вычисле-
ний при решении задачи возрастает невероятно быстро с увели-
чением числа параметров состояния, даже если на каждом шаге
требуется определить всего только одно управление. В равной
степени вычислительные трудности могут быстро стать непреодо-
лимыми при увеличении числа управляющих переменных, даже
в том случае, когда процесс описывается единственным пара-
метром состояния.
Как и раньше, начнем с рассмотрения некоторых частных задач.
11.2. Задача распределения с двумя ограничениями. Изучим
задачу, которая отличается от рассмотренной в § 10.2 только
тем, что в ней два ограничения, а не одно. Она формулируется
следующим образом:
п
2 0-2 jXj
О, j—\все целые;
п
найти max z— S
п
(ПЛ)
11.2. Задача распределения с двумя ограничениями 437
Здесь все и bi предполагаются целыми положительными чис-
лами. К такому виду сводится, например, задача о загрузке
подводной лодки запасными частями при наличии как объем-
ных, так и весовых ограничений.
Рассматриваемая задача естественно трактуется как п-шаго-
вый процесс распределения ресурсов, в котором на /-м шаге
выбирается величина Xj. Когда значение Xj определено, величи-
ны tZijXj и a2jXj определяют соответственно количество ресурсов
первого и второго типов, предназначенных для использования в
/-м способе производства *)• Однако в данном случае состояние
системы не определено до тех пор, пока не задано количество
обоих видов ресурсов. Следовательно, в этой задаче имеется два
параметра состояния — по одному для каждого вида ресурсов.
Коль скоро введены два параметра состояния, становится
совершенно ясным, как можно найти решение поставленной за-
дачи с помощью динамического программирования. Аналогично
тому как это было сделано в § 10.2, определим последователь-
ность функций *
A*Qi>b)= max 'Sfjtxj), /= 1, 2, ..., л, (11.2)
Л- — xk
где максимум берется по неотрицательным целым числам, удо'
влетворяющим условиям
(Н.З)
Тогда, так же как и в § 10.2,
Л,(^, £2) = max Л(*1), (11.4)
0<х, <6,
Л* (In &2) — max [/j (xft) + Лй_1 (|j — 5г — Д2Л)]>
£ = 2, 3, .... л, (11.5)
и
z* — h.n{bx, b2), (11.6)
где
Ш}- <11J>
Одновременно cA*(gi, Ы определяется и величина Хн(Ь, Ь) —
управление, реализующее ЛН&Лг). На n-м шаге, определяя
Ап (^1, 62), мы одновременно находим х . Оптимальные значения
!) Значение этого термина совпадает со значением термина «способ»^
использованного в работе Л. В. Канторовича [15*]. — Прим, перев..
438 Гл. 11. Динамическое программирование 11
остальных управлений могут быть получены из таблиц зна-
чений Ь) с помощью соотношений
/ \
Xn-i = Хп-1\Ь\ ^2 ^a2,n-uXn-u]'
\ и=0 и=0 /
f=l,...,n—1. (11.8)
Заметим, что функции состояния Л&(Вь |2) выражают собой
максимальное значение целевой функции при использовании пер-
вых k способов производства при условии, что для распределе-
ния между ними имеются соответственно количества и ре-
сурсов первого и второго типов. g2) есть оптимальное зна-
чение xk при условии, что процесс состоит только из k шагов и
количество ресурсов, распределяемое на них, равно соответствен-
но gi и &
На первый взгляд может показаться, что трудности при ре-
шении рассматриваемой задачи ненамного больше, чем при
решении задачи, изученной в § 10.2. Однако это вовсе не так.
Дело в том, что теперь Ak и xk являются функциями двух пере-
менных. Напомним, что для задачи из § 10.2 было, вообще го-
воря, необходимо вычислять и табулировать Ak и xk при всех
| = 0, 1, ..., Ь. По тем же соображениям для данной задачи
может оказаться необходимым табулировать Л* (Bi, Ь) для всех
комбинаций gi и g2, когда ^ принимает значения 0, 1, ...,
а £2— значения 0, 1, ..., 62. Если gi и $2 могут принимать по
100 значений, то, вообще говоря, возникает необходимость в
табулировании g2) для 10 000 возможных комбинаций g4
и £2- Как и для задачи из § 10.2, очень трудно проследить зара-
нее, какие комбинации gi и £2 будут действительно необходимы
на каждом шаге (это, конечно, зависит от Ьх и 62). Таким обра-
зом, за исключением редких случаев, приходится табулировать
Afe(Sbb) Для всех возможных комбинаций g4 и g2- Однако для
определения каждого Ль(11, Ь) при заданных величинах и g2
должна быть выполнена максимизация по Хь. Итак, если и g2
могут принимать по 100 различных значений, на каждом шаге
должно быть выполнено 10 000 операций максимизации, в то
время как для соответствующей задачи из § 10.2 на каждом
шаге требовалось выполнить только 100 операций максимизации.
Следовательно, задача вычисления функции Л&(£1, g2) на 6-м ша-
ге решения требует по крайней мере в 100 раз большего объема
вычислений, чем это было нужно на 6-м шаге задачи из § 10.2.
Есть и другая трудность, которая возникает из-за того, что
функции AfeQi, |2) должны сохраняться в памяти вычислитель-
ной машины. Мы отмечали уже, что, если g4 и g2 могут прини-
11.3. Задача с двумя переменными управления
439
мать по 100 значений, таблица значений функции Л/Д^, £2) будет
содержать 10 000 значений. Если и |2 могут принимать по
1000 значений, таблица значений функции Afe(gi, g2) будет со-
держать 106 значений. Таким образом, размер таблиц, которые
надо хранить в памяти машины, быстро становится очень боль-
шим.
Оперативная память вычислительных машин в настоящее
время не превосходит 32 000 ячеек. Следовательно, даже одна
таблица значений функции Аь(£ь g2) может значительно превы-
сить объем оперативной памяти вычислительной машины, так что
потребуется использование магнитных лент, значительно умень-
шающих скорость, с которой могут быть проведены вычисления.
Несколько слов о возможностях решения задач динамиче-
ского программирования на современных вычислительных ма-
шинах. Задачи, содержащие только 2 параметра состояния, с
помощью больших машин обычно решаются без особого труда.
При наличии 3 параметров состояния часто и речи быть не мо-
жет о прямом решении задачи даже с помощью самых больших
машин. Объясняется это тем, что если даже каждое может
принимать только 100 значений, таблицы значений функций Л/г
будут содержать 106 значений и вычисление каждой таблицы
потребует в 10 000 раз больших усилий, чем в соответствующем
одномерном случае. Позднее мы увидим, что иногда возможно
свести число параметров состояния к одному. Благодаря этому
некоторые задачи, содержащие 3 параметра состоянйя, могут
быть решены на мощных вычислительных машинах. Задачи,
содержащие 4 и более параметров состояния, почти всегда пре-
восходят возможности современных машин.
В этом параграфе, рассмотрев простое обобщение задачи из
§ 10.2, мы столкнулись, возможно, с наиболее серьезным препят-
ствием, мешающим использовать динамическое программирова-
ние для решения задач. Этим препятствием является число
параметров состояния рассматриваемых задач. Если оно более
трех, использование динамического программирования в настоя-
щее время невозможно. При трех параметрах состояния реше-
ние может оказаться возможным, но в этом случае разумно
изучить различные методы его отыскания. Задачи, содержащие
два параметра состояния, обычно могут быть решены, но тре-
буют иногда в 100 раз большего машинного времени, чем ана-
логичные задачи с одним параметром.
11.3. Задача с двумя переменными управления. Для задачи
распределения ресурсов, рассмотренной в предыдущем парагра-
фе, характерно, что ресурсы не могли распределяться незави-
симо. Выбор величины определял количества ресурсов обоих
440
Гл. 11. Динамическое программирование II
типов, подлежащих распределению на /-м шаге. Мы рассмотрим
теперь несколько отличную задачу, в которой также имеются
два типа ресурсов, однако на каждом шаге они могут распреде-
ляться независимо, и доход от одного шага является функцией
количества обоих типов ресурсов, распределенных на этом шаге.
Таким образом, задача имеет следующий вид:
S «1 jXj < bx, Д a2jyj < b2,
у/^0, /'= 1, п, все Xj и yj—целые; (11.9)
п
найти шахг= ///)•
Эта задача снова может рассматриваться как п-шаговый
процесс принятия решений, но теперь на /-шаге необходимо вы-
бирать значения и Xj, и yj. Чтобы описать состояние системы,
имеющей k шагов, на этот раз необходимы два параметра, в
качестве которых мы выберем количества каждого типа ресур-
сов, распределяемых на этих k шагах.
Действуя, как обычно, определим функции состояния
k
Л*(£1Д2)= max 2 fj(Xj, у}), k=X 2, ..п, (11.10)
х1’ •••’ xk •z“1
где максимум берется по неотрицательным целым числам Xj и
у^ удовлетворяющим условиям
k у
S £1» ауУ] &2* (11.11)
Рекуррентные соотношения имеют вид
A*Qi> У = тах[Мх*, ^Л)Ч-АЛ_г(^ — aXkxk, £2-a2ftf/A)], (11-12)
k — 2, ..., п,
где Хп может принимать значения 0, 1, ..., а ук — зна-
чения 0, 1, ..., Максимум по xk и yh находится перебо-
ром их всевозможных комбинаций. Например, если каждое из
них может принимать 100 различных значений, то для нахожде-
ния максимума нужно просмотреть 10 000 величин •
11» £2) — fk(xk^ (£1 — aikxk> I2— й2&)* (П.13)
Таким образом, решение этой задачи требует значительно
больших усилий, чем задача из предыдущего параграфа, так
11.4. Случай непрерывности переменных
441
как теперь существенно возрастает трудность нахождения каж-
дого Лл(£ь &>).
Итак мы видим, что если на каждом шаге выбору подлежит
более одной переменной управления, вычислительные трудности
при решении задачи значительно возрастают. Задачи с двумя
переменными управления обычно удается решать только с по-
мощью больших вычислительных машин. Задачи с тремя пере-
менными управления иногда тоже находятся в рамках вычис-
лительных возможностей. Что же касается задач с четырьмя
и более переменными управления, то лишь очень редко в на-
стоящее время удается решить их численно.
11.4. Случай непрерывности переменных. В § 10.7 обсужда-
лись трудности, возникающие в
даче из § 10.2 непрерывны. Эти
задач с двумя или более пара-
метрами состояния или с дву-
мя или более переменными
случае, когда переменные в за-
же трудности характерны и для
<$2
управления.
Для задач, рассмотренных
в § 11.2 и 11.3, из непрерывно-
сти ФУНКЦИЙ fj(Xj) И Uj)
следует непрерывность функ-
ций СОСТОЯНИЯ Afc(gi, g2) по
переменным и |2. Доказа-
тельство этого утверждения,
аналогичное приведенному в
§ 10.7, читателю предлагается
провести в упражнении 11.1.
Если же функции fj не непре-
рывны, то при практическом
решении задачи необходимо
I
М,-
Р и с. 11.1.
рассматривать переменные как дискретные. Непрерывность
функций g2) позволяет проводить их интерполяцию с от-
носительной безопасностью. Обычно они бывают очень «поло-
гими», что позволяет выбирать при их табулировании сетку с
достаточно большим шагом. Интерполирование в случае функ-
ции двух переменных имеет некоторые особенности. Мы приве-
дем здесь вывод интерполяционной 'формулы первого порядка.
Пусть требуется вычислить Лй(£ь |2). Обозначим уже вы-
численные значения вблизи от этой точки через Лй(аь Pi),
Afe(ai, р2), Ль(а2, Pi) и Afc(a2, р2). Все эти точки отмечены на
рис. 11.1. Рассмотрим точку
(«о- ₽о) = (у (ai °2)’ У ’
442
Гл. 11. Динамическое программирование 11
являющуюся центром прямоугольника, изображенного на ри-
сунке. Заменяя в формуле Тейлора частные производные ко-
нечными разностями (§ 2.10), получаем следующее приближён-
ное соотношение: »
ЛА у «ь Лл (Оо, Ро) + ^~ао)- [Л, («2, р0) - ЛА (ар Ро)] +
+ Д^-1ЛИ«о. М-лИ«0, Pi)]- (11-14)
Неизвестные здесь величины Лл(а0, р0), л*(а2> ₽о), Лл(ап Ро)»
ЛА,(а0, р2) и Лл(а0, pj могут быть определены из приближен-
ных равенств
ЛЛ(ао, Po)^"j [уЧ(а1’ Р1) + Ал(«2» Р1) + АЛ(а1, Р2) + Л^(а2, р2)],
Л^(а2, Ро) — Ад,(ап р0)^
2" (а2’ (а2’ (а1’ (ttl’
Л^(а0, р2) — (а0, р^
^y[A^(«2, Р2)Н~Лл(а1, р2) — Ak (а2, РО— Лл(а1? Pj)].
Подставляя их в (11.14), получаем интерполяционную фор-
мулу
а /г г \ 1 Г1 (2^1 — а1 — аг) (2?2 — Pi — Р2) 1 д /р р \ ।
A*(£i, ё2)^f [1-----------------------------]ЛНа1> Р1) +
+ Н1 - лй (ар р2) +
+j [i + - -^?~Д'~р2)]л* («2. Pi)+
+ -И1 + (2S1 ~Д‘ ~ + (2Ь ~ Р1 ~ Рг) ] Ад, (а2, р2), (11.15)
которая легко программируется для вычислительной машины.
Отметим, что в ней используются все четыре близкие к (gb g2)
точки, в которых вычислена функция Л^(х, у).
Как и в модели, рассмотренной в § 10.2, стратегии xfe(gi,g2)
не обязательно являются непрерывными функциями от gi и
Если не известно заранее, что они непрерывны, табулирование
этих функций может не привести к цели. Значения х\ в этом
случае приходится вычислять непосредственно, проводя вычис-
ления от х* в обратном направлении, как это описано в § 10.7.
В случаях, аналогичных описанному в § 11.2, где на каждом
шаге определялась единственная переменная управления, зада-
ча максимизации хь может решаться в точности так, как описа-
но в § 10.7. Кроме того, если fj(Xj) —вогнутые функции, то от-
11.4. Случай непрерывности переменных
443
сюда следует вогнутость функций g2) и AA(gb g2). До-
казательства этих фактов проводятся несколько иначе, чем в
§ 10.8, и читателю будет предложено провести их в упражне-
нии 11.2. В этих случаях могут использоваться упрощенные при-
емы, обсуждавшиеся в § 10.8 и в упражнении 10.30.
Остановимся, теперь на задачах, в которых на каждом шаге
берется максимум по двум переменным. Если о функциях
Рис. 11.2.
Qfe(x&, tjk, ii, £2 )ничего не известно, то обычно начинают с раз-
биения той области плоскости xhyk, в которой разыскивается
максимум, с помощью сетки с большим шагом (см. рис. 11.2).
Затем в окрестности найденных относительных максимумов
поиск продолжается с помощью сетки с более мелким шагом.
Это также проиллюстрировано на рис. 11.2. Разумеется, с по-
мощью сетки с мелким шагом может быть найдено более точ-
ное значение максимума лишь в той области, где она исполь'
зуется. Отметим, что сравнения, необходимые для отыскания
абсолютного максимума, проводятся весьма просто, поскольку
каждый раз по вычислении Ял это значение сравнивается с пре-
дыдущим и в оперативной памяти сохраняется лишь большее
из них (вместе с координатами соответствующей ему точки).
Несколько труднее найти все относительные максимумы при пер-
воначальном использовании сетки с большим шагом. Чтобы вы-
яснить, имеет ли Я& в некоторой точке сетки относительный
максимум, следует сравнить это значение со значениями Яа в
444
Гл. 11. Динамическое программирование II
восьми соседних точках (на границах число соседних точек рав-
но пяти или трем).
Если все yj) в (11.9) выпуклые (вогнутые) функции, то
функции Qfe(xfe, yh\ gi,g2) и Aft(gi,g2) также будут выпуклыми
(вогнутыми). Читателю предлагается доказать это утверждение
в упражнении 11.3. Если функции fj^yj) выпуклые, из ре-
зультатов § 3.12 следует, что максимум Я& будет достигаться в
крайней точке выпуклого множества (в нашем случае — в углах
прямоугольника). Поэтому в данном случае для вычисления
Afc(gi,g2) необходимо вычислить значения лишь в четырех
точках.
Если же функции fj(Xj, yj) вогнутые, для определения макси-
мума также может быть использована упрощенная процедура
поиска. Рассмотрим случай, когда функции fj(xh yj) строго во-
гнутые, так что функции Я& также строго вогнуты (если это не
так, не будем ставить перед собой задачу отыскать все макси-
мумы). Покажем, как на этот случай может быть обобщен ме-
тод упражнения 10.30.
Процесс начинается с выбора двух значений х&, скажем ои
и а2, делящих отрезок, в котором может меняться xfe, примерно
на равные части. Используя одномерную процедуру поиска,
обсуждавшуюся в упражнении 10.30, находим
h (аО = max Qk (ап у*-, |2); h (л,) = max Qk (а2, yk-, у.
«k • 4
Тогда, если h(aj) >Л(а2),_точка максимума должна лежать
в прямоугольнике O^x^ag, (см. рис. 11.3). Если
бы максимум Я/г не достигался в этом прямоугольнике, это про-
тиворечило бы допущению о вогнутости Я^ (противоречие обна-
руживается при рассмотрении отрезка прямой, соединяющего
точку максимума Я& и точку, доставляющую значение Л (си)).
11.5. Линейное и динамическое программирование
445
Если /i(a2)>/i(ai), то точка максимума должна находиться в
прямоугольнике 0<г/й<62/Лгь. Наконец, если
й(а2) =/t(ai), то точка максимума лежит в прямоугольнике
оч^Хй-^схг, 0<Cz/fe^&2/«2h.
На следующем шаге выбираются два значения г/й, скажем
Pi и р2, делящие примерно на равные части интервал изменения
№. Теперь вычисляем
Л(РО = шах Q* (хй, рр Ij, |2); ЛГ(Р2) = max Q* (xft, р2; ^)-
хь хь
Тогда если Л(Р1)>й(р2), то точка максимума должна лежать
. в прямоугольнике 0^xfe^Ca2, 0<^//А<Ср2 (если на предыдущем
шаге выполнялось неравенство A(ai) >Л(а2); если /Г(р2) >/T(pi),
точка максимума должна быть в прямоугольнике 0<^х&<Са2,
^i^yk^b2/a2k (см. рис. 11.4); если Л(₽1)=Л(р2), точка максимума
лежит в прямоугольнике 0<J^<Ca2, и т. д. для других
возможных значений xk.
Далее выбираются два новых значения х&— назовем их аз и
а4,—делящие приблизительно на равные части полученный ин-
тервал изменения xh (например, 0^xfe<^a2) и т. д. Результатом
этой процедуры является последовательное сужение прямоуголь-
ника, содержащего точку максимума. Более того, на каждом
шаге, как правило, мы получаем два новых значения максимума
при максимизации по каждой переменной, поскольку вычислен-
ный ранее максимум обычно не находится в остающемся прямо-
угольнике.
Этот параграф иллюстрирует возможность применения чис-
ленных методов в том случае, когда переменные предполагают-
) ся непрерывными, имеется два или более параметров состояния
или несколько переменных управления, по которым отыскивает-
ся максимум. Для задач, рассмотренных в предыдущей главе,
гораздо более удобный подход состоит в том, чтобы считать пе-
ременные дискретными. Это остается справедливым и для за-
дач, изучаемых в этой главе.
11.5. Сравнение линейного и динамического программирова-
ния. Задача линейного программирования
п
х>0/ у=1, 2, п; (11.16)
п
найти max z = У CjXj
1
446
Гл. 11. Динамическое программирование II
может рассматриваться как n-шаговый процесс принятия ре-
шений, в котором на /-м шаге выбирается значение величины Xj.
Действительно, эта задача линейного программирования может
быть сформулирована как задача динамического программиро-
вания. Однако в качестве аргументов функций состояния по-
требуется т параметров состояния — по одному для каждого
ограничения. Для того чтобы сформулировать эту задачу как
задачу динамического программирования, введем обозначения
k
A*Qi> •••>£„) = max 2 k=\,...,n, (11.17)
xi..xk i-1
где максимум берется по неотрицательным Xj, удовлетворяю-
щим условиям
k
= Z=l, 2, tn. (11.18)
Тогда рекуррентные соотношения принимают вид
л* (£1, ..., |m) = max [ckxk -ь А*_1 (&! — alkxk,
xk
k — (11.19)
Рассмотрим теперь, в каком интервале может меняться xk.
Пусть / есть множество индексов i, для которых при
всех /. Тогда |г->0 при ограничение удовлетво-
ряется при произвольно больших Xj, а может быть отрица-
тельным. Следовательно, максимальное значение 0&, которое
может принимать xft, таково:
0^ = min|^|, i£I, или оо, если / пусто. (11.20)
Трудности использования динамического программирования
для решения таких задач связаны, конечно, с числом параметров
состояния. При наличии 100 ограничений потребуется 100 пара-
метров состояния. Если допустить, что каждый принимает толь-
ко 100 значений, то таблица значений функции должна бу-
дет содержать 100100 чисел. Это невообразимо большое число.
Читатель, знакомый с ЭВМ, может попробовать вычислить дли-
ну магнитной ленты, необходимой для хранения таблицы та-
кого объема. Если предположить, что в секунду вычисляется
106 значений А&, то для вычисления одной только таблицы Ай
потребуется примерно 10093 лет. Таким образом, ясно, что в
общем случае решение задачи линейного программирования со
значительным числом ограничений с помощью динамического
11.6. Транспортные задачи с двумя пунктами производства 447
программирования оказывается невозможным. Даже в случае
одного или двух ограничений гораздо более эффективным ока-
зывается симплекс-метод.
При решении задач линейного программирования с помо-
щью методов динамического программирования может встре-
титься и другая трудность. Если некоторые ац отрицательны,
то уже неверно, что наибольшее значение которое может по-
требоваться, есть bit В самом деле, если нет уверенности в том,
что задача имеет ограниченное решение, то нет оснований ду-
мать, что Bi будет ограниченным. Во всяком случае, очень
трудно указать точно область определения каждого £г- для /(£/.
11.6. Использование динамического программирования в
транспортных задачах с двумя пунктами производства. Рассмот-
рим транспортную задачу с двумя пунктами производства и п
пунктами потребления. Математическая формулировка ее такова:
п п
S'*"!/~ а1> 2^2; = ®2’
— /=1, 2, ..n; для всех Z,/; (11.21)
найти min z = S ctjXtj = 2 + c2jx2j).
h j j
Поскольку задача имеет специальную структуру, можно
сформулировать ее в терминах динамического программирова-
ниял используя значительно меньше параметров состояния, чем
потребовалось бы для общей задачи линейного программирова-
ния с тем же числом ограничений. Действительно, мы увидим,
что для определения функций состояния этой задачи потребует-
ся только один параметр состояния.
Будем понимать под задачей (11.21) n-шаговый процесс при-
нятия решений, в котором на /-м шаге определяется, какое ко-
личество продукта из первого и второго пунктов производства
посылается в /-й пункт потребления. Так как то
ясно, что количество продукта, посылаемое из первого пункта,
автоматически определяет количество, посылаемое из второго4
пункта. Рассмотрим задачу вида (11.21), в которой имеется k
шагов, и количества продукта в первом и втором пунктах рав-
k
ны соответственно | и ц. Поскольку т- е- Л —
7е 1
k
— 2 bj — £, то, выбрав мы тем самым определяем ц. Следо-
/-1
вательно, g есть единственный необходимый параметр состояния.
448
Гл. 1L Динамическое программирование II
Введем последовательность функций состояния
ЛА(|)== min S(cvxlyH-(?2yx2y), (11.22)
*11’ x\k •/==1
X21’ •••’ X2k
где минимум берется по неотрицательным удовлетворяющим
условиям
k k k
bj-Ь
(11.23)
= 7=1,..., k.
Рекуррентные соотношения принимают вид
(£) — т*п + c2k (Pk x\k) 4“ (£ xlk)], (11.24)
xik
k = 2t ..., n,
где xlk должно удовлетворять неравенству
О < xxk < min {£, bk\ (11.25)
и
k й-i
Xik = bk — xlft< 2 bk — I, T. e. x^Z-^bj. (11.26)
/-1 y-l
Это эквивалентно следующему соотношению:
{л-i ч
О, I— 2 <•*!*< min {£, Ьь\ = &ь- (11.27)
При проведении вычислений функция ЛД£) должна табули-
k
роваться при всех £ — 0, 1, ..*,2^/» попутно запоминаются
j1
также значения функции Хи(ё)- Отметим, что размер этих таб-
лиц будет возрастать с ростом k. На последнем шаге опреде-
ляется х*п (и, следовательно, х2л = Ьа — х*„). Остальные х*к
находятся из соотношений
n-i(ai 1. (11.28)
11.7. Использование множителей Лагранжа
449
Поскольку известно, что из целочисленности и bj следует
целочисленность интерполяции при вычислениях не по-
требуется.
Если значение 2#; велико, таблицы значений функций
Лй(|) и будут содержать большое количество чисел, но
обычно такая задача все-таки без особого труда решается на
вычислительной машине. Тем не менее даже в этом случае
метод динамического программирования не выдерживает кон-
куренции с другими методами решения транспортных задач.
Приведенная выше формулировка может все же оказаться
полезной при решении задач описанного типа с нелинейными
функциями затрат. Чтобы обобщить задачу на случай нелиней-
ных затрат, нужно заменить СцХц на С1Дхъ) и c2jX2j на
СгДхг;), где Cij(xij) и Ctj(X2j) —затраты на доставку Хц и X2j
единиц продукта в /-й пункт потребления соответственно из
первого и второго пунктов производства. Эти затраты могут
быть произвольными функциями. Решение в этом случае мо-
жет быть проведено точно так ж.е, как описано выше, исключая
отыскание минимума в (11.24), поскольку теперь нельзя
использовать выпуклость функций затрат. При нелиней-
ных затратах, как правило, предполагают заранее целочислен-
ность Хи, а поиск максимума в (11.24) осуществляется непо-
средственно.
Задачи с двумя пунктами производства и нелинейными тран-
спортными затратами могут достаточно хорошо решаться ме-
тодом динамического программирования, в то время как другие
методы в этом случае, вообще говоря, непригодны.
11.7. Использование множителей Лагранжа для уменьшения
размерности. Ранее было отмечено, что, когда число параметров
состояния больше двух, решение задач с помощью динамическо-
го программирования даже на современных вычислительных ма-
шинах становится по сути невозможным. Мы покажем сейчас,
что введение множителя Лагранжа позволяет иногда уменьшить
число параметров состояния на единицу.
Чтобы показать, как это делается, рассмотрим снова зада-
чу (11.1) для того случая, когда Xj непрерывны. Предположим
также, что fj(Xj) —неубывающие функции от Xj. Тогда ясно, что
для любого оптимального решения по крайней мере одно огра-
ничение должно выполняться в виде равенства. Часто еще до
решения задачи удается определить, какое именно ограничение
выполняется как строгое равенство. Пусть известно, что для
оптимального решения этим свойством обладает второе огра-
ничение. Решим тогда для фиксированного значения 1
29 Зак. 735
450
Гл. 11. Динамическое программирование II
следующую задачу:
7-1
ху>0, /=1, ...,га; (11.29)
п п
найти max zx = 2 (ху) — % 2
Решить ее гораздо проще, чем задачу (11.1), так как здесь
имеется только одно ограничение и, следовательно, необходим
один параметр состояния. Рекуррентные соотношения для функ-
ций состояния в этом случае принимают вид
Л* (У = max [fk (xk) — Ka2kxk + (£ — alkxk)], £ = 2, n.
xk
(11.30)
Докажем, что если оптимальное решение х* задачи (11.29)
удовлетворяет условию
п
то х* является оптимальным решением и для задачи (11.1). Оче-
видно прежде всего, что х* — допустимое решение задачи (11.1).
Обозначим оптимальное решение задачи (11.1) через х°. Тогда
п п
Z (х°) = 2 G (х°у) > 2 (Х‘) == Z (х*). (11.31)
Однако так как х* есть оптимальное решение задачи (11.29), то.
п п
zx (х‘) = z (х*) — А 2 a-2jx*i > 2 (х°) — 2 = г, (х°),
/«=1 .7-1
т. е., поскольку 2а2/х/= 2 = ^2’должно быть г (х*)<^г(х°).
Это противоречит неравенству (11.31). Следовательно, в случае
непрерывных переменных Xj величина х* есть оптимальное ре-
шение задачи (11.1).
Приведенные выше рассуждения делают возможным следую-
щий прием решения задачи (11.1) в случае непрерывности пере-
менных Xj. Фиксируется произвольное значение А и решается
задача (11.29). Если решение х* таково, что 2 = то х*
есть оптимальное решение задачи (11.1). Если 2 ^2’
выбирается новое значение Л и процесс повторяется. Далее
11.7. Использование множителей Лагранжа 451
используются оба значения X и найденные величины
чтобы с помощью линейной интерполяции (или экстраполяции)
оценить новое значение X, при котором должно выполняться
условие 2 = Ь2- Затем заново решается задача (11.29) с
использованием уже этого значения X. Следующее значение X
находится интерполяцией по трем точкам и т. д. Обычно для
решения задачи (11.1) бывает достаточно пяти или шести ите-
раций. 1
Эта процедура гораздо менее трудоемка, чем описанная в
§ 11.2. Количество вычислений, используемых при таком под-
ходе, будет соизмеримо с количеством вычислений при исполь-
зовании метода § 11.2 лишь в том случае, когда число итераций
с различными значениями X близко к 100. Суть приведенного
метода состоит в назначении некоторой цены на второй ресурс и
устранении ограничения на количество используемого второго
ресурса. Затем мы изменяем стоимость этого ресурса в целевой
функции до тех пор, пока используемое количество не станет
равным в точности Ь2. Эта интерпретация показывает, что если
для выбранного X выполняется неравенство ^a2Jx*j> bv то X
следует увеличить. Аналогичная процедура может использовать-
ся и при условии целочисленности х>. При этом, конечно, уже
нельзя требовать, чтобы одно из ограничений выполнялось как
строгое равенство.
Конечно, предложенный выше метод не является универсаль-
ным. В упражнении 11.4 приведен пример, когда не существует
числа X с желаемыми свойствами. Мы не приводили никаких
достаточных условий применимости этого метода. Такие усло-
вия, которые были бы достаточно общими и в то же время имели
бы практическую ценность, дать трудно. Однако соображения
гл. 6 могут быть использованы для доказательства того, что этот
метод применим, если переменные Xj непрерывны, а функции
fj(xj) вогнуты. Читателю предлагается провести доказательство
этого утверждения в упражнении 11.6.
На практике вопрос о применимости этого метода решается
методом проб. Если удается найти такое X, что исключенное
ограничение обращается в строгое равенство, тогда из сказан-
ного выше следует оптимальность полученного решения.
В некоторых упражнениях к этой главе предлагается пока-
зать, как подход, связанный с использованием множителя Лаг-
ранжа, позволяет упростить решение отдельных типов задач с
тремя ограничениями (три параметра состояния) путем сведения
их к ряду задач, но уже только с двумя параметрами состояния.
Мы закончим обсуждение метода, связанного с использова-
нием множителя Лагранжа, тем, что проиллюстрируем его
29*
452
Гл. 11, Динамическое программирование II
применение к транспортной задаче с тремя пунктами производ-
ства, п пунктами потребления и нелинейными функциями затрат.
Функции состояния на этот раз определим так:
k
AfcQl» Ь) = т*П 2 [Ci;(X17)4-C2;(X2y) + C3y (л:3у)],
по всем x.j 7 — 1
..., п, . (11.32)
где минимум берется по неотрицательным удовлетворяющим
условиям
2 xXj =
7=1
k
2 X2j~ Ь»
7=1
k k
2x3y=2ft7-^-^ (11.33)
7=1 7=1 7
Xl7 + X2j’^TX3j— bj,
7=1, 2, k.
Рекуррентные соотношения запи-
шутся следующим образом:
£2)= [Ci* 4"
Xlk’ X2k
-\-C2k (X2k) + C3k (bk — xXk — X2*) +
+ Aft_! ,|2 - Х2Й)1, (11.34)
где минимум берется по и x2h, удовлетворяющим условиям
о < Xlk < min (£р bk) = 0j; 0 < x2k < min (|2, bk) = 02.
xik^x2k^bk1
или
x3k — bk x2k
k
xik 2 ^7 £2
7=1
Область, в которой отыскивается максимум, изображена на
рис. 11.5. Функции Afe(gi, g2) должны табулироваться при всех
k
целых и |2, таких, что 2 Ь}.
j-i
11.7. Использование множителей Лагранжа
453
Для того чтобы использовать множитель Лагранжа, допустим,
что нет никаких ограничений на количество продукта, отправ-
ляемое из второго пункта, а вместо этого каждой отправляемой
отсюда единице продукта приписана определенная цена. Коли-
чество продукта, имеющееся в первом пункте производства,
задано. Так как нам неизвестно количество продукта, отправ-
ляемого из второго пункта, нельзя задать и объем перевозки из
третьего пункта производства.
Будем теперь решать задачу
^xxj = ax, xv4-x2y+x3y = Z>y) 7=1, все х/у>0;
(11.35)
Л п
найти min z = [Ciу (Л]7) 4- С2у (х2у) 4- С3у (х3у)14~ 2 х2/
j-\
для различных значений %, пока не будет найдено такое, что
оптимальное решение удовлетворяет условию У, x2j = а2. Отсюда
автоматически следует, что 2х3у = а3 = '%ibj — ах — а2 и най-
денное решение является оптимальным для задачи с тремя пунк-
тами производства.
Чтобы решить задачу (11.35), введем функции состояния
k
•A-fe(l) = no y?i 1^1/(Л'Ч)Н_С2у(Х2у)4-^2/ + С3у(Х3у)],
k=\, 2, ..., n, (11.36)
где минимум берется по неотрицательным xfy, удовлетворяющим
условиям
й
Sxv = |, х1у-Ьх2уЧ-х3у = &у, /=1, 2,..., п. (11.37)
Рекуррентные соотношения имеют тогда вид
(£) = т*п C2k + hx2k 4-
Xlk’ X2k
xik — Afc-j(I — k = 2, n, (11.38)
где xlk и x2k должны удовлетворять неравенствам
(£> ^)> xik~\~x2k (11.39)
30 Зак. 735
454
Гл. 11. Динамическое программирование II
Функции Лй(£) следует табулировать при всех целых £ = 0,
k
1,.... 3^.
7 = 1
Таким образом, задача с тремя пунктами производства и п
пунктами потребления может быть сведена к последовательно-
сти n-шаговых задач с единственным параметром состояния. Для
линейных задач описанный метод уступает по своей эффектив-
ности специальным приемам, разработанным для решения транс-
портных задач. Однако он может оказаться весьма полезным в
случаях, когда функции затрат нелинейны.
11.8. Замена оборудования. В § 10.16 было показано, что ди-
намическое программирование можно использовать при решении
некоторых типов задач о замене оборудования. Остановимся на
изучении двух несколько более сложных случаев. В модели,
описанной в § 10.16, каждый раз при принятии решения имелось
только две возможности — продолжать использовать имеющую-
ся машину или купить новую. Добавим теперь еще одну воз-
можность— капитальный ремонт имеющейся машины. Кроме
того, все функции, введенные в § 10.16, будем предполагать за-
висящими не только от возраста машины и года ее покупки, но
и от времени, прошедшего после последнего капитального ре-
монта. Для описания функций состояния теперь потребуется два
параметра — один для возраста используемой машины и второй
для числа периодов, прошедших с момента ее последнего капи-
тального ремонта.
Как и в § 10.16, пусть 1и — затраты на установку машины,
купленной в начале периода и; Cu(j,v) —ожидаемые эксплуа-
тационные затраты на эту машину (купленную в начале пе-
риода и) в /-й период ее использования, если последний капи-
тальный ремонт этой машины был в начале периода v (время,
необходимое для капитального ремонта, считается пренебрежимо
малым); Su(hv)—стоимость машины (купленной в начале
периода и) после / периодов использования, если последний ка-
питальный ремонт был в начале периода у; Hu(j,v) —затраты
на капитальный ремонт машины, купленной в начале периода и,
после j периодов использования, если последний капитальный
ремонт был в начале периода v. Если машина ни разу не была
в капитальном ремонте, v означает период ее покупки.
Функции состояния Afe(gi, Вг) имеют в этом случае смысл за-
трат на планируемый период, приведенных к началу k-ro пе-
риода, если начиная с k-ro периода принимаются оптимальные
решения, используемая машина имеет возраст gi периодов, а
последний капитальный ремонт ее происходил в начале перио-
11 8. Замена оборудования
455
да g2- Рекуррентные соотношения для этих функций имеют вид
Ck-(£i Ч-1 > £2) 4-aA#+i (£1 -f-1, £2) — продол-
жать использовать без капитального ремонта;:
Л z . . £2)+аЛ*+1 (^-Н, k)—
ЛЛ^, £2)= min{
капитальный ремонту
Л + k) — £2)-haAfc+i (1, k) —
купить новую машину..
(11.40)
Из-за наличия двух параметров состояния эта задача много
труднее, чем задачи, обсуждавшиеся в § 10.16. Однако, так как
минимум вычисляется довольно просто и значения никогда
не бывают слишком большими, подобные задачи без особого
труда могут решаться на вычислительных машинах. Конечно,
на практике могут встретиться значительные трудности при
определении функций затрат.
Другое обобщение, которое мы будем рассматривать, состоит
в том, что имеется возможность выбора между машинами раз-
личных типов. На этот раз исключается возможность капиталь-
ного ремонта, а можно лишь продолжать эксплуатировать имею-
щуюся машину или приобретать новую.
Пусть функции luv, Cuv(j) и Suv(j) имеют ранее введенный
смысл, а дополнительный индекс v определяет тип машины. Для
примера остановимся на случае машин двух типов, хотя беэ
особого труда можно решить задачу, где это число произвольно.
Функции состояния снова зависят от двух параметров — возра-
ста используемой машины, если эта машина первого типа,,
и аналогичной характеристики для машины второго типа.
Оба параметра не могут быть положительными одновре-
менно, так как в любой момент времени имеется лишь одна
машина.
Пусть снова Л^(В1, Вг) выражает затраты, приведенные к на-
чалу &-го периода, если в конце (k—1)-го периода в наличии
имелась машина данного возраста и данного типа, а решения,
принимаемые в начале £-го периода и во все последующие, были
оптимальны. Если в конце первого периода. имеется машина
первого типа, то параметр определяет ее возраст, а параметр
g2 полагается равным нулю. Наоборот, если имеется машина
второго типа, то определяет ее возраст, a.£i = 0. Отметим, что
для этой задачи, если и g2 могут принимать п значений, функ-
ция I2) принимает только 2п—1 значение, а не п2, как в
30*
456
Гл. 11. Динамическое программирование II
случаях, когда приходится рассматривать все комбинации
11 и g2.
Для изучаемой задачи можно описать состояние системы
с помощью лишь одного параметра состояния. Чтобы пояснить,
как это делается, допустим, что известно, что машину первого
типа нельзя использовать более десяти периодов. Определим
тогда параметр g так, что если g принимает значение от 1 до 10,
то это означает, что имеется машина первого типа возраста g.
Если g>10, то это машина второго типа, а ее возраст g—10.
Однако удобнее все же использовать два параметра состояния.
Чтобы иметь возможность выписать рекуррентные соотношения
для функций состояния, предположим, что (k—1)-й период за-
кончился и имеется машина возраста gi первого типа. Тогда эти
соотношения выглядят так:
O) = min
Ck-tt, 1 (li + l) + «Aj+i (£i -|-1, 0) — ис-
пользовать ту же машину;
Iki—Sft_?1Ji(b) + Cfti(l)-|-aAft+i(l, 0)—
(11.41)
купить машину первого типа;
Ik2—Sii-iu 1 (£,i) + Cj2(l)4-aA*+i (0, 1)—
купить машину второго типа.
Если вычисления проводятся с помощью вычислительной ма-
шины, то без труда может быть решена задача с десятью или
-более типами машин.
В‘ упражнении 11.8 читателю будет предложено сформули-
ровать задачу для случая, когда две машины используются одно-
временно. Решения, которые здесь, могут приниматься, следую-
щие: использовать те же машины, заменить одну или заменить
другую, заменить обе машины. На этот раз необходимы два
параметра состояния, причем приходится рассматривать всевоз-
можные комбинации значений этих параметров. В упражнении
11.9 предлагается обобщить формулировку на случай одновре-
менного использования т машин.
11.9. Некоторые задачи вариационного исчисления. В § 10.19
мы показали, как можно использовать динамическое програм-
мирование для отыскания численного решения задачи вариа-
ционного исчисления, заключавшейся в отыскании функции//(х),
Р
минимизирующей интеграл /= JFQ/, /, x)dx при условиях
а
а/(а) =0, i/(P) —Ь. Рассмотрим теперь более общую задачу, в ко-
11.9. Некоторые задачи вариационного исчисления 457
торой нужно определить m функций уДх), минимизирующих
интеграл
Р
’ J Ftyv •••> Ут’ y'v-’У'т, X)dx (11.42)
а
при заданных граничных условиях z/3(a)=aj, //;(₽)
Другими словами, требуется определить кривую в
(т+1)-мерном пространстве (элементами его являются точки
[х, у\, ..., z/n]), начинающуюся в точке a=[a, ai, ..., am], окан-
чивающуюся в точке b=[p, bi, bm] и такую, что взятый
вдоль нее интеграл (11.42) достигает минимума.
В принципе для решения этой задачи может быть использо-
вана та же вычислительная схема, что и в § 10.19. Интервал
разбивается п+1 точками хи=а+ыДх, и=0, 1, ..., п,
на п подинтервалов длины Дх. Для любЬй допустимой дуги обо-
значим Уз(хи) =yUj и заменим приближенно Уу(хи) через
(Уи+t, j—yUj)/&x. Исходная задача может тогда быть заменена
такой приближенной: определить значения т(п— 1) переменных
yUj, минимизирующих выражение
п
Т V R (и и Уи+ь 1 Уа1 Уц + \,т — Уит v \ A v
' — r • • •1— • • • • ’-------------------дх----• х«)
и«0
(и удовлетворяющих условиям = /=1, т.
Эта задача может быть сформулирована как задача динами-
ческого программирования с т параметрами состояния. Пусть
.... W = min ^Р{уиЪ...., Уап,-^--Уа',...
I Уи+1,т-Уат , (1144)
I где = a ynj = bj, /=1, ...; tn. Рекуррентные соотношения
записываются тогда в следующем виде:
Aft(ll....1т) =
I = min [/ф,..................U, ~ - +
’ yk+l, !>•••’ yk+l,m L
+ (^+1,и ...» m)]* Л = 0> !»•••» п — 2, (11.45)
....|т) = Д(^,..., .... Х«~^Х-
31 Зак. 735
458
Гл. 11. Динамическое программирование II
Отметим, что в этой задаче на каждом шаге приходится искать
минимум по т переменным и, кроме того, функции состояния
зависят от т параметров. При т>3 не может быть и речи о ре-
шении таких задач методом динамического программирования.
Трудности же при т = 2, как уже упоминалось выше, обычно
удается преодолеть.
Нередко при решении задачи минимизации интеграла (11.42)
приходится сталкиваться с тем, что величины Уэ(х) не незави-
симы, а удовлетворяют системе г (г<т) дифференциальных
уравнений
....Ут, y'v •••> Ут' х) = °> Z==l, 2.....г. (11.46)
Эти уравнения представляют собой ограничения для рассматри-
ваемой задачи. Покажем, каким образом может быть получено
численное решение задачи в этом случае. Снова рассматривается
приближенная задача (11.43), а ограничения (11.46) заменяются
приближенно алгебраическими уравнениями
/7 /,. Уи + 1, 1 Уи1 Уи+Ът Унт у. \____п
...» уит>---
Z=l, 2, г, Й = О, 1, п — 1, (11.47)
относительно уи^
Функции состояния Ль определим, как и выше, с тем лишь
добавлением, что yUj должны удовлетворять теперь уравнениям
(11.47). Рекуррентные соотношения снова определяются соотно-
шениями (11.45), но минимум теперь берется по //м-i, j, удовле-
творяющим уравнениям
Ci t #Л+Ь1 m— 5m у. \__Л
----Ах---’ •••’ ----Ах----’
i=l, .... г. (11.48)
Следовательно, наличие ограничений (11.46) лишь облегчает
решение задачи методом динамического программирования, так
как на каждом шаге они сужают область изменения z/b+i,Ко-
нечно, если функции Gi имеют сложный вид, точное определение
области изменения yk+lt j может оказаться затруднительным.
Другая часто встречающаяся на практике задача состоит в
отыскании кривой, начинающейся на некоторой поверхности
g-(x, z/i, ..., ут) =0, кончающейся в точке b и минимизирующей
интеграл (11.42), который на этот раз является интегралом с не-
фиксированным нижним пределом. При такой постановке кривая
начинается не в заданной точке, а в какой-то точке заданной
поверхности. В принципе и для этой задачи можно получить
приближенное решение методом динамического программирова-
ния. Вычисления ведутся по той же схеме с тем, однако, отли-
11.9. Некоторые задачи вариационного исчисления
459
чием, что, когда мы дойдем до Л&, для которого существуют yh
удовлетворяющие уравнению g(xk, ylf yh) =0, следует вы-
числять Aft для множества всех таких у\, ..., ук, и это необхо-
димо повторить для всех соответствующих значений xh. Тогда
наименьшее из этих Л/г может быть выбрано в качестве /* и ре-
шение, следовательно, будет получено.
Остановимся еще на одном классе задач вариационного
исчисления. Пусть требуется определить функцию двух перемен-
ных Ф(х, у), минимизирующую интеграл
а2 |32
/== J J IF’ х' y)'<txdy. (11.49)
«1 pj
Здесь функция ф(х, у) задана в прямоугольнике
показанном на рис. 11.6. Значения функции у) на
границе прямоугольника
считаются известными.
Эта задача снова может
быть приближенно замене-
на задачей динамического
программирования. Чтобы
получить ее, разобъем пря-
моугольник на рис. 11.6.
сеткой с узлами в вершинах
(хь z/j), z = 0, 1,..., m, j—
= 0, 1,..., n. Значения ф бу-
дут вычисляться только в
узлах сетки. Обозначим
ф(хг-, f/j) =фг;-. Заменим приближенно dty/dx и dty/ду отношения-
ми соответственно
дф __ Ф/+ь/--Ф// s <?Ф _ Ф/,/+1 —Ф//
дх И ду \у
Исходная задача приближенно заменяется следующей: найти
величины ф0-, минимизирующие функцию
m—1 л-1
<"=»)
М ;=0
при условии, что значения ф^ на границах заданы.
Если интерпретировать эту задачу как многошаговый про-
цесс принятия решений, можно, начав со значения уп = Р2, на
/-м шаге выбирать m— 1 значение из величин ф^ в узлах сетки,
принадлежащих очередной строке, пока не дойдем до z/o = ₽i.
Здесь нам потребуется m—1 параметров состояния,
31*
460
Гл. 1L Динамическое программирование II
Определим функции состояния следующим образом:
ЛН£1.....U-i)= (11.51)
т-l п-1
-- min L
по всем Ф,7^Ф/Й ~ ~
kx *ky 11
Ду
где = h и ф удовлетворяет граничным условиям. Рекур-
рентные соотношения имеют вид
т-1
min
по всем ф. ft+1
V1 р (£ li+irzli — &
Ax ’ ky
i—Q
+ (Ф1, £+i> • * •» Фт-i, z?+i) * > — 0, 1, ..., n 2, (11.52)
где величины ф0>*, Фт,*> Фо,*+р Фт.л+i заданы. Для имеем
ЛЛ-1(^п •••, £т-1)”
т-1
= S^(L-, ^Г~' Уп-г)^^У (11-53)
4=0
при заданных фм, Фо,«-j и К«-г
. Очевидно, что численное решение таких задач методом ди-
намического программирования не представляется возможным
из-за большого числа параметров состояния и переменных, по
которым берется минимум на каждом шаге. Однако даже прин-
ципиальная возможность применения к этим задачам аппарата
динамического программирования представляется интересной1).
11.10. Планирование выпуска продукции и задачи теории со-
здания запасов. Важный класс стохастических задач последова-
тельного принятия решений связан с планированием выпуска
продукции в течение некоторого промежутка времени, имеющим
целью минимизировать суммарные ожидаемые затраты на про-
изводство и хранение продукции, если спрос на нее в каждом
временном интервале предполагается случайной величиной.
!) В работах советских математиков Н. Н. Моисеева, Ф. Л. Черноусько
и др. (см., например, [19*] и [20*]) разработаны эффективные вычислительные
методы для решения задач вариационного исчисления того типа, который
рассматривается в этом параграфе. Некоторые из этих методов являются
дальнейшим развитием метода динамического программирования. — Прим.ред.
11.10. Планирование выпуска продукции
461
Будем считать, что решения о выпуске продукции делаются
периодически. Каждый раз при принятии решения учитывается
планируемый промежуток из п периодов. Спрос на продукт, Vj,
в /-й период считается случайной величиной с известной плот-
ностью распределения вероятности (^) и не зависит от спроса
в другие периоды.
Можно построить множество моделей разной степени слож-
ности в зависимости от того, сколько решений следует принимать
в начале каждого периода. Мы остановимся здесь только на двух
случаях.
В первом из них требуется принимать только одно решение
о размере выпуска продукции в каждый период. Предполагается,
что это решение автоматически определяет необходимое количе-
ство рабочей силы, продолжительность работы, запасы сырья и
другие параметры. Будем учитывать только ту продукцию, кото-
рая находится на складе производства. Пусть у$ есть величина
запаса в начале /-го периода. Если х$ есть количество продукта,
выпускаемого в /-й период, a Vj — величина спроса, тогда
yj+i = yj + xj — Vj. (11.54)
Рассмотрим теперь затраты, возникающие в /-й период. Пре-
жде всего это производственные затраты. Сюда входят зарплата,
стоимость сырья и т. п. Эти затраты зависят только от xj и бу-
дут обозначаться через Cj(Xj). Далее имеются затраты, связан-
ные с изменением объема производства. Они включают затраты
по найму, увольнению, реконструкции и т. д. Так как они зави-
сят от %;—Xj-1, мы будем обозначать их через Dj(Xj—Xj_i). На-
конец, имеются затраты на хранение продукции или штрафы за
неудовлетворенный спрос. Будем предполагать, что этот вид за-
трат зависит только от z/j+xj, и соответствующие средние затра-
ты в /-й период обозначим через Fj(yj+Xj).
Пусть Ak есть приведенные к началу 6-го периода ожидаемые
затраты за периоды от 6-го до /г-го при условии, что в начале
6-го периода и во все последующие принимаются оптимальные
решения. Заметим, что Ak будет зависеть и от.yhi и от xfe_i, т. е.
аргументами функции состояния являются два параметра со-
стояния. Тогда ясно, что рекуррентные соотношения записы-
ваются в виде
Ь)—т*п Ck(xk)-[-Dk(xk + +
xk
+« aa+i (•*>>£?+** — V^^(vk)dvk ,£ = 1......../г —1,(11.55)
462
Гл. 11. Динамическое программирование 11
где а — коэффициент приведения. Кроме того,
Лй(^, + + + (U.56)
хп
Мы можем найти оптимальное значение хь вычисляя
Л1(хо,*л). Так как интерес представляет только хь нет необхо-
димости запоминать таблицу |г) при &>2. Поскольку за-
дача содержит два параметра состояния, для ее численного ре-
шения требуется немало времени. Однако если планируемый
промежуток времени содержит 10—20 периодов, a gi и |2 прини-
мают каждое примерно по 30 значений, на мощных вычисли-
тельных машинах задача решается довольно быстро.
В качестве второго примера рассмотрим случай, когда коли-
чество выпускаемого продукта не определяет однозначно потреб-
ность в рабочей силе. Такая ситуация вполне реальна, так как
меньшая рабочая сила может компенсироваться большей про-
должительностью рабочего дня. Пусть означает количество
рабочей силы в /*-й период. Снова рассмотрим затраты в /-й пе-
риод. Это будет стоимость сырья Cj(xj), заработная плата
Sj(Wj), затраты на изменение величины рабочей силы
—Wj-i), затраты х?), вызываемые отклонением ве-
личины рабочей силы от той, которая является идеальной при
объеме производства xj, и, наконец, ожидаемые затраты на хра-
нение и неудовлетворенный спрос Fj(yj+Xj). На этот раз мы
предполагаем, что нет затрат, зависящих от —х^.
Как и в предыдущем случае, для решения потребуются два
параметра состояния. Ими будут здесь wh-i и yk. Теперь, однако,
на каждом шаге потребуется отыскивать значения двух пере-
менных управления. Пусть функция g2) определена, как и
ранее. Тогда рекуррентные соотношения запишутся следующим
образом:
(£i> £2) — m^n (хй) + (^k — £1) +
xk* wk
+xk) + Pk (I2 + xk) 4~
00
+ а/ лй+1(^»> U + — k = \, n— 1.
0
(11.57)
Численное решение на этот раз гораздо более трудоемко, чем
в предыдущем случае. Тем не менее на мощных вычислительных
машинах оно осуществимо.
11.11. Случай квадратичных затрат. Интересный случай возни-
кает, если попытаться в соотношениях (11.57) аппроксимиро-
11:11. Случай квадратичных затрат
463
вать все затраты комбинациями линейной и квадратичной функ-
ций от переменных управления. Почему именно это интересно,
станет ясно, из последующего обсуждения. Для начала рассмо-
трим упрощенную форму функций затрат. Прежде всего запишем
Ck (xk)= Со + CiXk:> Sk (wk) = Sq + S^. (11.58)
Представляется очевидным, почему выбрано именно такое пред-
ставление. Функцию Dk(wh—wk^i) представим в виде
= Do (wk — — A)2 + D2. (11.59)
Аргументация в пользу такой аппроксимации становится ясной
из рис. 11.7. На этом рисунке истинный график D* изображен
непрерывной кривой, а пунктирная линия изображает аппрокси-
мирующую параболу, задаваемую уравнением (11.59). Очевид-
но, что предложенная аппроксимация годится лишь при малых
|и)А—wk-i|. Лучшая аппроксимация получилась бы, если бьюсь
параболы не была параллельна оси Dk, но тогда Dk уже не пред-
ставлялось бы комбинацией линейной и квадратичной функций
от wk—Wk-1.
Будем считать, что для данного количества рабочей силы
существует наилучший объем производства EiWk и, если хк пре-
вышает EiWk, то это ведет к затратам из-за увеличения продол-
жительности рабочего времени. Функцию Ek(wk, хк) аппрокси-
мируем выражением
Ек (™k. хк) = Ео (хк — A®*)2 + E2xk + Ez-wk, (11.60)
где коэффициенты Ей, Eit E2 и E3 выбираются так, чтобы лучше
согласовать равенство (11.60) с эмпирическими данными.
464
Гл. 11. Динамическое программирование П
Неприятной особенностью этой формулы является то, что Ek
возрастает с уменьшением при чего, естественно, не
должно было бы быть. При уменьшении xk аппроксимация ста-
новится все более грубой.
Рассмотрим, наконец, функцию Fk. Вместо того чтобы аппро-
ксимировать затраты на хранение и неудовлетворенный спрос
в k-й период, будем аппроксимировать действительные затраты,
когда спрос равен Vk. Ситуация снова очень похожа на ту, ко-
торой соответствует рис. 11.7. В нашем случае затраты будут
зависеть от yk+Xk—vk и приближенно запишутся в виде
^o(yk^rxk vk 2~Л)(У*+1 — ^i)2 + ^2- (П-61)
Допустим, что в приведенных выше выражениях константы
были определены так, что все затраты неотрицательны незави-
симо от того, какие значения принимают xk, и vh, и что для
любого множества значений vh общие затраты за планируемый
промежуток времени положительны. Мы будем считать эти кон-
станты не зависящими от kf т. е. от номера периода, что типично
для практических задач.
Используя полученные выше представления для различных
видов затрат, можно записать затраты Kk в £-й период следую-
щим образом:
= °0 + ° Л + + G А + ° А + +
В упражнении 11.11 читателю, предлагается определить Gj как
функции от коэффициентов введенных выше функций затрат.
Для данных значений Vj приведенные затраты за планируе-
мый промежуток времени равны
(11.63)
где Шо и у\ заданы и
J J
Uj+i — У)Л~Х) Vj — У\ + 3xi 2 Vf (11.64)
Введем обозначения
х = .......х„], w = lwb ....
Г 1 г 1 (11.65)
u = [x, w], у = 1&. •••. Ул+ib
Тогда выражение (11.63) принимает вид
K=pH-hu4-u'Hu4-qy 4-y'Qy,
11.11. Случай квадратичных затрат
46д
где h и q — векторы-строки, а Н и Q — симметрические матри-
цы. В упражнении 11.12 предлагается выразить h, q, Н, Q и р
через коэффициенты Gj. Отметим, что ш0 появляется в h. Легко
видеть также, что выражения u'Hu и y'Qy представляют собой
положительно определенные квадратичные формы.
Введем теперь в рассмотрение вектор г=[гь ..., гп], где
J
Z = 1
Тогда из равенства (11.64) следует, что
у = г + Тх,
где
"1 0 0 0 ... 0"
1 1 0 0 ... 0
т== 1 1 1 0 ... 0
_1 1 1 1 ... 1 _
(11.67)
(11.68)
(11.69)
есть треугольная матрица, содержащая единицы на главной
диагонали и ниже ее. Эта матрица неособенная, так как ни один
из элементов главной диагонали не равен нулю. Введя вектор г,
мы тем самым отделили переменные Vj от переменных управле-
ния. Подставляя выражение (11.68) в равенство (11.66), полу-
чаем
К=₽ 4- hu 4- u'Hu + qr 4- qTx + r'Qr 4- 2r'QTx 4- x'T'QTx.
(11.70)
Квадратичная форма xT'QTx положительно определенная, так
как форма y'Qy положительно определенная, а Т — неособенная
матрица.
Введем теперь матрицу порядка 2п
М =
T QT 0
0 0 ’
(11.71)
Тогда u'Mu = x'T'QTx и квадратичная форма u'Mu неотри-
цательная. Запишем также
2r'QTx = (2r'QT, 0) u, (11.72)
<|Tx = (qT, 0)u. QI,73)
466
Гл. 11. Динамическое программирование II
Если h=(hb h2), где hi содержит первые п компонент вектора h,
то выражение (11.71) можно переписать в виде
/< = P + qr + r'Qr + (hj+qT + Sr'QT, h2)u + u'Ru, (11.74)
где R==H + M. Заметим, что квадратичная форма u'Ru как сумма
положительно определенной и неотрицательной форм является
положительно определенной.
Теперь, после того как проделаны все эти выкладки, можно
объяснить причину столь подробного изучения случая квадра-
тичных затрат. В следующем параграфе будет доказано, что
если приведенные затраты для планируемого промежутка вре-
мени при заданных значениях Vj имеют форму (11.74), a r'Qr
и u'Ru — положительно определенные квадратичные формы, то
вместо отыскания W\ и можно искать w* и х*. из условия ми-
нимума Л, определенного выражением (11.74), где Vj заменены
их средними значениями Другими словами, если мы игнори-
руем тот факт, что спрос является случайной величиной, а вме-
сто этого просто используем средние значения спроса, оптималь-
ные значения Xi и полученные при решении этой задачи, бу-
дут в точности такими же, как если бы мы считали спрос случай-
ным и находили решение из соотношений (11.57). Таким образом,
стохастическая задача последовательного принятия решений мо-
жет быть заменена детерминированной. В общем случае этот
результат, конечно, не верен. Он справедлив здесь лишь потому,
что затраты выражаются комбинациями линейных и квадратич-
ных форм. В гл. 5 отмечалось, что для принятия оптимального
решения в первый период обычно необходимо находить страте-
гии и для других периодов. Здесь мы встретились с ситуацией,
где это не необходимо.
Для определения до* и х* можно в случае квадратичных за-
трат решить детерминированную задачу динамического програм-
мирования, для которой рекуррентные соотношения записы-
ваются в виде
(1ь £2) — m^n \Pk (xz?) + $k (^) + — £1) + Ek (W xk) +
xk> wk
%>2~^TXk Hz?)]» k—\, 2, n— 1.
(11.75)
Из этих соотношений решение найти несколько проще, чем из
(11.57).
Однако в рассматриваемом случае лучше всего использовать
классические методы дифференциального исчисления. Все что
требуется — это приравнять нулю частные производные по х^ и
11.12. Доказательство эквивалентности
467
wi от функции Л, определяемой выражением (11.74). В полу-
ченной при этом системе линейных уравнений относительно Xj
и Wj можно исключить Xj и Wj при />1 и найти явное выраже-
ние Xj и через w0, #i и pj. Эти уравнения достаточно просты,
и нахождение явных выражений Xi и W\ не слишком трудно.
В упражнении 11.13 читателю предлагается найти структуру
матрицы R в (11.74) и подлежащие решению уравнения. Оказы-
вается,; что оптимальные значения Xi и W\ имеют вид
п п
х* = + Р2дао + 2 Y р S = + д2^0 + 2 е л (11.76)
/=1 J J
Как только коэффициенты pb р2, yj, Si, 62 и ej, не изменяю-
щиеся в дальнейшем, определены, единственное, что остается, —
это предсказать ожидаемый спрос для каждого периода, а потом
использовать эти формулы для получения х* и
При выводе равенств (11.76) не накладывались условия
неотрицательности всех Xj и Wj. Однако для большинства встре-
чающихся на практике ситуаций величины х* и w* автоматиче-
ски оказываются положительными. Мы не делали также попытки
учесть целочисленность переменных Wj. На практике это тоже
редко оказывается серьезным препятствием.
Правила принятия решений, определяемые соотношениями
(11.76), часто называются линейными правилами принятия ре-
шений, так как оптимальные значения Xi и линейно зависят
от остальных параметров. Рассмотренная модель производствен-
ного планирования, основанная на квадратичных затратах и,
следовательно, линейных правилах принятия решений, впервые
была разработана Хольтом, Модильяни, Мутом и Симоном. Ее
подробное изложение можно найти в книге [6]. Эти же авторы
на практике применили эту модель в нескольких промышленных
фирмах. Они утверждают, что применение оказалось успешным,
хотя не было возможности получить четких оценок того, какое
сокращение затрат оно вызвало.
11.12. Доказательство эквивалентности стохастической и де-
терминированной задач в случае квадратичных затрат. Мы хо-
тим доказать, что если r'Qr и u'Ru — положительно определен-
ные квадратичные формы, то значения х* и w*, полученные
путем минимизации выражения (11.74), когда Vj заменены их
средними значениями в точности такие же, как если бы ми-
нимизировались ожидаемые приведенные затраты за весь пла-
нируемый промежуток времени. При доказательстве нам не по-
требуется даже предполагать, что Vj — независимые случайные
величины. Если <p(t>i, ...» vn) есть совместная плотность
468
Гл. 11. Динамическое программирование II
вероятности v,, то ожидаемые приведенные затраты для задан-
ных значений Xj и Wj определяются формулой
ОО СО
z = / ... J Кф (т1( .... vn) dvx ... dvn. (11.77)
О о
Прежде всего покажем, как путем минимизации выражения
(11.77) находятся оптимальные решения для первого периода.
При этом мы будем считать хк и k>\, функциями от ук и
wk-i. Пусть и* есть вектор, содержащий оптимальные управ-
ляющие функции. Он имеет вид
u* = [x*. x2(z/2, wL), .... хп(уП, w*v
.....(11-78)
Через и обозначим произвольный вектор управляющих функций
и положим 6 = и — и*.
Пусть z — ожидаемые приведенные затраты, соответствую-
щие управлению u, a z*— минимальные затраты. Чтобы не пи-
сать далее знака интегрирования по случайным переменным,
будем просто обозначать через £{/} среднее значение любой
функции f от случайных переменных. Из (11.77) следует, что
z-z* = Е {(hi + qT4- 2r'QT, h2) u} —E {(hj 4- qT + 2r'QT, h2)u*}+
+ £{u'Ru) — E {(u*)'Ru*j- (11.79)
Подставляя u = u*-(-6, получаем
z — z* = E {(hi 4- qT Д- 2rQT, h2) 6} 4- 2E {(u*)' R6} 4- E {6R6} ==
= E{[(h14-qT4-2r'QT, h2)4-2 (u*)'R] 6} 4-E {6'R6). (11.80)
Так как z*—минимальные затраты, должно быть верно, что
z — z* >• 0, т. е. для всех 6
E{[(h1 + qT + 2r'QT, h2) + 2(u*)'R]6} +£{6'R6} >0. (11.81)
Получим отсюда необходимое условие оптимальности и*. Так
как (11.81) выполняется при всех 6, оно должно выполняться и
для 6= ±eet, где е мало. Тогда Е{6/Я6} = е2Гц>0, а первый член
в левой части соотношения (11.81) пропорционален е. Обозначим
Е ([(h14- qT 4- 2r'QT, h2) + 2 (u*)' R] ej = sy.
Таким образом, для достаточно малого е знак левой части нера-
венства (11.81) будет зависеть только от esi. Если Si=£0, то этот
знак может быть любым, что недопустимо, Необходимо, следо-
вательно, чтобы Sj=Q,
11.13. Стохастические задачи и марковские процессы
469
Мы можем повторить эти же рассуждения, полагая
6= ±ее2, .±‘ееп. Это приводит к следующему условию: для
оптимальности управления и* необходимо, чтобы s = 0, т. е.
Е {[(h, + qT + 2rzQT, h2) + 2(u*)' R]} =0. (11.82)
Отсюда, поскольку hi, q, T, Q, h2 и R не зависят от случайных
величин,
(hj+qT4-2£{r'}QT, h2)4-2£ {(u*)7} R = 0. (11.83)
Матрица R — неособенная, так как u'Ru — положительно опре-
деленная форма. Следовательно, из равенства (11.83) единствен-
ным образом определяется
£{(„’)}=_ | + qT + 2F (И QT, h2)'. (11.84)
Величины Xi и Wi не являются функциями случайных перемен-
ных. Следовательно, их оптимальными значениями для первого
периода будут соответственно первая и (п+1)-я компоненты
выражения (11.84).
Допустим теперь, что мы определяем Xi и минимизируя
функцию (11.74), где Vj в г заменены на так что г заменяется
на Е{г}. Тогда необходимые условия того, что вектор и миними-
зирует функцию Л, состоят в выполнении равенства
VuK=2u'R + (h1 + qT + 2£{r'}QT, h2) = 0,
откуда
u = — I R-1 (Й! 4- qT 4- 2Е {г') QT, h2)z. (11.85)
Но правые части равенств (11.84) и (11.85) одинаковы, так что
первая и (п+1)-я компоненты вектора и, найденные из (11.84)
и (11.85), совпадают, что и требовалось доказать.
Весьма удивительно, что оптимальное решение в первый пе-
риод не должно зависеть от распределения вероятностей а
зависит только от их средних значений. Этой особенностью мы
обязаны тому, что затраты квадратичны и относительно пере-
менных управления, и относительно Vj. Для случая одношаговой
задачи первым обратил внимание на этот факт, по-видимому,
Тейл [10]. Его результат был обобщен на случай n-шаговых за-
дач Симоном [9]. Дальнейшее обобщение снова было проведено
Тейлом [11].
11.13. Стохастические задачи последовательного принятия ре-
шений с бесконечным планируемым промежутком и марковские
процессы. Значительная часть рассмотренных нами стохастиче-
ских задач последовательного принятия решений относилась
к тем случаям, когда плотности распределения случайных
470
Гл. 1Г Динамическое программирование II
переменных и функции затрат могут меняться от одного перио-
да к другому. В таких ситуациях разумно рассматривать только
конечный планируемый промежуток времени. Однако, если плот-
ности распределения постоянны и затраты не меняются от
периода к периоду, можно рассматривать и бесконечный проме-
жуток. Иными словами, мы можем вообразить, что система
функционирует неограниченно долго, и учитывать влияние всех
последующих решений на решение, принимаемое в текущий мо-
мент. В дальнейшем мы сохраним предположение о независимо-
сти случайных переменных, относящихся к различным периодам.
В § 10.18 мы уже рассматривали ситуацию такого типа на
примере задачи о создании запасов. Тогда же было отмечено,
что для определения структуры оптимальных политик может
быть использовано динамическое программирование. Однако
применявшиеся там методы анализа не обеспечивали возможно-
сти непосредственного отыскания оптимальной политики (хотя
и было отмечено, что если оптимальной является /?г-политика,
то можно найти параметры R и г, минимизируя по этим пере-
менным функцию А(£))-
Сейчас мы рассмотрим другой подход к определению опти-
мальных политик для стохастических задач последовательного
принятия решений с бесконечным планируемым промежутком
времени. Мы покажем, что задача отыскания таких политик
может оказаться даже проще, чем в случае конечного проме-
жутка. Как и обычно, возможность применения метода ограни-
чена случаями очень малого числа параметров состояния. Огра-
ничения на их число несколько более жесткие, чем в предыду-
щих случаях.
Вместо того чтобы исследовать вопрос на примере какой-ни-
будь практической задачи, изучим довольно общий тип стоха-
стических задач последовательного принятия решений.
Будем предполагать, что решения принимаются в равноот-
стоящие моменты времени, интервал между которыми будем
называть периодом. Предполагается, что в начале любого пе-
риода система находится в одном из М различных состояний.
Мы не будем вводить здесь никаких .специальных параметров
состояния. Если имеется один такой параметр, то М различных
состояний будут соответствовать М различным значениям, кото-
рые может принимать этот параметр. В случае двух параметров
М состояний будут соответствовать всем возможным комбина-
циям значений, которые могут принимать параметры состояния,
и данному состоянию I сопоставляется определенная комбинация
значений этих двух параметров.
Обозначим через A(f) ожидаемую прибыль за все будущее
время, приведенную к началу периода, когда состояние системы
11.13. Стохастические задачи и марковские процессы
471
перед принятием решения есть i и оптимальные решения прини-
маются в начале этого и во все последующие периоды. Вели-
чина Л (г) не зависит от того, какой период мы рассматриваем,
так как планируемый промежуток времени предполагается бес-
конечным.
Кроме того, что мы не ввели явно никаких параметров со-
стояния, мы не будем явно вводить и переменные управления.
Нас интересует лишь правило, указывающее, что делать, если в
начале периода система находится в состоянии i. Это правило
не будет изменяться от периода к периоду. Если бы мы рассма-
тривали задачу о создании запасов, правило могло бы формули-
роваться, например, так: заказывать 5 единиц, если система в
состоянии 1; 4 единицы, если в состоянии 2; 0 во всех остальных
случаях.
Вообразим теперь, что все действия, которые можно пред-
принять, если в начале периода система находится в состоянии/,
перенумерованы. Вообще говоря, число Ni таких действий может
быть очень большим. При фиксированном I задача состоит тогда
в выборе оптимального действия из возможных. Оптимальная
политика, указывающая, что делать при каждом z, представляет
собой просто набор оптимальных правил для каждого конкрет-
ного i.
Если не вводить переменные управления, то следует найти
другой способ, позволяющий сопоставить каждой политике опре-
деленные затраты. Сделаем это так: как только выбрано неко-
торое действие, скажем zz, и известно, что период^ начинается
с состояния z, будем предполагать, что тем самым определяется
ожидаемая прибыль или убыток f (z, и) за данный период. Кроме
того, предположим, что при заданных i и и определены числа
Pij(u) —вероятности того, что система окажется в состоянии /
к началу следующего периода. Это предположение характерно
для всех рассматривавшихся ранее задач. Например, в задачах
о создании запасов, если состояние запасов до заказа есть i и
величина заказа равна и, то вероятность того, что состояние за-
пасов будет равно / в начале следующего периода, равна
О, если j > i + и,
— у), если у < / + и,
Рц(ч) —
где p(v) есть вероятность того, что спрос в данный период рав-
няется V.
При этих определениях функциональное уравнение для Л (г)
имеет вид
Л (z) — max
и
М
f(i, + Ау(и)Л(у)
/-1
1=1,..., М, (11.86)
472 Гл. 11. Динамическое программирование II
м
где S Pij (и) — 1 при всех и и и принимает значения 1, 2,...,
являющиеся номерами действий. Таким образом, и не обяза-
тельно связывать со значениями некоторой переменной. Как
обычно, а<1 есть коэффициент приведения.
Для рассмотренных задач характерно, что в начале каждого
периода система находится в одном из М состояний. Кроме того,
как только выбрано правило принятия решений, определяется
множество вероятностей перехода р^ (величина pij есть вероят-
ность того, что система, находящаяся в состоянии /, окажется в
состоянии / в начале следующего периода). Заметим, что pij со-
вершенно не зависит от того, как система пришла в состояние I.
Пусть qh(i) есть вероятность того, что система находится в со-
стоянии i в начале ft-го периода. Тогда
м
/=1, .... М. (11.87)
Процесс, стохастическое поведение которого может быть опи-
сано таким образом, называется марковским процессом. Каждая
из рассмотренных нами ранее стохастических задач последова-
тельного принятия решений обладает свойством марковского
процесса.
м
Выберем теперь произвольную из JJ политик управления
i = 1
системой, получаемую путем выбора для каждого состояния i
одного из Ni действий, возможных для этого I. Пусть при исполь-
зовании этой (не обязательно оптимальной) политики приведен-
ный к началу периода ожидаемый доход за все будущее время,
когда система в начале периода находится в состоянии f, есть
ft(f). Тогда по аналогии с уравнением (11.86), если /(/) есть со-
ответствующий ожидаемый доход за период, мы видим, что
справедливо уравнение
м
1=1, (11.88)
У = 1
где Pij — вероятности перехода, соответствующие данной поли-
тике.
Введем в рассмотрение матрицу Р—||рг;|| и векторы-столбцы
h = [A(l), ..., Л(М)]; f = [/(l), .... f(Af)J. (11.89)
Тогда уравнение (11.88) можно записать в векторной форме
h —f-|-aPh, (11.90)
ПЛЗ. Стохастические задачи и марковски# процессы 473
или
(I —aP)h = f, (11.91)
или
h = (I —аР)"Ч. (11.92) ,
Так как сумма элементов каждой строки матрицы Р равна еди-
нице и, следовательно, сумма элементов каждой строки матри-
цы аР больше нуля и меньше единицы, то из результатов, изло-
женных в {ЛА 3.22}, следует, что тем самым гарантируется су-
ществование обратной матрицы для I — аР. Следовательно, из
системы М линейных уравнений (11.92) можно однозначно опре-
делить h(i) для данной политики. Как будет показано ниже,
это замечание может помочь нам при отыскании оптимальной
политики.
Прежде чем перейти к обсуждению методов, позволяющих
найти оптимальную политику, отклонимся на миг от темы и по-
кажем, что доход от ^-шагового процесса сходится при неогра-
ниченном росте k. Вообразим, что мы выбрали некоторую, не
обязательно оптимальную политику и hk(i) есть доход, приве-
денный к началу первого периода процесса, начинающегося с
состояния i и длящегося k шагов. Тогда
h* = f + aPhfe_! и h! = f. (11.93)
Следовательно,
h2 = f + aPf, h3 = f + aPh2 = f + aPf + a2P2f,
или
\ _ (k—\ \
hft= Sa'P'f, P° = I. (11.94)
\/-o /
Так как сумма элементов каждой строки матрицы аР больше
нуля и меньше единицы, то из {ЛА 3.22} следует, что
2a'p' = (I-aP)_1. (11.95)
7=0
Следовательно, при k—> оо стремится к пределу h, равному
(I — <хР)-Н.
Вернемся теперь к задаче определения оптимальной поли-
тики и отыскания A(f) для рассматриваемой системы. Допустим,
что мы уже выбрали произвольную политику, которой мы при-
пишем номер 0, и обозначим соответствующие ей значения h, f и
Р через h(0), f(0) и Ро. Тогда равенство (11.92) запишется в
виде
h (0) = (I — aP0)~’f (0).
474
Гл. 11. Динамическое программирование II
Пусть процесс начинается с состояния I в первом периоде и
стратегия 0 используется во всех периодах после первого, но не
обязательно в первом. Для первого периода мы будем искать
решение, которое максимизирует ожидаемый доход при условии,
что в дальнейшем будет использоваться политика 0. К этому
мы придем, если найдем значейие и, максимизирующее выра-
жение
м
f(i, + 0),
где /г(/;0) есть /-я компонента вектора h(0). Эта процедура
выполняется для каждого i. В результате получается новая по-
литика (обозначим ее 1), которую следует использовать в пер-
вом периоде, а также соответствующие ей значения /(/, и) и
рц(и), которые в векторных и матричных обозначениях мы за-
пишем как f (1) и Рь Допустим теперь, что мы решили использо-
вать политику 1 во всех периодах. Тогда можно вычислить соот-
ветствующий ей приведенный доход по формуле
h(l) = (I-aP1)-,f(l).
Ниже будет показано, что политика 1 лучше или по крайней
мере не хуже, чем политика 0, т. е. h(l)>h(0). Описанную про-
цедуру можно повторить, допустив, что политика 1 будет исполь-
зоваться всюду, начиная со второго периода, и при этом допу-
щении определить наилучшую политику для первого периода.
Назовем эту политику второй. Тогда h(2)>h(l), и политика 2
не хуже, чем политика 1. Будет доказано также, что такой
итеративный процесс сходится к оптимальной политике за конеч-
ное число шагов.
Приведем теперь доказательства двух фактов, на которые мы
ссылались ранее. Допустим, что уже проделано г итераций опи-
санного выше процесса. Мы хотим показать, что h(r)>h(r—1).
Из метода, использованного для определения политики г, сле-
дует, что
f (г) + aPrh (г - 1) > f (г - 1) 4- aPr_ih (г — 1). (11.96)
Однако
h(r-l) = f(r-l) + aPr_1h(r-l),
h(r) = f(r) + aPrh(r). (11.97)
Введем обозначение
S = f(r)-f(r-l) + a(P,-P,_1)h(r- 1). (11.98)
11.13. Стохастические задачи и марковские процессы 475
Из неравенства (11.96) немедленно следует, что s^O. Далее,
6 = h (г) - h (г - 1) = f (г) — f (г — 1) + aPrh (г) - aPr _jh (г - 1 )=
= S + aPr [h (г) — h (г — 1)] = s + аРД (11.99)
или
6 = (I —aPr)-1s = (l + aPr + a2Pr+ ...)s =
= s + aPrs + a2P2s+ ... . (11.100)
Однако s>0, а каждый элемент матрицы Рг неотрицателен. Сле-
довательно, 6 = h(r)—h(r—1)^>0, что мы и хотели доказать.
Итак показано, что политика г по крайней мере не хуже, чем
политика г— 1.
Покажем теперь, что если нет улучшения при переходе от
итерации г к итерации г+1, то политика г (и г +1 тоже) являет-
ся оптимальной. Доказательство будем вести от противного. До-
пустим, что есть политика г*, такая, что h(r*)^>h(r), причем
строгое неравенство выполняется по крайней мере для одной
компоненты. Тогда
,h(r*) — h (г) = &* = (! — aP,)-1s* = s* + aP.s*4- .... (11.101)
где
S* = f(r*)-f(r) + a(Pt-P,)h(r).
Так как по крайней мере одна компонента вектора 6* положи-
тельна, из соотношения (11.101) следует, что и у s* имеется
хотя бы одна положительная компонента, например f-я. Однако
это противоречит тому, что при определении политики г+1 было
принято наилучшее решение для состояния z, так как, переходя
от г к г+1, мы заключили, что s = 0. Следовательно, итератив-
ный процесс должен сходиться к оптимальной политике. Так как
имеется лишь конечное число различных политик, сходимость
происходит за конечное число шагов.
Описанный только что прием отыскания оптимальной поли-
тики в случае большого числа параметров состояния встречает
те же трудности, что и методы, применявшиеся ранее для задач
с конечным числом шагов. Например, если имеется два пара-
метра состояния, каждый из которых может принимать 100 зна*
чений, в начале периода система может оказаться в одном из
10 000 различных состояний. Напомним, что на каждом шаге
итеративного процесса необходимо решать систему линейных
уравнений (11.92) с числом переменных, равным числу состоя-
ний, т. е. в нашем случае с 10 000 переменных. При этом в ма-
трице I—ссР может оказаться до 108 ненулевых коэффициентов.
Решение такой системы уравнений представляет исключительно
476 Гл. 11. Динамическое программирование 11
трудную задачу даже для самых мощных современных вычисли-
тельных машин.
В случае же трех параметров состояния, каждый из которых
может принимать 100 значений, придется решать уже систему
линейных уравнений с 1 000 000 переменных. В настоящее время
это абсолютно невозможно.
Метод, обсуждавшийся в этом параграфе, был разработан
Ховардом [7].
11.14. Пример. Проиллюстрируем сейчас использование изло-
женного в предыдущем параграфе итеративного метода на ре-
шении простого примера с двумя параметрами состояния и
двумя решениями, принимаемыми на каждом шаге.
Пусть раз в год предприятие, изготавливающее автомобили,
должно принимать решение о выборе модели автомобиля на
следующий год. Предположим, что в момент принятия решения
может быть только одно из двух состояний: 1) выпускаемая
модель продается хорошо, 2) выпускаемая модель продается
плохо. Если модель удачная, то на следующий год предприятие
может а) выпускать ту же самую модель или Ь) попробовать
что-нибудь новое. Если модель неудачная, то оно может с) ско-
пировать удачную модель конкурентов или d) попробовать что-
нибудь новое.
Допустим, что вероятности перехода для каждого состояния
и каждого решения таковы:
Л1(«) = 0,6, р12(а) = 0,4, Л1(6) = о,7, p12(Z>) = 0,3,
р21(с) = 0,4, р22 (с) = 0,6, p2l (d) = 0,5, p22(rf) = 0,5.
Здесь, например, рц(а) есть вероятность того, что изготовитель
остается в состоянии 1, если он находится в состоянии 1, и при-
нимает решение а), т. е. решение о выпуске прежней модели.
Обозначим через Rij(u) прибыль в млн. долл, в наступающем
году, если он начинается с состояния f, заканчивается состоя-
нием /ив этом году принимается решение и. Пусть
/?п(а) = 7, /?12(а)=1, /?„(&) = 5, /?12(Ь) = - 1,
$21 (^) == $22 (^) = 0, /?21 (</) = 5, /?22 (iZ) = — 2.
Если f(i, и) есть ожидаемая прибыль в наступающем году, когда
он начинается с состояния i и принимается решение и, то
f(l, а) = 0,6-7 + 0,4-1=4,6, f(l, Z>) = 0,7-5 + 0,3-(—1) = 3,2,
/(2, с) =0,4 -6 + 0,6- 0 = 2,4, f(2, d) = 0,5• 5 + 0,5-(—2) = 1,5.
Коэффициент приведения а возьмем равным 0,9.
11.14. Пример
477
Мы хотим определить оптимальное решение, которое следует
предпринимать в каждом состоянии для того, чтобы максими-
зировать приведенную величину всех будущих прибылей. НачнехМ
с выбора одной из (четырех) возможных политик. Пусть прини-
мается решение Ь) в состоянии 1 и решение с) в состоянии 2.
В обозначениях предыдущего параграфа это политика 0. Для нее
_ ч г ГО,7 0,31 Г 0,37 —0,27'
f(0) —[3,2; 2,4], ро==|О4 06]. * — аРо == |_036 0,46
Вычислим Л(1;0) и /г(2;0)—приведенные значения будущих
прибылей, если используется выбранная политика, а процесс
начинается с состояний 1 и 2 соответственно. Для этого нужно
решить систему уравнений (11.92), которая в нашем случае
имеет вид
0,37А (1; 0) —0,27Л(2; 0) = 3,2; — 0,36А(1; 0) + 0,46Л(2; 0) = 2,4.
Результаты решения таковы: Л(1; 0) =29,1, Л(2;0)=27,9. Опре-
делим далее другую политику, которая по крайней мере не хуже
используемой. Сделаем это, допустив, что политика 0 будет
использоваться во все периоды, начиная со второго, и при этом
условии найдем оптимальную политику для первого периода.
Если этот период начинается с состояния 1 и в нем используется
решение а), то приведенная прибыль равна
4,6 + 0,9[0,6й(1; 0) + 0,4А(2; 0)] =
= 4,6 + 0,9 [0,6 • 29,1 + 0,4 • 27,9] = 30,35.
В то же время, если принято решение Ь), имеем й(1; 0) =29,1.
Итак, если период начинается с состояния 1, решение а) более
предпочтительно для политики. Если период начинается с со-
стояния 2 и принимается решение с), имеем Л(2;0)=27,9, а для
решения d) — 1,5 + 0,9 • 0,5[А (1; 0) + h (2; 0^] = 27,2. Следовательно,
решение с) предпочтительнее. Новая политика, политика 1, со-
стоит тогда в том, что в состоянии 1 принимается решение а),
а в состоянии 2 — решение с).
Далее определяются приведенные значения всех будущих
прибылей при условии, что во все моменты времени используется
политика 1 и процесс начинается соответственно с состояний 1
и 2. Эти величины находятся из системы уравнений
0,46А(1; 1) — 0,36/z(2; 1) = 4,6,
— 0,36А(1; 1) + 0,46Л(2; 1) = 2,4.
Отсюда следует, что h(\\ 1) =36,25 и /i(2; 1) =33,6.
32 Зак. 735
478
Гл. И. Динамическое программирование II
Пусть теперь политика 1 используется во всех периодах, на-
чиная со второго, а для первого, учитывая это условие, найдем
оптимальное решение. Если период начинается с состояния 1
и используется решение а), для приведенной прибыли имеем
й(1; 1) =36,25, а если используется решение Ь), то прибыль равна
3,2 + 0,9 [0,7 • 36,25 + 0,3 * 33,6] = 35,43.
Следовательно, решение а) предпочтительнее. Если период на-
чинается с состояния 2 и используется решение с), то
Л(2; 1) =33,6, а если решение d), то прибыль равна
1,5 + 0,9 • 0,5 [36,25 + 33,6] = 33,0.
Итак, новая политика, политика 2, состоит в том, чтобы в со-
стоянии 1 принимать решение а), а в состоянии 2 — решение с),
т. е. в точности совпадает с политикой 1. Оптимальная поли-
тика, стало быть, найдена. Предприятие должно, если модель
оказалась удачной, продолжать выпускать ее в следующем году.
В противном случае оно должно скопировать удачную модель
конкурента. Заметим, что здесь оптимальная политика обладает
тем свойством, что для каждого состояния она максимизирует
выигрыш в наступающем году.
11.15. Оптимальность чистых стратегий. Обсуждение стоха-
стических задач последовательного принятия решений, прове-
денное в предыдущем параграфе, содержало допущение, что в
начале каждого периода, зная состояние системы в этот момент,
из конечного множества альтернатив может быть выбрано опти-
мальное решение, которого и следует придерживаться. Заметим,
что на практике так обычно и бывает, однако в теории игр и в
статистической теории принятия решений часто приходится рас-
сматривать более общие типы стратегий.
Допустим, что вместо того, чтобы выбирать конкретные реше-
ния, мы используем случайную игру. Это можно сделать, напри-
мер, связав выбор решения с исходом случайной игры, состоящей
в вытаскивании шара из урны. Пусть для системы, находящейся
в начале периода в состоянии I, выбрано решение и с вероят-
ностью viu, где Viu^b и Г1ри такой процедуре мы не
и
знаем, какое решение будет принято, до тех пор, пока не будет
разыграна соответствующая случайная игра. В связи с этим
возникает задача о выборе вероятностей ViU так, чтобы макси-
мизировать приведенные ожидаемые прибыли.
Если принятие решений определяется исходом некоторой слу-
чайной игры, мы будем говорить, что используется смешанная
1115. Оптимальность чистых стратегий
479
стратегия. Заметим, что чистая стратегия, состоящая в выборе
конкретного решения представляет собой частный случай
смешанной: для нее = viu — 0, если u4=uiz
Докажем теперь, что всегда есть по крайней мере одна
чистая стратегия, являющаяся опимальной для модели,
изучавшейся в § 11.13. Другими словами, нельзя увеличить
ожидаемые приведенные прибыли за счет введения смешанных
стратегий.
Доказательство этого довольно просто. Если допустимы сме-
шанные стратегии, мы определяем политику выбором множества
m
из 2 Nt чисел Viu, где и 21» определяющих ве-
Z=-l и
роятность принятия решения и, если система находится в состоя-
нии i. Пусть числа образуют оптимальную политику. Если
она обладает тем свойством, что для каждого i только одно
положительно (и, следовательно, равно единице), то мы имеем
чистую стратегию, и доказательство окончено. Покажем, что
если хотя бы для одного i два или более v*iu > 0, т. е. если стра-
тегия смешанная, то существует чистая стратегия, которая так
же хороша, как и эта смешанная.
Для политики, характеризуемой вероятностями v*ite ожидае-
мая прибыль в первый период равна
Г(0=2ИА«К„. (н.102)
и
а вероятность того, что, начав первый период в состоянии 1,
система окажется в начале второго периода в состоянии /, есть
(11.103)
Обозначим через ft*(i) величину приведенных прибылей за все
будущее время, если процесс начинается с состояния i и исполь-
зуется оптимальная политика. Множество величин й*(г) нахо-
дится путем решения системы уравнений
(I — aP)h*=f. (11.104)
Вернемся теперь к итеративному процессу, описанному в
§ 11.13, и предположим, что политика, определяемая числами
v*u, будет использоваться во всех периодах, начиная со второго.
Для первого же периода имеется свобода выбора. Если первый
период начинается с состояния Z, тогда для любых значений ViUl
32*
480
Гл И. Динамическое программирование II
характеризующих политику в первый период, приведенный ожи-
даемый доход составит
2 f и) viu + а 2 Pij («) Л* (/) = 2 17 (Л «) 4-
и и, j и L
4-а 2
Обозначим
Yft = max|7(Z, «)4-«3 А/(»)£’(/)] = f (Л ^)+«2
Так как то для любых viu, таких, что ViU^Q и2уги = 1,
справедливо неравенство
S [7 (А «) 4- ® 3 Pij (и) h* (/)J Vi} < 2 Wu = Nu-
Следовательно, для процесса, начинающегося с состояния чи-
стая стратегия v^ = l,*aiw = 0, если u=/=t, не хуже любой другой.
Для каждого состояния i мы приходим к тому же самому за-
ключению, что чистая стратегия не хуже любой из смешанных.
Таким образом, мы получили новую политику, являющуюся чи-
стой стратегией. Применяя доказанный результат к случаю,
рассмотренному в § 11.13 (читатель помнит, что там рассматри-
вался случай смешанных стратегий), получаем, что новая стра-
тегия по крайней мере так же хороша, как и исходная. Но
исходная смешанная стратегия была оптимальной, следователь-
но, в этом случае всегда существует по крайней мере одна опти-
мальная чистая стратегия.
11.16. Сведение к задаче линейного программирования. Пока-
жем, что поставленная в § 11.13 задача может быть решена ме-
тодами линейного программирования. Иными словами, мы
покажем, что величины A(i) являются решениями некоторой
задачи линейного программирования. Специфические свойства
этой задачи будут использованы для получения оптимальной
политики. Основой для построения соответствующей задачи ли-
нейного программирования послужит функциональное уравнение
(11.86), которое можно записать так:
м
Л (/) > f (/, и) 4“ a 2 Pij («) Л (/) для всех и, i = 1, ..., М.
(И.105)
Точное равенство, конечно, выполняется только для оптималь-
ного решения (или решений, если оптимальное решение не един-
11.16. Сведение к задаче линейного программирования 481
ственно). Неравенства (11.105) удобно переписать в виде
м
A(i)— а 2 А;(Й)Л(/)>НЛ а) для всех и,
(11.106)
м
Число всех таких неравенств равно 2 М- Рассмотрим теперь
1 = 1
любой йабор значений xj, удовлетворяющих условиям
м
xt — а 2 Ptj(u)х} f (i, и) всех и, i — 1, ..., M. (11.107)
Заметим, что величины A(f) являются решениями соотноше-
ний (11.107), причем для каждого I точное равенство будет вы-
полняться по крайней мере для одного и. Положим
х*=[Л(1), ..., Л(7И)], а через х обозначим любое другое реше-
ние (11.107). Пусть х=х* + 6. Тогда
М М '
Л('0 + 6/ —а 2 А;(«)л(/) —“ 2 «)
/=1
для всех Z, и. ’ (11.108)
Однако для каждого i имеется по крайней мере одно и — назо-
вем его Ui, — для которого
м
Л (z) — а 2 Pij (Hi) Л (J) = f (i, Hi).
7-1
Вычитая эти равенства из соответствующих неравенств (11.108),
вычисленных при и = получаем
м
2 Pij^bj > 0, 1 = 1, ..., м,
7=1
или
м
6/ — а 2 Pij («/•) 6,- = ^>0, Z=l,
/=1
Используя обозначение Р = Wpij(Ui) ||, получаем
(b-aP)6 = d,
или
•6 = (I — aP)-1d = d + aPd + a2P2d+ ... >0,
так как d>0 и каждый элемент матрицы Р не отрицателен. Итак,
мы доказали, что 6>0, т. е. что если х* есть вектор с компонен-
тами Л(0,то для любогох, удовлетворяющего условиям (11.107),
482
Гл. 11. Динамическое программирование II
выполняется неравенство х>х*. Следовательно, если нам удаст-
ся найти такое решение х* соотношений (11.107), что для лю-
бого другого решения х выполняется условие х>х*, мы тем
самым найдем A(t).
Покажем сейчас, что оптимальным решением задачи линей-
ного программирования, состоящей в минимизации функции
м
при ограничениях (11.107), где каждое ej может быть произволь-
ным положительным числом, является х*. Обозначим оптималь-
ное решение этой задачи через х0. Тогда х0=х*, если х>х0 для
всех других решений х. Это будет установлено, если мы сумеем
показать, что для каждого i найдется по крайней мере одно
такое ц, что х0 удовлетворяет (11.107) как точному равенству.
В этом случае можно будет рассмотреть любое другое решение
х0+ 6 и использовать приводившиеся ранее рассуждения, чтобы
показать, что должно выполняться неравенство 6>0. Чтобы до-
казать, что для каждого i найдется по крайней мере одно такое и,
что Хо удовлетворяет (41.107) как точному равенству, допустим,
что для г непусто, строгое неравенство выполняется при
каждом и. Покажем тогда, что можно найти новое решение
Xi=x0—р, р^>0, где по крайней мере одна компонента векторар
положительна. Для того чтобы это сделать, выберем для ка-
ждого i /> одно ограничение, которому х0 удовлетворяет как
точному равенству. Вектор Xi также должен обращать его в
точное равенство. Итак, должно быть
м
Pi- a'SiiPij(ui)pJ = O,
Далее выберем произвольное щ для каждого /€/> и допу*
стим, что
м
^-«2Л/(В/И = 1(/’ВЖ> ^z>0, Z£/>.
/=>=1 ‘
Попытаемся теперь найти pj так, чтобы эти ограничения выпол-
нялись как точные равенства, т. е. так, чтобы
м
^- pt-aу2Л/(и<)(х°/-Р>) = Ц/’ ui)' i^I>>
или
м
Pt - а 2 ptj (lit) pj = i^/>.
11.17. Двойственная задача линейного программирования
4S3
Итак, если мы сможем определить pj,
виям
удовлетворяющее усло-
м
— i£I>t
м
Pi — a^pij(ui)pj = gi, iQl>,
будет найдено новое решение, в котором для каждого i имеется
по крайней мере одно такое и, что (11.107) выполняется как
точное равенство. Это возможно, так как приведенная выше си-
стема уравнений имеет единственное решение
P = (I —aP)"*g>0,
где g имеет компоненты, равные gi для и равные нулю
для всех остальных i. Итак, мы имеем новое решение х1'=х0—р,
причем р>0 и по крайней мере одна компонента вектора р по-
ложительна. Но это приводит к противоречию, так как
zr = exj = z0 — ер < z0 = ех0,
и, значит, исходное решение х0 было не оптимальным. Следова-
тельно, для каждого i вектор х0 должен удовлетворять условиям
(11.107) как точным равенствам по крайней мере для одного и
и поэтому для каждого решения х имеем х>х0. Отсюда х0=х*,
что и требовалось доказать.
Итак, доказано, что величины A(i) являются оптимальным
решением задачи линейного программирования с ограничениями
(11.107) и целевой функцией (11.109). Чтобы определить опти-
мальную политику, остается лишь заметить, какие из ограниче-
ний (11.107) для оптимального решения выполняются как точ-
ные равенства. То и, при котором ограничение для состояния i
выполняется как точное равенство, и дает оптимальное решение,
если период начинается с состояния i.
11.17. Двойственная задача линейного программирования.
Следует заметить, что задача линейного программирования,
м
обсуждавшаяся в предыдущем параграфе, имеет 2 Ni ограни-
чений, число которых обычно намного превосходит число пере-
менных (которое равно М, т. е. числу состояний). Это наводит
на мысль, что следует решать не исходную, а двойственную к
ней задачу.
484
Гл. 11. Динамическое программирование II
Итак, имеется 2^/ двойственных переменных wiu и двой-
ственная задача записывается так:
= j= 1, 2, ..М,
и i,u
wiu^>0 для всех Z, и; (11.110)
найти max Z— 2 f (i, u)wiu.
i, и
Здесь ограничения имеют вид равенств, так как переменные
исходной задачи могут быть любого знака.
Из изложенного в § 2.5 мы знаем, что только те wiu могут
быть положительными в оптимальном решении двойственной
задачи, которые соответствуют ограничениям прямой задачи,
обращающимся в точные равенства на ее оптимальном^ решении.
Следовательно, положительными могут быть только те для
которых и является оптимальным решением, когда период на-
чинается с состояния г.
Можно дать интересную интерпретацию двойственной задачи
(11.110), для чего, однако, придется дать сначала несколько
иную интерпретацию исходной задачи. Будем рассматривать за-
дачу, в которой имеется М+1 различных состояний: М прежних,
а (А4+1) -е состояние таково, что если система приходит в него,
то процесс оканчивается, и, следовательно, система никогда не
может из него выйти. Это состояние мы будем обозначать сим-
волом 0. Допустим, что если система пришла в состояние 0,
прибыль за все будущее время равна нулю, т. е. А(0)=0.
Пусть 1—а есть вероятность того, что процесс окончится в
течение рассматриваемого периода, если период начался с од-
ного из состояний /=1, ..., Л1; соответственно а — вероятность
того, что процесс не прекратится. Величина рг-Ди) представляет
собой вероятность того, что если период начинается с состояния i
и принимается решение и, система окажется в состоянии / в
начале следующего периода при условии, что процесс не прекра-
тится, т. е. условную вероятность. Тогда вероятность того, что
в конце периода система окажется в состоянии /, если период
начинается с состояния i и принимается решение и, равна
арц(и), так как а есть вероятность того, что процесс не окан-
чивается. Если период-начинается с состояния /, то вероятность
того, что процесс окончится, т. е. система придет в состояние 0,
равна 1—а независимо от того, какое решение принимается.
Если определить теперь величину A(i) как ожидаемую при-
быль за все будущее время (не приведенную), если период
начинается с состояния /, и в начале этого и во все последую-
щие периоды принимаются оптимальные решения, то A(z)
11.17. Двойственная задача линейнего программирования 485
будет удовлетворять следующему функциональному уравнению:
Л(г)= тах|7(Л «) + «2 Ау(«)Л(/)4-(1 - а)А(0/| =
= maxр(/, и) + ® S Ау(«)л(/)]» 1 = М. (11.111)
Это в точности такие же уравнения, как и (11.86). Итак, мате-
матически новая задача эквивалентна исходной.
Интерпретируем теперь (11.110) в терминах новой задачи,
в которой учитываются не приведенные прибыли, а определена
вероятность 1—а окончания процесса на каждом шаге. Ранее
уже было показано, что даже если допустить использование сме-
шанных стратегий, то все же среди оптимальных будет по край-
ней мере одна чистая стратегия. Итак, пусть допускается воз-
можность использования смешанных стратегий и viu есть веро-
ятность того, что будет принято решение и, если период
начинается с состояния Z. Пусть, кроме того, ^(z) —вероятность
того, что й-й период начинается с состояния i (она будет зави-
сеть, конечно, от того, с какого состояния начинался первый
период). Тогда в соответствии с (11.87) получим
Чш 0) = aS qk 'ViuPij{4> = a 2 <7* (0 /= 1, . •., M,
I, и i
(11.112)
Ay = S 2а;=2®|11[2а/(«)]=1- (плз)
Так как а’^рц = а<\, то при n-^-oo (аР)"->0 (ЛА 3.22), и, сле-
/
довательно, если qft=(^A(l), ..., qk(M)), то
lim Ч*+я = Чй(аР)я = 0. (11.114)
rt->oo
Иными словами, вероятность того, что система окажется в одном
из состояний /=1, 2, ..., М в начале периода, с ростом номера
периода стремится к нулю. Причина этого, конечно, в том, что
имеется вероятность 1—а окончания процесса в каждый период,
так что вероятность окончания процесса, т. е. прихода системы
в состояние 0, приближается к единице при fe->oo.
Попробуем теперь несколько модифицировать ситуацию, так,
чтобы значение qh(i) стремилось к единице (а не кчнулю) при
£->оо. Для этого нам придется сделать так, чтобы процесс не мог
окончиться в течение любого периода. Мы сделаем это, предпо-
ложив, что если процесс оканчивается в течение какого-либо
периода, он возобновляется снова с начала следующего периода.
486
Гл. 11. Динамическое программирование П
Пусть рг- есть вероятность того, что процесс начинается с со-
стояния i при условии, что он окончился в предыдущем периоде.
Если мы хотим, чтобы процесс начался снова, если он окончился
в предыдущем периоде, надо потребовать, чтобы Spz = 1* Так
I
как (1—а) есть вероятность того, что процесс окончится в тече-
ние периода, то величина 8i=(l—a)pi выражает безусловную
вероятность того, что процесс начнется с состояния I в начале
периода.
При сделанном предположении в начале любого периода
система всегда будет в одном из состояний /, /=1, М. По-
пытаемся определить величину </(/), выражающую вероятность
пребывания системы в состоянии i в начале периода. Если ве-
роятность нахождения системы в начале периода в любом
состоянии i, f=l, 2, ..., 7И, не зависит от времени, то будем
говорить, что система находится в статистическом равновесии
или в установившемся режиме. Если система находится в со-
стоянии i в начале периода, то процесс либо происходил и
раньше, либо начался в этом периоде с состояния L Следова-
тельно,
м
q(j) = ^qtf)P4 + ^ (11.115)
1 — 1
или
q = q(aP)H-e.
Отсюда, так как матрица, обратная к матрице I—аР, существует,
q = 8(I-аР)"1. (11.116)
Итак, при нашей новой интерпретации процесса установив-
шиеся значения q(i) действительно существуют. Если они дей-
ствительно являются вероятностями и система всегда находится
в одном из состояний /, 1=1, 2, ..., Л4, в начале периода, то
м
должно быть Проверим это. Просуммировав соотно-
шения (11.115) по /, получим
(11.117)
или, используя равенство (11.113),
м м
(11.118)
11.18. Дополнительные обсуждения 487
Ранее мы определили в< как (1—а)р». Таким образом,
м м
2 е/ = (1 - а)2р/ = (1—«)
i = l /=1
М
и, следовательно, действительно 3<7(0 = 1-
v i = 1
Запишем теперь
(11.119)
так что wiu есть совместная установившаяся вероятность того,
что период начинается с состояния i и принимается решение и.
Так как 2^=1, то, используя соотношения (11.113) и
(11.115), можно записать
= (11.120)
u Z, и
®/в>0 для всех Z, и,
2®(в = 1. (11.121)
I, и
Снова вернемся к двойственной задаче (11.110) и дадим ее
интерпретацию. Допустим, что в этой задаче мы должны вы-
брать б^>0 так, чтобы 2jE/=1 — а. Тогда двойственные пере-
' ’ менные WiU можно интерпретировать в смысле, указанном выше,
’ как установившиеся вероятности того, что система окажется в
состоянии i в начале периода и принимается решение и. Двой-
ственная задача указывает, что оптимальные значения WiU на-
ходятся путем максимизации ожидаемой прибыли за период.
i
> 11.18. Дополнительные обсуждения. Двойственная задача
подсказывает несколько других вопросов, представляющих
интерес. Рассмотрим процесс, в котором а=1 и который никогда
не кончается, т. е. в начале каждого периода система находится
в одном из М состояний I, z = l, 2, ..., М. Тогда для этой систе-
мы все Л(0, если они определены как и прежде, неограниченно
велики. Допустим, однако, что вместо того, чтобы пытаться
максимизировать прибыль в течение всего будущего времени,
мы будем максимизировать ожидаемую прибыль за период (или,
что эквивалентно, среднюю годовую прибыль). Будем предпола-
гать также, что определяемые соотношениями (11.113), обла-
дают тем свойством, что, начав период с состояния /, можно
достичь любого другого состояния / (хотя, возможно, и не в сле-
дующий период). Математически это означает, что для каждого
488
Гл. 11. Динамическое программирование II
i и / существует и, которое может зависеть от i и /, такое, что
/-я компонента вектора ег-Рл положительна. (Марковские про-
цессы с такими свойствами называются эргодическими.) При
таком подходе существует единственный набор установившихся
вероятностей q(i), каждая из которых положительна и которые
удовлетворяют условиям
м
q = qP, = (11.122)
i «1
(Читателю будет предложено доказать это в упражнении 11.15.)
Из этого следует тогда, что процесс никогда не может окончить-
ся и, следовательно, нет необходимости вводить вероятности,
определяющие начало процесса, чтобы гарантировать существо-
вание положительных установившихся вероятностей g(i).
Определим теперь величины WiU как установившиеся вероят-
ности того, что система находится в состоянии i в начале пе-
риода и принимается решение и. Будем искать оптимальную по-
литику (т. е. величины wiu) так, чтобы максимизировать среднюю
прибыль за период. Это приводит к следующей задаче линейного
программирования:
2 Wju — 2 = 0, / = 1. 2, ..., м,
и I, и
(11.123)’
для всех Z, и;
найти max z — У f (i, и) wiu.
i, и
Оптимальная стратегия будет характеризоваться положи-
тельными значениями wiu- Обычно при данном i только одно
йУги>0 и тогда и есть то решение, которое следует принимать,
если период начинается с состояния L
Для системы, в которой имеется только 100 возможных со-
стояний, задача линейного программирования (11.110) будет
содержать 100 ограничений и не менее 100 переменных, тогда
как задача (11.123) будет иметь 101 ограничение и примерно
1000 переменных. Хотя задачи линейного программирования
такого размера и могут быть решены, все же они достаточно
велики. Для более реалистических ситуаций, когда имеется
1000 и более состояний, соответствующие задачи линейного про-
граммирования в настоящее время решены быть не могут.
Постановка задачи, учитывающей приведенные прибыли (или,
что эквивалентно, процессы, которые могут окончиться), в форме
11.18. Дополнительные обсуждения 489
задачи линейного программирования принадлежит Эпену [4], а
в форме (11.123) для случая а=1 была приведена Манне [8].
-Описанные выше приемы могут быть легко обобщены на слу-
чай динамических систем с конечным числом периодов, в кото-
рых вероятности перехода и, возможно, принимаемые решения
изменяются от периода к периоду. Примером ситуации, которую
мы имеем в виду, является динамическая модель системы со-
здания запасов, рассматривавшаяся в § 10.18. Будем полагать,
что в начале &-го периода система будет в одном из Mk состоя-
ний. Число состояний может изменяться от периода к периоду.
Предположим, что если k-й период начался с состояния/, можно
предпринять Nik различных действий. Решение будем обозна-
чать через и. Пусть fk(i, и) есть ожидаемая прибыль за k-й пе-
риод, если он начинается с состояния i и принимается решением,
a pij(U'k)—соответственно вероятность того, что система при
этом окажется в состоянии j в начале периода £+1. Будем
допускать возможность использования смешанных стратегий.
Впрочем, снова справедливо, что среди оптимальных будет по
крайней мере одна чистая стратегия. Доказать это утверждение
читателю предлагается в упражнении 11.16.
Обозначим через wkiu вероятность того, что система будет в
состоянии i в начале периода k и что будет принято решение и.
Будем считать, что планируемый промежуток времени состоит
из п периодов и что мы хотим максимизировать приведенную
ожидаемую прибыль за все время. Допустим, что нам известно
состояние системы в начале первого периода, будем обозначать
его г, и vru — вероятность того, что в начале первого периода
принято решение и. Тогда whiu и vru должны удовлетворять
следующим условиям:
1) = 0. 7 = 1,2,...,^, (11.124)
и и
2 — £) = 0,
и I, и
k — — (11.125)
2^=1, (11.126)
и
k = 2,...,n, (11.127)
Z, и
^ги>0 для всех ti\ для всех h и- (11.128)
При этих ограничениях мы хотим максимизировать приведен-
ную прибыль
* = 2i?i(r, «)^„4- 2ай-У*(Л (11.129)
и k, i, и
490
Гл. 11. Динамическое программирование П
Мы пришли к задаче линейного программирования, которая,
к сожалению, будет, вообще говоря, очень большой. Например,
в случае 10 периодов со 100 возможными состояниями в каждом
и 10 возможными решениями для каждого состояния задача
будет иметь около 1000 ограничений и 10 000 переменных. Как
уже отмечалось, задачи такого размера в настоящее время стан-
дартными методами решены быть еще не могут. Простая форма
ограничений делает возможным решение задачи с помощью спе-
циальных приемов, например таких, в которых используется
принцип декомпозиции. Однако даже тогда придется иметь дело
с задачами линейного программирования очень большой раз-
мерности. Значительно более эффективными при решении задачи
такого типа представляются вычислительные методы динамиче-
ского программирования.
Хотя мы и не нашли лучшего вычислительного метода, чем
динамическое программирование, нам по крайней мере удалось
показать, что задача последовательного принятия решений, рас-
сматривавшаяся в § 5.3, может ставиться как задача линейного
программирования, если только переменные считать дискрет-
ными.
11.19. Заключительные замечания о проблеме размерности.
В этой главе рассматривались главным образом применения
динамического программирования к решению задач многошаго-
вого планирования более чем с одним параметром состояния
или более чем с одной переменной управления, выбираемой
на каждом шаге. Было показано, что вычислительные труд-
ности возрастают очень быстро с ростом числа параметров со-
стояния, и в большинстве случаев при четырех и более пара-
метрах состояния эти трудности оказываются непреодолимыми
для существующих вычислительных машин. Задачи с тремя
параметрами состояния удается решать лишь в некоторых слу-
чаях.
Несомненно, задача делается еще труднее, если на каждом
шаге требуется находить более чем одну переменную управле-
ния. Трудности порождаются двумя причинами: 1) с ростом
числа параметров состояния резко возрастает необходимый
объем памяти машины; 2) для каждой возможной комбинации
параметров следует определить Л&, выполнив оптимизацию по
одной или более переменным.
В некоторых случаях, как мы видели, удается найти опти-
мальные политики с помощью итеративных методов или сфор-
мулировав задачу в виде задачи линейного программирования.
Однако ни то, ни другое не снимает и даже существенно не сни-
жает трудностей, порождаемых проблемой размерности.
Литература
491
В настоящее время достигнуты еще очень незначительные
успехи на пути преодоления указанных трудностей. Основная
трудность здесь комбинаторного порядка — необходимо рассма-
тривать все возможные комбинации параметров состояния. Опыт
показывает, однако, что, вообще говоря, очень большая часть
комбинаций этих параметров не оказывает в действительности
влияния на решение, так как либо вероятность их столь мала,
что ею можно пренебречь, либо они соответствуют заведомо
невыгодным ситуациям и должны быть отброшены. Можно на-
деяться, что будет разработан метод, который позволит исклю-
чить большое число этих комбинаций и даст возможность решать
задачу либо точно, либо приближенно, но рассматривая лишь
малый процент возможных комбинаций. В немногих случаях
удалось уже развить специальные приемы, отвечающие приве-
денным требованиям. Одним из примеров может служить сим-
плекс-метод линейного программирования. Пока, однако, в этом
направлении сделано еще оченьиоченьмало.
ЛИТ ЕР АТУ РА
1. Beckmann М. J., Production Smoothing and Inventory Control, Operat.
Res., 9 (1961), 456—476. В этой статье показано, как можно использо-
вать функциональные уравнения динамического программирования для
того, чтобы характеризовать свойства некоторой оптимальной политики
в случае двух переменных состояния.
. 2. Веллман Р., Динамическое программирование, ИЛ, М., 1960.
3. Веллман Р., Дрейфус С., Прикладные задачи динамического про-
граммирования, изд-во «Наука», М., 1964.
4. d’E р е п о и х F., Sur un probleme de production et de stockage dans
1’aleatoire, Rev. Frang. rech. operation, 4 (1960), 3—15.
5. G u i 1 b a u d G. Th., Programmes dynamiques et programmes lineaires.
Note sur un modele de R. Bellman, Cahiers du Bureau universit. rech. ope-
ration, 2 (1957).
* 6. Holt C., Modigliani F., Muth J., Simon H., Planning Production,
Inventories, and Work Force, Englewood Cliffs, Prentice-Hall, 1960.
7. Ховард P., Динамическое программирование и марковские процессы,
изд-во «Советское Радио», М., 1964.
8. Manne A. S., Linear Programming and Sequential Decisions, Manag.
Sci., 6 (1960), 259—267.
9. S i m о n H. A., Dynamic Programming Under Uncertainty with a Quadra-
tic Function, Econometrica, 24 (1956), 74—81.
10. T h e i 1 H., Econometric Models and Welfare Maximisation, Weltwirtschaft.
Arch., 72 (1954), 60—83.
11. Theil H., A Note on Certainty Equivalence in Dynamic Planning, Econo-
metrica, 25 (1957), 346—349.
12. Wagner H., On the Optimality of Pure Strategies, Manag. Sci., 6
(1960), 268—269.
13*. Веллман P., Процессы регулирования с адаптацией, изд-во «Наука»,
М., 1964.
14*.Беллман Р., Применение математического программирования к задаче
о коммивояжере, Кибернет. сб., вып. 9, изд-во «Мир», М., 1964, 219—222.
492
Гл. 11. Динамическое программирование II
15*. Канторович Л. В., Экономический расчет наилучшего использования
ресурсов, М., 1960.
16*. Хелд М., Карп Р., Применение динамического программирования к
задачам упорядочения, Кибернет. сб., вып. 9, изд-во «Мир», М., 1964,
202—218.
17*. Arrow К. I., Karlin S. and Scarf Н., Studies in Applied Probability
and Management Science, Stanford, Stanford University Press.
18*. Kaufman А., С r u о n B., La programmation dynamique, Paris, Dunod,
1965.
19*. Моисеев H. H., Метод динамического программирования в теории
оптимальных управлений, I; II, Журн. вычислит, матем. и математ. фи-
зики, 4 (1964), № 3, 485—494; 5 (1965), № 1, 44—56.
20*. Баничук Н. В., Петров В. М., Черноусько Ф. Л., Численное
решение вариационных и краевых задач методом локальных вариаций,
Журн. вычислит, матем. и математ. физики, 6 (1966), № 6, 947—961.
Упражнения
11.1. Для задач, рассмотренных в § 11.2 и 11.3, доказать, что если fj(Xj)
и Ь(хз>Уз)—непрерывные функции, то и А* (51,52) являются непрерывными
функциями от и |2.
11.2. Рассмотреть задачу математического программирования: Ах<^5,
0<x<d; найти maxz==f(x), где f(x)—вогнутая функция. Доказать, что
оптимальное значение z есть вогнутая функция от |. В какой связи нахо-
дится этот факт с результатами § 11.5 и 11.6?
11.3. Для задачи, рассмотренной в § 11.3, показать, что из выпуклости
(вогнутости) функций Уз) следует выпуклость (вогнутость) функций
Уъ\ 5ь 5г) И Ай(5ь 5г)•
11.4. Рассмотрим следующую задачу:
xt—х2==0, Xi -[-х2 3, Xi, х2^>0, xh х2 — целые;
найти max z = 2x1-|-3x2.
Показать, что не существует такого множителя Лагранжа %, что можно
найти оптимальное решение этой задачи, минимизируя функцию
2х} —|— Зх2 (-^i — xz)
при условии Xi4-X2<i3. [Указание. Заметим, что для любого X оптимальное
решение последней задачи есть (0, 3) или (3, 0), но никогда не равно (1, 1),
решению исходной задачи.]
11.5. Докажите, что если переменные в задаче предыдущего упражнения
могут меняться непрерывно, то X, обладающее указанным свойством, суще-
ствует. Изучите поведение разности S=xi — х2 как функции от %. Встре-
чаются ли здесь трудности при вычислении искомого значения % с помощью
метода последовательных приближений?
11.6. Для задачи из § 11.2 доказать, что в случае непрерывности перемен-
ных Xj и вогнутости функций fj(Xj) возможно применение метода, основан-
ного на использовании множителей Лагранжа. [Указание. Применить теорию
гл. 6, чтобы показать, что существует два множителя Лагранжа, при которых
функция Лагранжа имеет седловую точку. Далее, используя ту же теорию,
показать, что при подходящем выборе Xi функция Лагранжа получается преж-
ней, если рассматривать задачу максимизации функции z-pZi ai/X/j
при условиях Xj 0; a2jXj < b2.
Упражнения
493
11.7. Рассмотреть транспортную задачу с двумя пунктами производства
и пятью пунктами потребления. Ресурсы в пунктах производства равны
соответственно 10 и 15, а потребности — 7, 3, 5, 8 и 2 соответственно.
Транспортные затраты как функции объемов перевозок хц приведены в таб-
лице. Найти Хц.
4Xj2 2Х1з 5< 3xi5
4х21 2х22 5х^2 Зх24 ю 8*
11.8. Рассматривается задача о замене оборудования для случая одно-
временного использования двух машин. Возможные решения — продолжать
использовать обе машины, заменить одну или другую либо заменить обе.
Сформулировать задачу в терминах рекуррентных соотношений динамическо-
го программирования.
11.9. Обобщить ситуацию, рассматривавшуюся в задаче упражнения 11.8,
на случай, когда имеется т машин, а необходимый выпуск продукции за-
дается известной функцией времени (например, может быть задано, что вы-
пуск увеличивается на 5% в год).
11.10. Рассмотреть задачу вариационного исчисления, в которой отыски-
вается функция #(х), минимизирующая функционал
I — J F (у, у', х) dx
а
и удовлетворяющая ограничению
3
J G (У, У', х) dx = у.
а
Показать, что задача может быть решена методом динамического программи-
рования с использованием двух параметров состояния. Показать также, что
введение множителя Лагранжа позволяет свести ее к задаче с одним пара-
метром состояния.
11.11. В выражении (11.62) выразить Gj через коэффициенты, введенные
в функциях затрат.
11.12. Выразить h, q, Н, Q и р, введенные в выражении (11.66), через
коэффициенты Gj.
11.13. Определить структуру матрицы R в уравнении (11.74) и найти
уравнения, которые надо решить для отыскания и.
11.14. Показать, каким образом модель системы создания запасов, рас-
смотренная в § 10.18, может быть приведена к виду, изучавшемуся в §11.12.
Что является состояниями? Сколько их должно быть? Что представляют со-
бой решения? Определить рц(и) и f(i,u).
11.15. Доказать, что для эргодического марковского процесса установив-
шиеся вероятности q(i) существуют, единственны и каждое /y(Z)>0. [Указа-
ние. Вектор q должен удовлетворять уравнению q(I — Р)=0, где I — Р —
особенная матрица.] Показать, однако, что можно единственным образом
выразить q(i), /=1, 2, ... , М—1, через q(M) и что матрица, получающаяся
после вычеркивания последних строки и столбца из I — Р, неособенная и мо-
жет быть разложена в степенной ряд.
33 Зак. 735
494
Гл. 11. Динамическое программирование II
11.16. Доказать, что для динамической задачи с п периодами, рассмотрен-
ной в § 11.18, по крайней мере одна чистая стратегия будет оптимальной.
[Указание. Непосредственно построить эту стратегию, проводя вычисления в
обратном направлении, как это делается при численном решении задачи.]
11.17. Рассмотрим задачу, обсуждавшуюся в § 11.3. Пусть нам известно,
что Ху есть оптимальное значение Xj. Тогда, решая задачу
п
2 а*1У i .....«. yj— целые;
п
найти max zQ == 2 fj (jfy, у
7»i
получаем значения t/y. Далее, решая задачу
п
j=l, ...» п, ху —целые;
п
найти max = 2 // (*/» //)»
найдем значения Ху. Используя их, найдем Уу и т. д. Показать, что этот
итеративный метод таков, что z0 zx z2 , и поэтому значения z
сходятся к относительному максимуму z. На одношаговом примере показать
геометрически, что сходимость к абсолютному максимуму г не обязательна.
11.18. Показать, что если для решения задачи, обсуждавшейся в § 11.2,
применить метод, основанный на использовании множителя Лагранжа, как
это сделано в § 11.7, то выражение 2 a2jxj будет монотонно возрастать,
1
когда % меняется от — оо до оо. Здесь х$ — оптимальное решение задачи
(11.29).
11.19. Показать, как можно использовать множитель Лагранжа для ре-
шения задачи о загрузке судна типа рассматривавшейся в § 10.6 для случая,
когда имеется дополнительное ограничение на общий вес.
11.20. Показать, как можно использовать множитель Лагранжа для ре-
шения задачи надежности типа рассматривавшейся в § 10.6 при дополни-
тельном весовом ограничении.
11.21. Решить пример из § 11.14, сформулировав соответствующую задачу
линейного программирования с помощью метода, введенного в § 11.17.
11.22. Пусть известно, что ограничение, содержащее r/j, будет выпол-
няться как точное равенство для оптимального решения задачи (11.9.). По-
казать, как для упрощения решения этой задачи можно использовать множи-
тель Лагранжа. Заметим, что после введения множителя Лагранжа мы при-
ходим к задаче только с одним параметром состояния, однако на каждом
шаге приходится искать минимум по двум переменным. В каком интервале
может меняться у ft
11.23. Объяснить, почему задача, изучавшаяся в § 11.3, не может рас-
сматриваться как задача динамического программирования с 2п этапами.
11.24. Какая экономическая интерпретация может быть дана задаче ли-
нейного программирования, описываемой уравнениями (11.107) и (11.109)?
11.25. Доказать, что итеративный метод отыскания оптимальной политики,
который рассматривался в § 11.13, может применяться без модификаций,
если допустить возможность использования смешанных стратегий.
Упражнения
495
1126. В § 10.18 изучалась задача о создании запасов, в которой пред-
полагалось, что плотность распределения вероятности спроса в &-й
период известна для всех k из планируемого промежутка времени. Рассмо-
трим теперь другую ситуацию, когда эта плотность в &-й период может
быть одной из конечного числа различных функций <pik(Vk). Если она равна
q>ih(Vk), то будем говорить, что система находится в t-м состоянии спроса
в период k. Допустим теперь, что состояние спроса не может быть предска-
зано с определенностью. Однако если система находится в состоянии спроса I
в начале Z?-ro периода, вероятность, что в начале (&+1)-го периода состоя-
ние спроса будет /, равна pij(k). В остальном задача формулируется так же,
как и в § 11.18. Предполагая, что состояние спроса на первом шаге известно,
показать, как для решения такой задачи можно использовать динамическое
программирование. [Указание. В этом случае потребуется два параметра со-
стояния. Предположите, что в начале периода состояние спроса известно.]
Задачи такого типа рассматривались Игльхартом и Карлином [17*, гл. 8].
11.27. Выразить в явной форме через соответствующие значения парамет-
ров линейные правила принятия решений, обсуждавшиеся в § 11.11 при
условии, что: а) планируемый промежуток времени состоит из одного перио-
да; б) планируемый промежуток времени состоит из двух периодов.
33*
ИМЕННОЙ УКАЗАТЕЛЬ1)
Балинский (Balinski М. L.) 153
Баранкин (Barankin Е. W.) §3
Бауман (Bowman Е. Н.) 299
Беллман (Bellman R.) 15, 24, 359,
413
Бил (Beale Ё. М. L.) 23, 177, 290
Бомол (Baumol W.) 153
' Вайнгартнер (Weingartner Н. М.)
275
Вольф (Wolfe Р.) 23, 24, 222, 229,
230, 241, 251
Гилдрет (Hildreth С.) 23, 242, 244
Гильберт (Hilbert-D.) 88
Гирш (Hirsh W. Н.) 153
Гольштейн Е. Г. И, 29
Гомори (Gomory R.) 24, 255, 276,
277, 287, 298
Гурвиц (Hurwicz L.) 23, 353, 354
Данциг (Dantzig G. В.) 10, 23, 24,
140, 153, 174, 177, 178, 275, 277,
298
Джонсон (Johnson S.) 24, 275
Деннис (Dennis J. В.) 24
Дойг (Doig А.) 290
Дорфман (Dorfman R.) 23
Дрейфус (Dreyfus S.) 24, 219, 414
Зойтендейк (Zoutendijk G.) 24, 316,
318, 320, 337
Канторович Л. В. 437
Кун (Kuhn Н. W.) 23, 195г 200,
Курант (Courant R.) 88
Лемке (Lemke С.) 23, 140, 318
Лэнд (Land А. Н.) 281, 290
!) При составлении указателя н
в конце каждой главы. — Прим. ред.
Манне (Manne А.) 24, 277, 489
Марковиц (Markowitz Н.) 23, 24,
226, 277
Миллер (Miller С. Е.) 23, 140
Модильяни (Modigliani F.) 467
Моисеев Н. Н. 460
Мут (Muth J.) 467
Розен (Rosen J. В.) 24, 322, 338
Симон (Simon Н. А.) 467, 469
Таккер (Tucker A. W.) 23, 195, 200,
204
Тейл (Theil Н.) 469
Уайтин (Whitin Т. М.) 190
Удзава (Uzawa Н.) 23
Фалкерсон (Fulkerson D.) 24, 275
Фергюсон (Ferguson A. R.) 178
Франк (Frank М.) 23, 241, 251
Фример (Freimer М.) 219
Хартли (Hartley Н. О.) 148
Хаутеккер (Houthakker Н.) 23, 244
Хедли (Hadley G.) 190
Хилдрет (Hildreth С.) 23
Ховард (Howard R.) 476
Хольт (Holt С.) 467
Чарнс (Charnes А.) 23, 140, 229, 295
Черноусько Ф. Л. 460
Эпен (d’Epenoux F.) 489
Эрроу (Arrow К. J.) 23, 353, 354
Юдин Д. Б. 11, 29
учитывалась литература, приведенная
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Базис 35
ортонормированный 53
Вариационное исчисление 422, 456,
460
Вектор (строка, столбец) 32
— вводимый в базис 42
— выпуклая комбинация 50
— единичный 33
— исключаемый из базиса 42
— искусственный 43
— лексикографически положитель-
ный 282
— линейная зависимость 35
— нормальный к гиперплоскости 50
— нормированный 53
— ортогональность 34
— порождение пространства 35
— скалярное произведение 34
— сложение 33
— умножение на скаляр 33
— характеристический /собственный)
53
Вероятность перехода 472
Вольфа способ в квадратичном про-
граммировании 230
Выпуклая комбинация векторов 50
Гессиан 58
Гилдрета метод в квадратичном про-
граммировании 242
Гиперплоскость 50
— касательная 60
— опорная 52
Гиперповерхность 56
— вогнутая 97
— выпуклая 97
Гиперсфера 50
Гомори алгоритм для полностью це-
лочисленных задач 276
Гомори алгоритм для частично цело-
численных задач 287
Градиент 57
Градиентные методы 302
-----в задачах с линейными огра-
ничениями 303
-------линейном программирова-
нии 333
-------нелинейном программиро-
вании 337, 340
-----метод Эрроу—Гурвица 353
-----проективный метод 332
Двойственность в задаче максимиза-
ции 87
-----программировании квадратич-
ном 246
------- линейном 48
•• Детерминированные задачи последо-
вательного принятия решений 387
----- теории создания запасов 391
Динамическое программирование 15.
359
Евклидово пространство 34
Задача детерминированная см. Де-
терминированные задачи
— квадратичного программирования
13, 220
— математического программирова-
ния линейная 10, 11
--------нелинейная 11, 12
— оптимизации классическая 13
— приближенная см. Приближенная
задача
— стохастическая см. Стохастичес-
кие задачи
— с условиями очередности 266
— с фиксированными затратами 151
498
Предметный указатель
Задача с фиксированными затратами
сведение к целочисленной 255
— целочисленная 14, 254
Задача о бродячем торговце 271
----- выборе направления наиболь-
шего изменения функции 93
-----загрузке корабля 375, 434
----- замене оборудования 409, 454
-----запасах 184, 391, 414, 430, 495
----- использовании рабочей силы
387
-----капитальных вложениях 273,297
-----линии сборки 298, 299
-----надежности 428
----- нефтяной компании 190
----- планировании выпуска авто-
мобилей 476
----------конденсаторов 432
--------производства 194, 218, 430,
460
-----производителе продуктов 179,
261, 434
-----производстве деталей 71, 180,
301
-------- насосов 432
--------продукции с переналадкой
оборудования 156
----- подводной лодке 173, 372
-----раскрашивании карты 298
-----распределении допусков 376
-------- поставок 375
--------самолетов по маршрутам 178
--------средств на производство и
рекламу 423
----- реализации проектов и кален-
дарном планировании 266
-----снабжении морской базы 428
-----торговце одеждой 88, 172
-------- хлебом 153
— расписания 299, 300
— транспортная 159, 174, 434, 447,
452
Квадратичная форма 54
Квадратичные затраты 462
Конечные альтернативы в линейном
программировании 260
Куна — Таккера теорема 203
— условия регулярности ограниче-
ний 205, 206
Кусочно-линейная аппроксимация 117
Линейные правила принятия реше-
ний 467
Линия уровня 55
Максимум абсолютный (глобальный)
16, 65
— относительный (локальный) 16
— сильный 66
— слабый 66
— условный 73
Марковские процессы 472
Матрица, определения и основные
свойства 29—31
— конгруэнтная 53
— неособенная 37
— обратная 37
— ортогональная 53
— подобная 53
— расширенная система уравнений 38
— характеристический вектор, поли-
ном, число 53
Минимум 66
— условный 73
Многогранник выпуклый 52
Множество точечное, определение и
основные свойства 49—52
Множители Лагранжа 76, 79
---в линейном программировании
94
--- интерпретация 85
---использование для уменьше-
ния размерности 449
Неравенство Шварца (Буняковского)
34
Нормаль к поверхности 60
Ньютона метод отыскания стацио*
парной точки 69
Образ 39
Ограничения 10
— линейные 11 z
— сепарабельные 13
Октант неотрицательный 51
Ортогональное дополнение подпро-
странства 36
Отображение 39
Отрезок 50
Линейная зависимость 35
Линейное преобразование 39
Параметры состояния 371
Переменная (базисная, небазисная)
39
Предметный указатель
499
Переменная вспомогательная 40
— искусственная 43
— истинная 43
— управляющая 170, 371
Поверхность уровня 60
Подпространство 36
Политика 371
Полупространство (замкнутое, от-
крытое) 50
Порождение пространства вектора-
ми 35
Приближенная задача в 6-форме 129
-----в Х-форме 117
Принцип декомпозиции 140
— оптимальности Р. Веллмана 372
Проблема размерности 436, 439, 441,
446, 490
Производная функции 56
— частная 56, 57
— в направлении г 58
Прямая 50
Ребро множества 52
Решение базисное 39
-----вырожденное 39
— в прямом направлении 387
— в обратном направлении 387
— допустимое 16, 41
— тривиальное 39
/?г-политика 406
Седловая точка 88, 195
----- глобальная 196
-------достаточные условия 199
-------необходимые условия 198
Сечение 275
— Гомори 277, 290
— Данцига 277
,— Марковица и Манне 277
Симплекс-метод 40—44
— таблица 44
Симплекс-метод двойственный 49
Симплекс-метод модифицированный
44—47
------- таблица 45
Система координат 33
----- ортогональная 34
Средняя стоимость детерминирован-
ная 191
-----из-за неопределенности 191
Стационарная точка 69
----- при наличии ограничений 308
Стохастические задачи математиче-
ского программирования 171
Стохастические задачи многошаговые
184
-----одношаговые со случайностя-
ми в спросе 172
-------------в технологических ко-
эффициентах 180
----- последовательного принятия
решений 414, 460, 469
----- теории создания запасов 414
Стратегия 478
— смешанная 478
— чистая 479 }
Теорема о неявных функциях 62
— Тейлора 59
— Куна—Таккера 203
Точка множества внутренняя 50
----- граничная 50
----- крайняя 51
Точка перегиба функции 68
Точки множества смежные 52
Транспортная задача 159, 174, 434,
447, 452
Управление 371
Управляющая переменная 170, 37!
Условия регулярности ограничений
Куна—-Таккера 205, 206
Фактор производства 266
Фаркаша лемма 209
Фиксированные затраты 151
Франк и Вольфа метод в квадратич-
ном программировании 241
Функциональное уравнение 405
Функция 55
— вогнутая 97
-----максимум и минимум 108
— выпуклая 97
-----максимум и минимум 105, 106
— Лагранжа 76, 79
----- интерпретация 86
— линейная 56
— непрерывная 56
— сложная 58
— состояния 374
— строго вогнутая 98
-----выпуклая 98
— целевая, см. Целевая функция
Характеристический вектор 53
— полином 53
— уравнение 53
— число 52
&00 Предметный указатель
Хартли метод максимизации 148 Хаутеккера метод в квадратичном программировании 244 Чарнса способ в квадратичном про- граммировании 229
Целевая функция 10 линейная 11 нелинейная 12 параметрическая 230 сепарабельная 12 Целочисленные задачи линейного программирования 14, 254 Цикл 407 Экстремум функции 74 необходимые условия 74 Эрроу—Гурвица градиентный метод 353 Якобиан 62
ОГЛАВЛЕНИЕ
От редактора перевода................................................5
Предисловие . —................................................* . 7
Глава I. Введение................................................... $
1.1. Задачи математического программирования ............... 9
1.2. Типы задач , . . ................................И
1.3. Вычислительные методы ................................
1.4. Трудности, порождаемые нелинейностями.................
1.5. Краткий исторический обзор............................
1.6. Обзор дальнейшего содержания . . . ...................
Литература ....................................................
Упражнения.....................................................
Глава 2. Необходимый математический аппарат . ....................
2. 1. Матрицы и векторы....................................
2. 2. Системы линейных уравнений...........................
2. 3. Линейное программирование............................
2. 4. Модифицированный симплекс-метод .....................
2. 5. Двойственность .................................. •
2. 6. Выпуклые множества...................................
2. 7. Характеристические числа и квадратичные формы ....
2. 8. Функция п переменных.................................
2. 9. Частные производные ................................
2.10. Теорема Тейлора .....................................
2.11. Теорема о неявных функциях...........................
Литература ...................................................
Упражнения....................................................
Глава 3. Классические методы оптимизации и свойства выпуклых
функций ................................................65
3. 1. Введение ............................................ 65
3. 2. Максимум и минимум при отсутствии ограничений .... 65
502
Оглавление
3. 3. Пример ............................................70
3. 4. Условный максимум и минимум. Множители Лагранжа 73
3. 5. Общий случай.......................................79
3. 6. Случай неотрицательных переменных и ограничений в
форме неравенств ........................................82
3. 7. Интерпретация множителей Лагранжа..................85
3. 8. Интерпретация функции Лагранжа; двойственность .... 86
3. 9. Примеры ...........................................88
3.10. Выпуклые и вогнутые функции........................97
3.11. Примеры ........................................... 102
3.12. Максимум и минимум выпуклых и вогнутых функций . . . 105
Литература .................................................109
Упражнения .................................................. 109
Глава 4. Приближенные методы решения задач с сепарабельными
функциями ..................................................116
4. 1. Введение ......................... ............... 116
4. 2. Построение приближенной задачи и определение локаль-
ного максимума..........................................116
4. 3. Пример ......................................... 123
4. 4. Другая формулировка............................. 129
4. 5. Замена переменных для получения сепарабельности .... 132
4. 6. Случаи, когда локальный экстремум одновременно являет-
ся глобальным ....................................... . 136
4. 7. Использование принципа декомпозиции при наличии огра-
ничений сверху ....................................... 140
4. 8. Пример .......................................... 143
4. 9. Метод Хартли для максимизации функции на выпуклом
множестве при сепарабельных ограничениях ...... 148
4.10. Задача с фиксированными затратами . .............151
4.11. Пример задачи с^ фиксированными затратами.........156
4.12. Транспортные задачи с выпуклыми сепарабельными це-
левыми функциями........................................159
Литература .................................................163
Упражнения .................. . ......................... 164
Глава 5. Стохастическое программирование.......................170
5.1. Введение ..........................................170
5.2. Одношаговые стохастические задачи со случайностями, по-
являющимися только в спросе.............................172
5.3. Одношаговые стохастические задачи со случайными вели-
чинами в технологических коэффициентах....................180
Оглавление
503
5.4. Многошаговые стохастические задачи ..................184
5.5. Средняя стоимость из-за неопределенности.............191
5.6. Замена случайных параметров их средними значениями . . 192
Литература .................................................. 192
Упражнения .................................................. 193
Глава 6. Теория Куна—Таккера.....................................195
6.1. Введение ........................................ 195
6.2. Необходимые и достаточные условия для седловой точки 195
6.3. Теорема Куна—Таккера.................................200
6.4. Установление необходимых условий методом Куна—Таккера 204
6.5. Один частный случай и пример....................... 212
Литература .................................................. . 215
Упражнения .................................................. 216
Глава 7. Квадратичное программирование...........................220
7.1. Введение ...................................220
7.2. Решение задачи квадратичного программирования с отри-
цательно определенной формой x'Dx......................222
7.3. Окончание процесса в случае отрицательной определенно-
сти формы x'Dx............................................226
7.4. Способ Чарнса для случая неположительности квадратич-
ной формы................................................ 229
7.5. Способ Вольфа, использующий параметризацию целевой
функции ............................................. . . 230
7.6. Пример ..............................................234
7.7. Другие методы решения задач квадратичного програм-
мирования ................................................241
7.8. Двойственность в квадратичном программировании .... 246
Литература ...................................................249
Упражнения ................................................. 249
Глава 8. Целочисленное линейное программирование . ............. . 254
8. 1. Введение ........................................254
. 8. 2. Задача с фиксированными затратами..................255
8. 3. Определение глобального экстремума для приближенной
задачи в б-форме....................................256
8. 4. Определение глобального экстремума для приближенной
задачи в Х-форме........................................ 258
8. 5. Представление некоторых поверхностей...............260
8. 6. Конечные альтернативы .............................260
8. 7. Задачи с условиями очередности . . ................266
8. 8. Реализация проектов и календарное планирование .... 266
504
Оглавление
8. 9. Задача о бродячем торговце............. 271
8.10. Капитальные вложения фирмы............ .273
8.11. Решение целочисленных задач линейного программирова-
ния ..................... 275
8.12. Алгоритм Гомори для решения полностью целочислен-
ной задачи ....................................276
8.13. Доказательство конечности ...............281
8.14. Алгоритм для решения частично целочисленных задач . . . 287
8.15. Доказательство конечности для случая частично целочислен-
ной задачи.................................... 291
8.16. Пример ..................................291
Литература .......................................295
Упражнения ...................................... 296
Глава 9. Градиентные методы.......................................302
9. 1. Введение ..........................................302
9. 2. Случай линейных ограничений........................303
9. 3. Сходимость итерационного процесса............... . . • 309
9. 4. Геометрическая интерпретация ......................312
9. 5. Численное определение г............................315
9. 6. Градиентный проективный метод .....................322
9. 7. Геометрические иллюстрации . . 329
9. 8. Сравнение методов определения г....................332
9. 9. Решение задач линейного программирования с использо-
ванием градиентных методов .....................(........ 333
9.10. Задачи с нелинейными ограничениями................ 337
9.11. Градиентный метод для задач с сепарабельными ограни-
чениями ................................... 340
9.12. Определение допустимого решения......................347
9.13. Пример . .................................. 348
9.14. Некоторые дополнительные замечания о сходимости . . . 352
9.15. Градиентный метод Эрроу—Гурвица для вогнутого про-
граммирования .............................................353
Литература ....................................................355
Упражнения . ..................................................355
Глава 10. Динамическое программирование I.........................359
10. 1. Введение ..........................................359
10. 2. Сущность вычислительного метода....................359
10. 3. Эффективность метода ..............................367
10. 4. Основные свойства динамического программирования . . 369
10. 5. Численный пример ..................................372
Оглавление
505
10. 6. Несколько других практических примеров..............375
10. 7. Случай непрерывности переменных................... 378
10. 8. Случай выпуклости или вогнутости функций fj(Xj) . . . 383
10. 9. Детерминированные задачи последовательного принятия
решений ..........................................387
10.10. Простая задача об использовании рабочей силы ..... 387
10.11. Детерминированные задачи создания запасов............391
10.12. Случай, когда Ь(Хз>Уз)—вогнутые функции....394
10.13. Пример .........................................399
10.14. Функциональные уравнения для систем с бесконечным
числом шагов...................:...........................401
10.15. Явное решение функционального уравнения............406
10.16. Задачи о замене оборудования....................... 409
10.17. Стохастические задачи последовательного принятия ре-
шений .................................................... 414
10.18. Стохастическая динамическая модель в теории создания
запасов .................................................. 414
10.19. Динамическое программирование и вариационное исчис-
ление ................................................... 422
10.20. Программы для решения задач методом динамического
программирования на вычислительных машинах .... 426
Литература .....................................................427
Упражнения ................................................. • • • 428
Глава 11. Динамическое программирование II.........................436
11. 1. Введение ...........................................436
11. 2. Задача распределения с двумя ограничениями..........436
11. 3. Задача с двумя переменными управления...............439
11.4. Случай непрерывности переменных.....................441
11. 5. Сравнение линейного и динамического программирования 445
11. 6. Использование динамического программирования в тран-
спортных задачах с двумя пунктами производства .... 447
11. 7. Использование множителей Лагранжа для уменьшения
размерности ...............................................449
11.8. Замена оборудования..................................454
11.9. Некоторые задачи вариационного исчисления...........456
11.10. Планирование выпуска продукции и задачи теории соз-
дания запасов .............................................460
11.11. Случай квадратичных затрат..........................462
11.12. Доказательство эквивалентности стохастической и детер-
минированной задач в случае квадратичных затрат . . . 467
11.13. Стохастические задачи последовательного принятия реше-
ний с бесконечным планируемым промежутком и марков-
ские процессы....................................’.........469
506
Оглавление
11.14. Пример ..................................476
11.15. Оптимальность чистых стратегий......... 478
11.16. Сведение к задаче линейного программирования .... 480
11.17. Двойственная задача линейного программирования . . .483
11.18. Дополнительные обсуждения ............. 487
11.19. Заключительные замечания о проблеме размерности. . .490
Литература ........................................491
Упражнения ........................................492
Именной указатель .................... 496
Предметный указатель • 497
Дж. Хедли
Нелинейное и динамическое
программирование
Редактор В. В. Беличенко
Художник А. А. Бессонов
Художественный редактор
Б. И. Шаповалов
Технический редактор
Л. М. Харьковская
Сдано в производство 23/V 1967 г.
Подписано к печати 22/XI 1967 г.
Бумага кама мелован. 60х901/1б=15’,88. бум. л.
31,75 усл. печ. л.,
Уч.-изд. л. 29,45. Изд. № 1/4075
Цена 2 р. 30 коп. Зак. 735
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Ленинградская типография № 2
имени Евгении Соколовой
Главполиграфпрома
Комитета по печати
при Совете Министров СССР
Измайловский проспект, 29