Солитоны и инстантоны в квантовой теории поля - Раджараман Р.

Автор: Раджараман Р.
Теги: физика квантовая теория поля квантовая физика
Год: 1985
Похожие
Квантовая теория поля
Введение в квантовую теорию поля
Квантовая теория поля и топология
Квантовая теория поля в физике конденсированного состояния
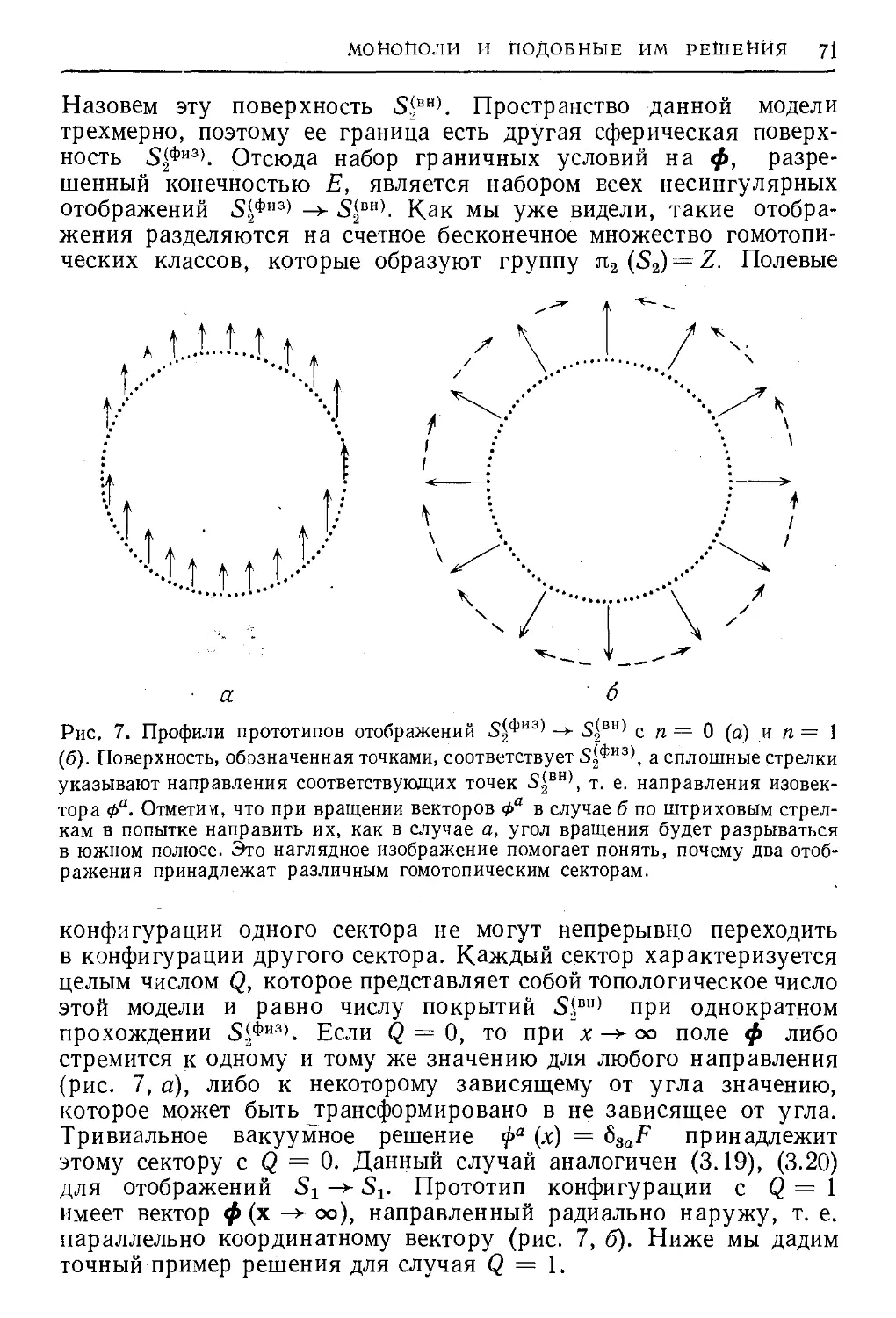
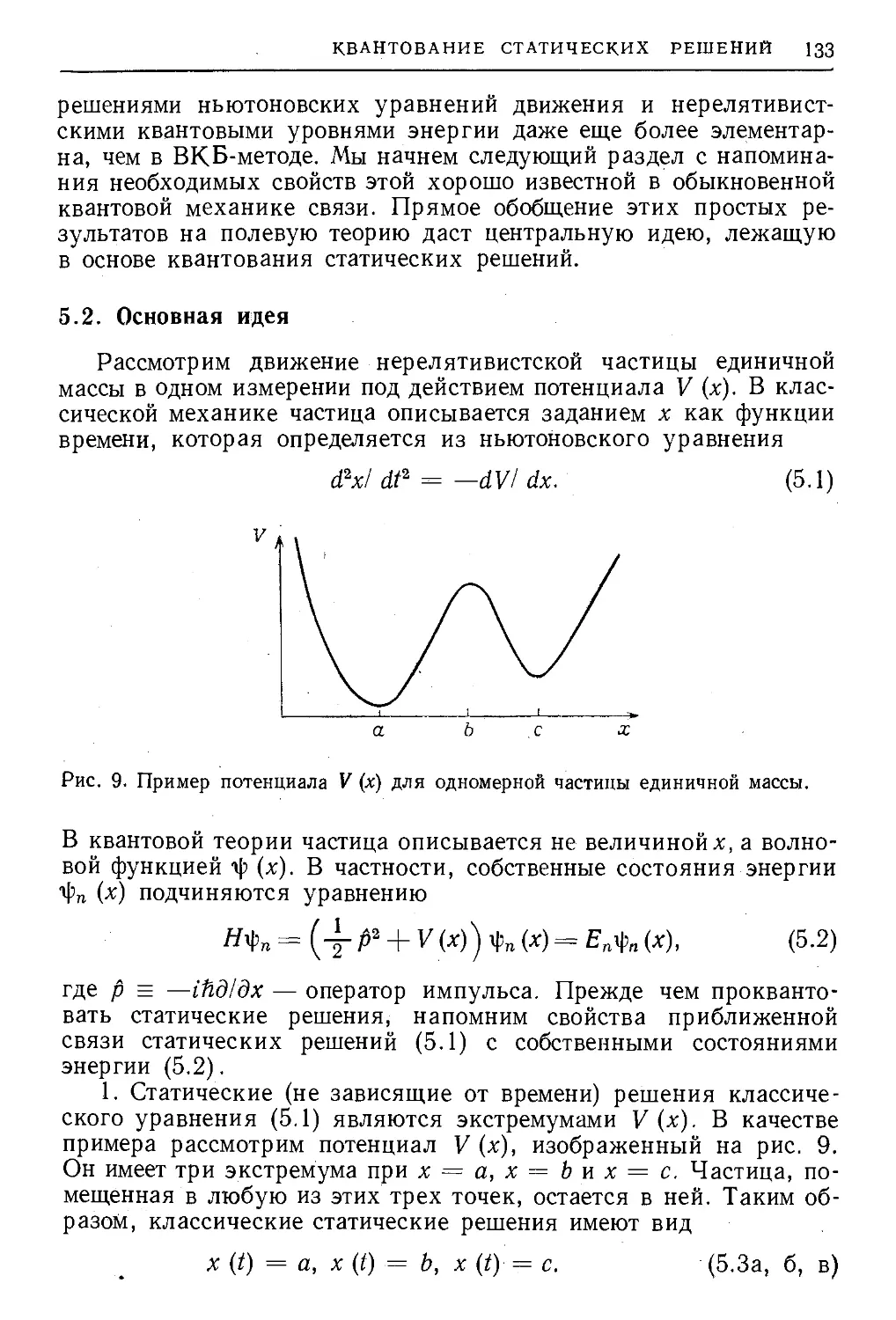
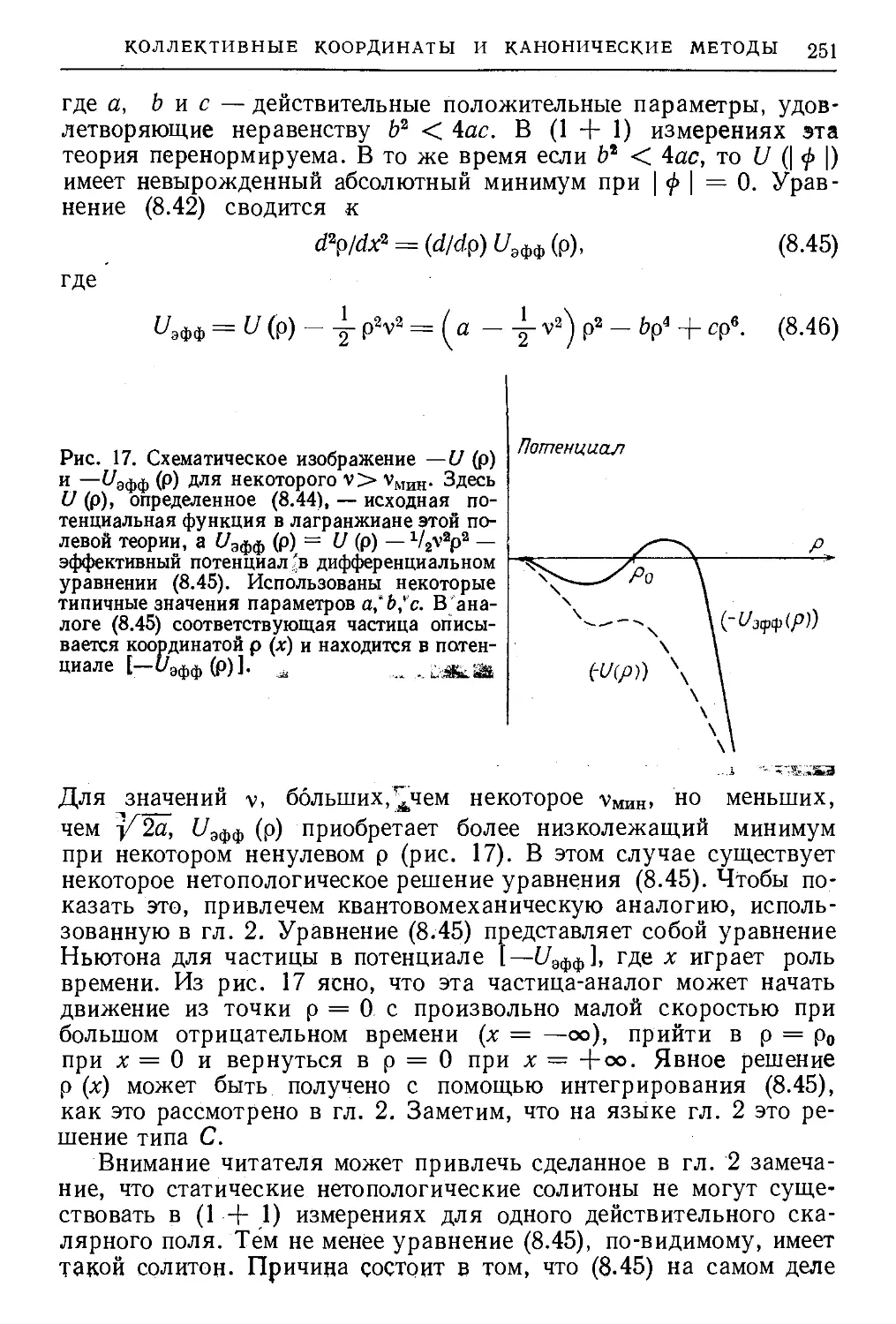
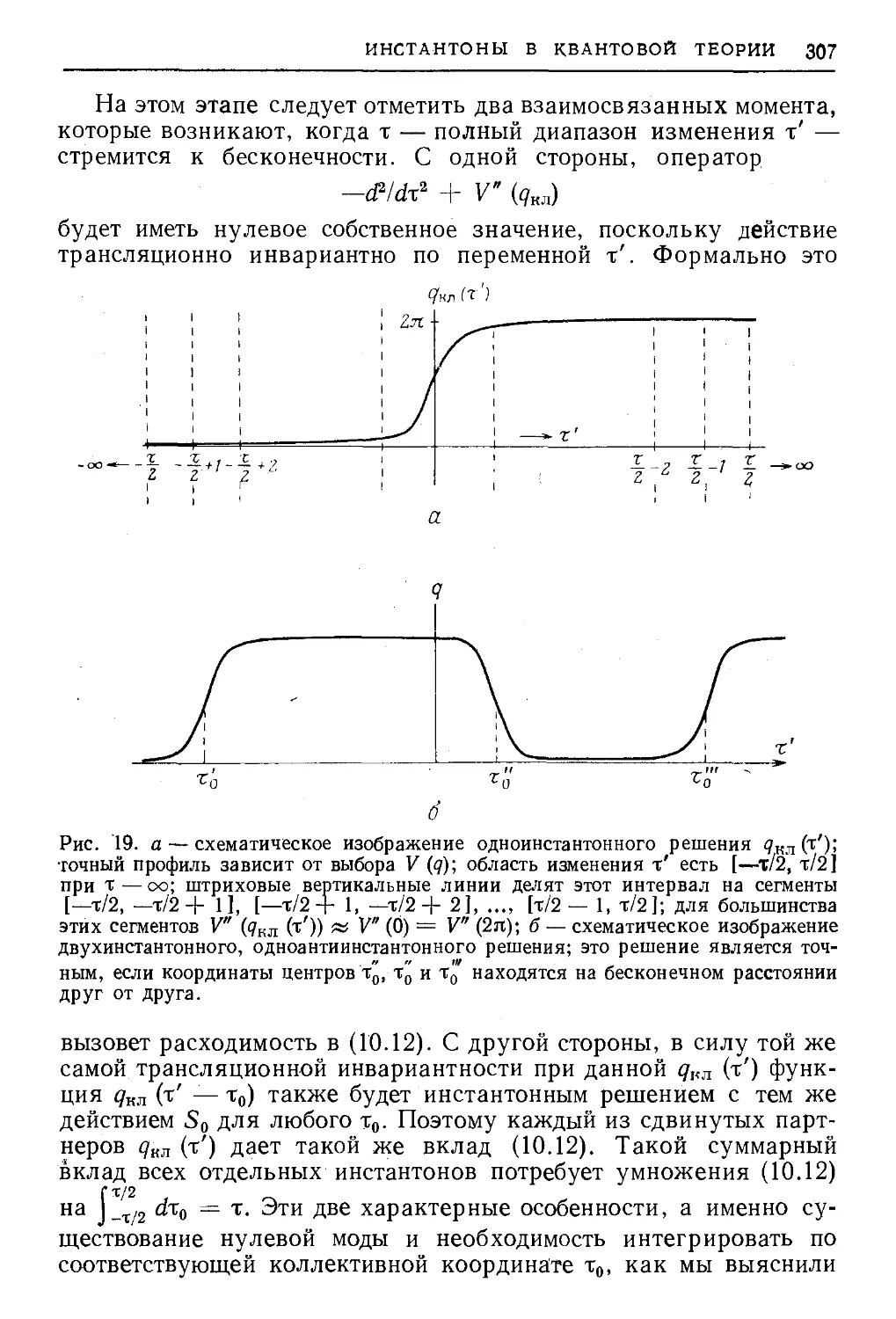
Текст
                    SOLITONS AND INSTANTONS
An Introduction to
Solitons and Instantons
in Quantum Field Theory
R. RAJARAMAN
Centre for Theoretical Studies,
Indian Institute of Science,
Bangalore 560012, India
North-Holland Publishing Company
Amsterdam-New York-Oxford
1982

Р. Раджараман
солитоны
и
ИНСТАНТОНЫ
в квантовой
теории
поля
Перевод с английского
канд. физ.-мат. наук А. А. Власова
и канд. физ.-мат. наук К. А. Свешникова
под редакцией
д-ра физ.-мат. наук О. А. Хрусталева
МОСКВА «МИР» 1985

1.1.К Т2.:\\
1МГ>
УДК 530.145
Раджараман Р.
Р15 Солитоны и инстантоны в квантовой теории поля. Пер.
с англ. —М.: Мир, 1985. —416 с, ил.
Монография индийского ученого является первым систематическим изло-
изложением теории квантовых солитонов и инстантонов и ее приложений к теоретико-
полевым и статистическим моделям. В относительно небольшом объеме охвачены
все аспекты и последние достижения этого бурно развивающегося в последнее деся-
десятилетие направления квантовой теории. Книга содержит необходимые предвари-
предварительные сведения для изучения вопроса и может служить также введением в проб-
проблему.
. Для научных работников в области квантовой теории и физики высоких
энергий, а также студентов и аспирантов.
_ 1704020000—394 -„ я_ , ББК. 22.31
Р 041 @1)-85 56~85' Ч- ' 530.1
Редакция литературы по физике
© North-Holland Publishing Company, 1982
© перевод на русский язык, «Мир», 1985

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Предлагаемая книга представляет собой превосходное введение
в теорию квантования полей в окрестности ненулевых класси-
классических решений. Читатель, не знакомый с этим предметом, обой-
обойдет в сопровождении искусного наставника одну из мастерских
современной физики, и если не останется в ней работать, то по
крайней мере значительно расширит свой кругозор.
Собранный в книге материал, как и стиль изложения, пол-
полностью отвечают ее назначению, поэтому представляется совер-
совершенно излишним снабжать монографию какими-либо подробными
примечаниями; то же самое относится и к довольно подробному
списку литературы, органично связанному с содержанием
книги.
Здесь же уместно подробнее осветить историю вопроса, изло-
изложенную в данной монографии слишком поверхностно. Это приво-
приводит к тому, что из поля зрения читателей полностью выпадают
важные работы, знакомство с которыми представляется нам со-
совершенно необходимым как для глубокого освоения материала,
так и для правильного понимания места упоминаемых в книге
исследований в современной квантовой теории поля.
Автор монографии полагает, что «за исключением важных,
но предварительных работ, появившихся в предыдущие десяти-
десятилетия, систематическое изучение этих вопросов началось только
в середине семидесятых годов». Такой приговор предыдущим
десятилетиям кажется слишком суровым. Дело в том, что отсчи-
отсчитывать их следует от момента рождения идеи квантования клас-
классического поля, когда выяснилось, что среди канонических преоб-
преобразований бозонного поля есть выделение очисловой составляю-
составляющей, поэтому оператор бозонного поля всегда потенциально со-
содержит классическое поле. Тогда же было обнаружено, что ра-
равенство нулю классической составляющей энергетически выгодно
только для свободного поля, поэтому квантование любой реаль-
реальной физической системы должно включать квантование бозонного
поля в окрестности классического поля. Если это поле можно
считать малым, то связанные с ним эффекты, как правило, удовлет-
удовлетворительно описываются в рамках стандартной теории возмуще-

.кипи: ргдлктог'л
пни, когда классическое поле в первом приближении считается
равным нулю. Однако даже в квантовой электродинамике —
триумфе теории возмущений — пренебрежение классическим по-
полем приводит к инфракрасным расходимостям, и возникающие
трудности удовлетворительно преодолеваются лишь после вы-
выхода за рамки теории возмущений. Хорошо известный метод
Блоха—Нордсика может служить примером достаточно система-
систематического исследования проблем, связанных с описанием кван-
квантовых эффектов в присутствии классического поля. Если класси-
классическое поле с самого начала нельзя считать малым, то возникает
задача последовательного описания свойств физической системы,
в которой главным эффектом является выделение классического
бозонного поля. Здесь уместно заметить, что среди имен людей,
размышлявших над этим вопросом, можно найти такие, как Вен-
цель, Паули, Боголюбов, любое исследование которых обычно
бывает как предварительным, так и окончательным. В частности,
решение задачи о последовательном выделении замороженного
бозонного поля в принципе было дано в работе Боголюбова
[П.
В «предварительных», а точнее классических работах по
квантованию в окрестности классических решений в первую
очередь рассматривался вопрос о восстановлении свойств сим-
симметрии гамильтониана системы, утрачиваемых после прямоли-
прямолинейного выделения из бозонного поля классической составляю-
составляющей, играющей роль внешнего поля. Именно этой цели служит
предложенное Боголюбовым каноническое преобразование, в ре-
результате которого среди новых переменных фигурируют функцио-
функционалы поля, играющие роль параметров группы симметрии. После
перехода к новым переменным удается построить регулярную
теорию возмущений, в которой с самого начала нет и речи о каких-
либо «нулевых методах».
Таким образом, прогресс семидесятых годов связан не Столько
с идейной стороной дела, сколько с более подробным изучением
свойств классических решений и привлечением к их анализу
новых для физики мощных математических методов (таких как
метод обратной задачи рассеяния). Однако изучение классической
части решения, каким бы интересным и сложным ни было это
занятие, есть составная часть общей физической задачи, поэтому
даже на этой стадии полезно помнить об общей структуре опера-
оператора поля. В «предварительных» подходах к проблеме сам форма-
формализм не позволяет забыть о ней, поэтому с этой точки зрения
многие рассуждения о связи классического и вторично кванто-
квантованного полей, о построении квантовых полей по классическим,
о постулатах для такого поля кажутся очевидными, а порой и
наивными. Пожалуй, наиболее трудная яасть теории квантования
около классических полей связана с усвоением смысла групповых

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
переменных 1). Здесь полезно иметь в виду, что после преобразо-
преобразования Боголюбова, например, классическое статическое решение
и (х) превращается в оператор и (х — а), где на преобразования
трансляций реагирует лишь групповая переменная а — функ-
функционал операторов поля. При этом трансляционная инвариант-
инвариантность связана вовсе не с тем, что и (х — а), как и и (х), — реше-
решение классических уравнений поля. Трансляционную инвариант-
инвариантность полной теории обеспечивает то обстоятельство, что теперь
а — оператор, который в данном случае реализуется как опера-
оператор умножения и выпадает из гамильтониана системы, и при
беглом взгляде его трудно отличить от переменной, имеющей
смысл координаты точки на действительной оси. Канонически
сопряженная а величина имеет смысл оператора полного импульса.
Классическая составляющая в формализме Боголюбова не яв-
является очисловой функцией; она не коммутирует с другими опе-
операторами поля, поскольку содержит в своем аргументе оператор.
Переменная х в аргументе классической составляющей безраз-
безразлична к преобразованиям сдвигов. Это обстоятельство полностью
разрешает возможные недоумения, связанные с возможностью
толкования наличия классической составляющей поля как про-
проявления протяженности частицы. Перестановочные соотноше-
соотношения между оператором а — координатой центра инерции системы
и оператором полного импульса — определяют а как величину
с непрерывным спектром, имеющую свойства координаты то-
точечной частицы. То, что воспринимается как протяженность
частицы, есть просто свойство некоторых состояний поля.
Заметим, что при изучении только классических свойств поля
соответствующие уравнения поля формулируются в терминах
переменных, безразличных к преобразованиям симметрии, в част-
частности к преобразованиям пространства-времени. Поэтому на
этой стадии аргументы классических полей можно подвергать
практически любым преобразованиям, не заботясь об их физи-
физическом смысле. С этой точки зрения, например, переход ко мни-
мнимому времени обоснован ничуть не хуже, чем соответствующий
стандартный переход в теории связанных состояний, поэтому
при учете этого обстоятельства появление инстантонов в реля-
релятивистски ковариантных теориях в значительной мере лишается
своей первоначальной таинственности.
Приведенные примеры достаточно убедительно показывают
необходимость представления общей структуры теории даже при
первоначальном прикосновении к ней. Библиографию работ,
применяющих метод Боголюбова к разнообразным задачам тео-
х) Если""с самого начала говорить на языке функционального интегрирова-
интегрирования, то этот вопрос формулируется как требование к структуре функционального
пространства задачи.

н ni'i ли< .кипи: ргдлкюрл ш-ренодл
рин ноля, а также обзор более ранних работ в этой области чи-
читатель может найти в статье [2], в которой также приведены
ссылки на исследования, устанавливающие связь между методом
Боголюбова и квантованием на произвольных гиперповерхностях
по Дираку. Эти работы в значительной степени проясняют гео-
геометрический смысл преобразования Боголюбова. Медленная
(после выделения равномерного движения по геодезическим груп-
группового пространства) зависимость групповых переменных от
времени позволяет установить аналогию между каноническими
преобразованием Боголюбова и методом Боголюбова—Крылова
в теории слабо нелинейных колебаний. На основе этой аналогии
в работе [3] предложен изящный метод релятивистски-ковариант-
ного квантования поля в окрестности классического решения
в терминах гейзенберговых полей. Наконец, в работе [4] метод
Боголюбова формулируется непосредственно в терминах опера-
операторов рождения и уничтожения бозе- и ферми-полей.
Приведенные здесь краткие замечания, призванные восста-
восстановить, насколько это возможно, истинную картину развития
метода квантования вблизи классических решений, а также обра-
обратить внимание читателя на работы, не отмеченные в монографии,
ни в коей мере не должны восприниматься как упрек: моногра-
монография, будучи задуманной как элементарное введение в предмет,
справляется с этой задачей вполне успешно и настоятельно реко-
рекомендуется как начинающему, так и более умудренному читателю,
для которого она будет хорошим современным справочником.
От автора и гл. 1—6 переведены А. А. Власовым, гл.7—11
и приложения переведены К. А. Свешниковым.
О. А. Хрусталев
ЛИТЕРАТУРА
1. Боголюбов Н. Н. — УАОД, 1950, т. 2 № 2, с. 3—24; Избранные труды, т. 2. —
Киев, Наукова Думка, 1970, с. 499—519.
2. Khrustalev О. A., Razumov A. V., Taranov A. Y. — Nucl. Phys., 1980, v. B172,
p. 44.
3. Свешников К. А. — ТМФ, 1983, т. 55, № 3, с. 361—384.
4. Тимофеевская 0. Д. — ТМФ, 1983, т. 54, № 3, с. 464—468.

ОТ АВТОРА
Всеми своими знаниями в этой области физики я обязан устному
и письменному общению с тремя людьми. Ими являются про-
профессора Сидней Коулмен, Роджер Дашен и Роман Джакив. Я им
очень благодарен.
Кроме того, очень полезными были обсуждения рассматри-
рассматриваемых вопросов со многими физиками из разных стран. Я бла-
благодарю их всех, и хотя практически невозможно перечислить
все имена, некоторые из них хотелось бы отметить особо. Это
профессора И. Аффлек, Н. Крист, Б. Хасслахер, А. Неве, Р. Шан-
кар, Дж. Стратди, Е. К. Дж. Сударшан, К. Б. Торн, Е. Дж. Вайн-
берг и Е. Виттен. Я также признателен профессорам X. Р. Криш-
намурти, Р. Нитянанда и С. Вадья за чтение частей рукописи и
полезные замечания. Я хочу выразить благодарность миссис
Радж Лакшми за помощь при чтении гранок. Вся ответственность
за оставшиеся опечатки лежит целиком на авторе.
Я благодарю Институт науки Индии за предложение написать
эту книгу, Центр аспирантуры Института за помощь при под-
подготовке рукописи к печати и мистера М. С. Нагараджа за эффек-
эффективную секретарскую помощь. Необходимо отметить гостеприим-
гостеприимство Принстонского института научных исследований, Гарвард-
Гарвардского университета и Массачусетского технологического инсти-
института, предоставивших мне возможность непосредственного обще-
общения с ведущими специалистами в этой области науки.
Наконец, я признателен моей жене Индире и моим родителям
за их поддержку.

ГЛЛ11Л I
ПРЕДИСЛОВИЕ И ВВЕДЕНИЕ
Несколько .отклоняясь от обычной практики, мы объединили
предисловие с вводной главой. Мы сделали это потому, что, как
нам кажется, обсуждение содержания книги — выбор рассматри-
рассматриваемых вопросов, уровень изложения и другие характеристики
и объяснения, обычно включаемые в предисловие, — полезнее
дать параллельно с кратким обзором и оценкой этой недавно
возникшей области науки.
Цель данной книги — дать информацию о релятивистских
квантовых теориях поля, начиная с классических решений соот-
соответствующих полевых уравнений. За исключением нескольких
важных, но предварительных работ, появившихся в предыдущие
десятилетия, систематическое изучение этих вопросов началось
только в середине семидесятых годов. Первым шагом в этом на-
направлении явилось нахождение решений все большего числа
классических релятивистских нелинейных волновых уравнений.
Сначала это было сделано для двумерных моделей одного ска-
скалярного поля, но вскоре классические решения (точные или
с хорошим приближением) были получены для некоторых систем
уравнений, включающих скалярные, векторные и дираковские
поля, для большего числа измерений.
В одном случае эти классические решения являются решениями
полевых уравнений в метрике Минковского, в другом они яв-
являются решениями евклидовых уравнений. В зависимости от
этого меняется их роль в квантовой теории. В обоих случаях важ-
важным свойством решений является их локализованность. В част-
частности, решения в пространстве Минковского имеют конечную
энергию с локализованной нерасплывающейся плотностью энер-
энергии. В большинстве случаев они перемещаются без искажения
формы с некоторой постоянной скоростью. Часто эти решения
называют солитонами, и мы будем использовать этот термин.
(Точнее говоря, их следовало бы называть уединенными вол-
волнами. Определение солитона накладывает более жесткие требо-
требования, которым не подчиняются многие наши решения. Различие
между этими двумя терминами подробнее разъясняется в сле-
следующей главе.) Тем, что они являются равномерно движущимися

ПРЕДИСЛОВИЕ И ВВЕДЕНИЕ Ц
нерасплывающимися пакетами энергии, солитоны напоминают
протяженные частицы, хотя они являются решениями нелиней-
нелинейных волновых уравнений. Элементарные частицы в природе также
представляют собой локализованные пакеты энергии; кроме того,
считается, что они описываются некоторой релятивистской тео-
теорией поля. Разумеется, полевая теория, описывающая элементар-
элементарные частицы, является квантовой теорией, в то время как соли-
солитоны прежде всего являются решениями классических полевых
уравнений. Это обстоятельство явилось предпосылкой для сле-
следующего этапа в развитии данного вопроса, на котором находи-
находилось соответствие между классическими солитонными решениями
любой полевой теории и состояниями протяженных частиц в кван-
квантовом варианте этой теории. Некоторого соответствия можно
было бы ожидать на основе интуитивных соображений, но по-
построение систематического аппарата для его установления яв-
является нетривиальной задачей. Процедуры установления такого
соответствия, которые могут быть названы «квантованием соли-
тонов», были развиты с использованием различных методов неза-
независимо несколькими группами теоретиков в период 1974—1975 гг.
Эти методы сводятся к обобщению на релятивистскую квантовую
теорию поля хорошо известного квазиклассического разложения
нерелятивистской квантовой механики. С помощью этого обобще-
обобщения при квантовании флуктуации поля в окрестности солитона
было показано, что '£ классическим солитоном следует связывать
не только квантовое состояние частицы-солитона, но и целый на-
набор возбужденных состояний. Такие свойства квантовой частицы-
солитона, как масса или формфакторы, получаются из соответ-
соответствующих свойств классического солитона с помощью регуляр-
регулярного квазиклассического разложения. Были разобраны такие
существенные технические трудности, как ультрафиолетовые
перенормировки квантовых флуктуации и проблемы нулевых
мод, связанные с непрерывными группами симметрии.
Как ответвление этих исследований возникла инстантонная
физика. Инстантоны — это локализованные классические реше-
решения с конечным действием евклидова варианта полевых уравне-
уравнений произвольной модели. Такие решения получены в точном
аналитическом виде для большого числа моделей, включая кван-
квантовую хромодинамику (КХД). На классическом уровне инстан-
инстантоны не очень отличаются от статических солитонных решений
не зависящих от времени полевых уравнений. В большинстве
случаев инстантоны модели вО измерениях являются статическими
решениями той же модели в D + 1 измерении. Но в отношении
их влияния на соответствующую квантовополевую теорию инстан-
инстантоны сильно отличаются от солитонов. Если последние приводят
к протяженным частицам, то первые ведут к туннельным эффек-
эффектам, которые могут существенно изменять структуру вакуумного

12 ГЛАВА I
состояния. Вакуумное состояние является краеугольным камнем
квантовой теории поля. Любые его изменения могут изменить
свойства теории. Например, в двумерной абелевой модели Хиггса
вакуумное туннелирование, вызванное инстантонами, приводит
к удержанию зарядов — эффекту, которого нельзя обнаружить
в стандартной теории возмущений. В КХД, где энергично искали
механизмы удержания кварков, надежды, что инстантоны могут
приводить к удержанию, не осуществились. Но даже в этом слу-
случае инстантоны дают существенный вклад в межкварковые силы.
Два свойства, присущие как солитонам, так и инстантонам,
делают их квантовые эффекты особенно интересными.
1. Большинство солитонов и инстантонов имеет непертурба-
тивную природу. Это означает, что они не могут быть получены,
если начинать с решений линейной части уравнений поля и рас-
рассматривать нелинейные члены по теории возмущений. Если клас-
классические решения сами по себе выходят за рамки теории возму-
возмущений, то возникающие при этом квантовые эффекты оказываются
также непертурбативными. Это не единственные и не первые
непертурбативные результаты, имеющиеся в теории поля, но они
означают важное продвижение вперед в исследовании квантовых
полей.
2. В типичном случае солитоны и инстантоны характери-
характеризуются некоторым топологическим индексом, связанным с их
поведением на пространственной бесконечности. Для солитонов
этот топологический индекс оказывается сохраняющейся вели-
величиной, которая в квантованной теории становится сохраняющимся
квантовым числом, характеризующим солитонное состояние. Та-
Такое топологическое квантовое число по своему происхождению
совершенно отлично от обычных нётеровских зарядов, связан-
связанных с непрерывными симметриями лагранжиана. В случае инстан-
инстантонов существование ненулевого топологического индекса ведет
к появлению набора вакуумных состояний, характеризуемых
вакуумным углом 9. Для математиков анализ гомотопий, кото-
которые возникают при описании этого явления, тривиален, но тот
факт, что такие соображения могут играть решающую роль в кван-
квантовой теории поля, представляет собой новое обстоятельство.
Большинство результатов в квантовой теории солитонов и
инстантонов получено квазиклассическим ВКБ-методом. Слово
«квазиклассический» означает, по мнению некоторых, что резуль-
результаты не вполне квантовополевые. В ответ следует отметить, что
результаты, полученные при учете солитонов и инстантонов,
в не меньшей степени квантовомеханические, чем результаты
стандартной теории возмущений. В самом деле, стандартная тео-
теория возмущений может рассматриваться как частный случай
квазиклассического метода, где квантуются флуктуации около
тривиального классического решения, в то время как в физике

ПРЕДИСЛОВИЕ И ВВЕДЕНИЕ 13
солитонов и инстантонов то же самое проделывается в окрест-
окрестности нетривиального непертурбативного классического реше-
решения. Это обстоятельство будет ясно из содержания гл. 5 и 6.
Хотя эти методы ведут к качественно новым результатам
в квантовой теории поля, основные физические идеи понять до-
достаточно легко. Большинство из них представляет собой обобще-
обобщение на теорию поля идей, с которыми мы уже знакомы по нереля-
нерелятивистской квантовой механике. Это весьма приятная сторона
данного вопроса. Разумеется, конкретные вычисления или стро-
строгие исследования солитонных (инстантонных) эффектов могут
быть сложны, но основные результаты можно оценить, не вда-
вдаваясь в технические подробности.
Сказав так много в похвалу предмета книги, мы должны также
очертить его рамки. Имеются два существенных ограничения:
1. Квазиклассический метод, рассматривает ли он солитоны
или инстантоны, требует выполнения условия слабой связи, поэтому
соответствующий параметр нелинейной связи должен быть мал. Это
требуется, даже если конечные результаты непертурбативны поэто-
поэтому параметру, как показано в различных частях этой книги. В не-
некоторых случаях оказывается, что квазиклассические ВКБ-резуль-
таты дают правильный ответ или хорошее численное приближение,
•даже если параметр связи велик; но это не может приниматься как
общая черта метода.
2. Метод, очевидно, требует знания прежде всего ряда нетри-
нетривиальных классических решений. Это означает, что для любой
данной модели локализованные несингулярные решения должны:
а) существовать и б) быть представимы либо в точной аналити-
аналитической форме, либо по крайней мере с достаточной точностью на-
наряду со своими свойствами стабильности.
Для ряда представляющих интерес случаев одно из этих тре-
требований или оба могут не выполняться. В частности, эти требо-
требования отчасти ограничивают применение солитонов и инстанто-
инстантонов к описанию адронных частиц, физические свойства которых,
как сейчас принимается, описываются КХД. Рассмотрим сначала
солитоны: КХД есть SU (З)-калибровочная теория, в которой
калибровочные бозоны взаимодействуют с ферми-кварками. Су-
Существуют различные способы квазиклассического разложения
в присутствии фермионов (гл. 9). Простейший путь — начать
с классических решений, для которых ферми-поле равно нулю.
В случае КХД это сводится к нахождению решений для самодей-
самодействующей системы калибровочных полей. К сожалению, дока-
доказано, что чисто калибровочная теория в C + 1) измерениях
не может иметь солитонных решений. Другой способ — проин-
проинтегрировать по фермионным степеням свободы и получить более
сложное эффективное действие для калибровочных полей. Для
такого эффективного действия до сих пор не найдено ни одного

14 ГЛАВА 1 /
/ '
точною солитониого решения. При описании адронов единствен-
единственная существенная польза солитонов получается при использова-
использовании еще одного варианта квазиклассической процедуры (гл. 9).
В этом случае начинают с классических решений связанных бо-
зон-фермионных уравнений поля, где термин «классический» для
поля со спином 1/2 означает замену его на с-числовую дираков-
скую волновую функцию. Даже здесь точные классические ре-
решения для КХД в C + 1) измерениях не найдены, но прибли-
приближенные решения привели к некоторому прогрессу в описании
адронов. Примером таких вычислений, которые часто называют
моделью «мешков», является «мешок» группы SLAC [24].
Рассмотрим теперь инстантоны. Классические инстантонные
решения имеются в явном аналитическом виде для системы само-
самодействующих полей Янга—Миллса (и при расширении для КХД).
Но в то время как квантовые эффекты этих инстантонов могут
быть рассчитаны, выполнение условия слабого взаимодействия
сопряжено с трудностями. Инстантоны КХД имеют любые раз-
размеры, т. е. они обладают масштабным параметром, который при-
принимает любые значения от 0 до <х>. Вычисление чисто инстантон-
ного эффекта требует интегрирования по их размерам. Но эффек-
эффективная (в перенормированном смысле) калибровочная константа
связи изменяется с масштабом расстояний. Есть указания, 4tq
она велика при больших масштабах расстояний. Следовательно,
для больших инстантонов должна быть большая константа
связи, что нарушает условие слабой связи квазиклассического
метода. Несмотря на эту трудность, были предприняты смелые
попытки получить с помощью инстантонов как можно больше
информации из КХД, но эти результаты сомнительны из-за
существования сильной связи.
Следует отметить, однако, что перечисленные трудности не
означают, что квазиклассический метод неверен в пределах уста-
установленных допущений, скорее эти допущения не полностью вы-
выполняются в КХД. Для множества других теоретико-полевых
моделей требуемые классические решения существуют и условие
слабой связи также выполняется. В этих случаях квазиклассиче-
квазиклассический метод приводит к важным непертурбативным резуль-
результатам. В нашей книге описаны многочисленные примеры та-
таких моделей. Эти примеры не являются неестественными или
изощренными, специально изобретенными для данной цели;
многие из них уже изучались как полезные с других точек зре-
зрения модели. Благодаря этим примерам квантовые солитонные
и инстантонные эффекты расширили наше понимание сложной
и многообразной структуры квантовополевых систем. Даже для
КХД это дало значительное количество полезной информации,
особенно о гомотопической классификации калибровочных пре-
преобразований и вакуумных состояний. Несмотря на проблемы,

ПРЕДИСЛОВИЕ И ВВЕДЕНИЕ 15
обусловленные сильной связью, которые ставят под сомнение
инстантонные вычисления в данной модели, эта информация,
по-видимому, имеет определенную ценность.
Данные вопросы, относящиеся к релятивистской квантовой
теории поля, представляют основной интерес для теории элемен-
элементарных частиц. Но солитонные эффекты изучаются также в ста-
статистической механике непрерывных систем. Формальное мате-
математическое сходство (евклидовой) квантовой теории поля и ста-
статистической механики находит при этом дальнейшее применение.
Исследования, о которых говорилось выше, начались в начале
семидесятых годов и в течение нескольких лет активно велись
во всем мире. Как часто случалось и раньше в теории элементар-
элементарных частиц, многие исследователи переключались на эту только
что появившуюся тематику, и за несколько лет было получено
большинство основных результатов и ограничений этого подхода.
В течение последних лет число новых работ по квазиклассиче-
квазиклассическому методу уменьшилось, и в большинстве этих работ рассма-
рассматриваются запутанные технические проблемы. Хотя писать книгу,
посвященную быстро развивающейся проблеме, — рискованное
предприятие, нам кажется, что настало время сделать такую по-
попытку. Тем не менее в качестве предосторожности большая часть
книги посвящена наиболее фундаментальным и проверенным
выводам. Последние исследования, содержащие новый, сложный
или противоречивый материал, излагаются кратко в небольших
абзацах в конце соответствующих разделов.
Структура книги следующая.
Первые три главы (гл. 2, 3 и 4) посвящены классическим соли-
тонным и инстантонным решениям. Нелинейные уравнения в част-
частных производных составляют основной предмет прикладной мате-
математики. Мы не будем обсуждать связанные с ними общие методы
и результаты, которые излагаются во многих обзорах и книгах.
Хотя мы и приводим вывод большинства классических решений,
особенно тех, которые недавно найдены в калибровочных тео-
теориях, С/^-моделях и т. д., мы не будем вдаваться в технические
подробности, такие, как метод обратной задачи рассеяния или
преобразования Бэклунда. Главная задача книги — изучение
квантовых эффектов, к которым приводят эти решения. Сами
классические решения следует считать заданными, хотя для
полноты изложения мы посвятим им три главы. В этих главах
основное внимание уделяется тем свойствам классических реше-
решений, которые важны в квантовых эффектах, рассматриваемых далее.
Затем в гл. 5—8 следуют методы1*; квантования солитонов,
которые приводят к квантовым частицам-солитонам и соответ-
соответствующим секторам в пространстве состояний. Сначала мы опи-
опишем квантование статического солитона, используя интуитивные
соображения. Далее формализуем его с использованием техники

16 ГЛАВА I /
7
функционального интегрирования и применим для квантования
периодических решений. Поскольку большинство учебников по
теории поля не рассматривают методы функционального интегри-
интегрирования, мы уделим место введению в эту технику, прежде чем
ее использовать. Будут рассмотрены также другие способы полу-
получения квазиклассических результатов, включая метод канони-
канонического гамильтониана. Разбираются такие технические вопросы,
как перенормировки ультрафиолетовых расходимостей и работа
с нулевыми модами. Эти процедуры иллюстрируются примерами
двумерных скалярных полевых теорий. В гл. 7 мы включили
также недавние точные результаты по 5-матрице для некоторого
класса двумерных теорий. Эта тема несколько выпадает из ква-
квазиклассической методологии, которая доминирует в остальной
части книги, но поскольку здесь существуют точные и изящно
выводимые результаты в моделях, связанных с солитонами, мы
не могли устоять"перед соблазном включить ее.
В гл. 9 методы функционального интегрирования и квази-
квазиклассические методы распространяются на ферми-поля. Для
обеспечения необходимого математического аппарата дается также
сжатое введение в грассмановы алгебры. Наконец, в гл. 10 и 11
рассматриваются квантовые эффекты инстантонов. Важное явле-
явление вакуумного туннелирования обсуждается в гл. 10 сначала
для простой квантовомеханической системы, затем для абелевой
калибровочной теории и в заключение для системы Янга—Миллса.
Инфракрасная проблема, связанная с большими инстантонами,
выделена в отдельный раздел. В гл. 11 рассматривается влияние
безмассовых фермионов на явление вакуумного туннелирования
и его связь с 0 A)-аномалией. Описано также влияние инстан-
инстантонов на силы между внешними зарядами и на борелеву сумми-
суммируемость ряда теории возмущений. Мы завершаем изложение
сводкой других исследований со списком литературы (разд. 11.5).
По замыслу — это текст элементарного уровня, предназна-
предназначенный для начинающих исследователей, студентов, а не для спе-
специалистов по теории, поля. Книга может быть также полезна фи-
физикам, работающим в других областях, которые хотели бы по-
понять основные идеи данной области физики. Мы не претендуем
на математическую строгость и полноту изложения в смысле
охвата всех работ, связанных с нашей основной темой. Приво-
Приводится около 350 ссылок на литературу, но, безусловно, некото-
некоторые работы могут оказаться неумышленно пропущенными. Основ-
Основное внимание уделено педагогическому разбору на максимально
простом уровне основных идей и методов, используемых в этой
области науки. Изложение включает большое число иллюстра-
иллюстративных примеров. Там, где возможно, мы начинаем с примеров
из нерелятивистской квантовой механики. Хотя считается, что
физика в таких ситуациях хорошо известна, тем не менее мы

ПРЕДИСЛОВИЕ И ВВЕДЕНИЕ 17
рассматриваем их достаточно подробно с той точки зрения, кото-
которая наиболее соответствует нашим целям. Мы хотим показать, что
многие понятия, лежащие в основе квазиклассического метода
теории поля, могут быть обнаружены в миниатюре в привычном
контексте элементарной квантовой механики. Этому приему мы
следуем как в случае солитонов, так и в случае инстантонов,
проводя детальный разбор их эффектов на типичных примерах.
К тому времени, когда проводились такие исследования,
квантовая теория разрабатывалась уже несколько десятилетий.
Нечего и говорить, что в работах по данной теме там, где это тре-
требовалось, использовались ранее полученные результаты и методы.
Поэтому в идеальном случае читатель должен хорошо знать ре-
результаты квантовополевой теории возмущений, калибровочной
теории и перенормировок. Однако такая подготовка не является
необходимой для понимания большей части излагаемого мате-
материала, который в целом самосогласован. Хорошая подготовка по
квантовой механике и общее представление о квантовополевых
методах в большинстве случаев будут достаточны. Конечно,
в нескольких местах, особенно в конце книги, не удалось обой-
обойтись без более сложного материала. Он включает использование
некоторых общих принципов квантовой калибровочной теории,
бегущей константы связи, асимптотической свободы, токовых
аномалий, принципов 5-матричной теории и т. д. Соответствующие
положения четко формулируются, но не выводятся. Они сами по
себе являются важными предметами изучения независимо от ква-
квазиклассического метода, и попытка ввести их со всеми подроб-
подробностями привела бы к серьезным отступлениям от основной темы.
Наконец, мы встретились с трудностью, связанной с отсут-
отсутствием каких-либо других книг на эту тему. Насколько нам
известно, во время написания данной книги не было ни одного
учебника, содержащего исчерпывающее изложение данного пред-
предмета. Однако мы много почерпнули из нескольких обзорных ста-
статей, в которых рассматриваются отдельные аспекты этого вопроса.
Обзор классических решений можно найти, например, в работах
Скотта и др. [309], Маханькова [239], Годдарда и Олива [167],
Актора [4]; по квантованию солитонов имеются работы Раджа-
рамана [289], Джакива [192], Коулмена [87], Фаддеева и Коре-
пина [131], по инстантонной физике—Коулмена [89], Марчиано
иПагельса [246], Олива [266], Сьюто [308], Джакива [1931. Все
наше изложение несет на себе влияние великолепных обзоров Коул-
Коулмена. Специально рекомендуем также обзор Фаддеева и Корепина
от нашего и может служить хорошим дополнительным чтением.
[Ссылки на другие хорошие обзоры, не рассматривающие ква-
квазиклассическую тематику, но имеющие отношение к нашему
обсуждению, приводятся в тексте.

ГЛАВА 2
КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ
ВОЛНЫ
2.1. Введение
Как подчеркнуто в гл. 1, нашей главной темой является квази-
квазиклассический метод во вторично квантованной релятивистской
теории поля. Иначе говоря, задавшись некоторыми или всеми
решениями системы классических релятивистских нелинейных
уравнений поля, мы обсудим методы, с помощью которых такие
решения могут быть использованы для изучения вакуума, одно-
частичных.состояний и других свойств соответствующей кванто-
квантовой теории поля. Способ получения таких классических решений
нас не особенно интересует. Разработано несколько впечатляю-
впечатляющих и сложных методов исследования решений нелинейных
волновых уравнений. Эти методы, примером которых является
метод обратной задачи рассеяния, сами по себе заслуживают
отдельной книги. Уже имеются отличные обзоры некоторых
методов, например, в книге Уизема [347] и в обзорной статье
Скотта и др. [309]. Мы отошли бы от основной темы данной книги,
если бы попытались детально их описать. Более того, знание ме-
методов получения классических решений не является необходи-
необходимым для понимания их последующего использования в кванто-
квантовой теории. Мы будем считать, что классические решения уже
получены.
Тем не менее для полноты изложения мы посвятим эту и сле-
следующие две главы исключительно классическим решениям. Так
как плодами релятивистской квантовой теории в основном поль-
пользуется физика элементарных частиц, мы сконцентрируем внима-
внимание на тех классических решениях, которые, насколько это воз-
возможно, напоминают классические протяженные частицы. В част-
частности, было бы хорошо найти решения, которые выглядят как
порции энергии, распространяющиеся без диссипации с постоян-
постоянной скоростью. Было бы еще лучше, если бы уравнения допускали
столкновения нескольких таких порций энергии, после которых
их первоначальные формы не изменялись бы по крайней мере
асимптотически по времени. Несмотря на сложность дифферен-
дифференциальных нелинейных уравнений в частных производных, реше-
решения с такими свойствами действительно существуют. Такие ре-
решения часто называют уединенными волнами и солитонами. Наша

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 19
первая задача — разъяснить значения этих двух терминов и
установить различия между ними. Мы приведем некоторые при-
примеры каждого типа решений. Будут описаны солитон синус-
Гордона, «кинк» теории ф*, монополь т'Хофта—Полякова,
инстантон и другие объекты, часто встречающиеся в современной
литературе. Будет дан и вывод этих решений в тех случаях, когда
он достаточно краток. Мы подчеркнем те черты решений, которые
важны для последующего квантования.
Хотя приведенные примеры относятся к релятивистским по-
полевым уравнениям и особенно важны в физике частиц, они инте-
интересны и сами по себе как решения довольно сложных нелинейных
дифференциальных уравнений .в частных производных. Некото-
Некоторые наши рассуждения и терминология могут быть применены
и к нерелятивистским системам. Поэтому мы надеемся, что со-
содержание этих первых глав заинтересует не только физиков,
изучающих элементарные частицы, но и специалистов в других
областях.
Прежде чем перейти к следующему разделу, скажем несколько
слов об обозначениях. В основном мы будем следовать стандарт-
стандартной ковариантной тензорной системе обозначений. Простран-
Пространственно-временные координаты представляются вектором
х* (ц = 0, 1, 2, 3; х° = d, х1 = х, х2 = у, Xs = z). Индексы
понижаются или повышаются метрическим тензором Минковского
guv = £**\ где g00 = —gu = —g22 = —g93 = 1 и g^ = 0 при
\л Ф v. Подразумевается суммирование по повторяющимся индек-
индексам; д„ обозначает пространственно-временные производные
dldx^. Иногда мы будем иметь дело с системами с меньшим числом
измерений. Например, большинство систем данной главы в двух
A + 1) измерениях —одном пространственном и одном времен-
временном; в этом случае индекс \i имеет значения только ц = О, 1.
Если в последующих главах использование компактных кова-
риантных обозначений существенно, в этой главе мы применяем
для пространственно-временной зависимости как явную форму
записиг так и ковариантную.
2.2. Уединенные волны и солитоны
Термины «уединенные волны» и «солитоны» относятся к опре-
определенным частным решениям нелинейных волновых уравнений.
Для более полного понимания таких решений напомним некото-
некоторые свойства простейшего из релятивистских волновых уравне-
уравнений, а именно уравнения
(±£1£)(х,Ц = О, B.1)
где ф (х, t) —действительное скалярное поле в A + 1) измере-
измерениях, ас — скорость света. Свойства этого уравнения хорошо

20 ГЛАВА 2
известны. Оно линейно и недисперсионно. Поэтому его решения
имеют два свойства, представляющие интерес для дальнейшего
рассмотрения.
1. Любая действительная «хорошая» функция вида / (х ± d)
есть решение уравнения B.1). В частности, если мы выберем ло-
локализованную функцию /, то можем построить локализованный
волновой пакет, который будет перемещаться с постоянной ско-
скоростью ±с и без искажения формы. Это, очевидно, связано с тем,
что плоские волны cos (kx ± (at) и sin (kx ± (at), где со = kc,
образуют полный набор решений уравнения B.1). Любая «хоро-
«хорошая» локализованная функция, например / (х —ct), может быть
записана в виде
/ (х - d) = j dk [аг (k) cos (kx -at) + a2 (k) sin {kx - erf)]. B.2)
Тот факт, что волновой пакет / (х —ct) движется без искажений
со скоростью с, связан с тем, что все его плосковолновые компо-
компоненты имеют одну и ту же скорость a/k = с.
2. Поскольку волновое уравнение линейно, то, если заданы
решения в виде локализованных волновых пакетов f1(x—ct)
и /г (х + ct), их сумма /3 (х, t) = fx (x — d) + /2 (х + d) также
является решением. При больших отрицательных временах
(t -> —оо) решение /3 (х, t) состоит из двух пакетов, широко раз-
разделенных и приближающихся друг к другу без существенных
искажений. При конечном времени t они сталкиваются. Но после
столкновения они асимптотически (при t -*■ оо) разделяются-на
те же два пакета, сохраняя свои первоначальные формы и ско-
скорости. Для системы B.1) это свойство выполняется также и для
большего числа пакетов.
Эти два свойства, а именно 1) сохранение формы и скорости
отдельного пакета и 2) асимптотическое сохранение формы и
скорости нескольких пакетов даже после столкновения, очевидно,
свойственны B.1), так как эта простая система уравнений линейна
и недисперсионна. Но типичные волновые уравнения во многих
разделах физики гораздо сложнее: они могут содержать нелиней-
нелинейные члены, дисперсионные члены и несколько взаимодействую-
взаимодействующих полей с числом пространственных измерений 1, 2 или 3.
Нас интересует вопрос: допускают ли такие уравнения, несмотря
на их сложность по сравнению с B.1), хотя бы некоторые решения,
обладающие первым свойством, а может быть, даже вторым свой-
свойством?
Заметим, что добавление к B.1) даже членов простейшего
вида стремится нарушить эти прекрасные свойства даже в A + 1)
измерениях. Рассмотрим, например, уравнение Клейна—Гордона
в двух измерениях
(□ + mW) ф (х, t) = (JL ^ - -gr- + mV ) ф (л, /) = 0. B.3)

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 21
Это уравнение еще линейно, и плоские волны cos (kx ± (at) и
sin (kx ± at) образуют полный набор решений. Но теперь со2 =
= &2с2 + т2с*. Таким образом, волны разной длины рас-
распространяются с различными скоростями со {k)lk, и уравнение
дисперсионно. Любой локализованный волновой пакет, имеющий
при t = 0 форму j dk [ax (k) cos kx + a2 (k) sin foe ], с течением
времени расплывается. Поэтому первое свойство отсутствует,
а следовательно, отсутствует и второе свойство. Если даже от-
отдельный пакет не может сохранить свою -форму, то не возникает
и вопроса о сохранении форм нескольких пакетов после столкно-
столкновения. Аналогичным образом рассмотрим добавление к B.1)
простого нелинейного члена:
<*• 0 + </>3(*. 0 = 0. B.4)
Не все решения этого уравнения известны, но с помощью числен-
численных или приближенных расчетов можно убедиться, что произ-
произвольный волновой пакет будет расплываться.
Тем не менее возможно, что для некоторых уравнений, со-
содержащих как дисперсионные, так и нелинейные члены, влияние
этих членов взаимно компенсируется" таким образом, что некото-
некоторые специальные решения будут обладать первым свойством.
Это может происходить в случаях одного, двух-и трех простран-
пространственных измерений, и такие решения неточно называют уединен-
уединенными волнами. Иногда может проявляться также и второе свой-
свойство. Эти решения называют солитонами.
Для получения более точного определения этих двух терми-
терминов необходимо количественно описать требования, которые до
сих пор качественно описывались как первое и второе свойства.
Такие свойства мы вывели из поведения волновых пакетов в ли-
линейных системах без диссипации типа B.1). Эти требования надо
обобщить так, чтобы включить как можно больше случаев реше-
решений, обладающих если не точно свойствами волновых пакетов B.1),
то по крайней мере существенными особенностями первого и
второго свойств. К сожалению, общепринятое определение со-
литонов и уединенных волн отсутствует. Разные авторы предла-
предлагают свои немного различающиеся варианты. Мы дадим теперь
рабочее определение, которое представляет собой компромисс
между этими вариантами. ■
Наше определение дается в терминах плотности энергии, а не
в терминах самих волновых полей, так как первая характеристика
более важна для интересующих нас систем. Это означает, что мы
ограничиваемся теми волновыми уравнениями (для любого на-
набора взаимодействующих полей фг (х, t), <j>2 (x, t), ...), которые
имеют соответствующую плотность энергии е (х, t), являющуюся

22 ГЛАВА 2
некоторой функцией полей ф1 (х, t). Ее пространственный
интеграл есть функционал Е (ф^ —сохраняющаяся полная энер*
гия. Большой класс уравнений, включающий полевые уравне-
уравнения физики элементарных частиц, удовлетворяет этому требо-
требованию. Так как физические системы обладают энергией, ограни-
ограниченной снизу, мы можем, не теряя общности, минимальное зна-
значение Е положить равным нулю. Задавшись этими рамками, мы
будем использовать прилагательное «локализованное» для тех
решений полевых уравнений, плотность энергии е (х, t) которых
в любой конечный момент времени локализована в пространстве,
т. е. конечна в некоторой ограниченной области пространства и
стремится к нулю на пространственной бесконечности достаточно
быстро, чтобы быть интегрируемой. Отметим, что для тех систем,
для которых Е [фг ] = 0 только в том случае, если фь (х, t) = О,
локализованное решение, определенное выше, имеют также и
сами поля, локализованные в пространстве. Например, уравне-
уравнение B.4) имеет соответствующую сохраняющуюся энергию
которая минимизируется при ф (х, t) = 0. Локализованные ре-
решения этой системы, если они есть, должны асимптотически стре-
стремиться к ф (х, t) = 0 при х -*■ ±оо для любого заданного I.
Производные йф1йх и йф/сН в этом пределе также должны обра-
обращаться в нуль. Напротив, уравнение
с2 dt* дх2
имеет соответствующую энергию
MZ)'+±&)'+±<r-M- <2-7>
Здесь Е [ф] минимизируется при ф (х, t) =±1. Это простейший
пример «спонтанного нарушения симметрии» в квантовом ана-
аналоге полевых систем. Теперь локализованное решение в любой
момент времени должно достигать ф = ±1 при х-*- ±<х>.
Дав определение понятия локализации в терминах плотности
энергии, определим уединенную волну как локализованное не-
несингулярное решение любого нелинейного уравнения поля (или
системы уравнений, если имеется несколько полей), плотность
энергии которого, будучи локализованной, имеет пространственно-
временную зависимость вида
e(x, /) = e(x-u/), B-8)
где и — некоторый вектор скорости.

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 23
Иначе говоря, плотность энергии должна двигаться без иска-
искажений с постоянной скоростью. Среди систем, имеющих соот-
соответствующую плотность энергии, это определение допускает
более широкий класс решений, чем определение, данное Скоттом
и др. [309], которое требует, чтобы сами поля имели такую про-
пространственно-временную зависимость в виде «бегущей волны».
Интересный пример заряженных уединенных волн, который
обсуждается в гл. 8, содержится в B.8), но он исключается опре-
определением Скотта и др. С другой стороны, их определение, данное
непосредственно в терминах полей, в принципе может быть при-
применено к системам, не имеющим соответствующей сохраняющейся
энергии. Мы не будем рассматривать такие системы. В то же время
наше определение более ограничено, чем определение Коул-
мена [87]. Он использовал термин «комок» для существенно не-
несингулярных решений с конечной локализованной энергией не-
независимо от того, подчиняются ли они B.8) или нет. Пример
с дублетным решением системы синус-Гордона (разд. 2.5), к со-
сожалению, исключается B.8), но включается Коулменом как
«дрожащий комок».1 Мы выбираем определение B.8) не потому,
что оно существенно лучше остальных, а потому, что оно опти-
оптимально для наших целей. Оно просто, довольно исчерпывающе
и позволяет определить солитоны приемлемо простым способом.
Отметим, что B.8) определяет уединенные волны с числом
пространственных измерений от одного и выше. Далее, любое
статическое (не зависящее от времени) локализованное решение
автоматически является уединенной волной со скоростью и = 0.
Многие уединенные волны, которые мы будем обсуждать, полу-
получаются как статические решения. Однако если для системы
с релятивистской (либо галилеевой) инвариантностью известно
статическое решение, то движущиеся решения тривиально полу-
получаются бустом, т. е. переходом в движущуюся координатную
систему.
Обратимся теперь к солитонам — уединенным волнам, отве-
отвечающим приведенному ниже дополнительному требованию, ко-
которое представляет собой обобщенный и более точно сформули-
сформулированный вариант упомянутого выше второго свойства. Рас-
Рассмотрим нелинейное уравнение (или систему уравнений). Пусть
оно имеет решением уединенную волну с плотностью энергии,
являющейся некоторой локализованной функцией е0 (х—ut).
Рассмотрим любое другое решение этой системы, состоящее в от-
отдаленном прошлом из N таких уединенных волн с произвольными
начальными скоростями и положениями. Тогда плотность энер-
энергии е (х, t) такого решения имеет вид
■N1
е(х, ^)-> 2j во(х — аг — U;0 при t-*—оо. B.9)

24 ГЛАВА 2
Заданная при t = —<х> эта конфигурация будет затем эволю-
эволюционировать во времени, следуя нелинейным уравнениям. Пред-
Предположим, что эволюция такова, что
N
е(х, *)-»■ .И 8о(х — аг -и^ + 6г) при г-*-+°°> B.10)
где 6г — некоторые постоянные векторы. Тогда такая уединен-
уединенная волна называется солитоном. Другими словами, солитонами
являются те уединенные волны, профили плотностей энергии
которых асимптотически (при t ->■ оо) возвращаются к своим
первоначальным формам и скоростям. Векторы 6г описывают
возможность твердого перемещения солитонов с их первоначаль-
первоначальных траекторий. Для солитонов такое перемещение является
единственным остаточным эффектом столкновений. Очевидно,
что это — замечательное свойство решений нелинейных полевых
уравнений.
Все солитоны являются уединенными волнами, но обратное,
очевидно, неверно. Добавочное требование B.10), накладываемое
на солитоны^ очень жестко. Поэтому лишь немногие из уравне-
уравнений, допускающих уединенные волны, обладают солитонными
решениями. Для нахождения решения данного нелинейного урав-
уравнения в виде уединенной волны достаточно найти любое локали-
локализованное решение, удовлетворяющее требованию B.8). Часто
это сделать трудно, но все же многие уравнения дают уединенные
волны. Однако для проверки того, что некоторое решение является
солитоном, необходимо найти не только это решение, но и беско-
бесконечно много зависящих от времени решений, состоящих из про-
произвольного числа солитонов, и проверить выполнение требова-
требований B.9) и B.10). Таким образом, определить, что данное нели-
нелинейное волновое уравнение обладает солитонными решениями,
очено трудно и еще труднее найти их в явной форме. Разработано
много мощных методов решения и исследования свойств уравне-
уравнений, допускающих солитоны. Это метод обратной задачи рассея-
рассеяния, преобразование Бэклунда, использование сохраняющихся
величин и т. д. Но хотя эти методы дают изящные способы иссле-
исследования таких систем, они не очень полезны для нахождения
новых уравнений, имеющих солитоны, или для определения,
обладает ли данное уравнение солитонами. Поэтому неудиви-
неудивительно, что найдено очень мало уравнений, допускающих соли-
солитоны. Несколько примеров содержится в обзоре Скотта и др. [309 ],
причем все в пространстве с одним измерением. Из них реляти-
релятивистским является только уравнение синус-Гордона. Это урав-
уравнение рассматривается в разд. 2.5 в качестве примера таких
систем.
По-видимому, большинство локализованных решений, обсу-
обсуждаемых в физической литературе, —уединенные волны. Ко-

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 25
нечно, нельзя исключить, что некоторые из них являются соли-
тонами, но при отсутствии информации о всех зависящих от вре-
времени решениях доказать это с определенностью нельзя. Можно
только отметить, что, так как требование B.10) очень жестко,
по всей вероятности, большинство из них являются только уеди-
уединенными волнами. К счастью, методы квантования классических
решений не зависят существенно от того, являются ли эти реше-
решения солитонами или уединенными волнами.
Четко определив различие между солитонами и уединенными
волнами (первые являются узким подклассом последних), необ-
необходимо заметить, что в большей части литературы оно затуше-
затушевывается. Уединенные волны часто называют солитонами, по-
видимому, потому, что последнее название более ясно и привле-
привлекательно. Хотя названия мало значат в физике, необходимо все
же различать, по крайней мере в классической теории поля, ре-
решения, удовлетворяющие требованию B.8), и решения, удовлетво-
удовлетворяющие, кроме того, требованиям B.9), B.10). В последующих
главах мы тоже поддадимся популярной тенденции использовать
название «солитон» для уединенных волн. Но по крайней мере
в этой главе различие будет сохранено.
2.3. Некоторые уединенные волны в двух измерениях
Приведем теперь некоторые примеры уединенных волн, на-
начиная с наипростейших. Как было отмечено выше, любое локали-
локализованное статическое (не зависящее от времени) решение является
уединенной волной. Таким образом, в этом разделе мы сосредото-
сосредоточим внимание на статических решениях в их простейшем проявле-
проявлении в случае скалярных полей в двух (одно пространственное +
+ одно временное) измерениях. Примеры с большим числом
измерений и с более сложными полями обсуждаются в следующей
главе. Рассмотрим скалярное поле ф (х, t), динамика которого
задается лоренц-инвариантной плотностью лагранжиана
■ &(x,t) = ±-(w-±.wr.-U(*)\ B.П)
здесь и далее точка и штрих обозначают дифференцирование по
времени и по пространственной переменной х соответственно,
а скорость света с положена равной единице. «Потенциалом» U (ф)
является любая неотрицательная функция от ф, достигающая
минимума —нуля при некотором значении или значениях ф.
Вариационный принцип
&l\dt J &х2£ (х, /))=0, B.12)

26 ГЛАВА 2
примененный к этому лагранжиану, приводит к волновому урав-
уравнению
U*='i-r = --%-(x,t). B.13)
Это волновое уравнение с нелинейными членами, завися-
зависящими от выбора U (ф). При изменении t уравнение сохраняет
функционал полной энергии Е, определяемый выражением
оо
Е[ф]= J <** [4W'+T(f )
Пусть абсолютные минимумы функции U (</>), являющиеся также
ее нулями, достигаются в М точках (М ^ 1). Иными словами,
пусть
1/(ф) = 0 для ф = g<i\ i = \ М. B.15)
Тогда функционал энергии достигает минимума, когда поле
Ф (х, t) постоянно в пространстве-времени и принимает любое
из этих значений, т. е.
Е [ф ] = О
тогда и только тогда, когда
ф(х, t) =gU), i= 1, .... М. B.16)
Нас интересуют статические решения, для которых уравнение
B.13) принимает вид
У <*) = -g. = + .*£-<*). B.17)
Уединенная волна должна иметь конечную энергию и локализо-
локализованную плотность энергии. Согласно B.15), ее поле должно при-
приближаться при х -*• ±<х> к одному из значений gW. Если U (ф)
имеет единственный минимум при ф — g, то наше решение ф (х) ->
-*■ g при х -> ±оо. Если существует несколько вырожденных
минимумов (М > 1 в BД5)), то ф (х) стремится к любому из зна-
значений g-(t> при х-*- —оо и к тому же или другому значению g-<'>
при х -*■ +оо.
Удовлетворяя этим граничным условиям, решим уравне-
уравнение B.17) для ф (х). Так как B.17) —обыкновенное дифферен-
дифференциальное уравнение второго порядка, оно может быть просто
решено в квадратурах для любого U (ф). Но прежде чем решать
его, полезно заметить, что B.17) имеет механический аналог.
Механические аналоги статических решений были указаны мно-
многими авторами (см., например, работы [81, 87, 145]). Если счи-
считать переменную х «временем», а ф — координатой точечной ча-
частицы с единичной массой, то уравнение B.17) представляет.собой

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 27
просто второй закон Ньютона для движения частицы под дей-
действием потенциала [—U (ф)]. Решение ф (х) описывает движение
этой частицы-аналога. Полная «энергия» движения, сохраняю-
сохраняющаяся при изменении «времени» х, дается выражением
W= l-Wldxf ~ U{ф). B.18)
Граничные условия, рассмотренные выше, требуют, чтобы при
х -*■ ±оо U (ф) -> 0 и йф/dx -> 0. Следовательно, W = 0. Энер-
Энергию W частицы-аналога не следует путать с энергией исходной
системы Е, определяемой выражением B.14). Для статического
решения ф (х) энергия Е равна
и, несомненно, дает полное «действие» движения частицы-аналога.
Таким образом, наше статическое решение соответствует неко-
некоторому движению частицы с конечным действием и нулевой энер-
энергией. Наконец, умножая B.17) на ф' и интегрируя, получаем
гф'ах, или ±(ф'Г = и(ф). B.20)
Поскольку ф' и U (ф) обращаются в нуль при х = —оо, постоян-
постоянная интегрирования равна нулю. Уравнение B.20) представляет
собой теорему вириала для частицы-аналога.
Вооружившись этой механической аналогией, рассмотрим сна-
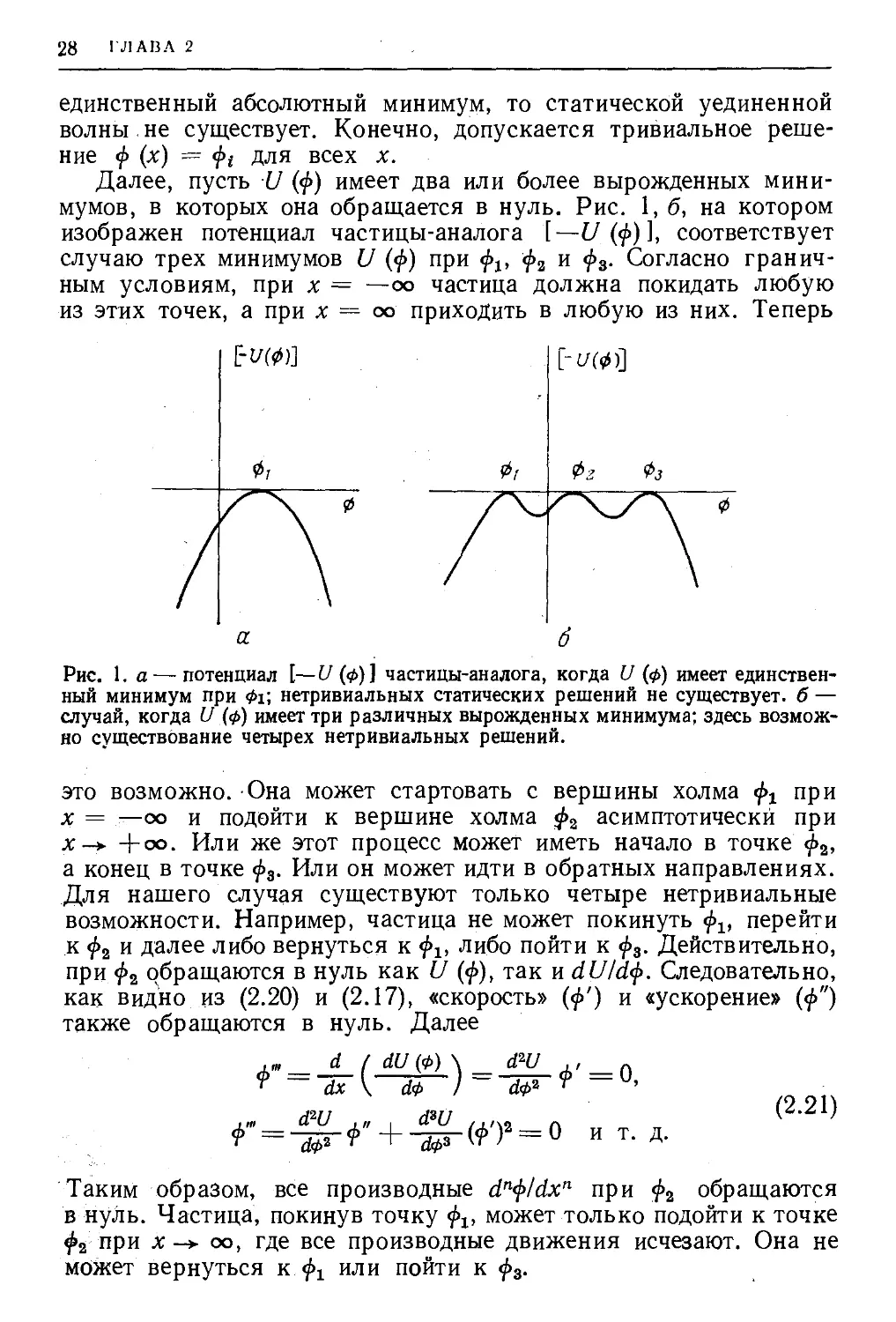
сначала U (ф) с единственным минимумом при^>*= фг: U (<^) = 0.
Тогда частица-аналог находится в потенциале [—U (ф) ], изобра-
изображенном на рис. 1, а. Потенциал имеет максимум при ф = фг
и отрицателен для всех остальных значений ф. Граничные усло-
условия требуют, чтобы траектория с нулевой энергией начиналась
и кончалась в точке ф = фг в бесконечно удаленном прошлом и
будущем (х = ±оо). Но достаточно взглянуть на рис. 1, а, чтобы
заключить, что такое нетривиальное движение невозможно!
Если частица сдвинется с точки ф = фг в любом направлении,
то назад она не возвратится. Ее кинетическая энергия уже ни-
никогда не будет нулевой, так как ее полная энергия W, равная
нулю, всегДа больше потенциальной энергии [—U (<*)]. Следо-
Следовательно, частица никогда не сможет остановиться и повернуть
назад к фг. В терминах статического полевого решения ф (х)
это означает, что, фиксировав граничное условие ф = фг, &ф!<Хх —
= 0 при х = —оь, его нельзя уже удовлетворить при х — +оо
для нетривиального несингулярного решения. Таким образом,
не решая точно уравнение B.17) и не вдаваясь в детали поведе-
поведения U (ф), мы приходим к заключению, что если U (</>) имеет

28
ГЛАВА 2
единственный абсолютный минимум, то статической уединенной
волны не существует. Конечно, допускается тривиальное реше-
решение ф (х) = <j>t для всех х.
Далее, пусть U (ф) имеет два или более вырожденных мини-
минимумов, в которых она обращается в нуль. Рис. 1,6, на котором
изображен потенциал частицы-аналога [— U (<j>)], соответствует
случаю трех минимумов U (ф) при <j>v фг и ф3. Согласно гранич-
граничным условиям, при х = —оо частица должна покидать любую
из этих точек, а при х = оо приходить в любую из них. Теперь
Фг Фз
Рис. 1. а — потенциал [—U (</>)] частицы-аналога, когда U (ф) имеет единствен-
единственный минимум при Ф1\ нетривиальных статических решений не существует, б —
случай, когда U (ф) имеет три различных вырожденных минимума; здесь возмож-
возможно существование четырех нетривиальных решений.
это возможно. Она может стартовать с вершины холма фг при
х = —оо и подойти к вершине холма ф2 асимптотически при
х-> +оо. Или же этот процесс может иметь начало в точке <j>2,
а конец в точке ^>3. Или он может идти в обратных направлениях.
Для нашего случая существуют только четыре нетривиальные
возможности. Например, частица не может покинуть фг, перейти
к ф2 и далее либо вернуться к фъ либо пойти к ^>3- Действительно,
при ф2 обращаются в нуль как U (ф), так и dU/d<j>. Следовательно,
как видно из B.20) и B.17), «скорость» (^>') и «ускорение» (ф")
также обращаются в нуль. Далее
а (аи(Ф)\
dx \ с1Ф I
d3U
B.21)
Таким образом, все производные d^ldxn при ф2 обращаются
в нуль. Частица, покинув точку фг, может только подойти к точке
f2 при х-*- оо, где все производные движения исчезают. Она не
может вернуться к фг или пойти к ф3.

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 29
Итак, механическая аналогия помогает нам сделать следую-
следующие выводы: 1) если U (ф) имеет единственный абсолютный ми-
минимум, то статической уединенной волны не существует, 2) если
U (ф) имеет п отдельных вырожденных минимумов, то можно
получить 2 (п — 1) типов решений, соединяющих при измене-
изменении х от —оо до +<х> любые два соседних минимума. При этом,
естественно, подразумевается, что могут существовать также
тривиальные, не зависящие от Координат и времени решения.
Кроме этих общи^рассуждений, можно привести и точное ре-
решение B.17) в квадратурах. Из B.20) имеем
йф1йх = ± [2U (ф)], B.22)
-шш'- B-23)
Здесь постоянная интегрирования х0 есть любая точка в простран-
пространстве, где поле имеет значение ф (х0). Как следует из предыдущих
рассуждений, при х -> ±оо ф (х) достигает любых дЬух сосед-
соседних минимумов U (ф), а для промежуточных значений х ф (х)
лежит между этими двумя минимумами. Следовательно, U (ф)
обращается в нуль только при х -> ±оо и положительна при ко-
конечных х. Таким образом, подынтегральное выражение несингу-
несингулярно, за исключением предельных точек при х -> оо или х0 ->
-> —оо. Задавая х0 и ф (х0), можно в принципе получить решение
ф (х) явным образом, проинтегрировав B.23) и обратив получен-
полученный результат. На практике сделать это аналитически возможно
только для некоторых функций U (</>). Заметим, что изменение х0
при фиксированном значении ф (х0) только сдвигает то же реше-
решение в х-пространстве. Это отражает трансляционную инвариант-
инвариантность исходного уравнения B.13).
Проиллюстрируем этот метод на примере решения в виде
«кинка» теории ф* [101, 173, 283]. Плотность лагранжиана имеет
форму B.11), где
и(ф) = ±-Х(ф*-тУХ)*; B.24)
Здесь % и т2 — положительные константы. Уравнение Движения
ф - ф" = т*ф - Ц3 B.25)
такое же, как B.6), за исключением констант. Здесь U (ф) обра-
обращается в нуль в двух вырожденных минимумах ф — +т/-улХ.
Поэтому .локализованные решения должны стремиться к ±т/у"К
при х-> ±оо. Как это следует из сделанных выше выводов, ста-
статические решения могут быть Двух видов. Они могут начинаться

30
ГЛАВА 2
с <j> = —mlyr'k при х — —оо и кончаться на ф = т/уЛ при
х = оо или наоборот. В частности, для статического уравнения
ф" = dU/d<j> = Кф3 - т2ф, B.26)
используя B.23), можно получить решение в виде
ф (х)
^= ~1~ I ~Z^=—=
B.27)
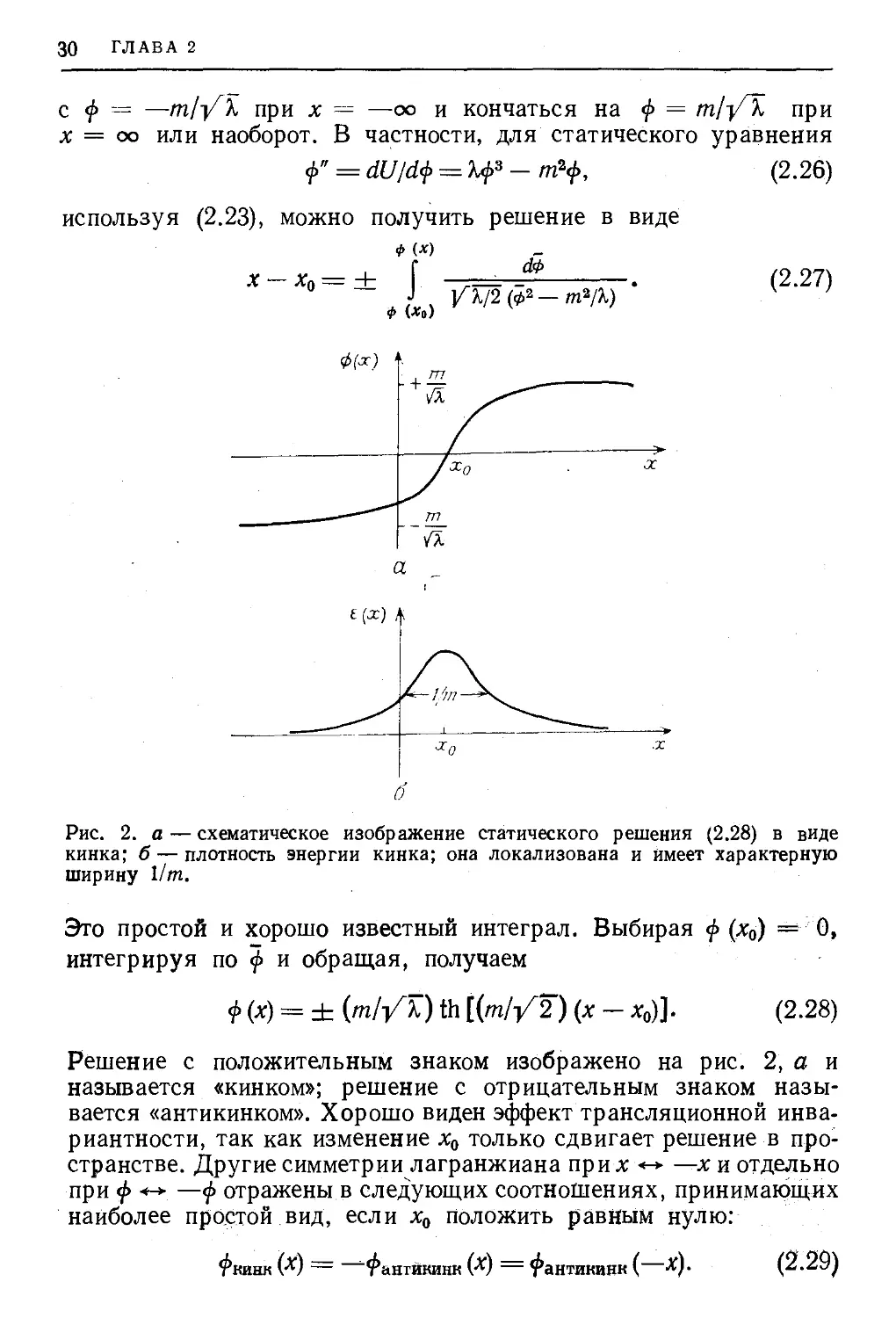
Рис. 2. а — схематическое изображение статического решения B.28) в виде
кинка; б — плотность энергии кинка; она локализована и имеет характерную
ширину 1/т.
Это простой и хорошо известный интеграл. Выбирая ф (х0) =0,
интегрируя по ф и обращая, получаем
ф(х) = ± (m/yT) th[(т//2) (* - дг0)]- B-28)
Решение с положительным знаком изображено на рис. 2, а и
называется «кинком»; решение с отрицательным знаком назы-
называется «антикинком». Хорошо виден эффект трансляционной инва-
инвариантности, так как изменение х0 только сдвигает решение в про-
пространстве. Другие симметрии лагранжиана при х <-»• —х и отдельно
при ф •*-*■ —ф отражены в следующих соотношениях, принимающих
наиболее простой вид, если х0 положить равным нулю:
гкинк W — ^тантйкинк W — уантикинк ( X).
B.29)

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 31
Плотность энергии кинка
г(х) = ±
используя B.22), находим
е (х) = (mV2K) sch4 [т (х - xJ/j/J] ■ B.30)
Плотность энергии кинка показана на рис. 2, б, где видно, что
она локализована около х0. Полная энергия кинка, называемая
иногда классической массой кинка Мкл, дается выражением
-!p-j£-; (9.31)
она конечна. Таким образом, кинк, а также антикинк — полно-
полноправные уединенные волны. Тем не менее они не являются соли-
тонами. Обычно, для того чтобы убедиться, что некоторые уеди-
уединенные волны не являются солитонами, т. е. что они не сохра-
сохраняются при столкновениях, необходима информация о завися-
зависящих от времени решениях, включающих несколько таких волн.
Но в данном примере двухкинковая конфигурация не может
даже существовать с конечной энергией, а тем более рассеиваться
некоторым заданным способом. Пусть первый кинк начинает дви-
движение из ф = —т/У^Х при х = —оо к ф = m/j/A. вправо. Если
за ним движется второй кинк, то последний должен стремиться
к ф = 2mlYX при х -> оо. Но это ведет к постоянному ненуле-
ненулевому значению плотности энергии при я-> оо и, следовательно,
к бесконечной полной энергии. Конечно, за кинком может сле-
следовать антикинк, возвращающий поле ф (х) к значению —т\-/Х.
Но здесь также численные вычисления показывают, что после
столкновения кинк и антикинк не сохраняют свои формы. Сле-
Следовательно, кинк есть уединенная волна, а не солитон. Он напо-
напоминает «комок» материи в том смысле, что представляет собой
статический самоподдерживающийся локализованный пакет энер-
энергии. Это сходство с протяженной частицей идет дальше: так как
система лоренц-инвариантна, исходя из заданного статического
решения B.28), преобразованием Лоренца можно получить ре-
решение в виде движущегося кинка. Помня, что ф — скалярное
поле, достаточно только провести преобразование координат
в B.28). Это дает
B.32)
где 1 >и > —1 —скорость. Подстановкой можно убедиться,
что это решение полевого уравнения B.25). Пространствен-
Пространственная ширина статического кинка в смысле плотности энергии B.30)

32 ГЛАВА 2
характеризуется величиной 1/т, тогда как соответствующая ши-
ширина движущегося кинка B.32) есть У\ — и?/т, как и должно
быть, согласно лоренцеву сокращению «комка» материи. Далее,
энергия зависящего от времени решения B.32) по B.14) есть
Е [фи] - J dx [ -i- (фи? + \ (ф'иТ + U (фи) ] =
—оо
= J
XS(
т
ОТ3 1 _ Мкл /9 qq\
где Мкл — энергия статического кинка B.31). Связь между
B.33) и B.31) отражает эйнштейновское соотношение между мас-
массой и энергией частицы. Поэтому неудивительно, что в кванто-
квантованном варианте теории кинку соответствует состояние частицы.
Другим важным свойством решения ^>Кинк (х) является его сингу-
сингулярность в точке обращения в нуль параметра нелинейности %.
Это свойство не может быть получено при разложении в ряд
по теории возмущений, начиная с линейного уравнения. Непер-
турбативность ^„инк приводит ко многим следствиям в квантовой
теории. Наконец, последнее свойство решения ^>кинк — «топологи-
«топологический» индекс — обсуждается немного ниже.
Очевидно, что такой же анализ можно провести для любой
функции U (ф) с вырожденными минимумами. Другим примером
является функция U (ф) = 1/2^>2 (ф2 — IJ. которая имеет три
вырожденных минимума при ф =0, ±1. Отсюда следует ожидать
четыре типа статических решений с граничными условиями
ф=[-1,0], [0,1], [1,0], [0,-1] при *=[—оо, оо].
В данном случае точные статические решения уравнения B.17)
имеют вид
1/2. B.34)
Все эти решения имеют локализованную плотность энергии и
конечную полную энергию. Примеры функции U (ф) с единствен-
единственным минимумом не имеют статических уединенных волн, как
это обсуждалось выше. Так, хорошо изученная полевая теория

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 33
с U (ф) = V2m2^>2 + V4^4, которая отличается от B.24) знаком
члена ф*, не имеет локализованного статического решения, кроме,
конечно, тривиального решения ф (х) = 0.
Перейдем на следующий уровень сложности, т. е. к статиче-
статическим решениям систем взаимодействующих скалярных полей
в двух пространственно-временных измерениях. Это приводит
нас к этапу, когда общих методов получения всех локализованных
статических решений данных полевых уравнений не существует.
Тем не менее некоторые решения, но, конечно, не все, могут быть
получены для класса таких лагранжианов [291 ] с использованием
метода пробных функций.
Вначале обсуждение идет так же, как и выше, с соответству-
соответствующим обобщением на случай системы взаимодействующих ска-
скалярных полей ф{ (х, f), i = 1, ..., N. Рассмотрим плотность лагран-
лагранжиана
N
(=1
где U ({^>j}) — некоторая функция всех фг, имеющая минимальное
значение, равное нулю. Полевые уравнения имеют вид
l, .... N. B.36)
Статические решения должны удовлетворять уравнению
B.37)
Это уравнение также имеет механический аналог. Теперь частица-
аналог движется с течением «времени» х в N измерениях с коорди-
координатами фг под действием потенциала [—U (ф^]. Требование
конечности энергии решения ведет к граничным условиям ф'{ = 0
для всех I и U (фс) = 0 при х ->• ±<х>. Для частицы-аналога это
опять соответствует траектории с конечным действием и нулевой
энергией в пространстве с Af измерениями, начинающейся и кон-
кончающейся в некоторых минимумах U (фг). Тем не менее имеются
два отличия от случая одного поля.
1. Там не существовало решения при наличии у U (ф) един-
единственного минимума. Это обусловлено тем, что частица, после
того как она оставила максимум [—U (ф)], имеет отрицательно
определенную потенциальную энергию и ненулевую кинетическую
энергию и поэтому не может остановиться и повернуть назад.
Для взаимодействующих полей в случае единственного минимума
U (ф{) также верно, что в любой другой точке Af-мерного ^-про-
^-пространства частица не может иметь нулевой скорости. Но несмотря
на это, она может пройти по замкнутой кривой и вернуться в исход-
2 Раджараман Р.

34 ГЛАВА 2
ную точку. Возможна соответствующая нетривиальная уединенная
волна. Это будет^ показано ниже на примере.
2. В отличие от уравнения B.17), которое решается в квадрату-
квадратурах, для системы дифференциальных уравнений B.37) не суще-
существует простого способа интегрирования. Здесь аналогия с меха-
механикой не помогает. Для заданного потенциала и граничных
условий в конечных точках нелегко проинтегрировать второй
закон Ньютона для движения в двух или более измерениях. Это
кажется удивительным, если иметь в виду долгую историю меха-
механики и многие классические учебники по теории орбит. К сожале-
сожалению, большая часть литературы посвящена «центральным по-
потенциалам». Здесь это соответствует системам, инвариантным
относительно вращения от одной точки <j>t к другой. Такая сим-
симметрия при вращениях в полевом пространстве согласно термино-
терминологии физики элементарных частиц называется «внутренней»
симметрией. При существовании внутренней симметрии ее можно
использовать аналогично тому, как используются полярные коор-
координаты в механике центральных потенциалов. В одной из после-
последующих глав мы рассмотрим отдельно внутреннюю симметрию
и «заряженные» уединенные волны. При отсутствии такой сим-
симметрии, даже если U (<j>i) представляет собой довольно простую
полиномиальную функцию, получить все решения уравнения
B.37) в общем виде невозможно. Но можно получить некоторые
решения для частных случаев, пользуясь следующей стратегией.
Разобьем задачу на две части. Сначала найдем «орбиту» ча-
частицы-аналога в Af-мерном пространстве, отвечающую граничным
условиям. Эта орбита есть одномерная кривая и определяется
N — 1 соотношениями между N координатами фг. Если орбита
известна, то движение вдоль орбиты, т. е. зависимость <j>t (х)
от х, может быть получено квадратурой, так как оно равносильно
движению вдоль одномерной кривой. Конечно, трудно найти
все орбиты, разрешенные данным потенциалом. Тем не менее для
многих типичных форм U (фг) оказывается достаточно нескольких
пробных орбит. Конечно, это не так хорошо, как если бы можно
было найти все орбиты для потенциала. Но во многих случаях
это дает некоторые точные решения.
Мы поясним эту процедуру на примере двух скалярных по-
полей фг и ф2, взаимодействие которых описывается потенциалом
U (^i> $*)• При этом частица-аналог перемещается в плоскости
\Фъ ФА- Пусть, например, U (фг, ф2) имеет два вырожденных
минимума в точках Р и Q плоскости {^>1; ^>а}> как показано на
рис. 3. (Обобщение на случаи большего числа минимумов или
взаимодействующих полей очевидно.) Будем искать разрешенные
потенциалом [—U (фъ ф2)] орбиты для частицы-аналога. Пусть
g (фъ ф2) = 0 B.38)

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 35
— уравнение орбиты. Тогда исключая х, можно -связать непо-
непосредственно орбиту с U (фх, ф2). Из B.38) имеем
Тогда
(■£■)*<«■-
B.39)
Фг
..••■ •(
Рис. 3. Типичные орбиты, соответствующие статическим локализованным реше-
решениям для случая двух взаимодействующих полей Ф\ и Фг и двух вырожденных
минимумов потенциала U (ф1у 02) в точках Р и Q. Орбиты типа В соответствуют,
согласно терминологии разд. 2Л, топологическим, а орбиты типа А — нетопо-
нетопологическим решениям. Орбиты типа С не описывают статические решения, но
могут играть роль в случае «заряженных» решений, обсужаемых в гл. 8.
При интегрировании
№J
B.37) получаем
B.40)
где Ai — постоянные
B.40) в B.39), имеем
интегрирования. Подставляя уравнение
дИ @1, 02)
50!
<* + *) = (*)'(J
at/
B.41)
Это уравнение орбиты, связывающее g (фг, ф2) непосредственно
с U (фх, ф2), в котором исключено х. Заметим, что эти интегралы
изменяются вдоль орбиты, так как фх и ф2 в подынтегральных
выражениях связаны соотношением B.38). Таким образом, B.41) —
интегродифференциальное уравнение орбиты, записанное через
потенциал. Ему может быть придана форма дифференциального
уравнения, но общий метод решения любого из этих уравнений
отсутствует. Это отражает трудности теории орбит, упомянутые
выше. Тем не менее можно выбрать разумные пробные функции
для орбиты B.38), подставить их в B.41) и попытаться удовлетво-
удовлетворить B.41) выбором параметров орбиты.
2*

36 ГЛАВА 2
Нахождение пробных орбит можно упростить, привлекая сде-
сделанные выше выводы. Периодические орбиты или орбиты, уходя-
уходящие в бесконечность, важные для истинно механических задач,
нас не интересуют, так как имеют бесконечное полное действие.
Конечную величину энергии уединенной волны имеют орбиты
с конечным действием и нулевой энергией, начинающиеся в мини-
минимумах Р или Q и кончающиеся в Р или Q. Пробные орбиты этого
вида могут быть двух типов (рис. 3). Орбиты типа А начинаются
и кончаются в одном и том же минимуме, описывая на плоскости
замкнутую кривую, тогда как орбиты типа В связывают различ-
различные минимумы. Орбиты типа С, когда частица покидает, скажем,
точку Р, переходит к некоторой точке R и возвращается по тому же
пути к точке Р, имеют конечное действие, но не разрешены динами-
динамикой. В точке поворота R частица должна иметь нулевую кинети-
кинетическую энергию и, следовательно, 0 = 0, так как ее полная энер-
энергия равна нулю. Но по предположению единственными нулями U
являются точки Р и Q. Таким образом, орбиты типа С не связаны
со статическими уединенными волнами, хотя они могут оказаться
существенными для некоторых зависящих от времени «заряжен-
«заряженных» решений, которые обсуждаются в гл. 8. Сейчас нам нужны
только орбиты типов А и В (если потенциал имеет единственный
минимум, то существует только тип А).
Процесс нахождения пробных орбит проще пояснить на при-
примере. Рассмотрим простой типичный для взаимодействующих
полей потенциал
Ц(фи f) = {tf-lLym2W4i-MW4 + ^ф\{ф\ - 0 d,
B.42)
где К, d и m2 > 0. В этот потенциал можно было бы ввести больше
параметров, сохраняя его полиномиальную форму, но их всегда
можно исключить изменением масштаба полей и пространственно-
временных координат. Эта модель типична и часто обсуждается
в литературе. Она состоит из двух ^>4-систем, одна из которых
имеет отрицательный член ф2, такой же, как в B.24), а другая —
положительный член ф2, входящий в последний член выражения
B.42). Таким образом, потенциал U (ф1г ф2) имеет два абсолют-
абсолютных минимума в точках {1, 0} и {—1, 0} в плоскости \фг, ф,,\.
Он обращается в нуль только в этих двух точках и всюду поло-
положителен, если К > (d — m2J. Тогда могут существовать орбиты
типов А и В. Так как потенциал имеет простую полиномиальную
форму, естественно искать орбиты в форме полиномов по ф. Для
орбит типа В, которые должны идти из одного минимума в другой,
рассмотрим семейство пробных орбит
<Ы = №>)" + « Ш2-1) = 0, B-43)

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 37
где а и п — некоторые параметры, которые надо определить.
Подставим B.43) в B.41) и проинтегрируем вдоль орбиты, начи-
начинающейся в точке (—1, 0); тогда в любой точке [фъ фг] орбиты
имеем
J dh (
Ц32 + йф2 {ф2 - 1)) ]. B.44)
Здесь постоянные интегрирования А1 и А2 в B.40) равны нулю,
так как интегралы имеют нижними пределами (—1, 0), где ф\
и ф'ъ обращаются в нуль в силу граничных условий. Исключая
с помощью уравнения орбиты B.43) ф1 вне и под интегралами,
получаем после интегрирования
,2 / , *2 \[ *Т tld п+2
Теперь остается только согласовать коэффициенты при одинаковых
степенях ф2 в обеих частях уравнения. Отсюда имеем два решения.
Первое решение
1) п = 2, а = A — 2т2Iй, % =-d (d — 2m2)/(l — 2m2)
B.46)
получается согласованием коэффициентов при ф\ и j>% соответ-
соответственно. Результирующее уравнение орбиты
представляет собой уравнение полуэллипса, соединяющего два
минимума U. Второе соотношение в B<46) есть ограничение на
параметры потенциала, которому необходимо удовлетворить на-
наряду с требованием положительности U. Подставляя данную
орбиту в полевые уравнения B.37), получаем
ф" = $-Ь+ dф22ф^ = 2т2 (ф3 - fr). B.47)
Это уравнение легко интегрируется (см. также [255 ]) и дает
(х) \(х0)],
(х) = ± [A - 2tn2)/d^2 sch [m(x - д0)]. (~ }

38 ГЛАВА 2
Таким образом, мы получили явное точное статическое решение
с конечной энергией системы полевых уравнений B.37) для по-
потенциала B.42).
Второе решение B.45) имеет вид
2) п = 1, т2 =2, % =8d/3, ее2 = (d — 3)/2d. B.49)
Соответствующая орбита есть параболическая дуга:
соединяющая два минимума U. Подставляя эту орбиту в B.37),
получаем
ф2 = т2ф2 + Ц\ + d<j>2 {<$ - l) = 2ф2-d [2d/(d - 3)]1/2 ф\ + -|- d<$,
B.50)
что можно записать в стандартной форме
ф2 = аф2-±Ьф22 + 2сф1 B.51)
выбирая соответствующим образом константы а, Ъ и с. Инте-
Интегрирование дает
(дг) = 1 - [2rf/(rf - 3)]1/2 ^»2 (дг).
Это новое точное решение в виде уединенной волны для потенциала
B.42), справедливое для другой области значений К, т2 и d,
чем решение B.48). Оба решения B.48) и B.52) типа В, имеют
кол околообразную форму для ф2 и форму кривой с перегибом для
фх, как показано на рис. 4, а. Для той же системы можно попы-
попытаться найти решение типа А, когда орбита начинается и кон-
кончается, например, в точке (—1, 0). Простейшим случаем является
эллипс:
+ 1)(а-ф1) = 0. B.53)
Он удовлетворяет уравнению B.41) при условиях
а = A + 4т2)/3, р = B - 4т2)/( 1 + 4щ2), d = C + 12т2)/D + 4т2),
_ (S-4m»)(l+4m») ,„ ,д,
л— (8 + 8т*)A-2т2) * ^ Oj
Эти соотношения просто получить, следуя процедуре, использо-
использованной в уравнениях B.44), B.45) для орбит типа В. Точные ре-

Классические солитоны и уединенные волны 39
шения опять можно найти исключением одного из полей системы
уравнений B.37) с помощью уравнения орбиты B.53). Это дает
B.55)
Фг /' \
Рис. 4. а — статическое решение B.48); решение B.52) имеет тот же общий вид.
но отличается в деталях; оба решения типа В; б — решение типа А B.56); это
статическое нетопологическое решение; при наличии только одного скалярного
поля такие решения не существуют.
Данное соотношение опять имеет стандартную форму B.51) и
при интегрировании приводит к
1 i i / \ 2а ■
где а, Ъ и с снова можно найти из сравнения B.55) и B.51). Другое
поле <f>2 (х) находим, используя уравнение орбиты B.53). Это
решение, схематически представленное на рис. 4, б, типа А и
интересно тем, что оно «нетопологично», т. е. при х -*• ±<х> имеет
один и тот же предел в отличие от остальных рассмотренных выше
решений. Но хотя B.56), несомненно, точное решение, его устой-
устойчивость при малых возмущениях требует отдельного обсуждения.

40 Глава i
Поскольку у решения отсутствует ненулевой топологический
индекс, предохраняющий от распада на рябь (плоские волны
малой амплитуды), оно вполне может быть неустойчивым [323].
Точные решения в виде уединенных волн B.48), B.52) и B.56)
относятся к одному и тому же потенциалу B.42), но к различным
значениям параметров m2, d и к. Этот потенциал выбран просто
в качестве типичного примера, использованного для пояснения
метода, хорошо работающего для многих других потенциалов
(см., например, [298]).
Основные недостатки рассмотренного метода следующие: 1) не-
необходимость подгонять орбиты, а не выводить их, 2) наличие
связей между параметрами потенциала, таких, как B.46), необ-
необходимых для существования решения. Последнее ограничение
возникло потому, что мы пытались строить особенно простые
орбиты. Орбиты с большим числом пробных параметров, воз-
возможно, уменьшат или даже исключат связи. Наконец, обобщение
этого метода на случай более двух взаимодействующих полей
очевидно, хотя при этом потребуются длительные алгебраические
вычисления. Вместо уравнения B.41) появятся (N — 1) уравне-
уравнений, связывающих орбиту с потенциалом.
2.4. Топологические индексы
Часто можно провести топологическую классификацию реше-
решений заданной системы уравнений. Возникновение этого понятия
в физике можно проследить по ранним работам Скирма [317],
Финкельстейяа и Мизнера [138] и Финкельстейна [137]. Более
современное и полное обсуждение данного вопроса можно найти
в лекциях Коулмена [87]. Основная идея уже упоминалась
в предыдущем разделе. Ее необходимо только выделить, форма-
формализовать и распространить на более сложные системы. Конкрет-
Конкретнее говоря, можно определить топологический индекс, сохраня-
сохраняющийся во времени. Как и другие сохраняющиеся величины,
он играет важную роль «квантового числа» состояний частицы
в соответствующей квантовой теории поля. Но он имеет совсем
другое, отличное от привычных сохраняющихся величин и кван-
квантовых чисел происхождение.
Напомним проведенное выше обсуждение скалярного поля
Ф (х, t) в двух измерениях. Пусть потенциал U (<j>) в B.11) имеет
дискретное (но не обязательно конечное) число вырожденных
абсолютных минимумов, в которых он обращается в нуль. Этому
удовлетворяют все примеры предыдущего раздела, а также си-
система синус-Гордона следующего раздела, имеющая дискретную
бесконечность вырожденных минимумов. Нас интересуют несин-
несингулярные решения с конечной энергией, частными случаями кото-
которых являются уединенные волны, и солитоны. Тогда, чтобы энер-

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 41
гия Е в B.14) была конечной, статическое или зависящее от вре-
времени поле должно стремиться к минимуму U (ф) в каждой точке
пространственной бесконечности для любого момента t. В одно-
одномерном пространстве пространственная бесконечность состоит из
двух точек х = ±оо. Рассмотрим, например, точку х = +°о.
Пусть в некоторый заданный момент t0
\imj>(x,t0) = j>(oo,t0) = j>1, B.57)
где фг — один из минимумов U (ф). Тогда с течением времени t
(вперед или назад, начиная от t0) поле ф (х, t) будет меняться
непрерывным образом в каждой точке х, следуя дифференциаль-
дифференциальному уравнению B.13). В частности, ф (оо, t) будет некоторой
непрерывной функцией t. С другой стороны, так как энергия
решения сохраняется и конечна, функция ф (оо, t) должна быть
всегда одним из минимумов V (ф), образующих дискретный ряд.
Она не может перескакивать от фг к одному из других дискретных
минимумов, так как непрерывно изменяется с t. Таким образом,
ф (оо, t) должна быть постоянной фг. Применяя те же рассу-
рассуждения к точке х = —оо, получаем, что ф (—оо, t) = фг не за-
зависит от времени и является минимумом U (ф), но в случае вы-
вырожденных минимумов не обязательно равна фг.
Следовательно, пространство всех несингулярных решений
с конечной энергией можно разделить на секторы, характеризуе-
характеризуемые двумя индексами, а именно не зависящими от времени зна-
значениями ф (х = оо) и ф (х =—оо). Эти секторы топологически-
не связаны в том смысле, что поля одного сектора не могут пере-
переходить непрерывным образом в поля другого, не нарушая требо-
требования конечности энергии. В частности, так как эволюция во
времени является примером такого непрерывного перехода, поле-
полевая конфигурация любого сектора с течением времени остается
внутри него. Естественно, при наличии одного минимума U (ф)
возможно только одно значение как для ф (оо), так и для ф (—оо);
поэтому существует только один сектор решений.
Для пояснения рассмотрим систему B.24) предыдущего раз-
раздела. Потенциал имеет два вырожденных минимума при ф —
----- (±т/у/к). Следовательно, все несингулярные решения с конеч-
конечной энергией такой системы, статические и зависящие от времени,
распадаются на четыре топологических сектора. Они характери-
характеризуются парами индексов (—т/у"!, т/-]/Т), (tn/Y^k, —m/i/X),
(■—mjу/~%, —m/y^X) и (m/|/X, т/У^Х), которые отвечают значениям
(^> (х = —оо), ф (х = +оо)). Таким образом, кинк, антикинк
и тривиальные постоянные решения ф (х) = + (m/т/Т) являются
членами четырех секторов. Полевая конфигурация, состоящая
из кинка, движущегося слева навстречу антикинку, идущему

42 ГЛАВА 1
справа, принадлежит сектору (—т/-/Х, —т/у^к). Даже если мы
не можем вычислить, что произойдет после их столкновения,
можно быть уверенным, что получающаяся полевая конфигурация
будет всегда оставаться в секторе (—m/j/^k, —m/j/X).
В литературе часто используется величина, называемая иногда
«топологическим зарядом». Здесь ее можно определить как
Q = (-/К/т) [ф {х = оо)~ф(х = — оо)] B.58)
с соответствующим сохраняющимся током
№ = (/Х/т) г^ дхф, B.59)
где использованы ковариантные обозначения
О
a e^v — антисимметричный тензор. Ясно, что
а„^ = 0, Q= j dxk0. B.60)
—оо
Величина Q есть просто разность двух индексов (у^Х/т) ф (оо)
и (т/Х/т)^>(—оо). Мы упоминаем здесь топологический заряд,
так как он является аналогом топологических индексов более
сложных систем, таких, как калибровочные теории в четырех
измерениях. Необходимо помнить, что, поскольку поле ф есть
измеримая физическая величина, для нахождения топологического
сектора необходимо знать не только Q, но также ф (оо) и ф (—оо).
Однако в тех случаях, когда физические величины зависят от
разности значений f а не от абсолютной величины ф, как это
имеет место во многих приложениях системы синус-Гордона,
Q становится истинно топологическим индексом. Уединенным
волнам с Q Ф 0 часто дают название «топологических». Волны
с Q = 0 — «нетопологические». Таким образом, кинк и антикинк
системы B.24) являются топологическими решениями, тогда как
тривиальные решения ф (х) = ± (m/j/'X) нетопологические. Один
из наших выводов последнего раздела, сформулированный с при-
применением данной терминологии, гласит, что для одного скаляр-
скалярного поля в двух измерениях нетривиальные статические решения
обязательно являются топологическими.
Отметим, что топологические индексы отличны от более при-
привычных сохраняющихся величин типа энергии, импульса, заряда
и т. д. Последние, как хорощо известно из классической и кван*

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 43
товой теории поля, связаны с существованием непрерывных
симметрии лагранжиана, таких, как временные сдвиги, простран-
пространственные сдвиги, «внутренние группы» и т. д. В отличие от этого
топологические индексы есть граничные условия, сохраняющиеся
вследствие конечности энергии, хотя во многих случаях эти ин-
индексы тесно связаны с определенного вида нарушением некоторой
симметрии. Пусть лагранжиан и U (ф) инвариантны при неко-
некотором преобразовании симметрии, действующем на ф (х). Если
U (ф) имеет единственный минимум в некоторой точке ф = ф0,
то значение ^>„ должно быть инвариантным при таком преобразо-
преобразовании. Но для получения нетривиальных топологических секторов
нужно иметь два или более вырожденных минимумов. В таком
случае при преобразовании инвариантен весь набор минимумов,
а не каждый минимум в отдельности. Например, система B.24),
имеющая четыре топологических сектора, допускает инвариант-
инвариантность U (ф) при ф «-»■ —ф. Но два минимума системы ф = —tn/j^k
и ф =т/>/^ в отдельности не инвариантны. Вместо этого они
переходят друг в друга. Это явление имеет большое значение
в квантовой теории и в статистической механике полевой системы
и носит название «спонтанное нарушение симметрии». К этому
явлению мы вернемся позднее, здесь же мы только рассматриваем
связь нетривиальных топологических секторов с существованием
нескольких вырожденных минимумов потенциала, что в свою
очередь связано со спонтанным нарушением симметрии.
Обобщение развитых идей на случай N взаимодействующих по-
полей фх (х, t) в двух измерениях очевидно. Пусть вырожденными
минимумами потенциала U (фъ ..., фк) являются некоторые дис-
дискретные точки Я'1), ..., Р<т) в N-иернои пространстве полей.
При х -у оо поля должны стремиться к любой из этих точек,
скажем к Я(г>, а при х-*-—оо — к другой из этих точек P<s>.
Эта пара точек PC) и P<s> характеризует частный топологический
сектор решений с конечной энергией. Если P<s> = PC"), то сектор
и его решения «нетопологические». Если /*<s> Ф РС">, то они
топологические. Мы показали в последнем разделе, что статические
нетопологические решения могут существовать для взаимодей-
взаимодействующих полей в двух измерениях, хотя для одного скалярного
поля они отсутствуют. Эти решения принадлежат к типу А,
одно из которых в качестве примера схематически изображено
на рис. 4,6.
Применительно к скалярным полям в двух измерениях понятия
топологических секторов и индексов выглядят слишком триви-
тривиальными. Но при переходе к более сложным системам в гл. 3,
таким, как калибровочные теории в четырех измерениях, приме-
применимы те же идеи. Это оправдывает предварительное знакомство
с такими понятиями в более простом контексте.

44 ГЛАВА 2
2.5. Решения системы синус-Гордона
Статические решения, рассмотренные в разд. 2.3, являются
лишь уединенными волнами, а не солитонами. Рассмотрим теперь
систему, которая дает солитоны по самому строгому определению,
приведенному выше. Она состоит из единственного скалярного
поля ф (х, t) в A + 1) измерениях, описываемого плотностью
лагранжиана
2 (х, t) = ±-(дцф) (д*ф) + KA){cos [(/ВД </>]-!}• B.61)
Эта система используется при исследовании широкого круга яв-
явлений, включающего распространение дислокаций в кристаллах,
скошенных волн в мембранах, магнитного потока в джозефсонов-
ских контурах, а также движение блоховских стенок в магнитных
кристаллах и модели элементарных частиц в двух измерениях.
Более детальные ссылки по этим применениям можно найти в об-
обзорах Скотта и др. [309] и Бароне и др. [26]. Разлагая плотность
лагранжиана в ряд по константе взаимодействия к, получаем
2 (дг, t) = 4- ад (&t) - 4- nfif + -±rr~- w + • • • • <2-62)
При к -*■ 0 это свободная система Клейна—Гордона, а член О (к)
связан с взаимодействием четвертого порядка (соответствующего
здесь притяжению). Но мы будем работать с полным лагранжиа-
лагранжианом B.61) и искать классические решения, непертурбативные по к.
Уравнение поля, получаемое из B.61), есть уравнение синус-
Гордона
□ ф + {тЧ Vk) sin [(/к/т) ф] = 0. B.63)
Эта система своим названием обязана наличию члена с синусом и
аналогией с уравнением Клейна—Гордона, что послужило поводом
для веселой дискуссии. Коулмен [§7] критикует это название
и цитирует слова Д. Финкельстейна о системе B.63): «Я сожалею,
что когда-то назвал ее уравнением синус-Гордона. Это была наша
с Джулио Рубинстейном шутка, и я никогда не использовал это
название в печати. К тому времени, когда он использовал его
в названии статьи, он уже был доктором философии и, следова-
следовательно, вне всякой критики». Но это историческое свидетельство
может только подлить масло в огонь дискуссии, так как Рубин-
стейн [297 ] в своей статье переадресовывает авторство названия
М. Крускалу.
Возвращаясь к уравнению B.63), упростим его заменой пере-
переменных
т) ф.

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 45
Плотность лагранжиана B.61) принимает вид
SB (х, t) = (/и4А) ~о" №цф) (д^ф) -)- (cos ф — 1) . B.64)
Уравнение движения имеет вид
-f* ig-+sin£fr 7) = 0, B.65)
а сохраняющаяся энергия равна
г, т3
Лагранжиан и уравнение поля имеют дискретные симметрии
га о—газ.
*(*, 0-**(*,./)+ 2л?я, .# = ...—2, -1, о, 1, 2,... .
В соответствии с этими симметриями энергия Е обращается в нуль
в точках абсолютного минимума
U (ф) = 1 - cos ф, B.68)
которыми являются
$(x,t) = 2Nn. B.69)
Как следует из нашего предыдущего анализа, все конфигурации
с конечной энергией, статические или зависящие от времени,
могут быть подразделены на бесконечное число топологических
секторов, каждый из которых характеризуется сохраняющейся
парой целых индексов (Л^, Л^2), соответствующих асимптотиче-
асимптотическим значениям 2Ыгп и 2N2n, достигаемым полем при стремле-
стремлении х к —оо и к +оо соответственно. Если по физическим сообра-
соображениям ф определено только по модулю 2я, как это происходит
в тех случаях, когда ф трактуется как угловая переменная, то
тогда имеет смысл топологический заряд
=ТЙГ J "*■§•
дх
—оо
Говоря, что ф определено по модулю 2я, мы считаем, что в любой
пространственно-временной точке можно взять ф (х, t) с точностью
2я. В других точках ф фиксировано требованием непрерывности.
Начнем со статических локализованных решений. Общие со-
соображения показывают, что для скалярного поля в одномерном

46 ГЛАВА 2
пространстве статические решения соединяют только соседние
минимумы U (ф), т. е. они должны нести заряд Q = ±1. Точные
решения легко получить, используя B.23):
Ф (х) Ф (х)
Интегрирование проводится просто и дает
ф (х) = 4 arc tg [ехр (х - х0)] = фоол (х - х0) B.72а)
или
ф (х) = — 4 arc tg [ехр (х - *„)] = фаш1К0Л (х - х0) = — ^сол. B.726)
Решение со знаком плюс B.72а) идет от ф = 0 к ф = 2я (рис. 5, а),
или (что эквивалентно) от 2я к 4я, от 4я к 6я и т. д. Оно соответ-
соответствует Q = 1 и часто называется солитоном системы. Второе
решение B.726) имеет Q = —1 и называется антисолитоном.
Каждый из солитонов имеет энергию Мс ~ 8тй/к, вычисляемую
подстановкой B.72) в B.66). Решения в риде движущихся соли-
солитонов можно получить, как и раньше, преобразованием Лоренца
B.72а), т. е. заменой (х — х0) на [(х — х0 — ut)/-]/\ — и2]. Реше-
Решение B.72а) несколько напоминает по форме рассмотренный выше
«кинк», хотя в деталях они различаются.
Но мы утверждаем, что в противоположность «кинку» решение
B.72а) является истинным солитоном согласно жестким требова-
требованиям B.9), B.10). Аналогично решение B.726) с Q =—1 есть
истинный солитон в полном смысле этого слова. Здесь мы назы-
называем его антисолитоном частично для того, чтобы отличить от
решения B.72а) с Q =1, а частично потому, что он связан с по-
последним симметрией ф<-+ — ф.
Эта система допускает и третий тип солитона, называемый
дублетом, или бризером, который будет описан ниже. Таким об-
образом, уравнение поля B.65) допускает не один, а три различных
типа солитонов.
Утверждение, что все эти решения действительно являются
солитонами, должно основываться на рассмотрении точных зави-
зависящих от времени решений уравнений поля, включающих произ-
произвольное число таких объектов после столкновения. К счастью,
для этого уравнения такие решения были в принципе получены.
Начнем с решения для солитон-антисолитонного рассеяния ^>Са
[280, 310] (см. также [297]). Это и несколько последующих
решений мы не будем выводить. Они являются точными решениями,

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 47
что легко проверить подстановкой в B.65). Так можно проверить,
что функция
(х, 1) = 4 arc tg
B.73)
Фса
t «О
Рис. 5. а — солитон синус-Гордона B.72а); б — три профиля решения фСа (х, t)
для солитон-антисолитонного рассеяния при больших отрицательных /, /= О
и больших положительных /; при /= 0 фСа обращается р нуль; в — солитон-
солитонное решение при /= 0.
удовлетворяет уравнению B.65). Легко найти ее асимптотическое
по времени поведение:
B.74,

48 ГЛАВА 2
где
А = (A -и2)/«Iпи. B.75)
Таким образом, в отдаленном прошлом решение описывает разде-
разделенные большим расстоянием солитон и антисолитон, сближа-
сближающиеся со скоростью 2и. Аналогично можно проверить, что
т /~ 7ч т /х + и(Т— А/2) \ , т /х-иG-А/2) у
B.76)
где опять рассматриваются ^сой и ^антисол с точностью 2я. В уда-
удаленном будущем решение ^>СА описывает ту же солитон-антисо-
литонную пару с такими же формами и скоростями. Единственное
изменение в исходной конфигурации B.74) заключается во вре-
временном сдвиге А, который представляет собой единственный оста-
остаточный эффект столкновения солитона с антисолитоном. При
сближении солитонов они при ? = 0 аннигилируют и поле исче-
исчезает всюду (рис. 5, б). Но при положительных значениях I оно
возникает вновь, асимптотически растет и разделяется на ту же
пару, как если бы вообще не было столкновения, за исключением
временного сдвига. Поскольку используются единицы, в которых
с = 1, то и <; 1, временной сдвиг А отрицателен. Качественно
говоря, это означает, что солитон и антисолитон притягивают
друг друга и взаимно ускоряются. Отметим, что соотношения
B.74)—B.76) удовлетворяют общим требованиям B.9), B.10),
предъявляемым к солитонам для специального случая столкнове-
столкновения солитона и антисолитона.
Существует аналогичное точное двухсолитонное решение
B.77)
показанное на рис. 5, в. В любой момент времени t оно изменяется
от —2я до +2я при изменении х от —оо до +оо и, следовательно,
принадлежит сектору с Q = 2. Отметим, что наши общие сооб-
соображения запрещали только статическим решениям принадле-
принадлежать секторам с $ Ф 1. Зависящие от времени решения могут
существовать во всех секторах. Решение B.77) также имеет про-
простое асимптотическое поведение при ?->- ±оо. Простые вычисле-
вычисления показывают, что аналогично ^сд решение ^>сс описывает
дйа солитона с Q = 1, движущиеся при ? = —оо навстречу друг
другу, а после столкновения уходящие друг от друга с теми же
скоростями, но со сдвигом во времени. Строго говоря, в B.77)
два солитона отскакивают друг от друга со скоростями, равными
ро модулю начальным скоростям, но противоположными по знаку.

КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 49
Это случай рассеяния назад. Но если по-прежнему рассматривать
поля с точностью 2я и не отличать первое решение, изменяющеся
от —2я до 0, от второго, изменяющегося от 0 до 2я, то асимптоти-
асимптотически не существует различия между рассеянием назад и вперед.
Наконец, вследствие симметрии ф *-+—~ф Фаа = —фес есть
антисолитон-антисолитонное решение. Точные решения B.74) и
B.77) указывают на то, что решения, названные нами солитоном
и антисолитоном, могут быть оба истинными солитонами. Но B.74)
и B.77) соответствуют случаям столкновений только двух таких
объектов. Точное определение B.9), B.10) требует аналогичного
поведения для произвольного их числа. Мы вернемся к этому
после описания решений фп (х, 7), называемых дублетами, или
бризерами. Можно проверить, что
также является решением уравнений поля. Здесь v — параметр,
несколько напоминающий и в B.73). В самом деле, превращая
действительный параметр и в ^>СА в мнимый и = iv, получаем
B.78), где по-прежнему ф„ — действительная функция. Если
считать, что и соответствует асимптотическим скоростям солитона
и антисолитона решения fCA, то под дублетом B.78) можно пони-
понимать «связанное» решение солитон-антисолитонной пары. Оче-
Очевидно, дублет является периодическим решением с периодом
х = Bn/-/T~fzP)/v.
Солитон и антисолитон осциллируют один относительно другого с
этим периодом. Профили ф „ (х, 1) для 0 >1> —т/4, (=0 и
0 <; ? <; т/4 очень схожи с изображенными на рис. 5, б профи-
профилями </>са- Но если в последнем случае пара С—А разделяется
на произвольно большое расстояние при ?-> ±оо, то в первом
случае солитоны могут разойтись только на конечное расстояние,
сохраняя всегда искажение своих форм вследствие взаимного
влияния и осциллируя один относительно другого. Существование
такого связанного состояния качественно понятно из того факта,
что пара fCA при рассеянии испытывает отрицательный временной
сдвиг B.75), означающий существование в среднем силы притя-
притяжения. С другой стороны, отталкивание при столкновении одного
солитона от другого, как это видно из асимптотического поведе-
поведения фес, указывает на существование силы отталкивания. Соот-
Соответственно связанной солитон-солитонной пары не существует.
Попытка положить и = iv в фсс приводит к комплексному,
а не к действительному решению, что недопустимо для нашей

50 ГЛАВА 2
действительной скалярной полевой системы. Это понятие сил от-
отталкивания и притяжения, заимствованное из механики частиц,
является здесь в лучшем случае весьма приближенным и справед-
справедливо только для больших расстояний, но оно приводит к пра-
правильным утверждениям о существовании связанных решений С—А
f „ и об отсутствии связанных решений С—С. К понятию сил мы
вернемся в гл. 3. Скажем несколько слов о статусе дублетного
решения как уединенной волны. Его плотность энергии, вычислен-
вычисленная по формуле B.66), не имеет пространственно-временной зави-
зависимости вида (х — ut), требуемого рабочим определением B.8)
уединенных волн. В B.78) решение дано в системе покоя, т. е.
центр решения находится в точке х = 0 для всех ?. Движущийся
дублет может быть получен из B.78) преобразованием Лоренца.
Но даже в системе покоя B.78) дублет имеет нетривиальную
зависимость от времени. Он осциллирует во времени для каждого
заданного х. Этим он отличается от солитона B.72), кинка и других
решений этой главы, которые статичны в системе покоя и удо-
удовлетворяют требованию B.8) в любой движущейся системе от-
отсчета. Тем не менее дублет удовлетворяет основным интуитивным
требованиям, предъявляемым к уединенным волнам: он имеет
локализованную конечную энергию и не диссипативен. В системе
покоя поле ограничено огибающей
±4arctg{(l/u)sch(jc/l +t'2)).
Следовательно, мы включаем его в набор уединенных волн, но
этот пример показывает недостаточность простого рабочего опре-
определения B.8) для многих интересных случаев.
Наше утверждение, что B.72а), B.726) и B.78) являются не
только уединенными волнами, но и солитонами, требует, чтобы
существовали зависящие от времени решения с произвольным
числом рассеивающихся солитонов, антисолитонов и дублетов,
которые при ?.-»-+оо превращаются сами в себя. Решения ^>сл
и ^сс дают часть требуемой информации. То, что такие решения
существуют, было показано в работах Абловица [3] и группы
Фаддеева [11, 127, 129, 362]. В результате проделанной работы
стали известны все зависящие от времени решения уравнения си-
синус-Гордона. Это очень впечатляющее достижение, которое стало
возможным благодаря использованию метода обратной задачи
рассеяния [149]. Многосолитонные решения не являются про-
простыми выражениями, такими, как ^са и ^>сс, записанные как
функции от ф (х, 1). Мы не приводим не только их вывод по методу
обратной задачи рассеяния, но даже сами выражения. Этот метод
так же, как и другие формальные и изящные свойства данного
примера, такие, как использование преобразований Бэклунда,

КЛАССИЧЕСКИЕ СОЛИТОНЫ Й УЕДИНЕННЫЕ ВОЛНЫ 51
существование бесконечного числа сохраняющихся величин и
т. д., представляет самостоятельный интерес, и его обсуждение
завело бы нас слишком далеко (см. начало этой главы). Однако
трудно устоять перед искушением без доказательств сделать неко-
некоторые короткие и качественные замечания.
Метод обратной задачи рассеяния по существу приводит к ис-
использованию переменных действие — угол, привычных для клас-
классической механики, описание которых можно найти в любом рас-
расширенном курсе этого предмета (см., например, [170]). Система
синус-Гордона дает конкретный пример использования этого ме-
метода, обобщенного на бесконечное число степеней свободы. Вместо
полевых переменных ~ф используется набор переменных |9 (р),
—оо < р < оо; qa, а = 1, 2, ...; цъ и р6, 6 = 1, 2, ...}, изменя-
изменяющихся в пределах 0 <: 6 < 2я, —оо <Г qa, qb <С оо, 0 <: рь <
<: 32ят2А. Это «угловые» переменные. Соответствующие сопря-
сопряженные переменные «действия», которые используются вместо
канонических переменных импульса я (х, 7) = (т*/к) дф (х, ~f)ldt,
образуют набор
\р{р), лежащий в [0, оо], Ра, Рь, оба в [—оо, оо]
и аь в [0, я/2]}.
В этих переменных можно показать, что гамильтониан системы
(т. е. интеграл энергии B.66)) имеет вид
—оо а
%[l 2V/2, B.79)
где Ms — масса солитона, т. е. его статическая энергия 8ms/k,
MD (аь) — энергия дублетного решения в системе покоя. Пере-
Переменная аь связана с внутренним движением дублетного решения.
Напоминаем, что даже в системе покоя дублет осциллирует с пе-
периодом х. Этой степени свободы отвечают сопряженные переменные
аъ и рь. Задача заключается в том, чтобы найти переменные дей-
действие — угол как функционалы от исходных переменных ф (х, 1)
и я (jc, ?), перейти к последним и показать, что гамильтониан
действительно имеет форму B.79). Даже в механике одной частицы
переменные действие — угол могут быть точно найдены только
для немногих случаев. Эта внушительная задача решается для
системы синус-Гордона преобразованием к линейной обратной
задаче. Линейная задача аналогична (но не в точности соответ-
соответствует) получению потенциала волнового уравнения Шредингера
из данных по состояниям рассеяния и связанным состояниям

§2 ГЛАВА 2
его решений, а не наоборот. Поэтому данный метод носит название
метода обратной задачи рассеяния. Здесь мы опускаем постановку
и решение обратной задачи. После получения соотношения B.79)
остальные шаги тривиальны. Заметим, что гамильтониан зависит
только от переменных действия, а не от углов, как и требовалось.
Поэтому он разделяется на сумму гамильтонианов свободных
релятивистских частиц. Три члена в B.79) имеют простую интер-
интерпретацию, если переменные действие — угол выразить через
первоначальные полевые переменные ф. Первый член соответ-
соответствует вкладу плосковолновых решений. Вспомним, что в пределе
слабого поля (малых ^>) данная система становится системой
Клейна—Гордона (уравнение B.62)), поэтому она допускает
плоские волны вида ^>0 exp [i (рх — У р2 + m2t)] с произвольной
малой амплитудой ^>0, распространяющиеся по всему пространству.
Каждая такая волна имеет энергию, пропорциональную-)//?2 + т2,
что отражено в первом члене B.79). Эта часть системы не отвечает
солитонам или уединенным волнам. Второй член соответствует
энергии солитонов (и антисолитонов, у которых такая же масса
М8). Поэтому индекс а в B.79) нумерует отдельные солитоны
и антисолитоны с импульсами Ра. Наконец, индекс Ь в последнем
члене нумерует дублеты с импульсами Ръ и массами MD (ab),
которые в системе покоя равны их энергиям, зависящим от пе-
периода внутреннего движения. Доказательство того, что эти соли-
тонные, антисолитонные и дублетные решения действительно
являются солитонами, заключается в разделении гамильтониана
на ряд членов, соответствующих свободным частицам, каждый
из которых связан только либо с плоской волной, либо с солитоном
(или антисолитоном), либо с дублетом.
Другим важным свойством системы является существование
преобразований Бэклунда. Примененные к системе синус-Гордона
[25, 2241 эти преобразования дают способ получения Af-солитон-
ных решений из решений с меньшим числом солитонов. Более
того, в данном методе требуется решать дифференциальные урав-
уравнения не второго порядка, а первого. Отметим, что уравнение
синус-Гордона, записанное в координатах светового конуса а =
= (х + 1I2 и р = (х — 1I2, имеет вид
д2ф/да dp - sin f = 0. B.80)
Пусть ф0 (а, р) — решение этого уравнения. Рассмотрим фг (а, р),
порожденное уравнениями преобразования Бэклунда
1-(ф1 + ф0)], -B.81а)
B.816)

КЛАССИЧЕСКИЕ СОЛЙТОНЫ Й УЕДИНЕННЫЕ ВОЛНЫ 53
где а — действительный параметр. Взяв производную д/др от
B.81а) и использовав B.816), получим
4~ (д2/до др) (ф1 — ф0) = cos [4" (^1 + Фо) ] sin [-у (& —
=-L sm ф,-1. s[n ф0. B.82)
Поэтому если </>0 (<*> р) — решение уравнения B.80), то и ^>х (а, р)
также является его решением. Точная функция </>х находится
интегрированием B.81) для заданной ф0. Например, возьмем
"/•о (°> р) = 0. Это точное (несолитонное) решение уравнения си-
синус-Гордона. Подстановка значения ф0 в B.81) дает
1 1 /1
- дфх/да = — а? дфх/др = a sin (-^- <
Интегрирование легко проводится и приводит к решению
^i (о, р) = 4 arc tg [exp (ao + р/а) ],
которое в первоначальных координатах \х, Ц записывается
в виде
где и — A — а2)/A + а2). Это односолитонное решение B.72а)
в системе, в которой оно движется со скоростью и. Таким образом,
из несолитонного решения преобразование Бэклунда порождает
односолитонное решение. Аналогичным образом можно последо-
последовательно получить многосолитонные решения. Существенная
часть этого метода, опущенная нами, которая предшествует исполь-
использованию B.81), заключается в доказательстве существования пре-
преобразований Бэклунда для системы синус-Гордона и нахождении
соответствующих уравнений B.81). Другое свойство системы
синус-Гордона заключается в наличии у решений бесконечного
числа сохраняющихся величин. Мы вернемся к данному свойству
в гл. 7. Читателей, интересующихся более полным обсуждением
метода обратной задачи рассеяния, преобразований Бэклунда,
сохраняющихся величин и т. д., отсылаем к обзору Скотта и др.
[309].
Чтобы использовать систему синус-Гордона для пояснения
квазиклассического метода в последующих главах, достаточно
знать, что B.72) и B.78) — точные решения уравнения поля B.65).
Что это так, читатель может просто проверить подстановкой реше-
решений в B.65). В гл. 7 мы поясним ВКБ-метод для квантования за-
зависящих от времени классических решений на примере дублетного
решения B.78). Мы выбираем дублет в основном потому, что он

54 ГЛАВА 2
является одним из немногих периодических локализованных ре-
решений релятивистской теории поля, полученных в аналитической
форме. То, что решения B.78) и B.72) также'солитоны, в какой-то
степени случайно. Благодаря этому некоторые ВКБ-результаты
оказываются точными и возможно построение точной 5-матрицы
системы (гл. 7). Но основной квазиклассический метод получения
связанных квантовых состояний из классических решений, опи-
описанный в гл. 5 и 6, требует только, чтобы эти решения были уеди-
уединенными волнами, т. е. локализованными недисперсионными реше-
решениями, а не обязательно солитонами в точном смысле этого слова.
Возможно, это является одной из причин, по которым термин
«солитон» в литературе часто распространяют и на уединенные
волны, независимо от того, удовлетворяют ли они жестким тре-
требованиям B.9) и B.10) или нет.

ГЛАВА 3
МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ
3.1. О многомерных решениях
В предыдущей главе мы работали в основном со скалярными по-
полями в A + 1) измерениях. Теперь нас интересуют более сложные
системы с большим числом измерений. Методов, пригодных для
решения нелинейных уравнений, настолько недостаточно, что даже
для скалярных полей заданной системы в A + 1) измерениях
в общем случае нельзя получить все зависящие от времени реше-
решения. Система синус-Гордона является скорее исключением, чем
общим правилом, и ее разрешимость обеспечивается почленным
разделением гамильтониана свободных частиц в соответствующим
образом выбранных переменных. Для большого числа типичных
систем, подобных двумерной теории </>4, такой успех вне досягае-
досягаемости. Конечно, если в двумерной теории ограничиться стати-
статическими в некоторой системе отсчета решениями, то в этой системе
отсчета оказывается существенным только одно (пространственное)
измерение и полевые уравнения превращаются в обыкновенные
дифференциальные уравнения. Более того, для трансляционно
инвариантных систем такие уравнения «автономны», т. е. не со-
содержат явно независимую переменную х, а содержат только поля
и их производные по х. Обычные автономные дифференциальные
уравнения второго порядка (даже системы таких уравнений)
решить не трудно, что подтверждается несколькими одномерными
статическими решениями, приведенными в предыдущей главе.
Но в случае двух или большего числа пространственных изме-
измерений даже статические решения подчиняются дифференциальным
уравнениям в частных производных. Эти нелинейные уравнения
решить труднее. Большинство реальных систем, например в фи-
физике элементарных частиц, включают нелинейно взаимодейству-
взаимодействующие скалярные, векторные и спинорные поля в C + 1) измере-
измерениях. Для типичных систем такого вида до сих пор нет системати-
систематического метода получения в аналитической форме даже одного
«етривиального классического решения. Те немногочисленные
точные решения некоторых сложных многомерных систем, кот'орые
приведены i этой и следующей главах, получены лишь для спе-
специально выбранных систем сУпомощью остроумных приемов,
упрощающих их полевце уравнения, Конечно, нетривиальнее

56 ГЛАВА 3
решения существуют для многих других моделей, но их аналити-
аналитическое получение представляет собой сложную задачу. Для таких
моделей приходится удовлетворяться теми общими свойствами
решений, которые удается получить, не решая полевых уравнений.
Поэтому в последующих разделах мы будем уделять внимание
прежде всего не самим точным решениям (если они существуют),
а общим свойствам классических решений. Важным общим свой-
свойством большого класса систем является возможность введения
гомотопической классификации и топологических зарядов. Другим
общим и полезным результатом является теорема вириала, с ко-
которой мы и начнем.
3.2. Теорема вириала
Эта очень полезная теорема [106, 188] приводит в основном
к отрицательному результату. Переходя от скалярных полей
в A + 1) измерениях, рассмотренных в гл. 2, к более реальным
системам, естественно начать со скалярных полей в пространствах
с большим числом измерений. Теорема вириала жестко ограничи-
ограничивает возможность существования в таких системах нетривиальных
статических уединенных волн. Из нее следует, что таких решений
не существует, когда число пространственных измерений 3 или
больше и когда лагранжиан имеет стандартную релятивистскую
форму '
2 (х, 0 = 4" (W) ■ (д»Ф) -и(ф (х, 0). C.1)
Здесь ф (х, /) = [$i (х, /); i = 1 AM — набор N взаимодей-
взаимодействующих полей в D пространственных и одном временном изме-
измерениях. В C.1) подразумевается скалярное произведение д^ф на
д^ф, т. е. суммирование по полевым индексам i. Потенциал
U (ф (х, /)), как и раньше, — некоторая неотрицательная функ-
функция, обращающаяся в нуль только в точках абсолютного мини-
минимума. Статическое решение ф (х) подчиняется уравнению
V20 = -g-(x), C.2)
где у2 ~ лапласиан в D измерениях. Это уравнение является
условием экстремума 8W = 0 функционала статической энергии
W [ф] = I сРх [±-ъф-\%ф + U (ф(х))] = Уг [ф] + V* [ф], C.3)
где функционалы Vx и V2 отвечают двум членам в правой части
соотношения. Заметим, что не только W, но также и Ух и V2
неотрицательны. Пусть фг (х) — статическое решение. Рассмо-
Рассмотрим однопараметрическое семейство конфигураций
&(x)=*i(kt). C.4)

МОНОГЮЛЙ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 57
Легко проверить, что
W [фк] = Уг [ф,Л + V2 [ф>,] = tf-^ [^1 + b~DV2 [фг1 C.5)
Так как ф1— экстремум W [ф], функционал W [фх] должен
быть стационарным по отношению к вариациям К, т.е.
(d/dk) W [фк] = О при X = 1. C.6)
Дифференцирование C.5) с учетом C.6) дает
C.7)
Поскольку Ух и У2 неотрицательны, для выполнения условия
C.7) при D 5== 3 необходимо, чтобы Ух [^Х] = К2 [#а] =0. Это
означает, что ф1 (х) постоянно в пространстве и является одним
из нулей U [ф]. Это решение тривиально, и, таким образом,
теорема запрещает нетривиальные изменяющиеся в пространстве
решения. Отметим, что данный вывод справедлив только для
статических решений и для лагранжиана вида C.1). Зависящие
от времени уединенные волны могут существовать для скалярных
полей в (D + 1) измерениях даже при D ^ 3 (гл. 8). Но теорема
указывает, что при поиске статических решений в реальном мире
C + 1) измерений необходимо рассматривать модели, состоящие
не только из одних скалярных полей. В разд. 3.4 исследуется
такая модель, включающая скалярные и векторные поля. Но
прежде полезно рассмотреть более простую модель, чтобы полу-
получить представление о некоторых важных идеях, которые потре-
потребуются в последующих разделах. Эта система состоит только из
скалярных полей, но в B + 1) измерениях.
3.3. Нелинейная О (З)-модель: изотропный ферромагнетик
Из уравнения C.7) следует, что при D =2 V2 [фх]= 0,
т. е. решение ф1 (х) для всех х есть один из нулей (которые яв-
являются также абсолютными минимумами) потенциала U(ф).
Если U (ф) и"меет только дискретные минимумы, то вследствие
непрерывности ф1 (х) должно быть тем же самым минимумом
U (ф) для всех х, т. е. не зависящим от х и тривиальным решением.
Если U (ф) имеет непрерывный ряд минимумов, то C.7) при D = 2
допускает зависящее от х решение, при котором ф меняется не-
непрерывно в пределах этого ряда минимумов.
Простейшим примером U (ф) с непрерывным рядом минимумов
является, конечно, U (ф) =0. Но такая модель слишком проста.
Уравнение для статического решения, получаемое из лагран-
лагранжиана C.1), имеет вид
0.. ■ C.8)

58 Глава 3
Несингулярными решениями этого уравнения являются только
константы. Однако можно ввести незначительное на первый
взгляд, но нетривиальное изменение модели, налагая ограничение
фф=1. Данная модель носит название нелинейной О (N)-
модели. Мы^рассмотрим случай Л/ = 3 и найдем, что он обладает
интересными решениями [30, 124, 318].
Нелинейная О (З)-модель состоит из трех действительных
скалярных полей ф(х, /) = {</>„ (х, /); а = 1, 2, 3} со связью
£^(х, Г)=ф.ф=1 C.9)
а
для всех значений (х, /). Динамика определяется плотностью
лагранжиана
=~т 2 2 {д»фа) {д^а) = т- w>
и уравненаем связи. Отметим, что ф можно считать вектором
во «внутреннем пространстве», т. е. трехмерном пространстве по-
полей; его компоненты имеют индекс а. Такие векторы необходимо
отличать от векторов в координатном пространстве, имеющих
лоренцевы индексы, например \i в C.10). Так, в C.10) под скаляр-
скалярным произведением понимается произведение д^ф как во вну-
внутреннем пространстве (обозначаемое точкой), так и в координат-
координатном (обозначаемое повторяющимися индексами (х). Мы обращаем
на это особое внимание, так как ниже будем часто работать с объ-
объектами, являющимися тензорами как в координатном простран-
пространстве, так и в некотором внутреннем пространстве, и различие
между ними необходимо тщательно учитывать. Отметим, наконец,
--что как лагранжиан C.10), так и связь C.9) инвариантны при гло-
глобальных вращениях О C) во внутреннем пространстве.
Уравнения поля получают из вариационного принципа Эй-
Эйлера—Лагранжа, примененного к действию, где связь учтена
введением множителя Лагранжа. Таким образом, находят экстре-
экстремум выражения
] C.11)
Отсюда получаются уравнения поля
^0*0+ ** = (□ + *) * = 0. C.12)
Множитель Лагранжа К (х, /) исключается с помощью уравнения
связи C.9):
C.13)

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 59
Рассмотрим пространство размерности 2 и ограничимся стати-
статическими решениями. Тогда после подстановки C.13) уравнения
поля принимают вид
0. C.14)
Сравним уравнение C.14) с уравнением C.8), получаемым в от-
отсутствие связи. Оказывается, что в отличие от C.8) уравнение
C.14) обладает интересными несингулярными решениями в двух
измерениях. Эти решения можно разбить по гомотопическим сек-
секторам, характеризуемым топологическим индексом. Основные
принципы данной классификации являются обобщением идей,
развитых в гл. 2 для более простого одномерного случая.
Энергия статического решения получается просто из лагран-
лагранжиана C.10):
±\ <у=1, 2. C.15)
Рассмотрим сначала решения с нулевой энергией («классический
вакуум»). Ясно, что они должны удовлетворять условию даф = 0
для всех х, т. е. ф (х) = фт, где ф@) — произвольный единичный
вектор во внутреннем пространстве. Хотя вектор ф@> не зависит
от х для решения с Е = 0, он может быть произвольно ориенти-
ориентированным во внутреннем пространстве, оставаясь при этом (в силу
условия C.9)) единичным. Таким образом, мы получаем вырожден-
вырожденное непрерывное семейство решений уравнения Е = 0, соответ-
соответствующих различным направлениям вектора фт. Так же как
для системы кинка B.24), это случай классического «спонтанного
нарушения симметрии». В задаче с кинком симметрия была дис-
дискретна (ф *~* —ф), поэтому существовало два дискретных решения
уравнения Е = 0, связанные этой симметрией. Здесь же мы
имеем случай непрерывной симметрии О C) и соответственно не-
непрерывное семейство вырожденных классических минимумов,
связанных друг с другом вращениями О C) во внутреннем про-
пространстве.
Найдем солитонные решения, т. е. решения с ненулевой, но
конечной энергией Е. Из C.15) ясно, что они должны удовлетво-
удовлетворять следующему условию, записанному в полярных координатах
(г, 0) в х-пространстве:
0 при г-+оо, C.16)
или
Итф(х) = ф1°\ C.17)
где опять ф<°> — единичный вектор во внутреннем пространстве.
Заметим, что при стремлении к бесконечности в координатном
пространстве по различным направлениям вектор ф (х) должен

60 ГЛАВА 3
достигать одного и того же предела фт. Иначе вектор ф будет
зависеть от угла 0 даже при г ■= оо, и угловая компонента гра-
градиента A/г) (дф/dQ) не будет удовлетворять условию C.16).
Поскольку ф (х) стремится к одному и тому же значению
фт в любой точке на бесконечности, физическая координатная
плоскость ^2 сжимается в сферическую поверхность 5|*из), т. е.
плоскость /?2 может быть отображена в сферическую поверхность,
причем окружность на бесконечности перейдет при этом в север-
северный полюс сферы. (Более точно это достигается при стереографи-
стереографическом отображении, см. ниже.) «Внутреннее пространство»,
т. е. пространство полей <j>a, в силу условия 2jo=i фа = 1 также
является сферической поверхностью единичного радиуса. Назовем
ее S<BH). Тогда любая статическая конфигурация ф(х) с конечной
энергией есть отображение 5<*из> в 5|вн).
Приведем без доказательства известный из топологии резуль-
результат. Все несингулярные отображения одной сферической поверх-
поверхности 52 в другую S2 могут быть подразделены на гомотопические
секторы. Отображения внутри одного сектора могут непрерывно
переходить друг в друга, но отображения двух различных секто-
секторов не могут непрерывно переходить друг в друга. Более того,
множество таких гомотопических секторов, или классов, счетно
и может быть охарактеризовано набором целых положительных и
отрицательных чисел и нуля. Точнее, эти гомотопические классы
сами образуют группу, изоморфную группе целых чисел. Фор-
Формально все это можно записать в компактном виде
я2 E2) =Z, C.18)
где пп (Sm) — гомотопическая группа отображений Sn -*■ Sm,
a Z — группа целых чисел (эти результаты и их доказательства
см. в классическом учебнике [321]).
Мы будем использовать иногда результаты типа C.18). Чита-
Читателям, не знакомым с ними, рекомендуем рассмотреть простейший
случай отображения окружностей в окружности. Пусть окруж-
окружность 5Х (задаваемая углом 6, определяемым с точностью 2я)
отображается в другую окружность 5Х (задаваемую Л). Отображе-
Отображение определяется непрерывной функцией Л F) с точностью 2я.
Рассмотрим, например, два таких отображения или функции
Ло F) = 0 для всех 6, C.19)
\ /6 для 0<8<л,
Л°^=ЬBя-6) для я<е<2я, <3-20>
где / — некоторый действительный параметр из интервала [0, 1 ].
Ясно, что при непрерывном уменьшении /до нуля второе отобра-
отображение непрерывно перейдет в первое. Интуитивно это также по-
понятно из рис. 6, б и е. Таким образом, два отображения принадле-

МОНОМИЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 61
жат одному гомотопическому классу. С другой стороны, рассмо-
рассмотрим отображение
Лх F) = 6 для всех 6. C.21)
Это также непрерывное по модулю 2я отображение, так как вместе
с 6 описывает полный круг и Лх. Но оно не переходит непрерывно
в C.19) или C.20). Это интуитивно понятно из рис. 6, г, кото-
который нельзя деформировать в рис. 6, б или в, не разрезая где-либо
окружность Л. Причина заключается, очевидно, в том, что в C.21)
вторая окружность «наматывается» на первую один раз, а в C.19)
\
\
Рис. 6. а — отображение одной окружности,
обозначенной сплошной линией, на другую,
обозначенную штриховой линией; 6 — три-
тривиальное отображение C.19), при котором
вся первая окружность отображается в точ-
точку на второй окружности; в — нетривиаль-
нетривиальное отображение C.20). Как 6 так и в имеют
нулевое число наматываний (Q = 0) и могут
быть непрерывно деформированы друг в друга
сжатием сплошной петли. Но отображение г
C.21) нельзя деформировать в б или в, не раз-
разрезая сплошной окружности.
и C.20) — нуль раз. Поэтому C.21) относится к отличному от
C.19) или C.20) гомотопическому классу. Два класса различаются
значением целого числа, называемого «числом наматываний»
2л
которое равно нулю для C.19), C.20), но равно единице для
C.21). Легко понять, что, наматывая вторую окружность произ-
произвольное число раз, можно получить счетное множество гомотопи-
гомотопических классов. Так,
Лп F) = п0 C.23)
является прототипом отображения класса Q = п. Отрицательные
значения Q получаются при наматывании в противоположном
направлении, например при замене 0 на —0 в C.23). Эти каче-
качественные замечания не доказывают, а скорее делают правдопо-
правдоподобным следующий результат:
ях (Sx) = Z. C.24)
Уравнение C.18) обобщает данный результат на отображения 52 -*
->-S2. Целым числом, характеризующим гомотопические классы

62 ГЛАВА 3
S2 -*■ S2, является обобщенное число наматываний, т. е. число раз,
которое одна сфера «обертывает» другую.
Таким образом, возвращаясь к нашей О (З)-модели, статиче-
статические конфигурации ф (х) с конечной энергией в двумерном про-
пространстве могут быть разделены на гомотопические секторы, ха-
характеризуемые некоторыми целыми значениями Q. Отметим, что
природа гомотопической классификации решений отличается здесь
от рассмотренной в гл. 2 на примерах кинка и системы синус-
Гордона. В этих примерах различные секторы отличались гра-
граничными значениями поля на пространственной бесконечности.
В О C)-модели роль граничных условий C.17) сводится только
к преобразованию координатного пространства к сферической
поверхности 5<*из). Граничные условия C.17) не определяют
однозначно граничное значение ф@>. Хотя вектор ф@> должен при-
принимать одно и то же значение во всех точках пространственной
бесконечности, он может иметь любое «внутреннее» направление.
Полевые конфигурации с различными направлениями ф<°> свя-
связаны непрерывным образом О (З)-вращениями во внутреннем
пространстве. Поэтому различный выбор фт не ведет сам по себе
к различным гомотопическим секторам О (З)-модели. Возникнове-
Возникновение секторов связано с поведением полей в пространстве, включая
внутреннее пространство. Полезно записать Q в виде интеграла
от полевых функций ф (х) аналогично C.22):
= Ж" J V
х
где ц = 1, 2 и v = 1, 2 — индексы декартовых координат, а знаки
произведения относятся к векторам внутреннего пространства.
Что это выражение определяет число наматываний (иногда на-
называемое топологическим индексом или числом), вытекает из
следующих соображений.
В силу условия 2ja^a = 1 сфера S2BH) во внутреннем про-
пространстве может быть описана двумя переменными {|х, £»}, на-
например сферическими углами вместо трех декартовых координат
фа. Существует хорошо известное выражение для элемента по-
поверхности сферы, связывающее декартовы и сферические пере-
переменные:
<о(вн) j2«. / 1 дФЬ дФс \ /о пг*\
dSa =dl [-^-^гвеаьс-щ^-щ^у C.26)
Тогда
, дФь dlr дФс dls
p e & дФъ

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 63
поскольку якобиан перехода от переменных \xlt хг\ к переменным
\llt £2} равен
C-28)
Подставляя C.26) в C.27), получаем
JS(B"), C.29)
так как фа — единичный вектор, нормальный к поверхности.
Вспоминая, что S<BH> — поверхность единичной сферы площади
4я, приходим к выводу, что Q определяет число поворотов вну-
внутренней сферы при вращении координатного пространства R?,
сжатого до 5|*из).
Данная гомотопическая классификация справедлива для любой
статической полевой конфигурации, для которой функционал
энергии C.15) конечен. Она не требует, чтобы поля были реше-
решениями полевого уравнения C.14). Решения с конечной энергией
образуют подмножество конфигураций с конечной энергией,и для
них справедлива та же классификация. Для нахождения неко-
некоторых решений произвольно выбранного Q-сектора воспользуемся
следующим остроумным приемом [30].
Начнем с тождества
J (Рх [(дпф ± е^ф X д,ф) ■ (д»ф ± е^ф х даф)] S» 0. C.30)
Оно справедливо в силу того, что подынтегральное выражение
есть скалярное произведение вектора в скобках на самого себя.
Раскрывая его, получаем
)-(d^) + 4v& X дуф)-епа(Ф X даф)) ^
±2 J (Px
Два члена в левой части равны друг другу, так как в силу связи
ф-ф= 1 и производной от нее ф- (дхф) — 0 выполняется равен-
равенство
Поэтому
2 J (Рх (дпф) ■ (дпф) ^ ±2 J йЧ^ф ■ (дпф х д,ф),
или
C.31)

64 ГЛАВА 3
Это неравенство устанавливает нижнюю границу энергии любой
статической конфигурации данного Q-сектора. Но статическое
уравнение поля C.14) получается из экстремума функционала
статической энергии C.15) при условии C.9). Так как конфигу-
конфигурация не может при непрерывном изменении перейти из одного
сектора в другой, экстремум можно искать отдельно в каждом
секторе. Для заданного Q-сектора энергия минимизируется при
выполнении равенства C.31). Это в свою очередь означает выпол-
выполнение равенства C.30), что возможно тогда и только тогда, когда
^ = ±е,^х(^). C,32)
Любая конфигурация, удовлетворяющая C.32) наряду с C.9),
минимизирует Е в некотором Q-секторе и, следовательно, автома-
автоматически удовлетворяет условию экстремума в виде полевого
уравнения C.14). Это легко проверить. Для любой конфигурации,
удовлетворяющей C.32), имеем
дп д„ф = ±6» (г^ф х drf) = ±e^v (
= К 1даф(ф-дуф) - ф(д,ф■ даф)] = ф(ф V20),
т. е. получаем уравнение поля. На последнем шаге использовано
соотношение
получаемое дифференцированием уравнения связи C.9). Любое
поле, удовлетворяющее C.32), удовлетворяет и C.14), но обрат-
обратное неверно. В принципе можно получить решения уравнения
C.14), не удовлетворяющие C.32). Они отвечают не абсолютному
экстремуму Е в соответствующем Q-секторе, а некоторым другим
экстремумам Е, например локальным минимумам. Нам достаточно
найти решения уравнения C.32). Заметим, что это уравнение
решить проще, чем исходное уравнение C.14). Оно является
дифференциальным уравнением первого порядка, тогда как
последнее является уравнением второго порядка.
Уравнение C.32) можно упростить специальным выбором
переменных. Напомним, что разрешенные уравнением связи
ф'ф = 1 значения ф образуют поверхность единичной сферы 5<ви>.
Спроецируем стереографически поверхность сферы на плоскость
и поставим в соответствие точкам первой декартовы коорди-
координаты а>! и со2 точек плоскости. Переменные сох и со2 связаны с пе-
переменными фа соотношениями
соа = Цу1( 1 - ф3), со2 - 2fc/( 1 - ф3), C.33)

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 65
где плоскость проекции выбрана параллельной плоскости \<(>1,
ф2\ и содержит южный полюс сферы. Полезно также построить
комплексную величину
со = сох + ш2 = 2 (ф1 + 1ф2)/A - ф3) = 2ф/A - фа),
где ф = ф1 + г</>2. Тогда
-g- = 2 [A - ф3) дхф + </> с^3]/A - № =
= [2/A - &J] (ЭД + Д&). C.34)
Но из уравнения C.32) имеем
Д Д C.35)
Подставляя C.35) в C.34), получаем
jCO = —(— JC/2CO, (o.oOj
что в терминах сох и со2 дает
дх1 дха ' дх2 дХ\ ' \ • /
(Напомним, что х1 и х2 — декартовы координаты нашего исход-
исходного двумерного физического пространства, а соа и со2 характери-
характеризуют плоскость во «внутреннем пространстве», на которую сте-
стереографически спроецирована сфера S|B«).
Уравнения C.37) представляют собой условия аналитичности
Коши—Римана со как функции от г* (верхние знаки) или г (ниж-
(нижние знаки), где z — х1 + ix2. Таким образом, любая аналитиче-
аналитическая функция со (г) или со (z*), записанная в первоначальных
переменных фа и х, автоматически удовлетворяет уравнению
C.32) и, следовательно, уравнению поля. При этом функция со,
аналитическая по г или по z*, не обязательно должна быть целой.
Хотя разрезы запрещены однозначностью фа (х), но возможны
изолированные полюсы со (z). Расходимость со в полюсах не
должна вызывать беспокойства, так как со'-»■ оо соответствует
«северному полюсу» 5<вн>, т. е. ф3 = 1.
Полезно выразить Е и Q через функцию со, аналитическую
по z. Имеем (вывод очевиден)
J A +1 со |2/4J ' ' 4л v '
Образец решения для произвольного положительного Q записы-
записывается в виде
со (г) = [(г — zo)/l]n, C.39)
3 Раджараман Р.

66 ГЛАВА 3
где п — любое положительное целое число, к — любое действи-
действительное число, аг0 — любое комплексное число. Так как C.39) —
аналитическая функция, то она, будучи выраженной через фа
и х, является точным статическим решением уравнений поля.
При лоренцевом преобразовании решения в движущуюся систему
отсчета мы получаем точное зависящее от времени решение не-
расплывающейся формы. Заметим, что исходная система лоренц-
инвариантна.
В C.39) со соответствует точке в пространстве полей, a z —
точке в координатном пространстве. Ясно, что для заданного
значения со существует п корней г. Поэтому решение принадлежит
сектору с Q = п. Это можно проверить подстановкой C.39)
в C.38). Получаем
п2 I ? 7 |2п—2 5,2/г
(;>i;i;vV' C-40)
После замены переменных
C.41)
интегрирование становится тривиальным и приводит к Q = п.
Следовательно, энергия Е — 4nQ = 4шг конечна. Ясно, что для
любых положительных п это точные решения, имеющие вид
уединенных волн.
Постоянные к и z0 (заменяющие координаты (л;хH и (х2H) соот-
соответствуют размеру и положению солитонного решения. Тот факт,
что решение существует для произвольных к и z0, a Q и Е от них
не зависят, отражает масштабную и трансляционную инвариант-
инвариантность. Подчеркнем, что выражение Е [ф] C.15) инвариантно
при х -*• х — а и х ->• кх.
Модель О C) интересна также в A + 1) измерениях. Было
показано [237, 281], что модель О C) в A + 1) измерениях так
же, как и система синус-Гордона, характеризуется наличием
бесконечного числа сохраняющихся величин и преобразований
Бэклунда, генерирующих решения. (В квантовом варианте было
показано, что модель асимптотически свободна, а сохраняющиеся
величины не имеют аномалий [236, 286].) Наконец, с помощью
бесконечного числа сохраняющихся величин была построена
точная факторизуемая 5-матрица [367]. Этот последний резуль-
результат обсуждается в одной из последующих глав. Статические ре-
решения в B + 1) измерениях справедливы и для модели в A + 1)
измерениях. В последней они существуют как инстантоны (гл. 4).
Кроме того, такая О (З)-модель и ее решения применяются в ста-
статистической теории изотропного ферромагнетика (разд. 3.6).

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 67
3.4. Монополь т'Хофта—Полякова
Теперь мы готовы рассмотреть статические солитонные реше-
решения в реалистическом случае C + 1) измерений. Из теоремы
вириала разд. 3.2 следует, что одни только поля спина нуль не
дают такого решения, необходимо вводить поля с высшими спи-
спинами. Поля спина 1/2 на этом этапе рассматриваться не будут.
Они являются ферми-полями, «классический предел» которых
требует специальной интерпретации и обсуждается в гл. 9. По-
Поэтому мы перейдем к полям спина 1, в частности к калибровочным
полям, важным для физики элементарных частиц.
Простейшим примером калибровочной теории в C + 1) изме-
измерениях является свободная электромагнитная система с калибро-
калибровочной группой U A). Она состоит из линейных уравнений Макс-
Максвелла и просто решается. Хорошо известно, что в отличие от A +
+ 1)-мерного линейного уравнения B.1) свободные уравнения
Максвелла в C + 1) измерениях не имеют решений, соответству-
соответствующих уединенным волнам. Любой локализованный пакет расплы-
расплывается. Солитонные решения возникают при взаимодействии элек-
электромагнитного поля с заряженными скалярными полями в B +1)
измерениях. К этому случаю мы вернемся позднее. Простейшим
примером "неабелевой калибровочной группы является SU B).
Эта группа соответствует триплету калибровочных полей, извест-
известных как поля Янга—Миллба [315, 359]. Этот триплет образует
сложную нелинейную систему, но было показано, что свободные
поля Янга—Миллса в C+1) измерениях также не обладают
уединенными волнами [88, 107, 272]. Они имеют интересные син-
сингулярные решения [360], но нас интересуют только несингуляр-
несингулярные решения с конечной энергией.
Расширим систему Янга—Миллса, введя взаимодействие полей
Янга—Миллса с триплетом скалярных полей, как это было сде-
сделано Джорджи и Глешоу [151]. В пионерских работах т'Хофта
[330] и Полякова [283] было показано, что такая модель имеет
несингулярное локализованное решение, обладающее некоторыми
замечательными свойствами. Этот раздел мы посвятим обсуждению
данной модели и ее статического солитонного решения. Неабелевы
калибровочные теории, одним из примеров которых является эта
модель, изучаются уже более двадцати лет. Хотя наше изложение
достаточно полно, читателю полезно предварительно познако-
познакомиться с основными характеристиками этих теорий, прежде чем
следовать нашему изложению. (Есть несколько хороших обзорных
статей и книг, см., например, [2, 42, 132, 326].)
Модель состоит из скалярных полей <f>" (х, t) и векторных
полей Л£ (х, t) в C + 1) измерениях. Индекс а = 1, 2, 3 есть
индекс внутреннего пространства, преобразующийся по локаль-
локальным (не зависящим от координат и времени) SU B)-преобразова-

08 IVIAHA 3
ниям, определенным ниже. Для любого заданного a фа является
скаляром, а А% (\i = 0, 1, 2, 3) — вектором относительно пре-
преобразований Лоренца. Плотность лагранжиана есть
2 (х, 0 = -\<&*?*\ + \ №) (DV) —tMW - F2J-
C.42)
Здесь «тензор поля» G% определяется как
G% = д»А% - dvAl + gtabcAlA%, -C.43)
а «ковариантная производная» й^ф" — как.
D^a = d^a + gzabcAb^. C.44)
(Ковариантные производные других триплетов полей, таких, как
Лд или G^v, определяются аналогично.) Действительные постоян-
постоянные gД > 0 и F являются параметрами модели. Поля А%, назы-
называются калибровочными, а поля фа в таком контексте называются
полями Хиггса, так как приводят к так называемому механизму
Хиггса (разд. 10.2).
Читателям, не знакомым с неабелевыми калибровочными тео-
теориями, этот лагранжиан может показаться сложным и надуманным.
Тем не менее он отвечает «калибровочной инвариантности», т. е.
инвариантен под действием SU B)-преобразований в каждой
точке пространства-времени. Эти преобразования определены
следующим образом:
^(х, t)~+[U(x, f)Utb(x, 0, C.45)
(LaAaX -**Ubd [LaAl + (t/g) Id^be {IT%, C.46)
где
[U(x, Qbc = [exp{-*L«8«(x, t)}]bc C.47)
—- произвольный член группы 5G B) в пространственно-времен-
пространственно-временной точке (х, t), записанный в матричном представлении 3X3.
(La)bc = 1гаьс — три генератора 5GB) в матричном представ-
представлении 3x3, / — единичная матрица, а 9а — групповые пара-
параметры, меняющиеся в пространстве-времени. Инвариантность
лагранжиана C.42) при калибровочных преобразованиях прове-
проверяется прямой подстановкой. Данные уравнения являются обоб-
обобщением на группу SU B) соответствующих положений электроди-
электродинамики с калибровочной группой G A).
В этом разделе мы рассмотрим некоторые классические стати-
статические решения данной системы, что представляет собой сложную
задачу, если учесть, что взаимодействуют 15 нелинейных полей
в C+1) измерениях.

МОНОПОЛИ И. ПОДОБНЫЕ ИМ РЕШЕНИЯ 69
Из лагранжиана C.42) следуют уравнения движения
D/j"^ = geabc (Dv<£6) фс, C.48)
О11О^фа=—1(фьфь)фа^-1Р2фа. C.49)
Ограничимся решениями, которые а) статические и б) удовлет-
удовлетворяют условию Л Л (х) = 0 для всех х, а. Тогда уравнения поля
принимают вид
= gzabc (О'фь) фс, C.50)
= —% (фьфь) фа + %Рфа, C.51)
где i, /== 1, 2, 3 — чисто пространственные индексы.
Мы ищем решения уравнений C.50), C.51) с конечной энер-
энергией. Эти уравнения намного сложнее уравнений поля, рассмо-
рассмотренных выше, но наш подход к задаче будет таким же: мы найдем
сначала решения для классического вакуума (с нулевой энергией).
Это позволит определить допустимые граничные условия, которым
должны удовлетворять конфигурации с конечной энергией. Затем
мы проведем гомотопическую классификацию этих граничных
условий. Наконец, среди конфигураций данного гомотопического
сектора будем искать решения с конечной энергией. Итак, найдем
нули энергии. Из лагранжиана просто найти выражение для со-
сохраняющейся энергии системы, которое для статических решений
с учетом того, что Л£ = 0, имеет вид
E=\d3x [-LGatjGaii + i-DtfDtj," + 4K(*V - р2У}• C-52)
Энергия достигает минимума и обращаетсй в нуль при
Л?(х) = 0, C.53)
р(х)р(х) = Р, C.54)
п,ф*=0, C.55)
что в силу C.53) сводится к дгфа = О. (Отметим, что первое усло-
условие C.53) достаточно, но не необходимо. Существуют другие ре-
решения Л?, сводящиеся к Л? = 0 калибровочными преобразова-
преобразованиями, которые дают Е = 0. Мы вернемся к этому вопросу в гл. 4.
Сейчас будем считать, что Л? = 0, и перейдем к условиям C.54),
C.55) для </>а.)
Условия для фа схожи с условиями модели О C) предыдущего
раздела. Они образуют вырожденное непрерывное семейство ре-
решений уравнения Е = 0. Для каждого из них ф = \фа\ имеет
определенную амплитуду F, но может иметь любое не зависящее
от х направление во внутреннем пространстве. Напомним, что
локальная калибровочная симметрия SU B) системы содержит
в себе глобальную (не зависящую от х) симметрию SU B), которая

70 ГЛАВА 3
в свою очередь для наших действительных скалярных полей ф
сводится к внутренней симметрии относительно вращений. Ре-
Решения семейства уравнений с Е — 0 C.53)—C.55) связаны друг
с другом такой симметрией.
Рассмотрим теперь конфигурации с ненулевой, но конечной
энергией Е. Сходство с нелинейной О (З)-моделью в некоторой
степени сохраняется и здесь, но теперь существуют и важные
отличия. Условия конечности Е заключаются, как и раньше,
в достаточно быстром стремлении полей на пространственной беско-
бесконечности к некоторой конфигурации с Е = 0. Из C.52) видно,
что эти условия на поле ф состоят в том, что при г = | х | -»- оо
г*/Югф-+0, C.56)
фф-^F2. C.57)
Как и в модели 0C), амплитуда ф достигает «вакуумного» зна-
значения F. Но в отличие от модели 0C) направление вектора ф
во внутреннем пространстве при стремлении к пространственной
бесконечности может быть разным. Это происходит потому, что
соответствующее уравнению C.16) модели 0C) условие C.56)
требует в отличие от первого равенства нулю ковариантной
производной Dj#, а не обычной производной д,ф. Рассмотрим
выражение C.44) для ковариантной производной и выразим ее
в сферических координатах \г, б, ф} и соответствующих компонен-
компонентах, б-компонента {йфа) определяется выражением
= ±^-+§еаЬсАьвфс. C.58)
Для того чтобы вся эта комбинация удовлетворяла условию
C.56), нет необходимости в стремлении дфа/дE к нулю при г ->- оо.
Производная дфа1д% может иметь ненулевой предел при г-»-оо,
если б-компонента калибровочного поля Ле входит в выражение
C,58) таким образом, что вся сумма C.58) стремится к нулю при
г-+оо. Это в свою очередь означает, что А\ убывает как \1г.
Аналогичное заключение справедливо для азимутальных компо-
компонент (grad фа) и А\. Тот факт, что некоторые компоненты А%.
при г -*- оо убывают лишь как 1/г, является следствием конеч-
конечности Е. Подынтегральное выражение в Е содержит произведе-
произведение GyG'"'', которое тогда убывает как 1/г4 и, следовательно,
интегрируемо.
Таким образом, в отличие от модели О C) конечность Е в дан-
данном случае позволяет полям фа (х) иметь на границе пространства
различные направления при условии, что 2а фафа ->- F2. Следова-
Следовательно, разрешенные значения фа на границе лежат на сфери-
сферической поверхности радиуса F во внутреннем пространстве.

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 71
Назовем эту поверхность 5<вн). Пространство данной модели
трехмерно, поэтому ее граница есть другая сферическая поверх-
поверхность S<*>. Отсюда набор граничных условий на ф, разре-
разрешенный конечностью Е, является набором всех несингулярных
отображений 5|*из) -»- 5*вн). Как мы уже видели, такие отобра-
отображения разделяются на счетное бесконечное множество гомотопи-
гомотопических классов, которые образуют группу it2(S2) = Z. Полевые
t 1.1. t t
\ ■
\
' :' :
ч
■а 6
Рис. 7. Профили прототипов отображений S|*) -> S^BH) с п = 0 (а) и я = 1
(б). Поверхность, обозначенная точками, соответствует S^*), а сплошные стрелки
указывают направления соответствующих точек S^BH\ т. е. направления изовек-
тора Фа. Отметим, что при вращении векторов Фа в случае б по штриховым стрел-
стрелкам в попытке направить их, как в случае а, угол вращения будет разрываться
в южном полюсе. Это наглядное изображение помогает понять, почему два отоб-
отображения принадлежат различным гомотопическим секторам.
конфигурации одного сектора не могут непрерывно переходить
в конфигурации другого сектора. Каждый сектор характеризуется
целым числом Q, которое представляет собой топологическое число
этой модели и равно числу покрытий SiBW) при однократном
прохождении 5^фи3). Если Q = 0, то при х -»- оо поле ф либо
стремится к одному и тому же значению для любого направления
(рис. 7, а), либо к некоторому зависящему от угла значению,
которое может быть трансформировано в не зависящее от угла.
Тривиальное вакуумное решение <j>a (x) = f>3aF принадлежит
этому сектору с Q = 0. Данный случай аналогичен C.19), C.20)
для отображений 5i -»- S^ Прототип конфигурации с Q = 1
имеет вектор ф (х -»- оо), направленный радиально наружу, т. е.
параллельно координатному вектору (рис. 7, б). Ниже мы дадим
точный пример решения для случая Q = 1.

72 глава 3
Заметим, что гомотопическая классификация конфигураций
данной модели с конечной энергией возникла целиком из гранич-
граничных условий для полей. В этом отношении данная классификация
отличается от соответствующей классификации в модели О C)
(хотя обе имеют одну' и ту же гомотопическую группу п2 E2))
и ближе по духу классификации моделей </>4 и синус-Гордона.
В последних пространство одномерно и различные секторы соот-
соответствуют различным значениям поля при стремлении х к —оо
или +оо. Например, в решении с кинком поле </> (л;) имеет разные
пределы при х -*■ ±оо. То же самое происходит в секторах с Q ф О
нашей калибровочной модели. При г->-оо по различным направ-
направлениям поле ф достигает различных пределов.
Мы ограничились рассмотрением статических конфигураций
с А% (х) = 0. Решение, которое мы получим несколько ниже,
также относится к этой категории. Но исходя из статического ре-
решения с А° (х) =0, можно получить калибровочными преобразо-
преобразованиями C.45), C.46) другие зависящие от времени решения с не-
ненулевым значением А%. Так как лагранжиан инвариантен при
калибровочных преобразованиях, а полевые уравнения^кова-
риантны, преобразованное решение также будет решением. Оно
будет иметь такую же энергию и топологический заряд, так как
энергия калибровочно-инвариантна и Q, как мы увидим ниже,
также.
Представим, как и раньше, топологический индекс в виде точ-
точного функционала от поля. Топологический ток &„, можно пред-
представить в виде [10]
kVL=(l/8n)eVLV(,ffiabed*f*de$>d°fi, C.59)
где
В силу антисимметрии е^ра имеем
0^ = 0, C.60)
Ясно, что сохранение тока следует из конструкции выражения
для k^ C.59), а не из динамики, т. е. формы лагранжиана или
уравнений движения. То же самое верно для тока B.59). Это
отражает отличие топологических зарядов и токов от привычных
нётеровских токов и зарядов, подчеркнутое в гл. 2. Определению
C.59) соответствует сохраняющийся заряд
Q = j (Pxk0 = -gL- j {гтг«ь< д& д& dhfa cPx =
=4г \
1 йЪЫё^ф'д&дър), C.61)
(физ)
Ь2

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 73
где i, /, k = 1, 2, 3 — пространственные индексы, а 5<*из)—
наша сфера на бесконечности координатного пространства. Для
того чтобы* убедиться, что C.61) является топологическим индек-
индексом отображения 5<*из) -»- SBBH\ введем для описания поверх-
поверхности 5|физ) параметры (а1; а2). Ими могут быть, например,
полярный и азимутальный углы. Перепишем тождество C.26)
для нашего координатного пространства;
(ра,=-^(Ра*Ыпгрд1£--$£-, p,q=l, 2.
Кроме того,
}фа = — iL . C.62)
Тогда
гл 1 Г jo I I nhr dxm дхп 7„ дФь даг дФс das \
о ЗХ J \ 2> иСС -р С/ССn OCtp f)x ОССg f)x I
***b 'Л*с
= 1 [
on J
Выражение C.63) имеет точно такую же форму, как C.25). Для
доказательства того, что Q есть топологическое число, достаточно
лишь повторить соответствующие рассуждения разд. 3.3.
Объясним теперь, почему решения данной модели называются
«монополями». Мы увидим, что с этими решениями можно связать
магнитный монопольный заряд. Он пропорционален Q — тополо-
топологическому числу, характеризующему решение.
Магнитные монополи как предмет исследования теоретиков
[111, 112, 307] и экспериментаторов имеют долгую историю. Мы
не будем в нее углубляться, а отметим лишь следующий хорошо
известный факт. В традиционной электродинамике уравнения
Максвелла для векторного потенциала А^ имеют вид
д^у = 4я/\ , C.64)
где
dvA», C.65)
^ =0 ' C.66)
и где /v — электрический ток. Введение магнитных зарядов и
токов требует добавления магнитного тока в правую часть урав-
уравнения C.66). В нашей неабелевой SU B)-калибровочной теории,
как можно показать, такой магнитный ток уже существует, и нет
необходимости модифицировать лагранжиан C.42) или уравне-
уравнения поля C.48), C.49).

74 ГЛАВА 3
Мы не связывали электромагнетизм с калибровочной моделью
C.42) и лишь отметили, что теория C.42) представляет собой обоб-
обобщение на группу SU B) U A)-калибровочной теории электро-
электромагнетизма. Но U A) является подгруппой группы SU B), по-
поэтому электромагнитную систему можно рассматривать как часть
более широкой системы C.42). На первый взгляд можно было бы
попытаться связать одно из трех калибровочных полей, скажем А%,
с электромагнитным полем. Но эта связь оказывается калибро-
вочно неинвариантной, так как различные поля Л£ перемеши-
перемешиваются при калибровочных преобразованиях C.46). т'Хофт пред-
предложил калибровочно-инвариантное определение тензора электро-
электромагнитного поля Fpy в терминах исходных полей:
a6>aD^6Dv^- C.67)
Можно проверить, что 1) это выражение калибровочно инва-
инвариантно и 2) в области, где фа = @, 0, 1), оно принимает вид
F^, = д,Л\ - dvA%. C.68)
Второе утверждение означает, что в специальной калибровке,
когда поля фа имеют одно и то же направление во внутреннем
пространстве, векторное поле вдоль этого направления можно
рассматривать как электромагнитное поле. В общем случае вы*
ражение C.67) определяет тензор поля. В отличие от обычной
электромагнитной системы C.64)—C.66) тензор C.67) имеет дуаль-
дуальный тензор с ненулевой дивергенцией. Небольшие преобразова-
преобразования позволяют получить из C.67) выражение
X <WadvFp° = (l/2g) ^vpoeebc д*ф« дРфь д^ = Dn/g) К, C.69)
где /гд — топологический ток C.59). Сравнивая это выражение
с выражением для электрического тока C.64), видим, что ма-
магнитным током является (l/g) 1г„. Магнитное поле, определяемое
обычным образом как Bt = 1/2е,-JhFik, удовлетворяет соотно-
соотношению
C.70)
Следовательно, полный магнитный монопольный заряд равен
C.71)
где Q — топологический заряд.
Отметим, что соотношение C.71) похоже на условие квантова-
квантования Швингера для магнитного заряда [307]. Однако оно не в точ-
точности такое же, да и не должно быть таким же. Последнее выво-

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 75
дится из квантовой теории, тогда как наши рассуждения были
строго классическими. Условие Швингера имеет вид
т = пП/q, п = 0, 1, 2 - C.72)
где Ь. = h/2n, h—постоянная Планка, q— электрический заряд
электрона. В C.71) Ь. отсутствует, a g — константа взаимодействия
в лагранжиане C.42)—C.44). Условие C.71) будет совпадать
с условием Швингера только в том случае, если некоторые кван-
тово-теоретические соображения позволят считать, что электри-
электрический заряд частиц, связанных с полем фа, равен q = gfi.
Так как тензор F»v в C.67) калибровочно инвариантен по
построению, то это справедливо и для к^, и для магнитного за-
заряда т. Читателя может смутить, что C.69) дает ненулевую ди-
дивергенцию тензора, дуального F^, тогда как выражение C.68),
к которому иногда можно привести F^v, есть чистый ротор и для
дуального тензора дает нулевую дивергенцию. Но C.68) следует
из C.67) только в областях, где <j>" имеет одинаковое направление
во всех точках внутреннего пространства. Согласно нашим рас-
рассуждениям о гомотопических классах, решения <j>a, начиная
с Q Ф 0, нельзя повернуть несингулярными калибровочными пре-
преобразованиями так, чтобы они имели одинаковое направление
во всем пространстве, как это свойственно конфигурации с Q = 0.
Таким образом, конфигурации с Q=£0 не могут быть записаны
в форме C.68) и, следовательно, должны иметь ненулевую дуаль-
дуальную дивергенцию в некоторых областях, связанных с существо-
существованием ненулевого магнитного заряда.
Эти общие соображения просто пояснить на примере конфи-
конфигурации с Q = 1, исследованном т'Хофтом и Поляковым. Рас-
Рассмотрим для статического решения следующий анзац:
F(x) = ba(x{/r)F(r), C-73)
Aa{(x) = Bat,(xJ/r)W(r), Л?(х) = 0, C.74)
где г = | х | и i, /, а = 1, 2, 3. Пусть F (г) и W (г) отвечают сле-
следующим граничным условиям при г -»- оо:
F(r)^F, W(r)^l/gr. C.75)
Функции F (г) и W (г) должны удовлетворять уравнениям поля
C.50), C.51). F — константа лагранжиана C.42). В силу C.75)
анзад удовлетворяет всем требованиям, сформулированным выше,
в том числе граничным условиям C.56), C.57). Очевидно, что
C.73), C.74) описывают конфигурацию с Q = 1. В C.73) внутрен-
внутреннее направление фа параллельно направлению ха, как показано
на рис. 7, б. Это — однозначное отображение 5<*из> в 5<вн). Оно
соответствует Q = 1, что можно легко проверить, подставляя
C.73) в определение Q C.61). Можно вычислить соответствующее

76 ГЛАВА 3
этой конфигурации магнитное поле б,- = 1/^i]hFl'k при г ->- оо.
Поскольку Di<j>a->-0 при г-»-оо, по определению F^ C.67)
с учетом C.73)—C.75) получаем
В (х) x/gr\ C.76)
что соответствует магнитному полюсу величины \lg в согласии
со значением Q = 1. Так как А% = 0 и все поля не зависят от
времени, то Foi = 0 и электрического поля нет. Таким образом,
решение имеет только магнитный заряд и не имеет электрического
заряда.
Заметим, что мы еще не решили точно уравнения поля C.50),
C.51). Эти уравнения, как и большинство систем нелинейных урав-
уравнений в трех пространственных измерениях, решить не просто.
Основную часть нашего обсуждения составил топологический
анализ, основанный исключительно на граничных условиях.
Замечательно, что, не решая самих уравнений, можно получить
так много информации о некоторых свойствах решений. В част-
частности, для анзаца C.73), C.74) мы использовали пока только
специально выбранную тензорную форму и граничные условия
C.75). Для нахождения функции F (г) и W (г) нужно подставить
анзац в уравнения поля. Анзац «сферически-симметричен», т. е.,
если не учитывать простых тензорных множителей, зависит
только от радиальной переменной г. Благодаря этому упрощению
дифференциальные уравнения, в частных производных C.50),
C.51) сводятся к обыкновенным дифференциальным уравнениям.
.При подстановке C.73), C.74) в уравнения поля после некоторых
вычислений получаем
*K£ r)_ 1) + fp{r)K{r)t (з.77)
£
--= 2Н (г) К2\г) + Ш (г) (~Р- - r2F2) , C.78)
где
, К (г) = 1 _ grW {r)t H(r)~grF(r). C.79)
Выражаясь специальным языком, это система связанных «неавто-
«неавтономных» дифференциальных уравнений. Хотя эта система намного
проще исходных полевых уравнений, решить ее все еще не просто.
Однако было показано [54, 288], что в пределе X -»- 0 при фик-
фиксированных g и F уравнениям C.77), C.78) удовлетворяют осо-
особенно простые функции
Отметим, что, хотя при Х-уО последний член лагранжиана C.42)
обращается в нуль, он все же влияет на решение через граничные

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЕ 7?
условия C.57) и C.75). Для получения точного статического ре-
решения в пределе К -*■ 0, принадлежащего сектору с Q = 1 и име-
имеющего магнитный заряд \lg, нужно подставить функции C.80)
в анзац C.79), C.73) и C.74).
В пределе "к -у 0 модель наряду с простым аналитическим ре-
решением для одиночного монополя C.80) обладает и другими
прекрасными свойствами. В частности, Богомольный [54] вывел
неравенство, связывающее энергию статической конфигурации
с ее топологическим индексом, схожее с результатом C.31) для
модели О C). При К = 0 для статического решения с Л^ = 0
энергия C.52) сводится к
= \
_L (G?. - гфОкфаJ + j Aiel7JG?Af°. C.81)
i.i.a
Второй член можно записать в виде
i-гцк0ацОк<1>а = j dhdk D BtjkGW1) =
(^?) C.82)
используя тождество DjO1^ = 0, где GaiXV — дуальное поле:
8at" = Vje^^Gpa. Это тождество следует из C.43), C.44) (см.
вывод евклидова аналога D.20) в гл. 4).
Рассмотрим калибровочно-инвариантныи электромагнитный
тензор F^y C.67). При г -*■ оо для любой конфигурации с конеч-
конечной энергией D^" -»- 0 и фа ->- ^>а//:'. Тогда магнитное поле,
получаемое из C.67), асимптотически имеет следующий вид:
Bk = -^EkiiFif -у A/2F) mfittitf-
Используя его, перепишем C.82) в виде
F & dakBk = 4nmF = 4n {Q/g) F,
где т — магнитный заряд, связанный с гомотопическим индек-
индексом Q соотношением C.71). Тогда энергия в C.81) записывается
в виде
Е = ^ + j dh 2 4- (G?/

78 ГЛАВА 3
В любом заданном Q-секторе энергия достигает минимума тогда
и только тогда, когда поля удовлетворяют «условию Богомоль-
Богомольного»
G?/ = ef/*D^e. C.84)
Очевидно, что эти результаты схожи с соотношениями C,31),
C.32) для модели О C). Если полевая конфигурация удовлетво-
удовлетворяет условию Богомольного C.84), то она минимизирует статиче-
статическую энергию в соответствующем Q-секторе и, следовательно,
является классическим решением в этом секторе. В частности,
для Q = 1 можно проверить подстановкой в анзац C.73), C.74),
что решение Прасада—Зоммерфельда C.80) удовлетворяет C.84).
Следовательно, знак равенства в C.84) означает, что монополь
имеет массу 4nF/g. Заметим, что так же, как кинк в гл. 2, моно-
монополь тем тяжелее, чем меньше константа взаимодействия g.
Для; Q > 1 или К Ф 0 аналитические решения неизвестны.
Численные вычисления и некоторые высказанные т' Хофтом и
Поляковым соображения указывают на то, что несингулярное
(Q = 1)-решение с конечной энергией существует, даже если
X ф 0. Более строгое исследование существования таких решений
было проведено Тюпкиным и др. [339].
Помимо всех его других интересных свойств монопольное ре-
решение является во всяком случае решением в виде уединенной
волны модели C.42), представляющей собой довольно сложную
систему взаимодействующих полей в C + 1) измерениях, Но нет
никаких оснований считать, что это решение есть солитон в смысле
строгого определения, приведенного в гл. 2.
3.5. Еще о монополях и дионах
В предыдущем разделе мы привели гомотопические соображе-
соображения, ведущие к мультимонопольным секторам модели C.42).
Мы также подробно рассмотрели одномонопольное решение.
Отметим, что для модели C.42) и для ее обобщений была прове-
проведена большая работа в области монополеподобных решений. За
недостатком места мы не можем обсуждать здесь ее так же под-
подробно, как мы обсудили основное монопольное решение. Нам
придется удовлетвориться общим обзором этих исследований,
снабдив его некоторыми качественными замечаниями и ссылками
на литературу. (Более подробное обсуждение и ссылки на лите-
литературу можно найти в обзорах [4, 245].)
Вскоре после получения одномонопольного решения модели
C.42) Джулиа и Зи [206] указали, что эта модель обладает также
дионами, т. е. объектами с электрическим и магнитным зарядами.
Напомним, что монопольное решение, описываемое анзацем
C.73), C.74), не имеет электрического заряда. Так как А% = 0,

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 79
а поля не зависят от времени, для электрического поля выпол-
выполняется условие
где /^v — калибровочно-инвариантныи электромагнитный тен-
тензор C.68). Джулиа и Зи предложили решения, являющиеся ста-
статическими, но с ненулевым значением А%. Они обобщили анзац,
включив в него
Aa0 = xaJ(r)/gr2
с граничным условием J (г) -у О при г -> 0. При этом поля Л?
и фа имеют прежнюю форму C.73), C.74). Вместо C.77), C.78)
для J (г), Я (г) и /С (г) получаются уравнения
г2 d2/C/dr2 = К (К2 — /2 + Я2 — 1),
r42H/dr2 = 2Я#2 + Ш [(Я2/^2) - r2F2],
г2 d2//dr2 = 2J/C2.
Тогда электрический заряд записывается в виде
q= jd3x(div E) = — — jdr-^-. C.85)
о
Точные решения можно опять найти в пределе W0 [54, 288].
Они имеют вид
*m=th"m
где у — произвольная действительная постоянная. Подставляя
это решение в C.85), получаем
q = Dл/£) sh 7. C.87)
Асимптотическое магнитное поле остается таким же, как C.76),
поэтому решение имеет магнитный заряд т — \lg. Очевидно, что
эти уравнения при у — 0 сводятся к уравнениям, описывающим
монополь т'Хофта — Полякова. Швингер [307] и Цванцигер
[368] доказали, что если существуют различные типы частиц,
несущие магнитный и электрический заряды (т; и qt соответ-
соответственно), то они должны подчиняться условиям
= Nn. C.88)
Ппименяя эти условия к монополю (q = 0, т = \lg) и диону
^ —- Dn/g) sh у, т = l/g), получаем соотношение
2) sh у = #Й, C.89)

80 ГЛАВА 3
которое, вообще говоря, не выполняется, так как постоянная у
решения C.86) может быть любым действительным числом. Это,
очевидно, связано с тем, что наши рассуждения были классиче-
классическими, тогда как условия Швингера—Цванцигера получены из
квантовых принципов и их можно применить только после кван-
квантования нашей теории (см. [191, 336]).
Монопольные и дионные решения, описанные выше, были
статическими. Как было показано выше, понятие топологических
монопольных секторов не ограничено только статическими ре-
решениями. Зависящие от времени периодические решения с ма-
магнитными и электрическими зарядами, для которых топологиче-
топологическое число может быть непосредственно связано с поведением ка-
калибровочных полей Л^, а не скалярных полей фа, были недавно
рассмотрены Кристом и Джакивом [83]. Росси [294] связывает
монопольное решение зависящим от времени калибровочным пре-
преобразованием с последовательностью инстантонов Янга—Миллса.
Тот факт, что в решениях типа C.73), C.74) внутренний ин-
индекс а связан с пространственными индексами i и /, дает интерес-
интересное направление исследований. Оно связано с возможностью
возникновения фермионных полей полуцелых спинов из бозонных
полей, а также с преобразованиями изоспина в спин. Отметим,
однако, что одно только перемешивание внутренних и простран-
пространственных индексов не имеет само по себе какого-либо особенно
глубокого смысла. Индекс а предназначен только для различения
трех скалярных полей фа. Все три поля фа могут существовать
в любой точке х, и нет никаких причин, препятствующих измене-
изменению соотношения между ними с изменением х. В этом случае
изовектор фа будет меняться по направлению с изменением х.
Случай, когда а остается одним и тем же для всех х, для тополо-
топологически нелинейных систем является скорее исключением, а не
правилом.
Но для монопольных секторов таких калибровочных теорий
перемешивание спиновых и внутренних индексов имеет, по-
видимому, глубокие следствия. Как показали Джакив и Ребби
[195] и Хазенфрац и т'Хофт [183], при взаимодействии системы
монополя с системой заряженных скалярных изодублетов возни-
возникает объект с полуцелым спином, хотя все начальные поля бо-
зонные. Соответствие этого интересного результата обычной спи-
спиновой статистике изучалось Голдхабером [168]. Вывод и обсужде-
обсуждение этих результатов читатель найдет в цитированных работах.
По поводу нашего замечания следует отметить, что указанные
следствия требуют гораздо большего, чем просто связи внутрен-
внутренних и пространственных индексов в решении типа C.73), C.74).
Многие другие свойства модели — спонтанное нарушение вну-
внутренней симметрии SU B), тот факт, что группа SU B) имеет ту

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 81
же структуру, что и группа вращений, а также то, что решением
является магнитный монополь, — дают вклад в эти результаты.
Конечно, эти результаты являются обобщением на монополи
калибровочной теории SU B) давно известного свойства точечных
монополей иметь при взаимодействии с точечными зарядами
аномальный угловой момент (см., например, [299]).
Анзац C.73), C.74), ведущий к одномонопольному решению
(Q = 1), сферически-симметричен. Гут и Вайнберг [179] (см.
также [140]) показали, что мультипольные решения нельзя полу-
получить из такого анзаца. Их необходимо искать среди функций, не
обладающих сферической симметрией [93,253, 267]. Патраскиу
[277] доказал, что для получения нетривиальных гомотопических
секторов рассматриваемого вида необходимо вводить дальнодей-
ствующие поля. Напомним, что. в нашем монопольном решении
одно из трех калибровочных полей Л£ убывает как \1г при г -> оо
по любому направлению. Более широкий вопрос о том, когда
калибровочные теории имеют нетривиальные гомотопические сек-
секторы, обсуждался в лекциях Коулмена [87] наряду с тем, как
могут быть «состыкованы» решения из различных секторов..
Распространение на случай высших представлений группы
50C) для скалярных полей (вместо триплетного векторного
представления C.42)) изучалось Шанкаром [311].
Распространение монополеподобных решений на высшие
5^/(п)-калибровочные теории рассматривалось во многих рабо-
работах, в том числе [18, 77, 92, 189, 201, 243, 315]. Недавно Вайн-
Вайнберг [343 ] описал в деталях монополи произвольных компакт-
компактных простых групп Ли.
Наконец, в очень интересном исследовании обобщенных моно-
монопольных решений высших калибровочных групп Олив и др.
[166, 167, 256, 265] указали на существование группы магнит-
магнитного заряда, дуальной исходной калибровочной группе. По-
видимому, эти две группы взаимно симметричны. Исходная ка-
калибровочная группа дуальна дуальной группе магнитного за-
заряда, поэтому было высказано предположение, что нётеровские
и топологические заряды в этих группах меняются местами.
Надеемся, что эти ссылки на литературу вместе с детальным
введением предыдущего раздела помогут интересующемуся чита-
читателю сориентироваться в растущем потоке литературы этой обла-
области физики.
3.6. Гомотопическое рассмотрение систем конденсированных
сред
В разд. 3.4 мы рассмотрели решения в виде уединенных волн
5^/B)-калибровочной теории в четырех измерениях. Аналогичный
анализ можно провести для многих других теорий. Хотя возмож-

82 ГЛАВА 3
ность получения точных решений в аналитической форме зависит
от конкретной модели, гомотопическая классификация конфигу-
конфигураций с конечной энергией может быть проведена для многих
моделей. Такая классификация применима также в системах кон-
конденсированных сред, например в жидких кристаллах, ферро-
ферромагнетиках, жидком гелии и сверхпроводниках с линиями тока.
Нетривиальные граничные условия использовались в некоторых
системах конденсированных сред задолго до того, как их ввели
в физике элементарных частиц и обобщили на релятивистские
системы и неабелевы калибровочные теории.
Мы не будем подробно обсуждать каждую из этих моделей, так
как для них справедливы принципы, использованные в предыду-
предыдущих разделах. Упомянем только некоторые модели и рассмотрим
гомотопическую классификацию их решений.
С этой целью приведем необходимые результаты по гомотопи-
гомотопическим группам из книги Стинрода [3211:
nn(Sn) = Z, C.90а)
nr,(Sm) = 0 при n<m, C.906)
пп (Si) = 0 при п > I, C.90в)
где пп (Sm) соответствует гомотопической группе отображения Sn
в Sm, a Z — группе целых чисел, т. е. отображения Sn -> Sn
разбиваются на дискретное бесконечное множество гомотопиче-
гомотопических классов, каждый из которых характеризуется целым числом.
Это справедливо для всех положительных целых п. В C.906)
и C.90в) нуль справа означает, что группа тривиальна, т. е.
в этих случаях все отображения могут быть деформированы
друг в друга.
Классическим примером в физике конденсированных сред, где
применяются такие гомотопические соображения, является система
трубок тока в сверхпроводниках второго рода. Но сначала на-
напомним, что мы выбрали неабелеву теорию C.42) в качестве ка-
калибровочной модели в C + 1) измерениях. Что было бы, если бы
мы выбрали вместо нее более простую абелеву калибровочную
модель? Абелев аналог C.42) описывается лагранжианом в (D + 1)
измерениях
2 (х, f) = - 4-^^v + 4" (ЭД* (&Ф) - 4-Ь (| ф |2 - ЯJ, C.91)
где ф (х, t) — комплексное скалярное поле, F^v — электромаг-
электромагнитный тензор F^ = 5цЛv — оИц и
О„ф = (д„-1еАг)ф. C.92)
Проводя такой же анализ, как выше, можно найти, что конфигу-
конфигурации с нулевой энергией имеют | ф (х, t) | = F и, следовательно,

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 83
конфигурации с конечной энергией должны удовлетворять усло-
условиям
\4>\->-F при х->оо, C.93)
Dvj> = (д^ф - ie-А^ф) -> 0 при х -»- оо. C.94).
Фаза комплексного поля на бесконечности не фиксируется этими
граничными условиями. Так как значения фазового угла а поля
ф = | ф | ехр (га) образуют окружность 5Ь граничные условия
отображают поверхность на пространственной бесконечности в Sx.
До сих пор мы не конкретизировали пространственную размер-
размерность D. Физически наиболее интересен случай D = 3, когда
поверхность на бесконечности есть 52. В силу C.90в) я3 Eг) = О,
т. е. все разрешенные граничные условия имеют тот же гомото-
гомотопический класс. Таким образом, для абелевой модели C.91)
при D = 3 не существует нетривиальных гомотопических секто-
секторов решений. (Это одна из причин, почему мы выбрали для об-
обсуждения в разд. 3.4 неабелеву SU B)-систему в трех простран-
пространственных измерениях.) Для абелевой модели то же справедливо
для всех D ^ 3, так как nD_x (SJ = 0 при Dij3. Только для
D = 2 (система с двумя пространственными и одним временным
измерениями) пространственной границей является Slf что ведет
к нетривиальной гомотопической группе пх (S]). Это знакомая
нам группа чисел наматываний. Число наматываний является
сохраняющейся величиной и постоянно даже для зависящих от
времени решений системы C.91) в B + 1) измерениях.
Эта абелева модель в B + 1) измерениях была детально изу-
изучена Нильсеном и Ольсеном [262 ], работу которых можно считать
предвестником монополя т'Хофта—Полякова. Нильсен и Ольсен
рассматривали эту систему для моделирования двухструнной
картины в физике элементарных частиц. Лагранжиан C.91)
является релятивистским динамическим аналогом процессов в ста-
статистической механике сверхпроводника второго рода, помещен-
помещенного в магнитное поле (см., например, [303]). При этом комплекс-
комплексное скалярное поле ф отвечает параметру порядка, а Лц — элек-
электромагнитное поле. Свободная энергия системы есть функционал
G [ф, Лц], имеющий в модели Ландау—Гинзбурга при темпера-
температуре' Т ниже критической температуры Тс следующий вид:
О[ф, AJ= \dx(±\<? - 1е\)ф\* + ±[\ф\*- F* ^
C.95)
здесь В = \ х А — магнитное поле. Отметим аналогию с га-
гамильтонианом системы C.91) для статических (или равновесных)
конфигураций с Ло = 0. Далее, если предположить инвариант-
инвариантность системы вдоль оси z (что приближенно справедливо для пла-
пластины сверхпроводящего материала, помещенного между пло-

84 ГЛАВА 3
скими полюсами магнита, поле В которого; направлено вдоль
оси z), то система становится существенно двумерной в плоскости
ху. Требование конечности энергии здесь заменяется требованием
конечности свободной энергии G. Для таких конфигураций в пло-
плоскости ху граничные условия, задаваемые C.95), тождественны
C.93), C.94) и имеют ту же гомотопическую группу пх (Sj). Суще-
Существование целого числа наматываний п связано с хорошо извест-
известным условием квантования потока. Напомним, что число наматы-
наматываний описывает число обходов фазой а окружности на простран-
пространственной бесконечности. Пусть окружность параметризуется 0,
тогда
2Л
о
Но, согласно условиям C.93), C.94), при |х| = г -> оо
+ {r,b)-+Fel*w, А^+(—1/е)(д^/ф)ш C.97)
Отсюда тангенциальная компонента Ав при г ->- оо равна
Поэтому
2j ±~§) A-d\ = +^x (поток), C.99)
о
где (поток) — полный магнитный поток через плоскость ху.
Мы видим, что требование, чтобы число наматываний п было це-
целым, равносильно «квантованию» полного потока через пло-
плоскость х-у, который становится при этом равным +2л/е, умножен-
умноженному на целое число.
Эффект квантования потока в сверхпроводниках хорошо
известен. Но может показаться странным, что мы получили его
из чисто классических соображений. Объяснение здесь анало-
аналогично приведенному выше в связи с условием квантования моно-
поля C.72). Как подчеркнул Коулмен [87], C.99) не является
точным условием квантования потока в сверхпроводниках. Пос-
Последнее имеет вид [303 ]
поток = 2nnfl/2q, C.100)
где 2<7 — заряд куперовской пары электронов. (Скорость света
положена, как и везде, равной единице.) В C.99) Й отсутствует,
а е — константа взаимодействия для лагранжиана C.91). Конечно,
лагранжиан C.91) допускает сохраняющийся заряд

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 85
но он не обязательно должен быть кратным е на классическом
уровне. Только в квантовом варианте теории константа взаимо-
взаимодействия е и заряд куперовской пары 2q связаны соотношением
2<7 —'eh, и C.99) становится условием квантования C.100).
Помимо этих общих топологических соображений хотелось бы
найти точные решения в различных секторах. Для этого ана-
аналогично анзацу C.73), C.74) для монополя рассмотрим цилин-
цилиндрический анзац
Аг = Ао = 0, Ав = А(г), <j> = F(r)e^, C.102)
где использованы полярные координаты (г, 0) на плоскости (х, у).
Граничные условия C.97) принимают вид
F (Г) -+F, А (г) ->■ п/ег. C.103)
Ясно, что этот анзац ведет к числу наматываний п. Уравнения
поля, получающиеся из C.95), с учетом анзаца C.102) сводятся к
C.104а)
- чг (т чг 1гЛ (г>0 + (еМ М - -г-)р W = °- <3- 104б>
Для произвольного "К аналитическое решение этой системы не-
нелинейных уравнений не известно. Но можно показать, что реше-
решения, если они существуют, экспоненциально быстро прибли-
приближаются к граничным значениям C.103). При г -> оо в C.1046)
можно подставить F (г) = F. Это делает данное уравнение линей-
линейным и решаемым, что приводит к следующему асимптотическому
поведению:
А (г) •-<■ (nfer) -\- const x exp (—eFr)/y г ■ C. !05а)
Подстановка C.105а) в C.104а) дает
F (г) F + const х exp (— y'T Fr). C.1056)
Г->ОО
Численные расчеты подтверждают существование несингулярных
решений с такими асимптотическими свойствами, причем, по-
видимому, по крайней мере решение с п = 1 (единичная вихревая
линия, или «трубка тока») является стабильным. Более общее и
строгое исследование существования таких решений проведено
Таубсом [325].
Заметим, что эти решения имеют конечный «размер» в двумер-
двумерной плоскости, т. е., как следует из C.105), Л„ и ^ при г -> оо
стремятся к своим граничным «вакуумным» значениям экспонен-
экспоненциально быстро. Магнитное поле, получаемое подстановкой
C.105а) в C.102) и C.92), также спадает к нулю экспоненциально

86 ГЛАВА 3
быстро nor. Все эти экспоненты имеют характерную длину, про-
пропорциональную F'1. Конечность размера связана с тем фактом,
что в отличие от О (З)-модели в разд. 3.3 или моделей Янга—Миллса
и СРп, которые изучаются в следующей главе, система C.91)
масштабно не инвариантна. Существование нетривиального реше-
решения с конечным размером в секторе с п = 1 данной модели
окажется очень полезным результатом,даже если не будет изве-
известна его точная аналитическая форма. Это решение исполь-
используется в гл. 10 для иллюстрации квантового эффекта инстан-
тонов.
Такие соображения применимы также к вихрям в гелии II,
где также параметром порядка является скалярное поле. Эта за-
задача в плоскости, перпендикулярной вихревой линии, сущест-
существенно двумерна, так что нетривиальная гомотопическая группа
пх (Sx) классифицирует конфигурации с такими вихревыми ли-
линиями. Вихревые линии здесь представляют собой так называемые
«линейные сингулярности». В то же время, так как л2 (Sj) = 0,
нетривиальных трехмерных секторов не существует, т. е. «точеч-
«точечные» сингулярности в Не II отсутствуют. В отличие от этого для
изотропных ферромагнитных систем с параметром порядка —
вектором намагниченности М — граничные условия допускают
различные направления единичного вектора m = М/| М |. Они
образуют поверхность 52, и, так как л2 E2) = Z, возможны то-
точечные сингулярности. Они аналогичны монопольным решениям
калибровочной теории SU B). Но ферромагнетик не имеет «ли-
«линейных сингулярностей», так как по C.906) пх E2) = 0. Другой
интересной системой является нематический жидкий кристалл,
характеризуемый вектором «директора» d при условии, что d
и —d неразличимы. Поверхностью вырождения в данном случае
является сфера S2, диаметрально противоположные точки которой
отождествлены. Такую структуру можно назвать Р2 = SJZ2,
и можно показать, что пх (Р2) =Z2. Таким образом, линейные
сингулярности могут существовать в таком жидком кристалле,
но они распадаются только на два, а не на дискретное бесконечное
множество гомотопических классов. Более детальное обсуждение
гомотопических свойств данных систем можно найти, например,
в работах [252, 337, 341].
Между приведенными выше примерами и более ранними при-
примерами, содержащими калибровочные поля, существует важное
различие. В последних примерах функционал энергии при сво-
свободной энергии включает ковариаятные производные скалярных
полей. При этом соответствующим выбором калибровочных полей
на бесконечности можно добиться обращения в нуль ковариант-
ных производных даже для зависящих от угла граничных условий
(см., например, C.94), C.97)). Таким образом, для конфигураций

МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 87
с конечной энергией возможны нетривиальные граничные усло-
условия. Но в жидких кристаллах, ферромагнетиках и т. п. калибро-
калибровочных полей нет. Здесь мы не привели выражения для свободных
энергий этих систем, которые можно найти в стандартной лите-
литературе по этим вопросам. Из данных выражений видно, что функ-
функционалы энергии включают только обыкновенные производные
от полей. Они не обращаются в нуль на бесконечности достаточно
быстро для нетривиальных граничных условий, и энергия таких
решений расходится в пределе бесконечного объема. Конечно,
реальные системы конденсированных сред имеют конечные объемы,
и энергия этих конфигураций остается конечной. Поэтому они
физически допустимы.
Другая возможность гомотопической классификации возникает
не из граничных условий, а из внутреннего поведения полей.
Мы видели это на примере модели О C) в разд. 3.3. Там присут-
присутствие члена (grad^J в энергии устраняло угловую зависимость
граничных условий в пределе бесконечного объема, но тем не
менее гомотопическая классификация, основанная на поведе-
поведении ф (х) при конечных х в двух пространственных измерениях,
была возможна. Следует отметить, что О (З)-модель полезна также
в физике твердого тела. Она представляет собой в некотором
смысле предел двумерного изотропного ферромагнетика. Поле
ф (х) соответствует спинам такой системы, а C.15) — гамильто-
гамильтониану. Белавин и Поляков [30], получившие решения для О C)-
модели, подчеркнули, что эти решения соответствуют метаста-
бильным «псевдочастицам», так как обеспечивают экстремум га-
гамильтониана. Так как частицы имеют конечную энергию, конеч-
конечная их плотность (порядка ехр (—ElkT)) всегда будет возбуждена
при любой самой малой температуре. Именно поэтому статические
солитонные решения с конечной энергией важны в статистической
механике систем конденсированных сред. Для О (З)-модели в двух
измерениях эти метастабильные состояния особенно важны. Хотя
их плотность при малой температуре мала, каждая «псевдоча-
«псевдочастица» может иметь произвольно большой размер в силу масштаб-
масштабной инвариантности гамильтониана C.15). Следовательно, они
могут занимать все пространство. Далее, каждая «псевдочастица»
с Q — 1 обладает спином ф, который может иметь произвольное
направление. Таким образом, Белавин и Поляков доказали, что
для такой системы дальний порядок нарушается при любой, даже
малой, температуре.
То, что солитоны играют важную роль элементарных возбуж-
возбуждений в термодинамике протяженных систем, было показано ка-
качественно Крумханслом и Шриффером [222]. Эта идея была
развита во многих работах (см. обзор [46]). Мы используем эти
соображения в гл. 10, рассматривая систему инстантонов в евкли-
евклидовой квантовой теории как инстантоцный газ,

ГЛАВА 3
3.7. Солитон-солитонные взаимодействия
Закончим наше изучение классических солитонов коротким
обсуждением их взаимодействий. Уже было подчеркнуто соответ-
соответствие единичного солитонного решения протяженной частице.
Найдем некоторое аналогичное соответствие между многосолитон-
ным решением и системой частиц. В частности, выясним, можно ли
аналогично случаю нескольких частиц хотя бы приближенно
описать динамику двух или большего числа солитонов, используя
потенциал взаимодействия, зависящего от расстояния между
ними.
Хотя некоторые модели обладают односолитонными решениями,
точные многосолитонные решения для большинства из них отсут-
отсутствуют. (Противоположные примеры типа модели синус-Гордона
редки.) Поэтому необходимо и полезно достичь качественного по-
понимания систем двух или более солитонов, используя интуитивные
аргументы и приближения. Так как наши уравнения поля нели-
нелинейны, суперпозиция односолитонных функций в общем случае
не будет решением. Но если солитоны достаточно далеки друг
от друга, их перекрытие мало. Тогда искажения каждого солитона,
вызванные нелинейными эффектами вследствие присутствия дру-
других, будут также малыми. Иначе говоря, можно ожидать суще-
существование решений (независимо от того, найдем ли мы их аналити-
аналитически или нет), соответствующих широко разделенным солитонам,
сохраняющим, за исключением небольших искажений, свою инди-
индивидуальность. В общем случае такие решения могут не быть ста-
статическими. Можно ожидать, что каждый солитон, воздействуя
на другие, не только их деформирует (поляризует), но и ускоряет.
Для того чтобы удержать солитоны на месте, необходимо вводить
дополнительные внешние силы.
Такую картину широко разделенных солитонов, схожую
с системой широко разделённых протяженных частиц, можно
реализовать в конкретной форме для специальных моделей.
В качестве простого примера возьмем кинки модели ф* B.25).
Граничные условия модели допускают конфигурации кинк —
антикинк, но точное решение такого вида неизвестно. Рассмотрим
не зависящее от времени уравнение этой модели
ф" ~Ц3 + т2ф = 0. C.106)
Как найдено в разд. 2.3, единственными решениями этого уравне-
уравнения с конечной энергией являются кинк, антикинк и тривиальные
решения ф = ±т/>/Х. Уравнение не имеет решений, которые
можно было бы рассматривать как широко разделенную статиче-
статическую пару кинк — антикинк. Это соответствует нашему ожида-
ожиданию, что кинк и антикинк взаимодействуют и не остаются стати-
статическими. Но если их удержать некоторой внешней силой, то стати-

МОНОПОЛИ.И ПОДОБНЫЕ ИМ РЕШЕНИЯ 89
ческое решение пары кинк — антикинк будет существовать. Такое
«удержание» можно провести следующим способом [280].
Рассмотрим вместо C.106) модифицированное уравнение ,
ф" - Щ3 + т2ф = a (R) {б (х - R/2) + б (х + #/2)}. C.107)
Правую часть можно рассматривать как две внешние силы, при-
приложенные к точкам х = ±R/2. В отличие от C.106) уравнение
C.107) обладает решением с конечной энергией, напоминающим
пару кинк — антикинк, разделенную расстоянием R. Решение,
конечно, имеет разрыв в точках х = ±R/2. Оно возникает только
в том случае, если величина внешних сил a (R) выбрана соответ-
соответствующим образом как функция от Р. Кинк и антикинк в этом ре-
решении искажены по сравнению с их первоначальными формами, но
искажение стремится к нулю при R->~oo. Все эти свойства соответ-
соответствуют нашим ожиданиям и аналогии с протяженными частицами.
Мы не будем рассматривать детали или вывод решения кинк —
антикинк (см. [289]). Уравнение C.107) интегрируется непосред-
непосредственно, при этом решение получается в эллиптических интегра-
интегралах. При подстановке этого статического решения в интеграл
энергии B.19) имеем [289]
Е (R) =-Ц^-£- - 8 V 2 4-ехр (- VYmR) +
-f-члены более низкого порядка по R. C.108)
Первый член есть масса покоя свободных кинка и антикинка.
Остальные члены можно отнести к потенциальной энергии взаимо-
взаимодействия V (R) пары кинк — антикинк
~ - (8 K2~m3A)exp(- V2 mR). C.109)
Отметим, что это взаимодействие 1) соответствует притяжению
и 2) является сильным при малом значении постоянных взаимо-
взаимодействия Х/т2. Аналогичный потенциал притяжения можно полу-
получить таким же способом для пары солитон — антисолитон модели
синус-Гордона. Мы привели выражение для потенциала C.109)
только для больших R, так как для малых R кинк и антикинк
теряют свою индивидуальность и, следовательно, V (R) перестает
иметь смысл.
(Потенциал C.109) напоминает потенциал одномезонного об-
обмена из квантовой теории поля. Действительно, в гл. 5 при кван-
квантовании этой теории выясняется, что она имеет мезон массы У 2т
и кинк-кинк-мезонную вершину порядка If-]/'К. Если вспомнить,
что две такие вершины появляются при обмене кинков мезоном,
и ввести для учета требований размерности множитель т, то
борновская амплитуда одномезонного обмена даст потенциал
V (R) = с (m3A) exp (— VJ mR),

90 fлайд 3
где с — безразмерная величина. Потенциал V (R) C.109) имеет
такую же форму, хотя он получен из чисто классической полевой
системы. Это пример свойства, которое обсуждается в гл. 5,
а именно того, что характерные черты непертурбативных солито-
нов в квантовой теории определяются в основном их классиче-
классическими аналогиями.)
Мантон [242, 243 ] подошел к проблеме межсолитонных сил
по-другому. Вместо того чтобы получать их из статического
потенциала, он умножает массу солитона на его ускорение, полу-
получаемое в присутствии другого солитона. Ускорение находится
построением решения в виде ф (х — V2fltf2), где ф (х) — статиче-
статическая солитонная функция. Считая ускорение а малым (разумное
предположение для достаточно разделенных солитонов), он на-
находит его значение, потребовав выполнимости уравнений поля
в низшем порядке по а. Он также показывает, что для случаев,
когда можно найти статический потенциал типа C.109), соответ-
соответствующая сила равна массе на ускорение солитона. Это усиливает
аналогию с ньютоновскими частицами и оправдывает введение
такого потенциала.
В первой из работ Мантон применил свод метод для определе-
определения силы, действующей между двумя монополями т'Хофта —
Полякова, что является более сложной задачей по сравнению
со случаем кинков. В частности, он получил следующий интерес-
интересный результат. Интуитивно можно ожидать, что два монополя
обладают дальнодействующей силой m2/R2, где т. — магнитньм
заряд каждого из них. Однако Мантон нашел, что в пределе Пра-
сада — Зоммерфельда (к -> 0 в C.42)) дальнодействующая сила
между монополями одинакового заряда обращается в нуль, а ме-
между монополями с противоположными зарядами удваивается по
сравнению с ожидаемым магнитостатическим значением. Причина
заключается в том, что в пределе К -> 0 в C.42) скалярное поле
безмассово. Обмен скалярным бозоном приводит к возникновению
силы притяжения О A/R2), компенсирующей магнитостатическое
отталкивание одинаковых монополей и увеличивающей магнито-
магнитостатическое притяжение монополей с противоположными заря-
зарядами. Эти соображения были развиты и обобщены О'Рейферти
и др. [268] на монопольные решения произвольных компактных
групп с хиггсовскими скалярными полями. Об изучении монополь-
дионных взаимодействий см. работу Джерсака и др. [202]. Силы
между рассмотренными выше вихрями абелевой хиггсовской
модели получены Шапошником [3021. Радж Лакшми [293] иссле-
исследовал силу, действующую между заряженными солитонами ком-
комплексных скалярных полей.

ГЛАВА 4
КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ
4.1. Что такое инстантон?
Термин «инстантон» относится к локализованным решениям с ко-
конечным действием классических евклидовых уравнений поля.
Евклидов вариант теории или системы полевых уравнений вво-
вводится заменой метрики Минковского giv (g00 — 1, gi! = —bi}
при i, j Ф 0; при всех остальных значениях^ = 0) на евклидову
метрику 8^v. Пространственно-временной координатный вектор
(л^мин (\i = 0, 1, 2, 3 в четырех измерениях) заменяется вектором
(^)евкл (ц. = 1, 2, 3, 4). Компоненты вектора (л^)евкл действи-
действительны, но евклидова теория инвариантна относительно О ^-пре-
^-преобразований, а не относительно преобразований Лоренца, т. е.
4
[X' X )евкл = 2j \X /евкл
ц=1
— инвариант. Соответственно лоренцев тензор заменяется
О D)-тензором. Например, вместо действительного векторного
поля (А»)Миа берется действительное поле(Л^)евкл, причем ОD)-пре-
образования оставляют (^4A^4A)евкл инвариантным. На индексы
«внутреннего пространства», такие, как а в уравнении C.10),
переход к евклидовой метрике не оказывает влияния. Поскольку
в евклидовой системе метрикой является 8^v, различий между
верхними и нижними пространственно-временными индексами нет.
Отметим, что это не просто замена обозначений. Евклидова
система — это не система Минковского, записанная в новых
переменных. Например, если (х^мин имеет четыре действительные
компоненты с инвариантом (х\ — х2), то {х^)евкл также имеет
четыре действительные компоненты, но с инвариантом BJt*2iI
Две системы различны. Но евклидову систему можно считать
аналитическим продолжением системы Минковского. Если взять
действительное время t = х0 системы Минковского и продолжить
его на мнимые значения, то (лч)евкл = И можно использовать
как четвертую компоненту евклидова координатного вектора
с неизменными остальными координатами х±, х2, х3. Тогда после
такого продолжения (хнл:и)е]кл будет связано с внутренним произ-
произведением МИНКОВСКОГО СООТНСШеНКеМ ^

92 ГЛАВА' 4
Аналогичное продолжение совершается для временных компонент
всех четырех-векторов. Для получения евклидова действия мы
аналитически продолжим действие Минковского и умножим его
на (—г), т. е. 5евкл = — i EМин)ПрОдолженное. Множитель (+-i),
не влияющий на классические уравнения, введен для удобства
в квантовом варианте теории. Кроме того, 5евкл с множителем
(—i) неотрицательно и напоминает функционал энергии стати-
статических конфигураций (см. ниже).
В качестве иллюстрации рассмотрим систему Клейна — Гор-
Гордона с действием
Ямин = \cU\dx[± (|fJ - -L (V*)« - т*ф*] D.1)
и уравнением поля
E) + m^ = 0. D.2)
Для получения евклидовой системы мы продолжим действитель-
действительное t на t = —ix4, а 5Мин — на 5евкл, используя соотношение
5еВкл = — *5мин- В результате евклидово Действие имеет вид
5евьл = J dxx \dx[-L (^J +.yW)a + trff ], D.3)
что приводит к евклидову уравнению поля
B2 + У2)ф-т2ф = 0. D.4)
В отличие от уравнения D.2), содержащего гиперболический
дифференциальный оператор, уравнение D.4) имеет эллиптический
оператор, допускающий другую систему действительных несин-
несингулярных решений.
Инстантоны есть локализованные решения таких евклидовых
полевых уравнений с конечным евклидовым действием. Может
возникнуть вопрос: почему нас должна интересовать эта евкли-
евклидова версия, если физически интересные системы погружены
в пространство-время Минковского? Ответ будет дан в гл. 10.
Мы увидим, что некоторые свойства квантовополевых теорий
в пространстве-времени Минковского удобно изучать, начиная
с классических решений евклидовой версии их полевых уравне-
уравнений. Одним из этих свойств является замечательный феномен
квантового туннелирования между вырожденными классическими
основными состояниями. Евклидовы инстантонные решения так же
важны для квантовых полевых теорий в пространстве-времени
Минковского, как классические солитонные решения. Роль ин-
стантонов в квантовой полевой теории, так же как роль квантовых
солитонов, прояснится при квазиклассическом разложении. Оно
начинается с классических решений теперь уже евклидовых поле-
полевых уравнений.

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ 93
В этой главе мы обсудим некоторые примеры инстантонных
решений на чисто классическом уровне. Более широкий вопрос
об их роли в квантовой теории будет рассмотрен в гл. 10 и 11.
На классическом уровне инстантоны не очень отличаются от
статических решений в пространстве-времени Минковского. Это
происходит из-за того, что статические решения зависят только
от пространственных координат, образующих евклидову под-
подгруппу пространства-времени Минковского. Действительно,
некоторые из уже полученных статических решений можно не-
непосредственно использовать как инстантоны систем с меньшим
числом измерений (разд. 4.4). Единственное отличие состоит в том,
что требование конечности энергии солитонов заменяется требо-
требованием конечности евклидова действия для инстантонов. Отметим,
что евклидово действие, такое, как в примере D.3), имеет струк-
структуру энергии конфигурации статического поля с числом измере-
измерений, увеличенным на единицу. Кроме того, при вычислении
квантовых эффектов инстантонов в гл. 10 и 11 мы увидим, что
вклад классического инстантона пропорционален ехр (—5евкл).
Если 5еЕКЛ бесконечно, то этот вклад исчезает. Таким образом,
по крайней мере в используемом квазиклассическом разложении,
имеют значение только решения с конечным евклидовым дей-
действием. За исключением этой замены статической энергии евкли-
евклидовым действием, при обсуждении классических инстантонов
мы будем следовать приведенному выше обсуждению статических
солитонных решений.
В следующих двух разделах мы рассмотрим инстантоны си-
системы Янга — Миллса. Именно с них работой Белавина и др. [30]
началось изучение инстантонов. Более того, неабелевы калибро-
калибровочные теории, пример которых дает система Янга — Миллса,
чрезвычайно важны в современных теориях элементарных
частиц. В разд. 4.4 и 4.5 мы обсудим инстантоны других систем.
В этой главе, если не оговорено другое, мы будем работать только
с евклидовыми системами. Поэтому индекс «евкл» мы опускаем.
4.2. Евклидовы конфигурации Янга—Миллса
Мы уже встречались в гл. 3 с полями Янга — Миллса Л£
в связи с монопольным решением. Тогда система включала также
«материальные поля» фа. Теперь мы их опустим и рассмотрим
SU B)-калибровочные поля А\ с самодействием. Для упрощения
записи полезно выразить три векторных поля А£, а = 1, 2, 3,
через матричные вектор-поля А^.
^^-Аа„(х), D.5)

94 ГЛАВА 4
где х заменяет (л^, х2, х3, л:4). Здесьg — константа взаимодействия,
задаваемая C.43), а оа — обычные спиновые матрицы Паули:
О 1 \ / 0 — i \ /1 О
i о)' «М, о )' «Цо -1
Точнее говоря, аа12 образуют три генератора двумерного пред-
представления группы SU B), являющейся калибровочной группой
нашей системы. Определенные соотношением D.5) антиэрмитовы
матрицы размерности 2x2 Лр,(л:)дают для каждого \i в каждой
точке (л:) ту же информацию, что и три поля Янга — Миллса
А% {х). Соответствующим образом определим матричный тензор
поля:
С применением этих матриц соотношения C.43), C.45), C.46)
упрощаются. Легко проверить, используя коммутационные соот-
соотношения [оа/2, оь/2] = 1гаЬсос12, что
бц^а^-аИц + Иц, av]. D.7)
Калибровочные преобразования C.45), C.46) формально не ме-
меняются при переходе к евклидовой метрике. Для матричного
поля Лр, они имеют вид
^ + UdJJ-^, D.8а)
G^-^UGpyJU-1. D.86)
Отметим, что, хотя C.45), C.46) были записаны в 3 х 3-предста-
влении групповых элементов U (x, t) и генераторов, то же пре-
преобразование справедливо для любых других представлений. Здесь
в соответствии с определением D.5) мы используем 2 х 2-пред-
ставление. Мы часто будем использовать тождество
dll(UU-1) = O = (dvU)U-1 + Udti(U-1). ■ D.9)
Другое преимущество такого матричного обозначения заключается
в том, что оно показывает очевидное сходство модели с электро-
электромагнетизмом, где калибровочной группой является абелева группа
U A). В последнем случае групповые элементы записываются
в виде U = е'а<*>, поля А^ (х) представляют собой числа, а не
матрицы, а соотношения D.7), D.8) сводятся к знакомым уравне-
уравнениям электромагнетизма.
Для евклидовой системы Янга — Миллса имеем четыре ма-
матричных поля А^ ([х = 1,2, 3, 4) в каждой евклидовой простран-
пространственной точке Хц (\х = 1,2, 3, 4). Евклидово действие выводят
из лагранжиана Минковского C.42) согласно описанной выше

Классические инстантонные решения 95
процедуре, опуская скалярное поле ф" и используя матричное
обозначение для А^. Оно имеет вид
Отметим, что константа взаимодействия g входит явно в действие
только через множитель —l/2g2. Остальная зависимость от g
вошла в масштаб поля А^ согласно определению D.5). Таким
образом, в классическом контексте величина константы взаимо-
взаимодействия не очень существенна, тогда как в квантовом контексте
величина действия, отнесенная к й, может играть важную роль.
Поэтому мы оставим множитель —l/2g2 в D.10). В результате
получаем следующее евклидово уравнение Янга — Миллса:
ОД, = a^v + [\, G^] = 0. D.11)
В этом матричном обозначении очевидно, что как действие, так
и уравнение поля инвариантны при калибровочных преобразова-
преобразованиях D.8).
Инстантонами Янга — Миллса являются решения уравнения
D.11) с конечным действием. Искать их мы будем так же, как
в рассмотренных выше примерах монопольных и других стати-
статических решений. Сначала найдем граничные условия, которым
должны удовлетворять все полевые конфигурации с конечным
действием (решения D.11) с конечным действием являются их
подмножеством). Основываясь на этих граничных условиях, мы
проведем гомотопическую классификацию. Это займет весь дан-
ный]*раздел. Собственно решения будут получены только в сле-
следующем разделе.
На первом этапе поиска конфигураций с конечной энергией
рассмотрим конфигурации с нулевым действием. В силу D.10)
равенство S = 0 возможно тогда и только тогда, когда G^v — 0.
Это уравнение имеет бесконечное множество решений для поля А^.
Ему удовлетворяет не только А^ = 0, но и любое другое поле,
полученное калибровочным преобразованием из А^ = 0. Эти
поля, называемые «чистыми калибровками», определяются выра-
выражением (см. D.8а))
(U-l(x)), D.12)
где U (х) в каждой точке х есть произвольный элемент группы
SU B) в ее представлении 2x2. Читатель может непосред-
непосредственно проверить, используя D.7), что D.12) дает G^ = 0.
Можно проверить также, что G^ = 0 всегда приводит к D.12).
Для конфигураций с конечной энергией из D.10) ясно, что
тензор G^ должен исчезать на границе евклидова 4-пространства,
т. е. на трехмерной сферической поверхности S£*H3) при г = оо,
где г = | х | = (х\ + х\ + х\ + х1I/2 — радиус в четырех изме-

96 ГЛАВА 4
рениях. Точнее, G(lV должен стремиться к нулю быстрее, чем \1гг
при г-> оо. Исчезновение G^ на S^a3) в свою очередь означает,
согласно D.12), что для А^ имеются следующие граничные усло-
условия:
lim Att(x) = limUdvU-1, D.13)
r->oo r-*-oo
где U — некоторый элемент группы, являющийся матричной
функцией. Основываясь на D.13), свяжем с каждой конфигура-
конфигурацией Лц, (х), которой соответствует конечное действие, групповую
функцию 0, определенную на сфере S<*H3) бесконечно большого
радиуса. Эту поверхность можно параметризовать тремя пере-
переменными а1; а2, а3, которыми могут быть, например, сферические
углы в четырех измерениях. Но если функция U зависит только
от аи а2, а3, то для нее не имеет смысла производная по радиусу,
тогда как в общем случае А^ (х) может иметь радиальную ком-
компоненту. Для преодоления этой трудности необходимо калибро-
вочно преобразовать А^ так, чтобы радиальная компонента везде
была равна нулю. Для этого рассмотрим А^ (х) с ненулевой ра-
радиальной компонентой Ат(х). Совершим калибровочное преобра-
преобразование, согласно D.8а), используя в качестве калибровочной
функции объект
U (а) = Р exp j dr'AT (x1) I. D.14)
Поясним обозначения в D.14). Эта функция является примером
«упорядоченных по траекториям» экспонент — очень полезной
конструкции в калибровочной теории [357]. Для заданной точки х
рассмотрим траекторию, которая для случая D.14) идет из начала
координат вдоль радиус-вектора. Компонентой А^, параллельной
траектории, является Ат. Таким образом, D.14) содержит криво-
криволинейный интеграл от А^ вдоль радиальной траектории.
Поскольку"поле А^ {х') — матрица, зависящая от х', такие ма-
матрицы для различных х' в общем случае не коммутируют и их
порядок следует определить. В D.14) порядок задается опре-
определением U в виде произведения экспонент exp (Ardr') от каждого
инфинитезимального элемента траектории, расположенных после-
последовательно от начальной точки (х = 0) до конечной точки х.
Символ Р обозначает, таким образом, «упорядочение по траекто-
траекториям». Вообще говоря, упорядоченная по траекториям экспонента
имеет вид Р (exp dx^AA, a D.14) является частным случаем.
Отметим, что, так как Лц (л:) — элемент алгебры Ли (см. D.5)),
О (х) для каждой точки х — элемент калибровочной группы.
Поэтому эту функцию можно использовать в калибровочных
преобразованиях.

КЛАССИЧЕСКИЕ ЙНСТАНТОННЫЕ РЕШЕНИЯ 97
Калибровочно преобразуем заданное А^ (х), используя калиб-
калибровочную функцию U (х). Радиальная компонента полученного
из D.8а) преобразованного поля А'^ (х) обращается в нуль. Полу-
Получаем
А'г (х) = UAr @)~1 - (drU) (f/)-1 =U[Ar- Ar] (f/)-1 = 0.
Поскольку действие калибровочно-инвариантно, А^ вместе с А^
обладает конечным действием. Комбинируя это с соотношением
А'г = 0, получаем граничные условия D.13) в виде
(A'v(x)) (ф„з) =U(au a2, а3)д^Ц-1 (аь а2, а3), D.15)
где U (а1; а2> аз) должна быть определена только на S<*H3>. Ниже
мы проведем гомотопическую классификацию функций U (аи
а2, а3). Будет показано (см. D.18)), что гомотопический индекс Q
можно записать в виде калибровочно-инвариантного интеграла
по полям. Таким образом, в интеграл можно подставить перво-
первоначальное поле Лр, ,(х) вместо калибровочно-преобразованного
поля Ali (x). Отсюда гомотопический индекс Q можно связать
с любой конфигурацией А^ (х) с конечным действием.
(Следует помнить, что U (а1; аа, а3), определенная только на
5<Физ), не может быть использована в качестве калибровочной
функции в несингулярных калибровочных преобразованиях. Для
последних необходима несингулярная во всем пространстве U (х).
Наша U (а1; а2, а3) в общем случае даже не будет граничным
значением несингулярной U (х). К этому важному замечанию,
сделанному Коулменом [89], мы вернемся еще ниже.)
Граничные условия D.15) допускают бесконечное множество
решений, связанных с различным выбором U (а1; а2, а3). Эти
функции можно классифицировать с помощью гомотопических
соображений. Так как матрицы U образуют двумерное предста-
представление SU B), функции U (а1; а2, а3) соответствуют отображе-
отображению S^H3) в групповое пространство SU B). Для классификации
таких отображений рассмотрим топологию группового простран-
пространства. По определению SU B) матрицы U образуют набор всех
унитарных унимодулярных матриц 2x2. Такие матрицы можно
однозначно записать в виде
tf=S<W D.16)
где s4 = / — единичная матрица 2x2, sh 2,3 = iau u, a ^ -
четыре произвольных действительных числа, удовлетворяющих
условию
2^=1. D-17)
4 Раджараман Р.

98 ГЛАВА 4
Таким образом, группа параметризована четырьмя действитель-
действительными переменными, удовлетворяющими условию D.17). Отсюда
групповым пространством является трехмерная поверхность еди-
единичной сферы в четырех измерениях. Назовем эту поверхность
S<BH>. Функция (/(«!, а2,'а3) отображает S**' в S3BH)-
Отметим сходство с обсуждением монопольной системы
в разд. 3.4. Там граничные условия отвечали отображению S2
в S2. Здесь мы имеем похожую ситуацию для трехмерных сфери-
сферических поверхностей. Из C.90) получаем, что соответствующая
гомотопическая группа я3 (S3) также изоморфна группе целых
чисел Z.
Следовательно, отображения S<*H3) -> S<BH) можно подраз-
подразделить на дискретное бесконечное множество гомотопических
классов, характеризуемых целым числом Q. Это целое число
часто называют индексом Понтрягина. Отображения одного класса
не могут быть непрерывно деформированы в отображения другого
класса.
Так как функции U (а1; а2, а3) можно классифицировать по
гомотопическим классам, конфигурации с конечным действием
Лр, (л:) также можно классифицировать по секторам, характеризу-
характеризуемым тем же индексом Q. Каждый сектор соответствует опре-
определенному гомотопическому классу U (ах, а2, а3), содержащемуся
в граничных условиях D.15) для А^. Поле А^ (х), принадлежащее
в 4-пространстве к определенному сектору Q, нельзя непрерывно
преобразовать в другой сектор, не нарушив конечности дей-
действия. Если это было бы возможно, то U («!, а2, а3), связанное
с граничным значением А^ (х), было бы также переведено из одного
гомотопического класса в другой, что невозможно по определе-
определению. Можно записать точный интеграл для индекса Понтрягина
в терминах полей аналогично тому, как это было сделано для
индекса Q монопольной системы:
Q = j Q (х) dH = - -^ \ d*x Tr [G^G^], D.18)
где дуальный тензор G^ определен следующим образом:
G)i\ — ~2 брлфо^ро- D.1У)
Докажем, что интеграл в D.18) действительно дает гомотопи-
гомотопический индекс Q. Доказательство будет несколько длинным, но
основная идея состоит в том, что Q есть «число наматываний»
сферы S£BH> на S|*H3', т. е. сколько раз групповое пространство
SUB) покрывает поверхность на бесконечности S|*H3). Мы хотим
показать, что интеграл в правой части D.18) дает это число на-

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ 99
матываний. Сначала запишем этот интеграл в виде поверхно-
поверхностного интеграла по S<*H3'. Начнем с очень полезного тождества
Dp.Gp.v ее дД^, + Ир,, Gpv] ==
[Л,,, (даА$ + ЛаЛэ)]} = 0, D.20)
где последнее равенство просто получается после раскрытия ско-
скобок и учета антисимметрии е^а^. Это тождество требует только,
чтобы тензор Gpv подчинялся определяющему уравнению D.7),
и не требует выполнения уравнения D.11). Отметим, что, когда
калибровочной группой является U A), а поля А^ — числа, а не
матрицы, тождество D.20) сводится к евклидову варианту второго
ковариантного уравнения Максвелла C.66). Используем D.20) для
записи «плотности Понтрягина» Q (х) через дивергенцию. Имеем
- 16я2<2 (х) = Tr [G^J = Тг [(д^Аъ - а„4) Gtiv +
+ (ДА- - AyAj g^] = Tr {(a^v - аул,о 6^ + лц hv, g^]} =
= Tr [a,A—а^№) G^v—vAv] = Tr [d^G^ - dv (ЛД„)], D.21)
где использовано свойство цикличности следа и тождество D.20).
Далее, разложим G^ в ряд в D.2.1). Получим
х) = Tr {EtlvaP l(d^Av) EаЛр + ЛаЛр) -
=Tr {e^vap [2^ (л,,5аЛр+ \AsAaA
D.22)
где использовано соотношение
ТГ [8pVa|3 (а,АУ ЛоЛр] = 1" Tr [^vap^ (i4Vi
которое следует из цикличности следа и антисимметрии
Получаем
Q(x) = d^, D.23)
где
/р = - A/8я2) ЕAтр Тг [ ЛУ (а«Лр + -| ЛаЛр)] . D.24)
Следовательно,
J f D.25)

100 ГЛАВА 4
Далее на поверхности на бесконечности S|*H3) наши конфигура-
конфигурации с конечным действием имеют Gap = 0, поэтому е|хтр5аЛр =
= —ецУорЛоЛр. Таким образом,
(j) йо^^Тт[А,АаА^. D.26)
ф)
5(физ)
Наконец, подставляя асимптотические выражения D.15) для полей
Лц, получаем
Q = - W Ф <KwPTr [(<Щ f/ (aaf/) f/ (aptf) (/-*]. D.27)
Таким образом, мы записали объемный интеграл D.18) как поверх-
поверхностный интеграл с подынтегральным выражением целиком в тер-
терминах группового элемента — функции U на S^H3>, соответству-
соответствующего произвольной конфигурации с конечной энергией. Далее
нам надо найти выражение для определения группового объема,
т. е. групповую меру; тогда мы сможем узнать, сколько раз обер-
обертывается группа вокруг S|*H3) для данной калибровочной функ-
функции U. Как уже было отмечено, параметризованное пространство
SU B) есть гиперсфера SJ,BH>. Ее можно параметризовать либо
четырьмя декартовыми переменными а^ D.16) со связью D.17),
либо (что эквивалентно) тремя независимыми переменными h,lt
£2 и £3. которыми могут быть, например, сферические углы в 4-про-
странстве. Элемент группы U соответствует некоторому значению
(£i> £2. Ы этих параметров. В окрестности U групповую меру
можно записать в виде
р (&, 12, У dtidtA D.28)
где плотность р (£1; £2> £з) должна удовлетворять свойству ин-
инвариантности d\x (U) при групповых трансляциях. Для пояснения
умножим U на любой фиксированный элемент группы U:
U' = UU. D.29)
Пусть U' соответствует параметрам (£|, ^2. Ш- Пусть набор эле-
элементов инфинитезимального объема d^d^d^ около (^, |2. Ы
занимает после умножения на 0 некоторый объем d^ld^d^.
Конечно, d^id^i*) не обязательно равен d\\ dh.2dh.3- Плотность р
должна быть такой, что
D.30)
Это требование представляет собой обобщение на непрерывные
группы свойства конечных групп сохранять число групповых

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ 101
элементов при умножении элементов на некоторый заданный
элемент. (Мы умножили на О слева. Получившийся результат
для группы SU B) справедлив также и для умножения справа.)
Этому требованию удовлетворяет следующий выбор р (Ei. £2> £з):
p(Ei, Еа, У = егдТг (U^-^U-^U-^), D.31)
где групповые элементы записаны в матричном представлении.
При умножении на U слева имеем
и=u-iur, u-l = (U
Тогда
p(Ei, Еа. Еа) = е,лТг ((f/Г1^-1-^"^^')-1 X
(^^^)^^§- D.32)
у dlp dlq д\г j dli д\] dlh v '
Ho
di; dl'q dl'r _
33.
где Det | 517^1 | —якобиан перехода от (Ei, E2. Ез) K (Ei. E2. Ез)-
Таким образом, D.32) сводится к
Р(Еь Е2, Ез) = р(Еь U, E3)Det|dS7dU
Следовательно,
Р (Е,, Е2, Ь) dEi rffe dEs = р (EI, E5, Е5) dE{ d£5 d£3. D.34)
Таким образом, мы видим, что выбор D.31) удовлетворяет требо-
требованию D.30). При подстановке D.31) в выражение D.30) послед-
последнее дает групповую меру.
Нам осталось показать, что поверхностный интеграл D.27)
для Q сводится к интегралу по групповой мере. Мы уже отметили
некоторое сходство между D.31) и D.27). Но в D.31) входят произ-
производные dUld\t, а в D.27) — производные дШдх^. Для избежания
недоразумений повторим, что три параметра £2 описывают группо-
групповое пространство. 2 х 2-матрицы U изменяются с изменением Ег.
что приводит к соответствующим производным в мере D.31).
С другой стороны, интеграл D.27) связан с полевой конфигура-
конфигурацией, граничные условия которой D.15) задают калибровочную

102 гллпл i
функцию U, определенную на S|*H3>. В этом случае групповые
матрицы и, следовательно, соответствующие групповые пара-
параметры £г сами являются функциями пространственных координат
х^ точек сферы S^H3>. Таким образом, в D.27) матрицы U можно
считать функциями от £г, которые в свою очередь являются функ-
функциями от Хц. Имея это в виду, запишем D.27) в виде
. x_p!__pL.|k.l. D.35)
dxv дха ахр J v '
Так как D.35) выражено в декартовых координатах х^ и декарто-
декартовых тензорах, полезно перейти от гиперсферы S|*H3> на бесконеч-
бесконечности к гиперкубу. Восемью сторонами куба являются поверхно-
поверхности Хц = +оо при [а = 1, 2, 3, 4. Отметим, что теорему Гаусса,
использованную в D.25), а также гомотопические выводы это
гладкое преобразование не затрагивает. Возьмем любую поверх-
поверхность гиперкуба, скажем л:4 = —оо. Ее вклад в интеграл D.35)
можно записать в виде
-1— [ dx dx dx~r Tr (l]-i*Ll]-i®Lv-i dU
D.36)
где m, n, l изменяются от 1 до 3. Но
Uj Ц l2dt*. D.37)
Следовательно, вклад поверхности л:4 = —оо в D.36) есть
' D-38)
т. е. интеграл по групповой мере с точностью, возможно, до по-
постоянного множителя, который мы рассмотрим ниже. Аналогич-
Аналогичные вклады дают все восемь поверхностей гиперкуба. Поэтому
их сумма D.35) записывается в виде
Q~\dt1 dtzdlsp(El 6,, Ы - j Ф (U). D.39)
Таким образом, выражение для Q, первоначально записанное
в D.18) как функционал от полевых переменных, сводится к ин-
интегралу по групповому пространству от групповой меры. По-
Поэтому Q, грубо говоря, пропорционально объему группового
пространства, заметаемого калибровочной функцией U при ее
изменении на S**113'. Из приведенного выше гомотопического
анализа следует, что при интегрировании по S^' групповое
пространство S^BH> может заметаться целое число раз. Тогда Q

КЛАССИЧЕСКИЕ ЙНСТАНТОННЫЁ РЕШЕНИЯ ЮЗ
пропорционально этому целому числу. Константа (—16л2)-1
в D.18) выбрана так, чтобы Q было как раз равно этому числу.
Это можно проверить на примере
Ux (х) = (*4 + iXjOj)l\ х | = U * s D.40)
Сравнивая с общим представлением D.16), видим, что калибро-
калибровочная функция отвечает условию а^ = х^, т. е. каждая точка
на S<*H3) отображается на «соответствующую» точку с такими же
сферическими углами сферы S^BH). Следовательно, гомотопический
индекс Q должен быть равен единице. Подстановка D.40) в D.27)
после небольших вычислений дает
<2=
5(физ)
3
Используя равенство da^ = dQx^ | х |2, где dQ — элемент телес-
телесного угла в евклидовом 4-пространстве, получаем
D-42)
так как полный телесный угол в 4-пространстве равен 2я2. (От-
(Отметим для дальнейшего, что этот пространственный интеграл
равен единице не только при | х | -> оо, но и для любого радиуса
\х\.)
Это подтверждает, что с множителем —1/16я2 в D.18) Q опре-
определяет число наматываний, и заканчивает наш набросок доказа-
доказательства того, что D.18) дает гомотопический индекс.
Отметим, что, так как выражение Тг Ю^О^] калибровочно-
инвариантно (см. D.86)), то калибровочно-инвариантно и Q, но
граничные условия D.13) не инвариантны. При калибровочном
преобразовании U' (х) граничные условия А^ ->■ Ид^ {И'1) D.8а)
заменяются на
л; -> и' (ид^и-1) (иг1 + и'д» (иг1 = (vu) в„ (uvy1. D.4.З)
Возникает вопрос, как это изменение согласуется с калибровоч-
калибровочной инвариантностью Q. В частности, не могли бы мы выбрать
U' = U-1, так что Лц = 0 на S<4>H3>? Если бы это было всегда
возможно, величина Q сводилась бы к нулю чисто калибровочным
преобразованием (см. D.26)) независимо от ее первоначального
значения и в нарушение ее калибровочной инвариантности. Ко-
улмен [87] изящно доказал, что нельзя выбрать U' = U-1, за
исключением случая, когда U принадлежит сектору с Q — 0.
Важное замечание, сделанное нами при обсуждении уравнения
D.15), заключалось в том, что функция U в граничных условиях
должна быть несингулярно определена только на сферической

104 ГЛАВА 4
поверхности S<*H3>. Она представляет собой функцию U (аи а2, а3)
параметров этой поверхности и не обязательно должна быть
граничным значением некоторой несингулярной калибровочной
функции, определенной во всем 4-пространстве. С другой сто-
стороны, функция U' (х) в D.43) преобразует поле во всем простран-
пространстве и должна быть несингулярной для всех х. Запишем U' (х)
как U' (| х |, alt a2, а3) в сферических переменных; U' должна
быть непрерывной функцией от | х | на семействе гиперсфер. Для
фиксированного | х \ U' есть функция от alt а2, а3. С изменением
| х | эта функция изменяется непрерывно. При | х | = 0 U' @, аи
а2, а3) не должна зависеть от аг, чтобы не быть сингулярной.
Следовательно, она должна быть постоянной матрицей. Любую
постоянную матрицу SU B) можно непрерывным образом полу-
получить из единичной матрицы. Собирая все это вместе, приходим
к выводу, что V (| х |, «!, а2, а3) для всех | х | может быть непре-
непрерывно приведена к единичной матрице. Полагая \х\—*оо,
находим, что граничное значение U' на S^H3> также может быть
непрерывно приведено к единичному элементу, т. е. оно принад-
принадлежит сектору с Q = 0. В этом случае V не может быть равна LJ-1
на S^H3>, если только сама функция U не принадлежит сектору
с Q — 0. Следовательно, если U принадлежит Q Ф 0, то ее нельзя
непрерывно продолжить до | х \ = 0, не наталкиваясь на син-
сингулярность. Например, функция иг в D.40) хорошо определена
на S^>H3>, но сингулярна при | х \ = 0.
Более точно из теории гомотопий следует, что если U имеет
индекс Qlt a U' — индекс Q2, то функция U'U принадлежит сек-
сектору с Qx + Q2- Мы видели, что, для того чтобы U' (х) определяла
допустимое калибровочное преобразование, ее граничное значение
на 5|ФИ3' должно соответствовать Q2 = 0. Тогда Qx + Q2 = Qlf
и на гомотопический индекс калибровочные преобразования
действовать не будут в соответствии с калибровочной инвариант-
инвариантностью выражения D.18).
Как и для случая монопольной системы, можно было бы про-
продолжить обсуждение гомотопических свойств евклидовой системы
Янга — Миллса, но мы остановимся на этом этапе. Отметим, что
наша классификация справедлива для всех конфигураций с конеч-
конечным действием независимо от того, являются ли они решениями
полевого уравнения D.11) или нет. Это уравнение нигде в нашем
обсуждении использовано не было. Наша следующая задача со-
состоит в поиске среди конфигураций с конечным действием не-
некоторого произвольного гомотопического сектора Q тех, которые
дают решение полевого уравнения. Точное решение с Q = +1
(или —1) назовем инстантоном (или антиинстантоном). Мы полу-
получим также точные решения с Q — N (или —N) при \ N \ > 1.
Они представляют собой мультиинстантоны (или мультианти-
инстантоны).

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ 105
4.3. Инстантоны Янга—Миллса
Прежде чем получить точные инстантонные решения евклидова
уравнения Янга—Миллса D.11), отметим, следуя Белавину
и др. [29], важность самодуальных и самоантидуальных конфигу-
конфигураций. Аналогичные соображения, также принадлежащие Бела-
Белавину и Полякову [30], мы использовали в более простом примере
модели О C). Начнем с тривиального тождества
. D.44)
(Заметим, что Gp,v в D.6) антиэрмитово для действительных полей
G£v) С учетом равенства Tr [G^G^] = Tr [G^G^] получаем
- J <Рх Tr [G^v] ^ + j Л Tr [G^G^],
или
S^(8nVg2)\Q\, D.45)
где S — евклидово действие D.10), a Q — гомотопический индекс
Понтрягина D.18). Неравенство D.45) справедливо для любой
конфигурации с конечным действием. Уравнение Янга — Миллса
D.11), как и любое полевое уравнение, можно получить из условия
экстремума действия S, следуя вариационному принципу
6S [А„] = 0. D.46)
Уравнение поля D.11) следует из уравнения D.46). Ясно, что
такую вариацию можно провести отдельно для каждого гомотопи-
гомотопического сектора, так как малые вариации не выводят поля из
соответствующего сектора. Поля, которые приводят к экстремуму
действия в некотором гомотопическом секторе, являются реше-
решениями D.11) в этом секторе. Из уравнений D.44), D.45) видно,
что абсолютное минимальное значение S (S = (вя2/^2) | Q |) до-
достигается в произвольном секторе Q при условии
£U VG iG. D.47)
Следовательно, самодуальные и самоантидуальные конфигурации
приводят к экстремуму S и, таким образом, являются решениями
D.11). Конечно, абсолютные минимумы S — не единственные
экстремумы действия. Поэтому наш вывод не доказывает, что все
решения D.11) самодуальны или самоантидуальны. Мы ограни-
ограничимся самодуальными и самоантидуальными решениями уравне-
уравнения D.47) и не будем рассматривать более общее уравнение D.11).
То, что поля, удовлетворяющие D.47), удовлетворяют также
D.11), можно проверить, привлекая доказанное выше тождество
D.20)
dAv = 0. D.48)

106 ГЛАВА 4
Ему удовлетворяет любой тензор вида D.7), но при G^ = ^
D.48) становится уравнением поля. Другое доказательство, ис-
использующее D.45), приводит к результату, что такие решения
действительно дают абсолютный минимум действия S в произ-
произвольном секторе Q. Отметим сходство вывода D.47) и соответ-
соответствующего условия C.32) в модели О C).
Прежде чем перейти к решению уравнения D.47), подчеркнем
роль евклидовой метрики в этом контексте. Тензор, дуальный
дуальному тензору, есть
SG ^^^- D.4У)
В евклидовой метрике имеем е^роероар = 2 [fy«Ap — бцр^аЬ
так что
0^ = 0^. D.50)
Соотношения D.49), D.50) можно символически записать в виде
■ . Ъ = e2G = G, D.51)
так как собственные значения оператора дуальности е равны +1.
Поэтому самодуальные и самоантидуальные конфигурации могут
существовать. С другой стороны, если бы метрика была метрикой
Минковского, то D.49) приняло бы вид
fJJG = —Gap. D-52)
Теперь собственные значения оператора дуальности равны ±t,
и самодуальных или самоантидуальных конфигураций не суще-
существует.
Найдем некоторые самодуальные (или самоантидуальные) ре-
решения уравнения D.47). Белавин и др. предложили простой вывод
одноинстантонного решения уравнения D.47). Но мы будем сле-
следовать методу, разработанному рядом авторов [91, 199, 200,
331, 350]. Этот метод дает сразу как одноинстантонные, так и
многоинстантонные решения. Многоинстантонные решения были
также получены другим способом Виттеном [354]. Используем
для калибровочного поля следующий анзац:
Л^ (х) = B(iv(9v(ln^>(x)), D.53)
где <j> (х) — скалярная функция, которую надо найти, 2^ — ком-
компоненты матрицы, построенной из матриц Паули следующим
образом:
0 -[-Оз —°2 —°i
—03 0 "f °i —°2
—о1 0
+0
3
D.54)

КЛАССИЧЕСКИЕ ЙНСТАНТОННЫЕ РЕШЕНИЯ Ю7
Эту матрицу можно компактно записать в виде [331 ]
2^ = ?'^о72, /=1,2,3, D.55)
где
e^v для ц, v=l, 2, 3,
..„ , D.56)
—8lii для v = 4. v '
Отметим, что матрица 2^ антисимметрична и самоантидуальна
по индексам. Нам потребуются следующие легко проверяемые
свойства 2цУ:
[2цо, 2vp] = t [б^2ар -f Ьра1^ — 6^2^ - б^цр], D.57а)
«wA = [б^Д-а + «vA* + 6аа2^], D.576)
— enva|32ap = — 2"nV. D.57в)
Используя эти тождества в анзаце D.53) для А^, получаем для
тензора поля выражение
G^ = Яо (д„да In ^ - д„ (In ^) 5a (In ф)) ~
- i\o (dvdo 1пф-д, (In ф) до (In ф)) ~ Ё^ (да In ф)\ D.58)
Дуальный тензор равен
(дада In f- 5a (In ф) da (In ^)) - 1 faP (do In ^)«] =
= t2v« (^ In ф - <?a (In ^) д„ (In ^)) - (fi - v) +
+ ^v^a(ln^). D.59)
Наложим условие самодуальности G^ = G^. Это дает
д* (до Щ) - (д„ In ф) (да In ^) = 5a (^ In ^) - (do In ф) (д„ In ^), D.60а)
= О. D.606)
Уравнение D.60а) удовлетворяется автоматически, а уравнение
D.606) можно компактно записать в виде
ПФ/Ф = О, D-61)
где [Ц\ф в евклидовой метрике есть дадаф. Нам осталось решить
уравнение D.61) для ф (х) и подставить решение в D.53). Для
несингулярной функции ф D.61) сводится к уравнению £]ф = 0,
которое допускает только тривиальное решение ф = const, веду-
ведущее к Лц = 0. Но при рассмотрении сингулярных ф (х) мы полу-
получаем интересные и в конечном счете несингулярные решения для

108 ГЛАВА 4
калибровочного поля. Возьмем, например, ф (х) = 1/| х |2. При
х Ф 0 эта функция удовлетворяет уравнению
0. D.62)
При х = 0 имеем □ A/| х |2) = —4я2б4 (х) в соответствии с теоре-
теоремой Гаусса:
ткA^г))^л2- D-63)
Поэтому даже при х = 0
= — 4п2 | л: |2б4(лг) = 0. D.64)
Следовательно, ф (х) — 1/| х |2 есть решение уравнения D.61);
решением также является функция более общего вида
^г D-65>
где atll и Ац - произвольные действительные постоянные1). Эти
решения при подстановке в D.53) дают после некоторого калибро-
калибровочного преобразования jV-инстантонные решения с гомотопиче-
гомотопическим индексом Q = N. Начнем с N = 0, что соответствует ф (х) =
= 1 и Л„ = 0. Это решение тривиально и принадлежит сектору
с Q = 0 (см. D.18) или D.26)).
4.3.1. ИНСТАНТОН
Рассмотрим теперь случай N = 1 в D.65). Используя у^ =
= (Хц — аш) и у2 = у^у^, получаем
ф(х)=1+кУ!?, D.66)
что ведет к
^ ^ D.67)
Отметим, что это решение сингулярно при у = 0. Но сингуляр-
сингулярность можно убрать соответствующим сингулярным калибровоч-
калибровочным преобразованием. Так как условие самодуальности и уравне-
уравнения движения калибровочно-ковариантны, полученная после пре-
1) Джакив и др. [199] записали Ф (х) в более общем виде J] S^/lх — ai |2>
который сводится к D.65) при Op^i -»- оо, ^^ -+оос условием ^2N_^_i/a%_^i =
= 1. Это решение имеет то преимущество, что оно конформно ковариантно.
Но мы будем использовать D.65), следуя т'Хофту (частное сообщение).

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ Ю9
образования функция также будет им удовлетворять. Соот-
Соответствующей калибровочной функцией является иг (у), где иг
определено в D.40). Действительно,
[U, (У)]'1^ [Ui (У)] = —2tS|lv (yv/y% D.68)
что можно проверить, подставляя D.40) в D.68). Таким образом,
D.67) можно записать в виде
\ (х) = [U,(у)]-1 д* [Ui(У)] уг%1ц ■ D-69)
После калибровочного преобразования с иг (у) получаем
А„ (х) -> Л^ (х) = [Ui (у)) [А„ + су [Ux (у)]-1 =
= - (W)u ^TW = Ui (^(/f) 1FTW'
D.70)
где использовано D.9). Для более явной записи пространственной
зависимости используем тензор 2^ — самодуальный аналог тен-
тензора 2^,,. Он определяется следующим образом:
3iV = V№2, D.71)
где
( e для ц, v= 1, 2, 3,
= -fvn = д ' D.72)
' 1 +6'^ для v = 4. к '
Аналогично D.68) тензор удовлетворяет соотношению
Ш, (У)] -^ [(/i (У)]'1 = -2/2^ -f-. D.73)
Калибровочно преобразованное решение, выраженное через 2^,
принимает вид
Это одноинстантонное решение. Хотя мы сначала получили син-
сингулярное решение D.67), а затем калибровочно преобразовали его
с помощью сингулярной калибровочной функции, окончательная
форма решения D.74) не имеет сингулярностей ни при каких
значениях х для любых кг ф 0. Данное решение обладает следу-
следующими свойствами:
1. При подстановке в D.7) оно приводит к тензору поля
Ч • D-75)

ПО ГЛАВА 4
Поскольку S^v — самодуальный тензор, тем же свойством обла-
обладает и G'nv Это подтверждает, что D.74) является решением евкли-
евклидова уравнения Янга — Миллса.
2. При х-у.оо решение ведет себя как «чистая калибровка»
A'il(x)-^Ul(x)dil[Uy(x)]~1 D.76)
в соответствии с граничным условием, налагаемым конечностью
действия. Действительно, действие решения есть
' s = - ф 16-x Tr [G-G-i = 1? 1 {f +V = +8я2/£2- <4-77)
3. Так как для этого решения G^,v = G^,v, то S = (8я2/^2) Q
и, следовательно, Q = +1. Это опять согласуется с нашим пре-
предыдущим утверждением D.42), что иг (х) принадлежит сектору
с Q= +1.
4. Точно так же можно вывести аналогичное самоантидуальное
решение, заменяя 2^ на И^ в анзаце D.53). Это ведет к замене
2ц„ на S^v в окончательном результате и дает решение
D.78)
Это решение самоантидуально, имеет Q = —1 и может быть на-
названо антиинстантоном.
5. Какое из двух решений D.74) и D.78) назвать инстантоном,
а какое — антиинстантоном, определяется соглашением. «Менее
тривиально, но также определяется соглашением, какое решение,
самодуальное D.74) или самоантидуальное D.78), связано с Q =
= +1. По нашему определению D.18), самодуальное решение
имеет Q = +1. Но мы могли бы точно также определить Q в D.18)
со знаком минус. Напомним, что Q обозначает число наматываний,
и произвольность знака Q связана с выбором положительного
направления наматывания.
6. Четыре-вектор а1м, в решении определяет «положение» ин-
стантона. Плотность действия в D.77) локализована вблизи
Ун = (х — ai)n = 0- В силу трансляционной инвариантности урав-
уравнения Янга — Миллса точку аг можно выбрать произвольным
образом. Точно так же константа klt определяющая «размер»
инстантона в смысле плотности действия, может быть выбрана
произвольной, но не нулевой. Эта свобода связана с масштабной
инвариантностью системы Янга — Миллса относительно преобра-
преобразований л"р, -> ta'p, и Ац -> ХАц при любом КфО. Точнее, если
^ц (х) — решение уравнения Янга — Миллса, то М№ (кх) также
его решение. Можно проверить, что решения с различными кг
в D.74) связаны таким масштабным преобразованием. Мы вер-

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ 1Ц
немея ниже к таким степеням свободы. Напомним, что решения
О (З)-модели имеют аналогичные степени свободы.
7. Одноинстантонное решение «существенно» сферически-
симметрично с центром в точке аг. За исключением тензора
^nv (х — fli)v. оно зависит только от (х — fljJ. Калибровочная
функция Uy, связанная с поведением решения при х ->■ оо, также
сферически-симметрична. Направление U1 в групповом простран-
пространстве S^BH) то же, что и направление радиус-вектора х^ в коорди-
координатном пространстве. В этом смысле инстантон напоминает рас-
рассмотренное выше монопольное решение с п = 1 в трех простран-
пространственных измерениях, где изовектор фа имеет при х -*- оо такое же
направление, как координатный вектор х.
8. Сингулярное при х = cty непреобразованное решение D.67) —
D.69) ведет себя вблизи этой точки как «чистая калибровка»
с калибровочной функцией U^1:
Ац (x)-vfZr1 (х — aijdyJJx (x — а\) при х-*-а\.
Поэтому мы могли избавиться от сингулярности соответствующим
обратным преобразованием Uy. Получаемое в результате А^ (х)
в D.74) обращается в нуль при х = а1.
9. Название «инстантоны» было предложено т'Хофтом [331],
так как в отличие от нелокализованных во времени солитонов
систем в пространстве-времени Минковского рассмотренные ре-
решения локализованы также и по х4 (мнимой временной
координате).
4.3.2 ЛГ-'ИНСТАНТОННЫЕ РЕШЕНИЯ
Они получаются подстановкой функции D.65) для произволь-
произвольного N в анзац D.53). Соответствующее калибровочное поле есть
\ (х) = f^vdv
L V ИЗ1 ""' ;j
" ■"- " "" N D.79)
где (r/;)^ = (х — а;)^, i, j = 1,2, ..., N. Используя тождество
D.68) для каждого yt, выражение D.79) можно представить в сле-
следующем виде:
N
К (х) = S UT1 (Уд дуУх Ш ft (x), D.80)
где

112 ГЛАВА 4
а Ui (уд — та же эталонная калибровочная функция с Q = 1
D.40) с аргументом г/; = (х — а{). Отметим, что
a - д - д
и» - дхр dix-aOv ■
Поле D.79) или D.80) формально является решением уравнения
Янга — Миллса, так как оно выведено из условия самодуальности.
Но, как и D.67), оно сингулярно. Поле имеет N сингулярностей
в точках х = at, i = 1, ..., N. Поскольку
[}(х)-^8и при х->~аи D.82)
Ail(x)-^-U:Tl (х— a^d^iUi (х — а{)] при х-+а{. D.83)
Таким образом, около каждой из сингулярностей jV-инстантонное
решение, так же как одноинстантонное решение D.69) около
своего центра, ведет себя как чистая калибровка. Действительно,
калибровочная функция U^1 та же, что и в одноинстантонном
случае. Следовательно, W-инстантонное решение можно считать
набором N отдельных инстантонов, формы которых при любых х
«поляризованы» вследствие влияния остальных инстантонов.
Вблизи ядра t-ro инстантона (х ж at) влияние остальных ин-
инстантонов пренебрежимо мало, и jV-инстантонное решение пред-
представлено в основном этим отдельным инстантоном.
Сингулярности в D.79) следует убрать соответствующим ка-
калибровочным преобразованием [259, 308], как это сделано в одно-
одноинстантонном случае. Уравнение D.83) подсказывает, что под-
подходящая калибровочная функция должна сводиться к t/j. (x — аг)
при стремлении х к любой из щ. Одной из таких функций является
UN(x) = (Zi + iZ-a)/yT^, D.84)
здесь
N
^(^) yt = x-at, D.85)
где рг — некоторые действительные константы. При yt -*• 0 для
некоторого i имеем
D.86)
Калибровочное преобразование А^ (х) с помощью UN (x) уничто-
уничтожает все сингулярности при х = щ. Имеем
Л; (х) = UN (х) (А» + д») Un1 (x), D.87)
(уд ц Ui (Уд + возможные конечные члены =
i [U\ (уд U\~l (уд] + конечные члены, D.88)

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ ИЗ
где использовано D.83) и D.86). Первый член обращается в нуль,
и сингулярность при х = at уничтожается. Это справедливо для
каждого значения at, i = 1, ..., N. Но существует еще опасность
появления новых сингулярностей, отсутствующих в первоначаль-
первоначальной функции D.79) и связанных с калибровочной функцией UN (х).
Очевидно, что UN (x) кроме сингулярностей при yifl = О имеет
еще одну сингулярность при 1^ = 0. У нас еще остались произ-
произвольными константы рг в определении 1^ D.85). На простом,
но важном примере было показано [158], что, когда все точки at
Рис. 8. Объем F8, равный объему
всего 4-пространства, за исключе-
исключением небольших сфер радиуса 8 с
центрами в точках а;. Полная по-
поверхность объема Vg представляет
собой сферическую поверхность на
бесконечности S^ и N сферических
поверхностей 0,- вокруг точек сц.
принадлежат прямой линии в евклидовом 4-пространстве, C,-
можно выбрать так, что 1^ никогда не обратится в нуль. Тогда
калибровочно преобразованное поле А^ (х) в D.87) будет несин-
несингулярным.
Покажем, что это решение соответствует индексу Понтрягина
Q = N (выше мы отметили, что решение представляет собой набор
N отдельных инстантонов). Так как А'^ (х) несингулярно, то
можно воспользоваться определением
16я2
J Тг КДЛ ctx,
D.89)
где G'^v — тензор поля, связанный с А'ц. Так как подынтегральное
выражение несингулярно, из области интегрирования можно
исключить N малых сфер с центрами в точках х = а{ и радиусами
е, причем е —>- 0. Для любого конечного малого е интегрирование
ведется по Vs — объему всего пространства, за исключением N
таких сфер (рис. 8). В объеме Ve даже первоначальное решение
А^ (х) D.79) несингулярно. Далее, в области Ve имеем
Тг
= Tr
D.90)

114 ГЛАВА 4
где Gnv относится к А^, так как А^ и А^ связаны калибровочным
преобразованием. Тогда
е_о
D.91)
Выражение D.91) имеет то преимущество, что для получения Q
не нужно точно вычислять А'ц (х) в D.87). Тензор G^, зависит
от более простого выражения для А^ D.79). Сингулярности А^ (х)
исключены из Ve, и мы можем применять теорему Гаусса с учетом
D.23). Заметим, что поверхностями, ограничивающими Ve, яв-
являются сферическая поверхность S«> при | х \ = оо и поверх-
поверхности at N малых сфер. Поэтому
Q = lim (ф ^da^-ф /ц da^ - фj^da^'- ■ ■ ■ - ф /„ doA , D.92)
где /ц — ток, определенный в D.24), а знаки минус соответствуют
вкладам внутренних поверхностей с учетом того, что do^ напра-
направлено.радиально наружу для каждой сферы. Так как при | х | ->■ оо
Ар (х) ведет себя как 1/|х|3, /^ убывает достаточно быстро, чтобы
I j^dOp было равно нулю. На малых сферах, где х прибли-
приближается к одной из точек аь А^ превращается в чистую калиб-
калибровку D.83) с калибровочной функцией U^1 (х — аг). Если А^ —
чистая калибровка, то (bj^da^ имеет вид D.27). Напомним, что
для калибровочной функции иг данный поверхностный интеграл
равен единице. Этот результат D.42) справедлив для сферической
поверхности любого радиуса. Если калибровочной функцией,
как в нашем случае, является U^1, то соответствующее значение
Ф/и^аи на каждой малой сфере очевидно равно —1. Поэтому
из D.92) получаем
Q = Hm [0 — (—1) — (—1)- • • — (—1)].
£-*-0
Предел при е -»- 0 теперь тривиален и дает Q = N.
Так как jV-инстантонные решения самодуальны, их действие
S = 8n2Q/g2 = 8n2N/g2 в N раз больше действия отдельного
инстантона. Это замечательное свойство решений нелинейного
полевого уравнения. Рассмотрим более знакомый случай стати-
статических уединенных волн в метрике Минковского. Статическое
решение с N уединенными волнами, разделенными конечным
расстоянием, если оно существует, вообще говоря, имеет энергию,
отличную от суммы энергий N таких изолированных уединенных
волн. Разность энергий связана с взаимодействием между уеди-

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЁ РЕШЕНИЯ Ц5
пенными волнами. Для нашей евклидовой системы понятия энер-
энергии не существует, но функционал действия 5, имеющий с ней
некоторое сходство, обладает замечательным свойством
5 (N инстантонов) = NS (один инстантон).
Формально это происходит потому, что все решения самодуальны
и в результате 5 ~ Q, но, возможно, это свойство имеет более
глубокое содержание.
На этом завершается наше обсуждение инстантонных решений
системы Янга — Миллса. Антисамодуальные Af-антиинстантонные
решения получаются сходным способом заменой S^v на S^ в ан-
заце D.53). Калибровочные теории в последнее время являются
объектом интенсивных исследований, и относительно их самих
и их инстантонных решений известно гораздо больше даже на
классическом уровне. Наше обсуждение в лучшем случае имеет
характер введения. Так, важное свойство инстантонов — поведе-
поведение при конформных преобразованиях — не было рассмотрено.
Оно в деталях исследовано Джакивом и Ребби [196] и Джакивом
и др. [199]. Это свойство мы только поверхностно затронули,
отметив инвариантность системы Янга — Миллса при растяже-
растяжениях. Действительно, система обладает симметрией под дей-
действием четырехмерной конформной группы преобразований с 15 ге-
генераторами, отвечающими 1) масштабным преобразованиям,
или преобразованиям растяжений, 2) четырем трансляциям,
3) шести О D)-вращениям и 4) четырем специальным конформным
преобразованиям
все это наряду с калибровочными преобразованиями, эффект
которых частично перекрывается с действием конформной
группы [196].
В этой связи возникает важный вопрос о числе степеней сво-
свободы Af-инстантонных решений, т. е. о том, сколько физически
различных решений можно получить из частного Л^-инстантонного
решения, используя симметрии системы, или, что эквивалентно,
сколько свободных параметров имеет общее Л^-инстантонное
решение. Рассмотрение начнем с одноинстантонного решения. Мы
уже получили пять свободных параметров X и а^, связанных
с симметрией при трансляциях и растяжении. Эффект остальных
генераторов конформной группы (О D)-вращения и специальные
конформные преобразования) можно исключить, как показали
Джакив и Ребби, калибровочными преобразованиями и трансля-
трансляциями. Пока существует калибровочная свобода, здравый смысл,
основанный на физических соображениях, говорит, что локальные
калибровочные преобразования не похожи на инстинные симме-

116 ГЛАВА 4
трии, например на пространственные вращения. Калибровочные
преобразования приводят не к физически новой системе, а к той
же системе в другой (калибровочной) трактовке. Поэтому необ-
необходимо сначала «фиксировать» калибровку некоторым калибро-
калибровочным условием, а затем выводить физические следствия. Исклю-
Исключением являются глобальные (т. е. не зависящие от х) калибровоч-
калибровочные преобразования. Было доказано (см. [89]), что они являются
истинными симметриями, так как ведут к законам сохранения.
Напомним, например, знакомые случаи изотопического спина или
глобальной заряженной ((£/ A)) симметрии в электродинамике.
В нашей SU B)-теории глобальная симметрия приводит к трем
новым степеням свободы, доводя общее число свободных пара-
параметров единичного инстантона до восьми. Из них решение D.74)
реализует только пять вследствие ограничений, накладываемых
анзацем D.53), который в свою очередь связан со специальной
калибровочной функцией Ut (х) (см. D.68)). Остальные три сте-
степени калибровочной свободы проявляются при замене функции
иг (х) на функции, связанные с ней глобальными вращениями
в групповом пространстве.
Если отдельный инстантон имеет восемь параметров, то для
Af-инстантонного решения можно ожидать 8N параметров. Мы уже
видели, что Af-инстантонное решение в окрестности каждой точки
at выглядит как одноинстантонное решение, или (что эквива-
эквивалентно) когда размеры 'к1 отдельных солитонов малы по сравнению
с расстояниями между ними Y\ ai — а; 12> Af-инстантонное ре-
решение выглядит как набор N почти неперекрывающихся отдель-
отдельных инстантонов. Это позволяет ожидать существования 8N пара-
параметров. Поскольку их число дискретно, можно предположить,
что оно не меняется при сближении инстантонов и увеличении их
перекрытия, когда параметры ^,г и at меняются гладким образом.
Число степеней свободы 8N можно свести к 8N — 3, если на физи-
физических основаниях не считать глобальные трансляции симметри-
симметриями системы. Отметим, что даже тогда имеет значение относитель-
относительная ориентация N инстантонов во внутреннем пространстве,
поэтому число параметров равно 8N — 3, а не 5N. Частное решение
D.79) имеет только 5N параметров из-за ограничений, наклады-
накладываемых анзацем D.53). Наши рассуждения слишком качественны,
чтобы их можно было назвать выводом. Однако то же число сте-
степеней свободы самодуальных решений было получено строгим
и изящным способом с помощью мощных математических методов
Атия и Уордом [14]. Читателям, интересующимся более глубоким
рассмотрением классических инстантонов, следует изучить ци-
цитированные выше работы, а также работы [15, 82].
Мы привели самодуальные или антисамодуальные решения.
Однако; как было подчеркнуто выше, вывод D.47) показывает

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ 117
только то, что такие функции являются решениями евклидова
полевого уравнения Янга — Миллса, но все решения не обяза-
обязательно должны быть самодуальными или антисамодуальными.
Можно было бы привести примеры типа «связанного решения
инстантон — антиинстантон», которое, если существует, имеет
Q = 0, но 5 > 0. Насколько нам известно, такие решения еще
не найдены, но отсутствует также и доказательство, что само-
самодуальные и антисамодуальные поля есть единственные решения
с конечным действием евклидовых уравнений Янга — Миллса.
Инстантоны Янха — Миллса привлекают внимание даже
на классическом уровне как интересные точные решения нетри-
нетривиальных нелинейных полевых уравнений. Еще более важную
роль они играют в квантовых калибровочных теориях. Эти
исследования, начавшиеся с работы т'Хофта [331], рассматривают-
рассматриваются в последних двух главах.
4.4. Инстантоны других моделей
Термин «инстантон», определенный в разд. 4.1, универсален.
Его можно использовать для евклидовых решений с конечным
действием любой модели. Такие решения играют важную роль
в соответствующей квантовой теории — они ведут к вакуумному
туннелированию и другим связанным с ним явлениям. В преды-
предыдущем разделе мы изучили инстантоны системы Янга — Миллса
в четырех измерениях, которые характеризуются гомотопическим
индексом. Аналогичные решения существуют для многих других
моделей, как более сложных, чем система Янга — Миллса, так
и более простых.
Возможно, простейшим примером является частица единичной
массы в потенциале V (q) с двумя ямами. В действительном
времени t лагранжиан имеет вид
L = ±(dq/dtr-±(q*~l)\ D.93)
Соответствующее «евклидово» действие и евклидовы уравнения
движения получаются продолжением t = —г'т, полагая 5евкл =•
= — г5Мин. Тогда
оо
SeBKn = J dx [±- (dqldxf + 4" (<72 - IJ] D-94)
— оо
приводит к уравнению
d^q/dx2 = dV/dq = q3 — q. D.95)
Отметим, что данное уравнение тождественно уравнению для ста-
статических решений теории </>4 Хиггса в A + 1) измерениях, рас-

118 ГЛАВА 4
смотренному в гл. 2 (в B.27) надо положить к = т = 1 и заме-
заменить ф на q, a x на т). Действие D.94) также равно энергии стати-
статической конфигурации теории </>*. Тогда нетривиальные решения
уравнения D.95) с конечным действием описываются теми же
функциями, что и статические решения теории </>* с конечной энер-
энергией, а именно кинк и антикинк:
<7(T) = ±th[(T-T0)//T]. D.96)
Они являются инстантонным и антиинстантоьным решениями
задачи с двумя ямами и, как показано в гл. 2, обладают тополо-
топологическими индексами +1. Этот индекс аналогичен индексу Пон-
трягина Q D.18). В гл. 10 мы увидим, что эти решения связаны
с квантовой амплитудой частицы, туннелирующей из минимума
потенциала q — —1 в минимум q = + 1.
Аналогично рассмотрим квантовый маятник, т. е. частицу
в потенциале V (q) = 1 — cos q. Классическое евклидово урав-
уравнение такой системы имеет вид
d2q/dr2 = sin q. D.97)
Оно идентично уравнению для статического поля двумерной си-
системы синус-Гордона (т. е. не зависящему от времени уравнению
B.65)). Евклидово действие маятника
оо
5= J dx \-^-(dqldxf+ I - cos?] D.98)
—-оо
равно энергии статической конфигурации с и ну с-Гордон а. Следо-
Следовательно, йнстантонное (антиинстантонное) решение D.97) будет
статическим солитонным (антисолитонным) решением системы си-
синус-Гордона. Мы используем маятник в гл. 10 для иллюстрации
важности инстантонов в квантовой теории.
Отметим, что эти примеры из механики частиц можно считать
одномерными (только во времени) скалярными полевыми теориями.
Их инстантоны являются статическими солитонами соответствую-
соответствующей полевой теории в двух A + 1) измерениях. Данная связь на-
наблюдается во многих других случаях.
Рассмотрим, например О (З)-модель в B + 1) измерениях,
которую мы обсуждали в гл. 3. Для нее получены статические со-
литонные решения с конечной энергией. Рассмотрим ту же мо-
модель в A + 1) измерениях. Ее евклидово полевое уравнение, оче-
очевидно, такое же, как статическое полевое уравнение C.14) B + 1)-
мерн.ой системы с евклидовым действием, задаваемым статической
энергией C.15) последней системы. Соответственно статические
решения B + 1)-мерной О (З)-модели в пространстве-времени
Минковского являются инстантонами A + 1)-мерной О (З)-мо-
дели. Что будет, если мы обобщим О (З)-модель на О (Л^)-модель

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ Ц9
с произвольным N >3, т. е. обобщим О (З)-модель на N скаляр-
скалярных действительных полей ф = \фа, а = 1, ..., N\ с фф =
= 2j^=i^a = 1? Рассмотрим статические солитоны в двух про-
пространственных измерениях. (Те же соображения справедливы
для инстантонов соответствующей A + 1)-мерной теории.) Будем
следовать логике разд. 3.3; граничные условия C.17) опять сжи-
сжимают евклидово двумерное пространство в поверхность сферы
5гфиз). Разрешенные условием £?Va = 1 значения поля при-
принадлежат поверхности гиперсферы Sn-\, погруженной в N из-
измерений. Следовательно, гомотопической группой локализован-
локализованных решений будет П2 (SN_j). Из C.90) видно, что эта группа
тривиальна, кроме случая N = 3. Поэтому нетривиальные ин-
стантОнные секторы двумерной О (А^)-модели существуют только
для N = 3. Ситуация не улучшается при переходе к более высо-
высоким пространственным размерностям, поскольку, как следует из
теоремы вириала разд. 3.2, динамика исключает нетривиальные
решения. Таким образом, результаты О (З)-модели нельзя обоб-
обобщить, переходя к О (А^-модели с N >3 (см. [110]). Мы вернемся
к этому вопросу ниже.
Обращаясь к калибровочным полям, рассмотрим инстантоны
электромагнитных систем, которые гораздо проще и более знакомы,
чем поля Янга—Миллса. Свободное электромагнитное поле без
источников, конечно, слишком просто. Оно линейно и точно на-
находится в отличие от поля Янга—Миллса, которое даже в отсут-
отсутствие источников является полем с самодействием. Поэтому рас-
рассмотрим электромагнитное поле, взаимодействующее с некото-
некоторым другим заряженным полем, например в абелевой модели
Хиггса C.91) в (£> + 1) измерениях. Из C.91) очевидно, что евкли-
евклидово действие системы конечно только в том случае, если соотно-
соотношения C.93) и C.94) выполняются на границе (D + 1)-мерной ев-
евклидовой области. Таким образом, область граничных значений
характеризуется S[BH) — окружностью фаз <j>. С другой стороны,
границей евклидова (D + 1)-пространства является So3'.
Поэтому гомотопическая классификация инстантонов основы-
основывается на группе nD EX). Из C.90) видно, что она нетривиальна
только для D = 1. Таким образом, в реальном случае C + 1)
измерений, когда инстантоны Янга—Миллса так важны, абелева
система C.91) не имеет нетривиальных инстантонных секторов.
Это одна из причин, почему мы выбрали для детального обсужде-
обсуждения инстантонов в четырех измерениях систему Янга—Миллса,
а не электродинамику. Электродинамические инстантоны с це-
целыми гомотопическими индексами существуют только в A + 1)
измерениях. Отметим снова, что получающиеся из C.91) полевые
уравнения в A + 1) измерениях будут такими же, как уравнения
статических полей данной системы в B+1) измерениях, если

|2() ГЛАНД !
работать в последней в калибровке Ао = 0. Ее координатам
(х, у) и полям (Ах, Аи) сопоставляются координаты (х, it) и
поля (Ах, IAq) евклидовых уравнений. Таким образом, мы уже
изучили инстантоны A + 1)-мерной абелевой модели Хиггса,
исследуя решения с вихревыми линиями в сверхпроводнике.
Из разд. 3.6 мы знаем о таких инстантонах так же много, как и об
инстантонах Янга—Миллса, за исключением точного аналитиче-
аналитического вида решений. Напомним (разд. 3.6), что численные расчеты
и исследования Богомольного [54] и Таубса [325] показали, что
несингулярные инстантоны действительно существуют в этой абе-
абелевой модели. Мы знаем их асимптотическое поведение C.105) и
точное выражение для гомотопического индекса C.99). Мы также
знаем, что они имеют конечные размеры, пропорциональные F'1,
в отличие от инстантонов Яьга—Миллса или модели О C), которые
могут быть произвольно большими в силу существования произ-
произвольного масштабного множителя D.74). Данное свойство абеле-
вых инстантонов модели Хиггса будет по достоинству оценено при
вычислении квантовых эффектов (гл. 10).
Следующей более сложной калибровочной теорией после
электромагнетизма является SU B)-теория Янга—Миллса, ин-
инстантоны которой мы уже детально рассмотрели. При рассмотре-
рассмотрении гомотопической классификации инстантонов калибровочных
теорий с высшими неабелевыми группами типа SU C), SU D)
и т. п. нет необходимости обсуждать каждую из них в отдель-
отдельности. Как отметил Коулмен [89], можно использовать сильную
теорему теории гомотопий [56]. Эта теорема утверждает, что
любое непрерывное отображение S3 в любую общую простую
группу Ли G можно непрерывно деформировать в отображение
S3 в SU B)-подгруппу группы G. Так как последние отображения
уже классифицированы с использованием п3 (S3) = Z, то, следо-
следовательно, классифицированы и первые в четырех евклидовых из-
измерениях. Как только произвольное отображение S3 -*■ G дефор-
деформировано в отображение S3 -*• SU B), можно непосредственно
применять всю нашу предыдущую классификацию последнего,
включая формулу для индекса Понтрягина и т. д. Этот результат,
справедливый для любой простой группы Ли, справедлив, в част-
частности, для всех SU (N). Если группа не простая, а состоит из про-
произведения простых групп, то необходимо провести отдельный ана-
анализ для каждой простой фактор-группы, т. е. получить набор
независимых SU B)-индексов Понтрягина для каждой такой
фактор-группы, характеризующий отображение S3 в данное про-
произведение групп. Далее, так как общая компактная группа Ли
представляет собой локально произведение абелевой группы
на простые группы, наш анализ SU B)-инстантонов в четы-
четырех измерениях справедлив и для более широкого семейства
групп.

КЛАССИЧЕСКИЕ ЙНСТАНТОННЫЕ РЕШЕНИЯ
Следует отметить, что инстантоны SU (А^)-калибровочных
групп с произвольным N имеют более чем академический интерес,
хотя существующие теории элементарных частиц используют
SU (А^)-калибровочные группы лишь с небольшими и конеч-
конечными N. (Принятая в настоящее время теория слабых и электро-
электромагнитных взаимодействий использует SU B) X U A)-калибро-
вочную группу, теория сильных взаимодействий использует
«цветную» группу SU C), некоторые теории, пытающиеся объеди-
объединить все эти взаимодействия, используют группы SU D), SU E)
или SU G).) Причина, почему SU (А^-калибровочные теории
с произвольно большим N могут быть важны, заключается в воз-
возможности так называемого l/W-разложения. Было убедительно
доказано [329, 356], что разложение в ряд по степеням \IN яв-
является хорошим приближением для квантовых SU (Af^калибро-
(Af^калибровочных теорий. В этом случае главный член в разложении соответ-
соответствует SU (А^)-теории с N-+oo.
Наконец, понятия солитонов и инстантонов были распростра-
распространены на общерелятивистские теории, см., например, [119, 159,
160, 184, 245, 300, 349].
4.5. CPN-модель
В гл. 3 мы упомянули, что О (З)-модель в A + 1) измерениях
имеет несколько интересных свойств, многие из которых схожи со
свойствами теории Янга—Миллса в C + 1) измерениях. Обе си-
системы дают инстантоны, характеризуемые целочисленными топо-
топологическими индексами. Процедуры получения этих решений
в разд. 3.3 и 4.3 также очень похожи; в обоих случаях мы сначала
выводили неравенства, которые давали нижнюю границу дейст-
действия 5, пропорциональную гомотопическому индексу Q. Мини-
Минимальность 5 вела к дифференциальным уравнениям первого по-
порядка (условиям «самодуальности»), которые затем решались.
Обе модели масштабно инвариантны и имеют инстантоны произ-
произвольного размера. (На квантовом уровне сходство сохраняется.
Хотя эти вопросы и выходят за рамки нашего исследования, сле-
следует отметить, что теории О C) и Янга—Миллса перенормируемы
и асимптотически свободны.) В то же время О (З)-модель сравни-
сравнительно проста. Она состоит только из трех скалярных полей
в двух измерениях с простым лагранжианом. Следовательно,
О (З)-модель, помимо того что она соответствует двумерным фер-
ферромагнетикам, является полезной пробной моделью, на которой
можно понять особенности более сложных неабелевых калибро-
калибровочных теорий. Но сходство отсутствует в одном отношении.
В разд. 4.4 мы отметили, что SU B)-систему Янга—Миллса можно
погрузить в более высокие SU (А^)-калибровочные теории и что
инстантонные решения продолжают существовать для произ-

122 глАёА 4
вольно больших N. Это позволяет сравнивать квантовые инстан-
тонные эффекты (методами, разработанными в гл. 10) с разложе-
разложением по большим Af [356, 357]. К сожалению, как указано выше,
соответствующее обобщение О (З)-моделей на О (А^)-модели не
дает инстантоны при N > 3.
Однако существует другое семейство скалярнополевых теорий
также в A + 1) измерениях, которые обладают всеми упомяну-
упомянутыми выше свойствами О (З)-модели, но в то же время дают ин-
стантонные решения даже для произвольно большого числа по-
полей N. Это так называемые СЯ^-модели [94, 120, 174]. Мы уви-
увидим, что для N = 1 С/5!-модель сводится к О (З)-модели. Для
больших N СЯ^-модель является лучшим обобщением, чем О (N)-
модель, в том смысле, что она продолжает давать инстантонные
решения. Несмотря на то, что эта модель предложена недавно,
для нее уже проведена большая работа в силу ее интересных
свойств. Этот раздел мы посвящаем описанию данной модели и по-
получению ее инстантонных решений [99, 356]. Наше рассмотре-
рассмотрение будет аналогично проведенным в предыдущих разделах.
СР (А^)-модель состоит из vV+1 комплексных скалярных
полей па (х), а — \, ..., JV + 1 в двух измерениях. Для полей
введем общее обозначение п (х) = \па (х)\. Так как нас интере-
интересуют инстантоны, мы будем работать в евклидовом двумерном
пространстве с координатами х = \xv x2\. Поля подчиняются
уравнению связи
JV+1
(п (*))* • п (х) = £ п'а (х) па (х) = 1 D.99)
и имеют плотность лагранжиана
2{х) = (д„п)*.(д„п) + (n*.^n) (n*-^n) D.100
с [х = 1, 2. После дифференцирования по х^ связь D.99) приво-
приводит к соотношению
n^n -f д„п*-п = 2 Re(n*-^n) = 0. D.101)
Таким образом, величина п*- д^п чисто мнимая, что мы будем
часто использовать.
Рассмотрим теперь набор пространственно-временных преобра-
преобразований
na(x)-+na(x)exp(i\(x)). D.102)
Фаза Л (х) зависит от х, но не зависит от индекса а. Все N + 1
поля умножаются на один и тот же фазовый множитель. При та-
таком преобразовании
дуП ->- (дуП -[- г'дцЛп) е'л, n^d^n ->■ п*.дцП -f id^A,
&{x)-+S?(x). D.103)

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ 123
Из этих соотношений ясно, что система обладает калибровочной
инвариантностью при U (^-преобразованиях D.102). Ситуация
несколько схожа с абелевой электродинамикой; так же как в элек-
электродинамике, будем считать «калибровочно-эквивалентными» все
поля, связанные только преобразованиями D.102). Лагранжиан
калибровочно-инвариантен. Набор N + 1 комплексных чисел,
подчиняющийся требованию калибровочной эквивалентности и
условию D.99), образует Af-мерное комплексное проективное про-
пространство. Отсюда обозначение CPN.
Калибровочная инвариантность становится более очевидной
при введении дополнительного векторного поля А^ (х); при этом
лагранжиан записывается в виде
SB(х) = дцп'-дцп + А1- 2Atl(in'-dt).n). D.104)
Экстремум действия 5 = j сРхЗ? (х) по А^ (х) приводит к урав-
уравнению
0 = dS/dA», = 2 (Лу, - т* • д^п).
Следовательно,
Atx=i(n*-dtxn). D.105)
Это уравнение связи для А^ (х). Поле А^ не описывает независи-
независимых степеней свободы, а полностью определяется п (х) с помощью
уравнения D.105). При подстановке D.105) в лагранжиан D.104)
(что допустимо для таких простых связей, см. [113]) получаем
лагранжиан D.100). Таким образом, два лагранжиана D.100) и
D.104) эквивалентны. Напомним, что n*-d,jn— чисто мнимая ве-
величина, тогда Лу, (х) —действительная величина.
(Системы D.100) и D.104) эквивалентны даже после квантова-
квантования. Это можно показать с помощью функциональных интегралов,
устранив при интегрировании квадратичную зависимость действия
от Лу,. Так как в этом разделе рассмотрение ведется на классиче-
классическом уровне, мы не будем дальше обсуждать этот вопрос, но отме-
отметим, что методы функционального интегрирования рассматри-
рассматриваются в последующих главах.)
Используя D.105) и D.101), лагранжиан D.104) можно запи-
записать в компактной форме
^(*) = (ад*-(ВД, D.106)
где
^11 = (^ + 1^I1. D.107)
При калибровочном преобразовании D.102) имеем

124 ГЛАВА 4
Теперь ясно видна калибровочная инвариантность лагранжиана
в форме D.106), а также аналогия со скалярной электродинами-
электродинамикой. Заметим, однако, что D.106) не является точным лагранжиа-
лагранжианом комплексных скалярных полей, взаимодействующих с элек-
электромагнитным полем. В D.106) отсутствует кинетический член,
связанный с Ац. Это происходит потому, что А^ (х) не является
независимым полем, а полностью определяется через п (х) урав-
уравнением D.105).
Евклидово полевое уравнение получается из экстремума дей-
действия
5= jd^(D(,n)*.(D(,n) D.109)
по п (х) с учетом связи D.99). Связь вводится в вариационный про-
процесс стандартно через множитель Лагранжа, т. е. ищется экстре-
экстремум S + J сРхк (х) (п*-п — 1). Отсюда получается уравнение
поля
DyZVi + кп = 0. D.110)
Множитель Лагранжа к (х) исключается с помощью соотношения
к = кп* ■ п = —п* • D^n,
что дает
Dvpvn-(n*-DVLDvn)n = 0. D.111)
Инстантоны являются решениями этого уравнения с конечным
действием. Мы получим их косвенно, как это делалось выше в дру-
других примерах, проведя классификацию конфигураций с конечным
действием.
Конечность действия D.109) требует, чтобы при г = | х\ -*■ оо
Для каждой компоненты па = \ па \ е'Фа это дает
1А»^а \па\ +lW«- D-113)
Отметим, что —iA^ в D.113) чисто мнимое и не зависит от а. Это
означает, что при г -*- оо имеем: 1) д^ \ па \ = 0 и 2) д^фа не зави-
зависит от а. Следовательно, граничное условие D.112) требует, чтобы
при г —*■ оо
п(лг)-^п(О)е'*(9), D.114)
где п<°> — произвольный постоянный комплексный вектор
с (п<°>)*-п@> = 1, а ф — обычный фазовый угол, который может
зависеть от угла в координатном пространстве Э, параметризую-
параметризующего границу пространства, которой в данном случае является

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ 125
окружность 5<*из>. Между тем разрешенные значения фазы ф
также образуют окружность S[BHK Следовательно, разрешенные
соотношением D.114) граничные условия образуют отображения
5<Физ)->-5<вн>. Мы уже знаем, что такие отображения распа-
распадаются на гомотопические классы, характеризуемые числом нама-
наматываний Q. Мы также знаем выражение для Q в виде
Свобода выбора постоянного единичного комплексного вектора
п<°> не отвечает еще одной гомотопической классификации. Отме-
Отметим, что лагранжиан обладает также глобальной (не зависящей
от х) симметрией SU (N + 1) помимо того, что подгруппа U A)
группы SU (N + 1) соответствует локальной калибровочной сим-
симметрии. С помощью глобальных SU (N -\- 1)-вращений можно не-
непрерывным образом переходить от одного значения п@> к другому.
Выражение D.115) можно записать в терминах А^. Поскольку
Э-компонента А^ есть
. i , д 1 йф
получаем
If If If
Q = —к— аНгЛе = — -д— ш-А = d^XE^yd^Ay. D.116)
5<физ) s№H3)
1 1
Это выражение можно переписать в виде
'Р„пу-(йуп). D.117)
Тривиальными вычислениями с использованием D.105) можно
убедиться в эквивалентности D.117) и D.116).
Далее, как и в предыдущих примерах, используем соответст-
соответствующее неравенство. Имеем
х (Dy.ii + i^D^nf. (ОуП ± ге^ад ^ 0. D.118)
После раскрытия скобок получаем
или
S^2n\Q\. D.119)
Уравнения D.112)—D.119) справедливы для любых конфигура-
конфигураций с конечным действием. Но если в D.118) имеет место знак
равенства, т. е. при достижении действием 5 минимального зна-
значения в произвольном Q-секторе, поле будет экстремумом действия

120 ГЛАВА 4
в данном секторе и будет удовлетворять уравнению поля. Знак
равенства в D.118) появляется при выполнении следующего ус-
условия:
. D.120)
Оно аналогично условию самодуальности D.47) или соотно-
соотношению C.32) для 0 (З)-модели. Все сделанные выше замечания
справедливы и здесь. Например, в отличие от исходного полевого
уравнения D.111) уравнение D.120) — дифференциальное первого
порядка, и его легче решить. Решения уравнения D.120), миними-
минимизирующие 5, автоматически удовлетворяют D.111), но обратное
неверно.
Для решения уравнения D.120) введем вместо п набор кали-
бровочно-инвариантных переменных. Напомним, что в силу
связи п*-п = 1 все поля па (х) не могут одновременно исчезать
в любой точке. Рассмотрим область R± координатного простран-
пространства, где, скажем, пг ф 0. В этой области определим
W(x) = n(x)/ni(x). D.121)
Отметим, что поля w (х) = \wa (х), а = 1, ..., N + 1} калибро-
вочно-инвариантны. Преобразование D.102) приводит к появле-
появлению одного и того же множителя ехр (гЛ (х)) в числителе и зна-
знаменателе D.121). Далее, w1(x) — 1 для любых х £ Rlt так что
существуют только N независимых калибровочно-инвариантных
комплексных полей wa. Это согласуется с размерностью CPN. Вне
области R± пх может обращаться в нуль, и тогда определение D.121)
неприменимо. Но в силу n* n = 1 должна существовать смежная
область R2, где отлична от нуля другая компонента, например п2.
Определим
w' = п/ла. D.122)
Можно убедиться, что п2 можно выбрать так, чтобы области R± и
R2 перекрывались в некоторой подобласти, где ни пъ ьи п2 не
обращаются в нуль. В этой подобласти w' и w связаны соотноше-
соотношением
w' = wn!/rt2. D.123)
Таким образом, мы можем определить поля \у(или w', w" и т. д.),
разделив х-пространство на перекрывающиеся области с различ-
различными определениями, которые можно аналитически продолжить
с одной области на другую, используя соотношения типа D.123)
в областях перекрытия. Данная процедура .определения полей
близка к той, которую обычно используют в теории калибровоч-
калибровочных полей при наличии монополей [358].
Уравнение D.120) локально, и мы будем решать его в произ-
произвольной области, скажем Rv где w определено согласно D.121).

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЁ РЕШЕНИЯ 127
Аналогичные рассуждения справедливы и для любой другой об-
области. При этом решения можно продолжить с одной области на
другую, используя соотношения вида D.123). Выразим уравне-
уравнение D.120) в переменных w. Имеем
Тогда D.120) принимает вид
D» (WaTll) = it^vDv (Wa.ni), п=\, . . ., N + 1,
или
WaD»^ -\- nidyWa = dbie^v (waDvni + nidvwa). D.124)
В силу D.120) первые члены в обеих частях уравнения D.124) со-
сокращаются. Остающиеся вторые члены разделим на пг ф 0 и по-
получим
ххюа, [г, v=l, 2. D.125
Отметим, что в D.125) входят обычные (dyWa), а не ковариантные
производные. Далее, так же как в модели О C), уравнение D.125)
представляет собой условие Коши—Римана. Взятое со знаком
минус в D.1^5) оно гласит, что wa является аналитической функ-
функцией z = xt -\- ix.2. Знак плюс соответствует wa, аналитической
ПО 2*.
Таким образом, мы нашли инстантоны. Любой набор аналити-
аналитических функций wa (z), a = 2, ..., N + 1 при wt = 1 является
решением уравнения D.120); решением является также любая
аналитическая функция ша (г*). В силу приведенных выше сообра-
соображений эти функции, переписанные в терминах п и х^, дают точ-
точные решения с конечным действием евклидова полевого уравне-
уравнения D.111).-Следовательно, эти функции являются инстантонами
данной модели.
В качестве точного примера рассмотрим одноинстантонное
решение. Выберем
w(z) = u + [(z-zo)A]v, D.126)
где u, v — пара ортонормированных комплексных векторов, удов-
удовлетворяющих УСЛОВИЯМ Mi = l, V1 = 1,
и* • и = v* • v = 1 и и* • v = 0.
Ясно, что D.126) образует набор аналитических функций и, сле-
следовательно, является решением. Константа к действительна и
соответствует «размеру» инстантона, а комплексное число z0 =
= (xi)o ~Ь г (Х2,)о соответствует его «положению» в плоскости z =
— *!■+ ix2. Свобода в выборе к и z0 отражает масштабную и транс-
трансляционную инвариантность действия D.109). Перепишем это ре-

I2H 1ЛЛПЛ I
шение, обратив D.121). С точностью до фазового множителя,
который всегда можно устранить калибровкой, D.121) приво-
приводит к
п = %w = w/| w |,
где
| w | = (w*-wI''2 = | ^ I..
При подстановке D.126) решение принимает вид
п(г) — ь + (г~г°)у D 127)
Легко проверить, что оно удовлетворяет полевому уравнению
D.111). На пространственной бесконечности при z -*■ оо
n(z)->(z/|z|)v =
Это удовлетворяет граничным условиям D.114) для фазового угла
ф (9) = Э. Решение принадлежит сектору с Q = 1 и описывает
отдельный инстантон. Антиинстантонное решение получается за-
заменой 2 на г*. (Отметим, что если бы мы опустили постоянный век-
вектор и в D.126), то соответствующая величина п = (г — г0) v/| z —
— z0 | была бы плохо определена при z = z0). Более сложный вы-
выбор w (г) дает мультиинстантонные решения.
Полезно записать А^ и Q, выраженные непосредственно через
w (г). Имеем
Лц = / (п* • д^п) = (i/2 | w |2) (w* • d^w - w • ^w*).
Используя соотношения Коши—Римана D.125), это можно све-
свести к
я W*-dvW + W-dvW* ,1 a i i 12 Iл ioo\
All=±eilv v2|^|2 = + -g- г„Л In | w |2. D.128)
Тогда
l AA, = ± 4r | *x П In I w |2. D.129)
В силу равенства в D.119) действие равно S = 2я| Q|. Несложные
вычисления при подстановке D.126) в D.129) подтверждают, что
Q = 1 и 5 = 2я.
В заключение установим связь СЯ^-модели с О (З)-моделью.
При N = 1 СЯ^-модель имеет два комплексных поля п^ и пг, свя-
связанные условием | % |2 + | п2 |2 = 1. Построим три поля фа, а = 1,
2, 3:
фа = «;(а°)рЛ) D.130)

КЛАССИЧЕСКИЕ ИНСТАНТОННЫЁ РЕШЕНИЯ 129
где аа — три матрицы Паули. В явном виде имеем
ф1 = 2 Re (лГл2), f = 2 Im (nf n2), </>3 = | m |2 — | n2 p.
Поля </>a действительны и удовлетворяют соотношению
Дальнейшими простыми вычислениями плотность лагранжиана
D.100) приводится к виду 2О (дц0а) Eц^а). Таким образом,
СЯ^модель есть О (З)-модель, записанная в терминах фа. Для
больших N CPjv-модели представляют собой лучшее обобщение
О (З)-модели, чем О (А^)-модели, так как они дают инстантоны
в двух измерениях для произвольного N.
Таким образом, мы видим, что СЯ^-модель, хотя и состоит
только из скалярных полей, обладает локальной калибровочной
инвариантностью. Она имеет инстантоны, во многом сходные с ин-
стантонами четырехмерной системы Янга—Миллса. Более общее
обсуждение нелинейных моделей, напоминающих калибровочные
теории, см. в работах [19, 59].
5 РаДжараМан Р.

ГЛАВА 5
КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ
5.1. Введение
В предыдущих главах приведены примеры локализованных клас-
классических решений нелинейных релятивистских уравнений поля.
Теперь мы можем обсудить связь таких решений с соответствую-
соответствующими квантовополевыми теориями. Оказывается, при опреде-
определенных благоприятных условиях можно установить соответствие
классических решений в пространстве-времени Минковского со
связанными состояниями и состояниями рассеяния квантовой тео-
теории. В частности, уединенные волны и солитоны (ниже для про-
простоты мы будем и те и другие называть солитонами) можно связать
с квантовыми состояниями протяженных частиц. Следующие не-
несколько глав посвящены исследованию этой связи, что не только
удовлетворит наш чисто академический интерес, но и даст новую
конкретную информацию о квантовой теории. Некоторые харак-
характерные величины квантовых состояний, например энергия или
формфакторы, могут быть разложены в квазиклассические ряды.
Мы увидим, что главные члены в этих рядах связаны с соответст-
соответствующими классическими решениями. Поэтому знание классиче-
классических солитонных решений при систематическом квазиклассиче-
квазиклассическом разложении дает некоторую информацию о квантовых со-
состояниях частиц. Более того, эта информация будет непертур-
бативной в смысле нелинейного взаимодействия, так как в наи-
наиболее интересных случаях непертурбативны соответствующие
классические решения. Заметим, что большинство классических
решений в предыдущих главах непертурбативны. Они становятся
сингулярными при обращении нелинейных членов полевых урав-
уравнений в нуль.
Евклидовы решения (инстантоны) также дают непертурбатив-
ную информацию о соответствующей квантовой теории, но в дру-
ном аспекте теории, связанном с вакуумными состояниями и эф-
эффектами туннелирования. Эти вопросы мы обсудим, как обещали,
в двух последних главах.
Начнем в этой главе с простейшего применения классических
решений в квантовой полевой теории — квантования статических
солитонных решений с целью получения непертурбативных кван-
квантовых состояний протяженных частиц. Формализм для такого

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 131
квантования развит в разных работах с помощью разнообразных
методов [62, 81, 101, 173, 284, 285]. Все эти методы, включающие
функциональные методы, методы канонического оператора и т. д.,
приводят к одному и тому же основному физическому результату.
Выбор того или иного метода отчасти является делом вкуса подоб-
подобно выбору среди методов дифференциального уравнения Шре-
дингера, фейнмановского интеграла по траекториям или комму-
коммутаторов Гейзенберга для рассмотрения задачи о гармоническом
осцилляторе. Для рассмотрения разных аспектов задачи мы будем
применять различные методы.
Мы уже отмечали, что односолитонное решение напоминает
даже на классическом уровне протяженную частицу. (Под «протя-
«протяженной» частицей понимается частица конечного, ненулевого
размера. Большинство частиц в природе, даже так называемые
элементарные частицы, по-видимому, являются протяженными,
хотя при теоретических вычислениях их часто приближенно счи-
считают точечными.) Как и протяженные частицы, наши солитонные
решения являются локализованными объектами с конечной энер-
энергией. В своих системах покоя они статичны, а в движущихся си-
системах движутся без дисперсии. При движении их формы испыты-
испытывают лоренцово сокращение (см., например, B.32)), а их энергия
Е при движении связана со статической энергией М знакомой ре-
релятивистской формулой Е = М1У\ —v2 (см., например, B.33)).
Эти особенности классических солитонов позволяют нам ожидать
существования некоторого соответствия с частицами и в кванто-
квантовой теории.
Эти ожидания оправдываются, но связь классических солитонов
с квантовыми частицами не совсем тривиальна. Грубое отождест-
отождествление классического решения с объектом типа волновой функции
квантовой частицы некорректно в силу ряда причин. Правильная
интерпретация более изощренна, хотя и проста по своей сути. От-
Отметив некоторое соответствие классических солитонов частицам,
в противовес этому заметим, что определение частицы в квантовой
теории внешне уводит далеко от классических решений полевых
уравнений. Чтобы оценить это замечание, напомним основные
отличия классической теории от квантовой. В первой поля яв-
являются с-числовыми функциями пространства-времени. Поля
описывают состояния классической системы, а их динамика опре-
определяется нелинейными дифференциальными полевыми уравне-
уравнениями в частных производных. Наши солитоны — только реше-
решения этих уравнений. Несмотря на сходство с физическими части-
частицами, понятие «частицы» не существует в классической полевой
теории.
В отличие от этого в квантовой теории поля понятие частицы
существует, но сами поля имеют другой статус. Они являются
5*

132 ГЛАВА 5
операторными функциями пространства-времени, а не с-числами,
и действуют на векторы в гильбертовом пространстве. Поля под-
подчиняются полевым уравнениям Гейзенберга," но решения этих
уравнений также являются операторами. Они не описывают со-
состояний квантовой системы. Состояния описываются векторами
в гильбертовом пространстве. В частности, «частицы» есть спе-
специальные векторы состояний, подчиняющиеся требованиям, ко-
которые мы накладываем на состояния частиц, исходя из квантового
релятивистского контекста. Нестрого говоря, частице в квантовой
теории соответствует дискретный гиперболоид спектра, т. е.
семейство собственных векторов операторов импульса и гамильто-
гамильтониана с собственными значениями Р и Е, подчиняющимися усло-
условию Е2 — Р2 = М2 с некоторым дискретным М. Кроме того,
требуется, чтобы соответствующие формфакторы данных состоя-
состояний были локализованы, что отражает свойство частиц описывать
локализованный комок вещества. Динамика состояний частиц,
как и динамика любых других векторов состояний, задается урав-
уравнением Шредингера, которое несколько отличается от полевых
уравнений. Поэтому понятие частицы в квантовой полевой теории
кажется достаточно далеким от классических решений полевых
уравнений. Действительно, при рассмотрении квантовой теории
поля в стандартных учебниках мало упоминается о связи между
частицами теории и решениями ее полевых уравнений, кроме
тривиального случая свободной полевой теории.
Конечно, эти два понятия связаны. Сама книга обязана своим
существованием данной связи. Сделанное в предыдущем абзаце
замечание дано с целью предостеречь от восприятия связи как
самоочевидной вследствие некоторого сходства частиц и класси-
классических решений. Для установления связи между ними необходимо
проделать еще некоторую работу.
К счастью, основные принципы, необходимые для установле-
установления корректной связи, по своей сути достаточно просты. Все, что
надо сделать, это воспользоваться такими известными из обычной
квантовой механики понятиями, как принцип соответствия и ква-
квазиклассическое разложение, связывающие квантовые уровни
с классическими орбитами при систематическом приближении, и
обобщить их на полевую теорию. Вероятно наиболее известным
примером такой связи в нерелятивистской квантовой мехнике
является ВКБ-метод и вытекающее из него условие квантования
Бора—Зоммерфельда. Это условие связывает избранные класси-
классические периодические орбиты с квантовыми уровнями энергии.
В последующих главах мы обобщим этот метод на полевую тео-
теорию и будем использовать периодические зависящие от времени
решения классических полевых уравнений. В данной главе мы
сконцентрируем внимание на более простой задаче квантования
статических решений. Аналогичная связь между статическими

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 133
решениями ньютоновских уравнений движения и нерелятивист-
нерелятивистскими квантовыми уровнями энергии даже еще более элементар-
элементарна, чем в ВКБ-методе. Мы начнем следующий раздел с напомина-
напоминания необходимых свойств этой хорошо известной в обыкновенной
квантовой механике связи. Прямое обобщение этих простых ре-
результатов на полевую теорию даст центральную идею, лежащую
в основе квантования статических решений.
5.2. Основная идея
Рассмотрим движение нерелятивистской частицы единичной
массы в одном измерении под действием потенциала V (х). В клас-
классической механике частица описывается заданием х как функции
времени, которая определяется из ньютоновского уравнения
d2x/ dt2 = — dVl dx. E.1)
v
a b с x
Рис. 9. Пример потенциала V (х) для одномерной частицы единичной массы.
В квантовой теории частица описывается не величиной х, а волно-
волновой функцией 1(з (х). В частности, собственные состояния энергии
•ф,1 (х) подчиняются уравнению
Щп =(-тР2 + V(x)) грп (х)=Епуп(х), E.2)
где р = —iud/dx — оператор импульса. Прежде чем прокванто-
вать статические решения, напомним свойства приближенной
связи статических решений E.1) с собственными состояниями
энергии E.2).
1. Статические (не зависящие от времени) решения классиче-
классического уравнения E.1) являются экстремумами V (х). В качестве
примера рассмотрим потенциал V (х), изображенный на рис. 9.
Он имеет три экстремума при х = а, х = b и х = с. Частица, по-
помещенная в любую из этих трех точек, остается в ней. Таким об-
образом, классические статические решения имеют вид
x(t) = a, x(t) = b, x(t) =c. E.3а, б, в)

134 ГЛАВА 5
Из них а и с дают минимумы (cPV/ dx2 > 0) и соответствуют ста-
стабильным статическим решениям, а решение b нестабильно. Начнем
с первого решения E.3а). Его можно назвать «классическим основ-
основным состоянием», так как оно отвечает решению с наинизшей
энергией, допускаемой для этой частицы классической механикой.
Полная энергия
E** = V(a). E.4)
2. В квантовой теории такое состояние не допускается. Прин-
Принцип неопределенности не позволяет частице иметь одновременно
нулевой импульс и фиксированное положение. Следовательно,
даже в основном состоянии (т. е. в состоянии с наинизшим собст-
собственным значением в E.2)) частица флуктуирует около х = а,
что приводит к энергии основного состояния
E0 = E™ + \ = V(a) + b0, E.5)
где Ао — квантовая поправка, обусловленная движением около
нулевой точки х = а.
3. Если потенциал около точки х = а приближенно можно
считать гармоническим, то можно использовать «разложение по
слабой связи». Разложим V (х) в ряд Тейлора в окрестности х ~ а:
= V(а) +±<*Цх - а)* + ±к3(х - af +±К(х - af + ■ ■ ■ .
E.6)
Тогда для волновых функций, удовлетворяющих условиям
К {{х - а)г) С со2 ((х - аJ), г = 3, 4, . . ., E.7)
где (...) обозначает математическое ожидание, эффекты негармо-
негармонических членов V (х) будут малы. Для достаточно малых Кг
низколежащие собственные состояния энергии, локализованные
в окрестности х = а, удовлетворяют условиям E.7), и для них
потенциал можно приближенно задать гармоническим, свойства
которого очень хорошо известны. Таким образом, энергии этих
низколежащих состояний можно представить в виде
E.8)
В частности, в данном приближении слабой связи энергия основ-
основного квантового состояния записывается в виде
Ео= V (а) + йсо/2 + О (К)- E.9)
4. Выражение E.9) описывает простейший случай связи кван-
квантовых состояний и классических решений. Слева стоит энергия
основного квантового состояния. Члены справа связаны с соответ-
соответствующим статическим классическим решением E.3а). Первый

Кёантованйё статических решений j35
член есть энергия этого классического решения. Во втором члене,
описывающем главную квантовую поправку, со отвечает классиче-
классической частоте устойчивого решения. Поправки О (кг), получаемые
из стандартной теории возмущений, включают только постоянные
%г и со, которые определяются производными потенциала при клас-
классическом решении х — а.
5. Не только энергия основного состояния, нр и энергии низ-
колежащих, слабовозбужденных состояний аналогичным образом
связаны с классическим решением соотношением E.8).
6. Энергия квантового состояния описывает только одно из его
свойств. Полная информация о состоянии содержится в волновых
функциях. Но в соответствующем приближении классическое ре-
решение дает и другие свойства волновой функции основного состоя-
состояния. Это происходит потому, что, хотя волновая функция г|H (х)
размазана по х, она все же в какой-то степени локализована около
классического решения х — а. Например, математическое ожида-
ожидание ее положения определяется выражением
\*xdx = a+..., E.10)
где точками обозначены поправки, связанные с константами не-
негармоничности Кг. Напомним, что величина а в E.10), хотя и мо-
может быть числом, но является статическим классическим реше-
решением E.3а), а слева стоит величина, характеризующая свойство
квантового основного состояния.
7. Повторим ту же процедуру для более интересного решения
х (t) = с E.3в). В классической механике это решение имеет
энергий
£кл = l/(c)j E.Ц)
которая больше V (а). Это решение аналогично классическим ста-
статическим солитонам в полевой теории. Они также описываются
статическими решениями с энергиями больше энергии классиче-
классических вакуумов соответствующих теорий поля. Хотя точка х — с
отвечает только локальному минимуму V (х), в ее окрестности
опять можно применить метод гармонического осциллятора, или
приближения «слабой связи»
V (х) = V (с) + 4- (о)'J (х - сJ + £ -ур (х - е)'. E.12)
8. Если опять К достаточно малы, то в окрестности х = с
негармоническими эффектами можно пренебречь. Построим се-
семейство состояний приближенно гармонических осцилляторов
с центром в точке х = с и с энергиями
Ёп- = V (с) + ft©' (п + -1-) + О (А,,). E.13а)

136 ГЛАВА 5
Если приближение справедливо, то наинизшее состояние имеет
энергию
E0 = V(c) + ±-tto' + O(K), E.136)
а математическое ожидание
(х)=с.+ О(К). E.14)
Таким образом, мы опять имеем приближенное описание собст-
собственных состояний энергии, связанных с классической энергией
статического решения V (с), причем (х) связано с самим решением
с (см. п. 9).
9. Теория возмущений, основанная на приближении гармони-
гармонического осциллятора, в, случае локального минимума х — с ис-
использует потенциал около х — с, как будто не существует другого
более глубокого минимума в точке х = а. В действительности мы
знаем, что волновые пакеты ямы х = с туннелируют в яму х = а
и наоборот. Следовательно, два набора уровней энергии переме-
перемешиваются. Но если Кг и К малы, то два минимума х = с, х = а
широко разделены большим потенциальным барьером. Таким
образом, туннелирование происходит медленно, и в результате
изменения собственных значений энергии малы. Другими словами,
туннелирование, если оно существует, является непертурбатив-
ным по параметрам^ и К- В любом конечном порядке разложе-
разложения по слабой связи набор уровней E.13) вблизи х — с можно
рассматривать отдельно от набора E.8) около точки х = а.
В теоретико-полевых приложениях мы будем рассматривать
примеры обоих типов — с туннелированием и без него. Примеры
явления туннелирования, связанные с инстантонами, рассматри-
рассматриваются в гл. 10. С другой стороны, распада состояний, построенных
в окрестности солитонных решений, вследствие туннелирования
не происходит. Это связано с наличием у солитонов ненулевого
топологического индекса, что эффективно возводит бесконечный
энергетический барьер между ними и вакуумными решениями.
Это объясняется в разд. 5.6.
10. В окрестности статического решения х (t) = b уровней не
существует, так как это решение нестабильно. Соответствующая
частота [(cPVl dx2)b]1/2 мнимая.
11. Очевидно, что при обращении в нуль гармонической по-
постоянной со вся процедура перестает работать. При этом условию
«слабой связи» E.7) нельзя удовлетворить никакими значениями %г.
В частности, следует отметить случай потенциала V (х), неза-
независящего от х. Хотя эта задача тривиальна, но она открывает
для нас новые свойства квазиклассического метода.
В данном примере все коэффициенты Тейлора ir и со обращают-
обращаются в нуль, и условие слабой связи E.7) становится бессмыслен-

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 137
ным. Соответственно вся физическая картина связи классического
статического решения с квантовыми уровнями нарушается. Хотя
каждая точка х = х0 теперь является классическим статиче-
статическим решением, собственные функции энергии не локализованы
около х = х0, так как потенциал не имеет необходимой для этого
кривизны в окрестности х = х0. Действительно, корректные соб-
собственные функции энергии eikx пробегают все точки оси х, и их
следовало бы связать не с отдельным статическим решением,
а с непрерывным семейством статических решений. Все это обус-
обусловлено существованием трансляционной симметрии, возникаю-
возникающей вследствие независимости V (х) от х.
Из этого примера следует, что если потенциал не зависит от
координаты, то соответствующая гармоническая частота со обра-
обращается в нуль и квазиклассический метод требует модификации.
Необходимую модификацию мы обсудим несколько ниже. Та же
проблема возникает при квантовании солитонов в полевой теории
в силу аналогичной причины — существования непрерывных
симметрии. Рассмотрение получающихся нулевых мод достаточно
сложно, и мы посвятим ему гл. 8. Но физическая идея, лежащая
в основе существования нулевых мод и их воздействия на квази-
классический метод, та же, что и в приведенном здесь тривиальном
примере. Отметим, что точные уровни энергии данной простой
задачи, когда V не зависит от х, можно представить в виде
я» = v + 4 Ыа. -<5Л5)
где рп — импульсы, т. е. квантовые поправки включают импульсы,
а не частоту, которая в рассматриваемом случае равна нулю. За-
Заметим, что импульсы сохраняются в силу трансляционной симме-
симметрии (которая привела к со = 0). То же справедливо в полевой
теории для каждой моды нулевой частоты, обусловленной непре-
непрерывной симметрией.
12. Возвращаясь к общему случаю потенциала V (х), завися-
зависящего от х, мы видим, что, если не возникает трудностей с обра-
обращением в нуль частоты со, с каждым статическим стабильным клас-
классическим решением можно связать набор собственных состояний
энергии. Квантование статических солитонов основано на обоб-
обобщении этих идей на теорию поля. Отмеченные выше специфиче-
специфические свойства, хотя и кажутся тривиальными, содержат зерно
важных черт солитонного квантования. Следует подчеркнуть, что
соотношения E.8), E.9), E.10) и E.13), E.14) справедливы только
при разложении по слабой связи, когда пренебрегают негармони-
негармоническими членами. Отметим, что негармонические члены в V (х)
приводят к нелинейным членам в уравнении движения E.1).
Следовательно, квантование статических солитонов в полевой тео-
теории справедливо только в том случае, если нелинейные взаимодей-

138 ГЛАВА 5
ствия малы. Тем не менее результаты могут быть непертурбатив-
ными. Это возможно, если само классическое решение непертур-
бативно. Оно определяет главные члены, как, например, в раз-
разложениях E,13), E,14), Методом теории возмущений рассматри-
рассматриваются только квантовые поправки.
В качестве промежуточного шага на пути к обобщению этих
идей на теорию поля рассмотрим систему с большим (но конечным)
числом степеней свободы. Представим пучок нерелятивистских
частиц с единичной массой в произвольном числе измерений,
описываемый декартовыми координатами х = (xlt ..,, xN), в по-
потенциале V (xlt ,.., xN), Пусть х = а — минимум (локальный или
абсолютный) потенциала V в Af-мерном пространстве. Тогда
х (t) = а является стабильным статическим классическим реше-
решением. Разложим V (хи ,.., xN) в окрестности xt = at:
V(x) = V (a) + -*-(*,- а,) (*, - а,)
+ -L (xt - а,) (Xj - а,) (хк - ak) [dxJ?}dXh } x=a + • • • • E.16)
Если производные V (х) третьего и более высоких порядков
при х = а малы (предел слабой связи), то можно построить
систему низколежащих состояний гармонического осциллятора
около точки х = а. Для этого диагонализируем матрицу вторых
производных ld2VldXi dxj]x==!t, заменяя переменные некоторыми
нормальными модами |г. Тогда в терминах |г задача сводится к си-
системе осцилляторов с частотами сог, где со? — собственные значе-
значения данной матрицы. (Если х = а действительно минимум, то
все со? положительны.) Эти моды связаны (слабо) через кубиче-
кубические и более высокого порядка члены в E.16). Состояние с наи-
низшей энергией, построенное в окрестности х = а, имеет энер-
энергию
N
£0 = V (а) + /_, ~2~йщ+ поправки. E.17)
Для более высоких возбужденных уровней (но не настолько вы-
высоких, чтобы нарушить приближение слабой связи) получаем
Е{пг) = ^ (а) + Й ^ ("' ~^ ~2~) Юг + П0ПРавки
1=1
Поправки к этим формулам получаются из теории возмущений.
Эти результаты являются простым обобщением задачи с одной
степенью свободы, причем набор собственных значений (со*J ма-
матрицы [д2У/дхг «5х;-]х=в заменяет число со2. Все сделанные выше

КбАйтовАнйё статических решений
замечания также тривиально обобщаются. Например, если одно
из значений сог- равно нулю (нейтральная стабильная мода), то
метод неприменим. Эту моду необходимо рассматривать отдельно.
Переходя к теории поля, начнем со скалярного поля <j> (х, t)
с лагранжианом
где, как и в гл. 2, U (ф) — произвольная функция ф, ограничен-
ограниченная снизу. Вместо конечного числа степеней свободы хъ ..., xN
мы теперь имеем непрерывное бесконечное множество степеней
свободы, т. е. значений ф в каждой пространственной точке х.
Но несмотря на это отличие, классическая динамика такой си-
системы аналогична механике частиц. Например, лагранжиан имеет
стандартный вид
L = Т [ф] — V [ф] E.19)
с кинетической энергией
\(^) E.20а)
и потенциальной энергией
У[ф] = \ dx [^(ЩJ + U (ф)] . E.206)
Уравнения движения Эйлера — Лагранжа имеют вид
д*ф (х, t)/dfi = — 6V \ф]/6ф (х, /), E.21)
где справа стоит функциональная производная. Напомним, что
координатами системы являются поля ф (х) и, следовательно,
энергия есть функция функций ф (х), т. е. функционал. Отметим
сходство полевого уравнения в форме E.21) с ньютоновским урав-
уравнением E.1). Статические решения уравнения E.21) также яв-
являются экстремумами потенциала в полевом пространстве и удов-
удовлетворяют условию
6V [ф]/&ф (х) = 0. E.22)
В частности, стабильные статические решения являются мини-
минимумами V так же, как в механике частиц.
Пусть ф (х) = ф0 (х) — один из таких минимумов. Разложим
V в функциональный ряд Тейлора в окрестности ф0:
E.23)
где использовано интегрирование по частям и г\ (х) = ф (х) —
—ф>0 (х); многоточие соответствует кубическим и более высокого

140 ГЛАВА 5
порядка по Т1 членам. Функциональный ряд Тейлора получается
последовательным взятием производных V [ф]. Оператор
(—у2 ~Ь cPUl йф2) в точке ф (х) = ф0 (х) является обобщением ма-
матрицы вторых производных V в E.16). Его собственные значения
и собственные функции определяются из дифференциального урав-
уравнения
[ ($)] ), E.24)
где щ (х) — ортонормированные «нормальные моды» флуктуации
в окрестности ф0 (х). Запишем [95]
Л (х, /) = ф (х, /) - ф0 (х) = S а @ у\л (х). E.25)
i
Тогда, используя E.23) и E.24), приводим лагранжиан E.18)
к виду
L = -у- 2 [с, (/I2 - (Vtfo] + 4" 2 ff'(W Ю|) + попРавки-
2
i
где сг = dc^/ dt, а поправки соответствуют третьей и более высо-
высокого порядка производным в ряду Тейлора E.23). «Приближение
слабой связи» здесь относится к поправочным членам при раз-
разложении E.26). Это приближение требует, чтобы амплитуды флук-
флуктуации л (х), а также третья и более высокие производные V [ф]
при ф = ф0 были малы. В низшем порядке приближения поправ-
поправками в E.26) пренебрегают. Тогда лагранжиан E.26) сводится
к лагранжиану набора гармонических осцилляторов с нормаль-
нормальными модами плюс постоянный член V [ф0]-
Соответственно в квантовой теории можно построить набор
состояний приближенно гармонических осцилляторов, располо-
расположенных в пространстве полей около ф0 (х), квантуя коэффициенты
нормальных мод с%. Энергии таких состояний определяются выра-
выражениями
E{"i} = V ["bi + й S ("' + 4") 0)' + П0ПРавки> • E-27)
где щ — номер возбужденной t'-й нормальной моды. Выражение
E.27) аналогично выражению E.13). Оно приближенно связывает
некоторые квантовые уровни с классическим решением ф0 (х).
Первый член есть просто классическая энергия статического ре-
решения ф0 (х). Второй член включает со; — частоты стабильности
ф0 (х). Отметим, что уравнение E.24) является классическим ли-
линейным уравнением устойчивости. Поправочные члены в E.27)
получаются стандартными методами разложения в ряд по теории
возмущений негармонических поправок в E.26). Подчеркнем
опять, что если одна из частот сог равна нулю, то приведенные
здесь простые соображения необходимо модифицировать.

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 141
Мы изложили основную идею построения связи квантовых
уровней с заданным стабильным классическим решением ф0 (х).
Полученные результаты справедливы только в рассмотренном
выше приближении слабой связи. В данной главе мы будем его
придерживаться. Решение ф0 дает либо абсолютный, либо локаль-
локальный минимум V [ф0]. Если ф0 — абсолютный (но, возможно, вы-
вырожденный) минимум, то он представляет собой «классический
вакуум» системы. В силу наличия члена (уфJ в V [ф] такой абсо-
абсолютный минимум должен быть пространственно независимым.
Квантовый уровень, построенный согласно рассмотренной выше
процедуре в окрестности такого абсолютного минимума, будет
вакуумным состоянием и квантом данной полевой теории. Для
иллюстрации рассмотрим типичный пример — теорию ф* с лагран-
лагранжианом
L = \ dx [± (^J - 4
Тогда
j dx
V [ф] = j
] E-29)
и статическое решение подчиняется уравнению
6V [ф]/бф (х) = —\2ф + тЧ + W = 0- E-3°)
Это уравнение имеет тривиальное статическое решение
фо(х, 0 = 0, У[фо = О] = О, E.31)
которое является абсолютным минимумом потенциала V [ф].
Потенциал V [ф], записанный в виде E.29), уже разложен в ряд
Тейлора в окрестности ф = 0. Вторая производная потенциала при
Ф = 0 дает оператор (—v2 + m2), уравнение на собственные зна-
значения которого
(_v* + ms)Tif(x) = a>?ii<(x) E.32)
тривиально решается и дает r\t (x) = L~3/2 exp (tk^-x), кг =
= 2nNtlL, где L -*■ оо и со| = к| + т2. Приближение слабой
связи подразумевает разложение по К. Набор уровней прибли-
приближенно гармонического осциллятора, построенный в окрестности
ф = 0, имеет энергии
{пй = V [ф0] + ft ^ VM+m* (л, + 4) + О (к) =
= ft ^ V k? + m2 (nt + -i-) + О (Я,). E.33)
к

142 глава 5
(В релятивистской квантовой теории часто используют единицы,
в которых ft = с = 1. Поскольку мы хотим выявить квазикласси-
ческую природу нашей теории, оставим ft, но положим с равным
единице. В этом случае параметр т имеет размерность (масса/ft).)
Наинизший уровень с nt = 0 является основным состоянием дан-
данной квантовой теории поля, т. е. вакуумным состоянием с энер-
энергией
Евгк = Е{0} = ^ А 2 /Ы + т1 +0 {%). E.34)
Следующее возбужденное состояние с модой кг- = 0 имеет энер-
энергию E^Ep^i.nt^oy
El = 4" П 2 VWT^rf -^-fttn + O (k) = Евак + hm + 0 (%). E.35)
Отметим, что Е{„г} может формально расходиться вследствие
бесконечного числа мод кг. Рассмотрение такой расходимости
с помощью перенормировок хорошо известно. Мы вернемся
к этому вопросу несколько ниже. Здесь же отметим, что в порядке
А,0 величина {Е{П1} — EBav) конечна. Таким образом, Ег — Евак
отвечает энергии одиночной квантовой частицы в покое, имеющей
массу ~ftm. Другие возбужденные состояния описывают кванто-
квантовую частицу, движущуюся с импульсом ftk, и т. д. Эти результаты
хорошо известны из стандартной теории возмущений. Мы их на-
напомнили здесь, чтобы подчеркнуть, что стандартную теорию воз-
возмущений можно рассматривать как частный случай нашего ква-
квазиклассического метода, когда используется классическое стати-
статическое решение, являющееся тривиальным абсолютным миниму-
минимумом потенциала V [<j>]. В этой главе нас интересуют новые резуль-
результаты, получаемые при применении этой процедуры для локаль-
локального минимума V [ф], т. е. для нетривиального зависящего от х
классического решения. К сожалению, модель E.28) не имеет
таких нетривиальных статических решений с конечной энергией.
Это ясно видно из соображений, приведенных в гл. 2 и 3. Поэтому
в следующем разделе мы рассмотрим для иллюстрации новых ас-
аспектов наших методов немного отличный пример, допускающий
нетривиальные статические решения.
Сначала сделаем некоторые замечания относительно доказа-
доказательства. В каждом случае мы разлагаем в ряд потенциал в окрест-
окрестности минимума и диагонализируем квадратичные члены. Это дает
сумму членов, отвечающих гармоническим осцилляторам, плюс
негармонические члены, которые, согласно предположению, не-
необходимо рассматривать по теории возмущений. После этого мы
просто постулируем результаты в главном порядке без соответ-
соответствующего вывода в силу того, что они являются непосредствен-

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 143
ным обобщением стандартных результатов для гармонического
осциллятора, имеющихся в любом элементарном учебнике по
квантовой механике. Другое дело поправки более высокого по-
порядка к этим уравнениям, которые требуют более осторожного
применения теории возмущений. Но в основном при квантовании
солитонов можно пользоваться результатами на уровне главных
квантовых поправок, т. е. в приближении гармонических осцил-
осцилляторов. Наш эвристический подход мы сохраним и в остающейся
части глав. Затем мы покажем, как можно формально вывести эти
результаты, используя функциональные или операторные методы.
5.3. Квантование кинка
Рассмотрим скалярное поле ф (х, t) в A + 1) измерениях
с лагранжианом, немного отличающимся от E.28), а именно
E.36)
Мы уже изучали эту систему на классическом уровне в гл. 2 и
знаем, что она дает статический кинк. Применим теперь к нему
квазиклассический метод предыдущего раздела. Потенциал си-
системы имеет вид
[И&)'И?)']- <537>
Статическое классическое решение удовлетворяет уравнению
Как мы видели в гл. 2, это уравнение дает тривиальные решения
ф (х, t) = dztnl-y^K и нетривиальные решения — кинки фк (х, t) =
= ± {miyV) th [т (x — а)/у^2]. Наш квазиклассический метод
можно применить к каждому из этих решений.
5.3.1. ВАКУУМ И ЕГО ВОЗБУЖДЕНИЯ
Начнем с тривиального решения фг (х, t) = m/-j/X. Разложим
в ряд потенциал в окрестности фг\
+ т /Г J ф3 dx + A- J ф* dx, E.39)
где f{x) = f (х) — фх (х) = ф(х) — т//Ъ и V tyj = О,

144 ГЛАВА 5
Если константа % достаточно мала, то можно рассматривать
кубичный и четвертого порядка члены в E.39) по теории возму-
возмущений. В низшем порядке в квадратичном члене вторая производ-
производная V [ф] при ф1 есть оператор (—д2/дх2 + 2т2) с собственными
значениями (kl + 2m2) и собственными функциями exp (iknx).
Разрешенные значения kn находим при нормировке
knL = 2шт, E.40)
где L стремится к бесконечности и 2*. -*■ (Ы2п) \ dk.
Используя все это, построим систему уровней приближенно
гармонического осциллятора в окрестности ф1. Наинизший из них
имеет энергию
^ ^ E.41)
где нуль отвечает классической энергии V [ф^. Это соответствует
вакуумному состоянию системы. Более. высокие возбуждения
аналогично E.33) обладают энергиями
E{Nn} = ft £ (Nn + -L) (kl + 2m2I/2 + О (К). E.42)
п
Мы имеем знакомую картину Л^„ квантов теории с импульсами
Шп. Их масса покоя в низшем приближении равна тЪ1у^2. Назо-
Назовем такую систему состояний, построенную в окрестности фъ
«вакуумным сектором». Так как эта процедура по существу кван-
квантует смещенное поле ф = ф — ф1 согласно стандартным методам
теории возмущений, в низшем приближении можно использовать
известный результат
@\ф(х, t)\0) = 0, _.E.43)
где | 0} — вакуумное состояние. Тогда
E.44)
Это аналог выражения E.10), представляющий собой еще одну
связь квантового вакуумного состояния с классическим решением
фг наряду с соотношением E.41).
Эти простые результаты также известны из традиционной тео-
теории возмущений, примененной к данной системе. Полученные
выше кванты являются некоторым типом частиц системы. Назовем
их для удобства «мезонами» модели. Ниже мы увидим, что данная
полевая теория дает кроме этих мезонов другой тип частиц, по-
получаемый при применении той же процедуры к кинку.
(Такой же набор вакуумного и многомезонных состояний
можно построить около ф% = —m/у^Х; от предыдущего он будет

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 145
отличаться только вакуумным значением @1 ф (х, t)\0) = ср2.
Эти два вакуума, рассматриваемые порознь, нарушают симме-
симметрию ф <-»• —ф исходного лагранжиана. Это один из простейших
примеров «спонтанного нарушения симметрии» — хорошо извест-
известного явления в квантовой теории поля. Мы не будем его здесь
подробно обсуждать и перейдем к нетривиальным решениям —
кинкам.)
5.3.2. КВАНТОВЫЙ КИНК И ЕГО ВОЗБУЖДЕНИЯ
Применим тот же метод к статическому кинку
фк (х-а)= (т//Г) th [m (х - а)//Т] E.45)
с энергией
У[фк] = Bу/¥/3)(пгУХ). E.46)
Это семейство солитонов с различными значениями а. Для опре-
определенности возьмем а = 0. Поскольку кинк представляет собой
статическое решение, удовлетворяющее E.38), он является экстре-
экстремумом потенциала V [ф]. При разложении потенциала по фк (х)
линейный член отсутствует в силу E.38). Поэтому имеем
4~ Л4), E-47)
где т) (х) = ф (х) — фк (х). Собственные значения оператора вто-
вторых производных V [ф] при ф = фк определяются из уравнения
X т]„ (л-) = к>1г\п (х). E.48)
Это уравнение, хотя и менее тривиальное, чем E.32), все же точно
решается. Заменой переменных z = тх/у2 оно сводится к урав-
уравнению типа уравнения Шредингера
U?) = -^(z). E-49)
Собственные функции и собственные значения этого уравнения
Шредингера хорошо известны [257]. Оно имеет два дискретных
уровня и непрерывный их континуум. Дискретными уровнями
являются
ю^ = 0, fjo(z)=l/ch2z, E.50а)
-L
т2, fjj (z) = sh z/ch2 z. ' E.506)

146 ГЛАВА 5
Непрерывный континуум уровней мы будем обозначать индексом q:
r\q (г) = ёч* C th2z.- 1 — ^ — Siqthz). E.50в)
Допустимые значения G в E.50в), как и допустимые значения kn
в E.40), фиксируются периодическими граничными условиями
в ящике длиной L при L -*■ оо. Отметим, что fj? (г) в E.50в) имеет
следующее асимптотическое поведение:
Л,(г) —exp[t(<7Z±-5-6fo))], E.51)
где
б (?) = —2arc tg [3^/B — ?2) ] E.52)
является фазовым сдвигом состояний рассеяния соответствующей
задачи Шредингера E.49). Длина ящика в переменных z —
= тх/у^2 равна mL/-\/2. Следовательно, периодические гранич-
граничные условия требуют, чтобы
qn(mL//Y) + 8(qn) = 2nn, E.53)
где п — любое положительное или отрицательное целое число.
Это фиксирует допустимые значения qn. В пределе L -»-оо до-
допустимые, значения образуют континуум, причем
E-54)
Используя нормальные моды, можно диагонализировать потен-
потенциал E.47) и лагранжиан в окрестности фк (х) в порядке А,0.
Необходимо только применить соотношения E.25), E.26), а также
E.50) для нормальных мод и их частот. Так как фк ~ О (l/j/k),
кубичные члены и члены четвертого порядка в E.47) будут по-
порядка у/~% и К соответственно. Согласно предположению, их необ-
необходимо рассматривать по теории возмущений. Следовательно,
в квантовой теории опять можно построить систему приближенно
гармонических состояний осциллятора в окрестности фк (х)
в пространстве полей. Можно также ожидать, что энергии состоя-
состояний равны (см. E.27), E.50))
оо
n 2 {Nn+-г
гг=О
2 VI trfi
ЗА ^\1-' I 2 / У 2 "* ' " ^j V ""■ ' 2
X
2 \l/2
X (-^-+2 +0(A,). E.56)

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ
Но здесь есть одна тонкость. Хотя этот анализ справедлив для
всех мод ел ^ 1 в E.50), он неприменим к моде с л = 0, так как
в E.50а) ю0 = 0. Мы уже неоднократно предупреждали о недо-
недопустимости использования разложения по гармоническим осцил-
осцилляторам при со = 0 в силу очевидных причин. В отличие от мод
с «^ 1, которые представляют собой чисто вибрационные моды
малых флуктуации, мода с п = 0 вообще не является вибрацион-
вибрационной. «Константа упругости» ю0 равна нулю. Соответственно кван-
квантовая волновая функция моды с п — 0 не локализована в окрест-
окрестности классического решения, а распределена по всему простран-
пространству. Та же проблема приводит при вычислениях к чисто техни-
техническим трудностям. Если попытаться непосредственно найти
поправки высших порядков к E.55) с учетом моды с п = 0, то
нулевая частота появится в знаменателе энергии, что приведет
к расходимостям.
Таким образом» строго говоря, прежде чем перейти к анализу
квантования кинка, мы должны научиться работать с такими
нулевыми модами. Хотя физические причины появления таких
нулевых мод легко понять (разд. 5.5), их систематическое рас-
рассмотрение требует достаточно сложных методов. Вся гл. 8 посвя-
посвящена рассмотрению таких нулевых мод. К счастью, состоя-
состояния E.55) можно исследовать, не вдаваясь в детали рассмотре-
рассмотрения нулевых мод. Для простоты мы это и сделаем здесь. Действи-
Действительно, большинство мод (за исключением моды с п = 0) являются
вибрационными, и квантовополевые волновые функции этих мод
приближенно соответствуют функциям гармонического осцилля-
осциллятора. Кроме того, выражение E.55) для энергии в порядке А,0
существенно не изменится, если мы сначала выберем ©0 ненуле-
ненулевым, а затем положим ю0 -»-0. Первый член не зависит от ©„,
а в следующем члене вклад моды с п = 0 обращается в нуль
при ю0 -»-0. Трудности возникают только в членах О (К), явно
не выписанных в E.55). Поэтому ограничимся пока порядком
О (к0) и продолжим наши бесхитростные рассуждения. Мы вер-
вернемся к качественному рассмотрению моды с п = 0 в разд. 5.5;
более полное изучение таких мод см. в гл. 8.
С этим условием перейдем к рассмотрению системы состояний
E.55), построенной в окрестности кинка в приближении малых К.
Представим следующую трактовку этих состояний, которая
подтверждается дальнейшими исследованиями этой главы.
1. Состояние с низшей энергией семейства E.55), соответ-
соответствующее \Nn =0}, можно рассматривать как состояние кинк-
частицы в покое. Заметим, что, хотя это состояние имеет наиниз-
наинизшую энергию в «кинк-секторе», т. е. в семействе E.55), оно не
является абсолютным основным состоянием, или вакуумом тео-
теории. Вакуум теории уже определен как состояние с наинизшей
энергией в «вакуумном секторе», т. е. в семействе E.42), построен-

148 ГЛАВА 5
ном в окрестности фг. Вакуумное состояние имеет энергию E.41),
меньшую, чем энергии всех других состояний семейств E.42) и
E.55) в порядке А,0. Таким образом, состояние {Л^п = 0} в E.55)
не является вакуумом и может рассматриваться как квантовый
кинк. Мы увидим, что он имеет свойства протяженной частицы.
2. Следующий, более высокий энергетический уровень E.55)
возникает в порядке А,0 при возбуждении моды ел = 1, т. е. при
Nx = I. Он имеет энергию
Ei=E[
~ т /—3~
i.N =oi =£о+ У -я-/ПЙ + О(Я,).
! In ( f Z
Это состояние можно интерпретировать как дискретное возбуж-
возбужденное состояние кинк-частицы. Более высокие возбуждения дан-
данной моды (Ыг > 1) дают более высокие возбужденные состояния
кинка. Связь основного состояния кинка с его возбужденными
состояниями аналогична связи основного состояния атома с воз-
возбужденными состояниями. Напомним, что атом по нашей терми-
терминологии также является протяженной частицей. Он обладает
дискретной энергией и локализованными формфакторами.
3. Остальные состояния семейства E.55), возникающие при
возбуждении мод с п ^ 2 (или, что эквивалентно, состояний
с Nq Ф 0 в E.56)), имеют другую интерпретацию. Их можно рас-
рассматривать как состояния рассеяния мезонов этой теории на
кинк-частице. Действительно, моды r\q E.50в) и их энергии пред-
представляют собой в порядке А,0 приведенные одночастичные волно-
волновые функции и энергии мезонов при рассеянии на кинке. В под-
подтверждение этой точки зрения отметим, что энергия возбужде-
возбуждения <7-й моды, согласно E.50в), равна
т. е. равна кинетической энергии мезона с импульсом umq/-]/2.
Напомним, что в данной теории мезон имеет массу i/2/пй. То,
что асимптотический импульс рассеянного мезона записывается
в виде fimqiyu, является следствием замены переменных z =
= /nx/i/2. Возвращаясь в собственных функциях r\q (z) в E.51)
к переменной х, получаем следующую асимптотическую форму:
exp [i ((qmx/yY) ± 6/2)],
что согласуется с асимптотической величиной импульса йт^/>/2.
Фазовый сдвиг б (q) является фазовым сдвигом для мезона при
рассеянии на кинке.
Можно заметить, что при трактовке этих состояний как со-
состояний рассеяния мезона на кинке в E.56) появляется только
кинетическая энергия мезона, а не кинка. Это происходит потому,

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 149
что с точностью О (А,0) кинк можно считать статическим; на его
статическом потенциале рассеиваются мезоны. Как мы увидим
из следующего раздела, это обусловлено тем, что масса кинка М
порядка AМ.). В пределе слабого взаимодействия кинк очень тя-
тяжелый и поэтому статичен. Главный член кинетической энергии
кинка имеет вид Р2/2М, т. е. порядка к, так как М ~ О A/А,).
Таким образом, в нашем рассмотрении в порядке А,0 справедлив
статический предел для кинк-частицы. Основываясь на данных
рассуждениях, можно полагать, что при возбуждении одной
моды из континуума (Nq=l для некоторого q в E.56)) мы получим
состояние кинк-мезонного рассеяния. Когда возбуждено не-
несколько таких мод, возникает состояние с несколькими мезонами
с соответствующими асимптотическими импульсами, рассеива-
рассеивающимися на кинке.
Такова наша интерпретация семейства квантовых состояний,
построенных в окрестности классического кинка, в приближении
слабой связи. В остальных разделах этой главы исследуем некото-
некоторые дальнейшие свойства таких состояний, что, как мы увидим,
подтвердит нашу интерпретацию.
5.4. Масса кинка и ее перенормировка
Получим точное выражение для массы квантовой кинк-ча-
кинк-частицы. Впервые это было проделано Дашеном и др. [101 ] в одной
из пионерских работ в этой области. Мы связали кинк-частицу
с наинизшим уровнем энергии системы E.55). Энергия уровня
определяется выражением
По =2т/2~т3/ЗА. + -i-ftm ]/ ±. + 1JJ Пт A<£ + 2)'/2 + О (Я,).
E.57)
Это выражение формально расходится. Бесконечные ряды 2?п
дают в пределе континуума E.54) квадратично расходящийся
интеграл. Это само по себе не должно нас беспокоить, так как
энергия вакуума E.41) также квадратично расходится. Физи-
Физически важна разность энергий между некоторым выбранным со-
состоянием и вакуумным состоянием. Эта разность находится вы-
вычитанием E.41) из E.57):
[т (U-
-№ + 2т2У'2]+О(Х). E.58)
'Гак как оба члена в квадратных скобках расходятся, вычитать
их необходимо осторожно, чтобы не потерять конечные вели-

150 fЛАЁА 6
чины. Рассмотрим ящик длины L. Тогда kn и qn, согласно E.40)
и E.53), связаны соотношением
. E.59)
Отсюда члены в квадратных скобках в E.58) принимают вид
{[*„ - 6n/LJ + 2т*У2 - Ц + 2т2I/2) =
= - {knbnlL) (kl + 2m2)-1'72 + О A/L2). E.60)
Переходя к пределу при L -*- оо и используя ^jk -*■ (L/2n) I dk,
получаем
СО
E.61)
Здесь б (k) выражено через k с использованием E.52):
-2 arctg (l^_%) + O(l/L), E.62)
где члены О (ML) можно опустить. Интегрируя по частям, полу-
получаем
После некоторых вычислений с учетом E.62) это приводит к вы-
выражению
2/2" т* , 1 -|/~Г.
Z7 С4
^0 ^вач — Qi 1 ~о~ у ~о~
ON £. J £.
- - г —
со
D/72/2 Г &р \Р *т~ £) | г\ /1 \ /С со\
— . .ГГг лг-т-г-л, 2~ГТГ + °^' E-6<3^
4л ]/ 2 J ]/ с2 + 4 (/52 + 1)
—оо
где в последнем интеграле использована переменная р = k "j/2/m.
Отметим, что, хотя квадратичная расходимость Ео устраняется
вычитанием £вак. выражение E.63) все же имеет логарифми-
логарифмическую расходимость в интеграле. Ее нельзя устранить добавле-
добавлением к лагранжиану бесконечной константы, так как E.63) опре-
определяет разность двух энергетических уровней. Тем не менее на
данном этапе вычислений эта расходимость не должна вызывать
беспокойства. Наоборот, ее и следовало здесь ожидать, а устра-

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ
ияется она с помощью нормального упорядочения гамильто-
гамильтониана.
Введение нормального упорядочения или перенормировки
теории было бы слишком значительным отступлением от нашей
основной темы. Появление «ультрафиолетовых» расходимостей
в квантовой теории поля вследствие определенного поведения
произведения операторов полей на малых расстояниях хорошо
известно в стандартной теории возмущений [53]. Известно также,
что они убираются добавлением к гамильтониану подходящих
«контрчленов». В этом разделе мы полагаем, что читатель знаком
с этой процедурой. В частности, нам потребуется перенормировка
только в смысле нормального упорядочения. Для теории <£4
в двух измерениях известно, что все появляющиеся расходимости
убираются нормальным упорядочением. Напомним, что гамиль-
гамильтониан теории E.36) имеет вид
где л (х, t) = <j> (х, t) — канонический импульс. В квантован-
квантованной теории операторы вида <j>2 (x, t), ф* (х, t) и т. п., а следова-
следовательно, и гамильтониан формально расходятся и плохо опреде-
определены. Поэтому энергетические уровни, вычисленные непосред-
непосредственно из гамильтониана, также будут расходиться. Именно
из-за этого появляется расходимость в E.63).
Данная проблема не связана прямо с кинком и его квантова-
квантованием. Гамильтониан E.64) имеют все состояния теории, в том
числе знакомы вакуумное и мезонные состояния E.41) и E.42).
Мы уже отмечали, что непосредственно вычисленная вакуумная
энергия E.41) расходится. Если бы мы вычислили массу мезона
в более высоком порядке (в низшем она равна -\/2пгй), то обнару-
обнаружили бы, что она содержит логарифмическую расходимость. Та-
Таким образом, устранение таких расходимостей существенно даже
в знакомом вакуумном секторе состояний. Оно достигается заме-
заменой гамильтониана на нормально упорядоченный ://:. В нашем
квазиклассическом рассмотрении трудно работать непосред-
непосредственно с нормально упорядоченной формой. Но последнюю
можно записать как первоначальную неупорядоченную форму
плюс некоторые контрчлены, так как
: ф* : = ф* - Аф2 - В, : ф2: = ф2 - Сл E.65)
где А, В и С — константы, равные бесконечности в теории воз-
возмущений. Следовательно, нормально упорядоченный гамильто-
гамильтониан можно записать в виде
Н\ = Н- J dx^dmY + D), E.66)
—9»

152 ГЛАВА 5
где константы dm2 и D можно найти стандартными методами тео-
теории возмущений. Для дт2 вклад порядка К следует из диаграммы
Фейнмана, приведенной на рис. 10:
дт* = »1 Т Ф = «л | Ъ
4л J /в2 + 2т2
—тл —Л
где тЛ — параметр обрезания импульса. Отметим, что в соот-
соответствии с нашим квазиклассическим рассмотрением мы привели
в явной форме зависимость однопетлевой диаграммы от h (см.
[85]). Мы не будем искать другую константу D, так как масса
а
+ 0A?)
Рис. 10. Однопетлевая диаграмма, определяющая массовый контрчлен dm2 в по-
порядке А,.по методу нормального упорядочения. Численные множители в E.67)
возникают в результате учета вклада каждого полевого оператора в Ф* (х), при-
причем каждому оператору соответствует своя линия диаграммы.
кинка содержит разность энергий двух уровней, и эффекты, свя-
связанные с D, сократятся. Хорошо известно, что контрчлены в E.66)
устраняют в любом порядке все ультрафиолетовые расходимости
в вакуумном секторе теории, включая расходимости энергий
вакуумного и одномезонного состояний. Мы сейчас покажем, что
эти же контрчлены устраняют логарифмическую расходимость
массы кинка E.63). Это очень хорошо, так как в перенормируе-
перенормируемой теории все физические величины должны быть избавлены от
ультрафиолетовых расходимостей одним и тем же набором контр-
контрчленов.
Замена Н на :#: E.66) приводит к появлению в потенциале
E.37) добавочных членов
Д V = — j dx (-1- дт2ф2 (х)
Изменяются классические энергии функций фк (х) и ф1 (х). Это
в свою очередь изменяет энергии квантовых уровней Ёо и £вак,
так как классические энергии определяют их главные члены.
В результате к E.63) добавляется величина
Д£о - ДЯвак = j dx [- -\-dtri {ф% - ф\) -(D- Dj] =
— CO
CO
= -i- dm? j dx (maA) A - th2 mx/ (/T) = dttfm \/ T/X. E.68)

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 153
Это главный вклад контрчленов в массу кинка. Остальные вклады
возникают вследствие а) квантовых поправок к производным
потенциала, которые также изменились, б) изменения самих
классических решений, так как полевые уравнения стали дру-
другими. Но это эффекты более высокого порядка (см. ниже замеча-
замечания 6).
Подставляя дт2 из E.67) в выражение E.68) и добавляя это
выражение к E.63), получаем перенормированную массу кинка
/И = (Д, + А£о) - (£вак + Д£вак) = 2 ^ "" +
f dp /—=№ J_) + 0(Xft«), E.69)
—л.
где в интеграле E.63) введено обрезание. Заметим, что оба подын-
подынтегральных члена ведут себя как \1р при р -*-оо, так что лога-
логарифмические расходимости сокращаются. Поэтому параметр обре-
обрезания Л можно устремить к бесконечности и взять интеграл.
В результате [101] имеем
М = B 1/Т/ЗА,) т3 + mft (-J- VW - 3/п VT) + О (КП2). E.70)
Это выражение определяет массу кинк-частицы, т. е. энергию
паинизшего состояния в окрестности кинк-решения после про-
недения нормального упорядочения. Сделаем следующие заме-
замечания.
1. Первый член в выражении для массы квантовой кинк-
частицы равен энергии классического статического кинка. Сле-
Следующий член отвечает главной поправке, связанной с кванто-
квантовыми флуктуациями. Соответственно первый член порядка й°,
а второй порядка й.
2. Главный член (энергия классического кинка) сингулярен
при К -»-0. Таким образом, наш результат непертурбативен.
Iiro нельзя получить по теории возмущений, исходя из вакуумного
сектора.
3. Тем не менее этот результат справедлив только в прибли-
приближении слабой связи. Его непертурбативная природа связана
исключительно с классическим вкладом. Квантовые поправки
получают по теории возмущений разложением по степеням К.
4. Таким образом, квазиклассическое разложение по степе-
степеням й и разложение в приближении слабой связи по степеням А, свя-
связаны друг с другом. Этого следовало ожидать. При элементарном

1$4 ГЛАВА 5
анализе размерностей в лагранжиане E.36) (в наших смешанных
единицах, где с = 1, а постоянная й выписывается явно) оказы-
оказывается, что отношение кй/т2 безразмерно. Именно оно является
безразмерным параметром разложения, а Ш/т2 С 1 есть усло-
условие слабой связи. Поэтому понятно, почему разложения по й
и по А, схожи при квантовании статического классического реше-
решения (см. также гл. 6).
5. В пределе слабой связи Ш1т2 <С 1 масса кинк-состояния,
благодаря наличию классического члена, намного больше массы
мезона, которая в порядке ЙА,0 равна >/2тй. Таким образом,
в нашем приближении кинк — гораздо более тяжелая .ча-
.частица, чем мезон.
6. При вычислении поправки E.68) к массе кинка мы учиты-
учитывали изменение энергии функции кинка E.45) из-за появления
контрчленов. Но мы не принимали во внимание, что сама функ-
функция кинка меняется по тем же причинам. Контрчлены добавляются
к лагранжиану и приводят к замене т2ф на (т2 + dm2) ф в урав-
уравнении поля. Поэтому в решении также т2 заменяется на (т2+дт2).
Запишем это изменение в виде
где, так как дт2 порядка О (А,й), Ьфк1фк также порядка О (Ш).
Таким образом, поправка к энергии кинка имеет явную и неяв-
неявную зависимость от дт2:
). E.71)
В E.68) мы включили отсюда только первый член, так как фк —
экстремум V и, следовательно, второй член в E.71) обращается
в нуль. Эффект 8фк ощущается только в порядке Й2А,. Те же сообра-
соображения справедливы для вакуумного решения фх. Таким образом,
вычисленное значение массы кинка E.70) верно в порядке й.
Это завершает наше обсуждение квантовой кинк-частицы.
Вычисления поправок более высокого порядка к массе см. в ра-
работах [108, 340].
5.5. Трансляционная мода
Хотя полное рассмотрение нулевых мод мы отложили до гл. 8,
теперь можно качественно рассмотреть природу и физические след-
следствия моды юо = О в E.50а). Наличие такой моды характерно
не только для кинк-решения. Нулевые моды возникают всегда,
когда квантуется зависящее от х статическое решение трансля-
ционно-инвариантной теории.

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 155
Напомним, что лагранжиан E.36), потенциал E.37) и уравне-
уравнение поля E.38) трансляционно-инвариантны. Рассмотрим про-
произвольную полевую конфигурацию ф0 (х), не обязательно явля-
являющуюся решением полевого уравнения. Как сама функция ф0 (х),
так и полученные из нее трансляциями функции ф0 (х — а) для
всех действительных а имеют одинаковую потенциальную энер-
энергию V [ф0 (х — а)], не зависящую от а. Функцию ф0 (х) можно
рассматривать как точку в пространстве полей, т. е. в простран-
пространстве функций ф (х). Аналогичным образом семейство получен-
полученных трансляциями функций ф0 (х — а) для всех а образует одно-
параметрическую кривую в том же пространстве. Все ее точки
имеют одинаковую потенциальную энергию V [ф0 (х)], поэтому
она является «эквипотенциальной» кривой. Понятно, что все
пространство полей состоит из таких эквипотенциальных кри-
кривых. (Некоторые из них могут быть тривиальными, состоящими
только из одной точки. Это соответствует случаю, когда ф0 (х)
не зависит от х; при этом все полученные трансляциями функ-
функции одинаковы.)
Рассмотрим кинк-функцию фк (х) = (m/|/X) th (тх/-[^2). Она
также принадлежит эквипотенциальной кривой семейства кин-
ков фк (х — а). Все точки кривой имеют одинаковую потенциаль-
потенциальную энергию V [фк (х — а) ] = B ут3)/ЗА,. Поскольку поле-
полевое уравнение E.38), решением которого является фк (х), трансля-
ционно-инвариантно, все функции, полученные трансляциями
из фк, принадлежат данной кривой. Ключевой момент заклю-
заключается в том, что хотя фк — экстремум V [ф] в силу своей ста-
статичности, фк не является минимумом V [ф] в полевом простран-
пространстве даже локально. Начиная с фк, мы можем двигаться вдоль
эквипотенциальной кривой без изменения V [ф]. Вдоль этой кри-
кривой данное кинк-решение имеет только «нейтральную» устой-
устойчивость. Вторая функциональная производная (а вместе с ней
и все производные) V [ф ] равна нулю, если смещение полей бе-
берется вдоль эквипотенциальной кривой. Это является причиной
пулевого собственного значения оператора второй производной,
что отражено в E.50а). Можно также проверить, что при инфини-
гезимальных трансляциях
Ь.фк = фк(х- 8а) - фк (х) = (-ба) дфк/дх -
= — 6a(m2//2X)sch2(/?u//2~). E.72)
С точностью до нормировочной постоянной это собственная мода
<о0 = 0 E.50а). Таким образом, нулевая собственная мода яв-
является касательной в точке фк (х) к эквипотенциальной кривой,
связывающей в пространстве полей все решения фк (х — а),
полученные с Помощью трансляций.

156 ГЛАВА В
Наличие этой моды © = 0 не имеет ничего общего с «безмассо-
«безмассовыми» полями. В нашей модели массовый параметр т не равен
нулю. Нулевая мода не связана также с «голдстоуновским бозо-
бозоном», хотя их происхождение имеет общие черты. Отметим, что
мода со = О E.50) является членом дискретного спектра собствен-
собственных значений в отличие от голдстоуновских бозонов, которые
дают нулевую частоту в качестве нижнего предела континуума
частот. Можно понять также, почему нулевые частоты не появ-
появляются при традиционном рассмотрении по теории возмущений
в учебниках теории поля (в отсутствие безмассовых полей). Как
мы отмечали, обычная теория возмущений эквивалентна разло-
разложению в окрестности тривиального не зависящего от х класси-
классического решения, т. е. в окрестности классической вакуумной
конфигурации. При квантовании, например, «вакуумного» сек-
сектора нашей модели в спектре частот E.41) не возникает нулевая
частота. Наинизшее собственное значение равно 2т2. Причина
заключается в том, что рассматриваемое классическое решение
Ф (х) — 0i — tnly^^ не зависит от х. При трансляциях оно остается
неизменным и не дает новых функций. Эквипотенциальная «кри-
«кривая» в этом случае состоит только из одной точки фх. С помощью
трансляций при неизменном V [ф] нельзя сместиться из точки фг.
Отсюда и следует отсутствие нулевой моды. Нулевые моды, свя-
связанные с трансляционной симметрией, возникают при квантова-
квантовании в окрестности классических решений только в том случае,
если сами решения не трансляционно-инвариантны, т. е. когда
они имеют нетривиальную пространственную зависимость.
Эти идеи легко обобщить на более сложные теории. Если мы
работаем не в одном, а в трех измерениях, то в общем случае
существуют три нулевые моды, связанные с тем, что нетривиаль-
нетривиальное решение можно подвергнуть трансляциям по трем незави-
независимым направлениям. Более того, если теория (но не решение)
инвариантна относительно вращений, то в силу аналогичной при-
причины существуют еще несколько нулевых частот: вращением дан-
данного решения мы можем получить другие близлежащие решения
с той же энергией. Наконец, если теория обладает непрерывной
внутренней симметрией, отсутствующей у данного решения, то
возникают еще нулевые частоты, каждая из которых связана
с соответствующим параметром группы симметрии. Такие моды
подробно рассматриваются в гл. 8.
Выяснив природу нулевых мод, перейдем к исследованию их
влияния на квантовые волновые функции, построенные в окрест-
окрестности классических решений. Для этого вернемся к примеру
кинка. Поскольку эта теория одномерная и не имеет непрерывной
внутренней симметрии, существует только одна нулевая мода,
связанная с трансляциями. Соответственно в E.50) все моды с п=6

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 157
ненулевые. Таким образом, за исключением трансляционной
моды, кинк является локальным минимумом V [<j>]. Представим
вид функции V [ф ] в полевом пространстве. Ее профиль в окрест-
окрестности фк напоминает ложбину. По дну ложбины идет эквипотен-
эквипотенциальная кривая, состоящая из фк и полученных из нее трансля-
трансляциями функций. По всем направлением, ортогональным экви-
эквипотенциальной кривой, потенциал возрастает. Следовательно,
построенные в окрестности фк в приближении слабого взаимодей-
взаимодействия собственные состояния энергии будут приближенно осцил-
ляторными по всем направлениям, кроме направления вдоль
трансляционной моды. Только вдоль этой моды потенциал V [ф]
не локализует волновую функцию. Аналогичная ситуация встре-
встречалась в элементарном примере, рассмотренном в разд. 5.2, п. 11.
Там мы имели одномерную частицу в тривиальном потенциале
V (х) = V. Так как потенциал не зависит от х, то эта задача обла-
обладает трансляционной симметрией. Любая точка х = х0 является
классическим статическим решением; точно так же и все осталь-
остальные точки, полученные трансляцией по х0, являются статическими
классическими решениями с той же энергией. Эквипотенциальной
кривой этой задачи является вся ось х. Следовательно, собствен-
собственные функции энергии exp (iknx) распределены по ^сей оси х.
Собственные значения энергии равны
Еп = У + ±-{ПК?. E-73)
Первый член дает классическую энергию статического решения
х @ = *о. а второй член можно рассматривать как квантовую
поправку, обусловленную (большими) флуктуациями вдоль оси х.
Свободное движение волновой функции по оси х приводит к появ-
появлению вклада от кинетической энергии в энергетические уровни.
В силу того что физика трансляционной моды в задаче с кин-
ком аналогична разобранной выше, следует ожидать, что воз-
воздействие трансляционной моды на уровни энергии приведет
к появлению вклада от кинетической энергии. Энергия кинка
и релятивистской теории равна j^M2 + Р2, где Р — импульс.
Но, как отмечено выше, кинк имеет очень большую массу порядка
A/А-). Поэтому его энергию можно представить как
Е (Р) = -/М2 + Р2 = М + РУ2М + • • • • E.74)
Главный член кинетической энергии порядка X. Таким образом,
следует ожидать, что трансляционная мода будет влиять на соб-
собственные значения энергии только в порядке X и выше через
вклады от кинетической энергии. Поэтому мы не учитывали эту
моду в последнем разделе, где выписывали члены только в по-
порядке V. Кроме того, при вычислении энергии кинка в порядке Х°

158 ГЛАВА 5
нет необходимости учитывать кинетическое движение кинк-
частицы. В этом приближении квантовый кинк покоится. Поэтому
мы считаем энергию кинка E.70) в порядке Х° «массой» квантовой
кинк-частицы. Эти замечания подтверждаются при более под-
подробном обсуждении в гл. 8.
5.6. Стабильность кинка и его форм факторы
Голдстоун и Джакив [173] при исследовании квантовых со-
состояний, построенных в окрестности статических солитонов,
предложили независимо ряд постулатов. Их постулаты обобщают
рассмотренные выше идеи и приводят к некоторым новым след-
следствиям, касающимся, в частности, формфакторов и устойчивости
солитонных состояний. Приведем эти постулаты в применении
к нашей теории <£4 в A + 1) измерениях. Ниже везде полагаем
Й = 1.
Постулат 1. Гильбертово пространство состояний теории
содержит кроме знакомого «вакуумного сектора» (т. е. вакуумного
и мультимезонных состояний) еще систему состояний в «кинк-сек-
торе», или «солитонном секторе». Последний распадается на сле-
следующие собственные состояния энергии-импульса:
а) состояния | Р) кинк-частицы с импульсом Р и энергией
Е = /р2 + М\
б) возбужденные состояния кинка \Р*) с импульсом Р и
энергией Е = >/Ра-|-М*2;
в) состояния рассеяния \.Р, kx, k2, ..., km), состоящие из
кинк-частицы и т мезонов с асимптотическими импульсами Р,
klt k2, ..-, km (число т изменяется от единицы до бесконечности);
г) состояния рассения \Р*, klt k2, ..., km), состоящие из
возбужденных кинка и т мезонов с асимптотическими импуль-
импульсами Р, kx, k2, ..., km.
Постулат 2. Кинк-сектор состояний ортогонален вакуумному
сектору и не связан с ним никаким локальным оператором. В част-
частности, квантовый кинк устойчив относительно распада на мезоны.
Постулат 3. Масса квантового кинка в пределе слабой связи
Х/т? -> 0 ведет себя как (const)A-.
Постулат 4. Матричные элементы полевого оператора Ф (х, t)
между этими состояниями зависят от X в пределе слабой связи как
(Р' | Ф | Р, к) и (Р' | Ф | Р*) ~ 0A),
и в общем случае
(Р\ Л,',..., к',\Ф\Р, *,,..., km)e~0Wl+m-l)/a), E.75)

Квантование статических решений
где индекс с обозначает связанную часть матричного элемента.
Здесь Ф (х, t) отвечает квантовому полевому оператору; для
классического поля мы используем обозначение ф (х, t).
Мы не будем обосновывать эти постулаты. Но мы увидим,
что они согласуются друг с другом и с развитыми выше идеями.
Набор состояний постулата 1 является набором построенных нами
состояний в окрестности кинка в приближении слабой связи.
Состояние \Р) — наинизшее состояние в выражении E.56), кото-
которое мы интерпретировали как квантовую кинк-частицу. Состоя-
Состояние | Р*) — возбужденное состояние, в котором возбуждена
только дискретная мода а>! = >^3/2/п, т. е. N1 = 1 и Nq = О
в E.56). Более высокие возбуждения этой моды (N± j> 2) неста-
нестабильны и распадаются на кинк и мезон. Напомним, что мезон
имеет массу >/2/пй, значение которое лежит в пределах между
ha>1 и 2ЙСЙХ. Зависимость от импульсов состояний \ Р) и \Р*)
в E.56) явно не видна, так как масса кинка порядка 1/1 и члены
кинетической энергии появляются только в порядке X. Наконец,
состояния \ Р, ku ..., km) и \ Р*, klt ..., km) отвечают воз-
возбуждениям мод континуума E.56) в отсутствие и при наличии
©!-возбуждения соответственно. Заметим, что этот постулат не
вводит новых типов состояний с возбуждениями нулевой моды ю0-
Это отвечает тому, что возбуждения вдоль этой трансляционной
моды только восстанавливают зависимость от импульсов состоя-
состояний кинк-сектора.
Постулат 2 более сильный. Кинк-сектор состояний построен
в окрестности решения фкжпк, которое не является абсолютным
минимумом V [ф]. В лучшем случае (т. е. без моды ю0) оно дает
локальный минимум. Априори только из энергетики можно ожи-
ожидать, что состояния, построенные в окрестности фкинк, будут
распадаться в состояния вакуумного сектора, построенные
в окрестности более низколежащего минимума фх. Действительно,
в приближении слабой связи все состояния кинк-сектора имеют
большую энергию, чем любое состояние вакуумного сектора, в
силу наличия главного члена в выражении E.56) порядка A/К).
Кинк-состояния оказываются аналогичными состояниям, постро-
построенным в окрестности х = с в простой задаче разд. 5.2, п. 9.
Но постулат 2 утверждает не только, что квантовый кинк
устойчив относительно распада в мезоны, но и что весь кинк-
сектор не связан с вакуумным сектором. Причина последнего
утверждения заключена в понятии топологической классифика-
классификации, обобщенном на квантовую теорию. Напомним, что мы клас-
классифицировали (гл. 2) все классические конфигурации с конечной
энергией теории ф* по топологическим секторам, основываясь на
разрешенных граничных условиях ф (х = оо, t) = ±m\Y^ и
</> (—оо, t) = ±mly^'k. Мы показали, что в классическом случае

|Ы) I Л \ИЛ
конфигурации не могут с течением времени перейти из одного
сектора в другой. Исходя из этого, мы определили сохраняю-
сохраняющийся топологический заряд Q. В квантовой теории используем
то же определение, заменяя ф (х, t) полевым оператором Ф (х, t):
j ^, *)_ф(_оо, *)], E.76)
где
/и = rm.v«3v<d, «ум. = 0. E.77)
Поскольку Ф (х, t) — эрмитов оператор, то заряд Q также эрми-
эрмитов. Он сохраняется по построению в силу E.77) и может быть
назван топологическим квантовым числом. Но вакуумный вектор
состояний строится квантованием флуктуации в окрестности
фг = -\-т1У'к. Точнее мы можем определить этот сектор как со-
состоящий из волновых теоретико-полевых функционалов *Р [ф],
обращающихся в нуль, если <f> (x) не подчиняется условиям
ф (оо) = ф (—оо) = /л/у7К. Следовательно, математическое ожи-
ожидание Q для любого состояния в вакуумном секторе равно нулю
(см., например, E.43) и E.44)). Аналогично состояния кинк-
сектора можно определить как состояния, волновые функционалы
которых обращаются в нуль, если не выполняются условия
ф (±°о.) = d=m/Y К. Эквивалентным образом этот сектор можно
определить как сектор с математическим ожиданием Q, равным
единице. Так как Q — сохраняющийся эрмитов оператор, кинк-
сектор с Q = 1 и вакуумный сектор с Q = 0 не только ортого-
ортогональны, но и не могут переходить друг в друга. В частности,
кинк-состояние, являющееся основным состоянием кинк-сектора,
устойчиво и не может распадаться на мезоны.
Рассмотрим далее произвольную локальную физическую
наблюдаемую A (t). Пусть
■ оо
--= J a(x, l)dx,
где а (х, t) не равно нулю только для некоторой ограниченной
области х при любом t. Тогда в силу условия причинности для
операторов, разделенных пространственноподобным интервалом,
для коммутатора при фиксированном времени t имеем
[A, Q]t= Hm-^- {[A, O(L)]t-[A, Ф(-Щ}=0. E.78)
£-*оо
Поэтому такой оператор А не может связывать секторы с различ-
различными значениями Q. Отсюда следует, что Q является чем-то типа
селектирующего квантового числа, отделяющего кинк-сектор
от вакуумного сектора [122].

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 161
Постулат 3 прост и полностью подтверждается нашим выво-
выводом массы кинка E.70). Утверждение постулата 4, что матричный
элемент ф между кинк-состояниями порядка 1/т/А-, будет явно
продемонстрировано ниже. Этого и можно было ожидать, так как
кинк-состояние строится в окрестности кинк-функций, которая
сама порядка l/j/А,. Остальные утверждения постулата 4 озна-
означают, что излучение или поглощение каждого мезона кинком или
возбуждение дискретной моды он приводит к появлению добавоч-
добавочного множителя УЪ. Это следует из формы потенциала V [ф]
в E.47). Кинк-сектор получается при квантовании смещенного
поля Ti (х) = ф (х) — фк (х). Эмиссия или абсорбция мезона кин-
кинком или возбуждение кинка через нормальную моду ©i возни-
возникает в теории возмущений через члены взаимодействия в E.47).
Главный член взаимодействия X I йхф^ц3 порядка |/ А-, если мы
вспомним, что </>^ ~ О A/|/Х).
Из данного обсуждения видно, что эти постулаты выражают
идеи, развитые в предыдущих разделах. Рассмотрим некоторые
другие их следствия, следуя Голдстоуну и Джакиву, применив-
применившим метод, развитый Керманом и Клейном [213] для многоча-
многочастичной задачи.
Определим функции f1 (x), /2 (x; k), /£ (x) соотношениями
(Р | Ф (х, 0)\Р')= J -g- ехр [I (Р - Р') u\h(x—a), E.79)
(Р,к\Ф(х, 0)|Р')= \~exp[i(P + k^P')a]f2(x-a; k),
—ОО
E.80а)
(Р* | Ф (х, 0) | Р') = } -|L ехр [i (Р - Р') а] /| (х - а). E.806)
В этих соотношениях зависимость от импульсов входит только
через комбинации (Р — Р') и (Р + k — Р'), что следует из транс-
трансляционной инвариантности. Рассмотрим уравнение движения
Гейзенберга для поля Ф (х, t)
t). E.81)
Оно похоже на классическое уравнение, но теперь Ф (х, t) — опе-
оператор. Возьмем от обеих частей E.81) матричные элементы при
6 Раджараман Р.

162 ГЛАВА Ь
t = О между кинк-состояниями | Р) и | Р') и вычислим их в глав-
главном порядке (l/-j/X). Первый член слева дает
, 0) в'"' |Т>'),„0) = - (£р - £р-J (Л|Ф (*, 0) | Р").
E.82)
Поскольку
этот член в главном порядке мы опустим. Остающиеся слева члены
при использовании E.79) дают
P-P')a]h(x-a). E.83)
Запишем вклад правой части в виде
—К 2 (Р | Ф (дг, 0) | л) (п | Ф (л:, 0) | п') (п' | Ф (*, 0) | Р'). E.84)
п, п'
Здесь | п) и | п') отвечают полному набору состояний кинк-сек-
тора, перечисленных в постулате 1. Вакуумный сектор состояний
можно не учитывать, так как, согласно постулату 2, эти два
сектора не связаны. В главный порядок из | п) и | п') дают вклад
по постулату 4 только кинк-состояния. Таким образом, в глав-
главном порядке E.84) можно привести к виду
-X £ (Р | Ф (х, 0) | Р") (Р" | Ф (х, 0) | Рт) (Рт | Ф (х, 0) | Р-) =
р", р1"
\ ехр [i (P ~ F) a] [h (x ~ а)]3" E-85^
Отметим, что оператор Ф3 (х, t) имеет ультрафиолетовые расхо-
расходимости, но эти расходимости возникают только в более высоких
порядках и их можно устранить нормальным упорядочением.
В главном порядке эти трудности не возникают.
| Таким образом, в главном порядке E.83) и E.85) равны друг
другу для любых значений Р, Р'. Следовательно, Д (х — а)
должно удовлетворять уравнению
(x-a) = -'k[h(X-a)f. E.86)
Это классическое полевое статическое уравнение, и его решение,
отвечающее граничным условиям кинк-сектора, имеет вид
fx (x-a) = {ml |/Г) th [т (х - а)/уТ] = <j>K(x~ a). E.87)

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 163
Тогда E.79) можно переписать в виде
(Р\Ф(х, 0)\Р')= \^
-j- члены более высокого порядка. E.88)
Это важный результат. Во-первых, он устанавливает соответ-
соответствие между классическим решением фк (х) и квантовыми со-
состояниями, построенными в его окрестности. Первое связано
со вторыми через математическое ожидание полевого оператора.
Сравним этот результат с соотношением E.14) для простой нере-
нерелятивистской задачи и с соотношением E.44) в вакуумном сек-
секторе, где опять классическое решение связано в главном порядке
с математическим ожиданием квантовой величины. Соотношение
E.88) очень похоже на них, за исключением того, что оно содер-
содержит не единичное решение, а интеграл по семейству классических
решений фк (х — а). Такая модификация связана с существова-
существованием вырожденного семейства трансляционных решений. Кроме
того, это отражает также наше интуитивное представление о раз-
размазанном вдоль трансляционной моды квантовом кинк-состоянии.
Так как фк <~~ О(\/\^Х), соотношение E.88) подтверждает
постулат 4. Наконец, E.88) можно обратить и записать
-|- члены более высокого порядка. E.89)
Это показывает, что классическая кинк-функция в главном по-
порядке X является «формфактором» полевого оператора Ф между
квантовыми кинк-состояниями. Более интересные формфакторы
связаны не с оператором Ф, а с физически более важными опера-
операторами плотности энергии, плотности топологического заряда
к т. п. Эти операторы содержат дФ/дх (или Ф2 — т2/Х). Из E.89)
ясно, что соответствующие формфакторы в главном порядке
нключают_(д</>^ (хIдх) и (ф\ (х) — т2/Х). Поскольку фк (х) ->
->+ml\^X при х->±оо, все эти формфакторы локализованы.
»то важный результат, так как он подтверждает интерпретацию
основного состояния кинк-сектора как протяженной частицы.
Такая частица имеет протяженные, но локализованные форм-
факторы. Для иллюстрации рассмотрим распределение плотности
шергии в кинк-состоянии, т. е. формфактор
8(х) = j d(P - Р')exp [i(Р - Р')х]{Р\Ж@, 0) | Р'), E.90)

164 ГЛАВА 5
— плотность гамильтониана, а П (х, t) = дФ (х, t)ldt. Вычислим
(Р | Ж (О, 0)|Р') в низшем порядке, подставляя полные наборы
состояний между полевыми операторами в E.91). В главный
порядок дают вклад только промежуточные состояния невоз-
невозбужденного кинка. Некинетические члены в (Р\Ж @, 0) | Р')
дают
= | -^ exp [i (Р - Р') а] <ГИЛ (-а), E.92)
где опущены промежуточные элементы вычисления, анало-
аналогичные проведенным в E.84), E.85), а также использован ре-
результат E.88); 8К!1 — плотность энергии классического стати-
статического кинка. Кинетический член в (Р | Ж @, 0)|Р') дает
(Р | i П2 @, 0) \P') = -L(P\ (дФ/dt? | Р')х^0 =
Р\Ф\Р') (Р" \Ф\П (Ер - £р») (ЕР. - ЕР.) = О (К).
Р"
E.93)
Это согласуется со сделанным выше утверждением, что кинети-
кинетическая энергия кинка появляется только в порядке X. Вкладом
E.93) в низшем порядке можно пренебречь по сравнению с E.92),
который порядка О A/Д-). Подставляя E.92) в E.90), получаем
8(х) = 8яп{х). E.94)
Таким образом, в низшем порядке формфактор энергии кинк-
состояния равен классической плотности энергии кинка, кото-
который, как мы видели в гл. 2, описывается локализованной функ-
функцией. Полная энергия ЕР кинк-состояния дается выражением
, 0)dx\P') =
= 2зй(Р-Р')(Р\Зв@,0)\Р'). E.95)
Следовательно,
ЕР = 2я(Р | Ж@, 0) | Р') = \dxS (х), E.96)
где <$ (х) — формфактор E.90). В низшем порядке О (\1%) E.96)
сводится к
\^-^. E.97)

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 165
Таким образом, мы воспроизвели согласующийся с E.70) ре-
результат: главный член квантовой энергии кинка равен его клас-
классической энергии.
Перейдем к функции /2 (х — a, k), определяемой E.80). Ее
можно вычислить точно так же, как Д (х — а), взятием матрич-
матричных элементов от операторного уравнения поля E.81). На этот
раз мы возьмем матричные элементы между чистым кинк-состоя-
нием | Р') и состоянием кинк плюс один мезон \ Р, k) и вычислим
их в главном порядке. Левая часть полевого уравнения дает
(Р, k | (д*/дР - д*/дх* - т2) Ф (jc, f) \P') =
= (Р, k\ (— (Ер + ак- EP.f - dW - m2)Ф(х, t) | P'). E.98)
Здесь щ —энергия мезона. Тогда в силу ЕР — Ер> = О (к)
главные члены E.98) при t = 0 принимают вид
(Р, k | (—©I - д2/дх2 - т2) Ф (х, 0) | Р') =
= \ -й-ехр[*7Р + к- Р') а](-<»1- т2 -^)fa(x-a; k). E.99)
Этот вклад в силу простулата 4 порядка О (Х°). Разложение пра-
правой части полевого уравнения по промежуточным состояниям
с использованием E.88) дает следующий главный вклад;
—ЗА, ^ (Р, k\<D(x, 0)\Р")(Р'\Ф(х, 0)\Р'")(Рп\Ф(х, 0)|/>')'=
Р", рт
W ехр [i (p + k~ Р') al ^ (* ~ а) ^2 (* - а> *)■ (
Множитель 3 возникает вследствие того, что внешний мезон мо-
может испустить любой из трех полевых операторов в произведе-
произведении Ф3 и эти возможности равновероятны. Так как E.99) равно
E.100) для произвольных Р, k и Р , отсюда получаем
\-д*1дх% - т2 + Щ\ (х - a)] ft (х -a;k) = <4h (* - а\ к). E.101)
Это уравнение E.48) для собственных значений оператора вторых
производных [82У/(Ьф8ф)]Фк. Таким образом, ©ft, введенная
в E.98) как энергия мезона, связывается с собственным значе-
значением в E.48), как мы и ожидали. Функция /2 (х, k) пропорцио-
пропорциональна соответствующей нормированной собственной моде % (х)
в E.48). Так как соотношение E.101) линейно, оно не фиксирует
константу пропорциональности. Используя знакомую бозонную
нормировку, мы положим
E.102)
Справедливость этого можно проверить с помощью уравнений,
куда /2 входит нелинейным образом, например с помощью кано-
канонических правил коммутации, которые'будут использованы ниже.

166 ГЛАВА 5
Полностью аналогичный результат справедлив для функции
/г (х — а) в E.80). Возьмем матричные элементы от уравнения
поля Гейзенберта между | Р') и | Р) и проделаем ту же процедуру,
что и выше. Мы снова получим уравнение для собственных зна-
значений, где теперь /2 (х — a; k) и со^ заменены соответственно на
ft (х — а) и о)! = М* — М. Поэтому ft (x — а) мы свяжем с диск-
дискретной модой с п = 1 в E.506) и аналогично E.102) положим
fS (x-a) = гц
Заметим, что если щ, т^ и цк рассматривать как полный набор
функций, то они должны удовлетворять соотношению
у\1 (х) vfi (у) -f V (х) л, (у) + S it W ЛА («/) = б (Д? ~ У), E.103)
так как функции !]„, включая ц0, образуют полный набор орто-
нормированных собственных функций эрмитова оператора в E.48).
Однако в полном наборе состояний кинк-сектора, перечисленном
в постулате 1, нет новых типов состояний, связанных с возбужде-
возбуждениями тH-моды. В то время как возбуждение т^-моды ведет
к | Р*), а %-мод — к состояниям мезон плюс кинк, флуктуации
вдоль т]0 дают только правильную зависимость названных со-
состояний от импульсов. Для проверки соответствия этого посту-
постулата с требованием, чтобы E.103) включало г\0, рассмотрим кано-
каноническое коммутационное правило
[Ф (х, t), (d/df) Ф (у, ОЬ=о = гё (х - у). E.104)
Возьмем матричные элементы между кинк-состояниями | Р) и
\Р'). Получим
(Р | [Ф (л, 0), (d/dt) Ф (у, 0)] | Р') =48 (Р - Р') б (х - у). E.105)
Это соотношение можно проверить, вычисляя матричные эле-
элементы с помощью полного набора промежуточных состояний кинк-
сектора. В главный порядок дают вклады только кинк, его воз-
возбужденное состояние и состояние кинк плюс один мезон, Чисто
кинковые промежуточные состояния дают
\i(EQ-Ep.)(P\<I>(x, 0)|<?)<0|Ф(*/, 0)\Р')~
-i (ЕР - EQ) (Р | Ф (у, 0) | Q) (Q | Ф (х, 0) | Р')\ =
- P')b] тР") - (/i(^- Ь)!Лх - a)exp[i(P -Q)b +
E-106)

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ
Во втором члене заменим переменную интегрирования Q на Q —
~ Р + Р' — Q. Тогда показатель экспоненты во втором члене
принимает вид i (Р — Q) b+i (Q —P') a = i(P — Q) a +i (Q —
— Р') Ъ. Таким образом, мы можем объединить два члена в один,
что дает
оо оо ' оо
1 J "& J "ё- j dQexp[i(P-Q)a+i(Q-P')b]x
—еОО
X Д (х - а) А (у - Ь) (Q-P'HQ-P) =
* ~ «>) (т А ОТ -
—ОО —еОО
E.107)
Кроме того, в силу E.87) и E.72) имеем
~h (x-a) = JL<j>K(X-a) = Ац0 (х - а), E.108)
где константа А определяется из условия нормировки ri0:
-^j *(-!£=!-)■_
в главном порядке. Таким образом, вклад чисто кинковых про-
промежуточных состояний в E.106) равен
оо
i J -^ exp [i (Р - Р') а] ц0 (х - а) % (у - а). E.110)
Нетрудно найти вклад промежуточных состояний, содержащих
кинк и один мезон. Заметим, что
(Р, k\(dO/dt)(y,
= i (ЕР - ЕР. + щ) | -g- exp [i (P + Л - />') 6] /2 (г/ - 6; Л), E.111)

168 ГЛАВА 5
где в низшем порядке (ЕР — Ер-) можно опустить по сравнению
с coft. Учитывая это, для членов кинка и мезона имеем
^ \{Р IФ (х, 0) | Q, k) (Q, k | (дФ/dt) (у, 0) |Р')- •
Q. k
-(Р\(дФ/Ш)(у, 0)|Q, *><Q, *|Ф(дг, 0)|Р'>} =
=l' J -w S 2£0*^ (* ~ a; A) /2 (^ ~a'k) exp l/ (P ~ pl) a] =
k
= i ^exv[i(P - P')a] 1^4(х - aLk(y-a)\. E.112)
Аналогичным образом вычисляется вклад промежуточных со-
состояний | Q*) возбужденного кинка:
-wехр I' <р - р'^а] [T]i <* ~
Все остальные промежуточные состояния в этом порядке не дают
вклада. Объединяя E.110), E.112) и E.113), мы видим, что в глав-
главном порядке левая часть соотношения E.105) дает
« J -^ exp [i (Р - Р') а] Г % (дг - а) %(# - а) + % (* - а) % (у - а) +
= «(/> — Р') б(лг — ^). E.114)
(Напомним, что по E.50) rj0 игц действительны.) Таким образом,
каноническое коммутационное соотношение E.105) выполняется,
хотя промежуточные состояния не включали набора состояний,
отвечающих Т10-моде. Член с ri0 в E.114), необходимый для пол-
полноты набора функций, эффективно учитывается в кинетической
энергии кинк-состояния в E.106)—E.110). Более полное рас-
рассмотрение коммутационных правил в солитонных секторах см.
в работе [322].
5.7. Заключительные замечания
Обсуждение предыдущего раздела показало, что постулаты,
связывающие солитонный сектор состояний с классическим кин-
ком, самосогласованы по крайней мере в рассмотренных след-
следствиях. Для иллюстрации нашего метода мы использовали при-
пример кинка модели E.36). Но те же методы можно применить для
квантования статических локализованных решений большого
класса теорий. Так стабильное статическое решение любой дру-

КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ 169
гой скалярной полевой теории в A + 1) измерениях квантуется
точно так же, как кинк. Система синус-Гордона, например, дает
статическое односолитонное решение в A + 1) измерениях. Его
можно проквантовать и получить односолитонный сектор состоя-
состояний, отличающийся от вакуумного сектора этой теории [102],
Нормальные моды системы состоят из обязательной трансляцион-
трансляционной моды и мод континуума. Для системы синус-Гордона нет
дискретной со1-моды, поэтому нет «возбужденного» солитонного
состояния, но в остальном наша интерпретация может быть не-
непосредственно применена.
Если модель рассматривается в B + 1) или C + 1) измере-
измерениях, то вычисления становятся более сложными. Мы имеем
больше нормальных мод, в том числе нулевых мод, связанных
с трансляциями и вращениями. Ультрафиолетовые расходимости
при большем числе измерений становятся сильнее, и для их устра-
устранения иногда приходится наряду с нормальным упорядочением
использовать нетривиальные перенормировочные контрчлены.
Далее, мы знаем из теоремы Деррика, что в C + 1) измерениях,
если имеются только скалярные поля, статического решения не
существует. Для получения статического классического решения
необходимо добавлять поля с более высокими спинами. Такие
поля вносят дополнительные трудности, хотя принципы трак-
трактовки и квантования солитонов остаются прежними. Например,-
монопольное решение, рассмотренное в гл. 3, включает скаляр-
скалярные и векторные поля с неабелевой калибровочной инвариант-
инвариантностью. Соответственно классическое полевое уравнение и лине-
линеаризованное уравнение на собственные значения для малых
флуктуации (аналог уравнения E.24)) необходимо решать после
фиксирования калибровки. Эти уравнения решить трудно. Мы
видели в гл. 3, что полевое уравнение C.50), C.51) было решено
Прасадом и Зоммерфельдом только для случая А. -*■ 0 и то доста-
достаточно нестрого. Насколько нам известно, аналитическое решение
для произвольных А. не найдено. Эти проблемы затрудняют (в от-
отличие от кинк-системы) аналитический вывод классических вы-
выражений для энергии монополя, формфакторов и т. п. и главных
квантовых поправок. Но нет оснований считать, что при фикси-
фиксированной калибровке и при решении соответствующих диффе-
дифференциальных уравнений "принципы квантования изменятся по
сравнению с примером кинка. Хотя все нормальные моды задачи
монополя еще не получены, на этом пути проделана значительная
работа, в частности, по определению нулевых мод задачи [6, 258].
При наличии фермионных полей (например, в модели «мешка»
SLAC [24]) ситуация принципиально другая. Фермионные поля
не имеют классического предела. Нестрого говоря, это происхо-
происходит в силу того, что большое число фермионов не может по прин-
принципу Паули находиться в одном состоянии и индуцировать почти

170 ГЛАВА 5
классическое поле. Таким образом, связь между «классическими»
полевыми уравнениями и соответствующими квантовыми тео-
теориями при наличии ферми-полей будет другой.
Квантование фермионных солитонов рассматривается отдельно
в гл. 9. Там мы увидим, что, несмотря на это отличие, исполь-
используются многие аналогичные методы с необходимой заменой знака.
Конечно, наше рассмотрение солитонного сектора было далеко
не строгим. Мы использовали приближение слабой связи,
которое вывели на основе разумных физических соображений,
обобщая гармоническое приближение нерелятивистской кван-
квантовой механики. Мы отдали должное также некоторым особен-
особенностям, свойственным полевой теории, — перенормировкам, то-
топологическим квантовым числам и нулевым модам. Несмотря на
это, наше рассмотрение было в лучшем случае« ознакомительным».
В гл. 6 мы дадим новый вывод уровней энергии солитон-
солитонного сектора с помощью функциональных методов. Однако этот
вывод ненамного строже проведенного здесь рассмотрения. Дей-
Действительно строгие доказательства дадут мощные методы кон-
конструктивной теории поля. Такие доказательства чрезвычайно
трудно построить. Даже существование спонтанного нарушения
симметрии для простой модели </>4 в двух измерениях было дока-
доказано только совсем недавно [ЮЗ, 114]. Солитонный сектор рас-
рассматривался Фролихом [148]. Такие строгие исследования ле-
лежат вне рамок данной книги. Нас вполне удовлетворяет тот факт,
что они подтверждают развитые здесь с помощью примитивных
методов идеи, а не противоречат им.
Мы получили квантовую солитонную частицу, исходя из клас-
классического солитона. Рассмотрение метода, в котором солитоны
связываются с когерентными состояниями, см. в работе [327].
В другом подходе Мацумото и др. [248] использовали солитоны
квантовой многочастичной теории в методе «бозонного преобра-
преобразования».

ГЛАВА б
ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ
6.1. Формализм интегрирования по траекториям
Удобным формализмом для изучения различных аспектов ква-
квазиклассического метода является квантовополевой формализм
интегрирования по траекториям. В предыдущей главе мы при-
привели некоторые квазиклассические результаты, не используя
функциональные интегралы. Это было возможно только потому,
что мы ограничились квантованием статических солитонных ре-
решений скалярных полей, что сводилось в приближении слабой
связи к изучению связанных гармонических осцилляторов.
Но для квантования зависящих от времени солитонных решений
или для изучения инстантонных эффектов использование функцио-
функциональных интегралов становится необходимым. Конечно, для этих
целей можно использовать другие методы, например метод ка-
канонических операторов, что мы и будем делать в некоторых раз-
разделах книги, но метод функциональных интегралов представ-
представляется, пожалуй, самым удобным.
Функциональные интегралы уже значительное время исполь-
использовались в теории поля, прежде чем их стали применять для
изучения солитонов и инстантонов. Основная область их приме-
применения включает исследование спонтанного нарушения симме-
симметрии с помощью «эффективного действия», получение функций
Грина из вакуумного функционала, вывод правил Фадцеева—
Попова в калибровочных теориях и многое другое. Нашей целью
не является Детальное изложение формализма функционального
интегрирования и различных его применений в квантовой теории
поля. Мы будем считать этот формализм заданным и будем исполь-
использовать его для рассмотрения специальных вопросов, связанных
с солитонами и инстантонами. Но для полноты изложения в этом
и последующем разделах мы дадим конспективное изложение
метода функциональных интегралов, необходимое для наших
целей. В качестве примеров будут выведены некоторые резуль-
результаты гл. 5. В других разделах и главах будут получены этим
методом новые результаты.
Функциональные интегралы теории поля представляют собой
обобщение интегралов по траекториям нерелятивистской кванто-
квантовой механики одной частицы. Поэтому начнем наше введение

172 ГЛАВА в
с краткого изложения последних. Рассмотрим простую одноча-
стичную систему гл. 5, т. е. нерелятивистскую частицу в одном
измерении с лагранжианом
L = -±-q*-V(q). F.1)
Соответствующий гамильтониан квантовой теории имеет вид
H = -Lp^V{q), F.2)
где р = —itidldq — оператор импульса. Тогда уравнение Шре-
дингера
ifi -^7-\p(q, t) = H\p(q, t) F.3)
утверждает, что заданная при t = О волновая функция ^ (q, 0)
при t = Т принимает вид
ф (q, Т) = ехр (- iHt/П) ф (q, 0). F.4)
Следовательно, квантовая амплитуда перехода частицы из q = qa
при t = 0 в q = qb при t — Т определяется выражением
K(qo> T\ qa, 0)ЕЕ(^ь|ехр(—iHT/H)\qa), F.5)
где | qa) и | qb) — собственные векторы оператора координат q.
Формулировка квантовой механики через интегралы по траекто-
траекториям дает альтернативный, но эквивалентный способ описания
этой амплитуды. (Ясное и детальное обсуждение формализма
интегрирования по траекториям можно найти в книге Фейнмана
и Хибса [136].) Следуя этому описанию, имеем
K(qb, T; qa, 0) = J S> Ъ{%а,%. гехр {(l/n)S[q(t)]\, F.6)
где
S [q®] = J d/L = J Л D- ^2 - V (</))
о о
— действие, a J й) [q (t)]Qa Qb т —интеграл 'по всем траек-
траекториям, т. е. по всем функциям'<7 (t), удовлетворяющим условиям
q @) = qa и q (T) = qb. Ниже часто будем опускать индексы qa,
qb, Т в ЯЬ [q\b qa т, но они подразумеваются. Интеграл по
траекториям есть' функциональный интеграл, более сложный,
чем обыкновенные интегралы. Тем не менее его можно рассматри-
рассматривать как предел бесконечного произведения обыкновенных инте-
интегралов. Траектория q (t) определяется заданием значения q для
каждого t. Следовательно, нестрого говоря, интеграл по траекто-
траекториям представляет собой произведение интегралов по q (t) для

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 173
каждого t. Точнее, заменим временной интервал [О, Т] дискрет-
дискретными эквидистантными точками t0 = 0, tlt t2, ..., tN^, tN = T,
где
tt _ tUl = e, Ыг = Т, F.7)
причем
Предел континуума достигается при е ->0, N -* оо, Afe — Т.
Тогда интеграл по траекториям F.6) записывается в виде
K(qb, T; qa, 0) = J Ф [(/(Olexp f -jj- J (-^-f -
1С Г Г
BN (T) | dq1 dq2 ■ ■ ■ dqN_x X
Nz=T
[+1
хехрНг> W"J'-i; -УНЦ^- в , F.8)
2е
где множитель BN (T), определяющий меру, выбирается так»
чтобы интеграл сходился и был соответствующим образом норми-
нормирован при е -* 0. Математические аспекты таких интегралов по
траекториям, включая их существование и связь с мерой Винера,
можно найти, например, в работе Гельфанда и Яглома [150].
Хорошо известно также, что формулировка квантовой механики
в терминах интегралов по траекториям эквивалентна более зна-
знакомым формализмам Шредингера и Гейзенберга. В частности,
два выражения F.5) и F.6) для К (qb, T\ qb, 0) дают один и
тот же результат. Это продемонстрировали в явном виде Фейн-
ман и Хибс [136] (см. также [2]). Мы будем считать установлен-
установленным, что формула F,6) и ее обобщение в теории поля дают физи-
физически корректные результаты.
Для нас чрезвычайно важна связь интеграла по траекториям
F.6) с уровнями энергии системы. Пусть | <£п) — нормированные
собственные функции гамильтониана с собственными значе-
значениями Еп. Введем в F.5) и F.6) полный набор промежуточных
состояний | <£„); тогда имеем
j Ф [q (t)] ехр \A/П) S [q (t)]} = (qb | exp (-ШТ/Щ qa) =
= У, (Чь I Фп) (Фп | Яа) ехр (~(ЕпТ/П). F.9)

174 ГЛАВА 6
В частности, если положить q @) = q (Т) = q0 и проинтегриро-
проинтегрировать по q0, то получим
G (Т) = Тг (ехр (-ШТ/П)) = ^ ехр (-1ЕпТЩ)=
П
СО
= J dfc<<70|exp(-i7f77ft)|</0) =
—со
со
= j dqo\£D[q(()]„.. qt.Tехр {(i/fl)S[q(m\. F.10)
Здесь след вычислен двумя различными способами — по соб-
собственным векторам энергии и собственным векторам координат.
Отметим, что интеграл по q0 добавляет еще один интеграл (по
значению q в конечной точке) к многократному интегралу по зна-
значениям q во всех промежуточных точках. Основной метод этой
главы относится к вычислению этого интеграла по траекториям
со следом в некотором приближении в форме ряда £п ехр (—iEn x
X Т/Л) и получению, таким образом, уровней энергии
Еп, Мы будем использовать квазиклассическое приближение,
которое для интеграла по траекториям сводится к хорошо из-
известному приближению стационарной фазы. Для пояснения
этого приближения рассмотрим многократный интеграл
оо оо оо
J Л/1 \dq2,.. j dqNg(q)exp[—if(q)], F.11)
•—со —со
где q отвечает набору \qx ... qN]. Пусть / (q) имеет одну стационар-
стационарную точку (экстремум) при q = а, и пусть g (q) достаточно мед-
медленно меняющаяся функция в окрестности q = а. Разложим
/ (q) в ряд в окрестности q = а. Линейный член в разложении
Тейлора отсутствует, так как а — экстремум. Пусть
f (q) = / (а) + т У1А№ + ° №> F-12)
где yt = qt — аг. Идея приближения стационарной фазы (ПСФ)
заключается в том, что, если экспонента ехр [—if (q) ] осцилли-
осциллирует достаточно быстро, то основной вклад в F.11) дает окрест-
окрестность стационарной точки q = а. Тогда в главном порядке при-
приближения членами третьего и более высоких порядков по t/i ряда
Тейлора F.12) можно пренебречь. Отсюда имеем
qi J dqt ... j dqNg (q) exp [—if (q)] «
» g (a) exp [—if (a)] J dyx ... j dyN exp ( — -i- iytAtjyj) =
= g (a) exp [-if (a)] (-^ )N/2 (Det A)'1'2. F.13)

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 175
Так как интеграл по траекториям в силу F.8) является много-
многократным интегралом, ПСФ можно также обобщить и на него*.
Пусть qKJI (t) — классическое решение системы, описываемой
лагранжианом F.1), начинающееся в точке q @) = ца и кончаю-
кончающееся в точке q (Т) = qb. Оно является экстремумом действия
S [q (t)], которое можно разложить в функциональный ряд
Тейлора в окрестности qKn (t):
т
S[q(t)]=S [qKil (t)] + 4" j <Uy (9 О (9 У (/) + О (у3), F.14)
о
где
— оператор, играющий ту же роль, что и матрица Atj в F.12).
В интеграле по времени проведено интегрирование по частям.
Применение ПСФ к этому интегралу по траекториям дает
« В' (Т)ехр \(ЦП) S [qKa (t)]} [Det О (t)y1/2, F.15)
где все множители с Bniu) и мера В включены в множитель В' (Т).
Детерминант оператора О (t) наиболее удобно вычислять с по-
помощью его собственных значений, как будет показано ниже.
Соотношения F.13) и F.15) конечно только приближенные, так
как опущены члены третьего и более высоких порядков по кван-
квантовым флуктуациям у (t). Справедливость этих результатов осно-
основывается на предположении о достаточно быстром осциллирова-
нии экспоненты подынтегрального выражения, необходимом для
того, чтобы основной вклад в интеграл давала окрестность ста-
стационарной точки экспоненты. Нестрого говоря, это происходит,
если действие S [^@1 велико по сравнению с й. Более точный
критерий быстрой сходимости разложения, главным членом
которого является F.15), достаточно сложен математически, и
мы его здесь не будем рассматривать. Отметим, что в главном
порядке вклад в интеграл по траекториям дает классическая траек-
траектория <7КЛ (t) и соседние с ней траектории. Это есть квазикласси-
квазиклассическое приближение. Квантовые эффекты учитываются в главном
порядке через множитель В' (Т) [Det О (t) ]~'/2. Следующие по-
поправки к F.15), включающие члены третьего и более высоких
порядков по у (t), можно получить по теории возмущений, моди-
модифицированной для формализма интегрирования по траекториям,

176 ГЛАВА 6
Но мы будем работать с главным членом разложения F.15).
Наконец, если подынтегральное выражение имеет несколько
стационарных экспонент (т. е. несколько классических траекто-
траекторий), то ПСФ утверждает, что каждая стационарная траектория
дает аддитивный вклад при условии, что эти стационарные траек-
траектории широко разделены. Если две стационарные точки близки,
то ПСФ неприменимо для одной из них.
В качестве упражнения рассмотрим кратко задачу о гармони-
гармоническом осцилляторе, для которого V (q) = co2^2/2. Тогда из F.10)
имеем
. F-16)
Пусть qKJI (t) — классическое решение, начинающееся в точке
<7кя @) = ?ои кончающееся в точке qKn (Г) — q0. Из элементарной
классической механики следует, что это решение — осциллятор
с действием
с \п п Т1— о,^2 sin2(co772) - 1(км\
Разложим S [q (t)] в ряд в окрестности qKJI (t). Пусть у (t) =
= q(t)— <7„л @ и у(О) = у (Т) = 0. Тогда
т
S[q(t)]=SKri[q0, qo, Л + \ J dty(t) (- ^- - со2) y(t). F.18)
Отметим, что так как действие осциллятора квадратично по q (t),
то в разложении F.18) отсутствуют члены третьего и более высо-
высоких порядков. Таким образом, мы можем получить точный ре-
результат, и нет необходимости использовать ПСФ. Тогда с учетом
F.15), которое для данного случая является точным соотношением,
имеем
G (T) = J dq0 exp \{ЦП) SKn [q0, q0, T]\^£>[y (t)] X
X exp I -4- f (It (-ftyO(t)y) =
• vn V2 ч
= j % exp {(i/Й) SKJ1 [q0, q0, T}} [Det 0 (l)YU2B' (T), F.19)
где О (t) = —dVdt2 — со2. Для нахождения оператора [Det О (t) ]
напомним, что он действует на функции у (t), удовлетворяющие

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 177
условию у @) = у (Т) = 0. Поэтому уравнение на собственные
значения имеет вид
Я2Я2 ,\ . / tint \
где п = 1, 2, ..., <х>. Поэтому
[DetO@r"»=
/2=1 ГС=1
F.21)
Бесконечное произведение в последнем уравнении сворачивается
и дает (sin coT/coT)/2. С учетом этого F.19) можно переписать
в виде
G(T) = jA70exp[(//ft)SKnfa0, q0, T)] В' (T)K(T)(«>T/s\n соГI/2.
F.22)
Множитель В' (Т) К (Т) чисто «кинематический», т. е. не содержит
динамику, которая здесь связана с частотой осциллятора со.
В частности, В' (Т) содержит меру lim BN (T) исходного опреде-
JV-»-OO
ления F.8), которую необходимо выбрать из условия правильной
нормировки. При подстановке выражения F.17) для классиче-
классического действия получаем
Т 1'2
тр)
Sln у
и A ) = В A) д (Т) аай ехр —jr-^ . , „. ——тр) =
= В' (Г) К (Т) (ЫПТI/2 2 ехр [-/ (n + i-) cor] =
= V ехр (-1ЕпТЩ). F.23)
/2=0
Отсюда ясно, что меру В' (Т) надо выбрать следующим образом:
В' (Т)К (Т) = BлШТ)-1/2. F.24)
15 этом случае мы получаем знакомые уровни гармонического
осциллятора
Еп = (п+ 1/2) Йсо. F.25)
Рассмотрим далее потенциал V (q) более общего вида. Пусть он
имеет минимум при q = а. Тогда, как было показано в последней
главе, q (t) = a —стабильное статическое классическое решение,
и окрестности которого можно построить уровни приближенно

178 ГЛАВА 6
гармонического осциллятора. Эти уровни получаются из инте-
интеграла по траекториям тривиальным обобщением предыдущего
вывода. Разложим V (q) в ряд в окрестности q == a:
V (q) = V (а) + «V/2 + О (q3)
S [q (*)] = -V(a)T + \ dt [
о
где q (t) = q (t) — а. Тогда для данного потенциала
G (T) = exp [—IV (a) T/fl]\dq0 \ 2>[q (*)] X
xexp -=■ ^гГ~^г
В отличие от F.16) в действии F.27) присутствуют члены третьего
и более высоких порядков по q (t), так как теперь потенциал не
является потенциалом гармонического осциллятора. Поэтому
воспользуемся ПСФ, что равносильно отбрасыванию этих кубич-
кубичных и более высокого порядка членов. Проделав это, мы сведем
F.27) к той же форме, что и F.16), за исключением множителя
ехр [—iV(a)T/H]. Таким образом, с учетом F.23) получаем
для данной задачи
ехР [~t
2; sin (соГ/2) ~
= % ехр {-A7Й)Т[У(а) + .Й(о(л+ 1/2I}. F-28)
п
Отсюда
Еп « V (а) + Па (п + 1/2). F.29)
Таким образом, мы вывели в формализме интеграла по траекто-
траекториям основной результат разд. 5.2, связывающий квантовые
уровни энергии со статическими классическими решениями.
Отметим, что пренебрежение негармоническими членами в F.26)
в ПСФ равносильно требованию малости коэффициентов негар-
негармонических членов по сравнению с со2, что является в точности
условием «слабой связи» разд. 5.2.
Прежде чем перейти к теории поля, завершим этот раздел
рассмотрением понятия евклидова интеграла по траекториям.
Запишем
; qat 0) = (qb | ехр | (—Ят/Й)| qa) =
= Е ЫФп) (Фп I qa) ехр (-Епг/П). F.30)

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД BRB 179
Этот объект можно рассматривать как аналитическое продолже-
продолжение амплитуды перехода F.5) на мнимое время. Кроме того, опера-
гор ехр (—Ят/й) сам хорошо определен для любых действитель-
действительных т, хотя и не является унитарным. Интегрирование по тра-
траекториям для данного объекта можно представить в виде
KE(qb, т; qa, 0)= [ 2>E[q(r')] ехр {(— l/fi)SE [^(т')]}, F.31)
где
— евклидово действие, введенное в гл. 4. Траектории q (т') на-
начинаются в точке <7 @) = qa и кончаются в точке q (т) = ^6.
Поскольку обе части F.31) — аналитические продолжения на
мнимое время обеих частей F.6), то можно полагать, что спра-
справедливо соотношение F.31). Эквивалентность F.31) и F.30)
можно также проверить. Евклидова мера ЗЬЕ [q (%')] отличается
от Ф [q (t)] в F.6) только множителем i. Евклидов интеграл по
траекториям F.31) в математическом смысле более обоснован,
чем интеграл в действительном времени F.6). В F.31) подынте-
подынтегральное выражение содержит действительную отрицательную
экспоненту, и сходимость интеграла для извилистых или очень
далеких (большие q (т')) траекторий математически более оче-
очевидна, чем в случае F.6). Евклидов интеграл по траекториям
потребуется при изучении инстантонов в квантовой теории.
При т'-> <х> евклидов интеграл по траекториям просто связан
с энергией основного состояния, так как
1\тКЕ(Яь, т: Яа. 0);=Шп У)(яь\
т >-оо Т->°° п
= Нт<</б|^0><^0|</а>ехр(-£01г/Й). F-32)
Поэтому
Тг [ехр (-Ят/Й)] =
= J dq0 J 2>Е [q (т')],0, ,„ t ехр {- A/Й) SE [q (т')]} t"^-exp (-Еот/П).
F.33)
Наконец отметим, что след Тг [ехр (—Ят/Й)] идентичен по струк-
структуре функции распределения Тг [ехр (—0Я)] статистической ме-
механики, где Р — обратная температура. Эта аналогия используется
и гл. 10 при обсуждении так называемого разреженного инстан-
юнного газа.

180 ГЛАВА в
6.2. Обобщение на полевую теорию
Понятие интеграла по траекториям можно формально обобщить
на квантовую теорию поля. Аналогом F.10) в теории поля для
случая одного скалярного поля ф (х, t) является выражение
G (Т) = Тг [ехр (—iHT/fl)] =
= \2>[ф (х, 01 ехр {{ЦП) S [ф (х, 0]}- F.34)
Здесь интеграл берется по всем полевым конфигурациям ф (х, t),
отвечающим граничным условиям, определенным ниже, а
т
'. 0)
— действие. Функциональный интеграл F.34), так же как F.8),
можно рассматривать как предел произведения обыкновенных
интегралов. Для этой цели необходимо заменить пространственно-
временной континуум (а не одно только время) точечной решеткой,
а затем перейти к пределу нулевого периода решетки. Суще-
Существование однозначного лоренц-инвариантного предела — более
сложная задача, чем в случае чисто временной решетки F.8),
так как необходимо рассматривать все виды (D + 1)-мерных
решеток в (D + 1)-мерной теории поля. Мы будем полагать,
что функциональный интеграл F.34) однозначно определен и
что над ним можно проводить манипуляции, аналогичные про-
проделанным в последнем разделе. Мы будем счигтать также, что функ-
функциональный интеграл дает «верный ответ» в том смысле, что он
приводит к Тг [ехр (—1НТ1П)] —результату, который можно
в принципе получить с помощью канонических операторных
методов.
Перейдем к граничным условиям на поле ф (х, t), определяемым
из условия его интегрируемости. Рассмотрим сначала граничные
условия во времени. Сравним F.34) и F.10). Так как след берется
по ехр {—ШТ/Н), положим ф (х, 0) = ф (х, Т) = ф0 (х) и затем
проинтегрируем по начальному значению поля ф0 (х) точно
так же, как мы интегрировали по q0 в F.10). Этот интеграл по
ф0 (х) явно не показан в F.34), но содержится в j SD [ф (х, t)]
наряду с интегралами по полям в промежуточные моменты вре-
времени. Затем рассмотрим граничные условия в пространстве,
которые также необходимы в теории поля. Наложим разумное
с физической точки зрения условие. Для его пояснения рассмо-
рассмотрим знакомую систему в A + 1) измерениях, описываемую
лагранжианом
2£ {х, 0 = 4- (дц^J — U (ф), F-35)

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 181
■'Де
U (j>) = ±- т*ф* + \ц\ F.36)
Здесь все конфигурации с конечной энергией должны удовлетво-
удовлетворять условию ф -у О при х —>■ + <х> для всех t. .Мы ожидаем, что
квантовое вакуумное состояние *P0 [<j>] локализовано в окрест-
окрестности ф = 0 и все состояния фоковского пространства W [ф]
существуют только для функций ф (х), удовлетворяющих условию
ф (<х>) = ф (—<х>) = 0. Соответственно функции в функциональ-
функциональных интегралах должны удовлетворять условию ф (<х>, t) =
= ф (—<х>, t) — 0 для любого t. С другой стороны, рассмотрим
случай спонтанного нарушения симметрии в кинк-системе, где
Тогда существуют четыре набора разрешенных граничных условий:
Ф(оо, t) = ±m/-/X, ф(—оо, t) = ±m/-/X,
как было показано в предыдущей главе, им соответствуют четыре
сектора квантовых состояний, которые не связаны друг с другом
в силу наличия селектирующего квантового числа. В этом случае
след Тг [ехр (—iHTIK)] можно брать по каждому сектору в от-
отдельности, а поля ф (х, t) в соответствующем функциональном
интеграле должны подчиняться граничным условиям рассматри-
рассматриваемого сектора. Например, если мы ищем след от ехр (—iHT/H)
в кинк-секторе состояний, то считаем, что поля в функциональном
интеграле подчиняются условию
ф(оо, t) = —ф(—оо, t) = m/-y^k
для всех t. Более сложные системы со спонтанно нарушенной
симметрией рассматриваются аналогичным образом.
Функциональный интеграл F.34) был записан для одного
скалярного поля. Для нескольких скалярных полей вводится
произведение таких интегралов (многократный функциональный
интеграл) по всем полям. В случае ферми-полей или калибровоч-
калибровочных полей ситуация усложняется. К этим случаям мы вернемся
и последующих главах.
Для иллюстрации функциональных методов выведем главный
результат гл. 5, согласно которому в приближении слабой связи
сектору уровней энергии ставится в соответствие статическое
солитонное решение. Рассмотрим, например, A + 1)-мерную тео-
теорию вида F.35) с некоторой функцией U (ф), допускающей ста-
стабильное статическое солитонное решение ф (х, t) = фкл (х). Так
как фкл (х) — экстремум потенциала

1в2 Глава б
а также и действия, то можно разложить
S[j>(x, *)] =
= -V[фкл]T + ±-\dx\dt[y(x, 0О(х, t)у(х, 0] + О (у*), F.37)
где
°* 9 *-£ + £-
У(Х, Ъ = ф(х, Ц-фпЛх).
Напомним, что функция ф (х, t) подчиняется пространственным
граничным условиям, соответствующим данному сектору, т. е.
тем же условиям, что и фкл (х). Поэтому у (х, t) удовлетворяет
условию у (±<х>, t) = 0. Приближение стационарной фазы для
функционального интеграла F.34), как и в предыдущем разделе,
равносильно пренебрежению кубичными и более высокого по-
порядка членами в F.37):
, t)]exp{(i/fi)S№(x, /)]}«
« exp (-W WKJ Т/П) J ^5 [у (х, /)] ехр ( - ± J dx J dt {yOy\) =
= В" (Т) ехр (-IV [фкл] Т/П) {Det [О (х, t)]\m. F.39)
Здесь В" (Т) — множитель меры, содержащийся в определении
j iZ5 [ф (х, I) ], которое мы до сих пор не раскрывали. Он выбирается
из условия правильной нормировки состояний. Для нахождения
оператора Det [О (х, t) ] по его собственным значениям, отметим,
что О (х, t) в F.38) является суммой члена, зависящего от t, и
члена, зависящего от х. Следовательно, его можно диагонализо-
вать отдельно в ^-пространстве и в х-пространстве. Пусть
— уравнение на собственные значения для зависящей от х части
оператора О (х, t) с граничными условиями уг (±°о) = 0. Урав-
Уравнение E.48) последней главы является частным случаем F.40)
для кинк-решения. Тогда
Г °о 
П Det (- Ж ~ шр)
1-1/2
{Det [О(х, 01Г1/2'= П Det ( )

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 183
Таким образом, детерминант свелся к произведению детерминан-
детерминантов гармонического осциллятора, рассмотренных в предыдущем
разделе. Используя результаты этого раздела, получаем
Тг [ехр (-ШТ/П)] « ехр (-IV[фкл] ТЩ) \\ BismlrT/2)) > F.42)
г
где множитель меры В" (Т) в F.39) опять выбирается так, чтобы
F.42) было справедливо в ПСФ. Перепишем это уравнение в виде
Тг [ехр (-ШТ/П)] я*
« ехр (-W [фкл] Т/П) П ( £ ехР [~iT^r (nr f 1/2)]) =
= £ ехр [- (iT/fl) (У[фкл] + £ Пщ{пг + 1/2))], F.43)
К}
где сумма £{« i берется по всем целым числам набора \пй, nv
п2, ...!. Следовательно, « этом приближении для уровней энергии
состояний, построенных в окрестности <£кл, получаем выражения
%} « V [фы] + % Пыг (nr -f 1/2). F.44)
Итак, мы вывели в качестве упражнения по функциональному
интегрированию основной результат последней главы. При этом,
конечно, физика осталась прежней и все качественные замечания
гл. 5 справедливы и здесь, но выраженные в терминах функцио-
функционального интегрирования. Например, пренебрежение в главном
порядке кубичными и более высокого порядка членами в F.37),
лежащее в основе ПСФ, есть не что иное, как приближение
«слабой связи» гл. 5. В общем случае сумма по всем нормаль-
нормальным модам в F.44) расходится, и эту расходимость необходимо
устранить добавлением в лагранжиан контрчленов. При этом
- \Ут(ф)<Н. F.45)
В ПСФ это ведет в главном порядке к замене V [фкл ] Т в F.39)
на \V [<£цл] + ^Кч [фкл]} Т, так что F.44) заменяется на
%} ~ V [фкд] + VK4 [фкл] + £ (пг + 1/2) /гсог. F.46)
г
Если теория перенормируема, то можно ожидать, что контр-
контрчлены устранят все расходимости в сумме по собственным часто-
частотам. Далее в гл. 5 мы отметили, что если любая из частот сол
исчезает из-за наличия некоторой непрерывной симметрии, что
происходит, в частности, для солитонных решений, то рассматри-

184 гллпл о
ваемый метод нуждается в модификации. Та же проблема суще-
существует и для настоящего метода по тем же причинам. Ее признаки
можно увидеть в F.42), где множитель \2i sin (cor772)}-* расхо-
расходится при сог -> 0. Главная же причина заключается в том, что
в этой ситуации ПСФ в своей простой форме не справедливо.
При этом решение фкл (х) .принадлежит непрерывному семейству
классических решений Р (а) [фкл (*)], где Р (а) —непрерывный
оператор симметрии, параметризованный переменной (перемен-
(переменными) а. Таким образом, фкл (х) не является изолированной
стационарной точкой S [ф], а принадлежит непрерывному се-
семейству стационарных точек, тогда как, вводя ПСФ, мы отметили,
что оно дает хорошее приближение только в том случае, если
стационарные точки достаточно широко разделены. Поэтому
нулевые моды, возникающие в силу существования непрерывных
симметрии, создают трудности и для настоящего метода, так же
как в гл. 5. Этого следовало ожидать, так как физический смысл
данного приближения тот же, что и в гл. 5. О том, как надо моди-
модифицировать эти методы при наличии нулевых мод, см. в гл. 8.
Из этих замечаний видно, что функциональный интеграл F.34)
дает энергетические уровни, связанные со статическим решением,
при тех же условиях и ограничениях, что и в предыдущей главе.
В полевой теории также можно ввести евклидов функциональ-
функциональный интеграл, обобщая соответствующим образом F.33). Имеем
Тг [ехр (-Ят/Й)] = \2)Е[ф(х, т')]ехр {-(l/ft)SBtf(x, т')]},
F.47)
где SE [ф (х, т')] — евклидово действие, введенное в гл. 4; в функ-
функциональном интеграле интегрирование ведется по начальным
и конечным значениям полей ^>0 (х) = ф (х, 0) = А (х, т). Так же
как в F.33), при т -> схэ основной вклад в след F.47) дает состоя-
состояние с наинизшей энергией данного сектора. Рассмотрим для
примера квантовое солитонное состояние в A + 1) измерениях,
являющееся состоянием с наинизшей энергией, построенным
в окрестности статического классического солитонного решения
фкл (х). Аналогично F.37) имеем разложение
= V [фяв] х + i- \ dx [ dx' [у (х, х1) 0Е (х, х') у (х, т') + О (у% F.48)
где
у(х, х')=ф{х, х')-фКЙ(х).

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 185
11ренебрежение членами О (г/3) в F.48) является гауссовским
приближением для F.47) и евклидовым аналогом ПСФ. В этом
приближении аналогично F.39) имеем
Тг [ехр (-Ят/Й)] « ВЕ (т) ехр (—У [фкл] т/Й) {Det [OE (х, т')]}/2,
F.50)
где ВЕ(х) —евклидова мера, аналогичная В" (Т) в F.39). Пере-
Перепишем F.50) в виде
Тг [ехр (-Ят/Й)] « В£(т)ехр {- [v [фяи]х/П + \ In Det O£]} =
где использованы собственные частоты нормальных мод F.40).
Объект tr In (—д2/дх'2 + со?) просто вычисляется при т-><х>.
Напомним, что собственные значения оператора —(<32/дт'2) для
наших граничных условий равны /г2я2/т2, п = 1, 2, ..., <х>. Поэтому
/г=1
где мы выделили расходящуюся часть интеграла. Эта расходя-
расходящаяся часть чисто кинематическая (не зависит от сог) и обращается
в нуль соответствующим выбором ВЕ (т). Мы включим ее в меру,
которую обозначим В'Е (т); тогда F.52) примет вид
где проведено интегрирование по частям. Подставляя это в F.51),
получаем
Тг [ехр (-Ят/Й)] ^ В'Е (т) ехр [- -£ (у [фкл] + £ -А согт)
F.54)

1ллвл в
Выбирая меру так, чтобы В'Е (т) = 1, для энергии квантового
солитона получаем выражение
^Ц. F.55)
Это наш старый результат, который можно сделать конечным до-
добавлением Укч [<j>KJI].
Все эти выводы являются примерами использования квази-
квазиклассического разложения для функциональных интегралов.
Новых результатов мы не получили, поскольку как в простран-
пространстве-времени Минковского, так ив евклидовом пространстве-вре-
пространстве-времени разлагали в ряд действие в окрестности статических решений.
Мы получим новые результаты при разложении в ряд в окрестности
классических решений, зависящих нетривиальным образом от t
(или т). В пространстве-времени Минковского это приведет к кван-
квантованию зависящих от времени солитонов, что рассматривается
в следующих разделах. В евклидовом пространстве-времени это
приведет к инстантонной физике, которую мы обсуждаем в гл. 10.
6.3. Условие Бора—Зоммерфельда
Квантование зависящих от времени решений в теории поля
проводится с помощью В КБ-метода, являющегося обобщением на
теорию поля условия Бора—Зоммерфельда. Это условие хорошо
известно в нерелятивистской квантовой механике и обычно вы-
выводится из дифференциального уравнения Шредингера. Обобщение
на теорию поля удобно проводить в формализме функционального
интегрирования. Сначала рассмотрим кратко вывод условия
Бора—Зоммерфельда для одночастичной системы на языке ин-
интегрирования по траекториям [44, 100, 180—182, 247].
Рассмотрим пропагатор системы F.2)
9(Е) = Тг (j~) = j. \dTG(T)exp (iET/П). F.56)
о
Полюсами 9 (Е) являются собственные значения энергии свя-
связанных состояний. Используя для G (Т) F.10), получаем
= j-\dT ехр (iET/П) \dqo\S> [q {t)]q @>^
>=*. x
X ехр \(i/fi)S[q(t)]\. F.57)
Условие квантования выводится из ПСФ для этого интеграла,
что является в рассматриваемом случае методом ВКБ. Сначала

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 187
разложим в ряд S [q (t)\ в окрестности некоторого нетривиаль-
нетривиального экстремума, т. е. зависящего от времени решения q'KJI (t),
удовлетворяющего уравнению
= Н^ = 0, F.58)
i де qin @) = q'Kll (Г) = q0. Для данного Т может существовать
несколько классических решений, удовлетворяющих граничным
условиям; мы будем их различать с помощью индекса /'. Разложим
S' [q (t) ] в ряд в окрестности q'^ (t) и для интеграла по траекто-
траекториям используем ПСФ, следуя уравнениям F.14), F.15). Сделаем
что для каждого решения q'Kn (t), j = 1, 2, ... в отдельности,
полагая, что они достаточно широко разделены для применимости
11СФ. Тогда имеем
G (Т) = ^ j dcl°exp (iSj [q0, q0, Т]Щ) A{, F.59)
где Sj [q0, q0, T] = S [я!кл] —действие ;'-го классического реше-
решения с началом и концом в точке q0, a
A{~jDet|-^-
Так как (d2V/dq2) ,- , вообще говоря, зависит от времени,
вычислить А{ труднее, чем в случае гармонического осциллятора
в разд. 6.1. Его вычисление приведено кратко в приложении А.
Для нахождения интеграла по q0 в F.59) применим опять ПСФ.
Стационарная экспонента должна удовлетворять условию
-= (^^» ** Ъ+4ьЫЯ* Яь. Л),|Г^Ь = -А + Л. F-61)
Последнее равенство следует из классической механики; рг и
/?2 — импульсы начала и конца траектории. Уравнение F.61)
показывает, что траектория на своих концах должна иметь не
только одну и ту же координату q0, но один и тот же импульс,
г. е. траектория должна быть периодической. Это не удивительно:
в конце концов интеграл по траекториям является многократным
интегралом по координатам qt в промежуточные моменты времени
F.8). Траектория общего вида имеет разрывы скоростей
(рис. 11, а). Но в ПСФ многократный интеграл J Пг dqt отбирает
классическую траекторию (рис. 11, б) со сглаженными углами.

188 ГЛАВА G
Это еще оставляет разрыв скоростей в точке q0. Но интегрирование
следа j dq0 сглаживает и этот разрыв в конечной точке
(рис. 11, в) и превращает траекторию в периодическую. (Для
простоты на рис. 11 показан случай двух измерений.)
Таким образом, F.59) сводится к сумме по всем периодическим
орбитам. Конечно, основной период (цикл) орбиты не обязательно
равен Т. Он может быть равен Tin, где п — произвольное целое
число, характеризующее число прохождений основной орбиты.
Рис. 11. а—■ неклассическая траектория общего вида, начинающаяся в точке
<7ol б — классическая траектория, отобранная приближением стационарной фазы
(ПСФ) для интеграла по траекториям; заметим, что острые углы (разрывы ско-
скоростей) сглажены ПСФ только в промежуточные моменты времени, так как инте-
интеграл по траекториям берется только по промежуточным значениям q.; в — пе-
периодическая классическая траектория; она отбирается ПСФ при интегрировании
следа по q0, которое сглаживает острый угол у q0. Для простоты на рисунке изо-
изображены двумерные орбиты.
Для данного Т G (Т) получает вклады от всех периодических
орбит с основными периодами, кратными Т. Заменим в F.59)
сумму по индексу /' на сумму по индексу п. Тогда
G (Г) = 2 ехр [(ЦП) nSKJI (Т/п)] Д{"> (T) &{2n) (T), F.62)
n
где A<n) —множитель из интеграла по q0 в ПСФ. Ясно, что дей-
действие для п прохождений орбиты равно п, умноженному на дей-
действие для одного цикла. Множители Аг, А2 вычислены в при-
приложении А:
АГ> (Т) & (П = т- (—^Н1/2 ехр (-Ш) (-^)W, F.63)
где .Екл —энергия периодической орбиты с периодом Tin. Окон-
Окончательно получаем
2
п О
п О
Хехр {^-[Ет + SKJT (т)]) (-1)", F.64)

, ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 189
где т = Tin — основной период цикла. Интегрирование по т
проведем также в ПСФ. Точка стационарной фазы теперь удовле-
удовлетворяет условию
Е = -dSKJdx = £кл, F.65)
где последнее равенство знакомо из классической механики.
Отметим, что Е является параметром в пропагаторе &(Е). ПСФ
отбирает ту периодическую классическую орбиту, энергия кото-
которой Екл = Е, Таким образом, период т и действие S данной ор-
орбиты фиксируются значением Е. Отсюда приближение стационар-
стационарной фазы для F.64) дает
=S т
. F.66)
Поскольку d2SKJdx2 = —dEldx, многие множители здесь сокра-
сокращаются:
-ix(E) exp
Й 1 -f exp [(i/ft) \
где
W (E) ~ S [x (E) ] + Ex (E) F.68)
— преобразование Лежандра для' S. 9 (E) имеет полюсы при
Е = Ет, которые удовлетворяют уравнению
W (Ет) = Bт + 1) лй, F.69)
где т — целое число. Вычет в каждом полюсе равен единице,
так как dWIdE = x. Таким образом, в ВКБ-приближении уровни
энергии определяются Ет, удовлетворяющими F.69). Это обыч-
обычное правило квантования Бора—Зоммерфельда [225], так как
- q2 - V + £) = J dtq2 = 2 J p dq, F.70)
0 0 Ql
где qx и q% — точки поворота классической орбиты.

190 ГЛАВА 6
Может показаться, что вычисление полюсов 'S (Е) дает уровни
энергии только в случае связанных состояний. Но если система
помещена в ящик с периодическими граничными условиями, то
все энергетические уровни дискретны и все орбиты ограничены.
Тогда описанный выше метод можно использовать для любого
уровня, а затем устремить размеры ящика к бесконечности.
В таком выводе подразумевается, что существует только одно
непрерывное семейство периодических орбит, параметризованное
переменной основного периода т, или, что эквивалентно, энергией
£кл (т). Иначе говоря, предполагается, что для любого т суще-
существует только одна орбита с основнЪш периодом т и эта орбита
дает вклад в интегрирование по dT в F.64) либо для однократного
(Т = т), либо для многократного прохождения (Т — пх). Это
позволяет заменить V. j dT на £jnn \ dx. Для типичных потен-
потенциалов «одной ямы» в одном измерении это предположение спра-
справедливо. Если потенциал V имеет несколько «ям» около различных
минимумов, то может существовать несколько семейств орбит,
т. е. орбит в различных областях с одинаковым основным перио-'
дом т. То же может происходить в двух или большем числе изме-
измерений. В таких случаях, если семейства орбит достаточно широко
разделены, ПСФ дает от каждого из них аддитивный вкладе & (Е).
Если в этом приближении член произвольного семейства удо-
удовлетворяет условию F.69), то он является уровнем энергии.
Более детальный анализ метода В КБ в формализме интеграла
по траекториям дан в работах Гуцвиллера [180—182], Берри
и др. (см. [45] и приведенные там ссылки) и Левита и Смилански
[232, 233].
6.4. Метод ВКБ в теории поля
Обобщим метод ВКБ сначала на несколько степеней свободы,
а затем на теорию поля, рассматриваемую как систему с'бесконеч-
с'бесконечным числом степеней свободы [100, 102]. Наше обобщение будет
формальным. Основные этапы те же, что и в разд. 6.3. Мы запишем
функциональный интеграл для пропагатора 9 (Е) = Тг [1/(Я —
— Н)\, а затем применим ПСФ, которое отберет зависящие от
времени классические периодические решения. Единственное от-
отличие заключается в том, что интегралы по квантовым флуктуа-
циям (аналогичные множителям А}") А|п) в уравнении F.62))
более сложны.
Рассмотрим, например, двумерную задачу —частицу в х —у-
плоскости с лагранжианом
L t у).

ФУНКЦИОНАЛЬНЫЕ MHTEfPAJibi И МЕТОД ВКБ 191
Тогда
оо
# (£) = jL j dTexp (iET/П)G (Г),
G{T) = \dx0 \dyo\s>[x(f)]
V о
-V(x, у)] J = \dr0 j" a>[r@]exp Mp |Л [4-r-r - V(r)] j, F.71)
где использовано компактное обозначение г = \х, у}. При при-
применении ПСФ к интегралу по траекториям отбираются класси-
классические орбиты, а применение ПСФ к интегралу j dr0 выбирает
из них периодические тривиальным обобщением F.61). Для
данного периода 7 дают вклад все периодические орбиты с
основными периодами Tin. Таким образом, в ПСФ мы мо-
можем записать
G G) « £ ехР VnS«* G/") Й1 J ^ № W1X
п
il4-^(—W-V')ttp\ F-72)
L о J
где SKn {Tin) — действие одного цикла периодической орбиты
Гкл' (О С ОСНОВНЫМ перИОДОМ Т = Tin, p (t) = Г @ — Гкл' @>
/ Ё1__1/Л = /'л -^2 &v \
\ дГ> 'v )if-\OiJ dt* dndrt)rW w'
а 3) [р (t)] включает интегрирование следа по dp @). Запишем
F.72) в виде
G (Т) « £ exp [wSHn G/п)/Й] A(n) (Г), F.73)
где А("> (Т) —аналог множителей Д<п> Д<"> в F.62). Он, как
и прежде, равен оператору {Det [—d2ldt2 — У"]}/2, но теперь
(—dj—V")—2Х2-матрица в \х — у\ -пространстве, являю-
являющаяся дифференциальным оператором, зависящим от времени.
Его вычисление требует использования теории Гамильтона—
Якоби, что в результате дает
( )'/2 ^ ^ (/2)]- F.74)

I !J 171 Л ИЛ G
где vi — «угол стабильности», определенный ниже. Вывод этого
выражения мы не даем (см. приложение А в работе [102]). Но можно
заметить, что F.74) похоже на одномерный результат F.63),
который мы вывели в нашем приложении А. Результат F.74)
отличается от F.63) только в двух отношениях.
1. Отсутствует множитель ехр (—inn). Напомним (см. при-
приложение А), что этот множитель дают сингулярные точки клас-
классической орбиты. Типичная периодическая орбита в двух изме-
измерениях (как на рис. 11, в) не имеет сингулярных точек, и данный
множитель отсутствует. В специальных случаях, когда орбиты
имеют сингулярные точки, такие множители следует ввести (на-
(например, для одномерных орбит в двумерной плоскости).
2. Результат F.74) содержит добавочный множитель
1/[2/ sin (nv1/2)]. Он соответствует, как мы покажем, квантовым
флуктуациям поперек орбиты. Угол стабильности vi определяется
следующим образом. Рассмотрим уравнение на нулевое собствен-
собственное значение оператора (—д2/д? — V"):
Здесь оператор представляет собой 2Х2-матрицу, а £ —двух-
компонентный вектор в х —//-плоскости. Отметим, что это урав-
уравнение является также «линейным уравнением устойчивости»
орбиты, т. е. гкл @, так же как и немного смещенное классиче-
классическое решение г'кл (t) = гкл @ + I (t), удовлетворяет уравнению
движения
—r-dV/dr = O. F.76)
Следовательно, малая деформация £ (t) в главном порядке удо-
удовлетворяет уравнению F.75). Два независимых решения урав-
уравнения F.75) обозначим 10 @ и Si (t). Каждое из них удовлетворяет
условию
|, (/ + т) = eiv% @ для всех /, F.77)
где vi — углы стабильности, т = Tin — основной период гкл (/)•
Уравнение F.77) выполн/яется в силу того, что оператор
(—д1 — V") сам периодичен с периодом т. Одно из этих решений
имеет вид
So (*) = "!■ г„л (*). F.78)
что можно проверить дифференцированием F.76). Так как гкл (t)
периодично, то периодично и £0 = гкл- Отсюда v0 = 0. Это нуле-
нулевое значение угла стабильности собственной функции F.78)
существует всегда и связано с инвариантностью уравнения дви-

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 193
жения относительно трансляций во времени. Отметим сходство
с нулевыми модами, с которыми мы встретились выше и которые
также связаны с некоторой непрерывной симметрией. Другой
угол стабильности vi, соответствующий второму решению £х (t),
в общем случае не равен нулю, что и отражено в результате F.74).
Так как мы не даем вывод выражения F.74), то поясним его
на примере. Рассмотрим потенциал простого вида
V (х, у) = V (х) + V8<oV, F.79)
где V (х) — некоторый одномерный потенциал, допускающий су-
существование семейства периодических по х орбит. Тогда V (х, у)
допускает семейство периодических орбит, целиком лежащих на
оси х:
х (() = хкл (t), y(t) = O, F.80)
где хцл @ обладает некоторым периодом т = Tin. Для данных
орбит задача разбивается на х-часть и «/-часть.
В этом случае матрица (cPVldrt drj)r факторизуется:
UdWldxXR 0
L 0 со2
Подставляя ее в F.75), находим следующее решение этого урав-
уравнения
удовлетворяющее условию \х (t + т) = еш%х (t). Таким образом,
угол стабильности в этом случае равен vi = сот и множитель флук-
флуктуации F.74) сводится к
где множитель (—1)" введен потому, что, как мы отметили выше,
орбита F.80) имеет две точки поворота. Именно такого множителя
флуктуации для орбиты F.80) в потенциале F.79) мы и ожидали,
основываясь на наших предыдущих рассуждениях. Полная за-
задача, включающая интеграл по траекториям F.71), фактор изуется;
более того, орбита F.80) целиком лежит на оси х.Следовательно,
множитель флуктуации равен произведению х-множителя и у-
множителя. Эффект флуктуации вдоль х-направления для ор-
орбиты на оси х уже вычислен в F.63) и в точности равен первому
множителю в F.81). Флуктуации вдоль оси у соответствуют
флуктуациям гармонического осциллятора (см. зависимость от у
в F.79), F.80)). Их эффект, вычисленный в F.22)—F.24), дает
второй множитель в F.81). Таким образом, в частном случае
F.79), F.80) выражение F.74) дает ожидаемый ответ.
7 Раджараман Р.

194 глава б
Для потенциала V (х, у) общего вида угол стабильности vi
определяется соответствующим обобщением сот. Так же как
мнимая частота со (со2 < 0) ведет к неустойчивости орбиты F.80)
в рассмотренном частном случае, мнимая часть vi ведет к неустой-
неустойчивости в общем случае. Это очевидно из F.77). Если vi имеет
мнимую часть, то lx it) растет с каждым циклом при стремлении t
либо к +оо, либо к —оо. Малые деформации теперь не остаются
малыми. Основываясь на физических соображениях, мы считаем,
что устойчивые квантовые состояния получаются только из
устойчивых классических орбит. Это отражено в уровнях энергии,
получаемых ниже; они становятся комплексными для комплекс-
комплексного Vi.
Вернемся к методу В КБ и перепишем F.74) в виде
F.82)
Подставляя F.82) в F.73) и F.71), получаем
п, р
Xexp (il [sM (т) + Ex -. (p + -i-) ftVl]) . F.83)
Дальнейшие шаги тождественны выводу F.64)—F.70) с соответ-
соответствующей модификацией результатов. ПСФ для интегрирования
по т отбирает для данных Е и р классическую орбиту, удовлетво-
удовлетворяющую условию
или
[ ±)^ = Е. F.84)
Напомним, что vi зависит от орбиты, т. е. vi = Vi (^кл (т))- Для
ПСФ F.83) дает
9 (Е) = ^ i Iif2lexp (-| Wp (£)) , F.85)
п, р
Wp(Е) = S (Екл) + Ех (£кл) - (р + -L) tlVl (Екл), F.86)
п, р
где

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 195
а .Енд —функция от Е F.84). Уровни энергии являются полюсами
9 (Е), соответствующими
WP(E) = 2тлП, т=1,2,-..., р = О,. 1, 2, ... . F.87)
Отметим, что уровни энергии F.87) характеризуются двумя це-
целыми числами тир. Это согласуется с нашим ожиданием, что
двумерное связанное состояние должно иметь два квантовых
числа. Квантовое число т в квазиклассическом приближении
соответствует числу полных волн, укладывающихся вдоль вы-
выбранной орбиты, а р отвечает поперечным возбуждениям орбиты.
Отметим, что квантовая энергия Е в F.84) не равна энергии
соответствующей классической орбиты Екл в отличие от одно-
одномерного случая F.65). Их разность (р + 1/2) й дх^дх можно
отнести к энергии поперечных к орбите флуктуации; эта возмож-
возможность отсутствует в одномерном случае. Напомним, что для част-
частного случая F.79), F.80) vi = сот и данный добавочный член
равен (р + 1/2) йсо, т. е. тому значению, которого следовало
ожидать для поперечных возбуждений типа гармонических.
Обобщение результатов F.84)—F.87) на несколько степеней
свободы и на теорию поля очевидно. Для N нерелятивистских
координат г (t) в F.71) отвечает Л^-вектору. ПСФ опять отбирает
периодическую классическую орбиту гкл (t). Оператор
представляет собой N X N -матрицу. Уравнение устойчивости
F.75) теперь имеет N независимых собственных функций |( (t)
с углами стабильности v/. Угол v0 опять обращается в нуль, так
как 10 = гкл, и если других симметрии нет, то остальные vt,
i = 1, ..., N — 1 вообще говоря отличны от нуля. В выражении
F.74) множитель [2/ sin (nvi/2) J заменяется произведением
N-l
П [2t sin (nv/^)],
отвечающим флуктуациям по N — 1 поперечным к орбите на-
направлениям. Далее результаты F.84)—F.87) обобщаются так:
N-1
^- = £, F.88)
а уровни энерги-и удовлетворяют соотношениям
W{Pl){E) = 2mnn, m = 0, 1, 2, ... , F.89)
Pi — 0, 1,2,..., для каждого i,

196 ГЛАВА 6
где
N—1
W{p.} (E) = S [Екл] + Ех (£кп) - g (Pi + 1/2) ftv,. F.90)
Мы отметили, что один угол стабильности v0 всегда равен нулю
в силу симметрии относительно трансляций по времени; если
других симметрии нет, то остальные углы вообще говоря не
равны нулю. Но если лагранжиан обладает другими непрерыв-
непрерывными симметриями, то они могут приводить к исчезновению не-
некоторых V/ точно так же, как они приводили к исчезновению
некоторых частот со* в предыдущей главе. В этом случае некоторую
периодическую орбиту гкл (t) можно непрерывным образом де-
деформировать с помощью оператора симметрии Р в близлежащие
периодические орбиты гкл = Ргкл, обладающие таким же пе-
периодом. Тогда соответствующая мода деформации % (t) =
= Гкл (t) — Гкл @ также будет иметь тот же период и, следова-
следовательно, нулевой угол стабильности. Такие симметрии, как и при
квантовании статических решений, приводят к трудностям в нашем
методе: множитель [2i sin (nvj/2)] расходится. Конечно, ре-
результаты ПСФ в главном порядке F.88)—F.90) при этом не изме-
изменяются. Мы будем работать только в главном порядке, но если
необходимо рассмотрение поправок более высоких порядков в слу-
случае нулевых углов стабильности, то метод необходимо модифи-
модифицировать. Более подробное обсуждение данной задачи можно
найти в приложении А работы [102], а также в гл. 8.
Помня об этих трудностях с нулевыми модами, обобщим наш
метод на теорию поля, рассматриваемую как систему с бесконеч-
бесконечным числом степеней свободы. Возьмем, например, скалярное
поле <j> (x, t) с действием
SKAf]=\dt \-L.l^YdK-V[4>]\, F-91)
где
V [<j>] = f dx Г-^- (V^>J + U (<j>) 1. F.92)
Тогда
oo
^ (£) = Tr ( F}_H) = 4r\dT exp (iET/ti) G (T), F.93)
где G (Т) определяется из функционального интеграла F.34).
Дальнейшие шаги формально те же. ПСФ опять отбирает класси-
классические решения </>кл (х, ^.Уравнение устойчивости (обобщение
уравнения F.75)) имеет вид
F.94)

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ 197
Так как </>кл (х, t) периодично с периодом т, решения удовлетво-
удовлетворяют условию
lt(x, t-\- T) = e'v*g; (x, t) для всех х, t. F.95)
Главное отличие заключается в том, что обычные периодические
граничные условия в ящике здесь приводят к бесконечному числу
независимых решений |г (х, t) с соответствующими v{. В резуль-
результате конечная сумма по индексу i в F.88)—F.90) теперь стано-
оо
вится бесконечной. Поэтому сумма Д] v, в общем случае может
расходиться, так же как сумма по нормальным частотам в преды-
предыдущей главе. В перенормируемой теории эту расходимость мож-
можно устранить введением обычных контрчленов. Таким образом,
применяя результаты F.88)—F.90) в полевой теории, будем счи-
считать, что в действие и энергию введены контрчлены. Поэтому
заменим F.88)—F.90) на
оо
(Pi + 1/2) ^Ж = Е' F-96)
о
W{p.} (E) = 2mntl, F.97)
где
оо
W{Pi) (Е) = SM [^>кл] + SK4 [фкл] + Ех (фкл) - I] (pt + 1/2) ftv,. F.98)
Здесь индекс «кч» обозначает вклад контрчленов, которые устра-
устраняют расходимости в бесконечных суммах. Уравнение F.96)
отбирает для данного Е и набора целых чисел \pt) классическое
периодическое решение </>кл. Тогда те значения Е, которые удо-
удовлетворяют F.97), F.98), дают перенормированные энергии свя-
связанных состояний. Эти уравнения мы поясним в гл. 7 на примере
модели синус-Гордона.
6«5, Заключительные замечания по методу ВКБ
В отличие от методов гл. 5 описанный здесь метод ВКБ позво-
позволяет квантовать не только статические классические решения,
по и решения, зависящие от времени. Однако работать с ним труд-
труднее, чем с методом квантования статических решений в приближе-
приближении слабой связи, описанным в гл. 5. Кроме того, что формулы
в методе ВКБ более сложны, требуется еще информация либо
о всех, либо о некоторых семействах точных зависящих от вре-
времени периодических классических решений. Для этих решений
необходимо вычислять, решая линейное уравнение устойчивости,

198 ГЛАВА 6
углы стабильности vt. Эти вычисления чисто классические, но
проводить их нелегко. Мы уже видели из предыдущих глав, что
решать нелинейные полевые уравнения даже статические, не
говоря уже о зависящих от времени, трудно. Однако, хотя полу-
получить классические решения и сложно, точно разрешить соответ-
соответствующую квантовополевую задачу еще сложнее. Лишь в редких
случаях можно решить квантовополевую задачу, не решая соот-
соответствующей классической задачи. Метод ВКБ позволяет полу-
получить некоторые приближенные кван-Говые результаты, если имеется
необходимая классическая информация. Но следует отметить,
что основное узкое место этого метода заключается в отсутствии
в настоящее время точных периодических классических решений
для большинства полевых теорий. Система синус-Гордона, кото-
которую мы используем в гл. 7, является редким исключением.
Если классические решения известны, то метод ВКБ является
более мощным инструментом, чем метод «слабой связи» гл. 5. Ко-
Конечно, в методе ВКБ также используют условие слабой связи, что-
чтобы получить хорошее приближение, поскольку членами третьего
и более высоких порядков по флуктуациям пренебрегают. Но'
классические решения, на которых основывается главное прибли-
приближение стационарной фазы, содержат важную непертурбативную
информацию. В отличие от статических решений, которые дают
информацию об областях минимума потенциала, набор всех пе-
периодических орбит дает информацию о всех его областях. Возьмем,
например, простой случай негармонического осциллятора (V (q) —
= (xJq2/2 + Xcplfy. Высоколежащие уровни энергии (для которых
метод ВКБ, вообще говоря, работает лучше) связаны с высоко-
высокоэнергетическими периодическими орбитами в областях, где не-
негармонический член Xq* больше гармонического члена a>2q2. Хотя
точно определить классические орбиты, необходимые для нашего
квазиклассического формализма, трудно, но они дают важную
непертурбативную информацию. Можно сравнить полученные
методом ВКБ уровни энергии для негармонического осциллятора
с найденными численно с хорошим приближением [216]. Оказы-
Оказывается даже в пределе сильного взаимодействия (X ^> со2) ВКБ-
приближение справедливо с точностью 1 % или лучше для всех
уровней, за исключением основного состояния, для* которого
точность составляет около 22 %. Метод ВКБ, конечно, точен
в пределе X ->0. Таким образом, по крайней мере в этом примере
ВКБ-результаты достаточно точны для большинства уровней
энергии и для большой области значений X. Трудно сказать, со-
сохранится ли такая точность для типичных задач теории поля,
но пример с негармоническим осциллятором дает повод для опти-
оптимизма. Действительно, для модели синус-Гордона результаты
окажутся точными. Правда, этот пример нетипичен в силу своих
специфических свойств. Для оценки точности метода его необ-

ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД BKfc 199
ходимо применить к большему числу полевых задач. Основная
трудность, возникающая при этом, заключается, как^мы отме-
отметили, в отсутствии точных периодических классических решений.
Сделаем еще одно последнее замечание о рассматриваемом
здесь и в гл. 5 квазиклассическом методе. С одной стороны, ква-
:шклассическое][приближение хорошо работает только в том слу-
случае, когда ft мало по сравнению, скажем, с действием для класси-
ческих|решений, используемых в этом методе. С другой стороны,
мы также подчеркнули, что метод требует выполнения условия
слабой связи, чтобы можно было отбрасывать члены третьего
и более высоких порядков по флуктуациям в ПСФ. Необходи-
Необходимость выполнения этих двух условий — малости й и малости
константы связи — можно продемонстрировать следующим об-
образом. Рассмотрим скалярную полевую теорию с потенциалом
U (ф) в виде
(j) F.99)
где g_— константа связи, малости которой мы требуем, ф = g<j>,
a U (ф) не зависит явно от g. Отметим, что этот вид потенциала
справедлив для^большинства рассмотренных выше моделей. На-
Например, для кинк-системы (уравнение E.36)) можно записать
*(P'n*№ (l/g*)[Lm*&l)*] F.100)
где g2 = Kim2 и ф = gф. Аналогично для системы синус-Гордона
(уравнение B.61)) имеем
U (ф) = (/в*Д) {1 - cos [WHm) ф]} = A/g3) [m2 A - cos ф)]. F.101)
Конечно U (ф) может зависеть от остальных параметров лагран-
лагранжиана, например от массы. Для потенциала вида F.99) действие
можно записать в виде
[ф (х, 0J = \di\dx [-г (<W -
= js- j dt j dx [±(д^Г - U (Щ = Jg-51ф1, F.102)
где S [^> ] не зависит явно от g. Рассмотрим любой типичный
функциональный интеграл нашего квазиклассического метода,
например встречающийся в уравнении F.34):
а (Г) - J 0> [ф (х, /)] ехр \{ЦЩ S[4>]\ =
= \£>[ф] ехр (^г SVf})=A\%[f] exp (iS [ф]1Пё^, F.103)

200 ГЛАЁА 6
где константа А возникает при замене Ф [ф] на Ф [f]. (Кон-
(Константа А может содержать бесконечные степени \lg, но так как
она^является общим множителем функционального интеграла,
то на физику она не влияет. Ее можно устранить соответству-
соответствующей переформулировкой меры функционального интеграла.)
Из^(б.ЮЗ) мы видим, что вся зависимость подынтегрального
выражения от ^заключена в комбинации {fig2)'1 в экспоненте.
Таким образом, для справедливости приближения стационарной
фазы требуется, чтобы комбинация fig2 была мала по сравнению
с действием S [</>кл] для стационарных орбит, т. е. классических
решений. Это точный критерий, который, конечно, удовлетво-
удовлетворяется, когда й и g2 малы.
Отметим, что, хотя мы использовали одно скалярное поле,
этот вывод справедлив для любого набора полей, если действие
можно записать в виде F.102). Например, для теории Янга—
Миллса действие можно представить в таком виде в терминах
соответствующим образом масштабно преобразованных матрич-
матричных полей Лц (см. D.10)). Для справедливости квазиклассиче-
квазиклассических результатов в этой теории опять требуется малость величины (
fig2. К сожалению, в чистой теории Янга—Миллса g (с соответ-
соответствующей перенормировкой) невозможно считать малым. Это
вызывает сомнение в квазиклассических результатах для такой
теории. Данная проблема обсуждается в разд. 10.5.

ГЛАВА 7
НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ
7.1. Спектр связанных состояний в теории синус-Гордона
Проиллюстрируем развитый в гл. 6 метод ВКБ, применив его
к двумерной модели синус-Гордона (СГ). Выбор модели СГ в ка-
качестве иллюстрации дает некоторые преимущества, но имеет и
одно неудобство. Преимуществ несколько. Мы уже рассмотрели
эту модель в гл. 2 на классическом уровне. Известны все класси-
классические решения этой модели, в частности семейство периодиче-
периодических решений получается в простой аналитической форме. По-
Последние представляют собой дублетные решения или бризеры,
задаваемые уравнением B.78). Они могут быть использованы как
исходные данные для метода ВКБ. Возникающая в результате
реализации этого метода алгебра оказывается легко поддающейся
обработке и удивительно простой. Кроме того, как мы упоминали
в гл. 2, система СГ является очень специфической системой с рядом
интересных свойств. В результате оказывается, что спектр свя-
связанных состояний, который дается методом ВКБ, является точ-
точным. Эта система также эквивалентна массивной модели Тирринга;
при этом солитонное состояние СГ отождествляется с фермионом.
Используя систему СГ для иллюстрирования метода ВКБ, мы
также воспользуемся случаем обсудить некоторые специфические
черты этой системы. Неудобство как раз в том и состоит, что
система СГ специфична. Некоторые аспекты полученных нами
результатов не типичны для метода ВКБ. Мы постараемся, на-
насколько это возможно, отделять аспекты результатов, специфич-
специфичные для системы СГ, от более общих выводов.
Будем следовать работе Дашена и др. [102], которые приме-
применили метод ВКБ для вычисления спектра связанных состояний
в системе СГ. Квазиклассическое квантование системы СГ было
также независимо проведено в серии работ Фаддеевым с соавто-
соавторами. (Некоторые ссылки на эти работы приведены в гл. 2; полный
список работ см. в статье [131 ].) Фаддеев и Тахтаджян [127]
решали классическое уравнение СГ путем определения переменных
действие — угол для этой системы. В этих переменных клас-
классический гамильтониан сводится к сумме вкладов от свободных
частиц (см. B.79)). После этого квазиклассическое квантование
проводится непосредственно, В частности, дискретный спектр

202 ГЛАВА 7
дублетов легко получить, если заметить, что угловая переменная,
ассоциируемая с дублетными решениями (обозначаемая р), имеет
компактную область изменения 0 <: р"ь <: 32я/п2Д (разд. 2.5).
Метод Фаддеева весьма изящен, но он приспособлен к специаль-
специальным системам типа модели СГ, для которых можно получить
полный набор переменных действие — угол. Вместо этого мы
выводим спектр СГ с помощью метода ВК.Б, поскольку этот метод
применим к более широкому классу систем. Процедура, иллю-
иллюстрируемая ниже примером СГ, может быть использована в любой
другой полевой теории независимо от того, обладает ли она сепа-
сепарабельностью гамильтониана и другими замечательными свой-
свойствами модели СГ, лишь бы имелось семейство периодических
классических решений.
Напомним обсуждение классической модели СГ в гл. 2. Плот-
Плотность лагранжиана B.61), приводимая здесь снова для удобства,
включает одно скалярное полеф (х, t) и определяется выражением
■ £(x,f) = -±-(<W - (>п%) {1 - cos [(У Цт) ф]}. G.1)
В гл. 2 мы изменили масштаб переменных: хп = тхп и ф =
= (}/~Х/т) ф, чтобы в результате исключить параметры т2 и X.
Но теперь мы сохраним исходные переменные, поскольку /п2 и X
имеют существенное значение в квантовом контексте. Подразуме-
Подразумевается, что классические результаты гл. 2 должны быть выра-
выражены через ф (х, t), прежде чем использовать их в этом разделе.
Потенциал U (ф) = (mi/X) {I — cos [(-/Xlm) ф]} имеет дискрет-
дискретные вырожденные абсолютные минимумы при ф = (т/у/~Х) Bпл),
п = —оо, ..., —1, 0, 1, ..., оо. Это приводит к спонтанному
нарушению симметрии в квантованной теории. Вакуумный сек-
сектор состояний может быть построен вокруг любого из этих мини-
минимумов. Для конкретности рассмотрим вакуумный сектор, по-
построенный вокруг ф = 0. Тогда лагранжиан может быть разложен
в ряд в окрестности ф = 0 по образцу B.62). В этом разложении
в порядке ^° система B.62) есть свободная полевая теория с бо-
зонной массой т (в отличие от системы кинка в гл. 2 и 5, где
бозонная масса равна yf2m). Энергия этого вакуумного состояния,
очевидно, равна
G.2)
В выражении G.2) и ниже мы будем полагать й = 1 в соответ-
соответствии с общепринятой практикой квантовой теории поля. Зави-
Зависимость квазиклассического разложения от й была явно показана
в предыдущих главах и может быть при необходимости введена.

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 203
В гл. 2jvibi привели также классические решения'модели СГ.
Односолитонное и антисолитонное решения B.72) являются ста-
статическими. Поэтому они могут быть проквантованы с использо-
использованием методов гл. 5, приводя к квантовым солитонным и анти-
солитонным частицам. Эта модель приводит также к «дублетным»
решениям, или «бризерам» B.78). Это непрерывное семейство
периодически зависящих от времени решений, и они могут быть
проквантованы методом ВК.Б, намеченным в общих чертах в гл. 6,
приводя к связанным состояниям. Кроме того, система СГ при-
приводит также к рассеивающимся решениям, содержащим произ-
произвольное число солитонов, антисолитонов и дублетов (таким, как
B.73) и B.77)). Эти решения не периодические (за исключением
артефакта помещения всей системы в ящик с соответствующими
периодическими граничными условиями). В квантованной теории
они соответствуют состояниям рассеяния. Чтобы получить спектр
частиц (связанных состояний) в СГ-теории, нужно проквантовать
только солитонное, антисолитонное и дублетное решения.
7.1.1. МАССА КВАНТОВОГО СОЛИТОНА
Определенный в B.72) СГ-солитон </>сол (х) является статиче-
статическим решением A + 1)-мерной скалярной теории поля, облада-
обладающим топологическим зарядом. Он весьма похож на кинковое
решение теории </>4 и может быть проквантован аналогичным
образом. Эта процедура тождественна .той, которая была прове-
проведена в гл. 5. Поэтому мы будем опускать детали и наметим только
основные этапы. В окрестности </>сол (х) может быть построен
сектор энергетических уровней, низший из которых есть кванто-
квантовая солитонная частица теории СГ. Ее масса состоит из класси-
классического слагаемого, за которым следуют квантовые поправки.
Энергия классического солитона, полученная в разд. 2.5 при
подстановке B.72) в B.66), есть
Якл №сол] = 8т»Д. G.3)
В главном порядке квантовые поправки получаются в терминах
частот нормальных мод второй производной потенциальной энер-
энергии. Потенциальная энергия есть
Частоты нормальных мод со? определяются уравнением

204 ГЛАВА 7
Это уравнение аналогично E.48). В порядке к0 квантовая поправка
к массе солитона Мсол дается выражением (разд. 5.4)
Т
Q
где [—VK4{f)] — контрчлен нормального упорядочения, кото-
который должен быть добавлен в лагранжиан. Для скалярного поля
в двух измерениях с взаимодействием без производных это един-
единственные расходимости. Здесь потенциал не является поли-
полиномом, но, поскольку косинус есть не что иное, как сумма экспо-
о
Рис. 12. а — типичный фейнмановский граф. приводящий к поправке от нормаль-
нормального упорядочения к константе четверного взаимодействия X; б — соответствую-
соответствующая поправка к от2; в — вклад низшего порядка в бот2.
нент, он может быть легко нормально упорядочен с помощью
стандартных методов. По существу используется хорошо извест-
известное тождество
еа+а+ = еа+еае 2 , если [а, а+] = с-числу.
Результат имеет вид [86, 102]
Этот результат также можно понять, разлагая cos ЦУ К/т)
в степенной ряд B.62) и строя диаграммы Фейнмана для функций
Грина. Как К, так и т2 вследствие отсутствия нормального упо-
упорядочения приводят к расходящимся поправкам, обусловленным
такими графами, как на рис. 12, а и б, соответственно. Но эти
поправки сокращаются в К/т2, что очевидно из примера этих
графов, которые содержат одни и те же петлевые интегралы.
Следовательно, единственное изменение в G.6), обусловленное
нормальным упорядочением, проявляется в замене множителя /п2
на (т2 — бт2). В низшем порядке бт2 определяется графом на
рис. 12, в, который дает
л
6^2 = — .А- Г i dk G.7)
О'

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 205
Кроме того, мы должны вычесть вакуумную энергию G.2), так же
как мы сделали в гл. 5. В результате получаем
оо
VK4 [ф] = -бт2 -£ j [ 1 - cos {¥£. ф)] dx - Евак. G.8)
Отсюда при использовании G.2) для главной квантовой поправки
к «солитонной массе» получаем выражение
G.9)
Дашен и др. [102] нашли все решения уравнения G.5) и подста-
подставили coQ вместе с бт2 из G.7) и фсол из B.72) в G.9). Результат
состоит в том, что выражение G.9) конечно при стремящемся
к бесконечности импульсном обрезании и равно (—т/я). Следо-
Следовательно, квантовая масса солитона есть
Мсол = 8т3/Х — т/я + О (Я,). G.10)
К этому солитонному состоянию применимы подробное обсуждение
и оговорки, приведенные в гл. 5. В частности, таким же образом
можно построить антисолитонный сектор состояний вокруг
&ттисо.т В силу симметрии ф -> —ф масса квантового анти-
солитона такая же, как Мсол.
7.1.2. МАССЫ ДУБЛЕТОВ
Дублетные решения имеют вид
фг(Х, t) = _arctg(/т2 - 1 cHmx^im). G.Ю
где просто выражено B.78) через ф (х, t) и период т. Переменная
т = /пт/2я безразмерна. Выражение G.11) дает непрерывное
семейство периодических решений, параметризованных периодом т.
Они могут быть проквантованы методом ВКБ, развитым
в разд. 6.4. Соответствующие энергии связанных состояний
определяются уравнениями F.96)—F.98). Все, что требуется,
это вычислить различные члены в этих уравнениях для реше-
решения G.11).
Классическое действие для этого решения за период равно
-1 . G.12)
б —ОО

206 ГЛАВА 1
При подстановке G.11) и интегрировании имеем
5„л [фт] = 32я (/геяД) [arc cos A/т) - /1^Л]. G.13)
Углы стабильности получаются из решений линейного уравнения
устойчивости
где
тц(*,* + т) = е'Ч (*,/). . G-15)
Дашен и др. [102] нашли все решения уравнения G.14), исполь-
используя следующую разумную идею. Вспомним из разд. 6.4, что ли-
линейное уравнение устойчивости удовлетворяется для любого ма-
малого .классического возмущения данного решения. Но для модели
СГ имеются точные классические решения, состоящие из произ-
произвольного числа дублетов. Рассмотрим решения с двумя дубле-
дублетами, где один из дублетов есть заданное ф% (х, t), а другой имеет
очень малую амплитуду и произвольную скорость. Таким обра-
образом, имеется бесконечное число точных решений, которые являются
малыми возмущениями данного фх. Используя их, Дашен и др.
выделили все независимые решения G.14) и соответствующие
углы стабильности. Мы не будем останавливаться на деталях, так
как решить линейное уравнение G.14) хотя и не легко, но ход
решения в принципе совершенно ясен. Результат имеет вид
v0 = 0, Vl = 0, G.16)
а далее следует континуум решений с
v,n = TT/ms + $, G.17)
где
Цп + б (qn) = 2пт\, G.18)
G.19)
Здесь L — полный объем, который стремится к бесконечности.
В этом пределе множество решений, характеризуемых qn, стано-
становится континуумом. Как и следовало ожидать, два угла стабиль-
стабильности равны нулю. Один нуль связан с обязательным решением
Ло (х, t) = (д Idt) фх (х, t),
рассмотренным в гл. 6. Другой связан с симметрией системы отно-
относительно пространственных вращений. Для произвольного реше-

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 207
ния фх (х, t) функция фх (х + 8а, t) есть также точное решение
с тем же периодом. Следовательно, гц1 (х, t) ~ [фх (х + Ьа, t) —
— Фх (х, t)yba имеет нулевой угол стабильности vx. Как мы неод-
неоднократно отмечали, если мы работаем только в главном порядке
по квантовым флуктуациям, то такие нулевые моды не создают
никаких проблем. В главном порядке ВКБ-результатов F.96)—
F.98) для энергий связанных состояний мы можем эффективно
не учитывать нулевые моды. Остальные углы, задаваемые в G.17),
не равны нулю.
Наконец, вклад от контрчлена есть
J
о
X
-f-\ dt \dx\l~cos
О -оо kn
где подставлены VK4 [ф] из G.8), G.7) и G.2). Таким образом, мы
собрали все ингредиенты, необходимые для подстановки в урав-
уравнения F.96)—F.98). Напомним, что эти уравнения определяют
энергетические уровни, характеризуемые главным квантовым
числом т и квантовыми числами pt, i = О, 1, ..., оо, определя-
определяющими поперечные к орбите направления. Чтобы получить основ-
основные дублетные связанные состояния, мы можем положить все
pi = 0 для любого данного т. Это аналогично приравниванию
Nn = 0 в E.55) для получения основного состояния кинка. Если
одно из рг Ф О, i > 1, то мы получаем более высокие возбуждения
непрерывных мод в G.17), G.18). Они соответствуют рассеиваю-
рассеивающимся решениям для дублетов с мезонами этой теории, совершен-
совершенно так же, как в секторе кинка в гл. 5. Когда все pt = 0 в
F.96)—F.98), мы имеем дело с комбинацией
Каждое из этих слагаемых приведено выше в явном виде. Мы
имеем
При L -> оо эта сумма с использованием G.18) может быть пре-
превращена в интеграл, который квадратично расходится. Эта квадра-
квадратичная расходимость сокращается с аналогичной расходимостью

208 ГЛАВА 7
в сумме по kn в SK4 G.20). Остающаяся логарифмическая расхо-
расходимость сокращается с другим слагаемым в SK4, пропорциональ-
пропорциональным бт2, приведенному в G.7). Во всем этом можно убедиться,
так же как в разд. 5.4, вычислив сначала SK4 [фс] 2~S?nv?n
при конечном объеме L и конечном импульсном обрезании Л.
Как и следовало ожидать в перенормируемой теории, расходя-
расходящиеся слагаемые сокращаются, приводя к конечному результату
при L, А ->■ оо, который имеет вид
sK, ы - -J- 2vi=4 Ci/f 2 ~l ~arccos il/^=
= — &/8nm>)SKAi>r] G.22)
при сравнении с G.13). Следовательно,
SKJI [фх] + Sm [фг] - 4 2 v, = A - V8nma) SK4 [^,] =
= C2я/7) [arc cos A/f) - /т2 — l], G.23)
где
^ G-24)
Это замечательно простой результат. Эффект от квантовых ВКБ-
поправок состоит просто в умножении классического действия
на общий постоянный множитель, не зависящий от т. Сравнивая
G.23) с G.13), мы видим, что в результате квантовых поправок
константа связи (к/т2) заменена «перенормированной» константой
связи у. По существу то же произошло и с солитонной массой
в G.10). В главном порядке мы можем написать
Мсол = 8т3/к — т/я = 8т/у. G.25)
Эти упрощающие черты специфичны для системы СГ. Они и не
типичны, и не существенны для работы метода ВКБ, но они де-
делают анализ спектра СГ весьма простым. Приводя результаты
G.13)—G.23), мы опустили значительное количество алгебраиче-
алгебраических деталей, поскольку они не содержат никаких новых принци-
принципов помимо тех, которые обсуждались в гл. 5 и 6. Более подроб-
подробные сведения см. в статье [102].
Если известен результат G.23), спектр связанных состояний
легко вычислить из F.96)—F.98). Когда все pi = 0, уравнение
F.96) дает
м, |О Ц, IV
,„ \Фг\ -Ь Оцц \Фх\ 77- 7 '
\л 1тч I кч 1гч 2 / |
Еагсcos

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 209
где следует помнить, что f = тт/2я. Приведенное уравнение свя-
связывает с произвольным Е (энергетической переменной в пропа-
гаторе 'S (Е) = Тг [1 1{Е — Я) ]) некоторое классическое реше-
решение фх (х, t), период х (Е) которого определяется этим уравне-
уравнением. Вспомним, однако, что Е не является классической энергией
этого решения. Последняя определяется как Екл = — (dSKJdx).
Разность между Е и Екл есть не что иное, как энергия нулевых
флуктуации в направлениях, перпендикулярных орбите.
При использовании G.23) и G.26) уравнение F.98) дает
W (Е) = SKJI [фг] + SK4 [фх] - -1 ^ v, + Ex (E) =
= C2я/у) [arc cos A/f) - j/f2 — 1 ] + C2я/у) т/т2 - 1 =
= C2я/у) arc cos A/f) = C2я/у) arc sin (Ey/l&m). G.27)
Наконец, условие квантования F.97) определяет уровни энергии
связанных состояний'при Е = MN, где
W (Мгт) = 2Nn,
или
MN = (lbm/y) sin (Ny/Щ, N = 1, 2, ..., <8я/у. G.28)
Формально условие квантования допускает все целые значения
W от 1 до оо, но при N > 8п/у мы выходим за пределы классиче-
классических дублетных решений, на которых базируются эти связанные
состояния. Чтобы это видеть, обратим G.26) и, используя G.28),
напишем
т (Мл-) = Bя/т) sec (Ny/Щ. G.29)
Здесь х (MN) — период классического дублета, соответствующего
jV-му связанному состоянию. Но классическое дублетное решение
соответствует связанной паре солитон—антисолитон, которые ос-
осциллируют друг относительно друга с периодом т. Дублеты су-
существуют только при 0 < х < оо. При х -> оо пара солитон—ан-
солитон—антисолитон стремится распасться. Из G.29) мы видим, что, когда
/V -> 8я/у снизу, х (MN) -> оо. Поэтому для N > 8я/у не сущест-
существует соответствующих классических дублетов и квантовых свя-
;анных состояний. Следовательно, G.28) справедливо только для
целых значений N, меньших 8я/у.
Таким образом, мы получили в G.28) конечный набор связан-
связанных состояний, соответствующих классическим дублетным реше-
решениям. Напомним, что классические дублеты имеют нулевой топо-
топологический заряд (фх (х, t)-*■ 0 при лс->±а>). Соответственно
псе связанные состояния в G.28) принадлежат вакуумному сек-
гору этой квантовой теории. Хотя изображенное на рис. 5, б клас-
классическое решение фх (х, t) выглядит как волновая функция нере-

210 ГЛАВА 7
лятивистского одномерного основного состояния, функция
фх (MN) (х, t) не является волновой функцией N-ro связанного
состояния в G.28). Напомним, что сейчас мы работаем с кванто-
квантовой теорией поля, волновыми функциями которой являются функ-
функционалы W [ф] от полей. Аналогичное предупреждение сделано
в гл. 5. Классические решения фх(мы) (х, t) имеют такое же от-
отношение к волновым функционалам основных состояний WN [ф],
как орбиты Бора к волновым функциям атома водорода.
На этом можно закончить иллюстрацию метода ВКБ в теории
поля с использованием системы СГ в качестве примера. Но ре-
результат G.28) имеет много интересных свойств, заслуживающих
специального рассмотрения. Эти свойства убедительно указывают
на то, что результат G.28) является точным для отношений масс.
7.2« Интерпретация дублетных состояний
При слабой связи (к/т2 <С 1) масса MN в G.28) может быть
разложена в ряд
у V 16 C!) A6K
Низшее из связанных состояний имеет массу
) G.31)
С другой стороны, СГ-лагранжиан, разложенный по степеням
к/т2, в нулевом порядке по (к/т2) дает (см. B.62)) свободную тео-
теорию поля с «элементарным» бозоном массы т. Когда взаимодей-
взаимодействие включено на малую величину, по стандартной теории воз-
возмущений масса «элементарного» бозона (после вычитания контр-
контрчленов нормального упорядочения) равна m + О (Я,2). Сравнивая
это с Mi, мы отождествляем низшее из дублетных состояний
с «элементарным» бозоном этой теории. Представляется неправдо-
неправдоподобным, что в вакуумном секторе может быть второе дискретное
состояние, отличное от элементарного бозона, масса которого
также сводится к т при слабой связи. Массы MN более высоких
состояний могут быть представлены в форме
MN = NMi [ 1 ~ 4" (V16m2J (N2 — 1) + О (k3)j . G.32)
Очевидно, что при слабой связи эти состояния можно.рассматри-
можно.рассматривать как квазисвободные связанные состояния N «элементарных»
бозонов с энергией связи
NMX - MN = -у Mi (к/16т2J (N3 - N) + О (к3). G.33)

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 211
11ри слабой связи квантовое число N обозначает число «элемен
гарных» бозонов в связанном состоянии.
Мы использовали слово «элементарный» в кавычках потому,
что при нашем выводе состояние N = 1 не имеет никаких специаль-
специальных отличительных черт по сравнению с другими. Все они появ-
появляются как семейство связанных состояний, основанных на клас-
классических дублетных решениях, и состояние «элементарного»
бозона как раз оказывается наинизшим. Дублетное решение,
соответствующее данному N, имеет вид (см. G.29) и G.11))
]■
Все они являются «бризерными» полевыми конфигурациями с об-
общим профилем, показанным на рис. 5, б. Конфигурация с N = 1
ничем не выделена по сравнению с другими. Эти результаты согла-
согласуются с представлением о «ядерной демократии», которую в те-
течение долгого времени отстаивали Чью и др. [80] как часть бут-
стрепного подхода к адронам. В этом подходе особое значение
придается отсутствию какого-либо фундаментального различия
между «элементарными» и «композитными» адронами. Интересно,
что наш метод подтверждает эту мысль в контексте теории поля,
когда можно было бы ожидать, что «элементарный» бозон, связан-
связанный с полем, играет особую роль.
Дашен и др. сравнили значения отношения масс MNIМх, най-
найденные методом В КБ и другими методами. Под последними мы
имеем в виду вычисления, проведенные для iV-бозонного связан-
связанного состояния с использованием теории возмущений и диаграмм
Фейнмана.
В порядке к теория СГ является А,</>4-теорией с притяжением
(см. B.62)), которая в нерелятивистском пределе соответствует
притягивающему взаимодействию между бозонами, задаваемому
выражением V (х) = — (к/8т2) б (л:). Так как при слабой связи
jV-бозонная энергия связи мала [О (Я,2)], ее можно вычислить,
используя нерелятивистское уравнение Шредингера для N тел
с б-образным потенциалом
..., xN). G.35)
(Напомним, что в низшем порядке масса бозона есть т.) Это урав-
уравнение допускает решение относительно его собственного значения
для основного состояния и дает
^ G.36)

212 ГЛАВА ?
что согласуется с ВКБ-энергией связи G.33) в главном порядке
О (X2). Сравнение можно продолжить, рассчитывая отношение
масс (УИ2 — 2М1)/М1 в старших порядках по X при помощи сумми-
суммирования фейнмановских диаграмм. Ряд Бете—Солпитера итери-
итерируется при использовании в качестве ядра упругой амплитуды
2 -> 2, точно вычисленной в порядке (Х/т2K из диаграмм Фейн-
мана. Суммируемые диаграммы показаны на рис. 13. Хотя в прин-
+ кроссинг-диаграммы
Рис. 13. Для получения связанного состояния М2 в амплитуде рассеяния М1-{-
+ Mi суммируется последовательность диаграмм Бете — Солпитера (а). Ядро
определяется в порядке X3 диаграммой б, а пропагатор задается в.
ципе этот диаграммный метод является просто теорией возмуще-
возмущений, на практике он в высшей степени нетривиален, поскольку
само ядро определяется в «двухпетлевом» порядке. Способ вычис-
вычислений описан в статье [102], и результат имеет вид
Шх-Мг _/ X у 4 / К \з ,
Mi ~~ V 16т2 / + п V
1 \ / А. \"* i г\ /л К\ /у Оу\
16т2
12
12
16т2
Метод ВКБ для этой величины дает выражение (см. G.28))
2Ml-M2 = 2 sin (у/16)-sin (у/8) =2[1 — cos(y/16)]. G.38)
Mi sin (у116) L \ч /i \ i
При разложении в ряд это точно согласуется с выражением по
теории возмущений G.37) вплоть до порядка Xi. Это удивитель-
удивительный результат. При сравнении нашего функционально-интег-

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 213
рального вывода приближения В КБ по методу стационарной фазы
с аналогичным выводом пертурбативного «петлевого» разложения
с помощью функциональных методов можно*ожидать, что эти два
метода согласуются на однопетлевом уровне. Согласие на двух-
петлевом уровне неожиданно и не будет иметь места для произ-
произвольной полевой теории. То, что ВКБ-результат согласуется с тео-
теорией возмущений вплоть до двух петель, есть другая специфиче-
специфическая черта теории СГ. Это также первое указание на то, что такие
В КБ-результаты для этой теории могут оказаться точными.
Заметим, однако, что это согласие с теорией возмущений имеет
место только для отношения масс. Когда по стандартной теории
возмущений вычисляется сама масса Мх с помощью расчета соб-
собственной энергии бозона в порядке к2, результат не совпадает
с разложением в ряд ВКБ-результата G.31). В той степени, в ка-
какой мы считаем В КБ-результаты точными для модели СГ, такое
совпадение имеет место только для отношения масс, а не для от-
отдельных масс в G.28). Такого ограничения следовало ожидать.
Всеобщий масштаб масс квантовой теории устанавливается при
нормальном упорядочении, которое заменяет т2 на т2 — Ьт2.
Процедура нормального упорядочения имеет неоднозначности
(см. [86]), связанные с массой, по отношению к которой произ-
производится упорядочение. Это элементарный пример ренормгруппы.
Исходя из этой неоднозначности, мы не можем ожидать, что метод
В КБ даст масштаб масс.
Система СГ обнаруживает и другое важное свойство. Для
слабой связи из результата G.32) мы видим, что MN только не-
немного меньше, чем NMX. В частности, MN > 2МХ при N ^ 3 и
малых к/т2. Поэтому уровни с N ^ 3, по-видимому, лежат в кон-
континууме из двух или больше частиц с N = 1. В обычном случае
мы ожидали бы, что эти высшие состояния несильно связаны и
распадаются на две или больше частиц с N = 1. Топологический
заряд не запрещает такие распады, поскольку все эти состояния
принадлежат одному и тому же вакуумному сектору (Q = 0). В са-
самом деле, тщательное исследование показывает, что в теории воз-
возмущений симметрия ф «-> — ф препятствует, например, распаду
М3 -> Мг + Мх. (Диаграммы Фейнмана имели бы нечетное число
внешних концов.) Но даже этот довод не запрещает такие распа-
распады, как УИ4 -> Мх + Mi, Мъ -*■ М2 + Mi и т. д. Что же пред-
предсказывает теория возмущений для амплитуд таких распадов?
Рассмотрим, например, процесс М4 -> Мх + Мх в системе центра
масс М4- В низшем порядке теории возмущений амплитуда этого
распада определяется древесными диаграммами на рис. 14. Эти
диаграммы получаются из стандартной теории возмущений при
разложении члена cos [(-/к/т) ф] в лагранжиане, как в B.62).
Напомним, что в низшем порядке система УИ4 в покое может рас-
рассматриваться как четыре покоящихся мезона, каждый массы т.

214 Г.МЛИА 7
Энергия-импульс двух мезонов в конечном состоянии, очевидно,
есть Bт, >/3m) и B/Л; —у^З/п). Тогда легко видеть, что фейнма-
новские графы на рис. 14, а, б и в дают вклады—iV/48m2,
—i№/96m2 и Л2/32/п2 соответственно. Сумма их равна нулю! Такой
же нулевой результат на уровне древесных графов может быть
установлен для других процессов, например таких, как Ме ->
-> 2М1; М8 -> 2МЪ Мъ -*■ ЗМХ и т. д. Если это справедливо
также и в высших порядках (некоторые неопубликованные рас-
расчеты однопетлевых поправок подтверждают это), то мы получаем
замечательный результат, состоящий в том, что все связанные со-
состояния MN стабильны, даже если топологический заряд и сохра-
V
/А
б в
Рис. 14. Диаграммы низшего порядка (древесные), дающие вклад в распад Mt-*-
-*■ Mi + Mi. Вершины получены из разложения косинуса в лагранжиане.
нение энергии не запрещают распад высших связанных состояний
в подходящие низшие состояния. Это еще одна специальная черта
системы СГ, по-видимому, связанная с существованием бесконеч-
бесконечного числа сохраняющихся величин, о котором упоминалось
в гл. 2. Заметим, что если этот результат верен во всех порядках,
то он подтверждает наше предположение, что ВКБ-отношение
масс является точным. В G.28) ВКБ-массы действительны и ди-
дискретны, что указывает на стабильность связанных состояний.
Нестабильность обнаруживалась бы по появлению мнимых доба-
добавок к MN за счет поправок высших порядков к ВКБ-результату.
Но если последний является точным, то поправок не требуется и
все связанные состояния стабильны.
До сих пор наши доводы в пользу точности ВКБ-отношения
масс были основаны на сравнении с результатами низших порядков
теории возмущений. Более убедительный довод для всех допу-
допустимых значений константы связи к/т2 (или у, что эквивалентно)
следует из рассмотрения S-матрицы системы СГ. Напомним, что
классическое дублетное решение можно рассматривать как свя-
связанную солитон-антисолитонную пару. То же, очевидно, справед-
справедливо для соответствующих квантовых состояний. А именно, массы
MN могут быть записаны через массу квантового солитона Мсол
G.25):
M.v = 2М0ОЛ sin (Ny/Щ < 2МСОЛ, N=1,2, ..., < 8я/у. G.39)

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 215
1:сли G.39) — точное выражение для отношения масс MNl2M0Oll,
то MN должны быть единственными полюсами на физическом листе
энергии в солитон-антисолитонной амплитуде рассеяния.
В разд. 7.5 мы покажем, как эта амплитуда может быть точно вы-
вычислена; при этом полюса появляются в точности при значениях
МЛг G.39) для всех допустимых значений константы связи у. Даль-
Дальнейшие свидетельства точности В КБ-отношений масс появляются
при использовании эквивалентности модели СГ и массивной мо-
модели Тирринга, которая обсуждается ниже.
7.3. Эквивалентность моделей СГ и МТ; бозонизация
Еще в шестидесятых годах Скирм [318, 319] исследовал си-
систему СГ в серии пионерских работ. Помимо прочего он предполо-
предположил, что квантовые солитоны СГ, хотя они и возникают в бозон-
пой полевой теории, могут быть эквивалентны фермионам, взаимо-
взаимодействующим через четырехфермионное взаимодействие. Но он
предсказывал такое отождествление только для некоторых значе-
значений константы связи, и его доводы были скорее предположением,
чем строгим доказательством.
Значительно позднее Коулмен [86], используя совершенно не-
независимые методы, строго установил такую эквивалентность в рам-
рамках теории возмущений. Рассмотрим модель СГ и массивную,мо-
массивную,модель Тирринга (МТ) в A + 1) измерениях, описываемые с по-
помощью лагранжианов
(cos [(-/l/rn) Ф] - 1}, G.40)
fr0> G,41)
где W — фермиевское поле, у*1 — матрицы Дирака в A + 1) из-
измерениях, а контрчлены нормального упорядочения включены
в параметры ml и mF. Предполагая, что обе эти теории сущест-
существуют, можно осуществить формальное пертурбативное разложе-
разложение каждой из них. Хорошо известно, что безмассовая модель
Тирринга (mF = 0) является точно решаемой [162, 205, 320, 328].
Тогда формально можно разложить массивную модель Тирринга
по степеням mF. Ясно, что такое разложение будет содержать
n-точечные функции составного оператора WW [220], с помощью
которых исследуется сектор с нулевым фермионным зарядом этой
модели. Система СГ также может быть разложена в пертурбатив-
ный ряд по степеням ml, т. е. выражена через n-точечные функции
от cos [(уИ/т) Ф]. Остающаяся невозмущенная часть лагран-
лагранжиана.^ есть не что иное, как свободное безмассовое поле и, сле-
следовательно, точно решается. (Замечание: для безмассового ска-

216 ГЛАВА 7
лярного поля в A + 1) измерениях имеются инфракрасные проб-
проблемы, которые должны быть обойдены в пертурбативном разло-
разложении). Центральный результат Коулмена состоял в явной демон-
демонстрации того, что эти два набора n-точечных функций совпадают
для всех п, и, следовательно, теория СГ эквивалентна сектору
с нулевым зарядом модели МТ при условии, что сделано следую-
следующее отождествление:
G.42a)
= 1/A+ £/я), G.426)
#" д,Ф = ¥уд¥ = f. G.42b)
Далее Коулмен показал, что гамильтониан модели СГ не ограничен
снизу при к/т2 > 8я, так что эта теория и отмеченная выше экви-
эквивалентность существуют только при к/т2 < 8я. Наконец, основы-
основываясь на этом явном доказательстве эквивалентности, он воскре-
воскресил предположение Скирма о том, что квантовый солитон модели
СГ может быть отождествлен с фермионом модели МТ.
Очевидно, что это выдающиеся результаты, устанавливающие
знак равенства между теорией бозе-полей и теорией ферми-полей
(бозонным сектором ее). Это отождествление СГ-солитона, возни-
возникающего в бозонной теории поля, с фермионом не нарушает тео-
теорему о связи спина со статистикой. Напомним, что в A + 1)
измерениях спина не может быть. Кроме того, в гл. 5 мы приво-
приводили доводы в пользу того, что квантовый солитон принадлежит
к совершенно отличному по суперотбору от вакуума сектору, от-
отличающемуся глобальным квантовым числом (граничным значе-
значением). Поэтому солитон не может быть рожден с помощью какого-
либо конечного произведения локальных полевых операторов
Ф (*i) ...Ф(х¥), действующих на вакуум. Следовательно, такое
солитонное состояние выпадает из сферы действия теорем, за-
запрещающих отождествление с фермионом. Вспомним, что
в разд. 3.5 мы намекали на подобную возможность в C + 1) из-
измерениях, исходя из превращения изоспина в спин.
Мы не будем здесь воспроизводить доказательство Коулменом
этой эквивалентности. Как мы уже говорили, его доказательство
точное и не имеет ничего общего с квазиклассическими методами.
По этой же причине оно несколько выпадает из нашей общей
тематики. Вместо этого мы будем считать его результат заданным и
используем его для дальнейшего подтверждения и уточнения
деталей наших квазиклассических соображений.
1. В модели МТ фермионный заряд Q равен
Q= J jodx= j IVFdx. G.43)

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОЁ
Отдельный фермион (f) имеет Q = 1, антифермион (f) имеет Q =
- —1, а связанное состояние фермиона и антифермиона имеет
Q = 0. Из соотношения эквивалентности G.42в) мы можем запи-
записать Q через СГ-поля:
дх пХ 2лт дх пХ' AА*>
—оо
Это не что иное, как топологический заряд модели СГ, аналогич-
аналогичный заряду E.76) в задаче кинка. Его значения равны +1 (—1)
для солитона (антисолитона) и нулю для связанных дублетных
состояний. Это согласуется с отождествлением СГ-солитона с МТ-
фермионом. (Строго говоря, эквивалентность этих моделей дока-
доказана только в секторе с Q = 0 МТ-модели. При применении соот-
соотношения G.44) к отдельному фермиону подразумевается, что мы
рассматриваем некоторую пару (ff) с полным зарядом Q = 0,
разводим заряды на большое расстояние друг от друга и исполь-
используем G.44) в окрестности каждого из них по отдельности.)
2. Запишем G.426) через перенормированную СГ-константу
связи у G.24)
_ Х/т* __ 8я . . -
\+2g/n ' V-*°>
мы видим, что, когда 0 < у < 8я, т. е. 0 < к/т2 < 4я, тиррин-
говская константа связи g положительна. С учетом обычной про-
процедуры определения знака силы в статическом пределе из лагран-
лагранжиана это соответствует притяжению между фермионом и анти-
фермионом. В одном пространственном измерении такая сила
притяжения независимо от того, насколько она велика, всегда
приводит по крайней мере к одному бозонному связанному со-
состоянию. Соответственно из G.28) мы видим, что для всех значе-
значений у в области 0 < у < 8я имеется по крайней мере одно солитон-
антисолитонное (дублетное) связанное состояние.
3. Рассмотрим предел слабой связи (у, к/т2 <^ 1) в модели СГ.
В силу G.45) это соответствует большому g, т. е. режиму сильной
связи в модели МТ. В этом режиме мы ожидаем сильного притя-
притяжения между f и f и большого числа связанных состояний ff. Это
находится в соответствии с G.28), где число солитон-антисолитон-
ных связанных состояний есть [8я/у], т. е. наибольшее целое
число, меньшее 8п/у. Когда у растет, g уменьшается. Соответст-
Соответственно число дублетных состояний в G.28) также уменьшается.
Наконец, когда у = 8я, т. е. к/т2 = 4я, уравнение G.45) дает
g = 0. Фермионы являются свободными. Заметим, что это как
раз то значение, при котором прекращает существование послед-
последнее остающееся связанное состояние Мх в G.28). Из G.39) мы
видим, что если у ->■ 8я, то Nlx -*■ 2уИС0Л, т. е. последнее остаю-

218 Глава f
щееся связанное состояние становится свободной парой из соли-
тона и антисолитона. Если считать, что СГ—МТ-эквивалентность
является точной, то тот факт, что в В КБ-результате G.28) свя-
связанные состояния также исчезают точно при у = 8я, когда тир-
ринговские фермионы становятся свободными, является дальней-
дальнейшим подтверждением предположения, что В КБ -результат яв-
является точным.
4. Когда у > 8я, g отрицательно. В модели МТ нельзя ожи-
ожидать никаких связанных состояний//, и соответственно все дуб-
дублетные состояния в G.28) исчезают. Отсутствие даже низшего
связанного состояния Мг является существенным. Напомним, что
мы связали это состояние с «элементарным мезоном» модели СГ.
Распространенное представление, основанное на теории возму-
возмущений, состояло в том, что для каждого поля имеется связанный
с ним сорт частиц (квантов возбуждений поля). При растущем
количестве непертурбативных результатов такие представления
не рассматриваются в общем случае как соответствующие дейст-
действительности. Очевидно, что случай у > 8я соответствует области
сильной связи модели СГ, где представления теории возмущений
могут быть отвергнуты. Одним таким примером является отсут-
отсутствие «элементарного» мезона модели СГ при у > 8 л. Квазиклас-
Квазиклассические ВКБ-методы имеют несколько слабых пунктов; но нали-
наличие таких важных непертурбативных результатов составляет
важное преимущество этих методов по сравнению с теорией воз-
возмущений. Напомним, что исчезновение состояния Мх из спектра
связанных состояний уже было задано В КБ-результатом G.28)
без обращения к теореме Коулмена об эквивалентности.
5. Тот факт, что g стремится к бесконечности, когда у -> О,
означает, что чем меньше СГ-константа связи, тем сильнее соли-
тон-антисолитонное притяжение. Такая обратная зависимость
снова находится в противоречии с результатами теории возмуще-
возмущений. Напомним, что в квантовой электродинамике в рамках тео-
теории возмущений силы между электронами и позитронами умень-
уменьшались бы при уменьшений постоянной тонкой структуры. Такое
обратное поведение межсолитонных сил не ограничено моделью
СГ и имеет место в более общем случае [125, 290]. Вспомним, на-
например, что в разд. 3.4 напряженность поля монополя, которой
пропорциональны силы между магнитными монополями, так-
также имеет в той теории обратную зависимость от константы свя-
связи 8-
6. Наконец, Коулмен показал, .что, когда %1т? > 8я,""кванто-
вая система СГ не имеет смысла, поскольку гамильтониан не огра-
ограничен снизу. Соответствующая катастрофа следует из наших
В КБ-результатов. Перенормированная константа связи у G.24),
от которой зависят последующие результаты, расходится при
Ш2 = 8я.

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 219
Это завершает наше обсуждение СГ-спектра масс, в котором
мы использовали метод ВКБ, присоединив к нему коулменовскую
теорему об эквивалентности. Некоторые из полученных данных,
такие, как точность ВКБ-результатов, эквивалентность модели
МТ и т. д., специфичны для системы СГ. Но другие, включая всю
процедуру вывода ВКБ-спектра, отождествление «элементарного»
бозона с одним из классических периодических решений, большие
межсолитонные силы в теории со слабым взаимодействием и т. д.,
не зависят от особенностей модели СГ. Подобные результаты мо-
могут оказаться справедливыми и для других моделей1).
7.3.1. БОЗОНИЗАЦИЯ
Эквивалентность моделей СГ и МТ есть динамический резуль-
результат, который зависит от точной формы двух лагранжианов. Но
отождествление в G.42а) и G.42в), в чьих терминах реализуется
эта эквивалентность, можно рассматривать как кинематическую
замену переменных. Оно может быть применено и к другим A +
+' 1)-мерным фермионным теориям. Сектор фермионной теории
с нулевым зарядом включает только билинейные формы, такие,
как ¥ (х) Ч (х), V (x) у^ W (х) и т.д. После соответствующей
ультрафиолетовой регуляризации они могут рассматриваться
как локальные бозе-поля. Все, что мы сделали в G.42а) и G.42в),
это заменили их на явные бозе-поля. Мы замечаем, что в G.42)
входит Ф, а также производная dv<D, но нет производных ферми-
поля W. Насколько мы можем видеть, это связано с тем фактом,
что ферми-поле подчиняется дифференциальным уравнениям пер-
первого порядка, граничные условия для которых требуют задания
только самого поля, а не его производных. В противоположность
этому бозе-поле подчиняется уравнениям второго порядка, кото-
которые требуют определения на границе как самого поля, так и его
производных. Уравнения G.42а) и G.42в) заменяют один набор
таких величин другим эквивалентным набором. Когда такая за-
замена проводится для модели МТ, возникающая в результате бо-
зонная теория поля оказывается моделью СГ. Такие шаги могут
быть предприняты для других двумерных фермионных моделей
независимо от того, ради чего это делается. Эту процедуру иногда
называют бозонизацией (см. [217]). Виттен [356] рассматривает
другую модель, в которой применялась бозонизация.
х) В последнее время развит квантовый метод обратной задачи рассеяния,
с помощью которого некоторые двумерные квантовополевые задачи, в частности
система СГ, решаются точно. Основные идеи этого метода содержатся в работе
[369* ]. — Прим. перев.

220 ГЛАВА 7
7.3.2. СОЛИТОННЫЕ ОПЕРАТОРЫ
В G.42) бозе-поле построено из (билинейных форм) ферми-
поля. Возможен также обратный процесс. Исходя из СГ-полевого
оператора Ф, Манделстам [2401 построил явную неполиномиаль-
неполиномиальную форму, которая может рассматриваться как ферми-поле ас-
ассоциированной модели МТ. Напомним, что в A + 1) измерениях
последняя имеет две компоненты. Рассмотрим в произвольный
момент времени t двухкомпонентное поле, определенное как
где
Чг,,,(*) = С1,,:ел«"(*):, G.46)
где С1;2 — константы, a Alt2 (х)— операторы, определяемые
как
j^( \\ ^ G.47)
Здесь |/Х//п — СГ-константа связи. Определим ¥£ (х) как сопря-
сопряженное к Wa (x). Исходя из канонических одновременных комму-
коммутационных правил
[Ф(х), Ф (*/)] = [Ф(х), Ф(у)} = 0,
[Ф (х), Ф (у)] = Я (х - у), G.48)
легко убедиться, что для х Ф у
Ы^х), А! (у)] = in [Q (х - у) - Q (у - х)} =
для х S у, G-49)
где 0 (х — у) — ступенчатая функция. Таким же способом можно
проверить, что
[Аа (х), Лр (у)] = in или —in G.50)
для всех а = 1, 2; р = 1, 2 и х Ф у. Тогда, применяя тождество
емем = eNeMe[M- щ, если [М, N] = с-числу, G.51)
к компонентам W в G.46), имеем

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 221
для всех а, р, когда х Ф у. Таким образом, построенные, согласно
G.46), поля Wa и ^Fp антикоммутируют, если х Ф у. Если х = у,
то вычисление более сложное, поскольку коммутатор G.49) не
является хорошо определенным, а произведение двух полей W
сингулярно при х = у. Этот случай следует рассмотреть при по-
помощи тщательно выполненной предельной процедуры х -*■ у при
подходящем выборе коэффициентов Сх, С2 в G.46). Это было сделано
Манделстамом, который получил результат
\Уа(х). ЗД)}+ = 0, {¥«(*), Wt(y)}+ = z8(x-y)8a^ G.53)
где { , ' }+ обозначает антикоммутатор, а г — константа
перенормировки. Поэтому поле W (х) в G.46) подчиняется анти-
антикоммутационным правилам для локального ферми-поля. Кроме
того, исходя из бозрнных коммутаторов G.48) легко убедиться,
что
G.54)
для х Ф у. Поэтому оператор W (х) увеличивает значение поля Ф
на 2пт/-у/к в области слева от х и оставляет его без изменений
справа от х. Таким образом, при применении к солитонному со-
состоянию [Ф (оо) —Ф (—оо) = 2nm/j^K] оператор W (х) сводит
его к состоянию в вакуумном секторе [Ф (оо) —Ф(—оо) = 0].
Отсюда следует, что Ч (х) помимо того, что оно является ферми-
полем, уничтожает солитон бозе-системы в соответствии с отож-
отождествлением солитона с фермионом. Конечно, W (х) изменяет поле
Ф на ступенчатую функцию. Ступенчатая функция может рассма-
рассматриваться как «точечный солитон», в то время как физическое со-
литонное состояние имеет некоторый «размер», на что указывает
классическое солитонное решение. Манделстам интерпретирует
свои W и ¥+ как операторы, которые уничтожают и рождают
«голые» точечные солитоны, которые приобретают конечный раз-
размер посредством взаимодействий. Доказательство того, что W
подчиняется уравнению поля массивной модели Тирринга, если
Ф удовлетворяет СГ-уравнению, читатель может найти в работе
Манделстама [211]. Более подробное обсуждение таких солитон-
пых операторов рождения см. в работах [129, 241, 306, 333].
Альтернативный подход предложили Бардакчи и Самуэль [21, 22].
7.4. Факторизация «S-матриц
Энергичное изучение солитонсодержащих полевых теорий
привело к побочному результату, представляющему значительный
теоретический интерес. Было показано, что для некоторого класса
квантовополевых теорий в A + 1) измерениях может быть точно
определена полная многочастичная 5-матрица. Более того, такие

222 ГЛАВА 7
5-матрицы обладают рядом привлекательных свойств. Во-первых,
любая многочастичная 5-матрица является упругой, т. е. число
.частиц любой данной массы и множество их импульсов остаются
после столкновения без изменений. Во-вторых, полная 5-матрица
факторизуется в произведение двухчастичных 5-матриц.
В-третьих, такие двухчастичные 5-матрицы подчиняются кубиче-
кубическому тождеству; этого тождества вместе с прошедшими проверку
временем принципами унитарности, аналитичности и кроссинг-
симметрии оказывается достаточным, чтобы привести в некоторых
моделях к точным аналитическим результатам для этих двух-
двухчастичных 5-матриц. Такие исследования начались с пертурба-
тивных или квазиклассических расчетов рассеяния солитонов в си-
системе GT [11, 128, 129, 194]. Впоследствии результаты вышли за
рамки таких приближений [210, 363, 365] и были предложены как
трчные результаты, выведенные на основе некоторых законов со-
сохранения, которым подчиняются исследуемые теории. Эти резуль-
результаты не ограничены только системой СГ и не требуют, чтобы рассеи-
рассеивающиеся частицы были солитонами при условии, что частицы
и их теории подчиняются двум приведенным ниже допущениям.
В этом и следующем разделах мы попытаемся дать объединенный
вывод этих результатов, полученных в ряде последних работ, а за-
затем проиллюстрируем его на примере СГ. При выполнении этой
задачи мы использовали хорошие обзоры Замолодчикова и Замо-
Замолодчикова [367] и Шанкара [312].
Напомним, что в гл. 2 мы упоминали о существовании беско-
бесконечного числа локальных законов сохранения для системы СГ.
Мы их не выписывали, и их явная форма нам не нужна. Для нас
важно только, что эти законы сохранения 1) локальны и 2) по-
порождают сохраняющиеся заряды, которые являются компонен-
компонентами лоренцевских тензоров возрастающего ранга. Для системы
СГ в этих свойствах можно убедиться, рассматривая явные выра-
выражения для этих токов [223]. Законы сохранения с таким же
свойством существуют также для нелинейной а-модели (т. е.
О (Л^)-модели в A + 1) измерениях, введенной в гл. 3) как на клас-
классическом [281], так и на квантовом [286] уровнях. То же самое
справедливо для других двумерных моделей (см. [209]).
Нашим отправным пунктом будет произвольная двумерная тео-
теория, в которой существуют такие законы сохранения. Пусть Q^ —
одна такая сохраняющаяся величина, которая является компо-
компонентой лоренцева тензора ранга N. Тогда значение этого%заряда,
действующего на начальное состояние произвольного процесса
рассеяния, когда все частицы находятся на большом расстоянии
друг от друга, определяется выражением
Qn\Pi, Ръ Рп)т = Ц <7л (еи k,)\px, р^ рп)ы, G-55)
1=1

несколько точных результатов 223
где pi — 2-импульс \еи kt\ 7-й частицы, a qN (eit kt) — некото-
некоторый полином N-то порядка по энергии и импульсу t'-й частицы.
Аддитивность вкладов отдельных частиц следует из локальности
закона сохранения; это означает, что QN — пространственный ин-
интеграл от некоторой локальной плотности. Тот факт, что эти
вклады представляют собой полиномы qN (et, /гг), следует из
свойств QN как лоренцева тензора. Обратим внимание, что в A +
+ 1) измерениях спин отсутствует, так что такие тензоры могут
быть построены только из энергии и импульса. Аналогично для
конечного состояния, состоящего из / вылетающих частиц, имеем
Qn\Pu P2 /?/}ощ = 2j Яы (e'f, k'i)\Pu p'2, ■■■, p'i)om- G.56)
Так как QN сохраняется,
igN(e',,k',)=tqN(ehkt). G.57)
/=1 i=\
Поскольку мы имеем бесконечное число сохраняющихся зарядов
QN возрастающего ранга N, мы имеем бесконечное число уравне-
уравнений вида G.57) с полиномами qN (e, k) возрастающего ранга. Они
должны разрешаться относительно 2 (п +/) переменных et, kit
е) и k}. Ясно, что эти уравнения в сильной степени переопределены
и в общем случае удовлетворяются только при выполнении усло-
условий
1 = п, G.58а)
множество \р\, ..., рп\ = множество \р\ р'п\. G.586)
При некоторых специальных значениях импульсов условия G.58)
можно обойти 'и удовлетворить G.57) для всех значений N; но
при этом нарушается аналитичность амплитуды рассеяния по
импульсным переменным. Следовательно, G.58) — единственное
решение. Из этого решения следует, что процесс существенно
упругий (полное число частиц не может измениться). Исходный
набор 2-импульсов должен быть таким же, как конечный набор.
Это не означает, что 5-матрица тривиальна. Если некоторые ча-
частицы в начальном состоянии имеют одинаковые массы, то они
могут обменяться импульсами в конечном состоянии или быть
замененными другими частицами той же массы. Но число частиц
каждой данной массы в отдельности должно сохраняться, чтобы
обеспечить тот же набор 2-импульсов.
На самом деле достаточно наличия двух таких тензорных
зарядов, чтобы получить G.58) (см. . [275, 286]). Для простоты
изложения мы предположили наличие бесконечного числа сохра-
сохраняющихся зарядов только потому, что в представляющих интерес
примерах, в которых имеется два заряда, имеется также и беско-

224 Глава 1
нечное число зарядов. Дальнейшим следствием этих сохраняю-
сохраняющихся зарядов является факторизация многочастичной 5-матрицы
в произведение двухчастичных 5-матриц. Рассмотрим, например,
столкновение трех частиц с начальными импульсами kx > k2 > k3.
Согласно G.58), результатом столкновения будет состояние из
трех частиц с тем же набором импульсов \kx, k2, k3\. Пространст-
Пространственно-временные диаграммы трех возможных вариантов соударе-
соударения показаны на рис. 15. Заметим, что мы намеренно провели
с1 6' а'
с' Ь' а' с' Ь'
t =°о
в
Рис. 15. Мировые линии для трех способов, которыми может происходить трех-
трехчастичное столкновение, когда импульсы упорядочены в виде йх> £г > Ьч. На
рис. айв S-матрица есть произведение трех двухчастичных S-матриц, на рис. б
содержится собственно трехчастичный процесс. Символы а, Ь, с, ... относятся к
индексам внутренней симметрии.
жирные мировые линии для этих частиц, чтобы показать, что они
имеют конечный, но не нулевой размер. На рис. 15, а и в они стал-
сталкиваются по двое, но в различных последовательностях, а на
рис. 15, б имеется собственно трехчастичное столкновение.
Тем не менее все эти три процесса приводят к одной и той же
амплитуде. Простейшим способом увидеть это является исполь-
использование соображений, связанных с перестановкой частиц [313].
Рассмотрим начальное состояние для некоторого большого отри-
отрицательного значения времени t, когда частицы находятся на
большом расстоянии друг от друга. Подействуем на это состояние
оператором exp (iaQN), где QN — любая из нетривиальных сохра-
сохраняющихся величин (тензорного ранга JV > 1) и й —действитель-
—действительный параметр. Заметим, что в квантовой теории Q_¥ — некоторый
оператор. Так как по предположению QN — интеграл от локаль-
локальной плотности, то он будет действовать по отдельности на каждый
из удаленных на большое расстояние друг от друга волновых
пакетов. Запишем волновой пакет j-й частицы в виде
IЬ (х)) = | J dk exp [ik (x - Xi)] f (k)),
G.59)

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 225
где волновая функция импульсного пространства f (k) есть любая
разумная функция, например гауссовой формы, локализованная
около k = kt. Конечно, эти частицы не являются точечными. Пере-
Переменные х и k обозначают координату и импульс центра масс ча-
частицы, или, точнее, ее «коллективные координаты» положения и
импульса. В приближении стационарной фазы можно видеть, что
||-; (х) локализована при х — xt. Тогда
| i|v (*)) = exp (iaQN) | i|j, (*)) =
\jdkexp[iaq(k)]exip[ik(x - xi)]f(k)), G.60)
где оператор QN, действуя на эту частицу, дает функцию qN (e, k),
которую мы записали как q (k), используя соотношение е2 = k2 +
Ь т\. Применяя снова к осциллирующей экспоненте условие ста-
стационарной фазы, находим, что/ф; (х) теперь локализована в окре-
окрестности
x = xt-a(dq/dk)hr G.61)
где мы учли, что f (k) локализована около среднего импульса k-t.
Ключевым моментом теперь является то, что если QN имеет не-
некоторый нетривиальный ранг, то q (k) будет нелинейной функ-
функцией от k и, следовательно, (dqldk)k. будет зависеть от kt. Поэтому
оператор exp (iaQN) перемещает i-ю частицу на величину
a (dql dk)k., которая зависит от ее среднего импульса kt. Таким
образом, когда exp (iaQN) действует на все исходное состояние,
он сдвигает частицы на различные расстояния, зависящие от их
импульсов. Делая параметр а произвольно большим, мы можем
изменять относительное положение любых двух частиц на произ-
произвольную величину.
Применим теперь этот сдвиг к трехчастичному столкновению
ira рис. 15. Ясно, что при сдвиге линии 3 относительно линий 1 и 2
мы можем перейти от рис. 15, а к рис. 15, б и рис. 15, в. Это имеет
следующие важные последствия:
1. Поскольку оператор QN сохраняется, он коммутирует с га-
гамильтонианом и, следовательно, 5-матрица не изменяется под
действием exp (iaQN). Отсюда следует, что амплитуды для трех
возможных последовательностей столкновения на рис. 15, а, б
и в равны!
2. Трехчастичная 5-матрица может быть записана в виде про-
произведения трех двухчастичных 5-матриц, как на рис. 15, а или в.
Даже случай рис. 15, б, когда имеется собственно трехчастичная
S-матрица, в силу симметрии относительно действия exp (iaQ*?)
сводится к факторизованной амплитуде (рис. 15, а или в).
3. Так как процессы, показанные на рис. 15, а и в, тождественны,
мы можем записать факторизованную амплитуду в двух различ-
8 Раджараман Р.

22G ГЛАВА 7
ных последовательностях, которые должны быть равны. Другими
словами,
5 A23) = 5 B3) 5 A3) 5 A2) = 5 ( 12) 5 A3) 5 B3), G.62)
где 5 (ij) — двухчастичные 5-матрицы. Поэтому не только трех-
частичная амплитуда факторизуется, но и сами двухчастичные
амплитуды должны удовлетворять кубическому тождеству G.62).
Заметим, что если 5 (ij) являются просто числами, то это кубиче-
кубическое тождество тривиально. Но, как мы отмечали, если некоторые
или все рассеивающиеся частицы имеют одинаковые массы (на-
(например, если они принадлежат к одному и тому же вырожденному
по внутренней симметрии мультиплету), то, согласно условию
G.58), 5 (ij) могут быть нетривиальными матрицами, связываю-
связывающими все вырожденные по массе частицы. В этом случае кубиче-
кубическое тождество G.62) является серьезным ограничением на саму
двухчастичную 5-матрицу.
То же доказательство может быть повторено для четырехча-
стичных и более высоких 5-матриц, чтобы показать, что они тоже
факторизуются в произведения двухчастичных S-матриц. Но неза-
независимых тождеств четвертого или более высоких порядков не воз-
возникает. Можно проверить, что сдвиг частиц и кубическое тожде-
тождество G.62) достаточны для факторизации высших многочастичных
амплитуд. Обратим внимание на решающую роль нетривиаль-
нетривиальности природы QN. Если бы мы использовали тривиальный случай
Qx = Р, где Р — оператор импульса (который в любой трансля-
ционно инвариантной теории всегда сохраняется), то q (k) = k и,
следовательно, все частицы сдвигались бы на одну и ту же вели-
величину а. Мы не можем изменить последовательность столкновений.
Для этого необходимо, чтобы QN было лоренцевским тензором
достаточно высокого ранга, так чтобы q (k) было нелинейным. Мы
использовали только одно такое QN. To обстоятельство, что инте-
интересующие нас примеры допускают наличие нескольких (или бес-
бесконечного числа) таких сохраняющихся зарядов возрастающей
сложности, только усиливает наши доводы. Несомненно, наш
вывод является до некоторой степени качественным. Например,
чтобы описать все возможные точки локализации каждой частицы,
мы использовали в G.59) волновую функцию от одной коорди-
координаты. Но ни явный вид распределения по импульсам / (к), ни явный
вид сохраняющейся величины QN не потребовался — исполь-
использовалось только минимальное следствие (которого достаточно),
заключающееся в том, что exp (iaQN) сдвигает различные частицы
на различную величину. Нет сомнений, что это доказательство
может быть представлено в более строгой форме. Следует упомя-
упомянуть, что задолго до этих теоретико-полевых результатов анало-
аналогичные соображения в пользу факторизации были развиты в более
простом контексте потенциалов из б-функций (см., например, [251]).

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 227
Таким образом, наш вывод состоит в том, что если двумерная
нолевая теория обладает сохраняющимися величинами достаточ-
достаточной сложности, то полная S-матрица является упругой и фактори-
чуется на двухчастичные S-матрицы, которые подчиняются куби-
кубическому тождеству G.62). Поэтому задача получения полной
.S-матрицы сводится к вычислению именно двухчастичной S-ма-
S-матрицы. Мы сделаем это для некоторых моделей в следующем раз-
разделе.
Наше обсуждение проведено для A + 1)-мерных моделей.
Нет особых причин для поиска C + 1)-мерных моделей с такими
необыкновенными свойствами S-матрицы. С одной стороны, Коул-
мен и Мандула [90] давно показали, что в C + 1) измерениях
S-матрица с такими сильными ограничениями, как те, которые
мы обсуждали, будет тривиальной. С другой стороны, в экспери-
экспериментальных данных по рассеянию при высоких энергиях неупру-
неупругие явления играют большую роль.
7.5. Несколько точных 5-матриц
В этом разделе мы покажем, как могут быть получены точные
выражения для полной S-матрицы для некоторого класса дву-
двумерных теорий, которые обладают необходимыми сохраняющи-
сохраняющимися величинами, удовлетворяющими приведенным выше требо-
требованиям. Все, что нам требуется найти, это двухчастичные S-ма-
S-матрицы. Высшие S-матрицы получаются с помощью факторизации.
Мы будем считать, что наши теории обладают некоторой внутрен-
внутренней О (N)-инвариантностью. Такой О (N)-инвариантностью обла-
обладают многие модели, в"том числе^система СГ, массивная модель
Тирринга, О (N)-сигма-модель и "модель Гросса—Неве, которая
описана в гл. 9. Мы считаем, что две исходные частицы принадле-
принадлежат некоторому векторному мультиплету относительно группы
О (N). Очевидно, что они имеют одинаковую массу М. Если не
учитывать случайных обстоятельств, все другие частицы массы М
в этой теории также будут принадлежать тому же мультиплету.
Следовательно, согласно G.58), конечное состояние должно также
состоять только из двух частиц, принадлежащих тому же вектор-
векторному мультиплету. Таким образом, мы ищем (с (pi) d (p'2)\S\ x
х a (pi) Ь (/?2)}> где pi и р\ — 2-импульсы и а, Ь, с, d (все изме-
изменяются от 1 до N) — индексы внутреннего пространства в этом
векторном мультиплете. Для вывода этой амплитуды привлечем
кубическое тождество G.62), а также хорошо известные принципы
S-матрицы теории. Детального развития S-матричной теории не
потребуется — нужны только основные свойства S-матрицы, та-
такие, как лоренц-инвариантность, аналитичность, унитарность и
кроссинг-симметрия. Мы считаем, что читатель хорошо знаком
с этими свойствами (см., например, [141]).
8*

228 ГЛАВА 7
Из лоренц-инвариантности следует, что помимо б-функций,
обеспечивающих сохранение энергии-импульса, S-матрица может
зависеть от 2-импульсов только через лоренцевы скаляры. На-
Напомним, что мы находимся в одном пространственном измерении,
когда невозможна никакая спиновая структура. В C + 1) изме-
измерениях обычно используются скалярные комбинации
s = (pi + p2f, t = (pi — p[f, u = (pi — p'2f, G.63)
причем
s + t + и = 4M2. G.64)
IV
Ill
]тв
л
[L
IV
in
a i 6
Рис. 16. a — s-плоскость с разрезом, на которой S-матрица аналитична; б — 9-
плоскость. Показано, что s-плоскость отображается на 0-плоскость в полосу
между Im G = 0 и Im G = я.
Эти определения применимы и вA + 1) измерениях, но в] отличие
от C + 1) измерений, где две из этих переменных могут независимо
изменяться в физическом процессе, в A + 1) измерениях может
независимо изменяться только одна из них. В системе центра
масс возможно только рассеяние вперед или назад. Следовательно,
s = (.ЕцМJ может меняться от 4М2 до оо, но при этом либо t = О
и и = 4М2 —s, либо и = 0 и t = 4М2 — s. Амплитуду рассея-
рассеяния можно записать в виде
(С (Р[) d (p'2)\ S | а (Р1) Ъ (ра)) = б (р[ - Pi) б (/72 - Р2) [cdSab (S)]. G.65)-
Это определяет порядок индексов cd по отношению к ab. \
Из свойства аналитичности следует, что S-матрица CdSab Щ
аналитична на s-плоскости с разрезом. Она может иметь на дей-
действительной оси между 0 и 4М2 полюсы, соответствующие связан-
связанные состояниям, и унитарные разрезы от 4М2 до оо и от —оо до О
(рис. 16, а). Она должна также подчиняться принципу отражения;
cA(s) = c!lSab(s-), G.66|
где звездочка означает комплексное сопряжение. Но бесконечное
число законов сохранения уже исключило неупругое рождени|

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 229
частиц. Следовательно, унитарные разрезы являются чисто упру-
упругими и кинематическими по происхождению. (Они возникают из-за
того, что импульсы являются двузначными функциями энергии и,
следовательно, s). Эти разрезы могут быть исключены с помощью
перехода к переменным быстроты 0г, определяемым через pi =
■-- \et, Ь]:
kt = MshQi, ei = MchQi. G.67)
Тогда
s = 4M2 ch2 @/2), где 0 = 0X - 02. G.68)
Тогда S-матрица является мероморфной функцией 0, обладающей
только полюсами, соответствующими связанным состояниям. При
замене переменных от s к 0 физический s-лист отображается в по-
полосу между Im 0 = 0 и 1га 8 = я, как показано на рис. 16, б.
Условие отражения G.66) для действительных 0 сводится к
cdS*ab(Q) = cdSab(-Q). G.69)
Перекрестные процессы а *->■ с и s «-» и, относительно которых
S-матрица должна обладать кроссинг-симметрией, для перемен-
переменной 0 сводятся к
в «- in — 0. G.70)
Эти результаты легко проверить. Далее мы используем О (N)-\m-
вариантность теории, учитывая, что частицы образуют некоторый
О (Л0-вектор. Разлагая cdSab @) по О (Л^)-инвариантным ком-
комбинациям, в общем случае мы можем написать
edSab Ф) = 6«А«А @) + 8аАА (9) + 6аАА (9)- G-71)
Запишем кроссинг-соотношения и соотношения унитарности в тер-
терминах этих Slt S2 и S3. Кроссинг-симметрия, которая переставляет
а ■>->• с и 0 «-»■ in — 0, дает
S2 @) = S2 (fit - 0), G.72)
Sx @) = S3 (fit - 0). G.73)
Полностью выписанное условие унитарности SS+ = 1 имеет вид
2] cdSef (Q)efSab (9) = 2] cdSef (fyabS'ef @) = bac6bd.
После подстановки сюда выражения G.71) это дает три соотноше-
соотношения
52 @) S2 (-0) + S3-@) S3 (-03) = 1, G.74)
S2 @) S3 (-0) + S3 @) S2 (-0) = 0, G.75)
j. @) Sx (—0) + Sx @) S2 (—0) + S2 @) Sx (—0) +
+ Sx @) S3 (-0) + S3 (9) Si (-0) = 0, G.76)

230 ГЛАВА 7
где использовано условие отражения G.69). Наконец, кубиче-
кубическое тождество G.62), которому должна удовлетворять двухча-
двухчастичная S-матрица, в матричных обозначениях имеет вид (см.
рис. 15, айв)
[b'c'Sef @')] [a'fSdc F + 0')] [deSab (9)] =
= Wa'Sed F)] x [cd'Sfa (в + в')] [ejSbc (в')]. G.77)
Здесь 0 = 0Х — 02, 0' = 02 — 03 и 0 + 0' = 0i — 0з, где вг —
скорости трех начальных частиц. После подстановки выражения
G.71) в это матричное уравнение оно сводится к набору незави-
независимых соотношений для функций Sx @), S2 @) и S3 @). Вывод
этих соотношений из G.77) производится непосредственно, но тре-
требует громоздких алгебраических преобразований. Результаты для
случая N — 2 несколько отличаются от результатов для случаев
N ^ 3. Это объясняется тем, что для N = 2 существует меньше
независимых трехчастичных комбинаций. Примем сначала, что
N 5г 3.. Коэффициент при Ьа'ьЬь>с§са в обеих частях G.77) дает
53 @) S2 @ + 0') S3 @') =
= S2 @) S3 @ + 0') S3 @') + S3 @) S3 @ + 0') S2 @'),
или в более компактном виде
S3S2S3 = S2SgS3 -f- S3S3S2, G.78)
где подразумевается, что во всех членах аргументами этих трех
Sj является соответственно 0, @ + 0') и Э'. Другие независимые
соотношения для случая N 5= 3 содержащиеся в G.77), имеют вид
St$1St = St&S1 + St$tp1, G.79)
030103 == <•oiOjjOi -p ibio3ibj -(- ibiib3ib3 -(- 010201 -(-
+ S^S^ + S1S1S1 + SsSsSv G.80)
Для Л^ = 2 существуют только два соотношения, а именно
S5S2S3 -|- SiS2S3 -|- S1S1S2 = SzSiSg -\- SzSsSa -f- SgSgS^, (' • ° 1)
osoio3 -p osO2O3 = о3озо,1 -р 03О8О2 -р 020301 -р О2О3оз ~р
+ 2S1S3SJ + SiS3S2 + S1S3S3 + S&Sx + SiSiSi. G.82)
Заметим, что в отличие от cdSab эти Slt S2, S3 не матрицы, а обычные
функции соответствующих переменных. Этих кубических тож-
тождеств вместе с условиями унитарности, кроссинга и аналитич-
аналитичности G.72)—G.76) достаточно для определения S-матрицы с точ-
точностью до неоднозначности, которая также может быть устранена
для конкретных моделей. Мы приведем вывод для случая N ^ 3.
Результаты для случая N — 2, которые получаются аналогичным
образом, будут также приведены ниже. Мы начинаем с кубиче.'

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 231
ских условий; возьмем G.78) и разделим обе части на S3S3SS> что
дает
.3,(8 + 6') _ ^9) S2 F')
Это означает, что
S2 (9)/S, F) = об, G.83)
где а — некоторая константа. Затем подставим в G.79) S2 (8)/а8
вместо S3 @) и. разделим обе части на SzSiSi, получим
„а _ Si (в') _ 3,(8 + 8')
aD —uWSxte + ey
Решением этого уравнения является
52 @) = - (об + Р) Sx @), G.84)
где р—другая константа. Используя G.83), G.84), запишем
G.80) только через, функцию Si и приравняем коэффициенты
при Sx (9) Sx @ + 0') Sx @'). Это дает простое соотношение
Р = (N — 2)/2. G.85)
Мы исчерпали все три кубических равенства G.78)—G.80) для
N ^: 3. Далее условие G.69) требует, чтобы
53 @)/S! @) = S2 (-0)AS3 (-0).
Отсюда
а* = — а = —iX, G.86)
где X — действительная величина. Отношение кроссинг-соотно-
кроссинг-соотношений G.72) и G.73) дает
или
Поэтому
Я = р/я = (iV — 2)/2я. G.87)
Отсюда
Таким образом, отношения Slt S2 и S3 полностью определены.
Чтобы определить какую-либо из этих функций в отдельности,
например S2 @), обратимся к условиям унитарности. Соотноше-
Соотношения G.75) и G.76), которые содержат только отношения St/Sj,
автоматически удовлетворяются полученными выше выражениями.
Остающееся условие G.74) требует, чтобы
5а (в) 53 (—6) A Ч- 1/Я2е2) = 1, G.89)

232 ГЛАВА 7
ИЛИ
S2 @) S2 (-0) = 02/@а + Д2), G.90)
где
А = 1/А- = 2n/(N —2). G.91)
Все, что нам нужно, это некоторая функция S2 @), которая удов-
удовлетворяет G.90) вместе с кроссинг-соотношением G.72). (Напом-
(Напомним, что до сих пор мы использовали только отношение этих
двух кроссинг-соотношений.) Ответ имеет вид
S2 @) = R @) R (in — 0), G.92)
где
R(e, s Г D^2) Г ("г/»)/г (^) Г <!±£Л). G.93)
Чтобы раскрыть тайну получения выражения G.93), обратим вни-
внимание на то, что простейшим решением уравнения G.90) было
бы Sr2 @) = 0/@ + г А). Но оно не удовлетворяет кроссинг-сим-
кроссинг-симметрии G.72). Мы можем попытаться исправить это, используя
выражение
которое кроссинг-симметрично, но не удовлетворяет унитарности
G.90). Унитарность восстанавливается умножением на еще один
множитель, а именно
2 \ > е +«д («я — е + iД) («я + е) '
но теперь кроссинг-симметрия снова потеряна. Мы можем продол-;
жать действовать таким образом до тех пор, пока не получим
бесконечное произведение сомножителей, которое в пределе должно
удовлетворять и унитарности, и кроссингу-симметрии. Результат
G.92), G.93) есть не что иное, как компактное представление такого,
бесконечного произведения с помощью Г-функций. Разумеется^
можно и непосредственно убедиться, что G.92) вместе с G.93|
удовлетворяет и унитарности, и кроссинг-симметрии. Заметим,;
что при N = 3, как внелинейной О (З)-модели, результат G.92|
сводится к :,
S2 @) = 0 (in - Q)/Bni — 0) (fit + 0). G.94|
Заметим также, что мы можем получить другое решение, замени!
в G.93) Д на —А, так как условие G.90) квадратично по Д.
Для случая N = 2 мы вместо G.78), G.80) используем соответ
ствующие кубические тождества G.81), G.82) и действуем тем ж<
способом. Вычисления и результат несколько более сложны,

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 233
принципы остаются теми же, что и в случае N ^ 3. Приведем
окончательный результат [367]
S3 @) = i ctg Dя2/у') cth Dя0/у') S2 @),
S1(e) = S,(iit-e), G.95)
S2 @) = B/я) sin Dя2/у') sh Dit6/v') sh Dit (in - 0)/y') (У @), G.96)
где
)ГA + —
R, @) = Г A6я/ + г8В) Г (l + 16я/ + '89)/г A6я/ +78я + '86
G.97)
X
G.98)
В этом решении у' —действительный параметр, пока не опре-
определенный. Этим решение отличается от результата для N ^ 3,
в котором независимых параметров нет. Это связано с тем фактом,
что в случае N = 2 имеются только два независимых кубических
тождества G.81), G.82) в отличие от трех тождеств G.78)—G.80)
для N > 3.
Когда Si, S2 и S3 известны, мы можем подставить их в G.71),
чтобы получить двухчастичную S-матрицу. Тогда полная много-
многочастичная S-матрица, содержащая произвольное число частиц
из О (А^)-векторного мультиплета, может быть записана благо-
благодаря факторизации в виде соответствующего последовательного
произведения двухчастичных S-матриц. Например, трехчастич-
ная S-матрица может быть получена из последовательности трех
двухчастичных S-матриц, соответствующих либо рис. 15, а,
либо рис. 15, в. Оба возможных варианта дают один и тот же
ответ, поскольку удовлетворены кубические тождества.
Но есть одна тонкость. Результат G.95)—G.98) для N = 2
и результат G.92), G.93) для N > 3 вместе со своим двойником,
соответствующим А *-♦ —А, могут быть названы «минимальными»
решениями для связей, обусловленных кубическими тождествами
и фундаменальными принципами S-матричной теории.' Но они
не являются единственными решениями. Предположим, что мы
умножили все три функции Sx @), S2 @) и S3 (8) на общий мно-
множитель

234 ГЛАВА 7
где ah — произвольные действительные константы и число мно-
множителей К также произвольно. Заметим, что / @) удовлетворяет
условиям / @) = / (in — 0), / @) / (—0) = 1. Следовательно,
когда S2 @) умножена на / @), она продолжает удовлетворять
G.90) и G.72). Остальные условия содержат только отношения
St @) и также будут выполнены. Поэтому, как в случае N = 2,
так и в случае N > 3, мы можем получить некоторое семейство
решений, умножая «минимальные» решения на множитель вида
G.99). Заметим, что множитель / @) приводит к дополнительным
полюсам при 0 = гай"в S-матрице, кроме тех полюсов,!которые
уже имеются в минимальных решениях. Полюса в S-матрице
соответствуют связанным состояниям, если они расположены
в области 0 < s < 4М2, т. е. на отрезке мнимой 0-оси, определяе-
определяемом как 0 <: Im 0 < я, Re 6 = 0. Следовательно, если какое-
либо из ah попадает в область 0 <: ah < я, то множитель / @)
может иметь важные следствия, указывая на другие связанные
состояния в системе.
Тот факт, что принципы аналитичности, унитарности и крос-
кроссинг-симметрии определяют S-матрицу только с точностью до
таких неоднозначностей, характерен не только для нашего рас-
рассмотрения. Это более общее свойство, которое известно уже в те-
течение некоторого времени. Такие неоднозначности называют не-
неоднозначностями Кастильехо, Далица и Дайсона (КДД) [75]
(см. также [141]). Кубические тождества наших систем эту не-
неоднозначность не устраняют, поскольку они содержат только
отношения St @), в--каждое из которых может быть введен один
и тот же множитель / @).
Наличия таких неоднозначностей (см. также [254]) в нашем
выводе и следовало ожидать. Напомним, что мы нигде не выписы-
выписывали лагранжиан или использовали все детали динамики. Мы
использовали лишь 1) наличие некоторых законов сохранения,
достаточных для обеспечения упругости и факторизации, 2) тот
факт, что рассеивающиеся частицы образуют векторный мульти-
плет в О (ЛО-инвариантной теории в двух измерениях, и 3) общие
принципы S-матричной теории. Может быть несколько полевых
теорий с различными лагранжианами, которые удовлетворяют всем
этим условиям, включая О (А^-инвариантность ПРИ заданном N.
Их динамика может быть различной и было бы удивительно, если
бы мы получили для них одну и ту же S-матрицу. Замечательно
уже то, что мы достигли таких результатов, основываясь на этих
общих требованиях без знания точного лагранжиана. Поэтому,
для того чтобы решить, вводить ли КДД-множители типа G.99),
и если вводить, то какие, мы должны ближе познакомиться с ди-
динамикой, исходя из конкретного лагранжиана исследуемой модели.
Такое же замечание относится к выбору значения свободного па-
параметра у' в случае N = 2 и к выбору между А и —Д_в случае N3

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 235
Чтобы показать, как это может быть сделано, рассмотрим рас-
рассеяние солитонов в хорошо нам знакомой теории СГ. Как мы
уже отмечали, эта теория обладает бесконечным числом локаль-
локальных законов сохранения, более чем достаточным для того, чтобы
обеспечить факторизацию. Эта теория также обладает скрытой
О B)-инвариантностью, хотя и неочевидной при беглом взгляде
на лагранжиан. Чтобы усмотреть эту симметрию в явном виде,
необходимо привлечь параметр «беспорядка» теории [207], что
выходит за рамки данной книги. Но мы можем воспользоваться
эквивалентностью теории СГ и массивной модели Тирринга (МТ),
обсуждавшейся в разд. 7.3. Модель МТ обладает хорошо извест-
известной U A)-симметрией относительно Y -veia Y. По существу это
О B)-симметрия с (V + W*)/2 и (*? — y¥*)/2it действующими как
О B)-дублет. Поскольку фермионы и антифермионы модели МТ
отождествлялись соответственно с солитонами и антисолитонами
модели СГ, есть основания предполагать, что если А и А обозна-
обозначают солитон и антисолитон, то
Ах = (А + Л)/2 и А2 = (А — A)l2i G.100)
образуют некоторый дублет относительно скрытой О ^-симме-
^-симметрии. Разложение S-матрицы по Slt S2 и S3 записывается теперь
в терминах О B)-тензоров. Индексы а, Ь, с и d в G.71) принимают
значения от 1 до 2. Физически более естественные понятия соот-
соответствуют А—Л-амплитуде рассеяния вперед (прохождения)
ST @), А — Л-амплитуде рассеяния назад (отражения) SR @)
и А—Л-амплитуде S @), для которой нет различия между рассея-
рассеянием вперед и назад. (Вследствие симметрии ф ■«-»■ —ф теории СГ
А—Л-амплитуда есть также S @).) Используя соотношение
G.100) между (Л, Л) и дублетом (Л1( Л2), легко убедиться, что
ST F) = Sx @) + S2 @), SR @) = Sx @) + S3 @),
S @) = S2 @) + S3 @). G.101)
Поэтому для вычисления Л—Л- и Л—Л-амплитуд рассеяния
мы можем использовать О B)-результат G.95)—G.98) для Sb
S2 и S3, но при этом необходимо соответствующим образом выбрать
константу у' и КДД-множители. Чтобы определить их, рассмо-
рассмотрим полюсы минимальной амплитуды G.95)—G.98). Эти полюсы
возникают из полюсов Г-функции. Существует много таких полю-
полюсов, но полюсы, соответствующие связанным состояниям, должны
попадать в физическую область @ < Im 0 < я, Re.0 = 0). Они
появляются из множителей Г A + г80Ау') и Г A — (8л + i8Q)/y').
Эти полюсы расположены в точках
1) 0П = ш?78, п = 1,2,..., <8я/у',
2) Qn = tn - iny'/8, я = 1, 2, .... <8л/у'. { '

236 ГЛАВА 7
С учетом G.68) второй набор в G.102) соответствует
sn = 4М* ch* (-£■ - iHl) = 4М* sin* (-31), G.103)
n= 1, 2, . .., <8я/у'.
Находясь в области 0 < s < 4М2, эти полюсы определяют поло-
положение связанных состояний. Первый набор, очевидно, соответ-
соответствует тем же связанным состояниям, проявляющимся как по-
полюсы в м-канале. Мы уже получили связанные состояния этой
теории при помощи ВКБ-метода в разд. 7.1, где мы также вы-
выдвинули аргументы в пользу утверждения о том, что полученный
там спектр связанных состояний точен. Этот спектр определяется
формулой (см. G.39))
M2=4M2sin2(ny/16), я=1,2 <8я/у, G.104)
где у — перенормированная константа связи теории СГ. Мы
видим, что этот спектр точно совпадает со связанными состоя-
состояниями G.103) нашей минимальной S-матрицы при условии, что
у' = у. Это не только помогает фиксировать параметр у' в S-
матрице, но показывает также, что для случая СГ может быть
достаточно минимального решения G.95), G.96) для О B) без
необходимости в дополнительных КДД-множителях. Правильность
минимального решения следует также из разбора случая у = 8я.
Тогда Si, S2 и S3 в G.95)—G.98) сильно упрощаются и для всех в
дают
ST (в) = S, @) + S, (в) = 1, SA F) = St @) + S3 @) = 0,
S@) = S2@) + S3@) = 1. G.105)
Это как раз то, что и должно было быть. Значение у = 8я соответ-
соответствует (разд. 7.3) g = 0, где g — константа связи для модели
МТ. Следовательно, мы ожидаем, что солитоны и антисолитоны
не испытывают никаких сил. Поэтому А—Л-амплитуда S равна
единице, так же как и А—Л-амплитуда прохождения ST, но А—А-
амплитуда отражения SR равна нулю. Далее, при у -у8я g ->-0
и наша S-матрица может быть разложена по степеням Bg/n) =
= (8я/у) — 1. Если это сравнить со стандартными вычислениями
по теории возмущений для рассеяния фермионов в модели МТ,
то результаты согласуются до порядка g3 включительно [346].
Эти доводы решительно указывают на то, что минимальное ре-
решение G.95)—G.98) определяет точную S-матрицу для рассеяния
солитонов (и антисолитонов) теории СГ.
Конечно, полная S-матрица этой системы также будет вклю-
включать рассеяние связанных состояний Мп друг на друге и на со-
литонах и антисолитонах. Для этих процессов Замолодчиков
[364] и Каровски и Тун [211] предложили вывод, основанный
на том обстоятельстве, что любое из этих связанных состояний Мп

НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 237
само является полюсом Л—Л-амплитуды. Отсюда Мп—Л-ампли-
гуда может быть получена как вычет в соответствующем полюсе
Л—Л—Л-амплитуды по относительной энергетической перемен-
переменной АА. Аналогично более сложная амплитуда, содержащая
несколько частиц Мп, Л и Л, есть снова вычет в соответству-
соответствующем произведении полюсов в подходящей мульти- Л—Л-ампли-
туде. Все мульти- Л—Л-амплитуды уже известны благодаря фак-
факторизации в терминах G.95)—G.98), так что амплитуды, вклю-
включающие связанные состояния Мп, также известны. Дальнейшие
сведения о том, как получаются эти вычеты, см. в работе [367].
С учетом этой дополнительной информации полнай СГ-матрица
рассеяния известна точно.
Можно попробовать разрешить аналогичным способом КДД-
неоднозначности для других О (^-инвариантных теорий. По-
видимому, в некоторых случаях работают минимальные решения.
Например, решение для N > 3 G.92), G.93), по-видимому, яв-
является правильным без дополнительных КДД-множителей для
нелинейной сигма-модели. Здесь мы не имеем ни точного спектра
связанных состояний для сравнения, ни возможности исполь-
использовать пертурбативную теорию возмущений. (Напомним из
разд. 3.3, что эта модель обнаруживает спонтанное нарушение
симметрии на классическом уровне. Но в квантовой теории не-
непрерывная симметрия не может нарушаться в A + 1) измере-
измерениях [84]. Направление поля ф во внутреннем пространстве
сильно флуктуирует, восстанавливая эту симметрию, и это на-
находит отражение в форме инфракрасных расходимостеи в теории
возмущений [238].) Но сигма-модель может быть атакована
с использованием l/Af-разложения; получаемые предсказания
согласуются с минимальным решением G.92), G.93) [365]. По-
Подобным же образом другое минимальное решение, а именно то,
в котором Д заменено на —Д в G.93), согласуется с результатами
l/Af-разложения в модели Гросса—Неве для N > 4 [355, 366}.
Приведенный выше вывод относится к рассеянию векторного
мультиплета некоторой О (Л/)-инвариантной теории. Те же прин-
принципы можно попытаться применить для других мультиплетов
других групп симметрии. Изменится основное тензорное разложе-
разложение G.71), и, следовательно, изменятся последующие уравнения.
Могут ли изменившиеся уравнения по-прежнему приводить к не-
некоторому решению, зависит от группы и мультиплета частиц.
Например, ГН-модель также приводит к «кинк-частицам» в до-
дополнение к ее элементарным фермионам, которые преобразуются
как спиноры относительно группы О (N). Точная S-матрица для
них получена с помощью этих принципов Шанкаром и Виттеном
1313], которые также получили S-матрицу для суперсимметричной
сигма-модели [314].

ГЛАВА 8
КОЛЛЕКТИВНЫЕ КООРДИНАТЫ
И КАНОНИЧЕСКИЕ МЕТОДЫ
8.1. Трактовка нулевых мод: простой пример
В разд. 5.5 мы рассмотрели основные физические причины появ-
появления в квазиклассическом методе флуктуационных мод нулевой
частоты, когда имеются непрерывные симметрии. В гл. 5 и 6
мы также несколько раз заметили, что в присутствии таких ну-
нулевых мод этот метод нуждается в модификации. Хотя нам уда-
удалось получить некоторые результаты (такие как уровни энергии
в солитонном секторе до О A°), где X — константа связи), не
уделяя специального внимания нулевым модам, последние будут
приводить к расходимостям в высших порядках до тех пор, пока
они не будут рассмотрены на иной основе, чем остальные моды
ненулевых частот.
В литературе описано много различных способов трактовки
нулевых мод (см., например, [t, 16, 81, 95, 130, 152, 153, 292,
335]). Многие из этих способов связаны с использованием коллек-
коллективных координат. (Понятие коллективных координат уже не-
несколько десятилетий применяется в теории многих тел; см.,
например, [52] 1).)
Эту главу мы посвятим обсуждению метода коллективных
координат. Такие координаты могут быть введены как в форма-
формализме функционального интеграла, так и в каноническом опера-
операторном формализме. Кроме того, в некоторых случаях коллек-
коллективные координаты могут быть явно определены как функционалы
от полевых переменных, в то время как в других случаях они
должны вводиться неявным образом. Мы попробуем проиллюстри-
проиллюстрировать эти различные возможности с помощью примеров. В част-
частности, мы изложим в разд. 8.3 и 8.4 канонический гамильтонов
формализм Криста—Ли, который вводит коллективные коорди-
координаты. Это даст нам возможность увидеть, как квазиклассический
метод работает в каноническом формализме, дополняя функцио-
функционально-интегральный подход, рассмотренный в гл. 6.
Мы начнем наше обсуждение, как и в других главах, с про-
простого примера из нерелятивистской квантовой механики, где
1) Метод коллективных переменных (точнее групповых переменных) был
сформулирован Н. Н. Боголюбовым в задаче о полкроне [370*]. — Прим. перев.

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 239
может быть продемонстрирована правильная трактовка нулевых
мод. Рассмотрим в двух измерениях некоторую частицу, поведение
которой управляется лагранжианом
i=|piLfe)V^(/4Ti). (8.1)
Этот лагранжиан инвариантен относительно некоторой непре-
непрерывной симметрии, а именно относительно вращений в плоскости
(хъ х2). Пусть V (~\f х\ -\-зф имеет минимум при некотором не-
ненулевом значении -\/х\^-х\ = R =£ 0. Ясно, что каждая точка Р
на окружности радиуса R будет классическим статическим ре-
решением. Предположим, что мы применяем квазиклассический ме-
метод гл. 5 для квантования статических решений. Этот метод вклю-
включает аппроксимацию энергетических собственных функций кван-
квантовой системы, исходя из волновых функций гармонического
осциллятора, сосредоточенных в окрестности любого заданного
классического решения, в нашем случае в окрестности любой
заданной точки Р на окружности радиуса R. Согласно этому
методу, уровни энергии должны иметь вид
2
E{nt, пг} — V (R) + ^ [tii + -^ йсог + высшие порядки,
где со? и col — собственные значения (d^Vldxi dXj)P. Легко видеть,
что благодаря вращательной симметрии одно из собственных зна-
значений со? равно нулю, в то время как другое определяется как
col = V (R). То обстоятельство, что (ох равно нулю, не создает
никаких проблем в первых двух слагаемых в Etni, пл- Можно
записать
Е{п,, пг) = V (R) -\- (пг -\- Va) йсо2 + высшие порядки.
Но в слагаемых высших порядков, где частоты а1 и со2 появляются
в энергетических знаменателях, как и в стандартной теории
возмущений, равенство нулю (лх приводит к расходящимся вкла-
вкладам. Эта техническая трудность является отражением того факта,
что частично нарушено основное предположение, стоящее за
квантованием статических решений. Стационарные квантовые
состояния этой системы не локализованы вокруг некоторого кон-
конкретного классического статического решения, т. е. в'окрестности
некоторой заданной точки Р на окружности радиуса R. Хотя
потенциал вблизи точки Р может быть приближенно квадратич-
квадратичным по радиальным смещениям, он .будет оставаться постоянным
по^отношению к угловым смещениям в силу симметрии. Следова-
Следовательно, собственные состояния гамильтониана, которые радиально
локализованы, растекаются в угловом направлении по всей

240 ГЛАВА 8
окружности. Их нельзя связать с какой-либо точкой на окруж-
окружности.
Таким образом, эта простая модель содержит все, в чем мы
заинтересованы, а именно нулевые моды флуктуации в квази-
квазиклассической процедуре, связанные с непрерывной симметрией.
Квазиклассический метод по-прежнему может быть применен,
но с некоторой модификацией для преодоления трудностей с ну-
нулевыми модами. Для этой простой модели требуемую модифика-
модификацию легко найти. Сначала декартовы координаты заменяются на
полярные координаты (г, 9). Преимущества последних очевидны,
но мы все же их перечислим, поскольку в теоретико-полевых
примерах коллективные координаты будут выбираться с учетом
аналогичных критериев. 1) Упрощается действие преобразований
симметрии—вращения изменяют только 9, так как г ортого-
ортогонально 9 и остается без изменений. 2) Вследствие вращательной
симметрии потенциал V = V (г) не зависит от 9; зависимость от 9
есть только в кинетической энергии, и она квадратичная:
L~-Lr* + ±-r*Q*-V(r). (8.2)
3) Канонический импульс, сопряженный 9, есть / = г29; в силу
симметрии он сохраняется. 4) Поскольку зависимость от 9 такая
простая, она может быть учтена точно без обращения к квази-
квазиклассическому приближению. При этом остается одномерная
задача по переменной г с некоторым эффективным потенциалом.
Теперь квазиклассический метод предыдущих глав может быть
применен только к этой одномерной задаче по переменной г,
которая больше не обладает какой-либо непрерывной симметрией;
исходная вращательная симметрия оставляет г без изменений.
Следовательно, при реализации квазиклассического метода не
останется никаких нулевых мод или связанных с ними трудностей.
Это основная идея, стоящая за модифицированной квазиклассиче-
квазиклассической процедурой в присутствии непрерывных симметрии и нуле-
нулевых мод. При подходящем обобщении такая процедура исполь-
используется в теоретико-полевых примерах, где коллективные коорди-
координаты играют ту же роль, что и переменная 9 здесь.
Для примера (8.2) легко выполнить точное вычисление зави-
зависимости от 9 как в формализме функционального интеграла, так
и в гамильтоновом формализме. Порождаемый (8.2) гамильто-
гамильтониан есть просто
Н = -i- р\ + /72/-2 + V (г), рг = г. (8.3)
Заметим, что координата 9 вообще не входит в выражение для Н.
Более того, в квантовом варианте мы можем искать собственные
значения энергии в любом данном /-секторе, так как орбитальный

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 241
момент сохраняется и, следовательно, коммутирует с гамильтониа-
гамильтонианом. В этом секторе одномерная задача (8.3) по переменной г
имеет эффективный потенциал УЭфф (г) = V (г) + /2/2г2, т. е.
обладает дополнительным центробежным слагаемым. Это допол-
дополнительное слагаемое в результирующей радиальной задаче яв-
является чистым эффектом нулевых мод угловых флуктуации, если
его рассматривать правильно, как это сделано выше.
Применим квазиклассический метод статического решения
к радиальной задаче (8.3) для произвольного заданного /. Класси-
Классическое статическое решение г (t) = R удовлетворяет уравнению
--£--() (8 4)
) (
dr )r-\ dr r £
В приближении гармонического осциллятора (гл. 5) соответству-
соответствующие квантовые уровни имеют вид
~ (п
где
ба = (^ВффЛП?. (8.6)
Заметим, что хотя г (t) = R — статическое решение результиру-
результирующей радиальной задачи (8.3), но оно также соответствует зави-
зависящему от времени периодическому решению исходной системы
(8.2) в следующем смысле. Следующие из (8.2) уравнения движе-
движения имеют вид
г — гё2 + dV/dr = 0, (8.7а)
(d/dt) (г2ё) = 0. (8.76)
Если мы положим г (t) = R и 9 = vt при v = l/R2, то уравнение
(8.76) автоматически удовлетворяется, а уравнение (8.7а) сво-
сводится к (8.4). Поэтому квазиклассический результат (8.5) можно
рассматривать так же, как разложение в ряд в окрестности за-
зависящего от времени решения, описывающего вращение по кругу
с орбитальным моментом /. Это находится в согласии с приведен-
приведенными выше интуитивными аргументами. Квантовая волновая
функция не остается локализованной в окрестности произвольного
заданного статического классического решения на плоскости,
а в силу вращательной симметрии стремится растечься в угловом
направлении. Следовательно, вращающееся зависящее от времени
классическое решение, которое включает в себя все точки, свя-
связанные друг с другом этой симметрией, будет лучшим классическим
пределом для квантовых стационарных состояний. К этому при-
приводит наш модифицированный квазиклассический метод.

242 ГЛАВА 8
Следует кратко остановиться на том, как такой же результат
может быть получен в формализме функционального интеграла,
поскольку мы видели, что этот последний предоставляет воз-
возможность непосредственного обобщения на теорию поля. Мы
ищем уровни энергии для произвольного заданного орбитального
момента /. Они определяются полюсами
j
2я <х>
Во (re eo|e-w+'i«|ro, 80>, (8.8)
где L — оператор орбитального момента, ft = 1, а след берется
в базисе полярных координат | г0, 90). Это можно записать в виде
Tr ( (eLSh) =' J dTeiETGi (T),
о
где
Gl(T)=\^\ dr0 j d%ro<r"«(r0, 90 + a\ e~l"T \r0, 80>; (8.9)
здесь для вращения конечного состояния использован оператор
eiLa. Запишем интеграл по траекториям для амплитуды (г0,
90 + a\e'iHT\ r0, 90) непосредственно в полярных координатах,
используя лагранжиан (8.2):
G,(r)= Ja>[r(/)]r(/)exp ij(|^-V(r))dlx
\ о /
■IT \
j da j -g- j S5 [9 (/)] exp t J D" ^^ - *в) Я . (8.10)
V о /
X
Здесь все пути идут из точки (г0, 90) при t = 0 в точку (г0, 90 + а)
при t = Т. Интегрирование по значению в конечной точке г0
включено в определение 2Е> [r(t)]. Наконец, так как а = 9 (Г) —
— 9 @) для всех траекторий, мы заменили а на j 9 dt в экспо-
о
ненте.
Заметим, что экспонента в угловом интеграле в точности ква-
квадратична по 9. Интегрирование по а и 90 равносильно интегриро-
интегрированию по конечным значениям траектории 9 (t) в дополнение

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 243
к промежуточным значениям. Поэтому интегрирование по углу
может быть выполнено точно и дает (с точностью до констант,
которые могут быть включены в меру)
где JXt обозначает произведение по всем моментам времени t.
После подстановки в (8.10) остается
Г Т 1
Gl(T)=\®[r(t)]exp U^dt^-Vir)-—)]. (8.11)
Таким образом, мы еще раз имеем радиальную задачу с эффектив-
эффективным потенциалом V (г) + /2/2г2. Теперь к этому радиальному
функциональному интегралу могут быть применены квазикласси-
квазиклассические методы гл. 5 и 6 без учета нулевых мод, так как теперь
вращательной симметрии нет. (При применении этого квазиклас-
квазиклассического метода в радиальной переменной существует дополни-
дополнительная техническая трудность, поскольку область изменения г (t)
простирается от 0 до оо, а не от —оо до +оо. Это приводит к так
называемой модификации Лангера. Мы здесь не будем обсуждать
эту трудность, поскольку она не связана с нашей основной целью—
трактовкой нулевых мод, которая уже достигнута интегрирова-
интегрированием по углу. Заинтересованные читатели могут обратиться
к работам [226, 257].)
Прежде чем оставить этот простой пример, рассмотрим послед-
последний вопрос, который касается хорошо известной неоднозначности
в упорядочении при переходе от классического гамильтониана
к квантовому гамильтониану. Выше мы преобразовывали пере-
переменные к полярным координатам непосредственно на классическом
уровне. На классическом уровне лагранжианы (8.1) и (8.2) со-
совершенно эквивалентны. Затем мы квантовали систему в форма-
формализме функционального интеграла непосредственно в полярных
координатах, что приводило к эффективному радиальному по-
потенциалу V (г) + /2/2г2. Предположим вместо этого, что мы кван-
квантуем систему в декартовых координатах. При этом лагранжиан
(8.1) приводит к уравнению Шредингера (при й = 1)
х2). (8.12)
Преобразовав с помощью г|з (г, 9) = [щ (r)/-y^r] eilQ это диффе-
дифференциальное уравнение к полярным координатам, легко убе-
убедиться, что Ui (г) подчиняется уравнению
~ "Г ilk + V <r) + - 27

244 ГЛАВА 8
Теперь центробежное слагаемое содержит дополнительную со-
составляющую —1/8г2 по сравнению с тем слагаемым, к которому
приводит полярный интеграл по траекториям в (8.11). Тот же
дополнительный член —1/8г2 можно также получить в формализме
функционального интеграла, если начать с интеграла по траек-
траекториям в декартовых координатах и затем заменить переменные
на полярные координаты, обращая внимание на сохранение пра-
правильного порядка бесконечномалых (детали см. в работах [118,
292]). Рассуждая с большей общностью, предположим, что мы
заменяем гамильтониан Я в (8.3) на гамильтониан
В = 4"Р' + /2/2''2 + У М + [А-. /(г)], (8. И)
где / (г) — некоторая функция г. На классическом уровне Н
тождественно Н, так как рг коммутирует с г. В квантовой теории,
когда [г, pr] = ih, Я отличается от Я на —ifif (r). Такие неодно-
неоднозначности при упорядочении указывают на то, что может суще-
существовать несколько квантовых гамильтонианов, соответствующих
одному и тому же классическому пределу. Для данной физической
системы, для которой предлагается квантовая теория, правильный
выбор определяется, конечно, тем, какой квантовый гамильто-
гамильтониан согласуется с экспериментальными данными для этой си-
системы. Правильной формой часто оказывается «стандартная де-
декартова форма»
в некоторых декартовых координатах \xi\. В этом случае, если
тот же гамильтониан требуется записать в каких-то других ко-
координатах \%i\, то лапласиан £;'d2/d;cf в гамильтониане (8.15)
переписывается через \\%\. Это приводит к единственному кванто-
квантовому гамильтониану в терминах \%i\. Переход от (8.12) к (8.13) —
пример такой процедуры (см. также [301 ]).
Это завершает наше обсуждение способов рассмотрения про-
проблем, обусловленных непрерывной симметрией и следующими из
нее нулевыми модами, на простом примере (8.1). Мы подчеркнули
существенные особенности этого примера, хотя они и очевидны,
так как в более сложном контексте полевых теорий мы будем
использовать аналогичные критерии при реализации правильного
подхода к нулевым модам. Роль переменной 9 там будут играть
коллективные координаты. В примере (8.1) элементарные геоме-
геометрические представления позволили немедленно идентифициро-
идентифицировать г и 9 как правильные координаты для решения проблемы
нулевых мод. Кроме того, (г, 9) явно заданы через исходные
координаты хх и хг. В некоторых теоретико-полевых случаях не-

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 245
обходимые коллективные координаты также могут быть написаны
явно как функционалы исходных полевых переменных: пример
приводится в следующем разделе. В более общей ситуации кол-
коллективные координаты должны вводиться неявным образом, как
это обсуждается в разд. 8.3 и 8.4.
8.2. Пример явной коллективной координаты
Рассмотрим теперь теоретико-полевой метод [292], посред-
посредством которого некоторые нулевые моды можно рассматривать
с помощью непосредственного обобщения процедуры, исполь-
использованной в разд. 8.1, т. е. с помощью нового набора координат,
явно определенных в терминах исходных полевых переменных.
Для иллюстрации этого метода рассмотрим комплексное скалярное
поле ф (х, t), управляемое плотностью лагранжиана
2(х, /) = ± (д^фУ (д»ф) ~-и(\ф|). (8.16)
До сих пор, пока U (| ф |) сохраняет перенормируемость теории
и допускает необходимые классические решения, используемые
ниже, явный вид 0 (| ф |) и размерность пространства могут
оставаться произвольными. Ясно, что этот лагранжиан инвариан-
инвариантен относительно действия глобальной симметрии U A):
ф(х,Ц-+е«*ф(х,(), (8.17)
где а не зависит от пространства-времени. Классическое уравне-
уравнение Лагранжа—Эйлера можно записать в виде
W-m-b <8Л8>
Для любого данного классического решения фка (х, t) уравнения
(8.18), как статического, так и зависящего от времени, в силу
симметрии U A) функция е'афкл (х, t) для любого действитель-
действительного а также является решением с той же энергией. Следова-
Следовательно, в окрестности любого классического решения будут об-
обсуждавшиеся выше нулевые моды флуктуации и связанные с ними
трудности. (Конечно, система (8.16) также инвариантна относи-
относительно действия пространственных трансляций и вращений. Это
приводит к появлению некоторых других нулевых мод. В дальней-
дальнейшем мы вернемся к рассмотрению этих мод, а пока рассмотрим
только нулевую моду, связанную с симметрией U A).)
Чтобы преодолеть эти трудности, сначала заменим перемен-
переменные на полярные поля р (х, t) и 9 (х, t), определенные формулой
ф(х, 0 = р(х, *)exp[i8(x, /)]. (8.19)

246 "ТГЛАВА 8
В терминах этих полярных полей лагранжиан (8.16) и полевое
уравнение (8.18) принимают вид
2 (х, t) = -i- (d^pf + i- р« (c^Of - U (р), (8.20)
□ р - р (дд9J + dt//dp = 0, (8.21 а)
дц (р2 д"9) = 0. (8.216)
С однопараметрической симметрией U A) связан сохраняющийся
заряд
Сохранение Q очевидно из (8.216). Как хорошо известно, в кван-
квантовой теории оператор Q порождает преобразования симметрии
(8.17), которые в терминах полярных полей имеют вид
р(х, /)->-р(х, t), (8.23а)
9(х, f)-*-Q(x, t) + a. (8.236)
Поскольку Q сохраняется и, следовательно, коммутирует с га-
гамильтонианом, мы можем искать собственные значения энергии
в любом заданном секторе с зарядом q. Они задаются полюсами
^тг) = i J dTe'BTGg(T), (8.24)
о
где
G, (Т) = Тг [г-'^в (Q _ 0] = J |L е-№ j д> [ро (х)] Ро (х) х
X j Ф [Йо (х)] (ро (х), 00 (х) + а | е-"»11 р0 (х), 90 (х)>. (8.25)
На последнем этапе след взят по собственным состояниям поля,
записанным в полярной форме, и для преобразования конечного
состояния по образцу (8.23) использован оператор с е{(*а. Окон-
Окончательно амплитуда перехода в (8.25) может быть записана как
теоретико-полевой интеграл по траекториям. Следовательно,
G"^ = J -щ- e'iqa J ^[р (х- t)] р(х- 9 J ^[Э (х> /)] ехр i's [р- е]Ь
(8.26)
где 1) все поля переходят из (р0 (х), 9(х)) при (=0 в (р0 (х),
90 (х) + а) при времени Т, 2) включено интегрирование по
Ро (х), 90 (х) и 3) S [р, 9 ] —действие в полярных полях, задавае-
задаваемое выражением
т
S [р, 9] = j dt j dx [-L @^J + _L p2 (д^2 + U(p)]. (8.27)

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 247
До этого момента рассмотрение было весьма непосредственным
обобщением того, что было сделано в простой задаче, рассмотрен-
рассмотренной в разд. 8.1, причем Q здесь играет ту же роль, что L там.
Но имеется одно существенное различие. В разд. 8.1 9 (t) —про-
—простая динамическая переменная, которая заменяется на 9 (t) + a
под действием однопараметрического вращения в плоскости.
Теперь же 9 (х, t) — поле, т. е. бесконечное число переменных,
по одному при каждом х. Между тем группой симметрии по-
прежнему является однопараметрическая группа U A). Поэтому
возникает желание найти некоторый подходящий набор коорди-
координат, описывающий 9 (х, t), такой, чтобы под действием преобра-
преобразования (J A) изменялась только одна из этих координат. Это
достигается использованием коэффициентов Фурье. Пусть
9 (х, t) = 2 bhn (t) exp (t-kB -x), .(8.28)
kn
где для простоты мы поместили систему в большой ящик, чтобы
волновые числа кп были дискретными. Под действием преобра-
преобразования (8.23) b0 (t) -»■ b0 (t) + а, в то время как все другие
коэффициенты Фурье с ненулевыми волновыми числами не ме-
меняются. Другими словами, если мы запишем (8.28) в виде
9(х, t) = bo(t) + Q(x, t),
где
9(х, t)= 2 Ьк (/) ехр (&„-х), (8.29)
то под действием преобразования (8.23)
Ьо (/) -* Ьо (/) + а, 9 (х, t) -> 9 (х, /), р (х, /) -»»р (х, /). (8.30)
К этому моменту должно быть ясно, что b0 (t) — именно та пере-
переменная, которая играет ту же роль, что и 0 (/) в разд. 8.1. Она
и только она меняется под действием преобразований симметрии
U A). Остальные переменные 9 (х, /) и р (х, /) (их бесконечно
много) не изменяются и в совокупности играют ту же роль, что
и г (t) в разд. 8.1. Переменная Ьо может быть названа «коллектив-
«коллективной координатой», связанной с рассматриваемой симметрией U A).
Это коллективная координата в том смысле, что она зависит от
исходного поля ф (х, t) для всех х. Действительно, Ьо может быть
явно записана через ф (х, t) при обращении ряда Фурье (8.28):
b0 (t) = (объем) J 9 (х, t) dx = (объем)'1 j dx Im (In <j> (x, t)). (8.31)
Записанное в переменных b0 (() и «оставшихся» переменных 9 (х, t)
л р (х, t) действие S [р, 9] (8.27) принимает вид
т
S [Ьо, р, 9] = J dt [ i- [60 (t)f A (t) + 6о @ Во @ j + S' [р, 9], (8.32)

248 ГЛАВА 8
где
т
S' [р, 9]]= J dt j dx I -L {d^f - U (p) + \ p2 (du8> I, (8.33)
A(t) = Jp2(x, t)dx, (8.34a)
B{t) = jpa(x, t)Q(x, ()dx. (8.346)
Запишем функциональный интеграл (8.26) через b0, p и 9 в виде
С, (Г) = J 0 [р (х, 0] Р (х, t) j ^ [9 (х, *)] ^ exp (tS' [р, 9]) j dfc0 @) х
Х J-^F J ^[&o@]exp [i (j [4-Л(Ово(О + 5(/)бо(О]л) - t^a],-
(8.35)
где J — якобиан, обусловленный заменой переменных. Все траек-
траектории b0 (t) идут из Ьо @) в Ьо (Т) = Ьо @) + а. Отсюда а =
= J 60 dt. Мы замечаем, что интеграл по всем траекториям b0 (t),
о
включая конечные точки, идентичен по форме интегралу по углу
в (8.10). Подынтегральное выражение также квадратично по й0,
и интегрирование может быть выполнено точно совершенно так
же, как при переходе от (8.10) к (8.11). Ясно, что результат имеет
вид
(8.36)
Таким образом, остается функциональный интеграл по «остав-
«оставшимся переменным» р (х, I) и 6 (х, t) с эффективным действием
в экспоненте
[q-i
5эфф [р, 8] = S' [р, 9] - [ dt [q Iff]> ее [ dtL^ [p, 9], (8.37)
-де
^фф [р, ё] ее f dx \\ {d^f - и (p) +_-!■ p2 (aue)»l -'
2 j pa dx
(8.38)
К функциональному интегралу (8.36) может быть применен
клазиклассический метод. Так как U (^-преобразование остав-
оставляет р (х, t) и 9 (х, t) без изменений, связанная с симметрией U A)

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 249
проблема нулевой моды больше появляться не будет. Эта мода
эффективно устранена посредством разделения переменных и
интегрирования по переменной b0 (t).
С помощью подходящей замены переменных мы в принципе
выполнили нашу задачу по учету нулевой моды, связанной с сим-
симметрией U A). На практике вычисление функционального инте-
интеграла (8.36) является трудным делом даже в приближении ста-
стационарной фазы вследствие сложности подынтегрального выра-
выражения в (8.36). Но, как мы отмечали в гл. 5 и 6, главный вклад
в уровни энергии дают сами классические решения, т.е. экстре-
экстремумы экспоненты S^ [p, 9]. Очень трудно вычислить из функ-
функционального интеграла (8.36) только квантовые поправки, обус-
обусловленные флуктуациями. Выясним, можем ли мы найти какие-
либо экстремумы 5Эфф [р, 9], решая уравнения
(б/бр(х, Q)Se(M,[p, 9]= 0, F/66 (х, 0MэфФ[р, 8] = 0. (8.39а, б)
Заданное в (8.37), (8.38) действие 5эфф [р, 91 является настолько
сложным, что представляется трудным даже решение классиче-
классических уравнений (8.39 а, б). Ясно, что они являются_нелинейными
интегродифференциальными уравнениями для р и 9. Тем не ме-
менее, возможно, что удастся найти одно нетривиальное решение,
которое к тому же имеет весьма привлекательную физическую
интерпретацию, с помощью ^следующей процедуры.
Можно проверить, что 9 (х, t) = 0 есть решение уравнения
(8.396), если р не зависит от времени. В этом случае уравнение
(8.39а) сводится к
-V-p (ж) + -g- - -^у^р-Р W = 0. (8.40)
Это уравнение по-прежнему имеет интегродифференциальную
форму. Но его решение может быть связано с некоторыми реше-
решениями исходных полевых уравнений (8.18) или (8.21). Рассмотрим
периодическое решение полевых уравнений вида
*(х, /) = pv(x)e-<*. (8.41)
Из (8.21а) мы видим, что pv (x) должно удовлетворять уравнению
-V3Pv (х) + (■^L)pv - v2Pv (x) = 0. (8.42)
Тогда ясно, что решение уравнения (8.42) pv (x) будет также
удовлетворять уравнению (8.40), если заряд q в (8.40) связан
с частотой v соотношением
q=v\pl(x)dx. (8.43)
Другими словами, решив уравнение (8.42) относительно возмож-
возможных значений v, мы разрешим (8.40) относительно собственных

250 ГЛАВА 8
значений q. Еще более важно, что зависящее от времени решение
(при 9 (х, t) = 0) эффективной задачи (8.39) связано с вращаю-
вращающимся решением (8.41) исходных полевых уравнений (8.21).
Вращение имеет место во внутреннем пространстве (фазы ф),
в котором действуетfрассматриваемая симметрия U A). Более
того, соотношение (8.43) показывает, что q, которое введено
в (8.25) в качестве заряда на квантовом уровне, должно быть
равно заряду классического решения (8.41). Короче, наш квази-
квазиклассический метод ставит в соответствие уровням энергии в за-
заданном зарядовом секторе классические решения, обладающие
тем же зарядом. С интуитивной точки зрения это весьма удовлетво-
удовлетворительно. Очевидно также, что в целом весь наш вывод весьма
близок простому примеру, рассмотренному в разд. 8.1._ Уравне-
Уравнения (8.40)—(8.43) соответствуют специальному случаю 9 (х, /) =
= 0. Конечно, уравнения (8.39) в общем случае имеют также
решения, в которых 9 (х, t) нетривиально. Эти решения очень
трудно вычислить, но для данного q решения с 9 (х, t) = 0 обла-
обладают наинизшей энергией (см. [228]).
В приведенном обсуждении предполагается, что локализован-
локализованные решения с конечной энергией уравнения (8.42) существуют
и могут быть получены. Но уравнение (8.42) по сложности не
сравнимо с (8.39) или (8.40). Оно представляет собой статическое
нелинейное волновое уравнение для действительного поля р (х)
с потенциалом £/афф (р) = U (р) —1/2 v2p2- Напомним, что та-
такие уравнения мы рассматривали в гл. 2 и 3. Без потери общности
можно считать, что U (| ф |) равно нулю в абсолютных минимумах.
Для того чтобы заряд (8.43) был конечен, поле р (х) = | ф (х) |
должно исчезать на пространственной границе. В то же время,
для того чтобы энергия решения
была конечна, U (| ф |) также должно быть равно нулю (т. е. до-
достигать своего абсолютного минимума) на пространственной
границе. Следовательно, U (| ф |) должно иметь свой абсолютный
минимум при | ф | = 0. Это означает, что рассматриваемая заря-
зарядовая симметрия не должна быть спонтанно нарушенной. Это
согласуется с требованием, чтобы оператор заряда был конеч-
конечным. Все это также означает, что солитонное решение уравнения
(8.42), которое мы ищем, на языке гл. 2 и 3 является нетопологи-
нетопологическим. Существование, устойчивость и другие свойства заряжен-
заряженных нетопологических солитонов в таких системах очень подробно
исследовали Ли с соавторами [142—145, 228]. В качестве при-
примера рассмотрим A + 1)-мерную задачу с потенциалом
+ c|*|a, (8.44)

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 251
где а, Ь и с — действительные положительные параметры, удов-
удовлетворяющие неравенству Ьг < 4ас. В A + 1) измерениях эта
теория перенормируема. В то же время если Ь* < 4ас, то U (| </> |)
имеет невырожденный абсолютный минимум при | ф \ = 0. Урав-
Уравнение (8.42) сводится к
cPp/dx* = (d/dp)UBw>(p), (8.45)
где
^эФФ = U(p)-±- р V = (а - ±- v») р2 - V + ф6. (8.46)
Рис. 17. Схематическое изображение —U (р)
и —^эфф (Р) Для некоторого v> vMHH. Здесь
U (р), определенное (8.44), — исходная по-
потенциальная функция в лагранжиане этой по-
полевой теории, а £/эфф (р) = U (р) — V2v2p2 —
эффективный потенциал'в дифференциальном
уравнении (8.45). Использованы некоторые
типичные значения параметров а,'Ь,'с. В ана-
аналоге (8.45) соответствующая частица описы-
описывается координатой р (х) и находится в потен-
потенциале 1-иэфф (р)]. ^ .... ,
Для значений v, больших,^чем некоторое vMhh. но меньших,
чем у^2а, иэфф (р) приобретает более низколежащий минимум
при некотором ненулевом р (рис. 17). В этом случае существует
некоторое нетопологическое решение уравнения (8.45). Чтобы по-
показать это, привлечем квантовомеханическую аналогию, исполь-
использованную в гл. 2. Уравнение (8.45) представляет собой уравнение
Ньютона для частицы в потенциале I— £/9(M,], где х играет роль
времени. Из рис. 17 ясно, что эта частица-аналог может начать
движение из точки р = 0 с произвольно малой скоростью при
большом отрицательном времени (х = —оо), прийти в р = р0
при х = 0 и вернуться в р = 0 при х = +оо. Явное решение
р (х) может быть получено с помощью интегрирования (8.45),
как это рассмотрено в гл. 2. Заметим, что на языке гл. 2 это ре-
решение типа С.
Внимание читателя может привлечь сделанное в гл. 2 замеча-
замечание, что статические нетопологические солитоны не могут суще-
существовать в A + 1) измерениях для одного действительного ска-
скалярного поля. Тем не менее уравнение (8.45), по-видимому, имеет
такой солитон. Причина состоит в том, что (8.45) на самом деле

252 ГЛАВА
не является статическим уравнением некоторого действительного
скалярного поля. Исходное поле Ф (х, t) есть комплексное скаляр-
скалярное поле, и решение, которое мы рассматриваем, имея форму
(8.41), на самом деле зависит от времени. Только модуль р (х)
является статическим и подчиняется уравнению (8.45).
Поскольку скалярные заряженные решения зависят от времени,
теорему вириала из разд. 3.2 применять нельзя. Нетопологиче-
Нетопологические солитонные решения уравнения (8.42) могут также суще-
существовать в более чем двух измерениях при подходящим образом
выбранных U (р), хотя их трудно получить в точной аналитиче-
аналитической форме. Детальное обсуждение вопросов существования та-
таких решений и их приблизительной формы приводится в цитиро-
цитированных выше работах Ли с соавторами, которые также рассматри-
рассматривают нетопологические солитоны для калибровочных полевых
систем в C+1) измерениях.
Возвращаясь к нашему квазиклассическому методу, можно
сделать два технических замечания.
1. В контексте простого примера разд. 8.1 мы отметили, что
если бы та система была первоначально проквантована в декарто-
декартовых координатах, а затем преобразована к полярным координатам,
то множитель Р/2г2 в эффективном потенциале заменился бы на
{I2 — V4)/2r2. Более сложным образом подобный эффект проявился
бы в настоящем случае, если бы мы записали функциональный
интеграл для Gq (Т) через «декартовы» поля Re Ф и Im Ф, а по-
потом перешли бы к р и Э (детали см. в работе [292]). Эти различия
не изменяют уровни энергии в первом порядке, а влияют лишь
на квантовые поправки.
2. Если бы система содержала другие поля кроме Ф (х, t),
то действие и полевые уравнения были бы более сложными. Но
основная процедура учета нулевой моды U A) осталась бы той
же самой. На дополнительные поля не влияет преобразование
симметрии (8.17), и они присоединились бы к р (х, t) и 0 (х, t) как
часть «оставшихся» переменных. Коллективная координата Ьо
может быть по-прежнему определена с помощью (8.31) и точно
проинтегрирована. В некоторых из цитированных выше работ
в добавление к комплексному полю Ф (х, t) включается дополни-
дополнительное действительное скалярное поле 0 (x, t). В нашем обсуж-
обсуждении мы опустили такие усложнения.
В заключение отметим, что описанный выше метод учета
U A)-нулевой моды привлекателен тем, что он предлагает прямое
обобщение простых физических идей, введенных в разд. 8.1. Кол-
Коллективная координата b0 (t) может быть определена в явном виде
как функционал от Ф (х, t) и точно проинтегрирована в функцио-
функциональном интеграле. Остающаяся задача обладает дополнитель-
дополнительным «центробежным» слагаемым, связанным с внутренними вра-
вращениями (последний член в (8.38)). Входящие сюда классические

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 253
решения были просто вращающимися решениями, обладающими
таким же .зарядом q, как и квантовые состояния. Этот метод мо-
может быть распространен также в некоторых случаях на неабе-
леву глобальную внутреннюю симметрию (см. [292]).
Большим недостатком этого метода, помимо громоздкости
функционального интеграла (8.36), является то, что он не может
быть применен ко всем типам нулевых мод, в частности к трансля-
трансляционным модам. Напомним, что даже для рассматриваемой здесь
модели вследствие трансляционной симметрии возникают допол-
дополнительные нулевые моды, которые мы не учитывали. Трудность
состоит в том, что неизвестно (по крайней мере мы не знаем),
как в явном виде определить трансляционную коллективную коор-
координату, т. е. определить такое X = X [ф (х) ], чтобы при варьи-
варьировании X можно было отличить некоторую данную конфигура-
конфигурацию ф (х) от ее сдвинутых конфигураций без изменения «формы»
поля. Для трансляционных симметрии коллективные координаты
должны вводиться неявным образом. Это описывается в последу-
последующих разделах.
8.3. Неявные коллективные координаты
Крист и Ли [81 ] разработали метод квантования солитонов
с использованием канонической гамильтоновой процедуры. Их
работа дополняет и объединяет результаты, описанные в преды-
предыдущих главах с использованием формализма функционального
интеграла. Этот метод также вводит коллективные координаты —
столько, сколько нужно для замены нулевых мод, обусловленных
непрерывными симметриями исследуемой модели. В этом методе
коллективные координаты не записываются явно как функцио-
функционалы от исходных полевых переменных. Они вводятся
неявно, но по-прежнему приводят к последовательному и изящ-
изящному квазиклассическому разложению.
Для сохранения простоты изложения мы опишем метод Кри-
ста—Ли в применении к моделям только с одной нулевой модой,
т. е. к теориям действительного скалярного поля в A + 1) изме-
измерениях, где единственной непрерывной симметрией, приводящей
к нулевой моде, является симметрия, обусловленная простран-
пространственными трансляциями. Формулируемый ниже метод рассмотре-
рассмотрения трансляционной нулевой моды был также независимо пред-
предложен Томбулисом [335] на несколько другом языке. Рассмотрим
стандартный лагранжиан для двумерного действительного ска-
скалярного поля, записанный в виде (см. уравнения F.109)—F.112))
= "F" J [т ^ ~ т
и #)]dx

254 ГЛАВА 8
через поле ф (х, t) с соответствующим образом выбранным масшта-
масштабом. Точкой и штрихом обозначены, как обычно, производные
по t и х соответственно. Преимущество записи лагранжиана
в виде (8.47) состоит в том, что в последующих вычислениях легко
следить за степенями параметра связи g, так как g2 появляется
только как общий множитель в (8.47). Кроме того, как отмечено
в конце гл. 6, степени % и g2 появляются совершенно одинаковым
образом. Поэтому нет необходимости следить за первыми, и мы
положим % = 1.
Вспомним сначала некоторые основные свойства системы
(8.47), используя рассмотрение, проведенное в предыдущих гла-
главах. Если U (ф) имеет вырожденные абсолютные минимумы, то
существует классическое статическое солитонное решение ^>кл (х) =
= а (х—X), удовлетворяющее условиям
o" + dU(o)/do=0, (8.48)
±\o'f = U{e). (8.49)
Его классическая энергия (масса классического солитона) равна
Мкл = V [а] = -1- J [ j- (o'f + U(o)]dx=±-\ (a'J dx = A/g2.
(8.50)
В силу трансляционной инвариантности а (х — X) — классиче-
классическое статическое решение для всех действительных X, но его
энергия A/g2 не зависит от X. Приведенная в гл. 5 процедура
квантования солитонов, не совсем отвечающая предъявляемым
требованиям, сводится к разложению
оо
f(x,() = o(x-X) + g%cn @ Лп (х - X), (8.51)
о
где цп (х — X) — набор ортонормированных собственных функ-
функций в уравнении
Напомним, что мы явно выписываем всю зависимость от g2. Все
величины ст (х —X), л\п (х —X), а>%, А и сп (t) не зависят от g,
т. е. порядка g°. Поэтому, когда лагранжиан (8.47) записывается
в координатах сп (t) вместо ф (х, t), он принимает вид

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 255
В порядке g° это не что иное, как совокупность гармонических
осцилляторов, и уровни энергии в солитонном секторе равны
= -р + 2 (Nn + т) w* + ° ^). (8-54)
п=0
Это главный результат, полученный в гл. 5. Неадекватность этой
процедуры состоит в том, что нормированная мода с п = 0, опре-
определяемая через
щ(х-Х) = AЦ/А)а'(х-Х), (8.55)
имеет нулевую частоту, что приводит к потенциальным расхо-
димостям в членах высших порядков в выражениях типа (8.54).
До сих пор мы лишь дали краткую сводку результатов, получен-
полученных в предыдущих главах. Теперь мы займемся проблемой нуле-
нулевых мод в рамках канонического гамильтонова формализма. Это
осуществляется с помощью преобразования переменной X, кото-
которая определяет положение солитона, в динамическую координату,
заменяющую координату нулевой моды с0. Это означает, что
вместо (8.51) мы разлагаем ф (х, t) в ряд в виде
ОО
<f>(x,t) = o(x-X @) + g I>qn @ Цп (х - X @)• (8.56)
Функции сг и цп те же, что и в (8.51), но в (8.56) опущено слагае-
слагаемое с п = 0. X(t) называется коллективной координатой, связан-
связанной с трансляционной симметрией. Стратегия состоит в том, чтобы
использовать X (t) и qn (t) (n > 0) как координаты системы
вместо сп (t) в (8.51). Ясно, что
<t> (x, 0 = (д/dt) 4>(x,f) = -[o' + g£ qn4n )X + g 2] ёпЧп- (8.57)
\ i / i
Для описания новых координат будем использовать компактное
обозначение ип, п = 0, 1, ..., оо, т. е. положим
uo(t) = X(t), un(t) = qn(t) для п^>0. (8.58)
Тогда слагаемое кинетической энергии в лагранжиане (8.47)
принимает вид
оо
= ^ J dx D У ) = -1 £ «АЯ-- (8-59)
'. /=-0

256 глава
где Di} — симметричная матрица, элементами которой (см. (8.57))
являются
Аи = -i- [ dx\ a' + g V qmr\'m , (8.60a)
s V i /
/
Don (п ф 0) = - -L J dx I а'
Dnm(n, m^0) = 8nm. (8.60b)
При этом мы использовали ортонормированность т)„ и также
ортогональность т)„ (n ^ 0) к % и поэтому к сг' в силу (8.55).
Все функции сг', ц'п и т]„ зависят от аргумента (х —X (t)). Но,
так как элементы D^- в (8.60) являются трансляционно-инвариант-
ными интегралами по х, то Dtj не зависят от X (t). Они являются
функциями только от \qn\- Аналогично потенциальная энергия
в лагранжиане также трансляционно-инвариантна и не зависит
от X (t). Мы можем записать ее в виде
V W = J dx [4-(fJ + U($)] = У(Ы)--^- + Y^Wn + O(g),
(8.61)
где использовано (8.56), (8.48) и (8.52). Слагаемое 0 (\/g) отсут-
отсутствует, поскольку а (х — X (t)) удовлетворяет (8.48). Поэтому
полный лагранжиан в переменных ut (i = 0, 1, ..., оо) имеет вид
2 йРч(Ы)й,-У(Ы). (8.62)
С. 1=0
Чтобы найти гамильтониан, будем искать канонические импульсы
яг (г = 0, 1, ..., оо), сопряженные координатам щ. Они равны
я* = dL/dut = Duuj. (8.63)
Следовательно, классический гамильтониан определяется фор-
формулой
Я = £ щщ -L= Yi-T^ (^Ь nJ + V (\4n\)- (8-64)
0 С, f=0

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 257
Для матричных элементов Dt], заданных в (8.60) с помощью
алгебраических преобразований, можно убедиться, что
(D-1)oo=l/D, {D~l)on = -DJD, n^O,
(D-\m = 8пт + DonDoJD, n, m ф 0, (8.65)
где D —детерминант матрицы Dtj, задаваемый выражением
D = Det Dt, = Doo + S D20n- (8.66)
Подставляя (8.60), получаем
2
(8-67)
Если мы разложим функцию (^ГУтЧт (х 4- X)) по полному
базисному набору цп (х — X), включшедему тH (х X)
= Л-'/2сг' (х — X), то (8.67) сведется
^ T (F ) (8'68)
где
a = Jt]0(jc —X) I 2 </„т^ (х - X)) dx. (8.69)
Используя детерминант D (8.68), можно подставить матричные
элементы (D)j;B (8.64), чтобы получить классический гамильто-
гамильтониан. Можно отметить следующие свойства этой процедуры.
1. Переменная нулевой моды отсутствует по той простой при-
причине, что она исключена с самого начала в разложении (8.56).
Но мы должны убедиться, что координата X (t), которая появ-
появляется вместо нулевой моды, не приводит к подобным же расходи-
мостям в старших порядках.
2. Как отмечалось выше, матричные элементы Dtj, а также
потенциальная энергия V—трансляционно-инвариантные инте-
интегралы и поэтому не зависят от X (t). Поэтому и0 (t) = X (t) всегда
отсутствует в гамильтониане (8.64). В гамильтониан входит
только сопряженный импульс я0. Это точный результат, не огра-
ограниченный каким-либо заданным порядком по g2. Следовательно,
9 Раджараман Р.

258 глава 8
сопряженный импульс я0 должен сохраняться во времени. Дей-
Действительно, я0 равен полному сохраняющемуся импульсу Р.
Мы имеем
= D00X + J] DOnqn = rto, (8.70)
где использованы (8.60) и (8.63). Поскольку коллективная коорди-
координата X (t) имеет смысл пространственного положения поля,
представляется весьма удовлетворительным, что сопряженный
ей импульс оказывается полным импульсом системы.
3. Используя равенство я0 = Р и (8.65), можно записать
классический гамильтониан (8.64) в виде
ОО
n=l n, m=l
(8.71)
4. Коллективная координата X (t) определена неявным обра-
образом с помощью (8.56), а не в явном виде как функционал ф (х, t).
Но это не мешает записать лагранжиан через X (t) и «оставшиеся»
координаты qn (t), n > 0.
До настоящего момента наше рассмотрение оставалось на
классическом уровне. Мы лишь заменили переменные ф (х, t)
на \Х (t), qn (t)\, избавившись тем самым от нулевой моды. В сле-
следующем разделе мы выполним квантование системы в этих пере-
переменных для получения уровней энергии в солитонном секторе.
8.4. Квантование солитонов с помощью канонических
операторных методов
Выполним квантование одномерной скалярной полевой теории
предыдущего раздела в координатах ип = (X; qn, n > 0) и их
канонических импульсах лп (Р; лп, п > 0). Квантование осуще-
осуществляется с помощью превращения ип и я„ в операторы, подчи-
подчиняющиеся одновременным каноническим коммутационным прави-
правилам (при Й = 1)
[ип @, пт (t)] = i8nm, [я„, ят] = [ип, ит] = 0. (8.72)

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 259
Напомним, что в исходных полевых переменных ф (х, t) в (8.47)
канонический коммутатор был бы обычным объектом
[ф (х, t), я {у, t)] = [ф (х, t), A/г«) ф (у, t)] = /б (х - у). (8.73)
Можно проверить, что два набора коммутаторов (8.72) и (8.73)
совместны. Как ф (х, t), так и ф (у, t) выражаются через ип (t)
и я„ (I) при помощи уравнений (8.56), (8.57) и выражения, обрат-
обратного (8.63). После простых алгебраических преобразований под-
подстановка коммутатора (8.72) приводит к (8.73). Эта совместность
важна, поскольку переменные ф (х, t) будут использоваться обыч-
обычным образом в вакуумном секторе, в то время как в солитонном
секторе мы будем использовать переменные ип. Классический
гамильтониан в переменных ип и я„ задан в (8.64) или в (8.71).
В квантовой теории должна быть разрешена неоднозначность
упорядочения в этом гамильтониане. Напомним, что в кинетиче-
кинетических членах в (8.64) множители (D'1)^ зависят от qn (хотя не за-
зависят от X) и не коммутируют с я„ при п > 0. Эти множители
должны быть упорядочены в некоторой конкретной последова-
последовательности. Вспомним короткое введение в проблему упорядочения
в конце разд. 8.1. Мы будем решать проблему, следуя плану,
предложенному там. Мы выберем квантовый гамильтониан в «де-
«декартовой» форме (в смысле, использованном в разд. 8.1) в исход-
исходных полевых переменных ф (х, t). Это означает, что мы конкрети-
конкретизируем квантовый гамильтониан в шредингеровском представле-
представлении следующим образом:
Н = 4- J (" (х)J dx + У [ф (х)], (8.74)
где я (х) —оператор импульса, сопряженный ф (х) ив соответ-
соответствии с коммутационным правилом (8.73) определяемый в шре-
шредингеровском представлении как функциональная производная
я (х) = —гб/б [ф(х)]. (8.75)
Это задает конкретную форму квантового гамильтониана. Напом-
Напомним также, что этот гамильтониан используется при стандартных
вычислениях в вакуумном секторе. Переход от переменных ф (х)
к переменным ип теперь может быть выполнен без какой-либо
неоднозначности с помощью превращения (функционального)
дифференциального оператора (8.75) в оператор, содержащий ип,
согласно стандартным правилам вычислений. Напомним, что
если бы имелся конечный набор переменных аг, i = 1, ..., N, то
лапласиан Si д2/да2с, записанный через другой набор коорди-
координат §с, имел бы вид
, /=1

260 ГЛАВА 8
где
N
/о 77 \
(8-77a)
В = Det flw. (8.776)
Нам следует обобщить это соотношение на бесконечное число
переменных, когда ф (х) для всех х заменяет щ, а ип заменяют
Рг. В этом случае матрица Btj имеет вид
дФ (х)
ШГ' ( }
Необходимые производные немедленно получаются из (8.56),
(8.58) и дают простой результат
Bti = Du, (8.79)
где Dtj —матрица, определенная в (8.60). Таким образом, га-
гамильтониан (8.74) сводится к
н==-T.t ■vwir(D'luVW-^ + v^)- (8-80)
п, т=0
В соответствии с коммутатором (8.72) мы положим
—id/dun = nn. (8.81)
Тогда, разделяя лп и ип на (Р; лп, п > 0) и (X; qn, n > 0) со-
соответственно и используя (8.65) для (D)^, имеем
1
(8.82)
Напомним, что Р коммутирует со всеми остальными слагаемыми,
поскольку они не зависят от X. Выражение (8.82) задает упоря-
упорядоченный квантовый гамильтониан в желаемых переменных.
Упорядочение осуществлялось посредством специального выбора,
но до сих пор не делалось никаких приближений, квазикласси-
квазиклассических или каких-либо других. Ясно, что в классическом пределе,
когда упорядочение не играет роли, (8.82) сводится к класси-
классическому гамильтониану (8.71). Далее вспомним, что импульс Р,
сопряженный% к коллективной координате X, является также
сохраняющимся полным импульсом и коммутирует с Н. Поэтому;
мы можем выбрать состояния, являющиеся собственными одно-
одновременно и для Я, и для Р. Начнем с собственного состояния Р =

КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ МЕТОДЫ 261
= 0, т. е. рассмотрим уровни энергии в системе центра масс.
Тогда гамильтониан сводится к
=0)=77П 2 nnUnmVD + ^^.\Km + V[\qn\]. (8.83)
2
п, т=\
Это выражение по-прежнему является точным в системе коорди-
координат Р = 0. Теперь начинается квазиклассическое приближение,
которое, как объяснялось в конце гл. 6, по существу является
разложением по степеням g. Рассмотрим зависимость от g различ-
различных слагаемых в (8.83). Главный член в D выражения (8.68)
есть A/g2, где А, задаваемое (8.50), есть с-число и коммутирует
с лп. Все DOn (n ф 0) не зависят от g. Потенциал V (\qn\) разло-
разложен в ряд в (8.61). Используя все это, мы можем определить
главные члены (О A/g2) и О (g°)) в Я. Ясно, что
Я(Р=о) = Яо + Я1( (8.84)
где
ф 2 $4(8-85)
а Нъ содержащее все остальные слагаемые в Я(р=0). порядка g
или выше. Квазиклассический метод может рассматриваться как
стандартная теория возмущений по степеням Hlt используя Но
как невозмущенный гамильтониан.
Щ В порядке g° можно пренебречь Ях; в этом случае уровни
энергии являются собственными значениями Яо. Тогда ясно, что
эти уровни имеют вид
что в точности согласуется до порядка О (g°) с результатом,
получаемым методом гл. 5 (положив со0 = 0 в (8.54)), где не пред-
предпринималось никаких специальных мер для учета нулевой моды.
Такое совпадение было обещано в гл. 5. Но если процедура гл. 5
должна приводить в высших порядках к проблемам с обраща-
обращающимися в нуль знаменателями, поскольку формализм содержит
нулевую моду, здесь же таких проблем нет. Поправки высших
порядков могут быть найдены при применении стандартной тео-
теории возмущений по степеням Н1. На практике это немного уто-
утомительно вследствие довольно сложного выражения для Н1 (я„,
qn), содержащегося в (8.83)—(8.85), но проблемы нулевых мод не
возникает, поскольку невозмущенный гамильтониан Яо (8.85)
содержит только ненулевые частоты. Единственный вклад коорди-
координаты X, которая заменяет нулевую моду, состоит в том, что она

262 ГЛАВА 8
вводит в гамильтониан зависимость от импульса, как показано
в (8.82).
Обратим внимание, что, хотя этот метод коллективных коорди-
координат отличен от методов, описанных в разд. 8.1 и 8.2, физический
смысл остается тем же. В рассмотренных там случаях может быть
найден эффективный гамильтониан или лагранжиан ((8.3)
в разд. 8.1 и (8.38) для задачи разд. 8.2), в которые коллективная
координата (Э в разд. 8.1 и Ьо в разд. 8.2) не входит. Единственный
вклад коллективной координаты состоял в том, что эффективные
лагранжианы содержали слагаемые, которые зависели от соот-
соответствующего сопряженного импульса (/ и q соответственно)
в квадратичной форме. Аналогично гамильтониан (8.82) не зави-
зависит от X, а только от оставшихся координат qn. Вклад X состоит
в добавлении к гамильтониану слагаемых квадратичной формы по
сопряженному импульсу Р.
Мы обсудили собственные значения энергии в системе Р = 0.
Чтобы получить спектр энергии для некоторого значения Р Ф 0,
в принципе нет необходимости возвращаться к полному гамиль-
гамильтониану (8.82). Можно просто привлечь лоренцеву инвариант-
инвариантность: для любого данного уровня энергии EiN > в системе покоя
имеется уровень у^Р2 ~\- Ehi \ для каждого ненулевого им-
импульса Р.
Мы описали лишь упрощенный вариант формализма Кри-
ста—Ли, который в полном виде применим для произвольного
числа измерений и может включать столько коллективных коор-
координат, сколько нужно для правильного учета всех непрерывных
симметрии данной проблемы, пространственных и внутренних.
В этом более общем случае такой подход осуществляется по тому же
плану, что и в йашем упрощенном варианте. Для некоторой задан-
заданной системы полей фх (х, t), ф2 (х, t), ... в произвольном числе
измерений (в совокупности обозначаемых ф(х, /)), на которой
задано действие некоторого набора непрерывных симметрии, клас-
классический солитон в общем случае имеет вид 0 (х, Хъ Х2, ■■■, XN),
где Xl XN—максимальное число произвольных параме-
параметров. Каждое решение принадлежит некоторому семейству реше-
решений, получаемых при варьировании Х{. Все семейство имеет
одинаковую энергию, так как Xt таковы, что изменение в любом
из Хг является результатом действия некоторой непрерывной
симметрии гамильтониана. Чтобы исключить нулевые моды,
связанные с такими изменениями, все эти Xt преобразуются в ди-
динамические переменные. Это означает, что производится раз-
разложение
ф (х, t) = о (х, X, ®, Х2 @, ..., XN @) +
+ g S Яп(ОЪ(х. #1 @, ■■■> Xn@). (8-87)

Коллективные координаты и канонические метоДы 263
где г\п (х, Хъ ..., XN) —полный ортонормированный набор при
условии, что все эти моды ортогональны ко всем нулевым модам.
Это означает, что они удовлетворяют условиям
i, Хъ ..., ХлО-т1го(х, X, Хл) = бтп, (8.88)
I ~dX~' ^п (х> %1 • • • Xn) dx = O для всех t = 1 N и всех п.
(8.89)
(В (8.88) и (8.89) подразумеваются скалярные произведения
между векторами г\ и о во внутреннем пространстве полей, и эти
векторы не следует смешивать с пространственной координа-
координатой х.) Динамическими переменными считаются Xt и qn. Задав
разложение (8.87), имеем
да , VI д \ дХ; , Vfi dqn
Zj(dxT 2jW7)ar lJ f(8.90)
1 = 1 \ П / . fl
что является обобщением (8.57). Тогда лагранжиан записывается
в терминах Xt, qn, Xt и qn, и непосредственно обобщаются все
остальные намеченные выше этапы рассмотрения. Дальнейшие
подробности этого общего формализма см. в работе [81], где
также приведено несколько приложений к квантованию статиче-
статических, а также зависящих от времени солитонных решений.
Наконец, метод неявных коллективных координат, описанный
в последних двух разделах в каноническом гамильтоновом форма-
формализме, может быть представлен также в формализме функцио-
функционального интеграла, в котором эти коллективные координаты
вводятся посредством некоторого варианта метода Фадцеева—
Попова [126]. Разумеется, физическое содержание в обоих форма-
формализмах одно и то же. В частности, Сакита, Жерве и Жевицки
развили эту процедуру в серии работ, в которых рассмотрены не
только квантовая энергия солитонов, но и рассеяние солитонов
(кроме уже цитированных работ этих авторов см. также [154,
155, 203]). Мы даем в приложении Б лишь беглый очерк того, как
неявная коллективная координата вводится в метод функциональ-
функционального интеграла для простого случая одномерной евклидовой
задачи.
Среди других работ, в которых рассматриваются нулевые
моды и (или) коллективные координаты, отметим работы [17,
79, 215, 249].

ГЛАВА 9
КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ
ДЛЯ ФЕРМИ-ПОЛЕЙ
9.1. Введение: грассмановы поля
До сих пор наше рассмотрение квазиклассического метода огра-
ограничивалось бозе-полями. На первый взгляд попытка перенести
эти методы на ферми-поля может показаться необоснованной.
С физической точки зрения, если классические бозе-поля имеются
в природе (например, электромагнитные волны, гравитационное
поле и т. д.), то классические ферми-поля отсутствуют по крайней
мере в том же смысле. Действительно, совокупность очень боль-
большого числа бозонов, находящихся когерентно в более или менее
одном и том же квантовом состоянии, может быть с хорошим
приближением описано классической теорией поля. Это не может
произойти с фермионами, поскольку принцип Паули запрещает
существовать в одном состоянии более чем одному фермиону.
С математической точки зрения классические бозе-поля описыт
ваются действительными (или комплексными) числами в каждой
точке пространства-времени. Вычисление таких переменных про-
производится привычными методами. В частности, функциональный
интеграл для бозонной квантовой теории поля, который представ-
представляет собой интеграл по классическим бозе-конфигурациям, яв-
является в точности пределом обычного с-числового кратного ин-
интеграла. В противоположность этому мы увидим, что хотя «клас-
«классический» предел ферми-полей может быть определен, он при-
приводит к антикоммутирующим полям. Исчисление таких объектов
сильно отличается от исчисления обычных коммутирующих пере-
переменных.
Учитывая эти глубокие различия между бозе- и ферми-полями
на языке их классического предела, можно задаться вопросом,
могут ли функциональные методы в общем и квазиклассический
метод в частности быть распространены на системы, содержащие
ферми-поля. Довольно интересно, что можно сделать и то, и
другое. Более того, многие результаты и промежуточные шаги
удивительно похожи на их аналоги для бозе-полей, за исключе-
исключением решающего знака минус. Эта глава посвящена введению
в такую технику для ферми-полей.
На первом этапе установим, что понимать под классическим
пределом квантовых ферми-полей, хотя полученное таким обра-

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 265
зом «классическое» ферми-поле не будет иметь такую же физи-
физическую значимость или экспериментальную достижимость, как
классические бозе-поля. Мы ограничимся полем Дирака со спи-
спином 1/2. Напомним, что квантовое бозе-поле, такое, как скаляр-
скалярное поле Ф (х, t), удовлетворяет одновременным коммутационным
правилам
[Ф (х, 0. (дФ/dt) (у, 0) = 1Ш (х - у), (9.1а)
' [Ф(х, /), Ф (у, 01 = КдФ/dt) (х, t), (дФ/dt) (у, 01 = 0. (9.1 б)
Неравенство нулю коммутатора (9.1а) — это то, что делает теорию
квантовомеханической. Классический предел соответствует й-> 0,
когда поле и его производные все коммутируют друг с другом и
ведут себя как обычные с-числа при любом (х, t). В противополож-
противоположность этому поле Дирака Wa (x, t) с каноническим импульсом
№а (х, t) удовлетворяет антикоммутационным соотношениям
\Wa (x, t), Wl (у, t)}+ = Йба„6 (х - у), (9.2а)
\Wa(x, t), ¥B(y, t)\+= {Wt(x, t), 4*5(у, Olf = 0. (9.26)
«Классический предел» может быть определен как ft -> 0, когда
все антикоммутаторы обращаются в нуль. В этом пределе Ч'и1?1'
не являются больше нетривиальными квантовыми операторами,
но они не являются и обычными с-числовыми полями, поскольку
антикоммутируют друг с другом вместо того, чтобы коммутиро-
коммутировать. Они могут быть названы грассмановыми полями. В качестве
прелюдии к развитию метода фермионного функционального
интеграла с использованием таких грассмановых полей пере-
перечислим некоторые основные свойства грассмановых чисел. Мы
дадим сжатую сводку некоторых свойств грассмановых алгебр,
необходимых для наших целей. Дальнейшие подробности см.,
например, в работе [37].
Рассмотрим набор из п объектов \аъ ..., ап\, подчиняющихся
соотношениям
\аь aj\+ = O для всех i, /. (9.3)
Очевидно, что \at, at\+ = 0 означает а\ = 0. Поэтому а? =
*= (a}) at = 0, а\ = 0 и так для всех более высоких степеней.
Следовательно, задав одно грассманово число ait можно по-
построить только две независимые функции от него, а именно (аг)° =
= 1 и at. Если заданы п независимых чисел аи ..., ап, то они
порождают следующие 2" линейно независимых функций:

266 ГЛАВА 9
1,
... ап.
Эти 2" независимых функций в совокупности образуют 2"-мер-
ное линейное пространство, называемое грассмановой алгеброй
Gn. Грассмановы числа at можно назвать генераторами этой ал-
алгебры. Произвольный элемент этой алгебры может быть записан
в виде
..., an) = /Ч S /ГЧ
где /°, /,
и т.д. —обычные (коммутирующие) с-числа,
/^2 (ру
Заметим, что в силу антисимметрии произведения at ... ат от-
относительно перестановки любых двух операторов а приведенное
выше разложение/ неединственно. К любому f\r)...,- всегда можно
добавить член, симметричный по двум индексам i, не изменив
/ (аъ ..., ап). Полезно рассматривать чисто «четное» и чисто
«нечетное» подмножества Gn. Элемент четного (нечетного) под-
подмножества содержит только четные (нечетные) произведения
чисел at:
S/&ад. + • • •.
(9.56)
Ясно, что четное подмножество коммутирует со всеми элемен-
элементами алгебры Gn, в то время как члены нечетного подмножества
антикоммутируют друг с другом. Это является отражением в ми-
миниатюре того факта, что четное число фермионов образует бозон,
в то время как нечетное число фермионов образует фермион.
Для грассмановых чисел развито и дифференциальное, и ин-
интегральное исчисления. Прежде чем их ввести, мы должны под-
подчеркнуть, что базисные генераторы алгебры \аъ .„, ап\ являются
дискретными объектами. Они не могут «непрерывно изменять свои
значения» ни в каком смысле в отличие, например, от действитель-
действительной переменной х, которая может принимать любое значение
от —оо до +оо. Хотя для грассмано'вых чисел будут развиты

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 267
понятия производных и интегралов с теми же обозначениями, что
и в обычном исчислении, эти производные и интегралы не имеют
обычной интерпретации в терминах бесконечно малых.
Например, производная формально определяется как
ddi/dcij = 6,; (символ Кронекера). (9.6)
Это соотношение есть просто определение символа в левой части,
и его нельзя рассматривать как отношение двух бесконечно
малых приращений. Несмотря на это, можно построить диффе-
дифференциальное исчисление, правила которого настолько близки
к правилам обычного дифференциального исчисления, насколько
это во'зможно себе представить. Например, производная от про-
произведения дается выражением
да
■p
. .. а1т) = bpil (а-ф^ . .. а,т) - Ьр,2 (а^ . . . а,т)
<9-7)
Таким образом, мы просто переставляем ар до тех пор, пока оно
не появится слева, и затем используем (9.6). Если ар вообще
отсутствует в произведении aix ... air, то производная равна
нулю. Ясно, что (9.6) задает левую производную, которую сле-
следует отличать от правой, определяемой как
К • • • ah) -k; = Ч К • • ■ 4_i) - 6*<г-1 (fl«ifl«r_,a*r) +
+ ... +(_i)r-i6pli(flji ... air). (9.8)
Действуя таким образом, можно установить согласованный набор
правил дифференциального исчисления. Но мы обратим внимание
на интегрирование, которое нам потребуется для наших фермион-
ных функциональных интегралов.
Мы начнем с одного грассманова числа а. Нам нужно опреде-
определить объект I daf (а) = I (/), где / (/) —с-число, для любой
функции / (а), принадлежащей алгебре Gv Напомним наше за-
замечание, что а нельзя рассматривать как непрерывную перемен-
переменную в том же смысле, что и Действительную переменную х. Со-
Соответственно интеграл не является «площадью под кривой / (а)»,
и нет никакого смысла в задании верхнего и нижнего пределов
в интеграле. Символ I daf (а) правильнее понимать как функцио-
функционал, который ставит в соответствие любому элементу / (а) грассма-
новой алгебры G1 с-число / (/). Но мы потребуем, чтобы он удо-
удовлетворял двум основным свойствам, которыми обладает обычный

268 ГЛАВА 9
Гоо
с-числовой интеграл J_oo dxf (x), а именно линейности и трансля-
трансляционной инвариантности. Это означает, что мы потребуем
+ b), (9.9а)
где b — другое произвольное антикоммутирующее число, и
2) J da [a/ (а) + Pg (а)] = a\ daf (а) + р J dag (a), (9.96)
где аир —произвольные с-числа. Мы уже выяснили, что для
одной грассмановой переменной а функция / (а) имеет общий вид
(/@) -f /<i)a), где /<°> и /A) —с-числа. Мы будем определять ин-
интеграл от нее как
/(/) = J da (/<°>+ /<Da) = /<!>. (9.10)
Это удовлетворяет требованиям (9.9) и для двух независимых
функций 1 и а сводится к
\da\ = 0, Jdaa=l. (9.11)
(Требование (9.9а) удовлетворяется, поскольку J da (a + b) =
= Jdaa + [Jdal] 6 = J da a.)
Далее, возьмем G2, порожденную a, и a2. Нам нужно опреде-
определить двойной интеграл I da1 I daj (аъ а^. Потребуем сначала,
чтобы dat также антикоммутировали, т. е.
{da,, daj\+ = \dai, a}\+ = 0. (9.12)
В G2 имеется только четыре независимые функции 1, аъ а2 и
аха2. В соответствии с (9.11) мы можем определить
J da1 J da2l = J da,. [ J da,!'] = 0,
J dat j da2a! = — j da2 [ j data^ = — J da2l = 0,
j dax j da,a2 = 1^1=0,
J da1 j da^a-^cUi = — j dax [ j do2a2j ax = — j da^ = — 1. (9.13)
Эти правила полностью определяют интеграл от произвольной
функции / (alt a2). Все эти положения обобщаются на Gn. Произ-
Произвольная функция / (аъ ..., ап) может быть записана как разложе-
разложение (9.4). Ясно, что в интеграле
\da1 Jda2 ...

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 269
дает вклад только последний член в (9.4). Все предыдущие
слагаемые содержат по крайней мере один dait не имеющий пары
из соответствующего at. Поскольку I da^ = 0, интеграл от
таких членов равен нулю. Последний член интегрируется с по-
помощью перестановки произведения а,- ... щп в виде апап_у ... ах
с соответствующим знаком. Поэтому
J da, \ da, ... \ dan (ati ... ain) = (- 1)р, (9.14)
. D I h> h> ■ • •> {'n \
где (—l)p—знак перестановки I , . ]•
\ tl, tl 1, •■., 1 /
Рассмотрим далее поведение интеграла при линейной «замене
переменных». Рассмотрим Gn, порожденную (аи ..., ап). Пусть
набор ф1У ..., Ьп) определен как
bi^Bifaj, (9.15)
где Btj — несингулярная с-числовая матрица. Очевидно, что на-
набор (blt ..., bn) на том же основании, что и (аи ..., ап), можно
рассматривать как набор генераторов алгебры Gn. Все bt подчи-
подчиняются тому же антикоммутационному правилу \bi, bj\+ = 0,
и любая функция / (аъ ..., ап), которая, согласно (9.4), может
быть записана как полином n-го порядка, может быть совершенно
также записана как полином по (Ьх, ..., Ьп). Мы уже знаем, что
единственным независимым п-кратным интегралом в Gn является
\da1 ... J dan (а^,^ ... а,) = 1. (9.16а)
Поскольку с тем же основанием алгебру можно было бы ввести
с использованием генераторов (blt ..., bn), мы имеем также
b, ... \dbn(bnbn-i ... M=l- (9-166)
Но, используя (9.15), получаем
' Vn-i ...Ь1 = (Det В) апап_х . . . av (9.17)
Таким. образом, (9.16а) и (9.166) взаимно согласованы только
в том случае, если мы введем якобиан следующим образом:
<й>х ... dbn = A/DetВ)dth ... dan. (9.18)
Заметим, что в аналогичном преобразовании для с-числового
интегрирования детерминант оказался бы в числителе.
Для наших целей важен интеграл от экспоненты. Очевидно,
"что е" = 1 + а, поскольку высшие степени а обращаются в нуль.
Поэтому, например,
J dat J <кцг-**га< = ^ da1 \ da2 (I - ка^) = Я, (9.19)

270 ГЛАВА 9
если использовать (9.13). Это может быть обобщено на кратный
интеграл с билинейной формой в показателе экспоненты. Рас-
Рассмотрим случай 2п генераторов (аъ ..., ап, аъ ..., ап), где мы
разбили генераторы на пары с помощью символов alt a^, а2, аг, ...
и т. д., чтобы согласовать с обычными обозначениями для опера-
операторов рождения и уничтожения. Но, хотя at и а1 имеют одинако-
одинаковые индексы, они являются полностью независимыми грассма-
новыми генераторами и а1 ни в каком смысле не является сопря-
сопряженным at. Рассмотрим интеграл
(п \
— £J uiAiflj I, (9.20)
i. /=i /
где Ai} —некоторая с-числовая матрица п X п, которая диа-
гонализируется при помощи преобразования
(В)ыАи(В-% = ХкЬк1, (9.21)
расс-
(9.22а)
где Яй —собственные значения Л. Мы определяем новые грасс-
мановы генераторы (blt 6Ъ Ь2, 52, ..., Ьп, 5п) как
и независимым образом
Bh = ((B^)-%iai, (9.226)
где Вт —транспонированная матрица В. Теперь заменим пере-
переменные на набор (bt, 5{). Если использовать (9.22) в (9.18), то
ясно, что
dS.db, •••■dgA=DetBJ[(Br)-,]^A ••• dandan =
= da1da1 ... dandan. (9.23a)
В то же время, используя (9.21), получаем
atAtjaj = 6kBklAi,BJ^bi = Ц Xk5kbk. (9.236)
k
Таким образом,
/ =j (dBldb1 ... dbndbn) exp /-
= П (f dBhdbhexp (~lhBhbh)) = Y\lh (используя (9.19)) =
k k
= DetA (9.24)
Сравните это с обычным с-числовым гауссовым интегралом от
п переменных (таким как в F.13)), значение которого пропор-
пропорционально A/Det ЛI'2. Тот факт, что в (9.24) входит Det A,

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 271
а не квадратный корень из него, обусловлен просто тем, что мы
имеем здесь In переменных, и матрица А, рассматриваемая как
2п X 2п-матрица, состояла бы из двух п х n-блоковых матриц Ац
вне диагонали. Но то обстоятельство, что Det А входит в числи-
числитель, а не в знаменатель, является следствием грассмановои при-
природы интеграла. Это различие окажется решающим в нашем по-
последующем анализе.
Следующий шаг состоит во введении грассмановых (т. е.
антикоммутирующих) полей. Мы отмечали, что грассмановы числа
(ах, ..., ап), порождающие алгебру Gn, правильнее всего рассма-
рассматривать как некоторые дискретные объекты, а не как переменные,
принимающие значения в некотором диапазоне. Это ограничение
не имеет места для произвольных элементов алгебры Gn. Произ-
Произвольный элемент / имеет с-числовые коэффициенты /@), /;1!, ...
в (9.4). Эти числа, конечно, могут непрерывно изменяться. Они
также могут зависеть от других с-числовых переменных, таких
как пространственные и временные координаты. В этом случае
элементы Gn также могут изменяться в пространстве-времени.
В частности, рассмотрим линейную функцию
/(х, 0=Е/Г)(х, t)at. (9.25)
i
Это наше антикоммутируйщее поле. Оно является функцией
пространственно-временных координат, но по определению анти-
коммутирующей
{/(х, 0, /(х', О1+ = 0. (9.26)
Заметим, что / (х, t) можно дифференцировать или интегрировать
по х или I. Эти операции подчиняются правилам обычного с-
числового исчисления, так как в этом случае изменяются только
с-числовые коэффициенты fi1) (x, t). Такие операции следует
отличать от взятия производных или интегралов по грассмановым
числам ах. Чтобы получить наше «классическое» поле Дирака,
рассмотрим грассманову алгебру с бесконечным числом генера-
генераторов, которые мы будем записывать в парных обозначениях
(ах, ах, а2, а2, ..., ап, ап; п -> оо). Под а-г и а-г снова понимаются
совершенно независимые грассмановы генераторы. Рассмотрим
также некоторый полный набор ортонормированных с-числовых
функций ф{ (х, t) в пространстве-времени, удовлетворяющий
условию
J dx J йЩ (х, 0 ф, (х, t) = б,/. (9.27)
Определим
w (х, о == I! ф{ (х, t) сц, ¥+ (х, 9 = S ф! (х, 9 й(- (З-28)
i i

272 ГЛАВА 9
По существу это наши классические поля Дирака. (Настоящее
поле Дирака имеет дополнительные усложнения, которые опущены
в наших обозначениях только в целях простоты. В обычных
обозначениях в теории квантового поля Дирака мы имеем раз-
разложение [50]
%(х, 0 = £ ф№ (х, 0bps + ф$£ (х, tLS, (9.29)
p. s
где ф^а (х, t) —спиноры, а — индекс спинорных компонент.
s — спиновый индекс, а (+) различает положительно- и отри-
цательночастотные подмножества полного набора функций.
В (9.28) спиновый индекс s вместе с р содержится в i, спинорный
индекс а опущен, а фр8 объединены в набор фг. Поэтому весь
набор аг в (9.28) обозначает классический предел как фермионных
операторов уничтожения bps, так и антиферм ионных операторов
рождения djs. Аналогичным образом набор at является класси-
классическим пределом полного .множества (&JS. dvs). Суммирование
по спиновым компонентам подразумевается в нормировке (9.27).
То обстоятельство, что ф} (х, t) в действительности являются
спинорами, не отменяет наших предыдущих аргументов, по-
поскольку спинор есть не что иное, как совокупность с-чисел.)
Наконец, мы готовы к построению основного функционального
интеграла, который нужен нам в теории поля Дирака. Рассмотрим
интеграл
G = } £> [¥+ (х, t)] 2) [W (х, /)] ехр {i J dx dt [¥+ (х, t) AW (x, *)]},
(9.30)
где А — дифференциальный оператор в пространстве-времени,
содержащий дираковские 7'матрицы. Напомним, что W — спи-
спинор, хотя спинорные индексы здесь опущены. Разложим W и W*,
согласно (9.28), как линейные комбинации аг и at соответственно.
Мера интегрирования определяется как
t)]= J
(9.31)
где i не индекс^ а -\/~—1. Оператор А определен на полной системе
ортонормированных с-числовых функций фг в (9.28). Если
Афь (х, t) — Ai$; (x, t), то подынтегральное выражение в (9.30)
принимает вид
ехр (i\dxj dtW+AW) = ехр (iajAjhah). (9.32)

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 273
Подставляя (9.31) и (9.32) в (9.30) и используя результат (9.24),
мы получаем
G = J П (idajdcij) exp (iajAjhah) = Det A. (9.33)
Множители i в мере (9.31) обеспечивают сокращение всех множи-
множителей i в (9.33). Заметим, что детерминант дифференциального
оператора оказался в числителе в отличие от соответствующего
результата для бозе-полей.
Заметим также, что как только получен результат (9.33),
грассмановы аспекты проблемы не играют более никакой роли.
Ответ в (9.33) зависит только от дифференциального оператора Л,
который определен на пространстве обычных с-числовых спинор-
ных функций. Чтобы вычислить этот ответ для различных А,
нам нужно .только решить обычное с-числовое уравнение на
собственные значения А. -
Мы рассматривали только билинейные формы по QV, Ч^)
в экспоненте (9.30). Такие задачи» как двумерная модель Тир-
ринга, приведут также к формам четвертого порядка по (W, W*),
но эти последние с помощью небольшой «ловкости рук» могут быть
сведены к билинейным формам (см. разд. 9.5). Таким образом,
мы получили весь необходимый математический аппарат для об-
обсуждения функциональных интегралов для ферми-полей.
9.2. Функциональный интеграл для свободного поля Дирака
Вспомним функциональный интеграл F.34), позволяющий вы-
вычислить Tr le~iHT ] для системы действительного скалярного
(бозе-) поля. Для комплексного скалярного поля ф (х, t), когда ф
и ф* можно рассматривать как две независимые переменные
вместо Re ф и 1т ф, уравнение F.34) тривиально обобщается
в виде
Тг [е-*нЧ =1&[ф* (х, /)]Ж>[ф(х, 01 exp(iS \ф, ф']), (9.34)
где S [ф, ф*.] —функционал действия. Теперь мы утверждаем,
что для поля Дирака справедливо весьма похожее функцио-
функционально-интегральное представление а именно
Тг [е-!НТ\ = К J 2> [Y+ (х, 013) [W (х, 01 exp (iS [W, ¥+]), (9.35)
где К — нормировочная постоянная и ¥, ¥+ — «классические»
грассмановы поля.
Мы начнем доказательство этого утверждения со случая
свободного квантового поля Дирака, когда собственные значения
гамильтониана уже хорошо известны из канонических оператор-

274 ГЛАВА 9
ных методов. Наше изложение представляет собой несколько из-
измененное доказательство, приведенное в приложении А работы
[103]. Действие для свободной дираковской системы в C+1)
измерениях имеет вид
т
So[V, ¥+] = Jdt JdxW(id -m)W =
о
T
= J dt J dx f ¥+ (x, 0 (i -|- + /a-V - pm) ¥ (x, /) I, (9.36)
0 I J
где мы используем стандартное обозначение для дираковских
матриц [49] и опускаем спинорные индексы. W = ор+Р, 5 = д№7'\
7° = Р и 7' = Р<*'\ Здесь Ти¥+ могут рассматриваться как грасе-
мановы поля. Применяя грассманово правило дифференцирования
(9.7), которое тривиально обобщается на поля, из условия
(S/SY+ (х, /)) So [W, ¥+] = 0 (9.37)
получаем уравнение Дирака
(id/dt + ia- V - Щ Ч (х, /) = 0. (9.38)
(Небольшое замечание. При изучении не квантованного вторично
уравнения Дирака в стандартных учебниках обычно под терми-
термином «дираковская волновая функция» понимают с-числовое спи-
норное поле, не учитывая грассмановых полей. Причина этого
будет объяснена ниже.)
Подставив (9.36) в (9.35), имеем
Тг [е-{н°т] = к\® [¥+] SD [¥] exp U j dt J dx (T+ (x, t) AW (x, t)) ,
(9.39)
где Ho —свободный дираковский гамильтониан, а А —оператор
А = id/dt + га-V — Р/п. (9.40)
Этот интеграл имеет вид (9.30), и из (9.33) следует ответ
(9.41)
где Я;- —собственные значения оператора А. Уравнение на соб-
собственные значения имеет вид
(id/dt + ia- V — Pm) ip (x, t) = Я\|з (х, t), (9.42)
где ap — четырехкомпонентный спинор с опущенным спинорным
индексом. В противоположность (9.38) здесь спинорная функция
(обозначенная через\р вместо W) есть с-числовой объект, а не грасс-

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 275
маново поле. Как отмечено выше, оператор А по существу дей-
действует в пространстве с-числовых спиноров, и его уравнение на
собственные значения будет сформулировано в этом пространстве.
Когда в учебниках изучается уравнение Дирака в качестве пре-
прелюдии в теории вторично-квантованного поля Дирака, фактически
изучается именно такое уравнение на собственные значения.
Решения уравнения (9.42) хорошо известны [49 ]. Запишем
i|) (х, 0 = L-3/2 exp [i (k • х - erf)] и (со, к), (9.43)
где и (со, к) — спинор. Подставив это выражение в (9.42), получим
условие на собственное значение
o-k.a-mP —Я| = 0, (9.44)
где этот детерминант берется в 4Х4-спинорном пространстве.
Это приводит к собственным значениям
Я = со ± ек, ек = V к2 + т2. (9.45)
Хорошо известно, что энергии ек есть собственные значения одно-
частичного свободного гамильтониана Дирака h0 = —ia-\ +
+ |3/л, А = id/dt — h0. (Здесь h0 не следует путать с Яо — га-
гамильтонианом всей полевой теории.) Для каждого (со, к) имеются
четыре независимых спинора, два вырожденных с Я = со + ек
и два с Я = со — ек. Таким образом, возвращаясь к (9.41), имеем
Тг [е-'".*1] = К П *■/ = К П (© + екJ (со - екJ. (9.46)
/ к, (о
Разрешенные значения к, которые, как обычно, задаются периоди-
периодическими граничными условиями в пространстве, есть kN = 2nN/L,
L ->-оо. Чтобы получить разрешенные значения со, необходимо
выбрать граничные условия на с-числовые функции при t = О
и t = Т. В бозонном случае естественным граничным условием
для следа является периодическое условие <j> (х, 0) — f (x, T).
В фермионном случае, как мы увидим ниже, правильный ответ
(т. е. тот ответ, который дается каноническими операторными
методами) получается при требовании антипериодичности по Т,
т. е. г|з (х, 0) = —г|з (х, Т). Тогда разрешенные значения со равны
со„Г = Bп+1)л, п = — оо, ..., —1, 0, 1, 2 оо. (9.47ч
Поэтому
Тг [е-'"*] = К П (П (со* + екJ (вк - со„J)- (9.48)
Но
(Х> <Х> <Х>
П (ек-сопJ= П (ек + со^J= Д 0* + со„J.

276 ГЛАВА 9
Следовательно,
Тг \е~
*1] = К П (П (<*« + екL
. (9.49)
к \_ п
Нормировочную постоянную К мы выбираем так, чтобы
* П П {Щ^У = П B4): (9-50а)
k п
Заметим, что множители Bп + 1) п/Т являются чисто кине-
кинематическими. Они не зависят от динамики, которая здесь пред-
представлена массой пг, содержащейся в еь. Кроме того (см. A.431.3)
в работе [175]),
п O+WfcH08^)- <9-5об>
Подставляя (9.50) в (9.49), получаем
Тг [е-1щц = Y[{2 cos \
П и+ехр (-^л4=
к
2р \~~iT
2ехр \~~i
Обозначение в (9.51) означает, что для каждого к имеется целое
число Пк, 0 <: Пк < 4. Сумма Л{"к} берется по всем возмож-
возможным наборам целых чисел [пи] = («ки «к2. ...) при условии
0 <: Пк < 4. Множитель С ({«к|) есть множитель комбинатор-
комбинаторного вырождения:
к
Очевидно, что (9.51) приводит к уровням энергии
Е{пк} = Ц (—2ek + лкек) , (9.52)
с кратностью вырождения С

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 277
Это в точности то, что мы ожидаем для свободной системы
Дирака. Состояние с наинизшей энергией (вакуумное состояние)
соответствует всем нулевым пи, и его энергия есть
£о=— 2 Ц ек.
к
Это имеет привычное объяснение как заполненное «море отрица-
отрицательной энергии». В этом море для каждого к имеются два фер-
миона с отрицательной энергией, соответствующие спиралкности
±1, каждый с энергией (—ek) = --у^к2 + тг. При необходимости
энергия Ео может быть исключена при нормальном упорядочении,
или, что эквивалентно, при добавлении константы Ео в лагран-
лагранжиан. Возбужденные состояния, которые получаются при нену-
ненулевых Пк, могут быть вырожденными. Для каждого импульса к
можно создать до четырех частиц, соответствующих фермиону
и (или) антифермиону со спиральностью +1 и (или) —1. Каждая
частица имеет ту же энергию еь, и, когда в импульсном простран-
пространстве имеется Пк частиц 0 < Пк < 4, кратность вырождения есть
4!/[(nk)!D — Пк)!]. Мы показали, что функционально-интеграль-
функционально-интегральное представление (9.35) в терминах грассмановых полей спра-
справедливо для свободного поля Дирака. До сих пор мы опускали
множители ft. Когда эти множители введены, (9.35) заменяется на
Тг [е-{НТ1Ц = К\ 2) [¥+] 3) [W] exp (iS pF, ¥+])/й), (9.53а)
где действие S сохраняется таким же, как прежде. Но мы изме-
изменим меру (9.31) соответственно на
j 3) [¥+] Ф pF] = j П (in dajdaj), (9.536)
i
чтобы функциональный интеграл по-прежнему был равен К Det A
с тем же оператором А, как прежде. Так как теперь Тг [eriH°Tifi ] =
= К Det А, уровни энергии (9.52) должны быть умножены на ft.
В этих обозначениях масса фермиона равна ft/n, где m — пара-
параметр в операторе А (9.40). В дальнейшем мы будем продолжать
опускать ft, но в тех случаях, когда это необходимо, мы будем
восстанавливать этот множитель.
9.3. Солитоны в присутствии ферми-полей
Функционально-интегральное представление (9.35) для
Тг [егснт ], которое мы только что провели для свободного поля
Дирака, имеет место также и для взаимодействующего поля Ди-
Дирака. Рассмотрим, например, поле Дирака, взаимодействующее
со статическим внешним скалярным полем <j> (x) с лагранжианом
взаимодействия
LB3 = g j dxW (x, t) V (x, 0 ф (x), (9.54)

278 ГЛАВА 9
где g — константа связи. С точки зрения физики мы знаем, чего
следует ожидать для спектра этой системы. Собственные энерге-
энергетические состояния должны снова состоять из суперпозиции
произвольного числа независимых фермионов и антифермионов
над вакуумом, так же как в (9.51), (9.52). Но энергия этих частиц
должна быть не чисто кинетической энергией ек = ]/ к2 -|- т2,
а определяться собственными значениями одночастичного га-
гамильтониана Дирака в присутствии статического внешнего поля
кф = — /а- V + Pm - g$f (x). (9.55)
Мы можем проверить, что функциональный интеграл (9.35) при-
приводит в точности к этому результату. Действие здесь есть
т
S = \dx\ dm (x, t) (t -i- + to- V - p (m - g<f> (x)) ¥ (x, t) =
о
т
= J dx j Л¥+ (x, О А Д (x, 0, (9.56)
о
где
Аф = id/dt + ia • V — P (m - gj> (x)) = id/dt - кф. (9.57)
Действие снова билинейно по ферми-полю и отличается от сво-
свободного дираковского действия (9.36) только заменой оператора А
на оператор Аф. После введения этого действия (9.56) в функ-
функциональный интеграл (9.35) мы получим аналогично (9.41)
Чт[е-снт] = КЪ&[Аф\. (9.58)
Вычисление Det [Аф] производится таким же образом, как в слу-
случае свободного дираковского поля. Мы не будем повторять все
шаги. Достаточно заметить, что Аф отличается от А только тем,
что содержит взаимодействующий одночастичный гамильтониан Нф
вместо свободного гамильтониана h0. Следовательно, в конечном
результате вместо собственных значений ек гамильтониана h0
окажутся собственные значения гамильтониана 1гф. Собственные
значения Нф определяются выражением
кф\ (х) = [-to• V + Р (т - gf (х))] / (х) = ef (x). (9.59)
Как и в случае свободного дираковского поля, собственные зна-
значения кф образуют пары е = ±ег (г = 0, 1 оо) за счет сопря-
сопряжения заряда. Это значит, что если задать собственную функцию
/V (х) с собственным значением ег > 0, то С ft (x) будет собствен-
собственной функцией с собственным значением —ег, где С = ра2 — ма-
матрица зарядового сопряжения в представлении
О <М „ // О
о, О

КВАЗИКЛЛССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 279
(см. [49]). Но в отличие от свободного дираковского поля, где
для каждых к и со были две вырожденные функции с различной
спиральностью, в присутствии внешнего поля ф в общем случае
такого вырождения для ег может не быть. Поэтому (9.48) заме-
заменяется на
Тг [е-'-"П = К Д (©„ + ег) (©„. - Er). (9.60)
п, г
Соответственно (9.51) превращается в
Тг [е-!"т] = К Det Аф = Ц С {\nr\) exp \-iT ( Ц (—вг + пггг))],
{",.} L \ r I \
(9.61)
где теперь 0 < пт < 2 и
Здесь, согласно (9.59), каждое £г == гг [ф] есть функционал от
ф (х). Уровни энергии определяются выражением
оо
£{*} = S (-er + nrsr). (Л.62)
Когда все nr = 0, мы снова имеем вакуум этой системы с запол-
заполненным ферми-морем энергии (JjT=o (—ег)). Когда некоторые
пг Ф 0, мы имеем фермион и (или) антифермион, для возникно-
возникновения каждого из которых требуется энергия +ег. Этого резуль-
результата мы интуитивно и ожидали. Условие 0 < пг < 2 означает,
что для каждого положительного значения ег может быть не более
одного фермиона и антифермиона. Потеря вырождения по спи-
ральности по сравнению со свободной задачей Дирака компенси-
компенсируется тем фактом, что индекс г здесь, грубо говоря, принимает
в два раза больше значений, чем импульс к в (9.51). Заметим, что
мы неявно предположили, что ни одно из значений ег не равно
нулю. Частные случаи, когда одно из гг равно нулю, рассматри-
рассматриваются в разд. 9.4.
На этом этапе мы не будем приводить соответствующие вы-
вычисления для зависящего от времени внешнего поля <j> (x, t).
В любом случае в такой ситуации не будет энергетических уров-
уровней, поскольку энергия не является сохраняющейся величиной.
Но ниже в этом разделе мы вычислим К Det Аф для зависящего
от времени <j>.
, Пусть теперь ф — не внешнее поле, а квантовое поле с дей-
действием вида
S = J dx dt [ -I (дцф)* - U (ф) -f T (id- m) V
= Sf-\-Srir + Sa, (9.63)

280 ГЛАВА 9
в очевидных обозначениях. Любая данная классическая конфи-
конфигурация f (х, t) может рассматриваться как внешнее поле, пока
речь идет о квантовой ферми-системе. Квантовая природа поля ф
затем учитывается, используя развитые в гл. 6 идеи, с помощью
интегрирования по всем конфигурациям ф (x, t). Иными словами,
~iHT] = к\&[ф] eiS* j SD [¥+] SD [W] el
Тг [e~iHT] = к\&[ф] eiS* j SD [¥+] SD [W] el (sv+s»*). (9.64)
Если скалярное поле ф заменено на векторное калибровочное
поле Лц с взаимодействием gWy^A^W, то последнее по-прежнему
остается билинейным по ферми-полю. Мы снова можем записать
Тг [e~iHT] = k\sD [Лц] ecsA j & [ip+] 3) [Т] е1 (в*+*вэ). (9.65)
Если А№ является калибровочным полем, то должны быть до-
добавлены слагаемые, фиксирующие калибровку (см., например,
[89], а также гл. 10), но это усложнение имеется уже и в отсут-
отсутствие ферми-полей. Ясно, что эта процедура имеет место также,
если ферми-поле взаимодействует с псевдоскалярным полем через
юкавскую связь. Если имеется несколько видов ферми-полей, то
мы просто получаем кратный интеграл по всем этим видам полей.
Таким образом, по существу мы рассмотрели все представляющие
интерес случаи в C -f- 1) измерениях. Заметим, что во всех этих
случаях действие содержит ферми-поля только билинейным об-
образом, так что в качестве математического аппарата достаточно
грассманова функционального интеграла (9.30). Напомним, что
в C + 1) измерениях ферми-поле не может самодействовать за
счет полиномиальных взаимодействий четвертого или более вы-
высоких порядков, поскольку такие теории не перенормируемы.
В (Г + 1) измерениях четырехфермионные взаимодействия пере-
перенормируемы. Мы рассмотрим отдельно эту возможность
в разд. 9.5.
Теперь, когда мы расширили функциональный интеграл для
Тг [eriHT ] вплоть до включения ферми-полей, следующий вопрос
состоит в том, могут ли квазиклассические методы также быть
распространены на такие случаи. Для чисто бозонного случая
эти методы возникают из приближения стационарной фазы в функ-
функциональном интеграле. Для грассмановых полей мы не вводили
соответствующего метода аппроксимации. Но он и не требуется,
поскольку действие билинейно по QP, ¥+) и фермионный функцио-
функциональный интеграл формально может быть точно вычислен с ис-
использованием (9.33). Когда это сделано, в (9.64) или (9.65) остается
чисто бозонный функциональный интеграл, для которого может
быть применено обычное приближение стационарной фазы. Осно-
Основываясь на этой идее, Дашен и др. [101 ] распространили квази-
квазиклассический метод функционального интеграла на фермионы.
[Другие методы получения квазиклассических результатов также

КВазИКЛассйчёскйе методы Для Фёрмй-полёй 281
могут быть распространены на фермионы. Например, Фридберг
и Ли [145] развили канонические операторные методы (введенные
в гл. 8 для бозе-полей) для учета ферми-полей. Джакив и Ребби
[197 ] еще в одном подходе применили метод Голдстоуна—Джакива
(описанный в гл. 5) усреднения полевого операторного уравнения
по постулированной системе солитонных состояний. Как и для
бозе-полей, эти различные методы приводят к эквивалентным
результатам. Мы будем работать с методом функционального
интеграла. ].
Рассмотрим пример системы (9.63); случаи векторного и псевдо-
псевдоскалярного полей трактуются аналогичным образом. Функцио-
Функциональный интеграл (9.64) имеет вид
Тг [е~снт] = к\ £>[ф] eiS* \® [¥+] 2) [¥]ехр [i\dt\ йх^Аф~Ч ) =
= К \ 3) [ф] е'5* Det [Аф] ='\sD [ф] е'5э*Ф [*], (9.66)
где теперь
Аф = id/dt f ia.-V-fiim-gA (x, 0). ' (9.67)
SS<M>[ф] = Бф [ф] -iln{KDet [Аф]}. (9.68)
Таким образом, остается бозонный функциональный интеграл,
в котором вклад от ферми-полей целиком содержится в эффек-
эффективном действии 5Эфф [ф]. Теперь мы можем применить к (9.66)
обычное приближение стационарной фазы. Пусть ф0 (х, t) — не-
нетривиальное локализованное решение уравнения
'1 1П
Тогда мы можем разложить в ряд 8эфф [ф] около ф0 (х, t) и за-
записать (9.66) в приближений стационарной фазы как
Тг [е~'"П « exp (tS84a, [^oD J & [У (х, /)] X
X exp [i\dx\ dty(l$$.)^ у] = exp («*«, Ш) Д,
(9.70)
где у (х, t) = ф (х, t) —ф0 (х, 0-
Заметим, что в противоположность чисто бозонной системе
здесь член в^ф [ф0] не является чисто классической величиной.
Как функционал S8$$ [ф], так и решение ф0 (х, t) содержат
квантовые эффекты от ферми-поля за счет оператора Аф, от которого
они зависят. Дальнейшие квантовые эффекты, обусловленные
флуктуациями бозе-поля ф около решения ф0, появляются за
счет множителя А. Этот множитель также неявно зависит от ферми-
поля через 5эфф и ф0.

2Й2 ГЛАВА §
Формально (9.70) дает ответ для спектра солитонного
сектора, ассоциированного с ф0 (х, t), в терминах детерми-
детерминантов линейных операторов. Как , только Det Аф вычислен,
"Язфф ["И известно и ф0 (х, t) может быть получено из (9.69).
Множитель Д является гауссовым интегралом, пропорциональным
[Det (^вэфф/Ьф Ьф)фа Ь1/2. Но практически эти вычисления весьма
трудны. За счет второго слагаемого в (9.68) 5Эфф [ф] в общем слу-
случае является неполиномиальным нелокальным функционалом,
особенно сложным, когда время Т конечно. Чтобы упростить
задачу, мы воспользуемся несколько менее удовлетворительным
приближением стационарной фазы, таким, которое, как будет
показано, в порядке ft приводит к тем же уровням энергии, что
и (9.70). Заметим, что если бы мы сохранили в нашем выводе
зависимость от ft, то (9.66) заменилось бы на
Тг [е-1™] = j SD ty\eS*lHK Det [Аф] = \®[ф] е'*9**[Ф]/П. (9.71)
Вместо того чтобы разлагать в ряд подынтегральное выражение
около экстремума S^, разложим его около экстремума Бф на
том основании, что в пределе малого ft e'5*/fi быстро осциллирует,
а К Det [Аф] меняется сравнительно медленно. (См. уравнение
F.13) как приближение к F.11).) Другими словами, пусть
фс (х, t) — солитонное решение уравнения
dU
Вместо (9.71) возьмем приближенное выражение
Тг [е-""У*] = exp (tS0[^]/ft) К Det [АФс] До, (9.73)
где
Доее \0\yfr /)]ехрD- \йх\<иУ[^)фау). (9.74)
Результат (9.73) легче вычислить и интерпретировать, чем (9.70).
Заметим, что фс, которое удовлетворяет (9.72), не что иное, как
классический солитон, который имела бы бозевская система в от-
отсутствие ферми-поля. Для простоты мы сначала возьмем в ка-
качестве фс статическое решение фс (х). Тогда
т
S, [фс] = -\dtdx [-^Ш2 + и(фе)] = -£кл ШТ, (9.75)
о
где Екл [фс ] — классическая масса солитона. Оператор АФс
в (9.67) для не зависящего от времени поля фс (х) является one-

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 283
ратором Дирака в статическом внешнем поле. Мы можем исполь-
использовать (9.61), чтобы написать
КDet [АФс] = S С (\пг}) ехр Г-iT 1 Ц (-в, + п*г)\ 1 , (9.
{пг} I \ г П
76)
где гг = ег [</>е ] — собственные значения одночастичного га-
гамильтониана Дирака (9.59) в присутствии фс (х). Наконец, До —
обычный множитель бозонных флуктуации, рассмотренный
в гл. 6. Мы можем записать его в виде (см. F.39)—F.43))
До =
ехр
L \р=о /
Np = Q, 1,..., оо,
(9.77)
где Юр = Юр [фс]—собственные значения оператора [—v2 +
+ (сРи/йфг)фс{х)]. Подставляя (9.75)—(9.77) в (9.73), получаем
Тг [е-"""/*] =
C({nr})exp [-
~8г + па) + ^ ((^р + 1 /2) ©р)) ] .
где 0
2и0<:Л^р
р
деляются из (9.78), равны
(9.78)
оо. Уровни энергии, которые опре-
опре- Екл
(-ег + лге
1 /2) (
o
(9.79)
Квантовые поправки расходятся. Эта расходимость может быть
устранена так же, как в чисто бозонных задачах в гл. 5 и 6, до-
добавлением к действию обычных контрчленов нормального упо-
упорядочения и перенормировки. Природа контрчленов зависит от
конкретной модели и пространственной размерности. В целом,
однако, контрчлены, являясь квантовыми вкладами, будут О (И)
по порядку величины. Мы можем записать все контрчлены, со-
содержащие как бозе-, так и ферми-поля, в форме fiSK4 и добавить
их к действию. В нашем приближении стационарной фазы в ок-
окрестности статической конфигурации фс (х) это, очевидно, при-
приведет к появлению в (9.73) множителя вида
ехр (iSm [фс]) - ехр (гТ£Кч
(9.80)

284- ГЛАВА 9
Соответственно результат (9.79) заменится на
Е{пг, Np) = Екл [фс] + ft С ^ **г + Y
\ г р I
~ ' (9.81)
Мы можем ожидать, что в перенормируемой теории для устране-
устранения всех расходимостей в солитонном секторе таким же образом
последовательно в каждом порядке будет достаточно тех же
контрчленов, которые добавляются в обычной теории возмущений.
Соответственно потенциально расходящиеся части в последнем
слагаемом в скобках в (9.81) должны сокращаться с Екч. Эти
уровни энергии можно интерпретировать так же, как уровни
в гл. 5. Они заполняют солитонный сектор состояний, ассоциируе-
ассоциируемый с фс (х). Мы начнем с предположения, что ни одно из сор
или ег не равно нулю. (Это предположение в общем случае не
верно; приведенная ниже интерпретация должна быть соответ-
соответствующим образом изменена — см. разд. 9.4.) Тогда наинизший
уровень в наборе (9.81) есть
^{NP="r=°} = iWooJI = ^кл ^ + Й ( У\ (~~6г) + ~~2~ А <Лр ~~ Екч\'
V г р ■ )
(9.82)
Это — масса основной квантовой солитонной частицы в присут-
присутствии поля Дирака. Сравнивая этот результат с соответствующей
задачей в отсутствие ферми-поля, мы видим, что решение фс,
его классическая энергия Екл [фс ], а также бозонная часть энер-
энергии нулевых колебаний 2Р1/2й(ор остаются без изменений. Это
происходит в силу природы приближения (9.73). Но масса кван-
квантового солитона теперь содержит дополнительный вклад, обус-
обусловленный энергией нулевых колебаний ферми-поля в виде
энергии заполненного ферми-моря. Более высокие уровни в (9.81)
соответствуют возбуждениям, которые теперь могут появляться
как в бозонных, так и в фермионных флуктуационных модах.
Единственная разница состоит в том, что в отличие от бозонных
мод любая данная фермионная мода может быть возбуждена
максимум дважды @ < пг « 2), что соответствует рождению
в этой моде одного фермиона и одного антифермиона, согласно
принципу Паули. Заметим, что ег — собственные значения одно-
частичного гамильтониана Дирака в присутствии фс (х) (9.59).
Поэтому до порядка й включительно солитон выступает как «фоно-
«фоновое поле» для фермионов. Квантовая природа поля ф ощущается
фермионами только в старших порядках. В следующем разделе
мы проиллюстрируем всю эту процедуру, используя специфиче-

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 285
скую модель, в которой фс (х), Екл [</>Д со,,, гг и ER4 ясно опре-
определены.
Солитонный сектор в присутствии ферми-полей может быть
также исследован в каноническом операторном формализме, как
это было сделано для случая чисто бозевских полей. Если ни одно
из (ор или гг не равно нулю, то разложение полевых операторов
имеет вид
Ф (х, t) = фе (х) + V (ар 1-i- flp (х) + afp -^L- п; (х)) , (9.83а)
где т)р (х) — нормальные моды бозонных флуктуации в окрест-
окрестности фс (х), и аналогично
ур (х, *) = £ [bre~%tfr+) (х) + dfe^f}.-* (хI» (9.836)
где /г*' (х) и ±ег = ±ег [</>с] — нормированные положительно-
и отрицательночастотные собственные функции одночастичного
гамильтониана Дирака (9.59) в присутствии фа. Исходя из ос-
основных антикоммутационных правил (9.2) для ферми-поля и ис-
используя обычную нормировку для fr±) (x), можно вывести стан-
стандартные антикоммутационные соотношения
\ЬГ, tf>)-h={dr, d?>)+ = 6rr;
все остальные антикоммутаторы обращаются в нуль.
Состояние с наинизшей энергией в солитонном секторе — ос»
новной квантовый солитон — в порядке ft соответствует тому,
что не возбуждена ни одна из бозонных и фермионных мод. Ясно,
что это состояние удовлетворяет условию
ар | сол) = Ьт | сол) = dT | сол) = 0. (9.84)
Нормально упорядоченный фермионный ток /№ (см. [50]) равен
Соответствующий заряд есть
~~~ b%-dHr)- (9.85)
Принимая во внимание (9.84), очевидно, что
<2|сол) = 0. (9.86)
Фермионные возбуждения получаются при действии, на |сол)
операторов Ь? или eft. Например, состояние Ь?0\сол) имеет

286 ГЛАВА 9
фермионное число, равное единице. Если мода г0 дискретная,
то это будет связанное солитонное состояние с фермионным чис-
числом, равным единице. Аналогичным образом <$0 \ сол) имеет
фермионное число, равное —1.
Следует отметить, что в (9,83)—(9.86) мы неявно предполо-
предположили, что ни одно из гг или сор не равно нулю. Мы сделали это
в целях простоты, чтобы дать предварительное представление
о солитонном секторе. В реальных случаях большинство гг и сор
не равно нулю, но некоторые из них обращаются в нуль. Разу-
Разумеется, это зависит от конкретной модели. Мы уже знаем, что
некоторые из сор равны нулю в силу непрерывных симметрии, та-
таких, как трансляционная инвариантность. Трактовка таких бо-
зонных нулевых мод и их следствия обсуждались в предыдущих
главах. Они влияют на уровни энергии только в следующем поряд-
порядке (О (й2)). В присутствии ферми-полей мы имеем дополнительную
возможность того, что некоторые из гг также могут обращаться
в нуль. Влияние такой фермионной моды с нулевой энергией рас-
рассматривается в следующем разделе.
Действия, ведущие от (9.73) к (9.81), справедливы для стати-
статического решения фк (х). Во многих случаях статического соли-
тонного решения может не быть. Возьмем, например, теорему
вириала, которая рассматривается в гл. 3. В таких случаях (а
также в случаях, когда статические решения существуют) по-
прежнему можно осуществить квазиклассическое разложение
в окрестности зависящих от времени периодических решений
(9.72). Для этого нужно применить полный метод ВКБ, развитый
в гл. 6. Мы будем работать с
оо
G (Е) = i \ dTeiET Tr [е~1»т] = Тг [ \/(Е - Н)].
о
Уровни энергии являются полюсами G (Е). Как только Tr [e'iHT ]
найдено, остальные шаги производятся так же, как в гл. 6. При-
Приближение (9.73) для Tr [e-iHT] все еще выполняется, когда фс
есть зависящее от времени решение с периодом Т. Но множители
(/С Det АФс) и До требуется вычислить для зависящей от времени
функции фс (х, t); Ао — чисто бозонный множитель, который уже
обсуждался в гл. 6. Когда фс периодична, мы видели, что мно-
множитель ((йрТ) для каждой бозонной моды заменялся на угол
стабильности vp. Сейчас мы покажем, что для фермионных мод,
содержащихся в К Det Аф , имеет место аналогичная замена
[103]. Уравнение на собственные значения для АФс теперь имеет
вид
[id/dt + /а• V - Р (ш - ёфс(х, 0)] Ф (х, 0 = Ц(х, t). (9.87)

КВАЗИКЛАССИЧЁСКИЁ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 287
Поскольку фс зависит от времени, мы не можем более записы-
записывать W (x, t) в виде e'Utf (х). Но рассмотрим уравнение Дирака
[id/dt + /а • V - р (т - g^>c (х, <)] /(х, 0 = 0. (9.88)
Поскольку оператор в (9.88) является периодическим с периодом Т,
можно найти решения fr (х, t), удовлетворяющие условию
fr(x, t + Т) = e~iarfr(x, 0 для всех х, L
Эти коэффициенты <хг называются «индексами Флоке». Сравни-
Сравнивая приведенное выше уравнение с F.95), мы видим, что индексы
Флоке аналогичны углам стабильности. Ясно, что
К г (х, t) = ехр [—1 (соп - ar/T) t] fT (x, t), (9.89)
где
соп = Bл + 1) я/Т
— собственные функции Аф , удовлетворяющие уравнению
(9.87) с собственными значениями
Более того, tyn>r (x, t) удовлетворяют условию антипериодич-
антипериодичности г|)„1Г (х, t + Т) = —1|з„, r (x, t) в соответствии с введен:
ным выше необходимым условием. Наконец, приведенное выше
соображение о зарядовом сопряжении снова показывает, что
все а появляются парами +<хг. Таким образом, аналогично (9.60),
(9.61) имеем
К Det Аф = П К ~ oilT) («„ + «г/Л =
п, г
= 2 С({пг})ехр Г-/ ( Ц (nAr -Or))] (9.90)
{пг} I \ г /J
со всеми положительными аг. Сравнивая с (9.76), мы видим, что
при переходе от статического решения фс (х) к периодическому
фс (х, t) место ггТ занимают индексы Флоке аг. (Заметим, что
если бы фс было статическим, мы могли бы записать fr (x, t) =
=е"'е^/г (х), и аг тривиально сводились бы к ег Т.) Вместо вычи-
вычисления гг мы должны теперь найти ат с помощью решения зави-
зависящего от времени уравнения Дирака. Когда аг найдены, ре-
результат (9.90) можно подставить в (9.73) и реализовать метод
ВКБ из гл. 6.
Наши результаты получены из приближения (9.73), где мы
разложили в ряд функциональный интеграл (9.71) в окрестности
точки стационарной фазы не всего подынтегрального выражения
е'5эфф/й> а только elS^ti. Мы сделали это для того, чтобы еде-

288 ГЛАВА 9
лать более простым последующий анализ, а также на том осно-
основании, что в пределе малых ft elS*ln является наиболее быстро
осциллирующей частью подынтегрального выражения. «Полное»
приближение стационарной фазы, когда разложение произво-
производится в окрестности экстремума 5Эфф, дано в (9.70), но, как мы
говорили выше, его труднее провести. Даже найти экстремум
ф0 (х, t), решая (9.69), значительно труднее, чем решать (9.72).
Причиной всего этого является дополнительный член —/ft x
х 1п (К Det Аф), который является нелокальным неполиноми-
неполиномиальным функционалом от ф. Но в порядке ft два приближения
(9.70) и (9.73) приводят к тем же энергетическим уровням (9.79).
Чтобы увидеть это, заметим, что S^ — 8Ф = —/ft In (/С Det Аф).
Поэтому решения ф0 (х, if) и фс (х, t), которые являются
экстремумами S3<j,<j, и 5>ф соответственно, также различаются'
на ф0 — фс = 8ф — О (ft). Это означает, что при данном ф0
соответствующее фс может рассматриваться как предел ■ ф0 при
ft ->• 0. Если включить зависимость от ft и контрчлены, то (9.70)
может быть записано в виде
-/ftlnA + ftSK4tfo]]}. (9.91)
Но
S,[fo] = S,[^] + F5,/6^e6^. + 0(A^) = S,[^] + 0(ft2), (9.92)
если использовать (9.72). Подобным же образом остальные члены
в экспоненте (9.91) уже имеют более высокий порядок по ft. По-
Погрешность, которая возникает при замене ф0 на фс и
Ф25афф/8фЬф)фо на (№8ф/8ф&ф)Фс, в этих членах будет еще более
высокого порядка. Эти замены сеодят (9.70) к (9.73). Таким об-
образом, улучшенное приближение (9.70) дает те же энергетические
уровни (9.81) до порядка ft включительно, но приводит к некото-
некоторым поправкам более высокого порядка. Несмотря на его слож-
сложность, некоторые авторы успешно применяли именно прибли-
приближение (9.70) для специфических моделей в пределе Т-*-оо [72, 103].
В другой популярной в этой области процедуре используется
классическое решение, при котором берется экстремум не от
Эф [ф] и не от полного S^ [ф], а от некоторой средней вели-
величины. Мы опишем этот метод для статических решений, когда
экстремум может браться между статическими конфигурациями
Ф (х). Для таких конфигураций подынтегральное выражение
в основном функциональном интеграле (9.66) может быть запи-
записано в виде
exp[t(S#-tln(/CDeti4,))] =
= 51
{nr}
(9.93)

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 289
Мы снова положили й = 1 и использовали (9.61). Но, если мы
возьмем экстремум от всей экспоненты в левой части и проведем
квазиклассическую процедуру, мы получим (9.70). Если мы возь-
возьмем экстремум только от S^, или, что эквивалентно, Екл [</>],
то мы получим приближение (9.73). Попробуем сделать нечто
среднее, взяв экстремум от Екл [ф] + Ъгпггг [ф]. Это выраже-
выражение, конечно, зависит от выбора фермионных чисел заполнения
\пг\. Настоящая процедура есть попытка выбора оптимального
экстремума в зависимости от чисел заполнения состояния, которые
мы исследуем. Энергия ферми-моря (Ег — гг [ф]) при взятии
экстремума не включается, но вычисляется в экстремуме. Нам
не известно удовлетворительного оправдания для этой процедуры,
кроме того, что это лучше, чем просто искать экстремум только
£кл [ф]- Напомним, крометого, что большая часть энергии ферми-
моря (все ее расходящиеся части) при добавлении контрчленов
сокращаются с ними.
Условие экстремума теперь имеет вид
[ф)\ = -у2 Ф \~
=-°- '(9.94)
Уравнение (9.94) можно переписать следующим образом. гг [ф] —
собственные значения одночастичного гамильтониана Дирака и
задаются в (9.59). Если ф изменится до ф + Ьф, то / изменится
до / + б/, а е — до е + бе. В первом порядке по бесконечно
малым (9.59) дает
{-to. V + Р (т - gf) \ б/ - g6#/ = бе/ + еб/. (9.95)
При взятии скалярного произведения с /+ и использовании нор-
нормировки J dxf^f = 1 получаем
или
6e[fl/ty(x) = g/*(x)P/(x) = gf(x)/(x). (9.96)
(Напомним, что / (х) — спинор с опущенными спиновыми индек-
индексами и в приведенных выше уравнениях подразумевается сумми-
суммирование по спинам; f = /fp.) Подставляя (9.96) в (9.94), находим
-V2 Ф + "£- = ~ё 2 "Mr, (9.97)
10 Раджараман Р,

290 ГЛАВА 9
где каждое fT удовлетворяет (9.59). Таким образом, мы получаем
совокупность связанных уравнений (9.59) и (9.97) для само-
самосогласованного решения относительно ф и fr. В простейшем
случае, когда только одна фермионная мода г0 однократно воз-
возбуждена, пг = б„0. Тогда уравнения (9.59) и (9.97) сводятся
к двум уравнениям
[-ta.V-bP[m-g*(x)]Mx) = e,0/,0, (9.98а)
-W = ~8frJr.. (9.986)
Приближение (9.72) для статического решения сводится к равен-
равенству нулю правой части (9.986), вследствие чего классическое
бозе-поле теряет всякую связь с ферми-полем. В (9.98) класси-
классическое бозе-поле и волновая функция Дирака />„ взаимосвя-
взаимосвязаны, что является той ценой, которую мы должны платить
за улучшение в приближении (9.94). Заметим, что уравнения (9.98)
имеют точно такой же вид, как уравнения Лагранжа—Эйлера,
которые мы получили бы для статического ф (х), исходя из лаг-
лагранжиана (9.63), если бы заменили ферми-поле W (х, t) на дира-
ковскую волновую функцию занятого состояния (i|v0 (х, t) =
= fr0 (x) ё~'Ег°*). Это придает связанным уравнениям (9.98)
некоторую интуитивную привлекательность. В самом деле, поле-
полевые уравнения с такой заменой ферми-поля на с-числовую дира-
ковскую волновую функцию часто вводились с самого начала
в квазиклассических вычислениях, особенно при создании моде-
моделей адронов. Наше обсуждение показывает уместность таких
уравнений в контексте систематического квазиклассического при-
приближения к исходной квантовополевой теории. Мы можем видеть
также пределы применимости таких уравнений. Эти два связанных
уравнения (9.98) получаются из условия (9.94) только тогда,
когда занята одна фермионная мода. Если занято N различных
мод, мы получаем N + 1 связанных уравнений (9.97) плюс N
уравнений вида (9.59), по .одному на каждое fr. Исходное при-
приближение (9.94), из которого получаются эти уравнения, также
не является экстремумом всего S^ [ф]. При взятии экстремума
была исключена энергия ферми-моря.
Несмотря на эти ограничения, уравнения (9.98) представляют
собой некоторое усовершенствование по сравнению с неспаренным
уравнением (9.72). Они все еще поддаются обработке, хотя решать
их труднее, чем (9.72). Такие уравнения решались и точно и чис-
численно для большого числа моделей. Помимо уже цитированных
работ см. [24] (знаменитый Мешок Станфордского линейного
ускорителя (SLAC)), [78, 229]. После того как найдено решение фс
связанных уравнений (9.98), остальная часть квази классического
метода реализуется так же, как и выше с помощью разложения
в ряд функционального интеграла (9.66) в окрестности фс.

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 291
9.4. О возможности существования солитонов с зарядом 1/2
Проиллюстрируем квазиклассический метод (9.72)—(9.81) кон-
конкретным примером. Выбранный нами пример приведет также кфер-
мионной моде с нулевой энергией и даст нам возможность обсу-
обсудить значение такой моды. Моделью будет теория размерности
A + 1), в которой кинковая система, рассмотренная в гл. 2 и 5,
взаимодействует с фермионами через плотность лагранжиана
2 (х, 0=4" (W —Т ^ ~ ^ + ^(i'^ W + gWW<t>- (9-99)
4
По сравнению с лагранжианом E.36) кинковой системы здесь
мы для простоты положили кинковый параметр К = т2 = 2.
Солитонный сектор этой системы (9.99) обсуждался Дашеном
и др. [101], которые также указали на существование фермион-
ной моды с нулевой энергией. Смысл такой моды был исследован
и связан с возможностью существования солитонов с зарядом
+ 1/2 Джакивом и Ребби [197].
К этой модели могут быть применены методы предыдущего
раздела, адаптированные к размерности A + 1). Нам требуется
лишь помнить, что Чг теперь двухкомпонентный спинор и имеются
только две матрицы Дирака. Мы используем представление
р = alt aL = 02. (9.100)
(Эквивалентно 7° = р = сг1и71 = P«i = кг3вд = / (dty° + dj/y1)-)
Прежде чем перейти к солитонному сектору, напомним, что в этой
модели вакуум имеет среднее значение (</>) = ±1. При таком ва-
вакууме элементарный фермион имеет массу tnF = \g (ф) | в низ-
низшем порядке за счет последнего члена в (9.99), даже если лагран-
лагранжиан не содержит явно члена с фермионной массой. Эта масса
всегда может быть выбрана положительной независимо от знака
(ф) или g, поскольку знак массового члена может быть всегда
обращен с помощью Ч1" ->• у^¥ = 7°71ЛР- Без потери общности
мы можем принять g > 0, (</>) = +1 и mF = g.
Учитывая все это, рассмотрим солитонный сектор и используем
приближение (9.73). Это приводит к результату (9.81) для уровней
энергии. Нам нужно лишь вычислить величины, входящие в (9.81)
а именно фе, Екл [фе], сор [^>с], гг [фс] и Екч [фе] для модели
(9.99). Статическое классическое решение фс (х) должно удовлет-
удовлетворять уравнению (9.72), которое теперь сводится к
й2фс/с1хг-2фс(ф1-1) = 0. (9.101)
Решением этого уравнения является не что иное, как прежняя
кинковая функция. Положив X = т2 = 2, а = 0в E.45), E.46),
имеем
Фс (х) = thx, (9.102a)
Екл 1фс] - 4/3. (9.1026)
10*

292 ГЛАВА 9
(Антикинк также является решением. Сектор состояний, постро-
построенных в окрестности антикинка, может быть рассмотрен анало-
аналогичным образом.) Величины сор в (9.81) являются не чем иным,
как частотами стабильности кинка и уже заданы в E.50). Энергии
ег [фс] фермионных мод при применении (9.59) удовлетворяют
условию
V/' (*) = i—iaid/dx - g№c (x)) fr (x) = erfr (x). (9.103)
Если мы запишем двух компонентный спинор в виде
то в представлении (9.100) условие (9.103) сведется к связанным
уравнениям
(-d/dx - 8фе (х)) iv(х) = егиг (х), (9.104а)
(d/dx - дфе (х)) иг (х) = e/v (*), (9.1046)
откуда следует
-Jr + §41 + 8 ^г) ur(x) = (--dW + g*tf + g(\ -ф1))иг(х) =
= z\ur{x), (9.105a)
(-d*/dx* + ?ф1 -g(l- ф1)) vr (x) = ejvr (x), (9.1056)
где мы использовали то обстоятельство (см. B.20)), что d<f>c/dx =
= -\/2U {фс) = 1 — ф1. Уравнения (9.105) точно решаются в эле-
элементарных функциях. По существу это не что иное, как пара од-
одномерных уравнений Шредингера в «потенциале» V (х) =
= 8*4>с ± 8 0 — фс) = g2 th2 x ± gsch2 x. При х -► ±оо V(х) -*■
-*■ g2. Поэтому собственные значения г2г содержат континуум
е? = g1 + k2r для ej > g2. Ниже g2 лежат дискретные уровни свя-
связанных состояний, которые могут быть найдены точно (см. [101,
257]) в виде
e? = 2/-g--r2, /- = 0, 1,..., <g. (9.106)
Заметим, что наинизший уровень есть е0 = 0. За исключением
его, для каждого ненулевого собственного значения е? из (9.105)
имеем пару собственных значений +ег гамильтониана Дирака
(9.103) в соответствии с приведенными выше общими соображени-
соображениями, основанными на сопряжении заряда. Тот факт, что непре-
непрерывный спектр начинается с er = g, также согласуется с тем об-
обстоятельством, что элементарный фермион имеет в этой модели
массу g.
Остается найти только £кч [</>с], требуемое в (9.81). Кроме
контрчленов (D + Vjd/n2^2), уже введенных в гл. 5 (см. E.66),

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 293
E.67)), мы будем иметь дополнительные контрчлены, обусловлен-
обусловленные присутствием в лагранжиане (9.99) ферми-поля. Они снова
имеют форму D + V2dm2 </>2. Здесь D — энергия фермионного
вакуума, т. е. D = £]Г(—е, [ф = 1 ]). Член V2dm2^>2 обусловлен
графом собственной энергии бозона, связанным с фермионной
петлей, а именно
У (9.107)
BяJ \ (k — g) (—й
В целом контрчлены, которые следует добавить к лагранжевой
плотности (9.99), имеют вид
3£т = D + D + V« (dm2 + йт5) </>2. (9.108)
В результате получаем
Екч [фс] = j dx [D + D + Va (dm2 + a»?) (^* (x) ~ 1)], (9.109)
где вклад от вакуумного значения ф = 1 вычтен так же, как
это сделано в E.68). Таким образом, мы собрали вместе все со-
составляющие, необходимые для вычисления уровней энергии
(9.81) в солитонном секторе, ассоциируемом с кинковой функцией
^>с (х). Вычисление энергий Е^Пг N j производится теперь не-
непосредственно применением алгебраических методов. В гл. 5
мы показали, что контрчлены J dx (D + V2dm2 (ф1 — 1)) устра-
устраняют расходимость в 2Р (VaCOp) (см. E.69)). Аналогично можно
проверить, что J dx (D Ц- V2 dm? (ф1 — 1)) устраняет расходи-
расходимость в S^o (—ег [</>с]), оставляя конечный ответ для энергети-
энергетического уровня Е<п n х при любых конечных числах заполне-
заполнения \nr, Np].
Вместо того чтобы проводить квазиклассическое разложение
в окрестности кинковой функции, можно попытаться разложить
в окрестности экстремума всего эффективного действия 5Эфф [ср],
содержащего вклад от моря отрицательной энергии. Это прибли-
приближение (9.70), и, как мы констатировали, пользоваться им значи-
значительно сложнее. Кемпбелл и Лиао [72] показали, как это может
быть проведено в аналитическом виде для модели (9.99). Заинте-
Заинтересованных читателей мы отсылаем к их статье, которая содержит
также обобщение на кирально инвариантные модели, когда фер-
мионное поле связано как со скалярным, так и с псевдоскалярным
полями
1 Возвратимся к нашему вычислению в кинковом секторе для
модели (9.99). До сих пор мы не уделяли специального внимания
тому факту, что наинизшая фермионная мода в (9.106) имеет
нулевую энергию. Энергетический спектр сам по себе не должен

294 ГЛАВА 9
измениться вплоть до порядка й в присутствии такой нулевой
моды. Можно просто подставить (ел=0) = 0 в (9.81). Но, как
доказали Джакив и Ребби [197], при этом оказываются сущест-
существенно затронутыми другие свойства состояний, ассоциируемые
с этими уровнями. Чтобы это увидеть, исследуем несколько дальше
нулевую моду (9.103). При е0 = 0 функции и0 (х) и v0 (х) в (9.104)
оказываются независимыми друг от друга, и их легко проинтегри-
проинтегрировать, что дает
«о (х) = «о exp \g j 4>с (*') dx' = и0 (ch *)«,
v0 (х) = v0 exp \—g j 6C (/) dx' = v0 (ch *)-«. (9.110)
Мы приняли, что g положительно. Очевидно, что v0 (x) нормиру-
нормируема, а «0 (х) нет. Поэтому мы должны положить ип = 0, и это
дает изолированное невырожденное решение для е0 = 0:
Заметим, -что fo/o = foaJo = 0. Поэтому решения фс (х) = th x
и / (х) = /0 (х) вместе по существу удовлетворяют связанным
уравнениям (9.98). Правая часть уравнения (9.986) просто обра-
обращается в нуль. Поэтому, если возбуждена только эта дискретная
мода г = 0 (пг = ЬГо), то фактически мы работаем с усовершен-
усовершенствованным приближением стационарной фазы (9.94), а не с (9.72).
Еще важнее то, что, поскольку /0 (х) невырождено, его зарядово-
сопряженное Cfo (x), которое также должно быть решением с ну-
нулевой энергией, должно совпадать с самим /„ с точностью до по-
постоянного множителя. Это означает, что f0 (x) должно быть заря-
дово-самосопряженным, если мы соответствующим образом вы-
выберем фазу в матрице зарядового сопряжения С. Это можно про-
проверить. В A + 1) измерениях при представлении (9.100) мы мо-
можем в качестве матрицы зарядового сопряжения использовать
С = (—03). Если задано произвольное решение (9.103) с энергией
ег, то легко убедиться, что fr = —сг3/> также является решением,
но с энергией —гг. Для решения (9.111) с е = 0, которое не вы-
вырождено, можно явно показать, что Cf0 = —03/о = /о-
Если бы не было зарядово-самосопряженнси фермионнои моды
с нулевой энергией, то мы могли бы разложить квантовое ферми-
поле, как в (9.836). «Основное солитонное состояние», т. е. основное
состояние в солитонном секторе, было бы тогда невырожденным
состоянием с зарядом Q = 0, удовлетворяющим (9.84). Но в при-

КВАЗЙКЛАССИЧЕСКЙЕ МЕТОДЫ ДЛЯ 6ЁРМЙ-П0ЛЕЙ 29S
сутствии самосопряженной нулевой моды (9.83), очевидно, из-
изменяется и принимает вид
У (х, t) = bofo(x) + £ (Ьге-'ег'$+) (х) + dU^'ft* (x)). (9.112)
Исходя из базисных антикоммутаторов (9.2) для полей, можно
убедиться, что Ьо подчиняется тем же стандартным антикоммута-
антикоммутационным правилам, что и br и dr:
\Ь0, Ч\+= 1. К br\+=\b0, br\+ = 0 и т. д.
Тогда тот же самый оператор заряда Q вместо (9.85) сводится к
Q = ±-\dxDt*V- Wf) = btb0 - -L + JJ (ЬЯ - dUr) ■ (9.113)
Состояние, в котором нет ни одной возбужденной фермионной
моды, теперь обозначим | сол —). По аналогии с (9.84) оно удов-
удовлетворяет соотношению
Ьо | сол — ) = ЪГ\ сол — ) = dr | сол — ) = 0. 1(9.114)
(Для простоты мы будем рассматривать только фермионные моды.
Бозонные возбуждения могут быть включены в рассмотрение,
как это сделано выше.) При всех пг = 0 и в отсутствие бозонных
возбуждений (Np = 0) это состояние | сол—) будет иметь ту же
энергию Мсол, задаваемую (9.82). Энергетические уровни вплоть
до О (й), как мы констатировали выше, не будут изменяться за
счет нулевой моды. Но в силу (9.113) и (9.114) заряд этого состоя-
состояния будет равен
<2|сол-) = ^-1 сол — >. (9.115)
Сопоставим это с «основным солитонным состоянием», введенным
выше в предположении, что ни одно из гг не равно нулю, для ко-
которого Q = 0. Далее возбудим однократно нулевую моду, т. е.
рассмотрим
|сол f ) = Ь+|сол — ). (9.116а)
Очевидно, что
Ьо | сол +■) = Ь0Щ | сол - ) = A - ЩЬ0) | сол ^ ) = | сол - ). (9.1166)
Поскольку возбуждается только мода с нулевой энергией (пг =
— fy-o, Np = 0, е0 = 0 в (9.81)), состояние | сЬл +) будет иметь
ту же энергию Мсол, что и | сол —). Но
Q | сол + ) = Щ | сол - ) = + 4" bt I сол - ) = ~ | сол + ) (Э. 117)
при использовании антикоммутационных правил для Ъ и d.
Поэтому и мы имеем два вырожденных состояния с наинизшей

296 ГЛАВА 5
энергией | сол ±) в кинковом секторе с зарядами ±1/2. Заметим,
что в отличие от мод с ненулевой энергией, которые появляются
парами ±ег, что приводит к 0 < пг < 2 в (9.76), нулевая мода
не вырождена. В разложении (9.60) Det Аф по собственным зна-
значениям она появляется только один раз. Поэтому для г = 0
0 «■ п0 < 1, т. е. эта мода может быть только однократно воз-
возбуждена. В силу этого | сол —) и |сол + ) являются двумя един-
единственными независимыми вырожденными состояниями наиниз-
наинизшей энергии в кинковом секторе. Более того, можно видеть, что
эти состояния являются зарядово-сопряженными друг другу.
Квантовополевой оператор зарядового сопряжения <$ преобра-
преобразует поля следующим образом:
, t) Я-1 = CY+ (х, t),
(9 11 R\
где С — матрица зарядового сопряжения, введенная ранее (см.
работу [50]; в наших обозначениях матрица С отличается от
матрицы этой работы множителем у0). Для разложения (9.112)
это сводится к
ШЪ-1 = dr, <вЪ\<в~х = d? для г =г 1,
Но оператор <$ унитарен и является симметрией гамильтониана
модели (9.99). Кроме того, | сол +) — единственное отличное от
| сол —) независимое состояние с той же энергией. Следовательно,
<в | сол - ) = а | сол - ) + р | сол + ), где | а |2 + | р |2 = 1, (9.120)
Но
(сол — \св\сол — ) = (сол -|- |bffi|сол — ) (используя (9.1166)) =
= (сол 4- \^К | сол — ) (используя (9.119)) =
= 0 ' (используя (9.114)).
Поэтому в (9.120) а = 0, Р = 1 и
^|сол-) = |сол + ). (9.121)
В результате мы имеет два вырожденных состояния | сол ±)
с наинизшей энергией в кинковом секторе, которые несут заряд
±1/2 и являются зарядово-сопряженными друг к другу. Каждое
является основной квантовой солитонной частицей. Фермионные
возбуждения каждого из этих двух состояний можно получить,
как и прежде, применяя остальные операторы рождения Ь? и $,
г Зг 1- Например,

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 297
при различных rt и различных pj приводит к состоянию с зарядом
(п — т — 1/2), сопряженным к которому будет состояние
с зарядом (т — п + 1/2). Оба они имеют одинаковую энергию,
равную
вплоть до порядка й включительно. Ясно, что все собственные
энергетические состояния в кинковом' секторе состоят из таких
пар зарядово-сопряженных состояний. Состояния внутри каждой
пары имеют одинаковую энергию, но противоположные по знаку
заряды. Все эти состояния имеют полуцелый заряд. Очевидно, что
это свойство не зависит от включения бозонных возбуждений.
Такое же рассмотрение может быть проведено отдельно в анти-
кинковом секторе, построенном в окрестности классического ан-
тикинкового решения (9.101).
Напомним, что модель (9.99) содержит также вакуумные сек-
секторы, построенные в окрестности ф = +1- В этих секторах фер-
мионные возбуждения над вакуумом являются обычными элемен-
элементарными фермионами и антифермионами, которые все имеют
заряды, когда используется тот же оператор заряда Q =
= 1/21 dx №+, ЧЧ. Конечно, мы могли бы прибавить к оператору
Q константу 1/2. Это превратило бы заряды в кинковом секторе
в целые, но тогда стали бы полуцелыми заряды в вакуумном сек-
секторе! Поэтому разница на полуцелое число между зарядами в ва-
вакуумном секторе, с одной стороны, и зарядами в кинковом сек-
секторе, с другой, представляется внутренним свойством, вызванным
присутствием самосопряженной моды с нулевой энергией (9.111).
Если бы мы могли провести эксперименты во всех секторах этой
двумерной модели, то это различие было бы измеримой величиной.
Например, если бы система (9.99) была помещена во внешнее
электромагнитное поле (добавлением слагаемого х1фА^ [*F, y^W]
к лагранжевой плотности (9.99)), то электрический заряд, который
обнаруживает поле А^, имел бы величину eQ. Частицы из кин-
кового сектора обладали бы полуцелым электрическим зарядом,
в то время как частицы из вакуумного сектора обладали бы целым
электрическим зарядом.
9.5. Дальнейшие замечания
Только что мы рассмотрели значение фермионной моды с ну-
нулевой энергией в кинковом секторе модели (9.99). Наличие та-
такой нулевой моды не является специфичным для кинкового ре-

298 ГЛАВА 9
шения или для модели (9.99). Из (9.110) видно, что решающим
свойством кинкового решения, которое делает возможной норми-
нормированную нулевую моду /0 (х), является то обстоятельство, что
фс (+оо) и <£с (—оо) имеют ненулевые значения противоположных
знаков. Любое другое топологическое решение с таким же свойст-
свойством также привело бы к такой нулевой моде. Это явление также
не ограничено рамками A + 1) измерений. Напомним, что в гл. 3
неабелева теория Хиггса в C + 1) измерениях (см. C.42)) привела
к решению в виде монополя т'Хофта—Полякова. Это также ста-
статическое решение, обладающее топологическим индексом. Джа-
кив и Ребби [197] включили в эту систему C.42) безмассовые
фермионы. Имеющиеся в секторе монополя расширенной теории
фермионные моды в соответствии с нашим общим методом будут
собственными функциями одночастичного гамильтониана Дирака
в фоновом поле классического монопольного решения. Джакив
и Ребби приняли, что фермионы являются изоспинорами относи-
относительно внутренней SU B)-группы теории, и нашли, что в данном
случае опять имеется невырожденная фермионная мода нулевой
энергии. Подобным же образом рассмотрим систему Янга—Миллса
в евклидовом четырехмерном пространстве, которая обсуждалась
в гл. 4. В ней возникли классические инстантонные решения,
обладающие топологическим индексом. Т'Хофт [331] показал,
что безмассовое уравнение Дирака в четырех евклидовых изме-
измерениях во внешнем поле Янг-миллсова инстантона снова поро-
порождает нулевое собственное значение. Мы рассмотрим этот вопрос
в гл. 11. Наличие фермионных нулевых мод в этих различных
примерах, содержащих некоторые топологические бозонные ре-
решения, очевидно, не является случайным совпадением. Мы знаем,
что это явление связано с фундаментальными математическими
теоремами [12, 13, 218], которые, однако, лежат далеко за рам-
рамками нашего изложения.
Все рассмотренные выше стабильные солитонные решения
классических уравнений бозонного поля обладали некоторым не-
ненулевым топологическим индексом. Это связано с тем, что по
крайней мере для тех классов лагранжианов, которые мы рас-
рассмотрели, видно, что статическим решениям необходим сохраняю-
сохраняющийся топологический индекс, чтобы они были стабильными отно-
относительно распада на тривиальные решения. Поэтому, когда эти
решения соединяются с фермионами, наличие фермионных нуле-
нулевых мод становится скорее правилом, чем исключением. Но
зависящие от времени решения в различных моделях, которые
мы изучали, не нуждаются в каком-либо топологическом индексе.
Напомним, что дублетные решения модели СГ удовлетворяют
условию ф (х, t) -*■ 0 при х -> +оо и являются нетопологическими.
Напомним также приближенные зависящие от времени решения,
данные для трехмерных моделей скалярного поля Фридбергом и

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 299
др. [142], где снова ф (х, t) -> 0 при х -> оо. В этих случаях,
когда поле Дирака вводится через юкавскую связь, нулевой фер-
мионной моды не должно быть вообще. (В контексте зависящих
от времени решений ф (х, t) под фермионными нулевыми модами
мы понимаем случаи, когда индексы Флоке обращаются в нуль).
Поэтому рассуждение разд. 9.3 может быть применено без из-
изменений. Детальные вычисления, использующие зависящие от
времени решения в C + 1) измерениях, см. в работе [1451.
Мы рассмотрели модели, в которых лагранжиан содержит поле
Дирака в билинейной форме. В эту категорию попадают все
представляющие интерес случаи в C + 1) измерениях, поскольку
взаимодействия, содержащие произведение четырех или более
ферми-полей, неперенормируемы. Это можно проверить с помощью
обычного подсчета степеней импульсов в диаграммах Фейнмана.
В A + 1) измерениях четырехфермионное взаимодействие пере-
перенормируемо. Типичным примером является модель
(9.122)
Сравним ее с другой моделью
S, (х, f)=W(id - т) W + gfWW - V2<£2, (9.123)
где ф (х, t) — скалярное поле. Легко видеть, что модели (9.122)
и (9.123) эквивалентны. Это можно показать как с помощью кано-
канонического метода, так и с помощью функционального интеграла.
Возникающие из Я?г (х, t) уравнения Лагранжа—Эйлера имеют
вид
ф(х, f) = gW(x, i)W(x,t), (9.124a)
(id -m)}¥ = —gfW. (9.1246)
Уравнение (9.124а) не является настоящим «уравнением движения»
для поля ф (х, t), поскольку в нем отсутствует производная по
времени от ф. Это происходит потому, что лагранжиан (9.123)
не содержит кинетического члена от поля ф. Поле ф не является
независимой степенью свободы в системе (9.123), и уравнение
(9.124а) является уравнением связи, которое фиксирует ф при
заданных W и Ц> для каждого (х, t). Стандартная теория связей
{113, 259], элементарным примером которой является (9.124а),
позволяет включить эту связь в лагранжиан. После того как ф
исключено из лагранжиана за счет введения в лагранжиан
(9.124а), мы получаем модель четырехфермионного взаимодействия
(9.122). Эта эквивалентность может быть показана также с помо-

300 ГЛАВА 9
щью функциональных интегралов. Применяя формулу (9.64)
к модели (9.123), имеем
Тг [е~шт] = j 2b Щ 3D [^+]3> meiS^exp [i \ dxdt(^> W - 1k
= \2D [¥+] 2b m etSv j 2b Щ exp {i j dxdt x
X [-1/, (ф - £ WJ + V2g2 ртJ }, (9-125)
где Sw = J dxd№ (id — m) W соответствует слагаемым от сво-
свободных фермионов в действии. Заменяя переменные <j> на <f =
— Ф —g'1±)XIr. можно точно взять интеграл по бозонам (экспонента
чисто квадратична), что дает некоторую не зависящую от дина-
динамики константу А. Тогда (9.125) сводится к
Tr [e-{HT] = AJ@ pF+] 2Ь V¥] exp (tSw + i j -5- g2 (WJ dx dt).
(9.126)
Это как раз то функционально-интегральное представление, ко-
которое мы должны были бы использовать для четырехфермионной
модели (9.122) с точностью до константы А, которая может быть
включена в нормировку. (Эти функциональные интегралы могут
быть использованы не только для определения уровней энергии,
но и для получения всех функций Грина теории при добавлении
членов с источниками (см., например, [2]).) Таким образом, мы
опять находим, что модели (9.122) и (9.123) эквивалентны.
Преобразовав модель (9.122) четырехфермионного взаимодей-
взаимодействия в модель (9.123), которая имеет только билинейные члены
по OF, Ч*1"), мы можем применить к последней методы, развитые
в предыдущих разделах. Эта процедура может быть тривиально
перенесена на другие перенормируемые четырехфермионные вза-
взаимодействия, такие, как 0Fy54'J- Требуется лишь вместо скаляр-
скалярного поля ф взять псевдоскалярное поле.
Используя этот метод, Дашен и др. [103] вычислили спектр
модели Гросса—Неве. Эта модель описывается лагранжианом
N / N \2
2 (х, 0 = V (VtidVj) +4 g2 У %V] - (9-127)
где /= 1, ..., N — индекс внутренней симметрии U (N), по
отношению к которой SB (x, t), очевидно, инвариантен. Гросс
и Неве [177] изучали эту теорию в пределе N ->■ оо и нашли,
что она приводит к спонтанному нарушению симметрии. Состав-
Составное поле ^¥jWj приобретает ненулевое вакуумное среднее. Это
делает возможным существование секторов с топологическими

КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 301
солитонами, и Дашен и др. вычислили энергетический спектр
в различных секторах, используя описанный выше квазикласси-
квазиклассический метод. С помощью тривиального обобщения модели (9.123)
система (9.127) оказывается эквивалентна лагранжиану
S' (х, t) = g Wj (id + 8ф) 40 - */яф*.
Мы знаем, как обращаться с этим лагранжианом. То обстоятель-
обстоятельство, что вместо одного фермиона имеется мультиплет из N фер-
мионов, легко учитывается в формализме функционального ин-
интеграла при использовании кратного интеграла по всем ферми-
полям. Это означает, что (9.66) заменяется на
Tr [ё~1нт] = \ф[ф] eS* J П (К® |>+] & [V,-]
X
X exp U j dldx 2 Ч$АфУ/\ = \4>[ф] exp (tS9(M, [ф]),
(9.128)
где
\ [ф] = S0 - IN In (K det АФ),
а Лф такое же, как в (9.67).
Остальные квазиклассические вычисления проводятся так же,
как в разд. 9.3. Дашену и др. [103] удалось реализовать прибли-
приближение «полной стационарной фазы» (9.69), (9.70), когда исполь-
используемое классическое решение является экстремумом полного эф-
эффективного действия, включающего энергию моря Ферми. Как
мы отмечали выше, это является технически трудной задачей;
детали читатель может найти в работе [103]. Но используемые
принципы квантования те же, что и в разд. 9.3. Многие из этих
принципов мы заимствовали как раз из работы [103].
В качестве заключительного замечания отметим, что с распро-
распространением наших методов на поля Дирака мы приобрели основ-
основной аппарат, необходимый для построения приближенных моделей
адронов с использованием квазиклассической теории поля. Изу-
Изучение выходящих за рамки теории возмущений солитонных секто-
торов с помощью квазиклассических методов является как до-
достаточно интересным, так и важным шагом вперед в теории х).
Но, как упоминалось во введении, дополнительным побудитель-
побудительным толчком к изучению таких методов является возможность
х) В частности, в последнее время обнаружено, что в рамках теорий «боль-
«большого объединения» электрослабых и сильных взаимодействий взаимодействие
фермионов с магнитными монополями т'Хофта — Полякова может приводить
к распаду протона [371 ]. — Прим. перев.

302 ГЛАВА 9
объяснения структуры и спектра адронов, поскольку известно,
что они являются протяженными частицами^ и, по-видимому,
должны описываться некоторой квантовой релятивистской тео-
теорией поля. Но, если различные солитонные решения и ассоцииру-
ассоциируемые с ними квантовые состояния, обсуждавшиеся в гл. 2—7,
полезны для иллюстрирования этой методологии, они не являются
реалистическими моделями адронов. Большинство примеров,
которые мы рассмотрели в этих главах, представляли собой дву-
двумерные модели скалярного поля. В разд. 3.3 мы провели изучение
примера калибровочной теории в C+1) измерениях, но он
обладал монопольным зарядом —интересным свойством, которое,
однако, отсутствует у реальных адронов. Еще более важно то,
что системы, обсуждавшиеся в предыдущих главах, не содержали
вкладов от ферми-полей, в то время как главной компонентой
адронов является фермионный кварк.
После того как мы включили в схему ферми-поля, мы имеем
достаточный теоретический фундамент для квазиклассических
моделей реальных адронов. Общепризнано, что адроны состоят
из кварков, удерживаемых вместе калибровочными бозонами.
В начальном приближении вместо векторных калибровочных бо-
бозонов можно использовать скалярные бозоны. Тогда мы имеем
типичную модель вида (9.63). (Если стремиться быть более реали-
реалистичными, то можно использовать калибровочные поля. Такая
процедура, являясь технически более сложной, основана на тех
же принципах, к которым присоединяются требования фиксиро-
фиксирования калибровки.) После задания модели в форме (9.63) или
(9.65) следует остальная часть нашего квазиклассического метода.
В частности, в большинстве случаев мы будем интересоваться ма-
малым числом низколежащих фермионных возбуждений. В хорошем
приближении барионы являются связанными состояниями трех
кварков, в то время как мезоны являются связанными состояниями
пары кварк—антикварк. Поэтому можно на реалистичных осно-
основаниях попробовать применить промежуточное приближение,
намеченное в общих чертах в конце разд. 9.3, когда классическое
решение удовлетворяет связанным уравнениям (9.97) и (9.59).
Более того, мы видели, что в главном порядке квазиклассического
разложения энергия, формфакторы и другие характеристики кван-
квантовой протяженной частицы определяются соответствующими свой-
свойствами самого классического решения. Поэтому в главном квази-
квазиклассическом приближении просто решаются классические свя-
связанные уравнения типа (9.98). Это сделано в нескольких статьях,
из которых выделяется работа [24], где из таких классических
решений вычислены некоторые свойства адронов, в том числе их
квантовые ■числа, формфакторы и др. Наше обсуждение в этой
главе обеспечивает теоретический фундамент для таких вычисле-
вычислений.

ГЛАВА 10
ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ
10.1. Инстантоны и периодический потенциал
В гл.4мы рассмотрели несколько примеров инстантонных решений.
Это были классические решения евклидовых уравнений движения
с конечным действием, и приведенные примеры простирались от
нерелятивистских одночастичных систем до релятивистских поле-
полевых систем, включая калибровочные теории. Из нашего обсуждения
на классическом уровне не следовала необходимость изучения
инстантонов, поскольку они являются решениями евклидовых
уравнений, когда переменная времени по существу комплексная.
Покажем теперь, что, несмотря на их евклидово происхождение,
инстонтоны могут играть важную роль в физике соответствующих
квантовых теорий.
Как и при квантовании солитонов, мы начнем с нерелятивист-
нерелятивистской квантовой механики и познакомимся с инстантонными эф-
эффектами в этом привычном контексте. Например, Поляков [287]
и Гильденер и Патраскиу [161] применили инстантонные методы
к частице в потенциале с двумя минимумами. Другим популяр-
популярным примером является задача о периодическом потенциале [89].
Для иллюстрации мы используем последний пример, так как он
представляет собой близкую аналогию инстантонной физике
в калибровочных теориях.
Рассмотрим частицу единичной массы, движущуюся вдоль
прямой в потенциале V (q), который удовлетворяет условию
V (q) = V (q + 2л) A0.1)
для всех q в интервале [—оо, оо]. Пусть минимумы^У (q) распо-
располагаются при q = 2Nn. Без потери общности положим V BNk) =
= 0. В качестве конкретного примера можно иметь в виду част-
частный случай
V (q) = 1 — cos q, A0.2)
,.но наши выводы будут справедливы для любого гладкого ограни-
ограниченного периодического потенциала с абсолютным минимумом
внутри каждого периода (рис. 18).
Задача о периодическом потенциале хорошо известна, особенно
в физике твердого тела, где она является моделью поведения элект-

304 ГЛАВА 10
ронов в одномерной решетке [219]. Хорошо известны следующие
свойства этой задачи, которые выводятся в квантовой механике
стандартными методами без обращения к инстантонам.
1. Разложим V (q) в окрестности минимума при q = 0. Пусть
г^г- (Ю.З)
Мы будем рассматривать низколежащие уровни этой системы
при условии слабой связи Яг <^ ®2- Это является также прибли-
приближением «сильной связи» для электронов в решетке. В этом прй-
Щ)
О
I
Рис. 18. Периодический потенциал V (q) с периодом 2я и минимумами при q =
= 2яЛГ.
ближении туннелирование волновых функций низколежащих
энергетических уровней от одной потенциальной ямы на рис. 18
к соседней мало. Если бы мы вообще пренебрегли туннелированием,
то могли бы построить волновую функцию основного состояния
и0 (q) в яме в окрестности q = 0 с некоторой энергией Ей. В на-
наинизшем порядке по Хт в A0.3) Ео = 1/2Н(л. Так как задача пери-
периодическая, мы могли бы построить также аналогичное основное
состояние «0 (q — 2Nn) в окрестности любого другого минимума
q = 2Nn также с энергией Ео. В отсутствие туннелирования мы
имели бы тогда бесконечнократно вырожденное основное состояние
с энергией Ео « V2ft(o.
2. На самом деле туннельные эффекты, хотя и малые, сущест-
существуют. Изолированный уровень Ео, который в отсутствие туннели-
туннелирования бесконечнократно вырожден, расщепляется в зону.
Соответствующие энергетические волновые функции в первом при-
приближении являются линейными комбинациями невозмущенных
волновых пакетов в отдельных ямах:
Фв(Ф= Е ем*щ(д - 2Nn), A0.4)
N=—oo
где 9 — параметр, нумерующий состояния в зоне. Коэффициенты
eiNB выбраны так, что состояния[A0.4) являются собственными

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 305
функциями унитарного оператора, реализующего симметрию
q -*-q + 2я, относительно которой гамильтониан инвариантен.
Под действием этой симметрии х)
фв(д + 2л) = е^фв(д). A0.5)
3. Теорема Блоха [51, 139] утверждает, что собственные функ-
функции энергии в периодическом потенциале должны удовлетворять
условию
*h(a) = e"«vh(q), A0.6)
где k — волновое число, a vh (q) периодична относительно сдви-
сдвигов |решетки, в нашем случае относительно q -^-q + 2it. Для
q -*-<7 + 2я условие A0.6) дает
e^j>h(q), A0.7)
что согласуется с A0.5) при отождествлении 2я& = 9.
4. Энергия уровней в низшей зоне дается выражением [218]
Eh да Ео — a (cos ka), A0.8)
где а — константа, га — период решетки. Используя для на-
нашего случая а = 2я, k = 9/2я и Ео да 1/2йо), мы можем записать
A0.8) в виде
Яеда^/аЙо) —acos8. A0.9)
Система содержит также зоны с большей энергией, но нас интере-
интересует только низшая зона, возникающая из расщепления основ-
основного состояния.
Покажем, как эти хорошо известные результаты могут быть
получены с использованием инстантонов и евклидовых функцио-
функционально-интегральных методов гл. 6. В конце обсуждения станет
ясно, почему при исследовании таких туннельных эффектов ква-
квазиклассическими методами евклидовы функциональные интегралы
(и поэтому инстантоны) более полезны, чем интегралы по траекто-
траекториям в действительном времени.
Рассмотрим евклидову амплитуду, определенную в F.30),
F.31), для перехода из q = 0 при т' = (—т/2) в q = 2я при т/ =
(+/2): /
т/2; 0, -т/2) = Bя | e-w* \ 0) =
A0.10)
х) Под термином «симметрия» автор подразумевает преобразования, обра-
образующие группу сдвигов q-*- q-\- 2n. — Прим. перев.

306 ГЛАВА 10
Здесь \фп) — собственные энергетические состояния, 10) и
и 12я) — собственные функции координаты (q), SE [q (%')] —
евклидово действие, и все пути идут из q (—т/2) = 0 в q (т/2) = 2я.
Мы рассматриваем зону с наинизшей энергией в нашей задаче
с периодическим потенциалом. В пределе больших т в сумме 2П
в A0.10) доминирует эта зона. Поэтому мы будем работать в этом
пределе. Подразумевается, что приводимые ниже выводы справед-
справедливы только в пределе т ->-оо, несмотря на то что мы приводим
в некоторых случаях зависимость от т.
Будем вычислять функциональный интеграл в A0.10) в квази-
квазиклассическом гауссовом приближении, разлагая SB [q (%')]
в окрестности его экстремумов. Эти экстремумы определяются
уравнением
Это классическое евклидово уравнение движения. Его решения
с конечным действием (удовлетворяющие условиям q (—.т/2) = 0,
q (т/2) = 2я при т -у оо) являются классическими инстантонами
этой системы. Антиинстантонное решение удовлетворяет усло-
условиям q (—т/2) = 2л, q (+т/2) = 0 при т ->-оо.
В гл. 4 мы отметили, что решения уравнения A0.11) с конеч-
конечным действием совпадают со статическими солитонами с ко-
конечной энергией в соответствующей скалярной полевой теории
с потенциалом V (q>) в A + 1) измерениях. В гл. 2 мы рассмотрели
существование и свойства таких классических солитонов. Объе-
Объединив результаты гл. 2 и 4, найдем, что инстантонное решение
уравнения A0.11) с конечным действием существует для любого
периодического потенциала формы, изображенной на рис. 18.
Пусть это решение qK!l (т') имеет действие SE [qKJ1 (%') ] = So.
Его график схематически показан на рис. 19, а. Нас интересует
его точная форма, которая зависит от деталей V (q), за исключе-
исключением того обстоятельства, что оно экспоненциально быстро стре-
стремится к нулю при т' -» оо и к 2я при т' ->- оо. Оно обладает то-
топологическим индексом
(Из обсуждения в гл. 2 мы знаем, что такие свойства имеют ме-
место. Для частного примера V (q) A0.2) этот инстантон будет та-
такой же функцией, что и СГ-солитон.)
Вычислим вклад от окрестности изолированного инстантон-
ного решения дкл (т') в функциональный интеграл в A0.10).
Используя гауссово приближение (гл. 6), получаем
где ВЕ (т) — множитель меры в функциональном интеграле.

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 307
На этом этапе следует отметить два взаимосвязанных момента,
которые возникают, когда т — полный диапазон изменения т' —
стремится к бесконечности. С одной стороны, оператор
-cP/dx* + V" (дкл)
будет иметь нулевое собственное значение, поскольку действие
трансляционно инвариантно по переменной т'. Формально это
о
Рис. 19. а ~ схематическое изображение одноинстантонного решения qK11 (т');
точный профиль зависит от выбора V (<?); область изменения т' есть [—т/2, т/2]
при т—оо; штриховые вертикальные линии делят этот интервал на сегменты
[—т/2, —т/2 + И, [—т/2 + 1, —т/2 + 2], ..., [т/2 — 1, т/2]; для большинства
этих сегментов V" (qKJI (т')) « V" (б) = V" Bя); б — схематическое изображение
двухинстантонного, одноантиинстантонного решения; это решение является точ-
точным, если координаты центров Tg, Tg и т0 находятся на бесконечном расстоянии
друг от друга.
вызовет расходимость в A0.12). С другой стороны, в силу той же
самой трансляционной инвариантности при данной #кл (т') функ-
функция #кл (т' — т0) также будет инстантонным решением с тем же
действием So для любого т0. Поэтому каждый из сдвинутых парт-
партнеров <7„п (т') дает такой же вклад A0.12). Такой суммарный
вклад всех отдельных инстантонов потребует умножения A0.12)
С г/2
на \_х/2 dx0 = т. Эти две характерные особенности, а именно су-
существование нулевой моды и необходимость интегрировать по
соответствующей коллективной координате т0, как мы выяснили

308 ГЛАВА 10
в гл. 8, отражают одно и то же явление. Как там отмечено, в этом
случае следует заменить координату нулевой моды на коллектив-
коллективную координату с помощью подходящей замены переменных.
В приложении Б мы покажем, как это можно сделать для настоя-
настоящего случая в формализме функционального интеграла. Резуль-
Результирующий вклад от всех отдельных инстантонов в A0.10) равен
(см. (Б. 14))
Bя| е-™| 0>lfо = e~s^JxBE(x) {Def [~d»;dx'' + V(?„Л)]Г1/2.
A0.13)
Здесь Def обозначает детерминант, из которого исключена нуле-
нулевая мода, / —множитель Якоби в (Б. 13), а подстрочное обоз-
обозначение A, 0) означает, что это вклад от одного инстантона без
антиинстантонов. Далее предстоят еще вклады. Следующий шаг
состоит в наблюдении, что в этой задаче инстантон имеет «конеч-
«конечный размер». Это означает, что инстантонное решение дкл (т' — т0)
для большинства значений т' весьма близко к тривиальным реше-
решениям, либо к q = 0, либо к q = 2я (см. рис. 19, а). Эта общая
черта, не зависящая от конкретной формы V (q), до тех пор пока
V" @) = со2 Ф 0. Только в некоторой конечной области измене-
изменения т' решение существенно отличается от 0 или 2я. Действие также
локализовано в этой области, за исключением экспоненциального
хвоста. Размер этой области, т. е. «размер инстантона», зависит
от таких параметров V (q), как со2, но не от т — полного интер-
интервала изменения т/, — который равен [—г1гх, V2t], причем т -*- оо.
Этот интервал можно разделить на подынтервалы [—1/2х, —1/2т +
+ 1], [—VaT+ I,— Va т + 2], ..., [V,t — 1, V2t]. Оператор erHxi*
и интеграл по траекториям в A0.10) могут быть записаны
как произведения соответствующих величин в подынтерва-
подынтервалах. В большинстве подынтервалов qKJI « 0 или 2я, V (дкл) я=
« ((PV/dq^K = со2 и оператор —дЬ + V" (<?„„)■« —дЬ + со2.
Величина дкл заметно отличается от 0 или 2я только в ко-
конечном интервале изменения т/, длина которого не зависит от т.
Поэтому мы можем записать
{Det'[-c& + Vfo™)]r1/8=i {Det(-^ + co2)}-1/2tf. A0.14)
Это уравнение просто определяет К, но смысл вышеприведенного
аргумента состоит в том, что К есть константа, не зависящая от т
при т—>-оо. Поэтому A0.13) превращается в
(-& + со
2)Г1/2. A0.15)
Мы уже знаем значение ВЕ(х) [Det (—дЬ + со2)]~1/2. Это не
что иное, как гауссов функциональный интеграл, который яв-
является аналитическим продолжением на т = IT функционального

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИЙ 309
интеграла гармонического осциллятора. Последний дается вы-
выражением F.19) в виде
В' (Т) {Det (—d2/dt2 - со2)}-1/2;
значение последнего (см. F.21) и F.24)) равно
/ 1 юг у/2
\ 2%ьШ sin at ) '
Заменяя т на IT, получаем
A0.16)
Таким образом,
/ m \ 1 /2
lim /9тг I /j—«т/й | o\/i л, p—Svluif(rl^L-\ Р—(л%/2 л л \j\
Это вклад от отдельных инстантонов.
Рассмотрим теперь конфигурацию, состоящую из инстантона,
локализованного в точке то, за которым следует антиинстантон
в точке то > то, за которым опять следует инстантон в точке
то 3> то (рис. 19, б). Конфигурация имеет правильные с точки
зрения нашей задачи граничные условия, а именно q (—оо) = 0,
q (оо) = 2я. До тех пор пока инстантоны разделены конечным
интервалом (вдоль оси т'), эта конфигурация в общем случае не
будет точным классическим решением. Но по мере того, как рас-
расстояния т0 — т0 и т0 — т0 растут, такая конфигурация все точ-
точнее удовлетворяет A0.11), поскольку перекрытие между инстан-
тонами становится произвольно малым. На самом деле это заме-
замечание справедливо для любого набора из пх инстантонов и п2
антиинстантонов, расположенных далеко друг от друга. До тех
пор пока п± — п2 = 1, граничные условия удовлетворяются.
Поскольку мы работаем в пределе т ->- оо, где т — размер области
изменения переменной т', такие конфигурации инстантонов с про-
произвольно большими расстояниями между ними являются допусти-
допустимыми. А именно, представляется очевидным, что инстантоны с рас-
расстоянием друг от друга больше R занимают бесконечно большее
фазовое пространство, чем инстантоны с расстоянием друг от
друга меньше R, для любого сколь угодно большого R.
Строго говоря, для любого конечного сколь угодно большого
расстояния друг от друга многоинстантон-антиинстантонные кон-
конфигурации не будут стационарными точками действия. Однако
первая производная 6S lq]/bq (т') очень мала и стремится к нулю,
когда расстояние растет. Следовательно, гауссово приближение
для подынтегрального функционала в окрестности такой кон-
конфигурации, где мы опустили эту первую производную, с ростом

310 ГЛАВА 10
расстояния будет все лучшим. Поэтому мы должны включить в на-
наше квазиклассическое разложение вклады от таких далеко раз-
разнесенных инстантонов и антиинстантонов (см. также [55]).
Вклад в Bя | е~Нх/п | 0) от таких асимптотически точных
многоинстантонных решений легко получить в рамках нашего
приближения, задав вклад от отдельного инстантона A0.17).
Поскольку пх инстантонов и п2 антиинстантонов далеко разнесены
друг от друга, каждый инстантон (или антиинстантон) дает в дей-
действие аддитивный вклад So. Каждый из них вносит в детерминант
множитель К, поскольку V" (qKJI) отличается от со2 в окрестности
каждого инстантона в одной и той же степени. Наконец, если рас-
рассматриваемые объекты далеко разнесены (т. е. расстояние между
ними значительно больше, чем размер инстантона), каждый ин-
инстантон (или антиинстантон) может быть локализован в любом
месте на оси т'. Поэтому интегрирование по точке его локализа-
локализации приводит к множителю /т. Разрешая каждому инстантону
находиться в любом месте на оси т', мы также включаем конфи-
конфигурации, в которых они недалеко разнесены. Но фазовое про-
пространство конфигураций, где некоторые инстантоны расположены
близко друг от друга, бесконечно мало по сравнению с фазовым
пространством конфигураций, где все они расположены далеко
друг от друга. Для инстантонов конечных размеров это чисто ки-
кинематическое утверждение о фазовом пространстве в пределе т ->-
-»--оо. Необходимо проверить, что динамика не опровергает
это утверждение. Мы сделаем это несколько ниже (см. замечание 4
в обсуждении ниже).
Таким образом, вклад от пх инстантонов и п2 антиинстантонов
в совокупности равен
ИтBя| е->™* 10>(П1,П1) =
Т->-оо
= [6„,_„2,,] ехр [~^ + ,"г) 8о/П] №)"'+"'г^/2 ^у\ A0.18)
где 6ni_na, 1 — символ Кронекера. Множители {Мп^) A/п2!)
появляются из-за неразличимости инстантонов. Мы разрешили
каждому инстантону находиться в произвольном месте на всей
оси т'. Ясно, что мы будем лишний раз учитывать конфигурации,
когда инстантоны просто меняются местоположением — отсюда
множитель MrixV. Такой же довод имеет место для антиинстантонов.
Заметим попутно, что в нашей задаче инстантоны и антиинстан-
тоны не должны обязательно чередоваться. Поскольку нулями
V (q) являются не только q = 0 или 2я, но и все q = 2Nn, возмо-
возможны конфигурации с конечным действием, где пх инстантонов и п2
антиинстантонов располагаются в произвольной последователь-
последовательности. Единственное требование, обусловленное граничными ус-
условиями, есть пх — п2 = 1. Этот случай следует отличать от за-

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 311
дачи о потенциале с двумя минимумами, который имеет только
два минимума, и, следовательно, инстантоны должны чередова-
чередоваться с антиинстантонами, чтобы сохранять действие конечным.
Возвратимся к нашей задаче. Полный вклад в квазиклассиче-
квазиклассическом приближении получается при суммировании A0.18) по пх
и п2:
Ш"°2 ^СГ* ■«■■-■■■■
A0.19)
Суммы по пх и п2 разделяются с использованием тождества
j -g-exp[-/e(n, - ла- 1)] = 6Й1_„,.,. A0.20)
о
После этого разделения суммы по ni и п2 тривиальны и дают
lira Bя | е-*«/* | 0) = Km Y Bя | фп) {фп | 0) е-£пт/* =
Т->-оо Т->-оо J—J
/2
2я
--1 <вт). A0.21)
Это наш главный результат. Можно заметить, что воспроизводятся
хорошо известные черты наинизшей энергетической зоны. Как
можно видеть из правой части равенства, низколежащие энерге-
энергетические уровни, которые преобладают в левой части A0.21)
при т—юо, образуют непрерывную зону, параметризованную
6, 0 < 6 < 2я. Энергия уровней в зоне, очевидно, равна
EQ = 1I.M-n{2JKe-s"lucoiQ). A0.22)
Это согласуется с выражением A0.9) при а = 2JKfie~s°/n в квази-
квазиклассическом приближении Bа — ширина зоны). При заданном
явно выражении для V (q) в принципе можно найти йнстантонное
решение qKJI (%'), его действие So [qKJI] и якобиан / = у So.
Константа Л' также может быть получена из A0.14) при исполь-
использовании собственных значений —д'^ + V" (<?Кл)- (Для потенциала
СГ A0.2), например, эти собственные значения есть не что иное,
как квадратные корни из частот стабильности СГ-солитона,
использовавшиеся в разд. 7.1.) Таким образом, наш квазиклас-
квазиклассический вывод в принципе позволяет вычислить ширину зоны.
Обращаясь к ассоциированным с энергетическими уровнями
A0.22) собственным функциям |^>е). мы видим из равенства
A0.21), что
Bя | фв) (фв | 0) = (е'в/2я) (ю/лй). A0.23)

312 ГЛАВА 10
Теперь ясно, что если бы нам надо было вычислить амплитуду
перехода {2Nn \ е-нх1П | 0), то весь предшествующий анализ
остался бы без изменений с единственной разницей, что П\ — п3 =
= N вместо 1. Это привело бы к замене eie в A0.21) на ешв. Таким
образом,
BNn | фв) {фв | 0) = (е«е/2я) (ш/яЙI/2.
Отсюда ясно, что
. -A0.24)
Это находится в согласии со свойством блоховских волн, задава-
задаваемым A0.5) или A0.7). Соотношение A0.24) задает квазипери-
квазипериодичность A0.5) волновых функций в точках q = 2Nn. Аналогич-
Аналогичное соотношение, связывающее фв (q) и фв (q + 2Nn) для
произвольного q, также может быть получено подобными квази-
квазиклассическими методами, если начинать с (q + 2Nn \ e-Hx/n\q).
Таким образом, мы снова вывели с использованием инстантон-
ных методов перечисленные выше основные свойства наинизшей
энергетической зоны в периодическом потенциале. Причина такая
же, как и в предыдущих главах. Аналогичными свойствами обла-
обладают полевые теории, особенно калибровочные теории, наиболее
удобным способом исследования которых являются евклидовы
функциональные интегралы и инстантоны. При соответствующем
обобщении наше упражнение по применению инстантонов в задаче
о периодическом потенциале может быть перенесено на эти более
сложные теории. Прежде чем перейти к калибровочным теориям,
представляется полезным сделать следующие замечания по по-
поводу приведенного выше вывода.
1. Мы использовали только классические решения с конечным
действием, а именно инстантоны и антиинстантоны. Формально
решения с бесконечным действием также являются экстремумами
евклидова действия. Но их вклад в квазиклассическом разложе-
разложении равен нулю. Заметим (см. A0.17)), что этот вклад пропорци-
пропорционален ехр [—SRa].
2. Поскольку мы изучаем туннельные эффекты, может быть
задан вопрос, почему мы не использовали амплитуду Bя | e-iHT/fi | 0)
в действительном времени для перехода со дна одной потенциаль-
потенциальной ямы в другую. В самом деле, спектральное разложение этой
амплитуды для действительного времени в принципе должно со-
содержать всю информацию, которую мы ищем, и мы использовали
такие амплитуды в предыдущих главах. Но оно неудобно для
квазиклассических разложений тех величин, которые мы сейчас
исследуем. Мы интересуемся туннельными эффектами на нижних
энергетических уровнях (т. е. расщеплением основного состояния
за счет туннелирования). Из гл. 6 очевидно, что соответствующее
квазиклассическое приближение включало бы низкоэнергетиче-

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 313
ские классические орбиты. Но допустимых классических низко-
энергетических траекторий, связывающих q = 0 и q — 2я, не
существует из-за наличия потенциального барьера между ними.
В противоположность этому, евклидов интеграл по траекториям
может быть разложен в окрестности решений евклидова уравнения
движения A0.11). Это евклидово уравнение тождественно ньюто-
ньютонову уравнению для соответствующей задачи с потенциалом
l—V(q)] в действительном времени. В потенциале [—V (q)]
точки q — 0 и q = 2я являются максимумами вместо минимумов,
и низкоэнергетическое решение должно существовать. Это и есть
инстантоны исходной задачи. Вот почему при изучении туннель-
туннельных эффектов на низколежащих уровнях с помощью квазиклас-
квазиклассического метода в игру вступает евклидов интеграл по траекто-
траекториям и инстантоны.
3. Наше вычисление может быть названо «приближением
разреженного инстантонного газа». Инстантоны, дающие вклад
в A0.21), мы рассматривали как одномерный газ частиц и анти-
античастиц, распределенных вдоль оси т/. Суммирование по пи п2
в A0.19) очень похоже на суммирование в функции распределения
очень разреженного газа частиц и античастиц в одном измерении
при условии, что полное «число частиц» П\ — п2 равно единице.
4. Важным предположением являлась разреженность инстан-
инстантонного газа, т. е. что инстантоны и антиинстантоны, дающие
вклад в A0.21), расположены далеко друг от друга. Решающим
аргументом в пользу этого является, очевидно, прежде всего то,
что инстантоны имеют конечные размеры. Для типичного пери-
периодического потенциала V (q) на рис. 18 с V" @) Ф 0 это справед-
справедливо. В некоторых полевых теориях, таких как двумерная абе-
лева модель Хиггса, которая обсуждается в следующем|разделе,
инстантоны снова имеют конечные размеры, так что при соответ-
соответствующем обобщении может быть применен наш вывод. Но для
теории Янга — Миллса в 4 измерениях, которая масштабно-
инвариантна, инстантоны имеют любые размеры. (Напомним
произвольный масштабный параметр \х в янг-миллсовских ин-
стантонах, полученных в гл. 4.) Поэтому для данной системы
приближение разреженного инстантонного газа наталкивается
на трудности, как мы увидим в разд. 10.5. Возвращаясь к нашей
задаче о периодическом потендиале, следует убедиться в том, что
именно разреженные конфигурации дают в пределе т -> оо глав-
главный вклад в A0.21). Зависимость от л в инстантонном вкладе
в A0.19) имеет вид (JK^e's°!n)n/n\ и достигает максимума, когда
п ж JK.xe~s"/n. Соответствующая «плотность инстантонов» есть
hlx = (JKe~s°/n)- Для малых й это как раз соответствует малой
плотности.
5. В выражении A0.22) второе слагаемое отражает эффект
туннелирования. Вследствие множителя ехр (—So/H) это слага-

314 ГЛАВА 10
емое обнаруживает ожидаемую экспоненциальную зависимость
от МП, а также от «высоты барьера». Напомним, что из уравнения
B.20), примененного к настоящему случаю, следует, что инстан-
тонное решение qKJI (%') подчиняется условию
— (<?клJ= У(^.л). где q«a = dqKJdx'.
Следовательно,
оо оо' 2п 2Я
So= \ (-у- йп + V) dx = j (qK]lfdx' = j ^кл^=| VWJq)dq.
—со .—со О О
A0.25)
Эта величина представляет собой высоту потенциального барьера
между 0 и 2я. Такая зависимость амплитуды туннелирования от
/ 2я
ехр \~~~n
V о
находится в согласии с общепринятыми результатами, получен-
полученными обычным методом [224].
6. Мы отметили сходство между инстантонами в этой задаче
и статическими солитонами соответствующей скалярной теории
поля в A + 1) измерениях. Хорошо известно, что в системах
в A + 1) измерениях при любой сколь угодно малой температуре
дискретная симметрия восстанавливается за счет образования
солитонов и антисолитонов («образования доменов»). Конкретный
пример по статистической механике квантовополевой теории см.
в работе [104]. Подобным же образом здесь инстантоны восста-
восстановили симметрию q -> q + 2я («для любого, сколь угодно ма-
малого й»). В отсутствие туннелирования волновая функция основ-
основного состояния ф0 была бы локализована в произвольной, но
только одной потенциальной яме, нарушая симметрию ф0 относи-
относительно q —<-G + 2я. Такое спонтанное нарушение симметрии
в системе с только одной степенью свободы на самом деле про-
произойти не может. Причина, конечно, в том, что обязательно будет
иметь место туннелирование, представленное здесь инстантонными
эффектами. В результирующей энергетической зоне B0.22) дей-
действительное основное состояние соответствует 6 = 0. Если под-
подставить 6 = 0 в соответствующую волновую функцию A0.5), то
последняя будет полностью симметричной относительно q —►
—►с? + 2я. Таким образом, инстантоны восстановили симметрию
основного состояния.
7. Сопоставьте задачу о периодическом потенциале (ЗПП),
которую мы только что рассмотрели, с тесно связанной с ней
задачей, когда частица расположена на единичной окружности,

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 315
задаваемой 0 < q < 2я, но с тем же лагранжианом L = 11гЦг —
— V (q). Частица на окружности (ЧНО) имеет такое же класси-
классическое уравнение движения и такое же дифференциальное урав-
уравнение Шредингера, что и ЗПП. Но квантованные уровни энергии
различаются. Это обусловлено тем, что координатное пространство
вместо всей действительной прямой состоит лишь из окружности
О < q < 2я и соответственно отличаются граничные условия.
В случае ЧНО точки q = 0 и q = 2я физически тождественны.
Естественное граничное условие, которое можно было бы пред-
предположить, состоит в том, что все волновые функции должны удо-
удовлетворять условию ф Bя) = ф @). В частности, это сводится
к выбору в качестве энергетических собственных функций только
тех блоховских волн из набора A0.5), для которых 0 = 0. Каждой
зоне уровней в ЗПП должен соответствовать только один уровень
(составляющая с 6 = 0) в случае ЧНО. Например, основное со-
состояние ЧНО есть составляющая с 6 = 0 из набора A0.22) с энер-
энергией
ПП BJKe-s°/n). A0.26)
Этот результат может быть также получен с использованием с са-
самого начала инстантонов. Поскольку классическое уравнение
для ЗПП и ЧНО одно и то же, в обоих случаях имеют место одни
и те же инстантонные решения. (В случае ЧНО многоинстантон-
ные решения должны пониматься в том смысле, что частица
несколько раз обходит окружность, пока т' меняется от —оо
до +оо.) Мы можем повторить такое же вычисление инстантон-
ного газа, как для ЗПП, с единственной разницей, что наложенное
в A0.19) условие пх — Щ = 1 может быть опущено. Любое реше-
решение с tii инстантонами и щ антиинстантонами, начинающееся
в q = 0, возвратится в q = (пг — п2) 2я, т. е. в ту же физическую
точку для всех Пг и п2. Таким образом, если мы опустим множи-
множитель 6П1-п„1 в A0.19), то экспоненциальные последователь-
последовательности будут уже независимы без обращения к A0.20). Результат,
очевидно, имеет вид
lim (q = 2я | *?-"*/« \ q = 0) = (со/яй)'/2 ехр (—У2(лт + e-s«^2//(T).
Т->-оо
A0.27)
Следовательно, воспроизведен энергетический уровень Ео
A0.26). Вычисления, основанные на инстантонах, важны и при
изучении туннелирования. Может показаться странным говорить
для ЧНО о туннелировании из физической точки q = 0 в нее же.
Но понятие туннелирования имеет смысл даже для ЧНО. В функ-
функциональном интеграле для амплитуды перехода из q = 0 в ту же
физическую точку имеются аддитивные вклады от классов путей,

316 ГЛАВА 10
которые обходят окружность нуль раз, один раз, два раза и т. д.
Например, за путь, который обходит окружность один раз, ча-
частица при переходе из 0 в 2я пересекает потенциальный барьер
один раз. При кратных обходах она пересекает барьер несколько
раз. Разумеется- соответствующие вклады в амплитуду перехода
могут рассматриваться как туннельные эффекты.
Для основного состояния в случае ЧНО выражение A0.26)
дает составляющую с 6 = 0 из энергетической зоны в ЗПП. Су-
Существует модификация, при которой, не меняя никоим образом
классическую физику ЧНО, мы можем изменить ее квантовую
энергию основного состояния так, чтобы привести ее в соответствие
с любой составляющей зоны ЗПП с 6 Ф 0. Изменим лагран-
лагранжиан ЧНО на
где 6 — действительная константа. Дополнительное слагаемое,
добавленное в A0.28), есть полная производная по времени.
Она не изменяет классические уравнения Лагранжа — Эйлера.
Но квантовые уровни изменяются, что можно предвидеть из
замены канонического момента р = q на р = q — 6/2я. При
различном выборе 6 в A0.28) получаются различные квантовые
теории, но каждая может рассматриваться как совершенно равно-
равноправная квантовая версия исходной классической системы ЧНО.
Как же дополнительное слагаемое в A0.28) изменяет наше инстан-
тонное вычисление для ЧНО? Классические инстантонные ре-
решения остаются прежними, но евклидово действие для отдельного
инстантона заменяется на
A0.29)
Так как антиинстантон движется вспять (q изменяется от 2я
до 0), его действие заменяется на So — /8. Легко усмотреть ре-
результирующую перемену в алгебре и убедиться, что выражение
A0.26) будет теперь заменено на
£в = -1- ftoo - 2JKne-s°'n cos 8.
Это выражение выглядит тождественным результату A0.22) для
ЗПП, но если в ЗПП все значения 6 являются значимыми, образуя
энергетическую зону, в случае ЧНО существует только одно
значение 6 для данной теории. Это значение параметра 8 в лаг-

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 317
ранжиане A0.28). Вместо целой зоны в ЗПП в случае ЧНО будет
только один уровень, хотя мы и можем изменять этот уровень,
варьируя параметр 6. Эта редукция числа уровней от зоны в ЗПП
к изолированному уровню в случае ЧНО находится в согласии
с тем обстоятельством, что первая имеет в бесконечное число раз
большее конфигурационное пространство.
Очевидно, что уровень Ев в случае ЧНО соответствует опре-
определенной блоховской функции фв с тем же значением 6. Эта функ-
функция подчиняется условию фв Bя) = е{вфв @), т. е. граничное
условие является лишь квазипериодическим (см. [40, 235, 236]).
Может показаться странным, что хотя точки 0 и 2я представляют
собой одну и ту же физическую точку, тем не менее фв Bя) Ф
ф фв @). Однако, как отметили Роте и Свиека [295, 296], вполне
возможно построить согласованную квантовую теорию для ЧНО
лишь с квазипериодическим граничным условием. Физическая
тождественность q = 0 и q = 2я находит отражение в том факте,
что матричные элементы физических операторов для фв Bя)
и фв @) одни и те же. Фазовый множитель eie в матричном эле-
элементе сокращается.
Мы столь подробно разобрали эти свойства ЧНО и отличия
последней от ЗПП потому, 470 аналогичное сравнение возникает
при изучении топологических вакуумов в калибровочных теориях
[40, 342]. Хотя явление вакуумного туннелирования в калибро-
калибровочных теориях и имеет некоторое сходство с ЗПП, по духу оно
ближе как раз ЧНО. Этот вопрос обсуждается в последующих
разделах.
8. В ЗПП туннелирование возвращает основному квантовому
состоянию дискретную симметрию гамильтониана относительно
q-+q-\-2л, хотя и нарушенную индивидуальными «классиче-
«классическими вакуумами» в q = 2Nn. В формализме функционального
интеграла это происходит посредством инстантонов. Можно задать
вопрос, что препятствует такому явлению в полевых теориях,
в которых известно, что некоторая дискретная симметрия спон-
спонтанно нарушается вакуумным состоянием. Рассмотрим, например,
хорошо знакомую A + 1)-мерную модель СГ. Ее потенциал
U (ф) = 1 —cos ф имеет такие же свойства, как и потенциал
ЗПП на рис. 18. Чтобы исследовать, имеет ли место в этой модели
туннелирование между соседними минимумами, предположим,
что мы вычисляем амплитуду (ф (х) = 2я | е~н% | ф (х) = 0) пу-
путем обобщения квазиклассического метода этого раздела на теорию
поля. Мы использовали бы теоретико-полевой евклидов функци-
функциональный интеграл с евклидовым действием
1/2(^«/') (д»ф)+ 1 -cos./.
И=1 /

318 ГЛАВА 10
где [i = 1,2 соответствует евклидову пространству-времени (хг =
= х, х2 = it). В квазиклассическом методе мы разложили бы поля
в окрестности решения евклидова полевого уравнения
V2 ф = sin ф, где V2 = д21дх\ + д21дх\. A0.30)
В соответствии с замечанием в гл. 4, это евклидово полевое урав-
уравнение является статическим полевым уравнением той же модели,
но в B + 1) измерениях. Инстантонами с конечным действием
этого евклидова уравнения A0.30) были бы как раз статические
решения с конечной энергией модели в B + 1) измерениях.
Но теорема вириала Деррика — Хобарта (разд. 3.2) запрещает
статические солитоны конечной энергии для этой модели в двух
пространственных измерениях. Поэтому уравнение A0.30) не
имеет инстантонов с конечным действием. Инстантоны с бес-
бесконечным действием уравнения A0.30) должны существовать,
но, как отмечалось выше, решение с бесконечным действием не
дает вклада в квазиклассическую туннельную амплитуду. Короче
говоря, мы видим, что по крайней мере в квазиклассическом
приближении в системах, подобных модели СГ в A + 1) измере-
измерениях, туннелирование между классическими минимумами не имеет
места, поскольку отсутствуют инстантоны с конечным действием.
То же замечание справедливо для кинковой системы, обсуждав-
обсуждавшейся в гл. 5, где U (ф) = 1/iK (ф2 — IJ. В этих системах в окре-
окрестности каждого потенциального минимума может быть построен
свой отдельный вакуум, который не туннелирует в другой. Сим-
Симметрия спонтанно нарушается.
Чтобы получить ненулевые туннельные эффекты в полевой
теории с помощью квазиклассических методов, мы должны найти
модели, которые допускают инстантоны с конечным действием.
В последующих разделах мы рассмотрим некоторые калибровоч-
калибровочные теории, обладающие этим свойством.
10.2. Топологические вакуумы в абелевой модели Хиггса
Обобщим теперь намеченный в общих чертах в предыдущем
разделе метод на калибровочную полевую теорию. Рассмотрим
так называемую абелеву модель Хиггса. Эта система состоит из
электромагнитного поля Лд (х, /), взаимодействующего с ком-
комплексным скалярным полем ф (х, /). Лагранжиан системы имеет
вид
z (х, о=- 4-vv+4- wr w) -~ъ(\ф\2~- f*y,
A0.31)
где F^ = д^Ау — dvA^, DJ> ее (дв — ieA^) ф, a F — действи-
действительная постоянная. Мы уже обсуждали свойства этой системы

инстантоны в Квантовой теории 319
на классическом уровне в разд. 3.5 и 4.4. Теперь мы рассмотрим
квантовый вариант этой теории [64, 67, 89].
Хорошо известно, что, согласно теории возмущений, в этой
системе должно проявляться знаменитое явление Хиггса [121,
178, 186, 187]. В этом явлении происходит спонтанное нарушение
симметрии U A) лагранжиана, но вместо соответствующего голд-
стоуновского бозона векторное поле приобретает массу и про-
продольную степень свободы в отличие от обычного фотонного поля,
которое было бы безмассовым и чисто поперечным. Такое поведе-
поведение ожидается в силу следующего аргумента. В теории возмуще-
возмущений благодаря последнему члену в A0.31) следует ожидать, что ф
приобретет нарушающее симметрию ненулевое вакуумное среднее
(ф)тк = Ре^, A0.32)
где постоянный фазовый угол а может принимать любое значение.
Обычно выбирают тот сектор состояний, где (f) = F действи-
действительно. Запишем ф в полярных координатах
ф(х, /) = р(х; 0^в(х.о. A0.33)
Так как в рамках теории возмущений мы работаем с полями, близ-
близкими к ф (х, /) = F Ф 0, такие полярные координаты являются
хорошо определенными. Напомним, что лагранжиан инвариантен
относительно U A)-калибровочных преобразований вида
ф(х, 0-^л<*-"<Нх, t), А»(х, О-^ДЛх, *) f A/е)д„А(х, I).
A0.34)
Мы выбираем Л противоположным по знаку и равным по модулю
фазовому углу 6 в A0.33), т. е. поля преобразуются в
ф(х, /)->р(х, /) = е-'в(х.<^(х> t),
В результате мы сделали поле ф действительным всюду. Заметим,
что Flxv = дцА'у — дуА'ц = F^v Так как лагранжиан калибро-
вочно-инвариантен, в терминах р и А'^ он принимает вид
3S = -1 F'^F'»" +1 (а, - ieAl) р (а" + 1еА'П р - | X (р2 - F2J.
Поскольку (р)вэк = (|^|)Вак = F, мы разлагаем р (х, /) = F +
+ Л (х- t); d^p = дцТ]. Тогда
A0.36)

320 ГЛАВА 10
Когда лагранжиан записан в такой форме, то можно сказать, что
система состоит из векторного поля массы eF и действительного
скалярного поля массы yr2'kFi. Пропавшая компонента ком-
комплексного скалярного поля «съедена» векторным полем с при-
приобретением массы и, следовательно, продольной компоненты
вдобавок к двум поперечным компонентам.
Этот качественный аргумент воспроизводит общепринятое
представление, что система A0.31) обнаруживает явление Хиггса.
В C + 1) измерениях мы не знаем ни одного повода для сомнений
в этом заключении. Однако в A + 1) измерениях, где гомотопи-
гомотопические соображения другие, мы увидим, что на самом деле явление
Хиггса отсутствует. На каком же этапе оказывается неверным
приведенное выше доказательство? По-видимому, оно явно не
зависит от пространственной размерности. Беда состоит в том,
что оно основано на теории возмущений в окрестности <j> = F
и Лд = 0, в то время как непертурбативные механизмы посред-
посредством инстантонных эффектов изменяют вывод в случае A + 1)
измерений. Этот и следующий разделы мы посвящаем демонстра-
демонстрации этого. В частности, мы обсудим структуру вакуума и найдем,
что она совершенно отлична от хиггсовского вакуума, сосредото-
сосредоточенного вокруг Лд = 0 и ф = F. Несмотря на сложность этой
модели по сравнению с задачей о периодическом потенциале
(ЗПП) разд. 10.1, сама физика и наше изложение ее весьма схожи
в обоих случаях. (На самом деле аналогия с частицей на окруж-
окружности (ЧНО) еще ближе, но для простоты мы начинаем с проведе-
проведения параллелей с ЗПП.)
Напомним, что в ЗПП энергия имеет минимумы на конфигура-
конфигурациях q (t) = 2Nn. В отсутствие туннелирования можно было бы
построить вырожденное семейство основных состояний, каждое
из которых локализовано в окрестности одного из этих миниму-
минимумов. Но туннелирование имеет место, и оно расщепляет эти вы-
вырожденные уровни в зону. Мы вычислили структуру этой энерге-
энергетической зоны, используя евклидову амплитуду для перехода
из одного минимума в другой. Эта амплитуда была вычислена
с использованием инстантонов в квазиклассическом приближении
к евклидову интегралу по траекториям. Теперь мы будем следовать
той же процедуре при соответствующем обобщении для двумерной
абелевой модели Хиггса, исходя из первоначального лагран-
лагранжиана A0.31).
Первый шаг состоит в идентификации конфигураций с мини-
минимальной энергией («классических вакуумов») этой системы, чтобы
вокруг них можно было построить подходящее вакуумное состо-
состояние. Ясно (см. разд. 3.5), что эта система имеет минимальную
(нулевую) энергию тогда и только тогда, когда
^(*) = /¥•<*• <>, Й^(х, 0 = 0 = F,,v(a, /), A0.37а)

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 321
что выполняется при
Л№ (х, t) = (Щеф) д„ф = (l/ie) (*-'«) дд (*«). A0.376)
Таким образом, мы имеем континуум классических минимумов,
каждый из которых характеризуется заданием функции е«а <*•<).
Обычное вакуумное среднее теории возмущений (ф (х, t)) =
= F, (Лд) = 0 принадлежит этому множеству, но это справед-
справедливо и для других конфигураций, полученных из них калибро-
калибровочным преобразованием A0.34). Конфигурации в A0.37) мы мо-
можем назвать «чистыми калибровками». Уже можно видеть, каким
образом могут потерпеть неудачу предсказания теории возмуще-
возмущений (включая возникновение явления Хиггса). В этом подходе
вакуум строится вокруг только одного из классических вакуумов
из множества A0.37), обычно вокруг ф (х, t) = F, Лд =0. Это
аналогично построению основного состояния в ЗПП вокруг одного
только минимума q = 0, в то время как правильное основное
состояние на самом деле размазано в волновые пакеты вокруг
всех минимумов. Подобным образом мы найдем, что здесь пра-
правильное вакуумное состояние производит выборку из всех клас-
классических вакуумов. Но анализ следует проводить очень осто-
осторожно, поскольку за счет калибровочной инвариантности мно-
множество конфигураций A0.37) несколько переполнено. Разберем же
этот вопрос.
Прежде всего мы замечаем, что классические вакуумы в A0.37)
включают как статические, так и зависящие от времени конфигу-
конфигурации, в отличие от хорошо знакомых примеров из механики
частицы (гармонический осциллятор, ЗПП и т. д.), где лагран-
лагранжиан имеет вид L = 1l2q2 — V (q) и, следовательно, энергия
минимизируется только статическими решениями. Но зависимость
от времени в A0.37) ложная и полностью определяется зависящей
от времени калибровочной свободой, содержащейся в A0.34).
Она может быть устранена частичным фиксированием калибровки
Ло (х, t) = 0. В дальнейшем мы будем работать в этой калибровке.
Совокупность классических вакуумов в A0.37) в калибровке
Л о = 0 сводится к не зависящему от времени набору
ф (х) = Feia<>x\
Ax(x) = -lr(e-^^)^r(e^^) = -^J^-. A0.38)
(Напомним, что в A + 1) измерениях при Ло = 0 остается только
одна составляющая, а именно Ах.) Равенство A0.38) задает полный
набор вырожденных статических конфигураций, которые мини-
минимизируют классическую энергию. Если бы не было больше ка-
калибровочной свободы, мы могли бы сказать, что набор A0.38)
11 Раджараман Р.

322 ГЛАВА 10
есть аналог набора координат q — 2Nn в ЗПП. Однако выбор
Ао = 0 не исчерпывает всю калибровочную свободу; остаются
допустимыми не зависящие от времени калибровочные преобра-
преобразования. Нам следует изучить точное содержание калибровочной
инвариантности относительно таких преобразований в кон-
контексте квантовой теории поля. В канонической гамильтоновой
процедуре в присутствии связей эта свобода, обусловленная не
зависящими от времени калибровочными преобразованиями, мо-
может быть прослежена до закона Гаусса
/ (х) = Div Е (х) - /0 (х) = dEjdx - -f ie (f*Dof - ф (ЭД*) = 0.
A0.39)
Напомним, что это уравнение является одним из уравнений Лаг-
ранжа — Эйлера, возникающих из лагранжиана A0.31). Но оно
не содержит производных по времени от электромагнитного поля
и является не настоящим уравнением движения, а уравнением
связи. В квантовой теории оно не может рассматриваться как
операторное уравнение, поскольку оно противоречит канониче-
каноническим перестановочным правилам. Эта трудность хорошо известна
(см., например, [50]). Одновременно правила коммутации дают
[Ех (*,), Ах (*2)]<=о = »в (*i - х2), [ф, Лд],=о
Следовательно,
[/ (*,), Ах (.г2)]«=о = i (д/дхО [б (а-, - х2)] Ф 0 A0.40)
и / (хг) как оператор не может обращаться в нуль. Поэтому закон
Гаусса накладывают на «физические» состояния как связь. «Физи-
«Физические» состояния определяются как подмножество состояний,
удовлетворяющих условию
Цх) | ^ф„з) = 0. A0.41)
Далее рассмотрим оператор
UA = exp D j A(x)I(x)dx), (Ю.42)
\ —со . /
где Л (х) — произвольная с-числовая функция. Тогда
. (Ю.43)

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 323
Предположим теперь, что мы ограничимся подмножеством функ-
функций, обозначаемых Л (х), которые удовлетворяют условию Л (х) ->
-*■ 0 при х ->+оо. Тогда £/~ может быть записано в виде
X = ехр D- } dx [(дхЕх -\ie (фЮоф - ф (Ц,
U
= ехр / | [я, (-^-) + я0* (-/Л^) + я0 (»Л^)] djf , A0.44)
I —с»
где в первом слагаемом проведено интегрирование по частям
с использованием условия Л (±оо) = 0 и
Поскольку я — канонические импульсы, которые заменяют со-
сопряженные поля, мы видим, что U~ является как раз тем опера-
оператором, который осуществляет не зависящие от времени калибро*
вочные преобразования, в квантовом контексте соответствующие
ф^фе~А(х)} f^fr'AW, Ах->Ах + {Ме)дхА. A0.46)
Таким образом, уравнение A0.43) показывает, что физические
состояния должны быть инвариантны относительно таких пре-
преобразований. Едва ли это незнакомый результат, но при таком его
выводе мы соблюдаем важное ограничение Л (+оо) = 0. Конечно,
калибровочные преобразования существуют и для произвольных
Л (х), не удовлетворяющих условию Л(±оо) = 0, и они оста-
оставляют инвариантными лагранжиан и гамильтониан. Но закон
Гаусса не обязательно требует инвариантности относительно него
всех волновых функционалов. Для редуцированного подмноже-
подмножества функций Л (х) калибровочные преобразования могут быть
названы «малыми калибровочными преобразованиями». Это назва-
название не означает, что Л (х) всюду мало, а лишь означает, что
Л (±оо) = 0. Калибровочные преобразования, которые не яв-
являются «малыми», будут называться «большими». Собственные
состояния полевых операторов \ф (х); Ах (х)) не являются физи-
физическими состояниями, поскольку они не инвариантны относи-
относительно U~, которое преобразует их в
11*

324 глава ю
Но, начав с | ф, Ах), можно построить калибровочно-инвариантное
физическое состояние, строя суперпозицию из всех состояний,
связанных малыми калибровочными преобразованиями:
I ф, Ах)фмз = \®[А (х)} U~A | ф, Д,), A0.47)
где интеграл берется по всем Л (х), таким, что Л (±оо) = 0.
Состояние \ф, Лж)фИЗ не является уже собственным состоянием
поля, но оно является максимально приближенным к последнему
объектом, который мы можем построить в физическом подпро-
подпространстве состояний. Другими словами, все это означает, что
совокупность всех полевых конфигураций \ф, Ах\ распадается на
классы эквивалентности, и внутри каждого класса элементы свя-
связаны друг с другом малыми калибровочными преобразованиями
Л (х). В результате ограничений за счет закона Гаусса координатами
системы являются только сами классы, а не индивидуальные кон-
конфигурации. Для каждого класса мы имеем физическое квазиполе-
квазиполевое собственное состояние \ф, Ах)ф-лч, определенное в A0.47). На-
Напомним, что все это обсуждение производится при условии А0=0.
Используя эти принципы, сравним нашу калибровочную поле-
полевую теорию с ЗПП. Каждый класс эквивалентности полевых
конфигураций (эквивалентных только относительно малых ка-
калибровочных преобразований) играет роль координаты положе-
положения q в ЗПП. В частйости, для заданных в A0.38) конфигураций
с нулевой энергией каждый класс эквивалентности таких кон-
конфигураций имеет аналогом одну из точек q = 2Nn в ЗПП. Таким
образом, необходимо идентифицировать различные классы экви-
эквивалентности, содержащиеся в множестве A0.38). Сейчас мы уви-
увидим, что классификация эквивалентности в множестве A0.38)
оказывается той же, что и его гомотопическая классификация.
Заметим, что для каждой функции eia M в силу A0.38) имеется
свой потенциал Ах. Для начала мы не наложили ограничений на
граничные значения а (х). Но вскоре мы увидим, что если мы нач-
начнем с конфигурации а (х) = 0, то могут иметь место только кван-
квантовые переходы к таким вакуумным конфигурациям, которые
удовлетворяют условию eia (±°°> = 1. Для удобства изложения
мы предвосхитим этот результат и ограничим eiaW условием
eia (±м) = 1 Условие ё°- (°°> = е'а <-°°> компактифицирует об-
область изменения аргумента —оо <х < оо, делая ее эквивалент-
эквивалентной окружности Si. Поэтому все такие функции eia(x) образуют
отображения Si в группу U A). Такие отображения, как мы знаем
из гл. 3, могут быть разбиты на гомотопические секторы, харак-
характеризуемые «числом оборотов» N, задаваемым выражением
^d*-=-^-M°°)-a(-oo)I. (Ю-48)

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 325
(Заметим, что в течение всего нашего обсуждения абелевых и не-
абелевых калибровочных теорий глобальные калибровочные пре-
преобразования (называемые иногда калибровочными преобразова-
преобразованиями «первого рода») рассматриваются отдельно от зависящих
от пространства-времени локальных преобразований на том осно-
основании, что первые являются истинными симметриями, приводя-
приводящими к сохраняющимся нётеровским зарядам. Напомним, что то
же положение принято в разд. 4.3 при подсчете инстантонных
степеней свободы. Аналогично подразумевается, что настоящий
анализ применяется после выделения глобальной калибровочной
группы. Иными словами, мы можем положить а (х = —оо) = О
для всех наших конфигураций. Но условие е{а (*=+<*>) = 1
по-прежнему допускает а (оо) = 2Nn, где N — в точности гомо-
гомотопический индекс в A0.48).
Более того, используя A0.38) и A0.46), для любого малого
калибровочного преобразования Л (х) получаем
а (х) -+а' (х) = а (х) + Л (х), A0.49)
так что
а'(±°°)==а(±°°) + Л( + °°) = а(±оо) и N' = N. A0.50)
Таким образом, под действием малых калибровочных преобра-
преобразований классические вакуумы остаются в том же гомотопическом
секторе. Обратно, все члены данного гомотопического класса
могут быть связаны малым калибровочным преобразованием.
Поэтому классификация классических вакуумов A0.38), основан-
основанная на «малой» калибровочной эквивалентности, становится такой
же, как описанная выше гомотопическая классификация. Каждый
класс характеризуется своим «числом оборотов» N и играет ту же
роль, что и один из минимумов потенциала (q = 2nN) в ЗПП.
При подходящем обобщении остающиеся шаги весьма похожи
на аналогичные шаги в ЗПП. Вокруг каждого гомотопического
класса N классических вакуумов мы можем построить пертурба-
тивное вакуумное состояние, т. е. теоретико-полевой волновой
функционал с минимальной энергией. Назовем эти состояния | N).
На них иногда ссылаются как на «топологические вакуумы», так
как их выделили с помощью топологических соображений. Они
являются теоретико-полевыми аналогами состояний волновых
пакетов и0 (q — 2Nn) в ЗПП (см. A0.4)). Вакуум теории возмуще-
возмущений, построенный вокруг ф (х) = F, А^ (х) = 0 (т. е. а (х) = 0,
N = 0), есть как раз состояние | N = 0). Суть в том, что подобный
топологический вакуум с той же энергией может быть построен
в каждом гомотопическом секторе N. Еще более важно, как мы
покажем ниже, что между ними имеет место туннелирование.
В результате ни один из этих топологических вакуумов | Af) не

326 ГЛАВА 10
является настоящим вакуумом. Истинные низкоэнергетические
состояния в главном порядке являются линейными комбина-
комбинациями этих пертурбативных топологических вакуумов, и выро-
вырождение по энергии разрушается.
10.3. Вакуумное туннелирование в абелевой модели Хиггса
Продемонстрируем теперь, что туннелирование между клас-
классическими вакуумами, принадлежащими различным гомотопиче-
гомотопическим секторам, действительно имеет место в двумерной абелевой
модели Хиггса. Мы осуществим это, вычисляя еще раз евклидову
амплитуду перехода, связывающую два таких вакуума, которая,
как отмечалось в гл. 6, может быть записана в виде евклидова
функционального интеграла. При этом мы получим также спектр
энергии правильных вакуумов этой теории.
Если бы не было усложнений, обусловленных калибровочной
инвариантностью, мы записали бы евклидов функциональный
интеграл, задающий евклидову амплитуду перехода для этой
модели, На основе принципов, намеченных в общих чертах в гл. 6.
Мы имели бы
G (т) = } £> [ф (х, т')] ® [ф* (х, т')] & [А„ (х, т')] exp(-SE [ф, ф*, A J)
A0.51)
где й = 1 и евклидово действие есть
оо т/2
sEty, Ф*. Aj= } dXl } dx2 [-Lf^v +
—оо —Т/2
] (Ю.52)
Здесь хг = х, х% = т' — евклидово «время», а ц, v принимают
значения от 1 до 2. Так как мы интересуемся вакуумным состо-
состоянием, то, как и в ЗПП, примем предел т -»-оо. Из-за перепол-
переполненности1), обусловленной калибровочной инвариантностью,этот
функциональный интеграл должен быть модифицирован. В пре-
предыдущем разделе мы изучали результат действия калибровочной
эквивалентности на языке теоретико-полевых волновых функци-
функционалов |^(ф, Лд)) в шредингеровском представлении. Теперь
мы для ясности представим соответствующее рассуждение с ис-
использованием функционального интеграла. Начнем с полной
-1) Термин «переполненность» применяется здесь автором в том смысле, что
в формальной функциональной мере интегрирования 2D [ф] SD [Ф*] SD [А^]
в A0.51) есть лишние переменные интегрирования, обусловленные калибро-
калибровочной инвариантностью, которые исчезают при наложении калибровки. —
Прим. перев.

ЙНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 327
калибровочной свободы относительно преобразований A0.34) без
какого бы то ни было фиксирования калибровки. Соответственно
классические конфигурации нулевой энергии являются полным
набором зависящих от пространства-времени «чистых калибро-
калибровок», заданных в A0.37). Рассмотрим возможные граничные
условия на поля в интеграле A0.51). Так как мы интересуемся
переходами из одного классического вакуума в другой, начальные
и конечные конфигурации (при т' = ±т/2, т ->■ с») должны быть
взяты в чисто калибровочной форме A0.37). Это аналогично усло-
условию в ЗПП, согласно которому все траектории идут из одного
минимума потенциала в другой. В дополнение к этому в теоретико-
полевом интеграле по траекториям должны быть также специально
оговорены граничные условия при х->-±°°. Согласно нашему
предписанию в гл. 6, мы будем требовать, чтобы все поля
в A0.51) стремились к конфигурациям с нулевой энергией (чистым
калибровкам) при *-»-±оо. Поэтому поля в A0.51) должны
стремиться к чисто калибровочному виду по всему периметру
евклидова пространства-времени. В двух измерениях этот пери-
периметр топологически эквивалентен окружности и может быть пара-
параметризован некоторым углом 0. Граничное условие теперь есть
граничное условие на периметре пространства-времени:
A0.53)
Каждый набор граничных условий на окружности эквивалентен
определению функции вида е1а(в). Как и прежде, такие функции
могут быть разбиты на гомотопические классы, характеризуемые
«числом оборотов» (см, C.96) и C.99))
2Я
■(* = -w\lS5-d» = -W<$A-(u=-£riF»*»*x. A0.54)
0 S,
Заметим, что
1. Эту гомотопическую классификацию и связанное с ней
число Q нельзя путать с гомотопической классификацией и свя-
связанным с ней числом N A0.48) в разд. 10.2. Обе включают отобра-
отображения некоторой окружности на группу U A). Но здесь окруж-
окружность есть граница евклидова пространства-времени в двух изме-
измерениях, и ettx(e) задает граничное условие на поля через их по-
поведение во времени. В разд. 10.2 мы обсуждали не зависящие
от времени чистые калибровки как функции только пространства,
компактифицированного в окружность. Поэтому Q и N различны,
но, как мы увидим, они могут быть связаны друг с другом в спе-
специальной калибровке.
2. Число N в A0.48) определено после того, как калибровка
была частично фиксирована. Напомним, что в разд. 10.2 мы поло-
положили Ао = 0 и eia (х) = 1 при х -*-±оо. Поэтому N имеет за-

358 ГЛАЙА 10
висящее от калибровки определение. В настоящем обсуждении
до сих пор калибровочного условия нет, и само Q является калиб-
ровочно-инвариантным, как следует из последнего выражения
в A0.54), в которое входит F^.
3. Гомотопический индекс Q и связанное с ним граничное усло-
условие A0.53) мы встретили в гл. 4 для той же модели. Там это усло-
условие возникало из требования конечности действия евклидовых
решений. Здесь мы не требуем, чтобы все конфигурации поля,
по которым производится интегрирование в A0.51), имели конеч-
конечное действие: в действительности правильно обратное утвержде-
утверждение. Можно показать [89 ], что такие функциональные интегралы
берутся преимущественно по полям с бесконечным действием.
В настоящем обсуждении мы пришли к тому же граничному усло-
условию не из конечного действия, а из общих требований, наклады-
накладываемых на поля на пространственно-временной границе в любом
функциональном интеграле типа вакуум — вакуум. Однако, по-
поскольку наши граничные условия такие же, как в гл. 4, они
совместны с конечностью действия. Поэтому множество допусти-
допустимых полей также содержит классические инстантоны системы
с конечным действием.
Вначале мы имеем один функциональный интеграл типа ва-
вакуум — вакуум для любого данного граничного условия, которое
в свою очередь задается функцией е'а(е), принадлежащей неко-
некоторому гомотопическому сектору Q. По всем полям, удовлетворя-
удовлетворяющим этому граничному условию, должно производиться интег-
интегрирование. По-видимому, имеется континуум таких функциональ-
функциональных интегралов, свой для каждой функции eiaW. Но это
утверждение требует проверки в случае калибровочной инва-
инвариантности.
Рассмотрим любое произвольное калибровочное преобразова-
преобразование из полного набора A0.34). Формально эти преобразования
имеют силу также в евклидовой метрике при замене t на т'. Пусть
калибровочная функция Л (х, %') имеет граничное условие
ШпЛ(.г, т') = Л (в), A0.55)
Г-*-оо
где (г, 0) — полярные координаты в плоскости (х, т'). Ясно, что
под действием этого преобразования
а @) -*-«' @) = а @) + Л @). A0.56)
Поэтому в общем случае граничная функция изменяется под дей-
действием калибровочного преобразования, и мы имеем другой функ-
функциональный интеграл. Но новый функциональный интеграл имеет
то же значение, что и старый. Так как действие A0.52) и мера
(не выписанная здесь в деталях) выбираются калибровочно-
инвариантным образом, интеграл имеет то же значение. Кроме

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 329
того, хотя а @) заменено на а' @), гомотопический индекс Q,
являясь калибровочно-инвариантным, не меняется. Это ясно из
выражения A0.54). (Л@) как граничное значение калибровочного
преобразования в пространстве-времени также принадлежит сек-
сектору Q = 0. Доказательство по существу то же, которое было
использовано в гл. 4 для системы Янга — Миллса. Отсюда сле-
следует, что а @) и а' @) принадлежат одному и тому же сектору Q.)
Обратно, любые два элемента а @) и а' @), принадлежащие од-
одному сектору Q, могут быть связаны калибровочным преобразова-
преобразованием при выборе Л @) = а' @) — а @).
Мы видим, что все функциональные интегралы, граничные
функции которых попадают в один и тот же гомотопический сек-
сектор Q, имеют совпадающие значения, связаны друг с другом ка-
калибровочными преобразованиями и, следовательно, калибровоч-
но-эквивалентны. Таким образом, вследствие калибровочной экви-
эквивалентности континуум таких интегралов сводится к дискретной
бесконечности обособленных классов, по одному для каждого
целого Q. Интегралы, принадлежащие различным секторам Q,
не связаны калибровочным преобразованием и в общем случае
различны. Отметим аналогию с ЗПП. Там соответствующие ампли-
амплитуды, связывающие любые два потенциальных минимума, равны
{(N + Q) 2я | е~Нх | 2я#). Эта амплитуда не зависит от N,
т. е. от начальных или конечных конфигураций, а зависит только
от Q, т. е. от разности граничных значений. Такую же роль в на-
нашей калибровочной теории играет гомотопический индекс Q.
(Чтобы усилить аналогию, ниже мы покажем, что в калибровке
Ао = 0 Q можно записать как разность между конечным и на-
начальным вкладами.)
Короче говоря, для каждого Q мы имеем отдельную ампли-
амплитуду, которая может быть вычислена с использованием любой
граничной функции еСа (е), принадлежащей данному сектору Q.
Конечно, даже после выбора определенной функции е(а <е) все
еще остается некоторая калибровочная свобода. Рассмотрим те
калибровочные преобразования, для которых функции Л (х, т')
на бесконечности обращаются в нуль, т. е. когда Л @) = 0. Тогда
при учете A0.56) граничная функция е'а(е) не изменяется. Следо-
Следовательно, множество полей, по которым производится интегриро-
интегрирование, остается тем же. Такие калибровочные преобразования
просто переставляют связанные калибровочными преобразова-
преобразованиями полевые конфигурации, каждая из которых дает один
и тот же вклад ехр (—SE [ф, Лц])- Хорошо известно, что жела-
желательно устранить этот избыток за счет прибавления члена, фикси-
фиксирующего калибровку. Этот аспект детально обсуждался еще
в литературе по доинстантонной калибровочной теории (см.,
например, [85]), и нет необходимости детально рассматривать
его здесь. Наиболее популярным выбором способа фиксирования

330 ГЛАВА 10
калибровки является добавление к действию фиксирующего
калибровку члена
v=- 4- j *х наJ- A0-5?)
Это калибровка Фейнмана; она устраняет остающуюся свободу.
Имея,это в виду, функциональный интеграл A0.51) в любом
данном секторе Q следует привести к виду
[G (t)]q = } \Ф [ф] Ф [ф*] 2) [ЛД]Ц (в) ехр [- (SE + S*K)], A0.58)
где все поля удовлетворяют граничному условию вида A0.53),
характеризуемому произвольной функцией aQ @), принадлежащей
гомотопическому классу Q. Мы можем выбрать любую подходя-
подходящую aQ @); это эквивалентно тому, что мы работаем в той ка-
калибровке, которая нам удобна. Чтобы согласовать наше обсужде-
обсуждение с разд. 10.2, мы можем предпочесть работать с Ао (х, %') = 0.
Выберем границу пространства-времени в виде прямоугольника
ABCD (рис. 20, а). Она топологически эквивалентна окружности,
и все наши доводы имеют силу. Индекс Q A0.54) есть не что иное,
как криволинейный интеграл
который берется в направлении обхода этого прямоугольника
по часовой стрелке. Поскольку Ао = 0, стороны AD и ВС не дают
вкладов в Q. Следовательно,
Q = n+ — N_, A0.59)
где
х(х, т'=±оо)Лг= JL | *г(-£),.=±вв (Ю.6С)
— с» —с»
при использовании A0.53) на АВ и CD. Поэтому, как говорилось
выше, в калибровке Ао = 0 Q равно разности между вкладами
при т' = ±оо. Выбор Ао = 0 допускает только статические
калибровочные преобразования. Мы используем эту не зависящую
от времени калибровочную свободу, чтобы Ах (вместе с Ао) обра-
обращались в нуль при т' = —с». Поэтому а (х, —с») = 0 на ли-
линии АВ. Вся калибровочная свобода исчерпана, и теперь
оо
= N.=^- \ dx(-^) ■ A0.61)
Так как Ао (х, т') = 0, на AD и ВС имеем

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 331
Отсюда на С и D должны быть ее же значения еСа, что и на В и Л
соответственно. На линии АВ еСа (*> = 1. Следовательно, (ela)D =
— (eia)c = 1. Поэтому в калибровке Ао — 0 амплитуда пере-
перехода связывает начальную конфигурацию а (х, —■ оо) = 0 только
с теми конечными конфигурациями (при т' = +оо), которые
D
А
г'
U
С
В
а
X - + оо
Z =- оо
Рис. 20. а — прямоугольник ABCD, изображающий границу двумерного евкли-
евклидова пространства-времени; б — гиперцилиндр, изображающий границу четы-
четырехмерного евклидова пространства-времени; он используетдя при обсуждении
системы Янга — Миллса; плоские поверхности наверху и внизу цилиндра сопо-
сопоставляются всему трехмерному х-пространству при %' — ±схз соответственно;
боковая цилиндрическая поверхность соответствует всем временам %' на простран-
пространственной бесконечности х -*• оо.
удовлетворяют условию eia <*' = 1 при х = ±оо. Напомним, что
в разд. 10.2 мы использовали этот факт как заданный с обещанием
привести доказательство ниже. В этой калибровке выражение
A0.61) показывает, что Q = Af+, где Af+ есть гомотопический ин-
индекс N, определенный в разд. 10.2 (см. A0.48)), примененный
к конечной конфигурации при т' = оо. Поэтому функциональный
интеграл может интерпретироваться как определяющий евклидову

332 ГЛАВА 10
квантовую амплитуду перехода (туннелирования) из конфигура-
конфигурации Аи = 0 (которая принадлежит сектору N = 0) при т' = —оо
в конфигурацию в некотором другом гомотопическом секторе
N = Q при т' = +оо.
Чтобы рассчитать эту туннельную амплитуду, мы должны
вычислить функциональный интеграл A0.58). Мы сделаем это
в квазиклассическом приближении, так же как в ЗПП. Мы раз-
разложим поля в окрестности экстремумов действия, которые удо-
удовлетворяют классическим евклидовым полевым уравнениям. Ре-
Решениями является совокупность инстантонов и антиинстантонов
этой модели. Напомним, что мы уже рассмотрели эти решения
в гл. 3 и 4. Первоначально они возникли в гл. 3 как статические
солитоны этой модели в B + 1) измерениях. Затем в гл. 4 мы
доказали, что солитонные решения в B + 1) измерениях можно
использовать как инстантоны в A + 1) измерениях при тривиаль-
тривиальной замене (х, у) и (Ах, Ау) на (х, %' = it) и (Ах, iAQ) соответ-
соответственно. Мы не получили точных решений, но в работе Таубса
[325] показано, что они существуют. Мы нашли их асимптотиче-
асимптотическое поведение C.105), которое показало, что эти инстантоны
имеют конечный размер порядка F. Они имеют конечное дей-
действие и гомотопический индекс, задаваемый в точности выраже-
выражением A0.54) для Q. Наконец, так как каждый инстантон имеет
Q = 1 и конечный размер (локализованную плотность действия
и локализованные электромагнитные поля F^v). совокупность
расположенных далеко друг от друга пг инстантонов и л2 анти-
антиинстантонов также является решением в секторе Q = пг — я2,
точным в пределе бесконечных интервалов. Получив эту инфор-
информацию, мы можем осуществить приближение разреженного ин-
стантонного газа совершенно так же, как это мы сделали для
ЗПП. То обстоятельство, что мы не знаем точного инстантонного
решения, как и в ЗПП, не имеет значения для наших целей.
Мы можем вычислить функциональный интеграл A0.58) для
любого Q. Выберем Q = 1, что является аналогом амплитуды
Bя | е~нх | 0), вычисленной в ЗПП. В квазиклассическом раз-
разложении дают вклады все решения с удаленными друг от друга
«1 инстантонами и л2 антиинстантонами и с «i — п2 = 1. При
очевидных обобщениях можно повторить все шаги, которые
в ЗПП привели от A0.10) к A0.21). Здесь мы эти шаги опустим,
но ответ, очевидно, имеет такую же структуру, как A0.21), и мо-
может быть записан в виде
2л
lim [G(t)]q=i == А \ ddetf> exp [(e-so2Bcos0 - С) Lx), A0.62)
т-« . . о •
где So — значение (SE + S$K) для отдельного инстантона, ai-^
->- оо — пространственная длина. Вместо множителя т в A0.21)

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 333
здесь мы имеем Lx, поскольку локализация каждого инстантона
может теперь принимать значения на всей плоскости (х, т').
Детальная структура множителей Л, В и С не важна для нашего
рассмотрения. При использовании обычного разложения ампли-
амплитуды перехода G (т) в терминах энергетических собственных
состояний A0.62) приводит при % -*■ оо к зоне низколежащих
уровней энергии, характеризуемых непрерывной переменной 0.
Каждый уровень соответствует плотности энергии
Ee/L = С — erS°2B cos 0. A0.63)
Мы видим, что она имеет такую же структуру, как зона A0.22)
в ЗПП. Ей может быть дана аналогичная интерпретация. Напом-
Напомним, что [G(t)]q=i в A0.62) играет роль (евклидовой) ампли-
амплитуды перехода из вакуумного сектора ciV = 0в сектор с N = I.
Поэтому, если считать, что So конечно, эти состояния из различных
гомотопических секторов обязательно туннелируют из одного
в другое. Следовательно, пертурбативные топологические вакуумы
| N), введенные в последнем разделе, перемешиваются друг с дру-
другом. Правильные уровни энергии в главном порядке являются
их линейными комбинациями. Правильные линейные комбинации
получаются при использовании тех же принципов, как в ЗПП.
Напомним, что там состояния в зоне имели вид A0.4)
1<Ы<?)>= S e"**\uo(q-2Nn)). A0.64)
N=— <x>
Коэффициенты должны были равняться еш& в сущности в силу
теоремы Блоха. Гамильтониан ЗПП не меняется под действием
преобразования q ~+q + 2я (осуществляемого унитарным опера-
оператором Т = е~12лР, где р — импульс). Отсюда [Т, Н] = 0, и соб-
собственные энергетические состояния являются также собственными
состояниями Т с некоторым унимодулярным собственным значе-
значением е'е. Линейные комбинации A0.64) выбирались таким обра-
образом, чтобы удовлетворять этому требованию. Применим соответ-
соответствующий вывод к абелевой калибровочной модели.
Рассмотрим зависящее от времени калибровочное преобразо-
преобразование с калибровочной функцией Лг (х), такой, что Аг (—с») = 0
и Лх (+оо) = —2я. (Например, Лх (х) = —я A + th x).) Клас-
Классические вакуумы в A0.38), характеризуемые некоторым eta(-x),
изменяются при этом преобразовании. В частности,
а(±оо)-»-а(±оо) +Л^ + оо),
# = A/2я)[а(оо)'--а(—оо)]->»#- 1. A0.65)
(Напомним, что только малые калибровочные преобразования
оставляют Af инвариантным. Но Лх (х) является большим ка-
калибровочным преобразованием, так KaKAx (оо) = —2я =£0.) One

334 рЛАЪА 10
ратор 7\, который осуществляет это преобразование, строится
при помощи добавления Аг (х) в последнее выражение в A0.44):
Г, = ехр (i \ [лх {дх\х1е) + я0* (-/A,
лф (/Л^)] dx\
Мы можем проинтегрировать первое слагаемое по частям и обра-
обратить последовательность действий в A0.44), но теперь поверхно-
поверхностный член остается, поскольку Аг (оо) Ф 0:
хехр |i-
= ехр[+Bш7в)£х(оо)]. A0.66)
При действии на физические состояния второй множитель в экспо-
экспоненте сводится к единице за счет закона Гаусса. Квантовый ва-
вариант A0.65) имеет вид
T1\N) = \N-l). A0.67)
Ясно, что 7\ играет здесь ту же роль, что оператор Т в ЗПП,
который заменяет и0 (q — 2nN) на и0 (q — 2я (Af — 1)). Далее,
поскольку оператор 7\ является калибровочным преобразова-
преобразованием, пусть даже и не «малым», он должен оставлять гамильтониан
инвариантным. Следовательно,
[ТЪН] = 0.
Операторы Н и 7\ могут быть одновременно диагонализованы,
и, как следует из A0.66), 7\ есть унитарный оператор, собственные
значения которого должны быть вида е№. Собирая все это вместе,
мы ясно видим, что в результате туннелирования линейными
комбинациями пертурбативных вакуумов | N), определяющими
истинные вакуумы, будут векторы
|в)= f; e^\N), A0.68)
JV=—оо
удовлетворяющие соотношению
оо
T1\Q)=%etNo\N-l) = el*\Q). A0.69)
—оо
Таким образом, мы получаем зону состояний, параметризованных
6 @ <: 0 <: 2я). Это в точности состояния из спектрального
разложения A0.62) с энергиями Е&, заданными в A0.63). Так как

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 335
состояния |0) являются истинными энергетическими собствен-
собственными состояниями, имеем
@ | е~т 10') = 2яб @ - 0') е~Еъ\
Отсюда получаем
= У, el (N~Miе (М I е~нх I ЛЛ (используя A0.68)) =
NM
NM
e~m|N)\ . A0.70)
I
Мы видели, что амплитуда перехода между топологическими сек-
секторами N и N -\- Q зависит только от Q и определяется функци-
функциональным интегралом A0.58). Поэтому, используя £N = 2л'б @),
получаем
-£ет=цт V е~'«° [ \£>[Ап] 3) [ф] 3) [^*]}Qe~<sfi+V). A0.71)
Так как
для всех полей, по которым берется интеграл в A0.71), мы можем
ввести множитель е"'^е, а также суммирование 2!q> под функ-
функциональный интеграл. Отсюда
X
lim e ябс = lim \D[A», f, £*]BCe« X
exp [- (SB + S$K + -^ J dSx/Viiv) ] • (Ю.72)
Здесь ^5 [Лц, ^>, <j>* ]BCeQ обозначает тот факт, что интегрирование
следует проводить по полям из всех секторов Q. Другими словами,
чтобы получить £е> мы можем просто проинтегрировать по всем
полевым конфигурациям, которые становятся чистыми калиб-
калибровками на бесконечности, не заботясь о проведении гомотопи-
гомотопической классификации, если мы используем модифицированное
зависящее от 0 действие 5е, определяемое как
Av (Ю.73)
Это равнозначно прибавлению к исходной лагранжевой плотности
A0.31) в пространстве Минковского дополнительного слагаемого
= (ев/4я) е^\ A0.74)

336. ГЛАВА 10
Этот результат открывает для нас альтернативный подход к 9-ва-
куумам. Можно с самого начала начинать с лагранжиана 9? +
+ Д5?е и вычислять вакуумное состояние с использованием функ-
функционального интеграла. В таком подходе 0 может рассматриваться
как параметр в лагранжиане (и в гамильтониане), и для каждого 0
мы имеем отдельную теорию с сектором состояний, вакуумом
которого является состояние | 0). В этом отношении состояния
|0) в этой калибровочной теории отличны от состояний |</>е)
в ЗПП. В ЗПП все состояния | </>е) в наинизшей энергетической
зоне были частью одного и того же физического спектра состояний.
Основным состоянием было только состояние с наинизшей энер-
энергией @=0), и более высокие 0-состояния были настоящими
возбужденными состояниями. В принципе частицу можно пере-
перевести из ее основного состояния 0 = 0 в высшие по 0 возбужденные
состояния, например облучая ее светом. В противоположность
этому в нашей калибровочной теории каждое состояние 10) есть
вакуум отдельного сектора состояний. Ни один калибровочно-
инвариантный оператор не может связать друг с другом состояния
из различных секторов 0 (см. ниже). Поэтому калибровочная
теория по своему духу ближе к частице на окружности (ЧНО
в конце разд. 10.1). При прибавлении к лагранжиану такой
частицы (см. A0.28)) зависящего от 0 члена мы можем превращать
ее основное состояние в любое, но только в одно из состояний
зоны ЗПП. Для любого данного 0 мы имели для ЧНО полное
гильбертово пространство состояний. При изменении 0, которое
является параметром в ЧНО, мы переходим к отличным друг
от друга лагранжианам со своими отдельными пространствами
состояний. Ситуация в нашей калибровочной теории в чем-то
аналогична.
Заметим, что, подобно дополнительному слагаемому в 10.28),
дополнительный 4jfeH Ai?e в A0.74), добавленный к лагранжевой
плотности, есть полная дивергенция: Ai?e = dil((e/2n)BilvAv).
Поэтому он не влияет на классические уравнения или на инстан-
тонные решения. Различные секторы 0 этих квантовых теорий
имеют один и тот же классический предел. Но дополнительное
слагаемое Ai?e нарушает симметрию по отношению к отражениям
Р, которой обладает исходный лагранжиан A0.31). В A + 1) из-
измерениях 1/2e|iV/'|iV есть в точности электрическое поле, которое
при отражении преобразуется как Ех -»—Ех. Аналогичное
замечание справедливо для симметрии относительно зарядового
сопряжения С. Это нарушение С и Р является одним из важных
следствий эффектов от квантовых инстантонов в этой модели.
Только в секторе 0 = 0, где Ai?e равно нулю, этот нарушающий
С, Р член отсутствует.
Утверждение, что различные 0-вакуумы принадлежат к об-
обособленным, физически изолированным друг от друга секторам,

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 337
можно подтвердить следующим аргументом. В калибровочной
теории предполагается, что все физические наблюдаемые и ассо-
ассоциируемые с ними операторы'должны быть инвариантны относи-
относительно всех калибровочных преобразований. Рассмотрим, в ча-
частности, преобразование 7\ A0.68). Любой физический оператор В
должен коммутировать с 7\. Отсюда
0 = (9 | [В, 7\] | 9') = (9 | В | 9') (е'-е- _ е*% A0.75)
Следовательно,
(9|В|9') = 0, если 9=^=9'. A0.76)
Ни один физический оператор не может связать состояние | 9)
с состоянием | 9'), и в этом смысле они являются вакуумами от-
отдельных секторов состояний. Читатель может быть обеспокоен
тем, что, с одной стороны, мы утверждали, что все физические
наблюдаемые коммутируют с «большим» калибровочным преобра-
преобразованием 7\, а с другой стороны, мы делали различие между
волновыми функциями \N) и | N + 1), которые связываются
друг с другом как раз оператором 7\. Здесь опять полезно про-
провести аналогию с частицей на окружности. Напомним, что там
q = 0 и q = 2я физически эквивалентны в том смысле, что все
наблюдаемые имеют одно и то же значение в q = 0 и q = 2я.
Но когда мы добавляем к лагранжиану зависящий от 9 член
A0.28), приводящий к квазипериодичному граничному условию,
мы имеем </>е Bя) Ф фе @). На аналогичном основании должен
рассматриваться статус вакуумов \N).
Подчеркнем, что интерпретация 9-вакуумов и их невырожден-
невырожденных энергий £е как обусловленных туннелированием между
топологическими вакуумами | N) является калибровочно-зависи-
мой интерпретацией. При определении состояний | N) мы исполь-
использовали калибровочные условия, сводящиеся к Ао = 0, а также
е*а (±оо) _ j дЛЯ статических классических вакуумов. Мы вы-
выбрали эту калибровку потому, что она предоставляет возможность
для привлекательной аналогии со значительно более простыми
квантовомеханическими проблемами ЗПП и ЧНО. В другой ка-
калибровке, однако, интерпретация в общем была бы другой. Этот
аспект подробно рассмотрели Бернард и Вайнберг [40]. Напри-
Например, в физической калибровке, т. е. когда Лц однозначно опре-
определяется через F^v, вообще нет остаточной калибровочной сво-
свободы. Классический вакуум один, и наша картина туннелирования
не имеет смысла. Тем не менее различные значения 9 и различные
секторы 9 могут существовать, поскольку мы можем исходить
из зависящего от 9 лагранжиана, прибавив слагаемое A0.74).
Полученные конкретные результаты, а именно существование
9-вакуумов и их энергий Е$, являются калибровочно-инвариант-
калибровочно-инвариантными. Наше калибровочно-неинвариантное обсуждение

338 ГЛАВА 10'
в разд. 10.2 не противоречит этим конкретным результатам,
которые получены при использовании функционального интеграла
A0.51), который зависит только от Q и калибровочно-инвариантен.
Наконец, независимо от того, в каком секторе 0 мы находимся,
соответствующее вакуумное состояние | 0) совершенно отлично
от пертурбативного вакуума, построенного вокруг <j> = F, Ап =
= 0. Поэтому явление Хиггса и связанные с ним свойства пер-
пертурбативного вакуума не должны иметь места. В следующей
главе мы явно увидим, что 0-вакуумы в этой модели допускают
кулоновское дальнодействие в отличие от явления Хиггса, где
поле Лц приобретает массу и приводит только к короткодейству-
короткодействующим силам.
10.4. Янг-миллсовский вакуум
Мы переходим, наконец, к инстантонным эффектам в квантовых
неабелевых калибровочных полях. Начнем со структуры вакуум-
вакуумного состояния в чистой системе Янга — Миллса, которая состоит
из трех 5£/B)-калибровочных полей Л^ (х, t), самодействующих
в C + 1) измерениях. На самом деле физика инстантонов была
изучена в этой системе, сначала на классическом уровне [29],
а вскоре после этого на квантовом уровне [64, 198, 331 ]. На на-
начальных этапах наши выводы по существу будут такими же,
как и в предыдущих разделах по абелевой модели Хиггса. Нам
требуется только повторить их в сжатой форме в контексте системы
Янга — Миллса. Но на последующих этапах появится важное
различие, которому мы уделим особое внимание. Наше рассмотре-
рассмотрение справедливо также для самодействующих калибровочных
полей из высших SU(Af)-rpynn.
Напомним, что мы уже ввели систему Янга—Миллса в гл. 4.
Мы будем использовать обозначения (см. D.5)—D.7)), в которых
А1 и G£v компактно записываются'через антиэрмитовы Bx2)-
матрицы Лц и G^v- Плотность лагранжиана имеет вид
ОИ- A0.77)
Она инвариантна относительно калибровочной группы SU B),
элементы которой есть е~А <х' *\ где для согласованности в обо-
обозначениях мы используем в качесте генераторов антиэрмитовы
Bх2)-матрицы Л (х, t) = (oa/2i) Aa (х, t). Под действием этих
преобразований (см. D.8))
Л^+е-л^ + а^еЛ. (Ю.78)
Как и в предыдущих разделах, мы будем работать в калибровке
Ао (х, i) = 0. Это условие по-прежнему допускает калибровочные
преобразования, порождаемые не зависящими от времени ма-
матрицами Д (х). Следовательно, множеством классических ваку-

ЙНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИЙ 333
умов этой системы являются статические чистые калибровки
Gnv = 0, или, что эквивалентно (см. D.12)),
а<х), A0.79)
гд^е а (х) — произвольная бесследовая антиэрмитова Bх2)-ма-
тричная функция. Далее, мы можем ограничиться теми a (x),
которые удовлетворяют условию еа <х> = 1 во всех точках | х | =
= оо на пространственной бесконечности. Основание для этого
такое же, как в абелевой модели Хиггса; несколько ниже мы
покажем, что вычисленное при помощи подходящего евклидова
функционального интеграла квантовое туннелирование связывает
конфигурацию а (х) = 0 только с теми классическими вакуумами,
которые удовлетворяют условию [еа(х)]х^<х> = 1. Поэтому
нам требуется рассмотреть только те классические вакуумы из
множества A0.79), которые удовлетворяют этому условию. По-
Поскольку [ех(х)]х^оо = 1, для таких функций трехмерное про-
пространство компактифицируется в поверхность гиперсферы Ss.
Каждая такая функция задает отображение этой сферы S3 в груп-
групповое пространство SU B). Как мы знаем из гл. 4, такие отобра-
отображения могут быть классифицированы по гомотопическим секто-
секторам, которые образуют гомотопическую группу я3 (SU B)) = Z.
Каждый сектор характеризуется целым числом — индексом Пон-
трягина. Этот индекс, который мы теперь будем обозначать N,
получается при непосредственном применении D.27) к компакти-
компактифицированному трехмерному пространству:
N = J „ [ d3x Tr [(eaV;e~a) (eaV,-e-a) (eaVfte~a)] stih. A0.80)
Короче говоря, наши классические вакуумы A0.79) могут быть
разделены на дискретную бесконечность секторов, каждый из
которых ассоциирован с данным гомотопическим классом N со-
соответствующего калибровочного группового элемента е~а(х).
Например, случай а (х) = 0, приводящий к А-г (х) = 0, при-
принадлежит классу N = 0. Пример класса Af = 1 соответствует
A\l)(x)=eaiVteai, A0.81)
где
A0.82)
Подставляя еа' <х> в A0.80), можно убедиться, что оно принад-
принадлежит сектору N = I. (Член Ыо3 добавлен для того, чтобы удов-
удовлетворить требованию еа <х> -> 1 при х-> оо. Без этого слагае-
слагаемого оно стремилось бы к —1. Все наше рассмотрение локальной
калибровочной инвариантности по сути дела проводится с точ-
точностью до общих глобальных калибровочных преобразований.

340 ГЛАВА 10
Поэтому достаточно того, чтобы еа <х> стремилось к некоторой
константе еа° при х-> оо. Для удобства мы выбрали еа« = 1.
Мы не будем углубляться далее в эти технические детали. Напом-
Напомним, что аналогичное утверждение относится к абелевой модели
Хиггса.)
Калибровочное преобразование, которое переводит N = 0-
конфигурацию с А; (х) = 0 в N — 1-конфигурацию с Л^1' (х),
очевидно, имеет вид
g1(x) = e-A.w, A0.83)
где А± (х) = а± (х). Согласно общим гомотопическим соображе-
соображениям, gx (x) также преобразует любой классический вакуум
сектора N в вакуум сектора (N + 1).
Вокруг каждого гомотопического класса N классических
вакуумов мы можем построить топологическое вакуумное состоя-
состояние | N). Состояния | N) из различных гомотопических секторов
калибровочно-неэквивалентны [67]. Причина та же, что и в абе-
абелевой модели Хиггса. Физический смысл калибровочной экви-
эквивалентности относительно не зависящих от времени преобразова-
преобразований (которые являются единственными, оставшимися в Ао = 0-
калибровке) снова определяется законом Гаусса. При обобщении
на теорию Янга—Миллса этот закон утверждает, что
/ (х) = DiG01 = dtFJ + [Ait El] = 0. A0.84)
Это одно из полевых уравнений, которые выводятся из лагран-
лагранжиана A0.77), но оно не содержит производных по времени и по-
поэтому является связью. Здесь Е' = Goi — «электрическое» поле
Янга—Миллса в 2х2-матричной форме. (Замечание: коммутатор
[А{, Е{] понимается в пространств 2х2-матриц. Его не следует
смешивать с коммутаторами операторов в гильбертовом простран-
пространстве квантовых состояний.) Так же как в электродинамике,
в квантовой теории Янга—Миллса уравнение A0.84) не может
рассматриваться как операторное уравнение. Оно должно быть
наложено на векторы физических состояний, которые должны
удовлетворять условию
£>г£'|Ч%из = 0. A0.85)
Для инфинитезимальных элементов е~бА |х) » 1 — 6Л (х) пре-
преобразование A0.78) сводится к
A0.86)
где Dj — ковариантная производная. Предположим на мгнове-
мгновение, что мы рассматриваем только те калибровочные функции Л(х),
которые удовлетворяют условию Л (х)-> 0 при х-у оо. В на-
наших матричных обозначениях канонический импульс, сопряжен-

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 341
ный Л г, равен B1 g2) £г. Следовательно, в квантовой теории опе-
оператор, порождающий калибровочные преобразования е~А{х),
имеет вид
U = exp (-p- J еРх Тг ((АЛ) £')) = exp (^- j d3x Tr (ADtE')),
A0.87)
где выполнено интегрирование по частям с использованием усло-
условия Л(х-> оо) = 0. В силу закона Гаусса A0.85) имеем
. A0.88)
Поэтому закон Гаусса индуцирует калибровочную эквивалент-
эквивалентность только относительно калибровочных преобразований, кото-
которые удовлетворяют условию Л (х-> оо) = 0. Но рассмотрим
преобразование g± (х) A0.83), которое переводит сектор N = п
в сектор N = (п -\- 1). Как ясно видно из A0.82), соответству-
соответствующая калибровочная функция Аг (х) = аг (х) не удовлетворяет
условию Аг (х-> оо) = 0. Поэтому состояния в различных гомо-
гомотопических секторах под действием закона Гаусса не становятся
калибровочно-эквивалентными.
Таким образом, мы имеем различные топологические вакуумы
| N) в каждом секторе. Они не являются истинными вакуумами,
поскольку они туннелируют один в другой. По крайней мере
в квазиклассическом разложении мы это можем предвидеть, по-
поскольку система Янга—Миллса допускает инстантонные решения
с конечным действием. Мы получили в явном виде эти решения
в гл. 4. Красивое доказательство того, что такое туннелирование
имеет место, дано Джакивом и Ребби [198]. Рассмотрим класс
полевых конфигураций
Л1Р)(х) = рл11)(х), A0.89)
где р —действительный параметр @ <: р < 1), а Л[-Х) —чисто
калибровочный классический вакуум в секторе N = 1 A0.81).
Для р = 0 и Р = 1 мы получаем чистые калибровки А-г = 0 и
А^= А\1) соответственно. Обе они приводят к G^ = 0 и, следо-
следовательно, к нулевой классической энергии. Для 0 < р < 1
Лр (х) не является чистой калибровкой. «Электрическое» поле G0'
по-прежнему равно нулю, поскольку ЛоР) = 0 и Л;Р) не зависит
от времени. Но «магнитное» поле Вг = V2 e,iihGik не равно нулю:
G,k= р (д/ЛГ - дкАП + р2 [Л}1 Y Ak1'] = (Р2 - Р) [А?\ A<kl)] ф
для 0<р< 1. A0.90)
Энергия пропорциональна I Tr (GjhGjh) cPx и поэтому не равна
нулю для 0 < Р < 1, но конечна, так как Л}1' убывает как 1/|х

342 ГЛАВА 10
при |х|-> оо (см. A0.82)). Поля А\^ образуют кривую в про-
пространстве-времени, когда Р изменяется от 0 до 1. Эта кривая,
соединяя два классических вакуума из секторов ^ = 0 и JV= 1
соответственно, создает не нулевой, а конечный энергетический
барьер между ними. Следовательно, мы можем ожидать кванто-
квантового туннелирования между этими двумя секторами. Этот довод
тривиально переносится на связь между двумя любыми секторами.
Ниже мы попытаемся провести вычисление туннельной ампли-
амплитуды с использованием функциональных интегралов. Пока же,
предвосхищая тот факт, что должно иметь место некоторое туннели-
рование, истинные вакуумы зададим линейными комбинациями
топологических вакуумов в виде
|9>.= £ eiN*\N). A0.91)
N— — OC
Множитель elNe возникает за счет тех же требований, что и в абе-
левой модели. Рассмотрим унитарный оператор U (gj, который
осуществляет калибровочное преобразование gx и дает
U(gi)\N) = \N+l). A0.92)
Так как [U (gj, H] = 0 и оператор U (g±) унитарен, собственные
состояния Н должны удовлетворять условию , U (gx) | 9) =
= е~'е|0), которое выполняется за счет A0.91). Наконец, если
В — произвольный калибровочно-инвариантныи оператор, то [В,
U Ы] = 0. Отсюда
0 = (9 | [В, U Ы) I 9') = (е~1в' - е~ш) (9 | В \ 9').
Поэтому
(В|В|9') = 0, если 9=^9'. A0.93)
Следовательно, все |9) являются вакуумами отдельных секторов
состояний и не переводятся друг в друга никаким калибровочно-
инвариантным оператором. Все дополнительные замечания, сде-
сделанные для абелевой модели в разд. A0.3), справедливы и здесь.
Обратимся теперь к евклидову функциональному интегралу,
который определяет туннельную амплитуду. Как и в предыдущих
моделях, поля А^ (х, т'), по которым производится интегрирова-
интегрирование, должны стремиться к вакуумным (чисто калибровочным)
конфигурациям на границе евклидова пространства-времени.
В данном случае этой границей является поверхность Ss. Так как
чисто калибровочное поле имеет вид Лц = е~а д^е"-, где е~а ■—
некоторый элемент SU B), каждое данное граничное условие
является отображением Ss -> [S.U B)]. Такие отображения снова

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 343
классифицируются по гомотопическим секторам. Ассоциируемый
с ними индекс Понтрягина Q уже получен в D.18), D.26):
Q = ~ ~Ш^ J Tr [(vAvld'x = -^L- j йо^раТг [Л,ЛРЛО]. A0.94)
Евклидов функциональный интеграл в секторе Q имеет вид
lim [G(T)]Q=\{®[Ail]\Qexp [-SeBIU1]. A0.95)
Евклидово действие SeBKn определено в D.10). Как и в абелевом
случае, в нем будут обычные слагаемые 5фК, фиксирующие кали-
калибровку (см., например, [85]), опущенные здесь для простоты.
Поля Ац, по которым производится интегрирование, должны удов-
удовлетворять некоторым граничным значениям на S3, которые при-
принадлежат сектору Q. Так же как в абелевой модели, этот функ-
функциональный интеграл является калибровочно-инвариантным и
зависит от индекса Понтрягина Q, который также калибровочно-
инвариантен.
Рассмотрим далее калибровку Ао = 0 и превратим границу
пространства-времени в большой замкнутый цилиндр (рис. 20, б).
Этот цилиндр является аналогом прямоугольника на рис. 20, а.
Две плоские поверхности цилиндра обозначают все трехмерное
пространство при т' = ±оо, в то время как цилиндрическая по-
поверхность обозначает пространственную границу (х -*■ оо) для
всех т'. В калибровке Ао — 0 цилиндрическая поверхность не
дает вклада в поверхностный интеграл для Q из A0.94). Отсюда
имеем
Q = N+~ N_,
где
Кроме того, можно использовать свободу в не зависящих от
времени калибровочных преобразованиях, чтобы положить а (х) =
= 0 (Л г (х) = 0) при т' = —оо. Тогда N_ = 0 и Q = N+. В этой
калибровке функциональный интеграл интерпретируется как
евклидова амплитуда перехода, связывающая сектор N = 0
с сектором N = Q. Наконец, рассмотрим боковую поверхность
цилиндра, где в калибровке Ао = 0
0 = Ао (х -v оо, т') = [е-а <"• т'> (<Э/<Эт') е^х' т')]х-*«,. A0.97)
Следовательно, 1еа <х' т'> ]х^оо не зависит от т'. Поскольку
в начальной конфигурации при т' = —оо мы выбрали еа(х'~оо) =
= 1, в конечной конфигурации при т' = +оо снова еа с-*00' f=«>) =
;= 1. Поэтому имеет место переход только к таким классическим

344 ГЛАВА 10
вакуумам, где еа(х)]х-*оо= 1. Таким образом, подтвержден
наш гомотопический анализ классических вакуумов, в котором
мы основывались на этом ограничении.
Наконец, по аналогии с A0.72) мы можем интерпретировать
0-вакуумы как вызванные зависящим от 0 слагаемым, добавлен-
добавленным к лагранжиану. При т -> оо имеем
(9|е-"*|9)= £ e-*W (N + Q \ e~^ \ N) =
N.Q
= 2яб @) 2 е~т \ & l\h e~seB™ =
Q
= 2яб @) j 3) HjBCe Q exp ( -SeBIUI + -^- j Tr (G^) d*x) .
A0.98)
Это равнозначно прибавлению к лагранжевой плотности в ме-
метрике Минковского A0.77) дополнительного слагаемого
Д^е = (9/16я2)Тг[О^5^]. A0.99)
Как и в абелевой модели, это слагаемое есть полная дивергенция
(см. D.21)—D.24)). Оно не влияет на классические уравнения
Янга—Миллса, но приводит к различным квантовым теориям
для каждого значения 9. Состояние 19) можно рассматривать как
вакуум соответствующей теории с построенным над ним гильбер-
гильбертовым пространством состояний. Это является альтернативным
способом понимания 9-секторов. Заметим, что
Tr [GnvGn = -i- ^vpa Tr [G^GpJ = Tr
где Et и Bt — неабелевы электрические и магнитные поля. При
обращении времени Et-> Et, в то время как Bt -> —Bt. Под
действием пространственного отражения Et -*■ —Еь в то время
как В-г -+ Вг. Поэтому под действием как обращения времени, так
и пространственного отражения дополнительное слагаемое A0.99)
меняет знак, в то время как исходный лагранжиан A0.77), про-
пропорциональный Tr (EtEt —Bfii), остается инвариантным. Следо-
Следовательно, при наличии дополнительного члена Ai?e B системе
нарушены симметрии Р и Т. Исключением является случай 9 = 0,
когда дополнительное слагаемое равно нулю.
До этого момента наше рассмотрение было весьма близким
к обсуждениям в предыдущих разделах. Это обусловлено тем, что
четырехмерная система Янга—Миллса имеет такую же гомотопи-
гомотопическую группу, что и двумерная абелева модель Хиггса. При
использовании компактных матричных обозначений для янг-
миллсовеких полей Лц (х) мы также придали многим из уравнений
вид, почти идентичный с абелерым случаем. По существу наш

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 345
анализ справедлив также с незначительными модификациями для
самодействующих калибровочных полей любой высшей группы
Si/ (N) в C+1) измерениях. Как упомянуто в гл. 4, любое
непрерывное отображение S3 в группу SU (N) может быть пре-
преобразовано в отображение в подгруппу SU B) группы SU (N).
Таким образом, нам требуется лишь выбрать подгруппу SU B)
группы SU (N) с соответствующими калибровочными полями
и повторить тот же анализ. Поэтому наше рассмотрение имеет
некоторую связь с квантовой хромодинамикой (КХД). Это SU C)-
калибровочная теория, в которую добавлены фермионы. При-
Присутствие фермионов, конечно, может привести к изменениям;
некоторые из них мы рассмотрим в гл. 11. Пока же вернемся
к системе SU B)-янг-миллсовских полей.
10.5. Инфракрасная проблема больших инстантонов
Если мы хотим действовать так же, как в абелевой модели
Хиггса, то на следующем этапе мы должны непосредственно вы-
вычислить туннельную амплитуду [G(t)]q и энергию 0-вакуума
в квазиклассическом приближении разреженного инстантонного
газа в функциональном интеграле A0.95). В гл. 4 мы получили
точные одноинстантонные решения для системы Янга—Миллса
с Q = 1 и конечным действием. Здесь также совокупность инстан-
инстантонов и антиинстантонов является решением в пределе бесконеч-
бесконечных интервалов между ними. Но существуют два различия между
этой системой и абелевой моделью Хиггса или ЗПП. Первое раз-
различие для наших целей не очень существенно. В отличие от абеле-
абелевой модели Хиггса система Янга—Миллса приводит к точным
многоинстантонным решениям, которые описаны в гл. 4. Однако,
хотя они и представляют на классическом уровне важные резуль-
результаты, точные многоинстантонные решения не влияют существенно
на функциональный интеграл. Это обусловлено тем, что в прибли-
приближении инстантонного газа в функциональном интеграле преобла-
преобладающую роль играет конечная плотность инстантонов и антиин-
антиинстантонов. Напомним, что в ЗПП мы в явном виде показали, что
эта плотность должна.быть конечна и пропорциональна ers°; тот
же аргумент справедлив и здесь. Конечная плотность означает
наличие бесконечного числа инстантонов в бесконечном объеме.
В сравнении с этим любое решение (точное или неточное) с конеч-
конечным числом инстантонов дает пренебрежимо малый вклад. На
языке газа-аналога конечное число инстантонов не обладает до-
достаточной энтропией. На самом деле даже лишь бесконечное число
инстантонов (конечная плотность) также не обладает достаточной
энтропией. Вспомним из ЗПП, что основному вкладу соответ-
соответствует также конечная плотность антиинстантонов. Таким обра-
образом, к сожалению, наши сведения о точных многоинстантонных

346 ГЛАВА Id
решениях не слишком полезны при вычислении функционального
интеграла. Достаточно данных для совокупности расположенных
далеко друг от друга инстантонов и антиинстантонов.
Но имеется более существенное различие между инстанто-
нами в ЗПП или абелевой модели Хиггса и инстантонами Янга—
Миллса: первые имеют фиксированный конечный размер, а послед-
последние могут иметь любые размеры. Напомним, что точный янг-
миллсовский инстантон D.74) содержит масштабный параметр Х±,
который может принимать любое значение 0<Х1<оо. Как
отмечалось в гл. 4, это связано с масштабной инвариантностью
лагранжиана Янга—Миллса. К сожалению, это свойство порож-
порождает некоторое сомнение во всем приближении разреженного газа.
Прежде всего можно задаться вопросом, имеют ли смысл в кон-
концепции разреженного газа изолированных инстантонов сколь
угодно большие инстантоны. Можно попытаться преодолеть эту
трудность, предположив, что, если задан инстантон произвольного
размера Klt пусть сколь угодно большого, мы можем считать, что
евклидов объем (Ут) значительно больше. Даже в предположении,
что это может быть сделано математически уд )Елетворительным
способом (упорядочивая между собой пределы Vt ->■ оо и Xj_ ->
->■ оо), имеются дальнейшие проблемы, если мы продолжаем поль-
пользоваться приближением разреженного газа. Напомним из гл. 4,
-что одиночный янг-миллсовский инстантон имеет в совокупности
восемь степеней свободы, т. е. задав определенное одноинстантон-
ное решение, мы можем получить другие при применении любой
из этих непрерывных симметрии. Четыре соответствуют простран-
пространственно-временным трансляциям, три —глобальным SU B)-вра-
щениям и одна —изменению масштаба. Каждая симметрия при-
приводит к нулевой моде в квантовых флуктуациях в окрестности
данного инстантона, для которой необходимо провести интегриро-
интегрирование по соответствующей коллективной координате. Следова-
Следовательно, если мы продолжаем пользоваться приближением разре-
разреженного газа, так же как в ЗПП или абелевой модели Хиггса,
мы получим набор вакуумных уровней (аналогичный A0.22)
или A0.63))
, оо
£е = — Vcos9e-S° \d'K12B(XJL), A0.100)
о
где мы по сравнению с A0.63) опустили несущественную не за-
зависящую от 0 аддитивную константу С; 50 — действие отдельного
инстантона, а V — объем трехмерного пространства. Заметим,
что интегрирование по глобальной SU B)-симметрии приводит
только к конечной константе, равной объему группы. Она вклю-
включена в 2В (к^, что также содержит все другие множители, обуслов-
обусловленные квантовыми флуктуациями в окрестности инстантона

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 347
размера Xt. Интегрирование по трансляциям приводит к расходя-
расходящемуся множителю V->oo, но это поддается удовлетворитель-
удовлетворительному объяснению, так как мы ожидаем, что вакуумные состояния
имеют конечную плотность энергии Ee/V. Но если расходится
интегрирование по размеру инстантона Хг (также коллективной
координате для масштабной симметрии), то никакая аналогич-
аналогичная интерпретация не может спасти данную ситуацию. Чтобы
увидеть, возникает ли такая расходимость, исследуем более тща-
тщательно, чем мы сделали для абелевой модели, множитель В (XJ.
По существу этот множитель включает детерминант, обусловлен-
обусловленный квантовыми флуктуациями. Последний есть экспонента от
суммы по всем ненулевым собственным значениям логарифма
второй производной от действия, вычисленной в окрестности фо-
фонового поля инстантона. Как и во многих других полевых теориях,
эта сумма по частотам включает ультрафиолетовую расходимость.
Напомним, что при вычислении в гл. 5 квантовой массы кинка
мы сталкивались с подобной ультрафиолетовой расходимостью
в сумме по частотам нормальных мод. В перенормируемой теории
такие расходимости устраняются перенормировочной процедурой.
Мы, очевидно, не можем здесь воспроизвести сложную проце-
процедуру перенормировки неабелевых калибровочных теорий. Она
подробно рассмотрена в доинстантонной литературе (см., напри-
например, [2, 85]). Мы не можем также воспроизвести здесь «герку-
«геркулесов труд» т'Хофта [332], который помимо прочего вычислил
квантовые флуктуации в окрестности инстантонного решения
после перенормировки (см. также [31, 76, 269]). На нашем ввод-
вводном уровне вполне достаточно напомнить следующие общие
свойства перенормировочной процедуры:
1. Мы вычисляем флуктуации в окрестности инстантонного
решения, а не в окрестности Ац = 0. Но ультрафиолетовые рас-
расходимости не искажаются гладким фоновым полем, поэтому
может быть использована стандартная процедура перенормировки.
2. Эта процедура содержит перенормировочную массу М,
от которой зависит перенормированное В (Хх). Так как Кг — един-
единственная помимо М размерная переменная,в системе (константа
связи g безразмерна), сравнивая размерности с обеих сторон
в A0.100), можно видеть, что В (Кг) должно иметь вид (l/Ц) f X
X (VW), где / — некоторая функция.
3. Так как g—единственный параметр в лагранжиане, за-
зависимость от М, обусловленная перенормировкой, возникает
целиком за счет замены g на «бегущую константу связи» gi^M)
в, A0.100). Заметим, что g безразмерна, и поэтому должна зави-
зависеть от М через комбинацию (%хМ).
Поэтому мы должны выделить в A0.100) зависимость от g,
которая до сих пор была неявной. Прежде всего заметим, что
в наших матричных обозначениях D.5)—D.7) действие D.10)

348 ГЛАВА 10
зависит от g только через общий множитель l/g2. В таком случае
замена переменных от нулевой моды на соответствующую коллек-
коллективную координату, как показано в приложении Б, приводит
к множителю Якоби, пропорциональному l/g. В приложении Б
рассматривается простой случай только однопараметрической
непрерывной симметрии и, следовательно, одной нулевой моды.
В настоящем янг-миллсовском случае имеется восемь нулевых
мод, которые следует заменить на соответствующие коллективные
координаты. Поэтому результирующий якобиан пропорциона-
пропорционален l/g8. В дополнение к этому действие отдельного инстантона
равно So = 8n2/g2. Таким образом, зависимость от g неперенор-
мированной энергии A0.100), неявно содержащаяся в выражении
A0.100), имеет вид
^-BKVe'. A0.101)
В перенормированном выражении для энергии нам нужно лишь
заменить g на g {ХХМ), чтобы получить зависимость от М.
В результате получаем следующее выражение для перенорми-
перенормированной энергии
Ев ?
где мы включили в В все другие константы. После открытия
асимптотической свободы [176, 282] мы знаем, что бегущая кон-
константа связи g (ХгМ) теория Янга—Миллса удовлетворяет соот-
соотношению
[2 ^М^ + высшие П°РЯДКИ по 8- (Ю- ЮЗ)
Поэтому для малых g имеем
где g0 — константа. Заметим, что, как только размер инстантона Хх
стремится к нулю, g также стремится к нулю и приведенная фор-
формула A0.104) является вполне удовлетворительной. Поэтому
для малых Кх подынтегральное выражение в A0.102) ведет себя
как
Это выражение обращается в нуль при Хг -> 0, и расходимость по
малым инстантонам в выражении A0.102) для плотности энергии
отсутствует. Если мы продолжаем использовать (без проверки)
тот же интеграл для больших инстантонов, то A0.102) будет иметь

ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 349
инфракрасную расходимость при Хг —> оо. Конечно, задаваемое
с помощью A0.103), A0.104) поведение константы связи справед-
справедливо только для малых g и, следовательно, малых Лх. В настоящее
время мы не знаем, как ведет себя g для больших кг. Мы можем
лишь сказать, что соотношение A0.104) приводит к увеличению
значений g при возрастании Къ и поэтому оно перестает быть спра-
справедливым. Короче говоря, по существу мы не знаем, является ли
интеграл A0.102) сходящимся или нет, а если он сходится, то
как его вычислить. '
В этой печальной ситуации можно воспользоваться одним из
нескольких возможных подходов (представленных в различных
частях библиографии). Оптимистической позицией было бы ожи-
ожидать, что в области больших Хг эффекты сильной связи, которые
мы сейчас не умеем вычислять аналитически, каким-то образом
сделают интеграл конечным. В настоящее время это всего лишь
надежда. Можно было также попытаться улучшить вычисления
путем учета поправок к пределу «идеального» разреженного инстан-
тонного газа. Одним видом улучшений было бы включение инстан-
тон-инстантонных эффектов, т. е. того факта, что при больших,
но конечных интервалах действие набора N инстантонов не есть
Л^-кратное действие отдельного инстантона. Включение таких
эффектов улучшило бы вычисления для больших инстантонов,
а также для области более высокой инстантонной плотности. Дру-
Другая возможность состоит в том, чтобы учесть решения, отличные
от инстантонов. В исходном квазиклассическом приближении
следовало бы использовать только решения евклидовых полевых
уравнений с конечным действием. Это и есть инстантоны. Но
такое приближение справедливо лишь в пределе слабой связи,
в то время как в системах, подобных теории Янга—Миллса,
имеются указания на то, что при больших расстояниях они
должны попадать в область сильной связи. Уже формула асимпто-
асимптотической свободы A0.104) смещает эффективную константу связи
в направлении больших значений при больших пространственных
масштабах. Конечно, эта формула не верна при сильной связи.
Но на основании того экспериментального факта, что кварки
не вылетают (или в лучшем случае редко бывают свободными,
если учесть очень малое число экспериментальных утверждений
о наблюдении кварков, [227]), имеется повод считать, что на боль-
больших расстояниях они связаны большими силами. Сейчас обще-
общепринято считать, что адроны описываются некоторой неабелевой
калибровочной теорией, причем наиболее популярным кандида-
кандидатом на эту роль является квантовая хромодинамика (КХД).
На этом основании можно ожидать, что янг-миллсовское взаимо-
взаимодействие также становится большим на больших расстояниях.
Заметим, что константа связи g2 играет ту же роль, что и темпе-
температура в аналоге из статистической механики, когда евклидов

350 ГЛАВА 10
функциональный интеграл сопоставляется статистической сумме.
В A0. 101) действие в экспоненте делится на g2 также, как энергия
делится на температуру в функции распределения. Рассмотрим
холодный газ каких-нибудь молекул. Когда температура растет,
в игру вступают конфигурации с более высокой энергией. Моле-
Молекулы распадаются на атомы, которые в свою очередь ионизи-
ионизируются в следующие составляющие элементы и т. д. Таким же
образом при малых g2 в нашем функциональном интеграле важную
роль играют инстантоны, которые являются классическими ре-
решениями с конечным действием (минимумами функционала дей-
действия). Но в области больших g2 могут выступить на передний план
конфигурации с большим действием, включая, возможно, конфи-
конфигурации с бесконечным действием. В этом духе Каллан и др.
[67 ] добавили вклад от «меронных» решений. Это решения для
системы Янга—Миллса с топологическим зарядом Q = 1/2 [105].
Так как Q не целое, то они имеют бесконечное действие, и мы их
не обсуждали в гл. 4. Но мерон-меронные конфигурации с конеч-
конечным расстоянием между ними имеют конечное действие при за-
заряде Q — 1. В этом смысле инстантон можно рассматривать как
связанную меронную пару. При больших g2 мы можем ожидать,
что инстантоны «распадаются на составляющие мероны». Оказы-
Оказывается, действие отдельного мерона логарифмически расходится
[67]. При наивном подходе можно ожидать, что мероны не дают
вклада, поскольку подынтегральное выражение имеет вид
ехр [—(действие)] и для меронов ведет себя как ехр [— (C/g2) In R],
где радиус евклидова пространства R стремится к бесконечности.
Но их энтропия (т. е. интеграл по местам их расположения) при-
приводит к множителю Ri = e*]nR, который может компенсировать
обрезающий множитель ехр [—(C/g2) In R ] для достаточно боль-
больших g2. Это качественное замечание должно быть проверено после
включения эффектов от флуктуации, что является весьма трудной
задачей. Однако подобное явление было доказано в физике твер-
твердого тела для некоторых двумерных систем, где энергия взаимодей-
взаимодействия также логарифмически расходится с расстоянием.
Меронные эффекты для системы Янга—Миллса подробно рас-
рассмотрены Калланом и др. [65, 67], которые также исследовали
неразреженный газ инстантонов с учетом некоторых их взаимо-
взаимодействий. Такие вычисления были проведены также для модели
0.C) и модели CPN в двух измерениях, в которых имеются ана-
аналогичные проблемы [38, 39, 134]. Для этих последних моделей
инфракрасная расходимость разреженного инстантонного газа,
по-видимому^ 'устраняется при учете этих улучшений. Помимо
приведенных выше качественных замечаний мы не будем обсуж-
обсуждать подробнее ни меронные вычисления, ни вычисления для
плотного инстантонного газа. Они достаточно сложны, а резуль-
результаты не до конца убедительны, по крайней мере для неабелевых

инстантоны ё Квантовой теории 351
калибровочных теорий в четырех измерениях. Действуя еще в одном
направлении, некоторые авторы предположили, что для систем
при конечной температуре инстантонные вычисления могут иметь
смысл, поскольку температура обеспечивает инфракрасное обре-
обрезание. Такие вычисления в модели CPN см. в работе [8]. Чита-
Читатели, интересующиеся изучением этих вопросов, отсылаются
к цитированным выше работам.
В противоположность перечисленным выше попыткам, возмож-
возможная более консервативная позиция состоит в том, чтобы заявить,
что для масштабно-инвариантных четырехмерных неабелевых ка-
калибровочных полей такие квазиклассические подходы тщетны.
В общем случае для квазиклассических методов необходима сла-
слабая связь, в то время как в этих калибровочных теориях неиз-
неизбежно появляется сильная связь на больших расстояниях.В функ-
функциональном интеграле для сильной связи (который аналогичен
высокотемпературной функции распределения) могут быть априори
существенными не только инстантоны или мероны, но по существу
все полевые конфигурации. Если ситуация такова, то любое ква-
зиклассическое вычисление, которое выделяет некоторое подмно-
подмножество (классических) конфигураций, может быть бессмысленным.
С точки зрения квазиклассических вычислений эта позиция яв-
является пессимистической, но она вполне может оказаться пра-
правильной. В защиту инстантонов следует отметить, что эта проб-
проблема — как обращаться с сильной связью на больших расстоя-
расстояниях — не является специфичной для таких квазиклассических
методов. Та же проблема встречается в большинстве исследований
по неабелевым калибровочным теориям, включая попытки дока-
доказать конфайнмент кварков. Недавно Виттен [356] предположил,
что ввиду этих проблем лучшим подходом может быть исполь-
использование l/iV-разложения, где N—индекс группы SU (N), и
доказал, что инстантоны исчезают в пределе больших N.
Следует подчеркнуть, что основная инфракрасная трудность
в инстантонных вычислениях существует только для масштабно-
инвариантных теорий, когда появляются инстантоны всех разме-
размеров. Для систем типа ЗПП, A + 1)-мерной абелевой модели
Хиггса или B + 1)-мерной модели Джорджи—Глэшоу (исследо-
(исследованной Поляковым [287]), где инстантоны имеют конечное дей-
действие и некоторый конечный размер, нет оснований отвергать
вычисления в приближении разреженного инстантонного газа.
Требуется только выбрать константу связи малой в масштабах
порядка инстантонного размера, и квазиклассическое приближе-
приближение должно дать хорошие результаты. К сожалению, физически
важная модель, а именно КХД в C + 1) измерениях, не попадает
в эту категорию. Здесь следует опять отметить, что, даже если
квазиклассические вычисления с использованием инстантонов,
меронов и т. д. для системы Янга—Миллса или КХД терпят

352 ГЛАЁА 10
неудачу, не вся информация, которую мы получили на этом пути
является неправильной или бесполезной. Точные одно- и много-
инстантонные решения для этих систем, конечно, существуют.
Гомотопическая классификация калибровочных преобразований
и классических вакуумов не имеет ничего общего с сильной или
слабой связью. Наконец, непрерывное семейство вакуумов, опи-
описываемое углом 0, также может существовать, несмотря на ин-
инфракрасные проблемы сильной связи. Напомним наш альтерна-
альтернативный способ введения 0-вакуумов. Можно просто начинать
с 9-зависимого семейства лагранжианов Э£ + A3?q, которые все
одинаково пригодны в качестве исходных для полевых уравне-
уравнений Янга—Миллса. Для каждого лагранжиана при заданном 0
квантовая теория может быть определена с использованием соот-
соответствующего действия в функциональном интеграле.Мы можем
оказаться неспособными вычислить функциональный интеграл
с использованием инстантонов ввиду проблем сильной связи.
Но до тех пор пока дают некоторый вклад конфигурации с
J Tr (G^G^) (Рх Ф О, мы можем ожидать, что слагаемое А3?в
будет приводить к различным теориям для каждого 0. Такой
0-вакуум можно рассматривать как вакуум соответствующего
гильбертова пространства состояний. Этот аргумент в пользу
С-вакуумов и 0-секторов состояний является только предположе-
предположением, но он не зависит от деталей инстантонных вычислений.

"ЛАВА 11
ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ
11.1. Инстантоны и конфайнмент
В предыдущей главе мы показали, как инстантоны и связанные
с ними гомотопические соображения могут резко изменить струк-
структуру вакуумного состояния в некоторых полевых теориях по
сравнению с пертурбативным вакуумом. Неудивительно, что
этому сопутствуют другие обусловленные инстантонами след-
следствия в поведении таких теорий. Одно из этих следствий отно-
относится к явлению «конфаинмента» (удержания кварков в адронах).
Мы уже касались этого явления в предыдущих главах. В при-
природе кварки, которые, как принято считать, являются состав-
составными частями адронов, наблюдаются редко, если вообще наблю-
наблюдаются. Принято считать также, что адроны, по всей вероятности,
описываются неабелевой калибровочной теорией, в которой кварки
взаимодействуют с калибровочными полями. (Наиболее популяр-
популярным кандидатом является квантовая хромодинамика, где кали-
калибровочная группа есть «цветная» группа SU C), которая выби-
выбирается так, чтобы не было спонтанного нарушения (разд. 11.2).
В больших моделях «большого объединения», которые являются
попыткой объединить сильные взаимодействия с электрослабыми
взаимодействиями, эта группа SU C) вложена в большую кали-
калибровочную группу.) Поэтому одной из наиболее важных задач
физиков, занимающихся теорией частиц, является выяснить,
можно ли доказать, что в таких калибровочных теориях кварки
испытывают дальнодействующую силу притяжения, достаточно
большую, чтобы удерживать их в адронах. Ясно, что такая сила
может возникнуть только за счет непертурбативных эффектов.
В теории возмущений силы между кварками, обусловленные обме-
обменом калибровочными бозонами, в C + 1) измерениях спадают
как Г/г2 совершенно так же, как в обычной электродинамике.
Как известно из электродинамики, такая сила не может удержи-
удерживать соответствующие заряды.
С самого начала одним из мотивов, обусловивших развитие
инстантонной физики, была надежда, что непертурбативные ин-
стантонные эффекты могут привести к такому конфайнменту
кварков (см. [285]). К сожалению, последующие исследования
обнаружили, что для квантовой хромодинамики в C + 1) измере-
12 Раджараман Р»

354 ГЛАВА11
ниях инстантоны едва ли приведут к удерживающему потенциалу
между кварками — по крайней мере не в прямолинейном вычис-
вычислении для инстантонного газа. Тем не менее интуитивное чувство,
что инстантоны должны порождать тенденцию к конфайнменту,
не является неправильным. В самом деле, в моделях с малым чис-
числом пространственных измерений может быть показано, что ин-
инстантоны осуществляют конфайнмент в том смысле, что они по-
порождают притягивающую энергию взаимодействия, которая про-
продолжает расти с расстоянием. Двумя известными примерами,
в которых может быть показано, что это происходит, являются
двумерная абелева модель Хиггса [66] и трех B + 1)-мерная
неабелева модель Хиггса [287]. Мы приведем первый пример,
поскольку он проще и большая часть черновой работы уже про-
проделана в разд. 10.3.
Напомним, что для этой абелевой двумерной модели Хиггса
теория возмущений предсказывает наличие явления Хиггса.
При этом явлении калибровочное поле имеет массу, пропорцио-
пропорциональную eF (см. A0.36)), что приводит к появлению короткодей-
короткодействующей силы, которая экспоненциально спадает на расстояниях
порядка (eF)'1. Но, как мы видели в разд. 10.3, правильные ва-
куумы не являются пертурбативными. Они являются 9-вакуумами,
получающимися при учете инстантонных (туннельных) эффектов,
которые непертурбативны. Соответственно можно ожидать, что
черты, ассоциируемые с явлением Хиггса, также отсутствуют.
В частности, мы покажем, что система будет содержать дально-
действующее электрическое поле. Когда в Э-вакуум помещены
две заряженные частицы противоположных знаков, на них дей-
действует притягивающий потенциал, линейно растущий по мере
увеличения расстояния между ними. Чтобы развести их на беско-
бесконечное расстояние друг от друга, потребовалась бы бесконечная
энергия, т. е. они находятся в конфайнменте.
Прежде чем мы покажем это, заметим, что даже в отсутствие
внешних зарядов Э-вакуум обеспечивает наличие постоянного
фонового поля. Рассмотрим среднее значение евклидова электри-
электрического поля (F12)e в 9-вакууме. Так как вакуум трансляционно-
инвариантен, имеем
(Fit (х, т'))в = (l/2Lx) ( J v/^v a'2x)9 = Bn/eLx) (Q)9, A1.1)
где Lx —> оо —объем евклидова пространства-времени, a Q —
«число оборотов» в A0.54). В формализме евклидова функцио-
функционального интеграла такое среднее значение дается выражением
j [ц] [2)ф] [3>ф*\ e-Q
[ [2МЙ] [2>ф] [3>ф*\ е~ V30

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 355
Напомним, что вакуумный функционал для Э-вакуумов включает
(см. A0.72)) сумму по полевым конфигурациям во всех секто-
секторах Q с весовым множителем ei0-e's, S ~ SE + 5фк. Знамена-
Знаменатель в A1.2) служит для нормировки. Следовательно,
<^м (JC, т'))е = Bn/eLx) (Q)9 =
= — Bni/eLx) (d/dQ) [—Евх] (используя A0.72)) =
= Bni/eLx) (d/dQ) [(С - 2Be~s° cos Q) Lx] (используя A0.63)) =
= Bni/eJBe-s°sinQ. A1.3)
Таким образом, мы видим, что Э-вакуум обладает постоянным
«фоновым» электрическим полем, которое не равно нулю, если
0 Ф 0 или я. Мнимый множитель i есть не что иное, как артефакт
евклидовой метрики, когда (F12)eBINI = i (F01)MHH.
Поместим в этот Э-вакуум два точечных заряда +q на боль-
большом, но конечном расстоянии L друг от друга и вычислим резуль-
результирующее изменение энергии. Способ осуществления этого ка-
либровочно- и лоренц-инвариантным образом был предложен
Вильсоном [353]. Рассмотрим этот способ в применении к нашей
задаче. Пусть в некоторой точке Р в евклидовой плоскости (х, х')
возникли два заряда ±q. Пусть они затем расходятся на расстоя-
расстояние X друг от друга, остаются неподвижными на этом расстоянии
в течение евклидова времени т, потом сближаются и аннигили-
аннигилируют в Q. Мировые линии этих двух зарядов вместе образуют
замкнутую петлю (рис. 21). Параметры петли L и т не следует
смешивать с L и т, которые задают размеры всего евклидова про-
пространства-времени, в которое помещена эта петля. Мы будем
работать в пределе, когда L,- т и т стремятся к бесконечности,
причем т > т. Расстояние L сохраняется большим, но конечным.
Взаимодействие некоторой внешней плотности тока /^ с по-
полем А^ описывается действием SB3 = I d2xjlxAll. В нашем
случае плотность тока /^ полностью обусловлена двумя точеч-
точечными зарядами, движущимися по периметру петли. Отсюда
jitd2x-> q dXp, где dx:]X описывает линейный элемент петли. Сле-
Следовательно, SE3 сводится к криволинейному интегралу по петле,
задаваемому выражением
SE3 = q ф Ар dXp, A1.4)
Это дополнительное действие, обусловленное внешними зарядами.
В формализме интеграла по траекториям это, очевидно, приводит
12*

356 ГЛАВА 11
к появлению в вакуумном функциональном интеграле дополни-
дополнительного множителя
($) A1.5)
(Даже в евклидовой метрике экспонента в W по-прежнему будет
иметь множитель i. Напомним, что i \А^ dx1* ]Мин = —i X
X [Ар dXp ]евкл' где знак минус учтен при выборе в интеграле
Рис. 21. Петля Вильсона. Заряды ±9 рождаются в Р и за (евклидово) время тх
расходятся на расстояние L. Затем они остаются в покое на время т: и, наконец,
сближаются за время %\ и аннигилируют. Величины гх и L конечны, а т*-»- оо.
Штриховой прямоугольник изображает границу пространства-времени.
по петле направления обхода против часовой стрелки на рис. 21.
Заметим, что множитель W, который можно назвать петлевым
множителем Вильсона, является калибровочно-инвариантным и
лоренц-инвариантным.) Поэтому вакуумный функциональный ин-
интеграл в присутствии этих зарядов имеет вид
\st>[Av, ф, Лвсе q {e-VQe№}.
Нормируем это выражение на обычный интеграл в отсутствие та-
таких зарядов и рассмотрим величину

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 357
Знаменатель, который является таким же, как в A1.2), даете~гРт.
В числителе мы имеем дополнительное взаимодействие, обуслов-
обусловленное внешними зарядами. Оно должно порождать дополни-
дополнительную потенциальную энергию AEQ (L) двух статических за-
зарядов, расположенных на расстоянии L друг от друга в течение
времени т. Конечным временем хх, которое требуется зарядам,
для того чтобы разойтись или аннигилировать (рис. 21), можно
пренебречь по сравнению с временем т, в течение которого они
находятся в покое, поскольку т—> оо. Следовательно, как мы
убедимся ниже, числитель дает ехр [— Евх — АЕв (L) т]. По-
Поэтому
£,|% D.7а)
или
A£e(Z) = lim-(l/T)ln(lPV A1.76)
Это и есть способ Вильсона для получения потенциальной энергии
двух внешних зарядов в зависимости от расстояния между ними.
Мы продолжим вычисление (W)e, используя приближение раз-
разреженного инстантонного газа, введенное в гл. 10. Это было
сделано Калланом и др. [66] (см. также [89]). Мы суммируем по
всем конфигурациям пх инстантонов и п2 антиинстантонов, рас-
расположенных на больших расстояниях друг от друга. На целые
числа пх и п2 не положено никаких ограничений, так как мы сум-
суммируем по всем Q = «! — п2 в A1.6). Знаменатель в A1.6) есть
обычный интеграл для вакуумной энергии. Как сумма по инстан-
тонам он, очевидно, имеет вид (см. гл. 10)
л -CLx V J(ni-".)8(ffi«~Sp)"'+"!
знаменатель = Ае 2j е г~^ —
= Ae"CLx exp B£LTcosfoTs°)> A1.8)
где константы А, В и С, которые по-прежнему не представляют
для нас интереса, те же, что и в гл. 10. Это дает обычную вакуум-
вакуумную энергию Ев в A0.63).
В числителе A1.6) мы имеем множитель Вильсона W, показа-
тель экспоненты которого содержит интеграл у A^dx^ по пе-
периметру петли на рис. 21. В результате числитель факторизуется
на части внутри петли и вне петли. Любая конфигурация, содер-
содержащая пх инстантонов, имеет:
а) некоторое число (п1)внутр инстантонов, находящихся пол-
полностью внутри петли (последнее замечание существенно, по-
поскольку инстантоны в этой модели имеют конечный размер);

358 ГЛАВА 11
б) некоторое число (п^^^11 инстантонов, находящихся пол-
полностью вне петли;
в) несколько инстантонов, пересекающихся с периметром петли.
Так как мы работаем в пределе больших L ит-> оо, отноше-
отношение площади петли к периметру велико, поэтому доля инстанто-
инстантонов категории «в» весьма мала, и мы будем ими пренебрегать.
Это замечание справедливо также для числа антиинстантонов п2.
Мы суммируем не только по всем % и п2, но и по всем возможным
положениям инстантонов и антиинстантонов для всех пх и п2.
Если мы обозначим такую сумму через Б{„ „ j, символически
можем записать
2 E A1-9)
{Пи пг) {„внут]
Кроме того,
{п.. "*} {„внутР) „внутр| {„внешн^ „-.,
К] • A1.10)
внутр J /
Член в квадратных скобках выглядит как число Q в A0.54),
но интеграл берется только по внутренней части петли. Следо-
Следовательно, это будет порождать число оборотов пвнутр — пвнутр
от внутренних инстантонов и давать нуль для внешних. Наконец,
в пределе х -> оо площадь внутренней части петли есть Lx в глав-
главном порядке по т. Принимая во внимание все эти соображения,
найдем, что в приближении инстантонного газа числитель A1.6)
будет равен
числитель - Ае~с1х( Е ехр [/ (<нутр-«2Внутр) (Q+2nq/e)] x
1
пвнутр+пвнутр
у \"~- ) I у
(<нутр)!(ивнутр)!
х/ Е ехр[/(«ГШН-«2НеШН)9]х
I ^внешн внешн
^внешн 4_лвн
B(Lx-L~x)e~s°) ' 2
(ивнешн)!(ивнешн)!
Л^Ст/- ехр {2Be~s° \{Lx -^ If) cos 9 f If co§ (9 + 2nqle)]}. A1.11)

ЕЩЁ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 35§
Мы использовали здесь тот факт, что внутренняя площадь равна Lx,
в то время как внешняя площадь равна (Lx — Lx). Деля выраже-
выражение A1.11) на A1.8), мы имеем для A1.6)
(№)9 = ехр {2Be~s°Lx [cos(Q + 2nq/e) - cosQ]}. A1.12)
Подставляя это выражение в A1.7), получаем
АЕе (L) = 2Be~s°L [cos 9 - cos(e -f 2nq/e)]. A1.13)
Наиболее важная черта этого результата состоит в том, что
при больших расстояниях L потенциальная энергия линейно
растет с ростом L. Это соответствует удерживающей силе, которая
остается постоянной на больших расстояниях. Заметим также,
что энергия A1.13) периодична по внешнему заряду q. При q =
= Ne, где N — произвольное целое число, эта энергия обра-
обращается в нуль. Удерживающая сила существует только для неце-
нецелых внешних зарядов (в единицах е). Естественное объяснение
состоит в том, что когда q = Ne, система рождает N заряженных
пар ±е между внешними зарядами ±<7 и экранирует последние.
Когда q/e нецелое, такое экранирование не является полным,
поскольку система может рождать только частицы с целочислен-
целочисленным зарядом; при этом сохраняется удерживающий потенциал
A1.13).
При такой интерпретации предполагается, что система может
рождать частицы заряда +е опять в противоположность пер-
турбативному результату механизма Хиггса (см. A0.36)), когда
остается только нейтральное скалярное поле т]. Кажется, что
инстантонные эффекты заставляют модель Хиггса вести себя
аналогично «нехиггсовой» модели. Под последней мы понимаем
модель, в которой константа F2 в исходном лагранжиане A0.31)
выбрана отрицательной. Такая модель есть не что иное, как обыч-
обычная скалярная электродинамика, которая имеет единственный
вакуум, частицы заряда ±е и стандартное кулоновское взаимо-
взаимодействие, которое в одном пространственном измерении также
линейно растет. Но существует решающая разница между линей-
линейным кулоновским потенциалом в нормальной нехиггсовой элек-
электродинамике в A+1) измерениях и линейным потенциалом
A1.13) в нашей модели. В первой мы ожидаем линейного потен-
потенциала уже на классическом уровне. Квантовый результат будет
существовать даже при й-*0. В противоположность этому в A1.13)
линейный потенциал экспоненциально мал по й. Заметим, что,
если бы мы сохранили зависимость от й, выражение A1.13) имело
бы множитель e~s<>/n. Таким образом, удерживающий потенциал
в абелевой модели Хиггса является в очень сильной степени не-
пертурбативным квантовым эффектом, обусловленным инстанто-
нами.

360 ГЛАВА 11
Подобное исследование может быть также проведено для не-
неабелевых калибровочных теорий. Петлевой множитель Вильсона
для неабелевых теорий [353] есть на что иное, как упорядочен-
упорядоченный по пути интеграл Р ехр (i (j) А^ dxA\ в матричном обозна-
обозначений для неабелевых калибровочных полей (определение «упоря-
«упорядочения по пути» см. в гл. 4). Используя это, Поляков [287]
исследовал инстантонные эффекты в конфайнменте в B+1)-
мерной неабелевой модели Хиггса. Эта модель более сложна,
чем наша абелева, такими же являются и расчеты, но Поляков
снова обнаружил линейный потенциал, обусловленный инстантон-
ными эффектами. Напомним, что в двух пространственных изме-
измерениях обычный классический кулоновский потенциал должен
расти с расстоянием только логарифмически.
Было бы весьма удобно, если бы инстантоны порождали такой
удерживающий потенциал в C + 1) измерениях либо для КХД,
либо для эталонного 5£/B)-янг-миллсовского случая. Напом-
Напомним, что, согласно гл. 4, хотя индекс Понтрягина Q для янг-
миллсовского случая является калибровочно-инвариантным, он
может быть записан как поверхностный интеграл от тока, который
локально зависит от калибровки.
где ill = ~rTr[ellvpoAvApAo]. A1.14)
Для инстантонов, расположенных далеко от петли Вильсона,
А^ — чистая калибровка на петле и может быть без изменения Q
преобразована калибровочным преобразованием в А^ = 0 на
петле. Полный «поток Понтрягина» j^da^ можно преобразовать
в тонкую трубку (по существу «струну» в четырех измерениях),
исходящую из инстантона, и эта трубка может быть выбрана так,
чтобы избежать пересечения с петлей. Тогда единственный вклад
в петлю Вильсона был бы обусловлен инстантонами вблизи пери-
периметра петли. Их вклады пропорциональны периметру петли,
а не 1т (в смысле экспоненты в A1.12)), поэтому никакой удержи-
удерживающей силы не порождалось бы (см. также разд. 11.5). Конечно,
это утверждение может быть сделано только для инстантонов
некоторого конечного размера. Для произвольно больших янг-
миллсовских инстантонов с ассоциируемыми с ними инфракрас-
инфракрасными проблемами сильной связи на нашем уровне обсуждения
какого-либо четкого утверждения сделать нельзя. Каллан и др.
[65, 67] выдвинули аргументы в пользу предположения о том, что
если в квазиклассические вычисления включить также меронные
конфигурации, то в результате мы получим удерживающий по-
потенциал. Понятие меронов мы ввели в сжатом виде в предыдущей

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 361
главе. Но как там отмечалось, обсуждение расчетов с меронами
выходит за рамки данной книги. Интересующиеся этим вопросом
читатели отсылаются к работам Каллана и др.
11.2. Связь безмассовых фермионов с КХД
Мы изучили вакуумную структуру чистой теории Янга —
Миллса, следующую из туннелирования между топологическими
вакуумами. Когда безмассовые поля со спином V2 взаимодей-
взаимодействуют с полями Янга—Миллса, они приводят к дальнейшим
изменениям свойств вакуумного состояния. Кроме того, что эта
система безмассовых фермионов, взаимодействующих с неабеле-
выми калибровочными полями, приводит к интересным теоретиче-
теоретическим следствиям, она имеет некоторую связь с адронной физикой
реального мира. Прежде чем изучать вакуумную структуру этой
системы, полезно кратко остановиться на этой взаимной связи.
Напомним, что мы периодически ссылались на квантовую хромо-
динамику (КХД) как на подающего надежды кандидата на роль
теории, дающей описание адронной физики. Опишем теперь под-
подробнее эту модель [146, 147, 276]. КХД есть неабелева калибро-
калибровочная теория в C + 1) измерениях. Калибровочной группой
(так называемой «цветной» группой) является группа SU C),
поэтому требуется восемь калибровочных полей Л£, а = 1, ..., 8.
Они могут быть представлены в совокупности с помощью анти-
антиэрмитовой ЗхЗ-матрицы аналогично тому, как это сделано для
системы Янга—Миллса. Пусть Яа/2 —эрмитовы бесследовые
генераторы SU C) в фундаментальном (ЗхЗ)-представлении. Они
удовлетворяют следующим коммутационным правилам
[Г/2, Kb/2] = iftckc/2, A1.15)
где fabc—структурные константы группы SU C), Тг (какь) =
= 2ЬаЬ. Тогда по аналогии с D.5) запишем
At,(x,i) = -§r^\aAl(x,t), A1.16)
а
где g — калибровочная константа связи. Тензорные поля фор-
формально определяются тем же уравнением, как в случае SU B),
а именно
G,lv = d,A-d,A-H4'|1I Av]. A1.17)
В КХД эти калибровочные поля взаимодействуют с несколькими
видами кварков со спином У2. Каждый вид кварков описывается
дираковским полем ¥^, где / — индекс «аромата», а — цветной
индекс, а спиновый индекс опущен. Индекс аромата /==1, 2, 3,
4 и т. д. обозначает соответственно кварки и (up), d (down),

362 ГЛАВА 11
s (странный), с (очарованный) и т. д. Полное число ароматов не
играет роли в нашем обсуждении. Мы не будем его конкретизи-
конкретизировать, так как продолжается открытие новых ароматов. Для
данного аромата/ ¥^ (а = 1, 2, 3) преобразуется по фундамен-
фундаментальному (триплетному) представлению цветной группы SU C).
Кварки имеют массы mf. В общем случае последние могут за-
зависеть от аромата, но не от цвета, который является точной калибро-
калибровочной симметрией модели. Калибровочно-инвариантная плот-
плотность лагранжиана для этой модели имеет вид
SB (х, 0 = . 2 Ж (гУХ - nifU Ц + -i Tr [G,VG^V], A1.18)
где
(DUU = (д„. + AW A1.19)
и всюду, где необходимо, подразумеваются единичные матрицы
3x3. Мы не будем подробно приводить всю экспериментальную
информацию, которая служит поводом для формулировки модели
A1.18) (см., например обзоры [246, 264]). Очень кратко можно
сказать, что тройная цветная симметрия кварков обусловлена
статистикой Ферми—Дирака, применяемой при построении ба-
рионов из трех кварков *). Требование, чтобы эта симметрия
была локальной калибровочной симметрией, возникает из свой-
свойства асимптотической свободы последней (в глубоко-неупругом
лептонном рассеянии на адронах кварки, по-видимому, являются
слабо взаимодействующими). Наконец, присутствие кварковых
полей с различными ароматами в A1.18) обусловлено открытием
различных семейств адронных резонансов, интерпретируемых
как связанные состояния кварков с этими различными ароматами.
Существуют также некоторые причины для того, чтобы поло-
положить массы кварков и и d (mf, f =1,2) равными нулю в началь-
начальном приближении. Косвенные данные по массам кварков застав-
заставляют считать, что тх и т2 много меньше, чем массы кварков с дру-
другими ароматами. Более того, когда т1 = т2 == 0, модель (П.. 18)
обладает дополнительными симметриями помимо цветной симме-
симметрии SU C). Безмассовые кварки и и d, очевидно, удовлетворяют
полевым уравнениям
УХ¥'=/(с^ + Л„)¥?=О, A1.20)
Y'(-a,1 + i411)/ = 0, A1.21)
г) Необходимость введения для кварков дополнительного квантового числа—
«цвета», обусловленная ферми-статистйкой кварков, впервые отмечена в работе
Боголюбова, Струминского и Тавхелидзе [372* J. — Прим, перев.

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 363
для / = 1, 2. В A1.20), A1.21) мы опустили цветной индекс в до-
дополнение к спинорным индексам. Рассмотрим теперь дублет
как изоспинор относительно группы SU B). Тогда легко убедиться,
что все шесть токов % (а112) yv- (I ± уъ) % сохраняются при учете
A1.20), A1.21), где а'/2 (г = 1, 2, 3) —обычные SU ^-генера-
^-генераторы, действующие здесь на %-спинор по запаху. Это показывает,
что теория обладает также киральной SU B) <gi SU ^-симме-
^-симметрией. (Появившиеся в последнем предложении группы SU B)
не следует путать с подгруппами SU B) цветной калибровочной
группы SU C). Эта киральная симметрия является глобальной
симметрией, действующей в пространстве запахов кварков и,
d, и не зависит от цветной группы.) Такая киральная SU B) ®
® SU B)-симметрия также подтверждается экспериментом. Ее
диагональная подгруппа SU B), ассоциируемая с тремя аксиаль-
аксиальными векторными токами, является обычной изотопической спи-
спиновой группой, которая, как хорошо известно, является хорошей
симметрией сильных взаимодействий. Остающаяся симметрия,
ассоциируемая с тремя аксиальными векторными токами, также
известна как хорошая симметрия, но она проявляется в спон-
спонтанно нарушенной форме. Учтя эту спонтанно нарушенную сим-
симметрию, мы рассчитываем обнаружить изовектор из трех псевдо-
псевдоскалярных бозонов Намбу—Голдстоуна [43, 171, 172, 260].
Три найденных в природе я-мезона отождествляются с этими бозо-
бозонами. Кроме того, киральная SU B) ® SU B)-симметрия привела
к множеству результатов по «мягким пионам», хорошо подтверж-
подтверждаемых экспериментами (см. обзор [7]). Конечно, на самом деле
пионы имеют малую, но ненулевую массу, указывающую на то,
что киральная симметрия SU B) (g> SU B) не является точной
симметрией и, что аксиальные векторные токи сохраняются только
приближенно. Это свойство может быть введено в модель A1.18)
приписыванием кваркам и и d малой массы. Но в первом прибли-
приближении SU B) (g> SU B) можно рассматривать как точную сим-
симметрию и положить тх и т3 равными нулю.
Заметим, однако, что выбор тх = тг = 0 порождает не только
желаемую киральную SU B) X SU B)-симметрию, но, по-види-
по-видимому, приводит к большей симметрии U B) ® U B). В допол-
дополнение к шести изовекторным токам, упомянутым выше, за счет
полевых уравнений A1.20), A1.21), по-видимому, должны сохра-
сохраняться два изоскалярных тока %у^ A ± у5) Х- Сохранение век-
векторного тока XTUOC> связанное с сохранением соответствующего
кваркового числа, физически приемлемо. Но аксиальный вектор-
векторный ток хт^ТбОС' связанный с симметрией U A) относительно

364 ГЛАВА 11
Wf -> gtovnp^ / = 1, 2, создает проблемы. Если эта симметрия
не является спонтанно нарушенной, то массивные адроны должны
появляться в дублетах по четности, чего они не делают. С другой
стороны, если эта симметрия спонтанно нарушена, то должен
быть соответствующий изоскалярный, лоренц-псевдоскалярный
голдстоуновский бозон. Но известный спектр мезонов не предо-
предоставляет подходящего кандидата на роль этого голдстоуновского
бозона. Конечно, мы не рассчитываем обнаружить, что в природе
такой бозон не имеет массы; те же поправочные слагаемые к квар-
ковым массам, которые делают киральную симметрию SU B) ®
® SU B) приближенной и приводят к некоторым массам я-ме-
зонов, должны также делать киральную симметрию U A) прибли-
приближенной. Но по оценке Вайнберга [344 ] масса этого бозона должна
быть меньше, чем !/3/пя, в то время как наинизшим изоскаляр-
ным Jp = 0~-мезоном в спектре частиц является т]-мезон, масса
которого около 4тя!
Это отсутствие в природе, с одной стороны, дублетов по чет-
четности, а с другой — подходящего голдстоуновского бозона, рас-
рассматривалось как серьезная проблема в КХД [147, 344]. Реше-
Решение этой проблемы было предложено т'Хофтом [331, 332] (см.
также [221, 271]; другую точку зрения, детально аргументи-
аргументированную, см. в работе [97]). Мы не можем рассматривать пред-
предложенное решение этой проблемы U A), но одна черта этой проб-
проблемы, которая приводит к различию между аксиальным вектор-
векторным U A)-током и аксиальным векторным SU B)-током в КХД,
состоящему в том, что первый допускает «аномалию», имеет отно-
отношение к нашему обсуждению структуры вакуума.
11.3. Подавление вакуумного туннелирования безмассовыми
фермионами
Предшествующее изложение можно рассматривать как квинт-
квинтэссенцию КХД с ударением на то обстоятельство, что имеется
веская причина считать в начальном приближении некоторые
кварки безмассовыми. Это побуждает нас к изучению системы
безмассовых фермионов, взаимодействующих с -неабелевыми ка-
калибровочными полями. В частности, мы сосредоточим внимание
на том, как явление вакуумного туннелирования, обсуждавшееся
в гл. 10, изменяется в присутствии безмассовых фермионов. Наше
рассмотрение будет проводиться не в терминах полной модели
КХД A1.18), а в терминах более простой «миниатюрной» модели
КХД (названной «младенческой» Коулменом [89], анализу кото-
которого мы будем следовать). Эта модель по-прежнему является неабе-
левой калибровочной теорией в C + 1) измерениях, но отличается
от полной КХД в двух отношениях.
1. В качестве калибровочной группы выбрана SU B), а не SU C).

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 365
2. Используются кварки только с одним ароматом. Они счи-
считаются безмассовыми и преобразуются по фундаментальному
(дублетному) представлению калибровочной группы SU B).
Калибровочно-инвариантный лагранжиан для этой миниатюр-
миниатюрной КХД очевидно имеет вид (спиновые индексы опускаются)
2 (х, t) = ¥а (i/DjaP ¥р + A/2/) Тг [О^СП, а, р, = 1, 2,
A1.22)
где G^v и D^ формально по-прежнему определяются в A1.17)
и A1.19), но теперь А^ —SU B)-поле Янга—Миллса, описывае-
описываемое матрицей 2x2, согласно D.5). Можно видеть, что модель
A1.22) содержит все существенные черты, которые нас интере-
интересуют. Она содержит безмассовые фермионы и аксиальный вектор-
векторный ток ¥ау^у5¥а, который, по-видимому, должен сохраняться
за счет полевых уравнений. Калибровочная группа SU B),
выбранная вместо SU C), упрощает вычисления без потери в бо-
богатстве гомотопической структуры. Из теоремы Ботта, на которую
мы ссылались в гл. 4, известно, что соответствующая гомотопи-
гомотопическая группа ns(SUC)) для полной КХД в любом случае
связана с я3 некоторой подгруппы SU B) группы SU C).
Мы будем исследовать вакуумную структуру и связанные
с ней черты модели A1.22), по существу комбинируя методы гл. 9
и 10. Ферми-поле не имеет с-числового классического предела,
а также вакуумного среднего. Поэтому множество «классических
вакуумов», вокруг которых должно строиться основное квантовое
состояние для A1.22), содержит только поле Янга—Миллса,
т. е. его чисто калибровочные конфигурации с нулевой энергией.
Мы уже классифицировали их по гомотопическим секторам N;
в любой данный момент времени и для каждого сектора N мы
можем построить «топологическое вакуумное» состояние | N).
Евклидова амплитуда перехода (N + Q | e~Hx \ N) опять опре-
определяется евклидовым функциональным интегралом в четырех
измерениях, где граничные условия на А^ характеризуются
калибровочно-инвариантным индексом Понтрягина Q. До этого
момента фермионы не влияли на анализ. Но значение амплитуды
(N + Q | е~Нх | N), конечно, изменяется в присутствии безмас-
безмассовых фермионов. Поле ¥ входит в евклидово действие, и по нему
должен браться интеграл в дополнение к калибровочному полю
в функциональном интеграле для этой амплитуды перехода.
Евклидово действие 5евкл, соответствующее лагранжиану A1.22),
имеет вид
5а + 5чг, SA = — g-j- J Тг (G(ivG(i
Sw = i j ¥у^¥/д: ее J W*M (AJ Wctx, A1.23)

366 ГЛАВА 11
где
MiAJ-i^ + A^y^. A1.24)
Слагаемые, фиксирующие калибровку, и цветные индексы для
простоты опущены; подразумевается, что они учтены. В евкли-
евклидовой метрике матрицы у^ выбираются эрмитовыми, удовлетво-
удовлетворяющими условию {у^, yv\+ = 8^. Матрица уъ = 7x727374 также
эрмитова с 7s = 1. «Туннельная амплитуда» между топологиче-
топологическими вакуумами \ N) и | N + Q) дается выражением
lim (N + Q|e~Hx \N) = \з)[АМ \.2> [¥+] 3>[^}e~s^^, A1.25)
где интегрирование по грассмановым полям ¥, ¥+ определено
в гл. 9. Зависимость действия от ферми-поля через S^r билинейна,
и, следовательно, интеграл по фермионам может быть взят точно.
По аналогии с (9.66) имеем
lim (N + Q\е~Нх\и)=.кЛя>[AJQе~8л Det [М (А»)], A1.26)
Т->-оо
где Кг — константа.
Покажем теперь, что этот интеграл в точности равен нулю.
Оператор М (А^) A1.24) есть оператор Дирака в присутствии
внешнего поля А^. Подобные операторы мы рассмотрели в гл. 9
(см., например, одночастичный гамильтониан Дирака (9.55)).
Мы видели, что в некоторых случаях, когда внешнее поле подчи-
подчиняется топологически нетривиальным граничным условиям, одно-
частичный гамильтониан Дирака имеет несколько собственных
значений с нулевой энергией. В настоящем случае, когда метрика
евклидова, оператор М (А^) A1.24) эрмитов и в некоторой сте-
степени похож на гамильтониан Дирака. Кроме того, поле А^ в опе-
операторе М (Ау) подчиняется нетривиальным граничным условиям,
характеризуемым индексом Q в A1.26). Неудивительно поэтому,
что когда Q ф 0, то М (А^) также имеет одно или больше нулевых
собственных значений. Как мы отметили выше (см. разд. 9.5 и при-
приведенные там ссылки на литературу), обращение в нуль таких
собственных значений связано с фундаментальными математиче-
математическими теоремами о спектральном потоке. Это также связано
с появлением здесь хорошо известного явления токовых аномалий.
Последние мы используем для вывода существования нулевых
собственных значений М (Лм).
Так как поле Дирака в A1.22) безмассовое, то полевые урав-
уравнения i (д^ + Лд) y^W = 0 = г¥ (—д^ + А^) у^, по-видимому,
формально сохраняют аксиальный векторный ток /д5 =
= ¥ (х) 7^75^ М в дополнение к векторному току /д =
= ¥ (х) 7ц¥ (х). Это означало бы наличие киральной симметрии

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 367
U A) ® U A). Но в действительности ток /д5 не сохраняется.
Билинейное произведение вида ¥ (х) ¥ (у) в квантовой теории
поля расходится при х ->■ у. Отсюда /д и /д5. которые, если поль-
пользоваться данным для них выше определением, оба содержат
произведение ¥ и ¥ в одной и той же точке, являются плохо
определенными в силу этой расходимости. Необходимо более
тщательно определить эти токи, слегка раздвинув соответствую-
соответствующие точки калибровочно-инвариантным образом [306]. Это при-
приводит к выражению
х+е/2 \ "I
f / л , '\ „,/ 1 N
pvn I | I A /~j v- I I IJJ i v" о
CAJJ 1 I V^U (ЛЛи,/ I I l Л —" ~л— С
x—e/2 J J
A1.27)
и аналогично для J^. Предел е-> 0 берется последним. Заметим,
что без упорядоченной по пути экспоненты по входящим в нее
калибровочным полям комбинация A1.27) не была бы калибро-
вочно-инвариантной относительно SU B)-преобразований
Ч*а (х) -* (е~А w)ag Ъ (х), А», (х) -у е~А (х) (Лц + д») е+А (х),
где А(х) — антиэрмитова матрица 2x2, использованная в A0.78).
Вычислив дивергенции/д и./^ определенных в A1.27), и следя
за сингулярными при е■->■ 0 слагаемыми, убеждаемся, что ток /д
по-прежнему сохраняется, а в дивергенции для /дб появляется
аномальное слагаемое
<Vhb = {i/8n2) Tr (GuvG^v). A1.28)
Мы не будем выводить это выражение, которое представляет
собой частный случай явления токовых аномалий, которое само по
себе является важным предметом исследований [5, 23, 32]; обзор
способов вывода этих аномалий см. в работе [190 ]. При сравнении
выражения A1.28) с выражениями в указанных работах следует
учесть, что множитель появляется за счет того, что мы работаем
в евклидЪвой метрике. Мы будем считать выражение A1.28)
заданным и исследуем его связь с явлением вакуумного туннели-
рования. В частности, мы используем эту аномалию для того,
чтобы установить существование нулевых собственных значений
безмассового оператора Дирака М (Лд) [61, 263, 305].
Мы подойдем к безмассовому случаю, начиная с массивного
квантового поля Дирака в присутствии внешнего поля А^, харак-
характеризуемого индексом Понтрягина Q. Для такой системы евкли-
евклидово действие есть
A1.29)

368 ГЛАВА 11
Наличие массового члена в A1.29) и в соответствующем полевом
уравнении, как хорошо известно и легко проверяется, приводит
к слагаемому —2т¥у5¥, явно нарушающему киральную симмет-
симметрию в d^J^, в дополнение к аномальному слагаемому. Заметим
также, что для внешнего поля Ап Тг Ю^б^] пропорционален
плотности Q (х) индекса Понтрягина, определенного в D.18).
Следовательно, для системы A1.29) выражение A1.28) заменяется
на
Vhb = - 2т ^¥ - 2tQ (x). A1.30)
Проинтегрируем A1.30) по евклидову объему и вычислим
евклидово вакуумное среднее. Левая часть равенства дает
>* (^евкл =0, A1.31)
где поверхностный интеграл на бесконечности обращается в нуль,
поскольку поле Дирака является массивным (короткодействую-
(короткодействующим), а А^ есть как раз внешнее поле в A1.29). Поэтому правая
часть A1.30) дает
0 = - 2т J (¥Т5¥)евкл Фх - 4i \ Q (x) d*x,
или
A1.32)
Вычислим вакуумное среднее j (¥y5¥) евкл d4x, используя евкли-
евклидов функциональный интеграл для системы A1.29). Имеем
(х)] Ф [V (х)] {e~s j A [f {у) уьЧ (у)]}
_ . — j ( 1
[4 (x)]e-s
где евклидово действие S определено в A1.29). Пусть fr (x)
спинорная собственная функция эрмитова оператора (Ш^
с собственными значениями кг, нормированная так, что
[//■' (x)fr (x) d*x = Ьгг-. Конечно, fT (x) также будет собственной
функцией (ШцУц — im), удовлетворяющей условию
(ШмТм - im) fT (x) = (K - im) fr (x). A1.34)

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 369
Как объяснялось в гл. 9, грассманово поле ¥ (х) мы представляем
в виде
W(x) = T1 arfr (д), ¥ (х) = 2 arfr (х), A1.35)
г г
так что
S = J ¥(х) (Ш^ - im) ¥ (jc) d*x = £ Mr (К - im). A1.36)
г
Отсюда при использовании меры (9.31) знаменатель A1.33) ста-
становится равным
J П (dardar) exp f — 2 arar (kr - im)\ = П (К - im). A1.37)
(По сравнению с мерой в (9.31) мы опустили множители i. Они
в любом случае сокращаются в числителе и знаменателе A1.33).
Мы можем также выбрать определение евклидовой меры без мно-
множителей г.) Используя разложение A1.35), числитель A1.33)
можно привести к виду
j П (dardar) П ехр [— а^ (Xr — im)] ( ^ asras \ fs- (у) y5/s (у) d*y\ =
г г \ss' )
= J П (dardar [I - arar (К - im)]) I £ as,as J fV (y) ysfs (y)diy) .
A1.38)
Напомним правила грассманова интегрирования из гл. 9. Когда
подыинтегральное выражение в A1.38) разложено в сумму произве-
произведений символов а и а, ненулевые интегралы дают только те сла-
слагаемые, которые содержат каждые а и а, один и только один раз.
Здесь это правило с необходимостью приводит к тому, что s = s',
и приводит A1.38) к виду
2 J dty tf' У) y^s (У)) П (К -im). A! .39)
Деля A1.39) на A1.37), для A1.33) получаем
f
(j ¥ (у) Т5¥ (у)
Напомним, что /г удовлетворяют условию
при
A1.41)

370 ГЛАВА II
Так как (iD^y^) антикоммутирует с уъ, функция yjr также будет
собственной функцией (iD^y^), но с собственным значением (—X,.).
Следовательно, согласно условию ортогональности A1.41),
j f sWs d*y = 0, если К Ф 0. A1.42)
Если некоторое Xs равно нулю, то /s и yjs вырождены и всегда
можно выбрать имеющую определенную киральность функцию Д.,
т- е- Te/s = +/s или —/s. Отсюда для любого нулевого собствен-
собственного значения ks J ]sy5fs d*y = + 1. В целом A1.40) сводится к
(j
= d/(- im)) (n+ - п_), A1.43)
где п+ (п_) —число собственных функций с нулевыми к и поло-
положительной (отрицательной) киральностью. Подставляя A1.43)
в A1.32), получаем
Q = n_-n+. A1.44)
Таким образом, начав с уравнения для дивергенции аксиального
тока A1.30), мы получили простое соотношение между числом
нулевых собственных значений оператора (iD^y^) и индексом
Понтрягина Q поля А^. Это соотношение выводится, исходя из
массивного поля Дирака, но A1.44) не имеет зависимости от т,
поэтому можно взять предел т -*■ 0 без каких-либо ограничений.
В частности, когда Q — ненулевой целое число, п+ и п. не могут
быть оба равны нулю. Следовательно, должно быть по крайней
мере одно нулевое собственное значение.
Вернемся теперь к функциональному интегралу A1.26) для
произвольного данного ненулевого целого Q. Каждая конфигу-
конфигурация А^ в функциональном интеграле обладает тем же индексом
Понтрягина Q, и мы показали, что iD^y^ должно иметь по край-
крайней мере одно нулевое собственное значение для каждого такого А^.
Ясно, что то же справедливо для оператора М (А^) = у4 (г^цТц),
использованного в A1.23)—A1.26). Следовательно, Det Ш (А^) ] =
= 0 для каждого А^ в функциональном интеграле A1.26), и этот
интеграл в точности равен нулю. Это в свою очередь означает, что
туннельная амплитуда lim (N + Q\e~H'v\N) обращается в нуль.
Т->оо
Явление вакуумного туннелирования, которое мы описывали
для чистой системы Янга —Миллса в гл. 10, подавляется при
добавлении безмассовых фермионов.
Следует отметить, что это явление было открыто т'Хофтом
[331 ], который получил в явном виде моду с нулевым собственным
значением оператора i (д^ + А^) у^ для специального случая,

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 371
когда полевая конфигурация А^ есть одноинстантонное решение.
Полученная им собственная функция имела вид
IU "т* \Л ./V} I
0 —некоторый пространственно-независимый спинор, X и
р —положение и размер одноинстантонного решения соответ-
соответственно. Читатель может проверить, что при подходящем вы-
выборе и о собственная функция A1.45) в' точности удовлетворяет
уравнению (дд + А^) yjo = 0, где в качестве А^ подставлено
одноинстантонное решение D.74). Отсюда ясно, что
Det [M (А^)] = 0 для одноинстантонной конфигурации и, сле-
следовательно, функциональный интеграл A1.26) равен нулю в ква-
зиклассическом разложении разреженного инстантонного газа.
Но полученный выше результат A1.44) является более общим.
Он означает, что Det M [А^] = 0 для каждой конфигурации А^
в A1.26), и, следовательно, функциональный интеграл в точности
равен нулю. Таким образом, этот результат не зависит от какого
бы то ни было приближения разреженного инстантонного газа
со связанными с ним проблемами, описанными в разд. 10.5.
Взаимосвязь между аномалией аксиального тока и подавлением
туннелирования может также быть показана иначе. Вернемся
на время в пространство Минковского, где уравнение аномалии
A1.28) принимает вид
д%5 = — A/8я2) Tr [G^G^] = 2QM (x, t). A1.46)
Здесь QM (x, f) — аналог плотности Понтрягина Q (х) для про-
пространства Минковского. Мы видели в D.23), D.24), что Q (х)
можно записать как чистую дивергенцию. Эта конструкция может
быть тривиально перенесена в пространство Минковского и дает
d^J 5 = 2QM (x, t)=^2dv"k A1.47)
где
Хотя из-за аномалии /и6 не сохраняется, но модифицированный
ток
7 . = /■ 9k Л 1 4Q1
очевидно сохраняется в силу A1.47). Соответствующий заряд
Qb=\70bd3x A1.50)

372 ГЛАВА 11
есть константа по времени и поэтому должен коммутировать
с гамильтонианом:
[Qe, Я] = 0. A1.51)
Заметим, что в то время как ток /дб является калибровочно-инва-
риантным за счет конструкции A1.27), ток /д6 таким не является.
Это связано с тем, что «топологический ток» k^, как мы отметили
в евклидовом контексте в гл. 4, калибровочно-неинвариантен.
Поэтому Q5 = Q5 — 2 J k0d3x есть сохраняющийся, но зависящий
от калибровки заряд. В частности, рассмотрим пример «большого»
калибровочного преобразования gly определенный в A0.83). Это
преобразование, которое переводит топологический вакуум | N)
в \N + 1). Под действием этого преобразования Q5 изменяется
вследствие изменения в J k0d3x. Это изменение может быть полу-
получено подстановкой преобразованного- калибровочного поля (ком-
(комбинируя. A0.78), A0.82) и A0.83)) в выражение A1.48) для k^.
Алгебраические преобразования для калибровочного преобра-
преобразования gi дают
и, следовательно,
(Напомним, что для статической чисто калибровочной конфигу-
конфигурации член I k0d3x есть как раз топологический заряд N A0.96),
который, как мы знаем, под действием gt заменяется на N + 1
в соответствии с A1.52). Для произвольного А^ J k0d3x не яв-
является уже целочисленным топологическим зарядом, но под
действием gt этот член по-прежнему изменяется на единицу, что
и приводит к A1.52).)
Топологический вакуум 10) соответствует сектору N — 0
калибровочного поля. Он, конечно, является также фермионным
вакуумом. Следовательно, Q610) = 0. Тогда
0> (за счет A1.52)) =2 | 1).
Действуя подобным образом далее, получаем
$5|Л0 = 2ЛЧЛО. (п-53)
Но [Q5, егНх] = 0 за счет A1.51); отсюда
0=(M|[Q5) e-

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 373
Поэтому
(M\e-"*\N)~8MN. A1.54)
Таким образом, мы еще раз приходим к выводу, что туннельная
амплитуда равна нулю, когда М Ф N. Стоящая за этим физика
состоит в следующем: состояние | М) связано с состоянием | N)
калибровочным преобразованием gx, действующим (М—N) раз.
Под действием этого преобразования Q5 в силу A1.52) должно
измениться. Но Q6 сохраняется. Следовательно, переходов из | N)
в любое другое состояние | М) не может быть.
Таким образом, ситуация такова, что топологические вакуумы
| N) : 1) являются состояниями с наинизшей энергией в соответ-
соответствующих гомотопических секторах, 2) вырождены по энергии
друг относительно друга (так как большие калибровочные пре-
преобразования также коммутируют с Я) и 3) не туннелируют
друг в друга, когда присоединяются безмассовые фермионы.
Можно задать вопрос, есть ли какой-нибудь смысл конструиро-
конструировать в этом случае 0-вакуум или состояния | N) могут служить
в качестве истинных вакуумов этой теории.
Каллан и др. [64] показали, что по-прежнему есть необходи-
необходимость в построении 0-вакуумов в качестве правильных вакуумов
вследствие свойства кластерного разложения — требования,
накладываемого на вакуум полевой теории. Пусть D (х) и В (х) —
два локальных оператора, скажем, при t = 0. Тогда свойство
кластерного разложения вакуумного состояния требует, чтобы
(вак | D (х) В (у) | вак) >- (вак | D (х) | вак) (как | В (у) | вак).
I X—У | ->-00
A1.55)
Мы увидим, что состояния | N) нарушают это условие для опе-
операторов с ненулевой киральностью. Можно сказать, что опера-
оператор В (х) имеет киральность с, если
[Q5) В(х)] = сВ(х). A1.56)
Ясно, что оператор В+ (х) имеет киральность —с. Например,
оператор </> (х) = ¥ (х) A — у5) ¥ (х) имеет киральность с = 2,
как это может быть проверено с использованием канонических
одновременных коммутационных правил. Рассмотрим теперь
матричный элемент произвольного оператора В (х) с ненулевой
киральностью 2с между топологическими вакуумами | N) и | М).
Имеем
2с (М | В (х) | N) = (М | [Q5, В (х)] \N) = 2(M-N)(M\B(x)\ N).
Поэтому
(M\B(x)\N)~6c. m-n. A1-57)

374 ГЛАВА 11
В частности,
(N\B(x)\N) = 0, так как сфО. A1.58)
Если бы вакуумы | N) удовлетворяли кластерному разложению,
то последнее с необходимостью приводило бы к
- lim
1 X—у|->оо
в силу A1.58). Но на самом деле этого не будет, так как если разло-
разложить ( N | В+ (х) В (у) | N) по промежуточным состояниям, то
получим ненулевой вклад (N | В+ (х) | N + с) (N + с \ В (у) | N).
В силу трансляционной инвариантности каждого матричного
элемента этот вклад равен (N | В+ @) | N + с) (N + с \ В @) | N)
и остается ненулевым при |х—у |->■ оо, нарушая кластерное
разложение. Основная причина состоит в том, что, в то время
как недиагональный матричный элемент (N + с\В | N) Ф 0, диа-
диагональный матричный элемент (N\B\ N) = 0. В противополож-
противоположность этому рассмотрим матричный элемент между состояниями
|в):
(9 |В19') = XI exp [i (NQ - MB')] (N\B\M) =
N. М
м
ic9](M-bc|B|M)~6(9-9'), (Ц.59)
так как для калибровочно-инвариантного оператора
В (М + с\В\М) не зависит от М. Следовательно, при разло-
разложении по промежуточным состояниям имеем
<9|В+(х)В(у)|9> —>jd9'<9|B+(x)|9')<9'|B(y)|9) =
I X—У |->-оо J
= <9|В+(х)|9)(9|В(у)|9), A1.60)
что согласуется со свойством кластерного разложения A1.55).
Короче говоря, хотя безмассовые фермионы и подавляют тунне-
лирование между топологическими основными состояниями | N),
истинные вакуумы являются их линейными комбинациями,
представленными состояниями | Q). Конечно, то обстоятельство,
что состояния | N) не туннелируют, должно проявляться в том,
что состояния | 9) по-прежнему вырождены по энергии. Это дей-
действительно так. Мы имеем
(91 е~Нх 19') = £ <Л/1 е~Нх \ М) exp [i (NQ ~~ MQ')] =
N. М
= Z(N\e-Hx\N)exp[iN(Q~-Q')], A1.61)
N

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 375
используя A1.54). Но, поскольку различные состояния \ N)
связаны Друг с другом большими калибровочными преобразова-
преобразованиями, которые коммутируют с Н, (N \ e~Hx\ N) не зависит от N.
Следовательно, A1.61) приводит к
(9 | e~Hx 19') = е^£°т £ exp [iN (9 - 9')] - 2я6 (9 ~~ 9') е~Е*\
N
A1.62)
Таким образом, вакуумы | 9) имеют одинаковую не зависящую
от 9 энергию Ео. Для A1.62) может быть написано функциональ-
функционально-интегральное представление, аналогичное A0.98); единствен-
единственное различие состоит в том, что теперь действие содержит также
ферми-поля, по которым должен браться интеграл:
Ge = Hm (91 е~Нх | 9> = 2я6 @) V е~т j 2 [¥*] 2 [W] 2 [A^q e~s=
Т->-ОО Q
= 2я6 @) j 3D [¥+] 2) [W] 2) [Л^все Q X
X ехр (- S + -jijL j Tr [G^v] d*x). A1.63)
Поэтому
(9 | j Tr {G^G^d^x 19) = -16nat-|-(lnGe) = 0, A1.64)
так как в силу A1.62) G9 не зависит от 9.
То обстоятельство, что все 9-вакуумы имеют одинаковую
энергию и все обладают равным нулю средним значением
Tr (G^vG^v), является отражением того факта, что в присутствии
безмассовых фермионов различные секторы 9 могут быть полу-
получены один из другого с помощью кирального вращения. Свя-
Связанный с этим преобразованием W -> eiay^ ток является опре-
определенным выше аксиальным векторным током /д5- Хотя при
лагранжиане A1.22) получается, что он сохраняется, мы видели,
что на самом деле аксиальный векторный ток обладает аномалией
(см. A1.28)). В результате под действием упомянутого выше
кирального преобразования евклидово действие изменяется (ана-
(аналогично обычным шагам, ведущим к теореме Нётер) на величину
AS = a j d^xd^b = -^г \
Tr
Сравним это с зависящей от 9 частью эффективного действия
в A1.63). Очевидно, что киральное вращение изменяет 9 на
6—2а. Поэтому различные секторы 9 связаны друг с другом как
раз киральным вращением, которое для безмассовых ферми-полей

376 ГЛАВА 11
есть просто переопределение полей. Отсюда следует эквивалент-
эквивалентность киральных инвариантов в различных секторах 0. Сопо-
Сопоставим это с чисто калибровочной полевой системой, рассмотрен-
рассмотренной в разд. 10.4. Там энергия Ев A0.100) и (ТгС/цД^е (полу-
(полученный при взятии логарифмической производной от A0.98) по 0)
зависят от 0, что свидетельствует о том, что различные секторы 0
не эквивалентны. Добавление безмассовых фермионов восстанав-
восстанавливает их эквивалентность.
11.4. Инстантоны и суммируемость по Борелю
Как мы видели, важной особенностью инстантонов является
то, что они приводят к непертурбативным результатам для физи-
физических величин. Этот аспект инстантонов находит свое отражение
также в их взаимосвязи с борелевской суммируемостью разло-
разложений теории возмущений. Мы посвящаем данный раздел демон-
демонстрации этой связи.
Рассмотрим некоторую квантовую систему, характеризуемую
параметром разложения ее. Пусть G (ее) — некоторая физическая
величина в этой системе типа ее вакуумной энергии или одной
из ее функций Грина. Для простоты мы опускаем зависимость
G (ее) от других переменных, кроме ее. В типичном случае теория
возмущений приводит для G (се) к бесконечному ряду вида
G(a)=lianan. A1.65)
п=0
Пусть теория перенормируема, так что ультрафиолетовые расхо-
расходимости устраняются в каждом порядке с помощью соответствую-
соответствующих перенормированных параметров. Мы можем тогда считать, что
каждое слагаемое ряда A1.65) конечно для любого конечного се.
При этом остается открытым вопрос о том, сходится ли бесконеч-
бесконечный ряд к конечному значению для представляющих интерес
значений се. Существует также неприятная возможность, что ряд
может расходиться Для любого сколь угодно малого се. Рассмотрим
в качестве примера квантовую электродинамику, где се —по-
—постоянная тонкой структуры, е2/4я. Вычисленные в низших поряд-
порядках, предсказания теории возмущений впечатляюще согласуются
с экспериментом. Тем не менее, как показал Дайсон [117], теория
возмущений для КЭД может на самом деле расходиться при пере-
переходе к высшим порядкам. Дайсон обратил внимание на то, что
когда се отрицательно (сколь угодно мало по модулю), пертурба-
тивный вакуум нестабилен. Он может распасться на электрон-
позитронные пары, и его энергия будет понижаться при расхо-
расхождении пар на большое расстояние друг от друга. (Напомним,
что Для отрицательных се противоположные заряды отталкиваются.)

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 377
В результате вакуумная энергия будет иметь мнимую часть для
всех отрицательных а и разрез вдоль отрицательной оси а с сингу-
сингулярностью при а = 0. Отсюда следует нулевой радиус сходи-
сходимости пертурбативных разложений в теории. В таком случае
согласие вычислений КЭД в низших порядках с экспериментом
должно быть отнесено за счет того, что ряд теории возмущений
является асимптотическим разложением правильного ответа.
Впоследствии подобная расходимость ряда теории возмущений
была обнаружена также в других моделях при оценке поведения
членов высших порядков в рядах (см., например, [34, 35,
57, 58, 234, 235, 273, 274]). Эти результаты показывают, что
имеется возможность того, что для многих представляющих инте-
интерес полевых теорий ряды теории возмущений могут расходиться
даже для сколь угодно малых ее.
Для некоторого заданного пертурбативного разложения, такого
как A1.65), радиус сходимости R определяется выражением
Коэффициенты ап для любого п в принципе могут быть получены
при вычислении подходящих фейнмановских диаграмм в этом
порядке, должным образом перенормированных. Очевидным путем
вычисления R является попытка вычисления ап для больших п
и оценка их поведения при п ->■ оо. Альтернативный способ полу-
получения информации о сходимости состоит в исследовании анали-
аналитических свойств функции Бореля, ассоциируемой с этим беско-
бесконечным рядом в борелевской процедуре суммирования. Эта про-
процедура также дает возможность «улучшения» сходимости ряда,
т. е. придания смысла G (ее) для некоторых | а | > R при аналити-
аналитическом продолжении. Вкратце идея такова. Используя соотно-
Гсо
шение п\ = Jo е~Чп dt, ряд A1.65) можно записать в виде
-'^а)пси. A1.66)
л=0
Намереваясь аналитически продолжать эту функцию, предполо-
предположим, что мы меняем местами суммирование и интегрирование,
и рассмотрим функцию
где
со
" а£-Л A1.68)
п=0

378 ГЛАВА 11
Функцию F (z) можно назвать функцией Бореля, ассоциируемой
с исходным рядом. Ключевым пунктом является то обстоятель-
обстоятельство, что ряд A1.68) обладает лучшей сходимостью, чем исходный
ряд A1.65), благодаря дополнительному множителю \1п\ в каж-
каждом члене. Пусть радиус сходимости исходного ряда A1.65) R
конечен и не равен нулю. Тогда радиус сходимости борелевского
ряда A1.68) R определяется как
1
~w
п\
l/n
jr\im(nl)~1/n = O, A1.69)
так как R > 0. В этом случае ряд A1.68) сходится для всех г,
и функция F (z) аналитична во всей плоскости г. Для всех поло-
положительных t F (la) может быть получена путем суммирования
A1.68) и подстановки в подынтегральное выражение в A1.67).
Тогда для тех значений ее, для которых интеграл существует, G (ее)
является хорошо определенной. Она называется борелевской
суммой исходного ряда A1.65). Когда | сс| < R, можно показать
(см., например, [348]), что G (ее) совпадает с G (се), т. е. что пере-
перемена местами суммирования и интегрирования при переходе от
A1.66) к A1.67) оправдана. Для тех значений се вне круга схо-
сходимости (| а | > R), для которых существует интеграл A1.67),
G (се) является аналитическим продолжением G (се).
Конечно, эта процедура требует, чтобы функция F (ta) была
несингулярной при всех 0 < t < оо для любого заданного се.
Когда R > 0, это удовлетворяется в силу A1.69). Борелевский
ряд буДет иметь бесконечный радиус.сходимости, и F (z) будет
аналитической во всей плоскости г. Когда же R = 0, это может
быть неправильно. Обратно, предположим, что мы задали физи-
физическую величину G (а) непосредственно в интегральной форме
A1.67) с некоторой F (at) в свернутом виде. Тогда мы можем
непосредственно исследовать аналитические свойства функ-
функции F (z). Если мы обнаруживаем, что F (z) имеет сингулярности
при некоторых конечных z, то борелевский ряд A1.68) имеет ко-
конечный радиус сходимости R и в силу A1.69) мы можем сделать
вывод, что радиус сходимости исходного пертурбативного разло-
разложения для G (а) равен нулю.
Применим эти идеи в квантовой теории поля, следуя т'Хофту
[334 ]. Мы будем работать в евклидовой метрике. Пусть ср (х) —
поле в D евклидовых измерениях. (Оно не обязательно должно
быть скалярным; <j> (x) может символически обозначать как ска-
скалярное, так и векторное поля.) Пусть (</> (xt) ... <f> (xn)) —неко-
—некоторая евклидова функция Грина теории. Она является также
функцией параметра связи а теории. Для определенности будем
считать параметр ее > положительным в физической области. (Для
КЭД а = еЩп > 0, для КХД а = g2, для системы СГ G.1)

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 379
а = Х/т2 > 0 и т. д.). С помощью функционального интеграла
функция Грина определяется как
f Я> [0 (X)] е- (Действие) ф ^ _ _ _ ф {xj
^. A1.70)
\ §> [Ф (х)] е
При использовании подходящим образом масштабно перенорми-
перенормированного поля ф (х) мы можем записать евклидово действие в виде
A/сс) S [</>], где зависимость от а выделена и S [</> ] положительно.
Как отмечалось в гл. 6, это может быть сделано для большинства
представляющих интерес моделей. Сначала рассмотрим числитель
и знаменатель A1.70). Числитель может быть записан в виде
N (а)= 2>[<j>(x)]exp[ -S [</>]) (ф .. . </>), (П-71)
где для простоты мы опустили зависимость от координат хъ ..., хп.
Из того факта, что в целях приведения действия к виду (l/a)S [</>]
мы могли изменить масштаб поля на а в некоторой степени, мы
можем ожидать появления бесконечного числа множителей а
в мере!) [е/> (х)] по сравнению с полем с неизменившимся масшта-
масштабом. Но эти множители будут присутствовать также в знамена-
знаменателе A1.70) и могут быть сокращены. Так как а и S [<j>] положи-
положительны, мы имеем тождество
a Jdffi(a/-S [£(*)]) =1. A1.72)
о
Подставляя это в A1.71), получаем
со
\ 3) [ф (x)]6(at - S [ф]) ехр (--i- S [ф]) (ф . . . ф) =
(at)e~l, A1.73)
о
где
FN (z) = \ @ [ф (л)] б (z — S [</>]) (ф ... ф). A1.74)
Таким образом, мы придали N (а) вид борелевского интеграла
с .точностью до общего множителя а, который не играет роли.
Подобный множитель появится и в знаменателе A1.70). Мы их
сократим.
Будем искать сингулярности функции FN (г), определенной
С помощью функционального интеграла A1.74). Функциональный

380 ГЛАВА 11
интеграл есть не что иное, как кратный интеграл по полю каж-
каждого х. Кратный интеграл с 6-функцией определяется как
\dyi... dyn& [z ~~ f {уъ ..., yn)] = § da\\f\-\ A1.75)
где правая часть есть интеграл по поверхности / (у) = z в «/-про-
«/-пространстве, а
Следовательно, интеграл A1.75) будет сингулярным для некото-
некоторого z = г, если | д/ | равно нулю всюду на поверхности / (у) = г.
Но | д/ | = 0 означает, что dfldyi = 0 для всех i. Таким образом,
интеграл A1.75) сингулярен в г, если функция f {уъ ..., уп) имеет
стационарную точку на поверхности /(у) = z. Обобщая это на
функциональный интеграл A1.74), мы видим, что борелевская
функция FN (z) сингулярна в z, если на поверхности S [<f>] — z
(в пространстве функций </> (х)) есть точка, удовлетворяющая усло-
условию
SS [^]/S^ (a:) = 0 для всех х. A1.76)
Но это не что иное, как евклидово уравнение поля, решениями
с конечным действием которого являются инстантоны. Поэтому,
если изучаемая полевая теория содержит инстантоны с конечным
действием, то борелевская функция FN (г) A1.74) имеет сингу-
сингулярности при тех конечных значениях z, которые равны значениям
действия этих инстантонов. Используя приведенные аргументы,
можно заключить, что пертурбативное разложение N (а) по сте-
степеням а имеет нулевой радиус сходимости. Аналогичный анализ
может быть повторен для знаменателя в A1.70), который мы
обозначим через D (ее). Функция Бореля FD (а), связанная cD (a),
также содержит сингулярности, обусловленные теми же инстан-
тонами при тех же значениях z. Следовательно, при разложении
в степенной ряд по a D (а) будет иметь нулевой радиус сходи-
сходимости. Тогда, исключая случайные обстоятельства, когда сингу-
сингулярности N (а) и D (а) при а = 0 в точности сокращаются, сте-
степенной ряд для отношения N (a)ID (а), который задает функцию
Грина (ф (xi) ... ф (хп)) в A1.70), также будет иметь нулевой
радиус сходимости.
Короче говоря, когда полевая теория допускает существование
инстантонов с конечным действием, пертурбативное разложение
ее функций Грина по степеням а не сходится для любого а».
Мы получили этот результат без явного вычисления коэффициентов
в старших порядках рядов теории возмущений. Заметим также,
что, хотя инстантоны и фигурировали в этом обсуждении, при
выводе мы не использовали квазиклассических приближений.

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 381
Конечно, наши квазиклассические инстантонные вычисления
в предыдущих^главах подтверждают этот общий результат.
Например, система Янга—Миллса содержит инстантоны с конеч-
конечным действием. В соответствии с этим мы нашли, что энергия ва-
вакуума для этой системы имеет существенную сингулярность, когда
параметр связи g2 равен нулю (см., например, A0.102) — A0.105)).
Это был всего лишь квазиклассический результат, но он показы-
показывает, что пертурбативное разложение этой энергии должно иметь
нулевой радиус сходимости. Аналогичные утверждения справед-
справедливы также для задачи о периодическом потенциале, для дву-
двумерной абелевой модели Хиггса и т. д.
Поучительно, также рассмотреть модели, которые не допу-
допускают действительных инстантонных решений с положительным
действием, но допускают комплексные решения с отрицательным
действием. Например, рассмотрим действительную скалярную
теорию в четырех измерениях с евклидовым действием (см. [133,
334 ])
Евклидово полевое уравнение
дЛ4> - 4>3/6 = ° - О1-78)
не может иметь действительных решений с конечным действием
в силу теоремы вириала, описанной в гл. 3. Но оно обязательно
имеет решение, если продлить <j> на комплексные значения.
Это решение имеет вид
./>(*) = ф/48/(*2 + Р2), A1.79)
где р —произвольный масштабный параметр (действие A1.77)
масштабно-инвариантно). Решение имеет отрицательное действие
S [«/>] = — 16я2. A1.80)
Если мы хотим исследовать определенную, согласно A1.74),
функцию FN (z) для комплексных г, мы должны продолжить
действительное поле <j> на комплексные значения, чтобы б (г —
— S [</>]) могло быть отличным от нуля. (Если исходное поле </>
само было комплексным (заряженным) полем с положительным
действием, то и Re <j>, и ln\ <f> должны быть продолжены
как комплексные значения, чтобы получить комплексное действие.)
В этом случае приведенное выше решение будет порождать син-
сингулярность при z = —16я2. Существование этой сингулярности
означает, что борелевский ряд имеет только конечный радиус
сходимости и исходный ряд теории возмущений имеет нулевой
радиус сходимости. Но, поскольку сингулярность в FN (z) имеется

382 ГЛАВА 11
только при отрицательных г, по-прежнему может существовать
возможность вычисления G (ее) в A1.67) для положительных ее,
если FN (z) для положительных z не имеет других сингулярностей,
не связанных с инстантонами. В этом случае мы можем считать
пертурбативный ряд суммируемым по Борелю в обобщенном
смысле. Исходный ряд теории возмущений, конечно, не имеет
смысла для произвольного ее, так как его радиус сходимости
равен нулю. Но вычисленная с помощью A1.67) функция G (ее),
если этот интеграл существует для некоторого се > О, может дать
имеющее смысл значение исследуемой физической величины.
Простым примером такого рода является степенной ряд
£(—1)"л!а". A1.81)
Его радиус сходимости, конечно, равен нулю. Соответствующая
функция Бореля имеет вид
-l)Bz"=Tqr7. (П.82)
Разумеется, она имеет сингулярность, но при z = —1. Поэтому
для положительных се >0 интеграл
по-прежнему существует. Функция G (се) может быть названа
борелевской суммой исходного ряда A1.81), но аналитическое
продолжение этого ряда не имеет смысла, поскольку последний
не существует ни в какой конечной области плоскости се. Если
в пертурбативном разложении физической величины возникает
такой ряд, как A1.81), то можно принять ту точку зрения, что,
хотя разложение по теории возмущений для произвольного се
не имеет смысла, исходная физическая величина может все же
быть хорошо определенной через борелевский интеграл типа
A1.83).
В противоположность этому, если имеется настоящий инстан-
тон, т. е. имеющий конечное положительное действие, как во всех
наших примерах в гл. 4 и 10, то F (г) сингулярно для некоторого
положительного z. Эта сингулярность для физических значений
се >0 попадает в область интегрирования борелевского инте-
интеграла. В этом случае пертурбативное разложение не является
суммируемым по Барелю. Но, согласно т'Хофту [334], даже
в таких случаях может сохраняться какая-то надежда. Даже если

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 383
сингулярность попадает для некоторого положительного t в инте-
интеграл A1.67), последний можно интерпретировать с помощью
подходящего аналитического продолжения, если только сингу-
сингулярность интегрируема. Например, мы видели, что вакуумная
энергия Янга—Миллса в приближении разреженного инстантон-
ного газа имеет зависимость от константы связи (g2 = ее) вида
С(а) = A/а1)е-8л2/а[1+О(а)]. A1.84)
Легко проверить, что формально
8я2)]. A1.85)
Сравнивая A1.85) с A1.67), мы видим, что соответствующая боре-
левская функция имеет вид
/?(z) = -gr[6(z^8n2)]. A1.86)
Она, конечно, сингулярна. Заметим, что в соответствии с нашим
общим результатом сингулярность появляется при 8я2, т. е. при
действии янг-миллсовского инстантона. Но эта сингулярность
интегрируема. Мы знаем, как интегрировать б-функцию или ее
производные. Поэтому, даже если инстантоны и порождают сингу-
сингулярности в функции Бореля на действительной положительной
оси, возможно, что функция по-прежнему будет интегрируема
и может привести к вычислению физической величины G (ее) как
функции а >0. Эти вопросы остаются открытыми. Кроме того,
хотя мы и показали, что инстантоны приводят к сингулярностям
в борелевской функции, мы не показали, что это единственные
сингулярности. В общем случае в F (г) могут существовать другие
сингулярности, не связанные с инстантонами. Все они должны
быть раскрыты до того, как можно будет окончательно установить
возможность суммирования по Борелю. Дополнительную инфор-
информацию по этим вопросам читатель может найти в лекциях
т'Хофта [334] и Крачфилда [98]. Распространение некоторых
из этих идей на случай включения ферми-полей см. в работе [273].
11.5. Дальнейшие разработки
Мы описали подробно основной непертурбативный вклад ин-
стантонов в вакуумную структуру соответствующей квантовой тео-
теории и несколько вытекающих из этого следствий. Разумеется, в этой
обширной области были проведен л дальнейшие исследования как
по уточнению и обобщению этих расчетов, так и в направлении
поиска более физических следствий инстантонов. В этом заключи-
заключительном разделе мы упомянем кратко некоторые из этих исследо-
исследований и приведем ссылки на литературу. ^

384 глава п
Одна группа расчетов связана с вычислением потенциала тяже-
тяжелых кварков, обусловленного инстантонами в КХД, с использо-
использованием вильсоновской петлевой функции. Эту функцию мы ввели
в разд. 11.1 в контексте двумерной абелевой модели Хиггса
и нашли, что она приводит в этой модели к удержанию зарядов в
присутствии разреженного инстантонного газа. Мы указали также,
что в C + 1)-мерной КХД подобное вычисление, к сожалению, не
приводит к удержанию кварков. Тем не менее инстантоны обус-
обусловливают существенный вклад во взаимодействие между тяже-
тяжелыми кварками, даже если этот вклад не увеличивается на боль-
больших расстояниях и не приводит кконфайнменту. Каллан и др. [67]
вычислили обусловленный инстантонами не зависящий от спинов
потенциал тяжелых кварков, используя неабелеву петлевую
функцию Вильсона. Эта процедура аналогична той, которую мы
использовали в разд. 11.1 для петли, соответствующей евклидо-
евклидовым мировым линиям пары qq. Эти авторы нашли потенциал,
который на малых расстояниях ведет себя как
V(R)~)\,27R* (^DftO, О1-87)
R-+Q J А,
О
где R — расстояние между кварками, Кг — размер инстантона,
a D (Кг) — «функция плотности» инстантонов размером Къ опре-
определяемая выражением
82 \6 / 8п2 \ /11 оо\
F^). (П.88)
Заметим, что по сравнению с янг-миллсовской функцией плотности
в A0.102) приведенная выше функция имеет степень (g)~12, а не
(g)~8. Это объясняется тем, что A1.88) соответствует калибровоч-
калибровочной группе SU C), связанной с КХД. Как отмечалось в гл. 4,
может использоваться тот же янг-миллсовский инстантон SU B),
но теперь этот инстантон имеет четыре дополнительные нулевые
моды за счет преобразований, обусловленных дополнительными
генераторами SU C). (На самом деле SU C) имеет на пять гене-
генераторов больше, чем SU B), но вращение, вызванное одним из
них, оставляет SU B)-инстантон инвариантным и не приводит
к нулевым модам.) Хотя этот потенциал на малых расстояниях
растет квадратично, Каллан и др. нашли, что на больших рас-
расстояниях он принимает постоянное значение
V (R) ~ (а + b/R). A1.89)
Таким образом, приближение разреженного инстантонного газа
в КХД не дает удерживающего потенциала. Константа а интер-

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 385
претируется как перенормировка массы, а константа b — как
перенормировка кулоновского потенциала. Впоследствии Каллан
и др. [69] выделили дополнительные зависящие от спина члены
(см. также [352 ]). Такой зависящий от спина потенциал, очевидно,
имеет значение в феноменологических моделях состояний кварко-
ния (qq). Привлекательной чертой, обнаруженной ими, было то,
что эти зависящие от спина члены могут быть получены из не
зависящего от спина члена A1.87) при взятии соответствующих
производных по R. Следовательно, зависящая от спина часть
зависит от меньших степеней R. Она оказывается постоянной
на малых расстояниях и убывает при R -> оо.
Заметим, что в A1.87) введено обрезание при ^с области изме-
изменения инстантонных размеров к1. Это является следствием инфра-
инфракрасной проблемы, которая отмечалась в разд. 10.5. В теории
Янга—Миллса (и, следовательно, также в КХД) инстантоны
могут быть всех размеров от 0 до оо. Поэтому, чтобы получить
конкретный результат, Каллан и др. ввели обрезание при Х^
которое они выбрали обратным типичному масштабу адронных
масс, когда эффективная константа связи g (kc) также мала.
Надежность такой процедуры, чувствительность результатов
к точному значению кс и возможные альтернативные способы
трактовки проблемы больших инстантонов до сих пор остаются
предметом оживленных споров. См., например, [9, 250]. Некоторые
другие подходы к влиянию инстантонов на динамику кварков
(включая легкие кварки) и их связанные состояния см. в работах
[63, 74, 116, 157, 324].
Другим привлекшим внимание аспектом является угроза
сильного нарушения симметрии Р и Т, обусловленная инстантон-
ными эффектами, и какой-либо надежный способ обойти эту
угрозу. Вспомним из разд. 10.4, что эффективный лагранжиан,
ассоциируемый с Э-вакуумами, в теории Янга—Миллса (см.
A0.98)) обладает зависящим от 0 дополнительным слагаемым и не
инвариантен под действием Р и Т, за исключением специального
случая 0 = 0. Аналогичное утверждение справедливо для цвет-
цветной калибровочной группы SU C) и становится уместным в реаль-
реальном мире в рамках КХД. В природе имеется нарушение как Р,
так и Т, но оно очень мало и в общепринятой интерпретации при-
приписывается слабым или суперслабым взаимодействиям. В таком
случае КХД, которая связана только с сильными взаимодейст-
взаимодействиями, должна сохранять Р и Т, т. е. вакуумный угол 0 должен
быть равен нулю. С другой стороны, если допустимо некоторое
0 Ф 0, наблюдаемая малости нарушения Т (оцениваемая по верх-
верхней границе электрического дипольного момента нейтрона) тре-
требует, чтобы 0 <: 10~5 [351]. Загадочным является механизм,
который заставляет 0 либо обращаться в нуль, либо быть неесте-
неестественно малым числом, меньшим, чем 10~5.
13 Раджараман Р.

386 ГЛАВА И
Одно из возможных объяснений состоит в том, что один из
кварков, взаимодействующих с калибровочным полем в КХД,
является безмассовым. В таком случае, как отмечалось в конце
разд. 11.3, различные секторы 0 эквивалентны и могут быть
сведены к 0 = 0 с помощью кирального вращения, восстанавли-
восстанавливая сохранение Р и Т в КХД. Но косвенные данные о массах
кварков по оценкам алгебры токов показывают, что, хотя кварки и
и d имеют малые по адронным масштабам массы, они, по-види-
по-видимому, не безмассовые. Учитывая это, Печчей и Квинн [278, 279 ]
предложили альтернативный механизм сохранения Р и Т, позво-
позволяющий всем кваркам иметь ненулевую физическую массу. Массы
некоторых кварков получаются при связывании их с хиггсов-
скими скалярами, которые должны приобретать ненулевое вакуум-
вакуумное среднее. Но скоро было выяснено [345, 351 ], что механизм
такого типа, включая спонтанно нарушенную симметрию U A),
приводит к существованию нового псевдоскалярного голдстоунов-
ского бозона. Он должен иметь нулевую голую массу, но за счет
взаимодействий в высших порядках приобретает конечную, но
малую физическую массу. Этот (пока гипотетический) легкий
бозон стал известен под названием «аксион». Вильчек [351 ] и
Вайнберг [345] сделали оценки различных свойств, которыми
должна обладать эта частица, и предложили экспериментальные
процессы, в которых она могла бы быть обнаружена (см. также
[169, 208, 358]). В частности, грубая оценка массы аксиона при-
приводит к значению около 100 кэВ. Были проведены некоторые экспе-
экспериментальные исследования с целью поиска этой частицы, но,
к сожалению, они пока привели к отрицательным результатам [28,
33, 115]. Если эта ситуация сохранится и окажется, что аксиона
в природе не существует, то потребуется найти какой-то другой
механизм подавления сильного нарушения симметрии Р и Т.
Предлагаются другие возможные механизмы, включая такие,
в которых имеется значительно более тяжелый аксион [20, 361 ].
В настоящее время полностью удовлетворительного объяснения
наблюдаемого нарушения симметрии Р и Т не имеется.
Между тем Каллан, Дашен и Гросс продолжили свои огромные
усилия по извлечению максимума возможных сведений о струк-
структуре реальных адронов с помощью инстантонных методов и свя-
связанных с ними приемов в КХД. Мы уже ссылались на их ранние
работы и использовали их при обсуждении основ инстантонной
физики. Их последующие работы [68—-70] выходят далеко за
пределы приближения разреженного инстантонного газа в на-
направлении уточнений и обобщений квазиклассического метода.
Среди сформулированных результатов имеются структура адро-
адронов, подобная мешку, возможное удержание кварков за счет
меронов и резкий подъем калибровочной константы связи g с рос-
ростом масштаба расстояний. Упомянутый последний резкий подъ-

ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 387
ем g, соединяющий области слабой и сильной связи в неабелевых
калибровочных теориях, был получен также Кройцем [96] при
компьютерном моделировании такой теории. Каллан и др. 170]
рассматривают результат Кройца как подтверждение их теорий,
основанных на инстантонах.
Противоположная точка зрения подвергает сомнению пользу
основанных на™инстантонах*'результатов в контексте КХД, в осо-
особенности из-за проблемы сильной связи и больших инстантонов,
описанной в разд. 10.5. Мы уже ссылались на работу Виттена
[356], в которой он предлагает l/jV-разложение как более осмыс-
осмысленное приближение к калибровочной SU (З)-теории и, кроме того,
доказывает, что инстантонные эффекты пропадают в главном
пределе N -> оо этого разложения. Однако Жевицки [204] нахо-
находит некоторые инстантонные эффекты, сохраняющиеся даже
в пределе N -> оо в C/V-модели (см. также [73, 261 ]).
Кроме этих фундаментальных вопросов, много работы было
проделано на техническом фронте инстантонной физики. В част-
частности, были разработаны методы вычисления инстантонных детер-
детерминантов, т. е. детерминантов квантовых флуктуации (бозонов
и фермионов) в окрестности инстантонных решений. Напомним,
что в гл. 5 мы подробно описали расчет такого детерминанта для
иллюстративного примера, когда мы вычисляли квантовые по-
поправки к массе кинка. В последующих примерах, особенно в тео-
теоретико-полевых решениях, таких как абелев вихрь Хиггса или
янг-миллсовский инстантон, мы не вычисляли соответствующие
детерминанты флуктуации. Они содержатся в множителях типа В
в A0.63) или В (Кг) в A0. Ш0), и их точное значение не требовалось
для нашего обсуждения. Если имеется желание изучить инстан-
инстантонные эффекты более детально, то вычисление таких флуктуа-
ционных детерминантов является существенным. Следуя пионер-
пионерской работе т'Хофта [332], большое число авторов изучили
поправки от квантовых флуктуации в присутствии инстантонов
для большого числа моделей. В дополнение к статьям, упомяну-
упомянутым в разд. 10.5, сошлемся на работы [38, 39, 41, 60, 230, 231, 270].
Как отмечалось в гл. 10, туннельные эффекты, которые мы
выводили в формализме евклидова функционального интеграла,
могут быть получены также в формализме реального времени
и при обобщении обычного уравнения Шредингера и его ВКБ-
приближения к теории поля. Результаты исследований такого
рода приведены в работах [36, 47, 48, 109, 156].
В разд. 10.5 мы ввели понятие меронного решения. Помимо
уже цитированных работ [67, 105] классические меронные реше-
решения, а также их роль в конфайнменте исследовались Глиммом
и Джаффе [164, 165]. Решения, интерполирующие мероны и ин-
сгантоны, были предложены Харом [214] для а-модели и Басея-
ном и Матиняном [27] для теории Янга—Миллса.
13*

ПРИЛОЖЕНИЕ А
Для любой классической орбиты множитель Дх в F.59) опреде-
определяется выражением
^(ii)A (A.I)
где
V" @ = V (д„я (/)), (А.2)
?нл (t) — классическая периодическая траектория с периодом Т и
у@) =у(Т) = 0. (А.З)
Здесь основным периодом траектории может быть не Т, a Tin
для любого целого п. Если выражение (А.1) записано на времен-
временной решетке, то оно есть не что иное, как гауссов кратный инте-
интеграл. Последний может быть вычислен точно, если мы можем
вычислить детерминант оператора (—d2/dt2 — V" (/)), который
появляется в экспоненте при граничных условиях (А.З). Чтобы
найти этот детерминант, мы диагонализуем его с помощью замены
переменных
\l$ (A.4)
где / (/) — решение уравнения на нулевое собственное значение
исследуемого оператора:
V" (/))/ (/) = 0. (А.5)
Обратное к (А.4) есть
\^dt'. <A.6)

ПРИЛОЖЕНИЕ А 389
Как может быть проверено прямой подстановкой, преимущество
такой замены переменных состоит в том, что
j D- у2 - 4- у ю *■)dt=I D*2)dt <А-7>
о о
Таким образом, в переменных z (t) действие ведет себя как действие
свободной частицы! Если время разбить на решетку /0 = О, /Х, ...,
^jv-i> tN = Т, как в F.8), то интеграл по траектории содержит
только Ylfsi1 dy (tt). Конечные точки у @) и у (Т) фиксируются
условием (А.З). Полезно включить дополнительное интегрирова-
интегрирование по yN = у (Т), умножив (АЛ) на
\=\dyN8(yN)=
—оо
\u\[\fr dil (А-8)
Когда (АЛ) умножено на (А.8) и переменные заменены на z (/),
мы имеем
(А.9)
где / — якобиан преобразования (А.4). Переходя на временную
решетку, получаем
, (АЛО)
где g = Bя/ейI/2 — правильный множитель меры. После замены
переменных на
bi-zt-z^, i=\ N (АЛ1)

390 ПРИЛОЖЕНИЕ А
это выражение факторизуется в произведение простых гауссовых
интегралов по bt и дает
If 2 N У]
J ~к^ ехр — т -|-/2 (Т) 2^, (е//?)) =
/ т \
dt \
'(О/-
о /
\-1/2
т^т • (АЛ2>
\ о /
Якобиан преобразования (А.4), которое есть уравнение Вольтерра,
получается через его ядро [150]:
/@ = ехр (-L\(t/f)dt) = exp ji-ln[/(T)// @)]J = [/ (T)/f @)]I/2.
(A.13)
Подставляя это в (А. 12), получаем
Т \-1/2
J^j- • (А.14)
\ о /
Эта величина просто связана с исходной классической орбитой
<7кл @- Заметим сначала, что
/ (*) =-Jf (<7кл @) (А. 15)
как некоторое решение (А.5). Поскольку орбита ^кл I (t) перио-
периодическая, имеем
/ (Г) = / @) = </кл @). (А. 16)
Кроме того,
[ d* - Г dt — од? di?KJ 2n? d<? ГА 171
J Pit) J (^кл@J~~ J (<?кл@K ~ J B(£-K)p ' l ;
0 0 ^i Qi
где классическая орбита могла совершить п оборотов по
основной периодической траектории за время Т, а цъ q2 — точки
поворота. В последнем равенстве мы использовали V242 = Е —■
— V (q) и опустили нижний индекс, указывающий, что все соот-
соответствует классической орбите. Имеем
Т = 2п
l2(E~V(q))f

ПРИЛОЖЕНИЕ А 391
Следовательно,
" ЁЭЧтг = —ж- (А-19)
[2 (Е - К)]3/2 ^£ V ;
it
Используя (А. 16)—(А. 19) в (А. 14), получаем
— г У/2 1 / dE\m
2fl\
Напомним, что q @) — конечная точка обоих концов траектории.
Для периодической орбиты q @) — просто одна из точек на орбите.
Когда А1 подставлено в интеграл для следа в F.59), мы получаем
« <п=§! «<°> «p (i « m) TJe- (- §■)'" (пТ ■
(А.21)
Но для замкнутой орбиты SKJI и dEldT не зависят от начальной
точки q @); кроме того, каждая орбита считается дважды, чтобы
учесть ее партнера с обращенным временем. Тогда
(А22)
есть период цикла.
Таким образом, мы имеем желаемый результат F.62), F.63), за
исключением фазового множителя е1яп. Он появляется из точек
поворота, сингулярную природу которых мы пока не учитывали.
Вблизи точки поворота, скажем q = q2, скорость q имеет нуль
Поэтому интеграл j dt/q2 = J dq/qs сингулярен, когда один
из двух пределов интегрирования достигает точки поворота,
хотя в целом объект вида qaqb\ab dqlqz, который появляется
J ча
в (А. 14), не расходится, когда либо qa, либо qb достигают точки
поворота. Это можно проверить, разлагая q = [2 (Е — V (q)) ]l/2
в окрестности точки поворота, в которой скорость имеет нуль
полуцелой степени. Но, хотя Ах конечно, оно приобретает допол-
дополнительные фазы, обусловленные скачкообразной структурой,
порождаемой сингулярностью q каждый раз, когда траектория
проходит через точку поворота. Обсуждение того, почему эта
фаза на одну точку поворота равна е'я/2, читатель может найти
в работах [212, 233]. Аналогичная фаза в волновой функции
возникает также при обычной трактовке метода ВКБ [225].
Для траектории, которая оборачивается п раз вокруг одной
и той же одномерной орбиты (т. е. имеет 2п точек поворота) ре-
результирующий фазовый множитель равен einn. Подставляя его
в (А.21), получаем результаты F.62), F.63).

ПРИЛОЖЕНИЕ Б
В гл. 8 мы видели, что, когда мы вычисляем квантовые поправки
к вкладу от классических решений, возникают нулевые моды,
обусловленные непрерывными симметриями, которые должны
заменяться на соответствующие коллективные координаты. Теперь
мы покажем, как эта замена может быть проведена для случая
однопараметрической трансляционной симметрии в формализме
функционального интеграла. Эта процедура служит небольшим
дополнением к обсуждениям в разд. 8.3 и 8.4, где использованы
канонические операторные методы. Мы проиллюстрируем эту
процедуру, используя простой пример одноинстантонного вклада
в одномерной квантовой механике. В частности, наше обсуждение
относится к задаче о периодическом потенциале (ЗПП) в гл. 10.
Мы выведем выражение A0.13), используя обозначения разд. 10.1.
Начнем с функционального интеграла в A0.10). Конечно, нас
интересует предел, когда евклидово время перехода т (т. е. область
изменения т') стремится к бесконечности. В этом пределе евклидово
действие в ЗПП трансляционно-инвариантно по %'; qKjl (т'—т0) —
инстантонное решение для действительных т0. Мы разложим
q {%') в ряд в окрестности qKJ1 (т' — т0) для произвольного задан-
заданного т0; тогда
<7(т') = <7кя.(т'-т0) + л(т'), (Б-1)
SE [Q СО] = SE [qKn (т' - т0)] + ± J л (т') Oi\ (т') dx' + 0 (if), (Б.2)
где
0= -
1«
(Б.З)
(т' - т0)] = j dx' (-i- (%iJ + V [qKB]) =
—oo
oo
= J dx' (-^т1J (согласно B.20)) = So. (Б.4)

ПРИЛОЖЕНИЕ Б 393
So не зависит от т0 в силу трансляционной инвариантности. Нор-
Нормальные моды флуктуации есть собственные функции г\п (т'—т0)
оператора О, удовлетворяющие условию
О'Цп (т' - т0) = а£т)„ (т' — т0). (Б.5)
В частности, нормированная функция
обладает нулевым собственным значением благодаря трансляцион-
трансляционной инвариантности. Нам нужно заменить интегрирование по этой
нулевой моде на интегрирование по точке локализации инстантона
т0. Это делается с помощью следующего приема [161 ], который
является вариантом метода Фаддеева и Попова [126]. Рассмотрим
тождество
j dxo8 I J ЛЧ (т' - T0) q (O j - R A (q) = 1, (Б.7)
где б [...] — б-функция Дирака от ее аргумента,
оо оо
A [q] = j -±- (rio (т' - то)) q (т') dx' = \ ц0 (т' - т0) ^ dx', (Б.8)
x'^0(x' ~xo)qKn(x'-xo). (Б.9)
Заметим, что в силу (Б.6)
«==[?L(^4)]tf:
и ле зависит от т0. Для конкретного потенциала V (q), использо-
использовавшегося в ЗПП, R есть 2я2/уА50. В тождестве (Б.7) мы неявно
предположили, что аргумент б-функции равен нулю только для
одного значения т0 для данной q (т'). Возможность наличия не-
нескольких корней и следствия рассмотрены в работе [185].
Рассмотрим евклидову амплитуду перехода в A0.10)
G = lim <2л | е~Нт/й |о> = j 0 [<}(т')]ехр (- y

394 ПРИЛОЖЕНИЕ Б
Подставим тождество (Б.7) в (Б. 10) и изменим порядок интегри-
интегрирования. Тогда
т/2
G = lim J dx0 [ S> [q (г')] exp ( - \ SE [q (x')]) x
в[(|^Ч(т'-То)<7(т'))-/?]Д(<7)- (Б. И)
x
Разложим ^ (т') в функциональный интеграл в окрестности
<7кл (т' — то) дая любого заданного т0, используя (Б.1) — (Б.4).
В главном гауссовом приближении
G = lim [ dxoe-s°/HA [qKa (х' - т0)] [ Sb h (x')j x
^°° -,/2 J
X exp ( - -L- J Лт'лбт,) б [ J -по (т' - т0) л (т') dx'] . (Б. 12)
В этом приближении мы пренебрегли членами О (tf) в экспоненте
и заменили q (%') на qKn {%' — х0) в A [q], как требуется в прибли-
приближении стационарной фазы, впервые введенном в F.13). В аргу-
аргументе б-функции мы использовали (Б.9), чтобы сократить слагае-
слагаемое R. Теперь все члены в интеграле по т0 в (Б. 12) не зависят
от х0. Поскольку So не зависит от х0, используя (Б.6) и (Б.4),
получаем
J = A [qKn (х' - xo)j = J ло (т' - т0) d^(^-T0) dx, = у^0. (Б. 13)
Наконец, хотя т0 и возникает в функциональном интеграле по
т] (т'), значение этого функционального интеграла не зависит от
т0. Это становится очевидно, если разложить т] (У) по нормальным
модам цп (т' —х0). в (Б.5) и записать функциональный интеграл
как кратный интеграл по коэффициентам разложения по модам.
Это как раз гауссов интеграл по всем функциям т] (т'), ортого-
ортогональным нулевой моде, и он может быть записан в виде ВЕ (т) х
X {Def [O]}-1/2, где ВЕ (т) — не что иное, как обычный множитель
меры в функциональном интеграле, a Def [б] = П„>0 со,2г —
детерминант О в пространстве, ортогональном этой нулевой моде.
Объединяя все это, приводим выражение (Б. 12) к виду
1/2. (Б. 14)

ПРИЛОЖЕНИЕ Б 395
Это как раз результат, приведенный в A0.13). Если мы сравним
(Б.14) с примитивным гауссовым приближением A0.12) (в кото-
котором не рассматривается тщательно нулевая мода), то увидим, что
нулевая мода заменена интегрированием по соответствующей
коллективной координате т0 с соответствующим якобианом / =
Как отмечалось в гл. 6, в большинстве представляющих интерес
случаев действие может быть записано в виде S [q] = (l/g2) S [q],
где g — константа связи, которая предполагается малой, a S [q]
в терминах подходящим образом перенормированной переменной q
не зависит от g. Следовательно, действие инстантона So имеет вид
So = S0/g2, и якобиан / в (Б. 13) пропорционален l/g. Мы проде-
продемонстрировали это только на примере одной нулевой моды, обу-
обусловленной трансляционной симметрией, но результат является
более общим (см., например, [89]). Для каждой нулевой моды,
которая заменяется на соответствующую коллективную коорди-
координату, якобиан приобретает множитель \lg.

ЛИТЕРАТУРА
1. Abbott L. F. — Nucl. Phys., 1978. v. B139, p. 159.
2. Abers E. S., Lee B. W. — Phys. Rep., 1973, v. 9C, p. 1. [Имеется перевод:
Аберс Е. С, Ли Б. В. Калибровочные теории. — В кн.: Квантовая теория
калибровочных полей. — М.: Мир, 1977.]
3. Ablowitz M. J., Каир D. J., Newell А. С, Segur H. —Phys. Rev. Lett.,
1973, v. 31, p. 125.
4. Actor R. — Rev. Mod. Phys., 1979, v. 51, p. 461.
5. Adler S. L. — Phys. Rev., 1969, v. 177, p. 2426.
6. Adler S, L. — Phys. Rev., 1979, v. D19, p. 2997.
^7. Adler S, L., Dashen R. F, —Current Algebras and Applications to Particle
Physics. — New York and Amsterdam: W. A. Benjamin Inc., 1968. [Имеется
перевод: Адлер С. Л., Дашен Р. Ф. Алгебра токов и их применение в физике
частиц. Пер. с англ./Под ред. Л. Д. Соловьева. — М.: Мир, 1970.]
8. Affleck 1. — Nucl. Phys., 1980, v. B162, p. 461.
9. Appelquist Т., Shankar R. — Phys. Rev., v. D18, p. 2952.
10. Arafune J., Freund P. G. 0., Goebel С J. — J. Math. Phys. (N. Y.1, 1975,
v. 16, p. 433.
11. Арефьева И. Я., Корепин В. Е. — Письма в ЖЭТФ, 1974, т. 20, с. 680.
12. Atiyah M., Singer I. — Ann. Math., 1968, v. 87, p. 484.
13. Atiyah M., Patodi V., Singer I. —Math. Proc. Camb. Phil. Soc, 1976, v. 79,
p. 71.
14. Atiyah M., Ward A. — Comm. Math. Phys., 1977, v. 55, p. 117.
15. Atiyah M. F., Hitchin N. J., Drinfeld V. G., Manin Yu. 1. —Phys. Lett.,
1978, v. 65A, p. 185.
16. Baacke J., Rothe H. J. — Nucl. Phys., 1977, v. В118, p. 371.
17. Babelon O. — Nucl. Phys., 1977, v. B131, p. 519.
18. Bais F. A., Weldon A. H. — Phys. Rev. Lett., 1978, v. 41, p. 601.
19. Balachandran A. P., Stern A,, Trahern G. — Phys. Rev., 1979, v. D19, p. 2416.
20. Baluni V. — Phys. Rev. Lett., 1978, v. 40, p. 1358.
21. BardakciK., Samuel S. — Phys. Rev., 1978, v. D18, p. 2849.
22. Bardakci K., Samuel S. — Phys. Rev., 1979, v. D19, p. 2357.
23. Bardeen W. A. — Nucl. Phys., 1974, v. B75, p. 246.
24. Bardeen W. A., Chanowitz M. S., Drell S. D., Weinstein M., Yan Т. М. —
Phys. Rev., 1975, v. Dll, p. 1094.
25. Barnard T. — Phys. Rev., 1973, v. A7, p. 373.
26. Barone A., Esposito F., Magee С J., Scott A. C. — Riv. Nuovo Cim., 1971,
v. 1, p. 227.
27. Басеян Ж. 3., Матинян С. Ж. — Письма в ЖЭТФ, 1980, т. 31, с. 70.
28. BechisD. J., Dombeck Т. №., Elsworth R. W., Sager E. V., Steinberg P. H.,
Tieg L. J., Yoh J. K., Weitz R. L. —Phys. Rev. Lett., 1979, v. 42, p. 1511.
29. Belavin A. A., Polyakov A. M., Schwartz A. S,, Tyupkin Yu. S. — Phys.
Lett., 1975, v. 59B, p. 85.
30. Белавин А. А., Поляков А. М. — Письма в ЖЭТФ, 1975, т. 22, с. 245.

ЛИТЕРАТУРА 397
31. Belavin A. A., Polyakov А. М. — Nucl. Phys., 1977, v. B123, p. 429.
32. Bell J. S., Jackiw R. — Nuovo Cim., 1969, v. 60A, p. 47.
33. Belotti £., Fiorini E., Zanotti L. — Phys. Lett., 1978, v. 76B, p. 223.
34. Bender С M., Wu T. T. — Phys. Rev., 1973, v. D7, p. 1620.
35. Bender С. M., Wu Т. Т. — Phys. Rev. Lett.,11976, v. 37, p. 117.
36. Bender I., Rothe H. J. — Nucl. Phys., 1978,>. B142, p. 177.
37. Березин Ф. А. Метод вторичного квантования. —M.: Наука, 1965.
38. Berg В., Luscher M. — Comm. Math. Phys., 1979, v. 69, p. 57.
39. Berg В., Luscher M. — Nucl. Phys., 1979, v. B160, p. 281.
40. Bernard С W., Weinberg E. J. — Phys. Rev., 1977, v. D15, p. 3656.
41. Bernard C. — Phys. Rev., 1979, v. D19, p. 3013.
42. Bernstein J. — Rev. Mod. Phys., 1974, v. 46, p. 7.
43. Bernstein J., Fubini S., Gell-Mann M., Thlrring W. — Nuovo Cimm., 1960,
v. 17, p. 757.
44. Berry M. V., Mount К. Е. — Rep. Prog. Phys., 1972, v. 35, p. 315.
45. Berry M. V., Tabor M. — J. Phys. A: Math. Gen., 1977, v. 10, p. 371.
46. Bishop A. R., Krumhansl J. A., Trullinger S. E. — Physica, 1980, v. ID, p. 1.
47. Bitar K., Chang S. J. —Phys. Rev., 1978, v. D17, p. 486.
48. Bitar K., Chang S. J. - Phys. Rev., 1978, v. D18, p. 435.
49. Bjorken J. D., Drell S. D. Relativistic Quantum Mechanics. — New York:
McGraw-Hill Book Co.; 1964. [Имеется перевод: Бьеркен Дж. Д., ДреллС. Д.
Релятивистская квантовая теория. Т. 1. Релятивистская квантовая меха-
механика. — М.: Наука, 1978.]
50. Bjorken J. D., Drell S. D. — Relativistic Quantum Fields. — New York:
McGraw-Hill Book Co., 1965. [Имеется перевод: Бьеркен Дж. Д., ДреллС. Д.
Релятивистская квантовая теория. Т. 2. Релятивистские квантовые поля. —■
М.: Наука, 1978.]
51. Bloch F. — Z. Phys., 1928, Bd. 52, S. 155.
52. Боголюбов Н. Н. Тябликов С. В. — ЖЭТФ, 1949, т. 19, с. 256.
53. Боголюбов Н. Н., Щирков Д. В. Введение в теорию квантования полей. —
М.: Наука, 1973.
54. Богомольный Е. Б. — Ядерная физика, 1976, т. 24, с. 449.
55. Bogomol'nyi Е. В. — Phys. Lett., 1980, v. 91В, p. 431.
56. Bott R. — Bull. Soc. Math. France, 1956, v. 84, p. 251.
57. Brezin £., he Guillou J. C, linn-Justin J. — Phys. Rev., 1977, v. D15, p. 1544.
58. Brezin E., Le Guillou J. C, linn-Justin J. — Phys. Rev., 1977, v. D15, p. 1558.
59. Brezin E., Mikatni S., linn-Justin J. — Nucl. Phys., 1980, v. B165, p. 528.
60. Brown L. S., Creamer D. B. — Phys. Rev., 1978. v. D18. p. 3695.
61. Brown L., Carlitz R., Lee С — Phys. Rev., 1977, v. D16, p. 417.
62. Cahill K. — Phys. Lett., 1974, v. 53B, p. 174.
63. CaldiD. C. — Phys. Rev. Lett., 1977, v. 39, p. 121.
64. Callan С G., Jr., Dashen R. F., GrossD. J. — Phys. Lett., 1976, v. 63B, p. 334.
65. Callan С G., Jr., Dashen R. F., GrossD. J. — Phys. Lett., 1977, v. 66B, p. 375.
66. Callan C.G., Jr., Dashen R.F., GrossD. J. — Phys. Rev., 1977, v. D16, p. 2526.
67. CallanC. G., Jr.. Dashen R. F., GrossD. J. — Phys. Rev., 1978, v. D17 p. r717.
68. CallanC. G., Jr., Dashen R. F., GrossD. J. — Phys. Rev., 1979, v. D19, p. 1826.
69. Callan С G., Jr., Dashen R. F., GrossD. J. — Phys. Rev., 1979, v. D20, p. 3279.
70. Callan С G., Jr., Dashen R. F., GrossD. J. — Phys. Rev. Lett., 1980, v. 44,
p. 435.
71. Callan С G., Jr., Dashen R. R., GrossD. J., Wilizek F., Zee A. — Phys. Rev.,
1978, v. D18, p. 4684.
72. CampbellD. K., Liao Y.-T. — Phys. Rev., 1976, v. D14, p. 2093.
73. Cant R. J. — Phys. Lett., 1980, v. 96B, p. 380.
74. Carlitz R. D., Creamer D. B. — Ann. Phys. (N. Y.), 1979, v. 118, p. 429.
76. Castillejo L., Dalitz R. H., Dyson F. J. — Phys. Rev., 1956, v. 101. p. 453,
76. Chadha S., D'Adda A., diVecchia P., Nichodemi F. — Phys. Lett., 1977, v. 72 B,
p. 103.

3:)8 ЛШТ-РЛТУРА
77. Chakrabarti A. — Nucl. Phys., 1975, v. B101, p. 159.
78. Chang S. J., Lee B.W.. Ellis S. D. — Phys. Rev., 1975, v. Dll, p. 3572.
79. Chang S. S. — Phys. Rev., 1978, v. D17, p. 2595.
80. Chew G. F., High Energy Physics, Les Houches, Ed. С de Witt and M. Ja-
Jacob. — London: Gordon and Beach, 1965, p. 189.
81. Christ N. H., Lee T. D. — Phys. Rev., 1975, v. D12, p. 1606.
82. Christ N. H., Weinberg E. J., Stanton N. K. — Phys. Rev., 1978, v. D18,
p. 2013.
83. Christ N. H., Jackiw K. — Phys. Lett., 1980, v. 91B, p. 228.
, p.
85. Coleman S. — in: Laws of Hacfronic Matter, Ed. A. Zichichi. — New York
84. Coleman S. — Comm. Math. Phys., 1973, v. 31, p. 2!
p.:
59.
and London: Academic Press, 1975.
86. Coleman S. — Phys. Rev., 1975, v. Dll, p. 2088.
87. Coleman S. — Classical lumps and their Quantum Descendants, 1975 Erice
Lectures published in New Phenomena in Sub-Nuclear Physics, Ed. A. Zi-
Zichichi. — New York; Plenum Press, 1977.
88. Coleman 5. —Comm. Math. Phys., 1977, v. 55, p. 113.
89. Coleman S. — in: The Whys of Subnuclear Physics, Ed. A. Zichichi. — New
York: Plenum Press, 1979.
90. Coleman S., Mandula J. —Phys. Rev., 1969, v. 159, p. 1251.
91. Corrigan E., Fairlie D. B. — Phys. Lett., 1977, v. 67B, p. 69.
92. Corrigan E., OliveD. I., Fairlie D. В., Nuyts /.— Nucl. Phys., 1976, v. В106,
p. 475.
93. Cremmer E., Schaposnik F., Scherk J. — Phys. Lett., 1976, v. 65B, p. 78.
94. Cremmer E., Scherk J. — Phys. Lett., 1978, v. 74B, p. 341.
95. Creutz M. — Phys. Rev., 1975, v. D12, p. 3126.
96. Creutz M. — Phys. Rev., 1980, v. D21, p. 2308.
97. Crewther R. — Riv. Nuovo Cim., 1979, v. 2, p. 63.
98. Crutchjield IT, W. Y. — Phys. Rev., 1979, v. D19, p. 2370.
99. D'Adda A., Luscher M., DiVecchia P. — Nucl. Phys., 1978, v. B146, p. 63.
100. Dashen R. F., Hasslacher В., Neveu A. — Phys. Rev., 1974, v. D10, p. 4114.
101. Dashen R. F.
102. Dashen R. F.
103. Dashen R. F
104. Dashen R. F.
Hasslacher В., Neveu A. — Phys. Rev., 1974, v. D10, p. 4130.
Hasslacher В., Neveu A. — Phys. Rev., 1975, v. Dll, p. 3434.
Hasslacher В., Neveu A. — Phys. Rev., 1975, v. D12, p. 2443.
Ma S. K., Raiaraman R. — Phys. Rev., 1975, v. Dll, p. 1499.
105. De Alfaro V., Fubini S., Furlan G. —Phys. Lett., 1977, v. 65B, p. 1631.
106. DerrickG. H. — J.Math. Phys.. 1964, v.5, p. 1252.
107. Deser S. —Phys. Lett., 1976, v. 64B, p. 463.
108. de Vega H. J. — Nucl. Phys., 1976, v. B115, p. 411.
109. de Vega H. J., Gervais J. L., Sakita B. — Nucl. Phys., 1978, v. B143, p. 125.
110. Din A. J., Zakrewski W. J. — Nucl. Phys., 1980, v. B168, p. 173.
111. Dirac P. A. M. — Proc. R. Soc. (London^, 1931, v. A133, p. 60.
112. Dirac P. A. M. — Phys. Rev., 1948, v. 74, p. 817.
113. Dirac P. A. M. — Can. J. Math., 1950, v. 2, p. 129.
114. Dobrushin R. L., Minlos R. A. — Func. Anal. Appl., 1973, v. 7, p. 324.
115. Donnelly T. W., Freedman S. J., Lytel R. S., Peccei R. £>., Schwartz M. —
Phys. Rev., 1978, v. D18, p. 1607.
116. Duncan A.— Phys. Rev., 1978, v. D18, p. 1988.
117. Dyson F. J. —Phys. Rev., 1952, v. 85, p. 631.
118. Edwards S. F., Gulyaev Y. V. — Proc. R. Soc, 1964, v. A279, p. 229.
119. Eguchi Т., Hanson A. J. — Phys. Lett., 1978, v. 74B, p. 249.
120. Eichenherr H. - Nucl. Phys., 1978, v. B146, p. 215.
121. Englert F., Broui R. — Phys. Lett., 1964, v. 13, p. 321.
122. Ezawa Z. F. — Phys. Rev., 1978, v. D18, p. 2091.
123. Ezawa T. — Phys. Lett., 1979, v. 81B, p. 325.
124. Фаддеев Л. Д. Препринт МПИ-ПАЕ/16. —Ленинград, 1974.
125. Фаддеев Л. Д. — Письма в ЖЭТФ, 1975, т. 21, с. 141.

ЛИТЕРАТУРА 399
126. Faddeev L. D., Popov V. N. — Phys. Lett., 1967, v. 25B, p. 29.
127. Фаддеев Л. Д., Тахтаджян Л. А. — ТМФ, 1974, т. 21, с. 160. [См. также:
Препринт ОИЯИ Е2-7998. — Дубна. 1974].
128. Фаддеев Л. Д., Кулиш П. П., Корепин В. £.— Письма вЖЭТФ, 1975, т. 21,
с. 302.
129. Фаддеев Л. Д., Корепин В. Е. — ТМФ, 1975, т. 25, с. 147.
130. Faddeev L. D., Korepin V. Е. — Phys. Lett., 1976, v. 63B, p. 435.
131. Faddeev L. D., Korepin V. E. — Phys. Rep., 1978, v. 42C, p. 1.
132. Славное А. А., Фаддеев Л. Д. Введение в квантовую теорию калибровочных
полей. — М.: Наука, 1978.
133. Fainberg V. Ya., Iofa M. Z. — Nucl. Phys., 1980, v. В168, p. 495.
134. Fateev V. A., Frolov I. V., Schwarz A. S. — Nucl. Phys., 1979, v. B154, p. 1.
135. Фатеев В. А., Фролов И. В., Шварц А. С. — Яд. физ., 1979, т. 8, с. 3.
136. Feynman R. P., HibbsA. R. Quantum Mechanics and Path Integrals. — New
York: McGraw-Hill Book Co., 1965. [Имеется перевод: Фейнман Р. П.,
Хибс А. Квантовая механика и интегралы по траектории. —М.;Мир, 1968.1
137. Finkelstein D. — J. Math. Phys., 1966, v. 7, p. 1218.
138. Finkelstein D., Mhner С — Ann. Phys. (N. Y.), 1959, v. 6 p. 230.
139. Floquet G. — Ann. de 1-Ecole Norm. Sup. B), XII, 1883.
140. Frampton P. — Phys. Rev., 1976, v. D14, p. 528.
141. Frauhchi S. Regge Poles and S-Matrix Theory. — New York: W. A. Benj-
Benjamin Inc., 1963.
142. Friedberg R., Lee T. D., Sirlin A. — Phys. Rev., 1976, v. D13, p. 2739.
143. Friedberg R., Lee T. D., Sirlin A. — Nucl. Phys., 1976, v. B115, p. 1.
144. Friedberg R., Lee T. D.. Sirlin A. — Nucl. Phys., 1976, v. B115, p. 32.
145. Friedberg R., Lee T. D. —Phys. Rev., 1977, v. D15, p. 1694.
146. Frihsch H.. Gell-Mann M. Proceedings of the 16th Internet. Conf. on High
Energy Physirs held in Chicago — Batavia, 1972. v. 2, p. 135.
147. Fritzsch H., Gell-Mann M., Leutwyler H. — Phy. Lett., 1973, v. 47B, p. 365.
148. Frohlich J. — Comm. Math. Phys., 1976, v. 47, p. 269.
149. Gardner С S., Greene J. M., Kruskal M. D. Miura R. M. — Phys. Rev.
Lett., 1967, V. 19. p. 1095.
150. Gel'fand J. M., Yaglom A. M. — J. Math. Phys., 1960. v. 1. p. 48.
151. Georgi M. Glashow S. L. — Phys. Rev. Lett., 1972, v. 28, p. 1494.
152. Gervain J.-L. Sakita B. — Phys. Rev., 1975, v. DM, p. 2943.
153. Gervais J.-L., Jevicki A., Sakita B. — Phys. Rev., 1975 v. D12. p. 1038.
154. Gervais J.-L., Jevicki A. — Nucl. Phys., 1976. v. B110, p. 93.
155. Gervais J.-L., Jevicki A. — Nucl. Phys., 1976, v. B110, p. 113.
156. Gervais J.-L., Jevicki A. —Phys. Rev., 1977, v. D16, p. 3507.
157. Geshkenbein B. V., Ioffe B. L. — Nucl. Phys., 1980, v. B166, p. 340.
158. Giambiaggi J. J., Rothe K. D. — Nucl. Phys., 1977, v. B129, p. 111.
159. Gibbons G. W., Perry M. J. — Nucl. Phys., 1978, v. B146, p. 90.
160. Gibbons G. W.. Hawking S. W. — Comm. Math. Phys., 1979. v. 66 p. 291.
161. Gildener E., Patrascioiu A. — Phys. Rev., 1977, v. D16, p. 423.
162. Glaser V. — Nuovo Cim., 1958, v. 9, p. 990.
163. Glimm J., JaffeA., Spencer T. — Comm. Math. Phys., 1975, v. 45, p. 203.
164. Glimm J., Jaffe A. — Phys. Rev. Lett., 1978, v. 40, p. 277.
165. Glimm J., Jaffe A. — Phys. Lett., 1978, v. 73B, p. 167.
166. GoddardP., Nuyts J., Olive D. — Nucl. Phys., 1977, v. B125, p. 1.
167. Goddard P., Olive D. — Rep. Prog. Phys., 1978, v. 41, p. 1357.
168. Goldhaber A. S. — Phys. Rev. Lett., 1976, v. 36, p. 1122.
169. Goldman Т., Hoffmann С M. — Phys. Rev. Lett., 1978, v. 40, p. 220.
170. Goldstein H. Classical Mechanics. — Reading, Mass., USA, Addison-Wesley
Publishing Co., 1950. [Имеется перевод: Голдстейн Г. Классическая меха-
механика. — М.: ГИТТЛ, 1957.]
171. Goldstone J. — Nuovo Cim., 1961, v. 19, p. 154.
172. Goldstone J., Salam A., Weinberg S. — Phys. Rev., 1962, v. 127, p. 965,

400 ЛИТЕРАТУРА
173. Goldstone J., Jacklw R. — Phys. Rev., 1975, v. Dl 1, p. 1486.
174. Golo V., Perelemov A. M. — Phys. Lett., 1978, v. 79B, p. 112.
175. Рыжик И. М., Градштейн И. С. Таблицы интегралов, сумм, рядов и про-
произведений. — М.—Л.: ГИТТЛ, 1951.
176. Gross D. J., Wilczek F. — Phys. Rev. Lett., 1973, v. 30, p. 1343.
177. Gross D. J., Neveu A. — Phys. Rev., 1974, v. D10, p. 3235.
178. GuralnlkG. S., Hagen С R., Kibble T. W. B. — Phys. Rev. Lett., 1964. v.13,
p. 585.
179. Guth A., Weinberg E. J. — Phys. Rev., 1976. v. D14, p. 1660.
180. GutzwillerM. — J.Math. Phys., 1967, v. 8, p. 1979.
181. Gutzwiller M.—3. Math. Phys., 1970, v. 11, p. 1791.
182. Gutzwiller M. — J. Math. Phys., 1971, v. 12, p. 343.
183. Hasenfratz P., 'tHooft G. — Phys. Rev. Lett., 1976, v. 36, p. 1119.
184. Hawking S. W. — Phys. Lett., 1977, 60A, p. 81.
185. Hietarinta J. — Nucl. Phys., 1980, v. B164, p. 343.
186. HiggsP. W. — Phys. Lett., 1964, v. 12, p. 132.
— "• ~ — -' ~ --~5, v. 145, p. "
187. Higgs P. W. —Phys. Rev., 1966, v. 145, p. 1156.
188. Hobart R. — Proc. Phys. Soc, Ю63, v. 82, p. 201.
189. Horvath Z., PallaL. — Nucl. Phys., 1976, v. B116, p. 500.
190. Jackiw R. — in: Lectures in Current Algebra and its Applications. Princeton,
N. J., USA, Princeton University Press, 1972. [Имеется перевод: Трейман С,
ДжакивР., Гросс Д. Лекции по алгебре токов. —М.: Атомиздат, 1977.]
191. Jackiw R. — in: Gauge Theories and Modern Field Theories. —Cambridge,
Mass., USA, M. I. T. Press, 1976.
192. Jackiw R. — Rev. Mod. Phys., 1977, v. 49, p. 681.
193. Jackiw R. —Rev. Mod. Phys., 1980, v. 52, p. 661.
194. Jackiw R., Woo G. — Phys. Rev., 1975, v. D12, p. 1643.
195. Jackiw R., Rebbi С — Phys. Rev. Lett., 1976, v. 36, p. 1116.
196. Jackiw R., Rebbi С — Phys. Rev., 1976, v. D14, p. 517.
197. Jackiw R., Rebbi С — Phys. Rev., 1976, v. D13, p. 3398.
198. Jackiw R., Rebbi С — Phys. Rev. Lett., 1976, v. 37, p. 172.
199. Jackiw R., Nohl C, Rebbi С —Phys. Rev., 1977, v. D15, p. 1642.
200. Jackiw R., Nohl C, Rebbi C. —Particles and Fields. — New York: Plenum
Publishing Co., 1978, p. 199.
201. Jacobs L. —Phys. Rev., 1976, v. D14, p. 2739.
202. Jersak J., Kiera M., Magg M. — Nuovo Cim., 1977, v. 40A, p. 269.
203. Jevicki A. — Nucl. Phys., 1976, v. B117, p. 365.
204. Jevicki A. — Phys. Rev., 1979, v. D20, p. 3331.
205. Johnson K. —Nuovo Cim., 1961, v. 20, p. 773.
206. Julia В., Zee A. — Phys. Rev., 1975, v. DM, p. 2227.
207. Kadanoff L., CevaH. — Phys. Rev., 1971, v. B3, p. 3918.
208. Kandaswamy J., Salomonson P., Schechter J. — Phys. Rev., 1978, v. D17,
p. 3051.
209. Karowski M. — Phys. Rep., 1979, v. 49 с. р. 229.
210. Karowski M., ThunH.-J., TruongT. Т., WeiszP. — Phys. Lett., 1977, v. 67B,
p. 321.
211. Karowski M., Thun H.-J, — Nucl. Phys., 1977, v. В130, p. 295.
212. Keller J. —Ann. Phys. (N. Y.), 1958, v. 4, p. 180.
213. Kerman A., Klein A. —Phys. Rev., 1963, v. 132, p. 1326.
214. Khare A. — J. Phys. A: Math. Gen., 1980, v. 13, p. 2253.
215. Khrustalev O. A., Razumov A. V., Taranov A, Yu. — Nucl. Phys., 1980.
v. B172, p. 44.
216. Kilpatrick J., Kilpatrick M. — J. Chem. Phys., 1948, v. 16, p. 781.
217. Kim S. Т., Woo С H. — Nucl. Phys., 1979, v. B155, p. 357.
218. KMis J. — Phys. Rev., 1977, v. D15, p. 2329.

ЛИТЕРАТУРА 401
219. Kittel С. Introduction to Solid State Physics. — New York, 1959. [Имеется
перевод: Киттгль Ч. Введение в физику твердого тела. Пер. с англ. —М.:
Наука, 1978.]
220. Klalber В. Lectures in Theoretical Physics, XA, Ed. A. Barut and W. Brit-
Britten. — London: Gordon and Breach, 1968.
221. Kogut J., Susskind L. ~ Phys. Rev., 1975, v. Dll, p. 3594.
222. Krumhansl J. A., Schrieffer J. R. — Phys. Rev., 1975, v. Bll, p. 3535.
223. Кулиш П. П., Нисимов Б. —Письма в ЖЭТФ, 1976, т. 24, с. 220.
224. Lamb G. L. 'Jr. — Rev. Mod. Phys., 1971, v. 43, p. 99.
225. Ландау Л. Д., Лифшиц Е. М. Квантовая механика. — М.: Наука, 1974.
226. Longer R. Е. — Phys. Rev., 1937, v. 51, p. 669.
227. La Rue G.,. F airbank W. M., Hebard A. F. — Phys. Rev. Lett., 1977, v. 38,
p. 1011.
228. -Lee T. D. Non-Topological Solitons. Columbia University Preprint Co.
2271-76. — Pisa, 1976.
229. Lee T. D., Wick G. С —Phys. Rev., 1974, v. D9, p. 2291.
230. Levine H. — Nucl. Phys., 1979, v. B157, p. 237.
231. Levine H., Yaffe L. G. ^ Phys. Rev., 1979, v. D19, p. 1225.
232. Levit S. Ph. D. Thesis submitted to the Weitzmann Institute of Science. —
Israel, 1978.
233. Levit S., Smilansky U.—Ann. Phys. (N. Y.), 1977, v. 103, p. 198.
234. Липатов Л. Н. — Письма в ЖЭТФ, 1976, т. 24, с. 179.
235. Липатов Л. Н. —Письма в ЖЭТФ, 1977, т. 25, с. 116.
236. Luscher М. — Nucl. Phys., 1978, v. В135, p. 1.
237. Luscher M., Pohlmeyer К. — Nucl. Phys., 1978, v. В137, p. 46.
238. Ma S.-K., Rajaraman R. — Phys. Rev., 1975, v. Dll, p. 1701.
239. Makhankov V. G. — Phys. Rep., 1978, v. 35C, p. 1.
240. Mandelstam S. —Phys. Rev., 1975, v. Dll, p. 3026.
241. Mandelstam S. —Phys. Rev., 1979, v. D19, p. 2391.
242. Manton N. S. — Nucl. Phys., 1977, v. B126, p. 525.
243. Manton N. S. — Nucl. Phys., 1979, v. В150, p. 397.
244. Marciano W., Pagels H. — Phys. Rev., 1975, v. D12, p. 1093.
245. Marciano W., Parsa Z., Pagels H. — Phys. Rev., 1977, v. D15, p. 1044.
246. Marciano W., Pagels H. — Phys. Rep., 1978, v. 36C, No. 3, p. 137.
247. Маслов В. А. — ТМФ, 1970, т. 2, с. 21.
248. Matsumoto H., Sodano P., Umezawa H. — Phys. Rev., 1979, v. D19, p. 511.
249. Matveev V. A. — Nucl. Phys., 1977, v. B121, p. 403.
250. McDougall N. A. — Phys. Lett., 1980, v. 89B, p. 397.
251. McGuire J. B. — J. Math. Phys., 1964, v. 5, p. 522.
252. Mermin N. D. — Rev. Mod. Phys., 1979, v. 51, p. 591.
253. Michel L., 0'Raifeartaigh L., Wali К. С — Phys. Lett., 1977, v. 67B, p. 198.
254. Mitra P. — Phys. Lett., 1977, v. 72B, p. 62.
255. Montonen С — Nucl. Phys., 1976, v. B112, p. 349.
256. Montonen C, Olive D. — Phys. Lett., 1977, v. 72B, p. 117.
257. Morse P., Feshbach H. Methods of Mathematical Physics. — New York: Mc-
McGraw-Hill Book Co., 1953. [Имеется перевод: Морс Ф. М., Фешбах Г. Ме-
Методы теоретической физики.—М.: ИЛ, 1958.]
258. Mottola Е. — Phys. Lett., 1978, v. 79В, p. 242.
259. Mukunda N., SudarshanE. C. G. Classical Dynamics: A Modern Perspective. —
New York: John Wiley and Sons, 1974.
260. Nambu Y. — Phys. Rev. Lett., 1960, v. 4, p. 386.
261. Neuberger H. — Phys. Lett., 1980, v. 94B, p. 199.
262. Nielsen H. В., Olesen P. — Nucl. Phys., 1973, v. B61, p. 45.
263. Nielsen N. K., Schroer B. — Nucl. Phys., 1977, .v. В127,'p.'493.
264. Novikov V. A., Okun L. В., ShifmanM. A., Vainshtein A. /., Voloshin M. В.,
Zakharov V. I. — Phys. Rep., 1978, v. 41C, p. 1.
265. Olive D. — Nucl. Phys., 1976, v. ВИЗ, р. .413.

402 ЛИТЕРАТУРА
266. Olive D. — Riv. Nuovo Cim., 1979, v. 2, p. 2.
267. О' Raifaertaigh L. — Lett. Nuovo Cim., 1977, v. 18, p. 205.
268. 0'Ralfaertaigh L., Park S. Y., Wali К. С — Phys. Rev., 1979, v. D20, p. 1941.
269. Ore F. — Phys. Rev., 1977, v. D16, p. 2577.
270. Osborn H., Moody G. P. — Nucl. Phys., 1980, v. B173, p. 422.
271. Pagels H. —Phys. Rev., 1976, v. D13, p. 343.
272. Pastels H. — Phys. Lett., 1977, v. 68B. p. 466.
273. 'Parisi G. — Phys. Lett., 1977, v. 66B, p. 167.
274. Parisi G. — Phys. Lett., 1977, v. 66B, p. 382.
275. Parke S. — Nucl. Phys., 1980, v. В174, p. 166.
276. Pati J. C, Salam A. — Phys. Rev., 1973, v. D8, p. 1240.
277. Patrasciou A. —Phys. Rev., 1975, v. D12, p. 523.
278. Peccei R. £>., Quinn H. R. — Phys. Rev. Lett., 1977, v. 38, p. 1440.
279. Peccei R. D., Quinn H. R. — Phys. Rev., 1977, v. D16, p. 1791.
280. Perring J. K-, Skyrme Т. Н. R. — Nucl. Phys., 1962, v. 31, p. 550.
281. Pohlmeyer K. — Comm. Math. Phys., 1976, v. 46, p. 207.
282. Politzer H. D. — Phys. Rev. Lett., 1973, v. 30, p. 1346.
283. Поляков А. М. — Письма в ЖЭТФ, 1974, т. 20, с. 430.
284. Поляков А. М. — Письма в ЖЭТФ, 1975, т. 21, с. 430.
285. Polyakov А. М. — Phys. Lett., 1975, v. 59В, p. 82.
286. Polyakov A. M. — Phys. Lett., 1977, v. 72B, p. 224.
287. Polyakov A. M. — Nucl. Phys., 1977, v. B120, p. 429.
288. Prasad M. K., Sommerfield С. Н. — Phys. Rev. Lett., 1975, v. 35, p. 760.
289. Rajaraman R. — Phys. Rep., 1975, v. 21C, p. 227.
290. Rajaraman R. — Phys. Rev., 1977, v. D15, p. 2866.
291. Rajaraman R. — Phys. Rev. Lett., 1979, v. 42, p. 200.
292. Rajaraman R., Weinberg E. J. — Phys. Rev., 1975, v. DM, p. 2950.
293. Raj LakshmiM. — Pramana, 1979, v. 12, p. 447.
294. Rossi P. — Nucl. Phys., 1979, v. B149, p. 170.
295. Rothe K. D., Swieca J. A. — Nucl. Phys., 1978, v. B138, p. 26.
296. Rothe K. D., Swieca J. A. — Nucl. Phys., 1979, v. B149, p. 237.
297. Rubinstein J.—J. Math. Phys., 1970, v. 11, p. 258.
298. RuckH. M. — Nucl. Phys., 1980, v. B167, p. 320.
299. Saha M. N. — Indian J. Phys., 1936, v. 10, p. 145.
300. Salam S., Strathdee J. — Phys. Lett., 1976, v. 61B, p. 375.
301. Salomonson P. — Nucl. Phys., 1977, v. B121, p. 433.
302. Schaposnik F. A. — Phy<=. Rev., 1978, v. D18, p. 1154.
303. Schrieffer J. R. Theory of Superconductivity. — New York: W. A. Benjamin
Inc, 1964. [Имеется перевод: Шриффер Дж. Теория сверхпроводимости.
Пер. с англ./Под ред. Д. А. Киржница. —М.: Наука, 1970.]
304. Schroer В., Swieca J. — Nucl. Phys., 1977, v. В121, p. 505.
305. Schwarz A. S. — Phys. Lett., 1977, v. 67B, p. 172.
306. Schwinger J. — Phys. Rev., 1951, v. 82, p. 664.
307. Schwinger J. — Phys. Rev., 1966, v. 144, p. 1087.
308. Sciuto S, — Riv. Nuovo Cim., 1979, v. 2, p. 16.
309. Scott A. C, Chiu F. Y. F., Mclaughlin D. W. — Proc. I. E. E. E., 1973,
v. 61, p. 1443.
310. Seeger A., Donth H., Kochendorfer A.—Z. Phys., 1953, Bd. 134, S. 173.
311. Shankar R. — Phys. Rev.', 1976, v. D14, p. 1107.
312. Shankar R. Yale University Preprint COO-3075-199. — Washington D. C,
1978.
313. Shankar R., Witten E. — Phys. Rev., 1978, v. D17, p. 2134.
314. Shankar R., Witten E. — Nucl. Phys., 1978, v. B141, p. 349.
315. Shaw R. Ph. D. Thesis — Cambridge University, UK, 1955.
316. Sinha A. —Phys. Rev., 1976, v. D14, p. 2016.
317. Skyrme T. H. R. — Proc. R. Soc, 1958, v. A247, p. 260.
318. Skyrme T. H. R. — Proc R. Soc, 1961, v. A262, p. 233,

ЛИТЕРАТУРА 403
319. Skyrme Т. Н. R. — Nucl. Phys., 1962, v. 31. p. 556.
320. Sommerfield С — Ann. Phys. (N. Y.), 1903, v. 26, p. 1.
321. Steenrod N. The Topology of Fibre Bundles. — Princeton, N. J., USA: Prin-
Princeton University Press, 1951. [Имеется перевод; Стинрод //. Топология ко-
косых произведений. Пер с англ./Под ред. М. М. Постникова. — М.: ИЛ, 1953. ]
322. Stelmann О. — Nucl. Phys., 1978, v. B145, p. 141.
323. Subbaswamy К- R., Trullinger S. E. — Phys. Rev., 1980, v. D22, p. 1495.
324. Suzuki M. — Phys. Lett., 1978, v. 78B, p. 466.
325. Taubes С. М. — Comm. Math. Phys., 1980, v. 72, p. 277.
326. Taylor J. C. Gauge Theories of Weak Interactions.— Cambridge University
Press, U. K., 1976. [Имеется перевод: Тейлор Дж. Калибровочные теории
слабых взаимодействий. Пер. с англ.'Под ред. Г. В. Ефимова. ■—М,: Мир,
1978.]
327. Taylor J. G. — Ann. Phys. (N. Y.), 1978, v. 115, p. 153.
328. Thlrrlng W. — Ann. Phys. (N. Y.), 1958, v. 3, p. 91.
329. 'tHooft G. — Nucl. Phys., 1974, v. B75, p. 461.
330. 'tHooft G. — Nucl. Phys., 1974, v. B79, p. 276.
331. 'tHooft G. — Phys. Rev. Lett., 1976, v. 37, p. 8.
332. 'tHooft G. — Phys. Rev., 1976, v. D14, p. 3432.
333. 'tHooft G. — Nucl. Phys., 1978, v. B138, p. 1.
334. 'tHooft G. — in: The Whys of Subnuclear Physics. — New York: Plenum
Press 1979.
335. Tomboulis E — Phys. Rev., 1975, v. D12, p. 1678.
336. Tomboulis E., Woo G. —Nucl. Phys., 1976, v. B107, p. 221.
337. Toulouse G., Kletnan M. — J. Physique Lett., 1976, v. 37, p. 149.
338. Treiman S. В., Wilczek F. — Phys. Lett., 1978, v. 74B, p. 381.
339. Тюпкин Ю., Фатеев В., Шварц А. — ТМФ, 1976, т. 26, с. 270.
340. Verwaest /. — Nucl, Phys., 1977, v. В123, p. 100.
341. Воловик Ж. Е., Минеев В. П. — ЖЭТФ, 1977, т. 45, с. 1186.
342. Wadia S., Yoneya Т. — Phys. Lett., 1977, v. 66B, p. 341.
343. WelnbergE. J. —Nucl. Phys., 1980, v. B167, p. 500.
344. Weinberg S. — Phys. Rev., 1975, v. Dll, p. 3583.
345. Weinberg S. — Phys. Rev. Lett., 1978, v. 40, p. 223.
346. Weisz P. — Nucl. Phys., 1977, v. В112, p. 1.
347. Whitham G. B. Linear and Non-linear Waves. — New York: John Wiley
and Sons, 1974. [Имеется перевод: Уизем Дж. Б. Линейные и нелинейные
волны. Пер. с англ./Под ред. А. Б. Шабата. —М.: Мир, 1977.]
348. Whittaker Е. Т., Watson G. N. A Course on Modern Analysis. — Cambridge
University Press, UK, 1920. [Имеется перевод: Ватсон Дж Н., Хитте-
кер Э. Т. Курс современного анализа.—2-е изд.—М.: Наука, 1962.]
349. Wilczek F. — Phys. Lett., 1976, v. 65B, p. 160.
350. Wilczek F. — in: Quark confinement and field theory. — New York: John
Wiley and Sons, 1977.
351. Wilczek F. — Phys. Rev. Lett., 1978, v. 40, p. 279.
352. Wilczek F., Zee A. — Phys. Rev. Lett., 1978, v. 40, p. 83.
353. Wilson K. G. — Phys. Rev., 1974, v. D10, p. 2445.
354. Witten E. — Phys. Rev. Lett., 1977, v. 38, p. 121.
355. Witten E. — Nucl. Phys., 1978, v. В142, p. 285.
356. Witten E. — Nucl. Phys., 1979, v. В149, p. 285.
357. Witten E. Lectures at Cargese Summer School. — Harvard Preprint
HUTP-79/A078, 1979.
358. Wu Т. Т., Young С N. — Phys. Rev., 1975, v. D12, p. 3845.
359. Young C. N., Mills R. — Phys. Rev., 1954, v. 96, p. 191.
360. Young C. N., Wu Т. Т. — in: Properties of Matter under Unusual Conditi-
Conditions, Ed. H. Mark, S. Fernbach. — New York: Interscience, 1968.
361. Young Т. С — Phys. Rev/Lett., 1978, v. 41, p. 523.
362. Захаров В. Е., Тахтаджян Л. А., Фаддеев Л. Д. — ДАН, 1974, т. 219, с. 1334.

404 ЛИТЕРАТУРА
363. Zamolodchikov А. В. — Comm. Math. Phys., 1977, v. 55, p. 183.
364. Замолодчиков А. Б. — ИТЭФ, Препринт 112. — M.: 1977.
365. Zamolodchikov А. В., Zamolodchikov Al. B. — Nucl. Phys., 1978, v. B133,
p. 525.
366. Zamolodchikov А. В., Zamolodchikov Al. B. — Phys. Lett., 1978, v. 72B,
p. 481.
367. Zamolodchikov А. В., Zamolodchikov Al. B. — Ann. Phys. (N. Y.), 1979,
v. 120, p. 253.
368. Zwanziger D. — Phys. Rev., 1968, v. 176, p. 1480 and 1489.
369*. Склянин Е. К., ТахтаджянЛ. А., Фаддеев Л. Д. — ТМФ, 1979, т. 40,
№ 2, с. 194—220.
370*. Боголюбов Н. Н. — УЛЩ, 1950, т. 2, № 2, с. 3—25; Избранные труды,
т. 2. — Киев: Наукова Думка, 1970.
371*. Рубаков В. Л. —Письма ЖЭТФ, 1981, т. 33, с. 658; Nucl. Phys., 1982,
v. B203, p. 311.
372*. Боголюбов Н. #., СтрцмЫский Б. В., Тавхелидяе А. Н. — Препринт
ОИЯИ Д-1968. — Дубна,' 1965.

ИМЕННОЙ УКАЗАТЕЛЬ
Абловиц (Ablowitz M. J.) 50
Актор (Actor R.) 17
Атия (Atiyah M.) 116
Аффлек (Affleck I.) 9
Бардакчи (Bardakci К.) 221
Бароне (Вагопе А.) 44
Басеян Г. 3. 387
Белавин А. А. 87, 93, 105, 106
Бернард (Bernard С. W.) 337
Берри (Berry M. V.) 190
Блох (Bloch F.) 6, 305, 333
Боголюбов Н. Н. 6, 7, 8, 238, 362
Богомольный Е. Б. 77, 78, 120
Вадья (Wadia S.) 9
Вайнберг (Weinberg E. J.) 9, 81, 337
Вайнберг (Weinberg S.) 364, 386
Вильсон (Wilson К. G.) 355—357, 360
Вильчек (Wilczek F.) 386
Виттен (Witten E.) 9, 106, 219, 237,
351, 387
Гельфанд Я. М. 173
Гильднер (Gildener E) 303
Гинзбург В. Л. 83
Глешоу (Glashow S. L.) 67
Глимм (Glimm J.) 387
Годдард (Goddard P.) 17
Голдстоун (Goldstone J.) 158, 161,
281, 363
Голдхабер (Goldhaber A. S.) 80
Гросс (Gross D. J.) 300, 386
Гут (Guth A.) 81
Гуцвиллер (Gutzwiller M.) 190
Дайсон (Dyson F. J.) 234, 376
Далиц (Dalitz R. H.) 234
Дашен (Dashen R. F.) 9, 149, 201,
206, 280, 291, 300, 301, 386
Деррик (Derrick G. H.) 169, 318
Джакив (Jackiw R.) 9, 17, 80, 108,
158, 161, 281, 291, 294, 298, 341
Джаффе (Jaffe A.) 387
Джерсак (Jersak J.) 90
Джорджи (Georgi M.) 67
Джулиа (Julia B.) 78, 79
Дирак (Dirac P. A. M.) 8, 274, 275,
277, 278, 283
Жевицки (Jevicki A.) 263, 387
Жерве (Gervais J.-L.) 263
Замолодчиков А. Б. 222, 236
Замолодчиков Ал. Б. 222
Зи (Zee A.) 78, 79
Зоммерфельд (Sommerfield С. Н.) 78,
90, 169
Каллан (Callan С. G.) 350, 357, 360,
361, 373, 384—387
Каровски (Karowski M.) 236
Кастильехо (Castillejo L.) 234
Квинн (Quinn H. R.) 386
Кемпбелл (Campbell D. К.) 293

406 ИМЕННОЙ УКАЗАТЕЛЬ
Керман (Kerman A.) 161
Клейн (Klein A.) 161
Корепин В. Е. 17
Коулмен (Coleman S.) 9, 17, 23, 40,
81, 84, 97, 120, 215, 216, 218, 227,
364
Крачфилд (Crutchfield W. Y.) 383
Крист (Christ N. Н.) 9, 80, 253, 262
Кришнамурти (Krishnamurthy H. R.) 9
Кройц (Creutz M.) 387
Крумхансл (Krumhansl J. А.) 87
Лангер (Langer R. Е.) 243
Ландау Л. Д. 83
Левит (Levit S.) 190
Ли (Lee T. D.) 250, 252, 253, 262, 281
Лиао (Liao Y.-T.) 293
Манделстам (Mandelstam S.)
Мандула (Mandula J.) 227
Мантон (Manton N. S.) 90
Марчиано (Marciano W.) 17
Матинян С. Г. 387
Маханьков В. Г. 17
Мизнер (Misner С.) 40
Миллс (Mills R.) 67, 86
220, 221
Паули (Pauli W.) 6
Печчей (Peccei R. D.) 386
Поляков А. М. 67, 78, 87, 105, 303,
351, 360
Попов В. Н. 171, 263, 393
Прасад (Prasad M. К.) 78, 90, 169
Радж Лакшми (Raj Lakshmi M.) 9, 90
Раджараман (Rajaraman R.) 17
Ребби (Rebbi С.) 80, 115, 281, 291,
294, 298, 341
Росси (Rossi P). 80
Роте (Rothe К. D.) 317
Рубинстейн (Rubinstein J.) 44
Сакита (Sakita В.) 263
Самуэль (Samuel S.) 221
Свиека (Swieca J. A.) 317
Скирм (Skyrme Т. Н. R.) 40, 215, 216
Скотт (Scott А. С.) 17, 18, 23, 24, 44
Смилански (Smilansky U.) 190
Стинрод (Steenrod N.) 82
Стратди (Strathdee J.) 9
Струминский Б. В. 362
Сударшан (Sudarshan E. С. G.) 9
Сьюто (Sciuto S.) 17
Намбу (Nambu Y.) 363
Неве (Neveu A.) 9, 300
Нильсен (Nielsen H. В.) 83
Нитянанда (Nityananda R.) 9
Нордсик (Nordsiek A.) 6
Олив (Olive D.) 17, 81
Ольсен (Olesen P.) 83
О'Рейферти (O'Raifaertaigh L.) 90
Тавхелидзе А. Н. 362
Таубс (Taubes С. М.) 85, 120, 332
Тахтаджян Л. А. 201
Тирри'нг (Thirring W.) 215
Томбулис (Tomboulis E.) 253
Торн (Thorn С.) 9
TyH(Thun H.-J.) 236
Т'Хофт ('tHooft G.) 67, 75, 78, 80,
108, 117, 347, 364, 370, 378, 382,
383, 387
Тюпкин Я. А. 78
Пагельс (Pagels H.) 17
Патраскиу (Patrasciou A.) 81, 303
Уизем (Whitham Q. В.) 18
Уорд (Ward A.) 116

ИМЕННОЙ УКАЗАТЕЛЬ 407
Фаддеев Л. Д. 17, 50, 171, 201, 202,
263, 393
Фейнман (Feynman R. Р.) 172, 173
Финкельстейн (Finkelstein D.) 40, 44
Флоке (Floquet G.) 287
Фридберг (Fridberg R.) 281, 298
Фролих (Frohlich J.) 170
Цванцигер (Zwanziger г).) 79, 80
Шанкар (Shankar R.) 9, 81, 222, 237
Шапошник (Schaposnik F. Л.) 90
Швингер (Schwinger J.) 79, 80
Шриффер (Schrieffer J. R.) 87
Хазенфрац (Hasenfratz P.) 80
Xap (Khare A.) 387
Хасслахер (Hasslacher В.) 9
Хибс (Hibbs A. R.) 172, 173
Хиггс (Higgs P. W.) 68
Хобарт (Hobart R.) 318
Яглом А. М. 173
Янг (Yang С N.) 67, 86

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аксион 386
Аналитичность 227, 228
Аномалия аксиального тока 364, 367,
368
Антиинстантон в задаче о периодиче-
периодическом потенциале 306
системе Янга — Миллса 110
Антикинк 30
Антикоммутирующие с-числа см.
Грассмановы числа
Ароматы 361, 362
Асимптотическая свобода 17
КХД 362
О (З)-модели 121
системы Янга — Миллса 348
Бегущая константа связи 348
Безмассовые фермионы 361—367
подавление вакуумного тун-
нелирования 364—367
Блоха теорема 305
Елоховские волны 312
Богомольного условие 77, 78
Бозонизация 219
Бора — Зоммерфельда условие 186—
190
Борелевская процедура суммирова-
суммирования 377
Борелевский ряд 378
обобщение 381, 382
Бореля функция 377, 378
для функций Грина 379
Бризеры (дублеты), классические 49,
201
— квантовые 205
Бэклунда преобразования 15, 52, 53
для системы синус-Гордона 52,
53
Вакуум 142—144
— абелевой модели Хиггса 320—326
— КХД с безмассовыми фермионами
371—375
— теории Янга — Миллса 342
Вакуумное туннелирование в абе-
абелевой модели Хиггса 332
теории Янга — Миллса 342
подавление безмассовыми фер-
фермионами 364
Вакуумный сектор состояний 144
в системе синус-Гордона 202
— угол 334
как параметр в лагранжиане
336
Вильсона петлевая функция (множи-
(множитель) в абелевом случае 355, 384
неабелевом случае 360,
384
Вириала теорема 56, 57
и евклидова модель СГ 318
О (З)-модель 57, 58
В КБ метод 186—198
в теории поля 190—197
и интегралы по траекториям
186—188
приближение слабой связи
197, 198
условие Бора — Зоммер-
Зоммерфельда 186
множитель Дх 388—391
точность 198
для теории СГ 213
Внутреннее пространство 58
вращение в нем 250
глобальные вращения 58
локальные преобразования 67
Гаусса закон 322—324, 340, 341
и калибровочная эквивалент-
эквивалентность 341
Гауссово приближение 185, 306
Голдстоуновские бозоны 156, 363
и симметрия SU B) X SU B)
363

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 409
Гомотопическая классификация в абе-
левой модели Хиггса 83
евклидовой системе Янга —
Миллса 97—104
жидких кристаллах 86
О (З)-модели 62
монопольных решений 71, 72
некоторые общие резуль-
результаты 82
отображение окружностей
в окружности 60, 61
Грассманова алгебра 266
генераторы 266
Грассмановы поля 265
— числа 265
Гросса — Неве (ГН) модель 227, 237,
300
определение 300
S-матрица 237
Групповая мера для SU B) 100—102
Зарядовое сопряжение 278, 294—296
матрицы 278, 294
оператор 296
Заряженные солитонные решения
250
Инстантоны 11, 91, 92
— абелевой модели Хиггса 119, 120
— калибровочных SU (Л^)-теорий 120
— отсутствие в О (Л0-моделях 119
— системы Янга — Миллса 95, 108,
119
— СРдг-модели 127
Интегралы по траекториям 172
и приближение стационар-
стационарной фазы (ПСф) 174, 175
Инфракрасная проблема больших
инстантонов 345—351
Дионы 79, 80
Дирака гамильтониан одиочастич-
ный 275, 278
— матрицы 274
— поле 273
функциональный интеграл 273,
274
Дублеты (бризеры) классические 19,
201
— как полюсы S-матрицы 235, 236
связанные состояния 209^211
— квантование 205
— квантовые масей 209
Евклидово действие 92, 94, 95
• для маятника 118
системы Клейна — Гордона
92
Янга — Миллса 94, 95
CPjy-модели 124
Евклидовы системы 91, 92
действие 92, 94, 95
уравнение поля 92, 124
функциональные интегралы
178, 179, 184, 185
• в теории поля 184, 185
Задача о периодическом потенциале
(ЗПП) 303—314
Калибровочные поля 68
матричные обозначения 93, 94
— преобразования абелевы 123
неабелевы 68, 94
не зависящие от времени 322,
323
Квазиклассический метод для кван-
квантования периодических решений
190—197
статических решений
143—170
и КХД 13, 14
ограничения 13, 199
Квантование зависящих от времени
солитонов 186
— магнитного потока в сверхпровод-
сверхпроводниках 84
— статических солитонов 130
Квантовая хромодинамика (КХД)
11—14, 349
«миниатюрная» модель 364
определение 361
— электродинамика (КЭД) 376
Кварки 361, 362
— ароматы 361, 362
— в КХД 361 .
— конфайнмент 353
Кинк теории 04 29
антикинк 30
квантование 143—149
классическое решение 30
масса квантового кинка
149—154
классическая 31
— непертурбативность 32

4Ю предметный Указатель
Киральная SU B) х SU B)-симме-
трия 363
и безмассовые кварки 363
нарушение 363, 364
Киральность операторов 373
Классический предел ферми-полей
264, 265, 272
Кластерное разложение 373—375
Коллективные координаты 238—263
в евклидовом функциональ-
функциональном интеграле 390—393
■■ модели U A)-симметрии 245,
246
нерелятивистской кванто-
квантовой механике 238—243
для трансляционной симме-
симметрии 255
якобиан 393
Конфайнмент 353
Кроссинг-симметрия 227
— для A + 1)-мерных О (^-моде-
(^-моделей 229
Кубические тождества для О (JV)-мо-
(JV)-моделей 230
S-матриц 226
Лангера модификация 243
Ландау — Гинзбурга модель 83
Локализованные решения 22
масса 78
обобщение на высшие груп-
группы 81
сила взаимодействия 90
топологический ток и заряд
72, 73 ,
Нелинейная О (З)-модель 58
Гомотопический анализ в двух
измерениях 60, 61
применение в теории ферро-
ферромагнетика 66
Неоднозначности КДД 234
устранение в модели СГ 235, 236
— моделях О (N) и ГН 237
Непрерывная симметрия в нереляти-
нерелятивистской задаче 239
Непрерывные симметрии 137
Нетопологические решения 39, 42
зависящие от времени 250
статические 39
Нормальное упорядочение 151, 152,
213
Нормальные моды флуктуации 138,'
140
Нулевые моды 137, 147, 154, 238, 245
фермионные 293, 294
и индекс Понтрягина 370
Обратной задачи рассеяния метод 15,
18, 24
для системы СГ 50
Массивная модель Тирринга (МТ) 215
О B)-симметрия 235
S-матрица 235, 236
эквивалентность модели СГ
215—217
Меронные решения 350, 386, 387
Механические аналоги нелинейных
уравнений 26—29, 33—36
Модель CPN 121, 122
инстантоны 127, 128
калибровочная инвариантность
123
■■ связь с О (З)-моделью 128, 129
Мопоноль ш'Хофта — Полякова 67—
78
гомотопический анализ 70—
72
и условие Богомольндгд 77,
78
квантования Швин-
гера 74
Переменные действие — угол 51, 52,
201, 202
Перенормировка массы квантового
кинка 149—154
— процедура 347
Понтрягина индекс 98, 339, 343, 347
— плотность 99
Потенциал тяжелых кварков 384
Приближение стационарной фазы
(ПСФ) 174—178
в теории поля 196
и условие Бора — Зоммер-
фельда 187—190
Принцип отражения 228, 229
Проблема U (I) 364
Разложение по степеням UN 121
Размер солитонов (инстантонов) в абе-
левой модели Хиггса 85

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 411
. ЗПП 313
О C)-модели 66
системы Янга — Миллса
ПО
CPjv-модели 127
теории Ф* 31
Разреженный инстантонный газ 313,
332
проблемы в теории Янга —
Миллса 346
Ряд теории возмущений 376
борелевская суммируемость
376
расходимость 377
Самодуальности условие 105, 106
аналоги в других моделях
126
Симметрия обращения времени и
аксионы 386
нарушение 344, 385
Синус-Гордона (СГ) система 44
антисолитон 46
двухсолитонные решения 46—48
дублеты (бризеры) 46, 49
квантование 203—209
классические решения 46—49
О B)-инвариантность 235
солитон 46
точная S-матрица 235, 236
эквивалентность массивной
модели Тирринга 215—217
Слабой связи условие (приближение)
134—141
и метод ВКБ 197, 198
система Янга — Миллса
349—352
S-матричная теория 17
в A + 1) измерениях 227—237
Солитонные операторы 220, 221
Солитонный сектор состояний 158
Солитоны 23, 24
— отличие от уединенных волн 24,
25
— системы синус-Гордона 46
квантование 203—205
Спонтанное нарушение симметрии
в О C)-модели 59
киральной симметрии
SU B) X SU B) 363
* A + 1)-мерной </>4-теории
22, 145
системе синус-Гордона
202
явлении Хиггса 319, 320
Стереографическая проекция 64
Toiuvioi мчсскис иикуумы .Ч2Г|, Mi'.'i
и к.i;k iс|>нс><• |>,| иижсмпс .17.1,
.474
— - подавление туниелировамия 364
туннелирование 332, 333, 342,
364
Топологический индекс или заряд 42
для монопольных решений 72,
73
О (З)-модели 60—62
-скалярных полей в A -\т 1)
измерениях 40—43
как квантовое число 160
соответствующий ток 42, 72
сохранение 41, 42
Точки поворота орбит 189
Точные S-матрицы 227—238
для модели ГН 237
теории синус-Гордона 235—
237
Трансляционная мода 154—157, 253
в инстантонном решении 307,
392—394
метод рассмотрения 253—258
Туннелирование 136, 304, 341, 342
— барьер 314, 342
— в абелевой модели Хиггса 326, 333
— — присутствии фермионов 370—
372
теории Янга — Миллса 341, 342
— подавление 374
Тэта-вакуумы и 9-секторы 336—339,
342, 354, 375
кластерное разложение 374
— фоновое поле 354, 375
Углы стабильности 192, 193
аналогия с индексами Флоке 287
в теории поля 196
Уединенные волны 22, 23
в A+1) измерениях 25—40
отличие от солитонов 24, 25
Унитарность 227
Упорядоченные по траекториям
экспоненты 96
Факторизация S-матриц 225
Фермионы из бозонных полей 80, 216
Ферми-поля, классический предел
264, 265
— функциональные интегралы 273
Флоке индексы 287
Формфакторы солитонных состояний
163, 164

412 ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Функциональные интегралы в теории
поля 180
гауссово приближе-
приближение 185
граничные условия 180
ПСФ 183
для абелевой модели Хиггса 330
теории Янга — Миллса 343
ферми-полей 273
Хиггса абелева калибровочная мо-
модель 82, 119, 318
, : вакуумное туннелирова-
ние 326
в B + 1) измерениях 83
— топологические вакуумы
325
явление Хиггса 319, 320
— механизм 68
— неабелева модель 67, 68
— поля (скалярные) 68
— явление 319, 320
Частица на окружности (ЧНО) 314—
317
аналогия с 9-вакуумом 336,
337
Цветная группа 361, 362
Цветной индекс 361, 363
Элементарный бозон 210, 211
Энергия связи системы СГ 210—212
ряд Бете — Солпитера
212
Ядерная демократия 211
Янга — Миллса система 93—104
— вакуумное туннелирование
342
закон Гаусса 340, 341
инстантоны 105
калибровочная эквивалент-
эквивалентность 341
калибровочные преобразо-
преобразования 94
проблема больших инстан-
тонов 345
топологические вакуумы 341

ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА 5
ОТ АВТОРА . 9
ГЛАВА 1. ПРЕДИСЛОВИЕ И ВВЕДЕНИЕ 10
ГЛАВА 2. КЛАССИЧЕСКИЕ СОЛИТОНЫ И УЕДИНЕННЫЕ ВОЛНЫ 18
2.1. Введение 18
2.2. Уединенные волиы и солитоны 19
2.3. Некоторые уединенные волны в двух измерениях 25
2.4. Топологические индексы 40
2.5. Решения системы синус-Гордона 44
ГЛАВА 3. МОНОПОЛИ И ПОДОБНЫЕ ИМ РЕШЕНИЯ 55
3.1. О многомерных решениях 55
3.2. Теорема вириала 56
3.3. Нелинейная О (З)-модель: изотропный ферромагнетик .... 57
3.4. Монополь т'Хофта — Полякова 67
3.5.|Еще о монополях и дионах 78
3.6. Гомотопическое рассмотрение систем конденсированных сред 81
3.7. Солитон-солитонные взаимодействия 88
ГЛАВА 4. КЛАССИЧЕСКИЕ ИНСТАНТОННЫЕ РЕШЕНИЯ 91
4.1. Что такое инстантон? 91
4.2. Евклидовы конфигурации Янга—Миллса 93
4.3. Инстантоны Янга—Миллса 105
4.3.1. Инстантон 108
4.3.2. N-инстаитонные решения 111
4.4. Инстантоны других моделей 117
4.5. CPjv-модель 121
ГЛАВА 5. КВАНТОВАНИЕ СТАТИЧЕСКИХ РЕШЕНИЙ ...... 130
5.1. Введение 130
5.2. Основная идея 133
5.3. Квантование кинка 143
, 5.3.1. Вакуум и его возбуждения . 143
5.3.2. Квантовый кинк и его возбуждения 145
5.4.тМасса кинка и ее перенормировка 149
5.5.|Трансляционная мода 154
5.6.*Стабильность кинка и его формфакторы 158
5.7. Заключительные замечания 168
ГЛАВА 6. ФУНКЦИОНАЛЬНЫЕ ИНТЕГРАЛЫ И МЕТОД ВКБ . . 171
6.1. Формализм интегрирования по траекториям 171
6.2. Обобщение на полевую теорию 180

414 ОГЛАВЛЕНИЕ
6.3. Условие Бора — Зоммерфельда 186
6.4. Метод ВКБ в теории поля 190
6.5. Заключительные замечания по методу ВКБ 197
ГЛАВА 7. НЕСКОЛЬКО ТОЧНЫХ РЕЗУЛЬТАТОВ 201
7.1. Спектр связанных состояний в теории синус-Гордона . . . 201
7.1.1. Масса квантового солитона 203
7.1.2. Массы дублетов 205
7.2. Интерпретация дублетных состояний . , 210
7.3. Эквивалентность моделей СГ и МТ; бозонизация 215
7.3.1. Бозонизация 219
7.3.2. Солитонные операторы 220
7.4. Факторизация S-матриц . 221
7.5. Несколько точных л-матриц 227
ГЛАВА 8. КОЛЛЕКТИВНЫЕ КООРДИНАТЫ И КАНОНИЧЕСКИЕ
МЕТОДЫ 238
8.1. Трактовка нулевых мод: простой пример 238
8.2. Пример явной коллективной координаты 245
8.3. Неявные коллективные координаты 253
8.4. Квантование солитонов с помощью канонических операторных
методов 258
ГЛАВА 9. КВАЗИКЛАССИЧЕСКИЕ МЕТОДЫ ДЛЯ ФЕРМИ-ПОЛЕЙ 264
9.1. Введение: грассмановы поля 264
9.2. Функциональный интеграл для свободного поля Дирака . . 273
9.3. Солитоны в присутствии ферми-полей 277
9.4. О возможности существования солитонов с зарядом 1/2 . . . 291
9.5. Дальнейшие замечания 297
ГЛАВА 10. ИНСТАНТОНЫ В КВАНТОВОЙ ТЕОРИИ 303
10.1. Инстантоны и периодический потенциал 303
10.2. Топологические вакуумы в абелевой модели Хиггса .... 318
10.3. Вакуумное туннелирование в абелевой модели Хиггса . . . 326
10.4. Янг-миллсовский вакуум 338
10.5. Инфракрасная проблема больших инстантонов 345
ГЛАВА 11. ЕЩЕ НЕСКОЛЬКО ИНСТАНТОННЫХ ЭФФЕКТОВ 353
11.1. Инстантоны и конфайнмент 353
11.2. Связь безмассовых фермионов с КХД 361
11.3. Подавление вакуумного туннелирования безмассовыми фер-
мионами 364
11.4. Инстантоны и суммируемость по Борелю 376
11.5. Дальнейшие разработки 383
ПРИЛОЖЕНИЕ А 388
ПРИЛОЖЕНИЕ Б 392
ЛИТЕРАТУРА 396
ИМЕННОЙ УКАЗАТЕЛЬ 405
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ . . ■ 408

УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее оформлении,
качестве перевода и другие просим присылать по ад-
адресу: 129820, Москва, И-110, ГСП, 1-й Рижский пер.,
д. 2, изд-во «Мир».

Р. РАДЖАРАМАН
СОЛИТОНЫ И ИНСТАНТОНЫ
В КВАНТОВОЙ ТЕОРИИ ПОЛЯ
Научн. редактор Н. Л. Телеснин
Мл. научн. редакторы:
Р. X. Зацепина, Г. Г. Сорокина
Художник Н. И. Василовская
Художественный редактор В. Б. Прищепа
Технический редактор В. П. Сизова
Корректор Н. А. Гиря
ИБ № 5217
Сдано в набор 02.11.84.
Подписано к печати 07.06.85.
Формат 60Х ЭО'/ц.
Бумага кн.-журн., имп.
Гарнитура литературная. Печать высокая.
Объем 13,00 бум. л. Усл. печ. л. 26,00 Усл.кр.-отт., 26,00. Уч.-изд. л. 26,
Изд. № 2/3389. Тираж 5000 экз. Зак. № 9. Цена 4 р. 20 к.
ИЗДАТЕЛЬСТВО «МИР»
129820, Москва, И-110, ГСП, 1-й Рижский пер., 2.
Ленинградская типография № 6 ордена Трудового Красного Знамени
Ленинградского объединения «Техническая книга» им. Евгении Соколово
Союзполиграфпрома при Государственном комитете CCGP
по делам издательств, полиграфии и книжной торговли.
193144, г. Ленинград, ул. Моисееико, 10.