А.С.Шварц
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ И ТОПОЛОГИЯ
В последние годы топология прочно вошла в математический арсенал физики.
С ее помощью сделано очень много, прежде всего в квантовой теории поля.
Открываются широкие перспективы для приложений топологии в других
областях физики. Основной целью настоящей книги является изложение
результатов квантовой теории поля, полученных топологическими методами.
Однако в ней освещены и некоторые топологические вопросы теории
конденсированных сред. Книга содержит также ориентированное на физиков
изложение основ топологии и необходимую информацию по теории групп и
алгебр Ли. Включение главы, посвященной основным лагранжианам,
используемым в физике элементарных частиц, делает книгу независимой от
учебников квантовой теории поля.
Для физиков, интересующихся применениями .топологии, и для математиков,
желающих ознакомиться с квантовой теорией поля и математическими методами,
используемыми в ней.
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ 5
ВВЕДЕНИЕ 7
ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ 11
Глава I. ОСНОВНЫЕ ЛАГРАНЖИАНЫ КВАНТОВОЙ ТЕОРИИ ПОЛЯ 14
§ 1. Простейшие лагранжианы 14
§ 2. Квадратичные лагранжианы 18
§ 3. Внутренние симметрии 20
§ 4. Калибровочные теории 25
§ 5. Частицы, отвечающие неквадратичным лагранжианам 28
§ 6. Лагранжианы сильных, слабых и электромагнитных взаимодействий 30
§ 7. Большие объединения 38
Глава П. ТОПОЛОГИЧЕСКИЕ МЕТОДЫ КВАНТОВОЙ ТЕОРИИ ПОЛЯ 41
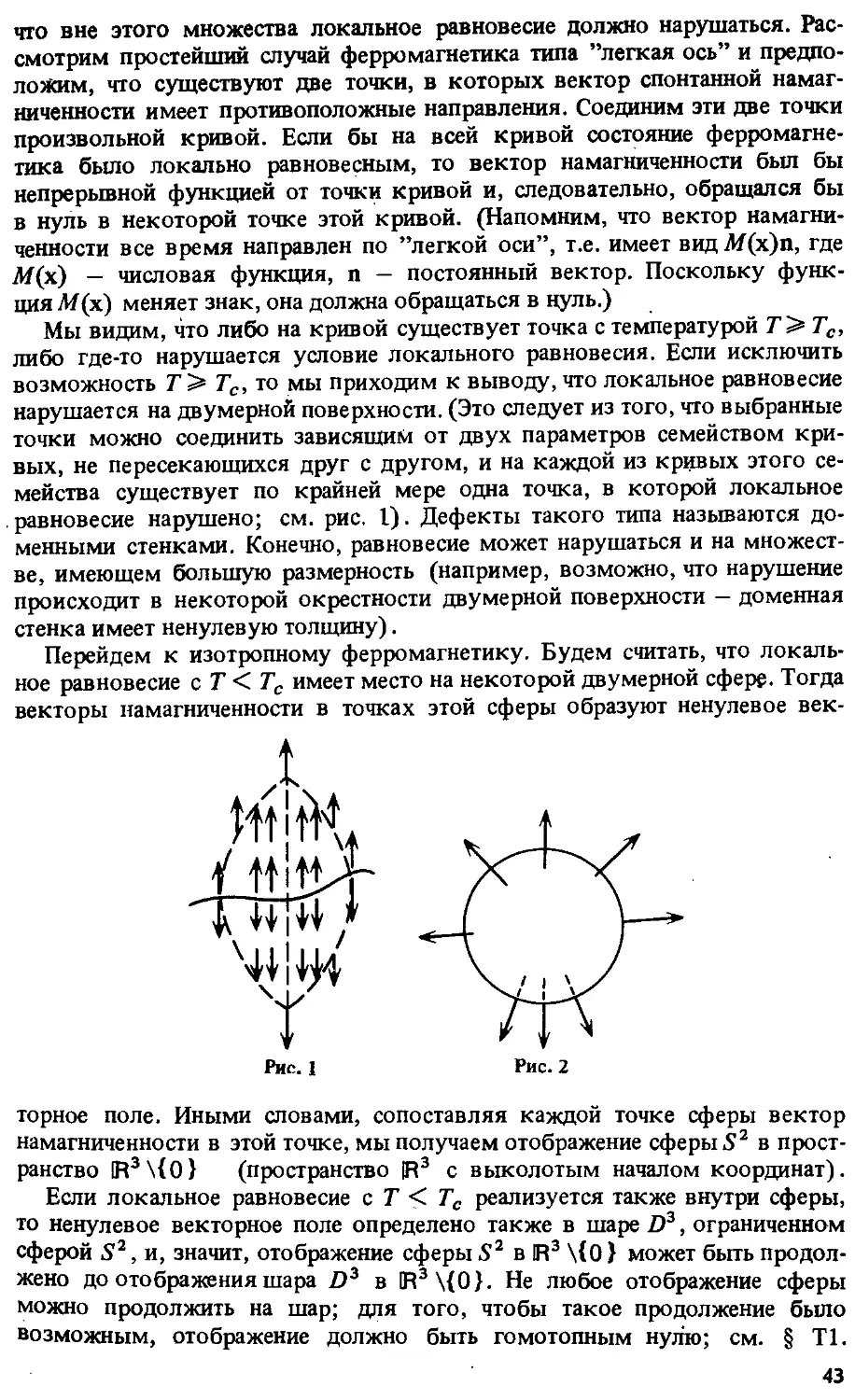
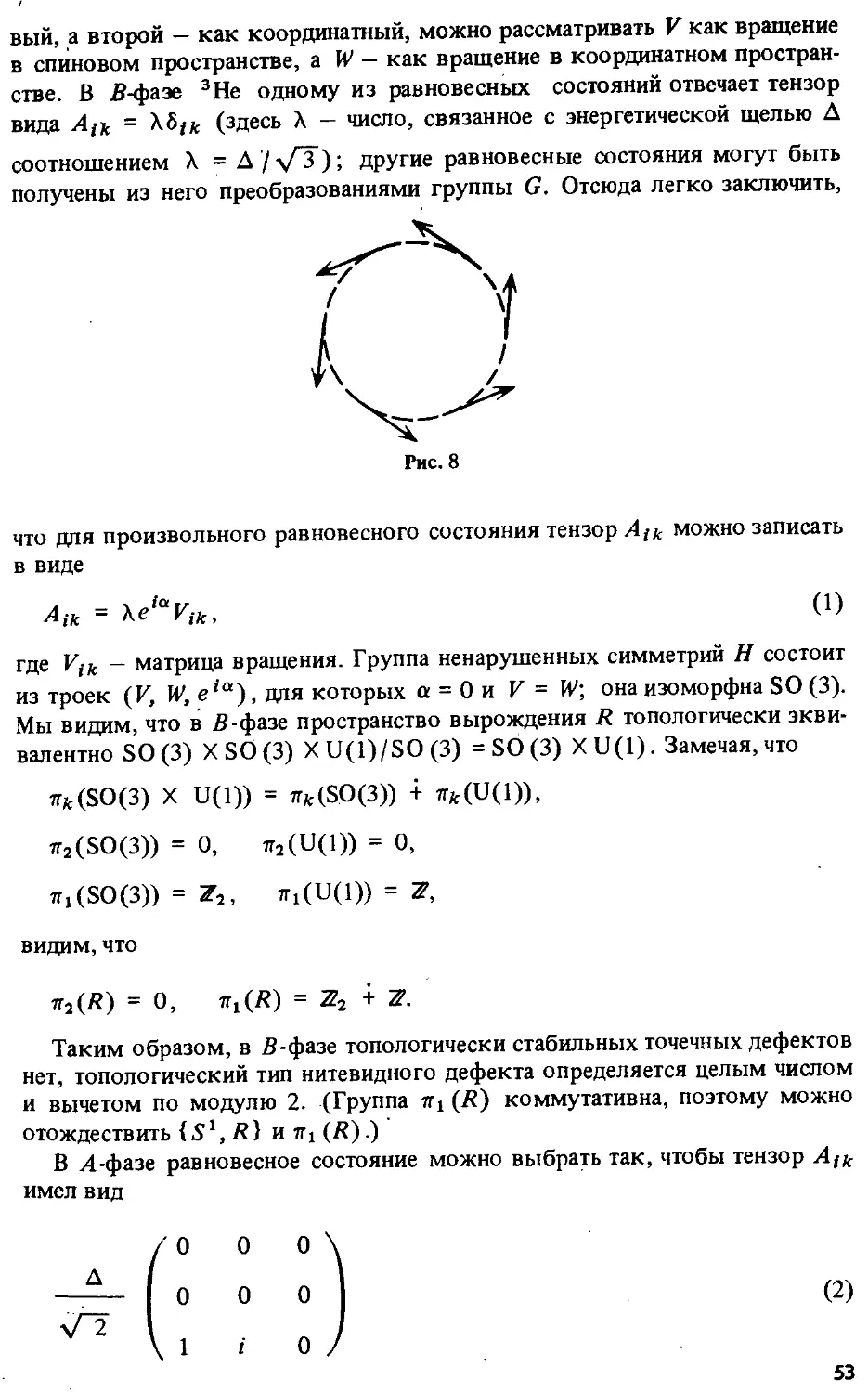
§ 1. Топологически стабильные дефекты 41
§ 2. Топологические интегралы движения 57
§ 3. Двумерная модель. Абрикосовские вихри 64
§ 4. Монополи Полякова-Хоофта 70
§ 5. Топологические интегралы движения в калибровочных теориях 76
§ 6. Частицы в калибровочных теориях 84
§ 7. Магнитный заряд 87
§ 8. Общие формулы для электромагнитной напряженности и 94
магнитного заряда в калибровочных теориях
§ 9. Экстремумы симметричных функционалов 99
§ 10. Симметричные калибровочные поля 100
§11. Оценка энергии магнитного монополя 110
§ 12. Топологически нетривиальные нити 114
§ 13. Частицы в присутствии нити. 120

§ 14. Нелинейные поля 127
§ 15. Многозначные функционалы действия 134
§ 16. Функциональные интегралы 139
§ 17. Применение функциональных интегралов в квантовой теории 145
§ 18. Квантование калибровочных теорий 152
§ 19. Эллиптические операторы 165
§ 20. Свойства эллиптических операторов. Индекс эллиптического 170
оператора
§ 21. Детерминанты эллиптических операторов 176
§ 22. Квантовые аномалии 180
§ 23. Инстантоны 187
§ 24. Число инстантонных параметров 199
§ 25. Вычисление инстантонного вклада 204
§ 26. Функциональные интегралы для теорий, содержащих фермионные 213
поля
§ 27. Инстантоны в квантовой хромо динамике 222
Глава Ш. ОСНОВЫ ТОПОЛОГИИ 228
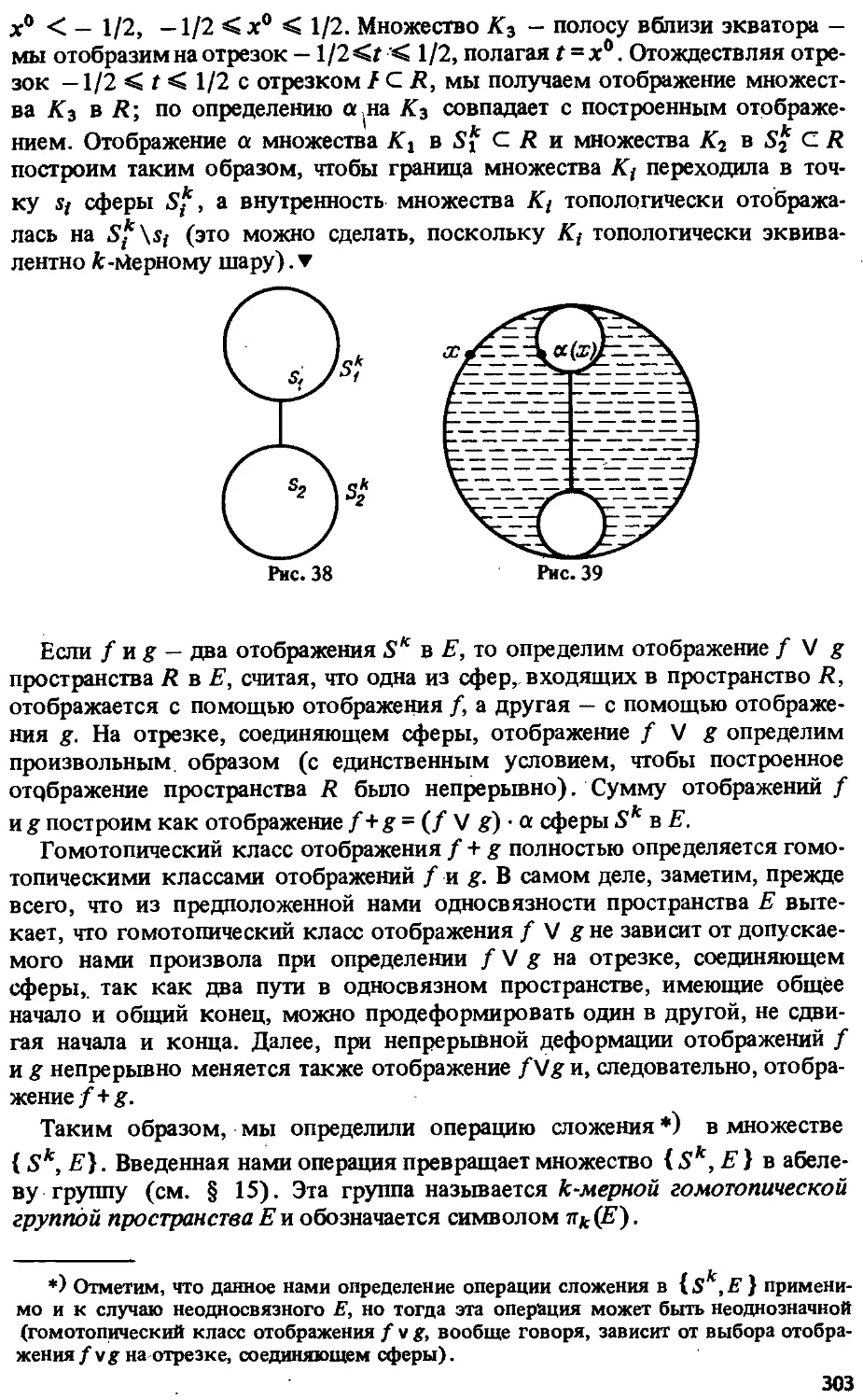
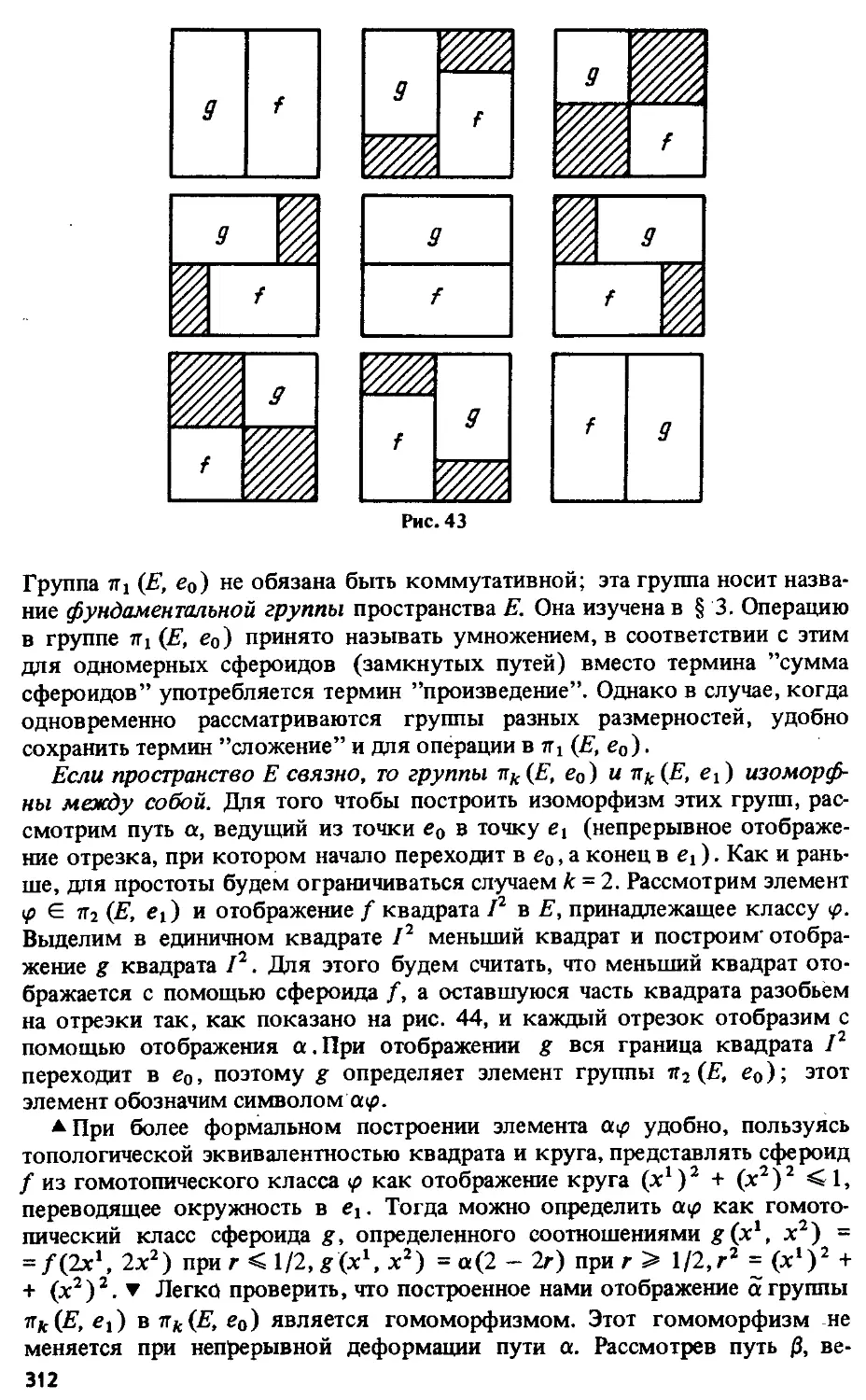
§1. Основные топологические понятия 228
§ 2. Степень отображения 242
§ 3. Фундаментальная группа 250
§ 4. Накрывающие пространства 255
§ 5. Многообразия 259
§ 6. Дифференциальные формы в евклидовом пространстве 265
§ 7. Гомологии и когомологии областей евклидова пространства. 274
§ 8. Гомологии и гомотопии 282
§ 9. Гомологии произвольных пространств 286
§ 10. Дифференциальные формы на гладком многообразии и гомологии
гладкого многообразия 294
§11. Гомологии римановых многообразий 298
§ 12. Гомотопическая классификация отображений сферы(основные
утверждения). 302
§ 13. Отображения сферы в неодносвязное пространство 306
§ 14. Гомотопические группы сфер. 308
§ 15. Гомотопические группы произвольных пространств 310
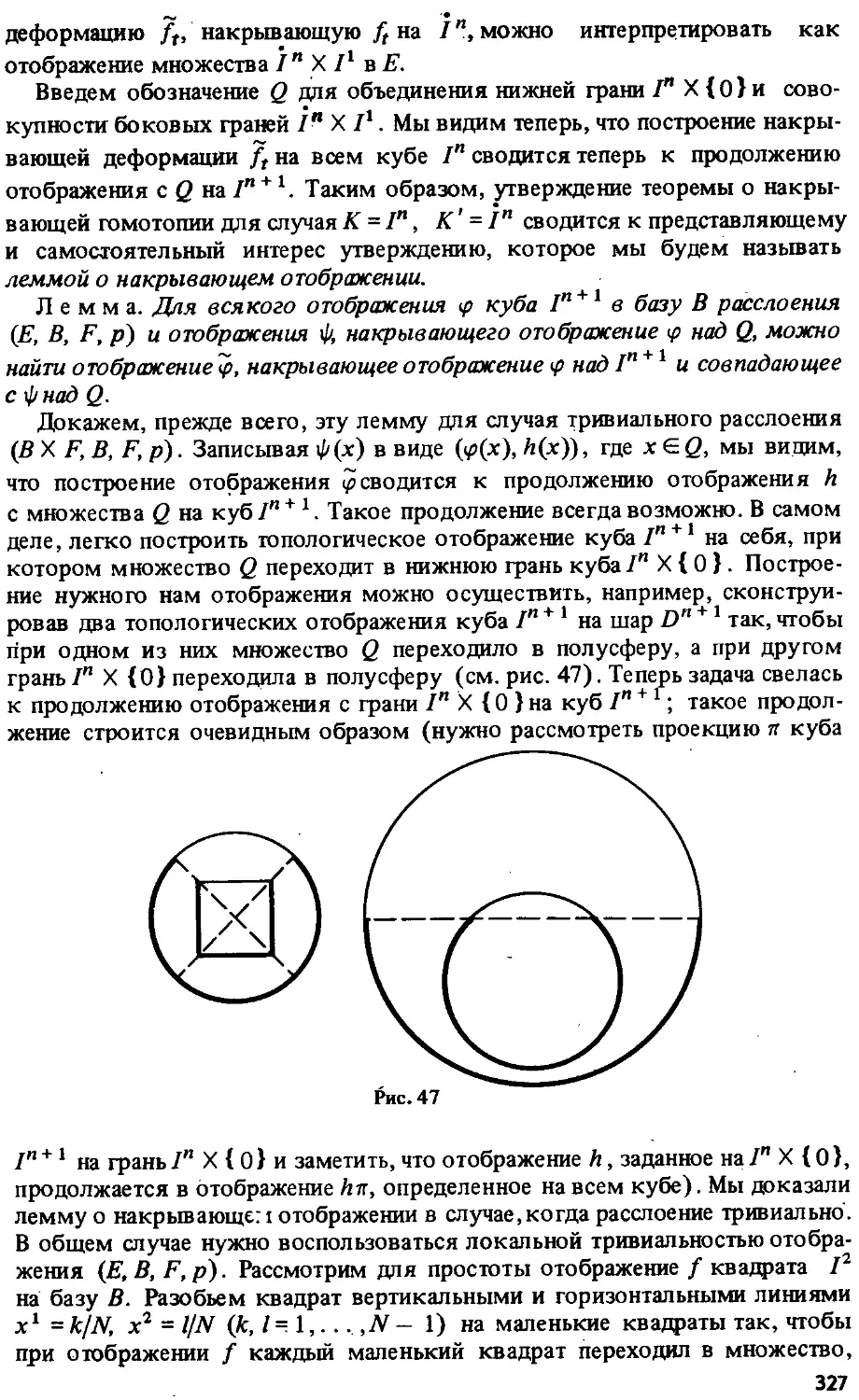
§ 16. Расслоенные пространства 315
§ 17. Связь между гомотопическими группами базы, слоя и пространства
расслоения 321
§ 18. Теорема о накрывающей гомотопии. Точная гомотопическая после 326
довательность
§ 19. Относительные гомотопические группы 332
§ 20. Гомотопические группы групп Ли и однородных многообразий 335
§ 21. Гомрлогии групп Ли и однородных многообразий 339
§ 22. Калибровочные поля и связности 346

§ 23. Калибровочные поля на многообразиях 353
§ 24. Характеристические классы калибровочных полей 356
§ 25. Геометрия калибровочных полей на многообразии 361
§ 26. Пространства калибровочных полей. Грибовские неоднозначности 363
Задачи 366
ПРИЛОЖЕНИЕ 370
§1. Топологические пространства 370
§ 2. Группы 372
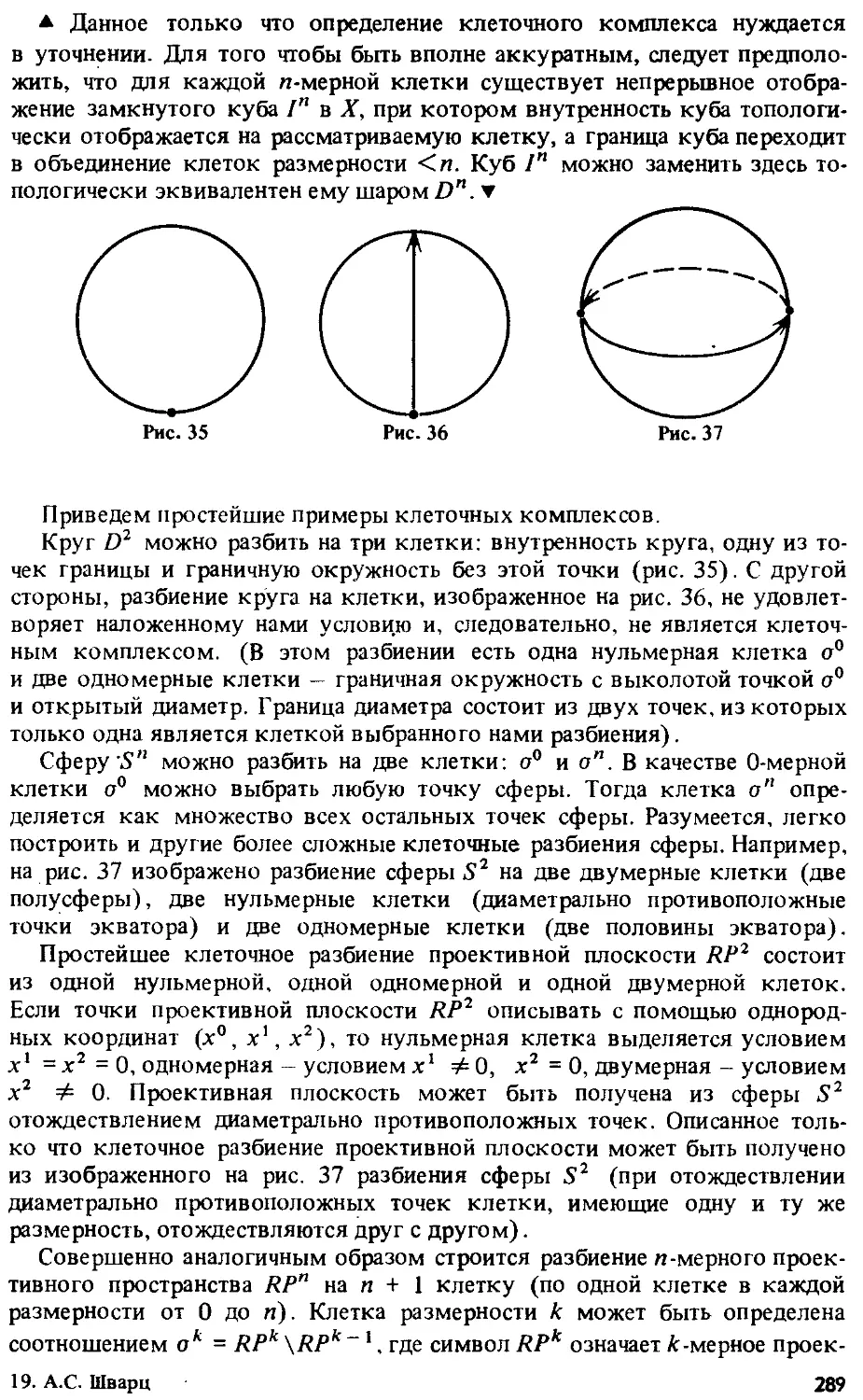
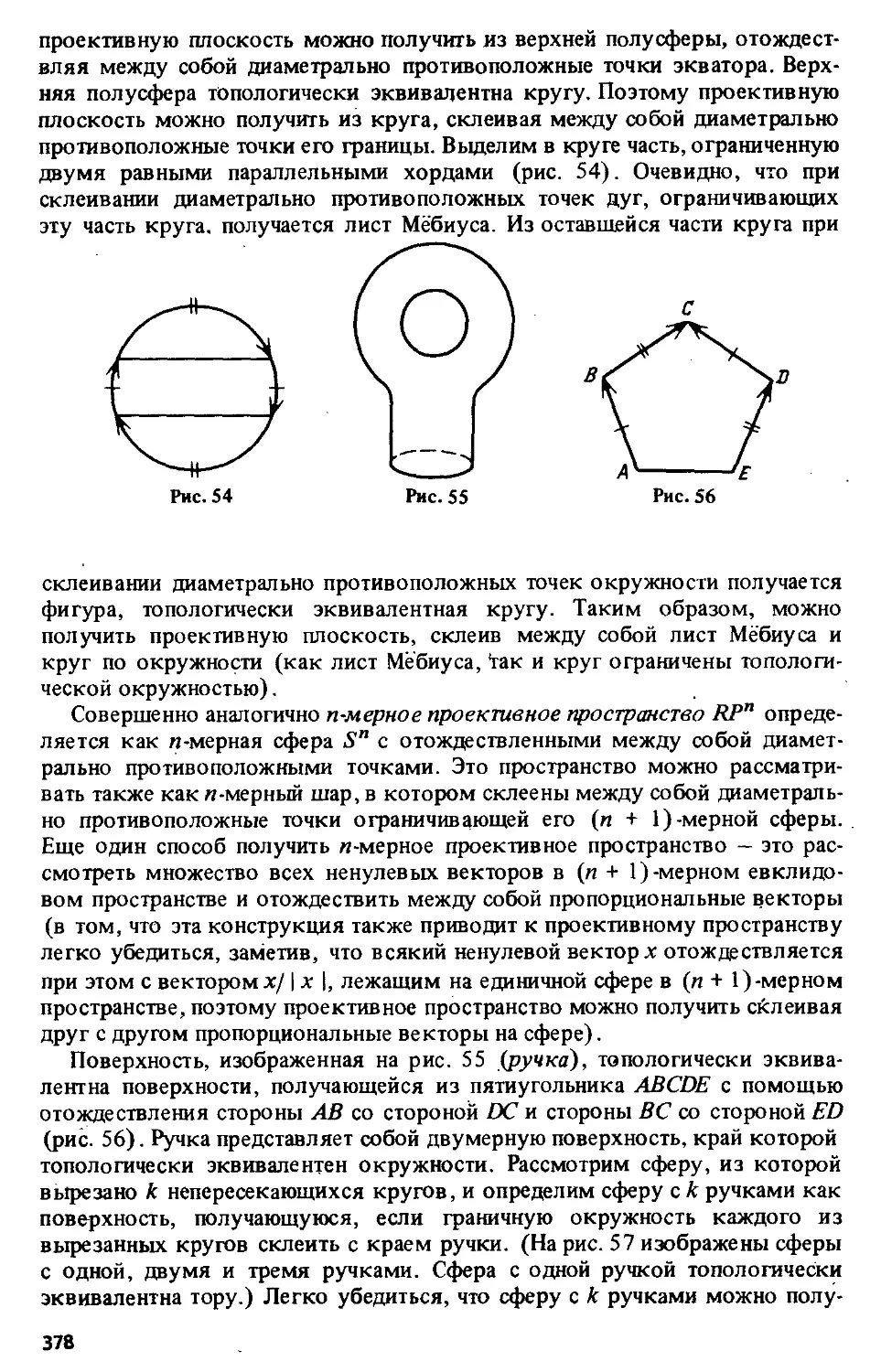
§ 3. Отождествление (наглядные примеры) 376
§ 4. Эквивалентность и отождествление 380
§ 5. Представления групп 381
§ 6. Действие группы на пространстве 387
§ 7. Присоединенное представление группы Ли 392
§ 8. Кватернионы 393
ЛИТЕРАТУРНЫЕ УКАЗАНИЯ 395
СПИСОК ЛИТЕРАТУРЫ 397
ПРЕДИСЛОВИЕ
В последние годы топология прочно вошла в математический арсенал физики.
С ее помощью сделано очень много, прежде всего в квантовой теории поля.
Открываются широкие перспективы для приложений топологии в других
областях физики.
Достаточно отметить, что топологические идеи играют важную роль в одном из
предложенных объяснений высокотемпературной сверхпроводимости. Топология
применяется также при анализе другого замечательного открытия последних лет
— квантового эффекта Холла.
Основной целью настоящей книги является изложение результатов квантовой
теории поля, полученных топологическими методами. Однако в ней освещены
некоторые топологические вопросы теории конденсированных сред.
Топологические понятия и теоремы, применяемые в физике, чрезвычайно
многообразны. В связи с этим в книгу пришлось включить большой объем чисто
математической информации.
Мне хотелось, чтобы книга была полезна разным категориям читателей. Чтобы,
с одной стороны, она была доступна студентам, знакомым только с основами
анализа, линейной алгебры и квантовой механики, а с другой стороны, была
интересна как специалистам по квантовой теории поля, так и математикам,
желающим ознакомиться с физическими приложениями топологии. Это
определило сложность структуры книги. Начало (гл.1) можно рассматривать как
введение в квантовую теорию поля. В ней описываются основные лагранжианы,
используемые в теории элементарных частиц. Центральная часть (гл. II)
посвящена приложениям топологии в квантовой теории поля. Далее следуют
топологическая часть (гл. Ш), которую можно рассматривать как учебник
топологии, рассчитанный на физиков, и Приложение. Ссылка вида § Т12
обозначает § 12 топологической части (гл. Ш), ссылки на главы I, II и Приложение

отмечаются буквами В, Ф и А соответственно. Куски текста, заключенные между
знаками А и V, можно при первом чтении пропустить.
К сожалению, ограниченность объема книги вместе с желанием сохранить ее
элементарный "учебный" характер привели к тому, что вне рамок книги оказались
многие чрезвычайно интересные физические результаты, полученные
топологическими методами. В частности, в книге не получила
отражения бурно развивающаяся в последнее время теория суперструны, хотя
топология играет в ее построении важную роль.
Глава П (как и гл. Ш) состоит из нескольких в значительной мере независимых
частей. В частности, § Ф1, посвященный топологически стабильным дефектам в
сплошной среде, формально почти не используется в дальнейшем. Далее, § Ф2 —
Ф8, Ф11 посвящены топологическим интегралам движения и топологически
Нетривиальным частицам, в частности магнитным монополям. В § Ф9, 10 дан
общий анализ симметричных калибровочных полей; этот анализ применен к
магнитным монополям. В § Ф12-Ф13 изучаются топологически нетривиальные
нити. В тесно связанных между собой §Ф14иФ15 исследуются нелинейные поля
и многозначные функционалы действия. В § Ф16, 17 рассматриваются
функциональные интегралы и их применение в квантовой теории; на этой основе
в § Ф18 изучается квантование калибровочных теорий. Далее, § Ф19, 20, 21
содержат необходимые для дальнейшего математические сведения об
эллиптических операторах и их детерминантах. В § Ф22 на базе этих сведений
анализируются квантовые аномалии. В § Ф23 —25'исследуются инстантоны в
калибровочных теориях. Наконец, в § Ф26 рассматриваются функциональные
интегралы в теориях, содержащих фермионные поля; в § Ф27 на этой основе
изучается вклад инстантонов в квантовой хромодинамике.
Для того чтобы получить минимальное представление о применении
топологических методов в квантовой теории поля, можно прочесть § Ф2—6 и
перейти к § Ф23, ознакомившись предварительно с § Ф16—18. Если читатель
интересуется топологически нетривиальными частицами и нитями, он может
после этого обратиться к независимым друг от друга § Ф7, Ф12 и Ф14, которые
могут быть дополнены § Ф11 (зависящим от §Ф7), § Ф13 (основанным на § Ф7,
12) и § Ф15, примыкающим к § Ф14. Читатель, интересующийся инстантонами,
должен обратиться к концу книги ( § Ф24-27), прочитав перед этим § Ф19—22.
Студенту разумно начать чтение книги с Приложения и § Т1, содержащих
необходимые для чтения гл. I и II сведения из теории групп и топологии. К гл. Ill
он может обращаться лишь для уточнения и доказательства результатов, на
которые есть ссылки в гл. П. Однако, конечно, читать будет легче при наличии
большей топологической информации; разумно ознакомиться прежде всего с
§Т12,16, 17. Специалист по квантовой теории поля, просмотрев Приложение, § Т1
и список определений и обо значений, может приступать непосредственно к
чтению гл. П. Математик может воспринимать гл. I как источник для
ознакомления с квантовой теорией поля, позволяющий приступить к изучению
физических приложений топологии.

ПРЕДИСЛОВИЕ
В последние годы топология прочно вошла в математический арсенал фи-
физики. С ее помощью сделано очень много, прежде всего в квантовой теории
поля. Открываются широкие перспективы для приложений топологии
в других областях физики.
Достаточно отметить, что топологические идеи играют важную роль
в одном из предложенных объяснений высокотемпературной сверхпроводи-
сверхпроводимости. Топология применяется также при анализе другого замечательного
открытия последних лет — квантового эффекта Холла.
Основной целью настоящей книги является изложение результатов кван-
квантовой теории поля, полученных топологическими методами. Однако в ней
освещены некоторые топологические вопросы теории конденсированных
сред. Топологические понятия и теоремы, применяемые в физике, чрезвы-
чрезвычайно многообразны. В связи с этим в книгу пришлось включить большой
объем чисто математической информации.
Мне хотелось, чтобы книга была полезна разным категориям читателей.
Чтобы, с одной стороны, она была доступна студентам, знакомым только
с основами анализа, линейной алгебры и квантовой механики, а с другой
стороны, была интересна как специалистам по квантовой теории поля,
так и математикам, желающим ознакомиться с физическими при-
приложениями топологии. Это определило сложность структуры книги.
Начало (гл. I) можно рассматривать как введение в квантовую теорию
поля. В ней описываются основные лагранжианы, используемые в теории
элементарных частиц. Центральная часть (гл. II) посвящена приложениям
топологии в квантовой теории поля. Далее следуют топологическая
часть (гл. III), которую можно рассматривать как учебник топологии,
рассчитанный на физиков, и Приложение. Ссылка вида § Т12 обозначает
§ 12 топологической части (гл. III), ссылки на главы I, II и Приложение
отмечаются буквами В, Ф и А соответственно. Куски текста, заключенные
между знаками а и Ў, можно при первом чтении пропустить.
К сожалению, ограниченность объема книги вместе с желанием сохра-
сохранить ее элементарный "учебный" характер привели к тому, что вне рамок
книги оказались многие чрезвычайно интересные физические результаты,
полученные топологическими методами. В частности, в книге не получила

отражения бурно развивающаяся в последнее время теория суперструны,
хотя топология играет в ее построении важную роль.
Глава II (как и гл. III) состоит из нескольких в значительной мере
независимых частей. В частности, § Ф1, посвященный топологически ста-
стабильным дефектам в сплошной сррде, формально почти не используется
в дальнейшем. Далее, § Ф2 — Ф8, Ф11 посвящены топологическим интегра-
интегралам движения и топологически Нетривиальным частицам, в частности
магнитным монополям. В § Ф9, 10 дан общий анализ симметричных калиб-
калибровочных полей; этот анализ применен к магнитным монополям.
В § Ф12-Ф13 изучаются топологически нетривиальные нити. В тесно свя-
связанных между собой § Ф14иФ15 исследуются нелинейные поля и много-
многозначные функционалы действия. В § Ф16, 17 рассматриваются функцио-
функциональные интегралы и их применение в квантовой теории; на этой ос-
основе в § Ф18 изучается квантование калибровочных теорий. Далее,
§ Ф19, 20, 21 содержат необходимые для дальнейшего математические све-
сведения об эллиптических операторах и их детерминантах. В § Ф22 на базе
этих сведений анализируются квантовые аномалии. В § Ф23 —25' иссле-
исследуются инстантоны в калибровочных теориях. Наконец, в § Ф26 рассмат-
рассматриваются функциональные интегралы в теориях, содержащих фермионные
поля; в § Ф27 на этой основе изучается вклад инстантонов в квантовой
хромодинамике.
Для того чтобы получить минимальное представление о применении
топологических методов в квантовой теории поля, можно прочесть
§ Ф2—6 и перейти к § Ф23, ознакомившись предварительно с § Ф16—18.
Если читатель интересуется топологически нетривиальными частицами и
нитями, он может после этого обратиться к независимым друг от друга
§ Ф7, Ф12 и Ф14, которые могут быть дополнены § Ф11 (зависящим
от §Ф7), § Ф13 (основанным на § Ф7, 12) и § Ф15, примыкающим
к § Ф14. Читатель, интересующийся инстантонами, должен обратиться
к концу книги (§ Ф24-27), прочитав перед этим § Ф19—22.
Студенту разумно начать чтение книги с Приложения и § Т1, содержа-
содержащих необходимые для чтения гл. I и II сведения из теории групп и тополо-
топологии. К гл. Ill он может обращаться лишь для уточнения и доказательства
резупьтатов, на которые есть ссылки в гл. II. Однако, конечно, читать будет
легче при наличии большей топологической информации; разумно ознако-
ознакомиться прежде всего с § Т12,16, 17. Специалист по квантовой теории поля,
просмотрев Приложение, § Т1 и список определений и обозначений, может
приступать непосредственно к чтению гл. П. Математик может восприни-
воспринимать гл. I как источник для ознакомления с квантовой теорией поля, поз-
позволяющий приступить к изучению физических приложений топологии.
Я обсуждал вопросы, затронутые в книге, со многими коллегами;
всем им, прежде всего С.П.Новикову, А.М.Полякову и Л.Д.Фаддееву,
внесшим большой вклад в этот круг идей, я искренне благодарен.
Пользуюсь случаем выразить признательность моим ученикам Ю.С. Тюпки-
ну, В.А.Фатееву, И.В.Фролову, Д.Б.Фуксу и особенно М.А.Баранову и
А. А. Рослому, оказавшим мне неоценимую помощь в работе над книгой.
Наконец, я хочу выразить глубокую благодарность моей жене Л.М. Кисей-
Кисейной за поддержку и помощь.

ВВЕДЕНИЕ
Под топологией понимается наука, изучающая непрерывные отображе-
отображения. С точки зрения топологии два пространства, которые могут быть
преобразованы одно в другое без разрывов и склеиваний, эквивалентны.
(Точнее, топологическая эквивалентность - это взаимно однозначное и
в обе стороны непрерывное соответствие.) Например, любое замкнутое
ограниченное и-мерное выпуклое множество топологически эквивалентно
и-мерному шару, его граница - границе шара ((и - 1)-мерной сфере).
Для того чтобы имело смысл понятие непрерывного отображения, доста-
достаточно, чтобы было определено расстояние между точками пространства
(чтобы пространство было метрическим). Более того, достаточно также,
если определено, какие точки пространства близки друг к другу (точнее,
определено понятие окрестности или предела). Тогда говорят, что
в пространстве введена топология. В физике постоянно приходится сталки-
сталкиваться с топологическими пространствами. В частности, пространство кон-
конфигураций и фазовое пространство в классической механике, множество
равновесных состояний, отвечающих данной температуре, в статистической
физике естественно наделяются топологией. В квантовой теории поля воз-
возникают также бесконечномерные топологические пространства. Это откры-
открывает возможности для применения топологии в физике. Конечно, то, что
интересует физика в первую очередь, — количественное описание физиче-
физических явлений — никак не сводится к топологии. Однако качественные
особенности явлений часто могут быть поняты с помощью топологических
соображений. В частности, если рассматриваемая физическая система и,
значит, связанное с ней топологическое пространство зависят от параметра,
то при некоторых значениях параметра скачком меняется топология.
Эти значения параметра отвечают качественному изменению в поведении
системы. (Например, значения температуры, при которых происходит изме-
изменение топологии множества равновесных состояний, являются точками
фазового перехода.)
В физике интересна не только (и не столько) топология возникающих
в ней пространств. Существенно важнее топологические свойства непрерыв-
непрерывных отображений пространств. Отображения топологических пространств
возникают в физике обычно как поля. (Например, если в области и-мер-
и-мерного пространства задано ненулевое векторное поле, то это поле можно
7

рассматривать как отображение области в множество ненулевых векторов.)
Особенно важную роль играют гомотопические инварианты непрерывных
отображений. Число (или какой-либо другой объект) называется гомотопи-
гомотопическим инвариантом отображения, если оно не меняется при бесконечно
малом изменении отображения. Точнее можно сказать, что гомотопические
инварианты не меняются при непрерывной деформации (гомотопии)
отображения (непрерывное изменение составляется из бесконечно малых
изменений).
В частности, если ненулевое векторное поле задано на плоскости вне не-
некоторого круга D, то ему можно сопоставить целое число л, показывающее,
сколько оборотов делает вектор при обходе по окружности, содержащей
->-
внутри себя круг D. (Если векторному полю Ъ{х,у). = (^, (х, у), ty2 (х,у))
сопоставить комплексную функцию Ф(г, у) = Ф, (/• costp, r.simp) +
+ /Ф2 (/• cos ^, r sin <j?), то ч'(/-,1/>) можно записать в виде ^{г, $) =
= A(r,tp)eia(-r>'('\ где а(г, у) при г Ф 0 - непрерывная функция.
Тогда а(г, 2 тг) - а(г , 0) = 2тгп, где и - целое число, показывающее,
сколько оборотов сделал вектор У(х, у).) Число п не меняется при непре-
непрерывном изменении векторного поля. т.е. является гомотопическим инва-
инвариантом. (Из определения ясно, что п должно меняться непрерывно, но це-
целое число может измениться только скачком.)
Рассмотрим, например, векторные поля, для которых: а) Ч') {х,у) = х,
Ъ2(х,у) =у: б) *i(x,y) = - v, *2(*,.v) =•*; а) %(х,у) = х2 - v2,
^2 (¦*>У) ~ 2ху. Им отвечают комплексные функции ^(г,^) = re1*,
*(/"»|Р) =re/(v? + n/2\ ty(r,ip) = r2e2llfi соответственно, и, следова-
следовательно, в первых двух случаях и = 1, в последнем п = 2.
Два отображения, для которых все гомотопические инварианты совпа-
совпадают, называются принадлежащими одному гомотопическому классу.
(Иными словами, отображения принадлежат одному гомотопическому
классу, если их можно соединить непрерьшным семейством отображений —
гомотопией.) Для Полей вместо термина "гомотопический класс" употреб-
употребляют термин "топологический тип поля". Для векторного поля, заданного
вне круга, описанный выше гомотопический инвариант является единст-
единственным. Иначе говоря, он полностью характеризует гомотопический класс.
(топологический тип) ненулевого поля. Если ненулевое векторное поле,
заданное вне круга, может быть непрерывно продолжено на всю плоскость,
то и = 0; в этом случае поле называется топологически тривиальным.
В общем случае число и можно интерпретировать как алгебраическое
число особых точек, возникающих при продолжении поля внутрь круга.
(К числу особых точек относятся как точки, в которых поле обращается "
в нуль, так и точки, в которых поле не определено.)
Физическая интерпретация сформулированных выше математических
утверждений может быть очень разнообразной. Например, можно рассмат-
рассматривать плоскость, на которой задано векторное поле как фазовое прост-
пространство системы с одной степенью свободы, и считать, что векторное поле
определяет динамику системы. Тогда топология позволяет получить
информацию о положениях равновесия (точках, где векторное поле обра-
8

щается в нуль). Если векторное поле интерпретируется как поле вектора
намагниченности, то его особые точки представляют собой дефекты
в ферромагнетике. Если комплексная функция Ф рассматривается как
волновая функция (параметр порядка) сверхпроводника, го особые точки
связаны с вихрями в сверхпроводнике.
В теории поля (как классической, так и квантовой) топологические
"соображения приводят к новому типу интегралов движения — к топологи-
топологическим интегралам движения. Такие интегралы движения возникают, если
каждому полю с конечной энергией удается сопоставить число, не меняю-
меняющееся при непрерывном изменении поля. (Это число является интегралом
движения, поскольку изменение поля с течением времени непрерывно.)
В частности, топологические интегралы движения могут существовать
в теориях, в которых есть бесконечное множество классических вакуумов
(классических аналогов основного состояния). В этих теориях топологиче-
топологические интегралы движения можно построить как гомотопические инвариан-
инварианты отображения бесконечно удаленной сферы в многообразие классических
вакуумов. Это отображение определяется асимптотикой поля на бесконеч-
бесконечности. Топологические интегралы движения могут существовать также
в случае, когда рассматриваемые поля принимают значения в нелинейном
многообразии, например на сфере.
Наиболее простые и важные физические приложения топологии связаны
с теорией гомотопий. Однако существенную роль играет также другая
часть топологии — теория гомологии. Она применяется непосредственно
(в частности, при анализе кратных интегралов, возникающих в физике,
например, при вычислении фейнмановских диаграмм) или как техническое
средство при построении гомотопических инвариантов. Теория гомологии
тесно связана с многомерными обобщениями формул Грина, Гаусса —
Остроградского, Стокса. (Эти обобщения удобно формулировать на языке
внешних дифференциальных форм, т.е. форм, в которых дифференциалы
считаются антикоммутирующими объектами.) Основными понятиями
теории гомологии являются понятия цикла (замкнутой поверхности) и
цикла, гомологического нулю (замкнутой поверхности, ограничивающей
поверхность, размерность которой на единицу больше). Например, в обла-
области [R3 \ Г, полученной из трехмерного пространства IR3 удалением неко-
некоторой замкнутой кривой Г, существуют одномерные циклы, не гомологич-
гомологичные нулю. Это очевидное утверждение можно формально доказать, рас-
рассмотрев магнитное поле тока, идущего по кривой Г. Напряженность Н
этого поля удовлетворяет условию rot H =0 вне Г. Если одномерный
цикл Г, в R3 \ Г является границей поверхности S, целиком лежащей
в R3 \ Г, то в силу теоремы Стокса
ф Н d\ = / rotH dS = 0.
г, s
Поэтому всякий цикл Г i, для которого § Н <1\ не равен нулю, не гомоло-
гичен нулю в IR3 \ Г.
При непрерывной деформации негомологичного нулю цикла снова полу-
получается негомологичный нулю цикл. Это замечание открывает путь к приме-

нению теории гомологии в теории гомотопий. Например, если у - отобра-
отображение окружности в рассмотренную выше область К3 \.Г, то ^Н<Л,
взятый по кривой, получающейся из окружности при отображении \р,
является гомотопическим инвариантом. (Это следует из теоремы Стокса.)
Еще одно важное понятие топологии, находящее применение в физике,—
это понятие расслоенного пространства. В математике и физике часто воз-
возникает ситуация, когда каждой точке Ъ некоторого пространства В сопо-
сопоставляется пространство Fb, зависящее от b G В. В случае, если все прост-
пространства Fb топологически эквивалентны друг другу, говорят, что объедине-.
ние Е пространств Fb является расслоенным пространством, пространст-
пространства Fb называются слоями, а В - базой. Например, если В - пространство
конфигураций механической системы, то, фиксировав точку этого прост-
пространства, мы можем рассмотреть всевозможные значения обобщенных ско-
скоростей (всевозможные векторы в рассматриваемой точке). Мы получим
зависящее от точки пространства конфигураций и-мерное векторное
пространство, где и — число степеней свободы. Объединение всех таких
векторных пространств является расслоенным пространством. Оно назы-
называется касательным расслоенным пространством для пространства конфи-
конфигураций В. Другой пример расслоенного пространства — это пространство
всех калибровочных полей, разбитое на классы калибровочно эквивалент-
эквивалентных друг другу полей. (Эти классы являются слоями, а множество всех
классов — базой расслоенного пространства.)
Часто возникает необходимость выбрать в каждом слое одну точку,
непрерывным образом зависящую от слоя (построить сечение расслоенного
пространства). В рассмотренных выше примерах понятие сечения до-
допускает физическую интерпретацию. Именно: сечение касательного рас-
расслоенного пространства можно рассматривать как векторное поле (поле
скоростей) на пространстве конфигураций. Для расслоения на классы
калибровочных полей построение сечения — это выбор калибровочного
условия. (Отметим, что для неабелевых калибровочных полей нельзя
выбрать калибровочное условие, выделяющее из каждого класса калибро-
калибровочно эквивалентных полей ровно одно поле. Это означает, что у соответ-
соответствующего расслоенного пространства нет сечения.) Расслоенные простран-
пространства не только непосредственно появляются в физических приложениях;
они играют также важную техническую роль при решении задач теории
гомотопий. Чрезвычайно важное в физике понятие калибровочного поля
тесно связано с понятием расслоенного пространства. Оно с математической
точки зрения зквивалентно понятию связности в главном расслоенном про-
пространстве (расслоенном пространстве, слоем которого является группа).
В настоящее время в физике широко применяются не только упомяну-
упомянутые выше топологические понятия, но и многие другие. В кратком введе-
введении нет возможности останавливаться на этих понятиях.

ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
\.{й | Y}— множество точек а, удовлетворяющих условию (или усло-
условиям) Y
Если/ - отображение А в В, то f(A) ={ f (а) I а&А) — образ множест-
ъаА,/'1 (х) ={а I aG A,f(a) = х}-прообраз точкиxGВ
Преобразование - взаимно однозначное отображение А па В
АХ.В ={ (х,у) I х&А,у&В) — прямое произведение множеств А л В
2. IR"(C") —и-мерное линейное действительное (комплексное) прост-
пространство, реализованное как пространство строк (или столбцов) из и дейст-
действительных (комплексных) чисел
Е — сопряженное пространство к линейному пространству h - (прост-
(пространство линейных функционалов на Е). Если / G Е — линейный функ-
функционал на Е, то значение функционала / на х обозначается f(x)=(f,x) и
называется скалярным произведением /их. Если А - линейный оператор
из ?\ в Ег, то сопряженный оператор А* действует из Е2 в Е х и опреде*
ляется соотношением < A*f,x) ^< f,Ax), f€E2, х€Ег. Для гильберто-
гильбертова пространства Е отождествляется с Е
ImА ={Ах |х ЕЕХ} — образ оператора
Кег А ={х | х €?*!, Ах = 0}- ядро оператора А
dim Е — размерность пространства Е
1{А) = dim Кег Л — число нулевых мод оператора Л
А/к = <. г | А | к) - матричные элементы оператора А, действующе-
действующего вЕ-
Sp.4 = 2< / I A I / > =Е\/ - след оператора А(X,-собственные значе-
значения)
3. Gx = G2 - изоморфизм групп GxkG2
Gi ^G2 — локальный изоморфизм групп Gx иС2
Если каждому элементу g группы G сопоставлено преобразование yg
пространства Xи >pgigi =>pgi -<^г (или *gigi =^i -4>gl), то говорят,
что задано левое ^ (первое) действие группы G на X
Nx ~ ( Vgfx) IS e G } — орбита точки х & X
Hx ~ ( S I Vg(x) =x,g €G}- стационарная подгруппа точки xGX
X/G — множество всех орбит группы G в X (факторпространство X
по G)

Правое действие подгруппы Н на G определяется формулой >рн Of) =
=gh, гдеgGG, hGH. Факторпространство G/H - множество орбит этого
действия (правых смежных классов)
Если Н — инвариантная подгруппа (т.е. подгруппа, инвариантная отно-
относительно внутренних автоморфизмов agh =ghg~1), то G/H снабжается
структурой группы (факторгруппы GnoH)
GL(«,IR) (GL(«, С)) - группа невырожденных действительных (ком-
(комплексных) матриц порядка и X и
U(«) = {а | а+а = аа* = I} — группа унитарных матриц -
SU(w)={a| а*а = аа* = 1, det a= 1} — группа унимодулярных унитар-
1ых матриц
О (и) = { а | ата~аат ~ 1} — группа ортогональных матриц
SO(n)={a \ата = аат = 1, det а = 1} - группа вращений
Sp(n) — симплектическая группа (см. § А8)
gl( и,IR ), jgl(«, С), u(n), su(«), so (и), sp(«) - алгебры Ли перечислен-
перечисленных матричных групп
# — алгебра Ли группы G ( § А2)
Tg(x) =gxg'i, g&G, xG& - присоединенное представление группы
G (§ А7)
ад(х) = [а, х], а& 8, х&^§ — присоединенное представление алгебры
Ли 8
4. Если А СХ, В CY, то отображение / пространства X ъ Y называется
отображением пары (Х,А) в пару (Y,B) в случае, когда/D) СВ
/о и /i принадлежат одному гомотопическому классу отображений X
в Y, если их можно соединить непрерывным семейством ft отображений X
в Y (деформацией или гомотопией). Аналогичное определение для отоб-
отображений пар
{ X, Y } — множество гомотопических классов отображений Хв Y
{X, А | Y, В) — множество гомотопических классов отображений (Х,А)
в (Y, В)
S"={x\ xGIR"+1, 11лг|! = 1}-я-мернаясфера,5= (-1,0 0) G5"
южный полюс сферы
л„(Х,Хо) ={Sn,s I -^,*o} — множество гомотопических классов отоб-
отображений сферы S" с отмеченной точкой s в пространство Хс отмеченной
точкой х0. При и> 1 множество п„{Х,Хо) превращается в группу — и-мер-
ную гомотопическую группу пространства X (§ Т15)
¦п„(Х,А) - относительные гомотопические группы (§ Т19)
5. Гладкое отображение — отображение, задаваемое бесконечно диф-
дифференцируемыми функциями
Гладкое многообразие М - пространство, в котором можно ввести
локальные системы координат, связанные гладкими преобразованиями
(§ Т5)
Дифференциальная (внешняя) форма степени к (Аг-форма) на М задает-
задается в локальных координатах формулой со = со,- ;.,-fccfac ' Л... Adx'k,
где Л — внешнее произведение дифференциалов (dxl Adx' = —dx' Л dx')
(§Т6,Т10)
12

Внешний дифференциал Ло = dafi... ik(x) Л dx'1 Л ... Adx к;
dw = 0 4^ форма со замкнута,
со = da ? форма со точна
Группа когомологий Н к(М) = Zk (М)/Вк (М) — факторпространство
пространства замкнутых форм по пространству точных форм (§ Т7, Т10)
Группа гомологии Нк(М) = Zk(M)/Bk{M) - факторгруппа группы
циклов (Аг-мерных замкнутых поверхностей) по группе циклов, гомоло-
гомологичных нулю (замкнутых поверхностей, ограничивающих (к + 1) -мерную
поверхность) (§ Т7, Т10)
Нк(М,А), Нк(М,А) — группы гомологии и когомологий с коэффи-
коэффициентами в абелевой группе Л (§ Т9, Т10)
6. Расслоение (E,B,F, р) - отображение р пространства Е на В, при ко-
котором прообразы всех точек (слои Fb=p~1 (Z>)) топологически эквива-
эквивалентны фиксированному пространству F (В — база, F — слой, р — проек-
проекция, Е — пространство расслоения) ( § Т16)
Е = В XF,p(b,f) = Z> €E В — тривиальное расслоение
Сечение расслоения — отображение q базы В в Е, для которого q F) G
&p-'{b)=Fb (J.e.pq=l) (§ Т16)
Если G действует на Е так, что все стационарные подгруппы тривиальны,
то расслоение (E,E/G,G,p) пространства Е на орбиты группы G называет-
называется главным (§ Т16)
Точная гомотопическая последовательность расслоения
• • ¦ -f«(^, ео)->7г„(?, ео)-я„0В, bo)-nrn_1(F, ео)- ...
(образ каждого гомоморфизма совпадает с ядром последующего) (§ Т18)
Расслоение, ассоциированное с главным расслоением (E,B,G,p), —
расслоение со слоем F, на котором действует G, склеенное из прямых
произведений Uf XF так же, как главное — из прямых произведений
U{ XG (§ Т25).
Все функции, отображения, многообразия, сечения расслоений предпо-
предполагаются гладкими, если не оговорено противное. (Однако все утвержде-
утверждения остаются справедливыми, если вместо бесконечной дифференцируемос-
ти предполагать дифференцируемость до некоторого конечного порядка,
зависящего от рассматриваемого вопроса. Обычно достаточно непрерыв-
непрерывной дифференцируемости или просто непрерывности).
7. Ац (х) — калибровочное поле (векторное поле, принимающее значе-
значения в алгебре Ли i§ калибровочной группы G )
WpV = Э^ Ар —дрАц + [Ац,Ар] —напряженность калибровочного поля
Vрф = (Эji + t(А,,))i/> - ковариантная производная поля $, преобра-
преобразующегося по представлению Т калибровочной группы G (символ t обозна-
обозначает представление алгебры Ли iS, отвечающее представлению Г группы G)
(§ В4, § Т22)
Пространственно-временной интервал в пространстве Минковского
записывается в виде
dxftdx>i=(dx0J -(dxf,
где х ° = t (как всегда, подразумевается суммирование по повторяющим-
повторяющимся индексам). Скорость света с полагается равной 1.
13

ГЛАВА I
ОСНОВНЫЕ ЛАГРАНЖИАНЫ КВАНТОВОЙ ТЕОРИИ ПОЛЯ
§ 1. Простейшие лагранжианы
Напомним, что классическую полевую теорию удобно задавать с по-
помощью функционала действия
S = f?dx, A)
где ? носит название плотности действия или лагранжиана. Лагранжиан яв-
является функцией от значений поля и его производных. Интегрирование в
A) происходит по всем пространственным переменным и по времени.
Уравнения движения получаются из принципа экстремальности действия:
вариация действия должна быть равна нулю при фиксированных гранич-
граничных условиях.
Перечислим простейшие лагранжианы, инвариантные относительно
группы Лоренца.
Прежде всего следует упомянуть лагранжиан свободного скалярного
поля кр (х)
„ч V i eV- B)
Соответствующее уравнение движения (уравнение Клейна—Гордона)
имеет вид
Решения этого уравнения движения могут быть представлены в виде су-
суперпозиции плоских волн
exp(-/Arx) = exp(-iAr°JC°+ikx), C)
где к2 = (к0J —к2 = а2. Отсюда легко получить, что при квантовании
лагранжиана B) получается теория, описывающая частицы массы ha.
(Плоской волне C) отвечает частица с энергией E = hk° и импульсом
р = hk и, следовательно,Е2 — р2 = т2 =h2a2.)
Отметим, что мы рассматриваем лагранжиан B) как классический.
В соответствии с этим он не содержит постоянной Планка h. Эта постоян-
постоянная появляется в выражении для массы квантовых частиц, возникающих
в квантовой теории, построенной по лагранжиану B), только потому,
что она содержится в постулируемых при квантовании канонических ком-
коммутационных соотношениях [7г(х),?(х')] = — iht>'(x-x)r. Это же замеча-
замечание относится ко всем другим рассматриваемым нами лагранжианам.
14

Часто уравнение Клейна—Гордона рассматривают как результат кванто-
квантования лагранжиана, описывающего свободную релятивистскую частицу.
(Поэтому процесс квантования уравнения Клейна—Гордона именуется вто-
вторичным квантованием.) Тогда постоянная Планка возникает в самом
уравнении Клейна—Гордона. Мы не придерживаемся здесь этой точки зре-
зрения. Начиная с этого места будем полагать h = 1.
Электромагнитное поле можно описывать с помощью потенциала^ (х).
При преобразованиях Лоренца поле Ац {х) преобразуется по векторному
закону. Два поля A'^ipc) и А^ (х), отличающиеся друг от друга на градиент
скалярной функции: А' =АI +Ъ11\, физически эквивалентны. Преобра-
Преобразование Ац -+Ац +Эц\ называется калибровочным преобразованием.
Тензор
Рцр - дрАр — Ър Ац
называется тензором электромагнитной напряженности; он не меняется
при калибровочных преобразованиях. Компоненты Fo t тензора F^ v "отож-
"отождествляются с компонентами Et электрической напряженности Е, а ком-
компоненты Fik связаны с компонентами Нк вектора магнитной напряжен-
напряженности Н; именно
Fi, = ei/k Hk (здесь /,/,* = 1,2, 3).
Лагранжиан электромагнитного поля может быть записан в виде
?=-1-FllvF^. D)
4
Пользуясь калибровочной инвариантностью, можно наложить на вектор-
н"ый потенциал А^ дополнительные условия таким образом, чтобы в каж-
каждом классе физически эквивалентных полей содержалось по крайней мере
одно поле, удовлетворяющее наложенному условию. Условия такого типа
называются калибровочными условиями. Например, можно наложить ка-
калибровочное условие Ъ цА11 =0 (условие Лоренца) или условие А0 =0,
div А = 0 (кулонова калибровка). Отметим, что кулонова калибровка
выделяет в каждом классе физически эквивалентных полей ровно одно
поле' (если потребовать убывания полей на бесконечности), в то время
как лоренцева калибровка не обладает этим свойством.
Уравнения движения, отвечающие лагранжиану D), имеют вид
Они совпадают с уравнениями Максвелла в пустоте. В кулоновой калиб-
калибровке каждому волновому вектору к отвечают две линейно независимые
плоские волны с частотой А:0 = I k I, удовлетворяющие уравнениям дви-
движения. (Плоская волна характеризуется волновым вектором к и векто-
вектором поляризации, ортогональным волновому вектору.) Отсюда можно
вывести, что при квантовании лагранжиана D) получается теория, описы-
описывающая частицы нулевой массы (фотоны). При каждом значении импульса
фотон может находиться в двух независимых состояниях.
15

Добавив к лагранжиану D) "массовый член" - а2 А^ А*, мы получим
лагранжиан
?=_ _ (d,1Avd'1Av-dllAvdvA>')+ - ^A^A», E)
описывающий массивное векторное поле. Отметим, что лагранжиан E)
уже не обладает свойством калибровочной инвариантности. При кванто-
квантовании этого лагранжиана возникает теория, описывающая векторные
частицы массы а; при заданном значении импульса р частица может нахо-
находиться в трех независимых состояниях. (Это следует из того, что при фик-
фиксированном значении волнового вектора есть три линейно независимые
плоские волны, удовлетворяющие уравнениям движения.)
Обратимся теперь к полям, преобразующимся по двузначным пред-
представлениям группы Лоренца. •* При квантовании этих полей следует поль-
пользоваться каноническими антикоммутационными соотношениями. Более
того, строго говоря, еще до квантования значения этих полей следует рас-
рассматривать как антикоммутирующие величины. Однако для наших целей
это уточнение почти везде не является существенным. Ў
Рассмотрим прежде всего поле, преобразующееся по двумерному ком-
комплексному представлению группы Лоренца L, т.е. являющееся двухкомпо-
нентным спинором <ра. (В группу Лоренца мы не включаем отражения.)
Из двух спиноров уа и х" можно составить скаляр еа(д^"х^^хи век-
вектор if а а11 ш х а - •fi 0м х. • (Напомним, что спинор х а = X а> комплексно со-
пряженный спинору ха> преобразуется как пунктирный спинор. Символ
а0 обозначает единичную матрицу, а матрицы а1 ,а2 ,а3 совпадают с матри-
матрицами Паули). Мы можем, таким образом, записать лагранжиан двухкомпо-
нентного спинорного поля у а в виде
? =
= - (уо^Ъ^у - Ъц^а11^ )+a(w+yy ). F)
Соответствующие уравнения движения
ibp ipa11 -аЩ- О
имеют решения в виде плоских волн
<р = и exp(-ikx),
где к2 =а2. Отсюда следует, что при квантовании лагранжиана F) полу-
получается теория, описывающая частицы массы т= а. Поскольку при кванто-
квантовании используются канонические антикоммутационные соотношения
эти частицы являются фермионами.
16

В квантовой теории поля заряженные частицы описываются комплекс-
комплексными полями; соответствующий лагранжиан должен остаэаться неизмен-
неизменным при умножении поля на комплексное число, по модулю равное едини-
единице. Лагранжиан F) при а Ф 0 не инвариантен относительно замены уa -»•
-+е'^<ра; поэтому ему отвечают нейтральные массивные фермионы (майо-
рановские нейтрино). При а = 0 лагранжиан F) описывает безмассовые
(вейлевские) нейтрино.
Чтобы построить лагранжиан, описывающий заряженные фермионы,
нужно использовать два спинорных поля ¦#>а и ха. Этот лагранжиан (лаг-
(лагранжиан Дирака) имеет вид
?= г(Эм ч?ам^ + ЭМ х а" X ) - т(.*Х + Х * )• G)
Вводя биспинор
¦о
где х . = е . • X "> можно переписать лагранжиан Дирака в форме
а а(?
(8)
(9)
где
О -~а\
)• (Ю)
Матрицы A0) удовлетворяют соотношениям
У У +У "у А5 • (П)
Четырехмерные матрицы -ум> для которых выполнены соотношения A1),
носят название матриц Дирака. Если в (9) заменить матрицы A0) на произ-
произвольные матрицы Дирака, то мы получим эквивалентный лагранжиан.
Двумерное комплексное представление группы Лоренца можно рассмат-
рассматривать как четырехмерное действительное представление этой группы.
Иными словами, двухкомпонентный комплексный спинрр уа можно
рассматривать как четырехкомпонентный вещественный спинор — майора-
новский спинор
В терминах маиорановских спиноров можно переписать лагранжиан F)
в виде (9), где уц - действительные матрицы, удовлетворяющие условию
A1) (действительные матрицы Дирака).
17

§ 2. Квадратичные лагранжианы
Рассмотрим простейшие лагранжианы, описывающие многокомпонент-
многокомпонентные поля. Начнем с лагранжиана
? = - ? a^aV - - ? k,,JJ, (i)
2 ( 2 i, i
описывающего и-компонентное скалярное поле ^ = (V1 >•••><?")• Этот
лагранжиан можно привести к более простой форме
? = 1- Е(Э^ЭУ-^УУ) B)
2 j
с помощью замены i/>' -> ? в/<У, где fly — ортогональная матрица. В самом
деле, при этой замене первое слагаемое в ? ("кинетическая часть" лагран-
лагранжиана) не меняет своего вида. С другой стороны, с помощью ортогональ-
ортогонального преобразования квадратичную форму ? к{цр'^ можно привести к
диагональному виду ? Рцр'\р1, где Vj — собственные значения симмет-
ричной матрицы кц. Мы видим, что в случае, когда квадратичная форма
? kjjtp'ip1 неотрицательно определена, лагранжиан A) описывает скаляр-
ные частицы с массами т,- = \fv~j. В случае если матрица кц имеет хотя бы
одно отрицательное собственное значение, гамильтониан интересующей
нас теории не является ограниченным снизу, и, следовательно, теория не
допускает интерпретации в терминах частиц. (Иногда говорят, что она
описывает частицы с мнимой массой — тахионы, добавляя при этом, что
таких частиц не существует.)
Совершенно аналогично исследуется квадратичный лагранжиан, описы-
описывающий многокомпонентное векторное поле — лагранжиан
? = ? - -
i 4
+ - Xk.fA'^A11'. • C)
2 i, /
Если симметричная матрица кц неотрицательно определена, то с помощью
диагонализации убеждаемся, что этому лагранжиану отвечают векторные
частицы с массами \fv{ где Vf — собственное значение матрицы кц.
Далее, рассмотрим квадратичный лагранжиан, описывающий п спинор-
ных полей,
? = ? 7(
+ 2 (MiiXiX,- + MuxiXi), D)
где M(j — симметричная комплексная матрица (массовая матрица). Лагран-
18

жиан D) с помощью унитарного преобразования Х| -*• Щ^ может быть
приведен к виду
/О// + Х/Х/), E)
где ntf > 0. Числа т/ имеют физический смысл масс. Можно найти числа
mj как собственные значения матрицы М* М. В самом деле, первое слагае-
слагаемое в D) не меняется при преобразовании Xt ~* ^//Х/ > где U = {Uit) —
унитарная матрица. Массовая матрица М = (Л//у) заменяется при этом пре-
преобразовании на UTMU, где UT — матрица, транспонированная к унитарной
матрице U. Легко видеть, что матрица М* М переходит в матрицу
и*м*ит*итми = и~1м
и, следовательно, собственные значения матрицы М* М не меняются. Это
замечание обосновывает указанный выше рецепт вычисления масс ntf,
если поверить утверждению, что лагранжиан D) может быть приведен
к виду E).
* Для того чтобы доказать это последнее утверждение, нужно проверить,
что выражение JC(x) ~ 2 Л///Х/Х/ — квадратичную форму на комплекс-
комплексном пространстве С" - можно привести к виду 2 w,-XiX; с помощью уни-
унитарного преобразования. Рассмотрим квадратичную форму
JT(x) = Л(х) +Jl(x) = Mkj(uk + ivk)(u, + ivf) +
+ Mfc/(Mfc - ivk) (u, - ivj)
на вещественном пространстве tR2". Очевидным образом С" можно рас-
рассматривать как И ; умножение на / в С" порождает в tR2" линейный
оператор /, удовлетворяющий условию /2 = -1-. Точке (хх, . . . , хп) =
= (mi + ivi,'. . . , и„ + ivn) G С" отвечает точка (i<i, »i, '¦ • ¦ , un, vn) G
€ tR2" > оператор/ переводит эту точку в (-иt, их -vn ,и„). Стандарт-
Стандартный базис в IR2" имеет вид ех, Jex, ..., е„, Jen, где et,'..., е„ — стандарт-
стандартный базис в С". Из соотношения JC(ix) = — Л(х) следует, что квадратич-
квадратичная форма Л"(х) на R 2" удовлетворяет условию
. F)
Эрмитову скалярному произведению в С" отвечает скалярное произведе-
произведение в IR2"; унитарные операторы в С" могут быть охарактеризованы как
ортогональные операторы в [R коммутирующие с/.Пользуясь скаляр-
скалярным произведением в !R2n, можно записать квадратичную форму Jf(x) в
виде Jf (х) = < Nx, х > , где N — самосопряженный оператор в Р2". Из F)
следует, что
NJ = -JN,
и, значит, по каждому собственному вектору х оператора ./V, имеющему
19

собственное значение X, можно построить собственный вектор Jx, имею-
имеющий собственное значение —Л. Это замечание вместе с обычными рассуж-
рассуждениями позволяет построить полную ортонормированную систему соб-
собственных векторов оператора N, состоящую из векторов xi,'Jxi,\ . .
. . . , хп, Jxn, которым отвечают собственные значения Xj, —Xj, . . . , Х„,
—X „, где \{ > 0. Рассмотрим ортогональный оператор, переводящий стан-
стандартный базис ei, Jex, . . . ,е„, Уеп в базис из собственных векторов опера-
оператора N. По построению это ортогональное преобразование коммутирует с
/ и, следовательно, может рассматриваться как унитарное преобразование
в С". Легко видеть, что построенное унитарноепреобразованиеявляется
искомым. Ў
§ 3. Внутренние симметрии
Под симметрией понимается преобразование полей, при котором функ-
функционал действия остается неизменным. Симметрия называется внутрен-
внутренней, если преобразование затрагивает только значения полей (но не ко-
координатные переменные!).
Рассмотрим, например, лагранжиан системы из п безмассовых скаляр-
скалярных полей у1 (х),..., у" (х).
?ь = ? - ЭМ*/Э*У. (О
i = 1 2
Очевидно, что этот лагранжиан (а следовательно, и отвечающее ему
действие) не меняется при преобразованиях вида
где а1, — ортогональная матрица.
Это означает, что лагранжиан A) обладает группой внутренних симмет-
симметрии О (и). (Этот факт был использован в предыдущем параграфе для
приведения к простейшему виду лагранжиана B.1)). Лагранжиан
? = ?ь - -тг ? (^J, C)
2 i=i
описывающий и невзаимодействующих скалярных полей одной и той
же массы, и лагранжиан
? = ?ь - Х( ? yf - аг? D)
i"= 1
также имеют группу внутренних симметрии О (и). Вместо того чтобы го-
говорить про п скалярных полей \р' (х), ..., у" (х), обычно удобно говорить
про и-компонентное скалярное поле у (х) = (кр1 (х), . . . , <рп (х)), прини-
принимающее значение в пространстве IR". Индекс i = 1, . . . , п называется изо-
изотопическим . индексом. Лагранжиан л-компонентного ' скалярного поля,
инвариантный относительно преобразований Лоренца, можно записать
в виде
jc = i <э^, э»у> - Щ*), ¦ E)
20

где < , > — стандартное скалярное произведение в 1R", a Ufa) =
= Ufa1, . . . , ip") - функция, заданная на пространстве R". (Лагранжианы
C) и D) можно рассматривать как частный случай лагранжиана E) при
т2
Щф) =— <^, у) и Ufa) = \(<(Д <р) -а2J соответственно.) Группа G,
состоящая из ортогональных преобразований пространства IR", является
группой внутренних симметрии лагранжиана E) в случае, если Ufa)
является G-инвариантной функцией на пространстве В" (т.е. U(gtp) =
= Ufa) для всех gGG, ye\R").
Можно говорить о группе внутренних симметрии также в случае, если
функционал действия задан на полях, принимающих значения в произволь-
произвольном многообразии М. Именно: группа G, действующая на М, называется
группой внутренних симметрии, если функционал действия не меняется
при соответствующих преобразованиях полей. (Очевидно, что преобразо-
преобразованию многообразия М, в котором принимают значения поля, отвечает
преобразование полей.) В частности, если и-компонентное скалярное поле
4>(х) может принимать значение только на сфере, выделенной условием
< if, ip ) = 1, то лагранжиан
JC = - <ЭМ^, 3>V> F)
имеет группу внутренних симметрии О (и).
Разумеется, можно говорить о внутренних симметриях не только в слу-
случае скалярных полей, но и в случае полей, преобразующихся по другим
представлениям группы Лоренца. Например, лагранжиан Дирака A.9),
как мы уже говорили, инвариантен относительно преобразования
ф(х) -у ф'(х) = е'аф(х). G)
Это означает, что лагранжиан Дирака обладает группой внутренней^ сим-
симметрии U(l). Симметрии G) отвечает интеграл движения Q = fd3x фу°ф,
имеющий физический смысл заряда.
Лагранжиан
1 _ _
?, = - S (H/o^ii - b^cfii,), (8)
2 / = 1
где !i, . . . , ?т — (двухкомпонентные) спинорные поля, очевидным обра-
образом инвариантен относительно замен ?,• ->• ы?/?;-, где иц - унитарная матри-
матрица. Таким образом, группой внутренних симметрии лагранжиана (8) слу-
служит группа U(w) (этот факт был использован при анализе лагранжиана
B.4)).
Лоренц-инвариантный лагранжиан, описывающий скалярные поля \р ,. ..
¦ ¦ ¦, ^" и спинорные поля ? х,..., %т, может быть записан в виде
? = ?b + ?f + Ant. (9)
где ?ь и ?f определяются соотношениями A) и (8),
Ant = 2 ГцкЬЫч?- Ufa)- (Ю)
И к
21

Если наложить дополнительное требование перенормируемости квантовой
теории,отвечающейA0), то следует считать, что U(tp) — полином степе-
степени <4:
Iffy) = af(f + fti/4V + c//fcv>V</ + d//k,v>WV- (И)
Отметим, что коэффициенты Гцк, btj, ... в A0) и A1) можно считать
удовлетворяющими условиям симметрии
Г#* = -Г/ffc, Ьц - bjt, ...
Если ?int = 0, то лагранжиан (9) имеет группу внутренних симметрии
О (и) X U(m), состоящую из ортогональных преобразований скалярных
полей и унитарных преобразований спинорных полей. В общем случае груп-
группой симметрии является подгруппа группы О (и) X U(m), состоящая из
преобразований, сохраняющих jCJn t.
Часто возникает вопрос об описании лагранжианов, для которых груп-
группа внутренних симметрии изоморфна данной группе G (например, груп-
группе SU B)).
Для этого прежде всего нужно реализовать группу G как подгруппу
группы О(и) X U(m) (т.е. построить изоморфное отображение группы G в
О (и) X U (/и). Пусть заданы гомоморфизмы Т\ и Г2 группы G в О (и) и
U(m) соответственно (т.е. заданы и-мерное действительное и т-мерное
комплексное представления группы G). Тогда можно построить гомомор-
гомоморфизм группы С в О(л) X U(m); сопоставив элементу g € G пару матриц
(Ti (g), Г2 (g))- Таким образом, задав представления 7\ и Г2, мы сопо-
сопоставляем элементу g e G внутреннюю симметрию лагранжиана ?ь + ?f,
при которой скалярные поля преобразуются по представлению Т\, а спи-
норные поля - по представлению Г2. Может оказаться, что элементу g Ф 1
отвечают единичные матрицы T%(g) и Г2(?), т.е. тривиальное пре-
преобразование внутренней симметрии. Тогда гомоморфизм группы G в
О (и) X \](т) не является изоморфизмом. Если фиксированы представле-
представления Ti и Tj. по которым преобразуются скалярные и спинорные поля,
то нетрудно выяснить структуру лагранжиана ?}п1) инвариантного отно-
относительно преобразований Tt (g), T2(g). (Соображения, основанные на
теории групп, позволяют перечислить инвариантные относительно, группы
G выражения, составленные из у и |, если известны законы изменения (р
и % при преобразованиях группы G.)
Рассмотрим, например, случай, когда G = SOC), скалярное поле пре-
преобразуется по трехмерному неприводимому представлению группы SOC),
а спинорное поле — по прямой сумме двух трехмерных неприводимых
представлений. (Иными словами, скалярные поля ^= (ipl, i^2,^3) обра-
образуют трехмерный вектор, а спинорные поля — два трехмерных вектора
Li = (?}, L\, L\) и L2 = (L\, L\, ?|). Из двух векторов Ai, A2 можно
составить единственный (с точностью до множителя) скаляр (Ai, A2) =
= 2 А\ А", линейно зависящий от At и А2. Из трех векторов At, А2, А3
а
можно составить единственный скаляр еаьсА\А\А%, линейно зависящий от
Ai, А2, А3; этот скаляр антисимметричен по Aj, А2, А3. Наконец, сущест-
существует единственный скаляр (А, АJ, являющийся полиномом четвертой
степени от компонент вектора А.
22

Воспользовавшись л ими замечаниями, мы без труда можем написать
наиболее общую форму для ?in t в интересующем нас случае:
+2 Ь0, U) +S
В общем случае, для того чтобы перечислить все способы, которыми
можно построить выражение вида A1), инвариантное относительно груп-
пые G, нужно выяснить, сколько раз содержится тривиальное (скалярное)
представление группы G в разложении Г?2', Т^3' и Г/4^ на неприводи-
неприводимые представления (символом Т *** здесь обозначена к-ая симметричес-
симметрическая тензорная степень представления 7"). Для того чтобы перечислить все
способы построения остальных членов в JCj n t, следует решить аналогичную
задачу для представлений т?2^ и Г] ® Т2^ ¦
Легко проанализировать все лагранжианы, имеющие группу симметрии
U(l). В самом деле, всякое комплексное представление группы U(l) раз-
разлагается на одномерные неприводимые представления. Это означает, что
с помощью унитарного преобразования мы можем добиться, чтобы спи-
норные поля ?i, . . . , %m преобразовывались под действием группы U(l)
по формуле
Ь, ¦* exp (in,a) %,, A2)
где П/ — целое число, которое мы будем называть U(l)-зарядом поля ?;-.
(Элемент группы U(l) мы записываем в виде е/а, где а — действительное
число.)
Инвариантный относительно группы U(l) квадратичный лагранжиан,
содержащий спинорные поля, может быть записан в виде
? = ?f + B МуЫ, + к.с), A3)
/
где Mfj может быть отлично от нуля только в случае, если щ + П/ = 0. Лаг-
Лагранжиан A3) очевидным образом распадается на сумму лагранжианов
?„,где символом ?„ обозначена часть лагранжиана A3), содержащая поля
с U(l)-зарядами, по модулю равными и. Для того чтобы выяснить к какой
наиболее простой форме можно привести лагранжиан ?„, введем вместо
полей с отрицательным U(l)-зарядом комплексно сопряженные им поля
(эти поля являются пунктирными спинорами с положительным U(l ^за-
^зарядом) .
Таким образом, лагранжиан ?„ при и > 0 записывается в виде
?п = 2 1- ($,о» ¦ ЭД- - Ъ^ ¦ о"|,) +
^ k +к.с), A4)
где ?, — спиноры, \к ~ пунктирные спиноры.
Пользуясь известными алгебраическими фактами нетрудно установить,
что с помощью унитарного преобразования полей можно сделать матрицу
23

а,к диагональной матрицей с неотрицательными элементами (унитарное
преобразование производится отдельно над полями ?;- и х*) •
* Чтобы доказать это утверждение, рассмотрим а/к как матрицу линей-
линейного оператора А, действующего из комплексного линейного пространст-
пространства Е в комплексное линейное пространство Е'. Нужный нам факт означает,
что в Е и в Е' можно выбрать ортонормированные базисы е) и е'к таким
образом, что в этих базисах матрица оператора А диагональна. Выберем в
качестве базиса е;- вЛортонормированный базис, состоящий из собственных
векторов неотрицательного самосопряженного оператора А*А. Если
A* Aej = Х/е/, где X/ > 0, то построим вектор е|, положив e'j = \j~VzAej.
Построенные таким образом векторы ортогональны и нормированы; это
следует из соотношения
< е'„ е)) = ХГ* Xj>A (Aeb Ae, > =
= Х-'^ХГ* (А+Аеи е,) = Xf^Xf^h,, = 6„.
Необходимый нам базис в Е' получаем произвольным образом, дополнив
систему векторов е\ = \т~1/гАе{ до ортонормирование го базиса^ т
Если матрица а)к — квадратная (т.е. в исходном лагранжиане было оди-
одинаковое число полей с U(l)-зарядом и и U(l)-зарядом — и), это означает,
что лагранжиан ?п распадается на несколько дираковских лагранжианов.
Если матрица а^к не является квадратной, то при приведении лагранжиана
A4) к простейшему виду с необходимостью возникают кроме дираков-
дираковских лагранжианов также лагранжианы, описывающие безмассовые (вей-
(вейлевские) нейтрино.
Таким образом, если фермион обладает зарядом относительно какой-
либо группы U(l) (например, электрическим, барионным, лептонным),
он описывается либо уравнением Дирака (если он обладает массой), либо
уравнением Вейля (если его масса равна нулю). Фермион может представ-
представлять собой массивное майорановское нейтрино только в случае, если он не
обладает никаким U(l)-зарядом (это объясняет особую роль уравнений
Дирака и Вейля в физике элементарных частиц).
Всякое действительное представление группы U(l) распадается в пря-
прямую сумму одномерных тривиальных и двумерных неприводимых пред-
представлений. Двумерные действительные представления группы U(l) полу-
получаются из одномерных комплексных представлений этой группы, если
комплексные представления рассматривать как действительные. Это озна-
означает, что с помощью перехода к новым полям представление группы U(l),
по которому преобразуются скалярные поля, можно привести к следую-
следующему простому виду
<^'-> е"Ча<р', (у = 1, ...,/•), у' -> ipi (у > г).
Новые поля if1, . . . , ifr следует считать комплексными скалярными поля-
полями; при действии exp (ta) € U(l) -комплексное поле i/ умножается на
ехр(/и/а), где и/; как и в случае фермионов, называется иA)-зарядом
поля ttf . Остальные скалярные поля мы считаем действительными; при
преобразованиях группы U(l) они не меняются, а их U(l)-заряд следует
считать равным нулю.
24

Лоренц-инвариантный лагранжиан, содержащий спинорные и скалярные
поля и инвариантный относительно группы U(l), может быть записан с
помощью формулы, аналогичной формуле A3); следует только потребо-
потребовать, чтобы каждый член лагранжиана содержал произведения полей, сум-
сумма U A)-зарядов которых равняется нулю.
§ 4. Калибровочные теории
Как мы уже говорили, лагранжиан Дирака A.9) инвариантен относитель-
относительно преобразования ф'(х) = С1ф(х), где ?/ = ехр(/а) (иными словами, груп-
группа U(l) является группой внутренних симметрии этого лагранжиана).
Этот лагранжиан не инвариантен относительно преобразований вида ф'(х) =
= и(х)ф(х), где U(x) = e\p(ia(x)) — функция, принимающая комплекс-
комплексные значения, по модулю равные единице. Однако можно рассмотреть
лагранжиан биспинорного поля, взаимодействующего с электромагнит-
электромагнитным полем А^ (х), и этот лагранжиан уже будет инвариантен относитель-
относительно преобразований ф'(х) - exp(ia(x)Li(x), если закон преобразования
электромагнитного поля выбрать в виде
где е - электрический заряд.
Для того чтобы включить взаимодействие с электромагнитным полем
существует простое общее правило: нужно производные Эм заменить на
VM = Эм — ieAp и добавить в лагранжиан слагаемое — — FllvFliv, где
4
Ffiv = b^Av — Ъ„Ац — напряженность электромагнитного поля. Это пра-
правило применимо всегда, если мы имеем дело с комплексным полем и лаг-
лагранжиан не меняется при умножении поля на ехр(га). Например, лагран-
лагранжиан комплексного скалярного поля у(х), взаимодействующего с элект-
электромагнитным полем Ац (х), имеет вид
1 т2 1
? = - (Эм Ч> - 1в4д Ф) (d»v*+ ieA»**)- w* - - F^FMV.
Рассмотрим теперь лагранжиан ?, обладающий группой внутренних сим-
симметрии G, т.е. инвариантный относительно преобразований вида у' (х) =
= 8Я> (х) > где я> (х) есть n-компонентное поле, G — группа, состоящая из п-
мерных матриц, g S G. Исходя из лагранжиана ?,, можно построить новый
лагранжиан Z, который инвариантен относительно более широкого класса
преобразований
где g (x) — функция, принимающая значение в матричной группе G. Имен-
Именно: в полной аналогии со стандартным способом введения электромаг-
электромагнитного поля, нужно заменить Эм на VM = Эм + еЛм (х), где Лм (х) - век-
векторное поле, принимающее матричные значения. Выражение VM носит наз-
название ковариантной производной. Закон преобразования поля А^ (х) сле-
25

дует выбрать так, чтобы имело место соотношение
V>'(*W(*)VM*(x), B)
где V д = Эм + еА'ц (х). Легко видеть, что соотношение B) диктует следую-
следующий закон преобразования:
'la1. C)
Из B) следует, что, заменяя Эм на VM, мы получаем, выражение ? инва-
инвариантное относительно преобразований if (х), А^ (х), задаваемых форму-
формулами A) и C). Существенно отметить, что в качестве Аи (х) достаточно
рассматривать не произвольные матричные функции, а лишь функции, при-
принимающие значения в алгебре Ли & группы G. В самом деле, если g (x) —
функция со значениями в матричной группе G, то матрица Эд g(x)g~1 (x)
принадлежит алгебре Ли & группы G. Если а €$, то gag~l €$. Из этих
утверждений следует, что закон преобразования C) не выводит за преде-
пределы алгебры Ли$. В частности, если G = U(m) — группа всех унитарных
матриц, то векторное поле А^ (х) принимает значение в множестве анти-
антиэрмитовых матриц. Легко проверить непосредственно, что преобразова-
преобразования C) переводят антиэрмитово поле А^ {х) снова в антиэрмитово поле.
Таким образом, по лагранжиану ?, обладающему группой внутренних
симметрии G, с помощью замены Эм на VM = Эм + еА^, где Ац {х) - век-
векторное поле, принимающее значение в алгебре Ли#, мы построили выра-
выражение Л, обладающее инвариантностью относительно преобразований
A), C) (локальных калибровочных преобразований). Поле А^ (х) носит
название калибровочного поля или поля Янга—Миллса. Оно является
обобщением электромагнитного поля. (Электромагнитное поле - с точ-
точностью до множителя — i — можно рассматривать как калибровочное поле,
отвечающее группе U A).)
Однако, если мы хотим рассматривать калибровочное поле А^ (х) по-
подобно электромагнитному как динамическое поле, мы должны добавить
к JC инвариантное относительно калибровочных преобразований выражение,
содержащее производные поля А^ (х). Для того чтобы построить такое
выражение, удобно исходить из замечания, что коммутатор ковариантных
производных может быть записан в виде
[V^V^v^ef^y, D)
где &pV = Эд/4,, - Э„ЛМ + е[Ац, Av] носит название напряженности ка-
калибровочного поля А^ (х). Из C) и D) следует, что
поэтому выражение
JCYM = ^ Sp V"
калибровочно инвариантно. Это выражение имеет физический смысл ла-
лагранжиана калибровочного поля А^ (х). Его нужно добавить к ? для то-
Л
го, чтобы получить лагранжиан ?, описывающий поле у(х), взаимодеи-
26

ствующее с калибровочным полем Лм (х). Говорят, что лагранжиан ?
получен из ? с помощью локализации группы внутренних симметрии G.
Группа G носит название калибровочной группы.
Нам будет удобно включить множитель е ("заряд"j в калибровочно<
поле. Тогда ковариантная производная запишется в виде VM = Эм + Лм
напряженность калибровочного поля в виде
Рцр = btlAv- д„Ац + [Ац,А„],
а в выражении для jCYm появится дополнительный множитель е'2.
Рассмотрим простой и в то же время важный пример указанной выше
конструкции. Пусть JC — лагранжиан, описывающий п-компонентное би-
спинорное поле, -лагранжиан A.9). Как мы знаем, всякое преобразование
ф'(х) - g\jj(x), где g € U(и), не меняет лагранжиана A.9). Это означает,
что по рассматриваемому лагранжиану можно построить лагранжиан
? = гфу11 (Эм + Лм)ф - тфф + — Sp F^f»", E)
Ае
где Ац принадлежат алгебре Ли группы U(n), т.е. удовлетворяют условию
антиэрмитовоети. Можно сказать, что лагранжиан E) получен из A.9)
с помощью локализации U(и)-симметрии. Существенно подчеркнуть, что
применяя процедуру локализации симметрии, не обязательно исходить
из полной группы внутренней симметрии лагранжиана. Можно применять
эту конструкцию к любой подгруппе группы внутренних симметрии. На-
Например, для лагранжиана A.9) можно ограничиться локализацией SU(«)-
симметрии. Тогда в выражении E) нужно считать, что матрицы А^ при-
принадлежат алгебре Ли группы SU(n), т.е. удовлетворяют кроме условия
антиэрмитовоети также условию Sp/l,, =0.
До сих пор мы предполагали в этом параграфе, что группа внутренних
симметрии G реализована как группа матриц, действующих в простран-
пространстве, в котором принимает значение многокомпонентное поле ^. Как
мы уже отмечали ранее, часто удобно считать, что группа G "лежит от-
отдельно": в пространстве, в котором принимает значение поле if, задано
представление Т группы G, а лагранжиан ? инвариантен относительно^
преобразований <р (х) =? T(g)y(x). Тогда конструкция лагранжиана ?
видоизменяется следующим образом. Под ковариантной производной
следует понимать выражение VM = Эм + tiA^), где t - представление ал-
алгебры Ли iS группы Ли G, отвечающее представлению Г группы G. Лаг-
Лагранжиан калибровочного поля нужно записывать в виде
где < , > — инвариантное скалярное произведение в группе Ли &, т.е.
скалярное произведение, удовлетворяющее условию {rga,rgb) = < a, b) ,•
где a, b Ei§ , g ? G, Tg - присоединенное представление группы G. (На-
(Напомним, что для матричной группы rg a -gag~l, а инвариантное скалярное
произведение можно определить формулой (а,Ь) = — Spaft.) Легко ви-
видеть, что лагранжиан ? инвариантен относительно локальных калибро-
27

вочных преобразований
(Это следует из закона преобразования ?^„ (х) = тг(х) ^„(х) для на-
напряженности калибровочного поля.)
В случае если группа G разлагается в прямое произведение групп
Gi и Сг, ее алгебра Ли %} представляет собой прямую сумму соответствую-
соответствующих алгебр Ли#г и &г. Это позволяет по инвариантным скалярным про-
произведениям < , } л и < , >2b#iH#2 построить зависящее от двух, па-
параметров семейство скалярных произведений в $:
(x,y) = \i <3с,^>! +\2<х,уJ
v
(мы обозначили через х и х проекции элемента х € & на #i и S?2) • Соот-
Соответственно, лагранжиан калибровочного поля со значениями в алгебре
Ли i§= f§i +f§2 содержит две константы связи:
JCYM = - ^2 < *М"> *"" >1 - ~^2 < Кг-' ?"" >2 •
В обшем случае алгебра Ли компактной группы Ли G разлагается в пря-
прямую сумму простых алгебр Ли; число параметров, от которых зависит
скалярное произведение в 9и, значит, число констант связи в лагранжиа-
лагранжиане калибровочного поля, равно числу алгебр в этом разложении.
§ 5. Частицы, отвечающие неквадратичным лагранжианам
Рассмотрим сначала лагранжиан, описывающий многокомпонентное
скалярное поле:
?=^2Эм^Э"/-Й/(^). A)
Представим его в виде
= Х- 2 Эм J Э" J - - 2 ки J j - Viip\ B)
где V(tfi) — полином, содержащий члены порядка > 3 по степеням ^. В
§ 2 было показано, что в случае, если матрица кц неотрицательно опреде-
определена, лагранжиану JC0 отвечают частицы, квадраты масс которых можно
найти как собственные значения матрицы kir Слагаемое F(i^) можно
учесть по теории возмущений; не изменяя качественной картины спектра,
оно приводит к поправкам для масс частиц. В случае, если матрица к{/-
не является положительно определенной, лагранжиан ?о не является ра-
разумным начальным приближением для теории возмущений. В этом слу-
случае разумно перейти от полей ч>1 (х) к новым полям х'(•*) ~ У1 С*) — с',
где константы с1 подобраны таким образом, чтобы квадратичная по х
часть лагранжиана ? допускала интерпретацию в терминах частиц (т.е.
28

чтобы она имела неотрицательно определенную матрицу ку). Для этого
достаточно выбрать с = (с1 с") таким образом, чтобы в точке с по-
полином W(y) принимал наименьшее значение. Например, если W (f) =
= aif2 + bip*, где а < 0, следует выбрать с = ±v— —• Перейдя к полю
26
X (х) =if (x) — с, мы получаем лагранжиан
а2
C)
который в нулевом приближении теории возмущений описывает части-
частицы массы т2 = — 4а. Точка с, в которой достигается минимум функции
W(if), носит название классического вакуума. Отметим, что классичес-
классических вакуумов может быть много; это явление обычно связано с наруше-
нарушением симметрии. (О нарушении симметрии говорят, если не все преобра-
преобразования, оставляющие инвариантным лагранжиан, переводят в себя класси-
классический вакуум. В частности, полином W (</>) = aif2 + by* инвариантен при
замене if -*¦ — if, но при а < 0 эта симметрия нарушается.)
В общем случае также можно найти спектр частиц, разлагая лагран-
лагранжиан вблизи классического вакуума и оставляя только квадратичные
члены. Однако в случае, если в теории имеются калибровочные поля,
следует наложить предварительно калибровочные условия, снимающие
калибровочную свободу в определении классического вакуума. Напри-
Например, рассмотрим лагранжиан
4
описывающий комплексное скалярное поле у, взаимодействующее с элект-
электромагнитным полем Ар. Здесь классический вакуум определяется усло-
условием \у\ -а, т.е. имеется целое семейство вакуумов у =дехр(/а). Од-
Однако все эти вакуумы калибровочно эквивалентны, поэтому мы можем
наложить калибровочное условие, снимающее вырождение классического
вакуума. В качестве такого условия разумно выбрать
Тогда лагранжиан D) примет вид
JE.= (Эм XJ - ХХ2 (X + 2аJ - X-F\v + е2 А\ (х + аJ, F)
где х (*) = Ч> (х) — О- Очевидно, что получаемый лагранжиан описывает
в нулевом приближении теории возмущений одну скалярную частицу
массы т = 2д\/Х и векторную частицу массы \Jlea. Заметим, что при
X = 0 лагранжиан D) описывает две скалярные частицы (с зарядами ± ё)
и одну безмассовую векторную частицу — фотон. При X > 0 происходит
нарушение U(l)-симметрии. Векторная частица становится массивной и
остается только одна скалярная частица. Это является проявлением так
называемого эффекта Хиггса. Эффект Хиггса имеет место также в неа-
белевых калибровочных теориях (подробнее см. в следующем парагра-
параграфе на примере модели Вайнберга—Салама).
29

Следует подчеркнуть, что описанная процедура нахождения спектра час-
частиц с помощью выбора подходящего начального приближения теории воз-
возмущений и дальнейшего применения теории возмущений основана на пред-
предположении, что поправки не меняют радикально спектра системы. Это пред-
предположение не всегда выполнено. Так, например, в квантовой хромо дина-
динамике (см. § 6) указанный выше рецепт приводит к предсказанию, что
фермионным и калибровочным полям должны отвечать частицы - кварки
и глюоны. Эти частицы не наблюдаются на эксперименте как свободные.
Тем не менее, рассмотрение кварков и глюонов оказывается очень полез-
полезным в области больших импульсов. Это связано с тем, что в квантовой хро-
модинамике теория возмущений работает тем лучше, чем больше участ-
участвующие в задаче импульсы (асимптотическая свобода).
§ 6. Лагранжианы сильных, слабых
и электромагнитных взаимодействий
Адроны можно считать состоящими из кварков. Каждый кварк харак-
характеризуется "цветом" (кварк может быть "желтым", "синим" или • "крас-
"красным") и "ароматом". В настоящее время обнаружено 6 "ароматов", кото-
которые принято обозначать буквами и, d, s, с, b, t. Кварки описываются с по-
помощью многокомпонентного биспинорного поля ф\ (верхний индекс ха-
характеризует "цвет" кварка и пробегает три значения, а нижний индекс
характеризует "аромат" и пробегает шесть значений).
Лагранжиан свободных кварков имеет вид
JC= 2 (*^>Э„**-1Ив*У**). A)
к d "
Поскодьку масса кварка зависит только от "аромата" (но не от "цвета"),
лагранжиан A) инвариантен относительно вращений в "цветовом прост-
пространстве" — преобразований вида ф'а' = g'j • ф'а, где glj — унитарная 3X3
матрица. Таким образом лагранжиан A) инвариантен относительно груп-
группы UC) и, тем более, относительно ее подгруппы SUC). Предполагается,
что сильные взаимодействия описываются лагранжианом jCch, получающим-
получающимся из A) с помощью локализации SU C)-симметрии (цветовой симмет-
симметрии) . Этот лагранжиан — лагранжиан квантовой хромодинамики - может
быть записан в форме
4h= 2 (/^7м(Эм5*+(/1^)фа"-/Иа^^) +
п, к. а
4g k,n a
- 2 та fa фа + — Sp f^f*". B)
Здесь поле А^ принимает значение в алгебре Ли группы SUC) (т.е. С4М)^ =
+ 2 ((Лм)™ (А„)к„ - {А„УЦ (АХ)- C)
30

Частицы, отвечающие полю Лм, носят название глюонов (от слова
"glue" - клей). Таким образом, основная гипотеза квантовой хромоди-
намики состоит в том, что взаимодействие между кварками осуществля-
осуществляется с помощью 8 векторных частиц — глюонов.
Часто удобно вместо биспинорных полей ф*а использовать спинорные
поля ?'а и Rf., считая, что биспинор ф1а состоит из спинора Lfa и пунктир-
пунктирного спинора, комплексно сопряженного спинору R". Отметим, что спи-
спинор ?д преобразуется при преобразованиях из цветовой группы SUC)
так же, как и ф'а (т.е. как вектор), а спинор/?" — как комплексно сопря-
сопряженная величина. (Для группы SU(n) величину, комплексно сопряженную
вектору, можно также рассматривать как вектор с нижними индексами —
ковектор.)
Построение теории, объединяющей слабые и электромагнитные взаимо-
взаимодействия, — теории Вайнберга—Салама — начнем с описания бозонного сек-
сектора этой теории. Будем считать, что имеется два комплексных скаляр-
скалярных поля ipl ,ф2 с лагранжианом
>>-т?2J. D)
Лагранжиан D) очевидным образом инвариантен относительно преобра-
преобразований из группы UB). (Матрица и S UB) преобразует поле у> = (<р1 ,<р2)
в поле </>', для которого ip'{ = и'- </>'; иными словами, поле <р являтеся дуб-
дублетом по группе SUB) и имеет 1ГA)-заряд, равный + 1). Мы можем стан-
стандартным образом включить взаимодействие поля </> с калибровочным
полем, принимающим значения в алгебре Ли группы UB) (алгебре мB)
всех антиэрмитовых матриц). Лагранжиан, описывающий взаимодействие
этих полей, имеет вид
где ^м<? = дyip + Ayif.Ay — антиэрмитова матрица, поле <р записывается
в виде столбца из полей у1, </>2. Отметим, что группа UB) не является
простой (UB) «* U(l) X SUB)), поэтому лагранжиан калибровочного
поля со значениями в алгебре Ли этой группы, содержит две константы
связи#! ng2:
1 1
где fnv — скалярная, a GyV — бесследовая часть напряженности ^„ ка-
калибровочного поля Ам:
Разложению группы UB) в произведение U(l) X SUB) отвечает разло-
разложение алгебры Ли антиэрмитовых матриц в прямую сумму алгебры Ли
матриц, не имеющих следа, и алгебры Ли скалярных матриц. В качестве
генераторов группы UB) удобно выбрать матрицы ill, ir1 /2, ir2/2, ii3II,
где т — матрицы Паули. Первая из этих матриц является генератором под-
подгруппы скалярных матриц, остальные - генераторы группы SUB). Поль-
31

зуясь разложением поля Аи по этим генераторам
1 1
•<4д = — '^д + — 'сд т,
2 2
можно записать лагранжиан E) в виде
1 1
? =
i
- —; (Эд bv - Э„ ?„J - —- (Эд с„ - Э„ с„ + [см, с„] J.
В теории, описываемой лагранжианом E), происходит спонтанное нару-
нарушение симметрии. В самом деле, минимум функции U(y) =X(< у,<р) ~г]2J
достигается при < у, у) = г\2. Выбирая в качестве классического вакуума
¦о
мы видим, что группа симметрии, оставляющих на месте клас-
сический вакуум (группа ненарушенных симметрии), состоит из матриц
вида
С ")¦
\0 1/
где |а| = 1, и, следовательно, изоморфна группе U(l). Генератор группы
ненарушенных симметрии, очевидно, может быть записан в виде —/A +т3).
Воспользовавшись тем, что поля, связанные калибровочным преобразо-
преобразованием, следует рассматривать как физически эквивалентные, мы можем
наложить на поля у1, у2 калибровочное условие i^1 = 0, Im<?2 = 0.
Разлагая лагранжиан E) по отклонениям от классического вакуума
</>о и оставляя только квадратичную по полям часть, мы получаем лагран-
лагранжиан
'2 1
+ -(Сд-йдJП2 +
¦(-)'-
4
1 2
2
1
4
+ - т?2Сд с^ - — (Эд bv - Э„й„J -
2 4^i
G)
^здесь с* = — (Сд ± /с2),
32

Для того чтобы найти массы частиц, описываемых лагранжианом G),
нужно диагонализовать этот квадратичный лагранжиан. Это можно сделать,
перейдя к полям
1
После перехода к новым полям квадратичная часть лагранжиана G) при-
принимает вид
jcqu = (Эд хJ - 4\Vx2 - {- (Эд w- - э„ w-) х
* - э„
1 2 1 r r 2
4 м " " м 4
4
Таким образом, лагранжиан G) описывает скалярную частицу массы
2\г), одну безмассовую векторную частицу (фотон) и три массивных век-
векторных частиц (одна из них имеет массу —]~\gi+g2, две другие -
V2
-р). Величина, соответствующая генератору —/A + т3) группы ненару-
у/2/ 2
шенных симметрии, имеет физический смысл электрического заряда.
Таким образом, электрический заряд - это иA)-заряд, отвечающий груп-
группе U(l) ненарушенных симметрии. (Он отличается от U(l)-заряда, отве-
отвечающего подгруппе U(l), входящей прямым множителем в SUB) X
XUA), - гиперзаряда). Отметим, что из (8) и E) видно, что электро-
glg2
магнитная константа связи равна е = . . (Часто вместо двух кон-
¦Jgt + г?
стант связи gx, g2 рассматривают электромагнитную константу е и угол
0W, определяемый соотношениями #, = elcosOw, g2 = e/sinSw. Угол
Sw называется углом Вайнберга; из эксперимента в w «20°).
Очевидно, что фотон и векторная частица, отвечающая полю ZM =
= (Сд — bfl)/\/gi+ g\ ¦ (Z-бозон), электрически нейтральны. Векторные
частицы, отвечающие полям И/д = ——— (см ± /см), носят названия W*-
2
бозонов. Они имеют электрический заряд ± 1.
Рассмотрим включение фермионов в модель Вайнберга—Салама. Для
того, чтобы описать представления группы UB) «= SUB) X U(l), по ко-
которым преобразуют фермионные поля, удобно характеризовать отдельно
поведение этих полей при преобразованиях из групп SUB) и U(l). (Ha-
33

помним, что неприводимое представление группы SUB) характеризуется
его размерностью, а неприводимое представление группы U(l) — целым
числом, которое мы назвали U(l)-зарядом). Оказывается, что лептоны в
модели Вайнберга—Салама описываются спинорными полями, которые
являются дублетами или синглетами по группе SUB). U(l)-заряды этих
полей (гиперзаряды) принимаются равными соответственно: У^оиЫ =
= - 1> ^sing = 2. Считая, что в модели имеется один дублет I" и один синг-
лет г, мы можем написать наиболее общий лоренц-инвариантный и имею-
имеющий группу внутренних симметрии UB) лагранжиан взаимодействия
спинорных полей 1а,г и скалярного поля <ра в виде
Ant =Г(!аГ*а+ТаГ*а), (9)
где i^,, la, V — поля, комплексно,сопряженные к у", 1а, г. (Напомним,
что мы считаем лагранжиан взаимодействия квадратичным по спинорным
полям и линейным по скалярным полям; см. C.10).). Полный лагранжиан
спинорных и скалярных полей имеет вид
JC-JCf + jCe+JCtat+jGieiMnt. 0°)
где Lf, Zb — безмассовые лагранжианы спинорных и скалярных полей,
•^seif-int = ~М^2 ~~ J?2J ~~ лагранжиан самодействия скалярного поля.
Лагранжиан модели Вайнберга—Салама (для случая одного поколения)
получается из лагранжиана A0) с помощью локализации группы внутрен-
внутренних симметрии UB) (т.е. с помощью замены производных на козариант-
ные производные и добавки лагранжиана калибровочных полей F)).
Отметим, что ковариантная производная поля I" может быть записана в
виде
а ковариантная производная поля г в виде
VMr = (aM+ibM)r.
Наложим, как и раньше, калибровочное условие у* - 0, 1пир2 = 0. Раз-
Разлагая лагранжиан Вайнберга—Салама по полю х = Ч>2 ~ V (т-е- п0 откло-
отклонениям поля if от классического вакуума) и оставляя только квадратич-
квадратичные по полям члены, мы получаем спектр частиц. Бозонная часть этого
спектра была описана выше. Для того чтобы найти фермионную часть
спектра нужно заметить, что массовый член имеет вид
fvl2r + к.с. (И)
Отсюда следует, что поле /' описывает безмассовую частицу (она отож-
отождествляется с электронным нейтрино), а поля 12,г вместе определяют
биспинорное поле, которому отвечает дираковская частицы массы ft\
(эта частица отождествляется с электроном).
Мы описали модель Вайнберга—Салама для одного поколения лептонов
(электрона и электронного нейтрино). Очевидным образом в эту модель
можно включить другие лептоны (мюон и мюонное нейтрино, т-лептон и
т-лептонное нейтрино). Для этого нужно считать, что в модели имеются
34

спинорные поля/f, I", 1%, а=\, 2, являющиеся дублетами по SUB) и
спинорные поля Г\,гг,гъ, являющиеся синглетами по группе SUB).
U A)-заряды этих полей следует полагать равными соответственно —1 и
+2. Лагранжиан взаимодействия спинорных полей /?, гк со скалярным
полем у" следует выбрать в виде
JC7= I /Х/^.^+к.с). A2)
/ = 1
Повторяя проведенные выше рассуждения, убеждаемся, что модифициро-
модифицированный описанным выше образом лагранжиан описывает три типа безмас-
безмассовых частиц (нейтрино) и три типа заряженных частиц с массами fit},
Отметим, что выражение A2) не является самым общим лагранжианом
взаимодействия полей 1"к, гк, у". Можно рассмотреть также взаимодействие
вида
JC7= I /*/,%*„+ К.С, A3)
/, к = 1
где flk -произвольнаякомплексная матрица.
Однако с помощью унитарной замены переменных лагранжиан A3)
приводится к виду A2). (Как показано в § 3 матрицу/lfc можно диаго-
нализовать, умножив слева и справа на унитарные матрицы.) Это означа-
означает, что в модели Вайнберга—Салама нет смешивания поколений лептонов.
Для того чтобы сделать нейтрино в модели Вайнберга—Салама массивными
нужно ввести в эту модель поля sx, s2, s3, являющиеся синглетами по
группе SUB) и имеющие U(l)-заряд равный нулю. При введении этих
полей утверждение об отсутствии смешивания поколений перестает иметь
место.
В объединенной теории сильных, слабых и электромагнитных взаимо-
взаимодействий калибровочная группа должна содержать как группу сильных
взаимодействия SUC), так и группу Вайнберга—Салама SUB) X U(l).
Таким образом, минимальной калибровочной группой в этом случае явля-
является группа SUC) X SUB) X U(l). Эта группа нарушается до группы
SUC) X U(l) с помощью дублета комплексных скалярных полей i^1, <?2,
преобразующегося как двумерный вектор относительно группы UB) «=
*** SUB) X U(l) и не меняющегося при преобразованиях группы SUC).
Поэтому бозонный сектор SUC) X SUB) X U(l)-теории отличается от
соответствующего сектора в модели электрослабого взаимодействия
только добавлением восьми калибровочных полей, отвечающих группе
SUC) (глюонных полей).
Фермионный сектор SUC) X SUB) X U(l)-модели содержит прежде
всего лептоны — поля, фигурирующие в модели Вайнберга—Салама. Они
остаются. неизменными при преобразованиях группы SUC) (являются
SUC)-синглетами). Кроме того, имеются поля кварков, преобразующиеся
по векторному или ковекторному представлению группы SUC) (по
представлениям 3 и 3). (Если кварки представлять с помощью биспинор-
ных полей 1//д, то все они преобразуются по векторному представлению
группы SU C). Однако нам удобнее работать со спинорными полями L'a и
Щ•) Поля кварков могут быть дублетами или синглетами по группе SUB).
35

Именно: предполагается, что поля кварков, преобразующихся по векторно-
векторному представлению группы SUC), являются дублетами относительно груп-
группы SUB) и имеют Щ1)-заряд равный 1/3. Кварки, преобразующиеся по
ковекторному представлению группы SUC), не меняются при преобразо-
преобразованиях группы SUB) (являются SUB)-синглетами), их U(l)-заряд может
быть равен — 4/3 или 2/3. Таким образом, кварковые поля преобразуются
по одному из представлений C, 2, 1/3), C, 1, 2/3) или C, 1, -4/3) (пер-
(первая из цифр характеризует закон преобразования относительно группы
SUC), вторая — относительно группы SUB), третья — заряд относительно
группы U A)).
Отметим, что U(l)-заряды кварков мы, следуя традиции, считаем дроб-
дробными - кратными 1/3. Это означает, .что кварковые поля преобразуются
по трехзначному представлению группы U(l). Разумеется, можно было бы
добиться целочисленности всех зарядов за счет переопределения генератора
группы U(l).
В минимальном наборе кварковых полей, способных описать современ-
современные экспериментальные данные, каждый из мулыиплетов C, 2, 1/3),
C, 1, -4/3), C, 1, 2/3) встречается трижды. (Другими словами, сущест-
существует три поколения кварков.) Таким образом, набор кварковых полей
состоит из спиноров L™, La, L™, Ral, Ra2,K3-Ki. Яа2, Яаз, где а =
= 1, 2, 3 — индекс, относящийся к группе SUC) (цветовой индекс), а =
= 1,2— индекс, относящийся к группе SUB), a U(l)-заряды полей L, R и
R равны соответственно 1/3, —4/3 и 2/3.
Для того чтобы построить лагранжиан SUC) X SUB) X иA)-модели,
нужно написать наиболее общий SUC) X SUB) X U(l)-инвариантный
лагранжиан ?, описывающий взаимодействие всех спинорных полей модели
и поля у01, а затем включить взаимодействие с калибровочными полями
(локализовать SUC) X SUB) X U(l)-симметрию в лагранжиане JC).
Часть лагранжиана ?, отвечающая лептонным полям и полю <р, была пост-
построена выше, поэтому мы должны описать только часть лагранжиана, отве-
отвечающую взаимодействию кварковых полей с полем ^. Легко видеть, что
инвариантными относительно группы SUC) X SUB) X U(l) являются
только выражения вида
и комплексно сопряженные им выражения. (Здесь <ра = еар<р®, Тра = <^а.)
Отметим, что поле Тр преобразуется по тому же представлению группы
SUB), что и поле </>, но имеет противоположный U(l) -заряд.) Отсюда
следует, что интересующая нас часть лагранжиана Z имеет вид
An, = 2 Aik L™Rak *a + Bik I?* Rak7pa) + э. с A4)
i, к
Используя унитарные замены кварковых полей
не меняющие свободной части лагранжиана, можно упростить вид матриц,
Ajk и Bik. Прежде всего, матрицу Ajk можно сделать диагональной: Ац =
= а.дц (см. § 2). Далее, с помощью преобразования полей R можно сделать
36

матрицу Вц эрмитовой (это вытекает из возможности записать любую
матрицу в виде произведения эрмитовой на унитарную). Однако после
этого еще остается возможность упростить матрицу Вц, проделывая преоб-
преобразования вида L?a ->• ukL?a, Rak ->• и~к Rak, к\,к ->• u~k Rak, где ик — ком-
комплексные числа, по модулю равные единице. Без ограничения общности
можно считать, что произведение чисел ик равно 1 (это следует из замечания,
что в случае, когда все ик равны между собой, матрицаВц не меняется).
Отсюда видно, что в случае двух поколений матрицу Вц можно сделать
действительной. (Двумерная эрмитова матрица В определяется двумя
действительными матричными элементами Вц и В22 и одним комплекс-
комплексным параметром В12 = В21. С помощью имеющейся у нас свободы мы
можем сделать этот параметр действительным.) В случае трех поколений
матрицу В, вообще говоря, нельзя сделать действительной. (Три комплек-
комплексных параметра В12 = В21, В13 = Вги В2Ъ - В32 нельзя сделать одновре-
одновременно вещественными, поскольку в нашем распоряжении есть только два
независимых вещественных параметра.)
Для того, чтобы проанализировать, какие частицы описываются интере-
интересующим нам лагранжианом, нужно, как всегда, разложить лагранжиан по
отклонениям от классического вакуума, оставить квадратичную часть и
диагонализовать ее. Для бозонного сектора и для лептонных полей соответ-
соответствующая процедура была уже проведена при анализе модели Вайнберга—
Салама. Чтобы выяснить, какие частицы отвечают кварковым полям ??а,
Rak и Rak, нужно диагонализовать соответствующий массовый член. Этот
член получается из A4) заменой поля &а на его вакуумное значение @, т?)
и имеет вид
Jt= 2 (AikLfRakV+BikLfRakv)+э.с. A5)
/, it = i
Для случая двух поколений A5) можно записать в виде
Л = 2 2
i. к =1
эх. A6)
(Матрицу А {к считаем диагональной: Aik = fl,-5,-fc) a Bjk — эрмитовой и
действительной.) Объединив спиноры L, Ь"*, L.%1, L%2 со спинорами, ком-
комплексно сопряженными к Ral, Ral, Ra2, Ra2 соответственно, в биспиноры
и" ,d'a?a ,s'a, можно переписать A6) в форме
•М =а117м"м +а2т]сс
+ bl2r}(cFs' +7d')
Далее, перейдем от биспиноров d',s' к биспинорам
d = d'cosec - s'sin0c, s = d'sin0c + s'cosflc.
Угол 0с можно выбрать таким образом, чтобы массовый член, выражен-
37

ный через поля и, с, d, s был диагоналей. При таком выборе поля и, с, d, s
соответствуют физическим кваркам. Угол вс, характеризующий смеши-
смешивание поколений, называется углом Кабиббо (из эксперимента следует,
°)
§ 7. Большие объединения
SUC) X SUB) X иA)-модель описывает одновременно сильные, сла-
слабые и электромагнитные взаимодействия, но не может рассматриваться
как единая теория этих взаимодействий, поскольку каждой из групп
SUC), SUB) и U(l) в ней отвечает своя константа связи. Действительное
объединение этих трех типов взаимодействия достигается в так называемых
теориях большого объединения. Модели большого объединения по мате-
математической структуре повторяют модель Вайнберга — Салама и SUC) X
X SUB) X иA)-модель, но они основаны на простой калибровочной группе
и поэтому в них фигурирует только одна константа связи. Возможность
обойтись всего одной константой связи возникает потому, что в кванто-
квантовой теории поля эффективная константа связи зависит от импульса. Точнее
говоря, даже в низшем приближении нельзя использовать при изучении
матрицы рассеяния константу связи, входящую в лагранжиан ("голую"
или "затравочную" константу связи). Ее следует заменить другим числом,
зависящим от характерного импульса частиц, участвующих в процессе
рассеяния.
а Квазиклассическое приближение отвечает в рамках теории возмуще-
возмущений использованию древесных диаграмм. (Разложение по h отвечает груп-
группировке диаграмм теории возмущений по числу замкнутых петель.) Од-
Однако, ограничение древесными диаграммами с голыми вершинами недоста-
недостаточно, хотя часто можно ограничиться рассмотрением древесных диаграмм
с "жирными" вершинами, т.е. вершинами, в которых "голая" константа
связи заменена зависящей от импульсов входящих линий вершинной
функцией. Если все импульсы в диаграмме по порядку величины равны
одному и тому же импульсу р, то можно считать, что в каждой из вершин
стоит одно и то же число (зависящее, конечно, от р). Это означает, что мы
можем пользоваться квазиклассическим приближением (т.е. древесными
диаграммами или, в следующем порядке, диаграммами с одной петлей),
считая, что константа связи зависит от р. Подробнее об этой зависимости
см. § Ф18. Ў
В SUC) X SUB) X иA)-модели зависимость эффективных компонент
связи от импульса такова, что при некотором значении импульса
(~1015 ГэВ) эти константы становятся близкими друг к другу. Поэтому
предполагается, что истинная калибровочная группа шире, чем группа
SUC) X SUB)X U(l), но ниже некоторой энергии симметрия нарушается
до SUC) X SUB) X U(l) (и далее, при энергиях порядка Ю2 ГэВ до
SUC)XUA)).
Существует много разных возможностей для выбора калибровочной
группы G, лежащей в основе теории большого объединения. Наименьшая
из возможных групп — это группа SUE). Мы остановимся немного под-
подробнее на БиE)-модели большого объединения. Бозонная часть этой моде-
модели состоит из двух многокомпонентных скалярных полей |^их, преобра-
38

зующихся соответственно по присоединенному B4-мерному) и вектор-
векторному E-мерному) представлениям группы SUE). (Конечно, в бозонную
часть модели входят и векторные калибровочные поля, принимающие
значение в алгебре Ли группы SUE).) Потенциал взаимодействия ска-
скалярных полей подбирается таким образом, чтобы классический вакуум
можно было выбрать в виде у = снр0, х = &Хо, где
-2/3
-2/3 О
-2/3
О 1
l/
Хо = 0 , A)
а и Ъ — действительные числа. (Поле if мы рассматриваем как эрмитову
матрицу с нулевым следом, а поле х — как столбец.) Группа ненарушен-
ненарушенных симметрии, отвечающая этому выбору классического вакуума, явля-
является подгруппой группы SUE), состоящей из блочно-диагональных мат-
матриц вида
I ч
(Здесь К — матрица третьего порядка.) Очевидно, что К — унитарная мат-
матрица, |/| = 1 и / • det АГ = 1; иными словами, К = ехр(-/'а)-Л, / = ехр(Зга),
А 6 SUC). Отсюда следует, что группа ненарушенных симметрии Я локаль-
/ 2тг / 2тг\
не изоморфна группе SUC) X U(l). I Если а = п—, А = expl in— 1,
то К = 1, / = 1, поэтому группа Н получается из SUC) X U(l) факториза-
факторизацией по подгруппе, состоящей из трех элементов. J Однако константы
а ~ 1015 ГэВ и b ~ 102 ГэВ выбираются таким образом, чтобы при боль-
больших энергиях нарушение симметрии, связанное с полем х, было несущест-
несущественным. При этих энергиях группа ненарушенных симметрии расширяется
до группы #0, состоящей из всех матриц h S SUE), коммутирующих
с матрицей i^0, т.е. из всех матриц вида
/ M
~ \ 0
0
If/' C)
где М - матрица 3 X 3, TV - матрица 2X2. Группа Яо локально изоморфна
группе SUC) X SUB) X U(l), поскольку h = йоехр(/а^о), h0 получается
из h заменой М на Мо ,N т No, detAf0 = detiV0 = 1, а <?0 определяется соот-
соотношением A). (Таким образом, ip0 является генератором группы U(l).)
Фермионный сектор 8иE)-модели состоит из спинорных полей фа
и каЪ, а, Ъ = 1,2, 5. При преобразованиях группы SUE) поле фа
является ковектором (вектором с нижним индексом), а поле каЪ - анти-
антисимметричным тензором. (Иными словами, фа преобразуется по представ-
представлению 5, а каЬ — по представлению 10.) Легко провести разложение этих
39

представлений по группе SUC) X SUB) X U(l). Будем обозначать индексы
1, 2, 3 первыми буквами греческого алфавита, а индексы 4, 5 - последни-
последними буквами. Тогда поле фа разлагается на неприводимые компоненты фа
и фт. Очевидно, что фа является SUC>TpmuieTOM, (точнее преобразуется
по ковекторному представлению 3 группы SUC)), БиB)-синглетом
и имеет U(l)-заряд (гиперзаряд), равный 2/3, а фт является SUC)-CHHrne-
том, 8иB)-дублетом и имеет и(])-заряд, равный — 1. Далее, поле каЬ
разлагается на неприводимые компоненты ка^ - е01® ру, кат и кто = eTav.
Очевидно, что р7 является 8иC)-ковектором, 811B)-синглетом и имеет
иA)-заряд равный -4/3. Далее, каг является 8иC)-вектором, SUB)-
дублетом и имеет иA)-заряд 1/3. Наконец, v является SUC)- и SUB)-
синглетом с иA)-зарядом 2. Мы видим, что представления группы SUC) X
X SUB) X U(l), получившиеся при • разложении представлений группы
SUE), фигурирующих в 5иE)-модели, совпадают с представлениями,
по которым преобразуются кварки и лептоны в SUC) X SUB) X U(l)-
модели. Отсюда можно заключить, что при энергиях в интервале 100 ГэВ <
<Е <IOIS ГэВ 8иE>модель сводится к SUC) X SUB) X иA)-модели.
Дальнейшее нарушение симметрии с помощью поля х- как мь' видели,
уменьшает группу симметрии до SUC) X U(l).

ГЛАВА II
ТОПОЛОГИЧЕСКИЕ МЕТОДЫ КВАНТОВОЙ ТЕОРИИ ПОЛЯ
§ 1. Топологически стабильные дефекты
Мы опишем сейчас применение топологии к классификации дефектов
(нарушений локального равновесия) в конденсированных средах. Воз-
Возможности приложения топологии связаны с тем, что во многих важных слу-
случаях состояние термодинамического равновесия оказывается вырожден-
вырожденным при температурах ниже некоторой критической температуры Тс. На-
Например, в ферромагнетике ниже критической температуры (точки Кюри)
возникает спонтанная намагниченность и вектор намагниченности М может
иметь различные направления в состоянии термодинамического равновесия.
В изотропном ферромагнетике вектор М при Т <ТС может иметь про-
произвольное направление; длина этого вектора зависит от температуры:
| М | = М(Т). Это означает, что при Т <ТС равновесные состояния изотроп-
изотропного ферромагнетика находятся во взаимно однозначном соответствии
с точками двумерной сферы S2. Иными словами, пространством вырож-
вырождения равновесного состояния для изотропного ферромагнетика является
сфера S2.
Для анизотропного ферромагнетика типа "легкая плоскость" вектор
спонтанной намагниченности М лежит в некоторой плоскости; длина его
снова зависит от температуры. В этом случае пространством вырождения
является окружность S1 (равновесные состояния находятся во взаимно
однозначном соответствии с точками окружности). Наконец, в ферромаг-
ферромагнетике типа "легкая ось" в равновесном состоянии возможны два значения
вектора намагниченности, отличающиеся друг от друга знаком. Пространст-
Пространство вырождения состоит в данном случае из двух точек (его можно рас-
рассматривать как нульмерную сферу 5°).
В общем случае множество всех равновесных состояний при фикси-
фиксированной температуре Т будем называть пространством вырождения и
обозначать символом R. Пространство вырождения Л можно рассматривать
как топологическое пространство; иными словами можно говорить о рав-
равновесных состояниях, близких друг к другу. (Нетрудно дать общее опре-
определение топологии в пространстве R; мы не будем этого делать, посколь-
поскольку в конкретных ситуациях всегда ясно, какие равновесные состояния
следует считать близкими.)
Структуру пространства вырождения обычно можно исследовать с
помощью теории Ландау фазовых переходов второго рода. Напомним,
41

что равновесное состояние определяется условием минимальности свобод-
свободной энергии. В теории Ландау предполагается, что равновесное состояние
можно найти, минимизируя свободную энергию не по множеству всех
состояний, а по множеству состояний, определяемому конечным числом
параметров (эти параметры носят название параметров порядка). Напри-
Например, для ферромагнетика параметром порядка является вектор намагни-
намагниченности М. В изотропном случае свойства симметрии позволяют заклю-
заключить, что свободная энергия является функцией от М2 и Г. При Т > Тс
минимум свободной энергии по М2 достигается при М = 0, при Т < Тс
этот минимум достигается при М2 = М2(Т) > 0. В случае одноосного крис-
кристалла малая анизотропная добавка к свободной энергии имеет при соот-
соответствующем выборе координат вид КМ\. Если К > 0, то минимуму
свободной энергии отвечает Mz = 0; поскольку свободная энергия остается
инвариантной относительно вращений вокруг оси г при Т <ТС множество
минимумов образует окружность. Мы имеем дело с ферромагнетиком
типа "легкая плоскость". При К < 0 свободная энергия достигает мини-
минимума, когда вектор М направлен по оси z (ферромагнетик типа "легкая ось").
Обычно вырождение равновесного состояния связано с явлением нару-
нарушения симметрии,. Так, например, функционал энергии для изотропного
ферромагнетика инвариантен относительно группы вращений SOC).
В то же время равновесные состояния характеризуются вектором М и,
следовательно, не обладают БОC)-симметрией; подгруппа группы сим-
симметрии, состоящая из вращений, оставляющих на месте фиксированный
вектор М, изоморфна группе SOB). В общем случае обозначим симво-
символом G группу преобразований, не меняющих функционала энергии, а сим-
символом Н — подгруппу группы G, состоящую из преобразований, оставляю-
оставляющих инвариантным фиксированное равновесное состояние е 6 R. (Груп-
(Группа Н называется в математике стационарной подгруппой элемента е е R,
а в физике — группой ненарушенных симметрии.) При преобразованиях
из группы G равновесное состояние снова переходит в равновесное состоя-
состояние. (Равновесное состояние находится из условия минимальности сво-
свободной энергии, а функционал свободной энергии, как и функционал
энергии, инвариантен относительно группы G.) Обычно приходится стал-
сталкиваться с ситуацией, когда два любых равновесных состояния можно
получить друг из друга с помощью преобразования из группы G. (Груп-
(Группа G действует на R транзитивно.) Физически это означает, что вырождение
равновесного состояния полностью обусловлено свойствами симметрии.
Если эта ситуация имеет место, то пространство вырождения R можно
отождествить с пространством смежных классов G/H (см. § А6).
Мы рассмотрим сейчас ситуацию, когда в некоторой области исследуемо-
исследуемого тела установилось локальное термодинамическое равновесие, т.е. в каж-
каждой точке можно говорить о температуре тела, но эта температура зависит
от точки. Если равновесное состояние вырождено, то при локальном термо-
термодинамическом равновесии будут зависеть от точки не только'температура,
но и другие параметры, характеризующие равновесное состояние (напри-
(например, вектор намагниченности для ферромагнетиков). Естественно считать,
что эта зависимость непрерывна.
Покажем, прежде всего, что, имея информацию о локально равновес-
равновесном состоянии на некотором множестве, мы иногда можем сделать вывод,
42

что вне этого множества локальное равновесие должно нарушаться. Рас-
Рассмотрим простейший случай ферромагнетика типа "легкая ось" и предпо-
предположим, что существуют две точки, в которых вектор спонтанной намаг-
намагниченности имеет противоположные направления. Соединим эти две точки
произвольной кривой. Если бы на всей кривой состояние ферромагне-
ферромагнетика было локально равновесным, то вектор намагниченности был бы
непрерывной функцией от точки кривой и, следовательно, обращался бы
в нуль в некоторой точке этой кривой. (Напомним, что вектор намагни-
намагниченности все время направлен по "легкой оси", т.е. имеет вид М(х)п, где
М(х) — числовая функция, п — постоянный вектор. Поскольку функ-
функция М(х) меняет знак, она должна обращаться в нуль.)
Мы видим, что либо на кривой существует точка с температурой Т> Тс,
либо где-то нарушается условие локального равновесия. Если исключить
возможность Т> Тс, то мы приходим к выводу, что локальное равновесие
нарушается на двумерной поверхности. (Это следует из того, что выбранные
точки можно соединить зависящим от двух параметров семейством кри-
кривых, не пересекающихся друг с другом, и на каждой из кривых этого се-
семейства существует по крайней мере одна точка, в которой локальное
. равновесие нарушено; см. рис. I). Дефекты такого типа называются до-
доменными стенками. Конечно, равновесие может нарушаться и на множест-
множестве, имеющем большую размерность (например, возможно, что нарушение
происходит в некоторой окрестности двумерной поверхности — доменная
стенка имеет ненулевую толщину).
Перейдем к изотропному ферромагнетику. Будем считать, что локаль-
локальное равновесие с Т < Тс имеет место на некоторой двумерной сфере. Тогда
векторы намагниченности в точках этой сферы образуют ненулевое век-
РИС. 1
Рис.2
торное поле. Иными словами, сопоставляя каждой точке сферы вектор
намагниченности в этой точке, мы получаем отображение сферы 52 в прост-
пространство !R3\{0} (пространство Р3 с выколотым началом координат).
Если локальное равновесие с Т < Тс реализуется также внутри сферы,
то ненулевое векторное поле определено также в шаре D3, ограниченном
сферой S2, и, значит, отображение сферы S2 в R3 \{0} может быть продол-
продолжено до отображения шара D3 в П3\{0}. Не любое отображение сферы
можно продолжить на шар; для того, чтобы такое продолжение было
возможным, отображение должно быть гомотопным нулю; см. § Т1.
43

(Отображение называется гомотопным нулю, если его можно непрерывно
продеформировать в отображение, переводящее всю сферу в одну точку.)
Например, если все векторы намагниченности, на сфере S2 направлены
по нормали к сфере (поле этих векторов имеет вид ежа, рис. 2), то нельзя
с помощью непрерывной деформации сделать все векторы поля параллель-
параллельными друг другу и, следовательно, нельзя продолжить это поле в поле
ненулевых векторов на ZK (см. § Т2). Это означает, что всюду внутри
сферы S2 не может быть локального равновесия с Т< Тс.
Равновесие может быть нарушено всего в одной точке; тогда говорят,
что мы имеем дело с точечным дефектом. Однако, нельзя исключить воз-
возможность того, что равновесие нарушено в нескольких точках или даже
в целой области (быть может, состоящей из нескольких связных компо-
компонент) .
Всякому отображению / сферы Sk « DR*+ 1 \{0} можно сопоставить
целое число и(/), не изменяющееся при непрерывном изменении отобра-
отображения /. Отображение /0 гомотопно отображению /У (т.е. /0 можно непре-
непрерывно продеформировать в Д) в том и только в том случае, если и(/0) =
= h(/i). Иными словами, множество { Sk, Kfc + 1\{0}} гомотопических
классов отображений сферы Sk в !Rfc + 1\{0} находится во взаимно одно-
однозначном соответствии с множеством целых чисел. (В § Т2 аналогичное
утверждение доказано для отображений Sk в Sk. Его можно перенести
на отображения Sk в IRfc + 1\{0}, воспользовавшись результатами § T1.)
В частности, отображение сферы Sk в [RAr + 1\{0} гомотопно нулю в том
и только в том случае, если n(f) = 0. Пользуясь этими утверждениями, сопо-
сопоставляем дефекту (множеству, где нарушено локальное равновесие)
в изотропном ферромагнетике целое число, характеризующее топологи-
топологический тип дефекта. Нужно окружить дефект сферой S 2 и сопоставить ему
целое число, определяемое векторным полем М(х), рассматриваемым
как отображение сферы S2 в И3 \{0}. Если это целое число не равно нулю,
то дефект называется топологически нетривиальным.
Наконец, обратимся к ферромагнетику типа "легкая плоскость". Рас-
Рассмотрим окружность, на которой имеет место локальное равновесие
с Т < Тс. Сопоставляя каждой точке окружности значение вектора на-
намагниченности в этой точке, мы получаем отображение окружности S1
в К2\{0} (напомним, что вектор намагниченности является ненулевым
вектором, лежащим в "легкой плоскости"). Если это отображение не го-
гомотопно нулю, то его нельзя продолжить в непрерывное отображение
круга D2, ограниченного окружностью 5',в R2\{0}. На окружность S1
можно натянуть однопараметрическое семейство непересекающихся друг
с Другом поверхностей, топологически эквивалентных кругу. Если век-
векторы намагниченности на S1 порождают негомотопное нулю отображение,
то на каждой из этих поверхностей должна -быть по крайней мере одна
точка, в которой нарушается локальное равновесие (или Т > Тс). Таким
образом, в предположении Т < Тс должна существовать целая линия,
состоящая из точек, в которых нарушено локальное равновесие (тополо-,
гически нетривиальный нитевидный дефект.).
Снова следует подчеркнуть, что равновесие может нарушаться не только
на линии, но и на множестве, имеющем большую размерность. Как пра-
44

вило, равновесие нарушается в малой окрестности некоторой линии. На-
Например, векторы намагниченности могут вести себя так, как это изобра-
изображено на рис. 3 — вне некоторой окрестности вертикальной линии имеет
место локальное равновесие (вектор намагниченности лежит в горизон-
горизонтальной плоскости — "легкой плоскости"), на линии вектор напряжен-
напряженности вертикален, а в окрестности происходит непрерывный переход от
горизонтального направления вектора намагниченности к вертикальному.
Рис.3
Важно отметить, что все дефекты, существование которых гарантиру-
гарантируется указанными выше соображениями, устойчивы, т.е. не могут исчезнуть
с течением времени. Рассмотрим для определенности топологически нетри-
нетривиальный дефект в изотропном ферромагнетике. На сфере S2, окружающей
этот дефект, векторы намагниченности М(х) задают негомотопное нулю
отображение этой сферы в IR3\{0}. Если с течением времени локальное
равновесие на сфере не нарушается, то это отображение непрерывно дефор-
деформируется. Это означает, что в начальный и конечный момент времени
отображения сферы гомотопны друг другу. По предположению в начальный
момент времени отображение сферы, определяемое векторами М(х), не-
негомотопно нулю; отсюда следует, что это же справедливо и в конечный мо-
момент времени.
Таким образом, при наложенных нами условиях внутри сферы
все время существует дефект (хотя, конечно, положение этого де-
дефекта может меняться). Более того, сохраняется не только сам дефект,
но и число, характеризующее топологический тип этого дефекта, поскольку
это число не меняется при непрерывном изменении поля М(х) на сфере,
окружающей дефект. Совершенно аналогичные рассуждения применимы
и в других рассмотренных нами случаях.
Перейдем к анализу общей ситуации. Будем считать для простоты, что
температура не зависит от точки. Тогда каждой точке области U, в которой
имеет место локальное равновесие, сопоставляется некоторая точка прост-
пространства вырождения R; иными словами, определено отображение / об-
области UbR.
Если сфера S2 лежит в области U, то отображение / определено на S2.
Если отображение / сферы S2 в R негомотопно нулю, то это отображение
нельзя продолжить на шар D3, ограниченный сферой S2. Это означает,
что внутри сферы S2 есть дефект - множество точек, в которых отсутст-
отсутствует локальное равновесие (т.е. имеются точки, не принадлежащие об-
области U).
Пусть теперь состояние рассматриваемой системы меняется с течением
времени таким образом, что локальное равновесие на сфере S2 сохраня-
45

ется. Тогда отображение /сферы S2 в R может зависеть от времени, но
эта зависимость должна быть непрерывной. Если два отображения можно
соединить непрерывным семейством отображений, то эти отображения
гомотопны (принадлежат одному гомотопическому классу). Мы ви-
видим, что гомотопический класс отображения не меняется с течением
времени.
Гомотопический класс отображения / характеризует топологический
тип дефекта. Так, например, в случае изотропного ферромагнетика R = S2
и гомотопический класс отображения / сферы S2 в R характеризуется
целым числом - степенью отображения (§ Т2). Это означает, что тополо-
топологический тип дефекта также можно охарактеризовать целым числом. Важ-
Важно отметить, что топологический тип дефекта не зависит от выбора
сферы S2. Точнее, пусть К — дефект, a S2 и 5| - две сферы, каждая иэ
которых содержит К и не содержит других точек, в которых локальное
равновесие нарушено. Тогда множества {S2, R ) и { S\ ,R) (множества
гомотопических классов отображений сфер S2 и 5| в R) можно отождест-
отождествить между собой. (Это вытекает из замечания, что сферу S2 можно не-
непрерывно продеформировать в сферу S2 таким образом, что в процессе
деформации сфера все время находится в области U, где есть локальное
равновесие.)
Из сказанного выше ясно, что топологический тип дефекта внутри сфе-
сферы S2 не меняется с течением времени, если на сфере все время сохраня-
сохраняется локальное равновесие.
Отметим, «по в множестве {Sk, R } гомотопических классов отобра-
отображений сферы Sk в пространство R может быть введена операция сложения.
Если пространство R односвязно, то эта операция оказывается однознач-
однозначной, и множество {Sk,R } является коммутативной группой относительно
операции сложения (§ Т12). Эта группа называется Ar-мерной гомото-
гомотопической группой пространства R и обозначается символом 7Г^(Л). В слу-
случае, если пространство R неодносвязно, операция сложения в { Sk,R),
вообще говоря, многозначна (§ Т12). Однако гомотопическая группа
7Гк(Л) по-прежнему может быть определена для любого к > 1; она оказы-
оказывается коммутативной при к > 2 у § Т15). Множество { Sk, R } для связ-
связного пространства R можно отождествить с множеством nk(R)liTi(R)
орбит группы iti(R), естественно действующей в nk(R). Иными словами,
{Sk, R) получается из irk(R) с помощью факторизации по Tii(R) (см.
§ Т13).
В связи с тем, что группа ni(R), вообще говоря, некоммутативна, опе-
операцию в этой группе и соответствующую многозначную операцию в мно-
множестве { S1 ,R } принято называть не сложением, а умножением.
Если U - область в Kfc+1, ограниченная снаружи fc-мерной сферой Sk
и изнутри двумя А;-мерными сферами Sk и Sk, a F — отображение облас-
области U в R, совпадающее на сферах Sk и Sk с отображениями ft и/2, а на
сфере Sk с отображением /, то гомотопический класс [/] отображения
равен сумме (точнее, одному из возможных значений суммы) гомотопи-
гомотопических классов [fi] и [f2] гомотопических классов отображений/! и/2;
46

см. § Т12. (Это утверждение можно при желании рассматривать как опре-
определение сложения в множестве { S к, R ) ) •
Укажем физическую интерпретацию сформулированного только что
предложения. Пусть в области U С IR3, ограниченной снаружи сферой S2
и изнутри сферами S2 и 5|, имеет место локальное равновесие. Обозначим
символом Kt дефект, расположенный внутри сферы SJ, символом К2 -
дефект внутри сферы 5| и символом К — дефект, состоящий из этих двух
дефектов (К = Кt U К2). Тогда, очевидно, на области U задано отображе-
отображение в пространство вырождения R. Гомотопический класс этого отобра-
отображения, рассматриваемого на S2, определяет топологический тип дефекта К,
а гомотопический класс этого же отображения, рассматриваемого на сферах
S2 и Sf, определяет топологический тип дефектов К\ и^2. Мы видим,
что топологический тип "составного" дефекта К равен сумме топологи-
топологических типов дефектов К\ и К2 (рис. 4). Поскольку операция сложения
многозначна, точнее было бы сказать что топологический тип дефекта К
равен одному из значений суммы топологических типов дефектов Ki и^2.
Сформулированное только что утверждение позволяет получить инфор-
информацию о динамике точечных дефектов. В частности, из него следует, что
при распаде точечного дефекта на два точечных дефекта сумма топологи-
топологических типов образовавшихся дефектов равна топологическому типу
распавшегося дефекта.
Если пространство R односвязно, как мы говорили, операция сложения
в множестве {S2,R} определена однозначно. Это означает, что топологи-
топологический тип "составного" дефекта однозначно определяется топологически-
топологическими типами составляющих его дефектов. Отметим, что это утверждение
справедливо также в случае, когда пространство R неодносвязно, но одно-
связна область U, в которой имеет место локальное равновесие. (Грубо
говоря, односвязность области U означает, что не существует нитевидных
дефектов.) В самом деле, если область U односвязна, то сфера S2, окру-
окружающая дефект, определяет элемент гомотопической группы я2 (U);
обозначим этот элемент символом а. (Мы используем то, что из
предложения односвязности U вытекает совпадение множеств {S2, 1/}и
тг2((/).) Каждой точке [/отвечает точ-
точка пространства R; отображение U
в R порождает гомоморфизм груп-
группы я2 (tA в я2 (R). Элемент группы
тг2(Л), отвечающий элементу аб
6и2(У) при этом гомоморфизме,
определяет топологический тип де-
дефекта. Элемент группы я2(/?), отве-
отвечающий составному дефекту, ра-
равен сумме элементов этой груп-
группы, отвечающих элементарным де-
дефектам.
Мы видим, что топологически не-
нетривиальные точечные дефекты мо-
могут возникать в случае, если сушест-
вуют негомотопные нулю отображе- Рис 4
47

ния сферы S* в пространство вырождения R. (Иными словами, прост-
пространство R неасферично в размерности 2.) Топологически нетривиальные
нитевидные дефекты могут возникать, если пространство R неодносвязно
(т.е. имеются негомотопные нулю отображения окружности S1 в Л), а то-
топологически нетривиальные дефекты, имеющие форму поверхности,
("стенки") — когда R несвязно. Пусть, например, локальное равновесие
нарушено на некоторой гладкой кривой или в малой окрестности этой
кривой (иначе говоря, дефект имеет форму нити или трубки). Выберем
в области локального равновесия U малую окружность S , охватывающую
эту кривую (рис. 5). Точкам области локального равновесия, в частности,
точкам окружности S1, сопоставлены точки пространства вырождения/?.
Топологический тип нитевидного дефекта определяется гомотопическим
классом отображения окружности S1 ъЯ; таким образом, топологический
тип можно рассматривать как элемент множества {S1, R). Множество
{S1, R } может быть отождествлено с множеством классов сопряженных
элементов в группе tti(R); см. § ТЗ. (Группа ^(R) действует на себя
с помощью внутренних автоморфизмов; множество (S1^) отождествля-
отождествляется с множеством орбит этого действия.) Если нитевидный дефект рас-
распадается на два нитевидных дефекта, то произведение топологических
типов образовавшихся дефектов ровно топологическому типу исходного
дефекта; точнее говоря, топологический тип исходного дефекта равен
одному из возможных значений произведения топологических типов обра-
образовавшихся дефектов. (Напомним, что в множестве {Sk,R) определе-
определена многозначная операция, которую в случае к - 1 принято называть умно-
умножением.) Доказательство этого утверждения совершенно аналогично, до-
доказательству соответствующего утверждения для точечных дефектов.
Рассмотрим в качестве примера нематическии жидкий кристалл. Прост-
Пространство вырождения такого кристалла совпадает с пространством
Рис.5
конфигураций двухатомной молекулы, состоящей из одинаковых атомов
(центр инерции молекулы считается фиксированным). С математической
точки зрения пространством вырождения является проективная плос-
плоскость RP2 - пространство прямых, проходящих через фиксированную
точку пространства IR3. Точку проективной плоскости RP2 можно задать
с помощью единичного вектора, определенного с точностью до знака,
иными словами, RPZ получается из сферы S2 отождествлением диамет-
диаметрально противоположных точек. Таким образом, в каждой точке, где
48

имеет место локальное равновесие, задан вектор, определенный с точ-
точностью до знака (такой вектор носит название директора). Проективная
плоскость неодносвязна: множество {Sl, RP2 } состоит из двух элементов
(т.е. все негомотопные нулю отображения окружности S1 в RP2 гомотоп-
гомотопны между собой).
В самом деле, irl(RP2) = Zj (см. § Т4). В силу коммутативности груп-
группы Zj каждый класс сопряженных элементов состоит только из одного
элемента и, следовательно, множество {S'.fl/'2} совпадает с множеством
Рис. 6 Рис. 7
Нитевидные дефекты в нематике носят называние дисклинаций. Мы
видим, что существует только один тип топологически нетривиальных
дисклинаций, отвечающий единственному нетривиальному элементу мно-
множества { S1, RP2 ). Поле директора в топологически нетривиальной дискли-
дисклинаций изображено на рис. 6. Пример топологически тривиальной дискли-
дисклинаций изображен на рис. 7. (На этих рисунках изображено поле директора
в плоскости, перпендикулярной плоскости нити.)-Для того чтобы иссле-
исследовать тип дисклинации, удобно воспользоваться тем, что замкнутый
путь в RP2 гомотопен нулю в том и только в том случае, если он накры-
накрывается замкнутым путем на сфере S2; см. § Т4. Иными словами, следует
вспомнить, что поле директора - это поле вектора, определенного с точ-
точностью до знака, и заметить, что поле директора на S1 гомотопически три-
тривиально в том и только в том случае, когда можно непрерывно выбрать
знак директора на всей окружности S1.
Гомотопическая группа ^(RP2) изоморфна группе тг2E2) = Z (см.
§ Т13 и § Т15). Это позволяет в случае, если область локального равно-
равновесия односвязна, сопоставить целое число каждому точечному дефекту.
При слиянии дефектов эти целые числа, характеризующие типы дефектов,
складываются между собой. Однако, если существуют нитеподобные де-
дефекты, область локального равновесия оказывается неодносвязнои. В этом
случае топологический тип точечного дефекта характеризуется неотрица-
неотрицательным целым числом. (Двум элементам группы rt2 (RP2 ), отличающимся
знаком, отвечает один и тот же элемент множества {S2,RP2} ;см. § Т13.)
Результат слияния двух точечных дефектов оказывается неоднозначным:
если сливаются дефекты с топологическими числами m м п, то может
получиться как дефект с топологическим числом m + и, так и дефект
с топологическим числом \т - п |. (Это утверждение вытекает из указан-
49

ного в § Т13 описания многозначной операции сложения в {Sk,RPk}.)
Например, два одинаковых топологических дефекта могут дать тополо-
топологически тривиальный дефект ("аннигилировать"), если один из дефектов
при приближении к другому обойдет вокруг нити.
Отметим, что кроме рассмотренных выше нематических кристаллов
(одноосных нематиков) могут существовать (пока не обнаруженные
экспериментально) двухосные нематические кристаллы. В нематическом
кристалле роль параметра порядка играет симметричный тензор еар, имею-
имеющий нулевой след. Группой симметрии является группа вращений SOC).
Для одноосного нематика минимум свободной энергии достигается на
тензоре, у которого два собственных значения совпадают; стационарная
подгруппа Я изоморфна группе О B). (Если главные оси тензора еаC
направлены по осям координат, причем собственные значения, отвечающие
осям х к у, совпадают, то группа Я состоит из вращений пространства И3,
переводящих в себя горизонтальную плоскость.) Отсюда ясно, что прост-
пространство вырождения R топологически эквивалентно пространству
SOC)/OB). Пространство SOC)/SOB) топологически эквивалентно S2
(см. § А6); отсюда следует, что SOC)/OB) = S2/22 = RP2. Впрочем,
соотношение R = RP2 можно получить и непосредственно, заметив, что
тензор с собственными значениями X, X, —2Х полностью характеризуется
главной осью, отвечающей собственному значению —2Х.
Однакб возможен вариант, когда минимум свободной энергии достигает-
достигается на тензоре еаC) все собственные значения которого различны; в этом
случае нематический кристалл называется двухосным. Считая, что главные
оси тензора еар совпадают с осями координат, видим, что стационарная
подгруппа Я в этом случае отождествляется с группой, состоящей из тех
вращений пространства IR3, которые переводят в себя каждую из коорди-
координатных осей. (Эта группа состоит из четырех элементов; ее нетривиальные
элементы h1>h2,h3 представляют собой преобразования, не меняющие
одной из координат и обращающие знак у двух других координат.)
Пространство вырождения R в данном случае топологически эквивалентно
SO C)/#. Для того чтобы исследовать топологию пространства R, заметим,
что пространство SO C) является накрывающим пространством простран-
пространства R (отображение пространства SOC) на SO C)/Я является четырех-
четырехлистным накрытием). Отсюда следует, что 7г2 (Л) = ^(SOC)) = О
(см. § Т15 или § Т17) и, следовательно, топологически нетривиальных
точечных дефектов не существует.
Для того чтобы вычислить группу 7Ti (R), удобно воспользоваться тем,
что существует гомоморфизм р группы SUB) на группу SOC); этот го-
гомоморфизм является двулистным накрытием. Очевидно, что пространст-
пространство R можно представить в виде SUB)/#, где Я - группа из восьми эле-
элементов, являющаяся прообразом группы Я при гомоморфизме р.
Легко проверить, что группа Я состоит из матриц ± 1, ±й1? ±h2, ± Л 3. где
hj = expli—Ojj = iOj (здесь а1; аг, а3 - матрицы Паули). Поскольку
группа SUB) односвязна, отсюда следует, что iti(R) = Н (см. §Т4 или
50

§Т17). Из соотношения A/, h/ht =—hj , вытекающего из коммутатив-
ности матриц Паули, видно, что элементы h\ и —ht являются сопряженны-
сопряженными элементами в группе Я. Группа Я разбивается на пять классов сопря-
сопряженных зтементов: два из них содержат по одному элементу A или —1),
а три — по два элемента (Л/ и -^Лу, / = 1, 2, 3). Отсюда следует, что мно-
множество {51,/? ) = {S1, SUB)/H} состоит из пяти гомотопических
классов.
Мы видим, что в двухосном нематике существуют четыре типа топологи-
топологически нетривиальных нитеподобных дефектов; Многозначная операция
умножения в множестве {S1,/?} определяется операцией умножения
в группе Ъ\ (К). Для того чтобы перемножить два элемента из {S1,R},
нужно взять по элементу из соответствующих классов сопряженности груп-
группы 7rt (R), перемножить их и рассмотреть класс сопряженности, к которо-
которому принадлежит произведение. (Конечно, этот класс может зависеть от вы-
выбора элементов в классах сопряженности.) Применяя этот общий рецепт
к случаю R = SUB)/#, видим, что при умножении класса сопряженности,
к которому принадлежат элементы hj и — hj, на себя может получиться
как класс сопряженности, содержащий 1 = А;- hj, так и класс сопряженно-
сопряженности, содержащий — 1 = hj{—hj). Во всех остальных случаях умножение
однозначно (например, А,А;- = ецк^к и принадлежит тому же классу со-
сопряженности, что и элементы{—h()hj, А,-(—А/), (—h{)(—
Информация об умножении в множестве {S1, R ) позволяет, как мы го-
говорили, получать информацию о распаде и слиянии нитевидных дефектов.
Если сливающиеся нити имеют разный топологический тип, то топологиче-
топологический тип образующейся нити может быть предсказан однозначно; если сли-
сливающиеся нити принадлежат к одному и тому же типу, это утверждение
не имеет места. (При слиянии нитей, тип которых описывается классом
сопряженности, содержащим элементы А,- и —А;, может получиться как
топологически тривиальная нить, так и нить, тип которой задается эле-
элементом — 1.)
Остановимся теперь на вычислении групп nt (R) и тг2 (Л) в общей си-
ситуации, считая, что вырождение равновесного состояния обусловлено свой-
свойствами симметрии (т.е. R может быть представлено в виде R = G/H,
где G — группа симметрии, Я — группа ненарушенных симметрии).
Группы ТГ{ (G/H) для i = 1, 2, 3 легко вычисляются (см. § Т20).
Приведем результаты вычисления групп 7Г2 (G/Я) и -п^ (G/H), считая, для
простоты, что группа G связна и односвязна. (Это предположение не огра-
ограничивает общности. Например, если G = SO C), то пространство SO C)/Я
топологически эквивалентно пространству SUB)/#, где Я = р'1 (Я) —
прообраз группы Я при гомоморфном отображении р группы SUB) на
51

S0C).) Легко проверить, что группа it2(G/H) изоморфна группе 7
а группа iti (G/H) изоморфна группе я0 (Я) = Я/ЯС, где Нс - максималь-
максимальная связная подгруппа группы Я (подгруппа, состоящая из элементов, ко-
которые можно соединить непрерывной кривой с единицей группы). Отсюда
вытекает в частности, что топологически нетривиальные точечные дефекты
существуют в том и только в том случае, если группа ненарушенных симмет-
симметрии Я неодносвязна, а топологически нетривиальные нитевидные дефекты
существуют в томи только в том случае, когда группа Я несвязна (т.е суще-
существуют дискретные ненарушенные симметрии).
Рассмотрим, например, сверхтекучие квантовые жидкости. В случа.е
сверхтекучего 4 Не единственной нарушенной симметрией является калиб-
калибровочная инвариантность. Группа глобальных калибровочных преобразова-
преобразований изоморфна группе U(l). (Волновая функция умножается при калибро-
калибровочном преобразовании на фазовый множитель eta.) Отсюда следует, что
пространство вырождения R в данном случае топологически эквивалентно
окружности S'. Это, конечно, вытекает и непосредственно из теории
Ландау — параметром порядка в данном случае является комплексное
число Ф; ниже точки фазового перехода равновесие достигается на окруж-
окружности |Ф| = с, где с - положительная константа. Поскольку я2 (S1) = О,
Ttl(S1) = ~Z точечных дефектов в 4Не нет, а нитевидный дефект может
быть охарактеризован с помощью целого числа. Физически эти дефекты
представляют собой вихри в сверхтекучем гелии. В самом деле, параметр
порядка в локально равновесном состоянии 4Не является комплексной
функцией ^(х) от координаты х. Топологическое число п, отвечающее ни-
нитевидному дефекту, с точностью до множителя 1/2тг совпадает с измене-
изменением фазы Ф(х) функции 'Ф(х) при обходе вокруг дефекта. Сверхтекучая
h
скорость \s выражается через фазу Ф(х) формулой \s = —УФ, откуда
т
ясно, что
1 т
п = $ v ф(х)</х = —— ф ysdx,
2 я г 2тгп г
где циркуляция берется по контуру Г, охватывающему нитевидный де-
дефект. Вихрь с п = 1 можно построить, положив в цилиндрических координа-
координатах Ф(г, чз, г) = a(r )etlf>. В этом случае сверхтекучая скорость направлена
по касательным к горизонтальным окружностям, имеющим центр на оси z
(распределение скоростей в горизонтальной плоскости изображено
на рис.8). Отметим, что топологические свойства сверхпроводника пол-
полностью совпадают со свойствами сверхтекучего 4Не.
Рассмотрим вкратце топологически стабильные дефекты в 3 Не. Пара-
Параметром порядка в этом случае является тензор Af^ — комплексный тензор
ранга 2. В пренебрежении спинорбитальным взаимодействием свободная
энергия инвариантна относительно группьГ G = SOC) X SOC) X U(l).
Элемент этой группы, определяемый тройкой (F, W, eia), где V = (Vu ),
W = (Wkr) — ортогональные матрицы,. переводит тензор Ацс в тензор
А,'к = eiaVilWkrAlr . Интерпретируя первый индекс у Aik как спино-
52

вый, а второй — как координатный, можно рассматривать V как вращение
в спиновом пространстве, a W — как вращение в координатном простран-
пространстве. В В-фазе 3Не одному из равновесных состояний отвечает тензор
вида Afk - \&tk (здесь X — число, связанное с энергетической щелью Д
соотношением X = A/V~3~); другие равновесные состояния могут быть
получены из него преобразованиями группы G. Отсюда легко заключить,
J
1
^~
Рис.8
что для произвольного равновесного состояния тензор
в виде
А№ = Xe'aVik,
можно записать
A)
где Vik - матрица вращения. Группа ненарушенных симметрии Я состоит
из троек (V, W,ela), для которых а = 0 и V = W; она изоморфна SO C).
Мы видим, что в В-фазе пространство вырождения R топологически экви-
эквивалентно SOC) XSOC) XUA)/SOC) =SOC) XUA). Замечая, что
rrfc(SOC) X
ffa(SOC)) = 0,
= ff*(S0C)) +
wa(U(l)) = 0,
видим, что
яа(Л) = 0, я,(Л) = Z2 + Z. '
Таким образом, в В-фазе топологически стабильных точечных дефектов
нет, топологический тип нитевидного дефекта определяется целым числом
и вычетом по модулю 2. (Группа ti\ (/?) коммутативна, поэтому можно
отождествить {S1, R) и 7гх (Л).) '
В Л-фазе равновесное состояние можно выбрать так, чтобы тензор
имел вид
B)
53
0
0
1
0
0
I
0
0
0

Преобразование (V, W, eia) e SOC) X SOC) X U(l), для которого V-
вращение на произвольный угол вокруг оси z, W. — вращение на угол а
вокруг оси z, принадлежит группе ненарушенных симметрии. (При враще-
вращении вокруг оси z в спиновом пространстве тензор B) не меняется, а при
вращении вокруг оси z в координатном пространстве на угол а этот тен-
тензор умножается на е~ia.) Мы видим, что в группе Я ненарушенных сим-
симметрии содержится подгруппа, изоморфная U(l) X U(l). Эта подгруппа
содержит все непрерывные ненарушенные симметрии (т.е. U(l) X.U(l)
является максимальной связной подгруппой группы Я). Кроме того,
в группе Я есть еще дискретные симметрии; именно, этой группе принад-
принадлежит любое преобразование (V, W, ei&), где V и W - вращения на угол я
вокруг горизонтальной оси, /3 — угол, образованный осью вращения W
с осью х (вращения V и W переводят ось z в себя, меняя ее направление
на обратное). Все дискретные симметрии могут быть получены из какой-ни-
будьоднойумножениемнапреобразования из U(l) XUA). Иными словами,
Я/иA) X U(l) состоит всего из двух элементов и, следовательно,
Я/иA) X U(l) =г2. Легко проверить, что
SOC) X SOC) X U(l)/U(l) X U(l) = S2 X SOC).
Отсюда видно, что R = S2 X SO C)/2г , т.е. S2 X SO C) можно рассматри-
рассматривать как двулистное накрытие пространства R. Односвязное пространство
S2 X SUB) является двулистным накрытием пространства S2 X SOC),
и, следовательно, четырехлистным накрытием пространства R. Отсюда
ясно, что я2 (Я) = я2 (S2 X SUB)) = тг2 (S2) + я2 (SUB)) = И, а группа
Tii (Л) состоит из четырех элементов. Нетрудно проверить, что группа
Tii (R) изоморфна группе Z4 вычетов по модулю 4; эта группа коммута-.
тивна, и, значит, множество {S1, R.) можно отождествить с группой ttj {R).
Таким образом, топологический тип точечного дефекта характеризуется
целым числом, а топологический тип нитевидного дефекта — вычетом по
модулю 4.
^ Интересные эффекты возникают, если на рассматриваемую систему
наложено слабое поле. Рассмотрим, например, одноосный нематик в маг-
магнитном поле. Равновесное состояние становится тогда невырожденным
(направление директора в равновесном состоянии должно совпадать
с направлением поля). Если магнитное поле приложить к жидкому
кристаллу, в котором есть точечный дефект типа, изображенного на рис.6,
то во всем кристалле, кроме трубочки, выходящей из дефекта, направле-
направление директора будет совпадать с направлением магнитного поля
(на рис. 9 изображены линии, касательные к направлению директора).
В общем случае наложение слабого поля (или учет слабого взаимодейст-
взаимодействия, например, спин-орбитального взаимодействия в 3 Не) приводит к вы-
выделению из пространства вырождения R некоторого подпространства R,
состоящего из состояний, остающихся равновесными в новой ситуации.
В состоянии локального равновесия каждой точке сопоставляется точка
пространства R. Однако при наших предположениях свободная энергия
54

в старых равновесных состояниях мало отличается от свободной энергии
новых равновесных состояний, поэтому разумно рассматривать также
состояния, локально равновесные в старом смысле. Мы будем говорить
тогда о частичном локальном равновесии. Если в области имеет место час-
частичное локальное равновесие, то каждой ее точке сопоставляется точка
пространства R. Так же, как раньше топологические соображения позволя-
позволяли доказать, что не могут исчезнуть точки, в которых локальное равновесие
нарушено, сейчас аналогичные соображения дают возможность утверждать,
Рис.9
что должны сохраниться точки, в которых нет полного локального равно-
равновесия, а есть только частичное. Пусть полное локальное равновесие наруше-
нарушено в некоторой точке (или в некоторой области), но там, где нарушено
полное локальное равновесие,имеет место частичное локальное равновесие.
Окружим эту точку (или область) сферой S2, на которой имеет место
полное локальное равновесие, и, следовательно, каждой точке этой сферы
сопоставлена точка пространства R. В шаре ZK, ограниченном сферой S2,
имеет место частичное локальное равновесие, и, следовательно, каждой
точке этого шара сопоставлена точка пространства R. Это означает, что
задано отображение пары (D3,S2) в пару (R, R), т.е. отображение ша-
шара D3 в R, при котором его граница переходит в R (см. § Т1).
(Разумеется, внутри шара могут быть точки, отображающиеся в R С R;
это соответствует тому, что внутри шара есть точки, в которых локальное
равновесие является полным. Конечно, в этих точках тем более есть частич-
частичное локальное равновесие.) Будем считать, что состояние системы меняется
с течением времени таким образом, что на сфере S2 все время остается
полное локальное равновесие. Будем предполагать, что частичное локальное
равновесие нигде не нарушается. Тогда отображение пары (ZK, S2) в пару
(R, R ) непрерывно меняется с течением времени, т.е. гомотопический
класс отображения пар не меняется. В частности, отсюда следует, что в слу-
случае, когда отображение пары (ZK, 5.2) в пару (R, R ) не гомотопно нулю,
точки, в которых нет полного локального равновесия, будут существовать
все время. (Отображение пары (D3,S2) в пару (R, R) гомотопно нулю,
если его можно продеформировать в отображение пар, переводящее весь
55

шар fl3 в Л, т.е. в отображение, отвечающее полному локальному рав-
равновесию .)
Таким образом, каждой точке (или области), в которой нарушено пол-
полное локальное равновесие, можно сопоставить гомотопический класс ото-
отображения пары (ZK,52) в пару (R,R), т.е. элемент множества
{D3, 5.2 | R, R}. В случае если пространство R связно и односвязно, мож-
можно отождествить множество { D3, 5? | R, R } с относительной гомотопиче-
гомотопической группой тг3 (Л, R ); для связного, но не односвязного пространст-
пространства R это множество получается из я3 (R, R ) с помощью факторизации
по действию группы iti(R) (см. § Т19).Если пространство R состоит
из одной точки (это означает, что наложенное возмущение полностью сни-
снимает вырождение), то относительная гомотопическая группа ti3(R, R)
совпадает с абсолютной гомотопической группой я.3(Л). В общем случае
группа тг3(R,R) может быть вычислена с помощью точной гомотопиче-
гомотопической последовательности ( § Т18):
R
i,
тг3(Л)
, R
, R
Л
тг2( R
i.
Если полное локальное равновесие нарушено на некоторой нити (или в тру-
трубочке, окружающей нить), то рассмотрим окружность S1, охватьтающую
Рис.10
нить, и ограниченный этой окружностью круг D2. Считая, что окруж-
окружности S1 имеет место полное локальное равновесие, а внутри круга частич-
частичное локальное равновесие, и сопоставляя каждой точке круга соответст-
соответствующую точку пространства вырождения, мы получаем отображение пары
(?>2,5?) в пару (R, R ). Гомотопический класс этого отображения не ме-
меняется с течением времени и определяет топологический тип рассматривае-
рассматриваемой нити. Таким образом, в этом случае топологический тип нити можно
56

рассматривать как элемент множества {D2,S} \R,R). Если простран-
пространство R связно и односвязно, это множество совпадает с относительной го-
гомотопической группой я2 (R, R ). Может оказаться, что нить, на которой
имеет место лишь частичное локальное равновесие, кончается на точечном
дефекте (рис. 9). Тогда элемент множества {D2, S} | R, R } не может быть
произвольным. В самом деле, отображение (D2,Si) в (R,R.) должно по-
порождать гомотопное нулю отображение 51 в R .(Это вытекает из замечания,
что на окружность 51 можно натянуть поверхность, топологически эквива-
эквивалентную кругу и целиком лежащую в области, где есть полное локальное
равновесие; см. рис. 10.) Ў
§ 2. Топологические интегралы движения
Начнем с простейшего примера. Рассмотрим одномерную частицу, дви-
двигающуюся в поле с потенциальной энергией V(x), и предположим, что
потенциальная энергия обращается в бесконечность в точке а (рис. 11).
Тогда очевидно, что частица не может преодолеть бесконечно высокий по-
потенциальный барьер в точке а; если она находилась в начальный момент
времени левее точки а, то она будет продолжать находиться левее точки а
все время.
Существенно отметить, что это утверждение имеет место как для класси-
классической, так и для квантовой частицы. Сформулированное только что ут-
утверждение можно переформулировать на несколько ином языке.
Рис. 11
Обозначим символом U множество, в котором может находиться интере-
интересующая нас частица. В нашей ситуации это множество несвязно (состоит из
двух компонент - лучей (-<», а) и (а, +.<»), и мы видим, что частица
остается в той компоненте, в которой она была в начальный момент време-
времени. (Напомним, что две точки принадлежат одной компоненте, если их
можно соединить путем — непрерывной кривой, начинающейся в одной
точке и кончающейся в другой.)
Рассмотрим теперь классическую систему с п степенями свободы,
описываемую функцией Гамильтона Н = Т + V, где кинетическая энер-
энергия Т является квадратичной функцией от импульсов, а потенциальная
57

энергия V(xl, ..., х") может обращаться в бесконечность в некоторых точ-
точках пространства IR". Предположим, что область U, в которой потенциаль-
потенциальная энергия конечна, несвязна — состоит из нескольких компонент
Ux Uk. Тогда очевидно, что классическая частица, находившаяся в на-
начальный момент времени в компоненте U{, во все последующие моменты
будет находиться в той же области (т.е. номер компоненты, в которой нахо-
находится частица, является интегралом движения). Аналогичное утверждение
верно и для квантовой системы, получающейся при квантовании рассмот-
рассмотренной только что классической системы. Именно, если волновая функ-
функция ф(х) отлична от нуля только в компоненте Uiy то это же верно для
волновой функции, получающейся при решении нестационарного уравне-
уравнения Шредингера с начальным условием ф(х). Область U, где потенциальная
энергия конечна, может рассматриваться как пространство конфигура-
конфигураций интересующей нас системы. Вместо того чтобы рассматривать
компоненты пространства конфигураций, можно рассматривать компонен-
компоненты фазового пространства, т.е. пространства, состоящего из тех точек
(Pi >•••. Pnf х-1 > ..., л:"), для которых функция Гамильтона конечна. Очевид-
Очевидно, что число компонент этого фазового пространства совпадает с числом
компонент пространства конфигураций. (Фазовое пространство можно
в данном случае рассматривать как прямое произведение IR " X U.)
Коснемся вопроса о нахождении основного состояния и слабо возбуж-
возбужденных состояний интересующей нас квантовой системы. Пусть наимень-
наименьшее значение потенциальной энергии V{x) достигается в точке х0.
Тогда вблизи х0 разложим потенциальную энергию в ряд Тейлора по откло-
отклонениям от этой точки:
где % = х-х0, W{%) = o(U|2).
Будем считать, что квадратичная форма кц%*%' не вырождена. Отбро-
Отбросив слагаемое W(%), мы получим гамильтониан многомерного гармониче-
гармонического осциллятора, уровни энергии которого определяются формулой
Ч, B)
где со; — собственные частоты, п = О, 1,2, ... Учитывая W(t-) по теории
возмущений, легко видеть, что поправка к уровням энергии имеет порядок
(A^hK'2, где N = шахи;. Отсюда ясно, что энергия слабо возбужденных со-
состояний определяется в квазиклассическом приближении соотношением
B). В частности, энергия Ео основного состояния в квазиклассическом при-
приближении равна V(x0) (точнее, Ео = V(x0) + -т h2со/ + O(t?/2)j ¦
Легко получить строгие оценки для энергии основного состояния.
Для того чтобы получить оценку сверху, удобно воспользоваться вариа-
вариационным принципом, взяв в качестве пробной функции волновую функцию
58

основного состояния гармонического осциллятора; уценка снизу очевидна:
Ео ^ V(xo). Существенно отметить, что подобные оценки можно без труда
провести также в случае, когда квадратичная форма кц ? %' вырождена.
Мы приходим к выводу, что и в этом случае в квазиклассическом прибли-
приближении Ео *** V(x0) (ошибка имеет порядок h).
При, отыскании основного состояния системы мы исходим из разложе-
разложения потенциальной энергии по степеням % = х — х0, где х0 - точка, в кото-
которой достигается наименьшее значение функции V(x). Можно ту же
процедуру провести, заменив точку абсолютного минимума дго любой точ-
точкой Xi, в которой достигается относительный минимум функции V(x).
Состояния, которые,мы при этом получим, будут, вообще говоря, квази-
квазистационарными. Например, для потенциальной энергии, изображенной
на рис. 12, волновая функция основного состояния осциллятора с потен-
потенциальной энергией — V"(хх)(х — ххJ будет квазистационарным состоя-
состоянием, время жизни которого определяется квазиклассическим коэффи-
циентом прохождения D = ехр ( / V 2 т (V (х) — Е ) dx ) через
V h а /
барьер между минимумами х0 и^; отсюда ясно, что это'время экспонен-
экспоненциально велико.
Ситуация меняется, если точка xi доставляет наименьшее значение по-
потенциальной энергии на одной из компонент области U (рис. 11).
Тогда сосредоточенные вблизи этой точки квантовые состояния являются
стационарными, а не квазистационарными (барьер, отделяющий точку хг
от точек, в которых потенциальная энергия имеет меньшее значение,
бесконечно высок). Повторяя проведенные выше рассуждения, можно
Рис.12
убедиться, что наименьшая возможная энергия квантовых состояний,
волновая функция которых отлична от нуля только в компоненте связ-
связности, содержащей точку xit в квазиклассическом приближении
равна U(xx).
В общем случае для того, чтобы изучить вопрос о топологических ин-
интегралах движения, нужно исследовать связность фазового пространства
.системы. (В фазовое пространство включаются только те точки, в которых
функция Гамильтона Я (р, х) конечна.) Ясно, что траектория классической
59

механической системы все время остается в той компоненте фазового про-
пространства, в которой она была в начальный момент времени, иными слова-
словами, номер компоненты связности может рассматриваться как интеграл
движения. Такие интегралы носят название топологических интегралов
движения. Можно убедиться, что топологические интегралы движения,
вообще говоря, сохраняются и после квантования системы. (В квантовом
случае вместо термина "топологический интеграл движения" употребляют
также термин топологическое квантовое число.)
Если фазовое пространство состоит из компонент связности Ult ..., U^,
и минимум функции Гамильтона на компоненте Uf равен Е{, то в квази-
квазиклассическом приближении минимальная энергия состояний с топологиче-
топологическим квантовым числом г равна Et. В частности, энергия основного со-
состояния равна значению функции Я в точке, где достигается абсолютный
минимум (т.е. равна тт{/Г!, ..., Ек}). Дня того чтобы получить в квази-
квазиклассическом приближении энергию слабо возбужденных состояний, нужно
разложить функцию Гамильтона в окрестности этой точки и оставить толь-
только квадратичные члены.
Топологические интегралы движения возникают не только в системах
с конечным числом степеней свободы, но и в теории поля. Рассмотрим в ка-
качестве примера теорию, описывающую скалярное поле у{х) = ^{t, x)
в одномерном пространстве, считая, что функционал действия записывает-
записывается в виде
S = / ?dxdt =
Мы употребляем обозначение ? для плотности действия (лагранжиана).
Тогда функционал энергии имеет вид
Q^ a*?dx, D)
Ъ?
где я(х) = = ip (x) — обобщенный импульс, отвечающий по-
а? (х)
лю чз (х). Под точкой фазового пространства следует понимать пару функ-
функций (тг(х), ч?(х)), для которой энергия D) конечна. Отметим, что функ-
функционал энергии в данном случае можно представить в виде Е = Т+ V, где
т = у ; n2d%,
x+x;(^-fl2Ju?x. E)
Слагаемое Т, квадратичное по обобщенным импульсам я(х), имеет физиче-
60

ский смысл кинетической энергии, слагаемое V, зависящее только от
обобщенных координат </э (х), - потенциальной энергии. Под конфигура-
конфигурационным пространством следует понимать множество полей </з (х), удовлет-
удовлетворяющих условию V [</з ] < °°.
Как фазовое пространство, так и пространство конфигураций в рассмат-
рассматриваемом случае несвязны — каждое из них состоит из четырех компонент.
В самом деле, для того чтобы обеспечить конечность*) выражения E)
мы должны предположить, что lim | </з(х) | = а. Отсюда следует, что
|х| ->»
поля с конечной энергией могут принадлежать к одному из следующих
четырех типов:
() = ?>(~°°) = а> 2) ?з(+°°) = — Ч>(—°°) = а;
3) ??(+«>) = — i/j(—оо) = — а; 4) ??(+°°) = ?>(~°°) = ~~а-
Поле одного типа нельзя непрерывным образом перевести в поле друго-
другого типа таким образом, чтобы все промежуточные поля имели конечную
энергию. (Тот факт, что при переходе от поля одного типа к полю другого
типа мы обязательно переходим через поле с бесконечной энергией озна-
означает, что поля разных типов разделены бесконечно высоким энергетиче-
энергетическим барьером.) С другой стороны, два поля, принадлежащие одному и
тому же классу, можно соединить непрерывным семейством полей
с конечной энергией. Мы видим, что четыре класса, на которые были раз-
разбиты поля i/j (х), являются компонентами связности пространства конфигу-
конфигураций. Фазовое пространство состоит из того же числа компонент, что и
пространство конфигураций. (Это вытекает из замечания, что всякую точ-
точку Gг(х), </з(х)), принадлежащую фазовому пространству, можно соеди-
соединить непрерывной кривой (т тг (х), </з (х) ), 0 < т < 1, с точкой @, </э (х).)
Наименьшее значение функционала энергии D) равно нулю; оно дости-
достигается при условии, что тг(х) = 0, a v? (х) = а или </з (х) = — а. Таким обра-
образом, минимум функционала энергии достигается в двух точках фазового
пространства, разделенных бесконечным энергетическим барьером.
(Эти точки фазового пространства носят название классических
вакуумов.)
Модель квантовой теории поля, получающуюся при квантовании систе-
системы, описываемой функционалом действия C), удобно исследовать с по-
помощью квазиклассического приближения.
Поскольку классические вакуумы разделены бесконечно высоким энер-
энергетическим барьером, каждому из них отвечает основное состояние кванто-
*) Отметим, что из конечности второго слагаемого в E), строго говоря, еще не
вытекает, что у (х) имеет пределы при х-> + °° их-* — «°. (Интеграл от функции мо-
может быть конечным, даже если эта функция не стремится к нулю при х -¦ °°.) Однако
если эти пределы существуют, то, очевидно, они равны ±а. Существование нужных
нам пределов можно доказать, использовав конечность также первого слагаемого
в E). Мы не будем проводить это доказательство, поскольку в физических вопросах,
видимо, можно считать, что рассматриваемые функции достаточно хорошо ведут себя
на бесконечности. В дальнейшем мы всегда будем предполагать, что функция
от п переменных стремится к нулю на бесконечности, если интеграл от нее по всему
пространству 1ВП конечен.
61

вой задачи (физический вакуум). Мы имеем здесь дело со спонтанным
нарушением симметрии (р (х) -»• — </? (х). По общему рецепту, для того что-
чтобы найти энергии слабовозбужденных состояний, нужно разложить функ-
функционал действия (или функционал энергии) по отклонениям от поля,
доставляющего минимум энергии (классического вакуума). Иными слова-
словами, вместо поля </э(х) следует рассмотреть поле ?(х) = ?>(х) —л или
поле %' (х) =?>(х) + а- Функционал действия, выраженный через поле % (х),
приобретает вид
где
Si = -4\aJ?dxdt-\f;
При квантовании функционала действия Squ мы получаем скалярные
частицы с массой т = 2а у/ 2 X h.
Неквадратичные члены Sj в условиях применимости квазиклассическо-
квазиклассического приближения дают малые поправки к энергии этих частиц. Аналогичные
рассуждения можно провести, производя разложение по отклонениям от
другого классического вакуума (т.е. по полю %'(х) = </з (х) + а).
Рассмотрим теперь минимум функционала энергии на компоненте фазо-
фазового пространства, для которой </э (— оо) Ф ^ (+ оо). Предположим для оп-
определенности, что </?(— оо) = - а, </?.( + оо) = а. Легко видеть, что интересую-
интересующий нас минимум равен
4\А2 __ ,
М = —— лД а3 F)
и достигается на функции
V>(x) = a th (д \/T\ (х - с)). G)
Это означает, что в квазиклассическом приближении наименьшая энергия
квантовых состояний, отвечающих рассматриваемой компоненте фазового
пространства, определяется соотношением F).
В квазиклассическом приближении полям G) отвечают квантовые час-
частицы, масса которых равна энергии этих полей (т.е. определяется форму-
формулой F)). Мы не будем останавливаться на доказательстве этого факта,
отметим только, что он имеет общий характер. Как мы уже говорили,
наименьшее возможное значение функционала энергии достигается на по-
полях, которые носят название классических вакуумов *). Во всех интере-
*) Мы всегда считаем, что энергия классического вакуума равна нулю (иными сло-
словами, энергия отсчитывается от энергии вакуума).
62

сующих нас примерах классические вакуумы являю» си трансляционно
инвариантными полями (не меняются при сдвиге). В квазиклассическом
приближении они связаны с основными состояниями квантовомеханиче-
ской полевой теории. Кроме классических вакуумов могут существовать
солитоны - поля с конечной энергией, доставляющие относительный
(локальный) минимум функционалу энергии. Эти поля не могут быть
трансляционно инвариантными, поэтому соответствующие минимумы
вырождены (функционал энергии не меняется при трансляции, поэтому,
если минимум достигается на поле </э (х), он достигается также на поле
tp (х — с)). В частности, поля G) можно рассматривать как солитоны.
Заметим, что солитон является не зависящим от времени решением клас-
классических уравнений движения. В интересующем нас релятивистски инва-
инвариантном случае с помощью преобразования Лоренца из не зависящего от
времени решения можно получить решение, изменяющееся с течением вре-
времени по закону s (х — \t), где v - константа (солитон со скоростью v).
а Отметим, что эта терминология отличается от принятой в математике.
В математической литературе принято называть решение уравнений движе-
движения, имеющее форму s (х — \t), уединенной волной со скоростью v, остав-
оставляя термин "солитон" для уединенных волн во вполне интегрируемых
системах. Ў
Солитон классической задачи по своим свойствам напоминает частицу.
В самом деле, солитон является локализованным решением уравнений
движения, форма которого не меняется с течением времени. (Солитон, как
и все рассматриваемые нами поля, имеет конечную энергию. Это означает,
что только в конечной части пространства солитон может существенно
отличаться от классического вакуума. В этой области локализована энергия
солитона.)
Оказывается, что в квазиклассическом приближении солитону отвечает
квантовая частица, масса которой равна энергии солитона. Вообще говоря,
эта квантовая частица не является стабильной, но во многих интересных
случаях ее стабильность гарантируется топологическими законами сохране-
сохранения. В частности, это имеет место, если солитон отвечает минимуму функ-
функционала энергии* на множестве всех топологически нетривиальных полей.
(Поле называется топологически нетривиальным, если его нельзя соединить
непрерывным семейством полей, имеющих конечную энергию, с классиче-
классическим вакуумом.) Подчеркнем, что изложенные выше утверждения приме-
применимы не только к одномерным, но и к многомерным полевым теориям.
Далее мы всегда будем пользоваться системой единиц, в которой h = 1.
Это вызвано в частности желанием не отклоняться от стандартных обозна-
обозначений, в которых коммутационное соотношение между обобщенным
импульсом тг(х) и обобщенной координатой </з(х) записывается в виде
[лг(х), i/j (х') ] = — 5 (х — х') .Если отказаться от условия h = 1, то следует
проводить квантование, пользуясь коммутационным соотношением
[я(х), i/j (х*) ] = — 5 (х — х') .Тогда массы частиц, отвечающих квадратич-
/
ной части действия, оказываются порядка h (например, в рассмотренной
63

выше модели они равны 2 a \J 2 X h). С другой стороны, масса частицы,
отвечающей солитону, определяется классической энергией солитона и,
значит, не содержит h. Таким образом, в пределе h-»-0 отношение массы
солитонной частицы к массе стандартных частиц стремится к бесконечно-
бесконечности. Можно показать, что в условиях, когда имеет смысл говорить о части-
частице, отвечающей солитону (т.е. в условиях, когда применимо квазиклассиче-
квазиклассическое приближение), это отношение всегда велико. В частности, в рассмот-
2
ренной выше модели интересующее нас отношение равно — a2h~1.
Соответственно условие применимости квазиклассического приближения
имеет вид a2jh > 1 или вид а2 > 1,если h = 1.
§ 3. Двумерная модель. Абрикосовские вихри
Приведем более сложные примеры теорий, обладающих топологически-
топологическими интегралами движения.
Рассмотрим прежде всего аналог функционала действия B.3) для дву-
двумерного случая:
S = f?d3x = -fdli4'blx^d3x--Xf(:\^\2-a2Jd3x, A)
2 8
где/1 = 0, 1,2, х= (x°,xl,x2) = (х°, х) G(R3, Эо = 9° = —5 = —, Э, =
= - Э' при / = 1, 2. (В A) вместо действительного скалярного поля</з мы
рассматриваем комплексное скалярное поле Ф; можно записать поле Ф
ввидеФ = ??1 + itp2 и сказать, что A) описывает двухкомпонентное ска-
скалярное поле (V1, V3! ) •)
Функционал энергии может быть выражен через обобщенные координа-
ты Ф(х) и обобщенные импульсы тг (х) = в виде
ЭФ()
E=T+V=-f\ir(x)\2d2x + -
2 2 LI dx
1
d2x
Ъх2
-a2Jd2x. B)
s
Снова энергия разбивается на кинетическую энергию Т = Т [яг] и потенциаль-
потенциальную энергию V = К[Ф]; пространство конфигураций состоит из полей
Ф(х), для которых V [Ф ] < оо.
Изучим сначала множество полей, для которых
ограничиваясь полями, достаточно хорошо ведущими себя при {х (—*¦ °°
Именно: мы будем считать, что в полярных координатах (г, <р) поле Ф(г, </з)
имеет конечный предел, когда г -*¦<», а </з не меняется:
lim Ф(г, i/j) = Ф(</з). D)
64

Наложим еще условие, что сходимость в D) равномерна по </э; тогда из
непрерывности поля вытекает непрерывность функции Ф(у). Из конечнос-
конечности интеграла C) следует, что | Ф(<^)| = а. Это означает, что функцию Ф(</>)
можно представить в виде Ф(<?) = аехр( — /а(</?)), где функция <*(</?) не-
непрерывна на отрезке [0, 2тг] и удовлетворяет условию
аBтг)-а@)=2тш, E)
вытекающему из соотношения Ф@) = ФBлг). Целое число п =и(Ф), фигу-
фигурирующее в соотношении E), характеризует топологический тип рассмат-
рассматриваемого поля Ф. (С геометрической точки зрения функцию Ф(</э) можно
рассматривать как отображение окружности, точки которой описываются
угловым параметром ip, в окружность | z | = а. Число п интерпретируется
как степень этого отображения; см. § Т1.) Будем предполагать, что при не-
непрерывном изменении поля Ф функция Ф(ч?), определяющая асимптотику
этого поля, также меняется непрерывно. Поскольку топологическое число
п (Ф) не меняется при непрерывном изменении функции Ф, оно не меняет-
меняется также при непрерывном изменении поля Ф(х). Мы видим, что совокуп-
совокупность полей, для которых интеграл C) конечен, распадается на компо-
компоненты, характеризуемые целым числом и. Примером поля, для которого
интеграл C) конечен и п = 1, является поле вида Ф(х) = a(r)ei{p, где
д(°°) = а. Из сказанного выше следует, что это поле нельзя соединить не-
непрерывным семейством полей, для которых интеграл C) конечен, с полем,
имеющем тривиальную асимптотику Ф(х) -*-а при | х | -*¦<*>.
Из приведенных только что рассуждений не следует, что в модели с
функционалом действия A) существуют топологические интегралы движе-
движения. Разумеется, из конечности энергии B) вытекает конечность интеграла
C), поэтому каждому полю с конечной энергией можно сопоставить целое
число п — топологическое число. Однако конечность энергии B) влечет
за собой кроме конечности интеграла C) также конечность интеграла
ЭФ " ,
х, а этот интеграл расходится для любого поля,
Эф
э!1
дх-
имеющего нетривиальную асимптотику. В самом деле, в полярных коорди-
координатах
2 dr
dip—,
Эх1
Ъх''
Ъг
ЭФ
и второе слагаемое логарифмически расходится, если не стремится к
dip
нулю при г -*•«>. Таким образом, всякое поле с конечной энергией B) то-
топологически тривиально (т.е. п = 0). Однако легко модифицировать функ-
функционал действия A) таким образом, чтобы существовали топологические
интегралы движения. Именно: следует включить взаимодействие с электро-
электромагнитным полем Лм, т.е. перейти к рассмотрению функционала действия
I- "~V4--Xfl I2 - 2*>2
12м 8
1
F)
65

где х = (х°, х\ хг) = (х°, х), х° =t, \ = дц -iAv, д, v = 0, 1, 2; FMV =
= ЪцАи — ЪиАц - тензор напряженности,. Н ~ ЪхАг - Ъ2А1 — магнитная
напряженность, (Ех, Еу) = (At — diAo, A2 — Ь2Ао} — электрическая на-
напряженность.
(Обычно записывают ковариантную производную ^ в виде Ъц + ieA^,
где е — электрический заряд; однако нам удобнее включить множитель е
в потенциал -4М). Функционал F) инвариантен относительно калибровоч-
калибровочных преобразований
ЛМ-*ЛМ-ЭМХ, Фч-Фе'\ G)
Пользуясь калибровочной инвариантностью, наложим на рассматриваемые
поля условие Ао = 0 (калибровочное условие). Тогда функционал энергии,
отвечающий функционалу действия F), запишется в виде
E=-J\7t\2d2x+f\-(\ V,*|2 +| V2*|2) + -X(|*|2 -a2J\d2x+EA,
2 I 2 8 >
1 (8)
где Ел= / (E\ + E\ + Й1) d2x — энергия электромагнитного поля (поля
2е2
Ф(лг), ^4i(x), Л2(лг) рассматриваются как обобщенные координаты, а
тг(х) = Ф(лг) и электрическая напряженность ?" = (Et, Е2) = А — как обоб-
обобщенные импульсы).
Легко убедиться, что пространство полей с конечной энергией распадает-
распадается на компоненты, характеризуемые целым числом п — топологическим чис-
числом поля ^(х). В самом деле, для любого п легко построить поле, обладаю-
обладающее конечной энергией. Например, для и = 1 можно положить
х1 +ix2
ф(х) = <*(/•) , <*(/•) = а при г >R,
Ло=0, А,= р(г)ец — , !',/= 1,2, /»(/•)= I при r>R.
При произвольном п удобно строить поле с конечной энергией в поляр-
полярных координатах. В частности, конечную энергию имеет поле
) = a(r)exp(in<?), А0 = О, А, = О, А^ = у(г), (9)
а(г) = я + C(/"), 7(О = - и + \(/"), функции C(г) и Х(л) достаточно быстро
стремятся к нулю при г -*°°. Энергия поля (9) в основном сосредоточена
в некотором шаре с центром в начале координат (радиус этого шара зави-
зависит от свойств функцийа(г) ну(г)).
Для того чтобы убедиться в конечности энергии поля (9), следует пере-
переписать функционал энергии (8) в полярных координатах:
f(\ r Ф | +
+ ~XS(\^\2-a22
(напомним, что мы положили я(х) = 0).
66

Заменив в функционале действия F) dbx на d4x и считая, что ji = 0,1,
2, 3, мы получаем теорию, описывающую поля в трехмерном пространстве.
В этой теории не существует топологически нетривиальных полей с конеч-
конечной энергией. Однако формулы (9) задают в цилиндрических координатах
(г, </э, z) топологически нетривиальные нити. (Аккуратное определение то-
топологически нетривиальной нити будет дано позже в § 11.) Поля, описыва-
описываемые формулами (9), не зависят от z, поэтому плотность энергии е(г, <р, z)
для такого поля также не зависит от z и, следовательно, полная энергия
бесконечна. Тем не менее эти поля представляют интерес, поскольку они
обладают конечной линейной плотностью энергии (энергия поля в области,
ограниченной двумя горизонтальными плоскостями, конечна). Более наг-
наглядно, можно сказать, что энергия рассматриваемого поля сосредоточена
в трубке, окружающей ось z.
Для поля, имеющего конечную энергию, топологическое число п с точ-
точностью до множителя B7т) совпадает с циркуляцией поля Лм по беско-
бесконечно удаленной окружности на плоскости х , х2 и, следовательно, с интег-
интегралом от магнитной напряженности Я пол1, х2:
„ = fAlxdx>x= JHd2x. A0)
2тг 2тг
Это проще всего проверить, перейдя к полярным координатам. Из конечно-
конечности энергии следует, что V^ = Э^Ф + iA^Ф -*¦ 0 при г -*-°°. Вспоминая, что
при г -к» поле Ф имеет асимптотику а ехр (- / X (v) ), видим, что
4„~ /*"• Э„Ф = Э„Х,
и, значит,
1 2тг 1 2тг 1
2i о ' 2тг о * 2ъ
* Для того чтобы это доказательство можно было сделать строгим,
следует потребовать, чтобы ковариантные производные быстро убывали
при | х | -*¦ °°. Достаточно предположить, что | УМФ |< const | х | ~ A + s > . В
полярных координатах тогда | УГФ| < constr~A+5), | V^K constr.
Если наложить калибровочное условие Аг = 0, то из неравенства | Э,Ф| =
= I Vr^| < const /-~A+5) легко вывести, что предел Ф(</э) = lim Ф(/", <р)
существует и | Ф(«р) — Ф(а, <^) I = I / br^(r, ip)dr \ <const r~s. Это позво-
ляет оправдать проведенные выше рассуждения в калибровке Л, = 0. Спра-
Справедливость соотношения A0) в других калибровках вытекает из калибро-
калибровочной инвариантности обеих частей A0). Ў
Таким образом, мы убедились, что пространство полей с конечной энер-
энергией (фазовое пространство) в модели с функционалом действия F) не-
несвязно — для каждого целого числа п существуют имеющие конечную
энергию поля с топологическим числом п, и два поля с разными топологи-
топологическими числами разделены бесконечно высоким энергетическим барье-
барьером. Квантовому состоянию в соответствующей квантовой теории также
можно сопоставить топологический интеграл движения, принимающий це-
67

лочисленные значения. Если этот интеграл движения (топологическое кван-
квантовое число) не равен нулю, то состояние является топологически нетри-
нетривиальным. В частности, могут существовать топологически нетривиальные
квантовые частицы.
Обозначим символом Е„(Х) точную нижнюю границу функционала
энергии на полях с топологическим числом п. Число Е„ (X) оценивает снизу
энергию квантовых состояний с топологическим числом п. Легко видеть,
что Ет + „ (X) < Ет (X) + Е„ (X). В самом деле, если есть два поля, имеющие
топологические числа т и п, то без ограничения общности можно считать,
что их энергии сосредоточены в далеких друг от друга областях. (Если
это не так, то мы можем параллельно перенести одно из полей; его энергия
и топологическое число при этом не изменяются). Из двух полей, обладаю-
обладающих этим свойством, можно образовать "составное" поле с топологическим
числом т + я и энергией, приблизительно равной сумме энергий; отсюда
следует нужное нам неравенство.
Мы докажем ниже, что Е„ = тг| п \а2 при X = е1. Эвристические рассужде-
рассуждения показывают, что Е„(X) < | п | Ех (X) при Х<е2 и что Еп (X) = | п | i?i(X)
при X > е2. (При X > е2 точная нижняя граница не достигается; наиболее
энергетически выгодными оказываются поля, составленные из далеких
друг от друга полей с топологическим числом п = ± 1.)
А Как мы говорили в § 2, для того чтобы исследовать в квазикласси-
квазиклассическом приближении топологически нетривиальные квантовые частицы,
нужно найти поля, доставляющие локальный минимум функционала энер-
энергии на множестве топологически нетривиальных полей. Нетрудно доказать
существование экстремалей функционала энергии (не зависящих от време-
времени решений уравнений движения), имеющих произвольное топологическое
число. Для этого следует заметить, что можно искать интересующие нас
экстремали в виде (9) (подстановка (9) проходит через уравнения движе-
движения). Точнее, если сначала написать уравнения Эйлера для функционала
F), а затем подставить в эти уравнения поле (9), мы получим те же урав-'
нения, что и при обратном порядке этих операций (т.е. мы можем сначала
подставить в F) поле (9), а затем проварьировать по функциям а (л),
у (г)). Этот факт легко проверить с помощью непосредственного вычисле-
вычисления.
Он может быть установлен также с помощью общих результатов § 10.
Для того, чтобы применить результаты § 10 следует заметить, что поле
(9) обладает симметрией относительно вращения в плоскости х, у (изме-
(изменение поля при вращении может быть скомпенсировано калибровочным
преобразованием). Точнее, при вращении на угол <р поле Ф умножается на
ein<P, а калибровочное поле не меняется; это эквивалентно калибровочно-
калибровочному преобразованию с не зависящей от точки калибровочной функцией пу
(глобальному калибровочному преобразованию). Обратно, всякое поле
(% А), преобразующееся таким образом (т.е. не изменяющееся при после-
последовательном выполнении вращения на угол ф и калибровочного преобра-
преобразования с калибровочной функцией — и</э),:может быть записано в виде (9).
Это замечание позволяет применить результаты § 10.
В силу сделанного выше утверждения, чтобы доказать существование
экстремали функционала F), имеющей произвольное топологическое чис-
число, достаточно проверить, что этот функционал, рассматриваемый только
68

на полях вида (9), достигает своего наименьшего значения. Для этого
можно воспользоваться теоремой о том, что непрерывная функция на ком-
компакте достигает наименьшего значения. (В подходящем гильбертовом
пространстве интересующий нас функционал слабо непрерывен, а шар в
гильбертовом пространстве компактен в слабой топологии).
Отметим, что поле (Ф ^, А ^ ), доставляющее минимум функционалу
F) на полях (9), не обязано отвечать локальному минимуму функционала
F), рассматриваемого на всех полях (хотя и является экстремалью этого
функционала). Мы покажем, что в случае X = е2 поле (Ф*"', А*-"*) отве-
отвечает наименьшему значению функционала на множестве полей, имеющих
топологическое число п, т.е. при X = е2
Эвристические рассуждения позволяют утверждать, что этот же факт имеет
место при X < е2, а также и при X > е2, и = ± 1, но не имеет места при X > е2,
| п | > 1. Таким образом, в квазиклассическом приближении при X > е2
полю (Ф^"\ А^) отвечает стабильная топологически нетривиальная час-
частица лишь при п = ±1 ; в то же время при X < е2 существуют стабильные
частицы с любыми топологическими зарядами.
Для того чтобы проанализировать случай X = е2, заметим, что в этом
случае выражение для энергии с помощью интегрирования по частям при-
приводится к виду
+ -| Vj*-/ V2*|2 +—— Я + -е2(|Ф|2 -a2) \d2x. (ll)
2 2е2 L 2 J )
Поскольку все слагаемые в A1), кроме первого, неотрицательны, а пер-
первое слагаемое по формуле A0) с точностью до множителя совпадает с то-
топологическим числом п, мы получаем, что Е > тта2 и что Е = тга2 в том и
только в том случае, когда подынтегральные выражения во всех интегралах
кроме первого равны нулю. Иными словами, значение энергии, равное
¦ппа2, достигается, если тг (х) = 0, Ё (х) = 0 и выполнены уравнения
V,*-/V24> = 0, Я+-е2(|Ф|2 -д2) = 0. A2)
Это поле, очевидно, доставляет наименьшее значение функционалу энергии
на полях (9) и одновременно функционалу энергии на множестве всех
полей с топологическим числом п > 0.
Случай и < 0 сводится к случаю и > 0 с помощью пространственного
отражения (функционал энергии при отражении инвариантен, а топологи-
топологическое число меняет знак). В результате мы получим оценку Е > тг| n | а2
и аналог уравнений A2) для полей, удовлетворяющих условию Е = тг| п\ а2.
Можно доказать, что система уравнений A2) и ее аналоги для п < 0 име-
имеют 2| п | -параметрическое семейство решений (калибровочно эквивалент-
эквивалентные решения отождествляются). Любое поле из этого семейства решений
Дает наименьшее значение функционалу энергии на полях с топологическим
числом п, поэтому вторая вариация функционала энергии относительно
69

каждого из этих полей неотрицательно определена. Можно доказать, что
вторая вариация функционала энергии относительно поля (^ ^, А ^ )
неотрицательна также, если Хе~2 меньше 1, но достаточно близко к едини-
единице. Отсюда следует, что поле (^(я*, А *л) ) отвечает минимуму.
С другой стороны, если Хе~2 больше 1 и достаточно близко к 1, вторая ва-
вариация функционала энергии перестает быть знакоопределенной и, значит, по-
поле (Ф^, А^"') не является даже локальным минимумом. Доказательство
основано на том, что нулевые моды оператора, отвечающего второй вариа-
вариации функционала относительно поля (Ф*"), А '"*), могут быть явно вычис-
вычислены при X = е2 (кроме нулевых мод, отвечающих калибровочному вырож-
вырождению, есть 2| п\ нулевых мод, отвечающих 2| п | -параметрическому семей-
семейству калибровочно неэквивалентных друг другу решений системы A2)).
Это позволяет исследовать по теории возмущений вторую вариацию для
Хе~2 близких к единице. Для этих X можно также сравнить ?"(* ^, А ^) и
|п | ?"(ФA), АA)); оказывается,чтоЕ(Ъ (п), А (п)) >\п |Е(УA>, А{1))
при X > е2 (т.е. поля, обладающие симметрией относительно вращений,
оказываются энергетически менее выгодными, чем поля, распадающиеся
на далекие друг от друга поля с и = ±1). Результаты, получающиеся при
Хе~2 близких к единице, согласуются с утверждениями, которые, как мы
говорили, по всей видимости, справедливы в общем случае. Ў
Рассмотренные выше математические задачи возникают не только в
квантовой теории поля, но и в статистической физике. (Более того, они по-
появились в статистической физике раньше, чем в квантовой теории поля.)
Дело в том, что функционал
Е = - /1 grad Ф +1А Ф |2 d3x +
+ -Х/(|Ф|2 -a2Jd3x+^—f\votA\2 d3x A3)
8 2е2
можно интерпретировать как функционал свободной энергии в модели
сверхпроводимости Гинзбурга—Ландау. (Здесь Ф(х) — комплексный па-
параметр порядка, А(х) — потенциал электромагнитного поля.) Исследован-
Исследованным выше экстремалям функционала (8) отвечают топологически не-
нетривиальные нити функционала A3) (абрикосовские вихри). В случае
X < е2 мы имели дело со сверхпроводником первого рода, при X > е1 —
со сверхпроводником второго рода.
§ 4. Монополи Полякова — Хоофта
Для того чтобы построить в трехмерном пространстве теорию, обладаю-
обладающую топологическими интегралами движения, начнем с рассмотрения
функционала действия
S = ^f(d^J d*x - \fW-a2J d*x, A)
где v? = (i/j', tp2, tfi3 ) — трехкомпонентное скалярное поле.
70

Функционал энергии в этом случае имеет вид
E = El+E2=-fn2(x)d3x + - f (grad$fd3x + \f ($2 - a2Jd3x, B)
где 7?(x) = <?(x) — обобщенный импульс, отвечающий обобщенной коорди-
координате if (х).
Исследуем сначала пространство полей <Д(х), для которых интеграл
S{t-a2fd*x C)
конечен. (Мы предполагаем что рассматриваемые поля непрерывны, сущест-
существует предел
lim ?(\n) = $(n) D)
для всякого вектора п и сходимость в D) равномерна, если п пробегает
множество векторов единичной длины.) При наложенных нами условиях
вектор Ф(п) непрерывно зависит от п. Из конечности интеграла следует,
что IФ (п) | = а, поэтому, рассматривая векторное поле Ф (п) на множестве
векторов единичной длины, мы получаем непрерывное отображение дву-
двумерной сферы, выделяемой уравнением | п| = 1, в двумерную сферу | Ф*| = а.
Каждому такому отображению сопоставляется целое число — степень
отображения (§ Т2). Это означает, что каждому полю^(х) отвечает целое
число — топологическое число поля, определяемое асимптотикой Ф*(п)
рассматриваемого поля. Топологическое число поля не меняется при непре-
непрерывном изменении поля <^(х). (Это вытекает из соответствующего утверж-
утверждения для степени отображения и из естественного поедположения, что при
непрерывном изменении поля <^(х) его асимптотика Ф (п) также меняется
непрерывно.)
Таким образом, множество полей, для которых конечен интеграл C),
несвязно — разбивается на компоненты, отвечающие различным значениям
топологического числа. Однако отсюда не следует несвязность пространст-
пространства полей, для которых конечен функционал энергии B), поскольку из
конечности интеграла / (gradi^J(i3x вытекает тривиальность асимптотики
поля ij?(х) (при стремлении х к бесконечности по любому лучу поле <р (х)
стремится к одному и тому же пределу). Это значит, что топологичеекое
число любого поля, для которого энергия B) конечна, равно нулю.
Для того чтобы получить из A) теорию, обладающую топологическими
интегралами движения, включим в нее поле Ам (х) = (А^, А\, А^), являю-
являющееся обобщением электромагнитного поля (это поле называется полем
Янга —Миллса или калибровочным полем). Именно, рассмотрим функцио-
функционал действия
^^4x, E)
где VM у(х) = дм ?(*) + [Аи (х), #(*)], f^ = Э^ А „ - Э^ + [Ам, А„]. Здесь
/i = 0, 1, 2, 3, символ [а, Ь] обозначает векторное произведение, а сим-
символ <а, Ь> — скалярное произведение векторов а, Ь. Переход от дейст-
действия A) к действию E) является частным случаем стандартной процедуры,
71

позволяющей по функционалу действия, обладающему группой внутрен-
внутренних симметрии, построить с помощью включения калибровочных полей
теорию, в которой эта группа внутренних симметрии локализована (см.
§ В4). В самом деле, функционал E) инвариантен относительно преобразо-
преобразований вида 1р'(х) = Vip(x), где V — ортогональная матрица. (Иными сло-
словами A) имеет группу внутренних симметрии S0C).) Действие E) об-
обладает уже локальной калибровочной симметрией. Иначе говоря, оно не
меняется при заменеip'(x) = V(x) <p(x), где V(х) —ортогональная матри-
матрица, гладко зависящая от х, если калибровочное поле Ам (х) преобразуется
соответствующим образом. А Калибровочное поле, вообще говоря, прини-
принимает значение в алгебре Ли группы внутренних симметрии. В данном случае
мы рассматриваем Ам (х) как трехмерный вектор, пользуясь тем, что ал-
алгебра Ли группы S0C) изоморфна алгебре Ли трехмерных векторов, в
которой операция определена как векторное произведение. Ў
Модель с функционалом действия E) представляет собой бозонную
часть модели, предложенной Джорджи и Глешоу для описания слабых
и электромагнитных взаимодействий. (Модель Джорджи - Глешоу содер-
содержит еще трехкомпонентное фермионное поле, преобразующееся по вектор-
векторному представлению группы SOC).) Модель Джорджи — Глешоу не может
в настоящее время (после открытия нейтральных токов) рассматриваться
как реалистическая; однако, ее структура близка к структуре теорий боль-
большого объединения, поскольку она, как и эти теории, основана на простой
калибровочной группе. Это делает ее анализ существенным для понимания
физики большого объединения.
Функционал энергии для действия E) может быть записан в виде
?=-/?2(х)Л + -/(^J</3л;+Х/(;?2 -a2Jcl3x+EYM, F)
$ ? % F3
Здесь ?"ум - функционал энергии для калибровочного поля. (Воспользо-
(Воспользовавшись инвариантностью относительно локальных калибровочных преоб-
преобразований, мы наложили калибровочное условие А0(х) =0.)
Пространство полей, для которых функционал энергии F) конечен,
несвязно. В самом деле, если энергия F) конечна, то конечен и интеграл
C), поэтому каждому полю с конечной энергией можно сопоставить це-
целое число п — топологическое число поля. С другой стороны, для каждого
п можно построить поле, имеющее топологическое число п и конечную
энергию. Например, для п = 1 можно положить
г G)
i4j(x) = 0, ?(x)=@(r)+e)n,-
X
где к, /, / = 1, 2, 3, г = | х |, п = —,а(г) и 0(г) - быстро убывающие функ-
ции, а@)= — 1, 0@) = -а. Здесь и далее мы полагаем vf(x) = 0, Е(х) = 0.
Это отвечает переходу от исследования фазового пространства к изучению
72

пространства конфигураций. Этот переход очевидным образом не влияет
на топологические свойства пространства.
Для того чтобы построить обладающее конечной энергией поле с лю-
любым топологическим числом и, рассмотрим произвольное векторное поле
Ф(п), определенное на множестве векторов единичной длины и удовлет-
удовлетворяющее условию I Ф(п) I = а. Используя поле $(п), построим поле ?(х)
вне единичного шара, положив <j?(x) = $(х/|х|). Калибровочное поле
Ам (х) подберем таким образом, чтобы ковариантная производная V^p(x) =
= Эм<^(х) + [Ам (х), <^(х) ] обращалась в нуль. Такое построение возможно,
поскольку в силу условия | Ф (п) | = а вектор р(х) ортогонален векторам
Э i^(x), Э 2<?(х), Э з<?(х). Именно следует положить
Ам(х)= [?(х), Эм
I (I
где Хм (х) — произвольные функции. Внутри единичного шара определим
поля (^(х), Ам (х) произвольным образом, наложив единственное условие
гладкости. Легко видеть, что энергия построенного поля конечна (по край-
крайней мере, в случае Хм (х) = 0). В самом деле, плотность энергии построен-
построенного поля вне единичного шара сводится к плотности энергии калибровоч-
калибровочного поля Ам (х). Конечность энергии калибровочного поля следует из
1
того, что оно может быть записано в виде А„ (х) = а„ (х/| х |) и, значит,
|х|
плотность энергии этого поля убывает как | х|~4.
Остановимся на физическом смысле топологического числа поля. Для
этого заметим, прежде всего, что каждый вектор ip может быть с помощью
вращения переведен в вектор, для которого </?' = <р2 = 0, </з3 = | <р\. Это под-
подсказывает, что на поле <^Г(х) естественно наложить калибровочное условие
??'(х) = ??2(х) = 0. Оказывается, однако, что такое калибровочное условие
заведомо нельзя наложить, если топологическое число поля отлично от
нуля. В самом деле, для поля, удовлетворяющего калибровочному условию
<рх = у2 = 0, асимптотика на бесконечности тривиальна: Ф(п) =Ф0 = @,0, а).
Если поле <^(х) допускает наложение калибровки </?' = </э2 = 0, то соответ-
соответствующая асимптотика 5>(п) имеет вид$(п) = F(n)$0. ГД? Р(п) - непре-
непрерывная функция, определенная на двумерной сфере | п| = 1 и принимающая
значение в группе SOC). Всякое отображение сферы S2 в SOC) гомотоп-
гомотопно нулю GT2(SOC)) = 0; см., например, § Т15). Отсюда следует, что
Ф (п) = V (п) $0 представляет собой гомотопное нулю отображение сферы
S2 в S2 и, значит, топологическое число поля <^(х) равно нулю. Таким
образом, мы видим, что поля, калибровочно эквивалентные полям, удов-
удовлетворяющим условию if1 = ip2 =0, топологически тривиальны. Имеет мес-
место и обратное утверждение: если топологическое число поля равно нулю,
то оно калибровочно эквивалентно полю, удовлетворяющему калибровоч-
калибровочному условию v?1 = v?2 =0.
Энергия поля <^(х) = Фо = @, 0, а) равна нулю. Поскольку функционал
энергии F), очевидным образом, неотрицателен, это поле доставляет наи-
наименьшее значение функционалу энергии. По общему правилу энергия рас-
рассматриваемого поля представляет собой квазиклассическое приближение
73

к энергии основного состояния (физического вакуума); естественно назы-
называть это поле классическим вакуумом. Для того, чтобы найти энергии
слабовозбужденных состояний, нужно разложить функционал действия по
отклонениям от поля с наименьшей энергией (классического вакуума) и
оставить только квадратичные члены. Продела-^ эту операцию с функцио-
функционалом действия E) мы получим для квадратичной части действия выраже-
выражение
+ ~ /((9mtjJ -8XeV)«*4*, (8)
где tj (лг) = ч?3 (х) - а. Квадратичный функционал действия при квантова-
квантовании приводит к теории, описывающей скалярную частицу массы 2a\f7k,
две векторных частицы с массами ag и одну безмассовую векторную части-
частицу. Эта безмассовая частица отвечает полю А\. Ее следует отождествлять
с фотоном, а поле А \ - с электромагнитным полем.
Мы имеем здесь дело с проявлением эффекта Хиггса. Классический ва-
вакуум $0 обладает в данном случае не SO C)-симметрией исходного лагран-
лагранжиана, а лишь SOB)-симметрией. Векторные поля, отвечающие нарушен-
нарушенным симметриям, приобретают массы.
Поскольку в калибровке tp1 = у2 = 0 поле А^(х) можно рассматривать
как электромагнитное, тензор F^v = d^Al — ЬиА^ можно рассматривать
в этой калибровке как тензор электромагнитной напряженности. Поставим
себе цель дать выражение тензора электромагнитной напряженности, не за-
зависящее от выбора калибровки. Легко видеть, что нужное нам выражение
может быть записано в виде
yv$)m. (9)
В самом деле, выражение (9), очевидным образом, калибровочно инва-
инвариантно; с другой стороны в калибровке ч?1 = у2 = О оно сводится к стан-
стандартному. Отметим, что напряженность (9) удовлетворяет уравнению
Максвелла
Э<, F^ + Эм Fvo + bvFotl = и.
(Это уравнение выполняется в калибровке ipx = <р2 - 0; в силу калибровоч-
калибровочной инвариантности оно верно всегда.)
В частности, для магнитной части напряженности Н = (F23, F3i,F12)
имеет место соотношение divH = 0. Выражение (9) для электромагнитной
напряженности имеет смысл и для топологически нетривиальных полей в
точках, где <?(х) Ф 0. (Использованный при обосновании этого выражения
переход к калибровке v?1 •= <р2 - 0 невозможен для топологически нетри-
нетривиальных полей сразу во всем пространстве; однако электромагнитная
напряженность определяется локальными свойствами поля, а в любой ма-
малой области, где поле <?(х) не обращается в нуль, переход к калибровке
V?1 =уз2 = 0 возможен.)
74

Воспользовавшись выражением (9) для FMl) можно связать топологи-
топологическое число с магнитным зарядом поля. Магнитный заряд определяется
соотношением
» = $HdS, A0)
где $HdS — поток напряженности Н через бесконечно удаленную сферу.
В классической электродинамике соотношение divH = 0 имеет место во
всех точках, поэтому магнитный заряд, определенный формулой A0),
всегда равен нулю. В рассматриваемой модели напряженность определена
только в тех точках, где <р(х) Ф 0, соответственно соотношение divH = 0
имеет место только в этих" точках. Это приводит к возможности существо-
существования полей с ненулевым магнитным зарядом. В частности, легко прове-
проверить, что для поля G)
и, следовательно, магнитный заряд равен 1. (Отметим, что принятое нами
определение полей Ам и напряженности FIIV отличается от стандартного
множителем 1/g. Если пользоваться обычным определением, то магнитный
заряд равен 1/&.) Мы видим, что для поля G) топологическое число совпа-
совпадает с магнитным зарядом. Оказывается, что совпадение топологического
числа с магнитным зарядом имеет место и в общем случае.
Проведем более подробный анализ понятий топологического числа и
магнитного заряда, из которого, в частности, будет следовать их совпаде-
совпадение. Заметим, прежде всего, что топологическое число поля <^"(х) можно
определить и в существенно более общей ситуации. Именно: достаточно
предположить, что вне некоторого шара ZK нет точек, в которых поле
<^Г(х) обращается в нуль. Тогда поле ip (х) на сфере S 2, внутри которой ле-
лежит шар D3, можно рассматривать, как отображение сферы S2 в прост-
пространство (R3, из которого выколото начало координат. Каждому такому
отображению можно сопоставить целое число (например, как степень
отображения сферы S2 в единичную сферу, переводящего точку х € S2
?(х)
в точку ). Это целое число мы будем называть топологическим чис-
IV 00 I
лом поля у?(х). Оно очевидным образом не зависит от выбора сферы S2, а
в случае, если поле имеет асимптотику Ф(п), совпадает с топологическим
числом, определенным ранее. Для интересующего нас топологического чис-
числа можно указать аналитическое выражение
4тт n<v \и>\Л
где интеграл берется по любой сфере, вне которой ^(х) не обращается в
нуль. (Вывод этого выражения намечен в § Т1 и в более общем случае
проведен в § Т8.)
75

Отметим далее, что формула (9) для тензора напряженности имеет
смысл во всех точках, где поле <^(х) не равно нулю. Поэтому магнитный
заряд может быть определен во всех случаях, когда поле<^(х)не обращает-
обращается в нуль вне некоторого шара D3 (т.е. во всех случаях, когда можно го-
говорить о топологическом числе поля ^(х)). При вычислении магнитного
заряда можно использовать любую сферу S*, содержащую .внутри себя шар
D (в силу теоремы Гаусса поток магнитной напряженности Н через все
такие сферы один и тот же).
Легко проверить, что магнитный заряд не меняется при непрерывном
изменении полей tp и Ам, лишь бы в процессе этого изменения поле ip все
время не обращалось в нуль вне некоторого шара. В самом деле, пусть
Ор(х, т), Ам(х, т))- семейство полей, непрерывно зависящее от парамет-
параметра т, 0 < т < 1, причем <^(х, т) Ф 0 при |х|> L. Рассмотрим поле
(<р(х, т (х)), Ам (х, т (х)), где т(х) - функция, равная нулю при | х| < 2L
и 1 при I х | > 3L. Выражая магнитный заряд этого поля один раз с помо-
помощью потока напряженности через сферу радиуса < 2L, а другой раз, исполь-
используя сферу радиуса > 2L, убеждаемся, что он совпадает с магнитным заря-
зарядом поля (^(х, т), Ам (х, т)) при т = 0 и при т = 1. Поскольку, с другой
стороны, поток напряженности не зависит от выбора сферы, мы видим, что
магнитные заряды полей Qp(x, т), Ам (х, т)) при т = 0 и т = 1 совпадают.
Теперь мы готовы доказать совпадение топологического числа поля tp,
задаваемого выражением A2), и магнитного'заряда. В самом деле, рас-
рассмотрим семейство полей Ор(х), тАр(х)), непрерывно зависящее от пара-
параметра т. Легко видеть, что при т =0 формула для магнитного заряда тако-
такого поля совпадает с выражением A2) для топологического числа поля
1р. Поскольку магнитный заряд не меняется при изменении т, это совпаде-
совпадение имеет место и при т = 1, т.е. для произвольного поля (ц>(х), Ам (х)).
(Отметим, что поле Qp(x), тАм(х)) может иметь бесконечную энергию,
даже если энергия поля (у?(х), Ам (х)) конечна. Однако это несуществен-
несущественно для проведенного выше рассуждения, поскольку магнитный заряд это-
этого поля имеет смысл.)
§ S. Топологические интегралы движения в калибровочных теориях
Существующие модели, объединяющие сильные, слабые и электромаг-
электромагнитные взаимодействия (модели "большого объединения" построены по
следующей схеме, повторяющей схему теории электрослабого взаимодей-
взаимодействия. Рассмотрим лагранжиан
? = ?0 - Гффу - и(д, A)
где ф = (ф1, ..., фт) — многокомпонентное фермионное полз, </з =
= (ip1, ..., tp") — многокомпонентное скалярное поле, а ?0 — свободный
лагранжиан этих полей. Будем предполагать, что рассматриваемый лагран-
лагранжиан инвариантен относительно группы внутренних симметрии G. Это озна-
означает, что поля ф и i/j преобразуются определенным образом при
преобразованиях группы G (принимают значения в пространстве некоторо-
некоторого представления группы G), а лагранжиан является скаляром относитель-
76

но этой группы (в частности, полином U(<p) и выражение Гфф<р =
-ГцкФ v Ф должны быть G-инвариантными). Из лагранжиана ? строит-
Л
ся лагранжиан ?, инвариантный относительно локальных калибровочных
преобразований, отвечающих функциям g(x), принимающим значения в G.
Именно, следует включить калибровочные поля А (х), принимающие зна-
значения в алгебре Ли 8 группы G, заменить в лагранжиане все производные
Эм ковариантными производными V^ и добавить слагаемое
(Здесь &ЦР =bilAv — Э„ЛМ + [Ам, A.v] — напряженность калибровочного
поля, <, > — инвариантное скалярное произведение в алгебре Ли #;
подробнее см. § В4.) Таким образом, под полем в теории, описываемой
Л
лагранжианом ?, следует понимать совокупность фермионного поля ф (х),
скалярного поля у (х) и калибровочного поля А (х). Поля, связанные ка-
калибровочным преобразованием, физически эквивалентны. Это позволяет
рассматривать не все поля; можно ограничить класс полей, наложив на них
какое-либо условие. Нужно только потребовать, чтобы каждое поле можно
было перевести с помощью калибровочного преобразования в поле, удов-
удовлетворяющее наложенному условию. (Условия такого типа называются
калибровочными.) Мы обычно будем использовать калибровочное условие
Ао = 0. Отметим, что наложение этого условия не полностью уничтожает
калибровочную'свободу: остается возможность совершать калибровочные
преобразования с функцией g (х), не зависящей от времени. (Соответствен-
(Соответственно, можно добавить к условию Ао = 0 еще дополнительные условия.)
Изучим вопрос о существовании топологических интегралов движения
¦ л
в теории, описываемой лагранжианом ?, полученным из лагранжиана ?
вида A). Заметим прежде всего, что фермионы несущественны в интере-
интересующей нас проблеме. Поэтому мы можем ограничиться только бочонной
частью лагранжиана
? = \
\ < V^, VV > Ufa) + jCYM. B)
Здесь ф(х) = (i/j1 (x), ...,1/?"(х))-и-компонентное, (принимающее значения'
в IR") скалярное поле, преобразующееся по представлению Г компактной
группы Ли G, калибровочное поле Ам принимает значение в алгебре Ли 5?
группы G, a V^i/j = Эм</з + t(A ^ч>, где / - представление алгебры Ли i§, от-
отвечающее представлению Г группы G. Множество точек и-мерного прост-
пространства, на которых функция ?/(</?) = Uty1,..., </з") достигает наименьшего
значения, будем называть множеством классических вакуумов и обозначать
буквой R. Будем предполагать, что R является подмногообразием прост-
пространства IR". Без ограничения общности можно считать, что наименьшее зна-
значение функции C/(ip) на R равно нулю (т.е. min ?/(</?) = 0).
Исследуем топологические свойства фазового пространства в рассматри-
рассматриваемой теории. Наложим калибровочное условие Ао = 0. Тогда функционал
77

энергии запишется в виде
Е = J d3x {у тг2 + \ }
(if / = 1, 2, 3). Здесь тг(лг) =1^(лг) — обобщенные импульсы, отвечающие
обобщенным координатам <р(х), a ?/(дг) = -At(x) = &io(x) пропорцио-
пропорционально обобщенному импульсу, отвечающему обобщенной координате
А{ (х). Фазовое пространство Р состоит из полей (яг(х), <р (х), Et (x), At (x)),
для которых конечен функционал C).
Очевидно, что число компонент фазового пространства Р совпадает
с числом компонент пространства Ро полей (</э(х), Ai(x)), на которых
конечен функционал
n, ftj >}, D)
где /, / = 1, 2, 3. Мы будем поэтому в дальнейшем рассматривать простран-
пространство Ро.
Рассмотрим отображение а, сопоставляющее каждой точке (ар1, ..., </зп)
пространства К" ближайшую к ней точку многообразия R. Как показано
в § Т5, на достаточно малой окрестности (R подмногообразия R отображе-
отображение а однозначно и непрерывно. Фиксируем эту окрестность.
Конечность функционала энергии D) требует, чтобы при | х| -+•«> поле
</з(х) приближалось к многообразию классических вакуумов R. Мы нало-
наложим поэтому на рассматриваемые поля условие, чтобы значения <р вне
некоторого шара D3 принадлежали описанной выше окрестности <R много-
многообразия R. (Иными словами, мы требуем, чтобы множество точек, для ко-
которых tp (x) ф (R, было ограниченным.)
Каждому полю <р (х) сопоставим гомотопический класс ? (</э) отображе-
отображения aip большой сферы S2 в R. (По сделанному предположению поле <р
отображает сферу достаточно большого радиуса в (R, а отображение а пере-
переводит (R в R). Этот гомотопический класс определяет топологический тип
поля </з(х). Мы будем часто называть ?(</з) топологическим зарядом
ПОЛЯ I/J.
В дальнейшем, рассматривая поля с конечной энергией, мы будем пред-
предполагать, что они "хорошо ведут себя на бесконечности". Точнее, мы будем
считать, что ковариантная производная V;</3 (x) стремится к нулю достаточ-
достаточно быстро:
I VfVp(x)| < const |хГA+6>, б > 0. E)
78

а В силу конечности энергии функция Vf<^(x) квадратично интегрируема.
Если Vf??(x) ~ |х|~а при | х|-+оо, то из квадратичной интегрируемости
вытекает, что а > 3/2. Это означает, что наложенное нами условие заведомо
выполнено, если скорость стремления функции Vf</?(x) к нулю более или
менее одинакова по всем направлениям. Ў Мы будем предполагать также,
что вдоль каждого луча X п., 1 п | = 1, 0< X < <» поле </э имеет конечный
предел Ф(п) = Urn ip(Xn) и достаточно быстро стремится к этому преде-
Л. -к»
лу: | Ф(п) — tp ( X п) | < const Х~ 6, 5 > 0. Отметим, что это предположение
выполнено, если калибровочное поле удовлетворяет требованию E) и ка-
калибровочному условию x'Aj = 0. В самом деле, тогда
\х'д{<р(х)\ = |дг' V,<p(x)| < const -1 jc Г6
и, следовательно,
9i/j(Xn)
ЭХ
const X
-A+8)
При наложенных нами условиях из конечности выражения D) вытекает,
что Ф(п) € R для любого вектора п0. Топологинеский заряд поля у можно
определять как гомотопический тип отображения Ф, определяющего
.асимптотику поля <р. (При этом Ф рассматривается как отображение сферы
|п| = 1 в R.) Это определение совпадает с указанными выше, поскольку
Ф(п) при больших X мало отличается от а</з(Хп) и, значит, гомотопический
класс отображения Ф совпадает с гомотопическим классом отобра-
отображения <7</з, рассматриваемого на сфере большого радиуса.
Если поле (</з, .4М) непрерывно зависит от параметра т и при каждом т
имеет конечную энергию, то его топологический заряд не зависит от т.
(Точнее, следует потребовать, чтобы при изменении параметра т в каждом
конечном промежутке нашелся такой шар D3, вне которого все поля из
семейства ут принимают значения в окрестности (R многообразия Л. Тогда
топологический заряд поля ipT можно вычислять с помощью отображения,
определяемого, полем </зт на границе этого шара.) В частности, поскольку
с течением времени поле меняется непрерывно, топологический заряд
поля, является интегралом движения. Иными словами, можно говорить
о топологическом заряде зависящего от времени поля <р(х) = ip(t, x), опре-
определяя его как топологический заряд поля tp(t0, х), где t0 — любое фикси-
фиксированное значение времени. (Мы предполагали, что для всякого конечно-
конечного отрезка времени [t0, t^] найдется такой iuapZK С !R3, что tp(t, x) S (R
для всех t0 < t < *i, х ф-D3.)
Группа G действует на многообразии классических вакуумов R. (Функ-
(Функция U(tp) инвариантна относительно группы G, поэтому преобразования
группы G переводят одну точку, в которой достигается наименьшее зна-
значение функции U, в другую точку, обладающую тем же свойством.) Мы
будем всегда предполагать, что группа G действует на R транзитивно, т.е.
каждый классический вакуум может быть получен из другого с помощью
преобразований группы G. (Иными словами, мы предполагаем, что вы-
вырождение классического вакуума полностью обусловлено инвариантностью
79

относительно группы G.) В этом случае R можно рассматривать как прост-
пространство смежных классов G/H, где подгруппа Я состоит из преобразова-
преобразований, оставляющих на месте фиксированный классический вакуум (см.
§ А6и§Т16).
Группа Я имеет физический смысл группы ненарушенных симметрии.
При сделанном нами предположении множество гомотопических классов
{S2, R} легко вычисляется. Будем считать, что группа G односвязна.
(Как объяснено в § Т20, это можно сделать без ограничения общности,
заменив в случае необходимости группу G ее универсальной накрываю-
накрывающей G.) Тогда гомотопическая группа я2 (R ) = я2 (G/Я) изоморфна груп-
группе 7Г1(Я) (см. § Т20). В случае, если группа Я связна, пространство Л =
= G/H односвязно и множество гомотопических классов { S2, R } можно
отождествить с гомотопической группой n2(R) = 74(Я), и, следовательно,
топологический тип поля определяется элементом группы 7тх (Я).
В моделях большого объединения группа Я локально изоморфна груп-
группе SUC) X U(l) (не нарушаются цветовая группа SUC) и электромагнит-
электромагнитная группа U(l)). Если Я = SUC) X U(l), то тг^Я) = w1(U(l)) = Z, т.е.
топологический заряд является целым числом. Позже мы увидим, что это
число можно отождествить с магнитным зарядом. В 81)E)-модели боль-
большого объединения эти утверждения сохраняют силу (как и во всех дру-
других имеющихся в литературе моделях), хотя группа Я лишь локально
изоморфна SUC) X U(l). Для того, чтобы вычислить группу iii(H) в слу-
случае, если Я локально изоморфна SUC) X U(l), следует найти гомоморфное
отображение односвязной группы SUC) X IR+ на Я. (Здесь IR+ — группа
положительных действительных чисел.) Тогда группа ttj (Я) изоморфна
ядру D этого гомоморфизма (это вытекает из соотношения SUC) X
X IR+/Z? = Я; см. § Т20). Для 8Щ5)-модели нужный нам гомоморфизм
сопоставляет паре (и, ехрХ), где и е SUC), expX G IR + , матрицу вида
/ Х\
(В 7.2), где К = и ехр ( -' ~ J. ' = ехР (' \) • Отсюда следует, что группа D
состоит из пар вида (ехр(/2 7гЛ/3), ехрB7гЛ)), где к - целое число, и, зна-
значит группа D изоморфна Ж (В группе D операцией является умножение,
ав ?- сложение.) Всякий замкнутый путь в Я с началом и концом в еди-
единице группы может быть записан в виде К = u(f) ехр — —
/ = ехр[/Х@], где 0 < t < 1, u(t) - непрерывная функция со значениями
в SUC), Х(Г) - непрерывная числовая функция. (Это следует из замеча-
замечания, что замкнутый путь в Я получается из пути в SUC) X fR+, соединяюще-
соединяющего единицу группы с одной из точек множества D при отображении SUC) X
X R+ в Я.) Гомотопический класс пути определяется целым числом
B7г)~1(ХA) -Х@)).Отметим, что гомотопический класс пути определяет-
определяется.только зависимостью числа /от t, т.е. замкнутым путем в группе U(l).
(Говоря более формально, можно построить отображение группы Я в U(l),
сопоставляя матрице (В 7.2) число / G U(l). Тогда при отображении груп-
группа 7Г!(Я) = Z изоморфно отображается на группу 7Ti(U(l)) = Ж. Точнее,
соответствующим друг другу элементам я^Я) и 74 (U(l)) отвечает одно
и то же целое число.)
80

В общем случае D является дискретной подгруппой центра группы
SUC) X 1R+. Этот центр изоморфен группе 23 + Р. где 23 - группа из
трех элементов, IR-группа действительных чисел. (Здесь 23> IR и 73 + IR —
группы, операцией в которых является сложение.) Всякая дискретная
подгруппа группы 23 + Я изоморфна либо И, либо "Z+ 23. Если
D = 2?3 + И, то Я = (SUC)/71Ъ~) X U(l). Это возможно только в случае, если
все скалярные поля преобразуются по представлениям группы SUC),
в которых центр ~Вг этой группы действует тривиально. В существующих
моделях эта возможность не реализуется и, значит, tfi(#) = Z.
В случае, если группа Я несвязна (имеются дискретные ненарушенные
симметрии), пространство R = G/H неодносвязно. Его фундаментальная
группа ttj(/?) изоморфна группе тго(Я) = Н/Нсоп, где Ясоп - группа не-
непрерывных ненарушенных симметрии (максимальная связная подгруп-
подгруппа группы Я) (см. § Т20). Множество { S2, R } можно получить как мно-
множество орбит группы Tti(R) = 7Г0(Я), действующей в группе ti2(R) = tii(H)
(см. § Т13 и § Т15). В § 5-8 мы будем считать, что группа Я связна:
анализ эффектов, возникающих в случае, когда имеются дискретные
ненарушенные симметрии, содержится в § 12, 13:
Отметим, что топологический заряд поля <р(х) не меняется при калибро-
калибровочном преобразовании. Это следует из замечания, что для калибровочно-
калибровочного преобразования, заданного с помощью функции g(x), можно найти
непрерывное семейство калибровочных преобразований ?т(х), соединяю-
соединяющее исходное преобразование с тождественным. А Если функция g(x)
определена на всем пространстве Я3, то это сразу вытекает из стяги-
стягиваемости пространства Я3. Однако, утверждение остается справедливым
также в случае, если функция #(х) определена только вне некоторого ша-
шара. Тогда область, на которой определена функция ?(х), гомотопически
эквивалентна сфере 52, и анализ отображений этой области в группу G
сводится к анализу отображений сферы 52 в G. Нужное нам утверждение
вытекает теперь из соотношения tt2(G) = 0, справедливого для любой груп-
группы Ли. Ў
Покажем, что в пространстве Ро полей (<р, А), имеющих конечную
энергию D), существуют поля произвольного топологического типа.
(Под топологическим типом поля (<р, А), естественно, понимается тополо-
топологический тип поля ip.) Иными словами, мы построим для каждого гомо-
гомотопического класса отображений сферы S2 в R такое поле <р, что его
асимптотика определяет этот гомотопический класс, и найдем для этого
поля \р такое поле А, что Е[у, А ] < °°. Рассмотрим произвольное гладкое
отображение а сферы S2, имеющей единичный радиус, в R и определим
скалярное поле при | х | > 1 формулой
—(тгг)-
Калибровочное поле 4м(х) при | х | > 1 зададим соотношением
1 " " («
81

где функция ам(п) подбирается из условия, чтобы ковариантная произ-
производная Vu \р была равна нулю при I х | > 1.
Внутрь шара I х I < 1 поля <р (х) и А^ (х) продолжаются произвольным
образом; единственное условие, которое налагается — это гладкость. Ко-
Конечность энергии построенного таким образом поля (<р,А) очевидна. {Вне
шара все слагаемые в выражении для энергии, кроме энергии калибровоч-
калибровочного поля, обращаются в нуль. Энергия калибровочного поля конечна, по-
поскольку напряженность этого поля убывает как I x | ~2.) Единственное,
что следует проверить, — это возможность подбора функции дм из условия
V = o.
А Приведем доказательство возможности такого выбора. Условие на
ковариантную производную может быть записано в виде
a(n + dn) = a(n) + r(^(n)) a(n) dn", G)
где | п | = 1 и (n,dn) = 0. Ясно, что для каждого п можно найти ам(п),
удовлетворяющее соотношению G). В самом деле, в силу транзитивности
действия группы G на R, любая точка R может быть получена из любой
другой с помощью преобразований группы G. Точка а(п + с?п), бесконечно
близкая к точке а (п), может быть получена из а (п) с помощью бесконечно
малого преобразования группы, т.е. элемента алгебры Ли. Этот элемент,
очевидно, линейно зависит от dn и, значит, представляется в виде а^ (n) dn11.
Выбор а^ (п) неоднозначен (можно, например, заменить ам (п) на ац (п) =
= а^ (п) + Ь^(п), где t (bu (n)) a(n) = 0, т.е. Ьц (п) принадлежит алгебре Ли
стационарной подгруппы элемента а(п). Поэтому возникает вопрос о воз-
возможности непрерывного выбора ац (п). Для того, чтобы гарантировать, что
существует непрерывно (даже гладко) зависящая от п функция ам (п),
удобно воспользоваться топологическими соображениями. Именно, следует
заметить, что при каждом п векторы а^(п), удовлетворяющие G), обра-
образуют линейное пространство Q(n) . Пространства Q(n) можно рассматривать
как слои расслоения, базой которого является сфера S2. Непрерывный
выбор пц (п) означает построение сечения этого расслоения. Сечение рас-
рассматриваемого расслоения существует, поскольку слой этого расслоения
стягиваем. Ў
Таким образом, мы установили, что пространство полей с конечной энер-
энергией распадается на компоненты, каждой из которых отвечает элемент
группы 7г j (Я) = 7Гг (К) ¦ Группа Wi (H) изоморфна прямой сумме несколь-
нескольких экземпляров группы 2? и конечной абелевой группы. Число экземпля-
экземпляров группы Z7, участвующих в этом разложении, равно размерности г центра
группы Н. (Это следует из замечания, что связная компактная группа Ли Н
локально изморфна произведению г экземпляров группы U(l) и компакт-
компактной односвязной группы Ли, см. § Т20). Мы видим, что топологический
тип поля можно охарактеризовать в интересующем нас случае с помощью
г целых чисел и нескольких вычетов. (Всякая конечная абелева группа
представляет собой прямую сумму вида ~2т_ + .. . + 2т/г, т.е. ее элемент
можно рассматривать как строку (&i,. . . ,к„), где kt — вычет по модулю
mt.) Эти числа и вычеты мы будем называть топологическими числами или
топологическими зарядами поля.
82

Существенно отметить, что топологический заряд можно определить не
только для поля, рассматриваемого во всем пространстве, но и для поля,
рассматриваемого в некоторой области VCIR 3, если только на границе Г
этой области поле достаточно близко к вакуумному (точнее, если на Г поле
принимает значение в окрестности (R многообразия R). Будем считать, что
топологический заряд поля <р в V определяется как гомотопический класс
?г Ор) отображения ар границы Г в R. Мы предположим, что граница Г
области V топологически эквивалентна сфере S2 и, значит, область V
вместе с границей Г топологически эквивалентна шару D3. Тогда можно
рассматривать ?гкак элемент группы тт2 (R) = 7Г,(#). Обозначим символом
Кр множество точек, лежащих внутри Г и удовлетворяющих условию
</>(х) ? (R. Если множество Кг пусто, то отображение (яр поверхности Г
в R продолжается на всю ограниченную сферой Г область V и, следова-
следовательно гомотопно нулю (т.е. fp =0). Далее, если К^ =Ky , то^г =fr >
иными словами, топологический заряд поля внутри Г полностью опреде-
определяется множеством Кт ¦ В самом деле, если Кг<) =КТ%, то можно найти
непрерьюное семейство топологически эквивалентных сфере поверхнос-
поверхностей Г,, соединяющее поверхности Го и Ti таким образом, что на всех
точках всех поверхностей <<?(х) ? <R. Это означает, что отображение о<р
определено на поверхности Гг, и, следовательно, гомотопический класс
отображения ар поверхности Г( в R не зависит от t. Топологический за-
заряд поля у аддитивен: если множество КГ является объединением непере-
непересекающихся множеств /Гр t и К^ г, то
Это соотношение можно вьюести из результатов § Т12.(Без ограничения
общности можно считать, что поверхности Г t и Г2 также не пересекают-
пересекаются и расположены внутри Г, тогда утверждение § Т12 можно применить к
области, ограниченной снаружи поверхностью Г, а изнутри — поверхностя-
поверхностями Г, иГ2.)
Для того, чтобы дать физическую интерпретацию аддитивности тополо-
топологического заряда, рассмотрим поле, энергия которого сосредоточена в об-
области D, состоящей из далеких друг от друга областей D\ и Di. Тогда вне
области D = D\ UZJ поле должно быть близким к вакуумному; иными
словами, можно считать, что вне D поле ip принимает значение в <R. Это поз-
позволяет определить топологический заряд поля <р в областях D,Di и Дг-
Аддитивность означает, что топологический заряд поля в области D являет-
является суммой топологических зарядов этого поля в ?>t и Lh. Отсюда следует,
«то топологический заряд является аддитивным интегралом движения.
До сих пор наши рассуждения были классическими. Однако, как мы го-
говорили в § 2, несвязность фазового пространства (существование тополо-
топологических интегралов движения в классической теории) обычно влечет за
собой существование топологических интегралов движения в соответствую-
соответствующей квантовой теории. Это справедливо и в рассматриваемой нами ситуа-
ситуации.
Отметим, что понятие топологического типа поля внутри поверхности Г
с математической точки зрения абсолютно аналогично определенному в § 1
понятию топологического типа дефекта локального равновесия. Точки, в
которых поле ip (х) принимает значение в области <R, следует считать анало-
83

гами точек, в которых имеет место локальное равновесие. Множество Кг —
это аналог множества точек внутри Г, в которых локальное равновесие
нарушено (дефекта локального равновесия). Доказательство аддитивности
топологического заряда повторяет рассуждения § 1.
§ 6. Частицы в калибровочных теориях
Проанализируем частицы, возникающие в теории, описываемой лаг-
лагранжианом E.2). Как обычно, для этого нужно разложить лагранжиан
в окрестности фиксированного классического вакуума <<?о, наложив пред-
предварительно калибровочное условие, устраняющее вырождение классиче-
классического вакуума. В качестве такого калибровочного условия разумно вы-
выбрать условие
<"р(х) = <Ро» (О
где а, как и выше, отображение, сопоставляющее точке <р Е 1R" ближай-
ближайшую к ней точку многообразия вакуумов R. Отметим, что отображе-
отображение а однозначно и непрерывно только в окрестности <R многообразия
R, поэтому наложение калибровки A) разумно лишь для полей, значения
которых лежат вблизи многообразия вакуумов. Вообще говоря, рас-
рассматриваемые нами поля удовлетворяют этому условию только для доста-
достаточно больших | х |, поэтому мы будем рассматривать калибровоч-
калибровочные преобразования, заданные не во всем пространстве [R3, а только
вне некоторого шара. (Функция g(x) ~g{t,x), осуществляющая калибро-
калибровочное преобразование, может зависеть от времени, однако, эта зависи-
зависимость несущественна в интересующих нас вопросах.) Поскольку много-
многообразие вакуумов R переходит в себя при преобразовании группы G, а
расстояние не меняется при этих преобразованиях, отображение о ком-
коммутирует с преобразованиями группы G:
oT(g) = T(g)o. B)
Иными словами, если точка <р' = о<р является ближайшей к tp точкой много-
многообразия R, то точка T(g)tp' является ближайшей к точке T(g)y. Соот-
Соотношение B) позволяет утверждать, что для всякой точки у ? <R.можно
найти такой элемент g € G, что T(g)y удовлетворяет калибровочному
условию A) (т.е. oT(g)y> = <р0). В самом деле, в силу предположенной
нами транзитивности действия группы G на Л, для любой точки многообра-
многообразия R, в частности для точки а<р найдется преобразование T(g), переводя-
переводящее эту точку в <р0 ¦ Замечая, что
мы получаем нужное нам утверждение.
Из сказанного выше следует, что всякое воле <р(х) можно перевести
в поле, удовлетворяющее калибровочному условию A), с помощью калиб-,
ровочного преобразования, отвечающего быть может разрывной функ-
функции g (x), Напомним, однако, что мы рассматриваем толькй калибровочные
преобразования, порождаемые непрерывными (даже гладкими) функция-
функциями ?,(х). Очевидно, что всякое поле, удовлетворяющее калибровочному
условию A), топологически тривиально, поэтому топологически нетри-
84

виальное поле не может быть переведено в поле, удовлетворяющее усло-
условию A), с помощью непрерывного калибровочного преобразования. (Как
было доказано выше, топологический тип сохраняется при калибровоч-
калибровочных преобразованиях, даже если функция g (х), осуществляющая калиб-
калибровочное преобразование, определена только вне некоторого шара.) От-
Отметим, однако, что всякое (даже топологически нетривиальное) поле
(f?(x) можно перевести калибровочным преобразованием в поле, удовлет-
удовлетворяющее условию A) во всякой стягиваемой области V С IR3 (если ко-
конечно, значения поля в этой области принадлежат множеству (R, на кото-
котором отображение а однозначно и непрерывно).
А Для того, чтобы убедиться в этом, рассмотрим для каждой точки х
множество #х элементов g ? G, удовлетворяющих условию T(g)oy = v»0-
Как мы видели, это множество не пусто. Легко проверить, что оно топо-
топологически эквивалентно стационарной подгруппе Я =Я(^0)- В самом деле,
если
(g)v() <р0, то
откуда g g~l €. H. Объединение всех множеств Ях можно рассматривать
как пространство расслоения, базой которого является область, где опре-
определено поле <р(х), а слоями являются множества Ях. Найти нужное нам
калибровочное преобразование - это значит в каждом слое Ях выбрать
элемент g (x), непрерывно зависящий от х, т.е. построить сечение расслое-
расслоения. Поскольку у расслоения со стягиваемой базой всегда существует сече-
сечение (см. § Т18), мы видим, что интересующее нас калибровочное пре-
преобразование действительно существует. Ў
Рассмотрим лагранжиан E.2) в калибровке A) в окрестности вакуума
Фо, оставляя только квадратичные по полям члены. В этот лагранжиан
войдет, очевидно, квадратичное по калибровочным полям слагаемое
< » C)
возникающее из члена — < V^ip, VM<p>. Это слагаемое дает массовые
члены для калибровочных полей. Всякий элемент А алгебры Ли 50 группы
G можно однозначно разложить в сумму элемента А1, принадлежащего
алгебре Ли Ж группы ЯСС, я элемента А", ортогонального (в смысле
инвариантного скалярного произведения) к подпространству Ж. Иными
словами, алгебра 8 разлагается в прямую сумму линейных подпро-
подпространств Ж и Ж1). Очевидно, что t (A')ip0 = 0 для A' G Ж. Разлагая ка-
калибровочное поле Ац(х) в сумму А'ц(х) + А1»(х),гдеА'ц(х) е Ж,А'1 (х) е
? Ж1, мы видим, что выражение C) равно
^<Г(Л;)^0, ГD"")^о>. D)
Эта означает, что калибровочные поля, отвечающие генераторам груп-
группы Я, остаются безмассовыми и после спонтанного нарушения симмет-
симметрии, а Если выбрать ортонормированный базис elt . . . , еп в алгебре Ли
iS группы G таким образом, что его первые векторы е1г . . . , е, лежат в
85

подалгебре К, то калибровочное поле Ац можно разложить по этому
базису: Аа = Ацвк. Массовый член для полей ^записывается в виде
, " 1
тцАрА'", где тц = — <t(et)^0,t(ef)^0). В частности, полям А», . . .
... . А'у. отвечают безмассовые векторные частицы поскольку mt1 = О,
если i < г или / <г. Массы других векторных частиц определяются как
собственные значения матрицы тц, г + 1</,/<п; см. § В2. Ў
Таким образом, в результате нарушения симметрии приобретают массу
п - г векторных полей, где п = dim G, г = dim Я, а и - г скалярных полей
исчезают при наложении калибровочного условия A). (Число степеней
свободы при этом не меняется, поскольку массивная векторная частица
имеет три спиновых состояния при заданном импульсе, а безмассовая —
только два.)
Те частицы, которые мы до сих пор исследовали, не исчерпьюают всего
спектра частиц, описываемых лагранжианом E.2). Их можно назвать
элементарными частицами или элементарными возбуждениями физическо-
физического вакуума. Могут существовать, конечно, связанные состояния элементар-
элементарных частиц. (В квантовой теории элементарные частицы отвечают полюсам
двухточечных функций Грина, а их связанные состояния — полюсам много-
многоточечных функций Грина.) Важно отметить, что в рассматриваемых нами
теориях должны существовать также частицы, которые можно назвать
топологически нетривиальными — частицы с ненулевым топологическим
зарядом. (Элементарные частицы и их связанные состояния имеют, как
легко видеть, нулевой топологический заряд.) Как мы уже говорили
каждому квантовому состоянию с конечной энергией, как и классическо-
классическому полю, можно сопоставить элемент группы тт2(К) = -Пх{Н), не меняю-
меняющийся при изменении этого состояния с течением времени (топологи-
(топологический заряд). С другой стороны, в квантовой теории поля предполагает-
предполагается, что любое состояние с конечной энергией при t -*¦+<*> распадается на
далекие друг от друга стабильные частицы. В силу аддитивности сумма
топологических зарядов этих частиц должна быть равна топологическому
заряду исходного состояния. Поэтому в случае, когда существуют топо-
топологически нетривиальные состояния (т.е. группа Я неодносвязна), сущест-
существуют также топологически нетривиальные стабильные частицы. Как мы
говорили, в теориях большого объединения топологический заряд можно
отождествить с магнитным зарядом; соответственно, топологически не-
нетривиальные частицы имеют магнитный заряд (являются магнитными
монополями).
± В случае, если ffi(#) Ф ~1, можно не только утверждать, что сущест-
существуют топологически нетривиальные частицы, но и оценить число стабиль-
стабильных топологически нетривиальных частиц. В самом деле, существуют
квантовые состояния с произвольными топологическими зарядами, и,
следовательно, любой элемент группы тг2(Л) = Л\(Ю может быть пред-
представлен в виде суммы топологических зарядов стабильных частиц. Для
каждой частицы существует античастица, топологический заряд которой
противоположен топологическому заряду частицы (как и все остальные
заряды). Поэтому каждый элемент группы тт\(Н) является линейной
комбинацией с целочисленными коэффициентами топологических зарядов
86

f ь • • •, is стабильных частиц, т.е. fi,...,?, — это система образующих
группы ттi(H). (Разумеется, деление на частицы и античастицы условно.
Однако, проведя это деление каким-либо образом, мы представляем лю-
любой элемент группы ni(ff) в виде линейной комбинации зарядов частиц,
а не античастиц.) Число элементов в системе образующих группы ^(Я)
не может быть меньше, чем размерность г центра группы Ли Я Мы при-
приходим к выводу, что в рассматриваемой теории существует как минимум
г типов стабильных топологически нетривиальных частиц. Ў
Отметим, что проведенные выше рассуждения нуждаются в некоторых
уточнениях. Дело в том, что мы неявно предполагали конечность числа
частиц, получающихся при распаде состояния с конечной энергией. Если в
теории существуют безмассовые частицы, то это предположение неоправда-
но. В рассматриваемой теории, однако, безмассовые частицы топологи-
топологически тривиальны, поэтому их существование не влияет на справедливость
проведенных выше рассуждений. (Оценка снизу для массы топологически
нетривиальных частиц будет получена в § 11.) Мы рассматривали выше
частицы, отвечающие лагранжиану E.2) — бозонной части лагранжиана
E.1). Как уже упоминалось, наличие фермионов несущественно в ин-
интересующих нас вопросах. Спектр ферми-частиц находится стандартным
способом по квадратичной части лагранжиана, разложенного по отклонени-
отклонениям от классического вакуума.
§ 7. Магнитный заряд
Остановимся прежде всего на случае, когда группа ненарушенных сим-
симметрии Я является связной однопараметрической группой. Заметим, что
группа ненарушенных симметрии всегда является замкнутой подгруппой
группы G и, следовательно, компактна. (Всякое замкнутое подпростран-
подпространство компактного пространства компактно.) Поскольку всякая связная
одномерная компактная группа Ли изоморфна группе U(l), мы видим,
что в нашем случае Я = U(l). Мы установили, что число калибровочных
полей, остаюшихся безмассовыми после нарушения симметрии, равно
размерности группы Я. Таким образом, в случае Я = U(l) остается одно
безмассовое йалибровочное поле; оно интерпретируется как электромаг-
электромагнитное поле. В калибровке F.1) потенциал электромагнитного поля мож-
можно отождествить с компонентой А1и = < Ац (х), ву) поля А^ (х), отвечаю-
отвечающей генератору ei группы Н =UA). Электромагнитная напряженность
выражается через потенциал А*и (х) обычной формулой
^W = VlW-^iD A)
Рассмотрим поле (<р(х), А^ (х)), считая, что в некоторой области ip{x)
принимает значение в многообразии вакуумов R и. что в этой области
Уцф(х) ~ 0- Тогда в калибровке F.1) поле А^ (х) принадлежит алгебре
Ли К группы Н = U(l), т.е. А^ (х) = А^ (х)ех. (В этой калибровке, оче-
очевидно, ip(x) = \р0 и, значит, VM((?(x) = ?Dм)<р0 = 0.) Мы видим, что в рас-
рассматриваемой калибровке
ft.WsVW«i- B)
87

и, значит
^V(*) = <^, (*),*• >• C)
(Напомним, что генератор в\ мы считаем нормированным:-1|е\ || = 1.)
Если энергия поля конечна, то при | х | -*<» поле у (jc) приближается к мно-
многообразию вакуумов, a VMip(x) стремится к нулю. Это означает, что мы
можем применять при | х | -+ °° соотношение B) для электромагнитной
напряженности. Таким образом на больших расстояниях выживает только
электромагнитная часть Р^и(х) тензора ^v(x). (Это связано с тем,
что оставшиеся калибровочные поля приобретают массу.)
В рассматриваемом нами случае Я = U(l) очевидно, что
п2 (R) = я2 (G/Я) = я, (Я) = тг, (U A)) = Ж.
Это означает, что топологический тип поля характеризуется целым числом-
топологическим зарядом. Мы покажем, что это целое число с точностью
до множителя можно отождествить с магнитным зарядом.
Прежде всего объясним, что следует понимать под магнитным зарядом
поля (<p(jc), i4M(jc)). Как уже говорилось, в калибровке F.1) можно
записать напряженность электромагнитного поля FMP (х) в стандартном
виде A). Для того, чтобы найти электромагнитную напряженность произ-
произвольного поля (<p(jc), Ац(х)) в точке х, нужно в окрестности точки х
перевести это поле калибровочным преобразованием в поле, удовлетворяю-
удовлетворяющее условию F.1), и вычислить напряженность полученного поля по фор-
формуле A). Отметим, что нужное нам калибровочное преобразование заве-
заведомо существует, если значение поля у в рассматриваемой точке принадле-
принадлежит фиксированной выше окрестности (R многообразия вакуумов. Выбор
этого калибровочного преобразования, конечно, неоднозначен. Однако,
полученные с его помошью калибровочные поля, удовлетворяющие ус-
условию F.1), связаны между собой калибровочным преобразованием.
Легко проверить, что функция g (jc) , осуществляющая это калибровочное
преобразование, принадлежит группе Я = U(l). (Если оу(х) = <р0 и
oT(g(x))tp(x) =(р0.товсилу F.2)
T(g(x)) oip(x) = T(g(x)) (A, = <Ро
и, значит, g(x) e Я = Я^о). Это означает, что поле А\ определено с точ-
точностью до обычной в электродинамике калибровочной эквивалентности,
а соответствующая напряженность Fy.v определена однозначно. Таким
образом, мы можем говорить об электромагнитной напряженности FMP (jc)
любого поля (<р(х), Ац (jc)) в тех точках, где значение поля у принадле-
принадлежит множеству (R. Позже мы укажем явную формулу, позволяющую вы-
вычислять электромагнитную напряженность поля (^ (jc) , А^ (х)). Сейчас
заметим только, что электромагнитную напряженность можно записать
в виде
Ъ
*)=
если <р(х) принадлежит многообразию вакуумов Л, a VM<p(jc) = 0 в ок-
окрестности точки х. Здесь мы обозначаем символом Л(<р) генератор ста-
стационарной подгруппы Ну точки <р € R, удовлетворяющий условию
|Л() = 1. В самом деле, выражение D) справедливо в силу C) в ка-
88

либровке F.1). С другой стороны, выражение D) калибровочно инвариант-
инвариантно, и, следовательно, справедливо и без условия F.1). Поскольку для по-
поля с конечной энергией на пространственной бесконечности <р (х) стремит-
стремится к многообразию R и VM<p(jc) -* 0, соотношение D) справедливо для
любого такого поля при х -+<». Точнее говоря, для такого поля следует
заменить D) соотношением
^)). E)
(Ввиду того, что значение поля <р(х) не принадлежит многообразию ва-
куумов R, а лишь близко к R, мы вместо h(ip(x)) подставляем значение
функции h (((?) на вакууме оц> (х), ближайшем к ^ (х).)
Электромагнитная напряженность удовлетворяет уравнению Максвелла
Эм FP а + Эр FOfi + Ъа F^p = 0; F)
это ясно из калибровочной инвариантности F^v и замечания, что уравне-
уравнение F) выполнено в калибровке F.1). В частности, магнитная напряжен-
напряженность Н = (F23, ^3i. ^12) удовлетворяет уравнению divH = 0. Это поз-
позволяет определить магнитный заряд любого поля (<р(х), Лм (*)), если
значения ц> (х) вне некоторого трехмерного шара принадлежат множ'ест-
ву ft. Именно, магнитный заряд определяется соотношением
Ш= — $HdS, G)
4w
где интеграл берется по любой двумерной сфере, внутри которой ле-
лежат все те точки, для которых *р(х) ? ft. (В силу соотношения divH = О
этот интеграл не зависит от выбора сферы. Однако, поскольку напря-
напряженность Н не всюду определена, рассматриваемый интеграл может быть
не равен нулю.) Для магнитного заряда поля с конечной энергией можно
указать также формулу *
Ш= — § < Й(х), h(atp(\)))dS, (8)
4тг
где 3?= (^23, ?)i. ^12), а интеграл берется по бесконечно удаленной
сфере. (Эта формула получается, если воспользоваться соотношением
E), верным на бесконечно удаленной сфере.) Легко убедиться, что маг-
магнитный заряд не меняется при непрерывном изменении поля (</> (х),
ЛДх)). (Мы предполагали, как и в § 5, что для каждой точки вне не-
некоторого шара значения поля у (х) в любой момент принадлежат мно-
множеству ft.) Иными словами, магнитный заряд является топологическим
числом поля ((<?(х), i4M(x)). Доказательство полностью повторяет дока-
доказательство аналогичного утверждения в модели Джорджи-Глешоу.
Как и в случае топологического заряда, при определении магнитного
заряда мы рассматриваем поле (<р, А^) в фиксированный момент времени
г, однако, заряд не зависит от выбора этого момента (это следует из неиз-
неизменности заряда при непрерывной деформации поля). Поэтому в даль-
дальнейшем мы будем считать, что рассматриваемые поля <р, /4М зависят толь-
только от пространственной переменной х.
Отметим, что можно говорить про магнитный заряд поля (<р(х),
¦<4ц(х))> заключенный внутри поверхности Г, на которой значения поля
89

V» (х) принадлежат множеству <R. Этот1 магнитный заряд Юг определяет-
определяется как Dn)~l fHdS. Легко проверить, что ГОГ не меняется при непре-
г
рывной деформации поля, если значения поля у на Г во время деформа-
деформации всегда принадлежат множеству (R.
Магнитный заряд поля (<р(х), 4м(х)) целиком определяется полем
?>(х). (Поле (<р(х), ^^(х)) имеет тот'же магнитный заряд, что и поле
(<р(х), у4м(х)), поскольку эти два поля можно соединить непрерывной
деформацией (<р(х), гЛм (х) + A - /).4М (х)), во время которой магнит-
магнитный заряд не изменяется.) Очевидно, что магнитный заряд Шг поля
(<р(х), Ац(х)) в области, ограниченной поверхностью Г,является функ-
функцией от топологического заряда поля у (х). (Если два поля <pi (x) и ipj (х)
имеют один и тот же топологический заряд, то определенные ими отобра-
отображения поверхности Г в (R можно соединить непрерывной деформацией. От-
Отсюда следует, что соответствующие магнитные заряды совпадают.) Более
того, можно утверждать, что магнитный заряд является линейной функцией
от топологического числа:
п»г(<?) = СГгОР)- (9)
Это вытекает из аддитивности топологического заряда и аналогичного
свойства магнитного заряда. Мы докажем, что С = р/4тг, где v определя-
определяется условиями е\р(уе%) = 1, exp(Xei) Ф 1 при 0 < X < v. (Можно ска-
сказать, что v - наименьшее положительное число, для которого exp(pei) = 1,
Геометрически v характеризуется как длина окружности Я = U A).)
В силу доказанного выше нам достаточно проверить равенство
) = -^Гг0М) (Ю)
47Г
хотя бы для одного топологически нетривиального поля м
Мы проверим это равенство в случае, если поле <р(х) принимает значе-
значения в многообразии R и выполнено соотношение VM <p (jc) = 0. (Отметим,
что соотношение A0) в обшем случае легко вывести и без соображений,
основанных на аддитивности заряда, поскольку любое поле можно про-
деформировать в поле, для которого мы проверим A0) непосредственно.)
Мы считаем, что поверхность Г топологически эквивалентна сфере
S2. На S2 можно ввести систему координат (р, а), где а — долгота, 0 <
<а<27Г, ар — расстояние до южного полюса, 0 <р < 1. Для южного полю-
полюса р = 0, для северного р = 1, а в обоих случаях произвольно. (Расстояние
от точки сферы до полюса можно понимать либо как расстояние bJR3,
либо как кратчайшее расстояние на поверхности сферы. В обоих случаях
нужно нормировать метрику так, чтобы расстояние между полюсами бы-
было равно 1.) Эта система координат порождает координаты на Г, кото-
которые мы также будем обозначать символами р, а. Пользуясь введенными
только что координатами, можно построить отображение / круга D2 на
Г, которое является топологическим внутри круга и переводит всю гра-
границу в одну точку. (Если считать, что круг D2 имеет радиус 1, то точке
круга с полярными координатами (р, а) следует сопоставить точку по-
поверхности Г, имеющую те же координаты в описанной выше системе).
Как следует из рецепта, изложенного в § Т 20, для того чтобы установить
90

взаимно однозначное соответствие между тг2 (R) и ttj (Я), следует найти
для отображения </> топологической сферы Г в R накрывающее его отоб-
отображение /3 круга D2 в G. Иными словами, нужно построить такое отоб-
отображение /}, чтобы было выполнено соотношение
Ч>(р,а)=Тф-1(р,а)Iро, A1)
где р, а в левой части равенства — введенные выше координаты на Г,
а в правой части - полярные координаты на D2, символ <р0 обозначает зна-
значение поля \р в северном полюсе поверхности Г (т.е. в точке, для кото-
которой р = 1,а произвольно).
а Чтрбы увидеть, что соотношение A1) эквивалентно соотношениям,
использованным в § Т20, следует вспомнить, что проекция расслоения
(G, GjH, Я, я) сопоставляет элементу g € G точку ir(g) = T(g~l)y0 e
? R = G/K Ў
Из A1) следует, что Т(в~1 A, а))<р0 = <Ро- Это означает, что отображе-
отображение 0 на границе круга D можно рассматривать как отображение окруж-
окружности S1 в Я - стационарную подгруппу элемента ^0- Сопоставляя эле-
элемент группы Vi (Я), определяемый этим отображением, элементу группы
Яг(в), определяемому отображением <р топологической сферы Г в Л,
мы получаем взаимно однозначное соответствие между -п^ (Я) и ir2 (R).
Таким образом, в интересующем нас случае Н = U(l) топологическое чис-
число поля <р можно определить формулой
у 1 а» ЭХ 1
Гг = -/-Л=-(ХB,г)-Х@)), A2)
" о Эа v
где Л (а) — непрерывная функция, задаваемая соотношением 0A, а) =
= ехр(—X(a)ei). (Каждый элемент окружности Я = U(l) можно одноз-
однозначно записать в виде exp(Xei), где 0 <\ < v. Рассматривая 2цр~*\ как
угловую координату на Я, получаем A2).)
Для того чтобы установить совпадение целого числа A2) с магнитным
зарядом, заметим, что, совершая калибровочное преобразование с функ-
функцией |3(р, а), можно перевести поле у в поле, равное <р0 на всей поверх-
поверхности Г за исключением северного полюса. (Здесь (р, а) рассматривают-
рассматриваются как координаты на Г. При р < 1 эти координаты определяют взаимно
однозначное соответствие между внутренностью круга и точками поверх-
поверхности Г с выколотым северным полюсом.) Это означает, что после калиб-
калибровочного преобразования интересующее нас поле удовлетворяет условию
F.1). В силу наложенного нами условия VMip = 0 после калибровочного
преобразования поле Лм становится полем А^, принимающим значение
в алгебре Ли подгруппы Я, т.е. А\ = дм ех. Поле ам можно рассматривать
как электромагнитное поле в калибровке F.1); электромагнитная напря-
напряженность выражается через ам стандартной формулой. Магнитный заряд
Wr с точностью до множителя Dтг)~ х совпадает с потоком магнитной на-
напряженности через поверхность Г. Интересующее нас поле не имеет осо-
особенностей; это значит, что мы можем выколоть из поверхности Г малень-
маленькую окрестность северного полюса, мало изменив при этом интересующий
нас поток. Точнее, если через Ге обозначить часть поверхности Г, для ко-
которой р < 1 — €, то при е -*¦ 0 поток через Ге стремится к потоку через Г.
91

Границей поверхности Ге является маленькая окружность Le. Легко ви-
видеть, что поток магнитной напряженности через Ге равен циркуляции по-
потенциала ам по этой окружности. Таким образом
Ш= lim —fHdS =
1 1 **
= — lim ?д„с?хм = — lim / ett(l - e,oi)du. A3)
4iT e-*O 4iT e-*O О
Символы ap (p, a), aa (p, а) обозначают компоненты векторного потенциа-
потенциала дм в координатах р, а на Г. Будем предполагать для простоты, что ка-
калибровочное поле Ац обращается в нуль вблизи северного полюса. Тогда
при калибровочном преобразовании из него получается поп*
Э
A'a(p,ot) = aa(p,a)ei = - — C l (p,a)C(p,a), p>\ -е.
да
Поскольку 0(р, а) -* CA, а) = exp(-X(a)ei) при р -> 1, мы видим, что
аа(р,Ы) ->Э\/Эаи,в силу A3),
mr= — (XBir)-X(O)). A4)
4я
Сравнивая A4) и A2), получим A0).
Покажем, что в рассматриваемых нами теориях электрический заряд
квантован, и установим связь между квантованием электрического и маг-
магнитного зарядов. В самом деле, электрические заряды частиц, отвечающих
полю if, определяются формулой — i'Xfc, где Хк — собственные значения опе-
оператора t(ei). (Напомним, что оператор f (ei) антиэрмитов, так что его
собственные значения чисто мнимы.) В самом деле, если ip = ~Ltpk fk, где
к
/i. • • •. fn - собственные векторы оператора t(ex), и из калибровочного
поля Ац отлична от нуля только его электромагнитная часть а^ (т.е. А^ =
(мм
к
Из соотношения exp (vet) = 1 вытекает, что
Значит, для всех собственных значений \к оператора f(et) выполнено ра-
равенство exp(pXfc) = 1. Отсюда следует, что
2тг
где п — целое число, т.е. электрические заряды равны — п. Таким овра-
оврага
зом, эти заряды являются целыми кратными числа 2я1>~1. Поскольку
магнитные заряды являются целыми кратными числа 1>Dтг)~1, мы видим,
что произведение электрического заряда произвольной частицы на магнит-
магнитный заряд любой другой частицы является полуцелым числом:
1
еп=~п. A5)
92

Подчеркнем, что мы пользуемся нестандартной нормировкой электро-
электромагнитного поля ам. Если перейти к стандартной нормировке, в которой
коэффициент при F2fiv в лагранжиане равен — 1/4, а не - 1/4#2, как у нас,
2-пп
то электрические заряды окажутся равными «Xfc? = g, а магнитные
v
v
заряды равными f, где и и f — целые числа, g - константа связи.
4irg
Из этого ясно, что соотношение A5) сохраняется и в стандартной норми-
нормировке.
Мы рассматривали до сих пор случай, когда группа ненарушенных
симметрии Я изоморфна группе U(l) . Переход к случаю, когда Я- произ-
произвольная связная группа, требует лишь небольших изменений в прове-
проведенных выше рассуждениях. Группа Я, как и всякая компактная группа
Ли, локально изоморфна произведению г экземпляров группы U(l) и одно-
связной компактной группы К. (Число г равно размерности центра алгеб-
алгебры Ли К группы Я.) В калибровке F.1) генератору каждой из групп U(l)
отвечает свой "электромагнитный" лотенциал и своя "электромагнитная"
напряженность: если е\,..., ег — генераторы сомножителей U(l), то
"электромагнитные" потенциалы определяются формуламиЛ* = < 4М, е* >,
напряженности выражаются через потенциалы стандартными формула-
формулами. В теориях большого объединения г = 1 и можно говорить об электро-
электромагнитном потенциале и соответствующей напряженности без кавычек.
При г > 1 мы также будем опускать кавычки.
Можно сказать, что электромагнитный потенциал ам = (Ац, е) отве-
отвечает каждому 'элементу е центра Z алгебры Ли Ж; среди этих потенциалов
есть г линейно независимых, отвечающих генераторам е\ ег. Электро-
Электромагнитную напряженность любого поля можно вычислить, перейдя с по-
помощью калибровочного преобразования к калибровке F.1), по формуле
^м" = Эм д„ - Э„ дм. Нетрудно проверить, что результат не зависит от вы-
выбора калибровочного преобразования. В самом деле, как мы говорили,
два разных потенциала Ац и А'ц, удовлетворяющих условию F.1) и ка-
либровочно эквивалентных между собой, связаны калибровочным преоб-
преобразованием с функцией, принимающей значение в группе Я. Отсюда сле-
следует, что поля ам = <i4M, е> и а'^ = (А'ц, е) связаны употребляющимся
в электродинамике калибровочным преобразованием и, значит, имеют од-
одну и ту же напряженность. Например, в случае бесконечно малого калиб-
калибровочного преобразования А'ц = Ац - Эм X - [А^, X], и нужное нам ут-
утверждение вытекает из замечания, что скалярное произведение комму-
коммутатора [Ац, X] на любой элемент из центра алгебры Ли равно нулю. Слу-
Случай конечного калибровочного преобразования для связной группы Ли
Я сводится к случаю бесконечно малого калибровочного преобразования.
Стандартным способом определяются магнитные заряды, связанные
с построенными только что тензорами электромагнитной напряженности.
С помощью рассуждений, аналогичных проведенным в § 4, можно доказать,
что магнитные заряды, построенные с помощью указанной только что
конструкции, не меняются при непрерывном изменении поля (являются
топологическими числами поля). С другой стороны, мы определили топо-
топологический тип поля,исследуя асимптотику скалярного поля <р. Тополо-
93

гический тип поля определяется тогда гомотопическим классом отобра-
отображения сферыS2 в многообразие вакуумов R (т.е. элементом множества
lS2,R)). Как мы говорили в § 5, множество {S2,R) в случае, когда
группа Н связна, отождествляется с группой тг2 {R) = tti (ff), которая
представляет собой прямую сумму г экземпляров группы Z и конечной
группы. Таким образом, существует г целочисленных топологических за-
зарядов — столько же, сколько мы построили магнитных зарядов. Отсюда
ясно, что магнитные заряды полностью определяют целочисленные тополо-
топологические заряды поля. (Кроме целочисленных топологических зарядов
могут существовать еше заряды, принимающие значения в одной из групп
Zm; они, конечно, не определяются магнитными.)
§ 8. Общие формулы для электромагнитной напряженности
и магнитного заряда в калибровочных теориях
В § 7 была указана формула G.5), позволяющая в случае, когда ста-
стационарная подгруппа Я одномерна, вычислять при х->°° электромагнитную
напряженность FMV (дс) поля с конечной энергией. С помощью этого соот-
соотношения получается выражение G.8) для магнитного заряда такого поля.
Однако, для того чтобы получить явное выражение для магнитного заряда
ntr (<р, А) поля в области, ограниченной поверхностью Г, необходимо
иметь формулу, дающую возможность непосредственно вычислить в любой
точке электромагнитную напряженность поля (<<?, Ам) без перехода к кали-
калибровке F.1). Для этого достаточно найти калибровочно инвариантное вы-
выражение, совпадающее с G.1) в калибровке F.1). Естественно искать нуж-
нужное нам выражение в виде
2" W, A)
где u)a6(ip) = -Wba(ip). (Первый член в A) совпадает с G.5). Второе
слагаемое обобщает соответствующий член в выражении для напряжен-
напряженности в модели Джорджи—Глешоу; см. § 4.)
Вводя обозначение
можно записать выражение A) в форме
Fiiv(x) - ( &рр(х)> Л(сг*р(х)) > + о>,р( \<р, V^v?). B)
Функции oiabiv) можно найти из требований
ы<р(х,У) = о>а1р(о,х, о.у), C)
Юф (t(A)tfio, t(B) ((?o) = — ([А, В] , Л(|р0)), D)
да" .
где о»обозначает дифференциал отображения а (т.е. (ст,х)° = —— • х ).
Условие C) сводит нахождение о>^ (jc, у) к случаю, когда <р G R, а век-
векторы jc, у касаются многообразия R. (Отображение а переводит точку <р в
точку многообразия Л, поэтому всякий вектор в точке <р переходит в ка-
касательный вектор к R.) Всякий вектор, касательный к R в точке ip0 € Л,
может быть записан в виде f (А)<ро> гДе A G S9 . Группа G действует тран-
94

зитивно на R. Это значит, что всякая точка <р ? R может быть получена из
ip0 ? R с помощью преобразования группы G. В частности, точка (^.беско-
(^.бесконечно близкая к ipo. может быть получена из <р0 с помощью бесконечно
малого преобразования группы G, т.е. с помощью элемента алгебры Ли $.
В самом деле мы видим, таким образом, что условие D) полностью
определяет о>^ (х, у) в случае, если <р ? R, а х и у касаются R и, следова-
следовательно, вместе с условием C) определяет со^, (х, у) для произвольных
<р, х, у. Рассмотрим, например, модель Джорджи—Глешоу. В этом приме-
примере отображение а сопоставляет вектору у ? [R3 точку а ~$/\ ~$\. Стационар-
Стационарная подгруппа точки <j? ? IR3 состоит из вращений с осью, направленной по
вектору y?. Отсюда ясно, что h(lp) =^/| ~$\ (это следует также из соотно-
соотношения Г (й (?))?= [?/1 ?1-^] =0).
Дифференциал отображения а(<р) задается формулой а, (<<?)]¦ =
= д/| ~ф | (б/ — | <р|~2 vV/}; используя это замечание, для (a.V^)'
имеем
Применяя эту формулу и формулу D), для и>^ (х, у) получаем
'yk
eijkjx'y
Это показьшает, лто A) согласуется с выражением D.9) для электромаг-
электромагнитной напряженности в модели Джорджи—Глешоу.
Проверим, что, выбрав o>au(<p) c помощью условий C), D), мы полу-
получим калибровочно инвариантное выражение для напряженности F^v{x).
Для этого заметим, что имеют место соотношения
Цаф), E)
T(g)y) = a)Jx,y). . F)
Соотношение E) влечет за собой калибровочную инвариантность перво-
первого слагаемого в B) (как W^v (x), так и h (op (jc) ) преобразуются по при-
присоединенному представлению при калибровочном, преобразовании, а ска-
скалярное произведение < , > инвариантно относительно присоединенного
представления). Аналогично из F) вытекает калибровочная инвариант-
инвариантность второго слагаемого в B). Для того, чтобы доказать E) заметим,
что стационарная подгруппа Н-р^^ элемента T(g)y получается из стацио-
стационарной подгруппы Др элемента ц> с помощью внутреннего автоморфизма
(если T{h)ip =<<?,то
Отсюда следует, что генератор стационарной подгруппы #г(?)<р полу-
получается из генератора стационарной подгруппы Н^ также с помощью внут-
внутреннего автоморфизма. Вспоминая, что присоединенное представление
действует с помощью внутренних автоморфизмов, мы видим, что соотно-
соотношение E) верно в случае, если <р е R. В общем случае это соотношение
95

вытекает из равенств
h(o(T(g)<p)) = h(T(g)*p) ^
(мы воспользовались соотношением F.2)).
Для того, чтобы проверить соотношение F), рассмотрим сначала случай,
когда <р = <р0 ? Я» а х = t {А)\р0,у = t{B)ip0 - векторы, касательные к Л
(в этом случае со^ (х, у) определяется условием D)). Заметим прежде
всего,что
T(g)t(A)<p = t(rg(A)) Tig)*. G)
Это следует из соотношений
Tig) T{\ + А) * = Tig) T{\ + A) T->(g) T(g) * =
1 +TgiA))Tig)<p =
g g
(мы воспользовались равенствами ГA +А)у = A +tiA))y, gA + A)g'x =
= 1+ Tg(A), верными для бесконечно малого А). Используя G), E) и
инвариантность скалярного произведения < , > относительно присоеди-
присоединенного представления rg, видим, что
(Jig) tiA ) ,po, Tig) ti В) (А,) =
iTgiA)) Tig) (A,, tiTgiB)) Tig) ф0) =
= -<[rgiA),TgiB)],
= -<Tg[A,B],
Проверка соотношения F) в общем случае сводится к рассмотренному
только что частному случаю с помощью F.2) и C).
Таким образом, калибровочная инвариантность правой части выраже-
выражения B) доказана. Для того, чтобы проверить, что формула B) дает пра-
правильное выражение для электромагнитной напряженности, нам осталось
убедиться, что в случае, когда выполнено калибровочное условие F.1),
правая часть B) сводится к стандартному выражению для электромагнит-
электромагнитной напряженности Ь^(х) - Э„дм(л:), где auix) = <i4/J(jc), й(^0)>-
Дифференцируя соотношение F.1), убеждаемся, что для полей, удовлетво-
удовлетворяющих калибровочному условию, имеет место соотношение
М = °
иными словами, о.Эм<р = 0. Таким образом, в калибровке F.1)
М, Av], h(<p0)) -
96

Мы воспользовались при преобразованиях соотношением
Оно сразу следует из соотношения F.2), примененного к случаю ? = 1+^4,
где А - бесконечно малое преобразование.
Таким образом, мы завершили доказательство того, что формула B),
где ^(х, у) задано соотношениями C), D), определяет электромагнит-
электромагнитную напряженность в случае, если Н = U(l). Та же формула может быть
использована для определения электромагнитной напряженности в случае,
если Н - произвольная несвязная одномерная группа. Однако в этом слу-
случае напряженность Fuv (x) может оказаться двузначной функцией, причем
эту двузначность нельзя будет устранить с помощью выбора однозначной
непрерывной ветви; подробнее см. в § 12. * Мы уже упоминали, что ге-
генератор h(ip) определен с точностью до знака, поэтому, строго говоря,
напряженность F^, заданная формулой B), также определена только с
точностью до знака. Фиксировав h(ip) для какого-либо значения у, мы по
непрерывности можем выбрать одно из двух значений h (<р) для всех <р е ft.
При Н = U(l) эта процедура позволяет определить непрерывную однознач-
однозначную функцию h (((?), заданную для всех <р е <R . Однако, в случае, когда Я
несвязная одномерная группа, эта конструкция может привести к противо-
противоречию, означающему неустранимую двузначность функции h{ip) и напря-
напряженности F ^„.г
Отметим, что конструкцию электромагнитной напряженности удобно
проводить на языке теории дифференциальных форм. В самом деле,
антисимметричному тензору cja &(<<?) можно сопоставить 2-форму cj=
1
= — waft(ip) dtp" л d^ . Соотношение C) означает, что,эта форма может
быть записана в виде cj = о*р, где р — С-инвариантная замкнутая 2-форма
на многообразии R. (В главном расслоении (С, G/H, Я) = (С, R, U(l))
можно построить G-инвариантную связность, т.е. калибровочное поле на
Н, изменение которого при преобразованиях группы G можно компенси-
компенсировать калибровочным преобразованием. Форма р интерпретируется как
напряженность этого калибровочного поля; см. § 10.)
Проанализируем теперь случай, когда стационарная подгруппа Я неодно-
неодномерна. Рассмотрим стационарную подгруппу Я = Я?,о элемента <р0 G R и
выберем элемент h0 алгебры Ли Ж группы Я, инвариантный относительно
присоединенного представления группы Я, т.е. удовлетворяющий условию
Tgh0 = h0 (8)
для всех g G Я. Если группа Я связна, то инвариантность относительно
присоединенного представления группы Я эквивалентна инвариантности
относительно присоединенного представления алгебры Ли ЗС. Поскольку
присоединенное представление а алгебры Ли определяется формулой
aji = [A, h], инвариантность элемента Ао относительно присоединенного
представления эквивалентна тому, что Ло принадлежит центру 2? алгебры
Ли Ж (т.е. коммутирует со всеми элементами этой алгебры).
Для элемента Ао ? Ж, удовлетворяющего требованию инвариантности
относительно присоединенного представления, можно построить функцию
97

на R, удовлетворяющую условию
h(TXg)*) = Tghto) (9)
и требованию
Л(<Ро) = Ло. A0)
(Соотношение (9) и транзитивность действия группы G на R позволяют
найти h(y) во всех точках R, если известно значение Л(<р) в точке <р0-
Равенство (8) гарантирует, что, определяя значение Л(<р) в точках с по-
помощью (9) и A0), мы не придем к противоречию.) Используя функцию
h (((?), мы можем построить со^ с помощью C), D) и определить электро-
электромагнитную напряженность соотношением B). Из (9), A0), F.2) выте-
вытекает, что выполнены соотношения E), F) и, следовательно, заданная
формулой B) напряженность калибровочно инвариантна. Проведенные вы-
выше рассуждения показывают, что в калибровке F.1) эта напряженность
определяется стандартным соотношением, в котором роль электромагнит-
электромагнитного потенциала играет а^ = < ,4 м, ft 0 > :
Fp.v = <V <4р> h0) - Э„ {Ац, h0 >.
Это означает, что построенная нами электромагнитная напряженность удов-
удовлетворяет уравнению Максвелла
Ъо FMp +, цикл, перест. = 0.
В силу калибровочной -инвариантности уравнение Максвелла удовлетво-
удовлетворяется и без предположения, что поле подчинено калибровочному условию
F.1).
Таким образом, в случае, когда стационарная подгруппа Я связна, по
каждому элементу Ао центра ЗС алгебры Ли Ж можно построить электро-
электромагнитную напряженность и соответствующий ей магнитный заряд (нес-
(несколько иным способом это доказано в предыдущем параграфе). Если центр
является r-мерной алгеброй Ли, то существует г независимых магнитных
зарядов. Вслучае.если группаЯнесвязна, элементл0 из центра алгебры Ли
К, вообще говоря, не удовлетворяет условию A0). Однако множество эле-
элементов вида Tg h0, гдеg&H, конечно. (Это следует из замечаний что тшй0 =
= Ло» если g принадлежит связной подгруппе Ясоп группы Я, а группа
Я/Ясоп конечна.) Обозначим число его элементов символом s. Определяя
функцию Л(<р) на Л с помощью условий (9) и ПО), мы получим s-знач-
ную функцию. В самом деле, если элемент <р е R представлен в виде
74?)Vo> т0 в силу (9), A0) h (<р) = rgh0. Если этот элемент может быть
представлен также в виде 7"(if)<po> то мы получаем Л(<р) = Гг-Ло- Элемент
т~й0 = TgTg-tgh0 может не совпадать с Tgh0 (т.е. мы не получаем одноз-
однозначной функции Л(<р)), но, поскольку Tg-tg~h0 может принимать только s
разных значений, мы видим, что соотношения (9) и A0) определяют h (if)
как s-значную функцию.
Таким образом, в случае, когда группа Я несвязна, напряженность FM1>
является, вообще говоря, многозначной функцией (см. подробнее в § 12).
98

§ 9. Экстремумы симметричных функционалов
Пусть дифференцируемая функция f(x) задана на линейном простран-
пространстве М, в котором действует линейное представление компактной группы
Ли G, и инвариантна относительно этой группы. Покажем, что G-инвариант-
ность функции f(x) можно использовать для отыскания стационарных то-
точек этой функции. Пусть N — множество, состоящее из всех точек, инва-
инвариантных относительно группы G. (Из линейности действия группы G
вытекает, что N является линейным подпространством.) Мы докажем, что
стационарные точки функции f на N являются одновременно стационарны-
стационарными точками этой функции на всем пространстве.
Важно отметить, что сформулированное только что утверждение сох-
сохраняет силу, если пространство М бесконечномерно. (Тогда вместо терми-
термина "функция" удобно употреблять термин "функционал", а вместо тер-
термина "стационарная точка" - термин "экстремаль".) Однако в бесконечно-
бесконечномерном случае необходимо уточнить требование дифференцируемости.
Именно, функционал следует считать дифференцируемым, если его прира-
приращение можно представить в виде
f(x + А) - f(x) = <A,h) + a(x,h), A)
' где ( , > — скалярное произведение, инвариантное относительно преоб-
преобразований группы G, a a (x, h) имеет более высокий порядок малости, чем
h (точнее, e~la(x, eh) -*¦ 0 при е-+Ои произвольном Л). Выражение 5/ =
= (A, h) называется вариацией / (или дифференциалом), а вектор А - гра-
градиентом в точке х; этот вектор обозначается grad/. Точка х стационарна,
если grad / = 0. Скалярное произведение, инвариантное относительно преоб-
, разований компактной группы G, всегда существует (см. § А5). Отметим,
что используемое нами понятие дифференцируемости в бесконечномерном
случае зависит от выбора скалярного произведения.
Приведем пример, иллюстрирующий применение свойств симметрии
функционала для отыскания его экстремалей. Рассмотрим функционал
)J d3x + / U(y>(x)) d3x, B)
определенный на полях ф (х), обращающихся в нуль на границе шара ?>3,
выделенного неравенством |х|<Л. В пространстве полей М, на котором
определен рассматриваемый функционал, введем скалярное произведение,
положив
<13х. C)
Приращение функционала B) можно представить в форме A) с А =
= — А\р + U1 (<р). Соответственно, условие стационарности (уравнение Эйле-
Эйлера) имеет вид — Д<р + U' (<р) = 0. Функционал B) и скалярное произведение
C), очевидным образом инвариантны относительно вращений. Точнее
говоря, группу SOC), действующую в(R3, можно рассматривать также как
группу преобразований пространства полей М, сохраняющую функционал
B) и скалярное произведение C). Роль множества JV играет совокупность
всех полей, не меняющихся при вращении (сферически симметричных по-
полей ip(| х|)). Мы можем утверждать, таким образом, что экстремаль функ-
99

ционала A), рассматриваемого только на сферически симметричных полях,
является экстремалью этого функционала, рассматриваемого на всех полях
из М. Это резко упрощает нахождение экстремалей, поскольку уравнения
Эйлера становятся из уравнений с частными производными обыкновенны-
обыкновенными дифференциальными уравнениями. Разумеется, нет никаких гарантий,
что сферически симметричные экстремали исчерпывают все экстремали
рассматриваемого функционала. Можно утверждать лишь, что часть реше-
решений полных уравнений Эйлера удается найти с помощью сферически сим-
симметричной подстановки (как говорят, эта подстановка проходит через
уравнения Эйлера).
Отметим, что при нахождении стационарных точек (экстремалей) нет
необходимости требовать, чтобы они были инвариантны относительно пол-
полной группы симметрии рассматриваемого функционала. (Например, мож-
можно рассмотреть функционал A) на полях, инвариантных относительно
группы SO B) вращений вокруг некоторой оси. Всякая экстремаль функ-
функционала, рассматриваемого на этом множестве, будет также экстремалью
на всем М.)
Докажем сформулированное в начале параграфа утверждение. Заметим,
прежде всего, что градиент функции/ в точке х0 S Л^ является вектором,
инвариантным относительно группы G. (Это сразу следует из соотношения
A), если воспользоваться G-инвариантностью функции / и скалярного
произведения.) Иными словами, grad/ € N. Предположение, что дг0 являет-
является стационарной точкой функции / на подпространстве N, влечет за собой
соотношение < grad f,h) = О для любого вектора h G N, в частности для век-
вектора А = grad/. Мы видим, что < grad /, grad/) = 0 и, значит, grad/ = 0.
А Теорема о стационарных точках инвариантных функций допускает
обобщение на случай функций, заданных на римановом многообразии М
(не обязательно конечномерном). Пусть дифференцируемая функция
/(jc) задана на гладком многообразии М, на котором действует компактная
группа Ли G, и инвариантна относительно этой группы. Рассмотрим мно-
множество N, состоящее из всех точек, инвариантных относительно группы G.
Тогда при некоторых условиях, которые обычно выполняются, стационар-
стационарные точки функции / на N являются одновременно стационарными точ-
точками функции на всем многообразии М.
Для того, чтобы сформулировать нужные нам условия, рассмотрим
произвольную точку х0 € N. По определению, группа G оставляет точку х0
на месте и, следовательно, переводит касательный вектор в точке хо в ка-
касательный вектор в той же точке. Действие группы G на касательные векто-
векторы можно рассматривать как линейное представление этой группы; обозна-
обозначим это представление буквой Т. Для точек, близких к хо, преобразование
\pg, отвечающее элементу # е G, может быть записано в виде
где опущенные члены имеют более высокий порядок малости по А. Из D)
видно, что для кривой, принадлежащей множеству N, касательный вектор в
точке х0 должен удовлетворять условию T(g)h = А при всех g € G. Иначе
говоря, этот вектор должен принадлежать линейному пространству ЛГ,
состоящему из G-инвариантных векторов (т.е. векторов, инвариантных от-
относительно представления Т группы G). Точку х0 € N будем называть
100

невырожденной, если в окрестности этой точки Nявляется многообразием,
и всякий вектор из пространства Ж касается Nb точке х0 (т.е. касательное
пространство к N совпадает с JT ).
Пусть теперь х0 —невырожденнаяточкамногообразияЛ^котораяявляет-
ся стационарной точкой для функции f(x), рассматриваемой только на N.
Тогда незначительная модификация рассуждения, приведенного выше для
линейного случая, показывает, что она является стационарной точкой функ-
функции /(х), рассматриваемой на всем многообразии М. В самом деле, в
силу компактности группы G можно ввести в касательных пространствах
к М скалярное произведение, инвариантное относительно группы G (иными
словами, М можно снабдить G-инвариантной римановой метрикой). Соот-
Соотношение A) сохраняет силу. Вектор grad / в точке х0 G N принадлежит в
рассматриваемом случае подпространству Ж (это вытекает из инвариант-
инвариантности функции й скалярного произведения). Из стационарности точки хо
на многообразии N следует, что (grad f,h) = О для любого вектора h, ка-
касательного к N. Для того, чтобы завершить доказательство, остается вспом-
вспомнить, что в силу предположения невырожденности любой вектор из под-
подпространства.^, в частности, вектор h = grad / является касательным к Ж
Проведенные только что рассуждения остаются справедливыми также в
случае, еслиЛГ — бесконечномерное многообразие. (Как и в случае, когда
М — бесконечномерное линейное пространство, дифференцируемость функ-
функционала следует определять с помощью соотношения A).)
Отметим, что доказанное утверждение сохраняет интерес также в случае,
когда множество N состоит из изолированных точек (является нульмерным
многообразием). Оно означает тогда, что G-инвариантная точка х0 является
стационарной точкой функции / в случае, если не существует G-инвариант-
ных касательных векторов в точке х0. Ў
§ 10. Симметричные калибровочные поля
Рассмотрим скалярные поля ip(x) - (^(х), ..., ip"(x)), взаимодейст-
взаимодействующие с калибровочными полями Ац(х), принимающими значение
в алгебре Ли X калибровочной группы К. Как мы видели, экстремали
функционала энергии связаны в квазиклассическом приближении с кван-
квантовыми частицами. Поэтому возникает вопрос о нахождении этих экстрема-
экстремалей. При решении этого вопроса оказывается полезным использовать
свойства симметрии функционала энергии. Этот функционал инвариантен,
с одной стороны, относительно локальных калибровочных преобразований,
а с другой стороны, относительно некоторых пространственных преобразо-
преобразований (в частности, относительно пространственных вращений). Полную
группу симметрии, порожденную группой локальных калибровочных
преобразований К°° и группой пространственных симметрии О, обозначим
символом L. В соответствии с общими утверждениями предыдущего пара-
параграфа, часть экстремалей функционала энергии можно найти, выделив под-
подгруппу G полной группы симметрии L и рассмотрев функционал энергии
на всех G-инвариантных полях. Тогда, по доказанному, экстремали функ-
функционала энергии на множестве G-инвариантных полей являются экстрема-
экстремалями этого функционала на множестве всех полей (условия, при которых
доказано используемое нами утверждение, как мы увидим, выполнены).
101

Наиболее простой способ выделения подгруппы G С L состоит в следую-
следующем. Рассмотрим произвольный гомоморфизм X группы вращений SO C)
в калибровочную группу К. Всякому элементу g e SOC) сопоставим
преобразование p(g) из группы L, получающееся, если сначала произвести
вращение g 6 SO C), а затем глобальное калибровочное преобразование,
отвечающее элементу Х(#) 6 I Очевидно, что отображение р группы
SO C) в L является гомоморфизмом, а его образ G\ — подгруппой
группы L.
Описанную только что конструкцию полезно слегка обобщить считая,
что X - двузначный гомоморфизм группы SO C) в К. Вместо двузначного
гомоморфизма группы SOC) в К можно рассматривать однозначный го-
гомоморфизм X группы SUB) в К. Каждому такому гомоморфизму отве-
отвечает подгруппа, состоящая из элементов группы L, представимых в виде
произведения, поворота p(g) и глобального калибровочного преобразова-
преобразования, отвечающего элементу Х(#) G К (здесь g e SUB), p — гомомор-
гомоморфизм группы SUB) на SO C)).
Поля, инвариантные относительно описанной только что группы G\,
разумно рассматривать как сферически симметричные в некотором
смысле. В самом деле, при пространственном вращении эти поля меняются,
но для каждого вращения можно подобрать глобальное калибровочное
преобразование таким образом, что в результате выполнения обеих преоб-
преобразований поле останется неизменным. Иными словами, изменение поля
при вращении может быть скомпенсировано калибровочным преобразова-
преобразованием. Способ компенсации задается гомоморфизмом X. Можно сказать,
что X определяет тип сферической симметрии. Число существенно различ-
различных типов сферической симметрии определяется числом гомоморфизмов
группы SOC) в группу К, не сопряженных друг другу. (Если два гомо-
гомоморфизма Ли X'группы SO C) в К сопряжены, т.е. связаны соотношением
Х'(?") = k\(g)k~1, где к G К, то из поля {у, А) с типом симметрии X
можно получить (у', А') с типом симметрии X1, подействовав на поле
(ip,A) элементом к группы К). Например,в случае, когда калибровочной
является группа SO C), можно рассматривать в качестве гомоморфизма X
либо тождественный гомоморфизм группы вращений SO C) на группу
К = SOC), либо гомоморфизм, переводящий всю группу вращений в еди-
единичный элемент группы К.
Опишем все поля (i^ (х), At (х)), i = 1,2, 3, инвариантные относительно
группы G\, определенной с помощью гомоморфизма X (поля с типом сим-
симметрии X). Заметим прежде всего, что эти поля удовлетворяют соот-
соотношениям
Г(Х00)?>(х) = ?>(irx), A)
g',T(X(g))A,(x) = A,(gx\ B)
где gt — матрица вращения g e SOC), T — представление группы К,
по которому преобразуется многокомпонентное скалярное поле <р, эле-
102

мент X (if) € К, как всегда, действует на калибровочное поле с помощью
присоединенного представления т. Из соотношений A), B) ясно, что все
значения полей tp (x), At (х) определяются, если известны значения полей на
неотрицательной части оси х3 (или на любом другом луче, исходящем из
начала координат). Это следует из того, что любую точку пространства R3
можно с помощью вращения перевести в точку, лежащую на выбранном
нами луче. Однако значения полей на оси х3 не являются произвольными.
Они не должны меняться при преобразованиях группы G\, отвечающих
вращению вокруг оси х3.
Иными словами, должны быть выполнены соотношения
TDg)Mr) = ?>(/"), C)
4 = Af(r), D)
где tp (r ) и Ai (г ) - значения полей в точке ('О, 0, г ), г > 0, g j - матри-
матрица поворота g вокруг оси х3. Переходя к бесконечно малым преобразова-
преобразованиям, можно переписать соотношения C), D) в виде
t(I3)v(r) = 0, E)
[1з,Аз(г)\ = О,
[h,Ai(r)] = А2(г), (в)
[h,A2{r)\ = -А,(г)
Здесь символ t обозначает представление алгебры Ли Ж, отвечающее пред-
представлению Т группы К. Символы /j, /2, /3 здесь и далее обозначают эле-
элементы алгебры Ли УС группы К, отвечающие бесконечно малым вращениям
вокруг осей х1, х2, х3.
Например, в случае, когда К = SO C), а X - тождественный гомомор-
гомоморфизм, из соотношений F) следует, что
Adr) =-
г
A2(r) = -(/JO0/2 - 7(Г)Л),
г
А3(г) = -а(гI3.
г
Если ?>(х) преобразуется по векторному представлению группы
К = SOC), то из E) видно, что ^(г) = ( О,О,- НО] (здесь <*(/¦),
0(г ). 7 (f ). %(? ) — произвольные функции.)
Как мы говорили, зная значения полей у, А. на оси х3, удовлетворяющие
условиям E), F), можно восстановить сферически симметричное поле
103

во всем пространстве с помощью соотношений A), B). В частности, если
К = SO C), X = 1, получаем
X
]7
G)
^ /, - y(r) eijk *— Ik.
(8)
Таким образом, при а = j3 = 0 мы приходим к полям, использованным при
анализе магнитных монополеи в модели Джорджи-Глешоу.
Важно подчеркнуть, однако, что нет никакой необходимости знать сфе-
сферически симметричное поле во всем пространстве - все интересные величи-
величины можно выразить через значения поля на оси х3. Покажем, например, как
вычислить энергию сферически симметричного поля. Прежде всего заме-
заметим, что плотность энергии &(х) рассматриваемого нами поля сферически
симметрична (т.е. зависит только от | х | = г). Это сразу следует из ка-
калибровочной инвариантности плотности энергии (при вращении поле
(ф(х), Af(x)) переходит в калибровочно эквивалентное и, стало быть,
плотность энергии не меняется). Таким образом, достаточно вычислить
&(х) только на оси х3 (точнее, на положительной части этой оси).
Через эти значения энергия запишется в виде
& = 4 я / &(r)r2dr.
о
(9)
Чтобы найти &(г) = & @, 0, г), нужно вычислить производные полей
в точках оси х3. Для этого следует записать соотношения A), B) в случае,
когда х = @, 0, г ) (точка х лежит на оси х3), a g - бесконечно малое вра-
вращение /i вокруг оси х1 или бесконечно малое вращение 12 вокруг оси х2.
Получаем
Эх2
X = (О, О, г)
Эх1
Эх2
X = (О, О, г)
X = (О, О, г) Г
X = (О, О, г)
(Ю)
lh,At(r)]},
\h,A,{r))).
(И)
104

С помощью соотношений A0), A1) убеждаемся, что Ё(г) можно предста-
представить в виде
[Wt(r), W3(r)] -
[W2(r),W3(r)} ^^)
or
A2)
где W,(r) = rA{(r), заряд e = 1.
Чтобы применить результаты предыдущего параграфа к отысканию
экстремума функционала энергии на полях (?>(х), At (x)), определим ска-
скалярное произведение полей (tp(x), At{xj) и &'(x),A'j(x)) как
/<^(x),/(x)>dx + f(At(x),A;(x))dx, A3)
где < , > в первом слагаемом обозначает инвариантное ркалярное произве-
произведение в пространстве представления Т, а во втором слагаемом — инвариант-
инвариантное скалярное произведение в алгебре Ли УС. (Мы считаем, что рассматри-
рассматриваемые поля достаточно быстро убывают на бесконечности; это гаранти-
гарантирует, в частности, существование интегралов, фигурирующих в A2).)
Преобразования группы G являются линейными преобразованиями прост-
пространства полей, сохраняющими скалярное произведение A3). Отметим, что
произвольные локальные калибровочные преобразования, в отличие от
глобальных, не являются линейными преобразованиями в пространстве
полей, однако, они представляют собой изометрии, т.е. сохраняют рас-
расстояния между полями, определенное с помощью скалярного произведе-
произведения A3).
Легко видеть, что функционал энергии дифференцируем на пространстве
полей, снабженном скалярным произведением A3). В силу доказанного
выше экстремали этого функционала, рассматриваемого только на G\-hh-
вариантных полях (т.е. на полях, имеющих тип симметрии X), являются
экстремалями функционала энергии на множестве всех полей. (Напомним,
что на G^-инвариантных полях функционал энергии приобретает вид (9),
где &(г) дается формулой A2).)
В частности, если калибровочная группа К является группой SO C),
гомоморфизм X является тождественным гомоморфизмом группы враще-
вращений SO C) в К = SO C), а у преобразуется по векторному представлению,
то функционал энергии (9) На сферически симметричных полях вида G),
105

(8) дается формулой
&= 4тг / -^([| B7 + 02 + Г2J + (а
+ (A +7J + /?2J?2 + VQ)r4 }. A4)
Таким образом, условия, позволяющие заключить, что экстремаль
функционала энергии, рассматриваемого только на симметричных полях,
является экстремалью этого функционала на множестве всех полей,
выполнены в нашей ситуации. В частности, мы видим, что экстремали
функционала A4) являются экстремалями функционала энергии в модели
Джорджи—Глешоу. Их можно рассматривать как сферически симметрич-
симметричные магнитные монополи в этой модели (точнее, как классические поля —
солйтоны, - отвечающие в квазиклассическом приближении частицам,
обладающими магнитным зарядом). Стандартные математические методы
позволяют доказать существование экстремалей функционала A2).
Оказывается, что и в других моделях сферически симметричные экстре-
экстремали можно рассматривать как магнитные монополи. Это вытекает из
утверждения, что топологический тип (и, следовательно, магнитный заряд)
сферически симметричного поля полностью определяется его типом сим-
симметрии. Докажем это утверждение. Напомним, что в силу определения,
данного в § 5, топологический тип зависит от поведения скалярного
поля tp(x) на бесконечности. Будем считать для простоты, что скалярное
поле имеет асимптотику i^(x) ~ Ф(х/1 х| ), где Ф(п) - отображение сфе-
ры | п | = 1 в многообразие вакуумов R = К/Н, а Я - группа ненарушен-
ненарушенных симметрии. Из свойств симметрии поля tp(x) (см. A)) вытекает, что
его асимптотика также обладает аналогичными свойствами
ФОгп) = Г(Хи))Ф(п) A5)
для любого вращения g G SO C). В частности, если n = k = @, 0, 1) — орт,
направленный по оси z (северный полюс сферы), a g — вращение вокруг
оси z, отсюда следует, что Х(#)Ф0 = Фо» где Фо = Ф(Ю- Иными словами,
X можно интерпретировать как отображение группы SO B) вращений
вокруг оси z в группу Я, состоящую из элементов группы К, оставляющих
на месте классический вакуум Фо. Группа SO B) топологически эквива-
эквивалентна окружности, поэтому гомотопический класс [X] отображения X
можно рассматривать как элемент группы ii\ (Я). С другой стороны, топо-
топологический тип скалярного поля определяется гомотопическим классом
отображения Ф, т.е. элементом группы тт2 (К) - я2 (К/Н), которая, как мы
знаем, изоморфна пг (Я) в случае, если группа К односвязна.
Покажем, что для сферически симметричного поля топологический тип
определяется элементом 2 [X] € яд (Я) = п2 {К/Н). (Операцию в группе
¦Пх (Я) мы называем сложением.) Точнее, мы будем доказывать несколько
более общее утверждение, применимое также в случае, когда тип симмет-
симметрии определяется двузначным гомоморфизмом X группы SOC) в К.
106

Поэтому Нам удобно будет считать, что тип симметрии определяется гомо-
гомоморфизмом X группы SUB); условие A) симметрии скалярного по-
поля if (х) заменится тогда соотношением
>(р(*)х) = n\(g)Mx), A6)
где #eSUB),p- гомоморфизм SUB) на SOC). Соответственно A5)
заменится на
. A7)
Из A7) следует, что
Х(^)Ф(к) = Ф(к), если pQr)k = k. A8)
Множество элементов группы SUB), удовлетворяющих условию
p(g)k = к, где к = @, 0,1), образует окружность, двулистно накрывающую
при отображении р группу SOB) CSOC) вращений вокруг оси z. Будем
обозначать эту окружность символом SO B). Из A8) ясно, что X переводит
SOB) в Я и, следовательно гомотопический класс [X] отображения X,
рассматриваемого на SO B), определяет элемент группы ^(Я) = тг2(К/Н).
Мы покажем, что топологический тип поля, симметрия которого определя-
определяется отображением X, описывается элементом [X] &и[{Н) = тг2(К/Н).
(Сделанное выше утверждение о топологическом типе поля с симметрией,
отвечающей гомоморфизму X, отсюда следует. В самом деле, если Х= Хр, то
[X] =2[Х], поскольку р является двулистным накрытием.) Как мы знаем
(см. § Т 20), для того, чтобы найти элемент группы я^ (Я), отвечающий
гомотопическому классу отображения Ф, нужно отыскать отображение Ф
круга D2 в К, накрывающее отображение Ф; тогда нужный нам элемент
является гомотопическим классом отображения Ф, рассматриваемого на
границе круга D2. Точнее, отображению Ф сферы S2 в R=K/H отвечает
отображение Фр круга D2 в R, где р — отображение кругаD2 на 5 2, перево-
переводящее всю границу в северный полюс к сферы S2 и топологическое на
внутренности круга. Отображение Ф накрывает отображение Ф, если элемент
Ф(х) G К переводит точку Фо G R в точку Ф( р(х)); иными словами
A9)
для всех
Мы найдем предварительно отображение ^ круга!J в SUB), удовлетво-
удовлетворяющее условию
р(?(*))к = р(*) B0)
для любой точки х G D2. Тогда нужное нам отображение Ф можно построить,
положив Ф(х) = Х(ф(х)). В самом деле, используя A7), A9), B0), видим,
что
Г(Ф(х))Ф0 = Г(Х(Ф(х)))Ф(к) = Ф(р(*(х))к) = Ф(р(х)).
Для х, принадлежащих границе S1 круга D2, имеем р(х) = к и, значит,
107

вращение р(Ф(х)) оставляет точку к на месте, т.е. Ф(х) принадлежит груп-
группе SOB).
Из явной конструкции отображения Ф, которая будет указана ниже,
следует, что У, рассматриваемое как отображение окружности S1 CD2
в окружность S1 = SO B), имеет степень 1. Вспоминая, что топологический
тип поля у(х) описывается гомотопическим классом [Ф] отображения
Ф = X* окружности S1 в Я, видим, что [Ф] = \Х]. (Это вытекает из замеча-
замечания, что описанное ниже отображение Ф является топологическим отобра-
отображением 51 на §0B).)
Нам осталось построить отображение ty. Это можно сделать, например,
представив круг D2 как множество комплексных чисел w, удовлетворяю-
удовлетворяющих условию | w | < 1 и положив
/ н> VI - I w \2Л
y-Vl-lwr w- )
(Для того, чтобы проверить, что отображение w-*' p(w) = р(Ф(м/))к
является топологическим внутри круга D2, нужно убедиться, что при
I w | < 1, | w'| < 1, w Ф w' точки p(w) и p(w') различны. Пользуясь тем,
4Top(g)k = p(g')k втоми только в том случае, еслиg' =gh, где h G SOB),
можно свести доказательство этого утверждения к замечанию, что
*(w')*(w) не принадлежит группе SOB), если \w\<l,\w'\<l,w Фм')
Суммируя доказанное выше, мы приходим к следующим утверждениям.
Пусть X - гомоморфизм группы SO C) в калибровочную группу К, 13 -
элемент алгебры Ли JC группы К, отвечающий бесконечно малому враще-
вращению вокруг оси z при этом гомоморфизме. Если /3 принадлежит алгебре Ли
стационарной подгруппы Н классического вакуума Фо, ю существует
экстремаль функционала энергии, имеющая тип сферической симметрии X.
Магнитный заряд экстремали определяется гомотопическим классом,
отображения, сопоставляющего точке окружности S1 с угловой координа-
координатой а, 0<а <2я элемент ехрBа/3)?#.
Доказательство первого из этих утверждений использует замечание, что
существуют поля с типом симметрии X, имеющие конечную энергию. (Это
замечание сразу следует из явного выражения A2) для функционала энер-
энергии.) Поле, на котором достигается наименьшее значение энергии среди
полей типа симметрии X, является нужной экстремалью. Тот факт, что
наименьшее значение энергии достигается, требует доказательства. Доказа-
Доказательство проводится стандартными в математике методами; однако, эти
методы выходят за рамки книги. Второе утверждение вытекает из замеча-
замечания, что порождаемое гомоморфизмом X отображение окружности SO B) С
С SOC) в группу К переводит точку с угловой координатой а в ехр(а/3).
Воспользуемся полученными выше результатами, чтобы исследовать
сферически симметричные магнитные мояополи в SU E)-модели большого
объединения. По доказанному для этой цели мы должны рассмотреть
всевозможные гомоморфизмы X группы SOC) в SUE), при которых
бесконечно малое вращение вокруг оси г переходит в элемент /3 алгебры
Ли стационарной подгруппы Н, состоящей, как мы знаем, из блочно диаго-
108

нальных матриц (В7.2). Без ограничения общности можно считать, что /3
является диагональной матрицей с элементами (iwij, irrii, im$, Ш4, /от5);
тогда указанное выше условие означает, что ms - 0. Магнитный заряд
поля с типом симметрии, определяемым гомоморфизмом X, вычисляется
как гомотопический класс отображения, сопоставляющего точке окружно-
окружности 5' с угловой координатой а матрицу
ехрBа/3) =
= diag(expB/#2i a),expBim2 a), expB/Vw3а),ехрB/#24а), expB/w5 a))GH
(т.е. диагональную матрицу с элементами expB//wjta) на диагонали).
Как следует из сказанного в § 5, гомотопический класс отображения S1 в Н
(а, следоватеяьно, также топологический тип и магнитный заряд поля с
типом симметрии X) определяется зависимостью от а элемента матрицы,
стоящего в четвертой строке и четвертом столбце. (Отображение группы Я
в U(l), сопоставляющее матрице (В7.2) элемент т GUA), порождает
изоморфизм групп 7Ti(#) и Я](иA)).) Таким образом, магнитный заряд
определяется гомотопическим классом отображения S1 в U(l), переводя-
переводящего точку с угловой координатой а в число expB/m4a). Мы приходим
к выводу, что магнитный заряд поля равен 2тА. Отметим, что этот резуль-
результат применим также в случае, когда X — двузначный гомоморфизм (а, стало
быть, rrif — полуцелые числа).
Отметим, что в определении магнитного заряда есть произвол, отвечаю-
отвечающий выбору знака у генератора электромагнитной группы U(l). Другой
выбор генератора приводит к отличающемуся знаком ответу для магнитно-
магнитного заряда.
Легко перечислить все возможные гомоморфизмы SOC) в SUE)
(все пятимерные представления группы SOC)). Простейшие варианты —
( ' 1 \ / i ' \
это случаи /3 = diaglO, 0, , — , 01, /3 = diaglO, 0, -, ,01 (они отвечают
пятимерному представлению, разлагающемуся в прямую сумму двумерно-
двумерного и трех одномерных). Магнитные заряды в этих случаях равны ±1. Легко
убедиться, что возможные значения магнитного заряда сферически симмет-
симметричных полей в 8иE)-модели равны 0, ±1, ±2, ±3, ±4. В самом деле,
всякое пятимерное представление группы SOC) разлагается в прямую
сумму неприводимых. Если представление приводимо, то возможные
размерности неприводимых компонент даются равенствами
5=4+1,5=3+1 + 1, 5 = 3 + 2, 5=2 + 2+1,
5 = 2 + 1 + 1 + 1, 5 = 1 + 1 + 1.+ 1+1.
Поскольку матричные элементы /3 в неприводимом представлении являют-
являются полуцелыми числами из интервала от -/ до /, где / связано с размер-
размерностью d представления соотношением d = 21+ 1, мы получаем, что магнит-
магнитный заряд сферически симметричного поля является целым числом из
интервала от —4 до +4. Далее, все числа из этого интервала реализуются
как магнитные заряды сферически симметричных полей (например, маг-
109

нитный заряд 4 отвечает неприводимому представлению, реализованному
так, что I3 = diag (- /, i,-2i,2i, 0)).
Воспользовавшись общим соотношением A2) можно без труда написать
выражение для энергии сферически симметричных полей в SU E)-модели.
§ 11. Оценка энергии магнитного монополя
Как мы уже говорили, для того чтобы найти в квазиклассическом приб-
приближении массу частиц, обладающих магнитным зарядом, нужно вычислить
минимум функционала энергии на множестве полей, магнитный заряд ко-
которых не равен нулю. Исследуем этот минимум сначала для моделей, в ко-
которых скалярное поле преобразуется по присоединенному представлению
калибровочной группы G. (К числу таких моделей относится модель
Джорджи-Глешоу.вкоторой G = SOC), и SUE)-Monenb большого объе-
объединения, когда мы ограничиваемся первым нарушением симметрии.) Та-
Таким образом, функционал действия интересующей нас модели имеет вид
5 =lK f
SKVt )
4е
+ 1Af(b^+[A^,ip],b^0+\A>1,ip])d4x-\fU(if)d'ix, A)
где <р и -<4д принимают значения в алгебре Ли i$ группы G, U(tp) — инва-
инвариантный полином на &, достигающий наименьшего значения на многооб-
многообразии классических вакуумов R.
Группа ненарушенных симметрии Я, отвечающая классическому вакуу-
вакууму 1^0, состоит из элементов g G G, коммутирующих с tpo- (Мы считаем,
чт группа G и, значит, ее алгебра Ли W реализованы матрицами; тогда при-
присоединенное представление определяется формулой Tg(tp) = gtpg~l.) В
группе Н есть однопараметрическая подгруппа Н^0', состоящая из элемен-
элементов вида ехр(а<р0) (подгруппа с генератором i^o)- Это подгруппа принад-
принадлежит, очевидно, центру группы Н. Мы будем рассматривать электромаг-
электромагнитную напряженность F^v и магнитный заряд ГО, отвечающие подгруппе
#*°\ (В модели Джорджи - Глешоу и SUE)-модели центр группы Я
одномерен, так что никаких существенно отличных возможностей для оп-
определения электромагнитной напряженности нет.) На больших расстояниях
интересующая нас электромагнитная напряженность записывается в виде
•Р
(Это следует из замечания, что hUp) = является нормированным гене-
II ?> II
ратором "электромагнитной подгруппы" группы ненарушенных симметрии
вакуума tp G R.) Мы можем поэтому записать магнитный заряд как (ум-
(умноженный на DЯ)) поток магнитной напряженности Н — вектора с ком-
компонентами Я" = - e"ikFfk = -ea'k(&jk> V>> U^H - через бесконечно
удаленную сферу. Отметим, что нормы всех классических вакуумов одина-
одинаковы, поскольку с помощью преобразований группы G можно перевести
110

фиксированный классический вакуум в любой другой, а при этих преоб-
преобразованиях норма сохраняется. Это позволяет считать, что II tp II = а = const
Преобразуя поток вектора Н(х) в объемный интеграл, получаем для
магнитного заряда выражение
ГО= /Hc?S = fbiei'k(fik,<p)-d3x. B)
4я 8я а
Заметим теперь, что
^ fjk, ц*)) = е'>к( fjk, V,*>
и, значит
т = feiJk<Ffk,Viv)-d3x. C)
8я о.
(Мы воспользовались тем, что для калибровочно инвариантной величины
( &}к> <р) обычная производная Э,-. совпадает с ковариантной производной
V/, и учли тождество Бианки e'/kV,- Wjk = 0; см. § Т22.) Далее восполь-
воспользуемся тем, что из соотношения / (с — Ъ, с — b\dx~> 0 следует неравенство
1
f<c,b)dx<-f(<c,c) + <b,b))dx, D)
причем равенство достигается только в случае с(х) = Ь(х) (здесь с (х) и
Ь(х) принимают значения в И"). Применяя это неравенство к векторам
¦— е*7'* &}к и V/ у, получаем, что
Че
f — eilk{fik,V^)dzx<
J d3x. E)
Интеграл, стоящий в правой части этого неравенства, отличается от энер-
энергии Е поля (up, у4м) только отсутствием слагаемого Ei = X/ U(tp) d3x.
Поскольку левая часть неравенства E) лишь множителем отличается от
е
магнитного заряда, мы получаем оценку ГО < (Е - Et). Иными сло-
4 па
вами,
E>4nta -+Ei, F)
е
причем равенство достигается только в случае
1 ... у
2еС ;*~ *' (-
111

Поскольку Ei > О, а магнитный заряд в принятой нами нормировке
принимает только целые значения, мы видим, что энергия поля, обладаю-
обладающего магнитным зарядом, допускает оценку
E>4w-. (8)
е
Покажем, что оценка (8) становится точной в пределе X -*¦ 0, если при
предельном переходе остальные параметры (е и а) остаются неизменными.
(Этот предел называется пределом Богомольного - Прасада — Зоммер-
фельда.) В рассматриваемом нами пределе Ei = 0, иными словами,
Е = ТТ^^' ^^х + ^/Щ-^Ц^^х. (9)
4е 2
А Отметим, что хотя мы можем отбросить слагаемое Е\ в функционале
энергии, от него остается след - благодаря тому, что при сколь угодно
малых X конечную энергию имеют только поля с асимптотикой t/>(x) -+R
на бесконечности, это условие следует сохранить и при X = 0. Ў Из прове-
проведенных выше рассуждений видно, что для полей, удовлетворяющих усло-
условию G), функционал (9) достигает своего наименьшего значения
EmiD(m)= 4пт-.
а
В частности, эти поля являются экстремалями функционала (9). (Наи-
(Наименьшее значение функционала (9) ищется на полях с асимптотикой
II tp (x) II ->• а на бесконечности и фиксированным значением магнитного за-
заряда да.) Нетрудно проверить, что уравнение G) имеет редиение. Напри-
Например, в модели Джорджи — Глешоу решением этого уравнения с ГО = I
является поле
sh ae | x |
\- I).
(Ю)
(Это поле получается, если искать решение уравнения G) в форме D.7).
Подстановка D.7) приводит к уравнениям первого порядка для а(г) и
Р(г), решение которых дает поле A0).)
Для произвольного натурального числа ГО можно доказать, что существует
B щ+2)-параметрическое семейство решений уравнения G) (калибро-
вочно эквивалентные решения отождествляются).
При X > 0 оценка (8) не является точной. Однако, в этом случае легко
получить двусторонние оценки для наименьшего значения энергии на полях
с магнитным зарядом ГО. Именно
4ящ -<Emin <4яГО - +ХС, A1)
е е
где С не зависит от X. Оценка снизу следует из F), оценка сверху получа-
112

ется, если выбрать в качестве пробной функции какое-нибудь поле, удов-
удовлетворяющее уравнению G).
Отметим, что величина ае в квазиклассическом приближении совпадает
с массой Mw заряженной векторной частицы (промежуточного векторного
бозона); см. § 4. Из оценки A1) следует, что масса магнитного монополя
по порядку величины равна е Af w.
Слегка модифицируя проведенное выше рассуждение, можно получить
оценку снизу для энергии поля, обладающего магнитным зарядом, в произ-
произвольной модели большого объединения. Напомним, что в таких моделях
для полей, обладающих конечной энергией, магнитный заряд можно опре-
определить как поток вектора —#' = — el/k< &к(х), A(i^x))> через бесконеч-
4эт 8я
но удаленную сферу (см. G.8)). Рассмотрим G-инвариантную гладкую
функцию <*0/>), равную единице в некоторой окрестности многообразия
классических вакуумов R и обращающуюся в нуль вне другой (большей)
окрестности многообразия R. а При построении функции <*(?>) можно
исходить, например, из функции p(tp), равной расстоянию от точки tp до
многообразия R. Тогда а(ц>) можно определить формулой а(<р) =j3(p(i^)),
где /3(р) - гладкая числовая функция, равная единице при р < е/3 и нулю
2
при р > — е. Число е доолжно быть выбрано таким образом, чтобы в е-ок-
рестности многообразия R функция p(tp) была непрерывной однозначной
фукцией. Ў Очевидно, что магнитный заряд можно определить также как
поток вектора А' = —е'; < Щь, a(ip)h(tp)) через бесконечно удаленную
8я
сферу, поскольку на больших расстояниях ?>(х) близко к многообразию
R, и, значит, а(<р(х)) = 1. Отметим, что вектор А' в отличие от вектора//*
определен при всех х. Действительно, элемент h(ip(x)) € i$ определен
только в случае, если ip(x) достаточно близко к многообразию R. Однако,
там, где этот элемент не определен, а(у(х)) = 0. Поэтому произведение
a(tp(x))h(y>(x)) также можно считать равным нулю. Преобразуя поток
вектора А' (х) в объемный интеграл, получаем
^/,</k, (*)(?) . A2)
8тг
Используя калибровочную инвариантность выражения < Щь, а((^)й(^)> и
повторяя рассуждения, приведшие нас к формуле C), получаем
«П= —/е*'*< fJk, V,(a^)^(^)))d3^. A3)
. 1
Применяя неравенство D) к функциям \[delik&ik и Vj(a(tp)h(tp)),
¦ч/Я"
получаем
W < Bс?/ < fjk, fJk)d3x +
16я
+ — / < V,(orfo)A(*)), Ч(а(^)Л(^))>d3x, A4)
d
113

где d — произвольное число. Из G-инвариантности функции а и из соотно-
соотношения h(jg(ip)) =Tgh(tp) вытекает, что
Ч*)'. A5)
Мы видим, что
где
Подберем теперь число т? таким образом, чтобы было выполнено неравен-
неравенство ga6(?>)i;a?b<7?2|?|2 привсех? (константут?можновыбрать не зави-
зависящей от <р,поскольку тензор gab(tp) отличен от нуля на ограниченном мно-
1
жестве). Полагая d = — г), получаем из A6) оценку
2е
4эт
< пе
^ 4я
Мы видим, что энергия Е($, А) поля (^, Лм), имеющего магнитный заряд
at, допускает оценку
Ю
Из полученной оценки вытекает, что масса магнитного монополя имеет
такой же порядок величины, как eA/w, где A/w — масса самой тяжелой
из векторных частиц. В самом деле, масса М^ по порядку величины равна
е\ а |, где | а \ — наибольшее из вакуумных средних компонент скалярного
поля?>. (Можно заменить здесь | а | длиной вектора $, отвечающего класси-
классическому вакууму.) С другой стороны, число т? равно lap1 (снова по по-
порядку величины). Это дает нужную оценку для массы магнитного моно-
монополя.
§ 12. Топологически нетривиальные нити
Мы видели, что в теориях большого объединения существуют тополо-
топологически нетривиальные поля (поля, которые нельзя свести к вакуумному с
помощью непрерывной деформации в классе полей с конечной энергией).
Грубо говоря, эти поля представляют собой образования, энергия которых
заключена в конечной области пространства и стабильность которых гаран-
гарантируется топологическими соображениями. В квантовой теории этим полям
отвечают стабильные частицы, обладающие топологическим зарядом. (Как
мы убедились, этот топологический заряд можно отождествить с магнит-
114

ным зарядом, а соответствующие частицы — с магнитными монополями.)
Мы покажем сейчас, что в теориях большого объединения могут существо-
существовать также топологически нетривиальные нити. На наглядном языке такие
нити описываются как образования, энергия которых заключена в не-
некоторой трубке и стабильность которых гарантируется топологическими
соображениями (простейшие примеры нитей описаны в § 3).
Нить можно определить как поле (tp, А^), существенно отличающееся
от вакуумного лишь в некоторой окрестности кривой линии Г. Точнее,
мы будем требовать, чтобы вне этой окрестности поле tp принимало зна-
значения в описанной в § 5 окрестности (R многообразия вакуумов R. Рас-
Рассмотрим окружность S1, охватывающую кривую Г и находящуюся в об-
области, где значения поля tp принадлежат <R (рис. 13) .Например,если Г—вер-
Г—вертикальная прямая и поле <р существенно отличается от вакуума в цилиндре
радиуса 5, то в качестве 51 можно выбрать горизонтальную окружность с
центром на прямой, имеющую радиус > 5. Поле tp, рассматриваемое на ок-
окружности S1, определяет отображение этой окружности в <R. Топологи-
Топологическим типом нити будем называть гомотопический класс этого отображе-
отображения или гомотопический класс отображения oip окружности S1 в многооб-
многообразие вакуумов R. А Эти два определения равносильны. В самом деле,
отображение а, сопоставляющее точке множества <R ближайшую к ней точ-
точку многообразия R, является гомотопической эквивалентностью, поэтому
с помощью этого отображения устанавливается взаимна однозначное со-
соответствие между множествами {S1, (R) и {S1,/?} гомотопических клас-
классов отображений окружности в (R и/? соответственно. Ў
Нить называется топологически нетривиальной, если ее топологический
тип является нетривиальным гомотопическим классом (т.е. отображение tp
окружности S1 в (R не гомотопно нулю).
Рис.13
Мы видели в § 3, что нити возникают в модели, описываемой лагран
жианом C.6). Рассмотрим еще одну простую модель, обладающую этим
свойством. Будем считать, что калибровочной группой является группа
G = SOC), а скалярное поле преобразуется по пятимерному неприводи-
неприводимому представлению группы SOC). (Иначе говоря, будем рассматривать
скалярное поле как симметричный тензор Ф1', i, j = 1, 2, 3, имеющий нуле-
нулевой след.) Выберем полином К(Ф) таким образом, чтобы многообразие
R состояло из матриц Ф", имеющих два одинаковых собственных значе-
115

ния X (число X фиксировано). Например, нужным нам условиям удовлет-
удовлетворяет полином
= a(Sp Ф2 - Ъг J + е Sp Ф3,
где е — достаточно малое число.
. Каждой матрице, имеющей два совпадающих собственных значения X,
сопоставим прямую линию, проходящую через начало координат и направ-
направленную по собственному вектору, отвечающему третьему собственному
значению — 2Х. Построенное соответствие взаимно однозначно. Таким об-
образом, многообразие R всех классических вакуумов в данном случае то-
топологически эквивалентно множеству всех прямых, проходящих через на-
начало координат в трехмерном пространстве. Иными словами, многообразие
R топологически эквивалентно двумерной проективной плоскости RP2.
Мы видим, что ttj {К) = 7Tt {RP г ) = ~к2 и, следовательно, множество { 51, R}
как и группа 7Tj(/?), состоит из двух элементов (см. § Т4).
Пример топологически нетривиальной нити в интересующей нас модели
дается соотношениями
D
A)
Ф(р,в) = о(р)К(--в)Ф0к1г
1
) L
Ар=Аг=О,
где р, d,z — цилиндрические координаты, Lz - элемент алгебры Ли группы
SOC), отвечающий бесконечно малому вращению вокруг оси г, У(в) =
- exp(Z,z0 ) - матрица вращения на угол в вокруг оси z, ФО — диагональ-
диагональная матрица с элементами X, X, '— 2Х; а(р) и /5(р) — числовые функции,
быстро стремящиеся к 1 при р -*•+«> и удовлетворяющие условиям а @) =
= C@) = 0. Функции а(р), /3(р) могут быть подобраны так, чтобы нить A)
удовлетворяла уравнениям движения. (Ниже будут указаны более общие
утверждения, справедливые в произвольной калибровочной модели.)
Мы всегда считаем, что вырождение классического вакуума полностью
обусловлено свойствами симметрии; это позволяет отождествить множест-
множества R и G[H, где Н— стационарная подгруппа точки <р0 S R. Если G одно-
связная группа, то группа Я1(Я) изоморфна группе яо(Я) =Я/ЯСОП.Таким
образом, всякой дискретной ненарушенной симметрииh&Hсопоставляет-
симметрииh&Hсопоставляется элемент группы tti(/?) (см. § Т20). Это соответствие строится следую-
следующим образом. Каждому пути g(t), 0 < t < 1, в группе G сопоставляется
путь
r(t)=T(g(t))<po B)
в R; всякий путь в R может быть записан в виде B). В случае если^(О) и
g A) (начало и конец пути g (t)) принадлежат Н, путь r(t) замкнут. В силу
односвязности группы G элемент [г] группы 7Ti(/?), определяемый путем
г (t), зависит только от концов пути g(t). Более того, пвскольку путям
if (О и g(t)h, где h € Я, отвечает один и тот же путь г (t) € R, элемент
[г] е 7Ti(i?) полностью определяется элементом g@)g~1(l). При непре-
непрерывном изменении элемента ?@)#-1A) элемент [г] не меняется. Это
116

означает, что существует соответствие между #/Ясоп и ni(R); легко про-
проверить, что это соответствие является изоморфизмом (см. § Т20).
Два элемента группы tti(/?) отвечают одному и тому гомотопическому
классу отображений окружности 51 в <R, если они сопряжены друг другу
(§ ТЗ). Таким образом, топологический тип нити задается элементом груп-
группы яо(Я), однако при этом сопряженные элементы отвечают одному и тому
же типу. (Множество {S',/?} отождествляется с множеством классов соп-
сопряженных элементов в группе тго(Я) = Н/Нсоп.) В свою очередь, элемент
группы Н можно рассматривать как элемент группы iro(#), помня при
этом, что два элемента группы Я, которые можно соединить между собой
непрерывной кривой, отвечают одному элементу группы яо(Я).
Рассмотрим несколько подробнее прямолинейные нити - поля, сосре-
сосредоточенные в окрестности прямой линии. (Если нить представляет собой
поле, сосредоточенное в окрестности кривой Г, то небольшой участок нити
можно считать прямолинейным в случае, когда толщина окрестности мно-
много меньше радиуса кривизны кривой.) Типичным примером прямолиней-
прямолинейных нитей являются поля (tp, А^), инвариантные при сдвиге вдоль оси z
и имеющие конечную линейную плотность энергии. Последнее условие оз-
означает, что энергия, заключенная между двумя горизонтальными плоскос-
плоскостями, конечна. Полная энергия поля в силу инвариантности при сдвиге
вдоль оси z бесконечна.
Для того чтобы линейная плотность энергии была конечна, нужно, в част-
частности, чтобы ковариантная производная V^ стремилась к нулю при удале-
удалении от оси z. Мы будем предполагать, что
V^< constp~{l+s\ C)
где р = \/х2 + у2 — расстояние до оси z. Будем считать также, что в ци-
цилиндрических координатах (р, 0, z) поле tp(р, в,z) = у (р, в) имеет предел
прир-> + °°:
Ф@) = lim ?>(p,0). D)
(В калибровке хАх + уАу = О существование предела вытекает из C);
более того, можно проверить, что I Ф@) — <р(р, 0I < const p~ . Это до-
доказывается так же, как соответствующие утверждения в § 3 и § 5.)
Функцию Ф@) можно рассматривать как отображение окружности в R;
топологический тип поля (^, Лд) очевидно совпадает с гомотопическим,
классом отображения Ф.
В случае прямолинейной нити (у, Лм), удовлетворяющей условию C),
топологический тип можно выразить через калибровочное доле А^. Имен-
Именно, отвечающий топологическому типу элемент группы Яо(Я) может быть
представлен в виде
a=(Pexp(-fA^ldx^)y1 =(Pexp(- / Ав<1в)У\ E)
о
где интеграл берется по бесконечно большой окружности, охватывающей
нить, символ Р ехр обозначает упорядоченную экспоненту, Ад =Ali Эхм/Э0—
компонента калибровочного поля в цилиндрических координатах (р,в,г),
117

отвечающая координате в. (Мы увидим ниже, что E) определяет элемент
группы Н - стационарной подгруппы элемента Ф@) Е R - я, следователь-
следовательно, определяет элемент группы Яо(Я).)
Элемент а можно определить также формулой а = lim a(p, 2я), где
а(р,в) — решение дифференциального уравнения
два(р,в)-а(р,в)Ав(р,в) = О
с начальным условием а(р, 0) = 1. (Иначе говоря,
а-1(р,е)=Рехр(- ?
о
Для того, чтобы доказать соотношение E), перейдем к пределу р
в соотношении
I V,e VI = I (Эе + ?(Ле (р, 0)))v I < const p~s,
вытекающем из C). Здесь t обозначает представление алгебры Ли, соот-
соответствующее представлению Т калибровочной группы G, по которому
преобразуется поле <р. Мы получим:
0, F)
где4е@) = lim Ae(p, 0). Из F) следует,что
Ф@)=Г(а-1@))Ф(О)( G)
е
где а*1 @) = Рехр ( - fAedd ). Поскольку ФBтг) = Ф@), мы видим, что
о
a = аBтг) принадлежит стационарной подгруппе Н элемента Фо. Пути
g (в) = а~х (в), 0 < в < 2тг, в группе G отвечает путь Ф(в) в R. Как было
объяснено выше, гомотопический класс пути Ф@) отвечает элементу груп-
группы #/#соп> определяемому элементом ^(О)^-1 B7г) =а"'@)аBя) =а€.Н.
Это доказывает соотношение E).
* Отметим, что в проведенном только что рассуждении мы использовали
дополнительное предположение, что существует предел Ад (р, в) при р-+°°..
От этого предположения можно избавиться за счет некоторого усложнения
доказательства. Ў
Для того, чтобы проанализировать в квазиклассическом приближении
квантовые аналоги нитей нужно найти нити, удовлетворяющие класси-
классическим уравнениям движения. Мы покажем сейчас, как в произвольном
топологическом классе найти прямолинейные нити, имеющие конечную
линейную плотность энергии и удовлетворяющие уравнениям движения.
Естественно искать такие нити в классе полей, обладающих в некотором
смысле аксиальной симметрией. Именно, мы будем рассматривать поля
(у, Ар), изменение которых при вращении на угол в вокруг оси z может
быть скомпенсировано глобальным калибровочным преобразованием,
отвечающим элементу ge = ехр(М0) e G. Здесь М - элемент алгебры Ли
& группы G; этот элемент определяет тип аксиальной симметрии. В ци-
цилиндрических координатах интересующие нас поля могут быть записаны в
118

виде
e,z) = ехр (Мв)Ав (р) ехр(М8),
Лг (р, 0, г) = ехр (Мв)А, (р) ехр (-Мв).
(Мы налагаем на поле (ц>, А^) дополнительное условие инвариантности при
сдвиге по оси z.) Для того, чтобы при в = 2тг формулы (8) давали тот же
ответ, что при 0=0, нужно потребовать, чтобы элемент а = ехр (—2пМ)
коммутировал с Ав (р), Ар(р),Аг (р) и чтобы функция ^ (р) удовлетворя-
удовлетворяла условию Т(а) <р(р) - ?> (р) • Чтобы поле (8) было несингулярным на оси
z, следует потребовать выполнения равенств Ар@) -Аг @) = 0. Будем счи-
считать, что у(р) = Фо + а(р), Ав (р) = М + /J(p), функции а(р), /3(р), Хр(^),
Xz(^) достаточно быстро стремятся к нулю прир -»•+<». Тогда линейная
плотность энергии е поля (8) конечна; это сразу следует из явного выра-
выражения для нее
2
+ 1
Эр
(9)
Экстремали функционала (9) удовлетворяют классическим уравнениям
движения. (Это можно проверить непосредственно или вывести из общих
результатов § 9.) Отсюда легко получить, что в любом классе аксиальной
симметрии существует нить, удовлетворяющая классическим уравнениям.
Такую нить можно найти и в более узком классе полей (8) с дополнитель-
дополнительными условиями Ар = Аг = 0, Ав (р) = Му (р), 7(р) - числовая функция.
Отметим, что топологический тип аксиально симметричной нити пол-
полностью определяется ее классом аксиальной симметрии (т.е. элементом
М G <§ ). В самом деле, топологический тип нити представляет собой гомо-
гомотопический класс отображения Ф@) = Г (ехр (Мв)) Фо, этому гомотопи-
гомотопическому классу отвечает элемент а = ехр (—2тгЛГ) S Н. Поскольку каждый
элемент абЯСС может быть представлен в виде ехр (-2пМ), мы видим,
что во всяком топологическом классе есть прямолинейные нити, имеющие
конечную линейную плотность энергии и являющиеся решениями уравне-
уравнений движения. Используя эти решения, легко построить криволинейные
замкнутые нити, удовлетворяющие уравнениям движения приближенно.
Квазиклассические рассмотрения позволяют построить с помощью этих
приближенных решений квантовые объекты, которые мы тоже будем назы-
называть замкнутыми нитями.
Изложенные выше соображения позволяют легко проанализировать
нити в конкретных моделях большого объединения. В частности, если ка-
калибровочная группа G односвязНа, то топологически нетривиальные нити
существуют в том и только в том случае, если есть дискретные ненарушен-
ненарушенные симметрии. Для случае G = SO (л) можно указать простой достаточный
11»

признак существования нитей. Именно, если скалярное поле преобразуется
по однозначному представлению группы SO (я) и существует односвязное
подмножество группы SO (л), содержащее подгруппу Я ненарушенных сим-
симметрии, го в модели существуют нити. Для того чтобы убедиться в этом,
следует прежде всего перейти от неодносвязной калибровочной группы
SO (л) к односвязной группе Spin (л) (универсальной накрывающей груп-
группы SO (л)). Многообразие вакуумов R = SO (л) /Я можно представить в
виде Spin (л)/Я, где Jf— подгруппа группы Spin (л), накрывающая груп-
группу Я. Из сказанного выше следует, что многообразие R неодносвязно в
том и только в том случае, если подгруппа Н несвязна. Разумеется, из не-
несвязности группы Я вытекает несвязность группыЯ; однако, группаЯможет
быть несвязной и в случае, если группа Я связна. В самом деле, каждой
точке группы SO (л) отвечает в Spin (л) две накрывающие ее точки. Если
группа Я связна, то в ней можно найти путь, соединяющий две точки, кото-
которые накрывают единицу группы SO (л). При отображении в SO (я) этот
путь переходит в замкнутый путь, негомотопный нулю в SO (и) и целиком
лежащий в Я. Однако, если Я содержится в односвязном подмножестве,
всякий замкнутый путь из Я гомотопен нулю в SO (и), а это значит, что
предположение о связности группы Я приводит к противоречию.
В SO A0)-модели большого объединения группа Н связна и содержит^
ся в односвязной группе SUE) С SOA0). Это означает, что группа Я
несвязна, и, следовательно, в SO A0)-модели существуют топологически
нетривиальные нити. В частности, генератору М группы SO B) С SO A0) ^
нормированному условием ехр BтгМ) = 1, ехр (вМ) Ф 1 приО< в < 2тг,
отвечает тип аксиальной симметрии, состоящий из топологически нетри-
нетривиальных нитей. (Если М рассматривается как генератор группы Spin A0),
то ехр BтгМ) Ф 1.)
Отметим, что топологически нетривиальные нити могут существовать
не только в моделях большого объединения, но и в моделях, описывающих
элекгрослабые взаимодействия. В стандартной модели Вайнберга—Салама
таких нитей нет, однако, можно доказать, что топологически нетривиаль-
нетривиальные нити существуют в модели Ли—Вайнберга, основанной на группе
SUC)X U(l). (Группа SUC)XUA) неодносвязна. Для того чтобы приме-
применить общие рассмотрения этого параграфа, ее нужно заменить односвязной,
но некомпактной калибровочной группой. Легче, однако, вычислить группу
71^G?) с помощью точной гомотопической последовательности.)
§ 13. Частицы в присутствии нити
Мы покажем сейчас, что частица при обходе вокруг нити может менять
свои квантовые числа. В частности, существуют модели, в которых при
обходе вокруг нити частица меняет электрический заряд. Такие модели не
являются реалистическими. Однако можно построить реалистические мо-
модели большого объединения, содержащие наряду с обычными частицами
слабо взаимодействующие с ними "зеркальные" частицы, и доказать, что
в этих моделях существуют нити, при обходе вокруг которых частица
превращается в зеркальную. (Такие нити в принципе можно было бы об-
обнаружить с помощью астрономических наблюдений).
120

Начнем для простоты с моделей, в которых группа ненарушенных сим-
симметрии Н одномерна. В этом случае, как было показано в § 8, электромаг-
электромагнитная напряженность F^ix) может быть записана в виде (8.1). В этой
формуле фигурирует функция h(cnp(x)), где hfa) обозначает генератор
одномерной группы Н^, состоящей из преобразований, оставляющих на
месте классический вакуум у, а - отображение, сопоставляющее каждой
точке множества <R ближайшую к ней точку многообразия вакуумов R.
В частности, для поля с конечной энергией F^,, (х) = ( &^„ (х), h(o<p(x)))
при | jc | -*¦ °° (см. G.5)). (Явный вид (8.1) электромагнитной напряжен-
напряженности F^i, не будет использован в дальнейших рассуждениях.) Мы уже
отмечали в § 7, что после наложения нормировочного условия генератор
Л(</>) определен с точностью до знака. Проанализируем вопрос о том, в
каких случаях эта двузначность может быть устранена.
Прежде всего заметим, что функция h (а<р (х) ), и вместе с ней электро-
электромагнитная напряженность F^v (x}, определены только на множестве V,
состоящем из тех точек х, для которых <р(х} G <R (т.е. поле <р (^доста-
(^достаточно близко к вакуумному). Если множество V односвязно, то из функ-
функции h(oip(x)), как и из любой другой многозначной функции на связном
односвязном пространстве, можно выбрать непрерывную однозначную
ветвь.
А Если функция задана на отрезке, то всегда можно построить однознач-
однозначную ветвь, разбив отрезок на маленькие части и выбирая нужную ветвь
последовательно на этих частях. В общем случае нужно фиксировать значе-
значение функции в одной из точек, соединить эту точку путями со всеми осталь-
остальными точками и выбрать непрерывную ветвь на каждом из этих путей.
В односвязном пространстве при продолжении по любому пути из точки х0
в точку xt мы получаем один и тот же результат. В самом деле, при не-
непрерывной деформации пути, ведущего из х0 в хi, результат не меняется,
а в силу односвязности всякий путь можно продеформировать в любой
другой, т
Далее, если пространство R односвязно (т.е. группа Н связна), те же со-
соображения позволяют вьщелить непрерывную однозначную ветвь функции
), определенной на <R , и, следовательно, однозначную ветвь функции
на V. Наиболее интересен случай, когда пространство R неодно-
связно и, следовательно, существуют топологически нетривиальные нити.
Тогда неоднозначность функции h(o*p(x)) и, следовательно, электромаг-
электромагнитной напряженности может оказаться неустранимой. Например, в опи-
описанной в предыдущем параграфе модели для поля A2.1), из функции
h(o<p(x)) нельзя выбрать непрерывную однозначную ветвь. Это очевидно
из явного выражения для h (oy (х))
(здесь Ло - генератор группы Н = ^(„>0)).
Для поля A2.8)
h(oy(p, в)) = ±ехр(Л/0)Л(о^(р))ехр(-Л/0).
Отсюда видно, что двузначность функции h(Oip(x)) неустранима в случае,
121

если
ahoof1 = -h0, B)
где a = exp (—2пМ), h0 — генератор группы U(l) СН = НЧ>^).
Условие B) является общим. Точнее говоря, поля, для которых дву-
двузначность электромагнитной напряженности неустранима, существуют,
если в группе ненарушенных симметрии Н можно найти элемент а "пере-
"переворачивающий" группу U(l) С Я (т.е. удовлетворяющий условию аиа'1 =
= и"-1 для любого элемента uE U(l) или, что то же самое, условию B),
где Ао — генератор группы U(l)). В самом деле,легко убедиться,что нуж-
нужными нам полями являются нити, топологический тип которых отвечает
этому элементу а. Точнее говоря, для этих нитей нельзя найти непрерывную
однозначную ветвь функции h {р*р (х) ). Если электромагнитная напряжен-
напряженность не обращается в нуль, отсюда следует неустранимость ее двузнач-
двузначности. Однако в случае, когда Fuv = 0, как, например, для поля A2.8),
электромагнитная напряженность с самого начала однозначна и о неустра-
неустранимой двузначности не может быть и речи.
Рассмотрим теперь электрический и магнитный заряды частиц, считая,
что вдали от частиц поля можно рассматривать как классические. Электри-
Электрический заряд частицы, по определению, с точностью до множителя D7т)
совпадает с потоком электрической напряженности через сферу, окружаю-
окружающую частицу. Аналогично, магнитный заряд частицы определяется через
поток магнитной напряженности. Однако, в случае, если частицы находят-
находятся в поле нити, удовлетворяющей условию B), где a — топологический
тип нити, эти определения электрического и магнитного зарядов неприме-
неприменимы (точнее, дают два отличающихся знаком значения этих зарядов,
поскольку двузначна электромагнитная напряженность). Несмотря на то,
что знаки электрического и магнитного зарядов не определены для отдель-
отдельной частицы, относительный знак может быть определен для пары частиц,
соединенных кривой линией (предполагается, что во всех точках кривой
имеет смысл говорить об электромагнитной напряженности, т.е. для всех
точек кривой значения поля у принадлежат множеству <R ). Рассмотрим
поверхность J2, заключающую в себе эту кривую, и множество, ограничен-
ограниченное снаружи поверхностью J2, а изнутри-сферами ?2а и Sl2, содержащими
частицы (рис. 14). Это множество односвязно, поэтому можно найти
однозначную ветвь тензора F^,,, непрерывную на этом множестве, и вы-
вычислить потоки (электрической или магнитной) напряженности через по-
поверхности ui и О2. Если эти два потока имеют один и тот же знак, мы
говорим, что обе частицы имеют (электрический или магнитный) заряд
одного знака. В противном случае заряды частиц считаем противополож-
противоположными. Относительный заряд частиц может зависеть от выбора кривой, сое-
соединяющей частицы, но не меняется при непрерывной деформации этой
кривой (если только при деформации кривая не выходит за пределы
множества U, на котором у (х) е <R ).
Будем считать, что рассматриваемое нами состояние существенно отли-
отличается от вакуумного только в окрестности некоторой замкнутой кривой
и в окрестностях нескольких точек. Это означает, что мы имеем дело с
нитью и несколькими частицами. (Можно было бы рассмотреть случай,
когда замкнутая кривая несвязна — это отвечает случаю, когда есть не-
122

сколько нитей.) Там, где состояние достаточно близко к вакуумному, мы
рассматриваем его квазиклассически, т.е. заменяем классическим полем.
Будем предполагать, что электромагнитная напряженность этого класси-
классического поля меняет знак при обходе вокруг нити. Тогда из сказанного
выше следует, что относительный знак зарядов действительно зависит от
выбора соединяющей эти заряды кривой. В самом деле, если частицы сое-
соединены кривыми 7i и 72. проходящими по разные стороны нити (рис. 15),
то относительный знак, отвечающий выбору кривой 7i> противоположен
Рис. 14 Рис. 15
относительному знаку, вычисленному с помощью кривой у2 • (Это связано
с тем, что при обходе по замкнутой кривой, составленной из кривой 7i и
пройденной в обратном направлении кривой 72 > напряженность меняет
знак.) Существенно отметить, что в случае, если относительный знак заря-
зарядов вычисляется все время с помощью одной и той же кривой 7>.но в ПР°"
цессе эволюции нить пересекает кривую, относительный знак зарядов ме-
меняется. В момент пересечения относительный знак зарядов нельзя вычис-
вычислять с помощью кривой 7- Изменение относительного знака при пересече-
пересечении связано с тем, что кривая переходит с одной стороны нити на другую.
Естественно условиться определять относительный знак зарядов с по-
помощью прямолинейных отрезков всегда, когда это возможно. Тогда можно
фиксировать знаки всех зарядов, фиксировав знак заряда одной из частиц.
Однако при этом заряд частицы будет изменяться, когда нить при движении
пересекает отрезок, соединяющий эту частицу с частицей, знак заряда ко-
которой заранее фиксирован.
Проведенные выше рассуждения наводят на мысль, что в рассматри-
рассматриваемых нами моделях заряд не сохраняется. Тем не менее можно дать такое
определение заряда, что закон сохранения в некотором смысле будет иметь
место. Для этого натянем на нить пленку, т.е. рассмотрим произвольную
поверхность, границей которой является та кривая, в окрестности которой
поле существенно отлично от вакуумного. Мы не будем исключать слу-
случая, когда есть несколько нитей, но тогда для простоты предположим, что
натянутые^ на них пленки не пересекаются. Удалим из пространства все
пленки, натянутые на нити, а также все точки, в которых электромагнитная
напряженность не определена. Тогда останется односвязное множество,
на котором можно выбрать непрерывную однозначную ветвь электромаг-
электромагнитной напряженности FMV. С помощью этой ветви определим электричес-
электрические и магнитные заряды частиц и нитей. (Заряд нити определяется как
умноженный на Dтг)"' поток напряженности через границу окрестности
123

пленки, натянутой на нить.) Из уравнений Максвелла следует, что опреде-
определенный таким образом заряд сохраняется. Тензор F^,, меняет знак при пе-
переходе через пленку, натянутую на нить, поэтому частица, пересекая эту
пленку, меняет знак заряда. Однако, изменение заряда частицы сопровож-
сопровождается соответствующим изменением заряда нити.
Ясно, что закон сохранения заряда нелокален*). (Заряд частицы зави-
зависит от случайного выбора пленки, натянутой на нить. Его изменение при пе-
пересечении пленки, конечно, не имеет физического смысла.)
Проведенные выше рассуждения касаются в равной мере электрическо-
электрического и магнитного зарядов. Оба типа зарядов определялись одинаковым об-
образом через поток напряженности. Вспомним, что приЯ =UA) магнитный
заряд совпадает с топологическим зарядом и проанализируем связь между
этими двумя видами зарядов, если Я — несвязная одномерная группа. В
общем случае топологический заряд поля в области, ограниченной поверх-
поверхностью Г, на которой поле достаточно близко к вакуумному, определяет-
определяется как гомотопический класс отображения этой поверхности в <R, то есть
как элемент множества {S2,®.} = {S2,R). (Мы предполагаем, что Г -
топологическая сфера.) Если Я = U(l), то пространство R односвязно,
{S2, R) = 7Г2 (R) = 2\ Однако, если Я - несвязная одномерная группа,
то пространств^ R = G/H неодносвязно. (Мы предполагаем группу G одно-
связной и, следовательно, л^ (R) - яо(Я) = Н/Нсоп.) Это означает, что
множество {S2, R) вообще говоря, нельзя отождествить с п2 (R) .=
= П\ (Я) = 2. Это множество получается из эт2 (Ю с помощью отождеств-
отождествления элементов, которые можно перевести друг в друга преобразованиями
из группы ttj (R), действующей на ;г2 (R~) (см. § Т 15). Легко понять, что
элемент группы ir-^ (R.) = Н/Неоп, определяемый элементом a G Я, три-
тривиально действует на пг (R) =Жъ случае, если преобразование и ¦+ аиа'1
не меняет элемента и € U(l) С Я. Если же а "переворачивает" группу
U(l) СЯ^.е.амоГ1 = м для и е U(l)), то элемент группы я2 (R), отве-
отвечающий целому числу т, переходит в элемент, отвечающий числу — т .-
Отсюда видно, что элемент множества {S2,R} характеризуется неотрица-
неотрицательным целым числом - топологический заряд определен с точностью до
знака. Это согласуется с тем, что знак магнитного заряда также не опреде-
определен (в силу двузначности магнитной напряженности).
До сих по мы занимались случаем, когда калибровочная группа G одно-
связна, а группа Н ненарушенных симметрии одномерна. Наши рассужде-
рассуждения без всякого труда обобщаются на случай, когда группа Я неодномерна,
но одномерен центр алгебры Ли этой группы. (Напомним, что тогда
электромагнитная напряженность определяется с помощью генератора это-
этого центра; см. § 7.) Эта более общая ситуация охватывает стандартные мо-
модели большого объединения, поскольку группа Я в этих моделях локаль-
локально изоморфна SUC) X U(l). Как мы говорили в предыдущем параграфе,
в моделях большого объединения могут существовать топологически не-
нетривиальные нити; нетрудно проверить, однако, что в них не может быть
нитей, при обходе вокруг которых электромагнитная напряженность ме-
*) Здесь ситуация аналогична общей теории относительности, в которой можно
сформулировать закон сохранения энергии, хотя нельзя ввести ковариантного поня-
понятия плотности энергии (нельзя говорить о локализации энергии).
124

няет знак Л Дискретная симметрия а, отвечающая топологическому типу
такой нити, должна была бы переводить электрон в позитрон. Однако, в
модели Вайнберга—Салама, которая при низких энергиях получается из
обычных моделей большого объединения, такой симметрии не сущест-
существует. Ў
Перейдем теперь к случаю, когда центр % алгебры Ли К группы Н имеет
размерность г > 1. В этом случае каждому элементу И e Z можно сопоста-
сопоставить с помощью формулы, аналогичной формуле -(8-1), свой тензор
электромагнитной напряженности. Для этого нужно использовать в форму-
формуле для электромагнитной напряженности функцию Л(?0> удовлетворяю-
удовлетворяющую условиям Л(сро) = Л и h(T(g)y) = rgh(ip). Как показано в § 7,
в случае если группа Н связна, существует однозначная функция й(^),
удовлетворяющая этим требованиям. Однако, в интересующей нас ситуа-
ситуации, когда существуют топологически нетривиальные нити, группа Н не-
несвязна и, следовательно, функция h(<p) и вместе с ней определенная с ее
помощью электромагнитная напряженность, вообще говоря, многознач-
многозначны. Легко видеть, что изменение функции h(cnp(x)) при обходе вокруг
нити связано с топологическим классом нити.
Будем обходить нить по замкнутой кривой, на которой значения поля
<р достаточно близки к вакуумному (i^ G (R ). Предположим для простоты,
что значения поля <р на кривой xt принадлежат многообразию вакуумов R
(это не меняет результата). Тогда поле у на кривой xt можно представить
в виде T(g(t))ip0> где t — параметр на кривой @ <f < \),g(t) - непре-
непрерывная функция от t со значениями в группе G,g@) = 1; через <?о обозна-
обозначается поле ^ в точке кривой, отвечающей t = 0 (в силу замкнутости кри-
кривой эта же точка отвечает t = 1). По определению, топологический тип нити
определяется элементом а = g~l A) ?Я = Н(у0). С другой стороны, не-
непрерывная ветвь функции h(ip(x)) на рассматриваемой кривой дается,
очевидно, формулой
h(t) = gi^hg-'itl
h(t) = hdp(xt)), h=h(fpo).
(Строго говоря, вместо ghg'1 для групп, не являющихся матричными,
нужно писать rgh.) При обходе нити по кривой xt значение h функции
hdfi(x)) заменяется на aha~l. Таким образом, если айсГ1 ФИ, тензор на-
напряженности изменяется при обходе вокруг нити.
Изложенные выше результаты представляют интерес для теорий, содер-
содержащих так называемые зеркальные частицы. Теории со стандартным набо-
набором элементарных частиц, как известно, не являются инвариантными от-
относительно пространственного отражения. Однако эту инвариантность
можно восстановить, введя в рассмотрение новые частицы, связанные со
стандартными с помощью пространственного отражения (зеркальные
частицы). Конечно, для того, чтобы введение зеркальных частиц не проти-
противоречило эксперименту, необходимо, чтобы взаимодействие этих частиц
со стандартными было очень слабым.
Нетрудно построить теории большого объединения, описывающие обыч-
обычные и зеркальные частицы. Связная часть группы ненарушенных симмет-
симметрии Н в теориях такого типа должна быть локально изоморфна группе
SUC) X U(l) X SUC) X U(l). (Как мы говорили, у всякой стандартной
125

частицы существует ее зеркальный аналог. Поэтому наряду с группами
SUC) и U(l), связанными с глюонами и фотоном, в группу ненарушенных
симметрии должны входить множители SUC) и U(l), связанные с зеркаль-
зеркальными глюонами и зеркальным фотоном.) Однако кроме связной части в
группу ненарушенных симметрии должна входить дискретная симметрия а,
переставляющая обычные и зеркальные частицы. По доказанному выше
это означает, что в теории существуют топологически нетривиальные нити,
отвечающие дискретной симметрии а. В теории с зеркальными частицами
есть два существенно различных тензора электромагнитной напряженности,
связанные соответственно с обычным и зеркальным фотонами (точнее,
с генераторами h^ и h2 двух групп U(l), содержащихся в Я в качестве
прямых множителей). Важно подчеркнуть однако, что при обходе вокруг
нити с типом симметрии а обычная напряженность переходит в зеркальную.
(Иначе говоря, эти две напряженности являются ветвями одной и той же
многозначной функции.) Это следует из соотношения оЛ j а~г = h 2.
Можно сказать, что в присутствии нити различие между обычными
и зеркальными частицами становится условным. Ситуация здесь полностью
аналогична ситуации в теориях с нелокальным сохранением электричес-
электрического заряда. Если в каком-то подмножестве трехмерного пространства нет
нитей (точнее, часть этого подмножества, на которой <р €Е <R , односвязна),
то в этом подмножестве есть два однозначных тензора электромагнитной
напряженности - обычный и зеркальный. Соответственно, в этом подмно-
подмножестве можно четко отделить стандартные частицы от их зеркальных парт-
партнеров (по крайней мере, если эти частицы участвуют в электромагнитном
взаимодействии). Однако, если обычная частица выходит из рассматри-
рассматриваемого подмножества, обходит вокруг нити и возвращается обратно,
то после возвращения она будет восприниматься как зеркальная. Это дает
повод назвать рассматриваемые нити "нитями Алисы". (Алиса могла по-
попасть в Зазеркалье, обойдя вокруг такой нити.)
Если бы нити Алисы существовали, они могли бы быть обнаружены
с помощью астрономических наблюдений, * Естественно думать, что то-
топологически нетривиальные нити, если они существуют, должны иметь
большую длину. Такие нити с необходимостью возникают на ранних ста-
стадиях развития Вселенной. Однако, те из нитей, которые имеют небольшую
длину,, в процессе эволюции должны исчезнуть — схлопнуться. Ў Каждый
астрономический объект может содержать частицы разной зеркальности.
Космологический анализ, проведенный М. Хлоповым, показывает, что
очень массивные объекты должны содержать примерно равное количество
обычных и зеркальных частиц, в то время, как объекты не слишком боль-
большой массы должны состоять в основном из частиц одного типа.
Если нить в процессе своего движения пересекает прямую линию, сое-
соединяющую Землю с галактикой, состоящей в основном из обычной мате-
материи, то галактика становится невидимой. Действительно, чтобы устано-
установить, является ли частица зеркальной или обычной, мы должны соединить
эту частицу кривой линией с частицей, которую мы условились считать
обычной, и рассмотреть ветвь тензора напряженности, непрерывную вдоль
этой кривой. Поскольку свет распространяется прямолинейно, мы должны
определять тип частиц в галактике, соединяя их с земными с помощью
прямых линий. Если галактика состоит как из обычной, так и из зеркаль-
126

ной материи, то после прохождения нити ее светимость, вообще говоря,
меняется*).
Подобный эффект будет иметь место и для соседних галактик, но с не-
некоторым запозданием (или с опережением). Таким образом, движение
нити порождает волну изменения светимости. (К сожалению, для дале-
далеких объектов существуют менее экзотические объяснения наблюдаемых из-
изменений светимости.) Движение нити может приводить к некоторым эффек-
эффектам даже в случае, когда наблюдаемый объект содержит примерно поров-
поровну обычной и зеркальной материи. Например, поскольку пульсации свети-
светимости для обычной и зеркальной компонент квазара независимы, прохож-
прохождение нити может вызвать быстрое изменение светимости квазара. (Воз-
(Возможно, этот эффект является объяснением резких изменений светимости,
которые трудно объяснить стандартными способами.)
Коснемся вопроса об изменении типа частиц при обходе вокруг нити в
произвольной модели. Если нет нити, то можно стандартным способом
классифицировать возникающие в модели частицы. Если же нити сущест-
существуют, то эта классификация применима в любой односвязной области,
не содержащей нитей. Пусть теперь частица выходит из рассматриваемой
области, обходит вокруг нити, топологический тип которой задается эле-
элементом а е Н, и снова возвращается в область. Группа ненарушенных сим-
симметрии Н очевидным образом действует на множестве стационарных со-
состояний интересующей нас системы; при этом одночастичные состояния
переходят в одночастичные. При действии дискретных ненарушенных сим-
симметрии может меняться тип частиц. Оказывается, что изменение типа части-
частицы при обходе вокруг нити управляется действием элемента а? Н, отве-
отвечающего топологическому типу нити. Для того, чтобы проверить это утвер-
утверждение, будем считать, что частица обходит вокруг прямолинейной нити
на достаточно большом расстоянии от нее по замкнутому контуру Г. Тог-
Тогда можно убедиться, что вектор состояния частицы после обхода умножит-
умножится на Р ехр ( - $Ац dx^).C другой стороны, в § 12 было доказано, что
г
выражение
а = (Рехр(- f A^dx11))-1
г
является элементом группы Н, отвечающим топологическому типу нити.
Это обосновывает сформулированное только что утверждение.
Отметим, что из доказанного только что факта "легко получить сделан-
сделанные выше утверждения об изменении электрического заряда и зеркаль-
зеркальности частиц при обходе вокруг нити.
§ 14. Нелинейные поля
В классической теории поля обычно изучаются поля, принимающие
числовые значения или поля, принимающие значения в пространстве IR"
(совокупность п числовых полей можно рассматривать как поле, прини-
принимающее значения в IR", — многокомпонентное поле). Мы будем рассматри-
рассматривать сейчас теории, в которых поля принимают значения в многообразии,
*) Конечно, мы говорим о галактиках только для определенности, те же рассужде-
рассуждения применимы и к другим астрономическим объектам.
127

обладающем нетривиальной топологией. Такие поля возникают в различ-
различных ситуациях. В частности, мы видели в § 1, что локально равновесное
состояние описывается полем, принимающим значения в пространстве вы-
вырождения R. Динамика локально равновесного состояния задается лагран-
лагранжианом, вид которого в значительной степени определяется свойствами
симметрии рассматриваемой системы. Если речь идет о квантовой статисти-
статистической физике, то этот лагранжиан также можно рассматривать как
квантовый.
Квантовую теорию поля можно интерпретировать как квантовую статис-
статистическую физику при нулевой температуре. Роль равновесного состояния
при нулевой температуре играет основное состояние. Поэтому под прост-
пространством вырождения R в квантовой теории поля следует понимать много-
многообразие всех основных состояний.
Рассмотрим, например, теорию, описываемую лагранжианом
? = \ Ь^Ь^ - V&), A)
где {f = (ip1, ..., <р") — и-компонентное скалярное поле. Наименьшая энер-
энергия реализуется в этом случае на постоянных полях, отвечающих минималь-
минимальному значению функции У (у). В частности, если V(y>) = Х((<р!J + ...
... + (<р"J - а2J, то наименьшее значение функции V(y) достигается
в точках пространства 0V, для которых (у1J + ... + (упJ = а2; эти точки
заполняют (и - 1)-мерную сферу S"~l. Минимумы функции V(y) и отве-
отвечающие им поля можно назвать классическими основными состояниями
или классическими вакуумами. Если классический вакуум существует
только один, то в квазиклассическом приближении ему отвечает квантовое
основное состояние, энергия которого отличается от энергии классического
вакуума поправками порядка h. В случае если классический вакуум вы-
вырожден, квантовые поправки к энергиям различных классических ваку-
умов могут быть разными. Тогда в квантовой теории вырождение основно-
основного состояния снимается полностью или частично. Отметим, впрочем, что
в наиболее важном случае, когда вырождение классического вакуума
полностью обусловлено свойствами симметрии, квантовые поправки'
к энергиям всех классических вакуумов одинаковы. Это означает, что
в квазиклассическом приближении каждому классическому вакууму
отвечает квантовое основное состояние.
Аналоги локально равновесных состояний мы будем называть голдстоу-
новскими полями. Таким образом, голдстоуновские поля, принимают зна-
значения в многообразии основных состояний R. Если вырождение основных
состояний полностью обусловлено действием группы внутренних симмет-
симметрии G (группа G транзитивно действует на R), то многообразие R можно
отождествить с факторпространством G/H, где Н - группа ненарушенных
симметрии. В этом случае голдстоуновские поля принимают значения в
однородном многообразии G/H. Голдстоуновские поля естественно счи-
считать медленно меняющимися. В самом деле, особая роль этих полей связана
с тем, что их энергия мало отличается от энергии основного состояния.
Рассматривать быстро меняющиеся в пространстве или во времени
голдстоуновские поля нет смысла, поскольку большие градиенты таких
128

полей давали бы большой вклад в энергию. Сделанные только что замеча-
замечания и требование релятивистской инвариантности позволяют записать
лагранжиан голдстоуновских полей в виде
? = {^W^V- B)
Здесь (ср1, ..., у") - локальные координаты на многообразии основных со-
состояний R, gtj (</>) = gjt (i^) - симметричное тензорное поле на многообра-
многообразии R. (Мы предполагаем, что координаты (*р1, ..., у") не меняются при
преобразованиях Лоренца, поэтому выражение A) лоренц-инвариантно.
Более того, это единственное лоренц-инвариантное выражение, квадратич-
квадратичное по производным Э^ср'.)
Для того, чтобы обосновать выбор лагранжиана голдстоуновского поля
в виде A), заметим, что из первых производных полей нельзя составить
линейное по этим производным лоренц-инвариантное выражение, а выраже-
выражения, имеющие более высокую степень по первым производным или содер-
содержащие старшие производные, для медленно меняющихся полей малы по
сравнению с B). (Исключение составляет выражение, линейное по вторым
производным, но оно с помощью интегрирования по частям может быть
приведено к'виду B).) Конечно, лагранжиан B) является приближенным;
имеющие более высокий порядок малости добавки к нему в некоторых
случаях оказываются существенными.
В случае, если для отыскания многообразия вакуумов применимо квази-
квазиклассическое приближение, то же самое приближение может быть исполь-
использовано для нахождения лагранжиана голдстоуновских полей. Именно,
следует рассмотреть исходный лагранжиан, считая, что поля могут прини-
принимать значения только в многообразии классических вакуумов. Например,
для лагранжиана A) с V(y>) = (Op1J + ... + О/1J - °2J лагранжиан
голдстоуновских полей имеет вид
? = | < ъ^, г?* >, C)
где значения поля <р связаны соотношением (i^1J + ... + (^"J =я2 (лежат
на сфере S"~l). Переходя на сфере к стереографическим координатам
тг1,..., п"~1, получаем для лагранжиана C) выражение
тг > = 2 (я'J D)
(а2 + < тг, я ) J ,- =
(стереографические координаты связаны с у1, ..., у" соотношением у1 =
= 2я'а2(а2 + <тг,я>)-1, 1 </< п, <р" =а(<тг,тг> - я2)(а2 + < тг, тг >)~1).
Лагранжиан C) очевидным образом- инвариантен относительно группы
SO(/j) . Поэтому то же можно сказать о лагранжиане D).
Симметричное тензорное поле g ц (<^) определяет метрику ds2 =
^ip на многообразии R. Требование положительности энер-
129

гии, отвечающей лагранжиану A), приводит к положительной определенно-
определенности тензора ?|/(<р). Таким образом, многообразие R представляет собой
риманово многообразие.
Пользуясь римановой метрикой на R, можно записать лагранжиан B)
в инвариантном виде
? = \ < Э„*, Э"* >, E)
где < , > —скалярноепроизведение,построенное по метрике в R. В случае,
если вырождение вакуума обусловлено действием группы, т.е. R = G/H,
риманова матрика на R должна быть инвариантной относительно груп-
группы G. Это означает, что тензорное поле g{j(<p) полностью определяется
своими значениями в какой-то точке у0 многообразия R. Более того, даже
в этой точке тензор gf]- не может быть выбран произвольным образом -
он должен быть инвариантным относительно стационарной группы Н
в этой точке. Иными словами, тензор g tj должен определять //-инвариант-
//-инвариантное скалярное произведение в пространстве Т^ (R) векторов, касательных
к R в точке <^о• В случае, если представление группы Н в пространстве
T^o(R) неприводимо, легко доказать, что //-инвариантное скалярное
произведение в T^o(R) единственно (с точностью до множителя).
Таким образом, в этом случае лагранжиан B) определяется по существу
однозначно (при умножении лагранжиана на числовой множитель уравне-
уравнения движения не меняются). Если G = SO(n), H=S0(n— 1), G/H =S"~1,
представление группы Н в пространстве касательных векторов к S"~l
является векторным представлением группы Н = SO (и — 1) и, следова-
следовательно, неприводимо. Это означает, что для полей, принимающих значения
на сфере S"~1, существует единственный (с точностью до множителя)
SO (и)-инвариантный лагранжиан вида B) (в стереографических координа-
координатах он принимает форму D) ).
Легко видеть, что лагранжиан B) описывает частицы нулевой массы
(точнее, полям «р-1, ..., у", фигурирующим в этом лагранжиане, отвечают
безмассовые частицы). Для того, чтобы убедиться в этом, нужно разложить
лагранжиан в окрестности какого-либо поля, не зависящего от координат:
<р(х) = (у},, ..., у"). (Такие поля играют роль классических вакуумов.)
Это оправдывает название "голдстоуновские поля" в применении к полям
ip1, ..., ip". а Напомним, что теорема Голдстоуна утверждает, что в случае,
если непрерывная группа симметрии G нарушается до группы Н, то в тео-
теории существует п безмассовых частиц, где п - число нарушенных генерато-
генераторов симметрии, т.е. п = dim G — dim//. В квазиклассическом приближении
этим частицам отвечают поля i^1,..., ^", принимающие значения в простран-
пространстве R = G/H. Теорема Голдстоуна неприменима к калибровочным
теориям, т
Остановимся теперь на топологических интегралах движения в теориях
с нелинейными полями. Функционал энергии, отвечающий лагранжиану B),
имеет вид
Е = у / (Л)*|1Г/+*</(*)Эв*|Эв*')<'3*. F)
130

где я/(х) = gij(<p)*p' — обобщенные импульсы, g*' (up) - матрица, обрат-
обратная к gtj (<р), а = 1, 2, 3. Как обычно при рассмотрении топологии прост-
пространства полей с конечной энергией можно считать, что щ (х) = 0; функцио-
функционал энергии приобретает тогда простой вид
Е = \ f gqto)bev%*!d*x. G)
Заметим прежде всего, что поля, стремящиеся к разным пределам по раз-
разным направлениям в пространстве 1R3, имеют бесконечную энергию. Точ-
Точнее, если поле <^(х) имеет асимптотику Ит <р(Хп) = Ф(п) для | п | = 1,
то, перейдя в интеграле G) к сферическим координатам, легко видеть, что
этот интеграл расходится в случае, если Ф(п) ^ const. Поэтому при рас-
рассмотрении полей с конечной энергией естественно считать, что эти поля
имеют предел при х. стремящемся к бесконечности
lim ^(x) = «д>. (8)
х -* °°
Поле <^(х) можно рассматривать как отображение пространства [R3
в R = G/H. Условие (8) означает, что это отображение может быть продол-
продолжено в непрерывное отображение на сферу S . (Напомним, что сфера S3
получается из пространства Ft3 с помощью присоединения к нему беско-
бесконечно удаленной точки. Определяя отображение сферы S3 в R, мы сопо-
сопоставляем бесконечно удаленной точке точку <р0 G R.)
Мы видим, что два голдстоуновских поля <^(х) = («p1 (х), ..., ^"(х)) и
<р(х) = (ч? 1 (х) <р "(х)) разделены бесконечно высоким энергетиче-
энергетическим барьером, если соответствующие отображения сфер негомотопны
друг другу. Иными словами, топологический тип голдстоуновского поля
определяется гомотопическим классом отображения сферы S3 в R = G/H.
В случае, если пространство R односвязно, можно отождествить это множе-
множество гомотопических классов с группой эт3 (R) - Тз (G/H) (о вычислении
группы n3(G/H) см. §Т21). Если R = S" (лагранжиан B) сводится
к лагранжиану D)), топологически нетривиальные поля существуют при
и = 3 и и =4. (Напомним, что n3(S2) =я3E3) = ~Z, см. § Т13.)
Отметим, что приведенные выше соображения о структуре пространства
полей с конечной энергией остаются справедливыми также в случае, когда
к лагранжиану B) добавлены члены, содержащие старшие производные.
Более того, только при наличии этих членов минимум функционала энергии
на множестве топологически нетривиальных состояний может быть отличен
от нуля, а Если значение функционала энергии G) на поле ^ (х) равно Е,
то значение этого функционала на поле ^(ах) равно оТ1/?. Устремляя а
к бесконечности и замечая, что поле ^ (ах) имеет такой же топологический
тип, как и поле <р (х), видим, что существуют поля со сколь угодно малой
энергией, имеющие произвольный топологический тип. т
Наиболее существенные физические приложения сформулированных
выше общих утверждений относятся к квантовой хромодинамике. В кван-
131

товой хромодинамике основными являются поля кварков — фермионные
биспинорные поля ф {{х). Здесь а= 1, 2, 3 — "цветовой" индекс, а / — ин-
индекс, отвечающий "аромату" кварка. При построении лагранжиана исходят
из свободного фермионного лагранжиана, считая, что масса кварка не зави-
зависит от цветового индекса. Этот лагранжиан инвариантен относительно "вра-
а а Ъ
щений в цветовом пространстве" преобразований вида \pf -*-Sb\j/., где мат-
рица Sa — унитарная матрица с определителем 1. (Иными словами, зта
матрица принадлежит группе SUC).) Обычным образом с помощью вклю-
включения калибровочных полей, принимающих значение в алгебре Ли группы
SUC), можно построить лагранжиан, инвариантный относительно локаль-
локальных калибровочных преобразований с группой SUC). Этот лагранжиан,
содержащий поля кварков и калибровочные поля (поля глюонов), назы-
называется лагранжианом квантовой хромодинамики (см. § В6). С его по-
помощью описываются сильные взаимодействия.
Массы двух наиболее легких кварков (м-кварка и d-кварка) близки
друг к другу. Если считать их совпадающими, то лагранжиан квантовой
хромодинамики инвариантен относительно SU B)-вращений в пространстве
а / а )
"ароматов", т.е. преобразований ф t -*¦ V,- фу-, где i, j .= 1, 2; Vt принад-
принадлежит группе SUB). Если массы двух легких кварков считать равными
нулю, то группа симметрии расширяется до SUB) X SUB). (Можно вра-
вращать в пространстве "ароматов" отдельно левые компоненты полей квар-
кварков с матрицей из группы SUB) и отдельно правые компоненты с другой
матрицей из той же группы.) Таким образом, при пренебрежении массами
двух легких кварков мы имеем группу симметрии SUB) X SUB).
Эта rpynrta спонтанно нарушается до группы SUB), отвечающей вращению
левой и правой компоненты с помощью одной и той же матрицы. Соответ-
Соответствующее пространство вырождения R = SUB) X SUB)/SUB) можнс
отождествить с группой SUB). а Заметим, что для произвольной груп-
группы G можно определить действие группы G X G на пространстве G, сопоста-
сопоставив каждому элементу (gi, g-г) *= G X G преобразование, переводящее
элемент g G G в gigg^1- Пары (glf g.2) € GX G, для которых g i =gi,
переводят в себя единичный элемент группы G. Это позволяет отождест-
отождествить факторпространство группы G X G по подгруппе, изоморфной G и
состоящей из элементов вида (g, g), с самой группой G. Ў
Группа SUB) топологически эквивалентна сфере S3. Таким образом,
в рассматриваемом случае tf3(SUB)) = я'зС^3) = ?• Это означает, что
топологический тип голдстоуновского поля характеризуется целым
числом.
Отметим, что при указанном в § Т1 отождествлении группы SUB) со
сферой S3, преобразования группы SUB) X SUB), действующие на
SUB), переходят во вращения сферы S3. Отсюда следует, что лагранжиан
голдстоуновских полей в рассматриваемом случае совпадает с лагран-
лагранжианом D) при и = 4. Соответствующие голдстоуновские частицы
отождествляются с ¦п-мезонами (при пренебрежении массами легких квар-
кварков я-мезоны являются безмассовыми).
132

Если, пренебречь массами трех наиболее легких кварков и, d и s, то
группа симметрии расширится до SUC) X SUC). Эта группа спонтанно
нарушается до подгруппы, состоящей из элементов вида (g, g) и изоморф-
изоморфной SUC). Пространство вырождения R = SUC) X SUC)/SUC) отож-
отождествляется с SUC). В силу соотношения tt3(SUC)) = 7t (см. § Т17)
топологический тип голдстоуновского поля снова определяется целым
числом.
Для того, чтобы построить лагранжиан голдстоуновских полей, мы
должны использовать метрику на R = SUC), инвариантную относительно
левых и правых сдвигов. Эта метрика определена с точностью до множите-
множителя и может быть представлена в виде
ds2 = const Spdgdg'1 = —const Sp (g'1 dgg'1 dg). (9)
В самом деле, касательное пространство к группе SUC) в единичном эле-
элементе группы отождествляется с алгеброй Ли suC) этой группы.
Поэтому нужная нам метрика определяется скалярным произведением
в suC), инвариантным относительно внутренних автоморфизмов
g -^hgh'1. Выражение (9) для метрики получается из замечания, что инте-
интересующее нас скалярное произведение с точностью до множителя дается
формулой (a, b) = Spab* = -Spab. Пользуясь (9), записываем лагран-
лагранжиан голдстоуновских полей в виде
? = const
-i
Вернемся к рассмотрению голдстоуновских полей в общем случае.
Заметим, что пространство полей, на которых определен функционал дейст-
действия, может быть несвязным. Добавление константы к функционалу дейст-
действия, конечно, не изменяет уравнений движения. В случае, если пространство
полей несвязно, константу можно выбирать по разному для различных ком-
компонент пространства полей; это приводит к важным следствиям. Будем
рассматривать голдстоуновское поле <^(х, t) = <pf (x) как путь в простран-
пространстве ? полей <р (х), зависящих только от х. При этом будем считать, что
поле <^(х) удовлетворяет условию (8), где у0 фиксировано; тогда i^(x)
интерпретируется как отображение сферы S3 в R, и & — как пространство
сфероидов в R (см. § Т15). Рассмотрим пространство $(^1,^2) голдстоу-
голдстоуновских полей ifit (x), совпадающих с полем фу (x) при t = 11 и с полем
1^2 (х) при t = 12 ¦ Это пространство можно интерпретировать как простран-
пространство путей в ?, соединяющих точки <^i (x) и <р2 (х) прострайства ?.
Пространство #(^1,^2) естественно возникает при вычислении матрич-
матричного элемента оператора эволюции — амплитуды перехода из <^i в <^2 —
за время t^ — t1. Именно, эта амплитуда представляется как функциональ-
функциональный интеграл от exp(/h"'S) по #(</>!, ^2) (см. § 17). Учитывая постоян-
постоянные слагаемые в функционале действия S, можно представить интересую-
интересующую нас амплитуду в виде
Ъ са f exp(ih-lS)Ildy(x,t), A0)
где S определяется лагранжианом B) (без включения константы), индекс
133

а нумерует компоненты Чва(^1, <Рг) пространства #(<0i, <^2)- Если
Vi = <^2> то эти компоненты находятся во взаимно однозначном соответ-
соответствии с элементами фундаментальной группы ttj ( &, <рй) и можно считать,
что индекс а пробегает эту группу. Из группового свойства операторов эво-
эволюции следует, что сар = саср. Случай tpt Ф кр2 сводится к случаю ipt =<?2.
поскольку пространство ^A^1,^2) либо пусто, либо гомотопически экви-
эквивалентно $(<Pi, <pi) (гомотопическую эквивалентность можно построить,
сопоставив произвольному пути X, соединяющему >р1 и <?2»ПУТЬ \ * v,
где v — фиксированный путь, ведущий из <р2 в у{). Группа -пу ( fi , <р%) изо-
изоморфна 1Тд (/?)• Этот изоморфизм очевиден, если \pt (х) = <^0. В самом де-
деле, путь <pt (x) в & можно интерпретировать как отображение четырех-
четырехмерного куба /4 в & (при каждом t мы рассматриваем сфероид <^,(х)
как отображение трехмерного куба I3 в R, переводящее всю границу
куба в <р0)- Эта интерпретация позволяет отождествить четырехмерные
сфероиды в R с замкнутыми путями в & , начинающимися и кончающи-
кончающимися в i?o• 'В общем случае следует учесть, что все компоненты простран-
пространства & гомотопически эквивалентны друг другу и, значит, группы
fi ( &> Vi) ПРИ различных <pi изоморфны. (Гомотопическая эквивалент-
эквивалентность порождается соответствием <р -*¦ у + р, где р — фиксированный
сфероид.)
Как говорилось выше, в случае если пространство R односвязно, каждо-
каждому полю с конечной энергией можно сопоставить элемент группы я3 (R),
характеризующий гомотопический тип этого поля. Если включить в лагран-
лагранжиан члены с высшими производными,' можно добиться, чтобы минимум
энергии на множестве топологически нетривиальных полей достигался на
некотором поле <р(х) — топологически нетривиальном солитоне.
Солитону ^ (х) отвечает в квазиклассическом приближении квантовая час-
частица. Чтобы выяснить, будет ли эта частица бозоном или фермионом,
нужно рассмотреть элемент а группы эт4 (R). определяемый суперпозицией
|^(я(х)) негомотопного нулю отображения X сферы S4 в S3 исолитона^,
рассматриваемого как отображение сферы S3 в R. Если коэффициент са
в A0), отвечающий элементу а из эт4 (R) = ™\ ( &) равен единице, то час-
частица — бозон, в противном случае са = — 1 и частица — фермион. Мы не бу-
будем останавливаться на доказательстве этого утверждения. В случаях
R = S3 и R = S2 мы имеем п3 (R) = Z, тг4 (/?) = ~&г- Суперпозиция отобра-
отображения S3 -*R с негомотопным нулю отображением S4 в S3 в этих случаях
определяет ненулевой гомоморфизм n3(R) в я4 (R) (см. § Т14, Т17).
Это означает, что частица, отвечающая солитону с нечетным топологическим
числом, будет фермионом в случае са = — 1 для ненулевого a €E тг4 (/?).
§ IS. Многозначные функционалы действия
В квантовой механике и квантовой теории поля различные величины мо-
могут быть представлены в виде функциональных интегралов по возможным
историям рассматриваемой системы (т.е. по возможным траекториям
в случае квантовой механики и.по возможным зависимостям полей от вре-
времени в случае квантовой теории поля). Множество историй, по которому
идет интегрирование, и вид подынтегрального выражения зависят от интере-
134

сующей нас величины (см. § 17); нам важно только, что в подынтеграль-
подынтегральное выражение входит экспонента от классического действия 5, умножен-
умноженная на мнимую единицу и деленная на постоянную Планка h. Отсюда сле-
следует, что функциональный интеграл может иметь смысл также в случае,
когда действие 5 является многозначным функционалом, если только
стоящее под интегралом выражение ехр(/ h^) представляет собой одно-
однозначный функционал. Иными словами, допустимо чтобы одной и той же
истории сопоставлялось несколько различных значений действия, сущест-
существенно лишь, чтобы все эти значения отличались на целое кратное величины
2 п h. Это условие на многозначные функционалы действия приводит к то-
тому, что константы, участвующие в выражении для действия, могут прини-
принимать только дискретный ряд значений (к квантованию этих констант).
Остановимся на некоторых примерах.
Прежде всего покажем, что условие квантования магнитного заряда
может быть получено из требования, чтобы имело смысл рассматривать
движение квантовой частицы в поле этого заряда. Напомним, что функцио-
функционал действия S классической частицы в электромагнитном поле, отвечаю-
отвечающий обычным уравнениям движения,
dxv
FQ A)
ds* bs
может быть записан в виде
s[*(т)] = -mfds-c JAU dx"; B)
здесь m — масса, е — заряд, ds - пространственно-временной интервал,
Ац - потенциал электромагнитного поля, возможная траектория хи(т)
определяется зависимостью времени х° и пространственных координат
х1, х2, хг от параметра т, где T0<r<ri. В случае если траектория х(т)
Является замкнутой конвой в пространстве Минковского (т.е. хц(т0) =
= х^(т1)), с помощью формулы Стокса можно переписать B) в форме
S[x(r)] = -mfds-- JF^dx" hdx" = - m fds - e f F, C)
2 г г
где Г - произвольная поверхность, натянутая на замкнутую траекторию
х(т), a F= — FpVdx*t\dxv - 2-форма, отвечающая напряженности элек-
электромагнитного поля. Напомним (см. § Т6), что в силу уравнений Максвел-
Максвелла форма F замкнута.
Если электромагнитное поле и вместе с ним форма F заданы во всем
пространстве Минковского, то форма F может быть представлена в виде
F = dA где A ^A^dx^.A^ — потенциал электромагнитного поля. Однако
нас интересует случай, когда электромагнитное поле задано не во всем
пространстве Минковского, а лишь в некоторой области V этого простран-
пространства. Именно этот случай реализуется, если есть магнитные заряды, по-
поскольку электромагнитное поле не определено в точках, где расположены
эти заряды. Если имеется точечный магнитный заряд, то траекторию его
движения можно рассматривать как кривую в пространстве Минковского;
135

область V получается исключением этой кривой из пространства Минков
ского.
Если форма F задана только в области V пространства Минковского,
то она может не быть точной (не представляться в виде F = dA); тогда можно
говорить о напряженности поля, но нельзя ввести потенциал поля, опреде-
определенный во всей области V. В этой ситуации не имеет смысла выражение
B) для действия частицы. Тем не менее, выражение C) не теряет смысла,
хотя и может принимать различные значения в зависимости от выбора
поверхности Г, т.е. становится многозначным функционалом. Легко видеть,
что разность между двумя значениями действия можно записать в виде
J F, где Г - замкнутая поверхность. В самом деле, разность между инте-
г
гралами / Fи / F, где П ,и Г2 — две поверхности, натянутые на замкнутую
г, г2
траекторию х(т), представляется как интеграл от F по замкнутой поверх-
поверхности Г, составленной из Га и Г2, при этом ориентация на Г выбирается сог-
согласованной с ориентацией на Fi и противоположной ориентации на Г2.
Мы видим, таким образом, что квантовая механика частицы в электро-
электромагнитном поле с напряженностью F может быть построена лишь в ситуа-
ситуации, когда для для любой замкнутой поверхности Г интеграл от F по Г
кратен2-rrhe'1 (только тогда функционал exp^'h S) будет однозначным).
В случае, если все точки поверхности Г отвечают одному и тому же значе-
значению временил0 интеграл от F по Г сводится к потоку магнитной напряжен-
напряженности через Г (в этот интеграл вносят вклад только пространственные
компоненты тензора напряженности F^J). Магнитный заряд Щр внутри Г
по определению отличается только множителем {4п)'х от этого потока.
Мы приходим, таким образом, к условию квантования магнитного заряда
h
П»г= — и, D)
2е
где п — целое число (см. § 7).
Отметим, что условие D) не только необходимо, но и достаточно для
того, чтобы функционал expO'h^) был однозначным, в случае, если
область V получена из пространства Минковского удалением мировых
линий одного или нескольких точечных магнитных зарядов. В самом деле,
легко проверить, что в этой ситуации всякая двумерная замкнутая поверх-
поверхность в V (двумерный цикл в V) гомологична поверхности, все точки
которой отвечают одному и тому же значению времени. Поскольку при
замене поверхности Г на гомологичную значение интеграла от F не меняет-
меняется, из условия D) вытекает, что для любой замкнутой поверхности этот
интеграл кратен 2irh.
Мы рассматривали до сих пор функционал действия C), определенный
только на замкнутых траекториях. Это ограничение несущественно: для
траекторий, начинающихся в фиксированной точке х(т0 )= *0 и кончающих-
кончающихся в фиксированной точке x(Ti)=xl, можно также найти многозначный
функционал действия, приводящий к уравнениям движения A). Именно,
следует фиксировать произвольную траекторию х(т) из интересующего
нас класса и для любой другой траектории х(т) определить действие фор-
формулой C), где Г теперь обозначает ориентированную поверхность, граница
136

которой состоит из кривой х(т) и пройденной в обратном направлении
кривой х(т ). Разные выборы траектории х(т) приводят к отличающимся
на константу функционалам действия. Повторяя проведенные выше рас-
рассуждения убеждаемся, что в новой ситуации выражение exp^ff'S) будет
однозначно при том же условии D).
Приведем сейчас общую конструкцию многозначных функционалов
действия для нелинейньрс полей (полей, принимающих значения в много-
многообразии). Будем считать для определенности, что интересующие нас поля
tp(\, t) зависят от трех пространственных переменных х и времени t (т.е.
заданы на пространстве Минковского); многообразие, в котором прини-
принимают значения эти поля, обозначим символом JI. Как говорилось в § 14,
наиболее простой лоренц-инвариантный функционал действия для таких
полей имеет вид A4.5); к нему можно добавлять более сложные члены,
содержащие высшие производные или высшие степени первых производ-
производных. Наложим на рассматриваемые поля требование, чтобы при х-»-00 поле
ср(х, t) имело предел (как упоминалось в § 14, это требование связано с
условием конечности энергии).
Далее будем считать, что время t изменяется в интервале от т0 до т^ и
что i^(x, r0) = <p(x, Ti) (ниже будет объяснено как избавиться от последнего
ограничения). Наложенные на поле tp(x, t) условия позволяют сопоставить
этому полю отображение многообразия S3 X S1 в многообразие Л. Дей-
Действительно, при каждом г поле <р(х, t) задает отображение 1R3 в JC ; это
отображение можно продолжить до отображения сферы S3, считая, что
сфера получается из (R3 присоединением бесконечно удаленной точки, и
сопоставляя этой точке 1 im <^(х, r). Условие <р(х, т0) = ?>(х, тх) обозначает,
что концы отрезка, который пробегает t, можно считать склеенными между
собой; иначе говоря, можно считать, что t изменяется на окружности.
При отображении, задаваемом полем ср, многообразие S3 X S1 переходит
в ориентированную замкнутую четырехмерную поверхность (цикл) в JC ;
этот цикл будем обозначать Z(tp).
Покажем, как по замкнутой 5-форме со в JI можно построить много-
многозначный функционал Sw(fp) от <р, который можно включить в качестве
слагаемого в выражение для действия. Именно, положим
SM= f со, E)
()
где Г(<^) — произвольная пятимерная ориентированная поверхность, грани-
границей которой служит цикл Z(cp). а Отметим, что такая поверхность может
не существовать, цикл Z(ip) может быть негомологичен нулю. Поэтому
нужно либо наложить на многообразие JU условия, гарантирующие сущест-
существование поверхности Г(<^), либо ограничиться рассмотрением полей, для
которых цикл Z(y) гомологичен нулю. Ў Значение функционала Sw может
зависеть от выбора поверхности Г(ср). Если Fi(^) и ГгО^) — две поверхно-
поверхности, границей каждой из которых служит цикл Z(*p), то
/ со - / со = / со, F)
г,ы i\(*>) г
где Г - замкнутая ориентированная пятимерная поверхность - пятимер-
пятимерный цикл. (Поверхность Г можно считать составленной из поверхности
137

Гц^) и из взятой с противоположной ориентацией поверхности Г2(^).)
Форма со называется целочисленной, если интеграл от нее по любому циклу
равен целому числу (см. § Т7).
Из F) следует, что для целочисленной формы со два значения функцио-
функционала Sw отличаются на целое число. Для того, чтобы включение в функцио-
функционал действия многозначного слагаемого 5W не мешало построению соответ-
соответствующей квантовой теории, нужно, как мы знаем, чтобы два значения
отличались на целое кратное постоянной Планка h - 2rrh; это означает,
что форма со должна отличаться множителем 2этпот целочисленной формы.
Иначе говоря, в действие можно включить слагаемое вида 2яЬ / со,, где
(>
со - целочисленная 5-форма.
Описанная только что общая конструкция приобретает физический инте-
интерес в случае, если с помощью нелинейного поля описывается квантовая
хромодинамика в низкоэнергетическом пределе. Напомним, что в кванто-
квантовой хромодинамике при пренебрежении массами трех самых легких квар-
кварков (и, d, s) симметрия SUC) X SUC) нарушена до SUC)-симметрии.
Это означает, что голдстоуновские поля, существенные при низких энер-
энергиях, принимают значения в многообразии R = SUC) X SUC)/SUC).
Многообразие R можно рассматривать как группу SUC), на которой дей-
действует группа SUC) X SUC) с помощью левых и правых сдвигов (преоб-
(преобразование, отвечающее элементу (Аь Й2)е SUC) X SUC), переводит
gG SUC) в high?). Таким образом, гол дето уновское поле — это матрич-
матричное поле g(x) = (g?(x)), удовлетворяющее условиям:g'1 (x)=g\x),detg(x) = 1.
Функционал действия для голдстоуновских полей должен быть лоренц-
инвариантным и SUC) X SUC)-инвариантным (т.е. инвариантным относи-
относительно левых и правых сдвигов на группе SUC)). Простейший функционал,
обладающий этим свойством, имеет вид
S = const / SpCM? du g -1) d *x G)
(cm. § 14). Однако, этот функционал обладает излишней симметрией,
нарушенной в квантовой хромодинамике. Именно, он инвариантен относи-
относительно преобразования g(x) ->¦ g~l (x). Если голдстоуновское поле g(x)
8
записано в виде g(x)= exp( 2 яДдг)\'), где А.1,...^8 - генераторы
i = 1
группы SUC), яДдг) — поля голдстоуновских мезонов, то преобразование
g-*g~l приобретает видэтДх) ->• — я,(х). Симметрия я,(х) -»¦ - я,(х) запре-
запрещает переход системы из четного числа мезонов в систему из нечетного
числа мезонов. Однако, в квантовой хромодинамике разрешен, например,
переход К+К"-* я+тг°я". Мы видим, что в функционале действия голдстоу-
голдстоуновских полей должно присутствовать слагаемое, нарушающее симметрию
g(x)-*¦ g'1 (x). В качестве этого слагаемого следует взять выражение E),
где со - 5-форма на SU C), определенная соотношением
1dg -Ibg -ibg -idg -i
w wg w8 wg
dg -idg ^
Xdy' bdy' hdyk Ndy1 Sdym (8)
(здесь к - произвольное действительное число).
138

Легко видеть, что форма со инвариантна относительно левых и правых
сдвигов на группе SUC) (более того всякая 5-форма на SU C), обладаю-
обладающая этим свойством, может быть записана в виде (8)). Отсюда ясно, что
со — замкнутая форма (см. §Т21); впрочем, замкнутость формы со, конеч-
конечно, нетрудно проверить и непосредственно. При к = 1 форма со является
целочисленной формой. Это означает, что постоянная к в (8) должна иметь
вид 2;глпгде п — целое число, если мы хотим, чтобы многозначность функ-
функционала действия не мешала построению квантовой теории.
Напомним, что поскольку 7T3(SUC)) = ^топологический тип голдстоу-
новского поля#(х)е SUC) определяется целым числом. Топологически
нетривиальному солитону g(x) в квазиклассическом приближении отвечает
квантовая частица. Доказывается, что эта частица будет фермионом, если
как топологическое число солитона, так и целое число п = кBпЪ)~1 нечетны.
Это позволяет отождествить солитоны с барионами.
§ 16. Функциональные интегралы
Под функциональным интегралом понимается интеграл по бесконечно-
бесконечномерному пространству. (Обычно это пространство является пространством
.функций от одной или нескольких переменных.) Для того, чтобы опреде-
определить функциональный интеграл, как правило, используют аппроксимацию
конечнократными интегралами. Например, пусть рассматривается функцио-
функционал F(ip), заданный на пространстве функций <р(?) от одной переменной t,
а < t < Ъ. Тогда можно рассмотреть этот функционал на множестве
непрерывных функций, линейных на каждом из отрезков [ti,t2],...
..., Uat-i> tN], где tt = а + iN~l(b -а). Пространство таких функций
конечномерно: всякая функция рассматриваемого типа определяется
конечным множеством чисел <р0 = <р(а), ..., <#\r-i = vO)v-i)> <ftv = Ч>Ф).
Это означает, что функционал F(<p) на интересующем нас множестве функ-
функций можно считать функцией конечного числа переменных i^i <pN
и рассмотреть интеграл JN от этой функции по переменным <?! ifijf.
Интеграл от функционала Ffy) естественно определить как предел интег-
интегралов jff при N-+°°:
J=fF[<p] П dy(T)= lim JN. A)
a < т < b If-* "
Однако во многих важных случаях нужный нам предел не существует.
Тогда разумно каким-то образом вьщелить из интеграла J^ расходящуюся
часть и понимать под функциональным интегралом предел выражения,
остающегося после выделения расходящейся части. Например, возможно,
что найдется такая константа С, для которой C~nJm имеет предел. Тогда
этот предел объявляется функциональным интегралом. (В этом случае
удобно переопределить JN, включив С в дифференциалы переменных,
по которым ведется интегрирование, т.е. понимать под d<pt произведение
Ч
Приведенное только что определение функционального интеграла может
быть модифицировано различными способами. Можно, скажем, сопостав-
сопоставлять каждой кусочно-линейной функции не значение функционала Fty)
на этой функции, а какую-то аппроксимацию этого значения. (Если функ-
139

ционап задается с помощью интеграла, можно вместо значения этого интег-
интеграла взять интегральную сумму, отвечающую выбранному нами разбиению
отрезка.) Оказывается, что во многих интересных случаях значение функ-
функционального интеграла зависит от выбора аппроксимации. Поэтому, строго
говоря, выражение / - fFQp)ndip(r) не имеет четкого смысла до тех пор,
пока не фиксирован предельный переход, с помощью которого это выра-
выражение определяется.
В случае, если функция <р(?) задана на всей прямой, при построении
конечнократной аппроксимации функционального интеграла следует
не только разбить прямую на малые отрезки, но и ограничить себя конеч-
конечным числом этих отрезков. Если функционал F[<p] определен на мно-
множестве функций у, зависящих от т переменных, то при построении ко-
конечнократной аппроксимации естественно заменить пространство DRm
решеткой и определять JN с помощью интегрирования по значениям функ-
функции ^ в конечном числе точек решетки (например, по значениям в точках
решетки, принадлежащим некоторому кубу).
Отметим, что в квантовой теории поля переход от функционального
интеграла / к его конечномерной аппроксимации JN тесно связан с про-
процедурой обрезания. Переход от функций, заданных на пространстве [Rm,
к функциям, заданным на дискретном множестве точек — решетке, экви-
эквивалентен обрезанию больших импульсов (ультрафиолетовому обреза-
обрезанию) ; ограничение конечным множеством точек решетки можно рассмат-
рассматривать как обрезание по координатам (инфракрасное обрезание).
Рассмотрим гауссовы интегралы — наиболее простые и важные среди
функциональных интегралов. Напомним, что гауссовым интегралом назы-
называется интеграл от экспоненты, в показателе которой стоит квадратичная
форма. В конечномерном случае имеет место формула
-- (Ax,x)\dx = Bn)Nl2(d
B)
где < , > - действительное скалярное произведение в Л^-мерном пространст-
пространстве, А — положительный самосопряженный линейный оператор. (Если ац —
матрица оператора А, то <Ах, х) - ацх 'х'.)
Будем приближать бесконечномерный гауссов интеграл
/= fexp(--Ux,x)Jdx C)
конечномерными интегралами
Jn= fexp(--<.ANx,x)Jdx, D)
где Aff — конечномерная аппроксимация линейного оператора А. Мы счи-
считаем, что оператор А действует в бесконечнрмерном гильбертовом прост-
пространстве; вектор х в C) пробегает это пространство. Оператор AN дейст-
действует в конечномерном пространстве, вектор х в D) пробегает это конечно-
конечномерное пространство. Например, если А - дифференциальный оператор,
действующий на функции в IR", то под А^ можно понимать оператор,
получающийся если заменить производные конечными разностями. Опе-
140

ратор AN действует тогда на функции, заданные на решетке в IR" (точнее,
на конечном числе точек такой решетки). Бели детерминанты операто-
операторов Aff имеют конечный предел при N -*¦ °°, естественно определить детер-
детерминант оператора А как предел этих детерминантов: det A = lim det Apf.
Бесконечномерный гауссов интеграл / следует считать равным (det4)~1/2.
(Интегралы JN не имеют конечного предела из-за множителей Bтг)ЛЛ'2;
как объяснено выше, разумно переопределить JN, включив эти множители
в дифференциалы. Тогда нужный нам предел будет существовать.) Соот-
Соотношение
/= fexp(--{Ax,x))dx = (deM)~1/2 E)
разумно сохранить в качестве определения бесконечномерного гауссова
интеграла и в случае, когда предела детерминантов операторов А^ при
и -> °° не существует. Однако в этом случае детерминант оператора А (точ-
(точнее, регуляризованный детерминант) следует определять другими спосо-
способами. Технически проще всего определение, основанное на понятии
f-функции оператора А. Будем считать, что самосопряженный оператор А
неотрицателен (т.е. {Ах, х) > 0)и имеет дискретный, спектр. Определим
f-функцию оператора/! формулой
r(s)=2X^s, F)
где \к пробегает ненулевые собственные значения оператора А. Форму-
Формула F) непосредственно задает f (х) только там, где ряд в правой части
сходится; однако, для других s можно определить f (s) с помощью анали-
аналитического продолжения. Если функция f(s) может быть аналитически
продолжена в точку s = 0, то определим det А с помощью формулы:
Xnd&tA = -
ds
s=0
(Это определение подсказывается соотношением — •
G)
= In A,.)
ds
а Если А — эллиптический оператор порядка г на т -мерном компакт-
компактном многообразии (см. § 19), то ряд F) сходится при Res > т/г. Функ-
Функция f (s), определяемая рядом F), продолжается в мероморфную функ-
функцию комплексной переменной s; эта функция не имеет особенности при
s = 0 и, значит, для определения детерминанта может быть использована-
формула G). Подробнее см. ниже § 20. Ў
Рассмотрим в качестве примера функциональный интеграл
-^/ [(V*J + т\2]
, (8)
где <р(х) — поле в В4, которое мы считаем убывающим на бесконечности,
V — четырехмерный градиент, Д = V2 — четырехмерный оператор Лапласа.
141

В силу E) этот интеграл равен (det(-A +/я2))/2. Для того, чтобы вычис-
вычислить f-функцию оператора А = — Д + /я2, удобно воспользоваться тож-
тождеством
7j /
r(s)o
(9)
T(s) о
Матричные элементы К(х, х0, t) = (х |ехр(—At)\x0 > оператора ехр(—
удовлетворяют уравнению
Э
— K(x,xo,t) = -AxK(x,xo,t) A0)
of
с начальным условием К(х, *р, f = 0) = 6(х - х0). В случае А = —Д + т2
это уравнение легко решается; ответ имеет вид:
K(x,xo,t)= -^^ exp(-m2r - (* ^о) ^. A1)
(Напомним, что мы наложили условие убывания на бесконечности.) Мы
видим, что
K(x,x,t)= ^-^-ехР(-т20. A2)
Для того чтобы найти Spexp(—At), нужно проинтегрировать К(х,х, t)
по dx; этот интеграл очевидным образом расходится. Чтобы получить ко-
конечный ответ, следует провести обрезание по координатам, т.е. считать,
что поле ip(x) задано в большом, но конечном ящике V. Тогда
m20. A3)
Это позволяет вычислить f-функцию с помощью (9):
= И—l—(rn2?-sTiL~2)- A4)
16я2 T(s)
Формула (9) применима только при Re s > 2, поскольку только при этом
условии сходится интеграл по t, однако формула A4) дает аналитическое
продолжение f-функции на все комплексные s, за исключением точек s = 1,
s = 2, в которых f-функция имеет простые полюса. Из A4) видно, что
A5)
f@)FЦ>"
32я
Часто представляет интерес не только регуляризованный детерминант опе-
операторов, но и асимптотика детерминантов решеточных операторов, аппрок-
аппроксимирующих исследуемый оператор. Детерминант оператора —Д + т2
становится конечным при введении ультрафиолетового обрезания (пере-
(перехода к решетке) и инфракрасного обрезания (ограничения объемом V);
142

важно исследовать асимптотику конечных детерминантов при снятии об-
обрезания. Эта задача вполне разрешима. Однако, технически много проще
заменить введение решетки так назьшаемым обрезанием по собственному
времени; результаты при этом существенно не изменяются. Будем назы-
называть детерминантом положительного оператора А, обрезанным по собст-
собственному времени, число dete4, определяемое равенством
оо оо
Indet?4 = 2 - / Г1 exp(-V)dt=-f Г1 Spexp(-At)dt. A6)
I С С
Для А = — Д + т2 из A3) и A6) видно, что
л 1 2
с ошибкой, стремящейся к нулю при е -> 0. Число, получающееся из A7)
выделением расходящейся при е -*¦ 0 части, будем обозначать In det 'A.
Подобно выражению detA = ехр(—?'@)) можно рассматривать det'yl
как регуляризованный детерминант оператора А. Из A7) ясно, что для
А=-А+т2
Vm* ,
In det Л = lndeM- j-r'(l). A8)
Это соотношение является частным случаем общего соотношения, которое
будет доказано в § 21.
К интегралу E) с помощью замены х -*¦ х + а сводится функциональный
интеграл
) ()) (d'm(Ab)J A9)
Далее, соображения, аналогичные примененным при исследовании интег-
интеграла E), приводят к формулам
fexp(-<Ax,*))dx = (deM)-1/2, BQ)
B1)
где А — самосопряженный оператор в гильбертовом пространстве.
Гауссовы интегралы появляются в квантовой теории поля при исследо-
исследовании квадратичных по полям лагранжианов. Однако они существенны
также при изучении более сложных лагранжианов, поскольку они возни-
возникают при приближенном вычислении соответствующих функциональных
интегралов методом стационарной фазы или методом Лапласа. Напомним,
что в конечнократный интеграл fexp(itt~1f(x))dnx при а -> 0 основной
вклад вносят окрестности стационарных точек функции f(x) (функ-
(функция f(x) считается действительной). Именно, для того чтобы найти основ-
143

ной член асимптотики рассматриваемого интеграла в случае, если ста-
стационарная точка единственна, следует разложить функцию /(дг) в этой точ-
точке по формуле Тейлора и, отбросив члены, имеющие порядок >2, взять
получившийся гауссов интеграл. Отсюда ясно, что асимптотика имеет вид
(»
/expl -f(x)dx
~ /(*o))(-27rm)n/2(d
-1/2
* expl - f(x0) )(-2nia)"'2[ det
B2)
где x0 — стационарная точка. (Если есть несколько стационарных точек,
то асимптотика дается суммой вкладов от этих точек.)
Аналогично получается асимптотика интеграла /ехр(—a~lf(xy)dx,
где /(х) - действительная функция, достигающая наименьшего значения
в точке х0. Основной член этой асимптотики дается формулой
-1/2
B3)
Аналоги соотношений B2) и B3) можно применять также в случае функ-
функциональных интегралов (хотя строго обосновать их затруднительно).
Отметим, что легко получить следующие члены в асимптотиках B2), B3).
Для этого нужно учесть члены порядка > 3, разложив экспоненту в ряд
по этим членам. Для функциональных интегралов соответствующие прибли-
приближения эквивалентны теории возмущений.
Определение функционального интеграла, данное выше, оказывается
не всегда достаточным. Иногда приходится использовать при определении
функционального интеграла процедуру, носящую в квантовой теории поля
название перенормировки. Пусть подынтегральное выражение в функ-
функциональном интеграле зависит от параметра X (быть может, векторного:
X = (X1, ..., XN)). Тогда аппроксимирующий конечнократный интег-
интеграл JN также будет зависеть от X. Может оказаться, что при фиксирован-
фиксированном X интеграл /дг(Х) не имеет конечного предела при N -> °°, однако,
удается подобратЕ такую последовательность \N значений параметра X,
что Jn(\n) имеет ненулевой конечный предел при N -*¦ °°. Этот предел
следует объявить тогда значением функционального интеграла. Разумеется,
могут существовать различные последовательности Х^у с требуемыми
свойствами. Тогда значение функционального интеграла определяется
неоднозначно; его можно считать зависящим от некоторого нового пара-
параметра ц, задающего предельный переход. (Параметр ц также может быть
векторным.) В квантовой теории поля параметры X1, ..., Х^, входящие
в подынтегральное выражение, имеют смысл голых зарядов или голых
масс) параметры, от которых зависит значение функционального интегра-
интеграла, называются физическими или одетыми (физические заряды, физичес-
физические массы).
144

§ 17. Применение функциональных интегралов
в квантовой теории
Величины, исследуемые в квантовой механике и квантовой теории поля,
можно выразить через функциональные интегралы; это представление
во многих случаях оказывается чрезвычайно удобным. Мы получим сей-
сейчас выражение некоторых важных величин через функциональные
интегралы.
Рассмотрим оператор
^Y ХаЛЬр. A)
i oq /
Функция
A(p,q) = Zan(q)p" B)
и
называется символом (точнее qp-символом) оператора A). Можно сказать,
Л
что оператор А получается из функции А(р, q) заменой координаты q
Л 1 Э
оператором координаты q и импульса р оператором импульса р =
/ bq
с условием, что операторы q пишутся левее операторов р. Переход от
Л
функции А(р, q) к оператору А можно рассматривать как квантование
классической физической величины А(р, q). Нетрудно проверить, что
— Л
функция / (q), получающаяся из функции f(q) при действии оператора А,
может быть записана в виде
1
/(<?)= -T-fA(p,q)f(eil)explip(q-qi)]dpdql. C)
л
Это означает, что матричные элементы (qi\A\q1) выражаются через
символ A(p,q) формулой
<<?2 1^4 l<7i>= —fA(p,q2)exp[-ip(ql - q2)]dp. D)
2я
Л
Отметим, что соотношение C) позволяет сопоставить оператор А функ-
функции А(р, q) также в случае, когда функция А(р, q) не является полино-
полиномом по переменной р.
Из соотношения C) легко вывести, что символ С(р, q) оператора
Л Л Л Л Л
С = А В выражается через символы А (р, q) и В(р, q) сомножителей АиВ
формулой
C(p,q)= -—fA(pi,q)B(p,ql)exp[-i(p1 -p)(<7, - q)] dp^dqx. E)
2я
Это соотношение мы используем, чтобы получить выражение интересных
для квантовой теории величин в виде функциональных интегралов. Рас-
л
смотрим оператор Я, имеющий символ Н(р, q), и найдем выражения
Л . Л
матричных элементов <^|ехр(-/7Я)|дг>оператора ехр(—/г#) в виде
145

функционального интеграла, * Оператор Н в приложениях имеет физичес-
физический смысл оператора Гамильтона квантовомеханической системы, а функ-
функция Н(р, q) интерпретируется как функция Гамильтона соответствующей
классической системы. Оператор ехр(-*7#) имеет смысл оператора эво-
эволюции квантовомеханической системы. Ў
Мы покажем, что интересующие нас матричные элементы могут быть
представлены в виде
{у | ехр(-г7Я) | х > = /ехр(/5) П dp (т)dn(r), F)
где
S [р (т),Я(т)] = / ( р(т) —— - H(p(r),q(r)))dr. G)
о \ dr /
(Функционал S интерпретируется как классическое действие вдоль фазо-
фазовой траектории р(т), <?(т).) В правой части равенства F) стоит функцио-
функциональный интеграл по траекториям р (т), q(r), 0 < т < t с условием q@) = x,
q(t) = у. Точный смысл выражения в правой части F) будет виден из до-
доказательства.
Для того, чтобы прийти к формуле F), воспользуемся соотношением
ехр(-/*Я) = (exp (-i -jj-jfy
(8)
и заметим, что при больших JV можно написать приближенно ехр ( -/—h
as
t л
« 1 — / — Н. Это позволяет утверждать, что символ оператора
N
этого
( * Л / f \
ехр I -I — Н ) приближенно равен ехр ( -/—Н(р, q) ); ошибка
\ N / \ N /
приближенного равенства убывает как N~2 при N -> °°. Отсюда с помощью
формул E), (8) получаем приближенное выражение для символа опера-
Л
тора ехр(-/7Я). Именно, с ошибкой, стремящейся к нулю при N -* °°,
можно записать символ G(p, q, t) оператора ехр(-г7Я) в виде
jy_1/exp(i2
pa{qa -<?„_!)-
- / -^ 2 Н(ра,<?„_,)) li'% dqa, (9)
N i i
где введены обозначения qo~<lN = q, Pn=P-
Из соотношения (9) можно с помощью D) получить приближенное
л
выражение для матричного элемента <j>|exp(—itH)\x). Оно по виду почти
совпадает с (9); различие состоит в том, что появляется дополнительное
интегрирование по pN = р и связанный с ним лишний множитель B я у1;
кроме того, граничные условия принимают вид q0 = x, qN = у. Таким
146

образом
(у \exp(-itH)\x)
1
N
/ /лг t n ч\
/expf ff S Pa(<7o-<7a-i)- —2 H(pa,qa_l)j)X
N N-l
X Yldpa П d?a) A0)
1 1
где q0 ~ x, Яы ~ У" Показатель в A0) представляет собой (с точностью
до множителя i) интегральную сумму для интеграла G), где траекто-
траектория q{f) начинается в точке х и кончается в точке у (на р(т) никаких гра-
граничных условий не накладывается). Это дает основание назвать предел
правой части A0) при N -»¦ °° функциональным интегралом от exp(iS)
по пространству траекторий р(т), q(r) с граничными условиями q@) = х,
q(t) = у. (Множитель Bя)-ЛГ мы уславливаемся включать в нормировку
дифференциалов.)
Совершенно аналогично получается выражение для матричных элементов
оператора ехр(—f#) в виде функционального интеграла
= exp[ifp(T)~—dT- fH(p(T),q(T))dT)ndp(T)dqj(T). A1)
\ о dr о /
Здесь, по-прежнему, интеграл берется по траекториям р(т), q(r) с гра-
граничными условиями q@) = х, q(t) = у. (Соотношение A1) можно непо-
Л. Л
средственно получить из F), заменив Н на Ш; такую замену можно еде-
Л
лать, поскольку на оператор Н не накладывалось условия самосопряжен-
самосопряженности.)
Важно подчеркнуть, что соотношения F), A1) остаются справедливы-
справедливыми для случая произвольного конечного числа степеней свободы; вывод
их основан на тех же соображениях. Символ дифференциального опера-
оператора
i=S 2 а''-\Ч)Гк , Э A2)
действующего в пространстве функций от п переменных ql, ..., q", опре-
определяется как функция от 2и переменныхfl1,... ,q", piy... ,р„:
A(p,q)=Z 2 я'1 - ik(q)P( ... pt A3)
Л
Как и раньше, оператор А получается из функции А (р, q), если заменить
переменные q1,..., qn операторами умножения на ql,..., q" (операто-
(операторами координат q1,..., q"), а переменные plt..., р„ - операторами
Pi = i~lbjbql (операторами.импульса); при этом операторы импульса
должны писаться правее операторов координат. Часто бывает полезным
понятие главного символа оператора А. Для дифференциального оператора
порядка г главный символ определяется как сумма тех слагаемых в пра-
147

вой части равенства A3), которые имеют порядок г по переменным Р\, . . .
¦¦¦,Рп-
Все доказанные выше соотношения практически без изменений перено-
переносятся на случай любого конечного числа степеней свободы. А Нужно, ко-
конечно, считать все переменные р, q векторными:
и всюду заменять Bя) -1 на Bя) ~", где и — число степеней свободы. Ў Бо-
Более того, аналоги соотношений F), A1) имеют место и для бесконечного
числа степеней свободы.
Рассмотрим важный частный случай, когда функция Гамильтона H(p,q)
квадратична по импульсам. Тогда интегралы по переменным р в форму-
формулах (9), A0) являются гауссовыми. Беря эти интегралы по стандартным
формулам (см. §16) и переходя к пределу N -+°°, мы получаем представ-
представление для <у |ехр(-itH) \х) и <у | ехр(- tH) \х> через функциональные
интегралы по траекториям в координатном пространстве. Например, если
где а1' (д) — положительно определенная матрица, то приближенное выра-
выражение A0) для < у | ехр (- i tH) \ x > имеет вид:
«/ехр (/2 - - aij{qa-i)(qa - qa-i)'(.qa - Яа-i)' ~ Т U (qa_1)jX
\ а 2. t /у /
ХП , d4l ¦¦ (Н)
/d''()
(Здесь введено обозначение a(q) = ay (q) для матрицы, обратной к a'1 (q).)
Это позволяет записать <у | ехр(-itH) \x) в виде функционального
интеграла
(у i ехр (-itH}\х > = / ехр (iS [q]) Пdq (т), A5)
где
S[q(r)] =fL(q(T),q(T))dT = f(^ atj(q)q'q1' - U{q)jdT A6)
— классическое действие вдоль траектории q (т) в конфигурационном про-
пространстве, интеграл берется по траекториям с граничными условиями
q@) = х, q{t) = у. Наличие множителей (deta(q)) I2 в A4) учитывается
тем, что в конфигурационном пространстве вводится элемент объема dq =
= y/deta(q) dq1.. .dq", отвечающий метрике ds2 = a,y(fl) dq1 dq'. Анало-
Аналогичные рассуждения приводят к формуле
, A7)
где
Seuci to(OJ = /( 7 an(q)qlq} + U(q))dT A8)
148

носит название евклидова действия. (Евклидово действие с точностью до
знака получается переходом от времени t к мнимому времени it.) Сле-
Следует подчеркнуть, что функциональный интеграл A7) существенно удоб-
удобнее в математическом отношении, чем интеграл A5). Это связано с тем,
что подынтегральная функция в A5) по модулю равна 1 и, значит, ин-
интеграл A5) сходится только потому, что подынтегральная функция ос-
осциллирует. Поэтому в квантовой теории все чаше пользуются интегралом
A7). Переход от A5) к A7) носит название евклидова поворота или
викова поворота; он связан с аналитическим продолжением по времени.
А Обычно оператор ехр (— tH) может быть определен для комплексных t
в полуплоскости Re t > 0, непрерывно зависит от г в этой полуплоскости
и аналитичен внутри полуплоскости. Матричные элементы < у \ ехр(- ш) 1 jc >
обладают теми же свойствами аналитичности, т Физическую информацию
можно с равным успехом получать из A5) и из A7), хотя оператор
ехр(—/ш) и имеет непосредственный физический смысл в отличие от
Л
оператора ехр (— tH). Например, из соотношения
= 2 ехр(-е„ t){y\n)(n\x),
где |п> — собственные векторы гамильтониана Я, е„ - соответствующие
собственные значения, вытекает, что при условии (у\0) Ф 0, @\х) Ф О
Л
асимптотика матричного элемента <^|ехр(— tH) \x) при ?Л-> +°° опре-
определяется энергией бо основного состояния 10> гамильтониана Н:
б0 = -Нт
f-v+oo f
Далее, статистическая сумма
Z№ = Spexp(-0/f) = ;<je|exp(-0i/)|je>dx A9)
Л
квантовой системы с гамильтонианом Н может быть представлена в виде
Zm = / ехр (- 5eucl [q (r)]) П dq (r), B0)
где интеграл берется по всевозможным замкнутым траекториям: 0 <
< г < C, q @) = q (/3). (Можно сказать, что функция q (f) удовлетворяет пе-
периодическим граничным условиям или что функция q(j) задана на окруж-
окружности.) Символ /3 обозначаем обратную температуру: /3 = Т'1.
Производяший функционал корреляционных функций при температу-
температуре Т = /З записывается в виде
B1)
где Z(|j) (/) — статистическая сумма в присутствии источника
Zm СО = / ехр (- (Seud [q] + Jq) П dq (r). B2)
(Здесь Jq = ///(т)?'' (т)с1т, функция /(т) носит название источника.)
* Соотношение B1) можно рассматривать как определение корреля-
корреляционных функций. Для того чтобы доказать, что это определение совпа-
149

дает со стандартным следует заметить, что
G(/) = 2 ?=1L / dTl. mJdTn с^-'»(т,,... ,т„ , ^
B3)
где
(т,) ... <?'«(rn) exp(-5eud [<?])П«/?(т), B4)
интеграл берется по замкнутым траекториям (q @) = q (j3) ).
Можно проверить, что при тг < ... < т„
0,1-^G,,....т„|Г) =
B5)
где ?'(т) = ехр(#т)?'ехр(—#т), < , >у обозначает среднее значение
по равновесному состоянию при температуре Т = /П1. Правая часть соот-
соотношения B5) является обычным определением корреляционных функ-
функций. Для того чтобы доказать B5), следует наложить на траектории в B4)
дополнительные условия q'k(Tk) = sk, проинтегрировать при этих допол-
дополнительных условиях, используя A7), а затем проинтегрировать по sit.,.
..., sn. Из B4) очевидно, что функции С^""''п(т1,..., т„ | Т) не ме-
меняются при перестановке Ti,..., тп, если одновременно переставляют-
переставляются индексы /j,..., in. Поэтому применяя B5), мы можем вычислить
G'1 '" (ti ,..., тп\Т) при произвольных значениях тх т„ (нужно
только переставить тх т„ так, чтобы они шли в порядке возрастания).
Функции G'n1""'l"(Ti,..., т„), получающиеся из Сп' л (ti, . .., т„ |7)
в пределе Т -*¦ 0, носят название евклидовых функций Грина (или функ-
функций Швингера). Они выражаются через средние значения произведений
q'n (т„) ¦... ¦ qli (тО по основному состоянию (времена т„,..., тх нужно
переставить в порядке убывания). При аналитическом продолжении из евк-
евклидовых функций Грина получаются обычные функции Грина (средние
значения по основному состоянию от произведений гейзенберговских опе-
операторов exp(iHt)qkexp(—iHt), расположенных в порядке убывания
времени).
Соотношения A5), A7), B0) можно применять и в случае бесконеч-
бесконечного числа степеней свободы (формально в этом легко убедиться с по-
помощью предельного перехода от случая конечного числа степеней сво-
свободы). Подчеркнем, однако, что расходимости, возникающие в. случае
бесконечного числа степеней свободы, обычно приводят к тому, что функ-
функциональные интегралы нельзя понимать буквально: аккуратное определе-
определение этих интегралов, должно включать процедуру перенормировки). т
150

Рассмотрим, например, квантовую статистическую сумму скалярного
поля с функционалом действия
B6)
считая, что введено обрезание по пространственным переменным х =
= (х1, х2, х3). (Символ g^" обозначает метрический тензор в простран-
пространстве Минковского, точка х принадлежит трехмерному кубу W; поле
<р (х) - у (t, x) удовлетворяет периодическим граничным условиям по трем
пространственным переменным.) Эта статистическая сумма Zv записы-
записывается с помошью функционального интеграла
где поле <р определено в четырехмерном яшике V, выделяемом условиями
О < t < C = 1/Г, х 6 (С, и удовлетворяет периодическим граничным усло-
условиям по всем четырем переменным. (Евклидово действие Seuci [у] полу-
получается из B6) заменой gM" на 5 м" и изменением знака перед U(tp). Интег-
Интегрирование при вычислении евклидова действия ведется по V.) Вместо то-
того, чтобы говорить о полях с периодическими граничными условиями,часто
удобно считать, что поля заданы на четырехмерном торе Г4 = S1 XS1 X
XS1 XS1.
Легко видеть, что плотность энергии основного состояния квантовой
системы, получающейся при квантовании классической теории с функцио-
функционалом действия B6), определяется формулой
} B8)
Это следует из замечания, что при Т -> 0 основной вклад в статистическую
сумму Zv = Spexp(-|3#) = 2exp(-j3e,-) дает слагаемое ехр(-Cео), от-
вечаюшее энергии е0 основного состояния в объеме W.
Если стремятся к бесконечности не все измерения яшика V, а только
пространственные, то формула B8) дает плотность свободной энергии при
температуре Т= (З. Производящий функционал корреляционных функций
в кубе W при температуре Т= (З задается формулой
ZV(J)
-^, B9)
где Zy (f) — статистическая сумма в присутствии источника. Функциональ-
Функциональный интеграл для Zy(J) отличается от функционального интеграла для
Zv добавлением к евклидову действию слагаемого fj(x)ip(x)dx. Как и
ранее, ^обозначает четырехмерный ящик 0 <Г<|3,хе ИЛ При предельном
переходе V -*¦ °° из функционала Gy (J) получается производящий функ-
15)

ционал для евклидовых функций Грина
G(J)= lim GV(J)=-E^- f Gn(xi,- ¦ ¦ ,xn)J(Xl) .. .J(xn)dnx.C0)
Из B5) следует, что евклидовы функции Грина могут быть представлены
в виде
Gn (*i,... ,*„) = <?(*i) - ..$(х„)H,
если xt = (т/, *,), тх > ... > т„. (Здесь <.. .>о - среднее по основному
состоянию. Символ *р(х) = $(т, х) обозначает полевой оператор, зави-
зависящий от пространственной координаты х и мнимого времени т). С по-
помощью аналитического продолжения по тх,..., т„ можно получить из
евклидовых функций Грина обычные функции Грина (средние значения
хронологических произведений гейзенберговских операторов поля по
основному состоянию).
Как подчеркивалось выше, в случае бесконечного числа степеней сво-
свободы мы сталкиваемся с ультрафиолетовыми расходимостями. Они вы-
выражаются в том, что нельзя непосредственно определить интересующие
нас функциональные интегралы предельным переходом от решетки. Нужно
еще в процессе предельного перехода менять параметры m и X, фигури-
фигурирующие в B6) (голую массу и голый заряд). Кроме того, нужно раз-
разделить J(x) на зависящее от шага решетки число z. (Вместо этого можно
перенормировать поле у (х), умножив его на z.) По теории возмущений
доказывается, что зависимость чисел m, X,z от шага решетки можно подоб-
подобрать таким способом, чтобы, выделив определенным образом расходя-
расходящиеся числовые множители, не зависящие от /, получить конечный ненуле-
ненулевой предел для Zv (J). При вычислении функционала Gv (J) расходяшие^
ся множители сокращаются. Это означает, что расходимости в функциях
Грина можно устранить перенормировкой массы т, заряда X и поля у (х).
§ 18. Квантование калибровочных теорий
Функционал действия в калибровочных теориях инвариантен относи:
тельно локальных калибровочных преобразований. Из-за наличия такой
большой группы симметрии лагранжиан теории оказывается вырожденным
(т.е. обобщенные скорости нельзя однозначным образом выразить через
обобщенные импульсы). Благодаря этому использование гамильтонова
формализма при квантовании оказывается затруднительным. Возникающие
трудности вполне преодолимы, но проще избрать обходной путь, основан-
основанный на использовании функциональных интегралов. Напомним, что в га-
мильтоновом формализме можно выразить физические величины с по-
помощью функциональных интегралов, в подынтегральном выражении кото-
которых фигурирует exp (iS) илиехр> (Seuc{), где S - функционал действия,
а ^eucl - функционал евклидова действия. Наша стратегия будет заклю-
заключаться в том, что мы, не обращаясь к гамильтонову формализму, постули-
постулируем, что аналогичное выражение справедливо в калибровочных теориях.
Для простоты будем рассматривать теорию калибровочного поля, не
взаимодействующего с другими полями (учет других полей не вызывает
каких-либо затруднений). Напомним, что функционал действия в калй-
152

бровочной теории имеет вид
S = - -'р JVV^ ^ар, ***> d*X, A)
где g^" — метрический тензор в пространстве Минковского. (Как всегда,
напряженность Уа^ калибровочного поля 4^, принимающего значения
в алгебре Ли 29 калибровочной группы G, определяется формулой &ар =
= ЪаАр - дрАа + [Аа,Ар], символ ( , > обозначает инвариантное ска-
скалярное произведение в алгебре Ли 29 . Если G - матричная группа, можно
считать, что <a, b> = -2 Sp (ab).
По определению, евклидово действие для полей Янга—Миллса полу-
получается из действия A) заменой g11" на 5м" (т.е. переходом от метрики
Минковского к метрике Евклида) и изменением знака. Менее формально
можно сказать, что евклидово действие получается из псевдоевклидова
заменой времени на мнимое время. Нам будет удобно рассматривать также
функционал евклидова действия для калибровочных полей на произволь-
произвольном римановом многообразии. Этот функционал определяется формулой
/MV * ?> dV /< f^ f°?)dV, B)
где &ali =ga>lgPv &nv>dV =\/det?aC d*x - элемент объема на римановом
многообразии. Отметим, что функционал B), как и рассмотренные выше
функционалы действия, инвариантен относительно локальных калибровоч-
калибровочных преобразований А^(х) ->А'^(х) =g(x)All(x) g'1 (х) -d^g^g'1 (x),
где g (х) — функция, принимающая значения в калибровочной группе G.
Рассмотрим функциональные интегралы
Zv = / ехр(-5еис1И])-ПЖ4(х), C)
2и(Ф) = 1ЧА) exp(-Seuc,H])IId4(je). D)
Здесь V— 4-мерный ящик, калибровочные поля А^(х) зада.ы в этом
ящике и удовлетворяют периодическим граничным условиям, евклидово
действие вычисляется при помощи интегрирования по V. Символ Ф(А)
обозначает произвольный калибровочно инвариантный функционал. Можно
взять, например Ф(А) = а(х,) ... о(х„), где а(х) = —- gfxag1'0 < faa (x),
*g
$ixv (x)) — плотность евклидова действия в точке х ? IR4. Другой воз-
возможный выбор: Ф(А) = Sp br, где Ьг — элемент калибровочной группы,
отвечающий параллельному переносу по замкнутому контуру Г
(Символ Р ехр обозначает упорядоченную экспоненту; см. § Т22).
Выражение C) будем называть статистической суммой в 4-мерном ящи-
ящике V,га отношение выражений D) и C) — евклидовым функционалом Гри-
Грина в ящике V. Из соотношения A7.28) видно, что предел выражения
V~l(— In Zy) при V-+°° следует интерпретировать физически как плот-
плотность энергии в основном состоянии. (Точнее говоря, при принятом здесь
подходе этот предел по определению является плотностью энергии в основ-
153

ном состоянии.) Аналогично, выражение
hm
h ()
v — °° Zy
в силу соотношений A7.29) и A7.30) разумно интерпретировать как
евклидов функционал Грина или евклидову функцию Грина (в зависи-
зависимости от выбора функционала Ф(А)). Например, при выборе Ф(^4) =
= a(jcj) . . . а(хп) выражение E) имеет физический смысл среднего от Т-
упорядоченного произведения o{xi) . . . о(х„) по основному состоянию.
Напомним, что временная координата точки х е Ft4 имеет смысл мнимого
времени. Под Г-упорядоченностью понимается упорядоченность по мнимо-
мнимому времени. Символ о(х) обозначает оператор, который должен был бы
отвечать величине а{х) в неиспользуемой нами операторной формулировке.
Заметим, что легко построить аналоги функционалов Zv nZv(i) для
случая, когда V — произвольное компактное риманово многообразие. Для
их определения в этом случае следует использовать те же формулы C),
D), считая, что ?eucit<4] '— это функционал евклидова действия на инте-
интересующем нас многообразии (см. B)). Рассмотренные выше функциона-
функционалы для ящика с периодическими граничными условиями можно считать
отвечающими 4-мерному тору (поскольку поле в ящике с периодическими
граничными условиями можно понимать как поле на торе).
А Отметим, впрочем, что для калибровочного поля термин "периоди-
"периодические граничные условия" можно понимать по разному: либо как требова-
требование, чтобы поля на противоположных стенках ящика совпадали, либо как
требование, чтобы эти поля были калибровочно эквивалентны. В первом
случае калибровочное поле имеет геометрический смысл связности в три-
тривиальном главном расслоении, базой которого является тор. Во втором
случае калибровочное поле интерпретируется как связность в произволь-
произвольном главном расслоении над тором. Аналогично, рассматривая калибро-
калибровочное поле на многообразии, мы, как объяснено в § Т 23, можем пони-
понимать его как связность в произвольном главном расслоении над этим
многообразием.т
Разумеется, функциональные интегралы C), D), как и все функцио-
функциональные интегралы, требуют аккуратного определения с помощью конечно'
мерной аппроксимации. Для того, чтобы построить такую аппроксимацию
можно воспользоваться следующими соображениями. Рассмотрим в IR4
кубическую решетку. Если в Ft4 задано калибровочное поле А^ (х), то
каждому ориентированному ребру у решетки можно сопоставить элемент
by калибровочной группы G, отвечающий параллельному переносу вдоль
этого ребра,
F)
Легко видеть, что при изменении ориентации ребра элемент Ьу заменяется
на обратный. Далее, при калибровочном преобразовании с калибровочной
функцией g (x) элемент Ьу преобразуется по простому закону
by = gixx)byg-l(x0), G)
где Хо и jci - начало и конец ребра у (см. § Т 22). Эти обстоятельства под-
154

сказывают, что в качестве решеточного аналога калибровочного поля ра-
разумно рассматривать функцию by, определенную на ориентированных реб-
ребрах решетки, принимающую значение в калибровочной группе G и удовлет-
удовлетворяющую условию Ъ_= by1 (здесь у обозначает ребро у, пройденное в
обратном направлении/.
Решеточным аналогом калибровочных преобразований являются пре-
преобразования вида G), где g(x) — функция, определенная на вершинах
решетки. Для того чтобы построить решеточный аналог действий, инва-
инвариантный относительно преобразований G), удобно сопоставить каждой
ориентированной двумерной грани а решетки элемент са группы G, полу-
получающийся при перемножении элементов Ьу, отвечающих ребрам, ограни-
ограничивающим рассматриваемую грань. Иначе можно сказать, что са - это
элемент группы G, отвечающий параллельному переносу по границе а гра-
грани а (т.е. са = Ь^). В рассматриваемом нами случае кубической решетки
двумерные грани являются квадратами. Заданной ориентации квадрата а
отвечает определенная ориентация ребер 7i > 7г > 7з, 74 > принадлежащих его
границе, и определенное направление обхода границы. Данное выше опре-
определение означает, что
са = byjjy^by^by^ , (8)
где произведение элементов Ьу. берется в порядке, определяющемся
ориентацией квадрата а (рис. 16).
Легко видеть, что при калибровочном преобразовании элемент са заме-
заменяется на сопряженный ему элемент группы G:
с'а = g(xo)cag~1(xo),
где х0 — начало ребра 7i • Если / — функция на группе G, не меняющаяся
при замене элемента g на сопряженный ему (/(kgk'1) =f(g)), то элемент
f(ca) не меняется при калибровочном преобразовании. Поэтому можно
построить калибровочно инвариантное действие, например, поставив в со-
соответствие каждому решеточному калибровочному полю Ьу сумму чисел
f(co)> отвечающих всем двумерным граням а.
А Отметим, что элемент са зависит от того, с какого ребра начать обход
границы квадрата а. (Можно было бы, например, заменить са на с"а =
= by by by by .) Однако, эта неоднозначность несущественна для нас,
поскольку два разных значения со являются- сопряженными друг к другу
элементами группы G (например, са = b~\tcabytи, значит f(co) =/(сст)).т
155

Легко подобрать функцию /(с„) таким образом, чтобы решеточная ка-
калибровочная теория аппроксимировала калибровочную теорию в непрерыв-
непрерывном пространстве. Например, если G—матричная группа, можно положить
f(g) = const Sp (g — lJ. В силу соотношения (§ Т 22) для маленького
квадрата а, ребра которого параллельны осям хд и х", имеем
са = I -а2 &»„,
где а - длина ребра решетки и, следовательно,
f(ca) = const я4 Sp #]•„. (9)
Это означает, что действие 2/(с„) при надлежащем выборе константы
а
аппроксимирует действие непрерывной калибровочной теории. Другой
возможный выбор решеточного действия отвечает функции f(g) =
= const Spg.
Если построено решеточное действие, то можно определить решеточный
аналог функциональных интегралов C), D), заменяя Seuci[y4] на его ре-
решеточный аналог
Sa(b) = ЕДс). . A0)
о
Интегрирование по калибровочным полпм следует при этом заменить
на интегрирование по их решеточным аналогам. Поскольку мы рассматри-
рассматриваем калибровочное поле в конечном объеме, мы имеем дело только с
конечным числом точек решетки и, следовательно, с конечным числом ре-
ребер. Для того чтобы задать функцию Ъу (решеточный аналог калибровоч-
калибровочного поля), нужно произвольным образом выбрать ориентацию на ребрах
решетки и сопоставить каждому ориентированному ребру у произвольный
элемент Ьу группы G. (Значение функции Ъу на ребрах противополож-
противоположной ориентации определяется наложенным выше условием Ь- = Ь~у.)
Таким образом, чтобы задать функцию Ьу, нужно фиксировать столько
элементов группы G, сколько есть ребер. Другими словами, функцию Ь^
можно рассматривать как элемент прямого произведения стольких экзем-
экземпляров группы G, сколько есть ребер. Инвариантное скалярное произведе-
произведение в алгебре Ли 'З порождает инвариантную метрику и, следовательно;
инвариантный элемент объема в группе G. Тем самым определяется и эле-
элемент объема в прямом произведении нескольких экземпляров группы G.
Интегрирование по решеточным аналогам калибровочного поля следует
производить, пользуясь именно этим элементом объема.
* Большая группа симметрии, имеющаяся у калибровочных теорий,
затрудняет не только работу в гамильтоновом формализме, но и вычисле-
вычисление функциональных интегралов C), D). В самом деле, применение тео-
теории возмущений к вычислению функциональных интегралов основано на
выделении из показателя квадратичной части и вычислении гауссовых
интегралов, в показателе которых стоит это квадратичное выражение.
Однако, поскольку в калибровочных теориях квадратичная часть лагран-
лагранжиана оказывается вырожденной из-за наличия бесконечномерной группы
симметрии, в прямом виде описанная процедура непригодна. Указанное
только что затруднение легко преодолеть, заметив, что интеграл по некото-
некоторому пространству от функции, обладающей группой симметрии, можно
156

преобразовать в интеграл по части этого пространства. Применив эту про-
процедуру к функциональным интегралам, возникающим в калибровочной
теории, мы получим интегралы, для которых теория возмущений может
быть построена так же, как в невырожденном случае.
Начнем с общего обсуждения интегрирования инвариантных функций
в конечномерном случае.
Пусть М — риманово многообразие, f{x) — функция на многообразии М.
Будем считать, что функция f(x) инвариантна относительно компактной
группы G, действующей на М, т.е. f(T{g)x) = /(*) Для любого преобразо-
преобразования T(g), отвечающего элементу g G G. Предположим, что все преобра-
преобразования T(g), g e G изометричны (сохраняют риманову метрику). Пока-
Покажем, что в этом случае
/Л*)«*М, (И)
м
где dn — риманов элемент объема, можно свести к интегралу меньшей
кратности. (Именно, кратность интеграла можно уменьшить на размер-
размерность орбиты группы G) Например, если f(x) сферически симметричная
функция на IR3, то интеграл по DR3 очевидным образом сводится к одно-
одномерному
ff(\x\)d3x = 4тг / f(r)r2dr. A2)
о
Ограничимся пока исследованием случая, когда группа G действует на
М свободно (т.е. все стационарные подгруппы тривиальны: Нх = 1). Рас-
Рассмотрим в М подмногообразие TV, пересекающее каждую орбиту группы G
ровно один раз. Тогда интеграл A1) можно преобразовать в интеграл
по многообразию jV. Проще всего это сделать с помощью так называемого
трюка Фаддеева—Попова. Будем считать, что многообразие TV задается
уравнениями
Fl(x) = 0,..., Fk(x) = 0. A3)
Эти уравнения предполагаются независимыми (иными словами, дифферен-
дифференциалы функций F1, . . . , Fk считаются линейно независимыми в каждой
точке х ? М). Систему уравнений A3) можно переписать в виде одного
векторного уравнения F(x) = 0, где F - отображение многообразия М в
IR*, сопоставляющее точке х ? М вектор (F1 (х), . . . , Fk(x)). Условие
независимости уравнений означает, что дифференциал Fx отображения F
является линейным оператором ранга к в каждой точке х ? М.
Определим функцию WF {x) равенством
WF(x) / 8(F(T(g)x))dg =1, A4)
где dg - инвариантный элемент объема на группе G, нормированный усло-
условием : объем V(G) группы G равен 1.
Тогда
/ fix) dfi= f WF(x) f(x) 8 (F(x)) d(i. A5)
M M
E-функция 5(F(x)) в правой части A5) превращает интеграл по М в
интеграл по многообразию N).
157

Для того, чтобы проверить соотношение A5), представим A1) в виде
двойного интеграла
/ Л*) Ф = fdn I dg Ях) WF(x) 8(F(T(g)*)) •
М М G
Сделав в двойном интеграле замену х = T(g)x и заметив, что функции
f(x) и WF (х) G-инвариантны, мы получим
/ /(*) ёц = fdfi f dg f{x) WF(x) 5(F( 5c)).
M M G
Беря интеграл по G, видим, что
Д = V(G) f WF(x)f(x)8(F(x))dn.
м м
Пользуясь условием нормировки V(G) = 1, убеждаемся в справедливости
соотношения A5).
Проведенное выше рассуждение относилось к конечномерному случаю.
Однако, мы будем применять окончательные результаты (соотноше-
(соотношение A5)) также и в бесконечномерной ситуации. При этом группа G уже
не будет предполагаться компактной. Часто удобно рассматривать правую
часть A5) как определение функционального интеграла, фигурирующего
в левой части этого равенства в случае, если подынтегральная функция
обладает бесконечномерной группой симметрии. Применим эти соображе-
соображения к интегралам C), D).
Подынтегральное выражение в них инвариантно относительно группы
С°°всех локальных калибровочных преобразований. Однако, эта группа
не действует свободно на пространстве всех калибровочных полей А ^ {х),
играющем роль многообразия М (см. § Т 26). Поэтому нам будет удобно
считать, что роль группы G в соотношении A5) играет группа G", состо-
состоящая из локальных калибровочных преобразований, порожденных такими
функциями g(x), для которых g(x0) = 1. Здесь jc0 - некоторая фиксиро-
фиксированная точка. Если поля заданы на евклидовом пространстве, то
под х0 удобно понимать бесконечно удаленную точку, т.е. налагать
условие lim g (x) = 1. Далее ради определенности мы рассматриваем поля
х -»~
на евклидовом пространстве. Группа Gq действует свободно на простран-
пространстве калибровочных полей (см. §Т 26). Мы должны выделить из прост-
пространства всех калибровочных полей Ац (х) множество N, пересекающее
каждую орбиту группы Gq ровно один раз. Сделаем это, наложив на рас-
рассматриваемые поля калибровочное условие Эм А11 (х) = 0. Строго говоря,
это условие удовлетворяет необходимым требованиям только в абелевом
случае. (В неабелевом случае вообще нельзя непрерывным образом вы-
выбрать по одному полю из каждой орбиты группы Gq ; см. § Т 26).
Однако, и в неабелевом случае можно использовать калибровочное
условие д цА11 (х) = 0 для построения теории возмущений. Это связано
с тем, что в теории возмущений играют роль только калибровочные поля,
мало отличающиеся от вакуумных. (Под вакуумным полем мы понимаем
поле с нулевой напряженностью, т.е. поле, калибровочно эквивалентное
нулевому.) Достаточно доказать поэтому, что два поля, удовлетворяющие
условию Ъ^А11 (х) = 0, нельзя связать калибровочным преобразованием
158

с функцией g(x) в случае, если эти поля достаточно близки к нулевому,
а функция g(x) близка к 1. Нелинейное уравнение для функции g(x)
в этом случае лишь малой добавкой отличается от линейного уравнения,
не имеющего нетривиальных решений и, следовательно, само имеет только
тривиальное решение. (В абелевом случае все уравнения линейны и никакие
предположения о малости полей не нужны.)
При применении соотношения A5) к интегралам C), D) роль функции
Wp (х) играет функционал W[A], определяемый соотношением
W\A] /6(ЭМ*)Пф = 1, A6)
где А^ = gA^g'1 - d^gg'1, интеграл берется по группе G? . Если поле
Ар, удовлетворяющее условию дц Ам = 0, достаточно мало, то, как мы
говорили, ЭмЛд = 0 только при g{x) = 1. Ввиду этого при вычислении
интеграла можно считать, что g (x) бесконечно мало отличается от единицы.
Замечая, что для бесконечно малого е (х)
Мы видим, что вычисление W[A] сводится к взятию интеграла
/5 (ЭдV е (*)) П de = det"» (Эд. V " ). A7)
(Здесь интегрирование идет по функциям е(х), пробегающим алгебру
Ли группы Gq.) Таким образом, применяя трюк Фаддеева—Попова, напри-
например, к функциональному интегралу D), мы можем переписать этот интег-
интеграл в виде
П dA. A8)
Для полученного функционального интеграла теория возмущений может
быть построена стандартными способами. При этом построении удобно
сделать замену Ац -^Л'ц = g~1Afl, где g — константа связи. Тогда в функ-
функционале действия исчезнет множитель ?~2, а напряженность J^,v заме-
заменится Hai ?"м„ = ЭМЛ„ — ЪуАц + g [Ац, Av]. Отметим, что ряд теории воз-
возмущений является рядом по g2, а не по g (поскольку в функционале дей-
действия фигурирует g2). Поэтому часто вместо g рассматривают величину
?2/4тг; эту величину также будем называть константой связи и обозначать
символом а (если нужно отличить ее от эффективной константы связи,
то будем называть а "голой константой связи" и обозначать abar).
В членах ряда теории возмущений по константе связи аъаг возникают
ультрафиолетовые расходимости. Для того чтобы устранить эти расходи-
расходимости, нужно сделать обрезание по импульсам (например, с помощью пере-
перехода к решетке) и затем снять обрезание (перейти от решетки к непрерыв-
непрерывному пределу), считая, что константа связи аьаг зависит от параметра
обрезания. Зависимость голой константы связи от параметра обрезания
обычно фиксируют требованием, чтобы эффективная константа связи в
некоторой точке (точке нормировки) принимала заданное значение а0. Ряд
теории возмущений можно перестроить в ряд по а0; тогда все члены ряда
теории возмущений для любой величины, имеющей физический смысл,
будут оставаться конечными при снятии обрезания (это означает перенор-
мируемость теории калибровочного поля) .Ў
159

Остановимся подробнее на переходе от решеточных калибровочных
теорий к непрерывному пределу. Для определенности будем считать, что
функционал действия решеточной теории задается формулой A0), где
f (с) = |3Sp (с2 - 1). (Калибровочная группа G считается матричной груп-
группой. Если группа G не является матричной, то можно положить / (с) =
= /3Sp с, где с — оператор, отвечающий элементу с 6 G в присоединенном
представлении.) Для такого функционала действия при надлежащем выбо-
выборе зависимости /3 от шага решетки а в пределе а -*¦ 0 из решеточного дейст-
действия получается действие непрерывной калибровочной теории. Однако
оказывается, что при этом выборе зависимости |3 от а не имеют разумного
предела физические величины, вычисленные с помощью решеточного дей-
действия. Поэтому приходится идти по другому пути, подсказываемому
теорией возмущений. Именно, зависимость |3 от а следует подбирать таким
образом, чтобы какая-либо из физических величин оставалась постоянной
при изменении а. Можно надеяться, что тогда все другие величины, пред-
представляющие физический интерес, будут иметь конечный предел при а -*
-*¦ 0. Корреляционные функции решеточной калибровочной модели экспо-
экспоненциально убывают при увеличении расстояния. (Этот факт строго до-
доказан для достаточно больших /3.) Скорость убывания характеризуется
корреляционным радиусом г (|3). В непрерывной теории корреляцион-
корреляционный радиус определяется наименьшей массой частиц, существующих в
теории. (Он равен обратной величине этой массы.) Поэтому при переходе
к непрерывному пределу разумно считать величину г (/3) не зависящей
от а. (Отметим, что зависимость Р от а, гарантирующую постоянство кор-
корреляционного радиуса при а -> 0, можно подобрать в силу того, что при
|3 -> 0 корреляционный радиус, измеренный в единицах шага решетки,
стремится к бесконечности.) Все остальные величины,имеющие физический
смысл, имеют конечный предел при избранной нами зависимости/3от а.
Мы получаем таким образом физические величины, отвечающие непре-
непрерывной калибровочной теории. Точнее, мы получаем целое семейство
теорий, зависящее от параметра, имеющего размерность длины — фикси-
фиксированного нами корреляционного радиуса. Подчеркнем, что исходный
лагранжиан непрерывной калибровочной теории зависел от безразмерной
константы связи, но в результате перенормировки мы получили семейство
теорий, зависящих от размерного параметра - корреляционного радиуса.
Вместо корреляционного радиуса нам будет удобнее характеризовать
теорию обратной к нему величиной т, имеющей размерность массы. (На-
(Напомним, что в принятой нами системе единиц h = с - 1 масса имеет раз-
размерность см.)
Все эти теории по существу эквивалентны друг другу - они отлича-
отличаются только выбором масштаба. Если, например, мы рассматриваем без-
безразмерную физическую величину, являющуюся функцией от импульсов
kt, . . . , кп, то, очевидно, что она будет зависеть только от отношений
ki/m, . . . , кп/т. В частности, эффективная константа связи а(к), рас-
рассматриваемая как функция от импульса к, является на самом деле функ-
функцией от к/т. (Определение эффективной константы связи можно дать
различными способами; однако сделанное выше утверждение справед-
справедливо при любом из этих способов, поскольку использует только сообра-
соображения размерности.)
160

В теории возмущений принято выражать эффективную константу связи
через ее значение в какой-либо фиксированной точке v — точке нормиров-
нормировки. Таким образом, константа связи оказывается функцией от импульса к,
точки нормировки v и значения константы связи в точке нормировки а0:
а(к/т) = а(к, и, а0), ао = а(и/т).
Мы видим, что вместо одного параметра т возникли два параметра и и
Oq. Ясно, что на самом деле эффективная константа связи зависит только
от некоторой комбинации параметров v и а0; иными словами, изменение
точки нормировки v можно компенсировать изменением а0. Этот факт
носит название ренорм-инвариантности.
Покажем, как, пользуясь теорией возмущений и ренорм-инвариант-
ностью, вычислить эффективную константу связи там, где она мала. По-
Поскольку в непрерывном пределе следует ожидать инвариантности отно-
относительно вращений, будем считать, что эффективная константа связи а не
зависит от направления вектора к и, следовательно, является функцией
от к2 jm2. Обратно, к2/т2 можно выразить через а. Легко убедиться, что
производная от а по In к2 зависит только от к2 \т2 и, значит, может рассмат-
рассматриваться как функция а
din a A9)
Функция |3 (а), фигурирующая в правой части A9), называется функ-
функцией Геллмана-Лоу. Очевидно, что /3 @) = 0 (для теории без взаимо-
взаимодействия эффективная константа связи равна нулю при всех к). Это оз-
означает, что разложение |3 (а) в ряд по а начинается с линейного члена
Р(а) = Ьа + ... B0)
Подставляя B0) в A9) , мы видим, что в случае, если членами высше-
высшего порядка в B0) можно пренебречь, имеет место соотношение
d\na
=
а
Отсюда
а (к2,
—
а2
V2,
= bd\nk2.
<*о) = ао1
- Ъ
к2
In—,
V2
B2)
где v — точка нормировки, а0 = а (и2, v2, а0) — значение эффективной
константы связи в точке нормировки. Подчеркнем, что соотношение B2)
справедливо там, где а (А) - малая величина, поскольку именно при этом
условии можно оставить в B0) только линейный член.
Коэффициент в B0) может быть явно вычислен по теории возмущений;
например, для калибровочной теории с группой G = SU(N) получается
,= _^ " B3)
2тг
(Для вычисления b могут быть использованы коэффициенты Сипи: см.
§ 25). Оказывается, что b < 0 для любой калибровочной теории с простой
некоммутативной группой G. Это означает, что в таких теориях соотно-
соотношение B2) применимо при больших А:2 и, следовательно, а -* 0 при&-*°°.
161

Это явление называется асимптотической свободой. (Если бы ока-
оказалось, что Ь > 0, то соотношение B2) было бы применимо при малых
к2 • никакой информации о поведении эффективной константы связи
при больших к2 из него нельзя было бы извлечь.)
Подчеркнем, что проведенные выше рассуждения с незначительными из-
изменениями применимы к любой перенормируемой теории, если функцио-
функционал действия этой теории масштабно инвариантен (не меняется при замене
х -> Хх). Требование масштабной инвариантности означает, в частности,
что лагранжиан не содержит массовых членов. Если теория асимптотически
свободна, то к ее лагранжиану можно добавить массовые члены, не нару-
нарушив при этом асимптотической свободы. (При больших импульсах вклад
массовых членов пренебрежимо мал.) При этом необходимо, конечно,
чтобы добавление массовых членов не нарушало перенормируемости.
А В дальнейшем нам будет удобно пользоваться не описанным выше
трюком Фаддеева-Попова, а его инвариантным аналогом. От множества JV,
фигурировавшего выше, мы требовали, чтобы оно пересекало каждую из
орбиг ровно один раз. Это значит, что существует взаимно однозначное
соответствие между множеством Nn множеством всех орбит. Мы укажем
сейчас, как непосредственно свести интегрирование G-инвариантной функ-
функции на римановом многообразии А/к интегрированию по множеству орбит
W = М/С Как и раньше, мы предполагаем, что М — риманово многообразие,
группа G компактна, преобразования группы G сохраняют риманову метри-
метрику. Стационарные подгруппы уже не будут предполагаться тривиальными,
однако, мы будем считать, что все стационарные подгруппы сопряжены.
(Это предположение не ограничивает общности, поскольку всегда можно
добиться его выполнения, выбросив из М множество точек, имеющее
нулевой объем.)
Заметим, прежде всего, что можно определить расстояние между орбита1
ми как расстояние между ближайшими точками этих орбит. Отметим, что
расстояние между орбитами можно определить также, как наименьшее
расстояние от фиксированной точки одной из орбит до точек другой орби-
орбиты. В самом деле, если минимум расстояния между точками орбит L { и L2
достигается для точек х G Lu у G L2. то, в силу изометричности преобразо-
преобразований группы 6', точки T(g) х и T(g)у также находятся на наименьшем'
расстоянии. Это означает, что. отыскивая пару ближайших точек, одну
можно считать фиксированной. При таком введении расстояния множество
орбит превращается в риманово многообразие. (Если х — произвольная
точка многообразия, L(x) — проходящая через нее орбита, а вектор dx
ортогонален к орбите L (х) в точке х, то расстояние между орбитами L (х)
и L(x + dx) равно длине вектора dx. Это следует из замечания, что геодези-
геодезическая в М. соединяющая ближайшие точки двух орбит, ортогональна к
обеим орбитам.)
Пользуясь римановой метрикой в мноюобразии орбит W можно опре-
определить элемент объема dv в этом многообразии. Объем орбиты L (х) отно-
относительно римановой метрики, порождаемой метрикой в М, обозначим
X(.v). Поскольку орбиты L (х) и L(T(g)x) совпадают, функция Х(х) инва-
инвариантна относительно группы G. Имеет место почти очевидная формула
f J\x)dv=ff{x)\{x)Jp, B4)
М W
162

где G-инвариантные функции f(x) и \(х) можно рассматривать как функ-
функции на W. Например, для SOC)-инвариантных функций в IR3 (сферически
симметричных функций) из B4) следует A2), если заметить, что Х(г) =
= Лиг2 - площади сферы радиуса г.
Для того, чтобы сделать формулу B4) эффективной, необходимо нау-
научиться вычислять функцию \(х) — объем орбиты. Будем считать, что в
алгебре Ли $ группы G фиксировано инвариантное скалярное произведе-
произведение, нормированное таким образом, что объем группы Gb индуцированной
этим скалярным произведением метрике на G равен 1. Для каждой точки
х S М определим линейный оператор &х, действующий из алгебры Ли *&
в касательное пространство >МХ к многообразию М в точке х. Именно,
будем считать, что этот оператор сопоставляет всякому бесконечно малому
преобразованию вектор, получающийся из х с помощью этого преобразова-
преобразования. Мы обозначим через D(x) детерминант оператора ?Г+Х Sfx. (Если
стационарная подгруппа нетривиальна, этот оператор вырожден; тогда
детерминант определяется как произведение ненулевых собственных значе-
значений.) Оператор &х обращается в нуль на алгебре Ли Жх группы Нх и
&х
ъЛ1х.Оператору невырожден;легко убедиться, что D(х) можно рассматри-
рассматривать также, как детерминант оператооа «Г*. ?FX. Мы покажем, что
Мх)-(О(х)I(У(Нх)Г, B5)
где объем V(HX) стационарной подгруппы Нх вычислен по римановой
метрике в G. Для того, чтобы убедиться в справедливости этого соотноше-
соотношения, рассмотрим факторпространство GjHx, снабженное римановой метри-
метрикой, индуцированной римановой метрикой в G. (Факторпространство G/H
является многообразием орбит группы//в G; расстояние между орбитами,
как и выше,определяется как расстояние междуих ближайшими точками.)
Орбита L (х) топологически эквивалентна многообразию G/Hx. Элементы
объема в L (х) и G/Hx различны, но отличаются толйко множителем, не
зависящим от точки орбиты. (Это следует из того, что оба элемента объема
инвариантны относительно группы G.) Для того, чтобы сравнить элементы
объема в L (х) и G/Hx, достаточно произвести это сравнение в одной из
точек многообразия G/Hx. Напомним, что для установления соответствия
между G/Hx и орбитой L (х) мы должны сопоставить каждому элементу
группыg&G точку T(g)х. При этом соответствии точки g и gh, где h SНх,
переходят в одну и ту же точку орбиты L (х). Иными словами, это постро-
построенное отображение порождает отображение G/Hxb L(x). Дифференциал
описанного только что отображения G в L(x) в точке g = 1 совпадает с
рассмотренным выше оператором $х, а дифференциал отображения
G/Hx в L (х) в соответствующей точке пространства G/Hx -с оператором
Fx. Отсюда следует, что элементы объема в GjHx и L (х) отличаются
множителем
Таким образом
B6)
163

Чтобы вычислить объем G/Hx, следует использовать B4) в случае Дх) =
= 1, М= G (пространство G/Hx можно представить себе как пространство
орбит группы Нх, действующей в G справа: все орбиты имеют один и тот
же объем). Мы убеждаемся, что
Замечая, что все подгруппы Нх сопряжены с фиксированной подгруппой Н,
видим, что все они имеют один и тот же объем. Таким образом
/ /(*) dn = (К(Я)Г ff(.x)(D(x)) ll2dv.
м w
В заключение применим инвариантную форму трюка Фаддеева—Попова
к вычислению статистической суммы для электромагнитного поля на
компактном римановом многообразии М. Функционал евклидова действия
в этом случае может быть записан в виде
ТУ" ( *". F) = 7-2(dA' dA ) =
= —(d+dA,A)=-(SA,A), B7)
где S= — d+d. Здесь напряженность ^рассматривается как 2-форма -
внешний дифференциал 1-формы .4, отвечающей потенциалу электромагнит-
электромагнитного поля. (Скалярное произведение форм понимается так, как это объясне-
объяснено в §ТП.) Ради простоты обозначений будем считать, что 2g2 = 1. Дейст-.
вие B7) инвариантно относительно калибровочных преобразований А -*А +
+ dg(x). Из этого следует, что квадратичная форма B7) бесконечнократно'
вырождена; соответственно оператор S =d+d имеет бесконечное число'
нулевых мод; этими модами являются 1-формы, удовлетворяющие усло-
условию dA = 0 (замкнутые 1-формы). Наложим на потенциал А калибровоч-
калибровочное условие d+ A = 0 (в координатах это условие записывается, в виде
VMM = 0; иными словами оно означает, что ковариантная дивергенция
вектораЛм равна нулю). Условие d +А = 0 выделяет в пространстве Г!
всех 1-форм многообразие N, которое можно отождествить с пространст-
пространством орбит калибровочной группы. (В самом деле, в каждом классе кали-
калибровочных полей существует ровно одно калибровочное поле, удовлетворя-
удовлетворяющее условию d +А = 0).
Метрика на многообразии орбит совпадает с естественной метрикой на
многообразии N. Действительно, многообразие iV очевидным образом
ортогонально каждой из орбит (это следует из соотношения (dg,A) =
= (g, d+A)=0, справедливого, если A S N). С другой стороны, как мы
знаем, расстояние между орбитами "измеряется по перпендикуляру" (если
тс и х + dx принадлежат близким орбитам и вектор dx ортогонален орбите
в точкех, то расстояние равно длине этого вектора). Таким образом, мы
можем применить инвариантную форму трюка Фаддеева—Попова, считая
что оператор &, фигурирующий в соотношении B5), совпадает с операто-
164

ром d. Мы получаем, что
= / ехр(- SeucI)(^)(det d+dI12 UdA. B8)
N
Конечно, применение соотношения B4) в бесконечномерном случае,
строго говоря, незаконно. По существу, мы должны рассматривать прове-
проведенное выше рассуждение как эвристические соображения, подсказываю-
подсказывающие, что правую часть равенства следует рассматривать как определение
не имеющего точного смысла интеграла в левой части этого равенства.
Отметим, что в правую часть B8) следовало бы включить множитель
К(#)~], где // — стационарная подгруппа группы калибровочных преобразо-
преобразований. В нашем случае эта стационарная подгруппа состоит из функций,
удовлетворяющих условию dg= 0, т.е. из постоянных функций; эта под-
подгруппа изоморфна 1R1. Объем ее, очевидным образом, бесконечен, поэтому
мы не включаем множитель V(H)~l в B8) (как и другие расходящиеся
множители). Оператор 5 на Л' имеет уже только конечное число нулевых
мод. В самом деле, нулевыми модами этого оператора являются 1-формы,
одновременно удовлетворяющие условиям dA = 0 и d+A = 0. Такие формы
называются гармоническими; их число совпадает с одномерным числом
Бетти Ь1 многообразия М (см. §Т11). Если й1 =0 (многообразие М ацик-
ациклично в размерности 1), то оператор 5 не имеет нулевых мод на Л'и инте-
интеграл от ехр(—5euci) no iVравен (det 5)'2 (подпространство Л' совпадает
в этом случае с пространством, натянутым на все собственные векторы
оператора S, отвечающие ненулевым собственным значениям). Отсюда
Z = (detSyll2(detd+dI/2 = (det(-A,)-1/adet(-A0), B9)
где At = -(d*d + dd*) и До = -d*d - операторы Лапласа на 1- и 0-формах.
Выражением B9) для статистической суммы электромагнитного поля
можно пользоваться и в том случае, когда Ь1 Ф0 (хотя в этом случае
наличие гармонических 1-форм — нулевых мод оператора d+d + dd+—
приводит к некоторым аномалиям; см. § 22) .т
§ 19. Эллиптические операторы
Напомним, прежде всего, что дифференциальный оператор второго
порядка
А= Ъа'(х)Ъ.Ъ. + %ь'(х)д. + с(х) A)
называется эллиптическим, если квадратичная форма 2 а'7 ?(-?;-является
знакоопределенной. Это определение без труда переносится на диффе-
дифференциальные операторы произвольного порядка. Именно, дифференциаль-
дифференциальный оператор А порядка к называется эллиптическим, если главный сим-
символ о(х, р) этого оператора обращается в нуль только при р = 0. Под глав-
главным символом оператора, как мы говорили, понимается та часть символа
оператора А, которая состоит из членов максимального порядка по р.
165

Таким образом, если оператор А имеет вид
А = _ Б _ а1'-'*^ ...Э,Л +..., B)
где многоточие обозначает члены, содержащие производные порядка мень-
меньше к, то главный символ оператора А равен
.--ft*. C)
Оператор Л можно считать матричным (т. е. считать, что его коэффи-
коэффициенты являются матрицами). Если коэффициентные функции операто-
оператора являются квадратными матрицами порядка г, то этот оператор дей-
действует в пространстве функций со значениями в fR*" (пространстве, эле-
элементами которого являются столбцы из г функций). Символ оператора
является в этом случае матричной функцией. Матричный оператор назы-
называется эллиптическим, если его главный символ о(х, р) является невырож-
невырожденной матрицей при р Ф 0.
Примерами эллиптических операторов являются оператор .Лапласа
Д = 2 2
и евклидов оператор Дирака
1 = И%
где у' - эрмитовы матрицы, удовлетворяющие условию
7'У + 7;У = 25';'
В пространстве размерности а матрицы у' имеют порядок 2", где п —
целая часть числа d/2 (иначе говоря, d = 2и или d= 2п + 1). Оператор Ди-
Дирака можно рассматривать как оператор, действующий на спинорные
функции — столбцы из 2" функций. Нетрудно проверить, что оператор
Дирака инвариантен относительно ортогональных преобразований. Точ-
Точнее, каждому вращению g e SO(d) можно сопоставить преобразование
спинорных функций ф(х) -*¦ ф' (х) = Sg$(g~ l х). (Матрицы 5^ образуют
двузначное 2"-мерное предствление группы SO(d) - спинорное пред-
представление.) При этом преобразовании имеет место соотношение
Можно рассмотреть также аналоги операторов Лапласа и Дирака на
римановом многообразии. Если метрический тензор обозначен через
gij(x), обратный ему тензор через g'1 (х), а соответствующая ковариант-
ная производная — символом V,-, то оператор Лапласа, действующий на ска-
скалярные функции, записывается в виде
Д = /''V,.V,. = V'V, = V(.V. D)
Таким образом, А<р ~ это ковариантная дивергенция вектора V'ip =
= 3'ip. Воспользовавшись обозначениями § Т11, оператор D) можно
записать также в виде Д- —8d.3p.ecbd— оператор внешнего дифференци-
дифференцирования, сопоставляющий скалярной функции <р 1-форму dy>, а 5 = d+ -
оператор, сопряженный d относительно скалярного произведения форм,
166

введенного в § Til. (Легко видеть, что 5 сопоставляет 1-форме Ajdx'
скалярную функцию В = V*Aj — ковариантную дивергенцию век-
вектора А,-.)
Оператор Лапласа Ак. пействуюший в пространстве А:-форм на рима-
римановом многообразии, определяется формулой
15)
(внешний дифферендиал d переводит г-формы в (г + 1)-формы, а сопря-
сопряженный ему оператор 5 = d* переводит г -формы в (г — 1)-формы; см.
§ Т 11).
На области U пространства IR" Аг-форма со = О}- ... ,-fc (*) dx'1 Л ... Л dx'k
задается с помощью ее коэффициентных функций со,^ ...,Л (х); если пред-
предполагать, что эти функции антисимметричны, то они сопоставляются
форме однозначно. Можно считать, таким образом, что оператор Ак опре-
определен на функциях со значениями в IRd ^fc-*, где d(k) = Скп— число коэф-
коэффициентных функций или, что то же самое, на сечениях тривиального
векторного расслоения (U X!Rd'*', U, lRd^^).Для общего «-мерного
многообразия М нельзя отождествить А:-форму с векторной функцией
(в каждой локальной системе координат мы имеем свои коэффициент-
коэффициентные функции). В этом случае следует рассматривать А;-форму как сечение
векторного расслоения со слоем Rd^J, оператор Ак действует в про-
пространстве таких сечений.
Этот пример привода; г к необходимости рассмотрения эллиптических
операторов, действующих в пространстве сечений Г(?) векторного рас-
расслоения ? (?", М, IRd), базой которого является «-мерное гладкое много-
многообразие М. Пространство такого расслоения склеено из прямых произве-
произведений Ui X R , где Ut - области bIR". Сечение tp расслоения % порождает
сечение *р,- в каждом из расслоений |/(f/,- XRd, t/,-,IRd). В локальных коор-
координатах сечения расслоения ?,- могут рассматриваться как функции со
значениями в pd. Это позволяет говорить о дифференциальных операто-
операторах в пространстве Г (?,-), состоящем из сечений расслоения ?,-. Для того
чтобы задать дифференциальный оператор в Г(?), нужно согласованным
образом задать дифференциальные операторы в Г (?,•). Оператор в Г(?)
называется эллиптическим, если все отвечающие ему операторы в простран-
пространствах Г(|() являются эллиптическими. Говоря проще, оператор в про-
пространстве векторного расслоения называется эллиптическим, если он эл-
эллиптичен в любой системе локальных координат.
Для того чтобы определить оператор Дирака на римановом многообра-
многообразии, удобно воспользоваться так называемым тетрадным формализмом.
В каждой точке «-мерного риманова многообразия М фиксируем и орто-
ортогональных и нормированных векторов е±,..., е„ (ортонормированный
репер). Координаты этих векторов будем обозначать е™ (индекс т носит
название мирового, а индекс а — внутреннего). Условие ортонормирован-
ности означает, что gmn(x) e^ei = Sab. Разлагая произвольный вектор
Ат по базису е\,..., еп, получаем координаты вектора в этом базисе Ат =
= А" е™. Для ковектора (вектора с нижним индексом) положим Ат =
= ет-Аа , где еат - матрица, обратная ке?\ Аналогично осуществляется пе-
переход от мировых индексов к внутренним для любых тензоров. В част-
167

ности, для ковариантной производной
4aAb = efebnVmA" = baAb+o>abcA\ F)
где шаьс носят название коэффициентов вращения Риччи. Легко проверить,
что ыаьс = — совсь. Мы видим, что при фиксированном а можно рассматри-
рассматривать соайс как элемент соа алгебры Ли антисимметричных матриц - алгеб-
алгебры Ли группы SO (и). Если задано представление Г группы SO (и), то анти-
антисимметричной матрице соа сопоставляется матрица wa в пространстве это-
этого представления. Говорят, что на римановом многообразии задана х-ком-
понентная величина Ф, преобразующаяся по .^-мерному представлению Т
группы SO (и), если закон преобразования этой величины при замене ре-
репера ех е„ на репер еа = ? aej,, где gjj — ортогональная матрица, имеет
вид
Для поля, преобразующегося по представлению Т, можно определить кова-
риантную производную соотношением
Величина, преобразующаяся по спинорному представлению группы SO (л),
называется спинором. В соответствие со сказанным выше мы можем оп-
определить ковариантную производную спинорного поля и записать опера-
оператор Дирака стандартным образом
Мы предполагали до сих пор, что ортонормированное реперное поле задано
на всем римановом многообразии М. Выбор такого поля не всегда возмо-
возможен. Однако, всегда можно покрыть М областями Ua, в каждой из которых
нужное нам поле существует. В пересечении областей Ua и V'$ имеются два
реперных поля, связанных соотношением е^ (х) = g(x, a, ff)be^{x),
где g (x, а, /3)* — ортогональная матрица. Поле величины, преобразующейся
по представлению Т, следует задавать в каждой облзсти Ua, подчиняя его
условиям согласования
= T(g(pc, C>
Для спинорного поля это определение требует уточнения, поскольку
спинорное представление двузначно. Чтобы имело смысл понятие спинор-
спинорного поля, нужно в каждом пересечении Ua П U$ выбрать одну из ветвей
двузначной функции T(g (х, а, 0)) (при этом требуется выполнение усло-
условия согласования T(g(х, а, у)) = T(g(х, а,C)) T(g(х, $,у)), еслих 6 Ua П
П Up П иу). Если такой выбор сделан, то говорят, что на многообразии
выбрана спинорная структура. Оказывается, что не на всяком многообра-
многообразии можно выбрать спинорную структуру.
Необходимым и достаточным условием для возможности введения спи-
норной структуры является обращение в нуль так называемого двумерно-
двумерного класса Шгифеля и>2. Если многообразие неодносвяэно, то спинорная
структура может быть введена разными способами. Эти способы находятся
во взаимно однозначном- соответствии с гомоморфизмами группы тгj (M)
168

в 2г или, 4fo то же, с элементами группы Я1 (Л/, Z2). В дальнейшем, говоря
об операторе Дирака, мы всегда будем предполагать, что на многообразии
введена спинорная структура.
Отметим, что спинорное представление группы SO (л) приводимо в слу-
случае, когда п четно. В самом деле, при этом матрица y"+l = — i"l2yx... 7"
является эрмитовой матрицей, антикоммутирующей со всеми У; в силу
соотношения y+1y"+1 = i ee собственные значения равны ±1. Простран-
Пространство всех спиноров разлагается в прямую сумму подпространств, состоя-
состоящих, соответственно, из спиноров, удовлетворяющих условиям уп+1ф =
= ф (правые спиноры) иуп+1ф = — ф (левые спиноры). Эти подпространст-
подпространства инвариантны относительно действия операторов спинорного представле-
представления. Из соотношения у"+1 % = — &7п+1 следует, что оператор р переводит
левые спиноры в правые и правые в левые.
Пользуясь евклидовым оператором Дирака можно ввести функционал
евклидова действия для уравнения Дирака по формуле
=(ф,?ф)-1т(ф. ф). G)
Здесь (»//], ф2) =/< ф\(х), ф2(х)) dxобозначает скалярное произведение
двух спинорных полей, построенное с помощью скалярного произведения
< , >, инвариантного относительно спинорного представления группы
SO (л). (При наложенном нами условии эрмитовости матрицу,- это скаляр-
скалярное произведение записывается как сумма произведений компонент одного
спинора на комплексно сопряженные компоненты другого спинора.)
Формула G) сохраняет смысл, если под ф понимать многокомпонентное
спинорное поле. (Тогда евклидово действие представляет собой сумму
слагаемых, отвечающих всем компонентам поля.) Мы будем считать, что
спинорное поле имеет к компонент (принимает значение в пространстве
С*). Тогда функционал действия G) инвариантен относительно группы
U(k) унитарных преобразований пространства С : замен фа -> и%ф%,
где a, b — номер компоненты (изотопический индекс), и% — унитарная мат-
матрица. Это позволяет стандартным образом ввести евклидово действие
фермионов, взаимодействующих с калибровочными полями. Именно,
если локализации подвергается подгруппа группы внутренних симметрии,
являющаяся образом компактной группы Ли G при гомоморфизме Т в
группу U(Л), то евклидово действие фермионного поля во внешнем калиб-
калибровочном поле Лд (х) записывается в виде
1т(ф,ф). (8)
Здесь, как всегда, Ац принимает значение в алгебре Ли группы G,t — пред-
представление алгебры Ли, отвечающее представлению Т группы G. Для того,
чтобы получить полный функционал евклидова действия, отвечающий
взаимодействию фермионных и калибровочных полей, нужно прибавить
к (8) функционал евклидова действия калибровочного поля.
Оператор
носит название оператора Дирака во внешнем калибровочном поле. Как
и обычный оператор Дирака он является эллиптическим оператором (вве-
169

вклада в A8.4) необходимо, как мы говорили, разделить на вклад от
инстантонов с топологическим числом q = 0 (вакуумных полей) в ин-
интеграл A8.3); этот вклад содержит множители g~l в количестве
dim?0 - dimG°° + 3. (Мы применяем B6), считая, г„ = 0, h0 = 3.) Пола-
Полагая dim&g = dim So» видим, что в формуле для g-инстантонного вклада
содержится 8q множителей g'1. Если G = SU(N), то, как сказано выше,
rq = 4Nq - (N2 - 1), hq = 0 при q > N/2; при 1 < q <N/2 имеем rq =
= 4q2 + 1, hq = (N - 2qJ; при q = 0, очевидно, r0 = 0, h0 = N2 - 1.
Пользуясь этими утверждениями, мы видим, что вклад от инстантонов с то-
топологическим числом q в A8.4), отнормированный как указано выше,
при любом q содержит множитель g~4Nq. При q = 1 интересующий нас
вклад записывается в форме B4), где g~s заменено на g~*N, а эффективная
константа связи g2 (X) определяется формулой
8тг2 8гг2 11 X
. B7)
3 Хо
Отметим, что одноинстантонный вклад B4) очевидным образом расхо-
расходится при Ф(А) = 1. Это означает, что соотношением B4) разумно пользо-
пользоваться лишь в случае, если множитель Ф(Л, а) подавляет вклад от инстан-
инстантонов больших размеров. Этого следовало ожидать, так как при Х-* °°
эффективная константа связи #(Х) перестает быть малой. Впрочем, не-
несмотря на упомянутую выше расходимость, было потрачено много уси-
усилий, для того чтобы проанализировать вклад инстантонов в статистичес-
статистическую сумму A8.3).
В общем случае, как будет показано в § 25, q -инстантонный вклад
при q > 1 может быть записан в виде
(Л)
'*' <28)
где интеграл берется по многообразию инстантонов (калибровочно экви-
эквивалентные инстантоны отождествлены),
At = d\ dA, At = l~d\ A - *)dA +dAd*A
— операторы Лапласа, действующие, соответственно, на функции и на 1-
формы со значениями в алгебре Ли калибровочной группы, dA — ковариант-
ный дифференциал, символ «обозначает переход к двойственной форме, ме-
мера d\iu порождается естественной метрикой на многообразии инстантонов,
а - константа, равная 4N для группы SU(/V). Детерминанты операторов
До4, Af в B8) регуляризуются с помощью обрезания по собственному
времени или с помощью f-функции (см. § 16 и § 21). (Нулевые моды
не учитываются при вычислении детерминантов.)
Из соотношения B8) можно получить выражение для одноинстантон-
ного вклада, заметив, что зависимость фигурирующих в ней детерминантов
от размеров инстантона может быть прослежена с помощью рассуждений,
примененных в конце § 21. (В силу трансляционной инвариантности эти
детерминанты не зависят от положения центра инстантона.) Мы не будем
проводить здесь соответствующего рассуждения, поскольку в § 25 содер-
198

вектору принадлежал подпространству 1тА. Это означает, что
г(А) = 1(А+). C)
Индекс эллиптического оператора А определяется соотношением
indexA=l(A)~r(A). D)
В силу C) индекс можно определить как разность числа нулевых мод
оператора А и сопряженного к нему оператора А+
index A = 1(А)- 1(А +). E)
Оказывается, что при непрерывном изменении эллиптического оператора
индекс оператора не меняется (если только во время изменения оператор
все время остается эллиптическим). Это утверждение будет следовать из
свойств эллиптических операторов, которые мы перечислим ниже. Оно
позволяет надеяться, что индекс эллиптического оператора можно вычис-
вычислить топологическими методами. Эта надежда оказывается справедливой -
существует теория, сводящая вычисление индекса к топологическим зада-
задачам (теория Атьи — Зингера). Мы не будем останавливаться на изложении
этой теории, но покажем, каким образом ценой удлинения вычислений
индекс может быть вычислен с помощью более элементарных средств.
Отметим только, что из неизменности индекса при непрерывном изменении
оператора нетрудно вывести, что индекс полностью определяется главным
символом этого оператора. (Два эллиптических дифференциальных опера-
оператора порядка г, отличающиеся только членами с производными порядка < г,
можно непрерывно перевести друг в друга, не изменяя членов со ставшими
производными. Поскольку эллиптичность оператора зависит только от глав-
главного символа, т.е. от членов со старшими производными, в этом процессе
эллиптичность сохраняется.)
Для того, чтобы получить аналитическую формулу, позволяющую вычис-
вычислить индекс, начнем с замечания, что индекс оператора может быть пред-
ствлен в виде
index A = 1(А+А) - 1(АА+). F)
В самом деле, если Af = 0, то, очевидно, A+Af = 0. С другой стороны, если
A+Af = 0, то (Af, Af) = (/, A+Af) = 0. Отсюда следует, что 1(А+А) =1(А).
Аналогично 1(АА + ) =1(А+).
Операторы А+А шАА+ являются неотрицательными эллиптическими опе-
операторами. Мы изучим сейчас операторы, обладающие этими свойствами.
Пусть В — неотрицательный эллиптический оператор. Тогда можно рас-
рассмотреть уравнение
Т-В*. G)
Это уравнение называют уравнением теплопроводности (по аналогии с
обычным случаем, когда роль оператора В играет положительный опера-
оператор, отличающийся только множителем от оператора Лапласа). Методы,
применяющиеся при изучении обычного уравнения теплопроводности,
позволяют установить, что уравнение G) при t > 0 имеет решение дЯя
любого гладкого начального условия, это решение единственно и являет-
171

ся гладкой функцией от параметра t и точки х?Л/. Оператор, ставящий
в соответствие начальному условию g € Г элемент g(t) ЕГ, получающий-
получающийся при решении уравнения G), обозначается символом ехр(— Bt). (Считая,
что к экспоненте от оператора можно применять обычные правила диффе-
дифференцирования, легко убедиться, что g(t) =exp(—Bt)g удовлетворяет урав-
уравнению G) с начальным условием #@) =g.)Можно доказать, что матрич-
матричные элементы < у\ txp(—Bt) I x) являются гладкими функциями при
t >0. Это позволяет утверждать, что оператор ехр(— Bt) имеет конечный
след. Более того, матричные элементы оператора R a exp (—Bt) R2, где
Ri, R-2 — произвольные дифференциальные операторы, также являются
гладкими функциями. Поэтому можно утверждать, что конечный след
имеет и этот оператор.
При изучении неотрицательного эллиптического оператора В оказывает-
оказывается очень полезной информация об асимптотике Sp ехр(—?/) при t -*+ 0
и ?->+°°. Асимптотика при t-*+°° становится очевидной, если предста-
представить Sp exp(—Bt) в виде суммы по собственным значениям:
Sp exp(-Bt) = 2 ехр( -1X,) = l(B) + 2 ехр(-ГХ,). (8)
Легко убедиться, что функция Spexp(-Sf) - 1(В) при t -*+°° стремится
к нулю по экспоненциальному закону.
Асимптотика выражения Sp exp(—iB) при t -*+0 имеет вид
2 4>k(B)tk, (9)
к
п и-2 л-4
где к пробегает числа — —; — , — ,... . (Символ п обозна-
г . г г
чает размерность многообразия М, а г — порядок дифференциального опе-
оператора 5.) Числа Ф/с(В) будем называть коэффициентами Силы. (Подроб-
(Подробнее о соотношении (9) и вычислении коэффициентов Фк(В) в случае,
когда В — оператор второго порядка, см. ниже.)
Для более общего выражения SpR ехр(-ГД), где R — дифференциаль-
дифференциальный оператор-порядка s, имеет место формула, аналогичная (9) . Именно,
асимптотика этого выражения при t ->+ 0 имеет вид
X*k(R\B)t-k, . A0)
" и-2/ и-27-2
где к пробегает множество чисел вида к = , ,.... а / -
г г
целая часть числах/2. Числа Ф*(/? I В) мы также будем называть коэф-
коэффициентами Сили.
Покажем, что индекс оператора может быть выражен через коэффициен-
коэффициенты Сили. Для этого заметим прежде всего, что операторы А +А и
АА+ и!Аеют одни и те же положительные собственные значения, причем
кратности этих собственных значений совпадают. (Если А +А f = X/, то
(АА+) (Af) =ХЛ/.) Используя этот факт и соотношение F), получаем
index X = Spexp(-M+,4)-Spexp(-M/f+) ' A1)
для любого положительного числа t. Переходя к пределу ?-> + 0в A1),
убеждаемся, что
index А = Ф0(А +А)-Ф0 (А А +). A2)
172

Отметим, что, используя соотношение A1) (или соотношение A2)), легко
получить сделанное выше утверждение о неизменности индекса при непре-
непрерывной деформации. В самом деле, можно проверить, что правая часть A1)
непрерывно меняется при непрерывном изменении оператора А. С другой
стороны, левая часть этого равенства является целым числом и поэтому
может измениться только скачком.
Остановимся коротко на вычислении коэффициентов Сили и индекса.
Рассмотрим прежде всего случай, когда В — скалярный эллиптический опе-
оператор второго порядка на «-мерном многообразии (т.е. В имеет форму
A9.1)). В этом случае можно искать асимптотику ( х I exp (—tB) I у)
при t -* О в виде
(х \exp(-tB)\y)^ ехр(- —'-— ]Z Ak(x, y)tk, A3)
\ t / к
где к пробегает значения — и/2, — и/2+ 1, —и/2+ 2,... (Мы пользуемся
здесь какой-либо фиксированной локальной системой координат.) Легко
проверить, что функция S(x,y) при фиксированном у должна удовлетво-
удовлетворять уравнению
dS Э5
Решением этого уравнения служит функция
S(x,y)= l- Pipe, yf, A5)
где р(х, у) — расстояние от х до у в римановой метрике ds2 = — а^ dxtdxk,
aik ~ матрица, обратная к а'к.
Выбрав 5 (х, у) в виде A5) и положив
(-Д,*)I/2, A6)
мы удовлетворим начальному условию
lim <x\exp(-tB)\y) = 8(x-y). A7)
t->+o
Для остальных функций Ак(х,у) из уравнения G) мы получим систему
уравнений, которую следует решать разложением по х-у (точка у все
время считается фиксированной).
Если известна асимптотика A3), то легко может быть найдена асимпто-
Л А
тика выражения Sp(R exp(-tS)) при t -* + 0, где R - дифференциальный
Л
оператор. В частности, мы будем рассматривать случай, когда R - диффе-
дифференциальный оператор нулевого порядка (оператор умножения на функцию
i?(x)); тогда
Sp(Rexp(-tB)) = f R(x)(x\exp(-tB)\x)dV. A8)
м
Таким образом, вычисление коэффициентов Сили сводится к нахождению
асимптотики выражения ( х I exp(-tB) \ x), которая в силу A3) имеет
вид
<* \exp(-tB)\x)=X%(x)tk, A9)
173

где %(х) = Ак(х,х), %(R\ В) = fR(x)Vk(x) dV. Описанная выше
процедура позволяет получить выражение для Ак (х, х) с помощью конеч-
конечного числа арифметических операций.
Указанный выше способ вычисления коэффициентов Сили принципиаль-
принципиально очень прост — он не требует взятия каких-либо интегралов и сводится
только к арифметическим операциям. Он применим не только для скаляр-
скалярных операторов второго порядка, но и для матричных операторов второго
порядка, главный символ которых является скалярной матрицей, напри-
например, для квадрата оператора Дирака. (Для матричных операторов в правой
части выражения A8) нужно заменить подынтегральное выражение на
TrR (д:) < jc | exp (—tB)\ x >, где Тг обозначает матричный след произ-
произведения матричных функций R(x) и < х |ехр(-?.б)| х >.) Однако вы-
вычисления, связанные с ним, довольно громоздки.
Эти вычисления были проделаны в общем виде для первых четырех
коэффициентов Сили. Приведем выражения, получившиеся для коэффи-
коэффициентов Ч?_2(.х)< Ф-ь*о(*) в случае, если многообразие четырехмерно.
Напомним, что мы предполагаем, что рассматриваемый эллиптический опе-
оператор имеет вид A9.1), где Ъ1 (х) й с(х) — матричные функции, ад'7 (х) -
скалярные функции. (Можно сказать, что а'' является матрицей только по
пространственным индексам /,/, но не по изотопическим индексам.) В силу
эллиптичности оператора квадратичная форма — а'1 (х) ptpj является зна-
коопределенной; без ограничения общности можно считать, что она
положительно определена. Это означает, что мы можем ввести риманову
метрику на многообразии М, положив ds2 =—aij(x)dxidx', где ац —
матрица обратная к а'1. Легко видеть, что для каждого из операторов
рассматриваемого нами класса можно найти такое калибровочное поле
А{ (х) на М, что этот оператор запишется в виде
В =„«?,?,-Е(х), B0)
где V,- — ковариантная производная по римановой метрике — atj(x) и
калибровочному полю А{ (х). Ковариантная производная Vy при действии
на поле Фа, имеющее только изотопический индекс, переводит его в поле
При действии ковариантной производной V,- на поле Ф'°, имеющее как
изотопический индекс а, так и пространственный индекс/, получается поле
где Г.у — символ Кристоффеля, построенный по метрике — д,у . Вычисления
показывают, что для оператора вида B0) коэффициенты Сили даются фор-
формулами
- <^( в) <22)
174

1
4тгJ
(-
1
30
1
- д
1
I
6
1
72
? Р + 1
2 1
180
р2 1
6
1
12
Здесь Rfjkb Rij>R ~~ тензоры Римана, Риччи и скалярная кривизна, &ц —
напряженность калибровочного поля Л,.
Выписанные только что соотношения могут быть применены также и
для операторов на «-мерном многообразии, если в них заменить D7гJ
на Dтг)"''2. В этом случае они, дают выражения для коэффициентов Сили
п п п
^>к(х) ПРИ к = — — ,——+ 1, — — +2. Из этих соотношений очевидным обра
зом получаются также формулы для коэффициентов Сили Ф^. (Переход
от Ф к(х) к Фк осуществляется с помощью взятия следа матрицы tyk(x)
и интегрирования по х.)
Покажем, как соотношения A2), B3) могут быть применены к вычис-
вычислению индекса евклидова оператора Дирака в калибровочном поле. (Мы
считаем, что снинорное поле преобразуется но представлению Гкалибровоч-
ной группы G. Определение оператора Дирака в калибровочном поле от-
отличается от стандартного определения заменой обычных производных на
ковариантные производные VM =ЭД + t (А м), где t — представление алгеб-
алгебры Ли Ч§, соответствующее представлению Т; см. § 19.
Будем рассматривать четномерный оператор Дирака. Этот оператор
разбивается на два оператора L и L + , действующие, соответственно, из
пространства левых спинорных полей в пространство правых спинорных
щшей и из пространства правых полей в пространство левых. В силу
самосопряженности и эллиптичности оператора Дирака операторы L и L +
являются сопряженными друг другу эллиптическими операторами. Нуле-
Нулевые моды оператора L можно назвать левыми нулевыми модами операто-
оператора Дирака У!, а нулевые моды оператора L + - правыми нулевыми модами
этого оператора. Таким образом, индекс оператора L можно интерпрети-
интерпретировать как разность числа левых и правых нулевых мод оператора Ди-
Дирака tQ .
Вычислим индекс оператора L, пользуясь соотношением A2). Ради про-
простоты будем рассматривать оператор Дирака на полях в четырехмерном
компактном многообразии с плоской метрикой (например на торе). Тогда
квадрат оператора Дирака rf дается формулой
1 1
- W(vMv,, + vvvM) - -
На левых и правых спинорных полях оператор W2 совпадает соответст-
соответственно с L + L nLL + . Вычисляя коэффициенты Сили с помощью формулы
175

B3), получаем
index/- = <t>0(L+L) - <t>0(LL+) =
32тг
Далее мы будем предполагать, что группа G — простая. Тогда можно вос-
воспользоваться соотношением
2 Tr (t(a) t(b)) = -ат<а, Ъ),
где а-? — число, называющееся индексом Дынкина представления 7";
см. § Т 21 (Мы предполагаем, что инвариантное скалярное произведение
< , > в алгебре Ли iS нормировано определенным образом (см. § Т 21).
Тогда число ат является целым.) Вводя обозначение
q(A) = -^ / < $,„, ^ *"><*«*, B4)
32тг
мы приходим к соотношению
index L = arq(A). B5)
Число q(A) называется топологическим числом калибровочного поля А
(см. § Т 24). Оно не меняется при непрерывном изменении калибровоч-
калибровочного поля. (Этот факт, доказанный в § Т 24, следует также из B4), по-
поскольку индекс оператора обладает этим свойством.)
Те же рассуждения, примененные к оператору Дирака на произвольном
четырехмерном компактном римановом многообразии, приводят к
формуле
index ^1f(( ^df))
24
= aTq(A) + - т(М),
о
где т(М) = / dV €^va^R^xp^ae ~ Челое число, не меняющееся
96тг
при изменении метрики на многообразии М. (Неизменность т(М) при
изменении метрики снова следует из аналогичного свойства индекса.)
Число т (Л/) носит название сигнатуры многообразия М.
§ 21. Детерминанты эллиптических операторов
Как мы говорили в § 16 детерминант (точнее, регуляризованный детер-
детерминант) неотрицательного оператора В может быть определен через f -(функ-
-(функцию этого оператора формулой In det В = —f'@). Это определение можно
применить в том случае, если f-функция f(s) = 2ХГ1 аналитически про-
продолжается в точку s = 0. Докажем, что для неотрицательного эллиптичес-
эллиптического оператора полюса аналитического продолжения функции f(s) нахо-
находятся в точках, отвечающих значениям показателя к в асимптотике B0.9)
176

n n — 2
выражения Sp exp (-tB) (т.е. в точках s = - — , - ,...). Вычет
г г
в полюсе s = к равен Vх (к)Ф_к(В), где Г(к) - значение Г-функции. При
s = О функция f(s) аполитична м f(O) = Фо (В) - 1(В). Отсюда следует
возможность определить det В с помощью f -функции.
Для того, чтобы исследовать поведение f-функции, воспользуемся со-
соотношением
^ VrX,)*. A)
Суммируя A) по всем не равным нулю собственным значениям операто-
оператора В, получаем
1 °°
*'(Sp exp(-tB)-l(B))dt. B)
/
T(s) о
(Для положительного оператора В мы уже использовали это соотношение
в § 17.) Чтобы B) имело место, необходимо, чтобы интеграл в правой
части сходился. В силу описанных выше свойств функции Sp exp (—tB)
(см. B0.8)) этот интеграл всегда сходится при больших t, а при t -* +0
он сходится для Re s > n/r. Представим функцию Sp exp (—tB) в виде
Spexp(-ffi)= 2 4>_k(B)rk+p(t), C)
k > 0
где в силу B0.9) \p(t) I <const • t при t -*+0. Разбив промежуток интег-
интегрирования в B) на промежутки [0, 1], [1, °°), получаем там, где справед-
справедливо соотношение B), формулу
f (s) =
I Ъ
P(s) \k > о s - k
\
t).
/
+ / (Sp exp (-tB) - l(B)) ts~ ldt + / p(t) -ts~l dt). D)
о о /
Очевидно, что правая часть соотношения D) определяет аналитическое
продолжение функции f (О в полуплоскость Re s > 0. Из D) ясна структу-
структура полюсов и вычеты в полюсах функции f (s). Особенность функции f (s)
при s = 0 оказывается устранимой в силу соотношения lim sT(s) = 1. Для
того, чтобы получить аналитическое продолжение функции f (s) в левую
полуплоскость Re s < 0, нужно использовать большее число членов асимп-
асимптотического разложения B0.9); нам это продолжение не понадобится.
Из соотношений D) можно получить следующее выражение для детер-
детерминанта неотрицательного эллиптического оператора:
In det В = I * -1 Ф^ к(В) + Г'A) (Ф0(Я) - 1(В)) -
к > О
- //-'(Spexp(-??)-/(?))Л-
1
- / r'(Spexp(-rfi)- 2 <i>_k(B)rk)dt. E)
О к > О
177

Другое определение детерминанта неотрицательного эллиптического
оператора подсказывается формулой
lndet A -In det Д = - / t~\Sp exp (-tA) - Sp exp (-tB)) dt, F)
о
справедливой для конечномерных положительных операторов. (Для того,
чтобы доказать эту формулу, следует выразить обе части равенства F)
через собственные значения операторов А и В и воспользоваться аналогом
формулы F) для чисел.) Для интересующих нас операторов интеграл
оо
ft'1 Sp exp (—tB) dt расходится на нижнем пределе. Чтобы получить
о
конечный результат, следует заменить нижний предел в этом интеграле на
е > 0. (В физической литературе эта процедура называется обрезанием по
собственному времени.) Мы будем говорить, что выражение
dete В = ехр ( - 2 / t ~l exp (-A,) dt), G)
где Л,- пробегает положительные собственные значения неотрицательного
эллиптического оператора В, получается из (бесконечного) детерминанта
оператора В с помощью обрезания по собственному времени. Выражение
для det6 В может быть переписано в виде:
lndete В = - / r!(Spexp(-^) -l{B))dt. (8)
с
Поскольку мы знаем асимптотику Sp exp (—tB) при t ->0, мы можем най-
найти асимптотику In dete В при е-*0. Легко видеть, что расходящаяся при
е ->• 0 часть In dete В может быть представлена в форме
- S к-*Ф_к(В)е~к +(Фо0В)-/(Д)Iпе. (9)
к > О
Конечная часть In det6 В будет обозначаться через In det' В. (Аккуратнее
можно определить In det' В как предел разности in dete В и выражения (9)
при е ->• 0.) Легко проверить, что In det В можно представить в форме
lndet' В = - / r^Spexpt-ri?) - 2 Ф_к(В) Гк -
О к > О
-0A -/)Фо(Я)-0(г- i)KB))dt. A0)
Сравниьая (:>) и A0) мы заключаем, что регуляризованный детерминант
det В, определенный с помощью f-функции несущественно отличается от
det' В, определяемого с помощью обрезания по собственному времени:
In det' В = In det Д'- Г'A) (Фо (Д)-/(?)). A1)
До сих пор мы рассматривали только детерминанты неотрицательных
эллиптических операторов. Детерминант произвольного эллиптического
оператора А может быть определен формулой
In det A = - IndexA+A. A2)
178

В заключение выведем соотношение, связывающее детерминанты опера-
операторов, отличающихся друг от друга численным множителем. Заметим преж-
прежде всего, что f -функции аВиВ связаны соотношением
f(s|«B) = сГ*Г(*|Д). A3)
(При больших s это вытекает из очевидной связи \'к = а\к между собствен-
собственными значениями операторов аВ и В; при остальных устанавливается с
помощью аналитического продолжения.) Дифференцируя A3) по s и по-
полагая s = 0, получаем
In det аВ = In det В + In a • f @ | В) =
= ln det В + In а • (Ф0(В) -/(?)). A4)
(Мы использовали здесь соотношение D).) Комбинируя A2) и A4),ви-
A4),видим, что для любого эллиптического оператора А
Indeta4 = Ый<АА+1па-(Ф0(А+А) -1(А)). A5)
Используем полученные только что формулы для того, чтобы проследить
за изменением детерминанта оператора Дирака в калибровочном поле
Ац (х) при масштабном преобразовании поля, т.е. при замене поля Ац (х)
на поле А^ (х) = ХЛМ (Xjc) . Ради определенности будем считать, что ин-
интересующий нас оператор Дирака задан на фермионных полях в четырех-
четырехмерном евклидовом пространстве. Преобразование W\, переводящее
фермионное поле ф (х) в поле ф ^ (х) = \2ф (Кх), сохраняет скалярное
произведение. Оно устанавливает унитарную эквивалентность операторов
xf = /f + ti/y) и хУ(Х) = \$ + ti/W)) (здесь как всегда t - представ-
представление алгебры Ли, отвечающее представлению калибровочной группы,
в пространстве которого принимают значения фермионные поля). Те-
Теперь, формально применяя соотношение A4), мы видим> что
In det#(x> = In detpr'^H In dettf - lnX • f @|#), A6)
откуда с помощью A5)
In det #a> = In det # +In Х-(/(#)--— Jd*x< ^„„.Я"). A7)
96rr
Применение A5) к операторам, определенным во всем евклидовом
пространстве, не вполне законно, так как мы все время предполагали,
что рассматриваемые эллиптические операторы заданы на компактном
многообразии. Для строгости необходимо ввести пространственное об-
обрезание, например, перейдя к рассмотрению полей, периодических по
каждой координате с периодом R (т.е. к рассмотрению полей на торе).
Поле Ар (х) нужно считать сосредоточенным в конечной области простран-
пространства. Чтобы соотношение A7) было вполне точным, нужно считать, что
в левой части детерминант вычисляется при параметре пространственного
обрезания \R, а все последующие выражения — при параметре R. Это ут-
утверждение можно применить также к случаю Ац (х) = 0, тогда оно поз-
позволяет найти зависимость детерминанта от параметра пространственного
обрезания. Обозначим через р (А) предел разности логарифма детерминан-
детерминанта оператора Дирака в калибровочном поле Ац и такого же оператора с
179

А^ = 0 при снятии пространственного обрезания (R -* °°). Тогда из сде-
сделанных выше утверждений ясно, что
?fltv,Fllv)d4x. A8)
96 7Г2
Это равенство следует рассматривать как более аккуратную запись соот-
соотношения A7).
Ясно, что проведенные выше рассуждения применимы и в других слу-
случаях, например, для оператора Лапласа в калибровочном поле.
§ 22. Квантовые аномалии
Принято говорить про аномалию в квантовой теории поля, если какое-то
соотношение, справедливое на классическом уровне, перестает быть вер-
верным после квантования.
Может случиться, например, что какая-то симметрия классического
лагранжиана перестает быть симметрией соответствующей квантовой
теории. В частности конформная инвариантность классического действия
не всегда влечет за собой конформную инвариантность соответствующей
квантовой теории.
Рассмотрим простейший пример — скалярное поле в обшей теории от-
относительности. Функционал евклидова действия этого поля запишем в виде
(О
Здесь ?Mj, — риманова метрика на четырехмерном многообразии М (при
переходе к евклидову действию псевдориманова матрика обшей теории от-
относительности заменяется на риманову). Символ R означает скалярную
кривизну, dV = \/g~d*x — элемент объема. Риманово многообразие М
будем предполагать компактным (это отвечает введению пространственно-
пространственного обрезания). Можно проверить, что функционал A) конформно инва-
инвариантен (т.е. не меняется при замене метрики g^v (х) на конформно эк-
эквивалентную ей метрику p(x)gfiV(x), если одновременно заменить <р(х)
на (р{х))~1!2 <р(х)). Как объяснено в § 17, величины, возникающие в
квантовой теории, могут быть выражены через функциональные интегралы,
подынтегральные выражения которых содержат ехр(—$). Рассмотрим ста-
статистическую сумму Zg, отвечающую функционалу A), т.е. функциональ-
функциональный интеграл
B)
Этот интеграл берется по пространству полей <р (х), снабженному скаляр-
скалярным произведением
Интеграл B) является гауссовым:
180

где
Sg = -A0 + ^R, E)
6
До — оператор Лапласа на функциях ip(x), построенный с помощью мет-
Л
рики gp,,, R — оператор умножения на R{x). Мы можем, таким образом,
выразить Zg через детерминант эллиптического оператора Sg
F)
Для того, чтобы проверить сохраняется ли конформная инвариантность
классической теории после квантования, сделаем в функциональном интег-
интеграле замену: у(х) -^ р(х)~1^2 у(х). Мы знаем, что подынтегральное выра-
выражение при этом не изменится, если одновременно заменить метрику g^ (x)
на p(x)g^v (x). Можно было бы ожидать поэтому, что статистическая сум-
сумма Zg не меняется при этой замене метрики (при конформном изменении
метрики). Однако, это ожидание не оправдывается. Дело в том, что, хотя
подынтегральное выражение не меняется, изменяется скалярное произ-
произведение C), по которому строится функциональный интеграл. (Грубо
говоря, меняется бесконечномерный элемент объема в функциональном
пространстве.) Именно этот эффект приводит к конформной неинвариант-
неинвариантности квантовой теории. Мы покажем сейчас, как вычислить вариацию
статистической суммы Zg при бесконечно малом конформном изменении
метрики. Это вычисление будет основано на общем утверждении о вариа-
вариации гауссова функционального интеграла в случае, когда меняется ска-
скалярное произведение в пространстве, по которому идет интегрирование.
Рассмотрим функциональный интеграл
Z = /exp (-§[/])<*/, G)
где § [f] — неотрицательный квадратичный функционал. (Этот интеграл
можно интерпретировать как статистическую сумму, отвечающую функ-
функционалу 8.) Будем считать, что при определении функционального ин-
интеграла используется зависящее от параметра и скалярное произведение
в пространстве, по которому ведется интегрирование. Тогда функцио-
функциональный интеграл G) тоже зависит от параметра м; мы его будем обозна-
обозначать поэтому символом Zu.
Найдем вариацию Zu при бесконечно малом изменении скалярного про-
произведения (т.е. при бесконечно малом изменении параметра и). Для этого
запишем, прежде всего, квадратичный функционал § в виде:
Slf]=<Su f,f)«, (8)
где Su — оператор, самосопряженный относительно скалярного произве-
произведения < , >„. Как объяснено в § 16, вычисление интеграла G) сводится
к вычислению детерминанта оператора Su:
Дифференцируя соотношение (8) по параметру и, получаем
~=-BuSu, A0)
аи
181

где Ви — оператор, описывающий изменение скалярного произведения
при бесконечно малом изменении параметра и,
d
du
Для того, чтобы вычислить вариацию Zu, мы вычислим сначала вариа-
вариацию Spexp(-5ur). воспользовавшись формулой A0). Очевидно, что
d ( dSu \
— Sp exp (- Su t) = Spl t exp (-- Sut) J =
du \ du /
d
= Sp(tBuSuexp(-Sut)) = -t — Sp(Buexp(-Sut)). A1)
dt
Соотношение A1) позволяет найти вариацию обрезанного по собственно-
собственному времени детерминанта оператора 5„ (см. B1.8)). Получаем
d d - dt
— In dete Su = - — / — Sp exp(-Su t) =
du du e t
d \dt
— Spexp(-5M0)— =
du / t
= / — Sp (Bu exp (- Su г)) dt = Sp (Bu exp (- Su f)) IГ - A2)
? af
Асимптотика правой части при Г -* °° управляется нулевыми модами опе-
оператора 5„. В самом деле, разлагая по собственным функциям </>„ опера-
оператора Su:
Sp Bu exp (- 5U f) = 2 < <р„ | Ви | vn > exp (- Х„ Г), A3)
н
видим, что в случае, если все собственные значения Х„ оператора Su по-
положительны, выражение A3) стремится к нулю при f->°°. Если же неотри-
неотрицательный оператор Su имеет нулевые моды, то
lim SpBHexp(-5ur)= 2 <«р„ | Ви \ipn > = SpBu ПE„), A4)
где оператор ПE„) осуществляет проектирование на нулевые моды опе-
оператора 5„. (Оператор ПE„), примененный к функции \р = Icnfe, дает
п
функцию ПE„)^/ = 2 с„1/)„, где суммирование ведется только по ну-
\„=о
левым модам.) Асимптотика правой части A2) при t -> + 0 для элиптичёс-
кого оператора описывается формулой B0.10). Напомним, что регуляри-
зованный детерминант In det' Su определяется с помощью выделения рас-
d ,
ходяшейся при е -*¦ 0 части из In dete5u. Считая, что — In det Su можно
du
182

d
получить выделением конечной части из — In det? Su, получаем
du
— In det' Su = - Фо Wu \SU) + SpBu П{Su). A5)
du
(Мы предполагаем, что Sp(Bu exp(— Su t)) при t -> + 0 имеет асимптотику
2 ^-k{Bu\Su)t'k. В частности, это условие выполнено, если оператор
к
Su является эллиптическим оператором на компактном многообразии,
а Ви — дифференциальным оператором.)
Проведенное выше доказательство не является строгим, хотя и при-
приводит к правильному ответу. (Вариация расходящейся части lndeteSu
могла бы давать вклад в вариацию конечной части.) Однако для эллип-
эллиптических операторов на компактных многообразиях нетрудно дать стро-
строгое доказательство, основанное на соотношениях B0.10) и B1.10). При
этом следует использовать тот факт, что из A1) вытекает формула
— Ф*Eи)=-*Ф*(В„|5и) A6)
du
для чисел ФкEм), определяющих асимптотику Spexp(- Su t) при f-* + 0.
Соотношение A5) можно записать также в виде
61ndet'5=-'*oEB|5') + SpEiJIIE)), A7)
где ЬВ — оператор, управляющий бесконечно малым изменением скаляр-
скалярного произведения,
§ < I/), <р' >
Соотношение A7) остается справедливым и в случае, если регуляри-
зованный детерминант определяется не с помощью обрезания по собствен-
собственному времени, а с помощью f-функции (т.е. при замене det'S на detS).
Из A7) вытекает формула для вариации статистической суммы G)
при бесконечно малом изменении скалярного произведения
51nZ= - 0toF?|S)-Sp(S?II(S))). A8)
Применим эту формулу для вычисления вариации статистической сум-
суммы B) при конформном изменении метрики. Как мы говорили, это вы-
вычисление сводится к нахождению изменения интеграла B) при изменении
скалярного произведения C). Легко видеть, что вариация скалярного
произведения при бесконечно малом конформном изменении метрики
gitv{x) A9)
дается формулой
y- B0)
(Мы учли, что поле меняется по закону Si/>(x) = —— 6p(x)ip(x). Таким
183

образом, оператор 8В, управляющий изменением скалярного произведения,
является оператором умножения на функцию 8р(х). Используя соотно-
соотношение B0.23), приведенное в § 20, мы получаем выражение для
/ 1 л\ 1 Л
Фо( ЬВI — До + ~ R \ Считая, что оператор — До + — Л не имеет нулевых
\ 6 / 6
мод, получаем
$%fS B1)
Таким образом, статистическая сумма B) конформно инвариантного
функционала A) меняется при конформном изменении метрики. Этот
факт носит название конформной аномалии.
Вариационная производная функционала действия по метрическому
тензору #м„ по определению отождествляется с тензором энергии-импульса
2 55
=-7=- —. . B2)
Из B2) можно получить выражение для среднего значения тензора
энергии-импульса по основному состоянию
2 51nZ
-7,- -. B3)
Из того факта, что функционал действия A) инвариантен при конформ-
конформном изменении метрики, вытекает, что след тензора энергии-импульса
в классической теории равен нулю:
Т» (х) = SiiV (х) Г"" (x) = — -^— gllP (x) = 0. B4)
\/g &gpv(x)
Мы использовали здесь то, что вариация функционала § при конформном
изменении метрики A9) равна
B5)
Отметим, что аналогичная формула справедлива для произвольного функ-
функционала. Используя аналог формулы B5) для функционала lnZ, а также
соотношения B3) и B1), видим, что
a0yb -Ra&Ra0 - До*). B6)
Таким образом, равная нулю в классической теории величина Т?(х) в
квантовой теории становится отличной от нуля. Часто именно это явление
понимают под конформной аномалией.
а Вычислим еще конформную аномалию для случая электромагнитного
поля. Как мы говорили в § 18, статистическая сумма в этом случае записы-
записывается следующим образом
Z = (det(-A1))-1/2det(-A0), B7)
184

где Д! = - (d* d + dd* ) - оператор Лапласа на 1-формах, До = —d*d -
скалярный оператор Лапласа. Мы хотим вычислить вариацию этой статисти-
статистической суммы при конформной вариации метрики. Вычисление основы-
основывается на общем результате, который нам будет полезен в дальнейшем.
Рассмотрим квадратичный функционал 8 [ f ], определенный на простран-
пространстве Pi и инвариантный относительно замены /-*•/" + Tg, где Т — линей-
линейный оператор, действующий из пространства Го в пространство Г^.
Примером такого функционала является функционал действия для
электромагнитного поля, инвариантный относительно калибровочных
преобразований. Оператор Т действует в данном случае из пространства
функций в пространство 1-форм (ковекторных полей) и переводит функ-
функцию g в 1-форму dg. Фиксировав скалярное произведение в Г, и ,Г0,
можно записать функционал $ в виде § [f ] = < Sf, f. >, где S — самосо-
самосопряженный оператор, и определить оператор Т*, сопряженный к Т.
Рассуждения, аналогичные проведенным в случае электромагнитного поля
(см. § 18), показывают, что статистическую сумму, отвечающую функцио-
функционалу $, разумно определить формулой
Z = (dclS)-ll2{detT*T?i2 =
= (det (S + ТТ* ))'u2dci T*T. B8)
(Во всяком случае, это определение разумно, если операторы S + ТТ* и
Т* Т являются эллиптическими, как мы будем предполагать дальше.)
Исследуем изменение статистической суммы B8) при бесконечно малом
изменении скалярных произведений в Го и Fj. (Как мы говорили выше,
решив этот вопрос, мы сможем исследовать аномалии.) Будем считать, что
в случае, когда изменение скалярных произведений в пространствах Pi и
Го описывается операторами 6/?! и ЬВ0 (т.е. 6</, g >,- = EBjf, g.){ =
= </, bBtg >,-, где </, g )t — скалярное произведение в Г,). Тогда вариа-
вариация статистической суммы может быть выражена соотношением
Sin Z = у0(в?, |п,) - |
где введены обозначения
Р(В\А) = Ч'0(В\А) - Sp(U(B)A),
? i = S Л ТТ*, п0 = Т+Т.
Доказательство этого соотношения в основном повторяет доказательст-
доказательство соотношения A8). Прежде всего следует проследить за вариацией опера-
операторов 5 и Г при изменении скалярных произведений. Легко убедить-
убедиться, что
S5 = -SBi ¦ S, C1)
5Г+ = T*8Bi - Sfi0- T* C2)
(последнее соотношение получается, если взять вариацию равенства
185

<T*f, g > о = </, Tg >,). Из выражений для 55 и ЬТ* получаем, что
5а, = -Sfii - S + TT*8Bt - ТЬВ0Т\ C3)
6а0 = Т*5ВХТ - dBQT*T. C4)
Используя соотношения
exp(-/aj)-r = Г-ехр(-Гпо), C5)
ехр(-/по).Г+ = Г*-ехр(-тО, C6)
expi-ta^-S = S-exp (-Га,), C7)
вытекающие из равенств а,Г=Га0, ао7' + =Г+а1, а, 5 = 5а,, получаем
if- - Spexp (-Гп,) + Spexp(-/no)j =
T r s
exp ( -fn,)) - Sp (SB0 exp (- fn0))). C8)
Теперь осталось заметить, что
5 f — — In detf n, + In dete ao\ =
oo / .
= - / y- 5 (- | Sp exp ( -rai) + Sp exp (- R:0)W
C9)
Подставив C8) в C9), получаем интеграл от производной, взяв который,
мы сведем исследование интересующей нас вариации к изучению асимпто-
асимптотик подынтегрального выражения.
Применим теперь соотношение B9) к изучению вариации статистический
суммы B7) при конформном изменении метрики. Роль операторов пг и
а 2 играют в этом случае операторы — Ь.г и —До- Бесконечно малое кон-
конформное изменение метрики g^ -*¦ A + a(x))gliV порождает изменение
скалярных произведений в пространствах 1-форм и О-форм (функций*),
186

описываемое операторами 5Вг = о и 5В0 = 2 о (здесь о— оператор умноже-
умножения на функцию о (х) ). Мы видим, что
51nZ = у
Число нулевых мод оператора Д,-, как мы знаем, равно /-мерному числу
Бетти Ь1 многообразия М. Если многообразие М ациклично в размерно-
размерности 1 и связно, то Ь1 =0, Ь° = 1. Нулевыми модами оператора До являются
постоянные функции. Очевидно, что
SpaII(A0) = V-1 fo(x)dV = у § In V,
где V = V (М) — объем многообразия М. Используя указанные в § 20 вы-
выражения для коэффициентов Сили, получаем
- 44RfiVR>lv + — R2 - 9AORJ.
§ 23. Инстантоны
Как мы говорили, различные величины в квантовой теории поля могут
быть выражены через функциональные интегралы, подынтегральное выра-
выражение которых содержит либо exp(iS), где 5 - функционал действия,
либо ехр(-5еис1), где Seucl - функционал евклидова действия.
Для приближенного вычисления этих интегралов можно использовать
метод стаилонарной фазы (в первом случае) или метод Лапласа (во втором
случае). Применение этих методов можно рассматривать как применение
квазиклассического приближения. В самом деле, возвращаясь к системе
единиц, в которой h Ф 1, мы видим, что в показателе экспоненты стоит
if\~1S или h-'Seuci, поэтому вычисление асимптотики при h ->0 может
быть проведено методами стационарной фазы или Лапласа.
Мы будем сейчас говорить об евклидовом случае. Применение метода
Лапласа требует нахождения наименьшего значения функционала 5 еис1 —
глобального минимума функционала 5eucl. Далее следует заменить вблизи
минимума функционал 5еис1 его квадратичной частью и вычислить полу-
получающийся гауссов интеграл. Можно применить аналогичную процедуру
не к глобальному минимуму, а к локальным минимумам функционала
5еис1. На первый взгляд получающийся вклад в функциональный интеграл
несуществен, так как он подавлен множителем ехр(- h AS), где Д5 -
187

разность значений 5eucl в локальном и глобальном минимумах. Тем не ме-
менее этот вклад представляет интерес, поскольку он приводит к поправкам,
выходящим за рамки теории возмущений. Кроме того, при вычислении
некоторых величин вклад от локальных минимумов является опре-
определяющим.
Локальные минимумы функционала 5еис1 называются инстантонами.
Нас будут интересовать в основном инстантоны в калибровочных теориях.
Однако мы начнем с рассмотрения инстантонов в простой квантово-механи-
ческой модели. Рассмотрим гамильтониан
р2
Н = + \(q2 - а2J A)
и соответствующее евклидово действие
Seuci = / \Ч\—) + М<72 ~ а2J\йт. B)
Потенциальная энергия U(q) = X (q2 — а2J имеет два минимума:
q = ±а — два классических основных состояния (классические вакуумы).
Эти же минимумы (точнее, функции q(r) = а и q(r) =— а) доставляют
наименьшее значение функционала B). Как было объяснено в § 2, исходя
из классического вакуума можно искать квантовое основное состояние,
заменяя сначала потенциальную энергию квадратичной, а затем учитывая
отклонения от квадратичное™ по теории возмущений. Действуя по этой
схеме, мы можем получить из двух классических вакуумов два основных
состояния гамильтониана A), имеющих одну и ту же энергию. Хорошо из-
известно, однако, что уровни энергии одномерного гамильтониана A) не вы-
вырождены. Кажущееся противоречие снимается тем, что вблизи каждого из
классических вакуумов мы имеем не стационарное, а лишь квазистационар-
квазистационарное состояние благодаря возможности туннельного перехода из одной ямы
в другую. Формально это сказывается в том, что ряды теории возмущений
расходятся, а энергия основного состояния неаналитична по h. Возмож-
Возможность туннельного перехода из одной ямы в другую приводит к тому, что
вместо двух основных состояний, переходящих друг в друга при замене q
ла — q, мы имеем два состояния — основное состояние с четной волновой
функцией и возбужденное состояние с нечетной волновой функцией.
Энергии этих двух состояний отличаются на экспоненциально малую
величину
Гп! / со3 \ .
Д Е = hco у ехр ( — 1, со = 2 а V 2 X . C)
тгХп \ 12 Xh/ W
В дальнейшем, как всегда, мы будем пользоваться системой единиц, в ко-
которой h = 1.
Попытаемся теперь исследовать гамильтониан A) с помощью евклидова
функционального интеграла. Основной вклад в этот функциональный
интеграл дают глобальные минимумы евклидова действия — классические
вакуумы q(r) = ±а. Однако кроме этих глобальных минимумов сущест-
188

вуют локальные минимумы функционала B) — функции
-<7(т) = ±s(t - с), D)
где
x(r) = ath(a\/TXr). E)
Значение функционала B) на функции D) равно -г- V 2 X а3, а Мы счи-
считаем, что функции q{r), на которых определен Seucl> заданы на всей чис-
числовой оси: — оо < г < + с». Строго говоря, нужно было бы сначала считать,
что эти функции определены на конечном промежутке, а затем устремлять
длину этого промежутка к бесконечности, т Отметим, что функционал B)
появлялся у нас уже раньше (в других обозначениях) как функционал
энергии B.4) одномерной полевой теории с лагранжианом B.3).
Функции D) интерпретировались как топологически нетривиальные
экстремали функционала энергии B.4). Эти функции дают минимум рас-
рассматриваемого функционала B) на классе полей, имеющих различные
пределы на бесконечности — топологически нетривиальных полей. Одну из
функций D) (скажем, отвечающую знаку " + ") будем называть инстанто-
ном, другую — антиинстантоном. (В смысле данного выше определения
инстантона как локального минимума функционала Seucl обе эти функ-
функции являются инстантонами.) Из функций D), являющихся стационарны-
стационарными точками функционала B), можно построить почти стационарные точки,
сшивая инстантонные и антиинстантонные решения, т.е. полагая, например,
ц{т) = s{t — c'i) при г < Ъ, q(r) = — s(r — с2) при т > Ъ (здесь ct<
< Ъ <с2); (рис. 17).
Аналогично строятся почти стационарные точки функционала 5еис1, со-
состоящие из нескольких чередующихся инстантонных и антиинстантонных
Рис. 17
решений. Эти почти стационарные точки иногда называют многоинстантон-
ными решениями. При вычислении функционального интеграла следует
учитывать все эти стационарные и почти стационарные точки функциона-
функционала 5еис,. Оказывается, что при этом можно воспроизвести ответ, полу-
получающийся элементарными квантово-механическими методами. Мы не бу-
будем воспроизводить этих вычислений. Отметим только, что значение
функционала 5еис1 на функциях D) в точности совпадает с показателем
экспоненты в C).
Из сказанного выше очевиден физический смысл инстантонов. Они яв-
являются решениями классических уравнений движения с мнимым временем
189

и описывают туннельный переход из одной ямы в другую (из точки
q = — а в точку q = d). Их учет в функциональном интеграле позволяет
исследовать явления, связанные с таким туннельным переходом. В частно-
частности, если мы хотим найти матричный элемент перехода из одного классиче-
классического вакуума в другой (матричный элемент ( — а | ехр (— Нт) \ а >,
т -*•«>), то в соответствующий функциональный интеграл топологически
тривиальные поля не вносят вклада. Это означает, что смешивание класси-
классических вакуумов происходит целиком за счет инстантонов.
Разумеется, в рассмотренной только что задаче использование инстанто-
инстантонов имеет только методический интерес — она существенно проще решается
элементарными методами. Однако инстантоны существуют и в более слож-
сложных случаях, и там их использование оказывается разумным. Это относит-
относится, например, к двумерному аналогу модели Джорджи—Глешоу (см. §4).
Очевидно, что евклидово действие в этой двумерной теории только обозна-
обозначениями отличается от функционала энергии в трехмерной модели
Джорджи—Глешоу. Это означает, что локальные минимумы функционала
энергии можно интерпретировать как инстантоны двумерной модели.
Топологически нетривиальные минимумы функционала энергии (магнит-
(магнитные монополи) можно рассматривать как топологически нетривиальные
инстантоны. (Инстантон называется топологически нетривиальным, если
его нельзя соединить с классическим вакуумом непрерывным семейством
полей, имеющих конечное евклидово действие.)
Перейдем к рассмотрению инстантонов в калибровочных теориях.
Предварительно мы исследуем структуру пространства калибровочных
полей в IR4, для которых конечно евклидово действие A8.2). Такие поля
на бесконечности близки к чисто калибровочным, т.е. имеют асимптоти-
асимптотику g'1(x)blig(x), где g(х) - функция со значениями в калибровочной
группе. * Для того, чтобы строго доказать это утверждение, нужно потре-
потребовать от рассматриваемых полей хорошего поведения на бесконечности.
Тогда из сходимости интеграла для евклидова действия следует, что
&nv(x) стремится к нулю достаточно быстро и, следовательно, поле с
нужной точностью можно рассматривать как чисто калибровочное. Ў Вся-
Всякому полю Лм с асимптотикой g'^xJS^^Jx) можно сопоставить гомо-
гомотопический класс отображения сферы большого радиуса в калибровочную
группу G, осуществляемого функцией g (х). Будем считать, что G - простая
некоммутативная компактная группа Ли. Тогда множество гомотопиче-
гомотопических классов отображений сферы 53 в G находится во взаимно однознач-
однозначном соответствии с множеством целы* иисел :
lS3,G) = n3(G) = Z F)
(см. § Т20). Таким образом, каждому полю с конечным действием со-
сопоставляется целое число — топологическое число поля. (Если G = SUB),
то, вспоминая, что группа SU{2) топологически эквивалентна сфере 53,
можно отождествить это целое число со степенью отображения S3 в S3.)
Целое число, сопоставленное полю, не меняется при непрерывном измене-
изменении поля, если в процессе изменения евклидово действие остается конеч-
конечным. Таким образом, пространство калибровочных полей с конечным
евклидовым действием распадается на компоненты, состоящие из полей
с одним и тем же топологическим числом. Оказывается, что топологиче-
190

ское число q поля Ац можно выразить аналитически с помощью формулы
V I** ^ < w Ю >
64я
± ^xi?^, *>">, G)
.32Я
где ^M" = — e^vpa &pO - антисимметричный тензор, дуальный к тензору
&ро. (Символ (а, Ь) обозначает инвариантное скалярное произведение в
алгебре Ли &, нормированное так, как указано в § Т21. В случае G =
= SU (и) это скалярное произведение определяется формулой {а, Ь) =
= -Spai.) Докажем соотношение G) для случая G - SUB) (об об-
общем случае, см. § Т23). Если G = SUB), элемент алгебры Ли можно
рассматривать как трехмерный вектор; в частности, Ац=(А1и, А\, А\~),
5ме = ф1^, F?p, F^,,). Легко проверить, что
где
j eabc.AbpAco) =
= e»vp°{A%F% - j eabcAavAbpAa)- (9)
Пользуясь этим соотношением, можно преобразовать четырехмерный
интеграл G) в интеграл по бесконечно удаленной сфере. Нетрудно убедить-
убедиться^ что для поля Аи, имеющего асимптотику g~lbug, интеграл по сфере
сводится к стандартному выражению для степени отображения g сферы S3
в SUB) = 53. (Слагаемым в правой части (9), содержащим Fapa, на бес-
бесконечности можно пренебречь.)
Воспользуемся соотношением G) для того, чгобы оценить снизу дейст-
действие для полей с фиксированным топологическим зарядом q. Нужную нам
оценку мы получим из соотношения
О ^ fd+xif^tf^J = 2/J4jc[(FmvJ ±< FMV, #M">]. A0)
В самом деле, из этого соотношения следует, что
8тг2
5 > —- \q\. A1)
g
Из вывода неравенства A1) видно, что знак равенства в A1) имеет место
в том и только в том случае, если
$»„ = #„„, q > 0, A2)
или
191

Поля, удовлетворяющие уравнению A2), называются самодуальными,
а поля, удовлетворяющие уравнению A3), - антисамодуалъными. Очевид-
Очевидно, что самодуальные и антисамодуальные поля являются экстремалями
евклидова действия. (Можно также непосредственно проверить с помощью
тождества Бианки (§ Т22), что из уравнений A2), A3) вытекают урав-
уравнения Эйлера для функционала A8.2) - евклидовы уравнения движения.)
Мы увидим, что существуют самодуальные поля с любым неотрицатель-
неотрицательным топологическим зарядом q и антисамодуальные поля с любым не-
неположительным зарядом q. Отсюда следует, что наименьшее значение
евклидова действия на полях с топологическим зарядом ц в точности рав-
8тг2
g
Для того чтобы построить само дуальное поле с q = 1 в случае G = SUB),
вспомним, что отображение
п -> и(п) = п° + i~on A4)
осуществляет тополо!ическую эквивалентное 1ь сферы S3 и группы SUB)
и, следовательно, имезг степень 1. (Здесь п = (и0, n) ? R4. \ п \г =
= (л0J + п2. а - (а1, а2, а3) - матрицы Паули.) Поэтому решение с
q = ! естественно искать в виде
При и(х) = \2(х2 + X2)"', где Л - произвольное число, мы действшель-
но получаем решение уравнения A2). Параллельный перенос переводит
самодуальное поле в самодуальное поле, поэтому мы получаем 5-пара-
5-параметрическое семейство решений уравнения с q = 1
\2 , / х -а \ / х- а \
А = ц-1 / JSnUl . A6)
м (х - аJ + X2 V I х - а I / М \\х-а\/
где и (и) определяется соотношением A4).
При пространственном отражении самодуальное поле переходит в
антисамодуальное, поэтому из полей A6) получается 5-параметрическое
семейство решений уравнения A3) с q = — 1. Оказывается, что описанные
только что поля исчерпывают (с точностью до калибровочной эквивалент-
эквивалентности) все решения с q - ±1. Самодуальные поля с q = 1 часто называю!
инстантонами: о самодуальных полях с q > 1 говорят как о q-инстантон-
ных решениях. Антисамодуальные поля с q = -1 называют антиинстанто-
нами. (С точки зрения общего определения, данного выше, все эти ноля
являются инстантонами.)
Отметим, что параметр X характеризует размер инстантона (или антиин-
стантона). а вектор а — положение центра инстантона. Для того чтобы
построить самодуальные поля с q = 1 в случае G = SU(jV), достаточно
заметить, что группа SUB) естественно вкладывается в SU(jV) (и соответ-
соответственно ее алгебра Ли — в алгебру Ли группы SU(AO) .Именно: можно рас-
рассматривать SUB) как подгруппу группы SU(jV), состоящую из матриц
192

вида
о
где А - 2 X 2-матрица. Мы можем поэтому рассматривать A6) как поле,
принимающее значение в алгебре Ли группы SU(/V). Оно, очевидно,
является самодуальным полем. Всякое решение уравнения самодуаль-
самодуальности с q = 1 для группы SUGV) калибровочно эквивалентно одному из
полей вида A6). Построение инстантонов с q = 1 в случае произвольной
простой компактной некоммутативной группы Ли G вполне аналогично.
При этом построении следует воспользоваться тем, что для любой такой
группы можно построить вложение группы SUB) в G, порождающее
изоморфное отображение группы ct3(SUB)) = Z на группу n3(G) (см.
§ Т20). Существование такого вложения позволяет рассматривать поле
A6) как решение уравнения самодуальности для группы G, имеющее еди-
единичный топологический заряд.
Более широкий класс само дуальных полей можно получить, используя
подстановку
Л а = (eaikbk-baib0)\nf, i, к =1,2,3,
-Л° = Эв1п/, A7)
где/ — произвольная функция. Поле A7) удовлетворяет уравнению само-
самодуальности, если функция / удовлетворяет четырехмерному уравнению
Лапласа (Э§ + V2)/=0.
В частности, если положить
я + 1 \f
f(x) = Б , A8)
i=i (х- xty
мы получаем самодуальное поле, имеющее особенности в точках хи . . .
.... xq+ t. Легко видеть, что эти особенности можно устранить с помощью
калибровочного преобразования, поэтому поле имеет конечную напряжен-
напряженность и конечное евклидово действие. Его топологический заряд равен q.
До сих пор мы рассматривали инстантоны в калибровочных теориях
в евклидовом пространстве. Разумно рассматривать также экстремали
евклидова действия на римановом многообразии. Как отмечалось выше,
при определении функциональных интегралов для евклидовых функ-
функций Грина следует произвести пространственное обрезание. Если при этом
наложены периодические граничные условия, то пространственное обреза-
обрезание эквивалентно рассмотрению калибровочных полей на 4-мерном торе.
Переход к полям на 4-мерной сфере 54 также можно рассматривать как
способ пространственного обрезания. Для инстантонов на римановом много-
многообразии применимы с незначительными модификациями рассуждения,
использованные выше в случае евклидова пространства. При этом под
тензором, двойственным к тензору S"aa, следует понимать тензор
193

где, как обычно, g обозначает детерминант метрического тензора gap.
Отметим, что уравнения A2) и A3) инвариантны относительно конформг
ного преобразования метрики gap(x) -*¦ g'ap(x) = p(x)gap(x).
Всякому калибровочному полю в IR4 можно сопоставить калибровочное
поле на сфере S4, определенное всюду, кроме северного полюса. (Для
того чтобы сделать это, нужно воспользоваться стереографическими коор-
координатами, позволяющими отождествить сферу S с выколотым север-
северным полюсом и IR4.) Наложенное нами условие, что поле в IR4 на бесконеч-
бесконечности близко к чисто калибровочному полю g~1(x)dtlg(x), означает,
что после калибровочного преобразования с функцией #(*) соответствую-
соответствующее поле на сфере можно непрерывно продолжить на Северный полюс.
(Подробнее см. § Т23.) Поэтому исследование калибровочных полей с
конечным евклидовым действием в R4 удобно проводить с помощью
перехода на сферу 54.
Чтобы задать калибровочное поле на 54 нужно согласованным об-
образом задать калибровочные поля А^\ А^ в двух системах координат,
покрывающих всю сферу. (Эти поля должны быть калибровочно экви-
эквивалентны там, где обе системы имеют смысл.) Геометрически калибровоч-
калибровочное поле на сфере интерпретируется как связность в расслоении, получен-
полученном из двух прямых произведений склеиванием с помощью функции,
устанавливающей калибровочную эквивалентность полей А^К А^.
Топологический тип этого расслоения однозначно определяет топологи-
топологическое число калибровочного поля (см. § Т25).
В стереографических координатах метрика на 54 конформно эквива-
эквивалентна метрике на ]R4, поэтому исследование уравнений самодуальности
и антисамодуальности в (R4 сводится к исследованию этих уравнений на
сфере 54. Мы покажем в следующем параграфе, что для G - SUB) при
любом q > 1 существует (Sq — 3)-параметрическое семейство имеющих
топологическое число q само дуальных полей HaS4, и следовательно, Ha[R4.
(Точнее говоря, после факторизации по калибровочной эквивалентности
множество решений уравнения само дуальности зависит от (Sq — 3) пара-
параметров.) Соответственно, при топологическом числе q < — 1 число пара-
параметров, описывающих калибровочно неэквивалентные решения уравне-
уравнения антисамодуальности, равно 8 | q | - 3.
Для того чтобы понять физический смысл числа 8^ — 3, рассмотрим
поле, которое вдали от точек д)( . . . , aq является чисто калибровочным,
а в случае, если точках близка к п{, имеет вид
X,- , / х - at \ / х - а( \ .
(х-щУ + Х2. \|дс-а, I/ \|х-а,-|/
где Vj G SUB), I х - в,-1 < I <?,- - а/1, X,- < \а( - а,- \ (грубо говоря, это
поле состоит из q далеких друг от друга одноинстантонных решений A6),
над каждым из которых совершен калибровочный поворот с матрицей
V/ 6 SUB)). Построенное нами поле является приближенным решением
уравнения самодуальности. Оно зависит от Sq параметров Dq параметров
п{, q параметров \[ и 3q параметров F/). Однако три из Sq параметров не-
несущественны (умножение всех матриц V( на одну и ту же матрицу
V G SUB) отвечает глобальному калибровочному повороту \\оппАц(х)).
194

Вблизи от построенных только что приближенных решений уравнения
самодуальности лежат точные решения этого уравнения. Подчеркнем,
что этот факт отнюдь не тривиален. В частности, из далеких друг от друга
инстантонных и антиинстантонных решений нетрудно построить приближен-
приближенные экстремали евклидова действия, но им не отвечают никакие точные
экстремали.
В случае G = SU(iV) ,N"> 2, пользуясь описанным выше вложением груп-
группы SUB) в SU(iV), поле B0) также можно рассматривать как приближен-
приближенное решение уравнения самодуапьности. Более того, можно считать, что
в B0) Vt G SU(iV) (т.е. поле B0) состоит из q далеких друг от друга
инстантонов, над каждым из которых совершен калибровочный поворот
с матрицей V{ G SU(A0). Полученное семейство приближенных решений
уравнения самодуальности зависит от 4Nq параметров. В самом деле, каж-
каждая матрица Vi определяется N2 — 1 параметром (т.е. dimSU(iV) =
= N2 - 1). Однако всякая матрица V из подгруппы SUB) С SU(N) ком-
коммутирует с (N — 2J-мерным семейством матриц. (Это семейство состоит
из матриц, удовлетворяющих условию Via = Vai = 0, если а < 2, i > 2,
иУаь = Х5Ой, если а, Ъ = 1,2.) Поэтому, хотя на первый взгляд поле B0)
зависит от (N2 — \)q + 5q параметров, реальное число параметров на
(N — 2J<? меньше. Можно доказать, что вблизи построенного только что
семейства приближенных решений лежит 4М?-мерное семейство точных
решений уравнения самодуальности с топологическим числом q. Более
того, всякое решение уравнения самодуальности с топологическим числом
q можно перевести в одно из полей, принадлежащих 4Л^-параметрическо-
му семейству, с помощью калибровочного преобразования из группы Go°.
Напомним, что калибровочные преобразования из G" определяются функ-
функциями g (х), обращающимися в единицу в фиксированной точке х0. В слу-
случае IR4 мы считаем, чтох0 = °°, т.е. полагаем
lim g(x) = 1.
Ограничение калибровочными преобразованиями из группы G" исклю-
исключает глобальные калибровочные преобразования. Если отождествлять
поля, получающиеся друг из друга с помощью любого калибровочного
преобразования, то число параметров, от которых зависит общее решение
уравнения самодуальности, уменьшится. Оказывается, что при топологиче-
топологическом числе q > N/2 число rq параметров, от которых зависит общее решение
уравнения самодуальности, равно ANq — (iV2 — 1). В самом деле, обозна-
обозначим через Ял группу, состоящую из калибровочных преобразований, не
изменяющих инстантон А. При переходе от отождествления инстантонов с
помощью группы G" к отождествлению с помощью группы всех калибро-
калибровочных преобразований G°° интересующее нас число параметров умень-
уменьшится на dimG — dim На, где А — инстантон общего положения. Можно
проверить, что в случае q > N/2 инстантон общего положения изменяет-
изменяется при любом калибровочном преобразовании (dimHA = 0) и, значит,
число параметров уменьшается на dimG = dimSU(/V) = N2 — 1. При
1 < q < N/2 можно доказать, что всякий инстантон А калибровочно экви-
эквивалентен полю, принимающему значения в алгебре Ли группы SUB<?)C
С SU (N), и вывести отсюда, что в случае общего положения dim HA =
195

= (N — 2qJ. (Число (N — 2qJ возникает как размерность группы
U(N — 2q), состоящей из элементов группы SU(iV), коммутирующих
с элементами подгруппы SUB<?). Мы видим, что интересующее нас число
параметров rq равно 4q2 + 1.
Покажем, что инстантонам в калибровочной теории также отвечает тун-
туннельный переход между классическими вакуумами. Будем пользоваться
калибровкой А о = 0. Тогда поле с наименьшей энергией (классический
вакуум) — это поле А((х), удовлетворяющее условию 5^ = 0 (г, / =
= 1, 2, 3). Всякое такое поле является чисто калибровочным, т.е. пред-
представляется в виде Aj(x) = g~l(x) dtg(x). Мы будем считать, что функ-
функция g (x) имеет предел при х -*¦ °°
Ит g(x) = So- B1)
X -> оо
Тогда функцию g (х) можно рассматривать как отображение сферы 53.
полученной из IR3 присоединением бесконечно удаленной точки в груп-
группу G. Ў Условие B1) можно обосновать с помощью предельного
перехода от конечного объема. Оно отвечает нулевым граничным условиям
на поле в конечном объеме. Периодическим граничным условиям отвечает
функция g(x), заданная на трехмерном торе Т3, т.е. отображение тора
Г3 в группу G. т
Всякой функции g(x), удовлетворяющей условию B1), и, следова-
следовательно, всякому классическому вакууму можно сопоставить целое число,
характеризующее гомотопический класс порождаемого этой функцией
отображения сферы S3 в G. (Напомним, что группу G мы считем простой
некоммутативной компактной группой Ли и, следовательно, { S3, G } = ^.)
Инстантоны отвечают туннельному переходу между классическими ва-
вакуумами, характеризуемыми различными топологическими числами.
В самом деле, можно считать, что инстантон подчинен калибровочному
условию Л о = 0 и на бесконечности имеет вид/4>1~ g ~1 (х) Ь ^ g (рс), где
g(x) = g(x, t) = 1 при xG R3,r ->-«> ипри-°° < t <°°,x -*°°; g(x,t) ->
-*g(x) приГ->+°°. (Выполнения этих условий можно добиться с помощью
калибровочного преобразования.) Если инстантон Ац (х, t) удовлетворя-
удовлетворяет наложенным только что условиям, то он описывает туннельный пере-
переход из классического вакуума Л,- = 0 в классический вакуум А( =g'1bi g.
В частности, поле A6) калибровочно эквивалентно полю, которое описы-
описывает туннельный переход из классического вакуума с топологическим
числом, равным нулю, в классический вакуум с топологическим числом,
равным 1.
Как мы говорили, инстантоны следует учитывать при вычислении функ-
функциональных интегралов вида A8.3), A8.4) методом Лапласа. Сущест-
Существенно, однако, что при вычислении инстантонного вклада только интеграл
по направлениям, ортогональным многообразию инстантонов, можно
заменять на гауссов; поэтому метод Лапласа сводит интеграл к интегралу
по многообразию инстантонов. Учитывая калибровочную инвариантность
и используя трюк Фаддеева — Попова, удается свести интеграл по беско-
бесконечномерному многообразию инстантонов к интегралу по конечному
числу параметров, характеризующих калибровочно неэквивалентные
друг другу инстантоны. Например, в случае G = SUB) вклад инстантонов
196

с топологическим числом q = 1 в интеграл A8.4) может быть записан в
виде
/Ф(Х,а)р(Х,д) d\ da, B2)
где Ф(Х, а) получается при подстановке в функционал Ф(А) инстантона
A7) с параметрами \,а;
ф = р(Х,д) d\ da B3)
— некоторая мера на многообразии инстантонов. Мера dfi может быть
выражена через бесконечномерные детерминанты. Подробнее задача о
вычислении меры на многообразии инстантонов будет изучена в § 25.
Заметим здесь только, что в случае q = 1 мера dn может быть найдена
из требования ренорм-инвариантности ответа. В частности, оказывается,
что при G = SUB), q = 1 инстантонный вклад с точностью до множителя
имеет вид
)^Л1 B4)
где g(X) — эффективная константа связи, отвечающая масштабу X (им-
(импульсу р = 1/Х). Она задается формулой
8тг2 _ 8тг2 22 X
_ _ __ jj^ B5)
**(X) g2 3 Хо
где Хо — точка нормировки. Мера X~s d\ dAa является мерой на много-
многообразии инстантонов, инвариантной относительно трансляций и растяже-
растяжений пространства IR4. (Более того, эта мера не меняется при произвольных
конформных преобразованиях пространства 1R4.)
Отметим, что интеграл A8.4) расходится; расходимости устраняются,
если разделить его на A8.3) и провести перенормировку. При вычислении
^-инстантонного вклада мы делим интеграл A8.4) на вклад в A8.3)
от топологически тривиальных полей, вычисленный методом Лапласа.
Множитель g'8 в B4) можно заменить на #(Х)~8, однако эта замена не яв-
является необходимой, поскольку мы ограничиваемся только основным
приближением метода Лапласа, а различие между g~e и #(Х)~8 играет
роль лишь в следующем приближении.
Остановимся коротко на происхождении множителя g~*. При фор-
формальном вычислении интеграла A8.4) методом Лапласа при интегрирова-
интегрировании по каждому направлению, ортогональному многообразию инстантонов,
возникает множитель #"'. Общее число этих множителей равно
dim &q - (rq + dim G °° - hq), B6)
где dim&g и dimG°° - (бесконечные) размерности пространства всех по-
полей с топологическим числом q и группы всех калибровочных преобра-
преобразований, Гд — число параметров, от которых зависит решение уравнения
самодуальности с топологическим числом q (после отождествления ка-
либровочно эквивалентных полей), hq — размерность подгруппы груп-
группы G°°, оставляющих на месте инстантон с топологическим числом q.
Мы не предполагали в формуле B6), что G = SUB). Если сделать это пред-
предположение, то га = 8<7 - 3, ha - 0 при q > 1. При вычислении инстантонного
197

вклада в A8.4) необходимо, как мы говорили, разделить на вклад от
инстантонов с топологическим числом q = 0 (вакуумных полей) в ин-
интеграл A8.3); этот вклад содержит множители g'1 в количестве
dim?0 - dimG°° + 3. (Мы применяем B6), считая, г0 = 0, h0 = 3.) Пола-
Полагая dimS, = dim Ёо. видим, что в формуле для <7-инстантонного вклада
содержится 8<7 множителей g~l. Если G = SU(N), то, как сказано выше,
rq = ANq - (N2 - 1), hq = 0 при q >N/2; при 1 < q <NB имеем rq =
= Aq2 + 1, hq = (N - 2qJ; при q = 0, очевидно, r0 = 0, h0 = N2 - 1.
Пользуясь этими утверждениями, мы видим, что вклад от инстантонов с то-
топологическим числом q в A8.4), отнормированный как указано выше,
при любом q содержит множитель g~4Nq. При q = 1 интересующий нас
вклад записывается в форме B4), где g'6 заменено на g~4N, а эффективная
константа связи ?2(Х) определяется формулой
8ст2 8тг2 11 X
B7)
g2 3 Хо
Отметим, что одноинстантонный вклад B4) очевиднымобразом расхо-
расходится при Ф(А) = 1. Это означает, что соотношением B4) разумно пользо-
пользоваться лишь в случае, если множитель Ф(Х, а) подавляет вклад от инстан-
инстантонов больших размеров. Этого следовало ожидать, так как при \-*- °°
эффективная константа связи #(Х) перестает быть малой. Впрочем, не-
несмотря на упомянутую выше расходимость, было потрачено много уси-
усилий, для того чтобы проанализировать вклад инстантонов в статистичес-
статистическую сумму A8.3).
В общем случае, как будет показано в § 25, q-инстантонный вклад
при q > 1 может быть записан в виде
*•' - - <28)
где интеграл берется по многообразию инстантонов (калибровочно экви-
эквивалентные инстантоны отождествлены),
Aj? =< dA, Af = ±d* A - *)dA +dAd*A
— операторы Лапласа, действующие, соответственно, на функции и на 1-
формы со значениями в алгебре Ли калибровочной группы, dA - ковариант-
ный дифференциал, символ «обозначает пере ход к двойственной форме, ме-
мера dpo порождается естественной метрикой на многообразии инстантонов,
о - константа, равная 4N для группы SU(/V). Детерминанты операторов
До1, А? в B8) регуляризуются с помощью обрезания по собственному
времени или с помощью f-функции (см. § 16 и § 21). (Нулевые моды
не учитываются при вычислении детерминантов.)
Из соотношения B8) можно получить выражение для одноинстантон-
ного вклада, заметив, что зависимость фигурирующих в ней детерминантов
от размеров инстантона может быть прослежена с помощью рассуждений,
примененных в конце § 21. (В силу трансляционной инвариантности эти
детерминанты не зависят от положения центра инстантона.) Мы не будем
проводить здесь соответствующего рассуждения, поскольку в § 25 содер-
198

жится несколько более общее рассмотрение, основанное на аналогичной
идее.
При квантовании калибровочной теории мы исходим из функционала
евклидова действия A8.1). Заметим, что, не изменяя классических урав-
уравнений движения, можно прибавить к этому функционалу слагаемое
i-0&,*?)= i-efd4x < fpt.fap > ^va0. B9)
В самом деле, как мы знаем, выражение B9) (так называемый 0-член)
только множителем отличается от топологического заряда, не меняется
при бесконечно малой вариации калибровочного поля, и, следовательно
не вносит вклада в уравнения движения. Можно прийти к тому же выводу,
заметив, что подынтегральное выражение в B9) является полной дивер-
дивергенцией. Однако на квантовом уровне введение в -члена приводит к сущест-
существенным эффектам. Это становится очевидным при вычислении инстантон-
ного вклада. В самом деле, ясно, что при наличии в -члена в выражении
для вклада от полей с топологическим числом q (в частности, в выраже-
выражении для <7-инстантонного вклада) появится дополнительный множитель
ехр(-16тг2<70г)-
Таким образом, в калибровочной теории возникает новый параметр в.
§ 24. Число инстантонных параметров
Основной целью этого параграфа будет подсчет числа параметров, от ко-
которых зависит <7-инстан энное решение на сфере 54. Однако, поскольку
большая часть рассуждений проходит для произвольного компактного
риманова многообразия М, мы начинаем с этой общей ситуации.
»Прежде всего повторим в удобных для нас бескоординатных обозначе-
обозначениях некоторые из рассуждений предыдущего параграфа. Пусть М — четы-
четырехмерное компактное ориентированное риманово многообразие, G -
простая компактная некоммутативная группа Ли. Калибровочное поле А
на многообразии М геометрически интерпретируется как связность в глав-
главном расслоении ?(?", М, G, р) с базой М (см. § Т22). Напряженность & по-
поля М рассматривается как 2-форма на М, принимающая значения в слоях
ассоциированного векторного расслоения %Т(ЕТ,М, & ,рт), где & — алгеб-
алгебра Ли группы G,nG действует на 8 с помощью присоединенного представ-
представления. Операция перехода к дуальному антисимметричному тензору в силу
соответствия между антисимметричными тензорами и формами порождает
некоторую операцию на формах; эта операция обозначается символом *.
1 1 ~
(Например, если f = -&a&dxa Л dxfi, то * f = -$a&dxa Л Л:*3, где
2 2
1
Vg?a0y6 ^yS ¦ Ecjma = aadxa есть 1-форма, то *а = —bapydxaf\
2 6
Л dx& Л dxy, где ba0y = y/geaeyS а6. Подробнее см. § Т 11.)
Евклидово действие калибровочного поля А с точностью до множителя
равно скалярному квадрату напряженности этого поля
f)= -L- f(f f«e)dK A)
4g2
199

(Скалярное произведение двух 2-форм / = —fapdxa Л dx^ и h =
1 2
= — hapdx* Л dxB, принимающих значения в слоях векторного расслоения,
определяется формулой (/, h) = /</ьр, ha0)dV.) Это определение приме-
применимо, если в слоях векторного расслоения задано скалярное произведение,
а на базе фиксирована риманова метрика. Аналогично скалярному произ-
произведению 2-<J)opM определяется скалярное произведение Аг-форм, см. § Т 1 ].)
Введенное в § Т 24 топологическое число калибровочного поля может
быть, очевидно, записано в виде
(*•*¦)• . B)
Используя соотношения (* f, *&") = (&,&) и (<f, *?) - (*f, f ), полу-
получаем, что
(F ± *f, f± *f) = 2{f, W) ± 2{f, *f) > 0. C)
Отсюда ясно, что (?", $f) >($',*&'), причем равенство выполнено только
в случае, если
*"= *f. D)
Мы видим, что S[A] > &n2g 2q и равенство достигается только в случае,
если выполнено уравнение самодуальности D). Аналогично, если q < 0,
то S[A] > 8n2g'2 \q\n равенство достигается только для полей, удовлет-
удовлетворяющих уравнению антисамодуальности
F=- *f. E)
Разумеется, проведенное только что рассуждение срочностью до обозначе-
обозначений совпадает с рассуждениями предыдущего параграфа.
Пусть А — калибровочное поле, удовлетворяющее уравнению самодуаль-
самодуальности D). Будем искать решение А' уравнения D), близкое к решению А.
Поскольку калибровочно эквивалентные решения следует отождествлять,
мы наложим на А' условие
d^(A'rA)=0. F)
снимающее калибровочную свободу. Напомним, что разность двух калибро-
калибровочных полей можно рассматривать как 1 -форму, принимающую значения
в слоях векторного расслоения %т (Ет, М, &, рт). Символ dA обозначает
ковариантный дифференциал (см. § Т22). Сопряженный ему опера-
оператор d*A можно рассматривать как ковариантную дивергенцию: если а =
, то
V ц обозначает ковариантную производную относительно римановой
метрики.
Итак, пусть для поля А' = А + а выполнено уравнение D) и условие F).
Тогда 1-форма а удовлетворяет уравнениям
P[dAa + ^[а,а])=0, G)
d\a = 0. (8)
200

Здесь введено обозначение Р = — A - ¦). Символ [а, а], где а =
определяется как 2-форма [я\,дм] dxx Л dx11.
Рассмотрим уравнения G) и (8), пренебрегая нелинейными членами
в G). В этом приближении уравнения G), 'й"* могут быть записаны в
форме
&а=0; (9)
здесь 5 - линейный оператор, преобразующий 1-форму в пару (/, А),
где / = PdA a — антисамодуальная форма (т.еТ форма, удовлетворяющая
условию /= — ¦/), а А— 0-форма dAa; все рассматриваемые формы
принимают значения в слоях расслоения %т. Пространство 1-форм бу-
будет обозначаться символом Fi, пространство 0-форм — символом Г0 и
пространство антисамодуальных 2-форм - символом Г2. Таким образом,
оператор 3 является оператором, действующим из Yx в Г2 + Го. Легко
проверить, что 3— эллиптический оператор.
Для этого необходимо заметить, что оператор 3 в локальных коорди-
координатах переводит 1 -форму a -a^dx^ в пару (/, А), где
f=^fXvdxx A dx\
f\u= - (Эх** - Э„вх) - -y/ge^vpadpaa + ..., ft = „ ,
отброшенные члены не содержат производных и не влияют на главный
символ оператора).
Таким образом, главный символ оператора 5" является матрицей линей-
ного оператора, переводящего дх в пару ( —(P\av - pva\ -
VpoPpaa), ip^a^ ). Этот оператор действует из пространства
размерности 4dimG в пространство такой же размерности. В самом деле,
а^ при каждом значении X = 1, 2, 3, 4 принимает значения в алгебре Ли.
Из компонент антисамодуального тензора Д» независимыми являются
только три, а 0-форма А имеет одну компоненту. Легко проверить, что глав-
главный символ оператора Sf является невырожденным линейным операто-
оператором и, следовательно, $ - эллиптический оператор. Строго говоря, для
того, чтобы иметь возможность говоритьоб эллиптичности оператора ff,
нужно представить пространства Vt и Гг + Го как пространства сечений
некоторых векторных расслоений. Переход к локальным координатам
определяет такое представление.
Риманова метрика в М и инвариантное скалярное произведение в #
как мы говорили, позволяют определить скалярное произведение форм,
принимающих значения в слоях расслоения ?т. Отсюда следует, что мы
можем ввести скалярное произведение в Fj и Г2 + Го и рассмотреть сопря-
сопряженный оператор 5"*, действующий из Г2 + Го в Fi. Легко проверить, что
оператор 2Г * переводит пару (/, A) G Г2 + Го в 1-форму d'Aj + dAh? Tj.
201

Для этого нужно воспользоваться соотношением
(PdAа, /) + (d*Aa, A) = {a,d*f) + (a,dA А).
Мы должны найти число решений уравнения (9), т.е. найти число l(SF)
нулевых мод оператора SF . Оценку для числа нулевых мод можно полу-
получить, вычислив индекс оператора аГ,
/E') = index S + /( О > index 5.
Индекс оператора 5 легко вычисляется с помощью известных тополо-
топологических результатов. Более длинное, но тем не менее вполне доступное
вычисление может быть проведено с помощью указанного в § 20 выраже-
выражения B0.12) индекса оператора через коэффициенты Сили. Ограничимся
для простоты случаем, когда Л/=54,аС= SUB). Тогда можно проверить,
что index & = 8<? -- 3 и. значит, l($") > 8q - 3,
Далее, можно доказать, что в рассматриваемом случае /( <0~*) = 0, т.е.
оператор 3~* не имеет нулевых мод.
Мы видим, что /(«О = 8q — 3. Иными словами, в линейном приближе-
приближении система уравнений G), (8) имеет (8q -3) -параметрическое семейство
решений. Отсюда можно вывести существование такого же семейства ре-
решений у нелинейной системы G). (8).
Вывод основан на бесконечномерном варианте теоремы об обратной
функции. Эта теорема относится к нелинейному уравневию вида W(x) = у,
где х принадлежит банахову пространству ?",, у - банахову пространст-
пространству Н2, a W - дифференцируемый нелинейный оператор, действующий из Ег
в Е2- Предполагается, что W(xo)= y0 и ищется решение уравнения W(x) = у.
где у близко к у0. В случае, когда дифференциал W оператора W в точ-
точке х0 является обратимым линейным оператором, доказывается, что
для у, близких к у0, существует единственное решение уравнения W(x) = y,
близкое к х0. (Грубо говоря, если линейный оператор W обратим, то
близкий к нему нелинейный оператор W тоже обратим.) Из сформулиро-
сформулированной только что теоремы об обратной функции можно вывести утвержде-
утверждение, относящееся к случаю, когда в условиях эгой теоремы дифферен-
дифференциал "Iff', хотя и не является обратимым, но обладает тем свойством, что
образ этого оператора совпадает со всем пространством Е2- Иными слова-
словами, мы предполагаем, что уравнение W (л-) = у имеет решение при лю-
любом у, но не предполагаем, что это решение единственно. Очевидно, чтс
решение уравнения W (х) = у образует /-параметрическое семейство, где
/ = I(W) - число нулевых мод оператора W. Можно показать, что тогда
решение уравнения W(x) = у, при у близком к у0, также образует /-пара-
/-параметрическое семейство. Для доказательства выберем / линейных функ-
функционалов /¦) (х) , . .., Г){х), подчинив их единственному условию, чтобы
они были линейно независимы на подпространстве, выделяемом уравне-
уравнением W (х) = 0 (в пространстве нулевых мод оператора Ш). Эти линей-
линейные функционалы задают отображение г пространств /Г, в fFt' (г(х)' =
= (г,(х), . . ., г,(х))). С помощью отображений W и г определяем отобра-
отображение W' пространства ?, в Е2 X р'. (Это отображение переводит х €Et
в пару (W(x), r(x)) е Е2 X IR'.) Из наложенных нами требований вытекает,
что дифференциал отображения W' в точке дг0 является обратимым линей-
линейным оператором, следовательно, по теореме об обратной функции, уравне-
202

ние W(x) = (у, г.) имеет решение для у, близких к у0, г, близких к нулю.
Поскольку всякое решение этого уравнения является решением уравнения
W(x) = у, мы получаем /-параметрическое семейство решений уравнения
W(x) = у для у, близких к у о (в частности, для у = у0).
Нам осталось заметить, что линейную систему G), (8) можно записать
в виде одного нелинейного уравнения Та = 0, где Т — нелинейный опера-
оператор, переводящий 1-форму j 6 Г) в пару (/, К) G Г2 + Го, где / =
= Р( dAa + — [а, а] ), h = d*Aa. Рассмотренный выше линейный опера-
оператор Sf является дифференциалом нелинейного отображения Т при а = 0.
Из соотношения 1C*) = 0 вытекает, что оператор «/"отображает Fi на
все пространство Г2 + Го. Это означает, что оператор Т удовлетворяет ус-
условиям, наложенным на оператор W в сформулированном выше утвержде-
утверждении. Мы можем, таким образом, сказать, что число параметров, от кото-
которых зависит решение уравнения Та = 0 (т.е. число параметров в решении
системы G), (8)), равно 1C)-
Отметим, что проведенные выше рассуждения нуждаются в некоторых
уточнениях. Как уже говорилось, все рассматриваемые функции, формы,
сечения расслоений мы, во избежание излишних оговорок, предполагаем
гладкими (бесконечно дифференцируемыми). Однако при этом ограни-
ограничении не удается превратить Pt и Г2 + Го в банаховы пространства с нуж-
нужными нам свойствами. Поэтому приходится несколько расширить эти
пространства. Можно, например, расширить пространство Г! до прост-
пространства 1-форм, коэффициентные функции которых имеют к производ-
производных, и производные порядка к интегрируемы с р-той степенью, где р > 4.
(Это пространство называется соболевским пространством и обозначает-
обозначается Wp.) Тогда на элементы Г2 + Го нужно наложить условие интегри-
интегрируемости производных порядка к — 1 со степенью р.
Вместо того чтобы исключать калибровочную свободу с помощью ус-
условия (8), можно говорить о многообразии инстантонов, в котором отож-
отождествлены калибровочно эквивалентные поля. Мы условимся обозначить
символом Nq бесконечномерное множество решений уравнения самодуаль-
самодуальности D), символом Rq будем обозначать множество, получающееся изЛ^
отождествлением калибровочно эквивалентных инстантонов. (Иными
словами, Rq — это множество орбит Nq/G°° группы локальных калибро-
калибровочных преобразований G°°.) Из сказанного выше следует, что для G =
= SUB), М = S4, q > 1 множество Rq имеет размерность 8q — 3.
Остановимся на случае произвольной простой компактной некомму-
некоммутативной калибровочной группы G. (Многообразие по-прежнему считаем
сферой S4.) В этом случае соотношение l(S ) =0 уже не всегда имеет
место. Заметим прежде всего, что /( ?F+) = 1C&*), где 3Sf+ - оператор,
переводящий пару (/, К) ? Г2 + Го в пару (Д^/, &{h), где Д^ =PdA d+A -
оператор, действующий в Г2, До = d\dA — оператор в Го- Отсюда следует,
что/E"+) =/(Д?)+/(Д$).
Аналогично, 1C~) = 1C+ 3) = /(Д?), где Д? =dAPdA +dAdA. Можно
доказать, что /(Д^) = 0 для любого инстантона на сфере 54. Число /(До) =
= l(dA) равно размерности подпространства ЖА в Го, состоящего из эле-
203

ментов, удовлетворяющих условию dA со = 0. Всякому элементу со ? Го от-
отвечает бесконечно малое калибровочное преобразование, определяемое
соотношением
ЬА = dA со.
(Иными словами, можно отождествить Го с алгеброй Ли & °° бесконечно-
бесконечномерной группы Ли G°° всех локальных калибровочных преобразований.)
Таким образом, ЖА состоит из всех бесконечно малых калибровочных
преобразований, не меняющих инстантона А. Можно сказать, что ЖА явля-
является алгеброй Ли группы НА, состоящей из всех калибровочных преобра-
преобразований, переводящих инстантон А в себя. В случае G = SUB) для инстан-
тонов с топологическим числом q > 0 группа НА тривиальна, а при q = 0
dimHA = dimЖА = 3. (Поле А = 0 не изменяется при всех калибровочных
преобразованиях, определяемых функцией, не зависящей от координат, —
глобальных калибровочных преобразований.) Если группа НА тривиаль-
тривиальна (т.е. 1(?~+) = сНтЗ€л = 0), инстантон называется неприводимым. Реше-
Решение уравнения само дуальности в окрестности неприводимого инстантона А
можно исследовать точно так же, как в случае группы SU B). Число па-
параметров, от которых зависит решение уравнений G), (8), если А - непри-
неприводимый инстантон,равно/( <?") = index &. В случае группы SU(«)
index S) = Anq - (n2 - 1),
где q - топологическое число. Если q > -п, то существуют неприводимые
инстантоны, и, следовательно, интересующее нас число параметров равно
4nq - (и* - 1). Отсюда следует, что
dimRq = 4nq~(n2 - I), q> — n.
Если инстантон приводим, то
= index &+d\mKA.
Таким образом, число нулевых мод оператора У зависит от размернос-
размерности группы НА. Инстантон называется регулярным в случае, если эта размер-
размерность не меняется при малом изменении поля А. Можно доказать, что раз-
размерность множества Rq равна / ( S) ) = index 5" + dim ЖА, где А - регуляр-
регулярный инстантон. Замечая, что
index ff = /(Д? ) - 1(АА ) - 1(АА ) = /(Д? ) - 1(АА),
dimJC4 =l(AA),
видим, что"
dim Rq = l(AA). A0)
§ 25. Вычисление инстантонного вклада
Как мы говорили, инстантоны существенны при вычислении функцио-
функциональных интегралов типа A8.3), A8.4) методом Лапласа. Напомним, что
метод Лапласа основан на разложении показателя экспоненты в окрест-
окрестности минимума этого показателя и вычислении гауссова интеграла, полу-
204

чающегося, если отбросить все члены в разложении, имеющие степень > 2.
В случае инстантонов мы сталкиваемся с ситуацией, когда минимум показа-
показателя экспоненты достигается не в одной точке, а на целом многообразии.
В этой ситуации метод Лапласа требует модификации, которая сейчас бу-
будет указана.
Рассмотрим интеграл
JK. A)
(Интеграл берется по и-мерному риманову многообразию М, символ dV
обозначает элемент объема на этом многообразии.)
Будем считать, что функция S (х) достигает своего наименьшего значе-
значения у на Аг-мерном многообразии N (т.е. S (х) > у для всех точек х & М к
S (х) = у при х ? N). Наложим на многообразие N (критическое многооб-
многообразие) условие невырожденности, т.е. потребуем, чтобы второй дифферен-
дифференциал функции S в каждой точке многообразия N был квадратичной формой
ранга п — к. Второй дифференциал функции S в точке х ? N нам будет удоб-
удобно записывать в виде d2S = — (S"dx, dx), где S" — самосопряженный
линейный оператор в касательном пространстве к М в точке х ? N. Тогда
.наложеннное нами требование означает, что оператор S" имеет ровно А: нуле-
нулевых собственных значений. (Очевидно, что всякий вектор, касательный к
N, является собственным вектором оператора S" с нулевым собственным
значением; поэтому оператор S" имеет не менее к нулевых мод.) Основ-
Основной член асимптотики интеграла A) npug -»-0 дается формулой
-v exp f-4V ^(*)(det ?"(*))~1/2ф, B)
где d/л — мера на N, задаваемая римановой метрикой, а детерминант вырож-
вырожденного оператора S" (х) понимается как произведение ненулевых соб-
собственных значений этого оператора. Для того, чтобы прийти к формуле B),
нужно заметить, что асимптотика интеграла A) определяется окрестностью
многообразия N и что при интегрировании по направлениям, ортогональ-
ортогональным N, можно пользоваться обычным методом Лапласа.
В случае если функции \р (jc) и S (х) инвариантны относительно компакт-
компактной группы Ли G, действующей на многообразии М, можно видоизменить
выражение B) для асимптотики интеграла A), Преобразование много-
многообразия М, отвечающее элементу g ? G, обозначим T(g). Будем считать,
что все преобразований T(g) сохраняют риманову метрику. Если со —
элемент алгебры Ли i$ группы G, то вектор, получающийся из точки х ?
? М при бесконечно малом преобразования и>, будем обозначать &хи>.
(Иначе говоря, Т{\ + и>)х-х + &хш.) Линейный оператор У х можно ин-
интерпретировать как дифференциал нелинейного отображения g -*¦ T(g)x в
точке g = 1. Инвариантное скалярное произведение ( , > в алгебре Ли
& группы G нормируем условием, чтобы объем группы G в соответствую-
соответствующей инвариантной римановой метрике был равен 1.
Многообразие N, на котором достигается минимум функции S, очевид-
очевидным образом инвариантна относительно группы G, так же как и функции,
205

фигурирующие в выражении B) для асимптотики интеграла A), Поэтому,
как было объяснено в § 18 (см. A8.24)), интеграл по Л^можно преобразо-
преобразовать в интеграл по пространству R = N/G орбит группы G в многообразии N.
В результате получаем главный член асимптотики интеграла A) при g -*-0
в виде
^4V C)
где
D)
Sxy'2, E)
d/к о — элемент объема в R, отвечающий естественной римановой метрике
в R, V(H) обозначает объем стационарной подгруппы группы G относитель-
относительно римановой метрики в G. (Мы предполагаем, что все стационарные под-
подгруппы сопряжены фиксированной подгруппе Н, поэтому все они имеют
один и тот же объем.)
Полезно отметить, что с помощью соотношений
det Dg = det S"(x)det $x $1 = det S" det <2~J Jx, F)
uetUxl=&etS'+S'x, G)
где Do = S" (x) + ffx 5X, Of = i x &x, можно записать Z (x) также сле-
следующим образом
Z(x) = (detD;Sr1/2(detn^). (8)
Для того чтобы проверить соотношение F), следует заметить, что из G-ин-
вариантности функционала S вытекает инвариантность второго дифферен-
дифференциала этого функционала в точке х ? N относительно преобразования dx -+
-+dx + 5~д.?, где % & &. Это свойство инвариантности влечет за собой соот-
соотношение S"?TX = 0, из которого, в свою очередь, вытекают равенства
S"$x$x = О, &X$~XS" = 0. Таким образом, для операторов S vl&xJx
можно найти общую полную систему собственных функций, на каждой из
которых либо S" > либо SFх&х имеет нулевое собственное значение. Пос-
Поскольку при вычислении детерминанта вырожденного оператора' мы при-
принимаем в расчет только ненулевые собственные значения, отсюда следует
F).
Применим сформулированные только что результаты об асимптотике
конечнократных интегралов с бесконечным числом минимумов к вычис-
вычислению инстантонного вклада в интегралы A8.3), A8.4). Роль функции
1
—— S(x) будет у нас играть функционал евклидова действия Seuci(A) =
g
1
= —— {§, &) , функции S (х) при этом отвечает функционал {$, $).
Ч
Если мы считаем, что интеграл берется по калибровочным полям с топо-
топологическим числом <7 >0 (пространство &q этих полей играет роль мно-
многообразия М), то роль многообразия N играет пространство Л^ всех реше-
решений уравнения самодуальности B4.4).
206

Для того, чтобы разложить евклидово действие по отклонениям от ре-
решения уравнения самодуальности, удобно переписать это действие в виде
и воспользоваться формулой для вариации напряженности при бесконечно
малом изменении калибровочного поля:
8&=dA8A A0)
(см. § Т24). Из этой формулы видно, что 8(f- *&) - 2PdA8A, где Р =
1
= — A — *). Пользуясь (9), получаем, что приращение евклидова действия
при бесконечно малом изменении самодуального калибровочного поля А
равно
ASeuci = —г(PdAbA,PdA8A) + . .. = —-(dAPdA8A, &4) + . .. , A1)
2g2 2g
где отброшенные члены имеют порядок > 2 по 8А.
Мы вычислили таким образом второй дифференциал функционала Seuci
в точках многообразия Nq. Роль оператора S", как мы видим, играет опера-
оператор dAPdA, действующий в пространстве Fi, состоящем из 1-форм со зна-
значениями в слоях расслоения ?т (Ет, М, &, рт). Далее, функционал 5еиС1
инвариантен относительно бесконечномерной группы G°° локальных калиб-
калибровочных преобразований. Ее алгебра Ли Э" может быть отождествлена
с пространством Го сечений расслоения %т. Действие бесконечно малого
калибровочного преобразования ые5?" =Гона калибровочное поле А
определяется формулой
8A=dAu. A2)
Это означает, что роль оператора ЯГХ в рассматриваемой задаче играет
оператор dA, действующий из Го =&°° в Fi, а оператору &%!зх отвечает
оператор dAdA.
Мы видим," таким образом, что выражению E) в общей формуле D)
соответствует в нашем случае выражение
ZA =(det(^^))-1/2det(^^I/2 =
= (detA?rI/2detA^, A3)
где Af = dAPdA + dAd+A, До = dAdA . (Отметим, что операторы Af и До
совпадают с операторами, рассматривавшимися в предыдущем параграфе.)
Алгебра Ли ЖА стационарной подгруппы НА состоит из элементов ш S
$°° = Го, удовлетворяющих условию dAш = 0 (т.е. из ковариантно пос-
постоянных сечений расслоения %т). Таким образом, размерность группы НА
равна числу нулевых мод оператора dA или, что то же, числу нулевых мод
оператора AJ> = dAdA. (Как мы видели, для G = SUB), q > 1 оператор
Д<? не имеет нулевых мод; при q = 0 есть три нулевые моды, отвечающие
глобальным калибровочным преобразованиям.)
Мы готовы теперь применить формально соотношение C) к вычислению
вклада инстантонов с топологическим числом q > 1 в функциональный
207

интеграл A8.4).Получаем
/ 8тг2
r
A4)
Здесь <2ц0 обозначает меру на многообразии инстантонов Л^, отвечающую ес-
естественной римановой метрике на этом многообразии. А Если А и А + а -
два инстантона, а -»• 0, то расстояние между соответствующими точками в
Rq равно (а + dA ip, a + dA ipI12, где у находится из условия d А (а + dA ip) =
= 0. В самом деле, поле А + а + dy получается из А +а с помощью бесконеч-
бесконечно малого калибровочного преобразования и вектор а + dAy ортогонален
орбите группы G°°, проходящей через А. Ў Почти все фигурирующие в A4)
выражения бесконечны. Например, dimSq и dimA^ — это (бесконечные)
размерности пространства Sq всех калибровочных полей и множества Л^
инстантонов с топологическим зарядом q, детерминанты бесконечномерных
операторов Д^ и Д$ также представляют собой расходящиеся величины.
Выражению A4) можно пытаться придать смысл, отбросив бесконечные
постоянные множители и заменив фигурирующие в A4) детерминанты на
соответствующие регуляризованные выражения (см. § 16). Такое рас-
рассмотрение уже позволяет заключить, что при интегрировании по многооб-
многообразию инстантонов ^следует пользоваться мерой dfx = ZAdn0,Tp,e ZA опре-
определяется формулой A3), в которой под детерминантами следует понимать
регуляризованные детерминанты. Однако более последовательно cfpeMHTb-
ся придать смысл выражению A4), перейдя сначала к решетке, а затем
устремляя шаг а решетки к нулю (снимая обрезание по импульсам).
Мы покажем сейчас, что эту программу можно провести для инстантон-
ного вклада в евклидовы функции Грина. Этот вклад, очевидно, записывает-
записывается в виде
¦(-?
A5)
где \(А) = ZA V(HA)~1, а Х@) дается той же формулой с А = 0. (Напом-
(Напомним, что евклидовы функции Грина получаются как частные от деления ин-
интегралов A8.4) и A8.3).) При вычислении интеграла A8.3) — статисти-
статистической суммы — мы считаем, что основной вклад вносят только инстан-
fоны с топологическим числом q = 0 — классические вакуумы.)
Число о в A5) равно &imNq — dimA^o- Это соотношение не имеет четко-
четкого смысла, поскольку размерности А', и А^ бесконечны. Однако, (бесконеч-
(бесконечную) размерность Nq можно представить в виде
dimNq = dim Rq + (dim G°° - dim HA) =
°\ A6)
(Мы воспользовались соотношением dim^ = t(AA), справедливым для
регулярного инстантона А (см. B4.10).) В частности
dimAr0 = dim^o+(dimG0° -dim#°) =
= dim G°° - dim G. A7)
208 .

Мы видим, что
т = dim Rq - dim Ro - (dim HA - dim H°) =
= l(AA) - /(Д^) - (/(Д?)-/(Д8)). A8)
Чтобы избежать рассмотрения бесконечных размерностей в этом рас-
рассуждении следовало бы перейти к решетке. Переход к решетке нужно со-
совершить и для того, чтобы придать смысл подынтегральному выражению
в A5). В частности, мы должны проследить за асимптотикой детерминан-
детерминантов решеточных аналогов Af (а) операторов Д/4 при а -»-0; не пытаясь ре-
решить эту не очень легкую (хотя, видимо, вполне доступную проблему)
мы заменим решеточное обрезание обрезанием по собственному времени
(см. § 21), считая, что асимптотика lndetA/4(a) совпадает с асимптоти-
асимптотикой lndeteA/*, где е = const a2. Пользуясь соотношением B1.9), мы мо-
можем тогда заключить, что при а -*¦ О
In det Д/ (а) « In detc Af =s
В решеточном случае, как мы говорили в § 18, аналогом калибровоч-
калибровочного поля служит функция by, определенная на ориентированных ребрах
решетки (мы считаем, что для каждого ребра фиксирована некоторая ори-
ориентация) . Интегрирование по пространству калибровочных полей Ау. за-
заменяется интегрированием по. произведению стольких экземпляров груп-
группы G, сколько есть ребер решетки. Элемент объема в этом произведении
определяется инвариантной римановой метрикой
ds2 = T,(b-ldby, b-xdby) A9)
у
(суммирование по всем ребрам решетки). Для того, чтобы установить
связь между элементом объема dfi0 в Rq и его решеточным аналогомс?До>
вспомним, что калибровочному полю у4м сопоставляется Ьу =
= Рехр (- fA^dx11). Если шаг решетки мал, то Ьу = 1 -Аца (мы считаем,
у
что ребро у направлено по оси хи). Пользуясь этим замечанием, представ-
представляем элемент длины A9) в форме
ds2 =а~2 /Шд, SA")dV = a-2(8A, SA). B0)
Отсюда видно, что
dna6~a-dimR4dno=a-l(A^dno. B1)
Далее, объем решеточного аналога группы НА следует вычислять с по-
помощью инвариантной метрики
ds2 = Z<pe1dPa,p-ldpa) B2)
о
в решеточном аналоге группы калибровочных преобразований G°°' Здесь
Ра, — элемент группы G, сопоставленный каждой вершине решетки (сум-
(суммирование по всем вершинам). Каждому калибровочному преобразованию
с функцией р(х) отвечает решеточное калибровочное преобразование;
14. А.С. Шварц 209

элемент длины B2) связан с метрикой в группе G°° соотношением
ds2 *>a~*f<p-l(x)8p(x). p-1(x)8p(x))dV. B3)
Это означает, что при введении решетки V(HA) следует заменить на
A
Теперь мы в состоянии исследовать асимптотику выражения Jq при
а ->¦ 0. Заметим прежде всего, что выражение \(А) d/j.ol\(O) при а -+0 имеет
асимптотику
const ехр( - (р(А) - р@)) In a), B4)
где
В самом деле, разность
(- — In det Д? (а) + In det Д^ (а) V
/ ' „ а \
— ( In det Д"(а) + In det Ao(a) )
\ 2 /
имеет при д-»-0 асимптотик^
1 \
-- (Фо( АА ) - 1(А?))+ (Фо(До ) - /(До )) Jin e-
~(~ ^ (Ф°(Л'} ~ /(А'}) + (Фо(Д») ~ 7(Дой)|п е =
= - (р(Л) - р@)) In а + (/(Д?) - 2/(Д^)) - (/(Д?) - 2/(Д8)) In a
(слагаемые, расходящиеся линейно и квадратично по е = а2, сокращаются).
Учитывая расходящиеся множители, содержащиеся в ф0 и V(HA)~t,полу-
V(HA)~t,получаем B4). Как мы видим, для того, чтобы при снятии решеточного обре-
обрезания выражение A5) стремилось к конечному пределу, зависимость го-
голой константы связи g от постоянной решетки а нужно выбрать ' таким
образом, чтобы выражение
—^— q+(p(A)-p@))\na
g (a)
iimcjiv/ конечный предел. Вычисляя коэффициенты Сили Ф0(Д^) и Ф0(Д01)
(см. § 20), получаем закон изменения g (a):
1 1 1 11
g2(a) g2 8тг2 6
где а — коэффициент, зависящий от калибровочной группы. Это — стан-
стандартный закон изменения голой константы связи, возникающий при пере-
перенормировке калибровочной теории. (Число g имеет смысл физической
константы связи, v - точка нормировки). Если закон измененияg (а) выб-
выбран н виде B6), то для инстантонного вклада в евклидовы функции Грина
210

в пределе а ->0 получаем конечный ответ
Ja «* constg~° expf г—)/ Ф(Л)бЬ>, B7)
\ а2 /о
\ о / Л о
где
= ZAV(HA)'1 =(det Af)-1/2(det Д^)К(ЯЛ)-!. B8)
Мы не включаем в общую константу не зависящие от А множители у @)
и V(HA)~l, поскольку они меняются при конформном изменении метри-
метрики, которое мы будем рассматривать далее. Для группы SU(m) имеем
а = 2и, а = 4nq. (Можно доказать, что в общем случае а = 2a.q.) Бесконечно-
Бесконечномерные детерминанты в B8) считаются регуляризованными так, как это
объяснено в § 21.
Вычисление этих бесконечномерных детерминантов представляет собой
нелегкую (хотя и разрешимую) задачу. Однако существенную информацию
о мере dv на многообразии инстантонов Rq можно получить, не вычисляя
детерминантов, а воспользовавшись конформной инвариантностью функ-
функционала действия A8.2) для калибровочного поля (легко видеть, что этот
функционал не меняется при замене римановой метрики-^ v (x) в много-
многообразии М на конформно эквивалентную ей метрику#^„(д:) = e°^g^v(pc)).
При конформном преобразовании метрики функциональный интеграл
A8.4) не остается неизменным. Как говорилось в § 22, этот факт носит
название конформной аномалии и связан с изменением скалярного произ-
произведения в пространстве полей, по которому идет интегрирование. Соот-
Соответственно изменяется также мера dv = y(A)dn0 • (у@))~1. Однако,
применяя результаты § 22, можно проследить за изменением меры dv при
бесконечно малом конформном изменении метрики многообразия М. При
этом удобно использовать то, что в силу B2.28) ZA можно интерпретиро-
интерпретировать как статистическую сумму квадратичного функционала SA (a) -
- {d\PdAa, а), инвариантного относительно преобразований а -*а + dAco.
Применяя соотношение B2.29), получаем выражение для вариации
ZA при бесконечно малом конформном изменении метрики 5?д„ =
(х)
b\nZA = -@(а|Д?) - ^Bа|До), B9)
где а — оператор умножения на а(х). Отсюда получается выражение для
вариации 8dy меры dn = ZA V(HA)~ 1 dfx0 =y(A)dn0 при бесконечно ма-
малом конформном преобразовании метрики
C0)
AMepa dfix) и объем V(HA) также изменяются при конформном изме-
изменении метрики. Их изменение управляется нулевыми модами операторов
Д? и До- Члены, отвечающие изменению меры dfj.o, сокращаются с вкла-
14* 211

дом нулевых мод в вариацию статистической суммы ZA. т Аналогичным
образом доказывается, что вариация у@) ПРИ конформном изменении
метрики равна
«7@) =Q-*(a|A?) - Ф(а|До))т@). C1)
Комбинируя C0) и C1) видим, что
0(|)
C2)
bdv =(-ФE|Д?) Ф(а|Д)
Вычисляя коэффициенты Сили (см. § 20), получим, что
bdv =( а/а(х)(Гм„, f"v)dv)dv. C3)
Ч 3847Г2 /
(Впрочем, ниже мы покажем, что при исследовании инстантонов в
IR4 можно обойтись уже использовавшимися выше коэффициентами
Фо(Д?), Фо(До)-)
Обратимся к случаю, когда М — сфера S4 с обычной метрикой. На
S4 действует 15-мерная группа конформных преобразований Q (преобра-
(преобразование х' ¦= у (х) назьшается конформным, если оно порождает конформ-
конформное изменение метрики: ds'2 - еа^ ds2). Благодаря конформной инва-
инвариантности уравнения само дуальности, действие группы Q на S4 порож-
порождает действие этой группы на многообразии Rq. Мера B8) не инвариантна'
относительно этого действия, однако соотношение C0) позволяет про-
проследить за изменением этой меры при преобразованиях группы Q. В слу-
случае q = 1 группа Q действует на Rq транзитивно, (т.е. любой инстантон
можно получить из любого другого с помощью конформного преобра-
преобразования.) Поэтому, исходя из соотношения C0), можно найти меру dv
на Rx однозначно с точностью до числового множителя. Собственно, мера
на Rq в случае М = S4 не представляет существенного интереса — пере-
переход к полям на 5"* был для нас лишь способом пространственного обреза-
обрезания и нам важен только предел формулы для инстантонного вклада в
случае, когда радиус сферы стремится к бесконечности (точнее, когда
размеры рассматриваемых инстантонов много меньше радиуса сферы).
При этом предельном переходе получается мера dp на множестве инстан-
инстантонов в IR4. Эту меру мы сейчас исследуем.
Как было выяснено в § 23, в случае G = SU(n) инстантоны с топо-
топологическим числом q = 1 характеризуются размером X и четырехмерным
вектором а, указывающим положение центра инстантона. Мера dv на
Rt записывается в виде dv = т(Х, a) d\ d4a. Ясно, что мера dv не ме-
меняется при параллельном переносе в 1R4, и, следовательно, функция
т(Х, а) не зависит от а. Далее, из C2) можно заключить, что вариация
212

/ 1 \
-4 1 + —а be
меры dv при растяжении jc -*\ 1 + —а к имеет вид
8dv = о/-Фо(Д^) — Фо(До) Ф0(Д?)
Фигурирующие в этой формуле коэффициенты Сили уже были исполь-
использованы выше. Получаем
11
§dv = — aqadv,
12
откуда при q = 1
/11 \d\ .
dv = const -expl—alnXJ—era.
Тем самым мы доказали приведенную в конце § 23 формулу для одно-
инстантонного вклада. В случае q = 2, G = SUB) многообразие Rq имеет
размерность 13 (dim R2 =8-2 — 3 = 13),а орбиты группы Q bR2 — раз-
размерность 12. Поэтому конформные свойства меры dp позволяют найти
эту меру с точностью до произвольной функции от одной переменной.
§ 26. Функциональные интегралы для теорий,
содержащих фермионные поля
В § 17 было показано, что многие важные физические величины в кван-
квантовой механике и квантовой теории поля могут быть представлены в
виде функциональных интегралов. В подынтегральные выражения этих
функциональных интегралов входит экспонента, в показателе которой
стоит функционал действия классической теории или его евклидов ана-
аналог (функционал, получающийся из классического действия при пере-
переходе к мнимому времени). Ь случае, если-теория содержит фермионы,
проведенные в § 17 рассуждения буквально не применимы. В частности,
это связано с тем, что нельзя говорить о классических фермионных полях.
В самом деле, в бозе-случае квантование основано на канонических ком-
коммутационных соотношениях
h
\Р/, Рк\ = [Qf, Як] =0. [Pj> Як] = Г 5/fc (О
или на эквивалентных соотношениях
[а,. ак] = [а], ак] = 0, [а,, а\] = h8Jk. B)
Из операторов, удовлетворяющих условию A), можно получить опера-
операторы, удовлетворяющие условию B), например, положив
(Як + Фк), "к = -р (Як -
В пределе fi -кооператоры рк, qk, ak, а*к становятся коммутирующими
и могут рассматриваться как классические величины. В то же время при
213

рассмотрении фермионов исходят из канонических антикоммутационных
соотношений
[af, ак ] + = [aj, ак] + = О, [ajt а*к]+ = h6/fe, C)
где [а, Ь]+ = аЪ + Ъа - антикоммутатор операторов а и Ъ. Ясно, что в пре-
пределе h -> 0 операторы ак и ак не становятся коммутирующими. Из этого
можно сделать вывод, что у фермионного поля нет классического предела.
Однако разумнее посмотреть на дело с другой точки зрения. Можно ска-
сказать, что в пределе h -*¦ 0 операторы ак и а\, удовлетворяющие условиям
C), превращаются в антикоммутирующие величины и интерпретировать
это как указание на то, что в классическом пределе фермионные поля
нужно рассматривать как поля, принимающие антикоммутирующие зна-
значения. Эта интерпретация оказывается чрезвычайно полезной. В частности,
представление физических величин в виде функциональных интегралов
можно перенести на случай, когда присутствуют фермионы, если только
соответствующим образом определить интегрирование по полям с анти-
коммутирующими значениями. Например, если рассматривается теория,
описывающая взаимодействие спинорного поля ф(х) и скалярного по-
поля <р(х), то производящий функционал евклидовых функций Грина может
быть записан в виде
_г. +1 z У, X, Х*1 ,...
Здесь Z[j, х, Х+] может интерпретироваться как статистическая сумма
в присутствии "источников"/, х-'
Z =/exp (-Seucl + /(/*+xV *+xK**)) П </*</* <ty+, E)
•Seuci= /("(^mVJ + Ф*&Ф + еФ*Фф + \<p4jdx4, F)
a iiS — евклидов оператор Дирака (см. § 19). В E) ф(х) и х(*) рассмат-
рассматриваются как поля, принимающие антикоммутирующие значения.
Аккуратное определение интегрирования по полям с антикоммути-
рующими значениями мы дадим позже. Сейчас мы ограничимся только
замечанием, что в наиболее интересных теориях функционал действия
зависит от фермионных полей квадратично, т.е. возникающие функцио-
функциональные интегралы по антикоммутирующим полям являются гауссовыми.
Как и в обычном случае, вычисление гауссовых интегралов по антиком-
антикоммутирующим полям сводится к вычислению детерминантов. Однако,
правила вычисления несколько модифицируются. (В то время как
в обычном случае при вычислении гауссова интеграла получается ответ
(det Л) ~ 112, где А — оператор, определяющий квадратичную форму в
показателе, при интегрировании по антикоммутирующим полям получа-
получается (det АI /2.)
Перейдем к точным определениям и формулировкам. Рассмотрим
символы е1,..., е", удовлетворяющие соотношениям
eae"=-e*V\ G)
и всевозможные выражения вида
— V V ОС, ОС Is /о\
и> - 2. 2 аа ...а <Г' ¦ ..еак. (8)
to, ak
214 к

Для выражений вида (8) естественным образом определяются опера-
операции сложения, умножения и умножения на число. (При этом, конечно,
используется соотношение G).) Мы получаем, таким образом, алгебру,
которая носит название грассмановои алгебры с образующими е1,... , е".
Более формально можно сказать, что грассманова алгебра — это ассоциа-
ассоциативная алгебра с единицей и образующими е1,..., е",удовлетворяющими
соотношениям G). Отметим, что всякий элемент грассмановои алгебры
может быть записан в виде (8), где коэффициенты д^ -ак антисиммет-
антисимметричны; такая запись единственна. Единственности записи элемента грас-
грассмановои алгебры в виде (8) можно добиться также, наложив усло-
условие, чтобы не обращались в нуль только те коэффициентыakai...aic,для
которых «! < а2 < . .. < Ofc.
Произведение четного числа образующих назьшается четным мономом,
линейная комбинация четных мономов — четным элементом грассмановои
алгебры. Аналогично определяются нечетные мономы и нечетные элемен-
элементы грассмановои алгебры. Из соотношений G) следует, что четный эле-
элемент грассмановои алгебры коммутирует с любым другим элементом;
два нечетных элемента антикоммутируют. Если в (8) а = 0 (т.е. всякое
слагаемое содержит хотя бы одно е <*), то найдется такое N, что со^ = О
(элемент со нильпотентен).
Выражение вида (8) напоминает полином от* переменных е1, . . . ,е".
Это приводит к мысли рассматривать элемент грассмановои алгебры как
функцию от антикоммутирующих переменных е 1,. . ., е ".Соответственно,
мы будем пользоваться для элемента грассмановои алгебры с образую-
образующими е1, . . . , е " обозначением со = со(е ) . Покажем, что для функции от
антикоммутирующих переменных можно определить аналоги обычных
Э со
операций анализа. Прежде всего определим частные производные ;~.
i ЭеА
Если со является мономом
со = eV> ...е°Ч . (9)
то будем полагать
Эсо
Всякий другой моном либо отличается от (9) только знаком, либо сов-
совсем не содержит е *. В этом посдеднем случае полагаем Эсо/Эе^ =0.На
произвольные элементы грассмановои алгебры распространяем операцию
Э /Э е * по линейности. Таким образом, для того, чтобы вычислить Э со/Эе * ,
если со представлена в виде суммы мономов, нужно в каждом из этих
мономов переставить е на первое место, воспользовавшись соотношения-
соотношениями G), а затем вычеркнуть е *.
Легко видеть, что имеет место соотношение
Э 9coj Эсо2
СОХСО2 = СО2 + COj . A1)
деК деК дех
(Здесь предполагается, что coi имеет определенную четность; знак "+"
соответствует четному coj, знак "—" нечетному.)
215

Определение интеграла функции от антикоммутирующих переменных
основано на соотношениях
fexdex = 1, fdex = 0. A2)
Кратный интеграл (интеграл по d"e = de" . . . del) понимается как пов-
повторный.
Из соотношений A2) следует, что fojd"e равняется нулю в случае,
если w является мономом степени < п. Интеграл от монома е . . . е °п
равен ± 1 в зависимости от четности перестановки alt . . . , а„. Если эле-
элемент грассмановой алгебры имеет вид (8), где коэффициенты а а . ак
выбраны антисимметричными, то
nla"l...n. A3)
Операция интегрирования может быть выражена через операцию диффе-
дифференцирования:
де" ... де1
Это следует из соотношения
Э" t
и из замечания, что при и-кратном дифференцировании монома степени
< п получается нуль.
Определенный только что интеграл обладает многими из привычных
свойств. Отметим, в частности, что имеет место формула интегрирования
по частям
dctJi дсоо
/ co2c/"e=+/wi d"e. A4)
Эех дех
(В A4) предполагается, что ojj имеет определенную четность; знак "—"
соответствует четной ш1г знак "+" нечетной.) Соотношение A4) сразу
следует из правила дифференцирования произведения A1) и замечания,
что
/ —J~ d"e = 0 A5)
для любого оо. (Чтобы получить A5) достаточно заметить, что Э cj/Э е х
является суммой мономов степени < и.)
Для интеграла по антикоммутирующим переменным имеет место ана-
аналог обычной формулы замены переменной. В частности, в грассмановой
алгебре можно заменить систему образующих е ', . . . , е" образующими
еа=Арер, где А% - невырожденная матрица. Элемент (8) может быть
выражен через образующие е1,.. ., е " соотношением
216

где новые коэффициенты аа а/с связаны со старыми соотношениями
Пользуясь A6), легко получить, что в случае, если коэффициенты в (8)
предполагаются антисимметричными, имеет место соотношение
<ГХ ... „ = det А а\^ .. „.
Это означает, что
/ы(б)</"е = fdetA-1 u(e)dne. A7)
Правило A7) линейной замены переменной в интеграле по антиком-
мутирующим переменным отличается от правила линейной замены перемен-
переменных в обычном интеграле тем, что детерминант замены входит в степени —1.
Мы не будем обсуждать здесь замену переменных в общем случае.
Отметим, только, что нам понадобится кроме линейной замены переменных
сдвиг аргумента в функциональном интеграле по антикоммутирующим
переменным, т.е. замена вида е" -> еа + C°, где 0° - антикоммутирующие
параметры. Аналог якобиана для этой замены равен 1.
Приведем простые примеры интегралов по антикоммутирующим пере-
переменным; ответы получаются непосредственно из определения
fexp(ae1e2)de2 de1 =a, A8)
/ехр( Z xaea)d"e = Xn-Xi- A9)
а = 1
Здесь а — число, Xi» • - • >Xn ~ антикоммутирующие объекты. Точнее,
можно считать, что подынтегральное выражение в A9) является элементом
грассмановой алгебры с образующими xi,. • •, Х«> е', • • • , с", но интегриро-
интегрирование проводится только по е1,. .. ,е". Выражение ехра, где а — четный
элемент грассмановой алгебры, определяется с помощью разложения в ряд
Тейлора. Именно, следует положить а= а0 +ffi, где ао — число, a ax —
нильпотентный элемент. Тогда ехр а - ехр а0 • B— а"). Рядв этом опреде-
определении содержит конечное число ненулевых членов.
Часто приходится рассматривать функции, зависящие как от обычных
(коммутирующих) переменных х1,.. . ,хт, так и от антикоммутирующих
переменных е1,. .. , е" (т.е. выражения вида (8), в которых коэффициенты
д? „ являются функциями от х).Интеграл /coc?mxс?"епонимается
как повторный. В частности, если со имеет вид (8), где коэффициенты
аа .. .а/с являются функциями отх и антисимметричны по «1...ак, то
/ соd mx dn е = п! JVJ n(x) dmx.
Наиболее важным типом интефалов по антикоммутирующим перемен-
переменным являются гауссовы интегралы-интегралы от выражения со = ехр а,
где а=— Сареае^ - квадратичное выражение по образующим е". Матри-
Матрицу Сар можно без ограничения общности считать антисимметричной. В даль-
217

нейшем это условие будет предполагаться выполненным. Нетрудно прове-
проверить, что
/exp ad"e = /ехр(- Са0еаеПAпе = VdetCaj3. B0)
Из A8) следует B0) для случая, когда о = \1е1 е2 +\г е3е4 + ...
Общий случай может быть сведен к этому частному с помощью линейной
замены переменной. Полезно отметить также более общую формулу
B1)
В B1), как ив A9), мы считаем, что Xi, • • ¦ , Х„ - антикоммутирующие
объекты, т.е. рассматриваем подынтегральное выражение как элемент
грассмановой алгебры с образующими х i > • • • > Х«. е' > • • • > е" (функцией
от антикоммутирующих переменных Xi, • ¦ ¦ , Х„,е', ¦ • • > е") ¦ '
Часто встречаются грассмановы алгебры, в которых задана операция
комплексного сопряжения (инволюция) : со -*¦ со. Обычно в таких случаях
алгебра имеет четное число образующих, попарно комплексно сопряженных
друг другу: е1 ."б1,..., е","ё". Действительными элементами грассмановой
алгебры (действительными функциями от антикоммутирующих перемен-
переменных еа, Та) называются элементы, не меняющиеся при комплексном сопря-
сопряжении. Отметим важный частный случай соотношения B1). Пусть а =
= Са0 eaW® - вещественная квадратичная форма, т.е. матрица С эрмитова.
Тогда
d"~ed"e = B2)
В написанной только что формуле, как и в формуле B1), матрица С пред-
предполагается обратимой.
Укажем модификацию соотношения B2) для случая, когда обратимость
матрицы С не предполагается. Обозначим через \р? ортонормированную
систему собственных векторов матрицы Сар, а через \к - соответствующие
собственные значения. Первые s из этих векторов будем считать отвечаю-
отвечающими нулевым собственным значениям. Тогда
/=^?1...^idet'Cexp(-xa(C-1)a0X0), B3)
где ffc=xaV^, det'C— произведение ненулевых собственных значений
матрицы С, а оператор С'1 для вырожденной матрицы С определяется как
оператор, имеющий в базисе >р" диагональные, элементы Х^1, если к > s,
и нулевые диагональные элементы при к <х. (Если П - оператор проекти-
проектирования на пространство нулевик мод оператора С, то оператор С можно
определить условиями С II = 0. СС'1 = С С= 1 - П.)
218

Доказательство соотношения B3) можно провести с помощью линейной
замены переменной
При этом следует использовать B1) и равенство
/ехр(Хаба + еаха) dnedne = XxXx ¦ •¦•ХИХЯ,
являющееся частным случаем формулы A9).
До сих пор мы рассматривали только грассмановы алгебры с конечным
числом образующих. В квантовой теории поля приходится иметь дело с
функциями от бесконечного числа антикоммутирующих переменных, т.е.
с элементами грассмановых алгебр, имеющих бесконечное число обра-
образующих.
Рассмотрим для определенности случай, когда образующие грассмановой
алгебры перенумерованы непрерывным параметром %. (Можно считать,
что % пробегает числовую ось или fc-мерное пространство.) Образующие
будем обозначать символом е(?); они считаются удовлетворяющими
соотношениям
e«i)e(fe) = -6(fa)e«1). B4)
Под элементами грассмановой алгебры с образующими е(?) будем пони-
понимать формальные выражения вида
« = 2/«*(*!, ¦••,6t)e«i).-.ettk)</*i ...d\k. B5)
(Это выражение получается из (8) если заменить дискретный индекс а
на непрерывный индекс ?, а суммирование по дискретному индексу инте-
интегрированием по %.) Соотношения B4) позволяют без ограничения общности
считать, что коэффициентные функции wfc(|b .. . , ?fc) антисимметричны
по ?i,..., ?fe.
Естественным образом определяется сложение и умножение элементов
вида B5). Можно сказать, что выражение B5) представляет собой функ-
функцию от бесконечного числа антикоммутирующих переменных е(?) или что
это выражение представляет собой функционал от функций е(?), прини-
принимающих антикоммутирующие значения. Следует подчеркнуть, что данные
только что определения не вполне аккуратны, поскольку мы не описали
класс функций wfc(?i,... ,|fc), которые могут фигурировать в B5) в
качестве коэффициентов. Нужные уточнения могут бьпь сделаны различ-
различными способами; мы не будем на них останавливаться.
Для функционалов от функций с антикоммутирующими значениями
можно определить дифференцирование и интегрирование. Интегрирование,
так же как и в случае функционалов от обычных функций, определяется
с помощью перехода к конечнократной аппроксимации. Точнее говоря,
следует в выражении B2) заменить интегрирование по непрерывному
параметру ? суммированием по конечной решетке, взять интеграл от
получившейся функции конечного числа антикоммутирующих перемен-
переменных и затем перейти к непрерывному пределу. Мы не останавливаемся
на выборе конечнократной аппроксимации и предельного перехода, по-
поскольку здесь нет существенных отличий от ситуации, описанной в § 16.
219

Формулы B0) - B3) для вычисления гауссовых интегралов переносят-
переносятся на рассматриваемый бесконечномерный случай. Например, формула
B0) приобретает вид
)«/6(O = (det СI'2, B6)
Л
где С - оператор с матрицей С{%, ?').
Для теорий, содержащих фермионы, можно указать представление
различных физических величин в виде функциональных интегралов, если
допустить к рассмотрению интегрирование также по функциям, принимаю-
принимающим антикоммутирующие значения. Именно: доказанные в § 17 утвержде-
утверждения с незначительными модификациями переносятся на случай, когда среди
полей рассматриваемой теории есть фермионные. Точнее, интересные
физические величины по-прежнему можно представить в виде функциональ-
функциональных интегралов, в подынтегральном выражении которых содержатся либо
exp(iS), где S — функционал действия, либо ехр(— 5euci), где Seuc\ —
функционал евклидова действия. Нужно только считатьфермиевские поля
в выражении для действия принимающими антикоммутирующие значения;
соответственно интеграл по этим полям следует понимать так, как это
объяснено в настоящем параграфе.
Например, статистическая сумма фермионного поля, находящегося во
внешнем калибровочном поле (рассматриваемом как классическое), может
быть записана в виде
Z = /ехр(- Seuci)n d1>+tty = det(# - im). B7)
Здесь мы считаем, что евклидово действие дается выражением A9.7).
Для устранения инфракрасных расходимостей в B7) следует сделать
инфракрасное обрезание, например, считая, что все поля заданы на ком-
компактном римановом многообразии. Ультрафиолетовые расходимости
устраняются с помощью описанной в § 21 регуляризации детерминанта.
Гауссов функциональный интеграл вычисляется с помощью формулы B6).
Функции Грина фермионного поля, находящегося во внешнем калибровоч-
калибровочном поле А, даются формулой
С„(х,,. •¦ ,х„; у1,...,у„\А) =
= Z-J]>(*!)... ф(хп)ф+(У1) ¦ ¦ ¦ ^+(^п)ехр(-5еис1)П^ + ^. B8)
(Точнее, формула B8) определяет 2и-точечную функцию Грина.)
Вместо этих функций Грина часто удобно рассматривать их производя-
производящий функционал
n^+cty. B9)
Вычисляя функциональный интеграл B9) с помощью бесконечномерного
аналога формулы B2), получаем
Gfo.tfl =expUv+(x)D(x>X'\A)r,(.x')dxdx'), C0)
где D(x, х' | А) = < х | (# - irrif1 | x').
Мы предполагали до сих пор, что рассматриваемый нами оператор Дира-
Дирака t-imve имеет нулевых мод. Если нулевые моды есть, то следует
220

считать, что Z = 0. Однако и при наличии нулевых мод может быть отличен
от нуля функциональный интеграл
1Ф(Х1)... ф(хп) ф\У1) ... ф+(^)ехр(-5еис1)П^+^.
Поэтому удобно по-прежнему определять функции Грина фермионного
поля формулой B8), полагая в ней Z = det (# - im), но считая, что при
вычислении детерминанта не учитываются нулевые моды (см. §21). Тогда
производящий функционал функций Грина может быть, как и раньше,
определен соотношением B9). Применяя бесконечномерный аналог фор-
формулы B3), мы получаем для этого функционала выражение
< х \(f - imj1 \x') v(x')dxdx'), C1)
где x,- = <i?,V,-> = j"i?+(x)ip(.(x)cfjc, ip((x) пробегает ортонормированную
систему нулевых мод оператора Дирака. Из C1) легко получается выраже-
выражение для функций Грина фермионного поля во внешнем калибровочном
поле. В частности, из C1) видно, что первой отличной от нуля функцией
Грина является 2х-точечная функция Грина, где s — число нулевых мод.
Эта функция Грина дается выражением
Gs(*!,. .. ,xs;yu... ,ys\A) ,
C2)
где символ asym обозначает антисимметризацию по хь . . . , xs и по ylt. ..
...,ys.
До сих пор наше рассмотрение относилось к полям в пространстве
произвольной размерности. Обратимся сейчас к фермионным полям нуле-
нулевой массы на 2п-мерном многообразии. В этом случае функционал евкли-
евклидова действия инвариантен относительно замены
+1) И*),
где 72и + 1 = — in4\У2 ¦ ¦ ¦ Угп- Однако, как видно из указанных выше фор-
формул, функции Грина, вообще говоря, не инвариантны относительно этого
преобразования. В самом деле, без ограничения общности можно считать,
что нулевые моды оператора Дирака, фигурирующие в выражении для
функции Грина, имеют определенную четность (являются либо левыми,
либо правыми). При этом разность числа левых и правых нулевых мод
интерпретируется как индекс оператора Дирака, рассматриваемого как
оператор на пространстве левых спиноров (см. § 20). Из указанной выше
формулы для функции Грина видно, что при замене C3) функция Грина
умножается на ехр(— 20(я_ - "+)), где и_ — число левых нулевых мод,
а и+ — число правых нулевых мод оператора Дирака. Пользуясь указан-
указанным в § 20 выражением B0.25) для индекса оператора Дирака, получаем,
что функция Грина умножается наехр(— 2&атЧ(АУ), где q(A) —топологи-
—топологическое число поля,
Gfalt... ,xa) = Gn(xlt... ,*„)ехр(- 2paTq{A)). C4)
Проведенные только что рассуждения можно рассматривать как вычи-
вычисление так называемой аксиальной аномалии для частного случая глобаль-
221

ных аксиальных (киральных) преобразований. Для полноты остановимся
коротко на более общей ситуации. Будем считать, что калибровочное поле
на 4-мерном многообразии содержит матрицу 7S> т-б- может быть записано
в виде
где поля Vy.(x) и WM(x) (векторная и аксиальная часть калибровочного
поля) принимают значения в алгебре Ли калибровочной группы. Евклидово
действие A9.7) инвариантно относительно калибровочных преобразований
фермионного поля ф(х)-> Т^(х))ф(х), если одновременно производится
калибровочное преобразование поля Ац(х). В случае если масса фермион-
фермионного поля равна нулю, возникает добавочная инвариантность относительно
аксиальных калибровочных преобразований. Бесконечно малые аксиальные
калибровочные преобразования имеют вид
Ч(со(х)У)ф(х), C5)
- iys Эмw(x) - iys Ид(х), со(х)], C6)
где со(х) — функция, принимающая значения в алгебре Ли калибровочной
группы. .
В то время как инвариантность евклидова действия относительно калиб-
калибровочных преобразований обеспечивает аналогичную инвариантность стати-
статистической суммы, аксиальная калибровочная инвариантность на квантовом
уровне нарушается (возникает аномалия). Точнее говоря, статистическая
сумма не меняется, если заменить поле А.^ на калибровочно эквивалентное
ему поле, но изменяется, если изменение поля А^ диктуется соотношением
C6). Как говорилось в § 22, возникновение аномалий связано с неинва-
неинвариантностью скалярного произведения. При калибровочных преобразова-
преобразованиях скалярное произведение фермионных полей сохраняется, в то время
как закон его изменения при аксиальном калибровочном преобразовании
C5) имеет вид
C7)
Рассуждения § 22 позволяют заменить вычисление вариации детерминан-
детерминанта оператора И/ при преобразовании C6) вычислением вариации этого
детерминанта относительно изменения скалярного произведения фермион-
фермионных полей по закону C.5). Пользуясь соотношением B2.17), получаем
51nZ = 51ndettf = - 5 1ndet#2 = ^
5 1net#
2 1 бтт
§ 27. Инстантоны в квантовой Хромодинамике
Напомним, что лагранжиан квантовой хромодинамики получается
из свободного фермионного лагранжиана
/#,-12 тг?Д- A)
с помощью локализации SU C) -симметрии.
Здесь при фиксированном / символ ^ обозначает трехмерный вектор,
каждая компонента которого является биспинором: W/ = {Ф}, ф2г, Ф^)-
222

Иными словами, рассматривая поля кварков i//*, где к характеризует
цвет, а /— аромат кварка, мы опускаем цветовой индекс к, считая ~§f век-
вектором в цветовом пространстве.
Евклидов функционал действия, отвечающий лагранжиану A), имеет
вид
S = /2 (< ~$fMf)~ imf( $f, 1f))dV, B)
где yif = (ф^, \ftj, фу), поле Ф$(х) принимает значение в пространстве спи-
норного- представления группы SO D), под $ понимается евклидов опе-
оператор Дирака. Евклидов функционал действия квантовой хромодинами-
ки, получающийся из B) локализацией SUC)-симметрии, может быть за-
записан в виде
S = f2(($f,V$f)-imf<1,f,$f))dV + SYM, C)
где 5ум ~ евклидов функционал действия для калибровочного поля А м,
принимающего значение в алгебре Ли группы SUC) (алгебре антиэрми-
антиэрмитовых 3 X 3-матриц с нулевым следом), N = 17м VM = 17м (<V + ^д) • (Дей-
ствие матрицы А^ на фу понимается как умножение этой матрицы на цве-
цветовой вектор-столбец фf.) Для того, чтобы представить функции Грина
квантовой хромодинамики в виде функциональных интегралов, следует
рассматривать фермионные поля, входящие в A) —C), как поля с анти-
коммутируюшими значениями. Например, евклидовы функции Грина мо-
могут быть определены как частные двух функциональных интегралов Zq
и Z, где
гф=;Ф[А, ф]е-3ПёАПс1фAф+, D)
Ф[А, ф] — калибровочно инвариантный функционал от полей Лд и \j/f,
функциональный интеграл Z (статистическая сумма) получается из D),
если положить Ф [А, ф] = 1. Можно считать, скажем, что
Ф[А,ф]=(Ьгф(х1),ф(х2)), E)
где Ьр =-Рбхр(—/у1д Лгд), Г — кривая, соединяющая точкиxt иЛг-Функ-
г
ционал E) калибровочно инвариантен и с его помощью можно построить
функцию Грина (двухточечную фермионную функцию Грина). Разумеет-
Разумеется, для того чтобы придать смысл функциональному интегралу D), нужно
сделать инфракрасное и ультрафиолетовое обрезания. Роль инфракрас-
инфракрасного обрезания может играть переход к рассмотрению полей на компакт-
компактном римановом многообразии (например, сфере). Ультрафиолетовое
обрезание может быть достигнуто с помощью введения решетки.
Без ограничения общности можно считать, что калибровочно инвариант-
инвариантный функционал ФИ, ф] имеет вид
Ф[Л ф] = ф(х,) ... ф(хт)ф+(у1) ... ф+(уп) V[A]. F)
(Все другие калибровочно инвариантные функционалы получаются как
линейные комбинации функционалов вида F).) Отметим, что из инва-
инвариантности относительно преобразований ф ~>е*аф, ф* -+е~"* ф* выте-
вытекает, что ненулевые функции Грина могут получиться только при условии,
223

что в F) т - п. В дальнейшем мы будем предполагать это условие выпол-
выполненным. Функцию Грина, отвечающую функционалу F), будем^называть
2л-точечной фермионной функцией Грина.
Подчеркнем, что мы рассматриваем только функции Грина, отвечаю-
отвечающие калибровочно инвариантным функционалам Ф[А, ф]. В частности,
это требование исключает возможность положить в F) V[A] = 1. (Функ-
(Функции Грина, отвечающие V[A] = 1, часто удобно рассматривать, но при этом
приходится фиксировать выбор калибровки.)
Функциональный интеграл по антикоммутируюшим полям ф, ф* явля-
является гауссовым и может быть вычислен по формулам предыдущего па-
параграфа. Например, применяя формулу B6.27), получаем для статистичес-
статистической суммы выражение
Z = / П det (# - irrif) exp (- SY м) П dA. G)
Для функционального интеграла D), где Ф[А, ф] имеет вид F), получает-
получается ответ
гФ = fGn (*i,... ,хп; у,,. .. ,у„ \А) V[A) X
X П det (# - imf) exp (- SYM) П dA, (8)
где Gn(xi,... ,х„; ух,..., у„ \А) - фермионная функция Грина во внеш-
внешнем калибровочном поле А. (Мы воспользовались формулой B6.28),
в которой, как мы говорили, детерминант оператора Дирака следует вы-
вычислять без учета нулевых мод.) Отметим, что как в G), так и в (8) опу-
опушены все индексы, отвечающие спину-и цвету.
Функциональные интегралы G) и (8) для Z и Z<j> можно вычислять
с помощью метода Лапласа. При этом вклад от полей с топологическим
числом q записывается в виде интеграла по многообразию инстантонов
с этим топологическим числом. Общее выражение для ^-инстантонного
вклада можно с помощью рассуждений § 25 записать в виде
/ 8тг2 \
Ja =g-°exp( -~T-q)f Gn(Xl,...,xn;yi,... ,у„ \A)V[A]dn,
J ( )
\ t /Rq
(9)
где
v(A)
"@)
v(A)= IIdet(# - imf)y(A) = П det(tf - /m^def1'2 Д?
(Мы сохраняем здесь обозначения § 25.) В (9) функции Грина и функцио-
функционал V[A] вычисляются в поле инстантона А).
-Если массы кварков малы, то можно написать
det ($ - imf)« mN{ det itA, A0)
где N — число нулевых мод оператора #,j, detJtf^ вычисляется без учета
нулевых мод.
Для того чтобы исследовать число нулевых мод оператора Дирака,
удобно воспользоваться теорией индекса (§ 20). В силу соотношения
224

B0.26) разность числа левых и правых нулевых мод оператора Т$ А (ин'
деке оператора Ю А, рассматриваемого только на левых спинорах) равна
3q, где q — топологический заряд поля А (Мы предполагаем, что простран-
пространственное обрезание проведено с помощью перехода к рассмотрению полей
на сфере или на торе и применяем формулу B0.26), учитывая, что сигна-
сигнатура этих многообразий равна нулю, а индекс Дынкина векторного пред-
представления группы SUC) равен 3.) Из сказанного выше ясно, что число ./V
нулевых мод оператора %А не меньше чем 3 | q |.
Если поле А является решением уравнения самодуальности B3.12)
или антисамодуальности B3.13), то число нулевых мод в точности равно
31 q I. В самом деле, в этом случае можно доказать, что у оператора $А
при q > 0 есть только левые нулевые моды, а при q < 0 — только правые
нулевые моды. Если, например, поле задано на торе и удовлетворяет урав-
уравнению самодуальности, то квадрат оператора Дирака на правых спинорах
дается формулой
V2=-VMV. . (И)
(Это вытекает из приведенной в конце § 20 формулы для #2 и соотноше-
соотношения -ем„рО7р7° = -7m1V75.) Замечая, что (ф, -VMVM\//) = (VM ф,
Vм ф), видим, что для правой нулевой моды оператора Дирака V рФ = 0.
Пользуясь связью напряженности &МУ с коммутатором ковариантных
производных, убеждаемся, что 1E-щ,)ф = 0. Если самодуальное поле
неприводимо (см. § 23), отсюда следует, что ф = 0. Мы видим, что для
инстантона А
del(VA -imf)^mj!lq{detVA, A2)
если масса кварка rrif мала. Это позволяет записать меру на многообра-
многообразии инстантонов в виде
^ A3)
где
7(A) = detVA (detAf r1/2detA^. A4)
В случае q = 1 получается следуюшее выражение для меры:
), A5)
где, как всегда, X — размер инстантона, который мы считаем много мень-
меньшим параметра пространственного обрезания, а — положение центра инстан-
инстантона, g(X) - эффективная константа связи:
2 г2 / 2 \
Соотношение A5) можно вывести из ренормгрупповых соображений.
Другой способ его получения основан на использовании приведенного
в конце § 21 вычисления изменения детерминанта оператора Дирака при
225

масштабном преобразовании калибровочного поля. Это вычисление
дает зависимость det flA от размеров инстантона. Нужная информация
об остальных детерминантах, фигурирующих в A4), получена в § 25.
Отметим, что этот способ вычисления одноинстантонной меры дает одно-
одновременно вычисление эффективной константы связи.
Остановимся подробнее на случае, когда один из кварков имеет нуле-
нулевую массу. В этой ситуациии вклад в статистическую сумму от топологи-
топологически нетривиальных полей исчезает. В самом деле, индекс оператора
Дирака в поле с ненулевым топологическим зарядом отличен от нуля. От-
Отсюда следует, что у оператора Дирака в таком поле всегда есть нулевые
моды и, значит, детерминант этого оператора обращается в нуль. Тем не
менее топологически нетривиальные калибровочные поля могут вносить
ненулевой вклад в функциональный интеграл D). Из результатов, приве-
приведенных -в конце предыдущего параграфа, следует, что 2л-точечная функ-
функция Грина оператора Дирака во внешнем калибровочном поле может быть
отлична от нуля только в случае п ~> N, где Л' — число нулевых мод опе-
оператора Дирака. Отсюда ясно, что вклад от полей с топологическим зарядом
q в 2п-точечную функцию Грина может быть отличен от нуля только в
случае и > 3 | q \. Мы видим, что топологически нетривиальные инстантоны
вносят вклад только в такие функции Грина, для которых п > 3. В част-
частности, в шеститочечную функцию Грина вносят вклад только инстантоны
с q = ± 1. С помощью B6.31) этот вклад выражается через нулевые моды
оператора Дирака в поле инстантона размера X с центром в точке а.
Отметим, что при нулевых массах кварков функционал действия кван-
квантовой хромодинамики инвариантен не только относительно преобразо-
преобразований ф -*¦ exp(ia)i//, но и относительно преобразований ф -> exp(fiys)\p
(последняя, инвариантность носит название киральной). Эти свойства сим-
симметрии сохраняются и после перехода к евклидову действию при соот-
соответствующей модификации определения кирального преобразования
(см. § 26). Существенно подчеркнуть, что учет инстантонного вклада
приводит к нарушению киральной U(l)-симметрии. В самом деле, мы
видели в конце § 26, что интересующая нас инвариантность нарушается
уже при вычислении функции Грина фермиона во внешнем калибровоч-
калибровочном поле, если только это поле имеет ненулевой топологический заряд.
Можно сказать, что инстантоны дают решение так называемой U(l)-проб-
U(l)-проблемы. Напомним, что в приближении безмассовых кварков нарушение
киральной инвариантности, связанной с вращениями в пространстве аро-
ароматов, приводит к существованию безмассовых голдстоуновских бозонов
(см. § 14). В реальном мире три первых кварка имеют малую массу,
и это ведет к приближенной киральной SUC)-инвариантности, нарушение
которой обеспечивает сушествование мультиплета из восьми псевдоскаляр-
псевдоскалярных мезонов сравнительно малой массы. По аналогии можно было бы
думать, что существует девятый легкий меэон, связанный с нарушением
описанной выше киральной U(l)-симметрии. Такой мезон отсутствует в
природе; необходимость объяснения его отсутствия составляет содержа-
содержание U A)-проблемы. Мы видим, что функции Грина, вычисленные с уче-
учетом инстантонного вклада, не инвариантны относительно киральной груп-
группы U(l), но не содержат каких-либо полюсов, отвечающих безмассовому
бозону, связанному с нарушением U(l)-симметрии.
226

Как и в случае чисто калибровочной теории, в лагранжиан квантовой
хромодинамики можно включить 0-член i — в -Jd*x{ ?д„, ^М">, не
меняя классических уравнений движения. Этот член снова приводит к из-
изменению вклада в функции Грина от полей с топологическим зарядом
q Ф 0. В этом вкладе (в частности в ^r-инстантонном вкладе), как и ранее,
появляется дополнительный множитель ехр(— \6it2q6i). Подчеркнем,
однако, что в случае нулевой массы кварков это изменение может быть
устранено с помощью переопределения фермионных полей. В самом де-
деле, как мы говорили, в случае нулевых масс кварков на классическом
уровне имеется киральная U(l)-инвариантность, нарушающаяся на кван-
квантовом уровне. Легко убедиться, что изменение фермионных функций Гри-
Грина при кирапьном U(l)-преобразовании компенсируется введением соот-
соответствующего 0-члена в лагранжиан. (При этом следует использовать
полученную в конце § 26 формулу для изменения функции Грина ферми-
она во внешнем калибровочном поле при интересующем нас преобразо-
преобразовании.) В реальном случае ненулевых масс кварков 0-член должен был
бы приводить к несохранению четности в сильных взаимодействиях; это
позволяет утверждать, что константа 0 близка к нулю.
227

ГЛАВА III
ОСНОВЫ ТОПОЛОГИИ
§ 1. Основные топологические понятия
Два пространства X и Y называются топологически эквивалентными
(гомеоморфными), если существует взаимно однозначное и в обе сторо-
стороны непрерывное соответствие между точками этих пространств *). (Такое
соответствие называется топологическим отображением или гомеоморфиз-
гомеоморфизмом.) Иными словами, два пространства топологически эквивалентны,
если одно можно перенести в другое без разрьшов и склеиваний (удобно
представлять себе рассматриваемые объекты сделанными из резины).
ll
\
\
А
А'
Рис.18
Рис.19
Рис.20
Например, два замкнутых отрезка конечной длины топологически экви-
эквивалентны (рис. 18). Прямая топологически эквивалентна открытому от-
отрезку конечной длины (топологическое соответствие между отрезком
(— тг/2; тг/2) и прямой может быть задано формулой х' = tgjc (рис. 19).
Аналогично открытый куб любой размерности топологически эквивалентен
евклидову пространству той же размерности (соответствие задается фор-
мулои х = tgx'; i = 1,..., и; — — <х' < — ; -°° <х ' <+«>. Окруж-
) Термин "пространство" здесь и'далее обозначает метрическое или топологичес-
топологическое пространство. Однако читатель, стремящийся к максимальной наглядности, без
существенного ущерба может представлять себе рассматриваемые объекты просто
как подмножества л-мерного евклидова пространства.
228

ность, из которой выколота одна точка, топологически эквивалентна
прямой, замкнутая дуга топологически эквивалентна замкнутому от-
отрезку (рис. 20). Аналогично «-мерная сфера S", из которой выколота
одна точка, топологически эквивалентна л-мерному евклидову простран-
пространству R" (рис. 21). Топологическое соответствие устанавливается стерео-
стереографической проекцией и аналитически может быть записано в виде
' =
Л 1-х'0' .
Если точка (х1,..., х") пробегает евклидово пространство, то точка
(х'°, х'1,..., х'") пробегает всю л-мерную сферу, определяемую урав-
уравнением (х'°J + ... + (х'пJ = 1, кроме точки A, 0,.... О, 0) - север-
северного полюса сферы. Числа х1,... , х" называются стереографиче-
стереографическими координатами точки (х'°,.-.., х'п) 6 X". Если точка сферы
(х'°,.. ., х'") стремится к точке A, 0,..., 0, 0), то соответствующая точ-
точка евклидова пространства^1,..., х") уходит на бесконечность: (х1J ¦+...
...+ {х"J ->°°. (Можно сказать, что стереографическая проекция уста-
устанавливает гомеоморфизм между сферой и евклидовым пространством,
к которому присоединена одна бесконечно удаленная точка.)
Описанное выше соответствие точнее было бы назвать стереографичес-
стереографической проекцией с центром в точке (—1,0,..., 0) - южном полюсе сфе-
сферы S". Аналогичным образом можно построить стереографическую проек-
проекцию с центром в любой точке сферы. В частности, стереографическая проек-
проекция с центром в северном полюсе определяется формулой
Всякое п-мерное ограниченное замкнутое выпуклое множество X тополо-
топологически эквивалентно п-мерному замкнутому шару. В самом деле, без
Рис. 21
ограничения общности можно предположить, что начало координат явля-
является внутренней точкой множества X. Проведем через начало координат
и точку х € X луч и обозначим через / (х) длину части этого луча, принад-
принадлежащей множеству X. Нужное соответствие задается формулой хт -
х
Граница выпуклого множества при этом соответствии перехо-
дит„ очевидно, в границу л-мерного шара (т.е. в (л - 1)-мерную сферу),
а внутренность выпуклого множества — в открытый л-мерный шар. Отсю-
229

да следует, в частности, что открытый и-мерный шар топологически эк-
эквивалентен открытому л-мерному кубу и, значит, топологически экви-
эквивалентен л-мерному евклидову пространству (это легко, конечно, про-
проверить непосредственно).
Интересные для физики примеры пространств, обладающих нетриви-
нетривиальной топологией, можно получить, рассматривая пространства конфи-
конфигураций простых механических систем. Так, например, пространство кон-
конфигураций двойного пространственного маятника (рис. 22) топологичес-
топологически эквивалентно произведению S2 XS2 двух двумерных сфер. * Первый
Рис.22
из составляющих маятник стержней закреплен в одном из концов, другой
его конец описывает сферу S2. При заданном положении первого стерж-
стержня положение второго также определяется точкой сферы S . Таким об-
образом, конфигурация маятника определяется парой ($i, s2)> где st и S2 —
произвольные точки сферы S 2. Ў
Положение двухатомной молекулы, состоящей из различных атомов,
описывается координатами центра инерции и сферическими углами, опре-
определяющими направление отрезка, соединяющего атомы. Это означает, что
пространство конфигураций топологически эквивалентно произведению
(R3 XS2. (Мы считаем, что молекула не меняет внутреннего состояния;
ее можно тогда рассматривать как твердый стержень.) Пространство кон-
конфигураций двухатомной молекулы, состоящей из одинаковых атомов,
топологически эквивалентно произведению IR3 XRP2. (При фиксирован-
фиксированном центре инерции положение молекулы определяется прямой, проходя-
проходящей через центр инерции. Благодаря тому, что атомы одинаковы, направ-
направление на этой прямой не задано. Вспоминая, что точки проективной плос-
плоскости RP2 находятся во взаимно однозначном соответствии с прямыми
в R3, проходящими через фиксированную точку, приходим к указан-
указанному выше описанию пространства конфигураций).
Иногда представляет интерес не топология пространства конфигураций,
а топология фазового пространства (точка в фазовом пространстве опи-
описывается обобщенными координатами и обобщенными импульсами).
Может оказаться полезным также рассмотрение топологии изо энергетичес-
энергетической поверхности в фазовом пространстве.
Разумеется, топологически нетривиальные пространства появляются в
физике и во многих других ситуациях. Например, пространство состояний
л-уровневой квантово-механической системы можно рассматривать как
комплексное проективное пространство СР"~1. (Состояние такой системы
описывается ненулевым вектором из л-мерного комплексного пространст-
230

ва С". Однако векторы, отличающиеся числовым множителем, следует
отождествить, поскольку они описывают одно и то же состояние.)
Фигура называется связной, если две любые ее точки можно соединить
путем. (Под путем, соединяющем точки х0 и xlt понимается семейство at
точек фигуры, непрерывно зависящее от параметра t, пробегающего отре-
отрезок [0; 1]. Иными словами, путь — это непрерывное отображение отрезка
в фигуру.)
Если фигура связна, то топологически эквивалентная ей фигура также
связна, иначе говоря, связность является топологическим свойством.
А В топологии связность пространства обычно определяется несколько
иным образом. Именно принято называть пространство связным, если его
нельзя разбить на два непересекающихся непустых замкнутых множества
(т.е. на два множества, каждое иа которых не содержит предельных точек
другого множества). Пространства, связные в указанном ранее смысле,
называются в топологии линейно связными. Легко проверить, что всякое
линейно связное пространство связно; обратное неверно. Простейшим
примерно связного, но не линейно связного пространства является множест-
множество на плоскости, представляющее собой объединение графика функции у =
= sin A/jc) и оси ординат. Однако связные пространства* представляющие
интерес для физики, оказываются всегда линейно связными. Мы в даль-
дальнейшем всегда будем использовать термин "связность",, имея в виду ли-
линейную связность, т
Всякая фигура распадается на связные куски (связные компоненты);
две точки принадлежат одной компоненте, если их можно соединить пу-
путем. Число компонент, на которое распадается фигура, является топологи-
топологическим инвариантом (не меняется при топологических преобразованиях).
Например, буква "Ы" состоит из двух компонент, а буква "Ё" из трех
компонент; очевидно, они негомеоморфны друг другу и ни одна из них
не может быть гомеоморфной букве А, которая связна (состоит из одной
компоненты).
Еще одним примером топологического свойства является компактность
(метрическое пространство называется компактным, если из любой после-
последовательности ее точек можно выделить подпоследовательность, имеющую
предел, принадлежащий тому же пространству). Известно, что подмно-
подмножество евклидова пространства компактно тогда, и только тогда, когда
оно замкнуто и ограничено. В частности, замкнутый шар компактен, поэто-
поэтому он негомеоморфен никакой области в евклидовом пространстве, в част-
частности открытому шару. (Под областью понимается связное открытое под-
подмножество евклидова пространства.)
Рассмотрим в качестве примера топологические свойства важнейших
матричных групп. (Множество всех квадратных матриц порядка п можно
рассматривать как векторное пространство размерности п2. Топология
в любом множестве матриц порождается топологией этого векторного
пространства.)
Группа GL(n, R) невырожденных действительных матриц порядка п
некомпактна и несвязна. Она состоит из двух компонент — матриц с поло-
положительным определителем и матриц с отрицательным определителем.
(Если матрица At зависит от параметра t непрерывно,det_d0 >0, det/li <
< 0, то непрерывная функция &z\.At должна обратиться в нуль при неко-
231

тором /, О < t < 1. Это доказывает, что матрица с положительным детер-
детерминантом и матрица с отрицательным детерминантом принадлежат разным
компонентам связности. Нетрудно проверить, что две матрицы, имеющие
детерминант одного и того же знака, можно соединить непрерывным се-
семейством матриц. Мы не будем приводить доказательства этого факта,
поскольку он будет следовать из общих результатов, сформулированных
в § 17). Группа О(п), состоящая из всех действительных ортогональных
матриц порядка и, компактна и несвязна; она также распадается на две
компоненты (матрицы с определителем 1 и матрицы с определителем - 1).
Ортогональные матрицы с определителем 1 образуют компактную связную
группу, которая обозначается символом SO (и). Группу SO (л) можно
рассматривать как связную компоненту группы О (и), которой принадле-
принадлежит единичный элемент этой группы. Группа U(«) комплексных унитар-
унитарных матриц порядка п компактна и связна. Этими же свойствами обладает
группа SU(n) комплексных унитарных матриц, имеющих определитель 1.
Группы U(l) и SOB) топологически эквивалентны окружности S1 (если
точка окружности S1 характеризуется угловой координатой <р, 0 <^> < 2я,
то ей отвечает одномерная матрица ei<p, принадлежащая группе U(l),
и поворот плоскости на угол if, принадлежащий группе SO B)).
Группа SUB) топологически эквивалентна сфере S3. В самом деле,
всякую матрицу, принадлежащую группе SU B), можно записать в форме
где комплексные числа х, у удовлетворяют условию |jc|2 +|j|2 = 1; счи-
считая, что х = х1 + ix2 и у = yi + iy1, это условие можно переписать в виде
Мы видели, что топологические свойства и топологические инварианты
могут быть использованы для доказательства негомеоморфности двух
фигур. К сожалению, соображения, основанные на связности и компакт-
компактности, позволяют установить негомеоморфность лишь в простейших слу-
случаях. Например, наглядные соображения показывают, что и-мерная сфера
негомеоморфна n-мерному шару (для того чтобы расстелить резиновый
мячик на плоскости, нужно проделать в нем дырку). Однако строго дока-
доказать это легко лишь в случае и = 1 (окружность не может быть гомеоморф-
ной отрезку, поскольку она остается связной после удаления любой ее точ-
точки, а отрезок этим свойством не обладает). Мы познакомимся позже с инва-
инвариантами, позволяющими доказать, что интуиция в большинстве случаев нас
не обманывает. (Речь идет о группах гомологии и гомотопических груп-
группах.) Разумеется, основная роль этих инвариантов состоит вовсе не в том,
чтобы строго доказать геометрически ясные утверждения; мы увидим, что
они позволяют получить многие важные и далеко не очевидные факты.
В топологии рассматриваются не только конечномерные фигуры (напри-
(например, подмножества евклидова пространства), но и бесконечномерные
объекты (в квантовой теории поля мы прежде всего сталкиваемся именно
с такими). Типичным примером интересного бесконечномерного объекта
является пространство непрерывных отображений одной конечномерной
фигуры в другую. Пространство непрерывных отображений X в Y обозна-
обозначается символом С(Х, У).
232

* Топологию в пространстве С(Х, Y) можно вводить разными способа-
способами. Мы будем считать, что топология в С(Х, Y) введена таким образом,
что последовательность отображений /„ сходится к отображению /, если
на каждом компактном подмножестве пространства X последовательность
/„ равномерно сходится к / (иными словами, С(Х, Y) наделяется тополо-
топологией равномерной сходимости на компактных множествах.) т
Особенно важна информация о связных компонентах пространства
С(Х, Y). Два отображения /0 и /] принадлежат одной компоненте прост-
пространства отображений С(Х, Y) в том и только в том случае, если сущест-
существует соединяющее их семейство отображений ft, непрерывно зависящее от
параметра t, пробегающего отрезок / = [0; 1]. (Семейство/, можно рас-
рассматривать как путь в пространстве С(Х, Y).) Отображения, принадлежа-
принадлежащие одной компоненте пространства отображений, называются гомотопны-
гомотопными друг другу; иначе можно сказать, что два отображения гомотопны
в случае, если одно можно непрерывно про деформировать в другое*).
Таким образом, все отображения X в Y разбиваются на классы гомотоп-
гомотопных друг другу отображений — гомотопические классы. Множество гомо-
гомотопических классов отображений X в Y будем обозначать символом
{X, Y }. (Можно сказать, что { X, Y } — это множество компонент прост-
пространства С{X, Y).
Если X состоит из единственной точки, то гомотопические классы отоб-
отображений X в Y находятся во взаимно однозначном соответствии с компо-
компонентами пространства Y. Для того чтобы убедиться в этом, достаточно
заметить, что в рассматриваемом случае пространство С(Х, Y) топологи-
топологически эквивалентно Y. (Каждому отображению X в Y сопоставляется точка
множества У, в которую переходит единственная точка пространства X.)
Менее тривиальный пример получаем, рассматривая отображения окруж-
окружности в плоскость с выколотым началом координат. Пусть /(а,/з) ~ отоб-
отображение окружности в плоскость, переводящее точку окружности с угло-
угловой координатой tfi в точку плоскости с декартовыми координатами х =
= cos tp — а, у = sin if — |3. Если а2 + /З2 ~Ф 1, то /(Q,0) можно рассматривать
как отображение окружности в плоскость с выколотым началом коорди-
координат! Легко проверить, что все отображения /(а,/з) с а2 + |32 < 1 гомотопны
друг другу. (Чтобы нродеформировать отображение f(a<t,p0) b/(Qii/3i),
достаточно найти внутри круга а2 + 02 < 1 путь (а (г), 0@), соединяющий
точки (ао,/Зо) и (ai»/3i); тогда семейство отображений/, =f(at,pt) мож-
можно рассматривать как деформацию отображения/(a )/3 ) в/(а >C ).) Ана-
Аналогично все отображения /(а>(з) с а2 + 02 > 1 гомотопны друг другу. Одна-
Однако очевидно, что отображение/(а г(з ) не может быть продеформировано
в отображение /(«, >(з ), если о& + Ро < 1, а\ +132 > 1; доказательство этого
факта будет намечено ниже. (Напомним, что мы рассматриваем/(а>(з) как
отображения в плоскость с выколотой точкой; конечно, если рассматри-
*> Иногда удобно предполагать, что параметр деформации t пробегает отрезок, от-
отличный от отрезка [0; 1). Например, если задана деформация ift. 0<f < 1. соединяю-
соединяющая отображения / и g. и деформация \!/f, 0 < Г < 1. соединяющая отображения g ah.
то деформацию pt, соединяющую / и А, можно задать на отрезке [0; 2], положив
Pf = ifit ПРИ 0 <f < I, Pt - $t-l ПРИ 1 <' <2. Однако за счет небольшого усложне-
усложнения формул всегда можно считать, что параметр деформации пробегает отрезок [0; 1 ].
233

вать /(а,/3) как отображения во всю плоскость, они все будут гомотопны
друг другу.)
а Деформацию ft(x) часто удобно бывает рассматривать как отображе-
отображение прямого произведения X X I в Y. (Каждой точке (х, t) G X XI сопос-
сопоставляется точка f(x, t) = /r(x) ? Y.) Произведение XXI называется ци-
цилиндром над X (если X — круг, то X XI можно представлять себе как кру-
круговой цилиндр, если Х- окружность, то XXI удобно представлять как боко-
боковую поверхность цилиндра). Множества, состоящие из точек вида (х, 0) и
(х, 1), называются соответственно нижним и верхним основаниями цилинд-
цилиндра. Отображения /0 и /, можно рассматривать как отображения, задан-
заданные соответственно на нижнем и верхнем основаниях,/о afi гомотопны,
если построенное таким образом отображение оснований цилиндра можно
непрерывно продолжить на весь цилиндр. Ў
Отображение пространства X в Y называется гомотопным нулю, если оно
гомотопно отображению, переводящему все X в одну точку пространства
Y. Если пространство Y связно, то все гомотопные нулю отображения го-
гомотопны друг другу; гомотопический класс этих отображений называется
нулевым.
Рассмотренные выше отображения f(a,p) окружности в плоскость с
выколотым началом координат гомотопны нулю при а2 + |32 > 1 (всякую
окружность, не содержащую внутри себя начала координат, можно стянуть
в точку, уменьшая ее радиус).
Отображение сферы S"~' в Y гомотопно нулю в том и только в том
случае, если его можно непрерывно продолжить на шар D", ограниченный
сферой S"~'.
В самом деле, если g(х',..., х") - отображение шара (jc1J +...
.. . + (хпJ < 1, a fi(xx,. .. , х") — отображение g, рассматриваемое на
сфере (х1J + ... + (У1J = 1, то формула
задает непрерывное семейство отображений сферы, соединяющее/) с отоб-
отображением, переводящим всю сферу в одну точку. Это означает, что всякое
отображение сферы S"~', которое можно продолжить на шар D", гомотоп-
гомотопно нулю. Обратное утверждение доказывается совершенно аналогично.
Геометрически очевидно, что тождественное отображение сферы S"~'
на себя не может быть продолжено до отображения шара D" в S"~l и, зна-
значит, негомотопно нулю. (Если граница резинового диска жестко закрепле-
закреплена, то, для того чтобы весь диск сдвинуть на границу, необходимо проде-
проделать в нем дырку.) Позже будет указано, как этот факт может быть стро-
строго доказан (§2).
Отметим, что существует топологическое отображение шара D" на куб
/", при котором сфера S"~l переходит в границу /" куба /". Отсюда следу-
следует, что отображение границы куба /" гомотопно нулю в том и только в
том случае, когда оно может быть продолжено на весь куб /".
Если всякое отображение окружности ь пространство X гомотопно
нулю, то пространство X называется односвязным. Если в односвязном
прстранстве X заданы два пути /0 и /i. соединяющих точки а и /3 (т.е. два
отображения отрезка [0; 1 ],удовлетворяющих условиям/0@) =/i@) =a.
/оО) = /i(l) = Р)< т0 можно продеформировать путь /0 в путь/! таким
234

образом, чтобы во время деформации начало пути все время находилось
в точке а, а конец - в точке 0. В самом деле, построим отображение ip гра-
границы квадрата 0 < / < 1, 0 <т < I в X, считая, что на верхней стороне
это отображение совпадает с Д, на нижней стороне с/о, а боковые стороны
переходят соответственно в а и 0. В силу односвязности это отображение
можно продолжить на весь квадрат; продолженное отображение <р задает
нужную нам деформациюft (т) = <р (/, т).
Если всякое отображение сферы Sk в пространство X гомотопно нулю,
то пространство X называется асферичным в размерности к (таким об-
образом, односвязность — это асферичность в размерности 1).
Две отображения любой фигуры X в выпуклое множество гомотопны
между собой (пространство отображений в выпуклое множество связ-
связно) . В самом деле, непрерывная деформация отображения /0 в отображе-
отображение /i может быть задана формулой
Отсюда следует, что всякое отображение пространства X в выпуклое мно-
множество гомотопно нулю; в частности, выпуклое множество асферично во
всех размерностях. Поскольку пространство IR" и шар D" можно рас-
рассматривать как выпуклые множества, эти утверждения применимы к
И"и?>".
Сфера S" асферична в размерностях < п. В самом деле, рассмотрим
отображение / сферы Sk, размерность которой к меньше чем п, в S". Выко-
Выколов из сферы точку, не принадлежащую образу отображения, мы можем
рассматривать / как отображения сферы Sk в сферу с выколотой-точкой.
Вспоминая, что сфера с выколотой точкой топологически эквивалентна
пространству IR" и что пространство IR" асферично во всех размерностях,
убеждаемся, что отображение гомотопно нулю.
* Проведенное только что доказательство нуждается в уточнении. Оно
применимо без всяких оговорок в случае, если/ — гладкое отображение:
тогда образ сферы Sk имеет размерность <^и, следовательно, при к < п
не может заполнять всех сферы S" (это следует также из леммы Сарда;
см. с. 243). Однако существуют непрерывные отображения сферы S ,
образ которых заполняет всю сферу S" (при к = 1 такие отображения носят
название кривых Пеано). Для того чтобы проверить, что непрерывное
отображение Sk в S" гомотопно нулю, следует заметить, что всякое непре-
непрерывное отображение гомотопно гладкому (см. § 2) и что в силу проведен-
проведенных выше рассуждений гладкое отображение гомотопно нулю. Ў
Рассмотрим теперь отображения окружности в окружность. Точки
окружности удобно описывать с помощью угловой координаты <р, считая,
Что <fi и \р + 2тг отвечают одной и той же точке окружности. Непрерывная
числовая функция f($), заданная на отрезке [0; 2тг],определяет непре-
непрерывное отображение окружности в окружность при условии
/Bя)-/@)=2дая, A)
где m — целое число. Всякое непрерывное отображение окружности в ок-
окружность может быть записано таким способом. Эта запись, конечно, не
единственна, однако две функции fiQp) и/2(^), определяющие одно и то
235

же отображение окружности, отличаются на целое кратное 2тг:
Число т, фигурирующее в условии A), называется степенью отображе-
отображения ; оно показывает, сколько раз одна окружность навернулась на дру-
другую. В самом деле, если, например, /(<р) монотонно возрастает (например,
/(<р). = ту), то уравнение /(у) = а имеет ровно один корень для любого а,
заключенного между /@) и /Bтг) = /@) + 2пт, и не имеет решений для
других а. Однако каждой точке окружности отвечает т значений угла а
в интервале [/@); /@) + 2/лт); это означает, что в каждую точку окруж-
окружности отображается ровно т различных точек (у каждой точки окружности
имеется т прообразов). Ситуация несколько сложнее, когда функция/(i/?)
немонотонна. Предположим для определенности, что т > 0. Тогда уравне-
уравнение /(у?) = а может иметь сколь угодно большое число решений (т.е. пря-
прямая у = а может много раз пересекать графику =/(^))- Обозначим сим-
символом т+ число решений, для которых /' (i?>) > 0 (график пересекает
прямую у = а, идя снизу вверх), символ w_ обозначает число решений,
для которых f (<р) < 0. (Мы считаем, что решений c/'(i?>) = 0 не сущест-
существует - график не касается прямой у = а.) Число т+ - т_ называется ал-
алгебраическим числом решений уравнения f(#) = а. Легко убедиться, что
для а в интервале [/@); /Bэт)) алгебраическое число решений равно 1.
В этом легко убедиться, заметив, что куски отрезка [0; 2тг], в которых
/(?>) < а> чередуются с кусками, в которых /(^) > а. В соответствии с
этим решения с / (^?) > 0 чередуются с решениями, для которых
/'(?>) < 0 (см. рис. 23). Для а, лежащих вне интервала [/@), /Bтт)),
алгебраическое число решений уравнения/^) = а равняется нулю. Снова
используя то, что каждой точке окружности отвечает т значений а в интер-
интервале [/@), /Bя)), мы видим, что алгебраическое число прообразов любой
точки окружности равно т (под алгебраическим числом прообразов пони-
понимается разность числа прообразов, для которых /'(^) > 0, и числа прооб-
прообразов, для котооых f (у) < 0). При непрерывном изменении отображения
его степень не изменяется, поэтому го-
гомотопные друг другу отображения име-
имеют одну и ту же степень. (Если отобра-
отображение меняется непрерывно, то его сте-
степень также должна меняться непрерыв-
непрерывно, однако в силу дискретности множе-
множества целых чисел степень отображения
может изменяться только скачком.) С
другой стороны, если отображения, оп-
определяемые функциями /0 и fi, имеют
одну и ту же степень п, то они гомотоп-
гомотопны; соединяющая их деформация задает-
задается формулой /, = tfi + A - г)/о (из
того, что рассматриваемые отображения
имеют одну и ту же степень, следует,
что ftBтт) =/,@) + 2irm и, значит,/, оп-
определяет отображение окружности в
Рис.23 окружность).
236

Таким образом, мы построили взаимно однозначное соответствие между
множеством {S1, S1) гомотопических классов отображений окружности
в окружность и множеством целых чисел. Несколько более сложные рас-
рассуждения позволяют сопоставить целое число — степень отображения —
каждому отображению и-мерной сферы в n-мерную сферу и показать, что
при этом также возникает взаимно однозначное соответствие между мно-
множеством гомотопических классов {S", S") и целыми числами (см. § 2).
Гомотопические классы отображений окружности в плоскость с выколо-
выколотой точкой также находятся во взаимно однозначном соответствии с мно-
множеством целых чисел. Для того чтобы убедиться в этом, заметим, что в
IR2\ {0} (в плоскости с выколотым началом координат) удобно ввести
полярные координаты (г, в), где 0 < г < °°, а угловую координату в мож-
можно считать пробегающей окружность S1. Отображение / окружности S' в
IR2\ {0} сопоставляет точке ip окружности S1 точку плоскостиfR2 — {0 }
с полярными координатами г = gy(v?), в = hf A/5); можно рассматривать^
как отображение S1 в луч 0<г<°°,айу — как отображение S1 в S1. При
деформации отображения / как gf, так и hf' также непрерывно деформи-
деформируются. Из сказанного следует, что отображения/ и/' гомотопны друг дру-
другу в случае, если^у гомотопному ийу гомотопно hf'. Поскольку gy всегда
гомотопно gf' (два отображения в луч гомотопны), классификация отоб-
отображений S1 в IR2\ {0} сводится к классификации отображений S1 в S1
Проведенные только что рассуждения допускают следующее обобщение.
Всякое отображение / пространства X в прямое произведение Y X Z можно
рассматривать как пару отображений (gf, hf), где#у - отображение X в Y,
a hf — отображение X в Z. Замечая, что при непрерывной деформации /
отображения gf и hf также непрерывно деформируются, видим, что каждо-
каждому гомотопическому классу отображений X в Y X Z сопоставляется гомо-
гомотопический класс отображений X в Y и гомотопический класс отображе-
отображений X в Z. Таким образом, существует взаимно однозначное соответствие
между {X, YXZ} и прямым произведением {X, Y} X {X, Z] .Замечая,
что Н"\{0} (пространство IR" с выколотой точкой) топологически экви-
эквивалентно прямому произведению сферы S"-1 на прямую В1, убеждаемся,
что существует взаимно однозначное соответствие между множеством
гомотопических классов {X, Sn~1} и {X, В"\{0} }. Из этого утвержде-
утверждения следует, что пространство R"\{0} , как и сфера S"~l, асферично в
размерности к, если к < и — 1. В частности, при п > 2 пространство
fR"\ {0 } односвязно. В то же время S1 и(Я2\{0} неодносвязны.
Прямое произведение двух окружностей топологически эквивалентно
тору (поверхности баранки). Для того чтобы убедиться в этом, нужно,
следуя рис. 24, сопоставить точке t тора точку t x окружности, лежащей
в горизонтальной плоскости (параллели тора), и точку t2 окружности,
лежащей в вертикальной плоскости (меридиана тора). В силу доказанно-
доказанного выше существует взаимно однозначное соответствие между множеством
гомотопических классов { 5', 5' X S'} и множеством {S^S'lX {s',51}.
Это означает, что гомотопический класс отображений окружности в тор
характеризуется парой целых чисел.
Два пространства У, и Y2 называются гомотопически эквивалентными,
если существуют такие отображения hx пространства У\ в У2 и И2 прост-
пространства У2 в Yi, что отображения hth2 и h2hx гомотопны тождественным
237

отображениям; Если пространства Yl и Y2 гомотопически эквивалентны,
то между множествами {X, Yt) и [X, Y2} можно установить взаимно
однозначное соответствие. В самом деле, легко построить отображение
hi множества 'X, Yt) в {X, Y2}, сопоставляя гомотопическому классу
отображения / пространства X в Yt гомотопический класс отображения htf
пространства X в Y2. Аналогично строится отображение Н2 множества
{ X, Y2 } в {X, Yi) . Отображения й\ и h2 взаимно обратны. В самом
Рис.24
деле, поскольку отображение hxh2 гомотопно тождественному, отображе-
отображение / гомотопно h\h2f. Это означает, что отображение h\h2 является тож-
тождественным; аналогично доказывается, что h2h^ также является тождест-
тождественным отображением.
Если пространство Y\ является подмножеством пространства Y2 и су-
существует деформация gt пространства Y2 в У,, при которой все точки
пространства Yt остаются на месте, то Yx и Y2 гомотопически эквивалент-
эквивалентны (роль отображения h 1 играет вложение Yx в Y2, роль отображения h2
играет g 1). Заметим, что нетрудно построить такую деформацию плоскос-
плоскости с выколотой точкой IR2\ {0} в окружность S1, положив в полярных
координатах gt(r> ?>) = (A — t)r + *¦> $)• Мы видим, что окружность гомо-
гомотопически эквивалентна плоскости с выколотой точкой, отсюда снова сле-
следует существование взаимно однозначного соответствия между множества-
множествами {S1, S1} и {S1, Р2\ {0 }}. Аналогично доказывается, что сфера S"~l
гомотопически эквивалентна п-мерному пространству с выколотой точкой.
Часто приходится рассматривать отображения одного пространства
в другое, подчиненные некоторым дополнительным условиям. Обычно эти
дополнительные условия накладываются на значения отображения на не-
некотором подмножестве. Пусть, например, в пространстве X выделено под-
подмножество А, а в пространстве Y — подмножество В. Отображение / прост-
пространства Хв Y называется отображением пары (X, А) в пару (Y, В), если
множество А при этом отображении переходит в В. Пространство всех
отображений пары (X, А) в пару (У, В) обозначим С(Х, А \ Y, В). Два отоб-
отображения пары (X, А) в пару (Y, В) называются гомотопными, если они
принадлежат одной и той же компоненте пространства С(Х, A\.Y, В)-
Иными словами, отображения/0 иД пары (X, А) в пару (Y, В) гомотоп-
гомотопны между собой, если существует соединяющее их непрерывное семейство
ft отображений пространства X в Y, для которого при каждой t выполнено
238

условие/,(А) С В,
Таким образом, пространство С(Х, А | У, В) отображений пары (X, А)
в (У, 5) распадается на гомотопические классы (классы гомотопных друг
другу отображений). Множество гомотопических классов отображений
пары (X, А) в пару (Y, В) обозначим символом {X, А \ Y, В}. Наиболее
интересен случай, когда X = D, Y = D" — шары, имеющие размерности,
соответственно, тип, а множества А иВ являются сферами, ограничиваю-
ограничивающими эти шары: А = Sm ~', В = S"~l.
Покажем, что гомотопическая классификация отображений в этом
случае сводится к гомотопической классификации сфер. Именно: сущест-
существует взаимно однозначное соответствие между множеством {[/", Sm~1\
If, S"~1 ) гомотопических классов отображений пары (Dm ,Sm~l) в пару
(D", S"~l) и множеством {Sm ~', S"~ } гомотопических классов отоб-
отображений сферы Sm~l в сферу S"~l. Отображение / пары (?/", Sm~1)
в пару (?>", S") переводит сферу Sm~A в S"; при деформации отоб-
отображения / соответствующее отображение сфер также непрерывно деформи-
деформируется. Мы видим, что множество {Lf1, Sm ~l | D", Sn~l } естественно
отображается в множество {Sm ~1, S"~l} . Проверим, что это отображение
является взаимно однозначным соответствием. Прежде всего заметим, что
всякое отображение у сферы Sm ~1 в S"~' может быть продолжено в отоб-
отображение/пары (iyn,Sm~f) в (Z)",^") по формуле
(Всякую точку шара мы записываем в виде (г, s), где г — расстояние точ-
точки до центра, as— точка сферы, лежащая на радиусе, проходящем через
рассматриваемую точку.) Отображение пар, определяемое описанной толь-
только что конструкцией, будем называть правильными. Легко видеть, что два
отображения пары (Dm, S) в (D", S"~l), совпадающие на Sm~1,
гомотопны друг другу. (Гомотопия определяется формулой ft =
= tf\ + A ~О/о) Отсюда следует, что всякое отображение пар гомотопно
правильному. Замечая, что правильные отображения пар гомотопны в том
и только том случае, если гомотопны порождающие их отображения сфер,
приходим к нужному нам утверждению.
Наряду с топологией — наукой, изучающей непрерывные отображения, —
развивается дифференциальная топология, в которой основным объектом
изучения являются гладкие отображения, а Слово "гладкий" здесь и в даль-
дальнейшем обозначает "бесконечное число раз дифференцируемый". На самом
деле практически все утверждения-дифференциальной топологии справедли-
справедливы и без предположения бесконечной дифференцируемое™; обычно дос-
достаточно существования однократных или двукратных непрерывных произ-
производных. Для краткости мы не будем уточнять, насколько можно ослабить
требование бесконечной дифференцируемости в формулируемых нами
утверждениях. Ў
Понятие гладкого отображения не имеет смысла в произвольном топо-
топологическом или даже метрическом пространстве. Однако оно заведомо
осмыслено для отображений областей пространства В". Отображение у об-
области Gt CIRm в область G2 С fa" может быть задано с помощью и функ-
239

ций от т переменных
уя ± <ра(х1,... ,хт),
где (х1,. ¦ ¦, хт) пробегает область Gj, а (у1,. . . ,у") принадлежит облас-
области G2- Отображение кр называется гладким, если все функции ^',. . . , ут
бесконечно дифференцируемы.
Взаимно однозначное гладкое отображение называется диффеоморфиз-
диффеоморфизмом (гладким преобразованием), если обратное к нему отображение
i?>~' также является гладким. (Иными словами, диффеоморфизм — это
взаимно однозначное и в обе стороны гладкое отображение.) В дифферен-
дифференциальной топологии диффеоморфизмы играют ту же роль, что гомеомор-
гомеоморфизмы в топологии. Если отображение B) является гладким преобразова-
преобразованием, то т = и и, следовательно, можно говорить о якобиане отображения ip
D(x\...,xn)
Из соотношения
D{y\ у") D(xl, х") _
D(x\...,xH) D(y\...,y")
вытекает, что якобиан гладкого преобразования отличен от нуля. Отсюда
следует, что якобиан диффеоморфизма ip области G{ на область G2 не
меняет знака. (Напомним, что под областью понимается связное открытое
множество. Якобиан D(<p) является непрерывной функцией на Gx; если
бы эта функция меняла знак, то в силу связности нашлась бы точка, где
она обращается в нуль.) В случае если якобиан D(<p) положителен, говорят,
что гладкое преобразование у сохраняет ориентацию, в случае если этот
якобиан отрицателен, говорят, что \р обращает ориентацию.
Понятия дифференциальной топологии имеют смысл не только для об-
области в евклидовом пространстве, но и для объектов, получающихся из
склеивания нескольких областей с помощью гладких преобразований. Эти
объекты носят название гладких многообразий (см. § 5). Лростейшим
примером гладкого многообразия является n-мерная сфера 5", которую
можно считать склеенной из двух экземпляров пространства К".
Два гладких отображения /0(*) и fi(x) называются гладко гомотоп-
гомотопными, если их можно соединить деформацией ft(x), гладко зависящей от
х и t. Если / гладко гомотопно g и g гладко гомотопно А, то / гладко го-
гомотопно h.
* В самом деле, если гладкая деформация \pt (х) соединяет отображения
f(x) и g(x), а гладкая деформация фг(х) соединяетg(x) и h(x), то глад-
гладкую деформацию pt(x), соединяющую f(x) и h(x), можно построить,
положив pt(x) = <p\(t)(x) ПРИ 0 <' <^. Pt(x) = ^М(г)(х) при Vz <t < 1.
Здесь \(t) и n(t) - гладкие функции, удовлетворяющие условиям Х@) =
= О, Х(Й) = 1, n('/i) = 0, ^A) = I. Чтобы гарантировать гладкость деформа-
240

ции pt(x) при t - Vi, следует предположить, что все производные функций
\(t) нцО) при t -}h обращаются в нуль. Ў
Всякое непрерывное отображение гомотопно гладкому; если два глад-
гладких отображения гомотопны, то они гладко гомотопны. Эти утверждения
позволяют ограничиться рассмотрением гладких отображений и гладких
гомотопий при решении задачи гомотопической классификации отображе-
отображений: для отображений сфер их доказательство будет намечено в § 2.
Мы уже упоминали выше, что гомотопический класс отображения сферы
в сферу той же размерности характеризуется целым числом — степенью
отображения. Из этого следует, что гомотопические классы отображений
сферы S"~l в IR"\{0} также находятся во взаимно однозначном соот-
соответствии с целыми числами. Покажем сейчас, как для случаев п = 2 и я = 3
получить аналитическое выражение для целого числа, характеризующего
гомотопический класс гладкого отображения 5" в [R"\ {0}. Заметим,
прежде всего, что всякой замкнутой поверхности Г в пространстве IR3,
не проходящей через начало координат, можно сопоставить поток § Е dS
векторного поля Е = х/| х |3 через эту поверхность. Поле Е можно интер-
интерпретировать как напряженность поля точечного заряда, расположенного в
начале координат. Это означает, в частности, что divЕ = 0 при х#0и, сле-
следовательно, в силу теоремы Гаусса § Е dSHe меняется при непрерывной де-
деформации Г, если только в процессе деформации она не пересекает начала
координат. Если Г — несамопересекающаяся поверхность, то f E dS равен
О в случае, когда начало координат не находится внутри Г, и равен ±4п,
если начало координат лежит внутри Г. Знак зависит от выбора ориентации
поверхности Г. В общем случае #Е Сравняется 4пт, где т — целое число.
(Это снова следует из теоремы Гаусса.)
Таким образом, всякой замкнутой поверхности Г, не проходящей че-
через начало координат, отвечает целое число
1 ] .V1 dx2 dx3 + х2 dx3 dxl + x3 dx4x2
mr= #EJS= § . C)
4w i' 4i r I x I
Дифференцируемому отображению / сферы Si bIR3\{0} сопоставим
число m(f) = niy, где Г =f(S2) — поверхность, в которую переходит сфе-
сфера S2 при отображении /. Переходя в интеграле C) от переменных х1,
х2, х3 к координатам %', |2 на сф^ере S2, получаем выражение
/'A)
э/2
91'
э/3
Э|'
э/3
э?2
э/3 э/3
V э/1
Э|> Э|2
э/1
э/2
э/1
Э|2
э/2
Э|2
^l1 dl2 =
1 1
~4V fJf\3~
(Э/с(?)/Э?2) d%1 d%2
241

(в качестве координат J-', |2 на сфере 52 можно выбрать, например, сфери-
сферические координаты). Целое число m(f) очевидным образом не меняется
при непрерывном изменении отображения / и, следовательно, характери-
характеризует гомотопический класс этого отображения.
Аналогичные соображения показывают, что целое число
1 -jc2 dxl +X1 dx1
m(f) = / =— f d( arctg
U) 2тг /(/) (x'J+(x2J 2 i \ *
I 2" /
=— f d( a
2тг i \
характеризует гомотопический класс гладкого отображения/ = (fl,f2)
окружности S' в/R2\ {0} . (Точка окружностиSl характеризуется угловой
координатой ip.) Соответствующие формулы для отображений S"~l в
IR"\ {0 } при и > 3 будут получены в § 8.
§ 2. Степень отображения
Рассмотрим систему и уравнений с т неизвестными
A)
f"(x\...,xm)=a",
или, короче,
/(*) = «, B)
где л: = (х1 хт ), Дх) = (/'(*),... ,/"(*)). Будем считать, что/, . . .
...,/" — гладкие функции, или, иначе говоря, отображение /, переводящее
точку х€.Щт в точку х' =f(x)€.IR", является гладким отображением
/л-мерного евклидова пространства Е = Вт в и-мерное евклидово простран-
пространство Е' = Щ". Будем предполагать, что
lim Дх) = °°. C)
Последнее условие означает, что / можно рассматривать как непрерывное
отображение от-мерной сферы в и-мерную сферу, поскольку, как мы виде-
видели в § 1, сфера представляет собой евклидово пространство, к которому
присоединена бесконечно удаленная точка. * Если (х1,. .. ,хт) и (а1, . . .
. .. , а") рассматривать как стереографические координаты на сфере; то
отображение переводит w-мерную сферу, из которой выколот северный
полюс, в и-мерную сферу без северного полюса. Если считать, что северный
полюс переходит в северный полюс, то условие C) гарантирует непрерыв-
непрерывность отображения / как отображения всей /и-мерной сферы в и-мерную. т
Два отображения рассматриваемого типа называются гладко гомотоп-
гомотопными, если существует гладкая деформация одного отображения в другое,
в процессе которой условие C) все время остается выполненным (точнее,
/о гомотопно ft, если можно соединить /0 и ft семейством отображений
/,, 0 < t < 1, таким образом, чтобы ft(x) гладко зависело от х, t и ft(x) -*¦ <»
при х -* °° равномерно по 0.
242

Мы займемся сейчас важным случаем т-пк покажем, что в этом случае
каждому отображению из описанного выше класса можно сопоставить
целое число (степень отображения), не меняющееся при деформации.
(При т=п можно отождествить пространство Е и пространство Е', однако
нам будет удобнее считать эти пространства разными.)
Поставим вопрос о числе решений системы уравнений A) или, что то же,
векторного уравнения B).
Назовем точку х е Е регулярной, если якобиан D(x) отображения /
в точке х не равен нулю
В противном случае точка х называется сингулярной.
Точка д??"' называется сингулярной, если по крайней мере один корень
уравнения f(x) = a является сингулярной точкой пространства Е; в против-
противном случае а называется регулярной точкой (отметим, в частности, что
в случае, если уравнение f(x) = а совсем не имеет корней, точка а регу-
регулярна) .
Имеет место следующее важное утверждение (лемма Сарда): объем
¦множества сингулярных точек пространства Е равен нулю *). Из леммы
Сарда вытекает, что регулярные точки образуют плотное множество в Е'.
Пусть а е Е' — регулярная точка. По определению каждое решение х
уравнения Дх) = д является регулярной - точкой в Е, т.е. якобиан D(x)
отображения / в точке х не обращается в нуль. Будем называть алгебраи-
алгебраическим числом решений уравнения Дх) = д разность числа решений, для
которых этот якобиан положителен, и числа решений, для которых якобиан
отрицателен. (Вместо термина "алгебраическое число решений уравнения
Дх)=д" мы будем иногда употреблять термин "алгебраическое число
прообразов точки а при отображении /".)
Можно доказать, что алгебраическое число решений уравнения Дх) = а
не зависит от выбора регулярной точки а€Е'. Это позволяет определить
степень отображения f как алгебраическое число решений уравнения Дх) =
= а, где а&Е' — произвольная регулярная точка. (Пользуясь геометриче-
геометрическим языком, можно сказать, что степень показывает, сколько раз накры-
накрыта точка д.)
В качестве примера рассмотрим в одномерном случае отображение
/(х) = х3— Зх (рис. 25). Сингулярными точками в Е являются точки х =
= ± 1, ъЕ' -точки а = ±2. Приа<- 2 и д>2 уравнение х3 - Зх=д имеет
одно решение и в этом решении /'(х) = 3(х2 — 1) >0. При — 2 < а < 2
уравнение х3 — Зх =а имеет три решения; для двух из них /'(х)>0, для
одного /'(х) <0. Таким образом, отображение Дх) имеет степень 1. Анало-
*) Пусть отображение /переводит множество ScEb множество S' СЕ'. Если /
взаимно однозначно, то объем 5'равен f\D(x) \dx; отсюда следует, что в случае,
S
если отображение произвольно, объем S' не превышает / \D(x) \dx. Применяя это
S
соотношение к случаю,, когда S — множество сингулярных точек в Е, S' — множе-
множество сингулярных точек в ?", видим, что объем S' равен нулю. (Это рассуждение не
является строгим, но из него легко сделать полное доказательство.)
243

гично устанавливается, что отображение f(x) = x*-x2 (рис. 26) имеет
степень 0. В двумерном случае рассмотрим отображение, переводящее
комплексное число z в zm"zn (мы отождествляем точки плоскости с ком-
комплексными числами). Если а = Аеш, А Ф 0, то прообраз точки а при иссле-
исследуемом отображении состоит из I т - п | точек z=re"t>, где гт + п = А,
(т - п)у=а + 2лк. Якобиан положителен при т>п и отрицателен при
т<п, поэтому степень отображения равна т-п.
Рис.25
Рис.26
Отметим, что в случае, когда степень отображения не равна нулю, урав-
уравнение f(x)=a имеет решение при любом а (если бы это уравнение не имело
решений при а = а0, то, вычисляя степень отображения с помощью регуляр-
регулярной точки а0, мы получили бы нуль).
Укажем сейчас аналитическую формулу для степени. Воспользуемся
при выводе известным соотношением
S(/(x)-a) = Z \ 6(х-хг(а)), D)
справедливым, если а - регулярная точка. (Через хг(а) здесь обозначены
корни уравнения f(x) = a; суммирование идет по всем корням. Через D(x),
как и раньше, обозначается якобиан det( df'l'dx').\
С помощью D) сразу получаем, что степень отображения /может быть
задана формулой
degf=fD(x)8(f(x)-a)dx, E)
где а - регулярная точка. В самом деле, из D) следует, что правая часть
E) равна
Бблее удобную
E) на гладкую
т.е. алгебраическому числу решений уравнения f(x) = a.
формулу для степени отображения получаем, умножив
функцию д(д), удовлетворяющую условию
244

и проинтегрировав по а. Эта формула имеет вид
degf=JD(x)n(f(x))dx F)
(соотношение E) справедливо только для регулярных а, но это не являет-
является препятствием для проведенного выше рассуждения, поскольку множе-
множество сингулярных а имеет нулевой объем). Для того чтобы гарантировать
существование рассматриваемых интегралов, удобно предположить, что
функция \к(а) финитна (обращается в нуль вне некоторого шара).
Соотношение F) можно рассматривать как новое определение степени
отображения; это определение мы будем называть аналитическим в отличие
от данного выше геометрического определения. Проведенные выше рассуж-
рассуждения показывают, что аналитическое определение степени совпадает с
геометрическим.
Если степень отображения определена аналитически, то нетрудно прове-
проверить, что она не меняется при гладкой деформации отображения. Проведем
доказательство этого утверждения. Достаточно доказать, что степень не
меняется при бесконечно малой вариации отображения. Удобно записать
F) в виде
. "J "J I.... in , п
)^-... -^ e- d х-
_r...1-7-e'.-WV G)
где, как обычно, е'«---'л= о, если среди индексов есть совпадающие,
e'i-'n = +i) если (/],...,*„) — четная перестановка, е'1''1" = — 1,
если (/j,... , /'„) — нечетная перестановка, e(i _ in = e'' •¦¦'". Тогда для
изменения степени при бесконечно малой вариации отображения / получаем
U bf'eh...in —Г • • • "А" е'"'''''" d"x
и! да'
a=f(x)
(y } >'¦¦'» dxil dxi7 ax-
о
Подьштегральное выражение здесь можно представить в виде —= А , где
дх'
1 df'* df'n
А' = и( f(x)) е, ,_ 8/' ¦ г- • • • —т- е"» ¦••'".
В силу финитности функции ц(а) можно считать, что в выражении для
deg/ интеграл берется не по всему пространству, а по шару большого
Э
радиуса. Преобразуя интеграл от дивергенции —т А в интеграл по границе
дх
этого шара, получаем, что б deg/= 0.
Покажем на простом примере, как с помощью понятия степени отобра-
отображения можно доказывать существование решений конкретного уравнения.
245

Рассмотрим уравнение
P(z,.J) = Q, (8)
где z — комплексное число, комплексная функция P(z, z) имеет вид
(,) e, . е>0.
Функция P(z, г) определяет отображение плоскости на плоскость (ком-
(комплексные числа отождествляются с точками плоскости R2, точке z сопо-
сопоставляется точка P(z, z)). Это отображение удовлетворяет условию C) и,
значит, принадлежит к изученному выше классу.
Деформация
Pt(z,z)=Azmzn + tr(z,z)
соединяет рассматриваемое отображение с отображением, определяемым
функцией P0(z, z) = Azm~zn. Это последнее, как мы видели, имеет степень
т — п, следовательно, ту же степень имеет гомотопное ему отображение
P(z, 1). В случае если тФ п, отсюда вытекает, что уравнение (8) имеет
хотя бы одно решение.
Заметим, что из доказанного утверждения вытекает, что алгебраическое
уравнение
aoz" + ciiz"-1 + ...+а„ =0
имеет хотя бы один комплексный корень (основная теорема алгебры).
Перейдем теперь к рассмотрению гладких отображений и-мерной сферы
в и-мерную. Введем на сфере (?0J + ... + (|"J = 1 стереографические
системы координат (х1,. .. ,х") и (je1,... ,3с") — одну с центром в
южном полюсе, другую с центром в северном полюсе (первая из них покры-
покрывает всю сферу за исключением северного полюса, а вторая —всю сферу
за исключением южного полюса).
Отображение одной сферы в другую называется гладким, если оно
задается гладкими функциями в этих координатах*). Далее все отображе-
отображения и все гомотопии будут предполагаться гладкими (даже если это не
будет отмечено явно); позже будет рассмотрен случай непрерывных ото-
отображений. Если / — гладкое отображение и-мерной сферы S" в л-мерную
сферу S", то понятия регулярной и сингулярной точек сфер 5" и S" опре-
определяются с помощью стереографических систем координат точно так же,
как и выше. Существенно отметить, что регулярность или сингулярность
Точки не зависит от выбора системы координат. Это следует из того,
что якобиан перехода от системы координат (х1, ... , х") к системе
(х1,... ,5с") не обращается в нуль**), и, стало быть, в случае если якобиан
отображения / не равен нулю в одной из систем координат, он не равен
*) Если точка сферы не совпадает с одним из полюсов, то в ее окрестности можно
пользоваться любой из рассматриваемых систем координат; поскольку переход от
одной системы к другой задается гладкими'функциями, гладкость отображения
не зависит от выбооа системы координат.
**) При определении стереографических координат, данном в § 1, этот якобиан
отрицателен. Однако нам удобнее видоизменить это определение так, чтобы якоби-
якобиан был положителен. Для этого можно, например, изменить знак у одной из коор-
координат.
246

нулю и в другой системе. Более того, заметив, что якобиан перехода от
(дг1,... ,х") к Eс1,.... л?") положителен, можно утверждать, что знак
якобиана отображения / также не зависит от выбора системы координат.
Это позволяет определить алгебраическое число решений уравнения Дх) = а,
где x?S", a — регулярная точка S", так же, как и раньше: как разность
числа решений с положительным якобианом и числа решений с отрицатель-
отрицательным якобианом. При определении алгебраического числа решений уравне-
уравнения Дх) = а не обязательно пользоваться стереографическими системами
координат; можно применять любые координаты на сфере, связанные
со стереографическими преобразованиями с положительным якобианом.
Мы будем говорить, что а -регулярная точка типа (г, s), если уравнение
/(х) = д имеет г решений с положительным якобианом и х решений с отри-
отрицательным якобианом (таким образом, алгебраическое число решений
уравнения f(x) =а равно г — s). Назовем степенью отображения / алгебра-
алгебраическое число решений уравнения/(х) = я, где а — регулярная точка. Для
того чтобы это определение было корректным, нужно доказать, что это чис-
число не зависит от выбора регулярной точки; мы опустим это доказательство.
Примеры отображений n-мерной сферы, имеющих произвольную степень,
проще всего построить с помощью понятия надстройки. Каждому отобра-
отображению / сферы S"~l в сферу Sk~1 сопоставим отображение Б/сферы S"
в сферу Sk, считая, что 2/совпадает с / на экваторе сферы S" и переводит
каждый меридиан сферы S" изометрично в меридиан сферы Sk. * Мы
считаем, что сфера S" определяется уравнением
Под экватором понимается подмножество сферы 5", выделяемое соотно-
соотношением |° = 0; очевидно, экватор можно рассматривать как (п — 1)-мер-
1)-мерную сферу. Под меридианом понимается лежащая на сфере полуокруж-
полуокружность, диаметром которой служит отрезок, соединяющий северный и
южный полюсы. Ў Аналитически можно записать отображение 2/ с по-
помощью формулы
где
Отображение ?/называется надстройкой над отображением /. Если к =п,
то степень отображения ?/ совпадает со степенью отображения /. В самом
деле, если относительно отображения/ точка а является регулярной точкой
типа (r,s), то любая точка, лежащая на меридиане, проходящем через а
(кроме северного и южного полюсов), является регулярной точкой типа
(г, s) относительно отображения X/.
Для того чтобы построить отображение сферы S" в 5", имеющее задан-
заданную степень q, заметим, что конструкция такого отображения очевидна
при и = 1. (Более того, для окружности легко построить отображение,
имеющее регулярные точки любого заранее заданного типа.) Взяв отобра-
отображение / окружности, имеющее степень q, и применив и — 1 раз операцию
247

надстройки, мы получим отображение 2" '/сферы S", имеющее ту же
степень.
Для степени отображения сферы S" можно указать аналитическую фор-
формулу, обобщающую соотношение F). В самом деле, повторяя проведенные
выше рассуждения, легко убедиться, что соотношение F) остается спра-
ведливым, если якобиан D(x) = detl — 1 вычисляется с помощью про-
проих'/
извольных систем координат на сферах S" и 5"; важно только, чтобы
эти системы координат были пригодны почти для всех точек сферы (как
стереографическая система координат, охватывающая всю сферу за исклю-
исключением единственной точки; при и = 2 можно взять обычные сферические
координаты в, tp, в которых непрерывность соответствия между точкой
сферы и ее координатами нарушается только на меридиане $ = 0). Функ-
Функция д, фигурирующая в F), должна быть гладкой функцией от коор-
координат на сфере S" и удовлетворять условию fji(a)da = 1, где интеграл бе-
берется по всем возможным значениям координат на S".
Для того чтобы гарантировать, что интеграл fn(a)da имеет смысл, нуж-
нужно дополнительно потребовать, чтобы при переходе к другим системам
координат на S" подынтегральное выражение оставалось гладкой
функцией.
Если на сферах S" и S" выбраны стереографические координаты
(х1, ..., х") и (хп, .. ., х'п), то степень отображения можно записать,
например, в виде
\дх'
deg/= /detl г b(x'(x))d"x.
ЧЭх7/
Если и = 2, то в сферических координатах степень отображения выражается
формулой
1 D(e,$)
deg/ = — // sine' dd
4тг D(§)
Пользуясь аналитическим определением степени отображения и повто-
повторяя проведенные выше рассуждения, приходим к выводу, что и в рассмат-
рассматриваемом случае степень отображения не меняется при гладкой дефор-
деформации. Имеет место и обратное утверждение — если два гладких отображе-
отображения имеют одну и ту же степень, то они гладко гомотопны.
До сих пор мы изучали только гладкие отображения сферы. Покажем,
что гомотопическая классификация непрерывных отображений сферы
сводится к гомотопической классификации гладких отображений.
¦ Заметим, прежде всего, что любое непрерывное отображение сферы S'"
в сферу 5" можно сколь угодно близко аппроксимировать гладким. Отсю-
Отсюда следует, что любое непрерывное отображение гомотопно гладкому,
поскольку два близких отображения гомотопны •). Далее, если два глад-
*) Имеет место следующее утверждение: если ни для какой точки xeSm точки
/о (*) и /i 00 не лежат на противоположных концах какого-либо из диаметров сфе-
сферы S" (т.е. угол между векторами /0(х) и /, (х) меньше 180°), то отображения /„
и /, гомотопны. Гомотопию легко построить, перетягивая /0 'BJ1", по меньшей из дуг
большого круга, проходящего через точки /0(х) и /, (х); еепи /0 и /, - гладкие
отображения, то эта гомотопия оказывается гладкой.
248

ких отображения /0 и f\ гомотопны, то их можно соединить гладкой гомо-
топией. В самом деле, непрерывную гомотопию /,(х), соединяющую /0
и Л, можно рассматривать как отображение произведения S'" X / в S";
аппроксимируя это отображение гладким, получаем гладкую деформа-
деформацию /,'(х). Эта деформация соединяет отображения f0 и//. Отображе-
Отображение /о аппроксимирует отображение /0 и поэтому гладко гомотопно /0;
аналогично // гладко гомотопно fx. Отсюда следует, что /0 гладко гомо-
гомотопно fi.
Мы можем теперь определить степень непрерывного отображения /
как степень гомотопного ему гладкого отображения. (Например, как сте-
степень гладкого отображения, достаточно близкого к /.) Из доказанного
следует, что определенная таким образом степень не зависит от произвола
в выборе гладкого отображения и что два непрерывных отображения го-
гомотопны в том и только в том случае, если они имеют одну и ту же степень.
Понятие степени отображения сферы имеет многочисленные и важные
приложения. Им можно воспользоваться, в частности, для доказательства
существования неподвижной точки отображения шара в себя.
Вспомним, прежде всего, что отображение /7-мерной сферы, которое
можно непрерывно продолжить на ограниченный этой сферой (п + 0-мер-
0-мерный шар, гомотопно нулю (т.е.. гомотопно отображению всей сферы в одну
точку).
Поскольку степени гомотопных отображений равны, а отображение
всей сферы в одну точку имеет степень нуль, мы видим, что отображение
сферы в сферу, имеющее ненулевую степень, нельзя продолжить на шар.
Этим утверждением можно воспользоваться для доказательства сле-
следующей теоремы о неподвижной точке.
Всякое отображение шара в себя имеет, по крайней мере, одну непод-
неподвижную точку.
В самом деле, пусть g — отображение шара в себя, не имеющее непод-
неподвижных точек (т.е. точек, удовлетворяющих условию g(x) = х). Тогда
можно определить отображение шара в сферу по формуле
х - g(x)
/с*)= -—Нт (9)
I х - g(x) |
(по условию знаменатель в (9) не обращается в нуль, поэтому форму-
формула (9) имеет смысл и определяет непрерывное отображение). Отображе-
Отображение /(*¦)> рассматриваемое только на границе шара, гомотопно тождест-
тождественному отображению 7(х) = х. В самом деле, отображение g переводит
шар в себя и, значит, сферу внутрь шара; таким.образом, вектор, идущий
из точки х в точку g(x), образует острый угол с вектором —х. Отсюда
следует, что для всех точек х, принадлежащих сфере, угол между векто-
векторами f(x) и i(x) = х не превосходит 90° и, значит, в силу сделанного выше
замечания отображения / и / гомотопны. Таким образом, степень отобра-
отображения /, рассматриваемого как отображение сферы, совпадает со степенью
тождественного отображения и, стало быть, равна 1.. С другой стороны,
отображение / продолжается на весь шар и, следовательно, имеет нулевую
степень. Мы пришли к противоречию, доказывающему, что лтображение g
имеет неподвижные точки.
249

В § 1 было показано, что всякое ограниченное замкнутое выпуклое
множество топологически эквивалентно шару. Можно утверждать поэтому,
что всякое отображение ограниченного замкнутого выпуклого множества
в себя имеет неподвижную точку. Известны многочисленные теоремы
о существовании неподвижных точек; доказанная теорема является прос-
простейшей из них.
§ 3. Фундаментальная группа
Путем в пространстве X называется непрерывное отображение отрезка
в пространство X. Образ начала отрезка называется началом пути, образ
конца отрезка - концом пути. Без существенного ограничения общности
можно считать, что все пути задаются с помощью отображения заданного
отрезка [а; Ь]. Иначе можно сказать, что путь — это непрерывная кривая
в пространстве X или непрерывное семейство точек, зависящее от пара-
параметра t, пробегающего отрезок.
Однако, говоря, что путь — это кривая, нужно помнить, что на этой кри-
кривой фиксирована параметризация с помощью действительного параметра.
Две кривые, совпадающие геометрически, но отличающиеся выбором па-
параметризации, определяют разные пути. Например, пути на плоскости,
задаваемые соотношениями
jc = cosr, у = sin r @<г<7г) A)
x = t, y = s/\-t2 (UK1), B)
определяют одну и ту же полуокружность, но мы их рассматриваем как
разные. Мы требуем, чтобы задающее путь отображение отрезка было
непрерывным, но не требуем, чтобы оно было топологическим. Иными
словами, мы допускаем самопересекающиеся пути и даже пути, в которых
какой-либо участок проходится несколько раз. Например, вполне допус-
допустимым является путь
х = cos nt, у = sin nt (О < t < 2 п, п — целое) C)
(окружность, пройденная п раз).
С понятием пути мы уже встречались при определении связного прост-
пространства. Напомним, что пространство называется связным, если для любых
двух его точек можно найти путь, соединяющий эти точки, т.е. путь с нача-
началом в одной из этих точек и с концом — в другой. В Дальнейшем в этом па-
параграфе будут рассматриваться только связные пространства.
Семейство путей fT(t), непрерывно зависящее от параметра т, назы-
называется гомотопией или деформацией путей, если все начальные точки
семейства совпадают между собой и все конечные точки также совпадают
между собой. Если параметр т меняется в пределах а < т < /3, то мы го-
говорим, что гомотопия соединяет два пути /<*(?) и fp{t). Два пути,
начинающиеся в одной и той же точке х0 и кончающиеся в одной и той же
точке *,, называются гомотопными (принадлежащими одному гомото-
гомотопическому классу), если их можно про деформировать один в другой
(т.е. соединить гомотопией) (рис. 27). Гомотопию/Т(Г) можно рассмат-
250

ривать как функцию, сопоставляющую каждой точке (t, т) прямоуголь-
прямоугольника { а < Г < Ь, а < т < ? } точку fT(t) - f(t, т) пространства X. Иначе,
гомотопия — это отображение прямоугольника в пространство X, пере-
переводящее сторону t = а в одну точку дг0 е X и сторону f = ie одну точку
Под замкну**1-** И7ГСЛ< понимается путь, у которого начало и конец
совпадают. Говорят, что замкнутый путь гомотопен нулю, если он может
быть продеформирован в нулевой путь (под нулевым путем понимается
11
а
Рис.28
отображение отрезка [а; Ь] в одну точку). Замкнутый путь можно рас-
рассматривать как отображение окружности. Действительно, если окруж-
окружность параметризовать угловой координатой $ @ < $ < 2 я), то*функция
/((?) на отрезке [0; 2 я], удовлетворяющая условию ДО) = /Bя), может
рассматриваться как непрерывное отображение окружности. Однако де-
деформация замкнутого пути и деформация отображения окружности —
это разные понятия. Ясно, что всякая деформация замкнутого пути может
рассматриваться как деформация отображения окружности. Однако дефор-
деформация отображения окружности, определяемая семейством функций /т(<^),
может рассматриваться как деформация замкнутого пути лишь в случае,
если точка /т@) = /тBтг) не зависит от т (по определению, при деформации
пути начальная и конечная точки должны оставаться неподвижными).
Тем не менее легко проверить, что замкнутый путь гомотопен нулю
тогда и только тогда, когда соответствующее отображение окружности
гомотопно нулю. В одну сторону это утверждение очевидно: если замкну-
замкнутый путь гомотопен нулю, то же самое можно сказать о соответствующем
отображении окружности. Если же известно, что отображение окружности
гомотопно нулю, то по доказанному в § 1 оно может быть непрерывно
продолжено на круг, ограниченный рассматриваемой окружностью. С по-
помощью этого продолжения деформация замкнутого пути в точку строится
очевидным образом: отображения нарисованных на рис. 29 окружностей
определяют нужную нам деформацию.
Напомним, что мы назвали пространство односвязным, если всякое
отображение окружности в это пространство гомотопно нулю, т.е. может
быть продолжено на ограниченный окружностью круг. Теперь мы можем
сказать, что пространство односвязно тогда и только тогда, когда всякий
замкнутый путь в нем гомотопен нулю.
251

Для определенности будем понимать в дальнейшем под путем отображе-
отображение отрезка [0; 1]. Рассмотрим в пространстве X все замкнутые пути,
начинающиеся и кончающиеся в фиксированной точке х0. Все такие пути
можно разделить на гомотопические классы: два пути принадлежат одно-
одному классу, если они гомотопны друг другу. А Заметим, что если путь/0(У)
гомотопен пути fi(t) (/0(f) ~ Л@)> аЛ@ ~ /г@> то> как легко про-
проверить, /о @ ~ /2 @. Кроме того, если /0 (Г) ~ Л (Г), то Д (t) ~ /0 @. Эти
свойства позволяют разбить множество всех путей на классы гомотопи-
гомотопической эквивалентности, т
Рис. 29
Множество гомотопических классов замкнутых путей в пространстве X
с. началами и концами в точке х0 обозначается символом тг) (X, х0). В слу-
случае если пространство X односвязно, это множество состоит из единствен-
единственного элемента.
Два пути, начинающиеся и кончающиеся в точке х0, можно перемножать:
произведение f * g путей fag получается, если сначала пройти по пути /,
а затем по пути g. Более формально, если пути fug рассматривать
как отображения отрезка [0; 1], то путь f * g задается отображением от-
отрезка [0; 1], совпадающим с /B1) на отрезке 0 < / < 1/2 и с gBt - 1}
на отрезке 1/2 < t < 1. Это произведение путей порождает произведение
гомотопических классов путей (чтобы проверить, что произведение гомо-
гомотопических классов определено корректно, необходимо убедиться, что
в случае, когда путь / гомотопен пути /', а путь g гомотопен пути g , произ-
произведение / * g гомотопно произведению /' * g'). Два произвольных пути,
вообще говоря, перемножать нельзя, но можно определить произведение
/ * g двух путей /и g, если конец / совпадает с началом g.
Нетрудно доказать, что множество гомотопических классов тт%(Х, х0)
с введенной только что операций умножения гомотопических классов
образует группу. Эта группа называется фундаментальной группой прост-
пространства X. Единичным элементом этой группы является гомотопический
класс гомотопных нулю путей. Если путь / принадлежит гомотопическому
классу [/], то путь /, пройденный в обратном направлении, принадлежит
гомотопическому классу [/]"'. В самом деле, произведение пути /на
тот же путь, пройденный в обратном направлении^ задается функцией,
равной fBt) при 0 < t < 1/2 и/B - 2г) при 1/2 < Г< 1. Деформация этого
пути в нулевой путь определяется формулой
252

при 0 < t < 1/2 и формулой
/т@=/«2-200-т))
при 1/2 <f < 1.
Вычислим, например, фундаментальную группу окружности. Рассмат-
Рассматривая путь с началом и концом в точке х0 € 5'как отображение окруж-
окружности, можно сопоставить ему целое число п — степень отображения (см.
§ 1). Поскольку гомотопные отображения окружности имеют одну и ту же
степень, мы получаем отображение множества ni(Si, х0) в множество
целых чисел ~Z. Можно доказать, что это отображение взаимно однозначно.
При перемножении путей степени соответствующих отображений окруж-
окружности складываются. Это означает, что группа iti(S1,x0) изоморфна груп-
группе Ж (Более простое доказательство см. в § 4.)
Фундаментальная группа может быть некоммутативной. Рассмотрим
в качестве примера плоскость с двумя выколотыми точками и на ней два
пути: путь /i, обходящий одни раз первую выколотую точку, и путь /2,
обходящий один раз вторую выколотую точку (рис. 30). Можно дока-
доказать, что путь ft * f2 негомотопен пути /2 * Д. Однако если пространст-
пространство X является топологической группой, то фундаментальная группа
ni(X, х0) коммутативна. Для замкнутых путей в топологической группе,
начинающихся и кончающихся в единице группы, можно определить умно-
умножение также с помощью групповой операции: произведение А = fg путей
/ и g определяется как путь h(t) = f(t)g(t). Нетрудно проверить, что путь fg
гомотопен пути f * g и, следовательно, новое произведение путей опреде-
определяет прежний закон умножения гомотопических классов. В самом деле,
путь / гомотопен пути /', который определяется формулой f'(t) = fBt)
при 0 < t < 1/2, f'(t) = 1 при 1/2 < t < 1. Путь g гомотопен пути g\ опреде-
определяемому формулой g'(i)=\ при 0</< Il2,g'(t) = gBt- 1) при 1/2 <
< t < 1. Очевидно чи путь f'g' совпадает с путем/* g. Поэтому путь fg
гомотопен пути / * g. Точно так же доказывается, что путь f*g гомотопен
пути gf. (Впрочем, можно не проводить доказательство заново, заметив,
Рис.30
что, изменив порядок умножения в группе, т.е. заменив групповую опе-
операцию hih2 операцией А, о h2 = A2Ai, мы снова получим групповую опера-
операцию, к которой можно применять предыдущие рассуждения.) Отсюда
получим, что в топологической группе X путь f * g гомотопен пути g * f,
т.е. группа jtj (X, х0) коммутативна.
Группа iti(X, x0) зависит, по определению, не только от пространст-
пространства X, но и от точки х0. Можно доказать, однако, что группы Hi(X, x0)
и пх(Х, х,), где xo,xt - различные точки, изоморфны. Построить указан-
указанный изоморфизм можно следующим образом. Рассмотрим путь а, идущий
из точки хп в точку Xi (напомним, что все пространства мы предпола-
253

гаем связными). Тогда всякому замкнутому пути/, начинающемуся и кон-
кончающемуся в точке *!, можно сопоставить путь а * f * а, начинающийся
в кончающийся в точке х0 (рис. 31). (Здесь и далее символ а обозначает
путь а, пройденный в обратном направлении.) Если путь /0 гомотопен
пути /i, то путь а * /о * а гомотопен пути а * Л * а и, следовательно,
определено отображение ni(X, xt) в vi(X, x0); это отображение обозначим
символом а. Нетрудно проверить, что отображение а является изомор-
изоморфизмом группы пх (X, х,) на группу wj (X, х0).
Рис.31
В самом деле,, это отображение является гомоморфизмом: путь а */*
* g *а гомотопен пути а * / *~a*a*g *~a, поскольку с* * а можно стянуть
в точку. Для того чтобы проверить, что отображение а взаимно однознач-
однозначно, следует убедиться, что отображение ~а группы 7Ti(X xt) в тт\{Х, х0)
обратно рассматриваемому отображению: аа = а а = I. Это нетрудно сде-
сделать, заметив, что путь сй*а */*а*а гомотопен / (снова стягивается
в точку путь а *а).
В случае когда х0 = xt, отображение а является автоморфизмом группы
Я! (X, х0); этот автоморфизм задается формулой
[«МаГ1 D)
(путь а в рассматриваемом случае замкнут, и ему отвечает элемент
[ а] ? 7Ti (X дг0); пути а отвечает элемент [а]"').
Построенный изоморфизм а зависит от выбора пути а (негомотопные
пути могут порождать разные изоморфизмы). Однако, в случае если фунда-
фундаментальная группа коммутативна, изоморфизм не зависит от выбора
пути. В случае х0 = xt это немедленно вытекает из формулы D). Общий
случай сводится к этому частному случаю с помощью соотношения 5/3 =
= а**^.
Непрерывное отображение h пространства X в пространство Y, пере-
переводящее точку х0 в точку у о, порождает гомоморфизм группы п^ (X, х0)
. в группу nt(Y, у о)- В самом деле, пути /(/) в пространстве X можно
сопоставить путь h(f(t)) в пространстве Y, причем гомотопные пути при
этом переходят в гомотопные пути, произведение путей переходит в произ-
произведение путей
254

§ 4. Накрывающие пространства
Понятие фундаментальной группы тесно связано с понятием накрываю-
накрывающего пространства. Под накрытием (или отображением накрытия) мы
будем понимать локально топологическое отображение h связного про-
пространства X на пространство Y. Если пространство Л' компактно, то локаль-
локально топологическое отображение можно определить как такое отображе-
отображение, при котором у каждой точки пространства X существует окрестность,
топологически отображающаяся в У, В общем случае это условие недо-
недостаточно, и нужно пользоваться следующим определением: отображение
h называется локально топологическим, если у каждой точки у е Y су-
существует такая окрестность U, что ее прообраз я "*(?/) можно разбить
на открытые подмножества, каждое из которых я топологически отобра-
отображает на U.
Пространство X называется накрывающим пространством. Если точка х
при отображении переходит в точку j;, то говорят, что х накрываетj/. Число
точек пространства X, накрывающих точку пространства Y (число про-
прообразов точки у)' называется числом листов накрытия. (Легко видеть,
что число прообразов не зависит от выбора точки у.)
Например, отображение w = z" (где w и z — комплексные числа) мож-
можно рассматривать как и-листное накрытие окружности | w| = 1 окруж-
окружностью | z | = 1. То же самое отображение можно рассматривать как
и-листное накрытие плоскости с выколотым началом координат другой
такой же плоскостью. Однако, отображение w = z", рассматриваемое на
всей плоскости, не является накрытием (оно не является локально топо-
топологическим в окрестности точки z = 0).
Отображение w = eiz, рассматриваемое как отображение действительной
оси на окружность | w| = 1, также является накрытием, только бесконечно-
листным. Это же отображение можно рассматривать как отображение на-
накрытия множества всех комплексных чисел на множество всех комплекс-
комплексных чисел, кроме 0 (пространствомX в данном случае является вся плос-
плоскость, а пространством Y — плоскость с выколотой точкой).
Трехмерное неприводимое представление группы SUB) отображает эту
группу на группу вращений (группу SOC)); в каждую ортогональную мат-
матрицу переходят при этом две унитарные матрицы и, значит, рассматривае-
рассматриваемое отображение является двулистным накрытием.
Важный класс накрытий получается с помощью следующей конструк-
конструкции. Рассмотрим конечную группу G, действующую в пространстве X сво-
свободно, т.е. таким образом, что xg Ф х для всякого элемента g e G, g Ф 1,
и всякой точки х G X (мы считаем, что группа G действует в X справа,
см. § А6). Тогда все орбиты группы G состоят из одного и того же числа
точек, совпадающего с числом элементов группы. Рассмотрим отображе-
отображение h пространства X в пространство Y = X/G орбит группы G, сопоставля-
сопоставляющее каждой точке ее орбиту. Очевидно, что это отображение является
конечнолистным накрытием. Накрытие, полученное с помощью такой
конструкции, называется главным, а группа G — группой этого накрытия.
В приведенной выше конструкции главного накрытия группу G можно
считать также и бесконечной дискретной группой, но тогда на действие
этой группы нужно наложить дополнительные условия, гарантирующие,
255

что отображение пространства X в пространство орбит будет накрытием.
Отметим, что умножение элементов группы К на элементы ее подгруппы
G справа можно рассматривать как свободное действие группы G в груп-
группе К. Поэтому в конструкции главного накрытия в качестве пространст-
пространства X можно брать группу К, а в качестве группы - ее дискретную подгруп-
подгруппу G.
Рассмотренные выше накрытия эквивалентны главным накрытиям. Так,
например, можно считать, что группа целых чисел действует на прямой:
целому числу и будем сопоставлять преобразование, переводящее число у
в число $ + 2тги. Многообразие орбит в данном случае топологически эк-
эквивалентно окружности. Полученное таким образом накрытие окружно-
окружности прямой линией эквивалентно построенному выше накрытию, задавае-
задаваемому отображением w = elz. Накрытие группы SOC) группой SUB),
описанное выше, может быть получено, если рассмотреть действие в груп-
группе SUB) ее подгруппы, состоящей из двух элементов: 1 и -1.
Рассмотрим накрытие h пространства Y пространством X. Очевидно,
что путь /, идущий из точки Х\ G X, которая накрывает точку у е Y, в
другую точку х2 € X, накрывающую ту же точку у G Y, переходит при
отображении в замкнутый путь hf. Говорят, что путь/ накрывает путь hf.
Можно доказать, что путь hf не гомотопен нулю (доказательство см. ниже).
Используя этот факт, можно получить следующее утверждение.
Если пространство X односвязно, то число элементов фундаменталь-
фундаментальной группы пространства Y совпадает с числом листов накрытия И. (Каж-
(Каждой точке х G X, накрывающей точку у ? Y, можно сопоставить гомотопи-
гомотопический класс замкнутых путей, получающихся при отображении h из путей,
ведущих из фиксированной точки х0, накрывающей у, в точку х.) Если
h — главное накрытие, то число листов накрытия совпадает с числом эле-
элементов в группе накрытия, поэтому из сформулированного выше утверж-
утверждения следует, что в случае, если пространство X односвязно, группа
ni(Y> У о) содержит столько же элементов, сколько содержит группа
накрытия. В этом случае имеет место также более сильное высказыва-
высказывание: группа iri(Y,y0) изоморфна группе накрытия.
Сформулированное только что утверждение позволяет вычислить фун-
фундаментальные группы окружности, плоскости с выколотой точкой и про-
пространства SOC). В самом деле, для этих пространств выше были построе-
построены односвязные главные накрытия (как показано в § I, группа SUB)
топологически эквивалентна сфере S3 и потому односвязна). Следова-
Следовательно, мы можем вычислить фундаментальные группы в этих случаях.
Видно, что для окружности и для плоскости с выколотой точкой фунда-
фундаментальная группа изоморфна группе целых чисел , а для группы SOC)
фундаментальная группа изоморфна группе из двух элементов И2 ¦
Наметим доказательство сформулированных выше утверждений.
Пусть /(г) - путь в пространстве Y, начинающийся в точке у, а х е X -
точка, накрывающая точку у. Тогда можно единственным образом по-
построить путь, накрывающий путь f(t) и начинающийся в точке х (если
путь f(t) замкнут, то накрывающий путь не обязан быть замкнутым,
но начало и конец накрывающего пути должны накрывать одну и ту же
точку). Для доказательства достаточно разбить путь / в пространстве Y
на маленькие куски и воспользоваться тем, что для достаточно малых
256

кусков утверждение очевидно в силу того, что накрытие является ло-
локально топологическим отображением. Далее, из аналогичных соображе-
соображений следует, что когда путь f(t) непрерывно деформируется в про-
пространстве Y, то накрывающий его путь непрерывно деформируется в
пространстве X; при этом начальная и конечная точки накрывающего пути
не меняются. (Это утверждение носит название леммы о накрывающей
гомотопии.) Таким образом, если два пути/о и/i в пространстве У гомо-
гомотопны, а накрывающие их пути исходят из одной и той же точки х, то
конечные точки накрывающих путей совпадают между собой.
Если пространство X односвязно, то два пути в пространстве X, начи-
начинающиеся в одной и той же точке х и кончающиеся в одной и той же точ-
точке х, гомотопны между собой и, значит, гомотопны накрываемые ими
пути. Таким образом, если фиксирована точка х ? X, накрывающая точку
7 6 У, то гомотопический класс замкнутого пути с началом и концом в
точке у характеризуется той точкой х пространства X, в которую приходит
накрывающий путь, начинающийся в точке х. Мы видим поэтому, что мно-
множество TTi(Y, у) находится во взаимно однозначном соответствии с мно-
множеством точек, накрывающих точку у.
Пусть теперь рассматриваемое накрытие является главным. Тогда все
точки, накрывающие данную точку у, получаются из фиксированной точ-
точки х с помощью действия элементов группы G. Нам будет удобно сопостав-
сопоставлять элементу g G G точку xg'1, лежащую над j>. Мы получаем при этом
взаимно однозначное соответствие между элементами группы G и точка-
точками, лежащими над у, и, следовательно, взаимно однозначное соответствие
между группами G и rr,(Y, у) (элементу g €. G отвечает гомотопический
класс замкнутого пути/ = hf, где /- путь, ведущий из х в xg ).
Покажем, что это соответствие является изоморфизмом групп G и
it\{Y, У)- В самом деле, рассмотрим в пространстве X путь/,, ведущий
из точки х в точку xgi1, и путь /г, ведущий из точки х в точку xg^1 ¦
Замкнутые пути в пространстве Y, накрываемые соответственно путями
/i и/2 , обозначим/1 и /;. Заметим, что путь /2' (t) =/г(^)^Г1 @<Г<1)
также накрывает путь /2 (точки /2(?) и /2(О при заданном t принад-
принадлежат одной орбите). Путь /, кончается в точке xgt1, а путь/г начинает-
начинается в этой точке. Поэтому можно определить произведение путей /, * /2 •
Л Л
Путь/, */2 накрывает путь/, */2 и кончается в точкеx{g^gi) ¦ Таким
образом, мы видим, что если при построенном выше соответствии гомо-
гомотопические классы путей /,, /2 отвечают элементам группы #,, #2, то
пути /, * /2 отвечает элемент jfi?2.
Сформулируем некоторые полезные утверждения.
А 1. Для всякого связного локально односвязного пространства Y
существует односвязное главное накрытие пространства Y (универсаль-
(универсальное накрытие), т.е. существует пространство X и дискретная группа G,
действующая свободно в X, такие, что пространство орбит топологически
эквивалентно пространству Y. Всякое односвязное накрытие эквивалент-
эквивалентно этому накрытию.
2. Всякое другое накрытие пространства Y эквивалентно накрытию,
получающемуся из универсального накрытия с помощью процедуры фак-
факторизации, описываемой следующим образом. Если Н - подгруппа груп-
257

пы G, то естественное отображение пространства Х/Н орбит группы Н
в X на пространство Y = X/G является отображением накрытия. Про
это накрытие говорят, что оно получается из универсального накрытия с
помощью факторизации.
3. Всякая локально односвязная топологическая группа Y может быть
представлена как факторгруппа односвязной топологической группы X
по дискретной инвариантной подгруппе G.
Легко проверить, что дискретная инвариантная подгруппа связной топо-
топологической группы принадлежит центру этой группы (т.е. ее элементы
коммутируют со всеми элементами группы). В самом деле, если g G G,
х е X, x(t) - путь, соединяющий элемент х с единичным элементом, то
путь x(t)gx~1(t) соединяет xgx'1 с элементом g. В силу инвариантности
группы G этот путь целиком лежит в G, в силу дискретности группы G
всякое непрерывное отображение отрезка в G переводит весь отрезок в
одну точку и, следовательно, xgx'1 = g. Из сказанного следует, что груп-
группа G, фигурирующая в утверждении 3, является подгруппой центра груп-
группы X. г
Рассмотрим теперь множество гомотопических классов отображений ок-
окружности в пространство Y. Всякий замкнутый путь можно рассматривать
как отображение окружности, однако, как мы уже говорили, два негомо-
негомотопных пути могут определять гомотопные отображения окружности, по-
поскольку, рассматривая деформацию замкнутого пути, мы считаем, что началь-
начальная точка пути (совпадающая с конечной) при деформации неподвижна, а при
деформации отображений окружности выполнение этого условия не требует-
требуется. Если на окружности фиксирована точка а, и при отображении/0 окружно-
окружности в пространство Y точка а переходит в точку у0, то это отображение окруж-
окружности порождает элемент [/0] из n^Y, y0). Если другое отображение
/i удовлетворяет условию /i(a) =У\, то можно доказать, что отображе-
отображения /о и /j гомотопны в том и только в том случае, если найдется такой
путь а, ведущий из точки у0 в точку 7i. что путь а */, * а гомотопен
пути /о (т.е. гомотопический класс [fi] при изоморфизме групп
Ti(T. У1) и Wj(F,у0), определяемом путем а, переходит в [/о]). В одну
сторону это утверждение очевидно: если путь a */j * а гомотопен пути/0,
то соответствующие отображения окружности гомотопны.
Из сформулированных выше утверждений вытекает, что всякое отобра-
отображение окружности в связное пространство Y гомотопно отображению,
переводящему точку а в фиксированную точку у^, и что два отображения
/о, /i, обладающие этим свойством, гомотопны тогда и только тогда, когда
соответствующие элементы [/0] и [/(] группы ni(Y, y0) связаны соот-
соотношением [/о] = М /i]X-1, где \ входит в iri(Y, y0). Иными словами,
всякому гомотопическому классу отображений окружности в Y сопостав-
сопоставляется класс сопряженных элементов в n^Y, y0). Построенное таким
образом соответствие между множеством гомотопических классов{ S1, У}
и множеством классов сопряженных элементов в Tt\(Y, yo) взаимно одно-
однозначно.
258

§ 5. Многообразия
Топологическое пространство М называется т-мерным многообразием
(точнее, топологическим многообразием), если у каждой точки этого про-
пространства существует окрестность, топологически эквивалентная области*)
пространства R. Топологическая эквивалентность подмножества много-
многообразия М и области пространства Шт позволяет ввести в этом множестве
координаты (и1,. . . , ит), считая координатами точки множества коорди-
координаты соответствующей точки пространства Шт; эта система координат
назьюается локальной системой координат в М. В многообразии М можно
ввести локальные системы координат так, чтобы для каждой точки много-
многообразиям имела смысл по крайней мере одна из этих систем.
Говорят, что М — гладкое многообразие, еслиЗ/ покрыто локальными
системами координат таким образом, что переход от одних координат к
другим задается с помощью гладких функций. (Разумеется, кроме локаль-
локальных систем координат, определяющих гладкое многообразие, в М можно
пользоваться и другими системами координат; существенно, однако,
чтобы все используемые системы координат были связаны друг с другом
гладкими преобразованиями.)
Примером от-мерного гладкого многообразия может служить действи-
действительное проективное пространство RPm или комплексное проективное
пространство СРт. Точка пространства RP т или СРт определяется нену-
ненулевым (гп + 1)-мерным вектором (дг°, . . . ,хт), состоящим соответствен-
соответственно из действительных или комплексных чисел; при этом векторы, отличаю-
отличающиеся только действительным (комплексным) числовым множителем,
отвечают одной и той же точке пространства RPm (пространства СРт).
Выделим в RPm подмножество U(, точки которого определяются вектора-
векторами, удовлетворяющими условию х' Ф 0. В Ut можно ввести координаты
|°0,..., ?('~l, ?|+1,..., %™у положив %[п= —j- при / Ф i. Множества
Uo Um покрывают вместе все RP m; переход от координат в Iff к
координатам в Uk задается гладкими функциями:
при
Таким образом, введение описанных только что систем координат пре-
превращает RPm в от-мерное гладкое многообразие. Совершенно аналогично
можно ввести координаты в комплексном проективном пространстве СРт.
Единственное отличие состоит в том, что (•' следует считать комплексны-
комплексными числами, поэтому СРт следует рассматривать как 2от-мерное много-
многообразие (т комплексных координат можно заменить 2т действительны-
действительными координатами). Числа х°,... ,хт называются однородными коорди-
*) Если у точки есть окрестность, топологически эквивалентная области простран-
пространства Ftm, то у нее, конечно, есть также окрестность, топологически эквивалентная
открытому шару пространства Ftm. Поскольку такой открытый шар топологиче-
топологически эквивалентен самому IRm, можно определить многообразие также, как простран-
пространство, каждая точка которого имеет окрестность, топологически эквивалентную Я.
259

нотами в RPm и CPm, а построенные выше, координаты в областях Ut -
неоднородными координатами.
Понятия, относящиеся к гладким многообразиям, удобно определять
с помощью локальных систем координат; при этом необходимо следить
за тем, чтобы эти понятия не зависели от выбора локальной системы.
Например, отображение / гладкого многообразия М в гладкое много-
многообразие М' называется гладким, если локальные координаты точки
f(x) S М' являются гладкими функциями локальных координат точки
х G М. (Это определение не зависит от выбора локальных систем коор-
координат в М и М', поскольку все рассматриваемые системы координат
связаны гладкими преобразованиями.)
Если мы определяем какую-либо величину в локальной системе ко-
координат, то мы должны задать правило пересчета этой величины из од-
одной локальной системы координат в другую. Конечно, от этого правила
пересчета необходимо потребовать выполнение следующего свойства:
при переходе от координат и к координатам и и затем от координат
и к координатам и должен получаться такой же результат, как при непо-
непосредственном переходе от координат и к координатам и. Например, век-
вектором в точке w-мерного многообразия М называется совокупность
m чисел ?', преобразующаяся при переходе от одной локальной системы
координат к другой по формуле
V'Dft, A)
где D'. — якобиева матрица перехода от координат и к координатам и в
рассматриваемой точке многообразия:
. Эй'
°; - и ¦ B)
Ковектором (вектором с нижними индексами) называется совокупность
пг чисел т}(., преобразующаяся по правилу
г?,- = л/т?,; . C)
это правило можно представить также в форме
V, = F',rir ' D)
где F'. — матрица, обратная к якобиевой матрице D'.
w ч E)
По ^-мерному представлению Т группы GL(w, IR) можно построить
закон преобразования fc-компонентной величины ц из одной координат-
координатной системы в другую, полагая
т? = T(D)n> F)
где D = (?>'.) - якобиева матрица. Если ^-компонентная величина tj, пре-
преобразующаяся по формуле F), задана в каждой точке многообразия М,
то говорят, что задано поле величины, преобразующейся по представле-
представлению Т. В частности, если Т — тензорное представление, мы приходим к
260

понятию тензора и тензорного поля в многообразии М. Закон преобразо-
преобразования тензора, имеющего к верхних и / нижних индексов, при переходе
к новой системе координат имеет вид
А',1 ¦ ¦ ¦ ;* = d'.1 ... D\kFm' ... Fmi A1' •¦•'*, G)
h- -Ik /, 'к 1, II »»i ..mi' v '
Ah • • • '* = Fh ... Flk />'« ... Df< A1,'-' '.*. (8)
Таким образом, тензор А1.1 !* преобразуется как произведение
Л---//
лA)--- А(к)а,\ ¦¦¦
к векторов и / ковекторов. В частности, для тензора, имеющего только
верхние индексы,
Л''-"'* = Lf; ... D\kAh--lk, (9)
для тензора, имеющего только нижние индексы,
А. . = Z>m' ... Dm'I . A0)
Всякое гладкое преобразование /многообразиям порождает преобразо-
преобразование тензоров и других величин, заданных на этом многообразии; это пре-
преобразование снова определяется соотношениями F) —A0), но теперь сле-
следует считать, что (м1, . . . ,йт) - это координаты точки, в которую пере-
переходит точка с координатами (к1, . .. , ит) при рассматриваемом нами пре-
преобразовании /. Существенно отметить, что соотношения (9) и A0) сохра-
сохраняют смысл и в случае, когда матрица D1. не является обратимой. Это
позволяет указать закон преобразования тензоров, имеющих только верх-
верхние или только нижние индексы, при произвольных гладких отображениях
многообразий (а не только при гладких преобразованиях). Пусть/— глад-
гладкое отображение многообразия М в многообразием', (и1 ит) —
координаты в М, (и1 цт ) — координаты в М'. Тогда всякому
тензору А с верхними индексами в М можно сопоставить тензор А в М' по
формуле (9), где D\ — якобиева матрица отображения /. Всякому тензо-
тензору А с нижними индексами вМ' можно сопоставить тензор А вМ, пользуясь
соотношением A0)*). Отображение тензоров с верхними индексами
(в частности, векторов), порождаемое отображением /, принято обозна-
обозначать символом /„. Для отображения тензоров с нижними индексами ис-
используется символ / *.
В случае если наМ' задано поле тензоров с нижними индексами, отобра-
отображение/* сопоставляет этому полю аналогичное поле наМ (каждой точке х
сопоставляется тензор, получающийся из тензора, заданного в точке/(х),
по формуле A0)). Отметим, что отображение /„ нельзя рассматривать
как отображение тензорных полей (точнее, тензорному полю на М с по-
* Тензор с нижними индексами называют ковариантным, сверхними-контрава-
риантным. Эти термины представляются неудачными, поскольку контравариантный
тензор переходит из М в М' , как и точки многообразия М, а ковариантный тензор
переходит в обратном направлении.
261

мощью отображения /, можно сопоставить в общем случае многозначное
тензорное поле на f(M) С М').
Под гладкой кривой в гладком многообразии М понимается отображе-_
ние отрезка в М, задаваемое в локальных координатах гладкими функ-
функциями
Вектор, касательный к гладкой кривой в точке u(t0), определяется как
строка из чисел
/du1 dum \
l , . . . , 1.
\# » = *, * * = *,/
Координаты касатель-
ного вектора в локальной системе координат и1, . . . , ит выражаются
через координаты этого вектора в локальной системе координат и1, ит
с помощью формулы
du1 Ъй' du1
dt (=f ди' dt
» «о - -о
Таким образом, касательный вектор к кривой можно рассматривать как
вектор в смысле данного выше определения.
В классической механике гладкие многообразия возникают как про-
пространства конфигураций механических систем. Обобщенные координаты
q1 q" представляют собой локальные координаты в пространстве
конфигураций. Из примеров, приведенных в § 1, ясно, что пространство
конфигураций может иметь сложную топологическую структуру; в част-
частности, не всегда можно ввести обобщенные координаты сразу во всем
пространстве конфигураций (т.е. не всегда это пространство топологиче-
топологически эквивалентно области в IR"). Обобщенные скорости q1, . . . , qn пре-
преобразуются как вектор при переходе к другим обобщенным координатам.
Обобщенные импульсы р,- = bL\bql образуют ковектор (здесь L =
= L (q, q) - функция Лагранжа).
Если в многообразииМ задано тензорное поле g/,(«), где gy — симмет-
симметричный тензор (gjj = g^), то можно определить длину кривой и = u(t)
с помощью соотношения
S =
t,
Выражение ds = \Jgtj (u)dul du1 носит название элемента длины. Экстрема-
Экстремали функционала 5 называются геодезическими. Тензор gtl- называется мет-
метрическим тензором. С помощью метрического тензора можно сопоставить
каждому вектору А1 ковектор At = gijA' и определить скалярное произ-
произведение векторов А1 и В' по формуле АВ = ?цА1. В' =А/В'. В случае, если
метрический тензор положительно определен (gjj (и)А А' > 0 для любо-
любого ненулевого вектора А), говорят, что он определяет риманову метрику
в М; многообразие М, снабженное римановой метрикой, называется ри-
мановым многообразием. Скалярный квадрат ненулевого вектора в рима-
новом многообразии положителен; это означает, что касательное про-
пространство можно рассматривать как евклидово пространство. Если тен-
262

зор gfj не является положительно определенным, то говорят, что он оп-
определяет псевдориманову метрику.
Гладкое многообразие называется ориентированным, если ориентации
локальных систем координат в нем согласованы (т.е. переход от одной ло-
локальной системы координат к другой всегда имеет положительный яко-
якобиан: det (Эй'/Эы') >0).
Не всякое гладкое многообразие ориентируемо (т.е. не всегда можно
покрыть его согласованными локальными системами координат). На-
Например, лист Мебиуса можно рассматривать как гладкое многообразие,
но это многообразие неориентируемо. (Мы считаем, что из листа Мёбиуса
удалены точки граничной окружности, поскольку у этих точек нет окрест-
окрестностей, топологически эквивалентных области евклидова пространства.)
Системы координат в RPm можно выбрать так, чтобы они были связаны
преобразованием с положительным якобианом при нечетном пг; это озна-
означает, что при нечетном m действительное проективное пространство ориен-
ориентируемо. При четном m многообразие RPm неориентируемо (неориенти-
(неориентируемость RP2 вытекает из того, что RP2 можно получить, склеивая лист
Мёбиуса и круг; см. § АА). Системы координат в СРт связаны преобразо-
преобразованием с положительным якобианом при любом т; следовательно,
СРт можно рассматривать как ориентированное гладкое многооб-
многообразие.
Обсудим, как выяснить, ориентируемо многообразие М или нет. Ради
простоты будем предполагать М связным (для того чтобы ориентировать
несвязное многообразие, достаточно выбрать ориентацию каждой из его
компонент). Пусть в множествах Uo,..., Ut,..., покрывающих М, вве-
введены локальные системы координат. Будем называть множества Ut и ?/,•
соседними, если пересечение С/,- и Uj не пусто. Если локальные системы
координат в двух любых соседних множествах ориентированы согласован-
согласованно, то М можно рассматривать как ориентированное многообразие. Если
же это условие не выполнено, будем пытаться изменить системы коорди-
координат в множествах Uf таким образом, чтобы добиться согласованности
ориентации. Начнем с множества ?/<>• Если ориентация локальной системы
координат в множестве U^, соседнем с Uo, не согласована с ориентацией
системы координат в Uo, изменим в Uk систему координат так, чтобы
ориентации стали согласованными (этого можно добиться, например,
с помощью перенумерации координат в Uk) ¦ Далее повторим ту же про-
процедуру для "соседей соседей" множества Uo (т.е. будем менять ориента-
ориентацию в соседях множеств Uk, ориентированных на первом этапе). Переходя
затем к "соседям соседей соседей" и т.д., мы в силу связности дойдем до
каждого из множеств U\ Ut При этом есть две возможности:
либо мы ни на каком этапе не придем к противоречию (тогда многообразие
М ориентируемо), либо на каком-то этапе возникает противоречие. (На-
(Например, для RP , согласовав ориентацию Ul и С/2 с ориентацией Uo, мы
на втором этапе видим, что U2 является соседом Ui, поэтому нужно сог-
согласовать ориентацию в t/2 с ориентацией в C/j. Однако при этом нам придет-
придется изменить уже введенную ориентацию в и2 и тем самым разрушить сог-
согласование с Uo.) Если возникает противоречие, то можно утверждать,
что ориентации множеств Ut нельзя выбрать согласованно; это означает,
что многообразием неориентируемо.
263

± В самом деле, если бы М было ориентируемым, то его можно было
бы покрыть множествами U'o,..., U\,..., в которых введены согласо-
согласованные системы координат. Всякое множество Uk пересекается по крайней
мере с одним из множеств U'j\ введем в Uk систему координат, согласо-
согласованную с системой координат в этом множестве ?/;'. Нетрудно проверить,
что введенные таким образом системы координат в множествах Uk согла-
согласованы между собой. Ў Отметим, что ориентация всех локальных систем
координат в связном многообразии однозначно определяется ориентацией
системы координат в Uo; поскольку область в 1R может иметь две ориен-
ориентации, это означает, что ориентируемое связное многообразие М может
быть ориентировано только двумя способами.
Если М и М' — компактные гладкие ориентированные /я-мерные мно-
многообразия, / — отображение М в М', то можно определить степень отоб-
отображения / как алгебраическое число прообразов регулярной точки х € М'.
(Понятия регулярной точки и алгебраического числа прообразов определя-
определяются так же, как в § 2. При этом можно пользоваться любыми система-
системами координат в М и М'. Необходимо только, чтобы координаты были сог-
согласованы с выбором ориентации в МиМ'; это обеспечивает независимость
знака якобиана при определении алгебраического числа прообразов от сис-
системы координат.) Так же как и для отображения сфер, два гомотопных
отображения имеют одну и ту же степень. Однако обратное утверждение
справедливо не всегда; можно сказать только, что два отображения, имею-
имеющие одну и ту же степень, гомотопны друг другу в случае, если М' топо-
топологически эквивалентно сфере.
Пусть на М выбрана система координат (м1,. .., «'"), применимая на
всем многообразии за исключением множества N, имеюшего нулевой
объем; систему координат (и'1,..., и'"'), обладающую аналогичными
свойствами, выберем также на М'. Тогда степень отображения /много-
/многообразия МьМ' может быть выражена формулой
. . . du
(^7
\Ъи'
где функция \р наМ' удовлетворяет условию
fv(un;. ..,u"")du'\..du'm" ¦
На функцию <р нужно наложить некоторые дополнительные условия (см.
§ 10); достаточно потребовать, например, чтобы \р обращалась в нуль на
множестве N', где координаты (и'1,..., и') не имеют смысла.
Доказательства всех сделанных только что утверждений повторяют
доказательства результатов § 2. Ниже (в § 10) будет дано определение
степени с помощью теории гомологии; в рамках этого олределения сфор-
сформулированные выше результаты становятся очевидными.
Подмножество Mi многообразия М называется п-мерным подмного-
подмногообразием, если в окрестности каждой точки в локальных координатах
(х1 хт) оно' может быть задано параметрическими уравнениями
где ipl —' гладкие функции и ранг матрицы ЪуЧЪи' равен п. Очевидно,
Mi можно рассматривать как многообразие, в котором и1,..., и" играют
роль локальных координат.
264

г
Имеет место следующее важное утверждение: для всякого подмно-
подмногообразия Mi многообразия М можно построить открытое множество
G С М, содержащее М i, таким образом, что вложение Mi в G является го-.
мотопической эквивалентностью. Наметим доказательство этого утверж-
утверждения для наиболее важного случая, когда М = IRm, а подмногообразие
Mi компактно. Покажем, что в этом случае в качестве множества G можно
выбрать е-окрестность Ue множества Mt, где е — достаточно малое поло-
положительное число. Под е-окрестностью здесь понимается множество точек,
удаленных от Mi менее чем на е. Расстояние р (х, Mi) от точки х до мно-
множества Mi определяется как минимальное из чисел р (х, у), где у пробе-
пробегает Л/,.Точнее, р{х, Mi) определяется как нижняя грань чисел р(х, у),
однако, в случае, если М] компактно, непрерывная функция р(х, у) от
у € Mi достигает нижней грани и, значит, для каждой точки х ?Мсущест-
?Мсуществует по крайней мере одна точка а(х) ? М( ,¦ удовлетворяющая условию
р(х, ск(х)) = р(х, М{). Оказывается, что можно найти такое б>0,что для
х, принадлежащих е-окрестности ?/е множествам!, точка а (х) единственна
и эта точка непрерывно (даже гладко) зависит от х. Легко продеформи-
ровать окрестность Ue, обладающую этим свойством, в множество Mi
таким образом, что точки множества Мх остаются на месте: достаточно
положить
а, (х)~ tx + A - t)ot(x).
Существование построенной деформации доказывает гомотопическую
эквивалентность окрестности Ue и множества Мх. Описанную только что
окрестность Ue часто называют трубчатой окрестностью подмногообра-
подмногообразия Mi.
Топологическое пространство М называется п-мерным многообразием
с краем, если у каждой из его точек есть окрестность, топологически эк-
эквивалентная пространству IR", или окрестность, топологически эквивалент-
эквивалентная полупространству в Ft" (т.е. множеству, выделяемому неравенством
(а, х) > 0, где а - ненулевой вектор) .Совокупность точекМ, для которых
нельзя найти окрестности, топологически эквивалентной [R", представляет
собой (п — 1)-мерное многообразие, которое называется краем много-
многообразия М. Например, шар D" является и-мерным многообразием с кра-
краем. Его краем служит сфера S"~ '.
§ 6. Дифференциальные формы в евклидовом пространстве
Мы займемся сейчас внешними дифференциальными формами, пред-
представляющими собой весьма удобный аппарат во многих вопросах матема-
математики и физики. Прежде всего заметим, что формула замены переменных
в кратном интеграле принимает чрезвычайно простой вид, если считать
дифференциалы координат антикоммутируюшими величинами. В самом
деле, в обычной записи
j [х ) ax .. . ctx — j f(ip (X)) | и (x) I ax .. . ax , A)
V и
D(x\...,x) /Э*\
где D(x) = ; = detl г ) — якобиан замены переменных
D(xl...,xn) \дх' ) ^
265

x' = ip (x). Будем рассматривать только замены переменных, сохраняющие
ориентацию (т.е. удовлетворяющие условию D(x) >0); тогда в A) можно
заменить \D(x) I на D(x). Мы покажем, что удобнее записывать кратный
интеграл
\ ... ,xn)dxl ... dxn B)
в виде
/ f(xl,...,x")dx1/\.../\dx", C)
и
где Л - знак так называемого внешнего произведения дифференциалов,
удовлетворяющего соотношениям
dx^dx' = -dx'/\dx'. D)
Считается, что для внешнего произведения выполнены обычные требования
ассоциативности и дистрибутивности; числа коммутируют с дифферен-
дифференциалами: Xdx = dx\. Если пользоваться обозначением C) для интеграла
B), то для замены переменных в интеграле нужно просто выразить подын-
подынтегральную функцию и дифференциалы координат через другие перемен-
переменные. Иными словами, имеет место соотношение
/ /(x')dx'1 Л.. .f\dx'"=ff(<p(x))dxn/\.. ./\dx'"'=
и' и
/Эх'1 Л /Эх'" ,.\
= 1ЯНх))(—Г dx'A Л.. .Л(-^ dxl"). E)
и ЧЭх'1 / \дх" /
4 Для того чтобы установить эквивалентность соотношений A) и E),
заметим, что из D) вытекает, что
dx'« /\...f\dxi"=ei'-i»dx1 f\.../\dx". F)
Вспоминая, что det (Л') = е'1 "¦1пА) ... А" , нетрудно вывести из F)
формулу ' "
(A\t Лс1' )Л...Л(/4^ dxin) = det (Afidx1 Л.. .Sdx",
доказывающую равносильность соотношений A) и E). Например, при и = 2
„ /Эх" , Эх'1 Д /Эх'2 , Эх'2 Д
dxn /\dx'2 =(—-dx1 + —- dx2)M—r dx1 + —т dx2) =
ЧЭх1 Эх2 / ЧЭх1 Эх2 /
/Эх'1 Эх'2 Эх'1 Эх'2\ , , Z>(x\x'2)
= (—Г Ч ~ —; ' —:)dxlbdx2= , , d
ЧЭх1 Эх2 Эх2 Эх1/ D(x\x2)
Отметим, что при замене переменных, для которой якобиан отрица-
отрицателен (т.е. ориентация области становится противоположной), интеграл ви-
вида C) меняет знак. Иными словами, интеграл C) следует рассматривать
как интеграл по ориентированной области.
Изложенные только что соображения показывают естественность рас-
рассмотрения выражений вида
'Л...ЛАс'*, G)
где Л — внешнее произведение дифференциалов. Выражение G) носит наз-
266

вание внешней дифференциальной формы степени к. Мы будем употреб-
употреблять также более короткие термины "внешняя форма степени к" или прос-
просто "fc-форма". Внешняя форма нулевой степени @-форма) - это просто
функция в рассматриваемой области. Внешние формы степени > л в л-мер-
ной области равны нулю, поскольку в них должно содержаться внешнее
произведение двух одинаковых дифференциалов, равное нулю в силу D).
Всякая внешняя форма степени л в л-мерной области может быть за-
записана в виде
cj=f(x)dxlA.../\dxn
(это следует из соотношения F)). Внешняя форма представляется в ви-
виде G) неоднозначно (мы видели это на примере л-форм в л-мерном прост-
пространстве). На коэффициенты внешней формы можно наложить условие
антисимметричности коэффициентов afi./.{ по индексам ily..., i^'. вся-
всякая внешняя форма записывается в виде G) с антисимметричными коэф-
коэффициентами и притом только одним способом. Например, 2-форма
ацйх1 Л dx1 совпадает с 2-формой -ац dx' Л dx* = -ацйх* Л dx' и, сле-
следовательно, равна 2-форме Ъц dx1 Л dx', имеющей антисимметричные коэф-
коэффициенты by = — (аи - uji). В общем случае из внешней формы можно
получить равную ей форму с антисимметричными коэффициентами с по-
помощью антисимметризации коэффициентов Д;,.../. по индексам i"i,...
..., 1^. Нам будет не всегда удобно считать, что коэффициенты внешней
формы антисимметричны; иногда полезно, например, представлять внеш-
внешнюю форму в виде
<о= 2 at fdx1* Л.. .Adx'x (8)
/,<...<ffc •- *
(пользуясь соотношениями D), всегда можно переставить дифферен-
дифференциалы в порядке возрастания индексов).
Мы считаем, что при преобразованиях координат дифференциалы dx'
преобразуются по стандартным формулам: dx'1 = (dx'llbx')dx'. Тогда
коэффициенты внешней формы со преобразуются как тензор с нижними
индексами (ковариантный тензор). Можно сказать, что внешние формы
находятся во взаимно однозначном соответствии с антисимметричными
тензорными полями. Можно рассматривать другой закон преобразования
внешних форм, который для сохраняющих ориентацию преобразований
координат совпадает с описанным выше, а для обращающих ориентацию
преобразований отличается знаком. Коэффициенты преобразуются тогда
как псевдотензор с нижними индексами.
Определим некоторые операции с внешними формами. При сложении
внешних форм, естественно, складываются их коэффициенты. Внешнее
произведение двух внешних форм определяется соотношением
(ail...ikdxil Л.. .Adxik)l\Q}Ji.;.jldx'i Л.. .Adx'') =
= ah...ik bh ...jjdx1* Л.. .Adjc'fc Л dx^ Л... AdA (9)
Отметим, что внешнее произведение Л-формы на /-форму является (к + /) -
формой. Внешнее произведение форм обладает свойствами ассоциатив-
ассоциативности и дистрибутивности; форма четной степени коммутирует с любой
267

другой формой; две формы нечетной степени антикоммутируют (послед-
(последние два утверждения объединяются равенством
где deg со обозначает степень формы со).
Дифференциал du> внешней формы G) определяется формулой
du> = dah ...lfcAdx'* Л ...Adx1'* =
Эд,- j
= —Ц1-* dx'Adx1' Л . . ./\dx'><.
Эх'
Если a{i...,- - антисимметрический тензор, то можно записать dco также
= biaii...ikdxi<> Adx1- Л. . .Adx^, A0)
в виде
где
— тензор, получающийся при антисимметризации тензора — . — .
Эх'°
Дифференциал обладает следующими свойствами:
A2)
A3)
Для того чтобы доказать A2), запишем d2o> в виде
•Л...
Л...
Эх'
= Эх1'Эх'
и заметим, что тензор ''•"'* симметричен по индексам i, /, поэтому
Эх' Эх'
его антисимметризация дает нуль. Соотношение A3) вытекает из правила
дифференцирования произведения и антикоммутативности дифферен-
дифференциалов.
Дифференциал 1 -формы А =А( dx' может быть записан в виде
1
dA =F= - Fjjdx'hdx', A4)
где
Fv=dtAJ-diAi. A5)
Дифференциал 2-формы a^-dx' Л dx' может быть представлен в виде
Sijk dx' Л dx'''Л dx k, A6)
268

Э fly
где Siik получается при антисимметризации тензора —г. В случае если
дх
atjr-ац,
1
Sijk = - (9fcfl,7 + 9,-fl/fc + Ъ,ак1). A7)
Отметим, что для 1-формы А ее коэффициенты At и коэффициенты
Fij ее дифференциала F = dA связаны так же, как электромагнитный
потенциал и тензор электромагнитной напряженности в четырехмерном
пространстве. Это подсказывает, что потенциал можно рассматривать как
l-форму, а тензор напряженности - как 2-форму; эти формы связаны
соотношением F = dA. Из соотношения d2A = 0 вытекает, что 2-форма
F, отвечающая напряженности, удовлетворяет условию dF = 0. Этот факт
равносилен уравнению Максвелла
a*Ftf + 3/FM + 3,i?/Jt=0. . A8)
В области U пространства IR3 1-формы, 2-формы и 3-формы могут быть
в декартовых координатах записаны в виде
со1 = co,dx' = co(x)dx, A9)
a>2 = Pl dx2 ЛЛс3 + Р2 dx3Ndxl+P3 dxl /\dx2 = РdS, B0)
w3 = Q dx1 J\dx2 Adx3, B1)
где со и Р - векторы, Q - скаляр. (Мы рассматриваем только преобразо-
преобразования координат, сохраняющие ориентацию, чтобы не делать различия
между векторами и псевдовекторами.)
Соотношения dco° =ш\ duI, = со2, dto2 = со3 могут быть представлены в
виде
ш= gradw0, B2)
Р = rot со, B3)
Q = div P. B4)
Здесь со0 - скалярная функция @-форма), со1, со2, со3 записаны с помощью
равенств A9), B0), B1). Соотношение d2 = 0 эквивалентно в DR3 равен-
равенствам rot grad со0 = 0, div rot со =0.
Рассмотрим теперь гладкое отображение <р области U в область (/'
Всякой форме
со' = a',,.../* dx'1*- Л...Adx'1'* B5)
в области {/'можно сопоставить форму co = ^*cj'b области С/,'положив
dxj *"Ay&;dx"")- B6)
(т.е. просто выразив в форме со'координаты х'и дифференциалы dx'
через х ndxno обычным формулам)*). В частности, функции /(*') в U1
*)Определенная только что операция >f* согласована с аналогичной операцией
над ковариантными тензорами, о которой мы говорили в § 5.
269

отвечает функция (<p*f)x = fQp (x)) в U (напомним, что функцию можно
рассматривать как 0 -форму).
Легко доказать соотношения
B7)
B8)
Если отображение <р представлено как суперпозиция отображений фх и
<р (теу(х) =<р($ (x)))tov* = vV*
Обратимся к интегрированию внешних форм. Определим интеграл
к -формы по ориентированной к -мерной поверхности, лежащей в п -мерном
пространстве. Если к = п, то, как говорилось выше, всякую к -форму можно
записать в виде
и интеграл этой формы по п -мерной ориентированной области U можно
определить как обычный п-кратный интеграл: /to = $f(x)dxl ...dxn.
Рассмотрим теперь произвольную ориентированную к -мерную поверх-
поверхность. Будем считать, что поверхность О,задана параметрическими-уравне-
параметрическими-уравнениями
хп = я>"(и); B9)
без существенного ограничения общности можно предполагать, что каждый
из параметров изменяется в отрезке [0; 1] (т.е. точка и = (и1,..., ы*) пробе-
пробегает к -мерный куб /*). Параметризация поверхности Q определяет отобра-
отображение куба/* на поверхность (точке и = (и1,..., и*) €/* соответствует
точка поверхности, которой отвечают значения параметров (и1,..., м*)). Это
отображение обозначим буквой у. Коротко можно записать параметри-
параметрические уравнения B9) в виде
х = ф).
Мы считаем отображение ip гладким; однако мы не предполагаем, что
это отображение взаимно однозначно (таким образом, разным значениям
параметров может соответствовать одна и та же точка поверхности). Будем
считать, что отображения у и >р' определяют одну и ту же ориентированную
поверхность, если можно найти такое гладкое преобразование X куба 1к,
имеющее положительный якобиан, что <р (м) = <р'(Х(и)). Тогда геометри-
геометрически поверхность, задаваемая отображением <р, совпадает с поверхностью,
задаваемой отображением v>' (т.е. множество точек вида <р(м), «е /*,
совпадает с множеством точек вида </(")• «6^); отличие состоит толь-
только в выборе параметризации. Преобразование X, связывающее две пара-
параметризации, носит название преобразования репараметризации; наложенное
нами условие положительности якобиана преобразования X означаёт.что X
сохраняет ориентацию.
Определим интеграл к -формы по к -мерной ориентированной поверх-
поверхности, заданной с помощью отображения <р, как интеграл от к -формы
270

<р* со по ^-мерному кубу Ik
f <o = f «p*w C0)
(как понимать интеграл в правой части C0), было объяснено выше).
Например, интеграл от формы atdy? по кривой О, (одномерной поверх-
поверхности), заданной параметрическим уравнением х' = ip'(u), определяется
соотношением
/а,Лс' = /«,(*(«<)) ^- du.
п о Эй
Интеграл от формы а>= — a^dx' J\dx' по двумерной поверхности ?2,
определяемой параметрическим уравнением х' = у1 (и1, и2 ), равен
- faifdx* /\dx' =
2 n
1 /Э<р' Э^' Э/ Э<р
= - /в|/(<Р(и))( -Ч -т - А —г
2^ ; ЧЭм1 Эм2 Э«2 Эй1
11 Э<р' Э.р' , ,
= SSaij(^(u)) — -Tduidu2
оо Эм1 Эй
(последнее равенство справедливо при условии ац = - ац). Аналогичные
вычисления дают для интеграла от Л-формы G), где д^ ,-fc — антисим-
антисимметричный тензор, по поверхности, заданной параметрическими уравне-
уравнениями B9), выражение
= *!/... /в,- . ,к(#{и)) — ...-irdul...duk.
оо Эй1 Ъик
Интеграл от формы не зависитотвыборапараметризации ориентированной
поверхности (это вытекает из указанного выше правила замены перемен-
переменных в интеграле от Л-формы по fc-мерной области и соотношения (<рХ)* =
= xv).
Мы предполагали до сих пор, что рассматриваемые поверхности парамет-
параметризуются точками Куба/*. Часто приходится рассматривать поверхности,
разбитые на конечное число кусков, каждый из которых параметризуется
точками куба; тогда интеграл от формы по поверхности определяется
как сумма интегралов по этим кускам. При естественных условиях на
разбиение интеграл не зависит от способа разбиения и от выбора параметри-
271

заций отдельных кусков (иными словами, интеграл аддитивен и инвариан-
инвариантен относительно репараметризации).
Например, сферу S2 в Ft3 можно параметризовать стандартным образом
с помощью сферических координат \р, в (О < \р < 2я, 0 < в < я). Параметри-
Параметризация неоднозначна на меридиане 0=0, однако это не мешает определять
интеграл от 2-формы по сфере с помощью этой параметризации. (Неодно-
(Неоднозначность параметризации на подмножестве, имеющем меньшую размер-
размерность, чем рассматриваемая поверхность, несущественна при вычислении
интеграла.) Отметим, что можно выбрать на сфере другие сферические
координаты e',tp'; тогда переход от координат в, у к координатам в', $'
будет разрывен на кривой линии. Это показывает, что разумно допускать
разрывные преобразования репараметризации, требуя, однако, чтобы
множество точек разрыва имело меньшую размерность, чем поверхность;
при таких репараметризациях значение интеграла также не меняется. Нако-
Наконец, можно разбить сферу S2 на части, например на верхнюю полусферу
х3 >0 и нижнюю полусферу х3<0, и выбрать параметризацию отдельно
на каждой из частей (например, выбрать в качестве параметров долготу
\р, 0 <ip <2я, и величину г = \/(х1J + (*2J, 0<г<1); пользуясь этими
параметризациями, мы приходим к тому же значению интеграла.
Поверхность,совпадающая геометрически с ?2, но снабженная противо-
противоположной ориентацией, будет обозначаться — ?2. Очевидно, что при измене-
изменении ориентации поверхности меняется знак интеграла от формы по поверх-
поверхности
/ со = - /со.
-« п
Символ т?2, где т - натуральное число, обозначает поверхность ?2, повто-
повторенную т раз. Если т — отрицательное целое число, то поверхность mCL
считается совпадающей с | т \ (— ?2). Имеет место соотношение
/ w = т / со.
тп "
Если i7j и fi2 — Две поверхности, то естественно определяется поверхность
?2 = ?2j +ft2- В случае если поверхности ?2а и п2 не перекрываются, то
определение суммы J2i •+ ?22 очевидно. Если J2X и J22 имеют общую часть
?23> т0 ?2i+?22 определяется как сумма непересекающихся кусков
(?2, \?23) + (?22 \?23)+ 2?23- Из аддитивности интеграла вытекает соотно-
соотношение
/ co=/w+/co.
n, + n2 п, п2
В частности, если из является и-формой, то свойство аддитивности пока-
показывает, что / из можно интерпретировать как объем и-мерной области ?2 С U.
п
Если мы хотим, чтобы объем области $2, ориентированной так же, как и
U, был неотрицателен, следует наложить на форму со дополнительное усло-
условие. Именно если
со = fix)dx1 A ... Л dx" = — /(*) б, ,- dx^ Л ... Л dx'",
272

то функцию f(x) нужно считать неотрицательной. Форму со называют
элементом объема в области U.
Основное свойство интеграла выражается соотношением, связывающим
интеграл от формы dcono поверхности ?2 с интегралом от формы со по
границе д?1 поверхности П:
fdu= /со. C1)
а ъа.
Для того чтобы придать точный смысл формуле C1), нужно определить
ориентацию границы ЭП ориентированной поверхности ?2. (Напомним, что
имеет смысл только интеграл от формы по ориентированной поверхности.)
Прежде всего определим ориентацию границы Э/* куба/*. Куб/* выделя-
выделяется неравенствами 0 < t' < 1, ; = 1, . . . , к. Его граница Э/* состоит из 2к
кубов размерности к — 1. Каждому числу /, 1 </<&, можно сопоставить
два (к — 1)-мерных куба/*~ ' и /*~ ', выделяемых соотношениями /' = 1
и tl = 0 соответственно. Числа tl,..., 11~], tl+ i ,...,?* можно рассматри-
рассматривать как координаты в /Д~' и в /Д,. Этот выбор координат порождает
определенную ориентацию кубов /*~! и /Д. С помощью выбранных
таким образом ориентации можно определить ориентацию границы куба /*
Именно будем считать, что введенная выше ориентация куба /Д~' согласо-
согласована с ориентацией границы куба /* при / четном и противоположна этой
ориентации при / нечетном; ориентация куба/* согласована с ориента-
ориентацией поверхности Э/* при / нечетном и противоположна — при / четном.
Для того чтобы определить ориентацию границы Э?2 поверхности ?2, нужно
параметризовать ?2 точками куба /*; тогда описанная выше ориентация
поверхности 3/* задаст ориентацию поверхности Э?2.
Чтобы доказать соотношение C1), проверим его сначала в случае, если
?2 есть А:-мерный куб /*, а со является (к — 1)-формой. Заметим, прежде
всего, что (к - 1)-форму в А:-мерной области можно представить в виде
co=I(-l)'~ V(*)^*' Л.-.Л^' Adx'+1 Л... Л (Ух*.
Легко видеть, что
/ ах'
Замечая, что
/^Лсл..
/* ' /* Ъх1
и, производя в / -м слагаемом интегрирование по dx\ приходим к соотно-
соотношению
/dco = S(-l)'-1( / со- / со). C2)
'if, 'to*
(Для того чтобы проинтегрировать по dx\ удобно переставить dx' на пер-
273

вое место; при этом возникает множитель (—1) .) Из указанного выше
описания ориентации границы куба 7* следует, что интеграл в правой части
C2) совпадает с интегралом от ш по Ык. Мы видим, что соотношение
C2) эквивалентно C1) для ?2=/*.
Общий случай сводится к только что рассмотренному с помощью соот-
соотношений C0) и B7):
f daj = f y*(du>) = f d(*p*u>)= f ip*a)= f to.
n ik ik ык да
Соотношение C1) является обобщением известных формул Гаусса,
Остроградского, Стокса. В самом деле, применяя это соотношение к фор-
формам степени 1 и 2 в трехмерном пространстве и используя B2) — B4),
получаем •
/ rot cS dS = f to dx,
/ divPdF= / ?dS.
Здесь ?22 — двумерная поверхность в !R3, J23 — трехмерная область.
§ 7. Гомологии
и когомологии областей евклидова пространства
• Ориентированную А>мерную замкнутую поверхность (поверхность,
не имеющую границы) будем называть fc-мерным циклом. В частности,
граница любой (к+ 1)-мерной поверхности является к-мерным циклом.
Если к -мерный цикл z в области f/ограничивает (к+1) -мерную поверхность
Ц, лежащую в области U (т.е. z = Э?2), то он называется гомологичным
нулю в этой области. Говорят, что цикл zx гомологичен циклу z2 в (/,
если можно найти такую ориентированную поверхность ?2, лежащую в U,
что Э?2 =zi — z2- ж Напомним, что —z2 обозначает поверхность, отличаю-
отличающуюся от z2 выбором ориентации; поэтому соотношение Э?2 -zx — z2 =
= Zj+ (—z2) означает, что граница поверхности ?2 состоит из поверхности
Zj и поверхности z2, взятой с противоположной ориентацией, т Если цикл
Zj гомологичен циклу z2 в U, пишут zx ~z2; иногда мы будем говорить,
что циклы Zj и z2 можно соединить пленкой. В частности, если цикл z2
может быть получен из цикла ZiC помощью непрерывной деформации,
то эти циклы гомологичны друг другу. (Поверхность, заметаемую циклом
во время деформации, можно рассматривать как пленку, соединяющую
циклы.) Область называется ацикличной в размерности к, если каждый
^-мерный цикл является границей (к +1)-мерной поверхности. В частности,
пространство IR" ациклично в любой размерности к>0. Это следует, напри-
например, из того, что пространство IR" и, значит, всякий лежащий в нем цикл
можно продеформировать в точку.Впрочем, поверхность, ограничивающую
тщкл в R"^, легко построить и непосредственно. Построение поверхности,
ограничивающей одномерный цикл в IR3, ясно из рис. 32; это построение
легко обобщается на многомерный случай. Всякая п-мерная область аци-
ациклична в размерностях > п.
Одномерный цикл - это замкнутая кривая, на которой выбрано направ-
направление. (Конечно, эта кривая может самопересекаться и состоять из несколь-
274

ких кусков). Рассмотрим в качестве примера циклы на плоскости, из ко-
которой выколота точка. Окружность с центром в вьжолотой точке является
циклом, не гомологичным нулю. Доказательство этого очевидного факта
может быть основано на следующем соображении. Рассмотрим на плоскос-
плоскости, из которой выколото начало координат, 1-форму
ydx-xdy
х2 +У2
Легко проверить, что dco= 0. Если бы окружность S1 с центром в начале
координат была границей области $2, то в силу формулы Грина C1) мы
получили бы
/ со = / со = / dw = 0.
sl да п
В то же время явное вычисление дает /со = 2тг, и, следовательно, рассматри-
sl
ваемая окружность не гомологична нулю. Всякий цикл на плоскости с вы-
выколотой точкой гомологичен kS1, где к — целое число, 51 — описанная
только что окружность. Доказательство основано на замечании, что плос-
плоскость с выколотой точкой можно непрерывным образом продеформиро-
вать в окружность с центром в выколотой точке (см. § 1). При этой де-
деформации всякий одномерный цикл деформируется в пройденную несколь-
несколько раз окружность; поскольку деформация переводит цикл в гомологич-
гомологичный ему цикл, это означает, что всякий одномерный цикл гомологичен
kS1.
Соображения, с помощью которых мы устанавливали негомоло-
гичность нулю окружности на плоскости с выколотой точкой, допускают
очевидное обобщение. Для того чтобы их сформулировать, введем следую-
следующие понятия, важные и сами по себе. Форма со называется замкнутой,
Рис.32
если йоэ = 0. Форма со называется точной в области U (или формой, кого-
мологичной нулю в области U), если в этой области найдется такая фор-
форма о, что со = da. Из соотношения d2 = 0 следует, что всякая точная форма
замкнута. Говорят, что форма cot когомологична форме со2 в области U,
если их разность cot — со2 когомологична нулю (т.е. сох — со2 =dd). Отме-
Отметим, что операция взятия дифференциала формы аналогична операции вы-
вычисления границы поверхности. Понятие замкнутой формы аналогично по-
275

нятию цикла и понятие точной формы — понятию цикла, гомологичного
нулю. Если г = ЭП, dco = О, то из соотношения F.31)следует, что / со = 0.
г
Иными словами, интеграл от замкнутой формы по циклу, гомологичному
нулю, равен нулю.
Может случиться, что цикл z не гомологичен нулю, но существует такое
целое число пг, что цикл mz гомологичен нулю. Тогда из /со = m /со сле-
mz z
дует, что / со = 0 для любой замкнутой формы со. К соотношению /со = 0
z z
можно прийти также в случае, если г — произвольный цикл, а со = da.
(Тогда /со = fda = / а = 0.) Мы приходим к выводу, что соотношение
z z д z
где z - цикл, со - замкнутая форма, влечет за собой, что форма со не кого-
мологична нулю {не точна),а цикл z не гомологичен нулю (более того,
не гомологичен нулю никакой цикл вида mz, где тп — целое число, m Ф 0.)
Сделанное только что* утверждение допускает обращение. Точнее, имеет
место следующее предложение.
1. Для того чтобы замкнутая k-форма в области Uбыла точной, необхо-
необходимо и достаточно, чтобы ее интеграл по любому циклу, лежащему в облас-
области U, был равен нулю.
2. Если интеграл от любой замкнутой формы в области U по циклу z
равен нулю, то найдется такое целое число тп, что цикл mz гомологичен
нулю.
Совокупность этих двух утверждений называется теоремой де Рама.
Мы не будем приводить ее доказательства, хотя и будем ее часто использо-
использовать.
Мы говорили выше, что для форм в IR3 вычисление дифференциала сво-
сводится к привычным операциям векторного анализа. Пользуясь соотноше-
соотношениями F.22) - F.24), видим, что 1-форма со1 в области (/CFt3, записан-
записанная в виде со1 = d?dx, замкнута в случае rot со = 0 и точна в случае, если
со — потенциальное векторное поле (со = grad<p, где <р — скалярная функ-
функция). Если 2-форма со2 в такой же области имеет вид со2 =PdS, то она
замкнута, если div P = 0, и точна в случае, когда существует векторное
поле со, для которого Р = rot со. Наконец, всякая 3-форма uii=Qdxl Л
Adx2 /\dx3 в области I/C1R3 замкнута и точна: можно найти векторное
поле Р, удовлетворяющее условию Q = div P. (Точность всякой 3-формы
в C/CIR3 связана с тем, что в Uнет трехмерных циклов.)
Напряженности Е электростатического поля отвечает точная 1-форма
Е d\=—dtfi, где <р — скалярный потенциал. Напряженность Н статическо-
статического магнитного поля удовлетворяет уравнению rot H = 0 в области, где
плотность тока равна нулю. Таким образом, форма Hdx в этой области
замкнута, однако не является точной. В самом деле, интеграл этой формы
по замкнутой кривой Г (циркуляция вектора Н ) дается формулой
4я
f Hdx=— /,
г с
276

где / — сила тока, проходящего через поверхность, ограниченную кривой Г.
Если / Ф О, то замкнутая кривая является не гомологичным нулю одномер-
одномерным циклом в области, где нет токов. Пусть, например, магнитное поле
создается линейным током силы /, текущим по оси г. Если Г — горизон-
4я
тальная окружность с центром на оси г, то f Hdx =— / и, значит, эта
г с
окружность является не гомологичным нулю циклом в области U, получен-
полученной из 1R 3 удалением оси г. Циркуляция напряженности Н по любому дру-
4я
тому циклу в области Vравна т — /, где т - целое число. Этот очевидный
с
факт можно доказать, заметив, что всякий цикл в {/гомологичен пройден-
пройденной несколько раз окружности Г. (Область f/можно непрерывным образом
продеформировать в окружность, и при этой деформации каждый цикл де-
деформируется в несколько раз пройденную окружность). В частности, соле-
соленоид, осью которого является ось z (рис. 33), гомологичен т раз пройден-
пройденной окружности, где т — число витков в соленоиде.
Совершенно аналогично, если магнитное поле создается линейным то-
током силы /, текущим по замкнутой несамопересекающейся кривой С в
IR3, то циркуляция напряженности по любому циклу Г в IR3\C равна
4я
т — /, где т — целое число, носящее название коэффициента зацепления
Рис.33
циклов С и Г в IR3. Пользуясь обычной формулой для напряженности:
/ [d\\ (r -г')]
Н(г) = -# Л ,,3Л ,
ее 1г- г I3
получаем для коэффициента зацепления
Аи г с I г — г г
4я г с
Ir-r'f
.' 13
277

Отметим, что из этого выражения очевидна симметричность коэффициента
зацепления: т(С, Г) = т(Т, С).
Напряженности Е можно сопоставить также 2-форму EdS. В силу соот-
соотношения div E = 4тгр, где р — плотность заряда, эта форма замкнута в об-
области, где нет зарядов. Однако эта форма не обязательно точна в рассмат-
рассматриваемой области: если в области есть замкнутая поверхность ?1, внутри
которой расположен ненулевой заряд q, то
/
п
Поверхность ?2 является тогда циклом, не гомологичным нулю в области,
где нет зарядов.
Сопоставляя магнитной напряженности Н 2-форму HdS, мы получаем
точную форму: в силу равенства Н = rot А, где А - векторный потенциал,
эта форма является дифференциалом 1-формы Adx. Отметим, однако,
что само существование векторного потенциала следует из того, что divH =
= 0 во всем пространстве IR 3, а в В 3 всякая замкнутая форма точна.
Перейдем к рассмотрению дальнейших примеров. Пусть U — область в
пространстве IR3, полученная удалением из этого пространства начала ко-
координат. Тогда сфера S2 с центром в начале координат является циклом,
не гомологичным нулю в U; это вытекает из соотношения
s* Ixl3
X
A)
Форма dS = Е dS отвечает напряженности точечного заряда, поме-
I х| 3
щенного в начало координат, соотношение divE = 0 при хФО означает,
что эта форма замкнута. Следствием соотношения A) является также то,
х
что замкнутая форма 7~^S не является точной в U. Всякий цикл
I х|3
в области U гомологичен циклу mS2, где т — целое число. Это вытекает
из возможности непрерывно продеформировать всю область U в сферу
S2. Можно проверить, что всякая замкнутая 2-форма в Uкогомологична
форме вида —:——dS, где q — действительное число. (Например, это
I х|3
можно вывести из теоремы де Рама).
Если U - область, полученная из tR3 удалением нескольких точек ai,...
..., а„, то можно доказать, что всякий цикл в этой области гомологичен
линейной комбинации с целочисленными коэффициентами циклов S2,...
... ,S%, где S2 — сфера, содержащая внутри себя точку я( и не содержа-
содержащая других выколотых точек. Всякая замкнутая 2-форма в рассматри-
рассматриваемой области когомологична линейной комбинации форм
I х - а, |3
с действительными коэффициентами. Иначе говоря, всякая замкнутая
х — а;
2-форма когомологична форме вида EdS, где E='Eqt ^ —
I х-а, | 3
278

напряженность, порождаемая зарядами qi,...,qn в точках а1;...,а„.
Мы не будем доказывать этих фактов; заметим только, что из соотноше-
соотношения
вытекает, что линейная комбинация циклов S?,... ,5„2 не гомологична
х — a j х — а„
нулю и линейная комбинация форм —z~-dS, • • •, z dS
I х-ах |3 | х-а„| 3
не когомологична нулю. (Мы подразумеваем,что не все коэффициенты ли-
линейных комбинаций обращаются в 0.) Утверждение о когомологичности
любой замкнутой формы линейной комбинации форм B) следует- из
аналогичного утверждения для циклов и теоремы де Рама.
Рассмотрим теперь область, полученную из IR" удалением одной или
нескольких точек. Ситуация для (п— 1)-мерных циклов и (и— 1)-форм в
этой области совершенно аналогична описанной выше ситуации для дву-
двумерных циклов и 2-форм в IR3. В частности, всякий (и- 1)-мерный цикл в
области, полученной из Ft" удалением одной точки, гомологичен mS"~1,
где т — целое число, Sn~1 — сфера, окружающая удаленную точку. Всякая
(и — 1) -форма в этой области когомологична форме q со, где
. . dx1 Л.-.ЛЛс'-1 Adxi+1 Л.. .J\dx"
Всякий fc-мерный цикл, 0 < к < п — 1, гомологичен нулю в пространстве
CR", из которого удалено конечное число точек. В самом деле, как мы уже
говорили, этот цикл является границей (к + 1)-мерной поверхности в IR".
Если эта поверхность проходит через некоторые из выколотых точек,
то в случае к + 1 < п с помощью малого сдвига можно добиться того, что
поверхность, ограничивающая рассматриваемый нами цикл, не будет про-
проходить через выколотые точки. Мы видим, что цикл гомологичен нулю
в интересующей нас области. Из доказанного только что утверждения и
теоремы де Рама следует, что всякая замкнутая Л-форма точна при 0 <
< к < п— 1 в пространстве IR", из которого удалено конечное число точек.
Число линейно независимых замкнутых, но не точных Л-форм называет-
называется fc-мерным числом Бетти области Uи обозначается через bk (U). Точнее,
если сушествует s замкнутых Л-форм coj,..., cos таких, что всякая замк-
замкнутая Л-форма со может быть однозначно записана в виде
со = (*! о?! + ... + as (x>s + a,
то число Бетти равно s (здесь ait... ,as — действительные числа, а —
точная Л-форма).
Например, для пространства И" все числа Бетти равны нулю (кроме
нульмерного). Если C/=IR"\{0}— и-мерное пространство, из которого вы-
выколота одна точка, то Ьк=0 при кФО, и—1, Ь°=й"~1=1 (всякая
замкнутая (и— 1)-форма когомологична форме вида qto, где со опреде-
определяется соотношением C), т.е. может быть представлена в виде qo> + da).
279

Для и-мерной области Ьк(U) =0 при к>п (в и-мерной области всякая
Л-форма равна нулю при к > п).
Можно определить Л-мерное число Бетти так же, как максимальное чис-
число линейно независимых негомологичных нулю циклов. Точнее, Ък равно
максимальному из чисел s, для которых можно найти fc-мерные циклы
z 1,..., z,, так чтобы всякий цикл вида mx z i + ... + ms zs был не гомоло-
гомологичен нулю. (Здесь тх,. . ., ms - целые числа, не обращающиеся в нуль
одновременно.) Доказательство эквивалентности определений чисел Бетти
через замкнутые формы и через ^-мерные циклы может быть получено с
помощью теоремы де Рама (см. ниже).
Перейдем теперь к определению групп гомологии и когомологий. Гово-
Говорят, что два ^-мерных цикла принадлежат одному классу гомологии облас-
области U, если они гомологичны друг другу в U (т.е. могут быть соединены
пленкой). Множество всех циклов разбивается на классы гомологии. Это
следует из того, что отношение гомологичности циклов обладает свойства-
свойствами рефлексивности, симметрии и транзитивности: z ~ z; если Zj ~z2,
то zi ~ z i; eoiHZ] ~ z2,Z2 ~ z3)to Zi ~z3.
Если z i ~ z \ и z2 ~ z 2, то z i + z 2 ~ z\ + z 2; это позволяет определить
сложение классов гомологии. жЕсли цикл Zj принадлежит классу гомоло-
гомологии [zj], а цикл z2 принадлежит классу гомологии [z2], то [zt] + [z2]
определяется как класс гомологии, содержащий цикл Z\ +z2- Из сказан-
сказанного выше следует, что так определенный класс гомологии не зависит от
выбора циклов z^ и z2. т Легко проверить, что совокупность классов го-
гомологии с определенной таким образом операцией сложения является
абелевой группой; эта группа называется А;-мерной группой гомологии
области U и обозначается символом Hk(U). Группа гомологии Н^(Щ
может быть определена также как факторгруппа Zic(U)/Bic(U), где
%к(Ю — группа всех ^-мерных циклов в области U, a Bk(U) - группа
всех ^-мерных циклов, гомологичных нулю в U. Ацикличность области U
в размерности к означает, очевидно, тривиальность А;-мерной группы гомо-
гомологии (Нк (U) = 0).
Из сформулированных выше утверждений следует, что Нк(В") =0 при
к>0. Если F - конечное множество, то #fc(lR"\jF) =0 при 0<к<п,
группа Hn_l (JR"\F) изоморфна прямой сумме f экземпляров группы
"Z, где f — число точек в множестве F.
Группа когомологий определяется совершенно аналогично группе гомо-
гомологии; следует лишь заменить классы гомологии ^-мерных циклов на
классы когомологий замкнутых &-форм. (Две замкнутых Л-формы ш1 и
шг принадлежат одному классу когомологий, если они когомологичны
друг другу, т.е. их разность является точной формой.) Более формально,
fc-мерная группа когомологий Н k (If) может быть определена как фактор-
факторгруппа Zk(U)/Bk(U), где Zk(U) -группа замкнутых форм, Bk(U) -
группа точных форм. Отметим, что формы можно не только складывать,
но и умножать на действительные числа; это позволяет рассматривать
Z * (U), В k (U), Н * (U) не только как группы, но и как векторные прост-
пространства над полем действительных чисел. Размерность векторного прост-
пространства Н k (U) равна, очевидно, числу Бетти bk.
280

Заметим, что определенное в § 6 умножение форм порождает умноже-
умножение классов когомологии. Если ^-мерный класс когомологии [со] содер-
содержит fc-форму со, а /-мерный класс когомологии [о] содержит /-форму о,
то произведение этих классов когомологии определяется как (fc + /)-мер-
ный класс когомологии, содержащий форму со Л о. Это определение не
зависит от выбора форм со и о; если со — со = б/т,о—5 = dp, то
со Л о — со Л ~а = d(j Л о? + (-\)кш Лр + т hdp).
Определим скалярное произведение класса гомологии [г] и класса
когомологии [со] с помощью соотношения
<[z],[co]) = /co, D)
z
где z — цикл из класса гомологии [z ], со — замкнутая форма из класса
когомологии [со] (из F.31) вытекает, что правая часть не зависит от
выбора цикла z и формы со).
Следующие утверждения устанавливают связь между группами гомоло-
гомологии и группами когомологии.
а) Если [со] GHk(U) и для любого класса гомологии [z] &Hk(U)
скалярное произведение < [z], [со] > = 0, то со = 0.
б) Если [z] &Н)с(и) и для любого класса когомологии [со] ? Hk(U)
скалярное произведение { [г], [со] ) = 0, то найдется такое целое число
т, что т\г\ =0.
Эти два утверждения можно рассматривать как другую формулировку
теоремы де Рама (см. выше). Форма со называется целочисаенной, если ее
интеграл по любому циклу z является целым числом. Можно доказать,
что любая форма когомологична линейной комбинации целочисленных
форм. Класс когомологии целочисленной формы называется целочислен-
целочисленным классом когомологии; из сказанного выше следует, что любой класс
когомологии является линейной комбинацией целочисленных классов
когомологии.
Отметим, что гомологии и когомологии в приведенной выше формули-
формулировке теоремы де Рама не вполне симметричны. Для того чтобы добиться
полной симметрии, нужно разрешить рассмотрение формальных комби-
комбинаций вида Е<7,-?2,-, где qt - действительные числа, Г2,- - поверхности в
U. Такие комбинации носят название цепей с действительными коэффи-
коэффициентами. Для них можно определить понятие границы, полагая Э 2д,-?2,- =
= Гс7,-Э ?2,-, и, следовательно, понятия цикла и цикла, гомологичного нулю.
Используя такие циклы, определяем группу Hk(U,Щ) — группу гомоло-
гомологии области U с действительными коэффициентами. Эту группу можно
рассматривать как векторное пространство над полем действительных
чисел.
Всякий цикл в смысле использовавшегося выше определения можно,
конечно, рассматривать как цикл с действительными коэффициентами.
Отсюда следует, что существует гомоморфизм р группы Н^(Ц) в группу
Нк{11,№). При этом классу гомологии f e.Hk(U), имеющему конечный
порядок (т.е. удовлетворяющему условию mf = 0 для некоторого тФО),
отвечает, очевидно, нулевой класс гомологии в Я^(с7,1Л) (если'wz =
281

= Э ?2, то z = Э {— Ш j. Группа Hk(U,\R) полностью определяется группой
Hk(U). Именно если ?!,...,?, — максимальная линейно независимая
система элементов группы Hk(U), то элементы p(?i), . • , p(?s) состав-
составляют базис векторного пространства Нк(Ц ?R).
Естественным образом определяется скалярное произведение класса
гомологии [z] eHk(U,\R) и класса когомологий [со] GH *(?/)• Утверж-
Утверждение теоремы де Рама означает, что это скалярное произведение не вырож-
вырождено (т.е. для любого ненулевого [и] GHk(U) найдется такое [z] G
eHk(U,\B), что ( [г], [ы] > ФО, и для любого ненулевого [2] GHk(U)
найдется такое [ы] ?Н* (U), что < [г], [ы] > Ф 0).
Если для элементов двух векторных пространств можно построить не-
невырожденное скалярное произведение, то их размерности равны. Отсюда
следует, что dim Hk(U,JR) = dim Н к(U). Это означает, что число Бетти Ьк
можно интерпретировать не только как dim Hk (U), но и как dim Hk (?/, IR).
Тем самым обосновывается указанное выше определение Ък как макси-
максимального числа линейно независимых негомологичных нулю циклов.
§ 8. Гомологии и гомотопии
Рассмотрим гладкое отображение f области U в область V. При этом
отображении всякая замкнутая поверхность Л в области U переходит в
замкнутую поверхность ?2' в области U'; две поверхности, гомологичные
друг другу, переходят в гомологичные поверхности (пленка, соединяю-
соединяющая два цикла в U, переходит в пленку, соединяющую соответствующие
циклы в U'). Это означает, что всякому классу гомологии a G Hk (U)
можно сопоставить ^-мерный класс гомологии в ?/'; этот класс будем
обозначать символом f „а. Таким образом, гладкое отображение f облас-
области U в область U' порождает гомоморфизм fm группы Hk(U) в группу
или').
Если ?2 — цикл размерности к в области U, a f0 и Л — гомотопные глад-
гладкие отображения области U в область U', то ^-мерные циклы f0 (Q.) и
fх (?2) гомологичны друг другу. В самом деле, если ft — деформация
отображения f0 в отображение /\, то (fc + 1) -мерная поверхность, заме-
заметаемая образом поверхности О в процессе деформации ft, представляет
собой пленку, соединяющую циклы f0 (?2) и ft A2) (см. рис. 34).
Мы видим, таким образом, что гомотопные отображения f0 и /\ порож-
порождают один и тот же гомоморфизм групп гомологии:
(/о). =(/¦.).•
Заметим далее, что, в случае если к -формы ш^ и со2 принадлежат одному
и тому же классу когомологий области U', формы f*(^\ и f*oj2 принад-
принадлежат одному и тому же классу когомологий области U; это следует из
соотношения f*d = d f* (мы по-прежнему считаем, что f — гладкое отоб-
отображение U в U'). Таким образом, мы можем сопоставить отображению f
гомоморфизм f * группы когомологий Н k (?/') в группу когомологий
Hk(U).
282

Если [со] енк(и'),[о] ен'(г/'),то
/•(М л [о])=/•[«] лГМ;
это вытекает из соотношения F.28).
Гомоморфизм /„ групп гомологии тесно связан с гомоморфизмом / *
групп когомологий. Для того чтобы установить эту связь, воспользуемся
соотношением
;/*со= ; со, О)
Г /(Г)
где со — произвольная fc-форма в 17', а Г — произвольная fc-мерная поверх-
поверхность в U. (Соотношение A) мгновенно вытекает из определения интегра-
интеграла от fc-формы. В самом деле, если поверхность Г задается с помощью
отображения tp куба 1к, то поверхность /(Г ) задается отображением f\p.
По определению
Г jk /(Г) Jc
Замечая, что y*f* = (fy)*, получаем A)). Применяя A) к случаю,
когда Г — цикл, со — замкнутая форма, видим, что для класса гомологии
[Г] EHic(U) и класса когомологий [со] GHk(U) выполнено соотноше-
соотношение
<ЛМ,[Г]> = <М,Л[Г]>. B)
Если со — замкнутая fc-форма в области U', а /0 и ft — гладко гомотоп-
гомотопные отображения области с7в область U', то формы /"„"со и f*u> принад-
принадлежат одному и тому же классу когомологий, иными словами, отображе-
отображения /о и fi порождают один и тот же гомоморфизм групп когомологий.
Это важное утверждение сразу вытекает из соответствующего утверждения
для групп гомологии и описанной выше связи между гомологиями и кого-
мологиями.
Рис.34
А Приведем также непосредственное доказательство нужного нам ут-
утверждения. Проверим, прежде всего, что при бесконечно малой вариации
8f гладкого отображения f вариация б/*со формы /"*со когомологична
нулю. Будем считать для простоты обозначений, что к = 2. Тогда
ь> = <*ц(у)с1у* Ady',
где ац = -а^. Если отображение f переводит точку х= (х1,... ,х") е U
в точку y=(y1,...,ym) = (f1(x) fm(x))eu', то форма со в
283

U' переходит в форму
f*CO = aiJ(f(x))dfi/\df
в области U. Вариация формы f * со при бесконечно малом изменении
отображения f имеет вид
dfco = -^- bfk{x) df Л df + аЛ f(x)) dbf Л df +
Ъук
+ aii(f(x))dfibddf = -p- bfk{x)df Ndfl*
ay*
+ 2aii(f(x))d6fi/\df>'.
Форма со замкнута, поэтому в силу соотношения F.17)
дд,у _ dakj daik
Ьу' ду/
и, значит,
ban , . . Э#ь,- ,
—— 8fkdf Л df = —— S fkdf Л df +
Ьук Эу/
+ -^ S /•fed/'/ Л df = 5/-feifflfc,- Л df + 5/fc Л d/' Л daik =
byi
= 2daij8fi /\df.
Мы получаем
bf* со = 2datj Sf' Л rf/' + 2a,7 c?6 /"' Л d/-'.
Теперь очевидно, что
bfco = da, C)
где
a=2aij(f(x))8fi df.
Из соотношения C) немедленно вытекает, что формы f0* со и f* со когомо-
логичны. В самом деле, если/", — гладкая гомотопия, соединяющая отобра-
отображения /о и fx, то
1 ЪПсо t / bti \
f?co-f0*to = f —^— dt = df [2ач(Ш) -f- df) dt.
0 at о \ at /
Применим доказанное только что предложение к случаю, когда f0 —
тождественное отображение пространства IR", а /2 — отображение, пере-
переводящее все 1R " в одну точку. Эти отображения гладко гомотопны; пред-
представляя замкнутую форму со в [R " в виде co = ft*co- f0* со, видим, что любая
замкнутая форма вИ" точна, т.е. Н к (Р") = 0 (это утверждение было вы-
высказано выше без доказательства). т
Отметим, что описанную в настоящем пункте связь между гомологиями
и гомотопиями можно использовать дпятого, чтобы сопоставлять непрерыв-
284

ным отображениям числа, не меняющиеся при непрерывной деформации
(т.е. строить гомотопические инварианты непрерывных отображений).
В самом деле, если область U^ отображается в область U2, со — замкнутая
форма в области U2, a z - цикл в области U±, то число
ff*to = / "
г Яг)
не меняется при непрерывной деформации отображения f. Например, если
со - форма в области U2 =IR"\{0}, определенная соотношением G.3),
то из сформулированного только что утверждения вытекает, что число
/со = / —1-—- ^•••а" f^df* A...Adfin.
/(z) z (И- 1)! 1/Г'2
не меняется при непрерывном изменении отображения / области Ux в
1В"\{0}. Заметим теперь, что интеграл от рассматриваемой нами формы
«я"/2
со по сфере с центром в начале координат равен . (Вычисление
Г (л/2 + 1)
проще всего провести, используя то, что на сфере единичного радиуса ин-
интересующий нас интеграл сводится к интегралу от формы со' = ?(— 1) 'х' X
Xdx1 Л. . . Adx'~l Adx' + l Л... Adx", получающейся, если положить
| л: | =1 в со. Преобразуя интеграл от со' по сфере в интеграл от d со =
= п dxl Л... Adx" по шару, получаем, что / со = иК„, где V п =
ТГ"'2 S
— объем шара единичного радиуса в и-мерном пространстве.)
Мы видим, что интеграл от формы о= (nVn) ~1со = п~1я"""^2Г(/г/2 + 1)со
по сфере равен 1 и, значит, интеграл от этой формы по любому циклу в
ffi" \ {0} является целым числом (т.е. класс когомологий этой формы
является целочисленным). Соответственно
Г(л/2+1) е<! ¦•¦<* ,- ,• ,
f о= —— Г——— f ' df2 A Adf"
является целым числом (цикл z предполагается целочисленным). В случае
Ux =IR"\{0}b качестве цикла z естественно взять сферу S", внутри
которой находится начало координат. Таким образом, каждому отобра-
отображению f области Ux =1R"\{0}b U2 =[R"\{0 }сопоставляется целое число
f(.s
Л-1,
Г(и/2 +1) 6'.-'» ,,
(и-1)! ft"-i IfCv^l"/2
bfin
fi-i
djr"' A... Adx
Отображению f пространств IR"\ {0} сопоставляется отображение единич-
285

ных сфер, определяемое формулой / (х) = . Легко убедиться,
что число и(/) совпадает со степенью deg/ отображения / . Поскольку
гомотопический класс отображений сфер полностью характеризуется сте-
степенью, а сфера 5" гомотопически эквивалентна пространству R"\{0},
отсюда следует, что гомотопический класс отображений пространств
[R " \ {0 } полностью характеризуется числом и (/ ). (Доказательство сов-
совпадения и(/) и deg /' можно провести с помощью аналитического выраже-
выражения для степени. Другой способ доказательства состоит в проверке соот-
соотношения n(f) =deg/' для одного из отображений в каждом гомотопи-
гомотопическом классе; поскольку как «(/), так и deg/' не меняется при дефор-
деформации, это дает совпадение и(/ ) и deg f' во всех случаях.)
§ 9. Гомологии произвольных пространств
В § 7 были определены группы гомологии областей n-мерного прост-
пространства. При определении этих групп мы рассматривали гладкие поверх-
поверхности, лежащие в этих областях, и их границы. Отметим, прежде всего,
что это определение можно модифицировать, отказавшись от требования
гладкости рассматриваемых поверхностей; при этой модификации мы
приходим, к тем же группам гомологии. В самом деле, негладкий цикл
(поверхность, не имеющая границы) гомологичен гладкому циклу. (Не-
(Негладкий цикл можно сколь угодно близко аппроксимировать гладким.
Аппроксимирующий гладкий цикл гомологичен исходному, поскольку его
можно непрерывно продеформировать в исходный цикл.) Аналогично,
если два гладких цикла можно соединить негладкой пленкой, то существу-
существует также соединяющая их гладкая пленка.
Указанное только что модифицированное определение групп гомологии
применимо для произвольного пространства в отличие от первоначального
определения. В самом деле, понятие гладкой поверхности имеет смысл
не только для областей в IR", но и для гладких многообразий, однако
в произвольном пространстве оно лишено смысла. В то же время в произ-
произвольном пространстве мы можем рассматривать поверхности, параметри-
параметризованные непрерывным образом с помощью точек ^-мерного куба или
же состоящее из нескольких частей, каждая из которых допускает подоб-
подобную параметризацию. Группа гомологии Нк(Х) определяется стандартным
образом как факторгруппа группы ^-мерных циклов (поверхностей,
не имеющих границы) по подгруппе циклов, гомологичных нулю (циклов,
ограничивающих некоторую (к + 1)-мерную поверхность).
Простейшие свойства групп гомологии, описанные в § 8 для гомологии
л-мерных областей, остаются справедливыми и в общем случае. В част-
частности, всякое непрерывное отображение f пространства X в пространст-
пространство Y порождает гомоморфизм /, группы Нк(Х) в Hk(Y). (Всякий цикл
при отображении / снова переходит в цикл, гомологичные циклы перехо-
переходят в гомологичные циклы.) Если отображения /0 и fx пространства X
в Y гомотопны, то соответствующие гомоморфизмы групп гомологии
(/о). " (/i). совпадают, * Гомотопию ft, соединяющую /0 и fx, можно
рассматривать как отображение F произведения X X / в Y. Цикл z X О
286

в нижнем основании цилиндра X X / гомологичен циклу 2 X 1 в верхнем
основании цилиндра X X /; пленка, соединяющая эти циклы, состоит из
точек (х, t), где х принадлежит циклу 2, a t е / = [0; 1]. Если цикл z при-
принадлежит классу гомологии [z] e Нк(Х), то при отображении F цикл
г X 0 переходит в цикл из класса гомологии (/о). [z] , а цикл z X 1 в цикл
из класса гомологии (ft). [г]. Как мы уже говорили, циклы 2 X 0 и 2 X 1
гомологичны в X X /, откуда следует, что классы гомологии (/о), [г]
и (Л ).' И совпадают, т
Из очевидного соотношения
(Лг). =¦/.*. (О
следует, что группы гомологии гомотопически эквивалентных пространств
совпадают. В самом деле, если пространства X и Y гомотопически экви-
эквивалентны, то существуют такие отображения / пространства X в Y и g
пространства Y в X, что отображения fg и gf гомотопны тождественному.
Отсюда следует, что {fg)t = 1 и (gf)m = 1. Пользуясь соотношением A),
убеждаемся, что ftgt = 1 и gtft = \. Таким образом,/, и ?* - обратные
друг другу гомоморфизмы. Отсюда следует, что /, — изоморфное отобра-
отображение группы Hk(X) на Hk(Y); аналогично g, изоморфно отображает
Hk{Y) на Нк(Х).
Вычислим группы гомологии в некоторых простейших случаях. Займем-
Займемся прежде всего нульмерными группами гомологии. Всякую точку х0 е X
можно рассматривать как нульмерный цикл. Если две точки х0 их, при-
принадлежат одной и той же компоненте пространства X, то соответствующие
нульмерные циклы гомологичны друг другу. (Путь xt, 0 < t < 1, соеди-
соединяющий х0 и х,, можно рассматривать как одномерную поверхность,
граница которой равна хг - х0. Это означает, что циклых0 их, гомоло-
гомологичны друг другу). Таким образом, для связного пространства X цикл,
отвечающий всякой точке х, гомологичен циклу, отвечающему фиксиро-
фиксированной точке х0 G X. Всякий нульмерный цикл пространства X может
быть представлен в виде линейной комбинации
ntiXi + .. . + mrxr B)
циклов, отвечающих точкам xlt ..., хг ? X. Для связного пространства X
цикл. B) гомологичен циклу (w, + . .. + mr)x0, где х0 - фиксированная
точка пространства X. Отсюда следует, что для связного пространства X
группа Н0(Х) изоморфна группе целых чисел Z. Аналогичные рассужде-
рассуждения показывают, что, в случае если пространство Л'несвязно, группаН0(Х)
изоморфна прямой сумме s экземпляров группы Z, где s — число компо-
компонент пространства X.
Сфера Sk, как мы знаем, гомотопически эквивалентна пространству
IRfc + 1 с выколотой точкой. Гомологии последнего пространства были
описаны в § 7. Пользуясь этим описанием, получаем
H0(Sk) = Hk(Sk)=Z,
Hi(Sk)=0 при 1Ф0, k. { )
Пространство В**1 с s выколотыми точками гомотопически эквива-
эквивалентно букету из s сферЗ* (объединению s экземпляров сферы 5*, каждая
пара из которых имеет одну общую точку, принадлежащую сразу всем
287

сферам). Поэтому группы гомологии букета из s сфер Sk тривиальны
в размерностях / Ф 0, к, а ^-мерная группа гомологии изоморфна прямой
сумме s экземпляров группы Z.
До сих пор мы рассматривали в этом параграфе только группы гомо-
гомологии с целочисленными коэффициентами. Так же, как и в § 7, можно
определить группы гомологии с действительными коэффициентами. Более
того, можно определить группы гомологии с коэффициентами в произволь-
произвольной абелевой группе G, разрешив рассмотрение линейных комбинаций
вида 2g,-S2,-, где ?2, - поверхности в интересующем нас пространстве X,
gj — элементы группы G (такие комбинации носят название цепей прост-
пространства X с коэффициентами в G, с их помощью можно стандартным об-
образом определить группы Нк(Х, G) гомологии пространства X с коэф-
коэффициентами в G). Однако определение когомологий с помощью внешних
форм не может быть применено к произвольному пространству, хотя оно
годится не только для областей в 1R", но и для любых гладких много-
многообразий (см. § 10).
Вычисление гомологии пространства удобно производить, разбивая
это пространство на более простые. Сейчас мы определим специальный
тип разбиений — клеточные разбиения и покажем, как с помощью этих
разбиений можно вычислить группы гомологии. Точнее, мы определим
понятия групп гомологии и когомологий клеточного разбиения и вычис-
вычислим эти группы для простейших клеточных разбиений различных прост-
пространств. Далее, мы наметим доказательство того, что группы гомологии
клеточного разбиения совпадают с определенными ранее группами гомо-
гомологии пространства и, следовательно, не зависят от выбора клеточного
разбиения. Группы когомологий также не зависят от выбора клеточного
разбиения; это позволяет определить группы когомологий пространства
как группы когомологий одного из клеточных разбиений этого прост-
пространства.
Множество называется клеткой, если оно топологически эквивалентно
пространству F". (Можно также определить клетку как множество, топо-
топологически эквивалентное «-мерному открытому шару или открытому
кубу, поскольку открытые куб и шар гомеоморфны R".)
Пусть пространство X разбито на конечное число непересекающихся
клеток разных размерностей. Мы будем рассматривать только такие раз-
разбиения, для которых граница каждой клетки состоит из клеток меньшей
размерности, принадлежащих рассматриваемому разбиению. Такие раз-
разбиения называются клеточными разбиениями или клеточными комплекса-
комплексами. Пространство, для которого можно построить клеточное разбиение,
называется полиэдром. (Мы предположили, что в клеточном разбиении
имеется конечное число клеток. Можно рассматривать также клеточные
разбиения, состоящие из бесконечного числа клеток. Тогда все сформули-
сформулированные ниже утверждения остаются справедливыми, если наложить
на клеточное разбиение некоторые дополнительные условия, всегда вы-
полняющиесяв интересных для физики примерах.)
Максимальная размерность клеток клеточного комплекса называется
размерностью комплекса. Объединение клеток размерности <д назы-.
вается q-мерным остовом клеточного комплекса и обозначается симво-
символом*".
288

а Данное только что определение клеточного комплекса нуждается
в уточнении. Для того чтобы быть вполне аккуратным, следует предполо-
предположить, что для каждой и-мерной клетки существует непрерывное отобра-
отображение замкнутого куба /" в X, при котором внутренность куба топологи-
топологически отображается на рассматриваемую клетку, а граница куба переходит
в объединение клеток размерности <и. Куб I" можно заменить здесь то-
топологически эквивалентен ему шаром D". т
Рис.35
Рис. 36
Рис.37
Приведем простейшие примеры клеточных комплексов.
Круг D2 можно разбить на три клетки: внутренность круга, одну из то-
точек границы и граничную окружность без этой точки (рис. 35). С другой
стороны, разбиение круга на клетки, изображенное на рис. 36, не удовлет-
удовлетворяет наложенному нами условию и, следовательно, не является клеточ-
клеточным комплексом. (В этом разбиении есть одна нульмерная клетка а0
и две одномерные клетки — граничная окружность с выколотой точкой а0
и открытый диаметр. Граница диаметра состоит из двух точек, из которых
только одна является клеткой выбранного нами разбиения).
Сферу " можно разбить на две клетки: а0 и а". В качестве 0-мерной
клетки а0 можно выбрать любую точку сферы. Тогда клетка а" опре-
определяется как множество всех остальных точек сферы. Разумеется, легко
построить и другие более сложные клеточные разбиения сферы. Например,
на рис. 37 изображено разбиение сферы S2 на две двумерные клетки (две
полусферы), две нульмерные клетки (диаметрально противоположные
точки экватора) и две одномерные клетки (две половины экватора).
Простейшее клеточное разбиение проективной плоскости RP2 состоит
из одной нульмерной, одной одномерной и одной двумерной клеток.
Если точки проективной плоскости RP2 описывать с помощью однород-
однородных координат (л:0, х1 , х2), то нульмерная клетка выделяется условием
х1 - х2 = 0, одномерная — условиемх1 ФО, х2 = 0, двумерная - условием
х2 Ф 0. Проективная плоскость может быть получена из сферы S2
отождествлением диаметрально противоположных точек. Описанное толь-
только что клеточное разбиение проективной плоскости может быть получено
из изображенного на рис. 37 разбиения сферы S2 (при отождествлении
диаметрально противоположных точек клетки, имеющие одну и ту же
размерность, отождествляются друг с другом).
Совершенно аналогичным образом строится разбиение и-мерного проек-
проективного пространства RP" на п + 1 клетку (по одной клетке в каждой
размерности от 0 до п). Клетка размерности к может быть определена
соотношением о* = RPk \RPk ~', где символ RPk означает А:-мерное проек-
19. А.С. Шварц 289

тивное подпространство, выделяемое в однородных координатах (х°, ...
..., х") условием хк + 1 = .. . = х" = 0. Топологическую эквивалентность
клетки ак и пространства Ffc можно установить, введя в ак координаты
Та же конструкция позволяет построить клеточное разбиение комп-
комплексного проективного пространства СР". В этом случае разбиение состо-
состоит из (п + 1)-й клетки размерностей 0, 2, 4,..., 2п. (Конструкция клеточ-
клеточного разбиения остается прежней, но клетка а2к = СРк\СРк~1 имеет
размерность 2к, поскольку однородные координаты являются комплекс-
комплексными числами.)
Покажем, как, зная клеточное разбиение полиэдра X, можно вычислить
группы гомологии этого полиэдра. Фиксируем ориентацию каждой из кле-
клеток клеточного разбиения. Клеточной цепью будем называть формальную
линейную комбинацию клеток этого разбиения с целочисленными коэффи-
коэффициентами. Если все клетки в этой формальной линейной комбинации
fc-мерны, будем говорить, что цепь имеет размерность к. Так, например,
для клеточного разбиения сферы S2, изображенного на рис. 37, можно
рассматривать двумерные цепи a^ol + аго\, одномерные Ъха\ + Ъга\
и нульмерные с^аХ + с20°. Естественно определяется сложение цепей
и умножение цепи на целое число. Это позволяет рассматривать множество
клеточных цепей как абелеву группу. Группа к-мерных клеточных цепей
обозначается символом Ск (X) или, короче, Ск. Границу каждой ^-мерной
клетки можно рассматривать как (к — 1)-мерную цепь*). Это позволяет
сопоставить каждой ^-мерной цепи сок (к — 1)-мерную цепь дсок — гра-
границу цепи ь)к. Именно если шк = Sa,a*. то
Эы* = 2a,- baf. D)
Сопоставляя цепи со цепь Эсо, мы получаем гомоморфизм группы fc-мер-
ных цепей Ск в группу (к - 1)-мерных цепей Ск_х. Этот гомоморфизм
будем обозначать символом Э^. (Если размерность цепи, границу которой
мы рассматриваем, очевидна из контекста, то вместо символа Ьк будем
употреблять символ Э.)
Рассмотрим, как действует гомоморфизм Э для описанного выше раз-
разбиения сферы S2. При соответствующем выборе ориентации клеток этого
*> Каждой А-мерной клетке о сопоставляется (к - 1)-мсрная цепь За =
= ?a/Oj ~~ , где о/ - это (к - 1)-мерные клетки, лежащие в замыкании а
к
клетки о ¦ По определению клеточного комплекса существует отображение ку-
к к
ба / на о , устанавливающее топологическую эквивалентность внутренности куба
к
и а . Если отображение является топологическим также на границе куба, то а,- = ±1;
знак а,- определяется выбором ориентации клеток а{ ~ и а*. В общем случае а,-
к *
показывает, сколько раз граница куба покрывает клетку о,- при рассматриваемом
к
отображении (с учетом знаков). Строгое определение цепи да довольно громозд-
громоздко; мы не будем на нем останавливаться, поскольку в интересующих нас примерах
нахождение этой цени не вызывает затруднений!
290

разбиения имеем
Таким образом, гомоморфизм Э на группах С2, Clt Co определяется
соотношениями
= (а1 -а2)о\ + (<*! -а2)а\,
0>, - Ъ2)о% -(Ь, - Ъ2)о\, E)
Клеточная цепь со называется клеточным циклом, если ее граница равна
нулю (Эсо = 0). Подгруппа группы Ск, состоящая из циклов, называется
группой к-мерных циклов и обозначается Zk. Клеточный цикл со назы-
называется клеточно гомологичным нулю, если он является границей клеточ-
клеточной цепи (т.е. существует клеточная цепь о, для которой со = да). Группа
k-мерных циклов, гомологичных нулю, обозначается символом Вк. Иначе
можно сказать, что Zk - это ядро гомоморфизма Ък, а Вк — образ гомо-
гомоморфизма Э к +1 ¦
Группа гомологии клеточного разбиения пространства X определяется
как факторгруппа Zk/Bk. Можно доказать что эта группа гомологии сов-
совпадает с группой гомологии Нк(Х), определенной выше. Отсюда, в част-
частности, следует, что в случае, когда рассматриваются два клеточных раз-
разбиения пространства X, построенные по этим разбиениям группы гомоло-
гомологии изоморфны.
Вычислим группы гомологии пространств, для которых выше были
построены клеточные разбиения. Для клеточного разбиения сферы S",
состоящего из двух клеток о" и о0, имеем Эо" = 0, Эо° = 0. Это означает,
что любая и-мерная цепь ко" и любая нульмерная цепь ко0 представляют
собой циклы, т.е. Zn = 2?,Z0 = Ж Гомологичных нулю циклов не существу-
существует, поэтому Я„E") = Z, Я0E") = Z, остальные группы гомологии три-
тривиальны (Hk(S°) =0, кФ 0, и).
Покажем, что для сферы S2 тот же результат получается, если восполь-
воспользоваться клеточным разбиением рис. 37. Из соотношений E) вытекает,
что всякий двумерный цикл в этом разбиении имеет вид к (а\ + о|). Одно-
Одномерные циклы имеют вид к (а\ + Oj), нульмерные циклы - вид ki о? +
+ к2 о\. Всякий одномерный цикл гомологичен нулю (он является грани-
границей цепи ка\). Нульмерный цикл гомологичен нулю в случае, если^1 +fc2
равняется нулю (он служит тогда границей цепи кх а\). Таким образом, для
рассматриваемого разбиения
Z2=-Z, Я2=0, Z1=Bl=I, Z0=Z4Z, 50=Z.
Мы приходим к группам гомологии двумерной сферыЯ2E2) = Я0E2) = Z,
Hi($ ) = 0; эти группы совпадают с группами гомологии, полученными
выше с помощью другого клеточного разбиения.
Для разбиения проективной плоскости RP2, построенного выше, да2 =
- 2а1, да1 = 0, да2 = 0. (Эти соотношения проще всего получить, рас-
рассматривая клеточное разбиение RP2 как полученное из клеточного раз-
разбиения сферы S2 и замечая, что при преобразовании, переводящем точку
291

сферы в диаметрально противоположную, клетка а\ переходит в клет-
клетку а\ с той же ориентацией, т.е. цепь ко\ переходит в цепь ка\.) Таким
образом, двумерных циклов в рассматриваемом разбиении нет. Всякая
одномерная цепь и всякая нульмерная цепь являются циклами, циклы
вида 2 к а1 гомологичны нулю в силу соотношения 2 к а1 = д(ка2). Мы
получаем
= 0, H1(RP2)=Z2, H0(RP2)=Z.
Совершенно аналогично вычисляются группы гомологии проективного
пространства RP". Можно проверить, что в этом случае да' = 0, если /
нечетно; до{ = 2а' ~1, если / четно, iФ 0.
Отсюда Н21 _1(RPn) = *2 при 2i -К л, H^^RP") = t при 2/-1 =
= n,H0(RPn) = Z, остальные группы гомологии тривиальны.
Для комплексного проективного пространства СРп все цепи являются
циклами. (В построенном нами клеточном разбиении нет нечетномерных
клеток, поэтому do2i= 0.) Таким образом, Z2j = Жпри 0 <i <и , B2j =
= 0. Мы видим, что Н2.(СР") =^при 0 < / <п, остальные группы гомо-
гомологии равны нулю.
Мы рассматривали до сих пор только цепи с целочисленными коэффи-
коэффициентами. С тем же успехом можно рассматривать цепи и группы гомо-
гомологии с коэффициентами в произвольной абелевой группе G. (Операцию в
G мы называем сложением.) Группу fc-мерных цепей клеточного комплекса
X с коэффициентами в группе G будем обозначать символом Ck(X, G). Легко
видеть, что эта группа изоморфна прямой сумме а^ экземпляров группы G,
где ак — число Л:-мерных клеток:
Ск{Х, G) = G +... + G . F)
ак
Стандартным образом определяется гомоморфизм Ьк группы Ck{X*G)
в (??_ (X,G). Определяя группу циклов Zk{X,G) как ядро гомоморфиз-.
ма Ьк , а группу Вк (X, С)циклов, гомологичных нулю, как образ гомо-
гомоморфизма \+1, мы приходим к понятию ^-мерной группы гомологии
^(X,G)/Bk(X,G) клеточного разбиения пространства X с коэффициен-
коэффициентами в G; эта группа не зависит от выбора клеточного разбиения и совпа-
совпадает с введенной выше группой Нк(Х, G).
Полностью повторяя приведенные ранее рассуждения, убеждаемся, что
Я„E",С) = Я0E",С) = G, G)
Я2. (СР", G) = G , 0 < i < п . (8)
Остальные группы Hk(Sn, G) rHk(CPn,G) тривиальны. Существенное от-
отличие возникает для гомологии пространства RPn. Например, в случае G =
= 2i любая цепь в RPn является циклом. (Соотношение 3(fcff21 ) =
= 2ko2t~l остается справедливым, но для к& Ж2 имеем 2к =0). Отсюда сле-
следует, что Н. (RP", Z2) = 2г2при0</ < и.Если в качестве группы коэф-
коэффициентов рассматривается группа R действительных чисел, то вее группы
гомологии пространства RP" тривиальны за исключением нульмерной
292

группы гомологии и группы Нп (RPn, (R) при и нечетном (группа
H2m+1(RP2m + 1, IR) изоморфна Р). В самом деле, четномерных циклов с
коэффициентами в IR не существует, а всякий нечетномерный цикл немак-
¦и-
симальнои размерности гомологичен нулю в силу соотношения
= ко2г~ 1 для любого fcSIR.
АДля произвольной группы G имеем H2.+1(RPn, G) = G/2Gnpn 0<
<i<^— ,Hn(RPn, G)=G при и нечетном, H2J(RPn,G)=G2 приО</<и/2.
(Мы пользуемся обозначениями 2G для подгруппы группы G, состоящей
из элементов, представимых в виде 2g, где^еС, и обозначением G2 для
подгруппы, состоящей из элементов порядка 2, т.е. элементов, удовлетво-
удовлетворяющих условию 2g = 0 ). Ў
Наметим доказательство совпадения групп гомологии, построенных по
клеточному разбиению пространства X, и введенных ранее групп гомоло-
гомологии. Достаточно проверить, что всякий цикл гомологичен клеточному
циклу, и что, в случае когда клеточный цикл гомологичен нулю в обычном
смысле, он клеточно гомологичен нулю. Заметим, прежде всего, что первое
их этих утверждений можно считать очевидным для fc-мерных циклов в
^-мерном клеточном комплексе. (Грубо говоря, Л:-мерный цикл в fc-мер-
ном комплексе не может содержать какую-то из ^-мерных клеток лишь
частично). Второе утверждение представляется столь же очевидным для
^-мерных клеточных циклов в (?+1) -мерном комплексе (если граница
(к+1) -мерной цепи в (к+1) -мерном комплексе лежит в t-мерном остове
комплекса, то эта цепь должна состоять из целых (?+1) -мерных клеток и,
следовательно, может рассматриваться как клеточная цепь).
Рассмотрим теперь fc-мерный цикл в клеточном комплексе размерности
больше к и покажем, что его можно продеформировать в ^-мерный цикл,
нежащий в ^-мерном остове клеточного комплекса. Для того чтобы постро-
построить нужную деформацию, следует заметить, что, в случае когда fc-мерный
цикл частично расположен внутри клетки размерности больше к, можно
построить непрерывную деформацию этого цикла, при которой часть цикла,
расположенная внутри клетки, переходит на границу клетки, а остальная
часть цикла остается на месте. (Построение такой деформации легко провес-
провести, пользуясь замечанием, что замкнутый куб, из которого выколота
внутренняя точка, можно продеформировать в границу куба таким обра-
образом, что точки границы остаются неподвижными). Повторяя последова-
последовательно описанный только что процесс "сдувания" цикла с клеток большой
размерности, мы деформируем любой fc-мерный цикл в гомологичный
ему цикл в ^-мерном остове клеточного комплекса. Рассматривая Л:-мер-
Л:-мерный остов как ^-мерный клеточный комплекс и вспоминая, что fc-мерный
цикл в таком комплексе гомологичен клеточному циклу, получаем, что
любой цикл гомологичен клеточному.
Точно так же, если ^-мерный клеточный цикл гомологичен нулю, то ог-
ограничивающую его (Аг+1)-мерную цепь можно "сдуть" с клеток размернос-
размерности > к+1 и получить цепь, ограничивающую интересующий нас цикл и ле-
лежащую в (к+1) -мерном остове клеточного разбиения. Таким образом, рас-
рассматриваемый нами fc-мерный клеточный цикл гомологичен нулю в
293

-мерном комплексе и, следовательно, как мы говорили, клеточно
гомологичен нулю.
Намеченное выше доказательство совпадения групп гомологии, по-
построенных без помощи клеточного разбиения, с клеточными группами
гомологии далеко от строгости. Более того, не является строгим само
определение клеточных групп гомологии. Дело в том, что мы рассматри-
рассматривали границу ^-мерной клетки как линейную комбинацию клеток размер-
размерности к—\. Сама возможность такого представления границы fc-мерной
клетки, строго говоря, требует доказательства. Аккуратное определение
групп гомологии клеточного комплекса и их совпадения с группами гомо-
гомологии, построенными выше, мы опустим.
§ 10. Дифференциальные формы на гладком многообразии
и гомологии гладкого многообразия
Напомним, что гладкое многообразие можно покрыть локальными си-
системами координат, связанными между собой гладкими преобразованиями.
Для того чтобы задать дифференциальную форму на многообразии, нужно
задать дифференциальные формы согласованным образом в локальных си-
системах координат. (Если (х , ..., х") и (х11 х'п) — две локальные
системы координат, то формы aijt ..., { (x)dxii Л ... Л dx'k и
вух тш. jk(x) dx''1 Л ... Л dx''k считаются согласованными при условии
Эх1'' Эх'*
¦)
В качестве примера рассмотрим сферу S". Мы видели в § 1, что на сфе-
сфере с помощью стереографической проекции можно ввести две системы
координат (х1 х") и (х 1, ...,х'"),/связанные преобразованием
(первая из этих систем покрывает всю сферу за исключением северного
полюса, а вторая — всю сферу, за исключением южного полюса).
Задав форму ы в координатах (х1,...,*") формулой
а в координатахх'1, ...,х'п — формулой
A+2(ж"J)"
...Л Л'-, A')
мы получим форму, определенную на всей сфере. (Эта форма имеет гео-
геометрический смысл элемента объема на сфере.)
Более общий пример — форма объема на произвольном ориентирован-
ориентированном многообразии с метрикой, которая задается в локальных координа-
294

тах метрическим тензором gy . Эта форма определяется соотношением
со = y/Jdx1 Л...Л<?с" = - y/g~et ,„ Лс'« Л ... Л Лс'",
и! "
где# — определитель матрицы gtj. Для того чтобы проверить, что написан-
написанное соотношение определяет форму на всем многообразии, нужно заме-
тить,что при переходе к новым координатам х'1, ..., х " метрический тен-
тензор преобразуется по формуле
g'ij = Т,к T}gkl ,
где Т? =Ъхк/дх"; т.е. матрица^-получается из ^.умножением на
матрицу Тк, с одной стороны, и на транспонированную к ней матрицу, с
другой стороны. Из этого следует,что
гт / дхк\
и, следовательно, y/g = (det ;f j \/g в случае, если переход к новым
/ Ъхк \
координатам сохраняет ориентацию (т.е. det— >0j. Вспоминая, что
\ Ьхп /
dx1 Л ... Л dx" =det—^dx'1 Л ...Л dx'n,видим,что
\fgdx1 Л .... A dx" = у/р'dx'1 Л...Л dx'n.
Все операции с дифференциальными формами, рассмотренные в § 6,
переносятся на дифференциальные формы, определенные на произвольном
гладком многообразии М; свойства этих операций такие же, как в евкли-
евклидовом пространстве.
Определение групп когомологий Hfe (Af) с помощью дифференциальных
форм также обобщается без труда. Определение групп гомологии Нк (M,G)
гладкого многообразия М с коэффициентами в абелевой группе G можно
дать двумя способами: с помощью гладких поверхнбстей и с помощью по-
поверхностей,, не обязательно обладающих свойством гладкости (см. § 9).
Оба способа приводят к одним и, тем же группам гомологии. Теорема де
Рама остается справедливой для "Произвольного гладкого многообразия;
в силу этой теоремы можно рассматривать векторное пространство Hfc (Af)
как пространство, сопряженное к Нк (М,Щ.
Так же как и в § 8, гладкое отображение / многообразия М в многообра-
многообразие М' порождает гомоморфизм /, групп гомологии многообразия М в
группы гомологии многообразия М' и гомоморфизм /* групп когомоло-
когомологий многообразия М' в группы когомологий многообразия М. Повторяя
рассуждения § 8, убеждаемся, что гладко гомотопные отображения /0 m/i
порождают совпадающие гомоморфизмы: fо =/*, (/о) «= (Л) »• .
Существенно отметить, что непрерывное отображение/ также порождает
гомоморфизмы /, и /* групп гомологии и когомологий, при этом гомо-
295

морфизмы /, и / ¦ не меняются при непрерывной деформации отображения
/. В самом деле, всякое непрерывное отображение одного гладкого много-
многообразия в другое гомотопно гладкому отображению, два гомотопных глад-
гладких отображения гладко гомотопны (доказательства этих факторов для
сфер намечены в § 2, в общем случае доказательства аналогичны). Это поз-
позволяет определить гомоморфизмы/,и/*, порожденные непрерывным ото-
отображением /, как гомоморфизмы отвечающие гладкому отображению f,
гомотопному отображению /. (Это определение не зависит от выбора ото-
отображения/ : если/ и/"—' два гладких отображения, гомотопных ото-
отображению /, то /' гомотопно и, значит, гладко гомотопно /", отсюда
следует,что ft = /",/'* =/"*'•") Если отображение / гомотопно глад-
гладкому отображению/, а отображение g — гладкому отображению g', то из
гомотопности отображений / и g вытекает гомотопность и, следовательно,
гладкая гомотопность отображений /'и #'. Мы видим, что /« = /'» =
= g* = g*, f* = /'* = g"' = g*; это означает, что гомоморфизмы групп
гомологии и когомологий не меняются при непрерывной деформации.
Как мы говорили, гомологии гладкого многообразия -М можно опреде-
определить с помощью поверхностей, не обязательно являющихся гладкими. Если
пользоваться этой модификацией определения групп гомологии, то сразу
ясно, что непрерывное отображение порождает гомоморфизм групп гомо-
гомологии и что два гомотопных непрерывных отображения порождают один и
тот же гомоморфизм (это было отмечено в § 9). Однако для групп когомо-
когомологий, определяемых с помощью дифференциальных форм,непосредствен-
форм,непосредственное определение гомоморфизма / *, порождаемого непрерывным отображе-
отображением /, невозможно; приходится использовать гладкую аппроксимацию
этого отображения, как это было сделано выше.
Отметим очевидные, но важные соотношения
Если многообразия Ми М' гомотопически эквивалентны, то их группы го-
гомологии и когомологий изоморфны. Доказательство этого факта для групп
гомологии, основанное на соотношении B), приведено в § 9. Для групп ко-
когомологий применимы совершенно аналогичные рассуждения, следует
только заменить соотношение B) соотношением B().
Если М - компактное л-мерное ориентированное многообразие (напри-
(например, сфера), то само это многообразие можно рассматривать как л-мерный
цикл. Класс гомологии этого цикла называется фундаментальным классом
гомологии многообразия и обозначается символом [М]. Очевидно (и может
быть строго доказано), что для связного многообразия М всякий п-мерный
класс гомологии кратен [М]; отсюда следует, что группа Нп (М) изоморф-
изоморфна группе целых чисел и класс [М] является образующей этой группы.
Отметим, что понятие степени отображения может быть сформулировано
в гомологических терминах. В самом деле, пусть/— отображение л-мерного
связного компактного ориентированного многообразия Mi в и-мерное
связное компактное ориентированное многообразие M2,f* —гомомор-
—гомоморфизм групп гомологии, порождаемый отображением/. В силу сказанного
выше класс гомологии /,Wi] кратен классу гомологии [М2]. Иными
296

словами,
ГЛМх\=ч[Мг\, C)
где q — целое число.
Будем называть q степенью отображения /. Легко понять, что q совпадает
со степенью, определенной в § 2 для случая отображения сфер и в § 5 для
общего случая. В самом деле, число q показывает, сколько раз многообра-
многообразие М1 накрывает многообразие М2 при отображении /. Мы видим, что гео-
геометрический смысл числа q совпадает с указанным в § 2 геометрическим
смыслом степени отображения.
Мы знаем, что гомоморфизм /» не меняется при деформации отображе-
отображения /. Отсюда сразу следует, что степень отображения/, определенная фор-
формулой C), не меняется при деформации отображения/.
Покажем, что аналитическое выражение для степени немедленно полу-
получается из данного только что определения. Пусть и-форма со на многообра-
многообразии М2удовлетворяет условию
/о>=1. D)
Из соотношений
Ям,) и,
/ со = q fco = q
/(Л/,) м,
вытекает, что
Я = ff'tJ. E)
Введем в многообразиях Mt и М2 системы координат (х1, ..., х")
и (х'1, .. ., х'") таким образом, чтобы они имели смысл всюду, кроме
множеств Nt С Mj и N2 С М2, имеющих нулевой объем. Форму со в коор
динатах (х ",..., х'") можно записать в виде
co = .p(x'1,...,x'")dx'1 Л ... Л dx'n,
условие D) означает, что
f<p(x')dx'x ...dx'"= 1.
Форма /*со тогда запишется в виде
/•(«)= ^(f(x))det(~-^dx1 Л ... Л dx".
Соотношение E) означает, таким образом, что
Я = M/(*))det (-^7) dxl • • • <ЬН. F)
Это соотношение F) совпадает с указанным ранее аналитическим выраже-
выражением для степени (см. § 5).
297

Мы можем теперь указать наиболее естественные условия применимости
соотношения F): функция у(х') должна быть такой, чтобы форму
y(x')dxn Л ... Л dx'n можно было продолжить в гладкую форму,
определенную на всем многообразии Мг.
Описанная в § 6 операция умножения внешних форм в области прост-
пространства IR" инвариантна относительно замены координат в области. Это
позволяет определить умножение внешних форм на гладком многообра-
многообразии М. Свойства этой операции на многообразии такие же, как в IR". В част-
частности, класс когомологий произведения замкнутых форм не меняется
при замене этих форм на когомологичные им формы. Это позволяет опре-
определить произведение классов когомологий [со] ? Нк(М), [о] е Н'(М) как
класс когомологий [со] • [о] = [со Л о] S Hfc + '(M).
Таким образом, в прямой сумме H(Af) векторных пространств Нк(М)
определена операция умножения. Мы можем поэтому рассматривать ЩМ)
как алгебру; алгебра ЩМ) называется алгеброй когомологий многооб-
многообразия М.
§11. Гомологии римановых многообразий
Рассмотрим л-мерное ориентированное риманово многообразие М.
Мы будем предполагать это многообразие компактным. Мы уже говори-
говорили, что на римановом многообразии существует форма объема
G}=y/gdxi Л ... Л dxn=—VJe, , dx'1 Л ... Л dx'n, A)
, л! '¦"
где g = det g,j - детерминант метрического тензора #,/. Коэффициентные
функции y/ge{ {п формы объема образуют, очевидно, антисимметрич-
антисимметричный тензор ранга и, определенный на всем римановом многообразии.
Существование этого тензора позволяет для каждого антисимметрическо-
антисимметрического тензора ранга к определить дуальный к нему антисимметричный тензор
ранга п — к. (Мы все время рассматриваем антисимметричные тензоры
с нижними индексами.)
Тензор, дуальный к антисимметричному тензору F,- _ (fc, определяется
формулой
*л •••/«-* = 77>/?*/,.../„-*',...^''¦¦'*> B)
(иными словами, для того чтобы перейти к дуальному тензору, нужно
поднять у тензора F^ ik индексы с помощью метрического тензора и
свернуть с тензором \fgeti ,n).
В частности, в четырехмерном многообразии (и = 4) вектору Ft дуален
тензор ранга 3
Рцк = y/geqkiF1, C)
а антисимметричному тензору F^ дуален тензор
Fik = -\fgeiki,Fil. D)
298

Отметим, что
Fi2 = n/F*134, F23 = sftFiA, Fl4 = VgF23, Fl9 =
Вообще,
З..../,.-*"*^11-'*. E)
где (/'i ijt) — индексы, остающиеся после удаления из множества
A и) индексов (fi .../„_*), а знак определяется четностью пере-
перестановки (/i,...,}„-k,h,- Jk)-
Скалярное произведение двух антисимметричных тензоров ранга к
определяется формулой
<F,G) = fFii_ikGl>-'ki/gd"x. F)
Легко проверить, что
Flt...tk(x)Ft>-tk(x)y/g >0 G)
(это соотношение становится очевидным, если заметить, что для каждой
точки х0 можно выбрать систему координат, в которой g;jt(*o) = $tk)-
Из G) вытекает, что {F, F) > 0 и (F, F) - 0 лишь в случае F = 0.
Поскольку fc-формы (дифференциальные формы степени к) находят-
находятся во взаимно однозначном соответствии с антисимметричными тензора-
тензорами ранга к, все понятия, введенные для антисимметричных тензоров,
можно перенести на формы. В частности, всякой форме
можно сопоставить дуальную ей (и - К) -форму
•"¦"оГ^Г^-'-**'1 Л ••л *'""* (8)
(здесь и далее к обозначает степень формы <о).
Скалярное произведение тензоров, определенное выше, порождает ска-
скалярное произведение форм; легко проверить, что
<<о,оУ> = /со Л »со'. (9)
м
Отметим соотношения
»»со = (-l)*("-fc)co, A0)
•<* СО, * ф) = <СО,(^>. A1)
Кроме оператора внешнего дифференцирования d, сопоставляющего к-
форме со (к + 1)-форму dсо, на римановом многообразии можно ввести
оператор б = (— l)nk + n+l * d *, сопоставляющий fc-форме со (Л — ^-фор-
^-форму Sco = (— 1)"к + " +1 * d * со. Легко проверить, что операторы dub сопря-
сопряжены, т.t.
<бсо,со'> = <co,rfco'> A2)
для любой?-формы со и (к — 1)-формы со'.
299

В самом деле,
<5со,со') = /бсоЛ »сУ = (-) ;
м м
= (-l)nk+n + l f d*u.A со'.
м
Замечая, что
rf(*co Л со') = с?(*со) Л ш' + (-1)п-к *и> Л du>',
*ш Л do/ =(-l)("-fc)fcdco' Л »со
и интеграл от формы d(* со Л со') по циклу М равен нулю, получаем A2).
Если многообразие М четномерно, то S = - * с? *, d= * S *.
Определим оператор Лапласа А с помощью формулы
A = (d + 8J=d8+8d. A3)
Легко проверить, что действие оператора Д на функции (формы степени
нуль) задается соотношением
А/= —^-^(s/ggli^-ff) ¦ A4)
/]Г Ьх1 \ Ьх' /
Оператор Лапласа самосопряжен и коммутирует с операторами d, 8 и *:
Ad = dA,
А8 = 8А, A5)
Д* = *Д.
Форма со называется гармонической если Дсо = 0. Если со — гармоничес-
гармоническая форма, то, очевидно,
0= < Дсо, со) = <c?co,Jco> + <со, со) =0,
откуда Jco = 0, б со .= 0; обратно, из соотношений с?со = 0, бсо = 0 вытекает
гармоничность формы со.
Докажем сейчас следующее утверждение (теорему Ходжа).
Каждая замкнутая форма когомологична одной и только одной гармо-
гармонической форме.
Поскольку гармоническая форма замкнута, из этого утверждения вы-
вытекает, что элементы группы Нк(М) находятся во взаимно однозначном
соответствии с гармоническими ^-формами, а ^-мерное число Бетти Ьк
совпадает с числом линейно независимых гармонических fc-форм.
Доказательство теоремы Ходжа основано на замечании, что всякую
форму со можно однозначным образом представить в виде
со = со'+ Дсо", A6)
где со' — гармоническая форма, а со" — форма, ортогональная ко всем гар-
гармоническим формам. В самом деле, разложим со по ортонормированной
системе собственных векторов оператора Д (мы рассматриваем компакт-
компактное многообразие, поэтому Д имеет только дискретный спектр). Отделяя
в разложении формы со часть, отвечающую собственным векторам с нуле-
300

вым собственным значением, получаем представление этой формы в виде
0} = со' + а, где ш — гармоническая форма, а а = 2с,-\pt, где ^ - собствен-
собственные векторы оператора А с ненулевыми собственными значениями: Ащ =
Xf, X, =? 0. Очевидно, что
^ A7)
Л/
(Разумеется, сходимость ряда A7) надо доказьшать; это доказательство
нетрудно провести.)
Оператор, сопоставляющий форме а> форму а/, фигурирующую в A6),
обозначим символом Я, а оператор, сопоставляющий форме а> форму оз" —
символом G. (Иначе говоря, Н — это оператор ортогонального проектиро-
проектирования на пространство гармонических форм Ж, а оператор G определяется
условиями со - Ню + ДСо), форма Gcj ортогональна Ж.) Из того, что
оператор А коммутирует с d, следует, что операторы Н и G также комму-
коммутируют с d. Заметим теперь, что всякая замкнутая форма а> когомологич-
на гармонической форме #а>. В самом деле, если dcj = 0, то
= Ни> +d8Gu> + 8Gdco= Hto
т.е. w когомологична #а>. Далее, если гармоническая форма а представле-
представлена в виде da, то
<а,а> = (a,da) = <5а,а> =0
и, значит, а = 0. Отсюда видно, что форма может быть когомологична толь-
только одной гармонической форме; это завершает доказательство теоремы
Ходжа.
В качестве примера рассмотрим применение теоремы Ходжа к вычисле-
вычислению когомологий и-мерного тора Т". Тор определяется как произведение п
окружностей; иначе говоря, точка тора задается строкой (s1, ..., s"),
где s* пробегает окружность S1. Вводя на каждой окружности угловой
параметр <р, пробегающий отрезок [0; 2п], можно характеризовать точку
тора числами (ip1, ..., (/>"). Риманову метрику на торе определим соот-
соотношением
таким образом, локально тор устроен так же, как евклидово пространство.
Можно проверить, что базис пространства гармонических &-форм на торе
состоит из форм вида dip'1 Л ... Л dy>'k, где i'i < ... < ik. Таким об-
образом, Л-мерное число Бетти и-мерного тора равно С*.
Теорема Ходжа обычно применяется не для вычисления групп когомо-
когомологий, а для получения информации о гармонических формах, исходя
из известной уже информации о группах когомологий. Например, оче-
очевидно, что для связного многообразия нульмерное число Бетти Ь° равно 1.
Отсюда вытекает, что'на римановом многообразии не существует никаких
гармонических функций @-форм) кроме констант. (Напоминаем, что мы
все время считаем многообразие компактным.)
301

Отметим также, что из теоремы Ходжа можно вывести, что для гладкого
ориентированного компактного и-мерного многообразия Л-мерное число
Бетти Ък совпадает с (и - к)-мерным числом Бетти Ь"~к. В самом деле,
введем в рассматриваемом многообразии риманову метрику (это всегда
возможно; см. § 16). В силу соотношения *Д = Д* оператор * переводит
гармонические формы степени к в гармонические формы степени (и - к);
из A0) вытекает, что соответствие между гармоническими формами сте-
степени к и (и - к) взаимно однозначно и, стало быть, Ък = Ьп~к.
В заключение заметим, что, пользуясь взаимно однозначным соответст-
соответствием между формами и антисимметричными тензорами, можно перевести
все сказанное выше на тензорный язык. В частности, операторы d, 8, А
можно считать операторами, действующими на антисимметричные тензоры;
например, если а -г- тензор ранга к, j3 = 5 а, то
(т.е. оператор Ь = d* можно интерпретировать как ковариантную дивер-
дивергенцию) .
§ 12. Гомотопическая классификация отображений сферы
(основные утверждения)
Во многих проблемах математики и физики возникает задача о гомото-
гомотопической классификации отображений At-мерной сферы Sk в какое-то
пространство. Напомним, что два отображения сферы Sk в пространство Е
принадлежат одному гомотопическому классу (гомотопны), если их мож-
можно соединить непрерывным семейством отображений (продеформировать
одно в другое). Целью этого параграфа является изучение множества
iSk, Е } гомотопических классов отображений сферы Sk в Е. Ранее в § 1
и 2 эта задача была исследована для случаев Е = |Rm и Е = Sr, r> к; мы
установили, что множество { Sk, Rm}, а также множество { Sk,Sr} при
г > к состоят из единственного элемента, а гомотопический класс отобра-
отображения Sk в Sk характеризуется целым числом (степенью отображения).
В настоящем параграфе мы сформулируем (отчасти без доказательств)
важнейшие факты о гомотопических классах отображений сферы; некото-
некоторые из пропущенных доказательств будут приведены в § 13—15. Будем
предполагать, что пространство Е связно и односвязно. Тогда для двух
гомотопических классов отображений Sk в Е можно определить сумму
этих классов с помощью следующей конструкции. Обозначим символом R
пространство, состоящее из двух fc-мерных сфер Sk и Sk и отрезка /,
соединяющего точку Sj сферы Sk с точкой s2 сферы Sk (рис. 38). Постро-
Построим отображение а сферы Sk на R, стянув полосу вблизи экватора сферы
в отрезок (рис. 39).
а Для того чтобы определить отображение а более формально, разобьем
сферу Sk, определяемую уравнением (х0J + (х1J + ... + (хкJ = 1 на
множества К^, К2, К3, выделяемые соответственно неравенствами х0 > 1/2,
302

x° < — 1/2, — 1/2 < x° < 1/2. Множество К3 — полосу вблизи экватора —
мы отобразим на отрезок —1/2 <? < 1/2, полагая t = х°. Отождествляя отре-
отрезок — 1/2 < f < 1/2 с отрезком 1С R, мы получаем отображение множест-
множества К3 в R; по определению а,на К3 совпадает с построенным отображе-
отображением. Отображение а множества К^ в Sk С R и множества К2 в Sk С R
построим таким образом, чтобы граница множества Kt переходила в точ-
точку S/ сферы Sk, а внутренность множества Kt топологически отобража-
отображалась на Sf\Si (это можно сделать, поскольку Kj топологически эквива-
эквивалентно А:-мерному шару). Ў
х
Рис.38
Рис.39
Если fag — два отображения SK в Е, то определим отображение / V g
пространства R в Е, считая, что одна из сфер, входящих в пространство R,
отображается с помощью отображения /, а другая — с помощью отображе-
отображения g. На отрезке, соединяющем сферы, отображение / V g определим
произвольным образом (с единственным условием, чтобы построенное
отрбражение пространства R было непрерьшно). Сумму отображений /
и g построим как отображение /+? = (/ V ?) • а сферы Sk в Е.
Гомотопический класс отображения f+g полностью определяется гомо-
гомотопическими классами отображений /a g. В самом деле, заметим, прежде
всего, что из предположенной нами односвязности пространства Е выте-
вытекает, что гомотопический класс отображения f V gne зависит от допускае-
допускаемого нами произвола при определении / V g на отрезке, соединяющем
сферы,, так как два пути в односвязном пространстве, имеющие общее
начало и общий конец, можно продеформировать один в другой, не сдви-
сдвигая начала и конца. Далее, при непрерывной деформации отображений /
и g непрерьшно меняется также отображение f\fg и, следовательно, отобра-
отображение /+g.
Таким образом, мы определили операцию сложения *) в множестве
{ Sk, Е}. Введенная нами операция превращает множество { Sk, Е } в абеле-
ву группу (см. § 15). Эта группа называется k-мерной гомотопической
группой пространства Е и обозначается символом лк (?").
*) Отметим, что данное нами определение операции сложения в {S ,Е } примени-
применимо и к случаю неодносвязного Е, но тогда эта операция может быть неоднозначной
(гомотопический класс отображения / v g, вообще говоря, зависит от выбора отобра-
отображения / v g на отрезке, соединяющем сферы).
303

Мы уже говорили, что множество {Sk, Sm} при к < т состоит из
единственного элемента (т.е. irk(Sm) = 0). Всякому гомотопическому
классу отображений сферы Sk в Sk отвечает целое число — степень отобра-
отображения (см. § 2), это соответствие представляет собой изоморфизм груп-
группы irk(Sk) и группы целых чисел Ж. (Доказательство того, что степень
суммы отображений равна сумме их степеней получается мгновен-
мгновенно из геометрического определения степени.) Отображение / прост-
пространства Е в пространство Е' порождает гомоморфизм /„ группы
пк(Е) в группу пк(Е'). а Всякому отображению g сферы S в Е
сопоставляется отображение fg сферы Sk в Е'. Если деформация
gt соединяет отображения g0 и g% , то деформация fgt соеди-
соединяет отображения fg0 и fgx, поэтому построенное соответствие определя-
определяет отображение /« множества ттк{Е) = { Sk, Е } в irk(E') - { Sk,E'}.
Из соотношения figVg') = (fg)V(fg') следует, что/, - гомоморфизм. Ў
Гомотопным отображением f0 и ft отвечают совпадающие гомоморфизмы:
(/о), = (Л)»- Композиции отображений отвечает композиция отвечающих
им гомоморфизмов:
(#)• = /А- A)
Отсюда вытекает, что гомотопические группы двух гомотопически экви-
эквивалентных пространств изоморфны друг другу. (Доказывается, это так же,
как аналогичный факт для групп гомологии; см. § 8.)
Отметим следующее полезное утверждение: eaiug - отображение сфе-
сферы Sk в себя, f - отображение Sk в Е, то
[fg \= (deg*)•¦[/] B)
(символы [/] и [fg ] обозначают элементы группы тгк(Е), отвечающие
соответственно отображениям f и fg, degg обозначает степень отображе-
отображения g). В самом деле, [fg ] = ft [ g ], а элемент [g] ? nk(Sk), отвечаю-
отвечающий отображению g, равен сумме degg экземпляров элемента группы
77fc(Sk), отвечающего тождественному отображению Sk на себя.
Заметим в заключение, что к данному выше определению сложения го-
гомотопических классов отображений сферы Sk можно прийти, рассматривая
отображения областей пространства IRfc+1. Рассмотрим в пространстве
k
множество U, ограниченное извне сферой Sk, а изнутри сферами Sk
и Sk (рис. 40). Пусть F — отображение множества U в односвязное прост-
пространство Е. Обозначим символом /0 (соответственно fx и /2) отображе-
отображение F, рассматриваемое только на сфере Sk (соответственно на сферах Sk
и Sk), гомотопические классы этих отображений будем обозначать симво-
символами [/oj, [fi], [/г]. Таким образом, [/0], [Л], [/а] можно рас-
рассматривать как элементы группы 7rfc (E). Мы покажем сейчас, что
[/о ] = [Л ] + [/а ]• C)
В самом деле, будем считать пространство R, участвующее в данном
выше определении суммы элементов множества{Sk, Е)= ггк{Е), вложен-
304

ным в U (см. рис. 41). Отображение F на R С U можно рассматривать как
отображение Л V /г, поскольку оно совпадает с /\ на S* и с /2 на S*.
Далее, заметим, что отображение а сферы S* на Л2, построенное в § 12,
гомотопно в U тождественному отображению S* на So- Это означает, что
существует такое непрерывное семейство at отображений сферы Sk в U,
что (*i совпадает с а, а а<) является тождественным отображением (мы
отождествляем сферы Sk и So). Построение деформации af ясно из
Рис.40
Рис.41
Рис.42
рис. 42. Для того чтобы доказать соотношение C) нам осталось заметить,
что семейство Fat отображений сферы Sk в Е соединяет отображения
Fao=/o hFo, = (/0V/i)o.
Соотношение C) допускает очевидные обобщения. Прежде всего, можно
перенести это соотношение на отображения множества U, ограниченного
извне сферой So, а изнутри сферами Sк,..., Sk. Если F - отображение мно-
множества U в односвязное пространство Е, то
[fo] = [ft]
D)
г^е \fi\ - гомотопический класс отображения F, рассматриваемого толь-
только на сфере Sk.
Пространство Е можно считать неодносвязным. В этом случае сумма
классов [/ij + ... + [/„] определена неоднозначно; соотношение D) озна-
означает, что [ /о ] является одним из возможных значений этой суммы.
Наконец, вместо множества U описанного выше типа, можно, конечно, рас-
рассматривать любое топологически эквивалентное ему множество.
Мы приходим к следующему общему выводу. Пусть U — замкнутая об-
область пространства Шл, внешняя граница которой топологически эквива-
эквивалентна сфере, а внутренняя граница состоит из нескольких множеств, топо-
топологически эквивалентных сфере, F — отображение множества U в произ-
произвольное пространство Е. Тогда гомотопический класс отображения F, рас-
рассматриваемого на внешней границе, равен сумме гомотопических классов
отображений, порождаемых отображением F на компонентах внутренней
границы.
305

§ 13. Отображения сферы в неодносвязиое пространство
Как мы уже говорили, для неодносвязного пространства Е данное выше
определение сложения элементов множества {Sk, E.} не является одно-
однозначным (оно зависит от выбора отображения / V g на отрезке 1С R).
Тем не менее рассмотрение многозначной операции сложения оказывается
полезным.
Нахождение множества { Sk, E. } при к > 2 и операции сложения в нем
для неодносвязного пространства может быть сведено к решению аналогич-
аналогичной задачи для односвязного пространства. Сведение, основано на следую-
следующей лемме.
Пусть р: Е -*¦ Е - отображение накрытия (см. § 4), / - отображение
связного односвязного пространства X в Е, переводящее точку х0 е X
в точку ео 6 Е. Тогда для точки ео G Е, накрывающей точку ео, найдется
одно и только одно отображение f пространства X в Е, переводящее х0
в е0 и накрывающее отображение f. (Термины " е0 накрывает е0",
"/ накрывает /" означают, что р(е0) =е0, p.f = f.)
Сформулированная только что лемма была доказана в § 4 для путей
(отображений отрезка). Построение накрывающего отображения в общем
случае сводится к случаю отрезка. В силу связности пространства X точку
х & X можно соединить путем x(t) с точкой ха. При отображении / этот
путь переходит в путь f(x(t)) в пространстве Е. Точку /(х), очевидно,
можно построить как конечную точку пути, начинающегося в е0 и накры-
накрывающего путь f(x(t)). Это построение приводит к результату, не зави-
зависящему от выбора пути x(t), поскольку конечная точка накрывающего
пути не меняется при деформации пути в пространстве Е. (В силу одно-
односвязности пространства X различные возможные пути x(t) принадлежат
к одному гомотопическому классу.) Лемма доказана.
Рассмотрим отображение р пространства Е в Е, являющееся главным на-
накрытием. Напомним, что для главного накрытия Е = E/G - пространство
орбит дискретной группы G, свободно действующей в Е, — отображение р
сопоставляет точке х ? Е ее орбиту, т.е. р(х) =р(х' )|если х' =xg, g.G G
(мы считаем, что G действует в Е справа). Докажем следующее ут-
утверждение.
Если пространство Е односвязно, то
{Sk,E) = {Sk,E}/G при к > 2. A)
(Действие группы G в Е очевидным образом порождает действие этой
группы в множестве { Sk, E), поэтому можно говорить о пространстве ор-
306

бит {S , E}/G этого действия. Равенство A) следует понимать как взаим-
взаимно однозначное соответствие между множествами.)
Для того чтобы доказать соотношение A), заметим прежде всего, что
отображению у сферы Sk в Е можно сопоставить отображение р<р сферы
Sk в Е; если отображение ip' получается из отображения у с помощью
преобразования g € G, то Pip'(x) =p>p(x). Отображение р порождает, та-
таким образом, отображение п множества {Sk, E.}/G в {Sk, E). Поскольку
всякое отображение Sk в Е при к > 2 в силу леммы накрывается отобра-
жением Sk в Е, образ этого отображения совпадает со всем множеством
{Sk, Е). Далее, если для двух отображений <р и у' сферы S* в Е отображе-
отображения pip и pip гомотопны, то, применяя лемму для случая X = Sk X /, мож-
можно для гомотопии между отображениями ptp ир^' найти накрывающую ее
гомотопию. Существование этой гомотопии позволяет установить, что
отображение ip гомотопно такому отображению ip", что р*р*(х) =ру"(х).
Отсюда следует, что ip"(x) = y'{x)g, где ? € G и, значит, гомотопические
классы отображений у и ip' получаются друг из друга с помощью преобра-
преобразования группы G. (Из соотношения р*р'(х) =р<р"(х) по определению ото-
отображения р следует, что tp"(x) = 4>'(x)g(x), g(x) € G. Однако в силу не-
непрерывности рассматриваемых нами отображений и дискретности груп-
группы G функция g(x) является константой: g(x) =g.) Это доказывает, что
построенное нами отображение множества {Skr E)/G на {Skf E) является
взаимно однозначным соответствием.
Применяя A) к случаю Е = S1, Е = U\X,G = 12, получаем ^(S1) = О
при к > 2.
Вычислим с помощью соотношения A) множество {Sk, RPk), где RPk
есть fc-мерное проективное пространство. Пространство RPk можно рас-
рассматривать как пространство орбит группы 72г, действующей на сфере Sk.
Единственное нетривиальное преобразование группы 27j является централь-
центральной симметрией, т.е. переводит точку х ? Sk в диаметрально противопо-
противоположную точку — х ? Sk. Пространство орбит группы 2F2 получается из Sk
с помощью отождествления диаметрально противоположных точек и,
следовательно, совпадает с RPk.
Действие группы 2?2 на Sk порождает действие этой группы на {Sk, Sk);
легко видеть, что нетривиальное преобразование группы Zj переводит ото-
отображение степени т в отображение степени (— 1)к+1т. (Это вытекает из
замечания, что степень центральной симметрии равна (—l)fc + 1.) Таким об-
образом, при к нечетном действие 72г ra{Sfc, Sk) тривиально; пространство
орбит lsk, Sk)/ ~2г отождествляется с { Sk, Sk} и, следовательно, соотно-
соотношение A) дает взаимнооднозначное соответствие между {Sk, RPk) и мно-
множеством целых чисел. При к четном нетривиальное преобразование груп-
группы ~2г переводит отображение Sk на Sk, имеющее степень т, в отображе-
307

ние степени — т; орбиту группы Щ в {Sk, Sk) = 77можно охарактеризо-
охарактеризовать с помощью целого неотрицательного числа. (Если т > 0, то орбита
состоит из двух чисел т и — т, если т = О, орбита состоит только из нуля.)
Таким образом, при четном к множество {Sk, RPk) можно отождествить
с множеством ^+ целых неотрицательных чисел. При к > 2 всякое отобра-
отображение Sk в RPk можно представить в виде ру, где ip - отображение Sk в
Sk, p — накрытие пространства RPk сферой Sк; при к нечетном отображе-
отображения ру>1 и Рфг гомотопны тогда и только тогда, когда степени отображений
ipi и 1/>2 совпадают, при к четном отображения ptpi и ру2 гомотопны при
условии | deg ^i I = I deg ip2 |.
Отметим, что в обоих множествах, фигурирующих в A), определена
многозначная операция сложения, а Существование такой операции
в {Sk, Е.) было отмечено в начале этого пункта. Сложение в {Sk, Е.}
порождает сложение в пространстве орбит {Sk, E.)/G: суммой а + /3 орбит
а и /3 объявляется орбита, содержащая сумму элементов, принадлежащих
соответственно орбитам а и /3. Орбита а + /3 зависит or выбора этих элемен-
элементов, поэтому определенная таким образом операция многозначна. Ў Легко
проверить, что построенное выше соответствие между множествами
{Sk,E) и {Sk, E.}/G согласовано с определенными в этих множествах
многозначными операциями.
Применяя это утверждение к случаю Е = RPk, мы видим, что при чет-
четном к множество {Sk, RI*k} можно отождествить с множеством 2?+ со
следующей операцией сложения: сумма чисел тЕ. 77+ и п ? 7?+ принимает
два значения m + п и | пг — п \. При нечетном к операция в {Sk, RPk)
однозначна и множество { Sk, RPk) с этой операцией изоморфно груп-
группе ~2.
Отметим, что соотношение A) в принципе применимо к вычислению
множества {Sk, E.) и операции сложения в этом множестве для любого,
неодносвязного пространства Е. (Нужно применить это соотношение
к универсальному накрытию, см. § 4.)
§ 14. Гомотопические труппы сфер
Задача о полном вычислении групп 77^E") до сих пор не решена. Однако
эти группы исследовались в многочисленных работах, и полученная в этих
работах информация с лихвой покрывает запросы физики.
Опишем, прежде всего, некоторые конструкции, позволяющие по одним
элементам гомотопических групп сфер строить другие.
В § 2 по каждому отображению / сферы Sm в S" было построено ото-
отображение Б/ сферы Sm+1 в S"+i (надстройка над отображением /).
Сопоставляя гомотопическому классу отображения / гомотопический
класс отображения Б/, мы получаем отображение группы itk(Sm) в груп-
Легко проверить, что это отображение является гомоморфизмом; этот
гомоморфизм называется гомоморфизмом надстройки и также обозначает-
308

ся символом Б. Доказывается, что гомоморфизм надстройки отображает
группу 77-fc(Sm) на всю группу Tfc + 1(Sm + l) при условии к < 2т — 1;
если к < 2 т — 2, то Б является изоморфизмом (теорема Фрейденталя).
По элементу a G nn(Sk) и элементу /3 е ^m (S71) построим элемент
а ° /3 ? 77т E*) как гомотопический класс отображения /# — композиции
отображений fug, принадлежащих соответственно гомотопическим клас-
классам а .и /3. Иначе говоря, а ° /3 = /,/3, где /6 а. Вспоминая, что Д - гомо-
гомоморфизм, видим, что
а о (C, + /32) = а о 01 + а о /32.
Мы уже отмечали, что 7rfcE") = 0 при к < п , 7rfcE") = ~Z, ^(S1) = О
при к > 2. Остановимся подробнее на группах ТзE2), тг4E3), гг4E2).
Приведем, прежде всего, пример негомотопного нулю отображения сферы
S3 в S2 (т.е. отображения, которое нельзя стянуть в точку). Будем считать,
что сфера S3 задана уравнением |zil2 + |z2|2 = l, где zltz2 - ком-
комплексные числа. Сопоставим точке (г1гг2) G S3 комплексное число
z = z I /z2. При этом мы получаем отображение сферы 53 на множество
комплексных чисел, к которому присоединена бесконечно удаленная точка
(точкам сферы, для которых z2 = 0, сопоставляется бесконечно удаленная
точка). Вспоминая, что множество комплексных чисел с присоединенной
к нему бесконечно удаленной точкой можно рассматривать как сферу S2,
видим, что построенное нами отображение h является непрерывным (даже
гладким) отображением S3 в 52. Отображение h называется отображением
Хопфа. Мы докажем впоследствии (§ 17), что гомоморфизм /г, группы
7rfcE3) в 7rfcE2), порождаемый отображением Хопфа h, является изомор-
изоморфизмом при к > 3. Отсюда следует, в частности, что группа rr3(S2) изо-
изоморфна группе я3E3) и, значит, изоморфна группе целых чисел Z7. Иными
словами, каждому отображению / сферы S3 в S2 можно сопоставить
целое число, зависящее только от гомотопического класса этого отображе-
отображения, — инвариант Хопфа отображения /. Два отображения S3 в S2 гомо-
гомотопны тогда и только тогда, когда их инварианты Хопфа совпадают. Инва-
Инвариант Хопфа отображения h равен 1, и, значит h негомотопно нулю.
Займемся теперь отображениями сферы S44 в S3 и в S2. Можно доказать,
что все негомотопные нулю отображения S4 в S3 гомотопны друг другу.
Иными словами, группа n4(S3) состоит всего из двух элементов, т.е. изо-
изоморфна 2?2. Примером негомотопного нулю отображения сферы 54 в S3
может служить надстройка 2 h над хопфовским отображением h сферы
S3 в S2. (По теореме Фрейденталя гомоморфизм 2 отображает 773(S2)
на 7г4E'3). Ядром этого гомоморфизма служит подгруппа, состоящая из
элементов, имеющих четный инвариант Хопфа.)
Группа тт4E2) изоморфна группе 7T4(S3), и, следовательно, изоморфна
Zj; изоморфизм между группами я4E2) и 774(S3) осуществляется ото-
отображением ht. Это следует из уже упоминавшихся результатов § 17.
Примером отображения, относящегося к единственному ненулевому гомо-
гомотопическому классу, может служить отображение h о Б И.
309

Все гомотопические группы пт (S*) за исключением групп irm Em) и
n4ra-i (S2m) состоят из конечного числа элементов. Группа я4m_i (S2m)
является прямой суммой группы 71 и конечной группы (как говорилось
выше, 77m(Sm) =У).
§ 15. Гомотопические группы произвольных пространств
В § 12 было показано, что, в случае если пространство Е связно и одно-
связно, в множестве гомотопических классов {Sk, E.) можно определить
операцию сложения. Было отмечено, что введение этой операции превра-
превращает множество { Sk, E.) в абелеву группу, которая называется гомотопиче-
гомотопической группой пространства Е и обозначается 77> (Е).
В настоящем параграфе мы определим гомотопические группы в более
общей ситуации, докажем некоторые свойства этих групп и выясним, как
связаны гомотопическая группа тт^(?") и множество {Sk, Е)ъ случае,если
пространство Е неодносвязно.
Рассмотрим пространство Е, в котором фиксирована точка е0. Будем
называть к-мерным сфероидом отображение сферы Sk в Е, при котором
южный полюс сферы переходит в точку е0. Два сфероида /0 и fx назы-
называются гомотопными (/о ~ /i)> если один из них можно непрерывно про-
деформировать в другой, т.е. существует семейство сфероидов ft, непре-
непрерывно зависящее от параметра t @ < / < 1) и соединяющее сфероиды /0
и fx. (Может случиться, что существует непрерывное семейство ft отобра-
отображенной сферы Sk в Е, соединяющее отображения /0 и fx, но это семейст-
семейство нельзя подобрать таким образом, чтобы при каждом t южный полюс
сферы переходил в е0. Тогда /0 и fx гомотопны как отображения сфер,
но негомотопны как сфероиды.) Если /0 ~ fx, то fx~ /о. если /0 ~ /ь
fx ~ /г, то /о ~ f2> поэтому множество всех сфероидов разбивается на
классы гомотопных друг другу сфероидов (гомотопические классы).
Множество всех гомотопических классов Л-мерных сфероидов в простран-
пространстве Е будем обозначать символом Як{Е, е0). Нульмерная сфера S0 со-
состоит из двух точек, которые мы будем называть южным и северным
полюсами. По определению сфероида южный полюс отображается в точ-
точку е0, поэтому нульмерный сфероид определяется той точкой пространст-
пространства, в которую переходит северный полюс. Два нульмерных сфероида
гомотопны между собой, если соответствующие им точки можно соединить
непрерывной кривой (путем) в пространстве Е (т.е. эти точки принадлежат
одной компоненте связности пространства Е). Таким образом, число эле-
элементов множества ло(Е, е0) равно числу компонент пространства Е.
Гомотопическое множество Лк(Е,ео) можно превратить в группу при
к > 1. Эта группа называется к-мерной гомотопической группой и обозна-
обозначается тем же символом. Определение операции в множестве iik(E, ео)
удобно сформулировать, несколько модифицировав данное выше определе-
определение сфероида. Именно мы будем понимать под ^-мерным сфероидом ото-
отображение единичного ^-мерного куба 1к в пространство Ё, при котором вся
граница куба 1к переходит в точку е0. (Мы считаем, как всегда, что куб/*
310

выделяется неравенствами 0 <= х1 < 1, ..., О <** < 1.) Легко построить
взаимно однозначное соответствие между сфероидами в новом и старом
смыслах, воспользовавшись тем, что сферу можно получить из куба,
отождествляя между собой все точки, принадлежащие границе куба.
В самом деле, фиксируем отображение а куба /* на сферу Sk, при котором
вся граница куба переходит в южный полюс сферы, а внутренность куба
топологически отображается на сферу, из которой выколот южный полюс.
Если / — отображение сферы Sk в Е, при котором южный полюс переходит
в точку-е0 (сфероид в старом смысле слова), то композиция /а отображе-
отображений / и а будет сфероидом в новом смысле слова. Построенное соответ-
соответствие взаимно однозначно, и мы можем поэтому пользоваться в случае
необходимости новым определением сфероида.
Определим операцию в множестве лк(Е, <?0), считая, для определенно-
определенности, что к = 2. Куб 1к при к = 2 представляет собой квадрат. Если заданы
два сфероида / и g, то их сум. " / + g определим как такое отображение
квадрата, которое на левой половине квадрата совпадает с отображением /,
а на правой половине - с отображением g. (Точнее говоря, для того чтобы
определить сфероид / + g на левой половине квадрата, мы аффинно ото-
отображаем левую половину квадрата на весь квадрат и затем применяем
отображение /; отображение / + g на правой половине квадрата получает-
получается аналогичным образом с помощью отображения g.) Более формально
ртображение И = f + g определяется соотношениями
И(х\хг) = /(г*1,*2) при (Хх1 < 1/2, 0 < х2 < 1,
h(xl, х2) = gBxl -1, jc2) при 1/2 ^х1 <1, 0 <*2< 1.
Легко проверить, что из / ~ /', g ~ g', следует / + g ~ /' + g\ поэтому
бписанное только что сложение сфероидов позволяет определить сложение
гомотопических классов. Нетрудно убедиться, что сложение гомотопичес-
гомотопических классов ассоциативно. Гомотопический класс тривиального отобра-
отображения /о (т.е. отображения, при котором весь квадрат /2 отображается в
точку ео) является нулевым элементом, поскольку для всякого сфероида /-
сфероид / + /о<гомотопен сфероиду /. Для элемента ч> € л2 (Е, е0) сущест-
существует противоположный элемент. (Если по сфероиду / построить сфероид g
соотношением ?(х\ х2) =/A — х1, х2), то сфероид f + g гомотопен три-
тривиальному. Поэтому гомотопические классы сфероидов / и g в сумме
дают нуль.) Мы видим, что операция сложения в множестве л2 (Е, е0) пре-
превращает это множество в группу. Совершенно аналогичные соображения
позволяют определить операцию в множество ^(i1, ео) при к > 1 и дока-
доказать, что это множество является группой относительно введенной опера-
операции. При к > 2 группа лк(Е, е0) коммутативна. Проведем доказательство
для случая к = 2 (в общем случае доказательство совершенно аналогично).
Для доказательства необходимо проверить, что сфероид f + g гомотопен
сфероиду g + /. Последовательные этапы деформации, переводящей f + g
в g +/, показаны на рис. 43 На этом рисунке заштрихованные части квадра-
квадрата отображаются в точку ео, те части квадрата, на которых написана буква
/ или g.нужно аффинно отобразить на единичный квадрат и затем этот
квадрат отобразить в Е соответственно с помощью отображения / или g.
311

a
f
9
1
1
f
И
f
3
jj
а
ш
ш
f
1
f
ш
f
а
ш
a
и
ц
f
I
a
f
I
f
9
Рис. 43
Группа п-ц (Е> eo) не обязана быть коммутативной; эта группа носит назва-
название фундаментальной группы пространства Е. Она изучена в § 3. Операцию
в группе 7Ti (E, ео) принято называть умножением, в соответствии с этим
для одномерных сфероидов (замкнутых путей) вместо термина "сумма
сфероидов" употребляется термин "произведение". Однако в случае, когда
одновременно рассматриваются группы разных размерностей, удобно
сохранить термин "сложение" и для операции в 7Гх (Е, е0).
Если пространство Е связно, то группы ;rfc{Е, ео) и п^(Е, е^) изоморф-
изоморфны между собой. Для того чтобы построить изоморфизм этих групп, рас-
рассмотрим путь а, ведущий из точки е0 в точку ej (непрерывное отображе-
отображение отрезка, при котором начало переходит в е0, а конец в е\). Как и рань-
раньше, для простоты будем ограничиваться случаем к = 2. Рассмотрим элемент
<р 6 Яг (Е, Cj) и отображение / квадрата /2 в Е, принадлежащее классу i/>.
Выделим в единичном квадрате /2 меньший квадрат и построим' отобра-
отображение g квадрата /2. Для этого будем считать, что меньший квадрат ото-
отображается с помощью сфероида /, а оставшуюся часть квадрата разобьем
на отрезки так, как показано на рис. 44, и каждый отрезок отобразим с
помощью отображения а.При отображении g вся граница квадрата 1г
переходит в е0, поэтому g определяет элемент группы п2 (Е, е0); этот
элемент обозначим символом aip.
а При более формальном построении элемента а^ удобно, пользуясь
топологической эквивалентностью квадрата и круга, представлять сфероид
/ из гомотопического класса ip как отображение круга (х1 J + (д:2J <¦ 1,
переводящее окружность в ех. Тогда можно определить щ как гомото-
гомотопический класс сфероида g, определенного соотношениями g(xl, x1) =
= fBx\ 2x2) npnr<ll2,g(xl,x2) =аB - 2г) при г > 1/2,г2 = (х1J +
+ (х2J. Ў Легко проверить, что построенное нами отображение а группы
TijciE, ex) в як(Е, е0) является гомоморфизмом. Этот гомоморфизм не
меняется при непрерывной деформации пути а. Рассмотрев путь j3, ве-
312

дущий из d в е0, мы можем построить отображение 0 группы Жк{Е, е0) в
пк(Е, ei). Если путь/3 представляет собой путь а, пройденный в обратном
направлении, тоа-0=1,/3-а=1. (Это можно доказать, заметив, что, про-
проходя сначала путь а, а затем путь /3, мы получим замкнутый путь а • j3, го-
гомотопный нулю. Отсюда следует, что а • |3 = а • /3 = 1. Аналогично j3 • а = 1.)
Это показывает, что 5 является изоморфизмом групп пк (Е, ео) и тгк (Е, е\).
Рис.44
В случае если е0 = е\, путь а можно представлять себе как одномерный
сфероид; этот сфероид порождает автоморфизм а группы пк(Е, е0). Авто-
Автоморфизм а зависит только от гомотопического класса замкнутого пути
а. Замечая, что а ¦ /3 = а ¦ 0, заключаем, что группа тг, {Е, е0) действует на
группе лк(Е, е0). (Каждому элементу группы nt (E, е0) отвечает автомор-
автоморфизм группы лк(Е, e0), произведению элементов n-j (E, е0) соответствует
произведение автоморфизмов.)
Исследуем теперь связь между множеством { Sk,E ) и группой
1Гк(Е, ео)¦ Рассматривая сфероид как отображение сферы Sk и замечая, что
гомотопные сфероиды представляют собой гомотопные отображения сфе-
сферы, видим, что существует естественное отображение группы тгк(Е, е0)
в множество { S , Е). Если пространство Е связно, то это отображение
является отображением на все множество { Sk, Е}. Для того чтобы прове-
проверить это утверждение, заметим, что для любого пути а и сфероида/ сферои-
сфероиды f и af можно рассматривать как гомотопные отображения сферы; гомо-
топия между / и af задается формулой ft = atf, где путь at представляет
собой часть пути а, соединяющую точки а@) и а (Г) (более формально
можно определить at соотношением ctt(r) =аG,т),0<т<1). Отметим,
что, в случае если путь а не замкнут, нельзя даже ставить вопрос о гомотоп-
гомотопности / и af, если f и af рассматриваются как сфероиды (а не как отобра-
отображения сфер).
Если путь а замкнут, то может случиться, что сфероиды f и af не гомо-
гомотопны; однако отвечающие им отображения сферы всегда гомотопны. Как
мы говорили выше, группа ttj (Е, е0) действует в группе ^(Е, е0); из
сказанного только что следует, что два элемента группы ттл (Е, е0), принад-
принадлежащие одной и той же орбите группы 7г! (Е, е0), определяют один и тот
же элемент множества {S , Е). Таким образом, существует отображение
множества орбит пк (Е, ео)Ы\ (JE, е0) на множество {Sk, E). Можно про-
проверить, что это отображение взаимно однозначно. В частном случае, когда
пространство Е односвяэно (группа 7Ti (E, е0) тривиальна), мы получаем
взаимно однозначное соответствие между тгк(Е, е0) и {Sk, E). Таким об-
313

разом, в этом важном случае мы можем считать, что в {5*, Е) есть груп-
групповая операция и отождествлять { Sk, E}c Л-мерной гомотопической груп-
группой. Такое отождествление можно произвести также в случае, если Е —
связная топологическая группа.
Напомним, что в § 12 для связного односвязного пространства Е в мно-
множестве { Sk, E } была введена операция сложения. Без труда проверяется,
что соответствие между 77> (Е, eo)vi{Slc,E) согласовано с операциями сложе-
сложения в этих двух множествах. Это позволяет утверждать, что группу пк (Е),
определенную в § 12 для связного односвязного пространства Е, можно
отождествить с группой лк(Е, е0). В случае к = 1 построенное выше дейст-
действие группы 771 (Е, е0) на лк(Е, е0) может быть определено формулой
Мы видим,что преобразования,отвечающие элементам ttj (E, во), являются
внутренними автоморфизмами группы tti (Е, е0) и, стало быть, орбитами
рассматриваемого действия являются классы сопряженных элементов
группы 7Ti (Е, е0). Если группа ni(E, e0) коммутативна, то каждая из
орбит состоит из единс!венного элемента, и, следовательно, можно
отождествить П\ (Е, е0) с множеством {S1, Е}.
В дальнейшем в случаях, когда это не может привести к путанице, мы
будем писать ттк (Е) вместо лк (Е, е0).
Отметим, что построенное выше взаимно однозначное соответствие
между множествами лк(Е, eo)jrri (E, е0) и {Sk,E} позволяет свести вы-
вычисление множества [Sk, Е) для неодносвязного пространства Е к анало-
аналогичной задаче для односвязного накрытия Е пространства Е. В самом деле,
если точка ео накрывает точку ео, то гомоморфизм р,, порождаемый
отображением накрытия р, является изоморфным отображением группы
¦пкф, е0) на пк(Е, е0) при к > 2 (см. § 17). Замечая, что ггк(Ё, ео) =
= {Sk, E), мы можем отождествить {Sk,E}/ffi (Е, е0) и {Sk, E). В дру-
других терминах это утверждение доказано в § 13. (Если Е — односвязное
главное накрытие E = E/G, то группа G изоморфна ni(E, ео); см. § 4.)
Остановимся на связи между гомотопическими группами и группами
гомологии. Всякий Л-мерный сфероид можно рассматривать как Л-мерный
цикл. Если два сфероида гомотопны, то отвечающие им циклы гомологич-
гомологичны, поскольку при деформации сфероид заметает поверхность, граница
которой состоит из циклов, отвечающих рассматриваемым сфероидам.
(Более формально можно определить класс гомологии, отвечающий сфе-
сфероиду /, как образ фундаментального класса гомологии сферы SK при
гомоморфизме/,. Если сфероиды fug гомотопны, то /. = g,, поэтому два
гомотопных сфероида определяют один и тот же класс гомологии.) Мы
построили, таким образом, отображение ттк(Е, е0) в Нк(Е, 2"). Легко про-
проверить, что это отображение является гомоморфизмом. Имеет место сле-
следующая теорема, принадлежащая Гуревичу.
Если пространство Е асферично в размерностях < к (т.е. п1 (Е, е0) =
= 0 при i < к) и к> 2, то гомоморфизм группы пк (Е) в группу Нк (Е, 2?)
является изоморфизмом этих групп.
Мы не будем приводить доказательство теоремы Гуревича.
314

§ 16. Расслоенные пространства
Рассмотрим отображение р пространства Е на пространство В. Простран-
Пространство Е разбивается на непересекающиеся множества - прообразы точек
пространства В. (Напомним, что под прообразом (точнее, полным про-
прообразом) точки Ъ G В понимается совокупность всех точек, которые.пере-
которые.переходят в Ъ при отображении р.) Прообраз точки Ъ мы будем обозначать сим-
символом р (Ь) или Fb. Будем говорить, что отображение р пространства Е
на В определяет расслоение, если прообразы всех точек b GBтопологичес-
GBтопологически эквивалентны между собой. Множество Fb = р (Ь) называется слоем
над точкой Ъ. Пространство В называется базой расслоения, Е - пространст-
пространством расслоения, а отображение р - проекцией расслоения. Если слои рас-
расслоения топологически эквивалентны пространству F, то F называется ти-
типичным слоем расслоения или, короче, слоем расслоения. Расслоение с
пространством Е, базой В, типичным слоем F и проекцией р обозначается
(Е, В, F, р) или просто (Е, В, F).
Начнем с простейших примеров. Рассмотрим ортогональную проекцию
прямого кругового цилиндра на основание. Эта проекция определяет рас-
расслоение; базой этого расслоения является круг, а слои топологически экви-
эквивалентны отрезку. Это же отображение, рассматриваемое на боковой по-
поверхности цилиндра, порождает расслоение, базой которого является
окружность (рис.45).
Лист Мёбиуса естественно отображается на окружность, которую удоб-
удобно представлять себе как среднюю линию листа Мёбиуса. Это отображение
определяет расслоение, у которого база топологически эквивалентна
окружности, а слой — отрезку (рис. 46).
Рассмотрим подмногообразие ?1 размерности k в пространстве К" (мож-
(можно считать, что ?2 — поверхность, не имеющая особых точек). Определим
Рис.45
Рис.46
пространство Г(П) как множество всех векторов, касающихся поверх-
поверхности $2 в какой-либо из ее точек. Каждому вектору е G Т(?1) сопоста-
сопоставим точку многообразия J2, в которой этот вектор касается ?1. Построен-
Построенное отображение пространства Г(П) на О. обозначим символом р; это
отображение порождает расслоение, слоем которого служит множество
векторов, касающихся данного подмногообразия в фиксированной точ-
точке. Таким образом, типичным слоем является пространство IR*. Описан-
Описанное расслоение называется касательным расслоением подмногообразия Л
(точнее, векторным касательным расслоением). Его можно модифициро-
315

вать, рассмотрев не все касательные векторы, а только касательные векто-
векторы, имеющие единичную длину (тогда слой топологически эквивалентен
сфере Sk~1) или только ненулевые касательные векторы (тогда слой то-
топологически эквивалентен пространству IR*, из которого выколото начало
координат).
Заменив в определении касательного расслоения пространство
пространством N(?1) векторов, ортогональных к ?2, получим определение
нормального расслоения подмногообразия ?1. Слой нормального расслое-
расслоения топологически эквивалентен \R"~k (или сфере S"~k~1, если ограни-
ограничиться нормальными векторами единичной длины.)
а Нормапьное расслоение компактного подмногообразия ?1 можно опи-
описать также следующим образом. Рассмотрим трубчатую окрестность Ue
многообразия О, (см. § 5). Напомним, что для всякой точки х G Ue су-
существует одна и только одна ближайшая к ней точка а (х) многообразия
?1; все точки окрестности Ue, ближайшие к т< чке у??1, могут быть одно-
однозначно записаны в виде у + т), где т? — вектор, нормальный к О, в точке у
и имеющий длину < е. Мы видим, что отображение а окрестности Ue на
О, представляет собой расслоение, слоем которого является открытый
(п - к)-мерный шар. Множество Ue можно отождествить с подмножест-
подмножеством пространства N(€1) (точке х G Ue сопоставляется нормальный век-
вектор х — а(х) в точке а(х) 6 ?2); отображение а переходит при этом
отождествлении в проекцию нормального расслоения. Отображение а, рас-
рассматриваемое на множестве Vs точек, удаленных от О, на расстояние 5,
где 5 — фиксированное число, удовлетворяющее условию 0 < 5 < е, являет-
является расслоением со слоем S"~k~l, это отображение отождествляется с
нормальным расслоением со слоем S"~lc~1. (Отметим, что Kg можно рас-
рассматривать как границу трубчатой окрестности Us.)v
Ради наглядности мы определили выше касательное расслоение только
для подмногообразия пространства ?R". Можно определить касательное
расслоение для произвольного гладкого и-мерного многообразия М. В
этом случае Т{М) состоит из всех векторов в М. Слой касательного рас-
расслоения над точкой у G М определяется как множество всех векторов
в точке у. Поскольку в фиксированной локальной системе координат век-
вектор А задается п числами (А1. . . . , А"), типичным слоем служит [R".
Аналогичным образом строится кокасательное расслоение гладкого много-
многообразия М; пространство Т* (М) этого расслоения состоит из всех ковек-
торов в М.
Отметим, что пространства Т(М) и Т*(М) естественно возникают в фи-
физике: функцию Лагранжа L (q, <7)системы с конфигурационным пространст-
пространством М следует рассматривать как функцию на Т(М); в случае если функ-
функция Лагранжа не вырождена, соответствующую функцию Гамильтона
Hip, q) следует рассматривать как функцию на Т*(М). (Обобщенные ско-
скорости q 'образуют вектор, а обобщенные импульсы р,- = bL/dq' — ковек-
тор. Если функция Лагранжа вырождена, то ковектор pt не произволен
и, значит, функция Гамильтона задана лишь на части многообразия Т* (М).)
Проекция pi прямого произведения В X F на первый сомножитель по-
порождает расслоение с базой В и слоем F. (Напомним, что прямое произве-
произведение В X F определяется как совокупность пар (b,f), где Ъ G В, f G F;
316

проекция pi сопоставляет точке (b, f) G В X F точку b G В.) Расслоение
(E, В, F, p) называется тривиальным, если оно эквивалентно прямому
произведению т.е. существует топологическое отображение X простран-
пространства Е на В X F, при котором слой над точкой Ь&Вв расслоении(Е, В, F, р)
переходит в слой над той же точкой в расслоении (BXF,B, F,px). (Иначе
говоря, отображение X должно удовлетворять условию р, X =р). Отображе-
Отображение X называется тривиализацией расслоения.
Расслоение (Е, В, F, р) называется локально тривиальным, если у каж-
каждой точки базы найдется окрестность, над которой это расслоение тривиаль-
тривиально. (Иными словами, для каждой точки b G В можно найти такую окрест-
окрестность U, что существует топологическое отображение Ху множества р'1 (U)
на U X F, удовлетворяющее условию PiXy = р.) Практически все встре-
встречающиеся в физике расслоения являются локально тривиальными. В даль-
дальнейшем мы обычно не будем проверять локальную тривиальность рассмат-
рассматриваемых нами расслоений, хотя это необходимо было бы делать, посколь-
поскольку локальная тривиальность существенна при построении содержательной
теории расслоений и в дальнейшем всегда предполагается.
Если для каждой точки b & В в слое Fb, лежащем над Ь, выбрана точка,
непрерывно зависящая от Ь, то говорят, что задано сечение расслоения
(Е, В, F, р). Точнее, под сечением понимается непрерывное отображение q
базы В в пространство расслоения Е, удовлетворяющее условию pq (b) = b.
Образ базы В при отображении q представляет собой подмножество прост-
пространства Е, пересекающее каждый слой ровно в одной точке; геометричес-
геометрически удобно представлять себе сечение как это подмножество.
Сечения тривиального расслоения находятся во взаимно однозначном
соответствии с непрерывными отображениями базы в слой. В самом деле,
если ip — непрерывное отображение В в F, то отображение q, переводящее
точку 6?Вв пару (Ь, <p(b)) G В XF, можно-рассматривать как сечение
расслоения (В X F, В, F, рО; всякое сечение может быть получено с по-
помощью этой конструкции.
Если В — окружность S1 ,F - отрезок /-, то прямое произведение S1 X /
можно представлять себе как боковую поверхность цилиндра; сечение
тривиального расслоения (S1 X /.51,/ , pt) геометрически представляется
как непрерывная кривая, пересекающая каждую из образующих цилиндра
ровно один раз.
Среднюю линию листа Мёбиуса можно рассматривать как сечение описан-
описанного выше расслоения, пространством которого является лист Мёбиуса,
базой — окружность S1, слоем — отрезок / . Отметим, что это расслоение
имеет сечение, хотя и не является тривиальным.
Сечение векторного касательного расслоения многообразия М представ-
представляет собой касательное векторное поле на Л/. Если модифицировать опреде-
определение касательного расслоения, рассматривая только ненулевые векторы,
то сечением будет ненулевое касательное векторное поле на М. Заметим,
что на сфере S2 всякое касательное векторное поле обращается в 0 хотя бы
в одной точке сферы ("теоремао еже"); это означает, что у модифицирован-
модифицированного описанным выше способом касательного расслоения к. сфере нет ни
одного сечения.
Можно доказать, что сечение существует у всякого расслоения, слой
которого стягиваем. Более того, если база Л-мерна, то сечение существует у
317

всякого расслоения, слой которого асферичен в размерностях < к (см. § 18).
Эти утверждения часто позволяют получить важную информацию.
Покажем, например, что на любом гладком многообразии М можно
ввести риманову метрику. Для этого рассмотрим расслоение, базой кото-
которого является М, а слоем над точкой х G М служит множество положитель-
положительно определенных симметричных тензоров ранга 2 в точке х. Риманову
метрику на М можно интерпретировать как сечение этого расслоения.(Для
того чтобы задать риманову метрику, нужно в каждой точке М задать
положительно определенный симметричный тензор ранга 2.) Слой рассмат-
рассматриваемого расслоения стягиваем, поскольку этот слой можно рассматри-
рассматривать как выпуклое множество в линейном пространстве всех тензоров
ранга 2. Отсюда следует, что сечение всегда существует. Это доказывает
существование метрического тензора, непрерывно зависящего от точки
многообразия. (Этот тензор можно аппроксимировать тензором, гладко
зависящим от точки, и получить в результате бесконечно дифференци-
дифференцируемую риманову метрику на М.)
Всякое расслоение, база которого стягиваема (например, топологически
эквивалентна шару), имеет сечение. (Доказательство см. в § 18.) Более
того, всякое такое расслоение эквивалентно тривиальному.
Отметим, что всякое локально тривиальное расслоение можно склеить из
тривиальных расслоений. В самом деле, рассмотрим покрытие базы В рас-
расслоения (Е, В, F, р) открытыми множествами Ut.... Lfc, над каждым
из которых расслоение тривиально. Для каждого из множеств Ut выберем
топологическое отображение \ множества UtXF нар~1(С/<) .переводящее
слой Ъ X F тривиального расслоения в слой расслоения (Е, В, F, р) над точ-
точкой Ы Если Ъ GUj П Uj , то на Ъ X F определены как отображение \ , так
и отображение X/. Построим для каждого bGU{ О U/ топологическое
отображение у,. ~ слоя F на себя, потребовав, чтобы точка А;- (р, /)
совпадала с точкой X,- (^.7(/,/>/)• (Иначе можно сказать, что -у* =
= (\ ) ^у > гДе fy - это отображение Xt рассматриваемое на слое b X F.)
Легко проверить, что
ь _ ь ь
yU, /)• 7(i,fc) V,/) ' ¦ W
если b&Ui C\UkC\Uj. Очевидно, что пространство Е можно склеить из
прямых произведений Ut X F, отождествляя точку (Ь, /) ? Ц X F с точкой
ф, f.')^Ut X F, если/= 7Ь(/,/) /, b СЦ П Ц . Далее, по любому
семейству отображений 7*(*,/) .удовлетворяющих условию A), можно
построить локально тривиальное расслоение, склеивая произведения Uf X F
между собой по описанному выше закону.
Мы говорили выше, что сечения тривиального расслоения находятся во
взаимно однозначном соответствии с функциями на базе, принимающими
значение в слое. Отсюда следует, что сечение локально тривиального рас-
расслоения можно интерпретировать как набор функций qt , определенных
на множествах Ut , принимающих значение в слое F и подчиненных усло-
условию согласования
Я,(Ь)=у*и)Я{(Ь). B)
318

Рассмотрим в качестве примера касательное расслоение многообразия М,
Если в области Ц С М введены локальные координаты (х1, ..., х"),
то касательный вектор определяется в этих координатах с помощью п
чисел (в1, ..., а"). Это означает, что над Щ касательное расслоение
эквивалентно тривиальному. Закон преобразования векторов из
одной координатной системы в другую определяет правила склеивания
прямых произведений Щ X1R" (иными словами, отображение yft ^
пространства IR" на себя состоит в умножении на якобиевую матрицу пере-
перехода от одних координат к другим в точке Ь).. Для того чтобы задать
сечение касательного векторного расслоения (векторное поле), нужно
задать его в каждой локальной системе координат и подчинить условиям
согласования там, где имеют смысл сразу две системы координат.
Если пространство Е разбито на непересекающиеся подмножества, каж-
каждое из которых топологически эквивалентно фиксированному пространст-
пространству F, то можно построить расслоение с пространством?"и типичным слоем F,
Базой этого расслоения является пространство В, получающееся из Е,
если отождествить между собой точки, принадлежащие одному и тому же
подмножеству рассматриваемого семейства. (Напомним, что существует
естественное отображение Е на В; это отображение является проекцией
рассматриваемого расслоения).
Пусть, например, в пространстве Е действует топологическая группа G.
Тогда Е разбивается на непересекающиеся множества — орбиты группы G.
Если е G Е, то можно построить непрерывное отображение а группы G на
орбиту точки е, положив a(g) = <pg(e) • Мы обозначаем через ^преобра-
^преобразование пространства Е, отвечающее элементу g & G), Напомним, что
группа G действует на Е, если каждому g e G сопоставлено преобразова-
преобразование <pg пространства Е, так что tpg gi = *Pgi*Pg1 (группа действует слева) или
^i Щг = ^s-i У%\ (гРУппа действует справа). Орбитой точки е называется
множество точек вида <^(е), g?G. Стационарной подгруппой Не точки е
называется множество элементов группы g, оставляющих на месте точку е
(т.е. g?He, если ^(е) =ё). В случае если стационарная подгруппа точки
тривиальна, отображение а является взаимно однозначным. Если, кроме
того, группа G компактна, то отображение а является топологическим.
Мы убеждаемся, что в случае, когда компактная группа G действует на Е
таким образом, что все стационарные подгруппы тривиальны, можно
утверждать, что все орбиты топологически эквивалентны группе G. Этот
же факт имеет место в большинстве интересных для физики случаев так-
также при отказе от условия компактности группы G. Мы видим, что разбие-
разбиение пространства Е на орбиты в рассматриваемой ситуации является рас-
расслоением; расслоения, полученные с помощью этой конструкции, назы-
называются главными.
В проведенных выше рассуждениях можно было с равным успехом
считать, что группа G действует на Е слева или справа; однако, изучая
главные расслоения, удобнее предполагать, что группа G действует на Е
справа. Таким образом, мы считаем, что каждой точке е G Е и элементу
g?G сопоставлена точка egGE; тривиальность стационарных подгрупп
означает, что eg?=e для любых ef±E, g?*l. (Если все стационарные под-
подгруппы тривиальны, то говорят, что группа G действует на Е свободно.)
319

Легко видеть, что главное расслоение, у которого есть сечение, три-
тривиально. В самом деле, если отображение q базы В в Е является сечением
главного расслоения (Е, В, G, р),то можно построить отображение X прямо-
прямого произведения В X G на пространство Е, полагая Х(Ь,?) = q(b)g; это
отображение порождает эквивалентность тривиального расслоения
(В X G,B, G, pi) и расслоения {Е, В, G, р).
Если стационарная подгруппа Не точки е G Е нетривиальна, то су-
существует непрерывное взаимно однозначное отображение /3 факторпрост-
ранства GjHe на орбиту точки е (см. § А6). В случае когда G/He компакт-
компактно, отображение /5 является топологическим. Это же верно во всех инте-
интересных для нас случаях и без предположения компактности G/He. Мы
будем предполагать поэтому, что орбиты топологически эквивалентны
факторпространствам G/He. Если все подгруппы Не сопряжены друг дру-
другу, то все пространства G/H€ топологически эквивалентны; в силу сде-
сделанного выше предположения это же справедливо для всех орбит группы G.
Таким образом, в исследуемой ситуации разбиение пространства Е на орби-
орбиты порождает расслоение.
Рассмотрим, например, действие подгруппы Я на группе G. (Ради опреде-
определенности будем считать, что Н действует на G справа, т.е. yh (g) =gh для
h EH, g e G.) Тогда все стационарные подгруппы тривиальны и разбиение
группы G на орбиты группы Н (правые смежные классы) является рас-
расслоением с пространством G, слоем 7/и базой G/H.
Если группа G транзитивно действует на пространстве Е (т.е.Е — одно-
однородное многообразие), то можно построить отображение а группы G на Е,
сопоставив элементу g G G точку *ря(е0), где е0 - фиксированная точка
пространства Е. Прообразы точек пространства Е при отображении а топо-
топологически эквивалентны стационарной подгруппе Не<1. Отображение а можно
рассматривать, таким образом, как расслоение с пространством G, слоем
Не и базой Е. Это расслоение, по существу, совпадает с построенным вы-
выше расслоением группы G на правые смежные классы подгруппы HeQ
(см. § А 6).
Приведем некоторые конкретные реализации описанных выше общих
конструкций.
Рассмотрим многообразие Vnk, точками которого являются ортонорми-
рованные системы из к векторов в и-мерном евклидовом пространстве IB".
Группа О (и), действующая в пространстве IB", переводит ортонормиро-
ванную систему векторов снова в ортонормированную систему. Поэтому
можно рассматривать группу О (и) как группу преобразований много-
многообразия Vnk.
Любую ортонормированную систему из к векторов можно перевести
в любую другую такую систему с помощью ортогонального преобразо-
преобразования. Это означает, что группа О (и) действует на Vnk транзитивно. Ста-
Стационарные подгруппы группы О (и), действующие в Vn%k, изоморфны
О(п-к). (Если (ег,..., ек) е Vn^k, то можно дополнить систему
векторов et,..., ек до ортонормированного базиса еи...,ек,ек + 1,...,е„ в IB".
Ортогональное преобразование, переводящее систему векторов ех,...,ек
в себя, сводится к ортогональному преобразованию в (п-к) -мерном
подпространстве, натянутом на векторы ек+1;...,еп.). В силу сказанного
выше пространство VnJc топологически эквивалентно пространству смеж-
320

ных классов (О(л)/О(п-к); существует расслоение (О(и), Vn k,O(n—k)),
имеющее пространство расслоенияО(п), базу Vnk и слойО(й-л).
В многообразии У„гк, можно определить также действие группы О(к) :
всякой ортогональной матрице Ar-го порядка {а{} сопоставляется преобра-
преобразование, переводящее систему векторов (еь...,е'к) 6= Kn>ft в систему векто-
векторов (e'i,..'., e'fe) G Vnk где е\ = a^e,-. Все стационарные подгруппы
группы О(Аг) тривиальны, поэтому действие О(к) в Kn>Jt порождает главное
расслоение пространства Vn<k со слоемО(к). База этого расслоения отожде-
отождествляется с многообразием Gntk, состоящим из Ar-мерных подпространств
и-мерного пространства (две точки многообразия V nJk принадлежат одной
и той же орбите группы О(к), если соответствующие системы векторов
порождают одно и то же fc-мерное подпространство пространства Ft").
Многообразие Gnk можно отождествить с факторпространством
O(n)/O(fc) X О(п-к). Длятого чтобы убедиться в этом, достаточно заметить,
что группа О (и), действующая в 1R", переводит fc-мерное подпространство
в fc-мерное подпространство, и, следовательно, может рассматриваться
как группа преобразований пространства Gnk. Группа О(н) действует в
Gnk транзитивно. Замечая, что стационарные подгруппы этого действия
сопряжены группе О(к) ХО(п~к), получаем, что Gnk = O(«)/O(fc) X"O(«-fc).
(Группа О(к) XO(«-fc) естественным образом вкладывается в О(и) как
группа преобразований, преобразующих отдельно первые к координат и
последние п-к координат.)
§ 17. Связь между гомотопическими группами базы,
слоя и пространства расслоения
Для вычисления гомотопических групп удобно пользоваться теорией
расслоенных пространств. Для расслоенного пространства (?", В, F, р) су-
существует связь между гомотопическими группами пространств Е, В и F,
часто позволяющая найти гомотопические группы одного из этих прост-
пространств, если известны гомотопические группы двух других. Сейчас мы
сформулируем ряд утверждений, связывающих гомотопические группы
пространств Е, В и F, и покажем, как эти утверждения применяются к вы-
вычислению гомотопических групп конкретных пространств. Позже мы по-
покажем, что эти утверждения можно' вывести из одной общей теоремы (тео-
(теоремы о точной гомотопической последовательности), и наметим доказа-
доказательство этой теоремы (§ 18). Будем писать тгк(Е), пк(В), nk(F), имея в
виду 1тк(Е, е0), 1тк(В, b0), irk(F, е0), где Ьо ?Д F =р~1{Ь0),е0<г F. Знак
равенства означает изоморфизм групп. Случай к = 0 не исключается из
рассмотрения, однако в этом случае, вообще говоря, в no{E), no(B), яо^)
нельзя ввести групповую операцию. Знак равенства, в котором участвует
одно из этих множеств, означает взаимно однозначное соответствие двух
множеств.
Предложение 1. Если Е - В X F - произведение пространств В
и F, то группа irk (Е) изоморфна прямой сумме групп -лк (В) и irk (F).
Для того чтобы доказать это утверждение, заметим, что всякий сфероид
/ в Е может быть записан в виде (/], /2), где fx — сфероид в В, /г — сфе-
сфероид в F. При непрерывном изменении сфероида / сфероиды/i,/г также
меняются непрерывно. Таким образом, элементу а е пк(Е.) сопоставляется
321

пара («i, а2),где а^& пк(В),а2 ? я*(^) - гомотопические классы сферои-
сфероидов /i, /2; легко видеть, что это сопоставление взаимно однозначно.
Предложение 2. Если база В расслоения (Е, В, F, р) асферична в
размерностях к и к + \,т.е. пк{В) =nk+l(B) = 0,Tonk(F) = пк(Е).
Для того чтобы уточнить связь между nk(F) и лк(Е), заметим, что вло-
вложение слоя F и Е определяет гомоморфизм группы nk(F) в пк(Е) (всякий
сфероид в F можно рассматривать как сфероид в Е). Если -пк (В) = 0, то
всякий сфероид в Е гомотопен сфероиду в F; иными словами, построен-
построенный гомоморфизм отображает nk(F) на лк(Е). Если nk+J (В) = 0, то любой
А:-мерный сфероид в F, гомотопный нулюв Е, гомотопен нулю также в F,
т.е. гомоморфизм nk(F) в пк(Е) является изоморфизмом nk(F) и под-
подгруппы группы irk (E).
Предложение 3. Если слой F расслоения (Е, В, F, р) асферичен
в размерностях к - 1 и к, т.е. irk_x(F) = irk(F) =0,то лк(Е) = лк(В).
Раскроем это утверждение более подробно: отображение р порождает
гомоморфизм ттк(Е) в пк(В) (сфероиду / в Е сопоставляется сфероидpf в
В). Этот гомоморфизм является изоморфизмом пк(Е) и подгруппы груп-
группы пк(В), если nk(F) = 0; в то же время он является отображением на
всю группу ик (В), если ик_ i (F) = 0.
Предложение 4. Если пространство Е асферично в размерностях
к — \ и к,то лк {В) = пк _! (F ).
Для того чтобы построить этот изоморфизм, рассмотрим (Аг — ]) -мерный
сфероид / в слое F. В силу асферичности Ев размерностях к - I этот
сфероид гомотопен нулю в Е. Это означает, что существует отображение g
А:-мерного шара в пространство Е, совпадающее на границе этого шара, т.е.
на сфере Sk~ , со сфероидом /. Отображение pg переводит fc-мерный шар
в базу В, причем вся граница этого шара переходит в одну точку; такое
отображение можно рассматривать как fc-мерный сфероид в В. Используя
асферичность пространства Е в размерности к, легко убедиться, что гомото-
гомотопический класс этого сфероида зависит только от гомотопического класса
сфероида /Мыполучили, таким образом, отображение Tk~i{F) в як(В);
можно доказать, что это отображение является изоморфизмом.
Отметим, что предложение 4 применимо и в случае к = I. В этом случае
оно означает, что при условии связности и односвязности пространства
Е имеет место соотношение ЭТоСО = ^liB). Знак равенства здесь означает
существование взаимно однозначного соответствия между ЯоСО и tfiC^)-
Предложение 5. Если пространства В и F связны (по(В) = 7го(^) =
= 0), то пространство Е также связно. (Это следует из предложения 3.)
Приведенные выше утверждения применимы, в частности, в ситуации,
когда слой является дискретным пространством, например, состоит из
конечного числа точек. Мы будем считать Е связным пространством. (Тогда
пространство Е расслоения с Дискретным слоем F можно рассматривать
как накрывающее пространство пространства В; см. § 4.) Дискретное
пространствоF асферично в размерностях > I. Применяя предложение 3,
убеждаемся, что для расслоения с дискретным слоем
nk{E)=vk(B)
при к > 2. Из предложения 4 следует, что в случае, когда пространство Е
односвязно, имеет место соотношение iro(F) = ях(Л); иными словами,
число элементов в группе tii(B) равно числу точек в слое.
322

Предложение 6. Если (Е, В, F, р) - главное расслоение со связ-
связным односвязным пространством Е, то группа л1(В) изоморфна группе
no(F) = F/Fcon, где Fcon - максимальная связная подгруппа группы F
(связная компонента единицы в группе F).
Доказательство этого предложения может быть сведено к исследован-
исследованному в § 4 случаю, когда группа расслоения дискретна. В самом деле, пос-
поскольку группа F свободно действует в Е, это же справедливо для ее под-
подгруппы Fcon. Мы можем, таким образом, рассмотреть главное расслоение
(Е, E/Fcon, Fcon), базой которого является пространство орбит E/Fcon.
Группа Fcon является инвариантной подгруппой группы F; из этого следу-
следует, что преобразования группы F переводят одну орбиту группы Fcon в
другую (если два элемента ех, е2 S Е принадлежат одной орбите группы
Fcon, т.е. е2 = ej, f €. Fcon, то для любого g e F имеем e2g = eigtjg^fg)
и, значит, eig и e2g принадлежат одной орбите группы Fcon). Мы видим,
что группа F действует на пространстве орбит E/Fcon. При этом элементы
группы Fcon С F переводят каждую орбиту в себя; это означает, что груп-
группа F/Fcon также действует на E/Fcon. Легко проверить, что действие груп-
группы F/Fcon на E/Fcon свободно и что пространством орбит этого действия
является пространство E/F.
. Таким образом, существует главное расслоение (E/Fcon, E/F,. F/Fcon)
с дискретным слоем F/Fcon. Пространство E/Fcon связно и односвязно
(односвязность вытекает из предложения 4: ¦ni(EIFco^ ~n0(Fcon) =0).
Главное расслоение с дискретным слоем и связным пространством рас-
расслоения можно рассматривать как главное накрытие. Это позволяет приме-
применить результаты § 4; учитывая односвязность пространства E/Fcon, полу-
получаем, что n^E/F) =F/Fcon.
Перейдем теперь к рассмотрению примеров. Рассмотрим отображение
прямой [R1 на окружность S1, определяемое формулой z = exp(iV) (бес-
конечнолистное накрытие окружности). Рассматриваемое отображение
является расслоением с дискретным слоем; поэтому можно утверждать,
что
nk(S1)=nk<fr1) = 0 A)
при к > 2. Таким образом, у окружности S1 есть только одна нетривиаль-
нетривиальная гомотопическая группа 7Г1E1) = ~Z. Замечая, что группы SO B) и
U(l) топологически эквивалентны окружности S1, видим, что
7TfcE1)=0 B)
где к > 2.
Далее, трехмерное представление группы SUB) можно рассматривать
как двулистное накрытие группы SOC) группой SUB) (расслоенное
пространство с пространством SUB), базой SOC) и слоем, состоящим
их двух точек). Группа SUB) топологически эквивалентна сфере S3
(см. § 1) и, следовательно,
7r*(SUB)) = 0 C)
при к = 1 и к = 2,
г. D)
323

Используя утверждения § 17, видим, что группа тгх (SOC)) состоит из двух
элементов (т.е.7^(80C) = Z'2)),
I E)
при к > 2. В частности,
тг2 (SOC)) = 0, я3 (SOC)) = Ж F)
Для того чтобы вычислить группы 7Tfc(SOD)), заметим, что существу-
существует гомоморфизм группы SUB) X SUB) на группу SO D) (см. § А8).
Этот гомоморфизм является двулистным накрытием (расслоением со сло-
слоем из двух точек). Мы видим, что 7Tfc(SOD)) = irk(SUB) X SUB)) при
к > 2. Используя предложение 1 и соотношение tfk(SUB)) = 7tk(S3), по-
получаем
G)
при к > 2. В частности,
tf2(SOD)) = 0, я2(БОD)) = Z© Z (8)
Рассмотрим теперь расслоение (SO (и), 5", SO (и - 1)). (Это расслое-
расслоение порождается транзитивным действием группы SO(/.) на Sn~1: эле-
элементу g €Е SO (и) сопоставляется точка сферы iS", в которую преобразо-
преобразование g переводит фиксированную точку сферы.) Замечая, что 7ГкE"-1) =
= 0 при к < л — 2, и применяя предложение 2, получаем, что
) (9)
при к < п - 2. Таким образом, я2(8ОC)) =tf!(SOD)) =.. . =
т.е.
))=г2 A0)
при п > 3.
Далее, я2(8ОD)) = n2(SOE)) = ... Вспоминая, что я2(ЯОD)) = 0, ви-
видим, что
7T2(SO(n))=0 A1)
при всех п.
Пользуясь предложением 5 и расслоением (SO (и), Sn~l, SO (и - 1)),
по индукции устанавливаем, что группа SO(n) связна. Отсюда сразу следу-
следует, что группа О (и) состоит из двух компонент.
Группа GL(m) гомотопически эквивалентна О(п), а группа GL+(n)
матриц порядка я X п , имеющих положительный детерминант — группе
SO (л) (см. § 1). Группа GL+(n) изоморфна произведению группы IR+ =
= QL,+ A) положительных чисел и группы SL(m). (Каждая матрица # €Е
е GL+(m) однозначно представляется в виде g = ХЛ, где h S SL(n), X e
е IR + .) Отсюда следует, что группа SL(n) гомотопически эквивалентна
GL+(/i) и, следовательно, гомотопически эквивалентна SO(n). Это поз-
позволяет всю полученную информацию о гомотопических группах группы
SO (и) перенести на группы GL(n), GL+(n) и SL(n). В частности, группа
GL+(n) связна, а группа GL(m) состоит из двух компонент. (Этот простой
факт неоднократно использовался выше.)
324

Из соотношения 7Tfc(SOB)) = 0 при к > 2 следует, что можно применить
предложение 3 к расслоению (SO C), S2, SO B) ). Получаем, что
7rk(SOC)) = *k(S2) A2)
при к > 3 и, значит,
nk(S3)=nk(S2). A3)
Последнее утверждение можно получить и более прямым путем, заметив,
что построенное в § 14 хопфовское отображение сферы S3 на S2 является
расслоением со слоем S1; это расслоение называется хопфовским. Приме-
Применяя к хопфовскому расслоению (S3, S2, S1) предложение 3, снова прихо-
приходим к соотношению A3).
Существенно отметить, что изоморфизмы гомотопических групп, кото-
которые мы построили и будем строить далее, могут быть описаны геометричес-
геометрически. Например, изоморфизм групп яЛE3) и irk(S2) при к > 3 осуществ-
осуществляется с помощью отображения й», где h — хопфовское отображение.
Иными словами, при этом изоморфизме гомотопический класс отображе-
отображения / сферы Sk в S3 отвечает гомотопическому классу отображения hf
сферы Sk в S2. (Следствия из этого общего утверждения, получающиеся
при к = 3,к = 4, сформулированы в § 14.)
Для того чтобы исследовать гомотопические группы 7Tfc(SU(H)), ис-
используем расслоение (SU(/i), S2", SU(n — 1)). Можно рассматривать
группу SU(/i) как группу преобразований и-мерного комплексного про-
пространства С". Орбитами группы SU(h) в С" являются Bи - 1)-мерные
сферы | z! |2 +... + \zn\2 = const, поэтому можно считать, что SU(n)
транзитивно действует на S2"~1. Нужное нам расслоение получается, если
каждому преобразованию g S SU(n) сопоставить точку, которую# перево-
переводит в фиксированную точку сферы S2n~l. Применяя предложение 2 к рас-
расслоению (SUOO.-S^""'^!^ - 1)), находим
*k(SU(n-l)) = irk(SU(n)) A4)
при к < 1л - 2. Отсюда и из соотношений 7T2(SUB)) = 0, ct3(SUB)) = 2"
получаем, что
7T2(SU(«)) = O A5)
для всех п и
тг3(8и(и))=г A6)
для п > 2.
Применяя предложение 5 к расслоению (SU(n), 52", SU(n-l)), no
индукции проверяем, что группа SU(n) связна.
Группа U(и) изоморфна U(l) X S\J(n)/^n^всякую унитарную матрицу
можно п способами записать в виде и = Xs, где X — комплексное число, по
модулю равное 1, X" = detu, s & SU(n)). Из этого следует, что группа
U(n) связна, тг^Щл)) = 7^A1A)) = Z", nk(U(n)) = nk(SU(n)) при к > 2.
а Используя расслоение (Sp(n), S4", Sp(n - 1)), получающееся, если
заметить, что группа Sp(n) действует в n-мерном кватернионном прост-
пространстве Q" и орбитами этого действия являются сферы S4", видим,
что
) A7)
325

при к < An — 2. Вспоминая, что группа Sp(l) топологически эквивалентна
сфере 53, убеждаемся, что
Ti(Sp(n)) = 0, *2(Sp(n)) = 0, n3(Sp(n))=X A8)
при всех п. Ў
§ 18. Теорема о накрывающей гомотопии.
Точная гомотопическая последовательность
Все утверждения, использованные для вычисления гомотопических
групп в предыдущем параграфе, могут быть доказаны с помощью теоремы
о накрывающей гомотопии, которая сейчас будет сформулирована.
Пусть (Е, В, F, р) - локально тривиальное расслоение, / - отображение
метрического пространства К в базу В этого расслоения. Тогда для всякого
отображения f пространства К в Е, накрывающего отображение /, и вся-
всякой деформации ft отображения / найдется деформация ft отображения J,
накрывающая деформацию ft. (Напомним, что отображение / накрывает
отображение /, если pf = /, т.е. для любой точки х €Е К точка f(x) принад-
принадлежит слою над точкой /(х). Аналогично деформация ft накрывает дефор-
деформацию/,, если pft =ft).
Мы докажем сейчас теорему о накрывающей гомотопии в случае, когда
К - полиэдр. В этом случае утверждение теоремы о накрывающей гомото-
гомотопии может быть усилено следующим образом.
Пусть / - отображение полиэдра К в базу В расслоения (Е, В, F, р).
Тогда для всякого отображения f полиэдра К в пространство Е, накрываю-
накрывающего отображение f, и всякой деформации ft отображения f можно найти
накрывающую ее деформацию fr отображения ]\ более того, если накры-
накрывающая деформация ft каким-либо образом выбрана на подполиэдре К'
полиэдра К, ее всегда можно продолжить в накрывающую деформацию ft
всего отображения ft.
Отметим, что в случае, если рассматриваемое расслоение тривиально
(т.е. Е можно отождествить с В X F, а отображение р — с проекцией В X F
на В), отображение /пространства К в Е, накрывающее отображение /,
переводит точку хSК в точку (f(x),g(x))&B X F, где g(x) — произволь-
произвольное отображение пространства К в F. Усиленное утверждение теоремы
о накрывающей гомотбпии для прямого произведения сводится к лемме
о продолжении гомотопии.
Если g — произвольное отображение полиэдра К в пространство F, gt —
произвольная деформация отображения g, рассматриваемого на подполи-
подполиэдре К' С К, то эту деформацию можно продолжить в деформацию отобра-
отображения g на всем полиэдре К.
В случае когда полиэдр К совпадает с кубом /", а полиэдр К' — с грани-
границей / " куба/", усиленное утверждение теоремы о накрывающей гомотопии
можно переформулировать, воспользовавшись замечанием, что деформация
ft отображения куба /" естественным образом отождествляется с отобра-
отображением \р куба I" + * = /" X Г1. Отображение /, накрывающее отображение
/=/о. можно рассматривать как отображение грани/" X {0)в Е. Наконец,
326

деформацию ft, накрывающую ft на / ", можно интерпретировать как
отображение множества /" X /' ьЕ.
Введем обозначение Q для объединения нижней грани I" X { 0 } и сово-
совокупности боковых граней I" X I1. Мы видим теперь, что построение накры-
накрывающей деформации ft на всем кубе /" сводится теперь к продолжению
отображения с Q на /" +1. Таким образом, утверждение теоремы о накры-
накрывающей гомотопии для случая К =1", К' = I" сводится к представляющему
и самостоятельный интерес утверждению, которое мы будем называть
леммой о накрывающем отображении.
Лемма. Для всякого отображения у куба I" +1 в базу В расслоения
(Е, В, F, р) и отображения ф, накрывающего отображение у над Q, можно
найти отображение у, накрывающее отображение <р над In + 1 и совпадающее
с фнад Q.
Докажем, прежде всего, эту лемму для случая тривиального расслоения
(В X F, В, F, р). Записывая ф(х) в виде (<?(*)> ^(*)). гДе х е??> мы видим,
что построение отображения ip сводится к продолжению отображения h
с множества Q на куб/" +1. Такое продолжение всегда возможно. В самом
деле, легко построить топологическое отображение куба /" + 1 на себя, при
котором множество Q переходит в нижнюю грань куба/" X { 0 }. Построе-
Построение нужного нам отображения можно осуществить, например, сконструи-
сконструировав два топологических отображения куба /" + ' на шар D" +1 так, чтобы
при одном из них множество Q переходило в полусферу, а при другом
грань /" X {0} переходила в полусферу (см. рис. 47). Теперь задача свелась
к продолжению отображения с грани /" X { 0 } на куб /" + ; такое продол-
продолжение строится очевидным образом (нужно рассмотреть проекцию п куба
Рис. 47
/" +1 на грань/" X { 0} и заметить, что отображение h, заданное на/" X {0},
продолжается в отображение йя, определенное на всем кубе). Мы доказали
лемму о накрывающс: i отображении в случае,когда расслоение тривиально.
В общем случае нужно воспользоваться локальной тривиальностью отобра-
отображения (Е, В, F, р). Рассмотрим для простоты отображение / квадрата I2
на базу В. Разобьем квадрат вертикальными и горизонтальными линиями
х1 = k/N, х2 = l/N (к, I = 1,... ,N — 1) на маленькие квадраты так, чтобы
при отображении / каждый маленький квадрат переходил в множество,
327

над которым рассматриваемое расслоение тривиально. Отображение /,
накрывающее отображение /, определено на множестве Q (т.е. на нижней
стороне квадратах = 0 и на боковых сторонах квадратах1 = 0, х1 = 1).
Будем считать, что отображение / уже построено при х2 <l/N. Построим
отображение / произвольным образом на отрезках х1 = k/N, l/N < x2 <
<(/+ l)/N (такое построение возможно в силу леммы, примененной к
случаю тривиального расслоения). Далее, с помощью той же леммы продол-
продолжим отображение /на квадратики k/N^x1 <(Аг + \)/N, l/N <x2 <(/+ l)/vV.
Теперь отображение /определено для всех точек, удовле^оряющих усло-
условию х2 <(/+ l)/iV. По индукции получаем отображение /на всем квадра-
квадрате I2. Доказательство леммы для куба произвольной размерности прохо-
проходит по той же схеме.
Отметим, что лемма о накрывающем отображении остается справедли-
справедливой, если заменить в ней куб /" +1 шаром D" +1, а множество Q — полусфе-
полусферой (это ясно из существования топологического отображения куба /" +'
на Dn * \ отображающего Q на полусферу).
Перейдем теперь к доказательству теоремы о накрывающей гомотопии.
Заметим, прежде всего, что утверждение этой теоремы в случае, когда
полиэдр К совпадает с кубом /", а подполиэдр К'— с границей/" куба /",
как мы говорили, эквивалентно лемме о накрывающем отображении и,
следовательно, уже доказано. Общий случай очевидным образом сводится
к этому частному случаю. Именно, нужно производить построение накры-
накрывающей деформации на клетках полиэдра К, начиная с клеток меньших
размерностей. Точнее, доказательство проводится индукцией по размер-
размерности К. По предположению индукции можно считать, что накрывающая
гомотопия задана на объединении полиэдра К' и r-мерного остова Кг
полиэдра К. Шаг индукции состоит в продолжении деформации на (г + 1) -
мерный остов Kr+1. Это продолжение можно строить отдельно на каждой
(г + 1)-мерной клетке, пользуясь тем, что для каждой такой клетки суще-
существует отображение куба/г+1 на замыкание клетки, являющееся тополо-
топологическим внутри куба.
Отметим, что из теоремы о накрывающей гомотопии сразу следует, что
у расслоения (E,B,F,p) со стягиваемой базой В всегда существует.сечение.
(Достаточно применить эту теорему для случая, когда / - отображение
базы В в точку b&B, a ft — деформация, соединяющая отображение /
и тождественное отображение базы В на себя). Для случая главного рас-
расслоения существование сечения сразу влечет за собой тривиальность этого
расслоения.
Доказательства всех утверждений § 17 можно провести с помощью
однотипных рассуждений, основанных на теореме о накрывающей гомо-
гомотопии.
Проверим, например, что, в случае если пк(В) = 0, всякий сфероид в Е
гомотопен сфероиду в F. Сфероид в Е будем рассматривать как отображе-
отображение g сферы S" в Е, переводящее точку sGS" в е0. Отображение f=pg,
переводящее точку sGS" в точку Ьо ~р(ео), можно рассматривать как
сфероид в В. В силу сделанного выше предположения сфероид / гомото-
гомотопен 0, т.е. существует деформация /, этого сфероида, удовлетворяющая
условию fi(x) = b0 для всех x(ESn. Деформация /г, накрывающая дефор-
328

мацию ft, может рассматриваться как деформация сфероида g в сфероид /i.
Замечая, что p(/i(*)) =/i(x) = *o. убеждаемся, что сфероид /i можно рас-
рассматривать как сфероид в слое Fb , лежащем над точкой Ьо. Мы доказали,
таким образом, что при условии п„{В) = 0 всякий л-мерный сфероид в Е
гомотопен сфероиду в F.
С помощью теоремы о накрывающей гомотопии можно получить также
более сильные утверждения, чем содержащиеся в §' 17. Именно, можно
построить так называемую точную гомотопическую последовательность
расслоения. Заметим, прежде всего, что с помощью этой теоремы можно
определить гомоморфизм 5 группы яп(В,Ьо) в группу nn-i(F, eo)> где
F= Ff, — слой, лежащий над точкой b0, e0 &F.
Для того чтобы построить гомоморфизм 5, рассмотрим сфероид в базе
В, задаваемый отображением / куба I в В, переводящим границу куба
1"вЬ0.
В силу леммы о накрывающем отображении можно накрыть отображе-
отображение / отображением / куба /" в Е. Отображение / переводит границу куба
в слой F над точкой Ьо. Поскольку граница куба / " топологически экри-
валентна сфере Sn~1, отображение / множества /" в F можно интерпрети-
интерпретировать как (л — 1)-мерный сфероид в F. Гомотопический класс этого
сфероида зависит от гомотопического класса сфероида / в В; поэтому
описанная только что конструкция порождает отображение группы
пп(В, Ьо) в nn-\(F, во)', это отображение обозначается символом 5. Не-
Нетрудно проверить, что 5 является гомоморфизмом при л > 2.
Отметим, что часто удобно при построении отображения 5 интерпрети-
интерпретировать сфероид / в базе как отображение шара D", переводящее границу
шара S"~l в Ьо.
Рассмотрим теперь следующую последовательность групп и гомомор-
гомоморфизмов :
... -* irn(F, е0) '^ *„(?', ео)"± я„(Д Ьо) 4 я„_ ,(F. е0) ^ ... A)
Символ р, обозначает отображение, порождаемое проекцией р пространства
Е на В: отображение /, порождается вложением слоя F в Е. Легко прове-
проверить, что композиция двух соседних гомоморфизмов в последовательности
A) равна0:
/».|.в0, /,5=0, 5р. =0. B)
А Если сфероид в .слое F рассмотреть как сфероид в пространстве Е, а
затем спроектировать в базу Я, то мы получим отображение сферы в одну
точку Ьо; это означает, что р./, = 0. При построении гомоморфизма 5 мы
исходили из отображения /, рассматриваемого как отображение /"в F;
поскольку /по построению является отображением куба /"в F ясно,
что отображение f множества /" в F гомотопно нулюв?\ Отсюда следует,
что /,5*0. Наконец, если гомотопический класс а ? !Гк(В) имеет вид р,0,
где Р&пк(Е), то, выбрав сфероид Лиз гомотопического класса ft мы
можем построить сфероид / из класса а, положив /= ph. Тогда отображе-
отображение /, использованное при построении класса 5а, можно отождествить с h ;
поскольку И переводит /" в точку, мы видим, что 5а = 0 и, значит, 5р, = 0.
329

(Мы рассматривали здесь сфероиды Ли/ как отображения кубов.) т
Из соотношения B) вытекает, что
Im/, CKerp,, ImSCKer/,, Imp, С Ker 5. C)
Оказывается, что имеет место более сильное утверждение:
Im /, = Ker р,, Im 5 = Ker /,, Im p, = Ker 5. D)
Иными словами, в последовательности A) ядро каждого гомоморфизма
совпадает с образом предыдущего гомоморфизма. Последовательность
•••^Л + 1 у*п ¦* Ап_1^... E)
групп Ап и гомоморфизмов Х„ назьшается точной, если Im Х„+ j совпадает
с КегА„. Таким образом, соотношения D) означают, что последователь-
последовательность A) точна. Эта последовательность называется точной гомотопиче-
гомотопической последовательностью расслоения.
В последовательность A) удобно включать также гомотопические мно-
множества яо(^. е0),То{Е, <"о). iro(B,bo), не наделенные структурой группы.
В каждом из этих множеств есть выделенный "нулевой" элемент, отвечаю-
отвечающий тривиальному гомотопическому классу. Это позволяет говорить о
ядрах участвующих в последовательности A) отображений также и в слу-
случае, когда эти отображения не являются гомоморфизмами. Соотношения
D) справедливы для всех членов последовательности A), в том числе и
для последних ее членов:
...->nl(B,bo)->no(F,eo)->iro(E,eo)^r:o(B,bo)^O. F)
Доказательство точности гомотопической последовательности расслое-
расслоения состоит из цепи тривиальных рассуждений; эта цепь оказывается доста-
достаточно длинной, поскольку приходится проверять отдельно каждое из соот-
соотношений D).
Докажем, например, первое из этих соотношений. Нам осталось прове-
проверить, что Кегр, С Im/,. Пусть гомотопический класса сфероида /принад-
/принадлежит Ker р.. Это означает, что сфероид h = р/гомотопен нулю в В; дефор-
деформацию сфероида И в точку обозначим ht. Построим деформацию /г отобра-
отображения /, накрывающую деформацию ht. Она связывает отображение /0 =/
с отображением /\, накрывающим h\. Поскольку образом отображения h i
является точка Ьо, образ отображения fx лежит в слое над этой точкой. Это
означает, что сфероид / в пространстве Е гомотопен сфероиду fx в слое F,
т.е. гомотопический класс сфероида /принадлежит множеству Im/,. Таким
образом, Kerр, = Im/,. Остальные соотношения D) доказываются анало-
аналогично. В § 19 будет намечено несколько иное доказательство точности
гомотопической последовательности.
Сейчас мы покажем, каким образом из точности последовательности A)
вытекают предложения § 17. Начнем с предложения 2. Если база В асфе-
асферична в размерности k (т.е. пк(В) = О), то гомоморфизм р, группы л^Е)
в лк(В) переводит все элементы группы пк(Е) в нулевой элемент (единст-
(единственный элемент группы пк(В)). Это означает, что ядро отображения р,
состоит из всей группы п^Ф)- В силу точности гомотопической последова-
последовательности это ядро совпадает с образом гомоморфизма /,, и, значит, /,
отображает nk(F) на все лк(Е).
330

Далее, образ группы чгк(в) = 0 в группе JTjt_i(F) при отображении 5
состоит только из нулевого элемента. В силу точности гомотопической
последовательности это означает, что ядро отображения /. группы ff*_i(F)
в лк(Е) состоит только из нулевого элемента; иными словами, i. изоморф-
изоморфно отображает nk^i(F) на подгруппу группы я*_!(?"). Если пк(В) =
* njc+iiBy = 0, то из доказанных только что утверждений вытека-
вытекает изоморфизм irk(F) = vk(E). Доказательство предложений 3 и
4 проводится совершенно аналогично. Отметим, что при этом пред-
предложение 4 получается в следующем уточненном виде: если простран-
пространство Е асферично в размерности к, то гомоморфизм б отображает
группу 7rfc + 1B?) на всю группу itk(F), а группа пк(В) изоморфно
отображается при этом гомоморфизме на подгруппу группы nk_l (F).
Отметим, что рассуждение, примененное выше при доказательстве
соотношения B), имеет общий характер. Именно предположим, что в
точной последовательности E) групп А„ и гомоморфизмов Х„ одна из
групп тривиальна, например, пусть Ак = 0. Тогда гомоморфизм Xfc_ t
является изоморфизмом группы Ak-i и подгруппы группы Ак_2, а гомо-
гомоморфизм Хк + 2 отображает группу Ак + 2 на всю группу Ак+1. Если в
точной последовательности Ак = Ак+з -0, то гомоморфизм Х^ + 2 является
изоморфизмом группы Ак+1иАк + 2-
Точная гомотопическая последовательность может быть использована
для вычисления гомотопических групп также в случаях, когда предложения
§ 17 оказываются недостаточными. Покажем, например, как можно вычи-
вычислить группы п з (SO (и) ). Мы видели в § 17, что п 3(SOC)) = Т, я3 (SOD)) =
= 2?+ Ж Далее, из A7.9) следует, что tt3(SO(m)) =7t3(SOE)) при -и >5,
поэтому вопрос сводится к вычислению группы tt3(SOE)). Рассмотрим
точную гомотопическую последовательность расслоений (SOE), SA, SOD)):
^ тг4E4) 4. tt3(SOD)) ^ *3(SOE)) ^
II II II II G)
->¦ S -* 2?+ Я -> тг3 (SOE)) -* 0 -»¦
Из точности последовательности G) вытекает, что i.отображает ?r3(SOD))
на w3(SOE)), причем ядром этого отображения служит образ гомомор-
гомоморфизма 5. Отсюда следует, что ff3(SOE)) = tf3(SOD))/Im5. Каждому це-
целому числу т отвечает элемент [т] гомотопической группы n^S*) =? И,
каждой паре целых чисел тх, т2 — элемент [mi, m2] гомотопической
группы я3 (SO D)) = г+ Я.
Непосредственные геометрические рассмотрения показывают, что при
гомоморфизме 6 элемент [т] S я4E4) переходит в элемент [т, т] е
е jt3(SOD)). Отсюда следует, что tf3(SOD))/Im6 = ~Z и, следовательно,
tf3(SOE)) = 77. Мы установили таким образом, что 7T3(SO(n)) = Упри
и>3, п?=4.
В случае, если у расслоения существует сечение, точная гомотопическая
последовательность упрощается. В самом деле, в рассматриваемом случае
гомоморфизм р, отображает группу п„(Е, е0) на всю группу тг„{В, Ьо);
иными словами Imp, = пп(В, Ьо). В самом деле, если q - сечение, то
p(q(b)) ~.b, и, значит, р,(я*(х)) = х W любогох S я„(Д Ьо). Из соот-
соотношения Ьпр. = Кег 6 вытекает, что 5 переводит всю группу я„(Я, Ьо)
331

в нулевой элемент группы Jrn_x (F, е0). Это позволяет получить из точной
гомотопической последовательности расслоения короткую точную после-
последовательность
I, р*
О -»¦ nn(F, е0) ¦* пп(Е, е0) -> я„(Д Ьо) -+ 0.
Из полученной точной последовательности вытекает, что /. изоморфно
отображает nn(F, е0) на подгруппу группы пп(Е, е0). Отождествляя
ЯпО*. во) с этой подгруппой, видим, что группа пп(В, Ьо) изоморфна
факторгруппе пп(Е, eo)/4,(F, e0).
§ 19. Относительные гомотопические группы
Более прозрачное доказательство теоремы о точности гомотопической
последовательности расслоения может быть получено с помощью понятия
относительной гомотопической группы.
Пусть Y - подмножество пространства X, х0 е Y. Будем называть от-
относительным сфероидом отображение шара D" в пространство X, пере-
переводящее границу шара — сферу S"~l — в подпространство> Y, а южный
полюс s сферы S"~ в точку х0. Два относительных сфероида называют-
называются гомотопными, если их можно соединить непрерывным семейством,
состоящим из относительных сфероидов. Множество гомотопических
классов относительных сфероидов обозначается символом тг„(Х mod Y, х0).
При п >2 в множестве itn(X mod Y, х0) можно ввести операцию,превраща-
операцию,превращающую это множество в группу — л-мерную относительную гомотопиче-
гомотопическую группу. При п > 3 группа пп(Х mod Y, х0) коммутативна. Сфероид,
переводящий весь шар D" в точку дс0. называется нулевым сфероидом.
Любой сфероид, переводящий шар D" в подпространство Y, гомотопен
нулевому сфероиду (или, короче, гомотопен нулю). Гомотопический
класс нулевого сфероида является нулевым элементом группы
тг„(X mod Y, х0) при п > 2.
Для того, чтобы определить сложение в множестве 7Г„ (X mod У, х0),
удобно модифицировать определение относительного сфероида. Именно,
под относительным сфероидом можно понимать отображение куба I" в
пространство X, переводящее куб/" в подпространство Y, а остальную
часть границы куба в точку х0- (Куб 1"~1 рассматривается как грань
куба /", выделяемая уравнением х" = 0.) По всякому сфероиду в старом
смысле можно построить сфероид в новом смысле по следующей конструк-
конструкции. Рассмотрим отображение а куба /" на шар D", при котором внутрен-
внутренность куба /"топологически отображается на внутренность шара D",внут-
D",внутренность куба /" топологически отображается на сферу S"~l с выко-
выколотым южным полюсом, а остальная часть границы куба /" переходит в
южный полюс сферы 5". Если у — сфероид в старом смысле слова,
то отображение <ра является сфероидом в новом смысле слова. Построен-
Построенное соответствие между сфероидами старого и нового типов взаимно
однозначно, поэтому при определении о'тносительной гомотопической
группы можно с равным правом пользоваться любым иэ приведенных
выше определений.
Пользуясь относительными сфероидами в новом смысле, можно опре-
определить операцию сложения в множестве irn(Xmod Y,x0) точно так же, как
332

это было сделано в § 14 для множества vn(X, х0). Доказательство ком-
коммутативности группы 7Tn(jifmod Y, х0) при п > 3 аналогично проведенно-
проведенному в § 14 доказательству коммутативности группы п„(Х, х0) при п > 2.
Рассмотрим, как связаны между собой группы я„(Г, х0), п„(Х, х0)
и п„(Х mod Y, х0). Заметим, прежде всего, что «-мерному относитель-
относительному сфероиду можно сопоставить (и — 1)-мерный сфероид в простран-
пространстве Y. (Если относительный сфероид реализован как отображение шара
D", то это же отображение, рассматриваемое только на границе S"~1
шара D", является сфероидом в пространстве Y.) Очевидно, что гомотоп-
гомотопным относительным сфероидам отвечают гомотопные сфероиды в Y; мы
построили, таким образом, отображение множества п„(Х mod Y, х0) в мно-
множество nn_1(Y, x0). Это отображение обозначается символом Э. При
п > 2 отображение Э является гомоморфизмом (часто этот гомоморфизм
называют граничным гомоморфизмом). Далее, всякий сфероид в про-
пространстве Y может рассматриваться как сфероид в пространстве X. Мы
получаем, таким образом, гомоморфизм группы nn(Y, x0) в группу
лп(Х, х0); этот гомоморфизм обозначим символом /, (гомоморфизм
/, можно рассматривать как гомоморфизм, порождаемый вложением /
множества Y в пространство X). Наконец, всякий сфероид в пространст-
пространстве X можно рассматривать как относительный сфероид; при этом возни-
возникает отображение / множества гтп(Х, х0) в irn(X mod Y, х^). Для п > 2
отображение / является гомоморфизмом.
Рассмотрим теперь последовательность групп и гомоморфизмов:
э '» / э
(У) *¦ п„(Х,х0)-* nn(XmodY,x0) -> тг„_,(Г, х0)^...
О)
Легко видеть, что композиция любых двух соседних гомоморфизмов в
этой последовательности равна 0:
/7. = 0, Э/ = 0, 1.3 = 0. B)
Например, если отображение ц> шара D" является относительным сфе-
сфероидом, то то же отображение, рассматриваемое только на границе шара,
является сфероидом в Y, гомотопным 0 в X. (Напомним, что сфероид,
определяемый отображением сферы S"~1, гомотопен 0 в случае, если это
отображение сферы можно продолжить на шар, ограниченный сферой
S"~ \ Отображение ip на сфере S"~1 по построению продолжается на
шар ?>".) Таким образом, мы видим, что /„Э = 0. Столь же просто прове-
проверяются и равенства //. = 0, Э/ = 0.
Из соотношений B) вытекает, что
Imi, С Ker/, Im/ С КегЭ, 1тЭ С Kerf,.
Оказывается, что на самом деле верны соотношения
Im/, = Ker/, Im/ = КегЭ, Im Э = Ker/,. C)
Иными словами, образ каждого гомоморфизма в последовательно-
последовательности A) совпадает с ядром предшествующего гомоморфизма.
Проверим, например, что Im Э = Кет /,. Поскольку мы уже знаем, что
Ьп Э С Кег /,, нам осталось проверить, что для всякого гомотопического
класса а е тг„_ i (Y, х0), удовлетворяющего условию /.а = 0, найдется
333

такой класс /3 € пп(X mod Y, x0) . для которого Э/J = а. Пусть отображение/
сферы S" в Y является сфероидом из класса а. Соотношение /ёа = О
означает,, что отображение / можно продолжить в отображение /' шара D"
в X. Это отображение можно рассматривать как относительный сфероид.
Очевидно, что для гомотопического класса jj относительного сфероида
/ выполнено соотношение 3C = а.
Соотношения C) означают, что последовательность A) точна. Эта по-
последовательность называется точной гомотопической последовательностью
пары (X, У). Отметим, что члены последовательности A), отвечающие
малым значениям п, не снабжены структурой группы; однако, утвержде-
утверждение о точности последовательности сохраняет смысл и для этих членов,
поскольку в них есть нулевой элемент (класс, состоящий из гомотопных
нулю сфероидов).
Пусть Ьо — точка базы В расслоения (Е, В, F, р); слой Fb , лежащий
над точкой Ьо, будем обозначать просто F. Естественный гомоморфизм
группы п„(ЕmodF,e0) в группу п„(В,Ь0) обозначим символом р.
(Мы обозначили через е0 произвольную точку в слое F. Если относи-
относительный сфероид / принадлежит гомотопическому классу a G
е тг„ (?" mod F, е0), то отображение pf можно рассматривать как сфе-
сфероид в базе В. Класс pa ? я„(Я, Ьо) определяется как гомотопиче-
гомотопический класс сфероида pf.)
С помощью теоремы о накрывающей гомотопии нетрудно доказать,
что гомоморфизм р является изоморфизмом:
я„(Е modF, е0) = *„(В, Ьо). D)
Соотношение D) позволяет получить из точной гомотопической последо-
последовательности пары (Е, F) описанную в предыдущем параграфе точную го-
гомотопическую последовательность расслоения (Е,.В, F, р)
Для того, чтобы проверить соотношение D), заметим прежде всего,
что отображение р отображает п„(Е mod F, е0) на всю группу пп(В, Ьо).
В самом деле, будем рассматривать сфероид в В как отображение g
шара D", переводящее границу шара S"~ * в Ьо, и по лемме о накрываю-
накрывающем отображении построим накрывающее отображение g шара D" в Е.
Выберем g так, чтобы точка s переходила в е0; поскольку g переводит
границу шара в слой над Ьо, можно рассматривать g как относительный
сфероид Е mod F. Гомотопический класс [g] e ^(^modF, e0) сфероида
g при гомоморфизме р переходит в гомотопический класс [g] G п„(В, Ьо)
сфероида g: поскольку сфероид g произволен, это доказывает нужное
нам утверждение. Далее рассмотрим гомотопический класс [/] €Е
€ ъ„(Е mod F, е0), переходящий при гомоморфизме р в нуль. Сфероид
/ из этого класса переходит при отображении р в гомотопный нулю сфе-
сфероид pf в базе. Деформацию сфероида pf в точку Ьо можно по теореме
о накрывающей гомотопии накрыть деформацией сфероида/. Полученный
в результате деформации сфероида/ относительный сфероид отображает
весь шар D" в слой F над точкой Ьо и, следовательно, гомотопен нулю.
Мы видим, что Кег р = 0 и, следовательно, р изоморфно отображает
я„(ЕmodF, е0)тп„(В,Ь0).
Отметим, что соотношение D) остается справедливым и при условии
и < 1, когда множество п„(Е mod F. е0) не наделено структурой группы;
334

тогда оно означает, что отображение р является взаимно однозначным
соответствием между irn(EmoAF, e0) и я„B?, *<>)•
Всякий относительный сфероид jfmod Y можно рассматривать как
отображение пары (Z)n, S" ) в пару (X, Y). (Напомним, что отображе-
отображением пары (Dn, 5") в пару (X, Y) называется отображение шара/)" в
X, переводящее сферу S"~l в Y, см. § 1.) Гомотопные сфероиды порожда-
порождают гомотопные отображения пар; однако, обратное утверждение не спра-
справедливо (деформация/, отображения пары (D", S") в пару (X, Y)
может р'ассматриваться как деформация сфероидов лишь в случае, если
ft (s) = х0 при каждом t). Таким образом, существует естественное отобра-
отображение множества {Dn, S"~1\X, Y} гомотопических классов отображе-
отображений пар в множество пп(Х mod Y, х0). Легко проверить, что множество
{Dn, S" \Х, Y) отображается на все множество пп(Х mod Y, х0), если
Y связно, и что это отображение взаимно однозначно, если Y односвязно.
(Отсюда, в частности, следует, что в случае связного односвязного Y между
множеством я„ (Xmod Y, х0) для разных х0 существует естественное
взаимно однозначное соответствие. Это позволяет писать п„(Х mod Y)
вместо я„ (X mod Y, дс0); впрочем, так часто делают и для произвольного Y,
если это не может привести к недоразумениям.) Если Y — произвольное
связное пространство, то {D", S"~1 \ X, Y} получается из я„(X mod Y,х0)
факторизацией по ni(Y, х0) (т.е. как множество орбит группы я,(У, х0),
естественно действующей в я„ (X mod Y, хо) ¦ Иными словами, связь между
{D",Sn~l \X,Y)итг„ (Xmod Y,х0) аналогична связи между { S", Е) и
пп(Е, е0) (см. § 15).
В § 1 было построено взаимно однозначное соответствие между мно-
множествами { Dm, Sm '" * | D", S" ~ *} и {Sm ~ x, S"~x}. Из этого результата
вытекает, что
' irn(Dn modS"-1) = ят_1E"-1).
§ 20. Гомотопические группы групп Ли
и однородных многообразий
Заметим прежде всего, что изучение топологии однородных многообра-
многообразий сводится к изучению связных однородных многообразий. Если одно-
однородное многообразие несвязно, то все его компоненты топологически эк-
эквивалентны друг другу: в самом деле, если точка х i принадлежит одной
связной компоненте, а точка х2 — другой связной компоненте однородно-
однородного многообразия, то преобразование группы, переводящее jcx в х2 уста-
устанавливает топологическую эквивалентность между рассматриваемыми
двумя компонентами.-
Всякая связная группа Ли гомотопически эквивалентна своей макси-
максимальной компактной подгруппе; это позволяет при изучении гомотопи-
гомотопических и гомологических групп ограничиться компактными группами Ли.
Аналогично, при рассмотрении однородных многообразий достаточно
исследовать компактные однородные многообразия. Однородное много-
многообразие G/H, где G и Н — связные группы Ли, гомотопически эквивалент-
эквивалентно Gc/Hc, где Gc, Hc - максимальные компактные подгруппы групп GuH.
335

Мы не будем приводить доказательств этих утверждений. Укажем только
некоторые примеры. Группа GL+(n, IR) невырожденных преобразований
с положительным детерминантом гомотопически эквивалентна своей
максимальной компактной подгруппе SO (и). Группа GL(h, (D) невырож-
невырожденных комплексных матриц гомотопически эквивалентна группе U(n).
(Гомотопическую эквивалентность в этих случаях легко построить с по-
помощью процесса ортогонализации Грама—Шмидта.) Группа Лоренца L го-
гомотопически эквивалентна своей максимальной компактной подгруп-
подгруппе SOC).
Алгебра Ли компактной группы Ли разлагается в прямую сумму про-
простых алгебр (§ А7), поэтому компактная группа Ли локально изоморфна
прямому произведению простых групп Ли. Единственная простая компакт-
компактная коммутативная группа Ли U(l) локально изоморфна группе положи-
положительных вещественных чисел (R + . Отсюда следует, что связная компактная
группа Ли G локально изоморфна односвязной группе КХ [R + , где К -
произведение односвязных простых компактных некоммутативных
групп Ли, a R" - прямое произведение п экземпляров группы \Bt. Это
позволяет представить группу G в виде
G = КХ K"+/D,
где D — дискретная инвариантная подгруппа. Из результатов § 4 вытекает,
что D = itx(G) и что подгруппа D коммутативна (более того, принадлежит
центру группы К XIR" ) •
- Замечая, что отображение группы К X IR" на группу G является расслое-
расслоением с дискретным слоем (накрытием) и используя предложения 1 и 3 из
§ 17, получаем
щ(С) = nt(KXV\1)= щ(К) A)
при / > 2 (пространство IR" стягиваемо, поэтому tffflR") = тг,(Р") = 0).
Если группа К является произведением групп L i, . . . , Lr, то в силу пред-
предложения 1 из § 17
*,(*)= ifi&i) + ...+ »,(!,). B)
Поэтому вычисление гомотопических групп компактных групп сводится
к вычислению гомотопических групп простых односвязных компактных
некоммутативных групп. Можно доказать, что всякая простая односвяз-
ная компактная некоммутативная группа L асферична в размерности 2
(т.е. п2 (L ) = 0), а трехмерная гомотопическая группа группы L изоморфна
группе целых чисел (n3(L) = It). Для классических групп Ли эти утвержде-
утверждения доказаны в § 17. Мы не будем останавливаться на общем доказательст-
доказательстве. Из сформулированных только что утверждений вытекает, что любая
группа Ли G асферична в размерности 2 (ir2(G) = 0). Группа ^(G) &m
любой группы Ли G изоморфна прямой сумме нескольких экземпляров
группы 72'. (Если компактная группа G представлена в виде К X IR+/Z),
где К — произведение г простых некоммутативных компактных групп,
то группа я3(Ст) изоморфна прямой сумме т экземпляров группы У.)
Вычисление гомотопических групп однородного многообразия G/H
удобно проводить с помощью расслоения (G, G/H, H) (см. § 16). Если
G - связная односвязная группа, то число элементов в группе nr(G/H)
336

равно числу компонент группы Я. Это следует из предложения 3 § 17.
Более того, можно утверждать, что группа -n^G/H) изоморфна фактор-
факторгруппе группы Я по группе Ясоп, состоящей из всех элементов группы,
которые молено соединить путем с единичным элементом. Для того чтобы
доказать последнее утверждение, следует применить предложение 6 § 17
к расслоению (G, G/H, Я). Далее, если группа G односвязна, соотношения
n1(G) = тг2(С) - 0 позволяют применить предложение 4 § 17. Из этого
предложения следует, что
тг2(С/Я) = я, (Я). . C)
Укажем геометрическое описание элементов групп -n^iG/H) и it2(G/H),
пользуясь приведенным в § 17 описанием изоморфизмов, фигурирующих
в предложениях 4 и 6.
Соответствие между компонентами группы Я и элементами группы
nl(G/ff) устанавливается с помощью следующей конструкции. Рассмот-
Рассмотрим путь у в G, начинающийся в произвольном элементе h группы
ЯСС и кончающийся в единице группы G. При естественном отобра-
отображении группы G на G/H путь у переходит в замкнутый путь !р. В силу
односвязности группы G, два пути, соединяющие точку h и единицу
группы, гомотопны между собой, поэтому гомотопический класс пути $>
не зависит от выбора пути </?. Таким образом, каждому элементуАеЯмы
сопоставили элемент группы ni(G/H); этот элемент будем обозначать
символом р(й). Легко проверить, что гомотопический класс р(А) не из-
изменяется при непрерывном изменении точки h. Таким образом, каждой
компоненте связности группы Я сопоставляется элемент группы ¦п1 (G/Я).
Нетрудно доказать, что p(AjA2) = p(hi)p(h2); иными словами, р явля-
является гомоморфизмом группы Я в ni(G/H). (В случае, если Я— дискретная
группа, это следует из результатов § 4. В общем случае доказательство
повторяет рассуждения § 4.) Ядром гомоморфизма р служит группа Ясоп,
которую можно охарактеризовать как максимальную связную подгруппу
группы Я. Таким образом, группа тг^С/Я) изоморфна факторгруппе
группы Я по группе Ясоп.
Мы рассматривали до сих пор группу ¦n1(G/ff) в случае, когда G —
односвязная группа (т.е. ограничивались случаем однородного много-
многообразия, на котором транзитивно действует односвязная группа). Заметим,
что это предположение по существу не ограничивает общности. В самом
деле, всякая группа Ли G может быть представлена в виде факторгруппы
односвязной группы Ли G по дискретной подгруппе N центра группы G
(см. § 4). Группу G можно рассматривать как универсальную накрываю-
накрывающую группы G; отображение накрытия q является гомоморфизмом, ядром
которого служит подгруппа N. Если группа G транзитивно действует на
однородном многообразии М = G/H с помощью преобразований <pg, то
можно определить транзитивное действие группы G на М, сопоставив
каждому элементу g ?G преобразование <?ч(г)- Стационарной подгруп-
подгруппой этого действия является подгруппа Я = q~l(H), накрывающая стацио-
стационарную подгруппу Я группы G. Очевидно, что Я = H/N. Мы видим, что
М = G/H = G/H. Отождествление многообразий GjH и G/H позволяет огра-
ограничиться при изучении однородных многообразий многообразиями, на ко-
337

торых транзитивно действует односвязная группа. В частности, ni(M) =
= Н/Нсоп.
Построение изоморфизма C) можно осуществить следующим образом.
В силу того, что группа G односвязна, всякое отображение окружности
S1 в Н можно продолжить в отображении круга D2 в G. Рассматривая
замкнутый путь а в Я как отображение окружности, мы строим отображе-
отображение 0 круга D2 в G, совпадающее на границе с выбранным нами путем в Я.
При естественном отображении я группы G в G/H вся группа Я переходит
в одну точку. Отсюда следует, что отображение тг/3 круга D2 в G/H пере-
переводит границу круга в одну точку и, следовательно, определяет элемент
группы v2(G/ff). В силу соотношения n2(G) = 0 построенный элемент
группы п2 (G/H) не зависит от выбора отображения /3 и полностью опре-
определяется гомотопическим классом пути а. Таким образом, мы построили
отображение группы iJi(ff) в ir2(G/ff). Это отображение является изомор-
изоморфизмом групп тг,(Я) и я2(С/Я).
В случае, если группа G неодносвязна, описанная выше конструкция при-
применима не к любому пути в Я, а только к такому пути, который гомото-
гомотопен нулю в G. Это означает, что отображение в тг2(СуЯ) определено не на
всей группе П\ (Я), а только на ядре гомоморфизма группы ni (Я) в ni (G),
порожденного вложением Я в С Это отображение является изомор-
изоморфизмом:
я2 (G/Я) = Ке^тг, (Я)
Существование описанного только что изоморфизма мгновенно вы-
вытекает из точной гомотопической последовательности расслоения
n2(G/H)
О
Для того, чтобы вычислить группу тг3(С/Я) удобно применить точную
гомотопическую последовательность расслоения (G, G/H, Я). Эта после-
последовательность имеет вид:
-*¦ тг3(Я) -»¦ тг3(С) -*¦ тг3(С/Я) -
Вспоминая, что 7Г2(Я) = 0, мы видим, что гомоморфизм р„ отображает
группу 7Г3(<7) на всю группу 7Г3(С/Я). В силу точности последовательно-
последовательности ядро гомоморфизма рт совпадает с образом гомоморфизма /» группы
ir3(ff) в 7Г3(С).Мы видим, что
тг3(С/Я)= я3(С)/1т/.. D)
Группы тгзС^) и 7Г3(Я) могут быть вычислены описанным выше способом.
Поэтому вьиисление группы n3(G/H) сводится к исследованию гомо-
гомоморфизма /,. Это исследование будет проведено в следующем параграфе.
Из доказанных в § 17 соотношений A7.9), A7.14), A7.17) следует,
что группы 7rfc@(m)), nk(U(m)), nk(Sp(m)) при достаточно больших
m стабилизируются (перестают зависеть от ni). Эти не зависящие от m
группы обозначаются соответственно символами тг^ (О), я^ (U), тг^ (Sp);
338

они называются стабильными гомотопическими группами классических
групп. Имеют место соотношения
), nk(O)= Jrfc+4(Sp) = яЛ + 8(О) E)
(теорема периодичности Ботта). Применяя соотношения E) и используя
равенства
tto(U) = 0, пгф) = S,
я0(О) = Я2, 71,@) = 2Г2, тг2(О) = О, 7Г,(О) = Z, F)
я4(О) = 0, тг5(О) = 0, я6(О) = 0, тг7(О) = Z-,
можно полностью вычислить группы nk(O), ^k(U), 7rfc(Sp).
§ 21. Гомологии групп Ли и однородных многообразий
Будем рассматривать гомологии гладкого многообразия М, на котором
транзитивно действует связная компактная группа Ли G. Стационарную
подгруппу будем обозначать символом Н. (Мы уже отмечали, что всякое
связное односвязное однородное многообразие гомотопически эквивалент-
эквивалентно многообразию описанного только что типа. Это означает, что наложенные
нами ограничения несущественны в задаче о вычислении групп гомологии и
когомологий.)
Будем изучать группу когомологий H*(iM). Эта группа (точнее векторное
пространство) определяется как факторгруппа группы Zk (M) все.х зам-
замкнутых fc-форм по группе Я* (М) всех точных (когомологичных нулю)
fc-форм. Мы покажем, что при вычислении когомологий достаточно рас-
рассматривать только инвариантные формы. Иными словами, группа Н\ (М)
изоморфна факторгруппе Zfnv (M)IB?ny (M), где Z\ny (M) и fifnv (M) -
группы инвариантных замкнутых k-форм и инвариантных точных к-форм
соответственно.
Проверим прежде всего, что всякая замкнутая fc-форма когомологична
инвариантной замкнутой fc-форме. Заметим, что замкнутая форма со кого-
когомологична замкнутой форме (<ру)*со (как всегда, символ %pg обозначает
преобразование многообразия М, отвечающее элементу g&G). В самом
деле, в силу связности группы G элемент g можно соединить кривой с еди-
единичным элементом группы G, поэтому преобразование ipg гомотопно
тождественному преобразованию. Отсюда следует, что для любой замкну-
замкнутой формы со форма (ipg)* со когомологична со (при гомотопных преобразо-
преобразованиях <#g и (pi = 1 форма из переходит в когомологичные друг другу
формы (ipg)* со и со). Таким образом, можно найти форму ag, для которой
(ipg)*u>- u)=dog. A)
По каждой форме и> построим инвариантную форму со с помощью
усреднения по группе
u=f(#g)*udg; B)
здесь символ dg означает инвариантный объем на группе G, нормированный
условием fdg = 1, Для того, чтобы проверить инвариантность формы со,
339

заметим, что .
Ой )* w = / (vh)*(ipg)* и dg p
(Мы заменили интегрирование по g интегрированием по hg и воспользо-
воспользовались инвариантностью элемента объема при этой замене.) Форма oJ ко-
гомологична форме со . Для того, чтобы в этом убедиться следует проинте-
проинтегрировать соотношение A) по группе G:
w = / (</>у)* coufc = /(со + dog) dg - Jojdg + fdogdg = oj+ d fag dg
(при преобразованиях использовано условие нормировки fdg = 1).
^ Приведенное доказательство не вполне аккуратно, поскольку мы не
проверили, что форму ag можно выбрать так, чтобы интеграл Jag dg имел
смысл. Эту неточность легко устранить, показав, что ag можно считать
кусочно-гладкой функцией от g. у
Рассуждение, совершенно аналогичное приведенному выше показывает,
что в случае, если инвариантные замкнутые формы ш1 и со2 когомологич-
ны, можно найти такую инвариантную форму р, что
ш2 -Ui =dp.
В самом деле, если <х>2 — ш\ =dr, го можно получить нужную форму р с
помощью усреднения формы т:
dp = d f fogfrdg = f (upgY (dT)dg=f(<pgf (w2 - Wi) dg = co2 - со,.
Доказанное утверждение позволяет ограничиться при вычислении Нк(М)
инвариантными формами.
Для описания инвариантных fc-форм на однородном многообразии доста-
достаточно описать антисимметричные тензоры ранга к в какой-либо точке этого
многообразия, инвариантные относительно стационарной подгруппы Н этой
точки.*) (Вместо антисимметричных тензоров можно рассматривать анти-
антисимметричные полилинейные формы, инвариантные относительно стацио-
стационарной подгруппы.) Мы видим таким образом, что вычисление групп Нк(М)
для однородного многообразия М сводится к задаче линейной алгебры.
Вычислим, например, таким способом когомологии сферы 5". В этом
случае G = SO (п + 1), Н= SO(«). Задача сводится к нахождению антисим-
антисимметричных тензоров ранга к в и-мерном пространстве, инвариантных отно-
относительно группы SO (и). При кФО, кФп таких тензоров не существует,
при к = п существуют инвариантные тензоры вида \eti ...,-„; им отвечают
инвариантные формы на Sn. Эти формы замкнуты, как и все и-формы на
S". Мы видим, что линейное пространство Н"E") одномерно: Н"E") = R1.
Антисимметричные тензоры ранга 0 — это скаляры. Таким образом,
H°(S") = R1.
Особенно удобно вычислять описанным выше методом гомологии
групп Ли. Компактную группу Ли G можно рассматривать как однородное
многообразие, на котором действует rpyiflra GX.G. (Элемент (tfi.g^) e
6 G XG переводит убСв gigg^1-) Формы на G, инвариантные относитель-
•) Нужно пользоваться тем.что инвариантные/t-формы находятся во взаимно одно-
однозначном соответствии с инвариантными антисимметричными тензорными полями.
(Мы все время рассматриваем здесь тензоры с нижними индексами.)
340

но этого действия, - это двусторонне инвариантные формы (формы, не
меняющиеся как при левых, так и при правых сдвигах). Они находятся
во взаимно однозначном соответствии с антисимметричными тензорами
(или антисимметричными полилинейными формами) на алгебре Ли &
группы G, инвариантными относительно присоединенного представления.
(Касательное пространство в единичном элементе группы отождествляется
с алгеброй Ли $, стационарная подгруппа единичного элемента изоморфна
группе G и действует на $ с помощью присоединенного представления.) Мы
докажем, ниже, что всякая двусторонне инвариантная форма на G замкну-
замкнута; отсюда следует, что элементы группы Hk(G) находятся во взаимно
однозначном соответствии с двусторонне инвариантными формами на G.
Таким образом задача вычисления групп Н* (G) эквивалентна задаче об
описании антисимметричных тензоров в $, инвариантных относительно
присоединенного представления. Отметим, что из этого факта вытекает, что
группы Нк (G) зависят только от алгебры Ли и, следовательно, не меняются
при замене G на локально изоморфную ей группу.
^ Приведем доказательство того факта, что всякая двусторонне инва-
инвариантная форма со на группе G замкнута. Рассмотрим отображение а груп-
группы G на себя, определяемой формулой
o(g) =g'1-
Если форма со двусторонне инвариантна, то форма а*со также обладает
этим свойством. (Легко видеть, что o(hg) = o(g)h ~l, o(gh) =h~1o(g),
т.е. при отображении а левые сдвиги переходят в правые, а правые — в ле-
левые. Поэтому а переводит левоинвариантные формы в правоинва-
риантные, правоинвариантные - в левоинвариантные, а двусторон-
двусторонне инвариантные — снова в такие же формы). С другой стороны
отображение о переводит единичный элемент группы в себя и, следова-
следовательно порождает отображение а* алгебры Ли & в себя. (Алгебра отождест-
отождествляется с касательным пространством к G в единичном элементе.) Нетруд-
Нетрудно проверить, что а*я=— а для sG^, (Если g = 1 + а, где а бесконечно
мало, то a (g) =g~l = 1 - а.) Отсюда следует, что тензор ранга к в $ умно-
умножается на (— 1) при преобразовании а. Мы получаем, что
a*co=(-l)fcco C)
для любой двусторонне инвариантной формы со . (В единичном элементе
группы G инвариантная /г-форма характеризуется антисимметричным
тензором ранга к. В силу доказанного выше, соотношение C) справедливо
в единичном элементе. Но поскольку обе части равенства C) являются
инвариантными формами, это соотношение справедливо везде, так как
инвариантная форма полностью определяется своим значением в единичном
элементе) . Из равенства C) сразу следует, что форма со замкнута. В самом
деле, дифференциал dco формы to является, очевидно, двусторонне инва-
инвариантной (к + 1)-формой и, значит,
a*(tfco) = (- l)k+ldco. D)
С другой стороны из соотношения a*d = da и равенства C) видно, что
o*(du>) = t1a*w = (-\)kdcj. E)
Из сравнения D) и E) следует dto = 0.
341

Отметим, что для широкого класса однородных пространств — так
называемых симметрических пространств — также можно утверждать,
что всякая инвариантная форма замкнута. Доказательство полностью пов-
повторяет рассуждения, проведенные выше для случая групп.
Односвязное однородное многообразие G/H называется симметри-
симметрическим, если в алгебре Ли # группы G можно выбрать базис A i, ... ,hr ,
v i vp таким образом, чтобы А х А г представляли собой базис
подалгебры ЗС, отвечающей стационарной подгруппе Н, и чтобы имели
место соотношения
[Ль А/] =
[hi, va] =
Ki, U k'<r ,l< a, (t, 7 < p.
Тогда линейное отображение X алгеоры iS на себя, определяемое соотно-
соотношениями A(Aj) = ht, X (v a) =va, является автоморфизмом алгебры ??.
Без ограничения общности можно считать, что группа G односвязна. Авто-
Автоморфизм X алгебры ?? порождает автоморфизм X соответствующей одно-
связной группы G. Из того, что X оставляет на месте элементы алгебры
Ли ЭС, отвечающей группе Н, следует, что X оставляет на месте элементы
группы Н. Напомним, что мы предположили односвязность многообразия
G/H; из этого предположения вытекает связность группы Н. Мы видим,
что автоморфизм X порождает отображение многообразия G\H на себя.
(Если ^,?2 G G,h еЯи?1 =?2А, тоХС?!) =^(?2)^(Л) = ^(ЫЛ •
Это значит, что два элемента, принадлежащие одному смежному классу
по Н, переходят при отображении X в элементы, обладающие тем же свой-
свойством.) Порождаемое автоморфизмом X отображение многообразия
G/H следует использовать вместо отображения о при доказательстве
замкнутости G-инвариантной формы на G/H.
Отметим, что чаще всего встречающиеся однородные многообразия
(сферы, многообразия Грассмана, многообразия Штифеля и т.д.) являются
симметрическими пространствами, т
Остановимся на группах гомологии групп Ли в размерностях < 3. Из
теоремы Гуревича (§15) вытекает, что для односвязной группы Ли G
имеют место соотношения
Я,(СУ) =H2(G,Z) = О,
я3(с, г) = 7Г3(С).
Если G — компактная группа Ли, то, как мы уже говорили, группа я3 (G)
является прямой суммой г экземпляров группы Z, где г — число неком-
некоммутативных алгебр Ли в разложении алгебры Ли ?? группы G в прямую
сумму простых алгебр Ли. Отсуда следует, что трехмерное число. Бетти
группы G равно г. По теореме де Рама (§9) размерность векторного
пространства НЭ(М) также равна г. В силу описанного выше соответствия
между элементами групп когомологий и инвариантными антисимметрич-
антисимметричными тензорами это означает, что в алгебре # существует ровно г линейно
342

независимых антисимметричных тензоров ранга 3, инвариантных относи-
относительно присоединенного представления группы G. В частности, если G —
простая некоммутативная компактная группа, то всякий инвариантный
антисимметричный тензор ранга 3 в алгебре Ли этой группы имеет вид
^•fapy гДе fafiy ~ структурные константы группы в некотором базисе,
ортонормированием относительно инвариантного скалярного произведения
в ??, X — вещественное число. Соответствующая тензору fapy полилиней-
полилинейная форма на 5? может быть записана в виде
(X, \У,А)=Га&уХаУ&2*
или в виде
-Sp(X;LH, *]), G)
если G = SU(/i) (см. §А7). Обозначим через со инвариантную 3-форму на
группе G, отвечающую тензору fapy- Инвариантное скалярное произве-
произведение в алгебре Ли простой компактной группы Ли определено с точностью
до множителя; мы воспользуемся этой свободой для того, чтобы нало-
наложить на форму со условие
/со = 1, (8)
z
z
где z — трехмерный цикл, принадлежащий классу гомологии, являющему-
являющемуся образующим элементом группы Н3 (G, ~Z). Тогда для всякого цикла
Г имеет место соотношение
/со = т,
г
где т — целое число, отвечающее классу гомологии цикла Г. (Напомним,
что для простой некоммутативной односвязной компактной группы Ли
H3(G, Z) = Ж) В частном случае G = SU(n), нормированное должным
образом скалярное произведение в алгебре Ли этой группы - алгебре анти-
антиэрмитовых матриц su(/i) —, определяется формулой
{х'у) = b (+
и форма со дается соотношением
_ 1 _! _! _,
Для произвольной группы форма со может быть записана в виде
со = (g^dgA [g-ldghg-ldg\ ), A1)
где скалярное произведение < , > нормировано условием (8). (Выражение
g ~l dg можно рассматривать как левоинвариантную форму на группе G,
принимающую значения в алгебре Ли ?? •). Отсюда следует, что выраже-
выражение A0) является левоинвариантной числовой формой на G'. С другой
стороны A0) в точке g = 1 совпадает с инвариантной трилинейной фор-
¦'О формах со значениями в векторном пространств и операциях с такими фор-
формами см. §22.
343

мои G). Отсюда следует, что A0) на самом деле двусторонне инвариант-
инвариантная 3-форма).
Образующий элемент группы H3(S\J(n)) определяется циклом, отве-
отвечающим многообразию S = SUB), стандартным образом вложенному
в SU(n). (Это следует из доказанного в § 17 утверждения, что вложение
SUB) в SU(n) порождает изоморфизм групп w3(SUB)) и jr3(SU(n).)
Это обстоятельство позволяет ограничиться случаем и = 2 при проверке
того, что скалярное произведение (9) в алгебре su(n) нормировано соот-
соотношением (8). Для и = 2 непосредственное вычисление показывает, что
форма A0) совпадает с формой объема на SUB) = S3, нормированной
условием обращения в 1 полного объема группы SUB). Это доказывает
соотношение (8) для группы SUB) и, стало быть, для произвольной груп-
группы SU(n). Отметим, что с помощью формы со легко выяснить к какому
гомотопическому классу относится отображение g (х) сферы S3 в груп-
группу G. Именно, целое число, отвечающее этому гомотопическому классу
в силу изоморфизма 7Г3(С) = 72, дается формулой
n(g)= / «= fg'oj. A2)
g(S3 > S3
(Ввиду изоморфизма 7Гз(С) = H$(G, Я) число и Of) совпадает с целым
числом, отвечающим классу гомологии цикла g(S3). Форма g*oo полу-
получается из со с помощью подстановки функции g(x) вместо точки g G G.)
В частности, для группы G = SU(n)
n{g)= -^ fSp(g-1(x)dg(x)[g-1(x)dg(x)Ag-1(x)dg(x)])dX.
4Sir2 s3 ¦
В дальнейшем нам будет удобнее нормировать скалярное произведе-
произведение в алгебре,Ли простой компактной группы Ли условием
/ = 1, A3)
24тг
.2
2
поскольку тогда скалярное произведение в алгебре su (и) выглядит очень
просто: (х, у > = 2 Sp xy+ = —2 Sp xy. Проанализируем теперь гомомор-
гомоморфизм Т„ группы H3(G, ~S) в группу Я3(§, 72), порождаемый гомоморф-
гомоморфным отображением группы G в группу G. Будем предполагать, что G и
G — простые некоммутативные односвязные компактные группы Ли.
(Это предположение не приводит к существенному ограничению общно-
общности, так как любая связная группа Ли гомотопически эквивалентна ком-
компактной группе, а компактная группа Ли локально изоморфна прямому про-
произведению простых групп Ли.) В рассматриваемом нами случае H3(G, Ж)=Ж,
#з (G, И) = 72, поэтому интересующий нас гомоморфизм Т', можно интер-
интерпретировать как гомоморфизм группы "Z в 72. Всякий такой гомомор-
гомоморфизм сопоставляет каждому числу к е ~2 число mk е 72, где тп - целое
число. Число /?? называется индексом Дынкина, гомоморфизма Т груп-
группы G в группу 'G'. Этот индекс может быть легко вычислен, если в- алгебрах
Ли # и # групп G и G введены инвариантные скалярные произведе-
произведения, нормированные условием (8) или A3). Именно, справедливо сле-
344

дующее соотношение:
т = —
где t - гомоморфизм алгебры ?9 в 5?, порождаемый гомоморфизмом Г
группы GbG, ахиу- произвольные элементы алгебры #. Доказательст-
Доказательство равенства A4) основано на замечании, что выражение
(t(x),t(y)) = <х,у)' A5)
можно рассматривать как инвариантное скалярное произведение в алгеб-
алгебре ??, поэтому выражение A5) только численным множителем ц отлича-
отличается от нормированного скалярного произведения (х, у) в f§ :
* (х,уУ - ц(х,у >.
Далее f'a&1 = nfapy, и' =/ju. (Здесь f'apy и fa&y - тензоры структур-
структурных констант, построенные по скалярным произведениям (,)' и (,>,
о/ и ш — соответствующие 3-формы на 59.) С другой стороны легко про-
проверить, что со' = T*oj, где B есть З-фор^ма в ^.построенная по нормиро-
нормированному скалярному произведению в ?9. Мы видим, что T*Z> = ды. Для
того, чтобы доказать соотношение A4), нужно убедиться, что т = ц;
этот факт следует из равенств
т = / cj = /Г*2> = //iw = М- . A6)
Т\z z z
Сформулируем без доказательства некоторые общие утверждения,
касающиеся структуры групп когомологий Hfc(G) группы Ли G. Опре-
Определенное в § 10 умножение классов когомологий позволяет рассматри-
рассматривать прямую сумму групп Нк(G) как алгебру - алгебру когомологий
группы G. Эта алгебра когомологий оказывается изоморфной грассмано-
вой алгебре с г образующими, где г — ранг группы G. Иными словами,
существуют такие нечетномерные классы когомологий еь . . . , ег, что
всякий элемент алгебры когомологий однозначно представим в виде
г
2 2 at t.et .. . et.,
k = о /,... ik * ' *
где коэффициенты ati. -/fc - антисимметричны по индексам i\, . . . , ik.
Размерности образующих elt . . . , ег для классических групп даются со-
соотношениями.
dimefc = 2>t + 1 для G = SU(r+ \\
dime* = 4k- 1 для G = S0Br+ 1),
dime* = 4fc— 1 при k <'.'r, dimefc = 2r- 1 для G = S0Br),
dim ek = 4k - 1 для G = Sp(r).
345

§ 22. Калибровочные поля и связности
Пусть G - группа Ли, 5? - ее алгебра Ли. Под калибровочным полем
понимается векторное поле Ац, принимающее значение в алгебре Ли ??.
(Мы рассматриваем в этом пункте калибровочные поля, определенные
в области U пространства IR".) Поле Ац является вектором с нижними
индексами (ковектором). Если в алгебре Ли выбран базис ех, . . . , ег,
тополеЛм(х) можно представить в видеЛм(х) = А*(х)ек, где.4д(х) -
числовые векторные поля. Таким образом, векторное поле Аи со значе-
значениями в алгебре Ли можно рассматривать как совокупность г числовых
векторных полей.
Пусть ф(х) - поле, принимающее значения в пространстве представле-
представления Т группы G. (Иными словами, ф преобразуется по представлению Т
группы G.) Ковариантная производная VM ф поля ф(х) определяется фор-
формулой:
^Ф = д^ф + ЦА^ф, A)
где символ t обозначает представление алгебры Ли$, отвечающее пред-
представлению Т группы G.
Напряженность &^„ калибровочного поля Ац определяется соотно-
соотношением:
Уду = ЪрА,, — ЭуЛм + [/1м,/1у]. B)
Легко видеть, что
(VMV,- V,VM)^ = 1^„)ф. , C)
Калибровочное преобразование определяется функцией g(x), прини-
принимающей значения в группе G. Поле ф(х), преобразующееся по представле-
представлению Т группы G, изменяется при калибровочном преобразовании по фор-
формуле:
D)
Закон изменения калибровочного поля Ац(х) при калибровочном пре-
преобразовании дается соотношением:
А'м(х) = т(g(x))А»(х) - (дм g)g'1 (x), E)
где т — присоединенное представление группы G.
Легко видеть, что
^(x). F)
Здесь V'^ обозначает ковариантную производную по полю А'ц. (Собствен-
(Собственно, закон преобразования калибровочного поля выбирается так, чтобы
было выполнено соотношение F).)
Напряженность &'цг, поля А м связана с напряженностью $-ци поля Ац со-
соотношением
*>„(*) = г(?(х))^(х). G)
(Это можно вывести, применяя соотношение C) для величины ф, пре-
преобразующейся по присоединенному представлению.)
346

Поле А ц называется чисто калибровочным, если оно калибровочно эк-
эквивалентно полю, тождественно равному нулю. Иными словами, поле
является чисто калибровочным, если оно может быть представлено в
виде
A^x) = g-1(x)dltg(x). (8)
Из соотношения G) следует, что напряженность чисто калибровочного
поля тождественно равна нулю. Оказывается, что в односвязной обла-
области верно и обратное утверждение: если ^,„ = 0, то поле имеет вид (8).
Понятие калибровочного поля является обобщением понятия электро-
электромагнитного поля. Именно, электромагнитное поле можно рассматривать
как калибровочное поле, отвечающее коммутативной группе Ли U(l).
Формулы, определяющие напряженность калибровочного поля и калибро-
калибровочные преобразования, сводятся для группы U(l) к стандартным фор-
формулам теории электромагнитного поля:
и v "~ ц v v ^ ji >
По каждому калибровочному полю можно построить связность, т.е.
правило переноса величины, преобразующейся по представлению груп-
группы G, вдоль кривой. Точнее говоря, каждой кривой Г можно сопоставить
элемент ЬГ группы G так, чтобы были выполнены условия;
1) если кривая Fj начинается в точке а0 и кончается в точке я1; кри-
кривая Т2 начинается в точке ах и кончается в точке аг, кривая Г составлена
из кривых Г! и Г2, то
Ъг = bTjbTi, (9)
2) если Г — бесконечно малая кривая, соединяющая точки х и х + dx, то
bT = l-A^dx». A0)
Покажем, что эти условия определяют Ьг. Пусть кривая Г задана с по-
помощью параметрического уравнения х = х (t), 10 < t < t \. Обозначим сим-
символом Г (а) часть кривой Г, отвечающую значениям параметра в интер-
интервале t0 < t < а. Тогда
dbT(a) / dx" \
-P^ = -UM—-)ьг(а). A1)
da \ do /
Соотношение A1) получается, если заметить, что кривая Г (а + d а) состоит
из кривой Г (а) и бесконечно малой кривой, соединяющей точки х(а) и
х(а + da). Уравнение A1) вместе с начальным условием ЬГ(, ) = 1
позволяет найти br = br(fj).
Используя понятие упорядоченной экспоненты, можно записать Ьг
в виде:
/ т' dx" \ / \
A2)
Отметим, что Ьг очень просто преобразуется при калибровочном пре-
преобразовании поля Ац. Именно, если Ьг и Ьр построены по калибровоч-
347
Ьг = Рехр(-/ Аи da )= Pexpl - fA^dx" ).
\ tQ do / \ г /

ным полям А м и Лм, связанным соотношением E), то
'(те Л ПТ»
тде х0 и Xi — начало и конец кривой Г. Соотношение A3) можно доказать
сначала для бесконечно малых кривых с, помощью A0), а затем распро-
распространить на произвольные кривые с помощью (9).
С помощью Ьг можно определить перенос величины ф, преобразующей-
преобразующейся по представлению Т, вдоль кривой Г, полагая, что ф(х0") переходит в
Ф(Хг)= Т(Ьг)ф(х0). A4)
Здесь Хо - x(t0) — начало, a *j = x(tt) — конец кривой Г. При переносе
вдоль кривой Г (о), определенной выше, ф(х0) переходит в ф(х(о)) =
= Г(Ьг(а)) Ф (*о); легко видеть, что
d ( dx" \
— ф(х(р)) = -НЛм(х(а)) —- )ф(х(о)). A4')
da \ do /
Рассмотрим в качестве кривой Г бесконечно малый прямоугольник
со сторонами, направленными по осямхц их" соответственно. Нетрудно
проверить, что в этом случае:
ЪГ= 1 -$nvdS +..., A5)
где dS — площадь прямоугольника и отброшенные члены имеют более
высокий порядок малости чем dS. Для доказательства этого соотношения
нужно представить Ьг как произведение элементов Ьг., где Fi, Г2» Г3, Г4 —
стороны прямоугольника, и вычислить Ьг. с точностью до второго поряд-
порядка по длине стороны Г,- (например, с помощью соотношения A2)).
В случае, если Г — произвольная бесконечно малая замкнутая кривая,
можно доказать следуюшее обобщение соотношения A5) :
*г =1-^ f»vdo»v +..., A6)
где da^" - бивектор, отвечающий поверхности, ограниченной кривой Г
(бесконечно малую замкнутую кривую можно считать плоской;, в плос-
плоскости, где лежит Г, она ограничивает область; символ do**" обозначает
площадь проекции этой области на плоскость, натянутую на оси /и/).
Отметим, что калибровочное поле определяет параллельный перенос в
прямом произведении U X G. Будем считать, что группа G действует на точ-
точки пространства V X G с помощью правых сдвигов (элементу g ? G со-
сопоставляется преобразование, переводящее точку (х, h) G U X G в точку
(х, h)g = (x, hg)). Пространство U XG расслаивается на орбиты группы G;
эти орбиты находятся во взаимно однозначном соответствии с точками
х Е U. Таким образом, мы получаем расслоение (U X G, U, G, р); проек-
проекция этого расслоения переводит точку (х^ й) е U X G в точку х G U. По
кривой Г в U, начинающейся в точке х0 €Е V и кончающейся в точке
jtj? У, можно построить отображение слоя над точкой х0 в слой над точ-
точкой Xi; именно точке (Xq, h) сопоставляется точка (xi, brh). Заметим,
что построенное только что отображение Хг слоя над х0 в слой над *i
коммутирует с правыми.сдвигами на элементы группы G: если при ото-
348

бражении Хг точка (х0, Л) переходит в (xlt h'), то точка (х0, hg) пере-
переходите (Xi.h'g).
Рассматривавшееся выше расслоение (U X G, U, G) является тривиаль-
тривиальным главным расслоением (см. § 16). Существенно, что калибровочное
поле порождает параллельный перенос слоев также в произвольном три-
тривиальном расслоении вида (U X F, U, F), где F — пространство, на котором
действует группа G. (Мы будем считать, что G действует на F слева с по-
помощью отображений T(g).) Параллельный перенос слоев в этом расслое-
расслоении переводит точку (*о>/) над началом кривой Г в точку (jci, T(br)f)
над концом кривой Г. В наиболее важном случае, когда F - пространство
линейного представления Т группы G, сечения расслоения (U X F, U, F)
отождествляются с полями, преобразующимися по представлению Т, а
операция параллельного переноса тесно связана с операцией ковариантно-
го дифференцирования. В частности, если поле у (х), преобразующееся по
представлению Т, удовлетворяет на кривой Г соотношению
dx»
?м**) "Г" =0>
da
то при параллельном переносе вдоль Г точка (х0, </>(х0)) переходит в точ-
точку (*i,(/>(*i)) (это следует из A41)).
Введем важное понятие группы голономии калибровочного поля. Фик-
Фиксируем точку х0 и рассмотрим элемент ЬГ, построенный по калибровоч-
калибровочному полю Ац и кривой Г, начинающейся и кончающейся в точке х<>. Мно-
Множество таких элементов образует подгруппу группы G (это немедленно
следует из соотношения (9)). Построенная таким образом подгруппа
Н(х0) называется группой голономии калибровочного поля в точке х0.
Группы голономии двух калибровочно эквивалентных полей сопряжены
друг другу. (Если калибровочная эквивалентность между полями А'ц и
Ац осуществляется функцией g (х), то для всякой кривой Г, начинающейся
и кончающейся в х0, в силу соотношения A3) имеем b'r =g (xo)brg~l(xo))
Отсюда следует, что в случае, когда поле Ац калибровочно эквивалентно
полю А'ц, принимающему значения в алгебре Ли подгруппы Gx группы G,
группа голономии поля Аи содержится в подгруппе, сопряженной подгруп-
подгруппе G\. В случае, если область U односвязна, можно доказать, что справедли-
справедливо и обратное утверждение: для всякого поля Ац можно найти калибро-
калибровочно эквивалентное ему поле А'ц, принимающее значения в алгебре Ли
группы голономии поля Ац. В частности, если Ьг = 1 для любой замкну-
замкнутой кривой Г, то группа голономии состоит только из единичного элемен-
элемента и, следовательно, поле Ац калибровочно эквивалентно полю А'ц= 0.
(Этот факт мы уже отмечали раньше.) Из соотношения A5) следует, что
для любых индексов ц, v элемент W^v (x0) алгебры Ли & принадлежит
алгебре Ли группы голономии калибровочного поля Ац в точке х0 ¦
а Установим теперь связь описанных только что конструкций с приня-
принятым в математике определением связности в главном расслоении. Заме-
метим, прежде всего, что касательное пространство к многообразию U X G
в точке (х, 1) может быть отождествлено с пространством И" X 5?, по-
поскольку алгебра Ли # отождествляется с касательным пространством к
группе G в единичном элементе. Выделим в линейном пространстве IR" X 5?
349

подпространство &(x,i)> состоящее из точек вида (?, —Av (х) %"), где
% = (? *,. . . , %") € R". При сдвиге на элемент g € G точка (*, 1) перехо-
переходит в (х, g), а касательное пространство к U X G в точке (х, 1) переходит
в касательное пространство в точке (х, g). Подпространство касательного
пространства к U X G в точке (х, #), получающееся из &(x,i)» обозначим
символом 5(Хг8). Подпространства вида &(Хд) > полученные описанным
только что способом, будем называть горизонтальными подпространства-
подпространствами. Эти подпространства задают в тривиальном главном расслоении
(?/ X G, U, G, р) связность в принятом в математике смысле этого слова.
Напомним, что связность в главном расслоении (Е, М, G) можно задать,
выделив в каждой точке е&Еподпространство $е касательного простран-
пространства к Е в точке е. Подпространства 5е называются горизонтальными
подпространствами. При преобразованиях из группы G горизонтальное под-
подпространство должно переходить в горизонтальное подпространство. Кроме
того, следует потребовать, чтобы касательное пространство к Е было прямой
суммой горизонтального пространства 5е и пространства, касательного
к слою, — вертикального подпространства.
Отметим, что с помощью связности можно определить процесс подня-
поднятия кривой из базы В главного расслоения в пространство Е этогб расслое-
расслоения. По определению поднятая кривая — это кривая, лежащая над кривой
Г и касающаяся в каждой точке горизонтального подпространства. Для
тривиального главного расслоения можно дать следующее конструктивное
определение поднятой кривой.
Пусть Г С U — кривая с параметрическими уравнениями х = x(t), t0 <
<?<?i. Обозначим символом Г (а) часть кривой Г, отвечающую значениям
параметра в интервале t0 < t < а. Перенося точку (x(t0), А), лежащую в
слое над началом кривой Г (а), вдоль кривой Г (а), мы получим точ-
точку (х(а), ЬГ(О)А), лежащую в слое над концом кривой Г(а). Точки
(х(а), ^г(о) А), где /0 < а < f i, образуют кривую в U X G, лежащую над
кривой Г. Процесс перехода от кривой Г к этой кривой называется подня-
поднятием кривой Г с помощью связности, т
При изучении калибровочных полей удобно пользоваться дифферен-
дифференциальными формами, принимающими значения в линейном пространстве.
Пусть V — линейное пространство размерности г. Под К-значной внеш-
внешней дифференциальной s-формой на области U CFt" понимается выражение
вида
w = cj^j ... \s dxx* Л ..- Л dx^11,
где "а . а, — функции, заданные на U и принимающие значения в V.
Если Vi,..., vr — базис в К, то форму со можно представить в виде
о = oj"va,
где ш1,..., о/ - числовые дифференциальные формы.
Таким образом, К-значная форма может рассматриваться как совокуп-
совокупность г числовых форм of, где индекс а (внутренний или изотопичес-
изотопический) пробегает г значений.
Калибровочному полю А^ можно сопоставить 1-форму
А = A^dx» , A7)
350

принимающую значение в алгебре Ли -9; нам часто будет удобно отождест-
отождествлять калибровочное поле с этой 1-формой. Если поле А'ц калибровочно
эквивалентно полю Ам, то соответствующие 1-формы связаны соотно-
соотношением
A' = T(g)A ~(dg)g-1,
А = T(g-y)A' + g~ldg.
Если поле А^ калибровочно эквивалентно нулю, то отвечающая ему форма
имеет вид
А = g-*dg
(эти соотношения эквивалентны E), (8)).
Напряженность калибровочного поля 5^„ можно рассматривать как
2-форму
&= - W^dx» Ndxv = dA + -[А А А], A8)
2. 2.
также принимающую значения в #. Выражение [А А А], фигурирующее
в A8), расшифровывается как [Ац,А„] dx"Adxv.
Ковариантный дифференциал dAco формы со, принимающей значения в
пространстве представления Т группы G, определяется формулой
¦ dAoi = dco + t(A) A со. A9)
* Ковариантный дифференциал определяется по отношению к калибро-
калибровочному полю Ац. Символ t обозначает представление алгебры Ли &, отве-
отвечающее представлению Т группы G. Если е\, . .. , ег — базис алгебры Ли &,
(Е™){, . . . (?"Г)г — матрицы преобразований t(e{), . . ., t(er) в некото-
некотором базисе пространства представления- Т, то в этом базисе
(t(A) A uf = (EZ^Aldx» А сЛ B0)
Символ d обозначает обыкновенный внешний дифференциал. Ў
В частности, если со есть 0-форма (т.е. просто функция), то
dAco = Vyco'dxy. BJ)
Если Г-форма cj = u^dx*1, то
dA<» =\ (ул"м - V^K)dxx A dx». B2)
Вообще, коэффициентные функции формы dAoo получаются с помощью
ковариантного дифференцирования коэффициентных функций формы со и
последующей антисимметризации. Иными словами, вычисление ковариант-
ковариантного дифференциала производится по тем же правилам, что и вычисление
обычного внешнего дифференциала с заменой обычных производных на ко-
вариантные. Пользуясь этим замечанием и соотношением C), легко прове-
проверить, что
d\ со = f(F) Л со. B3)
Здесь У обозначает 2-форму, отвечающую напряженности калибровочного
351

поля А,
= (Ekm)a - WLdx» J\dxv B4)
2
— матричнозначная 2-форма,
(t(f) Aw)m = - (Ekm)a Wa dx> Л dxv Л сЛ
2
Ковариантный дифференциал 2-формы $¦ , отвечающей напряженности,
равен нулю:
dAf = 0. B5)
Это важное соотношение носит название тождества Бианки; используя
связь между ковариантным дифференциалом и ковариантными производ-
производными, можно переписать B5) в виде
Vp %v ¦+ VM 9V9 + V,, fPll = 0. B6)
Доказательство тождества B5) удобнее всего основывать на замечании,
что для любой точки х можно найти калибровочное преобразование поля
А(х) в калибровочное поле А'(х), обращающееся в нуль в точке х. Для
поля А'{х) тождество Бианки в точке х очевидно; в силу сделанного за-
замечания отсюда вытекает тождество Бианки в общем случае.
Рассмотрим некоторые операции с векторно-значными формами. Если
в пространстве V определено скалярное произведение < , >, то естест-
естественно определяется скалярное внешнее произведение (ь)\ Л cj2> форм
cjj и cj2, принимающих значения в V. Это произведение является число-
числовой формой; если в базисе Vi, . . . ,vr пространства К скалярное произве-
произведение записывается с помощью матрицы hab (т.е. (va, vb) = hab), то
(cjj Л cj2 > = hab(J{ Л cj2,
где cjj, cj2 — компоненты форм cjj и cj2 в базисе Vi, . . . , vr. Мы будем
считать, что cji есть р-форма, а ш2 — g-форма, тогда < ш\ Л со2 > являет-
является числовой (р + ^)-формой.
В случае, если в пространстве V действует представление Т группы G,
имеет смысл говорить о ковариантных дифференциалах dAu)i и dAco2 форм
с^!, о?2 относительно калибровочного поля А, принимающего значения в
алгебре Ли группы G. Если скалярное произведение ( , > инвариантно
относительно представления Т, то легко проверить соотношение:
Соотношение B7) следует из соответствующей формулы для числовых
форм (см. § 6) и соотношения
<(t(A) Л cji) Л cj2 > - (-l)P <ш, Л (t(A) Л w2)> = 0, B8)
вытекающего из инвариантности скалярного произведения < , > .
352

§ 23. Калибровочные поля на многообразиях
Гладкое многообразие М можно считать склеенным из областей про-
пространства IR". Мы уже определили выше понятие калибровочного поля в
области пространства IR". Для того, чтобы задать калибровочное поле в
многообразии М, следует задать калибровочные поля в каждой из облас-
областей, из которых склеено М, наложив при этом некоторые условия согла-
согласования.
Перейдем к точному определению. Пусть гладкое многообразие М
покрыто областями Ult . . . , Uk, . . . , для каждой из которых задан глад-
гладкий гомеоморфизм на область пространства IR". Будем считать, что во
всех областях Ult. . . , Uk, . . . заданы калибровочные поля, принимающие
значения в алгебре Ли i§ группы Ли G; нам будет удобно представлять
эти поля с помощью 1-форм А (^ , . . . , А ^ . В области ?/,- П Uj заданы
одновременно поля А ^'^ яА*-''; будем говорить, что поля/1 **', ...,А^к'
задают калибровочное поле в многообразии М, если поле А(| * калибровоч-
но эквивалентно полю А *'* в области ?/,- П Uj для всех /,/ = 1,2 А:.
Иными словами, мы требуем, чтобы нашлись такие функции gfj (х), опре-
определенные на множествах Ut П Uj и принимающие значения в калибровоч-
калибровочной группе G, что*)
Мы предположили, что для областей Ult . . . , Uk фиксированы отобра-
отображения на области пространства й"; эти отображения позволяют ввести
координаты х1цу, . . . , х"^ в областях ?/,-. Калибровочное поле в области
U/ задается в этих координатах как векторное поле/4^- (*(,), • • • »*",-) )•
Условие согласования полей А^ и А^ на области Ut П Uj выглядит
следующим образом. Мы требуем, чтобы поле А^' * (х (,-),..., х",-)) было
калибровочно эквивалентно полю
(Соотношение B) означает, что поле А^' ^ преобразуется при переходе к
другой системе координат как ковектор.)
Мы видим, что определение калибровочного поля на многообразии в
терминах 1-форм
оказывается более простым; это связано с тем, что при определении с по-
помощью форм нет необходимости явно вводить координаты в областях
Vx Uk,...
В качестве примера рассмотрим калибровочные поля на сфере S". Бу-
Будем считать, что сфера 5" покрыта двумя стереографическими системами
*' Подчеркнем, что в A) и подобных ему соотношениях не подразумевается
суммирование по повторяющимся индексам, если эти индексы обозначают номер
области.
353

координат *(!)»••¦ t *"i) и XB)..... x"B) с центрами в северном и
южном полюсах сферы. Переход от одних координат к другим задается
формулой
ХB)
где Х(а) = (Х(а) *"<*))• Калибровочное поле на сфере задается с
помощью двух полей Л<° (X(i), . . . , х"A)) и А^2) (х\2) *))>
при этом поле А^ (*(i), . . . , х"^ ) должно быть калибровочно эквива-
эквивалентно полю
jP <f\hv ¦¦•• «B)) =
w
при 2 (*(i)J ^0. Из C) видно, что поле А^ (х'A) *"i)) имеет
на бесконечности асимптотику
(здесь С„ G ?? не зависит от х). Таким образом, поле А^ {х\^ х(i))
калибровочно эквивалентно полю, имеющему на бесконечности асимпто-
асимптотику D), и значит, убывающему на бесконечности не медленнее, чем
|Х(!) | ~2. Отсюда следует, что само поле А^ имеет на бесконечности
асимптотику ^"'Э^, где g — функция, осуществляющая калибровочную
эквивалентность между полями A Ji(*(i),..., x"i)) и А\{х (i),... ,x"i)).
Полученные результаты можно интерпретировать следующим образом.
Вместо калибровочного поля на сфере 5" можно рассматривать калибро-
калибровочное поле Ац (х1, . . ., х" ) в пространстве И", калибровочно эквивалент-
эквивалентное на бесконечности достаточно быстро убывающему полю. Однако обыч-
обычно удобнее обратный прием: если калибровочное поле на И" с достаточной
точностью является на бесконечности чисто калибровочным, его разумно
продолжить на S" и рассматривать как калибровочное поле на S".
Выше мы рассматривали поля и формы, преобразующиеся по представ-
представлению Т калибровочной группы G (т.е. принимающие значения б простран-
пространстве V этого представления), для случая, когда областью определения слу-
служила область в DR". В гладком многообразии М, покрытом областями
Ui, . . . , Uk, . . . мы определим поле (или форму), преобразующееся по
представлению Т, как совокупность полей (форм) cj*1' со* *
заданных соответственно в областях ?/1( . . . , t/k, ... и калибровочио
эквивалентных в областях Ut П Uj. ИЙаче говоря, требуется, чтобы для
каждой пары индексов i, / = 1 к нашлась гладкая функция gtj (x)
на Uj П Uj, принимающая значения в калибровочной группе G и удовлет-
удовлетворяющая условию
354

Если рассматривается одновременно калибровочное поле на много-
многообразии и поля или формы, преобразующиеся по представлению калибро-
калибровочной группы, мы всегда будем считать, что функции gtj, фигурирующие
в соотношениях A) и E),одни и те же. Если это условие выполнено, то с
помощью калибровочного поля А можно определить ковариантный диф-
дифференциал dAu> формы со, принимающей значения в пространстве представ-
представления V и заданной на многообразииМ как совокупность форм d^O) со*' *,
определенных в областях Ut Uk. (Мы считаем, что форма со опреде-
определена с помощью форм со*1* на областях Ut, а калибровочное поле/1 — с
помощью калибровочных полей А''* на этих областях.)
Поле <р, заданное на М и принимающее значения в пространстве V пред-
представления Т, можно рассматривать как 0-форму со значениями в этом про-
пространстве. Поэтому высказанные выше соображения позволяют опреде-
определить ковариантный дифференциал такого поля. Дифференциал поля у
представляет собой 1-форму на М со значениями в V. Эта форма задается
с помощью 1-форм VX(? *' * dx^t у, заданных в областях Ut\ (Здесь Vx =
= Эх + t(AJf)) — ковариантная производная, вычисленная с помощью ка-
калибровочного поля А *' *.)
Напряженность W калибровочного поля А на многообразии М опреде-
определяется как совокупность 2-форм &W, где fr^1 * - напряженность кали-
калибровочного поля А^' на U(. Как всегда, напряженность W является 2-фор-
мой, преобразующейся по присоединенному представлению группы G.
Существенно отметить, что калибровочное поле на гладком многообра-
многообразии нельзя рассматривать как 1-форму на этом многообразии (закон
преобразования A) отличается от закона преобразования 1-форм).Однако,
разность двух калибровочных полей А иА является 1-формой, преобразую-
преобразующейся по присоединенному представлению группы G. (Мы предполагаем,
что функции gtj, участвующие в определении полей А и А, совпадают;
тогда из A) следует, что Л(/) -AU) =T(gii(x))(A(-n ~AU)).)
В § 22 были введены различные операции с формами, принимающи-
принимающими векторные значения, для случая, когда эти формы определены в облас-
области пространства [R". Все эти операции без труда переносятся на случай
форм, определенных на гладком многообразии. (Например, если со и
а — две формы на М, заданные с помощью совокупностей форм со*'*
и а*'* на областях U{, то скалярное внешнее произведение (и Л о)
определяется как совокупность форм <со*'' Л а*1* > на ?/,-. Для того,
чтобы доказать корректность этого определения, следует проверить, что
формы < со*'* Ла*'*> и<со*;* Ло*^Ъ согласованы нужным образом на
Ut n Uj; это легко сделать.
Всюду в этом- пункте мы исходили из фиксированного разбиения мно-
многообразия М на области Ult , . . , Uk. Разумеется,одно и то же калибровоч-
калибровочное поле может быть определено с помощью различных разбиений мно-
многообразия М на области. Пусть Л*1* Л* * — калибровочные поля,
определенные на областях Ul, . . . , Uk и калибровочно эквивалентные на
областях Uj П Uj, а Л*1*, . . . , А^ — калибровочные поля, определенные
на областях {/|,...,{/, и калибровочно эквивалентные на Us О Um. Тогда
355

поля АA), . . . ,А{к) иполяЛA),. .. ,Л(/) задают одно и то же кали-
калибровочное поле на многообразии М в случае, если Л(>) калибровочно
эквивалентно A(s) на областях Ut n L/j.
Отметим в заключение, что в области t/ C1R", как и в произвольном
многообразии, можно определить калибровочное поле, разбив эту об-
область на меньшие области Ult . . . , Uk и задав в этих областях 1-формы
ЛA),... ,А(к) .удовлетворяющие условия согласования A). Такоеопре-
деление калибровочного поля на области является более общим, чем ис-
использованное в § 22, иными словами, поле, заданное с помощью семейства
форм АA), . . . , А(к), не всегда можно задать с помощью одной 1-формы,
определенной на всем U. Соответствующий пример содержится в § 24
(там показано, что поле магнитного заряда в 1R3\ {0}не может быть опи-
описано с помощью векторного потенциала, определенного на всей области
!R3\ { 0 } ). В дальнейшем, если не оговорено противное, рассматривая кали-
калибровочное поле в области f/ClR", мы будем предполагать, что оно задается
одной 1-формой (иначе говоря, для калибровочных полей в области мы
пользуемся определением § 22).
§24. Характеристические классы калибровочных полей
По калибровочному полю можно построить ряд числовых замкнутых
форм, которые носят название характеристических форм. Характеристи-
Характеристические формы не меняются при замене калибровочного поля на калибро-
калибровочно эквивалентное ему поле. Классы когомологий этих форм носят наз-
название характеристических классов. Характеристические классы не изме-
изменяются при непрерывном изменении калибровочного поля. Это утвержде-.
ние позволяет с помощью интегрирования характеристических форм со-
сопоставить калибровочному полю числа, не меняющиеся при непрерывном
изменении поля {топологические числа поля).
Простейшим примером характеристической формы является напряжен-
напряженность ^калибровочного поля, принимающего значения в алгебре Ли груп-
группы U(l). В самом деле, мы видели выше, что напряженность можно интер-
интерпретировать как 2-форму со значениями в алгебре Ли. В интересующей нас
ситуации алгебра Ли отождествляется с множеством действительных' чисел
1R1, а ковариантный дифференциал формы ^сводится к обычному диффе-
дифференциалу. Из тождества Бианки (9) вытекает поэтому, что W- замкнутая
2-форма. В рассматриваемом случае калибровочное поле можно отождест-
отождествить с электромагнитным полем; соотношение dS--^> является просто
одним из уравнений Максвелла. Если калибровочное поле задано на области
в пространстве 1R3, то форму $• можно интерпретировать как магнитную
напряженность, а интеграл от этой формы по двумерной замкнутой поверх-
поверхности можно отождествить с потоком магнитной напряженности через по-
поверхность, т.е. с магнитным зарядом.
Остановимся на этом подробнее. Обычн© электромагнитное поле зада-
задается антисимметричным тензором Fag, которому можно сопоставить замк-
замкнутую 2-форму ^=2" Fop dxa Л fit**3 (см. §6) .Если область U, в которой за-
задано электромагнитное поле, ациклична (например, совпадает со всем
пространством Минковского), то формаF точна, т.е. может быть представ-
356

лена в виде &=dA, где А = Л adxa интерпретируется как электромагнитный
потенциал. Если такое представление невозможно, то область U следует
покрыть ацикличными областями U^,..., Uk, . . . (например, взяв в качест-
качестве этих областей шары, лежащие в U) и в области Uk найти форму А^,.
удовлетворяющую условию S-~dA^. В пересечении ?/,• C\Uj имеем
d(A^ - А^~) = 0; в случае, если это пересечение ациклично (например,
если области Uk являются шарами), можно утверждать,что А^ — А"' =
= d\(l'l). Это означает,что в смысле §23 поляЛ1 >,..., А( ',... задают ка-
калибровочное поле, принимающее значения в алгебре Ли группы U(l)
(элементы алгебры Ли группы U(l) мы отождествляем с чисто мнимыми
числами; интересующее нас калибровочное поле задается 1-формами,
получающимися из А^\ ...,А^к\... умножением на мнимую единицу).
Рассмотрим в качестве примера замкнутую форму
<- х x1dx2 Adx3 + x2dx3Adx1 +x3dx1Adx2
f-*u'dS-g~ s? ¦
Эта форма определена при условии х = (х1, х2, х3)Ф0, т.е. в области
К3\{0}(если считать момент времени t фиксированным). Как говорилось в
§ 7, эта форма не является точной. Однако, хотя 3- нельзя представить в
виде dA во всей области 1R3\{O}, нужное нам представление возможно в
любой области, получающейся из Р удалением луча, исходящего из начала
координат. Например, если из Р3 удалить положительную часть оси х3,
то можно положить
А= к dx ^{Ы2 2dl)
gr ^3{х ).
W |х|-х3 /
По определению магнитный заряд внутри замкнутой поверхности равен
(с точностью до множителя Dтг)~') потоку магнитной напряженности
Н через эту поверхность, т.е. интегралу от^по поверхности (напомним, что
при фиксированном t форма Нравна Н dS). Форму ^можно интерпретиро-
интерпретировать как напряженность поля, создаваемого магнитным зарядом g, сосре-
сосредоточенным в начале координат, форму А — как потенциал этого поля.
(Этот потенциал сингулярен на луче, поэтому, строго говоря, нужно зада-
задавать интересующее нас поле семейством потенциалов, определенных в
разных областях). В обычной электродинамике электромагнитное поле
должно быть задано во всем пространстве Минковского. Отсюда следует,
что магнитный заряд всегда равен нулю. Это утверждение, однако, не
справедливо в единых теориях сильного, слабого и электромагнитного
взаимодействий, поскольку в них электромагнитное поле является вторич-
вторичным объектом и может быть определено не всюду.
В случае, если G — некоммутативная компактная группа Ли, можно опре-
определить замкнутую 4-форму как скалярное внешнее произведение 2-формы
$"на себя. Напомним, что в алгебре Ли & группы G можно ввести инва-
инвариантное скалярное произведение < , >; форма <^Л^"> определяется с по-
помощью этого скалярного произведения. Если G - компактная матричная
группа Ли, то форма <?"Л#) может быть записана в виде
357

Замкнутость формы <?7\ ?"> вытекает из соотношения B.10) и тождества
Бианки B.9) :
d(f/\9r)=<dAfbSr)+{3r/\dA$r)=0. A)
Мы будем называть форму (&А &) четырехмерной характеристической
формой, а ее класс когомологий - четырехмерным характеристическим
классом.
Покажем, что класс когомологий формы (S-A9-) не меняется при непре-
непрерывном изменении поля А. Достаточно проверить, что этот класс не меня-
меняется при бесконечно малом изменении поля А. Если калибровочное поле
А заменено на калибровочное поле А + 8А, где 6.4 — бесконечно малая
1-форма, то напряженность^заменяется на #"+ 8&, где
6 W= dA 8А = d8A + [A, 8А]; B)
это легко получить из соотношения B2.18). (Напомним, что калибровоч-
калибровочное поле на многообразии задается с помощью полей А^ на областях ?//
и что, рассматривая несколько калибровочных полей на многообразии, мы
молчаливо предполагаем, что функции^-, задающие калибровочную ¦экви-
¦эквивалентность полей Л О иА^ на Ut л U/ не зависят от выбора калибровочно-
калибровочного поля.)
Поэтому вариация формы < SFA ?) может быть записана в виде:
f 8A A f). C)
Отсюда видно, что
b(fA&) = Zd{bAAf). D)
В самом деле, в силу B.10) и B)
5 <&А Л ?">= <dA 8Ahf)- <8A /\dAf)= <8fAf).
Случай конечного изменения поля А, как всегда, сводится к случаю беско-
бесконечно малого изменения.
Отметим, что из доказанного следует, что форма <^Л^"> когомологична
нулю (т.е. четырехмерный характеристический класс равен нулю) в случае,
если рассматривается калибровочное поле на области U С IR". (Это стано-
становится очевидным, если заметить, что непрерывное семейство полей At =tA
соединяет произвольное калибровочное поле А с полем А = 0.) Для того,
чтобы явно выписать 3-форму, дифференциалом которой служит форма
<^Л?"), заметим, что напряженность &t поля At = tA дается форму-
формулой
ft = tdA+-t2[AJ\A] =tf+ -(t2 -t)[AAA].
Из D) вытекает, что
L
= df 2{A/\ \tf+-(t
о \ I 2
6 E)
358

Отметим, что проведенное только что доказательство не проходит для
калибровочных полей, заданных на произвольном многообразии, посколь-
поскольку в этом случае нельзя определить поле At = tA. (Если калибровочное
полеЛнамногообразииЛ/ определяется с помощью полей А О на областях
Uf С М, то калибровочные поля tA ^ ^ и tA ^'' не обязательно калибро-
вочно эквивалентны на U/ C\Uj-, мы не можем поэтому задать поле Ы на
М с помощью семейства полей tA *' ^.) Однако, очевидным образом спра-
справедливо следующее утверждение: если А и А — калибровочные поля на
многообразии М, заданные с помощью полей А^ и.А*-'' на областях Uf,
калибровочная эквивалентность полей А ^'* и A\j' определяется функ-
функциями gtj и калибровочная эквивалентность полей А *'' и А^'^ определяет-
определяется теми же функциями, то характеристические классы полей А и А
совпадают (для доказательства достаточно заметить, что поля А а А
можно соединить непрерывным семейством калибровочных полей At =
= tA+ (l-t)A).
Если М — четырехмерное компактное ориентируемое многообразие,
то число
F)
м
называется топологическим числом поля А. Из. сказанного выше следует,
что q (А) не меняется при непрерывной деформации поля А. (В этом мож-
можно убедиться, например, заметив, что F) представляет собой скалярное
произведение четырехмерного характеристического класса и класса гомо-
гомологии [М] многообразия М). Если многообразие М некомпактно, то ин-
интеграл F) может расходиться. Для того, чтобы выражение F) имело
смысл, достаточно предположить, что напряженность $ обращается в нуль
вне некоторого компактного подмножества многообразия М. Если поле
А непрерывно меняется таким образом, что в процессе этого- изменения
напряженность поля вне некоторого компактного множества/?С Мостает-
Мостается равной нулю, то топологическое число q(A), определенное формулой
F), не меняется. В самом деле, в силу соотношения D)
8q(A) = / 54FAF) = 2 fd
D D Г
(Мы предполагаем, что множество D ограничено, гладкой замкнутой по-
поверхностью Г; это можно сделать без ограничения общности.)
Проанализируем топологическое число калибровочного поля, заданного
на пространстве IB4, считая, что напряженность поля равна нулю вне шара
?>4 (т.е. поле калибровочно эквивалентно тривиальному вне шара). Топо-
Топологическое число в рассматриваемом случае можно записать в виде
q(A) = f <?ЛГ>=- / (fa0, fy6)dxaAdxl3/\dx^J\dx6 =
В4 4|R«
= ]f<^ap, ?rb>ea^Sd*x. G)
Во всех этих соотношениях можно заменить интеграл по IB4 интегралом
по D*. Для q (А) можно указать также выражения в виде интеграла
359

на сфере S3 = Э?>4 :
q(A)=-- f3(AA[AAA]> , (8)
(чтобы получить это выражение, следует воспользоваться соотношением
E), преобразовать интеграл по ?>4 в интеграл по S3 и учесть, что $= О
на S3). Вне шара?>4 поле/1 калибровочно эквивалентно нулю, т.е. может
быть представлено в виде A.7), где g(x) - .функция со значениями в
группе G.
Из результатов § 21 вытекает, что при описанной в § 21 нормировке
скалярного произведения в алгебре Ли условием B1.13) число
f<AA[AAA])= —— fig'1 dgA[g~l dgAg-1 dg])
48тг2 s* 48*2 s
является целым числом,характеризующим гомотопический класс отображе-
отображения g сферы S3 в группу G. Это показывает, что определение топологи-
топологического числа q(A) разумно изменить, введя в F) дополнительный мно-
1
житель ——, обеспечивающий целочисленность топологического числа. На-
Навет2
чиная с этого места мы будем определять топологическое число формулой
?(Л) = тт !<***>• (9)
Отметим, что топологическое число q(A) поля А, заданного .на р4, мо-
может быть определено также в случае, когда напряженность SF не обращается
в 0 вне шара, а лишь убывает достаточно быстро при | х\ -*-°°. Топологи-
Топологическое число д(А) не меняется при непрерывном изменении поля А я в
этом случае (это доказывается с помощью легкой модификации прове-
проведенных выше рассуждений).
Если напряженность & быстро убывает, то поле А совпадает асимптоти-
асимптотически с чисто калибровочным полем (т.е. имеет асимптотику A ^g~ldg,
где g (х) — функция, принимающая значения в группе G). Из соотношения
E) вытекает, что формула (8) справедлива теперь в случае, если интеграл
в ней берется по бесконечно удаленной сфере. Отсюда следует, что топо-
топологическое число поля А определяется гомотопическим классом функ-
функции g (x), рассматриваемой как отображение сферы большого радиуса
в группу G. 1
Отметим, что целочисленность топологического числаq{A) =
Sir
имеет место также для полей, заданных на произвольном компактном
многообразиям. В случае, если М = S4, это вытекает из проведенных выше
рассуждений, поскольку, как мы видели в § 23, калибровочное поле
на 54 можно рассматривать как поле на В4 с некоторыми условиями убы-
убывания на бесконечности. Общего доказательства мы проводить не будем.
Заметим, что при построении формы < &А $•) и топологического чис-
числа q(A) компактность группы G была не слишком существенна. Важно
только, чтобы в алгебре Ли ?? группы G существовало инвариантное ска-
скалярное произведение (не обязательно положительно определенное).
360

В алгебре Ли простой компактной группы Ли скалярное произведение
определено однозначно (с точностью до множителя) и мы имеем дело с
одним топологическим числом. В общем случае в алгебре Ли инвариантное
скалярное произведение может быть построено существенно различными
способами; тогда каждому из этих способов отвечает свое топологическое
число. Например, алгебра Ли группы SO D) (алгебра всех антисимметрич-
антисимметричных тензоров ранга 2 в R4) разлагается в прямую сумму алгебры Л +
самодуальных тензоров и алгебры Л _ антисамодуальных тензоров. (На-
(Напомним, что дуальный тензор А'к задается формулой А' = — €lkm"J4m"t
самодуальность и антисамодуальность определяются соотношениями А'к =
= ± А'к. Алгебры Ж+ и А_ изоморфны алгебре suB). Пользуясь этим за-
замечанием, легко построить в каждой из этих алгебр инвариантное скаляр-
скалярное произведение, удовлетворяющее условию B2.13)
(.A, B)± = -2Sp(AtB±).
Произвольное инвариантное скалярное произведение в алгебре so D) мо-
может быть записано в виде
<А, В) = \+(А+, Я+>+ + \_<Л_, 5_>,
1 1
где А+= - (А + А), А_= - (А -А) обозначают самодуальную (антиса-
2 2 '
модуальную) часть тензора А соответственно.
Пользуясь этим выражением для скалярного произведения, можно
построить два целочисленных топологических числа для калибровочного
поля со значениями в алгебре Ли so D):
q±T<FF,Ff>-
8тг 4
Вместо чисел q+ и q~ обычно удобно рассматривать два других целых
числа
^T A0)
(q+q-)
(П)
Эти числа называются соответственно числом Понтрягина и числом Эйлера
калибровочного поля.
§ 25. Геометрия калибровочных полей на многообразии
Мы видели в § 22, что калибровочное поле на U С R" определяет связ-
связность (правило параллельного переноса в прямом произведении UXG).
Покажем сейчас, что калибровочное поле на многообразии М порождает
связность в главном расслоении с базой М. Кривизна этой связности отож-
отождествляется с напряженностью калибровочного поля. Пусть калибровоч-
калибровочное поле А на гладком многообразии М задано с помощью калибровочных
361

полей А ^ХК ..., А *"* на областях Ult...,, Un в М. Тогда каждое из полей
A(i * определяет правило параллельного переноса в Ut X С Для того, чтобы
геометрически интерпретировать поле А, следует склеить между собой
прямые произведения Ц X G таким образом, чтобы было корректно опре-
определено правило параллельного переноса в пространстве Е, получающемся
при склеивании J7t X G,..., Un X G. Правила этого склеивания очевидным
образом диктуются функциями g{/ (х), определяющими калибровочную
эквивалентность А^'^ иу)*'' в Ut П U/. Именно, точку (и. И) 6 U,- X G
следует считать склеенной с точкой (и, h') € Ut X G, если и 6 Ut П Uj,
h'=gi,(u)h.
Для того, чтобы описанное только что правило склеивания было кор-
корректно, необходимо потребовать выполнения соотношений
gi/(x)gik(x) = gik(x) A)
при x&U j
Легко убедиться, что функции gti (x) gjk(x) устанавливают калибро-
калибровочную эквивалентность между АA) я А ^к\ если gt/ задает калибровоч-
калибровочную эквивалентность между А^'^ иЛ*", a gjk - калибровочную экви-
эквивалентность между А^'^ иЛ^^.Отсюда следует, что соотношение A) заве-
заведомо справедливо в случае, если функция, устанавливающая калибровоч-
калибровочную эквивалентность между А ^ и/l'*' в Ut П Uj П Uk> существует толь-
только одна. Мы всегда будем предполагать соотношение A) выполненным.
Описанное выше пространство Е можно рассматривать как пространство
главного расслоения, базой которого является М, а слоем — группа G.
В самом деле, на каждом пространстве {/,- X G группа G действует с по-
помощью правых сдвигов, причем склеивание согласовано с действием груп-
группы G. (Если («, И) склеено с (и, й'), то (и, hg) склеено с (и, h'g).) Как мы
говорили, правило склеивания выбрано таким образом, чтобы калибровоч-
калибровочное поле определяло параллельный перенос слоев построенного только
что главного расслоения вдоль кривой на базе. Для того, чтобы убедиться,
что выбранное нами правило склеивания действительно обладает этим свой-
свойством, нужно рассмотреть параллельный перенос над ?/,- П Uj. Этот парал-
параллельный перенос можно определить как с помощью поля А *' *, так и с
помощью поля А ('"*; проверим, что мы получаем при этом согласованные
результаты. В самом деле, если Г — кривая из U, П Uj, то при параллель-
параллельном переносе точек (х0, h) 6 t/,- X С вдоль этой кривой с помощью поля
Л(|) мы получаем точку (jcj, b^h), где b^ = Рехр (- / А^ dx"). Точ-
Точка (х0, h) склеивается с точкой (х0, gtj (х0) И), а точка (х i, b ?' * h) - с точ-
точкой (xi, gtj (Xi) b^h). Согласованность параллельного переноса и склеи-
склеивания следует теперь из соотношения
вытекающего из B2.13). Пусть F - пространство, на котором действует
группа G. (Для определенности считаем, что G действует слева с помощью
преобразований Г(?).) Если (?, М, G) - главное расслоение, то под ассо-
ассоциированным с ним расслоением со слоем F понимается расслоение,
пространство которого Е склеено из пространств Ut XF таким же образом,
362

как пространство Е склеено из Ut X G. Точнее говоря, мы считаем, что Ер
получается из U\ X F,..., Un X F с помощью отождествлений
Сечение ассоциированного расслоения может быть отождествлено с се-
семейством функций щ , определенных на множествах ?/,-, принимающих зна-
значения в F и удовлетворяющих условиям согласования:
где и G U{ П V). В физике обычно приходится иметь дело со случаем, ког-
когда F — линейное пространство, T(g) - линейное представление группы G.
Тогда понятие сечения ассоциированного расслоения может быть отождест-
отождествлено с понятием поля, преобразующегося по представлению группы G
(см.§ 23).
Как мы говорили в § 22, калибровочное поле на области {/определяет
не только правило параллельного переноса в U X G, но и правило парал-
параллельного переноса в U X F, если группа G действует в F. Отсюда следует,
что калибровочное поле на многообразии определяет параллельный пере-
перенос не только в главном расслоении, склеенном из множеств Ux X G, но и
в ассоциированном расслоении, склеенном из множеств Ц X F. В случае,
если F — пространство линейного представления группы G, параллельный
перенос в ассоциированном расслоении тесно связан с операцией ковариант-
ного дифференцирования поля, преобразующегося по представлению груп-
группы G.
В § 24 показано, что 4-форма (?"л $F) (где W — напряженность калибро-
калибровочного поля, < , > - инвариантное скалярное произведение в алгебре
Ли 9 группы G) замкнута и определяемый ею класс когомологий не ме-
меняется при непрерывной деформации калибровочного поля. Две связности
в одном и том же главном расслоении очевидным образом могут быть
переведены одна в другую с помощью непрерывной деформации. (Отож-
(Отождествляя рассматриваемые связности с калибровочными полями А и А,
можно построить нужную нам непрерывную деформацию по формуле At =
= А + t(A -А).) Отсюда следует, что класс когомологий формы ( f h §)
не зависит от выбора связности и, следовательно, определяется только
главным расслоением (Е, М, G, р). Этот класс когомологий называется
четырехмерным характеристическим классом.
§ 26. Пространства калибровочных полей
Грибовские неоднозначности
В этом параграфе мв! проанализируем топологическую структуру прост-
пространств калибровочных полей. Рассмотрим сначала пространство So тополо-
топологически тривиальных калибровочных полей на многообразии М (связностей
в тривиальном главном расслоении (М X G, M, G, р)). Это пространство
очевидным образом стягиваемо, поскольку его можно рассматривать как
линейное пространство. Нетривиальная топология возникает после отож-
отождествления калибровочно эквивалентных полей. Выделим из группы G°°
всех (локальных) калибровочных Преобразований подгруппу с?, состоя-
состоящую из преобразований, которые определяются функциями g (x), удовлет-
363

воряющими условию g(x0) - 1. (Здесь х0 — фиксированная точка много-
многообразия М). Группа G" действует свободно на пространстве &0- Для того
чтобы доказать это, вспомним, что каждому калибровочному полю А и
кривой у на многообразииМ мы сопоставляли элемент by = Р exp (—fA^dx^ )
7
калибровочной группы G. Закон преобразования элементов by при калиб-
калибровочном преобразовании, отвечающем функции g(x), имеет вид Ьу =
= S (*2) byg~l (хО, где Xi и х2 — начало и конец кривой у. Из этого закона
преобразования ясно, что группа G% действует свободно на ?0- В самом де-
деле, если калибровочное преобразование переводит в себя калибровочное
поле А, то для любой кривой у имеем by = g (х2) byg~1 (Xi). Выбирая кри-
кривую так, чтобы она начиналась в точке х0, а кончалась в произвольной точке
х, видим, что by = g (x) by, т.е. g(x)= I. Группа G°°, вообще говоря, не дей-
действует свободно на &о- Например, если калибровочное поле А^ принимает
значения в алгебре Ли Ж подгруппы Я группы G, ag 6 G - элемент, комму-
коммутирующий со всеми элементами подгруппы Н, то калибровочное преобразо-
преобразование, порожденное функцией g (x) = g (глобальное калибровочное преоб-
преобразование), оставляет на месте поле А м. Этот пример является в некотором
смысле общим. В самом деле, если поле А^ переходит в себя при калибро-
калибровочном преобразовании, определяемом функцией g (х), h#(xi) Ф 1, то Ьу =
= #(Xi) byg (Xi) для любого контура у, начинающегося и кончающегося
в Xj. Множество элементов Ьу, отвечающих таким контурам, образуют
группу голономии #(xi) (см. § 22). С помощью калибровочного преоб-
преобразования поле с группой голономии H(Xi) может быть преобразовано в
поле, принимающее значение в алгебре Ли этой группы; это сводит общую
ситуацию к рассмотренному выше примеру. Из приведенных только что
рассуждений ясно, что на полях общего положения (полях с группой голо-
голономии, совпадающей с G) группа G°° действует свободно.
Пространство S30 орбит группы G" в ?0 является, очевидно, базой
расслоения со слоем Gq и пространством расслоения &0- Задача о непре-'
рьшном выборе калибровочного поля из каждой орбиты группы G~ экви-
эквивалентна задаче о построении сечения описанного только что расслоения.
В случае, если у расслоения есть сечение, всякий элемент гомотопической
группы базы получается при естественном гомоморфизме из некоторого
элемента гомотопической группы пространства расслоения (именно,
элемент а получается из элемента q,a, где q — сечение). Поскольку в рас-
рассматриваемой ситуации я,- (&о) = 0» мы видим, что тг;($H) = 0, если су-
существует сечение (здесь / > 1). С другой стороны, из предложения 4 §17
или иэ точной гомотопической последовательности видно, что тг/0©о) =
= 7ri-i (С"). Отсюда ясно, что сечение может существовать только в случае,
когда все гомотопические группы пространства GJT тривиальны. Если мно-
многообразие М топологически эквивалентно сфере 5", то гомотопическая
группа ^(GJ") изоморфна группе %+n(G^. В самом деле, в этом случае
СЦ" можно отождествить с пространством отображений куба /" в G, пере-
переводящих всю границу /" куба /" в единичный элемент группы G. (Это
следует из замечания, что сфера 5" получается из /" при склеивании всей
границы в одну точку.) Элементы гомотопической группы пк (GJST) удобно
представлять как гомотопические классы отображений куба /* в Gj,
переводящих его границу/* в единичный элемент группы G™. Такое отобра-
364

жение сопоставляет точке и е /* функцию gv (x) со значением в G опре-
определенную на /" и удовлетворяющую условию gv (х) =1, если у€/*,
х&1" или v €/fc, хб/". Рассматривая пару (х, и) 6/"XT* как точку ку-
куба /n+fc, мы видим, что интересующие нас отображения куба 1к в G% на-
находятся во взаимно однозначном соответствии с отображениями куба 1п+к
в G, переводящими всю его границу f"+k = }"XIk u/"X/fc в единичный
элемент группы G. Гомотопические классы отображений куба 1"+к по
определению образуют группу -nn+k(G). Это означает, что группа
изоморфна группе 7rfc+n(G). Если G — компактная неабелева группа, отсю-
отсюда можно вывести, что на сфере S", п > 0 нельзя непрерывным образом
выбрать одно калибровочное поле из каждой орбиты группы G°? (т.е. нель-
нельзя наложить калибровочное условие, полностью снимающее калибровочную
свободу). В случае сферы S3 это сразу следует из соотношения п0 (G?) =
= 7г3 (G) Ф 0. В случае М = S4, G = SU(«) нужное нам заключение можно
получить из соотношения 7rt (С~) = тг5 (SU (и)) =?0. Общее доказательство
сводится к проверке того, что у компактной неабелевой группы G есть
ненулевые гомотопические группы сколь угодно большой размерности;,
мы не будем проводить этой проверки.
Сформулированные только что результаты относились к проблеме
непрерывного выбора калибровочного поля из орбит группы G?. Одна-
Однако с помощью тех же методов легко изучить вопрос о непрерьшном выборе
поля из орбит группы G°°. Группы G°° уже не действует свободно на
пространстве калибровочных полей ?0> но удалив из &0 поля с группой
голономии Я, не совпадающей с G, мы получим подпространство полей
общего положения &о, на котором G°° уже действует свободно. Удале-
Удаление подмногообразия, задаваемого бесконечным числом уравнений, не
влияет на гомотопические группы, поэтому я,- (&о) = ^i (&'o) = 0- Это
позволяет установить отсутствие сечения у расслоения пространства &о
на орбиты группы G°° в случае, когда калибровочные поля определены на
сфере S", п > 0 и принимают значения в алгебре Ли компактной неабеле-
неабелевой группы G.
Калибровочные поля на tR" при условии достаточно быстрого убывания
на бесконечности, как мы замечали, можно рассматривать как поля на S".
Используя это обстоятельство легко убедиться, что калибровочное условие
диА* =0 в неабелевом случае не полностью снимает калибровочную свобо-
свободу (это явление носит название грибовской неоднозначности). Точнее
говоря, можно найти два поля Лм и Ам, удовлетворяющие условиям
дцА"=0, дцА*=0,но связанные* калибровочным преобразованием с
функцией g(x), стремящейся к единице на бесконечности. Подчеркнем,
однако, что на IR" существуют калибровочные условия, выделяющие ров-
ровно одно поле из каждой орбиты группы G" или группы G°°. Например,
условия х^А м(х) = 0, А м@) = 0 выделяют ровно одно поле из каждого
калибровочного класса.
Мы рассматривали до сих пор для определенности случай топологически
тривиальных калибровочных полей (связностей в тривиальном расслое-
расслоении). Однако, все результаты переносятся на случай топологически нетри-
нетривиальных калибровочных полей (связностей в произвольном главном
расслоении). Например, можно вместо &0 рассматривать пространство
?„ калибровочных полей с топологическим числом и на сфере S4. Прост-
365

ранство &„ также является стягиваемым (деформация в точку опреде-
определяется формулой At = A— t)A + M*°)). Это позволяет с минимальными
изменениями повторить все проведенные выше рассуждения и прийти к -тем
же основным выводам.
Задачи
1. Произвести топологическую классификацию букв.
2. Доказать, что открытое круговое кольцо {а2 < х2 + у2 < b2 ,z = 0)
топологически эквивалентно однополостному гиперболоиду z2 = х2 +
+ у2-а2.
3. Проверить, что поверхность эллипсоида топологически эквивалентна
сфере.
4. Доказать, что пространство конфигураций твердого тела с закреплен-
закрепленной точкой топологически эквивалентно группе SOC) вращений трех-
трехмерного пространства.
5. Проверить, что группа SOC) топологически эквивалентна трехмер-
трехмерному проективному пространству RP*.
6. Доказать что гомотопический тип букета *) связных пространств
Xi,..., Х„ не зависит от выбора отмеченных точек в этих пространствах.
7. Доказать, что букет пространств Xt и Х2 гомотопически эквивалентен
пространству, состоящему из пространств Xlt Х2 и отрезка, соединяющего
точки, отмеченные в пространствахXi,X2.
8. Доказать, что тело в IR3, ограниченное сферой с к ручками, гомото-
гомотопически эквивалентно букету из к окружностей.
9. Доказать, что область IR3\F, получающаяся из [R3 удалением конечно-
конечного множества F, гомотопически эквивалентна букету из к двумерных
сфер, где к — число точек в F..
10. Доказать, что всякий граф гомотопически эквивалентен букету
из окружностей. (Под графом понимается одномерный клеточный
комплекс.)
11. Доказать, что кватернионное уравнение
qm +l(q) =0
имеет хотя бы одно решение в случае, если / (q) — полином степени < т.
(В частности, это утверждение справедливо для уравнения вида q2 +
+ Tiutqbi + с = 0.)
12. Доказать, что отображение сферы 53 на себя, определяемое формулой
q = qm, имеет степень т. (Мы рассматриваем здесь сферу 53 как мно-
множество кватернионов, удовлетворяющих условию II ^ II = 1.)
13. Доказать, что нечетное отображение сферы S2n в себя имеет нечетную
степень. (Отображение / называется нечетным, если оно переводит диамет-
диаметральные точки сферы в диаметрально противоположные: f(—x) - —/(х).)
14. Построить двулистное накрытие листа Мёбиуса круговым кольцом.
Показать, что бесконечную полосу можно рассматривать как бесконеч-
нолистное накрытие листа Мёбиуса.
*) Букетом .Л^и... U'Jfn пространств ЛГ,,.„, Х„,в каждом из которых отмечена
одна точка, называется объединение этих пространств, в котором все отмеченные
точки склеены в одну точку.
366

15. Доказать, что проективная прямая не гомотопна нулю на проективной
плоскости RP2. (В однородных координатах х°, х1, х2 наЛР2 проектив-
проективная прямая выделяется уравнением х2 = 0. Она топологически эквивалент-
эквивалентна окружности и, следовательно, может рассматриваться как замкнутый
путъвЯР2.)
16. Доказать, что универсальные накрывающие всех замкнутых поверх-
поверхностей, кроме сферы и проективной плоскости, топологически эквива-
эквивалентны плоскости IR 2.
17. Пусть конечная группа G свободно действует на ориентируемом глад-
гладком многообразии М. Доказать, что пространство орбит M/G является
ориентируемым многообразием в том и только в том случае, если все
преобразования группы G сохраняют ориентацию (все преобразования
группы G предполагаются гладкими).
18. Доказать, что фундаментальная группа букета из m окружностей яв-
является свободной группой с m образующими. (Элементы а^ ат на-
называются образующими группы G, если любой элемент группы предста-
представим в виде произведения элементов at и а] К Если между образующи-
образующими элементами группы нет никаких соотношений, кроме вытекающих
из тривиальных соотношений д,- • а~A = а'^ • п{ = 1, то группа называется
свободной группой с образующими ах,..., ат)\
19. Доказать, что фундаментальная группа связного графа является сво-
свободной группой, имеющей Ь1 образующих, где Ь1 — одномерное число
Бетти.
20. Доказать, что фундаментальная группа wj (X) полиэдра X изоморфна
фундаментальной группе его двумерного остова X2.
21. Доказать, что гомоморфизм фундаментальной группы tfi (X1) одно-
одномерного остова X1 полиэдра X в группу тг! (X), порождаемый вложением
X1 в X, отображает tti (X1) на всю группу nt (X).
22. Доказать, что фундаментальная группа сферы с к ручками изоморфна
группе с образующими а\,Ь\,..., а^, Ь^, связанными соотношением
пхЬуп! 'ftГ1 •. . akbkukibk1 = 1. (Иными словами, эта группа изоморфна
факторгруппе свободной группы с образующими al3bi пк,Ьк по
подгруппе, порожденной элементом at Ъ i ef1 Ь{1 ... акЬкак 1 Ьк 1.)
Указание. Воспользоваться клеточным разбиением,изображенным
на рис. 58.
23. Показать, что фундаментальная группа полиэдра X может быть зада-
задана как группа с г образующими и s соотношениями, где г — одномерное
число Бетти одномерного остова полиэдра X, a s — число двумерных кле-
клеток в X. (Иначе говоря, iry (X) может быть представлена как факторгруп-
факторгруппа свободной группы с г образующими по подгруппе, порожден-
порожденной s элементами.)
24. Доказать, что естественное отображение группы Ъ\ (X) в одномер-
одномерную группу гомологии Hi (X, Ж) является отображением на всю груп-
группу Hi {X, Z). (Каждый путь можно рассматривать как одномерный цикл.)
25. Доказать, что одномерная группа гомологии Ht (X, 71) полиэдра X изо-
изоморфна факторгруппе группы ttj (X) по ее коммутанту (т.е. по подгруппе,
порожденной элементами вида aba ~lb~1)
26. Доказать, что для всякого гладкого многообразия существует глад-
гладкое вложение (гладкое взаимно однозначное отображение) этого много-
367

образия в пространство OR^ для достаточно большого N. (Имеет место
более точный результат: «-мерное гладкое многообразие может быть глад-
гладко вложено в пространство Р .)
27. Доказать, что группу SO (и) можно рассматривать как ориентируемое
1
гладкое многообразие размерности - п (п - 1), а группу U (и) — как ориен-
ориентируемое гладкое многообразие размерности п2.
28. Показать, что односвязное многообразие ориентируемо.
29. Показать, что для всякого неориентируемого многообразия суще-
существует ориентируемое двулистное накрытие (точнее, можно построить
ориентируемое многообразие М и отображение М на М, являющееся дву-
двулистным накрытием).
30. Доказать, что комплекснозначная 1-форма
f(z)dz = f(x,y)(dx+idy)
замкнута в том и только в том случае, если функция/(г) является ана-
аналитической функцией от комплексной переменной z = х + iy. Вывести
из этого замечания стандартное выражение интеграла ot/(z) dz по зам-
замкнутому контуру через вычеты аналитической функции /(z) в особых
точках внутри контура.
31. Доказать формулу интегрирования по частям
/ СО* Л diO1 = / Ш* Л ы' - (-l)fc / do}* л ш'
гэг г
(здесь со* н со' обозначают соответственно Л-форму и /-форму, символ Г
обозначает (к + 1 + 1)-мерную ориентированную поверхность).
32. Вычислить группы гомологии области трехмерного пространства
ограниченной сферой с к ручками.
33. Вычислить степень гомоморфного отображения группы SUB) на
группу SOC).
34. Построить клеточное разбиение полнотория (тора с внутренностью)
и вычислить с помощью этого разбиения группы гомологии.
35. Вычислить группы гомологии многообразия Fn2 состоящего из еди-
единичных векторов, касательных к сфере S"~ .
36. Пусть А — ортогональное преобразование пространства [Rm, удовлет-
удовлетворяющее условию А" = 1, Ак Ф 1 при 0 < к < п. Доказать, что группа G,
состоящая из преобразований А0, А1,..., А"~х, свободно действует
на сфере S С tRm в случае, если для всякого собственного значе-
значения Я преобразования А выполнено условие Xfc Ф 1 при 0 < к < п. Вы-
Вычислить фундаментальную группу и группы гомологии пространства
Sm~ljG в случае т = 4, G свободно действует на S3. (В этом случае
S3/G называется линзовым пространством.)
Указание. В случае свободного действия тг^ (Sm ~ 1 /G) = G; при-
применяя теорему Гуревича и двойственность Пуанкаре, вычисляем группы
гомологии многообразия S3/G. Можно также произвести вычисление с
помощью клеточного разбиения; этот метод пригоден в общем случае.
37. Пусть fug- два и-мерных сфероида в топологической группе G. До-
Доказать, что сфероид h, полученный из сфероидов /, g с помощью группо-
группового умножения (Л (л:) =/(x)g (x)), гомотопен сумме сфероидов / и g.
368

38. Построить расслоение, база и слой которого топологически эквива-
эквивалентны окружности, а пространство является неориентируемой двумер-
двумерной поверхностью. Доказать, что эта поверхность (бутылка Клейна) то-
топологически эквивалентна сфере, в которую вклеено два листа Мёбиуса.
39. Проверить, что хопфовское расслоение E3, S2, 51) не имеет сечений.
40. Построить расслоение, сечения которого можно отождествить с fc-фор-
мами на многообразии М.
41. Рассмотрим пространство Е путей на связном гладком многообразии
М, начинающихся в фиксированной точке х0. Показать, что, сопоставляя
каждому пути а 6 Е его конец, мы получаем расслоение, базой которого
является М, а слой топологически эквивалентен пространству О, (Af) путей,
начинающихся и кончающихся в х0 (пространству петель). Проверить,
что пространство Е стягиваемо.
42. Показать, что для пространства О, путей на многообразии М, на-
начинающихся и кончающихся в точке х0, имеет место соотношение
43. Доказать, что 7r,(FnA:) = Опри i < п — к.
Указание. Доказывается по индукции с помощью расслоения
(*Vfc + i. vn,k.,.s"-"-*).
44. Доказать, что для грассманова многообразия Gntk fc-мерных пло-
плоскостей в пространстве Р " при / < п — к имеет место соотношение
Указание. Воспользуемся расслоением (FHi k, Gn< k, О (к)).
45. Доказать, что для любой двумерной замкнутой поверхности, кроме
сферы и проективной плоскости, гомотопические группы размерности
> 2 тривиальны.
4E. Рассмотреть точную гомотопическую последовательность расслоения
(Уп, 2, S"~1, S"~2) и показать с ее помощью, что при п четном
ти-2 (У„,2) = г, а при и нечетном тг„_ 2 ^„j) = 7!2-

ПРИЛОЖЕНИЕ
§ 1. Топологические пространства
Мы будем говорить, что множество Е является топологическим прост-
пространством , если в нем определено понятие открытого множества, удовлетво-
удовлетворяющее условиям 01,02.
01. Пересечение конечного числа открытых множеств открыто.
02. Объединение любого числа открытых множеств открыто.
Поскольку в метрическом пространстве определено понятие открытого
множества, всякое метрическое пространство можно рассматривать как
топологическое пространство. С помощью понятия открытого множества
в топологическом пространстве стандартным образом определяются поня-
понятия окрестности и предела. Непрерывность отображения одного топологиче-
топологического пространства в другое может быть определена как и для метрических
пространств с помощью понятия окрестности. Можно также сказать, что
отображение v? топологического пространства X в топологическое прост-
пространство Y непрерывно, если полный прообраз i^ (U) всякого открытого
множества U S Y является открытым подмножеством пространства X.
Отображение у называется топологическим (или гомеоморфизмом), если
оно взаимно" однозначно и в обе стороны непрерывно (т.е. непрерывно как
само отображение у, так и обратное отображение *р-1)- Множество F С Е
называется замкнутым, если его дополнение Е \ F открыто. Легко прове-
проверить, что объединение конечного числа замкнутых множеств замкнуто,
пересечение любого семейства замкнутых множеств замкнуто. Если все
точки сходящейся последовательности х„ принадлежат замкнутому множе-
множеству F, то предел этой последовательности также принадлежит множест-
множеству F. Всякое подмножество Е' топологического пространства Е можно
рассматривать как топологическое пространство. (Множество U С Е'
считается открытым в Е', если найдется такое открытое множество V С Е,
что V П Е' ~ U.) В дальнейшем без всяких дополнительных оговорок мы
считаем, что в пространстве, определенном как подмножество топо-
топологического пространства, топология введена описанным только что
способом.
Если наложить на топологические пространства только указанные выше
аксиомы, то сходимость к пределу и другие понятия могут обладать раз-
различными патологическими свойствами. В частности, может оказаться, что
370

последовательность имеет два различных предела. Для того, чтобы исклю-
исключить подобные патологии обычно накладывают дополнительные требова-
требования — так называемые аксиомы отделимости. Можно потребовать, напри-
например, чтобы пересечение всех окрестностей точки состояло из единственной
точки. Тогда каждое множество, состоящее из одной точки, оказывается
замкнутым. Обычно налагают более сильное требование, чтобы у двух лю-
любых точек пространства существовали непересекающиеся окрестности
(аксиома Хаусдорфа). Если это условие выполнено, то последовательность
не может иметь более одного предела. Все конкретные пространства, кото-
которые встречаются в этой книге, удовлетворяют не только аксиоме Хаусдор-
Хаусдорфа, но и более сильным требованиям этого рода. Поэтому всюду, кромв
§ А4, мы будем предполагать, что рассматриваемые нами топологические
пространства удовлетворяют аксиоме Хаусдорфа.
Топологическое пространство называется дискретным, если каждая его
точка является открытым множеством. Например, дискретным является
пространство, состоящее из всех целых точек числовой прямой. Всякое про-
пространство, состоящее из конечного числа точек, дискретно. (В самом деле,
дополнение к одноточечному множеству состоит из конечного числа точек.
Ло сделанному выше нами предположению каждая точка замкнута и,
значит, замкнуто любое конечное множество — как объединение конечного
числа замкнутых множеств.) Всякое отображение дискретного пространст-
пространства в любое топологическое пространство непрерывно.
Топологическое пространство Е называется компактным, если из всяко-
всякого открытого покрытия пространства Е можно выбрать конечное -подпо-
-подпокрытие. (Под открытым покрытием понимается такое семейство откры-
открытых множеств {Ua }, что каждая из точек х € Е принадлежит хотя бы од-
одному из множеств Ua .Условие компактности означает, что из открытого
покрытия Ua можно выбрать конечное число множеств Uai, „., Uan, кото-
которые также покрывают пространство Е.) Если пространство Е компактно,
то из всякой последовательности х„ & Е можно выбрать подпоследователь-
подпоследовательность, сходящуюся к точке из Е. Для метрических пространств верно также
обратное утверждение. Компактное подмножество Е пространства Е1
замкнуто в Е'. Всякое замкнутое подмножество компактного пространст-
пространства является компактным пространством. Если у - непрерывное отображе-
отображение компактного пространства Е в пространство Е1', то образ $(Е) прост-
пространства Е при отображении у является компактным пространством.
Если ip — взаимно однозначное непрерывное отображение компактного
пространства Е на пространство Е', то <р — топологическое отображение
(т.е. обратное отображение v? также непрерывно). Под прямым произве-
произведением Ei X Е2 множеств Ех и Е2 понимается множество пар (е1г е2),
где ех G Ei, e2 6 Е2. Если Е^ и Е2 — топологические пространства, то
в Ei X Е2 также естественным образом вводится топология. (Множество
U С Ei X Е2 следует считать открытым, если оно может быть представлено
как объединение множеств вида Ux X U2,rjxe Ui и U2 -открытые множе-
множества в Ei и Е2 соответственно.) Отображение у прямого произведения
Ei X Е2 в Е можно рассматривать как функцию ?"(е1> е%), принимающую
значения в Е и зависящую от двух переменных, пробегающих соответствен-
371

но Ei и Е2 ¦ Непрерывность отображения у означает, что функция <р непре-
непрерывна по совокупности переменных. Если пространства Et и Е2 компакт-
компактны, то пространство Ех X Е2 также компактно.
§ 2.Группы
Пусть для любых двух элементов множества G определено их произведе-
произведение, являющееся элементом того же множества. Если a G G, Ъ 6 G, то
произведение этих элементов будем обозначать символом а • Ъ или просто
аЬ. Элемент е G G называется единицей, если для любого а 6 G имеют
место равенства:
а- е = е¦ а = а.
Элемент b G G называется обратным к а 6 G, если произведения а ¦ b и
b-а являются единицами. Элемент обратный к а, обозначается а.
Если произведение, определенное в множестве G, ассоциативно (т.е.
(а- Ь)-с = а -(b-с)), обладает единицей и каждый элемент множества
имеет обратный, то говорят, что множество G является группой. Нетрудно
проверить, что в группе есть только одна единица и каждый элемент имеет
только один обратный; при этом из соотношения а ¦ b = e вытекает, что
b -а = е. Отображение у группы G в группу G называется гомоморфным,
если оно переводит произведение в произведение (т.е. у(а -b) =ip(a)-ip(b)).
"Отображение у называется изоморфным, если оно гомоморфно и взаимно
однозначно. Вместо терминов гомоморфное и изоморфное отображение
употребляются также термины гомоморфизм и изоморфизм. Если гомо-
¦ морфизм v? группы G в себя является изоморфизмом, то он называется
автоморфизмом. Любой элемент g 6 G определяет автоморфизм о^
группы G по формуле:
ag(h) = ghg-1. A)
Автоморфизмы, определяемые формулой A), называются внутренними.
Множество Н С G называется подгруппой группы G, если произведение»
двух любых элементов а & Н, b 6 Н снова принадлежит Н и для любого
элемента а & Н обратный ему элемент также принадлежит Н. Подгруп-
Подгруппа Н называется инвариантной, если вместе с каждым элементом h G Н
элемент вида ghg'1 также принадлежит Н для любого g G G. (Иначе мож-
можно сказать, что подгруппа называется инвариантной, если она переходит в се-
себя при всех внутренних автоморфизмах.) Говорят, что два элемента h j,
A2?G сопряжены друг другу, если существует внутренний автоморфизм,
переводящий hi в А2 (т.е. А2 = gh1g~1 ,тдр g^ G). Аналогично, две под-
подгруппы Я е G, Я* S G называются сопряженными, есди существует
внутренний автоморфизм, переводящий Я в Я'. Образ Im <p гомоморфиз-
гомоморфизма v? группы G в группу G' (т.е. множество элементов вида y(g),
где g & G), очевидно, является подгруппой группы G'. Множество элемен-
элементов группы G, переходящих в единицу группы G' при гомоморфизме у,
называется ядром гомоморфизма v> и обозначается Кег кр (иначе говоря,
372

Ker v? = v? (e)). Легко убедиться, что ядро гомоморфизма является инва-
инвариантной подгруппой группы G. По всякой инвариантной подгруппе
Н С G однозначно (с точностью до изоморфизма) можно построить груп-
группу G1 и гомоморфизм группы G на G1, ядро которого совпадает с Н.
Эта группа G1 обозначается G/H и называется факторгруппой G по Н
(подробнее см. в § А6). Группа G называется коммутативной или абеле-
вой, если два любых элемента glf g2 6G коммутируют (т.е. gt • g2 =
- Si • g\)- Для коммутативных групп часто употребляют термин "сложе-
"сложение" вместо "умножение", термин "нуль" вместо термина "единица",
термин "противоположный элемент" вместо термина "обратный элемент".
Множество действительных чисел IR является коммутативной группой,
если в качестве операции в этом множестве рассматривать обычное сложе-
сложение. Множество положительных действительных чисел IR+ является ком-
коммутативной группой относительно обычного умножения. Отображение, со-
сопоставляющее действительному числу х положительное число ехр х, пред-
представляет собой изоморфизм этих двух групп.
Совокупность всех преобразований множества X образует группу,
если под произведением двух преобразований понимать результат их
последовательного выполнения:
Эта группа называется группой преобразований множества X. Множество
всех невырожденных и-мерных матриц (матриц с ненулевым детерминан-
детерминантом) образует группу относительно обычного умножения матриц.
Эта группа обозначается GL(h, [R) (или короче GL(n)). Если рассматри-
рассматриваются невырожденные матрицы с комплексными элементами, то употреб-
употребляется обозначение GL(n, С). Гомоморфизм группы G в GL(«, IR)
(или в GL(/i, (С)) называется действительным (комплексным) и-мерным
представлением группы G (подробнее см. § А5). Подгруппа группы
GL(n, IR), состоящая из ортогональных матриц, обозначается символом
О (и), а подгруппа группы GL(n, (С), состоящая из унитарных матриц, —
символом U (и). Если рассматриваются подгруппы групп О (и) и U (и),
состоящие из матриц с определителем 1, то употребляются обозначения
SO (и) и SU(rt). Введенные выше обозначения используются также для
соответствующих групп линейных преобразований. (Напомним, что при
перемножении линейных операторов их матрицы также перемножаются.
Поэтому каждая подгруппа группы линейных преобразований изоморфна
подгруппе группы невырожденных матриц — матричной группе.) Группа
линейных преобразований четырехмерного пространства, сохраняющих
пространственно-временной интервал
ds2 = (dx° J - (dx»J - (dx2 J - (dx3 J = gik dx ldx k,
называется полной группой Лоренца. Термин "группа Лоренца" мы оставим
для подгруппы полной группы Лоренца, состоящей из преобразований с
матрицей я*, удовлетворяющей условиям det а'^ = \,а%> 0. (Можно сказать,
что группа Лоренца L состоит из преобразований Лоренца, не обращающих
времени и не содержащих пространственных отражений.)
373

Под топологической группой, понимается группа G, которая одновремен-
одновременно является топологическим пространством. При этом требуется, чтобы
операция умножения и операция взятия обратного элемента были непре-
непрерывны. (Операция умножения в G может рассматриваться как отображение
прямого произведения G X G в G, непрерывность умножения означает,
что это отображение непрерывно.) Подгруппа топологической группы так-
также может рассматриваться как топологическая группа. Любая матричная
группа (т.е. любая подгруппа группы GL (и, (С)) является топологической
группой.
Под прямым произведением групп Gx и G2 понимается множество
Gi X G2 пар (g\,gi), где#1 ?Gbj2 ? G2, с умножением, определяемым
формулой (gi, ft. )•(&'> ft) =fei -81,82 ¦ Si)- Если Gi и G2 - топологичес-
топологические группы, то Gt X G2 также можно рассматривать как топологическую
группу. Если группы Gj и G2 абелевы и операция в них обозначается зна-
знаком +, то вместо термина "прямое произведение" употребляется термин
"прямая сумма", сложение в прямой сумме Gi + G2 задается формулой
(?ь Ы + fe'bft) = fei +81,82 +g2)-
Топологическая группа G называется и-мерной (или и-параметрической)
группой Ли, если топологическое пространство, на котором определена
групповая операция, является л,-мерным многообразием (т.е. у каждой точ-
точки пространства G есть окрестность, топологически эквивалентная прост-
пространству [R"). Доказано, что в этом случае в пространстве [R" можно ввести
локальные системы координат таким образом, что групповая операция и
операция взятия обратного элемента будут задаваться гладкими функция-
функциями. (Отсюда следует, что G можно рассматривать как гладкое многообра-
многообразие; см. § Т5.) Примерами групп Ли могут служить группа невырожден-
невырожденных комплексных матриц GL(n, (С) и подгруппы этой группы (например,
GL (и, fft), U (и), SU(«), SO(«)). Эти подгруппы называются матричными
группами Ли.
Под алгеброй Ли понимается линейное пространство Л с операцией
[а, Ь] , удовлетворяющей аксиомам дистрибутивности [ha + \xb, с] =
= \[а, с] +fi [b, с], антикоммутативности [а, Ь] = — \Ъ, а] и тождеству Яко-
би [а, [Ь, с] ] + [Ь, [с, а] ] + [с, [а, Ь] ] = 0 (здесь а,Ъ,с^Л, \,\i- числа).
Если JL- действительное (комплексное) пространство, то алгебра Ли назы-
называется действительной (комплексной). Мы будем рассматривать только
действительные алгебры Ли. Примером алгебры Ли может служить мно-
множество всех комплексных (или всех действительных) квадратных матриц
порядка и с операцией коммутирования: [a, b] =ab - Ъа. (Сложение матриц
и умножение их на действительные числа определяются стандартным обра-
образом.)
Понятия подалгебры алгебры Ли, прямой суммы алгебр Ли, гомоморфиз-
гомоморфизма алгебры Ли определяются аналогично соответствующим понятиям для
групп. Например, отображение t алгебры Ли Л\ в алгебру Ли Л2 называ-
называется гомоморфизмом, если оно согласовано с имеющимися в алгебре Ли
операциями (т.е. линейно и удовлетворяет условию t([a, b]) = [t(a), t(b)]
для всехд, ftS^j).
Всякой группе Ли G можно сопоставить алгебру Ли 8 . Как линейное
пространство эта алгебра Ли совпадает с касательным пространством в
единичном элементе группы Ли (см. § Т5). В случае, если G — матричная
374

группа Ли, ее алгебра Ли i§ может рассматриваться как линейное подпрост-
подпространство пространства матриц. Операция [a, t] вводится как операция ком-
коммутирования матриц: [a, b] =ab - Ьа. (Это определение корректно, пос-
поскольку операция коммутирования не выводит из касательного црост-
ранства.)
Группам GL(«, С), GL (n, IR) отвечают алгебры Ли gl (и, С), gl (и, Ш)
всех комплексных или вещественных матриц. Группе U (и) отвечает алгеб-
алгебра Ли и (и), состоящая из комплексных антиэрмитовых матриц. (Это вы-
вытекает из замечания, что для элемента 1 + а & U (и) бесконечно близкого к
единичному, условие унитарности A + д)A+д+) = 1 приобретает вид
а + а+ = 0). Алгебра Ли su (и) группы SU (и) состоит из бесследовых анти-
антиэрмитовых матриц, алгебра Ли so (и) группы SO («) - из вещественных
антисимметричных матриц.
Представления групп Ли тесно связаны с представлениями алгебр Ли.
Под «-мерным комплексным представлением алгебры Ли понимается го-
гомоморфизм этой алгебры в алгебру Ли gl (n, С) (алгебру Ли всех комплекс-
комплексных матриц). Аналогично, действительное представление определяется как
гомоморфизм в алгебру gl (и, (R). Всякому представлению Т группы Ли
G отвечает представление t соответствующей алгебры Ли 8. Имеет место
также более общее утверждение: каждому гомоморфизму группы Ли Gi в
группу Ли G2 отвечает гомоморфизм соответствующих алгебр Ли. Чтобы
построить этот гомоморфизм напомним, что отображение одного гладкого
многообразия в другое порождает отображение векторов в первом много-
многообразии в векторы во втором многообразии (см. § Т5). В частности, го-
гомоморфизм группы Gi в G2 порождает отображение алгебры Ли^, состоя-
состоящей из касательных векторов kG, в единичном элементе группы, в алгеб-
алгебру Ли i§2. Доказывается, что это отображение является гомоморфизмом
алгебр Ли.
Две группы Ли Gx и G2, имеющие одну и ту же алгебру Ли i§ , локаль-
локально изоморфны. АПод локальным изоморфизмом понимается взаимно
однозначное соответствие между окрестностями единицы в группах G1 и
G2, сохраняющее операцию умножения. Мы пишем Gx - G2, если группы
Gx и G2 изоморфны, и Gj * G2, если группы Gt и G2 локально изоморф-
изоморфны, т Среди групп Ли, которым отвечает алгебра Ли &, есть одна и только
одна, односвязная группа Ли Go. Для любой другой группы G с той же
алгеброй Ли можно найти гомоморфизм группы Go на G, ядро которого
является дискретной подгруппой группы Go (эта подгруппа принадлежит
центру группы Go, т.е. ее элементы коммутируют со всеми элементами
группы Go). Группу Go можно рассматривать как универсальную накры-
накрывающую группу группы G (см. § Т4). В качестве примера заметим, что
группа U (и) локально изоморфна односвязной группе IR+X SU(«). Гомо-
Гомоморфизм группы [R+ X SU(«) на Щл) можно построить, сопоставив паре
(еа,u)G.R+X. SU(n) матрицу е'аи 6Щп). Ядро этого гомоморфизма явля-
является дискретной подгруппой группы fft+ X SU(«), изоморфной группе целых
чисел Z (иными словами, Щи) можно получить как факторгруппу [R+ X
X SU(«) no Z'). С другой стороны группа U(«) локально изоморфна
U(l) X SU(n) (например, это следует из локального изоморфизма групп
X SU(n) и R+ X SU(«)).
375

На всякой компактной топологической группе G можно единственным
(с точностью до множителя) способом построить инвариантную меру. Это
означает, что можно ввести понятие интеграла по G, удовлетворяющее
условию
/ f(gh)dg = Sf(hg)dg = Jf(g)dg
G G G
для любой непрерывной функции / на G и любого h&G. Иначе говоря,
на пространстве непрерывных функций может быть определен линейный
функционал (интеграл), инвариантный как относительно левых, так и отно-
относительно правых сдвигов (т.е. относительно преобразований L)t(g)= hg и
Rh (g) = gh). Инвариантную меру на компактной группе можно одно-
однозначно фиксировать, потребовав, чтобы группа имела единичный объем
(fdg = 1). Мы не будем останавливаться на общей конструкции инвариант-
G
ной меры. Отметим только, что такая мера легко может быть построена в
наиболее важном случае матричной группы G. Именно, в этом случае
в алгебре Ли # группы G можно ввести скалярное произведение (х,у) =
= — Spxy, инвариантное относительно внутренних автоморфизмов:
(g~1xg,g~1yg) ~{x,y). Это скалярное произведение порождает в G метрику
ds2 <g~ldg, g-1 dg) = -Sp (g-1 dg) (g-1 dg),
инвариантную относительно левых и правых сдвигов; элемент объема,
отвечающий этой метрике, задает инвариантную меру.
§ 3. Отождествление (наглядные примеры)
Мы опишем сейчас процесс, с помощью которого из одного топологиче-
топологического пространства можно получить другие. Этот процесс состоит в том,
что некоторые точки исходного пространства склеиваются между собой —
отождествляются. Он очень часто используется в книге. Начнем с несколь-
нескольких простых примеров, в которых этот процесс в высшей степени нагляден.
Рис.48
Рис.49
Рассмотрим прямоугольник и склеим между собой две противоположные
стороны этого прямоугольника. Если склеивание происходит без перевора-
переворачивания (рис. 48), то после склеивания мы получим поверхность, тополо-
топологически эквивалентную боковой поверхности цилиндра. Поверхность,
получающуюся если склеивание противоположных сторон прямоугольника
произвести "с переворачиванием", называют листом Мёбиуса (рис. 49).
Если у боковой поверхности цилиндра склеить между собой верхнее и
376

нижнее основания, то получится поверхность тора (рис. 50). Ту же самую
поверхность можно получить из прямоугольника, склеив левую сторону
с правой, а нижнюю с верхней (рис. 51).
Если у круга отождествить между собой все точки ограничивающей
его окружности, то получится поверхность, топологически эквивалентная
сфере (рис. 52).
-#-
Рис.50
Рис.51
Если у шара в трехмерном пространстве отождествить между собой
все точки его границы (двумерной сферы), то получится пространство,
топологически эквивалентное границе шара в четырехмерном простран-
пространстве — трехмерной сфере.
Далее, рассмотрим квадрат,разбитый на вертикальные отрезки (рис.53).
Будем считать, что все точки, лежащие на одном и том же вертикальном
отрезке, склеены между собой. При таком склеивании из квадратд получа-
получается отрезок. Это можно понять, заметив, что каждому вертикальному
отрезку после склеивания отвечает одна точка, т.е. после отождествления
мы получаем пространство, точками которого являются вертикальные
отрезки. Очевидно, что существует естественное взаимно однозначное
соответствие между вертикальными отрезками и точками, лежащими
на нижней стороне квадрата, которое непрерывно в обе стороны (т.е.
близким отрезкам отвечают близкие точки и обратно). Это и означает,
что после рассматриваемого нами склеивания точек квадрата получается
отрезок.
Рис. 52
Рис.53
Рассмотрим теперь двумерную сферу S2 и отождествим между собой
диаметрально противоположные точки этой сферы. Поверхность, га?лУ^"
чающаяся в результате такого отождествления, называется проективнои
плоскостью и обозначается символом RP2. Иными словами, точкой прРек-
тивной плоскости является множество, состоящее из двух диаметрах(ьно
противоположных точек сферы. Для того, чтобы представить проектов НУ10
плоскость более наглядно заметим, что все точки, лежащие ниже экватРРа>
отождествляются с точками, лежащими выше экватора. Это означаем что

проективную плоскость можно получить из верхней полусферы, отождест-
отождествляя между собой диаметрально противоположные точки экватора. Верх-
Верхняя полусфера топологически эквивалентна кругу. Поэтому проективную
плоскость можно получить из круга, склеивая между собой диаметрально
противоположные точки его границы. Выделим в круге часть, ограниченную
двумя равными параллельными хордами (рис. 54). Очевидно, что при
склеивании диаметрально противоположных точек дуг, ограничивающих
эту часть круга, получается лист Мёбиуса. Из оставшейся части круга при
Рис. 54 Рис. 55 Рис. 56
склеивании диаметрально противоположных точек окружности получается
фигура, топологически эквивалентная кругу. Таким образом, можно
получить проективную плоскость, склеив между собой лист Мёбиуса и
круг по окружности (как лист Мёбиуса, так и круг ограничены топологи-
топологической окружностью).
Совершенно аналогично п-мерное проективное пространство RP" опреде-
определяется как и-мерная сфера S" с отождествленными между собой диамет-
диаметрально противоположными точками. Это пространство можно рассматри-
рассматривать также как «-мерный шар, в котором склеены между собой диаметраль-
диаметрально противоположные точки ограничивающей его (и + 1)-мерной сферы.
Еще один способ получить «-мерное проективное пространство — это рас-
рассмотреть множество всех ненулевых векторов в (и + 1)-мерном евклидо-
евклидовом пространстве и отождествить между собой пропорциональные векторы
(в том, что эта конструкция также приводит к проективному пространству
легко убедиться, заметив, что всякий ненулевой вектор х отождествляется
при этом с вектором х/ | х \, лежащим на единичной сфере в (и + 1)-мерном
пространстве, поэтому проективное пространство можно получить склеивая
друг с другом пропорциональные векторы на сфере).
Поверхность, изображенная на рис. 55 (ручка), топологически эквива-
эквивалентна поверхности, получающейся из пятиугольника ABCDE с помощью
отождествления стороны АВ со стороной DC и стороны ВС со стороной ED
(рис. 56). Ручка представляет собой двумерную поверхность, край которой
топологически эквивалентен окружности. Рассмотрим сферу, из которой
вырезано k непересекающихся кругов, и определим сферу с к ручками как
поверхность, получающуюся, если граничную окружность каждого из
вырезанных кругов склеить с краем ручки. (На рис. 57 изображены сферы
с одной, двумя и тремя ручками. Сфера с одной ручкой топологически
эквивалентна тору.) Легко убедиться, что сферу с к ручками можно полу-
378

Рис.57
читьиз 4Л-угольникаЛ i5iCi/?l . . . AkBkCkDk, отождествляя DtCt сЛ,-5,- и
Ац-xDj с BjQ (см. рис. 58) (здесь г = 1,.... к, точку Ак+1 считаем сов-
совпадающей с Ai).
Рассмотрим снова сферу с к вырезанными кругами и вклеим вместо
вырезанных кругов к листов Мёбиуса (край листа Мёбиуса топологически
эквивалентен окружности; мы отождествляем этот край с границей выре-
вырезанного круга). Построенную только что поверхность — сферу, в которую
Рис.59
вклеены к листов Мёбиуса - можно получить также из 2&-угольника гак,
как это изображено на рис.59 для к = 1, 2, 3. (В 2к-утопъш1к.е АХВ1А2В2...
... AkBk сторона А{В{ отождествлена со стороной Bi^1At. Здесь / = 1,.. .
..., к; мы считаем, что Ак +1 =Alt Bk + i = Вх). Для того, чтобы доказать,
что полученная из 2&-угольника поверхность является сферой с к вклеен-
вклеенными листами Мёбиуса, следует заметить, что лист Мёбиуса может быть
получен из треугольника ABC, в котором сторона АВ отождествлена со
стороной ВС (см. рис. 60). (В самом деле, разрезая треугольник ABC по
высоте ВК и склеивая АВ и ВС мы получаем стандартное представление
листа Мёбиуса в виде прямоугольника, у которого одна из сторон1 склеена
с перевернутой противоположной стороной).
379

Всякая замкнутая поверхность топологически эквивалентна либо сфере с
ручками, либо сфере, в которую вклеены несколько листов Мёбиуса. (Под
замкнутой поверхностью мы понимаем здесь компактное множество,
каждая точка которого имеет окрестность, топологически эквивалентную
кругу.)
§ 4. Эквивалентность и отождествление
Во многих вопросах физики и математики два разных объекта разумно
рассматривать как эквивалентные в некотором смысле. Например, в кван-
квантовой механике состояние частицы или системы частиц можно описывать
с помощью ненулевого вектора, принадлежащего комплексному гильбер-
гильбертову пространству (вектора состояния). Однако, два вектора ф' и 4>, про-
пропорциональные друг другу, физически эквивалентны, т.е. описывают одно
и то же состояние. Электромагнитное поле можно описывать с помощью
векторного потенциала А м (х), но в этом случае потенциалы A J, (х) и А^ (х),
получающиеся друг из друга при помощи калибровочного преобразования
(т.е. связанные соотношением А^(х) =Ajl(x) + 6м\(х)), физически экви-
эквивалентны.
Общее понятие эквивалентности определяется следующим образом.
Говорят, что в множестве X задано соотношение эквивалентности, если
для любых двух элементов х G X, у 6 Y указано, эквивалентны они друг
другу (х ~ у) или не эквивалентны (х ~f- у). При этом соотношение экви-
эквивалентности должно удовлетворять требованиям рефлексивности х ~ х,
симметрии (если х ~ у, то у ~ х) и транзитивности (если х ~ у, у ~ z, то
х ~ z). Если в множестве X задано отношение эквивалентности, то для
всякого элемента х S X можно рассмотреть совокупность Nx элементов,
эквивалентных х. Множество Nx носит название класса эквивалентности
точки х. Легко проверить, что классы эквивалентности двух элементов
множества X либо совпадают, либо не пересекаются (если х ~ у, то Nx =
=Ny,.Bпротивном случае множество Nx C\Ny пусто). Таким образом, отно-
отношение эквивалентности в множестве X порождает разбиение этого множест-
множества на непересекающиеся подмножества (классы эквивалентности). Обрат-
Обратно, если задано разбиение множества X на непересекающиеся подмножест-
подмножества, то этому разбиению сопоставляется отношение эквивалентности: два
элемента считаются эквивалентными, если они принадлежат одному и тому
же подмножеству.
Если в множестве X задано отношение эквивалентности, то разумно
отождествить между собой эквивалентные элементы. Иными словами,
по множеству X и отношению эквивалентности следует построить новое
множество X, ^элементами которого являются классы эквивалентности.
Говорят, что X получено из X отождествлением (или склеиванием) эк-
эквивалентных точек. Наглядные примеры отождествления были описаны в
предыдущем параграфе. В- частности, считая эквивалентными точки квад-
квадрата 0 < х < 1, 0 <у < 1, имеющие одну илу же абсциссу, мы получаем раз-
разбиение квадрата на классы эквивалентности — вертикальные отрезки.
Разбиение двумерной сферы на множества, каждое из которых состоит
из пары диаметрально противоположных точек, порождается отношением
эквивалентности, при котором каждая точка х эквивалентна самой себе
(х ~ х) и диаметрально противоположной точке (х ~ —х).
380

Существует естественное отображение я множества X на X; именно,
каждой точке х 6 ^сопоставляется ее класс эквивалентности Л^. Отобра-
Отображение я называется отображением отождествления. Всякому отображению
g множества Хв множество Z можно сопоставить отображение g = gn
множества X в Z. Очевидно, что отображение g переводит эквивалентные
точки в одну и ту же точку. Обратно, если отображение / пространства X
в Z "склеивает" эквивалентные точки (переводит две эквивалентные точ-
точки в одну и ту же точку), то^ можно найти такое отображение Л множества
X в Z, что / = Ля (т.е. / = А). Например, если X есть и-мерная сфера S",
в которой считаются эквивалентными диаметрально противоположные точ-
точки, то всякая четная функция переводит эквивалентные точки в одну и ту
же точку, поэтому всякая четная функция на сфере X = S" порождает
функцию на проективном пространстве X = RP ".
Если задано отображение р множества X на множество Y, то по этому
отображению естественно строится отношение эквивалентности в X (точ-
(точки х i, х2 6 X следует считать эквивалентными, если р (х i) =р (х2 )). Клас-
Классами эквивалентности в данном случае являются прообразы точек у G Y
(каждой точке у ? Y сопоставляется ее прообраз — множество р~1(у),
состоящее из всех точек, которые переходят в у при отображении р). Мы
видим, что в рассматриваемой ситуации существует взаимно однозначное
соответствие между X и Y.
Если множество X является топологическим пространством, то в мно-
множестве X классов эквивалентности также естественно вводится топология.
Именно, топология в X определяется таким образом, чтобы отображение
g пространства X в произвольное топологическое пространство Z было
непрерывным в том и только в том случае, если отображение g = gn прост-
пространства X в Z непрерывно. В частности, считая, что Z = X, g — тождествен-
тождественное отображение, мы видим, что отображение ^пространства X в X долж-
должно быть непрерывным. Конкретно^опология в X может быть описана сле-
следующим образом. Множество U СХ следует считать открытым, если его
прообраз n~l(U) С X открыт в X Существенно отметить, что определен-
определенная таким образом топология в X может не удовлетворять аксиомам от;
делимости; в частности, одноточечные подмножества пространства X
будут замкнутыми множествами в том и только в том случае, если все клас-
классы эквивалентности являются замкнутыми подмножествами пространства
X. В интересных для физики случаях топологии в 1С, как правило, не обла-
обладают патологическими свойствами.
§ 5. Представления групп
Если каждому элементу группы G сопоставлено линейное преобразова-
преобразование Tg векторного пространства Е таким образом, что произведению эле-
элементов группы G отвечает произведение соответствующих им преобразо-
преобразований:
^8182 ~ ^?i Tg2 > (О
то говорят, что задано линейное представление группы G. Иначе можно
сказать, что линейным представлением группы G называется гомоморфизм
группы G в группу GL (E) всех линейных преобразований пространства Е.
Пространство Ё называется пространством представления группы G.
1 381

Подпространство Е' пространства Е называется инвариантным подпрост-
подпространством представления Tg, если все операторы Tg переводят подпростран-
подпространство Е' в себя. Очевидно, что операторы Tg, рассматриваемые только в Е',
образуют представление группы G в Е . Если в пространстве Е не существу-
существует нетривиальных инвариантных подпространств, то представление Tg на-
называется неприводимым (под нетривиальным подпространством понимает-
понимается подпространство, не совпадающее с Е или с подпространством, содержа-
содержащим только нулевой вектор). Если Tg (соответственно Г|) — представле-
представление группы G в пространстве Ei (в пространстве ЛГ2), то прямая сумма
представлений Tg и Т\ определяется как представление Tg группы G в
пространстве Ех +Е2, задаваемое формулой:
где ei & E1,e2 6 Е2. Представления Tg и Т\ называются эквивалентными,
если существует изоморфное отображение а пространства Ех на прост-
пространство Ei, удовлетворяющее условию
aTg = Г|а.
Представление Tg называется унитарным в случае, если все операторы
Tg унитарны, и ортогональным в случае, если все операторы Tg ортогональ-
ортогональны. (Разумеется, для того, чтобы имело смысл говорить об ортогональ-
ортогональности или унитарности операторов Tg следует предположить, что Е являет-
является действительным или комплексным гильбертовым пространством.)
Если F — инвариантное подпространство ортогонального или унитарного
представления Т, то его ортогональное дополнение F± также является ин-
инвариантным подпространством. Представление Т порождает представления
рассматриваемой группы в пространствах F и Fi ; оно эквивалентно пря-
прямой сумме этих представлений.
Для всякого представления Т компактной группы G в пространстве Е
можно найти скалярное произведение в пространстве Е, не меняющееся при
преобразованиях Tg. Иными словами, при подходящем выборе скалярно-
скалярного произведения в Е всякое представление компактной группы является
ортогональным или унитарным (в зависимости от того было ли Е действи-
действительным или комплексным пространством) *). Из сделанного только что
замечания вытекает, что всякое конечномерное представление компактной
группы G эквивалентно прямой сумме неприводимых представлений.
Особенно важную роль играют в физике представления группы Лоренца
L. Это связано с тем, что закон преобразования физической величины из
одной инерциальнои системы отсчета в другую описывается представлением
группы Лоренца. В самом деле, если какой-то физический объект (точка,
поле и т.д.) описывается в какой-то инерциальнои системе К с помощью
совокупности и чисел (<fii,..., <р„), то в другой инерциальнои системе К'
он будет описываться другими числами {\р\,..., <р'„). Эти новые числа
должны выражаться через старые (должно существовать правило пересчета
величин из одной системы отсчета в другую). Мы будем предполагать, что
(<p'i,..., ifi'f,) выражаются через (<рх уэ„) линейно. Поскольку переход
*) Для того чтобы построить инвариантное скалярное произведение в Е, нужно
взять произвольное скалярное произведение и усреднить его по инвариантной мере
dg на группе G.
382

от одной инерциалыюй системы отсчета к другой описывается преобразова-
преобразованием Лоренца, мы видим, что всякому g 6 Z, отвечает линейное преобразо-
преобразование Tg величин (<pi,..., уэ„). Соотношение A) очевидным образом
выполняется. Оно означает просто, что, пересчитывая физическую величину
сначала из системы К в систему К', а затем из системы К' в систему К",
мы получим тот же результат, что и при непосредственно пересчете из сис-
системы К в систему К".
Приведем примеры представлений группы Лоренца (примеры физичес-
физических величин). Под скаляром понимается величина, не зависящая от выбора
системы координат: иначе говоря, скаляр преобразуется по тривиальному
одномерному представлению группы L (все операторы Tg являются еди-
единичными операторами). Под вектором (точнее, контравариантным век-
вектором или вектором с верхними индексами) понимают величину
(А0, А1, А2, А3), преобразующуюся при переходе из одной инерциальной
системы отсчета в другую так же, как координаты:
" 'k B)
где а'к - матрица преобразования Лоренца.
Под ковектором (ковариантным вектором или вектором с нижними
индексами) понимается величина (А 0, А и А2, Аъ), преобразующаяся по
закону
A't = b*Ak, C)
где bfa'k = 5/. (Иначе говоря, матрица преобразования ковектора являет-
является обратной транспонированной матрицей к матрице преобразования Лорен-
Лоренца.) Примером ковектора является величина ду/дх1, где у — скалярное
поле. Тензором (точнее, контравариантным тензором второго ранга) А
называется величина, преобразующаяся как произведение В'Ск векторов
В* и С*:
1к 1т. D)
Аналогично определяются законы преобразования тензора А( %, имеющего
два нижних индекса, и тензора А*, имеющего один нижний и один верхний
индексы
А\к = Ъ\ЪЧ!Аы, E)
А? =а№А1т. F)
Тензоры второго ранга А\, А^, А'к можно рассматривать как матрицы;
в матричных обозначениях законы преобразования D), F) принимают
вид
А' = аАаТ, А'
Можно определить также понятие тензора, имеющего произвольное число
верхних и нижних индексов. Из инвариантности пространственно-времен-
пространственно-временного интервала ds2 = gijkdxidxk при преобразованиях Лоренца вытекает,
что метрический тензор gtk является инвариантным тензором (не меняется
при переходе к другой системе отсчета) :
='a}ak"gtm.
383

Из инвариантности четырехмерного объема при преобразованиях Ло-
Лоренца вытекает инвариантность тензора е;д/ при преобразованиях Ло-
Лоренца. (Полностью антисимметричный тензор е{/к, равен +1, если (/, /,
к, /) — четная перестановка, равен — 1, если (/',/, к, 1) — нечетная переста-
перестановка, и нулю, если два индекса совпадают.)
Законы преобразования B—6) определяют представления груп-
группы Лоренца. Существенно отметить, что эти законы могут быть приме-
применены также в случае, когда а\ является произвольной матрицей (не обя-
обязательно матрицей преобразования Лоренца.) Таким образом, законы
B—6) задают представление любой матричной группы. В частности,
законы B, 3) определяют соответственно векторное и ковекторное пред-
представления группы GL(«, IR), если а'{ рассматривать как произвольную
невырожденную действительную матрицу порядка п, а числа А' и А/
считать действительными A < / < и). В случае, если д' — комплексная
невырожденная матрица и А1, А/ комплексны, формулы B, 3) задают
векторное и ковекторное представления группы GL(«, С). Отметим, что
в комплексном случае можно рассматривать также законы преобразова-
ния, отличающиеся о1* законов B, 3) заменой матриц ак, 6, на
комплексно сопряженные матрицы:
A'f=aU*. G)
Л} = ъ\Ак. (8)
О величинах:, преобразующихся по законам G, 8), говорят как о векторах
и ковекторах с пунктирными индексами. Более широкий класс представ-
представлений матричных групп получается, если рассматривать тензоры, имеющие
произвольное число верхних и нижних индексов. (В случае, если группа
состоит из комплексных матриц, каждый индекс может быть обыкновен-
обыкновенным или пунктирным.)
Для группы Лоренца векторное и ковекторное представления эквива-
эквивалентны между собой; представления, определяемые формулами D, 5, 6)
также эквивалентны друг другу. Это следует из того, что мы можем опус-
опускать индексы с помощью метрического тензора gkl, например вектору А'
сопоставляется ковектор Ак = g/^A1, тензору Ats сопоставляется тензор
А кг = gklgrsA'*.
Для групп GL(/i, IR) и GL(«, (t) представления, определяемые форму-
формулами B, 3, 7, 8), не эквивалентны друг другу. Представления B, 3, 7, 8)
неприводимы. Представления D, 5, 6) приводимы. Например, подпрост-
подпространства, состоящие соответственно из симметричных (Atk = Akl) и анти-
антисимметричных (Aik = — Aki) тензоров инвариантны относительно группы
всех невырожденных матриц. В пространстве представления F) можно
выделить инвариантное подпространство, состоящее из тензоров вида \6^
и тензоров, имеющих нулевой след (удовлетворяющих условию А\ - 0).
Описанные только что инвариантные подпространства неприводимы отно-
относительно группы GL(«, 1R) или GL(/i, I).
Всякое представление группы Лоренца может быть реализовано с по-
мощьда тензоров (точнее, всякое представление этой группы эквивалентно
384

представлению группы в одном из инвариантных подпространств тензор-
тензорного представления). Однако, понятие представления можно расширить,
отказавшись от требования, чтобы каждому элементу группы отвечало
ровно одно преобразование Tg (допустив к рассмотрению многозначные
представления). Тогда у группы Лоренца появляются представления ново-
нового типа — двузначные представления. Простейшие из этих представлений
имеют комплексную размерность 2, т.е. сопоставляют каждому элементу
группы Лоренца комплексную двумерную матрицу. Двумерные матрицы,
отвечающие элементам группы Лоренца, имеют определитель 1 (т.е. при-
принадлежат группе SLB, (D)).
Вместо того, чтобы описывать двузначное отображение группы Лоренца
в SLB, С), нам будет удобно построить обратное отображение группы
SLB, С) в группу Лоренца. Будем исходить из представления группы
SLB, С), построенного с помощью тензоров, имеющих один обычный
и один пунктирный индекс; если рассматривать такой тензор как матрицу,
то интересующее нас представление сопоставляет матрице a G SLB, С)
оператор Та в пространстве матриц, определяемый формулой
(9)
Легко видеть, что эрмитовы матрицы образуют инвариантное подпрост-
подпространство представления (9). Двумерные эрмитовы матрицы образуют че-
четырехмерное действительное векторное пространство; такая матрица
может быть охарактеризована с помощью четырех действительных чисел
а1Ь д22, Re<*i2. Ima12. Нам будет удобнее рассматривать вместо этих
чисел числа
х° = -(Дц+а22), х1 = Rea12,
x2=-Ima12> x3 = -(Дц-Д22).
л
Иными словами, мы будем записывать эрмитову матрицу Хв виде
л / х° +х3 х1 -ix2 \ п _
Х= ( 1 1 о , ) =х° +ха , A0)
\ х1 +ix2 х° -х3 / к '
где ^} = (о1, о2, о3) — матрицы Паули:
о/ V/ о/ \о -1
1 ,
Заметим, что х' = — Sp(o'X), где а0 = 1. Преобразование (9) будем
рассматривать как представление группы SLB, С) в пространстве эрми-
эрмитовых матриц. Легко видеть, что операторы этого представления не меняют
детерминант эрмитовой матрицы:
detTa(A)=det(aAa*) = detadeU deta+
При описанном выше соответствии между эрмитовыми матрицами
и векторами (х°, х1, х2, х3) детерминант матрицы X переходит в
385

(x0J — (x1J — (x2J - (x3J. Рассматривая преобразования (9) как преобра-
преобразования четырехмерного пространства с координатами (х°, х1, х2, х3),
мы видим, что они сохраняют пространственно-временной интервал (х0J —
— (х1J — (х2J — (х3J; иначе говоря, они являются преобразованиями
Лоренца. Таким образом, мы построили гомоморфизм группы SLB, С)
в полную группу Лоренца. Точнее, этот гомоморфизм отображает SLB, (С)
на группу Лоренца L (как объяснено в § Т1 группу L можно рассматривать
как компоненту связности полной группы Лоренца; поскольку группа
SLB, С) связна, ее образ содержится в L). Ядром построенного только
что гомоморфизма группы SLB, С) на L является группа "Z?2 (в единич-
единичное преобразование Лоренца переходит кроме единичной матрицы матри-
матрица-1).
Рассмотрим теперь отображение группы L в группу SLB, <П), обратное
построенному только что отображению SLB, (E) на L. Это отображение
двузначно: каждому элементу группы L отвечает пара матриц, отличающих-
отличающихся знаком. Его можно рассматривать как двузначное двумерное представ-
представление группы. Это представление называется спинорным, а двухкомпонент-
ные величины, преобразующиеся по этому представлению, называются
спинорами. Величины, комплексно сопряженные спинорам, называют
пунктирными спинорами. (Вместо терминов спинор и пунктирный спинор
употребляют также термины левый и правый спинор.)
Отметим, что при построенном нами гомоморфизме группы SLB, С)
в группу L подгруппа SUB) группы SLB, (П) отображается на подгруп-
подгруппу SOC) группы L. В самом деле, если матрица a G SLB, С) унитарна, то
и, значит,
SpTa(X)=SpX.
При описанном выше соответствии между эрмитовыми матрицами
и четырехмерными векторами след матрицы переходит в удвоенную нуле-
л
вую компоненту вектора: SpX = 2x°. Поэтому преобразования Лоренца,
отвечающие унитарным матрицам, сохраняют х°; это означает, что они
являются ортогональными преобразованиями трехмерного пространства
с координатами (х1, х2, х3). Таким образом, мы построили трехмерное
ортогональное представление группы SUB); обратное отображение можно
4 рассматривать как двузначное двумерное представление группы. SOC).
Построенное соответствие между группами L и SLB, (С) позволяет рас-
рассматривать каждое представление группы L как (быть может, двузначное)
представление группы Лоренца. Неприводимые представления группы
SLB, (С) легко описать. Каждое такое представление задается с помощью
двух целых чисел р и q (р > 0,. q > 0). Оно может быть реализовано в
пространстве тензоров, имеющих р обычных индексов, q пунктирных ин-
индексов и симметричных отдельно по обычным и пунктирным индексам.
(Не имеет значения, рассматриваем мы тензоры с верхними или нижними
индексами. В самом деле, антисимметричные тензоры еа(з и е^ • инвариант-
инвариантны относительно группы SLB, С), и мы можем опускать и поднимать
индексы с помощью этих тензоров, что позволяет установить эквивалент-
эквивалентность тензорного представления с верхними индексами и тензорного пред-
386

ставление с нижними индексами.) В случае, если р + q четно, описанное
представление группы SLB, (С) порождает однозначное представление
группы Лоренца; при р + q нечетном соответствующее представление
группы Лоренца двузначно.
Понятие тензора тесно связано с понятием тензорного произведения
представлений. Если величина М ^ (М', ..., Мт) преобразуется по пред-
представлению Ti группы G (Т.е. вектор (М1, .... Мт) принадлежит прост-
пространству Et представления 7^), а величина N= (N1,... ,N") преобразуется
по представлению Т2 группы G, тъ по определению величина с компонен-
компонентами Ма ¦ Nb преобразуется по^ен/зорному произведению Гх ® Т2 представ-
представлений T"i и 7*2. Более аккуратно, для двух линейных пространств Еу и Е2
определяется тензорное произведение этих пространств Ех ® Е2 как
пространство, состоящее из формальных линейных комбинаций вида
Б са6еаA) ® ейB), где е,A) , е^ - базис в ?,, а е\2\ ..., елB) - базис
Ь
а, Ь
в Е2. Представление Ту ® Т2 действует в Et ®?121изменяяко°рдинатысай
по формуле
где (Г/С?))^ — матрица оператора Ti(g) в фиксированном выше базисе
в Е{. Отметим, что определение тензорного произведения пространств
и представлений не зависит от выбора базиса. Очевидно, что представление
группы тензорами ранга к является тензорным произведением к экземп-
экземпляров векторных представлений.
§ 6. Действие группы на пространстве
Говорят, что группа G действует на множестве Е (точнее, G действует
на Е слева), если каждому элементу g e G сопоставлено преобразова-
преобразование ipg множества Е таким образом, что
Иными словами, группа G действует на Е, если задан гомоморфизм этой
группы в группу всех преобразований множества Е. Наиболее важен слу-
случай, когда группа G реализована как группа преобразований множества Е
(т.е. фиксирован изоморфизм группы G и некоторой подгруппы группы
преобразований). Тогда говорят, что группа G действует на Е эффективно.
Если Е — векторное пространство, а все преобразования ipg линейны,
то Действие группы G на Е можно рассматривать как линейное представле-
представление группы G. В общем случае в физической литературе термин "действие
группы" заменяют термином "нелинейное представление группы".
Если каждому элементу g группы G сопоставлено преобразование ipg
множества Е таким образом, что
то говорят, что G действует на Е справа. Если задано правое действие группы
G на Е, то можно построить левое действие G на Е, сопоставив элементу
g 6 G преобразование \ ~ <pg_, (из соотношения (#, g2)~l = g'2l • g~\ выте-
вытекает, что \ig2 =*(glglyi =Vg-i1g? =\t •**,)• Это замечание позволяет
387

свести изучение правого действия <pg группы G на Е к изучению левого
действия Xg. Можно было бы вообще не вводить понятия правого дейст-
действия; однако, во многих случаях удобно пользоваться этим понятием.
В случае, если группа G действует слева, вместо фЛх) часто пишут
просто gx; условие A) означает тогда,что имеет место тождество (gig2)x =
= gi(g2x). В случае правого действия вместо yg(x) пишут xg; условие B)
означает, что x(gxg2) = (xgt)g2.
В случае, если топологическая группа G действует на топологическом
пространстве Е, мы всегда будем считать, что это действие непрерывно
(т.е., что <Pg(x) непрерывно по совокупности переменных g G G, x G Е).
В дальнейшем, говоря, что группа G действует на Е, мы будем иметь
в виду, что G действует на Е слева (если не оговорено противное). Всякую
матричную группу (подгруппу группы GL(«, (R)) можно рассматривать как
группу линейных преобразований пространства IR" (т.е. матричные группы
эффективно действуют на IR").
Если в множестве Е действует группа G, то в этом множестве естествен-
естественно вводится отношение эквивалентности. Именно, две точки Xi 6 Е, х2 ? Е
считаются эквивалентными, если одну можно получить из другой с помо-
помощью преобразования группы G (т.е. если х2 ~^>g{xi), где gG.G). Класс
эквивалентности Nx точки х G Е называется орбитой точки х. (Иначе
можно сказать, что орбита точки х состоит из всех точек, которые можно
получить из х с помощью преобразований группы.) Орбиты двух разных
точек, принадлежащих Е, либо совпадают, либо не пересекаются, т.е. мно-
множество Е разбивается на орбиты. Множество всех орбит группы G в про-
пространстве Е обозначается символом E/G. Если Е — топологическое прост-
пространство, то в множестве E/G естественно вводится топология (подробнее
см. § А4). Однако, эта топология может не удовлетворять аксиомам отде-
отделимости (в частности, для того, чтобы все точки в E/G были замкнутыми
множествами необходимо потребовать, чтобы все орбиты группы G были
замкнуты). Простейший пример возникающих таким образом патологий
получается, если рассмотреть группу GL(«) невырожденных матриц поряд-
порядка п как группу линейных преобразований пространства IR". В этом случае
имеются всего две орбиты: одна состоит только из нулевого вектора,
а другая — из всех остальных векторов. Пространство орбит IR"/GL(«)
состоит из двух точек, из которых только одна является замкнутым мно-
множеством.
В случае, если любая точка множества Е может быть получена из любой
другой точки с помощью преобразования группы G, говорят, что G дейст-'
вует на Е транзитивно (в этом случае орбита любой точки совпадает со
всем множеством Е, а множество E/G состоит из единственного элемента).
Отметим, что указанные выше определения применимы как в случае
левого, так и в случае правого действия группы; это же относится и к
определению стационарной подгруппы, которое мы сейчас дадим.
Стационарной подгруппой Нх точки х G Е называется множество элемен-
элементов группы G, оставляющих точку х на месте; иными словами h ? Нх,
если <рн(х) =х. (Множество Нх, очевидно, является подгруппой группы G.)
Если h 6ЯХ и x' = tpg(x), то ghg~l 6ЯХ-. Напомним, что преобразование
0Lg, переводящее элемент h в ghg~l, называется внутренним автоморфиз-
автоморфизмом группы G. Можно сказать, что группа Н^ (х) получается из Нх с помо-
388

щью внутреннего автоморфизма. Мы видим, что стационарные подгруппы
точек, принадлежащих одной и той же орбите, изоморфны; более того, они
сопряжены друг другу (две подгруппы называются сопряженными, если
одна получается из другой с помощью внутреннего автоморфизма).
Рассмотрим некоторые простейшие примеры.
Каждой трехмерной ортогональной матрице А с определителем 1 сопо-
сопоставляется вращение х' = Ах трехмерного пространства вокруг оси, прохо-
проходящей через начало координат. Это соответствие определяет действие
группы SOC) ортогональных матриц с определителем 1 в пространстве IR3.
Орбитами этой группы являются двумерные сферы с центром в начале
координат; само начало координат также можно рассматривать как орби-
орбиту, состоящую из единственной точки. Пространство орбит топологически
эквивалентно лучу. Каждая ортогональная матрица оставляет на месте
начало координат 0. поэтому стационарная подгруппа точки 0 совпадает
со всей группой SOC). Стационарная подгруппа точки х^О состоит из
вращений вокруг прямой, соединяющей точку х с началом координат; эта
стационарная подгруппа изоморфна группе SO B) (вращения йокруг оси
можно рассматривать как вращения в плоскости, ортогональной этой оси).
Совершенно аналогично можно рассматривать группу SO (и) (группу
и-мерных ортогональных матриц с определителем 1) как группу преобразо-
преобразований пространства 1R". Орбитами этой группы являются (п — 1)-мерные
сферы. Стационарная подгруппа точки @, 0, . . . , 0, г ), где гФО, состоит
из матриц {а/к} ? SO(n), у которых апп = 1,аПАг = д*п= 0 ПРИ к Ф п.
Матричные элементы такой матрицы, находящиеся в столбцах и строках
с номерами 1,. 2, ...,«- 1, образуют ортогональную матрицу порядка
и — 1, имеющую детерминант 1. Мы видим, что стационарная подгруппа
рассматриваемой точки изоморфна группе SO (и — 1). Это же верно для
любой точки х G. (R", х Ф 0, поскольку всякая такая точка принадлежит
орбите точки @, 0,..., 0, |х|), а стационарные подгруппы всех точек,
принадлежащих одной орбите, изоморфны.
Определим действие группы GLA,|R) действительных чисел, отличных
от нуля, на пространстве [R" с выколотым началом координат, сопоставив
каждому действительному числу ХФ0 преобразование, переводящее точку
(дг1,... , x")Gp"\ {0} в точку (Хх1,.. ., Хх"). В этом случае орбитами
являются прямые, проходящие через начало координат. Пространство
орбит может быть отождествлено с действительным проективным простран-
пространством RP"~* (см. §АЗ).
Аналогично можно определить действие группы GLA, С) (группы
отличных от нуля комплексных чисел) в пространстве С" с выколотым
началом координат. Пространство орбит получается при отождествлении
точки (л:1 х") G С" \{0} с точками вида (сх1,..., сх"), где с G С ,
сФО. Это пространство называется (и — 1)-мерным комплексным проек-
проективным пространством и обозначается СРп~х. Стационарные подгруппы
всех точек в двух последних примерах тривиальны (состоят только из
единичного элемента).
Рассмотрим еще один пример. Обозначим символом Gn % множество
^-мерных линейных подпространств и-мерного векторного пространства R".
Всякой и-мерной невырожденной матрице отвечает линейное преобразова-
преобразование пространства IR"; при этом линейном преобразовании ^-мерное про-
389

странство переходит в fc-мерное подпространство. Мы можем рассматри-
рассматривать, таким образом, группу GL(n) всех и-мерных невырожденных матриц
как группу преобразований множества Gn к. Всякое fc-мерное подпростран-
подпространство можно перевести в любое другое fc-мерное пространство с помощью
линейного преобразования. Это означает, что группа GL(n) действует на
Gn k транзитивно. Стационарная подгруппа, отвечающая плоскости a G
G Gn> k, изоморфна группе матриц вида
где А, В, С - матрицы размерности (и - к) X (и - к), к X (л - к), к X к
соответственно.
Рассмотрим теперь произвольную группу G и подгруппу Н С G. Можно
определить действие подгруппы Н на группе G двумя разными способами.
При левом действии группы Н на G каждому элементу А ? Н сопостав-
сопоставляется преобразование Lh> переводящее элемент g G G в Lft(_g) = hg.
При правом действии Н на G элементу h G Н сопоставляется преобразова-
преобразование, переводящее g G G в Rh(g) = gh. Орбиты левого действия назы-
называются левыми смежными классами подгруппы Я, орбиты правого дейст-
действия — правыми смежными классами. Пространство правых смежных клас-
классов мы будем обозначать символом G/H и называть факторпространст-
вом G по Н. Отметим, что между левыми смежными классами и правыми
смежными классами существует взаимно однозначное соответствие: если
#i & G и g2 ? G принадлежат одному и тому же левому смежному классу,
то g'i1 и g2l принадлежат одному и тому же правому смежному классу
(если h G Я, gx = hg2, то g~^ = g~21h, A G Я). Это позволяет не
вводить отдельного обозначения для пространства левых смежных классов.
Сопоставив каждому элементу g G G содержащий его правый смежный
класс, мы получаем отображение а группы G на множество G/H. Можно
сказать, что G/H получается из G отождествлением элементов, отличаю-
отличающихся умножением справа на элемент из Н (т.е. gt ~ g2,ecnn g2 = gth,
h ? Я); отображение а представляет собой отображение отождествления.
Естественно поставить вопрос, можно ли ввести в G/H операцию умно-
умножения таким образом, чтобы G/H было группой относительно этой опера-
операции, а отображение а - гомоморфизмом. Необходимым и достаточным
условием для возможности ввести такую операцию оказывается инвариант-
инвариантность подгруппы Я. В самом деле, если можно ввести требуемое умноже-
умножение, то Я будет ядром гомоморфизма а и, следовательно, инвариантной
подгруппой. С другой стороны, если Я — инвариантная подгруппа, то мы
можем определить произведение смежных классов Xj и Х2 как смежный
класс, содержащий gig2, где gt G\t и g2 & \2. (Из инвариантности под-
подгруппы вытекает, что этот смежный класс не зависит .от выбора элементов
#1 и g2. В самом деле, если g\ = gyh^, g\ = g2h2, где hlfh2 6 H, то
iiii = gig2h,rmh = g21h1g2h2 €Я.)
Отметим, что в случае, если Н — инвариантная подгруппа и gi.gi^- G
принадлежат одному и тому же правому смежному классу по Н, то они
принадлежат одному и тому же левому смежному классу по Н (если
390

Si ~ S\h, h 6 Я, то g2 = h'gi, где h' = g^A^I1 6 H). Таким образом,
множество G/H, где Н — инвариантная подгруппа, естественным образом
превращается в группу; эта группа называется факторгруппой группы G
по. подгруппе И. Факторгруппу G/H можно рассматривать как группу G,
в которой отождествлены между собой элементы, отличающиеся множите-
множителем, принадлежащим к группе Я. Например, если G = ~Z — группа целых
чисел по сложению, а подгруппа Я состоит из чисел, кратных целому чис-
числу/и (Я = т 2), то два числа принадлежат одному и тому же смежному
классу, в случае, если они дают один и тот же остаток при делении на т
(сравнимы по модулю т). Факторгруппа 2?/тЯ состоит из т элементов.
Она называется группой вычетов по модулю т и обозначается Zm.
Множество Е, в котором транзитивно действует группа G, называется
однородным пространством. Всякую орбиту группы G, действующей
в каком-либо множестве, можно рассматривать как однородное простран-
пространство. Например, мы видели выше, что орбитами группы SO (и), действую-
действующей в 1R", являются (и — 1)-мерные сферы; это значит, что сферу S"~1
можно рассматривать как однородное пространство относительно действия
группы SO (и).
Фиксируем точку е0 в пространстве Е, на котором транзитивно дей-
действует группа G. Обозначим символом К(е) множество элементов
группы, переводящих точку е0 в точку е (иначе говоря, g G К(е), если
tfg (е0) = е). Множество К(е0) совпадает со стационарной подгруппой точ-
точки е0; эту стационарную подгруппу обозначим символом Я. Если
g G K(e), h S Я, то gh G К{е). Если glf g2 S К(е), то ^ = g2h,
где h G Я. Иными словами, К(е) можно рассматривать как правый смеж-
смежный класс группы G по подгруппе Я. Таким образом, мы получаем
взаимно однозначное соответствие между точками пространства Е и множе-
множеством правых смежных классов G/H.
Если Я — произвольная подгруппа группы G, то в множестве правых
смежных классов G/H можно определить левое действие группы G с по-
помощью умножения слева на элементы группы G. Если смежный класс
К G G/H содержит элемент gt G G, то преобразование \pg, отвечающее
элементу g G G, переводит X в смежный класс, содержащий ggi. Этот
смежный класс не зависит от выбора элемента g G X (если g2 - g\h,
где h G Я, то gg2 = ggyh,vi, значит, gg2 и ggt принадлежат одному и
тому же смежному классу). Построенное действие группы G на множест-
множестве G/H транзитивно. Из проведенных выше рассуждений следует, что тран-
транзитивное действие группы G в произвольном пространстве Е эквивалентно
описанному только что действию. Точнее говоря, можно построить такое
отображение р пространства G/H на Е, что \pgp = pyg (здесь символом <pg
обозначается действие группы G в Е, а символом "!pg - действие группы G
в G/H). Если G — топологическая группа, то отображение р пространства
G/H на Е является взаимно однозначным непрерывным отображением;
во всех интересных для нас случаях это отображение непрерьшно в обе сто-
стороны. В частности, сфера S"~x топологически эквивалентна факторпрост-
ранству SO (я)/SO (и - 1).
391

§ 7. Присоединенное представление группы Ли
Всякая группа G действует на самой себе с помощью внутренних авто-
автоморфизмов. Точнее, сопоставляя каждому элементу g € G преобразование
h -*¦ ghg~l, мы получаем действие группы G на множестве G. Если G -
группа Ли, то описанное действие порождает линейное действие группы G
на алгебре Ли 9 группы G - присоединенное представление группы G.
(Единичный элемент группы переходит в себя при внутренних автоморфиз-
автоморфизмах, поэтому эти автоморфизмы порождают преобразования множества
касательных векторов в единичном элементе группы G.) Для матричной
группы Ли G алгебра Ли 8 также реализуется матрицами и присоединен-
присоединенное представление rg переводит элемент х € & в rg(x) = gxg'1. Если G -
компактная группа Ли, то как мы говорили, в пространстве всякого пред-
представления существует инвариантное скалярное произведение. Применяя это
утверждение к присоединенному представлению, мы видим, что в алгеб-
алгебре Ли & компактной группы Ли G существует скалярное произведение
< ¦ , • >, удовлетворяющее условию < тя(хг), rg(x2) } = < хх, х2 > (инва-
(инвариантное скалярное произведение). Рассматривая rg для элементов груп-
группы G бесконечно близких к единичному, т.е. полагая g = 1 + h, й G 3? ,
получаем Tl+h(x) =x + [h, x]. Это означает, что-присоединенному пред-
представлению группы G отвечает представление алгебры Ли & , задаваемое
формулой h -> oh (x) = [h, х]. Записывая условие инвариантности ска-
скалярного произведения в # ддя g = 1 + h, h G i§ получаем < {h, x, ], x2 > +
i- <x,, [ h, x2 ] > = 0. Отсюда следует, что выражение ([х, у], z), где х,у, z&&,
антисимметрично по х, у, z. Это выражение можно рассматривать как
G-инвариантную антисимметричную полилинейную форму Сполилиней-
ность обозначает линейность по всем аргументам). Выбирая в 5§ ортонор-
мированный базис elt ..., е„ и переходя от элементов х, у, z к их коорди-
координатам ха, уа, za в этом базисе, записываем < [х,у], z ) в виде
fapyXay^zP, где /а/37 - антисимметричный G-инвариантный тензор.
(Этот тензор можно интерпретировать как тензор структурных констант:
fapy = <[еа, ер],еу).)
Если линейное подпространство Ж алгебры Ли 8 переходит в себя при
присоединенном представлении алгебры 2> (является инвариантным под-
подпространством этого представления), то ah(x) = [h,x] S К для любых
h G !§, х G Ж. Это значит, что Ж является инвариантной подалгеброй ал-
алгебры i§. Неприводимость присоединенного представления алгебры Ли
означает, что алгебра 'З проста (не содержит нетривиальных инвариантных
подалгебр). Если & — алгебра Ли компактной группы Ли G, то из сказан-
сказанного в § А 5 следует, что присоединенное представление алгебры i§ разла-
разлагается в прямую сумму неприводимых представлений. Отсюда видно, что
алгебра $ разлагается в прямую сумму простых алгебр Ли. Группа Ли,
алгебра Ли которой является простой, также называется простой.
Все компактные простые группы Ли проклассифицированы. Всякая такая
группа локально изоморфна либо одной из групп, принадлежащих к клас-
классическим сериям SU(«), n>2, SO (и), п > 2, пФА, Sp(«), n> 1,либо
одной из так называемых исключительных групп G2, F^,E6, Еп, Е^,
392

§ 8. Кватернионы
Алгеброй кватернионов называется четырехмерное векторное простран-
пространство, в котором определено ассоциативное умножение по формуле:
(ао,а) (bo,b)-(aobo -ab, аХ Ь + доЬ + Ьоа)-
(Мы записываем кватернион в виде (<*o> а), где а о — действительное чис-
число, а — трехмерный вектор. Символы ab и а X b обозначают соответствен-
соответственно скалярное и векторное произведение трехмерных векторов.) Каждое
действительное число можно рассматривать как кватернион (числу а со-
сопоставляется кватернион {а, 0)). Умножение кватерниона на кватернион,
отвечающий действительному числу, сводится к умножению четырехмерно-
четырехмерного вектора на число
(в, 0)(Ь0,Ъ) = (Ьо,Ъ)(а,0) = (аЬо, аЪ).
Отсюда следует, что кватернион 1 = A, 0) является единицей алгебры ква-
кватернионов (для любого кватерниона а имеем \-а=а • 1 = а). Введем обо-
обозначения:
/ = @,1,0,0), / = @,0,1,0), /t = @,0,0,1).
Кватернионы 1, /, /, к образуют базис в векторном пространстве. Иными
словами, каждый кватернион может быть записан в виде ao+a1i+a2j +a3k.
Легко проверить, что
// = —// = к, /к = —kj = /', ki = —ik ~ /,
Кватернион (а0, —а) называется сопряженным кватерниону а = {ао,я) и
обозначается а". Легко проверить, что
Действительное число у/а20+ а2 называется нормой кватерниона и обозна-
обозначается || а Ц-. Легко проверить, что
\\ab\\ = || а || • || Ъ ||.
Из соотношения A) следует, что
а а
\а\\2 \\.a\\'
а = 1.
Это означает, что для всякого ненулевого кватерниона можно построить об-
обратный кватернион а по формуле
lall2 '
393

Множество кватернионов, имеющих единичную норму, является группой
относительно кватерниончого умножения; эта группа обозначается симво-
символом Sp(l). Группа Sp(l) является простейшей в серии классических
групп Sр (и). Для того, чтобы определить группу Sp(/i) рассмотрим
и-мерное кватернионное пространство <2" (пространство, точками которого
являются строки, состоящие из п кватернионов). Пространство Q" можно
рассматривать как 4 и-мерное действительное пространство. Всякой матри-
матрице {aj) порядка и X и, элементами которой являкпсл кватернионы,
сопоставим преобразование пространства, определяемое формулой
Я''= a',qf, B)
где (<Д ..., q") G Q", (qtl, ..., q'") e g". Группа Sp(«) состоит из
преобразований вида B), удовлетворяющих условию ? || q'' Ц 2 =2 \\q' ||2
(иначе можно сказать, что группа Sp(«) состоит из преобразований ви-
вида B) - кватернионных линейных преобразований, являющихся одновре-
одновременно ортогональными преобразованиями 4 «-мерного действительного
пространства).
Группа Sp(l) изоморфна группе SUB); изоморфизм можно получить,
сопоставив кватерниону а0 + a^i + д2/ + <*3к матрицу
а0 +a3i iat +аг \
\ -*
I = а0 + iaa,
iax - а2 а0 - a3i J
где а = (о1, а2, а3) — вектор из матриц Паули. (Проверка основана на за-
замечании, что матрицы /а1, id1, ia3 удовлетворяют тем же соотношениям,
что и кватернионы /', /, к.)
Всякой паре (а, Ь) кватернионов, удовлетворяющих условию \\a\\ =
= || Ъ || = 1 (т.е. a G Sp(l), Ъ Е Sp(l)), сопоставим преобразование 7\в>й)
множества всех кватернионов Q, определяемое формулой
Из соотношения || aqb'1 || = ||а || ¦ || q || ¦ || Ь'1 || = || q \\ следует, что преоб-
преобразование 71(Д( й) является ортогональным преобразованием четы-
четырехмерного пространства Q. Легко проверить, что, сопоставляя паре
(а, Ь) ? Sp(l) X Sp(l) преобразование 71(Д( ^ , мы получаем гомомор-
гомоморфизм Т группы Sp(l) X Sp(l) на группу SOD). Ядро этого гомомор-
гомоморфизма изоморфно группе <?2 (оно содержит, кроме единичного элемента,
элемент- (—1, —1)). Таким образом,
SOD) = Sp(l) X Sp(l)/ Z2 = SUB) X SUB)/Z2 .
Гомоморфизм Т переводит подгруппу группы Sp(l) X Sp(l), состоя-
состоящую из элементов вида (а, а), в подгруппу SOC) С SOD). (Это вытекает
из соотношения Г(а# вI=в-Ьв=1.)
394

ЛИТЕРАТУРНЫЕ УКАЗАНИЯ
Впервые топологически нетривиальные частицеподобные решения для
нелинейных моделей были рассмотрены Скирмом [1]. Для более общих
нелинейных моделей такие решения были изучены Финкелыптейном [2]
с помощью теории гомотопических групп. Всеобщий интерес к роли части-
цеподобных классических решений в квантовой теории поля был вызван
в 1974 г. работами Фаддеева и Тахтаджяна [3] (связь солитонов и кванто-
квантовых частиц в одномерных моделях), Полякова [4] (общее утверждение
о связи квантовых частиц и классических решений в квазиклассическом
приближении, магнитные монополи) ;'тХоофта [5] (магнитные монополи),
Нильсена и Ольсена [6] (струны), Зельдовича, Кобзарева и Окуня [7]
(доменные стенки). В многочисленных работах была исследована связь
классических решений и квантовых частиц [8]. В настоящей книге мы
не останавливаемся на подробном анализе этой связи. Частицеподобные
классические решения были построены в различных моделях теории поля
[9]. Почти сразу же было выяснено, что для изучения частицеподобных
решений очень полезны топологические методы [10]. Дальнейший толчок
к применению топологии в квантовой теории поля дало открытие инстанто-
нов [11], исследовавшихся затем в многочисленных работах. Позже найде-
найдены другие важные приложения топологии, в основном оставшиеся за
пределами книги (исключением является анализ многозначных функциона-
функционалов действия) . Следует упомянуть, в частности, изучение спина и статистики
частиц, отвечающих солитонам [12], открытие того факта, что в присутст-
присутствии магнитных монополей резко ускоряется распад протона [13], новый
тип аномалий, связанный с топологическими свойствами пространства
полей (глобальные аномалии) [14]. При изучении нарушения суперсиммет-
суперсимметрии очень полезным оказалось введенное Виттеном [15] понятие индекса
.суперсимметричной теории, аналогичное понятию индекса эллиптического
оператора. Отметим, что проникновение топологии в физику оказалось
взаимовыгодным — соображения, идущие из квантовой теории поля,
привели к новым топологическим результатам [16]. Успешное применение
топологии в квантовой теории поля стимулировало изучение топологичес-
топологическими методами дефектов в сплошной среде [11]. С математической точки
зрения возникающие там задачи во многом сходны с топологическими
задачами, к которым приводит квантовая теория поля, поэтому настояшая
395

книга открывается параграфом, посвященным топологически стабильным
дефектам локального равновесия. Перечислим коротко работы, на которых
основано изложение топологических вопросов квантовой теории поля в
настоящей книге. Изучение одномерных моделей и модели Джорджи-Гле-
шоу в § 2 и § 4 основано на работах [4], [5], содержание § 3 - на работах
[18]. Топологический анализ магнитных монополей в калибровочных
теориях (§ 5-8) следует работам [10а], [19], а оценка энергии магнитного
монополя (§ 11) -статьям [18], [20]. Анализ топологически нетривиаль-
нетривиальных нитей (§ 12, 13) основан на работах [21]. Исследование симметрич-
симметричных калибровочных полей в § 10 следует [22], см. также [23]. Топологи-
Топологический анализ нелинейных полей (§14) восходит к [2], а изучение много-
многозначных функционалов действия (§ 15) - к [24], [12в]. Материал § 23
и § 27 основан на [11], [25], [26], [27], а § 24, 25 - на [26].
Приведенные выше ссылки относятся только к применениям топологии
в квантовой теории поля. Этим применениям был посвящен ряд обзорных
статей и книг [28]. Основы топологии излагаются в книгах [29]. Из
учебников по квантовой теории поля следует упомянуть [30].

СПИСОК ЛИТЕРАТУРЫ
1. Skyrme T.H.R. II Ргос. Roy. Soc. - 1958. - V. A247. - P. 260.
2. Finkehtein D. // J. Math. Phys. - 1966. - V. 7. - P. 1218.
3. Фаддеев ЛД., Тахтаджян Л.А. II ТМФ. - 1974. - Т. 21. - С. 160.
4. Поляков AM. II Письма в ЖЭТФ. - 1974. - Т. 20. - С. 430.
5. 'tHooft G. И Nucl. Phys. - 1974. - V. В79. - P. 276.
6. Nielsen H.B., Olesen P. // Nucl. Phys. - 1973. - V. B61. - P. 45.
7. Зельдович Я.Б., Кобзарев ИМ., Окунь Л.Б. // ЖЭТФ. - 1974. - Т. 64. - С. 3;//
Phys. Lett. - 1974. - V. 50 В. - Р. 340.
8. a. Dashen R.F., Hasslacher В., Neveu A. // Phys. Rev. - 1974. - V. DIO. - P. 4114;
V. DIO. - P. 4130; - 1975. - V. Dll. - P. 3434 , V. D12 - P. 2443.
б. ФаддеевЛ.Д.,Корепин B.E. 11 ТМФ. - 1975. - T. 25. - С 147; // Phys., Lett. -
1976.-V. 63 B. -P. 435;//Phys. Rep. - 1978. -V.42C. -P. 1.
в. Тюпкин Ю.С., Фатеев ВА., Шварц А.С. // ДАН СССР. - 1975. - Т. 221. - С. 70;
// ЯФ. - 1975. - Т. 22. - С. 622.
9. Махонькое ВТ. И Phys. Rep. - 1978. - V. 35 С. - P. 1.
10. а. Тюпкин Ю.С., Фатеев ВА., Шварц А.С. Ц Письма в ЖЭТФ. - 1975. - Т. 21. -
С. 91.
б. Переломов AM., Монастырский М.И. // Письма в ЖЭТФ. - 1975. - Т. 21. -
С. 94.
в. Arafune J., Freund P.G.O., Goebel C.J. // J. Math. Phys. - 1975. - V. 16. - P. 433.
11. а. Поляков AM. II Phys. Lett. - 1975. - V. 59 B. - P. 82.
б.Белавин АА., Поляков AM., Тюпкин Ю.С., Шварц А.С. II Phys. Lett. - 1975. -
V. 59 В. -Р. 85.
12. a. Finkehtein D., Rubinstein J. //J.Math. Phys.-1968.-V.9.-P. 1762.
б.ШварцА.С. //Ill Школа физиков ИТЭФ. - Москва.: 1975. - Вып. I: - С. 78.
в. Witten Е. II Nucl. Phys. - 1983. - V. В223. - P. 422. - P. 433.
13. Рубеков А. И Письма в ЖЭТФ. - 1981. - Т. 33. - С. 645.
14. Witten Е. Ц Phys. Lett. - 1982. - V. 177 В. - Р. 324. // Commun. Math. Phys. -
1985.-V. 100.-P. 197.
15. Witten E. II Nucl. Phys. - 1982. - V. B202. - P. 253.
16. а. Шварц А.С. 11 Commun. Math. Phys. - 1979. - V. 67. - P. 1.
6. Donaldson S.K. // J. Dfff. Geom. - 1983. - V. 18. - P. 279.
17. а. Воловик Г.Е., Минеев ВЛ. // Письма в ЖЭТФ. - 1976. - Т. 23. - С. 647; -
Т. 24. - С. 605.
б. Toulouse G., Kleman М. // J. Phys. Lett. -1976. -V. 37. - P. 149.
18. Богомольный Е.Б. // ЯФ. - 1976. - Т. 24. - С. 449; // Phys. Lett. - 1980. -
. V. 91 В.-P. 431.
19. Шварц А.С. II Nucl. Phys. - 1976. - V. В 212. - Р. 358.
20. Романов В.Н., Фатеев В. А., Шварц А.С. // ЯФ. - 1980. - Т. 32. - С. 1138.
21. а. Тюпкин Ю.С.. Шварц А.С. // Phys. Lett. - 1980. - V. 90 В. - Р. 135.
5. Шварц А.С. И Письма в ЖЭТФ. - 1981. - Т. 34. - С. 555; // Nucl. Phys. - 1982. -
V. В 208.-P. 141.
397

22. а. Шварц А.С. // Commun. Math. Fhys. - 1977. - V. 56. - P. 79.
б. Романов В.Н.,Тюпкин Ю.С, Шварц А.С. // Nucl. Phys. 1977. - V. В 130.-P. 209.
23. л.БурланковДЕ. // ТМФ. - 1977. - Т. 32. - С. 326.
б. Bais F.A.,Primack Y.R. II Nucl. Phys. - 1977. - V. B123. - P. 253.
в. Wilkinson ?»., Goldhaber A.S. // Phys. Rev. - 1977. - V. D16. - P. 1221.
24. а. Новиков СП. 11 УМН. - 1982. -T. 5. - С 3.
6. Deser S., Jackiw R., Templeton S. II Phys. Rev. Lett. - 1982. - V. 48. - P. 975.
25. 't HooftG. II Phys. Rev. Lett. - 1976. - V. 37. - P. 8. // Phys. Rev. - 1976. -
V. D 14. - P. 3422.
26. Шварц А.С. //Phys. Lett. - 1977. - V. 67 B. - P. 172 // Commun. Math. Phys. -
1979. -V.64. -P. 233.
27. БелавинАА., Поляков AM. 11 Nucl. Phys. - 1977. - V. В 123. - P. 429.
28. a. GoddardP., OliveD. II Rep. Piog. Phys. - 1978. - V. 41. - P. 1357.
б. Coleman S. // The Whys of Subnuclear Physics. - N.Y.: Plenum Press, 1979. - P. 50.
в. Eguchi Т., Gilkey P.B., Hanson A.J. // Phys. Rep. - 1980. - V. 66C - P. 213.
r.Jaffe A., Taubes С Vortices and monopoles. - Boston: Biikhausei, 1980. - 291 p.
а. Nash Ch., Sen S. Topology and geometry for physicists. - London: Acad. Press,
1983. ^350 p.
e. Раджараман Р. Солитоны и инстантоны в квантовой теории поля. - М.: Мир,
1985-416 с.
29. а. Болтянский ВТ., Ефремович ВА. Наглядная топология. - М.: Наука, 1983. -
158 с.
б. Милнор Дж„ Уоллес А. Дифференциальная топология. - М.: Мир, 1972. - 278 с.
в. Рохлин ВА., Фукс Д.Б. Начальный курс топологии. - М.: Наука, 1977. - 488 с.
г. Хъюзмоллер Д. Расслоенные пространства. - М.: Мир, 1970. - 442 с.
д. Дубровин Б А., Новиков СП., Фоменко А.Т. Современная геометрия. Методы
и приложения. - М.: Наука, 1986. - 7-60 с.
30. а. Боголюбов Н.Н., Ширков Д.В. Введение в теорию квантованных полей. - М.:
Наука, 1984. - 600 с.
б. Ахиезер А.И., Берестецкий В.Б. Квантовая электродинамика. - М.: Наука,
1969. - 624 с.
в. Ициксон К., Зубер Ж.Б. Квантовая теория поля. - М.: Мир, 1984. - 848 с.
г. Волошин М.Б., Тер-Мартиросян КА. Теория калибровочных взаимодействий
элементарных частиц. - М.: Энергоатомиздат, 1984. - 296 с.

ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ
ВВЕДЕНИЕ •.
ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
Глава I. ОСНОВНЫЕ ЛАГРАНЖИАНЫ КВАНТОВОЙ ТЕОРИИ ПОЛЯ. . . .
§ 1. Простейшие лагранжианы
§ 2. Квадратичные лагранжианы
§ 3. Внутренние симметрии
§ 4. Калибровочные теории
§ 5. Частицы, отвечающие неквадратичным лагранжианам
§ 6. Лагранжианы сильных, слабых и электромагнитных взаимодействий".
§ 7. Большие объединения
Глава II. ТОПОЛОГИЧЕСКИЕ МЕТОДЫ КВАНТОВОЙ ТЕОРИИ ПОЛЯ . .
§ 1. Топологически стабильные дефекты
§ 2. Топологические интегралы движения
§ 3. Двумерная модель. Абрикосовские вихри
§ 4. Монополи Полякова-Хоофта
§ 5. Топологические интегралы движения в калибровочных теориях....
§ 6. Частицы в калибровочных теориях
§ 7. Магнитный заряд
§ 8. Общие формулы для электромагнитной напряженности и магнитного
заряда в калибровочных теориях
§ 9. Экстремумы симметричных функционалов
. § 10. Симметричные калибровочные поля
§ 11. Оценка энергии магнитного монополя
§ 12. Топологически.нетривиальные нити
§ 13. Частицы в присутствии нити
§ 14. Нелинейные поля
§ 15. Многозначные функционалы действия
§ 16. Функциональные интегралы
§ 17. Применение функциональных интегралов в квантовой теории
§ 18. Квантование калибровочных теорий
§ 19. Эллиптические операторы
§ 20. Свойства эллиптических операторов. Индекс эллиптического опера-
оператора
§ 21. Детерминанты эллиптических операторов
§ 22. Квантовые аномалии >
§ 23. Инстантоны
§ 24. Число инстантонных параметров

§ 25. Вычисление инстантонного вклада 204
§ 26. Функциональные интегралы для теорий, содержащих фермионные
поля 213
§ 27. Инстантоны в квантовой хромодинамике 222
Глава III. ОСНОВЫ ТОПОЛОГИИ 228
§ 1. Основные топологические понятия 228
§ 2. Степень отображения 242
§ 3. Фундаментальная группа 250
§ 4. Накрывающие пространства 255
§ 5. Многообразия 259
§ 6. Дифференциальные формы в евклидовом пространстве 265
§ 7. Гомологии и когомологии областей евклидова пространства 274
§ 8. Гомологии и гомотопии 282
§ 9. Гомологии произвольных пространств 286
§ 10. Дифференциальные формы на гладком многообразии и гомологии
гладкого многообразия 294
§ 11. Гомологии римановых многообразий 298
§ 12. Гомотопическая классификация отображений сферы (основные
утверждения) 302
§ 13. Отображения сферы в неодносвязное пространство 306
§ 14. Гомотопические группы сфер 308
§ 15. Гомотопические группы произвольных пространств 310
§ 16. Расслоенные пространства 315
§ 17. Связь между гомотопическими группами базы, слоя и пространства
расслоения 321
§ 18. Теорема о накрывающей гомотопии. Точная гомотопическая после-
последовательность ; 326
§ 19. Относительные гомотопические группы 332
§ 20. Гомотопические группы групп Ли и однородных многообразий .... 335
§ 21. Гомрлогии групп Ли и однородных многообразий 339
§ 22. Калибровочные поля и связности 346
§ 23. Калибровочные поля на многообразиях 353
§ 24. Характеристические классы калибровочных полей 356
§ 25. Геометрия калибровочных полей на многообразии 361
§ 26. Пространства калибровочных полей. Грибовские неоднозначности . . 363
Задачи 366
ПРИЛОЖЕНИЕ 370
§ 1. Топологические пространства 370
§ 2. Группы 372
§ 3. Отождествление (наглядные примеры) 376
§ 4. Эквивалентность и отождествление 380
§ 5. Представления групп 381 •
§ 6. Действие группы на пространстве 387
§ 7. Присоединенное представление группы Ли 392
§ 8. Кватернионы 393
ЛИТЕРАТУРНЫЕ УКАЗАНИЯ 395
СПИСОК ЛИТЕРАТУРЫ ,397