Текст
Г. НЕЙБЕР
КОНЦЕНТРАЦИЯ
НАПРЯЖЕНИЙ
ПЕРЕВОД С НЕМЕЦКОГО
| Н. Н. ЛЕБЕДЕВА |
ПОД РЕДАКЦИЕЙ ПРОФ. А. И. ЛУРЬЕ
ОГИ 3
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1947 ЛЕНИНГРАД
Редактор И, К, Снитко,
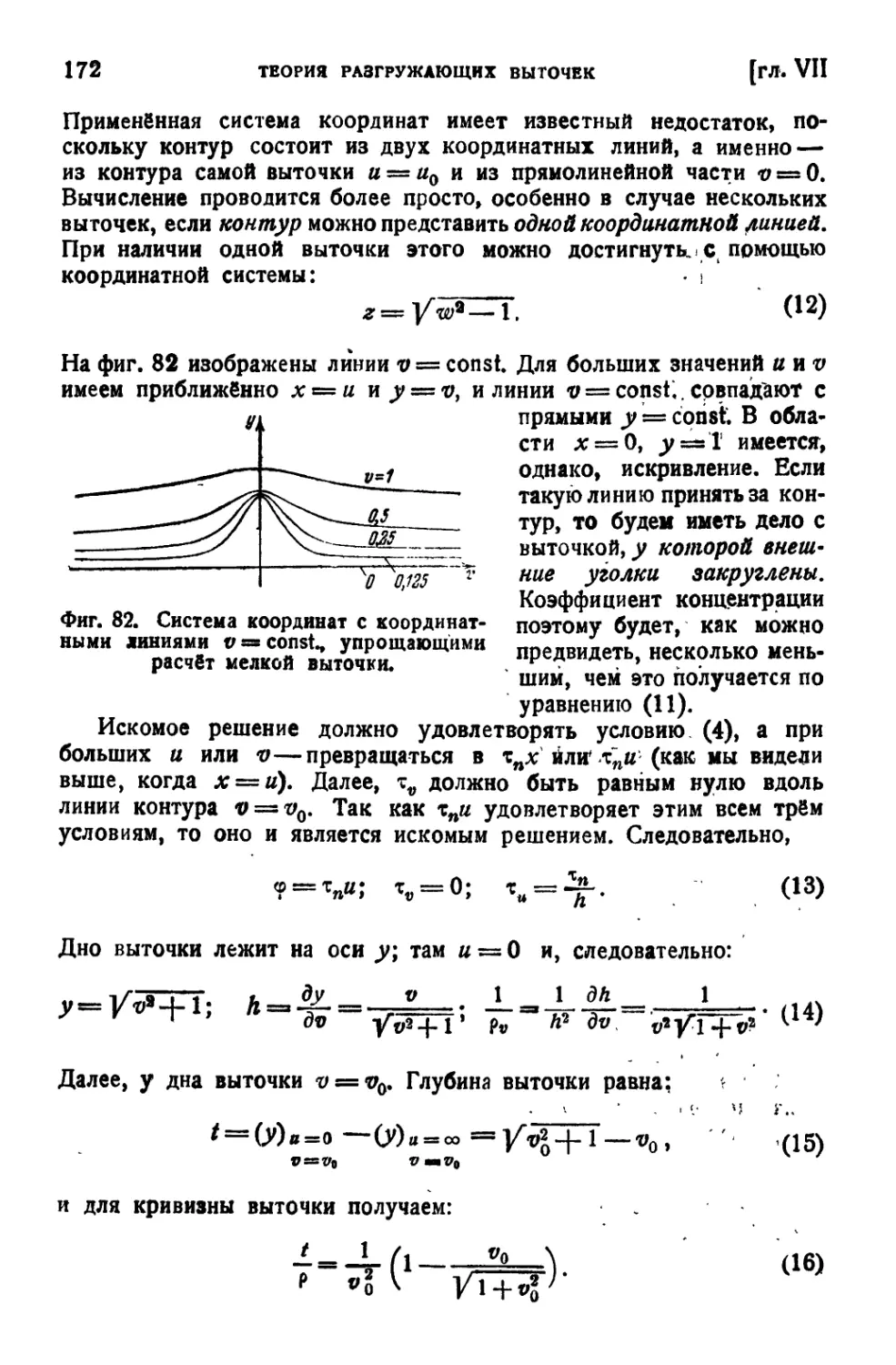
Технический редактор Я. А, Тумаркина.
Подписано к печати 27/1-1947 г, Печ. л, 123/*. Авт. л. 13,15. Уч.-изд. л. 13,60*
Тип. зн. в печ. л. 49.000. Тираж 10 000 экз. А 117.5. Цена 8 р. 25
Переплёт 1 р. 50 к. Зак. № 3475.
4-я типадпрафия им. Бвг. Соколовой треста ? «Пюляграфкнига» ОГ ИЯа
при Совете Министров ООСР. Ленинград, Измайловский ор., 29.
ОГЛАВЛЕНИЕ
Предисловие .......................... 0
Глава I.
Введение.
1. Старое учение о прочности материалов . ..................... ?
2. Требования, предъявляемые к точному расчёту на прочность... 8
Глава II.
Основные понятия учения о концентрации.
1. Коэффициент концентрации............................. • 10
2. Закон затухания........................................... 11
3. Основные формы выточек..................................... 11
4. Коэффициент концентрации для выточки любой глубины • • 12
Глава П1.
Основные данные из теории упругости.
1. Уравнения равновесия в напряжениях................ . • . 16
2. Деформации ................................................ 20
3. Деформации в криволинейных координатах................. 22
4. Закон Гука................................................. 26
5. Вывод основных уравнений.................................. 29
6. Выражение компонентов перемещений и напряжений через три
функции .... •............................................... 30
7. Вычисления в криволинейных координатах .... *.............. 34
г Глава IV.
Теория концентрации в плоской задаче.
1. Основные уравнения.......................• 40
2. Двусторонняя внешняя выточка................................ 47
3. Односторонняя глубокая внешняя выточка...................... 57
4. Круглые и продолговатые отверстия в очень широком fстержне . 63
5. Мелкая внешняя выточка..................................... 74
6. Построение номограммы для коэффициента концентрации у внешних
выточек, у круговых и продолговатых отверстий любых размеров 82
7. Концентрация напряжений у выступов......................... 84
Глава V.
Теория концентрации напряжений в пространственной задаче.
1. Основные уравнения.......................................... Г9
2. Решение уравнения Лапласа в эллиптических координатах .... 94
о. Глубокая внешняя выточка на теле вращения................... 99
4
ОГЛАВЛЕНИЕ
4. Мелкая внутренняя выточка иа теле вращения при отсутствии
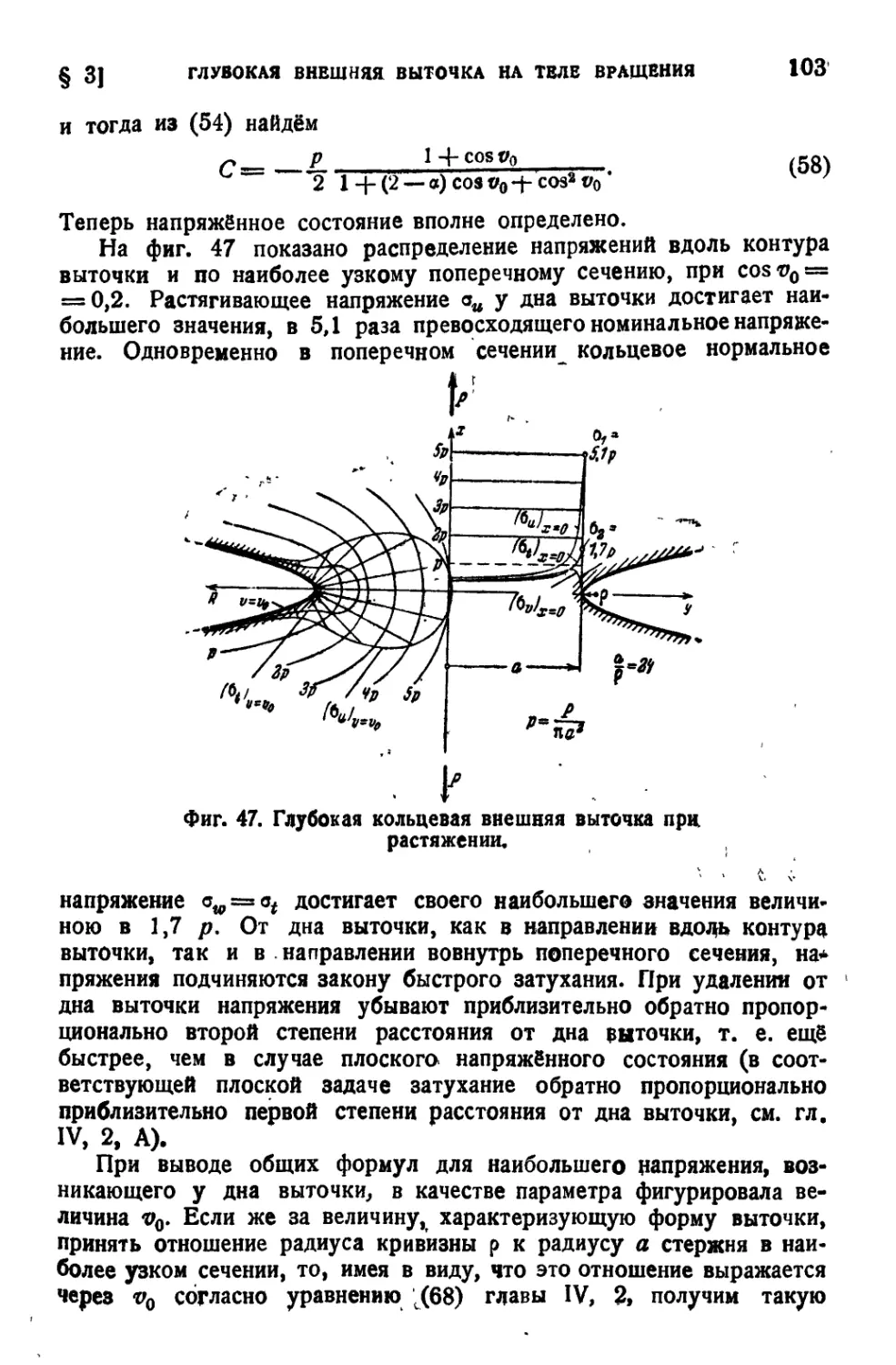
сверления................................................... 118
5. Выточка на теле вращения при двухмерном напряжённом состоянии 147
6. Построение номограммы для коэффициентов концентрации напря-
жений в выточках любых размеров . .......................... 158
Глава VI.
Теория влияния выточек призматического типа.
1. Основные уравнения....................................... 162
2. Сплошное поперечное сечение (стержень с продольным пазом) . 161
3. Тонкостенное полое поперечное сечение.................... 165
4. Валы с поперечными отверстиями ......................... 167
Глава VII.
Теория разгружающих выточек.
1. Разъяснение понятия...................................... 169
2. Разгружающие выточки при кручении....................... 170
3. Общие свойства коэффициента концентрации при наличии разгру-
жающих выточек.............................................. 175
Глава VIII.
< < Теория выточек с острыми углами.
1. Неприменимость классической теории упругости к выточкам с
острыми углами и причина этого............................... 176
2. Новая воображаемая модель . •.............................. 177
3. Коэффициент концентрации для выточек с острыми углами ... 178
4. Переход от закруглённой выточки к выточке с острым углом . . 183
5. Влияние деформации у основания выточки..................... 184
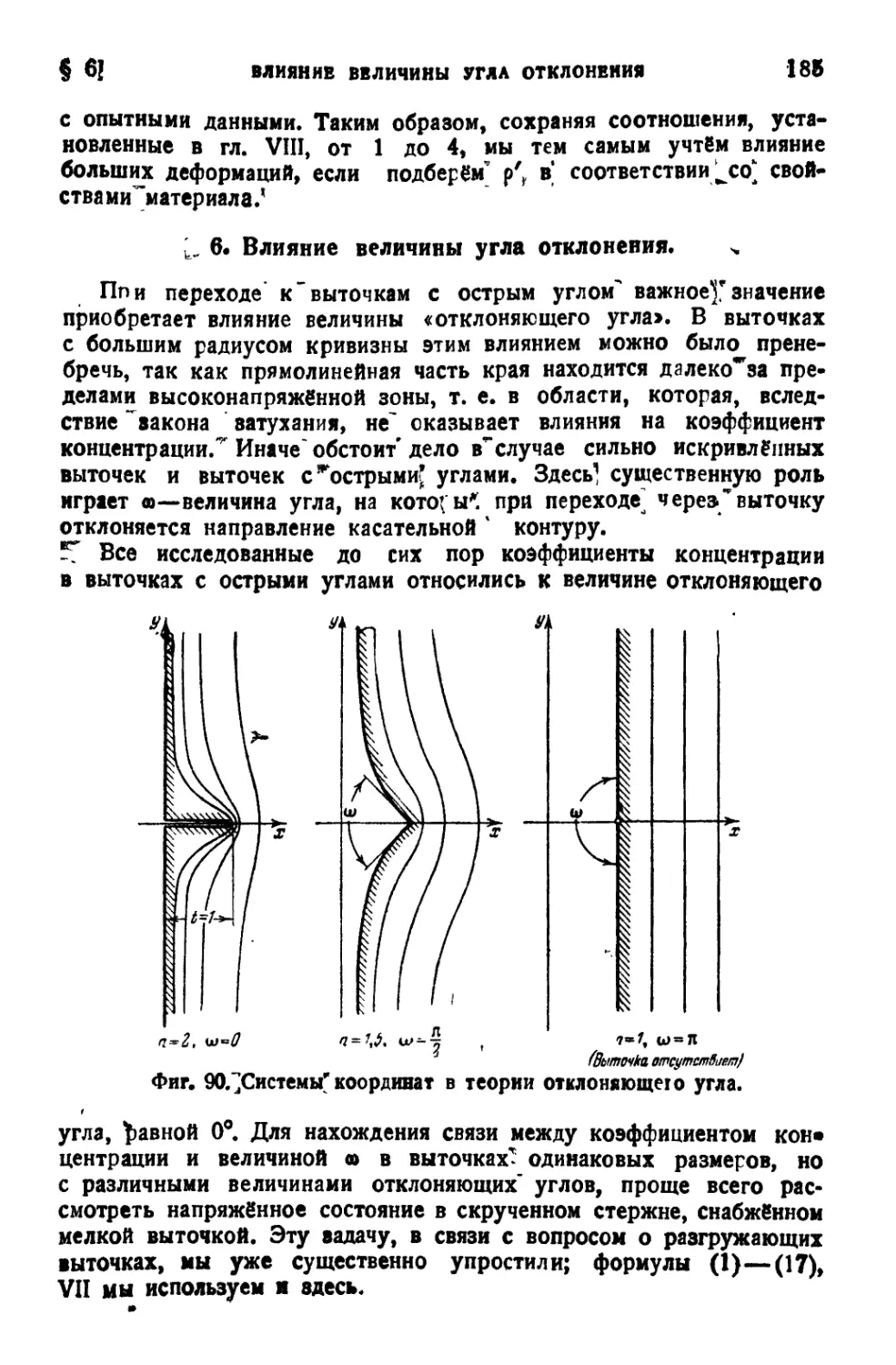
6. Влияние величины угла отклонения........................... 185
7. Общий технический коэффициент* концентрации................ 188
Глава IX.
Сравнение теории с результатами экспериментальных
исследований напряжений.
1. Измерения удлинений.............................. . 190
2. Фотоупругие измерения напряжений.................... 193
Глава X.
Номограммы для] коэффициентов концентрации.
1. Объяснения к номограммам для коэффициентов концентрации . . 197
2. Примеры . . ........................................ 197
Предметный указатель................................... 203
ОТ РЕДАКТОРА РУССКОГО ПЕРЕВОДА.
Настоящий перевод книги Нейбера «Kerbspannungslehre» был
выполнен доцентом Ленинградского Государственного Университета
Н. Н. Лебедевым, павшим в боях во время защиты Ленинграда
в 1941 году.
Книга Нейбера содержит значительное число принадлежа-
щих автору результатов, относящихся к решению плоских и про-
странственных задач теории упругости о распределении напряжений
в местах резкого изменения геометрической формы нагруженной
детали. Конструктор и расчётный инженер найдут в этой книге
ценные указания и сведения. Книга будет также полезна при изу-
чении теории, упругости, как содержащая интересный и практически
важный материал, иллюстрирующий применение общих методов и
уравнений этой науки. Изложение основных уравнений теории
упругости в книге Нейбера тяжеловесно и не отличается доста-
точной чёткостью и необходимой строгостью. Для читателя, имею-
щего в своём распоряжении руководства по теории упругости
П. Ф. Папковича, Л. С. Лейбензона, Лява и С. П. Тимошенко, это
обстоятельство, по нашему мнению, не имеет существенного зна-
чения.
22 октября 1946 г.
А. И. .Дуры.
ИЗ ПРЕДИСЛОВИЯ АВТОРА.
Современная техника требует в ряде случаев максимального
уменьшения веса конструкций и сооружений. Возможность осущест-
вления этого требования тесно связана с точным знанием действи-
тельного распределения напряжений в частях конструкций и соору-
жений; без такого знания надёжный расчёт на прочность невозможен.
Однако точное определение напряжений в телах сложной формы
является весьма трудной задачей. Обычно она решается экспери-
ментальным путём, чаще всего на модели тела. Естественно, что такой
путь рещения задачи не обладает общностью. Поэтому желательно
развитие теоретических способов определения распределения напря-
жений в телах сложной формы. Такая попытка делается в настоящей
книге.
Г. Нейбер.
ГЛАВА I.
ВВЕДЕНИЕ.
1. Старое учение о прочности материалов.
В начальный период развития машиностроения при определении
размеров частей машин довольствовались простыми соотношениями
между размерами отдельных частей. Например, диаметр вала паровой
машины определялся как некоторая доля диаметра цилиндра. При из*
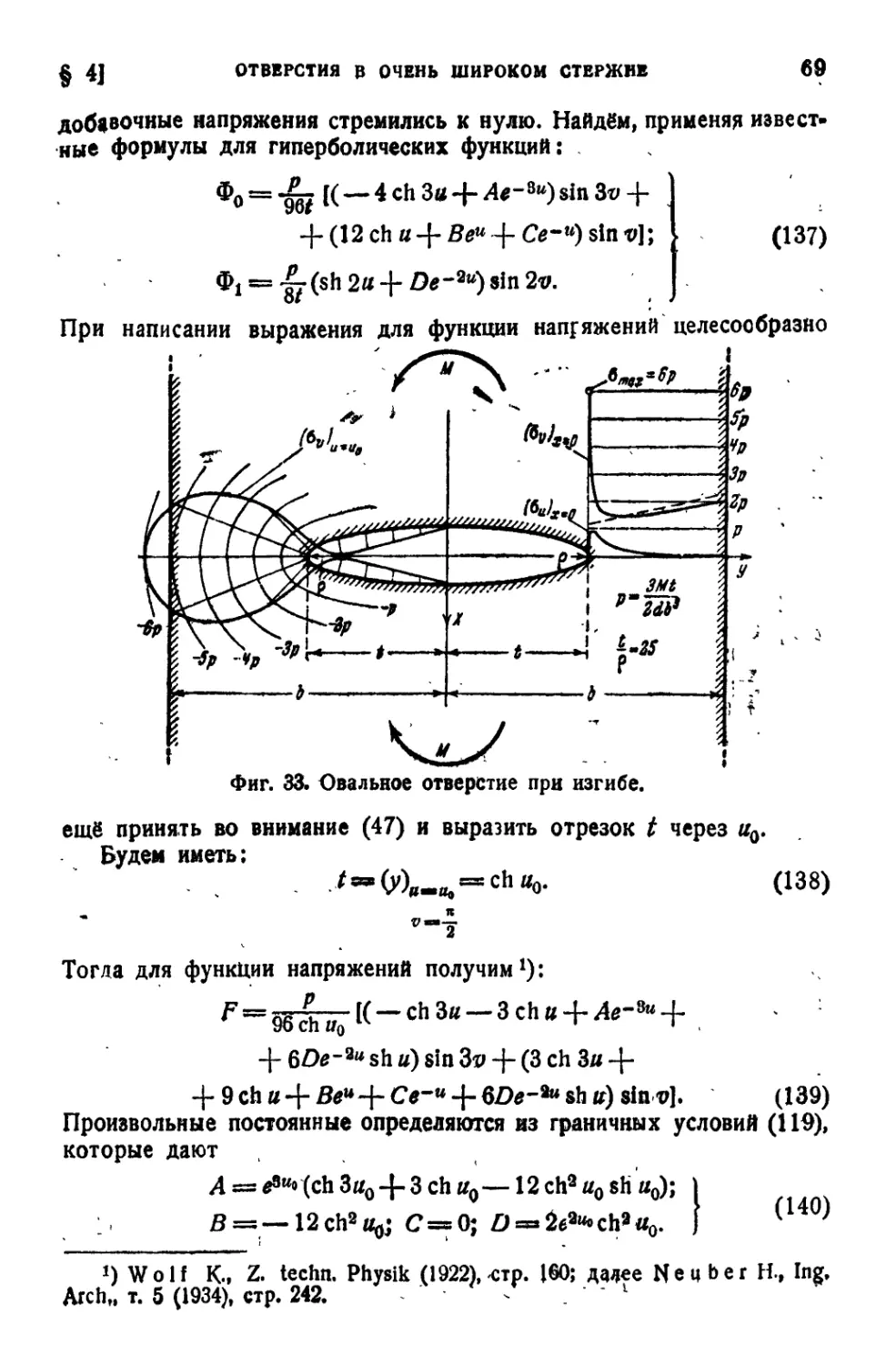
вестной простоте условий эксплоатации и постройки этот примитив*
ный способ расчёта был вначале достаточным, но по мере дальней*
шего развития техники, при всё более увеличивающемся различии
в характере и в величине действующих усилий, от него пришлось
отказаться.
Потребовался переход к другим методам. Стали определять, хотя
бы в грубом приближении, основные силы, действующие , на
отдельные части машины, и в соответствии с этими силами выби-
рать поперечные сечения нагруженных частей. Позднее было введено
понятие о допускаемом нанряжении, которое и до сих пор лежит
в основе технического учения о прочности. Бах был первым, кто уста-
новил численные, величины допускаемого напряжения (в этом со-
стоит одна из его заслуг), которые затем и вошли в употребление.
В применении к обычным строительным материалам в области задач
массового машиностроения эти величины до сих пор играют важную
роль. При этом основываются на предположении, что по поперечному
сечению детали напряжения распределяются плавно, без скачков. Так
например, прямолинейный закон распределения напряжений, имеющий
место только при простом растяжении и , при изгибе призматических
стержней, кладётся в основу расчёта непризматических тел. При та-
ком расчёте действительное напряжённое состояние и соответствую-
щие ему наибольшие напряжения, являющиеся причиной разрыва,
остаются неизвестными. Не было также установлено ни расчётных
ни экспериментальных методов для определения действительного
напряжённого состояния.
. Это старое учение о прочности, основанное главным образом на при-
менении элементарных формул, могло быть приемлемым, и то отчасти,
Для машин, неподвижно укреплённых на месте.
8
ВВЕДЕНИЕ
[гл. I
2. Требования, предъявляемые к точному расчёту
на прочность.
В настоящее время, вследствие грандиозного развития техники
и в особенности производства быстроходных машин, вес которых
должен быть минимальным, а нагрузка на отдельные части — макси-
мальной,— высказанные только что расчётные положения становятся
недопустимыми. Повышение прочности строительных материалов воз-
можно только в относительно узких пределах и, идя только этим
путём, требуемым условиям далеко нельзя удовлетворить. На помощь
приходит научное исследование, которое в полной мере выявляет зна-
чение геометрической формы элемента конструкции и указывает ме-
тоды правильного выбора этой формы для достижения наиболее бла-
гоприятного, с точки зрения прочности, распределения напряжений.
Опытные измерения деформаций и применение методов фотоупругости
дали возможность выявлять действительное напряжённое состояние,
возникающее в элементах конструкций. Обнаружено, что наличие не-
равномерного распределения напряжений в значительной мере обу-
словлено резкими изменениями формы поверхности тела. Исследова-
ние влияния этих резких изменений с^ормы на характер распределе-
ния напряжения составляет содержание учения о местных напряже-
ниях (о концентрации}. Поскольку разного рода резкие изменения
формы деталей машины обусловлены обычно конструктивными сообра-
жениями, удачный выбор формы этой детали позволяет лишь умень-
шать неравномерность в распределении напряжений, но не полностью
устранить её; наибольшие напряжения удаётся также уменьшить лишь
частично. Поскольку, таким образом, приходится иметь дело с нерав-
номерно распределённым напряжённым состоянием, а методов его опре-
деления наука о сопротивлении материалов не даёт, настоятельно
необходимой является проблема выработки основных методов точ-
ного выявления действительного напряжённого состояния.
Рядом с этим первым требованием идёт второе. Элементарное уче-
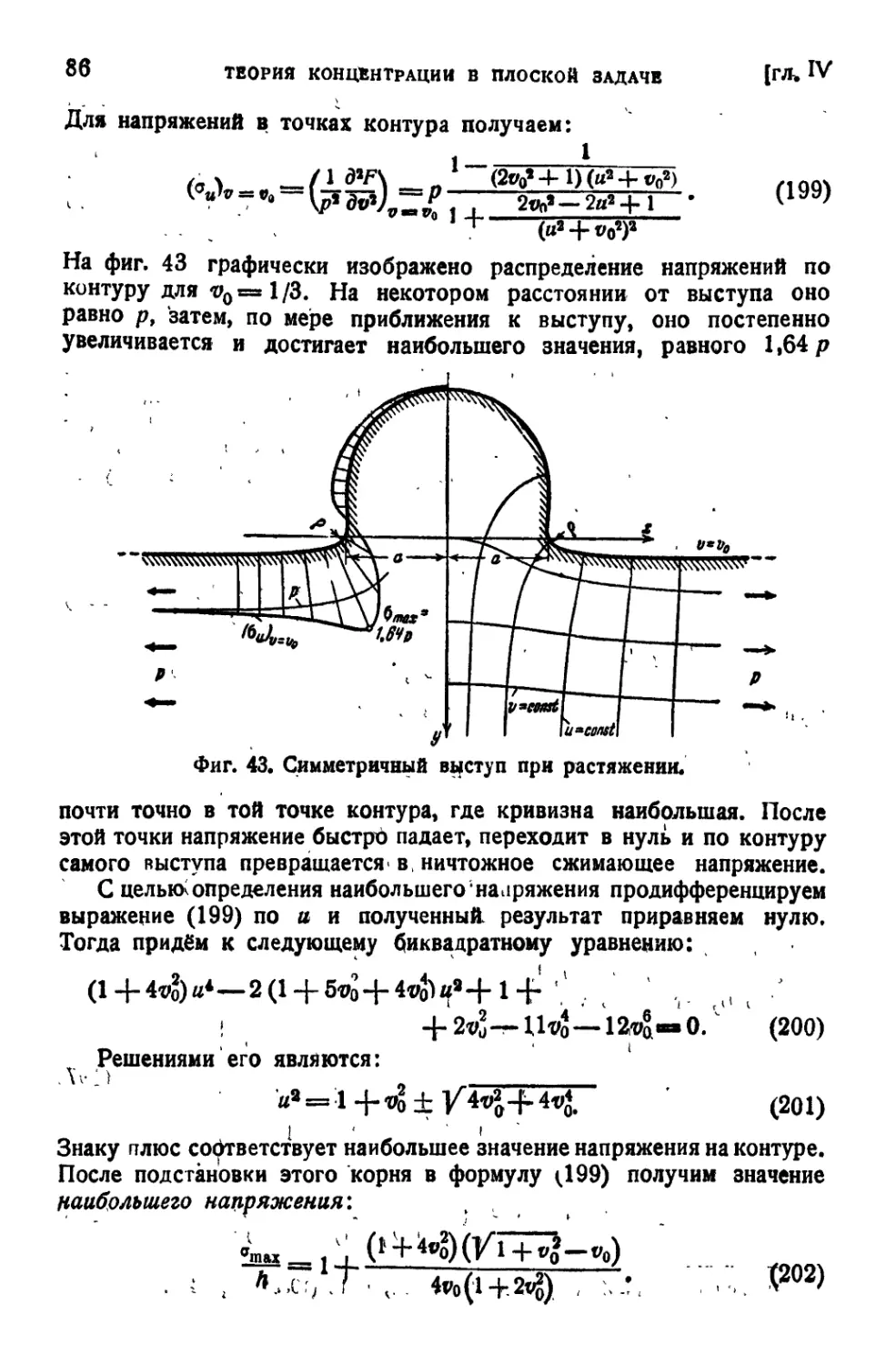
ние о сопротивлении материалов обычно имеет дело только с простым
линейно распределённым напряжением; в таких же условиях произ-
водились и испытания материалов, причём определялись величины,
характеризующие прочность только для образцов простой формы.
Чтобы знать действительные соотношения, нужно определять вели-
чины, характеризующие прочность подопытных образцов слож-
ной формы, т. е. при наличии концентрации. Только при этом
условии можно правильно судить о прочности строительных ма-
териалов, работающих в состоя ши нелинейно распределённых на-
пряжений.
Наконец, при пользовании уточнёнными способами расчёта, нужно,
чтобы силы, положенные в основу расчёта, были определены с пре-
дельной точностью; необходимо точно определить наибольшее и наимень-
шее значения рабочих нагрузок, включая и добавочные силы, вызван-
§ 2] ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ТОЧНОМУ РАСЧЕТУ НА ПРОЧНОСТЬ 9
ные температурой и напряжениями от монтажа. Успех обеспечен
только тогда, когда и это третье условие будет удовлетворено.
Настоящая книга ставит целью удовлетворить первому требованию,
являющемуся одновременно наиболее неотложным из перечисленных
трёх требований; в ней изложены методы выявления действительного
напряжённого состояния. Здесь будут изучаться напряжения с нели-
нейным распределением, вызванным концентрацией. Предварительно
даются общие основные положения учения о местных напряжениях
(о концентрации).
гл'ава II.
ОСНОВНЫЕ ПОНЯТИЯ УЧЕНИЯ О КОНЦЕНТРАЦИИ.
1. Коэффициент концентрации.-^
Для того чтобы конструктор мог с наибольшей лёгкостью полу-
чить представление о действительном напряжённом состоянии, целесо-
образно ввести в употребление отношение действительно наибольшего
напряжения к напряжению, которое дают элементарные методы ра-
счёта\Що предложению А. Тума (А. ТИиш)^напряжение, получающееся
по элементарным формулам старого учения о прочности, называют
номинальным напряжением.
В ближайшем отделе мы покажем, что если материал тела упруг,
а поверхность тела в области выточки не очень сильно искривлена х),
то отношение действительного наибольшего напряжения к номи-
нальному не зависит ни от абсолютной величины номинального напря-
жения, ни от материала.
Как известно, упругие свойства материалом сохранены до тех пор,
пока он следует закону Гука. Это условие с достаточным прибли-
жением выполняется пока нагрузка не очень велика и наибольшее
напряжение не превосходит предела упругости. За пределом упругости
отношение наибольшего напряжения к номинальному, вследствие зна-
чительного отклонения от закона Гука, не остаётся более постоян-
ным, а существенным образом зависит от материала тела.
Отношение наибольшего напряжения (ттах), не превосходящего
предела упругости, к номинальному напряжению (тп), назовём коэф-
фициентом концентрации и обозначим буквой ак. Величина зави-
сит определённым образом от формы элемента конструкции и ог
типа напряжённого состояния. В соответствии с нашим определением
имеем:
= (1)
Для нормальных напряжений употребляют, как известно, вместо
t букву а.
*) В случае сильно искривлённых выточек, и особенно при наличии за-
острений, коэффициент концентрации зависит также и от материала,
см. гл. VIII.
ЗАКОН ЗАТУХАНИЯ
11
§ 2]
Так как для назначения величины поперечного сечения, по кото-
рому определяется номинальное напряжение, существуют различные
возможности, необходимо при оценке величины коэффициента кон-
центрации всегда указывать способ определения номинального напря-
жения.
2. Закон затухания.
С целью наглядного ознакомления читателя с существом учения
о концентрации сформулируем теперь же его основной закон. Далее,
при решении конкретных задач, мы всегда будем находить подтверж-
дениэ этого закона.
Резкое повышение напряжений, с которым встречаются при ре-
шении всех задач о концентрации, всегда сопровождается значитель-
ным уменьшением напряжений вблизи зоны концентрации. Чем больше
максимальное напряжение в месте концентрации, тем резче наблю-
дается затухание напряжений при удалении От наиболее напряжённой
зоны. До некоторой степени здесь можно говорить о законе со,про-
тивления влиянию концентрации. Назовём его законом затухания.
Закон затухания проявляется особенно резко в случае пространст-
венного напряжённого состояния, как будет пбказайо в гл. V.
\/Разгружение напряжённой области путём устройства особой вы-
точки может явиться одновременно также Средством, позволяющим
уменьшить наибольшее напряжение, существовавшее в соседстве
с этой областью. Если, например, мы имеем дело с деталью ‘Машины,
в которой устройство выточки вызывается конструктивными соббра-
жениями, то устройством вблизи неё второй выточки можно добиться
существенного уменьшения максимального напряжения У К этому эф-
фекту разгружения путём устройства Нескольких выточек мы вернёмся
в гл.* VIII.
Законы затухания полезно также иметь в Ниду и при ‘дбЬу5кде-
нии формы выточки. На максимальное напряжение существенно’вНйяет
только та часть поверхности выточки, которая находится в вЫсРко-
напряжённой зоне. Форма детали на дбстаТочНо'м удалении От
выточки не оказывает влияния на величину максимального напря-
жения в окрестности выточки. Из Этого следует, Мпример, что
для круглой выточки в первую очередь Важна кривизна у''её осно-
вания, В то время как влияние боковых углов йтрВет лишь второ-
степенную роль.
3. Основные формы выточек.
Перед тем как приступить к решению задач, относящиеся ‘к уче-
нию о влиянии выточек, полезно привести разделение мточек На
основные типы. В зависимости от внёШйей формы будем разделять
выточки на: 1) мелкие и глубокие, 2) Внешние к внутренние,3) еди-
ничные и многократные и, наконец, 4) 'круглые и угловые (фиг. 1).
12 ОСНОВНЫЕ ПОНЯТИЯ УЧЕНИЯ О КОНЦЕНТРАЦИИ [гл. II
симметричную относительно
Однократна», круглая, Глубокая
мелкая
В зависимости от вида напряжённого состояния будем далее раз-
личать:
плоскую концентрацию напряжений (в плоских стержнях и пло-
скостях);
>си пространственную концентрацию
(например, при выточках на телах
вращения) и
призматическую концентр ацию
(например, в случае вала с клино-
видным пазом).
Кроме перечисленных может встре-
титься целый ряд других случаев,
где имеется усложнённая форма, ко*
торую не представляется возможным
непосредственно свести к вышеука-
занным основным формам. Однако,
как правило, коэффициент концен-
трации в этих случаях можно вычи-
слить по известным коэффициентам
ипичным примером является выточка
произвольной глубины. Коэффициент концентрации такой выточки
можно определить по коэффициентам для мелкой и глубокой выто-
чек. Предлагаемые при этом способы расчёта, вследствие их широ-
кого применения, имеют очень важное значениеЙ< должны быть поэтому
изложены уже здесь.
Кольцевая Внешняя Кольцевая Внутрен'
няя
Многократная Остроугольная
Фиг. 1. Различные формы выточек.
концентрации основных форм.
4. Коэффициент концентрации для выточки
любой глубины.
В качестве примера рассмотрим растянутый стержень с двумя
выточками, расположенными симметрично относительно оси стержня
(фиг. 2). В стержне без выточек существует равномерно распределён-
ное напряжённое состояние. Наличие мелкой выточки влечёт за собой,
в силу закона затухания, искажение поля напряжений только в не-
посредственной окрестности выточки; в достаточном от неё удалении
напряжённое состояние, как до образования выточки, так и после
её осуществления, остаётся равномерно распределённым. Как следует
из расчётных соображений, — на этом мы остановимся подробно
в гл. IV,—при определении коэффициента концентрации следует
принимать во внимание только те параметры, которые характеризуют
контур искажённой области, т. е. в данном случае только глубину t
и радиус кривизны р выточки. Напротив, ширина стержня не оказы-
вает существенного влияния на коэффициент концентрации в мелкой
выточке. Этот ход рассуждений допустим в тех случаях, где t до-
статочно мало в сравнении с шириной b стержня. Предельное зна-
чение, к которому стремится коэффициент концентрации в этом слу-
§ 4] КОЭФФИЦИЕНТ КОНЦЕНТРАЦИИ ДЛЯ ВЫТОЧКИ ЛЮБОЙ ГЛУБИНЫ 13
чае, представляет коэффициент концентрации для мелкой выточки.
Это предельное значение мы будем обозначать буквой
С другой стороны, если речь идёт об очень глубокой’выточке/то
искажение поля напряжений простирается на всё наиболее узкое
поперечное сечение стержня. При подсчёте коэффициента концент-
рации в этом случае следует принять во внимание, кроме радиуса
кривизны, ещё и ширину стержня в наиболее узком поперечном
сечении; вследствие предположенной симметрии мы можем ввести
в рассмотрение не всю, а только половину ширины наиболее узкого
поперечного сечения. Её мы обозначим буквой а. Влиянием глубины’
выточки теперь, в отличие от предыдущего, можно пренебречь, так
как, согласно закону затухания, напряжения по направлению к внеш-
ней грани очень быстро убывают. Коэф-
фициент концентрации здесь можно пред-
ставить как функцию безразмерного отно-
шения у. Тот факт, что коэффициент
концентрации при большой глубине не
зависит от неё, теоретически подтвер-
ждается тем, что при бесконечно боль-
шой глубине получается конечное, зави-
а
сящее только от отношения у , значение-
коэффициента концентрации. Это предель-
ное значение, представляющее коэффи-
циент концентрации для глубокой вы-
точки, мы обозначим буквой atk.
Как мы увидим в ближайшем отделе,»
оба предельных значения можно найти
либо совершенно точно, либо рассчитать4*
с достаточным приближением, исходя из
простых соображений.. Для того чтобы
по этим предельным значениям найти пра-
вильную величину коэффициента для вы-
точки любой глубины, возвратимся опять
к фиг. 2. Начиная с мелкой выточки,
в растянутом стержне будем последо-
вательно осуществлять всё более глубокие
ковый радиус кривизныХ/Ог линии, перпендикулярной к оси стержня
в точке против дна выточки, будем каждый раз откладывать коэф-
фициент концентрации, отвечающий соответствующей выточке.
Абсцисса полученной таким образом диаграммы, отсчитанная слева
направо, изображает собой величину а, отсчитанная с другой сто-
роны— справа налево — t. В качестве абсцисс мы можем выбрать
также безразмерные величины а/p и //р, так как радиус кривизны счи-
таем постоянным.
Фиг. 2. Растянутый стер-
жень с двусторонней сим-
метричной выточкой.
выточки, имеющие одина-
14 ОСНОВНЫЕ понятия УЧЁНИЯ о концентра [гл. II
Коэффициент концентрации вблизи точки — =з 0, — = А должен
р Р р
совпадать» с предельным, значением afk; с другой стороны, вблизи
точки у —— , у=?0 коэффициент должен совпадать с предельным
значением afk. В обеих точках коэффициент концентрации равен 1,
ибо для i — 0 исчезает, вытрчка, а для у->0 наиболее узкое сече-
ние делается настолько малым, что, в предположении постоянства
радиуса кривизны, окрестность наиболее узкой части стержня можно
рассматривать как призматический стержень. В окрестностях обеих
предельных точек кривая изменения коэффициента концентрации
должна сливаться с каждой из кривых, относящихся к обоим пре-
дельным случаям. В промежуточных точках, так как край, находя-
щийся на конечном расстоянии, ослабляет влияние выточки, кривая
изменения коэффициента концентрации проходит ниже этих гранич-
ных кривых. Этим условиям, можно удовлетворить, определяя коэф-
фициент концентрации ак из следующей формулы:
(2)
(3)
... L,+ 1
(«*-1)2 («ГЙ-1)2^
или
аА = 1 н—
Как следует из (2):
lira (<**) = lim (<х*) = «/*-
afk^ I
Таким образом, совпадение с предельными кривыми на границах
действительно имеет место. Далее, если «/%>«#, то знаменатель
всегда больше, чем —1, и в результате с другой
стороны, если то знаменатель больше, чем atk—1 и
а^<а/%<а^.\/Гаким образом, кривая изменения коэффициента кон-
центрации, определяемая вышенаписанной формулой, проходит всегда
внутри области, ограниченной предельными кривыми. Вместо показа-
теля степени 2, фигурирующего в формуле (2), можно было бы,
конечно, взять другой показатель, например 3; но эксперименталь-
ные исследования показывают, что действительная зависимость отве-
чает показателю 2.V
Выражение для коэффициента концентрации в выточке любой
глубины, полученное таким путём, имеет ещё то преимущество, что
допускает простое изображение в виде номограмм. Пусть —1 и
atk—1 являются катетами.прямоугольного треугольника. Тогда <хЛ— 1
равна высоте этого треугольника (см. фиг. 3). Доказательство сле-
дует из уравнения:
(«^- 1)(«ft -1) = («ft- 1)/(«fft~l)2 + («ft-l)2. (5)
§ 4] КОЭФФИЦИЕНТ КОНЦЕНТРАЦИИ ДЛЯ ВЫТОЧКИ ЛЮБОЙ ГЛУБИНЫ 15
которое вытекает непосредственно из уравнения (3). Выражения,
стоящие в обеих частях уравнения (5), представляют удвоенную
площадь треугольника; налево — как произведение катетов, направо —
как произведение гипотенузы на высоту.
При пользовании номограммами можно
избежать опускания перпендикуляра, если
провести взамен этого окружность из
центра, помещённого в вершине треуголь-
ника; тогда радиус той окружности, ко-
торая касается гипотенузы, определяет
коэффициент концентрации. Пример такого
построения дан на фиг. 104, где показаны
различные номограммы для коэффициен-
тов концентрации, в частности номо-
грамма для коэффициента концентрации
Фиг. 3. Зависимость между
коэффициентами концентра-
ции для выточек — мелкой,
глубокой и любой глубины.
растянутых плоских стержней с двусто-
ронними симметрично расположенными внешними выточками. Стрелки
указывают, как следует использовать номограмму (см. гл. X).
После этих предварительных соображений о сущности концент-
рации обратимся к основам теории упругости; это даст нам необхо-
димый математический, аппарат для выявления действительного на-
пряжённого состояния.
ГЛАВА III.
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ.
Сначала мы приведём основные уравнения равновесия в напряже-
ниях и рассмотрим геометрические условия протекания деформации.
Связывая уравнения напряжений и деформаций, мы приходим
к основным уравнениям теории упругости, которые мы решаем с по-
мощью функции, содержащей три переменных. Необходимые расчёты
выполняются в криволинейных координатах, что оказывается удобным
при решении задач о распределении напряжений в выточках.
1. Уравнения равновесия в напряжениях.
Фиг. 4. Напряжения в прямоугольной
системе координат.
Пусть на элемент поверхности dF действует сила dP. Тогда от-
dP
ношение называют напряжением, действующим на площадку dF.
Если~напряжение направлено'по нормали к площадке, то его назы-
вают нормальным напряжением. Если же оно действует в направ-
лении, лежащем в плоскости
самой площадки, то его на-
зывают касательным напря-
жением.
Для установления усло-
вий равновесия положим
в основу декартову систему
координат х, у, z и рас-
смотрим элемент объёма
с рёбрами dx, dy, dz, па-
раллельными координатным
осям (см. фиг. 4). Напря-
жения мы будем обозначать,
вообще, буквой х. С целью
уточнения обозначения при-
меняют, как известно, два индекса, из которых первый указывает на-
правление напряжения, а второй направление нормали к площадке.
Так например, представляет собой напряжение, действующее на
площадку у — const, но направленное вдоль оси х, т. е. оно является
касательным напряжением. С другой стороны, хуу есть напряжение
§ П
УРАВНЕНИЯ РАВНОВЕСИЯ В НАПРЯЖЕНИЯХ
17
которое действует на площадку у = const, в направлении оси у;
поэтому здесь мы имеем дело с нормальным напряжением; вообще,
там, где фигурирует два одинаковых индекса, всегда имеем дело
с нормальным напряжением. Для нормальных напряжений^вместо
и т. д. пишут короче <зя и т. д.
Напряжения мы условимся считать положительными, если на
площадки х -\-dx — const, у -|- dy — const, и z-j-dz = const, они
действуют в направлении координатных осей, а на площадки х = const.,
y=i const, и д== const, в направлениях, противоположных координатным
осям. В силу этого условия нормальные растягивающие напряжения
считаются положительными, в то время как сжимающие напряжения—
отрицательными. При составлении уравнений равновесия в напряже-
ниях необходимо учитывать, что напряжения, действующие на пло-
щадки x-f-dx — const., у 4~ dy = const, и z -|- dz = const., бесконечно
мало отличаются от напряжений, действующих по площадкам
х = const, _у = const, и z = const. Так например, по площадке
x-j-dx = const, действует нормальное напряжение dxi
тогда как на площадке х — const, действует <зя. На фиг. 4 указаны
только те напряжения, которые действуют вдоль оси х. Это сделано
с тем, чтобы не загромождать рисунка.
Силы, действующие на элемент объёма, мы получим простым
умножением напряжения на величину площадки, по которой оно
приложено, что на фиг. 4 уже и сделано. Условие равновесия, устра-
няющее движение в направлении оси х, тогда даёт *)
+ ^-dy) dxdz-^-
+ (ТО» + dz) dx dy == a^dy dz -J- -^dz dx -f- t^dx dy. (1)
Напряжения o^, взаимо уравновешиваются и выпадают из
уравнения; остаются только производные от напряжений. Если все
члены разделим ещё на dx dy dzy то получим первое из трёх сле-
дующих уравнений равновесия:
-^.4. jlyy, 4. .~а%. — о
дх ду dz ’
I дъуг । дтуХ
ду ~ dz * дх =0,
। дггх г n
dz ^'^дГ^^ду u’
(2)
Второе и третье из этих уравнений получаются точно таким же
образом из условий равновесия, устраняющих движение в направле-
х) В предположении отсутствия объёмных сил (например, силы веса,
центробежных сил, инерционных и т. п.). {Прим, ред)
2 Зан. 8475. Г. Нейбер.
18
основные данные из теории упругости
[гл. Ill
ниях осей у и z. Их можно также получить из первого уравнения
посредством циклической перестановки индексов х, у, z.
При выполнении уравнений (2) наш элемент объёма не может
передвигаться ни в одном из направлений. Но тело, с приложенной
к нему пространственной
системой сил, находится
в равновесии только
тогда, когда, кроме пре-
дыдущих трёх уравнений,
выполнены ещё три усло-
вия, устраняющие враще-
ние этого тела.
Мы обратимся к фиг. 5,
изображающей собой про-
екцию нашего элемента
объёма на плоскость ху,
^xgdzix
Фиг. 5. Равновесие касательных напряжений.
|
и исследуем условия, при
которых элемент не может
вращаться вокруг оси,
параллельной oz и проходящей через точку М—центр рассматри-
ваемого объёма. Достаточно учесть только те силы, момент которых
относительно выбранной оси не равен нулю (только эти силы и обо-
значены на фиг. 5). Уравнение моментов относительно точки М тогда
даёт:
или
^Xt=sха>к~{~"2 ty’ W
Члены с множителями dx и dy отбрасываем, как имеющие выс-
ший порядок малости. Таким образом мы приходим к первому из
трёх следующих уравнений:
= == хгу> ~ ‘'а»"
Второе и третье из этих уравнений, получающиеся из первого цик-
лической перестановкой значков, устраняют вращение элемента
тела вокруг двух других осей, проходящих через точку М и парал-
лельных Оу и Ох. Таким, путём мы вывели замечательное свойство
симметрии касательных напряжений, которое выражается в возмож-
ности перестановки индексов у касательных напряжений. Речь идёт
о так называемой теореме взаимности касательных напряжений.
Таким образом установлены все условия равновесия напряжений,
отнесённых к координатам х, у, z. Но остаётся ещё открытым вопрос
о тех напряжениях, которые действуют по любым наклонным пло-
щадкам. На этот вопрос можно ответить также из рассмотрения
§ 1]
УРАВНЕНИЕ РАВНОВЕСИЯ В НАПРЯЖЕНИЯХ
19
условий равновесия. Наклонной плоскостью, характеризуемой нор-
малью X, отсечём от нашего элементарного объёма угол, как по-
казано на фиг. 6. Напряжение, действующее по вновь проведён-
ному сечению, может иметь направление х. Мы его .обозначим по-
этому буквой тхХ. На остальных площадках, пусть действуют напря-
жения, заранее нам известные из рассмотрения
объёма. Ради простоты, напряжения, действую-
щие на каждую из площадок, приведём к одной
равнодействующей. Рассмотрим одну из трёх
площадок. Пусть на неё действует напряжение
т^, где р и v обозначают соответственно на-
правления напряжения и нормали к площадке.
Направления ц и v при этом считаются положи-
тельными, если они направлены к элементу,
а направления х и X, наоборот, положительны,
если они направлены от элемента. Сами напря-
жения, в соответствии с принятым правилом зна-
ков, должны считаться положительными, если
они действуют наружу от тела. При установле-
равновесия элемента
Фиг. б. К определе-
нию произвольно ори-
ентированных напря-
жений.
нии условий равновесия, устраняющих движение элемента в направле-
нии х, прежде всего нужно умножить напряжение на площадку F*, по
которой оно действует, чтобы получить силу. Но F' представляет
собой проекцию площадки F и поэтому равно произведению из F
на cos (X, v), где через (X, v) обозначен угол между направле-
ниями X и v. От силы, полученной таким путём, переходим к её
составляющей в направлении х. Для этого умножаем её ещё на
cos (х, р). Следовательно, та доля величины тхХ, которая должна
уравновешивать напряжения действующие по площадке F',
равна cos (х, р) cos (X, v). Если напряжения действуют по всем
трём площадкам, то индекс v нужно последовательно заменить на
х, у и z и результаты сложить; при этом индекс р каждый
раз .должен обозначать направление результирующего напряжения,
действующего на соответствующую площадку. Можно и не рас-
сматривать этой результирующей, если взамен неё сложить резуль-
таты действия её составляющих по осям х, у, zt т. е. последова-
тельно полагая р равным х, у, г. Тогда получим следующую двой-
ную сумму:
«= 5 2 V cos <х‘ н) cos (X, v).
В развёрнутом виде она состоит из девяти слагаемых. Вследствие
теоремы о взаимности касательных напряжений число их умень-
Изртся до шести. Направление х можно либо совместить с направле-
нием X, либо считать эти направления взаимно перпендикулярными.
В первом случае получаем выражение для нормального напряжения,
Действующего на выбранное сечение, во втором случае — выражение
Для касательного напряжения.
2*
20
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ
[гл. Ш
Для большей ясности приведём пример: пусть все напряжения,
отнесённые к координатам х, у, z, равны нулю, кроме Какие
напряжения возникают тогда в сечениях, составляющих угол в 45°
с осями х и Соответственно этому, на фиг. 7 в плоскости х, у
проведены направления 1 и 2. Тогда имеем:
тп = а, = COS(1, X) cos (1, у) 4- xyx cos (1,у) cos (1, х),
т12 — ~а>у сов (1, х) cos (2, у) + nyai cos (1,у) cos (2, х),
т2а == а2 = cos (2, х) СОЗ (2, у) 4- Трда cos (2„у) cos (2, х).
Но так как
cos(l,x) = cos(l,y) = cos(2,j) = — cos (2, х) = ~^=.,
из (7) получаем:
°1 = х1ву> °а = хацр т19 “ О»
(7)
(8)
(9)
т. е. в сечениях, составляющих угол в 45°, с осями х и у в этом
случае существует либо простое растяжение, либо простое сжатие.
Все эти чисто статические соотношения справедливы для любого
материала. Лишь при установлении связи между напряжениями
и геометрическими характеристиками
деформации мы должны принять во
внимание упругие свойства мате-
риала.
2. Деформации.
Буквами Е, ц, С мы обозначим
компоненты в направлениях коорди-
натных осей вектора перемещения,
которое претерпевает любая точка
Фиг. 7. Напряжения при чистом
сдвиге.
упругого тела, находящегося в условиях напряжённого и деформи-
рованного состояния, вызванного внешними силами. Знание в каждой
точке тела вектора перемещения помогает однозначному определению
деформированного состояния всего тела. По компонентам перемеще-
ния можно определить соответствующие им величины деформаций —
относительные удлинения и относительные сдвиги. Под относитель-
ным удлинением понимается отношение абсолютного удлинения беско-
нечно малого линейного элемента к его первоначальной длине. Обо-
значим его буквой а и используем при этом индексы, указывающие
первоначальное направление растянутого линейного элемента.
Относительный сдвиг представляет собой величину изменения
первоначально прямого угла. Его мы обозначим буквой 7 с двумя
индексами, указывающими первоначальные направления сторон пря-
мого угла. Последовательность индексов не играет при этом никакой
роли.
§ 2]
ДЕФОРМАЦИИ
21
В дальнейшем изложении теории деформаций нужно обратить
внимание на то, что, вследствие значительной сопротивляемости
строительных материалов воздействию внешних сил, деформации,
в большинстве случаев, имеют настолько малые значения, что их
квадратами, по сравнению с величинами самих деформаций, всегда
можно пренебречь, как имеющими высший порядок малости. Важней-
Фиг. 8. Сдвиги в прямоугольной
системе координат.
шим выводом, проистекающим отсюда, является закон наложения.
Согласно этому закону, последовательность наложения одного дефор-
мированного состояния на другое не отражается на конечном состоя-
нии, и величины деформаций, отнесённые к одной и той же коорди-
натной системе, алгебраически складываются. Имея в виду этот
закон, мы будем сначала обращать
внимание только на перемещение Е.
По величинам деформаций в/ и т. д.,
возникшим только от перемещения Е,
мы затем легко найдём те части общей
деформации, которые происходят только
от перемещения nq или С. И тогда,
согласно закону наложения, простым
сложением этих составных частей по-
лучим полное выражение для компо-
нентов деформации. За начало коорди-
нат выберем точку О элемента объёма,
в которой пересекаются рёбра О А = dx\
OB = dy и OC=*dz (см. фиг. 8).
Вследствие перемещения Е точка О
перемещение Е уже увеличится, вследствие изменения координаты х
на dx, на бесконечно малую величинуАналогичные заклю-
чения можно сделать для точек В и С. Отрезок dx передвинется
по своему направлению в положение О'А' и, кроме того, претерпит
перейдёт в О'. В точке А
относительное удлинение
s® dx дх
(Ю)
(И)
(12)
Отрезок dy переместится в положение О'В' и одновременно повер-
нётся. Изменение прямого угла АОВ, обусловленное этим вращением,
и есть сдвиг Так как малый угол можно заменить его танген-
сом, то получим
'ay dy ду 9
Аналогично определяется уменьшение угла АОС
. 5+-ж-&-;. а;
dz dz
22
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ [ГЛ. Ш
Относительное удлинение ребра ОВ,
поворота, равно
* dy
появляющееся вследствие его
(13)
и, следовательно, его можно считать равным нулю, так как величи-
/ 08
ной\'0у/ по сРавйению с* единицей мы пренебрегаем. То же самое
можно сказать об отрезке ОС, т. е. величину е/ можно также
считать равной нулю. Легко видеть, что и относительный сдвиг
7^ можно рассматривать как величину высшего порядка малости.
Заменой $ на их на у получим те части величин деформа-
ций, которйе вызываются компонентом перемещения т|. Аналогично
поступаем для получения слагаемых компонентов деформаций, вы-
званных перемещением' тр Совокупность всех этих слагаемых даёт
полное представление о величине деформации
г 8_±1 ₽ вл
® “ дх ’ У~ ду ' dz ’
v -Aj-JZL 7 -±Lj_A
ду ' дх ’ ’ дг ду ’
•ея? дх'дг'
(14)
Важную величину представляет собой объёмное расширение, рав-
ное отношению увеличения объёма элемента к первоначальному
его объёму. Обозначив объёмное расширение буквой е, получим;
. dx (1 + U (1 + е») rfg (1 + е.) — dx dy dz , j 5)
dxdydz ’ ' '
Так как произведение относительных удлинений является величи-
ной высшего порядка малости, то получаем
e = + + + (16)
т. е. относительное изменение объёма равно сумме относительных
удлинений в трёх взаимно перпендикулярных направлениях.
Таким образом, мы выразили компоненты деформаций через
компоненты перемещений в декартовых координатах. При вычисле-
нии распределения напряжений в выточках большим преимуществом
обладают криволинейные координаты. Поэтому мы теперь выведем
соответствующие формулы и в ьтих координатах.
3. Деформации в криволинейных координатах.
Перейдём к криволинейной ортогональной системе координат и,
v, w; при этом и, <о, w считаем непрерывными и дифференцируемыми
функциями х, у, z. Обратно, функции х, у, 2 предполагаются
§ 3]
ДЕФОРМАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
S3
непрерывными и дифференцируемыми по щ и, w; иначе говоря,
имеются уравнения:
х = х(и, t/, w), у—у(ц, «0; г = г(«, tr, w). (17)
ди
Фиг. 9. Линей-
ный элемент в
криволинейных
координатах и
его х-составля-
ющая.
Под направлением и будем понимать направление нормали к поверх?
пости м —const.; считаем его положительным» если оно направлено
в сторону увеличения параметра «. Переместимся вдоль и на линей-
ный элемент dsu. Параметр и изменится, при этом на du, В силу
ds
предположений о дифференцируемости, производная в каждой
точке имеет вполне определённое значение, которое мы обозначим
буквой длина элемента равна поэтому hudu. Величина h^iu
представляет собой расстояние между поверхностью и = const, и, сосед-
ней с ней, для которой и изменяется на величину da. Вследствие
различной кривизны обеих поверхностей' расстояние hudu для
каждой точки поверхности будет различным, несмотря
на то, что du имеет во всех точках одну и ту же
бесконечно малую величину. Это учитывается мно-
жителем ки, который мы поэтому и называем коэф-
фициентом искажения. Коэффициенты искажения
в направлениях v и та>, совпадающих с нормалями
к поверхностям. v=* const, и w = const, мы обозна-
чим соответственно буквами hv и hw. Соответствую-
щие им линейные элементы тогда равны hvdv
и hKdw.
Угол между двумя направлениями будем обозна-
чать, как и выше, указывая эти направления; так
например, (х, и) является углом между направле-
ниями х и и. Косинус этого угла получается тогда из линей-
ного элемента hudu и его составляющей на ось х (см. фиг. 9).
Аналогичные соображения справедливы для углов, (у. и) и (^» и)>
равно как и для углов, образованных направлениями и и w и коор-
динатными осями. Мы получаем:
. cos (х, и) = -£- 4^-,
4 ’ ’ Ли ди ’
cos (у, и)= т- ,
'л’ 7 hu ди ’
(18)
cos (г, и) = 4—
v /<« ди
И т. д.
Символом «ит.д.» мы выразили то обстоятельство, что можно
написать ещё две системы уравнений, получающиеся из предыдущей
Сменой буквы и на v и w. По известной теореме аналитической
геометрии имеем
cos2(x, н)-f-cos*(у, «)4-cos9(a, а) = 1 (19)
и т- д.
24
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ [ГЛ. III
Если выражение (18) для направляющих косинусов подставим в (19),
то получим:
и т. д.
Эти соотношения, по уравнениям (17), дают возможность вычис-
лить коэффициенты искажения.
Перемещения в направлениях и, v и w обозначим буквами <7,
V и W. Согласно закону наложения величину U можем получить
сложением составляющих перемещений 5, т), С в направлении (7. То
же самое справедливо и для перемещений V и W. Составляющие
найдём простым умножением на соответствующие направляющие
косинусы, в результате чего получим:
t7=Uos(x, zz)-|-'ncos(y, «) + С cos (г, я) и т. д. (21)
или, имея в виду (18),
(22)
hu \ ди ’ 1 ди г ди J 4
и т. д. При замене в этом уравнении буквы и на v или w следует
также одновременно U заменить на V или 1Г.
Компоненты деформаций содержат в себе прежде всего такие
слагаемые, которые получаются из уравнений (14), если в них
ввести лишь новые обозначения координат, линейных элементов и
перемещений. Обозначив эти слагаемые буквами ем' и т. д., получим
, 1 at/ . ' — 1 ^t/ I
8“ hu ди * - hv dv • hu ди * *
и т. д. При этом криволинейные координаты мы в первом приближе-
нии рассматривали как прямолинейные. Компоненты деформации
являются малыми величинами и, казалось бы, изменениями таких
малых величин, обусловленными криволинейностью координатной
системы, можно пренебречь, как малыми высшего порядка; однако,
сделав это, мы совершили бы принципиальную ошибку. При выводе
выражений для компонентов деформаций в декартовых координатах
у нас остались только бесконечно малые приращения компонентов
перемещений: и т. д., а сами перемещения выпали. Действи-
тельно, в тех слагаемых деформаций, которые проистекают от этих
малых приращений, криволинейность вызывает эффект высшего
порядка; но для самих перемещений это обстоятельство уже не
имеет места. В то время как в декартовых координатах постоянные
перемещения ц, С не вызывают никаких деформаций в теле (упру-
гое тело перемещается при этом как абсолютно твёрдое тело), в кри-
волинейных координатах, вследствие кривизны, при постоянных
перемещениях U, V, W это становится возможным. Как мы увидим
§ 3]
ДЕФОРМАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
25
Фиг. 10. Деформация в криво-
линейных координатах.
далее, происходящие при этом деформации не являются пренебре-
жимо малыми, так как они вызываются не малыми приращениями
перемещений, но самими перемещениями. u Величины этих
деформаций мы обозначим буквами е/'
и т. д. Их нужно сложить со слагае-
мыми из уравнения (23), чтобы полу-
чить полные деформации.
Рассмотрим элементарную пло-
щадку, принадлежащую поверхности
UZ==3 const и изображённую на фиг. 10.
Угловым точкам этой площадки при-
дадим постоянные перемещения U.
Ребро ОВ, направленное по v, имеет
длину hv dv. При перемещении эле-
мента ОВ. на длину kudu в положе-
ние АС' его длина увеличится на
f^—dvdu, т. е. он приобретёт относи-
тельное удлинение du. Относи-
он
тельное удлинение, соответствующее перемещению элемента О В на
величину (У, .получим умножением предыдущего выражения на отноше-
U
ние г—
hu du 9
т. е.
(24)
С другой стороны,
первоначально прямой
„ „ _ U dhv
~ huhv ди
при перемещении ребра ОВ в положение АС
угол между этим ребром и направлением и
увеличится на малый угол dfi, который равен ~ du. Увеличение
прямого угла соответствует при этом отрицательному относительному
сдвигу. Сдвиг у' соответствующий перемещению на величину СУ,
U А
опять получим умножением на тогда будем иметь:
Я И
у _________
~ hutiv dv •
(25)
Остальные слагаемые компонентов деформации найдутся рассмотре-
нием элемента площадки, взятого на поверхности '□= const. Мы по-
лучим их из (24) и (25) заменой v на w:
а " _ U "__ _ U 3hu /пЯЧ
w ~huhw du 9 — huhw dw •
Прочие слагаемые, вызванные постоянным перемещением СУ, являются
величинами высшего порядка малости.
К только что полученным выражениям добавляем согласно закону
наложения слагаемые, соответствующие постоянным перемещениям
26
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ
[гл. III
V и W; они получаются из (24), (25) и (26) заменой в них- буквы а
на v и w. К результату добавляем затем слагаемые по уравнениям
(23); выражение для относительного сдвига можно при этом несколько
преобразовать. Окончательно получим следующие выражения для
компонентов деформации:
““ Лм\ да “Г hv dv Тhw dw)•
hv dv \huJ'hu dtt\hv)
(27)
и T. Д.
При выводе формулы для объёмного расширения следует обратить
внимание прежде всего на то, что у нашего криволинейного элемента
длины рёбер, идущих в одном и том же направлении, отличаются
друг от друга. Но поскольку разница длин, так же как и при
оценке компонентов деформаций, вызывает весьма малый эффект,
при вычислении изменения объёма можно положить в основу средние
длины рёбер kw kv, kw по направлениям я, о и w.
Относительное изменение объёма тогда окажется равным:
g _. ku (I ~Ь cu) (I ~Ь £t?) (I ~b *«,) (28)
откуда, пренебрегая произведениями относительных удлинений, по-
лучим:
« = 8и+ев+®и, (29>
т. е. объёмное расширение и в криволинейных координатах равно
сумме относительных удлинений *).
Итак, мы записали деформации и в криволинейных координатах.
Ознакомимся теперь с соотношениями, которыми связаны между
собой компоненты напряжений и деформаций.
4. Закон Гука.
Закон Гука устанавливает пропорциональность, с одной стороны,
между нормальными напряжениями и относительными удлинениями и,
с другой стороны, между касательными напряжениями и относитель-
ными сдвигами.
*) Приведённый в этом параграфе вывод выражений (27) для составляю-
щих деформации в криволинейных косрдинатах, конечно, мало убедителен;
по нашему мнению, он является, однако, удачной попыткой- объяснить
наглядно структуру этих формул. Точный вывод читатель может найти
например, в «Математической теории упругости» Лява (ОНТИ, 1936), стр. 6'
и след. (Прим, ред.)
§ 4]
ЗАКОН’ ГУКА
27
Сначала представим себе, что существует только нормальное
напряжение <зх. Тогда в направлении этого напряжения вызывается
относительное удлинение
<0, = ^-, (30)
где Е представляет собой модуль упругости. Одновременно в каждом
из двух поперечных направлений возникает относительное сжатие,
имеющее величину
ОЛ»
8у = 8«=“^Ё'-
(31)
Коэффициент т в уравнении (31) называют пуассоновым числом.
Для металла его можно считать равным 10/3. Если действуют одно-
временно все три нормальных напряжения, то путём наложения
получаем:
(32)
Если мы эти выражения подставим в уравнение (16), то для объём-
ного расширения получим
1 /, 2\, . . ч
(33)
Сумму трёх нормальных напряжений, фигурирующую в (33), мы
в последующем коротко будем называть объёмным напряжением.
Далее, касательные напряжения пропорцио-
нальны соответствующим сдвигам, я коэффи-
циент пропорциональности называется модулем
сдвига. Его мы обозначим буквой G. Имеем:
Хху = &(xyi ^уг — @1ух> ~ (34)
Из этой связи между компонентами на-
пряжений и деформаций вытекает, что закон
наложения, применявшийся до сих пор только
к деформациям, справедлив также и для
Фиг. 11. Связь'между
растяжением и сдви-
гом.
напряжений.
Три введённых выше постоянных Е, т, О связаны между собой
важным соотношением. Это соотношение проще всего получить из
следующих соображений. Если действует только' касательное напря-
жение то квадрат, рёбра которого до деформации были парал-
лельны осям х и у и имели длину Ь, после деформации превра-
щается в ромб (см. фиг. 11). Абсолютное удлинение диагонали,
28
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ
[гл. III
выраженное
вании (34)
ь
через относительный сдвиг, равно ^ху —— , что на осно-
"г 2
можно заменить выражением с другой сто-
роны, в III, I мы видели, что в сечениях, проведённых под углом 45°
к рёбрам, этому чистому сдвигу соответствует состояние простого
растяжения или сжатия. В направлении одной диагонали квадрата
возникает растягивающее напряжение = т^, а в направлении
другой диагонали — сжимающее напряжение аа = — т^. Следова-
тельно, в соответствии с уравнением (32), диагональ претерпевает
относительное удлинение г* == А. — А. <з3) = А А.) и> зна.
чит, абсолютное удлинение диагонали равно AJpL (1 -f- 2) xxv. При-
равнивая между собой оба полученных нами выражения для абсолют-
ного удлинения диагонали, мы получим соотношение между тремя
упругими постоянными
г— Е
G (
2(14
(35)
Применим это соотношение для того, чтобы несколько преобразовать
уравнения (32). Первое из этих уравнений напишем в виде:
= F [0 + (°® + ’у + ’«)]• (36)
В правой части уравнения (36) фигурирует объёмное напряжение,
которое, согласно уравнению (33), можно выразить через объёмное
расширение. Тогда получим
т
Решив это уравнение относительно <зх, найдём:
= <38)
1 -4- —
и, имея в виду соотношение (38), окончательно напишем:
?®.= 2о(в®+^) (39)
И т. д.
Аналогично, в криволинейных координатах
°и= 20 2^ = (40)
и т. д.
§ б]
ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ
29
5. Вывод основных уравнений.
Мы возвратимся к основным уравнениям равновесия (2), первое
из которых имеет вид:
двя> I I ^хг___о /4<\
дх' ду dz ’ ***>
Для нормального напряжения из уравнений (39) и (14) получаем:
=»=2О(В + ^=2)' <«>
Для касательных напряжений и согласно уравнениям (34) и
(14), имеем:
^=о(гг+й)- ’-.= с(й-+й)- («’
Подставив выражения (42) и (43) в уравнение (41), получим:
* дх*'т — 2 дх ду* ' дх ду^ dz*^ дх dz~~ и‘
Ради краткости введём оператор
А— & I & I 52 ZAKS
Д “ дх* "Г" ду* “Ь dz* ’ (4б)
Далее, дифференцированием по х уравнения (16) найдём:
д± , д*п <(П__де
дх* ‘ дх ду' дх dz дх * ' '
в результате получаем первое из следующих трёх уравнений:
Л” 1 т ’"Г т — 2 дх -0; 1
. , т де + — 2 ду = 0; (47)
АГ 1 т &е ' т — 2 dz = 0.
Эти три уравнения, вместе с уравнением:
дх ' ду' dz
являются основными уравнениями теории упругости, здесь исполь-
зуемыми. Если они выполнены, то удовлетворены все уравнения,
которые мы выше привели не только для перемещений, но также
и для компонентов деформаций и напряжений.
Нужно только разыскать наиболее простые способы, с помощью
которых можно найти решения этих основных уравнений. В даль-
нейшем изложении мы покажем, что компоненты перемещения могут
быть выражены помощью предложенного мною решения по методу
трёх функций, при этом таким «образом, что основные уравнения
будут всегда удовлетворены.
30
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ
[гл. Ill
в. Выражение компонентов перемещений и напряжений
через три функции.
Уже Максвелл *) выразил компоненты перемещений и напряжений
через три функции и установил дифференциальные соотношения
между этими функциями. Однако он не дал общих выражений, пред-
ставляющих собой решение этих уравнений теории упругости. Другими
авторами избирался тот же самый путь, причём дифференциальным
соотношениям, существующим между функциями, удалось удовлетво-
рить в интегральной форме. Так например, выражение, данное
Е. Треффц 9), содержит интегрирование по х в декартовых координа-
тах. В другом случае,задачу теории упругости сводили к решению
контурной задачи теории потенциала 8). Каждый из ответов, получен-
ных таким образом, хотя и представлял математически безукоризнен-
ное решение задачи, но применение этих ответов было связано со
столь большими вычислениями, что для определения пространственного
напряжённого состояния в выточках они применения найти не могли.
В противоположность этому найденное мною *) б) новое решение
имеет то преимущество, что вычисления перемещений и напряжений
не требуют интегрирования. Решение это содержит одну простран-
ственную функцию напряжений, которая выражена через три гар-
монические функции. Вследствие симметрии системы уравнений срав-
нительно просто дать ход вычислений и в криволинейных коорди-
натах. В ряде случаев удалось получить решение даже в замкнутой
форме.
Моё выражение перемещений через три функции имеет форму *)
205—57+* 2 * * * 6”ф';
2а''1=--г?+2«ф>;
2ОС= — д^--|-2«Ф8,
(49)
где F обозначает пока неизвестную пространственную функцию на-
пряжений. Ф2, Ф8 являются гармоническими функциями, т. е.
они удовлетворяют условиям:
Д®1 а Дф2 = ДФ3 = 0. (50)
*) Maxwell, С., Scf. Pap., Paris, т. 2 (1927), стр. 198.
2) Е. Треффц, Математическая теория упругости, ОНТИ, 1934
стр. 80—84.
8) Korn A., Math. Ann., т. 75 (1914), стр. 497.
*) N е u b е г Н., Z. angew. Math. Meeh., т. 4 (1934), стр. 203.
6) Ранее Нейбера это решение было получено Г. Д. Гродским и
П. Ф. Попковичем, см. Попкович П. Ф., Теория упругости, Оборонгиз
1939, стр. 120—131. (Прим, ред.)
§ 61 КОМПОНЕНТЫ ПЕРЕМЕЩЕНИЙ И НАПРЯЖЕНИЙ
31
Чтобы получить уравнение, связывающее эти функции с функцией
напряжений Ft подставим выражения (49) для перемещений в основ*
ные уравнения* (47). Тогда, принимая во внимание (50), получим
\(dF\ 4- 2G ” де-0-
~^\дх) + 20 т—2 дх
-А® + 2°^^=^
-О + «>^-=0.
(51)
Последние уравнения, после изменения порядка дифференцирования,
можно написать также в виде
(52)
Ж-(2О^2 =
Отсюда следует, что выражение, стоящее в скобках, не зависит от
координат х, у, г, т. е.
2 О е—ДF = const. (53)
Постоянная величина в правой части (53) не существенна и, поло-
жив её равной нулю, получим:
2Ge^(l-^yF. (54)
С другой стороны, подставив выражения (49) для компонентов пере-
мещений в выражение для е [уравнение (48)], получим:
20е= » W »-.2 №
дх2 1 дх ду2 1 ду dz* dz 9 4 '
или, вводя обозначение оператора:
2Ое=_ДГ+2«(^. + ^+^). (56)
Воспользовавшись теперь соотношением (54), найдём:
(2“4)ДГ=2аЙ&+^Г-*-ф)- (57)
\ fn / \ ОХ ’ оу ' 0Z / х '
Тем самым мы получили искомое соотношение между функцией
напряжений и тремя гармоническими функциями. В то время как
соответствующее уравнение в прежних решениях предлагается
32
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ [ГЛ. Ill
только в интегральной форме, полученному здесь уравнению
можно удовлетворить очень простым способом. Именно, положим
Г=Ф0-|-хФ1-[-^Фа-}-гФ3,'‘ ' (58)
где Фо удовлетворяет уравнению • ‘
ДФо = О. (59)
Тогда будем иметь
ДР==ДФ04- хДФ1 + 2^ + ^ДФ24-2^4-гДФ3 4-2^. (60)
В силу (50) и (59) это уравнение приводится к виду
4F“2(l!+^+»- (6»
Найденное значение ДГ подставим в уравнение (57), тогда получим
значение а
* = 2(' v)- 162)
Таким образом мы удовлетворили всем требуемым условиям. Найдём
теперь ещё выражения для компонентов напряжений.
Нормальные напряжения мы получим из уравнения (42), если
в них вместо Виа подставим их выражения, согласно (49) и (54).
В результате найдём
„ — 1_ 2Ge дЧ'А<)ПдФ1 1 °* 20дх +и_2 = <^ + 2а дх ~1 - — Др т (63)
и т. д. Из уравнения (62) выразим ~ через а: 1
т 1 2 • (64)
Тогда уравнения (63) перепишутся в виде
+ №5)
И т. д.
Но, с одной стороны, по определению:
ад. дЧ> , д*Р . дЧ-'
№ ~~ дх* “Ь ду" й?2 • <б6>
С другой стороны, по (61)
J_Ape । дФг L ^$3
2 дх 1 1 ду 1 dz * \v< J
Таким образом выражение (65) окончательно можно записать в виде
х ду2 dz2 \ дх dy dz) '
и т. д.
§ 6] компоненты ПЕРЕМЕЩЕНИЙ И НАПРЯЖЕНИЙ 33
Непосредственно из (43) и (49) получаем выражения для касатель-
ных напряжений
W । -/дФ1 ,
z<w дх о(у "г дх
и т. д. СлёдуеТ при этом обратить внимание на то, что циклическую
перестановку индексов нужно производить и у функций Фр Ф9 и
Ф8. Легко убедиться, что выражения (68) и (69) удовлетворяют
уравнениям равновесия (2). Точно так же удовлетворяются все
остальные уравнения, которые можно получить комбинированием
уравнений (2), (14), (33), (34) и (39) i).
Замечательным является то, что в общем случае любого напря-
жённого состояния, без нарушения общности рассуждений, одну из
(четырём) гармонических функций можно принять равной нулю. Это
утверждение проще всего доказать следующим образом. Положим:
<70)
При этом Ф8', Ф9', Ф/ и Фо' являются четырьмя новыми гармони-
ческими функциями. Если напряжённое состояние определено функ-
циями Фо, Ф1( Ф3, Ф8, надлежащим образом выбранными, то по
уравнениям , (70) легко найти новые введённые нами функции; так
например, Ф8' получается непосредственно из уравнения
^Г=ф8> (71)
а Ф8', и Фо' определяются из уравнений (70) соответственно по
Ф8, Фр Фо и ф8'., Дифференцированием легко убеждаемся, чго вве-
дение новых гармонических функций не противоречит уравнениям
(50) и (59).
С помощью (58) для функции напряжений получаем:
Р = Фо-j-хФх -f-_уФ24~дФ8 = 2аФ8'Фо'4-хФ/ 4-^Фа’. (72)
Применив теперь эту подстановку к формулам (49), получим:
205=—^(Ф0'4-хФ1'4-уФа')4-2аФ1'; I
2GT] = — (Фо' 4- хФ/ 4-.уФа')4- 2аФ2'; [ (73)
2<Кв“ +^')- |
П См. Феппль А. Л., Сила и деформация, I часть, стр. 29-^41.
Треффц, Математическая теория упругости, стр. 33—36.
3 8ав. 8476. Г. НеЯбер.
34
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ [ГЛ. Ill
В результате оказывается, что перемещения не зависят от функции
Ф8'. Функция Ф8' была нужна для определения Фа', Ф/ и Фо'. На
конечный же результат эта функция не оказывает влияния; она, в
известной степени, уже учтена функциями Ф2', Ф/ и Фо', к кото-
рым перешла роль функций Фа, Ф! и Фо. Этим доказано, что на-
пряжённое состояние в общем случае может быть описано только
тремя функциями. В выражениях (49) сразу можно считать одну из
функций Фп Ф9 и Ф8 равной нулю. Наконец, посредством другой
подстановки, убедимся, что и Фо можно считать равной нулю.
А именно, положим .
Тогда будем иметь
2G$ = - (жФ/ +>Фа' 4- гФ8') -|- 2ДФ/; ’
2GT) = - №' 4-уФа' + лФ8') 4- 2аФа';
(74)
(75)
2GC== - а4-(хф1'+>фз'+2ф8')+2афв'-
В последних выражениях функция Фо' больше не фигурирует. Так
как три функции Ф/, Фа', Ф8' входят точно так же, как ранее вхо-
дили функции Фх, Фа и Ф8, то этим доказывается возможность, без
нарушения общности рассуждений, функцию Фо считать сразу равной
нулю.
Итак, в действительности необходимы только три гармонические
функции, причём безразлично, какую из четырёх функций считать
равной нулю. Следовательно, одной определённой гармонической
функции соответствуют три различных напряжённых состояния, кото-
рые, за редкими исключениями, не могут быть даны какими-либо
другими функциями. Следовательно, многообразие упругих напря-
жённых состояний, в общем случае соответствует трёхкратному
многообразию гармонических функций.
7. Вычисления в криволинейных координатах.
Наиболее существенным требованием, которое ставится при вы-
числении напряжений, является необходимость удовлетворить гра-
ничным условиям. Последние налагают определённые ограничения
на величины напряжений в точках, находящихся на поверхности тела.
Например, на свободной от внешних нагрузок поверхности тела
эти напряжения обращаются в нуль. Так как поверхность, ограни-
чивающая тело, вообще искривлена, то удовлетворить условиям
§ 7]
ВЫЧИСЛЕНИЯ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
35
на поверхности в декартовых координатах не легко. Напротив, если
использовать такую криволинейную систему координат, координатные
поверхности которой содержат и поверхность тела, изображаемую,
например, уравнением и = и0, — в смысле определения, данного
в III, 3, — то в точках этой поверхности обращаются в нуль все
напряжения с индексом и, т. е. *)
®« = 0, = ‘tuw = 0 Для и = “о- (76)
Вследствие этой простой формы граничных условий мы предпочи-
таем проводить вычисления в криволинейных координатах.
С основами вычислений в криволинейных координатах мы уже
ознакомились в III, 3. Преобразуем теперь к криволинейным коор-
динатам выражение (49). Для этого возвратимся к формулам (22)
для перемещений U, V и IF:
и т. д. Подставив сюда выражения (49) для £, т), С, получим:
2аи= £[(-£++(-£+ 2аф’)я-+
+ (—гг+2аф»)<7г|- (78)
и т. д. На основании равенств
dF dF dx . dF dy . dF dz .
da e dx da * dy da + dz du и т‘ (?9)
получаем
<S°)
Эти уравнения, дающие компоненты перемещения в криво-
линейных координатах, почти столь же просты, как и уравнения
в декартовых координатах.
Дальнейший ход вычислений заключается в установлении формул
для относительных удлинений [см. (27)]:
1 ГЗУ . V dhu . W ЗЛ„]
“ А« L^u dv "f* л«в Л» J И Т‘ Д‘
Отсюда получается объёмное расширение [см. (29)]
=®« ®«4” ®«о»
а затем, по формулам (40) и (62), и нормальные напряжения
’u = 2G(8#-[-^=ie) ит. д.
*) Предполагается, что поверхность и == aQ свободна от внешних нагру-
зок. (Прим, ped.)
3*
36
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ
[гл. Ш
По формулам (27) и (40) находятся касательные напряжения:
’-=с[Ы®+Ы(£)] и'-д- <84)
Таким образом установлены все соотношения, которце необходимы
для вычисления напряжений по функциям напряжений в криволиней-
ных координатах.
Ход вычислений, приведённый выше, предполагает, что в первую
очередь должна быть решена задача определения перемещений,
а затем уже и напряжений. Однако в большинстве случаев напряже-
ния проще вычислять непосредственно из функций напряжений.
Правда, некоторые свойства перемещений, как, например, однознач-
ность и непрерывность, имеют существенное значение при выборе
функций Фп Фа, Ф8 и Фо, но, как правило, не является необходимо-
стью определять сами перемещения; как вытекает из (49), (58) и (80),
свойствами однозначности и непрерывности должны обладать сами
функции Фп Ф2 и Ф8 и производные и т. д.; или же в криво-
линейной системе координат — и т. д. При этих условиях одно-
значность и непрерывность перемещений обеспечена. Поэтому мы
обыкновенно будем пользоваться несколько более коротким способом
вычислений, дающим непосредственно сами напряжения. Для этого
перемещения из (80) подставим в (81) и (84). Ради краткости вве-
дём в употребление следующие операции:
1 дли д .______
dflw2 hu ди \hu ди) ‘ huh^ "Sv dv ' huh^ dw dw И T’ Л'
(85)
d2 d2 _l 1 a / 1 d\_________=
dnudnv dnvdnu “ hu du \hv dv) hu2hv dv du
e hv dv\hu du ) huhj du dv^
<2hu du \hv2 dv ) ‘ 2hv dv \hu ' *
Остальные получаются циклической перестановкой букв и, ф, w.
Получаемые далее выражения можно ещё существенно упростить.
Рассмотрим для этого частный случай
= const. = С; Фо=— хС; Ф2 = 0; Ф8=0; Г*=*0. (87)
Все компоненты перемещения, кроме в этом случае равны нулю,
а £ равно:
S = ’ (88)
Следовательно, все точки тела перемещаются в данном направлении
на одинаковую величину, т. е. тело остаётся жёстким, и в нём де-
формаций никаких не возникает. Действительно, в этом случае
§ 7J
ВЫЧИСЛЕНИЯ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
37
исчезают все компоненты деформаций. Но и в криволинейных коор-
динатах при жестком перемещении тела компоненты деформаций
также должны обратиться в нуль. Значит, слагаемые в выражениях
для деформаций ем, fut) и т. д., содержащие Фп фа, Ф8, должны
исчезать. Отсюда следует *:
" ’• <89>
с циклической перестановкой букв и, v,w и x,y,z.
Чтобы получить окончательные формулы для нормальных напря-
жений, требуется еще выразить через функции напряжений объёмное
расширение. Из (54) и (62) имеем:
2Ge = («—1) ДГ и 2Ge - (1 — -|) ДГ. (90)
Для нормальных напряжений получаем:
d*F 2а /дФ1 дх
дп£ ' Л„4 \ ди ди
<91>
и т. д. Для касательных напряжений найдём:
__ d2F , а /дФхдх . d$idx дФ8ду , дФъду ,
дпидп„ huhv \ да dv' dv. du ‘ du dv ' dv ди '
. ЭФ8да . ЗФ8йг\ znc.
★ih+lfli) и т- л <92)
Сравнивая найденные выражения с соответствующими форму-
лами в декартовых координатах, т. е. с соотношениями (65) и (69),
3» д*
видим, что операции ^-^-соответствуют вторым производным
в некоторой декартовой системе координат, оси которой и', v', w'
в рассматриваемой точке совпадают по направлениям с осями и,
о, w криволинейной системы координат. Это соображение разъяс-
няет соотношения (89) с другой точки зрения.
Общие условия равновесия (6) оказываются здесь также удо-
влетворёнными; это станет очевидным, если обратить внимание на
то, что между дифференциальными операторами в декартовых коор- * 84
*) Подставив в (80) значения F, Ф1( Фа, Ф8 согласно (87) и воспользо-
вавшись (81) и (85), получим первое соотношение (89), а воспользовавшись
84) и (86)—второе соотношение. (Прим, ред.)
38
ОСНОВНЫЕ ДАННЫЕ ИЗ ТЕОРИИ УПРУГОСТИ
[гл. HI
цинатах х, у, г ив двух любых направлениях х и Л существуют
легко выводимые соотношения:
__e2Scos(x, н) cos (X, ,
д д V? V' / \ \ д (93)
2 2 cos (х, р) cos (X,
Наконец, можно вообще показать, что напряжение, действующее
в направлении х и приложенное к площадке с нормалью X, выра-
жается через функции напряжений следующим образом:
_______Э2/? . /ЭФх дх . дФ1 дх . ЭФ» dy ЭФ» ду ЭФ» дг .
Эпхд«х ' а \Элх дп\ дпх дпх dn*oni' дп\ •" дпж дп\
«*>
Здесь *) или означают дифференцирование вдоль прямых,
которые в рассматриваемой точке совпадают с направлениями х и X
Для того чтобы определить функцию напряжений, следует найти
соответствующую гармоническую функцию, т. е. такую, для кото-
рой оператор А равен нулю. Необходимо, следовательно, знать вид
этого оператора в криволинейных координатах. Проще всего это
получить, использовав выражение для объемного расширения. В де-
картовых координатах мы имели [ср. (56)]
2Ge = -AF+2«@+^ + ^). ОЗ)
Следуя уравнениям (80), (82), учитывая также уравнения (85), (86)
и (89), получим такое выражение для объемного расширения в кри-
волинейных координатах
9Г । &F । &F\ । 2»/ЭФ»Эх , ЭФ» Эу , ЭФ8Эг\ ,
e=xz х.дп^'дп^ ' dn1Bi)'~ hu*\da да' ди ди' ди .ди)'
. 2а/ЭФХ Эх дФ^ду ЭФ8Эг\
' \ да да~* да да ' да да)'
, 2а (дФ1 дх ЭФ2 ду , ЭФ» dz \
' Л»2 \ dw dw ' dw dw‘ dw dw)' ’ '
Сравнение между собой слагаемых в правых частях (95) и (96), не
содержащих а, даёт оператор:
Л__ э« ! Э2 , Э*
дп^ dnS1~ dnw*’
(97)
х) Как и в формулах (93). (Прим, ред.)
§ 7]
вычисления в криволинейных координатах
39
Если значение каждого из операторов, согласно уравнению (85),
подставить в уравнение (97), то после небольших упрощений най-
дём:
а = 1 f \ I д (huftu & \ I & f
А htlhKhw \ hu du)'dv\hv dv)'~ dw\ hw dw)\
(98)
С другой стороны, из сравнения слагаемых, содержащих множи-
тель 2а, имея ещё в виду соотношение (61), получим выражение
для ДГ, применяемое с большой пользой для определения нормальных
напряжений:
АР—о । дфг । - 2 । дФ^ду । дФ8'д.г^ , '
£ \ дх ~г" ду ‘ dz ) hj \ ди ди диди' ди д л ) '
_1_2 /дФ1 дх । дФ8 ду дФ8 дг\ ,
*" Ло? \ dv dv' dv dv' dv dv) T
2 (d<btdx дФ,ду дФ8
‘ \ dw dw • 3w dw ' dwdw/’ '
К вопросу о надлежащем выборе гармонических функций, т. е.
таких, для которых оператор (98) обращается в нуль, мы вернёмся
при решении отдельных задач. При этом мы всегда будем выяснять
ход рассуждений, сразу приводящий к правильному выбору функций.
Перейдём теперь к рассмотрению задач по определению напря-
жений в выточках,' и начнём со случая плоской задачи.
ГЛАВА IV.
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ.
1. Основные уравнения.
Чтобы получить основные уравнения, относящиеся к случаю
плоской задачи, предположим, что компоненты деформаций и напря-
жений зависят только от двух координат, скажем, от х и у. Общие
выражения, полученные нами в III, 6, принимают здесь специальную
форму. Четыре гармонические функции, из которых Фа мы сразу
положим равной нулю, зависят только от х и у, ЧТобй и функция
напряжений не зависела от г, нужно также положить‘функцию Ф8
равной нулю, что вытекает из уравнения (58). Мы получим тогда
Фо^ФфС*, У)"> $1 Ф»(*> j)5 Фав0; Ф8»0; |
Г=Ф04-хФг |
Выражения (49) для перемещений примут вид:
2^=-^+2«ФР
2<*1=~^
с=о.
(2)
Чтобы получить наиболее простое выражение для напряжений, вве-
дём новые гармонические функции ф/ и ф0' ио формулам:
Ф1 ~ ЪГ ’ ф° “ аФ1/ Ф°‘ 00
Имеем по уравнению (1):
Далее положим для сокращения записей:
(4)
<5)
§ 1]
ОСНОВНЫЕ УРАВНЕНИЯ
41
Таким образом получаем:
Р = Р'4-аФ/;
2G$= — ^(F'-аФ/);
1 2(Ь1=-^(Р'Ч-аФ1');
С = 0. J
Выражения для напряжений проще всего получить из (68) и (69).
Обратив внимание на то, что Дф\ =» 0, получим:
ff’-F' gif'
°* e дх* ду2
д2Ф'
а дх2 ’
dV'
x<e»~~~Sx^y> т®«в°; v—°
Благодаря равенству * F кр/________л дгФ/
дх2
для нормального напряжения <зв получим
ог =
или, как это следует из (7),
(7)
(8)
(9)
(Ю)
Таким образом мы пришли к плоскому деформированному состоя-
нию, для которого в направлении оси z компонент перемещения
равен нулю, но не равно нулю нормальное напряжение. Еслч речь
идёт о плоской пластинке, ограниченной поверхностями z = const.,
то по этим поверхностям должны действовать нормальные напряже-
ния
На практике наиболее важным является так называемое плоское
напряжённое состояние, для которого в направлении оси z не равно
нулю перемещение, но зато исчезает нормальное напряжение. Что-
бы удовлетворить этим требованиям, необходимо ввести некоторую
пространственную функцию напряжений.
Опять применим гармонические функции Ф/ и Фо', зависящие от
х и у. Однако теперь надлежащим образом должна быть введена
координата z. Положим
_4-4а + а«/ 9д»Ф1' „дФ/Х
«О---в(4-а) И +
। 2 — а д*Ф1' . 4 - ,
+4=1151*5+4=5 ф>
(И)
ж 4 аф1
ф1 = а(4-а) Э7
-4 +2д dw
а (4 —а) дх2
42
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ
[гл. IV
В последних выражениях через d обозначена толщина пластинки,
а её срединная плоскость предполагается совпадающей с плоскостью
г = 0 (см. фиг. 12.) Можно легко убедиться, что функции Фо, Ф1
и Ф8, введённые таким путём, суть пространственные гармонические
функции. Для функции напряжений найдём:
<12>
Снова положим:
(13)
Тогда 2(Н)
" р = + <16>
Для перемещений будем иметь:
2О; = _ 2.1 дх 1 >'+ 2— а । 2(4 —а)* ~4—аф1 ]>
20т| = ду 2 —а 2(4 —а) (16)
2ОС = 2- -гДГ /
4 — а
Из (68) и (69) получим затем выражения для компонентов напряжений:
(17)
При выводе (17) принято во внимание равенство ДФ/ = 0. Для тонких
пластинок толщина d мала в сравнении с остальными размерами.
1 1 Фиг.”12. Координаты
в пластинке.
Так как плоскость г = 0 является сре-
динной плоскостью пластинки, то коорди-
.d
наты ; значит г может принимать
лишь малые значения, и в первом при-
ближении членами d9 и z- мы можем пре-
небречь. Сравним теперь уравнения (17)
с уравнениями (7). Легко убедимся, что, как
в случае плоской деформации, так и в слу-
компоненты напряжения
чае плоского напряжённого состояния,
одинаково выражаются через функцию F'.
§ П
ОСНОВНЫЕ УРАВНЕНИЯ
43
Для толстых пластинок только что указанные приближённые
соотношения перестают совпадать в каждой точке, но для средних
значений напряжений, т. е. для
d
2
ит-д-
з
они остаются справедливыми, так как
d
j(g-z>)<fe = O, (19)
—£
и мы получим
PF' - ffip _
°*= ду* • ~ дх”- ’ ~ дхду ‘
(20)
Эти соотношения для компонентов напряжений, выведенные нами ранее
для плоского деформированного состояния, оказываются справедли-
выми и для случая плоского напряжённого состояния, если ввести
в рассмотрение средние по толщине значения напряжений. Важно
заметить, что эти напряжения становятся независящими от коэф-
фициента Пуассона.
В этом отделе мы будем заниматься исключительно плоским
напряжёнными состоянием, причём, ради простоты, под су и
будем понимать средние по толщине пластинки значения напряжений.
Далее, вместо F', Фо' и соответственно будем писать F, Фо
и Фг Таким путём и получим следующие основные уравнения для
плоского напряжённого состояния
Р = Фо + *Фр Фо = Фо (х, у); ]
21
Дфо==О; ДФ1 = 0. j
. d2F дгР ,ооч
°» = дх25 lW“ дхду ’ <22)
Следовательно, функция напряжений F соответствует функции, уста-
новленной в плоской задаче теории упругости Г. Б. Эри и называе-
мой его именем. Таким образом напряжения выражаются через вто-
рые производные по координатам от функции напряжений. Как мы
увидим, введение этой функции даёт ещё следующее преимущество.
Из условий на поверхности, выраженных в напряжениях, можно
вывести определённые граничные условия для самой функции напря-
44
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ
[гл. IV
жений и, значит, она вполне определяется еще до того, как най-
дены эти напряжения.
Для вывода этих упрощённых граничных условий рассмотрим
условия равновесия сил, приложенных к треугольному плоскому
Фиг. 13. Граничные условия в пло-
ском напряжённом состоянии.
Далее, согласно уравнениям (22),
элементу (рис. 13) с гранями dx,
dy, параллельными координатным
осям, и гранью ds. На грань ds
в направлениях х и у действуют
силы dX и dY. На гранях dx, dy
jsfitocnywt силы, вызванные на-
пряжениями Ядр яу и х^у. Из усло-
вия равновесия, устраняющего дви-
жение в направлении оси х, сле-
дует
dX= — я^у xxydx. (23)
Аналогично, получим:
d Y = яуйх — x^ydy. (24)
найдём
dX~ ^d^~dxlydx-----
Проинтегрируем эти уравнения вдоль кривой f, целиком располо-
женной в области тела и соединяющей точки Pt и Ра (см. фиг. 13).
Пусть Л/1>2, Тиа, УЪ2 соответственно представляют момент и проек-
ции сил, возбуждаемые действием части тела, лежащей левее (и выше)
кривой Pt Ра, на часть, расположенную с правой стороны этой кри-
вой (и ниже). Получим
2
+ (27)
2 2
гм=?>'=р©=®,-®.- <28>
1 1
Момент сил относительно точки х = 0, j = 0 равен:
2 2
Af1>a - / [х dY—y dXf= f [xrf(^)+X(^)] =
1 0
(29)
§ 1]
ОСНОВНЫЕ УРАВНЕНИЯ
45
Для грани, свободной от внешней нагрузки, непосредственно полу-
чаем:
const; const. (30)
дх ’ ду
В качестве последнего шага к разысканию уравнений, которые по-
служат для решений отдельных задач, дадим ещё выражение компо-
нентов напряжений через функцию напряжений в криволинейных
координатах. При этом мы используем тот факт, что исследуемые
соотношения не зависят от коэффициента Пуассона [ср. (7), (20) и
(22)], силу чего коэффициент Пуассона, а значит, и постоянную а,
мы можем считать любым числом. С целью упрощения вычислений
положим а равной нулю. Так как окончательный результат от а не
зависит, то, принимая это частное значение, мы не введём никакой
ошибки.
В декартовых координатах мы уже установили, что связь между
функцией напряжений и напряжениями, действующими в пластинке,
одинакова как в плоском напряжённом состоянии, так и в плоской
деформации. Но при а —0 также не существует разницы между
плоской деформацией и общим пространственным напряжённым со-
стоянием, если только принять во внимание независимость от коор-
динаты z. По этой причине мы можем сразу же исходить из про-
странственного напряжённого состояния и соотношений, уже выве-
денных для него в криволинейных координатах, но при условии,
что функция напряжений зависит только от двух координат:
F=F(u, v), (31)
причём третья координата чи принимается равной чв = г', из III,
(20) следует:
Из (91), полагая а = 0, получим:
I аг. &F I АГ
+ dn^^F’
Из III, (97), с учётом (31), имеем:
дп^'дп*'
Подстановка (34) в (33) даёт:
__ d*F __ d'F
*~~dnv*’ а’~дп,?'
(33)
(34)
(35)
46
Теория концентрации я плоской задаче
[гл. IV
Подставив значения операторов по и, и пи из (85) III и имея в виду
(31), получим следующие окончательные выражения для нормальных
напряжений:
1 д /1 af\ 1 д,1« dF
hv dv \h„ dv) ' ди du ’
_ 1 d /1 , 1 dhudF
°® hu du \hu du) "1“ dv dv ’
(36)
Выражение для касательного напряжения получается непосредственно
из (92) и (86) главы III
'_______1 д/1 dF\ . _±_д_Кд_Р
“» huди\hv dv) ' hu2hv dv да' ' '
Оператор А, данный уравнением (98), при /zw=l, принимает здесь
следующую форму:
(38)
hu \_du\hu ди/ 1 до УД, до/J 4 '
С целью использования граничных условий (26) — (29) нам необ-
дЕ dF
холимо выразить в криволинейных координах и По извест-
ит?
ной теореме дифференциальной геометрии величину можно пред-
ставить как компонент по оси х вектора grad F\ компоненты этого
вектора по двум взаимно-перпендикулярным направлениям и и v
будут:
dF \_dF dF l_dF qcn
dsu = hu да И dsv = hv dv * ' '
Компоненты вдоль оси x получим простейшим путём, умножая эти
величины на соответствующие косинусы:
g = cos (х, и) L + COS (X, -о) i- . (40)
Аналогично
g=coS0,a)^+coS(y,.)^. (41)
Вместо направляющих косинусов подставим их выражения из (18)
отдела III, 3, и тогда окончательно найдём
dF 1 dx dF 1 dx dF 142'1
дх = ftu2 ди ди й„2 dv dv ' ' '
dF__J_dydF ._t_d^dF /43)
ду hu2 да ди ~1~ ftw2 dv dv'
Эти соотношения мы могли бы получить из III, (99), считая в них
Фа == ф# = О или Ф£ = Ф8 = 0.
§ 2]
ДВУСТОРОННЯЯ ВНЕШНЯЯ ВЫТОЧКА
47
При расчёте удобнее пользоваться такими криволинейными коор-
динатами, для которых коэффициенты искажения равны друг другу.
Это будет иметь место, если при х«=х(а, t>) и у=у(и9 v) выпол-
няются условия:
—-+-^ дХ — л-дУ (Л1\
да до* dv ди' ' '
Тогда действительно, как вытекает из (31),
= h.
(45)
Такую криволинейную систему координат называют изометрической
сетью. Уравнение ЛФ —Ов этой системе координат принимает про-
стую форму
агф <)2ф ' ,
а«2 dv* °’ (46)
весьма облегчающую разыскание гармонических функций. Вследствие
формального сходства формы написания этого уравнения в декарто-
вых и изометрических координатах, гармонические функции как
в той, так и в другой координатной системе можно определять оди-
наковым образом.
Как известно, в декартовых координатах вещественная или мни-
мая часть всякой аналитической функции f(x -j- iy) является гармони-
ческой функцией. Равным образом, и в изометрических координатах
a, v вещественная и мнимая части комплексной функции/(а-|-й>)
являются гармоническими функциями.
2. Двусторонняя внешняя выточка.
Пользуясь фиг. 14, рассмотрим случай очень глубокой симмет-
ричной, двусторонней выточки. В I, 4 было отмечено, что при
увеличении глубины коэффи-
циент концентрации прибли- ----—
жается к предельному значе- Xх
нию, не зависящему от глу- /
бины выточки. Определение / s> /
этого предельного значения /
является целью последующего X-______I
рассмотрения. При этом для I________у I 1г
каждого вида нагрузки будет '
проведено исследование напря- Фиг. 14. Глубокая двусторонняя внеш-
жённого состояния. В силу за- няя выточка,
кона затухания существенное
влияние на коэффициент концентрации оказывает только кривизна
У дна выточки. Форма выточки в остальной её части мало влияет на
коэффициент концентрации, поэтому мы её выберем так, чтобы
48
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ
[ГЛ. IV
результат достигался наиболее простым вычислительным процессом.
Именно, мы возьмём выточку в форме гиперболы, чтобы иметь воз-
можность воспользоваться эллиптическими координатами
х — sh и cos v, у = ch и sin и (47)
Отсюда имеем:
и)2+Ш2"^ («)
Следовательно, линии и = const, являются эллипсами, а линии
v = const. — гиперболами.
Далее, из (32) получаем величины коэффициентов искажения
йи2 = й„9 = А9 = ch3 и cos3 v -|- sh3 и sin3® =
= ch3ft(l —sin9®)-]- (ch3 и — l)sin3® =
= ch9 a—sin9 ® s= ch9 a — 1 -f- cos9 ® =
= sh9 и -|- cos9 ®. (49)
Оба коэффициента искажения равны друг другу. Поэтому введённая
система координат является изометрической, вследствие чего можно
пользоваться простой формой (46) уравнения ДФ = 0.
Соотношения (42) и (43) переходят в следующие:
g = l[ch«cos®g-sh«sin®^]'; (50)
^ = l[shasin®^4-ch«cos®^]. (51)
Контур выточки изображается гиперболой с параметром ®0, а в соот-
ветствии с уравнением (30) з- и должны быть постоянны при
ох оу
V = Z±V0.
Общее решение этой задачи мы теперь разложим на несколько
таких решений, чтобы для каждого из них при интегрировании на-
пряжений, действующих по наиболее узкому сечению согласно урав-
нениям (27) — (29), получалась неравной нулю только одна из трёх
равнодействующих величин Х^г, Ухд, Mip Таким образом задача
распадается на три, соответствующие простому растяжению, чистому
изгибу и чистому сдвигу.
А. Простое растяжение. В этом случае функцию напряжений тре-
буется определить так, чтобы отличалась от нУлЯ тблько равнодей-
ствующая Л1,2.
Мы возьмём *):
&o — A(yv — xw)-|-Bch и сое®; Ф1 = Ап (52)
и, как легко убедиться, условие (46) будет выполнено.
N е ti b е г Н., Z. angew. Math. Meeh., т. 13 (1933), стр. 439.
ДВУСТОРОННЯЯ ВНЕШНЯЯ ВЫТОЧКА 49
Поэтому F = Ayv -|- В ch и cos v, (53)
или, согласно (47), F = ch и (Av sin v В cos v). (54)
По уравнению (50) найдём в первую очередь Получим:
*£= 8h“ch-« Xsta>A (55)
дх Л2 \ /
На ненагруженной грани v = ± v0 производная должна быть пси
стоянной. Из этого условия получается соотношение между А и В*.
B = Asin8v0. (56)
др
Далее по уравнению (51) найдём производную
£sh9 и sin к (Av sin v -|- В cos v) -f*
-f- ch8 и cos v (Av cos v -|- A sin v — В sin v)J (5?)
или, имея в виду (49),
+ ---адГ>>О (Atgv—Big v —Belg v). (58)
Подставим сюда В из (56). Тогда получим:
у- = аГо -f- sin8 v0 cig v etg v (cos81»0—cos8®)! . (59)
n dF
Отсюда видно, что при o=±=±z®0 производная-^ также постоянна.
Таким образом, контур свободен от внешних нагрузок.
Мы перейдём теперь к исследованию поля напряжений в попе*
речном сечении стержня. Для этого необходимо принять во внима-
ние соотношения (27), (28) и (29). В них индексу 2 соответствует
значение <»с= а индексу 1 значение v = — и0. При этом ока-
жется, что У1>2 и ЛТ1,2 равны нулю. Неравную нулю равнодействующую
напряжений Л1,2 умножим на толщину d пластинки, чтобы получить
величину внешней растягивающей силы, которую мы обозначим
буквой Р. Имеем:
j — 2 А (®0 -f- sin v0 cos т>0).
(60).
Таким образом функция напряжений для данной задачи определена,
и можно перейти к вычислению напряжений по формулам (36) и (37).
Выражения для напряжений можно существенно упростить, если
4 Зак. 3475. Г. ®ейбер.
50
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ 8АДАЧЙ
[гл.VI
иметь в виду (49). Не приводя промежуточных вычислений, даём
окончательные формулы
А . (п . COS2 СМ—cos20\
«и=л»ch «c°s «(2 Ч-----;
, ov г=а ch и cos v (cos2 V — cos2 т*0);
t«0 = Sh e Sin ® (cos2 v0—cos2 v).
(61)
С целью сравнения ввеаём номинальное напряжение, равное сред*
нему нормальному растягивающему напряжению по наиболее узкому
поперечному сечению стержня:
(62)
Величина а равна половине ширины наиболее узкой части стержня
(фиг. 14). В нашей координатной системе за единицу длины при*
нято значение
(v)«=o=l, (63)
v =i —
2
поэтому
e“(0Meo“Sinvo, • (64)
v = v,
таким образом можно положить:
Р — 2d sin vop. ; (65)
Если это значение подставить в (60), то для постоянной А, имеющей
размерность напряжения, получим следующую формулу:
Р v04-sin t»0cosv0 * '
На фиг. 15 дано распределение напряжений при tgo0 = 2. Вдоль
контура, начиная от дна выточки, в обе его стороны имеет место
быстрое затухание напряжений, что подтверждает закон затухания,
сформулированный в II, 2. В наиболее узком сечении график напря-
жения аи в некоторой части располагается ниже пунктирной линии,
соответствующей номинальному напряжению/ но затем, при прибли-
жении к дну выточки, напряжение быстро увеличивается и у дна
выточки достигает наибольшего значения, превосходящего номи-
нальное напряжение в 2,65 раза. Выражение для наибольшего на-
пряжения, возникающего у дна выточки, мы получим из (62) и (66):
«• (0“\=0t= Р Po+sinVco»»» ’ <67
иг
ДВУСТОРОННЯЯ внешняя ВЫТОЧКА
•1
её- «КРИВИЗНОЙ ВЫТОЧКИ». i
На основании уравнения гиперболы (48) имеем —,—~
± = tga®0; costf0 ,- * ~ > sin vo
Р т/ ±4-1
• (.68)
₽
р
Следовательно, vQ можно выразить через л/р, и тогда (67) перейдёт в
На фиг. 16 дана зависимость максимального напряжения от кривизны
выточки. Для малой кривизны, т. е. для малою —, можно пока*
Фиг. 16. Наибольшие на-
пряжения в глубокой
двусторонней внешней
выточке при растяжении
Фиг.' 15. Глубокая двусторонняя внешняя выточка
при растяжении.
зать, что траектории главных напряжений обладают свойствами
линий тока. В отношении этого вопроса отсылаем читателя к лите*
ратуре!).
В. Чистый изгиб. При чистом изгибе отличается от нуля только
Afi^. Этому условию удовлетворяют следующие выражения для функ*
ций 2):
фо в Ach 2asin 2v-j-Bv; Ф|Я=—4Ash«sino, (70)
х) Neube'r H., Ing. Arch., т. 6 (1935), стр. 325.
^NeuberH., Ing. Arch, t. 5 (1934), стр. 239.
4»
ТЕОРИЯ' КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ [ГЛ‘
являющихся, решением уравнения (46)., Функция напряжений буД£Т
иметь вид: .
F — A sin 2v 4- Bv. (71)
В соответствии с (50) и (51) получим
dF sh и sin v л n f П\
— (2Аcos2о4-В);, »
\ < > (72)
* dF* ch и cos v i л .; D4
=»--------------- (2Д cos 2v -p B).
Следовательно, если
B== -r-24cos2o0, (73)
та контур окажется ненагруженным, и при v=±Vq обе произвол*
ные превращаются в нуль. Затем, из, (27) № (28) непосредственно
следует равенство нулю И У),г. Из (29) получаем величину Afi.2,
равную, согласно определению, внешнему моменту /И, делённому на
толщину d пластинки. Имеем
№,2= 7= -(F)+,. + (F)-t,0= “2(4 Sin2®o + B^). (74)
(76)
Подставив сюда значение В из (73), найдём:
i : f | АЛ
у-1 ^t=!—2A(sin2o0 — г^совг^о). (75)
С. помощью. (36) и (37) компоненты напряжений получим; в форме:
1 _• 1 .<(„==.^sin2-»(cos2-»0—cos2o);
, л
; *ш> — м 8,12" (cos — cos ZVq)'
<i п
Номинальное напряжение вычисляем по элементарной формуле изгиба
°п~2аг0. Р*
Теперь из (75) можно получить значение А, имеющее размерность
напряжения. Принимая во внимание (64), получим:
. ____ sln»t>0_____
л~ р3(з№ь—2t/oCQs2tQ;
На фиг, 17 показаны графики, распределения напряжений для tg*oo= 2.
Пунктирная линия соответствует прямолинейному закону распреде*
ления напряжения, ио элементарной теории сопротивления материа*
лов. Напряжение <зи сначала (около оси стержня) лежит ниже этой
линии и затем при приближении к дну выточки быстро, увеличи-
ДВУСТОРОННЯЯ внешняя выточил
!«3
$ 2J
ваётся, достигая 'на контуре (у 'дна вытдчки) удвоенной величины
номинального напряжения. -
Из-формулы (68) получаем выражение для Максимального напря-
жения'.
, а -/а
7
gnrak_ P P__________ - . /79)
T 3[l/7 + (7-1)arqtei/r7]
На фиг. 18 Графически изображена зависимость Найболв'феГЪ на-
пряжения от л/р. f !’s
ЗЯ
4
(80)
(81)
Фиг. 18. Наибольшие напря-
жения в глубокой двусторон-
Фиг. 17. Двусторонняя глубокая Внешняя, ней внешней .вытечке гфи
выточка при изгибе. ' изгибе.
С. Чистый сдвиг. В случае чистого сдвига функции берутся в виде *)
Фо =» A sh и sin if; &t==Bv; Г
F = sh и (4 sin v Ц- Bo cosfl). J
По формуле (51)'находим ~ r
Поэтому граничные условия требуют, чтобы
А==—Bcbs9o0.
dF
Выражение для получаем по формуле (50):
dF i г
= -jp- [ch9 и cos v (4 sin v 4- Bo cos o) —
— sh2 a sin fl(4 cost»-J- 5 cos о—Biasing)),
’) N e'u b e г H., Ing.'Arch., r. 5 (1939); стр, 240.
(82)
(83)
54 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ [ГЛ. IV
или, согласно (49) и найденному нами выражению для А, имеем:
=я В Го—cos9 о0 tgo + te v (со®9 —cos9• (8^)
л . dF
Отсюда видно, что для о = ±t»0 величина оказывается постоям»
ной и. значит, условия на поверхности выполнены.
Соотношения (27)—(29) показывают, что в этим случае исчезают
Алд и Му#. Единственная, отличная от нуля, составляющая напря*
жений К1.2, умноженная на 4. даёт перерезывающую силу, которую
мы обозначим буквой V. Будем иметь:
К1.2 м — — « 23 (t»0 — sin cos о0). (85)
Для напряжений получим следующие выражения:.
В . . / о । cos’ V — cos’ vn \
= -fp sh ц sin о 2 4 £5 J ;
«0 = sh и sin v (cos9 v0—cos9 v);
Tu® = *^r ch и cos v (cos9 v0—cos9 o).
(86)
В качестве номинального напряжения здесь целесообразно взять
среднее касательное напряжение по наиболее узкому поперечному
сечению:
'•“TST “*p' Ф7)
(88)
Затем из (85), с учётом (64), получим:
д. _ g Sin t>0
” V0 —sin VjCOS V0 •
На фиг. 19 показан график распределения напряжений для
случая tgv0==7. Наибольшее напряжение в этом случае возникает
не у дна выточки, а на некотором очень небольшом удалении от
него. В самом узком поперечном сечении имеется только касатель»
ное напряжение Касательное напряжение в средней части стержня
меньше среднего касательного напряжения. Но при перемещении
к контупу 'недалеко от него напряжение быстро увеличивается и
в точке вблизи контура достигает своей наибольшей величины.
После этой точки оно быстро убывает. Аналогично ведёт себя вдоль
контура выточки напряжение а„. На большом расстоянии от дна
выточки оно имеет очень малую величину, но по мере приближения
к дну выточки оно постепенно увеличивается и недалеко от него
достигает наибольшей величины; в точке у дна выточки оно
делается равным иулю, -из растяжения переходит в сжатие и опять
недалеко от дна принимает ту же самую наибольшую величину
(численно), после чего быстро убывает.
§ 2]
ДВУСТОРОННЯЯ ВНЕШНЯЯ ВЫТОЧКА
55
Пунктирная линия соответствует параболическому распределению
касательного напряжения, даваемому элементарной формулой сопро-
тивления материалов для случая стержня, не имеющего выточки.
Фиг. 19. Двусторонняя глубокая внешняя выточка при сдвиге.
От этого напряженного состояния резко отличается состояние,
имеющееся в действительности.
Найдём наибольшее значение напряжения ow. Вдоль контура
выточки имеем:
Ы,.п^-2В^, „-2Й81„г, • (89)
Это выражение зависит только от в и принимает экстремальное
значение в тех точках, где равна нулю. Вычислим
(РиЪ-*, *= — Ksh’« + cos’ v0) ch и —
—2 sh8 и ch и] = 0. (90)
Отсюда получим:
sh’a = cos8®0; shzz= ±cosv0. (91)
Максимальное растягивающее напряжение соответствует знаку
плюс. Оно возникает в точке, определяемой абсциссой ж [ср. (47),
(64) и (68)]:
Я — з!1«С05®0 = С089‘00=*а-Ц^- = —-7^~а (92)
56
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ
(ГЛ. IV
и вычисляется по выражению:
(93)
Для того чтобы определить наибольшее касательное
ние, найдём ~uv для точек, лежащих в наиболее узком
Имеем: ' ’
/ ч __ о cos’vq-- cos3 у
\ UV/W = 0 cos^ V *
напряже-
сечении,
(94)
Это выражение зависит только от v. Поэтому вычислим произ-
водную от (т„Ф)а.=о по %>:
-о=[cos8® • 2 sin vcos v 4-
+ (cos.2 oa—cos2 о) 3 cos2 о sin о] =0; (95)
найдём:
cosai» = 3co$2oa; |
со8 г>= +|ЛГсОзг)0. I
Наибольшее касательное напряжение возникает поэтому в точке
[ср. опять (47), (64) и (68)]:
1 _______'_____________/13
j.= ,ln»=yi-I3cM>4>e.eli^^2L_aV -!-j- ;\Э7)
здесь оно равно:
. = —-----------JJ.—г . (98)
Р f о . Д Г о -Г о
При ~^2 максимум ти„ находится в точке j> = 0 и вычисляется
по формуле: , , , ,
а .ГТ
1I0H. =-_________P-J-_р--------=-. (99)
-*Га । 1 । а1
V 7+1L(7+1)arctgF "VjJ
На фиг. 20 приведена зависимость наибольшего напряжения от кри-
визны выточки.
Общий улучай совместного действия изгибающего момента и
перерезывающей сил£1 получается посредством наложения обоих полу-
§ 3] ОДНОСТОРОННЯЯ ГЛУБОКАЯ ВНЕШНЯЯ ВЫТОЧКА 57
ценных выше решений. Как мы видели, наибольшее напряжение на
контуре выточки при чистом изгибе лежит у дна выточки, а при
-чистом сдвиге — возле него. Поэтому, чтобы получить точное зна-
чение наибольшего напряжения при изгибе в общем случае, нельзя,
строго говоря, просто складывать между собой наибольшие ; напря-
жения, 'получающиеся при чистом изгибе и сдвиге. Место и величину
наибольшего напряжения нужно определить из графика напряжений,
Фиг. 20. Наивысшие напряже-
ния в двусторонней глубокой
внешней выточке при сдвиге.
б
Фиг. 21. Наибольшие напряжения при попе-
речном изгибе.
построенного посредством наложения двух графиков в отдельности
для изгиба и сдвига. Пример такого наложения дан на фиг.21.
Ради ясности чертежа, напряжения нанесены на развёрнутый контур
выточки. Истинное наибольшее напряжение оказывается на очень
незначительную величину меньше суммы огаах t ~Ь Зшах э отдельных
наибольших напряжений.' Поэтому в большинстве случаев оказы-
вается вполне допустимым вводить в расчёт просто сумму
отдельных наибольших напряжений, получающихся при, изгибе и
при сдвиге.
3. Односторонняя глубокая внешняя выточка.
Представим себе теперь, что стержень с двусторонней выточкой
рассечён вдоль оси х на две части. Тогда каждая из полученных
частей будет представлять собой _.
стержень с одной внешней выточкой
(фиг. 22). Как мы увидим ниже,
применение такого метода рассече-
ния позволяет по функциям напря-
жений для стержня с двусторонней
выточкой получить достаточно точ-
ный способ расчёта, служащий для
определения напряжённого состояния
в плоском стержне с односторонней
Фиг. 22. Односторонняя глубокая
выточка.?
выточкой. Конечно, здесь мы имеем дело только лишь с прибли-
жённым методом, так как вдоль оси х где теперь, собственно говоря,
58
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ [ГЛ. IV
должна быть свободная от внешней нагрузки грань, имеются извест-
ные небольшие напряжения. Но поскольку в данном случае речь
Фиг. 23. Односторон-
няя глубокая внешняя
выточка при растя-
жении искривлённого
стержня.
идёт об определении напряжений только в окрест-
ности дна выточки, которые обусловлены
в первую очередь полем напряжений в наиболее
узком поперечном сечении, характер сил, возни-
кающих вдали от дна согласно закону затухания,
имеет второстепенное значение. Здесь поэтому
точному выполнению граничных условий можно
предпочесть простоту вычислений.
Мы будем исходить из трёх вышерас-
смотренных функций напряжений. Но, при опре-
делении равнодействующей сил, действующих
по поперечному сечению согласно уравне-
ниям (27) — (29), теперь индексу 2 будет со-
ответствовать новый контур, для которого
^ = 0. Так как речь идёт о наиболее узком
сечении, то мы должны далее считать
А. Чистое растяжение. В сснову положим
функцию напряжений для плоского растянутого
стержня е двусторонней выточкой. Из (54) и (56) получим выраже-
ние равнодействующих усилий
—XiA = A (v0 -J- sin cos t»0); ।
Kba=0; Af12 — Д sin3^. J ' ?
f
Введём опять растягивающую силу Р
P=-X12d. (101)
Если за номинальное напряжение принять среднее напряжение по
наиболее узкому поперечному сечению, т. е.
♦ V
°» =<102)
то для постоянной А получается то же самое значение, что и для
стержня с двусторонней выточкой [ср. (66)]. Поэтому выражение
(69) для наибольшего напряжения сохраняет силу и для стержня
с односторонней выточкой. Однако это справедливо только тогда,
когда линия действия силы Р удалена от оси х на совершенно
определённое расстояние е (ср. фиг. 23). Величина Af13, умноженная
на толщину d пластинки, очевидно, должна быть равна моменту
§ 3] ОДНОСТОРОННЯЯ ГЛУБОКАЯ ВНЕШНЯЯ ВЫТОЧКА 59
силы Р относительно точки у»0, т. е. Р • е. Отсюда, принимая
во внимание (64) и (68), получаем;
а __ Мцй — _
6----р
sin2 Ур_______
Vq + Sin Vq COS Vq
(103)
На фиг. 24 графически изображена зависимость величины от у.
Уравнение (69) для наибольшего напряжения справедливо только
тогда, когда расстояние между линией действия силы Р и гранью,
не имеющей выточки, соответствует этой зависимости.
Если положение линии действия силы Р неизвестно, то удобнее
пользоваться другим условием, определяющим применимость формулы
(69). Оно основывается на рассмотрении деформации стержня.
В основе наших рассуждений лежит метод рассечения стержня
с двусторонней выточкой на две части. Этот метод предполагает,
Фиг. 25. Односторон-
няя глубокая внеш-
няя выточка при рас-
тяжении, если линия
действия силы прохо-
дит посредине наибо-
лее узкого сечения.
что компоненты напряжений и деформа-
ций симметричны относительно оси х.
Вследствие этого перемещение т; вдоль
оси х обязано быть равным нулю,
Фиг. 24. Расстояние е линия действия
силы от прямолинейного края, отне-
сенное к ширине а наиболее узкого
сечения.
мула (69) применима и в том случае, когда устранена возмож-
ность искривления прямолинейной грани стержня.
Выше рассмотренное решение соответствует только частным слу-
чаям. Рассмотрим теперь более общий случай чистого растяжения.
60
ТВОРИЯ ЦОНЦВНТРАЦИИ В ПЛОСКОЙ ЗАДАЧВ
(г«- IV
Предположим, что линии действия силы Р удалена на расстояние
от грани, не имеющей выточки (фиг. 25). К функции напряже-
ний, соответствующей растяжению стержня с двусторонней выточкой,
требуется добавить вторую функцию, соответствующую чистому
изгибу того же стержня. Появляющуюся в связи с этим новую
постоянную обозначим буквой А'.
Тогда из (54), (55), (59), (71) и (72) для равнодействующих
напряжений получим: 1
“ =А («о + sjn f0tcos О—4'sin2 ц0;
П.а=О;
= A sin2 Vq -j- A' (2oQ cos 2p0 — sin 2t»0).
(104)
Выражения (101) и (102) для полного растягивающего усилия и для
номинального напряжения остаются справедливыми и здесь. Момент
Л<18, умноженный на d, в соответствии с, нашим предпрложением,
должен быть равен Р-^. Поэтому^ принимая во внимание (64),
получим
— •Vi,а®* у— Р s ® ^о> " 2 Р 2 * (1^5)
Если подставим эти выражения в уравнение (104), то получим
два уравнения, из которых определяются постоянные А » А'
4 Л' sin op (у0 + sin Vq cos Vq) — 2 sin9 o0.
* A e sin3Pp — sin v0 cos Vp-j- t»pcos2t»p ’
д_0__________________sl«?o . ,
♦ * A* *
Vo + sin Vp cos Vot-41-j. s:n2 ?0
(Ю6)
Наибольшее напряжение, возникающее у дна выточки, вычисляется
по уравнениям (61) и (76)
W = ^V0-8A'tgo0. (107)
После подстановки сюда значений постоянных из (106) получим
отм как функцию о0. Выразив Затем v0 с помощью (68) через у, по-
лучим аюах как функцию кривизны выточки. В результате будем
иметь довольно сложное выражение для ашах, которое можно су-
щественно упростить, если использовать коэффициенты концентрации
для стержня с двусторонней выточкой. Обозначим буквами и а3
соответственно коэффициенты концентрации в стержне с двусторонней
глубокой t внешней выточкой, находящемся, в условиях простого
ОДНОСТОРОННЯЯ ГЛУБОКАЯ внешняя ВЫТОЧКА
6.1
растяжения
сать:
[см. (69)1 и чистого изгиба [см. (79)]* Тогда- можем напич
°шах
Р
(108)
где
(109)
Зависимость наибольшего
жена на фиг/26.
напряженияГот — графически изобра-
В. Чистый изгиб/Наложением функций напряжений, соответствую-
двусторонней выточкой, легко.
щих растяжению и изгибу стержня^с
получается решение задачи ©.напря-
жениях в стержне с односторонней
Фиг. 26. Наибольшее напряжение
в односторонней глубокой внеш-
ней выточке при растяжении,
если линия действия силы прохо-
дит посредине наиболее узкого
сечения.
Фиг. 27. Односторонняя
глубокая внешняя выточ-
ка при изгибе.
«1 — 2С
дится в состоянии чистого изгиба (фиг. 27). Уравнения (104) в общем
виде устанавливают равнодействующие напряжений по наиболее узкому
сечению. Здесь пойдёт речь только лишь о дополнительных условиях,
характеризующих чистый изгиб. При чистом изгибе обращается
в нуль ^2, а умноженный на толщину d, должен быть равен
моменту внешних сил, т. е.
Я1,2.= 0; = (НО)
За номинальное напряжение мы возьмём напряжение, вычисленное'
по элементарной формуле изгиба'.
бЛТ z111.
Щ1)
62 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ 8АДАЧЙ [ГЛ4 IV
Тогда из (104) получим
А'___________________Po+sln opcosPo .
A isin2v0
л=_£______________*____________
6 . A' 2v0cos2o0 —sin 2р0
1+Л sin2v0
(П2)
Если полученные здесь выражения подставим в (107), то найдём
наибольшее напряжение., С помощью (68), при использовании опять
коэффициентов <xt и <х2, найдём:
(ИЗ)
Зависимость наибольшего напряжения от кривизны выточки пред*
ставлена на фиг. 28.
С. Чистый сдвиг. В этом случае нас (см. фиг 29) непосредственно
к цели приводит функция напря*
жений, соответствующая чистому
сдвигу для стержня с двусторонней
выточкой. Мы вернёмся к урав*
Фиг. 29. Односторонняя
глубокая внешняя вы-
точка при сдвиге.
Фиг. 28, Наибольшее напря*
жение в односторонней глубо-
кой внешней выточке при
'.изгибе.
нениям (80)—(84) и уравнению (86). Для результирующихн апряжений
в этом случае получаем
ЛГ1.3 =“ 0; Yifl 543 В (и0—sin v0 cos v0); Mip = 0. (114)
умноженная на d с учётом знака, должна быть равна перере-
зывающей силе:
(115)
g отверстия в очень Широком стержне 63
За номинальное напряжение опять возьмём среднее касательное на-
пряжение по наиболее узкому сечению'.
’.-й-* <116>
Для постоянной В из уравнения (114) получается снова то же зна-
чение, что и в случае стержня с двусторонней выточкой [ср. (88)].
Поэтому формулы (93) и (99) для наибольшего нормального и ка-
сательного напряжений остаются справедливыми и для стержня
с односторонней выточкой.
Рассмотренные до сих пор задачи относились к определению
коэффициента концентрации в глубоких внешних выточках. Для
определения коэффициента концентрации в общем случае нам необ-
ходимо ещё найти коэффициент концентрации в стержне с мелкой
внешней выточкой. Однако, прежде чем обратиться к задачам из этой
области, необходимо рассмотреть ещё другую группу задач, отно-
сящихся к учению о концентрации напряжений в случае плоской
задачи. Мы имеем в виду изучение влияния отверстий различной
формы на распределение напряжений в тонких стержнях. Полученные
при этом результаты сослужат известную службу позднее, при рас-
смотрении мелких внешних выточек.
4. Круглые и продолговатые отверстия в очень широком стержне.
Как показано на фиг. 30, мы здесь будем заниматься плоским
стержнем, снабжённым круговым или продолговатым отверстием с
центром, расположенным на оси стержня. При наличии продолговатого
отверстия предполагается, что длинная ось от-
верстия или совпадает с осью стержня, или
перпендикулярна ей.
Все эти три случая можно рассмотреть
одновременно, принимая, что отверстие имеет
эллиптическую форму. Длину полуоси эллипса,
перпендикулярную оси стержня (за ось стержня
принята ось х), обозначим буквой /, а радиус
кривизны кривой в конце этой полуоси буквой р.
Тогда, при t > р, имеем продолговатое отвер-
стие с длинной осью, перпендикулярной оси
стержня, при / = р—круговое отверстие и,
Фиг. 30. Круглые и
овальные отверстия
в очень широком
стержне.
наконец, при /<римеем отверстие, удлинённое
в направлении оси стержня.
Поместим начало координатной системы ху
в центр отверстия стержня так, чтобы полуось t
отверстия совпадала с осью у. Затем, с по-
мощью соотношений (47), (48) и (49), перейдём к эллиптическим
координатам. Контур эллиптического отверстия обозначим буквой uv
64. ТЕОРИЯ КОНЦЕНТРАЦИИ в плоско* ЗАДАЧЕ
[гл. IU-
При разыскании функций напряжений мы всегда будем исходить'
из элементарного напряжённого состояния, возникающего в стержне-
без отверстия. К функции напряжений, соответствующей этому эле*
ментарному состоянию, добавим другую функцию, дающую как раз
такое искажение напряжённого состояния, какое создаётся при наличии
отверстия. Так как речь идёт о таком распределении напряжений,
при котором контур отверстия свободен от внешних нагрузок, то
в точках, лежащих на этом контуре, напряжения1 в стержне без от-
верстия и добавочные напряжения должны взаимно уничтожаться.
При удалении от отверстия добавочные напряжения должны быстро
Фиг. 31. Растяжение стержня с овальным отверстием,
расположенным поперёк оси стержня.
убывать, что Соответствует закону затухания. Падение добавочных
напряжений должно быть настолько быстрым, чтобы на сторонах
у —+Ь стержня {Ь — половина ширины стержня, фиг. 31) они, по
сравнению с элементарными напряжениями в стержне без отверстия,
были пренебрежимо малыми. Если отношение у достаточно велико,
то добавочные напряжения на гранях стержня можно считать прак-
тически равными нулю. Можно полагать, что на этих гранях суще-
ствуют только напряжения, соответствующие стержню без отверстия,
удовлетворяющие граничным условиям на Сторонах у = ±Ь стержня.
Таким образом мы должны позаботиться о выполнении граничных
условий только лишь на контуре и0 отверстия. При отсутствии внешних
нагрузок на этом контуре имеем условия:
— = Const.—Ct, = const.=Са, (117)
которые и должны выполняться при и —и^. В нашем случае эти ус-
ловия можно ещё несколько упростить. Если к функции F добавим
ОТВЕРСТИЯ В ОЧЕНЬ ШИРОКОМ СТЕРЖНЁ 6S
выражение Qx — С^у, то напряжения, получаемые двукратным диф-
ференцированием F [см. (22)J, от такого добавления остаются неизмен-
ными. Однако граничные условия примут теперь более простую форму
(
В силу уравнений (50) и (51) эти условия запишутся в криволинейных
координатах в виде: , .
1 = °’ = ; 019)
Такие упрощённые условия можно написать только для одного кон-
тура; в случае же нескольких контуров этого упрощения получить
нельзя. При двусторонней выточке, где требуется выполнение гранич-
ных условий на двух контурах, мы поэтому их не применяли.
Произвольные постоянные, входящие в функцию добавочных напря-
жений, а также и величина напряжений на контуре отверстия зависят
от Ор. Но каждому значению и0 соответствует совершенно определён-
ная форма эллипса, и значит, вполне определённая величина отноше-
ния-^-. Из уравнения эллийса (48) получаем:
~ = cth2«0; chw0= ; shw0=^=. (120)
Отсюда й0 можно выразить через Считая теперь, что — больше,
меньше, или, наконец, равно единице, мы получим решение для наших
трёх форм отверстия. Мы опять дадим решение отдельно для растя-
жения, изгиба и сдвига.
А. Чистое растяжение. Будем исходить из функции напряжений,
дающей решение для растянутого стержня, не имеющего отверстия.
Пусть Р—полное растягивающее усилие, приложенное к стержню.
Так как половина ширины сгержня обозначена буквой Ь, то напря-
жение в нём равно
<12»
Оно соответствует нормальному напряжению <з№> напряжения же и
равны нулю. Поэтому функцию напряжений следует взять в виде:
2=*=-^ V2
причём
‘1’о = |(У2—*2) и >( (122)
5 Зак. I*. Нейбер.
66 теория концентрации в плоской задаче |гл. IV
Тогда из уравнений (22), действительно, получим
^ = 0. (123)
Выразим Фо и Ф} в эллиптических координатах [ср. (47)]; применяя
известные формулы, получим
Фо — -^(1—ch 2и cos 21»); Фд = sh и cos v. (124)
Включим теперь сюда такую добавочную функцию, чтобы напря-
жения, ей соответствующие, стремились к нулю при увеличении и,
т. е. при удалении от отверстия. Окончательные выражения могут
быть взяты в виде:
Фо = - j [ 1 Аи -|- ( — ch 2а 4* &еcos 2v];
» , <12б>
Фх s* у (sh и -[- Се-*) cos v.
Можно легко убедиться, что эти функции удовлетворяют уравне-
нию (46). Функция напряжений теперь представится в виде:
F «{1 4-ch 2«2Дя+2Се-« sh и-f-
4-[—ch2а—1 -\-2Be-*u-\-2Ce-us\iu} cos2г»]. (126)
Граничные условия (119) при и = ип приводят к уравнениям:
2 sh 2а0 4- 2Л 4- 2Се-9и° = 0;
— ch 2а0— 14- 2Ве-*и*-\- 2Се-«* sh а0 = 0;
—2 sh 2а0—4Ве-2"» 4~ 2<?в-9“« = 0.
(127)
Умножим второе из этих уравнений на 2 и сложим с третьим.
Тогда получим уравнение для определения С; из третьего уравнения
определим затем постоянную В, наконец из первого—постоянную А.
Найдём
Л = —1 —ch2a0; В = 1 в’«»4--|—С= 14-е9Ч (128)
Так найденное решение впервые иным путём было получено С. Е.
Inglis!).
Важно прежде всего найти распределение напряжений на контуре
отверстия. В соответствии с граничными условиями в точках контура
исчезают напряжения и <зи9, Нормальное напряжение о(„ действую-
щее в точках на контуре, выражается формулой
(’Л-л, = (sh 2н0 — 1 — в9"» cos 2v). (129)
*) 1 n g 1 i s G E., Trans. Inst. Naval Archiv, London, t. 60 (1913), стр. 219.
£ отверстия В ОЧЕНЬ ШИРОКОМ СТЁРЖЙЕ б?
На фиг. 31 даны графики распределения напряжений ири cth к0 =
-5, или при —и 25. Напряжение на контуре достигает своего
максимального значения, равного Пр в конце большой полуоси,
т. е. у дна выточки. При перемещении вдоль контура, начиная с этой
точки, напряжение быстро убывает,, меняет знак и в точке на оси
стержня делается равным—р.
Распределение напряжений вдоль оси у точно так же даёт пред*
ставление о характере напряжённого состояния около выточки.
Напряжение ov при даётся формулой:
(<Л=| “p+f 3)(1 +
ch u0 cth ы J. (130)
Как видно из графика на фиг. 31, начиная с точки на контуре, где
имеет наибольшее значение, при движении к грани пластинки оно
очень быстро уменьшается, приближаясь к величине р. Что касается
напряжения то, в соответствии с граничными условиями, на кон*
туре оно равно нулю, затем несколько увеличивается, достигает
максимума и на некотором расстоянии от контура снова прибли*
жается к нулю. Касательное напряжение в точках оси у, вслед*
ствие симметрии, равно нулю.
Для наибольшего напряжения, возникающего у дна выточки,
получаем выражение:
(«Л-ц,« “Р О + 2 cth «о)- С130а)
Отсюда, имея в виду (ISO), получим формулу для коэффициента
концентрации в растянутом стержне с отверстием, имеющим форму
эллипса, большая ось которого перпендикулярна оси. стержня'.
^-==14-2|ЛГ (131)
Для кругового отверстия при / = р имеем:
^- = 3. (132)
Уравнение (131) справедливо и тогда, когда большая ось вллипса
параллельна оси стержня. В этом случае радиус р очень велик,
в большинстве встречающихся в практике случаев равен даже беско*
нечности, так что <з„„ = р.
Можно было бы думать, что в случае продолговатого отверстия
расположенного вдоль оси стержня (фиг. 30), т. е. при — < 1, наиболь-
68
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОЙКОЙ ЗАДАЧЕ
(гл. V1
шие напряжения возникают у конца большой оси, длина которой
пусть будет f. Однако для напряжения, возникающего в этой
точке, из (129) получаем
(133)
v-0
Фиг. 32. Наибольшие напряжения
в растянутых стержнях с овальным
отверстием.
отверстия в точке контура, лежа*
щей на оси стержня, возникает
сжимающее напряжение величи-
ною р, независимо от величины
радиуса р в этой точке.
Отсюда следует, что для
всех рассмотренных нами здесь
форм отверстия наибольшее на*
пряжение возникает в тех точ-
ках контура, о которых ка-
сательная к контуру парал-
лельна направлению растяже-
ния стержня.
Зависимость наибольшего на-
пряжения от. радиуса кри-
визны, представленная формулой
(131), графически изображена на
фиг. 32.
В. Чистый изгиб. При чи-
стом изгибе стержня без отвер-
стия функция напряжений пред-
ставляется формулой:
Л причём Фо= ^-(/ —3^); фх — р. ху. 034)
откуда для напряжений получаем
(135)
Таким образом, напряжение еш следует прямолинейному закону эле-
ментарной теории изгиба. За номинальное напряжение р принимается
напряжение от изгиба в точке, удалённой на расстояние i от оси
стержня. Обозначив изгибающий момент буквой М, можем написать
F-W- <13в)
Выражения (134) напишем в эллиптических координатах. Затем
добавим к ним другие функции, но так, чтобы можно было удо-
влетворить граничным условиям и чтобы при и достаточно большом
§ 4]
отверстия в ОЧЕНЬ ШИРОКОМ СТВРЖИВ
«9
добавочные напряжения стремились к нулю. Найдём, применяя извест-
ные формулы для гиперболических функций: .
% = —4 ch Зе -J- Ae~Su) sin 3v 4-
4- (12 ch е 4- Beu 4- Ce-«) sin о];
Ф| = ~(sh 2a 4" sin 2u
(137)
При написании выражения для функции напгяжений целесообразно
ещё принять во внимание (47) и выразить отрезок t через е0.
Будем иметь:
= ch «о- (138)
Тогда для функции напряжений получим1):
F“s^K-dl3“-3cl'“+'4‘-’“+.
4"67>e"a“sha)sin3o4"(3ch3a4_
4- 9 ch и 4- Be* 4~ Се~и 4- CDe-*4 sh a) sin o], (139)
Произвольные постоянные определяются из граничных условий (119),
которые дают
А = «в»» (ch 3a0 4- 3 ch a0—12 ch9 a0 sh a0); 1
В = —12^1^; C==0; Z> = 262^ch2a0. } ^140^
J) Wolf K., Z. techn. Physik (1922),-стр. 160; далее Netiber H-, Ing,
Arch,, t. 5 (1934), стр. 242. / 1
70
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ
[гл. IV
На фиг. 33 даны графики распределения напряжений для случая,
когда ctha0==5 или //ря»25. У дна выточки имеет место значитель-
ное повышение напряжения и = 6р. При перемещении от дна
выточки вдоль контура, а также и вдоль оси у напряжение быстро
убывает. Пунктирная линия соответствует элементарной теории изгиба
при учёте ослабления стержня в результате' высверливания отверстия.
Для наибольшего напряжения, возникающего у дна выточки, по-
лучим формулу:
’ши=*» (6v)0=0o Р (1 + cth «q) (141)
v«=9Q*
или, HQ основании (120) '' ;
- (142)
Зависимость наибольшего напряжения от//р графически изображена
на фиг. 34.
Для' кругового отверстия имеем:
^=2. (143)
Когда продолговатое отверстие расположено параллельно оси
стержня, концентрации напряжений около отверстия не получается.
[При р -> со amax = р. У дна выточки
(ось х) напряжение в этом случае будет
равно нулю.]
С. Чистый сдвиг. Стержень теперь
нагружен таким образом, что в се-
чении. х = 0 имеются; лишь касатель-
ные напряжения. Полная перерезываю-
щая сила в сечении пусть будет V.
Номинальное напряжение здесь мы бу-
дем вычислять по формуле
V
Р-&Г- (>«>
ЙГ-,™ р "растай сраше
изгибе. касательное напряжение в стержне9
не имеющем отверстия. Полное ре-
шение задачи опять будет состоять из элементарного решения для
стержня без отверстия и добавочных функций, исчезающих при боль-
ших значениях и. Элементарное решение даётся функциями
фо = ^г(3ху8 —Зх8^ —6^®ху);
I. ' I ч
(145)
(147)
написать
§ 4] ОТВЕРСТИЯ В ОЧЕНЬ ШИРОКОМ СТЕРЖНЕ 71
Согласно (145) найдём соответствующие напряжения:
- (Н6)
Действительно, в сечении х = 0 имеется лишь касательное напря-
жение, а грани у = Ъ свободны от внешних нагрузок.
Выразим функции Фо и Ф, через эллиптические координаты и,
добавив соответствующие функции, напряжения от которых затухают
вдали от отверстия, придём к следующим выражениям:
Фо = [(—3sh 4« -f- Де-4») sin 4о-f-
4-12 (1 — 4й9) sh 2« 4- Be-9» sin 2о];
©t = [(4 ch 3« 4" Се-8») sin3o4-
4-(-12 ch «4-De-») sin о].
Принимая во внимание (138), функцию напряжения можем
в следующем виде *): ..........
, ——-я-------{[—sh4«—2 sh 2«4*
128 g) ch’ ио1
-p^e-4»4“Ce-8»sha] sin 4-04~ [2sh4«4“
4- 4(1 —12 g)a ch9 »0) sh 2« 4- Be-2» 4-
4- Ce~8“ sh a -|- De-» sh »] sin 2n }.
Из граничных условий получим:
А = — 24е4**> sh9 e0 ch9 «0;
В = -Эбе2»* g)’ sh9 «о ch9 и0;.
С=8е2“«(2е9“«— l)ch9«0;
D = ( 24е9“« 4 g)’-1) ch9 «0.
Графики- распределения... напряжений для //р = 25 и b/t = 3 даны
на фиг. 35. Напряжение на контуре отверстия достигает своего ма-
ксимума в точке, очень близкой к дну выточки. Точно также и ка-
сательное напряжение, действующее в сечении х = 0, достигает сво-
его максимума* в точке, расположенной вблизи контура.
При определении каждого, из этих максимумов напряжений целе-
сообразно пренебречь членами с д9. Ошибку, проистекающую от
этого, при достаточно большой ширине стержня можно считать пре-
(148)
(U9)
1) N е u b е г Н., Ing. Arch., т. 5 (1934), стр. 243.
72 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ [ГЛ* IV
небрежимо малой. Это пренебрежение особенно допустимо в тео-
рии расчёта стержней, ослабленных отверстиями, когда ширина
стержня относительно велика и если идёт речь прежде всего об опре-
делении предельного значения коэффициента концентрации, соот-
ветствующего стержню с сравнительно большой шириной.
После некоторых 'преобразований функция напряжений запи-
шется в виде:
F= — [ch 2 (и — м0) — 11е2“» sin 2v, (150)
а напряжение на контуре будет,
. ч ' /Г З’А Зр 2u sin 2v ziki\
( > - > =₽7 т ♦ ’sh«n0+cos’ll•
Своего наибольшего значения бно достигает там, где выражение
== — Ksha ио+cosS ®)’2 со8 2®+sin8 2vJ (152)
делается нулём, т. е. при
’ cos2t»—— пД- или cosv = (153)
«h2eo Vch2«0
Наибольшее напряжение на контуре равно
U . с У' Р . : ;
§ 4] ОТВЕРСТИЯ В ОЧЕНЬ ШИРОКОМ СТЕРЖНЕ 73
и имеет место в точке, удалённой от оси у на расстояние
(155)
В сечении х=»0 касательное напряжение выражается формулой:
1 ( d“F dF\
(T“K\ei = sh2« \dudv ~ U до)о=^- ="!
= ^[-4sh2(«-«0)-2cth«(ch2(a-»0)-l)]. (156)
Точку с наибольшим касательным напряжением мы получим, если
приравняем нулю продифференцированное по и выражение (156).
Не приводя промежуточных выкладок, дадим выражение для рас-
стояния от оси у до точки, где достигает максимума:
Наибольшее касательное напряжение равно
^тах о - -----------
Т (У^-1)9
(157)
(158)
Зависимость каждого из максимальных напряжений от //р пока-
зана на фиг. 36.
Для кругового отверстия
Za&5. = 6; Ъ^. — 2. (159)
При совместном действии чистого изгиба и сдвига справедливо то,
что говорилось ранее для глубокой внешней выточки, именно:
наибольшее напряжение на контуре отверстия меньше на очень не-
значительную величину суммы наибольших напряжений, вызванных
порознь изгибом и сдвигом (ср. фиг. 21).
Для продолговатого отверстия, параллельного оси стержня, су-
щественно повышение напряжения только лишь вследствие сдвига.
Мы введём опять отношение t'/р' большой оси t' к новому радиусу р*
кривизны в точке на её конце. Как известно, для эллипса! справед-
ливы равенства:
Наибольшие напряжения мы получим так: в (154) и (158) заменим
//р на p'/f, Уравнение (154) тогда перейдёт в следующее:
^“1(/У+2+у^).. (1«1)
74
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧВ
[гл. IV
Точно с таким не успехом мы могли бы заменить //р на f /р'. Де-
лая такую замену в выражении (158), мы получим наибольшее ка-
сательное напряжение, но не в сечении х = 0, а в сечении у = 0.
Действительно, сделав вычисления для этого сечения, получим
т. е. то же самое выражение (158\ в котором //р заменено на/'/р'.
Итак, для продолговатого отверстия, расположенного вдоль оси
стержня, нагруженного поперечной си-
лой, для наибольшего напряжения спра-
ведливы те же формулы, что и для
продолговатого отверстия, перпендику-
лярного оси стержня, при условии, что
//р заменено на f//.
Перейдём теперь к группе задач,
относящихся к мелким внешним выточ-
кам. Как мы видели выше, по значе-
ниям коэффициентов концентрации для
мелких и для очень глубоких выточек
можно вычислить коэффициент концен-
трации для выточки любэй глубины.
5. Мелкая внешняя выточка.
Применительно к фиг. 37 мы теперь
будем заниматься либо стержнем ши-
рины b с односторонней мелкой внеш-
ней выточкой, либо стержнем ширины
2Ь с двусторонней внешней выточкой.
Фиг. 36. Наибольшие напря-
жения у овального отверстия
при сдвиге.
Вследствие закона затухания напряжённое состояние в точках
стержня, достаточно удалённых от выточек, не отличается от того,
какое существует в стержне без вы-
точек, поскольку отношение b[t мы
считаем достаточно большим. По-
этому мелкая односторонняя выточка
не оказывает влияния на распреде-
ление напряжений в точках на дру-
гой прямолинейной стороне стер г ня,
и разыскивая функцию, соответ-
ствующую искажению напряжений
выточкой, быстро убывающих по
всем направлениям от неё и являя;- Фиг. 37. Односторонние и двусто-
щихся добавочными к напряжениям роцние мелкие внешние выточки,
§ 5]
МЕЛКАЯ ВНЕШНЯЯ ВЫТОЧКА
75
в стержне без выточки, можно не принимать во внимание гранич-
ных условий на прямолинейной грани стержня, так как они выпол-
нены для первоначальной функции напряжений. В случае стержня
с двусторонней выгочксй к этой первоначальной функции напря*
жений нужно добавить функции, учитывающие искажение напряже-
ний выточками на обеих гранях стержня; Поэтому, если получено
решение для стержня с односторонней выточкой, то найденный
коэффициент концентрации может быть использован и для стержня
с двусторонней выточкой, поскольку при этом добавочные функции
напряжений взяты одинакорыми. Но, при определении номинального
напряжения, нужно в случае двусторонней выточки пользоваться
другой формулой.
А. Чистое растяжение. Будем пользоваться системой криволи-
нейных координат:
, > )I = V- и2ц_с2 . (163)
На достагочном удалении от точки х = 1, у = 0 линия и = const,
совпадает с линией х = const. Вблизи точки х = 2, y = Q линия
« = const, искривляется, образуя впадину, имеющую характер вы-
точки.
Аналогичное поведение имеет ортогональная система линий
о = const. На левой стороне фиг. 38 нанесены линии « = const, и
V — const.
Функция напряжения в- случае чистого растяжения стержня
в направлении оси у с интенсивностью р имеет вид:
F = -?r-x2, причем Фо = 0; Ф. =•£•*• (164)
Перейдбм теперь к криволинейной системе координат и посред-
ством надлежащим образом подобранной добавочной функции поста-
раемся удовлетворить граничным условиям в. точках контура мелкой
7,6 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ [ГЛ. IV
„выточки. При разыскании гармоничных функций следует учесть, что
мы опять здесь имеем дело с изометрической сеткой, ибо
V V - -1 + >7^1 (165)
и, значит, гармонические функции удовлетворяют дифференциаль-
ному уравнению (46).
Решениями являются:
Ф°— g (Л+ Си2+ + D(«« + »«)«)’
= у (« + 2^75+ Б •
(166)
Функция напряжений представится в виде:
M2 + w2 + (а2 + и«)2“1"?1“Ь5и + Си2 + ^“^
ryf 1 2и3 I р(- и3 Г ц2
/V«24-v2 (M2 + v2)V^ \«24-v2^(u2 + i
Значение «, соответствующее контуру, мы обозначим буквой и0.
Если произвольные постоянные, содержащиеся в функции F, опре-
делить теперь так, чтобы она содержала множитель («— «0)а, то
тем самым мы удовлетворим граничным условиям (119) в точках
и = ий. Этот ход рассуждений приводит к следующим значениям
ипрозвольных постоянных:
Л = Во«; В—2ад |
п ц2о . р 1 4t>o2 I
и~ 2uo»—I’ с — ]
Подставив эти выражения в (167), получим F в виде:
F-y(« — ^[1 — (2ао? —l)(«2 + v2)]’ (169)
Так как первые производные от F в точках контура обращаются
в нуль, то для напряжения в этих точках получаем:
।_____________1________
-D (2«o*-l)(«oa + v*) П7(п
— \fti ,д1р)ц±щ — Р . , 2v»~2«о2+1 •
Распределение* ов- по контуру при и = ]/2* показано на фиг. 38. На
некотором расстоянии от выточки напряжение делается равным но-
минальному напряжению р, затем, при приближении к выточке, оно
несколько уменьшается, а непосредственно около выточки напряге-
МЙЛКАЯ ВЙЕШНЯЙ ВЫТОЧКА
11
51
ние быстро увеличивается, достигая у дна выточки величины, рав-
ной 3,33 р.
Для наибольшего напряжения из (170) получаем следующее вы*
ражение:
Яд2 (2д§)2 — 1) — 1 Яд2
(°Л=“« —’max—Р п/ — 2и^+\ ‘ 2я02—1 “
- - (2яд2+1)(я02-1)Яд2 „ Яд2(2яд*+1) , П7П
~~Р (2я02-1)(Яд2-1)2 “р (2я02— 1)(яд«-1) у111)
Параметр в0 в формуле (171), имеющий тесную связь с формой вы-
точки, целесообразно заменить отношением глубины t выточки к ра-
диусу ьривизны‘р в точке у её два. Величины t и р вычисляются по
уравнению контура, получающемуся в параметрическом виде из (163)
при « —я0.
Глубина t получается как разность значений х в точке у дна
выточки (i> = 0) и в точке, удалённой на бесконечность (» = со):
/=«(х)в—И|) —(Х)и-,а()=аяо Ио = —-. (172)
Для определения радиуса кривизны лучше всего применить соотно-
шение, вытекающее из выражения для коэффициента искажения.
Пусть <р есть угол между касательной к кривой и некоторым фи-
ксированным направлением, например, осью х. Тогда, как известно,
кривизна кривой будет:
1 ду
Р ~ ds ’
где р—радиус кривизны, a ds — элемент длины кривой. Но можно
показать, что кривизна выражается через коэффициент искажения.
Эта зависимость (на выводе её мы здесь останавливаться не будем)
для, кривизны линии « = const, имеет вид1):
1 1 dhv
р ди *
Коэффициент искажения при ®=±=0 получим из (165):
— A s= 1 -^2" •
Поэтому кривизна у дна выточки равна
2.
р \й2 ди Л=о 1 \Я (йог—1)2
I1 “272
• (174)
(175)
(176)
x)F0ppl L. u. NeuberH., Festigkeitslehre mittels.Spannungsoptik,
стр. 91. Mtinchen, u. Berlin: R. Oldenbourg, 1935.
Теория концентраций в плоской задаче (гЛ.' IV
Отсюда, после умножения на глубину выточки, получим:
и далее
t 2
(ao’-l)2 ’
^“1+тй-
(177)
(178)
Найденное значение «02 подставим в (171); для наибольшего напря-
жения и для коэффициента концентрации получим простую фор-
мулу: .
^=3/’v-1+o. ,/a'j (179)
+ У 2p
Фиг. 39. Наибольшие напряжения
в мелкой внешней выточке при
растяжении.
Эта зависимость коэффициента концентрации от радиуса кривизны
графически изображена на фиг. 39 (пунктирная кривая). Однако ре-
зультаты, полученные таким путём, практически применить к мелкой
выточке (фиг. 37) непосредственно
нельзя, поскольку полученное реше-
ние относится к случаю выточки со
скруглёнными углами, что вытекает
из характера применяемой системы
координат (фиг. 38), в которой
острые углы на кривых ««const,
отсутствуют; можно ожидать, что
коэффициент концентрации, вычис-
ленный по формуле (179), будет
несколько ниже того, который имеет
место в выточках с острыми углами,
встречающимися во многих практи-
ческих случаях. Но и для последнего
случая : в нашем распоряжении есть
ещё одно простое приближённое
решение.
Именно, применение метода рас-
сечения к достаточно широким стерж-
ням, имеющим продолговатое от-
верстие и рассмотренным нами в IV, 4,
даёт приближённое решение для
мелких внешних выточек с острыми
внешними углами. Мы будем исхо-
простого растяжения стержня и пред*
днть из решения для случая
ставим его рассечённым вдоль оси л: (фиг. 31). В точках проведён-
ного сечения касательные напряжения равны нулю, а нормальные
напряжения оу при перемещении от выточки быстро убывают.-Так
§ МЁЛКАЯ ВНЙШНЙЯ ВЫТОЧКА 79
как эти напряжения действуют перпендикулярно растягивающей
силе, то в первом приближении можно не учитывать их влияние на
наибольшее напряжение, возникающее у дна выточки. Это наиболь-
шее напряжение обусловливается в первую очередь растягивающим
напряжением <за. Поэтому нельзя ожидать большой ошибки, если при-
нять одинаковыми коэффициенты концентрации в растянутом стержне
с продолговатым отверстием и в стержне с мелкой внешней
выточкой, имеющем острые углы х). Соответствующая кривая начер-
чена на фиг. 39. Как и следовало ожидать, коэффициент концентра-
ции в мелкой внешней выточке с острыми углами оказывается не-
сколько большим по сравнению с коэффициентом концентрации в вы-
точке с закруглёнными углами.
Номинальное напряжение р представляет, как было замечено
вначале, равномерно распределённое растягивающее напряжение в той
части стержня, где отсутствуют выточки. Оно равно
Р = £Г или р = (180)
в зависимости от того, имеется в виду односторонняя или двусторон-
няя выточка.
В. Чистый изгиб. Элементарной функцией напряжений в случае
чистого изгиба мы уже пользовались (134). Для того чтобы выра-
зить её в нашей координатной системе (163),
нужно произвести поворот координатных
осей и перенос их начала. Ось стержня
теперь идёт по направлению оси у, на рас-
стоянии х— и0 -f- от неё (стержень с
одной выточкой, фиг. 40), в то время как
ранее в IV, 4 ось стержня совпадала с осью х.
Мы должны поэтому заменить у на
ио"Ь_|----*» а * на у. При этом можно
отбросить постоянные и линейные члены,
Фиг. 40. Односторонняя
мелкая внешняя выточка
поскольку они на напряжения не оказывают при изгибе.
никакого влияния. Номинальным напряже-
нием является максимальное напряжение при изгибе стержня (ши-
рины Ь)\
Ш
(181) **)
**) Эти приближённые рассуждения подтверждены в работе F. О. Maun*
sell [Stresses in a Notched Plate under Tension. Phil. Mag. VII, 21, 1936 r.,
стр. 765 - 773J. Строгое решение для полукруглой выточки, полученное там
с по) ощью рядов Фурье, даёт для коэффициента концентрации значение 3,
которое вычислено с большой точностью.
80 теория концентрации в плоской задаче (гл. IV
Таким путём получим следующую элементарную функцию напряжений:
= (182)
Поскольку мы имеем в виду определение коэффициента концентрации
в мелкой выточке, то область искажённого выточкой напряжённого
состояния мала по сравнению с высотой Ь, или высота Ъ велика по
сравнению с остальными величинами, фигурирующими при расчёте.
Поэтому в случае мелкой выточки можно пренебречь как малыми
теми членами, которые содержат множитель 1/Ф. (Влияние высоты
стержня, которое 'исчезает в случае мелкой выточки, снова учиты-
вается в окончательной номограмме коэффициентов концентрации
для выточек любой глубины.) Если теперь в (182) пренебречь чле-
нами, содержащими множитель 1/Ь, то получится та же элементар-
ная функция напряжений, что и при простом растяжении [см. (164)].
Дальнейший ход выкладок поэтому будет точно такой же, как
и в случае простого растяжения. Таким образом, в случае мелких
выточек коэффициенты концентрации при чистом изгибе и при
простом растяжении одинаковы.
К тому же результату придём и в случае двусторонней выточки.
Но только здесь, если считать ширину стержня равной 2Ь, номиналь-
ное напряжение следует вычислять по формуле:
P = W‘ (183)
С. Чистый сдвиг. Элементарная функция напряжений для чистого
сдвига даётся уравнением (145). Имея в виду стержень с односто-
ронней выточкой, заменим в выражении для функции напряжений Ь/2
вместо b и в соответствии с нашей координатной системой у на
. b
«о + у—х> а х на У> после чего получим:
2^{[" +3 («о+4)^9-з(«о+4)2^+(«о+-
-Р[«о+4-х]4 <184)
или, пренебрегая линейными членами,
F = Ц. (х®—2 и.х) у -J- (- + 3«ох2 - 3«0W (185)
Номинальное напряжение, как и ранее, представляет собой среднее
касательное напряжение в стержне, не имеющем выточки (перерезы-
вающая сила V):
f-W- <186>
МЁЛКАЯ ВНЕШНЯЯ ВЫТОЧКА
81
§ 51
Перейдя к координатной системе (163), можно точно решить и эту
задачу с помощью надлежащим образом подобранной добавочной
функции, соответствующей напряжениям, быстро убывающим при
Фиг» 41. Односторонняя мелкая внешняя
выточка при сдвиге.
увеличении и. Распределение
касательного напряжения по
поперечному сечению стержня
получается таким, как оно
представлено на фиг. 41. Иска-
жение напряжений, возникаю-
щее от добавочной функции,
быстро уменьшается по всем
направлениям от дна выточки,
и в стержне устанавливается
тот же параболический закон
распределения касательного на-
пряжения, который имеет место
в стержне без выточки. Вблизи
контура выточки возникает
относительный максимум касательного напряжения, занчительно
меньший (при не очень искривлённом контуре) того, который суще-
ствует в середине стержня и который равен
<и« = 1.5р. (187)
Это вытекает из структуры функции напряжений. Так как элемен-
тарная функция напряжений (185) состоит из двух выражений, из
которых одно содержит множитель 1/Ь, а другое 1/д3, то и полное
решение представляется в виде суммы двух выражений такого же
типа. В случае мелкой выточки b велико по сравнению с другими
размерами выточки, и слагаемым с множителем 1/да можно прене-
бречь, как малой величиной. Поэтому функция напряжения для
мелкой выточки содержит множитель \fb. Этот же множитель содер-
жит и выражение для напряжения т'ти,
вания
от её
_______________________________возникающего вблизи осно-
выточки; кроме того, зависит от глубины t выточки и
радиуса кривизны р. Следовательно,
<188>
случае мелкой выточки с не очень большой кривизной это выра-
жение, благодаря множителю 1/д, всегда меньше 1,5. Подобным же
образом и выражение для наибольшего напряжения, возникающего
вдоль контура выточки, содержит множителем tfb.
Аналогичные соображения справедливы и для стержня с двусто-
ронней выточкой. Наибольшее касательное напряжение и здесь
получаемся, если р не очень мал, равным 1,5 р, где под р теперь
нужно понимать выражение:
так как'высота балки равна 2Ь.
6 Зак. 3475. Г. Нейбер.
В
(189)
82 ТЕОРИЯ КОНЦЕНТРАЦИЙ В ПЛОСКОЙ ЗАДАЧЕ (ГЛ. W
в. Построение номограммы для коэффициента, концентрации
у внешних выточек, у круговых и продолговатых
отверстий любых размеров.
\ л
При вычислении коэффициента концентрации, для внешних выто-
чек и продолговатых отверстий любых размеров мы. будем исходить
из соображений, изложенных в II, 4, при этом коэффициент концен-
трации будет определяться по известным уже предельным его зна-
чениям для мелкой и глубокой выточек.
А. Двусторонняя внешняя выточка. Предельные значения коэф-
фициента для глубокой выточки при растяжении и изгибе вычисляются
из соотношений (69) и (79) с номинальными напряжениями, вычисляе-
мыми по формуле (62) или (77). Предельные значения для мелкой
выточки при растяжении и изгибе даются формулой (131). При вычис-
лении коэффициента концентрации в выточке любой глубины является
существенным, чтобы в мелкой выточке в основу расчёта было поло-
жено то же самое номинальное напряжение, как и в глубокой
выточке. Так, например, при растяжении стержня с мелкой выточ-
кой, за номинальное напряжение, вместо
2W 2ad\ b)*
Р
Следует взять для идеально мелкой выточки во всех рас-
чётах, а значит, и при вычислении номинального напряжения, отно-
шением у мы должны пренебрегать по сравнению с другими вели-
чинами. Только тогда и получится, что кривая коэффициента кон-
центрации мелкой, выточки располагается выше кривой действитель-
ного коэффициента (см. фиг. 2), соответственно условию ак < afk.
Связанное с уменьшением ширины поперечного сечения стержня
введение множителя (1----при последовательном применении хода
рассуждений, указанного в П, 4, полностью скомпенсировало бы
влияние «глубокого коэффициента концентрации»; последнее же,
конечно, должно быть учтено при разрешении этой задачи. Поэтому
номинальное напряжение и для мелкой выточки должно быть рас-
считано по наиболее узкому поперечному сечению.
Для теории, относящейся к выточкам любой глубины, случай
чистого сдвига является в некотором отношении исключительным,
так как наибольшее напряжение возникает здесь не у дна выточки.
С другой стороны, точный расчёт для мелкой выточки даёт, как
было объяснено в IV, 5, С, совершенно другие соотношения при
сдвиге, чем при изгибе и растяжении. Точный расчёт этого исклю-
чительного случая оказывается поэтому крайне сложным, и здесь
мы его опустим. Однако во многих случаях расчёта можно доволь-
ствоваться вышеизложенной теорией для глубоких выточек.
$ б] ПОСТРОЕНИЙ НОМОГРАММЫ ДЛЯ КОЭФФИЦИЕНТА КОНЦЕНТРАЦИИ 83
В. Односторонняя внешняя выточка. Предельные значения коэф-
фициентов для глубокой выточки при растяжении и изгибе даны фор-
мулами (108) и (ИЗ), в которых номинальные напряжения вычисляются
согласно (102) и (111). В случае мелкой выточки при растяжении и из-
гибе справедлива формула (131), причём номинальное напряжение,
как следует из вышесказанного, должно оставаться, тем же самым.
Случай чистого сдвига и здесь представляет исключение. Для него
в первом приближении применима теория односторонней глубокой
выточки.
С. Круговые и продолговатые отверстия. Предельные значения
коэффициентов концентрации для круговых и продолговатых отверстий
при очень малых значениях отношения а/d («глубокая выточка») можно
вывести из теории односторонней внешней выточки, если представить
себе стержень составленным из двух
стержней с односторонними выточками
(фиг. 42) и считать их не очень искрив-
лёнными за исключением. области вблизи
отверстия. В отделе IV, 3, А мы полу-
чили решение для односторонней глубокой
выточки при условии, что прямолинейная
грань стержня (она соответствует здесь
внешней грани стержня) совершенно не
искривляется. Если исключить ближайшую
окрестность отверстия, то этому условию,
в первом приближении, удовлетворяет
здесь рассматриваемый нами случай.
Поэтому для «глубокого коэффициента концентрации» в продол-
говатом отверстии при растяжении стержня прежде всего следует при-
нимать соотношение (69). Но, кроме того, должно учесть также влия-
ние ближайшей к отверстию окрестности, ибо ведь там-то и прояв-
ляется рассматриваемое нами влияние выточек. Из чисто геометри-
ческих соображений можно ожидать, что при деформации области
около отверстия внешняя грань искривится так, что вогнутость её бу-
дет направлена вовнутрь, и значит, в этой области имеются добавоч-
ные напряжения от изгиба. С целью учёта этой части напряжений,
коэффициент концентрации мы представим в виде:
e ®i 0 90)
где а, относится к (69), а а8—к (113) и представляет слагаемое,
создаваемое изгибом. Постоянная С, полученная из сравнения с ре-
зультатами измерений по методу фотоупругости, согласно A. Hennig’y
равна 0,8. Мы к этому возвратимся в гл. VII. Для определения зна-
чения коэффициента концентрации мелкой выточки (<м< лкого коэф-
фициента концентрации») нужно пользоваться (131). Номинальное
напряжение вычисляется по (102).
Фиг. 42. Овальное отверстие
как глубокая выточка.
6*
84 тйоГйя койцкйт^АЦий в пдобкой задаче (гл. IV
При чистом изгибе для определения «глубокого коэффициента кон*
центрации» снова спр ведлива формула (190), так как в прехельном
случае, при очень мал^х значениях а/й, мы имеем здесь на одной
сторо е стержня только растяжение, а на другой сi ороне только сжа-
тие. Но минальным напряжением является теперь элементарное напря-
жение от изгиба у дна выточки
°n 2(b^fi)d * (191)
При малых значениях а/b эта формула переходит в
М
’=33. (192)
где представляет собой растягивающую силу» приложенную к одной
стороне стержня, и таким образом соответствует формуле (.102) для
номинального напряжения. Но при малом tjb формула (191) даёт
(193)
что совпадает с выражением (136) для номинального напряжения.
Следовательно, для <мелкого коэффициента концентрации» применима
непосредственно формула (142).
Чистый сдвиг стержня с продолговатым отверстием и с произволь*
ной высотой опять является исключительным случаем, для которого
не сущее вует таких простых акономерностей, какие имели место
для растяжения и изгиба. В большинстве случаев можно обойтись
результатами Или гл. IV, 3, С, или гл. IV, 4, С.
Номограммы для коэффиц ентов концентрации, построенные таким
образом для внешних вьпочек и продолговатых отверстий, помещены
нафиг. 104. Порядок пользевания номограммой указывается стрел*
ками. В остальном отсылаем к гл. X, где на определении коэффици-
ента концентрации мы останавливаемся более подробно.
7. Концентрация напряжений у выступов.
В задачах, которыми мы занимались до сих пор, уже чисто
интуитивно можно было ожидать повышения напряжений, обусло-
вленного ослаблением поперечного сечения в результате устройства
выточек и отверстий. В противоположность этому мы обратимся
теперь к рассмотрению случаев; где повышение напряжений вызы*
вается не удалением материала, а наоборот, его добавлением.
Мы рассмотрим плоский растянутый стержень, имеющий по бокам
маленькие выступы.
В качестве контурной линии целесообразно использовать линию
т» = const, координатной системы- (163), которую мы обозначим
§ 7]
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ У ВЫСТУПОВ
85
через ^о- Линия v = const для больших и (или х) превращается
в прямую, совпадающую с у в const (сравни фиг; 38 и 43к Вблизи
х = 2, у = 0 происходит всё же искривление, имеющее характер
выступа. Стержень простирается в, направлении оси х< и, за исклю-
чением непосредственной окрестности маленького выступа, равномерно
растягивается интенсивностью р. Для стержня без выступа мы имеем
функцию напряжений:
причём Ф0^=^(у3—^; Ф1 = -^х. (194)
Эту функцию выразим в криволинейной системе координат, опреде-
ляемой у авнениями (163), и добавим к ней надлежащим образом
выбранную другую функцию так, ч обы 1) в точках v = vQ внеш-
няя нагрузка была равной нулю, 2) при увеличении и и v напря-
жения, соответствующие этой функции, быстро убывали и чтобы
удовлетворялось дифференциальное уравнение (46). Тогда получим
следующие выражения:
ф» = 7 ~ - 2 + (SrS5 + Л + в’+
195)
Функция напряжений представится в виде:
^,вф°Л_лФ1 = т[®> 0*+»» +
+X+S’+C^+D(-Fb+<??W)+ "
Граничным условиям' проще всего удовлетворять, если так опре-
делить произвольные постоянные, чтобы.функция напряжений содер-
жала ножитель (v— ®0)а.
Это будет иметь место*, если положим" • 11
п . -зй-1 _ —ке-1 <197)
£) == -р?---; £«= р-.
2ti’+l 2»о+1
Функция напряжений окончательно) принимает форму1):
/-”= Г!----—J-------1. (198)
2 °, L : (2^+1)(«* + «’)]
*) N е u b е г НZ, angew. Matty. Meeh., т. 13 (1933), стр. 440,
86 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПЛОСКОЙ ЗАДАЧЕ (гл*
Для напряжений в точках контура получаем:
!____________________________________________L
(„) _ /1 (2t>0« 4- 1) (и» + Уо2) П99ч
- ( Г*’’ - ХР1 , 2%»-2««+1 ’ (199)
(а’ + »о4)’
На фиг. 43 графически изображено распределение напряжений по
контуру для т>0 = 1/3. На некотором расстоянии от выступа оно
равно р, затем, по мере приближения к выступу, оно постепенно
увеличивается и достигает наибольшего значения, равного 1,64 р
Фиг. 43. Симметричный выступ при растяжении.
почти точно в той точке контура, где кривизна наибольшая. После
этой точки напряжение быстро падает, переходит в нуль и по контуру
самого выступа превращается в. ничтожное сжимающее напряжение.
С целый определения наибольшего напряжения продифференцируем
выражение (199) по в и полученный, результат приравняем нулю.
Тогда придём к следующему биквадратному уравнению:
(1+4^)а‘—2(l + 6«b4-4®j)f+l-F , ,(1 J
! 4-2^-т-11^—12-ио—О. (200)
Решениями его являются: 1
=1 -f- По ± /4^+ 4v<. (201)
Знаку плюс соответствует наибольшее значение напряжения на контуре.
После подстановки этого корня в формулу ^199) получим значение
наибольшего напряжения'. , ,
O^oXVi + pq—pq)
. ; , .Г • v . М(1+.2р§) , ..
§ 7]
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ У ВЫСТУПОВ 87
Каждой величине р0 соответствует свое очертание контура. Характе-
ристикой этого очертания может здесь служить отношение половины
ширины выступа а к наименьшему радиусу кривизны р контура.
Под шириной выступа мы должны понимать расстояние между
теми точками контура, вблизи которых возникает наибольшее напря-
жение. Однако для того, чтобы определение было однозначным,
за эти точки мы возьмём те, для которых касательная к контуру
параллельна оси у, т. е., где
= <203>
Отсюда получаем требуемое значение и:
«х2 = 7 (1 — 2V + V • (204)
и, значит,
а = (х)„+ 20о0*—8о0*-(1 -8о09М. (205)
V « Vo
Для радиуса кривизны контура в любой его точке, в соответствии
с (174), получим:
= =________2v0(3a2 —v0»—1)
р V*2 дсгД „ [(иг _|_ Voi)« 4. 2р0* — 2а« -f-1]’
(206)
Чтобы получить точку с наименьшим радиусом кривизны р, опять
выражение (206) нужно продифференцировать по а, а затем прирав-
нять нулю. Тогда найдём:
«а9=14-0 (207)
После подстановки этого значения «а2 в (206)
получим следующую наибольшую кривизну
контура:
(2о8>
Фиг. 44. Наибольшие на-
Из этого выражения и из (205) найдём:
лл « л л * _ «л/ пряжении в ииммстрич*
1 + 20р02—8t>p4—(1 — 8ор2)'» /плач ном выступе при растя-
2(l + ®os) ’ ' женин.
Отсюда вытекает, что каждому значению о0 соответствует вполне
определённое значение а/p. Зависимость наибольшего напряжения
от а/p графически изображена на фиг. 44.
Таким образом показано, что и выступы влекут за собой зна-
чительное повышение напряжения; это повышение происходит не на
самом выступе, но в непосредственной окрестности около него.
88 теория концентрации в плоской задаче [гл. IV
Наибольшее напряжение, как и в задачах с выточками, зависит
от кривизны контура и, при некоторых обстоятельствах, может
достигать очень больших .значений.
Можно указать еще большое количество других плоских^ задач,
решение которых может быть получено подобным образом и пред*
ставляется либо в замкнутой форме, — как в тех случаях, которые
мы здесь рассмотрели,—либо с помощью бесконечных рядов.
В рамках настоящей книги — вследствие разнообразия мате*
риала—другие плоские задачи мы больше рассматривать не будем
и обратимся теперь к главной области учения о концентрации напря-
жений—к учению о влиянии выточек в случае пространственного
напряженного состояния.
ГЛАВА V.
ТЕОРИЯ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ В ПРОСТРАНСТВЕННОЙ
ЗАДАЧЕ.
!• Основные уравнения.
Для изучения концентрации напряжений в пространственной задаче
будет применён общий метод, изложенный в гл. III, 7. Из беско-
нечно большого количества задач, принадлежащих этой группе
мы здесь займёмся, конечно, только лишь небольшой их частью
Именно, предметом нашего
исследования будут являться
выточки, сделанные на телах
вращения. Такого типа тела
с выточками встречаются в
частях машин в самой разно-
образной форме. Как мы уви-
дим, решение задач о влиянии
выточек на тела вращения даст
возможность сравнить между
собой плоское и пространствен-
ное напряжённые состояния,
а из связи между этими груп-
пами зааач можно установить
общие закономерности. Каю
и ранее, мы займёмся сначала
глубокими и мелкими выточ-
ками, а затем указанными Фиг. 45. Глубокая внешняя и мелкая
в гл. II, 4 способами опре- внутренняя кольцевые выточки без осе-
делим коэффициент концентра- < вого отвеРстия*
ции для выточки любой глу-
бины. , Замечательно то, что задачи определения напряжений, ’ как
в мелкой внешней выточке на теле вращения, так и во scexi внеш-
них и внутренних выточках с большим осевом сверлением, можно
<;читИь задании двумерными ' (доказательство ; этого мы дадим
в гл. V, 5). В прбтивоположность этому, для обоих предельных слу-
чаев— глубокой.внешней выточки Интеле вращения, .и [мелкой вну-
тренней выточки без осевого отверстия (фиг. 45)—можно Ъжидать
90 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ. V
существования пространственного напряжённого состояния. В силу
этого главная задача настоящей главы состоит в точном определении
напряжений в этих двух предельных случаях при различных видах
внешних нагрузок.
Вследствие закона затухания коэффициент концентрации зависит
главным образом от кривизны поверхности выточки у её дна, бла-
годаря чему форму поверхности выточки в остальной её части
выберем так, чтобы получился наиболее простой.ход расчёта. Именно,
поверхность внешней глубокой выточки в дальнейшем заменяется
гиперболоидом вращения, а поверхность мелкой внутренней выточки —
эллипсоидом вращения. Тогда при решении задач можно пользоваться
эллиптическими координатами. Положим,
х = sh и cos v; у = ch и sin v cos w, \
г = ch zzsin sin w. J.
Поверхность « — const является эллипсоидом, поверхность 9 == const—
гиперболоидом вращения вокруг оси х и поверхность w —const —
плоскостью, проходящей через ось х. По уравнениям (20) гл. Ш,
3 вычислим прежде всего коэффициенты искажения hu, hv, ti„. Со-
гласно (1)| тогда получим:
hu = hv = h — J/sh2 и-|- cos2»; hw — ch и sin-v. ‘(2)
Компоненты перемещения вычисляем по уравнениям (80) гл. Ш, 7,
которые, если принять во внимание (1) и (2), перейдут в: !
2G£J=-j-{ —^-|-2a[$1ch«cost»-f-shyfnt>^$acosw-f-'
2GV=> у [ — 4~2a £—sh zz sin t' j-ch a.cos я(фасозл»-|-
,, , , .......... . ,• ' ' (3)
2GW=X $»C05W)- '
it . , К ‘
Нормальные напряжения вычисляем по-уравнениям (91) гл. Ill, 7,
откуда имеем: п . ,,,>>
‘ ~ [sh “ch +sitl ®cos ? sf]+0 ~ I) ДЛ+
[ch и cos 9 4- sh и sin V ^COS j;
$ 1J ' основные УРАВНВНИЯ 91
“ - да - да [sh “ ch “ £ + Sin v cos v Я + 0 “ I)л F +
t 2a Г । » dOi . , / 0Ф« . дФа!
+ ^2 —shtt sin IF _^+ ch и cos (cos ;
£[(ak~ £-*£+<’-
Уравнение (99) переходит в следующее:
д/7 == да [ch “cos v Sr+cos w S2+sln w +
4-shasin v(—:r^4-cosw^rr + sinw^-'j-h
1 ; \ oo 1 . ou ' ou ) 1
, /sin v chaW. ЭФ2 дФ8\1
Соответственно уравнениям (92) гл. III касательные напряжения
получаем в виде: . . ‘
1 d2F I 1 Г Ь U ! д/7! .
•'«e=—ft5^+ft4[sh«ch«^—sint>cos®5JJ-f-
4- £ [ch и cos v(^ 4- cos + sin + sh и sin v ( — +
, +cosw^+sln®^8)];
т ______L-^f-L-^Vb-F—tffa-^ч- ' :
vw fichu do \sin v dw) h [ * dw ‘
! 4-ctgx/(cosw~2 + sinw^) — sinw^ + cosw-^aj; (6)
T«« = Й (dFJ dw) + T [ct® 43 $ +th " (cos w +
1 +8inw^’)-slnw^+cosw^r]-
> . 1 . । 1
Чтобы иметь возможность рассмотреть' также внутреннюю выточку,
Имеющую!вид сферы, выпишем ещё аналогичные' выражения в сфе-
рических координатах. Эта система координат даётся уравнениями:
x = acost>; _y=KSiri‘ncosw; ’ / 1
! t zea asin'asin-ok , ,
(и ж= const -H сфера, v = const—конус, w = const—плоскость, про-
92
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
[r«j V
ходящая через ось x). Получим:
hu = 1; hv = и; hw =» w sin
, dF
2QU=± — 4-2а[Фх cos и-j-sin *0 (Фд cos До 4” sin w)l*>
2GV== — 2« [ — Фх sin 4“ cos cos w +
(8)
(9)
2OW
<’u =
-ж^+2«(-фа81п^+ф8со8да);
^+(1-
4-2«[cos<.-gi4-
' ' дФ2 . . дФв\1
cos до-s—2 + sin до-г-5) ;
„ du 1 . ди /19
i)"’
дФ2
cos до -
\dF 1 &F ctgvdF
и du a2sin2vda^ u* dv
4* —Y"~ f — sin до ^2. cos до :
41 ~ и sin v \ dw ~ dw / ’
. cos w дф2 j» sin w дф8\ .
' и <ЙГ п и do / *
4^+“’®т+$,п4й!)-
2 ( . дФ» дФа\
—— fsin‘K»-j3-2—cosw -г-5):
и sin v \ dw dwj*
d / 1 dF\ . / 1 дфц i дФ« .
T“" “ - й(« Л.) + «.4» ’ 4 -JF +cos" si- +,
+ thOT4®«J+aS1nt<-^4^^ + —
1 • du 7 >1 ч du ( 1 w dv 1 и dv г
_____d ( 1 dF\ । 2.Г_дФх .
j «2dp\sinvdw ' uj_
+ctg V (co^ w;ddp+Sih w 2;) - Sin -f- cos. w ;
_____1 d fl 4fx r fctg v дф! ? ,
,u¥> sin v Зй \ и dw) ' “ "ЭйГ*
, coswd^ .sinw^8_ J dp , cosW!^»l.
, ’ и dw ” и dw ' du ‘ д» J
и da а2 dv2
sin
dv
(Ю)
Л/7 = 2 COS V
I
ЙФ2
Г. (И)
основный Уравнений
93
§ il
Пусть поверхность внешней выточки очерчена По гиперболо-
иду t»0. Тогда компоненты напряжений, действующие на этой поверх-
ности, должны превращаться в нуль, и мы придем к следующим
граничным условиям:
в„=»0; = ,твИ( = 0 для v==Vq. (12)
В случае внутренней выточки поверхность очерчена по эллипсо-
иду и0 и граничные условия имеют вид:
°« = °; = т««>=0 ДЛЯ а = «0. (13)
Дадим ещё выражение некоторых интегралов, встречающихся в после-
дующих задачах. Они получаются из
внешними усилиями, приложенными к
напряжениями, действующими по
любой из поверхностей, с помощью
которой мысленно отсекается эта
часть тела. Компоненты равнодей-
ствующей внешних сил по осям х,
у или z обозначим буквами Pe, Pg |
и Pit а компоненты момента сил от-
носительно координатных осей бук-
вами Ма, Му и Mt.
В случае внешней выточки рас-
сечение следует произвести по по-
верхности и — const (площадь сече-
ния обозначим через F). Равнодей-
ствующая напряжения действующего на
щадке с рёбрами hvdv и hwdw равна силе величиною dv dv>
(см. фиг. 46 . Чтобы получить Рш, нужно проинтегрировать в пре-
делах поверхности составляющую предыдущей силы по оси х. Вме-
сто того, чтобы рассматривать равнодействующую напряжений, можно
использовать компоненты её в направлениях и, v и «г, т. ё. вместо у
подставить последовательно «, v, w. Тогда получим:
цСоз(х, у.) hv hwdvdwnr. д.
F'lftu, v, я»
условий равновесия между
какой-нибудь
части тела и
#4
Фиг. 46. К
потоков в
*sr*
определению силовых
кольцевой внешней
выточке.
элементарной пло'
(Н)
Выражения для Ру и Рв получим отсюда циклической перестановкой
букв х, у, г.
Момент М& относительно оси х получается посредством инте-
гри ования моментов составляющих напряжений по осям у и г отно-
сительно оси х (плечи моментов соответственно z и у). Если вместо
равнодействующей напряжений снова использовать её компоненты
в направлениях ut v, w, то получим;
/I 2 (У cos (*» Р) — * cos (у, р)] hv hw dv dw и т. д. (16)
F И«» ut if, w ‘
Циклической перестановкой букв х, у, г получим далее Му и М.
94
Теория концентрации в пространственной задаче [гл. V
В случае внутренней выточки рассечение проще всего произве-
сти по поверхности х = const. Тогда нужно интегрировать напряже*
ния 'гу, действующие на элемент dy dz. Из условий
равновесия получим интегралы
(16)
— р — — — — •
и т. д.
Циклической перестановкой подчёркнутых букв из этих выра-
жений получаются все нужные соотношения.
Мы будем теперь предполагать, что из этих шести интегралов
только один отличен от нуля. Тогда задача о напряжениях в общем
случае распадается на шесть частных задач, которые в совокупно-
сти дают напряжённое состояние, вызванное шестью компонентами
внешней пространственной системы усилий. Так как мы в даль-
нейшем будем заниматься телами вращения (ось х совместим с осью
симметрии тела, см. фиг. 45), то компоненты Pv и Р„ точно так же,
как М? и М„ вызывают в теле одинаковое напряжённое состояние.
Число частных решений сокращается поэтому до четырёх (растяже-
ние, изгиб, сдвиг и кручение). Однако перед тем как обратиться
к этим задачам, мы должны найти гармонические функции, которые
необходимо знать при вычислении напряжений.
2. Решение уравнения Лапласа в эллиптических координатах.
Возвратимся снова к уравнению (98) гл. III, 7. Если подставим
в него коэффициенты искажения из уравнений (2), то оно, написан-
ное в эллиптических координатах, примет вид:
дф = 'S’ [dS ТГ (ch “ + ST S (s,“ ’ 4г)+
<17>
Функцию Ф будем искать в виде произведения трёх функций
Л(а)»А(®) и А («9, каждая из которых зависит только от одной
переменной:
ф«А(а)-А(«)-АМ <18)
_ Л*ДФ
Тогда из -ф =0 следует
/tchu "dtf Aslntr dv“(’ln^ +
i 1 ( I 1 \ */,________л /194
: ' ‘“Ts ChM — k }
§ 2] РЕШЕНИЯ УРАВНЕНИЯ ЛАПЛАСА В ЭЛЛИПТИЧЕСКИХ КООРДИНАТАХ 96
Первый член (19) зависит только от «, второй — только от о.
Вследствие этого уравнение (19) может быть удовлетворено только
тогда, когда третий, член состоит из двух слагаемых, из которых
одно зависит* только от и, а другое—только от о. Это возможно
лишь при условии —--уА-== const; постоянную обозначим через—я’.
Таким путём уравнение (19) распалось на два слагаемых, одно из
которых содержит «, а другое—•о. Так как их сумма равна нулю,
то каждое из них либо равно нулю, либо равно некоторым посто-
янным, одинаковым по величине, но противоположным по знаку. Эту
постоянную обозначим через v>(v-{-l).
Окончательно получим следующие три дифференциальных урав-
нения:
-0;
dk^(che-&)+[dfc-v(v-
^r(s,n *4г)+[—ж-<v-
-Э+«аА==о-
(20)
Как хорошо известно, решением третьего уравнения (20) является:
/8 = cn sin яте 4* cos над. Что касается первых двух уравнений, то
посредством подстановки либо сЬи = Х, либо sin v ~ А их можно
привести к одному и тому же виду:
1) ww+(2k+ + d]/w_о, р1)
ибо
^=shB^. = ]As_l± иля
= (И)
Решение здесь удобнее всего искать в виде степенного ряда. Част-
ное решение, соответствующее показателю v, ищем в такой форме:
••• (23)
Подстановкой в уравнение (21) получим: ,
(А8— 1) [v (v—1) А*-8+a, (v — 2) (v—3) А*-* -f-
_j_ _4) — 5)А*~° 4~ • • •] 4~ (2А — 1) (vA’-i -f- at (v — 2) A’-94-
4~Я*С*— 4) A’-64~ • • •] 4~|дг—*(*4“ О] -f*ЛаА*-94-
4-л4А»-<4-...]=.0. (24)
96
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ 'ЗАДАЧЕ [ГЛ. V
Приравнивая нулю коэффициенты при -одинаковых степенях X для
определения постоянных av aitполучин следующие уравнения:
{v(v—1)-|-2v—*(*4-1)} Хч==0;
{— v(v—1) — уЧ-л’Ч-МО*- 2)(v — 3)4“2(v—'2) —
-v(v4-i)iB’-a=o;
{a2[-(v-2)(v — 3)—(v-2)4-n*] 4- n4[(v-4) (v-5)4~
4- 2 (V—4)—v (v 4-1)]} A’-4 «= 0
и T. Д. '
(25)
Первое уравнение выполняется тождественно; из второго опреде-
ляется аа, из третьего —л4 и т. д. Полученные выражения для по-
стоянных аа, e4«. i подставим в (23); тогда получим основную
форму (а) частного решения, соответствующего индексам я, v:
я’)[О-2)«—я«)
2-4(2ч— 1)(2м—3)
А'-4—... (26)
Если v-f-1 л | = 0, 2, 4, 6,... (чётные, положительные), то основная
.форма (а) превращается в конечный ряд.
Для положительных нечётных v 4~ In I основная форма (а) предста-
вляет бесконечный ряд. Однако с помощью формулы бинома
МХоДХ) -» - 44 4? + • • • = (27)
снова можно основную форму (а) представить в конечном виде, раз-
делив её на этот ряд. Таким путём получим основную форму (р):
Nn. (А) - х’-84*
+ 2 • 4(2v —1)(2у —3) Х
при у-]-|я| = 1, 3, 5, 7..., превращающуюся в конечный ряд.
При отрицательных v4-|n|, нужно прибегнуть к помощи
функции: ..
...=
Тождество этой функции с arc ctg]/k2—1 легко доказывается по-
средством дифференцирования. Именно:
да—•• (а»)
§ $ РЕШЕНИЕ УРАВНЕНИЯ ЛАПЛАСА В ЭЛЛИПТИЧЕСКИХ КООРДИНАТАХ 9?
С другой стороны,
^-(arcdg /*=1) _ _ _1_. ___1=. (31)
Равенство правых частей непосредственно следует из разложения
по биному. Эта функция даёт теперь возможность, при отрицатель*
ных v~Hnl> написать функцию Nn,t(X) в конечном виде, именно:
АГ», (X)arcctg/^=T + Af (А)}, (32)
где С—постоянная, а Л4(А)— степенной ряд, являющийся конечным
при v 4“ | л | как чётном, так и нечётном отрицательном (в последнем
случае при выделении множителя У У?—1). Таким образом приходим
ещё к двум основным формам.
При v 4-1 п | == — 2, — 4, — 6,... (отрицательные, чётные) полу-
чается основная форма (т):
(X) =
О 42)» —л2
2(2v-|-3)
[(у + 2Р--^][(, + 4)^-Я»] I 1/KZT-P
+ 2-4(2v + 3)(2v-f-5) Л + ...Jarcctg уА — 1 4
4" а^-'*-®4- 4- •.« 4* j,—»
где
п9== — 1;
П - 1 042)2-п\
3 . 2(2ч43) ’ : *
а 1 0 42У-Л» [Q4 2? -л2] [044?-л21
6 15^3 2(2^43) 2 • 4 (2ч 4 3) (2ч 4 5)
и т. д.
(33)
(34)
При у4-|й| = — 1, —3, —5... (отрицательные, нечётные)
получается основная форма (8):
N m________1 । (^41)2-^
№л(А)_ й_ъи|[л 4- 2(2ч43) Л
[р+^-^ц^Зр-^
~ 24.(2ч43)(2ч45) А
47[^--’4-^—’^^. 4-a_ai_1vu]V7TZTi|i (35)
где
п_____2 041?-'»*.
«5— з 2(2ч43) ’
„ 1_ ;18___2 041)«-л» [041?-/14 (043)2-«21
ю’- 15 3 2(2ч43) 2-4(2ч43)(2ч45)
И т. д.
7 Зак. £475. П 'Нейбер.
(36)
93 .. ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
[ГЛ. V
Например:
ЛГа-в (X) = — 3 {/Х^Т arcctg /ХаГГГ— 1}. |
’ ^о,-# (М “ 4 {[Х2 -Ц]arcctg ~ /хзтгу |. | (37)
При составлении общего решения уравнения Лапласа следует
иметь ввиду, что при замене v на — (v-f-l) постоянная 1), вхо-
дящая в'(20), не меняет своего значения; поэтому такая замена не
даёт новых решений. Важно ещё отметить, что случаю п — 0, v — О
соответствует решение
' ’ ^o4o(tA«)[%oo^(»(sin®) + ^ooM).-l(sin •»)]===«, ,
м;: [аоо+ *оо ( 1п f^cosv + £)]’
которое не остаётся конечным при о = 0. Добавляя решение Лап-
ласа In (у2-{-г9), можно однако при надлежащем подборе постоян-
ных получить решение, остающееся при *0 = 0 конечным.
§ з] ГЛУБОКАЯ ВНЕШНЯЯ ВЫТОЧКА НА ТВЛВ ВРАЩВНИЯ 99
Тогда получим:
Ф:= Nnft (?h и) [«»•» ^4ii» (sin ®) Н“ (sin ®)] X
х [Сп sin nw 4- dn cos nw] -|- «0,0 (In ch и -|- In sin «)). (38)
Очень часто встречающуюся функцию jVq,-i (ch й) == arcctg (sh «)
ради краткости мы будем обозначать буквой Т.
Чтобы иметь возможность изучить случай сферической внутрен-
ней выточки, необходимо рассмотреть также гармоцические функции
в полярных координатах. Посредством такого же хода рассужде-
ний, что и выше, и имея в виду (7) и (8), мы получим уравнение
Лапласа в виде:
и2 L ди \ ди) * sin v dv \ dv ) 1
1 —а 0, (39)
: sin* v dw* J ' '
а его общее решение в виде:
Ф = 2 Е4** 1вя-* (sin 4f)'Vbn>-> (sin mX
CO-
Xp».si,n nw-\-dnzoz пда^-|-до>0 (in в-j-dn sin »). (40)
На стр. 98 дана таблица значений яду, которые приходится брать
в рассматриваемых ниже задачах.
3. Глубокая внешняя выточка на .теле вращений.
А. Чистое растяжение. При разыскании надлежащих функций
необходимо прежде всего иметь ясность о характерных свойствах
исследуемого напряжённого состояния. Целесообразно при этом ис-
ходить из интегралов (14) и (15). При чистом растяжении равны нулю
все интегралы за исключением интеграла, дающего Про-
стоты ради мы здесь будем писать Р вместо Рж. Выражение (14)
напишем в развёрнутом виде, а затем используем формулы (18)
гл. III, 3 для направляющих косинусов. Тогда получим:
Л : I
что, согласно соотношений (1) и (2) ддя нашей координатной си-
стемы, преобразовывается к виду:
Р «=; J j' I ch и cos V—sh и sin v Ch и sin vdvdw.' (42)
о о L ,
7*
i6o Теория КОНЦЕНТРАЦИИ в ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [гл. V
Координату к, которая соответствует поверхности рассечения u = const
и по которой мы будем распространять интеграл, можно вы*
бирать произвольно; интеграл должен' иметь постоянное значение,
не зависящее от и. Например, мы можем считать и очень большим
(-> оо). Тогда sh и = ch и = ёи = h, и равенство (42) переходит в
Р = J J -j- е2“ (ом cos ф—tuv sin sin « duo. (43)
oo
Таким образом, и в подинтегральной функции входив только
в виде множителя е9“. При этом условии интеграл Может не за-
висеть от и только тогда,, когда напряжения при большой вели-
чине а будут пропорциональны но это произойдёт только лишь
й том Случае, если функции, через которые выражаются иапряжения,
имеют для v следующие наивысшие значения: v = О для Фо и v = — 1
для ФР Кроме того, ещё возможны меньшие значения v; для нас,
однако, здесь будет достаточным взять значение № —2 для Фо.
В силу условий осевой симметрии, которая имеет место как для
напряжений, так и для деформаций, в решении не должна фигури-
ровать координата w. Отсюда следует, что Фа и Ф3 можно считать
равными нулю. В Фо и Фх должно далее положить я = 0.
В слагаемых, зависящих от v, нужно считать равной нулю или
апч, или Ьпз. При этом нужно руководствоваться требованием, чтобы
внутри тела и в частности при v — 0 рассматриваемые решения оста-
вались конечными. Избегнуть -бесконечных решений возможно также
путём надлежащего наложения обоих решений. Здесь для п = 0,
v = 0, согласно (26) (основная форма а) и (29), получается:
ро.о-Но.0 (-М In 0 +1)] rfq jF;ao,o(ln ch M-]-lnsin^. (44)
Выбором постоянных (>о,о — — “До,о> отсюда можно полу-
чить функцию ’ '
До,о (inch «-fin (1-|- cos vj], (45)
Которая при t> = 0 Остаётся конечной.
Для v = —- 2 и для v = — 1 можно избегнуть бесконечности, при-
нимая соответствующие аЛ|, равными'нулю. Таким образом получаем
следующие выражения, дающие решение задачи: <*
k Фо =,4 [In ch и -|- in (1 cq^ »)] -[- В (Г sli zt — 1) cos p; ) '
' I (46)
Ф1 = CT-, Фа = 0; Ф8 = 0; T= arcctg (sh«). ’ J
§ 3]
ГЛУБОКАЯ ВНЕШНЯЯ ВЫТОЧКА НА ТВЛВ ВРАЩЕНИЯ
101
В соответствии с (58) гл. III, 6 для функции напряжений будем,
иметь выражение:
F = A [lnch«-f-ln(1 -f-coso)J-|-B(rsha—l)cos«4"
4- CFsh a • cos <o. (47)
Найдём теперь AF, необходимое при вычислении нормальных напря»
жений. Из (5) получаем:
AF =----2 У v-. (48)
Далее, необходимо рассмотреть особо выражения, содержащие-^
в уравнениях (4) и (6). При этом для краткости вводится обозна«
чение sh8«-j-cos8o==ch2«— sin8veft2. Получим:
-l-(sh и ch й-|£ + sin vcos v ^-) =
== -^[А 4- (В 4- Q (Г sh и -1) cos +
4-t-[-^4-B4-Ccos9^;
1 / . . dF . dF\ (49)
(sh и ch и sin v cos о
— ----|-B(—Teh «4-th «) —
Л4 1 1 cos v • 4 1 '
— CT ch a] 4—И*a I—A 4“ В 4* C cos8 v].
Выражения (4) и (6) не содержат в себе более никаких неизвест-
ных. Получаем следующие выражения для нормальных напряжений:
,.=^г{лт.,+а^+с(-2-.+^) «Ц-К
+-т-{—4+B+Ccos!l,}:
=¥-{-д-гт^+<’-псН +
+ COS V | . п л п I
——<А —В — С cos8 ;
1 ( . / о । cos v \ D cos v .
— । -|. cos v ) В ch2 и
. +c(a_i__^_)coso}.
Касательные напряжения имеют вид:
th и sin v
А2
П^пг+(’-1)с+
4—“ А 4~ В 4“ С cos2 v'j |, „tyw == 9> 0-
(51)
^uv
102 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ, V
Остаётся определит!» произвольные постоянные из граничных уело*
вий (12). Так как в выражениях для av и коэффициенты чле-
нов, которые содержат должны обращаться в нуль при ‘Р = ф0>
то мы получим четыре уравнения. Но третье уравнение является
следствием первого, а второе следствием четвёртого и, значит, всего
имеем два уравнения, из которых найдём
4 = (<х—1) (1 -j- cos о0) С; В = А — Ccos2^0. (52)
Для определения постоянной С теперь мы перейдём к определению
равнодействующей усилий, действующих по сечению, проходящему
через выточку. Для этого воспользуемся интегралом (42). Если принять
во внимание соотношения (52) то, действительно можно показать, что
этот интеграл имеет постоянное значение для всякого а и от и не
зависит. Однако эти вычисления мы здесь опустим и для простоты
будем предполагать а = 0, т. е. интегрировать будем по наиболее
узкому поперечному сечению тела. Для него h cos р и (42) при-
нимает значение:
2 2х
Р= j* J (<зм)в—о sintFcosvrfodws^
«о
Я
ЗГ 2ж
ШВ — аС I В—41 , ,
^е-<гм~тsinocostJdtodw»
cos V 1 cos9 V I
V 4 J
^2k[(B-«C) (1-cos^0) + (B-4) (53)
или, согласно (52)
P = 2itC (1 — cos o0)' [ — 1 -J- — 2) cos — cos9 o0]. (54)
Вследствие безразмерное™ нашей координатной системы вместо Р
мы должны ввести некоторую величину, имеющую размерность
напряжения; в качестве последнего возьмём номинальное напряжение,
равное среднему напряжению по’ наиболее узкому поперечному сече-
нию (радиуса а):
; <“>
Радиус а наиболее узкого поперечного сечения согласно (1) равен
a = (/ja+^)^=0=^ slno0, • (56)
V—Vt • I
так что
I P=^irsin2O0=/>ic (1—cos v0) (1-f-cos^p); (57)
ГЛУВОКАЯ ВНЕШНЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ
103
§ 3]
и тогда из (54) найдём
с __________________р_________1+cqspq
G 2 1 -|- (2 — a) cos ®0 -f- cos2 «о '
Теперь напряжённое состояние вполне определено.
На фиг. 47 показано распределение напряжений вдоль контура
выточки и по наиболее узкому поперечному сечению, при cos®0 =
= 0,2. Растягивающее напряжение у дна выточки достигает наи-
большего значения, в 5,1 раза превосходящего номинальное напряже-
ние. Одновременно в поперечном сечении^ кольцевое нормальное
(58)
Фиг. 47. Глубокая кольцевая внешняя выточка при
растяжении.
напряжение <sw = at достигает своего наибольшего значения величи-
ною в 1,7 р. От дна выточки, как в направлении вдоль контура
выточки, так и в направлении вовнутрь поперечного сечения, на*
пряжения подчиняются закону быстрого затухания. При удалении от 1
дна выточки напряжения убывают приблизительно обратно пропор-
ционально второй степени расстояния от дна рыточки, т. е. ещё
быстрее, чем в случае плоского напряжённого состояния (в соот-
ветствующей плоской задаче затухание обратно пропорционально
приблизительно первой степени расстояния от дна выточки, см. гл.
IV, 2, А).
При выводе общих формул для наибольшего напряжения, воз-
никающего у дна выточки, в качестве параметра фигурировала ве-
личина о0. Если же за величину, характеризующую форму выточки,
принять отношение радиуса кривизны р к радиусу а стержня в наи-
более узком сечении, то, имея в виду, что это отношение выражается
через v0 согласно уравнению J68) главы IV, 2, получим такую
104 теория концентрации в пространственной задаче [гЛ. V
формулу для наибольшего напряжения
7(°“Ъ„“ = р “Я?/f+1 +
а для наибольшей величины кольцевого нормального напряжения
формулу:
Р = Р ~~N р [и У у + 1 “I" °’5] ’ (60)
"=7+s-/'f+1+2' (61)
Точная зависимость величин наибольших напряжений от кривизны
выточки графически представлена на фиг. 48.
Фиг.'48. Наибольшие напряжения
в глубоких кольцевых внешних
выточках при растяжении.
В. Чистый изгиб. Для решения
задачи о напряжённом состоянии
при чистом изгибе возвратимся снова
к интегралам (14) и (15), харак»
теризующим силовой поток, прохо-
дящий сквозь поперечное сечение.
Мы предположим, что момент дей-
ствует в плоскости ху и в соот-
ветствии с этим будем считать, что
все интегралы, за исключением того,
который определяет Л1„ равны
нулю. Вместо М, будем теперь
писать М. Применяя уже много
раз использованные выражения для
направляющих косинусов, получим:
^)]*А*** №2)
или; благодаря (1)' и (2),
2к
М J (оя s|nv coso cos w — tuv sh и ch и cos w +
Ash a cos o’sin w] ch и sin vdvdw, (63)
§ 3] ГЛУБОКАЯ ВНЕШНЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ Г05
На далёком расстоянии от наиболее узкого поперечного сечения
sh«»ch« в = ЛгиУл;8+<у9-|-.га. Тогда подинтегральная
функция содержит множитель е8". Так как интеграл не должен
зависеть от к, то для больших значений и напряжения должны быть
обратно пропорциональными е8“. Из этих соображений заключаем
о наивысшем значении v, которое имеют слагаемые, зависящие от
а, — именно: v = — 1 для Фо и v = — 2 для Фх и Ф8. Кроме того,
можно использовать функции с меньшими значениями v. Далее, из ра-
венства нулю остальных интегралов можно ожидать, что выражения
и т(И) содержат множителем cos г», т. е. что сп = 0 и в Фо и Ф,
следует брать только л= 4~1> а в $а—только п = 0.
Так как внутри области, в частности при v = 0, решение должно
оставаться конечным, то следует считать равными нулю. Исклю-
чение представляет функция со значением v = — 1, «= 1, а именно:
+ bi>-i1 ctgcos w.
Оба слагаемые этого выражения при v = 0 превращаются в беско-
нечность. Но если мы положим = — ibit-v то получим с
точностью до постоянного множителя, выражение
coswl — cos» cosw sin»
ch в tin » ~* ch и 1 -f- cos »
(64)
остающееся конечным.
Мы получим решение задачи, если к вышеуказанным функциям
добавим ещё функцию со значением v =— Зи п,— 1 для Фо. Тогда
определим следующие выражения ’):
Ф —,Л sin»cosw . .
° лсй«(1-|-соз»)
4- в| ch и (Tsh и — 1) 4- ^4— 1 sin v cos v cos w,
L 3ch и J ’
Ф, ш C(Tch в—th «) sin V cosw;
®9 = O(TshB — 1) cos », Ф8 = 0.
Функция напряжений приобретает вид:
F = sin . cos , cos » [ете05^1 + см„j+
+ (B + C+O)ch«(rsli
-------H.-----
») к e u I» e'r H., Ing.-Arch., t. 6 (1935), стр. 133
(65)
(66)
106 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ* V
Опуская промежуточные вычисления, для компонентов напряжений
окончательно получим:
«« s.lnv-c.°y-£^g {-2 ch и (Г sh «-1) [В + (1 -а)(С+ D)] +
+тй [ - iSTwsrij - т а - 6С+<2+’> °]+
।. 1 Г____24_______. 2. п । nX] I
' ch® a [cos v (l-f-cos о) ‘ 3 о'т' ]'
+ л^(Л + Т 2Ccos91’+D sin9wX5
ro«lnt>cosrcosw|2 ch M(r sh u_ 1} [B _|_(1 __e) (C+ D)1 +
—ft4nz(4+iB+2Ccos9t,+D8in9t,)};
__sin о cos t> cos w f l Г 4 (2 4- со» v) ।
°w ~ ft« |ch B [co8 v (J cos V)t T .
_fi(—24- 2a) C-f-(l — a)D]
_L 1 __— в___осЧ
' ch» u k cos v (1 + cos v) 3 * )f *
v = 84T w {[(rsh g~ l)(l~2cosM -
Tcos2v"]rDI , rwi . ।
sh и J t5 + П a) (C + D)^ "t ch» и [(1 + co»v)»“" 3
4-(-l 4-а)с]-Ьуг(д+ yB4-2 Ceos?v-\-Dsin8®)};
xvw « (Г Sh « -1) [B 4- (. 1 - a) (C+D)J +
+ ch»a [(14- cos о)2 “ T * 1 + e)C’]}5
= 5os^s!ng> ch « - th u) [B + (1 - a) (C+ D)} 4-
I »h a ( ______24______ 2 n __ qz"»\\
^chsuk cosv(l + cosv) 3 ° . Jf
(68)
Из граничных условий (12) для постоянных А, В, С, D непос-
редственно получим восемь уравнений, так как коэффициенты в каж-
дом из слагаемых, содержащих в каком-нибудь виде переменную и
при ® = ®0, должны быть равны нулю. Некоторые из этих уравнений
оказываются тождествами % вследствие этого количество их умеш,-
§ 3] ГЛУБОКАЯ ВНЕШНЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ 107
шается до трех, из которых находим :
Д= —^2в(1—а) (1 + cos о0)9;
B~-(l-a)(C+D); '
ry
c= %-'[—3a 4- 2 (1 — a) cos +(4 ~ «) cos3 ^ol»
где
Ni«2cosvQ[2(1 — «) + (4—a)cosv0].
Постоянную D получим из интеграла (63), причём в нём целесооб*
разно положить « = 0. В результате имеем:
—____________________________________________ (70)
Ni it(l—cosv0),2a[64-4(4—a)cosv0-f-2(5—2a)cos2 v0-}-(4—a)cos* Vol ’ ' 7
Номинальное напряжение в этом случае вычисляется по элементарной
формуле изгиба:
м_______________________4Л4 _ /*71 \
<71>
Применяя формулу (56) и вводя кривизну у дна выточки ±=tgsv0,
получим окончательно следующую формулу для наибольшего на*
пряжения при изгибе, возникающего у дна выточки:
’=(’+=Д 4 (/I+7 +•>) [’ 7 -
4+4-4+7]. (72)
где
. 14- —
Л7в,з(441)+(1+Л)1/г±4-1+------------н=- (73)
\ р ' / \ ' mJ V р 1 р/
Точно так же наибольшая величина нормального напряжения аю,
возникающая у дна выточки, вычисляется по формуле:
=£’^Г2/д77+1 + »1. (74)
t>=v0 л 4 р ,L« г р 1 'mJ
w=0
На фиг. 49 показано распределение напряжений для -=>8 и
1 ?
— = 0,3. В левой части фигуры, внизу, дан график распределения
напряжения по контуру выточки. Этот график является характерным
для закона затухания. В верхней части показано распределение
Напряжений по наиболее узкому поперечному сечению. Пунктирная
108 ТЕОРИИ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ V
линия соответствует прямолинейному закону распределения напряже-
ний. Напряжение от изгиба, при приближении к дну выточки, резко
увеличивается, достигая в точке у дна выточки 2,4 кратной вели-
каны напряжения, получающегося по элементарной теории.
Линии, начерченные в правой части фигуры, соответствуют ли-
ниям одинаковых напряжений аи. По ним можно распознать об-
Смени? * Сечение и~0 -
Фиг, 49, Глубокая кольцевая внешняя выточку при изгибе,
ласть с наибольшими напряжениями, представляющую собой узкий
поясок, простирающийся вдоль контура сечения.
На фиг. 50 дана зависимость между наибольшими напряжениями
Oj и аа и кривизной выточки при трёх различных значениях пуас-
СОКОВОЙ ПОСТОЯННОЙ. \ '
С. Чистый сдвиг. Если, наиболее узкое сечение стержня с внеш-
ней выточкой находится в условиях чистого сдвига, то из интегралов
(,14} нужно положить равными нулю все, за исключением того, ко-
торый даёт перерезывающую силу. Ей мы обозначим V (вместо Pv)
и будем считать направленной вдоль оси у. Получим:
| (°««sh ° sin vcos w4-ch и cos® cos w—
: й sin w) ch u sin “p (75)
М1
Глубокая внешняя выточка йА телй вращений ,
10§
При очень больших значениях и в подинтегральной функции появ-
ляется множитель в2" и, следовательно, при больших и напряжения
должны быть обратно пропорциональными величине е9“. Отсюда для
наивысших значений v получается следующее: v=0 для ф0 и v = —1
Фиг. 50. Наибольшие напряжения в глубоких внешних кольцевых
выточках при изгибе.
для и Ф2. В остальном остаётся справедливым сказанное при
решении предыдущей задачи, т. е. с„ = 0, п = 1 для Фо и Фп а
« = 0 для Фа. Для устранения бесконечно больших значений коэф-
фициенты аП1 опять нужно считать равными нулю. Исключение пред-
ставляет случай v = 0, л=1, для которого получаем функцию вида:
th и [а1Л i ctgt> -р1Л cos w.
Оба слагаемые этой функции при *0 = 0 превращаются в бесконеч-
ность. Цо если положить а1Л1 = —bw то, с точностью до по-
стоянной) множителя, получим1 пригодное решение:
th « cos w *= th и У — cost». (76)
sin о 1 -|- cos v ' ‘ ’
Если k вышеупомянутым функциям добавим ещё функцию с парамет-
ром v = — 2, п s= 1 для - Фо, то удастся получить строгое ре-
шение! задачи. Мы будем иметь следующие выражения для функций:
,Ф0 е» A th и у, C03t, 4-В (Т ch и — th «) sin v cos t»;
, . । , (77)
! ch a(1 4-cost») ’ >8«»0.
< 110 ТЕОРИЙ .КОНЦЕНТРАЦИЙ И ЙРОСТРАНСТВВННОЙ ЗАДАЧЕ |г<Л« V
По ним находим функцию напряжений:
F^Sin oc<w 4- В(Тch и - tM) + с‘^^ +
-f-Dfchaj. (78)
Минуя промежуточные выкладки, для напряжений получаем следую-
щие выражения:
..=S^lb«[c(-S-.+n^)+D(-2-.)d-?
I 1 (2Л______2о । 2Ccoscf \ । 1 / а __
~*~ch2a\l 4-cosv • 14-cosv/ * й2\
— 2В Ceos2 v — Dsin8t^j;
__sin о cos о» ±1_ Г А । „, ,i 2а (
As •««[ (1 cos v)2 +С' 1 + * l + cosv"!"}
+ (l+Lso)0 + D(~ 1 + ®) “ ДЛ — 2В +
-]-Ccos2x> — Dsin8o^J;
_ sin О СО* HL. Г A i Л t 1 \ I
°w — As ‘ ika[(I + cos.t»)2’;C\ 1 4 а~(l-f-cos»)274
cosuM А *^Гх.« ч ~ 1-L(x 1 .
'см« = _т?_{т_г—:—F-C (1—a)cosv—2a — —— 4~
“® л4 (1 -jf-^cosiv 1 -L ' x ’ 14-cosvJ 1
+ °(‘— »”’+5й'[-лт^ +
+ с(«ео>«-1-«+тт^)]-е-^(А-2В+
4~Ccose,p—£>sin8t»^|; ,,(80)
. sh и sin v sitt w vf:. , . . Л
t««’ “ Л ch2 a (14- cos Sp [Л + 14-A 4- «.cos J;
_ sinw Г J л C(l + d)cost» . n . , . .
5«w “ Mini L 1-pcoso 1.4- cos «—r/> (-114 a) ±
+ЙЬ^-М+»Т^й)]'
Длд четырёх содержащихся в решении постоянных из граничных
условий получим сначала щесть уравнений. Но их число уменьшается
§ 3] .ГЛУБОКАЯ ВНЕШНЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ Lili
до трёх, из которых найдём:
А — С(1 — а — а cosvj,
D — C
1 , , . а8—2а
5----1- 1 —а 4- ---СОЗ о0
I — а 1 1 1 — а u
.-1 “ (1-а)(1+ «»?о)] '
(81)
Постоянная С определяется затем из интеграла (75), где величину и
целесообразно считать равной нулю. В качестве номинального напря-
жения возьмём среднее касательное напряжение по наиболее узкому
поперечному сечению, именно:
(82)
Тогда, с учётом (56), будем иметь:
с _ />(1—«ЩЧ-созор)8
а(1 — eos»o)[2 + (2—‘a) cos op]
(83)
(84)
Интересно отметить, что наибольшее касательное напряже»
ние возникает не в сечении w, а в сечении w = —. Обозначим это
напряжение через и с помощью (68), IV, получим:
. ( 1 . 1V,/TV7 . Л
*1 ~ (г«и>)в = о “ р—-
*
В сечении те = 0 существует только лишь относительный макси-
мум та касательного напряжения т«0, определяемого уравнением:
(ти„)п _ a =S аС Г 1+(1—«)СОЗ»0 _ етЧ
Wee0 (1—a)(l + COSOp) L COSO cos8о
(1 — g) COSOp(l -f-СОЗОр)!
COS V (1 -f СОЗ о) J* ' '
Для определения точного положения этого максимума несколько
упростим сначала выражение (85)^ положив в нём а = 1 (и ------
т=±=2). Тогда:
значит,
Z V 1 + СОЗ Рр____СОЗ8 О —COS8 Уо
' “ „Zo ”(^ — СОЗ Ор) (2-|-COS Ро) cos8 о
В этом последнем выражении мы узнаём ту же самую
мость от о, которая была установлена в соответствующей
(86)
зависи-
плоской
112 теория концентрации и ПроОтраиСтйенной задаче [гЛ. V
задаче [см. IV, (94)]. Поэтому максимум та лежит в том же самом
месте, как и при плоском напряженном состоянии'.
г— 1/
со$'»=±уг3cos «о? У=*ау —. (87)
7
Если выражение (85) исследовать при других значениях постоянной а,
то окажется, что положение максимума t2 с достаточной точностью
можно1 считать неизменным и совпадающим с предыдущим, опреде-
лённым уравнениями (87). Для вычисления величины та в уравне-
нии (85) положим поэтому cos к = )/3 costal получим:
соз^ = Уз COS v9
W = 0 , , j
При — С 2 наибольшее напряжение имеет место на оси (v = 0),
а величина его равна
*2 — (Tw)«®о “ Р
w 0
W = 0
2(t+V 7+1 + 1)
(89)
Далее, в сечении ® = 0, в точке, очень близкой к дну выточки
и лежащей на ёё поверхности, напряжение аи достигает максимума.
Для этого напряжения сначала получаем выражение:
‘ w SS3 0
at'sin «о ’ЬцГ. а —Г2 ч?1п2»0]
= (а— 1)(1cosVq) ft’ [ '’сЕ’ТГ]
(90)
Бодее точное исследование показывает также и здесь, что расстоя-
ние от точки,, где возникает <зи до наиболее узкого поперечного
Сечения можно с достаточной точностью определять по той же самой
формуле, как и при плоском напряжённом состоянии [ср. гл. IV,
формулу (92)], а именно: : г
v . J . <
sh и = zt cos v0,
(91)
§ 3]
ГЛУБОКАЯ ВНЕШНЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ
из
Если подставим эти
разований, получим:
~ (°w)sh a —cos — Р
v~-v0
w == О
значения в (90), то, после небольших преоб-
Кольцевое нормальное напряжение достигает своего наибольшего
значения в той же самой точке и вычисляется по формуле:
а2 “ (°w)sh и —cos v0 = Р
V «=» 2>0
W в 0
• (93)
На фиг. 51 показано распределение напряжений для у == 8, ~ = 0,3
в меридиональном сечении, проходящем через силу V. Внизу,
Фиг. 51. Глубокая внешняя кольцевая выточка при сдвиге; слева меридио-
нальное сечение, проведённое через силу V, и эпюра напряжений; справа
поперечное сечение и линии напряжений.
налево, мы видим графики распределения напряжений на поверхности
выточки. Они достигают своего наибольшего значения в непосредствен-
ной окрестности у дна выточки. В наиболее узком поперечном се-
8 Пак. В475. Гф дейбер.
114
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
[ГЛ. V
чёнии преобладающее значение имеет касательное напряжение; непо-
средственно около поверхности выточки оно достигает своего наиболь-
шего значения. Пунктирная линия соответствует случаю — = 0.
Направо начерчены линии касательных напряжений в поперечном
сечении. Они располагаются по преимуществу параллельно направлению
силы I/.
На фиг. 52 для той же самой выточки показано меридиональное
сечение, перпендикулярное направлению силы. Касательное напря-
Фиг. 52. Глубокая кольцевая внешняя выточка при сдвиге (см. фиг. 51);
слева продольное сечение, перпендикулярное к силе V; справа поперечное
сечение с линиями равных напряжений сдвига.
жение возрастает чрезвычайно быстро. У дна выточки, где оно на-
правлено параллельно контуру, оно достигает своего наибольшего
значения. Эта область, очевидно, является наиболее напряжённой.
По направлению внутрь, а также и вдоль контура выточки касатель-
ные напряжения быстро затухают.
Направо начерчены линии одинаковых касательных напряжений
в поперечном сечении. Зона с наибольшим касательным напряжением
представляет собой полоску, расположенную в окрестности точки,
где касательная к контуру параллельна направлению силы V.
Линии равных касательных напряжений, так же как и выше-
упомянутые линии касательных напряжений, можно получить после
§ 3| глубокая внешняя выточка на теле вращения 115
того, как определена равнодействующая касательных напряжений
в рассматриваемом сечении. К этому вопросу мы ещё вернемся при
рассмотрении мелких внутренних выточек на теле вращения и в гла-
ве V, 4, С укажем простые способы её получения.
io го зо
Фиг. 53. Наибольшие напряжения в глубоких кольцевых
внешних выточках при сдвиге.
На фиг. 53 показана зависимость между наибольшим напряжением
и кривизной выточки. /
Д. Чистое кручение. В этом случае те интегралы (14) и (15),
которые не определяют крутящего момента, нужно положить равными
нулю. Обозначив крутящий момент буквой М (вместо МЛ, получим
по уравнению (15)
о о
+ Й ~z h* dv dw' t94)
В нашей координатной системе уравнение переходит в следующее:
«в
М — 2тс ft:wwh ch8и sin2® dv, (95)
0
Так как при больших значениях и в подинтегральной функции по-
является множитель е3,‘, напряжения будут обратно пропорциональ-
8*
116 ТЕОРИЯ КОНЦЕНТРАЦИИ ft ЦрОСТРАНСГВЕНПОЙ ЗАДАЧЕ [гЛ. V
ными величине е3“. Соответственно этому для v можно брать сле-
дующие наибольшие значения:
v=-l для Фо и v = —2 для Фр Фа и Ф8.
Задача о кручении тел вращения является известной классической
задачей теории упругости. В этом случае напряжения получаются
независимыми от коэффициента Пуассона* *). Эту задачу легко решить,
исходя из наших общих выражений, положив
Фо = О; Ф1==0 (96)
и
Ф2= —f(ut о) sin w; Ф8 =/(«,<») cos «*. (97)
Отсюда следует, что:
F = 0. (98)
Соотношения (3) дают:
£7=0; V=0; W = ^f(u,v), (99)
т. е. тело закручивается вокруг его оси. Из (4) и (5) далее следует
ctt = 0; % = 0; а„=0. (100)
Наконец, из (6) получается:
т _0 т |
т (f^\ I ° °
TUU> —« h du\chu)' J
Для рассматриваемой задачи достаточно взять функцию с v = —2.
Так как в выражении (97) фигурирует cosw, то нужно считать
п=1. С целью получения конечных решений нужно опять положить
ап, В результате придём к следующему выражению:
/(«,т>) = Я(ТсЬа—thu)sin-». (102)
С этой функцией мы уже имели дело в задаче об изгибе. Для напря-
жений получим9):
<w = o; (ЮЗ)
Интеграл (95) даёт
г’ 4
М = —4ла С] sin8 vdv= —-g-waC(cos8 v0 — 3 cost’0-|- 2) =
4
= —2-itaC<2-{-coS'V0)(l — cost>0)2. (104)
*) См., например, А. и Л. Ф ёппль, Сила и деформация, т. II, стр
111-112. ОНТИ, 1936.
*) Результат впервые был получен Пёшлем См. Z. angew. Math. Meeh.,
т. 2 (1922), стр. 137.
§ 3] ГЛУБОКАЯ ВНЕШНЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ 117
Поминальное напряжение вычисляем по формуле:
2/И
тса3==^’ (Ю5)
Тогда, имея в виду, что a==sinv0, находим постоянную С\
С— Зр Sin Ур (1-hCOSVo)
8а(2 + cos Vo) (1— cosVo) ‘
Для наибольшего касательного напряжения, возникающего у дна
С * '
Фиг. 54. Глубокая кольцевая внешняя выточка при
кручении.
выточки, получим, наконец, следующую формулу, введя в неё кривиз-
ну выточки
(Ю7)
В правой части фиг. 54 показано распреде-
ление напряжений по наиболее узкому по-
перечному сечению, (вверху) и вдоль контура
выточки (снизу); ,в левой же части этой
фигуры начерчены линии напряжений. Они
Фиг.[55/Наибольшие на-
пряжения в глубоких
кольцевых внешних вы-
' точках при кручении.
идут в направлении линии «, так как существует только напряже-
ние которое и играет роль главного напряжения.
Зависимость наибольшего напряжения от кривизны выточки дана
на фиг. 55.
118 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ. V
4. Мелкая внутренняя выточка на теле вращения при отсутствии
сверления.
Перейдём теперь ко второй группе задач, решение которых тре-
бует применения общих методов. В начале этой главы уже было
замечено, что задачи о глу-
бокой внешней и мелкой
внутренней выточках в теле
вращения, не имеющем осе-
вого сверления, принадле-
жат к числу задач о про-
странственном напряжённом
состоянии.
Фиг. 56. Граничные условия цилиндра. Ради простоты вычисле-
ний внутреннюю мелкую вы
точку возьмём в форме эллипсоида (ср. фиг. 45). В соответствии
с определением, глубина выточки, которую мы опять обозначим
буквой Z, предполагается малой в сравнении с радиусом Ъ стержня:
(Ю8)
Умелым применением этого неравенства отдельные решения можно
существенно упростить, если придержияаться следующего порядка
вычислений: для каждого вида напряжённого состояния определяется
прежде всего напряжённое состояние в стержне без выточки; при
этом на поверхности стержня должны быть выполнены следующие
граничные условия, вытекающие из уравнений равновесия заштрихо-
ванного элемента стержня (фиг. 56), одна грань которого совпадает
с поверхностью самого стержня:
zxydz — О,
a/z—т^ = 0;
—<3tdy =0;
или благодаря равенству :
при _у9 -J- г2 = Z>2 (109)
ПРИ Р = Л (110)
Вторая часть решения заключается в определении так называемых
напряжений возмущения. Здесь требуется вычислить искажение рас-
пределения напряжения, обусловленное наличием в стержне внутрен-
ней выточки, и определить это искажение так, чтобы в совокупности
с напряжениями в стержне, не имеющем выточки, были удовлетво-
рены граничные условия (13) на поверхности выточки (u = w0). Эти
напряжения возмущения, подчиняющиеся закону затухания, и создают
концентрацию напряжений,
§ 4]
МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ
119
В точках внешней поверхности стержня, которые, вследствие (108),
находятся очень далеко от зоны искажения, напряжения возмущения
совсем затухают и не оказывают влияния на граничные условия (110).
Вместе с этим для мелкой внутренней выточки оказываются выпол-
ненными все граничные условия.
А. Чистое растяжение. В случае чистого растяжения стержня,
не имеющего выточки, напряжённое состояние в нём можно выра-
зить с помощью функций следующего вида:
= + 2х*1;
Ф2 = 0; Ф8 = 0.
(111)
Согласно (111) и (58) главы III для F имеем:
/7== 274ЧтК2-«)СУ9 + ^) + (2а-2)х2]. (112)
z V»
Напряжения получаем по формулам (68) и (69) газы Ш
^у = ~'гу = tyz === ~gx === (113)
Следовательно, величина р представляет собой равномерно распреде-
лённое растягивающее напряжение в стержне. Если обозначим силу,
растягивающую стержень, через Р, то
Р
Р ~ яЬг •
Сначала мы рассмотрим сравнительно простой частный случай, именно
тот, когда внутренняя выточка ограничена сферой. Из этого част-
ного случая читатель может отчётливо уяснить намеченный выше
ход вычислений.
Частный случай t = р. Используем уравнения (7) для того, чтобы
выразить функции Фо, Фп Ф2 и Ф3 в сферических координатах:
Фо = Т(та-“2(3^^-2); ]
\ > (П5)
Ф1 = 5~« costr; Ф2 = 0; Ф8 = 0. |
Сопоставляя их с общим выражением (40) для гармонической функ-
ции, легко устанавливаем, Что мы имеем дело с функциями v = 2;
и = 0 и v= 1, /г = 0 при /?п>7 = 0. К этим функциям нужно добавить
новые, которые бы соответствовали напряжениям, удовлетворяющим
граничным условиям (13). Этим свойством обладают функции, зави-
сящие подобным же образом от v и -о/, но иначе зависящие от и. Их
мы получим, если заменим v на — v— 1, т. е., если положим у = —3,
вместо 2 в функции Фо и у = — 2 вместо 1 в Фх, и если, вместо
^ = 0, положим далее дп^ = 0. Кроме того, следует принять во
120 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ. V
внимание, что функция Фо при v = — 1 и и = 0 также
пригодной. Таким образом подобранные функции дают
*» - «• +(32) + 4;
*x=[rz^“+§lcos«: *s=°; Ф«=0-
оказывается
решение:
(116)
Функция напряжений будет:
Р = Г й« -L Ц — -1 si n9 v 4-
г [2(4 — в) ‘ aj •
I (а—УР „2 2В | d I О.
4 — а и3 • и ’ и*
. 017)
Отсюда, согласно (10), найдём ДГ, а затем и нормальные напряжения:
! , 24В 2А , (—6—2a) С .
' р' и6 и» "г и» ’
Г . 21В , (1—a)Cl ,2 12В .
«. = [?+—+'~y-|sl" ’—1Г+
, Л , (-1+2QC .
"Т” и3 ' И3 ’
_Г15В
°W — I И5
. (3—3«)С1 . 2
Sm9®
12В I
и5 "Г
, А I (-142a) С
"Г и3 "Г й8
По (11) найдём касательные напряжения
( —44-а)С1 ,
----— sin V COS V
ил J
~VW--- О» -------О'
(118)
(Н9)
Для трёх вошедших в эти выражения произвольных постоянных из
граничных условий получим три уравнения, пользуясь которыми на-
ходим следующие значения постоянных (ради простоты положено
«0« 1):
л = (-йхй£;5 = ггт; С=а4-- (120>
i 2 (4 + 5a) ’ 4 4- 5a ’ 4 + 5a ' 7
Для наибольшего напряжения, возникающего у дна выточки, полу-
чим следующее:
( = 2,04р для “ = 0,3). (121)
§ 4] МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ 121
Кольцевое нормальное напряжение достигает максимума в той же
точке
ч 3(8 —5а)
°2 — — 2 (4 .J. 5а) Р —
з( —1Н“) ,
= -----5^Р(=О,14/> для 1 = 0,3). (122)
2(7-£)
Эти результаты вполне совпадают с теми, которые были полу-
чены (другим путём) ещё в 1908 году A. Leon х). Для этой сим-
метричной относительно оси нагрузки A* Leon’y удалось найти реше-
ние путём постепенного удовлетворения отдельным уравнениям тео-
рии упругости.
Общий случай. В том общем случае, когда поверхность выточки
имеет любую кривизну, решение получается непосредственно с помо-
щью аналогичных функций, но в эллиптических координатах. Индек-
сам v и п следует давать здесь те же значения, что и в предыду-
щем случае.
Однако при выборе отдельных гармонических функций нужно
теперь руководствоваться уравнением (38). Вследствие этого полу-
чим выражения:
*о = { ^4-J) (ch9 “ ~ у)+B[(3ch9« — 2) Г-3 sh «]} X
Х(3 sin9® — 2)-|-4 Г;
Ф1 = { 4’2Г£8*1 и-]-С[Тsh и — 1] | cos®;
Ф2 — 0; Ф3 = 0.
(123)
Отсюда для функции напряжений получается:
F= К4 — За)ch9e — 24-2а]sin9®
+ [(« — 1) ch’ « + (1 J2a)] + ЛГ4- В[(3 cha«—2) Г—3 sh и] X
X (3 sin9 ® — 2) -|- С [ Г sh9 и — sh и] cos9 ®. (124)
Опять вычислим сначала член Д/7, необходимый для определения
нормальных напряжений, и члены с множителем имеющиеся
!) A. Leon, StOrungen d$r Spannungsverteilung. Wien, 1908.
122 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ. V
в выражениях для а„, <з„ и tuv. Согласно (4), (5) и (6) найдём
= | j~jch3«-|-2C,[rch9K—sh«] | 4
। sin- v J 2p о л*?' 1 •
' Л2 ( 4 — а ’
1Г . <_ dF , , dFl
^sh«chw^ + sinocos«^-J =
= р | ^£=^psh9M-f-B[—12 rsh9a412sha]4
4-C[2Tsh9«—shrill +S-^ ( 4r“^tpch2« + 5‘r^P +
* 1J I I 4 — а r 14 — ar 1
+ 5 [(18 ch9 и — 12) T— 18 sh'aj 4 2C[ — Tsh9 а 4 sh aj} 4
+’s-Jr{-4-4e-Csh2“};
1ft « dF . dF~\
-rd shtfch^-s-sin-0 cos ^3- =
/i4L vv duj
= I l=^psh«chtt-|-B[18ch'e(Tsh« —1) +
+ аМИ~2си(™“-1)-ж] 1 +
+^!л+4Я+С8Н’“} •
Используя эти соотношения, для нормальных напряжений
чим:
att=^{pch9M-^^ + B,[12Tch9«-12sh«- ’
— “l -Ti-l + d aTch9«4-(l—a)sh«4- ^-11 +
• ch2«J 1 L I \ / j ch2ujj 1
+ -3Д — pch2« + e[( — 18ch9«4-6)r-f- 18sh«4-
(125)
-4^-li+^r I —A—4B—Csh9«
ch1 и Jf 1 M i j ’
°” = лИб[~ 6rch2“ + 6 sh «] -4- c[(2 — a) Teh9 «-f-
4-( — 3 + a)sh«]| + ^|psh9«-^B[(18ch9ii —
— 12) T — 18 sh m] 4- C [(-2 + 2a) Tch9 и — aT-|-
+ (2— 2a)sh m]|-J-4 + 4B-|-Csh9M |;
полу-
(126)
§ 4]
МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ
123
+ с[(2-«)(ГсЬ««-5Н«)-^] + -!!^!!.|в[бГ-
-6^]+с[(-2+^г+ет]};
Касательные напряжения вычислим с помощью формул (6):
(126)
р__,sin |—pshachw -f"5 [—18T sh u ch «4*
+ 18 ch и — -j- C [(2 — 2a) T sh и ch и (— 2 -f-
+ 2,)cb в + l=i]} + (Л + 4B+ Csh’«j,
’ ^UW
Произвольные постоянные, содержащиеся в решении, нужно теперь
определить так, чтобы были удовлетворены граничные условия (13).
Положим для краткости:
ch4 uQ sh (T)u=Uq— ch9 я0 sh2 «0 = g. (128)
Введём ещё в рассмотрение глубину выточки
(y)UssUo = ch = t. (129)
JC
2
Используем зги обозначения и в выражении для (aw)u=u0 прирав-
няем нулю коэффициенты слагаемых, зависящих от v. Получим
следующие уравнения:
',/2+-й4![’~1+ 4|+4‘2^ ~4+4]+
+ <?[«-£- + /»-А]} = 0;
-^+44° [-18 4+6 4+12 - 4]+
+ с[(2-2»)^-+(-2 + «)-^— 3 + « + Ц1-]}-0;
— а — 45 4-С[—г24- 1]=о.
Отсюда найдём произвольные постоянные:
(130)
л_ р sh uu/* м - |6^2 4- (4а — 2) g 4- 4/4 — 4а/2];
д_ Р sh в- к [(2 — а)^4- 2/44- ( — 3 4-а)/2]; • (131)
r__ р sh [6^—12/2],
124
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
[ГЛ. V
где
= 6 [( — 4 a)g2 - 6g/4 + 8g/2 4- 4/« — 4/4J.
Если эти значения подставим в (127), то увидим, что гра-
ничным условиям удовлетворяют и касательные напряжения, т. е.
мы удовлетворили всем условиям. Теперь можно перейти к вычис-
лению наибольших напряжений.
Как и можно было ожидать, наибольшее напряжение возникает
у дна выточки в направлении растяжения стержня. Если вместо
параметра й0 ввести кривизну выточки по формулам
-y-=ctha«0; ch«0 = ! / J?_________, shu0 = -r=2______, (132)
F ”p 1 V "p 1
то наибольшее напряжение вычислится по такой формуле:
если — >1,
Р
и
Кольцевое нормальное напряжение достигает максимума тоже у дна
выточки и равно .
а2=(°w)«=w0 = ——4-1,5----------1~ F—fo,5 4~
* N р \т р 1 * т 1 L \ 1
Vss~2
i-|_JL1cI. (136)
' m f p 1 m J J 4 '
От данного решения можно снова перейти к частному случаю -~== 1.
Для этого полученное решение нужно разложить в ряд, а затем
совершить предельный переход. Тогда получим формулы, полностью
совпадающие с (121) и (122).
МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЙ
125
§ 4)
На фиг. 57 даны графики распределения напряжений при --=26,
в правой части по наиболее узкому поперечному сечению, а в ле-
Фиг. 57. Кольцевая внутренняя выточка при растяжении.
вой — вдоль контура вы:очки. Напряжения по всем направлениям от
дна выточки очень быстро зату-
хают, примерно, обратно пропорцио-
нально третьей степени расстояния
от дна выточки. В точках, уда-
лённых от оси стержня на рас-
стояние, равное двум глубинам вы-
точки, существует уже приблизи-
тельно такое же напряжённое со-
стояние, как и в стержне без вы-
точки. В силу этого удаление
внешнего контура от выточки, при-
нятое на фиг. 57, может считать-
ся вполне достаточным. Изменение
обоих наибольших напряжений, в за-
висимости от кривизны выточки,
изображено на фиг. 58.
В. Чистый изгиб. Решение для
случая чистого изгиба заключает
в себе прежде всего элементар-
ную задачу об изгибе сплошного
цилиндра. Эта простейшая задача
Фиг. 58. Наибольшие напряже-
ния в мелких кольцевых внут-
ренних выточках при растяжении.
решается с помощью функций
126
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
[гл. V
следующего вида:
Ф‘= <2=.-(4-4”)'<’
Фа = -ДГа)г;- О2 + — 2х2);
4 2а (4—а) t v 1 z’
ф9==0.
(137)
В соответствии с (58) главы III отсюда получаем:
Р
(4-а)/
F =
-з+2^]-(138)
Напряжения вычисляем по (68) и (69) главы III:
— Р > 0y~°z —“ та?у ~ Zyz —’ Zzx — 0 39)
Но м и н аль ное напр яжение
тарное напряжение при
Оно равно
р представляет, следовательно, элемен-
изгибе сплошного цилиндра в точке у = 1.
(140)
Чтобы получить исходные данные для построения функций, соот-
ветствующих напряжению возмущения, начнём, как и в предыдущей
задаче, с частного случая, когда выточка образована сферической
поверхностью.
Частный случай /==р. С целью упрощения будем считать глу-
бину выточки равной единице [сравни (7)]:
= (у)и=^и0 — и$ = !•
(141)
w-02
Функции, заданные формулами (137), выразим теперь в сферических
координатах, определяемых уравнениями (7). Сопоставлением функ-
ций (137) с общим выражением (40) гармонической функции в сфе-
рических координатах найдём, что в функциях, содержащихся в вы-
ражениях (137), мы имеем дело со случаями v = 3, п==1, для Фо;
v = 2, п = 1 для Ф1 и v = 2, п = 0 для Ф2, причём Ьт = 0. Доба-
вочные функции должны соответствовать напряжениям, с помощью
которых можно бйло бы удовлетворить граничным условиям (13).
Это достигается с помощью функций, которые от v и w зависят так же,
как и функции (137), но в слагаемых, зависящих от и, значок v за-
§ 4j МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ГЕЛЕ ВРАЩЕНИЯ 127
меняется на —v— 1. Решение получим, если добавим ещё функ-
цию ф0 при v = — 2, п=1. Имеем поэтому:
фо __ |~ и9 -J- (5 sin3 гл — 4 sin n)cos w-f-
д
-|—j- sin v cos id;
“ (142)
ф1e sin V cos v cos w;
a> + #] <3 s,n’ ’ -2); *’ “ °-
С помощью соотношений (7—11) получим
функцию напряжений:
^=[т“(4-4 +3^-]
44t4H”3+2”)“’+4-4+4-24]si"scos^ <143>
нормальные напряжения:
Г 100В . 16 + « _ 48 + За <1 . » .
<з =1 — ри------R- 4-----г— С------+— D sin8 v cos id +
“ L r и6 1 и* и‘ J 1
. Г 64 । 80В Н4-2а„ . 36D1 .
_|_ |рИ__ -У + ---------Т_с + -JJJ-j sin v cos w;
% = [р« - 65В (1 + а) 1 цб д4 С+ 3 4-За рЛ q . —D sin3 v cos w -
. [34_ 50В , 1+2а_1 .
’ 1 а4 и* 4 4~ С sin vcos w; 1 и4 1 9
(144)
_[35B 5—5а —15+15а _1 . ч ।
°«> — 'I---c H-------jjr— D J sin ® cos w -f-
, [34 30B , — 3+4(1^ . 12—12а .
"Г |7T--«Г '---Ji-с Н----й4~- D\ sm fcosw
касательные напряжения:
VU1>
r»„-L 75В _L ~9 + «+ • 27-За+] • 9
~Ри~Т н-------с -[--------D Sin2 HCOS11COS ID +
I [34 20В t з + а „ , —6 + 6а
“Г[«г-'йг_1'“«г С“*----3—£ cos Я cos w;
» ___| 10В । — 2+а п । 6 — 6а р, 1
ч« — I п----------ь D cos v sin v sin in;
_[ 25В , З + а . —9 + 9а 1. „ . .
— I----у Н-----С Н----------D Sin2H Sin ID +
-I Г ЗА 4-29^ З+а г г 6 — 6а1 л
Ч [ 7^ + ----С~Г~~&~ ^Js'nw.
(145)
128
теория Концентраций в пространственной Задаче
[гл. V
Граничные условия (13) дают шесть уравнений для произвольных
постоянных. Два из этих уравнений тождественны между собой, а
одно из них можно рассматривать как следствие остальных, так что
остаётся четыре независимых уравнения, содержащих четыре произ-
вольных постоянных. Решение этих уравнений при «0™1 даёт:
__ 4 —9а — 7а*
“ 12а (12 +7а) р9
_ 12 + 63а
12а (12 +7а) Р'9
Р .
12 +7а 9
4 — 7а
U~ 12а (12 +7а) Р*
(146)
Как и можно было ожидать, наибольшее напряжение от изгиба
возникает у дна выточки. Найдём:
5(17----)
’< = («.>„, =-7----<!47>
-г Ч13- -S')
0=0
Кольцевое нормальное напряжение достигает максимума там же и
выражается формулой:
----("_'£} Р при -F = 0’3)- <148)
’“7 4 V3- т )
w=0
Общий случай. В общем случае^ при наличии выточки любой
кривизны, как и при простом растяжении, достаточно пользоваться
функциями, аналогичными прежним. Таким образом, мы возьмём
функции с теми же значениями п и v, но только теперь будем исхо-
дить из гармонической функции (38). Так как мы применяем эллип-
тические координаты, определённые уравнениями (1), то глубина
выточки равна:
/ = (у)а-«. =ch«0. (149)
К
2 •
<07=0
Для краткости, положим:
(150)
Тогда
Фо = V"1 }Х(Ch3“~ICh “)+ s[(5ch8«-
— 4ch«)T—5sh«che-]--|- th и (5sin8г» —
— 4 sin г»)cos a,-f"''ЦТch и — th и)sin v cosw;
(151)
§ 4]
МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ
129
[(^4 + 4?)Xsh и ch и + C(sh и ch и Т~ ch и +
Ф1 —' I 2а (4— a) v 1
I 1 .
4- 4~ТЛ— ) Sin V cos V cos w\
О СП U / J
(1 = Г( ch*и - 4 4-D [(3 ch*и -2) Т-3sh «Iх
1 * I 2а (4—а; \ о / J
X(3sin2 v — 2); Ф3 = 0.
(151)
В соответствии с этим функция напряжений принимает форму:
F~ _ ^)ch8 и 4- (— 3 + 2а) ch и ] sin» v Ц-
*4" £( — 3 4- 2«) ch8 и4-2+_^_24а_ Cj1 w J s|n v}cos w_|_
4- A [ch и T — th u] sin cos w 4*
4- В £(5 ch3 и — lchu)T — 5 sh и ch « § th и J X
X (5 sin3 v — 4 sin v) cos ® 4 C £(ch3 и — ch и) T—
— sh и ch и 4* -g- <h и j sin v cos2 v cos w 4*
4~D[(3ch8 и — 2ch«) T—3shuch«](3sin8t>—
— 2slot»)cosw. (152)
По формулам (4) и (5) вычисляем далее нормальные напряжения;
для краткости записи их выражений снова введём величину А2.
Найдём:
а„ = g ch8 и sin v cos2cos w 4- 2A 3-in 7°s w ( —-
~ sin3 d cos w —15 ch8a 4" U ch «) T-f-
-[ 15shrzch« — th « 4--y£f[^|-(--^7- sin v cos w £(12 ch8 и —
— 8ch) Г—12sh«ch« - +
' 15 ch3 и 15 Л2 J 1
Q |Г "I
4-^5 sin8 ncoswjl (6 — 4а) ch3 «4-(—64-За) ch а Г4“
4- ( —6 -j- 4а) sh и ch и 4-^2 — -0 th и — +
+ sin v cos w —44- За) ch8«-}~ (4 — 2а) ch«j Т4~
4- (4—За)sh и ch и th « 4- __-3_2_[ +
9 Зак. 3475. Г. (Нейбер.
130
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
[гл. V
+ sin3 t»’cos <w |£(—9-}- 6a)ch3« 4-(5 — 5a)ch «jT-f-
-}-(9 — 6a) sh «ch + a) th a} -|-
+ sin v cos w |£(8 — 5a) ch3 и -f- (— 4 -f- 4a) ch и J T 4-
+ (~8 + 5a)sh«ch и4 ( —|aJtha--2-sl?^2ch“|; (153)
p' 1 o 1 . « . Л . sin V cos w .. . -
a« =5= sh2 и ch a sin8 v cos w 4- 2 A --- th и -4-
v ft* Л4 •
+ -^-sin3t» cos те» £(15 ch8« —12 ch «) T—
]10 Q Г
+ -^5- sin v cos те» I (— 11 ch3 и 4*
-|-8 ch a) T-|- 11 sh«ch«— 4 Ц~Ь
+ ^5 sin8 v cos те» {£( — 6 4- 4a) ch8 и 4* (4 — 3a) ch и j 1 -|-
+(6 — 4a) sh «ch и -f- yth + sin v cos те» X
X{[(6 — 3a)'ch8«4"(“44-2a)ch«] 7*4.( — 64-
+ 3«)>h“^“—S-th“+sT^} +
4-^ sin3 т» cos те» ££(9— 6a) ch3 «-|"( — 8 -J- 5a) ch и j T-\-
4- (— 94“ 6a) sh a ch « -f- (2 — a) th «| 4-
+ sin v cos no |£(— 5 4- 5a) ch8u -f" (4 — 4a) ch « J T-{-
+ (5 — 5a)shach« + (-4+y)th«4- 2 “ } 1
% —2Л Sl2\r?h3WgS~ + 10 5 sint»cosTe»( — ch«T +
+th “++is^ot)+c sin ®cos 4(2 ~a) (ch “ T~
.. ч 2sha , ( 2,2 \tha 2she 1 .
th“) 3ch3« + \ з + з a) Л2 3A»ch3«]“r
4-6Dsint»cosTe»[(l—a) (chuT—th«— Yl •
§ 4] МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ J31
Выражения для касательных напряжений получим по формулам (6),
причём, ради краткости, опять введём А2:
. о 1 nACOSbCOSW .
xuv == — sh и ch2 и sin2 v cos cos w + 2 A--------[-
- f- 12Д sin2 cos v cos wjj — 15 ch2 « 4) sh u
4-15 ch2 и — 9—зЗЯГц] + Цг cos * cos w (4 ch2 a 8h “ T~
— 4 ch2 « + 4 + шг0 + & sin2© cos © cos да {£(6—-
— 4a) ch2 a — 2 a j sh и T-J- (т- 6 -f- 4a) ch2 и -j- 4 —
+ + S cos ©cos да [(-2 +a) X
Xch2ashaT4-(2-a)ch2a—i + + +
sin2 ©cos ©cos да {£(—9 6a) ch2a-J-2—2a j sh a T-f-
4*(9 — 6a)ch2a — 5 4~ 4a } 4~ 7J5 соз©сов’да£(2 — 2a)ch2и sh и T-\-
+ (-2 4-2«)ch2a-^+^]; (154)
T«W e "Jf" [(5 Ch2 и — 4) T— 5 sh a 4- 3^“] sin « cos © sin да -f-
4- sin © cos © sin да (2 — a)f— sh8a T-J- sh a—~ 4.
1 л 4 3ch2n/ 1
4“^jf sin © cos © sin да^[(3— 3a)ch2a — 24-2a] T4-
+ (—3-f- 3a)sh и|;
T«W= -~2hSu sta^shachaT— ch a 4-^2—4.
"Ь15 c"h^ a) (6 s,n2 + 4 sin w [<2~ a) (sh a ch a T —
—Ch“ + jck) + ^] cos2©4-^sinw(l —
—• a)(8h a ch a T— ch a 4- 3^) (з sin2 ©v—2 ).
Из граничных условий получим восемь уравнений; при этом в
выражении для нужно положить равными нулю коэффициенты при
sin8 v cos w sin v cos w sin v cos w .
Л2 ’ Л* И Л* ’
132
ТЙОРИЯ КОНЦЕНТРАЦИИ в ПРОСТРАНСТВЕННОЙ задаче
[гл. V
Л . sin2 V cos V Cos W COS V COS w
в выражении коэффициенты при -------------——-------------------
COS VCOSttl
и при -----; а в выражении для xuw приравнивать нулю сле-
. - sin* v sin w sin w
дует коэффициенты при -----— и при ——. Однако, два из этих
уравнений тождественны друг другу; далее, три из них являются
следствием остальных^ так что независимыми между собой остаются
четыре уравнения, т. е. столько же, сколько и неизвестных. Для
краткости, обозначим:
! 3 ch4 и0 [sh и0 (Л —11 + ch2 «0 = g; 1
«=«• I
ch «0 = t; |
(155)
£{£[£(4— а)+ 20 ch2 u0 —16 —4а] —
— 32ch2iz0+16—4а} —16ch2«0==M (156)
Тогда получим:
л= — -|5 + (-2PD,
10B = -^^{g[g(l-a)(2-a) + (10-8a)l2-4+
+ 4а] + 4/2|; (157)
С *= Зр‘8а£ "° { g [ g (2 — 2а) + Ю12—4 + 4а] + 4/2 } ;
6D |g( — 2 + а) - 10*2 + 4 + 2а] — 412}.
Наибольшее напряжение <зи в точке у дна выточки равно:
’=<4-..=# {* [^(10<а ~2а> - ж-+
° = Т +16 —4al —16/2 у. (158)
’ ю = 0 J ; ) -
Кольцееое нормальное напряжение достигает, наибольшего зна-
чения также у дна выточки и равно:
«а = (^аш1в. = ^^^(10^ + 8-8а) + 4/2]. (159)
• Ж
W — о
§. 4]
МВЛКЛЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ
133
Если принять во внимание равенства (1321, то уравнения (158)
и (159) дадут наибольшие напряжения в функции ; при этом
Г
t Г
(160)
где под с подразумевается величина, определяемая формулой (134).
Если полученные выражения разложить в ряд по степеням — 1,
то предельным переходом, устремляя у к 1, найдём полное соот-
ветствие. с ,(147) и (148) (такого вида вычисления проведены
в гл. V, 4, D). t
Распределение напряжений по контуру выточки при .— =10,
— .= 0,3 дано на фиг. 59. Этот пример замечателен не только тем,
что, вследствие выточки, возникает очень большой максимум напря-
жений, но прежде всего тем, что напряжение в изогнутом стерж-
Фиг. 59. Кольцевая внутренняя выточка при изгибе;
не может оказаться большим внутри, на поверхности выточ*
к и, а не на наружной поверхности стержня. Из линий одинако-
вых напряжений aw, начерченных на фиг. 59 (направо), совершенно
очевидно, с какого места устанавливается прямолинейный закон рас-
пределения напряжений. В расстоянии от оси х, равном удвоенной
глубине выточки, влияние? внутренней выточки на распределение
134
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
[гл, V
напряжений едва заметно, и стержень ведёт себя там практически
i
как сплошной цилиндр. Отношение , которое необходимо для то-
го, чтобы можно было применять теорию мелкой внутренней выточ-
ки, и которое строго математически должно быть исчезающе малым,
Фиг.’бОлНаибольшие^напряйсения'в мелких кольцевых’внутренних
выточках при изгибе.
практически может быть и не очень малым; однако предыдущее
решение при этом будет оставаться достаточно точным.
На фиг. 60 дана зависимость наибольшего напряжения от кри-
визны выточки и от коэффициента Пуассо'на.
С. Чистый сдвиг. Решение задачи о сдвиге при наличии мелкой
внутренней выточки основывается на тех же общих правилах, что
и в случае задачи об изгибе.
Возьмём сначала сплошной цилиндр, сечение х—0 которого
находится в условиях чистого сдвига. Решение для него даётся
посредством следующих функций:
у(у‘+^~4**>:
<Ра Х( — 2 д-зА. Ф3 = 0.
“ а (5—а)Ь! 1 3 / *
(161)
§ 4] МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ 135
F = — рху-}
(5ЙуИ<4-2а> 0'В 9+*2) + 4fta- 1) 5 /162>
a® = 4(5—ху; °р —
(163)
Д у2 (а — 1)*2А. г л-т ("" 6+2а)р tt~ /Чпл\
Ъ — Р\1 “75— (5 —а)^)’ V — 0’ т«* (5-а)^ Уг‘ <1б4)
Легко убедиться, что условия (НО) на поверхности выполнены.
Из (164) вытекает, что р есть касательное напряжение, действую-
щее в точке на оси сплошного цилиндра. Обозначим перерезываю-
щую силу в стержне буквой V. Согласно (16) найдём:
V = Р„ = f dy dz = p J j* [ 1 — £ — <**• (165)
F F
Интегралы f fу* dydz и fz9dydz представляют собой, как изве-
F F
it
ctho, экваториальные моменты инерции; каждый из них равен -у ;
интеграл JJ dydz равен площади поперечного сечения; таким обра-
F
зом получаем:
_5 —a V Зт + 2 V
Р~~4 — а nb*~2m + 2 it*2’
(166)
В дальнейшем нужно опять выразить предыдущие решения через
криволинейные координаты в соответствии с избранной выточкой.
Именно, в частном случае при t = р для сферической выточки—через по-
лярные координаты, а в общем случае — через эллиптические коор-
динаты.
Частный случай t — p. После перехода к координатной системе
(7) получаем функции, которые можно рассматривать как часть общей
потенциальной функции (40) с определёнными значениями п и v. При
разыскании поля добавочных напряжений мы будем сразу пренебре-
гать членами с коэффициентом . В рамках теории мелкой выточки
при определении коэффициента концентрации в конце вычислений
этими членами всё равно мы должны были бы пренебречь. Поэтому
речь идёт теперь только о том, чтобы на напряжённое состояние
^—р наложить другое напряжённое состояние, причём такое, по-
средством которого удовлетворяются граничные условия (13).
При составлении же выражений для функций, описывающих на-
пряжённое состояние стержня с выточкой, подверженного изгибу
силой, в конечном счёте для функций Фо, Ф1( Фа нужно снова
принять их выражения (161).
Вместо (161) при этом пренебрежении получаем только одну
функцию
35
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
[ГЛ. V
Фо = —рху~—ри? sin v cos v cos w, (167)
которая соответствует случаю п— 1, v = 2. В качестве добавочной
функции к Фо прежде всего может явиться функция с параметрами
п=1 и v==—3. Однако добавление этой функции недостаточно, и
мы должны добавить ещё функции Фх при n=l, v =—2 и Ф2,
при п ==» 0, v = —2, дающие в выражениях для напряжений слагае-
мые, одинаковым образом зависящие от v и w.
Тогда получим:
Фо = Г —+ sinvcosvcosw: Ф, = Д;sintfcosw;
Фа = §со^; Ф3 = 0.
Функция напряжений будет иметь вид: } <
•у_ Г а I Л I В -|- С1 .
Г = —---------------I sin ®cos® cos та.
Нормальные напряжения вычислим по формуле (10): .
°« = [2Р — — Чг (s + С)] sin v cos v cos w;
зю=[ — 2pH-^ + ^^(B-|-C)l sinvcos®cosw;
(168)
(169)
(170)
<Jw = [|r4'^r^(s+c)] sin V COSH cosта.
Соответственно (I!) выводим, наконец, формулы для касательных
напряжений:
Ч, = [р + (В + q]cos 2® cos та 4-
. -|_^(В-С)со8та;
%«, = [р — (# + О] s>n v sin та;
[4 Л 2 -4- <х гх , 2® — 2 .
—р------г-----Х-В-4---5— С cos®sinw.
г u5 u3 • ‘ u3 J
(171)
Постоянные определяются из граничных условий и принимают
следующие значения:
В-=С; (172)
причём, ради простоты, положено м0 = /= 1. Максимальное каса-
тельное напряжение возникает у дна выточки в точке, где каса
§ 4] МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ 137
тельная к контуру параллельна направлению сдвига. Там оно равно:
15(1--) 1
=------22/р(=1,91р при 1 = 0,3). (173)
”=«'=2- 7~т
Вдоль оси у касательное напряжение достигает относительного
максимума; оно равно:
, ч . । - Р Г 24 . 5(4—«)~|
4-f-5a|_ И» J*
Дифференцируя это выражение по и и приравнивая результат нулю,
найдём точку, где достигает относительного максимума
(175)
Вставив это значение и в (174), для относительного максимума полу-
чим выражение:
( = 1,09 р при 1 = 0,з). (176)
Нормальное напряжение av, действующее на поверхности, до-
стигает при -й = — ~ w = 0 (и =з uQ = 1) своего максимума, рав-
ного:
---р ( = 2,73р при 1 = 0,3 ). (177)
? й*
В том же самом месте действует наибольшее кольцевое напряжение
ow> численно равное:
; . f
аа = —( = О,82р при 1-=0,з) . ’ (178)
7 т
Общий случай. Для выточки любой кривизны нужно выразить
использованные выше функции в эллиптических координатах, сохра-
няя те же значения показателей пну. Получим
Фо = ^ — р sh и ch «4", A ch и ch ц 1 з сЬи)]
•• X sin к cost» cos w; . (179)
<1>! = В [ch и Т— th й] sin vcos w;
O8i=C[sh«T— f] cost»; Ф8 = 0.
138 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ. V
Здесь члены, содержащие множитель —, сразу опущены. Функция
напряжений имеет вид:
(180)
ilnv cos т> cost».
Нормальные напряжения вычисляем по формулам (4) и (5). При
этом опять пользуемся сокращенной записью, введя величину Ла.
s h 2«—(4 4- (1 — а) (в 4- С) )(sh 2« Т— 2 ch л) 4-
+(т ± 2В) dhMsln* cos ® cos w+
+ -Ц(—25 + Оch « 4- (у + 2В) 4й sin v cos V COS tv;
°»=M“psh2"+IA4"(1—a)(fi+C)lx
X (sh 2tf T— 2 ch й)4- — 2^4- (2—a) <?] 757 4-
1 Г /ЧА \ 1 iv
4- ьг (2B — C)ch и — (-£4- 2B) Bsin<o cos vcosw;
» Л» Iх z V C 1 »»ll
Вычисляя касательные напряжения по формулам (6), найдём:
cos w I ьа .
Tiw = —^“jPch3a4-
4- [4 4-(1 — a)(B 4-C)J(—ch9« Г4- sh «) 4-
+ (2В-С)811»} + ';°!’У'с{-рсЬ2« +
+ l4+(l—«)(B+C5I(ch2aT—2sh»)+
+ [-!+(— Пв1ет} + *Ь“тЛ(-2в + С)<*’« +
(181)
>in V COS V cos w.
(182)
= Цр sh « + [4 + (1 — <x)(B-b C)J(— sh »T+1)+
+ [ “* 5 + (* ~~ В]ж } sin v 8in w>
-Uw = £{—Pch I»4- [A 4-(1 —a) (S + <?)](ch a T—
— th и) — 4- 2в1 тлД! cos v cos w.
МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ
139
§ 4]
Граничные условия сначала приводят к шести уравнениям для опре-
деления постоянных, вошедших в решение. Действительно, в выраже-
нии для о„ мы должны приравнять нулю (для « = а0) коэффициенты
sinvcosv cost» sinvcosv cosW „„„ _
при -------------- и при ------, в выражении для —
. . cost» sin2» cost» „ cost»
коэффициент при —jp -» при------------- и при ; в выраже-
, , cos V cos W „
нии приравнивается нулю коэффициент при------------. Два из
шести уравнений тождественны, кроме того два других уравнения
являются следствием остальных, так что в конце концов остаются
независимыми только три уравнения. Из них находим следующие зна-
чения постоянных
А = з(у—ch2«0)c; В = —
/>ch2 и»
(183)
ch2 я0 arcctg (sh e0) + sh «о
-|-2sh«0
При вычислении максимумов напряжений опять в качестве параметра
целесообразно ввести кривизну контура, согласно (132). Кроме того,
для краткости, введём обозначение:
-27+2}, (184)
где с определяется формулой (134).
Для наибольшего касательного напряжения получаем:
°s5)
Координата точки в сечении it) = 0, v — , где возникает наи-
большее касательное напряжение, с достаточной точностью опре-
деляется уравнением sh и == ]/з sh и^ или
-" = Ж5^1 + ЗзЬ"«„ = «
р
140
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
[ГЛ. V
Само наибольшее напряжение в этой точке равно
Напряжение аи достигает максимума на внешней поверхности при
w — 0, а также при
cos V —
sh и0
Yeh 2 uQ
или x =
t sh2 rzn
chn0 )^ch 2r70
и равно:
Кольцевое нормальное напряжение достигает максимума в том же
месте и равно
(188)
Разложением в ряд можно показать, что при tf/p = 1 получаем
полное соответствие последних ^вух формул с формулами (177) и
(178). (та совпадает только для ш = 3; отклонение для других зна-
чений т объясняется приближённым определением точки, где имеет
место макеймум.) На фиг. 61 и 62 показано распределение напря-
жений для т/р е 10, 1//tz = 0,3. Характерные особенности в
этом случае в основном те же, что и в случае внешней. выточки.
На фиг. 61 налево (осевое сечение в направлении сдвига) очень
ясно видно, как напряжения ow и хи1} вблизи дна выточки прини-
мают наибольшее значение, но в точке самого дна всё же делаются
равными нулю. На фиг. 62 слева дано распределение касательного
напряжения в сечении* перпендикулярном к направлению сдвига. Как
это имело место в задачах растяжения и изгиба, при отсутствии
выточки напряжение распределялось бы равномерно; наличие же
выточки очень сильно искажает напряжённое состояние и при пере-
мещении к краю сильно увеличивает величину напряжений. Наиболь-
шая концентрация имеет место в точке, где касательная к контуру
совпадает с направлением сдвига.
На правой стороне обеих фигур начерчены траектории касатель-
ных напряжений и линии их одинаковых значений по всему попереч-
ному сечению. Равнодействующую касательных напряжений (^v)resJ
необходимую при вычерчивании траекторий касательных напряжений
§ 41
[мелкая Внутренняя выточка на телё вращений
141
Фиг. 61. Кольцевая внутреняя выточка при сдвиге; слева—сечение в пло-
скости силы V с эпюрой напряжений;£справа—поперечное^сечениехс линия-
ми напряжений сдвига.
Фиг. 62. Кольцевая внутренняя выточка при сдвиге; слева—продольное сече-
ние, перпендикулярное к направлению сдвига, с эпюрой напряжений; справа
— поперечное сечение с линиями равных напряжений сдвига.
142
ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ
[гл. V
и их одинаковых значений в поперечном сечении, можно определить
по компонентам и (которые нам известны) следующим простым
способом. Как вытекает из (182), мы можем положить
•'«в = (’«Л=о cos в (т«Х=«/2 sin w. (189)
Фиг. 63. Определение
равнодействующей ка-
сательных напряжений.
Значения ("цД^жо и (тси,)«>=«/2 Уже даны на левой стороне обеих фигур
в виде кривых. Для того чтобы найти теперь в какой-нибудь точке Р
поперечного сечения, центр которого принят
за начало О координат, равнодействующую ка-
сательных напряжений, как по величине, так и
по направлению, отложим в направлении оси jz,
во-первых, значение (т„с)и=0, соответствую-
щее у — ОР, во-вторых, значение
соответствующее z — ОР. Получим точки
А и В фиг. 63. Затем на отрезке АВ, как
на диаметре, построим окружность; пусть
прямая, параллельная ОР и проходящая че-
рез точку В, пересекает эту окружность в
точке С. Тогда PC изображает собой равно-
действующую касательного напряжения как
по величине, так и по направлению.
Для доказательства проводим линии, изо-
бражённые на фиг. 63 пунктиром; точки их
пересечения обозначим буквами D и Е.
Так как касательные напряжения тмв и
с одной стороны, по определению, должны
итти вдоль направления w и перпендикулярно
к нему, а с другой, благодаря (189), являются
компонентами РА и РВ, то они и будут
изображаться отрезками PD и РЕ (у на чертеже указан знак
минус, так как в направлении этого напряжения координата w убы-
вает). Но по построению PD и РЕ являются компонентами равно-
действующего касательного напряжения PC.
На фиг. 64 дана зависимость всех максимальных напряжений от
кривизны выточки.
D. Кручение. Здесь опять имеет место особый случай, предста-
вленный уравнениями (96) и (97). Прежде всего для сплошного ци-
линдра, не имеющего выточки, напишем:
Фое=О; Ф1==0; Ф2— ‘ая&Г хг>
8 аяо* ’
(190)
(191)
<,«=<3,e0.=V=°;
_ 2Afz . т _ 2Л4у
Х«*гс“= лМ ’ lrt— яМ ’
§ 4] МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ 143
где под М понимается крутящий момент, для которого должно быть
выполнено равенство (16) с заменой Мх на М. Доказательство этого
положения основывается на [элементарных формулах сопротивления
материалов.
Фиг. 64. Наибольшие напряжения в мелких кольцевых внутренних ,
выточках при сдвиге.
В этой сравнительно простой задаче мы начнём сразу с общего
случая, не выделяя частный при /=»р. Перейдём поэтому к эллип-
тическим координатам; получим:
Фв __ _ Ф»
COSW Sinw
2Af '
г—г sh и ch и sin v cos о.
anb*
(192)
Член sh и. ch и, зависящий от и, на основании общего выражения
(38) потенциальной функции соответствует значениям я « 1, v = 2.
144 ТЕОРИЙ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАЦАЧЕ [ГЛ. V
Дополнительные функции получаем заменой v =±= 2 на v = — 3; в резуль-
тате имеем - f
Фз Фа 2Л4 Г « « । л t i «
- -----= —rr sh a ch и -4- A (sh и ch и T—
co3w sinw аяМ L v
— ch и 4- -s-TTT-Yl s*n cos
1 O,Ch It /J 7
®! = 0; Фо = О; F = 0. '
Отсюда, согласно (4), (5) и (6), найдём: .
== % 2=2 аа>г= 0>
^uv== 0 > - -
— |sh«cha-|-4(shucha Т—
= [сЬ9« + л (ch®“ г—sh “ —
---“У1 s*n v cos '°’
3 ch2 и/J . ’
(193)
(194)
(195)
В качестве номинального напряжения введём напряжение кручения
сплошного цилиндра в расстоянии t от его оси.
Тогда по (129) имеем —
','‘=7=ЖГ <197>
Граничное условие (13) длд дос/однроЙ А даёт следующее значение:
: + . ... (198)
Наибольшее напряжение возникает у дна вытрчкй и равно 7
тт« в — (Tw)u=«o = f + Shuochu0 (*h tt° ch “o(7)«=mo
§ 4] МЕЛКАЯ ВНУТРЕННЯЯ ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ 145
После введения кривизны выточки, согласно (132), и обозначения с
из (134), это выражение можно записать в форме
/1 \2
„ 2( — — 1 )
__________\Р_______/ __ ' (200)
Распределение напряжений для t/p = 26 дано на фиг. 65. Для внеш-
него края — радиус Ь цилиндра можно принять равным 2 t, так как
Фиг. 65. Кольцевая внутренняя выточка при кручении.
на такое расстояние "уже влияние выточки не распространяется. Макси-
мальное напряжение, возникающее на контуре выточки и равное 2,9 р,
„ превосходит напряжение на поверхности цилиндра, где оно равно 2 р.
Вдоль поверхности, особенно по направлению к оси, касательные
напряжения очень быстро убывают. Осевое сверление с малым ради-
усом очень мало исказило бы напряжённое состояние, так как мате-
риал вблизи оси стержня почти не деформируется. Налево указаны
линии напряжений, дающие в каждой точке направление равнодей-
ствующего касательного напряжения. Эти линии проще всего найти
путём разыскания сначала дифференциального уравнения д^я них, а
затем путём его интегрирования. Так как компоненты и и и линей-
ного элемента линии напряжений ;относятся друг к другу так же,
как компоненты и и v касательного напряжения, то имеем:
du
h dv dv
10 Зак. M75. Г. (Нейбер.
(201)
146 ТЕОРИЯ кон центрАЦИИ В ПРОСТРАНСТВЕННОЙ задаче [гл. V
Если вместо компонентов и подставить их выражения(194),
то после интегрирования получим следующее уравнение для линий
напряжений:
£ ch4 a-f-A (ch4 иТ— ch9 и sh и — ysh «)jsin4 v = const. (202)
Зависимость наибольшего напряжения от кривизны выточки '.дана
на фиг. 66. Наибольшее напряжение для частного случая /==>р,
который особо мы здесь не рассматриваем, получим из (200) по-
средством предельного перехода. При этом, для краткости, положим:
Тогда
и, наконец,
______________________24*
р 3(1+2?-Н»)(1- 1 + ^. . 50-3
2да________ 1
I9’ + * * * + • • •
Полож / = р, т. е. 0 = 0, для шаровой выточки получим:
'с»« = —
р 4’
(203)
(204)
(205)
(206)
в чём легко убедиться, исходя и из сферических координат.
Мы видели, что во всех случаях нагружения цилиндра с внутрен-
ней выточкой вместо
Фиг. 66. Наибольшее напря-
жение в мелкой кольцевой
внутренней выточке при
1 кручения.
номинального напряжения, отнесённого
к наиболее узкому поперечному сечению*
вводится в расчётные формулы в качестве
сравнительной величины напряжение р
в сплошном цилиндре. Максимальное нат>,
пряжение всегда получалось умножением
этого напряжения р в сплошном цилиндре
на коэффициент, зависящий только от кри-
визны t/p и являющийся коэффициентом
концентрации мелкой выточки. Вследствие
закона затухания искажение в распределе-
нии напряжений делается незаметным уже
на сравнительно небольшом расстоянии
от оси, так что в известных пределах
можно использовать теорию мелкой вы-
точки, как приближённую теорию для выточек любой глубины. На
фиг. 57, 59, 61, 62 и 65 это принято во внимание, и внешняя
ЙЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ
147
§ 5]
поверхность взята на расстоянии только лишь b — 2t, или 31.
Этот ход мысли приводит веб же только к приближённому способу,
при котором обязательно имеется большая или меньшая ошибка.
Ослабляющее влияние внешней поверхности может быть учтено при
этом лишь надлежащим выбором номинального напряжения р, так
например, при кручении можно принять p = (l —ф).хп' Этот спо-
соб часто, но, вообще говоря, не всегда, даёт достаточно точные
значения. Влияние внешнего радиуса b должно учитываться тем, что
кроме коэффициента концентрации мелкой выточки нужно опреде-
лить коэффициент глубокой выточки и наложить их друг на друга
по способу, указанному в 11,4. Ниже мы увидим, что существенное
влияние оказывает также осевое внутреннее сверление, которое
должно быть учтено посредством третьего предельного значения
коэффициента концентрации.
В следующем параграфе мы займёмся определением всех тех предель-
ных значений коэффициента концентрации, которые необходимы для
полного исследования выточек на телах вращения. Соответствующие
этим выточкам напряжённые состояния располагаются на достаточном
удалении от оси стержня и вследствие этого могут считаться
двумерными.
5. Выточка на теле вращения при двухмерном напряжённом
состоянии.
Мы будем различать следующие четыре случая:
1) Мелкая внешняя выточка (фиг. 67,
2) Мелкая внутренняя выточка при большом осевом отверстии
(фиг. 68, 1<с).
3) Глубокая внешняя выточка при большом осевом отверстии
г (фиг. 69, а<Сс)-
4) Глубокая внутренняя выточка (фиг. 70,
Первые два случая, точно так же как и последние два, можно
рассматривать вместе, так что с этой точки зрения мы будем разли-
Фиг. 67. Мелкая кольце-
вая внешняя выточка.
Фиг. 68. Мелкая кольцевая
внутренняя выточка при
большом осевом отверстии.
чать только лишь мелкую и глубокую выточку. Области с искажён-
ным выточками напряжённым состоянием во всех этих случаях
10»
148 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ. V
лежат на большом расстоянии от оси, вследствие чего напряжённое
состояние можно приближённо считать плоским.
Фиг. 69. Глубокая
кольцевая внеш*
няя выточка при
большом осевом
отверстии.
Фиг. 70. Глубокая
кольцевая внутрен-
няя вытояка.
Мы будем пользоваться цилиндрическими координатами, положив
Д! = х; y = rco$W', Zaarslnw. (207)
Обратимся к соотношениям, справедливым для любых криволиней-
ных координат. Из (20), Ш, 3 получим, заменив и буквой х, a v
буквой г, значения коэффициентов искажения
Лд, — 1J hr — 1 *, j-xi г*
Оператор Лапласа Д берём ив (98), Ш, 7
л_ а4 , J4 . 1 д , 1 а4
а*4 "г Зг4 “г г дг "Г Г2 З®4 ’
(208)
(209)
Для ДГ точно так же, как и для напряжений, из (91) и (92), Ш, 7
можно вывести следующие выражения:
ЛГ=2@+еоз»«г-^^+
+ Л (210)
d4F , а\А„ . о д
а>~ 2^AF^“2<xaГ,
°г=3- + y)^+2«(cosw^ 4-sinw^ ;
§ 5J
ВЫТОЧКА НА ТЕЛВ ВРАЩЕНИЯ
149
- == -ст + “ (^+сош^ +sin ;
e(^_sinw*h +
7^-s,n^+coswT&)-
'iw
(211)
'xW г дх dw
1 d’F
Отсюда легко получить формулы, относящиеся к частным видам
напряжённого состояния.
А. Чистое растяжение. При чистом растяжении, в силу осевой
симметрии, функции Ф2 и Ф3 можно считать равными нулю, а для
остальных функций воспользуемся подстановками, ранее использо-
ванными при рассмотрении плоского деформированного состояния
фовЛ+«фр ф* = ^; фа = ф» = °;
фо+х^г=г; фовф'о(*>г); (2i2)
Ф{ = Ф' (х, г); Дф' = ДФ,' = 0.
Тогда
F = Фо 4- хФ, = F' 4- аФ;. (213)
Как уже было отмечено, область возмущения напряжённого состоя-
ния, в которой требуется вычислить предельные значения коэффи-
циента концентрации, удалена на большое расстояние от оси, и, зна-
чит, размеры в направлениях х и г можно рассматривать как малые
в сравнении с самым г. Поэтому при вычислении можно принять;
г=оо, вследствие чего оператор Д перейдёт в
Дг=^-4-^_ (214)
дх2 г ф-2 ’ '
т. е. в оператор Лапласа на плоскости х, г. Из (210), принимая во
внимание, что ДФ' = 0, следует
AF — 2д2ф'1- 2д2ф/1 Г2Ш
дг=др = ^+^ = 2~----------------2"^- (215)
Учитывая'это последнее равенство и точно также полагая в (211)
г = со, найдём:
&F' 1 л, I „ч.
AV ' (216>
Та:г = дхдг ’ Хг* “ 0* С®“ °'
150 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ. V
Следовательно, напряжения здесь выражаются через функцию на пря-
жений так же, как и при плоском деформированном состоянии.
Этим и доказано, что в данном случае речь идёт о плоской задаче.
Проведение вычислений поэтому излишне, так как соответствующее
решение было получено в гл. IV. Для коэффициента концентра-
ции в случае мелкой выточки можно пользоваться уравнением (131),
IV, 4, а для глубокой выточки применима формула (190), IV; 6.
Для максимального значения напряжения aw, которое обозначим
буквой а2, из (216) при ar = 0 (свободный контур) получается зна-
1 ь
чение — <зх. При этом нужно иметь в виду следующее: соотноше-
ние (216), выведенное в предположении, что область с искажённым
напряжённым состоянием находится на большом расстоянии г от оси,
справедливо только лишь для напряжений, подчиняющихся закону
затухания, т. е. для самих местных напряжений, и несправедливо
для первоначального напряжённого состояния ада = ап, в стержне
при отсутствии выточки, когда кольцевое нормальное напряжение
равно нулю. При вычислении максимального напряжения а2 нужно
поэтому вместо <зх поставить не а только приращение at — an,
вызванное самой выточкой; тогда получим:
' (217)
В. Чистый изгиб. Заметим, что и этом случае напряжённое
состояние зависит не только от х и г, но также и от координаты w.
Как следует из задач, рассмотренных уже в V, 3, В и V, 4, В,
функции Фо и Фх в этом случае содержат множитель cos w и мы можем
положить:
Фо = <Ро (х> r) cos w> (•*> r) cos (218)
Применение оператора (209) приводит тогда к следующему диффе-
ренциальному уравнению для <р0 и ®,: ' 4
(219)
дх* ' дг* * г дг г* ‘0 rz \ /
Положив здесь г = <х>, опять получим потенциальное уравнение
в плоскости х, г, т. е. появляющийся при изгибе множитель cosw
(в соответствии с простым растяжением) не вызывает никаких изме- .
нений в структуре основных дифференциальных уравнений. При
решении задачи можно снова принять Ф3 и Ф8 равными нулю, и
поэтому остаётся справедливым т’от же ход рассуждений, что и
в задаче о простом растяжении; значит, коэффициенты концентра- ’
ции в этих двух случаях одинаковы. >
С. Чистый сдвиг. Из рассмотренных в V, С, 3 и в V, 4, С
задач о сдвиге следует, что Фо и Ф, содержат множитель созте>, а
функция Ф2, которую теперь считать равной* нули? нельзя, зависит
§'5]
ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ
1:51.
только от х и г. Для установления номинального напряжения необ-
ходимо найти прежде всего напряжённое состояние в полом цилин-
дре с внутренним радиусом с, с внешним — Ь, работающем на сдвиг.
Оно представляется следующими функциями
Ф, = С | - (44- с‘) (»• -I л)-
' bW х 1
-------cosw;
а г I 9
. (220)
^“4Л)+Т7] cos w;
= *8 = 0.
F = С { - (й® -|- с») хг + [(4 - 2а) хг* +
cosw; (221)
AF = -=^— xr cos w, (222)
которые дают следующие 'компоненты* напряжений
ад, = С 4- xrcos w; ог = 0; aw = 0;
C^’-j-c8——r9jcosw; xrw«=sO;
т<и»= —с8— ^-j-^^lslnw.
L rs 1 5 — a J
Если обозначим перерезывающую силу буквой V, то путём сравне-
ния с элементарной теорией изгиба найдём
С ~ 4^7 я(й«—е4) • (224)
Напряжённое состояние в полом цилиндре, даваемое предыдущими
формулами, представляет одновременно первую ступень на пути
к вычислению напряжений в цилиндре с выточкой, поскольку пока
ещё не учтена кривизна выточки и область около наименьшего по-
перечного сечения может приблизительно рассматриваться как часть
полого цилиндра. В случае внешней выточки величина Ь при этом
тождественна с с-\-а, а для внутренней выточки с тождественна
с b—а. Во всех точках зоны около выточки величина г примерно
одинакова и приближённо равна расстоянию от оси до дна выточки.
Изменение г в рассматриваемой области можно считать 'пренебре-
жимо малым но сравнению с самим г. Если для точки у дна выточки
примем х = 0, то и величина х в сравнении с b или, с пренебре-
152 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ задаче [гл. V
жимо мала. В результате в зоне около выточки получим следующее
первоначальное напряжённое состояние
° X °Г °И> "хг
(225)
vIU=°; ^=^sInw»
(226)
где номинальное напряжение гп для случая внешней выточки
играет роль Ь) равно:
=3 (^япо)г= Ь
v'[(®+^k+(i+^-)<c+a)S
(227)
w-2
для случая же внутренней выточки (роль с играет Ь — а) таково:
*'[(з+Э,+(|+^>-‘->°]
(228)
»
Можно показать, что при учёте влияния выточки это простое напря-
жённое состояние претерпевает изменения только лишь в том смысле,
что изменяется напряжение xxw9 а также появляется напряжение xrw.
Последнего достаточно для удовлетворения граничным условиям,
Нормальных же напряжений при этом не возникает. Положим:
Ф0 = [Л?-^'4-Г-^- + (1"-2«) <Po]cOSW;
Ф^-^-совте; Ф2 = --^г—у-; Ф3 = 0>
(229)
причём <р0 должна зависеть только от х и г, a <p0cosw — гармони-1
ческая функция. Функция <р0 удовлетворяет дифференциальному
уравнению: » i
•А?о-§=<Н ’ (230)
откуда следует, во-первых, что
и, во-вторых, после дифференцирования, что: _
’ + ^0. (232)
\ or / or 1 Г® Л \ '
Теперь легко видеть, что Фо, Ф1 .и Ф2 действительно1 являются гар-
моническими функциями. > » < '
§ 5J ВЫТОЧКА ИА ТЕЛЕ ВРАЩЕНИЯ 153
Функция напряжений имеет вид:
F =—2a?ocos<a' (AF = O). (&38)
Тогда напряжения будут:
Оа! = 0, аг = — 2а А (>-) cos W,
®w = 2a^r(’-^.)cosw,
v' \ г / /озлл
= -^c°sw, 'rw = «(^T-7^ + ^)sinw>
^»=a®Trsinw-
(236)
Положим теперь г =s оо и для простоты введём новую функцию
д<Ро
. <р = а .
т dr
Тогда получим:
aa? = Qr ~ = *
d<p . d? .
^=•^•81"®; = ^не-
согласно (232) при г== со, функция ср удовлетворяет потенциальному
уравнению в плоскости х, г. Теперь и разыскание напряжений воз-
мущения оказывается чрезвычайно простым.
В случае мелкой, выточки речь идёт о том, чтобы на элемен-
тарное напряжённое состояние тамо = тп sin w, которому соответст-
вует функция га — хпх, наложить подходящее добавочное напряжён-
ное состояние так, чтобы поверхность выточки была свободной
от нагрузки. Для этого перейдём к эллиптическим координатам
и положим
а = Ь— г (или г — c) = ch «sin®;
x = sh« cos a
Как следует из (236), компонент по оси х касательного напряже-
ния, действующего в сечении w = const, получается дифференциро-
ванием функции ср sin w по х, а компонент по оси г—дифферен-
цированием по г. Следовательно, для получения компонента в на-
правлении и или о нужно брать производную также по направле-
ниям и или -о. Поэтому в криволинейных координатах (III* 3)
имеем: ,
-fesinw’’ T-=K^sinw- (238)
Выбранные здесь эллиптические координаты уже были использованы
нами при решении ряда задач. Относительно коэффициентов искаже-
154 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ. V
ния, которые вследствие изометрии равны друг другу, отсылаем к (49),
IV, 2. Для <р применимо простое потенциальное уравнение (46), 1V, 1.
В случае мелкой выточки контур цилиндра, содержащий выточку,
состоит из прямой 8 = 0 или
Фиг. 71. Мелкая кольцевая выточка
с большим расстоянием от оси при
сдвиге или кручении (ср. фиг. 67 и 68).
*у = 0 и из кривой, по которой
очерчена выточка и которую мы
примем за эллипс, обозначенный
буквой Поэтому должны быть
удовлетворены два граничных
словия:
У®ю)««о = “ 0* (239)
Элементарная функция
<р = тп x = Tnshtfcos^
уже удовлетворяет первому из этих
условий, что налагает такое же
условие и надобавочную функцию,
., и значит, последняя точно таким же
образом должна зависеть от v; с другой стороны, она должна удо-
влетворять закону затухания, т. е. для больших и — обращаться в нуль,
и, наконец, удовлетворять потенциальному уравнению на плоскости;
всем этим условиям удовлетворяет функция a"ttcosv. Положим
=== тм (shi иЦ-cos и
Отсюда
= —Л^~м)со5^ sin w;
= -у (— sh и — Ае~и} sin v sin w.
Второе граничное условие даёт
(240)
(241)
А » ch и0<
(242)
Параметр uQ выражается через глубину выточки и через её радиус
кривизны (см. IV, 41) по формуле cthtf0==j/ —.
ДлясШп0 = 5 распределение напряжений изображено на фиг. 71.
Наибольшее напряжение возникает у дна выточки, где касательное
напряжение достигает шестикратного значения. Вообще, для наиболь-
шего напряжения получаем:
. * стах == ~ и0 = tn(l-|-cth«0) = Tn(l + j/rI). (243)
ижжад = я/2
Такой же, коэффициенту концентрации был уже найден для продоль-
ной выточки в стержне при изгибе (см. фиг. 34).
§ 5] ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ 155
В случае глубокой выточки, в противоположность тому, что
имело место для мелкой выточки, речь идёт не о том, чтобы на
заданную элементарную функцию наложить добавочную функцию,
а о самостоятельном разыскании функции напряжений, удовлетворя-
ющей одновременно граничным условиям на внутреннем и внешнем
контурах и определяющейся посредством их однозначно. Вследствие
существования выточки один из этих контуров искривлён, и так
как рассматривается область, близкая к дну выточки, то он может
быть изображён в виде гиперболы Другой контур образуется
прямой е = 0, или *0 = 0. Следовательно, нужно удовлетворить
двум граничным условиям:
СчЛ « о = ^; (xw)v m = 0. (244)
Единственным решением задачи является то, для которого касатель-
ное напряжение обращается в нуль не только на обоих конту-
рах, но и повсюду, именно:
<р = Л«; TMW = -4sinw; tw = 0. (245)
Остаётся определить постоянную А. Перерезывающая сила, с точ-
ностью до знака, должна быть равна сумме составляющих напряжений
по оси у, действующих в произвольном сечении, взятом между краем
ti = 0 и краем v — За такое сечение примем поверхность й =
= const; получим:
v 0=1 ~ ’/ J т««»cos Су» w) dF—J* f sin vodF- (246)
F F
Здесь элемент dF площади представляет собой малый прямоуголь-
ник с рёбрами hv dv и hw dw. Но коэффициент искажения hw равен
расстоянию г от оси, которое по предположению велико по сравне-
нию с толщиной а в наименьшем поперечном сечении и, следова-
тельно, при интегрировании (246) может считаться постоянным, при
внешней выточке равным с, а при внутренней — Ъ. Таким образом
для внешней выточки получается:
V — J Jsin whdvcdw — Amv0. (247)
0 0
Номинальное напряжение для глубокой выточки можно получить из
(227) путём предельного перехода при а -> 0. Будем иметь
____
т.са ’
но в нашей координатной системе
а = (®)и= о = sin t»0’ (249)
V ем V9
156 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ ЗАДАЧЕ [ГЛ. V
и, следовательно,
V == 1гстге sin v0. (250)
Наконец, (247) даёт
A = (251)
К этому же результату мы пришли бы и для внутренней выточки.
На фиг. 72 дано распределение напряжений для tg'p0='|/8-
Фиг. 73. Наибольшее напряжение
в глубоких кольцевых выточках с
большим расстоянием от оси при
сдвиге или кручении.
У дна выточки 1 имеет место . значительный максимум напряжений,
равный 1,8 тп. Вообще для максимального напряжения получается:
_ — т _ - tgpo
Tmax v ^uw/u «О
V = 0О
w= тс/2
Параметр vQ связан известным образом с радиусом кривизны и
с толщиной в наименьшем поперечном сечении (см. (68), IV, 2);
окончательно получаем:
»о
(252)
/ а
ттах__ Р
arctgl/" ±
r Р
Фиг. 73 поясняет эту зависимость.
D. Чистое кручение. В задаче о кручении целесообразно при-
нять следующие выражения для функций напряжений, упрощающие
расчёт:
(253)
Фо = О; ®j==0;
Фа = —(x,r) sin w;
®» = 7?(V)cos®.
(254)
§ 5] ВЫТОЧКА НА ТЕЛЕ ВРАЩЕНИЯ
Откуда получаем:
’ F = 0,
и формулы (211) дают
Оду - ® »
Xrw~’d7 7 ’ Xxw дх*’
или, при Г = со
д<р __ду
xrw ~дг’ Х)В”>~'дх'
157
(255)
(256)
(257)
Эти выражения отличаются от (236) множителем fin w; следова-
тельно, ход вычислений такой же, как и в задаче о сдвиге и мржно
сразу сказать, что, также получаются равными х) и коэффициенты
концентрации для мелкой выточки, т. е. Для глубокой
выточки," вследствие требуемого при определении постоянной А
интегрирования, требуется особое доказательство. Возьмём
ср = Лxuw = у x^w = 0. (258)
Момент напряжений относительно оси х вычисляется по формуле
М = (259)
Элементарная площадка dF, как и в разделе С — прямоугольник
с рёбрами hvdv и kwdw, причём hw — r—постоянная, которую можно
считать равной для внешней выточки с, а для внутренней Ь\ для
внешней выточки получаем:
Ж =.[ fauwcihdvd‘W = 2i4c8it‘»0. (260)
Номинальное напряжение для этого напряжённого состояния соответ-
ствует элементарным формулам кручения и, следовательно, вычи-
сляется по формуле для внешней выточки:
2М(с+а)
п it[(c-|-a)4 —с*] ’
для внутренней выточки
_ 2М(Ь — а)
— пр4_(г,_й)4] •
х) Для полукруглой выточки (/==р) коэффициент концентрации, следо-
вательно, равен 2. Это соответствует и результатам W tilers [Z. Math. Phy-
sik, т. 55 (1907), стр. 227] и Sonntag [Z. angew. Math. u. Meeh., t. 9,(1929),
стр. 1].
158 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ задаче [гл. V
Путем предельного перехода, устремляя а 0, для глубокой внешней
выточки из (261) получаем
<263'
Отсюда, применяя (249), выводим
41 = 2irc2 sin ,votn. (264)
Наконец, подстановкой в (260) находим:
Л = ^ГТ»' <265>
Это же соотношение получилось бы и для внутренней выточки; оно
тождественно с уравнением (251), полученным в случае сдвига. Сле-
довательно, имеет место совпадение также и коэффициентов кон-
центрации.
6. Построение номограммы для коэффициентов концентрации
напряжений в выточках любых размеров.
Для определения коэффициента концентрации в выточках любых
размеров воспользуемся методом, указанным в гл. II, 4. Этот метод
предполагает заданными коэффициенты концентрации как для мелкой,
так и для глубокой выточек; но они нам уже известны.
А. Внешняя выточка. В случае глубокой выточки при растя-
жении нужно пользоваться формулой (59) с номинальным напряжением
(55), а при изгибе—уравнением (72) с номинальным напряжением (71).
Для сдвига справедливо выражение (84), причём в качестве номиналь-
ного напряжения служит касательное напряжение на поверхности
цилиндра, не имеющего выточки (только тогда удовлетворяется
условие atlt -> 1 при -> 0); значение его получается из (84) и (82)
_ 1 + “ у
при —«=»0 и оказывается равным --------® СИЛУ того’ чт0 это
, т
номинальное напряжение отличается от величины р, выражение (84)
,1 + 1
нужно умножить ещё на--------и тогда получается правильное зна-
1 + -
1 т
чение коэффициента концентрации для нашей номограммы. Наконец,
для кручения нужно применить уравнение (107) с номинальным на-
пряжением (105).
В случае мелкой выточки для изгиба и для растяжения остаются
справедливыми соотношения (131), IV, 4; для сдвига и кручения мы
нашли выражение (243). Так как максимальное напряжение при
§ 6] ПОСТРОЕНИЕ НОМОГРАММЫ ДЛЯ КОЭФФИЦИЕНТОВ КОНЦЕНТРАЦИИ 159
сдвиге возникает у дна выточки, то в противоположность. плоской
задаче здесь этот случай не представляет никаких исключений.
В. Внешняя выточка в полом цилиндре. При наличии осевого
отверстия к предыдущим предельным значениям добавляется ещё
одно, именно предельное значение коэффициента концентрации для
глубокой внешней выточки при большом осевом сверлении, кото-
рая рассмотрена в V, 5. Это вновь появившееся предельное значение
обозначим буквой atb. Общий закон для коэффициента концентрации,
установленный в II, 4,. требуется соответственно расширить.
Прежде всего для большого осевого отверстия имеем
+ (266)
Здесь tty зависит от t[o, atb от а/p. С уменьшением отверстия должно
выделиться слагаемое, соответствующее предельному значению коэф*
фициента концентрации глубокой выточки без отверстия, т. е. atk
Этого можно достичь, если принять следующее выражение для ко-
эффициента концентрации:
= (V4-1)2 + (“»- О’~(«ft-l)2 + («a--~l)2' (267)
а±с вместо а
С уменьшением к нулю отверстия а-\-сг^а в выражении (267)
исчезают члены, содержащие atb, а формула (267) принимает вид
(2) гл. II, 4. С другой стороны, при большом отверстии с делается
очень большим, а вместе с этим- большими становятся и ко-
эффициенты а<ь, ай, в которых а заменено на а-\-с, а обе дроби,
в знаменатель которых они входят, делаются изчезающе малыми.
Коэффициент концентрации для больших отверстий опять принимает
форму (266), из которой мы и исходили. Так как в уравнении (267)
оба добавочных слагаемых к формуле (266) зависят от одной и той
же переменной , то, естественно, вместо них, в качестве вспо-
г
могательной величины ввести новый коэффициент концентрации, за-
висящий от Иными словами, положим
Ё№~1)2 ” (^О2 ’ (268)
a -f- с вместо а
после чего выражение (267) принимает форму
(«* — !)’= (V*—I)5 *" 1)2 + («л-1)2 • (269)
Это уравнение показывает, что выражение для коэффициента кон-
центрации в конечном счёте нужно составить, зная не только коэф-
фициент концентрации при большом осевом отверстии, выражаемый
160 ТЕОРИЯ КОНЦЕНТРАЦИИ В ПРОСТРАНСТВЕННОЙ задаче [гл. V
согласно (266) через и atb, но используя и вспомогательный
коэффициент ah, определяемый по (268).
При растяжении за номинальное напряжение принимается среднее
напряжение по наиболее узкому поперечному сечению, равное
ж[(д 4- g)2—c*] • Для опРеделения предельного значения коэффициента
atk служит уравнение (59), для atk справедливо (131), IV и, наконец,
для <xtb формула (190), VI.
В случае изгиба номинальное напряжение равно ;
atk вычисляется по (72), — пр (131), IV; atb— по 190, IV.
При сдвиге номинальное напряжение вычисляется по (227). Для
1 + т
atk справедливо (84), причём его нужно умножить ещё на —=• ;
. 1+-
. • ' 1 т
для dfk воспользуемся (243), наконец, для — (253).
При кручении номинальное напряжение вычисляется по (261),
atk — по (107), —по (243) и <xtb— по (253).
С. Внутренняя выточка. При больших продольных осевых
отверстиях коэффициент концентрации определяется только через
два предельных значения atft и «я, из которых первое зависит от
а I
-, второе от —; например, при растяжении справедливо для первого
(190), IV, для второго—(131), IV (ср. V, 5). При устремлении ра-
диуса отверстия к нулю величин^ должна теперь дать пре-
дельное значение мелкой внутренней выточки без продольного
осевого отверстия. Этому условию мы удовлетворим, вводя вспо-
могательный коэффициент концентрации ал; именно положим:
Г__________1 , 1 , 1___
- (fltk -1)2 («гь -1)2 ф («л -1)2 ’
/•4- с . ’
где ак зависит только от —и вычисляется по формуле:
1 _ 1 .1
(«л-1)2 («гл-,1)2 (уь-1)2'
t + с вместо t
В случае с = 0, действительно, вместо получим а^; с другой
стороны, при больших с выражение fyi делается исчезающе
малым, так что требуемые условия тоже удовлетворены. При ра-
стяжении для имеет место выражение (133). В качестве номиналь-
р
ного напряжения служит Здесь b = а -|-1 -f- с (фиг.
68 и 70). * Я
(270)
(271)
§ 61 построении номограммы для коэффициентов концентрации 161
При изгибе номинальное напряжение вычисляется по формуле
♦ Для «tic и в/ъ справедливы те же самые формулы,
как и при растяжении, но а^й вычисляется по (158).
При сдвиге номинальное напряжение определяется по (228),
atk — из (253), — из (243); для справедливо (185), причбм
его нужно разделить на 2, так как относительная величина (166)
теперь равна половине номинального напряжения [см. выражение (228)
при b — а = 0].
В случае кручения для номинального напряжения справедливо
(262), а^д. и вычисляются как и при сдвиге, а по формуле
(200).
Номограммы коэффициентов концентрации для внешней и внут-
ренней выточек на теле вращения, полученные таким образом, по-
мещены на фиг. 104 и 105. Способ использования номограмм по-
ясняется указанными на чертежах стрелками, а также примером,
помещенным в отделе X. Для расстояния дна выточки от оси
(a-j-c или целесообразно принять общее обозначение г.
Мы заканчиваем на этом учение о влиянии выточек на распре-
деление напряжений в случае пространственной задачи и переходим
к следующему отделу теории концентрации напряжений. В силу
особого характера распределения напряжений этот отдел также тре-
бует детального рассмотрения. Мы имеем в виду влияние выточек
призматического типа.
11 Зак» &4I76. Г. Нейбер.
ГЛАВА VI.
ТЕОРИЯ ВЛИЯНИЯ ВЫТОЧЕК ПРИЗМАТИЧЕСКОГО ТИПА.
1. Основные уравнения.
С целью нахождения формул, пригодных для призматических
стержней, возвратимся опять к общим уравнениям Ш, 6. Мы имели
— । д*р । дФ8
°а> “Г Т а \^х ду
дг )
и т. д.
причём
Далее,
о
Г = Ф0-|-хФ1+уФ24-гФ8 и а = 2——.
ДФ0 = ДФХ = ДФ9 = ДФ8 = 0.
(1)
(2)
(3)
В последующих выкладках мы будем считать ось х совмещён-
ной с осью призматического стержня, ось у направим по линии
Фиг. 74. Деформация элемен-
тарной призмы при 'кручении.
действия перерезывающей силы (фиг.
74), а ось z совместим с нейтральной
линией поперечного сечения стержня.
В главе V, с помощью уравнений
(111) —(113) и (137)—(139), было
уже показано, что при чистом растя-
жении и при чистом изгибе призматиче-
ского стержня в нём возникает только
напряжение аф. В этих двух случаях
элементарный способ расчёта остаётся
совершенно строгим при любой форме
поперечного сечения стержня, ибо
здесь компоненты напряжения с инде-
ксами у и z равны нулю и граничные условия на незагруженной бо-
ковой ^поверхности стрежня удовлетворяются. Иначе обстоит дело при
сдвиге и при'кручении.
При частот сдвиге общее решение можно привести к более
простой форме следующим способом (подобные выражения мы уже
§ Q
ОСНОВНЫЕ УРАВНЕНИЯ
163
имели в V, (161)—(164)). Положим
Ф0 = -Т?^) + 4^7[(-4+у«-2«9)(^8-^) +
+ (- 8 + 8а — 2а*)(хуг2—
ф1 = 4(4^ар [2а О'*2—4> + 4 О “ а) О'*2—^2)] +
+ ’7<?0'> *);
Ф9 = 47?=ф/ <4 — 2а) (ХУ2 + хг* — У *8):
Ф3 = 0.
(4)
Здесь ср является гармонической функцией, зависящей от у и z.
Легко убедиться, что эти выражения удовлетворяют уравнениям (3).
Согласно уравнению (2)
F = 4 (4~:8)j[(4 ~ 2 “) (^3 + х^2) + (4 а - 4) ’ <®>
и из (1) получаем
0^ = 0} (5g = О,
=§+4(4L)j- [(-8+2 а)/+(4 -2 *)*];
- —г ,
ьу* — v> *я?е •
(6)
Распределение нормальных напряжений <зя подчиняется прямолиней-
ному закону элементарного учения сопротивления материалов, но
возникают касательные напряжения и которые должны быть
подчинены граничным условиям.
При частом кручениа удобнее всего принять следующие выра-
жения для функций:
Фо=“^?0»*); ®!=4?0,*); Ф2=тхг; фз=-?*у- (7)
Отсюда, согласно (2)
/=• = 0,
и (1) переходят в:
°® ~ = ®г = = )
^г/с=§ + оа*;
= Й —0V,
(8)
(9)
11*
164 ТЕОРИЯ ВЛИЯНИЯ ВЫТОЧЕК ПРИЗМАТИЧЕСКОГО ТИПА [ГЛ, VI
где & является углом закручивания, отнесенным к единице дли-
ны стержня. Для В из фиг. 74 получаем соотношение
= (10>
но оно уже удовлетворено, ибо здесь [ср. (49), III, 6J
ду +2e®t) —
С = ^(—§7 + 2 «фа) = & ху.
(И)
Сначала займёмся изучением влияния выточек в сплошном призмати-
ческом стержне.
2. Сплошное поперечное сечение (стержень с продольным
пазом).
1 Займёмся в первую очередь мелкой выточкой. При этом будем
предполагать, что в ближайшей окрестности от места, где должна
быть сделана выточка, контур в первом приближении можно считать
прямолинейным (фиг. 75). Для касательных напряжений на этом ме-
" У*
Фиг. 75. Вал с мелким про-
дольным пазом при сдвиге или
кручении.
сте, поскольку в нём у и г имеют
совершенно определённые значения,
из (6) или (9) получаются выражения:
’«,=|р+С1; ’~=Й+С>' <12>
где Сх и С8—постоянные; их можно
не писать, так как к <р можно доба-
вить слагаемые Тогда
«чеем
ОЗ)
Предельный переход, необходимый для
последовательного рассмотрения «мел-
кой выточки», требует теперь, чтобы
эта простая зависимость (13) была
принята не только в том месте, где сделана выточка, но также и
внутри зоны искажения, занимающей небольшую область. Для вы-
числения местных напряжений мы поэтому применим непосредствен-
но соотношения (13), встречавшиеся нам в подобной форме уже
неоднократно [см. (236) и (257), V, 5]. Дальнейший ход вычислений
поэтому уже ясен. Распределение напряжений показано на фиг. 71.
Коэффициент концентрации выражается в форме
*п
(14)
ТОНКОСТЕННОЕ ПОЛОЕ ПОПЕРЕЧНОЕ СЕЧЕНИЕ
165
§ 3] ------------------------
Согласно приведённому ранее выводу, за номинальное напряжение
нужно принять касательное напряжение в стержне без выточки в со-
ответствующей точке.
Для примера рассмотрим цилиндр с продольным пазом (фиг.
• 75). Если выточка расположена на нейтральной линии поперечного
сечения, то при сдвиге номинальное напряжение вычисляется по
формуле
_2
т V
Т «««•
•п
(15)
При кручении имеем
2AfT
т» = 'кР' *
(16)
Фиг. 76. Рассмотрен-
ный Веберомособый
случай:край состоит
из двух кругов, с
центром меньшего
круга на • контуре
большего.
Что касается глубокой выточки, сравнимой с размерами попереч-
ного сечения, то ещё до настоящего времени ие создано теории.
Для случая кручения, однако, существует реше-
ние, данное С. Weber *) и относящееся к слу-
чаю круговой выточки. Контур образуется
двумя кругами, причём центр меньшего круга
предполагается лежащим на контуре большего
(фиг. 76).
Для малых значений с]Ьрешение (14)(/ — р) очень
хорошо соответствует решению Вебера,"ибо в том
и другом случае для коэффициента концентрации
получается величина 2. Для выточек, которые
нельзя считать мелкими, всё же коэффициент кон-
центрации в первом приближении можно вычислять
по ф°РиУле (14), но в качестве номинального
напряжения нужно брать касательное напряжение
на контуре стержня без выточки. Этим путём
некоторое повышение коэффициента концентрации компенсируется
понижением номинального напряжения.
3. Тонкостенное полое поперечное сечение.
В тонкостенных полых поперечных сечениях расчёт упрощается
постольку, поскольку касательные напряжения в стенке, без учёте
влияния выточки, можно считать равномерно распределёнными по
толщине стенки. Вследствие этого для вычисления номинального на-
пряжения всегда оказывается достаточным рассмотреть лишь условия
статики.
Ч W е b е г С., Lehre der Verdrehungsfestigkelt. VDI-Forsch.-Heft, Nr. 249.
Berlin: VDI-Verlag, 1921.
166 теория влияния выточек призматического типа [гл. VI
На фиг. 77 изображено поперечное сечение, симметричное отно-
сительно оси у и имеющее повсюду одинаковую толщину стенок.
Для определения касательного напряжения в точке А при сдвиге
цилиндр рассекаем на обеих его сторонах в соответствующем месте
плоскостями, параллельными оси х и перпендикулярными к поверхно-
сти стенки. Рассмотрим часть стержня длиною dx. Тогда из условий
равновесия следует
2xd dx = J— dxy df> (17)
где f—площадь, заштрихованная на фиг. 77. Если подставить <зх из
(6), то получится известная формула:
где S—Статический момент площади / относительно нейтральной
линии, J—момент инерции всего поперечного сечения относительно
той же нейтральной линии.
Фиг. 77. Условия равновесия в по-
лом симметричном сечении.
Фиг. 78. Продольный паз
в полом сечении.
В случае кручения, вычислив момент напряжений относительно
произвольно выбранной точки, получим известное соотношение:
Мт
(19)
где F— площадь, ограниченная средней линией стенки..
Если теперь в области точки А образовать внешнюю или внут*
реннюю выточку в виде продольного паза (фиг. 78), то вследствие
уменьшения толщины стенки от d до а касательное напряжение
повышается до величины (из условий равновесия) при сдвиге
при кручениг
n~4aj'
Мт
(20)
(21)
§ 4] ВАЛЫ С ПОПЕРЕЧНЫМИ ОТВЕРСТИЯМИ 167
Эти величины, полученные в предположении равномерного распре-
деления напряжений по наиболее узкому поперечному сечению,
примем за номинальные напряжения.
С целью вычисления возникающих в действительности неравно-
мерно распределённых напряжений обратимся снова к основным
соотношениям (6) и (9). В случае сплошного поперечного сечения
зона искажений в сравнении с остальными размерами поперечного
сечения при предельном переходе к мелкой выточке могла считаться
настолько малой, что делались справедливыми простые соотно-
шения (13). Аналогично можно поступить также и в случае тонко-
стенного поперечного сечения. Вследствие малой толщины стенки
зона искажений здесь также простирается на область, которую
можно считать очень малой в сравнении с остальными размерами
поперечного сечения, так что при решении задачи опять приходим
к соотношениям (13). Так как имеет место (за исключением несу-
щественного множителя sin w) совпадение формул (13) и (236) главы V,
то данные в главе V решения для глубокой и мелкой выточки
применимы непосредственно и в рассматриваемом случае. Следова-
тельно, значения коэффициента концентрации для мелкой выточки
равно
l + V^/p, а для глубокой выточки ------Метод определения
arct«y 7
коэффициента концентрации для выточки любой глубины виден из
номограмм фиг. 103 и 104.
4. Валы с поперечными отверстиями.
Валы и стержни с поперечными отверстиями представляют собой
исключительный случай, так как здесь мы не имеем уже призмати-
ческого тела и, вследствие этого, основные уравнения настоящего
отдела неприменимы. Но, как показал Л. Фёппль *), такого типа слу-
чаи можно рассмотреть, исходя из соотношений, имеющих место
при плоском напряжённом состоянии.
Если, например, имеется в виду тонкостенный полый вал с по-
перечным отверстием, радиус которого мал в сравнении с радиусом
самого вала, то при кручении налицо плоское напряжённое состояние,
ибо при этих предположениях зону искажения можно рассматривать
как часть плоскости. Поэтому здесь идёт речь о плоскости, рабо-
тающей на сдвиг. Решение этой задачи нами было уже дано в гл. IV, 4.
Следует лишь обратить внимание на то, что в качестве номиналь-
1) Fappl L., Z. VOI, т. 65 (1921), 3, стр. 497.
168 теория влияния выточвк призматического типа [гл. VI
ного напряжения должно быть взято касательное напряжение
в стержне без отверстия, где оно должно быть таким
. 2^
Х»» —к(М—в<) ’
(22)
В расчёте на. сдвиг, сделанном для соответствующей плоской задачи
(см. IV,’ (144)г—(146)), нужно заменить р на 3/2 р. Поэтому для
продолговатого отверстия (фиг. 79) максимальное напряжение, возни-
Фиг. 79. Пустотелый вал с попереч- Фиг. 80. Вал с поперечным отвер*
; । ным отверстием. стием..
кающее на контуре вблизи* дна выточки в виде растягивающего на*
пряжения (см. IV, (155) и . фиг. 35), определяется формулой:
* *
gmax'o er 1 •»// I Д - .
' . "ГГ p ‘
(23)
таким образом для кругового отверстия(/yf-р) максимальное напря*
жение получится в четыре раза больше номинального.
Этот же самый способ рассуждения ‘ с достаточно хорошим
приближением можно применить к сплошным.валам (фиг. 80, см. также
вышеуказанную работу Л. Фёппль).
ГЛАВА VII.
ТЕОРИЯ РАЗГРУЖАЮЩИХ ВЫТОЧЕК.
1. Разъяснение понятия.
До сих пор мы занимались разысканием напряжённого состояния,
обусловленного выточкой заданной формы. , В настоящем отделе
ход мысли будет обратным: теперь будут разыскиваться не напря-
жения при заданной форме контура выточки, а наоборот, — форма
контура при заданном и по возможности минимально искажённом
напряжённом состоянии. Конечно, решение этой второй основной
задачи непосредственно связано с наличием решения первой.
Форма детали, правда, чаще всего конструктивно предопреде-
ляется наперёд, но всё же конструктор её выбирает до некоторой
степени произвольно. В большинстве случаев путём конструктивно
незаметных, несущественных изменений можно достичь улучшения
в распределении напряжений, а вместе с этим и увеличения проч-
ности детали. Пусть, например, мы имеем дело с круглым сплошным
валом, который из чисто конструктивных соображений должен быть
снабжён кольцевой выточкой, а в остальной части быть совершенно
гладким (фиг. 67). Распределение напряжения на валу, который,
допустим, закручивается, вследствие наличия выточки значительно
искажается, и у дна выточки существует значительное повышение
напряжений. Предположим теперь, что в конструктивном отношении
вполне допустимо вблизи первой выточки сделать ещё вторую.
Правда, на первый взгляд кажется, что в результате этого вызывается
дальнейшее и как будто ненужное повышение напряжений в новом
месте. Это действительно так, но — и на это мы обращаем внима-
ние— это второе произвольное повышение напряжений вызывает
уменьшение первого. Наглядно выражаясь, эффект выточек распро-
страняется теперь на обе области, и притом так, что повышение
напряжений в обоих местах теперь меньше, чем в случае суще-
ствования единственной, конструктивно необходимой, выточки.
Можно достаточно наглядно пояснить это явление, пользуясь
представлением о силовом потоке, создаваемом в детали внешними
силами, к ней приложенными и распространяющимся вдоль детали.
Удобство состоит в частности в том, что, не4 требуя детального
рассмотрения упругого состояния, это понятие непосредственно приво-
170 ТЕОРИЯ РАЗГРУЖАЮЩИХ выточек [гл. VII
дит к очень отчётливому пояснению явления: линия давления (сило-
вой поток) отклоняется (в разбираемом случае) второй выточкой
в сторону и внутрь. Влияние выточки после того, как проходящий
силовой поток уже отклонён, возрасти больше уже не может.
Явление разгружения можно объяснить и строго теоретически,
не прибегая к помощи этих представлений. С этой целью нужно
сослаться на неоднократно уже упомянутый закон затухания (см. II, 2).
Затем имеется теоретически доказанное свойство (см. IV и V) всех
выточек, с одной стороны, в области у дна выточки вызывать по-
вышение напряжений, а с другой стороны, в более далёкой области
вызывать уменьшение напряжений. Хотя новая выточка в месте, где
она сделана, и вызывает повышение напряжений, но, однако, в окрест-
ности, в том числе и у дна первой выточки, она вызывает разгрузку.
Удачным расположением таких добавочных выточек конструктор
имеет возможность благоприятно влиять на концентрацию напря-
жений и разгрузить опасные зоны детали. Такого типа дополнитель-
ные выточки, сделанные только лишь с целью выравнивания распре-
деления напряжений, называют (начиная с A. Thum’a) разгружа-
ющими выточками.
2. Разгружающие выточки при кручении.
Эффект разгрузки при наличии нескольких выточек мы пред-
ставим теперь аналитически с помощью методов математической
теории упругости. Одновременно мы установим
сочх свойства коэффициента концентрации несколь-
fx'O ких выточек.
кХкх.44^ В качестве примера возьмём скрученный
- х вал> который имеет несколько мелких выточек
Фиг. 81. Однократная либо в форме продольного паза, как изобра-
мелкая выточка. жено на фиг. 75, либо в форме выточек, окру-
жающих вал, как на фиг. 67. В обоих случаях
сделанные ранее для мелких выточек выводы приводят к соотноше-
ниям (см. V, (257) или VI, (13)) *)
где предполагалось, что, в соответствии с фиг. 81, ось х направлена
вдоль контура, а ось у перпендикулярно к нему. Одинаковый индекс
у обеих касательных напряжений, который соответствовал бы третьему
координатному направлению, ради простоты опущен. Функция <р
зависит только от х и у и удовлетворяет уравнению
^,2 V >
i) Thum A. u. Н. О s с h a t z, Steigerung der Dauerfestigkeit be! Rund-
Staben mit Queibohrungen. Forjchg. Ing.-We»., t. 3 (1932), стр. 87.
V соотно-
(3)
координа-
(4)
И V можно
§ 2] РАЗГРуЖАЮЩИВ ВЫТОЧКИ ПРИ КРУЧЕНИИ 171
Положим в основу рассмотрения изометрическую сеть, введя между
декартовыми координатами х, у и криволинейными и,
шения (см. IV, I)
Эх _ ду . дх ду
ди dv * dv ди
Тогда дифференциальное уравнение (2) в криволинейных
тах принимает следующую форму
д2? . „
ди* dv* ’
По известным теоремам теории функций под величинами и
подразумевать вещественные и мнимые части функции/(х-|~ О*)
комплексного переменного, где Z — У — 1.
Если положим
= «4-Z« = w, (5)
то между комплексными функциями г и w существует зависимость:
z » х 4- 1у = /(w) =/(«-(- Zn). (6)
Коэффициенты искажения в направлениях и и v оказываются равными
между собой и вычисляются по формуле:
Для радиусов кривизны ри и pv линий и — const и ® = const,
соответственно (174), IV, при hu — hv = h, (знак кривизны можно
здесь не учитывать) имеем:
_1____l_dh_ J________1 dft (Л\
ри k* ди ' pv h* dv ' ' '
Касательное напряжение вдоль линии и *= const, или v = const, полу-
чается из ? посредством формул (см. (238), V):
« Л ди ’ v~' h dv • W
В некотором расстоянии от выточки решение для 9 должно пре-
вращаться в Это выражение соответствует стержню без выточки и
одновременно даёт здесь номинальное напряжение.
Сначала предположим, что имеется одна выточка. Если она очер-
чена по эллипсу, то к цели приводит эллиптическая система
координат
z = sh w; х = sh и cos -п; у = ch и sin (10)
Решение было уже дано в V, 5, С. Коэффициент концентрации
получается равным:
172
ТЕОРИЯ РАЗГРУЖАЮЩИХ ВЫТОЧЕК
[гл. VII
Применённая система координат имеет известный недостаток, по-
скольку контур состоит из двух координатных линий, а именно—•
из контура самой выточки и = и0 и из прямолинейной части о — 0.
Вычисление проводится более просто, особенно в случае нескольких
выточек, если контур можно представить одной координатной линией.
При наличии одной выточки этого можно достигнуть, с, помощью
координатной системы: • ।
г = — 1. (12)
я
О 0,125
Фиг. 82. Система координат с координат-
ными линиями v =» const., упрощающими
расчёт мелкой выточки.
На фиг. 82 изображены линии о = const. Для больших значений и и о
имеем приближённо х — и и у = и линии •»=const,, совпадают с
прямыми у = const'. В обла-
сти х = 0, у = 1 имеется,
однако, искривление. Если
такую линию принять за кон-
тур, то будем иметь дело с
выточкой, у которой внеш-
ние уголки закруглены.
Коэффициент концентрации
поэтому будет, как можно
предвидеть, несколько мень-
шим, чем это получается по
уравнению (11).
Искомое решение должно удовлетворять условию (4), а при
больших и или v—превращаться в тпх йли тям-(как мы видели
выше, когда х = и). Далее, должно быть равным нулю вдоль
линии контура ‘0 = v(i. Так как тп« удовлетворяет этим всем трём
условиям, то оно и является искомым решением. Следовательно,
? = = г„ = ^-. (13)
Дно выточки лежит на оси
у; там «г=0 и, следовательно:
у 1 _ 1 д/г 1
yv2_|_ 1 ’ pv = ft2 dv, v’yT+o?
Далее, у дна выточки v = v0. Глубина выточки равна;
/ = (у)»=о —(у)„ = со
(15)
(16)
и для кривизны выточки получаем:
-=4fi—ЛЧ
§ 2]
РАЗГРУЖАЮЩИЕ ВЫТОЧКИ ПРИ КРУЧЕНИИ
173
Коэффициент концентрации находим2изж(13)
«>=^Ч=Цу1+’’Г- <17)
Исключение параметра w0 из (16) и (17), наконец дабт
(-;;)• “8>
При выточках большой кривизны, т. е. при больших //р, коэф-
фициент концентрации возрастает (чего и следовало ожидать)
и может быть вычислен по
формуле: .
Фиг. 83. Контур о многократной вы-
точкой.
даёт всегда несколько меньшее значение, чем фор-
в силу вышеупомянутого закругления
= (19)
что для больших t/p находится
в хорошем соответствии с (11).
В остальном полученная фор-
мула (18)
мула (11), что происходит
внешних углов.
После этих предвари-
тельных соображений пе-
рейдём к изложению самой
теории эффекта разгрузки.
Введём теперь новую си-
стему координат, соответ-
ствующую контурус несколь-
кими выточками (фиг. 83).
При этом будем рассма-
тривать бесконечно боль-
шое число выточек равной
глубины, удалённых друг
от друга на расстояние Ь.
Расчёт опять будем вести
для закруглённых внешних
углов, чтобы иметь возмож-
ность представить контур
в виде одной координатной
линии; именно положим:
cosz = Xcosw. (20)
Фиг. 84. Линии v « const (одновременно
это линии напряжений и координатные
линии) для контура с многократной вы-
точкой.
На фиг. 84 даны линии
я = const, для случая X = 2.
При больших у они соответствуют у — const., в то время как по мере
приближения к оси к всё больше и больше заметным становится
периодически повторяющийся выступ. Соотношения (13) остаются
174
ТЁОРНЯ РАЗГРУЖАЮЩИХ ВЫТОЧЁК
(гл. VII
справедливыми также и здесь. При х = и — О имеем:
у = arc ch (К ch v);
___ду____ ksh» .
dv ch2v— 1 ’
± = ± = (xi! — 1) ch о
p h" dv A. sh2 v "|/А.2 ch2 »— 1"
(21)
Для дна любой выточки нужно принять
При дальнейшем расчёте обратим главное наше внимание на соотно-
шение, получающееся для коэффициента концентрации при большой
Фиг. 85. Коэффициент разгрузки у в за-
висимости от отношения удалённости
выточки b[t.
кривизне выточки. Тогда из сопоставления с формулой (1 ^выведен-
ной для единственной сильно искривлённой выточки, можно будет
судить об эффекте разгрузки. Для малых v0 получаем:
t — (y)u=0
1 _ /X2 —1
р X sh2 v0
Из этого следует:
— (j)» = «/2 = arcch А;
V = Vo
__ J__/Х^т_
aji h X sh vQ
V—1 1
К р
(22)
“a- =*
th/
Р
(23)
или, принимая во внимание, что при выборе координатной системы
< Ъ
за единицу длины был принят отрезок —, получаем:
Ь
dh-5
(24)
§ 3] общие Свойства коэффициента концентрации 175
Сравнение с (19) показывает, что эффект разгрузки выражается
посредством множителя cth • Это число, зависящее только
от отношения b/t, т. е. от удалённости выточек, мы назовём коэф-
фициентом разгружения и обозначим буквой Он изображён
на фиг. 85; начиная с нуля—при бесконечно близких между собой
выточках—он затем постепенно повышается и при бесконечно уда-
лённых друг от друга выточках достигает 1, а коэффициент концен-
трации опять превращается в тот, какой был для единственной
выточки; действительно, уравнение (24) при b * оо превращается в (19).
3. Общие свойства коэффициента концентрации
при наличии разгружающих выточек.
Для того чтобы выработать общую точку зрения на коэффициент
концентрации при наличии разгружающих выточек, обратимся снова
к соотношениям (24) и (19). Переход от одной выточки к нескольким
можно трактовать как уменьшение глубины. Роль действительной
глубины t при нескольких выточках играет действительная глубина,
умноженная на коэффициент разгружения у
(25)
Точные вычисления показывают, что этот ход мысли приводит
к достаточно удовлетворительным результатам; вследствие этого
в предыдущих формулах действительную глубину t следует просто
заменить условной tw.
Таким образом, например, при нескольких выточках с острыми
внешними углами для коэффициента концентрации при кручении
и при сдвиге будем иметь:
«А=1 + /'^ (26)
а, соответственно,, при растяжении и изгибе
a^l-^j/^. (27)
ГЛАВА VIII.
ТЕОРИЯ ВЫТОЧЕК С ОСТРЫМИ УГЛАМИ.
1» Неприменимость классической теории упругости к выточкам
с острыми углами и причина этого.
Все предыдущие исследования имели в своей основе исключительно
классическую теорию упругости. Теперь перейдём к группе задач,
решение которых делает необходимыми соображения, приводящие
на границу возможности применения основ классической теории
упругости и даже за пределы этой границы, к новой теории.
В то время как при выточках не слишком малого радиуса клас-
сическая теория упругости ещё достаточна, при сильно искривлённых
выточках или даже при острых углах она приводит к совершенно
неправильным результатам. Так например, для коэффициента концен-
трации мелкой выточки при сдвиге или при кручении была найдена
Пусть, например, радиус кривизны составляет
только 1/10000 глубины. Тогда коэффициент концентрации должен бы
быть равным 101, что является невероятным. Аналогичные обстоя-
тельства имеют место для всех остальных выведенных выше коэф-
фициентов концентрации. При исчезающе малом радиусе кривизны
коэффициент концентрации делается пропорциональным j/”. Для
выточки с углами поэтому получается физически невозможное,
бесконечно большое значение. Мы здесь, очевидно, переходим границу
области возможного применения классической теории и, чтобы притти
к целесообразным основам расчёта, необходимо установить новый
критерий для оценки действительных свойств материала.
Но перед тем, как подойти к этой нелёгкой задаче, следует
объяснить причины, в силу которых оказываются несправедливыми
основы предыдущей теории. Возвратимся обратно к гл. III, где были
выведены основные соотношения для напряжённого и деформиро-
ванного состояния. В качестве мысленной модели нам служил при
этом — что имеет уже основное значение — бесконечно малый эле-
мент с рёбрами dx, dy, dz. Предположения, молчаливо сделанные
о бесконечной делимости вещества, его бесструктурное™ и т. д.,
представляют, очевидно, критерий применимости классической теории
§ 2] НОВАЯ ВООВРАИНЕМАЯ МОДЕЛЬ 177
упругости. До тех пор, пока дело идёт о мало искривлённом кон-
туре, или — точнее говоря—пока радиус кривизны поверхности
повсюду достаточно велик в сравнении с кристаллами вещества,
до тех пор не делается заметной ошибки, ибо при мало искри-
влённой поверхности напряжения, которые зависят от граничных
условий, существенно изменяются только в пределах больших обла-
стей, но не внутри участков, имеющих такой же порядок малости/
как и кристалл. Получается поэтому, что при слабо искривлённой'
поверхности структура вещества не оказывает влияния на распреде-
ление напряжений, а вместе с этим также и на коэффициент концен-
трации.
Совсем иначе обстоит дело при сильно искривлённой поверх-
ности. Тогда имеют место изменения напряжений даже в пределах
очень малых областей. Применимость классической теории упругости
обусловлена теперь тем, чтобы вещество даже в области порядка
кристалла можно было рассматривать как бесструктурное, ' а это
противоречит существованию самого кристалла.
Это соображение, привёденное нами в качестве причины непри-
менимости старого учения, указывает нам одновременно путь к новой
теории,
2. Новая воображаемая модель.
Мы только что видели, что не всегда допустимо рассматривать
бесконечно малый элемент. Требуется перейти к тому, чтобы пользо-
ваться в качестве воображемой модели элементом конечных размеров.
Представим себе теперь материал построенным из сплошных
маленьких, но всё же конечных частичек. Последовательное проведе-
ние этой мысли даёт новые условия как доля равновесия, так и дефор-
мации. При этом следует условиться об определённой форме части-
чек, а также уяснить себе вопрос о сущности упругих деформаций
её, о характере сил, передающихся на соседние частицы, и т. д.
Одним словом, нужно сделать ряд предположений, которые харак-
теризовали бы свойства материала. В результате этих основных пред-
посылок будут получены новые уравнения теории упругости, кото-
рые— в соответствии с конечностью частицы — будут иметь вид
не дифференциальных, а разностных уравнений. Решение отдельных
задач будет связано с применением теории конечных разностей.
После этого замечания читателю, которому, может быть, приходи-
лось самому решать гармонические задачи с помощью теории
конечных разностей, наверное станет сомнительной практическая
выполнимость расчёта, ибо, как известно, такого типа задачи тре-
буют огромного количества времени. В действительности, этот путь
был бы почти безнадёжным, но, как мы увидим, он и не является
необходимым.
Старое учение теряет свою применимость только ведь в зонах
с резким изменением напряжений, но, согласно закону затухания,
12 Эак. Г. ;Нейбер.
178 ТВОРИЯ ВЫТОЧЕК С ОСТРЫМИ УГЛАМИ [гл. VIII
такие зоны сравнительно невелики. И было бы преувеличением
совсем отбрасывать старую теорию, поскольку она в остальных обла-
стях хорошо применима. На фотив, мы используем её в качестве
надёжного аппарата в тех сравнительно больших зонах конструкции,
где имеется лишь плавное изменение напряжений и где разностный
метод был бы слишком утомителен. Таким образом также и при
сильно искривлённом контуре можно ещё . пользоваться классиче-
ской теорией упругости, но в самих зонах искажения нужно положить
в основу новую воображаемую модель.
. Расчёты показывают далее что с хорошим приближением
при помощи старой теории можно рассматривать даже и часть зоны
искажения. Удаётся получить пригодные результаты даже и тогда,
когда новая модель применяемся только к месту, лежащему в непо-
средственной близости от пункта искажения напряжений. Именно,
оказывается, что величина коэфф щиента концентрации в выточке с ост-
рым углам стоит в ближайшей связи с величиной частички; эта вели-
чина принимает на себя роль новой постоянной материала. И после
того как . эта постоянная определена опытным путём, практически
возможная ошибка в определении коэффициента концентрации опять
устраняется, даже и при пренебрежении новой мысленной моделью
в остальной зоне искажения напряжений.
3. Коэффициент концентрации для выточек с острыми углами.
Определение коэффициента концентрации в выточке с острым
углом,', согласно вышесказанному, может быть выполнено следующим
путём. Мы исходим из решения задачи методами классической тео-
рии упругости, именно, мы предполагаем, что — как и в выше разо-
бранных примерах—распределение напряжений для переменного ра-
диуса кривизны выточки найдено. У дна выточки мы применяем далее
новую воображаемою модель и вообразим там частичку шириной е.
Частичка предполагается настолько малой, что напряжения, дей-
ствующие по её поверхности, можно считать пэстоянными. Новые
значения напряжений мы получаем через осреднение старых значе-
ний на поверхности частицы. В качестве примера разберём прежде
всего мелкую вы точку при сдвиге, или при кручении.
А. Мелкая выточка с острым углом при сдвиге или при кру-
чении. Соответственно соотношениям (24D и (212), V, в наиболее
узком поперечном сечении действуют следующие напряжения:
(*««) <=0, (-•д = ^(sha-b ch и0 <**-»). (1)
' ' /-. W=2
В наиболее узком сечении ft=sha. Если ещё воспользоваться тем,'
что e-“ = ch« — sh«, то мы получим:
— tvw = tw (1—e“«she0-|-e’‘1>ch«()ctha). (2)
§ S3] коэффициент чеонцгн'|РМ1йи>^яя ЯЙДчЖк с^ЪФПыми углами ff9
Веснэяйуемея «ев^рь эдивй йбордйнйтбй.^о^&ййв
ch и == 1 -j- р» (3)
|i увеличивается от дна выточки—угловой точки — в направлении
«’(фиг. Фф.^Дли ^вычисления коэффициента’кбнцеР'^^ии^Яы'УдчЙе
с'ЪстрЫм углспгможно^ограничиться‘'Определением
его предельного значения при е-малом, так что
координату j*, которая может изменяться от О
дЪ*е, 'ерЯЗу'tib&tfo'picCMafptiWb-как'МДДУю ве-
личину. Поэтому будем учитывать только наимень-
шйе степени р. и дбпусТим, ЧТ'о
ch а ск 1; sh и ==.)/2щ cthA»,^
Величину а0 (соответствующую угловой точке мелкой
выточки) положим сразу равной нуЛо. 1ГогДа
—т =-4|=* (5)
"Фйг. «86 ВЬйбра-
жаемая модель для
I остро-
угольной выточки
при сдвиге или
кручении.
Напряжение в выточке с острым углом представляет, согласно пред-
ШМтвующим разъяснениям, среднее ’Значение напряжений вдоль от-
резка а и вычисляется, следовательно, так:
Если ещё принять во внимание значение единицы длины ввыбран-
ной координатной системе
ch-l/j) = 1 ав /, (7)
то получим (следующее «'предедвмбе -йШ^ёние для коэффициента кон-
центрации в выточке с острым углом
(8)
Сращивая это с предельным значением укоэффициента кон-
цёНтраЦии 'ЙруМВйЙ WflWrfft сМ5тбном йскривлении --(см. (&43)
гл. V}, НиДЯМ, WO we&rio ^рьдауда ИрИвизны теперь‘заяилаеттюло-
'•Vtiffd ЫирйЛы зЛеШММарной '^dchiddu.
’В ‘Ka’tfStirtfe йругд?о НрйМё'ра рассмотрим ШгЬЧку.
В. Глубокая выточка с острым углом при ДВуМёрйоМ напря-
жённом ’состоянии при сдвиге и Мрй чфучейии. Рассмотрим глу-
бокую вйточку, раэобранйую в V, fe, С. -ДЛя осейого еёченйя, пер-
ИР
180 т1ория выточвк с острыми углами (гл. VIII
пендикулярного к направлению сдвига, ранее выполненный расчёт
дал' следующие напряжения:
(^«w)w= л ; с»=о. (9)
В наиболее узком сечении Л = cos о. Опять введём новую коорди-
нату, отсчитываемую от' угловой точки выточки, положив г(фиг. 87)
slno=(l— I*). (10)
Мы можем брать только малые значения р, поэтому можно положить:
cos о == ]/"2р и tew = ^==-. (11)
Напряжение в угловой точке определяется так:
(12)
о
Постоянная А получается из (251), V, при о0 = -к-:
а=^- (13)
2
Если принять во внимание, что а»$1по0 = 1, то для коэффициента
концентрации'получим:
Фиг. 87. .Воображаемая мо-
дель для глубокой остро-
угольной выточки при сдви-
.ге или кручении.''
из гл. IV, 2, А, в наиболее
дующие напряжения:
Сравнивая это с предельным значением для сильно искривлённой
выточки, которое согласно <253) гл. V при* большом а/p оказалось
2 _/ л „
равным —1/ —, видим, что и в этой
1С г р t
задаче величина р заменяется через у.
Такое же исследование проведём теперь
для более Гсложного напряжённого со*
стояния.
С. Растяжение стержня,Снабжённого
двусторонней глубокой выточкой с угло-
выми точками. В случае стержня с дву-
сторонней выточкой, вследствие существо-
вания двух главных напряжений, расчёт
существенно затрудняется. Как следует
узком поперечном сечении-возникают еле-
КОЭФФИЦИЕНТ КОНЦеНТРАЦИИ для выточек С ОСТРЫМИ УГЛАМИ 161
Координатную систему выбираем так же, как и в предыдущих зада-
чах, следовательно, опять применимы соотношения:
sin ===== 1 —|л; cos 17= ]/2р..
(16)
Так как в (15) фигурирует член с cosa<o0, то необходимо ввести
|л0—расстояние края от точки |i = 0; только после выполнения
интегрирования следует положить |ло = О (если бы мы сразу поло-
жили = ~ и Но = 0> т0 У Дна выточки было бы аш = ау и <зу на
контуре не исчезало бы. Поэтому предельный переход к выточке
с угловой точкой следует совершить здесь только после выполнения
интегрирования).
Следует ещё отметить, что нижним пределом интеграла здесь
должно служить не непосредственно
несколько меньшее значение — |лх
(фиг. 88); именно, нижний предел инте-
грирования нужно выбрать так, чтобы
напряжение после интегрирования
исчезало, как требует граничное усло-
вие. Интегрирование следует выпол-
нить для обоих напряжений, ибо, как
и в классической теории упругости,
так и здесь, напряжения на нашей мо-
значение jjl = ^0 для края, а
Фиг. 88. Воображаемая модель
для глубокой остроугольной
* выточки при растяжении.
дели должны удовлетворять граничным
условиям. Но это возможно лишь при
условии, что в качестве нижнего пре-
дела интегрирования взято не |л0, но ~
несколько меньшее значение. Хотя р.о и играет роль координаты
контура, но мы вынуждены нашу частичку представить выдвинутой
из слоя контура на маленький отрезок с тем, чтобы <зу
удовлетворяло граничному условию. Это маленькое выдвижение,
исчезающее снова после предельного перехода к выточке с острым
углом, объясняется тем, что в наших рассуждениях мы выну-
ждены внезапно перейти от дифференциального исчисления к исчи-
слению в конечных разностях.
Некоторый малый отрезок, который в дифференциальном исчисле-
нии является бесконечно малым, в разностном исчислении имеет при
этом конечное значение.
Так как имеет тот же порядок малости, что и у., то, как и
выше, можно положить
cos
(17)
йосле чего напряжения переходят в
(18)
182
ТЖОВШЬ ВЫТОЧВЮ СОСТРЫМИ- УТЛАМЙ |гж V111
М»»пдешф.вввг$ь найдём. напряжение^ в-угловой*точке-. Получим
1«+н
ъЧМ-**
В процессе предельного перехода к выточке с,острым. умом з„сохра?
няет постоянное значение, в то время как и р/, которое всегда
М£ДОД&чодустремляются^к нулю. Поэтому мы можем ещё'до
пррдел.ьвдгр .перехода,пренебречь веддчинамж-Ро и рр по сравнению
€ в. Тогда (19) перейдёт в
(20)
Но-, это напряжение-должнопудовлетворять граничному условию, т. е.
исчезнуть. Отсюда^ддя ’/p1j получается . квадрададе. ypaWLWIW^
Hi——° Ф)
c.W»11 __
/Н1 “ 1 /Г; (22)
Н1 .доджадь^тн,меньше че^.^^тр.здерь,нужц^,прдад»мть.
во.,вдтни^только .первый кор^ь.,
Вычислим теперь напряжение, Подь^Й. звдх
Klh.
Подожидг.т^верь <р0 полу чиж ддяо наибольшего- напряжения в уг-
ловой точке значение
ол = 2Л}/'|. (24)
Постоянную А получим из (66), IV, при
(25)
Падаход от ЗАкг^лвинваш^гйяки к^ыТОтюлйтгым углом Ua
ЗиамнА коэффициент. коацеитрацим» вьугдоной- тоэмо- равен-
Для сравнения выпишем.. коэффициент концентрации при сильно
искривлённом/ контуре, который при- больших а/p, согласно (6$ty,
1У, .име*Т вид
а «Ь/ГЗ'. (27)
«г Pi-
Опять оказывается, что в выточке с; острым углом» ррль. радиуса
криризны.играет величина е/2.
Тот же с<мый закон можно установись) для г остальных напря-
жённых состояний, относящихся к вытрчкам. Однако разобранных
примерев-достаточно-для- того, чтобы на#ти коэффициент концдн-
трации"в- выточках-с острыми -углами?
Ради-простоты -вместо-е/2 введё^-г енерь., р'. Ддя\ коэффициента
концентрации в_выточке-с- острым углом играет, таким образом,
решающую роль величина р'. Соответственно нашей ч теории, кото-
рая». основывается.! на .- учёте» влияния- структуры, величина р', как*
половина-ширины элементарной частички,- введённой- в расчёт,•„ свя-
зана с структурой материала, т. е. р'/ддя .различных материалов-.,
вообще-принимает различные значения».ТакнМсобразамт здесь». дело
идёт о новой постоянной-материала, имеющей размерность длины.
Как-- мы -покажем/ в -ближайшем- отделе,- для-сталн- р'' равно/ прибли-
зительно, полмиллиметра» Коэффициент: концентрации-при\. переходе^
к'вытопкам»с-острыми углами»- таким>'Образо<щ зависит'от'-ма*
териала?
4.' Переход от закругл^нноЙ выточки к выточке
с. острым, углом,.
Значение, р'=*Д; соответствует.- идеальному» материалу! класса*
челкой, теории»-унруэоодцС. нмбмьцюйлупрртюйичувдевительносгвю;*.
прн:(возрастанци t р' чувзтвителввюстьхубызаетг Поэтому»•величину^
однаайём упру^ойпуаствитвлмоспгыя.гвытонки^ Лриослабенискри-ь
вдёщда вытонках:.(р -^велико) ,сдедует лолдаоваться |велмчиной жоэф-
фидиента концднграции.ьдляиидеадьнаго- материала.) с уменеиинмвмлр-
дая/.техниче^кмх материалов;! коэффициент .-койценарацци^постепенно
умяньшдется/дбо .коэффициент комцецтрацииутехническихыежэериалош
при»:уменьшающемсяhp .стр]емится1нелК(.бескенянноаги, аакикоэффи*
цненту конщентраоди в«тонки с острым/углом», какинаивысшему -пре*
дельному ¥ значению. Чтобы ндэычишштьъв каждом» отдельном .случае!
коэФФиииаН)?. концентрации., закруглйинойи вытоякм^ с-, применением»
нашей воображаемой модели, воспользуемся законом, перехода^
аналогичным тому, каццм . мы подьаодадись- в. случай; мелких
184 теория выточек с острыми углами (гл. УШ
и глубоких выточек, и обеспечивающим здесь переход от идеаль-
ного значения а' («к)р'-о к значению <xe = (ak)pe0 для выточки
с острым углом. Кривая перехода приближается, как видно из фиг.
89, к^обеим предельным кривым. Так как согласно теории идеаль-
”ный коэффициент концентрации
Р **
Фиг. 89. .Изменение ^техническою
коэффициента концентрации от гра-
ничного значения для случая идеаль-
ной упругости до граничного значе-
ния для выточки с острым углом.
для малого-’р-делается пропорцио-
нальным У 1/р, то для перехода
к выточке с острым углом следует
принять следующую формулу:
+ ,28Ч
i + yj- (28)
В ближайшем отделе мы уви-
дим, что эта формула очень хоро-
шо совпадает с результатами
опытов.
5. ^Влияние деформации у осно-
вания выточки.
^Нужно здесь отметить ещё
один недостаток классической тео-
рии^упругости, При выводе основных уравнений (Ш, 2) мы имели
в виду такую деформацию, при которой происходит только лишь
ничтожное изменение формы. Вследствие этого при выводе уравне-
ний равновесия (Ш, 1) можно было положить в основу состояние
тела до деформации. Совсем недавно Л. Фёппль1) показал, что
для выточек, деформации около которых велики, т. е. велики коэф-
фициент концентрации и кривизна выточки, это предположение
перестаёт быть приемлемым. Отнеся уравнения равновесия к дефор-
мированному состоянию и введя соответствующие постоянные
материала, Л. Фёппль показал, как можно, следуя этому ходу мысли,
объяснить уменьшение коэффициента концентрации в выточке
с острым углом. Таким образом, мы опять приходим к тому, что
для получения практически применимых результатов старая теория
должна быть в известной мере дополнена. Поскольку и учёт
влияния деформации и введение в рассмотрение нашей модели,
учитывающей структуру материала, разными путями приводят
к одинаковым выводам (в обоих случаях речь идёт об уменьшении
коэффициента концентрации сильно искривлённой выточки), можно
принять за основу один из этих двух путей, при условии, если
надлежащим образом выбрать постоянную материала в соответствии
*) FOppl. L, Ing.-Arch., т. 7 (1936), стр. 229.
§ 6!
влияние величины угла отклонения
188
с опытными данными. Таким образом, сохраняя соотношения, уста-
новленные в гл. VIII, от 1 до 4, мы тем самым учтём влияние
больших деформаций, если подберём' р'г в' соответствии ^со} свой-
ствами’материала.'
6. Влияние величины угла отклонения.
Ппи переходе к’выточкам с острым углом' важное}’ значение
приобретает влияние величины «отклоняющего угла». В выточках
с большим радиусом кривизны этим влиянием можно было прене-
бречь, так как прямолинейная часть края находится далеко'"за пре-
делами высоконапряжённой зоны, т. е. в области, которая, вслед-
ствие закона затухания, не' оказывает влияния на коэффициент
концентрации/ Иначе' обстоит’ дело в“случае сильно искривлённых
выточек и выточек с’’острыми’ углами. Здесь} существенную роль
играет «—величина угла, на котог ы*. при переходе} через’выточку
отклоняется направление касательной ' контуру.
Т Все исследованные до сих пор коэффициенты концентрации
в выточках с острыми углами относились к величине отклоняющего
Фиг. 90.^Системы’ координат в теории отклоняющего угла.
угла, равной 0°. Для нахождения связи между коэффициентом кон*
центрации и величиной « в выточках’ одинаковых размеров, но
с различными величинами отклоняющих" углов, проще всего рас-
смотреть напряжённое состояние в скрученном стержне, снабжённом
мелкой выточкой. Эту задачу, в связи с вопросом о разгружающих
выточках, мы уже существенно упростили; формулы (1)—(17),
VII мы используем и здесь.
Мб
tboi«wh'Wto4bkz сметными углами
[гл. ФШ
-Систему чмодепнют ‘«весь weo «выбрать так, чтобы ;в ->шле
КбврДИнвТНйх ЛИПЙЙ' имелась'кривая, оТвеЧй-юЩЗя вДОоЧке?с'у?И&е&й
точкой 'и 'ямббй1 величиной отклоняющего ’yiw> -Э»у -условию
можно удовлетворять, положив:
” ~ :х.'-л (29)
Тогда линия ««=0 изображает такую контурную линию (фиг. 90).
При ле2гугол,равен 'нулю, При «в=1'5 он равен4)6®, наконец,
при л =1,угол равен18б° (и вообще выточка отсутствует). У дйа
выточки с. угловой точки ц>е‘О, г='1 в 'ближайшей к выточке
окрестности положим ««‘l-J-a’i, и из (S9), пренебрегая высшийи
степенями zlt получим nzi<==tri. ‘Волее подробное исследование
даёт отсюдадля величины отклоняющего угла ‘формулу:
»ге.(2^->^к. (30)
При больших значениях z приближённо ле®>, т. е. х •== == и.
Искомая функция <р должна быть гармонической, т. е. должна
удовлетворять дифференциальному уравнению (4), VII; далее, для
больших и или v она должна переходить в т„>'(соответственно
:feT„, тг = 0). Наконец, xv должно' быть равным нулю вдоль
любой контурной линии u*=u0 (мы рассматриваем сначала’закруг-
лённую выточку). Решение представится в виде
•?—г„ = 0; % “-у* (31)
У дна выточки о ==» 0. Из этого следует
*—>+“"! (32)
Если теперь составить известным уже нам ' способом напряжение
в выточке с угловой точкой, то для коэффициента концентрации
получаем
«.*=4н( "^rfxe4 f (“)*-*+•'*
1 1 ±
ЧО+тГ-Я"- (33)
Отсюда, при п = 2, т. е. при угле отклонения 0°, для коэффициента
концентрации получаем
4~ '(84)
Решив >егаоситеяьно >майдём
1
7— 2
б]
ВЛИЯНИЕ ВЕЛИЧИНЫ УГЛА ОТКЛОНЕНИЯ
187
.Подставляя это значение 1/е в (33),
зависимость между коэффициентом
любом другом значении со
получим окончательно искомую
концентрации при со = 0° и при
1
(36)
При этом, в соответствии с (30), п и ш связаны между собой ураз-
нением
п = 2 —(37)
На фиг. 91 дана номограмма, построенная согласно предыдущим
результатам. Если, например, коэффициент концентрации при ш==0а
Фиг.91. Зависимость коэффициента концентрации для выточки с острым
углом от отклоняющего угла в номографическом представлении.
«о с отклоняющим углом 90°, определяется так: от точки авг=7
перемещаемся направо и вниз по кривой, соответственно указаниям
стрелки, до пересечения с вертикалью, дающей 90°; проведя от этой
точки пересечения горизонталь влево, мы можем отсчитать искомый
*в = 3,8.
На первый взгляд кривые на номограмме кажутся почти прямыми.
Коэффициент концентрации уменьшается почти равномерно с умень-
шением отклоняющего угла. Если обратить внимание на то, что с воз-
растанием отклоняющего угла увеличивается также и скругление внеш-
них углов, в соответствии со свойствами выбранной системы координат
(фиг. 90), то следует ожидать, что для технических выточек с резко?
выраженными внешними углами при возрастании отклоняющего угла
коэффициент концентрации не сотль сильно убывает. Это говорит
ютом, что кривые на номограмме ещё больше Должны приближаться'
к прямым линиям для технических выточек. Для практического Поль-
188 ТЕОРИЯ ВЫТОЧЕК С ОСТРЫМИ УГЛАМИ • [гл. VIIF
зования мы примем в основу поэтому прямолинейный закон, которому
соответствует в определенной области зависимость-
as== Н [(®s)<u=o (38У
очень хорошо соответствующая уравнению (36). Кроме того, это-
уравнение хорошо подтверждается и опытами, на что будет указано
в ближайшем отделе.
7. Общий технический коэффициент концентрации.
Уравнение (38) нужно ещё согласовать с уравнением (28) так,,
чтобы получился общий технический коэффициент концентрации,
соответствующий нашим требованиям, установленцым вначале. Иско-
мое уравнение для коэффициента концентрации должно в частности-,
удовлетворять требованию, чтобы с возрастанием радиуса кри-
визны влияние отклоняющего угла убывало. Возвратимся снова,
к отделам IV—VI, где выведены выражения для коэффициентов кон-
центрации, которые непосредственно справедливы для идеального-
материала при р = 0. Эти коэффициенты мы обозначили через
С уменьшением р до нуля они делаются пропорциональными p^l/p, »
можно положить:
(«* (39>
Подстановкой в (28) получаем
Vv
мало— 1 у—г (40)>
+А _
(в числителе можно пренебречь единицей по сравнению с j^l/p).
Отсюда' предельным переходом к р—>0 получаем коэффициент кон-
центрации для выточки с угловой точкой при отклоняющем угле;,
равном 0°. Мы получиМ:
(«Х=о=14-с (41>
Если подставить это в (38), то найдём
(42>
Сравнение (42) с (41) приводит прежде всего к заключению, что»
для получения общего коэффициента концентрации нужно только
лишь букву с заменить на с. Но это привело бы к выводу,,
противоречащему теории, что отклоняющий угол оказывает заметное:
влияние на коэффициент концентрации и при больших р.
§ 7] ОБЩИЙ ТЕХНИЧЕСКИЙ КОЭФФИЦИЕНТ КОНЦЕНТРАЦИИ 189
Вторая возможность установления общего коэффициента___кон-
центрации наиболее простым способом состоит в замене VW на
те — со _ /1
—-— у у; этим путём можно удовлетворить условию, связан-
ному с влиянием отклоняющего угла; (28) тогда переходит в
ай = 1+------(43)
1+-2-1/ X
те — со г р
Действительно, теперь при большом радиусе кривизны влияние бо*
кового угла ничтожно мало, что мы. и утверждали в предыдущих рас-
суждениях; теперь в знаменателе величина —-у делается ма-
лой по сравнению с . 1, и ш, следовательно, не оказывает больше
никакого влияния на коэффициент концентрации. При уменьшении
радиуса кривизны влияние отклоняющего угла, напротив, делается
постепенно веб более значительным и, наконец, при выточке с угло-
вой точкой, когда р = 0, получается уравнение (42).
Кроме того, г уравнение (43) вполне согласуется с результатами
опытов и представляет собой поэтому основное уравнение для тех-
нического коэффициента концентрации.
Для быстрого определения а/ — коэффициента концентрации для
идеального материала—служит номограмма (фиг. 104 и 105). Точно
так же и уравнение (43) можно представить в виде номограммы. Для
этой цели служит диаграмма на фиг. 106. Правила пользования вы-
текают из указаний стрелок; читателя отсылаем ещё к примеру,
приведённому в' отделе X.
Мы перейдём теперь к изложению результатов экспериментальных
исследований и сравним их с формулами, полученными здесь.
ГЛАВА IX.
СРАВНЕНИЕ ТЕОРИИ С РЕЗУЛЬТАТАМИ
ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ НАПРЯЖЕНИЙ.
1., Измерения удлинений.
Обыкновенными экстензометрами невозможно определить дей-
ствительно возникающие у дна выточки большие удлинения, а зна-
чит, и само наибольшее напряжение. Сконструированный Е, Preuss !)
В; 1912 .г, прибор подходит, к этому требованию уже ближе, но всё
же ещё не избавляет от ошибок. Только в 1932 г. G. Fischer9) раз-
вил способ измерения, испробованный на многих опытах и дающий.
с достаточной точностью, величину наиболь-
шего напряжения у дна выточки. Способ этот
состоит в определении перемещений ^.отдель-
ных точек вдоль прямой .линии, внесением,
величин перемещений в качестве ординат на.
прямой, где производились измерения, по-
лучают так называемую кривую, перемеще-
ний, из которой можно определить измене-
ние’ удлинений так’же и в тех точках пря-
мой, которые недоступны непосредственной
Фиг. 92. Выточки, иссле- установке экстензометра. Измерения,Гпрове-
дованные Фишером. данные Фишером, на выточках в [случае
плоского изгиба стержня признаны* всеми
специалистами как весьма надёжные, и поэтому мы их используем
для сравнения с теорией.
Речь при этом будет итти, с одной стороны, о выточке с угло-
вой точкой, но при различных отклоняющих углах, с другой стороны,
о закруглённых выточках (фиг. 92). Для односторонней выточки при
изгибе теория даёт (IV, б, В):
лГк — 1 + 2 ~~ »
r I
(1)
i) Preuse Е., VDI-Forsch.-Heft, Nr. 126; Z. VDI, т. 56 (1916), стр. 1349
и 1780.
s) F1 а с h е г G., Kerbwlrkung an Blegestaben. Berlin, VDI-Verlag, 1932.
§ 1]
ИЗМЕРЕНИЯ УДЛИНЕНИЙ
191
(аА — О.
!)»+(«»-IF ’
Чтобы определить ещё неизвестную величину р', установим прежде
всего коэффициент концентрации выточки с'угловой точкой. При очень
малых р, aiki а вместе с этим также и atk—1 переходят в:
^-1 = 1/!^./ L = |/о,663—.
** 3(тс2—8) гр V Р
Если в (3) подставим это значение, а для — 1 — значение |/ 4 у, то
получим:
Наконец^ после подстановки в (4) найдем:
j Г 0/63 —
1+ ц.-Л-у/'Н 1/ 1+0,|«^’ <6)
—<о Г Р г /
192 СРАВНЕНИЕ С РЕЗУЛЬТАТАМИ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ [ГЛ. IX
Отсюда предельным переходом при р -> 0 получим коэффициент
концентрации для выточки с угловой точкой
а8= 1
гс— ш Г 0,663 а
* у 14.0,166 у р'
(7)
Опыты над выточками с угловой точкой относились к стержням, у
которых были размеры^ = 95 мм, /=15 мм.
Фиг. 93. Коэффициенты кон-
центрации выточек с острым
углом при достоянных глу-
бине. выточки и ширине
стержня, но при переменном
отклоняющем угле, соответ-
ственно уравнениям (38)
главы VIII и (7) главы IX
II и по данным Фишера.
Фиг. 94. Коэффициент
концентрации при пере-
менной глубине выточки
и постоянных радиусе
кривизны и ширине стер-
5«hh.j
Фиг. 95. Коэффициент кон-
центрации при переменном
радиусе кривизны и посто-
янных глубине выточки и
* ширине стержня.
Фиг. 96. Коэффициент} кон-
центрации для полукруг-
лых выточек при перемен-
ном радиусе и постоянной
ширине стержня.
Коэффициенты концентрации,
в зависимости от отклоняющего
соответствующие опытам, ложатся,
угла, с достаточной точностью на
§ 2] ФОТОУПРУГИВ ИЗМЕРЕНИЯ НАПРЯЖЕНИЙ 193
прямую, которая при о)==к проходит через а8=1, а при со = у—
через а8 = 5 (см. фиг. 93). Соответствие с нашим уравнением (7)
получается при р' = 0,48 мм. Испытания проводились на специальной
стали с временным сопротивлением в 65 кг/мм*.
Найдя таким путём значение р', можно теперь сравнить с теорией
результат измерения Фишера на закруглённых выточках. Будем при
этом отклоняющий угол считать равным нулю. На фиг. 94 показано
изменение коэффициента концентрации при переменной глубине, но
при постоянном радиусе кривизны; фиг. 95 соответствует перемен-
ному радиусу кривизны по постоянной глубине, наконец, на фиг. 96
дана кривая для полукруглой выточки с переменным радиусом, но
с постоянной шириной стержня. Теоретические кривые для коэффи-
циента концентрации определены при этом по номограммам. Значе-
ния коэффициентов концентрации, полученные из опыта, все нанесены
на фигуре. Отклонение от теоретических кривых не превосходит точ-
ности опыта, так что теория вполне подтверждается.
2. Фотоупругие измерения напряжений.
Фотоупругий метод, получающий за последние годы всё большее
и большее значение, представляет неоспоримо самое лучшее и самое
эффективное вспомогательнсе средство исследования плоского напря-
жённого состояния. Относительно основ этого метода отсылаем
к соответствующей литературе1). С помощью этого метода кроме
траекторий напряжения получаются также и сами напряжения, а
именно, на контуре из непосредственных измерений, а внутри — либо
графическим, либо аналитическим расчётом.
Первая задача о местных напряжениях, решённая оптическим
путём, состояла в определении распределения напряжений в уголке.
На поляризационной установке, находящейся в Мюнхене, Н. С.
v. Widdern, Н. Kurzhals и L. Kettenacker2) под руководством L. FOppl’a
разобрали подробно эту задачу. Сравнить их результаты с теорией,
однако, нельзя из-за отсутствия пока строгого теоретического реше-
ния этой задачи.
Однако сравнение мы можем провести, пользуясь исследованиями
Е. Armbruster’a* * * 8), выполненными в Мюнхене и относящимися к стержням
с выточками; исследованию здесь подвергались изгибаемая балочка
с односторонней выточкой (фиг. 97) и растянутый стержень с дву-
сторонней выточкой (фиг. 98). Результаты опытов при переменном
*) FOppl L. u. Neuber, Н., Festigkeilslehre mittels Spannungsoptik,
Mfinchen u. Berlin, 1935.
*) См. предыдущих) сноску.
8) Armbruster E., Einfluss der OberflSchenbeschaffenheit auf den Span-
nungsverlauf und die Schwingungsfestigkeit. Berlin, 1931.
13 Зак. 3475. Г. Нейбер.
194 сравнении с результатами экспериментальных исследований [гл. IX
дадиусе кривизны, но при постоянных глубине выточки и отклоняю-
щем угле сопоставлены на фиг. 99 и 100 с теоретическими коэф-
фициентами концентраций. Последние вычислялись по номограммам
(фиг. ЮЗ и 104), и значение р' принималось равным 0,48 мм,
В случае балочки, работавшей на изгиб (фиг. 99), совпадение
удовлетворительное, тем более, если принять во внимание, что при
Фиг. 97. Исследованная
Армбрюстером изгибаемая
балочка с односторонней
выточкой.
Фиг. 98. Исследованный Арм-
брюстером растянутый стер-
жень с двусторонней выточкой.
ничтожной ширине балочки в 20 мм нельзя достигнуть очень боль-
шой точности опыта. Значение рх = 0,48 мм поэтому остаётся
Фиг. 99. Сравнение опытов Армбрюстера на
изгиб с теорией коэффициента кснцентрации.
приемлемым и для флинт-
гласа, который употреб-
лялся при фотоупругих
исследованиях.
В случае растяжения
стержня (фиг. 100) значе-
ния ; коэффициентов кон-
центрации, полученные из
опыта, располагаются по-
всюду выше теоретиче-
ской кривой. Если при-
нять во внимание, что
практически простое рас-
тяжение осуществляется
только приближённо и что всегда существуют некоторые напряжения
от изгиба, о чём известно каждому занимающемуся фотоупругими
исследованиями, то такое отклонение нас не должно удивлять. Пред-
положим, например, в болте, посредством которого в приспособлении
Армбрюстера производилось растяжение стержня, возникают несимме-
тричные силы трения, вызывающие небольшое смещение линии растя-
жения относительно оси стержня. Пусть величина смещения в наи-
более узком сечении достигает 3% ширины 2а (почти около 0,98 мм).
Тогда в результате этого появляются изгиб стержня и наибольшее
§ 21
Ф0Т0УПРУГИЕ ИЗМЕРЕНИЯ НАПРЯЖЕНИЙ
195
напряжение, поскольку коэффициент концентрации при изгибе
равен 6, увеличивается на 18%, т. е. действительное номинальное
напряжение в этом случае равно 1,18 величины теоретического зна-
чения. При ничтожной ширине стержня в 20 мм эти числа вполне
правдоподобны. Если
учтём эту поправку к ре-
зультатам опытов Арм-
брюстера, то получим —
как видно из фиг. 100, —
значения, очень близкие
к теоретической кривой.
Следующий ряд иссле-
дований, проведённых
точно так же в Мюнхен-
ской лаборатории А. Неп-
nig’oM *), относится к рас-
тянутому стержню с цен-
тральным круговым от-
верстием, как изображе-
Фиг. 100. Сравнение опытов Армбрюстера на
растяжение с теорией коэффициента концен-
трации.
но на фиг. 101. Для сравнения экспериментальных данных, относя-
щихся к коэффициенту концентрации, с теорией отсылаем к рас-
суждениям главы IV, 6, С. Коэффициент концентрации глубокой
Фиг. 101. Исследованный
Г еннигом растянутый
стержень с центральным
отверстием.
Геннига на растяжение стержня
с центральным отверстием.
выточки в этом случае составляется из значения 04— двусторонней
глубокой внешней выточки при растяжении и слагаемого от изгиба,
которое получается из коэффициента концентрации а3 односторонней
глубокой внешней выточки при изгибе, умноженного на некоторый
коэффициент С. Этот коэффициент, согласно опытам, проведённым
Hennig'oM, равен 0,8. Доказательство этого следует из фиг. 102, где
*) Н е n n i g A., Forsch. Ing.-Wes. (1933), стр. 53.
13*
196 СРАВНЕНИЕ С РЕЗУЛЬТАТАМИ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ [ГЛ. IX
изображена кривая для коэффициента концентрации, получающаяся
теоретически (р\= 0,48 мм). Как видно, она близко % подходит
к коэффициентам концентрации, полученным экспериментально.
Ещё целый ряд дальнейших исследований мы найдём в литера-
туре по экспериментальным исследованиям напряжений. Но и отме-
ченных работ уже достаточно, так как речь идёт только о сравне-
нии теории с экспериментом, относящимся к напряжениям в вы-
точках.
В последней главе, мы, исполняя обещание, останавливаемся под-
робнее на уже неоднократно упомянутых номограммах для коэффи-
циентов концентрации, которые дают возможность определять легко
и быстро коэффициент концентрации также и математически менее
подготовленному читателю.
ГЛАВА X.
НОМОГРАММЫ ДЛЯ КОЭФФИЦИЕНТОВ КОНЦЕНТРАЦИИ.
1. Объяснения к номограммам для коэффициентов концентрации.
Общий обзор всех случаев, которые рассматривались уже в теории,
даёт фиг. 103. В левой части дана сводка существенных признаков
соответствующих выточек; отклоняющий угол, который находится
всегда одним и тем же образом (см., например, фиг. 98), ради
простоты не обозначен. В первом столбце указан вид нагрузки,
а во втором — формулы, по которым вычисляется номинальное напря-
жение. Причём, в последних двух формулах введены обозначения:
S— статический момент верхней половины поперечного сечения
относительно нейтральной оси,
J — момент инерции всего поперечного сечения относительно
той же оси,
F — площадь контура, ограниченная средней линией.
Следующие столбцы поясняют применение номограмм фиг. 104
те - / t ~ Г а ~ / г
и 105; в заголовках указаны параметры у у, у у и у у
(радикалы введены для лучшего отсчёта по номограмме). Буквы
в столбце!/ — указывают, каким рядом чисел {а или Ь) нужно поль-
* Р >_
зоваться на фиг. 104 при отсчёте значений у у. Числа обозначают
нужную кривую (именно, для j/* у направо по фиг. 104, а для у—
направо по фиг. 105). Из фиг. 104, или, для выточек на телах вра-
щения, из фиг. 104 и 105, получаем сразу коэффициент концентрации
а'к для идеального материала. Влияние структуры и боковых углов
определяется затем ещё по номограмме на фиг. 106. Правила пользо-
вания лучше всего разъяснить на примерах.
2. Примеры.
А. Двусторонняя внешняя выточка при изгибе. Дано: р = 2,5 мм,
t — 15 мм, а = 95 мм. Отсюда получается:
/2 = 2,45,
-=6,16.
₽
Виды выточе е Вид напряжения Формулы номинальных напряжений IfaoaMemfti W? для л>ел- плдиточег Рсранетры для глу- (Ши.тдыПМ1< '?'арамгтрь и^пряСс^- ?-.Г“ у5—
Ряды чисел Кридые КрЛе
,-1ф да РастяЖение _Р_ 2d, а Ъ Г —
Изгиб змв Zda* ь 2 —
дач *# РастяЖение р da ъ 3 —
Изгиб 8МВ da* ь И
j* . ♦ . t q 1 ч Г 1 1 РастяЖение Р Zda ь 5 --
«! Изгиб 3MBt Zdlb’-t3) а 5 —
Son-' \vh9 РастяЖение р not Ь 6 —
—йк ~~П S Изгиб чмв па3 Ь 7 —
Сдвиг 1,23У яаг а 8 —
1т=0,3 Кручение гиТ па3 а 9 —
l! 1Л | - г р РостяЖение р п(гг-с2) Ь 5 1
Изгиб ЧЧдГ- nfrW b 5 2
’ Т_ " н рИ/^да Сдвиг uirw n(r^cv/ а Ю 3
1__ т~ :/7,J Кручение 2Мр г п^-сУ а 10 ц
I .1 РостяЖение Р п1Ь2-гг) b 5 5
4Ш Изгиб ЧНвг nft^ry Ъ 5 6
С№и &.Пг-иЗггН ntbVJ а 10 7
Кручение 2Мтг п(Ь^гУ а 10 8
Сдвиг V паг а 10 —-
Кручение -Нт. 2паг^ а 10 —
Любое симме- s тричное пусто- телое сечение Сдвиг И 2aJ а 10 —
Кручение Mr 3! 2aF а 10 —
\1) 3-статический момент верхней половины поперечного сечения относительно нейтральной оси
J- момент инерции всего поперечного сечения относительно той Mv оси
?<' плоцадь контура, ограниченная средней линией /------)
Фиг. 103. Перечень задач о напряжениях в выточках, решаемых припомощи
номограмм коэффициентов концентрации по фиг. 104—106.
Фиг. 104. Номограмма для определения идеального коэффициента концентрации.
ПРИМЕРЫ
Фиг. 105. Номограмма для кольцевых выточек с осевым отверстием.
§
Примеры
201
Как вытекает из указаний на фиг. 103, для
ваться рядом чисел а для 1/ — — кривой
~ нужно пользо-
2. Начинаем таким
образом двигаться на фиг. 104 от у -—==6,16 по вертикали вверх
до пересечения с кривой 2. Затем проводим налево горизонтальную
линию до пересечения с осью диа(раммы. Эту последнюю точку
пересечения соединяем с точкой |/Г?- = 2,45, находящейся на гори-
зонтальной оси; при этом нужно отсчёт производить по ряду чисел Ь.
Фиг. 106. Номограмма *для< о пределения технического коэф-
фициента концентрации.
Эта прямая касается круга, указывающего коэффициент концентрации
а; = 4,28.
Правильность этого способа следует из того, что радиус круга,
который касается указанной прямой, является высотой прямоуголь-
1
202 номограммы для коэффициентов концентрации [глЛХ
ного треугольника с катетами —1 и atk— 1. Следовательно,
действительно мы имеем дело с той зависимостью между предель-
ными значениями коэффициентов концентрации, которая требовалась
согласно П, 4 и была объяснена на фиг. 3.
Если имеем дело с материалом при р' = 0,48 мм, то -^±±±0,44.
Отклоняющий угол пусть будет 90°. Тогда при пользовании фиг. 106
будем смещаться по горизонтали налево в уровне /£=0,44 и вер-
тикально вниз при значении ш = 0,5 тс. Через точку пересечения
проводим луч, идущий к правому нижнему углу. Затем двигаемся
снизу от а'л = 4,28 под углом 45° вправо и вверх до пересечения
с этим лучом; из точки пересечения проводим вниз вертикаль и от-
считываем на оси окончательный технический коэффициент концен-
трации ал = 2,73. Доказательство согласованности этого способа по-
строения с уравнением (43), VIII, основывается на подобии соот-
ветственных треугольников.
В. Внешняя выточка с осевым отверстием при изгибе» Дано
р = 4 ММ, а = 13 леи, 1 = 85 мм, г = 25 мм, р' = 0,48 мм, а = 90°.
Находим
£ = 2,50; /£-0,35.
По вышеописанному уже способу, при у — (ряд чисел Ь) и у —
(кривая 5), из фиг. 104 найдём прежде всего ak, которое оказывается
равным 3,60. Здесь идёт речь о значении ак при большом осевом
отверстии, т. е. для (а^у = <»•
Теперь переходим к фиг. 105 и смещаемся вверх по вертикали
при значении /~— — 2,50 до пересечения с кривой 2, затем налево
по горизонтали до пересечения с осью. Последнюю точку пересече-
ния соединим прямой с точкой (а^)гтоо = 3,60, лежащей на другой
оси. Круг, которой касается эта прямая, даёт а* = 2,08. Из фиг. 106
по этой величине уже вышеуказанным путём при /"£ = 0,35 и
«=•£ получаем окончательное значение ай=1,63.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Вал с поперечным отверстием 167
Взаимность касательных напряже-
ний 18
Выкружки, см. выточки
Выступы 84
Выточки 11
— большой и малой кривизны 51
— внешние глубокие двусторонние
47, 53, 55, 147, 148, >155, 158
--------односторонние 57
-----у тел. вращения 99, 147,159
— внутренние глубокие 148, 155,160
-----мелкие у тел вращения 118»
147, 153
— мелкие 74, 148, 153
— многократные 173
— призматического типа 162
— произвольной глубины 12, 13
— разгружающие 169
— с острыми углами 176
— у тел вращения 87
Глубина выточки 12, 63, 74, 89, 123,
128, 172, 175
Граничные условия 19, 44, 45
Гука закон 26
Деформации в криволинейных ко-
ординатах 22, 25, 35
— компоненты — 22
Дно выточки 13, 47, 53, 64, 67, 71,
169
Закон Гука 26
— затухания И, 90, 170
— наложения 21, 27
— перехода от глубоких к мелким
выточкам 12—14
--------закруглённых к заострен-
ным выточкам 183, 184
Изгиб поперечный при глубоких
внешних выточках 57
— чистый при глубокой выточке 51,
61, 104
— чистый при мелкой выточке 79,
125
-----тел вращения 150
-----с отверстиями 68
Искажение, коэффициент — 23, 24,
40, 47.
Компоненты деформаций 22, 24, 37
—» напряжений 28, 30, 43
— перемещений 22, 29, 30
Концентрация напряжений 8
-----в плоской задаче 40
-----пространстве 89
-----у выступов 84
Коэффициент искажения 23, 24, 47,
— концентрации 10, 12
-----выточки глубокой 13
-----для двухсторонней глубокой
выточки 82
-------любой глубины 14, 15
-------- мелкой 12
--------при изгибе 53, 57
--------растяжении 51
--------сдвиге 50
--------односторонней глубокой вы-
точки 83
—---------------при изгибе 62
------------------растяжении 61
------------------сдвиге 56, 63
--------мелких выточек 82, 158
--------при изгибе 78, 80
----------------растяжении 77, 78
----------------сдвиге 81
--------отверстий 83
----------при изгибе 62
----------растяжении 67, 68
-------------сдвиге 56, 63
--------стержня с продольным па-
зом 164
--------тел вращения 158—160
--------ПрИ ИзГИбе Ю7, 128,
132
Коэфициент концентрации для тел
ПТ^НбЯ154ПРИ кРУчении И?»
— 7"*-----------растяжении 104,
120, >121, 124
204
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Коэффициент концентрации для тел
вращения при сдвиге 111, 136,
137, 139, 454
-------тонкостенных полых сече-
ний 167
-----, зависящий от отклоняющего
угла 187, 188
-----при остроконечных выточках
179—183
-------разгружающих выточках
171-175
-----технический 188, 189
-----у вала с поперечным отвер-
стием 168
-------стержня с выступами 86 -
— разгружения 174
Кривая изменения коэффициента
концентрации 14
Кривизна выточки 51, 172
Кручение стержней с глубокой вы-
точкой »115
-------мелкой выточкой 142
-------остроугольной выточкой
178, 179
-------продольным пазом 164
-------разгружающей выточкой
170
Линии давления 169
— тока 51
Метод трёх функций 30
Модель для остроугольных выточек
177, 179
Напряжение 16
— возмущения 116
— допускаемое 7
— касательное 16, 18, 19
— местное 8
— номинальное 10, 50
— нормальное 16, 17
— объёмное 27
— при криволинейной системе коор-
динат 28, 36, 37
-----прямоугольной системе коор-
динат 16
— через гармонические функции
32
Отверстия круглые 63
— овальные 64
— продолговатые 63
Паз 164
Пластинки толстые 43
—; тонкие 42
Радиус кривизны выточки 12.
Растяжение при глубоких внешних
выточках 48, 58
------- мелких выточках 75
-------отверстиях 65
— стержней с остроугольными вы-
точками 180
— тел вращения с выточками 103,
119, 149
Сдвиг в прямоугольной системе
координат 21
— относительный 20, 22
— при глубоких выточках 53, 62
----мелких — 80
— наличии остроконечных выточек
178, 179
------- —; отверстий 70
— стержней с пазом 164
— тел вращения 108, 150
Силы инерции 17
— объёмные 17
Теория выточек призматического
типа 162
— концентрации в плоскости 40
-------пространстве 87
— упругости 16
----, основные уравнения-------29
Технический коэффициент концен-
трации 188, 189
Траектории главных напряжений 51
— касательных — 140, 141
- равных — 108, 113, 114, 133, 141
Удлинение относительное 20
Уравнение Лапласа 94
— равновесия 17
Формы выточек 11, 12, 47, 48, 77,
79, 119, 126, 135, 154
— отверстий 63, 64, 68
Фотоупругость 8, 83, 191
Функции гармонические 30
— напряжений 30
— Эри 43
Цилиндр с продольным пазом 164
Эффект разгружения 11
ОПЕЧАТКИ
Стра- ница Строка Напечатано Должно быть По чьей вине
3 3
ИЗ 6 св. (т+2Г : ОГ [ Тип.
145 З'св. 1 Сл -© 1 — 5 — р V
154 11 св. J'vw) (xvw) V
168 6 сн. V- /“7 ' р
188 19 св. (ак )р—мало = с у р *
190 4 сн. -/"7 У р •
3uu 847*