Автор: Флетчер К.
Теги: гидромеханика механика жидкостей и газа механика физика гидродинамика
ISBN: 5-03-001881-6
Год: 1991
Текст
Вычислительные методы
в динамике жидкостей
С. A. J. Fletcher
Computational Techniques
for Fluid Dynamics 1
Fundamental and General Techniques
With 138 Figures
Springer-Verlag
Berlin-Heidelberg New York
London-Paris «Tokyo
К. Флетчер
Вычислительные методы
в динамике
жидкостей
В двух томах
Том 1
Основные положения и общие методы
Перевод с английского
A. И. Державиной
под редакцией
B. П. Шидловского
Москва «Мир» 1991
ББК 22.253
Ф71
УДК 532 + 681.3
Флетчер К-
Ф71 Вычислительные методы в динамике жидкостей: В 2-х
томах: Т. 1: Пер. с англ. — М.: Мир, 1991. —504 с, ил.
ISBN 5-03-001881-6
Двухтомник по современной вычислительной гидродинамике, на-
написанный известным австралийским специалистом, знакомым читате-
читателям по переводу его «Численных методов на основе метода Галёркина»
(М: Мир, 1988). Анализ задач проводится с позиций получения чис-
численного решения, выделяются актуальные нерешенные проблемы. При-
Приводятся программы на Фортране, реализующие излагаемые методы.
Двухтомник может использоваться и для решения сложных практиче-
практических задач, и как учебное пособие по вычислительной гидродинамике.
Для математиков-вычислителей, гидромехаников, физиков, аспи-
аспирантов и студентов вузов.
Редакция литературы по математическим наукам
ISBN 5-03-001881-6 (русск.) © Springer-Verlag Berlin Heidelberg 1988.
ISBN 5-03-001880-8 A11 rights reserved. Authorized transla-
ISRN Ч Ч4П 1R1S1 2 ГаншЪ tion from EnSlish language edition pub-
ISBN 3-540-18151-2 (англ.) Hshed by Springer-Verlag, Heidelberg,
New York, Tokyo
© перевод на русский язык,
А. И. Державина, 1991
От редактора перевода
Применение вычислительных методов в естественных нау-
науках получило в последние 3—4 десятилетия очень широкое рас-
распространение. Можно смело утверждать, что подобный «чис-
«численный» уклон в процессе теоретического исследования многих
классов задач не только не снизил качества подобных исследо-
исследований, но и придал им более жизненный колорит, существенно
приблизив результаты к требованиям инженерной практики.
Динамика жидкости и газа представляет собой одну из тех
областей знания, где подходы, основанные на применении вы-
вычислительных методов, оказались особенно плодотворными и
позволили получить продвижение в решении ряда проблем,
•считавшихся до этого неразрешимыми. Действительно, такие
особенности уравнений гидроаэродинамики, как нелинейность,
высокий порядок (особенно в отношении пространственных за-
задач) и возможность появления разрывных решений, зачастую
делают именно численный метод исследования наиболее пред-
предпочтительным и эффективным. Как раз это обстоятельство и
привело к появлению термина «вычислительная гидроаэроди-
гидроаэродинамика», обозначающего по существу некую самостоятельную
и бурно развивающуюся область науки.
В нашей стране вычислительная гидроаэродинамика имеет,
пожалуй, не меньшее распространение, чем во многих разви-
развитых странах. Тем не менее у нас ощущается определенный не-
недостаток монографической литературы в этой области, нередко
восполняемый переводами зарубежных изданий. Так, в свое
время большим успехом пользовался русский перевод книги
П. Д. Роуча «Вычислительная гидродинамика» (М.: Мир, 1980).
Однако эта книга к настоящему времени существенно устаре-
устарела и не может считаться удовлетворительной ни по освещению
гидродинамических процессов, ни по набору описанных в ней
численных методов.
Недавно вышедшая в русском переводе книга Д. Андерсона,
Дж. Таннехилла и Р. Плетчера «Вычислительная гидромехани-
гидромеханика и теплообмен» (М.: Мир, 1990) вполне удовлетворительно от-
отражает современный уровень гидроаэромеханики, однако,
От редактора перевода
к сожалению, ограничивается лишь описанием конечно-разност-
конечно-разностных методов.
Книга, предлагаемая нами читателю, представляет собой
первый том двухтомной монографии и выгодно отличается как.
современным уровнем изложения, широтой охвата физических
задач, так и разнообразием методов их численного решения.
Автор книги — известный австралийский ученый К. Флетчер —
знаком советским читателям не только по публикациям в перио-
периодической печати, но и по изданному в СССР переводу его книги
«Численные методы на основе метода Галёркина» (М.: Мир,.
1988), которая пользуется успехом у читателя.
Поскольку автор достаточно подробно излагает основное
содержание своей книги в предисловии, мы ограничимся здесь
оценкой некоторых ее отличительных черт.
Особенность предлагаемой книги состоит в том, что автор*
не углубляется в теоретическое обоснование излагаемых ме-
методов, ограничиваясь в этом отношении лишь анализом точ-
точности аппроксимации. Вместе с тем он подробно описывает
технику применения каждого конкретного метода, а также ана-
анализирует его положительные и отрицательные качества, уде-
уделяя при этом особое внимание оценкам точности и экономич-
экономичности. Невозможно переоценить и тот факт, что изложение си-
систематически подкрепляется и иллюстрируется программами на
языке Фортран, а также результатами расчетов по этим про-
программам.
Настоящий, первый том книги посвящен описанию практи-
практически всех методов решения наиболее характерных задач w
приемам реализации этих методов. Готовящийся к изданию вто-
второй том будет связан с более подробным изложением примене-
применения численных методов к определенным классам гидроаэродина-
гидроаэродинамических задач.
Есть все основания надеяться, что книга будет с интересом
встречена инженерами и научными работниками, занимающи-
занимающимися вычислительной гидроаэродинамикой, а также принесет
пользу аспирантам и студентам старших курсов тех специаль-
специальностей, где изучается механика жидкости и газа, и в особен-
особенности численные методы решения задач в этой области.
В. П. Шидловский
Предисловие
Предлагаемое вниманию читателя двухтомное издание яв-
является учебным пособием, предназначенным для студентов,
специализирующихся по техническим наукам и прикладной ма-
математике. Это пособие ставит своей целью ознакомление чита-
читателя с теми методами, которые доказали свою эффективность
в различных областях вычислительной гидроаэродинамики
(ВГАД), и разработку методики для успешного использования
этих методов. В т. 1 излагаются некоторые основные представ-
представления, а также наиболее общие методы, пригодные для чис-
численного исследования любых разновидностей течения жидкости
л газа. В т. 2 описываются специальные методы, приме-
применимые к изучению различных видов течения, имеющих инже-
инженерно-техническое значение, причем многие из этих методов
пригодны и для исследования конвективной теплопередачи.
Красной нитью сквозь все содержание книги проходит идея
о том, что конкурирующие подходы, используемые при решении
задач вычислительной гидроаэродинамики и основанные, на-
например, на применении конечных разностей, конечных элемен-
элементов, а также спектральных методов, тесно связаны между со-
собой и могут рассматриваться как отдельные части некоторой
единой структуры. Опыт, полученный автором при занятиях
со студентами, указывает на то, что именно с помощью такой
трактовки студент может наиболее глубоко разобраться как в
положительных, так и в отрицательных качествах того или ино-
иного численного метода.
Благодаря включению в текст 24 вычислительных программ,
а также примеров и задач данная книга окажется пригодной
также и для сформировавшихся исследователей или работни-
работников, желающих практически овладеть численными методами
без специального обучения. Содержание книги охватывает на-
наиболее современные методы и подкреплено более чем 300 ри-
рисунками, а также 500 названиями в списке литературы.
Применительно к большинству учебных заведений содер-
содержание т. 1 соответствует программе вводных курсов по ВГАД
на втором или третьем году обучения. Содержание т. 2
соответствует программе спецкурсов, читаемых по прикладным
Предисловие
разделам ВГАД на более поздней стадии обучения. Что касается
сформировавшегося исследователя или инженера-практика, то
такому читателю рекомендуется прочитать т. 1 и прорешать
все предлагаемые там задачи, прежде чем приступить к форму-
формулировке своей собственной программы по ВГАД. Содержание
т. 2 станет для такого читателя более ценным, после того как
он приобретет некоторый опыт по ВГАД в процессе работы над.
своей программой.
Предполагается, что читатель хорошо знаком с такими разде-
разделами прикладной математики, как численное решение линейных:
или нелинейных алгебраических уравнений, а также обык-
обыкновенных дифференциальных уравнений. Материал по этой те-
тематике можно найти в книгах [Dahlquist, Bjorck, 1974], [For-
sythe, Malcolm, Moler, 1977] l\ [Carnaghan, Luther, Wilkes^
1969]. Предполагается также, что читатель обладает опреде-
определенными знаниями по гидроаэродинамике. Такого рода знания
можно почерпнуть из книг: Streeter, Wylie «Fluid Mechanics»,
Panton «Incompressible Flow», Batchelor «An Introduction ta
Fluid Dynamics»2) и др.
Включенные в книгу программы для ЭВМ приводятся здесь
с учебной целью, а также для того, чтобы читателю было легче
составлять свои собственные программы либо путем исполь-
использования аналогичных построений, либо с помощью модифика-
модификации приводимых программ. Если иметь в виду, что человек*
практикующийся по вычислительной гидроаэродинамике/ с оди-
одинаковой вероятностью может как воспользоваться готовой про-
программой, так и набросать свою собственную, то желательно
обладать некоторым опытом переделки имеющихся программ,,
хотя бы самых простых. Автор книги может предоставить же-
желающим гибкий диск, пригодный для компьютеров фирмы
«ИБМ» и содержащий соответствующие программы.
Распределение материала в первом томе осуществлено сле-
следующим образом. В гл. 1 предлагается введение в вычислитель-
вычислительную гидроаэродинамику (ВГАД), в котором читатель получит
представление о том, почему ВГАД столь важна для науки и
практики, о характере решаемых при этом задач, а также о
том, как реализуются цели, поставленные перед ВГАД. Урав-
Уравнения, служащие для описания течения жидкости, обычно-
имеют форму дифференциальных уравнений в частных произ-
производных. Поэтому в гл. 2 описываются дифференциальные урав-
1) Имеется перевод: Форсайт Дж., Малькольм М., Моулер К. Машинные-
методы математических вычислений. — М.: Мир, 1980.
2> Две первые книги малоизвестны советскому читателю, а книга
Дж. Бэтчелора «Введение в динамику жидкости» переведена на русский*
язык в издательстве «Мир» в 1973 г.
Предисловие
нения в частных производных различного типа, приводятся со-
соответствующие граничные условия и дается краткий обзор тра-
традиционных методов решения.
Построение численных решений расчленяется на два этапа —
приведение дифференциальных уравнений в частных производ-
производных к системе алгебраических уравнений и решение этих алге-
алгебраических уравнений. Первый этап, называемый дискретиза-
дискретизацией, рассматривается в гл. 3, где особый акцент делается на
точности аппроксимации. В гл. 4 обеспечивается теоретический
базис, достаточный для того, чтобы те или иные численные ре-
решения можно было должным образом соотнести с «точным»
решением, как правило неизвестным. В гл. 5 вводится пред-
представление о методах взвешенных невязок, служащих средством
для исследования и сравнения между собой методов конечных
элементов, методов конечных объемов и спектральных методов
в качестве альтернативных средств дискретизации. Характер-
Характерные способы решения алгебраических уравнений, получаемых
в результате дискретизации, описываются в гл. 6. Совокуп-
Совокупность гл. 3—6 обеспечивает наиболее существенный информа-
информационный базис.
Одномерное уравнение диффузии, рассмотренное в гл. 7,
представляет собой простейшую модель для описания течения
жидкости с высоким уровнем диссипации. Это уравнение ис-
лользуется для того, чтобы противопоставить друг другу яв-
явные и неявные методы, а также чтобы обсудить методику чис-
численного представления граничных условий, формируемых по-
посредством производных. Если пространственная размерность
больше или равна двум, то для эффективного построения чис-
численных решений обычно требуется воспользоваться методикой
расщепления; различные варианты такого расщепления опи-
описываются в гл. 8. Конвективные (или адвективные) процессы
при течении жидкости, а также эффективные приемы их чис-
численной оценки рассматриваются в гл. 9. Конвективные члены
уравнений оказываются обычно нелинейными, и дополнитель-
дополнительные трудности, связанные с этой нелинейностью, рассматри-
рассматриваются в гл. 10. Общие приемы, разрабатываемые в гл. 7—10,
используются при построении специальных методов, служащих
Для исследования разнообразных видов течения жидкости или
особенностей их поведения, как это и показано в гл. 14—18
т. 2 книги.
При подготовке данного учебного пособия я прибегал к по-
помощи многих специалистов. В частности, я хотел бы поблаго-
поблагодарить д-ра К. Сриниваса, Нам-Хью Чжо и Зили Жу за
<то, что они прочитали текст рукописи и внесли множество
10 Предисловие
полезных предложений. Я благодарен ДжунДжеффери за подго-
подготовку иллюстраций очень высокого качества. Выражаю особук>
благодарность Сьюзен Гонзалес, Лин Кеннеди, Мариту Агудо
и Шейн Гортон, которые успешно справлялись как с каприз-
капризным автором, так и с трудноуправляемыми процессорными
устройствами, за перепечатку рукописи и ее пересмотренных
вариантов с похвальной точностью, скоростью и терпением.
Мне приятно отметить вдумчивую помощь и профессиональ-
профессиональную компетентность проф. В. Бейгльбёка, г-жи Кристины*
Пендль, г-на Р. Михельса и их коллег в издательстве Springer-
Verlag, проявившиеся при подготовке данного учебного посо-
пособия. Наконец, я выражаю глубокую признательность моей
жене Мэри, неизменно поддерживавшей меня и несшей бремя-
«книжной вдовы» со своим обычным достоинством.
Сидней, октябрь 1987 г. К. Флетчер
Глава 1
Введение
в вычислительную гидроаэродинамику
В данной главе предлагается обзор вычислительной гидро-
даэродинамики (ВГАД), причем основное внимание уделяется
эффективности затрат, производимых в процессе разработки.
Приводится описание некоторых характерных приложений,
позволяющих продемонстрировать возможности ВГАД. Вы-
Выявляется характерная структура уравнений гидроаэродинами-
гидроаэродинамики и иллюстрируется процесс превращения этих уравнений в
-алгоритмы, реализуемые на ЭВМ. Наконец, внимание читателя
привлекается к некоторым наиболее важным источникам ин-
информации более высокого уровня.
§ 1.1. Преимущества вычислительной гидроаэродинамики
Процесс установления гидроаэродинамики как науки, а
также развития практических приложений этой науки начался
и продолжался еще со времен Ньютона. Теоретическое разви-
развитие гидроаэродинамики концентрируется в основном на по-
построении и решении определяющих уравнений, пригодных для
различных типов течения жидкости или газа, а также на изу-
изучении разного рода аппроксимаций по отношению к этим урав-
уравнениям.
Определяющие уравнения ньютоновской гидроаэродинами-
гидроаэродинамики — нестационарные уравнения Навье — Стокса — известны
уже в течение 150 лет или даже более. Однако разработка уко-
укороченных форм этих уравнений (гл. 16) по-прежнему остается
областью активных исследований, так же как и проблема за-
замыкания осредненных по Рейнольдсу уравнений Навье — Сток-
Стокса (см. п. 11.5.2), применяемых в теории турбулентности.
В областях неньютоновской гидроаэродинамики, описания
химически реагирующих потоков и двухфазных течений теоре-
теоретические разработки находятся пока что не на столь высоком
Уровне.
Экспериментальная гидроаэродинамика сыграла важную
роль при проверке справедливости и установлении пределов
пригодности различных аппроксимаций по отношению к
12 Гл. 1. Введение в вычислительную гидроаэродинамику
определяющим уравнениям. Аэродинамическая труба, применяе-
применяемая как оборудование для проведения эксперимента, является
эффективным средством моделирования реальных течений.
Традиционно эта труба сыграла роль альтернативы натурным
измерениям, позволившей снизить затраты. В процессе проек-
проектирования конструкций, существенно зависящих от поведения
потока, например при проектировании самолета, натурные из-
измерения как элемент этого процесса не оправдывают себя эко-
экономически.
Устойчивое повышение скорости существующих ЭВМ и объ-
объема их памяти, начавшееся в 1950-х гг., привело к возникно-
возникновению вычислительной гидроаэродинамики (ВГАД). Эта ветвь
гидроаэродинамики дополняет ее экспериментальную и теоре-
теоретическую ветви, представляя собой альтернативное и экономи-
экономически эффективное средство моделирования реальных течений.
В качестве такового ВГАД предоставляет возможности про-
проверки теоретических приближений к таким условиям, экспери-
экспериментальное моделирование которых невозможно. Например,
эксперименты в аэродинамических трубах ограничиваются
определенным диапазоном чисел Рейнольдса, которые оказы-
оказываются обычно на один или два порядка величины меньше на-
натурных чисел.
Еще одно преимущество вычислительной гидроаэродинами-
гидроаэродинамики состоит в том, что при желании можно отбросить те или
иные члены определяющих уравнений. Тем самым открывается
путь к опробованию теоретических моделей или, наоборот, вы-
выявляются новые пути теоретического исследования.
Появление более эффективных ЭВМ стимулировало инте-
интерес к ВГАД, а последняя в свою очередь обеспечила сущест-
существенное повышение эффективности вычислительной техники.
В результате ВГАД стала к настоящему времени наиболее
предпочтительным средством проверки качества альтернатив-
альтернативных разработок в авиационной промышленности, в промыш-
промышленности турбодвигателей и в несколько меньшей степени в
автомобильной промышленности.
Суммируя выводы работ [Chapman et al., 1975; Chapman
1979, 1981; Green, 1982; Rubbert, 1986], можно утверждать, что
ВГАД позволяет получить пять важнейших видов преимуще-
преимущества по сравнению с экспериментальной гидроаэродинамикой:
1) время предварительной подготовки при проектировании
и при разработках существенно уменьшается;
2) ВГАД позволяет моделировать условия течения, не вос-
воспроизводимые при экспериментальных испытаниях на моде-
моделях;
§ 1.1. Преимущества вычислительной гидроаэродинамики \3
3) ВГАД позволяет получить более широкую и подробную
информацию;
4) стоимостная эффективность экспериментов на основе
ВГАД по сравнению с испытаниями в аэродинамических тру-
трубах непрерывно повышается;
5) применение методов ВГАД позволяет снизить потреб-
потребление энергии.
Согласно сложившейся традиции, длительные времена пред-
предварительного этапа проектирования были связаны с необходи-
необходимостью осуществления следующих последовательных этапов:
составления проекта, создания модели, испытаний в аэродина-
аэродинамической трубе и составления скорректированного проекта.
Создание модели оказывается зачастую наиболее медленной
стадией этого процесса. Использование хорошо отлаженной
программы по методике ВГАД позволяет испытывать серию
альтернативных проектов (например, с различной геометриче-
геометрической конфигурацией) в широком диапазоне значений парамет-
параметров, таких, как число Рейнольдса, число Маха, угол отклонения
потока. Расчет каждого варианта может потребовать около
15 мин на таком суперкомпьютере, как CYBER-205 или
CRAY-2. Возможности оптимизации проектирования существен-
существенно ограничиваются способностью проектировщика к восприя-
восприятию и оценке численных результатов. На практике ВГАД ока-
оказывается чрезвычайно эффективной на ранней стадии отбора
среди конкурирующих вариантов проектной конфигурации.
Однако подтверждение окончательного выбора проектного ва-
варианта все же достигается посредством испытаний в аэродина-
аэродинамической трубе.
Рабберт [Rubbert, 1986] обращает особое внимание на тот
факт, что если пакеты стандартных программ ВГАД исполь-
используются с максимальной эффективностью, то скорость примене-
применения методов ВГАД при повторном проектировании второ-
второстепенных элементов конструкции оказывается достаточно
большой. При этом Рабберт приводит пример, касающийся по-
повторного проектирования внешнего контура кабины самолета
«Боинг-757» с целью размещения тех же конструктивных эле-
элементов, что и в кабине «Боинга-767», но при минимизации вре-
времени смены пилота. Как указывает Рабберт, методы ВГАД
позволили определить такую внешнюю форму кабины, которая
была внедрена в производство еще до того, как была предпри-
предпринята какая-либо ее экспериментальная проверка в аэродина-
аэродинамической трубе.
Характерным ограничением для испытаний в аэродинами-
аэродинамической трубе является достижимое при этом число Рейнольдса
14 Гл. 1. Введение в вычислительную гидроаэродинамику
(натурные испытания обычно исключаются). За пределами
возможностей большинства экспериментальных установок ока-
оказывается также диапазон очень высоких температур, обуслов-
обусловленный взаимосвязью проблем теплопередачи с проблемами
обтекания. Это особенно явственно выделяется при решении
проблем сгорания, когда дополнительный уровень сложности
создается за счет изменения химического состава среды. Далее,
некоторые разновидности неустановившегося движения жид-
жидкости или газа не удается должным образом моделировать при
экспериментах, особенно если движение сопровождается неста-
нестационарными изменениями геометрии, как это имеет место для
некоторых задач биологической аэродинамики. Кроме того,
многие проблемы геофизической аэрогидродинамики оказы-
оказываются слишком большими или слишком отдаленными в про-
пространстве или во времени, чтобы быть доступными экспери-
экспериментальному моделированию. Так, например, потоки, возни»
кающие в нефтяных резервуарах, в принципе невозможно
подвергнуть точным экспериментальным измерениям. С другой
стороны, проблемы астрофизической гидроаэродинамики яв-
являются слишком отдаленными в пространстве, тогда как фор-
форма кривых, определяющих погоду, должна быть определена до
того, как она реализуется. Все эти разновидности движения
жидкости или газа являются подходящими для исследования
численными методами.
Такие экспериментальные установки, как аэродинамическая
труба, оказываются весьма эффективными с целью получения
глобальной информации, например, о значениях полной подъ-
подъемной силы и полного сопротивления, действующих на тело,
или о распределении давления на характерных участках его
поверхности. Однако нахождение детальных экспериментальных
распределений скорости и давления по всей области, окру-
окружающей тело, было бы чрезвычайно дорогостоящим и потребо-
потребовало бы очень много времени. ВГАД дает возможность полу-
получить эту детальную информацию без каких-либо дополнитель-
дополнительных затрат и, следовательно, позволяет дать более полное
представление о тех гидроаэродинамических процессах, кото-
которые здесь должны иметь место.
Возможно, наиболее важным побудительным стимулом к
расширению применения ВГАД является тот факт, что для
большинства вариантов модели основного потока применение
методов ВГАД оказывается значительно дешевле, чем прове-
проведение испытаний в аэродинамической трубе, причем со време-
временем эта разница в стоимости будет даже возрастать. Улучше-
Улучшение характеристик средств вычислительной техники достига-
достигалось до сих пор одновременно со снижением стоимости этой
§ 1.1. Преимущества вычислительной гидроаэродинамики 15
техники. В результате для определенного численного алгорит-
алгоритма и определенной задачи обтекания относительная стоимость
численного моделирования подвергалась до настоящего време-
времени существенному снижению (рис. 1.1). Параллельно с улуч-
улучшением характеристик средств вычислительной техники про-
происходило и улучшение эффективности численных алгоритмов
для решения заданной проблемы (рис. 1.2). Сочетание этих
10
ол
0.01
0.001
-IBM 650
™h 7090
CDC
-
—
i i 1 i i i
7094
ш 1 IBM 360-50
^-t i 360-Б7
6400:::5t* 370-195
6600#/"^5^ /S^Ti
360-91 7600 ^^jL '
1.4 ^
1/10 каждые 8 лет
I i i i i I i i i i I i i t i I
AR
CRAY
/
1 1 1
1
3SP
^ASF
1 i i i i i
I 1955 1960 1965 1970 1975 1980 1985
О _
Годы выпуска новых компьютеров
Рис. 1.1. Относительная стоимость вычислений по заданному алгоритму и
для заданного вида течения (согласно обзору [Chapman, 19791; воспроизве-
воспроизведено с разрешения AIAA).
двух факторов приводит к непрерывному повышению стоимост-
стоимостной эффективности методов ВГАД. В противоположность этому
стоимость осуществления экспериментов продолжает расти.
Повышение качества вычислительной техники и вычисли-
вычислительных алгоритмов привело, кроме того, к уменьшению по-
потребления энергии, необходимой для численного моделирования
течений. И наоборот, необходимость моделирования физи-
физических условий, приближающихся к предельным, с более высо-
высокими числами Рейнольдса, более высокими числами Маха и с
более высокой температурой, привела к увеличению потребле-
потребления энергии, требуемой для проведения экспериментов.
Хронологически развитие вычислительной техники в тече-
течение последних тридцати лет было направлено на создание более
быстрых машин с увеличенной памятью. Современный супер-
суперкомпьютер такого типа, как CYBER-205 [Levine, 1982], спосо-
способен действовать со скоростями до 400 мегафлоп. Один мегафлоп
соответствует одному миллиону арифметических операций
с плавающей запятой в секунду. Суперкомпьютеры последних
выпусков, такие, как NEC SX2 [Fernbach, 1986], способны
16
Гл. 1. Введение в вычислительную гидроаэродинамику
действовать со скоростями, превышающими 1000 мегафлоп.
Повышение скорости осуществляется в первую очередь за
счет сокращения цикла машинного времени, т. е. времени, по-
потребного для выполнения каждого цикла логических операций.
Если CYBER-205 имеет временной цикл 20 не B0-10~9 с), то
временной цикл машины NEC SX2 составляет 6 не.
Характерная операция, как, например, сложение с плаваю-
плавающей запятой, может быть разбита на некоторое число логиче-
Улучшение качества
компьютеров
х
5 Ю2
& 10
г
О
Улучшение качества
численных методов
2-мерные уравнения Навье - Стокса
С^ с осреднением по Рейнольдсу
Чч^- (Re=107)
Течение, зависящее
от времени
2-мерное
трансзвуковое
65
70
Годы
75
65
Рис. 1.2. Относительная стоимость в зависимости от качества техники и ка-
качества вычислительных алгоритмов (согласно обзору [Chapman, 1979]; вос-
воспроизведено с разрешения AIAA). ;
ских операций, для исполнения каждой из которых требуется
один машинный цикл. Если одна и та же операция типа сложе-
сложения с плавающей запятой должна последовательно применяться
к большому числу элементов некоторого вектора, то жела-
желательно иметь дело с каждой из логических операций последо-
последовательно, однако добиваться одновременного выполнения раз-
различных логических операций, связанных с каждым элементом
вектора. Таким образом достигается значительное перекрытие
операционных циклов и существенное ускорение суммарного
времени выполнения задания, если только вычислительный ал-
алгоритм способен использовать подобный принцип трубопро-
трубопровода.
Такие современные суперкомпьютеры, как члены семей-
семейства CRAY, а также CYBER-205, обладают специальными век-
векторными командами, использующими формат трубопровода.
Однако некоторые части программы не могут подвергнуться
§ 1.1. Преимущества вычислительной гидроаэродинамики 17
такой обработке, так что эффективная оперативная скорость
может составить всего 10—20 % от максимально достижимой
(согласно оценке) скорости [Fernbach, 1986].
Способность довести суммарную скорость выполнения зада-
задания до предела, поставленного возможностями техники, час-
частично зависит от способности операционной системы и компи-
компилятора к векторизации вычислительного алгоритма, а частично
от выбора таких вычислительных алгоритмов, которые по своим
свойствам поддаются подобной векторизации [Ortega, Voigt,
1985]. Придание вычислительному алгоритму такой структуры,
которая позволяет реализовать векторизацию, представляет со-
собой важную тему для исследования, но выходит за пределы
данной книги. По-видимому, долгосрочная тенденция будет
идти в направлении создания таких операционных систем и ком-
компиляторов, которые обеспечивали бы проведение векторизации
при условии, что пользователь мало заботится о соответствую-
соответствующей модификации основного алгоритма.
Если архитектура ЭВМ соответствует принципу трубопро-
трубопровода и имеется эффективная программа векторизации, а вре-
временной цикл машины сделан сколь возможно малым, то глав-
главным средством дальнейшего повышения оперативной скорости
является внедрение множественных процессоров, действующих
по принципу параллелизма. В настоящее время суперкомпью-
суперкомпьютеры [Fernbach, 1986] конструируются так, что они имеют до
восьми процессоров, работающих в параллельном режиме. Тео-
Теоретически это должно было бы обеспечивать восьмикратное по-
повышение скорости. Как показывают предварительные экспери-
эксперименты Стивенса [Stevens, 1986] с двухпроцессорной машиной
CRAY-X/MP, при численной реализации наиболее характерных
программ ВГАД можно добиться повышения скорости, получая
от 75 до 95 % теоретически возможного максимума.
Идея о введении некоторого набора процессоров, каждый
из которых оперирует с отдельным элементом вектора, сыгра-
сыграла важную роль при разработке более эффективной архитекту-
архитектуры компьютеров [Hockney, Jesshope, 1981]. Компьютер Illias-IV
имел 64 параллельных процессора и достигал суммарной опера-
оперативной скорости, сравнимой со скоростями машин CRAY-1 и
CYBER-205, хотя временной цикл этого компьютера составлял
целых 80 не. Сравнительные достоинства процессоров, работаю-
работающих по принципу трубопровода и параллельному принципу, в
общем виде обсуждаются в работах Левина [Levine, 1982], Ор-
теги и Фойта [Ortega, Voigt, 1985], а более подробно — в работе
Хокни и Джессхоупа [Hockney, Jesshope, 1981].
Разработка более объемистых и более дешевых модулей па-
памяти стимулируется существенным коммерческим интересом
2 К. Флетчер, т. 1
18 Гл. 1. Введение в вычислительную гидроаэродинамику
по отношению к хранению и обработке данных. Для приложе-
приложения к ВГАД важно, чтобы вся программа, включая команды и
набор переменных, сохранялась в основной памяти. Это связа-
связано с тем, что скорость передачи данных из вторичной (диско-
(дисковой) памяти в основную намного меньше, чем скорости обмена
между основной памятью и узлами процессора. В прошлом
именно объем основной памяти определял предел сложности
исследуемых задач ВГАД.
Весьма впечатляющей является хронологическая последо-
последовательность в возрастании объема памяти суперкомпьютеров.
У машины CDC-7600 (проект 1970 г.) объем памяти составлял
4-Ю5 64-битовых слов. Компьютер CYBER-205 (проект 1980 г.)
обладает памятью в 3-Ю7 64-битовых слов, а, согласно про-
программе NAS [Bailey, 1986], ожидается, что к 1990 г. будут
действовать суперкомпьютеры с основной памятью объемом .в*
109 64-битовых слов.
Значительный прогресс в создании миникомпьютеров в
1970-х гг. и микрокомпьютеров в 1980-х гг. обеспечил альтерна-
альтернативный путь к формированию стоимостно-эффективной ВГАД.
Появление микрокомпьютеров с 32-битовой памятью свиде-
свидетельствует о том, что ограниченная возможность доступа к ос-
основной памяти уже не является препятствием к применению»
микрокомпьютеров. Следовательно, относительная дешевизна
оперативной памяти указывает на возможность эффективного ре-
решения больших задач с помощью микро- или миникомпьютеров.
Основное отличие микрокомпьютеров от полногабаритных машин
состоит в их значительно более медленном временном цикле, а
также в их упрощенной и менее эффективной архитектуре.
Объединение многих сравнительно маломощных параллель-
параллельных процессоров рассматривается как весьма эффективный
путь к решению сложных задач ВГАД. Каждый из таких процес-
процессоров может базироваться на применении вполне стандартных
микрокомпьютерных компонентов, что приведет к возможно ма-
малой стоимости системы. Типичная система такого рода —
PAX-128 — описана в докладе Хосино [Hoshino, 1986]. Эта си-
система имеет 128 процессорных узлов, каждый из которых
базируется на микрочипах типа Motorola-68000, действующих
со сравнительно медленным временным циклом, равным 500 не.
Несмотря на это, система PAX-128 способна развивать скорость
до 4 мегафлоп.
Сравнительно медленное действие систем, базирующихся на
микрокомпьютерах, может компенсироваться допущением бо-
более длительных времен счета. Если для рутинной проектно-рас-
четной работы 15 мин на суперкомпьютере является, по-види-
по-видимому, общепринятой нормой [Bailey, 1986], то в процессе ис-
§ 1.2. Характерные практические задачи
19
следований и разработок времена счета на микрокомпьютере
порядка одного дня могут оказаться вполне приемлемыми. Это
даже дает преимущество исследователю, работающему в об-
области ВГАД, предоставляя ему достаточное время для интер-
интерпретации результатов и подготовки к расчету дополнительных
вариантов.
I
I
Моделирование
с крупными
вихрями •
Возможность в 1989 г. (прогноз)
Уравнения Навье- Стокса
с осреднением по Рейнольде/
АС —самолет
W—крыло
А —профиль
0ДС1 0.01
0.1 1 10 10* 10э
Скорость компьютера, мегафлоп
105 106
Рис. 1.3. Требования со стороны ВГАД к скорости компьютеров и объему
памяти (согласно [Bailey, 1986]; воспроизведено с разрешения Japan Society
of Computational Fluid Dynamics).
Весьма обнадеживающими являются прогнозы на будущее,
касающиеся скорости компьютеров и объема их памяти. Как
свидетельствуют оценки, сделанные в работах [Chapman, 1981;
Bailey, 1986; Fernbach, 1986], к 1990 г. можно ожидать воз-
возрастания скорости компьютеров до 104 мегафлоп, а объема
основной памяти — до 1000 мегаслов. Как предполагается, это-
этого будет достаточно (рис. 1.3) для полного расчета установив-
установившегося вязкого (турбулентного) сжимаемого потока вокруг ле-
летательного аппарата.
20 Гл. 1. Введение в вычислительную гидроаэродинамику
§ 1.2. Характерные практические задачи
В настоящее время вычислительная гидроаэродинамика, и
в особенности ее инженерные приложения, находится в такой
стадии своего развития, когда «задачи, связанные со сложной
геометрией, могут решаться при наличии простых физических
условий, а задачи, связанные с простой геометрией,— при
сложных физических условиях» [Bailey, 1986]. Ниже приво-
приводятся характерные примеры таких задач.
1.2.1. Сложная геометрия, простые физические условия
Распределение давления по поверхности типового сверх-
сверхзвукового военного самолета демонстрируется на рис. 1.4. Числа
Маха невозмущенного потока составляет 1.8, а угол атаки ра-
равен 8°. Самолет состоит из фюзеляжа, обтекателя кабины, за-
борников двигателя, киля, основного дельтовидного крыла и
Рис. 1.4. Распределение давления по поверхности типового военного само-
самолета. Линии равного давления с АСР = 0.02 (согласно [Arlinger, 1986]; вос-
воспроизведено с разрешения Japan Society of Computational Fluid Dynamics).
передних (фальшивых) крыльев. Кроме того, плоскости управ-
управления у задней кромки дельтовидного крыла отклонены вверх
на угол 10°. В каждой из плоскостей поперечного сечения, по-
последовательно расположенных в направлении вниз по потоку,
необходимо иметь приблизительно 19 000 узловых точек. Слож-
Сложность геометрии предъявляет серьезные требования к проце-
процедуре формирования расчетной сетки. Арлингер [Arlinger, 1986]
пользуется алгебраической техникой формирования сетки, ос-
основанной на применении трансфинитной интерполяции (см.
п. 13.3.4).
Течение предполагается невязким и повсюду сверхзвуковым,
так что можно воспользоваться явной маршевой схемой в на-
направлении невозмущенного потока. Это эквивалентно той
§ 1.2. Характерные практические задачи 21
процедуре, которая описана в п. 14.2.4. Явная маршевая схема
здесь особенно эффективна, причем расчет всего поля течения
требует 15 мин на компьютере CRAY-1. Для дискретизации
исходных уравнений используется метод конечных объемов
(§ 5.2). Как подчеркивает Арлингер, ключевым элементом,
необходимым для эффективного получения результатов, яв-
является гибкая и универсальная техника формирования рас-
расчетной сетки.
1.2.2. Упрощенная геометрия,
более сложные физические условия
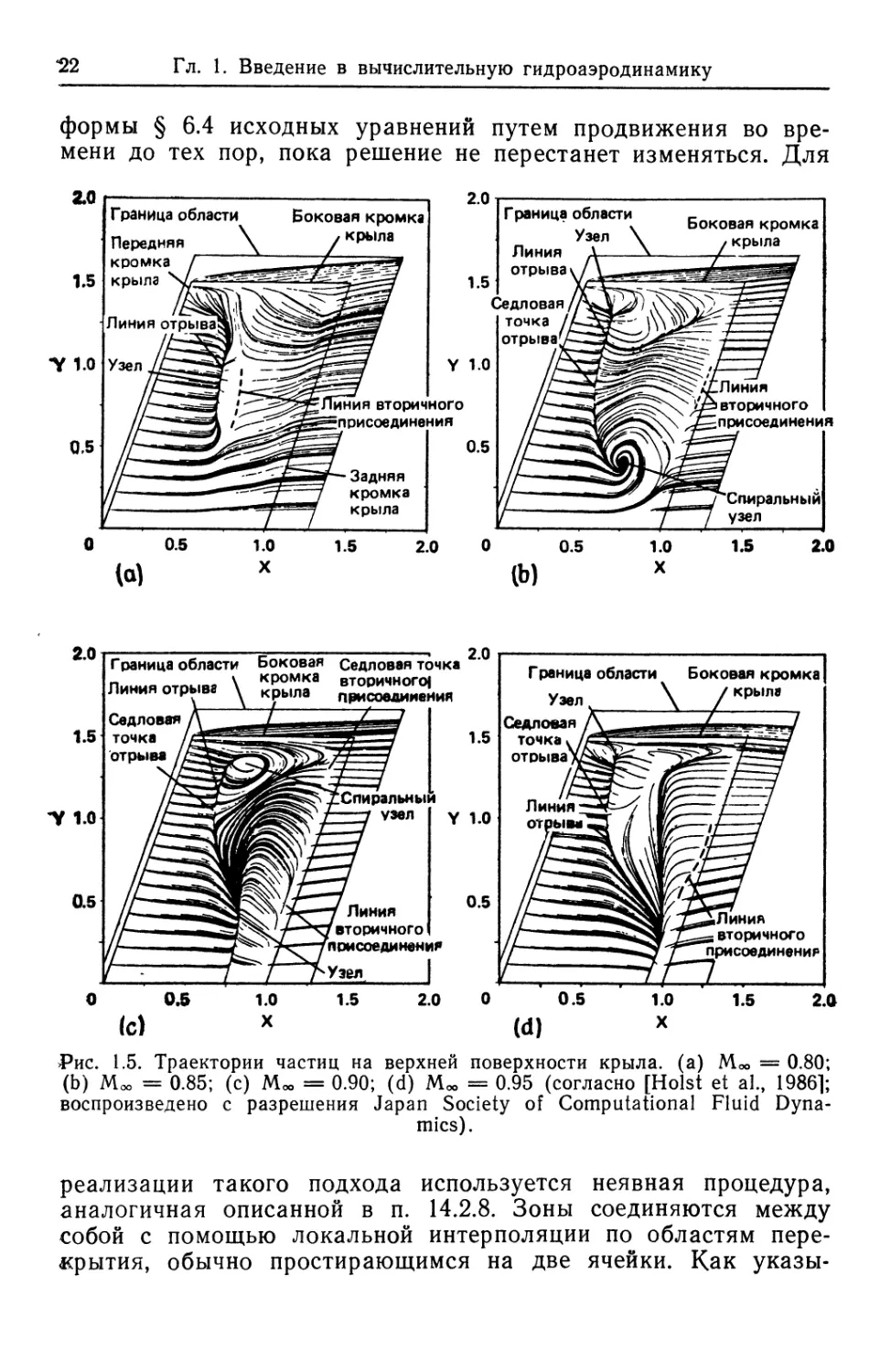
На рис. 1.5 показаны предельные траектории частиц на
верхней поверхности трехмерного крыла при возрастающих
числах Маха М» невозмущенного потока. Предельные траекто-
траектории частиц соответствуют тем картинам на поверхности, кото-
которые могли быть получены экспериментально с помощью
масла. Результаты, показанные на рис. 1.5, получены путем
расчета [Hoist st al., 1986] трансзвукового вязкого обтекания
крыла под углом атаки 2° с относительным удлинением, рав-
равным 3, и с числом Рейнольдса, рассчитанным по длине хорды
и равным 8-106.
При этих условиях над крылом формируется ударная волна,
взаимодействующая с пограничным слоем на верхней поверх-
поверхности и создающая обширную зону отрыва. Эта область отры-
отрыва изменяется и расширяется по мере увеличения Моо. Влия-
Влияние области потока, примыкающей к боковой кромке крыла,
делает картину отрыва существенно трехмерной. Терминология,
применяемая в надписях на рис. 1.5 (спиральный узел и т. п.),
соответствует классификации, принятой при описании трехмер-
трехмерного отрыва [Tobak, Peake, 1982].
Для построения решения требуется трехмерная сетка, со-
состоящая примерно из 170 000 точек, распределенных по четы-
четырем, частично перекрывающим друг друга зонам. Две зоны, рас-
расположенные непосредственно над крылом и под ним, имеют
сетку, измельченную в нормальном направлении с целью точ-
точного предсказания возникающих здесь очень больших градиен-
градиентов скорости. В этих двух зонах решаются уравнения Навье —
Стокса для тонкого слоя. Такие уравнения содержат только те
вязкие члены, которые связаны с направлением нормали и слу-
служат примером упрощенных уравнений Навье — Стокса
(гл. 16). В двух зонах, удаленных от крыла, течение предпо-
предполагается невязким и подчиняющимся уравнениям Эйлера (см.
п. 11.6.1).
Решения для каждой из узловых точек сетки во всех зонах
строятся по маршевой схеме на основе псевдонестационаржш
-22
Гл. 1. Введение в вычислительную гидроаэродинамику
формы § 6.4 исходных уравнений путем продвижения во вре-
времени до тех пор, пока решение не перестанет изменяться. Для
Граница области
Передняя \
Боковая кромка
крыла
2.0
Граница области
Узел \
Линия ^ Л-
отрыва v
Боковая кромка
/ крыла
2.0
1.5
-V1.0
0.5
Граница области Боковая Седловая точка
Линия отрыв, \ *рГ
Седловая
2.0
точка
отрыва
О 0.5
(с)
Спиральны i
узел
1.5
Y 1.0
Граница области Боковая кромка
Узел, \ /крып'
Седловая
Линия
ВТОРИЧНОГО
поисоединений
Узел I
точка
отрыва
1.0
X
1.5
2.0
,Линия
вторичного
присоединения
1.5
2.0
Рис. 1.5. Траектории частиц на верхней поверхности крыла, (а) М«> = 0.80;
(Ь) Моо = 0.85; (с) Моо = 0.90; (d) Moo = 0.95 (согласно [Hoist et al., 19861;
воспроизведено с разрешения Japan Society of Computational Fluid Dyna-
Dynamics).
реализации такого подхода используется неявная процедура,
аналогичная описанной в п. 14.2.8. Зоны соединяются между
собой с помощью локальной интерполяции по областям пере-
перекрытия, обычно простирающимся на две ячейки. Как указы-
§ 1.2. Характерные практические задачи 23
вает Холст, устойчивые решения получаются даже тогда, когда
очень большие градиенты пересекают границы зон.
В результате включения в анализ эффектов вязкости дан-
данная задача относится к существенно более сложному поведе-
поведению течения, и ее решение требует применения гораздо более
сложного вычислительного алгоритма, чем это было для зада-
задачи, рассмотренной в п. 1.2.1. Однако форма расчетной области
здесь значительно проще. Кроме того, расчетная сетка форми-
формируется здесь по зональному принципу, что обеспечивает луч-
лучший контроль за размещением узловых точек.
1.2.3. Простая геометрия, сложные физические условия
Для иллюстрации этой категории задач вместо инженерно-
технического примера выбран метеорологический. На рис. 1.6
представлен трехдневный прогноз распределения давления и
температуры (схема (Ь)) при 850 мбар (примерно 5000 футов)
по сравнению с данными измерений (схема (а)). Погодные
фронты показаны на основе косвенных данных, так как расчет-
расчетная схема обладает слишком грубым разрешением для того,
чтобы провести прямой расчет этих фронтов. Рассчитанный
прогноз дает картину погоды, весьма близкую к ее истинному
развитию.
Определяющие уравнения [Cullen, 1983], вообще говоря, не
учитывают вязкость, но принимают во внимание влияние ветра,
температуры, давления, влажности, поверхностных напряжений
на суше и на море, эффект подогрева, эффект осадков и дру-
другие эффекты [Haltiner, Williams, 1980]. Уравнения, как прави-
правило, записываются в сферических полярных координатах, рас-
расположенных параллельно земной поверхности, с добавлением
нормализованной координаты для давления, которая перпенди-
перпендикулярна земной поверхности. В результате трудности, связанные
с нерегулярностью границ вычислительных областей, а также
с формированием сетки, сводятся к минимуму.
Как указывает Каллен, показанные на рис. 1.6 результаты
были получены на сетке 192 X 80 X 15 с использованием яв-
явной расщепленной конечно-разностной схемы с продвижением
решения во времени. Это позволяет полностью хранить всю сет-
сетку в основной памяти. Для получения трехдневного прогноза
используется 288 шагов по времени, что требует 71/2 мин про-
процессорного времени на компьютере CYBER-205.
Как отмечает Каллен, основная трудность для проведения
Достаточно точного крупномасштабного прогноза на срок бо-
более 3—4 дней состоит в получении начальных данных, имею-
имеющих достаточно высокое качество. Что касается более тонких:
Гл. 1. Введение в вычислительную гидроаэродинамику
Рис. 1.6. Сравнение кривых распределения и температуры при 850 мбар.
(а) Измерения; (Ь) прогнозы (согласно [Cullen, 1983]; воспроизведено с раз-
разрешения Academic Press).
§ 1.3. Структура уравнений 25
местных прогнозов, то здесь возникают дополнительные труд-
трудности, связанные с необходимостью предотвращения «заглаты-
«заглатывания» внутреннего решения возмущениями, идущими от гра-
границ, а также с необходимостью точного представления огром-
огромных местных градиентов, соответствующих фронтам.
Для моделирования глобальной циркуляции, и в особенно-
особенности для построения долгосрочных прогнозов, можно применить
спектральный метод (§ 5.6), хорошо согласующийся со сфери-
сферической полярной геометрией. Вообще говоря, спектральные ме-
методы являются более экономичными, чем конечно-разностные
или конечно-элементные, при сравнимой точности расчетов, па
крайней мере для глобальных прогнозов. Применение спектраль-
спектральных методов к прогнозированию погоды кратко обсуждается
в книге Флетчера [Fletcher, 1984], а более подробно — в работе
Бурке и др. [Bourke et al., 1977].
Приведенные выше примеры дают наглядное представле-
представление о современном состоянии ВГАД. Что касается будущего,
то Бейли [Bailey, 1986] утверждает, что «для решения задач*
связанных одновременно и со сложной геометрией, и со слож-
сложными физическими условиями, требуются более мощные ком-
компьютеры с большим объемом памяти».
§ 1.3. Структура уравнений
Общая черта всех тех задач гидроаэродинамики, которые
рассматриваются в данной книге, состоит в том, что жидкость
может считаться непрерывной средой. Вследствие такого ус-
условия описание поведения жидкости может быть осуществле-
осуществлено посредством представления скорости и термодинамических
параметров как непрерывных функций времени и пространства.
Применение принципов сохранения массы, импульса и энер-
энергии позволяет получить систему дифференциальных уравнений
в частных производных (см. гл. 11) для скорости и термодина-
термодинамических переменных как функций времени и координат. Если
сформулировать граничные и начальные условия, соответствую-
соответствующие данному виду течения и типу дифференциального уравне-
уравнения в частных производных, то математическое описание за-
задачи будет завершено.
Многие гидроаэродинамические задачи связаны с разви-
развитием взаимодействия между конвекцией и диффузией. Простой
пример такого рода схематически представлен на рис. 1.7, где
показано распределение температуры жидкости в трубе в раз-
различные моменты времени. Предполагается, что жидкость дви-
движется слева направо с постоянной скоростью и и температура
в поперечном сечении трубы постоянна.
Гл. 1. Введение в вычислительную гидроаэродинамику
Температура как функция х и / определяется уравнением
дТ , дТ д2Т
= 0 при
О-1)
Если провести соответствующее обезразмеривание переменных,
то граничные и начальные условия примут вид
(**, 0 = 0, A.2)
cos пху — 0.5 < х < 0.5,
и, х <^ — и.о, х ^> и.о.
Уравнение A.1) и условия A.2) — A.3) обеспечивают матема-
математическое описание задачи. Член ад2Т/дх2 представляет собой
1.0
Г
XL -1.0
1.о г f=a5A
т
1.0 х 2.0
¦V-1
хк
xL -1.0
1.0 г t=1-°/"
1.0 х 2.0
XLV -1.0 0 1.0 х 2.0 xF
Рис. 1.7. Одномерное распределение температуры.
диффузионный член, а величина a — коэффициент тепловой
диффузии. Этот член несет ответственность за распределение
области ненулевой температуры вправо и влево; если коэффи-
коэффициент а мал, то и полоса распространения мала. Методика вы-
вычислений в применении к уравнениям, содержащим подобные
члены, рассматривается в гл. 7 и 8.
Член идТ/дх — конвективный член, несущий ответственность
за то, что распределение температуры целиком сносится впра-
вправо с известной скоростью и. Принципы обращения с этим чле-
§ 1.3. Структура уравнений 27
ном, а также с полным уравнением переноса A.1), рассматри-
рассматриваются в гл. 9. Если размерность задачи превышает единицу,,
то оказывается, что и конвективные, и диффузионные члены
связаны с каждым из исследуемых направлений (см. § 9.5) -
Если учесть, что величина и известна, уравнение A.1) яв-
является линейным по Т. Однако если решение строится для поля
скоростей, то необходимо рассмотреть уравнения с нелинейны-
нелинейными конвективными членами. Прототип для нелинейности по-
подобного рода задается уравнением Бюргерса (см. § 10.1)
?+•?—&•-•• <'-4>
Наличие нелинейного члена иди/дх способствует тому, что
при очень малых а развиваются очень большие градиенты из-
изменения и. Наличие таких градиентов приводит к необходи-
необходимости измельчения сетки, и в результате наличие нелинейности
нередко влечет за собой необходимость введения дополнитель-
дополнительного уровня итерации в вычислительный алгоритм.
Некоторые проблемы гидродинамики и теории теплопереда-
теплопередачи определяются решением уравнения Лапласа
Это имеет место для течения невязкой несжимаемой жидкости
в отсутствие завихренности, и тогда величина ф представляет
собой потенциал скорости (см. § 11.3). Уравнение Лапласа со-
соответствует наиболее характерному виду уравнения, опреде-
определяющего равновесие системы или решение стационарных за-
задач (см. гл. 6). Кроме того, уравнение Лапласа обладает тем
специальным свойством, что у него есть простые точные реше-
решения, которые можно складывать между собой (осуществлять
суперпозицию), так как само уравнение линейно. Наличие этих
свойств используется при применении методов, описываемых
в§ 14.1.
Многие гидроаэродинамические задачи связаны с опреде-
определением более чем одного искомого переменного, что приводит
к необходимости рассмотрения систем уравнений. Так, напри-
например, одномерное неустановившееся течение невязкой сжимае-
сжимаемой жидкости подчиняется уравнениям (см. § 10.2)
= 0, A.6а>
М.
28 Гл. 1. Введение в вычислительную гидроаэродинамику
где Р — давление, а Е — полная энергия, приходящаяся на еди-
единицу объема и определяемая выражением
? = 7ZT + 0.5pii»f A.7)
в котором у — отношение удельных теплоемкостей. Несмотря
на нелинейность уравнений A.6), их структура подобна струк-
структуре уравнения A.4) без диффузионных членов. В широком
лредставлении стратегия численного решения, разработанная
для скалярных уравнений, будет применимой и к системам урав-
уравнений.
Для тех гидроаэродинамических задач, где в рассмотрение
необходимо включить осредненные свойства турбулентности,
структура концептуального уравнения может быть представ-
представлена в виде
dt ' дх дх \ дх
где коэффициент а является теперь функцией искомой пере-
переменной и, a S представляет собой член типа источника, содер-
содержащий добавочные вклады за счет турбулентности. Однако
для полной ясности необходимо отметить (см. п. 11.4.2 и 11.5.2),
что турбулентные течения являются по меньшей мере двумер-
двумерными, а зачастую и трехмерными и что для описания таких
течений необходимо иметь систему уравнений.
§ 1.4. Обзор общих принципов вычислительной
гидроаэродинамики
Весь процесс выявления практической информации, касаю-
касающейся задач, связанных с течением жидкости или газа, схе-
схематически может быть представлен на рис. 1.8.
Определяющие уравнения (см. гл. И) для течений, пред-
представляющих практический интерес, оказываются обычно столь
сложными, что получить их точное решение невозможно и не-
необходимо строить численное решение. При использовании вы-
вычислительных методов исходные дифференциальные уравнения
в частных производных заменяются системой алгебраических
уравнений, в результате чего для получения решения можно
воспользоваться вычислительной машиной. В данной книге
будут изложены вычислительные методы, служащие для по-
построения и решения систем алгебраических уравнений.
При применении локальных методов типа методов конечных
разностей, конечных элементов и конечных объемов алгебраи-
алгебраические уравнения связывают между собой значения искомых
§ 1.4. Общие принципы вычислительной гидроаэродинамики 29
переменных в группе соседних узловых точек. При этом под-
подразумевается, что сетка, состоящая из дискретных точек, рас-
распределена по всей вычислительной области во времени и в
ДЛЯ КАЖДОГО ЭЛЕМЕНТА ЖИДКОСТИ
Сохранение массы =ф-
Второй закон Ньютона =>•
для движения
Сохранение энергии s>
Уравнение состояния
1
уравнение
ности,
уравнения
уравнения
Стокса,
уравнение
Решить
неразрыв-
Эйлера, )
Навье — }
j
энергии
уравнения
с граничными усло-
условиями
] Распределение скорости:
Распределение давления:
Распределение плотности:
; Распредедение температуры:
и (х, у, z, 0. v (х* У> *> 0,
w (ху у, z, /)
р (х, у, z, t)
р (х9 у, z, t)
Т(Х, у, 2, t)
Определить характеристики
течения:
отрыв потока,
секундный расход,
теплопередача,
силы, действующие на тело
(напряжение трения, сопро-
сопротивление, подъемная сила),
коэффициенты полезного дей-
действия (для турбины, диф-
диффузора)
Рис. 1.8. Обзор общих принципов вычислительной гидроаэродинамики.
пространстве. На этом основании процесс превращения непрерыв-
непрерывных определяющих уравнений в систему алгебраических уравне-
уравнений называют обычно процессом дискретизации (см. гл. 3). При
применении такого глобального метода, как спектральный,
30 Гл. 1. Введение в вычислительную гидроаэродинамику
искомые переменные заменяются обычно амплитудами, относя-
относящимися к различным частотам.
Алгебраические уравнения, к которым приводит процесс
дискретизации, могут быть получены следующим образом. Ха-
Характерное конечно-разностное представление уравнения A.1)
имеет вид
At ^ 2 Ах ~ Ах2 ' ^ ^
где х = jAx и t = nAt.
Если решение известно во всех узловых точках х\ на вре-
временном слое м, то уравнение A.9) можно использовать для со-
составления алгоритма, служащего для определения Г", т. е. на-
написать
rptl+l ТП ( U At \ (грП rptl \ , / О, At \ (rptt OT.rt . rptl \
Ti = Ti — {TAx~J ^+1 "" Г/-^ + 1"Л^"J V!~l ~ 2T* + Г'+"-
A.10)
Повторное обращение к формуле A.10) позволяет получить
решение во всех внутренних узловых точках Хи на временном
слое п + 1. Увеличение п на единицу и подстановка значений
Тп+Х в правую часть выражения A.10) позволяет осуществить
маршевое передвижение дискретного решения во времени.
При применении локального метода, например конечно-раз-
конечно-разностного, число узловых точек, необходимое для построения до-
достаточно точного решения, зависит, как правило, от размер»
ности, геометрической сложности и величины градиентов изме-
изменения искомых переменных. Для определения течения вокруг
самолета в целом может потребоваться сетка, состоящая из
10 млн точек. В каждой из узловых точек необходимо запоми-
запоминать каждую из искомых переменных, а также некоторые вспо-
вспомогательные переменные. При рассмотрении турбулентного сжи-
сжимаемого трехмерного течения указанный подход может при-
привести к необходимости введения от 5 до 30 искомых переменных,
приходящихся на каждую узловую точку. Для обеспечения эф-
эффективного расчета все эти переменные должны храниться в
основной памяти.
Если учесть, что для большинства задач гидроаэродинами-
гидроаэродинамики определяющие уравнения являются нелинейными, процесс
построения численного решения обычно ведется посредством
итераций. Иначе говоря, решение для каждого искомого пере-
переменного в каждой узловой точке последовательно подправля-
подправляется посредством обращения к дискретизованным уравнениям.
Процесс построения итераций оказывается нередко эквивалент-
§ 1.5. Литература для дополнительного чтения 31
ным продвижению решения на некоторый малый шаг во време-
времени (см. гл. 6). Число итераций или шагов во времени может
варьироваться от нескольких сот до нескольких тысяч.
Сам процесс дискретизации вносит в расчет ошибку, кото-
которую в принципе можно уменьшить за счет измельчения сетки,
если только дискретные уравнения такого типа, как уравнение
A.9), являются надежным представлением исходных опреде-
определяющих уравнений (см. § 4.2). Если численный алгоритм, реа-
реализующий итерацию или продвижение во времени, является
к тому же устойчивым (см. § 4.3), то численное решение мо-
может быть сделано сколь угодно близким к истинному решению
определяющих уравнений за счет измельчения сетки, при ус-
условии что это допускается ресурсами вычислительной машины.
Хотя, как правило, решение ищется в форме набора дискрет-
дискретных узловых значений, все же некоторые методы, как, напри-
например, конечно-элементные и спектральные методы, вводят в яв-
явной форме непрерывное представление численного решения.
В тех случаях, когда исходная физическая задача в силу свое-
своего характера обеспечивает плавность, указанные методы не-
нередко дают большую точность по отношению к каждой неиз-
неизвестной, входящей в дискретизованные уравнения. Эти методы
кратко обсуждаются в гл. 5.
§ 1.5. Литература для дополнительного чтения
Предлагаемое пособие ставит своей целью дать введение
в вычислительные методы, подходящие для решения задач гидро-
гидроаэродинамики. Более подробную информацию можно найти в
других книгах, обзорах, журнальных статьях и трудах кон-
конференций.
Рихтмайер и Мортон [Richtmyer, Morton, 1967] строят общие
основные теории для анализа вычислительных методов, приме-
применяемых в гидроаэродинамике, и обсуждают конкретные конеч-
конечно-разностные методы, используемые для исследования невяз-
невязкого сжимаемого потока. Роуч [Roache, 1976] исследуех. вязкое
отрывное течение для условий сжимаемой или несжимаемой
жидкости, но сосредоточивается при этом на конечно-разност-
конечно-разностных методах. В более позднее время Пейре и Тейлор [Peyret,
Taylor, 1983] рассмотрели вычислительные методы в примене-
применении к различным разделам гидроаэродинамики, делая наи-
наибольший крен в сторону конечно-разностных и спектральных
методов. Холт [Holt, 1984] предлагает описание чрезвычайно
мощных методов анализа течения в пограничном слое, а также
невязкого сжимаемого течения. Бук [Book, 1981] рассматривает
конечно-разностные методы в применении как к инженерной, так
32 Гл. 1. Введение в вычислительную гидроаэродинамику
и к геофизической гидроаэродинамике в условиях, когда диф-
диффузионные механизмы отсутствуют или играют очень малую
роль.
Томассе [Thomasset, 1981], Бейкер [Baker, 1983] и Гловин-
ский [Glowinski, 1984] анализируют вычислительные методы,
основанные на методе конечных элементов, а Флетчер [Flet-
[Fletcher, 1984] излагает технику применения конечно-элементных
и спектральных методов. В статье [Haltiner, Williams, 1980]
обсуждаются вычислительные методы, применяемые в геофизиче-
геофизической гидроаэродинамике.
В обзорных статьях [Chapman, 1975, 1979, 1981; Green,
1982; Krause, 1985; Kutler, 1985] обсуждается, на что в настоя-
настоящее время способна инженерная ВГАД и каковы ее перспекти-
перспективы в будущем. Эти статьи имеют явный уклон в направлении
приложений к авиации и космическим исследованиям. Обзор
более общего характера дан Тёркелем [Turkel, 1982]. В обзоре
Каллена [Cullen, 1983] рассматривается современное состоя-
состояние метеорологической ВГАД. Обзорные статьи по конкретным
разделам вычислительной гидроаэродинамики появляются
в серии Annual Reviews of Fluid Dynamics, в серии лекций
Института им. Кармана, а также в серии монографий, вы-
выходящей в издательстве «Пайнридж Пресс». В настоящей кни-
книге не затрагиваются более утонченные вычислительные методы,
применяемые для расчетов на векторных и параллельных
компьютерах. Однако исчерпывающий обзор исследований в
этой области дают Ортега и Фойгт [Ortega, Voigt, 1985].
Журнальные статьи по соответствующей тематике появ-
появляются в журналах: AIAA Journal, Journal of Computational
Physics, International Journal of Numerical Methods in Fluids,
Computer Methods in Applied Mechanics and Engineering, Com-
Computers and Fluids, Numerical Heat Transfer, Journal of Applied
Mechanics, Journal of Fluids Engineering. Наиболее важными
трудами конференций являются следующие: International Confe-
Conference Series on Numerical Methods in Fluids Dynamics, AIAA
CFD Conference Series, GAMM Conference Series, Finite Elements
in Flow Problems Conference Series Numerical Methods in Lami-
Laminar and Turbulent Flow, Conference Series, а также многие дру-
другие специализированные конференции.
Глава 2
Дифференциальные уравнения
в частных производных
В данной главе будут разработаны процедуры, служащие
для классификации дифференциальных уравнений в частных
производных, т. е. отнесения их к эллиптическому, параболи-
параболическому или гиперболическому типу. Каждый из этих типов
уравнений будет изучен как с математической, так и с физи-
физической точки зрения с целью демонстрации их важнейших ха-
характерных особенностей и тех разновидностей течения, при ко-
которых встречается тот или иной тип уравнения.
Определяющие уравнения гидроаэродинамики (см. гл. 11)
представляют собой дифференциальные уравнения в частных
производных, содержащих первые и вторые производные по
пространственным координатам и лишь первые производные
по времени. Производные по времени входят в уравнения ли-
линейно, но пространственные производные часто появляются в
нелинейной форме. Кроме того, если не считать специального
случая потенциального течения, обычно приходится иметь де-
дело не с одним уравнением, а с системой определяющих урав-
уравнений.
§ 2.1. Основные положения
Для линейных дифференциальных уравнений в частных
производных второго порядка с двумя независимыми перемен-
переменными можно предложить некоторую простую классификацию
[Garabedian, 1964]. Так, например, в случае дифференциально-
дифференциального уравнения в частных производных (ДУЧП) вида
где коэффициенты от А до G — постоянные, можно различить
три разновидности такого уравнения:
Эллиптическое В2 — 4АС < О,
Параболическое В2 — 4ЛС = 0, B.2)
Гиперболическое В2 — 4АС > 0.
3 К. Флетчер, т. 1
34 Гл. 2. Дифференциальные уравнения в частных прооизводных
Очевидно, что классификация связана только с высшими про-
производными по каждому из независимых переменных.
В случае двумерного установившегося потенциального те-
течения сжимаемой жидкости, обтекающей тонкое тело, опреде-
определяющее уравнение, аналогичное уравнению A1.109), имеет вид
(l-Mi)^r + -g- = 0. B.3)
Применение критериев B.2) свидетельствует о том, что урав-
уравнение B.3) эллиптическое в случае дозвукового течения
(Моо < 1) и гиперболическое — в случае сверхзвукового тече-
течения (Моо > 1).
Если коэффициенты от А до G, входящие в уравнение B.1),
являются функциями х, у, и, ди/дх или ди/ду, критерии B.2)
могут использоваться, как и прежде, если при этом значениям
Л, В и С давать локальную интерпретацию. Это означает, что
классификация определяющих уравнений может изменяться по
мере попадания в различные участки вычислительной области.
Определяющее уравнение для установившегося потенциаль-
потенциального течения сжимаемой жидкости, т. е. уравнение A1.103),
при применении двумерных естественных координат можно за-
записать в форме
где оси sun параллельны и перпендикулярны к местному на-
направлению линии тока, а параметр М—местное число Маха.
Применение критериев B.2) на локальной основе показывает,
что уравнение B.4) является эллиптическим, параболическим
или гиперболическим, если М < 1, М = 1 или М > 1 соответ-
соответственно. Характерная картина распределения местных чисел
Маха М в случае обтекания крылового профиля или лопасти
турбины показана на рис. 11.15. Характерная особенность, свя-
связанная с возможностью изменения типа определяющего урав-
уравнения в различных участках вычислительной области, пред-
представляет собой один из главных усложняющих факторов при
численном исследовании трансзвукового течения (см. § 14.3).
При анализе упрощенных разновидностей течения (см.
п. 11.2.6) тип уравнения может измениться. Определяющие
уравнения для двумерного установившегося течения несжимае-
несжимаемой вязкой жидкости, т. е. уравнения A1.82) — A1.84), при от-
отсутствии членов du/dt и dv/dt являются эллиптическими. Одна-
Однако введение приближения пограничного слоя приводит к пара-
параболической системе ДУЧП, т. е. к уравнениям A1.60) и A1.61).
§ 2.1. Основные положения 35
Применительно к тем уравнениям, которые можно предста-
представить в форме B.1), классификация ДУЧП может быть прове-
проведена путем проверки с использованием критериев B.2). Когда
же это невозможно, например в случае системы ДУЧП, для
надлежащей классификации приходится обычно проверять по-
поведение характеристик (см. п. 2.1.3).
Грубо говоря, различные категории ДУЧП могут ассоции-
ассоциироваться с различными типами гидроаэродинамических задач.
В общем случае задачи, содержащие зависимость от времени^
сводятся к решению либо параболических, либо гиперболиче-
гиперболических ДУЧП. Параболические ДУЧП определяют собой тече-
течения, обладающие тем или иным механизмом диссипации, на-
например такие, где существенны вязкие напряжения или тепло-
теплопроводность. В этом случае решение будет гладким, а градиенты
с течением времени будут уменьшаться, если только гранич-
граничные условия не зависят от времени. Если же диссипативные
механизмы отсутствуют, то решение будет сохранять постоян-
постоянную амплитуду в случае линейности ДУЧП и будет даже воз-
возрастать в случае его нелинейности. Такое решение характерно
для течений, определяемых гиперболическими ДУЧП. Эллипти-
Эллиптические ДУЧП обычно определяют собой задачи, относящиеся
к установившимся или к равновесным состояниям. Однако при
исследовании некоторых установившихся течений приходится
иметь дело с параболическими ДУЧП (установившееся тече-
течение в пограничном слое) и с гиперболическими ДУЧП (устано-
(установившееся невязкое сверхзвуковое течение).
2.1.1. Природа корректно поставленной задачи
Прежде чем продолжать обсуждение формальной классифи-
классификации дифференциальных уравнений в частных производных,
имеет смысл и формулировку задачи, и построение алгоритма
рассмотреть под углом представления о корректно поставленной
задаче. Задача, связанная с решением определяющих уравне-
уравнений вместе со вспомогательными (начальными и граничными)
условиями, является математически корректно поставленной,
если выполняются следующие условия:
1) решение задачи существует,
2) решение является единственным,
3) решение непрерывно зависит от вспомогательных данных.
Вопрос о существовании решения обычно не создает каких-
либо трудностей. Исключение составляет введение точных ре-
решений уравнения Лапласа (см. § 11.3), когда в некоторых изо-
изолированных точках решение может не существовать. Так,
36 Гл. 2. Дифференциальные уравнения в частных производных
например, оно не существует в центре источника, при г = rs и
при использовании A1.53). Зачастую на практике удается из-
избежать столкновения с этой проблемой путем расположения ис-
источника за пределами вычислительной области, например внут-
внутри тела, показанного на рис. 11.7.
Обычная причина неединственности связана с несоответ-
несоответствием вспомогательных условий типу определяющего ДУЧП.
Для уравнения потенциала, определяющего невязкие безвихре-
безвихревые течения, а также для уравнений пограничного слоя надле-
надлежащая форма начальных и граничных условий хорошо уста-
установлена. Для уравнений Навье — Стокса хорошо известны над-
надлежащие условия на твердой поверхности, однако существует
некоторая неопределенность относительно надлежащего выбо-
выбора граничных условий вдали от тела. В общем случае недооп-
недоопределение граничных условий приводит к неединственности,
тогда как их переопределение — к получению нефизических ре-
решений вблизи соответствующей границы.
Можно указать на некоторые проблемы обтекания, для кото-
которых множественность решений может ожидаться в силу физиче-
физических причин. К таким проблемам уже нельзя применять выше-
вышеприведенные критерии корректности математической постанов-
постановки. Именно такая ситуация нередко возникает при рассмотре-
рассмотрении течений, испытывающих переход от ламинарного состояния
движения к турбулентному. Однако при надлежащем пред-
представлении о гидроаэродинамике обычно удается идентифициро-
идентифицировать такие виды течений, расчет которых может быть услож-
усложнен из-за необходимости заботы о корректной постановке мате-
математической задачи.
Третий из перечисленных выше критериев требует, чтобы
малое изменение начальных или граничных условий влекло за
собой лишь малое изменение решения. Довольно часто вспомо-
вспомогательные условия вводятся в типовой вычислительный алго-
алгоритм в приближенной форме. Следовательно, если третье ус-
условие не выполняется, то ошибки, введенные вместе со вспомо-
вспомогательными данными, будут распространяться во внутреннюю
область, вызывая тем самым быстрый рост решения, особенно
для гиперболических ДУЧП.
Вышеуказанные критерии обычно приписывают Адамару
[Garabedian, 1964]. В дополнение к этому мы могли бы про-
провести простую параллель и потребовать, чтобы для корректно
поставленного расчета выполнялись следующие условия:
1) вычислительное решение существует,
2) вычислительное решение единственно,
3) вычислительное решение непрерывно зависит от при-
приближенных вспомогательных данных.
§ 2.1. Основные положения 37
Процесс построения вычислительного решения может быть
представлен схематически так, как это сделано на рис. 2.1.
Здесь термин «вводимые данные» соответствует приближенно-
приближенному представлению начальных и граничных условий. Если гра-
граничные условия формулируются для производных функции и,
то некоторая ошибка будет вноситься за счет приближенного
лредставления этих условий. Вычислительный алгоритм, как
правило, строится на основе определяющего ДУЧП (см. § 3.1)
и должен быть устойчивым (см. § 4.3), чтобы выполнялись все
три вышеприведенных условия.
Вводимые
данные, а
Вычислительный
алгоритм,
Вычислительное
решение, U
Рис. 2.1. Построение вычислительного решения
Таким образом, для проведения корректно поставленных вы-
вычислений необходимо, чтобы не только задача для исходного
ДУЧП со вспомогательными условиями была корректно постав-
поставлена, но чтобы и алгоритм был также корректно поставлен (ус-
(устойчив). При этом подразумевается, что приближенное реше-
решение, полученное в результате корректно поставленного расчета,
будет в определенном смысле близко к точному решению кор-
корректно поставленной задачи. Этот вопрос будет рассматривать-
рассматриваться в § 4.1.
2.1.2. Граничные и начальные условия
В результате проведенного в п. 2.1.1 обсуждения корректно
поставленных задач и корректно поставленных вычислений ста-
становится ясно, что вспомогательные данные являются в опре-
определенном смысле отправной точкой для получения внутренне-
внутреннего решения, в особенности по отношению к задачам о распро-
распространении. Если мы не делаем различия между временем и
пространством как независимыми переменными, то вспомога-
вспомогательные данные, вводимые на контуре dR (рис. 2.2), через по-
посредство вычислительного алгоритма (основанного на ДУЧП)
«экстраполируются», обеспечивая тем самым построение реше-
решения во внутренней области R.
Вспомогательные условия определяются как относящиеся к
одному из трех классов:
1) условие Дирихле, например u = f на dR,
2) условие Неймана (для производной), например ди/дп =
= f или ди/ds = g на dR,
38 Гл. 2. Дифференциальные уравнения в частных производных
3) смешанное условие, если условие Робина, например
ди/дп + ku = /, к > 0 на dR.
При формулировке вспомогательных условий B) и C) сим-
символ д/дп обозначает производную по внешней нормали.
При рассмотрении большинства течений, требующих для
своего анализа решения уравнений Навье — Стокса в прими-
примитивных переменных (иу v, p и т. д.), по меньшей мере одна со-
составляющая скорости задается на
Vn s ^^^^ границе втекания. Это дает гра-
\^ ^^ ничное условие Дирихле для ско-
скорости. По отношению к уравнению
для потенциала скоростей, опре-
определяющему течение невязкой сжи-
сжимаемой жидкости, условие дф/дп =
= 0 на поверхности тела является
условием Неймана. Смешанные
условия редко встречаются в гидро-
Рис. 2.2. Вычислительная об- аэродинамике, однако встречаются
ласть R. в теории конвективной теплопере-
теплопередачи. С вычислительной точки зре-
зрения вспомогательные условия Дирихле могут быть постав-
поставлены точно, если только функция f является аналитической. Од-
Однако при постановке условий Неймана или сломанных условий
вносятся ошибки (см. § 7.3).
2.1.3. Классификация с помощью характеристик
По отношению к дифференциальным уравнениям в част-
частных производных с двумя независимыми переменными клас-
классификация, т. е. отнесение к эллиптическому, параболическому
или гиперболическому типу, может быть осуществлена за счет
предварительного отыскания характеристических направлений,
только вдоль которых определяющие уравнения позволяют нахо-
находить полные дифференциалы.
Для одного ДУЧП первого порядка с двумя независимыми
переменными
a + bJc
в каждой точке существует единственная вещественная харак-
характеристика, причем характеристическое направление определяет-
определяется соотношением (см. рис. 2.5)
§ 2.1. Основные положения 39
Вдоль характеристического направления уравнение B.5) при-
приводит к соотношениям
du _ С du _ С /9 7ч
Уравнение B.5) является гиперболическим ДУЧП, и соотноше-
соотношения B.7) могут быть проинтегрированы как обыкновенные диф-
дифференциальные уравнения вдоль линий сетки, определяемой
соотношениями B.6), если только начальные данные заданы
на линии, не являющейся характеристикой.
То же самое представление о характеристических направ-
направлениях может быть использовано и в связи с изучением ДУЧП
второго порядка с двумя независимыми переменными, такого,,
как B.1). Так как из условий B.2) следует, что тип ДУЧП
определяется лишь коэффициентами при высших производных,
то уравнение B.1) удобно записать в виде
^ ^ + С-Й- + # = 0, B.8)
' ду2 ' ' х '
где Н включает в себя все члены с первыми производными и
без производных из уравнения B.1), а коэффициенты Л, В и
С могут быть функциями х и у. Для каждой точки области мож-
можно построить два направления, вдоль которых интегрирование
уравнения B.8) связано только с полными дифференциалами.
Существование этих (характеристических) направлений имеет
непосредственную связь с классификацией ДУЧП.
Для простоты представления введем следующие обозначе-
обозначения:
P — E1L о — — /? — — <? — д2п Т — дЧ (9 <п
Внутри рассматриваемой области располагается кривая К, на
которой Р, Q, R, S, Т и и удовлетворяют уравнению B.8). По
направлению касательной к К дифференциалы Р и Q удовлетво-
удовлетворяют соотношениям
B.10)
B.11)
уравнение B.8) может быть записано как
H = 0. B.12)
В соотношениях B.10) и B.11) величина dy/dx определяет
угол наклона касательной к К. Используя B.10) и B.11), из
40 Гл. 2. Дифференциальные уравнения в частных производных
уравнения B.12) можно исключить R и Т\ тогда получим
*И?)!-ВШ+СНИ?)+"]?+<?}=<>•
B.13)
Если выбрать dy/dx таким образом, что
то уравнение B.13) приводится к более простому соотношению,
связывающему dP/dx и dQ/dx, а именно
Два решения уравнения B.14) определяют два характеристи-
характеристических направления, на которых выполняется соотношение
B.15). Если сравнить B.14) с B.2), то ясно, что уравнение
B.8) является
1) гиперболическим ДУЧП, если существуют две вещест-
вещественные характеристики,
2) параболическим ДУЧП, если существует одна вещест-
вещественная характеристика,
3) эллиптическим ДУЧП, если характеристики комплексны.
Таким образом, дискриминант В2 — 4АС определяет не только-
тип ДУЧП, но и свойства характеристик.
Пока что исследование типа ДУЧП проводилось с исполь-
использованием декартовых координат. Возникает важный вопрос —
может ли преобразование координат такого рода, какой будет
описан в гл. 12, изменить тип дифференциального уравнения
в частных производных?
Таким образом, вместо (х> у) вводятся новые независимые
переменные (g, ц), причем предполагается, что преобразова-
преобразования 1 = 1(ху у) и ц = ц{х, у) известны. Производные преобра-
преобразуются по формулам типа (см. § 12.1)
ди о ди . ди /Л 1^?v
иГ = |*Ж+ТЬ^Г' B.16)
где 1х === дЦдх и т. д. После некоторых манипуляций уравне-
уравнение B.8) приводится к виду
A'w + B'-?k+c/J?r + H'=0> <2Л7>
где
В' = 2А1хцх + В (%хцу + Ъ„1ь) + 2С1уцу, B.18)
§ 2.1. Основные положения 41
После этого дискриминант В2 — 4АС преобразуется к форме
В2 - 4АС = Р [(ВО2 - 4Л/С/], B.19)
где якобиан преобразования ] = 1)Хцу — 1Уч]х. Формула B.19)
приводит к важному результату, гласящему, что классифика-
классификация ДУЧП остается одной и той же, будет ли она определена
в декартовых координатах по уравнению B.8) или же в коор-
координатах (g, ц) по уравнению B.17) с формулами B.18). Та-
Таким образом, введение преобразования координат не изменяет
типа ДУЧП.
Распространение принципа исследования характеристик на
уравнения более чем с двумя независимыми переменными ока-
оказывается менее полезным. В случае т измерений следует рас-
рассматривать (т—1)-мерные поверхности. Тем не менее иссле-
исследование коэффициентов при старших производных в принци-
принципе может дат^ь полезную информацию. Например, в случае
трех измерений уравнение B.8) будет заменено на уравнение
B.20)
Необходимо найти такое преобразование ? = ?(*, У у 2Ь Ч =
= ц(х, у, г), ? = ?(х, у, г), в результате которого исчезли бы
все смешанные производные по (g, tj, ?). Такой подход не го-
годится в случае более чем трех независимых переменных, но
тогда удобно заменить B.20) на уравнение вида
где N — число независимых переменных, а коэффициенты a}-k
заменяют коэффициенты от Л до f в B.20). Упомянутое ра-
ранее преобразование, выполняемое с целью избавления от сме-
смешанных производных, эквивалентно нахождению собственных
значений К матрицы А, имеющей элементы а/*.
Следуя Честеру [Chester, 1971], можно дать следующую
классификацию:
1) Если какое-либо из собственных значений К равно нулю,
уравнение B.21) является параболическим.
2) Если все собственные значения отличны от нуля и имеют
одинаковый знак, уравнение B.21) является эллиптическим.
3) Если все собственные значения отличны от нуля и все,
кроме одного, имеют одинаковый знак, уравнение B.21) являет-
является гиперболическим.
42 Гл. 2. Дифференциальные уравнения в частных производных
Для случая трех независимых переменных Хелвиг [Hellwig,
1964] предлагает эквивалентную классификацию, основанную
на значениях коэффициентов при производных в преобразо-
преобразованных уравнениях.
При числе независимых переменных, превышающем два,
часто можно получить полезную информацию относительно
свойств дифференциального уравнения в частных производных,,
рассматривая двумерные поверхности, т. е. путем выбора не-
некоторых определенных координатных значений. Так, например,
характер уравнения B.20) можно установить в плоскости
х = const, временно замораживая все члены с производными
по л: и рассматривая полученное таким образом уравнение как
уравнение для функции двух независимых переменных.
2.1.4. Системы уравнений
Как показывает исследование, проведенное в гл. 11, опреде-
определяющие уравнения для гидроаэродинамических задач часто
составляют систему, а не приводятся к одному уравнению. Си-
Система из двух ДУЧП первого порядка с двумя независимыми
переменными может быть представлена в виде
А» Ж + в» -W + Л« & + В'2 W = ?» B'22)
* + * + A % + B ? (
Учитывая, что и и v являются функциями х и у, можно записать
следующие соотношения:
При решении задачи, показанной на рис. 2.3, предполагается,
что решение уже было определено в области ACPDB. Как и
прежде, в точке Р ищутся два направления dy/dx> вдоль ко-
которых появляются только полные дифференциалы du и dv.
Для системы уравнений B.22) и B.23) это эквивалентно на-
нахождению таких множителей L\ и L2, что
Lx X B.22) + L2 X B.23) => m{ du + m2 dv = LXEX + L2E2. B.26)
Раскрытие членов, входящих в соотношение B.26), позволяет
получить соотношения
L,Ап + L2A2l = mx dxy LXBXX + L2B2l = mx dy,
LxBl2 + L2B22 = m2 dy.
§ 2.1. Основные положения
43
После исключения mi и т2 и перегруппировки членов получаем
Г (Ап dy - Вп dx) (A21 dy - В2Х dx) I Г Lx 1 _
L (Л12 dy - Bl2 dx) (A22 dy — B22 dx) \lL2\ ' ( ]
Учитывая, что система однородна по отношению к L/, необхо-
необходимо выполнение условия
det [A dy - В dx] = 0, B.29)
чтобы получить нетривиальное решение. В вышеприведенном
примере условие B.29) принимает форму
— ^21^12) \~~fa ) — (^11^22 — ^21^12 Н" ^11^22 —
dy
~ B2lBi2) = 0.
B.30)
Уравнение B.30) имеет два решения и характер решений за-
зависит от дискриминанта
DIS = (ЛИВ22 - А2[В{2 + Л22ВП - Л12В21J -
- 4(ЛПЛ22- A2lAl2)(BnB22-B2lBl2)t B.31)
от которого зависит также и классификация системы уравне-
уравнений B.22), B.23). Различные возможности указываются в
табл. 2.1.
Решение, подлежащее расчету
Начальные условия
Рис. 2.3. Схематическое представление вычислительной области для задачи
о распространении.
На характеристиках производные ди/дх, ди/ду, dv/dx и
dv/ду определяются неоднозначно. По существу при пересече-
пересечении характеристик могут возникать разрывы нормальных про-
производных, тогда как тангенциальные производные при этом
непрерывны.
44
Гл. 2. Дифференциальные уравнения в частных производных
Таблица 2.1. Классификация уравнений B.22), B.23)
DIS
Положительный
Нулевой
Отрицательный
Корни уравнения
B.30)
2 вещественных
1 вещественный
2 комплексных
Классификация
системы B.22), B.23)
Гиперболическая
Параболическая
Эллиптическая
В качестве использования вышеприведенной классифика-
классификации можно привести следующий пример. Определяющие урав-
уравнения для двумерного потенциального течения сжимаемой
жидкости (уравнения A1.103)) могут быть переформулированы
за счет введения составляющих скорости, что дает
ди
uv \ ди
)
uv
а также
ди
dv
dv
v2 }\ dv n /9
B.33)
Уравнения B.32) и B.33) имеют такую же структуру, как
B.22) и B.23). Конкретизация выражения в правой части
B.31) дает
DIS = 4 (М2 - 1), где М2 = (и2 + v2)/a2,
и свидетельствует о том, что система B.32) и B.33) является
гиперболической, если М > 1. Этот результат совпадает с тем„
который мы получили при рассмотрении уравнения для потен-
потенциала течения сжимаемой жидкости B.4). Именно этого и сле-
следовало ожидать, так как, несмотря на то что уравнения по фор-
форме различаются, они определяют одну и ту же физическую си-
ситуацию.
Построение, применявшееся для вывода уравнений B.28)
и B.29), может быть обобщено применительно к системе из
п уравнений первого порядка [Whitham, 1974]. Уравнение
B.28) заменяется уравнением
= 0, k=l, ..., п. B.34)
Свойства системы [Hellwig, 1964] зависят от решения урав-
уравнения B.29) следующим образом:
1. Если получено п вещественных корней, то система яв-
является гиперболической.
§ 2.1. Основные положения 45
2. Если имеется v вещественных корней, причем 1 ^ v ^
^.п— 1, а комплексные корни отсутствуют, то система являет-
является параболической.
3. Если не получено ни одного вещественного корня, то си-
система является эллиптической.
Для больших систем некоторые корни могут быть комплекс-
комплексными, а некоторые — вещественными; в таком случае система
является смешанной. Наиболее важно устанавливать различие
между эллиптическими и неэллиптическими системами диффе-
дифференциальных уравнений в частных производных, так как эл-
эллиптичность не допускает времениподобного поведения решения.
Поэтому система уравнений будет считаться эллиптической, если
только появляются комплексные корни.
Данная выше классификация распространяется и на систе-
системы уравнений второго порядка с двумя независимыми перемен-
переменными, так как путем введения вспомогательных переменных
можно получить систему большего числа уравнений первого
порядка. Существует, однако, риск, что обе матрицы А и В
окажутся особыми, так что во избежание поведения с вырож-
вырождением понадобится рассмотреть некоторые комбинации данных
уравнений [Whitham, 1974].
Применительно к системам, где число независимых перемен-
переменных превышает два, уравнение B.29) может быть частично
обобщено следующим образом. Систему уравнений первого по-
порядка с тремя независимыми переменными можно представить
в виде
A47 + B|r + C-!i- = D' B-35)
где символом q обозначается вектор, составленный из п иско-
искомых переменных. Уравнение B.35) приводит к получению ха-
характеристического полинома порядка п [Chester, 1971]:
det [А Хх + ЪХу + CXZ] = 0, B.36)
где Хх, Ху и Xz определяют нормальное направление к поверх-
поверхности в точке (х, у, z). Уравнение B.36) обобщает уравнение
B.29) и дает условие, что данная поверхность является харак-
характеристической. Ясно, что если характеристическая поверхность
является вещественной, то уравнение B.36) должно иметь ве-
вещественные корни. Если получено п вещественных корней, то
система является гиперболической.
Можно задать вопрос, какой характер имеет данное диф-
дифференциальное уравнение в частных производных по отноше-
отношению к определенным направлениям. Например, полагая
46 Гл. 2. Дифференциальные уравнения в частных производных
XX = XZ = 1 и разрешая уравнение относительно Ху, установим,
что уравнение B.35) является эллиптическим в направлении
у, если при этом появляются мнимые корни. Ясно, что каждое
направление можно исследовать по очереди.
Ниже предлагается простой пример системы уравнений,
формируемой из уравнений Навье — Стокса для установивше-
установившегося течения несжимаемой жидкости в двух измерениях. В без-
безразмерных обозначениях эта система имеет вид
ux + vy = 09 B.37а)
иих + vuy + px-1^ (ихх + иуу) = О, B.37Ь)
uvx + vvy + py — -^ (vxx + vyy) = 0, B.37c)
где ux = ди/дх и т. д., Re — число Рейнольдса, а и, v, p — иско-
искомые переменные. Уравнения B.37) приводятся к форме систе-
системы уравнений первого порядка за счет введения вспомогатель-
вспомогательных переменных R = vx, S = vy и Т = иу. Таким путем вместо
B.37) получим
ux + vy = 0,
— Ry + Sx =0,
S, +Т. =0, <2'38>
SJRe — Ту/Re + Px = uS — vT9
— ^,,/Re - Sy/Re +py = uR — vS.
Задача, приведшая к системе B.38), была выбрана так, чтобы
избежать возникновения особенностей у матриц А и В в урав-
уравнении B.35). Характер вышеприведенной системы уравнений
определяется путем замены д/дх на Хх и д/ду на Ху и прирав-
приравнивания нулю определителя получаемой алгебраической си-
системы, т. е. так, как это сделано в B.36). Результат получается
таким:
Xl(ll + Xlf = O. B.39)
Если положить Ху = 1, то выясняется, что величина кх мнимая.
Если же положить Хх=1, то мнимые корни появляются для
7у.у. На этом основании делается вывод, что система B.37) эл-
эллиптическая.
Изучение общей проблемы классификации дифференциаль-
дифференциальных уравнений в частных производных можно продолжить, сле-
следуя руководствам [Garabedian, 1964; Hellwig, 1964; Courant,
Hilbert, 1962; Chester, 1971].
§ 2.1. Основные положения 47
2.1.5. Классификация с помощью анализа Фурье
Классификация дифференциальных уравнений в частных
производных с помощью характеристик (см. п. 2.1.3 и 2.1.4)
связана с интерпретацией корней характеристического полино-
полинома, например, по B.36). Эти корни определяют характеристи-
характеристические направления (или поверхности, если речь идет более чем
о двух независимых переменных).
Однако тот же самый характеристический полином можно
получить, если дифференциальное уравнение в частных про-
производных подвергнуть анализу Фурье. В этом случае сами кор-
корни имеют другую физическую интерпретацию, хотя классифи-
классификация дифференциального уравнения в частных производных
по отношению к характеру этих корней остается той же самой.
Подход при помощи анализа Фурье полезен для систем таких
уравнений, в которых фигурируют производные выше первой,
так как при этом подходе отпадает необходимость в построе-
построении промежуточной системы большего числа уравнений перво-
первого порядка. Подход, основанный на анализе Фурье, дает, кро-
кроме того, указание на ожидаемую форму решения, например,
будет ли оно колебательным, с экспоненциальным ростом и т. п.
Это свойство используется в гл. 16 в процессе определения
того, могут ли устойчивые численные решения укороченных
форм уравнений Навье — Стокса быть получены с помощью
единственного марша по пространству.
Предположим, что решение однородного скалярного урав-
уравнения второго порядка
^ ^+С-Й- = 0 B.40)
ду2 v '
отыскивается в форме
оо
\ Y B.41)
/ = — оо k~ — оо
Амплитуды различных мод определяются при этом с помощью
граничных условий. Однако характер решения будет зависеть
от коэффициентов (ox)j и (oy)k, которые могут оказаться ком-
комплексными. Если коэффициенты Л, В и С не являются функция-
функциями и, то соотношение между ах и оу остается одним и тем же
Для всех мод, так что в выражении B.41) нужно рассмотреть
только одну моду. Подстановка в B.40) при этом дает
-Ао*х-Вояоу-Со1 = 0, или
B.42)
48 Гл. 2. Дифференциальные уравнения в частных производных
Здесь фигурирует характеристический полином относительно
Gx/оу, эквивалентный тому, который появлялся в B.29). Свой-
Свойства дифференциального уравнения в частных производных
B.40) зависят от свойств корней, а следовательно, и от Л, В и
С, как это было в B.2).
Подход с помощью анализа Фурье позволяет из главной
части определяющего уравнения получить тот же самый харак-
характеристический полином, который получался при анализе ха-
характеристик. Однако если предположить, что величина оу ве-
вещественная, то форма решения в направлении у оказывается
волнообразной. После этого решение, соответствующее харак-
характеристическому полиному B.42), полученному из полного урав-
уравнения, позволяет судить о форме решения в направлении х.
Изучение формы B.41) свидетельствует об аналогии с оп-
определением преобразования Фурье [Lighthill, 1958], имеющим
вид
оо оо
й (вх> °у)= \ \и (х> У) СХР (— 1<*хХ) ехр (— iayy) dx dyy B.43)
— оо —оо
или в общепринятом обозначении й = Fu.
При анализе свойств дифференциальных уравнений в част-
частных производных следует воспользоваться следующими резуль-
результатами:
Таким образом, характеристический полином можно получить,
подвергая преобразованию Фурье все члены определяющего
уравнения. В качестве примера укажем, что уравнение B.40)
преобразуется к форме
[A (iaxf + В (iejoy) + С AауJ} й = 0, B.45)
откуда непосредственно следует B.42). Характеристический по-
полином, вывод которого проведен с помощью преобразования
Фурье, часто называют символом дифференциального уравне-
уравнения в частных производных.
Способ построения характеристического полинома, основан-
основанный на преобразовании Фурье, остается пригодным, если Л,
В или С являются функциями независимых переменных. Если
же Л, В или С представляют собой функции искомых перемен-
переменных, то перед введением преобразования Фурье эти коэффи-
коэффициенты необходимо заморозить на их локальных значениях.
§ 2.1. Основные положения 49
Применение подхода на основе анализа Фурье к системам
уравнений можно проиллюстрировать с помощью рассмотрения
уравнений B.37). Если заморозить коэффициенты и и v в урав-
уравнениях B.37Ь) и B.37с) и провести преобразование Фурье для
иу v и р, получим следующую однородную систему алгебраиче-
алгебраических уравнений:
iax iay 0-
IGy
to,
\W
X v =0, B.46)
из которой получается характеристический полином det [ ] =
= 0, т. е.
К + Gl) V (иах + ту) + (№ К + °1)] = °- B-47>
Однако в левой части B.47) содержится комплекс i (uax +
-\-vey), связанный с первыми производными и и v. С другой
стороны, свойства системы B.37) определяются ее главной
частью, из которой явным образом исключены все производные,
кроме высших. В данном случае B.47) совпадает с B.39) и
приводит к выводу о том, что система B.37) является эллип-
эллиптической. При сравнении B.46) с B.38) становится ясно, что
подход с помощью анализа Фурье позволяет обойти проблему
построения эквивалентной системы уравнений первого порядка,
связанную с возможностью того, что эта система будет особой.
Корни характеристического полинома, полученного с по-
помощью анализа Фурье, интерпретируются здесь таким же обра-
образом, как при методе характеристик, примененном для определе-
определения типа дифференциального уравнения в частных производных.
Альтернативная классификация, основанная на величине наи-
наибольшего корня характеристического полинома, описывается
Гельфандом и Шиловым [1967].
Подход, основанный на применении анализа Фурье, исполь-
используется в § 16.1 для определения свойств решения, строящегося
с помощью единственного маршевого прохода вниз по потоку.
В этой ситуации эквивалент уравнения B.47) основан на со-
хранеции всех членов определяющего уравнения, а не только
«го главной части.
4 К. Флетчер, т. 1
50 Гл. 2. Дифференциальные уравнения в частных производных
§ 2.2. Гиперболические дифференциальные уравнения
в частных производных
Простейшим примером гиперболического ДУЧП является
волновое уравнение
J*!L-<*L — 0 B 48>
dt2 дх2 ~U* KZ'™}
При начальных условиях и(х, 0)=sinn.x;, du/dt(x, 0) = 0 и гра-
граничных условиях и@, t)=u(l, t) = 0 уравнение B.48) имеет
точное решение
и (х, /) = sin пх cos nt. B.49)
Характерной чертой линейных гиперболических ДУЧП является
отсутствие затухания.
Уравнение конвекции, рассматриваемое в § 9.1, является ли-
линейным гиперболическим ДУЧП. Уравнения, определяющие
неустановившееся невязкое течение, являются гиперболически-
гиперболическими, но нелинейными, так же как и уравнения, определяющие
установившееся сверхзвуковое невязкое течение.
2.2.1. Интерпретация с помощью характеристик
Гиперболические ДУЧП порождают вещественные характе-
характеристики. В случае волнового уравнения B.48) характеристиче-
характеристические направления определяются соотношениями dx/dt = ±1-
t
к с
Область
^ влияния /
ос-характеристиках / j3-
а/
/область\
мвисимости>
1
D
4
1
характеристика
*Pi~~ Li «•» U/j ¦+¦ ь\ X
Рис. 2.4. Характеристики волнового уравнения.
Характеристики, проходящие через точку Р в плоскости (х, t)r
показаны на рис. 2.4.
Для системы уравнений B.32), B.33) имеются две харак-
характеристики, определяемые соотношением
dx L a2 V а2
§ 2.2. Гиперболические ДУЧП
51
Ясно, что форма характеристик зависит от локального решения,
причем в общем случае они будут искривленными [Courant,
Friedrichs, 1948].
В случае гиперболического ДУЧП первого порядка B.5)
через каждую точку проходит единственная характеристика
dt/dx = А/В (рис. 2.5). Если А и В — постоянные, то характе-
характеристики представляют собой
прямые линии. Если же А и
В являются функциями от и,
х и /, то характеристики ис-
искривляются. В случае линей-
линейного уравнения конвекции,
рассматриваемого в § 9.1, от-
отношение В/А как раз соответ-
соответствует скорости. В случае
Наклон = А/В
Рис. 2.5. Характеристики для гипер-
гиперболического ДУЧП первого порядка,
уравнение B.5).
потока, как это показано на
трехмерного установившегося
невязкого сверхзвукового те-
течения характеристическая по-
поверхность образует конус во-
вокруг местного направления
рис. 11.14.
Имея дело с гиперболическими ДУЧП, можно воспользо-
воспользоваться характеристическими направлениями для построения
расчетной сетки, на которой выполнялись бы условия совмест-
совместности типа соотношения B.15). Именно это положено в осно-
основу метода характеристик, излагаемого в п. 2.5.1. В силу при-
причин, которые будут обсуждаться в п. 14.2.1, упомянутый метод
представляет сейчас в основном исторический интерес.
2.2.2. Интерпретация на физической основе
Как было отмечено выше, гиперболические ДУЧП связаны
с такими задачами о распространении, когда диссипация от-
отсутствует. Появление вещественных характеристик, таких, как
на рис. 2.4, свидетельствует о том, что возмущение решения и
в точке Р может повлиять на поведение решения только в об-
области CPD. И наоборот, решение в точке Р подвержено только
влиянию возмущений, идущих из области АРВ.
Кроме того, если начальные условия заданы при t = О, т. е.
на линии АВ на рис. 2.4, то этих условий достаточно, чтобы
единственным образом определить решение в точке Р. Для слу-
случая уравнения B.48) это можно продемонстрировать следую-
следующим образом.
Введем новые независимые переменные по формулам
? = * + /, r\ = x-t; B.51)
4*
g (х) = 0.5 Is (х) - J T (г) dr\ + D,
52 Гл. 2. Дифференциальные уравнения в частных производных
тогда из B.48) получим уравнение
°
которое имеет общее решение
и& Л) = /(&) +«Г (Л), B.53)
где / и g — произвольные дважды дифференцируемые функции.
Если для уравнения B.48) решается чистая задача с началь-
начальными значениями, то надлежит установить начальные условия
и (х, 0) = S (х), |f (х, 0) = Т (х). B.54)
Можно показать [Ames, 1969], что при ? = 0
B.55)
где С и D — постоянные интегрирования. Тогда из представле-
представления B.53) следует, что общее решение уравнения B.48) с на-
начальными условиями, соответствующими B.54), имеет вид
x+t -1
\ T(r)dr^. B.56)
В частности, если точка Р имеет координаты (Xi,ti), то реше-
решение в этой точке представляется в виде
и(хи /,) = 0.5 \s(xi + ti) + S(xi-ti)+ \ T(r)drl B.57)
L x.-ti J
т. е. решение в точке Р однозначно определяется начальными
условиями, заданными на линии АВ (рис. 2.4).
Для гиперболических уравнений не существует диссипатив-
ного (или сглаживающего) механизма. Отсюда следует, что
если начальные (или граничные) данные содержат разрывы,,
то эти разрывы вдоль характеристик будут передаваться во
внутреннюю область без размывания, если только уравнения
линейны. Это согласуется с результатом, отмеченным в п. 2.1.3
и гласящим, что разрывы нормальных производных могут воз-
возникать только при пересечении характеристик.
§ 2.2. Гиперболические ДУЧП 5$
Здесь следует подчеркнуть, что если рассматриваются урав-
уравнения, определяющие сверхзвуковое невязкое течение и яв-
являющиеся гиперболическими, то для согласования с тезисом
об изэнтропичности течения разрывы должны быть слабыми..
При сверхзвуковом невязком изэнтропическом течении опреде-
определяющие уравнения B.32) и B.33) порождают характеристиче-
характеристические направления, заданные соотношением B.50). Если реше-
решение таково, что характеристики сливаются вместе, то резуль-
результатом будет неединственное решение [Whitham, 1974]; на
практике при этом возникает ударная волна. Однако при пере-
переходе через ударную волну имеет место изменение энтропии, а
это противоречит допущению об изэнтропичности течения, на
котором основано использование уравнений B.32) и B.33). По-
Поэтому ударная волна образует границу (внутреннюю или
внешнюю) той области, в которой справедливы уравнения
B.32) и B.33).
2.2.3. Надлежащие граничные (и начальные) условия
В п. 2.2.2 было отмечено, что в случае волнового уравнения
B.48) начальные условия B.54) оказываются пригодными и в
зависимости от протяженности участка АВ будут единствен-
единственным образом определять решение в области АРВ (рис. 2.4).
Имеется также возможность введения граничных условий (см.
п. 2.1.2), которые могут быть заданы, например, на линиях
CD и EF на схеме рис. 2.8.
Здесь мы заново рассмотрим уравнения B.22) и B.23),.
так как эти уравнения непосредственно применимы к описанию
сверхзвукового невязкого течения (при соответствующем вы-
выборе коэффициентов Ап и т. д.), зададимся вопросом, как над-
надлежащим образом следует подобрать вспомогательные усло-
условия, чтобы иметь возможность получить единственное решение
уравнений B.22) и B.23). Характеристические направления,,
соответствующие эквиваленту уравнения B.50), будут в даль-
дальнейшем называться характеристиками аир. Вначале будут
рассмотрены три случая, показанные на рис. 2.6.
Случай, показанный на рис. 2.6(а), эквивалентен тому, что
было показано на рис. 2.4. Это означает, что данные относи-
относительно значений и и v на кривой АВ, отличной от характери-
характеристики, будут единственным образом определять решение вплоть
до точки Р. В случае, показанном на рис. 2.6 (Ь), кривая АВ
не является характеристикой, однако AD является характери-
характеристикой р. В этом случае значения и или v должны быть заданы
на одной из кривых, а на другой — соответственно v или и*
Следовательно, в точке А известны и и, и v. Аналогичная
54 Гл. 2. Дифференциальные уравнения в частных производных
/^-характеристики
r-характеристики
Случай (а)
/^-характеристики
а-характеристики
(<Х -характеристики
Рис. 2.6. Конкретизация вспомогательных данных для уравнений B.22) и
B.23) в случае их гиперболичности.
§ 2.2. Гиперболические ДУЧП
5S
ситуация имеет место в случае, показанном на рис. 2.6(с), за
исключением того, что здесь и АВ, и AD являются характе-
характеристическими кривыми.
Уравнения B.22) и B.23) могут интерпретироваться как
соответствующие неустановившемуся течению, если только у
заменить на t. Если рассмотреть (рис. 2.7) вычислительную об-
область х ^ 0 и t ^ 0, то видно, что решение в точке Р, близкой
к границе х = О, частично определяется граничными условиями.
th
Заданы и\л v
X
Рис. 2.7. Граничные условия для уравнений B.22) и B.23) в нестационарной
интерпретации.
на линии АС, а частично — начальными условиями на АВ\ при
этом предполагается, что определяющие ДУЧП являются ги-
гиперболическими. Надлежащими вспомогательными условиями
для этого случая будут задание и и v на линии АВ и задание
v или и на линии АС.
Эти два примера, показанные на рис. 2.6 и 2.7, иллюстри-
иллюстрируют общее правило для гиперболических ДУЧП, состоящее
в том, что число вспомогательных условий равно числу харак-
характеристик, направленных внутрь рассматриваемой области
[Whitham, 1974]. Выбор направления вдоль характеристики
должен быть сделан в соответствии с определенными правила-
правилами. Для задач с зависимостью от времени положительным
направлением будет направление роста времени. Для много-
многомерных гиперболических задач об установившемся течении»
сформулированных в примитивных переменных, одна из харак-
характеристик («ассоциированная» с уравнением неразрывности) со-
совпадает с локальной линией тока. Таким образом, посредством
граничной точки эта характеристика определяет свое положи-
положительное направление и указывает положительное направление
для других характеристик, проходящих через ту же точку.
56 Гл. 2. Дифференциальные уравнения в частных производных
§ 2.3. Параболические дифференциальные уравнения
в частных производных
Параболические ДУЧП встречаются при рассмотрении тех
задач, где включены некоторые диссипативные механизмы, та-
такие, как вязкостное напряжение или теплопроводность. Клас-
Классическим примером параболического ДУЧП является уравне-
уравнение диффузии или уравнение теплопроводности
Уравнение B.58) будет использовано для демонстрации раз-
различных вычислительных методов в гл. 7.
При начальном условии и = sin лх и граничных условиях
м@, t)=u(l, t) = 6 уравнение B.58) допускает точное ре-
решение
и (х, t) = sin лх ехр (— лЧ). B.59)
Экспоненциальное затухание, демонстрируемое формулой
B.59), являет собой контраст в сравнении с осциллирующим
решением B.5) волнового уравнения B.48).
Уравнение переноса (см. § 9.4 и 9.5) представляет собой
линейное параболическое ДУЧП, а уравнение Бюргерса, рас-
рассмотренное в § 10.1, является нелинейным параболическим
ДУЧП. Однако преобразование Коула — Хопфа (см. [Fletcher,
1983]) позволяет превратить уравнение Бюргерса в уравнение
диффузии B.58). Уравнения Навье— Стокса для неустановив-
неустановившегося течения являются параболическими. Эти уравнения ис-
используются как при решении нестационарных задач, так и в
тех случаях, когда псевдонестационарная формулировка (см.
§ 6.4) вводится для решения стационарной задачи. Если иметь
в виду строго установившееся течение, то пограничные слои
(гл. 15) и сдвиговые слои, как правило, определяются посред-
посредством параболических ДУЧП, причем направление потока
играет времениподобную роль. Многие из упрощенных ва-
вариантов уравнений Навье — Стокса (гл. 16) определяются по-
посредством параболических ДУЧП.
2.3.1. Интерпретация с помощью характеристик
Если интерпретировать уравнение B.58) как уравнение
B.8), с заменой у = t, то выявляется, что А = 1, В = С = 0,
так что уравнение B.58) оказывается параболическим. Как по-
показывает решение уравнения B.14), здесь имеется единствен-
единственное характеристическое направление, определяемое соотноше-
соотношением dt/dx = 0. Характерная вычислительная область для урав-
§ 2.3. Параболические ДУЧП
57
нения B.58) представлена на рис. 2.8. В противоположность
ситуации, возникавшей для гиперболических уравнений, при
переходе через линию t = U производные функции и всегда
остаются непрерывными. Характеристики не играют здесь та-
такой значительной роли, как это было для гиперболических урав-
CXV^S^^^^
Рис. 2.8. Вычислительная область для параболического ДУЧП.
нений. Для параболических ДУЧП не существует эквивалента
методу характеристик. Ясно, что если построить вычислитель-
вычислительную сетку, следуя локальным характеристическим направле-
направлениям, то никогда не удастся осуществить продвижение решения
во времени.
2.3.2. Интерпретация на физической основе
Для параболических задач характерны такие решения, ко-
которые реализуют маршевое продвижение во времени, но созда-
создают рассеяние в пространстве. Так, например, возмущение ре-
решения, введенное в точке Р (см. рис. 2.8), может оказать влия-
влияние на любую часть вычислительной области, соответствующую^
условию t ^ U. Однако при этом величина возмущения быстро
уменьшается по мере удаления от точки Р. В случае установив-
установившегося течения в двумерном пограничном слое (гл. 15) харак-
характеристики идут по нормали к направлению течения и здесь не
создается влияния в направлении вверх по потоку.
Появление диссипативного механизма косвенно указывает'
также и на тот факт, что даже если начальные условия содержат
разрыв, то решение во внутренней области всегда будет оста-
оставаться непрерывным. Дифференциальные уравнения в частных
производных, определяющие решение более чем в одном про-
пространственном направлении и являющиеся параболическими па-
отношению ко времени, становятся эллиптическими в стационар-
стационарном состоянии (если только стационарное решение существует)..
Ъ8 Гл. 2. Дифференциальные уравнения в частных производных
2.3.3. Надлежащие граничные (и начальные) условия
Для уравнения B.58) необходимо ставить начальные усло-
условия Дирихле, например
и (л:, 0) = щ{х) при 0 < х < 1. B.60)
Надлежащими граничными условиями могут быть
и |L(i,f) = A(O. B.61)
На границах CD и EF (см. рис. 2.8) допустима любая комби-
комбинация условий Дирихле, Неймана или же смешанных (см.
я. 2.1.2). Однако при задании граничных условий Дирихле же-
желательно обеспечить их непрерывную стыковку с начальными
условиями в точках С и Е. Невыполнение этого требования
приведет к решению, содержащему очень большие градиенты
вблизи точек С и Е, а это может создать трудности с реализа-
реализацией вычислительного алгоритма. В случае систем параболи-
параболических ДУЧП задание начальных условий на линии СЕ и гра-
граничных условий на линиях CD и EF необходимо вводить для
.всех искомых переменных.
§ 2.4. Эллиптические дифференциальные уравнения
в частных производных
В гидроаэродинамике эллиптические ДУЧП ассоциируются
со стационарными проблемами. Простейший пример эллипти-
эллиптического ДУЧП дает уравнение Лапласа
|? + -0- = О, B.62)
которое определяет потенциальное течение несжимаемой жид-
жидкости. При граничных условиях
Ф (х, 0) = sin пх, Ф(х9 l)==sinnA:exp(— я), ф@9 у) =
уравнение B.62) допускает решение
Ф (*. У) = sin nx ехР (— %У) B-63)
в области 0 ^ х ^ 1, O^f/^1.
Уравнение Пуассона для функции тока A1.88), определяю-
определяющее двумерное завихренное течение, является эллиптическим
ДУЧП. Как отмечалось выше, стационарное уравнение Навье —
Стокса и стационарное уравнение энергии также являются эл-
эллиптическими уравнениями.
§ 2.4. Эллиптические ДУЧП
Для эллиптического ДУЧП второго порядка, представлен-
представленного в форме B.1), существует важный принцип максимума
[Garabedian, 1964]. А именно как максимальные, так и мини-
минимальные значения ф должны достигаться на границе dR, если
не считать того тривиального случая, когда величина ф по-
постоянна. Принцип максимума полезен для проведения проверки
того обстоятельства, что численные решения эллиптических
ДУЧП ведут себя надлежащим образом.
2.4.1. Интерпретация с помощью характеристик
В случае ДУЧП второго порядка, представленного в общем
виде B.1), о котором известно, что оно эллиптическое, т. е. для
него 4АС <С В2, характеристики будут комплексными и их не-
невозможно показать в вычислительной области (последняя счи-
считается вещественной). При рассмотрении эллиптических задач:
в гидроаэродинамике идентификация характеристических на-
направлений не может оказаться сколько-нибудь полезной.
2.4.2. Интерпретация на физической основе
Наиболее важная особенность, касающаяся эллиптических
ДУЧП, состоит в том, что возмущение, внесенное в точке Р
(рис. 2.9), оказывает влияние на все другие точки в вычисли-
Заданы
ф или д<р/дп
Рис. 2.9. Характерная область для эллиптического ДУЧП.
тельной области, хотя вдалеке от точки Р это влияние будет
малым. Тем самым косвенно утверждается, что при попытке
отыскания численных решений эллиптических задач необходи-
необходимо рассматривать глобальную область. В противоположность
этому параболические и гиперболические ДУЧП можно решать
<60 Гл. 2. Дифференциальные уравнения в частных производных
прогрессивно-маршевым путем, отталкиваясь от начальных ус-
условий. Разрывы в граничных условиях для эллиптических
ДУЧП сглаживаются внутри области.
2.4.3. Надлежащие граничные условия
Тот факт, что любая точка внутри области способна ока-
оказать влияние на все другие точки рассматриваемой области,
влечет за собой вывод о том, что граничные условия необходи-
необходимо ставить на всех границах (см. рис. 2.9). Граничные условия
могут представлять собой любую комбинацию условий Ди-
Дирихле, Неймана или смешанных (см. п. 2.1.2). Однако если на
всех границах поставить условие Неймана d<t>ldn = f(s)y где
символ п соответствует внешней нормали, а 5 измеряется вдоль
контура границы, то необходимо позаботиться о том, чтобы
формулировка таких граничных условий не противоречила
определяющему уравнению. С помощью теоремы Грина полу-
•чим
fds=- J V2j>dV. B.64)
dR R
;Ясно, что если определяющее уравнение представляет собой
уравнение Лапласа или уравнение Пуассона, то соотношение
B.64) косвенно указывает на наличие дополнительного гло-
глобального ограничения, налагаемого на формулировку гранич-
граничного условия Неймана. Если уравнение B.62) характеризует
установившееся потенциальное течение несжимаемой жидкости,
причем ф представляет собой потенциал скорости, то величина
f точно соответствует нормальной скорости. Таким образом, в
случае установившегося потенциального течения несжимаемой
жидкости условие B.64) совпадает с условием сохранения мас-
массы A1.7). Численная реализация условия B.64) обсуждается
в п. 16.2.2. Для систем эллиптических ДУЧП граничные усло-
условия должны ставиться на всех границах, для всех искомых пе-
переменных.
При рассмотрении параболических и гиперболических
ДУЧП путем применения разложения в ряд всегда возможно
получить некое локальное решение в непосредственной бли-
близости от границы. Попытка проделать то же самое, имея дело
с эллиптическим ДУЧП, приводит, как правило, к получению
бесконечно возрастающего решения, и это имеет непосредствен-
непосредственную связь с тем фактом, что постановка задач для эллиптиче-
эллиптических ДУЧП оказывается некорректной, если граничные уело-
шия не заданы на некоторой замкнутой границе.
§ 2.5. Традиционные методы решения 61
§ 2.5. Традиционные методы решения
В данном разделе дается краткое описание трех методов
решения, которые могут быть названы прекомпьютерными, так
как они требуют только ручных расчетов или расчетов на при-
примитивных машинах. Эти методы хорошо работают примени-
применительно к простым модельным задачам, однако оказываются ме-
менее эффективными по отношению к более сложным уравнениям,
-определяющим течение жидкости или газа. Тем не менее иногда
эти методы полезны, так как помогают подсказать метод ре-
решения или получить некое приближенное или же локальное ре-
решение.
2.5.1. Метод характеристик
Этот метод применим только к гиперболическим ДУЧП.
Он описывается здесь применительно к ДУЧП второго порядка
с двумя независимыми переменными
| Л || + Я = О. B.65)
уг v '
дх2 ' дх ду
Решение уравнения B.14) позволит получить два корня
% = F и ?-0. <2-66>
Для двух соседних точек на характеристиках, определяемых
соотношениями B.66), условие совместности B.15) может быть
лриближенно представлено в виде
A -^j АР + С AQ + Н Ьу = 0. B.67)
Можно напомнить, что, как это было указано в п. 2.1.3, Р =
= ди/дх и Q = ди/ду, и, следовательно, для тех же двух сосед-
соседних точек
B.68)
Будем предполагать, что и, Р и Q известны вдоль некоторой
границы, не являющейся характеристикой (рис. 2.10). На на-
начальном этапе неизвестны ни решение, ни положение таких
внутренних точек, как d и е. Из соотношений B.66) можно по-
получить два соотношения для определения положения точки d.
Эти соотношения таковы:
У*-Уа = Рш1(ха-ха), B.69)
Уа-Уь=Оьа{ха-хь)9 B.70)
где _ _
Fad = 0.5 (Fa + Fd)9 Gbd = 0.5 (Gb + Qd).
62 Гл. 2. Дифференциальные уравнения в частных производных
По существу, кривые линии ad и bd были заменены здесь пря-
прямыми линиями, определяемыми путем осреднения наклона пер-
первоначальных линий в концевых точках.
Если величины xd и yd известны, то из уравнения B.67)
можно найти Ра и Qd с помощью соотношений
AadFad (Pd - Ра)
AbdGbd (Pd - Pb)
^ (Qd - Qa)
Cbd (Qd - Qb)
Wad (yd - Уa) = 0, B.71)
ЛЫ (yd - yb) = 0. B.72)
При известных Pd и Qd можно воспользоваться формулой
B.68), чтобы получить ud:
— Ua = Pad (*d — *a) + Qad (Ud — У a)-
B.73)
На практике, чтобы получить xdi yd, Pd, Qd и ud, уравнения
B.69) — B.73) следует решать с помощью итераций. В каче-
& -характеристики
^-характеристики
Рис. 2.10. Метод характеристик.
стве начальной итерации используются следующие аппрокси-
аппроксимации:
~Fad = Fa, Gbd = Gb и т. д. B.74)
Как правило, если точка d расположена не слишком далеко от
а и Ь, достаточно провести две или три итерации. Метод реали-
реализует маршевое продвижение вдоль сетки, построенной на ло-
локальных характеристиках, определяемых в свою очередь как
часть общего решения. Приведенная выше формулировка опи-
описывается в гидроаэродинамических терминах в работе Бело-
церковского и Чушкина [Belotserkovskii, Chushkin, 1965].
Метод характеристик имел широкое применение при иссле-
исследовании одномерных нестационарных газодинамических задач,
§ 2.5. Традиционные методы решения
63
а также при изучении установившегося двумерного сверхзву-
сверхзвукового течения невязкого газа. Однако этот метод становится
слишком громоздким, если его распространять на случай трех
или четырех независимых переменных или если в потоке воз-
возникают внутренние ударные волны.
2.5.2. Разделение переменных
Этот метод может применяться к ДУЧП любого типа. Для
иллюстрации применения метода рассмотрим уравнение диф-
диффузии
ди д2и /о -.
в области, показанной на схеме рис. 2.11. На той же схеме по-
0 хчХ^х^\^^хххххч>чХХ>чххч>чХХ>7Г
Рис. 2.11. Начальные и граничные условия для уравнения B.75).
казаны начальные и граничные условия. Метод состоит в вве-
введении общего расщепленного решения
и(х, t) = X(x)T(t). B.76)
Подстановка в B.75) дает
d2X
4рг+ **-<>, B.77)
¦§.
B.78)
где А,— произвольная постоянная. Уравнение B.77) имеет бес-
бесконечный набор решений вида
Xk(x) = Aksmkx, B.79)
где X = k2, &=1, 2, 3, ... и Ak — постоянные, определяемые
€ помощью граничных и начальных условий. Далее, уравнение
B.78) также имеет бесконечное число решений вида
Tk(t) = Bkexp(-k2t), B.80)
64 Гл. 2. Дифференциальные уравнения в частных производных
где постоянные Bk должны определяться из начальных и гра-
граничных условий. Подстановка выражений B.79) и B.80) в
формулу B.76) позволяет получить общее решение в форме
оо
и(х, 0=Е Cksinkxexp(—k2t). B.81)
Выражение B.81) удовлетворяет граничным условиям задачи.
Постоянные Ck определяются путем удовлетворения началь-
начальным условиям
оо
Е Ck sin kx = и (х9 0) = / (х), B.82)
k=\
т. е.
Ck = — [ f (s) sin ksds. B.83)
0
По отношению к данной конкретной задаче вклады от множи-
множителей ехр(—k2t) очень малы при больших k и / > 0. Поэтому
в разложении B.81) обычно бывает необходимо сохранить
лишь 10 или 20 членов.
Принцип разделения переменных связан с возможностью
выбора такой системы координат, при которой dR совпадает
с координатными линиями. При этом предполагается также,
что операторы в ДУЧП могут быть разделены. Отсюда сле-
следует, что хотя метод достаточно эффективен при решении мо-
модельных задач, он все же нечасто находит прямое применение
к решению относительно сложных уравнений, определяющих
движение жидкости или газа, при этом нередко в областях
неправильной формы. Тем не менее интересное обсуждение дан-
данного метода проводится в книге Густафсона [Gustafson, 1920].
2.5.3. Метод функции Грина
Для ДУЧП, записанного в обобщенной формулировке
Lu = f9 B.84)
решение в принципе может быть построено путем «обращения»
оператора L. Решение представимо в интегральной форме:
u(p)=\G{p,q)f{q)dVq, B.85)
где G(p, q)—функция Грина. В общем случае функция G(p,q)
содержит информацию, эквивалентную информации в операто-
§ 2.5. Традиционные методы решения 65
ре L, а также информацию о граничных условиях и области
вычислений. Следовательно, главная трудность, возникающая
при использовании метода функции Грина, состоит в определе-
определении того, какой именно должна быть эта функция в примене-
применении к данной конкретной задаче. Последующее вычисление
интеграла в B.85), как правило, не вызывает затруднений.
Функцию Грина можно построить для таких сравнительна
простых линейных уравнений, как уравнения Лапласа и Пуас-
Пуассона. Например, точечный источник единичной мощности в трех,
измерениях имеет функцию Грина
S(p,q) = (№nrpq, B.86)
где rpq — просто расстояние между р и q. Эта формула по су-
существу эквивалентна двумерному потенциалу скорости, задан-
заданному формулой A1.53) при т=\. После выполнения требуе-
требуемого дифференцирования получим
q) = b(p, q), B.87)
где б(р, q)—дельта-функция Дирака, центрированная в точке
р, a V^ — лапласиан, вычисленный при q. Свойство дельта-
функции Дирака таково, что
\w{q)b{Piq)dVq = w{p) и 6(р, q) = 0, если р Ф q. B.88)
Функция w(q) из B.88)—произвольная гладкая функция.
Процедура решения может быть окончательно определена,
если воспользоваться вторым тождеством Грина:
J (uv2v - vу2и) dV + J [и |~ - v |jj-) dS = 0. B.89)
R dR
Пусть в интересующей нас ситуации функция иу входящая в
левую часть соотношения B.89), отождествляется с решением
уравнения Пуассона
Sj2u= — f в области /?, и = 0 на контуре dR B.90)
и
v = G(p, q) = S(p, q) + g(p,q) при v = 0 на dR, B.91)
В результате соотношение B.89) приобретает форму
B.92)
5 К Флетчер, т. 1
66 Гл. 2. Дифференциальные уравнения в частных производных
Функция g(p, q) выбрана так, что V2qg = 0 в области R и
G(P> <7) = 0, когда точка q лежит на OR. В результате с по-
помощью B.88) и B.92) получим решение
u(p)=\G(p,q)f(q)dVq. B.93)
Метод функции Грина неявно используется при построении па-
панельного метода (см. § 14.1) и почти непосредственно исполь-
используется в методе граничных элементов (см. п. 14.1.3).
Для некоторых эллиптических ДУЧП можно построить не-
некий эквивалентный вариационный принцип и применить проце-
процедуру Рэлея — Ритца [Gustafson, 1980]. Такая методика яв-
является стандартной при применении метода конечных элемен-
элементов к исследованию механических конструкций, однако те эл-
эллиптические ДУЧП, которые встречаются в гидроаэродинами-
гидроаэродинамике, обычно не имеют эквивалентной вариационной формы.
§ 2.6. Заключение
В данной главе мы рассмотрели классификацию ДУЧП по
принадлежности к гиперболическому, параболическому или
эллиптическому типу. Все эти три типа встречаются при раз-
различных упрощенных вариантах определяющих уравнений гид-
гидроаэродинамики (гл. 11). Впрочем, системы уравнений могут
иметь также и смешанный тип. Гиперболические ДУЧП обыч-
обычно ассоциируются с задачами о распространении без диссипа-
диссипации (волнообразное движение остается незатухающим), а па-
параболические ДУЧП — с задачами о распространении при на-
наличии диссипации. В гидроаэродинамике диссипация обычно
порождается членами с вязкостью или теплопроводностью. Эл-
Эллиптические ДУЧП ассоциируются со стационарными зада-
задачами.
Каждый из типов ДУЧП требует задания различных гра-
граничных (и начальных) условий и нуждается в применении опре-
определенной методики решения. Например, метод характеристик
является «естественным» для гиперболических ДУЧП с двумя
независимыми переменными. Для нелинейных уравнений, опре-
определяющих гидроаэродинамические процессы, классификация
ДУЧП может подвергаться локальным изменениям. С учетом
этого граничные условия должны подбираться так, чтобы не
нарушалось соответствие классификации ДУЧП вблизи гра-
границы.
§ 2.7. Задачи 67
При исследовании установившегося двумерного сверхзву-
сверхзвукового течения вокруг хорошо обтекаемого тела определяющи-
определяющими уравнениями служат уравнения Навье — Стокса, которые
в силу появления вторых производных являются строго эллип-
эллиптическими в той интерпретации, какая предлагается в п. 2.1.2.
Однако подобная классификация не принимает во внимание ве-
величины тех членов, от которых зависит результат. В самом
деле, члены с вязкостью имеют значение только вблизи поверх-
поверхности, где вязкая диссипация в направлении вдоль по потоку
на один порядок величины меньше, чем вязкая диссипация по-
поперек потока; определяющие уравнения в этой зоне являются
смешанными — параболически-гиперболическими. Вдали от те-
тела все члены с вязкостью малы и система уравнений является
эффективно гиперболической. Когда появляются ударные вол-
волны, то очень большие градиенты по направлению удаления от
тела становятся причиной того, что члены с вязкостью (и с
теплопроводностью) приобретают существенное значение и
определяющие уравнения становятся локально эллиптическими
(в пределах, соответствующих толщине ударной волны). Этого
достаточно, чтобы заменить разрывное решение (в невязкой
аппроксимации) на решение с очень большим градиентом, но
непрерывное.
Совершенно очевидно, что строгая математическая класси-
классификация определяющих ДУЧП должна сочетаться со знанием
тех физических процессов, которые исследуются, чтобы за счет
такого сочетания обеспечить постановку правильных граничных
условий и выбрать надлежащую методику численного расчета.
§ 2.7. Задачи
Основные положения (§2.1)
2.1. (а) Проведите преобразование уравнения Лапласа д2ф/дх2 -\-
+ д2ф/ду2 = 0 к обобщенным координатам | = g(*, у), ц = г\(х, у) и по-
покажите, что полученное в результате уравнение является эллиптическим.
(Ь) Проведите преобразование волнового уравнения дгф\др— д2ф/дх2 = 0
к обобщенным координатам g = g(/, х), r\ = r\(t, x) и покажите, что полу-
полученное в результате уравнение является гиперболическим.
2.2. Проведите преобразование уравнения Кортвега — де Вриза [Jeffrey,
Taniuti, 1964]
ди , ди , д3и .
к эквивалентной системе уравнений первого порядка за счет введения вспо-
вспомогательных переменных р = ди/дх и т. д. Обоснуйте вывод, что полученная
система уравнений является параболической.
€8 Гл. 2. Дифференциальные уравнения в частных производных
2.3. Безразмерные уравнения, определяющие установившееся течение не-
невязкой несжимаемой жидкости, имеют вид
ди , ди , др
г— + и-г \-—— = 0,
д* ду дх
дх ду
ди ,
dv . dv . dp
дх ду ду
Установите тип этой системы дифференциальных уравнений в частных про-
производных.
Гиперболические ДУЧП (§ 2.2)
2.4. Покажите с помощью исследования, что ДУЧП второго порядка
д2и/дх dt = 0 является гиперболическим. Рассмотрите эквивалентную систему
ди . dv Л
dt дх
Обоснуйте вывод, что эта система гиперболическая и оси х и t являются ха-
характеристиками.
2.5. Рассмотрите модифицированное волновое уравнение
Покажите с помощью исследования, что это уравнение является гипербо-
гиперболическим. Рассмотрите соответствующую систему уравнений
¦яг *
$•-?¦-«• <•»>
Покажите, что эта система является гиперболической, и определите характе-
характеристические направления. Какова связь между уравнением B.94) и системой
B 95)? Объясняет ли форма этой связи наличие добавочной характеристики
у системы B.95) ^
2.6. Определяющие уравнения для одномерного неустановившегося из-
энтропического течения невязкой сжимаемой жидкости имеют вид
др , иду рди
dt ^ дх ^ дх "" '
ди l „ ди л Х др — о
где р = kpy и а2 = YP/p- Здесь а — скорость звука. Покажите, что эта си-
система гиперболическая и характеристики задаются соотношениями dx/dt =
§ 2.7. Задачи 69
Параболические ДУЧП (§ 2.3)
2.7. (а) Проведите преобразование уравнения дф/dt — ад2ф/дх2 = 0 к эк-
эквивалентной системе путем введения вспомогательной переменной р — дф/дх.
Покажите, что эта система параболическая.
(Ь) Проанализируйте таким же образом уравнение дф/dt — а(д2ф/дх2 +
-f д2Ф/ду2) =0 и покажите, что оно является параболическим.
2.8. Рассмотрите уравнение переноса du/dt + 2сди/дх — dd2u/dx2 = 0 с
начальными условиями и(х, 0) = exp (chid) и граничными условиями
,и@, t) — exp(—c2t/d) и иA, t) = (d/c)du/dx(\, t). Покажите, что это урав-
уравнение параболическое и определите его решение.
2.9. Уравнения, определяющие установившееся течение, в пограничном
слое несжимаемой жидкости на плоской пластине, могут быть записаны
в виде
ди . dv
дх ^ ду '
ди , ди 1 д2и Л
дл: d# Re ду2
Покажите, что эта система параболическая и укажите подходящий вариант
начальных и граничных условий для и и v.
Эллиптические ДУЧП (§2.4)
2.10. Рассмотрите уравнения
*L+*L= |fi_^L = 0< B>96)
дх ду ду дх
Покажите, что эта система является эллиптической (а) непосредственно,
(Ь) путем введения переменной Ф, где и = дф/дх и v = дф/ду.
2.11. Покажите, что выражения и = х/(х2 + у2), v = y/(x2 + y2) пред-
представляют собой решение системы B.96).
2.12. Покажите, что уравнения
ди , ди ( д2и , д2и \ Л
дх ду \ дх2 ду2 )
dv , dv ( d2v , d2v \ Л
дх ду \ дх2 ду2 )
образуют эллиптическую систему и что этим уравнениям удовлетворяют вы-
выражения
и == -2 \ах + аъу + k {exp [Л (* - х0)] + ехр [-? (д: - jc0)]} cos (ky)]/(Re D),
v = -2 [a2 + а3АГ - Л {exp [k (x - дроI + exp [-k (x - jc0)]} sin (^)]/(Re D),
где
D = [aQ + axx + a2y + аъху + {exp [k (x — x0)] + exp [—k (x — x0)]} cos (ky)]
и a0, ai, аг, #з, k и Xq — произвольные постоянные.
Традиционные методы (§ 2.5)
2.13. Рассмотрите решение уравнения д2ф/дх2 + д2ф/ду2 = 0 на единич-
единичном квадрате с граничными условиями
Т @, у) = 0, Г A, f/) = 0, Г (х, 0) = Го (*), Г (х, 1) = 0.
70 Гл. 2. Дифференциальные уравнения в частных производных
Примените метод разделения переменных для получения
оо
Т (х, у)=^Ак sin (knx) sh [kn (у - 1)],
/2=1
где
B7УЬ0 [(-!)*-1]
k ~~
sh (kn)
2.14. Уравнение дф/dt — ад2ф/дх2 = О необходимо решить в области-
О ^Г л; ^ 1, / > О с граничными условиями Ф@, t) = О, 0A, t) = <f>R и на-
начальным условием Ф(х, 0) = 0. Покажите с помощью метода разделения пе-
переменных, что решение имеет форму
20д (—1)* ехр (—k2n2at) sin (knx)
k=\
2.15. Покажите, что выражение
1 ( (х — уJ \
. ехр ( — v у/ )
у*
представляет собой функцию Грина для задачи теплопроводности, рассмо-
рассмотренной в задаче 2.14, путем демонстрации того, что при фиксированном у
это выражение удовлетворяет уравнению B.75).
Глава 3
Предварительные сведения
о приемах вычислений
В данной главе будет сделан обзор некоторых из основных
вычислительных приемов, используемых при решении задач
гидроаэродинамики. При решении конкретной задачи будут из-
известны исходные уравнения (гл. 11) и соответствующие гра-
граничные условия (гл. 11 и 2). Для получения приближенного ре-
решения исходных уравнений с заданными граничными условия-
условиями используются вычислительные приемы.
Например, при исследовании трехмерного нестационарного
течения несжимаемой жидкости следовало бы построить реше-
решение для скорости и давления, т. е. рассчитать и(ху у, z, t),
v(xy у у zy t), w( x, у у Zy t) и р(Ху у у Zy t) Процесс построения вы-
вычислительного решения состоит из двух этапов, схематически
Исходные ДУЧП
и граничные
условия
Дискрети-
Дискретизация
Система I
алгебраических"^
уравнений "
г
Алгоритм
решения
Приближенное
решение
и (х, у, z, t)
и т. д.
Рис. 3.1. Процесс построения вычислительного решения.
показанных на рис. 3.1. На первом этапе дифференциальные
уравнения в частных производных, описывающие непрерывный
процесс, а также вспомогательные (граничные и начальные) ус-
условия преобразуются в дискретную систему алгебраических
уравнений. Этот первый этап называется дискретизацией (см.
§ 3.1). Процесс дискретизации легко идентифицируется, если
используется конечно-разностный метод (см. § 3.5), однако он
несколько менее очевиден при применении методов конечных
элементов, конечных объемов, а также спектральных методов
(см. гл. 5).
В процессе замены отдельных членов исходных уравнений,
представляющих собой частные производные, алгебраическими
выражениями, связывающими узловые значения на конечной
сетке, вносится некоторая ошибка. Методика такого выбора
алгебраических выражений, который приводил бы к малым
72 Гл. 3. Предварительные сведения о приемах вычислений
ошибкам, рассматривается в § 3.2. Достигаемая при этом точ-
точность представления дифференциальных членов анализируется
в § 3.3 и 3.4. Не менее важной, чем ошибка в представлении
дифференциальных членов исходного уравнения, является
ошибка самого решения. В § 3.5 дается простая конечно-раз-
конечно-разностная программа, позволяющая непосредственно оценить
ошибку решения.
При обсуждении нестационарных задач процесс дискрети-
дискретизации часто отождествляется с преобразованием исходной си-
системы дифференциальных уравнений в частных производных
в систему обыкновенных дифференциальных уравнений по вре-
времени. Это можно было бы считать оправданным с учетом того,
что приемы решения обыкновенных дифференциальных урав-
уравнений (см., например, [Gear, 1971]) настолько хорошо извест-
известны, что дальнейшее обсуждение уже не требуется. Однако при
применении конкретного метода систему обыкновенных диффе-
дифференциальных уравнений следует превратить в соответствующую
ей систему алгебраических уравнений и получить таким спо-
способом вычислительное решение.
Второй этап процесса решения (см. рис. 3.1) требует, что-
чтобы алгоритм решения уравнения обеспечил построение реше-
решения системы алгебраических уравнений. На этом этапе также
может вноситься некоторая ошибка, однако она обычно пре-
пренебрежимо мала в сравнении с ошибкой, вносимой на этапе
дискретизации, если только метод не является неустойчивым
(см. § 4.3). Методы, применяемые при решении систем алгеб-
алгебраических уравнений, обсуждаются в гл. 6. Как правило, си-
системы уравнений возникают при решении задач об установив-
установившемся течении. Что касается задач о неустановившемся тече-
течении, то применение явных методов (см., например, п. 7.1.1)
может свести этап решения уравнений к алгоритму, состояще-
состоящему не более чем из одной строки.
§ 3.1. Дискретизация
Чтобы преобразовать исходное уравнение в частных произ-
производных (или систему таких уравнений) в систему алгебраиче-
алгебраических уравнений (или обыкновенных дифференциальных урав-
уравнений), можно выбрать один из нескольких вариантов. Наиболее
общепринятыми являются метод конечных разностей, метод ко-
конечных элементов и спектральный метод. Способ осуществления
дискретизации зависит также от того, рассматриваются ли про-
производные по времени (в применении к задачам с зависимостью
от времени), или же уравнения, содержащие только простран-
пространственные производные.
§ 3.1. Дискретизация 73
На практике дискретизация производных по времени осу-
осуществляется почти исключительно с использованием конечно-
разностного метода. При дискретизации пространственных
производных используется, как правило, метод конечных раз-
разностей, конечных элементов, конечных объемов или спектраль-
спектральный метод.
3.1.1. Преобразование производных
в дискретные алгебраические выражения
Для иллюстрации процесса дискретизации рассмотрим
уравнение
дТ д2Т ,~ п
которое определяет нестационарный процесс теплопроводности
в одном измерении. Символ Г соответствует температуре, сим-
символ а — коэффициенту теплопроводности. Черта сверху символи-
символизирует точное решение. Характерные граничные и начальные ус-
условия, соответствующие уравнению C.1), имеют вид
T(O,t) = b, f(l, t) = d, C.2)
Т (х, 0) = То (х), 0 < х < 1. C.3)
Наиболее прямой путь дискретизации состоит в замене произ-
производных эквивалентными им конечно-разностными выражения-
выражениями. Так, например, с помощью представлений C.21) и C.25)
уравнение C.1) можно заменить уравнением
77+'-т7 «(^-277 + 77+,)
It
Размеры шагов А/, Дх, а также смысл нижнего индекса / и
верхнего индекса п указываются на рис. 3.2. В уравнении
C.4) символ Tf соответствует значению Т в узле (/, п).
Как это явствует из самого процесса дискретизации, пре-
превращающего уравнение C.1) в уравнение C.4), задача о на-
нахождении точного (непрерывного) решения Т{ху t) оказалась
замененной на задачу о нахождении совокупности дискретных
значений Г/, т. е. приближенного решения в каждом из узлов
(/, п) (см. рис. 3.2). Ясно, что при этом возникают две связан-
связанные между собой ошибки — ошибка аппроксимации и ошибка ре-
решения. Ошибка аппроксимации, вносимая за счет дискретизации
уравнения C.1), будет рассматриваться в § 3.3 и 3.4. Ошибка,
соответствующая разнице между приближенным решением и
точным решением (ошибка решения), будет изучена в § 4.1.
74
Гл. 3. Предварительные сведения о приемах вычислений
Истинное значение приближенного решения в промежуточ-
промежуточной точке между узлами сетки отнюдь не очевидно. Согласно
интуитивному представлению, решение должно плавно изме-
изменяться в промежутках между узловыми точками. В принципе
решение в некоторой точке (хп tr), не совпадающей с узлом,
может быть построено путем интерполяции значений, соответ-
соответствующих решению для окружающих узловых точек. Как мы
АХ 2Ах (j-i)Ax
Рис. 3.2. Дискретная сетка.
(J-1) Arc
увидим в дальнейшем (см. § 5.3), этот интерполяционный про-
процесс является автоматически встроенной частью метода конеч-
конечных элементов.
Ясно, что если уравнение C.1) является дифференциальным
уравнением в частных производных, то уравнение C.4) алгеб-
алгебраическое. Если посмотреть на рис. 3.2, то с помощью уравне-
уравнения C.4) можно получить формулу (или алгоритм) для опре-
определения неизвестного значения Г/ + 1 в зависимости от извест-
известных значений Г" на п-м временном слое, т. е. найти выражение
ГП+\
1 =
C.5)
Чтобы построить полное численное решение на временном
слое (п + 1), следует применить формулу C.5) ко всем узлам
j = 2y ..., /—1, предполагая при этом, что граничные условия
пП+1
Дирихле обеспечивают данные о значениях Тп\ и Т]
3.1.2. Производные по пространству
Мы уже имели возможность видеть, как конечно-разност-
конечно-разностный метод дискретизирует производные по пространству, на-
например как величина д2Т/дх2 в уравнении C.1) превращается
§ 3.1. Дискретизация 75
в выражение (Г/_1 — 2Г" + Г^+О/Дл:2, входящее в уравне-
уравнение C.4).
Метод конечных элементов (см. § 5.3) позволяет достичь
дискретизации за счет первоначального предположения о том,
что локальное решение для Т допускает интерполяцию. Далее
это локальное решение подставляется во взятый с соответст-
соответствующим весом интеграл от всех членов исходного уравнения.
Типичный результат такого действия при использовании ли-
линейных элементов на равномерной сетке имеет следующий вид:
Да:
V • /
Если разделить обе части уравнения C.6) на Дл:, то результат
получится аналогичным по своей структуре выражению C.4).
Вывод уравнения C.6) приводится в п. 5.5.1.
В спектральном методе (см. § 5.6) используются предполо-
предположения, аналогичные предположениям метода конечных элемен-
элементов, за исключением того, что предполагаемая форма решения
для Т имеет вид
Г^Е */(<)*/(*), C.7)
где cij(t)—неизвестные коэффициенты, определяемые в процес-
процессе построения решения, а ф}(х)—известные функции х (см.
§ 5.6). Окончательная форма дискретного представления урав-
уравнения при использовании спектрального метода может быть
записана как
где Pj — известные алгебраические коэффициенты.
Какой бы метод ни применялся для осуществления дискре-
дискретизации, процесс последующего решения уравнений, например
с использованием выражения C.5), применяется непосред-
непосредственно к алгебраическим уравнениям и является в некотором
смысле не зависящим от способа дискретизации.
3.1.3. Производные по времени
При замене dT/dt в уравнении C.1) на одностороннее раз-
разностное выражение (Г/ + 1 — Т*})/М используется информация
только с временных слоев п и п + 1. В силу того что время из-
76 Гл. 3. Предварительные сведения о приемах вычислений
меняется только в положительном направлении, информация
с временных слоев с номерами п + 2 и больше нам недоступна.
В уравнении C.4) пространственная производная д2Т/дх2 аппро-
аппроксимировалась на временном слое п, в силу чего получился яв-
явный алгоритм для определения 77+1. Если бы пространственные
члены аппроксимировались на временном слое я+1, то полу-
получился бы следующий неявный алгоритм:
- S71/-/ + A + 25) Г"+1 - sT]tl = Т", C.9)
где 5 = aAt/Ax2. Уравнение C.9) можно решить, если рассмат-
рассматривать его как часть системы уравнений, полученной из C.9)
путем записи данного уравнения для всех узлов / = 2, ...
...,/-1 (см. §7.2).
Если в уравнение C.1) подставить формулу с центральной
разностью (Г/ + 1 — Г/~1JД/, то можно построить следующий яв-
явный алгоритм для определения Г"+1:
тп+х = тп-\ + Bащьх2) (Г?-! - 277 + T?+i). (ЗЛО)
Алгоритм C.10) является более точным, чем формула C.5) т
однако и более сложным, так как охватывает данные не с двух
слоев, а с трех: п— 1, п, п + 1. Этот частный вариант алгорит-
алгоритма оказывается непрактичным, так как он неустойчив (см.
п. 7.1.2). Однако в применении к другим уравнениям, напри-
например к уравнению конвекции (см. § 9.1), использование цент-
центральных разностей по времени приводит к устойчивым алго-
алгоритмам.
Существует некоторый альтернативный подход к дискрети-
дискретизации производных по времени, построенный на связи с обык-
обыкновенными дифференциальными уравнениями. Уравнение C.1)
можно записать в виде
4r=Lf> <зл1>
где L — дифференциальный оператор ад2/дх2. После дискрети-
дискретизации по пространству уравнение C.11) принимает вид
^Г = 1-аТ„ C.12)
где La — алгебраический оператор, полученный в результате
пространственной дискретизации. Совокупность уравнений
C.12), записанных для каждого из узлов, представляет собой
систему обыкновенных дифференциальных уравнений по вре-
времени. Отсюда следует, что к уравнениям C.12) может быть в
§ 3.2. Аппроксимация производных
77
принципе применена любая методика интегрирования обыкно-
обыкновенных дифференциальных уравнений (см. [Gear, 1971]). Во-
Вообще говоря, результат интегрирования можно записать в
форме
ч =¦
LaTfdt'.
C.13)
Вычисление интеграла в C.13) по схеме Эйлера дает выра-
выражение
/ =Tj + [LaTj] A/, C.14)
тождественное выражению C.5), если La — конечно-разност-
конечно-разностный оператор, фигурирующий в уравнении C.4). Вследствие
ошибок, связанных с введением оператора пространственной
дискретизации La, использование формулы интегрирования
очень высокого порядка для подстановки в C.13) обычно не
дает каких-либо преимуществ. Некоторые из наиболее эффек-
эффективных алгоритмов решения подобных задач рассматриваются
в § 7.4.
§ 3.2. Аппроксимация производных
В § 3.1 были приведены типичные алгебраические формулы,
позволяющие проиллюстрировать технику дискретизации про-
производных, подобных д2Т/дх2. Здесь демонстрируется процесс по-
построения таких алгебраических формул, сначала при помощи
разложения в ряд Тейлора, а потом — при помощи некоторой
общей процедуры. В каждом случае нетрудно оценить ошибку,
обусловленную процессом дискретизации.
3.2.1. Разложение в ряд Тейлора
В качестве первого шага по пути к разработке алгоритма
расчета тех значений Г, которые могут фигурировать в урав-
уравнении C.1), выразим производные Т по пространству и време-
времени в узле (у, п) через значения Т в близлежащих узлах. Для
реализации этого процесса воспользуемся разложениями в ряды
Тейлора типа
т=0
кхт Г дтТ1п
m\ L dxm J/ •
JT--Z
\ дтТ
ml L dtm
Т-
C.15)
C.16)
78 Гл. 3. Предварительные сведения о приемах вычислений
Эти ряды могут быть оборваны после любого числа членов,
причем возникающая в результате ошибка (ошибка аппроксима-
аппроксимации) определяется в основном следующим членом разложения,
если только Ах <С 1 в разложении C.15) или если Д/< 1 в раз-
разложении C.16). Следовательно, можно написать
^ + IJ + О (Лх% C.17)
Интерпретация остаточного члена О (Ах3) сводится к тому,
что, как предполагается, существует некоторая положительная
постоянная Ку зависящая от f, такая, что разность между зна-
значением Т в узле (/+ 1, п) и первыми тремя членами правой
части C.17), рассчитанными в узле (/, п) оказывается численно
меньше величины КАх3 для любых достаточно малых Ах. Ясно,
что связанная с такой аппроксимацией ошибка будет быстро
уменьшаться по величине по мере уменьшения Ах.
Обращаясь к выражению C.17), нетрудно видеть, что ко-
конечно-разностное представление дТ/дх можно получить непо-
непосредственно. Действительно, перегруппировка членов в C.17)
дает __ _
€]; G777)M*05а4#]> C.18)
[€]; =
Очевидно, что использование конечно-разностной подстановки
обеспечивает точность О (Ах). Дополнительные члены, фигу-
фигурирующие в правой части C.18), называются в дальнейшем
ошибкой аппроксимации. Выражение в правой части формулы
C.19) называется аппроксимацией с разностью вперед. Если
разложить величину Т?-\ в ряд Тейлора в узле (/, п) и пере-
перегруппировать члены, то можно построить аппроксимацию с
разностью назад:
Г-Г
Idx ],
C.20)
Как и C.19), эта аппроксимация вносит ошибку О (Ах). Гео-
Геометрическая интерпретация выражений (ЗЛ9) и C.20) дается
на рис. 3.3. Формула C.19) оценивает [дТ/дх]*} через наклон
линии ВС, тогда как формула C.20) дает ту же оценку посред-
посредством наклона АВ.
Формулы C.19) и C.20) были получены с помощью раз-
разложения в ряд Тейлора по пространству. Разложение в ряд
§ 3.2. Аппроксимация производных
79
Тейлора по времени — формула C.16)—может быть использо-
использовано для построения аппроксимации с разностью вперед
I
L dt J/
М
которая вносит ошибку О (At), если только предположить, что
А/<1 и что производные высших порядков ограничены.
3.2.2. Аппроксимация общего вида
Конечно-разностные выражения, приведенные в п. 3.2.1, были
построены с помощью простых перестановок в единственном
Т(х)г
Ах —Н
X;
Рис. 3.3. Различные варианты конечно-разностного представления дТ/дх.
разложении в ряд Тайлора. Более последовательная методика
построения разностных аппроксимаций сводится к тому, чтобы
начать с некоторого общего выражения типа
=аТ"- ¦+ьТ"+сТ°+'
C-22)
где постоянные а, Ъ и с подлежат определению, а член О(Ахт)
будет указывать на степень точности получаемой аппрокси-
аппроксимации.
Используя формулу C.15), можно написать
C*23)
jL, + ЬТ? + сТ?+] = (а + Ъ + с) Т? + (- а + с) Ах [^
Полагая а + b + с = 0, (—а + с) Ах = 1, получаем а = с —
¦— 1/Ajc и & = —2с + 1/Ах для любого с. Выбирая с так, чтобы
80 Гл. 3. Предварительные сведения о приемах вычислений
обратился в нуль третий член правой части формулы C.23),
получаем наиболее точную аппроксимацию из всех возможных
вариантов с подбором трех параметров. Таким образом, имеем
с = —-а = A/2)Дл: и Ъ = 0. Подстановка этих значений в C.23)
дает
дТЛп 1 / =п ,fn \ Л*2 Г д*Т -Iя
Следовательно, центрированная (или центральная) разност-
разностная аппроксимация для [дТ/дх]" имеет форму
C.24)
2Д*
с ошибкой аппроксимации О(Дх2). Очевидно, что центрирован-
центрированная разностная аппроксимация вносит ошибку аппроксимации
более высокого порядка, чем аппроксимации с разностями вперед
C.19) и назад C.20). Формула C.24) оценивает [df/дх]] по на-
наклону линии АС на рис. 3.3.
Если по аналогии с C.22) воспользоваться подобным же
представлением для [д2Т/дх2]", то получим следующую центри-
центрированную разностную формулу:
Тот же самый прием с использованием представлений типа
C.22) может быть применен для построения односторонних
разностных формул, если только вводить разложения в окрест-
окрестности соответствующих узлов. Этот же прием можно исполь-
использовать и для вывода многомерных формул, а также разност-
разностных формул для неравномерных сеток (см. п. 10.1.5).
3.2.3. Трехточечная асимметричная формула для [дТ/дх]"
Общий прием построения алгебраических формул для
аппроксимации производных (см. п. 3.2.2) используется для
вывода трехточечного одностороннего представления производ-
производной [дТ/дх]" В качестве исходного выражения вместо C.22)
берется следующее общее представление:
-g-]* = аТ] + М7+, + сТU + О (Д*т), C.26)
§ 3.2. Аппроксимация производных 81
где параметры а, Ь и с подлежат определению. Величины
77-н и Г/+2 разлагаются в ряд Тейлора около / (см. п. 3.2.1).
Подстановка этих разложений в C.26) и перегруппировка чле-
членов позволяет получить
C.27)
Путем сравнения левой и правой частей соотношения C.27)
нетрудно установить, что для получения наименьшей ошибки
параметры а, Ь и с должны удовлетворять следующим усло-
условиям:
1 ЬАх2.сB А*J .
Отсюда получаются значения параметров:
1.5 - 2 0.5
и ~ Их * ° ~ tax n L Ax
и, следовательно,
дТ 1П —1.577 + 2Г^+1 - 0.577+2
Ах2 Г а3Г I"
что согласуется с результатом, показанным в табл. 3.3 (см.
стр. 84). Данная формула вносит ошибку аппроксимации О(Дл:2),
как и формула C.24) с центрированной разностью.
Если в представление C.26) ввести большее число членов,
например
!?]" ~ аТ? + й7+1 + cfU + dfU + ef 7+4,
то добавочные условия для определения коэффициентов от а
до е могут быть получены из соотношения C.27), модифици-
модифицируемого при помощи требования, что коэффициенты при про-
производных высшего порядка обращаются в нуль. Однако схемы,
основанные на дискретизации повышенного порядка, зачастую
встречаются с более строгими ограничениями, связанными с
устойчивостью (см. § 4.3), чем это было для схем с дискретиза-
дискретизацией низкого порядка. Следовательно, альтернативная страте-
стратегия сводится к тому, чтобы некоторые из коэффициентов от а
до е позволяли уменьшить ошибку, а другие — улучшить ус-
устойчивость. Подобный же подход принимается при построении
схем для решения обыкновенных дифференциальных уравне-
уравнений (см. [Hamming, 1973]).
6 К. Флетчер, т. 1
82 Гл. 3. Предварительные сведения о приемах вычислений
§ 3.3, Точность процесса дискретизации
Дискретизация необходима для того, чтобы превратить ис-
исходные дифференциальные уравнения в эквивалентную им
систему алгебраических уравнений, для решения которых мож-
можно воспользоваться вычислительной машиной. Если исключить
тот случай, когда соответствующее точное решение имеет пре-
предельно простую аналитическую форму, то процесс дискретиза-
дискретизации обязательно вносит некоторую ошибку. Так, например,
центрированная разностная формула C.24) является точной
для полиномов вплоть до квадратичных, тогда как односторон-
односторонние формулы C.19) и C.20) точны лишь для линейных поли-
полиномов. О точности можно судить по тому факту, что все члены
ошибки аппроксимации оказываются равными нулю для поли-
полиномов достаточно низкого порядка.
В общем случае ошибка конечно-разностного представле-
представления производной может быть определена с помощью разложе-
разложения в ряд Тейлора в окрестности того узла, где оценивается
величина производной (см. п. 3.2.2), тогда как оценка главного
члена остатка дает достаточно хорошую аппроксимацию ошиб-
ошибки, если только элемент сетки имеет достаточно малый раз-
размер. Однако окончательная оценка членов ряда Тейлора воз-
возможна только тогда, когда известно точное решение.
Более прямой путь сравнения точности различных алгебра-
алгебраических формул сводится к рассмотрению простой аналитиче-
аналитической функции типа Т = ехр х и к сравнению значения произ-
производной, полученного аналитически, со значением, найденным
по дискретизационной формуле. В табл. 3.1 демонстрируется
подобное сравнение для значений dTjdxL оцениваемых в точке
х = 1 при аналитической функции вида Т = ехр х\ размер шага
составляет Дл: = 0.1. В общем случае трехточечные формулы,
будь то симметричные или асимметричные, оказываются зна-
значительно более точными, чем двухточечные формулы с раз-
разностями вперед или назад, однако значительно менее точными,
чем пятиточечная симметричная формула. Как очевидно из
табл. 3.1, если величина Ах достаточно мала, то главный член
ряда Тейлора (Р. Т.) дает хорошую оценку ошибки.
Типичные алгебраические формулы для оценки d2T/dx2 при
х = 1.0 для значений функции Т = ехр х приводятся в табл. 3.2.
Значения функции оцениваются с интервалом Дл: = 0.1. Как
и ранее, трехточечная симметричная формула является точной,
однако теперь трехточечная асимметричная формула оказы-
оказывается неточной. Как и при оценке качества формул для пер-
первой производной, главный член ряда Тейлора обеспечивает до-
достаточно точную оценку ошибки.
Таблица 3.1. Сравнение формул для вычисления df/dx при .v = 1.0
Вариант формулы
Точная
Трехточечная
симметричная
Разности вперед
Разности назад
Трехточечная
несимметричная
Пятиточечная
симметричная
Алгебраическая формула
(f — jf/_i)/2A*
(Ff + l-Tf)/Ax
(f^T^/Ax
(-1.571, + 2Tj + l -0.57\+2)/A*
G\ 2"~"8^ i+8^~ l — f.+2)/\2Ax
[?l
2.7183
2.7228
2.8588
2.5868
2.7085
2.7183
Ошибка
0.4533ХЮ
0.1406ХЮ
-0.1315X10"°
—0.9773ХЮ
-0.9072ХЮ
Главный член ряда
Тейлора
0.4531 ХЮ~2
0.1359ХЮ"
-0.1359X10"°
—0.9061 ХЮ"
—0.9061 ХЮ~5
Таблица 3.2. Сравнение формул для вычисления d2T/dx2 при х = 1.0
Вариант формулы
Точная
Трехточечная
симметричная
Трехточечная
несимметричная
Пятиточечная
симметричная
Алгебраическая формула
L dx* J/
2.7183
2.7205
3.0067
2.7183
Ошибка
0.2266ХЮ
0.2884ХЮ
—0.3023ХЮ
Главный член ряда
Тейлора
0.2265Х10"
0.2718ХЮ
-0.3020ХЮ
84
Гл. 3. Предварительные сведения о приемах вычислений
Алгебраические формулы для главных членов выражений,
определяющих ошибку аппроксимации, приводятся в табл. 3.3
и 3.4. Эти формулы получены так, как в п. 3.2.1,— путем раз-
разложения в ряд Тейлора в окрестности /-го узла. В табл. 3.3
приняты обозначения: Txxx = d?T/dx3 и т. д. Для данного кон-
конкретного примера (Т — ехрх) имеем ТХХХ = ТХХХХ и т. д. Следо-
Следовательно, величина ошибки в первую очередь зависит от сте-
степеней Ах. А отсюда вытекает, что по* мере уменьшения Ах сле-
следует ожидать, что при использовании пятиточечной формулы
ошибка аппроксимации будет уменьшаться гораздо быстрее,
чем при использовании двухточечных формул с разностями
вперед или назад.
Таблица 3.3. Главный член ошибки аппроксимации
(алгебраическое представление): dT/dx
Вариант формулы
Трехточечная
симметричная
Разности вперед
Разности назад
Трехточечная
несимметричная
Пятиточечная
симметричная
Алгебраическая формула
(Т +1-Г ,)/2Ax
G\ + 1 — Т.укх
(Т. — 7, j)/A*
/„1.5f. + 2f" -0.5Г. )/Д*
J /+ 7 +
(f — 87\ +87\ —
— Г 2)/12 Ал:
Главный член
ошибки аппрокси-
аппроксимации
Ьх>Тххх/6
ЬхТхх/2
- ЬхТхх/2
- Ах*Тххх/3
- Ьх*Тххххх/ЗО
Таблица 3.4. Главный член ошибки аппроксимации
(алгебраическое представление): d2T/dx2
Вариант формулы
Трехточечная
симметричная
Трехточечная
несимметричная
Пятиточечная
симметричная
Алгебраическая формула
(f 2Г +Г+1)/Дх^
G—27. +7". уд*2
/__ y + 1б7 — зог +
Главный член
ошибки аппрокси-
аппроксимации
Ах2Тхххх/\2
АхТххх
§ 3.3. Точность процесса дискретизации 8S
Причина большой ошибки, связанной с трехточечной асим-
асимметричной формулой и показанной в табл. 3.2, становится оче-
очевидной из рассмотрения табл. 3.4, на которой видно, что глав-
главный член ошибки аппроксимации имеет в этом случае всего
лишь первый порядок точности.
Как видно из табл. 3.1 и 3.2, существует тесная корреляция
между непосредственно рассчитанной ошибкой и ошибкой
аппроксимации. На этом основании следует ожидать, что не-
непосредственно рассчитанная ошибка будет уменьшаться вместе
с Ах по такому же закону, как это показано в табл. 3.3 и 3.4.
Этот вывод подтверждается и результатами, показанными на
рис. 3.4 и 3.5. Если построить графики в логарифмической
шкале, то градиент результатов, касающихся сходимости, т. е.
скорость сходимости, соответствует определенной степени Ах.
Как это ясно из данных, приведенных на графиках, в рассмот-
рассмотренных нами различных случаях ожидаемая скорость сходи-
сходимости подсказывается теми выражениями главных членов ошиб-
ошибки аппроксимации, которые приведены в табл. 3.3 и 3.4. Оценку
скорости сходимости можно по-прежнему основывать на дан-
данных об ошибке аппроксимации, даже если точное решение не-
неизвестно.
3.3.1. Сравнение формул высокого и низкого порядков
Если судить по тем результатам, которые были изложены
выше, то может показаться, что во всех случаях следует поль-
пользоваться формулой высокого порядка на мелкой сетке. Одна-
Однако это впечатление обманчиво. Во-первых, расчет по формуле
высокого порядка охватывает большее количество точек и,
следовательно, оказывается менее экономичным, чем расчет па
формуле низкого порядка. С точки зрения практической пер-
перспективы та точность, которая может быть достигнута при за-
заданном времени исполнения, или вычислительная эффектив-
эффективность, более важна, чем просто точность; точность же всегда
можно повысить за счет измельчения сетки. Вычислительная
эффективность рассматривается в § 4.5.
Во-вторых, формулы высокого порядка обладают сравни-
сравнительно небольшим преимуществом в точности перед формула-
формулами низкого порядка в случае грубой сетки, однако такое пре-
преимущество становится значительно больше, если сетка мелкая.
Однако при решении некоторой конкретной задачи нередко
случается, что требуемый уровень суммарной точности резуль-
результатов соответствует именно грубой сетке или же применение
грубой сетки необходимо из-за ограничений на машинную
память либо на время исполнения. Превосходство формул
Гл. 3. Предварительные сведения о приемах вычислений
высокого порядка, выявляемое на рис. 3.4 и 3.5, зависит еще и
от гладкости точного решения. Решения, соответствующие
сверхзвуковым течениям невязкой жидкости, могут содержать
Пятиточечная
симметричная
схема
10
-lg?
# Трехточечная
симметричная
схема
Разности вперед
0Л 0.8 1.2 1.6 2.0
tgAx
Рис. 3.4. Результаты, касающиеся сходимости при вычислении dT/dx;
?= \[dT/dx]FD/[dT/dx]ex-l\.
10
Пятиточечная
симметричная
схема
Трехточечная
симметричная
схема
Разности вперед
0,4 0.8 1.2 1.6 2.0
-lg их
Рис. 3.5. Результаты, касающиеся сходимости при вычислении d2Tjdx2\
Е = \[d*T/dx]™l[d4ldx%x - 11.
разрывы, связанные с наличием ударных волн (см. [Liepmann,
Roshko, 1957]). Если решение оказывается разрывным в пре-
пределах того интервала, на котором используются алгебраиче-
алгебраические формулы, то формула высокого порядка не будет давать
§ 3.3. Точность процесса дискретизации
87
существенно большую точность. Это можно видеть на примере
точного решения, показанного на рис. 3.6.
Использование трехточечной симметричной формулы:
Использование пятиточечной симметричной формулы:
fx^ = -7/A2 Дх).
Если учесть, что, согласно точному решению, [dT/dx]x=i =
= —оо, то пятиточечная формула не дает заметного преиму-
преимущества в точности по сравнению с трехточечной формулой.
1.0 х
Рис. 3.6. Разрывное (точное) решение.
Для задач о течении вязкой жидкости при больших числах
Рейнольдса (т. е. при малой естественной диссипации) реше-
решений с разрывами быть не может, но могут возникать очень
большие градиенты. Если градиент достаточно велик, а сетка
достаточно грубая, то схемы высокого порядка не приносят
преимуществ. Это можно проиллюстрировать на примере
функции у = th[k(x—1)], которая представлена графически
на рис. 3.7 для трех значений параметра k. Очевидно, что су-
существует градиент, центрированный в точке лг=1, величина
которого возрастает вместе со значением параметра k. Первая
производная dy/dx оценивалась при х = 0.96 с использованием
трехточечной и пятиточечной симметричных формул (см.
табл. 3.1) для уменьшающихся значений Ах при к = 5 и 20.
Результат демонстрируется на рис. 3.8. Нетрудно заметить,,
что пятиточечная формула обеспечивает преимущество в точ-
точности только тогда, когда сетка является достаточно мелкой.
Требуемая степень измельчения возрастает по мере того, как
градиент становится больше (возрастающее значение k). Для
некоторых промежуточных значений Ал: пятиточечная формула
Гл. 3. Предварительные сведения о приемах вычислений
Рис. 3.7. Аналитическая функция у = th[k(l—х)].
6r
<
Пятиточечная
,o симметричная
схема
0Л 0.8 1.2 1.6 2.0
-1дЛж
0Л 0.8 1.2 1.6
-igAar
Пятиточечная
симметричная
о схема
,• Трехточечная
симметричная
схема
2.0
Трехточечная
симметричная
схема
о'
/
-41
0.
,о Пятиточечная
симметричная
схема
t> Трехточечная
симметричная
схема
I
0.4 0.8 1.2 1.6 2.0
о Пятиточечная
ST симметричная
» Трехточечная
симметричная
схема
4 0.8 1.2 1.6 2.0
Рис. 3.8. Сходимость конечно-раз- Рис. 3.9. Сходимость [d2y/dx2]FD:
ностного значения [dy/dx]FD: влияние влияние гладкости решения;
гладкости решения; Е = "—'-'--" «^-'-^
Е= \[dytdx]FD/[dyldx]ex-\\.
§ 3.4. Представление волн 89
дает менее точную оценку производной. Соответствующее срав-
сравнение оценок второй производной демонстрируется на рис. 3.9.
Очевидна та же самая общая тенденция, а именно что формула
высокого порядка обеспечивает заметное улучшение только
тогда, когда сетка является измельченной.
В тех случаях, когда встречаются резкие градиенты, фор-
формулы высокого порядка дают намного большие значения про-
производной, чем формулы низкого порядка. Как следствие этого*
на заданной сетке члены высокого порядка в выражении ошиб-
ошибки аппроксимации уменьшаются не с такой большой скоростью,
как в случае, когда соответствующее точное решение является
гладким. В силу той же самой причины, если только сетка не
сделана очень мелкой, величина высшей производной в глав-
главном члене выражения для ошибки аппроксимации при дискре-
дискретизации высшего порядка может оказаться настолько большой,,
что суммарная ошибка будет сравнима с той, которая полу-
получается при дискретизации низкого порядка.
В качестве общего замечания примем во внимание, что в
силу причин, обсуждаемых в § 9.4, следует использовать ди-
дискретизацию по крайней мере второго порядка. Использование
дискретизации более высокого порядка может быть оправдано^
лишь в некоторых особых обстоятельствах.
§ 3.4. Представление волн
При многих явлениях, связанных с течением жидкости, дви-
движение обнаруживает волновой характер. Поэтому с концеп-
концептуальной точки зрения оказывается полезным рассматривать
точное решение так, как если бы оно распалось на отдельные
свойственные ему компоненты Фурье. В этой связи возникает
вопрос о том, будет ли процесс дискретизации с одинаковой
точностью представлять короткие и длинные волны.
3.4.1. Роль грубой структуры сетки
Метод конечных разностей заменяет непрерывную функцию*
g(x) вектором, составленным из узловых значений gj и соот-
соответствующим вектору, составленному из дискретных точек сет-
сетки Xj. Выбор надлежащего размера элемента сетки Ах зави-
зависит от гладкости функции g(x). Неудачный выбор иллюстри-
иллюстрируется на рис. 3.10(а), тогда как удовлетворительный выбор
показан на рис. З.Ю(Ь). Для получения достаточно точного
представления функции g(x)> показанной на рис. 3.10(а), по-
потребовался бы значительно более мелкий размер ячейки сетки,,
чем для такой g(x), которая показана на рис. ЗЛО(Ь).
•90
Гл. 3. Предварительные сведения о приемах вычислений
Представление Фурье для функции g(x) (которая предпо-
предполагается периодической) на интервале 0 ^ х ^ 2я имеет вид
g(x)=
gme
imx
C.28)
где t=(—1I/2, m — волновое число, a gm — амплитуда моды
9j
(a)
(b)
J I
Рис. 3.10. Дискретное представление g(x). Сетка — слишком грубая (а) и
удовлетворительная (Ь).
Фурье с длиной волны А, = 2л/т, задаваемая выражением (см.
[Hamming, 1973])
y(x)e-imxdx. C.29)
Вектору узловых значений gj также можно дать представление
Фурье, имеющее вид
*/ = ? gmeimiAx, C.30)
m=l
где модальные амплитуды gm задаются в виде
Z
C.31)
Дискретная природа сетки ограничивает диапазон длин волн,
поддающихся представлению. В частности, не могут быть пред-
представлены длины волн, более короткие, чем длина волны отсеч-
отсечки к = 2Ах. Это значит, что gj следует рассматривать как длин-
длинноволновую аппроксимацию функции g(x). Аналогично этому
Г?+1, т. е. приближенное решение, получаемое из C.5), сле-
следует рассматривать как длинноволновое приближение к точ-
§ 3.4. Представление волн 91
ному решению уравнения C.1). Этот аспект подвергается даль-
дальнейшему рассмотрению в § 9.2 и используется при обосновании
многосеточных методов (см. п. 6.3.5).
3.4.2. Точность представления волн
Чтобы получить представление о точности конечно-разност-
конечно-разностных аппроксимаций в тех случаях, когда следует ожидать вол-
волнообразного по своему характеру движения, рассмотрим при-
приложение к случаю прогрессивных волн, который задается в
виде __
Т(х, t) = Re {е["»<*-*'>1} = cos [m (х - qt)], C.32)
где i = (—1I/2, символ Re обозначает вещественную часть,
m — волновое число, как и в C.28), a q — скорость распростра-
распространения волны, движущейся в положительном направлении оси
х. В фиксированной точке х\ волновое движение является пе-
периодическим с периодом Р = 2я/(qm).
Если рассмотреть узел (/, /г), то в нем точные значения пер-
первой и второй производных Т выражаются в виде
|L = _ m sin [щ (x, - qtn)l C.33)
-g- = - m2 cos [m {Xj _ qtn)l C>34)
Выражение C.32) следует подставить в трехточечную формулу
что дает
Г—Т*
L дх J/
"dTj/^^Al (cos t tm (х)—Я*п)\+ A*}-cos {[m (Xj—qtn)]-mAx})=
= - m si" [m (xf - qtn)] sin (m ?jx)
mkx * V • /
В результате амплитудный фактор для представления первой
производной будет равен
AR(l) = i2^=i^L. C.36)
зрт [дТ/дх] mbx '
Пользуясь формулой C.32), получим центрированную раз-
разностную аппроксимацию для д2Т/дх2 в виде
7f7 f* [sin(mA*/2)]\2 Q_4
(mA,/2) J COS [/*(*;-?*„)]. C.37)
92 Гл. 3. Предварительные сведения о приемах вычислений
Амплитудный фактор для представления второй производной
имеет вид
**р-(¦*№&*¦)'¦ <3-38>
Как показывает изучение правой части формулы C.36), при-
применение конечно-разностной аппроксимации привело к изме-
изменению амплитуды производной. В случае длинных волн, когда
А>20Длг, амплитуда первой производной уменьшается за
счет умножения на коэффициент, равный 0.984—1.000, если
используется центрированная разностная аппроксимация.
Однако когда на длине одной волны располагается менее че-
четырех ячеек сетки (случай коротких волн), то амплитуда про-
производной составляет менее чем 0.64 от своего истинного зна-
значения. При длине_волны К = 20Ал: центрированное разностное
представление д2Т/дх2 уменьшает амплитуду в 0.992 раза.
Однако при длине волны К = 2Ах амплитуда второй производ-
производной уменьшается за счет умножения на 0.405. Как отмечалось
в п. 3.4.1, длинные волны воспроизводятся более точно, чем
короткие.
__Если сравнить разностную аппроксимацию вперед для
[дТ/дх]п по формуле C.19) с точным значением этой производ-
производной для функции Г, заданной формулой C.32), то мы найдем,
что ошибки вносятся как в значение фазы, так и в значение
амплитуды. Истинная величина амплитуды умножается на ко-
коэффициент [sin(m&x/2)/(mkx/2)], а уменьшение фазы опреде-
определяется коэффициентом тДх/2, что эквивалентно пространствен-
пространственному сдвигу вперед на Ах/2. Для приведенных выше примеров
ошибки по амплитуде и фазе исчезают при Ах-^О, т. е. в пре-
пределе длинных волн.
3.4.3. Точность формул высокого порядка
Как было указано в п. 3.4.2, представление о точности ди-
дискретизации можно получить, рассматривая прогрессивную
волну, движущуюся с постоянной амплитудой и скоростью q.
Точное решение задается формулой C.32). Здесь мы восполь-
воспользуемся тем же примером, чтобы проверить, будут ли разност-
разностные формулы высокого порядка воспроизводить волны с более
высокой точностью, чем формулы низкого порядка. Конкретно
мы будем сравнивать ^симметричные трехточечную и пятиточеч-
пятиточечную формулы для дТ/дх и д2Т/дх2, приведенные в табл. 3.1
и 3.2.
Действуя таким же образом, как при выводе формулы
,C.36), определим амплитудный фактор в применении к пяти-
§ 3.4. Представление волн
93
точечному симметричному представлению дТ/дх (см. табл. 3.1);
он равен
1\ ( 4 1 А \ sin m Дл: /о on\
) = (J - T cos m Ax) -ШГ- ¦ <3-39)
ШГ
Поведение выражения, определяемого правой частью C.39),
показано в табл. 3.5 применительно к длинным и коротким вол-
Таблица 3.5. Отношение амплитуд в случае прогрессивной волны
Производная
dT
dx
Производная
d*T
dx*
Схема
Трехточечная
метричная
Пятиточечная
метричная
Схема
Трехточечная
метричная
Пятиточечная
метричная
сим-
сим-
сим-
сим-
Отношение
амплитуд
Длинная волна
(X = 20Д*)
0.9836
0.9996
Длинная волна
(X = 20Д*)
0.9918
0.9999
Отношение
амплитуд
Короткая волна
(Я = 4Ax)
0.6366
0.8488
Короткая волна
(X = 2Д*)
0.4053
0.5404
нам. Амплитудный фактор в применении к пятиточечному пред-
представлению д2Т/дх2 (см. табл. 3.2) выражается в виде
=т {1 - °-25 [cos
sin
У • <3-40>
Поведение правой части C.40) в применении к длинным и ко-
коротким волнам показано в табл. 3.5. Показанные в этой таб-
таблице результаты свидетельствуют о том, что обе схемы дают
большую точность в случае длинных волн, причем особенно
хорошую точность обеспечивает пятиточечная схема. Однако
ни одна из рассмотренных схем не является особенно точной
в случае коротких волн. Этот результат согласуется со сде-
сделанными ранее замечаниями (см. § 3.3), касающимися сравни-
сравнительно малых преимуществ использования схем высокого по-
порядка на грубой сетке.
В процессе моделирования некоторой заданной волны из-
измельчение сетки (т. е. введение большего числа точек для
94
Гл. 3. Предварительные сведения о приемах вычислений
представления каждой длины волны) перемещает решаемую за-
задачу из области коротких волн в область длинных волн. Следо-
Следовательно, основной вывод, который можно сделать из изучения
табл. 3.5, состоит в том, что для точного расчета волнообраз-
волнообразных движений необходимо использовать достаточно мелкие
сетки.
§ 3.5. Метод конечных разностей
Как уже отмечалось в § 3.1, метод конечных разностей
основан на построении дискретной сетки (см. рис. 3.2), замене
континуальных производных в исходных дифференциальных
уравнениях с частными производными на эквивалентные им
конечно-разностные выражения и в перегруппировке членов
полученного алгебраического уравнения с тем, чтобы построить
алгоритм наподобие C.5). В данном параграфе все перечне-
ленные аспекты сведены воедино и предложена некоторая
простая конечно-разностная программа.
3.5.1. Концептуальная реализация
Различные шаги, совершаемые в процессе применения ме-
метода конечных разностей в некоторой заданной задаче, пред-
представлены схематически на рис. 3.11.
Сформи-
Сформировать
сетку
Задать началь
ные значения
искомых
переменных
Построить конечно-разностные
аналоги ДУЧП и граничные условия
переменных | J
• - - | -
Нет
Конечное
время
достигнуто
Скорректировать (если
необходимо) граничные
-л+1
значения Т
7
Для каждой внутренней
точки (j, п) провести
расчет по алгоритму
и получить. 7-
1
Процесс
|_Д^ ^.^«.??!iJ?i!l!!!
Решение
Рис. 3.11. Схема построения решения методом конечных разностей.
Процедура может быть конкретизирована, если применить
ее к нижеследующей нестационарной задаче о теплопровод-
теплопроводности (диффузии). Пусть теплоизолированный стержень
(рис. 3.12) в начальный момент имеет температуру Т(ху 0) =
§ 3.5. Метод конечных разностей 95
= 0°С. При ^ = 0 два горячих резервуара (Г=100°С) при-
приводятся в контакт с двумя концами стержня А и В. За-
Задача состоит в том, чтобы определить (численно) температуру
Т(х, t) любой точки стержня в любой последующий момент.
Исходным уравнением для этой задачи является уравнение
C.1), т.е.
dt дх2
Для решения этого уравнения необходимы начальные условия
C.3), роль которых состоит в задании начальных значений за-
Т0(х)
- 4 >
Задано Тд |^4NX4\\\ Изоляционный слой \NN\SSN^ Задано Тв
Т [ или » V»»
х=0 х=1
Рис. 3.12. Нестационарная теплопроводность в стержне.
висимого переменного Т°. (см. рис. 3.2). Один из простейших
конечно-разностных аналогов уравнения диффузии достигается
путем замены производной по времени аппроксимацией с раз-
разностью вперед, а производной по пространству — центрирован-
центрированной разностной аппроксимацией (см. п. 3.1.1). Это приводит
через посредство формулы C.5) к схеме с разностями, сдвину-
сдвинутыми вперед по времени и с центрированными по пространству
(ВВЦП)
77+1 = sT?-i + A - 25)Г? + sT?+u C.41)
где s = a&x/At2. Формула C.41) применяется ко всем внутрен-
внутренним узлам, где / = 2, ..., /—1. В случае типичной задачи о
теплопроводности граничные значения Г"+1 и Г/+1 задаются
лри помощи граничных условий C.2). Процесс решения повто-
повторяется по мере продвижения во времени (п = 1, 2, ...), пока
не достигается необходимое время окончания.
3.5.2. DIFF: нестационарная задача теории
теплопроводности (диффузии)
В п. 3.5.1 было дано качественное описание реализации
метода конечных разностей. Здесь будет описана соответ-
соответствующая программа расчетов на ЭВМ под названием DIFF.
96 Гл. 3. Предварительные сведения о приемах вычислений
1
2 С SOLVES ID TRANSIENT HEAT CONDUCTION EQUATION USING
3 С FTCS SCHEME,
4 С
5 DIMENSION TND1),DUMD1),TDD1),XD1),TED1)
6 С
7 С INPUT DATA;
8 С
9 С JMAX = THE NUMBER OF POINTS ALONG THE ROD
10 С МАХЕХ = THE NUMBER OF TERMS IN THE EXACT SOLUTION
11 С NMAX = THE MAXIMUM NUMBER OF TIME STEPS
12 С ALPH = THE THERMAL DIFFUSIVITY
13 С S = ALPH*DELT/DELX/DELX
14 С ТМАХ = THE MAXIMUM TIME
15 С
16 OPENA,FILE='DIFF.DAT')
17 OPENF,FILE='DIFF.OUT1)
18 READA,1)JMAX,MAXEX,NMAX,ALPH,S,TMAX
19 1 FORMATCI5fE10.3,F5.2.F5.0)
20 PI = 3.1415927
21 С
22 С TD = DIMENSIONAL TEMPERATURE
23 С TN = NONDIMENSIONAL TEMPERATURE
24 С
25 ОМАР = JMAX - 1
26 AJM = JMAP
27 DELX = l./AJM
28 DELT = DELX*DELX*S/ALPH
29 WRITEF,2)JMAX,MAXEX,NMAX,TMAX
30 2 FORMATC JMAX=\I5,' MAXEX»1,15,' NMAX=',I5,' TMAX=\F8.2)
31 WRITEFf3)S,ALPH,DELT,DELX
32 3 FORMATC S«\F5.3,' ALPH »' , E10.3, ' DELT -1 ,E10.3,
33 1' DELX = 'fE10.3,//)
34 WRITEF,4)S
35 4 FORMATC FTCS (EXPLICIT) SCHEME, * , 5X, ' S =\F5.3,//)
36 С
37 С SET INITIAL CONDITIONS
38 С
39 DO 5 J = 1,JMAP
40 5 TN(J) = 0.
41 N = 0
42 T = 0.
43 С
44 С SET BOUNDARY CONDITIONS
45 С
46 С EACH TIME STEP STARTS AT STATEMENT 2
47 С
48 6 TNA) = 1.
49 TN(JMAX) = 1.
50 IF(T .LT. O.Ol)TN(l) = 0.5
51 IF(T .LT. O.Ol)TN(JMAX) = 0.5
52 TDA) = 1OO.*TNA)
53 TD(JMAX) = 1OO.*TN(JMAX)
§ 3.5. Метод конечных разностей 97
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
С
С
С
С
С
С
С
С
С
С
С
С
С
С
с
с
с
7
8
9
10
11
12
13
14
COMPUTE F.D. SOLUTION
DO 7 J ¦ 2,JMAP
DUM(J) = (l.-2.*S)*TN(J) + SMTN(J-l) + TN(J+D)
CONTINUE
DO 8 J = 2,JMAP
TN(J) = DUM(J)
DO 9 J = 2,JMAP
TD(J) = 1OO.*TN(J)
T = T + DELT
WRITEF,10)T,(TD(J),J=1,JMAX)
FORMATC T= \F5.0,f TD»\11F6.2)
IF MAXIMUM TIME OR MAXIMUM NUMBER OF TIME-STEPS EXCEEDED
EXIT FROM LOOP
IF(K .GE. NMAX)GOTO 11
IF(T .LT. TMAX)GOTO 6
OBTAIN EXACT SOLUTION AND COMPARE
SUM = 0.
DO 13 J « 1,JMAX
AJ - J - 1
X(J) * DELX*AJ
TE(J) = 100.
DO 12 M = lrMAXEX
AM » M
DAM « B.*AM - 1.)
DXM * DAM*PI*X(J)
DTM = -ALPH*DAM*DAM*PI*PI*T
LIMIT THE ARGUMENT SIZE OF EXP(DTM)
IF(DTM .LT. - 87.)DTM = -87.0
TE(J) = TE(J) - 4OO./DAM/PI*SIN(DXM)*EXP(DTM)
SUM = SUM + (TE(J) - TD(J))**2
CONTINUE
WRITEFr14)T,(TE(J),J=1,JMAX)
FORMAT(/,f T= f,F5.0,f TE=f,11F6.2,//)
RMS IS THE RMS ERROR
AVS * SUM/U. + AJM)
RMS = SQRT(AVS)
WRITEFf15)RMS
FORMATC RMS DIF = f,Ell,4,//)
STOP
END
Рис. 3.13. Распечатка программы DIFF.
7 К Флетчер, т. 1
98
Гл. 3. Предварительные сведения о приемах вычислений
Программа DIFF применяет схему ВВЦП, определяемую соот-
соотношением C.41), к нестационарной задаче о теплопроводности
(диффузии), схематически изображенной на рис. 3.12.
Распечатка программы DIFF показана на рис. 3.13, а раз-
различные параметры, используемые в этой программе, описаны
в табл. 3.6.
Таблица
Параметр
JMAX
МАХЕХ
NMAX
ALPH
с
о
TIMAX
TD
TN
ТЕ
DX
DT
TIM
X
RMS
3.6
. Параметры, примененные в программе DIFF
Описание
Число точек по длине стержня
Число членов точного уравнения
Максимальное число шагов по времени
Коэффициент теплопроводности (диффузии) а
Максимальное время
Размерный массив температуры
Безразмерный массив температуры
Точный (размерный) массив температуры
Ах
At
Время
Координата, 0 < х ^ 1.0
Среднеквадратичная ошибка решения
Программа DIFF присваивает значения различным управ-
управляющим параметрам (строка 16), задает Ал: и Д^ и выводит на
печать различные параметры. На каждом шаге по времени
л+ 1 проводится расчет решения (см. схему на рис. 3.11) до
тех пор, пока не будут превышены значения NMAX или ТМАХ
(строки 72, 73). Затем рассчитывается точное решение (строки
74—91) по формуле
МАХЕХ
ТЕ
=100-
Это решение получено путем разделения
п. 2.5.2). Одновременно с помощью формулы
/JMAX
Z
« ч 1 -aBm-\Jn2tn
C.42)
переменных (см.
1/2
C.43)
§ 3.5. Метод конечных разностей
99»
рассчитывается среднеквадратичная ошибка. При начальных
условиях Т(х, 0)=0 и граничных условиях f@, /)=ГA, t) =
= 100 выдача ЭВМ, задаваемая программой DIFF и соответ-
соответствующая значению s = 0.5, демонстрируется на рис. 3.14 и,
показана графически на рис. 3.15.
JKAX- 11 МАХЕХ- 10 NMAX* 500 ТИАХ* 2999.00
S= .500 ALPH * .100Е-04 DELT « .500Е+03 DELX = .100Е+00
FTCS(EXPLICIT) CCKSME,
.500
3
6
.00
.00
.00
.13
.25
.00
.00
.00
.00
3.13
3
6
.00
.00
.00
.13
.25
6.
12.
17.
00
00
25
50
19
12
25
31
37
.00
.50
.00
.25
.50
25.00 50.00
50.00100.
56.25100.
62.50100.
65.63100.
00
00
00
00
Т= 500. TD= 50.СО 25.00 .00 .00
Т« 1000. TD=1CO.OO 50.00 12.50 .00
Т» 1500. TD=100.00 56.25 25.00 6.25
Т* 2000. TD-300.C0 62.50 31.25 12.50
Т» 2500. TD=100.00 65.63 37.50 17.19
Т« 3000. TD=100.00 68.75 41.41 21.88 10.16 6.25 10.16 21.88 41.41 68.75100.00
Т« 3000. Т1>100.00 68.33 41.53 22.49 11.68 8.25 11.68 22.49 41.53 68.33100.Оа
RKS DIF = .9418Е+00
Рис. 3.14. Типичная выдача по программе DIFF; s = 0.5.
О 0.5 х 1.0
Рис. 3.15. Решение уравнения D.41) при s = 0.5; устойчивое поведение.
Значение s, используемое в программе DIFF, служит для
задания шага по времени А/; значение шага по пространству
Ах = 0.1. При уменьшении 5 уменьшается А/, что ведет к
уменьшению среднеквадратичной ошибки решения. Последнее
очевидно и_з результатов, показанных в табл. 3.7 для условий
Г@, 0)=ГA, 0)=50. Результат, получаемый при s = 0.167.
соответствует специальному случаю и будет подвергнут даль-
дальнейшему обсуждению в п. 4.1.2.
Если обратиться к строкам 50 и_ 51 программы DIFF (см.
рис. 3.13), то увидим, что значения Г@, 0) и ТA, 0) получают-
получаются путем осреднения между тем, что задается начальными
7*
100 Гл. 3. Предварительные сведения о приемах вычислений
Таблица 3.7. Среднеквадратичная ошибка при t = tmax
s
0.5
0.3
0.167
Среднеквадратичная ошибка
Г @, 0) = Г A, 0)=50
0.492
0.187
0.00169
Среднеквадратичная ошибка
Т @, 0) = Г A, 0)=0
2.251
0.953
0.440
условиями, и тем, что соответствует граничным условиям. Эф-
Эффект задания Г @,0)= Г A,0)= 0 (т. е. в соответствии с началь-
начальными условиями) также демонстрируется в табл. 3.7. Очевидно,
что такое задание приводит ^существенному увеличению ошиб-
ошибки решения. Если положить Г@, 0)= ГA, 0)= 100, то ошибка
будет по своей величине аналогична той, которая получалась
при Г@, 0)=ГA, 0) = 0.
§ 3.6. Заключение
Как мы видели, дискретизация вносит некоторую ошибку,
представление о которой можно получить, рассматривая ошиб-
ошибку аппроксимации по крайней мере для метода конечных раз-
разностей. По-видимому, ошибка аппроксимации становится все
более точным критерием оценки ошибки решения по мере из-
измельчения сетки (см. п. 4.1.2).
Выбор конкретных формул для представления производных
может быть осуществлен путем последовательного исключения
тех или иных членов в выражении для ошибки аппроксимации
(см. п. 3.2.2). Однако такой подход нередко нуждается в моди-
модификации из-за необходимости выбирать некоторые коэффициен-
коэффициенты так, чтобы полученный алгоритм был устойчивым (см. §4.3).
Как видно из конкретных примеров, рассмотренных в § 3.3
и 3.4, если точное решение содержит разрывы или очень боль-
большие градиенты, то маловероятно, чтобы формулы высокого по-
порядка были существенно точнее формул низкого порядка. Кро-
Кроме того, при представлении волнообразных движений решения
с короткими волнами воспроизводятся менее точно, чем реше-
решения с длинными волнами.
Простая конечно-разностная программа DIFF, приводимая
в тексте, позволяет проиллюстрировать многие характерные
особенности метода конечных разностей. Как показано на кон-
конкретном примере, точность конечно-разностного решения урав-
уравнения диффузии весьма- чувствительна к тому, каким образом
учитываются разрывы, связанные с формулировкой граничных
§ 3.7. Задачи 101
и начальных условий. Вычислительные решения уравнения диф-
диффузии, построенные при различных схемах с различными гра-
граничными условиями, обсуждаются в гл. 7.
§ 3.7. Задачи
Аппроксимация производных (§ 3.2)
3.1. Воспользуйтесь методом аппроксимации общего вида (п. 3.2.2) для
определения коэффициентов от а до d, входящих в формулу
Какова ошибка аппроксимации, соответствующая данной формуле?
3.2. Трехслойная явная дискретизация членов уравнения dT/dt —
— асРТ/дх2 = 0 приводит к соотношению
— 2TJ+ \.ЬТ*}+{
At
A + d) (Tf_, - 2Tf + Г/+1)" d (Г,., - 2Tf + Ti+l)n~{ 1
Ax2 Ax2 J '
-.[
(a) Разложите каждый член этого соотношения в ряд Тейлора с целью
'определения ошибки аппроксимации всего уравнения при произвольных зна-
значениях d.
(b) Воспользуйтесь методом аппроксимации общего вида, чтобы выбрать
d как функцию s и чтобы схема имела при этом четвертый порядок точно-
точности по Ах. При решении этой задачи будут полезными формулы, следующие
за D.11).
Точность процесса дискретизации (§ 3.3)
3.3. Для случая у = sin лх/2 получите dy/dx при х = 0.5, выбирая Ах =
= 0.1 и используя формулы
dx ~ 2Ajc
dx
К } dx ~
dx ~ 12Ajc
после чего сравните точность полученных результатов.
3.4. Повторите решение задачи 3.3 со значениями Ад: = 0.05, 0.025, 0.0125
и определите, будет ли сходимость по изменению Ал: согласовываться с фор-
формой главного члена в выражении для ошибки аппроксимации. Для решения
этой задачи рекомендуется составить программу расчета на ЭВМ. Чтобы
уловить ошибку, связанную с применением схемы (с), может потребоваться
«счет с двойной точностью.
102 Гл. 3. Предварительные сведения о приемах вычислений
3.5. Для случая у = sin лх/2 получите d2y/dx2 при х = 0.5 со значе-
значениями Ал: = 0.1, 0.05, 0 025, 0.0125, используя формулы
после чего сравните точность полученных результатов и определите соответ-
соответствие сходимости с формой главного члена в выражении для ошибки аппро-
аппроксимации Для решения этой задачи рекомендуется составить программу рас-
расчета на ЭВМ, при необходимости применяя счет с двойной точностью.
Представление волн (§ 3.4)
3.6. Для случая прогрессивной волны
F(x, t) = cos [m (x — qt)]
покажите, что использование аппроксимации dT/dt « (Г^+1 — Г^)/А/ экви-
эквивалентно применению формулы
тогда как использование аппроксимации dT/dt « A.5Г"+1 — 27^ -+-
flyM эквивалентно применению формулы
-gl = ^1 sin ф&щЩ C sin {«[«_, (-
Покажите, что в пределе sin@.5mqAt) -+0.5mqAt и cos@.5m^A0 ->¦ 1.0 оба
вышеприведенных выражения эквивалентны между собой. Кроме того, пока-
покажите, что в пределе 0.5т^А^-^0 оба этих выражения совпадают с точной
оценкой величины dT/dt.
Метод конечных разностей (§ 3.5)
3.7. Модифицируйте программу DIFF путем использования для внутрен-
внутренних точек нижеследующей симметричной пятиточечной схемы:
-Г,_2/12 + 47^/3 - 2.57V + 4Г/+1/3 - Г/+2/12
дх2 ** Ах2
При j = 2 используйте формулу
dx2 ** ^x2
а также эквивалентную этой формулу для / = JMAX—1.
(a) Постройте решения для Але = 0.1 при s = 0.3, 0.2, 0.1.
(b) Какова точность решения в сравнении с точностью схемы ВВЦП?
§ 3.7. Задачи 103
3.8. Модифицируйте программу DIFF путем введения взамен схемы
ВВЦП следующей схемы:
О.бГ^-1 - 2Т*} + 1.577+1 a (rJL, - 2Г? + Т*}+1)
А* Ах* = °"
Для первого шага по времени используйте формулу с разностью вперед
по времени, т. е. dT/dt « (Тп+1 — Тп)/М.
(a) Постройте решения для Ал: = 0.1 при s = 0.5, 0.3, 0.1 и сравните их
*с решениями, построенными с помощью схемы ВВЦП.
(b) Проанализируйте изменение точности при уменьшении s и укажите,
насколько оно совпало с вашими ожиданиями. [Подсказка: следует рассмо-
рассмотреть выражение для ошибки аппроксимации, соответствующее задаче 3.2.]
Глава 4
Теоретические основы
На практике те алгебраические уравнения, которые полу-
получаются в результате описанного в § 3.1 процесса дискретиза-
дискретизации, формируются на сетке конечного размера. Исходя из вы-
выражений для ошибки усечения, данных в § 3.2 и 3.3, следует
ожидать, что более точные решения могут быть получены на
более мелких сетках. Этот аспект подвергается дальнейшему
рассмотрению в § 4.4. Однако если считать требуемую точ-
точность решения заданной, то с точки зрения экономичности мо-
может оказаться выгоднее решать задачу на грубой сетке с
помощью конечно-разностной схемы высокого порядка, чем при-
применять схему низкого порядка на мелкой сетке. Эти соображе-
соображения приводят к понятию вычислительной эффективности, изу-
изучаемому в § 4.5.
Важный вопрос, относящийся к вычислительным решениям,.
состоит в том, до какой степени мы можем гарантировать, что
вычислительное решение дифференциального уравнения (или
уравнений) в частных производных будет близко к точному
решению того же уравнения, а также при каких условиях это
вычислительное решение совпадает с точным. Очевидный от-
ответ на вторую часть этого вопроса состоит в том, что следует
требовать, чтобы приближенное (вычислительное) решение
сходилось к точному, по мере того как размеры элементов сетки
At и Ах уменьшались до нуля (см. § 4.1). Однако сходимость
очень трудно установить прямым путем, поэтому обычно ис-
используют обходной путь, такой, как на рис. 4.1. Этот обходной
путь связан с требованием о том, чтобы система алгебраиче-
алгебраических уравнений, полученных в результате процесса дискретиза-
дискретизации (см. § 3.1), была согласованной (см. § 4.2) с исходным
дифференциальным уравнением (или уравнениями) в частных
производных. Согласованность означает, что при помощи раз-
разложения в ряд Тейлора процесс дискретизации может быть
обращен с целью восстановления исходного уравнения (урав-
(уравнений). Кроме того, алгоритм, который служит для решения
алгебраических уравнений и, таким образом, позволяет полу-
получить приближенное решение 7, должен быть устойчивым (см.
§ 4.1. Сходимость
105
§ 4.3). В конце концов, чтобы судить о сходимости, привлекает-
привлекается псевдоуравнение
СОГЛАСОВАННОСТЬ + УСТОЙЧИВОСТЬ = СХОДИМОСТЬ. D.1)
Условия, при которых утверждение D.1) является точным,
обеспечиваются теоремой Лакса об эквивалентности (см. п. 4.1.1).
Исходное
дифференциал ь
ное уравнение
в частных
производных
ЦТ)
Дискретизация :
: Согласованность
Система ал-
алгебраических
уравнений
И
Устойчивость
Приближенное
решение Г
z= Сходимость —
при Ax,At->0
Точное
решение Т
Рис. 4.1. Концептуальная связь между согласованностью, устойчивостью и
сходимостью.
Крайне трудно получить теоретическую рекомендацию по
определению поведения решения на сетке конечного размера.
Строго говоря, большинство полезных теоретических резуль-
результатов применимо только в пределе, когда сетка сжимается до
нулевых размеров. Однако взаимосвязи, установленные между
сходимостью (§ 4.1), согласованностью (§ 4.2) и устойчивостью
(§ 4.3), также являются качественно полезными при опреде-
определении свойств вычислительных решений на сетках конечного
размера.
§ 4.1. Сходимость
Решение алгебраических уравнений (рис. 4.1), аппроксими-
аппроксимирующих заданное дифференциальное уравнение в частных про-
производных, называют сходящимся, если это приближенное реше-
решение приближается к точному решению дифференциального
уравнения в частных производных для любого значения не-
независимой переменной, по мере того как размеры ячеек сет-
сетки приближаются к нулю. Таким образом, мы требуем, чтобы
7/ ->f(xh tn) при Дл:->0, Д/->0.
Разность между точным решением дифференциального
уравнения в частных производных и точным решением системы
106 Гл. 4. Теоретические основы
алгебраических уравнений называется ошибкой решения и.
обозначается символом еп.\ таким образом,
e4 = T(xhtn)-Tnt. D.2)
Точное решение системы алгебраических уравнений является
приближенным решением исходного дифференциального урав-
уравнения в частных производных. Решение системы алгебраиче-
алгебраических уравнений точное, если в процессе вычисления в него не
внесено численных ошибок, например типа ошибок округления.
Как правило, величина ошибки e*j в (/, я)-м узле зависит от
размеров ячеек сетки Ах и А/, а также от значений тех высших
производных в данном узле, которые не были учтены при фор-
формулировке конечно-разностных аппроксимаций производных в
рассматриваемом дифференциальном уравнении.
Доказательство того, что решение системы алгебраических
уравнений сходится к решению дифференциального уравнения
в частных производных, в общем случае очень затруднительно
даже для простейших задач. Применительно к приближенному
решению уравнения диффузии с использованием простого алго-
алгоритма ВВЦП в форме C.41) доказательство сходимости при
s ^ 1/2 дается в работе [Noye, 1984]. Крайне трудно устано-
установить сходимость в тех случаях, когда дифференциальное урав-
уравнение в частных производных сложнее, чем уравнение диффу-
диффузии, а метод дискретизации не столь непосредствен.
Лишь немногие задачи гидроаэродинамики обладают точ-
точными решениями, а если таковых нет, то для вывода о сходи-
сходимости следует строить вычислительные решения на последова-
последовательно измельчаемых сетках (см. п. 4.1.2).
4.1.1. Теорема Лакса об эквивалентности
Для некоторого ограниченного класса задач можно уста-
устанавливать сходимость, пользуясь теоремой Лакса об эквива-
эквивалентности [Richtmyer, Morton, 1967]:
Если имеется корректно поставленная линейная задача с
начальными условиями и конечно-разностная аппроксимация к
этой задаче, удовлетворяющая условию согласованности, то
устойчивость является необходимым и достаточным условием
сходимости.
Несмотря на то что эта теорема сформулирована для ко-
конечно-разностной аппроксимации, она остается применимой
и к любой процедуре дискретизации, приводящей к появлению
узловых неизвестных, например к методу конечных элементов.
Теорема Лакса об эквивалентности очень важна, так как дает
возможность сравнительно легко установить устойчивость алго-
§ 4.1. Сходимость
107
ритма и его согласованность с первоначальным дифференциаль-
дифференциальным уравнением в частных производных, тогда как обычно
очень трудно установить сходимость получаемого приближен-
приближенного решения к решению упомянутого дифференциального урав-
уравнения.
Большинство «реальных» задач гидроаэродинамики нели-
нелинейны и представляют собой краевые задачи или же смешан-
смешанные задачи с граничными и начальными условиями, так что
теорема Лакса об эквивалентности не всегда строго применима.
Исходя из этого следует интерпретировать теорему Лакса об
эквивалентности как обеспечивающую необходимые, но не
всегда достаточные условия. «Уравнение» эквивалентности Лак-
Лакса, представленное в форме D.1), полезно для целей исключе-
исключения несогласованных дискретизаций и неустойчивых алгорит-
алгоритмов.
4J.2. Численная сходимость
Применительно к тем уравнениям, которым подчиняется
течение жидкости и газа, обычно невозможно теоретически про-
продемонстрировать сходимость. Однако для задач, обладающих
точными решениями, таких, как задачи, связанные с уравне-
уравнением диффузии, можно получить серию численных решений на
последовательно измельчаемых сетках и рассчитать ошибку ре-
решения. Сходимость означает, что ошибка решения должна
уменьшаться до нуля по мере того, как размеры элементов сет-
сетки приближаются к нулю.
Решения, полученные для программы DIFF (см. рис. 3.13),
были построены на последовательно измельчаемых простран-
пространственных сетках при Дл: = 0.2, 0.1, 0.05 и 0.025. Соответствую-
Соответствующие среднеквадратичные ошибки приведены в табл. 4.1 для
s = 0.50 и 0.30. Как видно из таблицы, среднеквадратичная
ошибка уменьшается примерно пропорционально Д*2. Основы-
Основываясь на этих результатах, можно сделать вполне оправдан-
оправданный вывод о том, что измельчение сетки должно приводить к
дальнейшему уменьшению среднеквадратичной ошибки и в
Таблица 4.1. Уменьшение среднеквадратичной ошибки
решения при измельчении сетки
s=ccA*/Aa;2
0.50
0.30
Среднеквадратичная ошибка
Дх=0.2
1.658
0.590
Дх=0.1
0.492
0.187
Дх=0.05
0.121
0.048
Дх=0.025
0.030
0.012
108
Гл. 4. Теоретические основы
lg (Лх)
-2.0 -1.8 -1.6 t -\А t Ч,2а О
-2
1/6
пределе при Ах (при фиксированном s), стремящемся к нулю,,
решение алгебраических уравнений должно сходиться к точ-
точному решению.
Установление численной сходимости является довольно до-
дорогостоящим процессом, так как при этом обычно необходима
использовать очень мелкие сетки. Учитывая, что в вышеупомя-
вышеупомянутом примере величина s сохраняется постоянной, при каж-
каждом уменьшении Ах вдвое шаг по времени уменьшается в че-
четыре раза. Ошибка решения, при-
приводимая в табл. 4.1, рассчиты-
рассчитывается при t = 5000 с. Отсюда
следует, что при 5 = 0.30 реше-
решение на самой мелкой сетке тре-
требует 266 шагов по времени,,
прежде чем будет рассчитана
ошибка решения.
Для уравнения диффузии
.-6 о» C.1) с нулевыми граничными
** значениями и начальным значе-
значением T(xfi)= Sinn*, O^x^l,
среднеквадратичная ошибка ре-
решения |e|rms изображается гра-
графически на рис. 4.2 как функция
Рис. 4.2. Численная сходимость размера ячейки Ах. Повышенная
для метода ВВЦП. степень сходимости (сходимость
четвертого порядка) выявляет-
выявляется очень четко при s = 1/6 в сравнении с другими зна-
значениями s ^ 1/2 (сходимость второго порядка), т. е. степень
сходимости пропорциональна Ах4 при 5 = 1/6 и пропорциональ-
пропорциональна Ах2 в остальных случаях. Как это будет показано в § 4.2,.
улучшенная степень сходимости при s = 1/6 должна ожидаться
на основании вида главного члена в выражении ошибки аппрок-
аппроксимации. Как правило, при достаточно малых размерах ячеек
Ал: и At ошибка решения будет уменьшаться подобно ошибке
аппроксимации при Длг-^О, А/->0.
§ 4.2. Согласованность
Говорят, что система алгебраических уравнений, получен-
. ная в результате процесса дискретизации, согласуется с перво-
первоначальным дифференциальным уравнением в частных произ-
производных, если в пределе, когда размеры ячеек сетки стремятся
к нулю, система алгебраических уравнений эквивалентна диф-
дифференциальному уравнению в частных производных в каждой
из узловых точек сетки.
-Ю
§ 4.2. Согласованность 109
Ясно, что наличие согласованности необходимо, если при-
приближенное решение должно сойтись к решению рассматривае-
рассматриваемого нами дифференциального уравнения в частных производ-
производных. Однако это условие не является достаточным, так как
даже если система алгебраических уравнений окажется эквива-
эквивалентной дифференциальному уравнению в частных производ-
производных при стремлении к нулю размеров ячеек, отсюда не сле-
следует, что решение данной системы алгебраических уравнений
будет стремиться к решению исходного дифференциального
уравнения. Например, если в программе DIFF задать s > 1/2,
то решение, использующее алгоритм ВВЦП по формуле C.41),
будет быстро расходиться.
Техника проверки на согласованность требует, чтобы точ-
точное решение было подставлено в полученные после дискрети-
дискретизации алгебраические уравнения с последующим разложением
всех узловых значений в ряды Тейлора в окрестности един-
единственной точки. Для наличия согласованности полученное вы-
выражение должно состоять из первоначального дифференциаль-
дифференциального уравнения в частных производных, сложенного с остаточ-
остаточным членом. Структура остаточного члена должна быть такой,
чтобы он обращался в нуль при измельчении сетки.
В данном параграфе мы проанализируем схему ВВЦП
(п. 4.2.1) и чисто неявную схему (п. 4.2.2) с тем, чтобы про-
проверить, представляют ли они согласованные дискретизации
уравнения диффузии C.1).
4.2.1. Схема ВВЦП
Схема ВВЦП C.41) использовалась нами в п. 3.5.2 для
получения решения одномерного уравнения диффузии. Подста-
Подстановка величины Г/, представляющей точное решение уравнения
диффузии в (/, п)-м узле, в приближенное выражение Т1} дает
Г?+1 = sfU + A - 25) Г? + sf/+i. D.3)
Нам необходимо определить, насколько близким является со-
соответствие соотношения D.3) уравнению диффузии C.1) в
(/, я)-м узле. Если каждый член соотношения D.3) заменить
разложениями в ряд Тейлора, построенными в (/, п)-м узле,
то после некоторых упрощений получим
Г ЛТ ЛП Г ?&Т ~\П
I^LJ _ а Y^r) + Enj = 0, D.4)
где
ПО Гл. 4. Теоретические основы
Как нетрудно видеть, дифференциальное уравнение в частных
производных D.4) отличается от уравнения диффузии C.1)
наличием добавочных членов, входящих в выражение для ве-
величины ?", называемой ошибкой аппроксимации. Происхож-
Происхождение этих_ добавочных членов связано с дискретизацией произ-
производных dT/dt и д2Т/дх2у выполненной соответственно по фор-
формулам C.21) и C.24).
Очевидно, что по мере того как размеры ячеек сетки ста-
становятся все меньше и меньше, ошибка аппроксимации Е1} в не-
некоторой фиксированной точке (х/, tn) будет стремиться к нулю.
В пределе, когда Дх->0, Д/->-0, алгоритм ВВЦП C.41) ста-
становится эквивалентным уравнению диффузии. Это свойство и
называется согласованностью.
В применении к алгоритму ВВЦП ошибка усечения в об-
общем случае имеет порядок О (А/, А*2). Однако если функция Г
удовлетворяет уравнению диффузии C.1), то она удовлетворяет
и уравнению
д2Т _ д д2Т _ д2 дТ _ 2 д*Т {А Rv
'ШГ~аЖ'дх^~а1хтЧГ~а дх* * *40'
Поэтому выражение для ошибки аппроксимации можно пере-
переписать в форме
Е1} = 0.5а A*2 (s -1) [Щ* + О (At2, Ах4). D.7)
Если s = 1/6, то первый член правой части вышеприведенного
выражения обращается в нуль и ошибка аппроксимации имеет
порядок О (At2, Ax4), или, что то же самое, при фиксированном
5, — порядок О (Ал:4). В этом случае по мере уменьшения раз-
размеров ячеек ошибка аппроксимации устремляется к нулю быст-
быстрее, чем при любом другом значении 5. Можно напомнить, что,
как указывалось в п. 4.1.2, при s= 1/6 ошибка решения также
приближается к нулю быстрее, чем при любом другом значе-
значении (рис. 4.2).
Из проведенных выше рассуждений ясно, что с помощью
таких же алгебраических манипуляций можно сделать вывод
о согласованности, а также о вероятной степени сходимости.
4.2.2. Чисто неявная схема
Здесь мы исследуем наличие согласованности при дискрети-
дискретизации по чисто неявной схеме G.20), примененной к уравне-
уравнению диффузии C.1). Чисто неявная схема определяется со-
соотношением
_ sT^+l + A + 25) Г/+l - sTftl = Tnf. D.8)
§ 4.2. Согласованность 111
Чтобы продемонстрировать согласованность, легче всего начать
с эквивалентной формы представления соотношения D.8), со-
соответствующей точному решению,
D9)
Во-первых, члены Г"-+/ и Т*}+\ разлагаются в ряд в окрест-
окрестности (/', м+1)~го узла и результат этого разложения под-
подставляется в D.9). Таким образом, получим
Во-вторых, члены Tf+] и [rXJC]"+1 и т. д., входящие в соот-
соотношение D.10), разлагаются в окрестности (/, п)-го узла. Это
дает результат
[ft]1; + (о.
- a [f«]; + A/ [f**,]? + @.5 A/2) [f««]; + ... + (-^-) ([f^]; +
M«+...)--=0. D.11)
В качестве следствий исходного уравнения получим
f f f f F^ D.12)
и используем тождество s = aAt/Ax2 или Ад:2 = aA^/s. На этом
основании уравнение D.11) приводится к виду
[ft-af^ + E^O, D.13)
где ошибка усечения выражается формулой
Очевидно, что если At стремится к нулю, то и ?/ стремится к
нулю, а уравнение D.13) совпадет с исходным уравнением. Это
означает, что соотношение D.8) согласуется с исходным урав-
уравнением.
112
Гл. 4. Теоретические основы
В выражении D.14) все производные по пространству были
преобразованы в эквивалентные им производные по времени.
С помощью уравнений D.12) можно выразить ошибку аппрок-
аппроксимации в зависимости только от пространственного размера
ячейки сетки и от пространственных производных, как в выра-
выражении по формуле D.7). Если сравнить формулу D.14) с фор-
формулой D.7), то ясно, что невозможно подобрать такое значе-
значение 5, которое позволило бы уменьшить ошибку аппроксимации
с использованием чисто неявной схемы до величины порядка
О (Ах4).
Из рассмотрения двух вышеприведенных примеров могло
бы показаться, что согласованность обеспечивается автомати-
автоматически. Однако попытки построения таких алгоритмов, которые
были бы одновременно точными и устойчивыми, могут иногда
приводить к потенциально несогласованным вариантам дискре-
дискретизации, как это имеет место, например, со схемой Дюфорта —
Франкела (см. п. 7.1.2).
§ 4.3. Устойчивость
Если при решении системы алгебраических уравнений (см.
рис. 3.1 и 4.1) возникают некоторые неконтролируемые воз-
возмущения (наподобие ошибки округления), то такие возмуще-
100
Т
50
5А00
0 0.5 х 1.0
Рис. 4.3. Решение уравнения C.41) при 5 = 0.6; неустойчивое поведение.
ния имеют тенденцию к затуханию. Устойчивое решение, по-
полученное с использованием схемы ВВЦП при 5 = 0.5, показа-
показано на рис. 3.15. Типичный неустойчивый результат (s = 0.6)
приведен на рис. 4.3. Оба этих результата были получены при
Дх = 0.1 и тех же начальных и граничных условиях, которые
использовались для графиков на рис. 3.15.
Из графика на рис. 4.3 видно, что на линии симметрии воз-
возникает колебание нефизического характера, которое распро-
распространяется затем в направлении границ. Амплитуда этого
колебания со временем возрастает.
§ 4.3. Устойчивость 113
Понятие устойчивости связано с ростом или затуханием
ошибок, вносимых в расчет на любом его этапе. В качестве по-
пояснения отметим, что здесь речь идет не об ошибках, обуслов-
обусловленных логическими неточностями, а о тех ошибках, которые
возникают вследствие неспособности компьютера дать ответы
с бесконечным числом значащих цифр. Практически каждый
расчет, выполняемый на ЭВМ, приводит к результату с конеч-
конечным числом значащих цифр, что на каждом шаге этого рас-
расчета вносит некоторую ошибку округления. Следовательно, вы-
вычислительная реализация алгоритма C.41)—это не Г/+1, а *Г/+1,
т. е. численное решение системы алгебраических уравнений.
Конкретный метод считается устойчивым, если кумулятив-
кумулятивный эффект всех ошибок округления, возникших в процессе
применения данного алгоритма, является пренебрежимо ма-
малым. Говоря более определенно, рассмотрим ошибки
$ = Т? — 9Т?9 D.15)
вносимые в узловых точках (/, л), где /= 2, 3, ..., /— 1 и
я = 0, 1, 2. Обычно крайне затруднительно определить точное
значение численной ошибки |" в (/, м)-й узловой точке при
наличии произвольного распределения ошибок в других
узловых точках. Однако можно дать оценку этой ошибки, поль-
пользуясь некоторыми стандартными методами, часть из которых
будет обсуждаться в данном параграфе. На практике числен-
численные решения оказываются, как правило, более точными, чем
это определяется упомянутыми оценками, так как при анализе
устойчивости нередко вводятся предположения о наихудших
возможных сочетаниях индивидуальных ошибок. Например,
можно предположить, что все ошибки имеют такое распреде-
распределение знаков, что их суммарный эффект будет аддитивным,
хотя на самом деле это не всегда так.
Применительно к линейным алгебраическим уравнениям,
полученным в результате дискретизации, можно показать, что
члены этих уравнений, характеризующие ошибку, удовлетво-
удовлетворяют тем же самым однородным алгебраическим уравнениям,
что и функция Т. Например, если используется схема ВВЦП,
определяемая алгоритмом C.41), то сказанное выше означает,
что фактическое вычисление *Г/+1 осуществляется на основа-
основании данных о *77_ь Т/ и *Т?+и так что
= 8
1) + A - 2s) (Т?) + s (Т,я+1). D.16)
Вспоминая, что точное решение алгебраических уравнений Г/
удовлетворяет уравнению C.41), и пользуясь формулой D.15),
8 К- Флетчер, т. 1
114 Гл. 4. Теоретические основы
с учетом D.16) получим однородное алгебраическое уравнение
Б?+1 = sE7-i + A — 2s) Б/ + ^Б/+1. D.17>
Если предположить, что заданы начальные и граничные зна-
значения, то все начальные ошибки |/, / = 2, 3, ..., /— 1, а так-
также граничные ошибки ?* и ?*, /г = 0, 1, 2, ..., в соответствии
с уравнением D.17) будут равны нулю. Если при расчете зна-
значения Тп\ в каком-то внутреннем узле не будут внесены те или
иные ошибки округления, то и результирующие ошибки реше-
решения останутся равными нулю.
Двумя наиболее общеупотребительными методами анализа
устойчивости являются матричный метод и метод Неймана^
В основе обоих методов лежит возможность предсказания, бу-
будет ли иметь место рост ошибки как разности между истин-
истинным решением численного алгоритма и фактически вычисляе-
вычисляемым решением, т. е. разности, учитывающей погрешности
округления.
Альтернативный вариант анализа устойчивости связан с
предположением о том, что начальные условия представляют-
представляются с помощью рядов Фурье. Каждая гармоника, или мода, ряда
Фурье будет возрастать или затухать в зависимости от вида
дискретизированного уравнения, которое, как правило, сама
порождает конкретную форму выражения для показателя рос-
роста (или затухания) соответствующей моды. Если данная мода
может неограниченно возрастать, то дискретизированное урав-
уравнение имеет неустойчивое решение. Эта интерпретация поня-
понятия устойчивости [Richtmyer, Morton, 1967] непосредственна
используется в методе анализа устойчивости, предложенном
Нейманом (см. п. 4.3.4 и 4.3.5). Неограниченный рост некото-
некоторой конкретной моды остается возможным, даже если дискре-
тизированные уравнения решаются точно, т. е. если ошибки
округления отсутствуют. Если же ошибки округления будут
внесены, то сама неустойчивая природа дискретизированных
уравнений будет вызывать неприемлемый рост ошибок. Сле-
Следовательно, методика анализа устойчивости дискретизирован-
дискретизированных уравнений будет оставаться одной и той же независима
от проявления присущей им устойчивости или неустойчивости.
4.3.1. Матричный метод: схема ВВЦП
Данный метод состоит в том, что система уравнений, опре-
определяющих распространение ошибки представляется в матрич-
матричной форме, после чего мы анализируем собственные значения
соответствующей матрицы. Для начала этот метод будет про-
§ 4.3. Устойчивость
115
иллюстрирован на примере схемы ВВЦП, реализуемой соглас-
согласно C.41).
Подставляя в D.17) значения / = 2, 3, ..., /—1 и заме-
замечая, что на границах ошибки равны нулю, т. е. что при всех п
-будет ?" = !" = О, получим
«.rt+1 «.At 1/1 О \ f-^
S/-1 =S5/-2 + A — 25)|/_i.
В матричной форме это можно записать как
Г+1 = АГ, /1 = 0, 1, ....
D.18)
D.19)
где А — квадратная матрица порядка / — 2, а %п — вектор дли-
длины / — 2; то и другое определяются выражениями
A - 2s) s
S A — 25) _
fc/l
s —
Можно показать, что при увеличении п ошибки %п остаются
ограниченными, если все собственные значения Хт матрицы А
различны и имеют абсолютные значения, меньшие или рав-
равные единице; иначе говоря, если
|Ят|<1 для любых X. D.20)
Далее формула (9.48) позволяет найти собственные значения
трехдиагональной матрицы А в виде
т=1, 2, .... /-2. D.21)
Условие устойчивости D.20) позволяет использовать только
такие значения 5, которые удовлетворяют двойному неравен-
неравенству
* SL D.22)
116 Гл. 4. Теоретические основы
Правая часть этого неравенства удовлетворяется при всех т и s,
тогда как для выполнения его левой части необходимо, чтобы
было
а это справедливо для всех т, если s ^ 1/2. Поэтому алгоритм
ВВЦП является устойчивым, если 5 ^ 1/2.
Форма матричного уравнения D.19) остается той же самой,
если в формулах D.18) будет фигурировать не вычислительная
ошибка, а само решение. Следовательно, матричному методу
можно дать и другую интерпретацию как методу, исследующе-
исследующему рост индивидуальных мод в представлении начальных ус-
условий с помощью ряда Фурье.
Как будет указано в п. 4.3.3, изменение характера гранич-
граничных условий при х = О и/или х = 1 приводит лишь к незначи-
незначительной модификации метода.
4.3.2. Матричный метод: двухслойная схема общего вида
В данном пункте мы покажем, как работает матричный
метод в случае двухслойной схемы общего вида, примененной
к уравнению диффузии. Эта схема, данная в форме G.24) „
имеет вид
<т»Л+ 1 ___ rntl
f At j - aCL*J7+1 - a A - P) LXXT4 = 0, D.23)
где LxxTf = (T}_{ - 2Tf + Г/+1)/Л*2.
В уравнении D.23) величина a — коэффициент тепловой
диффузии, тогда как параметр р контролирует степень неяв-
неявности (см. § 7.2). Численная ошибка D.15) определяется урав-
уравнением, эквивалентным D.23). Это уравнение записывается в
форме
- SR7+,1 + A + 25р) гг1 - sffiii=s A - р) б?- 1 +
+s(l-p)E/\i. D.24)
Уравнение D.24) пригодно для внутренних узлов. При нали-
наличии граничных условий Дирихле уравнения в концевых точ-
точках не требуются. Если уравнение D.24) повторить для всех
узловых точек, где / = 2, 3, ..., /—1, то в матричной форме
можно написать
АГ+1 = ВГ, D.25)
§ 4.3. Устойчивость
117
где
А =
+ 2sp - sp
— sp 1 +
-sp
- sp 1 + 2sP
— sp
l+2sp_
-2s(l-p) s(l-p)
s(l-p) l-2s(l-p) s(l-p)
s(l-p) l-2s(l-p) s(l-p)
s(l-P) l-2s(l-p)_
Алгоритм D.23) остается устойчивым, если величины собствен-
собственных значений матрицы А~!В не превышают единицы. С учетом
структуры матриц А и В это эквивалентно ограничению
|< 1.0. D.26>
Принимая во внимание симметричный трехдиагональный ха-
характер матриц А и В, можно получить аналитические выраже-
выражения для собственных значений [Mitchell, Griffiths, 1980]
= 1 + 2sp - 2sp cos (т^у) =
Следовательно, условие устойчивости имеет вид
ST =
1 — 4s A — Р) sin2 (/я/2 (/ — 1I
1 + 4sp sin2 [/я/2 (/ - 1)]
причем
ST=1
при
т. е. необходимо, чтобы 1—4s A — P)< 1 + 4sp, что удовлет-
удовлетворяется, и чтобы 1—4sA — Р)^—1 — 4sp, иначе говоря,,
чтобы 2>4s(l — 2р), или s ^ 0.5/A — 2р), если р < 0.5.
118
Гл. 4. Теоретические основы
Следовательно, если р < 0.5, то для устойчивости требует-
требуется, чтобы s < 0.5/A — 2р). Если р ^ 0.5, то алгоритм D.23)
является безусловно устойчивым. Весьма желательное свойство
безусловной устойчивости будет подробнее обсуждаться в § 7.2.
4.3.3. Матричный метод: граничные условия
для производных
Матричный метод может применяться и тогда, когда гра-
граничные условия имеют форму Неймана, т. е. когда они форму-
формулируются для производных. Предположим, что
--— = 6 при х = 0.
D.27)
Это условие можно реализовать путем введения фиктивной
точки Го, такой, что
или
= То — 26 А*.
Если это соотношение использовать для функции распределе-
распределения ошибок, то в сочетании ,с D.24) такой прием даст следую-
следующее соотношение, центрируемое в узле с номером 1:
<1 + 2sp)g*+1 - 2sp^+1 = [1 - 25A - Р)] &*+2s(l -p)g* - 2s6 Длг.
D.28)
Следовательно, если рассмотреть все подобные уравнения, то
А6Я+1 = ВГ + С, D.29)
где
А =
— «Р
—2sp
1 + 2sP —
С =
0
0
0
0
- sp 1 + 2sp - sp
-sp l+2sp_
1— 2s A— P) 2s A— p)
s(l-p) l-2s(l-p) s(l-p)
s(l-p) l-2s(l-p) s(l-p)
s(l-p) l-2s(l-p)_
§ 4.3. Устойчивость
119»
Как и прежде, для обеспечения устойчивости требуется, чтобы
ID-b)J<1-o.
В общем случае, когда нельзя получить явных формул для
собственных значений матрицы A-1B, D.29) удобно переписать
в виде
^+1 = Dr + AC, D.30>
где D = A~1B.
Максимальные собственные значения матрицы D можно
найти, пользуясь степенным методом [Carnahan et al., 1969].
Это потребует расчетов по формуле
повторяемых до тех пор, пока Xn+l не совпадет с X". Если
сходимость достигнута, то Хп+1 является собственным векто-
вектором, соответствующим максимальному собственному значению,,
которое определяется максимальным элементом вектора Xn+1.
Обычно на каждой итерации масштаб подбирается так, чтобы
максимальный элемент вектора Хп равнялся единице. Старто-
Стартовое значение Х° выбирается произвольно. Карнаган, Лютер и
Уилкс предлагают программу такого расчета и обсуждают воз-
возможные трудности, связанные с применением метода.
Применительно к двухслойной схеме общего вида D.23)
максимальные собственные значения матрицы D = А-!В для
граничных условий Дирихле и Неймана, поставленных в точке
х = 0, приводятся в табл. 4.2 для некоторого набора значений
р и s. Эти результаты были получены с помощью степенного*
Таблица 4.2. Данные о численной устойчивости
для двухслойной схемы общего вида
0.00
0.30
0.60
0.50
0.51
0.52
1.20
1.30
1.20
1.30
Граничные условия
Дирихле при х = 0
Максимальные собственные
значения
0.9660
-1.0053
— 1.0446
-0.9534
— 1.0161
0.9221
0.9159
Граничные условия
Неймана при jcs=O
Максимальные собственные
значения
0.9899
-1.0289
-1.0686
0.9753
-1.0273
0.9742
0.9721
1120 Гл. 4. Теоретические основы
метода. В случае граничного условия Дирихле в точке х = 0
результаты согласуются с требованием
J 2q , если
>обеспечивающим устойчивость (А,тах ^ 1). Ясно, что необходи-
необходимость выполнения граничного условия Неймана D.27) не-
несколько уменьшает устойчивость схемы при одинаковых зна-
значениях р и s.
4.3.4. Метод Неймана: схема ВВЦП
При определении критериев устойчивости наиболее обще-
общепринятым является метод Неймана, так как в общем случае
его легче всего применять и так как он самый непосредствен-
непосредственный и надежный. К сожалению, однако, этот метод можно при-
применять только для установления необходимого и достаточного
условия для линейных задач с начальными условиями и посто-
постоянными коэффициентами.
Как правило, практические задачи охватывают и перемен-
переменные коэффициенты, и различного рода нелинейности, и услож-
усложненные варианты граничных условий. А если что-то из этого
имеет место, то метод может применяться только локально и
при замораживании нелинейных членов. Для такой более об-
общей ситуации метод Неймана обеспечивает необходимые, но
не всегда достаточные условия устойчивости. Строго говоря,
метод применим только для внутренних точек. Однако метод
Неймана может дать эвристическую информацию о том, как
влияют граничные условия для производных на численную ус-
устойчивость, если этот метод применять по отдельности к тем
алгоритмам, которые используются на границах [Тгарр,
Ramshaw, 1976].
Метод Неймана состоит в том, что ошибки, распределенные
вдоль линий сетки на одном временном слое, разлагаются в
конечный ряд Фурье. После этого устойчивость или неустой-
неустойчивость вычислительного алгоритма определяется в зависи-
зависимости от того, будут ли отдельные компоненты Фурье для рас-
распределения ошибок затухать или возрастать при переходе на
^следующий временной слой. Итак, вектор начальной ошибки
выражается с помощью конечного комплексного ряда Фурье,
'так что в точке х\ ошибка определяется формулой
S/ = Z а*в'Ч / = 2, 3, ...,/- 1, D.32)
l
§ 4.3. Устойчивость Ш
где i'=(—1I/2 и 0т = тпАх. Ряд Фурье D.32) по виду совпа-
совпадает с тем, что было в выражении C.30), если не считать того,,
что здесь распределение ошибок на интересующем нас интер-
интервале 0 ^ х ^ 1 предполагается периодическим. Если учесть
линейность вычислительного алгоритма, достаточно изучить
распространение ошибки, обусловленное единственным членом
exp(i6m/) представления с помощью ряда Фурье согласно фор-
формуле D.32). Поэтому в дальнейшем обозначение 6т мы будем
писать без индекса т.
С учетом вида начального распределения ошибок решение
«ошибочного» уравнения D.17), соответствующего схеме ВВЦП,
ищется по методу разделения переменных в форме
^ = (G)Ve/, D.33>
причем в данной формуле зависимость данной компоненты
Фурье от времени включается в комплексный коэффициент
((/)", верхний индекс в символе которого подразумевает, что»
величина G возведена в степень п. Подстановка выражения
D.33) в уравнение D.17) позволяет получить уравнение
(G)rt+Ve/ = s(G)V*e(/-1} + A -2s)(G)Ve/ + s(G)Ve(/+1).
После некоторых алгебраических манипуляций получим
G=l— 4s sin2(9/2). D.34)
Величину G можно рассматривать как коэффициент усиления
моды Фурье с индексом га для распределения ошибок, соот-
соответствующий продвижению на один шаг вперед по времени;,
это подтверждается тем, что, как следует из D.33),
1Г'/|/ = О. D.35)
Можно отметить, что G является функцией 5 и 6. Иначе гово-
говоря, G(s, 9) зависит от размера элементов сетки, а также от
того, какая именно мода Фурье рассматривается, поскольку
s = aAt/Ax2 и 9 = тпАх. Ошибки будут оставаться ограничен-
ограниченными, если абсолютная величина G, называемая также избыт-
избытком, никогда не будет превышать единицу ни для каких мод
Фурье 9. Таким образом, общее требование устойчивости сво-
сводится к условию
|G|<1 при любых 9. D.36)
Как следует из D.34), требование устойчивости для схемы
ВВЦП гласит, что
— 1 < 1 - 4s sin2 (9/2) < 1 при любых 9, D.37)
122 Гл. 4 Теоретические основы
что справедливо, если 5 ^ 1/2. Этот результат совпадает с ре-
результатом, установленным с помощью матричного метода.
4.3.5. Метод Неймана: двухслойная схема общего вида
Здесь мы покажем, как проводится анализ устойчивости по
Нейману применительно к неявной двухслойной схеме общего
вида G.24). Ошибки округления, связанные с использованием
этой схемы, распространяются в соответствии с тем же урав-
уравнением
?П+\
у
<где
а A - р) LxA? = 0, D.38)
и а — коэффициент тепловой диффузии, ар — параметр, кон-
контролирующий степень неявности.
Для анализа устойчивости методом Неймана введем ряд
Фурье D.32), определяющий ошибку ? как разность между
истинным численным решением и численным решением, иска-
искаженным за счет ошибок округления; эта величина | опреде-
определяется формулой D.15). Поскольку уравнение D.38) линейно,
ш выражение для ?/ вводится единственная компонента Фурье,
так что
g?=(G)Ve/, D.39)
где i=(—1I/2, а / — номер узла сетки. С помощью подстанов-
подстановки получим
1яЛ*= (G)neteu~l)-2(G)neiQI+(G)nemi+l) =
В результате уравнение D.38) принимает вид
(O)"+'gW-(G)"«*e/ „Я/ГчШ-1-<6/ 2 (cos 9-1)
^ ap(U) e Ах2 -г
Деление всех членов на (G)Ve/ дает
G-l apG [2 cos 9 - 1)] , а A - р) [2 (cos 9 - 1)] _'_ п
.ИЛИ
! _ 4д A — Р) sin» (8/2)
Ь— 1 + 4sP sin2 (9/2) *
§ 4.3. Устойчивость 12$
Устойчивость имеет место, если \G\ ^ 1 при любом значении
8. Для предельных значений получаем
G = 1 при sin F/2) = О,
G = [l —4s(l — P)]/[l + 4*р] при sin @/2) = 1.
Если G<1, то 1 — 4sA — Р)<1 +4s0 или 5 > 0.
Если G>-1, то 1— 4s(l—P)> — I—4sp или s<0.5/A — 2р).
Вышеуказанные ограничения согласуются с теми результата-
результатами, которые приводятся в п. 4.3.2 и 7.2.2. Если рассматриваются
более сложные уравнения, то может оказаться необходимым
определить устойчивость при помощи формулы, эквивалентной
D.40), в некотором диапазоне значений 8, р, s и т. д. Зачастую
это проводится численно.
Если исследуются алгоритмы, имеющие дело с тремя слоя-
слоями по времени, т. е. такие, как в п. 7.2.3, то для установления
ограничений, обусловливающих устойчивость, следует решить
квадратное уравнение для G. Для большинства проблем гидро-
гидроаэродинамики необходимо рассматривать систему определяю-
определяющих уравнений. В этом случае вместо коэффициента усиления
G анализ устойчивости по Нейману приводит к матрице уси-
усиления G. При этом соответствующее условие устойчивости
имеет вид
\km 1^1.0 при любых т, D.41)
где Кт — собственные значения матрицы G.
В данном параграфе всегда предполагалось, что первона-
первоначальная физическая задача устойчива. Однако может случить-
случиться и так, что подлежащие расчету течения являются физиче-
физически неустойчивыми; такова, например, задача о переходе ла-
ламинарного течения в турбулентное. Для течений такого рода
решение, возрастающее со временем, должно быть приемле-
приемлемым. Чтобы получить возможность учета таких решений, мы
должны потребовать, чтобы величины собственных значений
при использовании матричного метода (п. 4.3.1) или коэффи-
коэффициента усиления при использовании метода Неймана (п. 4.3.4)
были меньше, чем 1 + О (At). Это условие заменяет неравен-
неравенства D.20) и D.36). Дальнейшее обсуждение этого вопроса
можно найти в книге [Richtmyer, Morton, 1967].
Более полное обсуждение вопросов устойчивости дискрети-
зированных уравнений имеется в книгах [Mitchell, Griffiths,
1980; Isaacson, Keller, 1966; Richtmyer, Morton, 1967], а также
в книге Рихтмайера и Мортона. Согласно общему мнению,
матричный метод определения устойчивости не столь надежен^
124 Гл. 4. Теоретические основы
как метод Неймана. Причины такого утверждения обсуждаются
в работах [Morton, 1980; Hindmarsh et al\, 1984] в связи с ис-
исследованием одномерного уравнения переноса (9.56). Проблема
устойчивости дискретизированных уравнений вблизи границ
лежит за пределами охвата данной книги (см. [Sod, 1985,
ch. 5]).
§ 4.4. Точность решения
Строго говоря, проведенное выше обсуждение проблем схо-
сходимости, согласованности и устойчивости касалось поведения
приближенного решения в пределе Дл:->0, Д/-^0. Однако на
практике приближенные решения строятся на сетке конечных
размеров и соответствующая точность имеет немаловажное
значение.
При определении согласованности, проведенном в § 4.2,
было получено явное выражение для ошибки аппроксимации.
Применительно к точному решению дифференциального урав-
уравнения в частных производных можно дать оценку точности
представления отдельных членов с производными, как это сде-
сделано в § 3.3. Совокупность таких членов, собранных вместе,
дает представление о том, насколько хорошо алгебраическое
уравнение согласуется с дифференциальным уравнением в
частных производных. Как и следовало ожидать на основании
изложенного в § 3.3, оценка главного члена в выражении ошиб-
ошибки аппроксимации для полного уравнения позволяет получить
достаточную оценку ошибки.
Как указывалось в § 4.2, порядок величины ошибки аппрок-
аппроксимации, как правило, совпадает с порядком величины ошибки
решения, если размеры ячеек сетки достаточно малы и если
начальные и граничные условия являются достаточно гладки-
гладкими. Как это нередко бывает, предполагаемое улучшение точности
(через ошибку аппроксимации) с применением схем высокого
порядка, по сравнению, скажем, со схемой второго порядка, не
достигается вследствие недостаточной гладкости начальных ус-
условий, сформулированных для данной конкретной сетки. Из-
Измельчение сетки очень часто позволяет вместе с применением
схемы высокого порядка получить и повышенную точность,
однако абсолютный уровень этой точности оказывается таким,
что он намного выше, а следовательно, и намного дороже, чем
это необходимо. Так, для инженерных целей может требовать-
требоваться точность в 1 %, если измерять ее в среднеквадратичной
ошибке. Схема четвертого порядка может продемонстрировать
свое преимущество в точности над схемой второго порядка
только при условии такого измельчения сетки, которое давало
<бы среднеквадратичную ошибку порядка 0.01 %. Пример по-
§ 4.4. Точность решения 125
лобного же влияния негладкости начальных данных на точ-
точность приводится в работе [Fletcher, 1983].
Для задач, описываемых гиперболическими дифференциаль-
дифференциальными уравнениями в частных производных, во внутренних час-
частях расчетных областей могут создаваться разрывы, а это за-
заметно ограничивает достижимую степень точности, если толь-
только возникающие разрывы не будут изолированы от остальной
части области и если не ограничиться поиском локального ре-
решения.
Один из путей определения точности конкретного алгорит-
алгоритма на сетке конечных размеров состоит в том, чтобы применить
этот алгоритм к решению родственной, но более простой зада-
задачи, имеющей точное решение. В этом отношении весьма полез-
полезным является уравнение Бюргерса (см. § 10.1), так как оно
моделирует конвективный и диффузионный члены уравнения
импульсов и так как его точные решения могут быть получены
для многих комбинаций начальных и граничных условий. Од-
Однако сама точность, помимо прочего, зависит от формулиров-
формулировки задачи, и тот алгоритм, который был достаточно точным
для модельной задачи, необязательно будет столь же точным
для первоначальной (и более сложной) интересующей нас за-
задачи.
Вторая методика оценки точности состоит в том, чтобы
строить решения на последовательно измельчаемых сетках (ис-
(исходя из предположения о наличии соответствующих вычисли-
вычислительных возможностей) и проверять, будет ли при таком по-
последовательном измельчении решение изменяться в рамках
заранее предопределенной степени точности. Тем самым предпо-
предполагается, что в пределе, когда А^, Да: и т. д.->-0, приближен-
приближенное решение будет сходиться к точному и что приближенное
решение на самой мелкой сетке может быть использовано вза-
взамен точного. Как правило, справедливость такого предположе-
предположения невозможно гарантировать в применении к «реальным»
задачам, а поэтому вычислительные решения полезно срав-
сравнить с надежными экспериментальными результатами (имею-
(имеющими известную степень точности) для той же самой задачи.
Например, можно воспользоваться данными о распределении
давления на поверхности тела, чтобы проверить, насколько
правдоподобным является решение на измельченной сетке.
Обычно, однако, экспериментальные данные по данной конкрет-
конкретной проблеме и с достаточными подробностями оказываются
недоступными в такой степени, чтобы позволить оценить гло-
глобальную среднеквадратичную ошибку.
Если предположить, что точность приближенного решения
^поддается оценке, то весьма важно рассмотреть и связанный
126 Гл. 4. Теоретические основы
с этим вопрос о том, как улучшить достигнутую точность. В са-
самом широком представлении ответ на этот вопрос может сво-
сводиться к тому, чтобы дать возможность выбора зависимых
переменных, например вместо скорости и давления взять зави-
завихренность и функцию тока. В качестве альтернативного вариан-
варианта может подойти возможность различного выбора независи-
независимых переменных. Например, использование полярных коорди-
координат будет давать более точные решения задачи о течении в
трубе, чем это было бы с декартовыми координатами при оди-
одинаковом числе узловых точек.
Можно ожидать, что в некоторых специальных случаях при-
применение схем высокого порядка или использование мелких се-
сеток могут привести к построению более точных решений. Од-
Однако введение таких мер вряд ли будет оправдано, если не
принимать во внимание время исполнения и, следовательно, вы-
вычислительную эффективность (см. § 4.5). На данном этапе мы
рассмотрим лишь один специальный прием, позволяющий
улучшить точность решения — экстраполяцию по Ричардсону.
4.4.1. Экстраполяция по Ричардсону
Как уже указывалось ранее (см. п. 4.1.2), численную де-
демонстрацию сходимости можно реализовать путем построения
последовательности решений на все более мелких сетках.
Ошибка решения на достаточно мелкой сетке уменьшается
вместе с размером ячейки так же, как ошибка аппроксимации
(см. табл. 4.1). Эта последняя особенность объясняет введение
экстраполяции по Ричардсону, используемой для улучшения
точности решения на конечной (но мелкой) сетке. Основная
идея состоит в том, чтобы сложить вместе взятые с соответ-
соответствующими весами решения на последовательно измельчае-
измельчаемых сетках, сделав это так, чтобы свести к нулю главный ттлен
суммарной ошибки аппроксимации. Однако форма выражения
ошибки аппроксимации связана с разложением в ряд Тейлора
по степеням локального размера ячейки. Поэтому неудивитель-
неудивительно обнаружить, что для эффективности экстраполяции по Ри-
Ричардсону последнюю следует проводить на сравнительно мел-
мелкой сетке.
Рассмотрим два решения уравнения диффузии, полученные
путем применения схемы ВВЦП с двумя вариантами шагов по
х, а именно Аха и Ax6, но при одном и том же значении s. Со-
Составное решение строится в виде
Тс = аТа + ЬТЬу D.42)
где а и Ь — коэффициенты, подлежащие определению. Разло-
Разложение членов в схеме ВВЦП, примененной к функции Тс в ряд
§ 4.4. Точность решения
127
Тейлора в окрестности (/, п) -го узла, дает
[Щ -а [Щ+а вд+ь ^1 =. °>
где, в силу формулы D.7), имеем
]—h
Если Ахь = &Ха/2, то' главный член ошибки усечения для со-
составной функции может быть сделан равным нулю при помо-
помощи формулы а + 0.256 = 0. Однако из D.42) ясно, что
а-\- b = 1. Поэтому а = —1/3 и Ь = 4/3, и, следовательно, со-
составное решение Тс = D/3) Г& — A/3)Га, как и следует ожидать,
имеет ошибку решения порядка О(Дд:4) на достаточно мелкой
сетке. Некоторые характерные значения среднеквадратичной
ошибки приводятся в табл. 4.3 при 5 = 0.5. Для наиболее мел-
мелких сеток ошибка убывает как О(Дл:4). Однако, несмотря на
то что применение экстраполяции по Ричардсону приводит к
ловышению уровня точности на мелкой сетке, для грубых се-
сеток имеет место обратная ситуация.
Таблица 4.3. Среднеквадратичные ошибки
при экстраполяции по Ричардсону (RE)
Схема
ВВЦП, s = 0.5
BBItfI,s = 0.5,RE
ВВЦП, s = 1/6
0.4915
0.9744
0.0017
Д*=0.05
0.0869
0.0104
0.542 X Ю~4
Д*=0.025
0.0153
0.634 X Ю~3
0.339 X Ю~5
Схема ВВЦП обладает необычным свойством — она может
обеспечить четвертый порядок точности без применения экстра-
экстраполяции по Ричардсону, а лишь за счет специального выбора
s = 1/6. Это не имеет места ни для чисто неявной схемы G.19),
ни для схемы Кранка — Николсона G.22), ни для каких-либо
других схем. Однако для обеих упомянутых схем можно обес-
обеспечить четвертый порядок точности с помощью экстраполяции
по Ричардсону. При выборе &хь = &ха/2 соответствующее это-
этому составное решение имеет форму
Те = D/3)Ть-A/3)Та9 D.44)
уже упоминавшуюся выше.
128 Гл. 4. Теоретические основы
В общем случае выбор коэффициентов а и b определяется
тем, какую степень по Ах имеет главный член в выражении
ошибки усечения (после эквивалентной замены At на Ах), а
также величиной отношения размеров ячейки Аха и Ахь. В ре-
результате получим
Если экстраполяцию по Ричардсону применить к какой-либо
нестационарной задаче, например определяемой уравнением
диффузии, то решения Ть и Та можно рассматривать как не-
независимые решения, построенные на разных сетках в тот конеч-
конечный момент времени, когда нам нужно рассчитать Тс. С уче-
учетом того обстоятельства, что экстраполяция по Ричардсону не
воздействует на решение на промежуточных стадиях его по-
построения, а лишь на окончательное решение, такой прием был
назван пассивной экстраполяцией по Ричардсону [Dahlquist,
Bjorck, 1974]. Если же после каждого шага по времени вычис-
вычисляется величина Тс и это решение рассматривается как на-
начальное, чтобы с его помощью рассчитать Та и Ть на следую-
следующем шаге по времени, то мы получим активную экстраполяцию
по Ричардсону (см. только что цитированную книгу).
Весьма поучительно провести сравнение различных схем, пе-
перечисленных в табл. 4.3, с точки зрения времени исполнения
решения (время центрального процессора). Для интегрирова-
интегрирования, проводимого на конечном интервале времени, упомянутое
время исполнения (execution time) может быть выражено как
ЕТ =
А* At 5 Дх3 *
где k — коэффициент пропорциональности. В результате имеем
Ь 1 s=0.5 = -д^Г , Ь 1 s=0.5, RE = д^з » Ы 5= 1/6 = -д^з~ •
Таким образом, можно видеть, что решение, соответствующее
ETs==0.5, re при Аха = 0Л, Ахь = 0.05, оказывается на 50 % точ-
точнее, чем решение, соответствующее ETs==0.5 при Ах = 0.025,
однако время его исполнения в семь раз меньше. Далее, реше-
решение, соответствующее ETs=i/6 при Ах = 0.05, примерно в две-
двенадцать раз точнее решения, соответствующего ETs=o.5, re при
Ахь = 0.025, при времени исполнения, в три раза меньшем.
Ясно, что использование экстраполяции по Ричардсону эффек-
эффективно, но в меньшей степени, чем в специальном случае
§ 4.5. Вычислительная эффективность 129
5 = 1/6. Однако такие специальные случаи весьма редки, в
особенности для более сложных уравнений и алгоритмов, чем
схема ВВЦП, примененная к уравнению диффузии.
§ 4.5. Вычислительная эффективность
Вопрос о том, какая точность может быть достигнута при
заданном алгоритме решения, связана с вычислительной эф-
эффективностью этого конкретного алгоритма. Вычислительную
эффективность можно определить как точность, достигаемую
в расчете на единицу времени исполнения. Таким образом,
алгоритм, при котором на грубой сетке достигается умеренная
точность, а время исполнения мало, может оказаться столь же
эффективным, как другой алгоритм, позволяющий получить
высокую точность на мелкой сетке и требующий большего вре-
времени исполнения.
Вычислительная эффективность СЕ может определяться
формулой
СЕ = А»/(вЕТ),
где 8 — ошибка приближенного решения, представленная в со-
соответствующей норме (например, в среднеквадратичной), а
ЕТ — время исполнения. Вычислительная эффективность — это
полезный критерий, позволяющий выяснить целесообразность
введения конечно-разностных схем высокого порядка или же
конечных элементов повышенного порядка.
Для большинства задач гидроаэродинамики применение
схем высокого порядка (например, четвертого или выше) с ко-
конечными разностями или применение конечных элементов по-
повышенного порядка (например, кубических или выше) не
является оправданным с точки зрения повышенной вычисли-
вычислительной эффективности, особенно в отношении трехмерных за-
задач. Однако во избежание чрезмерно большой численной дис-
диссипации и дисперсии (см. § 9.2) следует применять конечно-
разностные схемы как минимум второго порядка или же
линейные элементы.
При разработке различных вычислительных схем предпоч-
предпочтительно сравнение по вычислительной эффективности, а не
только по точности или только по экономичности. Если срав-
сравниваются вычислительные схемы, расчет по которым ведется
на одном и том же компьютере, то время исполнения может
измеряться непосредственно. Если нельзя установить время
центрального процессора, то следует обратить внимание на ре-
режим работы компьютера. Кроме того, нужно либо исключить,
либо оценить ту долю времени исполнения, которая тратится
на считывание данных и на печать результатов.
9 К. Флетчер, т. 1
130
Гл. 4. Теоретические основы
4.5.1. Оценка времени оперативного счета
В качестве альтернативы непосредственному замеру вре-
времени центрального процессора можно дать оценку времени
оперативного счета, получаемую из распечатки расчета и из
некоторых данных о сравнительном времени исполнения эле-
элементарных операций. Это может делаться на разных уровнях
сложности. Как было установлено, нижеследующий подход
дает вполне приемлемые оценки.
Первый шаг состоит в запуске программы, предназначен-
предназначенной для приближенного определения времени, затрачиваемого
на операцию каждого типа. Типичная программа такого рода
дается в приложении АЛ вместе с аналитическим описанием
соответствующей процедуры. Главная цель этой программы со-
состоит в определении относительного времени исполнения раз-
различных операций, поскольку такие времена могут варьировать-
варьироваться в широких пределах в зависимости от типа компьютера, опе-
операционной системы и компилятора. В табл. 4.4 приводятся
относительные времена исполнения для типичных вариантов
Таблица 4.4. Относительные времена исполнения для основных операций
Операция
Микрокомпьютер
(NEC-APCIV) !>
Супермикро-
Супермикрокомпьютер
(Masscomp
5400) 2)
Полногабаритный
компьютер
(CYBER-720) 3)
Сложение (FL) 4)
Вычитание (FL)
Умножение (FL)
Деление (FL)
Присваивание (=)
Оператор IF
Сложение (FX)
Вычитание (FX)
Умножение (FX)
Деление (FX)
Степень
SQRT
SIN
ЕХР
1.0
1.0
1.1
1.4
0.1
0.1
0.05
0.05
0.5
0.5
2.7
2.0
10.0
28.0
1.0
1.0
1.0
1.0
0.6
0.3
0.5
0.5
1.8
3.2
8.3
1.2
0.8
1.5
1.0
1.0
1.0
1.0
0.5
0.4
0.5
0.5
0.5
1.5
14.0
15.0
39.0
25.0
*) Microsoft FORTRAN 77, действующий при MSDOS (8086/8087 процессор с плавающей
запятой с ординарной точностью).
2) FORTRAN 77, неоптимизированный компилятор, действующий при UNIX (с ускори-
ускорителем плавающей запятой).
3) FTN5, неоптимизированный компилятор, действующий при операционной системе.
4) FL —плавающая запятая.
§ 4.5. Вычислительная эффективность 131
микрокомпьютера, супермикрокомпьютера и полногабаритного
компьютера, использующих язык Фортран.
Второй шаг состоит в том, чтобы идентифицировать важ-
важнейшие классы операций, вносящих вклады в суммарное время
исполнения. Результаты, приводимые в табл. 4.4 для компью-
компьютера NEC-APC IV, могут быть распределены по следующим ка-
категориям операций, которые целесообразно выделить:
(a) операции с плавающей запятой FL (floating point),
(b) операции с фиксированной запятой РХ (fixed point),
(c) присваивания, т. е. знаки равенства, R (replacements),
(d) логические операторы, т. е. IF, GOTO и т. д. (L),
(e) математические библиотечные функции, т. е. SIN, EXP
и т. д. (М).
Чтобы выразить время оперативного счета посредством
единственного числа, следует каждой из перечисленных выше
операций приписать некоторый относительный вес, так что, на-
например, время оперативного счета можно измерять через экви-
эквиваленты операций с плавающей запятой. Характерное распре-
распределение весов для компьютера NEC-APC IV соответствовало
бы формуле (основанной на данных табл. 4.4):
lFLeq = 20FX = 10R = 10L = 0.1М.
Для строк с 48 по 73 программы DIFF (см. п. 3.5.2), где сле-
следует исключить операторы WRITE, время оперативного счета
(operation count) получается следующим:
ОРСТ = [3FL + 6FX + 5R + 2L + (N* - 2) GFL+ I0FX+3R)] N,,
где Nx — число шагов по х> a N* — число шагов по /. Если
N* = 11, то время оперативного счета одного шага по времени
составляет ОРСТ = 74 FLeq. В процессе определения вышеука-
вышеуказанного времени оперативного счета для массива с индексами
выделялась одна операция с фиксированной запятой для зада-
задания значения индекса.
Оценки времени оперативного счета особенно полезны для
того, чтобы идентифицировать наименее экономичные части
программы, а также чтобы проводить сравнительные оценки
экономичности различных алгоритмов еще до составления и
опробования программы. Вследствие различия особенностей
быстродействия у различных компьютеров, а также усилий,
требуемых для получения точных результатов, прикидки вре-
времени оперативного счета наиболее эффективны тогда, когда их
используют для выяснения порядка величины различий во вре-
времени исполнения.
9*
132 Гл. 4. Теоретические основы
§ 4.6. Заключение
Для тех уравнений, которым подчиняется движение жид-
жидкости или газа, невозможно дать прямое подтверждение схо-
сходимости. Однако обычно нетрудно показать, что дискретизиро-
ванная форма уравнений является согласованной (см. § 4.2).
Обычно удается также показать, что «линеаризованный» ва-
вариант исходных уравнений обладает устойчивостью (см. § 4.3),
хотя обоснование этого может потребовать расчетов на ЭВМ.
Как следствие приведенных выше утверждений, теорема Лак-
са об эквивалентности обеспечивает необходимое, но недоста-
недостаточное условие сходимости. На практике для проверки устой-
устойчивости обычно требуется проведение численных расчетов.
Как матричный метод определения устойчивости, так и ме-
метод Неймана, строго говоря, применимы только к линейным
уравнениям, хотя оба метода дают некоторую информацию,
если нелинейность локально замораживается. Альтернативным
является энергетический метод, который может непосредствен-
непосредственно применяться к некоторым разновидностям нелинейных
уравнений. Описание этого метода приводится в книге [Richt-
myer, Morton, 1967].
Необходимо подчеркнуть, что реальные задачи гидроаэро-
гидроаэродинамики рассчитываются на конечных сетках и что те теоре-
теоретические свойства, которые основываются на допущении об
устремлении размера ячейки к нулю, могут оказаться нереали-
нереализуемыми на конкретной сетке конечного размера. Эта пробле-
проблема, по-видимому, в большей степени относится к схемам вы-
высокого порядка.
Разложение в ряд Тейлора, используемое для установления
согласованности (см. § 4.2), важно также и для получения яв-
явного выражения ошибки аппроксимации. Если учесть тесную
взаимосвязь между ошибкой аппроксимации и ошибкой реше-
решения, по крайней мере на мелкой сетке, то все, что делается для
уменьшения ошибки аппроксимации, будет, по-видимому,
уменьшать и ошибку решения. Это может навести на мысль о
специальном выборе s (=аД?/Лх2), как делалось при приме-
применении схем ВВЦП, или о выборе такой комбинации решений,
которая сводит к нулю главный член в выражении ошибки
аппроксимации, как при экстраполяции по Ричардсону
п. 4.4.1).
Для стационарных задач существует еще один прием, на-
называемый методом отложенной коррекции [Smith, 1965]. При
реализации этого метода рассчитывается предварительное ре-
решение, на основании которого оценивается главный член в вы-
выражении для ошибки аппроксимации. Затем этот член «добав-
§ 4.7. Задачи 133
ляется» к первоначальному дискретизированному уравнению
в качестве члена с источником и строится улучшенное решение.
В принципе это улучшенное решение может быть использовано
для новой оценки главного члена ошибки аппроксимации и весь
процесс может быть повторен заново. Обычно наилучшая вы-
вычислительная эффективность достигается с одним единственным
улучшенным решением.
Обращение в нуль главного члена в выражении ошибки
аппроксимации может быть использовано также при построе-
построении схем высокого порядка. После осуществления начальной
дискретизации главный член соответствующей ошибки аппрок-
аппроксимации дискретизируется и «добавляется» к первоначальной
схеме. Пример такого подхода приводится в п. 9.3.2.
Практические задачи гидроаэродинамики нередко требуют
построения вычислительного решения в сложных трехмерных
областях, где мы имеем дело с тысячами неизвестных узловых
значений. Применительно к таким крупномасштабным задачам
предварительное представление об относительной вычислитель-
вычислительной эффективности конкурирующих численных схем чрезвы-
чрезвычайно важно получить до того, как мы перейдем к основной
части вычислительного исследования. В книге [Finlayson,
1980] приводятся оценки затрачиваемой работы и сравнитель-
сравнительной точности для метода конечных разностей, метода конеч-
конечных элементов и метода ортогональной коллокации (см. § 5.1),
применяемых к решению обыкновенных дифференциальных
уравнений, а также к решению дифференциальных уравнений
в частных производных в одномерном и двумерном вариантах.
§ 4.7. Задачи
Сходимость (§ 4.1)
4.1. Модифицируйте программу DIFF путем использования вместо схемы
ВВЦП нижеследующей пятиточечной симметричной схемы. Для внутренних
точек используйте аппроксимацию
дх2 ~V 12 /-2+ 3 /-1 М1! + 3 /+1 12
а для / = 2 примените формулу
и эквивалентную этой формулу для / = JMAX—1. Это точно такая же мо-
модификация, какая требовалась для решения задачи 3.7.
(a) Постройте решения при s = 0.3 для Ах = 0.2, 0.1 и 0.05.
(b) Сравните степень уменьшения среднеквадратичной ошибки при убы-
убывании А* с тем, что имело место для схемы ВВЦП (см. табл. 4.1).
134 Гл. 4. Теоретические основы
4.2. Повторите задачу 4.1, заменяя схему ВВЦП в программе DIFF сле-
следующей схемой:
Для расчета первого шага по времени используйте следующую формулу с-
разностью по времени вперед:
дТ ^ тп+\ _т"
Это те же модификации, которые требовались при решении задачи 3.8.
Согласованность (§ 4.2)
4.3. Подтвердите путем проверки, что схема, предложенная в задаче 4.1,.
согласуется с исходным уравнением dT/dt — ад2Т/дх2 = 0. Соответствует ли
порядок ошибки аппроксимации той степени сходимости, которая была най-
найдена при решении задачи 4.1? Рассмотрите как внутренние точки, так и
точки (/ = 2, JMAX— 1), примыкающие к границе.
4.4. Проверьте согласованность схемы, предложенной в задаче 4.2. Яв-
Является ли степень сходимости, найденная при решении задачи 4.2, соответст-
соответствующей порядку ошибки аппроксимации?
Устойчивость (§ 4.3)
4.5. Примените анализ устойчивости по Нейману к определению пределов
устойчивости схемы, предложенной в задаче 4.1, для:
(a) внутренних точек,
(b) точек, примыкающих к границе, j = 2 и JMAX— 1. Может оказать-
оказаться удобным получить численную оценку выражения для амплитудного фак-
фактора \G\ при варьируемых значениях 0 и s.
4.6. Примените анализ устойчивости по Нейману к определению преде-
пределов устойчивости схемы, предложенной в задаче 4.2. Это потребует решения
квадратного уравнения относительно |G|.
4.7. Подтвердите правильность пределов устойчивости, найденных при*
решении задач 4.5 и 4.6, путем построения численных решений для «неустой-
«неустойчивых» значений 5.
4.8. Исследуйте устойчивость дискретизации уравнения dT/dt —
— ад^/дх2 = 0, основанной на представлении с разностью вперед для dT/dt
и на формуле, предложенной в задаче 3.1 для д2Т/дх2.
4.9. Примените матричный метод к схеме, предложенной в задаче 4.1Г
и определите пределы устойчивости путем численного расчета собственных
значений. Сравните результаты с теми, которые были получены при решении
задачи 4.5. Как изменятся пределы устойчивости, если одно из условий Ди-
Дирихле для функции Т заменить граничным условием Неймана?
Точность решения (§ 4.4)
4.10. Для схемы, рассмотренной в задаче 4.1, постройте алгоритм с экс-
экстраполяцией по Ричардсону, обращающий в нуль главный член выражения:
для ошибки аппроксимации. Определите численно, является ли эта схема бо-
более точной и может ли быть достигнуто теоретическое значение степени схо-
сходимости.
§ 4.7. Задачи 135
4.11. Для схемы, рассмотренной в задаче 4.2, постройте алгоритм с экс-
экстраполяцией по Ричардсону и сравните соответствующие численные решения
с теми, которые были получены при решении задач 4.1 и 4.2.
Вычислительная эффективность (§ 4.5)
4.12. Для схемы, предложенной в задаче 4.10, определите время опера-
оперативного счета и сравните с тем временем, которое соответствует схеме ВВЦП,
если с применением обеих схем достигается одинаковая точность.
4.13. Для схемы, предложенной в задаче 4.11, определите время опера-
оперативного счета и сравните с
(a) временем счета для схемы ВВЦП, если обе схемы дают одинаковую
точность,
(b) временем счета для схемы ВВЦП с экстраполяцией по Ричардсону.
4.14. Попытайтесь установить, какая из схем, рассмотренных в данной
главе, является «наилучшей», если принять во внимание вычислительную эф-
эффективность, ограничения на устойчивость и простоту составления про-
программы.
Глава 5
Методы взвешенных невязок
Методы взвешенных невязок (МВН) концептуально отли-
отличаются от метода конечных разностей тем, что МВН исходят
из предположения о возможности аналитического представле-
представления решения. Например, для построения решения уравнения
диффузии C.1) можно допустить представление приближенно-
приближенного решения в следующем виде:
Г= ?*/(')*/(*), E.1)
где а\ (t) — неизвестные коэффициенты, а ^/ (я) — известные
аналитические функции. Функции 4>j(x) часто называют проб-
пробными функциями, а решение в форме E.1)—пробным реше-
решением. За счет принудительно навязываемого характера анали-
аналитической формы решения в виде E.1) вносится некоторая ошиб-
ошибка, если только индекс / не делается произвольно большим.
При этом можно напомнить, что метод конечных разностей
определяет решение только в узких точках.
В § 5.1 дается информация о различных методах взвешен-
взвешенных невязок. Далее, в п. 5.1.1 некоторые из этих МВН приме-
применяются к решению простого обыкновенного дифференциально-
дифференциального уравнения, имея в виду обеспечить приемлемую базу для
сравнения. Метод конечных объемов, описываемый в § 5.2, тес-
тесно связан с методом подобластей (см. § 5.1). Однако по форме
представления дискретизации метод конечных объемов напо-
напоминает метод конечных разностей. Конкретные трудности при-
применения метода конечных объемов при наличии вторых произ-
производных перечисляются в п. 5.2.2, а в п. 5.2.3 приводится про-
программа для расчета под названием FIVOL, предназначенная
для решения уравнения Лапласа в области, имеющей непра-
неправильную форму.
В данной главе как метод конечных элементов, так и
спектральные методы развиваются на основе метода Галёрки-
на, который сам принадлежит к классу методов взвешенных
невязок. Описание метода конечных элементов и спектральных.
§ 5.1. Общая формулировка 137
методов реализуется в первую очередь через посредство спе-
специально разработанных примеров, позволяющих понять технику
применения этих методов. Указанные примеры продемонстри-
продемонстрируют также, по крайней мере в отношении метода конечных
элементов, наличие связи с некоторыми из конечно-разностных
методов, рассматриваемых к гл. 7—10. Более подробное обсуж-
обсуждение метода конечных элементов и спектральных методов дает-
дается Флетчером в книге [Fletc/ier, 1984].
В § 5.3—5.5 рассматривается метод-конечных элементов.
Вначале демонстрируется возрастающая точность линейной и
квадратичной интерполяций в одномерном и двумерном слу-
случаях, реализуемая при измельчении сетки. Характерные при-
примеры применения метода конечных элементов приводятся в
§ 5.4 и 5.5. Эти примеры включают программы расчетов под
названиями STURM для задачи Штурма — Лиувилля (см.
п. 5.4.2) и DUCT для задачи о течении вязкой жидкости в ка-
канале прямоугольного сечения (см. п. 5.5.2). Характерное свой-
свойство метода конечных элементов связано с легкостью его при-
приспособления к рассмотрению вычислительных областей непра-
неправильной формы; применение с этой целью изопараметрических
элементов рассматривается в п. 5.5.3.
Спектральный метод излагается в п. 5.6.1 в применении к
уравнению диффузии, где непосредственно используются гра-
граничные условия Дирихле. В п. 5.6.2 обсуждаются трудности ис-
использования граничного условия Неймана при применении
спектрального метода и отмечается возможность более общей
формулировки. Тесно связанный с этим псевдоспектральный
метод описывается в п. 5.6.3.
§ 5.1. Общая формулировка
Многие вычислительные методы можно рассматривать как
методы взвешенных невязок (МВН). Достаточно полное описа-
описание МВН и их приложения вплоть до 1972 г. можно найти в
книге [Finlayson, 1972]. Наше изложение рассчитано на то, что-
чтобы показать взаимосвязь методов конечных элементов, конеч-
конечных объемов и спектральных методов.
Исходной точкой для любого МВН является задание неко-
некоторого приближенного решения. Представление E.1) может
быть несколько расширено, если написать
Т (х, у, г, t) = Го (х, У, г, t) + ? a, (t) <j>f (х, у, г), E.2)
где функция То(х, у, z, t) выбирается так, чтобы удовлетворя-
удовлетворялись, причем по возможности точно, граничные и начальные
138 Гл. 5. Методы взвешенных невязок
условия. Аппроксимирующие (пробные) функции ф]{ху у> z)
предполагаются известными. В случае пространственной одно-
одномерности роль аппроксимирующих функций могут играть поли-
полиномы или тригонометрические функции, как, например,
ф. (х) = х*~1 или j>i (х) = sin jnx.
Коэффициенты uj(t) заранее неизвестны и их следует опреде-
определять путем решения системы уравнений, получаемых из исход-
исходного уравнения. При решении задач с зависимостью от времени
система обыкновенных дифференциальных уравнений (по вре-
времени) будет разрешаться относительно uj(t)\ для стационарных
задач будет решаться система алгебраических уравнений.
Предполагается, что исходное уравнение, например уравне-
уравнение теплопроводности, можно записать в виде
L(f) = f-aU = 0) E.3)
где чертой сверху обозначается точное решение. Если прибли-
приближенное решение E.2) подставить в уравнение {5.3), то послед-
последнее не будет тождественно удовлетворяться. Следовательно,
мы можем написать
L(T) = R, E.4)
где величина R будет называться в дальнейшем невязкой урав-
уравнения. В общем случае R является непрерывной функцией хг
у, z и t. Если параметр / сделать достаточно большим, то ко-
коэффициенты a}{t) можно выбрать таким образом, чтобы функ-
функция R оставалась малой во всей вычислительной области.
С целью определения коэффициентов а/(/) потребуем, что-
чтобы интеграл взвешенной невязки по всей вычислительной об-
области был равен нулю, т. е. чтобы выполнялось условие
\ J J Wm (х, у, z) R dx dy dz = 0. E.5)
Если положить m = 1, ..., М, то получится система уравнений
для определения а}. Для рассматриваемого здесь нестационар-
нестационарного случая это будет система обыкновенных дифференциаль-
дифференциальных уравнений. В стационарном случае получается система
алгебраических уравнений.
Можно отметить, что уравнение E.5) находится в тесной
связи со слабой формой исходного уравнения, т. е. с уравне-
уравнением
J J J
Wт (х, у, z) L (f) dx dy dz = 0, E.6)
§ 5.1. Общая формулировка 139
допускающим появление разрывов в точном решении [Lax,
Wendroff, 1960].
Различные варианты выбора весовой (поверочной) функции
Wm в уравнении E.5) приводят к построению различных мето-
методов, принадлежащих к классу методов взвешенных невязок.
Охарактеризуем кратко некоторые из этих методов.
A) Метод подобластей. Вычислительная область разделяет-
разделяется на М подобластей Z)m, могущих перекрывать друг друга,
причем полагают
1 внутри области Dm,
0 вне области Dm.
т*
Метод подобластей совпадает с методом конечных объемов
(см. § 5.2) по способу решения уравнения E.5). Уравнение
E.5) в сочетании с условиями E.7) обеспечивает необходимую
основу для выполнения законов сохранения на уровне дискре-
тизированного уравнения. Тем самым гарантируется реализация
тех свойств сохранения, которые присущи исходным уравне-
уравнениям. Это преимущество особенно важно при построении до-
достаточно точных решений, описывающих внутренние течения
или течения с ударными волнами.
B) Метод кол локаций.
Wm(x) = 6(x-xm), E.8)
где б — дельта-функция Дирака и х=(дс, у, г). Как показывает
подстановка E.8) в уравнение E.5), для метода коллокаций
характерно, что полагают R(xm) = 0. Следовательно, конечно-
разностные методы являются, по существу, методами коллока-
коллокаций без использования приближенного решения.
Особенно эффективной разновидностью данного метода яв-
является метод ортогональных коллокаций [Finlayson, 1980].
Этот метод основан на том, что аппроксимирующие функции
в представлении E.2) выбираются из числа ортогональных по-
полиномов, а неизвестными в E.2) служат узловые значения (ве-
(величины Т). Точки коллокаций выбираются из числа корней ор-
ортогональных полиномов, являющихся аппроксимирующими
функциями.
C) Метод наименьших квадратов.
140 Гл. 5. Методы взвешенных невязок
Принятие выражения E.9) эквивалентно тому, чтобы выпол-
выполнялось требование:
Величина \\ \ R2dxdydz является наименьшей.
D) Метод Галеркина.
т. е. весовые функции выбираются из того же семейства, что
и аппроксимирующие (пробные) функции. Если аппроксими-
аппроксимирующие функции составляют полную систему (в случае поли-
полиномов полная система имела бы вид 1, х2, х3, ..., хм), то урав-
уравнение E.5) показывает, что невязка ортогональна к каждому
элементу полной системы. Следовательно, по мере того, как
М стремится к бесконечности,_приближенное решение Т будет
сходиться к точному решению Т.
5.1.1. Приложение к обыкновенному дифференциальному
уравнению
Сравнение различных методов взвешенных невязок можно
провести, если построить решение обыкновенного дифферен-
дифференциального уравнения
JjL — y = O при.0<л:<1 E.11)
с граничным условием у = 1 при х = 0. Эта задача имеет точ-
точное решение у = ехр х.
Подходящее приближенное решение, эквивалентное выра-
выражению E.2), имеет вид
0=1 +Еву*7. E.12)
/-1
Это приближенное решение автоматически удовлетворяет гра-
граничному условию. В отличие от того, что было в случае E.2) у
коэффициенты а, в выражении E.12) постоянны. Подстановка
E.12) в уравнение E.11) дает невязку уравнения в виде
*=-l + Z а/0"*'-1-*0. <Блз>
Для определения коэффициентов а/ интеграл невязки, взятый
с некоторым весом по всей вычислительной области, прирав-
§ 5.1. Общая формулировка
141
нивается нулю. Следовательно, по аналогии с E.5) имеем
1
E.14)
Различные варианты метода взвешенных невязок реали-
реализуются за счет различного выбора весовых функций Wm(x).
Например, в методе Галёркина берется Wm{x) = \m при
т=1, ..., N. Вычисление интеграла E.14) при каждом зна-
значении т позволяет получить систему уравнений, которую мож-
можно представить в виде
SA = D. E.15)
Здесь вектор А составлен из неизвестных коэффициентов а/.
В случае метода Галёркина элемент матрицы S задается в
виде
(ЬЫ EЛ6)
а элемент вектора D — выражением dm = 1/m. Если задать
значение N = 3, то уравнение E.15) принимает вид
1/2
1/6
1/12
2/3
5/12
3/10
3/4
11/20
13/30
1FHH
JLa3J L 1/3 J
а решение этого уравнения записывается как
я, = 1.0141, а2 = 0.4225, а3 = 0.2817.
E.17)
E.18)
Подстановка E.18) в приближенное решение E.12) дает ре-
результат
у= 1 + 1.0141л: + 0.4225х2 + 0.2817л:3. E.19)
Сравнение этого решения с точным решением дается в табл. 5.1.
График изменения ошибки решения при различных значе-
значениях N показан на рис. 5.1. Ясно видно, что ошибка решения
быстро уменьшается по мере увеличения N. Как можно видеть
из табл. 5.1, среднеквадратичные значения ошибки решения, а
также невязки уравнения RTms, быстро уменьшаются при уве-
увеличении N. В общем случае точное решение задачи неизвест-
неизвестно и, следовательно, ошибку решения невозможно вычислить.
Однако оценить невязку уравнения вполне возможно, и это
142
Гл. 5. Методы взвешенных невязок
Таблица 5.1. Решения уравнения dyjdx — у = 0 по методу Галёркина
X
0.
0.2
0.4
0.6
0.8
1.0
Среднеквадратичная
ошибка решения
#rms
Приближенное решение
Линейное
1.0
1.4
1.8
2.2
2.6
3.0
0.2857
0.5271
Квадратичное
(ЛГ=г2)
1.0
1.2057
1.4800
1.8229
2.2349
2.7143
0.00886
0.0583
Кубическое
(W=3)
1.0
1.2220
1.4913
1.8214
2.2259
2.7183
0.00046
0.00486
Точное
решение
у=ехр(х)
1.0
1.2214
1.4918
1.8221
2.2251
2.7183
—
—
дает качественное представление о том, насколько близко дан-
данное решение к точному.
0.4
Рис. 5.1. Распределение ошибки для решения уравнения dy/dx
методу Галёркина.
— y = Q no
К решению уравнения E.11) применялись и некоторые дру-
другие разновидности метода взвешенных невязок из числа упо-
упомянутых в § 5.1. При N = 3 метод наименьших квадратов по-
§ 5.1. Общая формулировка
143
зволяет получить следующую систему уравнений, заменяющую
E.17):
1/3 1/4 1/5 -|га,-| I-1/2-.
1/4 8/15 2/3 ог = 2/3 . E.20)
1/5 2/3 33/35 J L a3 J L3/4J
Применение метода подобластей с интервалами от 0 до 1/3, от
1/3 до 2/3 и от 2/3 до 1.0 приводит к следующей системе урав-
уравнений:
г 5/18 8/81 11/324-11-0,-1 г 1/3
3/18 20/81 69/324 || а2 \ = \ 1/3 |. E.21)
L 1/18 26/81 163/324
JL3J l i/3 j
1.0
0.5
0.
0.
0.75
1.0
0.
0.625
2.0
Применение метода коллокаций при оценке невязки в точках
х = 0, 0.5 и 1.0 дает следующую систему уравнений:
E.22)
Значения а\, а2 и а3, полученные с помощью решения различ-
различными методами, приводятся в табл. 5.2, а соответствующие им
приближенные решения E.12)—в табл. 5.3.
Таблица 5.2. Сравнение коэффициентов в приближенных решениях
уравнения dy/dx — у = 0
Метод
Галёркина
Наименьших квадратов
Подобластей
Коллокаций
Оптимальной среднеквадратичной
невязки
Разложения в ряд Тейлора
Коэффициент
ах
1.0141
1.0131
1.0156
1.0000
1.0138
1.0000
пг
0.4225
0.4255
0.4219
0.4286
0.4264
0.5000
а%
0.2817
0.2797
0.2813
0.2857
0.2781
0.1667
Оптимальное в смысле среднеквадратичной величины ре-
решение получается за счет минимизации среднеквадратичной
ошибки с тремя неизвестными коэффициентами. Сравнение
144
Гл. 5. Методы взвешенных невязок
различных решений по методам взвешенных невязок целесооб-
целесообразно проводить именно с таким, а не с точным решением.
Ясно, что методы Галёркина, наименьших квадратов и подоб-
подобластей приводят к решениям, близким к оптимальным.
Точность метода коллокаций весьма чувствительна к выбору
контрольных точек. Если оценивать невязку при х = 0.1127,
0.50 и 0.8873, то получается решение, идентичное решению по
методу Галёркина.
Таблица
X
0.
0.2
0.4
0.6
0.8
1.0
Средне-
квадра-
квадратичная
ошибка
решения
5.3. Сравнение приближенных решений уравнения dy/dx ¦
Метод
Галёр-
Галёркина
1.0000
1.2220
1.4913
1.8214
2.2259
2.7183
0.000458
Метод
наимень-
наименьших
квадра-
квадратов
1.0000
1.2219
1.4912
1.8214
2.2260
2.7183
0.000474
Метод
подоб-
подобластей
1.0000
1.2213
1.4917
1.8220
2.2265
2.7187
0.000576
Метод
колло-
коллокаций
1.0000
1.2194
1.4869
1.8160
2.2206
2.7143
0.004188
Метод
опти-
оптимальной
средне-
квадра-
квадратичной
невязки
1.0000
1.2220
1.4915
1.8219
2.2263
2.7183
0.000434
Ряд
Тейлора
1.0000
1.2213
1.4907
1.8160
2.2053
2.6667
0.022766
-# = 0
Точное
решение
1.0000
1.2214
1.4918
1.8221
2.2255
2.7183
—
Решения, приводимые в табл. 5.3, изображаются графически
на рис. 5.2, и из графика ясно, что методы взвешенных невя-
невязок (за исключением, может быть, метода коллокаций) весьма
эффективно реализуют минимизацию ошибки решения по всей
области. В противоположность этому, метод разложения в
ряд Тейлора, обеспечивающий совпадение с точным решением
при х = 0.0, приводит к большой ошибке решения вдали от ну-
нулевой точки.
Различные методы взвешенных невязок подвергаются все-
всестороннему сравнению в книге [Fletcher, 1984], где автор де-
делает следующий вывод: «Метод Галёркина дает результаты
неизменно высокой степени точности, имея при этом столь же
широкий диапазон приложений, как и любой другой метод
§ 5.2. Метод конечных объемов
145
взвешенных невязок». В данной ситуации ценность метода Га-
Галёркина обусловливается тем, что он непосредственно приво-
0.002
-0.002
-0.004
-0,006
Метод подобластей
Решение
с оптимальным
L2,d
Рис. 5.2. Распределение ошибок для решений уравнения dy/dx — у •
строенных методами взвешенных невязок (N = 3).
0, по-
дит к методу Галёркина с конечными элементами, а также к
спектральному методу Галёркина.
§ 5.2. Метод конечных объемов
Вышеназванный метод подобен методу подобластей, если
не считать того, что здесь не вводится в явной форме какое-
либо приближенное решение наподобие выражения E.2). Этот
метод оказывается особенно компактным, если определяющие
уравнения включают только первые производные (см. п. 5.2.1).
Если же присутствуют и вторые производные (см. п. 5.2.2), то
требуются некоторые дополнительные операции.
10 К. Флетчер, т. 1
146 Гл. 5. Методы взвешенных невязок
5.2.1. Уравнения, содержащие только первые производные
Здесь мы проиллюстрируем применение метода конечных
объемов к решению уравнения первого порядка в общем виде
-jL + 4f-+# = O, E-23)
которое при соответствующем выборе q> F и G может пред-
представлять различные уравнения движения. Например, если по-
положить <7 = Р> F = 9tL и G = pv, то уравнение E.23) совпадет
с двумерным вариантом уравнения неразрывности A1.10).
J-l
Рис. 5.3. Двумерный конечный объем.
Применение метода подобластей к уравнению E.23) внутри
конечного объема ABCD, показанного на рис. 5.3, дает
ABCD
или, если применить теорему Грина,
[ H-nds = 0, E.25)
ABCD
где Н =(Л G). В декартовых координатах имеем
E.26)
Уравнение E.25) является не чем иным, как констатацией кон-
консервативности. В частном случае, если выбрать q = p, /7 = рй>
§ 5.2. Метод конечных объемов 147
<3 = рг;, уравнение E.25) совпадет с интегральной формулиров-
формулировкой закона сохранения массы. Следовательно, метод конечных
объемов сводится к дискретизации исходного уравнения, пред-
представленного в интегральной форме (см. § 11.2), в противопо-
противоположность методу конечных разностей, который обычно приме-
применяется к исходному уравнению в его дифференциальной форме.
Одним из приближенных представлений уравнения E.25)
может быть уравнение
DA
-?f(stql>k) + Y,(Fby-GAx) = O, E.27)
АВ
где $Ф — площадь четырехугольника ABCD, показанного на
рис. 5.3, причем #/, k есть величина, связанная со средним зна-
значением q внутри четырехугольника. В уравнении E.27)
= УВ — У А. &*АВ = *В — ХА,
Fab = 0.5 (Fu k_x + Fu k), GAB = 0.5 (G7, *_, + G/t k)
и аналогичные выражения для Аувс и т. д. Если «5$ не является
функцией времени, то уравнение E.27) принимает вид
a dqu kldt + 0.5 (F/t *_! + Fu k) ЬуАВ - 0.5 (GJt *_i + Gft k) ^xAB +
+ 0.5 (F/f k + Fi+lt k) Дг/вс - 0.5 (ОЛ k + O/+lt k)
+ 0.5 (F/t k + Flt k+l) &yCD ~ 0.5 (G7, k + G
+ 0.5 (F,.lt Л + FL k) byDA - 0.5 (G,.!,, + G;,,) SxDA == 0. E.28)
Если глобальная сетка (/, k) является нерегулярной, то запи-
записанное для конечных объемов уравнение E.28) обеспечивает
дискретизацию в декартовых координатах, без необходимости
введения обобщенных координат (см. гл. 12). Если же глобаль-
глобальная сетка является однородной и ее линии совпадают с линия-
линиями постоянных л: и у, то уравнение E.28) принимает вид
Ах Ay -jj-qi.k- 0.5 (G/t k_x + G7, *) Ад: + 0.5 (Ffy k + F!+u k) Ay +
+ 0.5 (O/f h + Од k+l) Ax - 0.5 (Ft_l9 k + Fl% k) Ay = 0,
или
что совпадает с аппроксимацией, полученной при представле-
представлении пространственных производных в E.23) с помощью цент-
центральных разностей.
10*
148
Гл. 5. Методы взвешенных невязок
Метод конечных объемов, который применялся для описа-
описания течения как несжимаемой, так и сжимаемой жидкостей
обладает двумя важными преимуществами. Во-первых, он об-
обладает хорошими консервативными свойствами (сохранение
массы и т. п.). Во-вторых, он допускает дискретизацию слож-
сложных вычислительных областей в более простой, хотя и не обя-
обязательно столь же точной форме, чем это позволяет изопара-
метрическая конечно-элементная формулировка (см. п. 5.5.3)
или введение обобщенных координат (см. § 12.2).
5.2.2. Уравнения, содержащие вторые производные
В п. 5.2.1 метод конечных объемов был приведен к решению
уравнения E.23), содержавшего только первые производные,
и привел к сравнительно просто получаемому дискретному вы-
выражению E.28). Если же исходное уравнение содержит вто-
вторые производные, то метод
у, конечных объемов нуждается
в некоторой модификации.
Эта ситуация будет про-
проиллюстрирована здесь на при-
примере построения решения
уравнения Лапласа
# + ¦§¦=0 E.30)
в вычислительной области, по-
показанной на рис. 5.4, с приво-
приводимыми ниже граничными ус-
условиями Дирихле:
на WX f=0,
на XY ф = sin Q/rXY,
на YZ ф= l/rYZ, E.31)
на ZW $=sinQ/rwz.
При таком выборе граничных условий уравнение E.30) имеет
точное решение
E.32)
Рис. 5.4. Вычислительная область для
решения уравнения Лапласа.
наличие которого позволяет непосредственно оценить точность
вычислительных решений.
Если бы уравнение Лапласа E.30) было записано в поляр-
полярных координатах, то показанная на рис. 5.4 вычислительная
область имела бы правильную форму. Однако благодаря
§ 5.2. Метод конечных объемов 149>
умышленной формулировке задачи в декартовых координатах
возникает возможность продемонстрировать способность мето-
метода конечных объемов оперировать с областями неправильной
формы, сохраняя при этом преимущество легко вычисляемого
точного решения. Программа FIVOL (см. п. 5.2.3) имеет до-
достаточно общую форму, позволяющую применить ее к обла-
областям других конфигураций, если только предварительно были
заданы внутренние узловые точки, например, с помощыо
приема, рассмотренного в п. 13.2—13.4.
Рис. 5.5. Конечный объем для деформированной сетки.
Следующий этап метода конечных объемов связан с при-
применением метода подобластей к уравнению E.30) в конечном
объеме ABCD, показанном на рис. 5.5, что дает
S K J) J 0, E.33)
ABCD ABCD
где
Следуя тем же путем, как и в п. 5.2.1, приближенное представ-
ление уравнения E.33) запишем в виде
т,
E.34>
150 Гл. 5. Методы взвешенных невязок
Различные приемы вычисления производных [дф!дх]{ k_l/2
и т. д. рассматриваются в книге [Peyret, Taylor, 1983].
Здесь величина [d<j>/dx]f k_lf2 вычисляется как среднее значе-
значение по площади B'BC'D'AA'B' на рис. 5.5. В результате по-
получим
ах J7 k__I/2 V, ^л'5'C'D' / J J V ox ) \ bA,B,c,D,) J
^^ J/,^-1/2 V5л'В'с^') ))\oy J * \ SA,B,C,D,) ) T
E.36)
и
j <t>dy « ^/, л-1Аул'В' + фвкув'с + 0/, kkyc'D' + <t>A&yD'A',
A'B'C'D'
а также аналогичное выражение для
Если сетка не слишком сильно деформирована, то
« — AycD' » А^/лв, А^/в'с « — А^'Л' » Аул-i, к и
к-\, к — ДулвД**-1, ft. E.37)
На этом основании выражение E.35) принимает вид
дфЛ _ А^^ @/. *-1 - 0/> fc) + Ayfe-b k (фв - Фа)
L дх J/ *-
_ i. fe
Если получить аналогичные выражения для [d^/dje]/+i/2, * и т. д.,
то уравнение E.34) можно записать в виде
Qab (Ь. *-i - Ь, *) + ^в (Фв ~ Фа) + Qbc (*/+i, fe - </•/, ft) +
+ Рве (Фс - Фа) + Qcd (Ф,, *+1 - */, fe) + ^CD (фо - фс) +
+ Qda (Ф/-1, fe - ^/, ft) + Рол (Фа ~ Фо) = 0, E.39)
где
^Ук-1, k)/SAB'
§ 5.2. Метод конечных объемов 161
Фигурирующие в E.39) значения фА, Ха, Уа вычисляются как
средние из четырех узловых значений вокруг данной точки. Так,,
например,
фА = 0.25 (ф1% k + ф,_и к + фни *_! + фи к_х).
Подстановка подобных выражений в уравнение E.39) приво-
приводит к следующему девятиточечному дискретному варианту
уравнения E.30):
0.25 (PCD - PDA) ф,_и k+l + [QCD + 0.25 (Рвс - PDA)] ф1% k+l +
+ 0.25 (Рвс - PCD) */ + i, *+i + [Qda +
+ 0.25 (PCD - PAB)] *7_lt k + (QAB - QBC + Qcd + Qda) */, k +¦
+ [Qbc + 0.25 (PAB - PCZ))] ф1+и k +
+ 0.25 (Рдл-Рдд) #/-!,*-! + [Q^ + 0.25 (PM-PTC)] #/.*-! +
+ 0.25 (Рлв - Явс) #/+lt л_, = 0. E.40>
Если положение узловых точек сетки определено, то входящие
в уравнение E.40) величины типа Qab, Рав и т. д. могут быть
вычислены раз и навсегда.
Для решения уравнения E.40) удобно применить последо-
последовательную верхнюю релаксацию (ПВР), описанную в § 6.3. Урав-
Уравнение E.40) может быть формально разрешено относительно*
Ф**к и, следовательно,
+1. * - {°-25 (Рсо - Рол) *,-., *+, + [Qcd +
+ 0.25 (Рвс - PDA) +jt k+l + 0.25 (Рвс - PCD
+ [Qda + 0.25 (PCD - РАВ)] ф,_и
+ [Qbc + 0.25 (РАВ - PCD
+ 0.25 (РАВ - Рвс) ф1+и *_,}7(Q^b + Qbc + Qcd + Qda),
E.41)
тогда как улучшенное решение выражается в виде
ФТк=Ф1к + Ь{ф1к~Ф1к), E.42>
где к — показатель релаксации (см. § 6.3).
Интересная особенность метода конечных объемов состоит
в том, что решение с граничными условиями Неймана (для
производных) может быть построено точно так же, как и в
случае граничных условий Дирихле, т. е. путем прямой под-
подстановки граничных значений в уравнение E.34).
162
Гл. 5. Методы взвешенных невязок
5.2.3. FIVOL: метод конечных объемов в применении
к решению уравнения Лапласа
Описанный выше метод реализован в компьютерной про-
программе FIVOL, распечатка которой приводится на рис. 5.6.
Основные параметры, используемые в программе FIVOL, опи-
описываются в табл. 5.4.
Таблица 5.4. Параметры, используемые в программе FIVOL
Параметр
JMAX
КМАХ
NMAX
RW
RX
RY
RZ
ТНЕВ
THEN
EPS
ОМ
PHI
PHIX
PHD
XA, YA
DXA
DXK
RMS
Описание
Число точек в радиальном направлении
Число точек в окружном направлении
Максимальное число итераций
rw (рис. 5.4)
гх (рис. 5.4)
гу (рис. 5.4)
rz (рис. 5.4)
Qwx (рис. 5.4)
Qzy (рис. 5.4)
Критерий сходимости ПВР
Показатель релаксации К в формуле E.42)
Ф
Ф
Ф*
Ха, У а
Ах а в
Axk-i,k
\\Ф* — 0nllrms, ||фп+1 — 0llrms
Программа FIVOL считывает и выдает исходные управ-
управляющие параметры (строки 1—25). Задается сетка, рассчиты-
рассчитывается начальное решение (для проведения ПВР), а также
точное решение (строки 38—53). Поскольку интерес представ-
представляет только сходящийся процесс решения, то точное решение
также использовалось в качестве одного из начальных реше-
решений для ПВР. Этот вариант приводит к быстрой сходимости
процесса по схеме ПВР. Задаются граничные условия (стро-
(строки 57—64); строго говоря, эта часть программы не является не-
необходимой, так как граничные условия уже были в неявной
форме учтены в строке 51.
На каждой стороне области задаются параметры, связан-
связанные с сеткой (Qab, Рав и т. д.); это отражено в строках 68—123.
2 С
3 С FIYOL APPLIES THE FINITE VOLUME METHOD TO THE SOLUTION OF
4 С LAPLACES EQUATION IN CARTESIAN COORDINATES ON A POLAR GRID*
5 С THE DISCRETISED EQUATION IS SOLVED BY SOR
6 С
7 DIMENSION XB1,21),YB1,21),QABB1,21),PABB1,21),QBCB1,21)^
8 1PBCB1,21),QCDB1,21),PCDB1,21),QDAB1,2l)rPDAB1r2X),
9 2PHIB1,21),PHIXB1,21)
10 С
11 OPENA,FILE»'FIVOL.DAT1)
12 0PENF,FILE«fFIV0L.0UT')
13 READA,1)JMAX,KMAX,NMAX
14 READA,2)RV,RX,RY,RZ,THEB,THEN,EPS,OM
15 1 FORMAT(815)
16 2 FORMAT(8E10.3)
IT С
18 WRITEF,3)
19 VRITEF,4)JMAX,KMAX,NMAX,EPS,OM
20 VRITEF,5)RV,RX,RY,*Z,THEB,THEN
21 3 FORMAT(! LAPLACE EQUATION BY FINITE VOLUME METHOD1,//)
22 4 FORMAT*' JMAX«\I2;f KMAX«M2,' NMAX*',I5,
23 15X,f BPS>',S10.3,' OM=\F5.3)
24 5 FORMATS RV«\F5,3/ RX«\F5.3.' RY»\F5«3,' RZ*f,F5.3r
25 15X,' ТДО»',Г5Л,' THEN-',F5.1,//)
26 С
27 JMAP - JMAX - 1
28 KMAP - KMAX - 1
29 AJM « JMAP
30 ARM - KMAP
31 DRVX » (RX - RV)/AJM
32 DRZY « (RY - RZ)/AKM
33 DTH - (THEN-THEB)/AKM
34 PI m 3.1415927
3$ С
36 С SET X( Y# EXACT AND INITIAL PHI
37 С
38 DO 7 К « 1,KMAX
39 AK « К - 1
40 ТНК - (THEB -l- AK*DTH)*PI/180.
41 CK « COS(THK)
42 SK « SIN(THK)
43 DR - DRVX -I- (DRZY - DRVX)*AK/AKM
44 RVZ * RW + (RZ - RV)*AK/AKM
45 DO 6 J * 1#JMAX
46 AJ « J - 1
47 R « RVZ + AJ*DR
48 X(J,K) « R*CK
49 Y(J,K) * R*SK
50 PHIX(JrK) = SK/R
51 PHI(J,K) s PHIX(J,K)
52 6 CONTINUE
53 7 CONTINUE
54 С
55 С SET BOUNDARY VALUES OF PHI
56 С
57 DO 8 J » 1,JMAX
58 РНШД) » 0.
59 PHI(J,KMAX) = PHIX(J,KMAX)
60 8 CONTINUE
Рис. 5.6. Распечатка программы FIVOL (начало).
«1
62
63
64
65
66
Ы
68
69
70
71
72
73
74
75
76
77
78
79
80
81
42
83
84
85
36
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
Ш
118
С
С
С
С
С
С
С
С
С
С
С
С
С
с
с
DO 9
К * 1,KMAX
PHIU,K) * PHIXA,K)
PHI(JMAX,K) * PHIX(JHAX,K)
9 CONTINUE
SET GRID RELATED PARAMETERS
DO 11 К « 2,KMАР
KM -
KP -
DO 1
JM *
JP «
XA «
YA ¦
XB »
YB »
xc «
YC *
XD «
К - 1
К + 1
0J« 2,JMAP
J - 1
J + 1
0.25*(X(J,K) + X<JMfK) + X<JM,
0.25MY(J,K) + YCJM,K) ¦ Y(JM,
0.254X(J,K) + X(J,KM) + X(JP,
0,25*(Y(J,K) + Y(J,KM) + Y(JPr
0.25*(X<J,K) + X(JP,K) + X(JP,
0.25*(Y(J,K) + Y(JP,K) + Y(JP,
0.25*(X(JfK) + X(J,KP) -»- X(JMr
YD « 0.25MY(J,K) ¦ Y(J,KP) + Y(JM,
SIDE AB
DXA
DYA
DXK
DYK
SAB
¦ XB - XA
« YB - YA
* X(J,K) - X(J#Krl)
¦ Y(J,K) - Y(J,K-1)
* ABS(DXA*DYK - DXK*DYA)
QAB(J,K) « (DXA*DXA + DYA*DYA)/SAB
PAB(J,K) » (DXA*DXK + DYA*DYK)/SAB
SIDE ВС
DXB
DYB
DXJ
DYJ
SBC
- XC - XB
m YC - YB
- X(J,K) - X(J+1,K)
* Y(J#K) - Y(JU,K)
* ABS(DYJ*DXB - DXJ*DYB)
QBC(J,K) « (DXB*DXB + DYB*DYB)/SBC
PBC(J,K) = (DXB*DXJ + DYB*DYJ)/SBC
SIDE CD
DXC
DYC
DXK
DYK
SCD
» XD - XC
« YD - YC
« X(J,K) - X(J,K+1)
« Y(JrK) - Y(J,K+1)
* ABS(DXC*DYK - DYC*DXK)
QCD(J,K) « (DXC*DXC + DYC*DYC)/SCD
PCD(j;K) * (DXC*DXK + DYC*DYK)/SCD
SIDE DA
DXD = XA - XD
DYD » YA - YD
DXJ - X(J,K) - X(J-1,K)
DYJ
« Y(J,K) - Y{J-1,K)
KM) -
KM) •
KM) •
KM) •
KP) •
KP) •
KP) ¦
KP) •
> X(J,KM))
? Y(J,KM))
ь X(JP,K))
> Y(JP,K))
1- X(J,KP))
? Y{J,KP))
1- X(JMrK))
b Y(JM,K))
Рис. 5.6 (продолжение).
119 SDA * ABS(DXJ*DYD - DYJ*DXD)
120 QDA(J,K) ¦ (DXD*DXD + DYD*DYD)/SDA
121 PDA(J,K) « (DXD*DXJ + DYD*DY^)/SDA
122 10 CONTINUE
123 11 CONTINUE
124 С
125 С ITERATE USING SOR
126 С
127 DO 14 N « 1,NMAX
128 SUM « 0.
129 DO 13 К « 2ДМАР
130 KM - К - 1
131 KP « К + 1
132 DO 12 J « 2,JMAP
133 JM « J - 1
134 JP * J + 1
135 PHD * 0.25*(PCD(J,K)-PDA(J,K))*PHI(JM,KP)
136 PHD = PHD + *QCD(J,K) + 0.25*(PBC(J,K)-PDA(J,K)))*PHI(J,KP>
137 PHD « PHD + 0.25MPBC(J,K)-PCD(J,K))*PHI(JP,KP)
138 PHD = PHD + (QDA(J,K) -I- 0.25*(PCD(J,K)-PAB(J,|O))*PHI(JM,K)
139 PHD * PHD + (QBC(J,K) + 0.25*(PAB(J,K)-PCD(J,K)))*PHI(JP,K)
140 PHD = PHD -I- 0.25*(PDA(J,K) - PAB(J,K))*PHI(JMДМ)
141 PHD » PHD -I- (QAB(J,K) + 0.25*(PDA{J,K)-PBC(J,K)))*PHI(J,KM>
.142 PHD » PHD + 0.25*(PAB(J,K) - PBC(J,K))*PHI(JPДМ)
143 PHD * PHD/(QAB(J,K)+QBC(J,K)+QCD(J,K)+QDA(J,K))
144 DIF * PHD - PHI(J,K)
145. SUM « SUM + DIF*DIF
146 PHI(JrK) « PHI(J,K) + OM*DIF
147 12 CONTINUE
148 13 CONTINUE
149 RMS = SQRT(SUM/(AJM-1.)/(AKM-1.))
150 IF(RMS .LT. EPS)GOTO 16
151 14 CONTINUE
152 VRITEF,15)NMAX,RMS
153 15 FORMAT(.' CONVERGENCE NOT ACHIEVED IN\I5,' STEPS\5Xf* RMS«9
154 1E12.5)
155 С
156 С COMPARE SOLUTION WITH EXACT
157 С
158 16 SUM = 0.
159 DO 21 К « 1ДИАХ
160 WRITEFr17)K
161 17 FORMAT(/,f K=f,I2)
162 DO 18 J * 1,JMAX
163 DIF = PHI(J,K) - PHIX(J,K)
164 SUM = SUM + DIF*DIF
165 18 CONTINUE
166 WRITEFr19)(PHI(J,K),J=1,JMAX)
167 WRITEF,20)(PHIX(J,K),J=1,JMAX)
168 19 FORMAT(f PHI*1,10F7.4)
169 20 FORMAT С PHX»1,10F7.4)
170 21 CONTINUE
171 RMS = SQRT(SUM/(AJM-1.)/(AKM-1.)>
172 VRITEFr22)NrRMS
173 22 FORMAT(/,' CONVERGED AFTER M3,1 STEPS\4X/ RMS«f,El2,5>
174 STOP
175 END
Рис. 5.6 (окончание).
156 Гл. 5. Методы взвешенных невязок
Итерационная процедура ПСР реализует расчет по формулам
E.41) (строки 135—143) и E.42) в строке 146, вычисляет
11^ — ^lirms (строка 149) и выходит из итерационного цикла
(строки 127—151), если выполнен критерий сходимости (EPS).
Затем выдаются на печать окончательное и точное решения
(строки 166—167), а также вычисляется и выдается на печать
величина \\ф — ф\\гт* (строки 171—172).
LAPLACE EQUATION BY FINITE VOLUME METHOD
JMAX« 6 KMAX» б NMAX« 50 EPS= .100E-04 OM-1.500
RV= .100 RX«1.000 RY»1.000 RZ= .100 THEB» .0 THEN* 90.0
K* 1
PHI= .0000 .0000 .0000 .0000 .0000 .0000
PHX= .0000 .0000 .0000 .0000 .0000 .0000
K* 2
PHI* 3.0902 1.2439 .7445 .5205 .3929 .3090
PHX= 3.0902 1.1036 .6718 .4828 .3768 .3090
K= 3
PHI= 5.8779 2.3473 1.4036 .9828 .7441 .5878
PHX= 5.8779 2.0992 1.2778 .9184 .7168 .5878
K= 4
PHI» 8.0902 3.1786 1.8990 1.3345 1.0163 .8090
PHX= 8.0902 2.8893 1.7587 1.2641 .9866 .8090
K= 5
PHI» 9.5106 3.6209 2.1680 1.5349 1.1802 .9511
PHX= 9.5106 3.3966 2.0675 1.4860 1.1598 ,9511
K= 6
PHI-10.0000 3.5714 2.1739 1.5625 1.2195 1.0000
PHX«10.0000 3.5714 2.1739 1.5625 1.2195 1.0000
CONVERGED AFTER 15 STEPS RMS= .13259E+00
Рис. 5.7. Типичная форма выдачи после прохождения программы FIVOL.
Типичная форма выдачи для случая сетки 6X6 представ-
представлена на рис. 5.7. Очевидно, что если начинать с точного реше-
решения, то процесс вычислений по схеме ПСР быстро сходится.
Основная причина большого значения ||^ — ^llrms связана с
большими изменениями решения вблизи rWz.
По мере измельчения сетки точность возрастает (табл. 5.5),
однако при этом для достижения сходимости требуется про-
§ 5.3. Метод конечных элементов и интерполяция 157
Таблица 5.5. Изменение ошибок решения
по методу конечных элементов при измельчении
сетки (rw = rz = 0.1, гх = Гу = 1.0, §wx = 0,
ezy = 90, © = 1.5)
Сетка
6X6
ихи
21X21
II *-* «rrns
0.1326
0.0471
0.0138
Число итераций
до сходимости
15
19
51
водить больше итераций по схеме ПВР. В случае однородной
прямоугольной сетки дискретизированное уравнение E.40)
вырождается в центрированную конечно-разностную схему.
обладающую сходимостью второго порядка, т. е. тем свой-
свойством, что введение в два раза более мелкой сетки (если она
уже была достаточно мелкой) уменьшает ошибку в 4 раза
(т. е. в 22). Применительно к показанным в табл. 5.5 резуль-
результатам для неоднородной сетки порядок сходимости оказывает-
оказывается меньше второго. Ожидается, что дальнейшее искажение сетки
еще более снизит скорость сходимости (см. задачу 5.4).
Метод конечных объемов широко применяется при иссле-
исследовании трансзвукового невязкого течения (см. § 14.3) и те-
течения жидкости (см. п. 17.2.3).
§ 5.3. Метод конечных элементов и интерполяция
Метод конечных элементов в начальной стадии своей раз-
разработки рассматривался как специализированная инженерная
процедура для построения матричных решений при расчетах
напряжений и смещений в анализе конструкций. Этому мето-
методу было дано солидное математическое обоснование после вве-
введения в рассмотрение потенциальной энергии системы и вариа-
вариационной интерпретации для метода конечных элементов.
Однако очень малое число задач динамики жидкости и газа
(или задач о теплопередаче) допускает свое представление в
вариационной форме. С другой стороны, во многих случаях ме-
метод Галёркина оказывается эквивалентным методу Ритца для
решения вариационных задач. Как следствие этого в боль-
большей части приложений метода конечных элементов к задачам
158 Гл. 5. Методы взвешенных невязок
гидроаэродинамики используется именно формулировка Галёр-
кина для этого метода. Здесь мы сосредоточимся исключительно
на галёркинской формулировке метода конечных элементов.
Традиционная инженерная трактовка метода конечных эле-
элементов дается в книге [Zienkiewicz, 1977]. Математические
аспекты и перспективы метода более подробно излагаются в-
книгах [Strang, Fix, 1973; Oden, Reddy, 1976; Mitchell, Wait,
1977]. Техника вычислений, преимущественно для приложений
метода конечных элементов к анализу конструкций, излагает-
излагается в книге [Bathe, Wilson, 1976]. Приложения традиционного
метода конечных элементов к гидроаэромеханике рассматри-
рассматриваются в книгах [Thomasset, 1981; Baker, 1983].
Если сравнивать с традиционным методом Галёркина, из-
изложенным в § 5.1, метод конечных элементов Галёркина обла-
обладает двумя чрезвычайно важными особенностями. Сначала
приближенное решение E.2) записывается непосредственно в>
форме комбинации узловых значений неизвестной функции, т. е.
T=I,T}<l>f(x, у, г). E.44)
Выражение E.44) может интерпретироваться как интерполя-
интерполяция по отношению к локальному решению в узловой точке Г/-
Благодаря тому что мы работаем непосредственно с узловыми
значениями неизвестной переменной, отпадает один уровень в
процессе вычислений на этапе решения уравнения (см. гл. 6)
и решение в узле приобретает прямой физический смысл. Кро-
Кроме того, становится легче видеть аналогию с методом конеч-
конечных разностей, а также становится более очевидной интерпре-
интерпретация метода конечных элементов в качестве средства дискре-
дискретизации (см. § 3.1) исходного дифференциального уравнения в
частных производных, представленного в континуальной форме.
Входящие в выражение E.44) аппроксимирующие функции
ф](х, у, z) часто называются в математической литературе
пробными или интерполяционными функциями, а в инженерной
литературе — функциями формы (при замене символа ф} на
Nj). Вторая важная особенность рассматриваемого метода со-
состоит в том, что аппроксимирующие функции ф}{х, у, z) выби-
выбираются почти исключительно из числа кусочно-линейных поли-
полиномов низкого порядка, причем выбор ограничивается ближай-
ближайшими элементами. Тем самым достигается сравнительно малое
число отличных от нуля членов, которые при их надлежащей
расстановке [Jennings, 1977, гл. 5] могут располагаться вбли-
вблизи главной диагонали матрицы уравнений. Это является важ-
важным на стадии решения уравнений (см. гл. 6), так как при
§ 5.3. Метод конечных элементов и интерполяция 159
подобной ситуации решение матричных уравнений будет более
экономичным.
Метод конечных элементов реализует дискретизацию на
двух этапах, каждый из которых вносит ошибки (хотя и не
всегда аддитивные). На первом из указанных этапов кусочно-
линейная интерполяция вводится по дискретным, или конеч-
конечным, элементам с целью связать локальное решение с узло-
узловыми значениями. Этот аспект будет исследован в данном
параграфе. На втором этапе используется построение со взве-
взвешенными невязками (см. § 5.1), ставящее целью получить
алгебраические уравнения для связки между узловыми значе-
значениями решения. Техника реализации второго этапа, а также по-
поведение решения иллюстрируются с помощью программ STURM
(п. 5.4.2) и DUCT (п. 5.5.2).
5.3.1. Линейная интерполяция
Одномерные линейные аппроксимирующие функции ф}{х)
показаны на рис. 5.8. Функция ф^х) принимает значения
ф/ = 0 при х <*/_!,
ф = L±. ПрИ х,х^.х^:х} (элемент А), E.45)
xi~~xl-\
Ф1 = 1 при х = xjy
X ~~ X
Ф^ = Х —х ПРИ xi^*x^xJ+i (элемент В), E.46)
(Ь¦ О ТТГ1И Y *^ Y ¦ •
Таким образом, функция ф\ отлична от нуля только в диапазо-
диапазоне х/_1 < х < */+1. Подобным же образом можно установить,
что аппроксимирующая функция ф\+х отлична от нуля только
между узлами / и / + 2.
В случае линейных аппроксимирующих функций выраже-
выражение E.44) принимает вид
Т = Т!_хф}_х+Т1ф! внутри элемента Л,
•(-Г/+1^/+1 внутри элемента В,
т. е. благодаря локальному характеру аппроксимирующих
•функций (см. рис. 5.8) в каждый элемент дают вклады лишь
по два члена. Внутри элемента А функция fa задается форму-
формулой E.45), а функция ф^х — формулой
*'-'в^т^г- E'48)
160
Гл. 5. Методы взвешенных невязок
Внутри элемента В функция ф}- задается формулой E.46), а
0 — формулой
X —
xl+i "~" xt
E.49)
Вышеописанное построение будет использовано для полу-
получения линейной интерполяции функции
д = 1 + cos @.5jut) + sin {nx) E.50)
в диапазоне 0 ^ х ^ 1. Поведение функции, определяемой фор-
формулой E.50), показано на рис. 5.9. Узловые значения у/ опре-
Элемент А Элемент В
Ь
1.0-
Рис. 5.8. Одномерные линейные аппроксимирующие функции.
деляются с помощью точного решения, т. е. yj = y(Xj). Внутри
же конкретного элемента местное решение ут, получаемое пу-
путем интерполяции, задается формулами
У\п = У}-\Ф1-\{х)-\-у1<1>1{х) внутри элемента Л,
Уш = yifj(x) + yl+ifj+i(x) внутри элемента В.
E.51)
Внутри элемента А ф/-г и ф/ задаются формулами E.48) и
E.45) соответственно. Внутри элемента В ф,- и ф}+\ задаются
с помощью E.46) и E.49).
Линейно-интерполяционное решение в форме E.51) пред-
представлено графически на рис. 5.9. Ясно, что при двухэлементном
делении интервала 0 ^ х <: 1 интерполяционное решение об-
обладает довольно большой неточностью в средних точках каж-
каждого элемента, например
х = 0.25: у = 2.63099, уш = 2.35356,
х = 0.75: у = 2.08979, у1а = 1.85355.
§ 5.3. Метод конечных элементов и интерполяция
161
Однако точность быстро возрастает по мере увеличения числа
элементов, на которые подразделяется интервал 0 ^ х ^ I
(см. табл. 5.6). Приводимая в табл. 5.6 среднеквадратичная
ошибка при линейной интерполяции уменьшается пропорцио-
пропорционально Ал:2, где Ад; — протяженность каждого элемента. Это
характерное свойство линейной интерполяции.
3.0г
2.0-
1.0
Формула E.50)
Квадратичная
интерполяция
/Линейная
интерполяция
0 0.5 1.0
х
Рис. 5.9. Одномерное конечно-элементное интерполяционное решение.
В этом месте читатель, впервые знакомящийся с этим мате-
материалом, может предпочесть перескочить через пункты, посвя-
посвященные квадратичной интерполяции и двумерной интерполя-
интерполяции, перейдя к рассмотрению процесса дискретизации, а
Таблица 5.6. Ошибки интерполяции выражения E.50)
по методу конечных элементов
Линейная интерполяция
Число
элементов
2
4
6
8
Среднеквадра-
Среднеквадратичная
ошибка
0.18662
0.04786
0.02138
0.01204
Квадратичная интерполяция
Число
элементов
1
2
3
4
Среднеквадра-
Среднеквадратичная
ошибка
0.04028
0.01599
0.00484
0.00206
11 К. Флетчер, т. 1
162
Гл. 5. Методы взвешенных невязок
также решения уравнений на примере уравнения Штурма —
Лиувилля (см. § 5.4).
5.3.2. Квадратичная интерполяция
Применение линейной интерполяции, иллюстриуемое на
рис. 5.8 и 5.9, налагает на приближенное решение некоторое
ограничение, состоящее в том, что оно должно изменяться меж-
между узловыми точками линейным образом. Как видим
(табл. 5.6), это обстоятельство в случае конечной сетки вносит
ошибку. Оценки подобных интерполяционных ошибок даются
Элемент В
Элемент А
i.Or
rj'+2
Рис. 5.10. Одномерные квадратичные аппроксимирующие функции.
в книге [Mitchell, Wait, 1977] и оказываются весьма полезны-
полезными, когда точное решение неизвестно. Если применить квадра-
квадратичную интерполяцию, то при тех же размерах сетки мы мог-
могли бы ожидать уменьшения ошибки интерполяции.
В качестве одномерной квадратичной аппроксимирующей
функции, показанная на рис. 5.10 функция ф}- задается следую-
следующим образом:
^/ = 0 при х < х*ъ
E.52)
при х> xj+2.
(элемент 5),
E.53)
§ 5.3. Метод конечных элементов и интерполяция 163
В этих аппроксимирующих функциях можно узнать интерпо-
интерполяционные функции Лагранжа. Получается, что <j>j = 1 в узле /
и Фз = 0 в узлах / — 2, / — 1, / + 1 и / + 2. При квадратичной
интерполяции выражение E.44) внутри элемента А принимает
следующий вид:
E.54)
а внутри элемента В — вид
Т = Т,ф, + Т1+1ф{+1 + Т1+2ф1+2, E.55)
т. е. внутри каждого элемента дают свой вклад только по три
члена.
Для модельной задачи, связанной с функцией E.50), под-
подходящая квадратичная интерполяция соответствует формулам
Уш = Ut-2$i-Ax) + *//-i^/-i(*) + y&i (x) внутри элемента Ау
Уш = yrfj (х) + yj+rff+i(x) + у1+2ф1+2(х) внутри элемента В,
E.56)
где предполагается, что внутри элемента А (х}-2 ^ х ^ Xf)
ф, х = ( хх*-> ) ( хх* ), E.57)
r/ V*/i-*/2/V*/i-*//
1 2
и аналогично для элемента В (xj ^ х ^ jc/+2).
Случай когда интервал 0 ^ х ^ 1 перекрывается единствен-
единственным квадратичным элементом, показан на рис. 5.9. Очевидно,
что квадратично-интерполяционное решение оказывается бо-
более точным, чем линейно-интерполяционное решение с тем же
числом узлов. Эффект измельчения сетки (т. е. увеличения
числа квадратичных элементов) сводится к быстрому умень-
уменьшению среднеквадратичной ошибки (см. табл. 5.6). Скорость
этого уменьшения, видная из табл. 5.6, пропорциональна Ах3
в случае квадратичных элементов. Следовательно, по мере из-
измельчения сетки квадратичная интерполяция становится все
более точной в сравнении с линейной интерполяцией.
В принципе допустимо использовать как кубическую интер-
интерполяцию, так и интерполяцию высших порядков, однако на
практике не принято пользоваться интерполяцией более
11*
164 Гл. 5. Методы взвешенных невязок
высокого порядка, чем квадратичная. Несмотря на то что ин-
интерполяция высокого порядка обеспечивает большую точность,
она приводит к системам уравнений, содержащим намного
больше ненулевых членов, чем при использовании интерполя-
интерполяции низкого порядка; следовательно, интерполяция высокого по-
порядка является более дорогостоящей в вычислительном отно-
отношении, особенно при двух или трех измерениях. Достижение
надлежащего баланса между точностью и экономичностью,
т. е. выбор методов обладающих вычислительной эффектив-
эффективностью (см. § 4.5), является одной из наиболее интересных
стратегических особенностей вычислительной гидроаэродинамики.
При измельчении сетки мы вправе ожидать, что ошибка ко-
конечно-элементного решения будет уменьшаться с такой же ско-
скоростью, что и интерполяционная ошибка. В общем случае при
заданной сетке ошибка решения будет больше, так как она
включает и дополнительную ошибку, обусловленную тем, что
решение в узловой точке не совпадает с точным решением.
Грубо говоря, применение линейных аппроксимирующих функ-
функций приводит к решениям, обладающим примерно такой же
точностью, что и решения, построенные с помощью конечно-
разностных методов второго порядка, тогда как применение
квадратичных аппроксимирующих функций приводит примерно
к такой же точности, что и применение конечно-разностных ме-
методов третьего порядка.
5.3.3. Двумерная интерполяция
Понятие конечных элементов, давшее название самому ме-
методу, становится более полезным, если число измерений пре-
превышает единицу. Так, при двух измерениях локальное реше-
решение интерполируется по отдельности внутри каждого из четы-
четырех элементов Л, В, С и Д окружающих узел (/, k) (рис. 5.11).
Приближенное решение, эквивалентное выражению E.44),
весьма удобно представляется с помощью введения координат-
координатной системы (?, т]), привязанной к элементу. При билинейной
интерполяции приближенное решение можно записать в виде
Г=ЕГ/*,Й, ч), E.58)
где для каждого элемента —1 ^ g ^ 1, —1 ^ ц ^ 1 (см.
рис. 5.11). Согласно выражению E.58), в каждый элемент вно-
вносят свои вклады по четыре члена. Аппроксимирующая функция
^(g, т|) приобретает форму
ф1 (I т)) = 0.25 A + Ы) A + Л/Л). E.59)
§ 5.3. Метод конечных элементов и интерполяция
165
Например, внутри элемента С, показанного на рис. 5.15, имеем
#, = 0.25A-6H-4),
#,-0.25A+6H ~Л).
откуда следует, что #/ = 1 при 6 = 1/» Л = Л* и #/ = 0 во всех
остальных узлах. На линиях постоянного 6 или Л аппроксими-
k+i tj=1
K+i
j-i
D
'j-l
A
с
j
В
K+l
'j+t
/с
J
k-1
Рис 5.11. Глобальная и локальная нумерация узлов.
рующие функции #/ обнаруживают такой же характер измене-
изменения, как и одномерные аппроксимирующие функции (см.
рис. 5.8).
Трехмерное изображение билинейной интерполяционной
функции, центрированной в узле (/, &), показано на рис. 5.12.
Рассматривая выражение E.58) и рис. 5.12, можно убедиться,
что функция Т остается непрерывной при пересечении границ
элементов; однако это не так по отношению к производным Т.
Как и в одномерном случае, внутри каждого конкретного
элемента можно определить двумерные биквадратные интерпо-
интерполяционные функции (рис. 5.13). Для лагранжевых элементов
приближенное решение, эквивалентное выражению E.44), при-
принимает форму
Г=ЕГ/#/F, г)), E.61)
166
Гл. 5. Методы взвешенных невязок
Рис. 5.12. Билинейная интерполяционная функция.
j-2
к+г
J-2
К+1
j-2
к
j-2
К-1
j-2
к-г
>i
К+2
•J-1
К+1
D
* А
•J-i
К-1
j-i
к-г
j
К+2
j
К+1
С
j
* В
j
К-1
j
к-2
•
'j+l
К+2
•J+1
К+1
i+»
К
#j+l
j+i
k-2
j+2
K+2
j+2,
K+1
J+2
К
ft
j+z
• i
> • <
> • <
Рис. 5.13. Двумерные квадратичные элементы Лагранжа.
§ 5.3. Метод конечных элементов и интерполяция 167
где биквадратные аппроксимирующие функции Лагранжа за-
задаются при помощи формул
Угловые узлы: $г (g, л) = 0.25g/g A + hi) Л/Л A + Л/Л).
Узлы в серединах
сторон (h = 0): ф1 (§, л) = 0.5 A -I2) т,/Л A + Л/Л).
Узлы в серединах
сторон (щ = 0): ф1 (g, л) = 0.5 A - ц2) Ы A + Ы).
Внутренний узел: фь (?, t\) = A — I2) A — г\2).
Как и прежде, квадратичные аппроксимирующие функции Лаг-
Лагранжа обладают интерполяционными свойствами, т. е.
$i = l, если g = g/, л = Ль
$1 = 0 во всех остальных узлах.
Поведение аппроксимирующей функции E.62) можно пред-
представить зрительно, придавая постоянные значения величинам
6 или ц; тогда эта аппроксимирующая функция будет вести
-себя подобно одномерной аппроксимирующей функции, изоб-
изображенной на рис. 5.10. Это обстоятельство следует из того фак-
факта, что двумерные аппроксимирующие функции Лагранжа
.представляют собой просто произведения соответствующих од-
одномерных аппроксимирующих функций. Данный факт дает
возможность сделать важные выводы, касающиеся интерполя-
интерполяции в более чем одном измерении, особенно в связи с построе-
построением схем, расщепляющихся по размерностям (см. § 8.3).
Двумерная интерполяция на конечных элементах будет
.проиллюстрирована здесь по отношению к функции
f = [1 — 0.8 cos @.5я*I [cos @.5ш/)], E.63)
вид которой показан на рис. 5.14 для области —l^x^l,
—1 <у < 1.
Эту область удобно расщепить на четыре элемента
(рис. 5.15), по отношению к которым решение должно интерпо-
интерполироваться билинейным образом при помощи девяти узловых
значений ft = f/.
Внутри некоторого конкретного элемента, например С, интер-
интерполяционное решение fin задается в виде
/in=?fi**($, Л). E-64)
где (|, у\)—локальная координатная система, связанная с эле-
элементом. Для элемента С имеем
g = 2jc — 1 и г\ = 2у— 1.
168
Гл. 5. Методы взвешенных невязок
Билинейные интерполяционные функции <pi задаются формула-
ми E.60), а чаще — формулами E.59).
Рис. 5.14. Двумерная функция f = [1 —0.8 cos @.5rtx)][cos@.5m/)].
в
4=1
у=0
?/=-1.0
0
х—-1»0 х—0 х=1.0
Рис. 5.15. Линейные элементы в двух измерениях.
Интерполяционное решение всего с четырьмя элементами
является не очень точным. Например, в точке х = 0.5, у = 0.5
/ = 0.45711, /in = 0.375.
Целиком интерполяционное решение для функции E.63) пока-
показано на рис. 5.16. Однако точность решения быстро возрастает
по мере увеличения числа элементов, покрывающих область
§ 5.3. Метод конечных элементов и интерполяция
169
(табл. 5.7). Показанные в табл. 5.7 результаты, относящиеся к
билинейной интерполяции, свидетельствуют о том, что средне-
среднеквадратичная ошибка уменьшается пропорционально Ах2
Таблица 5.7. Ошибки в случае двумерной
конечно-элементной интерполяции
Билинейная интерполяция
Число
элементов
4
16
64
Среднеквадра-
Среднеквадратичная
ошибка
0.08527
0.02199
0.00557
Биквадратичная интерполяция
Число
элементов
4
16
64
Среднеквадра-
Среднеквадратичная
ошибка
0.01199
0.00151
0.00019
Более точная интерполяция может быть достигнута за счет
применения биквидратичной интерполяции. Тогда каждый эле-
Рис. 5.16. Билинейная интерполяция функции E.63).
мент имеет девять узловых значений (см. рис. 5.13), которые
интерполируются с помощью выражения
fm=Z/i#/F.4), E-65>
где интерполяционные функции $/(?, т]) задаются с помощью
формул E.62). Как видно из табл. 5.7, элементы с биквадра-
170 Гл. 5. Методы взвешенных невязок
тичной интерполяцией являются более точными, чем элементы
с билинейной интерполяцией при сохранении одинакового чис-
числа узловых точек. Обращаясь к табл. 5.7, отметим, что 16 со-
соприкасающихся линейных элементов содержат такое же число*
узловых точек, как и 4 соприкасающихся линейных элемента.
По мере того как большее число квадратично-интерполируемых
элементов используется для покрытия области —l^x^lv
—1^#^1> среднеквадратичная ошибка убывает пропорцио-
пропорционально Ах3 (=Аг/3).
Аппроксимирующие функции Лагранжа могут быть введе-
введены и в случае трех измерений. При реализации трилинейной
интерполяции элементы в форме кирпичиков и имеющие по>
восемь узлов заменяют прямоугольные элементы с четырьмя
узлами, фигурировавшие при двух измерениях. В случае три-
квадратичной интерполяции элементы-кирпичики с 27 узлами,
заменяют прямоугольные элементы с 9 узлами в двух измере-
измерениях [Zienkiewicz, 1977]. При рассмотрении случаев двух и:
трех измерений введение кубической интерполяции и интерпо-
интерполяции более высоких порядков вполне возможно, но не пред-
представляет большого интереса вследствие большого числа взаи-
взаимосвязанных узлов [Fletcher, 1984].
Имеется возможность исключить центральный узел из квад-
квадратичного прямоугольного элемента, показанного на рис. 5.13;
это приводит к построению серендиповских элементов и к та-
такой интерполяции, при которой внутренние узлы не затраги-
затрагиваются. Введение таких элементов возможно при квадратичной
или имеющей более высокий порядок интерполяции и при лю-
любом числе измерений. Серендиповские элементы описываются
в книге [Zienkiewicz, 1977].
§ 5.4. Метод конечных элементов
и уравнение Штурма — Лиувилля
В п. 5.1.1 метод Галёркина был определен как принадлежа-
принадлежащий к классу методов взвешенных невязок. При введении фор-
формы приближенного (интерполяционного) решения, строящего-
строящегося по методу конечных элементов, т. е. выражения E.44), под-
подчеркивается, что неизвестными являются узловые значения, а
аппроксимирующие функции представляют собой кусочно-опре-
кусочно-определенные полиномы низкого порядка. Здесь мы применим ме-
метод Галёркина с конечными элементами к решению уравнения
Штурма — Лиувилля, имея в виду проиллюстрировать технику
реализации метода.
§ 5.4. МКЭ и уравнение Штурма—Лиувилля
171
5.4.1. Подробная формулировка задачи
Упрощенное уравнение Штурма — Лиувилля можно записать
з виде
d*Y y_
dx2 "T" J ~ Г
граничными условиями
sin (/-0.5) я*
dY
F@) = 0 и -2j(l)=0.
E.66)
E.67)
Для частного вида F, фигурирующего в правой части E.66),
точное решение задачи имеет вид
L
? I 1-нДл)«г sin К' ~ °-5> ««]• <5-68>
Метод Галёркина с конечными элементами начинается с
©ведения в качестве приближенного решения некоего пробного
J-1
х=0
Рис. 5.17. Задача Штурма — Лиувилля.
решения, эквивалентного выражению E.44), в виде
Г=?йГ,ф,(х), E.69)
причем функции ^/(х) представляют собой линейные аппрокси-
аппроксимирующие функции, которые в элементной системе координат
при х = хA) могут быть заданы выражениями (рис. 5.17)
Внутри элемента А:
Внутри элемента В:
= 0.5A+6), | = 2 [* ~(^;' +
?) = 0.5A — i), l=
E.70)
172 Гл. 5. Методы взвешенных невязок
Подстановка выражения E.69) в уравнение E.5) дает невяз-
невязку решаемого уравнения в виде
R = ^r + Y-F. E.71)
Использование уравнения взвешенных невязок E.6) при
№т(х) = фт(х) дает
1
Фт (х) (^r + Y-F)dx=0. E.72>
Можно отметить, что здесь интегрирование выполняется по об-
области 0 ^ х ^ 1. Если учесть, что в формуле E.69) решение
выражается через узловые значения У/, в уравнении E.72) не
могут появляться производные старше первой [Mitchell, Wait,
1977]. На этом основании используется интегрирование по час-
частям, приводящее к следующему соотношению:
Учитывая, что У@) = 0, нет надобности записывать уравнение
с т = 0 (см. рис. 5.17). Для т^1 имеем ^т@) = 0. При.
х = 1 dY/dx = O и поэтому формула E.73) принимает вид
Подставляя E.74) и E.69) в уравнение E.72) и проводя не-
некоторые перестановки, получаем
-11-0
Все члены, стоящие под знаками интеграла, известны, так что
E.75) представляет собой фактически систему алгебраических
уравнений, которую можно записать в векторной форме:
BY=G, E.76>
где Ьт>/, т. е. элемент матрицы В, выражается по формуле
С^) E<77>
§ 5.4. МКЭ и уравнение Штурма—Лиувилля
173
тогда как У/ есть элемент вектора Y, a gm — элемент вектора
G, т. е.
1
i>mF dx. E.78)
Правую часть формулы E.77) достаточно просто вычислить,
если превратить интеграл по х в интеграл по ?, взятый для каж-
Элемент В
Элемент В ^ ^
Элемент A J^tt" ^ХГ. Ун1 У)+г
Рис. 5.18. Вклады, соответствующие узлам и элементам и вносимые в дис-
кретизированные уравнения, (а) Линейная интерполяция; (Ь) квадратичная
интерполяция, угловой узел.
дого элемента по очереди (рис. 5.17). Если учесть, что функции
фт также задаются формулами E.70), то ненулевые вклады
дают только элементы, примыкающие к узлу / = т. Для узла
т = / вклад в расчет по формулам E.77) и E.78) дает толь-
только один элемент. Следовательно, матрица В является трехдиа-
гональной, т. е. отличны от нуля лишь нижеследующие члены
(KJ1)
Дх,
Ах,
E.79)
АХ:
АХ:
а для узла т = /:
Ах,
Ах.
Величины шагов Axj и
показаны на рис. 5.18.
174 Гл. 5. Методы взвешенных невязок
На первый взгляд, если учесть, что величина F известна из
вида уравнения E.66), правую часть в E.78) можно вычис-
вычислить непосредственно. Однако в более общем случае, когда F
известна, но является сложной функцией х, удобно провести
для F такую же интерполяцию, как и для У, т. е. записать
jt,(x), E.80)
где узловые значения F}- задаются непосредственно из уравне-
уравнения E.66). Подстановка формулы E.80) в выражение E.78)
дает
/ 1
>$«#/<**• E.81)
В случае линейных аппроксимирующих функций правую часть
формулы E.81) можно рассчитать в виде A^/^/—1)
а для т = /: gj = (Дх,/6) Fj_x + (Дху/3) Fj.
Рассматривая частный случай Ах,- = Ах/+\ = Ах, поучитель-
поучительно полностью выписать все члены уравнения E.76), разделив
их на Ах. В результате получим A ^ / ^ / — 1)
LU) r/-i+\j)Yi+ш г/+0 -
Очевидно, первая группа членов совпадает с конечно-разност-
конечно-разностным представлением d2Y_/dx2. Второй и третий члены соответ-
соответствуют оценке величин У и F в качестве средневзвешенных по
трем соседним узловым значениям. Набор весовых коэффи-
коэффициентов A/6, 2/3, 1/6) характерен для линейных элементов в
применении к однородной сетке.
С учетом трехдиагонального характера системы уравнений
E.76) имеется возможность экономного построения решения
путем использования алгоритма Томаса (см. п. 6.2.2).
Решения были получены при следующих значениях щ в
уравнении E.66):
fli = 1.0, а2=— 0.5, а3 = 0.3, а4==-0.2, а5 = 0.1.
§ 5.4. МКЭ и уравнение Штурма—Лиувилля
175
Для точек, разделенных одинаковыми интервалами, средне-
среднеквадратичная ошибка, полученная при различных значениях /,
Таблица 5.8. Среднеквадратичная ошибка
при решении упрощенного уравнения
Штурма — Лиувилля
/
6
11
21
41
81
Ах
0.2
0.1
0.05
0.025
0.0125
Hr-*Hrms
7.830 X Ю~3
1.860 ХЮ"8
0.447 X Ю~3
0.109 X Ю~3
0.027 X Ю
показана в табл. 5.8. Эта среднеквадратичная ошибка опреде-
определяется выражением
Уменьшение ошибки при уменьшении Ах, показанное в
табл. 5.8, пропорционально Ах2. Это согласуется с теоретически
предсказанным результатом для случая линейной интерполя-
интерполяции, причем имеет тот же самый порядок, как и для трехточеч-
трехточечных центрированных конечно-разностных формул (см., напри-
например, табл. 7.1).
5.4,2. STURM: программа расчета
по уравнению Штурма — Лиувилля
В п. 5.4.1 метод конечных элементов с линейной интерпо-
интерполяцией применяется к решению упрощенного уравнения Штур-
Штурма— Лиувилля E.66) с граничными условиями в форме E.67).
В данном пункте будет дано описание компьютерной програм-
программы STURM, предназначенной для получения конечно-элемент-
конечно-элементных решений задачи E.66) — E.67) при использовании линей-
линейной и квадратичной интерполяции.
В случае использования квадратичных интерполяционных
функций E.57) формулы E.77) и E.81) принимают следую-
следующую форму, пригодную для угловых узлов по внутренней части
176 Гл. 5. Методы взвешенных невязок
области:
в; = -
Особая форма выражений E.84) и E.85) является следствием
ограничений X/_i = 0.5 (х/_2 + */) и jc/+i = 0.5(jc/ + x/+2). Эти
ограничения могут быть ослаблены, что, однако, приведет к
усложнению алгебраических выражений.
В граничном узле m = J формулы E.77) и E.81) прини-
принимают вид
— 1 Да:.
E'86)
Подставляя E.74) и E.69) в уравнение E.72) и проводя не-
терполяции, но центрированных в узлах в середине сторон,
формулы E.77) и E.81) принимают вид
4 2 Ах,
»л-—
2 Ддс;
§ 5.4. МКЭ и уравнение Штурма—Лиувилля
177
Система уравнений E.76) является трехдиагональной, если
применяется линейная интерполяция, а в случае применения
квадратичной интерполяции — попеременно трехдиагональной
и пятидиагональной. Эффективные модификации метода исклю-
исключения по Гауссу могут быть использованы для решения урав-
уравнений E.76) в том или ином из указанных случаев и описы-
описываются в пп. 6.2.2 и 6.2.3.
Программа STURM применяет метод Галёркина с конеч-
конечными элементами к уравнению Штурма — Лиувилля E.66).
Распечатка программы STURM приводится на рис. 5.19. Основ-
Основные параметры, используемые в программе STURM, описы-
описываются в табл. 5.9.
Таблица 5.9. Параметры, используемые в программе STURM
Параметр
INT
IPR
NX
А
F
YEX
В
G
BANFAC
BANSOL
RMS
Описание
= 1, линейная интерполяция; =2, квадратичная интерполя-
интерполяция
= 0, выдать на печать лишь среднеквадратичную ошибку;
= 1, выдать на печать также и решение
Число точек в направлении оси х, включая х = 0 и х = 1.0
Коэффициенты щ в уравнении E.66)
Узловые значения для правой части E.66)
Точное решение F, формула E.68)
В в уравнении E.76)
G в уравнении E.76)
См. п. 6.2.3
См. п. 6.2.3
Среднеквадратичная ошибка
Программа STURM считывает (и выводит на печать) ис-
исходные управляющие параметры (строки 11—21). Задаются
значения х, точное решение, а также узловые значения функ-
функции F в правой части уравнения E.66) (строки 28—42). Вы-
Вычисляются вклады в матрицу В и вектор G в уравнениях E.76)
(строки 43—69) и проводится корректировка с целью учета гра-
граничных условий. Система уравнений E.76) с ленточной матри-
матрицей решается путем обращения к подпрограмме BANFAC
(строка 83), выполняющей факторизацию В в произведение
L-U, и обращения к подпрограмме BANSOL (строка 86) для
решения факторизованной системы. Распечатка и описание под-
подпрограмм BANFAC и BANSOL дается в п. 6.2.3. Далее рассчи-
12 К. Флетчер, т. 1
178 Гл. 5. Методы взвешенных невязок
1
2 С
3 С STURM COMPUTES THE SOLUTION OF THE STURM-LIOUVILLE PROBLEM,
4C P « Q - 1, F ¦ -SIG(AL*SIN(L-O.5)*PI*X), USING THE FINITE ELEMENT
1 5 С METHOD ON A UNIFORM GRID VITH EITHER LINEAR OR QUADRATIC
: 6 С INTERPOLATION.
7 С THE BANDED SYSTEM IS SOLVED WITH BANFAC, BANSOL (SECTIOH 6.2).
8 С
9 DIMENSION YF5),YEXF5),XF5),BE,65),GF5),FF5),AE),YDF5)
10 С
11 OPENA,FILE*1STURM.DAT1)
12 OPENF,FILE»'STURM.OUT*)
13 READA,1)INT,IPR,NX,A
14 1 FORMATCI5,5E10.3)
15 С
16 IF(INT .EQ. 1)VRITEF,2)
17 IFUNT .EQ. 2)VRITEF,3)
18 VRITEF,4)NX,A
19 2 FORMAT(' STURM-LIOUVILLE PROBLEM, FEMtLINEAR INTERPOLATION1)
20 3 FORMAT(f STURM-LIOUVILLE PROBLEM, FEMrQUADRATIC IHTrRFOLATION*)
21 4 FORMATC NX»\I3,' А»1,5Е10.3,//)
22 С
23 PI * 3.1415927
24 NXP = NX - 1
25 ANX « NXP
26 DX » l./ANX
27 DXS = DX*DX
28 С
29 С SET GRID, EXACT SOLUTION AND RHS(F)
30 С
31 DO 5 I « 1,NX
32 AI » I - 1
33 XU) » AI*DX
34 F(I) = 0.
35 YEX(I) = 0.
36 DO 5 L = 1,5
37 AL = L
38 . AL « (AL - 0.5)*PI
39 DUM = A(L)*SIN(AL*X(D)
40 F(I) » F(I) - DUM
41 YEX(I) « YEX(I) - DUM/U. - AL*AL)
42. 5 CONTINUE
43.С
44 С SET UP ARRAYS, В AND G
45 С
46 DO 7 I » 2,NX,INT
47 IM « I - 1
48 IF(INT .EQ. 2)GOTO 6
49 BA,IM) = 0.
50 BB,IM) » l.'/DXS + 1./6.
51 В(ЗДМ) = -2./DXS + 2./3.
52 BD,IM) = BBfIM)
53 BE,IM) = 0.
54 G(IM) = (F(I-l) + 4.*F(I) + F(M))/6.
55 GOTO 7
Рис. 5.19. Распечатка программы STURM (начало).
§ 5.4. МКЭ и уравнение Штурма—Лиувилля 179
3* 6 BA,IM)
57 BB,IM)
58 BC,IM)
59 BD,IM)
60 BE,IM)
0.
4.*A./DXS + O.D/3.
4.*<-2./DXS + 0.8)/3.
BB,IM)
0.
61 G(IM) • 0.4МГЦ-1) + 8.*F(D + F(I+D)/3.
62 Bd,I)
63 BB,I)
64 BC,I)
65 BD,I)
2.M-0.25/DXS - O.D/3.
2.M2./DXS + 0.2)/3.
2.M-3.5/DXS + 0.8)/3.
BB,I)
66 ыъ,:
67 Gd) « -0.1*(F(I-l)+F(I+3)) + 0.2*(F(I)^T(I+2)) ¦ 0.8*F(W)
68 G(I) « 2.*G(I)/3,
69 7 CONTINUE
70 С
71 С ADJUST FOR BOUNDARY CONDITIONS
72 С
73 BB,l) • 0.
74 B(l,2) » 0.
75 BOiNXP) « 0.5*BC,NXP)
76 BD,NXP) « 0.
77 BE,NXP) * 0.
78 IF(INT .EQ. l)G(NXP) * (F(NXP) + 2.*F(NX))/6.
79 IFdNT .EQ, 2)G(NXP) « 2.*(-0.1*F(NXP-l) + 0.2*F(NXP) + 0.4*F(NX))
80 С
81 С SOLVE BANDED SYSTEM OF EQUATIONS
82 С
83 CALL BANFAC(B,NXP,INT)
84 С
85 С
86 CALL BANSOL(G,YD,B,NXF,XNT)
*7 С
88 С
89 С COMPUTE RMS ERROR
90 С
91 SUM * 0.
92 DO 9 I « 2,NX
93 Y(I) * YD(I-l)
94 DY * Y(I) - YEXd)
95 SUM « SUM + DY*i>Y
96 IF(IPR .EQ. 0)GOTO 9
97 VRITEFf8)I,Xd),Yd),YEXd),DY
98 8 FORMATC I«f,I3ff X»\F7.5,' Y-4F7.5,1 YEX«I,F7.5,1 DY»'f
99 1F7.5)
100 9 CONTINUE
101 RMS * SQRT(SUM/ANX)
102 WRITEF,10)RMS,NX
103 10 FORMAT*//,* RMS«\E10.3,f NX»1,13)
104 STOP
105 END
Рис. 5.19 (окончание).
12*
180
Гл. 5. Методы взвешенных невязок
тывается и выводится на печать (строки 87—103) среднеквад-
среднеквадратичная ошибка как разность между значениями Y, выданны-
выданными после обращения к BANSOL, и точным решением.
Типичная выдача для случая линейной интерполяции при
Ад: = 0.125 представлена на рис. 5.20. Показанное решение со-
соответствует следующему набору коэффициентов щ в уравне-
уравнении E.66):
Л1 = 1.000, а2=—1.000, а3= 1.000,
а4=—1.000, а5= 1.000.
Результаты, показанные на рис. 5.20, свидетельствуют о том,
что в общем случае ошибка решения меньше вблизи границы с
условием Дирихле, чем вблизи границы с условием Неймана.
STURM-LIOUVILLE PROBLEM, FEM:LINEAR INTERPOLATION
NX= 9 A= .100E+01 -.100E+01 .100E+01 -.100E+01
.100E+01
1= 2 X= .12500 Y= .11631 YEX= .11721 DY=-.00089
1= 3 X= .25000 Y= .22691 YEX= .22733 DY=-.00042
1= 4 X= .37500 Y= .33732 YEX= .33833 DY=-.00100
1= 5 X» .50000 Y= .44403 YEX« .44633 DY=-.00230
1= 6 X= .62500 Y= .53796 YEX= .53943 DY=-.00147
I» 7 X= .75000 Y= .62765 YEX= .62899 DY=-.00134
1= 8 X= .87500 Y= .71190 YEX= .71739 DY=-.00549
1= 9 X=l.00000 У* .74987 YEX= .75848 DY=-.00861
RHS= .380E-02 NX= 9
Рис. 5.20. Типичная выдача после прохождения программы STURM.
В табл. 5.10 приводится сравнение среднеквадратичных оши-
ошибок решения при линейной и квадратичной интерполяции и при
измельчении сетки.
Таблица 5.10. Ошибки решения для задачи
Штурма — Лиувилля
Размер
ячейки,
Ах
1/8
1/12
1/16
1/20
Среднеквадратичная ошибка
Линейная
интерполяция
0.00380
0.00163
0.000904
0.000562
Квадратичная
интерполяция
0.00148
0.000178
0.000056
0.000023
§ 5.5. Другие приложения метода конечных элементов 181
Следует отметить такие особенности результатов, приводи-
приводимых в табл. 5.10:
1. Интерполяция высокого порядка (т. е. квадратичная)
оказывается лишь ненамного более точной, чем интерполяция
низкого порядка (линейная), если применяется очень грубая
сетка.
2. При измельчении сетки точность интерполяции высокого*
порядка возрастает с большей скоростью, чем для интерполя-
интерполяции низкого порядка.
3. Теоретические скорости сходимости оказались приближен-
приближенно достигнутыми (пропорционально Ах2 в случае линейной ин-
интерполяции и пропорционально Ах3 в случае квадратичной ин-
интерполяции).
Стоит напомнить, что при применении метода конечных эле-
элементов аппроксимирующие и весовые функции отличны от нуля
лишь внутри малой области, окружающей рассматриваемый
узел. Следовательно, метод конечных элементов является ло-
локальным методом. Как и в случае конечно-разностного метода,
уравнения (алгебраические), возникающие при использовании
метода конечных элементов, связывают между собой узловые
значения неизвестных лишь внутри малой области. Однако при
решении многомерных задач число охватываемых таким обра-
образом узлов для метода конечных элементов существенно больше,
чем для метода конечных разностей (см. § 8.3 и книгу [Flet-
[Fletcher, 1984].
§ 5.5. Другие приложения метода конечных элементов
В данном параграфе метод конечных элементов применяет-
применяется к решению уравнения диффузии (п. 5.5.1), уравнения Пуас-
Пуассона (п. 5.5.2) и уравнения Лапласа (п. 5.5.3). Первая из этих
задач позволяет проиллюстрировать обычную для метода ко-
конечных элементов практику, когда дискретизируются только
пространственные члены. Дискретизация члена с производной
по времени осуществляется как отдельный этап. Во второй за-
задаче вводятся две пространственные координаты, в результате
чего усложняется структура дискретизированных уравнений.
Третья задача дает представление о реализации изопараметри-
ческой формулировки, весьма полезной для вычислительных
областей неправильной формы.
5.5.1. Уравнение диффузии
Этот пункт посвящен применению метода конечных эле-
элементов к решению одномерного уравнения диффузии
182 Гл. 5. Методы взвешенных невязок
(теплопроводности)
au
в интервале 0 ^ х ^ 1_и t^ 0. Предполагается, что начальное
условие имеет фор^у Т(х> 0)=Т0(х), а граничные условия за-
записываются в виде Г@, t)=anT(l9t) = b.
Введение тех же самых линейных аппроксимирующих функ-
функций E.70), которые использовались в задаче Штурма — Лиу-
вилля, и такой же способ применения метода Галёркина с ко-
конечными элементами дают на однородной сетке следующий ре-
результат для внутренних узлов:
dt J,.! "T" 3 L dt J, "*" 6 L dt J/+1 Ax2 — U#
Для указанных выше граничных условий Дирихле не требуется
вводить дискретизированные уравнения у граничных узлов.
С учетом того что конечно-элементная формулировка при-
применяется только к пространству, член dT/dt в уравнении E.90)
подвергается такой же обработке, как и непродифференциро-
ванный (по пространству) член У в уравнении E.66). Не уди-
удивительно поэтому, что в E.91) и E.83) появляются одни и те
же весовые множители A/6, 2/3, 1/6). Если dT/dt заменяется
на ATn+l/&t, а последний член в левой части уравнения E.91)
вычисляется как средневзвешенная величина по отношению к
n-му и (п + 1)-му слоям по времени, т. е. так, как в уравнении
G.24), то результат принимает форму
+
(
3 V М /"^бЧ At
E.92)
где параметр р регулирует степень неявности. Уравнение
E.92) можно представить в следующей компактной форме:
л/— = а 1A — Р) L^r/ + р!^Г/ J = 0, E.93)
где АГ/4 = Г/+1 — Г/ и массовый, и разностный операторы
Мх и Lxx определяются соответственно формулами
А1, = A/6, 2/3, 1/6), Lxx = (l/Ax\ -2/Ax2, 1/Ajc2).
§ 5.5. Другие приложения метода конечных элементов 183
Сравнение с неявной конечно-разностной схемой G.24) по-
показывает, что единственная разница между ними состоит в том,
что член с производной по времени в конечно-элементном ва-
варианте разбит на слагаемые, определяемые в соседних узлах.
Уравнение G.24) может быть приведено к форме уравнения
E.93), если дать следующее определение массового оператора:
Afid = @, 1, 0).
Подобие структуры уравнения E.93) и уравнения E.90),
послужившего его прообразом, наталкивает на мысль о том,
что метод конечных элементов можно интерпретировать как по-
почленный процесс дискретизации наподобие конечно-разност-
конечно-разностного метода. Такая интерпретация изучается в приложении А.2
и используется в § 8.3.
После перестановки членов уравнения E.93) можно полу-
получить неявный алгоритм
(Мх - AtafiLxx) 77+1 = [Мх + А/а A - р) Lxx] Г?. E.94>
Важность структуры соотношения E.94) можно лучше оце-
оценить после прочтения § 7.2. Многократное применение соот-
соотношения E.94), центрируемого в каждом из узлов по очереди,
позволяет получить трехдиагональную систему уравнений, ко-
которую можно решить с помощью алгоритма Томаса (см.
п. 6.2.2).
Как будет видно далее, приравнивание р = 0 в случае
конечно-разностной схемы G.24) приводит к явному алгорит-
алгоритму. Это не так в случае рассматриваемой схемы вследствие «не-
«неявного» характера оператора Мх. Однако благодаря симмет-
симметричной природе операторов Мх и Lxx, из соотношения E.94)
все же можно получить явную схему, если сделать специальный
выбор М = Да:2/(бар).
Соотношение E.94) согласуется с уравнением E.90) при
ошибке усечения О (А/2, А*2), если р = 0.5, и обладает безус-
безусловной устойчивостью, если р ^ 0.5. При специальном выборе
Р = 0.5 соотношение E.94) было применено к анализу приме-
примера, рассмотренного в п. 7.2.5; результаты анализа приведены в
табл. 7.6.
5.5.2. DUCT: течение вязкости жидкости
в канале прямоугольного сечения
Здесь метод конечных элементов будет использован с целыа
представления в дискретной форме характерной двумерной за-
задачи. Полностью развитое ламинарное течение вязкой жидко-
жидкости в канале прямоугольного сечения (рис. 5.21) определяется
184 Гл. 5. Методы взвешенных невязок
уравнением импульсов в проекции на ось г\
где осевая скорость w(x, у) должна быть определена при за-
заданном градиенте давления dp/dz и заданной вязкости \i.
С точки зрения вычислений целесообразно привести E.95)
к безразмерной форме путем введения величин
E-96)
Тогда уравнение E.95) принимает вид (индекс nd опущен)
E.97)
дх2 ' ду2 • А—-
с граничными условиями
о> = 0 при х = ±1, у = ±\. E.98)
Следуя процедуре наподобие той, которая в п. 5.4.1 при-
применялась к уравнению Штурма — Лиувилля, для w вводится
пробное решение вида
w = Yj wdi (x9 у), E.99)
где 4>i{x, у)—двумерные интерполя-
интерполяционные функции, как правило, опре-
определяемые формулами, эквивалентны-
эквивалентными E.60) или E.62). Для данной
Рис. 5.21. Течение вязкой задачи на каждом из элементов будут
жидкости в канале прямо- введены билинейные интерполяцион-
угольного сечения. ные функции по схеме, представлен-
представленной на рис. 5.15.
Подстановка выражения E.99) в уравнение E.97), приме-
применение галёркинской формулировки в виде E.5) и E.10) и не-
некоторые простые перестановки приводят к следующей системе
алгебраических уравнений:
BW=G, E.100)
где компонентами вектора W являются неизвестные узловые
значения до,-, фигурирующие в "E.99), тогда как элементами
матрицы В являются выражения
^^^^ъ^<^^^
-1 -1
§ 5.5. Другие приложения метода конечных элементов 185
1
а компонента вектора G задается формулой
1 1
\tm\dxdy. E.102)
-1 -1
Параметр т соответствует номерам всех внутренних узлов,,
т. е. 2</<№Х—1, 2<Л<ЛГУ—1. Интегралы в E.101)
лучше всего вычислять для каждого элемента по отдельности,,
используя элементные координаты (?, г]), как в E.64). Нуле-
Нулевые вклады в глобальные интегралы в правых частях E.101)
и E.102) вносят лишь по четыре соседних прямоугольных эле-
элемента, окружающих узел т.
Структура выражений E.101) -и E.102) аналогична струк-
структуре выражений E.77) и E.78), если не считать того, что
интегрирование теперь ведется по двум измерениям вместо
одного. Интерполяционные функции ^(х, у) оказываются та-
такими, что вклады в интегрирование могут быть определены в
форме произведений одномерных интегралов (см. приложе-
приложение А.2).
В случае однородной сетки уравнение E.100) приобретает
особенно компактную форму
hk = -l, E.103>
где индексы /, k соответствуют глобальной сетке (рис. 5.11).
Операторы Lxx и Lyy в уравнении E.103)—это направленные
разностные операторы
Lxx = A/Д*2, -2/Дл:2, 1/Д*2),
Lyy = (l/\y*, -2/Ay>, 1/АуУ, {
а Мх и Му — направленные массовые операторы
МХ = МТУ = A/6, 2/3, 1/6); E.105)
наконец, символ ® обозначает тензорное произведение. Опера-
Операторы имеют следующий смысл:
Lxxwu k = др> .
Mywu k = A/6) wu k_x + B/3) wu k + A/6) wu k+u
J
Комплекс Мх ® LyyWjf k имеет аналогичную структуру.
186 Гл. 5. Методы взвешенных невязок
Трехточечная конечно-разностная дискретизация уравнения
E.97), эквивалентная данной, имеет вид
1
Ах2 "Г A*/2 "~ A
E.107)
и может быть представлена в форме E.103), если определить
JHxffd = AfJffd = (O, 1, 0).
Сами по себе массовые и разностные операторы, фигури-
фигурирующие в уравнении E.103), идентичны тем операторам, кото-
которые фигурировали в уравнении E.93). Главным отличием пер-
первого из указанных уравнений от второго является то, что в
результате интегрирования по двум измерениям возникает тен-
тензорное произведение одномерных операторов. Указанное отли-
отличие и обозначения массовых операторов были использованы в
§ 8.3. Более подробное обсуждение этих обозначений дается в
приложении А.2. Важность введенного обозначения состоит в
том, что оно позволяет осуществлять почленную конечно-эле-
конечно-элементную дискретизацию вполне аналогично тому, как это де-
делается в методе конечных разностей.
Систему уравнений, получаемую путем записи уравнения
E.103) для каждого внутреннего узла (/ = 2, ..., / — 1;
k = 2, ..., К— 1), очень удобно решать с применением ПВР
(см. § 6.3) подобно тому, как это делалось в п. 5.2.3. Чтобы
обеспечить согласование с распечаткой программы DUCT
(рис. 5.22), соответствующий алгоритм записывается в форме
w* k = 0.75 [1. + (PAR 1/6) X
X К_ьk+l + t«7+li k+l + wpl k_x + vfj+l k_x) +
+ PAR2 (wl k+l + <+'_,) + PAR3 («?+i A+«7+li 01/PAR1,
E.108)
$где
PAR1 = (b/aJ/\x2 + I/A/,
PAR2 = [- (b/aJ/Ax2 + 2/A#2]/3,
PAR3 = [2 (b/aJ/&x2 - l/A/J/3.
•С помощью соотношения E.108) определяется предваритель-
предварительное решение, а формула E.109) дает улучшенное решение
«7Л1 = Kk + *• К k - К *), E- Ю9)
где X — параметр релаксации согласно ПВР.
Вышеприведенная формулировка реализуется в программе
DUCT (рис. 5.22) с целью определения распределения скорости
в канале прямоугольного сечения (рис. 5.21). Программа
1
2 С.
3 € DUCT.FOR COMPUTES THE FULLY DEVELOPED YISCOUS LAMINAR FLOW IN К
4 С RECTANGULAR CHANNEL OF ASPECT RATIO, B/A (* BAR), BY FEH (LINEAR
5 С ELEMENTS) AND FDM OPT CENTERED DIFFERENCES).
6 С SOR IS USED TO OBTAIN ITERATIVE SOLUTION
7 С
8 DIMENSION WEXD1,41),WAD1,41)
9 С
10 OPENA,FILE»'DUCT.DAT')
11 OPENF,FILE*'DUCT.OUT1)
12 READA,1)NX,ME,NEM,IPR,ITMX,BAR,EPS,OM
13 1 FORMATEI5,3E10.3)
14 С
15 IF(ME .EQ. i)VRITEF,2)
16 IF(ME .EQ. 2)VRITEF,3)
17 2 FORMAT С DUCT FLOW BY FEM: LINEAR ELEMENTS')
18 3 FORMAT*f DUCT FLOW BY FDM: 3PT CEN. DIFF.1)
1* WRITEF,4)NX,NEM,BAR,ITMX,EPS,OM
20 4 FORMATC NX*\I3,f NEM«\I2,f B/A»a,F5.2,a MAX ITER «\I4,
21 1' CONY TOL » \E10.3,f OM » \F6.3,//)
22 С
23 PI * 3.1415927
24 NH « NX/2 + 1
25 NY * NX
26 NXP « NX - 1
27 NYP « NXP
28 ANX « NXP
29 DX * 2./ANX
30 DXS * DX'DX
31 DY « DX
32 DYS * DXS
33 BAS « BAR*BAR/DXS
34 PAR1 « BAS + l./DYS
35 PAR2 » B./DYS - BAS)/3.
36 PAR3 » B.*BAS - l./DYS)/3.
37 С
38 С SET UP EXACT AND INITIAL SOLUTIONS
39 С
40 DO 7 J « 1,NX
41 AJ « J - 1
42 X « -1. + AJ*DX
43 DO 5 К « 1,NY
44 AIC « К - 1
45 Y « -1. + AK*DY
46 С
47 CALL VEL(X,Y,NEM,PI,BAR,VD,QLX)
48 С
49 VEX(JrK) « WD
50 VA(J,K) * WD
51 5 CONTINUE
52 IF(IPR .EO. COGOTO 7
53 VRITEF,6)(VEX(J,K),K
54 6 FORMAT{• WE*•Д0F7.4)
55 7 CONTINUE
5S WRITEF,8)
57 $ FORMATC/)
Рис. 5.22. Распечатка программы DUCT (начало).
58 С
59 С ITERATE USING SOR
60 С
€1 DO 13 I a lilTHX
62 SUM « o.
63 DO 12 J * 2,NXP
64 JM ¦ J - 1
65 JP » J + 1
66 DO 11 К « 2,NYP
67 KM - К - 1
68 KP = К + 1
69 IF(ME .EQ. 2)GOTO 9
70 DUK * 1. + PAR1/6.*(WA(JM,KP) + WA(JP,KP) + WA(JM,KM) + VA(JP,KM)>
71 DUM « DUM + PAR2*(WA(J,KP) + WA(J,KM)) + PAR3*(WA(JM,K) +WA(JP,K))
72 WDD * O.75*DUM/PAR1
73 GOTO 10
74 9 DUH - 1. + BAS*(WA(JM,K) + VA(JP,K)) + (VA(J,KH) + WA(J,KP))/DYS
75 VDD * O.5*DUH/PAR1
76 10 DIF = VDD - VA(J,K)
77 SUH « SUM + DIF*DIF
78 VA(J,K) ¦ WA(J,K) + OM*DIF
79 11 CONTINUE
30 12 CONTINUE
Bl RMS * SQRT(SUM/(ANX-1.)/(ANX-1.))
«2 IF(RMS .LT. EPS)GOTO 15
*3 13 CONTINUE
84 VRITEF,14)ITMX,RMS
35 14 FORMAT С CONVERGENCE NOT ACHIEVED IN1,15,' STEPS \5X,
36 I1 ITER RMS * \E12.5)
87 С
38 С COMPARE SOLUTION VITH EXACT
39 С
SO 15 SUM * 0.
91 QL* « 0.
92 DO 18 J » 2,NXP
93 DO 16 К « 2,NYP
94 DIF « VA(J,K) - VEX(J,K)
95 SUM « SUM + DIF*DIF
96 QL » QL + WA(J,K)
97 16 CONTINUE
98 IFUPR .EQ. 0)GOTO 18
99 WRITEte,!?)(VA(J,K),K»2,NYP)
100 17 FORMATC VA=\11F7.4)
101 18 CONTINUE
102 QL « QL*DX*DY
103 RMS » SQRT(SUM/(ANX-1.)/(ANX-1.))
104 WRITEF,19I.RMS
105 VRITEF,21)VA(NH,NH),VEX(NH,NH)
106 VRITEFr20)QL,QLX
107 19 FORMAT(/r' CONVERGED AFTER \I3,f STEPS1,5X,'SOL RMS «\E12.5,//)
108 20 FORMATC COMP. FLOW RATE * I/E12.5,1 EXACT FLOW RATE » ',E12.5)
109 21 FORMATC W(C/L)*I,E12.5,1 WEX(C/L)«f ,E12,5,//)
110 STOP
111 END
Рис. 5.22 (окончание).
§ 5.5. Другие приложения метода конечных элементов
189
DUCT считывает (и выводит на печать) различные управляю-
управляющие параметры (строки 10—21). Задаются точное решение и
его начальная форма (строки 37—51). При решении данной за-
задачи число итераций по схеме ПВР не представляет интереса,
поэтому в качестве начальной формы решения по ПВР при-
применялось точное решение. Подпрограмма VEL (строка 47 на
1
2
3 С
4 С
5 С
6 С
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
SUBROUTINE VEL(X,Y,N,PI,BAR,V,QL)
FOR GIVEN X,Y COMPUTES AXIAL VELOCITY IN CHANNEL
AND COMPUTES THE FLOW RATE
CON = (8./PI/PI)**2
XAN * 0.5*PI*X
YAN « 0.5*PI*Y
W = 0.
QL * 0.
DO 2 I = 1,N,2
AI = I
CX = COS(AI*XAN)
DO 1 J « 1,N,2
AJ « J
CY = COS(AJ*YAN)
IJ » (I+J)/2 - 1
IF(IJ .EQ. O)SIG = 1.0
IF(IJ .GT. O)SIG = (-l.)**IJ
DEN = AI*AJM(AI*BAR)**2 + AJ*AJ)
DUM « SIG*CX*CY/DEN
V = V + DUM
QL ¦ QL + l./DEN/AJ/AI
CONTINUE
CONTINUE
V * CON*V
QL = A6./PI/PI)*CON*QL
RETURN
END
Рис. 5.23. Распечатка подпрограммы VEL.
рис. 5.22 и рис. 5.23) вычисляет точное решение, получаемое
по методу разделения переменных (см. п. 2.5.2), и имеющее
вид
p cos@.5^)cos@.5y^)J,
E.110)
*
8 2
= Ы
L
i-l, 3,5, ... / = 1,3,5, ...
NEX
NEX
1, 3,5, ... / = 1, 3,5, ...
где полный расход потока равен qt= \\ wdxdy.
190
Гл. 5. Методы взвешенных невязок
Далее программа DUCT (строки 58—83) ведет счет по фор-
формулам E.108) и E.109) с помощью итераций, пока величина
\w*{ ъ — w, А не станет меньше заданной малой величины
I! /» Л /¦ Л llrms
EPS. После этого (строки 87—106) решение сравнивается с
точным решением и выводится на печать. Основные параметры,
используемые в программе DUCT, приводятся в табл. 5.11.
Таблица 5.11. Параметры, используемые в программе DUCT
Параметр
NX
ME
NEM
IPR
ITMX
EPS
OM
X, Y
VEL
WEX
WA
WDD
RMS
QL
QLX
Описание
( = NY), число точек в направлениях х и у
= 1, метод конечных элементов с линейными элементами,
= 2, метод конечных разностей с трехточечной центриро-
центрированной схемой
Число членов в выражении для точного решения
Параметр управления печатью
Максимальное число итераций (ПСР)
Критерий сходимости (ПСР)
Показатель релаксации X (ПСР)
Безразмерные координаты х> у
Подпрограмма для вычисления точного значения скорости в
точке (х, у) и полного расхода
Точное значение осевой скорости w
Вычисленное значение осевой скорости w
1 Ш/. k - »/. к llrms' 1»/. k - *|/. *|ш»
Вычисленное значение полного расхода
Точное значение полного расхода qi
Таблица 5.12. Изменение точности решений по программе DUCT
по мере измельчения сетки (Ь/а = \)
Сетка
Метод
Конечных
элементов
Конечных
разностей
6X6
rms
0.007239
0.006480
0.5295
0.4949
и х и
rms
0.001571
0.001480
0.5540
0.5446
21 Х21
rms
0.000256
0.000205
0.5598
0.5583
Точное
значе-
значение
ь
0.5623
0.5623
§ 5.5. Другие приложения метода конечных элементов 191
Типичная выдача в результате прохождения программы DUCT,
предназначенной для решения с линейными конечными элемен-
элементами, полученного на сетке 6X6, показана на рис. 5.24.
Эффект измельчения сетки как для метода конечных эле-
элементов, так и для метода конечных разностей демонстрируется
DUCT FLOW BY FEM: LINEAR ELEMENTS
MX* 6 NEM=21 B/A« 1.00 MAX ITER = 30 CONV TOL * .1C0E-C1 О
VE= .0000 .0000 .0000 .0000 .0000 .0000
WE» .0000 .1386 .1926 .1926 .1386 .0000
WE* .0000 .1926 .2750 .2750 .1926 .0000
WE= .0000 .1926 .2750 .2750 .1926 .0000
WE» .0000 .1386 .1926 .1926 .1386 .0000
1ГЕ» .0000 .0000 .0000 .0000 .0000 .0000
VA= .1453 .1990 .1989 .1453
VA= .1990 .2842 .2842 .1989
1fA« .1989 .2842 .2842 .1989
WA= .1453 .1989 .1989 .1453
CONVERGED AFTER 10 STEPS SOL RMS « .72390E-02
V(C/L)= .28421E+00 WEX(C/L)= .27502E+00
СОИР. FLOW RATE = .52952E+00 EXACT FLOW RATE » .56227E+00
Рис. 5.24. Типичная выдача после прохождения программы DUCT.
в табл. 5.12. Очевидно, что оба метода имеют сходимость, про-
пропорциональную Ал:2, Д#2, причем метод конечных разностей
дает несколько меньшую среднеквадратичную ошибку, но не-
несколько большую ошибку по значению расхода потока qu
5.5.3. Вычислительные области неправильной формы:
изопараметринеское преобразование
В период приблизительно между 1965 и 1970 гг., когда ме-
метод конечных элементов впервые приобрел популярность, ши-
широко использовались треугольные элементы, так как именно
они позволяли моделировать сложные геометрические формы.
Эти треугольные элементы и соответствующие им интерполя-
интерполяционные формулы описываются в книге [Zienkiewicz, 1977].
Способность метода конечных элементов к рассмотрению
вычислительных областей, имеющих неправильную форму и
неоднородных, всегда была важной характерной чертой этого
192
Гл. 5. Методы взвешенных невязок
метода. Однако для моделирования сложных вычислительных
областей могут быть введены также и деформированные пря-
прямоугольные элементы через посредство применения изопара-
метрического преобразования. Предпочтение, отдаваемое пря-
прямоугольным элементам по сравнению с треугольными, объяс-
объясняется тем, что первые легче приспособить к взаимодействию
с программами формирования сеток (см. гл. 13), особенно в
трехмерных случаях. Тем не менее в работе [Jameson, Baker,
1986] разработана эффективная процедура, базирующаяся на
введении тетраэдральных элементов с целью моделирования
области, внешней по отношению к целому самолету.
4
В
^=1
р-1 2
Рис. 5.25. Изопараметрическое преобразование.
Характерная ситуация иллюстрируется на рис. 5.25. Элемен-
Элементы, показанные в физической плоскости (х, у), подверглись де-
деформации. Однако они без труда могут быть преобразованы в
элементы правильной формы в пространстве (?, г\), переход к
которому осуществляется по формулам (для случая билиней-
билинейной интерполяции)
E.112)
где (xi, у{)—координаты /-го угла элемента В в физическом
пространстве, а <?/(?, ц)—это те же самые билинейные аппрок-
аппроксимирующие функции, которые были определены формулой
E.59). Использование изопараметрического преобразования
оказывает влияние на вычисление интеграла E.5), содержаще-
содержащего взвешенную невязку.
WXY
§ 5.5. Другие приложения метода конечных элементов 193
В качестве примера применение метода Галёркина с конеч-
конечными элементами к задаче о решении уравнения Лапласа в
деформированной области (см. п. 5.2.3) приводит к линейной
системе уравнений, эквивалентной E.100), т. е.
BW=G. E.113)
Элемент Матрицы В задается выражением
WXYZ
где т — индекс узла, в котором центрируется весовая функция,
а / — индекс узла, вносящего свой вклад. В E.114) интегриро-
интегрирование выполняется по площади WXYZ (рис. 5.4). Однако для
того чтобы обобщить анализ на случай произвольных по форме
областей, прямое вычисление интеграла из E.114) в физиче-
физическом пространстве не будет пригодным.
Философия, стоящая за применением изопараметрического
преобразования, сводится к тому, что в преобразованном про-
пространстве (|, т]), где элементы имеют правильную форму, чис-
численная реализация интегрирования может быть проведена не-
непосредственно. Чтобы проиллюстрировать этот тезис, сосредо-
сосредоточим свое внимание на первом члене правой части E.114),
т. е. на интеграле
Производные дф^/дх и дф\\д\) связаны с производными
дф}/д1 и дф]/дг\ с помощью соотношения
где якобиан [/] соответствует выражению
J
Отдельные члены, входящие в якобиан, вычисляются с по-
помощью формул E.112). Например,
Из соотношения E.116) можно получить следующие явные
выражения для величины дф,/дх (и дфт/дх), входящей в
13 К. Флетчер, т. 1
194 Гл. 5. Методы взвешенных невязок
интеграл E.115):
Очевидно, что в E.115) имеем dxdy = det /dgrfrj. Подстановка
выражения E.119) в интеграл E.115) дает следующий вклад
в bmt / от каждого элемента:
e== \ J VditrMaf Л1п7 ~
Преимущество формулировки, основанной на изопарамет-
рическом преобразовании, сводится к тому, что все члены в
правой части E.120) являются функциями (|, х\), тогда как
элементы в пространстве (g, т|) имеют правильную форму, как
это и показано на рис. 5.25. Следовательно, для выполнения
интегрирования можно применить некий удобный прием, напри-
например квадратуру Гаусса [Isaacson, Keller, 1966]. Более подроб-
подробное описание изопараметрического преобразования и соответ-
соответствующей формулировки можно найти в книге [Zienkiewicz,
1977].
§ 5.6. Спектральный метод
Спектральный метод использует приближенное решение в
той же форме E.1), что и традиционный метод Галёркина. Как
и в традиционном методе Галёркина, аппроксимирующие и
весовые функции отличны от нуля во всей вычислительной об-
области. В этом отношении и спектральный метод, и традицион-
традиционный метод Галёркина являются глобальными методами [Flet-
[Fletcher, 1984]. В противоположность тому, что имеет место в ме-
методе конечных элементов, неизвестные коэффициенты a,j(t) в
приближенном решении E.1) не могут быть отождествлены с
узловыми значениями неизвестных.
Наиболее существенное отличие спектрального метода от
традиционного метода Галёркина состоит в том, что первый
из них использует в качестве аппроксимирующих и весовых
функций ортогональные функции. Аппроксимирующие и весо-
весовые функции являются ортогональными, если
Ф 0 при т = /,
= 0 при т ф /.
§ 5.6. Спектральный метод 195
Примерами ортогональных функций служат ряды Фурье, по-
полиномы Лежандра и полиномы Чебышёва.
В том примере, который мы вскоре разберем, будет видно,
что использование ортогональных аппроксимирующих и весо-
весовых функций упрощает структуру (обыкновенных дифферен-
дифференциальных) уравнений, получаемых при применении спектраль-
спектрального метода. Кроме того, при надлежащей постановке гранич-
граничных условий спектральный метод позволяет получить решения
очень высокой точности при сравнительно небольшом числе
членов в выражении приближенного решения, если только точ-
точное решение является достаточно гладким. Эти аспекты об-
обсуждаются в книгах [Fletcher, 1984; Canuto et al., 1987].
5.6.1. Уравнение диффузии
Технику реализации спектрального метода легче всего по-
понять на конкретном примере. Будет рассмотрено уравнение
диффузии __
дТ д2т п /с 1О1Ч
-5Г-«!?¦ = О E.121)
в вычислительной области O^x^l, так что будет возмож-
возможность провести непосредственное сравнение данного метода с
методами конечных разностей и конечных элементов. Гранич-
Граничные и начальные условия предполагаются следующими:
Г@, 0 = 0, f(l,t)=l и T(x9O)=sin(ax)+x. E.122)
Отправной точкой при использовании спектрального мето-
метода является введение приближенного решения
Т = sin (лх) + х + ? а, @ sin (jnx), E.123)
/-i
где cij(t)—неизвестные коэффициенты. Форма решения E.123)
автоматически удовлетворяет граничным и начальным усло-
условиям. Подстановка E.123) в E.121) позволяет найти невязку
R = Yj ["IF + a ti*)
Yj ["IF + a ti*)fl/J sin Unx) + ал;2 sin
/-1
Вычисление интеграла с весом, т. е. интеграла E.5) с весовой
функцией E.10), а именно
^ [sin (mnx)R]dx= 0,
о
13*
196 Гл. 5. Методы взвешенных невязок
дает
j~ + a(jnJaA \ [sin (mnx) sin (jnx)] dx +
-f- «я2 \ [sin (mnx) sin (nx)] dx = 0. E.124)
о
Преимущество использования ортогональных функций в E.124)
состоит в том, что первый из фигурирующих там интегралов
отличен от нуля, только если / = т, а второй интеграл не ра-
равен нулю, только если т= 1. Следовательно, уравнение E.124)
принимает форму
^L-f a(mnJam + rm = 0, /п=1, ...,/, E.125)
где
( ая2, если т = 1,
гт = \ Л _^, E.126)
т { 0, если тФ 1. х '
Решение уравнения E.125) можно записать непосредственно
в виде
После этого выражение E.123) принимает вид
Т = sin (ял:) е~апЧ + х, E.127)
который фактически является точным решением уравнения
E.121). Такой результат получился случайно благодаря спе-
специальному выбору граничных и начальных условий E.122).
Ситуация станет более реалистической, если начальное усло-
условие задать в виде
Xf \J) Эл — **Л , ^О. 1ZO^
а в приближенном решении E.123) комплекс sm(nx)+x за-
заменить на 5л: — 4х2. Применение спектрального метода с ус-
условием E.128) аналогично тому, что описывалось выше, за
исключением того, что формулы E.126) принимают вид
ii*Lt m= 1 3, 5, ...,
m E.129)
0, т = 2, 4, 6, ....
Если в уравнении E.125) величину dam/dt заменить формулой
с разностью вперед по времени (ап+{—аМ/Д/, то можно по-
§ 5.6. Спектральный метод
197
лучить следующий явный алгоритм:
ап+1 _ ап^ _ д/ ^(<х/пяJ Q^ + rV E.130)
В данном случае соотношение E.130) было проинтегрировано
с шагом Д? = 0.001. Результаты для различных значений / по-
показаны в табл. 5.13. В эту таблицу включены также точное ре-
решение Г и приближенное решение Ть, содержащее только ошиб-
ошибки, связанные со схемой численного интегрирования. Точное
Таблица 5.13. Спектральные решения уравнения E.121) при * = 0.5
X
0.00
0.02
0.04
0.06
0.08
О.Ю
0.12
0.14
0.16
0.18
, 0.20
Приближенное решение Т
1.500
1.314
1.162
1.037
0.935
0.851
0.782
0.725
0.679
0.641
0.610
/ = 3
1.500
1.347
1.199
1.075
0.973
0.889
0.820
0.764
0.717
0.679
0.648
/-5
1.500
1.338
1.191
1.067
0.965
0.881
0.812
0.755
0.709
0.671
0.640
Приближен-
Приближенное
решение
ТЬ
1.500
1.340
1.193
1.069
0.967
0.883
0.814
0.757
0.711
0.673
0.642
Точное
решение
Т
1.500
1.341
1.194
1.071
0.969
0.885
0.816
0.759
0.713
0.675
0.643
решение строится с помощью техники разделения переменных
(см. п. 2.5.2) и имеет вид
Т = х + 4 S {2/[B/ - 1) я]}3 sin [B/ - 1) пх] ехр {-а[B/ - 1)я]21).
E.131)
Приближенное решение Ть строится с помощью допущения о
том, что решение представляется в форме
Z
{2/[B/ - 1) я]}3 sin [B/ - 1) пх] Xf (t). E.132)
В результате подстановки в уравнение E.121) возникает не-
необходимость решить уравнение
dX,
E.133)
198 Гл. 5. Методы взвешенных невязок
Такое решение строится с помощью такой же разностной ап-
аппроксимации, какая делалась для ат в соотношении E.130) и
с тем же шагом по времени At = 0.001. Подстановка в E.132)
дает решение для ТьУ показанное в табл. 5.13.
Как показывают результаты, приводимые в табл. 5.13, ре-
решение Т становится более точным по мере увеличения /. Сле-
Следует, однако, помнить о том, что ошибка, отличающая Т от точ-
точного решения Г, происходит частично от аппроксимации, при-
присущей спектральному методу, а частично от ошибки за счет
разностной дискретизации производной по времени при построе-
построении численных решений для уравнения E.125). Что касается
разницы между двумя приближенными решениями, Т и Ть, то
она обусловлена исключительно ошибкой спектрального мето-
метода. Очевидно, что использование сравнительно малого числа
неизвестных в приближенном решении обеспечивает построе-
построение решения высокой точности. Это свойство характерно для
спектральных методов [Fletcher, 1984, гл. 6].
Приложения спектрального метода даны в п. 15.3.3 и
17.1.6. Традиционные области приложения этого метода отно-
относятся к глобальному метеорологическому моделированию
[Bourke et al., 1977], а также к прямому моделированию тур-
турбулентности [Orszag, 1977]. Обе эти области требуют исход-
исходных уравнений, включающих нелинейные члены, в особенности
для описания конвекции.
Желая, чтобы спектральный метод привел к эффективному
вычислительному алгоритму, необходимо ввести технику пре-
преобразования для учета нелинейных членов. Концептуально это
можно представить себе в форме введения локальных узловых
неизвестных Г/, заменяющих в выражении E.123) коэффи-
коэффициенты cij(t), тем самым представляя нелинейные члены в фор-
форме произведений Ti и а/, вычисляя затем заново коэффициенты
а}. Техника преобразований обсуждается в книгах [Fletcher,.
1984, гл. 5; Canuto et al., 1987].
5.6.2. Граничные условия Неймана
В п. 5.6.1 спектральный метод применялся к решению урав-
уравнения диффузии E.121) с граничными условиями Дирихле, что
привело к явной форме обыкновенных дифференциальных
уравнений E.125) относительно неизвестных коэффициентов
ат в пробном решении.
Теперь мы рассмотрим задачу с более трудными граничны-
граничными условиями для того, чтобы показать, что использование
спектрального метода нередко вызывает нужду в дополнитель-
дополнительных ухищрениях на этапе дискретизации. Пусть для конкрет-
§ 5.6. Спектральный метод 199
ности требуется решить уравнение диффузии E.121) в области
О ^ х ^1.0, t^O при начальном и граничных условиях
Т (х, 0) = 3 — 2х — 2л;2 + 2г\ E.134)
|f fl, 0=1.0. E.135)
Вместо того чтобы попытаться учесть начальное и граничные
условия в приближенном решении, как делалось в E.123),
введем общее приближенное решение вида
Т (х, t) = b0 (t) + t [<*j (t) sin B/я*) + Ь, (t) cos B/ях)]. E.136)
Чтобы выражение E.136) удовлетворяло граничным условиям
E.135), коэффициенты должны быть связаны соотношениями
? я/ Bя/) = - 2, ? Ь,- = 1. E.137)
С помощью E.137) коэффициенты а3 и bj могут быть исклю-
исключены из выражения E.136), что дает
/--1
Т = cos BJnx) + (^f) sin BJnx) + ? a, {sin [/ Bя;с)] -
/-1
- (i) sin [/ Bnx)]} + 2 a, {cos [/ Bях)] - cos [/ Bя*)]}.
/-0 E.138)
Реализация спектрального метода по Галёркину [Fletcher,
1984] требует, чтобы весовые функции в E.5) совпадали с
функциями, представленными в E.138), т. е.
Wm (x) = sin [m Bnx)] - (-^-) sin [/ Bя^)], 1 < m </ - 1
Подстановка E.138) в уравнение диффузии E.121) и расчет
согласно E.5) с учетом E.139) приводит к следующей систе-
системе обыкновенных дифференциальных уравнений:
do,
do, tn \—* j ( da г Л
-# + [а BятJ] am + Т2 у {-^f + [а Bл/J] а,\ = - 2а Bят),
'"=' E.140)
200 Гл. 5. Методы взвешенных невязок
f*
dt
/-1
+ [а Bя/пJ] Ьт + У №j- + [а Bя/J] Ь,} = а BnJf, E.141)
EЛ42)
У-о
Уравнения E.140) образуют систему связанных между собой
обыкновенных дифференциальных уравнений для определения
коэффициентов а/, не зависящих от обыкновенных дифферен-
дифференциальных уравнений E.141) и E.142) для определения коэф-
коэффициентов bj. Эти две системы решаются маршевым образом
по времени, чтобы предоставить значения aj(t) и bj(t), под-
подставляемые затем в выражение E.138), обеспечивая тем самым
численное решение Т(х, t).
Однако какой бы маршевый алгоритм ни был использован
при последовательном определении во времени коэффициентов
dj и bj, на каждом шаге по времени необходимо проводить на-
начальную факторизацию и матричное умножение. Если учесть,
что данная задача линейная и что достаточно точные решения
могут быть построены при сравнительно малом числе членов в
выражении приближенного решения E.136), добавочное время
исполнения алгоритма, связанное со взаимосвязанностью урав-
уравнений, не является чрезмерно большим.
Первоначальные значения aj и Щ получаются за счет под-
подгонки приближенного решения E.136) к начальному решению
E.134), т. е.
(x, 0)sinB/ji*)rfA;, &/ = 2$ Т(х, 0) cos B jnx)dx.
° E.143)
Численное решение данной задачи следует построить в зада-
задаче 5.17.
Имеется возможность воспользоваться альтернативной про-
процедурой, называемой тау-методом и тесно связанной с мето-
методом Галёркина. При использовании тау-метода весовые функ-
функции подбираются так, чтобы они соответствовали аппроксими-
аппроксимирующим функциям в выражении E.136), т. е.
Wm (х) = sin [m Bnx)}, 1 < m < / - 1,
W m (X) = cos [m Bnx)], l^m^J E'144)
Подстановка E.136) в уравнение E.121) и расчет согласно E.5)
на основе формул E.144) приводит к следующей системе
§ 5.6. Спектральный метод 201
обыкновенных дифференциальных уравнений:
Система уравнений E.145) является явной и имеет решения
ат @ = ат @)
1,
Ьт (t) = bm @) е-»»*»)»', 1< m < / E"Hb)
где am@) и bm@) определяются по формулам E.143), a aj(t)
и 6о(О удовлетворяют соотношениям E.137).
При решении данной задачи использование формул E.136),
E.137) и E.144) позволяет получить более эффективный алго-
алгоритм, чем применение спектрального метода Галёркина на осно-
основе формул E.138) и E.139). В общем случае тау-метод позво-
позволяет учесть трудные граничные условия с большей степенью
гибкости, чем это делает спектральный метод Галёркина (см.
п. 5.6.1). Описание тау-метода можно найти в книгах [Fletcher,
1984; Canuto et al., 1987].
5.6.3. Псевдоспектральный метод
Спектральный метод Галёркина (п. 5.6.1) приводит к весьма
точным решениям со сравнительно небольшим числом неиз-
неизвестных коэффициентов а; в выражении приближенного реше-
решения E.123). Однако при наличии нелинейных членов вычисле-
вычисление произведений приближенных решений отнимает очень мно-
много времени. Этот недостаток экономичности является причиной
использования метода коллокаций (см. формулу E.8)) вместо
метода Галёркина. Коллокация упрощает поиск решения в фор-
форме зависимости от узловых неизвестных значений подобно тому,
как это делают конечно-разностные и конечно-элементные ме-
методы, а не в зависимости от неизвестных коэффициентов а} в
приближенном решении. Явное использование узловых неиз-
неизвестных позволяет также осуществить более эффективный учет
граничных условий, чем это делается в спектральном методе
Галёркина. В литературе спектральный метод с коллокациями
принято обычно называть псевдоспектральным методом
[Orszag, 1971].
Применение псевдоспектрального метода будет проиллю-
проиллюстрировано здесь на примере решения уравнения диффузии
а 0 <5Л47)
202 Гл. 5. Методы взвешенных невязок
с начальным и граничными условиями
п(х, 0) = sin (ях) + х, й(—1, /)= — 1, йA, t)=l. E.148)
Производная по времени в уравнении E.147) дискретизирует-
ся с помощью конечно-разностной аппроксимации. Если для
указанной производной использовать разностную формулу Эй-
Эйлера, как в п. 5.6.1, то получается алгоритм
E.149)
Псевдоспектральный метод требует, чтобы соотношение E.149)
удовлетворялось в каждой из точек коллокации (лг/), и вводит
приближенное решение
JV+1
u(x,t)=Zak(t)Tk_l(x), E.150)
которое позволит вычислить пространственные производные.
Аппроксимирующими функциями в выражении E.150) служат
полиномы Чебышёва, определенные на интервале —1 ^ х ^ 1.
Полиномы Чебышёва позволяют точно определять производные
по пространству, и их обычно предпочитают тригонометриче-
тригонометрическим функциям, если функция и не является периодической.
Описание полиномов Чебышёва и общих вопросов их приме-
применения дается в книге [Fox, Parker, 1968]. Специальные рекур-
рекуррентные соотношения, связанные с применением спектрально-
спектрального и псевдоспектрального методов, приводятся в руководстве
[Gottlieb, Orszag, 1977].
Непосредственное использование выражения E.150) при-
приводит к следующему представлению d2u/dx2\j в уравнении
E.147):
I _ V а
В результате для перехода с временного слоя п на слой
п + 1 псевдоспектральный метод должен пройти через следую-
следующие этапы:
1) при заданном и^ вычислить а\ из выражения E.150);
2) при заданном с& вычислить [д2и/дх2]*} по формуле E.151);
3) вычислить ипЛх по формуле E.149).
Нетрудно видеть, что, хотя этап B) имеет место в спект-
спектральном пространстве, т. е. имеет дело с а*, этап C) реали-
реализуется в физическом пространстве, т. е. имеет дело с щ. Этап
§ 5.6. Спектральный метод 203
A) представляет собой преобразование перехода от физиче-
физического пространства к спектральному.
Эффективность псевдоспектрального метода зависит от того,
насколько экономично исполняются три указанных этапа. Вы-
Выясняется, что вычисление а\ по выражению E.150) требует
решения линейной системы Тая = urt, причем матрица Т плот-
плотная. Прямое применение метода исключения по Гауссу (см.
п. 6.2.1) для получения ап означает реализацию O((N + IK)
операций. К счастью, использование полиномов Чебышёва, вы-
вычисляемых в точках коллокации xj, заданных формулой
х, = cos [я (/ — 1)/N], E.152)
позволяет для вычисления а" воспользоваться быстрым пре-
преобразованием Фурье (БПФ), требующим O((N -f l)lg(# + 1))
операций. Быстрые преобразования Фурье [Cooley, Tukey,
1965] более подробно описываются в книге [Brigham, 1974].
Прямой расчет д2и/дх2 по формуле E.151) во всех точках
сетки требует проведения O((iV+lJ) операций. Однако ис-
использование полиномов Чебышёва дает возможность обраще-
обращения к различным рекуррентным соотношениям, что приводит к
некоторому уменьшению числа операций, необходимого для
полной реализации этапа B). В частности, пространственные
производные могут определяться непосредственно из полино-
полиномов Чебышёва, без их дифференцирования, а именно
^iW' EЛ53а)
¦S—E^i-iW- <5Л53Ь>
Явные соотношения между ау>, а{2) и ak в выражении
E.150) даны в работе [Gottlieb, Orszag, 1977]. Характерно, что
нижеследующие рекуррентные соотношения позволяют полу-
получить коэффициенты ар и а?2) с помощью O(N) операций:
а2, af = 0.5af + а*1*;
a(D ==/7@ =о аB) = аB) =0
un+\ — un+2 —и» un un+\ XJ-
В результате вычисление d2u/dx2\j с использованием БПФ мо-
может быть реализовано за O((N—l)lg(N—1)) операций.
204 Гл. 5. Методы взвешенных невязок
Ввиду экономичности каждого этапа псевдоспектрального алго-
алгоритма весь этот алгоритм оказывается весьма эффективным.
Эффекты нелинейных членов исходного уравнения псевдо-
псевдоспектральный метод учитывает особенно экономичным путем.
Рассмотрим уравнение Бюргерса A0.2) для невязкого потока
Если следовать той же процедуре, что и выше, то для пе-
перехода с временного слоя п на слой п + 1 псевдоспектральный
метод должен состоять из следующих этапов:
1) при заданном uf вычислить а% из выражения E.150);
2) при заданном а* вычислить [ди/дх]у по формулам E.153а),
E.154);
3) вычислить wnt = и*} [du/dx]f;
4) вычислить ип^х = uf — w1} А/.
Расчет нелинейного члена на этапе C) осуществляется в фи-
физическом пространстве, что позволяет избежать требующего
много времени умножения отдельных коэффициентов рядов,
таких, как E.150) и E.153).
Идея о применении преобразования, связывающего между
собой спектральное и физическое пространства с помощью
БПФ с целью эффективного расчета нелинейных членов, при-
применяется также и при использовании спектрального метода Га-
лёркина [Orszag, 1971]. Подробно анализируемый пример из
области метеорологии дается в книге [Haltiner, Williams, 1980].
В сравнении со спектральным методом Галёркина у псевдо-
псевдоспектрального метода имеется один недостаток. При необхо*
димости учета нелинейных членов псевдоспектральный метод
допускает возникновение побочных ошибок [см. Fletcher, 1984].
Это означает, что произведение двух рядов, неявно фигурирую-
фигурирующее на вышеуказанном этапе C), возбуждает возникновение
новых высоких частот, k?>N-\-\. Однако поскольку процесс
коллокации учитывает лишь N — 1 дискретную внутреннюю
точку, то высокие частоты должным образом не учитываются.
На практике происходит небольшое искажение амплитуд низ-
низкой частоты.
При рассмотрении физических задач с небольшой естествен-
естественной диссипацией интегрирование по времени может стать
неустойчивым вследствие накопления побочных ошибок, что со-
создает нелинейную неустойчивость. Такая проблема часто воз-
возникает при прогнозировании погоды. Для «технических» тече-
течений объем диссипации обычно достаточен, например из-за на-
§ 5.6. Спектральный метод 205
личия турбулентности, чтобы можно было игнорировать побоч-
побочные ошибки. В таком случае псевдоспектральный метод оказы-
оказывается обычно предпочтительнее, чем спектральный метод Га-
лёркина, вследствие большей экономичности первого и более
эффективного учета граничных условий в нем.
Спектральный метод Галёркина (см. л 5.6.1) строит реше-
решение целиком в спектральном пространстве, т. е. имеет дело с ко-
коэффициентами п\ в выражений E.123). Псевдоспектральный ме-
метод, описанный выше, работает частично в спектральном про-
пространстве, частично в физическом пространстве, с применением
БПФ для перехода из одного пространства в другое. Имеется
возможность дать такую интерпретацию псевдоспектральному
методу, чтобы его схема напоминала дискретизацию в физиче-
физическом пространстве, подобную тому, что осуществляется в ко-
конечно-разностном и конечно-элементном методах. Основные
этапы в ходе такой интерпретации, следуя работе [Ku, Hatziav-
ramidis, 1984], описываются ниже.
Узловые значения и* связаны со спектральными коэффи-
коэффициентами uk посредством соотношения E.150), которое в ком-
компактной форме может быть представлено в виде
11 = Та. E.156)
Коэффициенты а" явно выражаются через ип в форме
a = fu, E.157)
где элемент матрицы Т имеет вид
Ъ/-ТГ-Г7Гг»-1<*/>' <5158>
к /
причем
с, = 2*+, = 2, с,= 1, \<i<N+l.
Формулы E.153а), справедливые для всех точек сетки, можно
записать в виде
^ E.159)
Однако аA> можно связать с а посредством E.154), так что
a(i)==G(i)a> E.160)
где G*1) — это матрица (N + 1)Х(# + 1)> имеющая элементы
A) ( 0, если Аг>1 или k+l четное,
^ 2 (/ — 1)/^л во всех остальных случаях.
Коэффициенты d = 2, ck = 1 при А?5! 1.
206 Гл. 5. Методы взвешенных невязок
Ясно, что из соотношений E.159), E.160) и E.157) следует
|1 = TG<>fu = G<!>u. E.162)
Рассмотрение отдельного элемента вектора ди/дх свидетель-
свидетельствует о том, что соотношение E.162) дает непосредственно ди-
скретизационную формулу, выражающую ди/дх\,- через все
узловые значения щ. Это выглядит контрастом к трехдиаго-
нальной структуре матрицы G(l) при использовании центриро-
центрированного конечно-разностного выражения, моделирующего
du/dx\f.
Аналогичным образом, формулы E.153Ь) можно записать
в виде
Ц-=*Та<2> E.163)
и учесть, что
аB) = G<l>aW = G<I>G<l)a= G<2)a. E.164)
Элементы матрицы GB) могут быть вычислены с помощью
E.161). На основании E.163), E.164) и E.157) получим
^ = 6<2>u. E Л 65)
Матрицы GA) и GB) могут быть вычислены раз и навсегда
и введены в память. В результате все операции, скажем, на
одном временном слое выполняются в физическом простран-
пространстве.
Применение вышеуказанного построения к случаю уравне-
уравнения диффузии E.147) заменит этапы A) и B) на вычисление
[д2и/дх2]" с помощью соотношения E.165). Можно отметить, что
этот процесс требует O(N2) операций, тогда как этапы A) и
B) включают два быстрых преобразования Фурье и рекуррент-
рекуррентный процесс трудоемкостью O(N) операций. Вследствие допол-
дополнительных затрат времени на применение БПФ использование
соотношения E.165) является конкурентноспособными для N,
как правило, меньших 100 [Ku et al., 1987].
Если взять некий предельный случай N = 2 в выражении
E.150), то вышеуказанная псевдоспектральная процедура дает
такую же дискретизацию уравнения диффузии E.147), как и
схема ВВЦП C.4).
Явная матричная интерпретация псевдоспектрального ме-
метода будет рассмотрена в дальнейшем, в п. 17.1.6, в связи с
построением численных решений для течения несжимаемой
вязкой жидкости. Более сложные трактовки спектральных ме-
§ 5.8. Задачи 207
тодов в их различных аспектах можно найти в работах [Gott-
[Gottlieb, Orszag, 1977; Fletcher, 1984; Voigt et al., 1984; Peyret, 1986;
Canuto et al., 1987].
§ 5.7. Заключение
Метод взвешенных невязок обеспечивает общую основу для
сравнения многих приближенных методов (см. [Fletcher, 1984]).
Здесь были рассмотрены достаточно подробно метод Галёрки-
на с конечными элементами, спектральный метод Галёркина и
метод конечных объемов.
Методы конечных объемов и конечных элементов, так же
как и конечно-разностные методы, являются локальными ме-
методами. Следовательно, два первых метода приводят к дискре-
тизированным уравнениям с разреженными матрицами, хотя
обычно с менее разреженными, чем в случае конечно-разност-
конечно-разностного метода. Как метод конечных элементов в сочетании с изо-
параметрическим преобразованием, так и метод конечных объе-
объемов подходят для рассмотрения вычислительных областей непра-
неправильной формы. Кроме того, при применении обоих указанных
методов можно использовать обобщенные координаты (см.
гл. 12).
Дополнительное преимущество метода конечных объемов со-
состоит в возможности непосредственной дискретизации консер-
консервативной формы исходных уравнений (см. § 11.2). Это натал-
наталкивает на мысль о том, что дискретизированные уравнения
обеспечивают выполнение законов сохранения, если только
учесть ошибку дискретизации.
В противоположность вышеупомянутым спектральный ме-
метод является глобальным методом. Практически это делает его
методом, более трудным для реализации, однако позволяет
строить приближенные решения высокой точности при сравни-
сравнительно малом числе членов в выражении для приближенного
решения E.2). Относительные достоиинства методов конечных
разностей, конечных элементов и спектральных методов ана-
анализируются в книге [Fletcher, 1984]. Еще один мощный гло-
глобальный метод — метод ортогональной коллокации — сравни-
сравнивается с конечно-разностными и конечно-элементными метода-
методами в книге [Finlayson, 1980, гл. 4—6].
5.8. Задачи
Методы взвешенных невязок: общая формулировка (§ 5.1)
5.1. Уравнение d2y/dx2 + у = [1 — Ert/6J]sinE:rut/6) с граничными усло-
условиями у@) =0, у(\) = 0.5 необходимо решить в области 0 ^ х ^ 1.0, ис-
используя следующие методы взвешенных невязок:
208 Гл. 5. Методы взвешенных невязок
(a) метод Галёркина,
(b) метод подобластей @ ^ х < 0.5; 0.5 ^ х < 1.0),
(c) метод наименьших квадратов.
Приближенное решение представьте в форме
у = ах(х — а:3) + а2 (х2 — х3) + 0.5л:3.
Сравните численные решения с точным решением у = sin Eллг/6).
5.2. При надлежащем способе приведения к безразмерной форме уравне-
уравнение диффузии или теплопроводности может быть записано в виде
09 д*0 _л
dt дх*-""'
При начальном условии 0(#, 0) = sin (ял*) + х и граничных условиях 0@,
t) =0, 0A, t) =1.0 построить решения вышеприведенного уравнения в вы-
вычислительной области О^л:^ 1.0, 0 ^ tf ^ 0.20, пользуясь следующими ме-
методами:
(a) метод Галёркина,
(b) метод подобластей,
(c) метод коллокаций.
Следует использовать приближенное решение
лг
в = sin (пх) + х + ? ai @ (*' ~ xf+ll
/-1
Применение вышеуказанных методов взвешенных невязок к безразмерному
уравнению теплопроводности дает систему обыкновенных дифференциальных
уравнений относительно коэффициентов a,(t). Эти уравнения численно инте-
интегрируются маршевым методом.
Получите решения (после составления компьютерной программы) для
N = 3, 5, 7 всеми тремя методами и сравните точность и скорость сходимо-
сходимости. Точное решение этой задачи имеет вид 0 = sin (пх) е~л' + х.
5.3. Течение вязкой жидкости в канале прямоугольного сечения подчи-
подчиняется уравнению E.97):
дх2 ду2
с граничными условиями w = 0 при # = zfcl, # = zfcl. «Точное» решение
этой задачи дается формулой E.110), если величина NEX достаточно ве-
велика. Приближенные решения следует построить, пользуясь
(a) методом Галёркина,
(b) методом подобластей,
(c) методом коллокаций.
В качестве приближенного решения используйте выражение
N
форма которого подсказана видом предельных одномерных профилей скоро-
скорости (Ь/а = 0 и оо). Получите решения для N = I, 2 и 3 и сравните ре-
результаты с решениями, полученными в п. 5.5.2 методом конечных элементов.
§ 5.8. Задачи 209
Дайте комментарии, касающиеся точности в расчете на одну узловую неиз-
неизвестную, в связи с корректностью предполагаемого приближенного решения.
В этот анализ включите формулу E.110) с малыми значениями NEX, так
как это решение является одновременно и решением по Галёркину [Fletcher,
1984].
Метод конечных объемов (§ 5.2)
5.4. Постройте решения уравнения Лапласа в области, показанной на
рис. 5.4, используя программу FIVOL, для следующих значений параметров:
(a) г^ = 0.10, г^ = 4.00, /у =1.00, rz = 0.10, в^^ = 0, 6zy = 90;
(b) г^ = 0.10, гх
Для каждого варианта получите результаты на трех сетках: JMAX =
= КМАХ = 6, 11, 21. Сравните точность и скорость сходимости с результа-
результатами, приводимыми в табл. 5.5.
5.5. Модифицируйте программу FIVOL применительно к решению урав-
уравнения
Jte, _д?_ / д2Ф д2~
дх ду \ дх2 dt>
Источниковый член S может учитываться таким же образом, как и член
dq/dt в уравнении E.23). Испытайте программу для случая 5 = [cos B9) —
— sinB0)]/r2 путем получения решений для тех же самых значений парамет-
параметров, которые использовались для составления табл. 5.5. и а = 1. Сравните
решения с точным решением <? = (sin в)/г2. Граничные условия для вы-
выбранного выше значения S задаются формулами E.31).
5.6. Метод конечных объемов, описанный в § 5.2, необходимо применить
к ситуации, когда на линии WX задается граничное условие Неймана, а
именно
дФ
ду
1
wx
Остальная часть формулировки задачи та же, которая была дана в § 5.2,
при том (же точном решении.
Для получения уравнений, справедливых на линии WX, воспользуйтесь
той же процедурой, которая показана на рис. 5.5, но при этом используйте
«половинный» конечный объем, центрированный на WX и лишь простираю-
простирающийся внутрь вычислительной области. Соотношения, эквивалентные E.34),
могут быть получены непосредственно и аппроксимироваться так же, как в
программе FIVOL, за исключением того, что значение дф/дх\чгх можно полу-
получить из граничного условия. Член дФ1дх\^х удобно вычислить с помощью
трехточечной конечно-разностной аппроксимации, поскольку линия WX сов-
совпадает по направлению с осью х. Сделайте необходимые изменения в про-
программе FIVOL и испытайте при тех же условиях, какие были показаны в
табл. 5.5.
Метод конечных элементов и интерполяция (§ 5.3)
5.7. Примените линейную и квадратичную конечно-элементную интерпо-
интерполяцию к функции
g = A -f sin пх) е~2х в диапазоне 0 ^ х ^ 1.0.
14 К Флетчер. т. I
210 Гл. 5. Методы взвешенных невязок
Получите значения интерполированной функции для 3, 5, 9 и 17 равномерно
распределенных узловых точек внутри вычислительного интервала. Вычис-
Вычислите среднеквадратичную ошибку на основе 20 равномерно распределенных
точек в интервале 0 ^ х ^ 1.0 и покажите, что достигаются теоретически
предсказанные скорости сходимости.
5.8. Для функции, рассмотренной в задаче 5.7, выполните линейную и
квадратичную конечно-элементную интерполяцию на сетке, растущей по за-
закону геометрической прогрессии с показателем 1.2, для следующих вариантов
@ < Х5^ Хтгх):
(a) Ах = 0.2, 0.24, 0.288, 0.3456, ... ;
(b) Ах = 0.1, 0.12, 0.144, ... ;
(c) Ах = 0.05, 0.06, 0.072, ....
Завершите сетку, как только станет х > 1.0. В случае квадратичной интер-
интерполяции расположите каждую из средних точек так, чтобы **\ =0.5 (*у_з +
+ xj) и т. д. Вычислите среднеквадратичные ошибки на основе 201 равно-
равномерно распределенных точек и сравните со случаем интерполированного ре-
решения с приблизительно тем же числом равномерно распределенных внутри
данной области точек. Рассмотрите поведение решения и вклады в средне-
среднеквадратичную ошибку в различных частях вычислительной области и опреде-
определите, может ли интерполированное решение, имеющее заданную точность,
быть построено более экономичным образом за счет избирательного распо-
расположения узловых точек.
5.9. Получите решения с линейной и квадратичной интерполяцией на ко-
конечных элементах для функции
у = A + sin nx) e~2x sin (ny)
в вычислительной области 0^x^:1, 0 ^ у ^ \. Вычислите среднеквадра-
среднеквадратичную ошибку на однородной сетке, в пять раз более мелкой, чем самая
мелкая сетка с узловыми точками. Получите среднеквадратичную ошибку
для того же числа элементов, которое указано в табл. 5.7, и сравните точ-
точность и скорость сходимости с результатами, приведенными в табл. 5.7.
Метод конечных элементов; уравнение Штурма — Лиувилля (§ 5.4)
5.10. Как указано в приложении А.2, вклады в различные одномерные
конечно-элементные операторы соответствуют формулам
1 Г d<t>, 1
L
Покажите путем вычисления интегралов, что в случае линейных элементов
на однородной сетке вышеперечисленные операторы, будучи центрированы
в k-м узле, имеют значения
м ,12 1\г / 0.5 я 0.5 Ч , ( 1 2 1
мх -
5.11. Модифицируйте программу STURM так, чтобы она была пригодна
для граничных условий вида
Это потребует изменений в вычислении Ьт> / и gm при т = /, принимая во
внимание все ненулевые вклады, вносимые в соотношение E.73). Кроме того,
§ 5.8. Задачи 211
перед решением с помощью подпрограмм BANFAC/BANSOL необходимо бу-
будет провести некоторую перестройку трехдиагональной системы уравнений.
Испытайте сделанную модификацию путем численного решения уравнения
с граничными условиями у@) = 1, dy/dx(i) = —5л/12 в интервале 0 ^ х ^
< 1.0. Эта задача имеет точное решение у = cosEnx/6). Получите реше-
решения как с помощью линейной, так и квадратичной интерполяции при разме-
размерах сетки, указанных в табл. 5.10, и сравните достигаемую точность и ско-
скорость сходимости.
5.12. Примените метод Галёркина с конечными элементами, линейной и
квадратичной интерполяцией к решению уравнения
?-#-.
с граничным условием у@) = 1.0 в интервале 0 ^ х ^ 1.0. Эта задача имеет
точное решение у = ехр х. Решите неявные уравнения, используя подпро-
подпрограммы BANFAC/BANSOL, как в программе STURM. Получите решения на
однородной сетке с прогрессирующим измельчением, пока среднеквадратич-
среднеквадратичная точность не станет приближенно равной значениям, указанным в
табл. 5.3. Прокомментируйте относительные достоинства, такие, как точность
и вычислительная эффективность использования локальных аппроксимирую-
аппроксимирующих функций низкого порядка, как в методе конечных элементов, и глобаль-
глобальных аппроксимирующих функций высокого порядка, как в традиционном ме-
методе взвешенных невязок (см. § 5.1).
Метод конечных элементов — другие приложения (§ 5.5)
5.13. Получите решения для течения вязкой жидкости в канале прямо-
прямоугольного сечения, используя программу DUCT на сетке ИХ И, при раз-
различных значениях b/а, пока решение на центральной линии, проходящей по
меньшему размеру, не станет с точностью в 1 % среднеквадратичной ошибки
совпадать с одномерным параболическим профилем, а именно и = 1.5A —
-У2)-
5.14. Модифицируйте программу DUCT для решения уравнения Лапласа
в области 0 ^ х ^ 1.0, 0 ^ у ^ 1.0 при граничных условиях
w (х, 0) = cos @.5ях), w A, у) = 0, w (х, 1) = е°'5я cos @.5ях),
Эта задача имеет точное решение w = cos@.5nx)exp@.5jr#). Если к реше-
решению задачи применить метод конечных элементов, то расчет уравнений Га-
Галёркина, центрированных на линии х = 0, будет связан с интегрированием
лишь по двум соседним элементам. Для однородных граничных условий Ней-
Неймана формула E.101) остается в силе, так как все члены, возникающие
после интегрирования по частям, равны нулю. Покажите, что расчет урав-
уравнений Галёркина по двум соседним элементам не вносит изменений в Lyy,
однако вместо формул E.104) и E.105) следует использовать выражения
J_
3 ' "
14*
212 Гл. 5. Методы взвешенных невязок
Получите численные решения вышеуказанной задачи на сетках 6X6, 11 X
ХП и 21X21 и сравните точность решений по методам конечных элемен-
элементов и конечных разностей.
5.15. Модифицируйте программу DUCT для решения уравнения
дФ дФ д2Ф А дЧ _ п
"Wi~~di~a~M~~P ду2 ~и
в области 0 ^ х ^ 1.0, 0 ^ у ^ 1.0, при граничных условиях
Ф(х, 0) = ех/а, Ф(\, у)
* @, у) = е*/р, ф(х, 1) =
Это сочетание имеет точное решение Ф(х, у) = ехр(х/а)ехр(у/$). При зна-
значениях параметров а = 1.0, р = 1.0 постройте решения по линейной схеме
метода конечных элементов и по трехточечной схеме метода конечных раз-
разностей на сетках 6X6, ИХ И и 21X21. Сравните точность и скорость
сходимости для решений, полученных методом конечных элементов и мето-
методом конечных разностей.
Спектральный метод (§ 5.6)
5.16. Примените спектральный метод к решению уравнения диффузии
(как описано в п. 5.6.1) с начальным условием
Т(х, 0)==5jc~4jc2
и с граничными условиями Дирихле
т (о,о==о, F(i,o = i.
Покажите, что можно воспроизвести результаты, приводимые в табл. 5.13.
Получите также решения при / = 7 и 9, сравнив их с приближенным реше-
решением Ть и точным решением Т.
5.17. Примените спектральный метод к решению уравнения диффузии
с начальным условием
Т(х, 0) = 3 — 2х — 2х2 + 2хг
и со смешанными граничными условиями — Дирихле и Неймана (как в
§5.6):
ох
Получите численные решения при а = 1.0, используя значения / = 3, 5 и 7
в формуле E.136), вплоть до f = 0.1. Сравните численные решения с точным
решением
Г- 3 - 2х- I] ( I K sin [B/ - 1) пх] а- »/-*"»
чтобы определить скорость сходимости в зависимости от /. Подтвердите
путем численного расчета, что стационарное решение Tss = 3 — 2х дости-
достигается при доведении численного интегрирования до больших значений вре-
времени.
Глава 6
Стационарные задачи
Многие примеры из числа рассмотренных в гл. 3—5 содер-
содержали время в качестве независимой переменной, что принима-
принималось во внимание при построении алгоритмов. Однако многие
задачи гидроаэродинамики по самой своей природе являются
стационарными, а исходные уравнения по своему характеру
зачастую оказываются эллиптическими (см. § 2.4).
Как отмечалось в п. 3.1.2, для дискретизации уравнений
стационарного течения можно воспользоваться любым из трех
основных методов — конечных разностей, конечных элементов
или спектральным,— что приведет к системе уравнений
A(V)V = B, F.1)
где V — вектор, составленный из неизвестных узловых значе-
значений или из коэффициентов пробного решения E.2). Матрица А
содержит алгебраические коэффициенты, связанные с дискре-
дискретизацией и, вообще говоря, может зависеть от самого решения
(V). Вектор В составлен из алгебраических коэффициентов,
обусловленных дискретизацией, и из известных значений V,
например из тех, которые заданы граничными условиями.
Как правило, матрица A(V) является разреженной (содер-
(содержит мало элементов, отличных от нуля), причем ее ненулевые
элементы расположены вблизи диагонали, если используются
конечно-разностные или конечно-элементные методы. В случае
спектрального метода матрица A(V) будет наполненной (число
нулевых элементов мало). На рис. 6.1 элементы р9 q, r9 s m t
матрицы А связаны с соответствующими узловыми точками.
Элементы р и /, связанные с узлами (/, k-\- \) и (/, k— 1),
отодвинуты от диагонали этой матрицы на величину N — число
неизвестных узловых значений в направлении оси х.
Имеется возможность построить некоторый итерационный
процесс, позволяющий решить уравнение F.1) в его истинной
форме. Однако может оказаться более эффективным введение
внешней итерации, в процессе которой уравнение F.1) на каж-
каждом шаге превращается в линейное, так что можно восполь-
214
Гл. 6. Стационарные задачи
зоваться прямыми методами (см. § 6.2). К этому типу принад-
принадлежит и метод Ньютона,1 рассматриваемый в § 6.1.
Если матрица А не зависит от V, то требуется только один
этап внешней итерации, т. е. уравнение F.1) можно записать
в виде
AV = B. F.2)
Для решения уравнения F.2) можно применить как прямые ме-
методы (§ 6.2), так и методы итераций (§ 6.3). Если матрица А
хх х
ххх х
q rs
ххх
— q — r—s-k
H з j+i
XXX
XX J
Рис. 6.1. Типовое распределение отличных от нуля элементов матрицы А
после конечно-разностной дискретизации.
наполненная, то для осуществления непосредственного решения
уравнения F.2) применяются подпрограммы FACT и SOLVE,
описанные в п. 6.2.1 и использующие метод исключения по
Гауссу. Если матрица А трехдиагональная или трехдиагональ-
ная и пятидиагональная попеременно, то с помощью подпро-
подпрограмм BANFAC и BANSOL можно получить решение V также
с помощью гауссовского исключения, но значительно эффек-
эффективнее, чем при использовании подпрограмм FACT и SOLVE.
Для некоторых вариантов структуры А, таких, которые полу-
получаются при конечно-разностной дискретизации уравнения Пу-
Пуассона, могут быть применены специальные процедуры (см.
п. 6.2.6).
Применение итерационных методов (точечный Якоби, Гаус-
Гаусса — Зайделя и ПВР) иллюстрируется в п. 6.3.2 на примере
решения уравнения Пуассона, описывающего течение вязкой
жидкости в канале (см. п. 5.5.2). Исследуется влияние измель-
измельчения сетки на оптимальное значение показателя релаксации
и на скорость сходимости точечной ПВР. Демонстрируется об-
обобщение точечной ПВР на линейную ПВР и на неявную схему
переменных направлений (НПН), причем делается сравнение
с результатами точечной ПВР. Методы сопряженных градиен-
градиентов (п. 6.3.4), а также многосеточные методы (п. 6.3.5) описы-
описываются в первую очередь в качестве средств ускорения «клас-
«классических» итерационных процедур.
§ 6.1. Нелинейные стационарные задачи 215
Некоторые итерационные методы, будучи применены непо-
непосредственно к решению уравнения F.1), оказываются концеп-
концептуально подобными введению эквивалентной нестационарной
формулировки исходной задачи. Если считать, что нестацио-
нестационарное решение не представляет особой ценности, то можно мо-
модифицировать члены, зависящие от времени, таким образом,
чтобы сходимость к стационарному состоянию достигалась за
возможно более короткий промежуток времени исполнения.
Именно в этом состоит побудительный мотив для разработки
псевдонестационарных методов (см. § 6.4).
§ 6.1. Нелинейные стационарные задачи
Стационарные задачи гидроаэродинамики зачастую оказы-
оказываются нелинейными из-за характера конвективных членов или
несколько реже из-за зависимости от решения таких парамет-
параметров потока, как зависящая от температуры вязкость (типичный
пример).
Метод Ньютона с несколькими независимыми переменными
является потенциально полезным приемом решения стационар-
стационарных задач гидроаэродинамики с учетом его быстрой сходимо-
сходимости в случае попадания близко к истинному решению. Этот
метод будет проиллюстрирован здесь на примере решения двух
задач. Сначала будет решаться сильно нелинейная система
алгебраических уравнений. Далее будут рассмотрены двумер-
двумерные стационарные уравнения Бюргерса (см. § 10.4), так как
эти уравнения имеют точно такую же нелинейную структуру,
что и уравнения Навье — Стокса для несжимаемой жидкости
(см.§ 11.5).
6.1.1. Метод Ньютона
Метод Ньютона представляет собой мощное средство для
решения нелинейных уравнений, подобных F.1). Схематиче-
Схематическое представление этого метода дается на рис. 6.2.
Если уравнение F.1) переписать в форме
R = A(V)V-B = 0, F.3)
то основную формулу метода Ньютона можно записать в виде
1 R<*>, F.4)
где k — номер итерации, а Л(Л) — якобиан. Элемент матрицы
i{k) имеет форму
6R[h)
F-5)
216
Гл. 6. Стационарные задачи
Формулу F.4) можно переписать в виде
j(fc) ду<*+1> = — RW. F.6)
Векторное уравнение- F.6) представляет собой систему линей-
линейных уравнений, которую необходимо разрешить относительно
вектора поправки ДУ<*+1> = V<*+1) — V(fe) на каждом из итера-
итерационных этапов.
Начальное
решение
уМ, к = О
Вычислить
н(к)
Проверка
I
решение
Вычислить и
факторизовзть
—I
I
Заморозить
J
Вычислить
ду'*' =
-g^) R (к)
--. I
Рис. 6.2. Схематическое представление метода Ньютона.
Привлекательная особенность метода Ньютона состоит в
том, что он обнаруживает квадратичную сходимость, если
только текущая итерация достаточно близка к сходящемуся
решению Ус- Квадратичная сходимость означает, что
Vc|p. F.7)
Критерий сходимости метода Ньютона можно получить сле-
следующим образом (см. [Isaacson, Keller, 1966]). Если обращение
матрицы J@) обладает нормой, ограниченной величиной а, т. е.
если первый поправочный вектор AV(I) имеет норму, ограничен-
ограниченную величиной Ь, т. е.
и, кроме того, если R обладает непрерывными вторыми про-
производными, удовлетворяющими неравенству
N
С
N
§ 6.1. Нелинейные стационарные задачи 217
при всех V в области ||AV<1>||< 2b, и, наконец, если упомянутые
выше константы удовлетворяют соотношению
abc < 0.5, F.8)
то метод Ньютона будет сходиться к решению
lim V<*> = Vc,
fc-»oo
для которого R(V,) = 0 и || V<*> - Ус\\<Ь/Bк~1).
Здесь векторные нормы представляют собой максимальные
нормы, например | V | = max| Vt |, а матричные нормы — мак-
максимальные натуральные нормы, например
E
Следует заметить, что проверка выполнения неравенства F.8)
связана примерно с таким же объемом работы, как и попытка
решения самой задачи. Основная трудность при использовании
метода Ньютона состоит в том, что радиус сходимости Ь умень-
шается по мере увеличения Af [Rheinboldt, 1974], так что для
обеспечения сходимости величина V<0> должна быть близкой
kV,
• Наиболее существенная доля времени исполнения при при-
применении метода Ньютона уходит на факторизацию матрицы
№\ требуемую для решения уравнения F.6). Это время испол-
исполнения можно несколько уменьшить, если заморозить значение
J(*> на протяжении нескольких шагов Д&. Иначе говоря, фак-
факторизация матрицы J(*> будет нужна только один раз на про-
протяжении Ak шагов. Однако, как правило, для достижения
сходящегося решения понадобится при этом большее число ите-
итераций. Методы решения систем нелинейных уравнений, вклю-
включая метод Ньютона, обсуждаются в книге [Ortega, Rheinboldt,
1970].
6.1.2. NEWTON: температурный анализ работы
коллектора в виде плоской пластины
При анализе работы солнечного коллектора в виде плоской
пластины, схематически показанного на рис. 6.3, установление
энергетического баланса для поглотителя и двух стеклянных
крышек может потребовать решения следующей системы нели-
нелинейных уравнений, связывающих температуры поглотителя 7Ь
218
Гл. 6. Стационарные задачи
а также двух стеклянных крышек Т2 и Г3:
Кг = (Т* + 0.06823Г,) - (Ц + 0.05848Г2) - 0.01509 = 0,
#2 = (Г{+0.05848711 )-(Щ+ 0.11696Г2) + (Ц + 0.5848Г3) = 0, F.9)
#3 = (Т\ + 0.05848Г2) - B.05Г* + 0.2534Г3) + 0.06698 = 0.
Для упрощения операций при решении уравнений величины Гь
Т2 и Т3у входящие в уравнения F.9), соответствуют абсолют-
абсолютным температурам, деленным на тысячу.
Солнечное излучение
Температура
стеклянной
крышки 7"з
Температура
стеклянной
крышки 7*2
Температура
поглотителя
Рис. 6.3. Солнечный коллектор в виде плоской пластины.
Многокомпонентный метод Ньютона (п. 6.1.1), будучи при-
применен к уравнениям F.9), на каждом итерационном шаге k
требует решения уравнения
J(*)AT<*+O = --R(*) F.10)
относительно ДТ<*+1). Тогда решение выражается формулой
В уравнении F.10) /// = Л
Применительно к данной задаче имеем
D71 + 0.06823) - D71 + 0.05848) 0
J = D71 + 0.05848) — (871 + 0.11696) D71 + 0.05848)
0 D71 + 0.05848) — (8.271 + 0.2534)
F.11)
Решение этой задачи было представлено в алгоритмической
форме с помощью компьютерной программы NEWTON. Блок-
схема для программы NEWTON показана на рис. 6.4, а рас-
§ 6.1. Нелинейные стационарные задачи
Й19
печатки подпрограмм, указанных на этой блок-схеме, приво-
приводятся на рисунках 6.5—6.7. Различные параметры, используе-
используемые в программе NEWTON, расшифровываются в табл. 6,1.
Задать
начальные
значения Г
Вычислить
невязки
(RESID)
Выход
Сошлось ли решение?
Превышено ли
максимальное
число итераций?
Да
И
Нет
Инкремент
j(/c+ 1) _ j(k)
Решить
относительно
(SOLVE)
Факторизовать
якобиан
(FACT)
Вычислить
якобиан
(JACOB)
Рис. 6.4. Блок-схема программы NEWTON.
Невязки уравнений F.9) вычисляются с помощью подпрограм-
подпрограммы RESID (рис. 6.6), причем делается проверка (NEWTON,
строки 43—45), позволяющая остановить расчет, если средне-
Таблица 6.1. Параметры, используемые в программе NEWTON
Параметр
N
IT
ITMX
EPS
Т
R
RMSR
RMST
AJ
JPVT
DT
Описание
Число уравнений
Номер итерации
Максимальное число итераций
Максимально допустимая среднеквадратичная ошибка
Температура; зависимая переменная
Невязки уравнений F.9), сюда же вводится ДТ после воз-
возврата из подпрограммы SOLVE
Среднеквадратичная невязка
Среднеквадратичная ошибка решения, ЦТ—T||rms
Якобиан, J
Индекс строки с k-ч ведущим элементом (в подпрограмме
FACT), JPVT(#) = —1, если ведущий элемент равен нулю
AT, поправка к Т
1 С
2 С MEVTON APPLIES NEVTOiTS METHOD TO SOLVE Л NONLIKSAR 5YST1H 0?
3 С ALGEBRAIC EOUATIONS, R(T)
4 С RESID EVALUATES THE RESIDUALS
5 С JACOB EVALUATES THE JACOBIAN
6 С FACT FACTORISES THE JACOBIAN IHTO L.U
7 С SOLVE SOLVES THE LINEAR SYSTEM FOR DT
8 С
9 REAL*8 SUM,RMSR,RMS7,DSQRT
10 DIMENSION T<50),AJE0,50),P{50),JfVTEQ),TEX{50)
11 С
12 ОРЕМA,FILE»'NEVTON.DAT')
13 0PENF,FILE»'NEVT0H.0UT')
14 READ(l,l)N,im,i;PS
15 READA,2)(T(J),J=1,N)
16 R?ADU,3)(TEX(J),J*i,N)
17 1 FORMATBI5,E10.3)
IS 2 FORMATA0F5.2)
19 3 FORMATGF10.7)
20 С
21 ?RI7EF,4)N,ITMX,E?S
22 4 FORMATC NEVTONS METHOD FOR N *\I3,' ITXX= '13,* EPS» ',?10.
23 WRITE{6,5MT<J),J«1,N)
24 5 FORMATS INIT SOLN *\3F5.2,//>
25 AM » N
2$ IT » 0
27 6 CONTINUE
28 С
29 С CALCULATE RESIDUALS
30 С
31 CALL RESID(N,T,R)
32 С
33 SUM = 0.
34 DO 1 I * 1,N
35 7 SUM = SUM + R(I>*R{I)
36 RMSR = DSQRT(SUM/AN)
37 SUM = 0.
38 DO 8 I = 1,N
39 8 SUM = SUM + (T(I) - TKX(I))*»2
40 RMST = DSQRT(SUM/AH)
41 mTE{6,9)RMSR,RMS7,(MJ),J=l,5)
42 9 FORMATC RMS RH=f,D11.4,f RMS T ='^11.4/ R^'^Dii.l)
43 IF{RMST .LT. EPS)GOTO 12
44 IT = IT + 1
45 IF(IT .EQ. ITKX)GOT0 12
46 С
47 С CALCULATE JACOBIAH
48 С
49 CALL JACOB(N,T,AJ)
50 С
51 С FACTORISE THE JACOBIAN INTO L,U
52 С
53 CALL FACT(N,AJ,JPVT)
54 С
55 IF(JPVT(N) .EQ. -1)VRITEFДО)
56 10 FORMATC ZERO PIVOT DETECTED1)
57 IF(JPVT(N) .EQ. -DGOTO 15
§ 6.1. Нелинейные стационарные задачи 221
st
st
so
61
«2
C
«4
65
66
67
68
69
70
71
72
73
74
75
76
77
71
С
С
С
с
с
с
с
с
с
11
12
13
14
15
SOL?K FOR TIE COt«СЛОИ, ОТ
CALL SOLVE(N,AJ,JFVT,R)
INCREMENT T
DO 11 I ¦ 1,H
DT - -R(I)
T(I) - T(I) ¦ DT
GOTO 6
GENERATE OUTPUT
?RITEF,13)IT,RMST
FORMAT(//,' AFTER ',13,* ITERATIONS TIE IKS RESIDUAL IS' ',?12.S)
VRITEF,14)(T(I),I«1,N)
FORMATС Т • '7F10.7)
CONTINUE
STOP
WO
Рис. 6.5. Распечатка программы NEWTON.
квадратичная невязка оказывается меньше выбранного крите-
критерия или если превышено максимально допустимое число итера-
итераций. Подпрограмма JACOB (рис. 6.7) предназначена для рас-
расчета элементов якобиана матрицы F.11). Линейная система
F.10) решается в два этапа. Сначала якобиан факторизуется,
1 SUBROUTINE RESID(N,T,R)
2 С
3 С EVALUATES RESIDUALS REQUIRED BY NEWTON'S METHOD
4 С
5 DIMENSION TE0),RE0),T4E0)
6 С
7 DO 1 J « 1,H
8 DUM = T(J)
9 1 T4(J) * DUM*DUM*DUM*DUM
10 С * 0.05348
11 DUM = T4B) + C*TB) N
12 DAM = T4C) + C*TU)
13 R(l) * T4(l) + O.O6823*T<1) - DUM - 0.01509
14 RB) » T4U) + C*TA) - 2.*DUM + DAM
15 RC) = DUM - 2.05*T4C) - 0.2534*TC) + 0.06698
16 RETURN
17 END
Рис. 6.6. Распечатка подпрограммы RESID.
преобразуясь к форме LU с помощью подпрограммы FACT,
а затем преобразованная система решается согласно подпро-
подпрограмме SOLVE. Подпрограммы FACT и SOLVE описываются
в п. 6.2.1.
Форма представления решений уравнений F.9) показана
на рис. 6.8. Как свидетельствует решение, температуры поверх-
222
Гл. 6. Стационарные задачи
ности поглотителя и двух стеклянных крышек равны соответ-
соответственно 415 К A42°С), 379 К A06°С) и 334 К F1 °С). Для
среднеквадратичных значений ошибки и невязки характерна
1
2 С
3 С
4 С
5
6 С
7
8
Э
10
11
12
13
14
15
16
17
18
19
20
21
22
SUBROUTINE JACOB(N,T,AJ)
EVALUATES JACOBIAN REQUIRED BY NEWTON'S METHOD
DIMENSION TE0),AJE0,50),T3E0)
DO 2 I = 1,N
DO 1 J » 1,H
1 AJ(I,J) « 0.
DUH * T<I)
T3(I) * 4,*DUH*DUK*DUM
2 CONTINUE
С * 0.05848
AJA,1) « T3{1) + 0.06823
AJA,2) * - T3B) - С
AJB,1) « T3(l) + С
AJB,2> * - 2.*T3B) - 0.П6Э6
AJB#3) « T3C) + С
AJC,2) - T3B) + С
AJC,3) * - 2.05*T3C) - 0.2534
RETURN
END
Рис. 6.7. Распечатка подпрограммы JACOB.
примерно квадратичная сходимость по мере приближения к
сходящемуся решению, соответствующая формуле F.7). Этот
NEVTONS METHOD FOR N =
INIT SOLN = .30 .30
3 ITMX=
.30
10 EPS= .100E-04
RMS RH-
RMS RH«
RMS RH=»
RMS RH«
RMS RH=
.7023D-02 RMS T
.9400D-02 RMS T
.1317D-02 RMS T
.2372D-04 RMS T
.5353D-08 RMS T
.8307D-01
.2885D-01
.3148D-02
.4647D-04
.4867D-07
-.1216D-01
.1344D-01
.1738D-02
.2928D-04
.6588D-08
.6971D-09
.7722D-02
.1449D-02
.2881D-04
.5570D-08
-.1007D-0S
.4993D-02
.288SD-03
.4479D-06-
.3399D-08
AFTER 4 ITERATIONS THE RMS RESIDUAL IS
T = .4151283 .3794904 .3335792
.48667E-07
Рис. 6.8. Типовая выдача результатов по программе NEWTON.
пример показывает, насколько эффективным является метод
Ньютона при решении небольших систем сильно нелинейных
алгебраических уравнений.
§ 6.1. Нелинейные стационарные задачи 223
6.1.3. NEWTBU: двумерные нестационарные
уравнения Бюргерса
Нестационарная форма вышеупомянутых уравнений более
детально рассмотрена в § 10.4. Здесь же нам необходимо ре-
решить стационарные двумерные уравнения Бюргерса
_ да . _ дп 1 / д2п . д2п
dv dv 1 (d2v
с граничными условиями Дирихле для и и v, применяя с этой
целью метод Ньютона после дискретизации с помощью трех-
трехточечных центрированных разностных формул. Уравнение F.12)
можно записать в следующей дискретной форме:
Ruj, к = uj\ kLxUjy k + vj, kLyU^ k —g^- {Lxxuu k + LyyUjt k) = 0,
Rvjt k ^ uj\ kLxVj, k + V/, ~kLyVjf k — -j^- (LxxVjy k + LyyVjt k) = 0,
где
r» k ~ 2kx
F.14)
о -22-Y
by ' U) b )
' by2
Решение ищется в области, изображенной на рис. 6.9.
Граничные значения взяты из точного решения [Fletcher,
1983]
2 дФ _ 2 дФ /с 1С\
* y FЛ5)
где
~*о) + ^ -*•(*-*о) cos) (Лг/), F.16)
тогда как постоянные аь а2, аз, а4, as, X и лго подбираются так,
чтобы разнообразить поведение точного решения.
Если реализовать представление уравнений F.13) во всех
внутренних узлах, то получится 2(NX — 2) (NY — 2) уравнений,
которые должны быть разрешены относительно и/, & и vt\ k для
всех внутренних узлов. Процесс решения с использованием
224
Гл. 6. Стационарные задачи
метода Ньютона может быть символически представлен
формулой
¦•¦> = -R<»>, F.17)
где составляющими вектора Aq являются А#/, k, Аи/, *, а вектор
R имеет компоненты Ru]} k и Rv,, *, оцениваемые в каждом из
u=u(xT0), v=v[x>0)
Рис. 6.9. Вычислительная область для решения уравнений F.12).
внутренних узлов. Верхний индекс (я) используется для обо-
обозначения номера итерации. Якобиан J содержит такие члены:
F.18)
Аналогичные члены можно записать для Rvj, k.
Вышеприведенная формулировку задачи и ее решение реа-
реализуются в программе NEWTBU. Распечатки этой программы, а
также подпрограмм EXBUR для построения точного решения,
RESBU для расчета невязок согласно F.13) и JACBU для вычис-
вычислений по формулам F.18) приводятся на рисунках 6.10—6.13.
В табл. 6.2 расшифровывается смысл параметров, используемых
в программе NEWTBU.
dRuJt k/dUj_ly k = — 0.5ыд */Дл: — l/(Re Ал:2),
dRuu klduh k = B/Re) (I/A*2 + I/Ay2) + @.5/Ax) {uf+h k
dRuJy k/duJ+ly k = 0.5a/t k^x - l/(Re &x2),
dRuh k/dvif,_! = - 0.5i>/t ^/Ду ~ l/(Re Ay2),
dRuit k/dvh k+l = 0.5vJk/by - l/(Re Ay2),
л/а»/^ k = @.5/Ay) (му, л+1 — tt/t ft.,).
§ 6.1. Нелинейные стационарные задачи 225
1
2 С
3 С NEVTBU APPLIES NEWTON'S METHOD TO SOLVE BURGERS' EQUATIONS
4 С FOR U(X,Y) AND V(X,Y).
5 С EXBUR EVALUATES THE EXACT SOLUTION OF BURGERS1 EQUATIONS
6 С RESBU EVALUATES THE RESIDUALS
7 С JACBU EVALUATES THE JACOBIAN
8 С FACT FACTORISES THE JACOBIAN INTO L.U
9 С SOLVE SOLVES THE LINEAR SYSTEM FOR DT
10 С IRD CONTROLS READ/WRITE OF STARTING SOLUTION
11 С IPN IS THE INCREMENT FOR PRINTING ITERATIVE RMS
12 С
13 REAL*8 SUM,DSQRT,R,U,V
14 DIMENSION UB1,21),VB1,21),UEB1,21),VEB1,21),AE),KE0}
15 l,AJE0,50),JPVTE0),RDE0)
16 COMMON DX,DY,RE,NX,NY,DTI
17 С
18 OPENA,FILE*'NEVTBU.DAT1)
19 OPENF,FILE*1NEVTBU.OUT1)
20 OPENG,FILE* *NEVTBU.STO *)
21 READIED NX,NY, ITMX, IRD, IPN, EPS,REfOM,DT
22 READA,2)(A(J),J=1,5),AL
23 1 FORMATEI5,4E10.3)
24 2 FORMATEF8.2,F5.2)
25 С
26 NXP * NX - 1
27 NYP * NY - 1
28 N * (NX -2)*(NY - 2)*2
29 VRITEF,3)N,ITMX,IRD,IPN
30 3 FORMATC NEVTONS METHOD FOR N **,I3,5X,'ITMX*'.13,
31 I1 IRD*1,12,• IPN*1,12)
32 VRITEF,4)DT,EPS,RE#OM
33 4 FORMATC DT*\E12.5,f EPS*',ЕЮ.3 • RE*\E10.3,
34 I1 OM*\E10.3)
35 VRITEF*5)(A(J),J=l,5),AL
36 5 FORMATC A =\5F8.2,' AL*f ,F5.2,//)
37 С
38 С CALCULATE EXACT SOLUTION
39 С
40 CALL EXBUR(UE,VE,A,AL)
41 С
42 С GENERATE INITIAL SOLUTION
43 С
44 IF(IRD .LT. 2)GOTO 8 -\
45 С
46 С IRD * 2 OBTAIN STARTING SOLUTION FROM NEVTBU.STO (UNIT 7>
47 С
48 DO 7 К * 1,NY
49 READG,6)(U(K,J),J*1,NX)
50 READG,6)(V(K,J),J*1,NX)
51 6 FORMATA0F8<5)
52 7 CONTINUE
53 GOTO 11
Рис. 6.10. Распечатка программы NEWTBU (начало).
15 К. Флетчер, т. 1
55
56
57
58
59
€0
€1
62
*3
64
65
€6
67
68
69
70
71
72
73
74
75
76
77
78
79
«0
31
«2
83
Ы
85
87
S3
59
ЭО
91
Э2
•93
94
•95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
С
С
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
с
8
9
10
11
12
13
14
15
16
17
18
19
20
DO 10 J = 1,NX
DO 9 К = 1,NY
U(K,J) « UE(K,J)
V(K,J) ¦ VE(K,J)
CONTINUE
CONTINUE
DO 12 К » 1,NY
VRITEF,13)(UE(K,J),J»1,NX)
FORHATC UE»\7F10.4)
DO 14 К « 1,NY
VRITEF,15)(VE(K,J).J=1,NX)
FORHATC VE»\7F10.4)
AN * N
IT » 0
ITP » 0
ОИН = OH
DTI * l./DT
CONTINUE
CALCULATE RESIDUALS
CALL RESBU(U,V,R)
SUH » 0.
DO 17 I » 1,N
RD(I) * R(I)
SUH » SUH + R(I)*R(I)
RHS = DSQRK SUM/AN)
IF(IT CE, ITP)WRITEF,19)IT,RHS,(R(J)fJ«l#3)
FORHATC IT-M3.' RKS«\D11.4,f R»(,3D11.4
TEST FOR CONVERGENCE OR MAXIMUM NUMBER
OF ITERATIONS EXCEEDED
IF(RHS .LT. EPS)GOTO 23
IFUT -GE. ITP)ITP » ITP + IPN
XT - IT ¦ 1
IF(IT .EQ. ITHX)GOTO 23
IF(RMS .GT. 1.0E+03)GOTO 30
CALCULATE JACOBIAN
CALL JACBU(U,V,AJ)
FACTORISE THE JACOBIAN INTO L.U
CALL FACT(N,AJ,JPVTl,
IF<JPVT(N) .EQ; -l)VRITEF,20)
FORHATC ZERO PIVOT DETECTED1)
IF(JPVT(N) .EQ, -1)GOTO 30
SOLVE FOR THE CORRECTION, DT
CALL SOLVE(N,AJ,JPVT,RD)
INCREMENT U AND V
Рис. 6.10 (продолжение).
§ 6.1. Нелинейные стационарные задачи 227
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
С
С
С
С
21
22
23
24
25
26
27
28
29
30
DO 22 J = 2,NXP
DO 21 К = 2,NYP
ИВ = 2MK-2) + 2*(NY-2)*(J-2)
DU * - RD(MB+1)
DV * - RD(KB+2)
U(K,J) = U(K,J) + DU*CM
V(K,J) = V(K,J) ¦ DY*OM
CONTINUE
CONTINUE
GOTO 16
GENERATE OUTPUT
VRITEF,24)IT,RMS
FORMAT(//,' AFTER \I3,' ITEF
LD12.5)
DO 25 К = 1,NY
VRITEF,26)(U(K,J),J=1,NX)
FORMAT(f U«\7F10.4)
DO 27 К = 1,NY
VRITEFr28)(V(KfJ),J=1,KX)
FORMAT С V=',7F10.4)
IF(IRD .EQ. 0}GOTO 30
DO 29 К = 1,NY
VRITEG,6)(U(KrJ)fJ=1,NX)
VRITEG,6)(V(K,J),J=1,NX)
CONTINUE
CONTINUE
STOP
END
ITERATIONS THE RMS RESIDUAL IS
Рис. 6.10 (окончание).
Выражения F.13) вводятся в вектор R в следующем по-
порядке:
2, Ъ RV2,2)
а порядок введения скоростей в вектор q таков:
^2,3> У2,3> •••> U2,NY-l> V2yNY-U Щ, 2> У3,2> ••••
В качестве начального решения относительно п и v было
использовано точное решение уравнений F.12) со значениями
параметров п\ =а2 = 110.13, аъ = а4 = 0, а5=1.0, А, = 5,
Re = 10, ymax = я/30 и хо = 1.0. Однако с помощью програм-
программы NEWTBU, примененной на сетке 5X5, т. е. с 18 узловыми
неизвестными значениями и и у, не удается получить сходя-
сходящееся решение. Для получения такого решения необходимо
15*
228
Гл. 6. Стационарные задачи
Таблица
Параметр
NX, NY
ITMX
IRD
IPN
EPS
RE
OM
DT
N
UE, VE
A
U, V
R
RD
AJ
DU, DV
6.2. Параметры, используемые в программе NEWTBU
Описание
Число узловых точек в направлениях х и у
Максимальное число итераций
= 0, 1, вводит начальное решение, полученное с помощью
подпрограммы EXBUR
= 1, 2, записывает окончательное решение в файл
NEWTBU.STA
= 2, считывает начальное решение из файла NEWTBU.STA
Выдает на печать невязки через каждые IPN итераций
Максимально допустимая среднеквадратичная невязка
уравнений
Число Рейнольдса Re, формула F.13)
Показатель нижней релаксации со, формула F.19)
Шаг по времени, используемый в псевдонестационарном
варианте (§ 6.4)
Число уравнений, подлежащих решению
Точное решение п, v
аи ..., а5 в формуле F.16)
Зависимые переменные в уравнениях F.13)
Невязки уравнений F.13)
= R после возврата из подпрограммы RESBU; содержит
поправки Aq после возврата из подпрограммы SOLVE
Якобиан J в уравнении F.17)
Поправки для и и v; Aq в уравнении F.17)
подвергнуть нижней релаксации поправку
что применяется следующая формула:
(*+o =
= qCO -f
Это означает,
F.19)
при со = 0.15. Однако и в этом случае скорость сходимости
очень мала (см. данные на рис. 6.14). Такая ситуация не может
считаться необычной при применении метода Ньютона к дискре-
тизированным уравнениям, описывающим задачи гидроаэро-
гидроаэродинамики. А именно поправки, определяемые по методу Ньюто-
Ньютона, могут оказаться достаточно большими для того, чтобы те-
текущее решение вышло за пределы радиуса сходимости (см.
п. 6.1.1), если только эти поправки вводятся без изменений.
Вид формулы F.19) подсказывает соответствующую стра-
стратегию. Она состоит в том, что величина Aq(/Z+1>, получаемая в
результате решения уравнения F.17), определяет лишь на-
§ 6.1. Нелинейные стационарные задачи 229
правление поиска. Для трех значений со строятся новые реше-
.ния
я вычисляются соответствующие им невязки Rm+1). Для каж-
каждого значения оот рассчитывается среднеквадратичная невяз-
1
2 SUBROUTINE EXBUR(UE,VE,A,AL)
3 С
4 С CALCULATES THE EXACT SOLUTION OF THE TVO-DIMENSIONAL BURGERS1
5 С EQUATIONS USING THE COLE-HOPF TRANSFORMATION
6 С
7 DIMENSION AE),UEB1,21),VEB1,21)fPHB1,21)
3 COMMON DX,DY,RE,NX,NY
9 PI = 3.1415927
10 XZ = 1.0
11 YMAX = PI/6./AL
12 ANY = NY - 1
13 DY ¦ YMAX/ANY
14 ANX = NX - 1
15 DX = 2./ANX
16 DO 2 J = 1,NX
17 AJ * J - 1
18 X = -1. + AJ*DX
19 XD = X - XZ
20 DEX = EXP(AL*XD) + EXP(-AL*XD).
21 DDX = EXP(AL*XD) - EXP(-AL*XD)
22 DO 1 К = 1,NY
.23 AK = К - 1
24 Y = AK*DY
.25 SY = SIN(AL*Y)
26 CY = COS(AL*Y)
27 PH(K,J) = A(l) + AB)*X + AC)*Y + AD)*X*Y + AE)*DEX*CY
28 PHX = A{2) + AD)*Y + AE)*AL*DDX*CY
29 PHY = AC) + AD)*X - AE)*AL*DEX*SY
30 иЕ(К,а) = - 2.*PHX/PH(K,J)/RE
31 VE(K,J) = - 2.*PHY/PH(K,J)/RE
32 1 CONTINUE
33 2 CONTINUE
34 RETURN
35 END
Рис. 6.11. Распечатка подпрограммы EXBUR.
ка /?(m,+rmS> причем предполагается наличие квадратичной за-
зависимости /?w,+m!s от ©• Затем выбирается такое значение со,
а следовательно, и Aq(/Z+1), которое ведет к минимальному Rrms
для заданного направления поиска Aq(rt+1). Эта стратегия, од-
однако, может оказаться слишком доростоящей в вычислительном
смысле, если невязки Ru и Rv имеют сложные выражения.
230 Гл. 6. Стационарные задачи
В качестве альтернативной и более эффективной стратегии
по сравнению с применением формулы F.19) можно указать
на сочетание метода Ньютона с псевдонестационарной форму-
1
2 SUBROUTINE RESBU(U,V,R)
3 С
4 С EVALUATES RESIDUALS OF 2D STEADY BURGERS* EQUATIONS
5 С
6 REAL*8 R,U,V,CX,CY,CCX,CCY,DUM
7 DIMENSION UB1,21),VB1,21),RE0)
8 COMMON DX,DY,RE,NX,NY
9 С
10 NXP * NX - 1
11 NYP » NY - 1
12 CX = 0.5/DX
13 CY » 0.5/DY
14 CCX = l./RE/DX/DX
15 CCY » l./RE/DY/DY
16 NCT * 1
17 С
1$ DO 2 J = 2,NXP
19 JM « J - 1
20 JP = J + 1
21 DO 1 К = 2,NYP
22 KM « К - 1
23 KP * К + 1
24 DUM * CX*U(K,J)*(U(K.JP)-U(K,JM)) ¦ CY*V(K,J)*(U(KP,J)-U(KH,J)f
25 R(NCT) = DUM - CCXMUtK, JM)-2.*U(K, J)+U(K, JP)) - CCY*(U(KM,J)
26 1 - 2.*U(K,J) + U(KP,J))
27 DUM * CX*U(K,J)MV(K,JP)-V(K,JM)) + CY*V(K# J)* (V(KP, J)-V(KM, J)>
28 RCNCT+1) » DUM - CCX*(V(K,JM)-2.*V(KfJ)+V(K,JP)) - CCY*(V(KM,J*
29 1 - 2.*V(K,J) + V(KP,J))
30 NCT « NCT + 2
31 1 CONTINUE
32 2 CONTINUE
33 С
34 RETURN
35' END
Рис. 6.12. Распечатка подпрограммы RESBU.
лировкой той же задачи (см. § 6.4). Решение данной задачи с
помощью псевдонестационарного метода Ньютона излагается
в п. 6.4.1.
6.1.4. Квазиньютоновский метод
Другой вариант подхода к решению систем нелинейных ал-
алгебраических уравнений, часто называемый квазиньютоновским
методом, сводится к замене формулы F.4) соотношением
F.20>
2 SUBROUTINE JACBU(U,V,AJ)
3 С
4 С EVALUATES THE JACOBIAN OF THE 2D STEADY BURGERS* EQUATIONS
5 С
6 REAL*8 U,V,CX,CY,CCX,CCY
7 DIMENSION UB1,21),VB1,21),AJE0,50)
8 COMMON DX,DY,RE,NX,NY,DTI
9 С
10 N « (NX - 2)MNY - 2)*2
11 DO 2 J » 1,N
12 DO 1 X > 1,1
13 1 AJ(K,J) « 0.
14 2 CONTINUE
15 С
16 NXP * NX - 1
17 NYP « NY - 1
18 CX » 0.5/DX
19 CY = 0.5/DY
20 CXX * l./RE/DX/DX
21 CYY « l./RE/DY/DY
22 С
23 DO 7 J * 2,NXP
24 JM = J - 1
25 JP * J + 1
26 DO 6 К « 2,NYP
27 KM * К - 1
28 KP » К + 1
29 MB = 2MK-2) + 2*(NY-2)MJ-2)
30 LU « MB + 1
31 LV = MB + 2
32 ML = MB - 2*(NY - 2)
33 IF(ML .LT. 0)GOTO 3
34 AJ(LU,ML+1) = - CX*U(K,J) - CXX
35 AJ(LV,ML+2) = - CX*U(K,J) - CXX
36 3 AJ(LU,MB+1) » 2.*(CXX+CYY) + CX*(U(K,JP)-U(K,JM)) + DTI
37 AJ(LU,MB+2) = CY*(U(KP,J) - U(KM,J))
38 AJ(LV,MB+1) » CX*(V(K,JP) - V(K,JM))
39 AJ(LV,MB+2) * 2.*(CXX+CYY) + CY*(V(KP,J) - V(KM,J)) + DTI
40 MR = MB + 24NY-2)
41 IF(MR .GT. N-2)GOTO 4
42 AJ(LU,MR+1) * CX*U(K,J) - CXX
43 AJ(LV',MR+2) * CX*U(K,J) - CXX
44 4 MK = MB - 2
45 IF(MK .LT. 0)GOTO 5
46 AJ(LU,MK+1) = - CY*V(KrJ) - CYY
47 AJ(LV,MK+2) = - CY*V(K,J) - CYY
48 5 MT = MB + 2
49 IF(MT .GT. N-2)GOTO 6
50 AJ(LU,MT+1) = СУ*У(К,а) - CYY
51 AJ<LV,MT+2) = СУ*У(К,а) - CYY
52 6 CONTINUE
53 7 CONTINUE
54 С ' •' '
55 . . RETURN - • >
56 . ВД) , . . ч -
Рис. 6.13. Распечатка подпрограммы JACBU.
232
Гл. 6. Стационарные задачи
где матрица Н(/г) представляет собой аппроксимацию величины»
(JK*))-1, систематически модифицируемую на каждом итерацион-
итерационном шаге, так что она приближается к (J^)-1 по мере прибли-
приближения к сходящемуся решению. Модификация матрицы Н(Л>
на каждом шаге оказывается значительно более экономичным
NEWTONS METHOD FOR N = 18 ITMX=400 IRD= 1 IPN=2O
DT* .50000E+03 EPS» .100E-04 RE= .100E+02 OM= .150E+0&
Л* 110.13 110.13 .00 .00 1.00
UE»
UE»
UE»
UE»
UE*
VE»
VE»
VE»
VE»
VE»
IT*
IT»
IT*
It»
IT»
IT»
0
20
40
60
80
100
AFTER
U*
U«
U«
Us
U»
V»
V*
Y«
V«
Y«
.9990
.9990
.9990
.9989
.9988
.0000
.1317
.2679
.4142
.5774
RMS»
RMS»
RMS»
RMS»
RMS»
RMS»
.9586
.9583
.9572
.9553
.9524
.0000
.1277
.2598
.4010
.5577
.1496D+00
.2854D-01
.5504D-02
.1024D-02
.1892D-03
.3499D-04
115 ITERATIONS THE
.9990
.9990
.9990
.9989
.9988
.0000
.1317
.2679
•4142
.5774
.9586
.9605
.9603
.9577
.5524
.0000
.1282
.2605
.4017
.5577
R»
R»
R«
R*
R»
R»
.4888
.4863
.4786
.4655
.4462
.0000
.0753
.1515
.2297
.3109
-.2169D+00
-.8407D-02
-.3259D-03
-.1264D-04
-.4914D-06
-.1930D-07
RMS RESIDUAL
.4888
.4835
.4748
.4625
.4462
.0000
.0748
.1507
.-2290
.3109
.0559
.0565
.0584
.0614
.0657
.0000
.0090
.0179
.0266
.0349
.0991
-.0991
-.0991
-.0992
-.0992
.0000
.0012
.0023
.0034
.0045
-.2850D-01 -.2188D+0O
-.1105D-02 -.8483D-02
-.4288D-.04 -.3289D-03
-.1662D-05 -.1277D-04
-.647.0D-07 -.4977D-0S
-.2559D-08 -.1981D-b7
IS .98726D-05
0559
0567
0585
0615
0657
0000
0090
0179
0266
0349
-.0991
-.0991
-.0991
-.0992
-.0992
.0000
.0012
.0023
.0034
«0045
Рис. 6.14. Типовая выдача результатов по программе NEWTBU.
процессом, чем факторизация матрицы
может быть переписано в форме
Уравнение F.20^
F.
где вектор %{к) = H(/s)R(ft) может рассматриваться как опреде-
определяющий направление поиска. Скаляр ю<*> выбирают так, чтобы.
величина /^т^0 оказывалась минимальной в направлении по-
поиска %{к\ При больших N последнее свойство обеспечивает зна-
§ 6.2. Прямые методы для линейных систем 233
чительно больший радиус сходимости, чем при применении
обычного метода Ньютона. Характерный алгоритм, известный
как формула BFGS [Fletcher, 1980], позволяет строить сле-
следующее приближение V(A;+1) с помощью формулы F.21). В ре-
результате имеем
F#22)
Несмотря на то что матрица J является, как правило, разре-
разреженной, структура выражений F.22) свидетельствует о том,
ято матрица Н оказывается плотной. При k = 0 матрица
•Н@) полагается равной единичной матрице I.
Эффективность квазиньютоновских методов зачастую зави-
зависит от того, обладает ли матрица J некоторыми специальными
свойствами, такими, как положительная определенность [Jen-
[Jennings, 1977а]. Следовательно, применимость этих методов к
задачам вычислительной гидроаэродинамики должна исследо-
исследоваться для каждого случая отдельно. Значительная часть
литературы по квазиньютоновским методам связывает их приме-
применение с безусловной минимизацией (см., например, [Powell,
1976; Fletcher, 1980]). Обсуждение квазиньютоновских методов
в применении к специальным задачам можно найти в работах
[Broyden, 1965; Ortega, Rheinboldt, 1970; Shanno, 1983]. Ха-
Характерный вариант применения квазиньютоновского метода к
задаче гидроаэродинамики дается в работе [Engelman et al.,
3981].
§ 6.2. Прямые методы для линейных систем
Для эллиптических задач, описываемых линейными уравне-
уравнениями типа уравнений потенциального течения или тех, кото-
которые соответствуют промежуточным этапам метода Ньютона,
необходимо строить решение линейной системы алгебраических
уравнений
AV = В F.23)
относительно компонентов вектора V, где все элементы матри-
матрицы А и вектора В известны. Метод исключения по Гауссу
[Dahlquist, Bjorck, 1974] является предпочтительным средством
решения уравнений F.23), однако эффективность реализации
234 Гл. 6. Стационарные задачи
этого метода зависит от структуры матрицы А. Заслуживают
выделения три категории подобного рода матриц:
(a) Матрица А содержит лишь несколько или не содержит
совсем нулевых элементов. Тогда говорят, что матрица А пол-
полная или плотная.
(b) Матрица А содержит много нулевых элементов. Такую
матрицу называют разреженной.
(c) Матрица А содержит много нулевых элементов, причем
ее ненулевые элементы группируются вблизи главной диаго-
диагонали. Тогда матрицу А называют разреженной и ленточной.
Компьютерные программы, основанные на предположении
0 том, что матрица А является полной, оказываются более уни-
универсальными, но и более дорогостоящими в вычислительном
смысле. Такие программы могут использоваться в применении'
к разреженным и/или ленточным матрицам, однако для по-
последних категорий существуют специальные и притом более
экономичные процедуры. Какой бы ни была структура матри-
матрицы А, метод исключения по Гауссу должен применяться в два
этапа. Сначала матрица А факторизуется, превращаясь в ниж-
нижнетреугольную матрицу L и верхнетреугольную матрицу U в
качестве двух сомножителей. После этого факторизованная
форма уравнения F.23) решается как
UV = L-!B. F.24>
Вследствие структуры матрицы U процесс решения F.24) сво-
сводится к повторным подстановкам, осуществляемым после фор-
формирования комплекса L^B.
6.2.1. FACT/SOLVE: решение систем с плотными матрицами
Если матрица А плотная, то все ее элементы участвуют ш
образовании матриц L и U. Подпрограмма FACT (рис. 6.15}
реализует требуемую факторизацию по формуле LU = А. По-
Последующая серия подстановок согласно F.24) осуществляется
с помощью подпрограммы SOLVE (рис. 6.16).
На каждом шаге факторизации множество элементов из
текущего ряда k вычитается из элементов последующего ряда
1 с целью исключения и*. При этом вводится множитель
0«, klak, k> а величина а*, * называется ведущим элементом. Если
ведущий элемент равен нулю или очень мал, то исключение по
Гауссу либо не проходит вообще, либо дает очень неточные ре-
результаты. Во избежание этого вводится частичный отбор ве-
ведущего элемента. Для исключения Vk проводится поиск в k-m
столбце в интервале i = ft+l, N, ставящий целью найти»
§ 6.2. Прямые методы для линейных систем 235
1 SUBROUTINE FACT(N,A,JFVT)
2 С
3 С FACTORISES A INTO PERMUTED L.U SO THAT PERM*A « L*U
4 С JPVT(K) GIVES INDEX OF KTH PIVOT ROW
5 С SETS J?VT(N) = -1 IF ZERO PIVOT OCCURS
6 С
7 DIMENSION AE0,50),JPVTE0)
8 NM = N - 1
9 С
10 С GAUSS ELIMINATION WITH PARTIAL PIVOTING
11 С
12 DO 5 К = 1,NM
13 KP = К + 1
14 С
15 С SELECT PIVOT
16 С
17 L = К
18 DO 1 I = KP,N
19 IF(ABS(A(I,K)) .GT. ABS(A(L,K)))L = I
20 1 CONTINUE
21 JPVT(K) = L
22 S = A(L,K)
23 A(L,K) = A(K,K)
24 А(КД) = S
25 С
26 С CHECK FOR ZERO PIVOT
27 С
28 IF(ABS(S) .LT. 1.0E-15)GOTO 6
29 С
30 С CALCULATE MULTIPLIERS
31 С
32 DO 2 1= KP,N
33 A(I,K) = -A(I,K)/S
34 2 CONTINUE
35 С
36 С INTERCHANGE AND ELIMINATE BY COLUMNS
37 С
38 DO 4 J = KP,N
39 S = A(L,J)
40 A(L,J) = A(K,J)
41 A(K,J) = S
42 IF(ABS(S) .LT. 1.0E-15)GOTO 4
43 DO 3 I = KP,lT
44 A<I,J) = A(I,J) + A(IrK)*S
45 3 CONTINUE
46 4 CONTINUE
47 5 CONTINUE
48 RETURN
49 6 JPVT(N) = -1
50 RETURN
51 END
Рис. 6.15. Распечатка подпрограммы FACT.
236 Гл. 6. Стационарные задачи
1 SUBROUTINE SOLVE(N,A,JPVT,B)
2 С
3 С SOLVES LINEAR SYSTEM, A*X = В
4 С ASSUMES A IS FACTORISED INTO L.U FORM (BY FACT)
5 С RETURNS SOLUTION, X, IN В
6 С
7 DIMENSION AE0,50),JPVTE0),BE0)
8 С
9 С FORWARD ELIMINATION
10 С
11 NM = N - 1
12 DO 2 К « 1,NM
13 KP « К + 1
14 L « JPVT(K)
15 S = B(L)
16 B(L) = B(K)
17 B(K) = S
18 DO 1 I = KP,N
19 B(I) = B(I) -I- A(I,K)*S
20 1 CONTINUE
21 2 CONTINUE
22 С
23 С BACK SUBSTITUTION
24 С
25 DO 4 KA = 1,NM
26 KM = N - KA
27 К » KM + 1
28 B(K) = В(К)/А(КД)
29 S = - B(K)
30 DO 3 I = 1,KM
31 B(I) = B(I) + A(I,K)*S
32 3 CONTINUE
33 4 CONTINUE
34 B(l) = B(l)/A(l,l)
35 RETURN
36 END
Рис. 6.16. Распечатка подпрограммы SOLVE.
наибольший ведущий элемент щ, k (FACT, строки 17—24). Если
наибольший ведущий элемент равен нулю, то программа выдает
сигнал ошибки [JPVT(N)= — 1] и осуществляется возврат
к основной программе.
В предположении о том, что наибольший ведущий элемент
не равен нулю, осуществляется перестановка рядов (FACT*
строки 39—41), чтобы переместить наибольший ведущий эле-
элемент a/, k в положение (&, k). В каждом столбце / (/ = &+ 1^.
N) коэффициенты t-й строки (i=?+l, N) модифицируются
(FACT, строки 38—46) в соответствии с формулой
*,,. F-25)
§ 6.2. Прямые методы для линейных систем 237
Массивы хранятся в памяти вычислительных машин по столб-
столбцам (индекс i в а*,/). Поэтому наиболее целесообразно сделать
так, чтобы самый внутренний цикл подпрограммы FACT (стро-
(строки 43—45) реализовался по первому индексу.
Подпрограмма SOLVE прежде всего преобразует элементы
вектора В (строки 12—21) с целью взаимодействия с ведущей
строкой и модификации элемента bi, i = &+l, N, путем вы-
вычитания из него ведущей строки с соответствующим множите-
множителем, т. е.
что эквивалентно операции F. 25) в подпрограмме FACT. Окон-
Окончательное решение получается с помощью последовательных
подстановок, реализуемых посредством подпрограммы SOLVE
(строки 25—34). Это дает
Для экономии памяти решение V записывается на место исполь-
использованного массива и выдается уже как массив В.
Реализация исключения по Гауссу в два этапа, соответ-
соответствующих подпрограммам FACT и SOLVE, полезна в тех слу-
случаях, когда требуется строить решения для многих вариантов
величины В в правой части уравнения F.23). Это связано с
тем, что для выполнения подпрограммы FACT требуется
O(N3) операций, тогда как SOLVE требует O(N2) операций.
Обе эти подпрограммы, представленные в несколько расширен-
расширенной форме, подвергаются более тщательному обсуждению в
книге [Forsythe et al., 1977, разд. 3.3].
Как правило, при использовании спектральных методов
(§ 5.6) и панельных методов (§ 14.1) получаются матрицы А
с плотной структурой. В противоположность этому методы ко-
конечных элементов и конечных разностей приводят к матрицам
А разреженной структуры и, если используется методика рас-
расщепления (факторизации, § 8.2), матрицам узколенточной струк-
структуры.
Если матрица А разреженная, но не обязательно ленточная,
то исключение по Гауссу часто осуществляется при введении А
в память в форме одного массива, содержащего значения ац
вместе со связанным с ним индикаторным массивом IA, обеспе-
обеспечивающим информацию о положении точки (?, /). Основная
трудность, возникающая при программировании процесса гаус-
совского исключения с разреженными матрицами, связана с
вероятностью заполнения матрицы А. Иначе говоря, в процессе
238
Гл. 6. Стационарные задачи
исключения элементы матрицы А, первоначально равные нулю,
становятся отличными от нуля. Различные методы надлежа-
надлежащего представления А и IA обсуждаются в книгах [Jennings,
1977а, гл. 5; Duff, 1981], последняя из которых предла-
предлагает более высокий уровень анализа. Существуют пакеты про-
программ для реализации гауссовского исключения при разрежен-
разреженных матрицах; можно рекомендовать разработанные в Харуэл-
Харуэлле программы МА28 и т. д., рассмотренные в вышеназванной
книге Даффа.
6.2.2. Трехдиагональные системы: алгоритмы Томаса
Использование трехточечных конечно-разностных формул
или конечных элементов с линейной интерполяцией приводит
после расщепления (§ 8.2) к появлению матриц А в уравнении
F.23), имеющих трехдиагональную структуру. Использование
конечно-разностных схем более высокого порядка или конеч-
конечных элементов более высокого порядка приводит к ленточной
структуре А, где ширина области ненулевых элементов будет
больше. Алгоритм Томаса пригоден для решения уравнения
F.23) в случае трехдиагональной матрицы А. Обобщение алго-
алгоритма Томаса на случай пятидиагональной матрицы А описы-
описывается в п. 6.2.4. Если речь идет о системах уравнений, то
матрица А имеет, как правило, блочную (трехдиагональную)
структуру. Порядок действий в этом случае рассматривается в
п. 6.2.5.
Если ненулевые элементы располагаются вблизи главной
диагонали, то полезно рассмотреть те варианты исключения по
Гауссу, которые используют преимущества ленточной структу-
структуры А. Один из примеров такого варианта соответствует рас-
рассмотренной в § 9.3 задаче о конвекции — диффузии. Если вос-
воспользоваться формулами с центральными разностями, то при
обозначениях данного параграфа получается следующий алго-
алгоритм:
- A + 0.5Ясе11) t>f-i + 2vt - A - 0.5/Jcell) VM = 0, F.27)
при повторении которого по отношению к каждому узлу по-
получим
#2 b2 c2 ®2 d2
at bt
aN bN
. F.28)
§ 6.2. Прямые методы для линейных систем
239
где аг = — A+0.5#Сеп), bt = 2, С/ = —( 1—0.5Ясен). Ненуле-
Ненулевые значения d( связаны с членами типа источника или, как с
di и dN, с граничными условиями. Все элементы матрицы А,
кроме показанных выше, равны нулю. Можно отметить измене-
изменение некоторых обозначений по сравнению с п. 6.2.1, в частности
относящихся к Ь[.
Алгоритм Томаса для решения уравнений F.28) состоит из
двух частей (см. схему на рис. 6.17). Сначала уравнения F.28)
X X
XXX
XXX
X
• •
ххх
X X
•
•
X
X
X
X
X
X
X
^Прогонка
назад
Рис. 6.17. Алгоритм Томаса для решения трехдиагональной системы урав-
уравнений.
преобразуются к виду
с'
\с'2
1 с\
d'
1
т. е. из них исключаются коэффициенты а,-, тогда как коэффи-
коэффициенты bi нормализуются к единичным значениям. Для перво-
первого уравнения этой цели служат формулы
с\ = сЖ9 d\ = dxlbv F.29)
а для произвольно расположенного уравнения
di-aid'i-\
bi-aici-\
bf —
F.30)
240 Гл. 6. Стационарные задачи
Модификация уравнений по формулам типа F.30) проводится
в процессе прямой прогонки (рис. 6.17). Второй этап алгорит-
алгоритма сводится к обратной подстановке (обратная прогонка на
рис. 6.17), т. е. к использованию формул
Алгоритм Томаса чрезвычайно экономичен; он требует для
своего исполнения всего 5N — 4 операций (умножений и деле-
делений). Однако во избежание плохой обусловленности (и, следо-
следовательно, накопления ошибок округления) необходимо, чтобы
\bi\ > \di\ + \ci\. Как правило, использование расщепления
при решении многомерных задач (§ 8.2) приводит к трехдиа-
гональным системам уравнений, которые могут эффективно ре-
решаться при помощи алгоритма Томаса.
6.2.3. BANFAC/BANSOL: исключение по Гауссу
для узколенточных матриц
В тех случаях, когда матрица А имеет узколенточную струк-
структуру, для реализации исключения по Гауссу подходят" подпро-
подпрограммы BANFAC и BANSOL. Подпрограмма BANFAC
(рис. 6.18) выполняет прямую прогонку или несколько повто-
повторяющихся прямых прогонок, чтобы придать матрице А верхне-
верхнетреугольную форму. Подпрограмма BANSOL (рис. 6.19) пре-
преобразует правую часть F.23), а именно вектор В, и получен-
полученная система уравнения решается путем обратной подстановки.
Для случая INT = 2 подпрограммы BANFAC и BANSOL
составлены так, чтобы воспользоваться особым видом структу-
структуры матрицы А, полученным при использовании одномерных
квадратичных элементов. А именно матрица А оказывается по-
попеременно то «трехдиагональной» (три соседних ненулевых
элемента в одной строке), то «пятидиагональной» (пять сосед-
соседних ненулевых элементов в одной строке), что соответствует
уравнениям, связанным с узлами в серединах или в углах эле-
элементов соответственно (см. рис. 5.10).
В этом случае процесс факторизации (BANFAC) состоит из
двух прогонок. Первая прогонка воздействует только на «пяти-
диагональные» строки с целью исключения лишнего коэффи-
коэффициента ak, k-2- Вторая прогонка приводит матрицу к верхне-
верхнетреугольной форме. Конкретный вид реализации зависит от то-
того, связаны ли первое и последнее уравнения из системы F.23)
с узлами в серединах или в углах элементов. Граничные усло-
условия Дирихле соответствуют срединным узлам; граничные же
условия Неймана соответствуют угловым узлам. Читателю мо-
может оказаться полезным изучить часть программы, относящуюся
§ 6.2. Прямые методы для линейных систем 241
1
2 SUBROUTINE BANFAC(B,N,INT)
3 С
4 С FACTORISES BAND MATRIX ARISING FROM LINEAR OR QUADRATIC ELEMENTS
5 С INTO L.U
6 С
7 DIMENSION B<5,65)
8 IF(INT .EQ. 2)GOTO 2
9 С
10 С INT - 1, LINEAR ELEMENTS * TRIDIAGONAL SYSTEM
11 С
12 NP « N - 1
13 DO 1 J » 1,NP
14 JP * J + 1
15 BB,JP) « BB,JP)/BC,J)
16 BC,JP) « BC,JP) - BB,JP)*BD,J)
17 1 CONTINUE
18 RETURN
19 С
20 С INT » 2, QUADRATIC ELEMENTS - PENTADIAGONAL SYSTEM
21 С ASSUMES FIRST EQUATION FORMED AT MIDSIDE NODE
22 С
23 2 NH » N/2
24 DO 5 I « 1,2
25 JS = 3 - I
26 DO 4 J « JS,NH
27 JA « 2MJ-1)
28 IF(I .EQ. 2)GOTO 3
29 С
30 С I ¦ 1, FIRST PASS, REDUCE TO TRIDIAGONAL'
31 С
32 JB = JA + 2
33 BA,JB) * BA,JB)/BB,JB-1)
34 BB,JB) « BB,JB) - BA,JB)*BC,JB-1)
35 BC,JB) * BC,JB) - BA,JB)*BD,JB-1)
36 GOTO 4
37 С
38 С 1=2, SECOND PASS, REDUCE TO UPPER TRIANGULAR
39 С
40 3 JB = JA + 3
41 BB,JB-1) = BB,JB-l)/BC,JB-2)
42 BC,JB-1) » BC,JB-1) - BB,JB-l)*BD,JB-2)
43 IF(JB .GT. N)GOTO 4
44 BB,JB) » BB,JB)/BC,JB-1)
45 BC,JB) « BC,JB) - BB,JB)*BD,JB-1)
46 BD,JB) = BD,JB) - BB,JB)*BE,JB-1)
47 4 CONTINUE
48 5 CONTINUE
49 RETURN
50 END
Рис. 6.18. Распечатка подпрограммы BANFAC.
к высказанным положениям и начинающуюся с INT = 2, после
прочтения п. 6.2.4.
Примером использования подпрограмм BANFAC/BANSOL
как в случае трехдиагональных, так и попеременно трехдиаго-
16 К. Флетчер, т. 1
242 Гл. 6. Стационарные задачи
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
С
С
С
С
С
С
С
С
С
С
С
С
1
2
3
4
5
6
7
SUBROUTINE BANSOL(R,X,B,N,INT)
USES L.U FACTORISATION TO SOLVE FOR X, GIVEN R
DIMENSION RF5),XF5),BE,65)
IFUNT .EQ. 2)GOTO 3
INT = 1, TRIDIAGONAL SYSTEM
NP * N - 1
DO 1 J = 1,NP
JP * J + 1
R(JP) = R(JP) - BB,JP)*R(J)
X(N) = R(N)/BC,N)
DO 2 J = 1,NP
JA « N - J
X(JA) = (R(JA) - BD,JA)*X(JA+1))/BC,JA)
CONTINUE
RETURN
INT = 2, PENTADIAGONAL SYSTEM
ASSUMES FIRST EQUATION FORMED AT MIDSIDE NODE
SET IBC * 0 IF LAST EQUATION FORMED AT MIDSIDE NODE
SET IBC = 1 IF LAST EQUATION FORMED AT CORNER NODE
IBC » 1
NH = N/2
IFB*NH .EQ. N)R(N+1) » 0.
IFB*NH .EQ. N)BB,N+1) « 0.
DO 6 I =1,2
DO 5 J = 1,NH
JA = 2*J
DO 4 К = 1,1
JB = JA - 1 + К
R(JB) = R(JB) - B(I,JB)*R(JB-1)
CONTINUE
CONTINUE
NEN = NH - IBC
X(N) = R(N)/BC,N)
IF(IBC .EQ. l)X(N-l) = (R(N-l) - BD,N-1)*X(N))/BCrN-
DO 7 J * l,NEN
JA = N - 2*J + 1 - IBC
X(JA) « (R{JA) - BD,JA)*X(JA+1) - BE,JA)*X(JA+2))/B(
X(JA-l) = (R(JA-l) - BD,JA-1)*X(JA))/BC,JA-1)
CONTINUE
RETURN
END
Рис. 6.19. Распечатка подпрограммы BANSOL.
нальных/пятидиагональных матриц является решение задачи
Штурма —- Лиувилля (п. 5.4.2).
Полезная проверка правильности составления подпрограмм
решения уравнений F.23) состоит в том, чтобы после определе-
§ 6.2. Прямые методы для линейных систем
243
ния V заполнить левые части уравнений F.23) и убедиться в
равенстве левых частей правым. Это, однако, не гарантирует
точности построенного решения V, если матрица А плохо обус-
обусловленная, иначе говоря, если уравнения, составляющие систе-
систему F.23), близки к линейным. Плохо обусловленные системы и
их влияние на точность решения обсуждаются в книгах [Ge-
[Gerald, 1987; Dahlquist, Bjorck, 1974].
6.2.4. Обобщенный алгоритм Томаса
Применение конечно-разностных или конечно-элементных
схем повышенного порядка приводит к матрицам с более ши-
широкими лентами, чем трехдиагональная матрица. Однако не-
нетрудно провести обобщение алгоритма Томаса. Допустим, что
нам необходимо решить следующую пятидиагональную си-
систему:
b2 c2 f2
f3
et at bt ct ft
• • •
eN_x «лг-i bN
bN
Первый этап состоит в исключении всех элементов е„ что дает
b, с
<h b
a
¦i /i
2 C2
!3 К
/2
C3
fa
к
< п
__°w.
16*
244
Гл. 6. Стационарные задачи
где
F.32)
Следующий этап по существу совпадает с первым этапом обыч-
обычного алгоритма Томаса. Иначе говоря, все элементы а\ исклю-
исключаются, что дает
'2 '2
где
1 с"
F.33)
li ='
F.34)
*ibi-l
После этого для решения уравнений F.33) требуется обратная
подстановка следующего общего вида:
F.35)
Ji+V
Очевидно, что для решения пятидиагональной системы потре-
потребуются две прямые и одна обратная прогонки.
Различные этапы обобщенного алгоритма Томаса можно ин-
интерпретировать как серии операций (прямых прогонок), тре-
требуемых для приведения матрицы А к верхнетреугольному виду,
§ 6.2. Прямые методы для линейных систем
245
после чего с помощью обратных подстановок можно рассчитать
V. Ясно, что чем более широкую ленточную структуру будет
иметь матрица А, тем менее экономичным будет вышеописан-
вышеописанный алгоритм.
Если внутри самой ленты вкраплено достаточно большое
число нулей, то, как правило, более экономичными оказываются
некие альтернативные приемы обработки разреженных матриц
[Jennings, 1977a], хотя они вызывают больше трудностей при
программировании.
6.2.5. Блочные трехдиагональные системы
Описание алгоритма Томаса для решения трехдиагональных
систем дается в п. 6.2.2. Как правило, этот алгоритм следует
применять в тех случаях, когда единственное исходное уравне-
уравнение подвергается дискретизации с помощью неявного алгоритма
(§ 7.2). Однако многие задачи гидроаэродинамики описывают-
описываются системами уравнений (§ 10.2 и гл. 11). Попытки реализо-
реализовать неявные алгоритмы приводят тогда, как правило, не к:
скалярным трехдиагональным системам уравнений, а к блочным
трехдиагональным структурам. Однако алгоритм Томаса без:
труда распространяется и на действия в таких ситуациях.
Блочно-трехдиагональная система уравнений, эквивалент-
эквивалентная системе F.28), может быть представлена в виде
Ь, q
a2 b2 c2
а, Ь{
b*
v2
d2
, F.36)
v^ _
где а„ b/, cz- — субматрицы размера М X M, а V,- и d* суть М-
компонентные субвекторы. Число М соответсвует числу урав-
уравнений, записываемых в каждой точке сетки; например, для
трехмерного течения вязкой сжимаемой жидкости 7И = 5
(п. 11.6.3). Отсюда следует, что V; — субвектор решения, свя-
связанный с конкретной точкой сетки. Уравнение F.36)—система*
состоящая из Af блоков уравнений, причем каждый блок свя-
связанный с конкретной точкой сетки, включает в себя М урав-
уравнений.
Решение системы F.36) идет по методике, очень близкой
методике решения F.28). Сначала трехдиагональная матрица
246 Гл. 6. Стационарные задачи
блоков из F.36) преобразуется к верхнетреугольной форме за
счет исключения субматриц а/. По аналогии с F.29) первый
блок уравнений дает
с^^Г'сь d[ = (b{yldu F.37)
тогда как для блока общего вида имеем
'сг., dH^-'ld.-a^,}. F.38)
В выражениях F.37) и F.38) фигурируют явные выражения
обратных матриц. На практике более экономичный путь свя-
связан с решением TW-компонентной субсистемы; например, урав-
уравнение b?c^ = ct. решается относительно с'.. После выполнения
операций F.37) и F.38) уравнение F.36ч приобретает верхне-
верхнетреугольную форму при замене с, и d/ нас^ и d| и при замене Ьг
на единичную матрицу I.
Второй этап, эквивалентный применению формул F.31), тре-
требует обратных подстановок по формулам
v*=d;, v,. = d;-c;v,+1. F.39)
Как показывает подсчет, для реализации блочного алгорит-
алгоритма Томаса требуется ОEЛШ3/3) операций, что явно предпоч-
предпочтительно числу О((ЛШK/3), требуемому для реализации пол-
полного исключения по Гауссу. Однако если бы оказалось возмож-
возможным расщепить блочно-трехдиагональную систему F.36) на М
скалярных трехдиагональных систем, то полный подсчет по-
показал бы 0ENM) операций, т. е. грубо говоря, уменьшение
времени счета в М3/3 раз при N » М. В результате возникает
стимул к тому, чтобы построить неявные алгоритмы, которые
позволили бы части уравнений отделиться от системы в целом.
Вариант блочного алгоритма Томаса, описанный выше, изла-
излагается по книге [Isaacson, Keller, 1966].
6.2.6. Прямые алгоритмы решения уравнения Пуассона
Уравнение Пуассона, так же как и связанное с ним уравне-
уравнение Лапласа, достаточно часто встречается в гидроаэродина-
гидроаэродинамике, чтобы имело смысл исследовать возможности разработки
специальных процедур для решения дискретизированного урав-
уравнения Пуассона. Трехточечная конечно-разностная дискрети-
дискретизация двумерного уравнения Пуассона приводит к системе
уравнений типа F.23), для которой матрица А имеет форму,
показанную на рис. 6.1.
Для случая однородной сетки (Ах = ку), покрывающей
прямоугольную область O^x^l, O^y^l, один из блоков
§ 6.2. Прямые методы для линейных систем 247*
системы уравнений может быть записан в виде
IV,+1 = h*, Л=1 Af, F.40>
где М — число активных точек в направлении оси у. Каждый
вектор \k содержит N неизвестных значений Vj, *, связанных с
одной из линий сетки (у — Ук), направленной вдоль оси х.
Матрица g является трехдиагональной, имеет порядок N и от-
отличные от нуля элементы 1, —4, 1, относящиеся соответственно
к точкам (/— 1, &), (/, k) и (/+ 1, к). Вектор h* содержит все
те вклады в В из уравнения F.23), которые вносит в правук>
часть единственная линия сетки, идущая параллельно оси х,
т. е. у = ук.
При решении уравнения F.40) особенно эффективными
оказываются два метода — метод циклической редукции и ме-
метод разложения в ряд Фурье. Предпочтительная стратегия
[Swartztrauber, 1977] сводится к тому, чтобы вначале с по-
помощью циклической редукции уменьшить размер М в уравне-
уравнениях F.40), после чего строить решение редуцированной си-
системы с помощью разложения в ряд Фурье.
В процессе циклической редукции блок, расположенный в
k-й (четной) строке уравнения F.40), умножается на —g и
складывается с блоками в (k—1)-й и (&+1)-й строках с
целью исключения Vk-\ и V*+i. В результате получим
IV*_2 + g(I)V, + \Vk+2 = hi!\ (
где
gW = 21 - gg = (V21 + g) (V21 - g),
Этот процесс можно повторить требуемое число раз. После
осуществления / редукций уравнение F.40) приобретает форму
IV^2/ + g^V + IV,+2/ = h^, F.42>
где
gl = ~ Е (С - М), Pi = 2 cos [B* - 1) я/2'+'].
В принципе редукция может быть определена до тех пор,
пока граничные условия не позволят определить Vk-2i и \k+2?
[Dorr, 1970]. Затем с помощью обратных подстановок будут
определены все промежуточные векторы V*. На практике, одна-
однако, оказывается более эффективным завершить данный процесс
после / редукций, переключаясь на применение рядов Фурье.
248 Гл. 6. Стационарные задачи
Если на всех границах ставятся граничные условия Дирих-
Дирихле, то надлежащее представление в виде ряда Фурье будет
следующим:
Е() при k=*\ Mt, F.43)
где Mi — число линий сетки, параллельных оси х и оставших-
оставшихся в уравнениях F.42) после I редукций. Коэффициенты Us, к
определяются путем решения трехдиагональных систем вида
Us,k-i + W8,k + U89k+l = H8tk при s=l, ..., N, F.44)
тде
n
? (*„ yk) sin (ту$г). F.45)
величина ft(jt/, ун)—элемент вектора h(/> в уравнении F.42) и
F'46)
Быстрое преобразование Фурье [Cooley et ah, 1970; Brigham,
1974] применяется для нахождения неизвестных величин в со-
соотношениях F.43) и F.45). Слегка видоизмененные формы
этих соотношений, а также формул F.46) встречаются при
других вариантах граничных условий (Swartztrauber, 1977).
Для сетки, соответствующей случаю N = М, оптимальное
число циклических редукций дается в работе [Swartztrauber,
1977) в виде / = Iog2(log2^)—1. Комбинированный алгоритм
PACR(Z), впервые описанный Хокни [Hockney, 1970], требует
для своей реализации N2 log2 (log2 N) операций. При N= 1000,
1 = 2 алгоритм FACR(/) оказывается примерно в 30 раз бы-
быстрее, чем неявная схема переменных направлений (НПН, см.
п. 6.3.2), примененная к уравнению Пуассона. Реализация ал-
алгоритма FACR(/) на суперкомпьютерах обсуждается в книге
[Hockney, Jesshope, 1981], так же как и подходы к решению
дискретизированных уравнений Пуассона в трех измерениях
[Hockney, Jesshope, 1981].
Что касается подробного обсуждения прямых методов ре-
решения уравнения Пуассона, а также быстрого преобразования
-Фурье, то интересующийся читатель отсылается к книгам
[Hockney, Jesshope, 1981; Swartztrauber, 1977; Dorr, 1970], a
также к цитированным там источникам.
§ 6.3. Итерационные методы 249
Следует ясно отдавать себе отчет в том, что происхожде-
происхождение скорости циклической редукции и возможности представ-
представления с помощью ряда Фурье обусловлено симметричным ха-
характером и постоянством коэффициентов в дискретном вариан-
варианте лапласиана на равномерной прямоугольной сетке. В случае
сетки произвольной формы дискретизация уравнения Пуассо-
Пуассона, осуществляемая, например, в процессе применения метода
конечных объемов (§ 5.2) или метода конечных элементов с
изопараметрическим преобразованием (п. 5.5.3), или же исполь-
использования обобщенных координат (гл. 12), приводит к алгебраи-
алгебраическому уравнению с переменными коэффициентами. Напри-
Например, при введении обобщенных координат это уравнение мо-
может быть записано в виде
Я/, *У/-1, * + ъи kVi+u k + си kVl% *_, + йи *Уи л+1 + eU kvi, k = Л/, kr
F.47)
или, по аналогии с F.40), в виде
C*Vft_, + GkVk + D,V*+1 = h*. F.48)
Как и прежде, матрица Gk является трехдиагональной, а век-
векторы Ck и Dk содержат диагональные элементы. Однако для
уравнения F.48) не реализуется тот вариант исключений, ко-
который приводил к уравнению F.41).
Если к уравнению F.47) применить метод разложения в
ряд Фурье, то вместо трехдиагональной системы F.44) полу-
получится система уравнений для Us, k с плотной матрицей. Следо-
Следовательно, по отношению к уравнению F.47) метод разложения:
в ряд Фурье является не более экономичным, чем метод исклю-
исключения по Гауссу (п. 6.2.1), примененный непосредственно к это-
этому уравнению. В зависимости от выбора сетки уравнение
F.47) может включать также отличные от нуля вклады, свя-
связанные с узловыми точками (/—1, Л+1), (/—1, k—1)„
(/+1, k+l) и (/+1, ft-1).
§ 6.3. Итерационные методы
Итерационные методы можно применять непосредственна
к нелинейной системе уравнений F.1); однако проще несколь-
несколько видоизменить методику построения итераций, обращаясь к
линейной форме F.2). Все итерационные методы можно рас-
рассматривать как процедуры, предназначенные для последова-
последовательной модификации начальной аппроксимации, при этом си-
систематически приближаясь к решению. В общем случае про-
простые итерационные методы не обеспечивают сходимости, если
250 Гл. 6. Стационарные задачи
только матрица А, входящая в уравнение F.2), не включает
в себя больших элементов на главной диагонали, т. е. если не
выполняется условие F.52).
6.3.1. Общая структура методов
Общая структура итерационных методов для стационарных
задач будет выявлена, если уравнение F.2) переписать в
форме
(N-P)V = B, F.49)
где матрица N в некотором смысле близка к А, т. е.
« ||А||, но легко поддается численной факторизации; например,
матрица N может быть трехдиагональной. Уравнение F.49)
.можно переписать в виде
+ B, или
= N-ipv<»> + N-iB> или
где R{n) — вектор невязок уравнения на /г-м этапе итерации,
По мере приближения к точному решению величина \\Rn\\
стремится к нулю, так что контроль за поведением этой вели-
величины дает информацию о степени реализации сходимости. Ите-
Итерационный метод общего вида состоит из этапа начальной
аппроксимации, т. е. задания V<!), и этапов последовательного
улучшения аппроксимации с использованием формулы F.51).
Различные варианты метода отличаются друг от друга глав-
главным образом тем, как выбирается матрица N.
Схема F.51) будет обеспечивать сходимость, если спект-
спектральный радиус (т. е. величина максимального собственного
значения) для N-1P оказывается меньше единицы. Нередко
это условие соответствует более ограниченному условию о том,
что матрица А имеет свойство диагонального преобладания,
т. е.
\AJ!\>It\Atl\. F.52)
It
Одна из наиболее простых итерационных сх!ем для решения
уравнения F.2) носят название метода Якоби. При примене-
применении, этого метода
§ 6.3. Итерационные методы 251
где DI — диагональная матрица, тогда как L и U — строго ниж-
нижняя и верхняя треугольные матрицы соответственно. В резуль-
результате формула F.60) принимает вид
F.53)
Вышеописанная форма метода Якоби является неэкономичной,
так как требует слишком много итераций для достижения схо-
сходимости. Однако она может быть существенно улучшена за
счет применения приемов ускорения либо по методу Чебышёва
[Hageman, Young, 1981, гл. 4], либо по методу сопряженных
градиентов (см. п. 6.3.4).
Более эффективное улучшение метода Якоби обеспечивается
с помощью метода Гаусса — Зайделя, при котором в правую
часть формулы F.53) вводятся значения и(/*+1), если только
они известны. В этом случае
N = DI-L, P = U, F.54)
а эквивалентом формулы F.53) служит выражение
t
(+о = я, (в, - ? Ativ\+* - t+i Aitvf)JA ir F.55)
Как правило, итерации по Гауссу — Зайделю оказываются
вдвое быстрее итераций по Якоби, однако ускорению не под-
поддаются. Если матрица А обнаруживает диагональное преобла-
преобладание согласно условию F.52), то сходимость методов Якоби
и Гаусса — Зайделя гарантирована.
Метод Гаусса — Зайделя может быть существенно улучшен
с помощью последовательной верхней релаксации (ПВР), когда
у(я+1) определяется как средневзвешенная величина по отно-
отношению к v{.n) и (t^rt+1)) . Таким образом, схему ПВР можна
записать в виде
? д|/0(»+1) _ Jf)+i А^^/Ли + A - Л) vfK
F.56)
Коэффициент К — показатель релаксации. Для сходимости
ПВР необходимо выполнение условия 0 < К < 2. В обозначе-
обозначениях формулы F.51) схема ПВР соответствует принятию вы-
выражения
F.57)
252 Гл. 6. Стационарные задачи
Число итераций, требуемое для сходимости, чувствительно к
выбору Я. Оптимальный выбор обеспечивается принятием
значения
где [I — наибольшее собственное значение комплекса I —
DMA. Однако нахождение явного выражения для ^i может ока-
оказаться столь же дорогостоящим, как решение всей задачи в
целом. Поэтому предпочтительная стратегия состоит в том,
чтобы получить некую оценку значения ji уже в процессе реа-
реализации итераций согласно E.56). После этого формула F.58)
даст улучшенное значение X. Подробности этого процесса из-
излагаются в книге [Hageman, Young, 1981, гл. 9].
При хорошем выборе предварительного значения A,Opt схема
ПВР оказывается значительно более эффективной, чем метод
Якоби или метод Гаусса — Зайделя. Однако к ее первоначаль-
первоначальному варианту невозможно применить метод ускорения — ни
в форме метода Чебышёва, ни в форме метода сопряженных
градиентов. Но если провести небольшую модификацию для
получения метода симметричной последовательной верхней ре-
релаксации (СПВР), то введение приемов ускорения будет уже
возможным. Метод СПВР состоит из двух этапов. На первом
этапе применяется схема ПВР. На втором этапе итерация неиз-
неизвестных производится в обратном порядке с использованием
схемы ПВР при том же значении X, что и на первом этапе.
Метод СПВР соответствует следующему выбору матрицы N
в формуле F.51):
Следует подчеркнуть, что без применения приемов ускорения
метод СПВР оказывается менее эффективным, чем метод
ПВР.
6.3.2. Анализ течения в канале с помощью итерационных
методов
В данном пункте мы применим три итерационных метода —
методы Якоби Гаусса — Зайделя и последовательной верхней
релаксации (ПВР) к решению задачи о полностью развитом
ламинарном течении в канале прямоугольного сечения. Эти
три итерационных метода обсуждались в п. 6.3.1 в качестве
явных или точечных алгоритмов. Если воспользоваться алго-
алгоритмом Томаса (подпрограммы BANFAC и BANSOL, п. 6.2.3),
§ 6.3. Итерационные методы 253
то указанные итерационные методы могут быть использованы
и как неявные или линейные алгоритмы; линейные варианты
методов ПВР и НПН также будут описаны в данном пункте.
Рассматриваемый пример, касающийся течения жидкости
в канале, был использован ранее в п. 5.5.2 для иллюстрации
применения метода конечных элементов, причем была дана и
программа DUCT (рис. 5.22), позволяющая провести соответ-
соответствующий расчет на компьютере. Течение вязкой жидкости в
канале описывается безразмерным уравнением E.97):
/ Ъ \
1т J
с граничными условиями w=0 при х = ±\, у = ±\. Пара-
Параметр b/а характеризует форму сечения канала, показанную на
рис. 5.21. Трехточечная конечно-разностная дискретизация урав-
уравнения F.60) дает
F.61)
Если применить к решению уравнения F.61) схему Якоби
•{см. п. 6.3.1), то получится алгоритм
F.62)
тде индекс (п) означает номер итерации и PAR1 =(Ь/аJ/Ах2 +
Н- 1/Д#2. В схеме Якоби все значения в узловых точках в пра-
правой части формулы F.62) вычисляются на п-м итерационном
¦слое.
В схеме Гаусса — Зайделя узловые значения вычисляются
на самом последнем из предыдущих слоев итерации. Следова-
Следовательно, если итерации реализуют повторяющиеся прогонки в
направлении оси у (возрастающий индекс k) при последова-
последовательно изменяющихся значениях х (возрастающий индекс /),
то эквивалент формулы F.62), соответствующий схеме Гаус-
<са — Зайделя, принимает вид
F.63)
В схеме ПВР решение, соответствующее формуле F.63) и
обозначаемое теперь как w^\> комбинируется с предыдущим
254
Гл. 6. Стационарные задачи
решением
согласно соотношению
(+
- Я) wf\ =
X (я/Д -
F.64>
где Л — показатель релаксации. Если принять А,= 1, то полу-
получится схема Гаусса — Зайделя. Схема ПВР, примененная к
уравнению F.61) с учетом интервала 0 < X < 2, приведет к
сходящемуся решению.
Три указанных итерационных метода применялись также
и в сочетании с конечно-элементной аппроксимацией уравне-
уравнения F.60), которая была описана в п. 5.5.2. Например, экви-
эквивалент формулы F.63) соответствует формуле E.108).
Таблица 6.3. Число итераций до достижения сходимости
Якоби
0.8
0.9
КО (Г.-З.)
1.1
1.2
.3
.4
1.5
1.55
1.6
1.7
1.8
?* 7
«я 2
11 I
* Я вс ",
р* ** н О
41
39
33
28
24
21
18
15
12
11
11
14
21
?* Т
О Л о
Точеч]
но-раз
метод
(tol=
87
74
62
51
43
36
29
23
18
15
17
21
28
и? 7
Од о
я X
S» 7
Точеч!
но-эле
метод
(tol=
64
55
45
38
32
26
21
17
12
13
15
20
29
6 ?
**« ~
S3 X
о я —
« Н II
НПН
разнос
метод
(tol=
19
16
14
12
12
12
12
11
11
11
12
1 (О
S i
*« 2
^2 X
о* -
« ж II
НПН
элеме]
метод
(tol=
19
18
17
16
15
14
13
14
15
16
17
0.9
1.1
1.3-
1.7
2.1
2.S
2.8
3.3
3.7
4.1
4.5
В табл. 6.3 дается сравнение числа итераций, необходимо-
необходимого для достижения сходимости при решении задачи о течении
в канале с помощью программы DUCT на сетке размером
ПХП. Сходимость предполагается достигнутой, когда
||jR(/2>||rms < TOL. Результаты приводятся для двух значений
критерия TOL (tolerance). Решение, задаваемое в качестве на-
начального для итерационного процесса,— это точное решение
уравнения F.60). В случае сетки конечного размера это реше-
решение не совпадает с решением дискретизированного уравнения
§ 6.3. Итерационные методы
255
F.61). Выбор начального решения в форме w{j*\ = 0 требует
большего числа итераций, как это можно видеть из сравнения
результатов, показанных в табл. 6.3 и 6.4.
Таблица 6.4. Влияние степени измельчения
сетки на сходимость: задача о канале,
точечный ПВР (конечно-разностный метод)
Сетка
6X6
пхп
21X21
41X41
Оптимальное
к
1.30
1.55
1.74
1.86
Число итераций
до достижения
сходимости
(tol=i х ю~6)
12
23
41
79
Как показывают результаты, приводимые в табл. 6.3, схе-
схема ПВР с оптимальным значением X обеспечивает более быст-
-3.00г
-5.00-
-6.00
20
80
100
Рис 6.20, Динамика сходимости для точечного конечно-разностного метода
(TOL= 1 X Ю-6). . .
рую сходимость, чем схема Гаусса — Зайделя, которая в свою
очередь дает более быструю сходимость, чем схема Якоби. На
рис. 6.20> приводится график уменьшения среднеквадратичного
значения изменения решения, т. е. разности ^\x) ^\
256 Гл. 6. Стационарные задачи
в зависимости от номера итерации п при использовании конеч-
конечно-разностного метода.
Результаты, приводимые в табл. 6.3, свидетельствуют о
том, что точечный вариант метода конечных элементов (см.
формулы E.108), E.109)) дает более быструю сходимость, чем
точечный вариант метода конечных разностей при значениях
К ^ 1.7. Однако вычислительная работа, приходящаяся на одну
итерацию, для метода конечных элементов оказывается боль-
больше, так что при решении данной задачи этот метод не обяза-
обязательно будет эффективнее метода конечных разностей.
Все приведенные выше алгоритмы, соответствующие форму-
формулам F.62) — F.64), имели явную форму. Вполне возможно и
даже желательно отдельные группы узловых переменных рас-
рассматривать в неявной форме, если только получаемая система
уравнений будет поддаваться эффективному решению. По-
Последнее сможет быть достигнуто посредством формирования
трехдиагональных систем уравнений, связанных с каждой из
линий (линий постоянных k), параллельных оси х. В результа-
результате алгоритмическая запись уравнения F.61) принимает вид
Для решения этой системы удобно воспользоваться подпро-
подпрограммами BANFAC/BANSOL (п. 6.2.3). Учитывая, что в левой
части F.65) коэффициенты при ш(*> постоянны, применять
BANFAC требуется только для сеточной линии k = 2. Одна и
та же факторизация используется в подпрограмме BANSOL
для всех сеточных линий. Комбинация соотношений F.65) и
F.64) дает схему, известную как последовательная линейная
верхняя релаксация (ПЛВР).
Неявная схема переменных направлений (НПН), обсуждае-
обсуждаемая в книге [Varge, 1962, гл. 7], аналогична схеме ПЛВР, од-
однако направление счета по неявному алгоритму в этой схеме
меняется от итерации к итерации. Следовательно, вместо алго-
алгоритма, соответствующего F.65), используется следующий
двухэтапный алгоритм. На первом этапе решается следующая
трехдиагональная система, связанная с линиями постоянных
к, параллельными оси х:
- M^i. * + 0 + 2
§ 6.3. Итерационные методы 257
На втором этапе решается уже другая трехдиагональная си-
система, связанная с линиями постоянных /, параллельными оси у:
+ 0 + 2К
= Ху Ау> + Яхш</2(> к + A - 2*,) ш<:>, + Яяш'!>,, ь F.67)
где параметр Ку выбирается так, чтобы ускорить сходимость,
причем %х = (ЬАу/аАхJХу. Стратегические приемы для выбора
Ку обсуждаются в книгах [Varga, 1962; Wachpress, 1966].
Вышеописанная схема НПН эквивалентна схеме НПН,
описанной в п. 8.2.1. Формулы, сравнимые с F.66) и F.67),
могут быть получены и применительно к методу конечных эле-
элементов за счет принятия соотношений (8.35) и (8.36). Необхо-
Необходимое число итераций для конечно-разностного метода НПН
и конечно-элементного метода НПН демонстрируется в
табл. 6.3. Оба метода обеспечивают лучшую сходимость, чем
соответствующие точечные алгоритмы при неоптимальных зна-
значениях А.
Скорость сходимости сильно зависит от степени измельче-
измельчения сетки. По мере того как сетка измельчается, число итера-
итераций, приводящих к сходимости, возрастает, а оптимальное
значение К становится больше. Эта ситуация иллюстрирует-
иллюстрируется в табл. 6.4, построенной на основе начального решения
<>
Рассмотренные выше итерационные алгоритмы можно за-
записать в форме соотношения w<rt+1) = Gw(rt). Уменьшение ско-
скорости сходимости по мере измельчения сетки соответствует то-
тому, что максимальное собственное значение матрицы G при-
приближается к единице. Желательно, конечно, располагать теми
или иными средствами ускорения скорости сходимости. В кни-
книге [Hageman, Young, 1981] обсуждаются возможности приме-
применения в качестве приемов ускорения метода сопряженных гра-
градиентов и метода Чебышёва. Однако ни тот, ни другой из этих
методов при их применении к схемам Якоби или Гаусса — Зай-
деля не может обеспечить большей скорости сходимости, чем
использование схемы ПВР с оптимальным значением показа-
показателя релаксации Я. В качестве очень эффективного варианта
Хагеман и Янг рекомендуют применение схемы ПВР вместе
с адаптируемым алгоритмом для выбора Я. В их книге [Hage-
[Hageman, Young, 1981] приводится составленная для этой цели под-
подпрограмма. В книге [Jennings, 1977a] обсуждается возможность
использования с той же целью ускорения по Айткену.
17 К. Флетчер, т. 1
258 Гл. 6. Стационарные задачи
Следует отметить, что для эффективного применения выше-
вышеописанных итерационных методов решаемая задача должна
быть существенно эллиптической, т. е. в ее математическом
описании должны присутствовать вторые производные, но не
должно быть первых производных. Зачастую это приводит к
тому, что матрица уравнений (например, полученная из урав-
уравнения F.61)) является симметричной и положительно опреде-
определенной. Матрица А симметричная и положительно определен-
определенная, если \т = А и хгАх ,> 0 при всех х Ф 0.
Примерами уравнений, эффективно решаемых с помощью
вышеописанных итерационных методов, являются уравнение
Пуассона (для функции тока или давления), возникающее при
исследовании течений вязкой жидкости в переменных функция
тока — завихренность (§ 17.3), а также уравнение для потенциа-
потенциала, часто связанное с задачами о течении невязкой жидкости
(гл. 14) и, в частности, о трансзвуковых течениях (§ 14.3).
Если в задаче фигурируют первые производные существен-
существенной величины, то вышеописанные методы оказываются крайне
неэффективными и могут не обеспечивать сходимости. Если,
например, применять точечную схему ПСР с методом конеч-
конечных разностей к решению двумерных уравнений Бюргерса, рас-
рассмотренных в п. 6.1.3, на сетке 21 X И> то для сходимости
потребуется А, ^1.0. После 270 итераций невязки уравнений
снижаются примерно до 1.4 X Ю~5. Для сравнения укажем, что
приближенная факторизация в процессе нестационарного ме-
метода Ньютона (п. 6.4.1) приводит к той же степени сходимости
за 15 итераций.
Существенные члены с первыми производными возникают
в уравнениях импульсов, записанных в примитивных перемен-
переменных (§ 17.1), в уравнении переноса завихренности (§ 17.3), а
также в уравнении энергии (п. 11.2.4).
6.3.3. Существенно неявная процедура
Существенно неявная процедура (СНП) начинает анализ с
уравнения F.49), записанного с целью применения итерацион-
итерационного метода к стационарной задаче общего вида, и с помощью
факторизации расщепляет матрицу N на LU. В данном случае
матрица А получается за счет трехточечной центрированной
разностной дискретизации в двух измерениях. Структура мат-
матрицы А в этих условиях показана на рис. 6.1.
Как показано в работе [Stone, 1968], это можно сделать
так, чтобы получилось три диагонали в матрице L и три диаго-
диагонали в матрице U, элементы на главной диагонали которой
равны единице. Теперь если сформировать N = LU, то ясно,
§ 6.3. Итерационные методы 259
что матрица Р состоит из двух диагоналей, содержащих мно-
множители при fli+i,/-1 и У/_1,/+ь Для линейной системы уравне-
уравнений F.2) элементы матриц L, U и Р могут быть вычислены
раз и навсегда.
Алгоритм реализуется в два этапа. Сначала прямая про-
прогонка позволяет получить
F.68)
После этого осуществляется обратная подстановка
F.69)
Этот алгоритм весьма эффективен и часто имеет преимущество
перед схемой НПН, соответствующей формулам F.66) и F.67).
В работе [Schneider, Zedan, 1981] был разработан модифи-
модифицированный существенно неявный алгоритм (МСН), примени-
применимый к случаям пятиточечной или девятиточечной дискретиза-
дискретизации в двумерном пространстве, т. е. к случаю трехточечной
конечно-разностной дискретизации или к случаю линейной ко-
конечно-элементной дискретизации. Здесь будет описана пятито-
пятиточечная версия МСН. Что касается девятиточечной версии, то
интересующийся ею читатель отсылается к цитированной выше
работе Шнайдера и Зедана.
Алгоритм, использующий схему МСН, реализуется с по-
помощью формул F.68) и F.69). Однако вид матриц L, U и Р
отличается от того, что использовал Стоун. В алгоритме МСН
матрица L содержит по четыре ненулевых элемента в каждой
строке, тогда как матрица U имеет три ненулевых элемента вне
диагонали и единицу на диагонали, а матрица Р содержит два
элемента. Если нумерация элементов V соответствует сначала
возрастающим значениям /, а затем возрастающим значениям
&, то формула F.68) принимает вид
* + Р). k [о,н* *-, - «(-2*,. * + 2f/+1
Pi k [«/-2, *+i - «(-4 k + 20,.,, k + vh ft+1)f> -
[c/, *o/f ft_i + dlt kvl+u k_x + eu *»/_,, ft]<n+I>. F.70)
Обратная подстановка согласно F.69) реализуется в виде
№ ft(*/. Л+1. * + К *<>!-и *+i +'/. нЧ ,-ыГ (>
В формулах F.70) и F.71) коэффициенты с, d, e и / яв-
являются элементами матрицы L, коэффициенты g, h и t отно-
относятся к матрице U, а коэффициенты р1 и р2 — к матрице Р.
17*
260 Гл. 6. Стационарные задачи
Эти коэффициенты связаны с элементами матрицы А посредст-
посредством формул
=
=а\л -с/. Л. *-i -
Параметр a использован здесь для ускорения сходимости,
причем значение a = 0.5 близко к оптимальному. Как указы-
указывается в работе [Schneider, Zedan, 1981], схема МСН оказы-
оказывается, как правило, в два-четыре раза экономичнее, чем схема
СНП, и притом не требует перенумерации узлов сетки после
каждой итерации, как это имеет место в случае СНП.
Информация об использовании существенно неявных про-
процедур, по своей формулировке аналогичных изложенному выше,
имеется в работах [Rubin, Khosla, 1981; Zedan, Schneider, 1985;
Lin, 1985].
6.3.4. Методы ускорения сходимости
Различные методы итераций, описываемые в п. 6.3.1—6.3.3,
являются эффективными, но при решении некоторых задач об-
обнаруживают довольно медленную сходимость после того, как
невязка R испытает быстрое начальное уменьшение. Если
ошибку итерационного решения е = У<я) — Vе разложить в ряд
Фурье, то быстрое начальное уменьшение невязки соответст-
соответствует уменьшению амплитуды коротковолновых мод ряда
Фурье. Последующее уменьшение амплитуды длинноволновых
мод зачастую протекает со значительно меньшей скоростью.
Имеется, однако, возможность модифицировать уже рас-
рассмотренные нами итерационные методы для ускорения сходимо-
сходимости. Два наиболее эффективных для этого метода — это метод
ускорения по Чебышёву и метод ускорения с сопряженными
градиентами [Hageman, Young, 1981]. Здесь мы дадим описа-
описание важнейших особенностей метода ускорения с сопряжен-
сопряженными градиентами.
Первоначально будет предполагаться, что матрица А
в уравнении F.2) является симметричной и положительно оп-
определенной. Иначе говоря, при любом выборе х будет хгАх > 0.
§ 6.3. Итерационные методы 261
Дискретизация уравнения Лапласа с центрированными конеч-
конечно-разностными выражениями приводит к линейной системе
уравнений, для которой матрица А симметричная и положи-
положительно определенная.
Последовательность шагов при применении традиционного
метода сопряженных градиентов [Hestenes, Stiefel, 1952]
можно описать в следующем виде:
а(п+1)р(Я)э F.73)
Данный алгоритм оказывается сравнительно экономичным, так
как он требует только одного матрично-векторного умножения
на этапе F). Можно отметить, что невязка R(/l+1> вычисляется
рекурсивно по результатам шага B), а не из соотношения
rch-i) = в — AV<n+1>. За параметром р(я+1> ведется наблюдение
с целью уловить приближение сходимости. В отличие от схемы
ПВР (п. 6.3.1) метод сопряженных градиентов не содержит эмпи-
эмпирически подбираемых параметров.
В формулах F.73) вектор Р(я) определяет направление по-
поиска, которое в начале итерационного процесса задается равен-
равенством Р<°> = R@). Выбор параметра а<я+1) в формулах F.73)
гарантирует, что направления поиска Р<?> будут взаимно сопря-
сопряженными (ортогональными) в смысле выполнения условия
р<огАР(/) = 0 при 1ф^ F#74)
Кроме того, данный алгоритм обеспечивает, что R</)rR<» = О
при 1Ф\. Все эти особенности делают алгоритм весьма эффек-
эффективным и в отсутствие ошибок округления он мог бы способст-
способствовать построению решения системы из N линейных алгебраи-
алгебраических уравнений F.2) не более чем за N итераций. Параметр
№Л) в формулах F.73) выбирается так, чтобы эквивалентная
квадратичная функция
F (V) = 0.5VrAV — VrB F.75)
имела минимум в направлении Р<я> при V(n+l\
262 Гл. 6. Стационарные задачи
Если невязка R разлагается в ряд по собственным функциям
матрицы А, то можно установить, что каждый шаг метода со-
сопряженных градиентов воздействует таким образом, что как
бы приближенно исключает вклады от каждого из собственных
векторов по очереди [Jennings, 1977b]. Следовательно, если
некоторые из собственных значений А собраны в единую груп-
группу, то сходимость достигается менее чем за N итераций.
Если, кроме того, оказывается возможным произвести пред-
предварительное умножение отдельных членов уравнения F.2) так,
чтобы собственные значения полученной в результате матрицы
были сгруппированы более тесно, чем для матрицы А, а раз-
разброс собственных значений (А,тт, Ятах) был несколько умень-
уменьшен, то последующее применение метода сопряженных гради-
градиентов к «предварительно подготовленной» системе обеспечивает
более быструю сходимость. Наилучший вариант выбора конди-
кондиционирующего множителя состоит в умножении на А, так как
после этого решение будет тривиальным. Хорошим вариантом
является множитель N, фигурирующий в формуле F.51), со-
соответствующей итерационному методу решения стационарных
задач общего вида. На этом основании вместо F.2) запишем
NAV = NB. F.76)
Чтобы можно было применять вышеописанный вариант метода
сопряженных градиентов, необходимо комплекс N"!A сделать
симметричным. Этого можно добиться, формируя комбинацию
WN-^AW"*1, где матрица W обычно выбирается так, чтобы по-
получить WrW = N. В результате вместо F.76) получим
AV = B, F.77)
где
А = WN^AW1, V = WV, В = ^
Применение метода сопряженных градиентов к решению урав-
уравнения F.77) называют методом сопряженных градиентов с
предварительным кондиционированием. При хорошем выборе
N этот вариант приводит к более быстрой сходимости, чем не-
непосредственное применение метода к уравнению F.2).
На практике уравнение F.77) не формируется явным обра-
образом. Вместо шагов, соответствующих формулам F.73), дела-
делается следующее:
2) 6<Л+1> = 6<n> —
3)
§ 6.3. Итерационные методы 263
4) а<я+1> = р<л+1Ур<л>, F.78)
5) р(я+О — $(я+1) .J. a(n+\)p(nh
6)
В приводимой выше последовательности формул величины 6 и
R играют роль псевдоневязок, а значение величины р{п+1) слу-
служит критерием близости к сходимости.
Различные варианты выбора N, а следовательно, и W соот-
соответствуют различным итерационным схемам, рассмотренным
в п. 6.3.1. Таким образом, метод, основанный на применении
формул F.78), может интерпретироваться как основная схема
с ускорением по методу сопряженных градиентов. Альтернатив-
Альтернативный, но очень эффективный вариант предварительного конди-
кондиционирования можно построить путем приближенной фактори-
факторизации матрицы А и расщепления ее на нижнетреугольную и
верхнетреугольную матрицы L и U [Jackson, Robinson, 1985].
Для случая конечно-разностной дискретизации стационар-
стационарного уравнения переноса, не содержащего производной по вре-
времени (уравнение (9.81)), результирующая система уравнений,
эквивалентная F.2), не будет симметричной вследствие влия-
влияния дискретизированных членов с первыми производными
идТ/дх и идТ/ду. Метод сопряженных градиентов может быть
применен и к этому случаю при надлежащей модификации
[Axelsson, Gustafsson, 1979].
Одна из таких схем под названием ORTHOMIN, построен-
построенная в работе [Vinsome, 1976], описывается нами здесь. В при-
принятых автором обозначениях формулы F.78) заменяются сле-
следующими выражениями:
р()=6()+2 a(«>pw, F.79)
где
Sin) _ N- 1р(Я) (я. /) _
о -in к , a -
(zAp@)rp(i).
z_(N-iA)r .
У A) '
Если сохранить все члены под знаком суммирования в вы-
выражении для Р<я), то реализация метода потребует значитель-
264 Гл. 6. Стационарные задачи
ного объема памяти и будет весьма неэкономичнной. На прак-
практике схема хорошо работает при i = 0, ..., 4.
В работе [Markham, 1984] проводится сравнение различных
вариантов метода сопряженных градиентов с предварительным
кондиционированием для несимметричных систем уравнений.
Схема ORTHOMIN является эффективной, однако Маркхэм на-
находит, что метод дважды сопряженных градиентов [Fletcher,
1976], а также модификации этого метода обладают большей
эффективностью. Тем не менее в работе [Jackson, Robinson,
1985] утверждается, что методы минимальной невязки оказы-
оказываются эффективнее, чем метод дважды сопряженных градиен-
градиентов, если решаемая задача обладает значительной степенью
несимметричности. Таким образом, если матрица А имеет произ-
произвольную форму, то нельзя указать универсально предпочтитель-
предпочтительного метода сопряженных градиентов.
Имеется возможность симметризовать общую форму мат-
матричного уравнения F.2), заменяя последнее на
ArAV = ArB. F.80)
В общем случае данный подход не может быть рекомендован,
так как если матрица А в какой-то степени плохо обусловлена,
то к матрице АГА это будет относиться в еще большей степени
при вытекающей отсюда потере точности в процессе решения
F.80) относительно V. Однако в работе [Khosla, Rubin, 1981]
уравнения, описывающие поток несжимаемой вязкой, жидкости
вокруг кругового цилиндра при Re = 100, были решены путем
такой симметризации определяющих уравнений, как в F.80), и
применения схемы СНП (п. 6.3.3) В| сочетании с методом сопря-
сопряженных градиентов при предварительном кондиционировании.
Метод СНП как таковой требует приблизительно 240 итераций
для достижения сходимости на сетке 61 X 24, тогда как метод
СНП с вышеуказанным дополнением требует для достижения
сходимости всего около 40 итераций.
6.3.5. Многосеточные методы
Описываемые здесь методы применимы как к линейным си-
системам F.2), так и к нелинейным системам F.1). Типичный
вариант метода будет описан первоначально в применении к
линейным системам, а в дальнейшем будет описано и его рас-
распространение на случай нелинейных систем.
Многосеточные методы имеют дело с последовательностью
сеток, m = 1, ..., М> при отношении размеров ячеек сетки
A/Am = 0.5. Линейная система, решение которой нужно по-
§ 6.3. Итерационные методы 265
строить на наиболее мелкой сетке, записывается в виде
Ъм F81)
Приближенное представление Vм соответствует решению на
сетке, ближайшей в последовательности по степени грубости,
т. е. Vм-1. Подобным же образом решение Vm, построенное на
сетке промежуточного размера, является хорошим приближе-
приближением к решению на более мелкой сетке, ближайшей в последо-
последовательности к данной, т. е. к VM+1.
Если приближенный вариант решения уравнения
дт-иуи-1 = Bw+1 обозначить символом Vm+b a, так что
ут+1 = ym+1, a + дут + 1^ (Q ^
ТО
Am+1Ww+1 = Bm+1 - Am+1Vm+1'a = Rm+1. F.83)
Поправка Wm+1 и невязка (или дефект) Rm+l весьма близко
аппроксимируются поправкой и невязкой на ближайшей в по-
последовательности более грубой сетке, т. е. величинами Wm и
Rm, если только последние обладают достаточной гладкостью,
т. е. если амплитуды высокочастотных составляющих малы.
Наивысшая частота, поддающаяся представлению на дискрет-
дискретной сетке с ячейкой Ат, равна 2Ат (п. 3.4.1).
Релаксационные итерационные процедуры, подобные про-
процедурам Якоби, Гаусса — Зайделя и ПСР, описание которых
было дано в п. 6.3.1, на протяжении нескольких итераций уда-
удаляют высокочастотные компоненты. Но вот удаление низкоча-
низкочастотных компонент ошибки, а следовательно, и невязки яв-
является причиной слабой сходимости релаксационных методов
на фиксированной сетке.
Однако низкочастотная компонента на мелкой сетке стано-
становится высокочастотной компонентой на грубой сетке. Исходя
из этого, применяя многосеточные методы, стремятся восполь-
воспользоваться высокочастотным сглаживанием, присущим релакса-
релаксационным методам, следующим образом.
При заданной (т + 1)-й сетке для сглаживания высокоча-
высокочастотных компонент поправки и невязки делается несколько
(v1) релаксационных шагов. На основании F.83) это может
быть символически записано в виде
Wm+1'v' = RELAX1" (Wm+I, Am+1, Rm+1), F.84)
pm+l,v' pm+1 ^ дт+1ддгт + 1, v1
В случае линейной системы уравнений релаксация может быть
применена как к первоначальному уравнению F.2), так и к
266 Гл. 6. Стационарные задачи
уравнению F.83) с невязками и поправками. В случае нелиней-
нелинейных систем уравнений релаксация должна быть применена к
первоначальному уравнению F.1).
Распределение невязок Rm на m-й сетке вычисляется по
Rm+1'v' с помощью ограничительного оператора /JS+i. Это мо-
может быть символически записано в виде
l. F.85)
Надлежащие варианты ограничительного оператора будут ука-
указаны позднее. Процесс релаксации и ограничения продолжается
до тех пор, пока не будет достигнута самая грубая сетка, т. е.
т=\.
На наиболее грубой сетке с экономической точки зрения це-
целесообразно продолжать релаксацию (или использование лю-
любого другого итерационного метода) до тех пор, пока не будет
получена сходящаяся поправка W1. В качестве альтернативы
уравнение A!W! = R1 или F.2) может быть решено с помощью
прямого метода (§ 6.2). Можно отметить, что в общем случае,
если R1 отлична от нуля, то и W1 отлична от нуля.
Поправка W2 может быть получена из W1 путем пролонга-
пролонгации (интерполяции). Это символически изображается формулой
W2 = /iW1, или в более общем виде
w. F.86)
Надлежащие формы оператора пролонгации /m+1 будут ука-
указаны позднее. Затем на более мелкой сетке при т + 1 делается
еще несколько релаксационных шагов (v2), так что
Wm+1'v2=RELAXv2(Wm+1, Am+I, Rm+1), F.87)
прежде чем проводить пролонгацию на более мелкую сетку.
Один многосеточный цикл, берущий начало с наиболее мел-
мелкой сетки, т. е. с т = Af, состоит из серии повторных примене-
применений формул F.84) и F.85), пока не будет достигнута наиболее
грубая сетка, после чего строится точное или полное итераци-
итерационное решение уравнения A*WX = R1 и проводится серия пов-
повторных применений формул F.86) ц F.87) вплоть до вторич-
вторичного достижения наиболее мелкой сетки при т = М. Эта про-
процедура называется V-циклом и ее блок-схема приводится на
рис. 6.21.
Цикл повторяется заново до тех пор, пока не будет достиг-
достигнута удовлетворительная сходимость на наиболее мелкой сетке.
Если в качестве уравнения F.2) берется уравнение Пуассона
на равномерной сетке, то десяти циклов достаточно для того,
чтобы изменение решения для двух последовательных циклов
§ 6.3. Итерационные методы
267
уменьшилось до значения порядка 10~5. При проведении пер-
первого цикла величина Wm принимается равной ^первоначально
заданному предполагаемому решению на мелкой сетке Vм' а.
Прежняя
аппроксимация
y/V\tG
I
m=M,Wm=VM'a,Rm=BM
Л Wm'"=RELAX1'1(W,in A1? Rm)
m=m-l
Новая
аппроксимация
Нет
ro=m+l
t
1__ #
Решить A1 W1 = R1 точно
Прежняя
аппроксимация
Ограничение
Релаксация
Точное
решение,
m = 1
Новая
аппроксимация
Пролонгация
Рис. 6.21. Блок-схема для многосеточного V-цикла.
Ограничительный оператор С+и фигурирующий в фор-
формуле F.85), позволяет построить распределение невязок на бо-
более грубой сетке Rm по известному распределению невязок на
более мелкой сетке Rm+1. Простейшим выбором для физической
268 Гл. 6. Стационарные задачи
сетки при индексах / и ky соответствующих положению узловой
точки на грубой сетке в направлениях х и у соответственно, яв-
является непосредственное замещение R?,k = Rf,Xl- Такой про-
цесс устойчив и эффективен в вычислительном плане при реше-
решении существенно эллиптических задач, например для уравнения
Лапласа в п. 5.2.3. Однако для нелинейных задач со слабой эл-
эллиптичностью типа задач о течении вязкой жидкости с боль-
большими числами Re (гл. 17) более устойчивый выбор обеспечи-
обеспечивается с помощью пятиточечных и девятиточечных операторов
lm+\
[0201 Г1 2 1 I
2 82, 1242 F.88)
0 2 о J L1 2 1 J
Оператор пролонгации (интерполяции) из формулы F.86)
обычно базируется на билинейной интерполяции в двух измере-
измерениях. Так, например, если индексы /, k относятся к более грубой
сетке т, то
w?.k, F.89а)
wf± 1/2, * = 0.5 (wf. k + wf± i, *), F.89b)
, ft+i/2 = 0.25 (wf.k + wT+i * + otfft+i + w?+u *+i). F.89c)
Значения wm+l в точках (/, k ± 1/2) определяются так же,
как в формуле F.89Ь). Следует отметить, что узловые точки
(/, k) на более грубой сетке будут переобозначены индексами
B/ + 1, 2k + 1) на более мелкой сетке.
При решении нелинейных задач многосеточный метод мож-
можно сочетать с методом Ньютона (п. 6.1.1). На каждом шаге
ньютоновской итерации линейная система F.6) решается отно-
относительно поправки к решению. Многосеточный алгоритм, соот-
соответствующий рис. 6.21, может применяться в процессе итераций
при решении F.6).
Однако многосеточный метод может применяться и непос-
непосредственно к решению нелинейной системы F.1), без обраще-
обращения к методу Ньютона. При этом существенное отличие от ал-
алгоритма, схематически представленного на рис. 6.21, состоит
в том, что на этапе ограничения по формуле F.85) нужно огра-
ограничивать переброской на более грубую сетку т не только не-
невязку Rm+1>vl> но и приближенное решение vm+1'a. На /п-м
слое вместо решения уравнения F.83) ищется решение
уравнения
тш а m mCm+U. F.90)
§ 6.3. Итерационные методы 269
На практике решение Vm> a строится путем релаксации с по-
последующей переброской на более грубую сетку точного реше-
решения на самой грубой сетке, а затем релаксации и пролонгации
на все более мелкие сетки по аналогии со схемой, показанной
на рис. 6.21. Как только получено решение Vm>°, рассчиты-
рассчитывается поправка
которая затем пролонгируется на (т + 1)-ю сетку. После этого
подправленное решение, т. е. vw+1'a + /m+1Ww, релаксируется
в основном так же, как и в линейном случае, чтобы получить
+1 2
, V2
Схему решения нелинейной задачи называют методом пол-
ной аппроксимационной памяти (ПАП) [Brandt, 1977] в от-
отличие от метода поправочной памяти (ПП), описываемого на
рис. 6.21. Если учесть, что метод ПАП перебрасывает на более
грубые сетки и решение, и невязку, то его экономичность не-
немного ниже (на 5 % — 10 %), чем у схемы ПП; в общем случае
метод ПАП не должен использоваться при решении линейных
задач. Как и в случае метода ПП, эффективность этого метода
зависит от возможности сглаживания поправки к решению W
и невязки R.
Описание методов ПП и ПАП было начато с аппроксимации
решения на наиболее мелкой сетке, m = М, проходило через
V-цикл вплоть до самой грубой сетки и возвращалось обратно,
чтобы улучшить начальное решение. Такая стратегия является
вполне подходящей, если в нашем распоряжении имеется хоро-
хорошее приближение к решению Vм.
Если никакой информации о решении нет, то лучше начинать
с решения на наиболее грубой сетке, полученного либо непос-
непосредственно, либо с помощью обычных итераций. Для улучше-
улучшения решения с помощью интерполяции высокого порядка де-
делается переход на следующий уровень более мелкой сетки, а
затем проводятся г многосеточных V-циклов. Процесс интер-
интерполяции высокого порядка в сочетании с г многосеточными V-
циклами повторяется на последовательности все более мелких
сеток вплоть до m = Му а многосеточный V-цикл повторяется
до достижения сходимости.
Описанное выше составляет основу полного многосеточного
метода (ПМС), представляющего собой обобщение методов
ПАП и ПП. Схема метода ПМС показана на рис. 6.22 для слу-
случая линейной системы уравнений. Функция INT(Vm, m) симво-
символизирует кубическую интерполяцию Vm сначала в направлении ху
270
Гл. 6. Стационарные задачи
Решить А1 V1 = В1 точно
гл = 1
г = 0
а затем для всех узловых значений х(т+1) в направле-
направлении у. Функция MGI(Vm'r-1, Am, Bm) соответствует одно-
одному проходу через многосеточный V-цикл, показанный на
рис. 6.21.
Многосеточный подход можно рассматривать как прием
ускорения, подобный методу сопряженных градиентов (п. 6.3.4)
и примененный к основной итерационной схеме (п. 6.3.1—
6.3.3.). Другой вариант интерпретации состоит в том, что основ-
основная итерационная схема рас-
рассматривается как средство
сглаживания в рамках много-
многосеточного метода, так же как
она рассматривалась в каче-
качестве предварительного конди-
кондиционера по отношению к ме-
методу сопряженных градиен-
градиентов. Как и при ускорении по
методу сопряженных градиен-
градиентов, было найдено, что исполь-
использование неполной (приближен-
(приближенной) линейной факторизации
матрицы А, переводимой в
L-U, весьма эффективно в ка-
качестве сглаживающего процес-
процесса для соотношений F.84) и
F.87) [Sonneveld et al., 1985].
Это особенно справедливо в
случаях матриц А с сильной
асимметрией, например для за-
задач с преобладающим влия-
влиянием конвекции (гл. 9 и 10).
Подробное описание мно-
Vm'°=INT(Vm~J,m)
Vm'r=MGI(Vm'rH,Am,Bm)
Да
Решение уравнения А V "" — В™
госеточных методов дается в
Рис. 6.22. Блок-схема для метода трудах [Brandt, 1977; Stuben,
ПМС. Trottenberg, 1982; Hackbusch,
1985], а также некоторых
других авторов. Брандт, а также Штубен и Треттенберг при-
приводят написанные на языке Фортран программы по приме-
применению простого многосеточного метода к решению уравне-
уравнения Пуассона. Описание, данное здесь, следует в основном
Штубену и Троттенбергу. Приложения многосеточных методов
к решению задач о невязком течении приводятся в п. 14.2.9
и 14.3.5, а к проблемам течения вязкой несжимаемой жидко-
жидкости—в п. 17.2.3 и 17.3.1.
§ 6.4. Псвдонестационарный метод 271
§ 6.4. Псевдонестационарный метод
Альтернатива решению алгебраических уравнений, возни-
возникающих при дискретизации некоторой стационарной задачи, со-
состоит в построении эквивалентной нестационарной задачи и ре-
решении этой задачи маршевым методом вплоть до достижения
стационарного состояния. В подобных условиях время играет
роль итерационного параметра.
Таким образом, если провести дискретизацию уравнения
Лапласа
& + ?-«. F.92)
пользуясь центрированными конечно-разностными формулами
при Ах = Ау, то метод Якоби дает для внутренних узлов (на
сетке /, k типа, показанного на рис. 6.21) выражение
= 0.25 (оГ*+1 + vfk-, + vf\ k + vf\ ft). F.93)
Желая получить эквивалентное нестационарное уравнение,
следует заменить F.92) на выражение
Дискретизация с помощью конечно-разностных формул при
Ал: = At/ приводит к алгоритму
vtk = A - 45) vlk + s (vl k+l + vl k-x + vj+u k + v1-\. k), F.95)
где s = aAt/Ax2. Выбор 5 = 0.25 воспроизводит формулу F.93).
Таким образом, имеется очевидная связь между нестационарной
формулировкой и методом итераций, рассмотренным в § 6.3.
Важное преимущество нестационарной формулировки со-
состоит в том, что она позволяет воспользоваться различными
приемами расщепления, обсуждаемыми в § 8.2. Например, урав-
уравнение F.94) при его решении по методу НПН приводит к ал-
алгебраическим уравнениям (8.14) и (8.15). Решение этих урав-
уравнений строится путем решения подсистем уравнений, связанных
с каждой из сеточных линий, с помощью алгоритма Томаса
(п. 6.2.2). Этот процесс иллюстрируется на рис. 6.23.
Если учесть, что само нестационарное решение интереса не
представляет, обычно целесообразно выбрать такую последова-
последовательность шагов по времени, чтобы минимизировать общее чис-
число временных шагов, необходимое для достижения сходимости.
Вид упомянутой последовательности зависит от самой задачи,
однако, как правило, имеет характер геометрической прогрес-
прогрессии, причем диапазон изменения временных шагов соответст-
соответствует диапазону собственных значений, связанных с трехдиаго-
272
Гл. 6. Стационарные задачи
нальными матрицами, соответствующими сеточным линиям по
направлениям х и у [Wachpress, 1966, гл. 6].
При решении задач обтекания часто выясняется, что на од-
одних участках вычислительной области приближение к стацио-
стационарному состоянию идет значительно быстрее, чем на других.
При обтекании ступеньки, обращенной назад (п. 17.3.3), реше-
решение в области отрыва потока за ступенькой сходится значи-
значительно медленнее, чем в областях, удаленных от ступеньки.
Начальное
решение
Стадион
ное реше
V
Подобрать A t
(ускоренная
сходимость)
ар-
ние
i
1 "
1
Да
-
Прогонка по
направлениям х
}
V*=Vn+AV*
А А Прогонка
Г 1 по направ-
1 1 пениям
И у
эт
\
ЦуП-1 _ уП||
<?
т: 1
Алгоритм
(каждая се
лини
Томаса
точная
а I
Я;
Рис. 6.23. Псевдонестационарный метод с расщеплением для решения дву-
двумерной задачи.
В силу наличия пространственных вариаций скорости сходимо-
сходимости целесообразно дать следующую модификацию уравне-
уравнения F.94):
F.96)
где коэффициент с(х, у) подбирается эмпирически так, чтобы
выравнять скорость сходимости на различных участках вычис-
вычислительной области. После этого схема расщепления вводится
обычным образом (§ 8.2).
6.4.1. Двумерные стационарные уравнения Бюргерса
Здесь мы проиллюстрируем эффективность псевдонестацио-
псевдонестационарного метода путем сочетания его с методом Ньютона в при-
применении к решению двумерных стационарных уравнений Бюр-
§ 6.4. Псевдонестационарный метод 273
герса (п. 6.1.3). Уравнения F.12)' заменяются эквивалентными
им нестационарными уравнениями:
дп , _ дп , . дп 1
Ж "+" и дх + v ду Те
Дискретизированная форма уравнений F.97), эквивалентная
уравнениям F.13), имеет вид
=0. F-98)
где Rul^k и Rvffi определяются выражениями F.13).
Можно отметить, что стационарные члены представлены
выражениями на временном слое п+l. Это сделано для того,
чтобы псевдонестационарная форма была совместима с мето-
методом Ньютона и чтобы временной слой п + 1 был однозначно
эквивалентен итерационному уровню в методе Ньютона
(п. 6.1.1). Из рассмотрения выражений F.13) следует, что
Ruf у и Rv, . являются функциями и?\1, ип+} fe, i)n+> и т. д.
Поэтому разложение Ruffi и Rvffi в окрестности временного
(итерационного) уровня, как это делается в п. 8.2.2, позволяет
переписать уравнения F.98) в виде
Л//г+1
(Allf у
/• Л I П,.П I
0А„1, ;_";„ F.99)
где Аи = un+l — м"ит. д. Член q обозначает как и, так и v,
а индексы /, т соответствуют всем возможным значениям / и
k, для которых частные производные отличны от нуля. Иначе
говоря, 1 = 1—1, /, /+1; m=k—1, k, k+1. Уравнения
F.99) могут быть объединены в одно матрично-векторное
уравнение вида
(^)q = -R, F.100)
которое можно сравнить с уравнением F.17) при использова-
использовании обычного метода Ньютона. Выбор малых значений Д? со-
соответствует тому, что расширенный якобиан (I/Af + J)
приобретает большую степень преобладания членов, близких
к диагонали.
Уравнение F.100) обладает большей эффективностью в от-
отношении «нижней релаксации» в рамках метода Ньютона, чем
18 К Флетчер, т. 1
274
Гл. 6. Стационарные задачи
уравнение F.19). Типичная форма выдачи для решения урав-
уравнений Бюргерса, обеспечиваемого программой NEWTBU с
уравнением F.100), показана на рис. 6.24. Очевидно, что с
уравнением F.100) сходимость осуществляется намного быст-
быстрее, чем с уравнениями F.17) и F.19). В случае уравнения
NEVTONS METHOD FOR N = 18 ITMX= 50 IRD= 1 IPN= 5
DT= Л0000Е-01 EPS= .100E-04 RE= .100E+02 OM= .100E+01
A = 110.13 110.13 .00 .00. 1.00
UE=
UE=
UE=
UE=
UE=
VE=
VE=
VE=
VE=
VE*
IT*
IT=
IT=
IT=
IT=
0
5
10
15
20
AFTER
U=
U=
U=
U=
U=
Y=
Y=
V-
Y«
V*
.9990
.9990
.9990
.9989
.9988
.0000
.1317
.2679
.4142
.5774
RMS=
RMS=
RMS=
RMS=
RMS=
.9586
.9583
.9572
.9553
.9524
.0000
.1277
.2598
.4010
.5577
.1496D+00
.1756D-01
.2O63D-O2
.2465D-03
.2963D-O4
23 ITERATIONS THE
.9990
.9990
.9990
.9989
.9988
.0000
.1317
.2679
.4142
• 5774
.9586
.9605
.9603
.9577
.9524
.0000
.1282
.2605
.4017
.5577
R=
R=
R=
R=
R=
RMS
m
.4888
.4863
.4786
.4655
.4462
.0000
.0753
.1515
.2297
.3109
-.2169D+00
-.1071D-01
-.1072D-02
-.1160D-03
-.1308D-04
RESIDUAL
4888
4835
4748
4625
4462
0000
0748
1507
2290
3109
.0559
.0565
.0584
.0614
.0657
.0000
.0090
.0179
.0266
.0349
-.0991
-.0991
-.0991
-.0992
-.0992
.0000
.0012
.0023
.0034
.0045
-.2850D-01 -.2188L+00
-.2309D-02 -.170315-01
-.2097D-03 -.1748D-02
-.21O3D-O4 -.1905D-03
-.2219D-05 -.2157D-04
IS J
0559
0567
0585
0615
0657
0000
0090
0179
0266
0349
S3174D-05
-.0991
-.0991
-.0991
-.0992
-.0992
.0000
.0012
.0023
.0034
.0045
Рис. 6.24. Типичная выдача по результатам программы NEWTBU с уравне-
уравнением F.100).
F.100) скорость сходимости зависит от выбора А/. Если значе-
значение At велико, то сходимость идет так, как при обычном мето-
методе Ньютона. Однако в применении к двумерным уравнениям
Бюргерса это, по существу, означает расходимость (п. 6.1.3).
Если же значение Д? мало, то скорость сходимости оказывает-
оказывается меньше, но появляется преимущество, состоящее в значи-
значительном расширении радиуса сходимости. Тем самым преодо-
преодолевается главный недостаток метода Ньютона, отмечаемый в
табл. 6.5. Если уравнения решаются, то с учетом единствен-
единственности решения уравнений F.98) ясно, что при выборе доста-
§ 6.4. Псевдонестационарный метод
275
Таблица 6.5. Метод Ньютона
Преимущества
Недостатки
1) Быстрая сходимость (малое число итераций)
2) Может модифицироваться для устранения
многих явных недостатков
3) Можно воспользоваться приближенным ре-
решением
1) Малый радиус сходимости при большом чис-
числе неизвестных
2) Факторизация J на каждой итерации неэко-
неэкономична с вычислительной точки зрения
3) Факторизация J требует большого объема па-
памяти для хранения всех элементов
4) Метод расходится, если матрица J плохо
обусловлена
точно малого At решение будет построено, какова бы ни была
его приемлемая начальная аппроксимация.
Видоизменения программы NEWTBU, отражающие пере-
переход к уравнению F,100), содержатся в строках 36 и 39 под-
подпрограммы JACBU (рис. 6.13). Основные недостатки метода
Ньютона, отраженные в программе NEWTBU, связаны с не-
недостаточной экономичностью процессов формирования матри-
матрицы J и факторизации расширенного якобиана \\/At + J}. Фак-
Факторизация матрицы J требует O(N3) операций, что чрезвычайно
расточительно в случае больших N. Кроме того, по соображе-
соображениям экономичности необходимость хранения всех элементов
матрицы J в оперативной памяти влечет за собой строгое огра-
ограничение на максимальный размер тех систем уравнений, кото-
которые могут решаться.
Многие из элементов матрицы J равны нулю и только не-
некоторые из отличных от нуля имеют большие значения. Это
позволяет сделать вывод о том, что при решении данной зада-
задачи величины Ru и Rv существенно зависят от некоторых узло-
узловых неизвестных и]у k, 0/, *, но очень слабо зависят от других
узловых неизвестных. На этом основании желательно рассмот-
рассмотреть такие аппроксимации для матрицы J, которые охватили
бы сильную зависимость и проигнорировали бы слабую, если
только такой подход привел бы к уменьшенным якобианам или
к- таким структурам матрицы J, которые допускали бы эффек-
эффективную реализацию приближенной факторизации (см. § 8.2).
Возможная плата, которую пришлось бы уплатить за это, со-
состояла бы в увеличении числа итераций до достижения сходи-
сходимости. Однако если каждая итерация будет сама по себе доста-
достаточно экономичной, то упомянутая плата окажется приемлемой.
18*
276 Гл. 6. Стационарные задачи
В тех случаях, когда приемы приближенной факторизации
(расщепления), описываемые в § 8.2, применяются к решению
нелинейных задач, это можно связать с приближенной факто-
факторизацией уравнения F.100). Данный аспект проясняется и
развивается в § 10.4, где с помощью приближенной фактори-
факторизации уравнения F.100) строится решение двумерных уравне-
уравнений Бюргерса, т. е. решается поставленная здесь задача.
§ 6.5. Стратегические приемы
для решения стационарных задач
Для описания большинства задач гидроаэродинамики ис-
используются системы дифференциальных уравнений в частных
производных (гл. 11). Если рассматриваются задачи, связан-
связанные с потенциалом скоростей (§ 14.3), с функцией тока (§ 17.3),
или течения несжимаемой жидкости, связанные с изменения-
изменениями давления (§ 17.1 и 17.2), то, как правило, одно из опреде-
определяющих уравнений имеет матрицу с диагональным преоблада-
преобладанием. В некоторых случаях это уравнение может быть также
и линейным. Следовательно, здесь будут применимы итерацион-
итерационные методы (§ 6.3), в частности многосеточные методы
(п. 6.3.5), а также специальные прямые алгоритмы (п. 6.2.6),
если только сетка является однородной.
Когда роль зависимых переменных играют компоненты ско-
скорости или завихренность, то в определяющих уравнениях обыч-
обычно фигурируют нелинейные конвективные члены (гл. 10). Ди-
Дискретизация таких уравнений приводит к нелинейным системам
уравнений типа F.1), в которых нет диагонального преобла-
преобладания, если не считать случаев, когда диффузионные (вязкие)
члены значительно больше конвективных членов. Тогда, гово-
говоря о методе решения, следует выбирать между ньютоновским
или псевдоньютоновским алгоритмами и псевдонестационар-
псевдонестационарным алгоритмом, связанным с приближенной факторизацией.
Сравнительные недостатки и преимущества двух подходов сум-
суммируются в табл. 6.5 и 6.6.
При решении задач о течении вязкой жидкости с больши-
большими числами Рейнольдса (гл. 17 и 18) матрица J становится
плохо обусловленной и это нередко приводит к расходимости
метода Ньютона, даже если начальная аппроксимация соот-
соответствует сходящемуся решению с близкими параметрами.
В отношении некоторых задач ничего нельзя сказать a priori
относительно существования стационарного решения. Тогда
при введении нестационарной формулировки удается автома-
автоматически обнаружить осцилляционное псевдостационарное ре-
решение.
§ 6.6. Заключение 277
Таблица 6.6.
Преимущества
Недостатки
1)
2)
3)
4)
5)
1)
Псевдонестационарная формулировка при
приближенной факторизации
Каждая итерация экономична
Очень большой радиус сходимости
Малые требования по объему памяти (рас-
(расщепление делает сеточные линии взаимоне-
взаимонезависимыми)
Позволяет обнаруживать нестационарность
задачи
Можно воспользоваться приближенным реше-
решением
Медленная сходимость (требуется большое
число итераций)
Исторически метод Ньютона чаще использовался в сочета-
сочетании с методом конечных элементов, тогда как псевдонестацио-
псевдонестационарный подход с расщеплением чаще сочетался с методами
конечных разностей. Однако псевдонестационарный подход
можно интерпретировать с точки зрения приведения к диаго-
диагонально-расширенной системе уравнений, которую следует ре-
решать итерационными методами, как в случае уравнения F.100).
Следовательно, даже если расширенные системы уравнений не
имеют формального диагонального преобладания по признаку
F.52), они подходят для решения многосеточными методами
(п. 6.3.5) и обычно обеспечивают более быструю сходимость.
§ 6.6. Заключение
В данной главе был дан краткий обзор методов решения ал-
алгебраических уравнений, полученных после дискретизации
(§3.1), в первую очередь в применении к стационарным
задачам.
Те алгебраические уравнения, которые получаются при ди-
дискретизации определяющих уравнений гидроаэродинамики
(гл. 14—18), являются, как правило, нелинейными. В резуль-
результате оказывается неизбежным применение тех или иных ите-
итерационных процедур. Концептуально полезная идея состоит
во введении внешней итерации, позволяющей преодолеть нели-
нелинейную природу дискретизированных уравнений, так что на
каждом шаге этой внешней итерации решается линейная си-
система уравнений. Решение этой системы может строиться либо
прямыми (§ 6.2), либо итерационными методами (§ 6.3).
Во внешней итерации можно воспользоваться методом
Ньютона (п. 6.1.1) или псевдонестационарным методом (§ 6.4).-
278 Гл. 6. Стационарные задачи
Несмотря на то что метод Ньютона в окрестности решения
обеспечивает квадратичную сходимость, малый радиус этой
•сходимости при большом числе узловых неизвестных делает
данный метод в его основной форме менее эффективным, чем
псевдонестационарный метод.
При решении многомерных задач ценность неявных схем
расщепления (§ 8.2) прямо пропорциональна эффективности
решения систем уравнений с узколенточными матрицами
(п. 6.2.2—6.2.5) на каждом этапе внешней итерации.
Итерационные методы, используемые на каждом этапе внеш-
внешней итерации, оказываются обычно наиболее эффективными
для систем с сильным диагональным преобладанием. Это часто
имеет место при дискретизации уравнений, определяющих
трансзвуковое течение невязкого газа (§ 14.3), а это привело к
развитию специальных итерационных методов (п. 14.3.5). Од-
Однако характерная черта многосеточных методов (п. 6.3.5) со-
состоит в том, что они позволяют достаточно экономичным пу-
путем с помощью прямого метода строить решение на самой гру-
грубой сетке. Таким образом, многосеточные методы применимы
независимо от того, обладает ли матрица системы уравнений
диагональным преобладанием или нет.
§ 6.7. Задачи
Нелинейные стационарные задачи (§ 6.1)
6.1. При решении задачи о солнечном коллекторе с помощью программы
NEWTON модифицируйте эту программу так, чтобы матрица J, входящая в
уравнение F.10), рассчитывалась только через каждые р шагов. Сравните
'числа итераций до достижения сходимости и общие числа необходимых опе-
операций, получаемые при различных значениях р. Более разумно начинать с та-
такого решения для Т(о), которое требует для достижения сходимости большего
числа итераций, чем показанное на рис. 6.8.
6.2. Сделайте расчеты по программе NEWTBU для значений Re = 5, 2, 1.
Для каждого варианта выберите значение со, приводящее к наиболее быстрой
сходимости. Что бы вы могли сказать относительно зависимости от Re числа
итераций, нужного для сходимости? Можете ли вы скоррелировать эту зави-
зависимость с относительной величиной различных членов уравнений F.12), а
также с вытекающим отсюда преобладанием диагональных членов матрицы J
в уравнении F.17)?
6.3. Примените квазиньютоновский метод (п. 6.1.4) при Htti== \/Ji,i к
задаче о солнечном коллекторе. Положите Hi, / = 0 при i ф /. Сравните сум-
суммарное время счета с аналогичным временем при применении обычного ме-
метода Ньютона.
Прямые методы для линейных систем (§ 6.2)
6.4. Составьте компьютерную программу для решения уравнения F.27)
при Rceu = 0.5, пользуясь подпрограммами BANFAC и BANSOL для значе-
значений vj при /==2, ..., 10. Граничные условия: Vi = 0, vn = 1.0. Данная за-
§ 6.7. Задачи 279
дача имеет точное решение в форме (9.46).
vi = —0.0060834 + 0.00365 E/3)' при } = 1, ..., 11. F.101)
6.5. Пятиточечная схема, соответствующая схеме F.27), имеет вид
0 + «cell) V2 - 8 B + *cell) "/-1 + 3°°1 ~
~ 8 B " «cell) Vl + 0 - *cell) W/+2 = °- <6-102>
Видоизмените подпрограммы BANFAC и BANSOL применительно к решению-
пятидиагональной системы, получаемой из вышеприведенного уравнения.
Предположите, что заданы адекватные граничные условия, позволяющие
вычислить u/_2 и Vj-i на левой границе, а также v]+i и Vi+2 на правой гра-
границе. Проведите расчет по этой схеме при / = 3, ..., 9 и RCe\\ = 1.0. Вос-
Воспользуйтесь формулой
VI = (г10*/ - l) (е10 - 1) при XI = 0.1 (/ - 1), F.103>
чтобы получить граничные значения для уь v2i v10 и vn. Формула F.103)
выражает точное решение задачи, дискретная формулировка которой соот-
соответствует F.102). Следовательно, решение уравнения F.102) должно быть
близко к выражению F.103).
6.6. Составьте компьютерную программу для реализации решения блоч-
но-трехдиагональных систем уравнений с блоками 2X2. Проверьте работу
программы после дискретизации уравнений
^._2^. = 0 и ^.-05^-0 F.104>
dx2 dx dx2 dx
с граничными условиями Т = 0 и 5 = 1 при х = 0, Т = 2sh A), S = ch(l)
при х = 1, используя трехточечные центрированные конечно-разностные фор-
формулы. Получите решения внутри интервала 0 ^ х ^ 1.0 при Ах = 0.1. Точ-
Точное решение уравнений F.104) с приведенными выше граничными усло-
условиями Дирихле выражается в виде Г = 2 sh(jc), S = ch(jc).
Итерационные методы (§ 6.3)
6.7. Постройте решения для задачи о течении в канале (п. 6.3.2) в со-
соответствии с табл. 6.3 при условии применения методов Якоби, Гаусса — Зай-
деля и ПВР с конечно-разностной дискретизацией для значений b/а = 3 и
10. Какой эффект оказывает увеличение отношения сторон?
6.8. Видоизмените программу DUCT с целью введения схемы НПН, со-
соответствующей уравнениям F.66) и F.67), и подтвердите результаты, пока-
показанные в табл. 6.3. Сходимость нередко ускоряется за счет введения после-
последовательности итерационных параметров Я^1. Определите эффективность
следующего выбора для случая b/а = 1, Ах = Ау:
где N — число разбиений на каждой из сторон сечения канала. Формула
F.105) приводит к циклу, при необходимости повторяемому. Надлежащая-
стратегия для выбора последовательности итерационных параметров обсу-
обсуждается в книгах [Varga, 1962; Wachpress, 1966].
6.9. Примените к решению задачи о течении в канале (п. 6.3.2) алгоритм
МСН (п. 6.3.3) для условий, соответствующих табл. 6.3, и сравните число*
итераций, требуемых для сходимости, а также суммарное время счета с ре-
результатами, показанными в табл. 6.3.
280 Гл. 6. Стационарные задачи
6.10. Примените псевдонестационарный метод Ньютона (программа
NEWTBU) с расчетом элементов матрицы J только через каждые р итера-
итераций. Определите влияние р на сходимость и суммарное время счета.
6.11. Видоизмените программу NEWTBU так, чтобы отдельные элементы
матрицы J приравнивались нулю, если они меньше критерия TOL При
TOL = 10~5, 10~3, Ю-1 определите, сколько именно элементов J приравни-
приравнивается нулю и как изменяется число итераций, необходимое для сходимости.
Будет ли получаемая в результате структура расположения отличных от
нуля элементов матрицы J допускать возможность более эффективного ре-
решения уравнения F.100), чем с применением подпрограмм FACT и SOLVE,
например, с применением итерационного метода на основе соотношения
F.51)?
6.12. Можно ли сделать программу NEWTBU сходящейся быстрее за
счет использования последовательности Д?? Введите цикл с помощью гео-
геометрической прогрессии шагов по времени
где показатель прогрессии г « 1.2 и р « 5—40. Проведите эксперименты с
различными комбинациями Д/@), г и р.
Глава 7
Одномерное уравнение диффузии
Если говорить о перспективах развития вычислительных ме-
методов, то уравнение диффузии содержит тот же самый дисси-
пативный механизм, который обнаруживается при изучении
задач гидроаэродинамики со значительным влиянием вязкости
или теплопроводности. Следовательно, приемы численного ана-
анализа, эффективные для уравнения диффузии, позволят целе-
целенаправленно выбрать и надлежащие алгоритмы для решения
задач динамики вязкой жидкости (см. гл. 15—18).
В данной главе одномерное уравнение диффузии будет ис-
использовано для того, чтобы на примерах его решения разра-
разрабатывать явные и неявные схемы. При этом будет уделяться
внимание вопросам устойчивости и точности различных схем.
Будет рассмотрена также и проблема точного учета граничных
и начальных условий.
Ранее (см. § 2.3) мы вводили уравнение диффузии или
уравнение теплопроводности
#-<•#-» G.D
в качестве примера параболического дифференциального урав-
уравнения в частных производных, а также пользовались им для
иллюстрации процессов дискретизации (§ 3.1) и применения
конечно-разностного метода (§ 3.5).
В уравнении G.1) величина Т может рассматриваться как"
скорость, завихренность, температура или концентрация в за-
зависимости от того, рассматриваем ли мы диффузию импульса,
вихря, тепла или массы. Если Т — температура, то уравнение
G.1) определяет поток тепла в стержне, который теплоизоли-
теплоизолирован на боковой поверхности, но может передавать тепло
окружающей среде через свои концы (точки Л и В на рис. 7.1).
Обычно встречаются два типа граничных условий. Во-пер-
Во-первых, зависимая переменная задается как известная функция
времени. В обозначениях уравнения G.1) такое задание имеет
форму (для точки А)
Г@,*) = 6@- G.2>
282 Гл. 7. Одномерное уравнение диффузии
Это — граничное условие Дирихле (см. п. 2.1.2). На практике
b часто является константой. Во-вторых, можно задать про-
пространственную производную зависимой переменной. Примени-
Применительно к G.1) это можно записать в виде (для точки А)
4|-«U) = c(/). G.3)
Это — граничное условие Неймана (см. п. 2.1.2). Как и в слу-
случае граничного условия Дирихле, величина с часто является
константой.
7д или I j Тв или
дТд/дх (SSSSSS^ дТ /дх
х=0 х=1 В
Рис. 7.1. Одномерный нестационарный процесс теплопроводности.
Для получения единственного решения уравнения G.1) не-
необходимо задать также и начальные условия. Это может быть
сделано в форме
Г(*. 0) = Г0(*). G.4)
Точное решение Т(х9 t) удовлетворяет уравнению G.1), а так-
также условиям G.4) и G.2) или G.3), применяемым при х = 0
их =1.0.
С целью построения приближенного решения уравнение
G.1) подвергается дискретизации (§ 3.1), и полученное алгебра-
алгебраическое уравнение приводится к такой форме, которая позво-
позволяет составить алгоритм. Этот алгоритм дает возможность по-
получить решение на (п+1)-м временном слое (см. рис. 3.2)
по данным о решении, известном на n-м и на более ранних
временных слоях. Описание процедуры в целом дается в § 3.5.
§ 7.1. Явные методы
При использовании явных методов единственная неизвест-
неизвестная, например Г/+1, фигурирует в левой части алгебраической
формулы, полученной в результате дискретизации.
§ 7.1. Явные методы
283
7.1.1. Схема В В ЦП
Если для производной по времени ввести двухточечную раз-
разностную аппроксимацию со сдвигом вперед, а для простран-
пространственной производной — точечную аппроксимацию с
центральной разностью, то уравнение G.1) приобретает сле-
следующую форму:
Г1т1 0G7.1-277 + 774.,)
IP °
Ы IP — °-
Уравнение G.5) будет в дальнейшем называться схемой
ВВЦП (разности со сдвигом вперед по времени и центральные
л+1
ВВЦП
n+1
n-1
j-1 j j+1
Ричардсон
j-i j
Дюфорт — Франкел
П o-
j-1 j j+l
n-1
n+1
j-1 J j+l
J-l j j+1
Кранк — Николсон ТСЧН
Рис. 7.2. Активные узлы в алгебраических схемах для уравнения диффузии.
Линейный МКЭ,
Кранк —Николсон
по пространству). Как можно видеть, пространственная про-
производная была аппроксимирована на п-ы слое по времени, т. е.
на известном временном слое. Несколько преобразуя уравне-
уравнение G.5), получим алгоритм
Г?4 = s77-i + A - 25)Г? + s77+1, G.6)
где фигурирует параметр дискретизации 5 = aAtfAx2.
Узлы сетки, связанные зависимостью по формуле G.6), по-
показаны на рис. 7.2. Подстановка в уравнение G.5) функции Т,
т. е. точного решения уравнения G.1), и разложение каждого
из членов в ряд Тейлора относительно узла (/, п) (так же, как
в п. 3.2.1) дает _ _
" дТ д2т 1
Таблица 7.1. Алгебраические схемы дискретных вариантов представления уравнений
диффузии d7/dt — ад*Т/дх* =* О
Схема
Алгебраическая формула
Главный член
ошибки аппроксимации *
(Е)
Коэффициент усиления
О (вввД)
Усло-
Условия
устой-
устойчивости
Комментарии
ввцп
А*
— 4s sin2 I -rr
X
д4Т
дх4
Дюфорт —
Франкел
Tn+i_Tn-\
_J I \ТП
2 M Ax2 r/-1
" l^jj dx4
2s cos e;+'(i:-4s2jsin2eI/2
Нет
Д71
d+2s)
?"* rsT?
Кранк —
Николсон
•_.—•
._!_.
Трехслой-
Трехслойная чисто
неявная
•
1
Линейный
метод
конечных
элементов/
Кранк —
Николсон
LJJ
A 1*1"f* 1
/
„, (Т1+Т1 1=0
aL**\ 2 ) °
з дгу+1 1 дг^
2 Д/ 2 Д*
дгп+1
( Ах2 \ д4Т
1 - 2s sin2 F/2)
1 + 2s sin2 F/2)
B-3s) + cos6(l+3s)
B + 3s) + cos 6A-3s)
Нет
Нет
Нет
Г 1 2 1 \
х { 6 ' 3 ' 6 J
* Ошибка аппроксимации была выражена исключительно через Аде и производные по дс, как в методе модифицированного уравнения
(п. 9.2.2). Таким образом, алгебраическая схема эквивалентна уравнению дТ/dt — ad277d*2 + ? (Г)=0,
286 Гл. 7. Одномерное уравнение диффузии
где ошибка аппроксимации Е" определяется формулой
* д2Т А*2 дАТЛп . ~/А,2
а J + °<Л/
J/
Как можно видеть, имеет место согласованность (см. § 4.2)
уравнений G.5) и G.1).
Исходя из структуры главного члена в выражении для ?/>
схема ВВЦП будет считаться имеющей первый порядок точ-
точности по времени и второй порядок точности по пространству.
Однако следует помнить, что это утверждение, строго говоря,
справедливо только в пределе Д/->0, Ajc-^O. Практически ре-
решения строятся на сетке конечных размеров и величина таких
членов, как d2T/dt2, заранее неизвестна.
Как показывает анализ устойчивости по Нейману (§ 4.3) >
коэффициент усиления G выражается формулой
G=l-4ssin2(y),
где s = <xAt/Ax2 и 0 = пглАх. При любом значении Q и при
5^0.5 будет \G\ ^ 1. Следовательно, алгоритм G.6) будет
давать устойчивые решения, если 5 ^ 0.5. Ранее мы уже виде-
видели (см. п. 4.2.1), что при специальном выборе s=l/6 некото-
некоторые члены в выражении ошибки аппроксимации обращаются в
нуль, и тогда алгоритм G.6) дает ошибку аппроксимации по-
порядка О (At2, Ax4).
Вышеописанные свойства схемы ВВЦП при ее применении
к уравнению диффузии G.1) суммируются в табл. 7.1. Можно
отметить, что форма выражения ошибки аппроксимации, при-
приводимая в табл. 7.1, эквивалентна выражению G.7). Точность
численных решений, строящихся с использованием схемы
ВВЦП, показана в табл. 7.3.
7.1.2. Схемы Ричардсона и Дюфорта — Франкела
При построении алгоритма G.6) использование двухточеч-
двухточечной односторонней разностной формулы дает вклад первого
порядка в выражение ошибки усечения, а использование трех-
трехточечной центрированной разностной формулы — вклад второ-
второго порядка в то же выражение. Поэтому логическим усовер-
усовершенствованием алгоритма G.6) является схема
2А?
предложенная Ричардсоном (см. рис. 7.2). Однако, несмотря
на то что схема имеет порядок О {At2, Ax2), анализ ее устой-
§ 7.1. Явные методы 287
чивости по Нейману [Noye, 1983] показывает, что при s,>0
схема безусловно неустойчива. Таким образом, она не пред-
представляет практической ценности. Можно отметить, что заме-
замечание о неустойчивом поведении относится к уравнению в це-
целом. Если аппроксимация с центральной разностью для произ-
производной по времени применяется к уравнению конвекции (9.2),
то может быть получен устойчивый алгоритм (9.15).
Схему Ричардсона G.8) можно модифицировать так, что-
чтобы получить устойчивый алгоритм. Это достигается за счет
замены Т? в уравнении G.8) на 0.5 (Г" + Г/). В резуль-
результате получается уравнение
T/l + l nntl—\ ГгрП (rpfl~\ _i тП-\"\\ I ftl 1
ш
Уравнение G.9), известное как схема Дюфорта — Франкела
(см. рис. 7.2), можно преобразовать так, чтобы получился яв-
явный алгоритм
n~l
Схема Дюфорта — Франкела является трехслойной по вре-
времени во всех случаях, кроме s = 0.5, а в последнем случае она
совпадает со схемой ВВЦП. При использовании трехслойной
схемы нужно хранить в памяти данные на двух временных
слоях и возникает необходимость в альтернативной двухслой-
двухслойной схеме для реализации первого шага по времени.
Применение к уравнению G.10) анализа устойчивости по
Нейману (см. § 4.3) дает коэффициент усиления G, приведенный
в табл. 7.1. Так как при любом значении 0 и при s> 0 имеем
\G\ ^ 1, то схема Дюфорта — Франкела устойчива при лю-
любом значении At. Однако имеется некая цена, которую нужно
уплатить за этот весьма благоприятный результат, касающий-
касающийся устойчивости. Если в G.9) подставить точное решение, раз-
разложенное в ряд Тейлора относительно (/, п)-го узла, то в ре-
результате получится
Следовательно, для обеспечения согласованности необходимо,
чтобы Д?/Дл;->0, когда Д?->0 и Да:->0, т. е. для наличия со-
согласованности требуется выполнение условия Д? <С Да:. Однако
<x(At/AxJ = sAt, а при решении задач о диффузии ожидается,
что s имеет порядок О A). Поэтому схема Дюфорта — Фран-
Франкела согласуется с уравнением G.1), но будет неточной, если
288 Гл. 7. Одномерное уравнение диффузии
величина sAt велика. Альтернативная форма выражения ошиб-
ошибки аппроксимации (см. табл. 7.1) показывает, что если s =
= A/12I/2, то схема Дюфорта — Франкела дает ошибку ап-
аппроксимации О (Ах4). Соответствующая этому точность реше-
решения указывается в табл. 7.3.
Все же с практической точки зрения использование схемы
Дюфорта — Франкела влечет за собой серьезное ограничение
на величину Att даже несмотря на то что это ограничение свя-
связано с требованиями точности, а не устойчивости, как это было
со схемой ВВЦП.
7.1.3. Трехслойная схема
Явная форма трехслойной дискретизации уравнения G.1)
в общем случае записывается в виде
аТТх + ЬТ1 + сТ1} - (dLxxT? + eLxxT?~l) = 0, G.12)
где
Параметры а, Ь, с, d и е могут быть определены путем разло-
разложения каждого из членов уравнения G.12) в ряд Тейлора от-
относительно узла (/, п) и требования о том, чтобы уравнение
G.12) было согласовано с уравнением G.1). Примеры подоб-
подобных процедур даются в п. 3.2.2 и 3.2.3. Эта процедура по-
позволяет переписать уравнение G.12) в форме, содержащей
лишь две варьируемые константы у и р вместо пяти. В резуль-
результате уравнение G.12) заменяется на
А/ А*
- а [A - р) LxJi + ?ЬХХТ*}-1] = 0. G.13)
Разложение членов уравнения G.13) относительно узла (/, п)
указывает на согласованность данного уравнения с уравнением
G.1), причем ошибка аппроксимации выражается формулой
Ё\ = as A*2 -g- @.5 + Y + Р ~ -it) + О (Дх4), G.14)
где s = aAt/Ax2. В выражении G.14) все производные по вре-
времени заменяются производными по пространству посредством
использования исходного уравнения, как это сделано в
табл. 7.1.
Ясно, что уравнение G.13) имеет ошибку аппроксимации чет-
четвертого порядка, если постоянная р выражется по формуле
р = _0.5 -Y+ 1/A25). G.15)
§ 7.1. Явные методы
289
Из уравнения G.13) получается алгоритм
тле L'xxT, = T._1] l+
Оказывается, что алгоритм G.16) обладает лишь условной
устойчивостью, причем максимальное значение s, обеспечиваю-
обеспечивающее устойчивость, является функцией у. Это можно установить,
применяя к уравнению G.13) анализ устойчивости по Ней-
Нейману (см. § 4.3). При этом возникает необходимость решения
следующего квадратного уравнения относительно G:
G.17)
+ [Y — 20s (cos в — 1)] = 0.
Для обеспечения устойчивости необходимо, чтобы было \G\ ^
^ 1 при любых значениях в. В результате можно построить
график, показанный на рис. 7.3 и демонстрирующий границу
0.50
0.40
0.30
Неустойчивое
2.0
4.0
6.0
Рис. 7.3. Граница области устойчивости для схемы G.13) и формулы G.15).
области устойчивости в координатах у и s. При у = 0 уравне-
уравнение G.17) приводит к обусловленному требованием устойчиво-
устойчивости ограничению на s( s^O.34), более суровому, чем это де-
делает схема ВВЦП. Точность трехслойной схемы G.13) иссле-
исследуется в п. 7.1.4.
7.1.4. DIFEX численные результаты применения явных схем
В данном пункте сравниваются результаты применения схе-
схемы ВВЦП (п. 7.1.1), схемы Дюфорта — Франкела (п. 7.1.2), а
также трехслойной схемы (п. 7.1.3). Все три метода отражены
19 К. Флетчер, т. 1
1 С DIFEX SOLVES THE DIFFUSION (ID TRANSIENT HEAT CONDUCTION)
2 С EQUATION USING VARIOUS EXPLICIT SCHEMES
3 С
4 DIMENSION TND1),DUMD1),TDD1),XD1),TED1),TOLD1),ELC)
5 REAL*8 SUM,AVS,RMS,DSQRT,DMP
6 С
7 OPENA,FILE*•DIFEX.DATf)
* OPEN F,FILE='DIFEX.OUT)
$ *EAD(l,l)ME,IPR.JHAX,MAXEX,NMAX,ALPH,S,TMAX,T$TfGAN
10 1 FORMATEI5,E10.3,F5,3,3F5.2)
11 С
12 PI * 3.1415927
13 JMAP = JttAX - 1
14 AJN = JMAP
15 DELX = l./AJM
16 DELT = DELX*DELX*S/ALPH
17 С
18 IF(ME »EQ. 1)WRITEF,2)
19 IF(ME .EQ. 2)WRITEF,3)
20 IF(ME .EQ. 3)WRITEF,4)
21 2 FORMATС FTCS SCHEME',//)
22 3 FORMATС DUFORT-FRANKEL SCHEME1,//)
23 4 FORMAT(' 3-LEVEL, 4TH-0RDER SCHEME1,//)
24 VRITE<6,$)JMAX,MAXEX,NMAX,TMAX,TST,GAK
25 5 FORMATC JMAX«\I5,' MAXEXs',15,1 NMAX»',X$,
26 lf THAX-4F5.2,1 TST«\F5.2,f GAM«*,F5.2)
27 VRm<6,6)S,ALPH,DELT,DELX
2$ 6 FORMAT С ?=',F5.3,* ALPH = \E10.3/ DELT « %B1O.3#
29 1* DELX = \E10.3,//)
30 С
31 IF(ME .EQ. 2)AS - 2.*S/A.+2.*S)
32 IF(ME .EQ. 2)BS « A. - 2.*S)/A. + 2.*S)
33 IF(ME .NE. 3)GOTO 7
34 AS = (l.+2.*GAH)/U.+GAM)
35 BS = -GAM/U.+GAM)
36 CS = S/A.+GAM)
37 DS « 1.5 + GAM - 1./12./S
38 ES = -0.5 - GAM + 1./12./S
39 EL(l) = 1.
40 ELB) = -2.
41 ELC) = 1,
42 7 CONTINUE
43 С
44 С OBTAIN INITIAL CONDITIONS FROM EXACT SOLUTION
45 С
46 T = TST - 2.*DELT
47 DO 9 I * 1,2
48 T = T + DELT
49 С
50 CALL EXTRA(JMAX,MAXEX,D?LX,PI,ALPH,T,TE)
51 С
52 DO 8 J = 2,JMAP
53 IFU .EQ. l)TOL(J) * TE(J)/100.
54 IFU .EQ. 2)TN(J) « TE(J)/100.
55 8 CONTINUE
56 9 CONTINUE
57 С
58 С SET BOUNDARY CONDITIONS
59 С
Рис. 7.4. Распечатка программы DIFEX (начало.)
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
С
С
С
С
С
С
С
С
С
С
С
С
С
С
с
с
с
с
с
с
10
11
12
13
14
15
16
17
18
19
20
TOL(l) = 1.
TOL(JMAX) = 1.
TNA) = 1.
TN(JMAX) = 1.
TDA) = 1OO.*TNA)
TD(JMAX) = 1OO.*TN(JMAX)
N = 0
EACH TIME STEP STARTS AT STATEMENT 10
N * N + 1
IF (ME .EQ. DGOTO 15
IF(ME .EQ. 2)GOTO 13
ME = 3, 3-LEV., 4TH ORDER
DO 12 J =2,JMAP
DUM(J) * AS*TN(J) + BS*TOL(J)
DO 11 К » 1,3
KJ * J - 2 + К
DUM(J) = DUM(J) + CS*EL(K)*(DS*TN(KJ) + ES*TOb(KJ)>
CONTINUE
CONTINUE
GOTO 17
ME « 2, DUFORT-FRANKEL
DO 14 J = 2,JMAP
DUM(J) = ASMTN(J-l) + TN(J+1)) + BS*TOL(O)
GOTO 17
ME = 1, FTCS
DO 16 J = 2,JMAP
DUM(^) * (l.-2.*S)*TN(J) + S*(TN(J-1) + TN(J+1)>
CONTINUE
DO 18 J = 2,JMAP
IF(ME .GT. l)TOb(J) = TN(J)
TN(J) = DUM(J)
DO 19 J = 2,JMAP
TD(J) = 1OO.*TN(J)
T = T + DELT
IF(IPR .EQ. l)VRITEF,20)T,(TDr(J),J=l,JMAX)
FORMATC T= f,F5.2rf TD=\11F6.2)
IF MAXIMUM TIME OR MAXIMUM NUMBER OF TIME-STEPS
EXCEEDED EXIT FROM LOOP
IF(N .GE. NMAXKOTO 21
IF(T .LT. TMAX)GOTO 10
OBTAIN EXACT SOLUTION AND COMPARE
114 21 SUM = 0.
Рис. 7.4 (продолжение).
19*
292 Гл. 7. Одномерное уравнение диффузии
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
С
С
С
с
с
CALL EXTRA(JMAX,MAXEX,DELX,PI,ALPH,T,TE)
DO 22 J = 1,JMAX
DMP * TE(J) - TD(J)
SUM * SUN + DMP*DMP
22 CONTINUE
IFUPR .NE. l)?RITEF,20)T,(TD(J),J*l,JMAX)
WRITEF,23)T,(TE(J),J»1,JMAX)
23 FORMAT(/,f T» \F5.2,1 TE»',11F6.2,//)
RMS IS THE RMS ERROR
AVS * SUM/U. + AJM)
RMS * DSQRT(AVS)
WRITEF,24)RMS
24 FORMAT(f RMS DIF * f,Dll.4,//)
STOP
END
Рис. 7.4 (окончание).
в тексте программы DIFEX, распечатка которой приведена
на рис. 7.4 и которая является обобщением программы DIFF
(рис. 3.13).
Решения ищутся в вычислительной области 0^*^1.0 и
2.00 ^ t ^ 9.00 при начальных условиях, заданных при t =
= 2.00, с помощью точного решения C.42), деленного на 100.
Граничные условия имеют вид
t) = T(l, 0—1.0. G.18)
Представление о точности различных схем можно получить
путем оценки среднеквадратичной разности между численным
и точным решениями при Т = 9.00. Точное решение рассчиты-
рассчитывается с помощью подпрограммы EXTRA (рис. 7.5). Схема Дю-
форта — Франкела и трехслойная схема нуждаются в задании
начальных данных на двух слоях при t = 2.00 и t = 2.00 — Д*.
Основные параметры, используемые в программе DIFEX
(см. рис. 7.4), приводятся в табл. 7.2. Характерная форма пред-
представления решения, построенного с помощью трехслойной схе-
схемы на сравнительно грубой сетке, показана на рис. 7.6.
Точности различных вариантов решения, полученных при
использовании программы DIFEX, сравниваются в табл. 7.3.
Чтобы получить возможность сравнения трехслойной схемы
четвертого порядка в виде G.13) со схемами ВВЦП и Дюфор-
та — Франкела, использовалось два значения s: 5 = 0.3 и 0.41.
Кроме того, в таблицу включены два частных случая — ВВЦП
с s=l/6 и схема Дюфорта — Франкела с s=(l/12I/2. Оба
§ 7.1. Явные методы 293
этих случая соответствуют резкому уменьшению ошибки ап-
аппроксимации.
1
2 SUBROUTINE EXTRA(JMAX,MAXEX,DELX,PI,ALPH,T,TE)
3 С
4 С EXACT SOLUTION OF THE TRANSIENT HEAT CONDUCTION PROBLEM
5 С
6 DIMENSION XD1),TED1)
7 С
S DO 2 J * 1,JKAX
9 A J « J - 1
10 X(J) » DELX*AJ
11 TE(J) * 100.
12 DO 1 M - 1,MAXEX
13 AH * N
14 DAM = B.*AM - 1.)
15 DXM = DAM*PI*X(J)
16 DTM « -ALPH*DAM*DAM*PI*PI*T
17 С
18 С LIMIT THE ARGUMENT SIZE OF EXP(DTM)
19 С
20 IF(DTM .LT» - 25JDTM » -25.0
21 DTM - EXP(DTM)
22 IF(DTM .LT. 1.0E-10)GOTO 2
23 1 TE(J) « TE(J) - 400./DAM/PI*SIN(DXM)*DTM
24 2 CONTINUE
25 RETURN
2f END
Рис. 7.5. Распечатка программы EXTRA.
J-LETOi, 4TH-0RDER SCHEHE
JMAX* 11 MAXEX= 10 NMAX* 500 TMAX» 9.00 TST» 2.00 GAM* 0.00
S» .300 ALPH = .100E-01 DELT * .300E+00 DELX = Л00Е+00
T> 9.20 TD*100.00 84.12 69.80 58.45 51.16 48.65 51.16 58.45 69.80 84.12100.00
T» 9.20 TE«100.00 84.12 69.80 58.45 51.17 48.66 51.17 58.45 69.80 84.12100.00
RMS DIF = .4169D-02
Рис. 7.6. Типичная выдача результатов по программе DIFEX (начало).
При 5 = 0.3 схема ВВЦП обнаруживает скорость сходи-
сходимости второго порядка. Приближенное значение скорости схо-
сходимости было получено по данным об отношении величин сред-
среднеквадратичной ошибки на двух сетках: Да: = 0.1 и Аде = 0.05,
т. е.
Г = lg (RMSA*-o.l/lg (RMSд*-о.О5).
Схема Дюфорта — Франкела значительно точнее схемы ВВЦП.
294
Гл. 7. Одномерное уравнение диффузии
Таблица 7.2. Параметры, используемые в программе DIFEX
Параметр
ME
IPR
JMAX
МАХЕХ
NMAX
ALPH
S
ТМАХ
TST
GAM
TD
TN
TOL
ТЕ
DELX
DELT
EL
Т
X
RMS
Описание
= 1: схема ВВЦП
= 2: схема Дюфорта—Франкела
=3: трехслойная схема четвертого порядка
Управление формой выдачи; IPR=1 для решения ТО
Число точек в направлении х »
Число членов в выражении точного решения
Максимальное число шагов по времени
Коэффициент тепловой диффузии а
= aAx/At2
Максимальное время
Начальное время
Параметр у в соотношении G.16)
Размерный температурный массив
Безразмерный температурный массив Тп в G.16)
Безразмерный температурный массив Тп~х в G.16)
Размерный температурный массив точного решения
Ах
At
Коэффициенты в выражении разностного оператора Lxx
Время
Пространственная координата, 0 ^ х ^ 1.0
Среднеквадратичная ошибка решения
Это связано с близостью данного значения s к специальному
s = A/12I/2= 0.289, для которого достигается скорость сходи-
сходимости четвертого порядка. Трехслойная схема четвертого поряд-
порядка (при у = 0) оказывается менее точной, чем схема Дюфор-
Дюфорта—Франкела на грубой сетке (Д* = 0.20). Обычная тенден-
тенденция для схем повышенного порядка состоит в том, что для
выявления своих преимуществ в точности они нуждаются в бо-
более мелких сетках. По мере возрастания у точность трехслойной
схемы четвертого порядка на заданной сетке уменьшается, хо-
хотя четвертый порядок скорости сходимости приближенно со-
сохраняется. При 5 = 0.41 и y=1-0 трехслойная схема четвер-
четвертого порядка обнаруживает точность, сравнимую с точностью
схемы Дюфорта — Франкела на грубой сетке, но является су-
существенно более точной на мелкой сетке.
Результаты, показанные в табл. 7.3, свидетельствуют о том,
что построение схем повышенного порядка путем уменьшения
§ 7.2. Неявные методы
295
Таблица
Схема
ввцп
То же
»
Дюфорт —
Франкел
То же
»
Трехслойная
4-го порядка
То же
t 7.3. Численные решения
s
1/6
0.30
0.41
0.289
0.30
0.41
0.30
0.30
0.30
0.41
Y
0.0
0.5
1.0
1.0
уравнения G.1) с помощью
явных схем
Среднеквадратичная ошибка RMS
(Дх=0.2)
0.7266 X Ю~2
0.6439
1.2440
0.0498
0.0244
0.8481
0.0711
0.1372
0.2332
0.7347
(Дх=0.1)
0.4921 XI 0~3
0.1634
0.3023
0.2328 ХЮ
0.0136
0.2085
0.00416
0.00665
0.00916
0.0229
(Лх = 0.05)
0.3279 X Ю
0.0413
0.0755
0.1152Х10
0.00395
0.05250
0.00022
0.00029
0.00054
0.00140
Прибли-
Приближенная
скорость
сходимо-
сходимости
г
3.9
2.9
2.0
4.3
1.8
2.0
4.2
4.5
4.1
4.0
ошибки аппроксимации не представляет серьезных трудностей.
Такие схемы, как правило, дают повышенную точность на мел-
мелкой сетке, однако зачастую при ужесточении ограничений, свя-
связанных с устойчивостью. По отношению к нелинейным уравне-
уравнениям, определяющим движение жидкости, повышение точности
может оказаться не столь большим, как для уравнения диффу-
диффузии, обладающего в данной ситуации весьма гладким решением.
§ 7.2. Неявные методы
В случае применения неявных схем пространственный член
d2Tfdx2 в уравнении G.1) аппроксимируется, по меньшей мере
частично, на неизвестном временном слое (л+ 1). На практи-
практике это приводит к возникновению взаимосвязи уравнений для
каждого из узлов (/, м+ 1) на (п + 1)-м временном слое и к
необходимости решать систему алгебраических уравнений для
продвижения решения во времени.
7.2.1. Чисто неявная схема
Простейшее неявное конечно-разностное представление
уравнения G.1) имеет вид
тп+\ тп (тп+\ 9Тп+\ , тп+1\
296
Гл. 7. Одномерное уравнение диффузии
Для получения полезного алгоритма уравнение G.19) перепи-
переписывается в виде
—s77-i + A + 25)T*}+1 - sTniX\ = 77.
G.20)
В результате разложения в ряд Тейлора относительно (/, я)-го
узла выясняется, что эта схема имеет ошибку аппроксимации
Полученное выражение имеет тот же порядок, что и для явной
схемы ВВЦП, соответствующей уравнению G.5) при 5 Ф 1/6,
хотя постоянный множитель здесь несколько больше.
С помощью анализа устойчивости по Нейману (см. § 4.3)
получается следующее выражение для коэффициента усиления:
G = [l+ 25A— cosO)].
Если 5 > 0, то при любом 9 имеем \G\ ^ 1. Это означает, что
схема G.20) безусловно устойчива, выявляя тем самым свое
очевидное преимущество перед условно устойчивой явной схе-
схемой G.5).
Однако для решения уравнения G.20) необходимо рассмот-
рассмотреть как все узлы /, так и соответствующие уравнения. Таким
образом, может быть выписана матрица уравнений для неизве-
неизвестных значений Г"+1:
A+25) —5
—5 A+25) —5
—5
0+25) -5
X
X
тп+1 -
тп+1
тп+1
•
_ 77+/_
d2 '
d3
d,
-dj-x_
G.21)
§ 7.2. Неявные методы 297
В уравнении G.21) имеем
где значения Г?+1 и Г/+1 известны из граничных условий Ди-
Дирихле. Очевидно, что система уравнений G.21) является трех-
диагональной. Следовательно, для решения уравнений G.21)
можно воспользоваться алгоритмом Томаса (см. п. 6.2.2), тре-
требующим выполнения 5(/—2)—4 операций (учитываются
только операции умножения и деления).
На практике с учетом необходимости формирования урав-
уравнений решение неявной системы G.21) с помощью алгоритма
Томаса требует, как правило, вдвое большего компьютерного
времени, чем решение того же числа явных уравнений G.6).
Шаг по времени может быть сделан существенно большим, чем
предельное значение шага по времени для явной схемы, т. е.
Д/ехр = 0.5Дл;2/а; однако точность решения будет при этом
меньше.
7.2.2. Схема Кранка — Николсона
Альтернативный вариант неявного алгоритма для решения
уравнения G.1) соответствует схеме Кранка — Николсона (см.
рис. 7.2), которая имеет вид
Г/ Д~Г/ - a @.5LxxT* + 0.5LxxTfrl) = 0, G.22)
где
Г Ф / — 1 / *^ / -J- 1
J-XX* — д^2 '
Фактически эта схема аппроксимирует пространственную про-
производную на слое времени, промежуточном между п-м и (п +
+ 1)-м слоями, т. е. на временном слое (п + 1/2). Если выпол-
выполнить разложение в ряд Тейлора относительно точки (/, п +
+ 1/2), то мы найдем, что уравнение G.22) согласуется с
уравнением G.1) при ошибке усечения порядка О(А^2, Ах2).
Последнее представляет собой значительное улучшение по
сравнению как с чисто неявной схемой, так и со схемой ВВЦП,
поскольку обе они имеют точность лишь первого порядка по
времени.
Анализ устойчивости по Нейману показывает, что схема
Кранка — Николсона является безусловно устойчивой (см.
298 Гл. 7. Одномерное уравнение диффузии
табл. 7.1). Перестановка членов уравнения G.22) дает алгоритм
- 0.5sTl+l + A + s) Tf+l - O.bsTftl =
= 0.5s77-i + A - s) T1} + 0.5sT?+u G.23)
который можно сравнить с алгоритмом G.20). Если последова-
последовательно рассмотреть все пространственные узлы, то соотноше-
соотношение G.23) даст трехдиагональную систему уравнений, эффек-
эффективное решение которой может быть выполнено с помощью ал-
алгоритма Томаса.
Вследствие присущего ей второго порядка точности по вре-
времени схема Кранка — Николсона составляет основу очень по-
популярного метода решения параболических дифференциальных
уравнений в частных производных. Свойства схемы Кранка —
Николсона суммируются в табл. 7.1.
Можно получить обобщение уравнения G.22), если напи-
написать
_^_ _ а [A _ р) LxxTf + pi«77+1] = 0, G.24)
где
1 = 77+| —Г? и
В случае р = 0 получается схема ВВЦП, при р = 0.5 —
схема Кранка — Николсона, а при р = 1.0 — чисто неявная
схема.
Анализ устойчивости по Нейману, проводимый для уравне-
уравнения G.24), показывает возможность устойчивого решения при
- если 0<р< 1/2;
нет ограничений, если
Можно отметить, что схема Кранка — Николсона располагается
на границе области безусловно устойчивого режима. Для мно-
многих стационарных задач гидроаэродинамики эффективный путь
состоит в решении эквивалентной нестационарной задачи вплоть
до такого состояния, когда решение больше не изменяется (см.
§ 6.4). Однако нередко в различных частях вычислительной об-
области решение приближается к стационарному состоянию с
существенно различными скоростями; тогда говорят, что урав-
уравнения являются жесткими (см. § 7.4). К сожалению, схема
Кранка — Николсона в этой ситуации часто приводит к осцилли-
осциллирующему решению, которое, будучи в принципе устойчивым,
приближается к стационарному состоянию довольно медленно.
§ 7.2. Неявные методы 299
В этом отношении некоторые трехслойные по времени схемы
оказываются более эффективными, чем схема Кранка — Ни-
колсона.
7.2.3. Обобщенная трехслойная схема
Для уравнения диффузии можно составить обобщенную
трехслойную схему, охватывающую, в частности, и уравнение
G.24). Эта схема имеет вид
а 1A — Р) Lxxi j + pLxxl i \ = U, G.20)
где ДГП = Г/— Г/. Включение в схему дополнительного вре-
временного слоя влечет за собой повышенные требования к па-
памяти, чтобы хранить решение. Однако современная тенденция
сводится к тому, что компьютерная память становится дешевле
и больше по объему. Есть и второй эффект, связанный с необ-
необходимостью выделения дополнительного времени на исполне-
исполнение алгоритма, порядка 10—15%, нужного для обработки до-
дополнительных членов.
Особенно эффективная трехслойная схема получается, если
выбрать 7 = 0.5, р = 1.0. Эта схема имеет ошибку аппроксима-
аппроксимации О (А/2, Але2), является безусловно устойчивой, может ре-
решаться с помощью алгоритма Томаса и способствует затуханию
искусственно вызванных колебаний, обсуждавшихся ранее в
связи с упоминанием о жестких задачах. Мы будем называть
эту схему трехслойной чисто неявной (ТСЧН) и воспользуемся
ею в дальнейшем при обсуждении вопроса о приближенной
факторизации (см. § 8.2 и 8.3). Схема ТСЧН обладает полез-
полезным свойством Л-устойчивости (см. § 7.4).
Свойства некоторых из весьма многочисленных численных
схем для моделирования уравнения диффузии G.1) показаны
в табл. 7.1. Намного больше схем дается в книге (Richtmyer,
Morton, 1967].
7.2.4. Схемы повышенного порядка
Отправной точкой изложения в данном пункте является
дискретизированное уравнение G.25), модифицированное так,
чтобы охватить как конечно-разностные, так и конечно-элемент-
конечно-элементные трехслойные схемы. В результате уравнение G.25) заме-
заменяется на
- о [pL,J7+I + A - Р) Wjf] = 0, G.26)
300 Гл. 7. Одномерное уравнение диффузии
где
Д77+1=77+1-Г/,
Г, , — 27*,
™' / — Ах2
Стоит отметить, что уравнение G.26) по своей структуре по-
подобно уравнению G.13). При применении метода конечных эле-
элементов Мх = {^, j, j}, так что
Мх АГ, = -J- ДГ,_, + у ДГ, +-J-АГ/+1. G.27)
В случае метода конечных разностей Мх = {0, 1, 0}. Параметры
V и р могут быть подобраны так, чтобы обеспечить заданные
уровни точности и/или устойчивости. В п. 7.2.2 различным схе-
схемам соответствовало значение y = 0. Частный вариант выбора
7 = 0, р = 0.5 приводит к методу Кранка — Николсона. Ре-
Результаты как для конечно-элементной, так и для конечно-раз-
конечно-разностной форм метода * Кранка — Николсона приводятся в
табл. 7.3. Вариант выбора у = 0.5, р = 1.0 кратко обсуждается
в п. 7.2.3. В данном пункте параметр у будет рассматриваться
как свободный, но параметр р будет считаться функцией у.
Разложение членов уравнения G.26) в ряд Тейлора относи-
относительно узла (/, п) дает следующее выражение для главного
члена ошибки усечения:
^( ^?) G.28)
где оператор массы записывается в виде
Мх = {6, 1 —26, 6}. G.29)
Это выражение включает в себя как конечно-разностную (б =
= 0), так и конечно-элементную F=1/6) формулировки.
В выражении G.28) для ошибки аппроксимации исключены
все производные по времени, как это было сделано в табл. 7.1.
Рассмотренные ранее схемы (см., например, п. 7.2.3) соот-
соответствовали выбору р = 0.5 + У- Ясно, однако, что при выборе
G.30)
должна быть достижима точность четвертого порядка. Это
обстоятельство в свою очередь дает мотивировку выбора
Mx = {-j2> I», -jj}, так как при таком Мх и при р = 0.5 + V
получается ошибка аппроксимации четвертого порядка.
§ 7.2. Неявные методы 301
Уравнение G.26) последовательно применяется к каждому
узлу, что да^т трехдиагональную систему уравнений вида
А{Гп^\ + B,Tf+l + СМИ = A + 2Y) MJ7 - УМХТПГ1 +
+ (l-?)sL'xxTl, G.31)
где
ЛУ = СУ = A + YN —sp, BJ = (l
Несмотря на то что число операций, требуемое для решения
уравнения G.31), значительно больше, чем для чисто неявной
схемы или схемы Кранка — Николсона, данная схема оказы-
оказывается намного более точной (см. п. 7.2.5).
7.2.5. DIFIM: численные результаты применения неявных схем
В данном пункте проводится сравнение точности схемы по-
повышенного порядка G.31) с точностью неявных схем более
низкого порядка, а также явных схем низкого и высокого по-
порядков, рассмотренных в § 7.1.
Программа DIFIM представляет собой обобщение програм-
программы DIFF, направленное на построение численного решения
уравнения G.1) при граничных, условиях G.18) путем решения
последовательности уравнений G.31) так, чтобы решение про-
продвигалось во времени для всех внутренних узлов. Для решения
уравнения G.31) используются подпрограммы BANFAC и
BANSOL. Если учесть, что Л/, В/ и С/ не зависят от времени,
то обращение к BANFAC необходимо сделать лишь один раз,
на первом шаге по времени. Распечатка программы DIFIM при-
приведена на рис. 7.7. Программа DIFIM может работать по пяти
вариантам схем, приведенным в табл. 7.4 и соответствующим
различным представлениям р как функции у, а также различ-
различным вариантам оператора Мх. Случай 1, когда v —0> соответ-
соответствует схеме Кранка — Николсона G.26). Многие из основных
параметров, используемых в программе DIFIM, совпадают с
теми, которые применялись в программе DIFEX (см. табл. 7.2).
Дополнительные параметры приводятся в табл. 7.5. Типовая
выдача, характеризующая решение при ME = 3 и у = 0, пока-
показана на рис. 7.8.
Программа DIFIM использовалась для сравнения результа-
результатов применения различных методов, перечисленных в табл. 7.4.
Сравнительные данные приводятся в табл. 7.6 и относятся к
точности решения на различных сетках (А* = 0.2, 0.1 и 0.05)
при /=12.0. Эти результаты были получены при а = 0.01 и
1
2 С " /
3 С DIFIM.FOR SOLVES THE DIFFUSION EQUATION USING
4 С VARIOUS IMPLICIT SCHEMES
5 С
6 REAL*8 SUM,AVS,RMS.DSQRT,DMP
7 DIMENSION DUMF5),XD1),TED1),AE,65),DF5)
8 DIMENSION ELXO) ,EMXC) #TOLD1) ,TND1) ,TDD1)
9 С
10 OPENA,FILE»*DIFIM.DAT')
11 OPENF,FILE*'DIFIM.OUTf)
12 READA,1)ME,IPR,JMAX,MAXEX,NMAX,ALPH,S,TMAX,TST,GAM •
13 1 FORMATEI5,E10.3,F5.3,3F5.2)
14 С
15 PI = 3.1415927
16 JMAP = JMAX - 1
17 AJM = JMAP
18 DELX = l./AJM
19 DELT = DELX*DELX*S/ALPH
20 С
21 IF(ME .EQ. 1)WRITEF,4)
22 IF(ME .EQ. 2)VRITEF,5)
23 IF(ME .EQ. 3)WRITEF,6)
24 IF(ME .EQ. 4)VRITEF,7)
25 IF(ME .EQ. 5)WRITEF,8)
26 WRITEF,2)JMAX,MAXEX,NMAX,TMAX,TST,GAM
27 2 FORMAT(f JMAX»\ 15,* MAXEX=\I5,' NMAX=\I5,
28 V TMAX=\F8.2,f TST=\F5.2,g GAM«\F5.2)
29 WRITE (б, 3) S, ALPH,' DELT, DELX
30 3 FORMATCS» \F5.3,f ALPH • ',E10.3,v DELT » 'ЕЮ.З,
31 lf DELX * ',E10.3,//)
32 4 FORMATС DIFFUSION EQUATION: FDM-2ND',//)
33 5 FORMAT(' DIFFUSION EQUATION: FEM-2ND\//)
34 6 FORMAT С DIFFUSION EQUATION: FDM-4TH\//)
35 7 FORHATC DIFFUSION EQUATION: FEM-4TH1,//)
36 8 FORMATS DIFFUSION EQUATION: COMP1,//)
37 С
38 С IMPLICIT PARAMETERS
39 С
40 BET = 0.5 + GAM
41 IF(ME .EQ. 3)BET ¦ BET - 1./12./S
42 IF(ME .EQ. 4)BET « BET + 1./12./S
43 IF(ME .EQ. 1 .OR. ME .EQ. 3)EMXA) = 0.
44 IF(ME .EQ. 2 .OR. ME .EQ. 4)EMXA) = 1./6.
45 IF(ME .EQ. 5)EMXA) = 1./12.
46 EMXB) = 1. -*2.*EMXA)
47 EMXC) = EMX(l)
48 AD « EMXA)*A. +*GAM) - BET*S
49 BD ¦ EMXB)*A. + GAM) + 2.*BET*S
50 CD = AD
51 ELX(l) = 1.
52 ELXB) = -2.
53 ELXO) = 1.
54 JMAF = JMAX - 2
55 С
56 С OBTAIN INITIAL CONDITIONS FROM THE EXACT SOLUTION
57 С
Рис. 7.7. Распечатка программы DIFIM.
58
59
60
61
€2
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
С
С
С
С
С
С
С
С
С
с
с
с
с
с
с
с
с
\
9
10
11
12
13
14
15
16
17
Т ¦ TST - 2.*DELT
00 10 I ¦ 1,2
Т = Т + DELT
\
CALL EXTRA(JHAX,MAXEX,DELX,PI,ALPH,T,TE>
т
DO \f J « 2,JMAP
IF(t .EQ. l)TOL(J) « TE(J)/100.
IF<H .EQ. 2)TN(J) « TE(J)/100.
CONTINUE
CONTINUE
SET BOUNDARY CONDITIONS
TOL(l) = 1.
TOL(JMAX) ¦ 1.
TNA) - 1.
TN(JHAX) * 1.
TDA) = 1OO.*TNA)
TD(JMAX) * 1OO.*TN(JMAX)
N « 0
EACH TIME STEP STARTS AT STATEMENT 11
N = H + 1
SET UP THE TRIDIAGONAL SYSTEM OF EQUATIONS
DO 14 J » 2,JMAP
JH - J - 1
IF(N .GT. DGOTO 12
AA,JM) * 0.
AB,JH) - AD
ACfJM) * BD
AD,JM) * CD
AE,JM) - 0.
D(JM) * 0.
DO 13 К « 1,3
KJ « J - 2 + К
D(JM) = D(JM) + EMX(K)*(A. + 2.*GAM)*TN(KJ) - GAM*TOL(KJ))
D(JM) = D(JM) -1- S*ELX(K)*A.-BET)*TN(K4)
CONTINUE
CONTINUE
D(l) * D(l) - AB,1)*TNA)
D(JMAF) = D(JMAF) - AD,JHAF)*TN(JMAX)
SOLVE BANDED SYSTEM OF EQUATIONS
IF(N .EQ. UCALL BANFAC(A,JMAF,1)
CALL BANSOL(D,DUMrA,JMAFfl)
DO 15 J = 2,JMAP
TOL(J) = TN(J)
TN(J) = DUM(J-l)
DO 16 J « 2,JMAP
TD(J) « 1OO.*TN(J)
T ¦ T + DELT
IF(IPR .EQ. l)WRITEFf17)T,(TD(J),J=lfJMAX)
FORMATC T» f.F5.2 ' TD«M1F6.2)
Рис. 7.7 (продолжение).
304 Гл. 7. Одномерное уравнение диффузии
119 С
120 С IF MAXIMUM TIME OR MAXIMUM NUMBER OF TIME-STEPS EXCEED»
121 С EXIT FROM LOOP
122 С
123 IF(N .GE. NMAX)GOTO 18
124 IF(T .LT. TMAX)GOTO 11
125 С
126 С OBTAIN EXACT SOLUTION AND COMPARE
127 (C
128 18 CALL EXTRA(JMAX,MAXEX,DELX,PI,ALPfl,T,TE)
129 С
130 SUM * 0.
131 DO 19 J « 1,JMAX
132 DMP * TE(J) - TD(J)
133 SUM * SUM -I- DMP*DMP
134 19 CONTINUE
135 IF(IPR .NE. 1)VRITEF,17)T,(TD(J),J=1,JMAX)
136 VRITEF,20)T,(TE(J),J»l,JMAX)
137 20 FORMAT!/,f T» \F5.2,f ТЕ»1,11F6.2,//)
138 С
139 С RMS IS THE RMS ERROR
140 С
141 AYS » SUM/A. + AJM)
142 RMS - OSQRT(AVS)
143 VRITEF,21)RMS
144 21 FORMATS RMS DIF - \D11.4,//)
145 STOP
14$ END
Рис. 7.7. (окончание). >ЩЦ
начальном условии, соответствующем точному решению C.42)
при t = 4.5. Граничные условия Дирихле были наложены на Т
при х = 0 и 1.0. Приближенная скорость сходимости была полу-
получена такой, как в табл. 7.3.
DIFFUSION EQUATION: FEM-4TH
JMAX* 11 МАХЕХ- 10 NMAX- 500 ТМАХ» 12.00 TST- 4.50 GAM* .00
S- 1.000 ALPH * Л00Е-01 DELT - .100E+01 DELX * .100E+00
T* 12.50 TD-100.00 88.55 78.22 70.02 64.76 62.94 64.76 70.02 78.22 88.55100.00
?= 12.50 TE=100.00 88.54 78.21 70.00 64.74 62.92 64.74 70.00 78.21 88.54100.00
RMS DIF * .1522D-01
Рис. 7.8. Типичная выдача результатов по программе DIFIM.
Все результаты, приводимые в табл. 7.6, были получены при
s = 1.0. Методы, номинально имеющие второй порядок (слу-
(случаи 1 и 2), обнаруживают приблизительно второй порядок схо-
§ 7.2. Неявные методы
305
Таблица 7.4. Различные варианты, предусмотренные в программе DIFIM
Случай
(ME)
1
2
3
4
5
Метод
Конечно-разностный
порядка
Конечно-элементный
порядка
Конечно-р азностный
порядка
Конечно-элементный
порядка
Комбинированный
2-го
2-го
4-го
4-го
@, 1,
A/6,
@, 1,
A/6,
A/12
0)
2/3,
0)
2/3,
5/6,
1/6)
1/6) „
1/12)
Р
0.5+ Y
0.5+ Y
0.5 + y- l/A2s)
0.5 +у + 1/A25)
0.5+ Y
Таблица 7.5. Дополнительные параметры, используемые в программе DIFIM
Параметр
Описание
ME
GAM
BET
ЕМХ
ELX
AD, BD, CD
Параметр, определяющий выбор метода (см. табл. 7.4)
Параметр у, используемый в уравнении G.26)
Параметр р, используемый в уравнении G.26) и табл. 7.4
Массовый оператор Мх
Разностный оператор Lxx
Коэффициенты Ah Bj и С/ в уравнении G.31)
димости, тогда как методы, номинально имеющие четвертый
порядок (случаи 3, 4 и 5), обнаруживают сходимость четвер-
четвертого порядка. Это имеет место как при у = О, так и при у = 1.
Вообще говоря, увеличение у снижает уровень точности при
сохранении примерно той же скорости сходимости. При приме-
применении грубых сеток точность, обеспечиваемая схемами повы-
повышенного порядка (случаи 3—5), ненамного превышают ту, ко-
которая достигается со схемами более низкого порядка (случаи 1
и 2), в особенности при больших значениях у. Однако с приме-
применением мелкой сетки разница в точности оказывается сущест-
существенной. В случаях 3—5 сравнимая точность обнаруживается на
грубых и мелких сетках при y = 0. Однако при 7 = 1 случай 1
дает более высокую точность, чем случаи 3 и 5, особенно на
грубой сетке.
Сравнение некоторых явных и неявных схем приводится
в табл. 7.7 для случаев у = 0 и у = 1.0 при 5 = 0.41. Эти ре-
результаты были получены при t = 9.00 с начальным заданием Т
20 К Флетчер, т. I
306
Гл. 7. Одномерное уравнение диффузии
Таблица 7.6. Точность неявных схем (см. табл. 7.4) при решении
уравнения G.1)
Случай
(ME)
1
2
3
4
5
1
2
3
4
5
Y
0.0
0.0
0.0
0.0
0.0
1.0
1.0
1.0
1.0
1.0
Среднеквадратичная ошибка RMS
(Дх=0.2)
0.3895
0.8938
0.2393
0.2393
0.2393
2.090
1.760
2.367
1.395
1.867
(Лх=0.1)
0.1466
0.1787
0.01526
0.01522
0.01525
0.03003
0.2475
0.1246
0.09269
0.1087
(Д*=0.05)
0.03993
0.04185
0.00Ю53
0.000897
0.001034
0.03245
0.04668
0.008129
0.005912
0.007097
Приближен-
Приближенная
скорость
сходимости
г
1.9
2.1
3.9
4.1
3.9
3.0*
2.4
3.9
4.0
3.9
На основе отношения
при t = 2.00. На грубой сетке различные схемы обнаруживают
сравнимую точность. Однако на мелкой сетке неявные схемы
дают значительно большую точность.
Таблица 7.7. Сравнение
Метод
Конечно-разностный
2-го порядка, неявный
Конечно-разностный
4-го порядка, неявный
ВВЦП, явный
Конечно-разностный
2-го порядка, неявный
Конечно-разностный
4-го порядка, неявный
Конечно-разностный
4-го порядка, явный
Y
0.0
0.0
0.0
1.0
1.0
1.0
неявных и
явных схем
при s = 0.41
Среднеквадратичная ошибка RMS
(Л,-0.2)
0.7502
0.03718
1.2440
0.7625
0.6482
0.7347
(Лх-0.1)
0.2004
0.002407
0.30230
0.1681
0.03155
0.02290
(Да:=0.05)
0.05127
0.000206
0.07550
0.04938
0.00192
0.00140
Прибли-
Приближенная
скорость
сходи-
сходимости
г
2.0
3.5
2.0
1.8
4.0
4.0
Тот, вообще говоря, высокий уровень точности, который до-
достигается на мелких сетках, в известной степени отражает
гладкость точного решения и относительную простоту опреде-
§ 7.3. Граничные и начальные условия 307
ляющего уравнения. Как отмечалось в § 7.1, нельзя ожидать
столь же высокого уровня точности при рассмотрении задач
гидроаэродинамики. Однако целенаправленный подбор коэффи-
коэффициентов дискретизированного уравнения типа G.26), служащий
для уменьшения ошибки усечения, является вполне оправдан-
оправданным при условии достаточной устойчивости алгоритма. В об*
щем случае характеристики устойчивости неявных схем, улуч-
улучшенные по сравнению с характеристиками явных схем, позво-
позволяют проявить большую гибкость при выборе свободных
параметров, т. е. у и р в уравнении G.26).
§ 7.3. Граничные и начальные условия
В § 7.1 и 7.2 использовались граничные условия Дирикле,
и там, где начальные условия требовали задания данных на
двух слоях, эти данные обеспечивались за счет точного реше-
решения. В результате единственный источник ошибок в решениях
был связан с дискретизацией производных в определяющем
уравнении G.1). В данном параграфе будут рассматриваться
такие решения, в которых добавочные ошибки вносятся в про-
процессе реализации граничных и начальных условий.
7.3.1. Граничные условия Неймана
Разработанные нами пока что алгоритмы, как, например,
G.6), пригодны для расчета внутренних узлов. Чтобы восполь-
Л+1 о
X-=G х=О
Явный вариант Неявный вариант
Рнс. 7.9. Варианты реализации граничных условий Неймана.
зоваться этими формулами для граничных значений, таких, как
Г?4 на рис. 7.9, потребовалась бы информация о решении за
пределами вычислительной области. Поэтому нужно разработать
специальные формулы для использования на границах. Приме-
Применительно к граничным условиям Дирихле G.2) трудностей не
20*
308 Гл. 7. Одномерное уравнение диффузии
возникает. Там, где требуется значение Г"» делается подстановка
Тпх = Ъп на основании G.2).
Граничные условия Неймана в форме G.3) ставят перед ис-
исследователем белее серьезную проблему. Величина [dT/dx]ir
входящая в формулу G.3), может быть смоделирована посред-
посредством одностороннего конечно-разностного выражения с ис-
использованием информации лишь изнутри области. Результат
имеет вид
( + 1Г1)/ сп+\ G.32)
В типичном варианте приложения схема ВВЦП G.6) будет ис-
использована для определения значений Т?+] во всех внутренних
узлах, / = 2, ..., / — 1. На границе х = 0 формула G.32) дает
ГГ+1 = Г?+1~сп+1Ах. G.33)
Здесь важная проблема состоит в том, что соотношение G.33)
дает ошибку аппроксимации О (Ах), тогда как схема ВВЦП
имеет ошибку аппроксимации О (Ах2). Учитывая, что уравнение
диффузии является параболическим уравнением (см. § 2.3), по-
пониженная точность решения на границе окажет влияние на точ-
точность решения внутри области во все позднейшие моменты
времени.
На основании изложенного желательно представить условие
Неймана G.3) посредством такого алгебраического выражения,
которое имеет такую же ошибку аппроксимации, как и выраже-
выражение, используемое для внутренних узлов. Этого можно добиться
следующим образом. Формула G.3) моделируется соотноше-
соотношением
(Г? - Го )/B Ах) = сп. m G.34)
Чтобы добиться ошибки аппроксимации порядка О (Ах2), фор-
формула G.34) составлена со включением фиктивного узла @, я),
лежащего за пределами вычислительной области (рис. 7.9).
Однако если вычислительную область условно расширить так,
чтобы включить в нее указанную точку, то соотношение G.34)
может использоваться вместе с уравнением для точек внутрен-
внутренней области, таким, как G.5), записанным для точки A, п),
чтобы исключить из обоих уравнений Г?. Результат имеет вид
ТЧ+Х = - 25 Ахсп + A - 2s) Г? + 2s7t, G.35)
причем во всех точках области ошибка усечения имеет порядок
О (At, Ax2). Если во внутренних точках используется неявная
§ 7.3. Граничные и начальные условия 309
схема, например G.19), то соотношение G.34) записывается
для временного слоя п + 1 и в сочетании с уравнением G.20)
дает уравнение (см. рис. 7.9)
A + 2s) ГГ1 - 2sf2 + 1 = Тх - 2skxcn+\ G.36>
которое может рассматриваться как первое уравнение трехдиа-
гональной системы, эквивалентной системе G.21). Эта система
может решаться с помощью алгоритма Томаса. Построение, ис-
использованное для получения уравнений G.35) и G.36), пригод-
пригодно и в том случае, когда граничные условия Неймана ставятся
при х= 1 (см. рис. 7.1).
Можно ожидать, что использование различных формул на
границах приведет к изменению свойств, касающихся устойчи-
устойчивости. Строго говоря, более или менее прямолинейный анализ
устойчивости по Нейману (§ 4.3) применим только к уравне-
уравнениям для внутренних точек; тем не менее, согласно предполо-
предположению [Тгарр, Ramshaw, 1976], анализ по Нейману может
быть эвристически распространен и на границы. Альтернатив-
Альтернативный вариант определения устойчивости полной системы уравне-
уравнений, включая соотношения на границах, состоит в использова-
использовании матричного метода.
В применении к уравнению диффузии обсуждается возмож-
возможность применения матричного метода к схеме Кранка — Никол-
сона с различными граничными условиями [Mitchell, Griffiths,
1980]. Как было показано в этой работе, схема Кранка — Ни-
колсона с граничными условиями Дирихле является безусловно
устойчивой. С граничными условиями Неймана схема Кранка —
Николсона устойчива, однако одно из собственных значений
матрицы усиления равно единице, что дает осциллирующее ре-
решение. Для смешанного граничного условия общего вида необ-
необходимо вводить дополнительное ограничение на параметры гра-
граничного условия, чтобы обеспечить устойчивость.
7.3.2. Точность реализации граничного условия Неймана
Реализация граничного условия Неймана (п. 7.3.1), приме-
применяемого к уравнению диффузии, будет описана применительно
к некоторым из схем, упоминавшимся в § 7.1 и 7.2, причем бу-
будет указано, как влияет эта реализация на суммарную точность.
Решения уравнения диффузии
dj пд*т
а°
310
Гл. 7. Одномерное уравнение диффузии
будут строиться здесь в пространственном интервале 0.1
^ х ^ 1.0 при граничных условиях
U = с = 2 - 2я sin @.05я) ехр [— а (~J/] при х = 0.1,
Г = 2 при х =1.0.
Начальные условия выбраны в форме
T = Bx + 4cos@.5nx) при t = 0. G.39)
Данная задача имеет точное решение
Т = 2х + 4 cos @.5я*) ехр [- а (-?-J /], G.40)
которое будет использовано для оценки точности численного
решения.
Численные решения вышеописанной задачи были получены
•с помощью модифицированной формы программы DIFEX
(рис. 7.4). Среднеквадратичные ошибки для сеток различного
размера приводятся в табл. 7.8. Эти ошибки были рассчитаны
при t = 9.00. Чтобы избежать ошибок, связанных с реализацией
начальных условий, такие условия при t = 0.80 были сформули-
сформулированы при помощи точного решения G.40). Все решения, де-
демонстрируемые в табл. 7.8, были получены при значении s =
= 0.30.
Таблица 7.8. Явные схемы для внутренних точек с граничным
условием Неймана при дг = 0.1
Метод для
внутренних
точек
ВВЦП + G.32)
ВВЦП + G.34)
Трехслойный
4-го порядка
Y = 0+G.34)
Фор-
Формула
для
гра-
нич-
ничного
усло-
условия
G.32)
G.34)
G.34)
G.34)
0.1958
0.1753
0.4244
0.8684
Среднеквадратичная ошибка
=0.225
X
X
X
кг2
кг*
кг*
Дх=0.1125
0.07978
0.4235 X
0.9142 X
0.2034 X
10
10
10
RMS
Ах=0.05625
0.03539
0.1064 X
0.2144 X
0.4867 X
10
ю-3
Приб-
лижен-
лиженная
ско-
скорость
сходи-
сходимости
г
1.2
2.0
2.1
2.1
Сочетание реализации граничного условия в форме G.32)
со схемой ВВЦП дает, как видно из таблицы, сравнительно не-
неточное решение, точность которого возрастает с измельчением
сетки примерно по линейному закону. Таким образом, первый
§ 7.3. Граничные и начальные условия
311
порядок точности, связанный с применением формулы G.32),
превалирует над вторым порядком точности по пространству,,
свойственным схеме ВВЦП. Это положение подтверждается ха-
характером распределения ошибки для сетки с Ал; = 0.225, пока-
показанным в табл. 7.9. Точность решения является наименьшей при
л; = 0.1, т. е. там, где задается граничное условие Неймана, и
становится все более точным по мере приближения к точке
х= 1.00.
Таблица 7.9. Распределение ошибки для случая А* = 0.225
в табл. 7.8
Метод для
внутренних
точек
ВВЦП +
1 G ЧО\
ВВЦП +
+ G.34)
Трехслой-
Трехслойный 4-го
порядка,
+ G.34)
X
0.1
—0.3799
0.332 ХЮ~3
0.832 XI 0~2
0.325
-0.1989
—0.221 ХЮ~2
0.421 ХЮ~2
0.550
-0.08366
-0.272 XI 0~2
0.166ХЮ
0.775
-0.02610
-0.173 ХЮ"
0.572 ХЮ~3
1.000
0.000
0.000
0.000
Формула G.34), аппроксимирующая первую производную с
точностью второго порядка, может сочетаться со схемой ВВЦП
с целью получения алгоритма G.35), дающего решение при
# = 0.1. Среднеквадратичные ошибки для этого сочетания при-
приводятся в табл. 7.8. Очевидно, что построенные таким образом
решения более точны, чем при использовании аппроксимации
первого порядка G.32) для граничного условия Неймана. Со-
Соотношение G.34) дает ошибку аппроксимации второго порядка,
такую же, как и схема ВВЦП. Из табл. 7.8 видно, что рассмат-
рассматриваемое сочетание приводит к сходимости второго порядка.
Анализ распределения ошибок для этого сочетания, приводимо-
приводимого в табл. 7.9, показывает, что ошибка при х = 0.1, где задает-
задается граничное условие Неймана, меньше ошибки в любой дру-
другой точке.
Формула G.34), т. е. аппроксимация второго порядка для
граничного условия, может сочетаться с внутренней схемой
G.16) четвертого порядка. Это легче всего сделать за счет ис-
использования G.36) для явного выражения величины Т"
312 Гл. 7. Одномерное уравнение диффузии
и последующего применения формулы G.16), записанной для
узла 1. Среднеквадратичные ошибки для различных вариантов
измельчения сетки приводятся в табл. 7.8 с использованием двух
значений у. В общем случае рост y уменьшает точность. Второй
порядок ошибки аппроксимации, соответствующий формуле
представления граничного условия, достаточен для того, чтобы
ввести до второго порядка суммарную скорость сходимости.
Фактически точность, соответствующая обоим значениям у,
меньше точности схемы ВВЦП. Как показывает приводимое
в табл. 7.9 распределение ошибки, создаваемой трехслойной
схемой четвертого порядка, ошибка оказывается значительно
больше вблизи точки лс = 0.1, где задается граничное условие
с производной, однако вблизи точки х = 1.00 она меньше ошиб-
ошибки, создаваемой схемой ВВЦП.
В принципе можно ввести для dT/dx представление более
высокого порядка, чем G.34), связанное с информацией о доба-
добавочных узловых значениях Тп и т. д. Однако это повлекло бы
за собой не только усложнение алгоритма, но и необходимость
установления ограничений на величину s, обусловленных устой-
устойчивостью. Строго говоря, предпринимать такое исследование
стоило бы с помощью матричного метода (§ 4.3). Нередко вве-
введение повышенного порядка представления граничного условия
уменьшает рабочий диапазон s, связанный с действием внутрен-
внутреннего алгоритма.
Формулы G.32) и G.34), представляющие граничные усло-
условия с первым или вторым порядком точности, применялись так-
также и в сочетании с некоторыми неявными схемами, описанными
в § 7.2; ошибки соответствующих решений приводятся
в табл. 7.10. Среднеквадратичные ошибки рассчитывались при
t = 15.00. Точное решение G.40) было использовано для зада-
задания начального решения при / = 5.20. Приводимые в табл. 7.10
значения были получены при выборе s = 1.0. Два конечно-раз-
конечно-разностных метода второго и четвертого порядков, охваченные
табл. 7.10, соответствуют в табл. 7.4 значениям параметра ME,
равным 1 и 3.
Сочетание формулы первого порядка G.32) для представле-
представления граничного условия с конечно-разностной схемой второго
порядка дает суммарную скорость сходимости первого порядка
и точность решения, сравнимую с той, которую создает соответ-
соответствующая явная схема (табл. 7.8). Эта сравнимая точность до-
достигается вопреки повышенным значениям s, используемым
в неявных схемах. Тем самым обеспечивается косвенное под-
подтверждение того, что формула первого порядка для граничного
условия играет доминирующую роль в оценке среднеквадратич-
среднеквадратичной ошибки.
§ 7.3. Граничные и начальные условия
31$
Таблица 7.10. Неявные схемы для внутренних точек с граничным
условием Неймана при * = 0.1
Метод для
внутренних точек
Конечно-разност-
Конечно-разностный 2-го по-
порядка (МЕ = 1)
То же (МЕ = 1)
Конечно-разност-
Конечно-разностный 4-го по-
порядка, y = 0
То же, у = 1.0
Формула
для гра-
граничного
условия
G.32)
G.34)
G.34)
G.34)
Среднеквадратичная ошибка RMS
Дх = 0.225
0.1448
0.01478
0.00912
0.01478
Ах 0.1125
0.07138
0.00363
0.00223
0.00539
Дх=0,05625
0.03344
0.00087
0.00053
0.00141
Прибли-
Приближенная
скорость
сходи-
сходимости
г
1.1
2.1
2.1
1.9
Значительное уменьшение ошибки достигается за счет ис-
использования формулы второго порядка G.34) для представле-
представления граничного условия, в особенности на наиболее мелкой
сетке. Точность не столь велика, как та, которую дает сочетание
со схемой ВВЦП, хотя скорость сходимости имеет второй по-
порядок. Переход к схеме четвертого порядка для внутренних
точек, FDM-4TH, дает несколько более точное решение, но со
скоростью сходимости лишь второго порядка. При 7=1-0 точ-
точность оказывается меньше, чем при у = 0, что согласуется со
свойствами явной схемы.
Для получения скорости сходимости повышенного порядка
следует ввести более точное конечно-разностное представление
граничного условия Неймана при лс = 0.10. Такой процесс дол-
должен привести к необходимости совместного рассмотрения четы-
четырех или пяти узловых точек, а это повлечет за собой потреб-
потребность в модификации алгоритма Томаса для решения дискрети-
зированных уравнений с соответствующей матрицей.
7.3.3. Начальные условия
Начальные условия, представленные в форме G.4), не вызы-
вызывают каких-либо трудностей в случае двухслойной схемы, по-
подобной G.6) или G.20), если не считать границы, на которой
ставится граничное условие Дирихле. Может случиться так, что,
скажем, на границе х = 0 значение f@,0), определяемое на-
начальным условием, отличается от значения f @, 0), определяе-
определяемого граничным условием. Предпочтительная стратегия сводится^
314 Гл. 7. Одномерное уравнение диффузии
к тому, чтобы осреднить два значения Г@, 0) на первом
временном слое, п = 0, но вновь вернуться к надлежащему гра-
граничному условию в последующие моменты времени. В табл. 3.7
эта стратегия сравнивается с альтернативным путем, состоящим
в задании Г@, 0) на первом временном слое с помощью на-
начальных условий. Для данного конкретного примера видно, что
стратегия осреднения приводит к более точному решению.
Трехслойные схемы, подобные G.25), требуют задания ин-
информации на двух слоях; поэтому^ на начальной стадии интег-
интегрирования они нуждаются в замене. Роль такой замены долж-
должна сыграть двухслойная схема, достигающая той же или более
высокой точности. Следовательно, подходящей была бы трех-
трехслойная схема второго порядка, подобная схеме Кранка — Ни-
колсона. В качестве альтернативного варианта можно восполь-
воспользоваться схемой первого порядка по времени типа ВВЦП при
условии, что второй слой начальных данных рассчитывается на
мелкой сетке, тем самым компенсируя первый порядок точно-
точности. Для этой цели может быть полезной экстраполяция по Ри-
Ричардсону (п. 4.4.1).
§ 7.4. Метод прямых
Алгоритмы, разработанные в § 7.1, 7.2, при дискретизации
уравнения G.1) вводят дискретные формулы одновременно как
для производной по времени, так и для пространственной про-
производной. Это нередко позволяет добиться исключения членов,
определяющих соответствующие ошибки аппроксимации, повы-
повышая за счет этого порядок точности.
Однако альтернативный подход состоит в том, чтобы про-
пространственный член подвергнуть дискретизации первым, пре-
превращая, таким образом, дифференциальное уравнение в част-
частных производных в систему обыкновенных дифференциальных
уравнений для узловых значений. Если в уравнении G.1) зави-
зависимую переменную Т заменить на и, то в результате вышеопи-
вышеописанных действий получим
duf
uf a(u^^2ut + u/+l)
dt A*2 ~U)
где для дискретизации d2u/dx2 в уравнении G.1) было исполь-
использовано трехточечное конечно-разностное выражение второго
порядка. Процесс перехода от уравнения G.1) к уравнениям
G.41) является примером применения метода прямых [Holt,
1984], или полудискретизации.
Привлекательная черта метода прямых состоит в том, что
для решения полудискретной формы исходного дифференциаль-
дифференциального уравнения в частных производных можно воспользоваться
§ 7.4. Метод прямых 315
различными методами решения систем обыкновенных дифферен-
дифференциальных уравнений [Gear, 1971; Lambert, 1973; Seward et. al.r
1984]. Следует, однако, подчеркнуть, что построение полудис-
полудискретной формы вносит ошибку, связанную с пространственной
дискретизацией. В результате этого «наилучшим» вариантом
при выборе метода решения получаемой системы оказывается
обычно алгоритм более низкого порядка, чем если бы это была
система обыкновенных дифференциальных уравнений, не свя-
связанная с аппроксимациями. При решении задач с начальными
данными, описываемых обыкновенными дифференциальными
уравнениями, наиболее эффективными обычно оказываются
либо линейные многошаговые методы, либо методы Рунге —
Кутты.
Последовательное применение соотношения G.41) ко всем
внутренним узлам приводит к системе уравнений, записывае-
записываемых в виде
Au. G.42)
Если бы пространственный член уравнения G.1) был нелиней-
нелинейным, то уравнение G.42) можно было бы записать в более об-
общей форме
d/dt F. G.43)
Скалярные эквиваленты векторных уравнений G.42) и G.43)
имеют вид
du/dt = Лы, G.44)
du/dt = f. G.45)
Применяя к уравнению G.45) линейный многошаговый метод
общего вида, можно написать
т т
Z«i»'+l = A/ZPif+l, G-46)
где ищется решение «n+w. Если pw = 0, это решение получается
в явной форме; если же рт Ф О, то G.46) представляет собой
неявный алгоритм для определения ип+т.
Простейший случай, когда т= 1, приводит к соотношению
щип+1 + aou* = М (РоГ + Pif+1)> G.47>
которое охватывает, в частности, схему Эйлера (ai =—ao = 1,
Ро=1, pi=0),
un+l-un = Mfn. G.48)
Последняя формула, если ее применить к линейной системе
G.42) в форме G.41), совпадает со схемой ВВЦП, соответст-
316 Гл. 7. Одномерное уравнение диффузии
вующей уравнению G.5). Соотношение G.47) охватывает так-
также и трапецоидальную схему
un+i _ип = ы (o.5f + 0.5Г+1). G.49)
В применении к G.41) трапецоидальная схема совпадает со
схемой Кранка — Николсона в форме G.22).
Двухшаговый вариант схемы G.46) имеет вид
2 + a{un+l + аои" = Д* (pof + fcf+I + Р2Г2). G.50)
При применении к G.41) соотношения G.50) при р2 = 0 схема
G.50) позволяет получить явное решение и!}*2 и совпадает со
схемой G.12). Если р2=?*=0, то схема G.50) в применении к
G.41) охватывает как схему G.25), так и схему G.26). Напри-
Например, схема ТСЧН (п. 7.2.3) соответствует выбору <х2 = 1.5,
ai = —2.0, ao = 0.5, |Jo = Pi = 0, p2 = 1.0. Фактически все схе-
схемы, разработанные в § 7.1 и 7.2, могут рассматриваться как
принадлежащие классу линейных многошаговых методов.
При решении обыкновенных дифференциальных уравнений
используют линейные многошаговые методы более высокого по-
порядка (т. е. включающие большее число шагов), и притом в
варианте предиктор — корректор. В этом случае явная схема
обеспечивает предиктор, а неявная схема — соответствующий
корректор [Gear, 1971]. Однако если стратегия высокого по-
порядка применяется к системе уравнений, полученных в резуль-
результате полудискретизации дифференциального уравнения в част-
частных производных, например к системе G.41), то для хранения
информации о векторах nn+l и Fn+l необходим большой объем
памяти. Кроме того, использование схемы высокого порядка
для маршевого продвижения по времени было бы неэффектив-
неэффективным, так как если точное решение не является очень гладким,
то преобладающее влияние на ошибки решения будет, вероят-
вероятно, оказывать дискретизация низкого порядка пространствен-
пространственных членов.
Необходимость избежать хранения в памяти большого числа
решений, соответствующих предшествующим шагам по времени,
побуждает воспользоваться одношаговыми методами решения
полудискретных систем, такими, как методы Рунге — Кутты.
В применении к уравнению G.45) схема Рунге —Кутты общего
вида, содержащая R этапов, может быть записана в форме
? ? crfr, G.51a)
§ 7.4. Метод прямых 317
где
r = f(t + Шп y + MZ brsfs\ r = 1, 2. ...,/?, G.51b)
S=*l /
ar=Zbrs, r=l, 2, ...,/?. G.51c)
Формулы G.51) охватывают неявные схемы Рунге—Кутты,
неэкономичные в вычислительном плане, так как уравнение
G.51Ь) является нелинейным и должно решаться с примене-
применением итераций для каждого из значений fr и на каждом шаге
ло времени. Поэтому больший интерес проявляется к явным
схемам Рунге —Кутты, в которых верхние пределы суммиро-
суммирования в формулах G.51Ь) и G.51с) заменяются на г—1. Так,
например, схему Эйлера G.48) можно интерпретировать в ка-
качестве одноэтапной (?=1) явной схемы Рунге — Кутты при
С\= 1, &п = 0, ai = 0.
Существует бесконечное число двухэтапных явных схем
Рунге — Кутты второго порядка. Типичной схемой такого рода
является улучшенная схема Эйлера
Существуют и многочисленные трехэтапные явные схемы
Рунге — Кутты "третьего порядка [Lambert, 1973]. Нижесле-
Нижеследующая четырехэтапная и четырехшаговая схема Рунге —
Кутты четвертого порядка получила широкое распространение
при решении задач с начальными значениями, определяемых
обыкновенными дифференциальными уравнениями
^ ), G.53)
где
ит = ип + 0.5 Aff\ Г = / 0*+1/2, tf),
и" = ип + 0.5 A/f, Г = f (tn+m, tT)9
а— = ип + Д/Г, f" = f (tn, О-
Очевидно, что схемы Рунге — Кутты повышенного порядка тре-
требуют большего числа оценок для f. При решении таких полу-
полудискретных систем, как G.43), серия повторных оценок всех
членов, связанных с пространственной дискретизацией, зачас-
зачастую играет определяющую роль в подсчете суммарного време-
времени исполнения.
318 Гл. 7. Одномерное уравнение диффузии
Если скалярное уравнение G.44) рассматривается вместе
с начальным условием и(О)=ио, то соответствующее точное
решение имеет форму
u(t) = uoe" = uss. G.54>
Чтобы физическое решение соответствовало устойчивому про-
процессу в интервале 0 ^ / ^ оо, необходимо, чтобы Я ^ 0. Абсо-
Абсолютная устойчивость линейного многошагового метода G.46)
анализируется путем применения указанной схемы к уравне-
уравнению G.44) с последующим формированием полинома устой-
устойчивости
т
Е^-ЛД/рОг^О. G.55)
При заданном ЯД/ абсолютная устойчивость достигается [Lam-
[Lambert, 1973] тогда, когда все корни rs полинома G.55) удовлет-
удовлетворяют условию
|г,|<1. G.56)
Это условие в принципе эквивалентно ограничению, выполне-
выполнение которого требовалось для устойчивости решения дискрети-
зированного дифференциального уравнения в частных произ-
производных при применении анализа устойчивости по Нейману
(§4.3).
В случае схемы Эйлера абсолютная устойчивость дости-
достигается, если —2 г^ ЯД/ ^ 0. Поскольку Я < 0, это соответствует
условию Д/<2/|2|. Для трапецоидальной схемы абсолютная
устойчивость связана с условием ЯД/ < 0; следовательно, тра-
пецоидальная схема устойчива при любом выборе Д/.
Критерий абсолютной устойчивости, эквивалентный G.56),
описан в книге [Lambert, 1973] и приводит к ограничению
—2 ^ ЯД/ <; 0, относящемуся как к одноэтапной схеме Эйле-
Эйлера, так и к явной двухэтапной схеме Рунге—Кутты G.52).
Однако четырехэтапная явная схема Рунге—Кутты G.53)
имеет слегка расширенный интервал устойчивости —2.78 ^
^ ЯД/ < 0.
При применении метода прямых мы встречаемся с система-
системами обыкновенных дифференциальных уравнений. Следователь-
Следовательно, уместно проверить абсолютную устойчивость уравнений в
форме G.42). Как и прежде, можно получить полином устой-
устойчивости G.55), если вместо Я вводить Я* — собственные значе-
значения матрицы А. В общем случае величины Я& комплексные.
Однако чтобы задача имела физически устойчивое решение,
необходимо, чтобы вещественная часть Ял, т. е. ИеЯь, была по-
положительной.
§ 7.4. Метод прямых 319
Например, применение схемы Эйлера G.48) к уравнению
G.41) дает следующий критерий абсолютной устойчивости:
G.57)
Для системы из М уравнений, соответствующей представ-
представлению G.41), матрица А получается трехдиагональной и ее
собственные значения определяются формулами (9.48), т. е.
В результате наиболее строгое ограничение на величину Д/, вы-
вытекающее из условия G.56), имеет форму
с\ ^- 4а Д/ * / -- 0.5а /— Гг\\
—2 < jp~ или bd < -др-. G.59)
Таким образом, здесь получено то же самое ограничение
на величину Д?, обусловленное устойчивостью, как и для схемы
ВВЦП G.5). Этого и следовало ожидать, так как метод Эйле-
Эйлера с шагами по времени в применении к уравнениям G.41) со-
совпадает со схемой ВВЦП. Применение к G.41) трапецоидаль-
ной схемы G.49) приводит к ограничению Re^-Д^^О. Но так
как в силу G.58) Reta ^ 0, то ограничение на At отсутствует.
Трапецоидальная схема, примененная к G.41), совпадает со
схемой Кранка — Николсона G.22). Как можно предположить
на основании этих примеров, абсолютная устойчивость алго-
алгоритма решения системы обыкновенных дифференциальных
уравнений эквивалентна устойчивости алгоритма решения род-
родственной задачи о решении дискретизированного дифферен-
дифференциального уравнения в частных производных (§ 4.3).
Если система, полученная при помощи метода прямых, яв-
является нелинейной, например система G.43), то определение
устойчивости алгоритма зависит от собственных значений яко-
якобиана <9F/<3U. Однако сами собственные значения зависят от
решения и могут нуждаться в корректировке в процессе по-
построения решения.
Точное решение системы уравнений G.42), образуемой из
{7.41), может быть записано в виде
U=S «*A4 + USS, G.60)
где собственные значения Kk определяются формулами G.58),
а величины е* — соответствующие собственные векторы. Коэф-
Коэффициенты ak определяются начальными условиями Uo(#/). Как
ясно из формул G.58), диапазон изменения собственных значений
320
Гл. 7. Одномерное уравнение диффузии
довольно велик, особенно на мелкой сетке. Это наводит на мысль
о том, что вклады в решение различных собственных векторов,
отраженные в формуле G.60), будут затухать с различными ско-
скоростями.
Если для решения системы G.42) используется явная схе-
схема, то ограничение на величину шага по времени будет опреде-
определяться значением |Reta|max. Однако время, в течение которого
нужно проводить интегрирование, будет определяться значе-
значением |Reta|min. Отношение |Re^|max/|Re^|min называется ко-
коэффициентом жесткости. Если этот коэффициент очень велик,
порядка 104—106, то система
ШНЬЛ обыкновенных дифференци-
дифференциальных уравнений называется
жесткой. Яено, что для реше-
решения жестких систем желатель-
желательно иметь алгоритмы, несвязан-
несвязанные ограничениями на шаг по
времени.
Безусловная устойчивость
подобного рода гарантирует-
гарантируется, если численный метод об-
обладает А-устойчивостью [Dahl-
quist, 1963), т. е.. если область
его абсолютной устойчивости
включает в себя всю левую
полуплоскость ReA,-A?<0. Но
понятие Л-устойчивости содержит весьма высокое требование. Ни
одна из явных схем, будь то линейная многошаговая или схема
Рунге — Кутты, не является Л-устойчивой. Наивысший возмож-
возможный порядок из числа Л-устойчивых схем имеет неявная линей-
линейная многошаговая схема второго порядка.
Родственное, хотя и менее суровое понятие, связанное с ус-
устойчивостью, —- это устойчивость типа Л (a) [Widlund, 1967],
представление о которой иллюстрируется на рис. 7.10. Метод
обладает устойчивостью типа Л (а), если можно построить бес-
бесконечный клин, симметричный относительно отрицательной ве-
вещественной полуоси и имеющий угол полураствора а, внутри
которого метод является абсолютно устойчивым. Если все соб-
собственные значения матрицы А вещественны, что имеет место
для уравнения G.41), то численный метод, обладающий устой-
устойчивостью типа Л@), будет эффективным, даже если система
жесткая.
При построении решения задач об установившемся течении
численный алгоритм нередко основан на эквивалентной псев-
псевдонестационарной процедуре (см. § 6.4). Чтобы достичь ста-
Рис. 7.10. Устойчивость типа А (а).
§ 5.7. Заключение 321
ционарного решения наиболее эффективным путем, строятся
неявные схемы, основанные на известных свойствах, касаю-
касающихся устойчивости эквивалентных алгоритмов для обыкно-
обыкновенных дифференциальных уравнений [Beam, Warming, 1979].
Неявные алгоритмы такого рода (гл. 8—10, 14, 17 и 18) оказы-
оказываются обычно эквивалентными линейным многошаговым мето-
методам низкого порядка.
Процессы приспособления вычислительных алгоритмов к
специфическим свойствам векторных и параллельных процессо-
процессоров [Ortega, Voigt, 1985] возродили интерес к явным методам,
даже с целью построения стационарных решений на основе
псевдонестационарных формулировок. Такие формулировки
часто основаны на использовании схем Рунге — Кутты с мар-
маршевым продвижением по времени в сочетании с построениями
метода прямых (гл. 14 и 18).
§ 7.5. Заключение
Для одномерного уравнения диффузии были построены яв-
явные схемы, имеющие порядок вплоть до четвертого. Повышен-
Повышенные порядки точности достигались за счет взаимной компенса-
компенсации ошибок усечения, связанных с дискретизацией простран-
пространственного члена д2Т/дх2 на различных временных слоях п и
члена с производной по времени dT/dt в различных простран-
пространственных точках /. На практике при этом требуется сделать
такой специальный подбор свободных параметров, как в соот-
соотношении G.15), чтобы члены низкого порядка в выражении
для ошибки усечения стали тождественно равными нулю.
При использовании явных схем для получения устойчивых
решений обычно возникает необходимость выбора At, не пре-
превышающего некоторого максимального значения (посредством
ограничения на параметр s). Как правило, применение явных
схем повышенного порядка связано с более суровыми ограни-
ограничениями на At, обусловленными устойчивостью. В случае схе-
схемы Дюфорта — Франкела необходимо ограничивать величину
At, чтобы получить приемлемо точные решения, несмотря на то
что устойчивые решения могут быть получены при очень боль-
больших значениях At.
Неявные схемы часто позволяют добиться безусловной ус-
устойчивости ценой добавочных вычислительных усилий. До тех
пор пока неявную схему можно ограничить трехдиагональной
формой, суммарный вычислительный труд, вкладываемый в
нее, будет примерно вдвое превышать труд по решению на ос-
основе эквивалентной явной схемы. Включение дополнительных
членов на неявном (п+1)-м временном слое позволяет
21 К. Флетчер, т. 1 i
322 Гл. 7. Одномерное уравнение диффузии
проявить больше гибкости в построении схем повышенного по-
порядка. Однако, как свидетельствуют результаты (табл. 7.8),
для получения значительного улучшения точности может ока*
заться необходимым вводить мелкую сетку.
Если задача, описываемая уравнением диффузии, требует
задания граничного условия для производной, то возникают до-
дополнительные ошибки, связанные с дискретизацией граничного
условия. При решении задач, определяемых параболическим
дифференциальным уравнением, весьма важно, чтобы дискре-
дискретизация граничных условий с производными осуществлялась с
помощью формул такого же порядка точности, как и внутри
области.
При помощи дискретизации одного лишь пространственно-
пространственного члена исходное дифференциальное уравнение в частных про-
производных (ДУЧП) преобразуется к полудискретной форме,
сводящейся к системе обыкновенных дифференциальных урав-
уравнений (ОДУ) по времени. В результате различные алгоритмы,
разработанные специально для ОДУ, становятся пригодными
для решения ДУЧП. Подчеркивается, однако, что эквивалент-
эквивалентная система ОДУ содержит ошибки, обусловленные простран-
пространственной дискретизацией. Это обстоятельство несколько умень-
уменьшает стремление к использованию алгоритмов решения ОДУ,
имеющих очень высокий порядок. Обращение к полудискрет-
полудискретной форме оказывается удобным, когда для дискретизации про-
пространственных членов применяется спектральный метод (§ 5.6,
п. 15.3.3 и 17.1.6).
§ 7.6. Задачи
Явные методы (§7.1)
7.1. Выведите (а) формулу G.14), (Ь) уравнение G.17).
7.2. Проведите приближенный подсчет числа операций для схем ВВЦП,
Дюфорта — Франкела и трехслойной схемы четвертого порядка (у = 0) при
s = 0.30, затем сравните их вычислительную эффективность.
7.3. Постройте двухслойную пятиточечную схему, имеющую четвертый
порядок точности. В окрестности границ понадобятся несимметричные пяти-
пятиточечные формулы. С помощью анализа по Нейману проверьте устойчивость
данной схемы. Получите численные результаты (если возможно), подтвер-
подтверждающие необходимость ограничений, связанных с устойчивостью и со ско-
скоростью сходимости.
7.4. Рассмотрите уравнение G.13) с отрицательными значениями у, по-
поставив целью убедиться в возможности построения устойчивых и точных ре-
решений. В случае у = —0.5 может ли схема G.13) быть видоизменена так,
чтобы она походила на схему Дюфорта — Франкела, т. е. за счет изменения
Р-комплекса в дискретном представлении пространственной производной?
Если да, то установите, может ли быть построена устойчивая и имеющая вы-
высокую точность схема Дюфорта — Франкела?
§ 7.6. Задачи 323
Неявные методы (§ 7.2)
7.5. Выведите формулу G.30).
7.6. Примените анализ устойчивости по Нейману к системе G.31) с па-
параметром р, выраженным по формуле G.30), чтобы в плоскости yt s опре-
определить границу области устойчивого поведения для случаев: (а) 6 = 0,
(Ь) б = 1/12, (с) б = 1/6.
7.7. При б = 1/6, y = °» 0=1 и s = 1/6 схема G.31) становится яв-
явной. Сравните полученные для этого случая решения с теми, которые полу-
получаются с применением схемы ВВЦП. Исследуйте другие комбинации пара-
параметров, превращающие схему G.31} в явную.
7.8. С помощью программы DIFIM получите решения для случаев ME =
= 4, 5 при у = 0.5. Сравните точность и скорость сходимости с данными,
приводимыми в табл. 7.6.
7.9. Проведите приближенный подсчет числа операций для случаев МЕ=
= 1, 4 и у = 0 в табл. 7.6 и сравните вычислительную эффективность при
s = 1.0 с эффективностью схемы ВВЦП при s = 0.5 и схемы Дюфорта —
Франкела при s = 0.3.
Граничные и начальные условия (§ 7.3)
7.10. Видоизмените программу DIFEX, чтобы ввести и учесть в ней:
(а) граничное условие Неймана G.32) с первым порядком точности, (Ь) гра-
граничное условие Неймана G.34) со вторым порядком точности, и воспроиз-
воспроизведите результаты, приводимые в табл. 7.8.
7.11. Видоизмените программу DIFIM, чтобы ввести и учесть в ней:
(а) граничное условие Неймана G.32) с первым порядком точности, (Ь) гра-
граничное условие Неймана G.34) со вторым порядком точности, и получите
результаты, приведенные в табл. 7.10. При JMAX = 6 сравните распределе-
распределение ошибки с тем, которое приводится в табл. 7.9.
7.12. Для схемы Дюфорта — Франкела, начиная с точного решения
(подпрограмма ЕХТРА) при t = 2.00, введите схему ВВЦП на более мелкой
сетке по х и t для получения второго слоя начальных данных. При s = 0.3
и s = 0.5 сравните точность решения по схеме Дюфорта — Франкела с ис-
использованием схемы ВВЦП на начальном участке в момент времени t =
= 9.00 с решением, в котором два слоя начальных данных задаются точ-
точным решением при / = 2.00 и / = 2.00 — А/.
21*
Глава 8
Многомерное уравнение диффузии
Материал, изложенный в гл. 7, позволяет сделать общий
вывод о том, что для решения задач с существенным влиянием
диссипации, например определяемых одномерным уравнением
диффузии, неявные схемы оказываются более эффективными,
чем явные.
Распространяя неявные схемы на многомерные задачи и
желая при этом получить экономичные алгоритмы, необходи-
необходимо прибегать к специальным процедурам. Эти специальные
процедуры зачастую строятся на идее о том или ином способе
расщепления уравнения при использовании удобного коорди-
координатного базиса (§ 8.2, 8.3 и 8.5). Применение расщепляющих
построений требует особого внимания, если необходимо выпол-
выполнить граничные условия для производных (условия Неймана,
см. § 8.4). Приемы расщепления, разрабатываемые в данной
главе, применимы к методам конечных разностей, конечных
элементов и конечных объемов.
§ 8.1. Двумерное уравнение диффузии
Уравнение диффузии в двух измерениях имеет вид
дТ д2Т д2Т п
(8Л)
Для области, показанной на рис. 8.1, граничные условия Ди-
Дирихле записываются в виде
Т@,у, t) = a{y, t),
f(l,y,t) = b(y,t), (8.2)
f (x, 0, t) = c(x, t),
f(x,l,t) = d(x,t),
а начальные условия — в виде
f(x,y,0) = T0(x,y). (8.3)
§ 8.1. Двумерное уравнение диффузии
325
Типовые схемы явного и неявного счета, разработанные для
одномерного уравнения диффузии, в этом параграфе будут рас-
распространены на случай двух измерений, чтобы уяснить, будут
ли они непосредственно применимы.
8.1.1. Явные методы
Схема ВВЦП в двух измерениях имеет форму
ДГ
i, k
(8.4)
где
rptl
=
" 2!
f + Uk
и т. д.
Если придать этому вид алгоритма, то получим
Т/, fe = SxTf-i. k + A — 2Sjc — 25^) Г/, fe + 5jci/+l, ifc +
Syl j,k-\-\-Syl i, k+\> \*«o)
где 5^ = axht/Ax2 и 5y = ayAt/Ay2. Разложение в ряд Тейлора
в окрестности узла (/, kt n) свидетельствует о том, что уравне-
=1 j.
-1 j j+i
к-\
j=NX
J
Рис. 8.1. Двумерная область и граничные условия Дирихле.
тше (8.5) согласуется (§ 4.2) с уравнением (8.1) и имеет ошиб-
ошибку аппроксимации порядка О (At, Ax2, Дг/2).
Как показывает анализ устойчивости по Нейману, схема
(8.5) будет устойчивой, если
. (8.6)
Можно заметить, что если sx = sy = 5, то условие (8.6) дает
s ^ 0.25, а это ограничение более строгое, чем соответствующее
условие для одномерного условия (п. 7.1.1). Однако если для
получения достаточно точного решения приходится выбирать
326 Гл. 8. Многомерное уравнение диффузии
малый шаг по времени, то ограничительное условие на устойчи-
устойчивость может и не быть критическим.
Для случая а = ах = ау и Ах = Ау в книге [Mitchell, Grif-
Griffiths, 1980] предлагается обобщение схемы (8.4), т. е.
д^П + 1
—?*- - aLxxTl k - aLyyifk - a2 AtLxxLyyTl k = 0, (8.7>
которое устойчиво в диапазоне 0 < s ^ 0.5. Несмотря на то
что схема (8.7) девятиточечная, ее экономическую реализацию
можно осуществить в два этапа:
)Tlkj (8.8>
= A + « btLxx) fJt k. (8.9)
В случае трех измерений эта схема превращается в трехэтап-
ный алгоритм, при этом сохраняется «одномерный» диапазон
устойчивости 0 < 5 ^ 0.5. В отличие от этого трехмерная схе-
схема ВВЦП при Ах = Ay = Az остается устойчивой в диапазоне
0 < 5 ^ 1/6.
Одним из более интересных явных алгоритмов является ме-
метод «классики» [Gourlay, 1970]. В своем простейшем варианте
этот метод может рассматриваться как двухэтапная схема
ВВЦП. На первом этапе алгоритм (8.5) применяется ко всем
узловым точкам, для которых сумма /+& + ai четная; иначе
говоря, это относится к ячейкам сетки, соответствующим чер-
черным квадратам шахматной доски. На втором этапе нижесле-
нижеследующее уравнение решается для всех тех узловых точек, для
которых сумма / + k + и нечетная, т. е. применительно к бе-
белым квадратам «эквивалентной» шахматной доски.
A + 25, + 2sy) Ttk =TU + sx G?-+i! * + Tnitl k) +
Члены в правой части уравнения (8.10), определенные в момент
времени tn+u известны из результатов первого этапа. Простой
метод «классики» дает ошибку аппроксимации О (At, Ax2, Ау2),
однако в отличие от схемы ВВЦП он является безусловно ус-
устойчивым. Более подробное обсуждение серии методов «клас-
«классики» можно найти в книге [Mitchell, Griffiths, 1980].
8.1.2. Неявный метод
Действуя таким же образом, как и при решении одномерных
задач, можно построить неявную схему, для которой простран-
пространственные производные в уравнении (8.1) определяются на вре-
§ 8.2. Методы расщепления для многомерных задач 327
менном слое (/г+1). В результате получается алгоритм
- SxTfll k + A + 2sx + 2s,,) Ttk - s*77+i. к -
— SyTf, k-i — SyT", k+i = 77, k- (8.11)
Данная схема имеет ошибку аппроксимации О(Д?, Д*2, Ду2)
и является безусловно устойчивой. Однако трудность здесь за-
заключается в том, чтобы предложить экономичный метод реше-
решения уравнений, получаемых после применения схемы (8.11) к
каждому узлу сетки.
Обращаясь к уравнению (8.11), можно дать такую нумера-
нумерацию узлов, чтобы три члена находились на главной диагонали
или рядом с ней, тогда как два других члена были бы отделе-
отделены от трех упомянутых некоторым числом внутренних узлов
сетки (напримр, NX — 2 на рис. 8.1). Из сказанного следует,
что алгоритмом Томаса воспользоваться нельзя. Использова-
Использование обычного метода исключения Гаусса (п. 6.2.1) было бы
чрезвычайно неэкономичным; вариант исключения по Гауссу
для разреженных матриц также остался бы неприемлемо рас-
расточительным в применении к мелким сеткам.
§ 8.2. Методы расщепления для многомерных задач
Трудность, связанная с двумерной неявной схемой, может
быть преодолена путем расщепления алгоритма решения или
системы алгебраических уравнений на два полушага, дающих
в сумме продвижение на один шаг по времени. На каждом
полушаге неявная трактовка дается только членам, связанным
с определенным координатным направлением. Следовательно,
появятся только три неявных члена, которые могут быть сгруп-
сгруппированы в окрестности главной диагонали. В результате для
построения решения может быть использован чрезвычайно эф-
эффективный алгоритм Томаса. Суммарный процесс интерпрета-
интерпретации каждого шага по времени в форме последовательности бо-
более простых дробных шагов называется расщеплением (по вре-
времени).
8.2.1. Неявный метод переменных направлений (НПН)
Наиболее известным вариантом методики расщепления яв-
является неявный метод переменных направлений (НПН), пред-
предложенный в работе [Peaceman, Rachford, 1955]. Мы подробно
рассмотрим этот метод, а затем предложим более общий под-
подход, основанный на расщеплении.
Схема НПН для решения уравнения (8.1) записывается в
виде двух полушагов по времени, как будет показано ниже.
328
Гл. 8. Многомерное уравнение диффузии
На первом полушаге используется следующий вариант дискре-
дискретизации:
а на втором —
/, k r m* r rptl+1 s\
axLXxI j, k — UyLyyl j,k = U.
(8.12)
Af/2
В течение первого полушага решение Т известно на времен-
временном слое /г, но неизвестно на слое (п + 1/2), обозначаемое
Л+1
к-\
1
Прогонка
в направлении х
(постоянное к),
выполняемая
на 1-м шаге
по времени
j-i j i+i
ч^ -v г
Прогонка в направлении /
(постоянное/ ), выполняемая
на 2-м шаге по времени
Рис. 8.2. Реализация схемы НПН.
звездочкой. Однако неизвестные узловые значения Г* связаны
только с продвижением по направлению х (т. е. при постоян-
постоянном значении k на рис. 8.2). Уравнение (8.12) может быть пе-
переписано как одно уравнение из системы, а именно
0.5syTlk+i. (8.14)
Остальные уравнения той же системы формируются около дру-
других узлов той же строки k. Таким образом, решение полученной
системы уравнений дает промежуточное решение Т* k,
j = 2, ..., NX— 1, справедливое лишь для одного значения к.
Далее системы уравнений решают относительно T*k, / = 2, ...
..., NX — 1, для каждой строки, т. е. для k = 2, ..., NY — 1„
используя при этом алгоритм Томаса.
§ 8.2. Методы расщепления для многомерных задач 329
На втором полушаге используется уравнение (8.13), пред-
представляемое в виде
sy)Ttk - O.5s!,77.V+i =
sx)Tlk + 0.5sxr!+uk. (8.15)
В течение второго полушага решение на временном слое
п + 1 неизвестно, однако известно решение на промежуточном
временном слое, обозначенном звездочкой. Система уравнений,
связанных со всеми узлами, расположенными на одной сеточ-
сеточной линии вдоль направления у (фиксированное /) решается
относительно Г/.V, k = 2, ..., NY — 1. Процесс повторяется
для каждой из упомянутых сеточных линий, т. е. для / = 2, ...
..., NX—1.
Для проверки устойчивости схемы НПН следует применить
анализ устойчивости по Нейману, определяя коэффициент уси-
усиления для каждого полушага. Устойчивость полного шага по
времени определяется произведением двух коэффициентов уси-
усиления для полушагов, а именно
и —и и —
^ s.n2 {Qx/2) • x+2Sy sin2 (By/2) ' l°O'
Как показывает изучение формулы (8.16), при любом значении
Sat, sy, Qx и Gv получим \G\ ^ 1. Однако, рассматривая по от-
отдельности \G'\ и |G7/|, найдем, что если полный шаг по вре-
времени является безусловно устойчивым, то каждый из полуша-
полушагов устойчив лишь условно. Впрочем, интерес представляет
лишь полный шаг по времени.
Составная схема (8.12) и (8.13) согласуется с уравнением
(8.1) и обладает ошибкой аппроксимации порядка О (А/2, Дх2,
Аг/2). Второй порядок точности является следствием симметрии
схемы в точной аналогии с тем, как второй порядок точности
схемы Кранка — Николсона был следствием симметрии по от-
отношению к временному слою (п + 1/2).
Однако для достижения суммарной ошибки аппроксимации
порядка 0{ht2) необходимо для промежуточного решения T*fk
вводить граничные значения так, чтобы они были совместимы
с алгоритмами для внутренних точек (8.14) и (8.15). Напри-
Например, если ставятся граничные условия Дирихле, то задание
^nx, k=bl+l12 при х = 1 приводит к алгоритму с ошибкой
аппроксимации порядка О (А/). Чтобы ошибка аппроксимации
лолучила порядок О(Д?2), необходимо задать T*NX k с помощью
330 Гл. 8. Многомерное уравнение диффузии
соотношений (8.12) и (8.13), т. е. по формуле
Тж, k = 0.5 {hi + bTx) - 0.25 AtLyy {bTl - «). (8.17)
Аналогичная проблема возникает и при использовании схем
с приближенной факторизацией; надлежащие формы задания
граничных условий обсуждаются в п. 8.3.2 и § 8.4.
Таким образом, можно прийти к выводу, что схема НПН
для двумерного случая обладает требуемыми свойствами: без-
безусловно устойчива, имеет второй порядок точности и допускает
экономичный метод решения. Схема НПН распространяется
и на трехмерное уравнение диффузии, при решении которого
вместо алгоритмов (8.14) и (8.15) необходимо вести счет на
трех дробных шагах, каждый из которых занимает время Д^/3.
В случае трех измерений схема НПН оказывается экономичной,
имеет второй порядок точности по пространству, но является
лишь условно устойчивой. Для ее устойчивости необходимо,
чтобы sx, sy, sz ^ 1.5, где sz = azht/Az2.
8.2.2. Обобщенная двухслойная схема
Попытаемся теперь дать обобщение идеи расщепления. Не-
Неявная двухслойная конечно-разностная схема общего вида при-
применительно к уравнению (8.1) может быть записана в виде
_?*. _ A _ р) (ахЬххП к + ayLyyTl к) -
- Р (axLxxT??kl + aLyyT], к) = 0, (8.18)
где
/, k = Tj, k — T/, k-
Здесь величину ДГ/Д1 можно рассматривать как поправку
к решению на временном слое п, требуемую для продвижения
на временной слой (я+1). Для минимизации накапливающей-
накапливающейся ошибки округления полезно, чтобы величина ДГ^1 фигури-
фигурировала в явном виде в тексте компьютерной программы. Роль
коэффициента р в уравнении (8.18) состоит в задании опреде-
определенных весовых множителей при членах, соответствующих вре-
временным слоям п и (я+1); та же идея была использована и
при выводе уравнения G.24).
С помощью перестановки членов уравнения (8.18) можно
получить неявный алгоритм для определения ДГ/Д1. Вначале
член T?*k разлагается в ряд Тейлора в окрестности /г-го вре-
временного слоя в соответствии с формулой C.16), а именно
§ 8.2. Методы расщепления для многомерных задач 331
что можно аппроксимировать формулой
—±±) + О№. (8.19)
Подстановка формулы (8.19) в уравнение (8.18) дает
(axLxxT?. k + ayLyyTl k) - p {axLxx/ST?^+ayLyy Д77Д1) =0,
(8.20)
или после некоторой перегруппировки
[1 - р Д/ (axL« + ayLyy)] ATjft1 = A/ (a^L** + a^y) Г?. *. (8.21)
В левой части соотношения (8.21) фигурируют алгебраические
операторы, действующие как в одном, так и в другом направ-
направлениях. Чтобы можно было воспользоваться алгоритмом То-
Томаса, соотношение (8.21) заменяется другим соотношением,
получаемым в результате приближенной факторизации, а
именно
) A - Р ШуЬуу) Д27Л1 = А* (<*Д** + ^у^уу) Г/. *. (8.22)
Как показывает сравнение соотношений (8.21) и (8.22), в ле-
левой части последнего содержится дополнительный член
Отсюда следует, что соотношение (8.22) аппроксимирует (8.21)
с точностью О(Д?2).
На каждом шаге по времени выполнение соотношения
(8.22) может быть реализовано в форме двухэтапного алгорит-
алгоритма. Первый этап сводится к решению следующей системы урав-
уравнений, справедливых на каждой из сеточных линий, направлен-
направленных параллельно оси х (линии постоянного k на рис. 8.2):
A - Р btaxLxx) кТ], k = Д/ (axLxx + ayLyy) Т], *. (8.23)
Это уравнение служит для определения ДГ/, & что можно рас-
рассматривать как промежуточное приближение для ДГ/,"У. Если
Lxx представляет собой трехточечный оператор с центральной
разностью, то уравнения (8.23) будут иметь форму трехдиаго-
нальной системы, которая может быть эффективно решена с
помощью алгоритма Томаса (п. 6.2.2). На втором этапе ре-
решается следующая система уравнений:
A - р ШуЬуу) biff = bll ь (8.24)
332 Гл. 8. Многомерное уравнение диффузии
справедливая на каждой из сеточных линий, параллельных оси
у (линии постоянного / на рис. 8.2). Структура уравнений
(8.23) и (8.24) аналогична структуре уравнений (8.14) и (8.15),
характеризующих схему НПН. В случае уравнений более слож-
сложной формы основной вклад в суммарное время исполнения алго-
алгоритма вносит расчет всех пространственных членов в правых
частях уравнений (8.23). Реализация, рассматриваемая здесь,
требует лишь однократного расчета пространственных членов
на одном шаге по времени. В отличие от этого схема НПН тре-
требует проведения двух подобных расчетов. Алгоритм (8.23),
(8.24) предложен в работе [Douglas, Gunn, 1964].
Двухэтапный алгоритм (8.23), (8.24) является безусловно
устойчивым при р ^ 0.5 и имеет ошибку аппроксимации по-
порядка О (At2, Ах2, Ау2), если р = 0.5. Построение, связанное
с приближенной факторизацией, обобщается и на случай трех
измерений, причем в отличие от схемы НПН соответствующая
схема безусловно устойчива при р ^ 0.5.
Если изложенная здесь методика используется для построе-
построения решений стационарных задач в форме предельного стацио-
стационарного состояния решений для соответствующих нестационар-
нестационарных задач (§ 6.4), то полезно в уравнение (8.23) ввести опре-
определение
RHS = (axLxx + a'yLyy) Tnu k, (8.2б>
По мере приближения к стационарному решению величина RHS
стремится к нулю; следовательно, контроль за изменением
RHS даст возможность установить близость к стационарному
решению.
8.2.3. Обобщенная трехслойная схема
Обобщенная трехслойная неявная схема для решения одно-
одномерного уравнения диффузии задавалась в форме G.25). Соот-
Соответствующая трехслойная схема для случая двух измерений
записывается в виде
+ Р (axLxx + ayLyy) Ttk\ (8.26)
где
Если применить то же самое построение, которое использова-
использовалось для перехода от соотношения (8.18) к уравнениям (8.23)
и (8.24), то из (8.26) получится следующий двухэтапный ал-
§ 8.3. Схемы расщепления 333
горитм. На первом этапе соотношение
{axLxx + ayLyy) Tl k + ТГ+^Г АГ* * (8'27)
дает возможность получить трехдиагональную систему уравне-
уравнений, относящихся к каждой сеточной линии, параллельной
оси х.
На втором этапе каждого шага по времени используется сле-
следующее уравнение:
= Д7а *
При выборе специальных значений Р = 1, у = Ъ.Ь двухэтап-
ный алгоритм, заданный с помощью уравнений (8.27) и (8.28),
согласуется с уравнением (8.1) с ошибкой аппроксимации
О (At2, Ах2у Ау2) и является безусловно устойчивым. При реали-
реализации первого шага по времени (п = 0) необходимо восполь-
воспользоваться двухслойной схемой, подобной (8.23), (8.24).
Рассмотренные в этом параграфе схемы расщепления
естественным образом обобщаются и на случай трех измерений
[Mitchell, Griffiths, 1980]. Современный подход к процессам
расщепления, при котором неявное уравнение дополняется не-
некоторым членом, как правило, порядка О (At2) с целью осуще-
осуществления факторизации, подробно обсуждается в работе
[Gourlay, 1977]. При решении уравнения диффузии в двух или
трех измерениях имеется возможность применения схем рас-
расщепления повышенного порядка. Некоторые из таких схем рас-
рассматриваются в книге [Mitchell, Griffiths, 1980].
§ 8.3. Схемы расщепления и метод конечных элементов
Здесь мы будем применять метод Галёркина с конечными
элементами (§ 5.3) к решению двумерного уравнения диффузии
(8.1) с граничными и начальными условиями, заданными в
форме (8.2) и (8.3), и попытаемся определить, нуждаются ли
в модификации схемы расщепления, разработанные в § 2.8,
чтобы охватить конечно-элементную разновидность дискрети-
зированных уравнений. Воспользуемся элементами прямоуголь-
прямоугольной формы с билинейными интерполяционными функциями
типа E.59) внутри каждого элемента. Если метод Галёркина с
конечными элементами применяется на сетке, однородной в
334 Гл. 8. Многомерное уравнение диффузии
направлениях х и у, то после деления всех членов на ДхДу по-
получим
Мх ® Му [-§-], k = ахМу ® LXXT,9 k + ауМх ® LyyTit ку (8.29)
где знак ® обозначает тензорное (или внешнее) произведение
[Mase, 1971]; Мх и Му — массовые операторы соответствую-
соответствующих направлений, a Lxx и Lyy — разностные операторы тех же
направлений (см. приложение А.2). Массовые операторы по
направлениям имеют вид
Afx = (l/6, 2/3, 1/6), Му = (\/6, 2/3, 1/6)Г, (8.30)
а разностные операторы по направлениям — вид
L LЛ r (ЛL
(8.31)
Таким образом, член Му ® LxxTlt k дает девятиточечное пред-
представление производной д2Т/дх2. Обращаясь к рис. 8.3, получим
2 f Гу-мь-аГ/.^ + Гж^!
"*" 3 X Их* J "*"
+ 64 Z? Г (8-32)
Введенное ранее конечно-разностное представление, напри-
например в форме (8.4) и следующих за этим соотношений, может
рассматриваться в рамках соотношения (8.29), если опреде-
определить конечно-разностные массовые операторы по направле-
направлениям с помощью выражений
Mxd = (M[d)T = @, 1,0),
так что конечно-разностные выражения будут содержать толь-
только три члена.
Что касается дискретизации многомерных уравнений, про-
проводимой на основе конечно-элементного и конечно-разностного
подходов, то метод конечных элементов моделирует простран-
пространственные производные по данным, распределенным в преде-
пределах некоторой площадки, тогда как метод конечных разностей
моделирует те же производные по данным вдоль определенно-
определенного пространственного направления. Вообще говоря, конечно-
элементная формулировка более точна, но вместе с тем и ме-
§ 8.3. Схемы расщепления
335
нее экономична, так как связана с расчетом большего числа
членов.
Если вместо линейных лагранжевых элементов используют-
используются квадратичные лагранжевы элементы, то каждый из массо-
массовых и разностных операторов будет содержать уже по пять
членов, так что тензорное произведение типа Мх ® LyyTjt * бу-
Прогонка в направлении х
(постоянное к)
Прогонка в направлении у
(постоянное/)
(aj Конечно-элементная формулировка
Л+1?
Прогонка в направлении х
(постоянное А:)
Прогонка в направлении /
(постоянное/)
(Ь) Конечно-разностная формулировка
Рис. 8.3. Активные узлы для схем расщепления по уравнениям (8.23), (8.24)
или (8.39), (8.40).
дет содержать 25 членов. Однако такое выражение согласуется,
как правило, с представлением производной д2Т/ду2 с точ-
точностью до членов порядка О(Ау3).
8.3.1. Приемы расщепления конечно-элементных уравнений
Здесь будет изложено два способа расщепления конечно-
элементных уравнений. Первый из этих способов приводит к
алгоритму, аналогичному схеме НПН (8.14), (8.15). Второй
алгоритм сводится к выражению решения через поправки
Д71/,*, как по схеме (8.23), (8.24).
Так же как и при исследовании одномерного уравнения диф-
диффузии, в соотношение (8.29) будет вводиться конечно-разност-
336 Гл. 8. Многомерное уравнение диффузии
ное представление производной дТ/dt, а пространственные чле-
члены будут моделироваться средневзвешенными значениями для
п-то и (д + 1)-го слоев по времени. Таким образом, соотноше-
соотношение (8.29) заменяется выражением
Мх ® Му -±±- = (ахМу ® Lxx + ауМх ® Lyy) [A - ft) Г?, k + ргУДЧ-
(8.33)
Уравнение (8.33) представляет собой конечно-элементный
эквивалент уравнения (8.17). Расщепление типа НПН с конеч-
конечными элементами осуществляется путем введения в левую
часть уравнения (8.33) дополнительного члена
M*xayLxx ® Lyy [pV+1 - A - РJ Г],
так что это уравнение принимает вид
(Мх - а*р ЫЬХХ) ® (Му - аур MLyy) T^k =
= [Мх + ах A - р) Д/L**] ® [Afy + ау A - р) Д/L^] Г?, ь (8.34)
Решение уравнения (8.34) может быть весьма эффективно про-
проведено в два этапа. На первом из них соотношение
(Мх - а*р MLXX) Т], k = [Му + ау A - р) AtLyy] П k (8.35)
позволяет получить трехдиагональную систему на каждой из
сеточных линий, параллельных оси х. На втором этапе соот-
соотношение
(Му - а,р ULyy) Ttk = [Мх + «х A - Р) MLxx] т). к (8.36)
приводит к трехдиагональной системе на каждой из сеточных
линий, параллельных оси у.
При р = 0.5 единственным различием между конечно-эле-
конечно-элементной конструкцией типа НПН в форме (8.35), (8.36) и ко-
конечно-разностной конструкцией НПН вида (8.14), (8.15) будет
появление в первой из них массовых операторов. Конечно-эле-
Конечно-элементный алгоритм по схеме НПН является экономичным, имеет
второй порядок точности по времени и пространству и обла-
обладает безусловной устойчивостью при р ^ 0.5 + (б — 0.25) /s,
где б определяется по формуле (8.44), а вместо 5 можно ис-
использовать sx или sy.
Расщепление может осуществляться и другим способом.
При этом член Г/Д\ находящийся в правой части уравнения
(8.33), разлагается в ряд Тейлора в окрестности п-го времен-
временного слоя с отбрасыванием членов О(Д?2). После перегруппи-
§ 8.3. Схемы расщепления 337
ровки результат может быть записан в виде
{Мх ® Му - р А/ (ахМу ® Lxx + ауМх ® !„„)] ATft1 =
? . (8.37)
Если в левую часть уравнения (8.37) ввести дополнительный
член р2kt2axayLxx®LyyДТ/Д1, то получится расщепляющееся
уравнение
{Мх - р ШХЬХХ) ® (Afу - р A/%L^) Д77Д1 =
= Ы (ахМу ® L** + ауМх ® !„„) Г?, ь (8.38)
причем реализация расщепления включает соотношение
(Мх - р Шх Lxx) ЛГд k = А^ (ахМу ® L^ + ауМх ® Lyy) Г?, * (8.39)
для всех сеточных линий, идущих в направлении х> а также со-
соотношение
(Му - р ШУЬУУ) Д77Д' = XT], k (8.40)
для всех сеточных линий, идущих в направлении у.
Уравнения (8.39), (8.40) можно сравнить с уравнениями
(8.23), (8.24). Правая часть уравнения (8.39) требует больше-
большего времени для своего расчета, чем правая часть (8.23). Расчет
правых частей осуществляется на временном слое п. Как мож-
можно видеть из рис. 8.3, схема метода конечных элементов охва-
охватывает девять активных узлов на n-м слое по времени по срав-
сравнению с пятью активными узлами для схемы конечно-разност-
конечно-разностного метода. Однако процесс расчета членов уравнения (8.39),
а также реализация решения трехдиагональных систем урав-
уравнений для обеих формулировок различаются несущественно.
Как свидетельствуют вычислительные эксперименты, метод ко-
конечных элементов работает, вообще говоря, медленнее мето-
метода конечных разностей, но обычно обеспечивает более точное
решение.
Вычислительный алгоритм (8.39), (8.40) согласуется с урав-
уравнением (8.1) при ошибке аппроксимации порядка О (At2, A*2,
Af/2), если р = 0.5. Такие же уравнения по схеме с расщепле-
расщеплением будут получены, если вместо линейных лагранжевых эле-
элементов использовать квадратичные лагранжевы элементы
(п. 5.3.2); при этом, однако, операторы МХу Lyy и т. д. будут
содержать максимальное число членов, т. е. пять вместо трех
[Fletcher, 1984].
22 К. Флетчер, т. 1
338 Гл. 8. Многомерное уравнение диффузии
8.3.2. TWDIF: обобщенная схема для реализации расчетов
с конечными разностями или конечными элементами
Различные схемы расщепления, рассмотренные в п. 8.2.2,
8.2.3 и 8.3.1, могут быть объединены в одну обобщенную трех-
трехслойную схему, охватывающую как конечно-разностную, так и
конечно-элементную формулировки. Мы покажем это здесь
для области, изображенной на рис. 8.1.
Распределение температуры в области 0 ^ х ^ 1, 0 ^ у ^
^ 1 определяется уравнением (8.1) со специальными гранич-
граничными условиями
ПО, у,/) = 20
f A, у, 0 = 20 + 80 [у - е-™™2* sin @.5ш/)],
(
Т(х,0, /) = 20,
Т(х, 1, 0 =20+ 80[у — e-°*™2i sin@.5nx)].
Для данного примера существует следующее аналитическое ре-
решение:
Т = 20 + 80 [у — е-0***** sin @.5ях) sin @.5ш/)]. (8.42)
Обобщенная схема может быть введена за счет трехслойной
конечно-разностной дискретизации уравнения (8.29) при
а = ах = ау, что дает
= а(Му® Lxx + MX® Lyy) [A - р)П k + Wtkl (8.43)
т. е. соотношение, эквивалентное (8.26). Однако здесь массо-
массовые операторы (8.30) по координатным направлениям будут
представлены в обобщенном виде
Мх = My = {б, 1 — 26, б}. (8.44)
Ясно, что конечно-разностная схема (п. 8.2.2 и 8.2.3) соответ-
соответствует значению 6 = 0, тогда как конечно-элементная схема
(п. 8.3.1) соответствует значению б = 1/6.
После приближенной факторизации уравнения (8.43) полу-
получается следующий двухэтапный алгоритм, заменяющий (8.39)»
(8.40):
§ 8.3. Схемы расщепления 339
Первый этап
К - (тй^г)L J ^*=RHS"> <8-45)
где
,RHS" = [аЩМ„ ® L« + Afx <8> Lw) Г?, » + уМх ® Л1,ДГ?. J/(l + y).
(8.46)
Второй этап
К G^V) \ " - ^*• (8-47)
Для уравнений, формируемых в точках вблизи границ, нуж-
«о задать граничные значения величин ДГ* в (8.45) и ДГП+1 в
(8.47). Надлежащий вид этих граничных значений проще все-
всего определить путем свертывания (8.45) и (8.47) в одну ком-
комбинированную схему, получаемую за счет исключения ДГ*.
Тогда становится ясно, что требуемые для решения (8.47) гра-
граничные значения ДГ* могут быть получены непосредственно из
формул (8.41), тогда как граничные значения для ДГ* должны
вычисляться также из (8.41) через посредство обращенного со-
соотношения (8.47); например, в точке j=NX (л:=1) имеем
ЛГкх, * = [Af, - (-jt^j-) Lyy] ДГй?*. (8.48)
Если граничные условия (8.41) не зависят от времени, то для
ДГ* и ДГЛ+1 получаются нулевые граничные значения. Извест-
Известные граничные значения зависимых переменных ДГ* и ДГП+1
переносятся в правые части уравнений (8.45) и (8.47) соответ-
соответственно до решения уравнений.
Реализация вышеописанного алгоритма проводится с по-
помощью программы TWDIF (рис. 8.4). На первом этапе соот-
соотношение (8.45) приводит к трехдйагональной системе уравне-
уравнений, связанных с каждой из сеточных линий, идущих в направ-
направлении х. Эти уравнения решаются с помощью подпрограмм
BANFAC и BANSOL (рис. 6.18 и 6.19). Вычисление по форму-
формуле (8.46) реализуется в подпрограмме REDIF (рис. 8.5). На
втором этапе соотношение (8.47) служит средством получения
трехдйагональной системы уравнений, связанных с каждой из
сеточных линий, идущих в направлении у; система решается с
использованием подпрограмм BANFAC и BANSOL. Основные
параметры, используемые в программе TWDIF, описаны в
табл. 8.1. Типовая выдача результатов для случая конечно-раз-
конечно-разностной схемы Кранка — Николсона на грубой сетке показана
на рис. 8.6.
22*
1 С
2 С TWDIF APPLIES APPROXIMATION FACTORISATION TO SOLVE
3 С THE UNSTEADY HEAT CONDUCTION PROBLEM FOR T(XrY) .
4 С REDIF EVALUATES THE RIGHT-HAND SIDE.
5 С
6 REAL*8 SUMT,RMST,DSQRT,AN
7 DIMENSION TD1,41),DTD1,41),RD1,41),EMXC),EMYC),
8 1BE,41),RRTD1),DDTD1),SIXD1),SIYD1),YD1),ERRD1,41)-
9 COMMON DX,DY,EMX,EMY,NX,NY,R,T,DT
10 OPENd,FILE='TVDIF.DAT1)
11 0PENFfFILE='TWDIF.0UTf)
12 READd,l)IBC,NX,NY,ME,GAM,BET
13 READA,2)ALF,DTIM,DTMCH,TMAX
14 1 FORMATDI5,2F5.2)
15 2 FORMATDE10.3)
16 С
17 PI = 3.141592654
18 PIH = 0.5*PI
19 NXS = NX + 1
20 NYS « NY + 1
21 NXP = NX - 1
22 NYP = NY - 1
23 IF(IBC .EQ. DNXN = NXP
24 IFUBC .EQ. DNYN = NYP
25 IF(IBC .EQ. 2)NXN = NX
26 IF(IBC .EQ. 2)NYN = NY
27 NXPP = NXN - 1
28 NYPP * NYN - 1
29 AN = NXPP*NYPP
30 ANX = NXP
31 - DX = l./ANX
32 ANY = NYP
33 DY = l./ANY
34 SX = ALF*DTIM/DX/DX
35 SY = ALF*DTIM/DY/DY
36 EMX(l) = 0.
37 IF(ME .EQ. 2)EMXA) » 1./6.
38 IF(ME .EQ. 3)EMXA) = 1./12.
39 EMXB) * 1. - 2.*EMXA)
40 EMXC) = EMX(l)
41 DO 3 J = 1,3
42 3 EMY(J) = EMX(J)
43 VRITEF,4)NXfNY,ME,GAM,BET,SX,SY
44 4 FORMATC UNSTEADY HEAT CONDUCTION WITH NXrNY =',213,/,
45 I1 ME =\I3,' GAM ='^5.2,' BETA =',F5.2,f SX,SY =\2F6.3)
46 IF(ME .EQ. l)VRITEFr5)EMX
47 5 FORMATC APPROX. FACT., 3PT FDMr EMX=',3E1O.3)
48 IF(ME .EQ. 2)WRITEF,6)EMX
49 6 FORMATC APPROX. FACT., LINEAR FEM, EMX=*,3E10.3)
50 IFUBC .EQ. 1)WRITEF,7)
51 IF(IBC .EQ. 2)WRITEF,8)
52 7 FORMATC DIRICHLET B.C.')
53 8 FORMATC DIRICHLET AND NEUMANN B.C.1)
54 VRITEF,9)DTIM,DTMCH,TMAX
55 9 FORMATC DTIM =\Е10.3,* PRINT INT. =\Е10.3,' ТМАХ =\E10.3,//>
56 С
57 С GENERATE INITIAL SOLUTION
58 С
59 DO 11 J - 1,NX
60 AJ s J - 1
61 X * AJ*DX
62 SIX(J) = SIN(PIH*X)
Рис. 8.4. Распечатка программы TWDIF (начало).
63 DO 10 К « 1,NY
64 AK = К - 1
65 Y(K) = AK*DY
66 SIY(K) = SIN(PIH*Y(K))
67 10 T(K,J) = 8O.*(Y(K) - SIX(J)*SIY(K)) + 20.
68 11 CONTINUE
69 IF(IBC .EQ. DGOTO 14
70 DO 12 J « 1,NX
71 12 T(NYS,J) » T(NYP,J) + 160.M)Y
72 DO 13 К « 1,NYS
73 13 T(K,NXS) * T(K,NXP)
74 14 CONTINUE
75 GAMH * GAM
76 GAM » 0.
77 BETH в BET
78 BET * 0.5
79 TIM = 0.
80 TMCH * -0.00001 + DTMCH
81 DIM = - 0.5*ALE*PI*PI
82 DO 17 J « 1,NX
83 DO 15 К = 1,NY
84 DT(K,J) = 0.
85 15 R(K,J) = 0.
86 DO 16 К = 1,5
87 16 B(K,J) = 0.
88 17 CONTINUE
89 18 CCXA * BET*DTIM*ALF/DX/DX/A.+GAM)
90 CCYA « BET*DTIM*ALF/DY/DY/A.+GAM)
91 ТГАС = EXP(DIM*(TIM+DTIH)) - EXP(DIM*TIM)
92 С
93 CALL REDIF(ALF,GAM,DTIM,NXN,NYN)
94 С
95 С TRIDIAGONAL SYSTEMS IN THE X-DIRECTION
96 С
97 DO 21 К
98 DO 19 J
99 JM = J -
100 BB,JM)
101 BC,JM)
102 BDrJM)
103 19 RRT(JM)
2,NYN
2fNXN
L
EMX(l) - CCXA
EMXB) + 2.*CCXA
EMXC) - CCXA
R(K,J)
104 BB,l) = 0.
105 IF(IBC .EQ. 1)DT(K,NX) = - 8O.*SIY(K)*TFAC
106 IF(IBC .EQ. 1)DUM=(EMYA)-CCYA)*SIY(K-1)+(EMYB)+2^*CCYA)*SIY(K>
107 1 + (EMYC)-CCYA)*SIY(K+1)
108 IF(IBC .EQ. l)RRT(JM) = RRT(JM) + BD,JM)*80.*TFAC*DUM
109 IF(IBC .EQ. 2)DT(K,NXS) = DT(K,NXP)
110 IFdBC .EQ. 2)BB,JM) = BB,JM) + BD,JM)
111 BDrJM) = 0.
112 С
113 CALL BANFAC(B,NXPP,1)
114 CALL BANSOLtRRT^DT^B^NXPP,!)
115 С
116 DO 20 J = 2,NXN
117 JM = J - 1
118 20 R(KtJ) в DDT(JM)
119 21 CONTINUE
120 С
121 С TRIDIAGONAL SYSTEMS IN THE Y-DIRECTION
122 С
123 DO 24 J = 2,NXN
124 DO 22 К = 2,NYN
125 KM * К - 1
Рис. 8.4 (продолжение).
126
127
128
129
130
131
1>2
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155.
156
157
158
JL59
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
С
С
С
С
С
С
С
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
ВB,КМ) « EMY(l) - CCYA
В(ЗДН) = E.MYU) + 2.*CCYA
ВD,КИ) = EMYC) - CCYA
RRT(KH) = R(K,J)
BB,l) = 0.
IFUBC .EQ. 1)DT(NY,J) = - 8O.*SIX(J)*TFAC
IFUBC .EQ. l)RRT(KM) = RRT(KM) - BD,KM)*DT(NY,J)
IF(IBC .EQ. 2)DT(NYS,J) ¦ DT(NYP,J)
IF(IBC .EQ. 2)BB,KM) » BB,KM) + ВD,KM)
BD,KM) » 0.
CALL BANFAC(B,NYPP,1)
CALL BANSOL(RRT,DDT,B,NYPP,1)
INCREMENT T
DO 23 К = 2,NYN
KM = К - 1
DT(KfJ) * DDT(KM)
T(KfJ) s T(K,J) + DDT(KM)
CONTINUE
IF(IBC .EQ. 1)DT(NY,NX) » - 8O.*TFAC
IF(IBC .EQ. 2)DT(NYS,NXS) = DT(NYP,NXP)
TIM = TIM + DTIM
TFAC = EXP(DIM*TIM)
IF(IBC .EQ. 2)GOTO 26
DO 25 К = lfNY
T(K,NX) = 20. + 8O.*(Y(K) - TFAC*SIY(K))
T(NY,K) = 20. + 8O.*(l. - TFAC*SIY(K))
GOTO 29
DO 27 J » 1,NX
T(NYS,J) = T(NYP,J) + 160.*DY
DO 28 К = 1,NYS
T(K,NXS) = T(K,NXP)
GAM = GAMH
BET = BETH
IF(TIM .GE. TMCH)GOTO 30
IF(TIM .LE. TMAX)GOTO 18
GOTO 37
COMPARE WITH EXACT SOLUTION
TMCH = TMCH + DTMCH
SUMT = 0.
DO 33 KA = 1,NY
К * 1 + NY - KA
DO 31 J = 1,NX
ТЕ * 20. + 8O.*(Y(K) - TFAC*SIX(J)*SIY(K))
ERR(K#J) » T(K,J) - ТЕ
SUMT = SUMT + (T(K,J) - TE)**2
WRITEFr32)(T(K,J)fJ=l,NX)
FORMATC T=\11F7.3)
CONTINUE
DO 34 KA = 1,NY
К = 1 + NY - KA
VRITEF,35)(ERR(KrJ)rJ=1,NX)
rORMATC E=',11F7.3)
RMST * DSQRT(SUMT/AN)
WRITEF,36)TIMfRrtST
FORMATC TIME =\E11.4,' RMST >'fD11.4)
IF(TIM .LE. TMAX)GOTO 18
CONTINUE
STOP
END
Рис. 8.4 (окончание).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
С
С
с
с
с
SUBROUTINE REDIF(ALF,GAM,DT1M,NAN,NШ)
EVALUATES
UNSTEADY
DIMENSION
1DMXC,3),
1
2
3
4
5
COMMON DX
RIGHT-HAND SIDE OF THE
HEAT CONDUCTION EQUATION
DTD1,41),TD1,41),RD1,41),
DMYCr3),EMXC),EMYC)
,DY,EMX,EMY,NX,NY,R,T,DT
CCX = ALF/DX/DX
CCY = ALF/DY/DY
DO 1 I =
DMX(I,1)
DMX(I,2)
DMX(I,3)
DMYA,I)
DMYB,I)
DMYC,I)
DO 5 J =
DO 4 К =
RTD = 0.
DO 3 M =
MJ = J -
DO 2 N =
NK = К -
RTD = RTE
1.3
= CCX*EMY(I)
= -2.*DMX(I,1)
= DMX(I,1)
= CCY*EMX(I)
= -2.*DMYA,I)
= DMYA,I)
2,NXN
2,NYN
1,3
2 + M
1,3
2 + N
> + (DMX(N,M)+DMY(N,M))*T(NK,MJ)*DTIK
1 + GAM*EMX(M)*EMY(N)*DT(NK,MJ)
CONTINUE
R(K,J) =
CONTINUE
RETURN
END
RTD/A. + GAM)
Рис. 8.5. Распечатка подпрограммы REDIF.
UNSTEADY HEAT CONDUCTION WITH NX,NY = 6 6
ИЕ = 1 GAM = .00 BETA = .50 SX,SY = 1.000 1.000
APPROX. FACT., 3PT FDMr EMX= .000E+00 .100E+01 .000E+0O
DIRICHLET AND NEUMANN B.C.
DTIM = .400E+04 PRINT INT. = .240E+05 TMAX ¦ .250E+05
T^IOO.000
T=
T=
T=
T=
T=
E=
E=
E=
E-
E*
E=»
84.000
68.000
52.000
36.000
20.000
.000
.000
.000
.000
.000
.000
92.370
76.743
61.827
47.515
33.642
20.000
-.067
-.063
-.054
-.039
-.021
.000
TIME » .2400E+05
85.487
70.197
56.259
43.469
31.515
20.000
-.127
-.121
-.103
-.074
-.039
.000
80.024
65.002
51.839
40.259
29.827
20.000
-.174
-.166
-.141
-.103
-.054
.000
RMST = .
76.517
61.667
49.002
38.197
28.743
20.000
-.205
-.195
-.166
-.121
-.063
.000
75.309
60.517
48.024
37.487
28.370
20.000
-.216
-.205
-.174
-.127
-.067
.000
1294D+00
Рис. 8.6. Типовая выдача результатов, полученных с помощью программы
TWDIF.
344
Гл. 8. Многомерное уравнение диффузии
Таблица 8.1. Параметры, используемые в программе TWDIF
Параметр
ALF
GAM, BET
ЕМХ, EMY
ME
NX, NY
DX, DY
SX, SY
DTIM
DTMCH
TIM
TMCH
TMAX
T
ТЕ
DT
DDT
В
К
RMST
Описание
a = ax = ay в уравнении (8.1)
Y, P в уравнении (8.43)
MXy My в формуле (8.44)
= 1 — метод конечных разностей;
= 2 — линейный метод конечных элементов
Максимальное число узловых точек в направлениях х и у
Дл:, ку
sx и sy в уравнении (8.5)
А*
Интервал времени для выдачи на печать
Время
Сравнительное время для принятия решения о выдаче на
печать
Максимальное время
Узловое значение температуры Г* k в уравнении (8.43)
Величина Г, соответствующая (8.42)
ДГ? k в уравнении (8.46)
ДГу ^ и ДТ*"^1 после возврата подпрограммы BANSOL
Трехдиагональная матрица; левые части уравнений (8.45) и
RHSn в уравнении (8.46); также используется для хранения
в памяти Д7^ k из уравнения (8.47)
1|Г-Г||гт.
Программа TWDIF используется для сравнения работы ко-
конечно-разностных схем Кранка — Николсона, двухслойной чис-
чисто неявной (ДСЧН) и трехслойной чисто неявной (ТСЧН) с
работой конечно-элементной схемы Кранка — Николсона. Ре-
Результаты сравнения суммируются в табл. 8.2. При использова-
использовании трехслойной чисто неявной схемы (ТСЧН) расчет первого
шага проводится по схеме Кранка — Николсона. Кроме того,
в табл. 8.2 приводятся данные о среднеквадратичных ошибках,
полученных при применении модифицированной схемы Кран-
Кранка — Николсона со значением 6=1/12 в формуле (8.44).
Конечно-разностные схемы Кранка — Николсона и ТСЧН
обладают сравнимой точностью, особенно на мелкой сетке. Это-
Этого следовало ожидать, так как обе схемы имеют ошибки аппрок-
аппроксимации второго порядка. Очень точное решение по схеме
§ 8.3. Схемы расщепления
345
Таблица 8.2. Среднеквадратичные ошибки в случае граничных условий
-5
Дирихле при / = 24 000, а = 1 X Ю и sx = sy = 1.00
0.20
0.10
0.05
Кранк—Ни-
колсон,
метод
конечных
разностей
(МЕ=1),
<у=0, 0=0.50
0.02682
0.00648
0.00157
дсчн,
метод
конечных
разностей
Y=0. 0 = Г.ОО
0.40880
0.08874
0.02065
тсчн,
метод
конечных
разностей
0=~1.ОО
0.00306
0.00528
0.00150
Кранк —Ни-
колсон,
метод
конечных
элементов
(МЕ = 2),
Y=0, 0=0.50
0.03364
0.00686
0.00159
Кранк —Ни-
колсон,
6=1/12,
Y=0, 0 = 0.50
0.002820
0.000134
0.000082
ТСЧН, полученное на грубой сетке, рассматривается как ано-
аномалия. Двухслойная чисто неявная схема (ДСЧН) значитель-
значительно менее точна, и это соответствует свойственной ей ошибке
аппроксимации порядка О (At, Ал:2, Аг/2). Конечно-элементная
схема Кранка — Николсона обладает ошибкой аппроксимации
второго порядка и обнаруживает точность, сравнимую с точ-
точностью конечно-разностной схемы Кранка — Николсона. Одна-
Однако схема Кранка — Николсона со значением 6=1/12 в фор-
формуле (8.44) приводит к значительно более точным решениям
как на грубой, так и на мелкой сетках. Этого следовало ожи-
ожидать, так как данная схема имеет ошибку аппроксимации по-
порядка О (А/2, Ах\ А*/4).
Схемы, перечисленные в табл. 8.2, классифицируются как
девятиточечные. Однако расчет по подпрограмме REDIF для
конечно-разностных схем будет более эффективным, если счи-
считать, что каждый из операторов Мх и Му содержит лишь по
одному элементу, отличному от нуля. Следовательно, в под-
подпрограмме REDIF ненулевые вклады в массивы DMX и
DMY могут быть сгруппированы в трехкомпонентные
векторы.
Несмотря на то что конечно-элементная схема является фор-
формально девятиточечной, симметрия массовых операторов (8.44) у
а также тот факт, что расчет по формуле (8.46) необходима
проводить только при прогонках в направлении х, позволяют
воспользоваться описываемой ниже экономичной процедурой.
Сначала формула (8.46) переписывается в виде
RHS = Z {Lxxi> MYTV + MxV LYTV},
ri
(8.49)
346 Гл. 8. Многомерное уравнение диффузии
где
m—k—l m=k—l
и где, кроме того, m' = m — & + 2, Г = I — / + 2. MYT и
LYT — трехмерные массивы, связанные с узловыми точками
У— 1, / и / + 1, когда выражение для RHS центрируется в узле
(/, k). Структура формулы (8.49) следует из того, что в фор-
формуле (8.46) прежде всего рассчитываются все члены с опера-
операторами по у.
Однако расчет массивов MYT и LYT по формулам (8.50)
и (8.51) остается одним и тем же, будет ли галёркинский узел
расположен в точке /— 1, / или в точке /+ 1. Следовательно,
для большей эффективности целесообразно рассчитать только
MYT3 по формуле (8.50) и только LYT3 по формуле (8.51).
Значения MYT2 и MYTb нужные для подстановки в (8.49), бу-
будут получены путем сдвига значений MYT3 и MYT2, взятых из
расчета на предыдущем галёркинском узле, т. е. путем введе-
введения /—1 вместо /. Аналогичным образом определяются LYT2
и LYT,.
Вышеописанные приемы были использованы в работе
[Fletcher, Srinivas, 1984] при решении задачи о течении не-
несжимаемой вязкой жидкости вдоль обращенной назад ступень-
ступеньки при использовании переменных функция тока — вихрь, при-
применение которых обсуждается в п. 17.3.3.
§ 8.4. Граничные условия Неймана
В § 8.2 и 8.3 предлагается описание и реализация схем
*с расщеплением при граничных условиях Дирихле. Варианты
реализации граничных условий Неймана для одномерного урав-
уравнения диффузии, соответствующие первому или второму
порядку точности, рассмотрены в п. 7.3.1.
Здесь будут описаны процедуры для надлежащего сочета-
сочетания граничных условий Неймана со схемами расщепления, рас-
рассмотренными в § 8.2 и 8.3. Характерная задача о многокомпо-
многокомпонентной диффузии включает задание смешанных граничных
условий Дирихле — Неймана. Чтобы дать конкретный пример,
сохраним в прежнем виде первое и третье граничные усло-
условия из (8.2), заменив, однако, второе и четвертое условия на
§ 8.4. Граничные условия Неймана 347
следующие:
-—A, yf t) = g(y> t) и -*-(*> 1, t) = h(x, t), (8.52)
где g(y, t) и h{x, t)— известные функции.
8.4.1, Конечно-разностная реализация
Различные схемы, рассмотренные в § 8.2 и 8.3, имеют вто-
второй порядок точности по пространству. Граничные условия
Неймана (8.52), реализуемые со вторым порядком точности,,
имеют вид
Т 1>\ и — Т г
i-\,k
Граничные условия (8.53) будут реализовываться в сочетании
с применением обобщенной двухслойной схемы (п. 8.2.2).
Для точек, расположенных на границах А = 1 и у= 1, рас-
расчет правой части соотношения (8.23) может быть произведен
после того, как при помощи формул (8.53) будут введены до-
добавочные точки со значениями T/+i, * и Ти *+ь лежащие вне
пределов вычислительной области как таковой. Однако опера-
операторы в левых частях соотношений (8.23) и (8.24) требуют по-
построения поправок AT*+\tk и AT/.V+i- Это можно сделать с по-
помощью применения формул (8.53) на последовательности
интервалов по времени, т. е.
Д77+/, k = A77J-/, k + 2bxbgnk+\ (8.54a)
где
А^+1 = ёТх - Й> (8.54Ь)
Д77,+Д 1 = Д77Д1-! + 2 А*/ Д/гГ1. (8.54с)
Далее, чтобы провести расщепление двумерных операторов на
неявные одномерные, требуется с помощью формул (8.54) мо-
модифицировать соответствующие компоненты операторов Lxx и
Lyy. Так, при / = NX замена по формуле (8.54а) приводит к
следующему соотношению, заменяющему на первом этапе со-
соотношение (8.23):
, k = Ы (axLxx + ayLyy) Tnu k -
- 2 Ах A - а,р MLxxZ) (I - а,р MLyy) Agj+if (8.55>
:2
где L^c = {2, —2, 0}/Да:2. Однако на втором этапе соотношение
(8.24) используется без модификации. При k = NY соотноше-
348
Гл. 8. Многомерное уравнение диффузии
ние (8.23) используется на первом этапе в своем первоначаль-
первоначальном виде. Однако на втором этапе (8.24) заменяется соотноше-
соотношением
где L^ = {0, -2, 2}7Л*Л
Описанные выше процедуры были применены к расчету при-
примера, рассмотренного _ в п. 8.3.2 при граничных условиях
дТ/дхA, уу t) = 0 и дТ/ду(х, 1, /)=80, заменяющих соответ-
соответствующие граничные условия Дирихле. Однако при таком
специальном выборе граничных условий g и h в формулах
(8.52) представляют собой константы, так что правые части
соотношений (8.55) и (8.56) совпадают с правыми частями со-
соотношений (8.23) и (8.24). Точное решение для рассматривае-
рассматриваемого случая соответствует выражению (8.42). Решения были
получены при помощи схем, указанных в п. 8.3.2; среднеквадра-
среднеквадратичные ошибки приводятся в табл. 8.3.
Таблица 8.3. Среднеквадратичные ошибки в случае граничных
условий Дирихле/Неймана при t = 24 000, а = 1 X Ю~5 и sx = sy = 1.00
Ах{=Ау)
0.20
0.10
0.05
Кранк —Ни-
колсон,
мет'од
конечных
разностей
Y=0, 3=6.5
0.12940
0.03199
0.00779
дсчн,
метод
конечных
разностей
(МЕ=1),
Y—0, 0 = 1.0
1.58100
0.41120
0.10080
тсчн,
метод
конечных
разностей
Y=0.5,'
Р = 1.0
0.03985
0.02640
0.00744
Кранк — Ни-
колсон,
метод
конечных
элементов
(МЕ=2),
Y=0, 3=0.5
0.15720
0.03358
0.00788
Кранк—-Ни-
колсон,
6 = 1/12,
0.01341
0.00070
0.00021
Наблюдаемые тенденции аналогичны тем, которые относи-
относились к граничным условиям Дирихле (табл. 8.2), если не счи-
считать того, что при использовании всех методов уровень средне-
среднеквадратичных ошибок оказывается больше того, когда должны
удовлетворяться граничные условия Неймана. Типичное рас-
распределение ошибок показано на рис. 8.7. Видно, что наиболь-
наибольшие ошибки возникают на границах, где применяются гранич-
граничные условия Неймана, или вблизи таких границ. Аналогичный
эффект наблюдался в случае одномерного уравнения диффу-
диффузии (табл. 7.9), а также при решении задачи Штурма — Лиу-
вилля (§ 5.4). В тех случаях, когда все граничные условия от-
относятся к типу Дирихле, наибольшие ошибки возникают внутри
области в точках, наиболее удаленных от границ.
§ 8.4. Граничные условия Неймана 349
Интересная особенность результатов, приводимых в
табл. 8.3, относится к высокой точности данных, связанных со
схемой «четвертого порядка» для внутренних точек, когда в
формуле (8.44) имеем б = 1/12. Нелишне напомнить, что в
случае одномерного уравнения диффузии введение граничного
UNSTEADY HEAT CONDUCTION WITH NX,NY =6 6
HE = 2 GAM = .00 BETA = .50 SX,SY = 1.000 1.000
APPROX. FACT., LINEAR FEMr EMX= .167E+00 .667E+00 .167E+00
DIRICHLET B.C.
©TIM • .400E+04 PRINT INT. = .160E+05 TMAX ¦ .161E+05
T*100.000 88.775 78.650 70.614 65.455 63.677
T= 84.000 73.351 63.742 56.109 51.193 49.455
T= 68.000 58.954 50.790 44.300 40.109 38.614
T« 52.000 45.433 39.505 34.790 31.742 30.650
T* 36.000 32.549 29.433 26.954 25.351 24.775
T= 20.000 20.000 20.000 20.000 20.000 20.000
Е=
Е=
Е=
Е*
Е*
Е=
TIME
.000
.000
.000
• 000
•000
• 000
-
.000
.026
.035
.031
.017
.000
1600Е+05
.000
¦ 047
.063
.054
.031
.000
RHST »
.000
.057
.074
.063
.035
.000
.000
.047
.057
.047
.026
.000
.4710D-01
.000
.000
.000
.000
.000
.000
Рис. 8.7. Распределение ошибок с граничными условиями Дирихле и Неймана.
условия со вторым порядком точности ограничивало суммар-
суммарную точность даже при использовании схемы повышенного по-
порядка для внутренних точек.
8.4.2 Конечно-элементная реализация
При наличии определяющих уравнений, подобных уравне-
уравнению (8.1) и содержащих вторые производные, реализация гра-
граничных условий Неймана оказывает существенное влияние на
процесс дискретизации. В п. 5.4.1 это было проиллюстрировано
на примере решения одномерной задачи Штурма — Лиувилля.
Применение метода Галёркина с конечными элементами к
уравнению (8.1) приводит к нижеследующему интегральному
соотношению с весовыми функциями (§ 5.1):
^L)xdy. (8.57)
В отличие от рассмотрения, проведенного в § 5.1, в соотноше-
соотношение (8.57) не вводилось пргближенное решение для Т. Функция
Фт представляет здесь собой весовую функцию, связанную с
350
Гл. 8. Многомерное уравнение диффузии
галёркинским узлом. В связи с реализацией граничных усло-
условий Неймана представляют интерес два случая. Первый из них
относится к узлу т, расположенному на границе х = I
(рис. 8.1); второй случай, когда узел т расположен на грани-
границе у=\. Мы будем предполагать, что фт представляет собой
билинейную интерполяционную функцию (§ 5.3), хотя данный
подход справедлив по отношению к интерполяции любого по-
порядка. Вследствие локального характера функции фт(х, у) в
окончательную оценку членов уравнения (8.57) ненулевые
вклады вносятся только двумя элементами. Два случая, пред-
представляющие интерес, демонстрируются на рис. 8.8.
/т>й (гале'ркинский) узел
Элемент О
Элемент С
L
L
-1
Т
В
Т
В
R
Я
j
(b)
/77-й (галёркинский)
узел
к-\
Элемент С Элемент D
к-\
Рис. 8.8. Реализация метода Галёркина с конечными элементами у границ.,
(а) Граница х = 1; (Ь) граница у = 1.
В правой части уравнения (8.57) можно провести интегри-
интегрирование по частям. Иначе говоря, будем иметь
Если говорить о границе jc = 1, то лишь вычисление линейных
интегралов в (8.58) и (8.59) дает ненулевой вклад в каждый
элемент на границе R. Весовая функция фт равна нулю на
границах В и L элемента С, а также на границах L и Т эле-
элемента D. Вклад в линейный интеграл от границы В элемента
D тождественно погашает вклад от границы Т элемента С.
Для функций Г, фигурирующих в интегралах по площади,
вводятся общепринятые приближенные выражения
Z (8.60)
§ 8.4. Граничные условия Неймана 351
На основании (8.52) имеем dT/dx\x=i = g(t). Одномерная
.интерполяция функции g(t) вводится по формуле
g(t)=ZfVq(y)g)J(t). (8.61)
В случае интерполяции по Лагранжу ф1 (х, у) = ф* (х) <j>yq (у).
Вычисление различных интегралов в соотношениях (8.57) —
(8.59), выполненное на однородной сетке, после деления на
Дд:Ду дает
LxxTh k) + ауМх ® LvyTu k]. (8.62)
Соотношение (8.62) имеет такую же структуру, как и соотно-
соотношение (8.29) для внутренних точек, если не считать добавоч-
добавочного члена c&xMygk/kx, связанного с граничным условием Ней-
Неймана.
Если учесть, что вклады дают только два элемента, то опе-
операторы Мх и Lxx принимают вид
Операторы Му и Lyy совпадают с теми, которые определены
формулами (8.30) и (8.31).
Реализация граничного условия Неймана при у = 1 прово-
проводится аналогичным путем, если не считать того, что линейные
интегралы в (8.58) и (8.59) дают ненулевые вклады только на
границах Т элементов С и D (рис. 8.8 (Ь)). Результат, эквива-
эквивалентный (8.62), принимает вид
[мх ® Му •f-]/ k - [*ХМУ ® LxxTh k + a, {^L + MX® LyyTu к)] .
(8.64)
В соотношении (8.64) операторы Мх и Lxx задаются согласно
(8.30) и (8.31), а операторы Му и Lyy имеют вид
*«Ч°.—5?-. afT- (8'65)
Интересно сравнить, как осуществляется реализация гра-
граничных условий Неймана при использовании методов конеч-
конечных разностей и конечных элементов. Конечно-разностная фор-
форма, эквивалентная (8.29), записывается в виде
/'k ¦
(8*66)
352 Гл. 8. Многомерное уравнение диффузии
где операторы Lxx и Lyy соответствуют формулам (8.31). Вве-
Введение условий (8.53) на границе х = 1 позволяет получить
следующую локальную форму выражения (8.66):
Щ, k -2а* (-8-+L**Ti- 0+«лл. *• <8-67>
где L** задается теперь согласно (8.63), a Lyy— согласно (8.31)^
как и прежде.
Как уже было замечено при введении понятия о массовых
операторах (§ 5.5 и п. 8.3.1), эквивалентная конечно-разност-
конечно-разностная формулировка может быть построена за счет модифика-
модификации массовых операторов. Таким образом, массовые операторы
в соотношении (8.62) примут при этом вид
Mfxd = {0, 0.5, 0}, Mfyd = {0, 1, 0}г. (8.68)
Окончательная форма соотношения (8.62) совпадает с (8.67).
Следовательно, в случае билинейной лагранжевой интерполя-
интерполяции на прямоугольных конечных элементах оказывается воз-
возможным реализовать граничные условия Неймана при помо-
помощи метода Галёркина с конечными элементами путем введения
набора значений в добавочных точках Г/+1, k и Г/, к+и соответ-
соответствующих формулам (8.53), применяя при этом повсюду
формулу для внутренних точек типа (8.29). Следует подчерк-
подчеркнуть, что хотя такой подход целесообразен с точки зрения эф-
эффективности программирования, его следует применять после
того, как будет доказана эквивалентность.
Типичные результаты, полученные при помощи метода ко-
конечных элементов с граничными условиями Неймана дТ/дхA,
у у t) = 0 и дТ/ду(х, 1, t) = 80, приводятся в табл. 8.3. Общие
тенденции подобны тем, которые имели место при граничных
условиях Дирихле, за исключением того, что при наличии гра-
граничных условий Неймана ошибки, как правило, становятся
больше. Та же тенденция очевидна и по отношению к методу
конечных разностей.
§ 8.5. Метод дробных шагов
В применении к тем неявным методам, которые описывались
в данной главе, общая стратегия состояла в том, чтобы про-
провести дискретизацию, а затем переформулировать или моди-
модифицировать полученные алгебраические уравнения с целью
построения «одномерных» алгоритмов, подобных (8.27), (8.28).
Стратегия, альтернативная вышеописанной, состоит в рас-
расщеплении исходного уравнения, например (8.1), на пару урав-
уравнений, каждое из которых является локально одномерным.
§ 8.5. Метод дробных шагов 353
Тогда взамен (8.1) вводятся уравнения
°-5ж-"а^ = 0' (8-69)
0.5-§-- ах-g- = 0. (8.70)
Эти уравнения подвергаются дискретизации и решаются по-
следовательно на каждом шаге по времени. Этот класс мето-
методов был разработан советскими математиками и его подроб-
подробное описание дается в книгах [Н. Н. Яненко, 1971] и [Г. И. Map-
чук, 1974]. В книге [Mitchell,. Griffiths, 1980] эти методы
относятся к классу локально одномерных методов.
Явное представление уравнений (8.69) и (8.70) имеет вид
= A + ау btLyy) Tl ь (8.71)
Ttk = A + *x AtLxx) Ttk12. (8.72)
Если a = ax = ay, то данная схема совпадает со схемой (8.8),
(8.9). Алгоритм (8.71), (8.72) имеет ошибку аппроксимации
порядка О (At, Ах2, Ау2) и при Ах = Ау является устойчивым,
если s ^ 0.5.
Неявная реализация (8.69) и (8.70) по Кранку — Николсо-
ну имеет вид
A - 0.5ау AtLyy)Ttk12 = A + 0.5а, AtLyy)Tl k, (8.73)
A - 0.5а* AtLxx) Ttk = A + 0.5а, AtLxx) Tl+kU2. (8.74)
Соотношения (8.73) и (8.74) приводят к трехдиагональным
системам уравнений вдоль сеточных линий, параллельных у и
х соответственно; это значит, что решение может продвигаться
по времени экономичным образом с использованием алгоритма
Томаса. Схема (8.73), и (8.74) имеет второй порядок точности
по времени и пространству при надлежащем задании гранич-
граничных условий и безусловно устойчива как в двух, так и в трех
измерениях.
Уравнения (8.73) и (8.74) могут быть объединены в одну
составную схему за счет исключения 77,V/2, если только опе-
операторы Lxx и Lyy являются коммутативными; иначе говоря,
если одна и та же формула получается как за счет LxxLyyTnj*k2>
так и за счет LyyLxxTni*kn- Полученная таким образом со-
составная схема совпадает с составной схемой НПН, являющейся
результатом исключения Т* k из уравнений (8.12) и (8.13).
Однако принципиальное отличие данного подхода возни-
возникает при выполнении граничных условий. Если метод дробных
23 К. Флетчер, т. 1
354 Гл. 8. Многомерное уравнение диффузии
шагов применяется к двумерной области, показанной на
рис. 8.1, то условие Дирихле на границе х= 1, ГA, у, t)= b(y>
t) принято реализовать на промежуточном временном слое
в виде
Г&."*2 = 6"+ (8.75)
и аналогичные соотношения для граничных условий на других
границах. Такой путь выполнения граничных условий фактиче-
фактически приводит к снижению точности схемы в целом до первого
порядка по времени.
В работе [Dwoyer, Thames, 1981] исследуется проблема кор-
корректной реализации граничных условий в применении к дву-
двумерному уравнению переноса (§ 9.5). Как показано в книге
[Mitchell, Griffiths, 1980], корректное граничное условие при
х = 1, если используются уравнения (8.71) и (8.72), имеет вид
Гй^,2 = A + ау MLyy) Ы (8.76)
Это наводит на мысль о том, что при использовании схемы
(8.73), (8.74) подходящая форма промежуточных граничных
условий Дирихле при х = 1 может быть получена, если решить
уравнение
A - 0.5а^ MLyy) ГйхУ* = A + 0.5а„ AtLyy) Ы (8.77)
Можно отметить, что метод дробных шагов не позволяет по-
построить экономичный алгоритм путем введения поправок
ДГ/,"У, как можно было сделать с приближенной факториза-
факторизацией (п. 8.2.2 и дальнейший текст). Кроме того, метод дроб-
дробных шагов не дает возможности непосредственного вычисления
невязки по отношению к стационарному состоянию (см. фор-
формулу (8.25)), что играет важную роль при решении стационар-
стационарных задач с помощью псевдонестационарной формулировки
(§6.4).
§ 8.6. Заключение
Для многомерных параболических дифференциальных урав-
уравнений в частных производных, например для уравнения диф-
диффузии, неявные схемы являются более эффективными, чем
явные, в первую очередь благодаря присущему им более устой-
устойчивому поведению. Кроме того, неявная формулировка обеспе-
обеспечивает большую гибкость при построении схем повышенного
порядка [Mitchell, Griffiths, 1980].
Желая сохранить экономичность, свойственную алгоритму
Томаса, при переходе к многомерной неявной формулировке,
необходимо ввести ту или иную форму расщепления по на-
§ 8.7. Задачи 355
правлениям. Рекомендуемое построение сводится к тому, что-
чтобы представить уравнения в форме линейной системы по отно-
отношению к поправке ДГ/.V и ввести приближенную факториза-
факторизацию, например (8.22), чтобы иметь возможность воспользо-
воспользоваться многоэтапным алгоритмом, каждый из этапов которого
требует решения трехдиагональной системы уравнений.
Приближенная факторизация эффективна при применения
как конечно-разностного, так и конечно-элементного методов.
Появление массовых операторов по направлениям в конечно-
элементном алгоритме приближенной факторизации (8.39),
(8.40) дает возможность построения схемы, более точной по
пространству, путем выбора 6=1/2 в формуле (8.44). Повы-
Повышенная точность достигается как с граничными условиями Ди-
Дирихле (§ 8.3), так и с граничными условиями Неймана (§ 8.4).
Однако для сохранения точности второго порядка по време-
времени необходимо уделить особое внимание реализации граничных
условий для промежуточной поправки к решению ДГ* k, по-
появляющейся в процессе приближенной факторизации. Не-
Несмотря на то что методика реализации граничных условий Ней-
Неймана имеет концептуальные различия в зависимости от того,
применяется ли метод конечных разностей или метод конечных
элементов, форма соответствующих уравнений после дискрети-
дискретизации нередко оказывается структурно-эквивалентной.
Приемы расщепления (или приближенной факторизации),
разработанные в данной главе, после небольшой модификации
могут быт применены к двумерному уравнению переноса (§9.5),
двумерным уравнениям Бюргерса (§ 10.4), а также к уравне-
уравнениям, определяющим различные классы течения жидкости, осо-
особенно в тех случаях, когда необходимо решать уравнения
Навье —Стокса (см., например, п. 17.2.1 и 17.3.3, § 18.3 и § 18.4).
§ 8.7. Задачи
Двумерное уравнение диффузии (§ 8.1)
8.1. Примените анализ устойчивости по Нейману к схеме (8.7) и пока-
покажите, что эта схема устойчива, если 0 < s < 0.5
8.2. Для случая Ах = Ау определите ошибку аппроксимации для схемы
(8.7), если s = 1/6.
8.3. Модифицируйте программу TWDIF так, чтобы она была применима
к схеме (8.7) и проверьте путем расчетов теоретические результаты, соответ-
соответствующие задачам 8.1 р 8.2.
Методы расщепления для многомерных задач (§ 8.2)
8.4. Примените анализ устойчивости по Нейману к трехмерным эквива-
эквивалентам схемы НПН (8.14), (8.15) и схемы приближенной факторизации
(8.23), (8.24). Покажите, что трехмерная схема НПН является условно ус-
устойчивой, а схема приближенной факторизации — безусловно устойчивой
23*
356 Гл. 8. Многомерное уравнение диффузии
8.5. Модифицируйте программу TWDIF так, чтобы она была применима
к схеме НПН (8.14), (8.15) и сравните точность и экономичность этой схемы
с аналогичными качествами схемы приближенной факторизации для ME = 1,
у = о, |3 = 0.5.
8.6. Повторите сравнение, показанное в табл. 8.2, для случаев sx = sy =
= 0.5. и 1.5, объясните полученные результаты. Для варианта sx = sy = 0.5
сравните результаты с данными для схемы, рассмотренной в задаче 8.3.
Схемы расщепления и метод конечных элементов (§ 8.3)
8.7. Модифицируйте программу, составленную при решении задачи 8.5,
так, чтобы применить ее к конечно-элементному варианту схемы НПН (8.35),
(8.36), и сравните точность результатов с точностью решений, отраженных
в табл. 8.2.
8.8. Покажите, что схема (8.43), (8.44) при у = 0, Р = 0.5 эквивалентна
схеме
[1 - @.5а Л* - 6 Ах2) Lxx] T)k = [l + @.5а М + б Л*/2) Lyy] 7'* fe,
[l - @.5а Л* - б Л*/2) Lyy] Тп+? - [1 + @.5а М + 6 Л*2) Lxx] т], к.
Для специального случая б = 1/12 эта схема совпадает со схемой, имеющей
четвертый порядок по пространству и предложенной в работе [Mitchell,
Fairweather, 1964].
8.9. В программе TWDIF замените соотношение (8.48) за счет вычис-
вычисления значения ArNX ^ по формулам (8.41) при tn+i/2. Сравните точность
решения с результатами, приведенными в табл. 8.2.
Граничные условия Неймана (§ 8.4)
8.10. Модифицируйте программу TWDIF так, чтобы отразить реализацию
граничных условий Неймана в соответствии с данными, приведенными в
табл. 8.3. С помощью методов, указанных в табл. 8.3, получите решения для
случаев sx = sy = 0 5 и 1.5.
8.11. Модифицируйте программу, составленную при решении задачи 8.3,
так, чтобы получить решение с граничными условиями Неймана, сравнимое
со случаем, рассмотренным в табл. 8.3, но при sx = sy = 0.5.
8.12. Модифицируйте программу, составленную при решении задачи 8.5
для схемы НПН, так, чтобы получить решение для контрольного случая, на
основе которого составлена табл. 8.3. Сравните точность этого решения с
точностью, приведенной в табл. 8.3.
Метод дробных шагов (§ 8.5)
8.13. Модифицируйте программу, составленную при решении задачи 8.5,
так, чтобы применить ее к схеме (8.73), (8.74), и проверьте работу програм-
программы для данных, по которым составлена табл. 8.2.
8.14. Модифицируйте программу, составленную при решении задачи 8.12,
так, чтобы получить решение с условием Дирихле на границе х = 1, ис-
используя соотношение (8.77), и сравнить точность этого решения с точностью
метода дробных шагов.
Глава 9
Линейные задачи
с преобладающим влиянием конвекции
Для большинства задач обтекания движение жидкости яв-
является важным фактором, определяющим общий характер по-
потока. В уравнениях гидродинамики (гл. 11) движение жид-
жидкости характеризуется составляющими скорости иу v, w no
направлению декартовых координат х9 у, г. В одномерном
уравнении импульсов по направлению оси х
ди . ди \ . др д2и /Гк ! ч
составляющая скорости и входит в инерционный член
(du/dt + иди/дх), а также в член, характеризующий вязкую
диффузию \лд2и/дх2. Другими искомыми величинами являются
плотность р, давление р и вязкость |х.
Ранее при рассмотрении уравнения диффузии мы изучали
ловедение таких членов, как д2и/дх2. Теперь мы рассмотрим
конвективные члены типа иди/дх и обсудим, как с ними лучше
всего обращаться с вычислительной точки зрения.
Конвективный член обладает двумя не зависящими друг
ют друга особенностями, которые необходимо принять во вни-
внимание. Во-первых, этот член содержит первые производные по
пространственной переменной. При использовании для аппрок-
аппроксимации члена ди/дх симметричной трехточечной формулы в
решении возникают колебания нефизического характера, если
вязкий член оказывается малым в сравнении с конвективным.
Такое поведение связывают с воздействиями дисперсионного
типа (§ 9.2), проявляющимися через ошибку аппроксимации.
В применении к установившемуся течению мы исследуем это
явление в § 9.3.
Если при моделировании ди/дх используется несимметрич-
несимметричная алгебраическая формула, то, несмотря на нередко дости-
достигаемое улучшение гладкости получаемого решения, точность
аппроксимации ди/дх обычно оказывается на один порядок
ниже по сравнению с соответствующим представлением с по-
помощью симметричной алгебраической формулы, охватываю-
охватывающей то же самое число узловых точек. При использовании
358 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
несимметричных формул низкого порядка в ошибку аппрокси-
аппроксимации могут быть привнесены такие слагаемые, которые по
своей величине будут сравнимы с величиной важных физических
членов, учитываемых здесь.
Этот аспект решения будет принят во внимание в § 9.2 при
рассмотрении уравнения, описывающего чисто конвективный
процесс, в § 9.3 для уравнения стационарной конвекции — диф-
диффузии, а в § 9.4 для уравнения переноса. Уравнение переноса
получается из уравнения (9.1) путем линеаризации конвектив-
конвективного члена (т. е. путем замены иди/дх на гди/дх), пренебреже-
пренебрежения членом с градиентом давления др/дх и предположения
о том, что величины е и р известны.
Второй важной особенностью конвективного члена являет-
является его нелинейность по отношению к искомой переменной.
В случае сверхзвукового невязкого потока (п. 11.6.1) нелинейный
характер конвективных членов приводит к тому, что становит-
становится возможным появление ударных волн. Этот нелинейный ха-
характер конвективных членов мы будем обсуждать главным
образом в связи с уравнением Бюргерса в гл. 10.
§ 9.1. Одномерное линейное уравнение конвекции
Для исследования задач, связанных с конвекцией, рассмот-
рассмотрим следующее линейное уравнение:
где и — известная скорость, a f — пассивная скалярная вели-
величина, например температура. Уравнение (9.2) гиперболическое.
Его можно интерпретировать как некую модель для конвек-
конвективной части уравнения энергии A1.44).
Если величина и постоянна и положительна, то общее ре-
решение уравнения (9.2) можно записать в виде
T(x,t) = F(x-ut\ (9.3)
где начальное условие задается выражением
T(x,0) = F(x), (9.4)
причем функция F(x) известна. Если эта функция определена
во всем диапазоне изменения х, —оо ^ х ^ оо, то решение в
некоторой заданной точке (х\, t\) плоскости (лг, t) совпадает
с решением для точки с координатой хх — ut\ в момент време-
времени t = 0, т. е.
Т(хи tl) = F(xl-utl) = f{xl-utu 0).
§ 9.1. Одномерное линейное уравнение конвекции
359
Это показано графически на рис. 9.1. Решение Т оказывается
постоянным вдоль таких линий, как линия ЛВ, служащая ха-
характеристикой для этого уравнения (рис. 2.5).
9.1.1. Схема с разностями вперед по времени
, и центральными по пространству (ВВЦП)
Простейший алгоритм для решения уравнения диффузии
связан с использованием схемы ВВЦП согласно уравнению
<G.5). Соответствующее представление уравнения (9.2) с ис-
T(x,O)=F(:c)
ACXj-lftpO) X
Рис. 9.1. Зависимость решения от начальных данных.
пользованием разностей вперед по времени и центральных по
пространству будет иметь вид
2 tax
L (9.5)
Разностное уравнение (9.5) может быть представлено в форме
.алгоритма
77+1 = 77 - 0.5С G7+i - 77-1), (9.6)
аппроксимирующего уравнение (9.2) с ошибкей порядка О (А/,
Дл:2). Величина С, входящая в формулу (9.6), называется чис-
числом Куранта и определяется выражением
C = uj^. (9.7)
Если применить к алгоритму (9.6) анализ устойчивости по
Нейману, то для т-й компоненты начального распределения
ошибки получится коэффициент усиления в виде
G=l —/С sine. (9.8)
Ясно, что |G|^l при любых 9, так что алгоритм (9.6)
является безусловно неустойчивым. Можно вспомнить, что
360 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Таблица 9.1. Алгебраические схемы (дискретизация)
Схема
Алгебраическая форма
Ошибка аппроксимации Е *
(главные члены)
ввцп
+uLxT]=0
Си
Ах\ д2Т
дх2
(¦?¦)
Вверх по
потоку
тп+\
11 ~у|-1
д2Т
дх2
+.(*•!)
«Чехарда»
Лакса —
Вендроффа
дгп+1
"~дГ~
дАТ
дх*
Кранка —
Николсона
.-.-.
§ 9.1. Одномерное линейное уравнение конвекции
361
для уравнений конвекции дТ/dt + и дТ/дх = О
Коэффициент затухания G
@=:тяДх)
1 — 1С sin 6
1 _ с A — cos 9) — iC — sin 9
-/Csin9± A -C2sin29I/2
1 _ ic sin 9 - 2C2 sin2 (|-)
A - 0.5/C sin 9)/(l + 0.5/C sin 9)
Условие
устойчи-
устойчивости
Неустой-
Неустойчивая
C< 1
C<1
C<1
Нет
Замечания
с = «^
А*
L -1 > 2 ' 1
** 1 Ах2 ' Д*2 ' Дх2 j
362 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Схема
Алгебраическая форма
Ошибка аппроксимации Е *
(главные члены)
Трехслой-
Трехслойная,
полностью
неявная
—J—
1
3 Д7
rt+1
М
1 ATf
2 At "¦"
дх3
Линейная
КЭ/Кран-
ка — Ник ол
сон а
ш
Mx
At
¦ +
/ Ax2 \ d3T
lT2"J дх3
+ uLx
как в методе
* Ошибка аппроксимации Е выражена через Ах и производные по х,
эквивалентно уравнению дТ/dt -f и дТ/дх + Е (Т)=0.
эквивалентная схема ВВЦП была условно устойчивой в приме-
применении к уравнению диффузии. Благодаря отсутствию устойчи-
устойчивости следует сделать вывод, что схема ВВЦП практически
неприменима к решению задач о чистой конвекции. Для пол-
полноты информации свойства схемы ВВЦП в применении к урав-
уравнению (9.2) суммируются в табл. 9.1.
9.1.2. Схема с разностями против потока и условие КФЛ
Альтернативная схема может быть получена при введении
разностной формулы для дТ/дх со сдвигом назад в предполо-
предположении, что величина и положительна. Тогда дискретизация
уравнения (9.2) принимает вид
Г? цG7-77_,)
"¦ Ах '
или в алгоритмическом представлении
(9.9)
(9.10)
§ 9.1. Одномерное линейное уравнение конвекции
363
Таблица 9.1 (продолжение)
Коэффициент затухания Q
(в=тяД*)
1 ±4-iC + /8Csin9I/2
2(i + 'HTsine)
B + cose~ \.ЫС sin 6)
B +cos 6 + 1.5/CsinG)
Условия
устойчи-
устойчивости
Нет
Нет
Замечания
м / х 2 х \
модифицированных уравнений (п. 9.2.2). Таким образом, алгебраическое представление
В случае отрицательного и вместо (9.10) применяется форму-
формула 77+1 = A-|С|)Г/ +|C|77+i. Согласно формуле (9.10),
решение 77+1 определяется информацией из области, располо-
расположенной вверх по потоку от узла (/, п). Следовательно, схема
(9.10) будет упоминаться в дальнейшем как схема с разностя-
разностями против потока (табл. 9.1). Численные решения, полученные
на основе разностной схемы против потока, будут изложены в
л. 9.1.5.
Если применить к схеме (9.10) анализ устойчивости по Ней-
Нейману, то получится коэффициент усиления, показанный в
табл. 9.1. Решения получаются устойчивыми, если
С = и-^<1. (9.11)
Неравенство С ^ 1 называют обычно условием Куранта —
Фридрихса — Леей (КФЛ). Вообще говоря, это условие при-
применимо ко всем явным схемам для дифференциальных урав-
уравнений в частных производных гиперболического типа. С физи-
физической точки зрения условие КФЛ означает, что частица
364 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
жидкости за один шаг по времени At не должна продвигаться
более чем на один пространственный шаг Ах.
В частном случае при С=1 формула (9.10) дает
Т*}+l =Т?-\, что является точным решением уравнения (9.2);
это иллюстрируется на рис. 9.1.
Разложение точного решения в ряд Тейлора в окрестности
узла (/, л), подставленное в формулу (9.10), дает результат
дТ дТ д2Т д2Т
~л7—I" и ~л 1~ 0.5 At -гтг 0.5и Ах -^-т- + О (At2, Ax2) = 0. (9.12)
01 и X (jt (j X
Следовательно, формула (9.10) не противоречит уравнению
(9.2), но содержит в себе ошибку аппроксимации, главные чле-
члены которой имеют порядок О {At, Ax). Из уравнения (9.2)
получаем
дТ „ дТ д2Т ? 2 д2Т
dt ~ " дх ' dt2 """"- дх2 f
и, следовательно, уравнение (9.12) можно переписать в виде
+и 05«Дл:AС)|5 + О(А/2 А^2) 0
Если считать, что ошибка аппроксимации при использовании
формулы (9.10) имеет порядок О (А/2, Ах2), то вместо уравне-
уравнения (9.2) эта формула будет соответствовать уравнению
дТ . дТ , д2Т п /п л оч
~S7"+ w-5 а "т-2- = 0. (9.13)
Это значит, что использование двухчленного конечно-разност-
конечно-разностного представления дТ/дх со сдвигом вверх по потоку в соче-
сочетании с разностной формулой для dT/dt при сдвиге по вре-
времени вперед вносит искусственную (численную) диффузию с
коэффициентом а7 = 0.5аДхA — С). Ясно, что коэффициент ис-
искусственной диффузии обращается в нуль, когда С= 1; это и
не удивительно, поскольку формула (9.10) в таком варианте
соответствует точному решению.
Может показаться, что выбор А/, дающего С= 1, позволит
обойти проблему искусственной диффузии. Хотя это и дей-
действительно так в применении к линейному уравнению конвек-
конвекции, однако при рассмотрении нелинейных уравнений, подоб-
подобных уравнению Бюргерса (§ 10.1), когда скорость и (входящая
в выражение для С) изменяется в пространстве, невозможна
обеспечить равенство С = 1 во всех точках.
§ 9.1. Одномерное линейное уравнение конвекции 365
9.1.3. Схема «чехарда» и схема Лакса — Вендроффа
Применяя подход, использовавшийся ранее к уравнению
диффузии, попытаемся построить более точную модель урав-
уравнения (9.2) с помощью введения центральных разностей как по
времени, так и по пространству. Это приводит к схеме «че-
«чехарда»:
тп + \__тп-\ и(Тп Тп \
2L | v J + l J~lJ — о /q 141
_2 _ _|
2 А/ + 2 Ах
и соответствующему ей алгоритму
Формула (9.15) соответствует уравнению (9.2) с ошибкой
аппроксимации, имеющей порядок О (At2, Ax2). Применение к
(9.15) анализа устойчивости по Нейману дает коэффициент
усиления G, представленный в табл. 9.1. Как можно видеть,
\G\ = 1.0, если С ^ 1, однако при некоторых значениях В по-
получим \G\ > 1.0, если С > 1. Следовательно, если удовлетво-
удовлетворяется условие КФЛ, схема «чехарда» будет нейтрально устой-
устойчивой. Это и желательно, так как в этом случае решение не
затухает с течением времени; отметим, что на то же самое ука-
указывает и физический характер процесса конвекции согласно
(9.2).
Как нетрудно видеть, решение Г/+1, обеспечиваемое фор-
формулой (9.15), как бы перепрыгивает через решение Тп\\ отсюда
и название — схема «чехарда». Однако структура формулы
(9.15) указывает на то, что вычислительная сетка уподобляется
здесь шахматной доске; решение, строящееся для «черных»
полей», оказывается совершенно независимым от решения для
«белых полей». Это обстоятельство может приводить к появ-
появлению двух «расщепившихся» решений. Роуч [Roache, 1972]
обсуждает различные варианты стратегии для преодоления дан-
данного затруднения, одним из которых является осреднение ре-
решения по двум временным слоям, а именно п и /г + 1.
Халтнер и Уилльямс [Haltiner, Williams, 1980] провели
анализ применения схемы «чехарда» (9.15) к задаче с гармо-
гармоническим начальным условием, т. е. когда функция в правой
части формулы (9.4) принимает форму F(x)=exp(ijm&x),
где m — волновое число (§ 9.2). Они получили для (9.15) ана-
аналитическое решение, состоящее из двух волн или двух мод, про-
происхождение которых связано с тем, что формула (9.15) кор-
коррелирует между собой три временных слоя. Одна из этих мод
соответствует физическому решению, а вторая — это паразитная
«вычислительная» мода, распространяющаяся в направлении,
366 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
противоположном моде физического решения, причем величина
этой моды меняет свой знак на каждом шаге по времени.
В случае линейного уравнения конвекции вычислительную
моду решения можно подавить за счет выдлежащего выбора до-
добавочного слоя начальных данных, т. е. задавая не только Тп,
но и Тп~1. Однако в применении к нелинейным задачам вычис-
вычислительная мода, присущая решению по схеме «чехарда», мо-
может неограниченно развиваться и ухудшить перспективу
разделения решения на соседних временных слоях, о которой
упоминалось ранее. Стратегии такого типа, как осреднение, су-
существенно подавляют вычислительную моду, не оказывая за-
заметного воздействия на физическую моду.
Схема «чехарда» является трехслойной, и поэтому при ее
применении требуется некий альтернативный подход для реа-
реализации первого шага по времени. Эту схему рекомендуется
применять [Morton, 1971] для решения гиперболических задач,
например задач, описываемых уравнением конвекции (9.2); за-
заметим, что эквивалетная схема Ричардсона для уравнения
диффузии является неустойчивой.
Схема Лакса — Вендроффа представляет собой весьма эф-
эффективный (и популярный) алгоритм для решения уравнений,
описывающих течение невязкой сжимаемой жидкости (§ 10.2 и
п. 11.6.1). В применении к уравнению конвекции (9.2) схема
Лакса — Вендроффа совпадает с методом Лейза [Leith] (см.
[Roache, 1972]). Оба метода основаны на построении прибли-
приближения второго порядка для члена с помощью разложения в
ряд Тейлора, в результате которого получается представление
5Г~ и 0**Ж=Чг
После введения представления для д2Т/дх2 с применением
центральных разностей мы приходим к конечно-разностной мо-
модели для уравнения (9.2) по Лаксу — Вендроффу в форме
77+1 = Г? - 0.5С G7+1 - 77-0 + 0.5С2 (Г,я_, - 2Г? + Г/+0- (9.16)
Схема Лакса — Вендроффа согласуется с уравнением (9.2)
при ошибке аппроксимации порядка О (At2, Ax2) и является
устойчивой, если удовлетворяется условие КФЛ С ^ 1.0
(табл. 9.1). Численные решения с использованием схемы Лак-
Лакса — Вендроффа приводятся в п. 9.1.5.
9.1.4. Схемы Кранка — Николсона
Схема Кранка — Николсона оказывается весьма эффектив-
эффективной в применении к одномерному уравнению диффузии. В дан-
данном разделе конечно-разностные и конечно-элементные схемы
§ 9.1. Одномерное линейное уравнение конвекции 367
Кранка — Николсона применяются к одномерному уравнению
конвекции (9.2).
Конечно-разностная схема Кранка — Николсона может быть
записана в виде
1 д/ ' + и @.51*77 + 0.5L *Г?+1) = 0, (9.17)
где LxTj =(Tj+i — Tj-i)/2Ax. Из уравнения (9.17) получается
следующий трехдиагональный алгоритм:
—0.25С77+11 + Г/ + 1 + 0.25СГ/+11 = 0.25СГ/-1 + Т" — 0.25СГ/+ь
(9.18)
для которого можно построить эффективное решение с по-
помощью алгоритма Томаса (п. 6.2.2). Схема Кранка — Николсо-
Николсона согласуется с уравнением (9.2) и обладает погрешностью
порядка О (At2, Ax2). Анализ устойчивости по Нейману дает
коэффициент усиления G, показанный в табл. 9.1. Ясно, что
схема Кранка — Николсона является безусловно устойчивой.
Если к уравнению (9.2) применить метод конечных элемен-
элементов Галёркина с нелинейной интерполяцией по пространству,
то получается следующая система обыкновенных дифферен-
дифференциальных уравнений:
M*[ilrl + uLxTi = 0' (919)
в которую входит массовый оператор Мх = {-?, -|, ^}. Введе-
Введение разностного представления dT/dt по Кранку — Николсону
приводит к схеме
уП-\-1 'рП
Мх \t ' +uLx[0.5 {T? + Ti+i)] = 0, (9.20)
которую можно сравнить со схемой (9.17). Массовый оператор
можно представить в более общем виде, аналогичном формуле
(8.44), а именно
Мх^{6, 1-26, б}, (9.21)
где значение б = 1/6 дает конечно-элементную форму, а зна-
значение 6 = 0 — конечно-разностную форму. После подстановки
(9.21) в уравнение (9.20) получается трехдиагональный алго-
алгоритм
(б — 0.25С) T^l + A - 26) Г/+ 1 + (б + 0.25С) Т?$\ =
= (б + 0.25CO7-i + A - 26) Г? + (б - 0.25С) Т?+\. (9-22)
Реализацию этого алгоритма дает программа TRAN (рис. 9.8).
Конечно-элементная форма (9.20) обладает ошибкой аппрок-
аппроксимации порядка О (At2, Ax4). Следовательно, при достаточно
368 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
малых шагах по времени, когда погрешность решения опре-
определяется преимущественно пространственной дискретизацией,
конечно-элементная схема Кранка — Николсона дает более
точные результаты, чем конечно-разностный метод, построен-
построенный по аналогичной схеме. Происхождение ошибки аппрокси-
аппроксимации второго порядка, показанной в табл. 9.1, связано с трак-
трактовкой члена А/2 на основе модифицированного уравнения
(п. 9.2.2). Если величины Сии имеют порядок 0A), то член
Д^2 играет преобладающую роль при определении ошибки
аппроксимации. Конечно-элементная схема Кранка — Николсо-
Николсона (9.20) является безусловно устойчивой (табл. 9.1). Как
видно из табл. 9.1, при применении к уравнению диффузии ти-
типичные неявные схемы являются безусловно устойчивыми.
Однако применение неявных схем к гиперболическим уравне-
уравнениям не обязательно обеспечивает их преимущество. При ис-
использовании неявной схемы на заданном временном слое
п + 1 получается некая система связанных между собой урав-
уравнений. Поэтому любое возмущение, связанное, например, с
округлением и возникающее в одном из узлов (/, п), влияет на
решение во всех узлах (/, п+1) на следующем временном
слое. Такое поведение физически соответствует дифференциаль-
дифференциальному уравнению в частных производных параболического типа
(п. 2.3.2), подобному уравнению диффузии.
В противоположность вышесказанному возмущения в реше-
решениях для уравнений в частных производных гиперболического
типа (п. 2.2.2) распространяются с конечными скоростями. При
решении дифференциальных уравнений в частных производ-
производных гиперболического типа с помощью неявных схем обычно
возникают существенные неточности, если только величина М
(или величина С) достаточно велика. Если же величина Д/
мала, т. е. если для уравнения конвекции С ^ 1.0, то примене-
применение неявных методов не обеспечивает преимущества в устой-
устойчивости, хотя оно и может дать некоторое преимущество в точ-
точности, как это имеет место с конечно-элементной схемой Кран-
Кранка — Николсона.
9.1.5. Линейная конвекция усеченной синусоидальной волны
Чтобы проиллюстрировать особенности применения раз-
различных схем при решении уравнения (9.2), рассмотрим распро-
распространение синусоидальной волны. Это значит, что уравнение
(9.2) должно решаться при начальном условии
= sin (IOjxjc) при 0<*<0.1,
-0 при 0.1<*<1.0 (9'23)
§ 9.1. Одномерное линейное уравнение конвекции
369
и при граничных условиях
г (о, о = о, П1, о = о.
Точное решение, справедливое вплоть до t = 0.9/w, имеет вид
{=0, 0<x<tt/,
= sin [10я (х - ut)]9 и/ < * < itf + 0.1, (9.24)
= 0, ut + ОЛ <jc<1.0.
Кривые точного решения для значения « = 0.1, определенные
при / = 0 и 8, показаны на рис. 9.2. Синусоидальная волна
распространяется без уменьшения амплитуды со скоростью
01
i.e _
8.6 .
5.4 .
е.2
\ Точное
} решение
.1
F I
i I
Точное
решение
t~8.f
в.2
8.2 8.4 8.6* Ю.8 1.8
Рис. 9.2. Решение уравнения конвек- Рис. 9.3. Решение уравнения конвек-
конвекции с помощью схемы с разностями ции по схеме Лакса — Вендроффа при
против потока. С = 0.8.
Различные схемы, описываемые в п. 9.1.2—9.1.4, реализуют-
реализуются в программе TRAN, распечатка которой показана на рис. 9.8,
при а = 0. Эта программа обеспечивает построение численных
решений одномерного уравнения переноса и описана в
п. 9.4.3. В применении к данной конкретной задаче точное ре-
решение (9.24) рассчитывается с помощью подпрограммы EXSOL
(рис. 9.9).
Численные решения были получены для 41 точки, располо-
расположенной равномерно в пространстве на интервале 0 ^ х ^ 1.0,
при числе Куранта С = 0.8. Решение, полученное с помощью
программы TRAN при ? = 8.0 (т. е. после 40 шагов по времени)
в результате применения схемы (9.10) с разностями против по-
потока, показано на рис. 9.2. Численное решение имеет гладкую
форму, однако в сравнении с точным решением оно оказывается
24 К Флетчер, т. 1
370 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
размазанным (или диффузно сглаженным); это обстоятельства
соответствует введению членов с искусственной вязкостью, по-
подобно тому, как это имеет место в уравнении (9.13).
Решение с помощью схемы Лакса — Вендроффа (9.16) по-
показано на рис. 9.3 для значений t = 8.0 и С = 0.8. Можно на-
напомнить, что структура схемы Лакса — Вендроффа эквивалент-
эквивалентна структуре схемы ВВЦП (являющейся неустойчивой) прет
добавочных диффузионных членах, соответствующих формуле
05СА
Решение Лакса — Вендроффа характеризуется первичной
волной уменьшенной амплитуды, распространяющейся медлен-
медленнее точного решения, а также появлением вторичных волн в
i.e.,.. . «спутном следе» первичной
т
8.8 .
8.6 .
«спутном следе» первичной
$ jj волны. Если начальное усло-
]| Точное t\ Точное вие (9.23) представить в фор-
i \ решение j \ решение ме ряда Фурье, а индивиду-
индивиду(
j 1 t-9.8 j j t-8.8
li
альные слагаемые (моды) ре-
решения восстановить так, что-
f i j бы получить решение Лак-
* jVi ca — Вендроффа при / = 8.0,
А А / I ^ то УП0МЯНУтый «спутный след»
j ]# /\ М И * j ]# соответствовал бы коротко-
fe_/*Li jLLlL- IlJLI—1—* волновым слагаемым, рас-
** 8?г| ie.'4J el б] в.8 l.e
• у 1/ 1 / х
8.2
| ie.'4J el б] в.8 l.e пространяющимся медленнее,.
у 1/ 1 / х чем основное слагаемое. Вол-
* Ч М новой пакет, следующий за
Рис. 9.4. Решение уравнения конвек- ОСНОВНЫМ решением, принято
ции по схеме Кранка — Николсона называть «дисперсионным еле-
при С = 0.8. дом». Эта дисперсия будет
обсуждаться в § 9.2.
Можно отметить, что при С= 1.0 как схема с разностями
против потока, так и схема Лакса — Вендроффа воспроизво-
воспроизводят точное решение. В то же время неявные схемы, подобные
конечно-разностной схеме Кранка — Николсона, этого не де-
делают. Конечно-разностное решение Кранка — Николсона при
/ = 8.0 и С = 0.8 показано на рис. 9.4. Это решение содержит
первичную волну, распространяющуюся медленнее точного ре
шения, а также существенный дисперсионный след.
Соответствующее конечно-элементное решение Кранка — Ни-
Николсона несколько точнее, чем решение, показанное на рис. 9.4;
его максимальная амплитуда несколько больше, а дисперсион-
дисперсионный след — меньше. Однако при С = 0.8 и и = 0.1 преобладаю-
преобладающее влияние на ошибки оказывают члены, пропорциональные
А?2. При С = 0.1 и при больших значениях и более важную
роль начинают играть члены четвертого порядка по простран-
§ 9.2. Численная диссипация и дисперсия 371
сгву и конечно-элементная схема Кранка —- Николсона оказы-
оказывается значительно точнее других схем.
Особенности течения, показанные на рис. 9.2—9.4, будут
еще раз рассмотрены в конце § 9.2. Следует подчеркнуть, что
.для лучшего выявления некоторых проблем расчета течений
с преобладающим влиянием конвекции здесь были использо-
использованы сравнительно грубые сетки (Ах, Д?), а также относитель-
относительно «трудное» начальное условие. Однако остается в силе
утверждение о том, что построение численных решений чисто
диффузионного уравнения значительно проще, чем такого же
уравнения с конвективным членом.
§ 9.2. Численная диссипация и дисперсия
Многие явления в гидродинамике описываются системами
уравнений, которые обладают свойствами «гиперболичности»,
т. е. у них либо совсем отсутствуют диссипативные члены,
либо они имеют малый порядок. Для решений таких уравне-
уравнений характерным являются волновые пакеты, которые рас-
распространяются с постоянной либо слабо меняющейся амплиту-
амплитудой. Очень важно, чтобы численные схемы не вносили нефизи-
нефизическую диссипацию, как, например, при решении уравнения
(9.10) (рис. 9.2). Важно также, чтобы численные схемы не
влияли на скорость распространения волн, т. е. численные схе-
схемы не должны вносить искусственную дисперсию, приводящую
к результатам, показанным на рис. 9.4.
Решение, описывающее бегущую плоскую волну с диссипа-
диссипацией и дисперсией, можно представить в виде
p *e»>i', (9.25)
где Гатр — вещественная положительная величина, m — волно-
волновое число, связанное с длиной волны X соотношением X = 2я/т.
В выражении (9.25) величина р(пг) определяет скорость зату-
затухания амплитуды волны, a q{m)—скорость распространения
волны.
Если движение плоской волны (9.25) описывается линей-
линейным уравнением конвенции, то р(пг) и q(m) принимают зна-
значения р(пг) = 0 и q(m)=u, т. е. волны любой длины распро-
распространяются с постоянной скоростью и не затухают.
Весьма поучительно рассмотреть два уравнения, которые
близко связаны с уравнением конвекции (9.2), а именно
24*
372 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Уравнение (9.26) представляет собой уравнение переноса, ко-
которое будет рассматриваться в § 9.4, а уравнение (9.27) яв-
является линейным уравнением Кортевега де Вриза. Для плоских
волн, описываемых уравнением (9.26), входящие в решение
(9.25) параметры принимают вид
р (щ) = am2, q (m) = ы, (9.28)
т. е. затухание амплитуды волны определяется диффузионным
членом, а скорость распространения постоянная. Так как
т = 2лД, то короткие волны затухают быстрее, чем длинные.
Для плоских волн, описываемых уравнением (9.27), имеем
= о, q(m) = u — $m2, (9.29)
т. е. амплитуда волны не меняется, а скорость ее распростране-
распространения зависит от длины волны. Если имеются волны с разной
длиной, то они распространяются с различными скоростями,
т. е. диспергируют. Более значительным изменениям подвер-
подвергается скорость распространения коротковолновых возмущений
(большие т). Так, если р положительна, то короткие волны
движутся намного медленнее.
Формально теперь мы можем определить диссипацию как
затухание амплитуды плоских волн, а дисперсию как распро-
распространение плоских волн различной длины с разными скоростя-
скоростями q(m). Говоря о роли старших производных в уравнениях
типа (9.26) и (9.27), можно связать положительную диссипа-
диссипацию с появлением пространственных производных четного по-
порядка, умноженных на коэффициенты переменного знака. Ана-
Аналогично уменьшение скорости распространения волны можно
связать с появлением пространственных производных нечетного
порядка, умноженных на коэффициенты переменного знака.
При исследовании пригодности (§ 4.2) дискретизированного
уравнения, например (9.9), кажется, что разностный алгоритм
такой, как (9.10), эквивалентен исходному уравнению в част-
частных производных плюс ошибка аппроксимации на разностной
сетке. Но ошибка аппроксимации обычно связана со старшими
производными четного и нечетного порядков. Связь между дис-
диссипацией, дисперсией и старшими производными в ошибках
аппроксимации будет обсуждаться в п. 9.2.2.
9.2.1. Разложение в ряд Фурье
Количественные оценки диссипации и дисперсии численной
схемы, вносимые тем или иным вычислительным алгоритмом,
могут быть получены путем разложения точного и численного
решений в ряд Фурье. Так, для частного примера, рассмотрен-
§ 9.2. Численная диссипация и дисперсия 37&
ного в п. 9.1.5, фурье-разложение начального условия (9.23)
имеет вид
Т(х,0)= Е Тте^\
т= — оо
Используя метод разделения переменных (п. 2.5.2), точное ре-
решение в любой момент времени можно представить в виде ряда
оо
Т(х, 0= Е Tmeim <*-<>, (9.30)»
m— — оо
который восстанавливает точное решение (9.24). Фурье-компо-
Фурье-компоненты в (9.30) имеют постоянную скорость и амплитуду, так
как уравнение (9.2) не содержит диффузионных членов.
Аналогичным образом можно записать фурье-представление
и для решения конечно-разностного алгоритма, например схемы
против потока (9.10), в виде
оо
T(x,t)= Z Tme-p<<m^eim^-^m^\ (9.31>
m= -oo
Поскольку рассматриваемое алгебраическое уравнение (9.10)
является линейным, фурье-компоненты его решения могут рас-
рассматриваться независимо.
На одном шаге по времени Д/ волна, описываемая пг-й ком-
компонентой приближенного решения, пройдет расстояние q(m)At
с уменьшением амплитуды, которое определяется множителем
ехр [—p(m)At]. В течение того же промежутка времени гп-я
волна пройдет расстояние ukt с постоянной скоростью. Если к
вычислительному алгоритму предъявляется требование отсут-
отсутствия искусственной вязкости или дисперсии, то должно быть
р (щ) = 0, a q (m) = u.
Выражения для p(m) и q(m) можно получить подстанов-
подстановкой (9.31) в (9.10) и вычислением отношения амплитуд гп-й
компоненты фурье-представления на одном шаге по време-
времени, т. е.
т p-p(m)(t+At) im[x-q{m)(t + At)]
Q =i-^ f = p-[p(m) + tm^(m)]Af (9 32V
Tme"p{m)teim[x~qim)t] ' [?.oz}
Подстановка в (9.10) дает отношение амплитуд
Gm = 1 + С [cos (mkx) — 1] — iC sin (mA*). (9.33)
He удивительно, что оно в точности совпадает с выражением
(табл. 9.1), полученным при оценке устойчивости по Нейману
разностной схемы с разностями вверх по потоку (9.10).
374 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Из соотношений (9.32) и (9.33) получаем
| G \т = е-рсод* = 1 — 4СA — С) ът2@.ЬтАх). (9.34)
.Для устойчивого решения p(m)^0 неустойчивость может быть
связана с отрицательной диссипацией. Кроме того, выражение
(9.34) может служить мерой диссипации алгоритма (9.10). Па-
Параметр диссипации р(т) зависит как от С, так и от множителя
тАх, определяемого волновым числом. Коэффициент затуха-
затухания будет наибольшим при тАх = я, т. е. для более коротких
волн.
Скорость распространения волн q(m) связана с фазой фт
ютносительного затухания амплитуды Gm соотношением
• / \ \2 а —С sin (mkx) /о осч
фт - -тц (*,) Ы = arctg , +C[cos(^/_ ц . (9.35)
где фт — изменение фазы т-и волны на одном временном шаге.
Для точного решения
^>ех = —muAt = —Cm Ал:.
Таким образом,
^Г ~ ~ \ СгпЪ* ) g V 1+С [cos (тДх) - \]
Скорость волны (или эквивалентное изменение фаз) разностно-
разностного решения тем ближе к точному решению, чем меньше вели-
величина тДх, и ошибка растет при тАх-^п.
Если 0 < С < 0.5, то q (т) < и для больших т\х.
Если 0.5 < С < 1.0, то q(m)>u для больших тАх.
Различные разностные схемы, рассмотренные в § 9.1, при-
приводят к различным выражениям в правой части (9.33), что в
свою очередь приводит к различным значениям р{т) и q(m)
в (9.32).
Вводя фурье-разложение для точного и приближенного ре-
решений и рассматривая относительное изменение параметров
т-й гармоники, можно получить выражения для диссипации и
дисперсии численной схемы для любого значения величины
тАх. Мортон [Morton, 1971] использовал такой подход для
численных схем, рассмотренных в § 9.1.
Наименьшая длина волн, которую может представлять раз-
разностное решение к = 2Ах, что равносильно тАх = я. Длинные
волны соответствуют тАх-+0. Если разностная схема вносит
какую-либо диссипацию или дисперсию, то, как следует из
(9.26) — (9.29), можно ожидать, что короткие волны будут иска-
искажаться значительнее, чем длинные. С физической точки зрения
§ 9.2. Численная диссипация и дисперсия 375»
предпочтительней моделировать длинноволновые характеристи-
характеристики (малые тАх) точно и проверять, чтобы любые искусственно
вводимые коротковолновые характеристики затухали физиче-
физически и численно. Такая стратегия совпадает с анализом, приве-
приведенным в п. 3.4.2.
9.2.2. Метод модифицированного уравнения
Как мы уже видели, диссипацию и дисперсию можно свя-
связать с наличием вторых и третьих пространственных производ-
производных, как это было в уравнениях (9.26) и (9.27). Это предпо-
предполагает, что из анализа ошибки аппроксимации можно опреде-
определить диссипативные и дисперсионные свойства частного*
вычислительного алгоритма. Однако ошибка аппроксимации
должна интерпретироваться специальным образом.
Предположим, что L(r) = 0 — дифференциальное уравнение,
a La(T)=0 — алгебраическое уравнение, например (9.9). Сле-
Следовательно, в свете вышеприведенных рассуждений об ошибке
аппроксимации Еп\ можно написать
L (?) = La (?) - g} (f) = 0. (9.37>
Откуда для ошибки аппроксимации получаем
La (T) = L(T) + E (T) = 0, (9.38)*
где алгебраическое уравнение представлено в виде разложения
приближенного решения в ряд Тейлора. Уравнение (9.38) пре-
преобразуется таким образом, чтобы выражение Е(Т) содержало-
только пространственные производные. С этой целью уравне-
уравнение (9.38) неоднократно дифференцируется для исключения
производных по /, а также смешанных производных. Это не-
несколько другая ситуация, чем в уравнении (9.37), где ошибка
аппроксимации может улучшаться преобразованием L(f)=0.
Уравнение L (Т) + Е (Т) = 0 представляет собой дифферен-
дифференциальное уравнение с бесконечным числом членов. Оно назы-
называется модифицированным уравнением [Warming, Hyett, 1974],.
решение которого будет строиться с помощью алгебраического
уравнения при наличии соответствующих граничных условий..
Как и выше, это модифицированное уравнение можно исполь-
использовать для демонстрации точности вычислительного алгоритма.
В модифицированном уравнении производные нечетного по-
порядка связаны с дисперсией, производные четного порядка —
с диссипацией. Следовательно, рассматривая члены с производ-
производными наименьших четного и нечетного порядков в модифици-
модифицированном уравнении, мы можем судить о диссипативных и.
376 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
дисперсионных свойствах алгебраической схемы, но только для
больших длин волн. Это происходит в силу того, что модифи-
модифицированное уравнение получено на основе разложения в ряд
Тейлора, что предполагает малые значения Д^ и Дх. Однако,
• как отмечалось выше, именно длинноволновые характеристики
представляют наибольший интерес.
С помощью модифицированного уравнения можно показать,
что при использовании схемы Лакса — Вендроффа (9.16) для
решения уравнения (9.2) главный член в ошибке аппроксима-
аппроксимации имеет вид
Как отмечалось выше, схема Лакса — Вендроффа аппроксими-
аппроксимирует (9.2) с точностью до О (At2, Ах2). Из приведенного выше
выражения для ошибки аппроксимации видно, что дисперсия
имеет второй порядок, а диссипация — третий. Модифициро-
Модифицированное уравнение было использовано при получении выраже-
выражений для ошибки аппроксимации в табл. 7.1, 9.1 и 9.3, так что
можно оценить диссипацию и дисперсию численной схемы, свя-
связанные с длинноволновыми возмущениями (малые тАх).
Анализ разностных схем с помощью модифицированного
уравнения имеет еще и то преимущество, что он распростра-
распространяется и на нелинейные уравнения, в то время как фурье-
анализ (п. 9.2.1) применим только к линейным уравнениям.
В работе [Klopfer, McRae, 1983] используется метод модифи-
модифицированного уравнения для построения обобщенных схем
Лакса — Вендроффа при исследовании одномерного нестацио-
нестационарного распространения ударных волн, описываемых уравне-
уравнениями Эйлера A0.40).
При исследовании численных схем для уравнений гидроди-
гидродинамики (гл. 11) с помощью модифицированных уравнений тре-
требуется проведение существенных алгебраических преобразова-
преобразований. В этом случае формульные преобразования с помощью
ЭВМ, например MACSYMA, могут оказаться очень эффектив-
эффективными. Возможность формульных преобразований в вычисли-
вычислительной гидродинамике обсуждается в работе [Steinberg,
Roache, 1985].
9.2.3. Использование разложений в ряды Фурье
Рассмотрение ошибок аппроксимации, приведенных в
табл. 9.1 для разностной схемы со сдвигом против потока, схе-
схемы Лакса — Вендроффа и Кранка — Николсона в применении
к примерам, рассмотренным в конце § 9.1, очень упрощается,
§ 9.2. Численная диссипация и дисперсия 377
если обратиться к фурье-компонентам, входящим в решение.
Результаты, указанные на рис. 9.2—9.4 и в табл. 9.1, показы-
показывают, что значительная диссипация численной схемы эффек-
эффективно компенсирует малую дисперсию для разностной схемы
против потока и ослабляет часть дисперсионной ошибки в
решении Лакса — Вендроффа. В схеме Кранка — Николсона
преобладают дисперсионные ошибки, которые приводят к значи-
значительному замедлению распространения каждой из фурье-гар-
моник. Хотя все схемы Кранка — Николсона устойчивы, с уве-
увеличением числа Куранта ошибка растет как С2 (табл. 9.1).
Для малых С и, следовательно, малых At дисперсионная ошиб-
ошибка схемы Кранка — Николсона в конечных элементах
(табл. 9.1) значительно меньше, чем у других схем, рассмот-
рассмотренных в § 9.1.
Использование разложений в ряды Фурье и модифициро-
модифицированных уравнений позволяет построить более точные численные
схемы, уменьшающие ошибки диссипации и дисперсии. Это мож-
можно проиллюстрировать на методе Тейлора — Галёркина с ко-
конечными элементами [Donea, 1984]. Согласно этому методу,
сначала проводятся дискретизация по времени, которая для
уравнения (9.2) дает
тП+[7тП +uw=°- <9-39>
Однако более точное представление dT/dt на п-ы временном-
слое можно записать в виде
dt A^ dt 6 dt
Из (9.2) имеем
d2f _ 2 d2f d*f __ 2 d2 df
dt2 ~U dx2 • dt* ~U dx2 dt '
Следовательно, более точная (чем (9.39)) полудискретиза-
полудискретизация уравнения (9.2) дается выражением
Использование сетки с постоянным шагом и метода Галёр-
Галёркина с конечными элементами и линейной интерполяцией
(§ 5.4) приводит уравнение (9.40) к виду
[Мх - -? Ax2Lxx] (Tl+l - Г?) + CbxLtf - 0.5C2A/L^ = 0,
378 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
которое является обобщением схемы Лакса — Вендроффа (9.16).
Вид массового оператора Мх={-^9 -|-, —} вытекает из формули-
формулировки метода конечных элементов. Член (С2/б) Ьхх(т1+{ — Т*})
возникает из-за сохранения дополнительных слагаемых в разло-
разложении производной дТ/дх в ряд Тейлора. Уравнение (9.41) со-
содержит ошибку аппроксимации порядка О (At3, Ax3), что можно
сравнить со вторым порядком точности схемы Лакса — Вендроф-
Вендроффа (9.16). В работе [Donea, 1984] с помощью разложения в ря-
ряды Фурье исследованы дисперсия и диссипация схемы; найдено,
что уравнение (9.41) превосходит схему Лакса — Вендроффа для
всех длин волн и чисел Куранта в интервале 0 < С < 1.
Приведенная выше схема может быть обобщена введением
.дополнительных членов в рядах Тейлора для управления
(анти-)диссипацией и (анти-)дисперсией. В работе [Baker, Kim,
1987] выведена такая общая схема и названа формулировкой
Тейлора — Вика (ФТВ) метода Галёркина с конечными элемен-
элементами. ФТВ-алгоритм содержит четыре произвольные постоянные.
«Специальный выбор этих постоянных дает 17 хорошо известных
численных схем, сформулированных в методах конечных разно-
разностей и конечных элементов. Оптимальный выбор может быть сде-
сделан в принципе и для линейного уравнения конвекции (9.10). Од-
Однако для более общих гиперболических уравнений сохранения,
например уравнений Эйлера A0.40), оптимальным будет реше-
решение, которое обладает хотя и желательной диссипацией, но и
значительной дисперсией.
Мы можем сделать общий вывод о том, что следует избе-
избегать аппроксимационных формул первого порядка для произ-
производных. Аппроксимация первого порядка для п и производной
в исходном уравнении будет порождать пространственные про-
производные порядка (я+1) и выше в модифицированном урав-
уравнении (которое является эквивалентным решаемому исходно-
исходному уравнению). Это особенно важно для конвективных членов
(/2=1), так как введение фиктивных производных второго и
третьего порядков может существенно изменить характер ре-
решения.
§ 9.3. Стационарное уравнение с конвекцией и диффузией
Для многих задач обтекания диссипативные механизмы яв-
.ляются существенными только в узком слое, обычно вблизи
границы обтекания. Численные решения, построенные на сет-
сетках, приспособленных к основному потоку, часто начинают
осциллировать в пограничном слое, где точное решение претер-
§ 9.3. Стационарное уравнение
379
певает резкое изменение. Стационарное уравнение конвен-
конвенции — диффузии является полезным модельным уравнением, с
помощью которого можно проиллюстрировать это явление.
Это уравнение в безразмерных переменных имеет вид
d2T
Л (9.42)
dT
dx
dx2
= 0.
Оно выражает стационарный баланс между конвекцией и диф-
диффузией. Время не играет никакой роли. Если к (9.42) доба-
добавить граничные условия
Г@) = 0 и f(l)=1.0, (9.43)
то в интервале 0 ^ х ^ 1 точное решение можно представить
в виде
Т = [*>"*/« — 1.0]/[е"/а —1.0]. (9.44)
Это решение, приведенное на рис. 9.5, характеризуется постоян-
постоянно ш**=*-2> ?сеП=2
0.5
-0.5
точное решение
О О-А-О-Л-Ю-Л-О-А-g-Л
0.5
1.0
Рис. 9.5. Влияние числа Рейнольдса ячейки на решение уравнения конвек-
конвекции — диффузии.
ным распределением Т почти на всем интервале, кроме тонкого
пограничного слоя в окрестности х = 1.
9.3.1, Влияние сеточного числа Рейнольдса
Если использовать трехточечные центральные разности для
производных в (9.42), то получим следующий алгоритм:
- A + 0.5ЯСен) Гу., + 2Г, - A - 0.5flceii) Tf+l = 0, (9.45)
где /?сец = иАх/а, т. е. /?Ceii — число Рейнольдса (строго говоря,
Пекле), построенное на характерной длине ячейки Дл:.
380 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Разложение уравнения (9.45) в ряд Тейлора около /-го узла
показывает, что оно аппроксимирует уравнение (9.42) с точ-
точностью до О (Ах2). Разностная схема (9.45) является неявной,
но если выписать уравнение для всех узлов, то получается си-
система уравнений с трехдиагональной матрицей, для решения
которой могут быть использованы экономичные способы
(п. 6.2.2).
Для относительно простого случая точное решение (9.45)
можно представить в виде
(9.46)
где Ао и Во выбираются таким образом, чтобы удовлетворялись
граничные условия (9.43). Для случая и/а = 20 и Ах = 0.05,
0.1 и 0.02 решение (9.46) приведено на рис. 9.5. При Ах = 0.05,
что эквивалентно Rce\\ = 1, решение довольно хорошо согла-
согласуется с точным. При /?ceii = 2 (Ах = 0.1) решение совпадает
с точным везде, кроме пограничного слоя в окрестности х= 1.
Для более грубой сетки при /?Ceii = 4 решение не только яв-
является неточным, но и носит колебательный характер.
Из (9.46) видно, что колебательных решений не будет, если
/?ceii ^ 2. Полезно также связать поведение решения, показан»
ное на рис. 9.5, с собственными числами матрицы системы
уравнений (9.45), записанных с граничными условиями (9.43).
Эта система имеет вид
е.
b с
a b с
АТ = В,
т2
(9.47а)
a b с
a b
О
-сТ}
(9.47b)
где а = — A +0.5i?Ceii), b = 2 и с = — A — 0.5/?Ceii). Соб-
Собственные числа вышеприведенной трехдиагональной матрицы
•связаны с а, Ь и с следующими соотношениями:
к, = Ъ + 2 (ac)m cos (у^у), /= 1, 2, ...,/- 2. (9.48)
§ 9.3. Стационарное уравнение 381
Видно, что для того, чтобы собственные числа были веществен-
вещественными, необходимо удовлетворить условию ас ^ 0:
(l+0.5/?cell)(l-0.5#cell)>0 ИЛИ /?Се11<2. (9.49)
Таким образом, появление осциллирующих решений связано с
появлением комплексных собственных чисел.
Для матрицы А в (9.47а) общею вида ограничение на соб-
собственные числа X дается теоремой круга Гершгорина (см. [Jen-
[Jennings, 1977])
Таким образом, собственные числа матрицы А лежат в
кругах, связанных с каждым рядом матрицы А. Центр каж-
каждого круга определяется диагональю с элементами aiJy а ра-
радиус— суммой внедиагональных элементов каждого ряда. В ра-
работе [Carey, Sepehrnoori, 1980] применялась теорема круга
Гершгорина для анализа уравнений вида (9.47а) при различ-
различных значениях /?ceii. В интервале 0 < /?Ceii ^ 2 центр круга
Гершгорина лежит в точке {—2а/Дх2, 0} комплексной плос-
плоскости, имеет радиус 2a/Ax2 и все собственные числа располо-
расположены на отрицательной части вещественной оси. С увеличе-
увеличением Rce\u т. е. с уменьшением а, радиус круга уменьшается,
а центр перемещается к началу координат. При Rceu = 2 центр
круга расположен в точке (—w/Ajc, 0), радиус равен и/Лх =
= 2а/Ах2. При Rcen > 2 радиус остается постоянным, но центр
движется к началу координат и собственные значения являют-
являются комплексными. При /?сец = оо центр круга совпадает с на-
началом координат, а собственные значения становятся чисто
мнимыми величинами.
Ограничение RCe\\ ^ В для получения неосциллирующих ре-
решений применимо и к другим методам, в частности к методу
конечных элементов. В работе [Finlayoon, 1989] получено зна-
значение В для метода конечных элементов и метода ортогональ-
ортогональной коллокации. Однако обычно В меньше 10.
Следует подчеркнуть, что осциллирующие решения могут
появиться, если /?сец > В, а появятся ли они на самом деле,
зависит от геометрии потока и граничных условий. Например,
замедление потока перед препятствием часто порождает осцил-
осциллирующее решение при /?Сен > В. Однако для равномерного
или ускоряющегося потока можно построить неосциллирующее
решение и при RCe\\ > В.
Как и следовало ожидать, если для представления дТ/дх
в (9.42) использовать не центральные разности, а разности про-
против потока (Т,- — Tj-\)/&x, то осциллирующие решения не
382 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
возникают. Разностная схема со сдвигом против потока дает
вместо (9.45) следующий алгоритм:
- A + Ясен) Т^г + 2A+ 0.5tfCeii) T, - Г/+1 = 0. (9.50)
Из (9.48) видно, что схема против потока имеет вещественные
собственные числа при всех значениях Ясен- Решение с исполь-
использованием разностной схемы против потока для и/а = 20 и
Дх =-. 0.2 показано на рис. 9.6. Как и следовало ожидать, осцил-
1.0
0.5
-0.5
о ax=8.2,R ,,«4 (против потока)/
ш дх=8.2,1Г*|]«4 (центральная) /П
точное решение
0.5
1.0
Рис. 9.6. Решение уравнения конвекции — диффузии по схеме с разностями
против потока.
ляции в решении отсутствуют, но решение не является доста-
достаточно точным.
Разложение уравнения (9.50) в ряд Тейлора показывает,
что оно аппроксимирует (9.42) только с точностью О (Ах).
С точностью О (Ах2) (9.50) аппроксимирует уравнение
(Э.51)
т. е. использование разностей против потока приводит к по-
появлению искусственной диффузии 0.5/?Ceiia, аналогично тому,
как при использовании конечных разностей против потока для
уравнения конвекции тоже возникала искусственная диффузия
(см. (9.13)). Практически для получения достаточно точного
решения из (9.51) вытекает ограничение 0.5i?Ceii<l, которое
является более жестким, чем (9.49).
Если при х=\.О вместо условия Дирихле поставить гра-
граничное условие Неймана, то характер решения существенно не
изменится. Для больших значений и/а схема центральных раз-
разностей (9.45) приводит к решениям с еще большими осцилля-
циями, чем показанные на рис. 9.6.
§ 9.3. Стационарное уравнение 383
9.3.2. Схемы с разностями против потока
повышенного порядка точности
Именно колебательный характер решений, получаемых при
использовании трехточечных центральных разностей для пред-
представления dT/dx в (9.42), и диссипативная природа двухточеч-
двухточечной схемы с разностью против потока (9.50) наводят на мысль,
что для получения более точного решения необходимо исполь-
использовать четырехточечное представление для dT/dx. При и > 0
таким представлением может быть следующее:
-^•«аГ/_2 + 67'/_1 + с7'/ + Г/+1. (9.52)
•Следуя процедуре п. 3.2.2, получаем следующую схему:
Для отрицательных значений и соотношение (9.53) заменяется
на
dx 2Ax ^
Уравнение (9.53) умышленно записано в виде модификации
трехточечной схемы центральных разностей. Параметр q опре-
определяет степень модификации.
Разложение в ряд Тейлора около /-го узла дает
Таким образом, модификация может быть использована для
нейтрализации отдельных членов разложения в ряд Тейлора
для полного уравнения. В частности, при выборе q = 0.5 иск-
исключается член Ax2d3T/dx3 и схема (9.53) становится схемой по-
порядка О(Д;с3). В свете сказанного выше о связи раскачки ре-
решения с дисперсией и производными четного порядка можно
ожидать, что использование (9.53) с q = 0.5 и вместе с соот-
соответствующей дискретизацией для d2T/dx2 приведет к более точ-
точному решению с меньшей раскачкой, чем (9.45).
Использование формулы (9.53) при дискретизации (9.42)
приводит к следующему неявному алгоритму:
-f RcellTj^ -[l+(q + 0.5) /fceil] Tf_x + B + tftfcell) Tj -
- [l + (-J- - 0.5) Леей] TJ+l = 0, (9.54)
который сводится к (9.45) при q = 0. Структура (9.54) при-
приводит к решению более сложной четырехдиагональной матрицы.
384 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Для этой цели эффективным является использование обоб-
обобщенного алгоритма Томаса (п. 6.2.4) с / = 0. Требующиеся
для этого дополнения к подпрограммам BANFAC (рис. 6.18) и
BANSOL (рис. 6.19) указаны на распечатках программ
рис. 9.8 в строках 126—133.
Численное решение уравнения (9.54) с граничными усло-
условиями (9.43) можно сопоставить с точным решением, данным
формулой (9.44). Типичные результаты, полученные на грубой
сетке с Ах = 0.2, /?ceii = 4, для различных значений q приве-
приведены в табл. 9.2. Случай q = 0 совпадает с решением по трех-
трехточечной схеме центральных разностей (9.43), которая при-
приводит к осциллирующему решению, изображенному на рис. 9.5
и 9.6.
Таблица 9.2. Решение уравнений (9.42), (9.43) с использованием (9.54)
и грубой сетки
X
Точное решение
« = 0
4 = 0.5
4=1.0
<7= 1.5
0.0
0.0
о о о о
о о о о
0.2
0.0000
0.0164
0.0000
0.0000
0.0004
0.4
0.0000
—0.0328
-0.0003
0.0002
0.0032
0.6
0.0003
0.1148
0.0058
0.0036
0.0222
0.8
0.0018
—0.3279
-0.0760
0.0597
0.1491
1.0
1.0000
1.0000
1.0000
1.0000
1.0000
Случай q = 0.5 приводит к значительно более точному ре-
решению, хотя все еще слегка осциллирующему. Видно, что с
увеличением q решение становится более гладким, но с увели-
увеличением диффузии, подобно решению, полученному по двухто-
двухточечной схеме против потока (9.50), показанному на рис. 9.6.
На мелкой сетке при q = 0.5 получаются наиболее точные ре-
решения (не показаны).
Эквивалентное дифференциальное уравнение, в действи-
действительности решаемое по схеме (9.54), можно получить разложе-
разложением в ряд Тейлора в окрестности узла /. В результате
dT Ax d2T
dx /?-, dx2
Ax2 d*T
6 dx3
Ax4 d5T
120 dx5
... =0. (9.55)
Для практических задач, для которых типичны малые зна-
значения а/и, величина RCe\\ имеет порядок 0A) или больше. Это
§ 9.4. Одномерное уравнение переноса 385
означает, что формальная ошибка аппроксимации, вносимая
представлением (9.42) для производных, может различным об-
образом влиять на точность решения уравнения (9.54). Так, при
9=7^0.5 третий член в (9.55), по-видимому, будет оказывать
наибольшее влияние на точность решения. Отсюда следует, что
для задач с малым коэффициентом диффузии а конвективные
члены, подобные udT/dx в (9.42), должны аппроксимироваться
более точно, чем диффузионные.
Результаты, приведенные в табл. 9.2, согласуются с (9.55).
Видно, что увеличение q ведет к положительной диссипации.
Однако следует помнить (§ 9.2), что разложение (9.55) являет-
является более подходящим для описания длинноволновых возмуще-
возмущений. Из разложения (9.55) следует, что при q = 0.5 и /?Ceii =
= 1.0 разностная схема (9.54) формально является схемой
четвертого порядка. Однако для нелинейных задач конвекции
Ясен будет зависеть от локального решения, так что точности
четвертого порядка невозможно достигнуть во всей вычисли-
вычислительной области. Частный случай q = 0.375 был рассмотрен в
работе [Leonard, 1979] в связи с двумерной задачей, описанной
в п. 17.1.5.
Из анализа, приведенного в § 9.2 и 9.3, следует, что про-
пространственные производные нечетного порядка, входящие в
ошибки аппроксимации, связываются с колебанием решения,
а производные четного — с диссипацией или неограниченным
ростом в зависимости от знака стоящего перед производной
множителя. Тенденция вызвать колебания без потери амплиту-
амплитуды будет относиться к явлению типа дисперсии, хотя понятие
дисперсии, строго говоря, имеет смысл только для нестацио-
нестационарных течений. Если данное стационарное течение рассмат-
рассматривать как предел нестационарного (со стационарными гранич-
граничными условиями) на очень большом интервале времени, лю-
любые колебания типа дисперсии можно считать происходящими
из-за баланса между влиянием дисперсии и наложением гра-
граничных условий.
§ 9.4. Одномерное уравнение переноса
Одномерное уравнение переноса может быть записано в
виде
#+.?—?-«• <9-66>
где Т — пассивная скалярная величина (например, температу-
температура), подверженная конвекции с постоянной скоростью и(х, t) и
диффузии (рис. 1.7). Если Т —- температура, то а — коэффициент
25 К. Флетчер, т. 1
386 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
термодиффузии. Для анализа численного решения уравнения
(9.56) будем предполагать, что и и а — постоянные величины.
Как и уравнение диффузии (гл. 7), уравнение переноса является
строго параболическим (§ 2.3) и для него требуются граничные
и начальные условия того же типа, например G.2) — G.4), как
и для уравнения диффузии.
Однако при больших значениях и/а можно ожидать, что
в уравнении (9.56) будут преобладать первые два члена. Тогда
уравнение переноса будет проявлять свойства, аналогичные
уравнению конвекции (9.2). Следует напомнить, что точные
решения уравнения конвекции обычно имеют вид бегущей не-
незатухающей волны (без уменьшения амплитуды). Следователь-
Следовательно, при больших значениях и/а можно ожидать, что решения
уравнения переноса (9.56) будут иметь вид волны со слабым
затуханием.
На основе анализа уравнения конвекции с диффузией, ко-
которое является предельным для уравнения переноса, можно
также ожидать, что в приближенных решениях уравнения
(9.56) появятся пространственные волны, если будут использо-
использованы симметричные трехточечные алгебраические представле-
представления для конвективного члена при больших и/а.
В этом параграфе мы рассмотрим алгебраические схемы
(ВВЦП, Дюфорта — Франкела и т. д.), исследованные ранее
для уравнений диффузии и конвекции (§ 9.1), для того, чтобы
понять, вносит ли какие-либо новые трудности в численную
схему одновременное включение диффузии и конвекции в
уравнение.
9.4.1. Явные схемы
Применение схемы ВВЦП для аппроксимации (9.56) при-
приводит к алгебраическому уравнению •
г?*'-г? цG7+1-77_о а G7-1-2*7+ г?)
которое приводит к вычислительному алгоритму вида
77+1 = (s + 0.5C) 77_1 + A - 25) Г? + (s - 0.5С) Tni+U (9.58)
где 5 = aAt/Ax2 и С = uAt/Ax.
Из разложения в ряд Тейлора в окрестности узла (/, п)
следует, что схема (9.58) аппроксимирует уравнение (9.56) с
погрешностью порядка О (At, Ax2). Если алгоритм (9.58) рас-
рассматривать с точностью до членов порядка О (At2, Ax2)y то он
§ 9.4. Одномерное уравнение переноса 387
аппроксимирует уравнение
д! . дТ д2Т , М д2Т
—
<9-59>
т. е. в уравнение в частных производных, которое аппроксими-
аппроксимируется алгоритмом (9.59), включается дополнительный член, ин-
интерпретируемый выше как главный член ошибки аппроксимации.
Следуя методу модифицированных уравнений (§ 9.2), вторую
производную по времени можно исключить, заменив ее произ-
производными по пространству, что дает
дТ . дТ i ,.д2Т
А/2 А*2 \ дъТ
—-и—I>^
+ (о.5а2Д/ - <ш2Д/2 + 0.25u4Afi -a-^ + u2-^-) -§jr = 0, (9.60)
где а' = u2At/2. Таким образом, видно, что использование раз-
разностной схемы первого порядка точности по времени вносит
в уравнение переноса диссипацию и дисперсию первого поряд-
порядка. Для больших значений и/а член искусственной диффузии
а'д2Т/дх2 может оказаться сравнимым с физической диффу-
диффузией, если не ограничить величину At. Если величина д4Т/дх*
не является слишком большой, то маловероятно, что послед-
последний член в (9.60) будет существенным. Следовательно, огра-
ограничение на шаг по времени Л? дает
А/ < -|г или С2 < 25 или #Ceii (= -?) < -|-. (9.61)
Ясно, что имеется веская причина использовать схему второго
порядка точности по времени при решении уравнения пере-
переноса.
Напомним, что схема с разностями вперед по времени и
центральными по пространству приводит к алгоритму, который
условно устойчив для уравнения диффузии и всегда неустой-
неустойчив для уравнения конвекции. В табл. 9.3 приведен коэффи-
коэффициент усиления G для уравнения переноса, полученный на ос-
основе анализа устойчивости схемы по Нейману. Для устойчивых
решений \G\ ^ 1, что приводит к следующим ограничениям:
0<C2<2s<l. (9.62)
Соотношение (9.62) включает в себя «диффузионный» предел
(п. 7.1.1). Строго говоря, ограничение (9.62) допускает реше-
решения, для которых Ясен = u&x/a = C/s > 2.0, т. е. можно ожи-
ожидать появления осциллирующих решений. Из (9.61) также сле-
следует, что такие решения будут недостаточно точными.
25*
388 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Таблица 9.3. Алгебраические схемы (дискретизация)
Схема
Алгебраическая форма
Ошибка аппроксимации Е *
(главные члены)
ввцп
I
pfl + \
X
A + 2С2)]
дх*
Вверх по
потоку
+ „
_
д2Т
дх2
Дюфорт
Франкел
X [и Д*2/6 - 2а2С2/и]
дх*
Лаке —
Вендрофф
- [СаАх-и (Ал:2/6) A -С2)]Х
лзт
х + [са2
где а* = а + О.ЪиС Ал:
Кранк —
Николсон
* I
•—•—•
- aLxx) X
w(A*2/6)(l+0.5C2)
X
{Л^.},
- a (Aa:2/12) A + 3C2)
dx3
dx*
§ 9.4. Одномерное уравнение переноса
389
для уравнения переноса dT/dt + идТ/дх —
Коэффициент затухания G
(9=/ля Дх)
1 — 2s(l - cos 9) - iC sin 9
1 — Bs + С) A — cos 9) — iC sin 9
В ±[B2-8s(\ +2s)]1/2
B +4s)
где В = 1 + 4s cos 9 — i2C sin 9
1 — 2s* (Г*- cos 9) — iC sin 9,
где s* = a*A//A*2
1 _ s A — cos 9) — /0.5C sin 9
1 + s A — cos 9) + /0 bC sin 9
ad*Tfdx* = 0
Условие
устойчивости
0<C2<2s<l
С + 2s < 1
0<C2<2s*<l
Нет
Замечание
/?cell<2/C
ДЛЯ ТОЧНОСТИ
*ce.l< 2/U-С)
для точности
для точности
чтобы избежать
пространственных
осцилляции
чтобы избежать
пространственных
осцилляции
390 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Схема
Алгебраическая форма
Ошибка аппроксимации Е *
(главные члены)
3-слойная
чисто
неявная
3 ДГ?+1 1 АГ?
2 М 2 А/ ^
+ {uLx-aLxx}T»+l=0
Линейная
мкэ
Кранк —
Николсон
1 1 1
мх
X
— aLx
{Ir
Алгебраическая схема эквивалентна уравнению dT/dt + и дТ/дх — ад'Т/дх2 +
С/5 = ы Ах/а.
Если для представления (9.56) использовать, как в схеме
Ричардсона G.8), центральные разности по времени вместе с
центральными разностями по пространству, то полученный в
результате алгоритм будет безусловно неустойчив, если не по-
потребовать s = 0, что приведет к схеме «чехарда» (9.15) для
уравнения конвекции (9.2).
Схема Дюфорта — Франкела для уравнения переноса имеет*
вид
гя+1_
Г?"'
( грП фи
V7/ + l "" l 1 -1
Ал:2
= 0. (9.63)^
Анализ устойчивости по Нейману показывает, что если
число Куранта С ^ 1, то не требуется ограничения на 5. Из
разложения в ряд Тейлора в окрестности узла (/, п) следует,,
что в противоположность уравнению диффузии для аппрокси-
§ 9.4. Одномерное уравнение переноса
391
Таблица 9.3 (продолжение)
Коэффициент затухания Q
(8= тп\х)
1 ± ~ i [3 + 16s A - cos 9) + iSC sin 9]1/2
2(l+-|"[2s A " cos 6) + iC sin 9')
2 + 3 cos 9 — 3s A — cos 9) — П.5С sin 9
2 + 3 cos 9 + 3s A — cos 9) + П.5С sin 9
Условие
устойчивости
Нет
Нет
Замечание
^cell ^ 2'
чтобы избежать
пространствен-
пространственных осцилляции
^cell < 2»
чтобы избежать
пространствен-
пространственных осцилляции
мации схемы (9.63) уравнением (9.56) необходимо потребовать
At ^ Дл: (С2 ^> 1 в табл. 9.3), а это очень строгое ограничение.
Если для представления дТ/дх использовать центральные
разности вместо разностей против потока, то для положитель-
положительных и получим алгоритм
77+I = (s + C)TU + A - 25 - С) Г? + sr,\i.
(9.64)
Разложение в ряд Тейлора показывает, что (9.64) аппрокси-
аппроксимирует уравнение (9.56) с точностью О {At, Ax). Из выражения
для ошибки аппроксимации для схемы с разностями против
потока, приведенной в табл. 9.3, следует, что она вносит ис-
искусственную диффузию с коэффициентом а' = 0.5аДл;A — С).
Такой же член возникает и для уравнения конвекции
(табл. 9.1). Для получения точных решений уравнения пере-
переноса с помощью схемы с разностями против потока необходи-
необходимо потребовать, чтобы
а! < а или /?СеИ < { _с -
392 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Анализ устойчивости схемы (9.64) по Нейману дает коэф
фициент усиления G, который приведен в табл. 9.3. Необходи-
Необходимое условие устойчивости \G\ ^ 1 приводит к требованию
, (9.65)»
что эквивалентно неравенству
которое является значительно более строгим ограничением,
для уравнения диффузии (табл. 7.1).
В большинстве рассматриваемых до сих пор схем ограниче-
ограничения были связаны с тем, что необходимо получить достаточно*
точные решения, используя для производных аппроксимацион-
ные формулы первого порядка точности. Схема Лакса — Венд-
роффа (9.16) обладает вторым порядком точности как по вре-
временной переменной, так и по пространственной. Для уравнения:
переноса (9.56) схема Лакса — Вендроффа может быть интер-
интерпретирована как схема ВВЦП с модифицированной диффузией
а* = а A + 0.5C7?ceii). При /?сец -*¦ оо ошибки аппроксимации^
и условия устойчивости вновь возвращаются к указанным в-
табл. 9.1.
9.4.2. Неявные схемы
Использование неявных схем для уравнения диффузии бо-
более эффективно, поскольку для них не требуется выполнения-
условия устойчивости s ^ 0.5. Наиболее эффективная одномер-
одномерная двухслойная схема для уравнения диффузии, схема Кран-
Кранка— Николсона, здесь будет рассмотрена в применении к урав-
уравнению переноса. Строго говоря, данную схему следует описы-
описывать как трапецоидальную схему, поскольку первоначальная"
схема Кранка — Николсона была развита для уравнения диф-
диффузии. Однако названия — схема Кранка — Николсона и двух-
двухслойная — будут применяться время от времени к любой двух-
двухслойной схеме, в которой пространственные производные вы-
вычисляются симметрично относительно слоя (я+ 1/2) по времени..
Для уравнения переноса использование схемы Кранка —
Николсона дает разностное представление
/ / I ле
7. .-97.4-7... 7. .-97. -*-Т...^=(^ (9б^
§ 9.4. Одномерное уравнение переноса 393
которое можно переписать в виде алгоритма
— (s + 0.5C) 77+/ + 2(l+s)Г/+1 - (s - 0.5C)T]$l =
= (s + 0.5CO7-i + 2 A - 5) Г/ + (s - 0.5С) 77+i. (9.68)
"Почленное разложение (9.68) в ряд Тейлора в окрестности
узла (/, п) показывает, что этот алгоритм аппроксимирует урав-
уравнение (9.56) с погрешностью порядка О (At2, Ax2). Таким об-
образом, проблема искусственной диффузии, возникающая в схе-
схемах первого порядка, здесь отсутствует.
Анализ устойчивости алгоритма (9.68) по Нейману дает для
.коэффициента усиления G приведенные в табл. 9.3 выражения,
из которых видно, что они не накладывают никаких ограниче-
ограничений на критерий устойчивости для С или s. Но для отсутствия
осцилляции решения по пространству требуется удовлетворить
неравенство Rce\\ ^ 2.
Для длинноволновых компонент (малые тАх) решения
о свойствах диссипации и дисперсии вычислительных алгорит-
алгоритмов для уравнения переноса можно судить, исходя из выраже-
выражений для ошибки аппроксимации, приведенных в табл. 9.3.
'Обычно неявные схемы в этом смысле являются удовлетвори-
удовлетворительными. Физическая диссипация в системе приводит к умень-
уменьшению больших дисперсионных ошибок, связанных с коротко-
коротковолновыми возмущениями (/пАх-^я), возникающими в реше-
решении уравнения конвекции. В частности, конечно-элементная
-схема Кранка — Николсона, приведенная в табл. 9.3, обладает
малыми ошибками, связанными с дисперсией и диссипацией,
при малых значениях С. Для получения информации о коротко-
коротковолновых компонентах решения необходимо провести фурье-
анализ схемы (п. 9.2.1). Это будет применено к задаче о кон-
лзекции температурного фронта в следующем пункте.
9.4.3. TRAN: конвекция температурного фронта
Рассмотрим некоторые из описанных в п. 9.4.1 и 9.4.2 схем
применительно к задаче о конвекции со скоростью и темпера-
температурного фронта в жидкости с коэффициентом термодиффузии
а. Для больших значений числа Рейнольдса ячейки (строго
говоря, числа Пекле), RCe\\ = uAx/a, ширина фронта ограниче-
ограничена несколькими шагами по пространству (рис. 9.11) и все схе-
схемы,-описанные в п. 9.4.1 и 9.4.2, порождают осциллирующие
решения, в основном обусловленные дисперсионными ошибками
-схемы (§ 9.2).
Попытаемся построить две новые схемы, которые будут об-
обладать намного лучшими дисперсионными характеристиками.
394 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Обе схемы основаны на разностных формулах Кранка — Ни-
колсона для производной по времени. Первая схема представ-
представляет собой обобщение схемы Кранка — Николсона (9.20) с~
массовым оператором, которая применялась для линейного
уравнения конвекции (п. 9.1.5). В случае одномерного уравне-
уравнения переноса она дает
где Мх s {6, A—26), б}, a Lxx — условное обозначение для
трехточечных формул с центральными разностями. Параметр б
будем выбирать таким образом, чтобы уменьшить дисперсион-
дисперсионные ошибки схемы. Очевидно, что схема (9.69) приводит к трех-
диагональной системе уравнений, которая может быть решена
с использованием эффективных методов. Анализ устойчивости,
по Нейману показывает, что схема (9.69) устойчива при.
б < 0.25.
Что касается длинноволновых характеристик схемы, то, ис-
используя метод модифицированных уравнений (п. 9.2.2), видим,,
что система (9.69) эквивалентна следующему уравнению:
дТ . дТ д2Т . А 2 / 1 . С2 л\ д3Т
+ иа + иАл: { + V
(9.70>
Формально схема (9.69) является схемой второго порядка точ-
точности. Очевидно, что выбором б= 1/6 +С2/12 можно подавить
младший член с дисперсией в ошибке аппроксимации. Если,,
кроме того, С2 < 0.5, то младший диссипативный член будет
вносить положительную диссипацию в ошибку аппроксимации.
Однако при оптимальном выборе б для устойчивости схемы
требуется, чтобы С ^ 1.0.
Альтернативным средством для улучшения дисперсионных
свойств схемы является использование четырехточечной схе-
схемы Кранка — Николсона с разностями против потока
тп+\ _ тп
1 д, ' + («U4) - aLxx) 0.5 B7 + ТГ1) - 0, (9.71>
где при и ^ 0
1?>Г-0.Б <Г'+'~Г'-'> + у(Г/-»-ЗГ/^+8Г/-гж). (9.72).
Соотношение (9.72) представляет собой четырехточечный кон-
конвективный оператор, введенный в связи с рассмотрением ста-
стационарного уравнения диффузии — конвекции в п. 9.3.2.
§ 9.4. Одномерное уравнение переноса
395
Подстановка (9.72) в (9.71) приводит к четырехдиагональ-
ной системе уравнений, которая должна решаться на каждом
шаге по времени. Для этого требуется использовать обобщенный
алгоритм Томаса (п. 6.2.4). В программе TRAN обобщение
.алгоритма Томаса достигается за счет дополнительной прямой
прогонки (строки 126—133), сводящей систему к трехдиаго-
нальной форме. В данном случае обобщенный алгоритм Тома-
Томаса требует выполнения почти на 80 % операций больше, чем
обычный алгоритм Томаса. Схема (9.71), (9.72) устойчива при
q ^ —3//?Сен. Практически это условие не является ограниче-
ограничением, поскольку обычно интерес представляют только положи-
положительные значения q.
Эквивалентное уравнению (9.71) модифицированное урав-
уравнение (п. 9.2.2) имеет вид
<дт
дт
д2Т
12 ) дхъ
— U-
¦с1
12
t)s-+---=°- <973)
В (9.73) u&x3/Rce\\ = аДх2. Видно, что для потоков с /?Ceii ^> 1
<член с дисперсией дает наибольший вклад в ошибку аппрокси-
-2.0
Рис. 9.7. Начальные условия в задаче о распространении температурного
фронта.
мации. Этот член можно исключить выбором q = 0.5 + 0.25С2.
При таком выборе q и больших значениях i?Ceii диссипативный
член имеет наименьший порядок и вносит положительную дис-
диссипацию.
Приведенные выше схемы (9.69) и (9.71), а также схемы,
рассмотренные в п. 9.4.1 и 9.4.2, были использованы для реше-
решения задачи о распространении фронта температуры, иллюстри-
иллюстрируемой на рис. 9.7. При / = 0 задан скачок температуры в точ-
точке х = 0. В последующие моменты времени фронт движется
со скоростью и вправо и его профиль размывается под дей-
действием термодиффузии с коэффициентом а. Следовательно, в
396 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
С
С
с
с
с
с
с
1
1
2
3
4
5
6
7
8
9
10
1
11
TRAN SOLVES THE LINEAR TRANSPORT EQUATION USING
VARIOUS EXPLICIT AND IMPLICIT SCHEMES
DIMENSION RF5),TF5),TDF5),TEXF5),AE,65)
,DD),XF5)
OPEN(l,FILE=fTRAN.DAT1)
OPENF,FILE='TRAN.OUT')
READA,1ЖЕ,JMAX,NTIM,NEX,JPRrLN
READA,2)C,U,S,Q,EM
FORMATF15)
FORMATBF5.2,3E10.3)
IF(JPR .EQ. 1)WRITEF,3)
IF(JPR .EQ. 2)WRITEF,4)
FORMAT С PROPAGATING SINE-WAVE1)
FORMAT С PROPAGATING TEMP-FRONT1)
JMAF ¦ JMAX - 2
JMAP = JMAX - 1
AMP = JMAP
DX » 1.0/AMP
IF(JPR .EQ. 2)DX = 4./AMP
DT = C*DX/U
EL = LN
ALPH = S*DX*DX/DT
IF(ALPH .LT..1.0E-10)ALPH * 1.0E-10
KCEL = U*DX/ALPH
QQ = Q*C/3.
IF(ME .LT. 3)QQ * 0.
MQ = 0
IF(ABS(QQ) .GT. 0.000DMQ * 1
ATIM = NTIM
TIM = 0.
TIMAX = DT*ATIM
PI = 3.141592654
IF(ME .EQ. 1)WRITEF,5)ME
IF(HE .EQ. 2)WRITEF,6)ME
IF(ME .EQ. 3)VRITEF,7)ME
IF(ME .EQ. 4)WRITEF,8)ME
FORMATC ME = \I2,f FTCS DIFFERENCING')
FORMAT Г ME «',12,' LAX-VENDROFF •)
FORHATC ME = \I2,' EXPLICIT 4PT UPWIND1)
FORMAT С ME =',12,f GENERAL CRANK-NICOLSON1)
VRITEF,9)JMAX,NTIM,C,U,DX,DT
FORMATS JMAX=M3,' NTIM='/I3,t C*\F5.2/ и=§Д5.2^
.' DX=f,F5.3,' DT=\F5.3)
WRITEF,10)S,ALPH,RCEL,Q,QQ
writeF!idnex,ln',em
FORMAT(f S=\F5.2,' ALPH*',E10.3,f RCEL»! ^6.3,
.* Q=\F5.2,f QQ=',F6.3)
FORMATC- NEXSM5,1 EL«',I5,f EM=\E10.3)
Рис. 9.8. Описание программы TRAN (начало).
§ 9.4. Одномерное уравнение переноса 397
54 IF(ME .GT. 3)GOTO 12
55 SS = S
56 IF(ME .EQ. 2)SS = S + 0.5*C*C
57 AA = @.5*C + SS) + 3.*QQ
58 BB = 1. - 2.*SS - 3.*QQ
59 CC = -0.5*C + SS + QQ
60 GOTO 13
61 12 AA = EM - 0.25*C - 0.5*S - 1.5*QQ
62 BB * 1.0 - 2.0*EM + S + 1.5*QQ
63 CC = EM + 0.25*C - 0.5*S - 0.5*QQ
64 AE « EM +0.25*C + 1.5*QQ + 0.5*S
65 BE = 1. - 2.*EM - 1.5*QQ - S
66 CE = EM - 0.25*C + 0.5*QQ + 0.5*S
67 13 VRITEF/14)AA,BB,CC/AE,BE/CE
68 14 FORMATC AA=',F8.5,' BB=\F8.5,f CC=\F8.5,f AE=\F8.5,f BE*
69 1F8.5,' CE=\F8.5,/)
7p С
71 С INITIALISE T AND EVALUATE TEX
72 С
73 CALL EXSOL(JPR,JMAX,X,T,TEX,NEX,DX,U,ALPH,TIMAX,EL)
74 С
75 DO 16 J = 1,JMAX
76 DO 15 К = 1,5
77 15 A(KrJ) f 0.
78 16 CONTINUE
79 VRITEF,17)TIM
80 17 FORMAT С INITIAL SOLUTION, TIM =\F5.3)
81 VRITEFr18)(X(J),J=l,JMAX)
82 VRITEF,19)(T(J),J«l,JMAX)
83 18 FORMATC X='r12F6.3)
84 19 FORMATC T=f ,12F6.3)
85 С
86 С MARCH SOLUTION IN TIME
87 С
88 DO 26 N = 1,NTIM
89 IF(ME .GT. 3)GOTO 21
90 С
91 С EXPLICIT SCHEMES
92 С
93 D(l) « T(l)
94 DB) = T(l)
95 DC) = TB)
96 DO 20 J = 2,JMAP
97 IF(ME .EQ. 3)DD) = D(l)
98 D(l) = DB)
99 DB) = DC)
100 DC) « T(J+1)
101 T(J) = AA*DA) + BB*DB) + CC*DC)
102 IF(ME .EQ. 3)T(J) = T(J) - QQ*DD)
103 20 CONTINUE
104 GOTO 26
Рис. 9.8 (продолжение).
105 С
106 С TRIDIAGONAL SYSTEM FOR IMPLICIT SCHEMES
107 С
108 21 IF(MQ .EQ. 1)DIH = 1.
109 DO 22 J = 2,JMAP
110 .7Л * J - 1
111 AA,JM) = 0.5*QQ
112 AB,JM) = AA
113 AC,JM) = BB
114 AD,JM) = CC
115 R(JM) = AE*T(JM) + BE*T(J) + CE*T(J+1)
116 IF(MQ .EQ. 1 .AND. J .CT. 2)DIM = T(JM-l)
117 IFUIQ .EQ. l)R(JH) = R(JM) - 0.5*QQ*DIM
118 22 CONTINUE
119 R(l) = R(l) - AB,1)*TA)
120 IF(MQ .EQ. 0)GOTO 24
121 R(l) = R(l) - AA,1)*TA)
122 RB) = RB) - AA,2)*TA)
123 С
124 С REDUCE A TO TRIDIAGONAL FORM
125 С
126 DO 23 JM = 3,JMAF
127 JMM = JM - 1
128 DUM = AA,JM)/AB,JMM)
129 AB,JM) = AB,JM) - AC,JMM)*DUM
130 AC,JM) = AC,JM) - AD,JMM)*DUM
131 AA,JM) = 0.
132 R(JM) = R(JM) - R(JMM)*DUM
133 23 CONTINUE
134 A(l,l) = 0.
135 Ad,2) = 0.
136 24 AB,l) = 0.
137 AD,JMAF) = 0.
138 С
139 CALL BANFAC(A,JMAF,1)
140 CALL BANSOL(RfTD,A,JMAF,l)
141 С
142 DO 25 J » 2rJMAP
143 25 T(J) = TD(J-l)
144 26 CONTINUE
145 С
146 VRITEF,27)TIMAX
147 27 FORMAT С FINAL SOLUTION, TIM =',F5.3)
148 VRITEF,18)(X(J),J=1,JMAX)
149 VRITEF,19)(T(J),J=1,JMAX)
150 VRITEF,28)(TEX(J),J=1,JMAX)
151 28 FORMAT С TEX-M2F6.3)
152 SUM = 0.
153 DO 29 J = 2.JMAP
154 29 SUM = SUM + (T(J) - TEX(J))**2
155 RMS = SQRT(SUM/(AMP-1.))
156 VRITEFf30)RMS
157 30 FORMAT С RMS ERR=\E12.5)
158 STOP
159 END
Рис. 9.8 (окончание).
§ 9.4. Одномерное уравнение переноса 399
1 SUBROUTINE EXSOL(JPR,JMAX,X,T,TEX,NEX,DX,U,ALPH,TIMAX,EL>
2 С
3 С SETS THE INITIAL T SOLUTION AND FINAL EXACT (TEX) SOLUTION
4 С
5 DIMENSION TF5),TEXF5),XF5)
6 JMAP = JMAX - 1
7 PI» 3.141592654
8 IF(JPR .EQ. DXST = 0.
9 IF(JPR .EQ. 2)XST = - 2.0
10 DO 1 J = 1,JMAX
11 AJ = J - 1
12 X(J) = XST + AJ*DX
13 T(J) = 0.
14 • 1 TEX(J) = 0.
15 IF(JPR .EQ. 2)GOTO 3
16 С
17 С EXACT SOLUTION FOR PROPAGATING SINE-WAVE
18 С
19 JM = 0.1001/DX + 1.0
20 INC = U*TIMAX/DX + 0.001
21 DO 2 J = 1,JM
22 T(J) = SINA0.*PI*X(J))
23 JP = J + INC
24 2 TEX(J?) = T(J)
25 RETURN
26 С
27 С EXACT SOLUTION FOR PROPAGATING TEMP-FRONT
28 С
29 3 T(l) = 1.0
30 TEX(l) = 1.0
31 DO 5 J = 2,JMAP
32 IF(X(J) .LT. O.)T(J) = 1.0
33 IF(ABS(X(J)) .LT. 1.0E-04)T(J) = 0.5
34 DEM = 0.
35 DO 4 К = 1,NEX
36 AK = 2*K - 1
37 DUM = AK*PI/EL
38 SNE = SIN(DUM*(X(J)-U*TIMAX))
39 DIM = - ALPH*DUM*DUM*TIMAX
40 IF(DIM .LT. -20.)GOTO 5
41 4 DEM = DEM + (SNE/AK)*EXP(DIM)
42 5 TEX(J) = 0.5 - 2.*DEM/PI
43 RETURN
44 END
Рис. 9.9. Описание программы EXSOL.
каждый момент времени чем больше Rceu = иАх/а, тем круче
профиль температурного фронта.
Исходным уравнением в этой задаче является уравнение
(9.56). Для достаточно малых значений t можно задать сле-
следующие граничные условия:
Т (-2, t) =1.0, Т B, 0 = 0.0. (9.74)
400 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Точное решение этой задачи, найденное методом разделения
переменных, имеет вид
Т(х. O^O.S-A
kl
(9.75)
Различные схемы, которые заложены в программу TRAN, при-
приведены в табл. 9.4. Распечатка программы TRAN дана на
рис. 9.8, а основные параметры указаны в табл. 9.5. Точное ре-
решение дает подпрограмма EXSOL (рис. 9.9). Типичная выдача
результатов программы TRAN при использовании схемы Лак-
са — Вендроффа показана на рис. 9.10.
PROPAGATING TEMP-FRONT
HE « 2 LAX-VENDROFF
JMAX» 21 NTIM= 10 C- .25 U* .50 DX= .200 DT» .100
S= .25 ALPH= .100E+00 RCEL= 1.000 Q= .00 QQ= .000
HEX= 100 EL= 20 EM» .000E+00
AA= .40625 BB= .43750 CC= .15625 AE> .00000 BE= .00000 CE= .00000
INITIAL SOLUTION, TIM = .000
X»-2.000-1.800-1.600-1.400-1.200-1.000 -.800 -.600 -.400 -.200 .000 .200
X» .400 .600 .800 1.000 1.200 1.400 1.600 1.800 2.000
T« 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 .500 .000
T= .000 .000 .000 .000 .000 .000 .000 .000 .000
FINAL SOLUTION, TIM »1.000
X=-2.000-1.800-1.600-1.400-1.200-1.000 -.800 -.600 -.400 -.200 .000 .200
X= .400 .600 .800 1.000 1.200 1.400 1.600 1.800 2.000
T= 1.000 1.000 1.000 1.000 1.000 .999 .997 .991 .973 .934 .862 .747
T* .593 .422 ,261 .137 .059 .020 .005 .001 .000
*EX= 1.000 1.000 1.000 1.000 1.000 1.000 .998 .993 .978 .941 .868 .749
TEX» .588 .412 .251 .132 .059 .022 .007 .002 .000
RMS ERR» .44842E-02
Рис. 9.10. Типичная выдача по программе TRAN.
При /?ceii= 1.0 в табл. 9.6 дано сравнение решений, полу-
полученных как по явным, так и по неявным схемам. Все методы
приводят к гладким решениям, тогда как схема Лакса — Вен-
Вендроффа оказывается наиболее точной из явных схем. Наибо-
Наиболее точной из неявных схем является схема (9.71) с q = 0.5,
что соответствует 3-му порядку аппроксимации члена идТ/дх.
Расчеты по неявным схемам Кранка — Николсона для бо-
более высоких значений RCe\\ показаны в табл. 9.7 (/?Ceii = 3.33)
и табл. 9.8 (/?ceii = 100). В качестве эталона принята конечно-
разностная схема Кранка — Николсона. Решение по этой схе-
схеме является осциллирующим и выявляет добавочный скачок за
фронтом, который особенно хорошо виден при RCe\\ = 100
(табл. 9.8 и рис. 9.11). Видно, что две низкодисперсные схемы
§ 9.4. Одномерное уравнение переноса
401
ME
1
2
3
4
4
4
4
Таблица 9.4. Различные схемы, реализуемые программой
Описание
Схема ВВЦП (9.58)
Схема Лакса—Вендроффа (9.58) с s* = s + 0.5C2
TRAN
Явная 4-точечная схема с разностями против потока
(9.72); EX-4PU
Конечно-разностная схема Кранка — Николсона; б =
CN-FDM
Конечно-элементная схема Кранка — Николсона; б =
CN-FEM
Схема Кранка—Николсона с массовым оператором;
+ С2/12; CN-MO
= 0,
1/6,
6 =
4-точечная схема Кранка—Николсона с разностями вперед;
q = 0.5 + 0.25С2; CN-4PN
(9.57),
, = 0;
G = 0;
'1/6 +
6 = 0,
Таблица 9.5. Параметры, используемые в программе TRAN
Параметр
ME
ME
ME
ME
JMAX
NTIM
Описание
= 1; схема ВВЦП (9.58)
= 2; схема Лакса—Вендроффа (9.16)
= 3; явная 4-точечная схема с разностями вперед (9.57),
(9.72)
=4; обычная схема Кранка—Николсона (9.69), (9.71)
Число точек в интервале 0 ^ х ^ 1
Число шагов по времени
26 К- Флетчер, т. 1
402 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Таблица 9.5 (продолжение)
Параметр
TIMAX
JPR
JPR
NEX
LN
С
и
ALPH
S
RCEL
Q
ЕМ
DT, DX, X
Т
ТЕХ
АА, ВВ, СС
АЕ, BE, СЕ
А
BANFAC
BANSOL
R
TD
Описание
Время, при котором выполняется сравнение с точным ре-
решением
= 1; задача о распространении синусоидальной волны
= 2; задача о распространении температурного фронта
Число слагаемых N в (9.75), используемых в программе
EXSOL
Число слагаемых L в (9.75), используемых в программе
EXSOL
Число Куранта (9.11)
Значение и в (9.2), (9.56)
Коэффициент термодиффузии а в (9.56)
s = aAf/Ajt*
Число Рейнольдса ячейки, иАх/а, § 9.3
q в (9.53), (9.72)
б в (9.69)
Д*. Дх, х
Зависимая переменная в (9.2), (9.56)
Точное решение (9.24) или (9.75)
Коэффициенты перед Г"_1э Г" и Г"+1в явных схемах
Коэффициенты перед Т**1, Т*+1 и Г"*/ в неявных схемах
Элементы в трехдиагональной матрице (9.18)
Факторизация матрицы А к треугольному наддиагональному
виду
Решение уравнения AT = R для Г"+1
Правая часть трехдиагональной системы уравнений (9.22)
Решение для Г^+1, полученное в подпрограмме BANSOL
ч
Таблица &.6. Решение заДачй о температурном фронте при / = 1, ?сеп == 1,
С = 0.25, м = 0.5, Ах = 0.2, М = 0.05
Схема
Точное решение
ВВЦП
Лакса-Вендроффа
Явная 4-точечная
с разностями против потока
(EX-4PU), q = 0.5
Кранка—Николсона
с конечными разностями
(CN-FDM)
Кранка—Николсона
с конечными элементами
(CN-FEM)
Кранка—Николсона
4-точечная с разностями
против потока (CN-4PU),
<7 = 0.5
-0.40
0.978
0.981
0.973
0.976
0.981
0.977
0.976
-0.20
0.941
0.947
0.934
0.940
0.946
0.937
0.939
0.00
0.868
0.877
0.862
0.872
0.870
0.861
0.865
0.20
0.749
0.760
0.747
0.762
0.742
0.742
0.746
0.40
0.588
0.598
0.593
0.609
0.575
0.585
0.586
0.60
0.412
0.414
0.422
0.431
0.398
0.415
0.411
X
0.80
0.251
0.245
0.261
0.258
0.245
0.258
0.253
1.00
0.132
0.121
0.137
0.123
0.135
0.138
0.135
1.20
0.059
0.047
0.059
0.040
0.067
0.063
0.062
1.40
0.022
0.014
0.020
0.005
0.030
0.023
0.024
1.60
0.007
0.003
0.005
—0.003
0.012
0.007
0.008
Средне-
квадра-
квадратичная
ошибка
0.006
0.004
0.010
0.006
0.004
0.002
Таблица 9.7. Решение задачи о температурном фронте при t =» 1, #св11 = 3.33,
С «. 1, и = 1, А* — 0.1, Л/ = 0.1
Схема
Точное решение
Кранка—Николсона
с конечными разностями
(CN-FDM)
Кранка—Николсона
4-точечная с разностями
против потока (CN-4PU),
q = 0.75
Кранка—-Николсона
с массовым оператором
(CN-MO), б — 0.25
X
0.50
0.979
1.016
0.979
0.972
0.60
0.949
0.981
0.947
0.950
0.70
0.890
0.894
0.887
0.883
0.80
0.793
0.760
0.788
0.795
0.90
0.658
0.601
0.653
0.660
1.00
0.500
0.443
0.497
0.504
1.10
0.342
0.306
0.342
0.343
«. 1.20
0.207
0.200
0.212
0.206
1.30
0.110
0.123
0.117
0.109
1.40
0.051
0.073
0.056
0.052
1.50
0.021
0.041
0.023
0.022
Средне-
квадра-
квадратичная
ошибка
—
0.018
0.002
0.002
Таблица 9.8. Решение задачи о температурном фронте при t = 1, RCon = 100,
С = 1, и = 1, Д* = 0.1, At = 0.Г
Схема
Точное решение
Кранка—Николсона
с конечными разностями
(CN-FDM)
Кранка—Николсона,
4-точечная с разностями
против потока (CN-4PU),
q = 0.75
Кранка—Николсона
с массовым оператором
(CN-MO), б = 0.25
X
0.50
1.000
1.217
1.010
1.000
0.60
1.000
1.253
1.050
1.000
0.70
1.000
1.093
1.056
1.000
0.80
1.000
0.825
0.958
0.998
0.90
0.987
0.553
0.741
0.954
1.00
0.500
0.335
0.466
0.501
1.10
0.013
0.187
0.223
0.045
1.20
0.000
0.098
0.065
0.002
1.30
0.000
0.048
-0.007
0.000
1.40
0.000
0.022
-0.024
0.000
1.50
0.000
0.010
-0.018
0.000
Средне-
квадра-
квадратичная
ошибка
—
0.113
0.059
0.013
406 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
(9.69) и (9.71) являются эффективными при RCe\\ = 3.33 в по-
подавлении нефизических колебаний.
При Rce\\ = ЮО схема с массовым оператором при
6=1/6 + С2/12 дает крутой температурный фронт без осцил-
осцилляции. Четырехточечная схема с разностями против потока при-
приводит, однако, к более размытому фронту со слабыми колеба-
колебаниями решения перед и за фронтом. Расчетные точки по схеме
Кранка — Николсона с массовым оператором (CN-MO) пока-
показаны на рис. 9.11 только в тех случаях, когда они отличаются
от точного решения.
+ CN-FDH
о CN-4PU
о CN-MO
— точное решение
0.8
1.0
2.0
Рис. 9.11. Решение задачи о температурном фронте при /=1 и RCe\\ = 100
(обозначения см. в табл. 9.9).
Дополнительную информацию об относительных свойствах
двух схем (9.69) и (9.71) можно получить на основе фурье-ана-
лиза, как это было сделано в п. 9.2.1. Начальные данные пред-
представляются в виде рядов Фурье, и затем из разностного уравне-
уравнения находится отношение амплитуд Gm и фазового угла фт для
каждой моды Фурье 6т. В случае схемы Кранка — Николсона
с массовым оператором (9.69) получаем следующие выраже-
выражения:
[1 - B6 + s) A - cos 9m)]2 + @.5C sin 9mJ V/2
mJ ; '
Щ?т— [i — 26A —
_ Bб - S) (i - cos em)]2 + (o.5c
-C sin 8m [1- 26A- cos 9mI
26A — cos Qm)]2 - [0.5C sin 9m)]2 - [s A - cos 9m)]2 *
(9.77)
Соответствующие выражения для точного решения имеют вид
Gex, m = ехр [-СД%2/Ясеи], tg ^ех, „ = tg (-C9m). (9.78)
§ 9.4. Одномерное уравнение переноса
407
Таблица 9.9. Волновые характеристики решения при Rcen = 3,33, С = 1,0,
А* = 0.1
Схема
Кранка—Николсона
с конечными раз-
разностями (CN-FDM)
Кранка—Николсона
с массовым опера-
оператором (CN-MO)
Кранка—Николсона,
4-точечная с раз-
разностями против по-
потока (CN-4PU)
Точное решение
Кранка—Николсона
с конечными раз-
разностями (CN-FDM)
Кранка—Николсона
с массовым опера-
оператором (CN-MO)
Кранка—Николсона,
4-точечная с раз-
разностями против по-
потока (CN-4PU)
^m/^ex, m
^А72/'-'еХ, ttl
*-* т./ '-• ex, m
Фех, т
Фт
Фт
Фт
0.05
0.996
0.996
0.996
-9.00
-8.94
—9.00
-8 96
0.25
0.858
0.841
0.827
—45.00
—39.19
-45.37
-40.65
0.50
0.619
0.573
0.438
-90.00
-56.58
—100.21
-71.29
0.75
0.389
0.683
0.216
—135.00
-49.09
-164.20
-130.14
1.00
0.251
1.003.
0.231
—180.00
О.ОО
—180.00
-180.00
Таблица 9.10. Волновые характеристики решения при /?Сеи =100, С = 1
A 01
Схема
Кранка—Николсона
с конечными раз-
разностями (CN-FDM)
Кранка—Николсона
с массовым опера-
оператором (CN-MO)
Кранка—Николсона,
4-точечная с раз-
разностями против по-
потока (CN-4PU)
•„/*
Gm/Gex, m
Gm/Gex, m
Gm/Gex m
Ах =
0.05
1.000
1.000
1.000
0.1
0.25
0.995
0.994
0.958
0.50
0.984
0.980
0.674
0.75
0.970
0.967
0.277
1.00
0.961
1.000
0.010
408 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Схема
вт/л
0ех> т
Фт
Фт
Фт
0.05
-9.00
-8.94
-9.00
—8.96
0.25
-45.00
-38.94
—45.00
—40.27
0.50
-90.00
-53.13
—90.01
-61.30
0.75
-135.00
-38.95
-135.08
—73.14
1.00
Точное решение
Кранка—Николсона
с конечными раз-
разностями (CN-FDM)
Кранка—Николсона
с массовым опера-
оператором (CN-MO)
Кранка—Николсона,
4-точечная с раз-
разностями против по-
потока (CN-4PU)
-180.00
0.00
-180.00
—180.00
В табл. 9.9 и 9.10 приведены значения Gm/GeXtm и фт для раз-
различных Qm и соответствующих условиям табл. 9.7 и 9.8.
Для четырехточечной схемы Кранка — Николсона с раз-
разностями против потока (9.71) для Gm и фт получаем выраже-
выражения
г _ ( [1 - s* A - cos 9m)]2 + {0.5С sin 8m [1 + q A - cos 6m)/6]}2 y/2
m ~ \\\ + s* A - cos 9m)]2 + {0.5C sin 9m [1 + q A - cos 6m)/6]}2 ) '
—С sin 6П
- cos 8m)/6]
-cosem)]2-{0.5C sin9m[l
-cosem)/6]>*'
(9.79)
(9.80)
где s* = s + qC{l — cos9m)/3. Отношение амплитуд и фазовый
угол в зависимости от 0т при RCe\\ = 3.33 и 100 приведены в
табл. 9.9 и 9.10 соответственно.
Видно, что при Rceii = 3.33 (табл. 9.9) конечно-разностная
схема Кранка — Николсона плохо согласуется с точным реше-
решением по фазовому углу, особенно для коротких волн при
вт-^п. Наоборот, схема с массовым оператором и четырехто-
четырехточечная схема дают хорошее согласие с точным решением по
фазе. Обе схемы имеют тенденцию к диссипации для промежу-
промежуточных длин волн (9m ~ я/2), а четырехточечная схема являет-
является диссипативной и для коротких волн.
При Rcen = 100 (табл. 9.10) конечно-разностная схема
Кранка — Николсона сохраняет амплитуду при всех длинах
волн, но вносит значительные ошибки в величину фазового угла
при малых длинах волн. Это совпадает с осцилляциями темпе-
температурного фронта на рис. 9.11. Четырехточечная схема с раз-
разностями против потока дает ошибку в фазе для промежуточ-
§ 9.5. Двумерное уравнение переноса 40$
ных длин волн, компенсируя ее значительным затуханием ко-
коротковолновых возмущений. Из приведенного на рис. 9.11 соот-
соответствующего решения для температурного фронта видно, что
эта схема приводит к небольшим осцилляциям и сглаживанию
профиля температуры. Схема Кранка — Николсона с массовым
оператором сохраняет амплитуду, так же как и конечно-раз-
конечно-разностная схема, но, кроме того, дает хорошее согласование по
фазовому углу. Следовательно, резкий профиль температур на
рис. 9.11, соответствующий этой схеме, не является неожидан-
неожиданным.
Хотя вариация параметра б в схеме с массовым оператором
и параметра q в четырехточечной схеме против потока являют-
являются довольно эффективным средством уменьшения дисперсион-
дисперсионных ошибок, их влияние вытекает из дискретизации различ-
различных членов исходного ^уравнения (9.56). Массовый оператор
связан с производной dT/dt, а четырехточечная разность против
потока — с конвективным членом идТ/дх. Отсюда следует, что
стратегия выбора оптимального массового оператора непри-
непригодна для одномерного стационарного уравнения конвекции —
диффузии (§ 9.3). Однако в случае многомерных уравнений
переноса массовый оператор появляется в методе конечных эле-
элементов в связи с недифференцируемыми пространственными на-
направлениями. Следовательно, механизм изменения б в массо-
массовом операторе для уменьшения дисперсии имеет место как для
нестационарных, так и стационарных многомерных уравнений
переноса (§ 9.5).
Аналогичный приведенному выше фурье-анализ для обыч-
обычных конечно-разностной и конечно-элементной схем выполнен
в работе [Pinder, Gray, 1977] для одномерного уравнения пе-
переноса. Фурье-анализ схемы, основанной на использовании
представлений Тейлора — Галёркина, в применении к одномер-
одномерному уравнению переноса выполнен в работе [Donea et al.,
1984].
В данном параграфе использовались различные аналитиче-
аналитические методы, анализ устойчивости по Нейману, метод модифи-
модифицированного уравнения и фурье-анализ для исследования не-
некоторых общепринятых схем решения задач с преобладающим-
влиянием конвекции, а также для построения улучшенных схем..
§ 9.5. Двумерное уравнение переноса
Дополнительные трудности, возникающие при анализе мно-
многомерного уравнения переноса, сравнимы с теми, которые
имеют место при переходе от одномерного уравнения диффузии
к многомерному. В двумерном случае уравнение переноса имеег
410 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
вид
$
¦-<>¦
Явные схемы для уравнения (9.81) устойчивы при более жест-
жестких условиях, что было справедливо также и по отношению к
явным схемам для двумерного уравнения диффузии. Так, на-
например, двумерный вариант схемы ВВЦП (9.58) приводит к
алгоритму
T/.V = (sx + 0.5Сх) Г?.,, * + A - 2sx - 2s,) Tnu k +
+ (sx - 0.5Cx) 27+I. k + (sy + 0.5C,) П *_, +
+ (sy-0.5Cy)Tlk+i, (9.82)
где
sx = ax?*t/&x2, Cx =
sy = ауЫ/Ау2, Су =
Анализ устойчивости алгоритма (9.82) по Нейману дает сле-
следующие условия [Hindmarsh et al., 1984]:
(sx + sy) < 0.5, ? + $L < 2. (9.83)
Если Sx = 5У = 5, то для устойчивости должно быть s ^ 0.25, что
-В два раза меньше, чем в одномерном случае.
Другой серьезной проблемой многомерного случая являет-
является введение искусственной диффузии, в частности искусствен-
искусственной перекрестной диффузии, вводимой схемами первого поряд-
порядка. Как мы уже видели, использование разностей первого по-
порядка по времени и разностей против потока для конвективных
членов приводит к появлению членов с искусственной диффу-
диффузией и дисперсией. В двумерном случае эквивалентная разност-
разностная схема вносит члены с искусственной диффузией с коэффи-
коэффициентами
< = — 0.5ш\л: (С, - 1), < = -0.5иД# (С„ — 1). (9.84)
Ошибки, вносимые этими членами, особенно велики, когда
вектор скорости направлен под углом 45° к координатному на-
лравлению [de Vahl Davis, Mallinson, 1976]. Этот вопрос более
лодробно будет обсуждаться в п. 9.5.3.
§ 9.5. Двумерное уравнение переноса 411
9.5.1. Методы расщепления
При использовании неявных схем для двумерного уравне-
уравнения переноса удается избежать трудностей выполнения усло-
условий устойчивости, присущих явным схемам, но возникает про-
проблема получения эффективного решения неявных разностных
уравнений, точно так же как и для уравнения диффузии.
Здесь мы рассмотрим типичный случай приложения метода
расщепления к двумерному уравнению переноса. Применяя ме-
метод Галёркина с конечными элементами (§ 5.3) с билинейными-
прямоугольными элементами к уравнению переноса (9.81), по-
получим
xx
Мх ® Му [¦g-]/ k = [-иМу ®LX- vMx ®Ly + axMy ® Lx
+ ayMx®Lyy]T!tk9 (9.85)
где Lx**(-l, 0, l)/2Ax, Ly*m(l9 0, -l)T/2/iy и ^ ()
для равномерной сетки. Операторы LXXy Lyy и Му даются фор-
формулами (8.30) и (8.31).
Уравнение (9.85) можно сравнить с (8.29). Дополнительный
член в (9.85) возникает из-за наличия конвективных членов.
Однако массовые операторы по направлению в конвективных
членах ведут себя так же, как и для диффузионных членов.
Другими словами, для метода конечных элементов они оказы-
оказывают влияние на операторы Lx и Ly в перпендикулярном на-
направлении. Это следует из тензорного произведения ® и формы
операторов Мх и Му. Уравнение (9.85) можно обобщить, если
ввести определение
Мх = (Ьх, 1 - 2ЬХ, Ьх), Му = Fу, 1 - 26^, 6^, (9.86)
где 8Х и бу — параметры, которые могут выбираться из усло-
условий минимизации дисперсионных погрешностей аналогично
тому, как это делалось в п. 9.4.3 при выборе б в уравнении
(9.21). Выбор 8Х = 8У = 0 дает трехточечную конечно-разност-
конечно-разностную схему, выбор 6* = 6г/ = 1/6 приводит к линейной конечно-
элементной схеме.
При использовании трехслойного представления для dT/dt
уравнение (9.85) можно привести к виду
Мх <8> Му [A + у) -^- - у -^1] = A - Р) RHS" + р RHS"+\
(9.87)
где
RHS = - [Му® (uLx - axLxx) + MX® (vLy -ayLyy)]Thk.
412 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
Та же самая схема была использована для разностного пред-
представления (8.26) уравнения диффузии.
Вводя то же расщепление, которое применялось к (8.29),
получим следующий двухступенчатый алгоритм для решения
двумерного уравнения переноса:
* + ТТ7 Д' №х - axLxx)] йТ}9 k = (jfy) RHS" +
Ясно, что включение конвективных членов, т. е. uLx и vLy, не
избавляет от необходимости эффективного разбиения (9.87) на
совокупность трехдиагональных подсистем уравнений на каж-
каждом слое расчетной сетки.
Алгоритм (9.88), (9.89) аппроксимирует уравнение (9.81) с
ошибкой О(Д/2, Ах2, Д*/2); при этом для двухслойной схемы
у = 0, р = 0.5, а для трехслойной у = 0.5, р = 1. Та же точ-
точность достигается независимо от того, используется ли линей-
линейная конечно-элементная схема или трехточечная конечно-разност-
конечно-разностная схема для вычисления операторов Мх, Му> Lx> Lxx, Lyy Lyy.
Однако коэффициенты в выражении для ошибок аппроксимации
будут разными в разных случаях, причем конечно-элементный
метод дает более точные решения.
Анализ устойчивости схем (9.88) и (9.89) по Нейману дает
квадратное уравнение (в случае трехслойной схемы) для ко-
коэффициента усиления G, решение которого легко находится
численно. Результат расчета показывает, что при р ^ 0 обе
схемы безусловно устойчивы как в случае аппроксимации с
помощью бесконечных элементов, так и с помощью конечных
разностей.
9.5.2. THERM: задача о проникновении тепла
Метод расщепления, сформулированный в п. 9.5.1, здесь
будет использован для решения задачи о втекании холодной
жидкости в горячий двумерный канал с сечением очень боль-
большого удлинения. Вдали от боковых стенок канала распределе-
распределение температуры существенно двумерное и описывается ста-
стационарной формой следующего уравнения энергии:
дТ , д(иТ) . d(vT)
(990)
Ж + ~W~ + ду пх дх> аУ ду* —U'
где ах == ау = а — коэффициент термодиффузии. Уравнение
(9.90) записано в нестационарном виде для использования
§ 9.5. Двумерное уравнение переноса
413
стратегии псевдостационарных решений (§ 6.4). Если компо-
компоненты скорости и и v известны, то уравнение (9.90) представ-
представляет собой линейное двумерное уравнение переноса.
Уравнение (9.90) удобно решать в безразмерном виде, для
чего вводятся следующие безразмерные переменные:
Г—Го ,/_ и тш/_ vRe
Um Аэит
— JL Pr= 4aUm
Т' =
Tw — Го
2.5*
a Re'
f _
Pr =
a Re
k
(9.91)
где Го и L — температура на входе и на стенке, ит — средняя
осевая скорость, Re, Рг — числа Рейнольдса и Прандтля соот-
соответственно (п. 11.2.5). Такой выбор хг и других безразмерных
' х=хтах
Рис. 9.12. Расчетная область в задаче о проникании тепла.
переменных удобен тем, что температурный профиль разви-
развивается почти на одном и том же интервале х' для различных
Re. Если указанные выше безразмерные переменные подста-
подставить в (9.90), то получим то же самое уравнение в штрихованых
переменных с коэффициентами
В дальнейшем штрихи у безразмерных переменных будут опус-
опускаться.
Для расчетной области, показанной на рис. 9.12, зададим
следующие граничные условия:
Г@, у) = 0 при х = 09
дТ
дх=0 при x = xmax,
Т(ху ± 1)=1 при у = ± 1.
(9.93)
1 С
2 С THERM APPLIES APPROXIMATION FACTORISATION TO SOLVE
3 С THE UNSTEADY THERMAL ENTRY PROBLEM FOR T(X,Y) .
4 С
5 DIMENSION T<41,42),DTD1,42),RD1,42),UD1,42),VD1,42),
6 1ЕШЗ) ,EMYC) ,BE,65) ,RRTF5) ,DDTF5) ,CXC) ,CYC) ,TEXD2)
7 2,ALFA0),DYFLA0),CXQD)
8 COMMON CX,CXQ,CY,CCX,CCY,EMX,EMY,NX,NY,R,T,DT,U,V
9 DATA ALF/1.6815953,5.6698573,9.6682425,13.6676614,17.6673736,
10 121.6672053,25.6670965,29.6670210,33.6669661,37.6664327/
11 DATA DYFL/-0.9904370,1.1791073,-1.2862487,1.3620196,-1.4213257,
12 11.4704012,-1.5124603,1.5493860,-1.5823802,1.6122503/
13 С
14 OPENA,FILE=*THERM.DAT')
15 OPENF,FILE*1THERM.OUT')
16 READA,1)NX,NY,ME,ITMAX,GAM,BET,Q
17 READU,2)DTIM,EPS,RE,PR,XMAX
18 1 FORMATDI5,3F5.2)
19 2 FORMATCE10.3,2F5.2)
20 С
21 NXS = NX + 1
22 NXP = NX - 1
23 NYP = NY - 1
24 NYPP ¦ HYP - 1
25 NYH * NY/2 + 1
26 ANX » NXP
27 DX = XMAX/ANX
28 ANY = NYP
29 DY « 2./ANY
30 ALX = 10./RE/RE/PR
31 ALY = 1.6/PR
32 CXA)
33 CXB)
34 CXC)
35 CYA)
-0.5/DX
0.
0.5/DX
-0.5/DY
36 CYB) = 0.
37 CYC) = 0.5/DY
38 CXQ(l) » Q/DX/3.
39 CXQB) = -3.*CXQA)
40 CXQC) = -CXQB)
41 CXQD) = -CXQ(l)
42 CCX = ALX/DX/DX
43 CCY = ALY/DY/DY
44 IF(ME .N3. 2)Q = 0.
45 EMX(l) = 0.
46 IF(ME .EQ. 3)EMXA) = 1./6.
47 EMXB) » 1. - 2.*EMXA)
48 EMXC) = EMX(l)
49 DO 3 J « 1,3
50 3 EMY(J) = EMX(J)
51 С
52 IF(HE .EQ. 1)VRITEF,4)NX,NY,ME,ITMAX
53 IF(HE .EQ. 2)VRITEF,5)NX,NY,ME,ITMAX
54 IF(HE .EQ. 3)VRITEF,6)NX,NY,ME,ITMAX
55 4 FORMAT С THERMAL ENTRY PROBLEM: 3PT FDM, NX,NY =',213,* ME *f
56 112,' ITMAX =\I3)
57 5 FORMATC THERMAL ENTRY PROBLEM: 4PT UPWIND FDM, NX,NY =',213,
58 1' ME=',I2,' ITMAX*1,13)
59 6 FORMATC THERMAL ENTRY PROBLEM: LIN FDM, NX,NY «',213,' ME ='
60 112,' ITMAX =',I3)
61 VRITEF,7)GAM,BET,DTIM,XMAX,PR,RE,Q
62 7 FORMATC GAM =',F5.2,' BETA =',F5.2,' DTIM =',F6.3,' XMAX *'
63 1F5.2,1 PR=f,F5.2,' RE=\F5.1,' Q«f,F5.2,/)
64 С
65 С GENERATE INITIAL SOLUTION
66 С
Рис. 9.13. Описание программы THERM (начало).
67 DO 9 К = 1,NY
68 АК = К - 1
69 Y = -1. + AK*DY
70 T(K,1) = Y**32
71 T(K,NXS) = 1.
72 U(K.l) = 1.5M1. - Y*Y)
73 V(K,1) = 0.
74 DO 8 J = 2,NXS
75 U(K,J) = U(K,1)
76 V<K,J) = 0.
77 IF(J .EQ. NXS)GOTO 8
78 AJ = J - 1
79 T(K.J) = T(K,1) + AJ*DXMT(K,NXS)-T(K,1))/XMJ
80 8 CONTINUE
€1 9 CONTINUE
82 DO 12 J » 1,NXS
83 DO 10 К = 1,NY
84 DT(K,J) = 0.
85 10 R(K,J) = 0.
86 DO 11 К « 1,5
Zl 11 B(K,J) = 0.
Zя 12 CONTINUE
«9 GAMH = GAM
90 GAM = 0.
91 BETH = BE1
92 BET =0.5
93 ITER = 0
94 С
95 13 DBT * BET*DTIM/U.+GAM)
96 CXA = 0.5*DBT/DX
97 CYA = 0.5*DBT/DY
98 CCXA = DBT*CCX
99 CCYA = DBT*CCY
100 С
101 CALL RETHE(RMST,GAMrDTIM)
102 С
103 IF(RMST .LT. EPS)GOTO 24
104 IF(RMST .GT. 1.0E+04)GOTO 24
105 С
106 С TRIDIAGONAL SYSTEMS IN THE X-DIRECTION
107 С
108 DO9 К = 2,NYP
109 DO 15 J = 2,NX
110 JM = J - 1
111 BB,JM) = EMX(l) - CCXA - CXA*U(K,JM)
112 BC,JM) = EMXB) + 2.*CCXA
113 BD,JM) = EMXC) - CCXA + CXA*U(K,J+l)
114 RRT(JM) = R(K,J)
115 IF(ME .NE. 2)GOTO 15
116 LST = 1
117 IF(J .EQ. 2)LST = 2
118 BA,JM) = 0.
119 DO 14 L=LST,4
120 LJ = J + L - 3
121 14 B(L,JM) = B(L,JM) + CXQ(L)*U(K,LJ)*DBT
122 15 CONTINUE
123 BB,l) = 0.
124 BBrJM) = BB,JM) + BD,JM)
125 BD,JM) = 0.
126 IF(ME .NE. 2)GOTO 17
127 С
128 С REDUCE TO TRIDIAGONAL FORM
129 С
Рис. 9.13 (продолжение).
130
131
132
133
134
135
136
137
13S
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
С
С
С
С
С
С
С
С
С
С
С
С
с
с
16
17
18
19
20
21
22
23
24
DO 16 JM = 3,NXP
JMM = JM - 1
DUM = BA,JM)/BB,JMM)
BB,JM) = BB,JM) - BC,JMM)*DUM
BC,JM) « BC,JM) - BD,JMM)*DUM
BA,JM) = 0.
RRT(JK) = RRT(JM) - RRT(JMM)*DUM
CONTINUE
B(l,2) =. 0.
CALL BANFAC(B,NXP,1)
CALL BANSOL(RRT,DDT,B,NXP,1)
DO 18 J = 2,NX
JM = J - 1
R(K,J) = DDT(JM)
CONTINUE
TRIDIAGONAL SYSTEMS IN THE Y-DIRECTION
DO 22 J = 2,NX
DO 20 К * 2,NYP
KM - К - 1
BB,KM) * EMY(l) - CCYA - CYA*V(KM,J)
BC,KM) ¦ EMYB) + 2.*CCYA
BD,KM) = EMYC) - CCYA + CYA*V(K+1,J>
RRT(KM) = R(K,J)
BB,l) = О.
ВD,KM) = 0.
CALL BANFAC(B,NYPP,1)
CALL BANSOL(RRT,DDT,B,NYPP,1)
INCREMENT T
DO 21 К = 2,NYP
KM = К - 1
DT(K,J) « DDT(KM)
T(K,J) = T(K,J) + DDT(KM)
CONTINUE
DO 23 К = 2,NYP
T(K,NXS) = T(KrNXP)
DT(K,NXS) - DT(K,NXP)
ITER = ITER + 1
GAM = GAMH
BET = BETH
IF(ITER .LE. ITMAX)GOTO 13
COMPARE WITH SEMI-EXACT SOLUTION:
SUM = 0.
DO 25 J = 2rNX
AJ » J - 1
X = AJ*DX
CALL TEXCL(X,TDX,PR,ALF,DYFLl
TEX(J) » TDX
IF(J .EQ. 2)GOTO 25
DIF = T(NYH.J) - TDX
Рис. 9.13 (продолжение).
§ 9.5. Двумерное уравнение переноса 417
190 SUM * SUM + DIF*DIF
191 25 CONTINUE
192 RMS = SQRT(SUM/(ANX-1))
193 VRITEF,26)ITER,RMST,RMS
194 26 FORMATC AFTER M3,1 ITERATIONS, RMS-RHS =\E10.3,
195 1' RMS-ERR =\E10.3)
196 WRITEF,27)(T(NYH,J),J=2,NX)
197 ,VRITEF,28)(TEX(J),J=2,NX)
198 27 FORMATC C/L TEMP -\11F6.3)
199 28 FORMATC EX TEMP =\11F6.3)
200 STOP
201 END
Рис. 9.13 (окончание).
Применение группового метода конечных элементов (§ 10.3)
[Fletcher, 1983] с линейной интерполяцией на прямоугольных
элементах приводит к системе обыкновенных дифференциаль-
дифференциальных уравнений
Мх ® Му [^-] .k = {My® \-Lx (uT) + axLxxT] +
'' +Mx<8>[-Ly(vT) + ayLyeT]},,k, (9.94)
которая отличается от (9.85) только тем, что в конвективные
операторы Lx и Ly входят и, v. Следовательно, двухступенча-
двухступенчатый алгоритм (9.88), (9.89) реализуется с помощью программы
THERM (рис. 9.13) с операторами Lx и Lyy действующими на
иТ и vT соответственно.
Программа THERM работает при любых заданных распре-
распределениях скорости. Одн'ако для проведения сравнения расчет-
расчетного профиля температуры с полуаналитическим решением
[Brown, 1960] предполагалось, что профиль скорости имеет
вид, характерный для полностью развитого течения:
и =1.5A — у2), 3 = 0. (9.95)
Чтобы избежать разрыва решения в точке Л, граничное усло-
условие в программе THERM задавалось в виде
У) = У32. (9.96)
Это дает профиль температуры на входе, который равен нулю
всюду, кроме угловых точек: х = 0, у = ±1.
Вычисление величины RHS" в (9.88) выполняет подпро-
подпрограмма RETHE (рис. 9.14). Основные параметры, использован-
использованные в программе THERM и подпрограмме RETHE, описаны
в табл. 9.11. Типичная выдача результатов программы THERM
приведена на рис. 9.15 для конечно-разностного метода с при-
приближенной факторизацией.
Решение на центральной линии сравнивается с полуана-
полуаналитическим решением [Brown, 1960], которое вычисляется
27 К. Флетчер, т. 1
418 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
С
С
С
С
С
SUBROUTINE RETHE(RMST,GAM,DTIM)
EVALUATES
RIGHT-HAND SIDE OF THE
TVO-DIMENSIONAL TRANSPORT EQUATION
REAL*8 RTD,SUMT,AN,DSQRT
DIMENSION
1DMXC,3),1
COMMON CX
NXP = NX •
NYP = NY -
DO 1 I = 3
DMX(I,1) "
DMX(I,2) -
DMX(I,3) =
DMYA,I) >
DMYB,I) ••
1 DMYC,I) :
SUMT - 0.
DO 6 J =2
DO 5 К = I
RTD = 0.
DO 4 N = :
NK = К - <
DO 2 M = :
MJ = J -
DTD1,42),TD1,42),RD1,42),UD1,42),VD1,42),
)MYC,3),EMXC),EMYC),CXC),CY<3)rCXQD)
CXQ^Y^CCX^CCY^EMX^EMY^NX^NY^^^T^^V
- 1
- 1
L,3
» CCX*EMY(I)
= -2.*DMX(I,1)
* DMX(I,1)
= CCY*EMX(I)
^ -2.*DMYA,I)
« DMYA,I)
,NX
I, NYP
L,3
г + n
L,3
г + м
DUM = DMX(N,M) + DMY(NrM) - CX(M)*EMY(N)*U(NK,MJ)
1 - CY(N)*EMX(M)*V(NK,MJ)
2 RTD = RTD
+ DUM*T(NK,MJ)*DTIM
1 + GAM*EMX(M)*EMY(N)*DT(NK,MJ)
MST = 1
IF(J .EQ.
DO 3 H = 1
MJ = J -
3 RTD = RTD
IF(J .EQ.
4 CONTINUE
2)MST = 2
1ST, 4
3 + M
- CXQ(M)*EMY(N)*U(NK,MJ)*T(NK,MJ)*DTIM
2)RTD = RTD - CXQA)*EMY(N)*U(NK,1)*T(NK,1)*DTIK
SUMT = SUMT + RTD*RTD
5 R(K,J) = 1
6 CONTINUE
AN = NXP*
^TD/A. + GAM)
(NYP-1)
RMST = DSQRT(SUMT/AN)/DTIM
RETURN
END
Рис. 9.14. Описание программы RETHE.
с помощью подпрограммы TEXCL (рис. 16.5, т. 2). Полуанали-
Полуаналитическое решение строится для приведенной формы уравнения
(9.90), в которой предполагается, что членом осевой диффузии
ахд2Т/дх2 можно пренебречь. Справедливость такого предпо-
предположения обсуждается в п. 16.1.4. Следует заметить, что
§ 9.5. Двумерное уравнение переноса
419
Таблица 9.11. Параметры, используемые в программе THERM
Переменная
ME
ITMAX
GAM, BET
q
NX, NY
DTIM
EPS
RE, PR
XMAX,
ALX, ALY
CX, CY
CXQ
EMX, EMY
T; U, V
TEX
TEXCL
DT
DDT
В
R
EMS; RMST
Описание
= 1, приближенная факторизация, 3-точечный конечно-раз-
конечно-разностный метод, AF-FDM
= 2, приближенная факторизация, 4-точечная схема с раз-
разностями против потока, q = 0.5, AF-4PV
= 3, приближенная факторизация, линейный метод конечных
элементов, 6 = 1/6, AF-FEM
Максимальное число итераций
Y, Р в (9.88), (9.89)
Параметр в 4-точечной схеме с разностями против потока.
Ях в (9.97)
Число точек в направлениях х и у
М
Допустимая величина RHS" в (9.88)
Число Рейнольдса, число Прандтля
Протяженность расчетной области по х
ах, ау в (9.90), (9.92)
Lx, Ly в (9.98), (9.89)
Приращение Lx при построении LAX
MXt My в (9.88), (9.89)
Температура; компоненты скорости по х и у
Температура на центральной линии (полуточное решение)
Вычисляет ТЕХ при заданном х и числе Прандтля Рг; тре-
требует задания ALF и DYFL; описывается в п. 16.1.4
ДГ* k в (9.88)
AfJt k и Д7^"У при возврате из BANSOL
4-диагональная и 3-диагональная матрицы; левая часть урав-
уравнений (9.88) и (9.89)
RHSn в (9.88), вычисляемая в RETHE; используется также
для запоминания AT у k в (9.89)
II tcil-Tcil II ч *> IIRHSrt||
М Ъ\Ь L/L ||rms » »rms
27*
420 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
получающееся полуаналитическое решение хорошо аппроксими-
аппроксимирует решение данной задачи везде, кроме окрестности входа
(х = 0) и малых значений Re. Из-за ограничений, налагаемых
на решение Брауна, оно будет называться посуточным в про-
программе THERM и табл. 9.12.
THERMAL ENTRY PROBLEM: 3PT FDM, NX,NY
•CAM - .50 BETA «1.00 DTIM - .200 XMAX
11 11 ME * 1 ITMAX = 25
2.00 PR» .70 RE=100.0 Q =
.00
AFTER 20 ITERATIONS, RMS-RHS = .857E-05 RMS-ERR » .180E-01
C/L TEMP = .459 .744 .881 .945 .975 .988 .995 .998 .999 1.000
EX TEMP = .493 .786 .'909 .962 .984 .993 .997 .999 .999 1.000
Рис. 9.15. Типичная выдача из программы THERM.
В табл. 9.12 и на рис. 9.16 приведены решения на централь-
центральной оси для относительно грубой сетки. Среднеквадратичные
•ошибки, приведенные в табл. 9.12, основаны на решении вдоль
центральной линии во всех точках, кроме / = 2, так как вблизи
входа х = 0 пригодность по-
полуточного решения становится
сомнительной.
В табл. 9.12 и на рис. 9.16
приведены также результаты
расчета, полученные с исполь-
использованием дискретизации
д(иТ)/дх четырехточечных раз-
разностей против потока вместо
оператора Lx в уравнении
(9.94) и эквивалентных ему
(9.88) и (9.89). Это та же са-
самая четырехточечная дискре-
дискретизация с разностями против
потока, которая обсуждалась
в п. 9.3.2 и 9.4.3. Корректное
ТЕМ
+ ЯР-FDM
О AF-4PU
¦ AF-FE.M
— точное решение
0.0
1.0
2.0
Рис. 9.16. Сравнение решений для
температуры вдоль центральной ли-
линии (обозначения см. в табл. 9.12).
рассмотрение двумерной зада-
задачи в целом означает, что четы-
четырехточечная дискретизация с
разностями против потока бу-
будет вводиться также и для d(vT)dy. Но это не было сделано в
программе THERM, поскольку в данном примере v = 0, и, сле-
следовательно, член d{vT)/dy не влияет на решение. Четырехточеч-
Четырехточечная схема с разностями против потока неприменима в точке
/ = 2 из-за трудностей задания подходящего значения Го, k.
Ясно, что все методы дают хорошее согласие с полуточным
решением ввиду грубости сетки. Особенно хорошо согласуется
422 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
линейный метод конечных элементов со стационарным модифи-
модифицированным уравнением, решение которого в действительности
и находилось.
Относительные характеристики построения массового опе-
оператора и четырехточечной дискретизации с разностями против
потока для конвективных членов можно сравнить, если рассмот-
рассмотреть стационарное модифицированное уравнение для схемы,,
которая включает в себя свойства обоих вариантов. Запишем
это уравнение
д(иТ) , d(vT) д2Т д2Т ,
~дх~ ¦+¦ ду ~пх дх2 аУ ду2 +
+ (иДл;2/6) {A - 2qx - 66,) -g
+ F6* - 0.5)//?Сеп, ,]-§?} +...+
{A - 2qy - 66,)^ +
Яу + F6, - 0.5)//?ceU, J^j + ...^О, (9.97)»
где qx и qy — свободные параметры, введенные в четырехточеч-
четырехточечную схему с разностями вперед, применяемую для дискретиза-
дискретизации членов д(иТ/дх) и d(vT)/dy соответственно. Параметры
6* и 8У заменяют б в определениях Мх и Му (9.94). Числа Рей-
нольдса ячейки определяются в виде
? (9-98).
В рассмотренном примере v = 0, так что /?Сеи, у = 0. В противо-
противоположность случаю для уравнения конвекции — диффузии Rceu,x
является функцией координат.
Из (9.97) ясно, что при выборе qx = qy = 0.5, 6* = 6У = 0
либо qx = qy = Q, 6^ = 6, = -^- производные третьего порядка,,
дающие дисперсию, будут исключены. Однако последующее
рассмотрение диссипативных членов с производными четверто-
четвертого порядка несколько отличается, особенно для больших чисел
Рейнольдса RCei\. Оба метода дают положительную диссипацию,
но в случае схемы с массовым оператором диссипация стре-
стремится к нулю с увеличением числа Рейнольдса ячейки, тогда
как для случая четырехточечной схемы с разностями против^
потока это не имеет места. Результаты табл. 9.12 представляют
решение уравнения (9.97).
§ 9.5. Двумерное уравнение переноса 423
9.5.3. Поперечная диффузия
При использовании двухточечной схемы с разностями про-
тив потока для конвективных членов в одномерной задаче воз-
шикает искусственная диффузия а'= 0.5 иДх (табл. 9.1 и 9.3)
для одномерной задачи. В случае многих переменных влияние
искусственной диффузии удобнее рассматривать в связи с ло-
локальным направлением потока. Так, в случае двух переменных
коэффициенты искусственной диффузии вдоль потока и в по-
поперечном к потоку направлении представляют больший физи-
физический интерес, чем коэффициенты искусственной диффузии
вдоль координатных направлений.
При а = а* = ау и и = v = const двумерное стационарное
уравнение конвекции — диффузии можно записать в виде
дТ . дТ ( д2Т . д2Т \ Л /л ллч
и-5—Ь v "и а ( -зт + тт ) = 0. (9.99)
дх ' ду \ дх2 ' ду2 ) v '
'.Будем предполагать, что для дискретизации производных
*дТ/дх и дТ/ду используется двухточечная схема с разностями
против потока, а для дискретизации д2Т/дх2 и d2T/dy2 — трех-
трехточечные центральные разности. Разложение в ряд Тейлора
членов полученного в результате дискретизации разностного
уравнения показывает, что оно с точностью О (Ах2, Ау2) аппрок-
аппроксимирует уравнение
«^+!На+<)-&-(а+<)!М' (9лоо)
тде с? = 0.5ыДл;, a'y = 0,5vAy.
Ясно, что уравнение (9.100) является непосредственным
обобщением одномерного уравнения (9.51) с той разницей, что
оно содержит искусственную диффузию по координатным на-
направлениям.
В уравнении (9.100) удобно перейти к координатной систе-
системе, связанной с касательным и нормальным к потоку направ-
направлениями. В результате получим
где
с^ = O.5<7 (A* cos3 a + Ay sin3 а),
а^ = O.5<7 (Ay sin а — Ал: cos а) sin 2а,
о!п = О.5<7 (Ал: cos а sin2 а + Ay sin а cos2 а).
В уравнении (9.101) s и п означают координаты по каса-
касательной и нормали к локальному направлению потока
424 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
соответственно. Кроме того, скорость равномерного потока q
направлена под углом а к оси х, так что
u = q cos а и i; = <7sina. (9.102)<
Первые три члена в уравнении (9.101) являются результа-
результатом непосредственного преобразования уравнения (9.99). По-
Последние три члена описывают искусственную диффузию. В слу-
случае Ах = Ау видно, что о!п будет максимальным при а = 45°
и нулевым, если направление потока совпадает с осью х или
у. И наоборот, искусственная диффузия вдоль линий тока мак-
максимальна при a = 0 или 90° и минимальна при a = 45°.
С первого взгляда может показаться, что искусственная
диффузия вдоль линий тока представляет большой интерес, так.
как при Ах = Ау l^l^0^ для всех a в интервале 0 ^ a ^
^ 90°. Однако для большинства течений производная d2T/ds2
очень мала всюду, кроме окрестности точки торможения. И на-
наоборот, для сдвиговых течений и пограничного слоя (гл. J6)
д2Т/дп2 ^> d2T/ds2 и производная д2Т/дп2 сравнима по величи-
величине с конвективным членом qdT/ds. Следовательно, поперечная
искусственная диффузия может вносить значительную погреш-
погрешность, если аппроксимация конвективных членов имеет недо-
недостаточно высокий порядок, а локальное направление потока не
совпадает с координатными линиями. В противоположность
этому методы, которые приводят к искусственной диффузии
только вдоль линий тока [Brooks, Hughes, 1982], весьма эф-
эффективны для построения неосциллирующих достаточно точ-
точных решений для многих гидродинамических задач.
Поперечная искусственная диффузия подробно изучалась
теоретически и экспериментально в работах [de Vahl Davis,
1976; Mallinson, 1976; Raithby, 1976; Griffiths, Mitchell, 1979].
§ 9.6. Заключение
В этой главе применялись последовательно различные чис-
численные методы, рассмотренные в гл. 7 для уравнения диффу-
диффузии, к линейному уравнению конвекции, стационарному уравне-
уравнению диффузии и уравнению переноса. Эти уравнения являются
модельными различной степени сложности для уравнений
(гл. 11), описывающих задачи гидродинамики. Соответствую-
Соответствующие методы будут применены в гл. 14—18 к определяющим
уравнениям гидроаэродинамики.
При исследовании модельных уравнений основное внимание
уделялось тому, как выделить численную дисперсию и диссипа-
§ 9.6. Заключение 425
цию и по возможности ее регулировать. Это особенно важно
при использовании алгебраических схем первого порядка точ-
точности в тех случаях, когда диффузия либо отсутствует, либо
много меньше по порядку величины, чем конвекция. В другой
ситуации, когда конвекция преобладет над диффузией, могут
возникать нефизические осцилляции, если для дискретизации
конвективных членов используется симметричная трехточечная
алгебраическая формула на грубой сетке. Однако введение
массовых операторов, которые привносят черты конечно-эле-
конечно-элементного метода, обеспечивает механизм контроля за колеба-
колебаниями дисперсионного типа. При использовании метода рас-
расщепления введенного в § 8.3, массовые операторы оказались
полезными при исследовании стационарных и нестационарных
многомерных задач.
Альтернативные способы контроля за осцилляциями диспер-
дисперсионного типа обеспечиваются введением четырехточечной ди-
дискретизации против потока для конвективных членов. Этот
прием оказывается эффективным, хотя он часто вносит допол-
дополнительные диссипативные члены более высокого порядка, кото-
которые могут оказаться существенными на грубой сетке. Четырех-
Четырехточечная дискретизация против потока может быть введена
и в неявные алгоритмы, но она приводит обычно к четырех-
.диагональным системам уравнений, которые могут быть реше-
решены с помощью алгоритма Томаса после сведения системы к
трехдиагональному виду. Это на 80 % увеличивает машинное
время по сравнению с тем, которое затрачивается на решение
>самого алгоритма Томаса. Использование четырехточечных
схем, кроме того, приводит к необходимости введения допол-
дополнительных граничных условий на входе или локального сведе-
сведения к трехточечной схеме.
Сопоставление различных методов, использованных в дан-
данной главе, показывает и сравнительную цену эффективности
метода модифицированных уравнений (п. 9.2.2) для построения
улучшенных алгоритмов. Поскольку в его основе лежит раз-
разложение в ряды Тейлора, этот метод дает информацию только
о длинноволновых характеристиках.
Для получения коротковолновых характеристик требуется
анализ Фурье (п. 9.2.1), который используется также и при
анализе устойчивости по Нейману (§ 4.3). Однако если метод
модифицированных уравнений допускает непосредственное об-
обобщение на нелинейные схемы и уравнения, то при использова-
использовании анализа Фурье требуется локальная линеаризация, которая
может привести к ухудшению эффективности метода для не-
.линейных задач гидроаэродинамики (гл. 10, И и 14—18).
426 Гл. 9. Линейные задачи с преобладающим влиянием конвекции
§ 9.7. Задачи
Одномерное линейное уравнение конвекции (§ 9.1)
9.1. Получите выражение для погрешности аппроксимации, указанной в
табл. 9.1 для схемы Лакса— Вендроффа.
9.2. Примените анализ устойчивости по Нейману к схеме Кранка — Ни-
колсона (9.22) с массовым оператором и убедитесь в выполнении условия
б ^ 0.25 для устойчивости схемы.
9.3. Примените программу TRAN для решения задачи о конвекции сину-
синусоидальной волны с помощью схемы Кранка — Николсона с массовым опера-
оператором и сравните полученные решения с приведенными на рис. 9.2—9.4.
Численная диссипация и дисперсия (§ 9.2)
9.4. Примените анализ Фурье (п. 9.2.1) к одномерному уравнению кон-
конвекции для следующих схем: A) схемы с разностями против потока, B) схе-
схемы Лакса — Вендроффа, C) конечно-разностной схемы Кранка — Никол-
Николсона при С = 0.8 и Ад: = 0.5. Получите результаты, эквивалентные приве-
приведенным в табл. 9.9, причем для этого рекомендуется составить программу
расчета на ЭВМ. Проанализируйте решения, показанные на рис. 9.2—9.4,.
относительно фурье-разложений.
9.5. Примените метод модифицированных уравнений: A) к схеме с раз-
разностями против потока, B) к схеме Лакса — Вендроффа, C) к конечно-раз-
конечно-разностной схеме Лакса — Вендроффа для анализа одномерного уравнения
конвекции и подтвердите результаты, приведенные в табл. 9.1. Сравните
расчетные характеристики с анализом Фурье задачи 9.4 и результатами, по-
показанными на рис. 9.2—9.4.
9.6. Постройте обобщенную трехслойную схему, эквивалентную (8.26),.
для одномерного уравнения конвекции. Примените метод модифицирован-
модифицированного уравнения с произвольными у и р и определите, имеется ли возмож-
возможность их оптимального выбора для минимизации ошибок, связанных с дис-
дисперсией и диссипацией. Внесите изменения в программу TRAN, включив в
нее эту задачу, и проверьте ее действие на задаче о конвекции синусоидаль-
синусоидальной волны.
Стационарное уравнение конвекции — диффузии (§ 9.3)
9.7. Включите схему центральных разностей (9.45) и схему с разно-
разностями против потока (9.50) в программу расчета и подтвердите результаты,,
приведенные на рис. 9.5 и 9.6.
9.8. Проведите расчет по программе, составленной в задаче 9.7 с гра-
граничным условием Неймана dT/dx = g при х = 1.0. Выберите g таким обра-
образом, чтобы точное решение было близко к решениям, приведенным на
рис. 9.5 и 9.6. Сравните решения с полученными для случая, когда задана*
граничное условие Дирихле.
9.9. Получите симметричные пятиточечные схемы для dT/dx и d2T/dx2r
минимизируя ошибку аппроксимации, оставляя в каждом выражении по од-
одному параметру. Примените эту схему к решению конвективного уравнения
диффузии с граничным условием Дирихле (9.43). Используйте точное реше-
решение (9.44) для получения требуемого граничного условия. Измените подпро-
подпрограммы BANFAC и BANSOL для решения системы с полученной в резуль-
результате пятидиагональной матрицей. Полученные решения сравните с приведен-
приведенными в табл. 9.2 и определите, будет ли выбор двух подходящих параметров^
приводить к более точным, но устойчивым решениям.
§ 9.7. Задачи 427
> Одномерное уравнение переноса (§ 9.4)
9.10. Примените метод модифицированного уравнения к дискретиза-
.циям Лакса — Вендроффа и Кранка — Николсона для одномерного уравне-
уравнения переноса и подтвердите результаты, приведенные в табл. 9.3.
9Л1. Для явной четырехточечной схемы с разностями против потока, т. е.
(9.71) с заменой 0.5 (Г" + Г"+1) на Tf в пространственном операторе, вос-
воспользуйтесь методом модифицированного уравнения для определения опти-
оптимальной величины q. Примените анализ устойчивости по Нейману для опре-
определения критериев устойчивости. Проведите расчет по программе TRAN с
оптимальным q, если схема устойчива, при условиях, данных в табл. 9.6, и
•сравните полученные результаты.
9.12. Измените программу TRAN, включив в нее трехслойную чисто не-
неявную схему (табл. 9.3). Решите задачу о распространении температурного
-фронта (п. 9.4.3) для повышенных чисел Рейнольдса ячейки и определите
эмпирически границу, до которой не появляются осцилляции решения. По-
Повторите все расчеты по схеме Кранка — Николсона с конечными разностями
и конечными элементами.
.Двумерное уравнение переноса (§ 9.5)
9.13. Примените метод модифицированного уравнения к схеме Кранка —
.Николсона с массовым оператором для двумерного уравнения переноса (9.81)
и определите оптимальные значения дх и 8У в (9.86) для минимизации дис-
.персионных ошибок.
9.14. С помощью программы THERM сравните приближенную фактори-
:зацию с помощью конечно-разностной схемы AF-FDM, четырехточечной схе-
схемы с разностями против потока (AF-4PU) (q = 0.5) и метода конечных
-элементов (AF-FEM) для числа итераций, достаточных для сходимости. Про-
Проделайте это для трех маршевых алгоритмов: (а) Y = 0» Р — 0-5; (Ь) Y = 0»
р = 1; (с) у = 0,5, р = 1 и на сетках 11 X 11 и 21 X 21.
9.15. На основе табл. 9.12, решения задачи 9.14 и дополнительных реше-
решений, полученных из программы THERM, сравните вычислительную эффектив-
эффективность трех методов приближенной факторизации: конечно-разностного ме-
метода (AF-FDM), четырехточечной схемы с разностями против потока (AF-
•4PU) и метода конечных элементов (AF-FEM).
Глава 10
Нелинейные задачи
с преобладающим влиянием конвекции
В гл. 9 были рассмотрены линейные задачи с преобладаю-
преобладающим влиянием конвекции. Как было показано там, процесс
дискретизации уравнений, и в особенности их конвективных
членов, требует особой осторожности во избежание появления
фиктивных членов с высшими производными (если иметь в
виду модифицированное уравнение), которые по своей величи-
величине могут оказаться сравнимыми с членами определяющего
уравнения, важными по своему физическому смыслу. Эта
проблема особенно серьезна при введении двухточечных раз-
разностей со сдвигом вверх по потоку.
Установление связи производных высокого порядка в моди-
модифицированном уравнении (п. 9.2.2) с процессами диссипации
и дисперсии позволяет построить более точные вычислительные
алгоритмы. Например, четырехточечные системы со сдвигом"
вверх по потоку позволяют избежать чрезмерных осцилляции,
связанных с дисперсией (п. 9.3.2 и 9.4.3), без введения нежела-
нежелательной диссипации, как в случае двухточечной схемы со сдви-
сдвигом вверх по потоку.
Конвективные члены, входящие в уравнение энергии
(п. 11.2.4), являются линейными, если известно поле скоростей.
Однако конвективные члены уравнений импульсов (п. 11.2.2 и
11.2.3) существенно нелинейны. В данной главе рассматривают-
рассматриваются дополнительные осложнения, связанные с нелинейной кон-
конвекцией. Подходящую для этой цели модель обеспечивает од-
одномерное уравнение Бюргерса, так как оно обладает конвек-
конвективной нелинейностью той же самой формы, что и уравнения
Навье —Стокса для несжимаемой жидкости (§ 11.5), и допу-
допускает легко вычислимые точные решения для разнообразных
комбинаций начальных и граничных условий.
В процессе применения анализа устойчивости по Нейману
конвективную нелинейность необходимо нейтрализовать. Эта
осуществляется путем временного замораживания коэффициен-
коэффициентов при производных, фактически зависящих от решения. При
анализе нелинейных вычислительных алгоритмов можно вос-
воспользоваться методом модифицированного уравнения [Klopfer,.
§ 10.1. Одномерное уравнение Бюргерса 429
McRae, 1983J, однако появление произведений производных
высшего порядка делает процесс построения схем повышенной
точности менее конкретным и надежным (п. 10.1.4), чем это
было для линейных уравнений (п. 9.4.3).
Нелинейный характер конвективных членов обусловливает
появление больших градиентов зависимых переменных. Это
наводит на мысль об использовании неоднородных сеток, ло-
локально измельченных в окрестности быстрых изменений реше-
решения. Влияние неоднородности сетки на ошибку аппроксимации
и точность решения кратко анализируется в п. 10.1.5. Этот во-
вопрос более подробно обсуждается в гл. 12.
Определяющие уравнения гидроаэродинамики (гл. 11)
обычно имеют структуру систем, являясь при этом нелинейны-
нелинейными. Дополнительные осложнения, связанные с построением вы-
вычислительных алгоритмов для систем нелинейных уравнений,
подвергаются предварительному рассмотрению в § 10.2.
Как мы видели ранее (гл. 5), метод Галёркина с конечными
элементами приводит к точным и экономичным алгоритмам
для решения линейных задач с преобладающим влиянием кон-
конвекции (п. 9.1.4, 9.4.3 и § 9.5). Однако учет конвективной нели-
нелинейности является потенциально неэкономичным в условиях
многомерности или при использовании интерполяции повышен-
повышенного порядка. Недостаточная экономичность может быть пре-
преодолена за счет применения группового метода конечных эле-
элементов; описание этого метода дается в § 10.3.
Схемы расщепления, рассмотренные в § 8.2, 8.3 и 9.5, рас-
распространяются на двумерные уравнения Бюргерса в п. 10.4.2.
Как и их одномерный вариант, двумерные уравнения Бюргер-
Бюргерса допускают без труда строящиеся точные решения, по край-
крайней мере для предельного стационарного состояния, позволяя
тем самым осуществлять прямые оценки точности конкретных
вычислительных алгоритмов (п. 10.4.3).
i § 10.1. Одномерное уравнение Бюргерса
Одномерное уравнение Бюргерса [Burgers, 1948] имеет вид
дп , - дп д2п ~ /1Л 1Ч
-rr + U-z ^-з-2- = 0. (ЮЛ)
dt дх дх2 у '
Уравнение Бюргерса аналогично уравнению переноса (9.56),
если не считать того, что здесь конвективный член является
уже нелинейным. Это та же самая форма нелинейности, кото-
которая имеет место и в уравнениях импульсов (п. 11.2.2 и 11.2.3).
Чтобы подчеркнуть упомянутую связь с уравнениями импуль-
импульсов, коэффициент диффузии а из уравнения (9.56) был заменен
430 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
на коэффициент кинематической вязкости v в уравнении A0.1).
Более глубокий анализ уравнения Бюргерса проводится
в работах [Fletcher, 1983a; Whitham, 1974].
10.1.1. Физическое поведение
Если из уравнения A0.1) удалить «вязкий» член, то в ре-
результате получим невязкое уравнение Бюргерса
^ + й|| = 0, A0.2)
которое можно сравнить с уравнением (9.2). Наличие нелиней-
нелинейности в уравнении A0.2) позволяет развиваться непрерывным
Рис. 10.1. Формирование неоднозначного решения невязкого уравнения Бюр-
Бюргерса A0.2).
решениям. На рис. 10.1 дается схематическая иллюстрация то-
того, как происходит этот процесс. Конвекция переносит волну
слева направо, и на рисунке показаны решения для последо-
последовательности значений времени t = 0, U, ti- Точки на волне, где
значения и больше, подвергаются более быстрой конвекции и
в конечном итоге опережают участки волны, конвектируемые
с меньшими значениями п. Чтобы уравнение A0.2) имело един-
единственное решение (и приносило результат, имеющий физиче-
физический смысл), необходимо постулировать возникновение ударной
волны (линия аЪ на рис. 10.1), при переходе через которую п
изменяется разрывным образом.
Сравнимая с этой схемой эволюция волны для «вязкого»
уравнения Бюргерса A0.1) показана на рис. 10.2. Вязкий член
уд2п/дх2 производит двоякое воздействие. Во-первых, он умень-
уменьшает амплитуду волны при возрастании t (точно так, как и для
уравнения переноса). Во-вторых, он предотвращает развитие
многозначных решений, подобных показанным на рис. 10.1.
§ 10.1. Одномерное уравнение Бюргерса
431
Вышеупомянутые особенности делают уравнение Бюргерса
очень подходящей моделью для проверки работы вычислитель-
вычислительных алгоритмов для описания таких течений, где предвидятся
либо очень большие градиенты, либо ударные волны. Роль
этого уравнения как средства для проверки действия вычис-
вычислительных алгоритмов облегчается за счет применения пре-
преобразования Коула — Хопфа [Cole, 1951; Hopf, 1950], позво-
позволяющего строить точные решения уравнения Бюргерса для мно-
многих комбинаций начальных и граничных условий. Примеры
использования уравнения Бюргерса с такими целями приводятся
Рис. 10.2. Эволюция решения уравнения Бюргерса A0.1).
в работе [Fletcher, 1983a]. В п. 10.1.4 с помощью уравнения
Бюргерса демонстрируются различные вычислительные алго-
алгоритмы для расчета течений с преобладающим влиянием кон-
конвекции.
Существует альтернативный подход к обращению с нели-
нелинейным конвективным членом. Он требует, чтобы уравнение
A0.1) было переписано в консервативной, или дивергентной,
форме
dt дх дх2 ' \i\j.vj
где Р = 0.5п2. Группы членов наподобие F естественным об-
образом возникают при выводе уравнений, определяющих течение
жидкости (п. 11.2.1), и нередко подвергаются прямому моде-
моделированию в вычислительных алгоритмах, особенно при иссле-
исследовании течения сжимаемой жидкости (§ 14.2 и 18.3). Та же
идея используется и при формулировке группового метода ко-
конечных элементов (§ 10.3).
Наличие нелинейного конвективного члена в уравнении
A0.2) способствует также вознкновению побочного эффекта
432 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
(aliasing). Если начальное условие п(х, 0), относящееся к
A0.2), разлагается по соответствующим компонентам Фурье,
как это было сделано при выводе уравнения (9.30), то после-
последующая эволюция решения, определяемого уравнением A0.2),
приведет к быстрому расширению спектра длин волн с замет-
заметными амплитудами, реализуемому через посредство произведе-
произведений компонент Фурье, появляющихся из-за наличия нелинейного
члена пдп/дх.
Когда решение строится на сетке с размером ячейки Ах>
наименьшая длина волны, которую можно различить, равна
2Ах. Энергия, связанная с волнами, длина которых меньше
2Дх, выявляется в связи с волнами большой длины. Это явле-
явление называется побочным эффектом [Hamming, 1973]. К со-
сожалению, коротковолновые вклады в решение, подвергнутые
побочному эффекту, искажают истинный характер длинновол-
длинноволновой части решения и даже могут привести к неустойчивости
(которую называют нелинейной неустойчивостью) в тех слу-
случаях, когда интегрирование уравнений проводится на очень
больших интервалах времени, как, например, при численной
реализации прогноза погоды.
Следует напомнить (§ 9.2), что при наличии любого вида
диссипации — физической или численной — амплитуда корот-
коротковолновой части решения весьма существенно уменьшается;
в этом случае ошибки, порождаемые побочным эффектом, ока-
оказываются минимальными. Именно такая ситуация складывает-
складывается для большинства инженерных задач гидроаэродинамики,
когда, как правило, имеет место физическая диссипация. Одна-
Однако многие классы геофизической гидродинамики характери-
характеризуются конвекцией волновых пакетов при очень малой физи-
физической диссипации или ее отсутствии. В этих условиях побоч-
побочный эффект, а также нелинейная неустойчивость, может пред-
представлять серьезную проблему.
10.1.2. Явные схемы
Конечно-разностное представление уравнения A0.1) в соот-
соответствии со схемой ВВЦП имеет вид
Дополнительный множитель unt у конвективного члена пред-
представляет собой локальное решение в узле (/, п). Это решение
имеется в нашем распоряжении, а поэтому различные схемы
(например, схема Дюфорта — Франкела и др.), предложенные
§ 10.1. Одномерное уравнение Бюргерса
433
для решения линейного уравнения переноса (§ 9.4), могут быть
применены и к решению уравнения Бюргерса.
Представления об ошибке аппроксимации и о модифициро-
модифицированном уравнении также могут быть распространены на не-
нелинейные уравнения типа уравнения Бюргерса. При примене-
применении анализа устойчивости по Нейману дополнительный мно-
множитель и1! у конвективного члена временно замораживается,
так как анализ устойчивости, строго говоря, применим только
t=0
\t=0.36
V
.0 0
50
1
1.0
X
Рис. 10.3. Точное решение уравнения Бюргерса.
к линейным уравнениям. Несмотря на то что применение ана-
анализа по Нейману к нелинейным уравнениям не поддается стро-
строгому обоснованию, выяснилось, что на практике такой анализ
эффективен.
Вполне очевидный вариант применения схемы ВВЦП к
уравнению A0.3), эквивалентный A0.4), принимает вид
к?
Т
- = 0. A0.5)
Алгоритм, составленный на основе A0.5), является составной
частью программы BURG (рис. 10.4) для случая ME = 1.
Потенциально более точная модель конвективного члена
строится с помощью четырехточечной дискретизации со сдви-
сдвигом вверх по потоку. Такая модель применялась к эквивалент-
эквивалентному линейному конвективному члену в п. 9.3.2 и 9.4.3. Четы-
Четырехточечная дискретизация dF/dx со сдвигом вверх по потоку
вводится посредством замены (Fj+i — Fj-i)/2Ax в уравнении
28 К. Флетчер, т. 1
1 С
2 С BURG SOLVES BURGERS EQUATION FOR A PROPAGATING 'SHOCK*
3 С
4 DIMENSION RF5),UF5),UDF5),UEF5),AE,65)
5 1,EFD),XF5)rAAB),BBB),CCB)
6 OPENA,FILEs * BURG.DAT')
7 OPENF,FILE»f BURG.OUT•)
8 READA,1)ME,JMAX,NTIM,XMAX,AD
9 READA,2)C,S,Q,EM
10 1 FORMATCI5,2E10.3)
11 2 FORMAT(F5.2,3E10.3)
12 С
13 JMAF » JMAX - 2
14 JMAP « JMAX - 1
15 AMP « JMAP
16 DX * 2.*XMAX/AMP
17 DT * C*DX
18 SA » AD*C*C
19 ALPH = S*DX*DX/DT
20 IF(ALPH .LT. 1.0E-10)ALPH = 1.0E-10
21 RCEL = DX/ALPH
22 QQ « Q*C/3.
23 IF(ME .LT. 3)QQ « 0.
24 MQ « 0
25 IF(ABS(QQ) .GT. 0.0001)MQ = 1
2S ATIM = NTIM
27 TIM = 0,
28 TIMAX = DT*ATIM
29 PI = 3.141592654
30 С
31 VRITE<6,3)
32 3 FORMAT(• PROPAGATING SHOCK WAVE(BURGERS EQUATION)*)
33 IF(ME .EQ. 1)WRITEF,4)ME
34 IF(ME .EQ. 2)VRITEFt5)KE
35 IF(ME .EQ. 3)VRITEF/6)ME
36 IF(ME .GE. 4)VRITEF,7)ME
37 4 FORMATEH ME =,12,ЗХД8Н FTCS DIFFERENCING)
38 5 FORMATEH ME =,I2,3X,13H LAX-VENDROFF)
39 6 FORMATEH ME »,I2,3X,20H EXPLICIT 4PT UPWIND)
40 7 FORMATEH ME »,I2,3X,23H GENERAL CRANK-NICOLSON)
41 WRITEF,8)JMAX,NTIM,C,DX,DT,XMAX
42 8 FORMATC JMAX«\I3/ NTIM«f,I3,f C«f,F5.2,
43 1' DX«\F5.3,f DT«f,F5.3,f XMAX«'fF5.2)
44 VRITEF/9)S,ALPHfRCEL,Q,EM/SA
45 9 FORMATC S«\F5.2,' ALPH»1 ,E10.3,f RCEL»1 ,F6.1# f Q»
46 Г ЕМ^ЧГб.З,1 SA=\E10.3)
47 С
48 IF(ME .GT. 3)GOTO 10
49 Ш1)
50 BBA)
51 CCA)
52 IF(ME
53 AAA)
54 BBA)
55 CCA)
56 AAB)
57 BBB)
0.5*C + 3.*QQ
- 3.*QQ
-0.5*C + QQ
NE. 2)GOTO 11
0.
0.5*C
-0.5*C
С
-С
58 CCB) » 0.
Рис. 10.4. Распечатка программы BURG (начало).
»59 GOTO 11
60 10 ЛАA) »И + 0.5*S
61 ВВA) « 1.0 - 2.0*ЕН - S
62 ССA) « ЕЙ + 0.5*S
63 11 VRITEF,12)AA,BB,CC
64 12 FORMATC AA«\2F8.5,f BB-',2F8.5,a CC»1.2F8.5,/)
65 С
66 С INITIALISE U AND EVALUATE UEX
67 С
68 CALL EXSH(JMAX,X,U,UE,DX,XMAX,ALPH,TIMAX)
69 С
70 UDA) » U(l)
71 UD(JKAX) * U(JMAX)
72 DO 14 J « 1,JMAX
73 DO 13 К « 1,5
74 13 A(K,J) * 0.
75 14 CONTINUE
76 WRITEF.15)TIM
77 15 FORMAT Г INITIAL SOLUTION, TIH »\F5.3)
78 VRITEF,16)(X(J),J«l,JMAX)
79 VRITEF,17)(U(J),J«l,JMAX)
BO 16 FORMAT С X»\12F6.3)
81 17 FORMATC U«\12F6.3)
82 С
83 С MARCH SOLUTION IN TIME
84 С
85 DO 27 N = 1,NTIM
36 IF(ME .GT. 3)GOTO 21
«7 С
48 С EXPLICIT SCHEMES
89 С
90 IP » 1
91 18 IF(IP .EQ. l)EF(l) « 0.5*U(l)*U(l)
*2 IF(IP .EQ. 2)EFA) « 0.5*UD(l)*UD(l)
93 EFB) » EFA)
94 EFC) * EFB)
95 IFUP .EQ. 1)EFD) * 0.5*UB)*UB)
96 IF(IP .EQ. 2)EFD) « 0.5*UDB)*UDB)
97 DO 20 J * 2,JMAP
98 IF(ME .EQ. 3)EFA) « EFB)
99 EFB) * EFC)
100 EFC) » EFD)
101 IFUP .EQ. 1)EFD) * O.5*U(J+1)*U(J+1)
102 IF(IP .EQ. 2)EFD) * 0.5*UD(J+l)*UD(J+l)
103 DUM « S*(U(J-1) - 2.*U(J) + U(J+D)
104 IF(ME .NE. 2 .OR. IP .EQ. 2)GOTO 19
105 JP « J+l
106 IF(J .EQ. JMAP)JP * J
107 DUM » 0.5*DUM+O.5*S*(U(J)-2.*U(J+l)+U(JP+l))+0.5*(U(JP)-U(J))
108 19 UD(J) « U(J) + AA(IP)*EFB) + BB(IP)*EFC) + CC(IP)*EFD) + DU!t
109 IF(ME .EQ. 3)UD(J) « UD(J) - QQ*EFA)
110 20 CONTINUE
111 IF(ME .NE. 2 .OR. IP .EQ. 2)G0T0 25
112 IP « IP + 1
113 GOTO 18
Рис. 10.4 (продолжение).
28*
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
С
С
С
С
С
С
С
С
С
21
22
23
24
25
26
27
28
29
30
31
TRIDIAGONAL SYSTEM FOR IMPLICIT SCHEMES
IF(MQ .EQ. DDIM = Ud)
DO 22 J = 2,JMAP
JM =« J - 1
IF(JM .NE. DDIM = U(JH-l)
AA,JM) = 0.5*QQ*DIM
AB,JM) = EM - 0.5*S - (O.25*C + 1.5*QQ)
AC,JM) « 1.0 - 2.0*SM + S + 1.5*QQ*U(J)
AD,JM) = EM - 0.5*S + @.25*C - 0.5*QQ)
IF(ME .NE. 5 )GOTO 22
AB,JM) = AB,JM) - 0.5*SA*U(JM)
AC,JM) = AC,JM) + SA*U(J)
AD,JM) = AD,JM) - O.5*SA*U(J+1)
R(JM) = AAA)*U(JM) + BBA)*U(J) + CCA)
Rd) = R(D - AB,1)*UA)
IF(MQ .EQ. 0)GOTO 24
Rd) * Rd) - Ad,i)*ud)
RB) = RB) - Ad,2)*Ud)
REDUCE A TO TRIDIAGONAL FORM
DO 23 JM = 3,JMAF
JMM « JM - 1
DUM * A(l,JM)/AB,JMtf)
AB,vM) = AB,JM) - AC,JMM)*DUM
AC,0M) = AC,JM) - AD,JMM)*DUM
AA,JM) = 0.
R(JM^ = R(JM) - R(JMM)*DUM
CONTINUE
A(lfl) .- 0.
Ad,2) = 0.
AB,l) = 0.
AD,JMAF) = 0.
CALL BANFAC(A,JMAF,1)
CALL BANSOL(RfUD,ArJMAFrD
DO 26 J » 2,JMAP
IF(ME .LE. 3)U(J) = UD(J)
IF(ME .GT. 3)U(J) = UD(J-l)
CONTINUE
CONTINUE
VRITEF,28)TIMAX
FORMAT С FINAL SOLUTION, TIM *\F5.3)
WRITEF,16)(X(J),J-l,JMAX)
WRITEF,17)(U(J)fJ=lrJMAX)
VRITEF,29)(UE(J),J=1,JMAX)
FORMAT С UE=',12F,6.3)
SUM = 0.
DO 30 J = 2,JMAP
SUM = SUM + (U(J) - UE(J))**2
RMS = SQRT(SUM/(AMP-1.))
WRITEF,31)RMS
FORMAT(' RMS ERR=\E12.5)
STOP
END
Рис. 10.4 (окончание).
§ 10.1. Одномерное уравнение Бюргерса 43Г
A0.5) на оператор L{x]F, который в случае положительного и
имеет форму
LxF = Ш + ЗА^ ' A0*6>
В случае отрицательного и выражение A0.6) заменяется на
Формулы A0.6) и A0.7) имеют ошибки аппроксимации по-
порядка О (Ал:2) независимо от выбора q, за исключением случая:
9 = 0.5, когда эти ошибки имеют порядок О(Дл:3). Для рас-
рассматриваемой в п. 10.1.4 задачи о распространении ударной
волны явная четырехточечная схема со сдвигом вверх по пото-
потоку, соответствующая формулам A0.6) и A0.7), включена как
составная часть в программу BURG (рис. 10.4) для случая
МЕ = 3.
Уравнения, определяющие неустановившиеся одномерные
течения невязкой жидкости с ударными волнами (§ 10.2 и
14.2), по своей структуре аналогичны консервативной форме
невязкого уравнения Бюргерса, т. е.
ж+€=°> <1о-8>
где F = 0.5/г2. Ранее к линейному аналогу уравнения A0.8) в
форме (9.2) применялась схема Лакса — Вендроффа (9.16).
Ввиду нелинейности функции F замена d2u/dt2 на эквивалент-
эквивалентную производную будет значительно сложнее, чем это было в
п. 9.1.3. Так, из уравнения A0.8) следует
он д F д ( dF \ dF + ди * uF
UF*= ~~~ дх dt = "~ !дх \дТ) И ~дГ= IF = """ Л~дх~'
где А = дР/дп. В случае уравнения Бюргерса А = п. Исполь-
Использование вышеприведенных соотношений дает
дЧ д
dt2
Если_ ввести подходящую форму дискретизации для
d(AdF/dx)/dx, то при применении схемы Лакса — Вендроффа
к уравнению A0.8) получим
438 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
где в применении к уравнению Бюргерса Л/+1/2 = W/+1/2 =
= 0.5(и/ + и/-и) и т. д. Схема A0.10) обладает ошибкой ап-
лроксимации порядка О(Д/2, Да:2) и устойчива при
|итахД//Дл;| ^ 1.0.
С учетом явного появления якобиана А после полушагов
j— 1/2 и /+ 1/2 схема A0.10) является в вычислительном пла-
плане менее экономичной, чем эквивалентный алгоритм (9.16) для
линейного уравнения конвекции. Более экономичный метод вы-
вычисления получается в результате замены схемы A0.10) на
эквивалентный ей двухэтапный алгоритм
= 0.5(и? + «?+,) _ 0.5-Ц-(/ft., -F1}), A0.11)
«Г1 = «7 - ?
Формула A0.11) дает возможность получить промежуточное ре-
решение #*_1/2, обычно на временном слое (я+1/2)Д?, позво-
позволяющее вычислить F*+l/2 и т. д., подставляя результат в пра-
правую часть формулы A0.12). Двухэтапная схема A0.11),
A0.12) эквивалентна схеме (9.16), если F = u. Для упрощения
программирования значения F при / + 1/2 вводятся в память
на место F(j). Это сделано в программе BURG (рис. 10.4) для
варианта ME = 2.
В историческом плане [Richtmyer, Morten, 1967] двухэтап-
двухэтапный алгоритм A0.11), A0.12) оказался весьма успешным для
предсказания поведения невязкого сжимаемого потока. По-
Попытки распространить его на изучение потока с вязкостью, сде-
сделанные, например, в работе [Thommen, 1966], были не столь
удачными из-за формального снижения точности до порядка
О(Д?, Дл:2). В итоге результаты для стационарного состояния
были достаточно точными, но шаг по времени подвергался
ограничению, связанному с условием устойчивости Куранта —
Фридрихса — Леви. При решении нестационарных задач шаг по
времени необходимо было подвергнуть еще более суровому
ограничению, чтобы добиться приемлемой точности. Обобще-
Обобщение алгоритма A0.11), A0.12), сделанное Томменом и ставя-
ставящее своей целью дискретизацию уравнения A0.3), можно пред-
представить в форме
л;+1/2 = 0.5-(и? + и?+1) - 0.5 -g" (/=/+!
+ 0.5s [0.5 (a»_, - 2«« + *f+l) + 0.5 («; - 2«» + uf+i)], A0.13)
- 2м/
§ 10.1. Одномерное уравнение Бюргерса 439
где s = vAt/Ax2. Эта схема включена в программу BURG
(ME = 2). Из рассмотрения формулы A0.13) видно, что рас-
расчет члена с вязкостью охватывает четыре узловые точки; это
вызывает необходимость задания добавочных граничных усло-
условий для вычисления а/+2. Схема A0.13), A0.14) приводит к ус-
устойчивым решениям, если
At (Л2 At + 2v) < Ах2. A0.15)
Как указывается в книге [Peyret, Taylor, 1983], явный и прак-
практически приемлемый критерий получения устойчивого решения
имеет вид М ^ Ах2/Bv + \А\Ах).
Совокупность формул A0.13), A0.14) можно интерпрети-
интерпретировать в качестве одного из членов семейства Sp, Y, введенно-
введенного в работе [Lerat, Peyret, 1975]. Это семейство методов обсуж-
обсуждается в книге [Peyret, Taylor, 1983]. Родственное семейство
Sp для расчетов по невязкому уравнению Бюргерса обсуж-
обсуждается в п. 14.2.2. Параметр у определяет пропорцию распре-
распределения при вычислении члена с вязкостью, который в форму-
формуле A0.13) центрируется в узловых точках / и /+ 1. В случае
схемы Томмена а = E = у = 0.5.
Общая классификация разностных схем для решения не-
невязкого уравнения Бюргерса A0.2), включающая в себя и се-
семейство Sp, дается в работе [Yanenko et al., 1983]. Эта клас-
классификация охватывает также и неявные схемы, причем отно-
относится, в частности, к уравнениям Эйлера для одномерного
неустановившегося течения A0.40), A0.41). Яненко и его со-
соавторы описывают и дают ссылки на работы в отношении мно-
многих схем советского происхождения, малоизвестных западным:
авторам.
10.1.3. Неявные схемы
Применение неявных схем к нелинейным уравнениям типа
уравнения Бюргерса не является столь же непосредственным,,
как в случае линейных уравнений (гл. 9). Вариант неявной
схемы Кранка — Николсона в применении к уравнению A0.3)
принимает вид
= - 0.5L* (F? + F?+1) + 0.5vLxx (щ + и*}*1), A0.16>
где Аи»+1 = и»+1 —и», Lx = (—lt 0, 1)/2Д* и Lxx = (l, —2,
Чтобы воспользоваться чрезвычайно эффективным алгоритмом
Томаса (п. 6.2.2), необходимо свести соотношение A0.16) к
трехдиагональной линейной системе уравнений относительно»
-440 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
решения и}+1. Наличие неявного нелинейного члена /v+1 ста-
ставит при этом серьезную проблему.
Указанную проблему можно, однако, разрешить таким же
путем, который использовался при введении поправки к реше-
решению ДГ/+1, когда рассматривались схемы расщепления (§ 8.2).
А именно, проводится разложение F"+1 B РЯД Тейлора в окрест-
окрестности /г-го временного слоя. Тогда
ИЛИ
где А = [dF/duY} + щ применительно к уравнению A0.3). В ре-
результате схему A0.16) можно превратить в следующий трех-
диагональный алгоритм:
\Щ + иГ) (Ю.17)
или
иТХ + 0.5 А^ [Lx (и}и]+{) — vLxxu!}+{] =и} + 0.5v AtLxxunh A0.18)
В процессе вывода формулы A0.18) член LXF? сократился.
Будучи преобразованным к трехдиагональной форме, соотно-
соотношение A0.18) может быть записано в виде
П /1+1 ¦ itl /1+1 | П /1+1 лП /1А 1Л\
ujllj-\ -[- DjUj -j- CjUj+i = Uj, Aи.1У;
где
dl = - 0.25 (At/Ax) u?-i - 0.55,
dnt = 0.55а"-1 + A - 5) и? + 0.55И/+1 и 5 = v At/Ах2.
Очевидно, коэффициенты а1} и сп, являются функциями ип и
поэтому на каждом шаге по времени должны вычисляться за-
заново. Однако форма соотношения A0.19) позволяет осущест-
осуществить непосредственное использование алгоритма Томаса
(п. 6.2.2).
Неявная схема A0.18) имеет ошибку аппроксимации поряд-
порядка О (At2, Ax2) и является безусловно устойчивой в смысле
Неймана. Линеаризованная схема Кранка — Николсона A0.17)
может быть обобщена так, чтобы включить в нее массовые one-
§ 10.1. Одномерное уравнение Бюргерса 44$
раторы и четырехточечную дискретизацию конвективного чле-
члена со сдвигом вверх по потоку (п. 9.4.3). Следуя (9.69) и (9.71),.
обобщенный вариант дискретизации уравнения A0.3) по схеме
Кранка — Николсона записывают в виде
Мх (^-J = - 0.5L(*4) BF? + и1} АиГ1) + 0.5vL*. (и? + itf+l),
A0.20>
где My = {б, 1—26, б}, a L*4)F определяется формулой A0.6)
при положительном и. Ошибка аппроксимации для схемы
A0.20) имеет порядок О (At2, Ax2). В четырехдиагональной
форме представление A0.20) сводится к соотношению
ft ft -{• 1 I tl tl-\-\ I ifl tl ~b 1 I tl tl-\-\ itl i л r\ C\A\
ejUj-2 -{-ajUj-i -\-bjUj -\-CjUj+\ =df, A0.21>
где
n q_ kt n
d\ = — @.25 + 0.5?) -^- u"-i + б - 0.5s,
c\ = @.25 — -|) -У- uf+i + б - 0.5s,
$ = F + 0.5s) и/-1 + A — 26 - s) a/ + F + 0.5s) u"+i.
Четырехдиагональная система уравнений A0.21) может ре-
решаться с помощью обобщенного алгоритма Томаса (п. 6.2.4).
На практике четырехдиагональная система A0.21) сводится к
трехдиагональной форме (строки 134—144 на рис. 10.4), после
чего подпрограммы BANFAC и BANSOL применяются обычным
способом. Обобщенный алгоритм Кранка — Николсона A0.21)
включается в программу BURG при условии, что ME = 4 или
больше.
Устойчивые решения системы A0.21) получаются при
б ^ 0.25 и (/^0. Как можно было ожидать на основании из-
изложенного в п. 9.4.3, выбор специальных значений б и q будет
уменьшать колебания, связанные с дисперсией. Этот вопрос
затрагивается в п. 10.1.4.
10.1.4. BURG: сравнение численных результатов
В данном пункте различные явные (п. 10.1.2) и неявные-
(п. 10.1.3) схемы будут применены к решению задачи о распро-
распространении ударной волны, процесс которого определяется
442 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
«вязким» уравнением Бюргерса A0.3). При * = 0 ударная вол-
волна находится в точке л: = 0. Начальные условия имеют вид
щ(х) = й(х,0)=1.0 при -*тах<л:<0,
и0 (х) = п (*, 0) = 0 при 0<л:<л:тах. * ' '
Следующие граничные условия задаются при х = ±хтах:
п(-хтаху 0=1Д п(хтах> /) = 0. A0.23)
При указанной комбинации начальных и граничных условий
уравнение A0.3) имеет точное решение, представляемое в виде
оо / °°
г. \ \(Y ?W/1 />-0.5ReG //? / V />-0.5ReG//? (\C\ 9A\
— oo ' — oo
где
G(l;x, О^^аО^Ч- V и Re=l/v.
0
Выражение A0.24) представлено на рис. 10.3 в форме графи-
графиков для двух значений Re. При использовании выражения
A0.24) в качестве точного решения необходимо ввести ограни-
ограничения на время и на наименьшее значение Re таким образом,
чтобы граничные условия A0.23) были совместимы с точным
решением.
Различные схемы, описанные в п. 10.1.2 и 10.1.3, включают-
включаются в программу BURG (рис. 10.4), причем реализация той или
иной схемы осуществляется в зависимости от значения пара-
параметра ME в соответствии с табл. 10.1. Выбор параметров
•б = 1/6, q = 0 дает схему Кранка — Николсона, соответствую-
соответствующую групповому методу конечных элементов. Введение форму-
формулировки, связанной с этим методом (§ 10.3), необходимо для
осуществления явной дискретизации независимой переменной F.
Для построения решений уравнения A0.3) с малыми значения-
тли вязкости v желательно ввести в правую часть соотношения
A0.16) некий член с искусственной диссипацией; т. е. добав-
добавляется следующее выражение:
После линеаризации LXXF"'1 модифицированный вариант соот-
соотношения A0.20) представляется в форме
МхиГ1 + 0.5 & [L<4) Ш+1) - vLxxu?+l - va AtLxx {u]uT')] =
u?. A0.25)
§ 10.1. Одномерное уравнение Бюргерса
44$
Таблица 10.1. Различные схемы, расчет по которым включен в программу
BURG
ME
1
2
3
4
4
4
4
5
Описание
Схема ВВЦП A0.5)
Двухэтапная схема Лакса—Вендроффа A0.13), A0.14)
Явная четырехточечная схема со сдвигом
A0.7)
Кранк—Николсон, конечно-разностная; 6
обозначение CN-FDM
Кранк—Николсон, конечно-элементная; б
обозначение CN-FEM
Кранк—Николсон, массовый оператор; 6
обозначение CN-MO
Кранк — Николсон; 4-точечная, вверх по
в A0.20); обозначение CN-4PU
Обобщенная схема Кранка—Николсона
пация
вверх по потоку
= 0, q = 0 в
= 1/6, </ = 0в
= 0.12, </ = 0в
потоку; 6 = 0,
плюс добавочная
A0.6)v
A020);
A0.20);.
A0.20);
q = 0.S
дисси-
Параметр va подбирается эмпирическим путем. Подключение
к программе схемы A0.25) реализуется при ME = 5.
Различные параметры, используемые в программе BURG,
описываются в табл. 10.2. Вычисление точного решения па
формуле A0.24) осуществляется в подпрограммах EXSH
(рис. 10.5) и ERFC (рис. 10.6). Типовая форма выдачи резуль-
результатов, полученных по программе BURG с применением схемы
ВВЦП, показана на рис. 10.7.
Если коэффициент вязкости имеет значение v = 0.2, то ха-
характерное число Рейнольдса ячейки равно RCe\\ = u(l)Ax/\ =
= 1.0. Это наводит на мысль о том, что конвективный и дисси-
пативный члены уравнения A0.3) имеют одинаковый порядок.
Решения для случая Rceu = 1.0, полученные с помощью раз-
различных явных и неявных схем, предложенных в п. 10.1.2 и
10.1.3, приводятся в табл. 10.3. Все методы дают гладкие ре-
результаты. Схема ВВЦП является наиболее точной из явных
схем, а четырехточечная схема Кранка — Николсона со сдви-
сдвигом вверх по потоку и со значением q = 0.5 является наиболее
точной из неявных схем.
Характерные решения с вязкостью v = 0.03 (RCe\\ = 3.33)
приводятся в табл. 10.4. Конечно-разностная схема Кранка —
Николсона дает решение, для которого заметны покачивания
-444 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
Таблица 10.2. Параметры, используемые в программе BURG
Параметр
.ME
JMAX
NTIM
TIMAX
ХМАХ
AD
С
ALPH
S, SA
RCEL
Q
ЕМ
DT, DX, X
и
EF
UE
АА, ВВ, СС
А
R
UD
UD
Описание
= 1, схема ВВЦП A0.5)
= 2, двухэтапная схема Лакса—Вендроффа A0.13), A0.14)
= 3, явная четырехточечная схема со сдвигом вверх по по-
потоку A0.6), A0.7)
= 4, обобщенная схема Кранка—Николсона A0.20)
= 5, обобщенная схема Кранка—Николсона плюс добавоч-
добавочная диссипация
Число точек в интервале —хтах ^ х ^ хтах
Число шагов по времени
Время сравнения с точным решением
хтах в A0.22)
Искусственная диссипация va в A0.25)
Характерное число Куранта, С = u(\)At/Ax
Вязкость v в A0.3)
s = vAt/Ax2, sa = vaC2 (табл. 10.5)
Характерное число Рейнольдса ячейки, u(l)Ax/v
q в A0.6)
б в A0.20)
At, А*, х
Зависимая переменная, и в A0.3)
F в A0.3)
Точное решение, п в A0.24)
Коэффициенты-множители при f"_j и т. д. в явных схемах;
коэффициенты-множители при и"_ { и т. д. в неявных
схемах
Элементы четырехдиагональной матрицы A0.21)
Вектор, содержащий dу в A0.21)
Промежуточное явное решение; первый этап решения по
схеме Лакса—Вендроффа
Предназначено для w"+1 после возврата из подпрограммы
BANSOL
§ 10.1. Одномерное уравнение Бюргерса
445
1
2
3 С
4 С
5 С
б
7
8
9
10
11
12
13
14
15
16
17 С
18
19
20
21
22
23
24
25
26
27
28 С
29 С
30 С
31
32
33 С
34
35
36
37
38
39
40
41
42
43
SUBROUTINE EXSH(JMAX,X,U,UE,DX,XMAX,ALPH,TIMAX)
SETS THE INITIAL U SOLUTION AND FINAL EXACT (UEX) SOLUTION
DIMENSION UF5),UEF5),XF5)
JMAP = JMAX - 1
PI = 3.141592654
XST = -XKAX
DO 1 J = 1,JMAX
AJ = J - 1
X(J) = XST + AJ*DX
U(J) = 0.
1 UE(J) » 0.
U(l) = 1.0
UEA) = 1.0
DO 2 J = 2rJMAP
IF(X(J) .LT. O.)U(J) » 1.0
IF(ABS(X(J)) .LT. 1.0E-04)U(J)
0.5
AJ
XB
XA
PQ
PP
XB
XA
X(J)
- AJ
AJ - TIKAX
SQRT@.25*PI)
SQRT(PI*TIMAX*ALPH)
XB*PQ/PP
XA*PQ/PP
ERFC CALCULATES THE COMPLEMENTARY ERROR FUNCTION
CALL ERFC(XA,EXA)
CALL ERFC(XB,EXB)
SUMA ш
SUMB «
DUH ш
IF(DUM
IF(DUH
SUMC =
UE(J)
2 CONTXMUE
RETURN
END
pp*EXA
PP*EXB
O.5*(AJ-O.5*TIKAX)/ALPH
.GT. 20.)Dim = 20.
.LT.-20JDUH =-20.
EXP(DUM)
SUMA/(SUMA
Рис. 10.5. Распечатка подпрограммы EXSH.
дисперсионного типа, особенно за ударной волной. Схема Кран-
ка — Николсона с конечными элементами и четырехточечная
-схема Кранка — Николсона со сдвигом вверх по потоку дают
для указанного случая гладкие и точные решения. Ударная вол-
волна расползается примерно на девять узловых точек, так что
численные алгоритмы могут без труда уловить наличие резко-
резкого градиента и.
446 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
Если v = 0.001 (/?ceii = 10), то ударная волна становится
значительно более крутой (табл. 10.5 и рис. 10.8) и имеет тен-
тенденцию к возбуждению колебаний, связанных с дисперсией.
1
2 SUBROUTINE ERFC(X,ERC)
3 С
4 С COMPLEMENTARY ERROR FUNCTION
5 С
6 В » ABS(X)
7 IF(B .LT. 4)GOTO 1
8 D = 1.0
9 GOTO 2
10 1 С « EXP(-B*B)
11 T « l./U. ¦ 0.3275911*B)
12 D « 0.254829592*T - 0.284496736*T*T + 1.421413741*T*T*T
13 1 - 1.453152027*T*T*T*T + 1.061405429*T*T*T*T*T
14 D - 1. - D*C
15 2 IF(X .LT. 0.)D « -D
16 ERC * 1. - D
17 RETURN
18 END
Рис. 10.6. Распечатка подпрограммы ERFC.
В принципе можно построить схемы с пониженной диспер-
дисперсией, следуя при этом процедуре, изложенной в § 9.4 и связан-
PROPAGATING SHOCK WAVE(BURGERS EQUATION)
ME м I FTCS DIFFERENCING
JMAX- 21 NTIM= 20 C= .25 DX= .200 DT= .050 XKAX= 2.00
S« ,25 ALPH= .200E+00 RCEL= 1.0 Q= .00 EM* .000 SA= .О00Е-Ю0
AA= Л2500 .00000 BB= .00000 .00000 CC= -.12500 .00000
INITIAL SOLUTION, TIM = .000
Xp-2.000-1.800-1.600-1.400-1.200-1.000 -.800 -.600 -.400 -.200 .000 .200
X» .400 .600 .800 1.000 1.200 1.400 1.600 1.800 2.000
U» 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 .500 .000
U= .000 .000 .000 .000 .000 .000 .000 .000 .000
FINAL SOLUTION, TIM =1.000
X=-2.000-1.800-1.600-1.400-1.200-1.000 -.800 -.600 -.400 -.200 .000 .'20O
X= .400 .600 .800 1.000 1.200 1.400 1.600 1.800 2.000
U= 1.000 1.000 1.000 1.000 1.000 .999 .997 .991 .975 .940 .869 .751
U= .588 .407 .247 .132 .063 .027 .010 .003 .000
UE* 1.000 1.000 1.000 1.000 1.000 .999 .996 .989 .973 .937 .868 .75*
UE« .591 .409 .247 .132 .063 .027 .011 .004 .000
*MS ERR» Л4106Е-02
Рис. 10.7. Типичная выдача результатов, полученных с помощью программы
BURG.
ной с формированием модифицированного уравнения (п. 9.2.2) >
а также с таким выбором коэффициентов q или 6 в соотноше-
соотношении A0.20), который способствовал бы уничтожению коэффи-
коэффициента при производной наинизшего нечетного порядка. Нели-
Таблица 10.$. Решение дли распространяющейся ударной болйь* п?и / = 1.66,
М = 0.05
1.6, С=»6.2&, Ах = 6.26,
Схема
Точное решение
ВВЦП
Лаке — Вендрофф
EX-4PU, G = 0.5
CN-FDM
CN-FEM
CN-4PU, q = 0.5
X
-0.40
0.973
0.975
0.979
0.971
0.975
0.973
0.972
-0.20
0.937
0.940
0.943
0.936
0.939
0.936
0.936
0.00
0.868
0.869
0.869
0.869
0.867
0.865
0.867
0.20
0.753
0.751
0.748
0.757
0.747
0.748
0.753
0.40
0.591
0.588
0.583
0.598
0.582
0.589
0.593
0.60
0.409
0.407
0.403
0.415
0.403
0.411
0.410
0.80
0.247
0.247
0.244
0.248
0.246
0.252
0.247
1.00
0.132
0.132
0.131
0.129
0.135
0.136
0.131
1.20
0.063
0.063
0.063
0.069
0.067
0.064
0.063
1.40
0.027
0.027
0.027
0.025
0.030
0.027
0.028
1.60
0.011
0.010
0.010
0.009
0.013
0.010
0.012
Средне-
квадра-
квадратичная
ошибка
—
0.0014
0.004
0.003
0.003
0.002
0.0007
Таблица 10.4. Решение для распространяющейся ударной волны при t-
Дх = 0.10, Дг = ОЛО
1.00, /?Сец=»3.33, С =1.00,
Схема
Точное решение
CN-FDM
CN-FEM
CN-4PU, <7 = 0.5
X
0.00
1.000
0.998
1.000
1.000
0.10
0.999
0.995
1.000
1.000
0.20
0.995
1.020
0.999
1.000
0.30
0.969
1.021
0.986
0.980
0.40
0.847
0.814
0.846
0.847
0.50
0.500
0.438
0.491
0.501
0.60
0.153
0.157
0.153
0.144
0.70
0.031
0.043
0.023
0.022
0.80
0.005
0.011
0.002
0.004
0.90
0.001
0.003
0.000
0.001
1.00
0.020
0.001
0.000
0.000
Средне-
квадра-
квадратичная
ошибка
0.015
0.003
0.003
Таблица 10.5. Решение для распространяющейся ударной волны при
5а = 0.25, А* = 0.10, М = 0.10
2.00,
С = 1.00,
Схема
Точное решение
CN-FDM
CN-MO, 6 = 0.12
CN-4PU, q = 0.5
X
0.50
1.000
1.004
1.000
1.000
0.60
1.000
0.984
1.001
1.000
0.70
1.000
0.987
0.995
1.000
0.80
1.000
1.086
1.010
1.009
0.90
1.000
0.996
1.011
0.983
1.00
0.500
0.413
0.522
0.572
1.10
0.000
0.028
—0.046
-0.056
1.20
0.000
0.000
0.007
—0.007
1.30
0.000
0.000
—0.001
0.000
1.40
0.000
0.000
0.000
0.000
1.50
0.000
0.000
0.000
0.000
Средне-
квадра-
квадратичная
ошибка
0.020
0.009
0.015
§ 10.1. Одномерное уравнение Бюргерса
449
нейный характер уравнения A0.3) приводит к появлению мно-
многих добавочных произведений, не укладывающихся в рамки
дисперсионно-диссипативного образца, фигурирующего в п. 9.2.2.
Если построить эквивалентную линейную схему за счет локаль-
локального замораживания нелинейных коэффициентов, то получаются
следующие оптимальные значения коэффициентов б и q\
1 (Mu^xf
Oopt = -g" H 12
A0.26)
A0.27)
Очевидно, эти значения представляют собой естественное обоб-
обобщение оптимальных значений, полученных в п. 9.4.3 для тем-
фффффффффффффффффффффуфС
+ CN-FDM
OCN-4PU
¦ CN-MO
— точное решение
-1.0
0.0
1.0
2.0
Рис. 10.8. Распределение скорости при t = 2.00 и Rceu = 100. Обозначения
см. в табл. 10.1.
пературного фронта с конвекцией. Однако использование зна-
значений A0.26) или A0.27) в данном случае не является столь
же успешным, как в п. 9.4.3, преимущественно в силу влияния
добавочных нелинейных членов, присутствие которых не отра-
отражено в нашем анализе.
На основании изложенного здесь была принята альтерна-
альтернативная стратегия. Она сводится к эмпирическому выбору б и
q, а также к введению достаточно интенсивной искусственной
диссипации, способной ликвидировать большую часть ряби без
размазывания ударного фронта по чрезмерно большому числу
узловых точек. Результаты, приводимые в табл. 10.5 и на
29 К. Флетчер, т. 1
450 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
рис. 10.8, свидетельствуют об успехе этой стратегии и о том, что
даже конечно-разностная схема Кранка — Николсона дает до-
достаточно точные результаты при условии разумного примене-
применения искусственной диссипации.
Однако рассматриваемый пример является весьма подходя-
подходящим для использования искусственной диссипации, так как
точное решение дает постоянство повсюду, кроме ударной вол-
волны. Следовательно, большое значение va в соотношении A0.25)
не влияет на решение нигде, кроме ближайшей окрестности
ударной волны. Более разумный прием исследования состоит
в том, чтобы сделать va функцией решения, принимающей су-
существенно отличное от нуля значение только вблизи ударной
волны. Этот прием обсуждается в п. 14.2.3.
Расчет одномерного уравнения Бюргерса применительно к
внутреннему слою, подобному ударной волне (т. е. тонкому),
может быть проведен с помощью спектральных методов (§ 5.6).
Непосредственное применение спектрального метода Галёрки-
на приводит к решению, обнаруживающему глобальные коле-
колебания для случая девятичленного решения с полиномами Ле-
жандра при v = 0.01 [Fletcher, 1984]. В работе [Basdevant
et al., 1986] построены решения при v = 0.01/n с использова-
использованием спектрального тау-метода и метода коллокаций (псевдо-
(псевдоспектрального, см. п. 5.6.3) на основе полиномов Чебышёва.
Установлено, что без применения преобразования координат
следует использовать 256 точек коллокаций и тем самым из-
избежать появления решений колебательного типа. Делается вы-
вывод о том, что спектральные методы в силу их глобального ха-
характера не столь хорошо пригодны для расчета тонких внут-
внутренних слоев, как локальные методы типа метода конечных
разностей или метода конечных элементов.
10.1.5. Неравномерная сетка
Когда во внутренней области течения или вблизи границ
возникают очень большие градиенты, то для получения более
точных решений требуется измельчение расчетной сетки. Одна-
Однако если сетка остается равномерной во всей вычислительной
области, то измельчение сетки может оказаться неэкономичным
с точки зрения стоимости вычислений, в особенности для мно-
многомерных задач.
Очевидная альтернатива состоит в том, чтобы ввести сетку,
измельчаемую только на тех участках вычислительной области,
где ожидается появление резких градиентов. Техника построе-
построения подобного рода сеток обсуждается в гл. 13. Здесь мы изу-
изучим вопрос о применении неравномерных сеток к решению од-
§ 10.1. Одномерное уравнение Бюргерса 451
номерных стационарных задач, в первую очередь ставя своей
целью противопоставить ожидаемое улучшение точности реше-
решения благодаря локальному измельчению сетки возможному сни-
снижению порядка ошибки аппроксимации.
Уравнение конвекции — диффузии (§ 9.3)
в котором и и а — постоянные, а граничные условия имеют вид
Г@) = 0, 7A) = 1, при больших значениях и/а порождает
очень большой градиент вблизи точки х= 1 (рис. 9.5).
Локальное измельчение сетки вблизи х = 1 может быть
осуществлено за счет того, что размер ячейки изменяется по
закону геометрической прогрессии. Иначе говоря,
xJ+x — xJ = rx(xj — Xj_l) = rxkxi, A0.29)
где тх — коэффициент изменения сетки. Для конкретного при-
примера, показанного на рис. 9.5, значение гх меньше единицы,
что как раз и требуется, если желательно расположить больше
узловых точек вблизи границы л; =1.0. Как правило, значе-
значение гх сохраняется постоянным либо во всей вычислительной
области, либо в ее большей части.
Трехточечное представление производной dT/dx общего вида
для случая неравномерной сетки, приводящее к наименьшей
ошибке аппроксимации, может быть построено с помощью ме-
методики, описанной в п. 3.2.2. Разложение в ряд Тейлора всех
компонент этой трехточечной дискретной формулы в окрест-
окрестности точки Xj дает
dzT
¦•¦!¦
где коэффициент гх выражается согласно A0.29) и где Ах}- =
= Xj — Xj-\. Это представление имеет второй порядок, однако
вносит добавочную ошибку третьего порядка, исчезающую в
случае равномерной сетки (гх = 1.0).
Применение к уравнению A0.28) метода Галёркина с конеч-
конечными элементами и с линейной интерполяцией (см. п. 5.3.1)
приводит к «трехточечному» представлению dT/dx. Разложение
в ряд Тейлора для комплекса, соответствующего конечно-
29*
452 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
элементному трехточечному представлению dT/dx, имеет вид
T iA_\ — 1 ;_i | Ui . L±*j
-1-
x ^ 2 *г* 1' с/л:2 ^ 6 г^ + 1 dx* "*"
A0.31)
При таком представлении возникает диссипативный член пер-
первого порядка, знак которого зависит от того, возрастает или
уменьшается размер ячейки сетки по направлению положи-
положительного отсчета х. Очевидно, если величины (гх—1) или Ах,-
не малы, то влияние этого диссипативного члена при больших
значениях и/а может_быть существенным, если сравнивать его
с влиянием члена ad2T/dx2 в уравнении A0.28).
Трехточечное представление d2T/dx2 в A0.28), минимизи-
минимизирующее ошибку аппроксимации, соответствует следующей фор-
форме разложения в ряд Тейлора в окрестности точки Xji
[d2T kx,
1^ + НГ<'*-
Левая часть формулы A0.32) является также и результатом
линейной галёркинской конечно-элементной дискретизации про-
производной d2T/dx2. Очевидно, что применение неравномерной
сетки ведет к появлению ошибки аппроксимации первого по-
порядка.
Подстановка левых частей формул A0.30) и A0.32) в урав-
уравнение A0.28) приводит к следующей трехдиагональной схеме:
[0.5/?се11
^-^>/+1 = 0. A0.33)
Подстановка левых частей A0.31) и A0.32) в то же уравнение
приводит к несколько более простой трехдиагональной схеме
A0.34)
где Rce\\ = uAxj/a. Решения, построенные на основе схем
A0.33) и A0.34), были получены при и/а = 20 и И точках
внутри интервала 0 ^ х^ 1 и приводятся в табл. 10.6 и 10.7.
§ 10.1. Одномерное уравнение Бюргерса
453
В случае равномерной сетки, когда гх = 1, число Рейнольдса
ячейки /?ceii = 2; этот случай графически изображен на рис. 9.5.
Таблица 10.6. Изменение среднеквадратичной
ошибки в зависимости от гх для решений
уравнения A0.28) при и/а = 20
Среднеквад-
Среднеквадратичная
ошибка
A0.33)
A0.34)
гх
0.70
0.0338
0.0048
0.80
0.0276
0.0080
0.90
0.0319
0.0197
1.00
0.0455
0.0455
Таблица 10.7. Решения
неравномерной
Tt точное
7\ A0.33)
Г, A0.34)
уравнения A0.28)
сетки, гх = 0.8, /
с использованиек
i/a = 20
1
X
0.753
0.0072
0-0006
0.0035
0.827
0.0312
0.0111
0.0229
0.885
0.1010
0.0615
0.0879
0.932
0.2584
0.2050
0.2439
0.970
0.5480
0.5013
0.5376
1.00
1.0000
1.0000
1.0000
Средне-
квадра-
квадратичная
ошибка
0.0276
0.0080
В данном случае среднеквадратичная ошибка определя-
определяется преимущественно локальными ошибками у узловых точек,
близких к jc = 1. Мы видим, что уменьшение гх уменьшает
среднеквадратичную ошибку (табл. 10.6), причем решения по
схеме A0.34) оказываются значительно точнее, чем по схеме
A0.33). В силу того что гх < 1.0, использование схемы A0.34)
вносит положительную диссипацию. При использовании схемы
A0.33) выбор значения г* = 0.80 приводит к минимальной сред-
среднеквадратичной ошибке решения. Это соответствует относи-
относительно однородному распределению ошибки (табл. 10.7). При
коэффициентах изменения гх < 0.80 вблизи точки л: =1.0 ло-
локальная ошибка решения уменьшается, однако она возрастает
при малых значениях х. Отметим, что для более сложных опре-
определяющих уравнений и многомерных задач надлежащие значе-
значения коэффициента изменения сетки обычно попадают в интер-
интервал 0.8 <г*^ 1.2.
Использование неравномерной сетки при наличии большого
внутреннего градиента может быть проиллюстрировано на
454 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
примере использования модифицированной формы уравнения
Бюргерса
f. + (a-0.5)?-v|J-0. A0.36)
В сравнении с уравнением A0.1) сюда был введен дополни-
дополнительный член, —0.5дп/дх. При начальном и граничных усло-
условиях в форме A0.22) и A0.23) включение добавочного члена
эквивалентно допущению о миграции сетки вместе с ударной
волной, в результате которого ударная волна не движется по
отношению к сетке. В силу указанных свойств уравнение
A0.35) имеет исключительно простое стационарное решение
A0.36)
Уменьшение v приводит к обострению градиента, центрирован-
центрированного в точке х = 0. Уравнение A0.35) можно записать в кон-
консервативной форме
f-+f-'^-". 00.37)
где F = 0.b(u2— и). После проведения дискретизации получим
= vLxx («? + А«Г') - Lx (ff + -? А«Г'). (Ю.38)
где Lxx и Lx определяются формой левых частей A0.32),
A0.30) и A0.31), a dF/du = и — 0.5.
Применение представления A0.31) к dFJdx является при-
примером формулировки на основе группового метода конечных
элементов (§ 10.3), так как F представляет собой нелинейную
группу. Мы получаем следующую трехдиагональную систему
уравнений относительно Дм^+1:
{1 + bt [Lx (и - 0.5) - vl,J } Аи? = A* {yLxxu\ - LXF?). A0.39)
Процесс интегрирования уравнения A0.39) приближается до
тех пор, пока величина Да/+1 не станет пренебрежимо малой
в сравнении с решением уравнения (vLxxu}-— LxFj) = 0.
Для ударной волны, центрированной в точке х = 0, удобно
ввести сетку, размер ячейки которой возрастает по закону гео-
геометрической прогрессии как в положительном, так и в отрица-
отрицательном направлениях оси х, если отсчитывать от точки х = 0.
Решения, построенные на основе A0.30) и A0.31) для v = 0.08
и 11 точек внутри интервала — хтгх ^ х ^ хтах, приводятся в
табл. 10. 8 и 10.9. Для случая гх= 1.0 решения, соответствующие
Ясен = 5, основаны на условии иA)= 1.0.
§ 10.1. Одномерное уравнение Бюргерса
455
Таблица 10.8. Изменение среднеквадратичной
ошибки в зависимости от гх для решения
уравнения A0.39) при v = 0.008
Среднеквад-
Среднеквадратичная
ошибка
A0.30)
A0.31)
1.00
0.0084
0.0084
1.10
0.0093
0.0090
гх
1.20
0.0123
0.0082
.}J
1.30
0.0161
0.0068
Таблица 10.9. Решения уравнения A0.39) с использованием
неравномерной сетки при г* =1.3 и v = 0.08
и,точное
м, A0.30)
«,A0.31)
X
-1.368
1.000
0.999
0.999
-0.882
0.996
1.001
1.002
-0.509
0.960
0.993
0.967
-0.221
0.799
0.807
0.788
0.000
0.500
0.500
0.500
0.221
0.201
0.193
0.212
0.509
0.040
0.007J
0.033
0.882
0.004
-0.001
-0.002
1.368
0.000
-0.001/
0.001
Сред-
неквад-
ратич-
ная
ошибка
—
^00161
0.0068
Ошибки, приводимые в табл. 10.8, указывают на то, что
использование дискретизации для dF/dx в соответствии с левой
частью формулы A0.30) способствует уменьшению точности
с увеличением гх. В противоположность этому использование
формулы A0.31) вызывает уменьшение среднеквадратичной
ошибки при достаточно больших гх. Однако повышение точ-
точности при этом не слишком велико. При гх = 1.3 оба упомяну-
упомянутых решения сравниваются с точным решением в табл. 10.9.
При х = 0.0 оба решения точны, а наиболее заметные вклады
в среднеквадратичную ошибку приходят из четырех точек:
х = ±0.221, ±0.509.
Для применения метода неравномерных сеток к «реальным»
задачам о течении жидкости обычно необходимо провести
большое число численных экспериментов с целью наилучшего
выбора коэффициента изменения сетки гх, а также и схемы
дискретизации. При решении нестационарных задач с большими
456 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
местными градиентами может оказаться необходимым ввести
сетку, адаптирующуюся к локальному решению. Иначе го-
говоря, область локального измельчения сетки может изменяться
во времени. Подобного рода методы введения адаптивных се-
сеток [Thompson, 1984; Thompson et al., 1985] находятся за пре-
пределами данной книги.
Введение неравномерных сеток может потребоваться также
и там, где вычислительная граница не совпадает с локальным
характером сетки. В работе [Noye, 1983] предлагается обзор
традиционных приемов разрешения подобных ситуаций. Более
совершенный подход к решению задач с нерегулярными гра-
границами связан с использованием обобщенных криволинейных
координат (гл. 12), при введении которых вычислительная гра-
граница автоматически совпадает с сеточной линией.
§ 10.2. Системы уравнений
Материал, изложенный в § 10.1 ив предшествующих гла-
главах, относится к случаю существования единственного опреде-
определяющего уравнения. Однако гидроаэродинамические явления
обычно описываются посредством систем уравнений (гл. 11).
Исключением является течение невязкой несжимаемой жид-
жидкости, описываемое уравнением Лапласа (§ 11.3). Цель данно-
данного параграфа состоит в том, чтобы рассмотреть систему опре-
определяющих уравнений и применить к ней типовые приемы ди-
дискретизации, которые ранее уже применялись к случаю одного
определяющего уравнения.
Одномерное неустановившееся течение невязкой сжимаемой
жидкости определяется системой из трех уравнений: неразрыв-
неразрывности (п. 11.2.1), импульсов в направлении х (п. 11.2.2) и энер-
энергии (п. 11.2.4). После введения подходящих безразмерных пе-
переменных (п. 14.2.3) система уравнений может быть записана в
форме _ _
где
Y (V - 1)
|. A0.41)
+ 0.5ры2
В A0.41) р — плотность, и — скорость, р — давление, у — от-
отношение удельных теплоемкостей.
§ 10.2. Системы уравнений 457
Хотя зависимыми переменными являются р, и и р, дискрети-
дискретизация применяется непосредственно по отношению к q и К
Это будет проиллюстрировано здесь применительно к двух-
этапной схеме Лакса — Вендроффа A0.11), A0.12). В приме-
применении к уравнению A0.40) при этом получим
qJ+i/2 = 0.5 (q? + q?+I) - 0.5 ¦§. (F«+I _ F»), A0.42)
iF;-./2)- <10-43>
На каждом этапе построения решения величины р, и и р вы-
вычисляются по выражениям A0.41) для q, так что можно найти
и компоненты F.
В работе [Kjopfer, McRae, 1983] используется подход с по-
помощью модифицированного уравнения, ставящий целью коррек-
корректировку основной (дисперсионной) ошибки в результате при-
применения схемы Лакса — Вендроффа к решению уравнений Эй-
Эйлера A0.40), моделирующих одномерную задачу об ударной
трубе (задача 14.8). Полученная авторами схема является бо-
более точной, ее решения имеют меньшую тенденцию к колеба-
колебаниям, но, как правило, для обеспечения устойчивости этой схе-
схемы требуется задавать весьма малые значения Atmax.
Для решения систем уравнений можно строить и неявные
схемы. Так, например, схема Кранка — Николсона в примене-
применении к уравнению A0.40) будет иметь вид
q"+I " q/= - 0.25-g- [(F?+i - F?-i) + (F/Я - ВДI- (Ю.44)
Чтобы получить линейную систему алгебраических уравнений
для Aq^+1, нелинейные члены Fn+1 разлагаются в ряды типа
F«+i = F« + AAq«+i+ ? A0.45)
где A(=dFd/q) представляет собой матрицу 3X3, вычисляе-
вычисляемую с помощью A0.41). Конкретную форму матрицы А можно
получить из соотношения A4.99). После подстановки A0.45)
в A0.44) и перегруппировки членов получим
°25 А АЧ"+/ + 1Д<Г' + °25 АМШ
= -O.5-^-(F7+l-Fy_,). A0.46)
Уравнение A0.46) представляет собой блочно-трехдиагональ-
ную систему размерности 3X3 относительно Aq?+1, которую
можно решать с помощью блочного варианта алгоритма
458 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
Томаса (п. 6.2.5). Размерность блока 3X3 является прямым
следствием числа определяющих уравнений в каждой узловой
точке. Если из уравнений A0.46) получить Aq?+1, то решение
после м-го шага по времени вычисляется по формуле q?"M = qJl +
I
Устойчивость дискретизированной схемы, например A0.46),
может быть определена с помощью анализа по Нейману (§ 4.3)
так же, как это делается для скалярных уравнений. Учитывая,
что анализ по Нейману применим только для линейных урав-
уравнений, целесообразно линеаризовать уравнение A0.40) до ди-
дискретизации. Это значит, что получится уравнение
где А = dF/dq, как и было в формуле A0.45). Анализ устой-
устойчивости по Нейману проводится согласно процедуре, описанной
в п. 4.3.4, если не считать того, что вместо коэффициента уси-
усиления G, как в D.33), будет фигурировать матрица усиления
G. Для случая схемы Кранка — Николсона A0.46) результат
имеет вид
G = A + 0.5/-^- A sine)" (i_o.5/-^- A sine). A0.47)
Если собственные значения матрицы G обозначить через А,т, то
для устойчивости требуется, чтобы было |Ят| ^ 1.0 при любых
т. Устойчивость будет зависеть от локальной величины соб-
собственных значений матрицы А в A4.32). Если отвлечься от по-
появления матрицы Якоби А, структура выражения A0.47) ока-
оказывается весьма похожей на то, что было при применении схе-
схемы Кранка — Николсона к линейному уравнению конвекции
(табл. 9.1).
Система уравнений A0.40) более подробно рассматривается
в п. 14.2.3, гДе программа SHOCK формируется на основе
двухэтапной схемы Лакса — Вендроффа A0.42), A0.43) и схе-
схемы Мак-Кормака A4.49), A4.50). Типовое решение распро-
распространяющейся ударной волны показано на рис. 10.9 после
25 шагов по времени. Решение было построено с помощью рав-
равномерной сетки Ах = 0.01 в интервале 0^%^1.0. В момент
/ = 0 ударная волна располагается в точке х = 0.5; в после-
последующие моменты времени она распространяется вправо с без-
безразмерной скоростью ударного фронта, равной 1.195.
В уравнение A0.40) вводилась искусственная диссипация
с целью получения более гладкого решения. Форма членов с
искусственной диссипацией приводится в формуле A4.53). Гру-
§ 10.3. Групповой метод конечных элементов
459
бо говоря, это получается аналогично тому, как было при до-
добавлении некоего члена к одномерному уравнению Бюргерса
A0.3) с тем, чтобы получить уравнение A0.25). Однако вели-
величина v, являющаяся эквивалентом va в A0.25), представляет
собой функцию локального решения, так что она имеет сколь-
нибудь ощутимое значение лишь на ударной волне.
о Лаке—Вендрофф
(искусственная вязкость)
точное решение
0.4
0.5
>OOOOi
Рис. 10.9. Профиль распространяющейся ударной волны при
у= 1.4, v = 2 в A4.53).
1.5,
Сравнивая результаты, показаные на рис. 10.9, с результа-
результатами рис. 10.8, мы убеждаемся, что расчетный профиль удар-
ударной волны для «реального» определяющего уравнения является
менее крутым, чем для одномерного уравнения Бюргерса. От-
Отчасти это связано с относительной сложностью реальных урав-
уравнений, а отчасти отражает сравнительную точность схем Лак-
са — Вендроффа и Кранка — Николсона.
§ 10.3. Групповой метод конечных элементов
Метод конечных элементов был применен к задаче Штур-
Штурма — Лиувилля в § 5.4, к одномерному уравнению диффузии —
в п. 5.5.1, к двумерному уравнению диффузии —в § 8.3 и к дву-
двумерному уравнению переноса — в п. 9.5.2. Во всех этих слу-
случаях определяющие уравнения были линейными.
Однако определяющие уравнения гйдроаэродинамики
(гл. 11) содержат, как правило, нелинейные конвективные чле-
члены. В примитивных переменных эти конвективные члены об-
обладают квадратичной нелинейностью в случае течения несжи-
несжимаемой жидкости и кубической нелинейностью для сжимаемо-
сжимаемого потока. - _ ;
460 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
Обычный метод конечных элементов связан с введением от-
отдельного приближенного решения типа E.44) для каждой за-
зависимой переменной, фигурирующей в определяющем уравнении.
В случае применения метода Галёркина получаются многочис-
многочисленные произведения узловых значений зависимых переменных,
особенно большое число которых происходит от нелинейных
конвективных членов. Эта особенность является одной из при-
причин недостаточной экономичности метода конечных элементов
в применении к многомерным задачам [Fletcher, 1984].
Однако вклад в неэкономичность, который вносят нелиней-
нелинейные члены, можно аннулировать за счет введения группового
варианта метода конечных элементов [Fletcher, 1983b]. Этот
групповой вариант может применяться к решению любых не-
нелинейных задач, однако он особенно эффективен по отношению
к нелинейностям конвективного происхождения.
Формулировка группового варианта требует осуществления
двух шагов:
1) уравнения приводятся к консервативной форме, как, на-
например, уравнение A0.3);
2) одно и то же приближенное решение вводится для груп-
группы членов под знаком дифференцирования, например для F в
уравнении A0.3).
10.3.1. Формулировка одномерного группового варианта
Применение группового метода конечных элементов будет
проиллюстрировано на примере одномерного уравнения Бюргер-
са, представленного в консервативной форме A0.3). Отдельные
приближенные решения, эквивалентные E.44), вводятся для
и и F в уравнении A0.3) в виде
и = ? фгщ и F = ? <t>tFly A0.48)
где через Ft обозначается значение F в 1-м узле. Подстановка
в A0.3) и вычисление интеграла E.5) от невязки, взятой с ве-
весовой функцией Галёркина, приводят к системе обыкновенных
дифференциальных уравнений. В случае равномерной сетки эта
система записывается в виде
Мх [4f I + LxFt - vLxxUj = 0, A0.49)
При этом предполагается, что интерполяционные функции <j>i
в формулах A0.48) являются линейными. Если дискретизация
по времени соответствует схеме Кранка — Николсона, то соот-
§ 10.3. Групповой метод конечных элементов
461
ношение A0.49) дает алгоритм по схеме A0.20) при 6=1/6
и q = 0.
Если в выражение LxFj подставить зависимость F/ от и/, то
результат принимает вид
A0.50)
Применение обычного метода конечных элементов к уравне-
уравнению A0.1) приводит к следующей дискретной форме конвек-
конвективного члена:
ди (Ц/-
и
дх
A0.51)
Дискретизация линейнвх членов ди/дх и д2и/дх2 дает тот же
результат, что и в A0.49).
фффффффффффффффффФЗ
+ CN-FEM(C)
о CN-FEM(G)
— точное решение
-1.0
0.В
1.0
2.0
Рис. 10.10. Сравнение результатов применения обычного и группового методов
конечных элементов к решению одномерного уравнения Бюргерса при t = 2.0.
CN-FEM(C)—схема Кранка— Николсона для обычного метода конечных
элементов; CN-FEM(G)—схема Кранка — Николсона для группового метода
конечных элементов.
Дискретная форма представления, к которой приводит обыч-
обычный метод конечных элементов, сочеталась с разностной фор-
формой Кранка — Николсона для моделирования производной по-
повремени, и полученное на такой основе решение одномерного
уравнения Бюргерса обозначается на рис. 10.10 KaKCN-FEM(C).
Групповой вариант метода конечных элементов включается в
программу расчета в форме соотношения A0.20) при 6= 1/6 и
q = 0. Соответствующее решение обозначается на рис. 10.10 как
CN-FEM(G).
462 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
Решения, показанные на рис. 10.10, основаны на данных для
41 узловой точки, разделенных одинаковыми пространствен-
пространственными интервалами в интервале —2.0 ^ х ^ 2.0, и соответ-
соответствуют граничным и начальным условиям, рассмотренным в
п. 10.1.4. Число Рейнольдса ячейки /?сец основанное на и(\),
равно 5. Решение с помощью обычного метода конечных эле-
элементов обнаруживает область за ударной волной, где имеют
место более значительные колебания, чем для решения по груп-
групповому методу конечных элементов. В других зонах вычисли-
вычислительной области оба решения идентичны.
Поведение решений, полученных с помощью обычного и
группового методов конечных элементов в применении к одно-
одномерному уравнению Бюргерса, сравнивается в работе [Fletcher,
1983с] с точки зрения численной сходимости. В случаях линей-
линейной, квадратичной и кубической интерполяций оба варианта
дают сравнимую точность. При одном пространственном изме-
измерении и тот и другой варианты подобны друг другу в смысле
экономичности.
10.3.2. Формулировка многомерного группового варианта
Применение группового метода конечных элементов демон-
демонстрируется здесь на примере двумерных уравнений Бюргерса
A0.57), A0.58). Эквивалентная дивергентная векторная фор-
форма представления этих уравнений имеет вид
где
q = {и, v}, F = {и2, uv}, G = {uv, v2},
g Г0.бц(м» + о») 0.5р(ц» + РаI A0 53)
Наряду с приближенными решениями для и и v теперь вво-
вводятся добавочные приближенные решения для групп и2, uv,
v2 и для составляющих вектора S. Типовое приближенное ре-
решение (в случае применения прямоугольных элементов) имеет
вид
ZU). A0.54)
где ф(?, ц)—билинейные интерполяционные функции E.59).
Член (uv)i представляет собой значение комплекса uv в 1-й
узле.
§ 10.3. Групповой метод конечных элементов 463
Применение метода Галёркина с конечными элементами со-
согласно процедуре § 5.3 позволяет получить дискретизирован-
ные уравнения
Mx®My[^]fk = RHS, A0.55)
где
RHS = - Му ® Lx? - Мх ® Ly G +
+ v (Му ® Lxx + МХ® Lyy) q + Мх ® MyS. A0.56)
Стоит отметить подобие структуры полученных уравнений и
уравнений (9.85). В этом состоит особенность группового ва-
варианта; а именно на уровне, на котором проводится дискрети-
дискретизация, уравнения являются линейными, хотя и неопределенны-
неопределенными. Если узловые группы выразить через неизвестные узловые
переменные, то возникает нелинейность, но зато система ста-
становится определенной.
Как свидетельствует наличие тензорных произведений мас-
массового и разностного операторов, например Му ® LXF, в правой
части A0.56), групповой вариант метода конечных элементов
приводит к девятиточечной дискретизации производной д?/дх.
Строго говоря, эта дискретизация является всего лишь шести-
шеститочечной, так как один из элементов оператора Lx равен нулю.
Если обычный метод конечных элементов применить к урав-
уравнению A0.57), A0.58), то связующая способность окажется
значительно больше. Она определяется здесь числом узловых
групп, получаемых в результате дискретизации конвективного
члена.
Рост связующей способности будет приводить к увеличению
числа операций, а следовательно, и времени исполнения. Свя-
Связующая способность возрастает с увеличением размерности, с
введением более высокого порядка интерполяции, а также с
повышением порядка нелинейности в определяющем уравне-
уравнении. Чтобы дать правдоподобную оценку воздействия всех фак-
факторов на суммарное время исполнения алгоритма, в табл. 10.10
приводятся данные о числе операций.
Уравнения Бюргерса и уравнения Навье — Стокса для сжи-
сжимаемой жидкости (п. 11.6.3) обладают конвективными членами
с квадратичной и кубической нелинейностью соответственно.
Из табл. 10.10 видно, что для обычного метода конечных эле-
элементов с линейной интерполяцией связующая способность воз-
возрастает как с увеличением числа измерений, так и с повыше-
повышением порядка нелинейности. В отличие от этого связующая спо-
способность для группового варианта изменяется под влиянием
увеличения числа измерений, но остается неизменной при по-
повышении порядка нелинейности.
464 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
Таблица 10.10. Связующая способность и число операций для обычного
и группового вариантов метода конечных элементов с линейной
интерполяцией
Система
уравнений
Двумерная,
Бюргере
Трехмерная,
Бюргере
Двумерная,
вязкая, сжи-
сжимаемая, На-
вье — Стоке
Трехмерная,
вязкая, сжи-
сжимаемая, На-
вье — Стоке
Конвек-
Конвективная
нелиней-
нелинейность
Квадра-
Квадратичная
Квадра-
Квадратичная
Кубиче-
Кубическая
Кубиче-
Кубическая
Обычный МКЭ
связую-
связующая
способ-
способность
(конвек-
(конвективная
нелиней-
нелинейность)
49
343
225
3 375
число
операций
ДЛЯ
расчета
невязки
828
12 603
6 772
217 065
Групповой МКЭ
связую-
связующая
способ-
способность
(конвек-
(конвективная
нелиней-
нелинейность)
9
27
9
27
число
операций
для
расчета
невязки
206
1308
404
2 349
отноше-
отношение
чисел
операций
(обыч-
ное/груп-
ное/групповое)
4
9
17
92
Большая связующая способность впоследствии трансфор-
трансформируется в большое число операций, требуемых для расчета
невязки в стационарном состоянии. Предполагается, что систе-
системы обыкновенных дифференциальных уравнений, формируемые
с помощью дискретизации, интегрируются маршевым способом
по времени с использованием приемов расщепления, подобных
тем, которые были изложены в § 8.2, 8.3 и 9.5. Как правило,
на каждом шаге по времени вычисление стационарной невязки
RHS в соответствии с формулой A0.56) занимает около 50 %
времени исполнения. Вследствие этого подсчет числа операций
для вычисления невязки на одном шаге по времени приближен-
приближенно соответствует расчету полного времени исполнения.
Результаты, приводимые в табл. 10.10, свидетельствуют о
том, что групповой вариант метода конечных элементов ста-
становится все более экономичным в сравнении с обычным ва-
вариантом по мере возрастания порядка нелинейности или числа
измерений. Применительно к трехмерному течению вязкой жид-
жидкости групповой вариант позволяет рассчитать невязку стацио-
стационарного состояния с экономичностью, почти в сто раз превы-
превышающей экономичность обычного варианта. Это приближенно
соответствует пятидесятикратному улучшению суммарного вре-
времени исполнения алгоритма. Если вместо линейной интерполя-
§ 10.3. Групповой метод конечных элементов
465
ции используется интерполяция более высокого порядка, то от-
относительная экономичность группового варианта в сравнении
с обычным вариантом метода конечных элементов становится
еще больше.
Относительные времена исполнения, подсчитанные для обыч-
обычного и группового вариантов конечно-элементной дискретиза-
дискретизации двумерных уравнений Бюргерса и приведенные в
табл. 10.10, подтверждены на практике [Fletcher, 1983b]. Че-
Четырехкратное улучшение, показанное в табл. 10.10, соответ-
соответствует замеренному отношению времен исполнения, равному
два с половиной.
700г
6.00-
со
5.00-
3.00-
О = 3-FD
О =LF?(C)
? - LFEF)
а
о
8
О
0.20 0.40 0.60 0.80 1.00 1.20 1.40
ЧдОХ
Рис. 10.11. Свойства пространственной сходимости для разных вариантов дис-
дискретизации стационарных двумерных уравнений Бюргерса. 3-FD — трехточеч-
трехточечная конечно-разностная дискретизация; LFE(C)—обычный метод конечных
элементов с линейной интерполяцией; LFE(G)—групповой метод конечных
элементов с линейной интерполяцией.
В применении к стационарному двумерному уравнению
Бюргерса при v = 0.1 относительная точность группового и
обычного вариантов метода конечных элементов может быть
оценена на основании результатов, демонстрируемых на
рис. 10.11. Эти результаты были получены на равномерной сет-
сетке при Дл: = Ау. Среднеквадратичные ошибки уменьшаются по
мере измельчения сетки примерно с той же скоростью и для за-
заданной сетки имеют примерно ту же величину. Видно, что обе
конечно-элементные схемы точнее, чем трехточечная конечно-
разностная дискретизация уравнений A0.57) и A0.58).
30 К. Флетчер, т. 1
466 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
Суждение о сходимости схем основано на рассчитанном реше-
решении [Fletcher, 1983b], которое по сравнению с тем, что показана
на рис. 10.12, обладает более умеренным градиентом, но с более
отчетливой тенденцией развития в направлении оси х. Это ре-
решение затабулировано на рис. 6.14.
Рис. 10.12. Точное стационарное решение двумерных уравнений Бюргерса
A0.57), A0.58).
Групповой вариант исследовался также авторами работы
(Christie et al., 1981), которые называли его «аппроксимацией
произведений». Они показали, что для представительных мо-
модельных задач групповой вариант оказывается теоретически
столь же точным, как и обычный вариант метода конечных
элементов.
Общий вывод, который можно сделать, исходя из содержа-
содержания данного параграфа, сводится к тому, что групповой ва-
вариант метода конечных элементов должен быть предпочтен
обычному варианту этого метода с целью достижения приемле-
приемлемой экономичности, если дискретизация осуществляется по от-
отношению к нелинейным уравнениям гидроаэродинамики (гл. И)
§ 10.4. Двумерные уравнения Бюргерса 467
с числом измерений более одного. Однако нет оснований ожи-
ожидать, что использование группового варианта приведет к умень-
уменьшению точности решения.
§ 10.4. Двумерные уравнения Бюргерса
Подобно тому как одномерное уравнение переноса имеет
свой многомерный аналог (§ 9.5), так и одномерное уравнение
Бюргерса может быть обобщено на многомерный случай. Дву-
Двумерные уравнения Бюргерса имеют вид
- дй . дй ( дЧ . д2п \ л /1Л--ч
w + yv + ) 0 A0-57>
дй , - dv . - dv ( дЧ , дЧ \ п /1Л CQ4
Двумерные уравнения Бюргерса совпадают с двумерными урав-
уравнениями импульсов для ламинарного течения несжимаемой
жидкости (п. 11.5.1), если в последних пренебречь членами с
давлением.
10.4.1. Точное решение
Как и в случае одномерного уравнения Бюргерса, точные
решения могут быть построены [Fletcher, 1983d] с помощью пре-
преобразования Коула — Хопфа. При двух измерениях преобразо-
преобразование Коула — Хопфа связано с введением одной функции Ф,
через посредство которой входящие в уравнения A0.57) и
A0.58) функции п и v выражаются по формулам
-=-2у|Ф/^)> .= -2,т/ду) A059)
В результате уравнения A0.57) и A0.58) преобразуются в од-
одно-единственное уравнение
которое представляет собой двумерное уравнение диффузии
(8.1). При задании надлежащих граничных и начальных ус-
условий уравнение A0.60) имеет точное решение, которое при по-
помощи формул A0.59) может быть использовано для формиро-
формирования точных решений уравнений A0.57), A0.58).
Главный интерес представляет стационарное решение урав-
уравнений A0.57), A0.58). Поэтому будут отыскиваться точные
решения стационарной части уравнения A0.60), т. е.
# + 0
30*
-0. A0.61>
468 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
Приводимое ниже точное решение уравнения A0.61) обеспе-
обеспечивает значительную свободу контроля над соответствующими
решениями для скоростей, удовлетворяющими уравнениям
A0.57) и A0.58). Имеем
ф = п{ + а2х + а3у + аАху + аъ [еМ*-*о> + ?-*<*-*>] cos (Ху), A0.62)
где коэффициенты аи ..., а5, а также параметры X и х0 под-
подбираются так, чтобы придать надлежащие особенности точно-
точному решению. Если воспользоваться формулами A0.59), то со-
соответствующие точные решения уравнений A0.57), A0.58) при-
принимают вид
й= - 2v {а2 + аАу + Яа5 [«*<*-«,) - g-M*-*o)] CQS {ky)}
{ах + а2х + аъу + а<ху + а5 [в*<*-*о> + е-Мх-*о)] cos (ky)} >
, = - 2у {а3 + сцх - каь №<*-**> + е-Ш-*о)] s!n №y)}
{a+aAr + ar/ + aA:f/ + a[^(x-Xo) + ^~A'(x";:o)]cos(^)} '
Типичный вариант точного решения для стационарного «тече-
«течения» с очень большим внутренним градиентом показан на
рис. 10.12. Это решение получено при следующем выборе пара-
параметров:
a1 = a2= 1.3 ХЮ13, a3 = a4 = 0, as=1.0f /|ллкч
А = 25, Xo=lf v = 0.04. {10-65)
Точное решение A0.63), A0.64) особенно полезно для того,
чтобы оценить степень точности различных алгоритмов
[Fletcher, 1983c], как показано на рис. 10.11.
10.4.2. Схемы расщепления
Разработка схем расщепления для многомерных уравнений,
например двумерных уравнений Бюргерса, идет по пути, близ-
близкому к тому, который был указан в § 8.2, 8.3 и 9.5. Дополни-
Дополнительное усложнение вносит при этом нелинейность. Как прео-
преодолевается подобное усложнение, будет показано ниже с
помощью обращения к двумерным уравнениям Бюргерса, пред-
представленным в консервативной форме A0.52).
Уравнения A0.55), A0.56), представляющие собой дискре-
тизированную форму уравнения A0.52), соответствуют как груп-
групповому варианту дискретизации с конечными элементами, так
и конечно-разностной дискретизации, если массовые операторы
представить в таком виде:
Мх = F„ 1 - 26„ 6Х), Му = (в,, 1 - 26^, 6у)т, A0.66)
§ 10.4. Двумерные уравнения Бюргерса 469
как в (9.86). Выбор 6* = 8У = 0 дает обычную трехточечную
конечно-разностную дискретизацию; выбор же значений
bx = &y = -L дает групповой вариант метода Галёркина с ко-
конечными элементами, основанный на билинейной интерполяции.
Было бы возможно ввести трехслойную дискретизацию по
времени для уравнения A0.55), как это было сделано при вы-
выводе схемы (9.87). Однако здесь нас интересует использование
псевдонестационарной формулировки (§ 6.4) с целью получе-
получения решения для стационарного состояния. Поэтому мы вос-
воспользуемся приводимым ниже вариантом двухслойной чисто не-
неявной (v = 0, р=1) дискретизации по времени для уравне-
уравнения A0.55):
Ы4ЯГ1+l- A0-67)
Такая дискретизация приведет к схеме расщепления, эквива-
эквивалентной расширенному методу Ньютона (п. 6.4.1). Желая по-
получить из уравнения A0.67) линейную систему уравнений для
Aqtt+1, необходимо провести линеаризацию нелинейных членов
F, G и S в выражении A0.56) для RHS"+1; для этого осущест-
осуществляется разложение в окрестности n-го временного слоя, что
дает
A0.68)
где А, В и С вычисляются на основе выражений A0.53) в виде
A-iL-Г2" °\ *-™.-(v u \
dq- \V uj' dq—^0 2V ) '
+ у2) 2uv
2uv («2
После подстановки в уравнение A0.67) появляется возмож-
возможность построить следующую приближенную факторизацию:
[Мх + М (Lx\ - vLxx - 0.5М^С)] kq] k = At RHS", A0.70)
[My + At (LyB - vLyy - 0ШуС)} Aq»+i = AqJf,. A0.71)
Тот факт, что в уравнения A0.70) и A0.71) входят матрицы
Якоби А и т. д., делает уравнения блочно-трехдиагональными
вдоль сеточных линий, параллельных осям х и у соответствен-
соответственно. Так как матрицы А и т. д. зависят от решения, возникает
470 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
необходимость в проведении новой факторизации блочно-трех-
диагональной системы на каждой итерации п. Эффективное ре-
решение блочно-трехдиагональной системы строится с помощью
блочного алгоритма Томаса (п. 6.2.5).
Анализ устойчивости по Нейману применяется к схеме
A0.70), A0.71) после временного замораживания значений А
и т. д. Этот анализ показывает, что алгоритм схемы расщепле-
расщепления A0.70), A0.71) является безусловно устойчивым. На прак-
практике использование чрезмерно большого шага по времени мо-
может привести к нелинейной устойчивости.
Схема расщепления имеет ошибку аппроксимации порядка
О (At, Ах2, Ay2). Поскольку нас интересует только решение для
стационарного состояния, можно рассмотреть такие модифика-
модификации вида левых частей уравнений A0.70) и A0.71), которые
позволили бы достичь стационарного состояния при уменьшен-
уменьшенном объеме вычислений. В пределе стационарного состояния
RHS* = 0, так что никакая модификация левой части не мо-
может оказать влияния на решение для стационарного состояния,
даже если она и повлияет на нестационарное решение. Пред-
Предпочтительная стратегия сводится к такому выбору формы ле-
левых частей, чтобы на каждой итерации построение решения
было наиболее эффективным, однако чтобы можно было из-
избежать существенного увеличения числа итераций, необходи-
необходимых для достижения стационарного состояния.
Как отмечалось в п. 6.2.5, т скалярных трехдиагональных
систем могут быть решены более эффективно, чем одна блоч-
но-трехдиагональная система уравнений размерностью ту, т.
Уравнения A0.70) и A0.71) могут каждое в отдельности рас-
рассматриваться так, как если бы это были две последовательно
решаемые трехдиагональные системы. Для этого в формулах
A0.69) следует вычеркнуть члены, не попадающие на диаго-
диагональ. Дополнительная экономия может быть получена за счет
замены формул A0.69) на
) с0Ч^)( > <10-72>
о
Это означает, что одинаковые левые части могут быть исполь-
использованы для каждой из скалярных компонент уравнений A0.70)
и A0.71). Иначе говоря, левая часть должна подвергаться фак-
факторизации (подпрограмма BANFAC) лишь один раз для двух
решений (подпрограмма BANSOL) с различными правыми
частями A^RHS? и A/RHS?. Формулы A0.72) вместе с урав-
уравнениями A0.70) и A0.71) являются составной частью програм-
программы TWBURG (рис. 10.13).
1
2 С
3 С
4 С
5 С
б
7
8
9
10
11
12
13
14
15
16
17
18 С
19
20
21
22
23
24 С
25
26 С
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
TVBURG APPLIES APPROXIMATION FACTORISATION TO SOLVE
THE STEADY 2-D BURGERS' EQUATIONS FOR U(X,Y) AND V(X,Y)
DIMENSION RUB1r21),RVB1,21),UB1,21),VB1,21),UEB1,21),
1VEB1,21),BE,65),RRUF5),DDUF5),RRVF5),DDVF5),CXC),CYC),
2CXQD),CYQD),EMXC),EMYC),DMXC,3),DMYC,3),AE)
COMMON DX,DY,RE,NX,NY,CX,CXQ,CY,CYQ,DMX,DMY,EMX,EMY,RU,RV,U,V
OPENA,FILE=•TVBURG.DATf)
OPENF,FILE=fTWBURG.OUTf)
READA,1)NX,NY,ME,ITMAX,IPR.BET,QX,QY
READA,2)DTIM,EPS,RE,EM1,EM2
READA,3)(A(J),J=1,5),AL
1 FORMATEI5/3F5.2)
2 FORMATEE1O.3)
3 FORMATBE10.3,4F5.2)
NXP = NX - 1
NXPP = NXP - 1
NYP = NY - 1
NYPP ¦ HYP - 1
AN = NXPP*NYPP
CALL EXBUR(UErVE,A,AL)
СХA) =
CXB) «
CXC) »
CYA) »
CYB) «
CYC) »
CXQ(l)
CXQB)
CXQC)
CXQD)
CYQ(l)
CYQC)
CYQD)
CCX =
CCY =
IF (ME
IF (ME
EMX(l)
EMY(l)
IF (ME
IF (ME
EMXB)
EMXC) =
EMYB) =
EMYC) =
DO 4 I =
DMX(I,1)
DMX(I,2)
DMX(I,3)
DMYA,I)
DMYB,I)
4 DMYC,I)
-0.5/DX
0.
0.5/DX
-0.5/DY
0.
0.5/DY
= QX/DX/3.
= -3.*CXQA)
= -CXQB)
= -CXQ(l)
= QY/DY/3.
= -3.*CYQA)
= -CYQB)
= -CYQ(l)
l./DX/DX/RE
l./DY/DY/RE
NE. 2)QX = 0.
NE. 2)QY = 0.
= 0
= 0
EQ.
EQ.
= 1
3)EMXA)
3)EMYA)
= EMI
= EM2
- 2.*EMXA)
EMX(l)
1. - 2.*EMYA)
EMY(l)
1,3
= CCX*EMY(I)
= -2.*DMX(Ifl)
= DMX(I,1)
= CCY*EMX(I)
= -2.*DMYA,I)
= DMYA,I)
Рис. 10.13. Распечатка программы TWBURG (начало).
€0 IF(HE .EQ. 1)VRITEF,5)NX,NY,ME,ITMAX
61 IF(ME .EQ. 2)VRITEF,6)NX,NY,ME,ITMAX
62 IF(ME .EQ. 3)VRITEF,7)NX,NY,ME,ITMAX
63 5 FORMATC 2-D BURGERS EQUATION: AF-FDM, NX,NY »' ,213,f HE *%
64 112, • ITMAX«\I3)
65 6 FORMAT*1 2-D BURGERS EQUATION: AF-4PU, NX,NY »',2I3,* ME •',
66 112,' ITMAX*\I3)
67 7 FORMATC 2-D BURGERS EQUATION: AF-ИО, NX,NY *r,2I3/ KB »f,
68 112,' ITMAX«\I3)
69 VRITEF,8)BET,DTIM,RE,QX,QY,EMXA),EMYA)
70 8 FORMATC BETA»1 ,F5.2, • DTIM»1 ,F5.3, • RE«\F5.1,f QX«\T4.*
71 I,1 QY«\F4.2,f EMX«\F5.3,f EMY«',F5,3)
72 VRITEF,9)(A(J),J*1,5),AL,DX,DY
73 9 FORMAT С A* f,2E10>3,3F5,2,f AL«f,F5.2/ DX,DY«*,2F8.5,/>
74 С
75 С GENERATE INITIAL SOLUTION
76 С
77 DO 10 J « 1,NX
78 VA,J) » VEA,J)
79 V(NY,J) » VE(NY,J)
80 U{1,J) " UEA,J)
81 10 U(NY,J) * UE(NY,J)
82 DO 12 К « 2,NYP
83 U(K,1) * UE(K,1)
84 U(K,NX) * UE(K,NX)
85 V(K,1) « VE(K,1)
86 V(K,NX) * VE(K,NX)
87 DO 11 J * 2,NXP
88 AJ « J - 1
89 U(K,J) « U(K,1) + 0.5*AJ*DX*(U(K,NX)-U(K,X)>
90 11 V(K,J) « V(K,1) + O.5*AJ*DXMV(K,NX)-VAC,U)
91 12 CONTINUE
92 IFUPR .LE. DGOTO 17
93 DO 13 К » 1,NY
94 13 VRITEF,14)(UE(K,J),J*1,NX)
95 14 FORMATDH UE»,7F10.4)
96 DO 15 К « 1,HY
97 15 VRITEF,16)(VE(K,J),J=1,NX)
98 16 FORMATDH VE*,7F10.4)
99 17 DO 20 J « l.NX
100 DO 18 К « 1,NY
101 RU(K,J) « 0.
102 18 RV(K,J) * 0.
103 DO 19 К « 1,5
104 19 B(K,J) * 0.
105 20 CONTINUE
106 ITER » 0
107 С
108 21 DBT = BET*DTIM
109 CXA « 0.5*DBT/DX
110 CYA « 0.5*DBT/DY
111 CCXA « DBT*CCX
112 CCYA « DBT*CCY
113 С
114 CALL RHSBU(RMSU,RMSV,ME,DTIM)
115 С
116 IF(RMSU .LT. EPS)GOTO 34
117 IFiRMSU .GT. i;0E+04)GOTO 34
118 С
119 С TRIDIAGONAL SYSTEMS IN THE X-DIRECTIOH
120 С
Рис. 10.13 (продолжение).
121 DO 27 К * 2.NYP
122 DO 23 J « 2,NXP
123 JM » J - 1
124 JP * J ¦ 1
125 BB,JM) = EMX(l) - CCXA - CXA*U(K,JM) - O.5*EMXA)*DBT*RE*
126 1(U(K,JM)*U(K,JM) + V(K,JM)*V(K,JM))
127 BC,JM) = EMXB) + 2.*CCXA - 0.5*EMXB)*DBT*REMU(K,J)*U(K,J>
128 1 + V(K,J)*V(K,J))
129 BDrJH) » EMXC) - CCXA + CXA*U(K,JP) - 0.5*EMXC)*DBT*RE*
130 1(U(K,JP)*U(K,JP) + V(K,JP)*V(K,JP))
131 RRU(JH) = RU(K,J)
132 RRV(JM) « RV(K,J)
133 IF(ME .NE. 2)GOTO 23
134 LST = 1
135 IF(J .EQ. 2)LST = 2
13S BA,JH) = 0.
137 DO 22 L=LST,4
138 LJ = J + L - 3
139 22 B(L,JM) » B(L,JM) + CXQ(L)*U(K,W)*DBT
140 23 CONTINUE
141 BB,l) * 0.
142 BD,JM) = 0.
143 IF(ME .NE. 2)GOTO 25
144 С
145 С REDUCE TO TRIDIAGONAL FORM
146 С
147 DO 24 JM = 3,NXP
148 JMM » JM - 1
149 DWM = B(l,JM)/BBrJMM)
150 BB,JM) * BB,JM) - BC,JMM)*DUM
151 BC,JM) « BC,JM) - BD,JMM)*DUM
152 BA,JM) = 0.
153 24 RRU(JM) * RRU(JM) - RRiJ(JMM)*DUM
154 BUr2) * 0.
155 С
156 25 CALL BANFAC(B,NXPP,1)
157 CALL BANSOL(RRU,DDU,B,NXPP,1)
158 CALL BANSOL(RRVfDDV,B,NXPP,l)
159 С
160 DO 26 J = 2fNXP
161 JM = J - 1
162 RU(KfJ) = DDU(\JM)
163 26 RV(K,J) = DDV(JM)
164 27 CONTINUE
165 С
166 С TRIDIAGONAL SYSTEMS IN THE Y-DIRECTION
167 С
168 DO 33 J = 2fNXP
169 DO 29 К = 2,NYP
170 KM - К - 1
171 KP = К + 1
172 BB,KM) = EMY(l) - CCYA - CYA*V(KM,J). - O.5*EMYA)*DBT*RE*
173 hu(km,j)*u(km,j) + у(км,а)*у(км,а))
174 В(ЗДМ) = EMYB) + 2.*CCYA - 0.5*EMYB) *DBT*RE* (U(Kr J) *U(K, J,
175 1 + V(K,J)*V(K,J))
176 BD,KM) « EMYC) - CCYA + CYA*V(KP,J) - O.5*EMYC)*DBT*RE*
177 1(U(KP,J)*U(KP,J) + V(KP,J)*V(KP,J))
178 RRU(KM) = RU(K,J)
179 RRV(KM) * RV(K,J)
180 IF(ME .NE. 2)GOTO 29
Рис. 10.13 (продолжение).
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
20$
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
.221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
С
С
С
С
С
С
С
С
С
С
28
29
30
31
32
33
34
35
36
37
38
39
40
41
LST = 1
IF(K .EQ. 2)LST = 2
ВA,КМ) = 0.
DO 28 L=LST,4
LK = К + L - 3
B(L,KM) = B(L,KM) + CYQ(L)*V(LK,J)*DBT
CONTINUE
BB,l) « 0.
ВD,KM) = 0.
IF(ME .NE. 2)GOTO 31
REDUCE TO TRIDIAGONAL FORM
DO 30 KM = 3,NXP
KMM = KM - 1
DUM = BA,KM)/BB,KMM)
BB,KM) = BB,KM) - BC,KMM)*DUM
BC,KM) = BC,KM) - BD,KMM)*DUM
BA,KM) = 0.
RRV(KM) = RRV(KM) - RRV(KMM)*DUM
B<1,2) = 0.
CALL BANFAC(B,NYPP,1)
CALL BANSOL(RRU,DDU,B,NYPP,1)
CALL BANSOL(RRV,DDV,B,NYPP,1)
INCREMENT U AND V
DO 32 К = 2,NYP
KM - К - 1
U(K,J) = U(K,J> + DDU(KM)
V(K,J) = V(K,J) + DDV(KM)
CONTINUE
ITER » ITER + X
IF(ITER .LE. ITMAX)GOTO 21
COMPARE WITH EXACT SOLUTION
SUMU = 0.
SUMV = 0.
DO 36 J = 2,NXP
DO 35 К = 2,NYP
DU = U(K,J) - UE(K,J)
DV = V(K,J) - VE(K,J)
SUMU = SUMU + DU*DU
SUMV = SUMV + DV*DV
CONTINUE
RMSUE = SQRT(SUMU/AN)
RHSVE = SQRT(SUMV/AN)
WRITEF,37)ITER,RMSU,RMSVrRMSUE,RMSVE
FORMAT I* AFTER',13,' ITERATIONS, RMS-RHS='
I1 RMS-ERR=f,2E10.3)
DO 38 К = 1,NY
WRITEF,39)(U(K,J),J=1,NX)
FORMAT С U=',7F10.4)
DO 40 К = 1,KY
WRITEF,41)(V(K,J),J=1,NX)
FORMAT С V=f,7F10.4)
STOP
END
,2E10.3,
Рис. 10.13 (окончание).
§ 10.4. Двумерные уравнения Бюргерса 475
10.4.3. TWBURG: численное решение
Алгоритм, соответствующий схеме расщепления A0.70) г
A0.71), включен в качестве составной части в программу
TWBURG (рис. 10.13), предназначенную для получения ста-
стационарных решений уравнения A0.52) в вычислительной обла-
области — 1 ^ л: < 1, 0 ^ # ^ r/max, где f/max = л/бХ. Граничные
условия Дирихле получены из точного решения A0.63), A0.64).
Начальные условия получены путем линейной интерполяции
граничных условий в направлении оси х.
Основные параметры, используемые в программе TWBURG,.
описываются в табл. 10.11. Имеется возможность реализовать
решение уравнений A0.70), A0.71) в трех альтернативных ва-
вариантах. В случае ME = 1 для LXi Lxx и т. д. вводятся трехто-
трехточечные дискретизации с центральными конечными разностями и,
кроме того, полагается 6Х = 8У = 0. При ME = 2 четырехточеч-
четырехточечная дискретизация со сдвигом вверх по потоку, применявшаяся
ранее в п. 9.3.2, 9.4.3 и 9.5.2, используется как для LXi так и для
Ly. Для L{x используются четыре точки, начиная с (/ — 2, k)
и кончая (/+ 1, k)\ для Ly4)—четыре точки, начиная с
(/, k — 2) и кончая (/, k + 1). Для типового точного решения,
данные о котором приводятся на рис. 10.15, вблизи линии
х = 1 величина и отрицательна. Строго говоря, для вычисления
L(x4) в этой области должны использоваться четыре точки:
(/—1, А), ..., (/ + 2, k). Для упрощения программирования
в программе TWBURG этого не сделано. При ME = 3 пара-
параметры массового оператора 6* и 8У выбираются эмпирическим
путем, чтобы получить более точное решение.
Правая часть уравнения A0.70) вычисляется с помощью
подпрограммы RHSBU (рис. 10.14), а точное решение A0.63),
A0.64)—с помощью подпрограммы EXBUR (рис. 6.11) при
количестве элементов в массивах UE и VE, измененном на
21 X 21. В дополнение к этому в подпрограмме EXBUR (стро-
(строка 10) задается значение х0 согласно A0.65). Типовая выдача
результатов, полученных по программе TWBURG, приводится
на рис. 10.15.
Решения, полученные тремя указанными методами при вы-
выборе параметров согласно A0.65), приводятся в табл. 10.12 и
10.13 применительно к сетке 6X6. Соответствующие ошибки
решения в зависимости от х приводятся на рис. 10.16 и 10.17.
Даже на столь грубой сетке все методы дают сравнимую сте-
степень точности, причем наибольшие ошибки решения возни-
возникают в окрестности большого внутреннего градиента
(рис. 10.12). Исходя из результатов § 9.4 и п. 10.1.4, можно
ожидать, что больший разброс данных от разных методов
476 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
Таблица 10.11.
Параметр
ME
NX, NY
ITMAX
IPR
BET
QX, QY
DTIM, DX, DY
EPS
RE
EMI, EM2
A
CX, CY
CXQ, CYQ
EMX, EMY
DMX, DMY
U, V
UE, VE
DDU, DDV
RU, RV
RRU, RRV
В
RMSU, RMSV
RMSUE, RMSVE
Параметры, используемые в программе TWBURG
Описание
= 1, приближенная факторизация, 3-точечный конечно-
разностный метод, AF-FDM
= 2, приближенная факторизация, 4-точечная схема
со сдвигом вперед, AF-4PU
= 3, приближенная факторизация, схема с массовым
оператором, AF-MO
Число точек в направлениях х и у
Максимальное число итераций
>1, выдать на печать точное решение для и и v
Весовой коэффициент для п-го и (п + 1) -го временных
слоев равен 1 в табл. 10.12 и 10.13
qx и qy в 4-точечной дискретизации со сдвигом вперед.
А/, Ал:, Ау
Критерий значения || RHS^ fj в A0.70) для сходимо-
сходимости к стационарному состоянию
Число Рейнольдса Re = \/y
6х, Ьу в A0.66)
Коэффициенты аи ..., as в A0.65)
LXy Ly в A0.70) и A0.71)
Инкременты к Lx и Ly для формирования Lx\ Ly
Мхи Му в A0.70) и A0.71)
My$$Lxx, Mx®Lyy в A0.56)
Зависимые переменные
Точное решение (й, у), определяемое A0.63), A0.64)
Компоненты Aq* k и Aq^1 после возврата из BANSOL
Компоненты RHSn в A0.70); ячейки для временного
хранения Aq;. k
Одномерные компоненты RU, RV, требуемые для
BANSOL
4-диагональная или 3-диагональная матрица; левые
части A0.70) и A0.71)
Компоненты ||RHS/l||rms
"«-"И; \\v-v\\rms
1
2
3 SUBROUTINE RHSBU(RMSU,RMSV,ME,DTIM)
4 С
5 С EVALUATES RIGHT-HAND SIDE OF THE 2-D BURGERS1 EQUATION
6 С
7 REAL*8 RUD,RVD,SUMU,SUMV,AN,DSQRT
8 DIMENSION RUB1,21),RVB1,21),UB1,21),VB1,21),
9 1DMXC,3),DMYC,3),EMXC),EMYC),CXC),CYC),CXQD),CYQ<4)
10 2,FB),GB),ESB)
11 COMMON DX,DY,RE,NX,NY,CX,CXQ,CY,CYQ,DMX,DMY,?MX,EMY,RUrRV,U,V .
12 NXP = NX - 1
13 NYP - NY - 1
14 SUMU = 0.
15 SUMV ' 0.
16 DO 7 J =2,NXP
17 DO 6 К = 2,NYP
18 RUD = 0.
19 RVD * 0.
20 DO 2 N * 1,3
21 NK = К - 2 + N
22 DO 1 M * 1,3
23 MJ = J - 2 + M
24 F(l) = U(NK,MJ)*U(NK,MJ)
25 FB) = U(NK,MJ)*V(NK,MJ)
26 GB) = V(NK,MJ)*V(NK,MJ)
21 G<1) = FB)
:28 ESU) = 0.5*RE*U(NK,MJ)MFU) + GB))
.29 ESB) = 0.5*RE*V(NK,MJ)MF(l) + GB))
.30 DUM * CX(M)*EMY(N)*FA) + CY(N)*EMX(M)*GA)
31 RUD = RUD+(DMX(N,M)+DMY(N,M))*U(NK,MJ)+EMX(M)*EMY(N)*ESA) - DUH
32 DUM = CX(M)*EMY(N)*FB) + CY(N)*EMX(M)*GB)
33 1 RVD = RVD+(DMX(N,M)+DMY(N,M))*V(NK,MJ)+EMX(M)*EMY(N)*ES{2) - DUM
34 2 CONTINUE
35 IF(ME .NE. 2)GOTO 5
36 MST « 1
37 IF(J .EQ. 2)MST = 2
38 DO 3 M'= MST,4
39 MJ = J - 3 + M
40 RUD = RUD - CXQ(M)*U(K,MJ)*U(K,MJ)
41 3 RVD = RVD - CXQ(M)*U(K,MJ)*V(K,MJ)
42 IF(J .EQ. 2)RUD = RUD - CXQ(l)*U(K,1)*U(K,1)
43 IF(J .EQ. 2)RVD = RVD - CXQ(l)*U(K,1)*V(K,1)
44 NST = 1
45 IF(K .EQ. 2)NST = 2
46 DO 4 N = NST,4
47 NK » К - 3 + N
48 RUD = RUD - CYQ(N)*U(NK,J)*V(NK,J)
49 4 RVD = RVD - CYQ(N)*V(NK,J)*V{NKrJ)
50 IF(K .EQ. 2)RUD = RUD - CYQ(l)*UA,J)*VA,J)
51 IF(K .EQ. 2)RVD = RVD - CYQ{1)*VA,J)*V(lfJ)
52 5 SUMU = SUMU + RUD*RUD
53 SUMV = SUMV + RVD*RVD
54 RU(K,J) = RUD*DTIM
55 6 RV(KfJ) = RVD*DTIM
56 7 CONTINUE
57 AN * (NXP-DMNYP-1)
58 RMSU = DSQRT(SUMU/AN)
59 RMSV = DSQRT(SUMV/AN)
€0 RETURN
61 END
Рис. 10.14. Распечатка подпрограммы RHSBU.
478 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
2-D BURGERS EQUATION: AF-MO, NX,NY = б б ME * 3 ITMAX» 20
BETA= 1.00 DTIM* .010 RE= 50.0 QX= .00 QY= .00 EMX* .260 EMY« .260
A= .100E+14 Л00Е+14 .00 .00 1.00 AL=25.00 DX,DY* .40000 .00419
UE-
UE=
UE=
UE=
UE=
UE=
VE=
VE=
VE=
VE=
VE=
VE=
AFTER
U=
U=
U=
U=
U=
U=
V=
V*
V=
V=
V«
Y*
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
.0000
.1051
.2126
.3249
.4452
.5774
1.0000
1.0000
1.0000
1,0000
1.0000
1.0000
.0000
.1051
.2126
.3249
.4452
.5773
21 ITERATIONS, RMS-RHS
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
.0000
.1051
.2126
.3249
.4452
.5774
1.0000
1.0002
1.0003
1.0004
1.0003
1.0000
.0000
.1051
.2126
.3250
.4453
.5773
.5505
.5491
.5448
.5375
.5271
.5132
.0000
.0600
.1204
.1818
.2447
.3097
-.0333
-.0333
-.0333
-.0333
-.0333
-.0333
.0000
.0000
.0000
.0000
.0000
.0000
= .624E-04 .801E-05
.5505
.5426
.5349
.5275
.5203
.5132
.0000
.0586
.1180
.1790
.2425
.3097
-.0333
-.0354
-.0364
-.0365
-.0354
-.0333
.0000
-.0004
-.0008
-.0009
-.0007
.0000
0250
0250
0250
0250
CX250
0250
0000
0000
0000
0000
0000
0000
RMS-ERR
0250
0239
0233
0233
0238
0250
0000
0002
0004
0005
0004
0000
.0200
.0200
.0200
.0200
.0200
.0200
.0000
.0000
.,0000
.0000
.0000
.0000
= .449E-02 .120E-02:
.0200
.0200
.0200
.0200
.0200
.0200
.0000
.0000
.0000
.0000
.0000
.0000
Рис. 10.15. Типовая выдача результатов, полученных с помощью программы
TWBURG.
I
ID
+ АГ-РПМ
оAF-4PU
o.flF-MO
— точное решение
+ AF-FDM
о AF-4PU
¦ AF-МП
— точное решение
0.0
Рис. 10.16. Распределение ошибок для
решения и двумерного уравнения
Бюргерса при ylym*x = 0.4. Обозначе-
Обозначения см. в табл. 10.11.
Рис. 10.17. Распределение ошибок для
решения v двумерного уравнения
Бюргерса при у/утгх = 0 4. Обозна-
Обозначения см. в табл. 10.11.
§ 10.4. Двумерные уравнения Бюргерса
479
возникает при более сильных градиентах. Однако эти решения
свидетельствуют о том, что алгоритмы схем расщепления могут
быть без труда распространены на нелинейные уравнения и что
такие схемы, как AF-4PU и AF-MO, потенциально более точ-
точные, могут быть включены в программу при достаточно эконо-
экономичной реализации.
Таблица 10.12. Изменение и в зависимости от х при #/#тах — 0.4,
NX = 6, NY = 6
Точное решение
AF-FDM
AF-4PU,<7jc=1A
<^ = 0.0
AF-MO, 6Х =
= 6^ = 0.26
X
-1.00
1.0000
1.0000
1.0000
1.0000
-0.60
1.0000
1.0022
1.0003
1.0004
-0.20
0.5375
0.5221
0.5247
0.5257
0.20
-0.0333
-0.0322
-0.0326
—0.0365
0.60
-0.0250
-0.0250
-0.0256
—0.0233
1.00
-0.0200
—0.0200
-0.0200
—0.0200
Средне-
квадра-
квадратичная
ошибка
—
0.0066
0.0054
0.0045
Таблица 10.13. Изменение v в зависимости от х при
NX = 6, NY = 6
Точное решение
AF-FDM
AF-4PU, qx = 1.0,
^ = 0.0
AF-MO, 6* =
= Ьу = 0.26
X
-1 00
0.3249
0.3249
0.3249
0.3249
-0.60
0.3249
0.3251
0.3246
0.3250
-0.20
0.1818
0.1774
0.1781
0.1790
0.20
0.0000
0.0003
0.0003
—0.0009
0.60
0.0000
0.0000
—0.0002
0.0005
1.00
0.0000
0.0000
0.0000
0.0000
Средне-
квадра-
квадратичная
ошибка
—
0.0018
0.0015
0.0012
480 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
§ 10.5. Заключение
Вычислительные приемы, которые развивались примени-
применительно к уравнению диффузии в гл. 7 и 8, к уравнениям линей-
линейной конвекции и переноса — в гл. 9, были распространены
здесь на семейство нелинейных уравнений — уравнений Бюргер-
са — для одномерного и двумерного случаев. Уравнения Бюр-
герса содержат ту же самую форму конвективной нелинейно-
нелинейности, какая имеется во многих определяющих уравнениях дина-
динамики жидкости и газа.
При многих комбинациях начальных и граничных условий
уравнения Бюргерса допускают легко рассчитываемые точные
решения. В силу этого они представляют собой модельные
уравнения, подходящие для проверки разнообразных вычисли-
вычислительных методов. Применительно к одномерному уравнению
Бюргерса эта особенность была использована в п. 10.1.4 и
10.3.1, а применительно к двумерным уравнениям Бюргерса —
в 10.3.2 и 10.4.3.
Чтобы иметь возможность воспользоваться алгоритмом То-
Томаса, необходимо подвергнуть линеаризации конвективную не-
нелинейность. Такая необходимость выявляется как для неяв-
неявных одномерных схем (п. 10.3), так и для многомерных схем
расщепления (п. 10.4.2). Методика линеаризации без труда
распространяется и на системы уравнений (§ 10.2).
Анализ Фурье, непосредственная применимость которого к
линейным уравнениям была показана в п. 9.2.1 и 9.4.3, косвен-
косвенно используется и при анализе устойчивости по Нейману после
замораживания нелинейности. Подход, связанный с примене-
применением модифицированного уравнения (п. 9.2.2), остается приме-
применимым и к линейным уравнениям. Однако произведения про-
производных высшего порядка появляются при этом в достаточ-
достаточном числе и имеют достаточную величину, чтобы существенно
уменьшить точность определения диссипативных и дисперсион-
дисперсионных свойств. Оказывается обычно полезным в качестве проме-
промежуточного шага подвергнуть анализу эквивалентное линейное
уравнение, так как именно это уравнение часто обнаружи-
обнаруживает качественно эквивалентное диссипативное и дисперсион-
дисперсионное поведение. Построение более точных схем нередко тре-
требует использования определяющих принципов, выявленных с
помощью соответствующих линейных уравнений, при условии
внесения в них тех или иных эмпирических поправок.
Большинство вычислительных методов, разработанных для
линейных уравнений, могут быть распространены и на нели-
нелинейные уравнения. Однако, имея дело с нелинейными членами
конвективного типа, часто оказывается более целесообразным
§ 10.6. Задачи 481
использовать такие сохраняемые переменные, как, например,
функция F в уравнении A0.3). В тех случаях, когда это по-
полезно, сохраняемые переменные будут использоваться в
гл. 14—18.
Нелинейный характер определяющего уравнения делает не-
неэкономичным применение обычного метода Галёркина с конеч-
конечными элементами, особенно при решении многомерных задач и
при использовании повышенного порядка интерполяции. Это
затруднение преодолевается за счет представления уравнений
в консервативной форме и введения приближенных решений
для сохраняемых групп. Групповой вариант метода Галёркина
оказывается зачастую более точным, особенно в тех случаях,
когда консервативной форме представления определяющих
уравнений отдается предпочтение в связи с физическими особен-
особенностями задачи.
§ 10.6. Задачи
Одномерное уравнение Бюргерса (§ 10.1)
10.1. Примените к уравнению A0.20) анализ с помощью модифициро-
модифицированного уравнения. Нелинейные коэффициенты уравнения считайте при этом
замороженными и рассмотрите два случая: A) q = 0, B) 6 = 0. Покажите,
что оптимальные значения 6 и (/ задаются соотношениями A0.26) и A0.27)
соответственно.
10.2. Модифицируйте программу BURG так, чтобы реализовать конечно-
разностную дискретизацию уравнения A0.1) по схеме Кранка—Николсона и
сравните полученное решение с тем, которое соответствует конечно-разност-
конечно-разностной дискретизации уравнения A0.3) по той же схеме и при условиях, соот-
соответствующих табл 10.5. Как изменятся результаты этого сравнения, если
интегрирование будет продолжено до больших значений времени?
10.3. Модифицируйте программу BURG за счет введения в нее соотно-
соотношений A0.26) и A0.27) и сравните решения применительно к условиям, от-
относящимся к большим числа Рейнольдса ячейки и соответствующим
табл. 10.5.
10.4. Программа BURG может быть использована для получения ста-
стационарных решений уравнений A0.37) при F = 0.5 (w2— и). Введите соответ-
соответствующие изменения в общую трехслойную схему, эквивалентную схеме
(8.26), и постройте решения при A) у = 0, Р = 1; B) у = 0, р = 0.5;
C) у = 0.5, р = 1.0. Сравните числа итераций, требуемых для достижения
стационарного состояния в условиях, соответствующих табл. 10.9, но с ис-
использованием однородной сетки.
10.5. Для уравнения конвекции — диффузии A0.28) составьте программу
неравномерной дискретизации A0.30) — A0.32) и подтвердите результаты,
приводимые в табл. 10.6 и 10.7.
10.6. Разработайте четырехточечную дискретизацию на неоднородной
сетке со сдвигом вверх по потоку так, чтобы оставался один свободный па-
параметр (эквивалентный q). Предположите, что величина гх постоянна, но
не равна единице. Примените эту дискретизацию к модифицированному урав-
уравнению Бюргерса A0.37) с двухслойной чисто неявной маршевой схемой
A0.38). Сравните точность полученных при этом решений с тем, которое по-
показано в табл. 10.8 и 10.9 для различных значений свободного параметра.
31 К Флетчер, т. 1
482 Гл. 10. Нелинейные задачи с преобладающим влиянием конвекции
Системы уравнений (§ 10.2)
10.7. Модифицируйте программу SHOCK (рис. 14.17) с тем, чтобы реа-
реализовать в ней явную четырехточечную схему со сдвигом вверх по потоку,,
введенную в п. 9 4.3. Получите решения, соответствующие тем, которые
отражены на рис. 10.9, при искусственной диссипации, достаточной для по-
подавления чрезмерных колебаний. Для получения устойчивых решений может
оказаться необходимым использовать малое значение At (малое число Ку-
Куранта С). Сравните крутизну полученного профиля ударной волны с тем, ко-
который показан на рис. 10.9.
10.8. Обобщите конечно-разностную схему Кранка — Николсона A0 44)
с тем, чтобы разработать такую схему с массовым оператором при варьи-
варьируемом параметре 6 для системы уравнений A0 40). Модифицируйте про-
программу SHOCK (рис. 14.17) так, чтобы она работала по этой схеме, и срав-
сравните качество решения с тем, которое показано на рис. 10.9, при эмпирически:
подобранном значении б.
Групповой метод конечных элементов (§ 10.3)
10.9. Реализуйте в программе BURG расчеты по обычному методу конеч-
конечных элементов с разностной формой производной по времени, соответствую-
соответствующей схеме Кранка — Николсона, для одномерного уравнения Бюргерса и
сравните точность полученного решения с точностью, обеспечиваемой приме-
применением группового метода конечных элементов и схемы Кранка — Николсона
с массовым оператором, для условий, соответствующих табл 10 5
10.10. Оцените связующую способность и число операций для расчета не-
невязки с помощью обычного и группового вариантов метода конечных элемен-
элементов в применении к двумерным уравнениям Бюргерса с использованием ква-
квадратичной интерполяции.
10.11. Модифицируйте программу TWBURG так, чтобы получить воз-
возможность расчета по обычному методу конечных элементов в применении
к уравнениям A0.57) и A0.58), и сравните точность и экономичность такого
расчета с теми же параметрами для группового метода конечных элементов
в применении к уравнению A0.52), для условий, соответствующих табл. 10.12
и 10.13. Как изменится это сравнение при использовании более мелкой
сетки?
Двумерные уравнения Бюргерса (§ 10.4)
10.12. Составьте программу, основанную на подпрограмме EXBUR, для
построения таких точных решений двумерных уравнений Бюргерса, кото-
которые порождали бы более сильные внутренние градиенты, в то же воемя соз-
создавая умеренные градиенты переменной и в окрестности линии х = 1.
10.13. С помощью программы TWBURG получите решения на сетках
6X6, 11ХП и 21X21 для условий, соответствующих табл. 10.12 и 10.13,
при 0 < б*, Ьу < 0.30, 0 < qx, qy < 1 0 Решите вопрос об оптимальном вы-
выборе бх и 6у, а также qx и qy для каждого варианта сетки.
10.14. Проведите расчет по программе TWBURG для следующего на-
набора параметров: п\ = а2 = 0 01101, а3 = а4 = 0, а5 = 1 0, А, = 5, х0 = 1.0
и v = 0.1. Этот набор создает умеренный граничный градиент вблизи х =
= 1 0. Каков будет оптимальный выбор значений 6*, ду, а также qx, qy на
сетке 11ХП для данного варианта?
Приложения
§ АЛ. Эмпирическое определение времени исполнения
основных операций
На рис. АЛ приведена распечатка компьютерной программы
COUNT, дающей возможность приближенно определить време-
времена исполнения различных типов операций. Тип операции, соот-
соответствующей тому или иному значению параметра ICT, при-
приводится в табл. АЛ.
Таблица АЛ. Операции, учтенные в программе COUNT
ICT
1
2
3
4
5
6
7
S
9
10
11
12
Операция
Пустой цикл DO
Присваивание
Сложение и присваивание
Вычитание и присваивание
Умножение и присваивание
Деление и присваивание
Целочисленный оператор IF
Возведение в степень и присваивание
Извлечение квадратного корня и присваива-
присваивание
Синус и присваивание
Экспонента и присваивание
Сложение массивов и присваивание
Время исполне-
исполнения (с) для
JV=10 000
32.9
45.0
65.0
65.0
64.5
64.5
38.6
210
69.5
60
74.7
81.6
Для каждой операции выполняется пара связанных между
собой циклов DO. Внутренний цикл повторяет заданную опе-
операцию 1000 раз. Внешний цикл осуществляет повторение
внутреннего цикла N раз. Для достаточно большого N вре-
время, прошедшее от ввода параметров ICT и N (строка 15) до
вывода тех же параметров (строка 48), может быть определено
вручную. В качестве возможной альтернативы используется под-
подпрограмма, измеряющая время центрального процессора между
строками 15 и 48.
31*
484 Приложения
1 С COUNT FACILITATES THE DETERMINATION OF THE EXECUTION
2 С TIME FOR SPECIFIC OPERATIONS, DEPENDING ON THE VALUE OF ICT.
3 С N IS THE NUMBER OF OUTER LOOPS.
4 С
5 DIMENSION EA000),FU000),GA000)
6 С INTEGER A,B,C
7 В = 3.0
8 С = 1.0
9 IA = 8
10 DO 21 J = 1,1000
11 F(J) = 2.0
12 21 G(J) = 1.0
13 WRITE(*,22)
14 22 FORMATEX,'VALUE FOR ICT AND Nf)
15 READ(*,23)ICT,N
16 23 FORMATB15)
17 С
18 DO 14 I = 1,N
19 DO 13 J = 1Д000
20 С
21 GOTOA,2>3,4,5,6,7,8,9,10,11,12),ICT
22 1 CONTINUE
23 GOTO 13
24 2 A = J
25 GOTO 13
26 3 A = В + J
27 GOTO 13
28 4 A = В - J
29 GOTO 13
30 5 A = B*J
31 GOTO 13
32 6 A = B/J
33 GOTO 13
34 7 IF(I .GT. 0)GOTO 13
35 .GOTO 13
36 8 A = B**IA
37 GOTO 13
38 9 A = SQRT(B)
39 GOTO 13
40. 10 A = SIN(B)
41 GOTO 13
42 11 A = EtfP(B)
43 GOTO 13
44 12 E(J) = F(J) + G(«J)
45 13 CONTINUE
46 14 CONTINUE
47 С
48 VRITE(*,15)ICT,N
49 15 FORMATEX, ' ICT=' ,I7,5X, ' N=\l7)i
$0 STOP
51 END
Рис. АЛ. Распечатка программы COUNT.
§ А.2. Массовый и разностный операторы 485
Времена исполнения, приводимые в табл. АЛ, относятся к
супермикрокомпьютеру (Masscomp 5400), данные о действиях
которого даны в табл. 4.4. Время исполнения для ICT = 1 вы-
вычтено из данных для случаев ICT = 2 и ICT = 7. В остальных
случаях вычитается время для ICT = 2. Для операций с фик-
фиксированной запятой (FX), перечисляемых в табл. 4.4, активизи-
активизируется оператор целочисленности (строка 6), а вычисление
библиотечных функций (строки 38, 40 и 42) заменяется опера-
операторами CONTINUE, что сделано для выполнения оператора
GOTO (строка 21).
§ А.2. Массовый и разностный операторы
Как указывается в п. 5.5.1 и 5.5.2, метод конечных элемен-
элементов можно интерпретировать как средство почленной дискрети-
дискретизации, если только массовый и разностный операторы по на-
направлениям идентифицированы в явной форме. Происхождение
этих операторов в рамках метода Галёркина с конечными эле-
элементами (§5.1 и 5.3) будет показано здесь с двумерным уравне-
уравнением переноса (9.81)
дТ , дТ . д! д2! д2! п /А 1Ч
dt ' дх ' ду х дх2 у ду2 v '
Приближенное решение для Г вводится по формуле
T=ZTi<l>i(x,y)t (A.2)
* = i
где <f>i(x, у) — двумерные интерполяционные функции Лагран-
жа, эквивалентные функциям E.60). Выражение (А.2) подстав-
подставляется в уравнение (АЛ); согласно формулам E.5) и E.10),
вычисляется галёркинский интеграл от невязки с весом, и ре-
результат представляется в виде
Мх ® МУТ + иМу ® LXT + vMx ® LyT —
- ахМу ® LXXT - ауМх ® LyyT = 0, (А.З)
где символ ® обозначает тензорное произведение и f = dT/dt.
Символы Мх и Му соответствуют массовым операторам по на-
направлениям и определяются формулами
Af,={|.
1±Ll
486 Приложения
Разностные операторы по направлениям задаются формулами
г —1-°*. о Ш / -I-L A+г*> —!—1
* I Д* ' U) Дх J ' ^хх ~ \ Дх2 ' г* Дх2 ' гж Дх2 ) ' ,д
где г» и rj, — коэффициенты изменения размеров сетки,
гх = -Ш Ц r(/ = -f^±i——, (А.6)
xi~xi-\ Ук~~Ук-\
так что на равномерной сетке имеем гх = гу = 1.
Можно видеть, что имеет место почленное соответствие
между исходными уравнениями (АЛ) и дискретизированным
уравнением (А.З). Источник этого соответствия можно увидеть,
если рассмотреть в (АЛ) единственный член дТ/дх. Примене-
Применение к уравнению (АЛ) метода конечных элементов включает
следующий вклад от производной дТ/дх:
(А.7)
где знак Ye обозначает вклады от элементов, примыкающих
к узлу т. Интерполяционные функции Лагранжа фт можно
представить в форме произведений одномерных интерполяцион-
интерполяционных функций
(А.8)
где функции <j>^ и ф^ задаются формулами E.45) и E.46).
Следовательно, вклады в интеграл (А.7) можно расщепить на
компоненты по направлениям
Как результат этого можно ввести операторы
Lx,=
ДА7-1/2
где предполагается, что m-й галёркинский узел совпадает с
глобальной узловой точкой сетки (/, k)> так что
§ А.2. Массовый и разностный операторы 487
Таким образом, член дТ/дх в уравнении (АЛ) дискретизирует-
ся в форме Му <g> LXT. На глобальной сетке это приобретает вид
М. « L,T = i {'ышЪ-м) +
Там, где в определяющем уравнении (АЛ) появляется вторая
производная, применение интегрирования по частям приводит
к следующему определению оператора Lxx во внутренней точке:
х. (АЛ 4)
Определения, сравнимые с теми, которые даны в формулах
(АЛО), (АЛ1) и (АЛ4), могут быть получены и для Мх, Ly и
Lyy соответственно. На практике интегралы в формулах (АЛО)
и т. д. вычисляются путем введения координат (|, т]), связанных
с элементом, как это было с формулами E.58) — E.60). Для
линейных элементов
йт) при |т = ±1 и -1<Б<1. (А.15)
Формулы (АЛО), (А.11) и (АЛ4) применимы для интерполя-
интерполяции Лагранжа любого порядка. В случае квадратичной интер-
интерполяции операторы, выражаемые по формулам (А.4) и (А.5),
имеют по пять компонент, связанных с угловыми узлами, и по
три компоненты, связанные с узлами в серединах сторон.
Как очевидно из формул (А.5), форма операторов Lx и Lxx
аналогична тому, что имеет место при конечно-разностной ди-
дискретизации. В отличие от этого массовые операторы (А.4) ве-
ведут свое происхождение от интегральной природы метода Га-
лёркина. На этом основании при решении трехмерной задачи
производная дТ/дх дискретизируется в виде
дТ/дх ->МУ® Мг ® LXT. (A. 16)
Для элементов в форме кирпичиков с использованием трили-
трилинейной интерполяции вышесказанное позволяет заключить, что
оператор Му ® М2 ® Lx будет самое большее 27-точечным опе-
оператором.
При применении равномерной сетки существует связь между
ролью массовых операторов и разностными формулами Паде.
Вычисление дТ/дх по разностным формулам Паде с точностью
четвертого порядка осуществляется посредством решения
488 Приложения
трехдиагональной системы
1 /дТ\ 2 /дТ\ 1 (дТ
или
Mx-j^ = LJ. (A. 18)
Можно отметить, что здесь массовый оператор относится к тому
же направлению, по которому берется производная. В отличие
от этого при использовании метода Галёркина с конечными эле-
элементами получается
dT/dx->My®LxT (А. 19)
и появляется явная формула, имеющая связь с поперечным
направлением. Однако при использовании равномерной сетки
выражение (А. 19) также соответствует дискретизации четвер-
четвертого порядка точности.
Чтобы добиться четвертого порядка точности при дискре-
дискретизации д2Т/дх2, используя формулы, эквивалентные (А. 18)
или (А. 19), необходимо обобщить представление массового опе-
оператора, как это было сделано в (8.44), на оператор Мх =
= {6, 1—26, 6}. Выбор 6=1/12 обеспечивает четвертый по-
порядок точности (табл. 8.2).
Литература
Глава 1
Arlinger В. G. A986). Computation on Supersonic Flow Including Leading-
Edge Vortex Flows using Marching Euler Techniques. — In: Proc. Int. Symp.
Сотр. Fluid Dynamics, ed. by K. Oshima (Japan Computational Fluid Dy-
Dynamics Society, Tokyo). Vol. 2, p. 1—12.
Bailey F. R. A986). Overview of NASA's Numerical Aerodynamic Simulation
Program. — In: Proc. Int. Symp. Сотр. Fluid Dynamics, ed. by K. Oshima
(Japan Computational Fluid Dynamics Society, Tokyo). Vol. 1, p. 21—32.
Baker A. J. A983). Finite Element Computational Fluid Mechanics.—(McGraw-
Hill, New York).
Book D. L. (ed.) A981). Finite-Difference Techniques for Vectorised Fluid
Dynamics Calculations. — Springer Ser. Comput. Phys. (Springer, New York,
Berlin, Heidelberg).
Bourke W., McAveney В., Puri K., Thurling R. A977). Methods Comput Phys,
17, p. 267—325.
Chapman D. R., Mark H., Pirtle M. W. A975). Astronaut. Aeronaut., p. 22—35.
[Имеется перевод: Ракетная техн. и косм., 1980, № 2, с. 3—32.]
Chapman D. R. A979). AIAA J., 17, р. 1293—1313.
Chapman D. R. A981). In: 7th Int. Conf. Numer. Methods in Fluid Dynamics,
ed. by W. C. Reynolds, R. W. MacCormack, Lecture Notes in Physics, Vol. 141
(Springer, Berlin, Heidelberg), p. 1—11.
Cullen M.J. P. A983). J. Comput. Phys., 50, p. 1—37.
Fernbach S. A986). Performance Expectations for Future Large-Scale Scientific
Computers. — In: Proc. Int. Symp. Сотр. Fluid Dynamics, ed. by K. Oshima
(Japan Computational Fluid Dynamics Society, Tokyo). Vol. 1, p. 58—66.
Fletcher С A. J. A984). Computational Galerkin Methods, Springer Ser. Com-
Comput. Phys. (Springer. Berlin, Heidelberg). [Имеется перевод: Флетчер К.
Численные методы на основе метода Галёркина.—М.: Мир, 1988.]
Glowinski R. A984). Numerical Methods for Nonlinear Variational Problems,
Springer Ser. Comput. Phys. (Springer, Berlin, Heidelberg).
Green J. E. A982). In: Numerical Methods in Aeronautical Fluid Dynamics,
ed. by P. L. Roe (Academic Press, London), p. 1—32.
Haltiner G. J., Williams R. T. A980). Numerical Prediction and Dynamic Me-
Meteorology, 2nd ed. (Wiley, New York).
Hockney R. W., Jesshope С R. A981). Parallel Computers (Adam Hilger,
Bristol).
Hoist T. L, Thomas S. D., Kaynak U., Grundy K. L., Flores J., Chaderjian N. M.
A986). Computational Aspects of Zonal Algorithms for Solving the Com-
Compressible Navier — Stokes Equations in Three Dimensions. — In: Proc Int.
Sym. Сотр. Fluid Dynamics, ed. by K. Oshima (Japan Computational Fluid
Dynamics Society, Tokyo). Vol. 1, p. 113—122.
Holt M. A984). Numerical Methods in Fluid Dynamics, 2nd ed., Springer Ser.
Comput. Phys. (Springer, Berlin, Heidelberg).
Hoshino T. A986). Highly Parallel Computer PAX for Scientific Applica-
Applications. — In: Proc. Int. Symp. Сотр. Fluid Dynamics, ed. by K. Oshima
490 Литература
(Japan Computational Fluid Dynamics Society, Tokyo). Vol. 2, p. 183—194.
Krause E. A985). Comput. Fluids, 13, p. 239—269.
Kutler P. A985). AIAA J., 23, p. 328—338.
Levine R. D. A982). Sci. Amer., 246, p. 112—125. [Имеется перевод: В мире
науки, 1983, № 1, с. 16—29.]
Ortega J. M., Voigt R. G. A985). SIAM Rev., 27, p. 147—240.
Peyret R., Taylor T. D. A983). Computational Methods for Fluid Flow, Sprin-
Springer Ser. Comput. Phys. (Springer, Berlin, Heidelberg).
Richtmyer R. D., Morton K. W. A967). Difference Methods for Initial Value
Problems, 2nd ed. (Wiley, New York). [Имеется перевод: Рихтмайер Р. Д.,
Мортон К. Разностные методы решения краевых задач. — М.: Мир, 1972.]
Roache P. J. A976). Computational Fluid Dynamics (Hermosa, Albuquer-
Albuquerque, N. M.) [Имеется перевод: Роуч П .Дж. Вычислительная гидродинами-
гидродинамика. — М.: Мир, 1980.1
Rubbert P. E. A986). The Emergence of Advanced Computational Methods in
the Aerodynamic Design of Commercial Transport Aircraft. — In: Proc. Int.
Сотр. Fluid Dynamics, ed. by K. Oshima (Japan Computational Fluid Dyna-
Dynamics Society, Tokyo). Vol. 1, p. 42—48.
Stevens K. G. A986). Efficiency of CFD Algorithm on Multiprocessor Architec-
Architectures. — In: Proc. Int. Symp. Сотр. Fluid Dynamics, ed. by K. Oshima
(Japan Computational Fluid Dynamics Society, Tokyo). Vol. 1, p. 67—73.
Thomasset F. A981). Implementation of Finite Element Methods for Navier —
Stokes Equations, Springer Ser. Comput. Phys. (Springer, Berlin, Heidel-
Heidelberg).
TobakM., Peake D. A982). Ann. Rev. Fluid Mech., 14, p. 61—85.
Turkel E. A982). Comput. Fluids, 11, p. 121—144.
Глава 2
Ames W. F. A969). Numerical Methods for Partial Differential Equations (Bar-
(Barnes and Noble, New York).
Belotserkovskii O. M., Chushkin P. I. A965). In: Basic Developments in Fluid
Dynamics, ed. by M. Holt (Academic, New York), p. 1—126.
Chester C. R. A971). Techniques in Partial Differential Equations (McGraw-
Hill, New York).
Courant R., Friedrichs К. О. A948). Supersonic Flow and Shock Waves (In-
terscience, New York). [Имеется перевод: Курант Р., Фридрихе К. Сверх-
звуковые течения и ударные волны. — М.: ИЛ, 1950.]
Courant R., Hilbert D. A962). Methods of Mathematical Physics, Vol. II (In-
terscience, New York). [Имеется перевод: Курант Р., Гильберт Д. Методы
математической физики, т. 2. — М.: Гостехиздат, 1951.]
Fletcher С. A. J. A983). The Galerkin Method and Burgers' Equation. — In:
Numerical Solution of Differential Equations, ed. by J. Noye (North-Holland,
Amsterdam), p. 355—475.
Garabedian P. A964). Partial Differential Equations (Wiley, New York).
Гельфанд И. М., Шилов Г. Е. Некоторые вопросы теории дифференциальных
уравнений (Обобщенные функции, вып. 3). — М.: Физматгиз, 1958.
Gustafson К. Е A980). Partial Differential Equations and Hilbert Space Me-
Methods (Wiley, New York).
Hellwig G. A964). Partial Differential Equations, An Introduction (Blaisdell,
New York).
Jeffrey A., Taniuti T. A964). Nonlinear Wave Propagation with Application ta
Physics and Magnetohydrodynamics (Academic, New York).
Lighthill M. J. A958). Fourier Analysis and Generalised Functions (Cambridge
University Press, Cambridge).
Whitham G. A974). Linear and Nonlinear Waves (Wiley, New York). [Имеет-
[Имеется перевод: Уизем Дж. Б. Линейные и нелинейные волны. — М.: Мир, 1977.]
Литература 491
Глава 3
Gear С. W. A971). Numerical Initial Value Problems in Ordinary Differential
Equations (Prentice-Hall, Englewood Cliffs, N. J.).
Hamming R. W. A973). Numerical Methods for Scientists and Engineers, 2nd
ed. (McGraw-Hill, New York). [Имеется перевод: Хемминг Р. В. Численные
методы для научных работников и инженеров. — М.: Наука, 1968].
Liepman H., Roshko A. A957). Elements of Gas Dynamics (Wiley, New York).
(Имеется перевод: Липман Г. В., Рошко А. Элементы газовой динамики. —
М.: ИЛ, I960.]
Глава 4
Carnahan В., Luther H. A., Wilkes J. О. A969). Applied Numerical Analysis
(Wiley, New York).
Dahlquist G., Bjorck A. A974). Numerical Methods, trans by N. Anderson
(Prentice-Hall, Englewood Cliffs, N. J.).
Finlayson B. A. A980). Nonlinear Analysis in Chemical Engineering (McGrau-
Hill, New York).
Fletcher С A. J. A983). J. Comput. Phys., 51, p. 159—188.
Hindmarsh A. C, Gresho P. M., Griffiths D. F. A984). Int. J. Numer. Methods
Fluids, 4, p. 853—897.
Isaacson E., Keller H. B. A966). Analysis of Numerical Methods (Wiley, New
York).
jMitchel A. R., Griffiths D. F. A980). The Difference Method in Partial Diffe-
Differential Equations (Wiley, Chichester).
Morton K. W. A980). Int. J. Numer. Methods Eng., 15, p. 677—683.
Neye J. A984). Chap. 2 in Numerical Solution of Differential Equations,
ed. by J. Noye (North-Holland, Amsterdam).
Richtmyer R. D., Morton K. W. A967). Difference Methods for Initial-Value
Problems (Interscience, New York). [Имеется перевод: Рихтмайер Р. Д.,
Мортон К. Разностные методы решения краевых задач. — М.: Мир, 1972.]
Smith G. D. A965). Nonlinear Solution of Partial Differential Equations (Ox-
(Oxford University Press, Oxford).
Sod G A. A985). Numerical Methods in Fluid Dynamics (Cambridge Univer-
University Press, Cambridge).
Trapp J. A, Ramshaw J. D. A976). J. Comput. Phys., 20, p. 238—242.
Глава 5
Baker A. J. A983). Finite Element Computational Fluid Mechanics (McGraw-
Hill, New York).
Bathe K. J., Wilson E. L. A976). Numerical Methods in Finite Element Ana-
Analysis (Prentice-Hall, Englewood Cliffs, N. J.).
Bourke W., McAvaney В., Puri K., Thurling R. A977). Methods Comput. Phvs.,
17, p. 267—325.
Brigham E. O. A974). The Fast Fourier Transform (Prentice-Hall, Englewood
Cliffs, N J).
Canuto C.f Hussaini M. Y., Quateroni A., Zang T. A. A987). Spectral Methods
in Fluid Dynamics, Springer Ser. Comput. Phys. (Springer, Berlin, Heidel-
Heidelberg).
•Cooley J. W., Tukey J. W. A965). Math. Comp, 19, p. 297—301.
Finlayson B. A. A972). The Method of Weighted Residuals and Variational
Principles (Academic, New York).
Finlayson B. A. A980). Nonlinear Analysis in Chemical Engineering (McGraw-
Hill, New York).
Fletcher C. A. J. A984). Computational Galerkin Methods, Springer Ser. Com-
Comput. Phys. (Springer, Berlin, Heidelberg). (Имеется перевод: Флетчер К.
Численные методы на основе метода Галёркина. — М.: Мир, 1988.]
492 Литература
Fox L., Parker I. B. A968). Chebyshev Polynomials in Numerical Analysis
(Oxford University Press, Oxford).
Gottlieb D., Orszag S. A. A977). Numerical Analysis of Spectral Methods:
Theory and Application (SIAM, Philadelphia).
Haltiner G. J., Williams R. T. A980). Numerical Prediction and Dynamics Me-
Meteorology, 2nd ed. (Wiley, New York).
Isaacson E., Keller H. B. A966) An Analysis of Numerical Methods (Wiley,
New York).
Jameson A., Bader T. J. A986). Euler Calculations for a Complete Aircraft.—
In: Proc. Tenth Int. Conf. Numerical Methods in Fluid Dynamics, Beijing,
Lecture Notes in Physics, Vol. 264 (Springer, Berlin, Heidelberg), p. 334—
344.
Jennings A. A977). Matrix Computation for Engineers and Scientists (Wiley,
Chichester).
Ku H. C, Hatziavramidis D. A984). J. Comput. Phys., 56, p. 495—512.
Ku H. C, Taylor T. D., Hirsch R. S. A987). Comput. Fluids, 15, p. 195—
214.
Lax P., Wendroff B. A960). Commun. Pure Appl. Math., 13, p. 217—237.
Mitchell A. R, Wait R. A977). The Finite Element Method in Partial Differen-
Differential Equations (Wiley, Chichester).
Oden J. Т., Reddy J. N. A976). An Introduction to the Mathematical Theory
of Finite Elements (Wiley, New York).
Orszag S. A. A971). Stud. Appl. Math., 50, p. 293—327.
Orszag S. A. A977). Numerical Simulation of Turbulent Flow.— In: Hand-
Handbook of Turbulence, ed. by W. Frost, Т. Н. Moulden (Plenum, New York),
p. 281—313.
Peyret R. A986). Introduction to Spectral Methods, Lect. Ser. 1986-04, Von
Karman Inst. for Fluid Dynamics, Belgium.
Peyret R., Taylor T. D. A983). Computational Methods for Fluid Flow, Sprin-
Springer Ser. Comput. Phys. (Springer, New York, Berlin, Heidelberg).
Strang G., Fix G. J. A973). An Analysis of the Finite Element Method (Pren-
(Prentice-Hall, Englewood Cliffs, N. J).
Thomasset F. A981). Implementation of Finite Element Methods for Navier —
Stokes Equation, Springer Ser. Comput. Phys. (Springer, Berlm, Heidel-
Heidelberg).
Voigt R. G., Gottlieb D., Hussaini M. Y. A984). Spectral Methods for Partial
Equations (SIAM, Philadelphia).
Zienkiewicz О. С A977). The Finite Element Method, 3rd ed. (McGraw-Hill,
London). [Имеется перевод 1-го изд.: Зенкевич О. Метод конечных элемен-
элементов в технике. — М.: Мир, 1975.1
Глава 6
Axelsson О., Gustafsson I. A979). J. Inst. Math. Its Appl., 23, p. 321—337.
Brandt A. A977). Math. Comput., 31, p. 333—390.
Brigham E. O. A974). The Fast Fourier Transform (Prentice-Hall, Englewood
Cliffs, N. J.).
Broyden С A965). Math. Comput., 19, p. 577—593.
Cooley J. W., Lewis P. A. W., Welch P. D. A970). J Sound and Vibrations,
12, "p. 315—337.
Dahlquist G., Bjorck A. A974). Numerical Methods, trans, by N. Anderson
(Prentice-Hall, Englewood Cliffs, N. J.).
Dorr F. W. A970). SIAM Rev., 12, p. 248—263.
Duff I. S. A981). A Sparse Future. —In: Sparse Matrices and Their Uses,
ed. by I. S. Duff (Academic, London), p. 1—29.
Engelman M. S., Strang G., Bathe K. J. A981). Int. J. Numer. Methods Eng.,
17, p. 707-718.
Литература 493'«
Fletcher С. A. J. A983). Int. J. Numer. Methods Fluids, 3, p. 213—216.
Fletcher R. A976). In: Numerical Analysis, ed. by G. A. Watson, Lecture Notes
in Mathematics, Vol. 506 (Springer, Berlin, Heidelberg).
Fletcher R. A980). Practical Methods of Optimization, Vol. 1. Unconstrained
Optimization (Wiley, Chichester).
Forsythe G. E., Malcolm M. A., Moler С. В. A977). Computer Methods for
Mathematical Computations (Prentice-Hall, Englewood Cliffs, N. J.).
Gerald C. A978). Applied Numerical Analysis, 2nd ed. (Addison-Wesley, Read-
Reading, Mass.).
Hackbusch W. A985). Multigrid Methods and Applications, Springer Ser. Corn-
put. Math. (Springer, Berlin, Heidelberg).
Hageman L. A., Young D. M. A981). Applied Iterative Methods (Academic,
New York).
Hestenes M. R., Stiefel E. L. A952). Nat. Bur. Stand. J. Res., 49, p. 409—
436.
Hockney R. W. A970). Meth. Сотр. Phys, 9, p. 135—211.
Hockney R. W., Jesshope С R. A981). Parallel Computers (Adam Hilger,
Bristol).
Isaacson E., Keller H. B. A966). Analysis of Numerical Methods (Wiley, New
York).
Jackson C. P., Robinson P. C. A985). Int. J. Numer. Methods Eng., 21,
p. 1315—1338.
Jennings A. A977a). Matrix Computation for Engineers and Scientists (Wiley,.
Chichester).
Jennings A. A977b). J. Inst. Math. Its Appl., 20, p. 61—72.
Khosla P. K., Rubin S. G. A981). Comput. Fluids, 9, p. 109—121.
Lin A. A985). Int. J. Numer. Methods Fluids, 5, p. 381—391.
Markham G. A984). A Survey of Preconditioned Conjugate-Gradient-type
Methods Applied to Asymmetric Systems, CERL Report TPRD/L/AP
137/N83.
Ortega J. M., Rheinboldt W. C. A970). Iterative Solution of Nonlinear Equa-
Equations in Several Variables (Academic, New York).
Powell M. J. D. A976). A View of Unconstrained Optimization. — In: Optimiza-
Optimization in Action, ed. by L. C. W. Dixon (Academic, London), p. 117—152.
Rheinboldt W. C. A974). On the Solution of Large, Sparce Sets of Nonlinear
Equations, TR-324, University of Maryland.
Rubin S. G., Khosla P. K. A981). Сотр. Fluids, 9, p. 163—180.
Schneider G. E., Zedan M. A981). Numer. Heat Transfer, 4, p. 1 — 19.
Shanno D. F. A983). Comput. Chem. Eng., 7, p. 569—574.
Sonneveld P., Wesseling P., de Zeeuw P. M. A985). In: Multigrid Methods for
Integral and Differential Equations, ed. by D. J. Paddon, H. Holstein (Oxford
Science Publication, Oxford), p. 117—167.
Stone H. L. A968). SIAM J. Numer. Anal., 5, p. 530—558.
Stuben K., Trottenberg U. A982). In: Multigrid Methods, ed. by W. Hack-
Hackbusch, U. Trottenberg, Lecture Notes in Mathematics, Vol. 960 (Springer,,
Berlin, Heidelberg).
Swartztrauber P. N. A977). SIAM Rev., 19, p. 490—501.
Varga R. A962). Matrix Iteratve Analysis (Prentice-Hall, Englewood Cliffs,
N. J.).
Vinsome P. K. W. A976). ORTHOMIN, An Iterative Method for Solving
Sparse Sets of Simultaneous Linear Equations. — In: Proc. 4th. Symp. on
Reservoir Engineering (SPE of AIME, Los Angeles), p. 150-159.
Wachpress E. L. A966). Iterative Solution of Elliptic Systems and Applications
to the Neutron Diffusion Equations of Reactor Physics (Prentice-Hall, Engle-
Englewood Cliffs, N. J.).
Zedan M., Schneider G. E. A985). Numer. Heat Transfer, 8 p. 537—557.
494 Литература
Глава 7
Beam R. M., Warming R. F. A979). An Implicit Factored Scheme for the
Compressible Navier-Stokes Equations II: The Numerical ODE Connection,
AIAA Paper 79-1446.
Dahlquist G. A963). BIT, 3, p. 27—43.
Gear C. W. A971). Numerical Initial Value Problems in Ordinary Differential
Equations (Prentice-Hall, Englewood Cliffs, N. J.).
Holt M. A984). Numerical Methods in Fluid Dynamics, 2nd ed., Springer Ser.
Comput. Phys. (Springer, Berlin, Heidelberg).
Lambert J. D. A973). Computational Methods in Ordinary Differential Equa-
Equations (Wiley, Chichester).
Mitchell A. R., Griffiths D. F. A980). The Finite Difference Method in Partial
Differential Equations (Wiley-Interscience, New York).
Noye B. J. A983). In: Numerical Solution of Differential Equations, ed. by
J. Noye (North-Holland, Amsterdam).
Ortega J. M., Voigt R. C. A985). SIAM Rev., 27, p. 149—240.
Richtmyer R. D., Morton K. W. A967). Difference Methods for Initial-Value
Problems (Interscience, New York). [Имеется перевод: Рихтмайер Р. Д.,
Мортон К. Разностные методы решения краевых задач. — М.: Мир, 1972.]
Seward W. L., Fairweather G., Johnston R. L. A984). IMA J. Numer. Anal.,
4, p. 375—425.
Trapp J. A., Ramshaw J. D. A976). J. Comput. Phys., 20, p. 238—242.
Widlund О. В. A967). BIT, 7, p. 65—70.
Глава 8
Douglas J., Gunn J. E. A964). Numer. Math., 6, p. 428—453.
Dwoyer D., Thames F. A981). Accuracy and Stability of the Time-Split Finite
Difference Schemes, AIAA Paper 81-1005.
Fletcher C. A. J. A984). Computational Galerkin Methods, Springer Ser. Com-
Comput. Phys. (Springer, Berlin, Heidelberg). [Имеется перевод: Флетчер К.
Вычислительные методы на основе метода Галёркина. — М.: Мир, 1988.]
Fletcher С. A. J., Srinivas К. A984). Сотр. Meth. Appl. Mech. Eng., 46,
p. 313—327.
Gourlay A. R. A970). J. Inst. Math. Its Appl., 6, p. 375—390.
Gourlay A. R. A977). Splitting Methods for Time Dependent Partial Diffe-
Differential Equations. — In: The State of the Art in Numerical Analysis, ed. by
D. Jacobs (Academic, London).
Марчук Г. И. Численные методы в прогнозе погоды. — Л.: Гидрометиздат,
1967.
Mase G. Е. A971). Continuum Mechanics (McGraw-Hill, New York).
Mitchell A. R, Fairweather G. A964). Numer. Math., 6, p. 285—292.
Mitchel A. R., Griffiths D. F. A980). The Finite Difference Method in Partial
Differential Equations (Wiley-Interscience, New York).
Peaceman D. W., Rachford H. H. A955). SIAM J., 3, p. 28—41.
Яненко Н. Н. Метод дробных шагов решения многомерных задач математи-
математической физики. — Новосибирск: Наука, 1967.
Глава 9
Baker A. J., Kim J. W. A987). Int. J. Numer Methods Fluids, 7, p. 489—520.
Brooks A. N., Hughes T. J., R. A982). Comput. Methods Appl. Mech. Eng., 32,
p. 199—259.
Brown G M. A960). AIChE J., 6, p. 179—183.
Carey G. F., Sepehrnoori K. A98.0). Comput. Methods Appl. Mech. Eng., 22.
p. 2.O—4o.
Литература 495-
de Vahl Davis G., Mallinson G. D. A976). Comput. Fluids, 4, p. 29—43.
Donea J. A984). Int. J. Numer. Methods Eng., 20, p. 101 — 119.
Donea J., Giuliani S., Laval H., Quartapelle L. A984). Comput. Methods Appl.
Mech. Eng., 45, p. 123—145.
Finlayson B. A. A980). Nonlinear Analysis in Chemical Engineering (McGraw-
Hill, New York).
Fletcher С A. J. A983) Comput. Methods Appl. Mech. Eng., 37, p. 225—243.
Griffiths D. F., Mitchell A. R. A979). In: Finite Elements for Convection
Dominated Flows, ed. by T. J. R. Hughes (ASME, New York), p. 91 —
104.
Haltiner G. J., Williams R. T. A980). Numerical Prediction and Dynamics.
Meteorology, 2nd ed. (Wiley, New York).
Hindmarsh A. C, Gresho P. M., Griffiths D. F. A984). Int. J. Numer. Methods
Fluids, 4, p. 853—897.
Jennings A. A977) Matrix Computation for Engeneers and Scientists (Wiley,
Chichester).
Klopfer G. H., McRae D. S. A983). AIAA J., 21, p. 487—494.
Leonard B. P. A979). Comput. Methods Appl. Mech. Eng., 19, p. 59—98.
Morton K. W. A971). Proc. Roy. Soc. London, Ser. A, 323, p. 237—253.
Noye J. A983). Chap. 2 in Numerical Solution of Differential Equations,
ed. by J. Noye (North-Holland, Amsterdam).
Pinder G. F., Gray W. G. A977). Finite Element Simulation in Subsurface
Hydrology (Academic, New York).
Raithby G. D. A976). Comput. Methods Appl. Mech. Eng., 9, p. 75—94.
Roache P. J. A972). Computational Fluid Dynamics (Hermosa, Albuquer-
Albuquerque, N. M.). [Имеется перевод: Роуч П .Дж. Вычислительная гидродинами-
гидродинамика.—М.: Мир, 1980.]
Steinberg S., Roache P. J. A985). J. Comput. Phys., 57, p. 251—284.
Warming R. F., Hyett B. J. A974). J. Comput. Phys., 14, p. 159—179.
Глава 10
Basdevant C, Deville M, Haldenwang P., Lacroix J M., Onazzoni, Peyret R.,.
Orlandi P., Patera A. T. A986). Comput. Fluids, 14, p. 23—41.
Burgers J. M. A948). Adv. Appl. Mech., 1, p 171.
Christie I., Griffiths D. F., Mitchell A. R., Sanz-Serna J. M. A981). Inst. Appl.
Numer. Anal., 1, p. 253—266.
Cole J. D. A951). Q. Appl. Math., 9, p. 225—236.
Fletcher C. A. J. A983a). Chap. 3 in Numerical Solution of Differential Equa-
Equations, ed. by J. Noye (North-Holland, Amsterdam), p. 355—475.
Fletcher С A. J. A983b). Comput. Methods Appl. Mech. Eng., 37, p. 225—243.
Fletcher С A. J. A983c). J. Comput, Phys., 51, p. 159—188.
Fletcher С A. J. A983d). Int. J. Numer. Methods Fluids, 3, p. 213—216.
Fletcher С A. J. A984). Computational Galerkin Methods, Springer Ser. Com-
Comput. Phys. (Springer, Berlin, Heidelberg). [Имеется перевод: Флетчер К.
Численные методы на основе метода Галёркина. — М.: Мир, 1988.]
Hamming R. W. A973). Numerical Methods for Scientists and Engineers,
2nd ed. (McGraw-Hill, New York). [Имеется перевод: Хемминг Р. В.
Численные методы для научных работников и инженеров. — М.: Наука,.
1968.]
Hopf Е. A950). Commun. Pure Appl. Math., 3, p. 201—230.
Klopfer G. H., McRae D. S. A983). AIAA J., 21, p. 487—494.
Lerat A., Peyret R. A975) Rech. Aerosp., 1975-2, p. 61—79.
Noye J. A983). Chap. 2 in Numerical Solution of Differential Equations,
ed. by J. Noye (North-Holland, Amsterdam), p. 130—353.
Peyret R., Taylor T. D. A983). Computational Methods for Fluid Flow, Sprin-
Springer Ser. Comput. Phys. (Springer, Berlin, Heidelberg).
496 Литература
Richtmyer R. D., Morton K. W. A967). Difference Methods for Initial-Value
Problems (Interscience, New York). [Имеется перевод: Рихтмайер Р. Д.,
Мортон К. Разностные методы решения краевых задач. — М.: Мир, 1972.]
Thommen H. U. A966). Z. Angew. Math. Phys., 17, p. 369—384.
Thompson J. F. A984). AIAA J., 22, p. 1505—1523.
Thompson J. F., Warsi Z. U. A., Martin C. W. A985). Numerical Grid Gene-
Generation, Foundations and Applications (North-Holland, New York).
Whitham G A974). Linear and Nonlinear Waves (Wiley, New York). [Имеется
перевод: Уизем Дж. Б. Линейные и нелинейные волны. — М.: Мир, 1977.]
Yanenko N. N., Fedotova Z. I., Tusheva L. A., Shokin Y. I. A983). Comput.
Fluids, 11, p. 187—206.
Указатель сокращенных обозначений
БПФ (FFT) —
ВВЦП (FTCS) -
ВГАД (CFD) -
ДСЧН BLFI) —
ДУЧП (PDE) -
КН (CN) -
КФЛ (CFL) -
МВН (WRM) -
МО (МО) -
МСН (MSI) —
НПН (ADI) —
ОДУ (ODE) -
ПАП (FAS) -
ПВР (SOR) —
ПЛВР (SLOR) -
ПМС (FMG) -
ПП (CS) —
СНП (SIP) -
СПВР (SSOR) -
ТСЧН CLFI) —
ФТВ (TWS) -
быстрое преобразование Фурье 203, 206
схема, центрированная по пространству, со
сдвигом вперед по времени 107, 114, 283
вычислительная гидроаэродинамика 7 и далее
двухслойная чисто неявная схема 345
дифференциальное уравнение в частных произ-
производных 33 и далее
схема Кранка — Никольсона 366
условие Куранта — Фридрихса — Леви 363
методы взвешенных невязок 136
массовый оператор 185
модифицированная существенно неявная про-
процедура 259
неявная схема переменных направлений 256Г
327, 330, 336
обыкновенное дифференциальное уравнение
322
метод с полной аппроксимационной памятью
269
последовательная верхняя релаксация 186, 189,
251, 254, 257, 258
последовательная линейная верхняя релакса-
релаксация 256
полный многосеточный метод 269
метод с поправочной памятью 269
существенно неявная процедура 258
симметричная последовательная верхняя ре-
релаксация 252
трехслойная чисто неявная схема 283, 299
формулировка Тейлора — Вика 378
32 К. Флетчер, т. 1
Предметный указатель
Алгоритм расщепления, двухэтапный
(algorithm of splitting, two-stage)
332
Аппроксимация производных (appro-
(approximation to derivatives) 77—81
с разностью вперед (forward
difference approximation) 78, 83, 84
назад (backward ~ ~)
78, 83, 84
Аппроксимирующая функция, линей-
линейная (approximating function, linear)
159
Вюргерса уравнение (Burgers* equa-
equation) 223, 272, 429, 467
Векторизация вычислительного алго-
алгоритма (vector processing) 17
Галёркина метод (Galerkin method)
140
с конечными элементами (finite
element Galerkin method) 170—194,
459—467
групповой (group ~ ~
^ _) 459—467
Taycca—Зайделя метод (Gauss—Sei-
del ~) 251—255
Гаусса метод исключения (Gauss
elimination ~) 233, 234, 237, 238,
240
Граничные условия (boundary condi-
condition) 37, 53—55
Дирихле (Dirichlet ~ ~) 37,
38, 282, 307
Неймана (Neuman ~ ~) 37,
38, 198, 282, 307, 309—311, 346
Грина функция (Green's function)
64-66
Дискретизация (discretisation) 29,
71—77
Дисперсия численная (dispersion, nu-
numerical) 370—378
Диссипация численная (dissipation,
~) 370—378
Дифференциальное уравнение в част-
частных производных, гиперболическое
(partial differential equation, hyper-
hyperbolic) 33—35, 50, 66, 68
параболическое (~ ~
~ parabolic) 33—35, 56, 66, 69
эллиптическое (~ ~
~ elliptic) 33—35, 58, 66, 69
Диффузии уравнение (diffusion equa-
equation) 181—183, 281—356
Дюфорта—Франкела схема (DuFort—
Frankel scheme) 283, 286—288
Зональный метод (zonal method) 21 —
23
Изопараметрическое преобразование
(isoparametric formulation) 192—194
Интерполяция, биквадратичная (bi-
(biquadratic interpolation) 169—170
— билинейная (bilinear ~) 164—166
— двумерная (two-dimensional ~)
164—170
— квадратичная (quadratic ~) 162—
164
— линейная (linear ~) 159—161
Итерационные методы (iterative me-
methods) 248—270
Квазиньютоновский метод (quasi-
Newton method) 230—233
Конвекции уравнение (convection
equation) 358
Конвекции—диффузии уравнение
(convection—diffusion ~) 379
Корректно поставленная задача
(well-posed problem) 35—37
Предметный указатель
499>
Коула—Хопфа преобразование (Co-
(Cole—Hopf transformation) 431, 467
Кортевега-де-Вриза уравнение (Ког-
teweg de Vries equation) 67, 372
Коэффициент усиления моды Фурье
(amplification factor) 121
Кранка — Николсона схема (Crank—
Nicolson scheme) 283, 297—299,
366—368
Куранта—Фридрихса—Леей условие
(Courant—Friedrichs—Levi condi-
condition) 363
Лакса—Вендроффа схема (Lax—
Wendroff scheme) 360, 365
Лапласа уравнение (Laplace's equa-
equation) 27, 58, 65, 67
Навье — Стокса уравнения (Navier—
Stokes equations) 11, 29
для тонкого слоя (~ ~ ~-
thin layer) 21
осредненные по Рейнольдсу
(~ ~ ~ Reynolds-averaged) 11,19
укороченные (~ ~ ~ redu-
reduced form) 11
Начальные условия (initial conditions)
37, 53—55, 313—314
Невязка (residual) 138
Нелинейность квадратичная (nonli-
nearity quadratic) 463, 464
— конвективная (~ convective) 428'
— кубическая (~ qubic) 463, 464
Неустойчивость физическая (physical'
instability) 123
Ньютона метод (Newton's method)
215—222
Матрица ленточная (banded matrix)
234
— плотная (dense —) 234
— пятидиагональная (pentadiagonal
~) 243
— трехдиагональная (tridiagonal ~)
238
Метод дробных шагов (fractional
steps method) 352—354
— коллокаций (colocation ~) 139
— конечных объемов (finite volu-
volume ~) 45—157
разностей (finite difference ~)
94
элементов (~ elements ~)
157—170
с расщеплением (~ ~ ~
with splitting) 333—346
— наименьших квадратов (least-squa-
(least-squares method) 139
— полной аппроксимационной памяти
(full approximation storage ~) 269
— поправочной памяти (correction ~
~) 269
— прямых (method of lines) 314—
321
— ускорения с сопряженными гра-
градиентами (~ ~ acceleration with
conjugate gradients) 260—262
Методы взвешенных невязок (weigh-
(weighted residual methods) 136—212
Многосеточные методы (multigrid ~)
264—270
Модифицированное уравнение (modi-
(modified equation) 375, 376
Оператор массовый (mass operator)'
185
— разностный (difference ~) 185
Отложенной коррекции метод (defer-
(deferred correction ~) 132
Ошибка аппроксимации (truncation-
error) 78, 80, 81, 82, 84, 100
— решения (solution ~) 73, 124
— среднеквадратичная (rms ~) 98..
99. 107
Переменных направлений схема (al-
(alternative directions scheme) 256,
327—330
Переноса уравнение, двумерное (two-
dimensional transport equation) 410
одномерное (one-dimensional ~
~) 385
Побочный эффект (aliasing) 431, 432
Полудискретная форма ДУЧП (semi-
discrete form of PDE) 314
Пробная функция (trial function) 136
Пробное решение (~ solution) 136
Псевдонестационарный метод (pseu-
dotransient method) 271—276
Псевдоспектральный метод (pseudo-
spectral ~) 201
Пуассона уравнение ('Poisson equa-
equation) 58, 65, 246
Размер элемента сетки (grid cell"
size) 90
32*
500
Предметный указатель
Разностная формула, несимметричная
'(difference formula, asymmetric) 80,
83, 84, 87
центрированная симметричная
(~ ~ centered, symmetric) 80, 83,
84, 87
Расчетная сетка, ее формирование
(computational grid generation) 20,
21
Расщепления методы (methods of
splitting) 327—333, 468—470
Рейнольдса число, сеточное (cell Rey-
Reynolds number) 379
Ричардсона схема (Richardson sche-
scheme) 283, 286—288
Рунге—Кутты схемы (Runge—Kytta
schemes) 316, 317
Связующая способность (connectivi-
(connectivity) 463, 464
Серендиповские элементы (serendipi-
(serendipity elements) 170
Система уравнений, блочно-трехдиа-
гональная (block-tridiagonal system
of equations) 245
'Согласованность (consistency) 104,
105, 108—112
Спектральный метод (spectral me-
method) 194—206
"Существенно неявная процедура
(strongly implicit procedure) 258—
260
•Сходимость (convergence) 104 105—
108
Тау-метод (tau method) 200
Теплопроводности уравнение (heat
conduction eqution) 181—183
Томаса алгоритм (Thomas algorithm)
238—240
обобщенный (~ ~ generalized)
243, 244
Трехслойная схема (three-level sche-
scheme) 288, 289
обобщенная (~ ~ generalized)
— чисто неявная (~ ~ fully impli-
implicit) 299
Устойчивости анализ, матричный ме-
метод (stability analysis, matrix me-
method) 114—120
— — метод Неймана (~ ~ Neu-
Neumann's ~) 120—124
Устойчивость (stability) 105, 112—
124
Факторизация (factorization) 331, 355
Фурье анализ (Fourier analysis) 47—
49
— быстрое преобразование (fast Fou-
Fourier transform) 203
— преобразование (Fourier ~) 48,
49
Характеристик метод (method of cha-
characteristics) 61—63
Характеристики (characteristics) 38—
41, 50, 51
Циклической редукции метод (cyclic
rediction method) 247, 249
Чехарда схема (leapfog scheme) 365
Штурма—Лиувилля задача (Sturm—
Liouville problem) 170—180
Эйлера схема (Euler's scheme) 317,
318
— уравнения (~ equations) 21, 29
Экстраполяция по Ричардсону (Ri-
(Richardson extrapolation) 126—128
активная (~ ~ active) 128
пассивная (~ ~ passive)
128
Энергетический метод (energy me-
method) 132
Эффективность вычислительная (com-
(computational efficiency) 129—131
Якоби метод (Jacobi method) 250—
252
Оглавление
От редактора перевода 5
Предисловие 7
Глава 1. Введение в вычислительную гидроаэродинамику ... И
§ 1.1. Преимущества вычислительной гидроаэродинамики 11
§ 1.2. Характерные практические задачи 20
§ 1.3. Структура уравнений 25
§ 1.4. Обзор общих принципов вычислительной гидроаэродинамики . . 28
§ 1.5. Литература для дополнительного чтения 31
Глава 2. Дифференциальные уравнения в частных производных . . 33
§ 2 1. Основные положения 33
§ 2.2. Гиперболические дифференциальные уравнения в частных произ-
производных 50
§ 2.3. Параболические дифференциальные уравнения в частных произ-
производных 56
$ 2.4. Эллиптические дифференциальные уравнения в частных произ-
производных 58
§ 2.5. Традиционные методы решения 61
§ 2.6. Заключение 66
§ 2.7. Задачи 67
Глава 3. Предварительные сведения о приемах вычислений ..... 71
§ 3.1. Дискретизация 72
§ 3.2. Аппроксимация производных 77
§ 3.3. Точность процесса дискретизации 82
§ 3 4. Представление волн 89
§ 3.5. Метод конечных разностей 94
§ 3.6. Заключение 100
§ 3.7. Задачи 101
Глава 4. Теоретические основы 104
§ 4.1. Сходимость 105
§ 4 2. Согласованность 108
§ 4.3. Устойчивость 112
§ 4.4. Точность решения 124
§ 4.5. Вычислительная эффективность 129
§ 4.6. Заключение 132
§ 4.7. Задачи 133
Глава 5. Методы взвешенных невязок 136
§ 5.1. Общая формулировка 137
§ 5.2. Метод конечных объемов 145
502 Оглавление
§ 5.3. Метод конечных элементов и интерполяция 157
§ 5.4. Метод конечных элементов и уравнение Штурма — Лиувилля 17Q
§ 5.5. Другие приложения метода конечных элементов 181
§ 5.6. Спектральный метод 194
§ 5.7. Заключение 207
§ 5.8. Задачи 207
Глава 6. Стационарные задачи .... 213
§ 6.1. Нелинейные стационарные задачи 215
§ 6.2. Прямые методы для линейных систем 233
§ 6.3. Итерационные методы .... 249
§ 6.4. Псевдонестационарный метод 271
§ 6.5. Стратегические приемы для решения стационарных задач . . . 276
§ 6.6. Заключение 277
§ 6.7. Задачи 278
Глава 7. Одномерное уравнение диффузии ...... ... 281
§ 7.1. Явные методы 282
§ 7.2. Неявные методы 295
§ 7.3. Граничные и начальные условия 307
§ 7.4. Метод прямых 314
§ 7.5. Заключение 321
§ 7.6. Задачи 322
Глава 8. Многомерное уравнение диффузии 324
§ 8.1. Двумерное уравнение диффузии 324
§ 8.2. Методы расщепления для многомерных задач 327
§ 8.3. Схемы расщепления и метод конечных элементов 333
§ 8.4. Граничные условия Неймана 346
§ 8.5. Метод дробных шагов 352
§ 8.6. Заключение . . . ' 354
§ 8.7. Задачи 355
Глава 9. Линейные задачи с преобладающим влиянием конвекции . 357
§ 9.1. Одномерное линейное уравнение конвекции 35&
§ 9.2. Численная диссипация и дисперсия 371
§ 9.3. Стационарное уравнение с конвекцией и диффузией 378
§ 9.4. Одномерное уравнение переноса 385
§ 9.5. Двумерное уравнение переноса 409
§ 9.6. Заключение 424
§ 9.7. Задачи 426
Глава 10. Нелинейные задачи с преобладающим влиянием конвекции 428
§ 10.1. Одномерное уравнение Бюргерса 429
§ 10.2. Системы уравнений 456
§ 10.3. Групповой метод конечных элементов 459
§ 10.4. Двумерные уравнения Бюргерса " . 467
§ 10 5. Заключение 480
§ 10.6. Задачи 481
Приложения . 483
§ АЛ. Эмпирическое определение времени исполнения основных операций 483
§ А.2. Массовый и разностный операторы 485
Литература 489
Указатель сокращенных обозначений 497
Предметный указатель 498
Уважаемый читатель!
Ваши замечания о содержании книги, ее
оформлении, качестве перевода и другие про-
просим присылать по адресу: 129820, Москва,
И-ПО, ГСП, 1-й Рижский пер., 2, издательство
«Мир».
Учебное издание
Клайв Флетчер
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ
В ДИНАМИКЕ ЖИДКОСТЕЙ
В 2-х томах. Т. 1
Заведующий редакцией
академик В. И Арнольд
Зам зав редакцией А С. Попов
Ст научн редактор П Я Корсоюцкая
Мл. научн редактор Н С. Полякова
Художник О. С. Василькова
Художественный редактор В. И. Шаповалов
Корректор Т М. Подгорная
И Б № 7463
Сдано в набор 03.05.90. Подписано к печати 14.01.91.
Формат 60X88Vie Бумага офсетная № 2 Печать вы-
высокая. Гарнитура литературная. Объем 15,75 бум. л*
Уел печ л 31,50 Уел кр -отт 31,50 Уч -изд л 28,96.
Изд № 1/7168 Тираж 5000 экз Зак 524 Цена 7 руб.
ИЗДАТЕЛЬСТВО «МИР» В/О «Совэкспорткнига»
Государственного комитета СССР по печати
129820. ГСП, Москва, И-110, 1-й Рижский пер. 2.
Набрано в Ленинградской типографии № 2 головного
предприятия ордена Трудового Красного Знамени
Ленинградского объединения «Техническая книга»
им Евгении Соколовой Государственного комитета
СССР по печати 198052, Ленинград, Л-52, Измайлов-
Измайловский проспект, 29 Отпечатано в Ленинградской типо-
типографии № 8 ордена Трудового Красного Знамени Ле-
Ленинградского объединения «Техническая книга» им.
Евгении Соколовой Государственного комитета СССР
по печати 190000, Ленинград, Прачечный переулок, 6.