Вычислительные методы в задачах механики жидкости - Тейлор Т.Д., Пейре П.

1.2. Различные формы уравнений Навье—Стокса
1.2.2. Ортогональные криволинейные координаты
1.3. Уравнения Навье—Стокса для несжимаемой жидкости
1.3.2. Уравнения в переменных вихрь—функция тока
2.2. Решение обыкновенного дифференциального уравнения
2.2.3. Аналогия между итерационными процедурами и решением эволюционных уравнений
2.3. Аналитическое решение конечно-разностной задачи
2.4. Схемы направленных против потока разностей с коррекцией
2.5. Методы повышенного порядка точности
2.5.2. $M$-метод и неявный метод компактного оператора
2.6. Решение одномерного линейного параболического уравнения
2.6.2. Схемы с нецентрированными разностями
2.6.3. Центрально-разностная схема Дюфорта—Франкела
2.7. Решение одномерных нелинейных параболических и гиперболических уравнений
2.7.2. Методы решения уравнений при наличии вязкости
2.8.2. Неявный метод чередующихся направлений
2.8.3. Явные схемы для нелинейных уравнений в консервативной форме
2.8.5. Обобщенные методы чередующихся направлений
Глава 3. Интегральные и спектральные методы
3.2. Примеры применения метода конечных элементов для решения стационарных задач
3.3. Примеры применения спектрального метода для решения стационарных задач
3.4. Пример применения метода конечных элементов в нестационарном случае
3.5. Пример применения спектрального метода в нестационарном случае
Глава 4. Сопоставление численных методов
4.2. Конечно-разностный аналог спектрального метода
4.3. Простейший разностный аналог метода Годунова
5.2. Функция Грина и уравнения в переменных вихрь—функция тока
6.2. Уравнения Навье—Стокса для стационарного случая: метод искусственной сжимаемости
6.2.3. Сходимость к стационарному состоянию
6.2.6. Другие варианты метода искусственной сжимаемости
6.3. Уравнения Навье—Стокса для нестационарного случая
6.4. Примеры решения задач для физических переменных скорость—давление
6.4.2. Нестационарная горизонтальная струя в стратифицированной жидкости
6.5. Уравнения для переменных вихря и функции тока и методы их решения
6.5.5. Решение задачи для больших чисел Рейнольдса
6.5.6. Аппроксимация уравнения вихря, записанного в консервативной форме
6.5.7. Уравнения для нестационарного случая
6.6. Примеры решения уравнений для вихря и функции тока
6.6.2. Нестационарное обтекание кругового цилиндра
Глава 7. Использование метода конечных элементов для решения задач механики несжимаемой жидкости
Глава 8. Спектральные методы решения задач механики несжимаемой жидкости
8.2. Вязкая жидкость — ламинарные и турбулентные течения
Глава 9. Модели и расчеты турбулентных потоков
9.2. Моделирование крупномасштабных вихрей
9.3. Расчеты турбулентных потоков с использованием модели замыкания
10.1.2. Применения методов ячеек и конечных объемов
10.2. Разностные методы решения стационарных уравнений
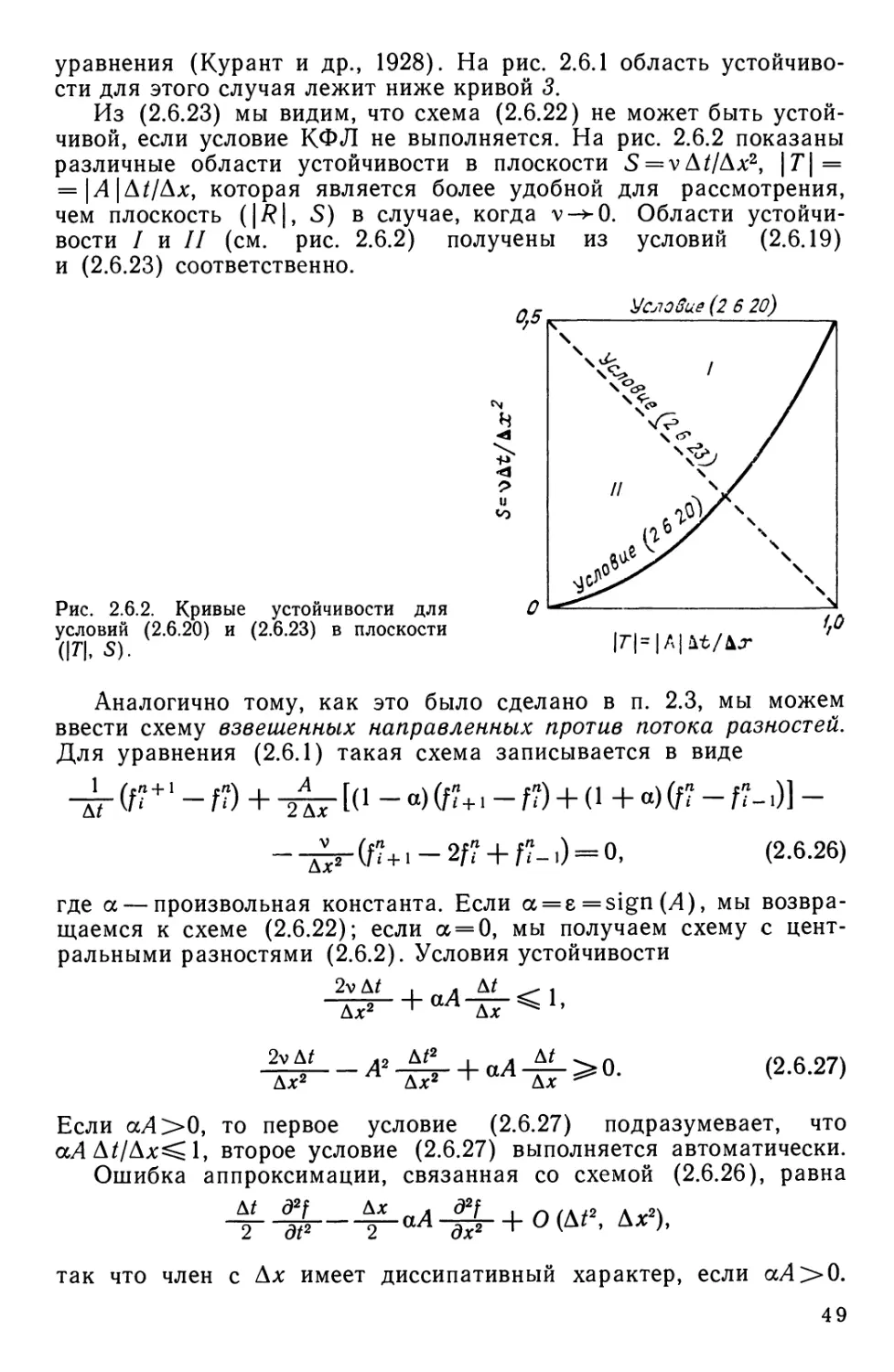
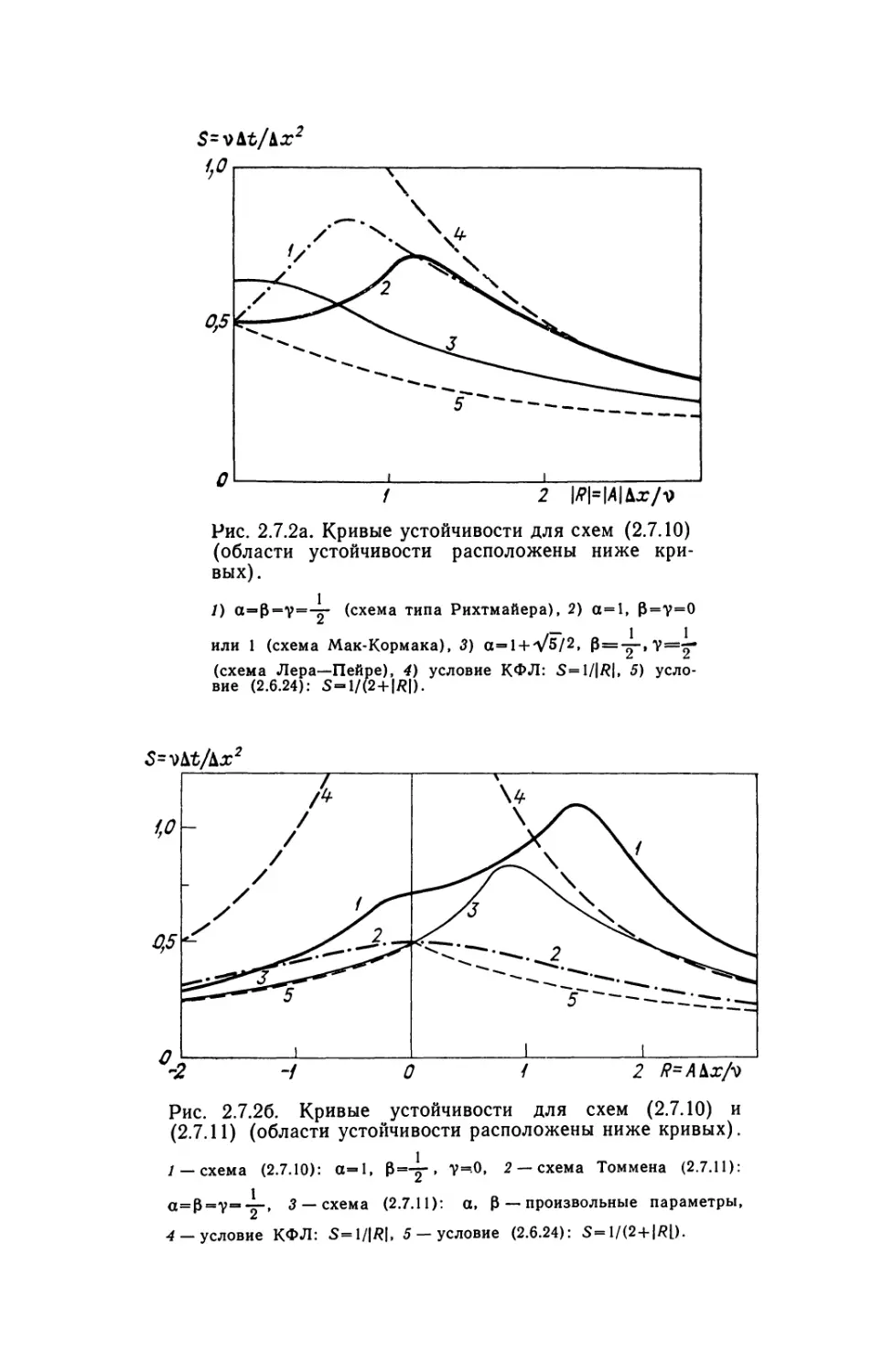
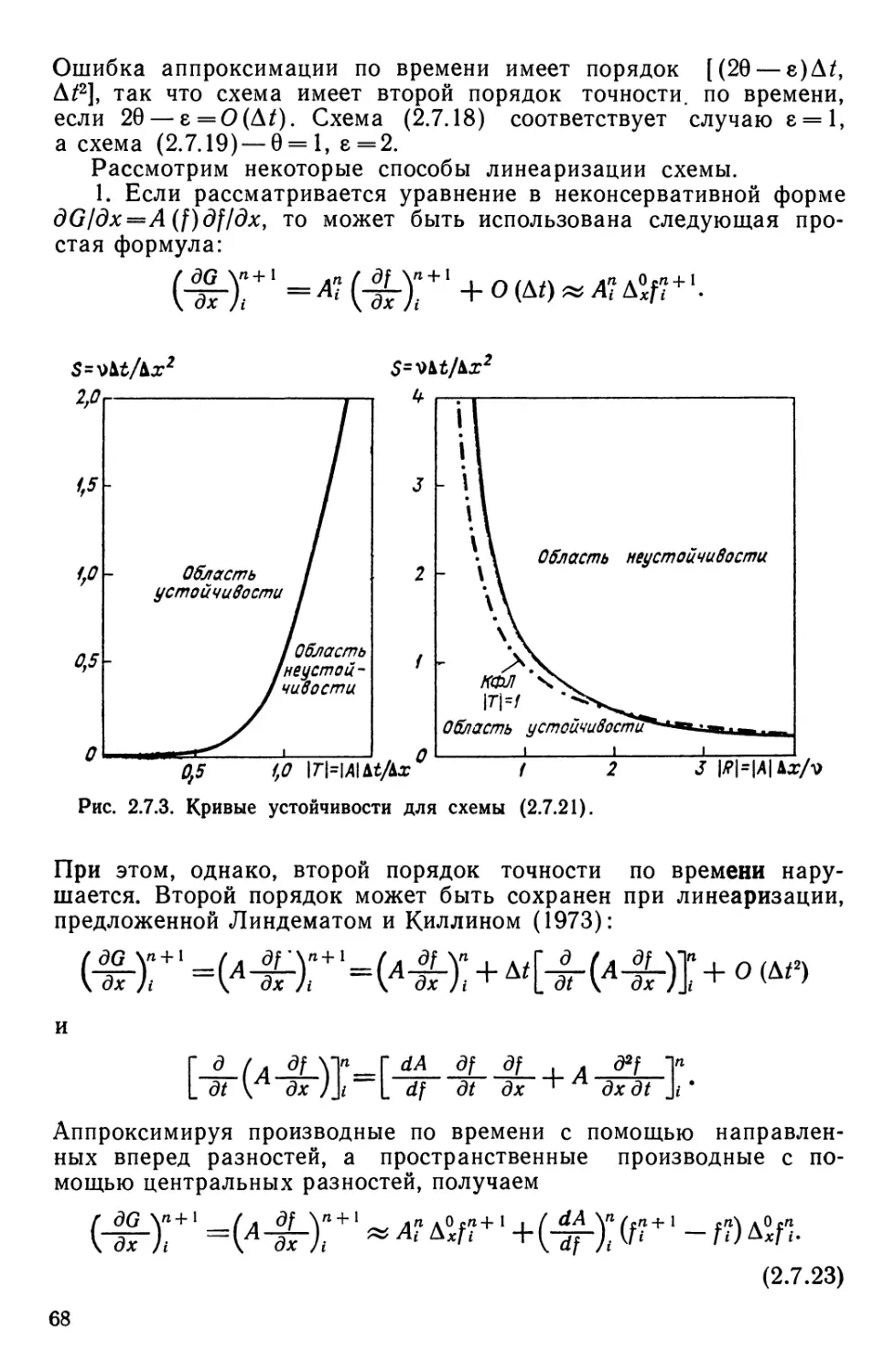
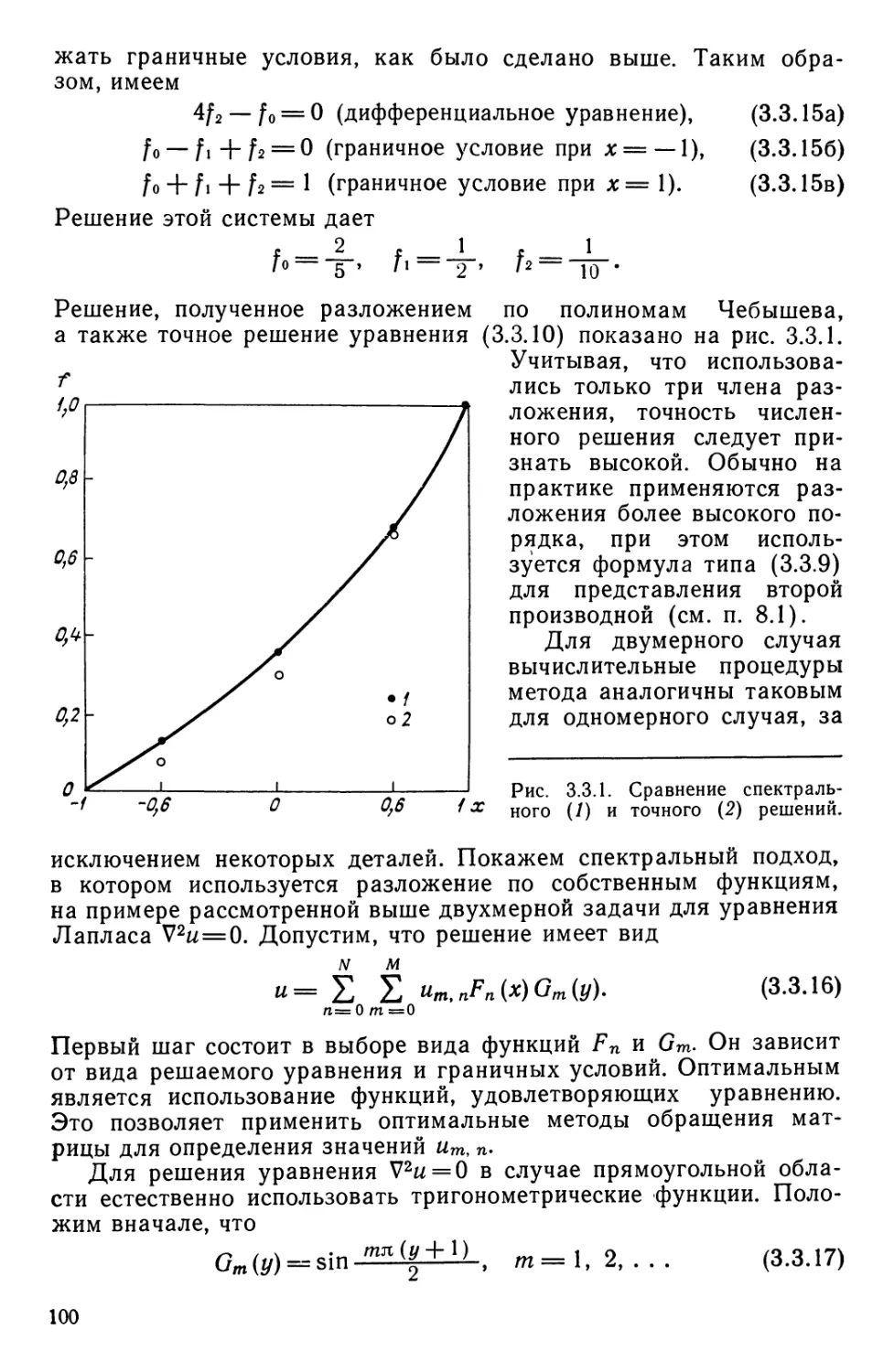
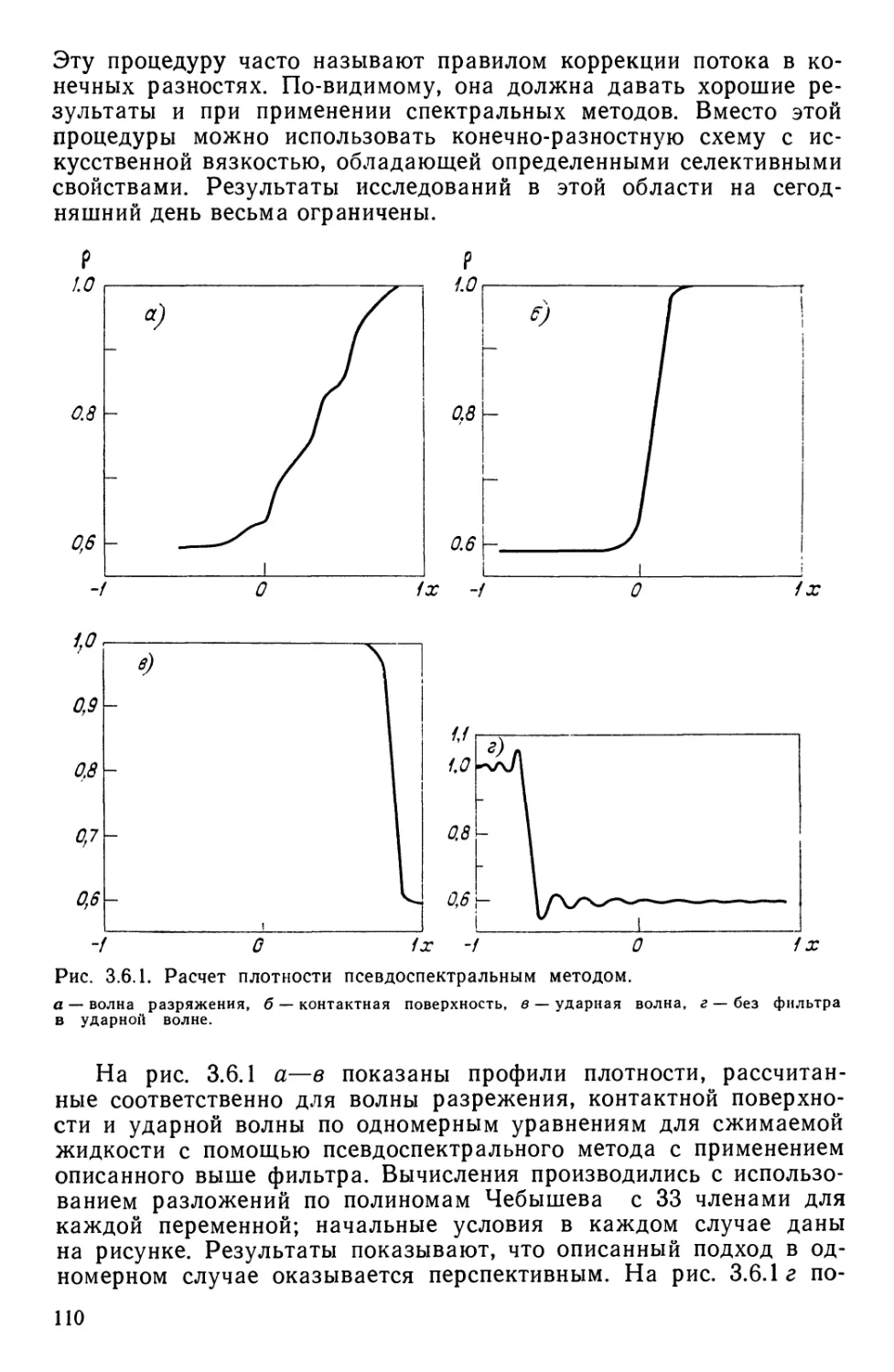
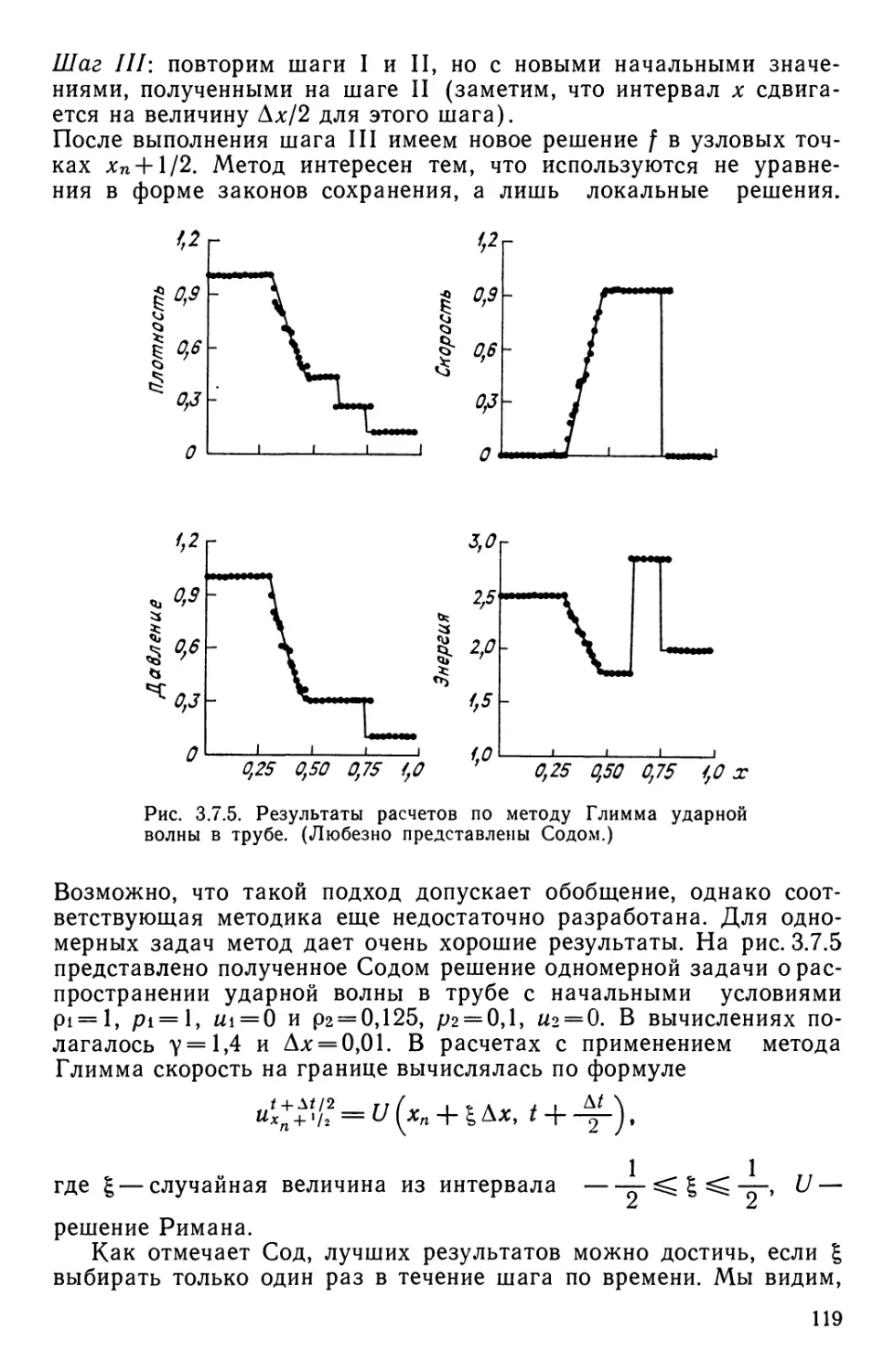
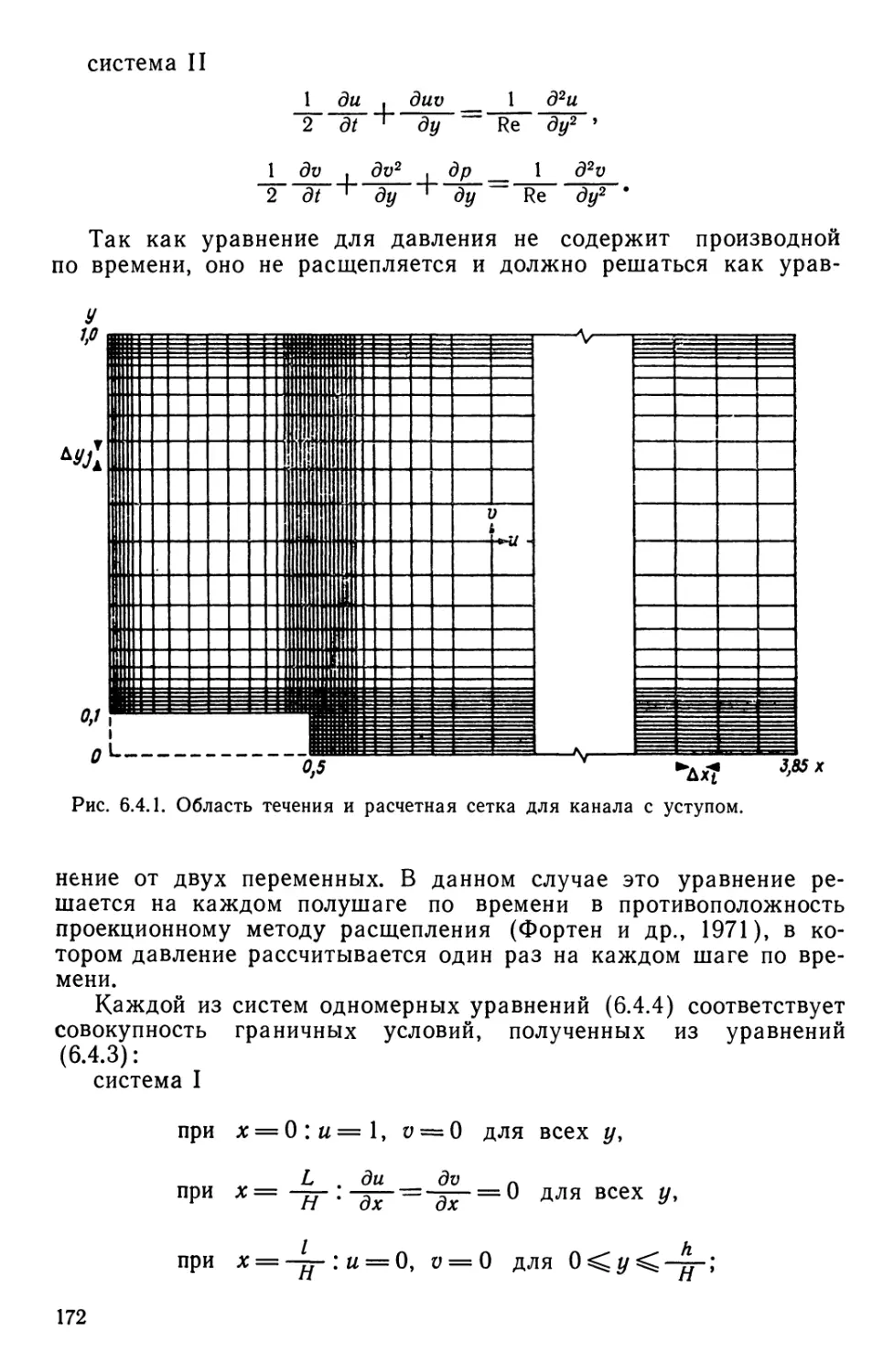
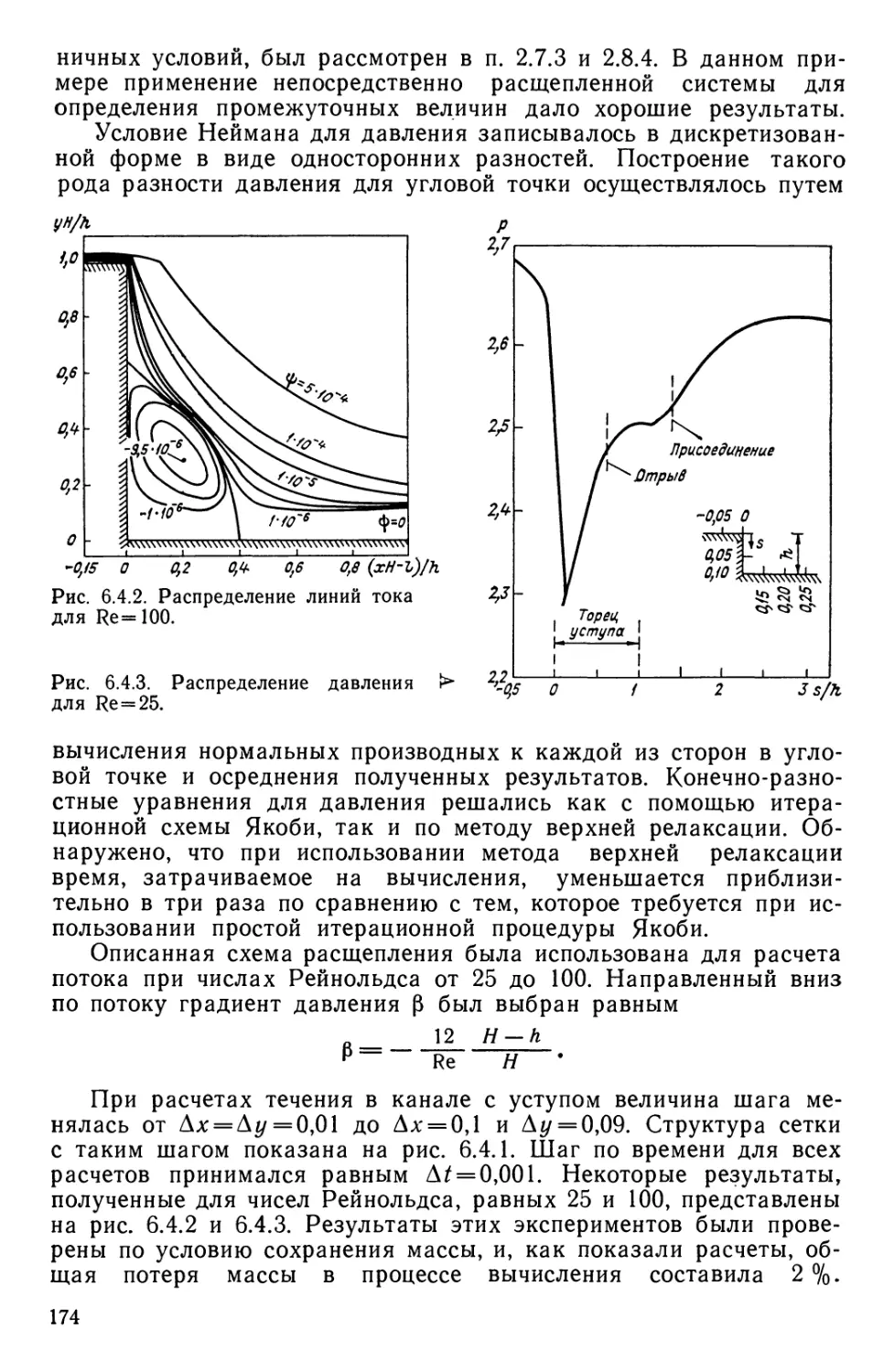
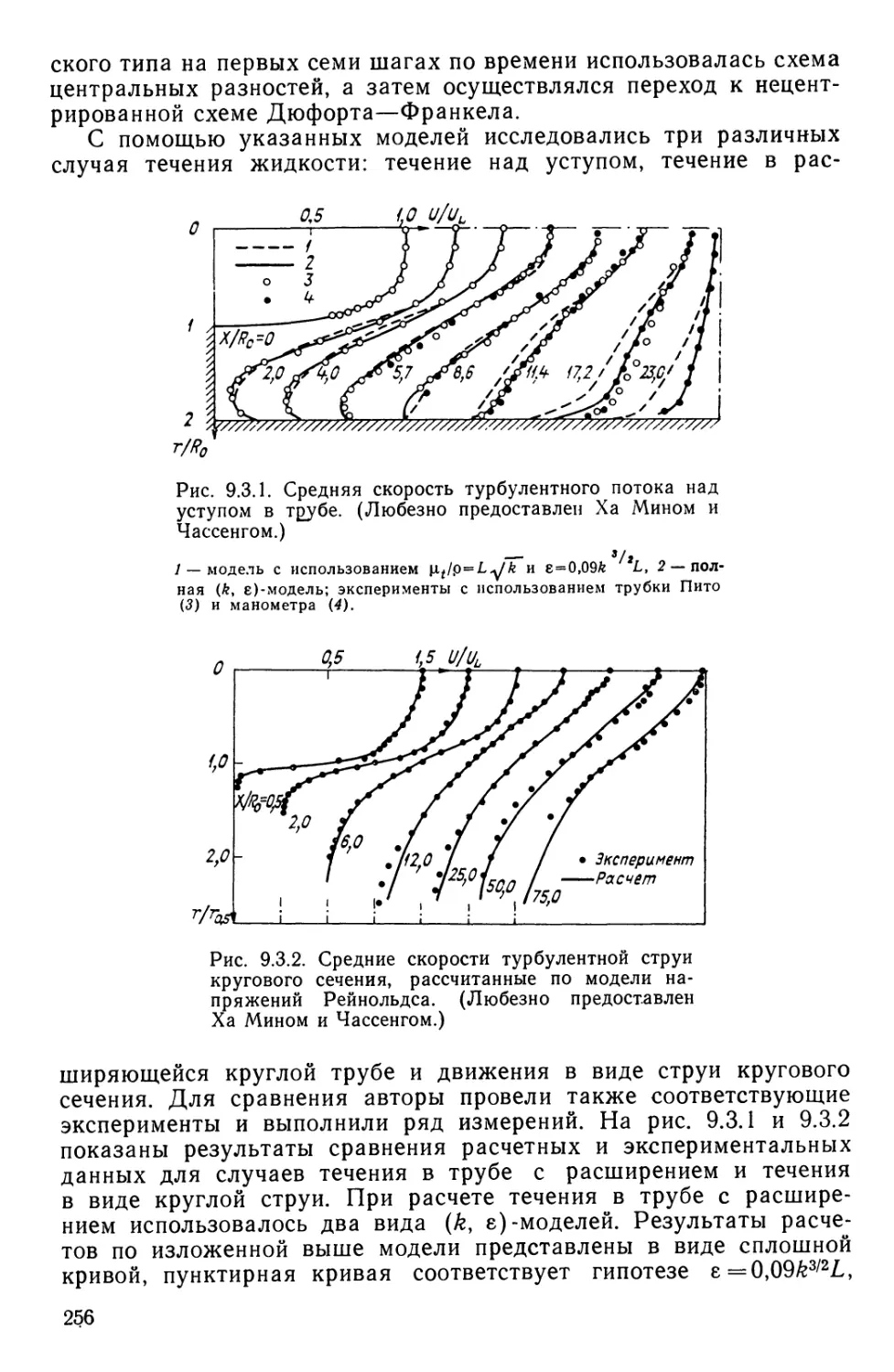
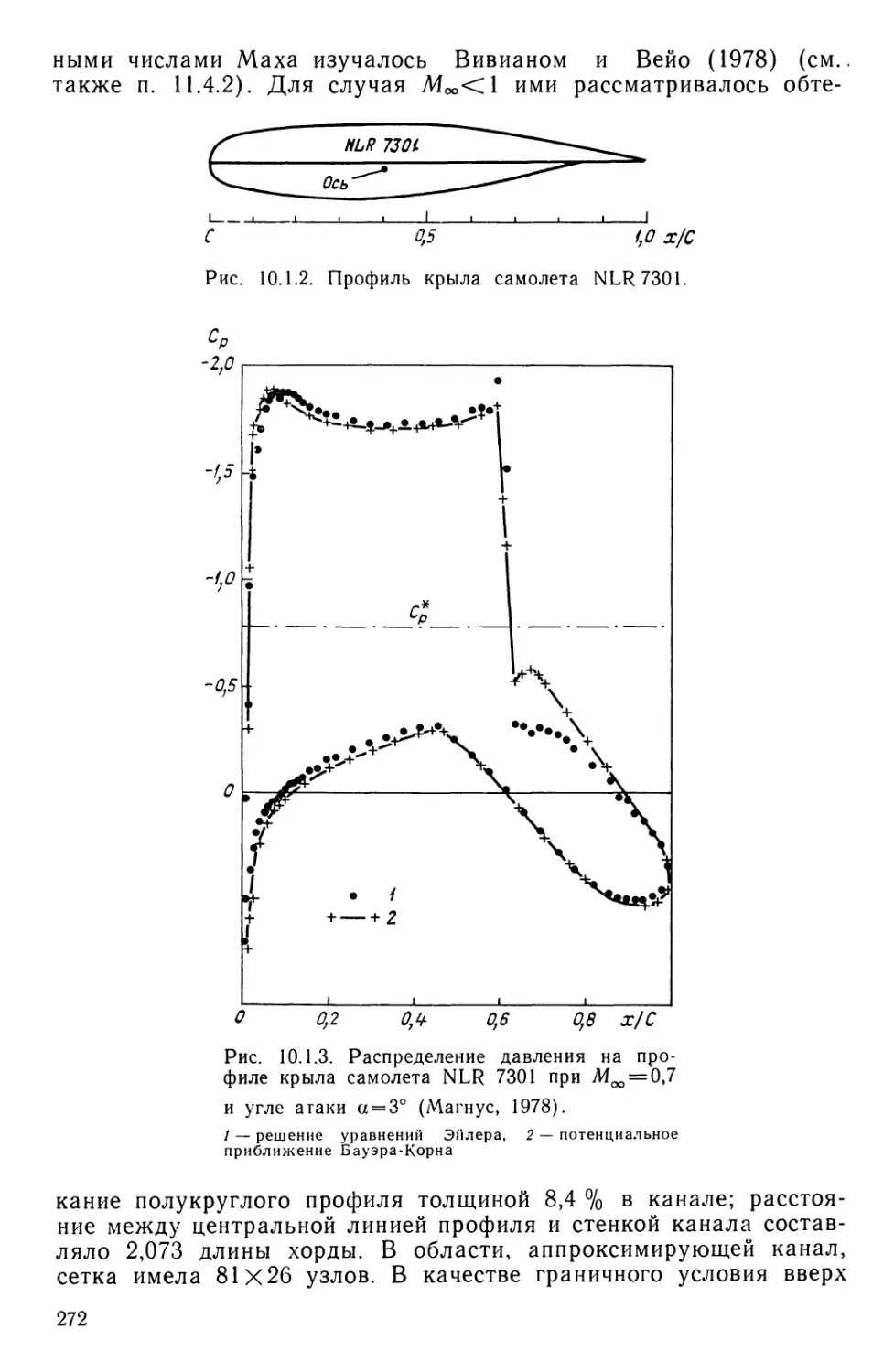
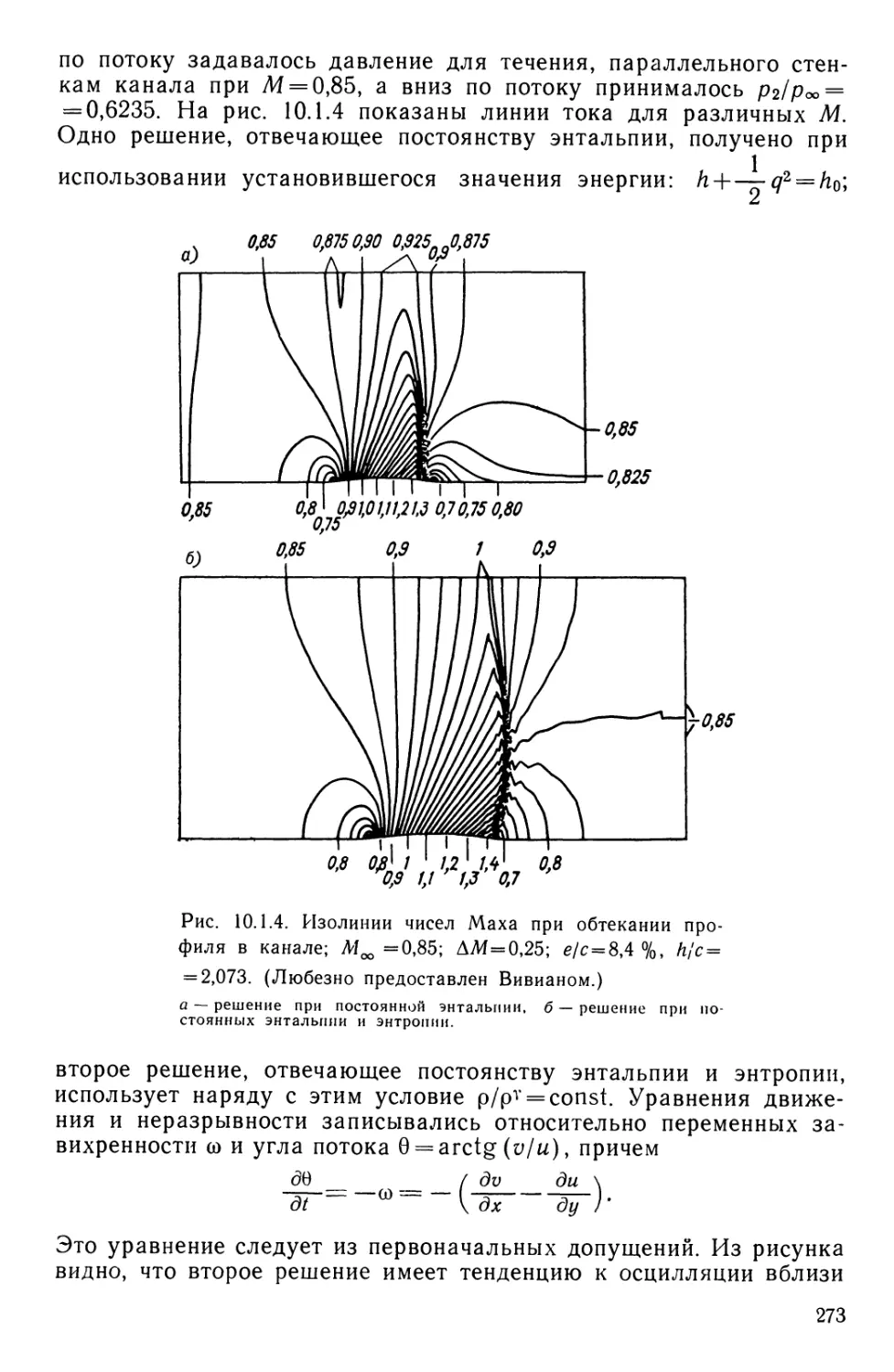
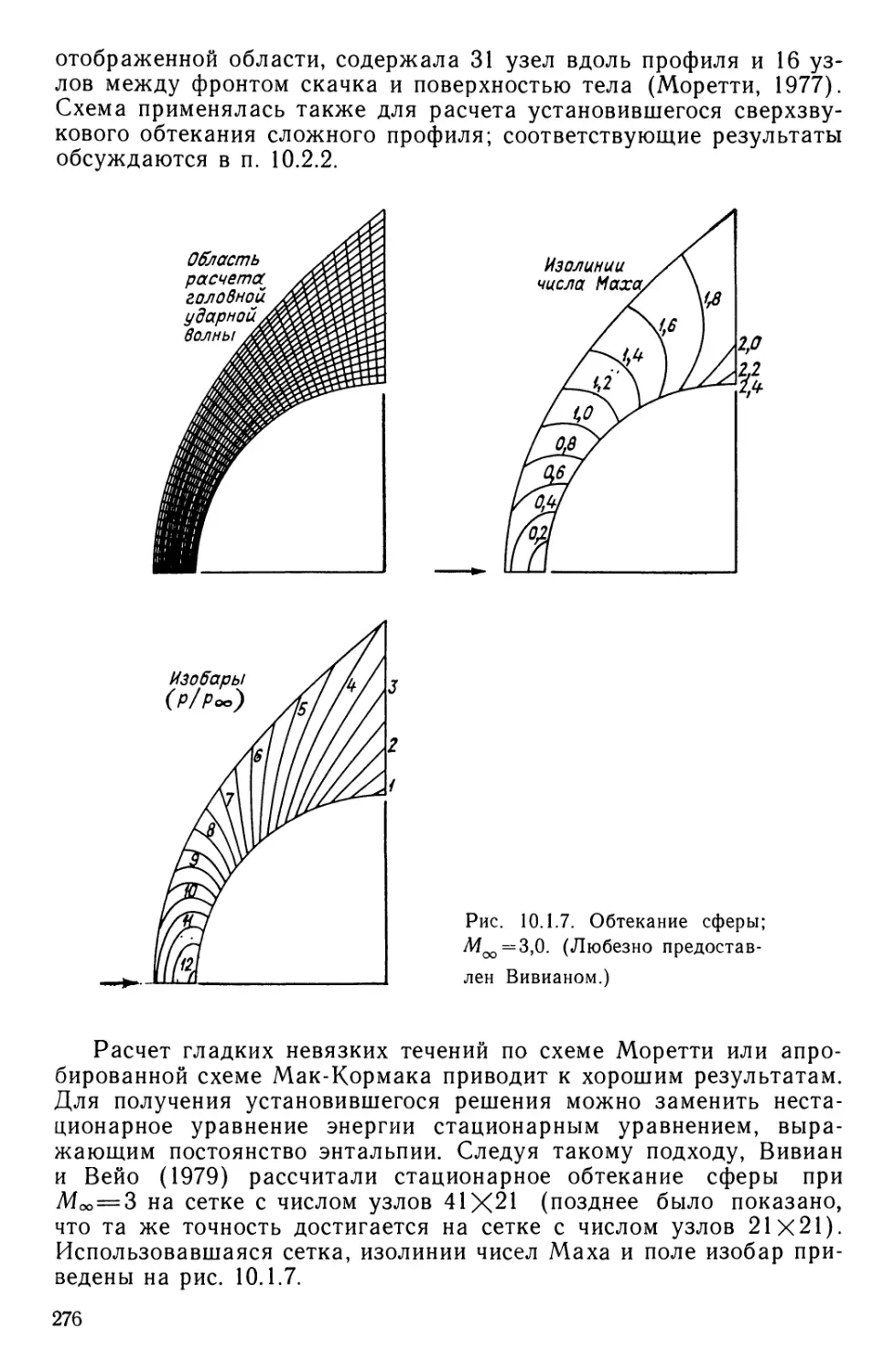
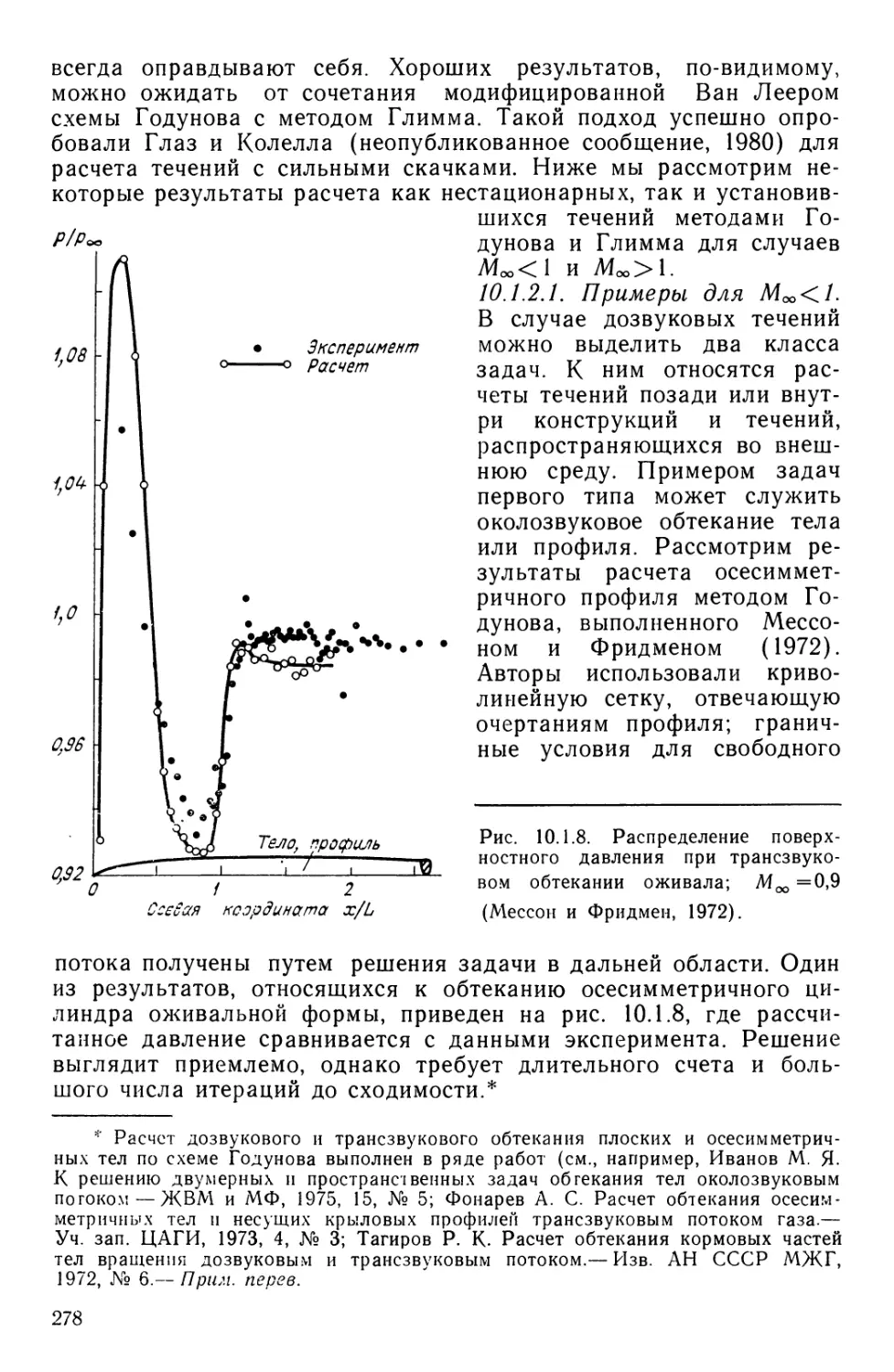
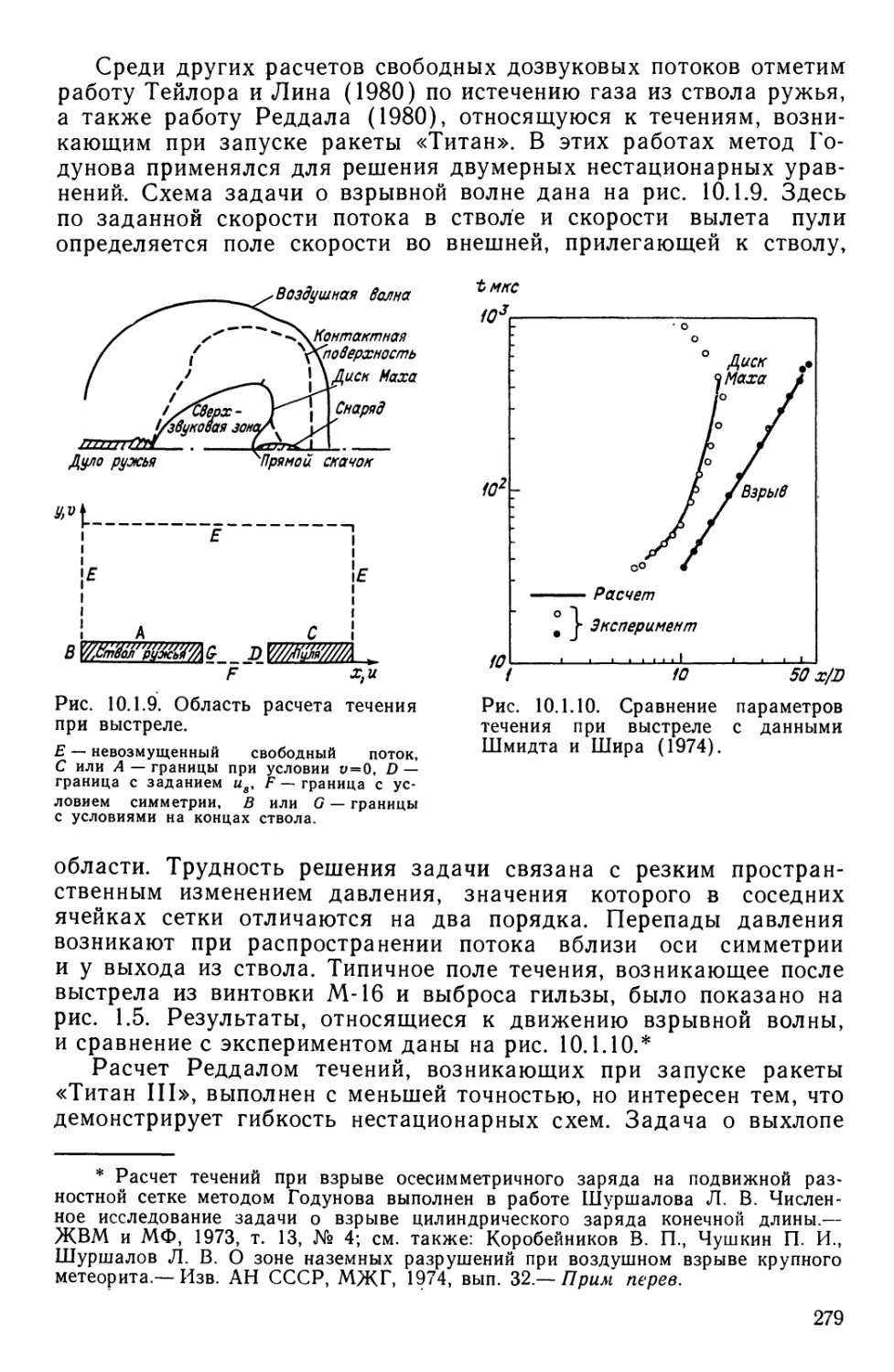
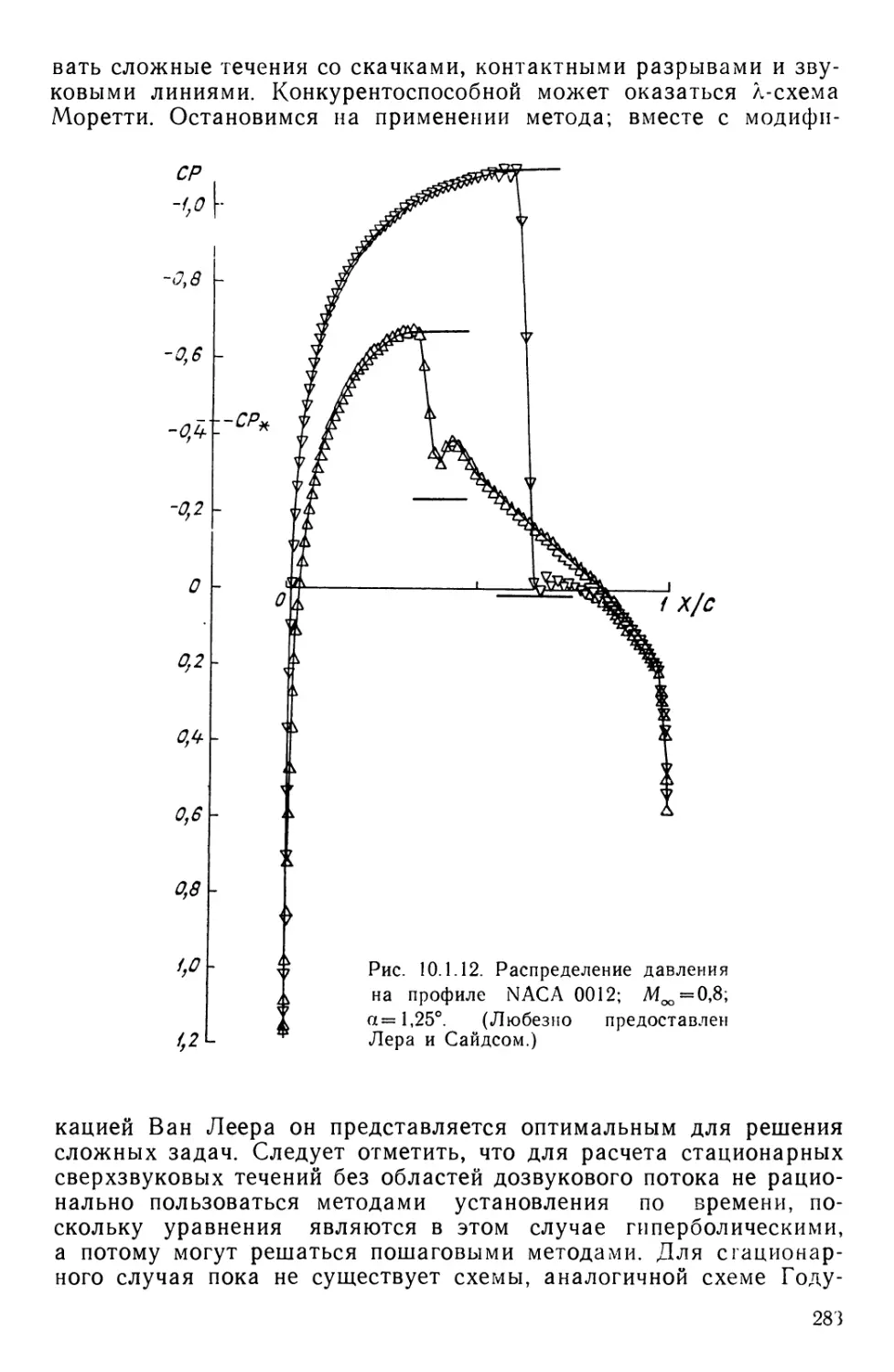
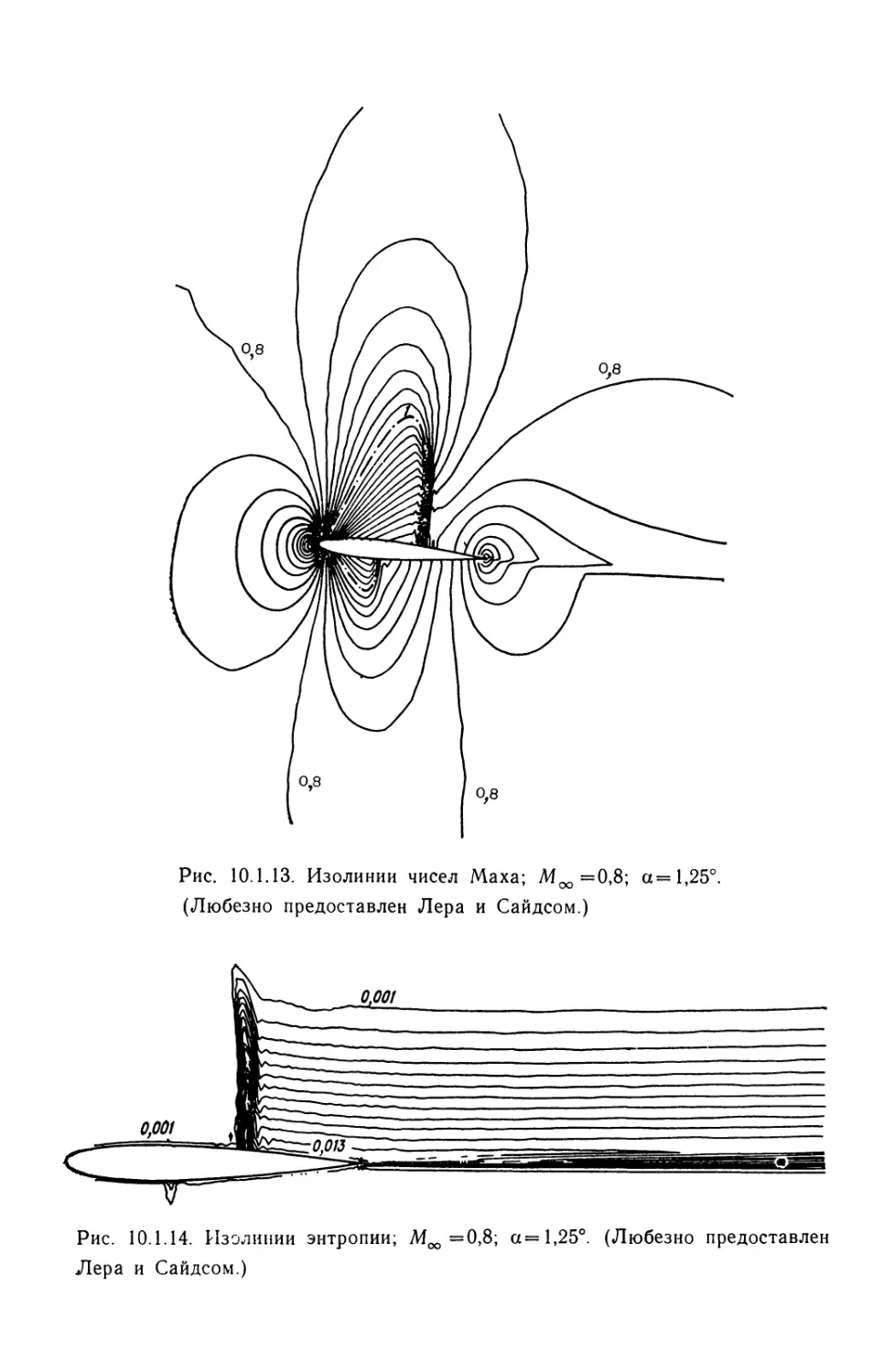
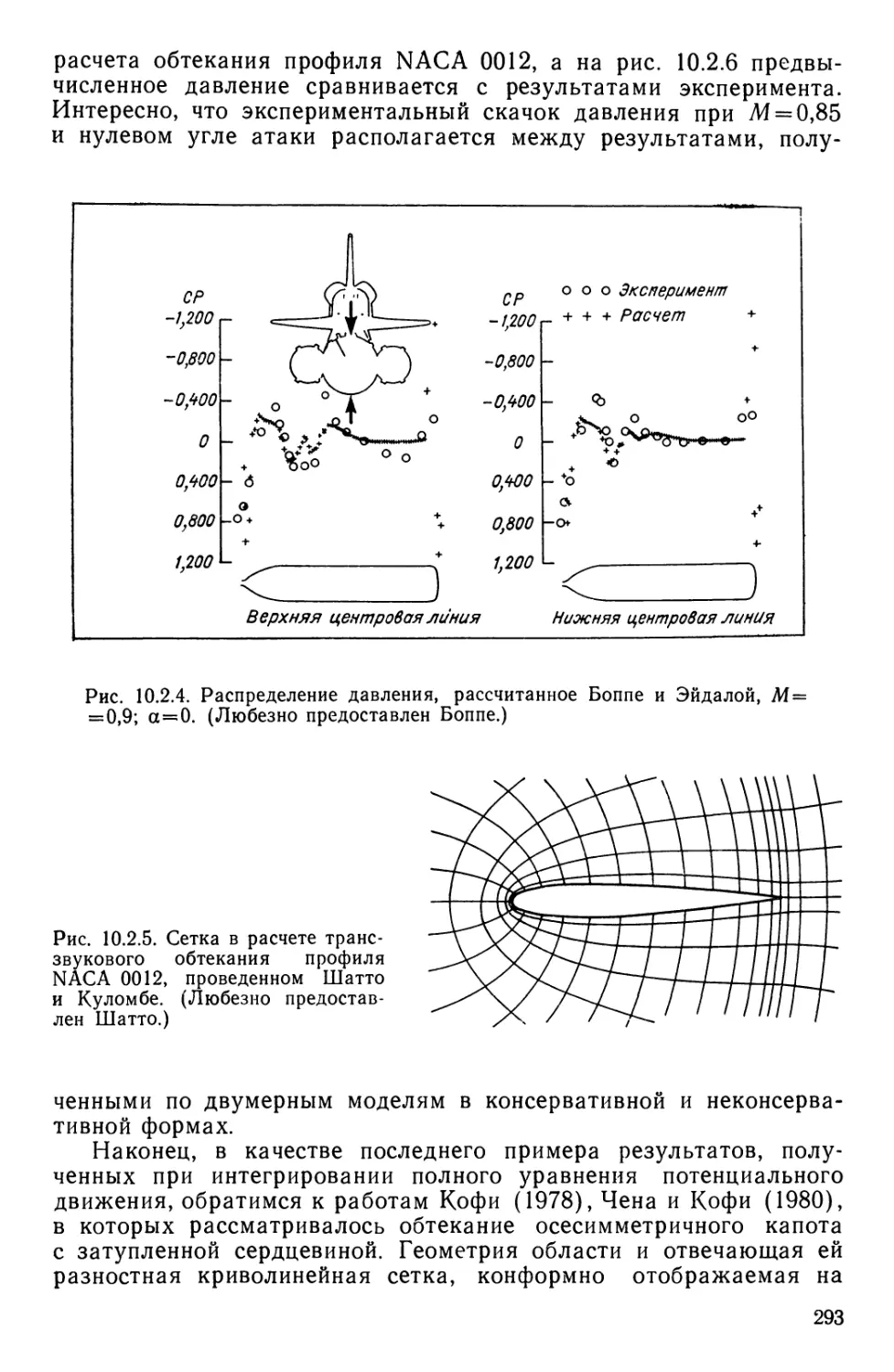
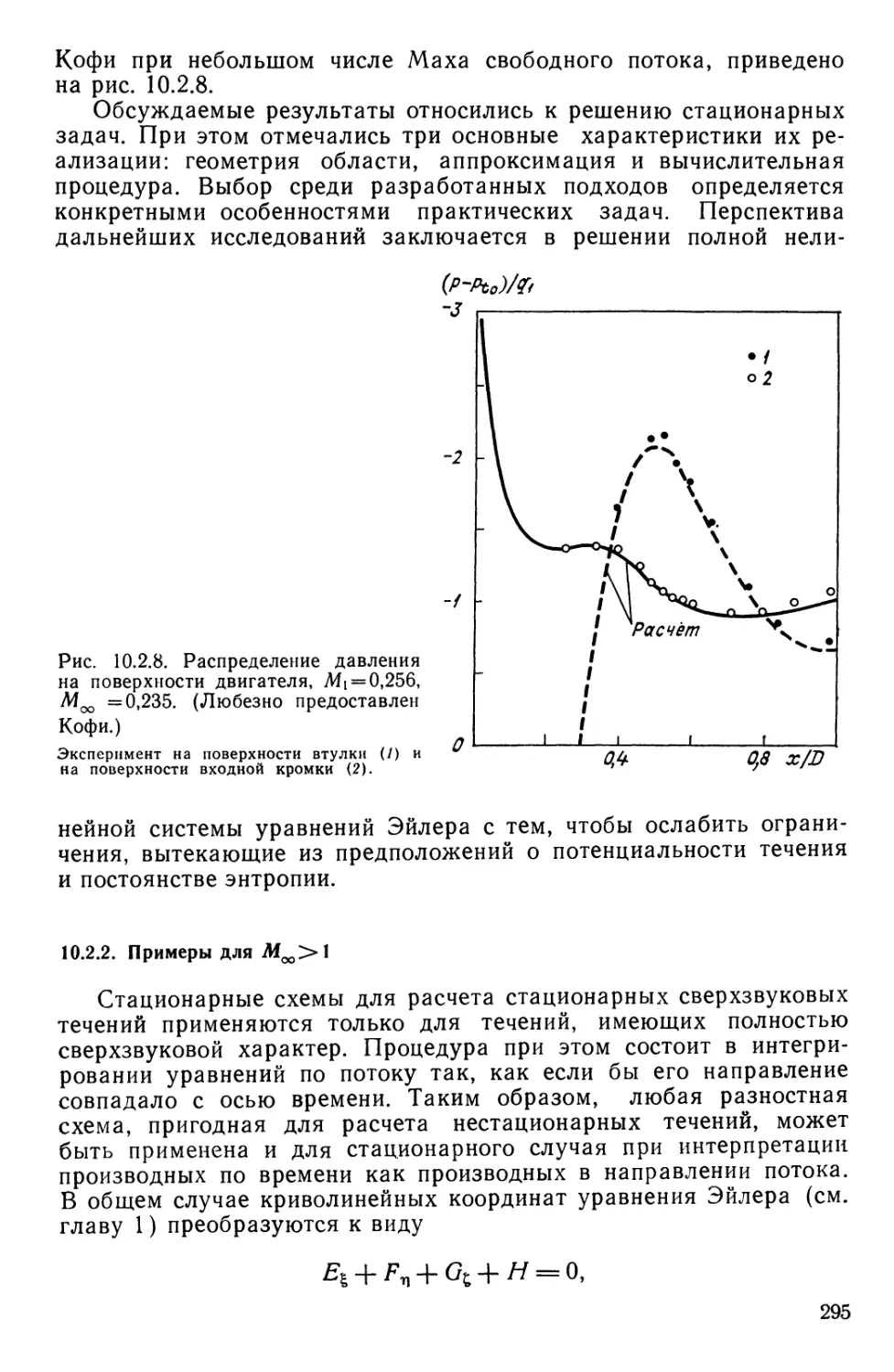
$10.2.2. Примеры для $M_\infty > 1$$
Глава 11. Течения вязкой сжимаемой жидкости
11.3. Разностные схемы на равномерной сетке в декартовых координатах
11.4. Разностные схемы в криволинейных координатах
11.4.2. Дискретизация в физической области
Приложение Б. Метод последовательности сеток
Приложение В. Метод сопряженных градиентов
$10.2.2. Примеры для $M_\infty > 1$$
Автор: Тейлор Т.Д. Пейре П.
Теги: движение жидкостей гидродинамика климат моделирование гидромеханика климатология геофизика переводная литература гидрометеоиздат прогноз погоды
Год: 1986
Похожие
Численные методы в примерах и задачах
Задачи и управления по курсу "Численные методы"
Численные методы решения задач электрофизики
Численные методы решения обратных задач математической физики
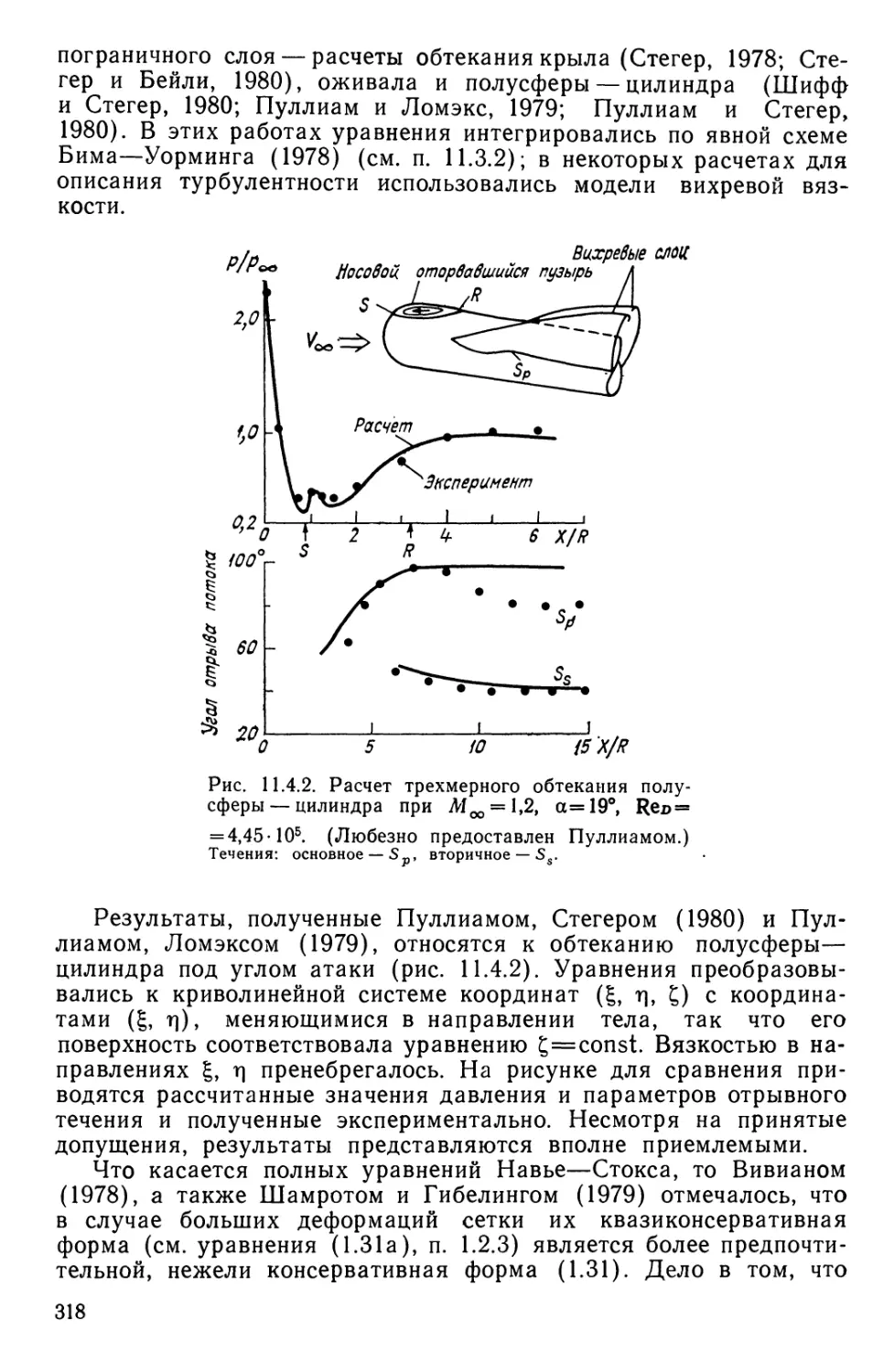
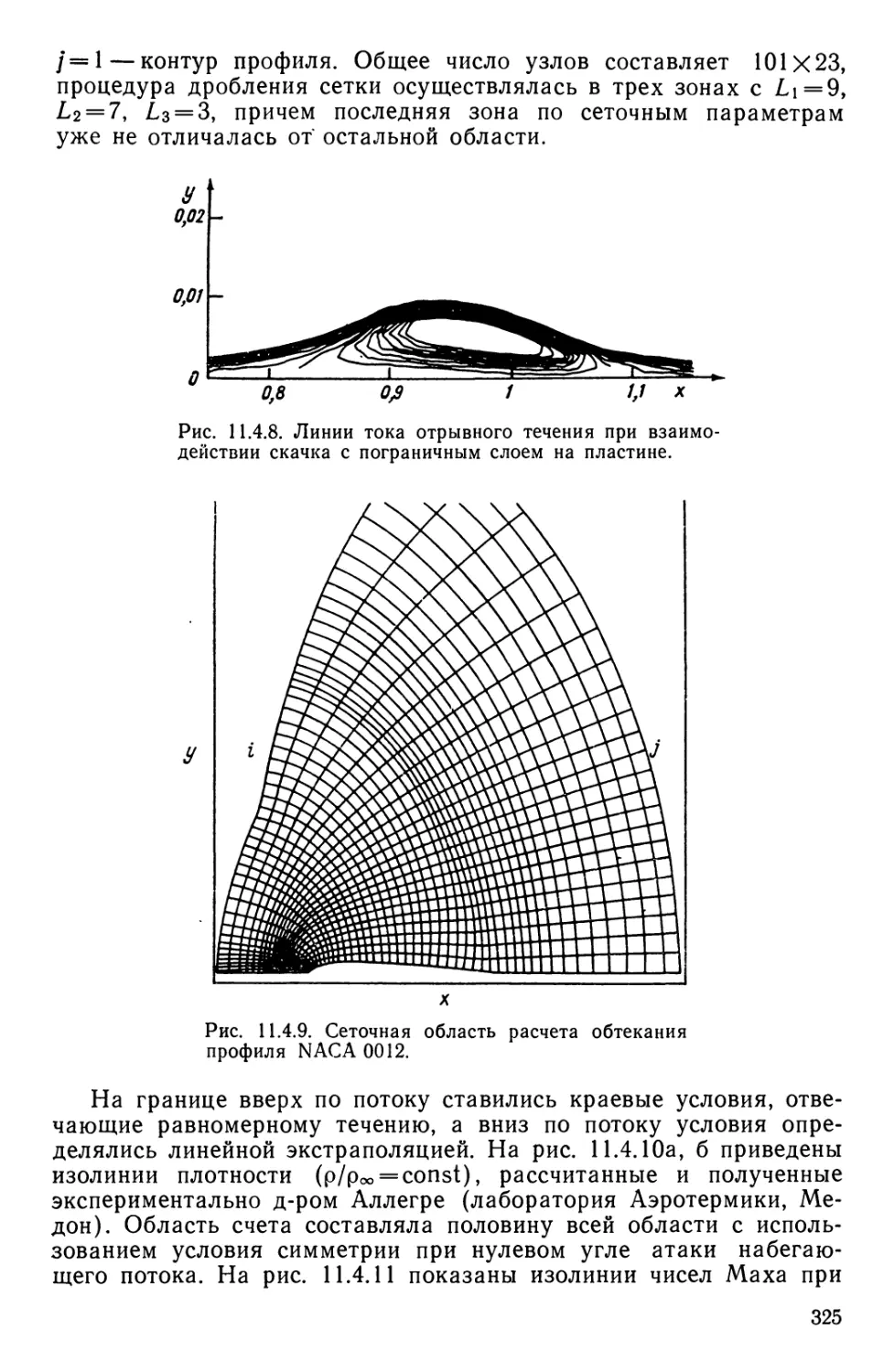
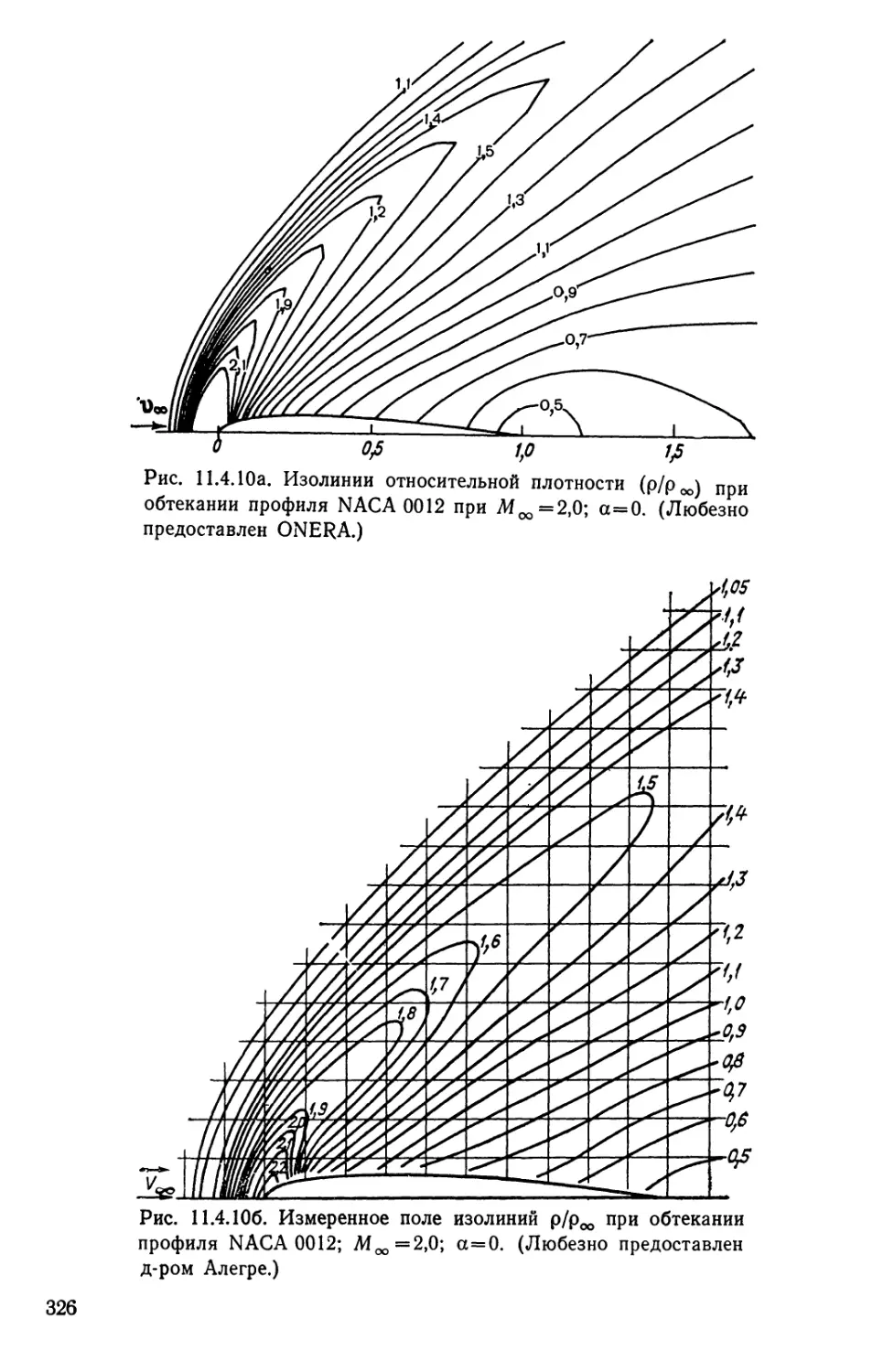
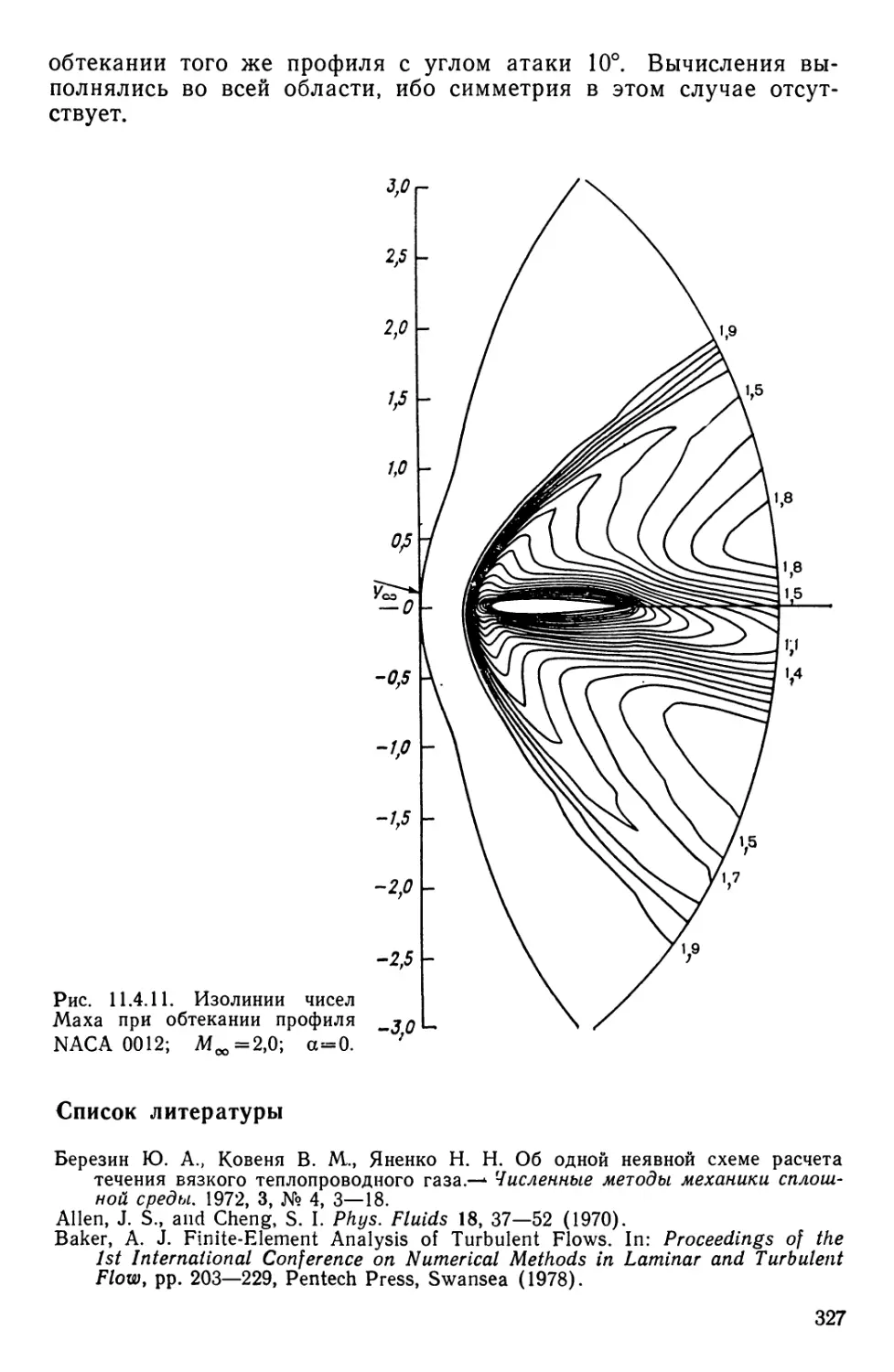
Текст
                    Роже Пейре
Томас Д. Тейлор
Вычислительные
методы в задачах
механики жидкости
Ленинград Гидрометеоиздат 1986

Roger Peyret
Thomas D. Taylor
Computational Methods
for Fluid Flow
With 125 Figures
ш
Springer-Verlag
New York Heidelberg Berlin

Роже Пей ре
Толлас Д. Тейлор
Вычислительные
методы в задачах
механики жидкости
Перевод с английского и редакция
Н. Е. Вольцингера, Л. В. Руховца, Б Е. Шнеерова
Ленинград
Гидрометеоиздат
1986

УДК 532.518.1
Книга состоит из трех частей. В первой части рассматриваются основные
свойства и различные варианты методов конечных разностей, конечных
элементов и спектральных методов, а также ряд специальных приближенных методов
решения уравнений гидромеханики. Во второй и третьей частях излагаются
многочисленные примеры практического применения этих методов для расчетов
ламинарных и турбулентных течений сжимаемой и несжимаемой жидкости.
Многие изложенные в книге методы нашли широкое применение в задачах
численных прогнозов погоды и моделирования климата.
Для гидродинамиков и специалистов геофизического профиля,
использующих численные методы моделирования течений жидкости.
П
1903040000-111
069(02)-86
14—86
© 1983 by Springer-Verlag New York Inc.
AU Rights Reserved
Authorized translation from English Ian-
guage edition published by Springer-Verlag,
Berlin, Heidelberg, New York, Tokyo
© Перевод на русский язык, Гидроме-
теоиздат, 1986

Предисловие переводчиков
Успехи гидродинамики в течение двух последних десятилетий обязаны прежде
всего развитию средств и методов вычислений. Впечатляющий перечень
направлений в этой обширной области, возникших и развивающихся на основе
численного моделирования, включает задачи прогноза погоды, взаимодействия океана
и атмосферы, гидрогеологии, газовой и космической аэродинамики. Теория
и практическое применение численных методов для гидродинамики превратились
в настоящее время в самостоятельную дисциплину.
Становление вычислительной гидродинамики происходило на основе
существовавшей к началу 60-х годов сравнительно небольшой группы методов и
элементов теории разностных аппроксимаций. Использовавшаяся в то время
вычислительная техника по характеристикам памяти и быстродействию уступала
современным машинам на два-три порядка. Тем более показательны ранние
успехи вычислительной гидродинамики, предложившей новый подход к решению
классических задач и новые области применения.
В последующие два десятилетия развитие осуществлялось в направлении
расширения и углубления гидродинамического описания с привлечением более
полных уравнений и отказом от ограничений, определяемых идеализацией
структуры движений. Разрабатывались модели турбулентности и имитировались
течения с различными режимами, химическими превращениями, излучением,
сосредоточенным энерговыделением и пр. Решение всех этих задач
обеспечивалось прогрессом вычислительной техники, характеризовавшимся увеличением
быстродействия и объема памяти вычислительных машин приблизительно в
десять раз каждые семь лет. Соответственно повышалась эффективность
численных методов и расширялся их арсенал.
Среди методов вычислительной гидродинамики конечно-разностные методы
по-прежнему доминируют. Это объясняется их применимостью к широкому
кругу физических задач в самой общей постановке. Вместе с тем почти каждая
задача требует модификации общего подхода, и разностные методы могут
оптимизироваться для отдельных задач. Это выражается в возможности
построения схем повышенной точности, схем с заданными диссипативными
и дисперсионными свойствами, с сохранением интегральных инвариантов,
сохранением монотонности, с выделением особенностей решения, с построением
адаптирующихся к решению сеток и др. Однако требования, предъявляемые к методу,
противоречивы. Так, повышение точности схемы увеличивает трудоемкость ее
реализации, уменьшает устойчивость, требует дополнительных краевых условий,
что существенно усложняет постановку разностной краевой задачи и т. д.
Разнообразие же и сложная структура реальных течений ведет к тому, что сфера
приложений любого метода, приспособленного для реализации некоторой модели
течения, неизбежно оказывается ограниченной. Результатом этого является
создание различных аппроксимационных конструкций, версий и модификаций
в рамках конечно-разностного подхода.
Обращение к методам, опирающимся на другие принципы дискретизации,
еще более расширяет возможности выбора средств решения задач с учетом
преимуществ и недостатков каждого подхода. Спектральные методы по
сравнению с конечно-разностными при одинаковом объеме вычислений обеспечивают
более высокую точность расчета и обычно не подвержены вычислительной
неустойчивости, однако они труднее реализуемы и применимы лишь в областях
простой геометрии; псевдоспектральные методы лучше приспособлены к решению
граничных задач и столь же точны, но связанное с их применением искаженное
представление спектра обычно ведет к вычислительной неустойчивости; конечно-
элементные методы снимают проблему расчета в областях неправильной
конфигурации, но они сложны, в гиперболических задачах обычно менее эффективны
и искажают фазу решения. Ограничения, присущие любому методу, заставляют
в каждом конкретном случае искать компромисс между требуемой точностью,
простотой реализации, ее стоимостью и другими факторами выбора. Но если почти
для любой задачи целесообразна своя модификация метода, то верно и то, что
часто такая задача может успешно решаться различными методами или их
сочетанием.
5

Все сказанное относительно многообразия методов, их ограничений,
допустимости и целесообразности разных подходов к каждой отдельной проблеме делает
очевидной необходимость ориентации в широкой панораме методов, получаемых
результатах и общем состоянии вычислительной гидродинамики. Этой цели
в определенной мере отвечает монография Р. Пейре и Т. Тейлора, перевод
которой предлагается читателю.
Книга состоит из трех частей. В первой части представлены наиболее
употребительные численные методы решения уравнений гидродинамики с
привлечением простейших элементов теории; существо самих методов поясняется на
конкретных примерах. Авторы прилагают заметные усилия для того, чтобы
облегчить усвоение темы, унифицировать материал, показать связь и внутреннее
единство различных подходов, однако изложение носит весьма нестрогий
характер. Две последующие части книги содержат примеры приложений
методов для решения задач динамики несжимаемой и сжимаемой жидкости. Здесь
отражен ценный практический опыт в области вычислительных аспектов
моделирования, таких, как особенности алгоритмов, сравнение их эффективности,
оптимизация расчетов, корректность граничных процедур, критерии устойчивости.
Благодаря удачно подобранным примерам и обширной библиографии работ
по вычислительной гидродинамике, выполненных преимущественно во Франции
и США, книга представляет по существу развернутый обзор исследований
по предмету. Таким образом, книга дает общее представление о методах
вычислительной гидродинамики и вместе с тем содержит свод рекомендаций, которые
могут быть использованы для успешного осуществления и оптимизации расчетов.
Это делает ее полезной для широкого круга читателей — от начинающего
вычислителя до квалифицированного специалиста.
При переводе устранены некоторые небрежные формулировки и исправлены
замеченные ошибки. Библиография книги почти не содержит ссылок на работы,
выполненные в СССР. Этот недостаток, сознаваемый самими авторами, особенно
ощущается при обсуждении методов решения задач газовой динамики.
Приводимые примечания в какой-то мере обращают внимание читателя на этот пробел.
Н. Е. Вольцингер,
Л. В. Руховец,
Б. Е. Шнееров

Предисловие
В этой книге делается акцент на вопросах практического
применения численных методов для решения задач динамики жидкости.
Поэтому мы ограничили математические выкладки и попытались,
насколько возможно, отразить сущность численных методов,
рассматривая простые математические модели.
Книга состоит из трех разделов. В первом разделе излагаются
основы численных подходов, применяемых для решения задач
механики жидкости. Здесь рассматриваются методы конечных
разностей, конечных элементов, спектральный метод, а также ряд
специальных методов.
Второй раздел посвящен решению задач несжимаемой
жидкости с помощью различных численных методов. Рассматривается
решение задач для ламинарных и турбулентных течений с
использованием методов конечных разностей, конечных элементов и
спектрального метода.
В третьем разделе книги излагаются методы решения задач
для сжимаемой жидкости. Этот раздел состоит из двух глав,
посвященных течениям невязких и вязких жидкостей. Приводится
ряд примеров.
Написание книги оказалось возможным благодаря помощи
ряда организаций и специалистов как в США, так и во Франции.
Многие исследователи предоставили нам свои материалы, и мы
попытались отразить их в этой книге. Если мы кого-то
непреднамеренно упустили, то мы сожалеем об этом.
В заключение мы хотели бы выразить особую благодарность
Генри Вивиану и управлению ONERA, которые предоставили
возможность для работы обоих авторов совместно с группой
вычислительных методов аэродинамики в ONERA, Шатильон, вблизи
Парижа.
Особую признательность мы выражаем Морту и Ральфу
Куперам из Управления морских исследований, Аль Лёбу (армия
США), Роберту Муру и Ричарду Хоглунду из DARPA, Филу Сель-
вину (военно-морские силы США) за поддержку исследований,
которые сделали возможным создание этой книги-
Мы выражаем также наши благодарности Вольфу Бейглбёку
и Генри Кёбенсу за предоставленную возможность публикации
этой книги в серии Шпрингер-Ферлаг и Джил Оуэне за
машинописные работы.
Наконец, мы хотели бы поблагодарить Аннет Пейре и
Франсуазу Тейлор за их поддержку в этом рискованном предприятии.
7

Часть I
Численные методы
Глава 1
Введение. Общие уравнения
Применение вычислительных машин в инженерных
расчетах привело к возникновению совершенно новой научной
области вычислительной гидродинамики. С развитием этого направ-
Футы
-50 -25 0 25 50 75 WO 125 150 175 (рутЫ
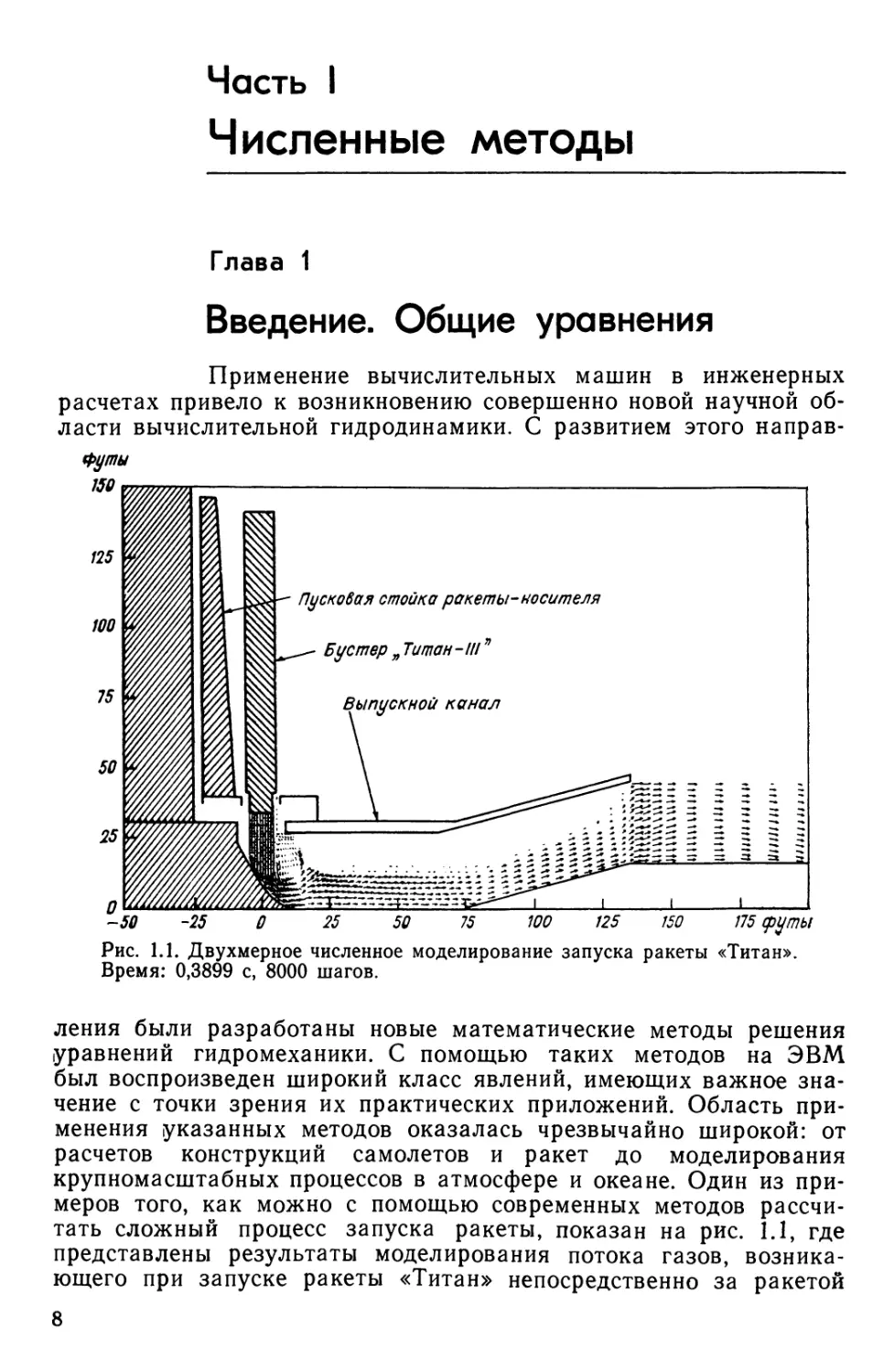
Рис. 1.1. Двухмерное численное моделирование запуска ракеты «Титан».
Время: 0,3899 с, 8000 шагов.
ления были разработаны новые математические методы решения
уравнений гидромеханики. С помощью таких методов на ЭВМ
был воспроизведен широкий класс явлений, имеющих важное
значение с точки зрения их практических приложений. Область
применения указанных методов оказалась чрезвычайно широкой: от
расчетов конструкций самолетов и ракет до моделирования
крупномасштабных процессов в атмосфере и океане. Один из
примеров того, как можно с помощью современных методов
рассчитать сложный процесс запуска ракеты, показан на рис. 1.1, где
представлены результаты моделирования потока газов,
возникающего при запуске ракеты «Титан» непосредственно за ракетой
8

и в отводном канале. Расчет потока производился путем решения
нестационарных уравнений невязкой жидкости с помощью метода
Годунова (1959). В последующих главах будет показано, как
проводить такие расчеты.
О 1 2 0 1 2 х
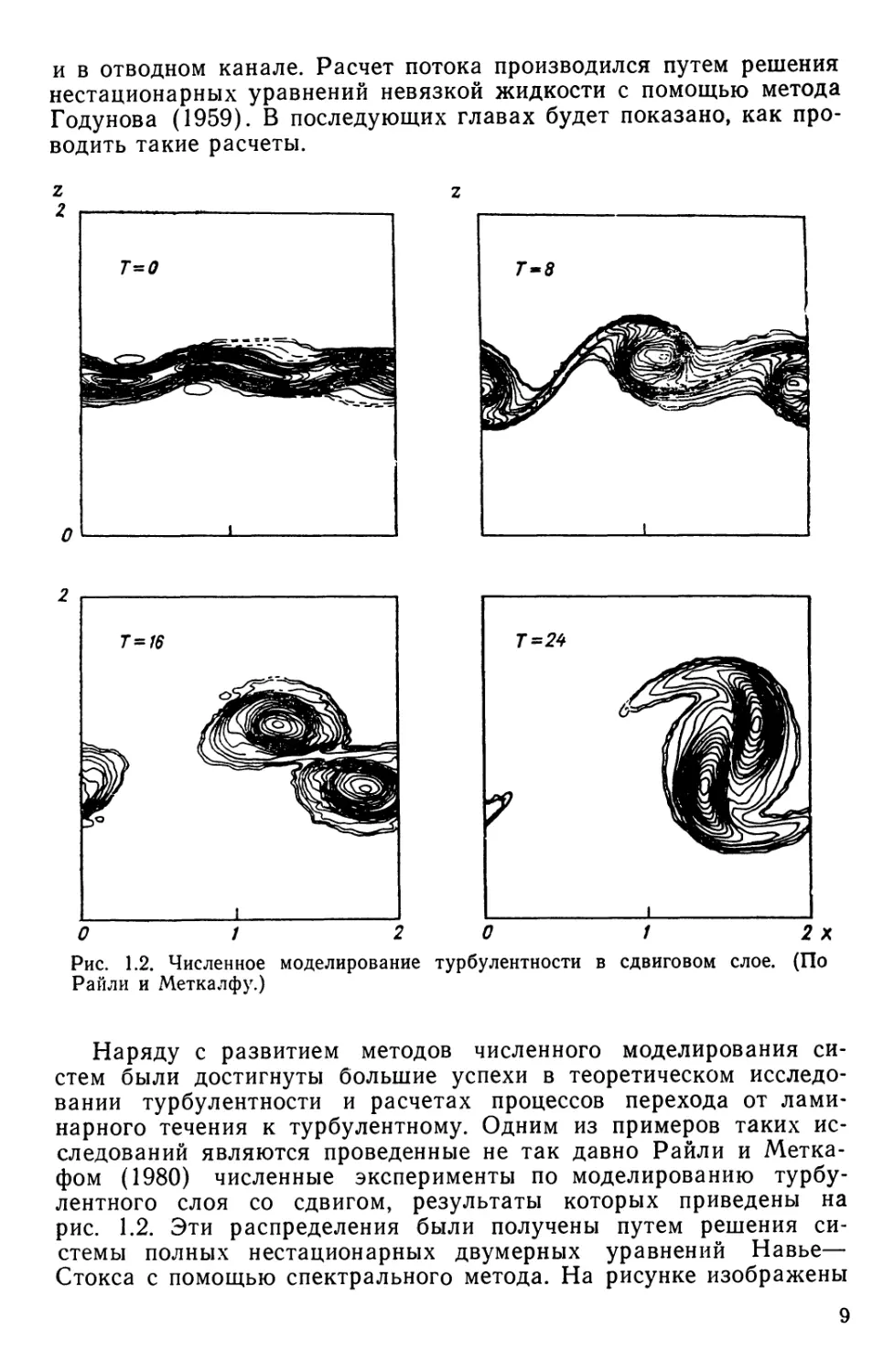
Рис. 1.2. Численное моделирование турбулентности в сдвиговом слое. (По
Райли и Меткалфу.)
Наряду с развитием методов численного моделирования
систем были достигнуты большие успехи в теоретическом
исследовании турбулентности и расчетах процессов перехода от
ламинарного течения к турбулентному. Одним из примеров таких
исследований являются проведенные не так давно Райли и Метка-
фом (1980) численные эксперименты по моделированию
турбулентного слоя со сдвигом, результаты которых приведены на
рис. 1.2. Эти распределения были получены путем решения
системы полных нестационарных двумерных уравнений Навье—
Стокса с помощью спектрального метода. На рисунке изображены
9

течения, полученные в результате осреднения турбулентных
пульсаций по времени. В качестве начального условия использовалась
неустойчивая мода, полученная теоретическим путем (Михалке,
1964). Отметим, что согласно прогнозу происходит закручивание
вихря. Эти примеры показывают, какие сложные движения
удается моделировать в настоящее время. Нет сомнения в том, что
в будущем можно будет моделировать и более сложные процессы.
Прогресс в развитии численного моделирования был достигнут
в известной мере благодаря конкуренции между
экспериментаторами и специалистами в области численного моделирования.
Первая серьезная дискуссия по этому вопросу была вызвана
статьей Чепмена, Марка и Петла «Вычислительные машины
вместо аэродинамических труб», опубликованной в 1975 г. В этой
статье было обращено внимание на то, что появилась общая
тенденция перехода к численному моделированию течений жидкости
с помощью вычислительных машин. В то время, когда появилась
эта статья, существовали определенные трудности, связанные как
с невысокой продуктивностью имевшихся тогда ЭВМ, так и с
недостаточной эффективностью методов расчетов.
Однако и вычислительная техника и численные методы быстро
развивались и за 10 лет, начиная с 1965 г., эффективность и в той
и в другой области повысилась примерно на два порядка (Чеп-
мен, 1979). Эта тенденция сохраняется, и в настоящее время для
получения предварительных оценок все в большей степени
используется моделирование с помощью ЭВМ для того, чтобы избежать
необходимости проведения дорогостоящих экспериментов.
Прогресс в области вычислительной техники до последнего
времени сводился, в основном, к увеличению скорости расчетов
на ЭВМ, однако в последнее время наметилась другая тенденция.
Быстродействие вычислительных машин уже не растет по
экспоненте, а остается почти постоянным, но зато очень быстро падает
стоимость вычислительных средств за счет применения новых
интегральных схем. В результате в самом ближайшем будущем
вычислительные машины с длительностью цикла в 10 не и памятью
в миллион слов будут стоить приблизительно 300 тыс. ам.
долларов. Это приведет к настоящей революции в научных
исследованиях, когда наряду с крупными вычислительными центрами будут
существовать сравнительно дешевые вычислительные комплексы,
которые могут быть использованы небольшими
исследовательскими группами для проведения сложных расчетов в области
динамики жидкости. В настоящее время устройства, которые
предназначены для такого рода расчетов, уже создаются как на
коммерческой основе, так и по правительственным заказам. В табл. 1
приведены для сравнения некоторые сведения о быстродействии,
эксплуатационных качествах и предполагаемой стоимости
некоторых ЭВМ, разрабатываемых в настоящее время в США.
Аналогичные ЭВМ находятся в стадии разработки также в Англии и
Франции. Рисунок 1.3 иллюстрирует падение относительной
стоимости запоминающих устройств и коммерческую доступность
10

памяти порядка одного миллиона слов. В результате можно
представить некоторую схему вычислительной машины, обладающей
огромными быстродействием и памятью, изображенную на
рис. 1.4. Время одного цикла для каждого процессора могло бы
составлять 10 не, а оперативная память — состоять из нескольких
миллионов слов. Такой прогресс в области вычислительной
техники несомненно приведет к еще более интенсивному развитию
численных методов механики жидкости.
Это в свою очередь вызовет новый подъем в численном
моделировании крупномасштабных процессов и создаст возможности
Рис. 1.3. Стоимость различных
видов памяти ЭВМ.
/ — магнитный барабан, 2 — диск с
неподвижными головками, 3 — память на
цилиндрических магнитных доменах,
4 — память на приборах с зарядной
связью, 5 — ферритовая память, 6 —
память на МОП-структуре, 7 —память на
биполярных элементах.
0,2 0,4 0,6 0,8
Стоимость, цент/Стъ
W
для получения более глубоких представлений о механизме
турбулентности и процессах перехода от ламинарного течения к
турбулентному.
Один из примеров эффективного использования новых
недорогих процессоров был приведен в недавно опубликованной статье
Таблица 1. Характеристики некоторых ЭВМ
ЭВМ
FPS
СДС 7600
CRAY-1
МКС
36*
40
80
мопзс
12(6)
40(10)
80 (25) **
СВБС
3000 ч
Несколько
суток
7 ч
Примерная
относительная стоимость
технического
оборудования
0,03
1,00
0,60***
Примечание: МКС — миллион команд в секунду; МОПЗС — миллион
операций над числами с плавающей запятой в секунду; СВБС — среднее время
работы без сбоя.
х Одна команда ЭВМ FPS содержит шесть независимых операций:
сложение с плавающей запятой, умножение с плавающей запятой, индексация,
разветвление, обмен между регистрами и обмен в оперативной памяти.
Модульные единицы системы FPS-AP могут быть собраны в большие системы с
высокой скоростью обмена в оперативной памяти.
"** Типичное и/или обычно получаемое быстродействие.
>х* Без стоимости управляющей ЭВМ.
11

Энсельма, Броше и Буассо (1981). Эти авторы, использовав
специализированную вычислительную машину с высокоскоростным
процессором, провели расчет потока в сверхзвуковом компрессоре
в два раза быстрее, чем на ЭВМ СДС 7600. Стоимость
использовавшейся вычислительной системы составила примерно 200 тыс.
ам. долларов.
Совершенствование вычислительной техники будет также
содействовать развитию численных методов. Тенденция будет со-
! Память на
1 магнитной
ленте и
1 диске
\Х
Главный,
компьютер.
Печатающее
\ус
/Г
1
тро
lepM
fucn.
йст$оу
инал,
пей.
s. /
Ч
Ч
Ч
ч
\
ч
ч
/
/
/
/
/
/
•
/
Матричный
процессор
Центральная
оперативная
память
Матричный
процессор
Матричный
процессор
Рис. 1.4. Схема недорогой вычислительной машины,
предназначенной для задач численного
моделирования.
стоять в отказе от методов, основанных на использовании
линейных и квадратичных функций при замене дифференциальных
уравнений конечно-разностными соотношениями. В этом
направлении уже достигнуты определенные успехи при решении ряда
задач с применением эрмитовых методов (Хёрш, 1975; Пейре, 1978)
и интерполяции с помощью сплайнов (Рубин и Хосла, 1977).
Кроме того, для решения с высокой степенью точности
нелинейных уравнений гидромеханики применяются разложения в ряды
Фурье или по полиномам Чебышева в сочетании с быстрым
преобразованием Фурье (Орзаг и Израэли, 1974). В случае двух- или
трехмерных задач эти методы дают возможность сократить время
расчетов более, чем на порядок по сравнению с методами
конечных разностей, поскольку для получения такого же разрешения,
как и в конечно-разностных методах второго или третьего
порядка точности, требуется меньшее число узлов сетки, чтобы
определить коэффициенты разложений. Такого рода
усовершенствованные методы были предложены недавно в работах Хедфогеля,
12

Робинсона и Шульмана (1980), а также Майерса, Тейлора и Мёр-
дока (1981).
Однако несмотря на ожидаемое расширение вычислительных
возможностей предстоит преодолеть немало трудностей,
возникающих при решении ряда прикладных задач в области
моделирования течений. К числу таких задач относится моделирование
движения двухфазной жидкости, а также сложных течений с
сильными скачками уплотнения и разрежения, рассматриваемых в за-
t-205MKc Воздушная
волна
" * l 4- ta
W'/'Л
yf^- + * '
y ^ £ £ ^ <£ '
t v £ ^ Z * '
~\+ ^r ^ Ж X X 4 i--. - >
I " -
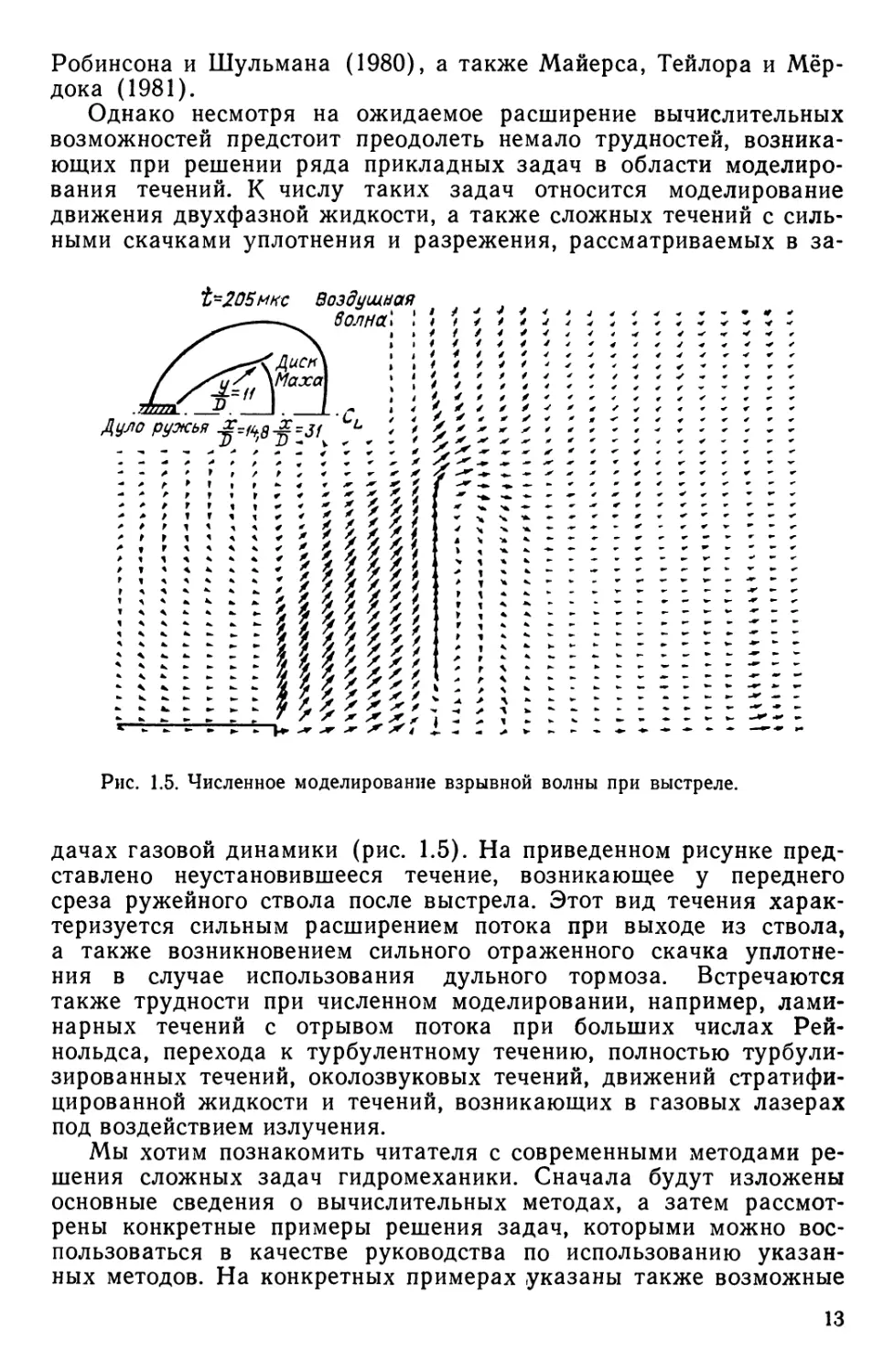
Рис. 1.5. Численное моделирование взрывной волны при выстреле.
дачах газовой динамики (рис. 1.5). На приведенном рисунке
представлено неустановившееся течение, возникающее у переднего
среза ружейного ствола после выстрела. Этот вид течения
характеризуется сильным расширением потока при выходе из ствола,
а также возникновением сильного отраженного скачка
уплотнения в случае использования дульного тормоза. Встречаются
также трудности при численном моделировании, например,
ламинарных течений с отрывом потока при больших числах Рей-
нольдса, перехода к турбулентному течению, полностью турбули-
зированных течений, околозвуковых течений, движений
стратифицированной жидкости и течений, возникающих в газовых лазерах
под воздействием излучения.
Мы хотим познакомить читателя с современными методами
решения сложных задач гидромеханики. Сначала будут изложены
основные сведения о вычислительных методах, а затем
рассмотрены конкретные примеры решения задач, которыми можно
воспользоваться в качестве руководства по использованию
указанных методов. На конкретных примерах указаны также возможные
13

ошибки, которые могут возникать при использовании
рассматриваемых методов. Мы стремились придать книге практическую
направленность, рассматривая ее как дополнение к другим книгам,
относящимся к тем же проблемам, например, монографиям Гот-
либа и Орзага (1977), Холта (1977), Рихтмайера и Мортона
(1967), Роуча (1973) и др., и поэтому намеренно избегали
пространных математических выкладок.
Начнем обсуждение с рассмотрения исходных уравнений,
которые будут в дальнейшей представлены в различных формах.
1.1. Уравнения Навье—Стокса
Движение сплошной среды подчиняется законам классической
механики и термодинамики: законам сохранения массы, количества
движения и энергии. Запись этих законов в инерциальной
(абсолютной) системе координат приводит к следующим уравнениям,
выражающим в интегральной форме законы сохранения массы,
количества движения и энергии соответственно:
-^-Spdü + SpV-Nd£ = 0, (1.1)
v 2
-4- \ 9Vdv+ J [(N • V)pV— Ntf]d£ = J ftdc, (1.2)
v S v
--g- J pEdv + J N . [pEV - (TV + q]dZ = $U • V dv. (1.3)
о S о
В этих уравнениях t — время, р — плотность, V — скорость
материальной частицы в абсолютной системе координат, Е — полная
энергия:
где е — внутренняя энергия; а — тензор напряжения; q — вектор
потока тепла; fe — внешняя сила, приходящаяся на единицу
объема; N — единичный вектор внешней нормали к поверхности S
объема v. Уравнение энергии справедливо в предположении, что
в рассматриваемом объеме v нет источников и стоков энергии.
Свойства среды не обязательно описывать непрерывными
функциями пространства и времени; в случае если они
непрерывны и дифференцируемы в некоторой области пространства
и времени, уравнения (1.1) — (1.3) в интегральной форме можно
преобразовать к эквивалентной системе уравнений в частных
производных:
-|L + v.(pV) = 0, (1.5)
-£- (pV) + V ■ (pVV - а) = U, (1.6)
4г{9Е) + V • (p£V - aV + q) = U • V. (1.7)
14

Полученные таким образом уравнения записаны в дивергентной,
или консервативной форме. Эквивалентная неконсервативная
форма этих уравнений имеет следующий вид:
-5P- + PV V = 0, (1.8)
p-^--v ■* = *.. (К9)
p-g a-W+Vq = 0, (1.10)
где D/Dt=d/dt+\-y есть оператор индивидуальной производной.
Вышеприведенные уравнения основаны на эйлеровом подходе
к описанию движения сплошной среды: величины,
характеризующие свойства среды (р, V и др.), рассматриваются как функции
временной и пространственных координат в декартовой системе
координат. Другое описание основано на лагранжевом подходе,
в котором зависимые переменные определяют характерные
свойства движущихся материальных частиц. Следовательно, эти
свойства описываются функциями времени и параметров,
используемых для идентификации отдельных частиц, например координат
частиц в некоторый фиксированный начальный момент времени.
Лагранжев или, точнее, смешанный лагранжево-эйлеровый
подход представляет собой интерес в задачах, в которых
рассматриваются различные среды с поверхностями раздела. Однако в целом
этот подход в механике жидкости применяется не столь широко,
как эйлеров, и поэтому здесь рассматриваться не будет.
Основными зависимыми переменными в уравнениях (1.1) —
(1.3) или (1.5) — (1.10) являются функции р, V и Е (или е). Для
получения замкнутой системы уравнений в нее необходимо
добавить соответствующие соотношения для тензора напряжений а
и для вектора потока тепла q. Мы будем рассматривать случай
ньютоновских жидкостей, т. е. таких, для которых тензор
напряжения есть линейная функция градиента скорости. Из этого
определения следует закон Ньютона для а, называемый также
законом Навье—Стокса:
а = -р1 + т, (1.11)
t = X(V • V)I + 2^defV,
где
defV = 4-[vV + (vV)<]
(символ t означает транспонирование тензора), р — давление,
т — тензор вязкого напряжения, X и \х — коэффициенты вязкости,
defV — тензор скорости деформации. Кроме того, предполагается,
что перенос тепла осуществляется в соответствии с законом Фурье,
т. е.
q = _£v7\ (1.12)
15

где Т—абсолютная температура; k — коэффициент
теплопроводности.
Для многих жидкостей, в частности для воздуха и воды,
законы Ньютона и Фурье выполняются с достаточной точностью.
Если ввести (1.11) в уравнения (1.9) и (1.10), то получим
соответственно:
p-^+VP = f* + !^V2V+(X + ^)V(V- V) +
+ (V • V)Vb + 2(defV)Vn, (1.13)
P^f + PV-V = 0-Vq, (1.14)
где Ф — функция диссипации:
ф = т . VV = MV • V)2 + 2fx(defV) • (defV). (1.15)
Другая форма уравнения энергии может быть получена путем
введения величины удельной энтропии s:
рГ^-^Ф-V.q. (1.16)
Переменные, определяющие состояние р, е, Т и р, связаны
термодинамическими соотношениями (в предположении, что имеет
место локальное термодинамическое равновесие). Мы рассмотрим
наиболее простой случай, когда все термодинамические свойства
могут быть получены из единственного фундаментального
соотношения, которое для сжимаемой жидкости имеет вид:
5 = s(p, е).
Из этого соотношения давление р и температура Т выражаются
через переменные р и е следующим образом:
'—р^Ш- г=1*к- <1Л7)
Важным частным случаем является случай совершенного газа,
в котором удельные теплоемкости ср и cv постоянны. Для такого
газа уравнения состояния имеют вид:
p = (Y-l)Pe, Y = -g-, (1.18а)
e = cvT. (1.186)
Коэффициенты вязкости и теплопроводности зависят от
локального термодинамического состояния; в большинстве случаев они
зависят только от температуры:
Х = Х(Т), \L = \i(T), k = k(T). (1.19)
16

В соответствии со вторым началом термодинамики функция
диссипации Ф не может быть отрицательной. Можно показать,
что это приводит к следующим условиям:
3A, + 24u>0, ^^о. (1.20)
Если же исключить явления внутренней релаксации, которые не
удовлетворяют принятому условию локального
термодинамического равновесия, то соотношение Стокса
3?, + 2jli = 0 (1.21)
является общепринятой аппроксимацией для таких процессов.
1.2. Различные формы уравнений Навье—Стокса
1.2.1. Уравнения в безразмерной форме
Сначала преобразуем приведенные в п. 1.1 уравнения в
безразмерную форму. Для того чтобы ввести безразмерные переменные,
получим характерные значения всех переменных, входящих в
уравнения Навье—Стокса, исходя из следующих основных
характерных величин: скорости V*, плотности р* и коэффициентов
вязкости jit* и теплопроводности é*.
Все другие характерные величины могут быть получены из
основных: L/V* для t, р*У*2 для a, p*V*2/L для fe, V*2 для е и Е
и р*У*3 для q. Уравнения (1.1) — (1.10) сохранят свой вид, если
в них безразмерные величины обозначить теми же символами,
которыми обозначались размерные величины. Далее мы используем
в качестве характерных величин p*V*2 для р и \x*V*/L для т.
Тогда соотношение (1.11) в безразмерной форме принимает вид
«—PI + -RT*.
T = MV * V)I + 2ndefV, (1.22)
где Re = V*Lç>*l[i*— число Рейнольдса.
Для случая совершенного газа вместо (1.12) получим
4 = -W*V*. (1.23)
где Pr = jA*Cp/é* — число Прандтля. Уравнение энергии (1.14)
сохранит свой вид в безразмерной форме, если величину Ф
определить как (t-VV)/Re. Введем безразмерные величины для
температуры и энтропии, используя характерные значения Г* и s* так,
чтобы s*r* = K*2. Тогда уравнения энергии (1.16) и состояния
(1.17) остаются неизменными в безразмерной форме. Для
совершенного газа с постоянными значениями удельных теплоемкостеи
17

уравнение состояния (1.18а) не меняется в безразмерной форме,
уравнение же (1.186) принимает вид
е = Т/[у(у-1)М*21
где Af* = V*/A/Y^* — число Маха. Если мы выберем s* = cVi
означающее, что съТ* = У*2, то получим е = Т.
1.2.2. Ортогональные криволинейные координаты
Рассмотрим теперь уравнения Навье—Стокса в ортогональной
криволинейной системе координат, фиксированной по отношению
к абсолютной системе координат. Обозначим эти координаты
через xt (г=1, 2, 3) и пусть а, ß, \ — локальные единичные
векторы, образующие тройку касательных к координатным линиям х\,
я-?, хг соответственно. Элементарное смещение ds может быть
представлено как
ds = hi dxx а + h2dx2p + hzdx3^y
где h\, h2i Аз — метрические коэффициенты. Компоненты скорости
по отношению к локальным осям обозначим через и\, u2j iiz-
Тогда
V = щек, + Щ$ + щу.
Уравнение неразрывности (1.5) может быть записано в виде:
здесь использовано правило суммирования по одинаковому
индексу.
Запишем уравнение для компонента количества движения в
направлении а, т. е. для pu\\ два других уравнения для ри2 и рыз
получаются циклической перестановкой.
Из уравнения для этого компонента количества движения
в форме (1.6) получаем
ж «•»■) + таг -эггСтг /,'ЛА!Г")+-W (r" 'S—
-^^-^{Г^-Г,,^)^,-.-, (1.25)
здесь £Гц — компоненты тензора %Г\
Тц = ptliUj + рЪц щ-*ч>
xij = X(V • V)ô,y + 2|i(defV)f/f
18

где ou — символ Кронекера;
V • V = , , . ^— (-:— hih2hzue),
h\h2hz дхе \ he ' 2 3 7'
Выражения для (def V)22 и (defV)33 получаются путем
циклической перестановки:
(defV),/(^/) = -[^-^r + -^
dxf
-râr(*-£-+*-£r)]- <'-26)
Уравнение энергии (1.7) принимает вид
-§г№) + »,»',<„ й,1т>|Ц[|>е + '"''"Ж'"""
-TfftHr&l}-«'-v- "•27)
Такие же преобразования можно применить и к другим
уравнениям, представленным в предыдущем разделе.
1.2.3. Плоские течения
Рассмотрим более подробно уравнения для двумерных плоских
течений. Эти уравнения могут быть выведены из
вышеприведенных, если выбрать плоскость, имеющую траектории движения,
в качестве координатной поверхности х3 = const. В этом случае
«з = 0, Аз = 1, д/дхз = 0\ х\ и х2 остаются ортогональными
координатами на этой плоскости.
Сначала мы запишем уравнение Навье—Стокса в декартовых
координатах х и у (х\=х, х2 = у, и\=иу U2 = v). Система из
четырех уравнений в дивергентной форме без учета внешних сил
может быть записана в следующем виде:
J?L_i_J^ + _|^ = o, (128)
dt ~ дх ~ ду
где /, F, G — четырехкомпонентные векторы. Векторы F и G
могут быть представлены в виде суммы двух членов:
G = GI--irGv, (1.29)
19

где Fi и Gi соответствуют невязкой части членов F и G, a Fv
и Gv — вязкой. Более точно:
î=
( р\
pu
pv
V7
, F,=
Fv =
/
o,=
/ p"
P"2 + P
рыи
V (p£ + p) и
\
pv
puv
pv2 + p
\(pE + p)vy
0
fxx
UXXX + VXxy +
de
dx
(1.30)
Gv =
lxt/
ЬУУ
UX xu + VXyy + •
de
ьху-Г"ъуу грт ~ fy
С учетом соотношения Стокса ЗА + 2jj, = 0 имеем
2 /Л du dv
lxy
_ 2 /0 du dv \
сх~ т^Ч z~d~x ду~)9
/ du . dv \
_2_ /9 dv du \
Теперь рассмотрим уравнения Навье—Стокса в произвольной
криволинейной системе координат (которые могут зависеть от
времени). Пусть т, £, ц — независимые переменные:
т = *, £ = £(*» #> '). Ч = Л(*. У> *)•
Тогда уравнения в полностью консервативной форме, как это
было показано Вивианом (1974), имеют вид
d'f , dF . dG _0
di "г л, —и'
от
(1.31)
20

где / = //D, D = d(l, к))/д(х, у) —якобиан преобразования,
*-И'-3-+''-е-+0-£).
3~И'-£ + '-Й- + <'-£)-
Производные первого порядка, входящие в Fy и Gv, могут быть
преобразованы аналогичным способом.
Уравнения (1.28) в квазиконсервативной форме можно
получить путем непосредственного применения правила цепочки:
/ à , JL JL _l JlL JL\ f a. (Jk <L j- JtL JL\ f л.
\дт ^ dt dl f dt дц )' "т~ V дх д\ ^ дх дц )г ^
+(^-ж+-^^)о-°- <'•»•«
Очевидно, что любую производную, входящую в вязкие члены Fv
и Gv, по правилу цепочки можно также преобразовать к новым
координатам.
1.3. Уравнения Навье—Стокса для несжимаемой жидкости
1.3.1. Уравнения в переменных скорость—давление
Течение несжимаемой жидкости характеризуется следующим
условием:
V • V = 0. (1.32)
Если это условие подставить в уравнение неразрывности (1.5), то
получим
^- + V.VP=0 или -75Г-0. (1.33).
Это означает, что плотность постоянна вдоль траектории
жидкой частицы. В большинстве случаев обычно предполагается, что
р постоянно, так что это условие выполняется тождественно
всюду. Для стратифицированных жидкостей уравнение (1.33)
часто используется с целью вычисления малых возмущений
плотности р' относительно средней постоянной плотности р0, так что
Р = ро + р/. Однако при применении такого подхода следует быть
осторожным. Необходимо быть уверенным в том, что он
согласуется со всеми уравнениями переноса.
В случае |л = const уравнение для количества движения (1.6)
преобразуется к виду
P [^Г + v * <VV)] + vp - ^V = '- ( l -34)
Здесь неизвестными являются скорость и давление, которые
можно определить из уравнений (1.32) и (1.34), что, однако, со-
21

здает некоторые трудности при решении задач для несжимаемой
жидкости, поскольку граничные условия обычно задаются только
для поля скорости. Наиболее прямой путь решения уравнений
относительно давления состоит в комбинировании уравнений (1.32)
и (1.34) для получения уравнения Пуассона относительно
давления в виде
V2p = g(tt, ü, w),
где g (u, v, w) —функция компонент вектора скорости. Это
уравнение следует решать при условии, что уравнение (1.34)
используется на каждой границе для получения граничного условия
относительно dp/dN — градиента давления по нормали к границе.
Однако если вязкость и вектор \е равны нулю, а поток является
•стационарным и безвихревым, то получим уравнение для
определения давления
р + -J- Р ("2 + v2 + ^2) = const.
Уравнение (1.34) можно привести к другому виду при
использовании условия (1.32):
p[4r+(V' V)v]+Vp-^tV2V = f,. (1.35)
Эта форма уравнения называется неконсервативной (или
конвективной) формой уравнений Навье—Стокса, в то время как (1.34)
является консервативной (или дивергентной) формой.
1.3.2. Уравнения в переменных вихрь—функция тока
Другой вид уравнений Навье—Стокса можно получить при
использовании вектора вихря скорости
(o = vXV. (1.36)
Уравнение для w выводится путем применения оператора вихря
к уравнению (1.35); при этом член, содержащий градиент
давления, исчезнет. В результате получаем
-g- + (V. V)co-(a>. V)V-vV2w = yVXf, (1.37)
где v = fi/p. Это уравнение обычно связано с уравнением для со-
леноидального вектора функции тока W, который определяется
с помощью соотношения
V = vX4l, (1.38)
(1.38) автоматически удовлетворяет условию несжимаемости
(1.32). Уравнение, описывающее связь между W и (о, можно
получить путем применения оператора вихря к (1.38) и
использования определения (1.36). Тогда
V24* + <d = 0. (1.39)
22

Эта связь наиболее интересна в том случае, когда вектор W
содержит лишь одну координатную компоненту. Это справедливо,
в частности, для плоских течений:
V = vX(Wk), (1.40)
где к — единичный вектор нормали к плоскости течения, ^¥ —
скалярная функция. В этом случае вихрь (о=сок и уравнения (1.37)
и (1.39) из векторных превращаются в скалярные:
-3T + (V -V)co-vV2co = ^vXfe, (1.41)
V2W + (û = 0. (1.42)
Так же как и в случае уравнений для скорости, уравнение (1.41)
называют уравнением вихря в неконсервативной (или
конвективной) форме. Уравнение вихря в консервативной форме имеет вид
-§Г + V • ( Vo)) -^2°} = 7vXt ( 1 -43>
Если в уравнении вихря для функции тока перейти к
безразмерным величинам путем введения характерных величин для вихря
со — V*/L9 для функции тока V*L, для масштаба по пространству
L и по времени t — L/V*, тогда в уравнениях (1.37), (1.41)
и (1.43) величина v = \x/ç> должна быть заменена обратным
числом Рейнольдса, т. е. величиной 1/Re = v/V*L. В правых частях
этих уравнений величина fe должна быть заменена на /eL/pV*2.
Отметим, что важной особенностью уравнений в переменных
вихрь—функция тока является то обстоятельство, что в них в
явном виде не входит давление.
Если, однако, необходимо определить давление вдоль линии
или границы, то следует проинтегрировать тангенциальную
производную от давления, которую можно получить из уравнения для
количества движения, записанного в координатах вдоль границы
или линии. Для определения всего же поля давления необходима
решать уравнение Пуассона, приведенное выше.
Список литературы
Годунов С К. Разностный метод расчета разрывных решений уравнений
гидродинамики. Матем. сборник, 1959, 47 (89), № 3, с. 271—308."
Chapman, D. R., Mark, H., and Pirtle, M. W. Astronaut. Aeronaut. 22—35 (1975).
Chapman, D. R. AIAA Paper 79-0129 (1979).
Enselme, M., Brochet, J., and Boisseau, J. P. Low-Cost Three-Dimensional Flow
Computations using a Mini-system; 5th AIAA Computational Fluid Dynamics
Conference. Paolo Alto, June 1981.
Gottlieb, D., and Orszag, S. A. Numerical Analysis of Spectral Methods. SIAM,
Philadelphia, 1977.
Haidvogel, D. В., Robinson, A. R. and Schulman, E. E. /. Comput. Phys. 34,
1—53 (198C).
Hirsh, R. J. Comput. Phys. 19, 90—109 (1975).
Holt, M. Numerical Methods in Fluid Dynamics. Springer, New York, 1977.
Michalke, A. /. Fluid Mecli. 19, 543—556 (1964).
23;

Myers, R., Taylor, T. D., and Murdock, J. /. Comput. Pliys. 34, 180—188 (1981).
Orszag, S. A., and Israeli, M. Ann. Rev. Fluid Mech. 6, 281—317 (1974).
Peyret, R. ONERA T. P. No. 1978—29, Chatillon, France (1978) and Proceedings
1st International Con], on Numerical Methods in Laminar and Turbulent Flow,
pp. 43—54. Pentech Press, Plymouth, U. K., 1978.
JRichtmyer, R. D., and Morton, K. W. Difference Methods for Initial-Value
Problems. Interscience, New York, 1967. (Рихтмайер P., Мортон К. Разностные
методы решения краевых задач. М.: Мир, 1972).
Riley, J., and Metcalfe, R. AIAA Paper 80-0274 (1980).
Roache, P. J. Computational Fluid Dynamics. Hermosa, Albuquerque, 1972.
(Роуч П. Вычислительная гидродинамика. M.: Мир, 1980).
Rubin, S. G., and Khosla, P. /. Comput. Phys., 24, 217—244 (1977).
Viviand, H. Rech. Aewsp. No. 1974-1, 65—78 (1974).
Глава 2
Конечно-разностные методы
Вплоть до недавнего времени при решении задач
динамики жидкости преобладали численные методы, основанные на
конечно-разностных аппроксимациях. Эти методы являются
достаточно эффективными и играют главенствующую роль при решении
многих задач. В этой главе мы попытаемся описать эти методы
и изложить их основные достоинства.
2.1. Дискретные аппроксимации
Пусть f (х)— функция, заданная на интервале а^х^Ь. Интервал
[а, Ь] дискретизируется с помощью точек сетки Хо — ау хи •••
..., xi, ..., Jtiv+i = ô, дискретное представление f(х) есть {/(а),
f(x\), ..., f(xi), ..., f(b)}. Если f (х) является решением
некоторой математической задачи, например решением
дифференциального уравнения, значения f (х,), как правило, не известны точно,
а являются результатом некоторой аппроксимации:
ft**f(xi).
Величина (jc/+i — xi) есть шаг сетки, и мы будем предполагать
для простоты, что этот шаг есть константа:
Дл: = (& — a)/(N+ 1), Xi = a + ibxt i = 0, ..., N + 1.
Производную га-го порядка от функции / (х) в точке хь
аппроксимируем следующим образом:
где коэффициенты а/ определяются с помощью разложения в ряд
Тейлора, J и J2 — целые числа, зависящие от порядка
рассматриваемой производной, а также от степени точности аппроксимации.
24

Если для т = \ мы рассмотрим аппроксимацию по трем
значениям fi, т. е. /1+/2=2, и примем, что /1=/2=1, то мы можем
записать общее выражение для производной:
df (xi) (\-a)fi + l+2afi-(\+a)fi-1 (2 j 2V
где a — произвольная константа. Ошибка такой аппроксимации
равна
q A* d2f Ах2 d3f
2 dx2 6 dx3 '
Придавая a определенные значения, получаем формулы для
стандартных разностей:
центральная разность (а = 0)
^Ш^^ fU2Lf'~f -А^ ошибка = О (А*2); (2.1.3а)
разность назад (а=1)
^ixt} ^ f'~zu~' sA^> ошибка = О (А*); (2.1.36)
разность вперед (а== — 1)
dfl*l) = fux~U =Axfi, ошибка = О (Ах). (2.1.3в>
Выбирая /i = 2, /2 = 0 и используя разложение в ряд Тейлора,
чтобы найти значения <zj, получим аппроксимацию второго
порядка точности
Jfe£L*-5S-(3f'-4f'- + /'-0. (2.1.4а)
Если /i=0, /2 = 2, также получим аппроксимацию второго порядка
точности:
df (**) „ -4fi + 4fi + i — fi+2 /о i 46V
Аппроксимацию четвертого порядка точности получаем, если
J \ =/2 = 2:
df (Xj) _ -/^, + 8/^,-8^., + ^., (9 - -v
~~3ï Î2A^ ' l^1'0'
Аналогичным образом можно определить аппроксимацию для всех
производных. Например, обычная разностная аппроксимация
второй производной имеет вид
d2f(xj) fUl-2ft + ft-i _л f. Г21в>
dx' ~ АХ2 —bxxtf ^-А-Ь)
ее точность О (Ах2).
25

Использование обозначений разностных операторов А0.,
Д+, Ахх, •-. очень удобно и позволяет легко проверить
справедливость следующих соотношений:
4-(Ах + AJ) = A°,
At — Д7 = Д*Д*л:,
А^Дх = АХХ.
Однако отметим, что Д^Ах^А**, поскольку
A A f fi + 2 — 2fi + fi-2
Ьх bxti — ^д^ '
2.2. Решение обыкновенного дифференциального уравнения
Рассмотрим в качестве примера простое дифференциальное
уравнение
A-^-v-g- = 0, 0<*<1, (2.2.1а)
f(0) = U0y f(l) = Uu (2.2.16)
где v=const>0 и А=А(х). Интервал (0,1) разобьем точками
Xi = iAx, t = 0... N+l. Обозначим через fi численную
аппроксимацию f {xi) в точке лт, конечно-разностная аппроксимация (2.2.1)
будет иметь вид:
AiA°xfi-vAxxfi = 0y /=1, ..., ЛГ, (2.2.2а)
fo = U09 /лг + 1 = 1/1. (2.2.26)
Использование центральных разностей приводит к ошибке
второго порядка по отношению к шагу сетки Ах. Уравнения (2.2.2)
представляют собой линейную алгебраическую систему, решение
которой дает N значений //. В данном случае соответствующая
матрица трехдиагональна, так что весьма эффективно может быть
использован прямой метод решения. Общий метод факторизации
приводит к простому алгоритму решения, который описан в
следующем пункте.
2.2.1. Метод факторизации
Этот метод предназначен для решения линейной алгебраической
системы
^F = G, (2.2.3)
где si* — трехдиагональная матрица, F — вектор неизвестных, G —
заданный вектор.
26

Рассматриваемый метод является частным случаем более
общего метода факторизации, в котором матрица <я£ представляется
в виде произведения двух треугольных матриц j? и Л, т. е. s4>=
= 3?М. Решение уравнения (2.2.3) получается затем в два этапа.
Вначале вычисляется вектор V из системы 3?V=G, затем
находится вектор F из системы MF = V. Это разложение имеет то
преимущество, что треугольные матрицы легко обращаются. В случае
трехдиагональнои матрицы метод применяется в соответствии со
следующим алгоритмом.
Пусть разностные уравнения, соответствующие уравнению
(2.2.3), имеют вид
aifi-i + bifi + cifi + l = dii ï=1, ..., N,
/o = f/o, f*+i = £/i. (2.2.4)
Для этих уравнений имеют место рекуррентные соотношения:
fi = Xtfl + l + Yt9 /=1, ..., N, .(2.2.5)
где коэффициенты Xi и У; легко находятся (путем
приравнивания):
Коэффициенты Х0 и У0 определяются из (2.2.4) и (2.2.5) при
i= 1. Сравнение этих двух уравнений дает:
Ь\ gi d\ — a\Uo
1 ~~ —Xi ~~~ У,
Сравнивая эти соотношения с уравнением (2.2.6) при условии
/= 1, получаем:
Х0 = 0, У0 = £/о.
Сначала с помощью (2.2.6) вычисляются коэффициенты Xi и Yi
(/=1, ..., N), затем — с помощью (2.2.5) искомые величины fit
при этом i изменяется от N до 1. Можно показать (Изаксон и
Келлер, 1966), что алгоритм устойчив по отношению к случайным
ошибкам, если выполняются следующие условия:
IM>k,|, 1Ч>|а*| + Ы ** = 2, ..., N.
\bN\ > \aN\, (2.2.7а)
которые выражают условия диагонального преобладания
элементов матрицы А = [aim], имеющего вид
K/l> Е Kml, /=1, ..., N, тф1. (2.2.76)
т=\
Для уравнений (2.2.2) условия (2.2.7а) удовлетворяются в том
и только в том случае, если
\А\Ьх < о
v
где |j4|A;c/v называется сеточным числом Рейнольдса.
27

2.2.2. Итерационные методы
Как было показано в п. 2.2.1, в случае трехдиагональной матрицы
прямой метод решения системы (2.2.3) весьма эффективен.
Однако поскольку в случае матриц общего вида часто применяются
итерационные методы, имеет смысл кратко рассмотреть некоторые
из них.
Метод Якоба. Значение fi на (/л+1)-й итерации дается с
помощью формулы (й,=^0):
î? + { = -gr(-aif?-i-cif?+l + di), ;=1, ..., N. (2.2.8)
Метод Гаусса—Зейделя. Значение fmM вычисляется с
использованием уже полученных значений на (га+1)-й итерации в
предыдущих точках. Так, если вычисления производятся при
возрастающих значениях /, то метод Гаусса—Зейделя описывается
формулой
f? + X =^(-aif?±xl -ctf?+x + dù /=1, ..., N. (2.2.9)
Метод последовательной релаксации. По этому методу сначала
методом Гаусса—Зейделя определяется предварительное значение
jrn+i^ а затем релаксационным путем, характеризуемым
положительным параметром о, находится окончательное значение /m+1
/Г + 1=соГГ + 1 + (1-о))/Г. (2.2.10)
Сходимость этих методов имеет место, если max|/™+1— fT\-*0,
когда m-+oo при любых начальных значениях f°r Для методов
Якоби и Гаусса—Зейделя достаточным условием сходимости
является строгое диагональное преобладание в матрице s£y т. е.
выполнение строгих неравенств в (2.2.7а) или в (2.2.76). Это
условие не всегда выполняется; например, оно не выполняется для
уравнения (2.2.2а). Однако это условие было бы выполнено, если
бы член, не содержащий производную Bf (ß>0), был бы
включен в левую часть уравнения (2.2.1а).
Поэтому другое достаточное условие сходимости, которому
легче удовлетворить, состоит в том, что матрица неприводима *
и имеет диагональное преобладание [условия (2.2.76)] со
строгим неравенством по меньшей мере для одного значения /.
Для метода последовательной релаксации известное условие
сходимости является более жестким: если матрица зФ симмет-
* Матрица является неприводимой, если решение соответствующей
алгебраической системы не может быть сведено к последовательному решению двух
систем более низкого порядка. Простые условия неприводимости могут быть
найдены из теории графов (см.: Варга, 1962).
28

рична и положительно определена, то метод сходится при 0<ш<
<2.
Мы отсылаем читателя к учебникам по численному анализу
для более детального изучения вопросов сходимости
итерационных процедур и, в частности, для определения оптимальных
значений параметра релаксации о).
Замечание. Описанные итерационные процедуры можно
представить в матричной форме следующим образом. В
предположении, что bi^Oy уравнения (2.2.4) после деления на Ъь можно
привести к системе вида (2.2.3), в которой на главной диагонали
находятся единицы. Тогда матрица s& может быть разложена
следующим образом:
где M и Л* — нижняя и верхняя строго треугольные матрицы,
соответственно имеющие только одну ненулевую диагональ. Метод
Якоби определяется с помощью формулы
Fm+l = (JC + jr)Fm + G;
метод Гаусса—Зейделя
{I-J[)Fm + { = NFm + G или
Fm + ■ = (/ - Ж)~х JfFm + (/ — Л)"1 G;
метод последовательной релаксации
Fm+ ' = j(Fm+l + JTFm + G,
Fm+l=coFm + l + (l— (ù)Fm.
2.2.3. Аналогия между итерационными процедурами и решением эволюционных
уравнений
Как было показано Гарабедяном (1956), существует аналогия
между некоторыми итерационными процедурами и решением
эволюционных уравнений. Если сопоставить формально индексу га
момент времени m At, то можно легко найти аналог каждой
процедуре, описанной выше, используя разложения в ряд Тейлора
как по пространству, так и по времени. Этот общий метод
определения ошибки аппроксимации конечно-разностной схемы для
уравнения, описывающего зависимость от времени, рассмотрен
в п. 2.6.
Таким образом, если разложения в ряды Тейлора выполнены
для каждого из уравнений (2.2.8), (2.2.9) или (2.2.10), то мы
получаем уравнение вида
*-8—»-£--*-£-• <2-2-">
где сохранены только главные члены. Коэффициент К зависит от
рассматриваемой итерационной процедуры. Сходимость итераци-
29

оннои процедуры эквивалентна существованию стационарного
решения уравнения (2.2.11). Необходимым условием этого является
условие параболичности уравнения (2.2.11) для />0. Для
метода Якоби:
K = /ta = 2v-$->0;
для метода Гаусса—Зейделя
* = ^з=-|$-(1 ~^4Р)>0> еслиЛД*<2^;
для метода последовательной релаксации
2 — со А Ал: \
2v ;•
Коэффициент К пр положителен, если A Ax/2v< (2 — са)/ох
Однако условие /С>0 не является достаточным для того, чтобы
численное решение уравнения (2.2.11), получаемое с помощью схем
(2.2.8) — (2.2.10), имело бы стационарный предел.
Дополнительным условием является устойчивость схемы, используемой для
аппроксимации уравнения (2.2.11). Устойчивость таких схем будет
рассмотрена в п. 2.6. Анализ устойчивости схем (2.2.8) — (2.2.10)
приводит к условиям, эквивалентным некоторым из условий
сходимости, упомянутым в п. 2.2.2.
Сопоставление различных выражений для коэффициента К
позволяет определить свойства сходимости итерационных процедур.
Например, если Л=0, мы получаем ЯГ-з=:"1Г^яи со^пр =
= (2 — со)/Сг=3. Из уравнения (2.2.11) ясно, что чем меньше /С,
тем выше скорость сходимости итерационной процедуры. В
частности, метод последовательной релаксации сходится быстрее, чем
метод Гаусса—Зейделя, если 1<а)<2. Отметим, что для
нахождения оптимального значения со необходимо выполнить более
сложный анализ (Гарабедян, 1956).
2.3. Аналитическое решение конечно-разностной задачи
Рассмотрим теперь дифференциальное уравнение
A-£r-v-£L = 0, 0<*<1, (2.3.1а>
с граничными условиями
f(0) = U0t f(l) = Ul9 (2.3.16)
где Л Hv — константы (v<0).
Решение этого уравнения имеет вид
/ = [/„ + ([/,- U0) е*1~1 , (2.3.2)
е — 1
30

где 6=A/v. На рис. 2.3.1 представлен график решения.
Существенная его особенность — наличие пограничного слоя толщиной
О ( | ô | ) при ô~^0. Этот пограничный слой локализуется вблизи
точки л; = 0, если ô<0, и вблизи точки jt=l, если ô>0.
Предположим, что уравнение (2.3.1) аппроксимировано с помощью
центральных разностей: первая производная с помощью А0,, вторая
производная с помощью Д.™. Получается следующая
конечно-разностная задача:
(2-R)fi + l-4fi + {2 + R)fi-l = 0t * = 1, ..., N, (2.3.3а)
fо = I/o, fA' + . = t/i, (2.3.36)
Рис. 2.3.1. График функции f.
где R— алгебраическое сеточное число Рейнольдса:
В простейших случаях, к каковым относится рассматриваемый
нами, решение разностной задачи можно получить аналитически.
Методы решения линейных конечно-разностных уравнений с
постоянными коэффициентами сходны с методами, используемыми
в теории обыкновенных дифференциальных уравнений (см.
например, Годунов и Рябенький, 1964).
Общее решение уравнения (2.3.3а) имеет вид:
fi = C\q\ + C2ql2,
(2.3.4)
где q\ и q2 — корни характеристического уравнения,
соответствующего (2.3.3а):
(2 - R) q2 - 4? + (2 + R) = 0, (2.3.5)
Ci и С2 — константы, которые определяются с помощью
граничных условий (2.3.36).
Корни (2.3.5)
^ = 1, *--|±f-,
31

константы имеют вид
г —л </i — I/o п _ Ut-Uo
Таким образом, решение (2.3.4) получаем в виде
4-1
?? + 1-1
/,- = 1/0 + (t/, - U0) J2+1 , . (2.3.6)
Рассмотрим предельный переход при Дх-^-О, когда Xi = iAx
фиксировано. Предполагая, что ô =0(1), имеем
i I 2 + ОД* у / 2 + ОД* у,/Д*
?2 = Ь-6Д* J = \Ъ-ЪЬх) =
= Л[1+^!£^ + 0(А/)]. (2.3.7)
Отсюда вытекает, что qlz аппроксимирует со вторым порядком
точности фундаментальное решение eàx дифференциального
уравнения (2.3.1а). В то же время заметим, что второе решение q\=\
точно совпадает со вторым фундаментальным решением
дифференциального уравнения.
Наконец из уравнений (2.3.6) и (2.3.7) получаем:
fi = î (xi) + A*2 (t/i - I/o) Ф (xi) + О (Ах% (2.3.8а)
Ф(*')=~ 12(/-1)2 [^(^-0-^-0^1 (2.3.86)
где f(xi) — точное решение. Остальные члены выражают ошибку.
Разложение (2.3.8) можно получить и другим способом. Для
этого рассмотрим дифференциальное уравнение, соответствующее
конечно-разностному уравнению (2.3.3), к которому применяется
разложение в ряд Тейлора (конструкция аппроксимационной
ошибки). Это уравнение имеет вид
df
dx
^+^-S—^)+<w>-°- <м.ч
Если мы ищем решение этого уравнения в виде
асимптотического разложения
F (*, Ах) = F0 (х) + AxF, (х) + Ax2F2 (х) + О (Ах3), (2.3.10)
Fo(0) = C/o, Fo(l) = Uu F}(0) = Fj(l) = 0 для /=1, 2,
то получим систему уравнений, определяющую различные F, (/ =
= 0, 1,2) из которой следует, что
^о (х) = /(*) — точное решение,
Л(*) = 0,
F2(x) = (Ul-U0)O(x).
32

Такой анализ лишен общности, однако он позволяет
установить связь между конечно-разностной схемой и ее
дифференциальным приближением (2.3.9)*.
Предположим, что Дх<^1, но ô не обязательно порядка
единицы, так что сеточное число Рейнольдса \R\ = | ô \Ах может быть
0(1). Отметим, что ^2<0, если |/?|>2. Это означает, что ql2
положительно для четных значений индекса i и отрицательно для
нечетных. Это обстоятельство (Роуч, 1972) объясняет наличие
осцилляции, которые могут появляться в численном решении при
|/?|>2. Напомним, что условие |#|<2 гарантирует диагональное
преобладание в матрице линейной алгебраической системы,
определяемой конечно-разностным уравнением (2.3.3).
Положим теперь, что первая производная аппроксимируется
по схеме с весами
-^r^^T^-^àî + il + ^^fi, (2.3.11)
где а — константа. Если а = 0, то получаем аппроксимацию с
помощью центральных разностей. Если же а = ±1, то имеем нецент-
рированные аппроксимации. Схема направленных против потока
разностей получается, если
а ==8, e = sign(/?).
Если аппроксимацию (2.3.11) использовать для уравнения (2.3.1) г
то численное решение /,- опять можно получить с помощью (2.3.4),
но при этом
2 + (1 + а)/г (2 3 12Ъ
Отметим, что <7г>0, если
a>(l--J-) = a0 или а <(—1 1-) = а, (2.3.13)
и осцилляции в решении не появляются. Эти условия гарантируют
также диагональное преобладание в соответствующей матрице
коэффициентов.
Если Ах«С1 и 6=0(1), то сеточное число Рейнольдса /? =
= б Дд:<с1 и условия (2.3.13) легко удовлетворяются. В этом
случае разложение, аналогичное (2.3.10), имеет вид
fi = f(xl)-ßJix{Ul-Uo)^ Ф(*/) + 0(Дх2), (2.3.14)
* О связи разностных схем с их дифференциальными приближениями,
см., например: Давыдов Ю. Н., Скотников В. П. Дифференциальные
приближения разностных схем (М., 1978); Шокин Ю. И. Метод дифференциального
приближения (Новосибирск, 1979).— Прим. перев.
33

дифференциальное приближение, аналогичное (2.3.9):
Л df „ dif аА* л <Pf ,
v-И, 0—А-
dx dx2 2 rfjc2 ^
+ -^-[-»-0—ï~S-]+0(^_a (2.3..5)
Отметим, что использование схемы взвешенных разностей
против потока приводит к ошибке порядка а ах и эта ошибка носит
диссипативный характер, если аЛ>0, т. е. если а и Л (или R)
имеют один и тот же знак. Если |/?|>2 (это случай, когда
использование направленных разностей против потока оправдано),
то а0>0 и cci<0, независимо от знака R. Поэтому представляется,
что необходимо использовать условия а>а0, если R>0> и а<аь
если /?<0. Этот последний вывод может быть получен более
строго, чем с помощью приведенных эвристических аргументов,
основанных на рассмотрении главной части ошибки аппроксимации.
Рассмотрим последовательно два случая /? = оДлг-*±оо
и/? = 0(1) при Дх->0.
В первом случае ищем значение а, которое дает точное
решение задачи (2.3.1) (Равьяр, 1979). Пусть а* является таким
значением. Тогда с^еРъ, т. е. q2 = e6Ax и
2о+п1а2&ЛХ =е6*Х- (2.3.16)
2— (1 + ct*)ôA* v 7
Отсюда
о 1 4- Р6 Ах
В случае когда Л>0, ô>0 и оДх-»- +оо,
2
а* ~ г-д 1- 1 + экспоненциально малые члены;
Но тогда а0=1—2/ôAjc и можно заключить, что (а* — а0)
экспоненциально стремится к нулю при бЛх-^+оо. Поскольку
а* есть значение а, которое дает точное решение, заключаем, что
в случае Л>0 следует брать а>а0.
Легко проверить, что аналогичный результат получим при
Л<0 путем замены а0 на ai. Таким образом, если Л<0, следует
брать a<ai.
Теперь рассмотрим более часто встречающийся на практике
случай: Дх<1, но R= (A/v)àx= оДх = 0(1). Из (2.3.12) следует,
что <72>1 независимо от знака R, если a>ao=l—2//?, и 0<^2<
< 1 независимо от знака R, если a<ai = — 1 —2/R.
Кроме того, çi2 = e'lnÇ2 = e(xi/Ax)ing2 Следовательно, если a>a0,
то ql2 стремится экспоненциально к бесконечности при Дх-^0
для любого значения iE [1, N] и фиксированном Xi = iAx. Легко
34

видеть, что fi~t/0 + экспоненциально малые члены. Если а<ссь
то (при Дх-^О) fi~U\ + экспоненциально малые члены. Если мы
вспомним (см. рис. 2.3.1), что пограничный слой существует
вблизи точки х = 0, если Л<0, и вблизи точки д*=1, если Л>0,
то можно заключить снова, что следует выбирать а>а0, если
Л>0, и а<аь если Л<0.
Кроме того, можно сделать один интересный вывод. Если
| ô |Лх = 0(1), то Ax = 0(|ô|_1). Отсюда следует, что первая
расчетная точка находится на границе пограничного слоя. В этом
случае, если выбор а делается в соответствии с вышеприведенными
выводами, численное решение хотя и не описывает пограничный
слой, но дает правильную аппроксимацию решения вне
пограничного слоя.
В заключение отметим, что некоторые интересные результаты,
связанные с аналитическим решением нелинейных
дифференциальных уравнений по схеме разностей против потока были получены
Ченгом и Шубиным (1978).
2.4. Схемы направленных против потока разностей с коррекцией
Пусть уравнение (2.3.1) аппроксимировано с помощью схемы на-
правленных против потока разностей (2.1.2) с а = sign/? для
первой производной. Такая аппроксимация приводит к
диагональному преобладанию матрицы, что позволяет использовать,
например, итерационную процедуру для решения. Получающееся
конечно-разностное уравнение имеет лишь первый порядок точности.
Однако точность второго порядка может быть достигнута, если
корректирующий член, определяемый на предыдущей итерации,
включается в общую схему с тем, чтобы при сходимости получить
центрально-разностную аппроксимацию. Такой метод коррекции
был рассмотрен в различных формах и для разных уравнений
Деннисом и Чангом (1969), Хосла и Рубиным (1974), Та Фуок
Локом (1975), Вельдманом (1973) и Пейре (1971). Этот метод
оказался весьма эффективным и в применении к уравнениям
Навье—Стокса.
Однако если решение осциллирует вследствие применения
центрально-разностной схемы, то метод коррекции, описанный
выше, не исключает таких осцилляции. Вводимый в целях
коррекции член должен выбираться таким образом, чтобы
получающаяся конечно-разностная схема была бы, во-первых, второго
порядка точности и, во-вторых, достаточно диссипативной, чтобы
подавить возможные осцилляции. Второе требование означает,
что в схему должен быть введен член с искусственной вязкостью.
Для иллюстрации сказанного рассмотрим нелинейное
дифференциальное уравнение, для которого итерационная процедура
естественна:
V-S--g (/)-£{- = 0, v = const >0, (2.4.1)
35

с соответствующими граничными условиями типа (2.3.16).
Уравнение (2.4.1) аппроксимируем следующим образом:
vAxxfi-giAxfi = 0, (2.4.2)
где gi=g(fi) и А* —любой конечно-разностный оператор,
аппроксимирующий производную первого порядка. Нелинейная задача
решается с помощью итерационной процедуры
v Axxf ? + [-g? A*xf? + ' = 0. (2.4.3)
Как было показано в п. 2.2.1 для случая А* =А° , матрица
системы (2.4.2) имеет диагональное преобладание тогда и только
тогда, когда
|gf|^L<2. (2.4.4)
Аппроксимация по схеме направленных против потока разностей,
обеспечивающая диагональное преобладание, определяется по
формуле
V*/* = 4" К1 - 8) А* + 0 + е) дх ] fr =(д° --g-Д*е A«) fi, (2.4.5)
где e=sign(g™).
Метод коррекции заключается в применении следующего
итерационного уравнения:
v А«/Г + ' - g? Alf? + ' = Л, (g?)f?t (2.4.6)
где разностный оператор Ax(g™) определяется так что
[gi А*, + Л, (gi)] /, = Jg- + О (Ах2).
Если оператор А* задан с помощью (2.4.5), то прямая процедура
определения Ах проста:
Л* (gi) fi = 4- д* I St I Axxf«. (2.4.7)
Эта процедура может порождать осциллирующее численное
решение. Более систематический способ построения
корректирующего члена состоит в отыскании оператора общего вида
1
/=-1
л,ы*-.Ел/1+/. (2А8)
где
36

Произвольные коэффициенты определяются из условий
подавления осцилляции и второго порядка точности аппроксимации.
Удовлетворение этим требованиям приводит к выражению
Л* (gi) fi = -g" ^xeëi kxxfi — AÀë (/S°xgi) • (bxxfl) —
-b*?&(bxxgi)-{Hxxfi). (2.4.9)
где 8 = sign(A°Ä^t), г = sign (Axxgi), a, ß — положительные
константы, которые определяют искусственную вязкость. С учетом
этого оператора
получающееся конечно-разностное f
уравнение (2.4.6) при
условии сходимости (fm+l = f™)
аппроксимирует следующее
дифференциальное
уравнение:
Л, d2î rr df
1,0
dx2
dx
+ Ax2X
4-tï
+ o|-
d*f
g d>f
dx* 3
dg I d2f
+
X
i dx \ dx2
d2g I d2f
dx3
f A*3ß X
0,5
dx3 dx2
O(A*4) = 0.
Рис. 2.4.1. Пример использования
метода направленных против
потока разностей с коррекцией.
Lx-0,1
•0=1/25
Точнее решение
' ?-$
Метод разностей
прогт/8 потока
о О О
• 1,0 О
Л 1,5 О
DO 0,51
Коррекция
0,5
1,0 х
Искусственная вязкость пропорциональна первой и второй
производным от g, однако член типа \gi\d2f/dx2 также можно было
бы включить. Заметим, что члены, содержащие g,
рассматриваются здесь как коэффициенты при производных от функции f.
Это несколько искусственно, и следовало бы учесть вид функции
g(f). В случае уравнения вихря, которое будет рассмотрено ниже,
/играет роль вихря, a g — скорости.
На рис. 2.4.1 показаны некоторые результаты, полученные для
случая g(f)=f, причем решение / удовлетворяет следующим
граничным условиям: /(0) = 1, /(1)=0. В этом случае точное
решение имеет вид
f(x) = Clîh(C2--%rx),
где Ci =
1 и Сг= 12,5, если v = 725.
37

2.5. Методы повышенного порядка точности
При решении некоторых задач точность второго порядка
оказывается недостаточной, и появляется необходимость в
использовании методов более высокого порядка точности. Часто
встречающиеся конечно-разностные аппроксимации могут быть получены
путем использования разностных формул типа (2.1.1). Однако чем
выше порядок аппроксимации, тем больше число используемых
точек дискретизации. Так, применение метода четвертого порядка
точности для уравнения (2.1.5) приводит к алгебраической системе
с 5-диагональной матрицей. Другой путь построения разностных
уравнений состоит в использовании так называемых
«компактных» методов. Целью этих методов является получение
аппроксимации высокого (в основном четвертого) порядка, приводящих
к решению алгебраических систем с трехдиагональной матрицей.
Мы рассмотрим эрмитов метод, Af-метод и неявный метод
компактного оператора (метод OCI — operator compact implicitv) (см.
Коллатц, 1966, 1972).
2.5.1. Эрмитов метод
В этом методе в качестве неизвестных в каждой точке
рассматриваются не только значения самой функции, но и ее производные
/', /''., ... Уравнения системы представляют собой соотношения
между функцией и ее производными в трех последовательных
точках. Эти соотношения называются формулами Эрмита. Как было
отмечено Коллатцом (1966), идея метода была предложена давно,
однако только в последнее время метод стал применяться для
решения задач динамики жидкости.
Общая трехточечная формула Эрмита для производных
первого и второго порядков записывается в виде
Нь= S (а,//+/+ *,/;+, +c/fï + /) = 0. (2.5.1)
Здесь aJ9 bj, Cj — константы, определяемые из следующего
условия: соотношение (2.5.1) должно представлять (с точностью до
некоторого порядка величины Ах) точное соотношение, которое
существует между любой регулярной функцией / (х) и ее двумя
первыми производными î'{x), f"{x) в трех точках Xi_i==(î—1 )Ах,
Xi = iAxf Xi+i= (i+ l)Ax. Практически выполняется разложение
в ряд Тейлора около точки х\ в уравнении (2.5.1), и мы получаем
Z ^ТГ = 0. (2-5.2)
k=o dx*
Если формула (2.5.1) была бы точной, то все Ak должны быть
равны нулю. На самом деле только конечное число (К) величин
Ak может быть приравнено нулю:
Ak = 0, ft = 0, ..., К. (2.5.3)
38

Максимально возможное значение К существенно зависит от
числа произвольных параметров, включенных в уравнение (2.5.1).
Если /С = 3, то удовлетворение четырех однородных уравнений
(2.5.3) оставляет пять неопределенных коэффициентов, и после
изменения обозначений параметров получаем:
.—-ЧИч-аЕ2-. ъ.,-±±$=ь-+,-*.
16Y ,40 , 16ß . А
_ 15ß + 8y Зр + 29 , 3a-7ß-5y , „ , Q
» — 7Г& AT » ôi = TZ t-p + Ь,
а,=
àx2 Ах ' ! Ах
c_1 = a-fß — y, с0 = 4а, с,=а — ß — у,
где произвольные параметры а, ß, у, р и 6 являются константами
и не зависят от Ах. Вышеприведенные выражения подставляются
в формулу (2.5.1), которую запишем в символической форме
Я, [а, ß, y, Р, в] = 0. (2.5.4)
Левая часть (2.5.4) однородна относительно параметров, так что
четыре из них можно выразить через пятый, который можно
принять равным единице. Ошибка <8, связанная с формулой (2.5.4),
может быть получена путем разложений в ряды Тейлора и имеет
вид
g = Jtf 9Г + -^ [3pfV + (За - 2Y) П +
■ A^5.(7e/VI-2ß/VII)+0(AA (2.5.5)
1 630
где римские цифры означают порядок производных.
В различных методах высокого порядка точности используются
формулы, которые можно получить непосредственно из общей
формулы (2.5.4). Некоторые из них будут описаны ниже.
Существуют и другие методы, которые могут использовать эту общую
формулу, например метод, основанный на аппроксимациях с
помощью сплайнов (Рубин и Хосла, 1977) или метод OCI (Саймент
и др., 1978).
Отметим также, что можно получить формулы Эрмита для
неравных шагов сетки (Адам, 1975).
Применим теперь эрмитов метод для решения задачи (2.3.1).
Уравнение (2.3.1а) аппроксимируем следующим образом:
Л/,' —v£ = 0, /=1,..., ЛЛ (2.5.6)
где f и /"— соответствующие аппроксимации df/dx и d2f/dxz
в точках дискретизации Xi = iàx, àx=l/(N+l). В уравнении
(2.5.6) неизвестными являются производные /'. и /". Два
дополнительных уравнения могут быть получены из соотношений,
39

связывающих эти производные с самой функцией. В обычных
конечно-разностных методах f. и f". могут быть явно выражены
с помощью формул типа (2.1.1). Здесь же вместо этого мы
рассмотрим две независимые формулы Эрмита:
Hi\au ßb Yi> Pi, 6,] = О,
Ht[a29 ß2, Y2, p2, e2] = 0, /=1, ..., N. (2.5.7)
Кроме того, для замыкания системы к граничным условиям
fo = U0y fN + l = Ut (2.5.8)
необходимо добавить соотношения Эрмита, записанные для
границ, или дифференциальное уравнение, записанное в граничных
точках и связанное с некоторыми соотношениями Эрмита.
Получающаяся алгебраическая система есть (3x3)-блочная
трехдиагональная; неизвестными являются векторы t|)i = (f/, f.,
f" ). Эта система решается методом матричной факторизации,
идентичным методу, описанному в п. 2.1 для простой трехдиаго-
нальной системы.
Рассмотрим теперь некоторые частные эрмитовы методы.
Неявная схема для вторых производных. Этот метод был
исследован и применен практически Хершем (1975) и Адамом
(1975). Он соответствует специальному выбору постоянных в
формулах Эрмита (2.5.7):
ai = ßi=Yi = 0> Pi = l. 6, = 0,
5
а2 = —, ß2 = 0, Y2=l> р2 = 92 = 0.
На основании этого получаем
f; + 1 + 4fî + fLi--|r(fi + i-f<-,) = 0f (2.5.9)
f; + I+10f; + fLi--^-(fi + i-2fi + fi_i) = 0. (2.5.10)
В этом случае система замыкается с помощью: а) граничных
условий (2.5.8); б) уравнения (2.5.6), записанного при / = 0 и i =
= N+l\ в) нецентрированных формул Эрмита:
tfi[0, 0, 0, 1, -1] = 0,
(2.5.11)
HN\p, 0, 0, 1, 1] = 0.
Соотношения (2.5.9) и (2.5.10) имеют четвертый порядок
точности, а соотношения (2.5.11)—только третий. Однако рост аппрок-
симационной ошибки вблизи границы, где заданы условия
Дирихле, не обязательно нарушает точность численного решения.
40

Было показано (Пейре, 1978), что ошибка численного решения
по отношению к точному решению в случае, когда £/0=1, £Л=0,
равна:
Ei = fi-f(xd = bx4-^-O(Xi) + 0(Ax5l /=1, ..., N, (2.5.12)
где Ф (xi) определено с помощью (2.3.86) и ô =A/v.
Решение задачи требует обращения (3x3)-блочной трехдиаго-
нальной матрицы. Однако можно уменьшить размерность блоков
(Адам, 1975) путем использования линейной комбинации (2.5.6)
в точках /—1, i, i+\ вместе с (2.5.10) для исключения вторых
производных /£_4 , \", f . В этом случае блоки имеют
размерность 2x2, а неизвестным является вектор tyi=(fi, /'.).
Этот метод был применен для решения уравнений Навье—
Стокса в форме уравнения вихря для функции тока Хёршем
(1975), Мета (1977), Добом и Та Фуок Локом (1978), Та Фуок
Локом (1980) (см. п. 6.6.2), Бонту и др. (1978), Леконтом и Пике
(1981), а также Рубиным и Хосла (1977) с использованием
аппроксимации на сплайнах. Для решения уравнений Навье—
Стокса в исходной форме этот метод применялся Эльзассером
и Пейре (1979), Эльзассером (1980), Гиа и др. (1979). В этом
случае было установлено (Эльзассер и Пейре, 1979), что более
практично не замыкать систему путем использования уравнения
для количества движения на границах, как это было сделано
выше для модельного уравнения (2.5.6) с целью избежать
вычисления градиента давления на границе. Для случая
дифференциального уравнения (2.3.1) это сводится к замене уравнения,
записанного в точках / = 0 и i = N, формулами Эрмита четвертого
порядка точности
Я,[1, % 3Д, 0, 0] = 0, Я„[1, -% 3Л, 0, 0] = 0. (2.5.13)
Главная часть ошибки в этом случае также дается формулой
(2.5.12).
Явная схема для вторых производных. Вторая производная
Î" может быть выражена через значения самой функции и ее
первой производной в соседних точках (Адам, 1977). Это
выражение может быть получено из общей формулы Эрмита (2.5.4) при
a = Y = 1 и ß =р=в = 0:
f" fi + 1 -" fi - 1 i о fi + l—2fi + fi-l icy с \ Л\
Это соотношение имеет четвертый порядок точности. Неизвестные
г|),= (fiy f ) находятся затем путем решения (2x2)-блочной трех-
диагональной системы, получаемой из уравнений (2.5.6),
соотношений (2.5.9) и (2.5.14), граничных условий (2.5.8) и
соотношений (2.5.11).
При решении задачи (2.3.1) использование такого метода
приводит к ошибке Ei = fi — f (xi) порядка Д#4, но несколько большей
41

по величине, чем (2.5.12). Однако если этот метод применяется
для решения такой сложной задачи, как решение уравнений
Навье—Стокса в переменных скорость—давление (Эльзассер,
Пейре, 1979), то явная формула (2.5.14) дает результаты,
сравнимые по точности с теми, которые получаются с применением
неявной формулы (2.5.10).
2.5.2. М-метод и неявный метод компактного оператора (метод OCI)
М-метод, использованный Краузе и др. (1976) для решения
уравнений пограничного слоя, отличается от двух вышеизложенных
методов тем, что вместо двух формул (2.5.7) используется четыре
формулы Эрмита. Эти четыре независимых соотношения:
tft[0, -1, 1, 0, 0] = 0, Я;[1, 0, 1, 0, 0] = 0,
Я;[0, 1, 1, 0 , 0] = 0, (2.5.15а)
tft[0, 0, 0, 1, 0] = 0 (2.5.156)
вместе с уравнением (2.5.6), записанным в точках /—1, /, /+1Д
приводят к системе из семи алгебраических уравнений, из
которых исключаются производные /,_i, /ь f/+i, //_i, /ь /*+i. В
результате получаем конечно- разностное уравнение, содержащее
только неизвестные f/_i, f/, /;+i. Это уравнение вместе с
граничными условиями (2.5.8) образует трехдиагональную систему,
которая легко может быть решена. Этот метод имеет четвертый
порядок точности, а ошибка Ei = fi — f (xt) сравнима с ошибкой
метода явного исключения, изложенного в п. 2.5.1.
Стандартный метод OCI, развитый, в частности, Сайментом
и др. (1978), приводит к конечно-разностному уравнению,
идентичному уравнению в УИ-методе. Однако способ вывода этого
уравнения отличается и может быть использован для вывода
обобщенного метода OCI (Бергер и др., 1980, Леконт и Пике, 1981).
Изложим этот метод применительно к общему линейному
дифференциальному уравнению второго порядка:
L{f) = G, 0<jc< 1, (2.5.16а)
f(0) = f/0, f(l) = £/,. (2.5.166)
Образуем линейную форму
ß^to + O + ß0L (fi) + ß-,L (/;-,) = а,/;*, + a0fi + а_^-,. (2.5.17)
Предположим, что параметры a/ и ß/ при / = 0, —1, 1 могут быть
найдены так, что уравнение (2.5.17) соответствует с точностью
до некоторого порядка точному соотношению между функцией
и ее производными, существующему благодаря
дифференциальному уравнению (2.5.16а). Заменяя в (2.5.17) величины L (f)
через G, мы получаем конечно-разностное уравнение
a.fi +, + a0fi + a-,/,-,« ß,Gi + , + ß<A + ß-iG<-i. (2.5.18)
42

Это уравнение вместе с граничными условиями (2.5.166)
приводит к линейной алгебраической системе с трехдиагональной
матрицей. Определение коэффициентов а/, ß/ производится таким же
образом, как и для формулы Эрмита (2.5.1)—путем разложений
в ряды Тейлора в (2.5.17). Получается уравнение, аналогичное
(2.5.2).
Стандартный метод OCI получается, если в уравнениях (2.5.3)
К = 4. Соответствующая система из пяти однородных уравнений
позволяет выразить пять коэффициентов а,- и ß/ через один
неизвестный, как это было отмечено ранее. Получающееся конечно-
разностное уравнение имеет четвертый порядок точности. Это
уравнение идентично соответствующему уравнению в М-методе.
Обобщенный метод OCI (Бергер и др., 1980) может быть
выведен путем использования трех уравнений Л* = 0, А = 0, 1, 2, и двух
уравнений Л д. = О (Ах4), & = 3, 4. При этом сохраняется точность
четвертого порядка и остается определенный произвол, который
может быть использован для получения некоторых
дополнительных специальных свойств, например диагонального преобладания
в матрице системы и дискретного принципа максимума.
2.6. Решение одномерного линейного параболического уравнения
Рассмотрим линейное параболическое уравнение
^ + X-|L--v-|^- = 0, 4 = const, v = const>0. (2.6.1)
Наиболее простой схемой, которая может быть использована для
решения этого уравнения, является явная схема
/П + 1 еП сП еП сП Г) р/1 | (П
i — li . л /t + l"~ /i-l It + 1 ~~ zli "Г ïi-
+ А " + i '*-' -v ,t + l AV "-1 =0, (2.6.2)
Д/ ' 2Ajc Ax2 v 7
где Ах и At— шаги по пространству и по времени соответственно,
так что плоскость (х, t) дискретизирована: x = iAx, t = nAt, где
i и п — целые. В уравнении (2.6.2) f^œf^Ax, tiAt). Численное
решение f", получаемое с помощью уравнения (2.6.2), должно
сходиться к точному решению f(iAx, nAt) уравнения (2.6.1),
когда А* и At->-0 в данной точке (iAx, nAt). Теорема
эквивалентности Лакса устанавливает, что для корректно поставленной
задачи с начальными условиями, соответствующей линейному
эволюционному уравнению, аппроксимированному с помощью
согласованной схемы, устойчивость является необходимым и
достаточным условием сходимости.
Теперь кратко определим согласованность и устойчивость.
Более строгие определения можно найти, например, в книге Рихт-
майера и Мортона (1967).
В общем виде уравнение (2.6.1) записывается
(-|- + L)f = 0, (2.6.3)
43

схема (2.6.2)
Л,/? + 1 + Ло/? = 0, (2.6.4)
где Ai и Ло — два разностных оператора, определяемых в данной
задаче следующим образом:
Л,Ь = //, = /,,
Aofi = [-/ + M (А А°х - v A«)] U; (2.6.5)
при этом / — есть единичный оператор и
дxfi = 2 л* (^ +1 — f ' - О»
àxxfi = -др- (ft +1 - 2/, + U - ,). (2.6.6)
Согласованность означает, что любое регулярное решение
(2.6.3) должно удовлетворять (2.6.4) с ошибкой, стремящейся
к нулю при Ал:, Д/->0. Эта ошибка называется аппроксимацион-
ной ошибкой и определяется с помощью выражения
8 = -±r[Alf(ibx9 (п + I) At) + A0f (i Ах, пМ)1 (2.6.7)
где / — регулярное решение уравнения (2.6.3). Согласованность
означает, что
|<Г| —О, когда Дх-^0 и А* — 0. (2.6.8)
Практически исследование согласованности выполняется путем
разложения в ряд Тейлора около точки /Да:, nAt.
В нашем случае
Л,/(/А*, (п+ l)At) = f + At 4L + -^L-g- + О (Д/3),
Ло/(/Дх, nbt) = -f + Abt[2L+ Ajf *{ +Q(As4)]-
-'4£-+J£~£-+°M-
Отсюда
® ~Vdf +Л дх v dx» J+ 2 dt* +
Первый член в правой части этого выражения равен нулю,
поскольку / есть решение (2.6.1). Ошибка аппроксимации имеет
порядок О (At, Ах2); поэтому схема согласована, и говорят, что она
первого порядка точности по времени и второго порядка по
пространству. Определение устойчивости, используемое в этой книге,
44

заключается в том, что если начальные данные, связанные с
уравнением (2.6.3), разложены в ряд Фурье по пространственной
координате так, что
оо
f(x> 0)= S F°(k)exp(ikx)9 где i = V^T, (2.6.10)
то любая компонента Fn+i(k), вычисленная по схеме (2.6.4), не
должна расти со временем.* Рассмотрим одну компоненту (2.6.10).
Конечно-разностное уравнение (2.6.4) допускает решение вида
fi = Fn (k) exp (i kl Ax), (2.6.11)
так что численное решение, аппроксимирующее точное решение,
может быть записано в виде
оо
f1= £ Fn(k)exp{ikiAx), (2.6.12)
k = — оо
где F0 задано по (2.6.10). Устойчивость означает, что |/7n(é)[
остается ограниченным для любых k и п-+оо. Вводя (2.6.11)
в (2.6.4), получаем выражение
giFn + x + goFn = 0
или
Fn + * = gF\ где £ = -=^- кгФО). (2.6.13)
Коэффициент g называется множителем перехода. Из (2.6.13) мы
получаем, что Fn+i = gn+iF° (где индекс п+\ в g есть показатель
степени). Поэтому условием устойчивости (условие фон
Неймана**) является
Ы<1 (2.6.14)
для любых значений k Ах, таких, чтобы 0^kAx^2n.
Вместо того чтобы проводить анализ множителя перехода g,
соответствующего схеме (2.6.2), мы исследуем устойчивость более
общей двухуровенной трехточечной схемы, аппроксимирующей
уравнение (2.6.1). Эта схема записывается в виде
aifïtl + aofl + l + a^fill = axfUx + a<>f? + a_if?_i, (2.6.15)
где коэффициенты a/ и a/ должны удовлетворять условию
(a, + a0 + a_,) — (a, + a0 + a_ô = 0,
выражающему тот факт, что в уравнение (2.6.1) входят только
члены с производными. Не теряя общности, мы можем положить
ai + a0 + a_, = a, + а0 + a_, = 1. (2.6.16)
* Точнее, существует ограничение на рост этих компонент; допустимым
обычно считается рост не быстрее конечной степени 1/Ал: при Ал:—>■ 0.— Прим.
перев.
** Собственно условием фон Неймана является |g|^l + 0(Af).
45

(2.6.17)
Вводя (2.6.11) в (2.6.15), получим выражение для множителя пе*
рехода
1 — (ai + fl-i) + (fli + a-i) cos kàx + i (ai — a-i) sin k Ax
^ 1 — (ai + a_i) + (ai + a_i) cos/e A* + i (ai — a_i) sin/г àx
После преобразований
i 12 * i vT {В' -B)X + C -С I
где
X = -9-0 — cos k Ах), В = 16a,a_i,
C = 4[(a1~a_I)2-(ai + a-i)],
В' = 16a,a _„ С7 = 4 [(a, — a_i)2 — (a, + a_,)].
Условие |g|^l выполняется тогда и только тогда, когда
(В' — В)Х + С' — С^0 для 0<Х<1,
что достигается, если
(С'-С)>0, ß'-ß + C'-C^O.
Эти условия, выраженные через коэффициенты (2.6.15), имеют
вид:
(ai — a-02 — (ai — a-xY — (a{ + a_i — a, — a_,) >0,
4 (djct-! — aja-i) + (cti — a-j)2 — (a{ — a-x)2 —
— (ai + a_, — a, — a_,) > 0. (2.6.18)
В частности, для схемы (2.6.2) мы имеем
(Xi = 0, a0=l, a_i = 0,
A А/ . v M
ai~" 2 àx "T" Ax2 '
2vA/
a0= 1
a_,=-
Ajc2 '
Л A/ . vA/
2 Ал: ~ A*2
Условия (2.6.18) в этом случае имеют вид
-^-<1 и -|£-<1. (2.6.19)
Если ввести сеточное число Рейнольдса R=AAx/v, то условия
(2.6.19) можно записать в виде
S<^- и S<4-' (2-6-20)
46

где S = v At/Ax2. Область устойчивости изображена на рис. 2.6.1
(область устойчивости лежит ниже кривой 1).
Отметим, что если S = 72, то схема (2.6.2) идентична методу
Якоби для решения алгебраической системы, получающейся из
разностного уравнения
AA°xfi-ViAxxfi = 0.
(2.6.21)
N
0,25V
\
\
\
\
\
/ S=f/2,S=2/R2
2 S = /(2+\R\)
3 Условие КФЛ, S<f/\R\[cM.(26.25)]
2 |y?| = M|Ax/v
Рис. 2.6.1. Кривые устойчивости для условий
(2.6.20) и (2.6.24) в плоскости (|/?|, 5).
Из рис. 2.6.1 видно, что если 5 = 72, то |#|^2, и это есть не что
иное, как условие диагонального преобладания для матрицы
системы (2.6.21).
2.6.1. Эффект неустойчивости
Положим, что вычисления производятся по схеме (2.6.2) и
значение Ах задано. Если значение At выбирается так, чтобы условие
(2.6.19) выполнялось, то получаемые результаты правильны
и ошибка численного решения имеет порядок ошибки
аппроксимации. Если же At выбрано слишком большим, так, что условие
(2.6.19) не выполняется, то численные результаты будут
осциллировать, причем рост этих осцилляции будет очень быстрым. После
некоторого числа временных шагов их амплитуды станут так
велики, что ЭВМ зарегистрирует «переполнение». Это явление
характерно для неустойчивости.
2.6.2. Схемы с нецентрированными разностями
Первое из условий (2.6.19) показывает, что для фиксированных
значений А допустимый шаг по времени тем меньше, чем меньше
значение v. Отсюда вытекает, что схему с центральными разно-
47

стями по пространству, описываемую уравнением (2.6.2),
затруднительно применять в случаях, когда v/A2 слишком мало, и
невозможно использовать вообще в случае уравнения адвекции (v =
= 0).
Одна из возможностей решения задачи заключается в отказе
от применения центрально-разностной аппроксимации для
производной первого порядка. С этой целью направление разности
определяется в зависимости от знака А. Предположим, что v = 0.
Уравнение (2.6.1) превращается в чисто адвективное уравнение,
и его общее решение есть f = y(f — At), где ср — произвольная
функция (определяемая начальными условиями).
Вид точного решения показывает, что / остается постоянной
вдоль характеристических прямых х — At = const, так что в
фиксированную точку (х, t) информация приходит по определенному
направлению, характеризуемому значением А. Поэтому при Л>0
информация распространяется в направлении х>0. Отсюда легко
понять, что в этом случае следует использовать разность,
направленную назад.
Если Л<0, информация распространяется в направлении x<0
и следует использовать разность, направленную вперед. Такая
аппроксимация называется направленной против потока
разностью.
Простейшая нецентрированная разностная схема для
аппроксимации (2.6.1) может быть записана в виде
-^r(fr1-/?) + -2^r[(l-e)(f?+,-f?) + (14-e)(f?-f?_,)]-
- -EP" (tf +1 - 2tf + ft- 0 = 0. (2.6.22)
где 8 = sign(i4). Эта схема является частным случаем общей
схемы (2.6.15), поэтому критерий устойчивости для нее выводится
из условий (2.6.18). В этом случае мы получаем только один
критерий
Л* = 0 *f , . , (2.6.23)
2v + Ал: | А | v '
или, вводя сеточное число Рейнольдса \R\:
vAt ^ 1
(2.6.24)
Область устойчивости располагается ниже кривой 2 в плоскости
(\R\, S) на рис. 2.6.1. Если v = 0, то критерий (2.6.23) принимает
вид
A'<-jT|- (2-6'25)
и называется условием Куранта—Фридрихса—Леей (КФЛ) и
является характеристикой явной дискретизации гиперболического
48

уравнения (Курант и др., 1928). На рис. 2.6.1 область устойчиво
сти для этого случая лежит ниже кривой 3.
Из (2.6.23) мы видим, что схема (2.6.22) не
чивой, если условие КФЛ не выполняется. На
различные области устойчивости в плоскости
= |Л|Д//Дл:, которая является более удобной
чем плоскость (|/?|, S) в случае, когда v->0.
вости I и II (см. рис. 2.6.2) получены из
и (2.6.23) соответственно.
может быть устои-
рис. 2.6.2 показаны
S = vA//Ax'2, \Т\ =
для рассмотрения,
Области устойчи-
условий (2.6.19)
Рис. 2.6.2. Кривые устойчивости для
условий (2.6.20) и (2.6.23) в плоскости
(m. S).
0,5
Условие (2 6 20)
H
«4
ч
\
\\ '
\°сЯ
^
\<г
ЧА
\
// \
\
N
\
\
\
\
N
N
|r|=|A|Ät/lJ-
'/*
Аналогично тому, как это было сделано в п. 2.3, мы можем
ввести схему взвешенных направленных против потока разностей.
Для уравнения (2.6.1) такая схема записывается в виде
At
Ajc2
.(f?+1-2f? + f?_,) = 0,
(2.6.26)
где a — произвольная константа. Если а = е =sign (Л), мы
возвращаемся к схеме (2.6.22); если а = 0, мы получаем схему с
центральными разностями (2.6.2). Условия устойчивости
2v А/ , л M ^ л
2vAt
Ajc2
Ад:2
-Л2
и2
Ajc2
Ajc
+ аЛ
Ajc
>0.
(2.6.27)
Если аЛ>0, то первое условие (2.6.27) подразумевает, что
аА àt/Ax^l, второе условие (2.6.27) выполняется автоматически.
Ошибка аппроксимации, связанная со схемой (2.6.26), равна
A/ d2f Ajc
аЛ
d2f
так что член с Ах имеет диссипативный характер, если аЛ>0.
49

Схема взвешенных разностей представляет интерес потому, что
она устойчива и при малых значениях v, а ее ошибка
аппроксимации может быть минимизирована за счет выбора такого
значения а, что a = Ysign (А), где 0<7<1.
Рассмотренные явные схемы легко реализуются, но условия
устойчивости накладывают определенные ограничения, особенно
тогда, когда коэффициент диффузии v мал. Эти ограничения
могут быть несколько уменьшены при использовании схем с
разностями против потока. Однако в этом случае точность по
пространственной координате уменьшается, за исключением случая
использования трехточечных нецентрированных разностей [типа (2.1.4а)
и (2.1.46)]. Использование таких разностей возможно, но при
этом возникает необходимость специального рассмотрения
дополнительных граничных условий.
Ниже, при рассмотрении схем для нелинейных параболических
уравнений, мы увидим, что можно построить явную схему второго
порядка точности как по пространству, так и по времени с
критерием устойчивости типа КФЛ и для v->0. Однако в качестве
следующей мы рассмотрим схему, которая часто используется для
нахождения стационарного решения задачи: схему центральных
разностей Дюфорта—Франкела. Эта явная схема обладает
хорошими свойствами устойчивости.
2.6.3. Центрально-разностная схема Дюфорта—-Франкела
Эта схема является трехуровенной по времени и для уравнения
(2.6.1) записывается в виде
ТдГ W —fi )+ ТАГ V* + 1 ~~ '1 - l) "~
--5?-[/7+i-(f? + I + /rI) + f7-i]-0. (2.6.28)
Легко видеть, что эта схема — явная, но не является
согласованной с исходным уравнением (2.6.1). Схема (2.6.28) может быть
записана в виде
ТАГ"' ""'' >>+ТАГ^ + 1~'''-1>,~~
-^(f7+i-2f7 + f?-i) + -5Jr(f? + I-2f? + f?-1) = 0. (2.6.29)
Последний член в (2.6.29) аппроксимирует выражение,
содержащее производную по времени:
v M2 d2f
Д*2 dt2 '
Поэтому схема (2.6.28) согласована с (2.6.1) лишь в том случае,
когда v At2/Ах2-* О при Д/->-0 и Ах-^0. Исследование
устойчивости схемы (2.6.28) осложняется тем, что она содержит три уровня
по времени. Эта схема не является частным случаем общей схемы
50

(2.6.15). Для исследования устойчивости рассмотрим решение
f1l = Fnexp(ukAx). Из (2.6.28) получаем
(1 + 2S) Fn + 1 — 2 (2S cos k Ах — i Т sin k Ах) Fn — (1 — 2S) Fn~l = 0.
Полагая, что Fn+l = gFn = g2Fn-\ получаем квадратное уравнение
для множителя перехода g:
(1 + 2S) g2 — 2 (2S cos A Ax — i Г sin £ Ax) g — (1 — 2S) = 0. (2.6.30)
Это уравнение можно получить и другим способом (см.
приложение А). Условие устойчивости требует, чтобы корни g
уравнения (2.6.30) удовлетворяли неравенству: |g|<;l для О^&Дл;^
^2я. Можно показать (используя теорему из приложения Л), что
устойчивость схемы Дюфорта—Франкела имеет место, если
выполняется условие КФЛ: [Tl^l. Таким образом, устойчивость
схемы не зависит от вязкости.
2.7. Решение одномерных нелинейных параболических
и гиперболических уравнений
Рассмотрим теперь конечно-разностные методы решения
уравнения вида
■з-ч-^—а--«. <"•■>
где v = const>0. Если v = 0, то уравнение (2.7.1) становится
гиперболическим и удовлетворяет закону сохранения:
4 + ^ = 0- (2-7-2)
В этом случае решение (2.7.2) допускает разрывы (слабое
решение). Если эти разрывы удовлетворяют неравенству, называемому
условием энтропии (Олейник, 1957; Лаке, 1957), то слабое
решение задачи с начальными условиями для —оо<[л:< + оо является
единственным. Более того, доказано (Олейник, 1957), что, если
v->0, то решение задачи (2.7.1) с некоторыми начальными
условиями стремится к слабому решению уравнения (2.7.2) с теми же
самыми начальными условиями.
Поэтому если v мало, то решение уравнения (2.7.1) будет иметь
тот же самый вид, что и решение уравнения (2.7.2) вне области,
примыкающей к границе. Например, в случае сжимаемой вязкой
жидкости, когда число Рейнольдса велико, в основном потоке
могут существовать узкие области с очень большими градиентами.
Если жидкость невязкая, эти области будут представлять собой
ударные волны, т. е. разрывы решения. Если же вязкость мала,
но не равна нулю, то толщина области с большими градиентами
настолько мала, что не может быть описана с помощью конечно-
разностной сетки и численное решение для вязкой жидкости
ведет себя подобно решению для идеальной жидкости. Поэтому
численная схема, предназначенная для решения уравнения (2.7.1)
51

с малыми значениями v, должна быть приспособлена к расчету
разрывных решений. По этой причине методы, обычно
используемые для решения (2.7.1), представляют собой не что иное, как
обобщение методов решения уравнения (2.7.2). Если v не мало,
так что решение является вязким всюду, могут применяться
методы, изложенные в п. 2.6. Схемы, рассматриваемые ниже,
относятся к решению одного уравнения, однако они могут быть без
труда распространены на системы уравнений.
2.7.1. Методы решения уравнений при отсутствии вязкости
Здесь мы кратко изложим некоторые явные схемы для решения
уравнения (2.7.2), в котором не учитывается вязкость. Вначале
прокомментируем методы первого порядка точности как по
пространственной координате, так и по времени. Эти методы основаны
на нецентрированной аппроксимации производной. К ним
относятся схемы направленных против потока разностей (Курант
и др., 1952), которые были описаны в п. 2.6, а также
мажорантные схемы, являющиеся обобщением схем направленных против
потока разностей на случай систем уравнений. Предположим, что
(2.7.1) есть гиперболическая система, так что все собственные
числа матрицы A (f) =dG (f)/df действительны. Матрица А (/)
может быть тогда представлена в виде суммы двух матриц A+(f)
и A~(f)y собственные числа которых все неотрицательны и все
неположительны соответственно. Схема разностей назад
используется затем для аппроксимации производной, относящейся к
матрице Л+, а схема разностей вперед — для аппроксимации
производной, относящейся к матрице А~. Мажорантные схемы для
уравнений, записанных в неконсервативной форме, были
предложены и исследованы Анучиной (1964), Яненко и Шокиным (1969).
Эти схемы были исследованы Уормингом и Бимом (1978) и Сте-
гером и Уормингом (1981) применительно к уравнениям,
записанным в консервативной форме.
Среди других методов первого порядка отметим схему Лакса
(1954), которая была одной из первых схем, позволившей
описывать разрывы. Лаксом и Вендрофом (1960) было показано, что
разрывные решения могут быть рассчитаны без специального
рассмотрения разрывов, если дифференциальное уравнение
рассматривается в консервативной форме (2.7.2) и если схема
консервативна.
Говорят, что двухуровенная явная схема консервативна, если
она имеет вид
f?+'ef7—£L[//(f?+/, .... f?_l+l)-H(f1+i-u .... /?-,)].
(2.7.3а)
где H — функция 2/ аргументов, каждый из которых должен для
согласованности удовлетворять условию
M(f, ..., f) = G{f) для любого /. (2.7.36)
52

Здесь описываются только такие схемы (улавливающие скачки).
Мы отсылаем читателям к книгам Рихтмайера и Мортона (1967)
и Моретти (1974) для ознакомления с методами (выделения
скачка), в которых ударные волны рассматриваются специальным
образом при явном использовании условий Рэнкина—Гюгонио.
Метод второго порядка точности для решения уравнений
невязкой жидкости был предложен Лаксом и Вендрофом в 1960 г.
Эта схема получается при использовании разложений в ряд
Тейлора по времени до членов третьего порядка, т. е.
f(x, t + M) = f(x, t) + ^M + ±-^-At2 + 0(M>). (2.7.4)
Производные df/dt и d2f/dt2 вычисляются с использованием
исходного уравнения (2.7.2)
df dG
dt = дх '
ô2f __ d2G __ д ( dG \_
dt2 ~~ дх dt ~~ " дх \ dt У
__ à (dG df\_ д (Лт dG\
~ дх \ df dt )— dx V4'' dx J*
Если эти выражения подставить в (2.7.4) и аппроксимировать
производные центральными разностями, мы получим схему Лакса—
Вендрофа:
+ ^г[Л?+.,.(0?+,-0?)-А"--/.(0?-0?-,)], (2.7.5)
где Ап определяется соотношением
Заметим, что схема (2.7.5) является частным случаем общей схемы
консервативной формы (2.7.3) при /=1 и
H (a, ft) = 4-[0(a) + 0(ft)]-^^(-i^)[0(a)-0(ft)].
Устойчивость такой схемы исследуется в предположении, что
A (f) = const. Тогда критерий устойчивости есть условие КФЛ:
И(/)|-^-<1. (2.7.6а)
В случае когда уравнение (2.7.2) является векторным, (2.7.6а)
заменяется на следующее условие:
1Ы/)|-£Г<1, k=l, ..., m, (2.7.66)
53

где Xk — собственные числа матрицы A(f). Это последнее
условие может быть представлено в геометрической форме: область
зависимости решения разностного уравнения должна содержать
в себе область зависимости решения дифференциального
уравнения (2.7.2).
В случае когда (2.7.2) есть векторное уравнение, схема (2.7.5)
требует вычисления матриц Л и At_ïf. Для того чтобы этого
избежать, Рихтмайер (1962) предложил двухшаговый вариант
схемы Лакса—Вендрофа. Такая модификация, которую часто на-
uê^rj
LÊA£J
п+1
/i+a-- Q г— о Ьт
Рис. 2.7.1. Положение узлов
вычисления предиктора fi.
зывают двухшаговой схемой Лакса—Вендрофа, в одномерном
случае при i4=const идентична исходной схеме (2.7.5). После
Рихтмайера было предложено еще несколько двухшаговых схем.
Схема, предложенная в 1969 г. Мак-Кормаком, получила
широкое распространение, поскольку она проста и обладает
некоторыми свойствами, полезными для расчета ударных волн.
В 1973 г. Лера и Пейре (1973b; 1974b; 1975) предложили
обобщение этих двухшаговых схем. А именно, они построили общий
вид схемы из класса схем со следующими свойствами:
1) явная консервативная схема;
2) двухшаговая, типа предиктор—корректор-,
3) трехточечная двухуровенная (решение /"+1 зависит от трех
значений / на уровне п)\
4) второй порядок точности по времени и пространству.
Схемы, обладающие всеми этими свойствами, образуют общий
класс схем, зависящих от двух параметров а и ß. Эти параметры
характеризуют положение точки, в которой вычисляется
предиктор fi (рис. 2.7.1). Эти схемы, обозначаемые S«, имеют
следующий вид:
fi = (l-ß)/? + ßf?+i —a-^r(0?+i—ОТ),
д<
.[(o-ß)G?+, + (2ß-l)G? +
/п + 1 рП
1 ~1' ~ ' 2а Д*
+ (l-a-ß)G?_, + G,-G,_,],
(2.7.7a)
(2.7.76)
где Gi= G (fi), афО.
54

Второй шаг (2.7.76) может быть записан в более удобном для
вычислений виде
^+1 = T^1-PHl-a-ß)/f_, + [2ß(l-ß)-a(l-2a)]/?-
-ß(o-ß)/?+,-(l-a-ß)fi_I + (o-ß)f*}--§^r(ö,-Ö<_,),
(2.7.76')
поскольку при этом не требуется хранение или перерасчет б™.
Отметим, что для схем (2.7.7а) и (2.7.76) соответствующая
функция Я, входящая в (2.7.3), такова, что /'= 1 и
Н{а, &) = -^L[(a-ß)G(a)-(I-a-ß)G(e)] +
+ -±-G{ßfl + (l-ß) &-а4гС°(«)-<? (*)]}'
В ллнейном случае, если A =dG/df = const, легко убедиться,
что все схемы Sa идентичны схеме Лакса—Вендрофа (2.7.5), где
^?+v* ==^£-1/2 =^' так что Условием устойчивости является (2.7.6).
Все конечно-разностные схемы, обладающие четырьмя
вышеуказанными свойствами, относятся к классу S^-схем. Если же
a = ß = V2, то предиктор вычисляется в центральной точке сетки:
это есть двухшаговый вариант схемы Лакса—Вендрофа,
предложенный Рихтмайером (1962). Если a=l, ß=72, мы получим
схему, предложенную Рубиным и Бёрстейном (1967). Более общие
схемы S* были рассмотрены Мак-Гиром и Моррисом (1973).
Схемы, соответствующие а=1 и ß=0 или ß = l, являются
двумя вариантами схемы Мак-Кормака (1969). Если ß = 0,
предиктор /; определяется в точках Xi = iAx и вычисляется с
помощью схемы разностей вперед, а fnt+i — с помощью разностей
назад. Если ß = l, // определяется в точках xi= (i+l)Ax и
вычисляется с помощью схемы разностей назад, а величина /^+1 — с
помощью разностей вперед.
Класс схем S<* и S« был рассмотрен Уормингом, Катлером
и Ломэксом (1973). Численные эксперименты (Лера и Пейре,
1973а, 19746, 1975) показали, что различные S«-схемы дают
неидентичные результаты, в частности, в случае ударных волн.
Некоторые из этих схем дают профили ударной волны с сильными
осцилляциями, другие — более регулярные профили, в некоторых
случаях — монотонные. Такие различия в поведении численных
решений появляются только в нелинейных случаях, поскольку при
A (f) = const все схемы идентичны.
Простой способ сравнения свойств различных схем состоит
в анализе так называемого «эквивалентного уравнения». Для
численной схемы, которая аппроксимирует дифференциальное
уравнение (2.7.2) с ошибкой р и о = At/Ах порядка единицы,
эквивалентным уравнением порядка q будем называть дифференциаль-
55

ное уравнение, которое аппроксимируется той же самой схемой,
но с ошибкой порядка qy где q>p. Следует ожидать, что схема
даст результаты, более близкие к решению эквивалентного
уравнения, чем к решению исходного уравнения.
Для получения эквивалентного уравнения вначале применяется
разложение разностного уравнения в ряд Тейлора аналогично
тому, как это делается при определении ошибки аппроксимации.
Затем производные по времени в членах, связанных с ошибкой,
исключаются путем замены их выражениями, которые
получаются повторным дифференцированием разложения * (подробнее
см.: Уорминг и Хайет (1974), Лера и Пейре (1975)).
В случаем схем (2.7.7а), (2.7.76) эквивалентное уравнение
третьего порядка запишется в виде**
dt ' дх 6 дх |/ ' дх2 2а df дх vr'
- aoG) -А. [(р - 1) f - aoG] + 2а2 J^-(-*L-)2}, (2.7.8)
где g Ах = ht. Теперь, если мы рассматриваем численнные
результаты, получаемые с помощью схемы, как аппроксимацию точного
решения дифференциального уравнения (2.7.8) с начальными
условиями исходной задачи, то изучение свойств уравнения
(2.7.8) должно дать информацию относительно поведения
численного решения. Такое изучение будет выполнено с целью
сравнения свойств различных схем Sa. Например, предполагая, что
G(f)=/2/2, получим эквивалентное уравнение (2.7.8) в виде
г-+-е-(4-)-^[«.-й-«.-г-э-+*(*л- <2-7-9>
где
Et = -±[(3-a)if + {2»-l)x\ + ß(1~ß) -l],
£, = -£[2(2-a)Ti + 2ß-l].
Теперь мы можем выполнить эвристическое изучение свойств
уравнения в частных производных (2.7.9) путем рассмотрения
* Т. е. рассматривается первое дифференциальное приближение с
исключением производных по t порядка выше первого. О классификации схем на
основе дифференциального приближения см.: Яненко Н. Н., Шокин Ю. И., Ту-
шева Л. А., Федотова 3. И. Классификации разностных схем одномерной
газовой динамики методом дифференциального приближения.— Численные методы
механики сплайных сред. Новосибирск, 1980, т. 11, № 2, с. 123—159; Яненко H.H.,
Шокин Ю. И, Компанией Л. А., Федотова 3. И. Классификация разностных
схем двумерной газовой динамики методом дифференциального приближения.
Препринт № 19—82, Институт теоретической и прикладной меахники, СО АН
СССР, 1982.— Прим. перев.
** См. работы Лера и Пейре (1974в, 1975) по общим гиперболическим
системам и приложениям к задачам газовой динамики.
56

тех эффектов, которые создают члены с четными и нечетными
высшими производными. Член Т\=Е\дъЦдхъ имеет дисперсионный
характер и приводит к дисперсионным осцилляциям в численном
решении. Если G(f)=Af, ^=const, то член Т\ является
единственным, который следует сохранить в правой части
эквивалентного уравнения. Это имеет место для всех 5^-схем. Член Т2 =
= —Е2 (gj)(gjr) может рассматриваться как диссипативный член
при E2(f)-~<.0 и антидиссипативный — при Е2 (f)—т~>0.
Таким образом, в зависимости от знака E2df/dx этот член может
оказывать положительное влияние путем демпфирования
возможных колебаний, создаваемых дисперсионными членами, или
отрицательное влияние, усиливая колебания. Дифференциальный
порядок третьего члена Es(df/dx)3 ниже дифференциального
порядка двух предыдущих членов, и поэтому эффект третьего члена
вообще незначителен, что было проверено с помощью численных
экспериментов.
В случае волны сжатия или ударной волны (df/dx<iO) схема
диссипативна, если £2>0. В случае же волны разрежения
(df/dx>0) схема диссипативна, если Е2<.0. Следовательно,
невозможно построить схему с хорошими диссипативными
свойствами для всех возможных случаев. Однако оптимальная схема
может быть определена с помощью следующих условий:
а) Е2 ^ 0 для любого ц из промежутка — 1 ^ ц ^ 1 ;
б) Мах (Е2) — минимален.
Условие «а» означает, что схема диссипативна для любой волны
сжатия или ударной волны, условие «б» — что эффект
положительности Е2 является слабейшим из возможных.
Единственной системой (а, ß), удовлетворяющей одновременна
условиям «а» и «б», является
Такая оптимальная схема дает профиль ударной волны с весьма
незначительными фиктивными колебаниями или даже без
таковых, когда дисперсионная ошибка Т\ достаточно мала, например,,
если ö = At/Ax выбирается так, что crmax|/| = l. Кроме того»
вследствие условия «б» скачок уплотнения размазывается по
минимальному числу узлов. Численные эксперименты показывают,
что для различных схем класса S« амплитуда колебаний остается
ограниченной даже в том случае, если схема не всюду
диссипативна в смысле (2.7.9). Для этих схем слабая неустойчивость,
возникающая за счет антидиссипативного члена 72, по-видимому,
балансируется эффектом члена
r4=-^-Gf(ö2f-l)-g-,
57

который появляется в эквивалентном уравнении четвертого
порядка. Это предположение подтверждается при сравнении
эквивалентных уравнений, соответствующих схеме Лакса—Вендрофа
(2.7.5) (где G=f2/2) и схеме центральных разностей по времени:
где о = At/Ах. Для обеих схем эквивалентное уравнение (2.7.9)
одно и то же, причем
^=-6^-^ £2 = -4(Зл2-1), £3 = аг1.
Однако для схемы с центральными разностями по времени
эквивалентное уравнение четвертого порядка не содержит члена
Г4, в то время как в схеме Лакса—Вендрофа он присутствует. Это
обстоятельство может дать ответ на вопрос, почему схема
центральных разностей по времени неустойчива в нелинейном случае.
По поводу других подходов к анализу неустойчивости в
нелинейном случае см. Рихтмайер и Мортон (1967), Крейс и Олигер
(1973).
Наконец, следует отметить, что наличие диссипативного члена
74 может также объяснить способность устойчивых схем S"
отбирать слабое решение, удовлетворяющее условию энтропии. Более
глубокое исследование свойств конечно-разностных схем,
основанное на анализе эквивалентного уравнения, можно найти,
например, в работах Хёрта (1968), Яненко и Шокина (1969), Уорминга
и Хайета (1974), Хартена и др. (1976), Лера и Пейре (1975),
Пейре (1977), Лера (1981).
На практике часто бывает необходимо добавить член с
искусственной вязкостью к какой-либо из схем, описанный выше. Такой
член может быть необходим: а) для выбора решения,
удовлетворяющего условию энтропии; б) для предотвращения
неустойчивости в нелинейном случае; в) для погашения фиктивных
колебаний в численном решении.
Концепция искусственной вязкости была введена фон
Нейманом и Рихтмайером (1950), разработана Лаксом и Вендрофом
(1960) и с тех пор используется в различных формах во многих
работах. В простейшем случае скалярного уравнения (2.7.2) с G =
=/2/2 введение искусственной вязкости по Лаксу—Вендрофу
заключается в добавлении к уравнению (2.7.5) или (2.7.76) члена
At/AxDi, где
D^-^tllfU^-flKn^-fD-ln-fi-Mîl-fl-dl
а % есть положительная константа порядка единицы. Тогда
условие устойчивости модифицированной схемы будет
.£.,„,<(,+-£-)*-?-
Это условие является более жестким, чем обычное условие КФЛ.
58

В рассматриваемом случае член с искусственной вязкостью
соответствует дискретной аппроксимации выражения
_LvAv2 д /1_Ф_
9
^-ê-d-s-i-s-).
которое представляет собой вязкий член типа
рассмотренного фон Нейманом и Рихтмайером. Для схем Sa с членом DL
эквивалентное уравнение (2.7.9) имеет тот же самый вид, за
исключением того, что член Е2 заменяется на член Е2, где
если^- < О,
если -^— > 0.
_ df дЧ
Член Т2 = —Е2—д—з~2~ не всегда имеет диссипативный характер,
если x>niax|£,2| для O^n^l. Далее будут рассмотрены и
другие способы гашения колебаний.
2.7.2. Методы решения уравнений при наличии вязкости
Двухшаговые явные схемы, которые аппроксимируют уравнение
с вязким членом типа (2.7.1) с ошибкой аппроксимации второго
порядка как по времени, так и по пространству, являются по
меньшей мере пятиточечными, а некоторые из них даже
семиточечными.
Таким образом, мы приходим к общему классу схем с
большим числом параметров. Однако если потребовать, чтобы эти
схемы не были существенно асимметричны по отношению к точке
Xi = iAx, число параметров может быть уменьшено. Если, кроме
того, рассматриваются только схемы, для которых второй шаг не
содержит значений fn и /*_2, мы получаем обобщение схем
(2.7.7а) и (2.7.76):
fi = si1) + va ^r [y (f?+2 - 2f?+1 + tf) +
+ (l-y)(ft+i-2f7 + f7-i)l (2.7.10a)
f? + l-SP> + -^|^[(2a-l)(/?+1-2f7 + /7_1) +
+ (l-fi)(f?+i-2fi + fi-l) + fi(fi-2fi-l + fi-2). (2.7.106)
В этих выражениях Si1) и S*® представляют собой соответственно
правые части уравнений (2.7.7а) и (2.7.76), т. е. «невязкую» часть
схемы. Правые части (2.7.10а) и (2.7.106) зависят от трех
произвольных параметров а, ß и у. Схемы такого вида будем
обозначать S" . К их числу относятся двухшаговые схемы Лакса—
Вендрофа ф = 7г) и схема Мак-Кормака (ß=0 и ß = l) при
условии 7==ß-
59

Пятиточечные схемы характеризуются условиями у(1—ß) =0,
(1—у) ß=0. Эти условия выполняются для схем S^0, Sati,
которые являются прямым обобщением «невязких» схем S<*, S^,
исследованных Уормингом, Катлером и Ломэксом (1973).
За.исключением этих схем, все остальные являются
семиточечными. Семиточечные схемы неудобны для решения краевых
задач, так как создаются трудности вблизи границ. Этот вопрос
будет более подробно рассмотрен позже.
В связи с такого рода трудностями, а также из-за того, что
часто возникает необходимость в отыскании лишь стационарного
решения уравнения (2.7.1), была предложена пятиточечная схема
первого порядка (At, Ах2) для нестационарного случая и второго
порядка (Ал:2) для стационарного (Томмен, 1966). Эта схема
явилась первым обобщением двухшаговой схемы Лакса—Вендрофа
Sl(j применительно к учету вязкости. Пятиточечные схемы,
обладающие указанными свойствами точности, обозначаются S*
и имеют следующий общий вид:
+ (l_Y)(f?+l-2tf+ /?-,), (2.7.11а)
/7 + 1 = S(/2)+v-gï-[/7+i-2/7 + /7-i]. (2.7.116)
Схема, предложенная Томменом (1966), была схемой S1/2V ,..
Схемы Sî/t, '/У2 и So, о или Sjj представляют особый интерес, так
как они обладают свойствами соответствующих невязких схем
и второй шаг (2.7.116) не включает вычисление вязкого члена
с fi. Это приводит к уменьшению времени счета и к увеличению
эффективности по сравнению с некоторыми другими схемами.
В связи со сложным представлением множителей перехода для
схем (2.7.10) и (2.7.11) точные критерии устойчивости неизвестны.
Однако численное исследование этих множителей возможно
и позволяет определить области устойчивости. На рис. 2.7.2а
и 2.7.26 изображены эти области для некоторых частных случаев
схем в плоскости R=AAx/v, S=v At/Ах2. Заметим, что обе схемы
(2.7.10) и (2.7.11) сводятся к схеме S" при v = 0, так что
критерий КФЛ есть необходимое условие устойчивости. В случае А=0
можно показать, что условие 2vA^A*2 является достаточным,
чтобы обеспечить устойчивость при v = ß и а^72. Для схемы
Томмена (a = ß=y = V2) точное условие устойчивости таково:
At(A2 At-\-2v) ^Ах2. Однако в качестве практического критерия
может быть использовано условие At^Ax2/(2v + \А \Ах) (см.
рис. 2.7.2а и 2.7.26).
Рассмотрим теперь параболическое уравнение
60

|/?|=H|Ax/v
Рис. 2.7.2a. Кривые устойчивости для схем (2.7.10)
(области устойчивости расположены ниже
кривых) .
/) a=ß=Y=-ö- (схема типа Рихтмайера), 2) а=1, ß=v=0
или 1 (схема Мак-Кормака), 3) a=l + V5/2, ß=—-,v—-5-
(схема Лера—Пейре), 4) условие КФЛ: 5=1/|/?|, 5)
условие (2.6.24): 5=1/(2+|/?|).
S=vAt/Ax'
2 R=ALx/v
Рис. 2.7.26. Кривые устойчивости для схем (2.7.10) и
(2.7.11) (области устойчивости расположены ниже кривых).
i —схема (2.7.10): а-1, ß=—. V=°. 2 — схема Томмена (2.7.11):
a=ß=Y=-r-, 3 — схема (2.7.11): а, ß — произвольные параметры,
4 -условие КФЛ: S-1/|Ä|, 5 - условие (2.6.24): S=l/(2+|/?[).

где v(/) — положительная функция от /. Это случай уравнений
Навье—Стокса для сжимаемой жидкости, когда вязкость зависит
от температуры. Если ввести фукцию G(f)
Q(f)**F(f)—»{f)-$r, (2.7.13а)
то уравнение (2.7.12) примет вид
df . dG
dt "*" дх
= 0, (2.7.136)
так что формально соответствующие численные схемы второго
порядка точности даются формулами (2.7.7а) и (2.7.76).
В этих схемах Gn. = G(f^) и Gi = G(fi) определяются
следующим образом:
мп
Gl^Fl—jir [(/?-/?_,) + y(fhi- 2/? + /?-,)], (2.7.14а)
ôi =U §- {(fi - f, -.) + [а + ( 1 - 2а) y] (ft +, - 2f, + fi -,)],
(2.7.146)
где Mn. и Mi являются аппроксимациями v (/) :
Ml= ._£ m/v(f?+/), Mi=XmjviJi+i). (2.7.15)
Константы m,- и m; должны удовлетворять условиям
Жт/=Дл=1 (2'7Л6а)
и
1 1 __
(2а-1) £ \Щ+ S М = 0. (2.7.166)
Отметим другой выбор величин М*\ и Mr.
который эквивалентен (2.7.15) с точностью до членов порядка
Д^2. Оба определения идентичны в случае, если v есть линейная
функция от /.
Схемы (2.7.14) являются пятиточечными тогда и только тогда,
когда а=1, ß произвольно, у = 0 или у = \. Среди таких схем
наибольший интерес представляют схемы Мак-Кормака с а=1, ß =
= 7 = 0, mi=m_i = 0, m-i = mj_= m0 = m0 = V2 или а=1, ß = Y=l,
m_1==/n1==0, m\ = m-i = m0 = m0 = V2. В этих случаях значения
в узлах локализуются симметрично по отношению к xi = i Ах
62

и точкам, в которых вычисляются окончательные значения. Это
обстоятельство устраняет некоторые из трудностей,
встречающихся при использовании схем вблизи границы.
Отметим, что при v = const схемы (2.7.10) и (2.7.14)
становятся идентичными при следующих условиях:
ч 1 о 1
а)а = -у, ß = —, у произвольно;
б) аф —, ß = a и y=1 или ß=l—а и у = 0-
Интересно отметить, что второй шаг (2.7.146) может быть
переписан в виде, аналогичном (2.7.76'), в то время как для схемы
(2.7.10) это возможно, если выполняются условия «а» и «б».
Таким образом, для уравнения (2.7.12) могут быть получены
пятиточечные схемы первого порядка точности в нестационарном
случае и второго порядка в стационарном случае, аналогичные
(2.7.11). Предварительное значение // на шаге — предикторе
определяется формулой (2.7.7а), в которой величина Gnt вычисляется
по формулам (2.7.14а), (2.7.15), (2.7.16а), а окончательное
значение }п+1 на втором шаге определяется по формуле
^ + 1 = ^_^L_[(a-ß)F?+1 + (2ß-l)F? + (l _a-ß)Ff_! +
+ h - F, _ ,] +-3&. [(v?+, + vf) (f4+, _ f?) _
_(v? + v?_,)(f?-/?_,)]. (2.7.17)
Отметим, что среднее значение ~(v/+i + v;) может быть
заменено на v[(f/+i + f/)/2].
2.7.3. О граничных условиях
При использовании многошаговых методов обычно возникает
проблема определения промежуточных значений вблизи границы.
Эта задача возникает и в случае метода расщепления (Яненко,
1971), когда конечно-разностное уравнение на каждом шаге не
согласуется с исходным. В неявном методе чередующихся
направлений, для которого имеет место согласование с исходным
уравнением на каждом шаге, также происходит рост ошибки
аппроксимации по времени в точках, примыкающих к границе (Фэйрвезер
и Митчелл, 1967), если точное зависящее от времени граничное
значение используется для определения предварительной
величины на границе.
Такое же явление возникает и при использовании некоторых
описанных выше методов типа «предиктор—корректор».
Рассмотрим, например, поведение схемы Мак-Кормака в первой точке
1=1 вблизи границы х=0у в которой значение функции известно:
63

f(0, /)=ф(/). Для вычисления f^+i необходимо знать /о. Если
используется граничное условие, т. е. если мы берем /0 =
= cp((n-\-l)At), ошибка аппроксимации в точке /=1 становится
порядка vAt/Ax, и эта потеря согласованности имеет место как
в нестационарном, так и в стационарном случае. Причина этого
заключается в том, что окончательная точность схемы
определяется как результат комбинации шагов предиктора и корректора.
Эта комбинация эффективна для определения значений во
внутренних точках, которые не содержат на шаге «корректор»
значений в граничных точках, получаемых из граничных условий. Такие
особенности имеют место главным образом в тех случаях, в
которых предварительные и окончательные значения определяются
в одних и тех же точках, поскольку появляется искушение
использовать граничное значение в качестве значения предиктора.
Для других схем, в которых ß=^0 или ß^l и которые подобны
центрированным (ß==-2~) схемам типа схемы Томмена,
предварительное значение /о не определяется на границе, а вычисляется,
как правило, с помощью модифицированного конечно-разностного
уравнения. Примером может служить использование (2.7.11а)
с 7 = 1, однако необходимо соблюдать осторожность при
вычислении значения fi (которое входит в расчет f^+1) с помощью той
же самой модифицированной схемы. Как было указано Ченгом
(1975), в методах, в которых оба шага соответствуют одному
и тому же конечно-разностному оператору, не происходит потери
точности. К числу таких схем можно отнести схемы Браиловской
(1965) и Аллена и Ченга (1970). В схеме Мак-Кормака благодаря
условию устойчивости, которое подразумевает, что vAt/AxœAxr
ошибка аппроксимации в точке /=1 становится порядка Ах,
В этом случае можно предположить, что разность между
численным и точным решением сохраняет порядок Ах2 всюду. Это
предположение, проверенное расчетами, основано на аналогичных
результатах, полученных Густафсоном (1975) для линейного
гиперболического уравнения.
Для линейного стационарного случая можно получить более
точные результаты. Рассмотрим стационарное решение уравнения
(2.7.1) для интервала 0<*<1 при граничных условиях /(0) = 1,
/(1)=0. Решение получено как предел при t-^oo численного
решения по схеме Мак-Кормака с предварительными значениями
вблизи границы, равными точным граничным значениям.
Конечно-разностная задача может быть решена явно так, как это было
изложено в п. 2.3. В предположении, что vAt/AxœAx, AAx/v<^lf
Дл:<^1, установлено, что ошибка численного решения имеет
порядок Ах2 всюду, даже вблизи границы, где ошибка аппроксимации
имеет порядок Ах. Этот результат находится в соответствии
с предложенной в общей теории Крейса (1972) оценкой скорости
сходимости численного решения краевых задач для обыкновенных
дифференциальных уравнений. Аналогичные результаты были по-
64

лучены Брамблем и Хаббардом (1962) при решении задачи
Дирихле для уравнения Пуассона.
Для схемы Мак-Кормака существует способ расчета, при
котором ошибка аппроксимации при любых условиях имеет второй
порядок малости. Этот способ заключается в вычислении
предварительного значения /0 путем использования либо схемы (2.7.10а),
модифицированной за счет применения нецентрированной
аппроксимации второго порядка для второй производной, либо схемы
(2.7.10а) при ß=0, Y = l- В последнем случае необходимо
вычислять окончательное значение fn+[ и соответствующие
предварительные значения /i и /2 с помощью этой же схемы при ß=0,
7=1. Отметим, что такой метод нельзя применить к уравнению
(2.7.12), аппроксимируемому схемами второго порядка (2.7.7а),
(2.7.76) и (2.7.146); за исключением случая, когда öt
определяется не с помощью (2.7.146), а по формуле
G^Ft
Ах
Такой метод приводит к первому порядку точности по
пространству. Другой эффективный путь решения основан на том, что два
варианта — при ß =7 = 0 и при ß = y = 1—имеют
противоположные по знаку главные части ошибок аппроксимации.
Таким образом, одновременно вычисляются два значения
^n+i,+ и ^и-1,- получаемые с помощью каждого из двух
указанных вариантов, окончательное значение определяется путем
осреднения fn+i = (fn1+1'++f?J+t'~)/2. Заметим, что два значения
предиктора, соответствующие этим двум схемам, должны быть
вычислены при 1 = 2.
Определенный произвол, существующий в описанных выше
классах схем, дает возможность применять к значениям в узлах
вблизи границы специальные подходы, позволяющие уменьшить
ошибку аппроксимации. Однако следует быть осторожным, чтобы
избежать потери устойчивости схемы на границе.
2.7.4. Неявные методы
Ограничения на шаг по времени, которые накладывают условия
устойчивости, относящиеся к явным схемам, часто бывают
слишком обременительными на практике, и поэтому все более
употребительными становятся неявные схемы, свободные от такого
ограничения. В случае одномерного линейного уравнения, как,
например, (2.7.1), можно записать двухуровенную схему
(/7 + ^ fi) + (Л Ag _ v Ахх) [9f7 + ! + (1 - 6) /?] = 0, (2.7.18)
часть ошибки аппроксимащ
[4-»№-■&■)]•
At
где 0^0^ 1. Главная часть ошибки аппроксимации равна
At д
65

Условия устойчивости имеют вид:
2(26—1)S+1>0, (26-1)T + 2S>0,
где S = 2v At/Ax2 и Т=А At/Ax. Эта схема представляет особый
интерес в случае 6 = 72 (схема Кранка—Николсона), поскольку
она имеет второй порядок точности и является безусловно
устойчивой. На каждом шаге по времени вычисления сводятся к
решению линейной алгебраической системы с трехдиагональной
матрицей.
Другой эффективной, безусловно устойчивой схемой второго
порядка точности является следующая трехуровенная схема:
-1^(3f7 + I--4f? + frl) + (ilAÎ-vA«)f7 + l=0. (2.7.19)
Как это было отмечено Рихтмайером и Мортоном (1967), такая
схема обладает лучшей способностью подавления
высокочастотных гармоник, чем схема Кранка—Николсона. Это свойство
может быть полезным в некоторых расчетах.
Обе схемы могут быть записаны в форме (называемой «Д»-
формой, см. Уорминг и Бим, 1978), которая особенно эффективна
при решении многомерных задач. Вводя оператор Ах =
=ЛД°,— vAxx и единичный оператор I, можем записать схему
(2.7.18) в виде
[/ + в ДГА,] А/? + 1 = -AtAxfl
f? + i-f7 + Af? + I.
Схема (2.7.19) запишется следующим образом:
[/ + ^л,]а/?+1==-~-^л^ + 4- Aft
f? + l = f? + Af? + l.
В литературе можно найти описания и других неявных схем для
линейных одномерных уравнений.
В случае нелинейных уравнений, представляющих для нас
основной интерес применительно к задачам механики жидкости,
если нелинейность рассматривается неявно, то возникает
необходимость использования итерационных процедур. Однако, по
возможности, следует избегать их применения.
Если член, описывающий вязкость, является преобладающим
по сравнению с нелинейным членом, неявность может быть
отнесена к вязкому члену. Для этого линейное уравнение (2.7.1)
может быть аппроксимировано с помощью центрально-разностной
схемы Кранка—Николсона:
_^_(f?+>_fr,)+A°xG?-^-Axx(f? + 4fr,) = 0. (2.7.20)
66

Эта схема имеет второй порядок точности как по времени, так и
по пространству и условием ее устойчивости является условие
КФЛ:
|Г| = |Д(/)|Д*/Д*<1,
где A=dG/df. Однако эта схема становится неустойчивой в
нелинейном случае, если v = 0. При этом возникают две
последовательности решений на сетках, что приводит к появлению осцилляции,
которые могут существовать также и при вязкости v, не равной
нулю, но не слишком большой, чтобы предотвратить
неустойчивость. Появление таких осцилляции, вообще говоря, можно
устранить путем осреднения численного решения через каждые 15—
25 шагов по времени. Возможным способом такого осреднения
в момент времени N At является, например, следующий (Орзаг
и Танг, 1979):
1) вычислить предварительное значение р[+1 в момент N+1
с использованием уравнения (2.7.20);
2) определить новое значение ff = -j (ff+1 + 2/f + fï~l) ;
3) вычислить новое значение f^+1 с использованием уравнения
(2.7.20), в котором fN заменено на ]**.
Такая процедура сохраняет второй порядок точности.
Другой схемой, которая может быть успешно использована
в случае, когда вязкость v слишком мала, является схема
Адамса—Бэшфорта—Кранка—Николсона:
-±-(fl+i-fl) + ^t№-Gr,)-^-^x(fl+l + fl) = 0. (2.7.21)
Схема имеет второй порядок точности, но неустойчива при v = 0.
Однако известно, что эта неустойчивость проявляется весьма
слабо. Такую схему рекомендуется применять в том случае, когда
v отлично от нуля. В аналитическом виде критерий устойчивости
для (2.7.21) использовать на практике неудобно, поскольку
характеристическое уравнение имеет комплексные корни. Однако
исследование, основанное на теореме Миллера (см. приложение А)
и на результатах расчетов, дает кривые устойчивости,
изображенные на рис. 2.7.3.
Схемы (2.7.20) и (2.7.21) являются условно устойчивыми.
Безусловная устойчивость может быть получена в том случае,
когда нелинейный член dG/dx вычисляется в момент времени
(tt-f 1)Д/ и затем линеаризуется обычным способом. Рассмотрим
нелинейные варианты схем (2.7.18) и (2.7.19), которые могут быть
записаны в виде
TS-[(l+e)(f? + l-f;) + (l-e)(f?-/?-')) +
(2.7.22)
67

Ошибка аппроксимации по времени имеет порядок [(29 — е)Д/,
Д/2], так что схема имеет второй порядок точности, по времени,
если 29 — e=0(àt). Схема (2.7.18) соответствует случаю е = 1,
а схема (2.7.19) —9 = 1, е=2.
Рассмотрим некоторые способы линеаризации схемы.
1. Если рассматривается уравнение в неконсервативной форме
dG/dx=A(f)df/dx, то может быть использована следующая
простая формула:
Область неустойчивости
Область устойчивости*
0,5 1,0 \Т\=\А\М/Ьх 1 2
Рис. 2.7.3. Кривые устойчивости для схемы (2.7.21).
J |Л>|=И| Алг/v
При этом, однако, второй порядок точности по времени
нарушается. Второй порядок может быть сохранен при линеаризации,
предложенной Линдематом и Киллином (1973):
/ dG у + 1 __
V дх
Г =№+'=№+"1МАМ+° <*<•>
№№)>[
dA df df
df dt дх
+ А
d*f
dxdt
-i
Аппроксимируя производные по времени с помощью
направленных вперед разностей, а пространственные производные с
помощью центральных разностей, получаем
(^)г ч^г ' ~ * *""'? * '+ш «+' -'»л;'"•
(2.7.23)
68

2. Если A(f) =Cf (С = const), то линеаризация
« Al AÎ/f + ' + Al * ' AÎf J - Al AÎf?
приводит ко второму порядку точности.
3. Для консервативной формы Брайли и Макдональд (1973,
1975), а также Бим и Уорминг (1976, 1978) предложили
следующую линеаризацию:
(^r=(-f?-)r+4<(w):+° <**'>• <»*■>
и окончательно
("fr)" + ' ж A°*G? + А°* IЛ? ^ + ' - AM' (2.7.24b)
Теперь, если (2.7.23) или (2.7.24в) подставить в выражение
(2.7.22), то получающиеся схемы с 6 = 72, е = 1 или 6=1, е = 2
имеют второй порядок точности и линейно безусловно устойчивы.
Однако применение метода факторизации к решению
соответствующей трехдиагональной алгебраической системы может
наложить некоторые ограничения на сеточное число Рейнольдса или
на шаги по времени (условие диагонального преобладания
матрицы). Например, условие диагонального преобладания для схемы
(2.7.22) с 8 = 7г, е = 1 и v = 0 имеет вид
(U?+i| + U?_1|)^<4.
Это условие вдвое слабее критерия КФЛ. Его можно не
принимать во внимание, если использовать другой способ решения
алгебраической системы, однако диагональное преобладание
должно иметь место, чтобы способствовать подавлению фиктивных
осцилляции при решении конечно-разностных уравнений.
4. Эффективная схема, которая приводит к матрице с
диагональным преобладанием без ограничений, была предложена Лера
(1979, 1981) для уравнений, не содержащих вязкости и
удовлетворяющих законам сохранения.
Этот метод нетрудно распространить на уравнения,
содержащие вязкость, если достаточно иметь только первый порядок
точности. Такую схему можно построить на основании разложения
в ряд Тейлора (2.7.24а). В (2.7.246) производная df/dt
выражается с использованием самого уравнения, т. е.
V dxdt ) дх V dt )~ дх L V дх дх* )У
69

Теперь, используя равенство dG/dx = Adf/dxy получим
Затем, чтобы не вводить третьи производные, пренебрежем вязким
членом в (2.7.25) и получим окончательное выражение
-5r0? + I-f?) + A°xOÎ—f-AH^AiG? + M?)2Ai/? + l]-
-^Axx(f'l + l + îl) = 0,
где Ai. _ fi + 42 — fi->/2
Л Л ( fi + 1 + fi
Л1 + Чг— Л\ 2
Ошибка аппроксимации по времени имеет порядок О (v At) и не
исчезает в стационарном случае. Второй порядок точности можно
восстановить, если сохранить вязкий член в (2.7.25) и определять
его на шаге я, но при этом теряется безусловная устойчивость.
В работах Лера (1979, 1981) вышеприведенная схема при v = 0
получена путем исследования общего класса неявных схем. В
заключение отметим, что, если функция G (/) обладает свойством
однородности, т. е. G(Xf) =XG(f) (как это имеет место в
уравнениях газовой динамики для идеального газа (см. Лера. и Пейре,
1974а; Бим и Уорминг, 1976; Уорминг и Бим, 1978), так что G =
=Afy то линеаризация (2.7.24в) дает
2.8. Многомерные уравнения
2.8.1. Явные схемы для адвективно-диффузионного уравнения
Рассмотрим двухмерное адвективно-диффузное уравнение
-w+A^-+Bw~ vv^=0' (2-8Л)
где Л, В и v (v>0) предполагаются постоянными.
Прямое обобщение явной схемы применительно к решению
уравнения (2.8.1) имеет вид:
^Г W+1' - fl /) + A A°xfl / + В A°yf?, / - v (Д„ + Ауу) fl j = 0, (2.8.2)
где fn . œf(iAx, j Ay, nAt) /, /, n — целые и
&xf i, j = 2Дл: (/« + ». / ~~ fl - !» /)»
(// + ../-2/,,, + /,_,,,),
70

Схема (2.8.2) имеет первый порядок точности по времени и
второй— по пространству. Для нее должен удовлетворяться
следующий критерий устойчивости*:
(H| + |ß|)2A*<4v,^<4-' где Д* = Ду.
Схема направленных против потока разностей, аналогичная
схеме (2.6.22), может быть записана для уравнения (2.8.1) в
следующем виде:
■irfàï ' - п, /)+4 к» -«л А*я '•+о +е») ^tf. /]+
+ -f-10 - ев) Л+f?, , + (1 + ев) А;/?, /] - v (Д« + A J ft ,• = О,
(2.8.3а)
где eA = sign(y4), eB = sign(ß) и
A* fi, / = -д^- (fi + I, / — fi, i),
bïfi.i=s-Zr(fi.i-ft-i.i).
&У fi,i = "д£~ (fi. /41 — fi, /),
Д» f/./ =-^-(/«./-f»./-i).
Если положить Дх = А«/, то критерий устойчивости для этой схемы
имеет вид
2.8.2. Неявный метод чередующихся направлений (метод ADI)
В тех случаях, когда предпочтение отдается неявным схемам
в связи с их свойством безусловной устойчивости, рекомендуется
выбирать те из них, которые приводят к решению трехдиагональ-
ных алгебраических систем (обычных — для скалярного
уравнения, блочных — для векторного уравнения). Неявный метод
чередующихся направлений (метод ADI — Alternaiting direction
implicit), предложенный Писменом и Рэчфордом (1955),
позволяет получать весьма эффективные неявные схемы. Этому методу
посвящено много работ, например статья Дугласа и Ганна (1964),
монография Яненко (1971) и Митчелла (1969).
* Здесь приведен один из возможных видов необходимого условия
устойчивости, следующий из ограничения на множитель перехода g схемы (2 8.2):
I g\ = {(l -4v ^4г)2 + (^-)2 И| + loi2}''2 < I.- Прим. перев.
71

Предположим, что Л и В в уравнении (2.8.1) не являются
постоянными, а зависят от переменной /. Метод ADI является двух-
шаговым и записывается в виде
-хгfr. / - fh) + (Л' А° - v А«) ^. I + (ßiд°* - v О /?. / = °>
(2.8.4а)
-S-(f "V - ^ /) + (^ А° - v A«) h. I + (В2 А° - v A J /?,+,' = О,
(2.8.46)
где Ль Л2, ßi, 5г — аппроксимации А и В. Значение предиктора
fi,j можно рассматривать как аппроксимацию точного решения
в момент времени (n + -x\At, если Ль Л2 и В\у В2 являются
аппроксимациями Л и В в соответствующие моменты времени.
Например, если требуется только первый порядок точности по
времени, то могут быть использованы простые выражения А\ =
= А2=А7}. и Bi=B2 = B" . Точность второго порядка
достигается в случае, когда Л и В — постоянны. Для точности второго
порядка по времени в общем случае соответствующими
аппроксимациями являются
Л, = CoAl+j! + (1 —со —с,) Al} + cxAnCi\
Л2 = (1 - со + сх + с2) Aï+j' + (со - d - 2с2) Al, + с2А^\
Вх = yoBl+j! +(1 — Vu —Yi) Bl i + Yiß"-/'.
B2 = (1 - Yo + vi + Y2) B7.V + (yo + Vi - 2Y2) ß?f / + У2В?~'1,
где Co, Ci, c2 и Yo, Yb V2 — произвольные параметры. Если c0 =
= Yo = 0, Ci + c2 = y\ + y2 = — 1, значения Л*+*, В"*1 не появляются
в уравнениях (2.8.4), так что оба шага (2.8.4а) и (2.8.46) не
связаны и могут быть решены раздельно. Если же шаги связаны друг
с другом, то необходимо использовать итерационную процедуру,
которая эффективна только при включении ее в глобальную
итерационную процедуру, как это делается при решении уравнений
Навье—Стокса для несжимаемой жидкости.
В случае когда Л и В — постоянные, можно показать, что
схема ADI безусловно устойчива. Однако следует помнить, что
при исследовании устойчивости не принимались во внимание
граничные условия и их наличие может нарушить безусловную
устойчивость (см. работу Бонту и др., 1978, посвященную
интегрированию уравнений Навье—Стокса).
Для решения трехдиагональной алгебраической системы на
каждом шаге (2.8Ла) или (2.8.46) можно применить, например,
метод факторизации. В этом случае условия диагонального
преобладания имеют вид
| Л, | Ajc/v < 2, |ß2|Az//v<2.
72

Если эти условия не выполняются, то ограничения,
накладываемые на шаг по времени
А*< . л .2лА*2 о » А^< , о^У 0 , (2.8.4b)
гарантируют диагональное преобладание.
Рассмотрим теперь кратко проблему граничных условий,
которая уже обсуждалась в п. 2.7.3. Предположим, что решение
ищется в прямоугольной области, границей которой является Г =
= riUr2 (Г1 и Г2 — части Г, параллельные осям у и х соответ-
ственно) с граничными условиями f(x, у, t)\ = ф(х, у, t). Для
решения алгебраической системы, соответствующей (2.8.4а),
необходимо иметь значения //,/ на IY Хотя Ji,j может рассматриваться
как аппроксимация точного решения, использование граничного
значения f/,/|г, =ср \х, у, (п + ^jAt\ приводит к большой ошибке
аппроксимации вблизи границы в случае, если ф существенно
зависит от t (Фейрвезер и Митчелл, 1967; Митчелл, 1969). Причина
этого объяснялась в п. 2.7.3. Лучший способ обойти эту трудность
заключается в определении граничного значения таким образом,
чтобы комбинация обоих временных шагов давала бы второй
порядок точности как в точках, примыкающих в границе, так и во
внутренних. Этого можно добиться, если значение //,/|
получать из самих конечно-разностных уравнений. Таким образом,
предполагая, что А\=А2 в уравнениях (2.8.4), вычтем (2.8.4а) из
(2.8.46). Тогда получим
h 1=4- (ft+/ '+к /)+-тA* к* A°* -v A") fà[ -
-(ßiAj-v A,,)/?,,]. (2.8.5)
Уравнение (2.8.5) позволяет найти значение /,-, / на Гь поскольку
значения fn . и fn+\ на этой границе известны.
Ограничения на шаг по времени, вводимые условием
диагонального преобладания, хотя и не являются слишком
обременительными, могут быть устранены, если для аппроксимации
первых производных вместо центральных разностей использовать
направленные против потока разности (в соответствии со знаками
А\ и В2). Однако в этом случае теряется второй порядок точности.
Возможный способ сохранить второй порядок точности для
стационарного случая заключается в применении нецентрированных
разностей с чередующимися направлениями на каждом шаге.
Соответствующая схема имеет вид
-JT(fi, / - П, /) + {Al, А*, - v Axxft,,) + (ß?, / А? - v А„) fl, = О,
(2.8.6а)
-& ifCÎ - h, /) + «, АГ - v А„) h,, + {ßl i A*, - v Aj f?,+, ' = О,
(2.8.66)
73

где
А? =4-10 + гА)А+-г(\ - ел)Ах],
eA = sign(A?tJ) (2.8.6b)
и аналогичные определения для Д* и А** с заменой Д± на А±
и г а на eB = sign(Bni .). Для нестационарного уравнения схема
имеет только первый порядок точности по времени; при
достижении стационарного состояния ошибка аппроксимации составляет
0(AtAx, AtAy, Ах2, ...). Отметим, что безусловная устойчивость
схемы сохраняется.
Изложенный метод предложен Пейре (1971) для решения
уравнений Навье—Стокса в случае несжимаемой жидкости и
применен Добом и Та Фуок Локом (1978) для решения уравнений в
переменных вихрь — функция тока.
2.8.3. Явные схемы для нелинейных уравнений в консервативной форме
Рассмотрим явные схемы типа предиктор — корректор, которые
представляют собой прямое обобщение одномерных схем,
рассмотренных в п. 2.7.1. Имеется много возможностей такого
обобщения. Мы отсылаем читателя к работам Лера (1981) и Лаваля
(1981а, б), в которых приводится достаточно полное описание
этих схем для случая невязкой жидкости, и к работе Пейре и Ви-
виана (1975), в которой рассмотрены некоторые обобщения для
случая учета вязкости. Здесь же мы рассмотрим схему второго
порядка точности, предложенную Мак-Кормаком (1969), и
обобщение этой схемы, ранее рассмотренное Томменом (1966) и
имеющее первый порядок точности для нестационарного состояния,
и второй порядок — для стационарного.
Рассмотрим нелинейное уравнение
Это уравнение можно рассматривать как двухмерную модель
движения вязкой сжимаемой жидкости с переменной вязкостью v(/).
Схемой Мак-Кормака для уравнения (2.8.7) является
h,, = fi, i - M Д+ (Fl, - Ml, A7fl,) - At A+ {Hl, - Nnt,, А~Ц ,),
(2.8.8a)
flY=±(ff,i + ft.i)--rMbï(jPi.i-Ml,,A£ft.,)-
—±-AtA; (н,,, - Nit, A+fi,,), (2.8.86)
74

где предварительное значение fi, / определяется в тех же самых
точках, что и окончательное значение f"+.1, Fi ,• = F (fi,,), #, ,- =
= H(hf)n
Ml j = m0< / + (1 - mo) v?_,,,,
<,= «ov"/ + (l-no)v"/_b
Mit j = ( 1 — m0) V/ +,, / + m0v/, /,
< / = v (/" /)
% i = v (ft. /)
#/, / = (1 — n0) vit / +1 + >Wi, /, (2.8.8b)
где m0 и no — произвольные константы. Мак-Кормак принял га0 =
= по^={/2', другой возможный вариант: m0 = no=l. Эффект выбора
сказывается только на ошибке аппроксимации. Другой способ
заключается в том, чтобы задать аппроксимацию членов вязкости
выражением
AÏ?./=v[mo/7,/ + (l-то)/?-!,/].
что идентично (2.8.8в), если v — линейная функция /.
Схема (2.8.8) является одним из четырех возможных
вариантов схемы Мак-Кормака. Другие варианты получаются из (2.8.8)
путем замены соответственно А+ на А~ и Д+ на Д~. Хотя не был
J х х у у
теоретически определен лучший вариант для вязкого случая, как
это было сделано для невязкого одномерного случая (Лера
и Пейре, 1974а, Ь), вероятнее всего, в выборе варианта важную
роль будет играть направление распространения ударной волны
(если v = 0 или v<^; 1).
Достаточно полное теоретическое исследование устойчивости
схемы (2.8.8) отсутствует. В невязком случае необходимое
условие устойчивости можно получить, исходя из общего требования,
чтобы область зависимости численного решения содержала
область зависимости точного решения. В результате получим
Д* =
Л* ' Ау
где A=dF/df и B = dH/df. При наличии вязкости это условие
может быть заменено на условие (2.8.36) в предположении, что
Как уже было отмечено, в одномерном случае преимуществом
схемы Мак-Кормака являются компактность и простота учета
граничных условий. Однако может случиться, что ее
несимметричная структура становится невыгодной, например при расчете
обтекания тела потоком. В этом случае центрированные схемы могут
быть более полезными. Кроме того, если ищется только
стационарное решение уравнения (2.8.7) или если первый порядок точ-
75

ности по времени считается достаточным, то могут быть
использованы схемы типа схемы Томмена (2.7.11) (Томмен, 1966).
В двумерном случае особенность метода Томмена, являющегося
одним из вариантов двухшаговой схемы Лакса—Вендрофа
(Рихтмайер, 1962), заключается в определении предикторов ff+i/2,/
и fу. . j_ в двух различных точках и использовании их в
разностях по х и у соответственно в невязкой части конечно-разностного
уравнения на втором шаге. На втором шаге вязкие члены
определяются с помощью значений fV-.. Это приводит к компактной
девятиточечной схеме, которая имеет первый порядок точности по
времени в нестационарном состоянии и второй порядок точности
(с отсутствием зависимости по At) в стационарном. Схема
Томмена может быть обобщена путем определения значений
предиктора/*., ft соответственно при х= (i+$x)àx, у=/Ду, t =
= (n+ax)At и x = iAx, y=(j+$v)Ay, t=(n+av)At (рис. 2.8.1).
Эта схема была предложена Лера (1981) для аппроксимации
уравнения, не содержащего вязкости. Вывод ее аналогичен выводу
схем (2.7.7). Общая схема записывается в виде
ftl = О - ß*) fi i + ß*/"+1./ - 0х At At Ff, j - ax At {yx0 [%x Д+ +
+(i-xx)A;)w+Ui+(i-yx)[»xAt + (i-»x)A;}Hil} +
+ ax At [гх AZ (Mf+,,, A+fU i. /) + 0 - «*) At « / A~xfl /)] +
+ a* A* [Yf A; (N7+i,, Atfhu /) + (1 - Y?) A;(Ä??. / A+f?. /)]; (2.8.9a)
fll = (l-tf)fll + fi«fli + 1-at>AtAtHli-a!'At{y%Wài +
+ (\-%v)A7]FÏ,i+l + (l-y$)[li!>AÎ + (l-v.!>)A7)Fll} +
+ avAt[е"Д-«/+1 A+f?,, + i) + 0 - *")*ti^li^fl/)1 +
+ av At У AJ (Ml,+, Atfl l+,) + (1 - yO A7 (M?-j Atfl,)]; (2.8.96)
fi*i ' - ft. I - -b?r{[(«X - ß') ^ + (ax + tf - 1)Д7] П, + A7H ,} -
—ё-{№ - ^ày +(a"+рУ -1)^] т- ' + А'"f- ') +
+ A* [A J (M?,i Atfl /) + A; (Ni, A+fl,)], (2.8.9b)
где
Fl,=F(jli) и М.,= Н(}0,
Ml j = E rrikvl+k, j, Z rtik = 1, m* = const,
ft=-i ft
i
N?,,= Yj «ftv"/ + ft, Z"*=1. «ft = const,
ft=-l ft
ÂÏ?./ 1-^7+,.,+ v?.,), ЛГ?.y l-(v?. # + , + v7.,). (2.8.9r)
76

Параметры a* ß* ух, ух À*, \хх и аналогичные параметры со
значком у произвольные. Они определяют различные схемы этого
класса. Схему Томмена (Томмен, 1966) можно получить при
условии, что все параметры полагаются равными i/2. Эта схема была
использована Магнусом и Иошихара (1975) для расчета
невязкого сверхзвукового течения. С этой же целью ее применили Лера
и Сайде (1981), которые все параметры, за исключением а* =
= 0^=1 + ^/5/2, полагали равными 72. Для случая v = 0 схемы
Мак-Кормака получаются при ах = аУ= 1.
Рис. 2.8.1. Сетка для обобщенной
схемы Томмена.
JW-
J~/
ь~/
-т- Ф
а,
47
(ЗхАх
LH
Схема разностей вперед, идентичная описанной с помощью
уравнений (2.8.8) при v = 0, получается при ßÄ = Y о = ßy = Т2^ = О
и \ix = \x,y=\. Другие варианты, упомянутые выше, соответствуют
следующим значениям параметров:
ß* = Yo = \ix = 0, $у = уу = hy = 1 — разности по х — вперед,
по у — назад.
ß* = yo = А,* = 1, ß17 = yiï = \iy = 0 — разности по х — назад,
по у — вперед.
ß* = Yo = §У = Y# = ! » Xх = ХУ = 0 — разности по x — назад,
по у — назад.
Отметим, что схема, определяемая значениями параметров ух0 =
= Хх==1Хх=уу = ху==1хУ== а* = аУ =1, ß*, ß^ = 0 или 1, очень
близка к схеме Мак-Кормака, но более устойчива (Лера, 1981).
В случае v=^0 вышеприведенный выбор параметров определяет
схемы, аналогичные схеме Мак-Кормака, но имеющие только
первый порядок точности по времени. Что касается условий устойчи-
77

вости, то мы укажем их для линейных случаев с отсутствием
вязкости при следующих значениях параметров: ух =Xx = \ix=yyQ =
=№=\ху = 1/2. Эти условия имеют вид
&х ' ' V8 А# л/8
При наличии вязкости условие (2.8.36) может служить
приближенным критерием устойчивости.
2.8.4. Явные методы расщепления
Способ применения общих одномерных схем с учетом вязкости
к многомерным задачам состоит в использовании явных методов
расщепления (Странг, 1968; Гурлей и Моррис, 1968, 1970; Мак-
Гир и Моррис, 1972; Лаваль, 1980, 1981а, b — для невязкого
случая; Мак-Кормак, 1971—для вязкого случая). Мы опишем здесь
метод расщепления, связанный со схемой Мак-Кормака (2.7.7)
и схемой (2.7.14) (при а=1, ß=7 = 0 или 1), применительно
к уравнению (2.8.7). Этот метод может быть распространен на
любую из схем общего класса, введенных выше. Разностные
операторы Lx (At) и Ly (At) определяются путем последовательного
применения одномерной схемы к членам с производными по х и по
у в уравнении (2.8.7). Таким образом сокращенное выражение
flJ = Lx{M)fli (2.8.10а)
соответствует двухшаговой схеме (2.7.7) (fx . отождествляется
с f7*4"1), где G = F — vdf/dx аппроксимируется с помощью схем
(2.7.14а) и (2.7.146). Аналогично выражение
flJ=Ly(At)flJ (2.8.106)
соответствует схеме, в которой х заменяется на у и G =
= H — vdf/dy.
Последовательное применение операторов Lx и Ly приводит
к схеме
fn^i{ = Lx(At)Ly(At)fni,h (2.8.11)
Только в особых случаях (в частности, для скалярного уравнения
с v = const) такая конечно-разностная схема имеет второй
порядок точности. В общем случае, когда (2.8.7) есть векторное
уравнение (например, уравнение Навье—Стокса для сжимаемой
жидкости), схема (2.8.11) не обладает вторым порядком точности.
Второй порядок точности может быть получен, если
рассматривать такие симметричные последовательности операторов, как
fiï ' ~ Ly (■%-)L* ("Г") L* ("Г") 1у ("f ) К '■ <2'8'12)
/?,+, ' = Ly (-£-) Lx (At) Ly (-Ц-) Ц ,, (2.8.13)
в которых сумма шагов по времени равна 2 At.
78

Метод расщепления по сравнению с двухмерными схемами
(2.8.8а) —(2.8.8в) или (2.8.9а) —(2.8.9г) имеет следующие
преимущества:
а) условия устойчивости представляют собой условия для
одномерных задач и, следовательно, являются менее
ограничительными, чем в двумерном случае;
б) в операторах Lx и Ly могут использоваться разные шаги
по времени применительно к следующей последовательности:
где М^\ есть целое число. Это представляет особый интерес
в случае, когда максимально допустимые шаги по времени в двух
направлениях —Atx и А^ —значительно отличаются друг от
друга (вообще говоря, вследствие различия между шагами сетки
Ах и Ау)у так как это позволяет производить вычисления в
каждом направлении с соответствующим максимальным шагом по
времени. Таким образом, если Aty<^Atx, схема (2.8.14) может
быть успешно использована путем выбора At = Atx и М, равного
наименьшему целому числу, такому, что M^Atx/2Aty. Однако,
если M слишком велико, могут возникать определенные
трудности (Мак-Кормак, 1971).
Основное неудобство при использовании метода расщепления
связано с учетом граничных условий. Поскольку на каждом шаге
по времени нет согласования с решаемым дифференциальным
уравнением, возникает проблема определения граничных условий
для промежуточных значений. Методы использования граничных
условий для схемы Рихтмайера (двухшаговая модификация схемы
Лакса—Вендрофа), аппроксимирующей уравнение без учета
вязкости, были предложены Гурлеем и Моррисом (1970) и Мак-Ги-
ром и Моррисом (1972). В общем случае при учете вязкости
обычный метод заключается в использовании точных граничных
условий для промежуточных значений искомых величин. Как
отмечалось в п. 2.7.3, такая процедура приводит к росту ошибки
аппроксимации вблизи границы (см. Яненко, 1970). Однако практически
этот рост не оказывает существенного влияния на точность
численного решения.
2.8.5. Обобщенные методы чередующихся направлений (методы ADI)
Для неявных схем, примененных к двух- и трехмерным
уравнениям, можно легко получить решения, если использовать
обобщенные методы ADI, позволяющие свести задачу к последовательному
решению линейных алгебраических систем с трехдиагональными
(простыми или блочными) матрицами. (Дуглас, и Ганн, 1964;
Яненко, 1971; Березин и др., 1972, 1975а, Ь; Линдемат и Килин,
1973; Брайли и Макдональд, 1973, 1975, 1977, 1980; Бим и Уорминг,
1978).
79

Рассмотрим кратко эти методы. Предположим, что неявная
схема может быть записана в виде
(/ + Л, + Л, + Аг) îlVk = Qfl. /. *, (2.8.15)
где Ах, Ay,k — разностные операторы, каждый из которых
соответствует производным только в одном направлении, и Q —
разностный оператор по любому из направлений, возможно, содержащий
смешанные производные. Операторы могут зависеть также и от
f7} . k , если исходное уравнение является нелинейным. Схемы
типа схемы (2.8.15) можно построить путем обобщения на
многомерный случай неявных схем, приведенных в п. 2.7.4. При этом
уравнение может быть векторным. Запишем уравнение (2.8.15)
в А-форме:
(1 + Ах + Ау + Л*)(f?//.'* - f". i.k) = Rfl. /. *, (2.8.16)
где R = Q — (f + Ax+Ay + Az). Уравнение (2.8.16) записано для
приращения f7}*} k— fn . k и решается с помощью обобщенного
метода ADI:
(/ + Л,) fithh = Rfli.k, (2.8.17а)
(/ +Л,)/Г/. * = £/.*. (2.8.176)
(/ +Л*) £*/.* =/Г/, л, (2.8.17b)
flVk = f7lhk + fTf.k. (2.8.17г)
На каждом шаге получается трехдиагональная система. Важные
рекомендации, связанные с решением таких систем, были сделаны
Брайли, Макдональдом (1980) и Нероном (1981).
Исключив промежуточные значения, получим
конечно-разностное уравнение, решаемое с помощью приведенного алгоритма.
Окончательное уравнение имеет вид
(/ + А,)(/ + Ау)(1 + Az){fï+f]k - fl ,. k) = Rfl hk. (2.8.18)
Это уравнение отличается от уравнения (2.8.16) членом
О (At2) у так как каждый оператор Ах, Ау, Аг имеет порядок
О (At). Отметим, что схема (2.8.18) не обязательно имеет те же
свойства устойчивости, что и схема (2.8.16).
Метод расщепления (2.8.17) устраняет трудности, связанные
с формулировкой граничных условий для промежуточных
значений в случае условий Дирихле. Предположим, что функция
f(x, у, г, t) известна на границе Г:
f(x, у, z, *)|Г = Ф(*> У> z> ')•
Пусть Гь Г2, и Г3 — части границы, параллельные плоскостям
(у, z), (х, z) и (х, у) соответственно. Уравнение (2.8.17г) дает
значения /**.*. на Г3, необходимые для решения (2.8.17в),
а именно
с*** I ( п+\ П \ I
//. /. а|Гз=ЧФ*,/. л —Ф«./. аЛГз-
80

Аналогично уравнения (2.8.17в) и (2.8.176) дают
f7, /. k |г2 = (/ + Л2) (ф?,"/,1 k — ф?, /, а) |г2,
fl /. * |г, = (/ + Л,)(/ + Л,)(qff.V * - Ф?, /, *) |г,
В частности, если ф не зависит от времени, то промежуточные
значения равны нулю на границе.
Заметим, что схема Писмена—Рэчфорда (2.8.4) для
двухмерного уравнения с Ai=A2 и B\=B2 может быть включена в общую
процедуру (2.8.17) с Л2 = 0 путем введения величины //,/ = /?.+
+— /*. г Граничное условие (2.8.5) становится тогда
идентичным вышеприведенному.
В заключение отметим, что в стационарном состоянии f71^ k —
— fn. k = 0, так что Rfn. k = 0 соответствует стационарному
конечно-разностному уравнению, отвечающему исходному
дифференциальному уравнению. Поэтому выражение Rf1} . . может рас-
сматриваться в общем случае как результат, полученный по
явной схеме
/*./. k — fi.j, k = Kfi,j, *,
аппроксимирующей исходное уравнение. С учетом этого правая
часть уравнения (2.8.16) может быть заменена на результат,
полученный по многошаговой явной схеме (Холландерс и Пейре,
1981; Лера, 1981).
Список литературы
Анучина H. Н. Разностные схемы решения задачи Коши для гиперболических
симметричных систем.—ДЛЯ СССР, 1964, 154, № 2, с. 247—250.
Березин 10. А., Ковеня В. М,., Яненко H H. Об одной неявной схеме расчета
течений вязкого теплопроводного газа.— В кн.: Численные, методы механики
сплошной среды, 1972, 3, с. 3—18.
Браиловская И. Ю. Метод расчета течений с сильным вязким взаимодействием.—
ДАН СССР, 1965, 162, № 1, с. 36—39.
Годунов С. К-, Рябенький В. С. Введение в теорию разностных схем.— М.: Физ-
матлит, 1962.
Олейник О. А. Разрывные решения нелинейных дифференциальных уравнений —
УМН, 1957. 12, 3(75), с. 3—73.
Шокин Ю. И. О методе первого дифференциального приближения в теории
разностных схем для гиперболических систем уравнения.— Труды
Математического института им. Стеклова, 1973, 122, с. 66—84.
Яненко H. Н. Метод дробных шагов решения многомерных задач
математической физики.— Новосибирск: Наука, 1967.
Adam, Y. Comput. Math. Appl. 1, 393—406 (1975).
Adam, Y. /. Comput, Phys. 24, 10—22 (1977).
Allen, J. S., and Cheng, S. I. Phys. Fluids 19, 37—52 (1970).
Beam, R M. and Warming, R. F. /. Comput. Phys. 22, 87—110 (1976).
81

Beam, R. M., and Warming, R. F. AIAA J. 16, 393—402 (1978). (PTK *, 1978,
№ 4, с 145—156.)
Berger, А. E., Solomon, J. M., Ciment, M., Leventhal, S. И., and Weinberg, В. С,
Math. Comput. 35, 695—731 (1980).
Berezin, Yu. A., Kovenja, V. M., and Yanenko, N. N. Lecture Notes in Physics,
Vol. 35, pp. 85—90, Springer-Verlag, New York (1975a).
Berezin, Yu. A., Kovenja, V. M., and Yanenko, N. N. Comput. Fluids 3, 271—281
(1975b).
Bontoux, P., Foiestier, В., and Roux, В. /. Mec. Appl. 2, 291—316 (1978).
Bramble, J, H., and Hubbard, В. E. Numer. Math. 4, 312—327 (1962).
Briley, W. R., and McDonald, H. An Implicit Numerical Method for the
Multidimensional Compressible Navier—Stokes Equations, United Aircraft Research
Laboratory Rep. M911363-6 (Nov. 1973).
Briley, W R.„ and McDonald, H. Lecture Notes in Physics, Vol. 35, pp. 105—110,
Springer-Verlag, New York (1975).
Briley, W. R., and McDonald, H. /. Comput. Phys. 22, 372—397 (1977).
Briley, W. R., and McDonald, H. /. Comput. Phys. 34, 54—73 (1980).
Cheng, S I. A Critical Review of Numerical Solution of Navier-Stokes Equations.
In Progress in Numerical Fluid Dynamics, Lecture Notes in Physics, Vol. 41,
pp. 78—225 Springer-Verlag, New York (1975).
Cheng, S. I., and Shubin, G. /, Comput. Phys. 28, 315—326 (1978).
Ciment, M., Leventhal, S. H., and Weinberg, В. С. /. Comput. Phys. 28, 135—166
(1978).
Collatz, L. The Numerical Treatment of Differential Equations, Springer-Verlag,
New York (1966).
Collatz, L. Hermitian Methods for Initial-Value Problems in Partial Differential
Equations. In Topics in Numerical Analysis, Proceedings of the Royal Irish
Academy Conference on Numerical Analysis, J. J. H. Miller, Ed., pp. 41—61,
Academic Press, New York (1972).
Courant, R., Friedrichs, К. С, and Lewy, M. Math. Ann. 100, 32—76 (1928).
(Курант P., Фридрихе К., Леви Г. О разностных уравнениях математической
физики. УМН, вып. 8, 1940, с. 125.)
Courant, R., Isaacson, E., and Rees, M. Commun Pure Appl. Math. 5, 243—255
(1952).
Daube, O., and Ta Phuoc Loc, /. Mec. 17, 651—678 (1978).
Dennis, S. С R., and Chang, G.-Z. Phys. Fluids 12, Suppl. II, 11.83—11.93 (1969).
Douglas, J., and Gunn, J. E. Numer. Math. 6, 428—453 (1964).
Elsaesser, E. Etude de Méthodes Hermitiennes pour la Résolution des Equations
de Navier-Stokes pour un Fluide Incompressible en Régime Stationnaire,
Thèse Doct 3iemc Cycle, Université Pierre et Marie Curie, Paris (1980).
Elsaesser, E., and Peyret, R. Méthodes Hermitiennes pour la Résolution
Numérique des Equations de Navier-Stokes. In Méthodes Numériques dans les
Sciences de l'Ingénieur, E. Absi and R. Glowinski, Eds., pp. 249—258, Dunod, Paris
(1979).
Fairweather, G., and Mitchell, A. R. SI AM J. Numer. Anal. 4, 163—170 (1967).
Garabedian, P. R. Math. Tables Aids Comput. 10, 183—185 (1956).
Ghia, K. N., Shin, С. T., and Ghia, U. Use of Spline Approximation for Higher-
Order Accurate Solutions of Navier-Stokes Equations in Primitive Variables.
In Proc. 4th AIAA Computational Fluid Dynamics Conference, pp. 284—291,
Williamsburg, VA. (1979).
Gourlay, A. R., and Morris, J. L. Math. Comput. 22, 715—720 (1968).
Gourlay, A. R., and Morris, J. L. /. Comput. Phys. 5, 229—243 (1970).
Gustaffson, B. Math. Comput. 29, 396—406 (1975).
Harten, A., Hyman, J. M., and Lax, P. D. Commun. Pure Appl. Math. 29, 297—
322 (1976).
Hirsh, R. S. /. Comput. Phys. 19, 90—109 (1975).
Hirt, С .W. /. Comput. Phys. 2, 339—355 (1968).
Hollanders, H., and Peyert, R. Rech. Aérosp. No. 1981-4, 287—294 (1981).
* PTK — журнал «Ракетная техника и космонавтика».
82

Isaacson, E., and Keller, H. Analysis of Numerical Methods, Wiley and Sons,
New York (1966).
Khosla, P. M., and Rubin, S. G. Comput j Fluids 2, 207—209 (1974).
Krause, EM Hirschel, E. H., and Kordulla, W. Comput. Fluids 4, 77—92 (1976).
Kreiss, H. O. MatH Comput. 26, 605—624 (1972).
Kreiss, H. O., and Öliger, J. Methods for the Approximate Solutions of
Time-Dependent Ptoblems. GARP Publ. series No. 10, Global Atmospheric Research
Program (1973).
Laval, P. С R. Acad. Sei. В, 204, 239—242 (1980).
Laval, P. C. R. Acad. Sei, В, 221,. 125—128 (1981a).
Laval, P. Schémas Explicites de Désintégration du Second Ordre pour la
Résolution des Problèmes Hyperboliques Non Linéaires: Théorie et Applications aux
Ecoulements Transsoniques. ONERA, Note Technique No. 1981-10 (1981b).
Lax, P. D. Commun. Pure Appl. Math. 7, 159—193 (1954).
Lax, P. D. Commun. Pure Appl. Math. 10, 537—566 (1957).
Lax, P. D., and Wendrcff, B. Commun. Pure Appl. Math. 13, 217—237 (1960).
Lecointe, Y., and Piquet, J. On the Numerical Solution of Some Types of Unsteady
Incompressible Viscous Flow. Second International Conference on Numerical
Methods in Laminar and Turbulent Flow, July 13—16, 1981, Venice, Italy.
Lerat, A. С R. Acad. Sei. A, 288, 1033—1036 (1979).
Lerat, A. Sur le Calcul des Solutions Faibles des Systèmes Hyperboliques de Lois
de Conservation a l'Aide de Schémas auf Différences. ONERA Publ. No. 1981-1
(1981).
Lerat, A., and Peyret, R. C. R. Acad. Sei. A, 276, 759—762 (1973a).
Lerat, A., and Peyret, R. C. R. Acad. Sei. A, 277, 363—366 (1973b).
Lerat, A., and Peyret, R. Comput. Fluids 2, 35—52 (1974a).
Lerat, A., and Peyret, R. Lecture Notes in Physics, Vol. 35, pp. 251—256, Springer-
Verlag, New York (1974b).
Lerat, A., and Peyret, R. Rech. Aerosp. 1975-2, 61—79 (1975).
Lerat, A., and Sides, J. Proceedings of the Conference on numerical Methods in
Aeiodvnamic Fluid Dynamics, Univ. Reading, March (1981).
Lindemuth, J., and Killeen, J. /. Comput Phys. 13, 181—208 (1973).
MacCormack, R. W. The Effect of Viscosity in Hypervelocity Impact Cratering.
AIAA paper No. 69—354 (1969).
MacCormack, R. W. In Lecture Notes in Physics, Vol. 8, pp. 151—163, Springer-
Verlag, New York (1971)
Magnus, R., and Yoshihara, H. AIAA J. 13, 1622—1628 (1975). (PTK, 1975, № 12,
с 93.)
Mehta, U. B. Dvnamic Stall of an Oscillating Airfoil. AGARD Conference
Proceedings No. 227, Unsteady Aerodynamics, Ottawa, Canada, pp. 23.1—23.32 (1977).
McGuire, G. R., and Morris, J. L. /. Inst. Math. Applic. 10, 150—165 (1972).
McGuire, G. R., and Morris, J. L. /. Comput. Phys. 11, 531—549 (1973).
Mitchel, A. R. Computational Methods in Partial Differential Equations. Wiley,
New York (1969).
Moretti, G. Proceedings of 1974 Heat Transfer and Fluid Mechanics Institute,
Stanford Press, Stanford (1974).
Neron M. Etude et Applicaton d'une Métode Implicite de Résolution des Équations
de Navier-Stokes pur un Fluide, en Compressible, en Coordonnées
Cylindriques. Thèse Doct.-Ingénieur, Université Pierre et Marie Curie, Paris (1981).
Orszag, S. A., and Tang, C.-M. /. Fluid Mech. 90, 129—143 (1979).
Peaœman, D. W., and Rachford, H. H. /. Soc. Indus. Appl. Math. 3, 28—41
(1955).
Peyret, R. C. R. Acad. Sei. A 272, 1274—1277 (1971).
Peyret, R. Résolution Numérique des Systems Hyperboliques. Application à la
Dynamique des Gaz. ONERA, Publication No. 1977—5 (1977).
Peyret, R. C. R. Acad. Sei A 286, 59—62 (1978a)
Peyret, R .A Hermitian Finite-Difference Method for the Solution of the Navier-
Stokes Equations. In Proceedings of the First International Conference on
Numerical Methods in Laminar, and Turbulent Flow, 43—54, Pentech Press,
Plymouth, UK (1978b).
Peyret, R., and Viviand, H. Computation of Viscous Compressible Flows Based
on the Navier-Stokes Equations. AGARDograph No. 212 (1975).
83

Raviart, P. Л. Métodes d'Éléments Finis en Mécanique des Fluides. Ecole d'Eté
d'Analyse Numérique, EDF, INRIA, CEA (1979).
Richtmyer, R. D. A Survey of Difference Methods for Non-Steady Gas Dynamics.
NCAR, Tech. Note 63—2, Boulder, CO (1962).
Richtmyer, R. D., and Morton, K. W. Difference Methods for Initial Value
Problems, Interscience, New York (1967). (Рихтмайер P., Мортон К. Разностные
методы решения краевых задач. М.: Мир, 1972.)
Roache, P. J. Computational Fluid Dynamics, Hermosa Publishers, Albuquerque,
NM (1972). (Роуч П. Вычислительная гидродинамика. M.: Мир. 1980.)
Rubin, Е. L., and Burstein, S. Z. /. Comput. Phys. 2, 178—196 (1967).
Rubin, S. G., and Khosla, P. K. /. Comput Phys. 24, 217—246 (1977).
Shokin, Y. I. In Lecture Notes in Physics, Vol. 59, pp. 410—414, Springer-Verlag,
New York (1976).
Steger, J. L., and Warming, R. F. J. Comput. Phys. 40, 263—293 (1981).
Strang, G. SLAM J. Numerical Analysis, 5, 506—517 (1968).
Ta Phuoc Loc, /. Mec. 14, 109—134 (1975).
Ta Phuoc Loc, /. Fluid Mech. 100, 111—128 (1980).
Thommen, H. U. Z. Angew. Math, Phys. 17, 369—384 (1966).
Varga, R. S. Matrix Iterative Analysis, Prentice-Hall, Englewood Cliffs, NJ (1962).
Veldman, A. E. P. Comput. Fluids 1, 251—171 (1973).
Von Neumann, J., and Richtmyer, R. D. /. Appl. Phys. 21, 232—257 (1950).
Warming, R. F., and Beam, R. M. SIAM—AMS Proc. 11, 85—129 (1978).
Warming, R. F., and Hyett, B. J. /. Comput. Phys. 14, 159—179 (1974).
Warming, R. F., Kutler, P., and Lomax, H. AIAA J. 11, 189—196 (1973).
(PTK, 1973. № 2, с 76.)
Yanenko, N. N., and Shokin, Y. I. Phys, Fluids 12, Suppl. II, 11.28—11.33 (1969).
Глава 3
Интегральные и спектральные
методы
В главе 2 были рассмотрены вопросы применения
конечно-разностных методов для интегрирования
дифференциальных уравнений динамики жидкости. Этой же цели могут служить
и другие методы, основанные, в частности, на подходах
интегрального типа, таких, как методы моментов, наименьших квадратов,
Галеркина, Рэлея—Ритца. Каждый из этих методов может
применяться либо к некоторой подобласти рассматриваемого течения,
либо ко всей области. Кроме того, употребляются и
псевдоспектральные методы, которые не опираются на интегральную
формулировку уравнений. Имеются специальные методы для
сжимаемой жидкости — методы ячеек, которые используют локальные
физические модели для каждой ячейки с целью получить
численный эквивалент интегральных законов сохранения. В этой главе
мы опишем методы, которые нашли широкое практическое
применение. Сначала рассмотрим методы интегрального типа.
Вообще говоря, такой подход основывается на двух формах.
Первая заключается в использовании вариационных
формулировок решаемой задачи (например, метод Рэлея—Ритца). Вторая
состоит в умножении уравнений сохранения, которые упрощенно
запишем как L(f)=0, на весовую функцию Wi и интегрировании
по некоторой пространственной области (взвешенная невязка).
84

Получающееся интегральное соотношение J L(/)№,ds = 0
используется как основа для решения. Методы решения могут быть
различными, но все они в конечном счете основываются на
некотором предположении относительно аналитической формы
решения с неизвестными константами или функциями. Решение в
предполагаемой форме с указанными неизвестными подставляется
в интегральное уравнение для получения соответствующих
уравнений для этих неизвестных.
Для того чтобы применить вариационный метод, необходимо
определить интеграл по рассматриваемой области
/ = \ \ F (*, у, /, fXi fy, . . .) dx dy,
такой, что его экстремум достигается на решении
дифференциальной задачи. В большинстве физических задач функционал /
вводится на основе энергетических соображений. Однако в общем
случае уравнений вязкой жидкости вариационный принцип не
установлен.* Поэтому указанный подход используется только
в определенных случаях (например, в случае безвихревого
потенциального течения или течения Стокса) и не очень просто
распространяется на более полные уравнения движения.
Более общим подходом, имеющим вариационный характер,
является упомянутый метод взвешенной невязки. Этот метод
приводит к интегральному уравнению путем умножения уравнений
движения на весовую функцию Wi и затем интегрирования по
области. Задается функциональная форма независимых
переменных с неизвестными коэффициентами, которая затем
подставляется в интегральное уравнение. Метод должен давать столько
уравнений, сколько имеется неизвестных. Это можно осуществить
двумя способами. Первый заключается в разбиении и
рассматриваемой области на N подобластей интегрирования для N
неизвестных, второй — в применении N весовых функций для N
неизвестных.
Первый способ приводит к методу конечных элементов,
второй— связан со спектральными методами. Такая классификация
является упрощенной, поскольку метод конечных элементов и
спектральный метод могут рассматриваться как единый метод,
применяемый несколько иным образом. К этим методам примыкают:
метод подобласти или интегральных соотношений (Wz = l), метод
моментов (Wi = xi), метод Галеркина (Wi = Fi, где Fi — одна из
функций, вводимых для представления решения), метод
наименьших квадратов (Wi = 2dL (f)/ôa,-, где а,-— неизвестные параметры
решения).
* Точнее, установлено, что такого принципа нет. Вариационные
формулировки для уравнений Навье—Стокса существуют либо при определенных
ограничениях (принцип локального потенциала), либо для стационарных уравнений
без инерционных членов, либо, наконец, для расширенной системы, включающей
сопряженные уравнения.— Прим. перев.
85

Каждому из перечисленных методов посвящено большое число
исследований. Обзор работ по интегральным методам и методу
моментов выполнил Холт (1977). В этой главе основное внимание
уделяется методу Галеркина и в меньшей степени — методу
наименьших квадратов. Мы не будем обсуждать отдельно методы
конечных элементов и спектральный, а рассмотрим их совместно
в п. 3.1. В отличие от метода коллокаций, использующего
сеточные значения в физическом пространстве, для собственно
спектральных методов решение определяется в спектральном
пространстве; в этой главе рассматривается также
псевдоспектральный метод, являющийся комбинацией методов коллокаций и
спектрального.
3.1. Методы конечных элементов и спектральные
Принцип, лежащий в основе метода конечных элементов и
спектрального метода, заключается в сведении исходных
дифференциальных уравнений в частных производных к системе
обыкновенных дифференциальных или алгебраических уравнений, которые
могут быть решены обычными методами. При этом процедура,
применяемая в спектральных методах, аналогична используемой
в аналитических методах решения линейных дифференциальных
уравнений в частных производных, когда решение ищется путем
разложения в ряд по некоторой системе функций.
Рассмотрим, например, простое уравнение
dt +Ж~У дх* (ÖAA)
в интервале O^x^L при некотором начальном и граничных
условиях. Запишем разложение вида
/V
/=Е ai(t)Fi(x)% (3.1.2)
/=о
где а,— неизвестные, a Fi (х) — так называемые базисные
функции. Представление (3.1.2) должно удовлетворять начальному
и граничным условиям, а также дифференциальному уравнению.
Если граничные условия не удовлетворяются непосредственно, то
задача сводится к выражению граничных условий в спектральном
пространстве, т. е. через величины au при удовлетворении
дифференциального уравнения. Это может оказаться достаточно
трудным для сложных задач динамики. Ниже мы рассмотрим
некоторые возможности решения такой задачи. Однако сейчас
предположим, что можно обойти проблему граничных условий.
Подставим (3.1.2) в (3.1.1) с целью определения величин щ. В
результате получим уравнение
N
S [aiFi + ai(F'i-vF"i)] = 0, (3.1.3)
где
' dCLl
86

Следующий шаг заключается в определении из этого уравнения
соотношений для величин щ. Это может быть выполнено путем:
1) приравнивания коэффициентов при каждой величине Fi
к нулю, 2) использования соотношений ортогональности, 3)
использования весовых функций Wi и интегрирования (3.1.3) с
весом по промежутку O^x^L в целях получения (jV+1)
уравнений для (W+1) известных.
Рассмотрим два первых случая. Для того чтобы приравнять
нулю коэффициенты или использовать ортогональность,
необходимо установить связь между F'— vF" и Fi. Обычно принимают
м
F'i-vFÏ= Z ïm,iFm. (3.1.4)
m=0
В некоторых случаях такое представление накладывает
ограничение на выбор полиномов в правой части. Предполагая, что (3.1.4)
выполнено, имеем
Z [a'iFi + щ Z ßm. iFm) = 0. (3.1.5)
;=o\ m=0 /
В этом соотношении можно приравнять к нулю коэффициенты при
Fi или определить условия ортогональности
\w(x)FiFidx = \r (3.1.6)
о чсУ» 1 — У»
где с/ — константы.
Каждая из этих процедур приводит к системе уравнений для
определения а,. В простейшем случае при ßm, ; = 0 для тф1,
приравнивая коэффициенты при каждом А к нулю, получаем
aî + fc.ia* = 0. (3.1.7)
В случае ßm>i = 0 для тф1-\-\ и тфг— 1 имеем
aî + e£-ifc.*-i+a* + ifc.£ + i = () (3.1.8)
(индексы сдвинуты, чтобы коэффициенты при одинаковых Fi
оказались приравненными к нулю). В задачах, встречающихся на
практике, такие соотношения могут быть более сложными. В этом
случае возникает необходимость в применении численных методов
для решения уравнений, определяющих щ.
Для иллюстрации сказанного примем в качестве Fi полиномы
Чебышева (при v = 0). Согласно (3.1.4), имеем
N
F'i= Z Vm,iFm, (3.1.9)
m=0
где коэффициенты ßm, i получаются из рекуррентного
соотношения
2Fm = Fm + i/(m + 1) - Fm-xl{m - 1).
87

Уравнение (3.1.3) принимает вид
Z [a'tFt + at S fim.iFm) = 0. (3.1.10)
i = 0\ m=0 /
Теперь с целью получить уравнения для а, коэффициенты при
Fi можно приравнять к нулю или использовать условие
ортогональности полиномов Чебышева. В последнем случае следует
нормировать задачу на отрезке —1^*^:1 (либо на 0^x^:1).
Введем новые переменные x = 2x/L—1 и t = 2t/M* Для новой
переменной х полиномы рассматриваются на интервале —l^x^l.
Умножим (3.1.10) на /VV1—х2, проинтегрируем по х и
используем соотношение
+ 1 ГО, /=#=*,
\ /rL-s FiFjdx = <я/2, ]=1Ф09 (3.1.11)
-1 V1~* U, j = i = 0.
Можно показать (см. Готлиб и Орзаг, 1977), что для
определения коэффициентов а, получают следующие соотношения:
а/H—- 2l, рар=0, а0 = 2, aL = 1 для / > 0. (3.1.12)
(р + i) —нечетное
Эти уравнения довольно сложны, и для их решения приходится
применять численные методы. Начальные условия для величин ai
можно получить путем разложения начальной функции f в ряд
по полиномам Чебышева. Коэффициенты при каждом слагаемом
Fi будут начальными значениями для а<.
До сих пор мы предполагали, что разложение удовлетворяет
граничным условиям. Допустим, что в нашем примере должно
выполняться краевое условие /=1 при х== — 1. Тогда к N
уравнениям для üi добавляется дополнительное условие
N
1 = Е ai(t)Fi(-\). (3.1.13)
i = 0
Такая задача является некорректной. В случае полиномов
Чебышева существует способ обойти эту трудность, однако при
использовании других координатных функций такая процедура
может оказаться не простой. Заметим, что для полиномов Чебышева
операция дифференцирования понижает порядок полинома,
причем в этом случае F0= 1, F\=x и F2 = 2a:2—1, ..., поэтому F' =
= 4F\ или Fg =4/7о. Поэтому уравнений, полученных путем
приравнивания коэффициентов или ортогонализации, будет
недостаточно для определения aNi если они содержат первую
производную. Их будет недостаточно для определения aN и cln-\, если
имеется и вторая производная. Для того чтобы задача
88

стала корректной, следует отбросить уравнение для aN и заменить
его уравнением (3.1.13). Уравнения (3.1.12) определяют величины
au • • •> cln-u а уравнение (3.1.13)—величину aN. Этот способ
называют тау-методом *. Его можно применять и для вторых
производных, однако при этом уравнение для aN-[ заменяется вторым
граничным условием, записанным аналогично (3.1.13). Следует
отметить, что при использовании явного метода интегрирования
по времени для получения величин аь ..., aN-\ величина aNi
входящая в член с наиболее высоким порядком в разложении, должна
определяться из граничных условий. Это означает, что указанный
член преобладает и может существенно влиять на устойчивость
решения. Об этой особенности удовлетворения граничных условий
следует помнить при использовании метода.
Приведенный пример в определенной степени специфичен,
однако он может оказать некоторую помощь при освоении метода
(более подробно этот пример рассмотрен в работе Готлиба и Ор-
зага (1977)). В работе Тейлора (1962) приводится более сложный
пример применения спектрального метода для решения задачи
о переносе массы при малых числах Рейнольдса с использованием
функций Бесселя и полиномов Лежандра.
Другим способом определения величин аг непосредственно из
дифференциального уравнения является интегрирование этого
уравнения с весом по интервалу а^х^Ь:
а а
Точки а и Ь должны лежать на отрезке (О, L), но могут
выбираться произвольно. Функции Wj (х) также могут выбираться
произвольными, что используется для получения уравнений,
определяющих величины а,. Подстановка (3.1.2) в (3.1.14) дает
n ь
£ \wj[a'iFi + ai(F'i-vF"i)}dx = 0, / = 0, . . ., N. (3.1.15)
/ = 0 а
Если Ь — a = L, то (3.1.15) позволяет построить спектральную
схему. Если интервал интегрирования Ь — a<L, то используется
метод ячеек или метод элементов. Для метода элементов
характерно, что число слагаемых мало для каждого элемента
и элементы могут перекрываться. Для схемы конечных
элементов, использующей метод Галеркина, функции Fj выбираются не
очень сложными, и в качестве Wj берутся обычно Fj. Для метода
конечных элементов разложение (3.1.2) имеет вид
/=Z tt(t)Fi(x)% (3.1.16)
* Более подробно о тау-методе см. Ланцош К. Практические методы
прикладного анализа. М., 1981.— Прим. перев.
89

где fi — значение f в узле /, а базисная функция Fi— кусочно-
непрерывная функция, отличная от нуля в ограниченной области
(функция с компактным носителем) со следующими свойствами:
( 1, i = m,
Условие (3.1.17) означает, что F% равно нулю всюду вне элемента.
Эти функции обычно являются линейными или квадратичными.
В силу условия (3.1.17) матрица системы уравнений,
определяющих //, оказывается сильно разреженной. Применение более
общих разложений типа (3.1.2) с расширенным шаблоном
увеличивает эффективность метода, поскольку с меньшим числом
членов удается получить ту же точность. Однако в этом случае
требуются дополнительные усилия для обращения матриц. Отметим,
что разложения по полиномам Чебышева обладают свойством
хорошей сходимости для большинства функциональных
представлений и позволяют применять быстрое преобразование Фурье,
связывающее коэффициенты и значения в физическом
пространстве. Поэтому эти полиномы очень полезны при решении
рассматриваемых задач.
В негалеркинских методах, как, например, в методе
наименьших квадратов, Wj уже не являются функциями с компактным
носителем. Этот метод основывается на определении интеграла от
квадрата невязки, возникающей при подстановке в уравнение
приближения f :
/= \\L(f)\2ds. (3.1.18)
s
Отыскивается минимум этого интеграла, представляющего собой
погрешность метода. Если функция f представлена в виде
полинома или ряда с неизвестными коэффициентами а*, то
отыскивается минимум интеграла по а*. При прямом подходе производная
от / по каждому а* приравнивается к нулю, т. е.
В этом выражении роль W{ играет величина 2dL(f)/dcii.
Другая возможность заключается в применении теории
оптимизации для функций полезности с целью минимизации интеграла
/. Этот подход применялся Бристо и др. (1978) в обширном
исследовании, посвященном методу конечных элементов (см. также
Бристо и др., 1979 и Перио, 1979). Метод является довольно
сложным, и приводимый ниже пример расчета течения
несжимаемой жидкости демонстрирует его суть и точность получаемых
результатов.
Представленные методы применялись здесь к нестационарному
уравнению, но они применимы и в стационарном случае. Отличие
состоит в том, что уравнения для коэффициентов в стационарном
90

случае обычно требуют обращения матриц, в то время как в
нестационарных случаях иногда можно использовать явные схемы
интегрирования с целью упростить или исключить такую
процедуру. Однако при использовании неявных схем для решения
требуются примерно те же затраты. Отметим, что и в стационарном
случае можно использовать схему интегрирования по времени.
Выше мы предполагали, что разложения можно применять и
при наличии граничных условий. Для отдельных задач, в которых
применяется спектральный подход в форме (3.1.2), это сделать не
просто. Однако разложение (3.1.16) метода конечных элементов
всегда позволяет включить в расчет значения в граничных точках,
что связано с сущностью самого метода. Поэтому, когда в случае
применения спектрального подхода возникают трудности,
связанные с граничными условиями, предпочтительнее решать задачу
в физическом пространстве. Для этого используется
псевдоспектральный метод, который будет рассмотрен ниже в этой главе.
Все приведенные рассуждения носили общий характер. Чтобы
показать особенности рассматриваемых методов — спектрального
и конечных элементов — рассмотрим простые примеры.
Результаты более сложных расчетов будут приведены ниже.
3.2. Примеры применения метода конечных элементов
для решения стационарных задач
В качестве первого примера рассмотрим обыкновенное
дифференциальное уравнение
-%r + f =0 (3.2.1)
с условием /=1 при л: = 0. Будем искать решение уравнения
в интервале 0^л:^1. Интегрируя уравнение по этому
промежутку с некоторым весом Wj, имеем
1
\wl(4r + f)dx = 0. (3.2.2)
Функцию / представим в виде ряда
f=E№(4 (3.2.3)
После подстановки (3.2.3) в (3.2.2) получим
/V 1
£ ft \wj(F'i + Fi)dx = 0, / = 1,..., N. (3.2.4)
i=l о
Таким образом, имеем систему алгебраических уравнений для
постоянных fi с коэффициентами bj, *, которые определяются
формулами
1
bi.i^lWjiF'i + Fddx. (3.2.5)
о
91

Для того чтобы система уравнений (3.2.4) имела единственное
решение, необходимо, чтобы число уравнений N равнялось числу
неизвестных в задаче. До этого момента спектральный метод и
метод конечных элементов не имеют различий. Теперь мы
рассмотрим каждый из этих методов в отдельности. Начнем с метода
конечных элементов.
В этом методе в качестве неизвестных fi рассматриваются
значения f в узловых точках. Их распределение является вопросом
выбора и в одномерном случае осуществляется просто. В
двухмерном случае узлы обычно выбираются в вершинах каждого
треугольного или четырехугольного элемента. Функции Fi(x)
являются линейными или квадратичными. Выберем линейный элемент
в интервале 0 ^ х ^ 1 так, что
Fl(x)=l-xt F2(x) = xy (3.2.6)
и примем
f = fi(l-x) + f#. (3.2.7)
Поскольку /=1 при лс=0, /ч = 1. Далее, полагая Wj = Fj, из (3.2.5)
получаем
b,,i=\Fi(F'i + Fi)dx. (3.2.8)
Ü
Следовательно:
1
bul = $(-x)(l-x)dx=--t-, bt,,=*$(l-x)(l+x)dx = -l-t
О о
1 1
62 ! = J (—х) xdx = J-, b2,2 = J *(1 + x)dx = -g-.
Так как fi уже определено граничным условием, для нахождения
/2 требуется только одно из уравнений (3.2.4), которое возьмем
в виде
2 1
£ U ) F2 {F\ + Ft) dx = 0, (3.2.9)
/ = i о
т. е. для определения /г используем весовую функцию F2.
Подставляя значения интегралов, получим
-4-f' + lH2 = 0' (3-2Л°)
откуда /2 = 0,4. Для точного решения уравнения (3.2.1) у=е~х
/2 = 0,368.
Нетрудно видеть, что основных усилий требует определение
.значений Ьц — коэффициентов матрицы результирующей системы
92

(3.2.4). Это и есть основная процедура при использовании метода
конечных элементов. В двухмерном случае коэффициенты bi,j
определяются двойными интегралами, которые распространяются
на элементы, представляющие собой обычно треугольники или
прямоугольники.
Теперь рассмотрим уравнение второго порядка
-g--f=0 (3.2.11)
с граничными условиями f=0 при х=—1 и / = 1 при х=1. В
качестве примера возьмем два элемента, как показано на рис. 3.2.1.
Рис. 3.2.1. Пример
одномерного конечного элемента. х-Ч
х=0
f?=f
х=/
Для решения используем линейные элементы и, следуя
общепринятым обозначениям, переименуем базисные функции F{ в N{.
Умножая уравнение на Nj и интегрируя по интервалу—1 ^ х ^
^ 1, получим
)М£г-г)**=°-
(3.2.12)
Интегрируя по частям и учитывая, что jVj = 0 при * = ±1, если
индекс / относится только к внутренним точкам, получим
d-irinr+N<f)dx==0- (з-2-13>
(•
Цель этого шага — уменьшить порядок производной в
уравнении, что является стандартным приемом в методе конечных
элементов. Следующий шаг состоит в выборе представления для
функции /. Мы можем сделать это в общем виде для всей
области или для каждого элемента в отдельности. Общая
формулировка допускает вычисление в каждом узле области. В данном
примере будем использовать поэлементное определение, а ниже
для двумерного уравнения рассмотрим общую форму
представления. Предположим, что для каждого элемента функция / имеет
следующий вид:
f=nN*{x)+UN\{x),
fu = fiN\l(x) + f2N2(x).
(3.2.14)
93

По определению, базисные функции Ni в узлах должны
удовлетворять условиям
ГО, 1фи
ЛМ*/)=(,э i = j (3.2.15)
Поэтому для интервала —1 ^ х ^ 0 полагаем
М0(х)==—х и N\(x) = (\ +х).
Для интервала 0 ^ х ^ 1 полагаем
N\1(x)=1—x и N2(x) = x.
Таким образом, рассматриваются три точки х = — 1, 0, 1, в
которых базисные функции удовлетворяют условию (3.2.15).
Подставим выражения для / (3.2.14) в (3.2.13) и проинтегрируем по
соответствующим интервалам:
С dN, Г dNa , dN\~\ \ dN, Г dN\< dN,].,
О 1
+ J Ni [f0NQ + fxN\\ dx + \ Nj [fMl + f2N2] dx = 0. (3.2.16)
-i о
В силу краевых условий /о = 0 и /2=1, т. е. требуется
определить только значение /i (/=1). В подробной записи имеем
о 1
j i[0 + f,]d*+J(-l)[f,(-l)+l]dx +
-1 Ö
0 1
+ \ (l+x)[0 + Ml + *)]d*+$(1-*Ш,(1-х) + *]<** = 0
-I 0
(3.2.17)
или
/i + /.-l+f. S (\ + x?dx + u\(\-x?dx +
-1
1
+ 5 x(\—x)dx = 0. (3.2.18)
о
Отсюда /i = 5/16 = 0,313. Точное решение (3.2.11) имеет вид: / =
= Ае~х + Вех, где К = егЧ(ег*— в2), В=—е2А и f\Xss0=i/(e-* + e) =
= 0,365.
Рассмотрим теперь общее представление (3.2.3) для двухмерной
задачи. В этом случае применение метода конечных элементов
связано с утомительной процедурой и на практике используются
94

вычислительные шаблоны. Рассмотрим, например, решение задачи,
представленной на рис. 3.2.2. Примем
u=YtNi{x9y)ui. (3.2.19)
i
Положим, что Ni являются линейными функциями и что
используются четыре прямоугольных элемента (рис. 3.2.3). Неизвестно
X =-/, y=f , — f Х=/, у=1
х=Ч,у=Ч
v=0
x=1,y=-f
Рис. 3.2.2. Пример двухмерного конечного
элемента.
Рис. 3.2.3. Узлы двухмерного конечного
элемента. 7
значение и лишь в центральной точке, ибо все другие точки
лежат на границах. Чтобы вычислить это значение, умножим
исходное уравнение на Nj и проинтегрируем по области. Получим
, Л2-. Л2.. \
(3.2.20)
.UOS-t-Sr)"«"*-0-
Интегрируя по частям и учитывая, что Nj = 0 на границе, получим
95

Если подставить разложение (3.2.19) в (3.2.21), то
Çn(-*L-£L + -*L-^)"<*.-0. <3.2.22>
Обозначая
+ 1 +1 • ХАТ
Г Г ( dNi dN; dNi am. \
C<-i = }l)i{-irJSr + ^^-)dxdy' (3-2.23)
5f{ Рис. 3.2.4. Нормализованные координаты
ч f конечного элемента.
имеем
£*/.**** = О, (3.2.24)
i
где ut для /=1... 8 известны и и=0 для /=1, 2, 6, 7 и 8.
Поэтому выражение (3.2.24) можно записать в виде
Cf, зЫз + си 4и4 + ci% 5и5 + си 9и9 = 0, (3.2.25)
где щ, ta, и5 известны. Однако возникает вопрос: какие значения
имеют из и иь— 1,0; 0,0 или 0,5. На это мы ответим позже.
Поскольку в (3.2.25) неизвестной является величина и% принимаем
/ = 9, так что необходимо вычислить с9,з> c9Ai с9г5 и с9,э (именно на
этом этапе расчеты становятся утомительными). Прежде всего
необходимо установить вид функций Ni в данной задаче. Отметим,
однако, что последующая процедура зависит не от характера
задачи, а лишь от конфигурации элементов. Для линейной базисной
функции Ni можно принять (Зенкевич, 1971):
Nt = -^{1+ 6Ы(1 + ml (3.2.26)
где li и r\i — соответствующие масштабные множители.
Переменные £ и т] меняются в пределах элемента так, как показано на
рис. 3.2.4. Заметим, что выражения для Ni меняются на каждом
элементе. В нашей задаче, вследствие симметрии, рассмотрим
96

только элементы 2 и 3 и узлы 3, 4, 5, 9. Для / = 9 базисные
функции имеют следующий вид:
N9 (элемент 3) = -J-(l-£)(1 + л). £ = -1+2*. r\=l+2y;
^9(элемент2) = ^-(1-^)(1-л), £ = -1+2*. л=-1+2у
или в координатах (*, у):
N9(3) = {l-x)(l + y),
N9(2) = (l-x)(l-y). (3.2.27)
Аналогично, можно показать, что
Nz{2) = xy, Л^4(3) = л:(1 + t/),
tf4(2) = *(l-y), #5(3) = -**/. (3.2.28)
Используя эти выражения, можно найти значения c2J-:
1 _ 1 _ ±_ _ 8
^9,3 о"» ^9, 4 ö~*> £9, 5 о > ^9, 9 ОТ •
Если эти значения подставить в (3.2.25), то получим
щ = -1- (и, + ы4 + "5). (3.2.29)
Теперь, если положить из = ^5 = 0,5 и щ=1, то получим
w9 = -j-. (3.2.30)
Это значение является правильным, что можно проверить
простым расчетом, применив разностную аппроксимацию исходного
уравнения Лапласа в центральной точке uq с учетом граничных
условий. Неопределенность в выборе значений в угловых точках
иг и и5 является затруднением и при использовании других
численных методов; такой выбор требует осторожности.
Приведенные примеры показывают особенности применения
метода конечных элементов. Прежде всего подчеркнем
необходимость применения численных процедур для вычисления
коэффициентов Cij. Эти процедуры должны быть построены в (g,
ri)-системе координат, так чтобы они могли легко применяться при
различной конфигурации области с использованием разбиения
области (х, у) на произвольные треугольники или прямоугольники,
трансформируемые в нормализованные регулярные элементы
(g, г\). Процедура образования сетки с целесообразным
расположением узлов допускает алгоритмизацию. В общем случае система
(3.2.24) является алгебраической системой для узловых значений
ии которые могут быть подходящим образом упорядочены с
целью упростить решение системы.
97

3.3. Примеры применения спектрального метода
для решения стационарных задач
Применим спектральный метод для решения уравнения (3.2.1),
которое уже решалось методом конечных элементов. Будем
считать, что функция / может быть разложена в ряд по полиномам
Чебышева, свойства которых рассмотрены, например, Фоксом и
Паркером (1968), Ривлиным (1974). В этом случае
f = f0Tl + fJ*l + f2Tl + ...i (3.3.1)
где Т* — полиномы Чебышева, которые рассматриваются в
промежутке O^x^l. Имеем
Т*о=1, ГТ = 2л: — 1, Г2 = 8д:2-8а:+1*. (3.3.2)
Если в (3.3.1) учесть только два члена, то
/ = /о + Ы2*-1). (3.3.3)
Из граничного условия следует, что
fo-1+f«. (3.3.4)
так что
/ = (!+/.) + /• (2* - 1) = (1 + /,) Т'о + fJÏ. (3.3.5)
Подставляя это выражение в уравнение (3.2.2), получаем
1 1
( 1 + /.) S Wj (То + ГО) dx + ft S W, (TV + TÏ) dx = 0. (3.3.6)
о 0
Теперь нужно выбрать функции Wj. Если использовать теорию
разложения по полиномам Чебышева, то получим
т*
Ух (1-х)
Напомним свойство полиномов Чебышева:
ГТ' |л'
-^ dx = \nß,
= 1 = 0,
= j^0, (3.3.7)
:/.
g Ух (1-х) . 0
Тогда из (3.3.6) с учетом того, что Т*'=0, Т*'=2Т*, находим
(l + f,)n + f,2ji=0 для / = 0,
(l + f.)0 + f,-2- = 0 для / = 1.
* Рассматриваются смещенные полиномы, определяющиеся из полиномов
Чебышева первого рода Тп(х) соотношением: Тп (х) = Тп(2х — 1).— Прим. ne-
рев.

Ясно, что второе уравнение ошибочно, ибо /i должно равняться
нулю, что невозможно. Это есть следствие усечения ряда. Из
уравнения для / = 0 получаем
/.=-4-' f=4—f*2*-1)- <3-3-8>
Для х=1 значение / = 0,333 сравнимо с точным решением / =
= 0,368. Эта процедура остается неизменной и при учете в
разложении более высоких степеней. В этом случае удобнее
использовать формулу, непосредственно дающую разложение для
производной (Готлиб и Орзаг, 1977):
/(*)=£ UT\ М. f (х) = f /fr? (*), (3.3.9а)
i = 0 i = 0
где
atf* =4 £ pfp, а0 = 2, а£ = 1 для i > 0. (3.3.96)
(Р+ 1) —нечетное
Рассмотрим теперь уравнение второго порядка
-S—/=0 (3.3.10)
с граничными условиями /(—1)=0 и /(1)=1. При решении этой
задачи будем учитывать три члена в разложении по полиномам
Чебышева в интервале —1 ^ х ^ 1:
f = foT0 + ÎJi + Î2T2. (3.3.11)
Подставляя (3.3.11) в (3.3.10) и учитывая, что для интервала
— l^x^l, Г0=1, Ti=x и Т2=2х2— 1, получим
4/2Г0 - (foTo + fxTx + f2T2) = 0. (3.3.12)
Используя условие ортогональности
+ 1
• dx = <jt/2t 1 = ]ф0, (3.3.13)
получим
4/2-/0 = 0, (3.3.14а)
/, = 0, (3.3.146)
/2 = 0. (3.3.14b)
Таким образом, мы имеем только тривиальное решение. Причина
этого состоит в том, что условия ортогональности для Т\ и Гг,
которые приводят к условиям (3.3.146) и (3.3.14в), являются
усеченными вследствие усечения ряда (3.3.11) на члене 7Y Если
в разложение добавить член с Г3 в (3.3.11), то уравнение
(3.3.146) уже не будет тривиальным. Однако следующее
уравнение, которое вводится из-за учета члена с fc, будет тривиальным.
Таким образом, ясно, что в случае использования полиномов
Чебышева последние два уравнения должны быть отброшены, ибо
они являются следствием редукции. Эти уравнения должны выра-
99

жать граничные условия, как было сделано выше. Таким
образом, имеем
4/2 — fo = 0 (дифференциальное уравнение), (3.3.15а)
/о — /i+/2 = 0 (граничное условие при х = — 1), (3.3.156)
/о + f 1 + Ь = 1 (граничное условие при х = 1). (3.3.15в)
Решение этой системы дает
2 1 1
/o = -g-. fi=—, /2 = ~кр
Решение, полученное разложением по полиномам Чебышева,
а также точное решение уравнения (3.3.10) показано на рис. 3.3.1.
Учитывая, что
использовались только три члена
разложения, точность
численного решения следует
признать высокой. Обычно на
практике применяются
разложения более высокого
порядка, при этом
используется формула типа (3.3.9)
для представления второй
производной (см. п. 8.1).
Для двумерного случая
вычислительные процедуры
метода аналогичны таковым
для одномерного случая, за
Рис. 3.3.1. Сравнение спектраль-
~f ~°;6 0 0,6 1 х ного (/) и точного (2) решений.
исключением некоторых деталей. Покажем спектральный подход,
в котором используется разложение по собственным функциям,
на примере рассмотренной выше двухмерной задачи для уравнения
Лапласа V2u=0. Допустим, что решение имеет вид
N M
«= S S Um.nFn(x)Gm(y)- (3-3.16)
tt=0 m =0
Первый шаг состоит в выборе вида функций Fn и Gm. Он зависит
от вида решаемого уравнения и граничных условий. Оптимальным
является использование функций, удовлетворяющих уравнению.
Это позволяет применить оптимальные методы обращения
матрицы для определения значений ит, п.
Для решения уравнения V2u = 0 в случае прямоугольной
области естественно использовать тригонометрические функции.
Положим вначале, что
Gm(y) = sm ""^+1> , /п=1, 2,... (3.3.17)
100
';и
0,8
0,6
о,«
0,2
п
' 1
X о
1
о2
I

Эта система функций автоматически удовлетворяет граничному
условию и=0 при у=±1. Выберем теперь вид функций Fn(x).
Здесь существует ряд возможностей; наиболее приемлемой
является та, при которой произведение функций Fn(x) • Gm(y)
удовлетворяет уравнению V2#=0:
V2(FnGm) = [K-(-^)2Frt]
Gm=0.
Это уравнение имеет решение:
Ьпехр
тл (х + 1)
+ спехр
тл (х + 1)
(3.3.18)
(3.3.19)
Для того чтобы удовлетворить условию и=0 при х= — 1,
положим
Ьп=-сп. (3.3.20)
Замечая, что функции Fn оказываются не зависящими от индекса,
можем записать (3.3.16) в виде
м
тл (х + 1) 1 Г тп (* 4-1)
и=2^ит jexp
т = \
-] —ехр[-
])х
Xsin
тл{у+\)
(3.3.21)
Это решение должно удовлетворять условию и = 1 при х = \\
M
1 = £ ит[ехр (-тл) - ехр (тл)]sin mTc(jj+1) . (3.3.22)
m = l
Для определения ит такое уравнение может быть эффективно
обращено численно с помощью быстрого преобразования Фурье.
В рассматриваемом простом случае, согласно формуле для
коэффициентов ряда Фурье, имеем
#т[ехр(—тл) — ехр(тл)]= j sin mjt^~t~ ) dy = -^-(l -cosmn).
тл
Замечая, что sh*= (ех — е~~х)/2, получаем окончательно
£-» тл L
1 — cos тл
sh тл
sh
тл (х + 1)
sin
тл(у+ 1)
(3.3.23)
(3.3.24)
Отметим, что для представления решения в виде ряда можно
выбрать и другие функции, однако тогда решение уравнений для
коэффициентов ит, п, вероятнее всего, потребовало бы численного
обращения матриц. Следует отметить также, что разрывы в
граничных условиях вызывают фиктивные осцилляции (явление Гиб-
101

бса). Такого рода особенности следует учитывать при применении
спектральных методов; к этому мы еще вернемся в п. 3.6.
Приведенные примеры использования спектрального метода и
метода конечных элементов показывают, что при спектральной
аппроксимации для отдельного элемента или комбинации
отдельных элементов с простыми функциями на элементе существенной
разницы между методами конечных элементов и спектральным
нет. Отметим возможность расширения спектрального подхода,
которая заключается в использовании аппроксимаций на
элементах с условиями сращивания (например, условием
непрерывности функции и некоторых ее производных). Основное различие
между двумя методами проявляется при уменьшении числа
элементов (обычно до одного) и увеличении числа членов в
спектральном разложении. Это может привести к увеличению
точности и уменьшению времени счета, если используется эффективная
схема обращения матриц.
До сих пор рассматривались примеры стационарных течений.
Однако задачи, в которых имеется зависимость от времени, могут
решаться и рассматриваемыми методами.
3.4. Пример применения метода конечных элементов
в нестационарном случае
При использовании методов спектрального и конечных элементов
для нахождения стационарного решения часто прибегают к
интегрированию нестационарного уравнения на длительный срок.
Рассмотрим уравнение вида:
-gr + 0(f, fX9 fy, fg9 x9y,z9 0 = 0.
Попытаемся найти значение f(t+At), используя значение f (t).
Выражение для G в этом уравнении содержит искомые функции и
их производные, которые следует аппроксимировать при
разбиении области на элементы некоторым рядом. Покажем это на
примере простого одномерного уравнения, отличающегося от (3.2.1)
наличием нестационарного члена;
-§h-ah-/=o <3-4Л>
с граничным условием / = 1 при х = 0. В качестве начального
условия полагаем f = 0 при £ = 0.
Для решения этого уравнения умножим его на весовую
функцию Wj(x) и проинтегрируем по х в интервале (xi, xi):
Хч Хг
4- S wifdx+S wi (ж+f)dx=°- <3-4-2>
Xi xx
102

Как и в стационарном случае, положим Wj = Fj и /4 = 1—х, F* =
= х; в первом приближении примем
f = fi{t)Fï{x) + f2{t)F2(x), (3.4.3)
так как /=1 при х = 0 для / > О, то /i = l для t > 0. Уравнение
(3.4.2) принимает вид
-^- j F2 (F, + F2f2) d* + \ F2 (F[ + ftF'2 + Ft + f2F2) dx = 0. (3.4.4)
Для стационарного случая при xi = 0 и X2= 1 в (3.2.8) мы имели:
1 1
^F2{F\ + F)dx=-±-% \F2(F'2 + F2)dx = ±. (3.4.5)
Поскольку
1 1
j FXF2 dx = -g-, J F2F2 d* = -i-, (3.4.6)
то
или
t(I4)+(4+W-« <3-4-7»
^-+4-/2-i=°- (3-4-8)
df ^ 2
Для того чтобы получить решение fi{t), это уравнение можно
проинтегрировать численно или аналитически. Решение,
полученное аналитически с учетом начального условия, имеет вид
f2 = ^-[l-e~T J- (З-4-9)
Величина f2 обращается в нуль при * = 0 и дает приближение
к стационарному значению, равному 0,4, для больших t.
В этом примере важно подчеркнуть еще раз, что граничное
условие заменило одно из уравнений для неизвестных, а именно
уравнение для /ч. Следует помнить, что такая процедура является
типичной.
3.5. Пример применения спектрального метода
в нестационарном случае
Уравнение (3.4.1) можно решить спектральным методом с
применением разложения по полиномам Чебышева с двумя членами,
аналогично тому, как это делалось в стационарном случае:
/ = М0 + М*)(2*-1). (3.5.1)
103

Если это выражение подставить в уравнение (3.4.2) вместе с
1Г , Г'-' F^T'-i (3.5.2)
' V*(*-i)
и положить Xi = 0 и xz= 1, то получим
-57-(/,я) + ^я + 2л/2 = 0,
-е-(Ьт-)+/«т—°- (3-5-3)
Граничное условие /=1 при л; = 0 дает
fi=l + /2. (3.5.4)
Очевидно, что задача переопределена и одно из уравнений
должно быть отброшено. Граничное условие не может быть опущено,
так что необходимо исключить одно из дифференциальных
уравнений. Из соображений точности следует исключить второе
уравнение. Причина этого изложена ранее (см. п. 3.1). Объединив
оставшееся уравнение с (3.5.3), получим
-^- + 3/,-2 = 0. (3.5.5)
Решение уравнения, обращающееся в нуль при / = 0, имеет вид
и=\(\-е~ы) (3.5.6)
и, следовательно:
/2=-(4-+-f «~80- (з-5-7)
При больших значениях t эти формулы дают стационарное
решение.
Отметим, однако, что /г не удовлетворяет начальному условию
при £=0. Это есть несогласованность, которая присуща методам,
использующим представление решения в виде конечного ряда, и
которая обязана переопределению системы уравнений для
коэффициентов ряда; связанную с этим погрешность можно уменьшить
с помощью т-метода (Ланцош, 1961). Такая особенность может
оказаться причиной осложнений в практических вычислениях (см.
Тейлор и Мёрдок, 1980). Рассмотрим, например, уравнение:
-§-+-§г =° (3-5-8>
при условиях / = 0 при / = 0 и f=\ при х = 0 для t> 0. Если для
его решения применить разложение по полиномам Чебышева с
явной схемой интегрирования по времени, то решение после первого
шага будет иметь вид, представленный на рис. 3.5.1. На этом же
рисунке приведены также точное решение и решение, полученное
104

методом коллокаций, показывающее, что расчеты в физической
области дают лучшие результаты (см. Тейлор и Мёрдок, 1980).
Поэтому, как уже отмечалось выше, следует быть осторожным при
u;w г—
1
N
'M
оА
г"
o,sV
Пй\—
1 Л П
1 Точное \
V" решение J * !
1 ; Ку^К~метод j
i i \ »
\\ / \ !
•1 / \ •
1 ' i i
1 \ 1 • \ \ 1
\ / 1 1
\ • /\Метод \ |
1* коллокаций l i
if * ' 1
.i it
ii * *
\ i \ i
\ i \ i \
\ 1 \ 1
\ 1 \ 1
^f ■ i Л-' î. 1
w
û;ô
iZa
Рис. 3.5.1. Сравнение точного решения с решениями,
полученными т-методом и методом коллокаций для
одного шага по времени (Д/ = 0,08).
применении т-метода с явной схемой интегрирования по времени.
Приведенные примеры интегрирования по времени одномерных
задач отразили основные особенности учета нестационарности при
применении спектрального метода и метода конечных элементов.
При переходе к многомерным задачам может лишь увеличиться
объем вычислений, но существо дела не меняется.
1Ö5

3.6. Псевдоспектральные методы
Кроме уже рассмотренных методов конечных элементов и
интегральных соотношений, спектрального метода, использующего
приближения Галеркина, существуют и другие спектральные методы,
а также метод ячеек, которые хорошо зарекомендовали себя при
решении задач гидромеханики. Рассмотрим эти методы кратко.
При решении задач динамики жидкости наиболее
эффективным оказалось одновременное применение методов коллокации и
спектрального, что получило название псевдоспектрального метода.
По сравнению со спектральным этот метод более эффективен и
в ряде случаев облегчает решение краевых задач. Чтобы
изложить сущность псевдоспектрального метода, рассмотрим
уравнение
dt + дх -v дх2 ' (ö'bA)
Предположим, что искомая функция / может быть представлена
в виде ряда
f=t U(t)Fi(x). (3.6.2)
Вместо того чтобы подставлять (3.6.2) в (3.6.1) и получать
уравнения для определения /;, проинтегрируем (3.6.1) по времени:
t + At
f(t + At,x)-f(t,x)= J (v-Ц—g-)d/. (3.6.3)
Если теперь подставить разложение (3.6.2) только в правую часть
уравнения (3.6.3), то мы получим связь между значениями / в
физическом пространстве и представлением этой функции в
спектральном пространстве. Правая часть может быть приближенно
вычислена с помощью квадратурных формул типа
t + At M
\ Gdt= £ bmG(tmt x)Att Af</i+l=-£±^-. (3.6.4)
t m=0
Это соотношение в совокупности с (3.6.3) может быть
использовано для определения f(t + At, х). Процедура характеризуется тем,
будет ли квадратура (3.6.4) неявной по времени или явной. Для
моментов времени, в которые значения f (t, х) известны, можно
использовать разложение / в форме (3.6.2). Тогда можно вычислить
0 0m. *)-(v-g-—§-) (3.6.5)
для каждого М<п+\.
Следующий шаг состоит в вычислении f(t + At) по формуле
M
f(t + Att x) = f(t, х)+ Z bmG(tm, х)Ы. (3.6.6)
m=0
106

Это легко выполняется, если fen+i=0, поскольку в этом случае
уравнение является явным. Однако если Ьп+1ф0> то необходимо
использовать какой-либо способ реализации неявной схемы.
Наиболее практичный путь связан с методом предиктор—корректор,
ибо он может быть применен даже в том случае, когда функция
G(t, х) достаточно сложна. При этом используется явный
предиктор для получения предварительного значения fp(t + At, х), затем
вычисляется G(t+At, х) в квадратурной формуле и находится
уточненное значение f(t + kt, х).
Другой подход основывается на том, что члены вязкости
являются линейными. Тогда вначале следует разделить линейные и
нелинейные члены в выражении для G(t, х). Затем можно
применить явную схему интегрирования по времени по отношению к
нелинейному члену и неявную — по отношению к линейному члену
вязкости. Аппроксимируем значения d2f/dx2 в момент t с помощью
спектрального разложения, d2f/dx2 в момент t + At представим на
сетке. Моршуазн (1981) разработал вариант такой процедуры и
с успехом применил его к расчетам различных видов течений.
Конечно-разностный предиктор и спектральный корректор можно
также применять и для решения уравнения Пуассона, как это
было показано в численных экспериментах Хёрша и др. (1982);
см. также Орзаг (1980). Другим вопросом, требующим особого
обсуждения, является проблема возникновения ошибок при
вычислении нелинейных членов. Эти ошибки называются ошибками
искаженного представления спектра. Возникают они при
перемножении двух спектральных разложений, например fdf/dx*.
При использовании псевдоспектрального метода обнаружено,
что явная схема интегрирования по времени Адамса—Бэшфорта
дает разумные результаты при решении задач невязких течений
с помощью разложений по полиномам Чебышева. Однако
существует некоторая неопределенность, относящаяся к выбору
оптимального шага по времени, с которым должны проводиться такие
расчеты. Готлиб и Орзаг (1977) предложили условие
устойчивости At^8/N2 (N — число спектральных членов). Спектральный
метод может рассматриваться как одноэлементное разложение
в интервале —1 ^ х ^ 1. Как следствие этого, оно содержит
информацию, которая позволяет любой точке в указанном интервале
«сообщаться» с другой точкой. Поэтому оказывается, что
временной шаг определяется приблизительно тем временем, которое
необходимо, чтобы волна распространилась по всему интервалу
— 1 ^ х ^ 1. В масштабной форме это означает, что t> равное
двум, является максимальным пределом. Экспериментальное
исследование псевдоспектрального метода, проведенное Майерсом,
Тейлором и Мёрдоком (1981), показало, что этот предел является
правильным и обеспечивает устойчивые результаты. Однако оп-
* Влияние такого искажения на сеточную аппроксимацию впервые
рассмотрено в работе: Phillips N. A. An example of nonlinear computational instability.
Atm. and Sea in motion. The Rockf. Inst. Pr. 1959. (Атмосфера и океан
в движении. ИЛ, 1963).— Прим. перев.
107

тимальное значение шага по времени с точки зрения точности и
устойчивости в настоящее время неизвестно, тем более, что
градиенты вблизи границ оказывают сильное влияние на шаг по
времени.
Псевдоспектральный подход имеет ряд достоинств. Во-первых,
он может обеспечивать требуемую точность аппроксимации по
пространственным переменным путем добавления членов в
разложение для f(ty х). Во-вторых, он позволяет без труда вводить
физические граничные точки. В-третьих, не требует трудоемких
квадратур, свойственных методу конечных элементов. В-четвертых,
допускает широкий выбор функций для разложений. И, наконец, при
расчетах сжимаемой жидкости метод легко применим в тех
случаях, когда использование других методов наталкивается на
трудности. В качестве функций для разложения могут использоваться
сплайны, полиномы Чебышева, синусы, косинусы и другие
функции. Однако, насколько это возможно, следует выбрать функции,
позволяющие использовать эффективные методы, такие, как
быстрое преобразование Фурье (БПФ) или методы типа сопряженных
градиентов для преобразований из физического пространства
в спектральное и обратно. Тейлор и др. (1981) показали, что
метод сопряженных градиентов может конкурировать с БПФ.
Дальнейшее исследование показывает, что предварительное
масштабирование матрицы с целью улучшения ее обусловленности может
сделать процедуру прямого матричного обращения
конкурентоспособной и для нестационарных задач.
Препятствием для применения метода БПФ может служить
неравенство пространственных шагов между узлами, которое
имеет место при использовании полиномов Чебышева. Однако при
использовании равномерной сетки и разложения по полиномам
Чебышева снижается точность определения коэффициентов при
обращении матриц. Ланцош (1956) показал, что более
правильный путь получения разложений по полиномам Чебышева с
равными расстояниями между узлами — это первоначальное
образование ряда по синусам и преобразование его с использованием
функциональных тождеств между синусами и рядами по
функциям Бесселя и полиномам Чебышева. Однако такой подход, по-
видимому, не дает преимуществ при практической реализации.
Следует соблюдать также осторожность при применении
псевдоспектрального метода к задачам, содержащим разрывы или
большие градиенты, поскольку в областях больших градиентов могут
возникать осцилляции (явление Гиббса). Поэтому при расчетах
могут использоваться фильтры, подавляющие шумы этого типа.
Орзаг и Готлиб (1980), а также Хедфогель (1980)
использовали спектральный метод с фильтром. В этом методе на первом
шаге находятся коэффициенты спектрального разложения,
которые затем умножаются на множители g*, имеющие вид
l-exp[-(iV2-/2)/iVg]
g'~ 1-ехр[-(лЭД)] '
108

где i — индекс члена в разложении, N — максимальный номер
члена, М) — регулирующий масштаб, обычно принимаемый
равным 2N.
Эксперименты с такого рода фильтрами показывают, что они
не всегда приводят к удовлетворительным результатам. Более
удовлетворительные результаты могут быть получены при
фильтрации в физическом пространстве по следующей формуле:
f но. = f стар + а {f. + _ _ 2fj + fj _ i)( (3 6 ?)
где о — коэффициент сглаживания, у определяет положение в
пространстве. Из полученных выше результатов, относящихся к
конечно-разностным методам, следует, что введение фильтра (3.6.7)
эквивалентно учету искусственной вязкости. Смысл применения
такого фильтра заключается в его селективности. Исследования
в этой области, проведенные Майерсом и др. (1981), а также
Тейлором, Майерсом и Альбертом (1981), позволили получить
селективные правила, которые, по-видимому, дают достаточно
хорошие результаты. Одно из этих правил относится к несжимаемой
жидкости, другое — к сжимаемой. Для несжимаемой жидкости
правило состоит в следующем: пусть задана точка Xj и
вычисленное значение f(xj); тогда
1 ) образуем величины 5 . \_ = f(Xj + \) — f(xf) и т. д.;
2) если S iS з <0и5 \ S з < О, то вводится коррекция
i + 2 J + ~2 i~T j~T
/"ob{Xj) = f {Xl) + 0,USj + i_ - sf_x_y
Для сжимаемой жидкости лучшим правилом, известным на
сегодняшний день, является правило коррекции потока, предложенного
Борисом и Буком (1976), а также Залесаком (1979). Это правило
состоит из следующих шагов:
1) уравнение интегрируется по времени для получения значения
/(/ + Д/) по значениям f(t) в N точках;
2) производится сглаживание f(t + At) по формуле
/, (t + M) = fi (t + At) + о [f/+1 (t + M) - 2/, (t + At) + f f _ , (t + AOÏ
3) производится «антисглаживание» f(t + At) по формуле
fj(t + At) = fj(t + At)-(D , -D Л,
где D 1 получается из следующего селективного правила:
D 1 =SmaxfO, minfSA i, \ Dl , I, SA 31;
i + T l l i-T | /+T| / + TJ
1 + 2
S = sign M ,V A , =fi + 1(t + At)-fj(t + àt).
(Vi)'
'•+-
109

Эту процедуру часто называют правилом коррекции потока в
конечных разностях. По-видимому, она должна давать хорошие
результаты и при применении спектральных методов. Вместо этой
процедуры можно использовать конечно-разностную схему с
искусственной вязкостью, обладающей определенными селективными
свойствами. Результаты исследований в этой области на
сегодняшний день весьма ограничены.
-/ 0 1x-f О
Рис. 3.6.1. Расчет плотности псевдоспектральным методом.
а — волна разряжения, б — контактная поверхность, в — ударная волна, г — без фильтра
в ударной волне.
На рис. 3.6.1 а—в показаны профили плотности,
рассчитанные соответственно для волны разрежения, контактной
поверхности и ударной волны по одномерным уравнениям для сжимаемой
жидкости с помощью псевдоспектрального метода с применением
описанного выше фильтра. Вычисления производились с
использованием разложений по полиномам Чебышева с 33 членами для
каждой переменной; начальные условия в каждом случае даны
на рисунке. Результаты показывают, что описанный подход в
одномерном случае оказывается перспективным. На рис. 3.6.1 г по-
110

казано распределение плотности для ударной волны, полученное
без применения фильтра. В заключение мы упомянем о методе,
предложенном Ланцошем (1956) и предназначенном для
уменьшения шума при разложении функций в ряд по синусам. Ланцош
(1956) предложил способ фильтрации рядов по синусам путем
усечения и затем умножения каждого коэффициента на множитель
_ sm[fa/(^ + l)]
£— W(N+l) *
где N+1 есть первый отбрасываемый член в ряде, i — индекс
члена. Такой способ устраняет явление Гиббса при расчете
ступенчатой функции. Аналогичный множитель предложен для
улучшения сходимости производной от ряда по синусам.
3.7. Метод конечных объемов (ячеек)
Метод конечных объемов или ячеек основан на представлении
рассматриваемого уравнения в интегральной форме. Область
решения делится на элементарные объемы, в пределах которых
проводится интегрирование уравнения. Такая процедура позволяет
учитывать сложную конфигурацию области, не вводя
криволинейную систему координат. Кроме того, метод обладает свойством
консервативности. В методе используются лишь координаты
угловых точек ячеек; при этом для определения ячеек могут быть
использованы и криволинейные координаты, не обязательно
ортогональные.
Опишем метод конечных объемов на примере уравнения
df . dF . dG
dt "• дх + ду
где
F = Fl(f)-v(f)-
= 0, (3.7.1)
äf
дх
G = C,(/)-v(/)-g-. (3.7.2)
Уравнение в интегральной форме (3.7.1) имеет вид
d
dt
\ fde + l H- Nds = 0, H = (F, G), (3.7.3)
qp tp
где QP — элементарная ячейка, граница которой есть Гр, и N —
единичный вектор нормали к Гр. Для определения интеграла вдоль
границы в декартовых координатах из (3.7.3) имеем
H - N ds = F dy - G dx. (3.7.4)
В случае криволинейной сетки (рис. 3.7.1) элементарная ячейка
представляет собой четырехугольник ABCD. Для аппроксимации
111

уравнения (3.7.3) в Qp используется осредненное значение fP
функции / по Qp в предположении, что fp локализуется в центре
Qp. Тогда уравнение (3.7.3) дает
где Sp — площадь ячейки ЙР; НАв, Ннс, HCd и Hda — потоки
через соответствующие стороны четырехугольника. Уравнение (3.7.5)
представляет собой обыкновенное дифференциальное уравнение,
описывающее эволюцию во времени среднего значения fp. Необхо-
N \
-4— \в
(hJ)
/ Рис. 3.7.1. Элементарная ячейка в ме-
/ тоде конечных объемов.
——— 2 1 — координатная сетка, 2 — грань ячейки.
димо также: а) определить потоки ЯАВ, НВс, HCd, Hda\ б)
ввести дискретизацию по времени в уравнение (3.7.5). Ограничимся
рассмотрением только пункта «а». С учетом (3.7.4) получим
Пав = Fab &Уав — Gab &Хав,
И вс = F вс &Увс — G вс Д#вс>
Ff CD = F CD kycD — G CD k*CD>
HDA = FDA /iyDA — G DA &xDAi (3.7.6)
где Fab, Gab, Fbc, Gbc, ...— соответственно средние значения F,
G по сторонам AB, ВС и др.,
&Хав = *в — Ха, &Уав = Ув — Уа,-.- (3.7.7)
(хА, У а) —координаты точки Л.
Рассмотрим теперь уравнение, следующее из (3.7.1) в
пренебрежении вязкостью (v = 0). Если через fi, j обозначить среднее
значение / по элементарной ячейке (рис. 3.7.2), то для
определения потоков можно использовать простые формулы
HAB = ±(Fi + lt, + Fl.,)byAB-±(Gi + UJ + Qi9i)bxAB. (3.7.8)
1 12

Аналогичные формулы могут быть записаны для потоков через
другие стороны элементарной ячейки. В случае однородной сетки
в декартовой системе координат эти выражения представляют
собой обычные формулы центральных разностей.
Аналогичным образом можно определить нецентрированные
схемы, предполагая, например, что среднее значение F по AB
имеет вид a\Fi, j+(l — ai)Fi+i, ;- вместо — (Ff+i, j + Fi, j), а среднее
Рис. 3.7.2. Сетка для метода конечных объемов.
значение по CD—(1—ai) Fi, j + ai/Vi, j вместо — (Fi, j + Fi-i, j).
Такие определения с «i = 0 или 1 были использованы в методах
конечных объемов Мак-Кормаком и Поллеем (1972), Риччи и
Инуе (1973) и Дейвертом (1975). В этих методах дискретизация
по времени основывалась на методе расщепления, связанного со
схемой предиктор—корректор (см. главу 2).
При наличии членов вязкости в уравнении (3.7.1) выражения
для потоков через границы ячеек содержат производные первого
порядка от функции f, поэтому необходимо определить средние
значения для этих производных. Рассмотрим выражение для
потока H АВ
113

Простой способ определения осредненных значений производных
(df/dx)AB и (df/dy)AB заключается в том, что они принимаются
равными средним значениям по ячейке Q' границей которой
является четырехугольник Г" = (Л', В', С, D') (см. рис. 3.7.2):
Q' г
где S' — площадь Q'. Остается определить криволинейные
интегралы по Г". Пусть
) fdy = fE куА'В' + ÎB ЬУВ'С + fp kyc'D' + fA ЬУD'A',
Г'
\ fdx=fE AxA>B' + fB àXB'C + fp A*C'D' + fA A*DM',
где
/£ = /» + !,/» fP = fi.i>
ÎA =-T-(fi + l./ + //./+ /*,/-l+ fi + i.f-i).
4
J_
4
ÎB = -r (fi + 1. /+ 1 + /*. /+ l + fi, i + fi+h i)
ЬУА'В> = — {ЬуАгВг + &УАв),
A*/C'D' = — (&УВА + At/CD),
Ьув'с = — (АуВхв + &Увс),
ЬУ D'A' = — (Ar/ол + &УАА')- (3.7.9)
Аналогично определяются АхА'в' и т. д. S'=—S;+i, j + S*. j), где
Si, j — площадь ячейки (/, /). Удобство этих аппроксимаций в том,
что они содержат только координаты вершин ячеек.
В качестве другой аппроксимации можно принять
А#л'В' = —kyc'D* = Ay ab, Аув'с = — AyD'A' = —AyPE (3.7.10)
и аналогично для АхА'в' и др. Кроме того, S' =АхреАуав —
— АхАВАуРЕ. Такая аппроксимация использует координаты
центров ячеек, определяемых как средние от координат вершин. Этот
результат можно получить и другим путем: предположим, что
114

центр ячейки (/, /) относится к криволинейной системе Цх, у) =
= const, г)(х, t/)=const (см. рис. 3.7.2). Производные df/dx и
dfldy могут быть выражены через производные от функции / по
5 и л:
àf _ 1 <?(/, У) àf _ 1 au, f) г _ a(jc, у) /q7in
ах - / а(б, л) • <ty — / a (g, л) ' a(g, л) # &•'•")
Производные по g, т), входящие в правые части (3.7.11),
аппроксимируются конечно-разностными отношениями, например:
/ам -JezJp. (JL\ - f*~fA гз7 12>
\ dl Jab- lE-lp ' \дц )ab^~ чв-г\а ' ^./.i^
Аналогично представляются производные по х и у. Подставляя
эти выражения в (3.7.11), имеем выражения для осредненных
производных (df/дх) АВ и (dfldy) ab, аналогичные тем, которые были
получены с использованием (3.7.10). Заметим, что значения £ и т|
в точках £, Р, Л, В и др. не входят в окончательные формулы:
геометрия сетки выражается только через кординаты вершин и
центров ячеек.
В случае однородной декартовой сетки обе аппроксимации
сводятся к центральным разностям.
Очевидно, что можно аппроксимировать производные в (3.7.12)
с помощью других конечно-разностных формул, например нецент-
рированных разностей, как это было сделано Дейвертом (1975).
До сих пор мы рассматривали общий подход. Теперь
остановимся подробнее на двух специальных методах, которые были
разработаны для случая сжимаемой невязкой жидкости.
3.7.1. Метод Годунова
Среди методов конечных объемов, применяемых для расчетов
течений сжимаемой жидкости, имеется метод, весьма удобный для
расчетов сложных течений невязкой жидкости при наличии
больших градиентов. Речь идет о методе, предложенном Годуновым
(1959). Он интересен тем, что основан на концепции
использования локальных решений одномерных физических задач для
расчетов многомерных течений. Чтобы представить основные
положения метода, рассмотрим одномерное нестационарное течение
сжимаемой жидкости, описываемое векторным уравнением:
-ÇL-1--??-—.0, (3.7.13)
dt ' дх
где
Здесь р — давление, р — плотность, и — скорость, y —
адиабатическая газовая постоянная.
115

Проинтегрируем уравнение (3.7.13) по промежутку (хи х*)
^r\fdx + F(x2)-F(x1) = 0, (3.7.14)
i
av
n-f
TL
Lx
J r
71+1
>-
Xfl-f xn
Xfl+1
Рис. 3.7.3. Распределение сохраняющихся величин.
f -[ fdx
затем определим осредненные величины с помощью выражения
(3.7.15)
Л, V Л, 1
Х\
Разделим область течения на элементы длиной Ах = хо — хи Если
описывать течение с помощью такого осреднения, то характери-
t ♦
Грань
Волна., у
бегущая влево
Контактная г
Волна,
'бегущая вправо
Состояние (n)
?п Рп "п
Рис. 3.7.4. Волновая диаграмма для задачи Римана.
стики течения в пределах каждого элемента будут постоянными,
но будут отличаться друг от друга на разных элементах. Эти
величины для некоторого момента времени t схематично показаны
на рис. 3.7.3. Основное положение метода заключается в том, что
по заданному начальному распределению можно вычислить потоки
в граничных точках из решения задачи Римана о распаде разрыва
(рис. 3.7.4) для переменных, осредняемых по сторонам
элементарных ячеек. Решение задачи Римана требует применения
итерационной процедуры.
116

В случае малых градиентов или акустической волны задача
может быть линеаризована, и окончательное выражение для
решения между состояниями п и м+1 (п — номер ячейки) имеет вид
иХ9 = й9--£*±^§±-, (3.7.16)
п — п (Ри)я+1-(рЦ)я П7т
Р*2 — Р2 0 , _ ,_ » (Ö./.1/J
2 VYP2/P2
Р,2 = р2- Цп+12 "* VvW* (3.7.18)
Эти соотношения используются для определения дозвукового
потока на границе, т. е. когда | w*|< VYP2/P2. В этом случае веер
характеристик является расходящимся. Если же
1«*| =
й Рп+х-Рп
2 VW2P2
>л/-^-- <3-7Л9>
т. е. в случае сверхзвукового потока, на границе следует
использовать соотношения
иХ2 = й2 "п + 12~"" , (3.7.20)
Р*,= рг- р"+1-р" , (3.7.21)
рХг = Ъ- Р''+<-Р" . (3.7.22)
Здесь предполагается, что сверхзвуковой поток движется слева
направо. В случае обратного направления индексы должны быть
переставлены. В этих выражениях индекс «2» означает осреднение
по состояниям п и д+1:
/2 = -2"(/я + /я + О-
Приведенные выражения для расчета плотности несколько
отличаются от тех, которые были получены Годуновым. Величины
в левых частях (3.7.16) —(3.7.18) и (3.7.20) —(3.7.22)
используются для определения потоков в уравнении (3.7.14). Уравнение
(3.7.14) интегрируется затем на шаг At по явной схеме. Это дает
новое распределение осредненных по ячейке величин и т. д.
Для решения двухмерной задачи используется метод
расщепления, что позволяет свести эту задачу к двум одномерным, для
решения которых применяются приведенные выше формулы.
Метод Годунова устойчив и сохраняет монотонность благодаря
сглаживанию, обязанному наличию градиентных членов в равенствах
(3.7.16) —(3.7.18) и (3.7.20) — (3.7.22). Градиентные члены
являются аналогами искусственной вязкости в конечно-разностном
методе. Эксперименты показывают, что при расчетах сильных
взрывных волн следует учитывать нелинейность в формулах, дающих
решение задачи Римана. Метод Годунова из-за повышенной устой-
117

чивости нашел широкое применение; сошлемся на работы
Тейлора и др. (1972) и Сода (1975), где показано, что метод
Годунова имеет ту же точность, что и многие конечно-разностные
методы второго порядка точности. Метод может быть рекомендован
для расчетов течений невязкой жидкости при наличии сложных
ударных волн.
Интересным развитием метода Годунова является метод,
предложенный Глиммом и исследованный Чориным (1976), Содом
(1978, 1980а, 1980b) и Колелла (1979). Достаточно подробно он
описан Содом (1980b). Этот метод не применяется к уравнениям
ни в интегральной, ни в разностной форме— в нем используется
решение задачи Римана на половинных шагах по времени и
случайная выборка.
3.7.2. Метод Глимма
Рассмотрим ту же одномерную задачу, которая рассматривалась
выше при изложении метода Годунова. В этой задаче область
разбивалась на ячейки длиной Ах и потоки на границах
вычислялись на основе решения задачи Римана с начальными значениями,
осредненными по границам ячейки. Методы Годунова и Глимма
идентичны только до этой процедуры. В методе Глимма не
используются исходные уравнения для вычисления новых значений
величин, относящихся к ячейке; вместо этого на следующем полушаге
по времени вновь решается задача Римана с начальными
условиями, являющимися решением предшествующей задачи в случайной
точке промежутка. Изложим ход решения с помощью графиков.
Шаг I: а) начальные условия б) решение задачи Римана.
Tav
1
71-/
71
Ах
п+1
Волна^
бегущая
влево
Состояние^
t \ Грань
]ячеини у
Контактная/
\ПОвенРп^У^лна,
?2 "сргучая вправо
\Pj / pL^^
Vn-j-i,Pnh,çCnh
ХП-1 XH XTL+1 __
Шаг II: Выполним случайную выборку решения между хп — Дх/2
и Хп + Дх/2 для получения новых средних начальных значений
в момент времени t+At/2.
Новые
^начальные
'условия в интервале
i_± i__ z
Ах Хъ Ах
2 2
xn-i ХП ХП+{
118

Шаг III: повторим шаги I и II, но с новыми начальными
значениями, полученными на шаге II (заметим, что интервал х
сдвигается на величину Дх/2 для этого шага).
После выполнения шага III имеем новое решение / в узловых
точках Хп+1/2. Метод интересен тем, что используются не
уравнения в форме законов сохранения, а лишь локальные решения.
h*
%0,9
<о
<^
1 0,6
Ъ
Л;
^ - ..
п
- i
Л
«L
\
V
л—•
1
— 1 ... i 1 1
0,25 0,50 0,75 1,0
0,25 0,50 0,75 1,0 х
Рис. 3.7.5. Результаты расчетов по методу Глимма ударной
волны в трубе. (Любезно представлены Содом.)
Возможно, что такой подход допускает обобщение, однако
соответствующая методика еще недостаточно разработана. Для
одномерных задач метод дает очень хорошие результаты. На рис. 3.7.5
представлено полученное Содом решение одномерной задачи о
распространении ударной волны в трубе с начальными условиями
pi = I, pi = l, wi = 0 и p2 = 0,l25, p2 = 0,l, W2 = 0. В вычислениях
полагалось Y=l>4 и Ax = 0,0l. В расчетах с применением метода
Глимма скорость на границе вычислялась по формуле
«£#/,'-£/(*. +S А*, < + -£-).
где \ — случайная величина из интервала
-T«s«T> "-
решение Римана.
Как отмечает Сод, лучших результатов можно достичь, если \
выбирать только один раз в течение шага по времени. Мы видим,
119

что результаты расчетов в одномерном случае оказываются
точнее тех, которые обычно дают разностные методы.
Список литературы
Годунов С. К. Разностный метод расчета разрывных решений уравнений
гидродинамики.— Матем. сборник. 1959, 47 (89), № 3, с. 271—308.
Boris, J. P., and Book, D. L. /. Comput. Phys. 20, 397—431 (1976).
Bristeau, M., Glowinski, R., Periaux, J., Perrier, P., Pironneau, O., and Poirier, G.
IRIA Laboria Rept. No. 294 (1978).
Bristeau, M., Glowinski, R., Periaux, J., Perrier, P., and Pironneau, O. Comput.
Meth. AppL Mech. Eng. 17/18, 619—657 (1979).
Chorin, A. J. J. Comput. Phys. 22, 517—533 (1976).
Collella, P. An analysis of the Effect of Operator Splitting and of the Sampling
Procedure on the Accuracy of Glimm's Method, PhD Thesis, University of
California, Berkeley (1979).
Deiwert, G. S. AIAA J. 13, 1354—1359 (1975). (PTK, 1975, № 10, с 120.)
Fox, L., and Parker, I. B. Chebyshev Polynomials in Numerical Analysis, Oxford
Press, London (1968).
Glimm, J. Commun. Pure AppL Math. 18, 697—715 (1965).
Gottlieb, D., and Orszag, S. A. Numerical Analysis of Spectral Methods, SIAM,
Philadelphia (1977).
Haidvogel, D. В., Robinson, A. R., and Schulman, E. E. /. Comput. Phys. 34, 1—53
(1980).
Hirsh, R. S., Taylor, T. D., Hadworny, M., and Kerr, J. Proceedings 8th
International Conference on Numerical Methods in Fluid Dynamics, Springer-Verlag,
New York.
Holt, M. Numerical Methods in Fluid Dynamics, Springer-Verlag, New York (1977).
Lanczos, С Applied Analysis, Prentice-Hall, Englewood Cliffs, NJ (1956). (Лан-
цош К. Практические методы прикладного анализа. М.: Физматгиз, 1961.)
McCormack, R. W., and Paullay, A. J. AIAA Paper 72-154, January (1972).
Morchoisne, Y. AIAA Paper No. 81-0109, Aerospace Sciences Mtg., St. Louis
(1981).
Myers, T., Taylor, T., and Murdock, J. /. Comput. Phys. 43, 180—188 (1981).
Orszag, S. A. /. Comput. Phys. 37, 70—92 (1980).
Orszag, S. A., and Gottlieb, D. In: Approximation Methods for Navier-Stokes
Problems, Lecture Notes in Mathematics, Vol. 771, pp. 331—398 Springer-Verlag,
New York (1980).
Periaux, J. Résolution de Quelques Problèmes Non linéaires en Aérodynamique
par des Méthodes d'Éléments Finis et de Moindres Carrés Fonctionnels. Thèse
de 3éme cycle, Université Pierre et Marie Curie, Paris (1979).
Rivlin, T. J. The Chebyshev Polynomials, Wiley-Interscience, New York (1974).
Sod, G. /. Comput. Phys. 27, 1—31 (1978).
Rizzi, A. W., and Inouye, M. AIAA J. 11(11), 1478—1485 (1973). (PTK, 1973,
№ И, с 27.)
Sod, G. A. SAE Tech. Paper No. 800288, Feb, (1980a).
Sod, G. A. Computational Fluid Dynamics with Stochastic Techniques. Princeton
University Report MAE No. 1479. Also presented at Von Karman Institute
of Fluid Dynamics Lecture, March 24 (1980b).
Taylor, T. Heat, Mass, and Momentum Transfer at Low Reynolds Numbers, Ph.
D. Thesis, University of California, Berkeley (1962).
Taylor, T., Ndefo, E., and Masson, B. S. J. Comput. Phys. 9, 99—119 (1972).
Taylor, T., and Murdock, J. In: Approximation Methods for Navier-Stokes
Problems, Lecture Notes in Mathematics, Vol. 771, pp. 519—539 Springer-Verlag,
New York (1980).
Taylor, T., Myeis, R., and Albert, J. Comput. Fluids, 9, 469—473 (1981).
Taylor, T., Hiish, R. S., and Nadworny, M. In Proceedings of the 4th GAMM
Conference on Numerical Methods in Fluid Mechanics, Paris (1981).
Zalesak, S. T. /. Comput. Phys. 31, 335—362 (1979).
Zienkiewicz, О. С The Finite Element Method in Engineering Science, McGraw-
Hill, London (1971).
120

Глава 4
Сопоставление численных методов
В предыдущих главах мы рассмотрели различные
численные методы, применяющиеся для решения задач динамики
жидкости. Не всегда легко удается сопоставить эти методы между
собой. Однако в ряде простых случаев можно привести некоторые
соотношения между конечно-разностным, интегральным и
спектральным методами. Для более сложных задач возможны только
качественные сопоставления.
4.1. Конечно-разностный аналог метода конечных элементов
В главе 3 проводилось сопоставление однотипных методов. В этой
главе мы сравним методы различных типов. Сопоставим сначала
методы конечных элементов и конечно-разностный. Лучше всего
это сделать путем получения конечно-разностных схем, исходя из
метода конечных элементов. Для этого рассмотрим простое
уравнение
Примем
dt ^ дх дх2 • V*-*-*)
f=ZiNJ(x)fl(t), (4.1.2)
где Nj(x) —одномерная базисная функция и fj(t) —сеточное
значение функции / в узлах. В соответствии с процедурой метода
конечных элементов получим уравнения
N N
i=i /=i
где
Pi. i = J NtNi dx>
0
r dNi
4i-i=\-dTNidx>
./—S
0
121

В случае линейных базисных функций вида
Н,-г
N,=
N• —
iVy —
#/ + .
=
х-
х1
=
Xj — X \
Ал:
-Xj-i
Да: 1
+ 1 — х :
Да:
X — Xf 1
Д* j
ДЛЯ JC/_i < *<*/,
ДЛЯ Х; ^ Jt <| */ + 1
можно показать, что выражения для коэффициентов уравнения
(4.1.3) имеют вид
О, 1Ф1$ i+ 1, / — 1,
76Да:, /=/ — 1,
Р'\/ = 1 2,
(4.1.5)
<7*\ / =
П,! =
(4.1.6)
(4.1.7)
7зД*, / = *',
I Ve Аа:, / = /+1;
( 0, /=£*', Î+1, /-1,
-'Л, / — ^* — 1,
о, / = /,
72, / = *'+1;
О, \фь, i+ 1, / — 1,
1/Дх, / = /—1,
—2/Д*, / = /,
{ 1/Д*. / = /+1.
Если выражения для коэффициентов подставить в уравнение
(4.1.3), то получим
d Г fi + i , 2ft , fi-i 1, // + ,-/,-, _ ff + i-2ff + ff-,
dt L 6 "Г 3 "*" 6 J"1" 2Да: "" Да:2
(4.1.8)
Это уравнение эквивалентно конечно-разностному уравнению
второго порядка точности, полученному ранее. Однако член с
производной по времени несколько отличается, поскольку представляет
трехточечное весовое осреднение функции /. Таким образом,
метод конечных элементов с выбранным базисом приводит к неявной
конечно-разностной схеме (4.1.8).
4.2. Конечно-разностный аналог спектрального метода
Аналогичный результат можно получить, используя для вывода
разностного уравнения разложение по полиномам Чебышева.
Предположим, что имеет место представление функции f в виде
ряда
f-Z М')Г/(*).
/=о
(4.2.1)
122

где Tj(x)—полином Чебышева степени /, a,j(t)—неизвестные
функции.
В этом разложении нормируем интервал—1<л:<1 и
положим f=fj-\ при *=—1, f=fj при *=0 и f=fi+\ при х=1.
Подставим (4.2.1) в уравнение (4.1.1); с учетом того что То = 1, Ti = x,
Тг = 2х2— 1, получим
(4.2.2)
(а'оТо + air, + а2Т2) 4
■ ахТ0 + 4а2Тх = 4а2Т0
Используя интегральное соотношение
J?i Vi-*2
0, 1ф\%
я, i = j = 0,
получим
a0 + ах = 4a2,
а\ + 4а2 = 0,
а2 =
= 0.
(4.2.3)
Последние два уравнения не могут выполняться, так как из них
следует, что аг = const и ai ~ constХ^ (результат усечения
разложения). Поэтому их следует отбросить. Это становится ясным,
если попытаться вывести разностное уравнение из этих трех
соотношений. Для этого необходимо связать величины ao, ai, аг со
значениями / в точках х=—1, 0, 1, что легко выполнить,
используя (4.2.1). Разрешая соответствующие уравнения относительно
üj, имеем
— ''+'+*' + ''- , ,4.2.4,
//+< — //-! _ A'f
(4.2.5)
ад= fz+.-^ + f,-,^ (4.2.6)
Подставляя эти выражения в (4.2.3), получим
J*-(-*L)-A.f, (4.2.8)
d (Д2/) = 0. (4.2.9)
dt
123

Уравнение (4.2.7) соответствует исходному уравнению и
эквивалентно дифференциально-разностному уравнению
d ( f/ + i+2// + f/-i \ , /, + ,-/,-, f/ + i-2f/ + /,-i
-)+
Л V 4 У ' 2Ajc — Ах2
(4.2.10)
Уравнение (4.2.10) можно интерпретировать двояко.
1. Оно определяет решение /j, если fj-\ и />i дают граничные
условия. В этом случае аппроксимация является весьма грубой
(Дх=1). Однако можно получить более точные уравнения
конечно-разностного типа, используя при разложении полиномы
более высокой степени. Заметим, что каждое из таких уравнений
связывает N узловых значений f (N — число членов в
разложении).
2. Оно определяет решение в элементарном интервале (Xj-i,
Xj+i) длины 2Ал: (Дл;<С1), преобразованном к интервалу (—1, 1).
В этом случае необходимо задать условия для коэффициентов а,}
в (4.2.1) с целью согласовать решение на общей границе двух
элементарных интервалов. Например, можно потребовать
непрерывности функции f и ее производной df/dx. Это дает
дополнительное уравнение, связывающее узловые значения функции f.
Разложения более высоких степеней потребуют дополнительных
условий согласования.
4.3. Простейший разностный аналог метода Годунова
Получим конечно-разностный аналог метода Годунова в
одномерном случае. Запишем уравнение сохранения в виде
-%Г + ^Г = 0, (4.3.1)
где / — сохраняющаяся величина и F — поток через границу х.
В схеме Годунова значение F на границе между ячейками п и
п+\ аппроксимируется с помощью соотношения
ri+./,- F» + ^ + ' (hn + t-hn). (4.3.2)
Поэтому разностная аппроксимация уравнения (4.3.1) имеет вид
fn(t + M) — fn(t) . ^П+'/Г^-'Ь _Q (4 3 3)
At * Ал: V • • /
или
fn(t + àt) — fn(t) j Fn+i-Fn-i (iin + x-2hn + hn-x) _q
At * 2 Ax Ax
(4.3.4)
Это уравнение является конечно-разностным аналогом исходного.
Дополнительный член имеет диссипативныи характер и оказывает
стабилизирующее влияние на результаты расчета.
124

Глава 5
Некоторые специальные методы
Наряду с уже рассмотренными методами конечных
разностей, конечных элементов и спектральным существуют и
другие численные методы, которые нельзя отнести ни к одному из этих
типов. Поскольку эти методы могут быть полезными в численных
расчетах, мы рассмотрим их в этой главе. При изложении методов
основное внимание уделяется практической стороне вопроса;
детали будут опущены. Сначала рассмотрим метод, применяемый
для решения задач, которые могут быть описаны
дифференциальными уравнениями Лапласа или Пуассона.
5.1. Метод решения задач потенциального течения
При решении ряда задач динамики несжимаемой жидкости
оказывается возможным использовать классический метод функции
Грина, опирающийся на интегральную формулировку уравнений.
К числу таких задач относится расчет потенциальных течений; при
этом с помощью функций Грина удается свести решение
трехмерной задачи к вычислению двухмерного поверхностного интеграла.
На это следует обратить внимание, так как может сложиться
впечатление, что при расчете потенциальных течений
использование конечно-разностного подхода наиболее предпочтительно.
Однако при практической реализации конечно-разностного аналога
исходных уравнений, несмотря на его простоту, могут возникнуть
трудности. Они могут быть связаны как со сложной
конфигурацией области решения, на границах которой должно выполняться
граничное условие
(п — направление нормали к границе), так и с большой
пространственной протяженностью области, когда необходимое число
узлов сетки столь велико, что превышает практические возможности
ЭВМ. Поэтому разностный метод не всегда является лучшим для
расчета потенциальных течений. Решение многих задач с
дозвуковым потенциальным потоком в сложной области можно свести
к интегральному уравнению, решение которого можно выполнить
с меньшими усилиями и дешевле. Такого рода метод решения был
разработан Хессом и Смитом (1964, 1966), Робертсом и Рандлом
(1972), Раббертом и др. (1967, 1972). Основу решения
применительно к уравнению для потенциального течения составляет
хорошо известный принцип суммирования источников, стоков и
диполей, приводящий к интегральному уравнению, описывающему
потенциал поля. Это можно сделать двумя способами. Первый
125

из них состоит в применении теоремы Грина, устанавливающей, что
потенциал в точке Р в пространстве вне поверхности s определяется
выражением
«pw—тк-Птт£
дц>(д)
Ч)
дп
X
1
r(P, я) J
ds +
ds.
J_
4л
1\ш
дп
X
(5.1.1)
где п — нормаль к поверхности 5 в точке q. На рис. 5.1.1
графически изображена каждая из переменных величин.
На поверхности 5 уравнение (5.1.1) превращается в
интегральное уравнение относительно ср(р), так как дср/дпд задано. Однако
Рис. 5.1.1. Представление переменных
задачи о потенциальном течении.
Хесс (1972) отметил, что это уравнение имеет не единственное
решение. Способ, вызывающий меньше возражений, основывается на
выражении для поверхностного потенциала, предложенного Кел-
логом (1953):
Ф(Р> = Й r(p\g) °Wds>
(5.1.2)
где a(q)—неизвестное распределение интенсивности источников.
Используя граничное условие оср/дп = 0 на поверхности и
учитывая скачок производной на ней (см. Келлог, 1953), получим
2^^-\\^[ттЬг]о{р)а8:
1р- Voo.
(5.1.3)
Это интегральное уравнение Фредгольма второго рода. Если
значения о(р) найдены из этого уравнения, то можно использовать
уравнение (5.1.2) для определения ср(р) и поля скорости из
соотношения V = grad(p. Если поле скорости известно, то давление
определяется из уравнения
P + ~ö-PooV2 =/?оо +-о-pooVL
(5.1.4)
126

Отметим, что метод одинаково пригоден как для внешних течений,
так и для течений внутри области при условии, что во втором
случае знак вдоль нормали меняется на противоположный.
Главное преимущество метода функции Грина заключается
в том, что он позволяет уменьшить на единицу размерность задачи
и обеспечить необходимую точность. Кроме того, узлы сетки
появляются только на границе области, которая принимается
конечной, даже если поле течения бесконечно. Метод позволяет
вычислить поле скорости и потенциал
с одинаковой точностью, которая,
однако, снижается в области
экстремальной кривизны
поверхности тела, где необходимо
измельчение сетки. Степень
измельчения зависит от точности,
с которой требуется приблизить
Рис. 5.1.2. Аппроксимация поверхности
с помощью плоских элементов.
поверхность при решении интегрального уравнения (5.1.3).
Аппроксимация интегрального уравнения имеет вид
2шт (р) - £ о, (Р)\\^ [тйЬг] ds=-n>-V~, (5.1 -5)
i At
где интеграл
вычисляется по элементу Ai. В некоторых случаях вычисление
этого интеграла связано с трудностями, поскольку эта процедура
зависит от конфигурации поверхности. Наиболее просто
интегральные коэффициенты уравнения (5.1.5) находятся в случае, когда
поверхность аппроксимируется плоскими элементами. Это дает
так называемое приближение первого порядка. Такая
аппроксимация поверхности показана на рис. 5.1.2. Ясно, что для поверхностей,
имеющих острые углы и малые радиусы кривизны, эта
аппроксимация становится неточной. Методы улучшения аппроксимаций
были предложены Хессом (1973), Робертсом и Рандлом (1972),
Крэгсом и др. (1973), которые учли характер потенциальных
решений вблизи ребер тел, отметив важность их влияния на
решение.
Процедура решения уравнения потенциального течения состоит
из следующих шагов:
1) аппроксимация рассматриваемой поверхности системой из N
элементов;
127

2) выбор одной точки р для каждого элемента, в которой должна
быть определена величина о(р)\
3) вычисление поверхностного интеграла для каждого элемента
1 ^ds. (5.1.7)
*.,-!!
дпр
г(р, q)
Здесь / обозначает точку р, в которой определяется нормаль к
поверхности. При p=q интеграл равен 2я. Для случаев двух и
трехмерных потоков Хесс разработал методы вычисления интегралов
(5.1.7). Он показал, что эти интегралы могут быть определены
путем вычисления потенциала и скорости, индуцируемых
поверхностным элементом источника единичной плотности в
некоторой точке пространства (более подробно см. работу Хесса и Смита
(1966));
4) составление уравнений
N
Е i4/t/ay = -nrVoo; (5.1.8)
х = 1
5) решение алгеабраических уравнений (5.1.8) методом
исключения Гаусса или каким-либо итерационным методом.
В принципе метод функции Грина является достаточно
простым, за исключением вычисления коэффициентов Лг-,,-. Для их
определения необходимо составлять специальные программы
расчета на ЭВМ. Если же они составлены, то решение сводится
к матричным преобразованиям, которые сами по себе могут
оказаться затруднительными. Метод функции Грина можно
использовать не только для решения задач расчета потенциальных
течений жидкости. Это относится и к задачам, формулируемым в
переменных вихрь—функция тока.
5.2. Функция Грина и уравнения в переменных вихрь—функция
тока
Уравнения, описывающие двумерное течение несжимаемой
жидкости, могут быть записаны в следующем виде (см. главу 1):
dû) , _ da) , _ d<ù 1 2
^г + »-эг + ^7=тгуЧ (5'2Л)
y*W + a, = 0, (5.2.2)
»=Т; Ü = -^T' <5-2-3)
где со — вихрь скорости, 4я — функция тока, и, v — составляющие
скорости в направлениях х и у соответственно. Уравнение для
функции тока может быть приведено к интегральному. С этой
целью используются некоторые сведения из теории потенциала. Пре-
128

жде всего можно записать решение уравнения в переменных
вихрь — функция тока в виде интеграла (см. Бэтчелор, 1967):
W = - -^- \ \ ©' In г dV9 (5.2.4)
где
г=л/(х-х')* + (у-уу9
dV = dx' dy\
g/ = cû(a;/, y')-
Здесь In г есть функция Грина для двумерного случая.
Из (5.2.4) можно получить выражения для составляющих
скорости:
°--+згй "~Р"' ■""■ <5-2-«>
Эти выражения используются для решения уравнения (5.2.1).
Можно однако добавить решения ин и Vh, удовлетворяющие
уравнению V2lF = 0. Получим
и = ир + uh, (5.2.7)
v = vp + vh. (5.2.8)
Эти выражения вместе с уравнением переноса вихря образуют
систему уравнений относительно и, v и œ. Граничные условия для и
и v удовлетворяются путем выбора соответствующих решений ин
и Vh- Имеются различные точки зрения относительно
необходимости учета последних слагаемых в (5.2.7) и (5.2.8). Томпсон и др.
(1973, 1974) показали, например, что если в случае вязкой
жидкости вихрь удовлетворяет граничным условиям, то однородные
решения необходимы только для удовлетворения условиям в
свободном потоке, т. е. Uh==Uoo и Vh = Voo. Смысл этого положения
заключается в возможности определить вихрь на границах таким
образом, чтобы удовлетворить одновременно граничным условиям
и уравнениям движения. В этом заключается основная проблема
для задач в рассматриваемой формулировке. Вообще говоря,
вихрь на границе получается путем разложения в ряд Тейлора,
исходя из определения (см. п. 6.5)
(0 = vXV. (5.2.9)
By (1975, 1976) исследовал этот вопрос и высказал
предположение, что граничные аппроксимации первого и второго порядка,,
возникающие при разложениях в ряд Тейлора, нарушают
интегральный закон сохранения вихря. Он предложил использовать
уравнения (5.2.7) и (5.2.8) на границе, чтобы получить
интегральное уравнение для вихря на поверхности.
129

Процедура решения задачи следующая:
1) уравнение (5.2.1) интегрируется по времени для получения
новых значений со в каждой внутренней точке области;
2) образуются соотношения
u=Uoo — -тг— / / -i 42-7-7 72- + ws, (5.2.10)
n it (x~~Xi) +(y — yi)
T/ 1 1 W (x-Xi)(ùijbxày /com
* = у- + -ъс\\ (х-*)* + (у-у,г +v° (5-2Л1)
с дополнительным требованием отсутствия особенности в точке
(/, /). В этих выражениях us и vs — поверхностные вихревые
потенциалы неопределенной интенсивности и со*, j — значения,
полученные на шаге 1;
3) соотношения шага 2 используются на границе и определяются
соответствующие вихревые потенциалы с тем, чтобы
удовлетворить граничным условиям.
Описанная процедура близка к методу Хесса и Смита (1966),
рассмотренному ранее. Нахождение us и vs может оказаться
трудоемкой процедурой. В некоторых случаях требуются
определенные усилия для получения достаточно точного решения. Однако
иногда можно предпочесть упрощенный подход Томпсона и др.
(1973, 1974), предположив, что us и v8 равны нулю, и вычислив
поверхностный вихрь по формуле
©,..,,., = п,..,,., X тЬ"["У| + 1- ' + 9V'-/]+ ° <Д*2>- <5-2Л2>
Различия в результатах, полученных с использованием формулы
Грина и приближений, аналогичных (5.2.12), рассматриваются
в п. 6.6.1.
Методы, рассмотренные до сих пор, излагались применительно
к нестационарным течениям. By и Вабах (1976), By и Рицк (1979)
предложили другой интегральный метод для решения задач в
различной формулировке применительно к стационарным и
нестационарным течениям [см. также By и Томпсон (1973)].
Независимо от применяемого метода проблема расчета
переходного режима сохраняется. Если точное переходное состояние
не интересует исследователя, а изучается лишь установившееся
состояние, то естественно предположить, что течение потенциально.
Основным преимуществом метода функций Грина является
применение интегральных уравнений, что способствует устойчивости
и зачастую уменьшению времени счета в случае, когда вихревая
область сравнительно невелика. В двухмерном варианте эти
преимущества не проявляются так явно, однако в трехмерном — метод
функции Грина сокращает время счета по сравнению с методом
конечных разностей. Но для окончательных выводов необходимы
дальнейшие исследования.
Для решения уравнения в переменных вихрь — функция тока
кроме метода функций Грина могут применяться и другие специ-
130

альные методы, например метод суммирования дискретных
вихрей, который мы рассмотрим ниже.
5.3. Метод дискретных вихрей
Использование метода дискретных вихревых элементов для
решения двухмерных задач несжимаемой жидкости было описано
различными авторами (см. Розенхед (1931), Биркгоф, Фишер (1959),
Чорин (1973), Милинаццо, Сафмен (1977), Мур (1976), Холд
(1979), Сафмен, Бейбер (1979), Леонард (1980)). Основная идея
этого метода заключается в представлении потока с помощью
дискретных вихрей, которые движутся вместе с потоком. Для
течения невязкой жидкости рассматривается уравнение вихря
-^-0, (5.3.1
которое означает, что завихренность остается постоянной в
движущемся элементе жидкости. Поэтому поток можно представить
как последовательность вихревых элементов. Траектории этих
элементов определяются скоростью течения:
-§-=«. <5-3-2>
-$- = *• (5.3.3).
Если скорости известны, то уравнения (5.3.2) и (5.3.3) можно
проинтегрировать. Если предположить, что поле течения состоит иа
совокупности точечных вихрей интенсивностью k\ в точках {х\у
Ух), то функция тока поля течения может быть представлена
в виде суперпозиции вихрей:
^=- -ег Zki In С(* -Xif +{у - у'п (5-3-4)
i
так как для единичного точечного вихря перемещение имеет вид
Ъ = - -И"ln г = - -%Г 1п И* - *# + (У - у№ (5.3.5)
Тогда поле скорости
—5-=--è-I-*^. <5-3-6>
dt " ду
ri. /
(<• ФI)
dt
где
ri i = (Xi - Xif + (yt — ygf.
131

Эти соотношения представляют собой уравнения траектории
каждого вихря. Их интегрирование позволяет получить положение
каждого вихря и, следовательно, определить поле скорости.
Однако применение метода встречает две трудности. Первая
заключается в том, что нельзя удовлетворить каким-либо заданным
граничным условиям; вторая — интегрирование уравнений может
приводить к стремительному росту решения вследствие наличия
особенности в правых частях уравнений при /->/. Чорин и Бернар
(1973) отметили, что эту трудность можно преодолеть путем
использования «капель» в местах расположения точечных вихрей,
т. е. использования соотношений
Г—g-ln|r|, |r|>ô
Чр=\ k (5.3.8)
и выбора ô таким, чтобы перемещение вихрей в течение
временного шага имело тот же порядок, что и разделение вихрей. Этот
выбор, однако, субъективен.
До сих пор мы рассматривали только случай невязкой
жидкости. Однако метод дискретных вихрей применялся также для
расчетов течений вязкой жидкости (Чорин, 1973). Процедура
заключается в применении метода со случайными вариациями
траектории. В настоящее время применимость такого подхода для
решения задач вязкой жидкости остается дискуссионной (Милинаццо
и Сафмен, 1977).
Применение общей концепции метода вихрей к свободным
течениям жидкости без твердых границ не вызывает
принципиальных трудностей, однако метод, позволяющий включать в
рассмотрение границы, недостаточно разработан. Для невязкой жидкости
можно принять условие отражения с целью исключить поток
через границу. Однако в случае вязкой жидкости вихрь
генерируется на границе и интенсивность источников и положение вихрей,
вводимых для удовлетворения уравнениям Навье—Стокса, не
определяются с достаточной точностью. Чорин (1978) исследовал
этот вопрос и предложил метод, который, по-видимому, применим
к пограничным слоям. Однако и в нем возникают трудности с
разделяющимися потоками.
Из сказанного следует, что метод вихрей нашел свое место
б ряде приложений, однако остается дискуссионным вопрос о его
значимости применительно к задачам вязкой жидкости.
Распространение метода на трехмерный случай также наталкивается на
трудности. Ребах (1977) разработал метод расчета трехмерных
течений, очень близкий по существу к методу вихрей. Описание
метода Ребаха можно найти как в его работе, так и в статье Ги-
ро-Валле и др. (1978).
Помимо метода дискретных вихрей существует метод,
сочетающий концепцию вихревой траектории с методом сеток для
определения функции тока (Кристиансен, 1973).
132

5.4. Метод облака в ячейке
Применение метода дискретных вихрей затруднено при наличии
особенностей, связанных с источником. Кроме того, применение
этого метода требует рассмотрения большого числа вихрей для
обеспечения достаточной точности расчетов. Метод, который, по-
видимому, сочетает лучшие свойства метода вихревых траекторий
и конечно-разностного способа решения уравнения в переменных
вихрь—функция тока, был предложен в работе Робертса и Кри-
hJ+t
ùh, j+1
Рис. 5.4.1. Веса для метода «облака .Ц-
в ячейке». hJ
*пУп
Aj
L+1jj
стиансена (1972). В этом методе интегрируются уравнения
траекторий для каждого вихря, т. е. уравнения:
dxn
dt
dyn
dt
■tin,
= Vn
(5.4.1)
(5.4.2)
Скорости определяются через функцию тока, а не путем
суммирования рядов. Численное решение уравнения для функции тока
строится путем использования осредненной по ячейкам
завихренности. Для решения применяется сетка, наложенная на поле
движущегося вихря. Завихренность в каждом узле сетки,
окружающем вихрь (рис. 5.4.1), локализованный в точке xn = Xi + ôjc, уп =
=Уз+ау> определяется с помощью нормирующих весов:
wi9j = (l — àx)(l —ày) = Aù Wi + UJ = 6x(l —6y) = A2;
witi + \ = (1 — Ьх) by = Л3; wi + lt j + l=öxöy = Л4, (5.4.3)
где
ô# = àx/àx, by = ày/ky.
Таким образом, в узлах сетки определяется завихренность,
создаваемая каждым вихрем. Далее уравнение для функции тока
у2\р4-о) = 0 (5.4.4)
133

решается любым методом — конечно-разностным, спектральным
или методом конечных элементов. Соответствующее граничное
условие для скорости должно быть задано с целью определить
функцию тока на границе области. После того как функция тока и,
следовательно, скорость определены в каждой точке сетки,
вычисляются скорости переноса вихревых элементов по формуле
ип = и (хп, уп) = Ахии I + А2щ + и / + Аъии / + 1 + М + 1, / +, (5.4.5)
и Vn — аналогично.
Далее интегрируются уравнения траекторий для
вихря:
Рассмотренный метод оказался весьма эффективным. Он успешно
применялся в работах Робертса и Кристиансена (1972), Кристи-
ансена (1973), а также Милинаццо и Сафмена (1977). Расчеты
показали, что для N=1000 (число вихрей) метод «облака
в ячейке» работает примерно в 20 раз быстрее метода
дискретных вихрей.
5.5. Метод характеристик
В последние годы при решении задач невязких сверхзвуковых и
неустановившихся течений сжимаемой жидкости широко
применяется метод характеристик. В этом методе используется тот факт,
что подобные течения могут быть описаны с помощью семейств
взаимно пересекающихся линий, вдоль которых распространяются
возмущения. Эти линии, называемые в одномерном случае
характеристиками, образуют вычислительную сетку, которая заранее
неизвестна и определяется в ходе вычислений *. Основная
особенность метода характеристик, затрудняющая его стандартную
реализацию, связана с тем, что в областях течений с большими
градиентами характеристики одного семейства сближаются и в
предельном случае пересекаются, т. е. вычислительная сетка
вырождается. Несмотря на то что преимуществом этого метода является
быстрота расчетов, в последние годы в связи с развитием новых
методов он используется все реже**. Однако его основные
положения не потеряли своей важности и часто применяются с целью
* В двумерном случае сетка образуется двумя семействами
бихарактеристик, на которых выполняются так называемые условия совместности; в
трехмерном — семействами характеристических поверхностей с выполняемыми
соотношениями совместности.— Прим. перев.
** Метод характеристик нашел широкое применение для расчета
сверхзвуковых течений с выделением ударных волн, в задачах оптимизации летательных
конструкций и др. (см. Белоцерковский О. М. и др. Численное исследование
современных задач газовой динамики. М., Наука, 1974; Воскресенский Г. П., Чуш-
кин П. И. Численные методы решения задач сверхзвукового обтекания тел.
Итоги науки и техники. Сер. Механика жидкости и газа. М., 1978). - Прим.
перев.
каждого
(5.4.6)
134

установления связей между решениями для внутренних точек
потока и его граничных значений. Они лежат и в основе методов
Годунова и Глимма, описанных выше. Рассмотрим основные
положения метода характеристик применительно к стационарному и
неустановившемуся случаям.
Рассмотрим сначала неустановившееся одномерное изэнтропи-
ческое течение сжимаемой жидкости. В этом случае основные
уравнения имеют вид:
др , дpu
dt ■ дх
:0, (5.5.1)
d9U Ь-зг(Р + РИя) = 0. (5.5.2)
dt
£- = const. (5.5.3)
Введем новую переменную — скорость звука с, определяемую
соотношениями
C2=rf/L <*= W-. (5.5.4)
dp р v '
Вместо исходной системы получим
"" +«-£-+4~Й-=0- (5.5.6)
dt ' дх ' р дх
Эти уравнения могут использоваться для вывода характеристик,
которые определяются как линии, на которых производные от
функций р и и не определены. Это достигается путем образования
системы уравнений, содержащей уравнения (5.5.5), (5.5.6) и
соотношения
du = -^dx + -^-dt, (5.5.7)
dp = -*-<** + -*-Л. (5.5.8)
Если решить эту систему относительно производных от р и \х и
найти условия, при которых эти производные становятся
неопределенными (т. е. приравнять нулю определитель системы), то мы
получим соотношения
-§-=и±с, (5.5.9)
с
-*-±А* = 0. (5.5.10)
135

Уравнение (5.5.9) называется уравнением характеристик.
Интегрирование этого уравнения дает сетку характеристик,
СОСТОЯщую из одной системы линий х= J (и + с) dt, пересекаемой дру-
t+At
гой системой линий х= J (и — с) dt (рис. 5.5.1). Вдоль характе-
t
ристики выполняется соотношение (5.5.10); положительный знак
сохраняется вдоль линии и + с, отрицательный — вдоль линии
t А
bx=(u+c)kt / \bx=(u-c)bt
—*-
х Рис. 5.5.1. Сетка характеристик.
и— с. С помощью этих уравнений и заданных условий в точках
1 и 2 можно найти положение точки 3 и значения р и и в этой
точке. Аналогичным образом можно, начиная от линии ^ = 0,
продвигаться шагами по времени. Сетка может стать нерегулярной,
что зависит от свойств потока и положения границ. Важно, что
вышеприведенные уравнения могут применяться для всех точек
течения и позволяют связать внутренние и граничные точки.
Для стационарных сверхзвуковых течений уравнения
характеристик выводятся аналогично, исходя из уравнений
(5.5.11)
(5.5.12)
(5.5.13)
(5.5.14)
JL- = const,
р
Можно показать, что уравнения характеристик имеют следующий
вид:
dy uv ± с д/ц2 + у2 — с2
dx и2 —с2
du
dx
dv
dx
+ v
+ v
dpu
dx
dv
du , 1 dp
dy * 9 dx
dv , 1 dp
dy ^ 9 dy
+^r=°.
--£-« o.
= 0,
= 0,
136

и вдоль характеристик выполняются условия
{и2 - с2) -ÎOL du + (v2 — с2) dv = 0.
Эти уравнения легко преобразовать к обычному виду (см.,
например, Липманн, Рошко (1957)).
Мы рассмотрели только применение метода характеристик для
решения одномерного нестационарного и двумерного
стационарного случаев, однако его можно применять и в многомерном
случае. Для этого существует целый ряд схем (см. Ферри, 1954;
Холт, 1956; Батлер, 1960; Холт, 1963; Клайн и Хофман, 1972; Рэ-
кич, 1967; Холт, 1974) *, однако на практике может применяться
метод расщепления, который позволяет свести многомерную
задачу к ряду одномерных нестационарных или двумерных
пошаговых задач. Мы не останавливаемся подробно на этих методах,
поскольку в книге для решения таких задач приводятся другие,
более простые и, по-видимому, более эффективные методы.
Сопоставление метода характеристик и конечно-разностной схемы
улавливания скачка на примере расчета трехмерного
сверхзвукового потока выполнено в работе Рэкича и Катлера (1972), в
которой показано, что расчет разностным методом выполняется
примерно в четыре раза быстрее.
В будущем метод характеристик, по-видимому, будет
использоваться в основном для корректного учета краевых условий путем
экстраполяции величин от расчетных точек в потоке сжимаемой
жидкости к неизвестным граничным точкам. Для этого требуется
провести характеристику через некоторую точку до ее
пересечения с границей и проинтегрировать соответствующее соотношение
вдоль характеристики. Объединив граничное условие с этими
результатами, можно определить поток в граничных точках.
Список литературы
Batchelor, G. К. An Introduction to Fluid Dynamics, Cambridge University Press,
Cambridge (1967).
Birkhoff, G., and Fisher, J. Circ. Mat. Palermo 8, 77—90 (1959).
Butler, D. С Proc. R. Soc. London A 1281, 255, 232—252 (1960).
Christiansen, J. P. /. Comput. Phys. 13, 363—379 (1973).
Chorin, A. J. /. Fluid Mech. 57, 785—796 (1973).
Chorin, A. J., and Bernai d, P. S. /. Comput. Phys. 13, 423—428 (1973).
Chorin, A. J. /. Comput. Phys. 22, 428—442 (1978).
Cline, M. C, and Hoffman, J. D. AIAA Paper No. 72—190 January (1972).
Craggs, J. W., Mangier, K. W., and Zamir, M. Aeronaut. Q. 24, February (1973).
Ferri, A. General Theory of High Speed Aerodynamics, Vol. 6, pp. 583—669,
Princeton University Press, Princeton, NJ (1954).
Guiraud-Vallée, D. et al. ONERA Report No. T. P. 1978—1, Chatillon, France
(1978). Also Proceedings of the Conference on Numerical Methods in Fluid
Dynamics. University of Reading, U. K., January (1978).
Hald. O. H. S J AM J. Numer. Anal. 16, 726—755 (1979).
* Обзор схем метода характеристик в многомерном случае — см.
упомянутую выше работу Г. П. Воскресенского, П. И. Чушкина.— Прим, перев.
137

Hess, J. L., and Smith, A. M. O. Douglas Aircraft Co. Rept. No. ES40622, March
(1962). Abbreviated version: /. Ship Res. 8, 22—44 (1964).
Hess, J. L., and Smith, A. M. O. Progress in Aeronautical Science, Vol. 8, pp. 1 —
138, Pergamon Press, New York (1966).
Hess, J. L., McDonnell-Douglas Corp. Rept. MDC15679—01, Loang Beach, October
(1972).
Hess, J. L., McDonnell-Douglas Corp. Engr. Paper 6060: Long Beach, California
(1973).
Holt, M. /. Fluid Mech. 1, 409—423 (1956).
Holt, M. The Method of Near Characteristics for Unsteady Flow Problems,
University of California, Berkeley, Rept. No. AS63-2, June (1963).
Holt, M. Recent Contributions to the Method of Characteristics for Three-Dimen-
sionai Problems in Gas Dynamics, University of California, Berkeley, Rept.
No. FM-74-2, Aprii (1974).
Kellogg, O. D. Foundations of Potential Theory, Dover Press, New York (1953).
Leonard, A. /. Comput. Phys. 37, 289—335 (1980).
Liepmann, H. W., and Roshko, A. Elements of Gasdynamics, Wiley & Sons, New
York (1957). (Липман Г. В., Рошко А. Эле.менты газовой динамики. М.,
1960.)
Milinazzo, F., and Saifman, P. G. /. Comput. Phys. 23, 380—392 (1977).
Moore, D. W. Mathematika 23, 35—44 (1976).
Rakich, J. V. AIAA J. 5, 1906—1908 (1967). (PTK, 1967, № 10, с 239.)
Rakich, J. V., and Kutler P. AIAA Paper 72—191 (1972).
Rehbach, С Rech. Aéros. No. 1977—5, 189—298 (1977).
Roberts, A. L., and Rundle, К. BAC (Weybridge) Rept. Aero. MA 19 (1972).
Roberts, K. V., and Christiansen, J. P. Comput. Phys. Commun. 3, 14—32 (1972).
Rosenhead L. Proc. R. Soc. Lond. A 134, 170—192 (1931).
Rubbert, P. E., et al. Vol. I, USAAVLABS Tech. Rept. No. 67—61A December
(1967).
Rubbert, P E., and Saaris, G. R. AIAA Paper No. 72—188 (1972).
Saffman, P. GM and Baker, G. G. Ann. Rev. Fluid Mech. 11, 95—122 (1979).
Thompson, Jr. J. F., Shanks, S. P., and Wu, J. С "Numerical Solution of 3-D Na-
vier-Stokes Equations in Integro-Differential Form" In Proceedings of the
AIAA Computational Fluid Dynamics Conference, Palm Springs, California,
July (1973).
Thompson, Jr. J. F., Shanks, S. P., and Wu, J. С AIAA J. 6, 787—794 (1974).
Wu, J. С AIAA Paper No. 75-47 (1975).
Wu, J. С AIAA J. 14, 1042—1049 (1976). (PTK, 1976, № 8, с 62.)
Wu, J. C, and Rizk, Y. M. Lecture Notes in Physics, Vol. 90, pp. 558—564,
Springer-Verlag, New York (1979).
Wu, J. C, and Thompson, J. F. Comput. Fluids 1, 197—215 (1973).
Wu, J. C, and Wahbah, M. M. Lecture Notes in Physics, Vol. 59, pp. 448—453,
Springer-Verlag, New York (1976).

Часть II
Несжимаемая жидкость
Эта часть книги посвящена задачам расчета потоков
несжимаемой жидкости. Существуют различные возможные
подходы к описанию таких движений, основанные на использовании
либо физических переменных скорость—давление, либо переменных
вихрь скорости—функция тока, либо уравнения переноса вихря.
Постановка задачи в физических переменных дает возможность
сравнительно легко распространить методы расчета плоского
потока на трехмерный случай. Основное затруднение при таком
подходе заключается в определении давления на границе
рассматриваемой области. В последующих главах показаны пути решения
этой проблемы.
Рассмотрены также задачи, в которых в качестве основных
переменных используются вихрь скорости и функция тока.
Трудность, возникающая в этом случае, связана главным образом
с необходимостью определения значения вихря на границе
области. Имеется целый ряд способов преодоления этой трудности, и
некоторые из них обсуждаются ниже. Неудобство использования
переменных вихрь скорости—функция тока состоит в том, что при
такой постановке задачи давление непосредственно не
рассчитывается и для определения этой величины необходимо производить
дополнительные вычисления.
Для случая трехмерного движения такие задачи не
рассматриваются, поскольку это требует обобщения используемых
методов. Подробности, касающиеся применения такого подхода,
можно найти в работах Азиза и Хеллумса (1976), а также Малин-
сона и Де Валь Дэвиса (1973, 1977); вопросы, связанные с
постановкой граничных условий, рассмотрены в статье Хирасаки и
Хеллумса (1970).
Заметим, что для решения двумерной задачи можно
воспользоваться только одним уравнением, записанным для функции тока.
Этот вопрос мы не рассматриваем и отсылаем читателя к
работам Бурсье и Франсуа (1969), Роуча и Эллиса (1975), Моршуазна
(1979),Чебеки и др. (1981).
Необходимо упомянуть еще об одном подходе, не нашедшем
отражения в этой книге. Речь идет об использовании переменных
вихрь—скорость. При этом необходимо рассматривать уравнение
переноса вихря, уравнение неразрывности и формулы,
определяющие вихрь через градиенты скорости. Дифференцируя уравнение
139

неразрывности и соотношение, определяющее вихрь скорости,
можно получить комбинацию этих двух уравнений. Это приводит
к эллиптическим уравнениям для составляющих скорости.
Примеры такого подхода рассмотрены в работах Фасела (1976) и
Денниса и др. (1979).
Список литературы
Aziz, К., and Heliums, J. D. Phys. Fluids 10, 314—324 (1967).
Bourcier, M., and François, С. Rech. Aérosp. No. 131, 23—33 (1969).
Cebeci, T., Hirsh, R. S., Keller, H. В., and Williams, P. G. Comput. Meth. Appl.
Mech. Engr. 27, 13—44 (1981).
Dennis, S. С R., Ingham, D. В., and Cock, R. N. /. Comput. Phys. 33, 325—339
(1979).
Fasel, M. /. Fluid Mech. 78, 355—383 (1976).
Hirasaki, G. J., and Heliums, J. D. Q. Appl. Math. 28, 293—297 (1970).
Mallinson, G. D., and De Vahl Davis, G. /. Comput. Phys. 12, 435—461 (1973).
Mallinson, G. D., and De Vahl Davis, G. /. Fluid Mech. 83, 1—31 (1977).
Morchoisne, Y. Rech. Aérosp. No. 1979-5, 293—306 (1979).
Richardson, S. M., and Cornish, A. R. H. /. Fluid Mech. 82, 309—319 (1977).
Roache, P. J., and Ellis, M. A. Comput. Fluids 3, 305—320 (1975).
Глава 6
Конечно-разностные методы
решения уравнений Навье—Стокса
6.1. Уравнения Навье—Стокса для физических переменных
Уравнения Навье—Стокса могут быть записаны в безразмерном
виде следующим образом:
^V . + A(V) + VP = -4r-V2V, (6.1.1а)
dt ■ ~v'' ' v Re
V V = 0, (6.1.16)
где выражение для A(V) определяется по-разному в зависимости
от того, в какой форме — консервативной или неконсервативной —
записывается адвективный член:
A(V) = v(W), (6.1.2а)
A(V) = (V-v)V. (6.1.26)
В декартовых координатах (х, у) составляющие а(и, v)> b(u>
v) вектора A(V)=ai + ôj, где V=(h, v), определяются по
следующим соотношениям:
я(и> v) = -^ {и2) + -щ- (uv),
Ъ (и, v) = -A. (uv) +Jjj- (о») (6.1 .За)
140

для (6.1.2а) и
/ v ди , ди
öx т ду '
b(u,v) = u-%r+v-^- (6.1.36)
для (6.1.26).
Типичной задачей, связанной с системой уравнений (6.1.1),
является задача с краевыми и начальными условиями, которая
формулируется следующим образом: найти решение V, р системы
уравнений (6.1.1) в ограниченной области Q с границей Г при
заданном на этой границе условии
V = Vr (6.1.4)
и значениях V в начальный момент времени £ = 0, равных
V = V°. (6.1.5)
Граничные значения Vr должны удовлетворять условию
J Vr-Nds = 0, (6.1.6)
г
где N — единичный вектор, направленный по нормали к Г, а
начальные значения V0 должны удовлетворять уравнению
V.V° = 0. (6.1.7)
При решении уравнений Навье—Стокса для скорости и
давления возникают следующие трудности:
1) уравнение у • V = 0, которое должно выполняться в любой
момент времени, не позволяет использовать какой-либо простой
явный метод, не требующий решения системы алгебраических
уравнений на каждом шаге по времени;
2) Отсутствует граничное условие для давления.
Ниже будут рассмотрены различные способы преодоления
указанных трудностей, которые были использованы для нахождения
конечно-разностных решений. Главы 7 и 8 посвящены изложению
процедур, используемых в методе конечных элементов и
спектральных методах. Начнем с рассмотрения метода искусственной
сжимаемости для стационарного потока.
6.2. Уравнения Навье—Стокса для стационарного случая:
метод искусственной сжимаемости
Уравнения Навье—Стокса для стационарного случая, полученные
из (6.1.1), записываются в виде
AW + vp-^v'V, (6.2.1а)
V • V = 0. (6.2.16)
141

Типичные краевые задачи для этих уравнений сводятся к
нахождению их решения в ограниченной области с заданными
значениями скорости V на границе
V = Vr. (6.2.2)
Вычислительные трудности, связанные с решением уравнений
Навье—Стокса для нестационарного потока, обусловлены
необходимостью удовлетворять на каждом шаге по времени
уравнению V- V = 0. В случае стационарного движения эту трудность
можно обойти с помощью так называемого метода искусственной
сжимаемости.
6.2.1. Описание метода
Этот метод был введен в 1965 г. Владимировой и др.* (см. также
Яненко, 1967) и в 1967 г. Чориным независимо друг от друга и
применялся ими в несколько различной форме. Метод основан на
том, что решение стационарных уравнений (6.2.1)
рассматривается как предел при tf-*oo, к которому стремится решение
системы нестационарных уравнений, образованной из
нестационарных уравнений движения и уравнения неразрывности с введенным
в него возмущением. В результате получается система
эволюционных уравнений, которые могут быть легко решены с помощью
обычных методов (явных или неявных).
Мы остановимся на методе Чорина. Тейлор и Ндефо (1970)
провели ряд расчетов с помощью метода, указанного в книге
Яненко, однако их попытки применить его для расчета течения
жидкости в канале не были успешными, и им пришлось решать
задачу с использованием уравнения Пуассона для давления.
Поэтому для установления пределов применимости этого метода
необходимо провести дальнейшие исследования. Метод Чорина
состоит в том, что вместо уравнения неразрывности
рассматривается следующее уравнение:
-^- + C2V.V=0, (6.2.3)
где с2 — произвольная постоянная. Решение этого уравнения не
имеет физического смысла, пока не достигнуто стационарное
состояние с d/dt = 0. Таким образом, условие V- V = 0
удовлетворяется только в случае сходимости. Метод, основанный на решении
системы уравнений (6.1.1а) и (6.2.3), может быть назван
псевдонестационарным методом, ибо переменная t, входящая в
последнее уравнение в качестве времени, не имеет физического
смысла.
* Владимирова H. Н., Кузнецов Б. Г., Яненко H. Н. Численный расчет
симметричного обтекания пластинки плоским потоком вязкой несжимаемой
жидкости.— В кн.: Некоторые вопросы вычислительной и прикладной математики.
Новосибирск: Наука, 1966, с. 186—192.— Прим. перев.
142

Параметр с2 в уравнении (6.2.3) необходимо выбирать таким
образом, чтобы обеспечить сходимость к стационарному
численному решению системы уравнений (6.1.1а) и (6.2.3) с граничными
условиями (6.2.2) и начальными условиями
V = V° при t = 0 и р = р° при t = 0, (6.2.4)
где V0 и р°—произвольные функции (при условии, что V- V° = 0).
Фортен и др. (1971) показали, что точное решение
нестационарной задачи Стокса, описываемой уравнениями (6.1.1а)г
(6.2.3), (6.2.2.) и (6.2.4), стремится к решению соответствующей
стационарной задачи Стокса.
Название «метод искусственной сжимаемости» (Чорин, 1967)
было выбрано потому, что уравнения (6.1.1а) и (6.2.3) можно
получить из уравнений Навье—Стокса для сжимаемой жидкости,
уравнение состояния которой записывается в виде
р = с2р, где с2 = const.
Фактически уравнение (6.2.3) обращается в уравнение (6.1.16)
при с~2->-0, и решение системы (6.1.1а) и (6.2.3) при c~2<d
можно рассматривать (Темам, 1969) как некоторое приближение
к нестационарному решению системы (6.1.1). Такой подход был
реализован Ганулисом и Тиррио (1976) с помощью метода
конечных разностей. Однако при этом могут возникнуть
вычислительные трудности, связанные с использованием очень больших
значений с2, и поэтому метод искусственной сжимаемости,
по-видимому, наиболее целесообразно применять при решении
стационарных задач. В этом смысле его можно рассматривать как
некоторый алгоритм построения специального итерационного метода
решения стационарной задачи.
6.2.2. Дискретизация
С целью дискретизации по пространству используем разнесенную
сетку для метода маркеров и ячеек (рис. 6.2.1), введенную Хар-
лоу и Уэлшем (1965), и рассмотрим весьма простую явную схему
дискретизации по времени. Тогда аппроксимация (6.1.1а) и (6.2.3)
будет иметь следующий вид:
1 /-Я+1 *.п \ 5 „п I А 1 ~п 1 г-,2 .П
-др1и/ + ,/а. } — Ui + 42, /Л" Я/ + 42, i+bxpt + 42* / =^rVhUi + i/2> /,
(6.2.5а)
1/Я+1 п \ \ ип , А 1 п
-дГ^°'» / + ,/2 — °£» / + W+ bi> l + lh + byPi. /+,/2 =
= ^-vb* /+«/2. (6.2.56)
-TT MV - ^ /) + г (Ai tf.V + АЯ+/0 = 0. (6.2.5b)
143

Здесь конечно-разностные операторы А1 , А1 и V£ определяются
х у П.
как
А*//, т = -д7~"(/' + 72, m — fl-42, m),
А^/,т = -д^-(//, m+ 42 — fl. т-ЧФ
Vifl, m = bxxfl. m + byyfl. m = К Ai + A* Ai) fl, ,
fl + l,m — 2fl,m + fl-l,m
&xx[ /, m =
À*/*///. m —
Ajc2
fl,m+l — 2//, m+ f/, m-l
(6.2.6)
7+/
J-'
\VL;j+f/2
Pij UL+f/2,j
L-f
Рис. 6.2.1. Сетка для метода марке-
i+t ров и ячеек (разнесенная сетка).
где /, m — либо целые, либо нецелые числа. Величины а* . и
'+72, /
Ь7} /з являются аппроксимационными выражениями для
операторов а (и, и) и b(u, v), определенных по (6.1.3). В случае
когда они используются в неконсервативной форме (6.1.36),
имеем
п п А 0 п ■ лп \0я
ai + 4*> / = И* + 1/2|/ /\xUi + i/2, j+ t>/ + i/„ j/\ylli + i/2, /,
*"/ + •/. = û?./ +«/.A^7./ + |/. + о?./ + «/.Д^?./ + |/а. (6.2.7a)
где
H'/rrTn + b /Ч'/Д^.У+'/Д ^./-'/2~1~ °< + l./-I/a).
Aü4/,
144
U/ + 1. m — //-1, m), Ayf/, m = 2 д» (/'. m + 1 — f/, m-l).
2 Да:

В случае когда используется консервативная форма (6.1.3а),
имеем
а?+./,. / = Ах {и)1+Ч2,1 + К (ио)?+ ■/.. />
ft?i/ + ./I = Ai(w)?(/ + ./I + Ai(o2)?l/ + ./if (6.2.76)
где
(u\i = -4(ui + 4*-i + ui-4*.if> (v2)i,i = — (vi, / + «/2+ о*. у-'/2)2,
(M0)/w=T-(a/ + v../ + i + M« + -/../)(°/ + i./ + '/.+ ^. / + -/J.
Все эти выражения имеют второй порядок точности
аппроксимации. Кроме того, последнее выражение (6.2.76) в достаточной
мере обладает свойством консервативности, поскольку
обеспечивает сохранение количества движения и кинетической энергии
(в случае Re_1 = 0) (Забуски и Дим, 1971).
6.2.3. Сходимость к стационарному состоянию
Метод искусственной сжимаемости применяют для того, чтобы
получить стационарное решение, удовлетворяющее условию
(6.2.8)
где е — малое число. То, что сходимость имеет место, следует из
двух фактов: 1) упомянутой выше сходимости при t-+oo решения
нестационарной задачи Стокса с возмущением к решению
стационарной задачи и 2) согласованности и устойчивости схемы (6.2.5)
(это следствие эвристического распространения теоремы Лакса
об эквивалентности). Согласованность следует из самого
построения конечно-разностной схемы.
Для того чтобы убедиться в устойчивости этой схемы,
проведем приближенный анализ. Аппроксимационные выражения,
полученные после линеаризации (6.2.7а) и (6.2.76), будут
идентичны, поэтому мы рассмотрим только (6.2.7а) в предположении,
что
^+ •/,./= Ä/./ + «/,= мо (const)-
»/./ + ./,-^ + I/fi/-ü0 (const).
На первом этапе опустим члены уравнений (6.2.5а) и (6.2.56),
включающие давление, так что уравнением дивергенции можно
145

пренебречь,* и каждое из двух уравнений движения примет вид
адвективно-диффузионного уравнения
fl+, ' = [/ - Д* («о А" + со Д°, - -^- Vi)] fi. i , (6.2.9)
где / — тождественный оператор.
Условия устойчивости этого разностного уравнения
записываются в виде
-f (K| + K|)2A*Re<l, (6.2.10)
4А' ■<!, (6.2.11)
Re Ал:2
где Дл; = Ду.
Второй этап приближенного анализа можно легко осуществить,
если пренебречь конвективным членом (ио = ио = 0) и оставить
члены с давлением. В этом случае схема примет вид
иПч»1 = {1 ^VÄ)rf+./,./-A/Aip7+./fi/f (6.2.12а)
^ + v. = (/-^-VÎ)o7,, + .,,-Af Aip7i/ + ./lf (6.2.126)
р? +х = pi, - Мс2(ДХ+/1 + А}*?."/ ')• (6.2.12в)
Спектральный радиус матрицы перехода для приведенной
выше схемы не превышает единицы, если удовлетворяются
следующие условия, полученные с помощью метода, указанного
в приложении А:
4Ч^Ыг+^)<1- *>°- (6-2лз)
В этом неравенстве содержится условие параболичности (6.2.11);
таким образом, условиями устойчивости являются соотношения
(6.2.10) и (6.2.13). Опыт расчетов показывает, что процесс
сходится быстрее, если с2 велико, но несколько меньше, чем с2 т>
определенное по (6.2.13).
Схема (6.2.5) может быть видоизменена с целью улучшения
сходимости и упрощения программирования (Фортен и др., 1971).
Эта модификация заключается в том, что в (6.2.5) используются
значения искомых величин, взятые в момент времени п+1 сразу
же после их вычисления (этот метод, являющийся не чем иным,
как схемой Гаусса—Зейделя, может быть частично неявным в за-
* Такой метод анализа может оказаться некорректным (см., например,
А. Касахара. О некоторых конечно-разностных методах решения
гидродинамических задач.— В кн.: Численные методы решения задач динамики атмосферы
и океана. Л., 1968, с. 157—167).— Прим. перев.
146

висимости от того, решаются ли эти уравнения одновременно или
последовательно). Например, уравнение (6.2.5а) с учетом (6.2.7а)
может переписать в виде
-£f\ui + xh,} — ui + xh> i)+ ui + 42,1 2ДЛ- •"
+ »/ + ■/,./ 2Â^ + -5J-lP/ + i./-P/./J-
1 ^?+3/2,/-2^+,/2t/+^//2,/
Re V bx2
+ Aï/2
причем здесь предполагается, что расчеты проводятся в порядке
возрастания значений индексов î и /.
Очевидно, что полученная таким образом схема на переходной
стадии уже не отвечает уравнениям (6.1.1а) и (6.2.3). Точнее
говоря, конечно-разностное уравнение (6.2.14) можно рассматривать
как аппроксимацию уравнения
„ ди . ди . ди . др 1 / д2ы . д2ы \ Л /с 0 л -ч
при
^-Hw+iïè?-)' (6-2Л6)
где Дл: = Ду. Уравнение (6.2.15) относится к параболическому типу
при / > 0 только в случае /С > 0. Это является необходимым
условием того, чтобы решение (6.2.15) имело предел при t-^oo.
Не проводя полного анализа сходимости модифицированной
схемы, можно тем не менее получить общее представление о
существовании такой сходимости. Если пренебречь конвективным
членом уравнения и слагаемым, содержащим давление,
указанный метод расчета превращается в метод последовательной
релаксации для решения уравнения Лапласа, причем в качестве
параметра релаксации берется величина co*=4Â//Re Ах2. Легко
проверить, что условие сходимости метода последовательной
релаксации 0 < со* < 2 есть не что иное, как условие К > 0 для случая
u=v = 0. Отметим, что критерий сходимости для этой
модифицированной полунеявной схемы в два раза менее ограничителен,
нежели условие (6.2.11).
Заметим также, что если 4+ (u + v)Re Ах > 0, то К< 1, т. е.
данная схема сходится к стационарному решению быстрее,
нежели согласованная схема (при том же At). Отмеченная здесь
вкратце аналогия между итерационной процедурой и
эволюционным уравнением уже обсуждалась в п. 2.2.3.
= 0, (6.2.14)
147

6.2.4. Аппроксимация граничных условий
Пусть Г является границей расчетной области, на которой заданы
значения скорости V, т. е. Vr=(ar, иг). Граничное условие для
давления р отсутствует. Если использовать разнесенную сетку для
метода маркеров и ячеек, то граница Г располагается таким
образом, как это указано на рис. 6.2.2. Вертикальная граница
проходит через точки, в которых определена горизонтальная
составил
Г
1>Г* Vf
■1
1
vr
Р У-1
р
► — Г
Рис. 6.2.2. Сетка для метода маркеров и
ячеек вблизи границы Г.
ляющая скорости и, а горизонтальная часть границы проходит
через точки, где определена вертикальная составляющая скорости v.
Поэтому давление р не определено на границе, и этот факт имеет
существенное значение: уравнение (6.2.5в) может быть без всяких
изменений записано для ближайших к границе точек. Алгоритм
(6.2.5а) —(6.2.5в) позволяет рассчитывать давление без ввода
специально относящихся к нему граничных условий.
Сетка для метода маркеров и ячеек хорошо приспособлена
для расчета давления, однако она не совсем удобна для расчета
скоростей. Как видно из рис. 6.2.2, определенные трудности
возникают при расчете vi или т, например: если vi рассчитывается
по (6.2.56), то в аппроксимационные выражения для blu, v) и
d2v
дХ2 вх°дит величина vo, т. е. значение скорости в точке, которая
лежит за пределами расчетной области. Можно указать
различные способы определения этой «внешней» величины vo.
Первый из них, так называемый метод отражения, состоит
в том, что скорость vr на границе Г определяется как среднее
значение между двумя скоростями vo и vu так что
t>o = 2i>r-op
(6.2.17)
т. е. vo определяется с помощью линейной экстраполяции.
Второй способ заключается в приближенном описании
производной в точке 1 (рис. 6.2.2) с помощью нецентрированных разно-
148

стей первого порядка точности. Так, для первой производной
используется выражение
dv
дх
1 (ü2+vi-2vv)^ (6.2.18а>
2 Ал:
а вторая производная определяется как
d2v
дх2
-*pr(v2-Svl + 2vT). (6.2.18б>
Фактически, с точки зрения удобства программирования
в точке 1 мы можем использовать обычную аппроксимацию с
центральными разностями и формулы (6.2.18а) и (6.2.186) для
определения величины v0. Так, для первых производных имеем
ÔV I V2— V0 1/1 о \
-ЗГ|,=-2д^=-2дГ(г'2 + 0--21'г)-
Это равенство дает величину vo такую же, как и (6.2.17).
Аналогичным образом соотношение
приводит к выражению
о0 = -§- (v2 — 6ü, + 8vr). (6.2.19>
Наконец, если используются нецентрированные разности второго-
порядка, мы получаем формулы
v0 = -3- (Щ — 6ü, + 8ür) для -£- (6.2.20a)
üq = g- (v3 — 5v2 + 15ü, — I6vr) для -^2- . (6.2.206)
Необходимо отметить, что если для аппроксимации вторых
производных в точке 1 используется (6.2.17), то связанная с этим
ошибка аппроксимации будет порядка 0(1). Иначе говоря, в точке
1 результирующее разностное уравнение (6.2.56) уже не отвечает
дифференциальному уравнению. Однако эта локальная потеря
согласованности вовсе не обязательно приводит к общему
уменьшению точности численного решения (Брамбль и Хаббард, 1962;
Крейс, 1972).
Исследуем теперь на простом примере влияние аппроксимации
граничных условий в случае использования разнесенной сетки.
Рассмотрим следующую задачу:
-g--o-~^ = 0, 0<х<1, 0 = const, (6.2.21а)
f(0) = t/0, f(\) = Ul. (6.2.216)
14$

Ее точное решение имеет вид
с, v _ (Щ — Ux) ехр (Ьх) + Цх — и0 ехр (Ô) (Q 2 ^
' ^ ' 1 — ехр (о) ' \ • • /
Отрезок [0, 1] разбивается промежуточными точками так, чтобы
концы отрезка попадали на середины ячеек сетки (рис. 6.2.3);
таким образом, Xi=(t —) Ах при / = 1, ..., N и Ax = l/N.
Аппроксимируем (6.2.21а) следующим образом:
(6.2.23)
• ' Т • L__
1 = 0 \ * = ' i=N i=N+1
LAx ^
Рис. 6.2.3. Распределение узлов сетки.
Величины /о и /jv+ь относящиеся к точкам, лежащим за
пределами рассматриваемого отрезка, рассчитываем по формуле (6.2.17)
/о = 2[/0 /b /N+1=21/! —fN.
Таким образом, ошибка аппроксимации конечно-разностного
уравнения (6.2.23) имеет порядок О (ах2) для 1 < i < N и 0(1) для
i=l или i = N. Система конечно-разностных уравнений задачи за-
лисывается следующим образом:
(fi + l-2fi + fi-l)--±g-(fi + l-fl-l) = 0, KKN, (6.2.24а)
(U - 3f, + 2Uo) - -^- (f2 + f i - 2t/0) = 0, (6.2.246)
(2Ul-3fN + fN-l)--^{2Ul-fN-fN-l)=0. (6.2.24b)
Решением этой задачи является
ft = £i?î + c2ql2y
где ci и qi — корни характеристического уравнения,
соответствующего (6.2.24а), а с\, сг — постоянные, определяемые из
соотношения (6.2.246) и (6.2.24в). Отсюда находим, что
•при
<7 = 2 + ôA*/(2 — ôAjc).
150

Путем разложения в ряд по Ах (Дл:->~0) в предположении,,
что Xi — фиксированное число, получим, что ошибка Ei равна
Ei = fi-f(xi) = Ax2(U0-Ui)W(xi) + O(Ax3)i 1</<ЛГ, (6.2.25).
где
Эта ошибка Ei имеет порядок О (Ал:2) повсюду, даже в точках
/ = 1 или i=N. В частности, в точке /=1 ошибка равна
Е=_ JWA. _J^1_ + о (Дд.). (6.2.26).
Этот результат наводит на мысль, что метод простого отражения
эквивалентен согласованной аппроксимации с помощью нецентри-
рованных разностей. В действительности, если использовать
указанные выше схемы аппроксимации первого и второго порядков,,
то мы получим ошибку порядка О (Ах2), но в точках,
расположенных вблизи границы, эта ошибка будет иметь порядок О (Ах3),
т. е. она будет на порядок больше величины, определяемой по
(6.2.26). Поэтому рекомендуется использовать согласованные
аппроксимации. Хорошие результаты, вообще говоря, получаются
при использовании трехточечных аппроксимаций (6.2.20а) для
dv/dx и d2v/dx2.
6.2.5. Уравнение Пуассона для давления
Метод искусственной сжимаемости можно рассматривать также
как некоторый итерационный метод решения стационарных
уравнений Навье—Стокса с использованием, в частности, уравнения
Пуассона для давления. Если с помощью уравнений (6.2.5а) и
(6.2.56) исключить из (6.2.5в) скорость в момент времени п+1, то^
последнее уравнение примет вид
Pli ' - PÎ. I - с2 àtMpl, = -с2 А* V* • [V - At (А - -jL- vïv) J .,
(6.2.27>
где
Vä = (Ax, A],), Vä = Д** + А,,.
В пределе при п ->■ оо, когда /??,"/1 = pi /, будет V/* • V" /= V/iX
X(VäV)" / = 0 и получающееся в результате уравнение
VaP*./ = —Vä • A<w (6.2.27а).
является аппроксимацией уравнений Пуассона для р, которая
получена следующим путем: взята дивергенция от обеих частей
уравнения (6.2.1а) и использовано уравнение (6.2.16), выражающее
тот факт, что V — бездивергентный вектор.
151

Для точек, расположенных вблизи границы, уравнение (6 2 27)
лринимает иной вид вследствие использования в уравнении
(Ь.2.5в) значении иг или vr . Например, для точек,
расположенных вблизи вертикальной границы (рис. 6.2.4), уравнение (6 2 27)
имеет следующий вид: ' '
+ Ai(tf./-Aftf.l + -!Lvi;«?./)], («./t>/-«r). (6.2.28)
bvz/г
->A7 4j
'Ai
[j-A
Wv/
67
j-f/2
i-0 1/2 1 = 1
V
1=2
Рис. 6.2.4. Расположение узлов
сетки вблизи вертикальной
границы Г.
Сравнивая это уравнение с уравнением (6.2.27), записанным для
точки (1, У), легко заметить, что (6.2.28) можно рассматривать как
уравнение (6.2.27)., записанное для точки (1, /) при граничном ус-
ловии
д*
■(p"/-Po"„)=-A/ + ^v^
Re
(6.2.29)
Это есть не что иное, как аппроксимация условия Неймана для
давления, полученного путем проекции уравнения движения
(Ь.2.1а) на нормаль к границе Г.
Необходимо отметить, что метод искусственной сжимаемости
ле требует рассмотрения ни о0>/±% , ни величины и^ ; для внеш-
!?АЙоотКИЛЧТО было бы необх°Димо при использовании уравнения
(Ь.2.2У). Преимущество данного метода состоит в том, что
условие Неймана для давления автоматически входит в численное
решение и этот факт согласуется с математической постановкой
задачи.
С этой точки зрения интересно обсудить влияние выбора сетки
на численное решение задачи. Для первой сетки, использованной
352

Чориным (1967) (рис. 6.2.5 а), скорость и давление определяются
в каждом ее узле. Преимуществом такой сетки являются ее
простота и то обстоятельство, что скорость определяется, в частности,
на границе Г, где эта величина обычно задается. В то же время
данная сетка имеет тот недостаток, что давление также должно
определяться на этой границе. Так как значение давления на
границе, вообще говоря, не задано, необходимо указать специальный
метод его расчета на этой границе.
На второй сетке (рис. 6.2.5 б), использовавшейся Кузнецовым
(1968), а также Фортеном и др. (1971), давление определяется
в узлах сетки, а скорость в центральной точке ячейки, однако гра-
1 U[
4 <
Р ,
Р
1 <
—
А—
р
<
Р
1—е 1
о
—о
f f oU .
Фи wV
1—g £ 1
Рис. 6.2.5. Расположение узлов сетки, принятое Чориным (а),
Кузнецовым, a также Фортеном и др. (б), для разнесенной сетки (в).
ница Г не проходит через узлы сетки. Поэтому давление уже не
надо определять на этой границе и можно использовать одни и
те же формулы для расчета всего поля давления.
Наконец, описанная выше сетка для метода маркеров и ячеек
(рис. 6.2.5 в) отличается от предыдущей расположением точек,
в которых определяется скорость. Некоторый недостаток этой сетки
состоит в том, что на каждой из сторон границы определяется
только одна составляющая скорости, так что вблизи границы
необходимо применять нецентрированные разности, как это
пояснялось в п. 6.2.4. Но это неудобство с лихвой окупается
преимуществами сетки для метода маркеров и ячеек в отношении расчета
давления.
Весьма полезно сравнить шаблоны сеток, используемые при
дискретизации уравнения Пуассона, с шаблонами, применяемыми
в методе искусственной сжимаемости. На сетках, представленных
на рис. 6.2.6, давление определяется во всех узловых точках,
а черные точки представляют собой те узлы, данные в которых
используются при аппроксимации уравнения Пуассона для точки Р
с использованием обычных центральных разностей. Как мы
видим, в первых двух случаях (а) и (б) существуют две не связа-
ных одна с другой системы точек, в которых определяется
давление. Это обстоятельство приводит к тому, что существуют два
решения для давления. Эти решения отличаются одно от другого
15S

произвольной постоянной, и, по-видимому, нет оснований считать,
что эти две произвольные постоянные обязательно должны быть
одинаковыми. Существование двух различных полей давления
может привести к возникновению осцилляции вычисленного
давления, однако градиент давления не является осциллирующей
функцией. Вычисленная скорость также не осциллирует. Необходимо
отметить, что при использовании специального метода, требующего
определения давления на границе Г, в случае использования сетки
на рис. 6.2.6 а или путем модификации аппроксимации V • V
вблизи Г в случае сетки на рис. 6.2.6 6, может возникнуть
взаимодействие (слабое) указанных полей. Из рисунка (6.2.5 в) видно,
*>
*)
*)
т 1 1 I 1 1 1 1 I 1 1 Г
I il т т т
1р 1р I \р \
т т 1 Т I т т т
-| 1 I \——А 9 [
è I I I 1 1 1 ' I ' ' 1
Рис. 6.2.6. Расположение узлов сетки при
решении уравнения Пуассона для давления.
что подобное явление разделения полей при использовании сетки
для метода маркеров и ячеек отсутствует и это делает ее очень
удобной для расчетов.
6.2.6. Другие варианты метода с введением искусственной сжимаемости
В п. 6.2.5 была представлена очень простая схема решения
уравнений, используемых в методе искусственной сжимаемости. В
некоторых случаях условия устойчивости могут стать слишком
ограничительными. К примеру, если Re очень мало (Re<Cl), то условие
(6.2.13) может привести к необходимости выбора весьма малых
значений At и с2, вследствие чего сходимость к стационарному
состоянию будет медленной. Если же Re очень велико, условие
(6.2.10) дает очень малое значение At. Численные эксперименты
показали, что этот метод чрезвычайно эффективен при Re,
меняющихся в пределах от 1 до 103 при условии разумного выбора
шагов сетки Дл: и Ау.
Рассмотрим теперь ряд схем, обладающих менее
ограничительными условиями устойчивости.
6.2.6.1. Схема центральных разностей Дюфорта—Франкела. Эта
схема была использована Чориным (1967) в предложенном им
J 54

методе искусственной сжимаемости. Схема может быть записана
в следующем виде:
1/М+1 П—\\,П I Л* я 1 гт2 п I
~~2ÂT\Ui + 42, \ — Ui + 42, f) + ^г + «/2. ]-Г &xpi + 42, j j^T" VhUi + i/2, / +
+ "V("Ä^+^-)A"^+,/2'/ = 0,
l/re + l га—l\|«n i »Ira 1 _2 га i
-2д7-^°г. /Ч-'/г — vi. i + 4*)-r t>i.i+4t + byPi. i + Чг Rj"Vftü'' / + '/г +
-YKT (P"+/' - P""/ ') + c2(A*< / + AX /) = °. (6-2-30>
где
Эта частично неявная схема обеспечивает устойчивость и не
приводит к вычислительным трудностям, ибо величины и^ . и
v^+i/ могут быть рассчитаны непосредственно по явной схеме.
Главная часть ошибки аппроксимации для первого уравнения
(6.2.30), например, равна
М2 / 1 . 1 \ д2и
Re Vax2 "» ày2 ) dt2
и стремится к нулю при приближении к стационарному состоянию.
Поскольку в схеме используются величины на трех временных
уровнях, трудно провести полный анализ устойчивости. Некоторые
результаты можно получить путем комбинирования теоретических
выкладок с расчетными данными в следующих двух случаях.
1. Для адвективно-диффузионного уравнения, аналогичного
(6.2.9), условие устойчивости имеет вид <y/2(u2Q+v20)l/2At/àx^:l
при Ау = Ах (Кашмен-Русин, 1984).
2. Для линеаризованных уравнений невязкой жидкости Чорин
получил условия (и20 + у20)1/з<с и у2(1 + у5)сД//Дл:<:1. Заметим,.
что Чорин выполнил этот анализ для совмещенной сетки (см.
рис. 6.2.5 а).
Один из недостатков схемы центральных разностей состоит
в том, что если члены, описывающие вязкость, отсутствуют, то для
нелинейного случая эта схема становится неустойчивой, и поэтому
при очень больших числах Рейнольдса следует ожидать
появления вычислительной неустойчивости.
6.2.6.2. Схема направленных против потока разностей. Условие
(6.2.10), которое становится весьма ограничительным в случае
больших чисел Рейнольдса, может быть смягчено, если для
аппроксимации конвективного члена A(V) использовать направлен-
155*

:ные против потока разности. При этом, однако, в случае
применения двухточечных нецентрированных разностей решение будет
иметь лишь первый порядок точности.
6.2.6.3. Неявные схемы чередующихся направлений.
Использование неявных схем чередующихся направлений сопряжено с более
громоздкими расчетами, поскольку при этом необходимо
производить обращение трехдиагональных матриц, однако эти схемы
обладают такими свойствами в отношении устойчивости, которые
зачастую делают их весьма эффективными. Рассмотрим уравнения
(6.1.1а) и (6.2.3), записанные в неконсервативной форме, и
введем обозначения
VÄ = K + '/.,y °/./ + ■/,)• Ph = Pi.r
Тогда неявная схема чередующихся направлений записывается
в виде
-д- ( V* - VX) + unh а; V, + vi a*;v2 -
- T^(a**Fa + A,i,VZ) + vtph = 0, (6.2.31a)
4-(vx+l~v,)+^Arv,+^A;vrl-
rt(a^Vä + A^Vä+1) + Vä+Pä = 0, (6.2.316)
^(pî+l-pî)+c2Vi;-VnH + l = 0, (6.2.31b)
где
Vä=(Ax, Ay), Ajf/, m =(//+!, m — fi,m)/kXt A^fi, m =
= (fl,m + \—fl,m)/by, kxfl,m = (fl,m — fl-Um)/àX И
kyfl, m = (fl, m — fl. m- l)/Ay;
Uh и Vh аппроксимируют и и v, как и в уравнении (6.2.7а).
Вообще говоря, конечно-разностные операторы,
соответствующие каждому из направлений, одинаковы на обоих шагах, т. е.
и, в частности,
Ах = А* , А„ = А„
a; = a7 = aî, д; = д7 = а°, (6.2.32)
причем операторы с центральными разностями А°х, А0 уже
были определены в п. 6.2.2. В этом случае можно усилить неявный
характер схемы (6.2.31), если на первом шаге рассчитать
вспомогательную величину рь, из уравнения с учетом искусственной
сжимаемости, а затем использовать это значение на втором шаге.
7156

На каждом шаге по времени задача сводится к решению
системы линейных алгебраических уравнений с трехдиагональными
матрицами. Обращение этих матриц легко выполняется с помощью
метода факторизации. Однако достаточное условие применимости
метода факторизации состоит в том, чтобы обращаемая матрица
удовлетворяла условиям (2.2.76). Если 0^|w£ |ReAx^2 и 0 =^
^ |и£ |ReA# =$ 2, эти условия выполняются. Если |a^|ReAjc>.
> 2, необходимо, чтобы имело место неравенство
Ы < . 2ReA*2 ; (6.2.33)
| unh I Re Ajc - 2
аналогичное условие должно выполняться, если |ü£|ReA*/>2.
Существует способ, помогающий ослабить условие (6.2.33). Он
заключается в использовании конечно-разностных операторов
с направленными против потока разностями для неявной части
схемы и операторов с разностями вниз по потоку для ее явной
части (Пейре, 1971). Таким образом, на каждом шаге по времени
получаются матрицы с диагональным преобладанием, и в случае
сходимости, т. е. для стационарного состояния, решение имеет
второй порядок точности. Именно
а*=4- К1 -е")А*+0 + 8") Д*1>
(6.2.34)
АГ = 4"[(1 + е«)А+ + (1 — ew)A^],
где eît = sign {unh), Д± определены выше, а выражения для А* и
А** аналогичны (6.2.34), если Д± заменить на А± а ги на ev =
= sign (vnh). На переходной стадии схема имеет первый порядок
точности, а при стационировании ошибка аппроксимации имеет
порядок О (AM*, At Ay, Ах2, ...).
Независимо от того, применяются ли соотношения (6.2.32) или
(6.2.34), условие устойчивости схемы (6.2.31), записанной для
разнесенной сетки (6.2.5в), имеет вид
д*<Л|£_ при Ах = Ау (6.2.35)
и может оказаться менее ограничительным, чем (6.2.33), если для
величины с выбрано достаточно малое значение. Путем численных
экспериментов было обнаружено, что это условие необходимо
изменить, приведя его к виду At<2ReXx2. Такое ограничение, по-
видимому, связано с влиянием граничных условий (см. п. 6.5.2 и
6.5.6).
157

6.3. Уравнения Навье—Стокса для нестационарного случая
Большинство общих методов, используемых обычно при решении
уравнений нестационарного движения, применяется для
определения давления путем решения уравнения Пуассона и расчета
скорости из уравнений движения. Примером такого метода является
метод маркеров и ячеек (Харлоу и Уэлш, 1965). Этот метод
первоначально был предложен для решения задач со свободной
поверхностью, но его можно применять и для расчета любого
течения несжимаемой жидкости. Аналогичный метод был разработан
Уильямсом (1969) для трехмерных задач, в которых
конечно-разностное уравнение Пуассона решалось с использованием
разложений в тригонометрические ряды.
Был предложен также метод (Чорин, 1968, Темам, 19696),
названный проекционным методом, который при использовании
явных схем в некоторых случаях совпадает с методом маркеров и
ячеек, однако по форме отличается от него.
Для решения нестационарных уравнений Навье—Стокса
успешно применялся также метод другого типа (Пейре, 1976). Он
основан на использовании метода искусственной сжимаемости на
каждом шаге по времени. Как уже было сказано, использование
метода искусственной сжимаемости эквивалентно решению
уравнения Пуассона для давления. Этот факт, справедливый, как было
показано для стационарного случая, имеет место также в
нестационарном случае, когда метод искусственной сжимаемости
реализуется в виде итерационной процедуры решения системы
нелинейных алгебраических уравнений, получающейся на каждом шаге
по времени.
Далее будет рассмотрен проекционный метод и показана его
связь с методом маркеров и ячеек в случае использования явной
схемы, а затем неявная итерационная схема. Наконец, несколько
слов будет сказано о методе возмущений, с помощью которого
недавно были получены интересные результаты.
6.3.1. Проекционный метод и метод маркеров и ячеек
6.3.1.1. Проекционный метод. Был предложен независимо Чориным
(1968) и Темамом (1969), а один из его вариантов с применением
явной схемы был разработан Фортеном и др. (1971). Этот метод
представляет собой метод дробных шагов первого порядка
точности по времени. На первом шаге вычисляется предварительное
значение V* по явной схеме
V д, + А (Vя) - -^- V2V» = 0, (6.3.1)
которая аппроксимирует уравнение движения без члена с
градиентом давления. Отметим, что здесь рассматривается только
дискретизация по времени.
153

Затем на втором шаге проводится коррекция V* с
использованием уравнений
V"+i-.V* . „ Л+1
M
Vp^l = 0y (6.3.2а)
V . V"+l=0. (6.3.26)
Если взять дивергенцию от левой части уравнения (6.3.2а) и
использовать уравнение (6.3.26), отражающее тот факт, что Vn+1 —
бездивергентный вектор, мы получим уравнение Пуассона
vy* + ' = -l-V • V*. (6.3.3а)
Граничное условие для р получается, если записать векторное
уравнение (6.3.2а) в проекции на единичную внешнюю нормаль
к границе Г. Таким образом мы получаем условие Неймана
где V* есть (пока еще не определенное) значение V* на Г.
Условие совместности в данном случае выражается в виде
-~- J V • V* ds = - -^- j (Vn + ' - V*) . Nds
й г
и выполняется тождественно вследствие наличия условия (6.1.6),
которое выражает тот факт, что полный поток на границе Г
равен нулю. Важно, что такая дискретизация по пространственным
переменным сохраняет вышеупомянутое условие совместности.
Итак, сначала из уравнения (6.3.1) получаем V*, затем, решая
задачу Неймана (6.3.3), находим pn+l и, наконец, по (6.3.2а)
рассчитываем Vn+1.
Прежде чем обсуждать аппроксимацию указанного граничного
условия и более подробно остановиться на соотношении для V*r,
скажем несколько слов относительно дискретизации по
пространственным переменным. Чорин (1968) использовал сетку,
показанную на рис. 6.2.5 а, Фортен и др. (1971) и Ладевез и Пейре
(1974)—сетку, изображенную на рис. 6.2.5 б. Однако,
по-видимому, этот метод оказывается более эффективным, если
используется сетка для метода маркеров и ячеек (рис. 6.2.5 в). В
последнем случае проекционный метод*, если не учитывать
граничные условия, становится тождественным методу маркеров и ячеек.
В случае когда для указанной выше сЗсемы центральных разностей
используется разнесенная сетка (см. рис. 6.2.5в), условия
устойчивости записываются в виде (6.2.10) и (6.2.11).
* Метод получил такое название из-за того, что векторная величина,
полученная на втором шаге, может рассматриваться как проекция векторного поля
(V*) на векторное подпространство с нулевой дивергенцией, удовлетворяющая
соответствующим граничным условиям.
159

Существенная особенность проекционного метода заключается
в том, что численное решение не зависит от величины V*. Это
утверждение основано на следующих двух фактах: 1) значение V*
во внутренних точках не зависит от V*, поскольку оно
вычисляется по явной схеме; 2) величина V*v появляется в задаче
Неймана (6.3.3) одновременно в правой части уравнения Пуассона
(6.3.3а) и в условии Неймана (6.3.36), и поэтому ее можно
сократить. Для того чтобы доказать это утверждение, достаточно
рассмотреть дискретизацию (6.3.3) для точек, расположенных вблизи
t/2,m,
0tm
f9m+i
Р 3/2, m
Lm
ifm-1
2,/n
Рис. 6.3.1. Положение точки P вблизи границы Г
при решении уравнения Пуассона.
границы Г, так как V* появляется только в уравнениях задачи,
относящихся к указанным точкам. Рассмотрим точку Р (рис. 6.3.1).
Аппроксимация (6.3.3а) в этой точке (/=1, j = m) может быть
записана так:
пП+1 ,
Р2, m
Ах \
, 1 ( Р?Л.' +
р1^
р?Л! •
PO, m
àx
1 ~~ P\% m
àx
nn+l _ nn+l
Pi, m Pi, m-
)
+
A»
A«/
_ 1 ( U*h, m
M \ A.
— Hr
'\, т + Чг
'], m-
4"
(6.3.4a)
Ax ' Ay
a условие Неймана (6.3.36) приближенно выражается в виде
1
АхЛРи т — рО, т)= —"д7"^Г — Ut).
(6.3.46)
Величина и* есть значение и* в точке (72, т). Легко видеть, что
если теперь величину р?4^— Р"+^ определенную из (6.3.46),
подставить в (6.3.4а), то неизвестная величина и* исключается из
обеих частей уравнения (6.3.4а). Отсюда можно заключить, что
решение не зависит от величины и*. В частности, мы можем
выбрать u*T = u7fi'i и тогда получим, что разность давления по нор-
166

мали к границе Г равна нулю на этой границе. Ясно, однако, что
условие обращения производной в нуль является чисто
вычислительным условием и это вовсе не означает, что реальный градиент
давления равен нулю.
Отметим, наконец, что если исключить V* из (6.3.1) и (6.3.2а),
мы придем к схеме
V*+IA7V* + А (v*)+*рп+' —wу2у"=°' {6-3-5)
которая аппроксимирует уравнение движения с первым порядком
точности по времени. Поэтому устойчивость проекционного метода
определяется условием устойчивости разностного уравнения,
полученного на основании (6.3.5). Обсуждавшиеся выше условия
устойчивости зависят, в частности, от того, какая схема (с
центральными или же направленными против потока разностями)
используется для аппроксимации конвективного члена A(V).
Уравнение (6.3.5) есть не что иное, как то самое уравнение, для
решения которого применяется метод маркеров и ячеек, изложенный
в п. 6.3.1.2.
Фактически проекционный метод является частным случаем
более общего метода расщепления, использовавшегося для
решения уравнений (6.3.5) и (6.3.26). На его основе можно получить
ряд способов решения уравнения движения. Другие возможности
обсуждаются в п. 6.3.1.3.
6.3.1.2. Метод маркеров и ячеек. При использовании метода
маркеров и ячеек, предложенного в 1965 г. Харлоу и Уэлшем,
сначала производится аппроксимация уравнения движения (6.1.1а)
а затем путем комбинирования аппроксимированных уравнений
движения для обеих составляющих скорости получается
уравнение Пуассона для давления. Уравнения (6.1.1) записываются
в виде
-дГ \Ui + 4*1 — Ui + !/2. i) + ai + 42, i + &xpi + i/„ / j^T VäH/ + i/2, / = 0,
(6.3.6a)
(6.3.66)
aU?,V + aXV = 0, (6.3.6b)
где все операторы определяются согласно (6.2.6).
Если теперь ввести величины w£+* f и »Т^+у«» определенные
соответственно из (6.3.6а) и (6.3.66), в условие несжимаемости
(б.З.бв), то получим уравнение
vipVii -Ai (4f -а" /+-W ri»* • /)+
+ А' (-%- - ЬЧ., + -щ- VU, ,), (6.3.7а)
161

которое представляет собой не что иное, как аппроксимацию
уравнения (6.3.3а). В результате единственное отличие этого способа
от проекционного метода состоит в том, что уравнение Пуассона
здесь записывается в ином виде, однако эти различия
распространяются и на аппроксимацию правых частей в тех случаях, когда
рассматриваются точки вблизи границы. Предположим, что
уравнение (6.3.7а) записано для точки Р (см. рис. 6.3.1), которой
соответствуют г = 1, / = т:
1
■\р2, m — *Р\, m + PC m) + Л 2 VPl, m + 1 — *Pl, m + p\,m-l) =
Ax2 \H*. m «Hi.m-r fu. m/ ~r Ay2
1 Г 1 / rz n \ y \ ( n n \1
—ÂF^3"2* m ~~ ö"/2' m'—5F^" m + ,/2"~ *" т-чХ (6.3.8a)
где
ö?i/ = a?i/-Re-IvK/ и в?,, = 6?./-Re-'vattf. y
Одновременно рассмотрим граничное условие для давления,
получаемое в результате проекции уравнения движения (6.1.1а)
на нормаль N к границе Г:
(-&-Г— [4- + *<V)-Tè-Wr N. (6.3.76)
Для точки Р уравнение (6.3.76) записывается в виде
а в дискретизированной форме
-д^ (PU +т - />о".+т) = -4" («7Î.'» - "'/.. «) - О?/,. ». (6.3.86)
где о,, т рассчитывается для уровня n, а не п+ 1.
Существенная разница между методом маркеров и ячеек и
проекционным методом заключается в том, что в (6.3.4) величина w*
считается неизвестной, подлежащей определению; однако для
суммы и71.. +Atä7}. , являющейся аналогом и*, необходимо
12, ТП '/2, ТП 1
ввести особую аппроксимацию величины ä71 m , в которую
входят не определенные пока значения и* m и и£ m±l/j . Вообще
говоря, эти величины определяются нецентрированной
аппроксимацией ä7}. т. Кроме того, часто используется упрощенная форма
(6.3.76)."™
Однако при рассмотрении уравнения (6.3.8а) мы можем
подставить в него выражение р*+^—Р^т' определенное из (6.3.86),
162

и убедиться в том, что anXj ш исчезает из обеих частей этого
уравнения. На основании этого можно заключить, что при данной
аппроксимации й™ т величины ип_ъ т и v* m+I/ могут быть
выбраны произвольными. В то же время v^ ч появляется также
и в 5 1 m+I/, но при этом возникает проблема, которая уже
обсуждалась в п. 6.2.4 и которая связана с использованием сетки для
метода маркеров и ячеек.
В заключение отметим, что численное решение, полученное
с помощью метода маркеров и ячеек, не зависит от вычисляемого
значения градиента давления на границе Г, взятого по нормали
к этой границе, при условии, что значение Щ ш согласовано с
аппроксимацией правой части уравнения Пуассона. Это условие
необходимо для того, чтобы сохранялась точная аналогия с
сокращением u*v в уравнении (6.3.4). Наконец, если ä1}, т принято
равным —(и71*1 — unT)/At, что соответствует специальному выбору
и1\, т» мы снова получаем равенство нулю градиента давления
на Г, нормального к этой границе.
Впервые однородное граничное условие для градиента
давления было использовано Фортеном и др. (1971) в проекционном
методе. Затем Истон (1972) предложил применить его в методе
маркеров и ячеек, и в совершенно ином контексте оно было
рассмотрено Амсденом и Харлоу (1970) в упрощенном методе
маркеров и ячеек (метод SMÂC).
6.3.1.3. Неявные схемы. В методах, рассмотренных выше, скорость
Vn+i вычислялась по явной схеме, поэтому, согласно условию
устойчивости аппроксимации уравнения параболического типа, шаг
по времени был ограничен. Это ограничение может быть снято,
если применять неявные схемы.
Например, используя метод маркеров и ячеек, Прахт (1971)
применил неявную схему для расчета члена, описывающего
вязкость, и явную схему для расчета конвективных членов; Девиль
(1974, 1975) использовал неявную схему в методе чередующихся
направлений. В проекционном методе неявная схема может
использоваться либо при вычислении вспомогательного поля
скорости V*, либо при аппроксимации по времени уравнения движения,
аналогичного (6.3.5). Первый вариант был рассмотрен в работе
Чорина (1968), в которой использовался метод чередующихся
направлений, и в работе Фортена и др. (1971), где применялся
метод дробных шагов, основанный на расщеплении операторов по
переменным х и у. Отметим, что, если V* вычисляется по неявной
схеме, вопрос о граничном условии для давления остается
открытым, как и в случае применения явной схемы. Точнее говоря,
предыдущее доказательство было основано на том, что
предварительные значения величины V* рассчитывались по явной схеме,
вследствие чего значения V* во внутренних точках не зависели от
значений V* на границе. Однако результаты теоретических исследо-
163

ваний, проведенных Темамом (1969b, 1977), показали, что
численное решение Vn+1, pn+l стремится к точному решению при Д^, Дл:
и Ду-^0, если V* на Г выбрано равным точному граничному
значению V7**1. Однако мы не знаем, как будет вести себя решение
в случае, если это последнее условие не выполняется.
Трудность, связанная с определением V* на границе, может
быть обойдена, если при расщеплении использовать какую-либо
неявную схему расчета. В качестве примера рассмотрим неявную
схему второго порядка точности (схема Адамса—Бэшфорта/Кран-
ка—Николсона):
у»+'-У" , ЗА»-А*-' , „^ + '/2 у»у»+|+ ysy*
At + 2 +Vp 2Ri = 0' <6'3-9)
V . V*+I=-0. (6.3.10)
Уравнение (6.3.9) здесь заменяет (6.3.5). Теперь применим метод
расщепления, аналогичный уже описанному, т. е.
У*-У* , ЗА*-А*-' У2У* п /ftQin
Ai + 2 2R^- = 0» (6'ЗЛ1>
\ГП+1 V* „.ill/ Т72\ГП+1
At +^+ /2-T^ = °» (6-3-12)
y . Vrt + 1 = 0. (6.3.13)
Беря дивергенцию от левой части уравнения (6.3.12) и учитывая
(6.3.13), получим уравнение Пуассона для давления
vy + ,/2 = -irv -V*. (6.3.14а)
Условие Неймана, как и ранее, получим путем проекции
(6.3.12) на единичную нормаль N к границе Г, т. е.
(■А-Г"-—Mv-'-v-HE^]-N- <6А146>
Повторяя те же рассуждения, что и для явной схемы, мы можем
утверждать, что решение /?n+,/2, Vn+1 не зависит от значения V* на
границе Г. Однако условие (6.3.146) содержит неизвестное
значение (V2Vn+1) • N на границе Г. Для аппроксимации этой величины
используется уравнение неразрывности, так что для границы х =
= const (см. рис. 6.3.1) получим
--[-еч-ж.+оз-х:1.- <б-з-'<=>
164

Затем производную по х аппроксимируем с помощью нецентриро-
ванной разности первого или второго порядка точности,
включающей известное значение dv/dy на границе. Такая процедура была
использована Моршуазном (1981). Ранее она была предложена
Прахтом (1971), который применил ее при реализации метода
отражения.
В случае использования метода расщепления, описываемого
уравнениями (6.3.11) — (6.3.14), вычислительный алгоритм сводится
к следующему: 1) уравнение (6.3.11) решается явно относительно
V*; 2) совместно решаются уравнение (6.3.12) с учетом
граничного условия для Vn+1 и уравнение (6.3.14) при произвольных
значениях V* на Г, что дает Vn+1 и рп+,/г. Это может быть выполнено
с помощью итерационного процесса путем попеременного
однократного применения итерации Гаусса—Зейделя для каждой из
величин.
В отношении устойчивости этого метода отметим, что если для
аппроксимации производных по пространственным переменным на
разнесенной сетке используются центральные разности второго
порядка точности, то полученная в результате схема обладает
значительно лучшими свойствами, нежели чисто явные схемы (см.
п. 2.7.4).
Изложенный выше неявный метод был проверен авторами на
тестовых примерах. Аналогичные системе уравнений (6.3.9) —
(6.3.10) схемы с использованием спектральных разложений по
пространственным переменным были рассмотрены для разных
вариантов метода расщепления Орзагом и Келсом (1980), Тейлором и
Мёрдоком (1980). Методы, использованные этими авторами,
изложены в главе 8.
6,3.1,4. Связь с методом искусственной сжимаемости. Интересно
отметить связь между проекционным методом (или методом
маркеров и ячеек, поскольку эти два метода тождественны в случае,
когда используется разнесенная сетка) и методом искусственной
сжимаемости, изложенным в п. 6.2. Предположим, что решение
уравнения Пуассона (6.3.3а) определяется с помощью простой
итерационной процедуры якобиевого типа
(6.3.15)
где m — номер итерации, X — параметр сходимости. Указанная
процедура будет в точности якобиевой, если
. * _ 1 Ал:2 Ar/2
А — До— 2 Ax2 + ày2 .
Отметим, что (6.3.15) сходится, если К ^ К0. Теперь, сравнивая
(6.3.15) с (6.2.27), заключаем, что если для вычисления стацио-
165

нарного решения уравнений Навье—Стокса используется
проекционный метод и если на каждом шаге по времени вместо
нахождения точного решения уравнения Пуассона для давления
производится лишь одна итерация при т==0, то указанный метод
становится тождественным методу искусственной сжимаемости при Х =
= с2Д£2. Разумеется, можно выполнять более одной итерации на
каждом шаге по времени, и тогда мы можем получить алгоритм,
который будет обеспечивать лучшую сходимость. В исследованиях
Фортена и др. (1971) и Ладевеза и Пейре (1974) на каждом шаге
по времени выполнялось 12 итераций.
6.3.2. Итерационный метод
Можно построить итерационный метод решения нестационарных
уравнений движения вязкой жидкости на основе: 1)
аппроксимации уравнений движения и неразрывности по неявной схеме и
2) решения полученной системы нелинейных алгебраических
уравнений с помощью итераций (Фортен, 1972, Пейре, 1976). Важным
свойством такого метода является его хорошая устойчивость, так
что шаг по времени может быть выбран исходя из требуемой
точности решения. Кроме того, строить неявные схемы второго
порядка точности по времени проще, чем явные схемы того же
порядка точности.
Весьма эффективной схемой является схема Кранка—Никол-
сона. Рассмотрим более общую двухуровенную схему, в которой
дискретизация по времени осуществляется следующим образом:
a/ +e[A(v-')—^—]+
+ (1-в)[А(Уя) ^1] + Vpn + T = 0, (6.3.16а)
V . ул+| = 0, (6.3.166)
где 6 — постоянная величина, 0 ^ Э ^ 1. Если 6 = 0, получаем
явную схему, а при 6 = 1 — чисто неявную схему. Схема Кранка—
Николсона соответствует значению 8 = 72. Число т, определяющее
момент времени (п-\-х) At(х > 0), произвольно, и его следует
выбирать так, чтобы уменьшить ошибку аппроксимации (6.3.16а).
Это обусловлено тем, что в уравнения Навье—Стокса не входит
производная по времени от давления, и поэтому давление
определяется с точностью до произвольного слагаемого, являющегося
. функцией времени. Главной частью ошибки аппроксимации (по
времени) для (6.3.16а) является
-f-!-{-3- + »|><V>--S4+*4
Эта схема имеет второй порядок точности аппроксимации по
времени, если 6=т=—. Если 6 = 0 или 1, данная схема имеет только
166

первый порядок точности и т может быть выбрано произвольным
образом (обычно принимают т= 1).
Для аппроксимации по пространственным переменным берется
разнесенная сетка, причем, как правило, используются
центральные разности второго порядка точности (см. п. 6.2.2). Если 0,<
< 7г, необходимое условие устойчивости схемы (6.3.16) есть
-W *£ЛУ < 2(1-26) ' (l"l + M)2A'Re<TAr.
При 6^— эта схема безусловно устойчива (в линейном прибли-
жении).
Если ввести дискретизацию по пространственным переменным,
как это описано в п. 6.2.2, уравнения (6.3.16а) и (6.3.166) на
каждом шаге по времени приводятся к системе нелинейных
алгебраических уравнений для неизвестных величин, представляющих
собой значения скорости и давления в узлах сетки, например
гс+1 „я+1 пп + х
И*+ 1/2, /, Vi, / + 1/2' Pi, j .
Введем обозначения
л +1 M +1 гг + т
Uh = Ui + xj2, /, Oä= Oif/ + i/2, ph = pi,i .
Тогда конечно-разностные уравнения, получаемые из (6.3.16),
можно записать в символической форме
Lu(uh, vhj рА) = 0, (6.3.17а)
L0(uh, vhi p/>) = 0f (6.3.176)
D(uht vh) = 0, (6.3.17b)
где (6.3.17a, 6) — уравнения движения, а (6.3.17в) — уравнение
неразрывности. Записав эти уравнения для всех узлов сетки,
располагающихся в рассматриваемой вычислительной области,
получим систему нелинейных алгебраических уравнений, которая
решается с помощью итерационной процедуры.
Довольно простая итерационная процедура может быть
представлена следующим образом (напомним, что m — номер
итерации):
m + l m , * г /m m m\ n 0 n
vZ + l-vZ + k2Lv(uZ, *?,"?) = 0, vl = vli + 42t
pZ + l-p?+XD(uZ + \ ü? + 1) = 0, р1 = рЧ+Г\ (6.3.18)
где &i, é2 и À,— параметры, которые необходимо выбирать таким
образом, чтобы обеспечить сходимость итерационного процесса.
Отметим, что приведенная выше итерационная процедура
представляет собой не что иное, как метод искусственной сжимаемо-
167

сти, применяемый на каждом шаге по времени. Необходимые
условия сходимости процесса (6.3.18) могут быть получены так же,
как это делалось при исследовании устойчивости метода
искусственной сжимаемости. Если k\=k2 = k, Ах = Ау и конвективные
члены равны нулю, то получим следующие условия:
-èr(-w+^M- + 2l)<l> *>о, я>о. (6.3.19)
Оптимальные значения k и Я, обеспечивающие минимальное
число итераций, необходимых для достижения сходимости
процедуры (6.3.18), находятся путем численных экспериментов.
Неизвестно, существуют ли теоретические обоснования выбора
оптимальных значений этих параметров. Соотношение (6.3.19)
показывает, что при данных Ах, At и к существует максимальное
значение À:
. _ Ах2 ( 28 , Ах2 \
Amax — -§g VHrT + TATJ'
из которого следует, что поскольку À>0, то
k ( 49 . Ах2 \-i
Ах2 < \ Re + 2 At ) *
Удобно брать величину k такой, чтобы она была порядка А*2,
и, как показывает опыт, наилучшая сходимость достигается в тех
случаях, когда X близко к Ащах (но не равно этому значению).
Именно выбор надлежащих значений параметров имеет наиболее
важное значение для этого метода, поскольку число итераций,
необходимых для обеспечения сходимости, в сильной степени
зависит от этого выбора. В конечном счете прежде, чем приступить
к расчетам по указанному методу, рекомендуется провести
большое число предварительных испытаний с целью определить
оптимальные значения параметров.
Для улучшения сходимости (в этом случае и вычислительная
программа окажется более простой) можно видоизменить
вышеуказанную итерационную процедуру путем использования в
каждом из соотношений (6.3.18) значения неизвестных на (т+1)-й
итерации сразу же после того, как они вычислены. В этом случае
процедура превращается в метод Гаусса—Зейделя, тогда как
предыдущий итерационный процесс был процедурой якобиевого
типа. Для такой модификации становится трудно исследовать
сходимость путем анализа устойчивости аналитическими
методами, поскольку элементы матрицы перехода являются
комплексными числами. Исследование собственных чисел матрицы
перехода можно выполнить расчетным путем.
Характерные значения параметров сходимости, используемые
при расчетах, приведены в п. 6.4.2.
В заключение заметим, что помимо двухуровенной схемы
(6.3.16а) можно использовать и другую форму дискретизации по
168

времени. Например, трехуровенная схема второго порядка
точности аппроксимации
1 .[ßVn + l - 4Vrt + Vn- '] + A (Vn+1) - VT**! +vp" +1 = 0,
2 A/ L~T - * -r ' j -r - v ' ; Re
V - Ул+, = 0,
(6.3.20)
с дискретизацией по пространственным переменным на
разнесенной сетке была успешно применена при решении ряда задач
(Чайлдрес и Пейре, 1976, Бланшон и Хартманн, 1979, Пейре,
1981).
Чисто неявная схема (6.3.20) безусловно устойчива. Если
итерационная процедура (6.3.18) применяется для решения уравнения
(6.3.20), то условия сходимости имеют вид
-Д^-(-^+4^Г + 2^)<1' ^>0, Я,>0. (6.3.21)
Преимущества этого способа перед схемой Кранка—Николсона
состоят в том, что, во-первых, программа получается более
экономичной и, во-вторых, более эффективно подавляются короткие
волны, а это может быть важно в тех случаях, когда решение
очень изменчиво (Рихтмайер и Мортон, 1967). В то же время, как
и в случае всех трехуровенных схем, с помощью схемы (6.3.20)
нельзя определить решение на первом шаге по времени при
заданном начальном условии. Поэтому для определения решения на
первом шаге по времени необходимо использовать другую схему.
6.3.3. Сопоставление различных методов
Как было отмечено ранее для метода искусственной
сжимаемости, изложенная в п. 6.3.2 итерационная процедура эквивалентна
решению уравнения Пуассона для давления, которое может быть
получено из уравнений (6.3.18) для u^+i и v%+i. Для того чтобы
связь между указанным методом и теми методами, которые были
изложены в п. 6.3.2, стала более понятной, приведем вывод
уравнения (6.3.18). Итерационная процедура для решения уравнений
(6.3.16) записывается в виде
Vrt + I'm + 1~Vn + I'm + é[vpn + T,m + Si(VAl + 1'm) + So(V;l)]=0,
(6.3.22а)
рп + т,т + \ _рп + т,т + 1у # уП + \,т + \=^ (6.3.226)
где
\ТП+\ Г V2Vn+X ~\
s,(v+')=-^- + e[A(v »+•)—ï-v__ ]t
s»(v"): xf + (i-e)[A(v»)—v-^f-].
169

Исключив теперь из уравнения (6.3.226) Vn+1-W+1> найденное из
(6.3.22а), получим
рп + т. т + 1 __ рп + т. m _ krfpn + T. m =
= _XV • [Vn + U m - kS^V1*1' m) - kSo(Vn)]. (6.3.23)
Это уравнение определяет специальную итерационную процедуру
решения уравнения Пуассона для давления, которое могло бы
быть получено путем применения оператора (V-) к уравнению
(6.3.16а). В случае сходимости при т-^оо уравнение (6.3.23)
принимает вид
Vy + T = -v • [Si(V" + 1)+So(Vn)], (6.3.24)
так как lim (V* Vn+1»w) =0. В частности, в случае явной схемы
т-> оо
при 6 = 0 мы имеем V-Si (V71*1) =(V- Vn+1)/A^ = 0. Поэтому
получаем уравнение Пуассона, которое обычно используется в
проекционном методе [уравнение (6.3.3а)] или методе маркеров и ячеек
[уравнение (6.3.7а)]. Отметим, что явная схема (0 = 0),
используемая в методе искусственной сжимаемости, была введена Чори-
ным (1968) и применялась, в частности, Вичелли (1971) и Лиу
(1976). Вичелли показал, каким образом можно изменить
вычислительный процесс, чтобы вместо процедуры якобиевого типа
(6.3.22) получить процесс Гаусса—Зейделя. Для того чтобы
завершить аналогию между итерационным методом в случае 0 = 0
(явная схема) и методом маркеров и ячеек или проекционным
методом, напомним, что если правильно записать правую часть
уравнения Пуассона и условие Неймана на границе, то численное
решение не будет зависеть от «внешнего» значения V0 в методе
маркеров и ячеек или значения V* на стенке в проекционном методе.
Такое «подобие» между видом правой части уравнения Пуассона
и условием Неймана автоматически выполняется в изложенном
неявном итерационном методе для любых значений 0. Этот
результат аналогичен полученному в п. 6.2.5.
6.3.4. Метод возмущений (штрафа)
Темам (1968) предложил следующий метод возмущений. Вместо
уравнения дивергенции (6.1.16) используется уравнение
ep+V-V = 0, 8>0, 8 — 0. (6.3.25)
В этом случае из уравнения движения можно исключить
величину р, так что (6.1.1а) и (6.1.16) заменяются одним уравнением
^_ + (v.v)v-^i^-^=--Ll^L, (6.3.26)
которое необходимо решить при условии е->0. Отметим, что член
в правой части (6.3.26) был введен для того, чтобы выполнялось
условие устойчивости. Темам (1968) доказал, что решение (6.3.26)
170

,-2 с [ du dv dv du \ /c A 14
стремится к решению (6.1.1) при е->-0. Несмотря на то что при
очень малых значениях е могут возникнуть вычислительные
трудности, этот метод успешно применялся Хьюзом и др. (1979),
а также Берковье и Энгельманом (1979) в сочетании с методом
конечных элементов (для 6ä10_2Aa:2) и был использован
Маршаллом и др. (1978) и Апсоном и др. (1980) при решении задач
свободной конвекции.
6.4. Примеры решения задач для физических переменных
скорость—давление
6.4.1. Стационарный поток над уступом
Для того чтобы показать, как находится конечно-разностное
решение задачи для исходных переменных, рассмотрим случай
стационарного решения в канале (Тейлор и Ндефо, 1971) с уступом
(рис. 6.4.1). При изучении этого течения применим метод
расщепления Яненко (1967) для решения уравнения с физическими
переменными (6.1.1а) и уравнения для давления
du dv _ dv ди
ду дх ду
Начальные и граничные условия, согласованные только для
стационарного случая, следующие:
при * = 0, 0<х<-~-, 0<*/<1:ы=1, о = 0; (6.4.2)
при х = 0, -£-<*/< 1 : и= 1, о = 0, -|^=-j^-äjr для *>0;
при * = -£-, 0<г/<1:^ = -^ = 0,^-=-р(соп81)для^>0;
при y = -ff Для 0 < х < -jj-, при у = 1 для 0 ^ х < -^ ; (6.4.3)
при у = 0 для -#-<*<-#- • и = 0, о = 0, -^-=-r7~^T'
/ л^ ^ h . л (\ ар 1 д2и
при х = -7Г для 0^y<t-R-:u = 0, о = 0, -^-——j-.
Здесь ß — заданный градиент давления для течения Пуазейля,
/ — расстояние от входного сечения до уступа, L — общая длина
канала, H — ширина канала и h — высота уступа.
В результате расщепления получим уравнения движения
в следующей форме:
система I
1 ди ди2 . др 1 д2и
~2~ dt + дх + дх Re дх2 '
1 dv t_äuy____ 1 d2a . ffi4 4ï
171

система II
1 du , duv
1 д2и
2 dt ^ ду ~~~ Re ду2 '
1 dv . du2 . dp 1 d2v
~Т~дГ+ ду "*" ду ~~ Re ду2 *
Так как уравнение для давления не содержит производной
по времени, оно не расщепляется и должно решаться как урав-
0,5 т +àif 3,8$ х
Рис. 6.4.1. Область течения и расчетная сетка для канала с уступом.
нение от двух переменных. В данном случае это уравнение
решается на каждом полушаге по времени в противоположность
проекционному методу расщепления (Фортен и др., 1971), в
котором давление рассчитывается один раз на каждом шаге по
времени.
Каждой из систем одномерных уравнений (6.4.4) соответствует
совокупность граничных условий, полученных из уравнений
(6.4.3):
система I
при я = 0 : и = 1, ü = 0 для всех уу
L . du dv г,
при х= -jgr:-^- ——- = 0 для всех у,
H * дх
l h
при x = -jj-:u = 0y v = 0 для 0<#<-jj-;
172

система II
при y=-jf для 0<х<-^-, (6.4.5)
при у = О для -ту- <^ х <; -7т- : ы = О, v = О,
при #=1 для 0< д:<-т7-: гг = 0, и = 0.
Процедура нахождения решения сводится к следующему.
1. Используя значения ип и vn для момента п At рассчитываем
вспомогательную величину р из уравнения (6.4.1) и граничных
условий, содержащихся в (6.4.3). Затем с учетом полученного р
система I интегрируется на полшага вперед по времени, в
результате чего получаем вспомогательные величины ü и v.
2. Вычисляется давление pn+1 так же, как и на первом шаге,
но уже с использованием ü и v. Наконец, путем интегрирования
системы II еще на полшага по времени с учетом üy v и pn+1
получаем un+i и un+i.
Для решения этих уравнений используется метод конечных
разностей. Скорость и давление определяются в узлах сетки.
Производные по пространственным переменным аппроксимируются
на неравномерной сетке (x/+i— Xi = Axi, yi+\— yi = Ayi) с
помощью центральных разностей в следующем виде:
(гагЛ. /= д* + д*-. • (6А6)
\dx2)i,j~Z AxiAXi-^Axi + ZiXi-i) ' (0.4./)
Для простоты используется явная схема интегрирования по
времени так, что
du о ü — un т
~дГ =—л/— для системы *»
du п un+l — u тт //- >i о\
= 2 г- для системы И. (6.4.8)
dt At
Для увеличения устойчивости можно применять неявную
аппроксимацию члена с вязкостью, так как уравнения,
полученные в результате расщепления, являются одномерными и легко
решаются с помощью метода факторизации.
Условия устойчивости приведенной выше схемы принадлежат
к типу соотношений для одномерного случая [см. уравнение
(2.6.19)]. Ошибка аппроксимации (без учета граничных условий)
имеет порядок О (At); уравнение для несжимаемой жидкости
удовлетворяется с точностью О (At2), Для стационарного случая
ошибка остается порядка О (At): этот факт характерен для
метода расщепления. Вопрос о точности, обусловленной' видом гра-
173

ничных условий, был рассмотрен в п. 2.7.3 и 2.8.4. В данном
примере применение непосредственно расщепленной системы для
определения промежуточных величин дало хорошие результаты.
Условие Неймана для давления записывалось в дискретизован-
ной форме в виде односторонних разностей. Построение такого
рода разности давления для угловой точки осуществлялось путем
ун/к р
Рис. 6.4.3. Распределение давления 1>
для Re = 25.
вычисления нормальных производных к каждой из сторон в
угловой точке и осреднения полученных результатов.
Конечно-разностные уравнения для давления решались как с помощью
итерационной схемы Якоби, так и по методу верхней релаксации.
Обнаружено, что при использовании метода верхней релаксации
время, затрачиваемое на вычисления, уменьшается
приблизительно в три раза по сравнению с тем, которое требуется при
использовании простой итерационной процедуры Якоби.
Описанная схема расщепления была использована для расчета
потока при числах Рейнольдса от 25 до 100. Направленный вниз
по потоку градиент давления ß был выбран равным
12 H-h
р— Re H
При расчетах течения в канале с уступом величина шага
менялась от Дх = Дг/=0,01 до Ал' = 0,1 и Аг/ = 0,09. Структура сетки
с таким шагом показана на рис. 6.4.1. Шаг по времени для всех
расчетов принимался равным А/ = 0,001. Некоторые результаты,
полученные для чисел Рейнольдса, равных 25 и 100, представлены
на рис. 6.4.2 и 6.4.3. Результаты этих экспериментов были
проверены по условию сохранения массы, и, как показали расчеты,
общая потеря массы в процессе вычисления составила 2 %.
174

На рис. 6.4.2 показано распределение линий тока вблизи уступа.
Отметим, что отрыв потока происходит не у верхней кромки
уступа, а ниже ее приблизительно на 2/3 высоты уступа. На рис. 6.4.3
показано локальное изменение давления в области течения. Здесь
давление на переднем торце уступа сначала резко уменьшается,
а затем начинает расти до тех пор, пока противоположно
направленный градиент не становится достаточно большим, чтобы
привести к отрыву потока.
Этот небольшой пример, поясняющий основы метода
расщепления, более подробно рассмотрен в работе Тейлора и Ндефо
(1971). Результаты исследования течения в области угла
приведены в работе Ладевеза и Пейре (1974).
6.4.2. Нестационарная горизонтальная струя в стратифицированной жидкости
Ниже приведен пример (Пейре и Ребурсе, 1981, 1982) решения
уравнений Навье—Стокса для физических переменных (с
помощью метода, изложенного в п. 6.3.2) в случае стационарной
У <
+D/2
1
А'
В'
,—^
-Л/2
В
у0
т2
1
1
1
те ;
г
1
1
1
1
1
с'
\l>
X1
X
А Т,
Рис. 6.4.4. Форма области.
С X
ламинарной струи, распространяющейся в полубесконечном
канале, заполненном стратифицированной жидкостью, которая
первоначально находится в состоянии покоя. Область, в которой
происходит движение, показана на рис. 6.4.4. Жидкость, которая
в начальный момент времени покоится в канале высоты 2#,
устойчиво стратифицирована по температуре:
г.(у)- (Г>Г/,)У +
т2 + т1
2Я
при Т2 > Г,.
Плотность р и температура Т связаны между собой согласно
уравнению состояния
Р = Ро[1 — Р*(Г —Го)] при Т0= Г1 + Г2 ,
где ß* — объемный коэффициент теплового расширения.
Начальные значения плотности р8(у) и давления р8(у) в жидкости соот-
175

ветствуют распределению температуры Ts(y). Давление
подчиняется закону гидростатики:
Ps(y) = -gPo[y --Тн-(т2- W] + const,
где g — ускорение свободного падения. В момент /=0 жидкость,
обладающая теми же физическими свойствами, что и та, которая
заполняет канал, начинает поступать в канал с максимальной
скоростью Uo через отверстие ВВ' (высоты D). Температура
поступающей жидкости постоянна и равна Г0, а ее плотность — р0, что
соответствует значениям этих величин в покоящейся
стратифицированной жидкости при у = 0.
Как это обычно делается при решении такого рода задач,
удобно ввести возмущения давления я и температуры в
относительно соответствующих величин ps и Ts в жидкости, находящейся
в покое. Вводятся также безразмерные переменные с
использованием в качестве масштабов следующих величин: L*=2D для
длины, L*/Uo для времени, Uo для скорости, p0f/g для давления
и (Т2 — Т\)/г) для температуры, где r)=H/D. Оставляя для
безразмерных переменных прежние обозначения, получим уравнения
Навье—Стокса в приближении Буссинеска в следующем виде:
dW +(V. V)V+V*-4? Ri0j = 0, (6.4.9)
dt ^^ v' ж ^ VJt Re
V • V = 0, (6.4.10)
* • ,V. V0 + V. J-^JÎ* 0, (6.4.11)
dt ' vw ' ' J RePr
где j — единичный вектор, направленный по вертикали, а число
Рейнольдса Re, число Ричардсона Ri и число Прандтля Рг
определяются согласно следующим соотношениям:
Re = -^f^, Ri = ß*g(-^
2 ^-^ Рг = -^-
2Я
В качестве начальных условий при / = 0 принимается, что
# = £/ = 0i = O. Граничные условия имеют следующий вид:
на ВВ' :и = (1 - 16#2)ф(/), и = 0, 0=-*/;
на AB и B'A':u = v = -?ß- = 0;
дх
на АХ и A'X':u = v = e = 0,
где ф(/) — функция, описывающая постепенное увеличение
скорости втекания жидкости: ф(0)=0, ф(/) = 1 при t^t0. Хотя
выбор конкретного вида ср (t) не влияет на установившееся
движение, число итераций, необходимых для решения этой задачи (по
методу, изложенному в п. 6.3.2) для переходного состояния при
t^to, во многом зависит от степени гладкости этой функции
176

(т. е. q/ (0) = <р' (/0) =0). Представленные здесь результаты
получены для случая, когда у (t) имеет вид полинома четвертого
порядка и to = 0,25.
Основная вычислительная трудность в решении данной задачи
связана с тем, что область течения не ограничена. Изложенное
ниже решение получено для ограниченной области с искусственно
заданной границей СС (см. рис. 6.4.4), а характеристики
течения на этой границе определяются на основе соответствующих
уравнений, описывающих свободное вытекание жидкости из
рассматриваемой области, которое препятствует распространению
возмущений вверх по потоку или возникновению вычислительной
неустойчивости. Эта задача, представляющая определенные
трудности даже в случае нестратифицированной жидкости вследствие
необходимости решения уравнений Навье—Стокса для
переменных скорости и давления, здесь усложняется из-за учета
стратификации жидкости и возможности распространения в ней
внутренних волн.
Вблизи границы СС поток является нестационарным в
течение всего рассматриваемого периода времени вследствие
существования вихрей, перемещающихся вниз по потоку, что делает эту
задачу существенно отличной от рассмотренной в п. 6.4.1 задачи
расчета стационарного течения типа Пуазейля. Разные способы
определения характеристик течения в сечении СС
рассматривались в работе Пейре и Ребурсе (1981). Наилучшие результаты
были получены при следующих условиях:
дх U' дх2 и'
ди , dv г, дк dv dv . 1 d2v . r».^
дх ' ду ду dt ду ■ Re ду2 '
Если включить эти условия в общую процедуру нахождения
решения задачи, то путем последовательных итераций можно получить
значения и, и, 0 и я в выходном сечении. Давление я находится
посредством интегрирования дп/ду вдоль СС при значении я=1
в ближайшем к точке С узле сетки.
Можно использовать другой метод (Као и др., 1978), который
состоит в том, что полубесконечный интервал 0^x<C<x>
заменяется конечным промежутком 0^л:<1 посредством
преобразования координат х=1—ехр(—ах)у a = const, а затем «на
бесконечности» при х=\ ставятся граничные условия для течения пуа-
зейлевского типа. Более полное обсуждение вопроса о выборе
«растянутых» координат проводится в работе Силлса (1969).
Для решения уравнений движения (6.4.9) — (6.4.11)
использовался метод, изложенный в п. 6.3.2, причем параметр
дискретизации был принят равным V2, что отвечает схеме Кранка—Никол-
сона. На разнесенной сетке (см. рис. 6.2.1) температура 9
определяется в центре ячейки и обозначается через 0 .+1/г /+1/я. Член,
описывающий в (6.4.9) вынуждающую силу, присутствует только
177

в уравнении для v и рассчитывается как среднее значение
соответствующих величин для моментов времени п и п+\ в точках
U + 2»/+2) и v ~" 2"»'"^"Зу1 Уравнение (6.4.11)
аппроксимируется в соответствии с той же схемой, что и уравнения
движения, за исключением того, что производные в конвективном члене
V-V® определяются с помощью пятиточечной схемы центральных
разностей четвертого порядка точности. Аппроксимация такого
высокого порядка используется для того, чтобы связанная с ней
ошибка была мала по сравнению с диффузионным членом
(RePO-^G.
тт п+\ п-\-\ п + \/2 лЯ-Н
Искомые величины tt/+i/2> /, ü*,/+i/2, pt.i и 0*+i/2, /+1/2,
обозначенные соответственно через Uh, Vh, Рк и 0^, вычисляются
с помощью итерационного процесса Гаусса—Зейделя,
описываемого уравнением (6.3.18) и вспомогательным уравнением для
температуры
ez+l-QZ + xE(uZ+\ vV+\ ©;r)=o,
причем параметр % должен удовлетворять условиям сходимости
^Ырг+ткг)^' *>° <А*-А*>- <6-4Л2>
Как видно из условий (6.3.19) и (6.4.12) целесообразно
использовать не сами параметры k, % и X, а величины a = k/Ax2, b =
= Х/Ах2 и с = к/Ах. Полученные путем численных экспериментов
характерные значения a, b и с, обеспечивающие сходимость
итерационного процесса, даны в табл. 6.4.1.
Таблица 6.4.1. Параметры сходимости
Re
10
100
250
Ах = Ау
1/10
1/16
1/16
M
1/50
1/64
1/64
а
0,40
0,75
0,82
ь
0,40
0,75
0,82
с
10,50
9,50
8,70
Предполагается, что сходимость имеет место при условии
max{|Lu|, \LV\, I-DI, \E\} ^0,25-10~2. Вообще говоря,
максимальную ошибку дает уравнение для v\ уравнение неразрывности
удовлетворяется с точностью до 10~3. Число итераций,
необходимое для обеспечения сходимости на каждом шаге по времени,
составляет примерно 35 для установившегося режима (^>^0. = 0,25)
при Re = 250, Ri = 64. Число итераций может возрасти до
нескольких сотен для начальной фазы движения (0</=^0). Для сетки
80x20 узлов (A# = Ay = Vi6) расчеты до конечного момента вре-
178

-0,8 h
4,0 X
Рис. 6.4.5. Распределение линий тока в различные моменты времени
для Re = 250, Ri-64, Pr=10.
а) /=0.50; б) /=1,50; в) /=2.0.

мени £ = 2(A/ = V64) требуют 45 минут работы центрального
процессора (на компьютере СДС 6600).
Предварительные численные эксперименты для конкретных
значений физических параметров задачи (Пейре и Ребурсе, 1982)
показали, что при этих значениях течение остается симметричным
относительно оси у = 0. В результате была принята гипотеза о
симметричности потока, и расчеты выполнялись только для половины
области течения жидкости. Результаты, приведенные на рис. 6.4.5
и 6.4.6, относятся к случаям Re = 250, Ri = 64, Рг=10 и Ri = 0
-1,2^0
4,0 х
Рис. 6.4.6. Распределение линий тока (/ = 2,0, Re = 250) в случае отсутствия
гравитационных эффектов, Ri = 0.
(нейтральная стратификация), t]=H/D = 2,3125 и £ = L/2Z) = 5.
На рис. 6.4.5 показано распределение функции тока в
различные моменты времени. Эффект стратификации становится
очевидным при сравнении рис. 6.4.5 с рис. 6.4.6, который показывает
картину течения при отсутствии силы тяжести. В последнем
случае вихри, возникающие вблизи входного сечения, остаются около
стенки и расширению линий тока препятствуют только стенки
канала. При наличии же стратификации вновь возникающие вихри
уносятся вниз по течению, а вместо них у входа возникают другие
вихри, которые имеют меньшие размеры и вращаются в
противоположную сторону. В результате этого струя располагается вдоль
оси канала между двумя рядами вихрей. Поскольку
последовательно расположенные вихри имеют противоположное
направление вращения, линии тока в области струи периодически
расходятся или сходятся. Поэтому соответствующая скорость течения
осциллирует, причем максимальные ее значения превышают
скорость при входе в канал. Необходимо отметить, наконец, что ско-
180

рость течения вне струи довольно мала (рис. 6.4.7), но это не
видно на приведенных выше рисунках, которые дают только
качественную картину движения.
0,5
L
л
-:М~>Л-
Ч
4-
1,0
1,5
2,0
У
3,0
i
)
/ I
'I
\
\
/
/
Рис. 6.4.7. Профили горизонтальной скорости и при
/) Re=250, Ri=0; 2) Re=250. Ri = 64. Pr=10.
3fi
/ = 2,0.
к
— /
•—2
4,0 X
6.5. Уравнения для переменных вихря и функции тока и методы
их решения
6.5.1. Уравнения для стационарного случая
Уравнения для переменных вихря и функции тока могут быть
записаны для случая плоского стационарного потока в виде
[lof)
1
Re
•V* <d =
= 0,
V2^ -f со = 0.
Здесь W — функция тока, a» — вихрь,
(6.5.1а)
(6.5.16)
V2=-
д2
д2
дх2
ду2
х, у — декартовы координаты, и и v — составляющие скорости V,
которые выражаются через функцию тока посредством
соотношений и=дхР/ду, v = —dW/dx. Чтобы замкнуть эту задачу,
необходимо к уравнениям (6.5.1) добавить соответствующие граничные
условия так, как это изложено в п. 6.5.3.
181

6.5.2. Псевдонестационарные методы
Для решения уравнений (6.5.1) были предложены различные
методы. Один из них основан на рассмотрении нестационарного
уравнения
4t + [l(40-t^V2]o = 0, (6.5.2а)
у2Чг + о) = 0 (6.5.26)
и решении этой эволюционной задачи с целью получения
стационарного решения при t-+oo. Хотя продолжительность расчетов до
получения достаточно малой производной d(ù/dt ограничена и
зависит от значения числа Рейнольдса Re = £/L/v, все же во многих
случаях расчетное время слишком велико, чтобы можно было
говорить о целесообразности применения этого метода.
Другой метод, по существу аналогичный нестационарному
методу, состоит в том, чтобы путем модификации получить два
взаимосвязанных параболических уравнения вместо системы,
состоящей из параболического и эллиптического уравнений. Для этого
используются следующие уравнения:
d(ù
dt
\-[l(V) ^Lv2]co = 0, (6.5.3а)
dt- a[V2*F + co] = 0, (6.5.36)
где а>0 — постоянный параметр. Преимущество такой
постановки задачи перед (6.5.2) заключается в том, что в последнем
случае можно использовать экономичную схему решения шаг за
шагом, в противоположность задаче (6.5.2), в которой на каждом
шаге по времени приходится решать эллиптическое уравнение
(6.5.26). Впрочем, в первой из указанных задач не обязательно
находить точное решение уравнения (6.5.26) на каждом шаге по
времени, поскольку нас интересует лишь стационарное решение.
Система псевдонестационарных уравнений (6.5.3) была,
по-видимому, впервые использована Бургграфом (1966) в сочетании
с явно—неявной аппроксимацией по времени. Вследствие наличия
явной части в примененной схеме, она сходилась только в тех
случаях, когда число Рейнольдса было достаточно мало.
Весьма эффективным методом решения указанной системы,
улучшающим сходимость, является неявный метод чередующихся
направлений (см. главу 2). В настоящее время этот метод
широко применяется как в первоначально предложенном виде
(Писмен и Рэчфорд, 1955), так и в обобщенной форме (Дуглас
и Ганн, 1964), использованной Малинсоном и Де Валь Дэвисом
(1973),
Если решение вычисляется для квадратной области Q, 0<х<С
<1, 0<*/<1, причем величины о?,/, uït /, и" / и -ф?, /
являются соответственно аппроксимациями со, и, v и W в точке xi =
182

= iAxy уэ=]'Ау и в момент времени tn = nAt, то схема
чередующихся направлений Писмена—Рэчфорда для уравнений (6.5.3)
может быть записана в следующем виде*:
-В" (*|. / - »?. /) + («?. / А°, - -^-) fi,, ; + (vi, Д° - 1%L) со?, , = О,
(6.5.4а)
-JT Kï ' - fii. ;) + («?. i А°х - -^-) ôi, / +
+ (</AÎ—ТГ)»?.Г"=0, (6.5.46)
-^- (U. / - W?. /) - а (д„Ф/. / + AyyWl , + со?,+ ') = 0, (6.5.5а)
_^_ (ч;«+ 1 _ {£. .) _ а (д^. . + A^« + I + 0» +1 ) = 0> (6-5.5б)
^' = iXV, <V = -A0,W?,V, (6.5.5b)
Без учета граничных условий эта схема чередующихся
направлений безусловно устойчива в линеаризованном случае. В работах
Бонту (1978) и Бонту и др. (1980) исследовано влияние
граничных условий на устойчивость с учетом эффекта взаимодействия
между ¥ и (о на границе рассматриваемой области.
В общем случае получающиеся на каждом шаге системы
линейных алгебраических уравнений решаются с помощью метода
факторизации (см. п. 2.2.1). Метод применим для любых А^ при
|u|ReAx^2 и |u|ReA*/^2. Однако если эти условия для числа
Рейнольдса, вычисленного для сеточных значений, не
выполняются, то шаг по времени определяется из условия (6.2.33). Хотя
такое ограничение не слишком сильно, поскольку Re велико, оно
может быть ослаблено, если использовать в (6.5.4а) и (6.5.46) не-
центрированные аппроксимации для ды/дх и ды/ду, определяемые
в соответствии со знаком и и v.
Для того чтобы матрица осталась трехдиагональной, такие
аппроксимации выражаются через двухточечные разности и
поэтому имеют точность лишь первого порядка. Чтобы получить
решение второго порядка точности для установившегося
состояния, можно воспользоваться схемой чередующихся разностей
(2.8.6). Такой метод был применен в работах Доба и Та ФуокЛок
(1979) и Та Фуок Лок и Доба (1981) для решения уравнения
вихря.
В заключение отметим, что схема чередующихся направлений
(6.5.4) — (6.5.5) может быть применена также и в тех задачах, где
используется уравнение (6.5.1а), записанное в консервативной
форме. В этом случае L (y¥)<ù = duiùldx + dv<ùldyy и для
аппроксимации этих производных могут быть использованы вычислитель-
* Конечно-разностные операторы определены в п. 6.2.2.
183

ные схемы, описанные в п. 6.5.6. При подстановке аппроксимаци-
онных выражений в (6.5.4а) и (6.5.46) входящие в них значения
составляющих скорости берутся для момента времени п.
6.5.3. Граничные условия
Граничное условие, используемое при решении уравнения (6.5.1)
в области Ù с границей Г, получается из соотношений для
физических переменных, приведенных в п. 6.1. Скорость V на Г, т. е.
V = V известна [уравнения (6.1.4) и (6.1.6)]. Записывая эти
граничные условия для функции тока, получим
V дх )т Vr w» V дМ h Vr т'
где N и т — соответственно внешняя нормаль и единичный
вектор, направленный по касательной к Г. Интегрируя первое из
приведенных уравнений вдоль Г, получим граничные условия на
Г в общей форме
xp = f(*. У), -Ж = 8(*> *)• (6-5-6а)
где / должно удовлетворять условию сохранения полного потока
\(\f . т)Л> = 0. (6.5.66)
г
Поскольку / и g не зависят от времени, то в методе
чередующихся направлений мы можем использовать одни и те же
граничные значения на обоих шагах. Поэтому задание W на Г,
а именно Ч^, / = "ЧРгЧ1 = f/, / при (*/, у/)еГЛ, дает возможность
вычислить Vi.j и Y7?4".1 во всей области Qh из уравнений (6.5.5а)
и (6.5.56). Проблема заключается в том, чтобы сформулировать
граничные условия для вихря. Это главная трудность,
возникающая при решении задачи в такой формулировке.
Укажем три способа решения этой задачи. Обозначим через
Фт+1 любую из величин ф, фп+1 или какую-либо другую величину,
полученную на (т+1)-й итерации. Предлагаются следующие
способы:
1) использовать условие cû™+1 = — (V2XF)T!l ;
2) использовать условие о)г+1 — cor — у\ \ш)г ~~S \ — О» где па"
раметр сходимости у положителен;
3) использовать формулу Грина для того, чтобы получить
столько дополнительных уравнений для со, сколько имеется
граничных точек.
Рассмотрим теперь поочередно все эти способы.
184

Способ 1. Рассмотрим часть границы Г, определяемую как
у = 0. Граничные условия на ней следующие:
¥(*. 0) = Ы*)> (6.5.7а)
^ = -go (х). (6.5.76)
Используя со = — (V2XF) , получим
co(,,0) = -^i^--^^L. (6.5.8)
Из уравнения (6.5.7а) имеем д2У¥(х, 0)/дх2 = 1^ (х). Теперь
необходимо найти значение второй производной д2У¥(х, 0)/ду2. В
общем случае для этого применяется разложение в ряд Тейлора.
Например, разлагая 4я (х, Ау) в ряд
Щх. Ау)-Щх, 0) + Ay^J^ + ^J^b^-+ ...
получим для точки (л:, 0) величину
с ошибкой О(Ау). Подставляя это выражение в (6.5.8), получим
формулу первого порядка точности
I (*, 0) = -f0 (х) - -А- [V (*, Ау) - /0 (а:)] ^g0 (х). (6.5.10)
(6.5.9)
(û!
В эту формулу входит неизвестная величина 4я (х, Д#), которая
определяет переход от значения со на границе к величине 4я
внутри данной области. Однако этот переход требует знания
4я (х, Ау) в предыдущий момент времени или на предыдущей
итерации.
Формула первого порядка точности (6.5.10) была предложена
Томом в 1933 г. и с тех пор часто использовалась (Брайен, 1963,
Гринспен, 1969).
Подобным же образом, используя разложение функции
4я (х9 2Ау) в ряд Тейлора, аналогичное (6.5.9), можно получить
формулу второго порядка точности. Путем линейной комбинации
разложений 4я (xt Ау) и 4я (х, 2 Ау) можно получить оценку
д2У¥ (х, 0)/ду2, имеющую точность второго порядка. Отсюда
получается следующее выражение для ®(х, 0) :
©(*, 0) = -fo(x) + -I±r[}¥(xi 2Ау)-8Ч(х, Ду) + 7Ы*)]-
" ■*,(*). (6.5.11)
ау
Эта формула второго порядка точности была использована
Уилксом (1963), Пирсоном (1965) и др. Другие формулы такого
185

же типа были рассмотрены Брайли (1971), Роучем (1972), Орза-
гом и Израэли (1974) и Гуптой и Манохаром (1979).
Еще одна формула второго порядка точности, в которую
входит не Ч? (ху 2Ду), а величина оо(х, Ду), была предложена
Вудсом (1954). В этом случае для определения д2Х¥ (х, 0)/ду2
использовалось разложение (6.5.9) с сохранением слагаемого с
производной третьего порядка дЗУ¥(х, 0)/ду3. Для оценки этого
последнего слагаемого использовалось уравнение
д2х¥ д2}¥
= —О)
ду2 — w дх2 '
которое после дифференцирования по у дает
дгчг(х, 0) _ дв>(х, 0) азу(х,0)
ду3 ду dx2dy
Учитывая, что
дх2 ду «•w
и
да> (*, 0) 1
ду "Äy-t®^» Ay) —©(*, 0)],
получаем следующее выражение:
<о(*. 0)--i?^L-^[V(xf Ay)-M*)]- "V^ -
3-^(x) + -^.ftW. (6.5.12)
Эта формула была, в частности, использована Ранчелом и др.
(1969), а также Боземаном и Дальтоном (1973).
Для того чтобы воспользоваться любой из формул (6.5.10),
(6.5.11) и (6.5.12), необходимо знать величины ^¥(х9 Ду)
и ^(х, 2Ду) или cû(x, Ду), относящиеся к уровню т. Кроме того,
как показывают численные эксперименты, во многих случаях
приходится применять процедуру релаксации. Поэтому если записать
формулы (6.5.10)—(6.5.12) в виде
ю(*. 0) = FpF(*f Ду), ¥(*, 2Ду), со (л:, Ду)], (6.5.13)
то значение о)т+1 на границе может быть определено следующим
образом:
Û>m+l = F\4Tm(x, Ду), Ч?т(х9 2Ay), сот(л;, Ду)],
o)m + ,=Yôm+, + (l — v)o)m, (6.5.14)
где у — параметр релаксации (0<у<1). Орзаг и Израэли (1974)
исследовали теоретические ошибки, связанные с применением
различного вида приведенных выше формул. В частности, было
обнаружено, что при использовании формулы первого порядка
186

точности (6.5.10) численное решение имеет ошибку второго
порядка по отношению к точному решению. Это еще раз
подтверждает тот факт (Крейс, 1972), что использование граничных
условий более низкого порядка точности теоретически не
обязательно должно вести к потере точности. Однако такое
утверждение справедливо только по отношению к порядку ошибки. Сами
же результаты, полученные по разным формулам, могут, как
показано в п. 6.6, отличаться один от другого. Гупта и Манохар
(1979) провели тщательное сравнение результатов, полученных
с применением указанных формул, для случая вынужденного
течения в полости. Результаты аналогичных сравнений изложены
в п. 6.5.8.
Способ 2. Был предложен Дородницыным и Меллером (1968)
и может быть представлен в виде
о>*+«(д, 0) = ©*(*, 0)-у[Ч"П{х> А^~~М*} +go(*)], (6-5.15)
если для аппроксимации производной по нормали д*¥ (х, 0)/ду
используются разности первого порядка. Очевидно, что можно
использовать также трехточечные разности второго порядка. В
случае сходимости, когда (о^+^о)^, выполняется условие
(д^/dN) =g. Параметр у должен быть выбран таким образом,
чтобы обеспечить сходимость метода. Такой анализ был выполнен
Израэли (1970, 1972).
Заметим, что оба приведенных выше метода связаны между
собой. Фактически, если использовать формулу (6.5.10) в
сочетании с процедурой релаксации (6.5.14), получим
со— (х, 0)-«И*, 0) --^{[^ X~hiX) +*<*>]+
+ -f-[fô(x) + <*m(x, 0)]}.
Это выражение совпадает с формулой (6.5.15) (если в ней у
заменить на 2у/Ау) при условии, что не учитывается член порядка
Ау, однако следует напомнить, что обе формулы (6.5.10)
и (6.5.15) имеют точность лишь первого порядка.
Способ 3. Он основан на использовании формулы Грина для
уравнения (6.5.16) применительно к области Ù' (рис. 6.5.1).
Формула Грина записывается в следующем виде:
pW(X, ix) = j0(x, у; X, \1)Ч2ЧГ(х, y)do +
+ I [*°(%S^fl) *(* у)-°ь * *• ^)^%^-]^
г и Г' L J
(6.5.16)
где G — фундаментальное решение уравнения Лапласа, так что
для двумерного случая
0(х9 у; X, fx) = 4-ln[(A:-^)2 + (y-^)2].
187

В качестве точки (А,, \х) может быть выбрана любая точка
плоскости (х, у) у а
{2л, если (X, \х) œ Q',
я, если (A,, ц) е= Г U Г',
О, если (A,, [i)<£Q'.
Текущими переменными в производных по нормали, стоящих под
знаком криволинейного интеграла, являются х, у. Рассматривая
точку (Ä,, ja), принадлежащую Г, и используя уравнение (6.5.16)
Рис. 6.5.1. Границы области Q'.
и граничные условия (6.5.6), на основании уравнения (6.5.16)
получим
л^-jOcorfa + j^
(6.5.17)
Если записать это уравнение для всех граничных точек (т. е. N т
точек), мы получим N дополнительных уравнений для со,
которые можно рассматривать как граничные условия. Здесь, как и
ранее, величины 4я и dW/dN, стоящие под знаком криволинейного
интеграла, взятого вдоль Г", неизвестны, но их можно оценить
для предыдущего момента времени или предыдущего шага
итерации. Аппроксимируя входящий в (6.5.17) интеграл по
поверхности, придем к следующему выражению:
\ G (х, у; А,, (ы) со (х, y)da^2l Ai> / (^ Iх) ®*. h
в котором суммирование производится по всем точкам
(находящимся внутри области Q' и на ее границах ГиГ"). Тогда из
уравнения (6.5.17) получаем
£A-,/(k, ix)(ùitl = Fm(Xt ix) для (Я,, ii) es Г, (6.5.18)
где Fm включает, в частности, слагаемое, зависящее от значений
ЧГг и (дЧг/дЫ)™, вычисленных на предыдущем шаге итерации
га. Простой способ получения граничных условий заключается
188

в вычислении (6.5.18) для каждой граничной точки с тем, чтобы
получить величину cû™+1 на границе с помощью итерационной
процедуры
со? + 1 = со? + y(Z Ai.fiùT. / - Fm). (6.5.19)
Здесь по-прежнему у — параметр сходимости, который должен
быть положительным.
Другой способ заключается в повторном вычислении (6.5.18)
для всех граничных точек с тем, чтобы получить систему
алгебраических уравнений, которая может быть записана в виде
ArXr + A/X/ = Fw, (6.5.20)
где X —вектор, элементами которого являются Nr граничных
значений со : X/ — вектор, соответствующий TV/ значениям со,,/
внутри области; А и А/ — матрицы размерностей соответственно
N XN и Л^/ХЛ^/, a F™ — вектор, соответствующий Fm(X, \i) из
уравнения (6.5.18). Далее, с помощью итерационной процедуры
(может быть, с использованием процесса релаксации)
ArXr+1 = -A/Xr + Fm
можно вычислить Х™+1 посредством только одного обращения
матрицы, т. е. использования А"1, вычисленной лишь один раз.
By и Вабах (1976) впервые предложили использовать формулу
Грина для получения дополнительных граничных условий. При
этом внутренняя граница Г" не рассматривалась,, так что
поверхностный интеграл вычислялся по всей области, за исключением
тех ее частей, где вихрь со обращался в нуль. Метод, основанный
на введении внутренней границы Г7, благодаря чему достигается
экономия машинного времени, был предложен и применен для
решения уравнений Навье—Стокса в работе Сеа и др. (1981).
6.5.4. Итерационный метод
Вместо того чтобы вводить фиктивное время и решать систему
уравнений параболического типа с помощью какого-либо метода,
предназначенного для решения нестационарных уравнений,
можно непосредственно решать систему эллиптического типа
(6.5.1) с помощью итерационной процедуры. Вначале уравнения
(6.5.1) аппроксимируются с помощью конечно-разностных
уравнений
[b*№./>--jf-]«*./-o. <6-5-21а>
VhVt.l + m. i = 0, (6.5.216)
189

где конечно-разностный оператор /^("Ч^, у), определяемый
следующим образом:
U (V,. у) = (Д°¥,. у) А' - (A^Fi, /) Д° = ut. у А ° + и*, у Д°, (6.5.22)
представляет собой аппроксимацию конвективного члена V-V
с помощью центральных разностей, a V* =АХх+АУу.
Конечно-разностные уравнения (6.5.21) имеют точность второго порядка.
Уравнения (6.5.21) решаются с помощью следующей
итерационной процедуры (Гринспен, 1969; Ранчел и др., 1969; Роуч,
1975), шаг которой определяется номером га. Предположим, что
значения Ч*™. и со?1, известны. Величины Ч1*™*1 и o^t1 опреде-
ляются следующим образом.
1. Вычисляется вспомогательная величина W™*1 из
соотношений
VhVT.V = -<*?. I Для (*,, */у)е=Йл (6.5.23а)
и
4?.V = ft.i Д^я (хьУ/)еГл. (6.5.236)
2. Определяется окончательное значение W™*1 по
релаксационной формуле
4?y = a4fctl + (l-a)W?th 0<а<1, для (*,, уд е= Q*.
(6.5.24)
3. Рассчитывается вспомогательное значение cù™*1 с
использованием соотношений
[Мч№) ë-]ô"/"1 = 0' (**, if/Jeft, (6.5.25а)
^^«Л.уСчГ4-1, cow), (*,, Уу)еГЛ, (6.5.256)
где величина F/, у определяется по граничным значениям вихря со.
4. Определяется окончательное значение юя+* по
релаксационным формулам
o>7:r1=ßc57:-ri+(i_Р)соГ!/, (*,. й)ейа,
co^r1=Y«"|1 + (l — Y)^/, (^й)еГа, (6.5.26)
где параметры релаксации ß и у соответственно для внутренних
и граничных точек не обязательно должны быть равны один
другому (0<ß, y^1).
При достижении сходимости итерационный процесс
заканчивается. Вопрос о выборе критерия сходимости довольно сложен.
Можно рассмотреть различные способы определения этих
критериев,
190

Простые критерии сходимости имеют следующий вид:
/?<■> = max (|^ + 1-W7|/|)<e4f)
«. /
7?П)=тах(К + '-со-/|)<е(0)
г де е^г и 8û) должны быть достаточно малы по сравнению со
средними значениями соответствующих величин. Могут быть
полезными относительные критерии сходимости, такие, как, например:
RV = л m + lh <£Ф (Ф = х1г или со),
max(l<!/ I)
в которые входят численные значения самого решения. При
рассмотрении некоторых сложных течений может случиться, что
итерационный процесс нахождения решения хорошо сходится во всей
области, за исключением отдельных изолированных точек,
например вблизи особых точек или, в более общем случае, в области
очень больших градиентов, где нельзя получить точного решения.
В этом случае лучше ввести осредненные критерии типа
г>(3) 1 V1 I m +1 m I ^
ИЛИ
^4)=(121ф^1-ф^Г)
2
ф»
где N— общее число точек, по которым производится
суммирование. Если используется такой критерий, возможно
нормализованный по отношению к максимальному значению \ymf\ |, то
рекомендуется проверить также выполнение указанных выше
критериев по максимальным величинам отклонений.
Наконец, необходимо весьма тщательно проверить, как
сказываются на решении различные параметры релаксации и
конечно-разностные формулы, выбранные с целью оптимизации
расчетов (влияние умножения на Re, на шаг сетки в какой-либо
степени и т. д.). Поэтому рекомендуется в случае, когда сходимость,
как предполагается, уже достигнута, определить невязки
уравнений, например в виде оценки по максимальному значению
/е-гД|[м*,,)--|-]»,,|}.
«ï>-m«(|v|*,,, + »,,,D.
Значения этих невязок, которые нужно сравнивать с
максимальными значениями самого решения, определяют степень точности
полученного решения конечно-разностных уравнений.
191

На каждом шаге итерационной процедуры (6.5.23) — (6.5.26)
приходится решать две системы линейных алгебраических
уравнений. A priori кажется, что эти системы могут быть решены
с помощью любого метода — прямого или итерационного. Однако
в таких случаях рекомендуется использовать итерационные
методы, поскольку решение этих систем является лишь внутренним
циклом глобальной итерационной процедуры. По мере
достижения сходимости глобального итерационного процесса разность
между двумя величинами, определенными на двух
последовательных шагах итерационной процедуры, уменьшается и,
следовательно, число итераций, необходимых для получения решения
системы линейных алгебраических уравнений (6.5.23) или (6.5.25),
непрерывно уменьшается. Более того, это число может быть
чрезвычайно мало (порядка единицы на последнем этапе глобального
итерационного процесса), если требуемая степень сходимости
итерационного процесса при решении систем (6.5.23) и (6.5.25) не
слишком высока (учитывая, что это лишь промежуточный
результат) .
Решение уравнения (6.5.23), как правило, не представляет
трудностей, поскольку это обычное уравнение Пуассона. При
решении (6.5.25) возникают проблемы обеспечения сходимости при
|M,-f/|ReAx>2 или |ü;,/|ReA*/>2, так как матрица системы
(6.5.25) уже не является диагонально преобладающей. Это
обстоятельство, возникающее в тех случаях, когда число Рейнольдса
слишком велико по сравнению с величиной, обратной шагу сетки,
долгое время не давало возможности получить численное решение
уравнений Навье—Стокса. В следующем пункте изложен общий
метод, позволяющий преодолеть эту трудность.
6.5.5. Решение задачи для больших чисел Рейнольдса
Изложенный здесь способ решения задачи при отсутствии
диагонального преобладания состоит в использовании нецентрирован-
ных разностей против потока для аппроксимации конвективного
члена V-Vo) (или в консервативной форме V(Vco)). Схемы с
применением такой аппроксимации были развиты Баракатом и
Кларком (1966), Ранчелом и др. (1967, 1969), Госменом и др. (1969),
Торренсом (1968) и Гринспеном (1969). Они включают оба
итерационных решения стационарной задачи или нестационарного
уравнения с дискретизацией по времени.
Оператор с центральными разностями L/l(4fi,/) в уравнении
(6.5.21а) заменяется выражением
Lh (Y,, /) = (ДХ /) А; - (Д^*. /) А;, (6.5.27)
в котором
д» _ 0-«У./)Д£ , (l + e?,/)AJ _ло Ajc «д ,fi - 9ft.
Ajc= 2 1 2 — A* 2 — Zt.jbxx9 (O.O.Jo)
192

где гу . = sign (Ui,j)= sign (A0 4?itj). Аналогичная формула
используется для Д*
_ (l-e?,/)A+ (l+e?f/)A- _л0
г~ 2 I" 2
= Аи,
Ау
е?,/Л^, (6.5.29)
где е^ . = sign (vit /) = sign (—Д0^ 4?it у).
Как указывалось в главе 2, такая дискретизация приводит
к матрице с диагональным преобладанием для любых чисел Рей-
нольдса; однако эти аппроксимации обладают точностью лишь
первого порядка. Можно по-прежнему достичь второго порядка
u=v=0
u=v=0
Рис. 6.5.2. Течение в полости.
u = v=0
точности, используя метод коррекции, описанный в п. 2.4. Тогда
(6.5.25а) заменяется уравнением
[û^tD-^jo^T^-Aft^r1)^/, (6.5.30)
в котором оператор A/l(xFyi+1) определяется следующим образом:
Ah(xYi, /) со,-, / = -g- Axe" /И/. / A**©*, J + -J- ДУ8?, /ü«. / А^^. / +
+ С, А^со/, у + С2 А^со/, у, (6.5.31)
Ci-
-j- Дх2ф„ A^i, / + -g- Axhu АххЩ, /,
C2 = -т- Ax2<p0 A°u/f / + -5- АЛ, A^ü/, /.
(6.5.32)
Если мы хотим, чтобы при сходимости сохранялось аппрокси-
мационное выражение с центральными разностями (6.5.22),
следует выбрать Ci = C2 = 0 или
фа = %и = фо = х0 = 0. (6.5.33)
Это соответствует коррекции, предложенной Деннисом и Чангом
(1969) и использованной, в частности, Вельдманом (1973) и Та
Фуок Лок (1975).
193

Если необходимо ввести искусственную вязкость, то можно
выбрать следующие значения:
<pw = —2аиё" I при аи = const > 0 и ё" i = sign (Д° щ, /),
Хы = — 2ßwi"/ при ßM = const >0 и e"/ = signOW*,f/). (6.5.34)
Аналогичные соотношения используются для величин,
соответствующих переменной у. Так, полагаем
фо = —2аД у и Х0 = —2ßüe?, /. (6.5.35)
Особый интерес представляет, в частности, выбор значений ф
и х ПРИ расчете возвратного течения в замкнутой области
(рис. 6.5.2). Если положить
<P,i = -2ë?t/, XW = 2Î"/, <p0 = -2ê?l/f X0=2e?i/f (6.5.36)
то значения вихря на стенках, ограничивающих область, не
войдут в выражения, аппроксимирующие V-V<d в точках,
ближайших к границе. Благодаря этому исключается возможность того,
что итерационный процесс будет расходиться или появятся
осцилляции решения, вызванные очень большими значениями вихря
на границе AB или вблизи угловых точек А и В.
6.5.6. Аппроксимация уравнения вихря, записанного в консервативной форме
Уравнение вихря, записанное в консервативной форме, имеет вид
V .(Vcû)--^_ = 0, (6.5.37)
а в дискретизированной форме
2
V* • (V©),. / - V^'' = 0. (6.5.38)
Обычно используются два вида аппроксимаций нелинейного члена
V(Vo)). Аппроксимация первого типа с применением центральных
разностей для нелинейного члена, записанного в консервативной
форме, определяется так:
Va (Vcd);, , = Д° (и©)/, / + Д° (wo),, /. (6.5.39)
Соответствующая схема с разностями против потока
записывается в виде
Vä (V(d)£. у = А* (г/со)/, / + A* (V(ù)it /, (6.5.40)
где
д: (и©),, , = -L [(1 - е?, /) At (шо),. / + (1 + с?, /) AJ (и©),,,] =
= Д°(шо)/, / — — Д*е" / Ахх {u(ù)it /, (6.5.41)
194

и аналогичным образом определяется А*. Касаясь вопроса
о том, является ли матрица s^=[ait m], связанная с уравнением
(6.5.38) матрицей с диагональным преобладанием, следует
указать, что имеет место следующее неравенство:
|а/,/1 ^ '
a;,m|<l + 0(ReAA:3), Д* = Д#.
m
m Ф I
Обычное условие диагонального преобладания не содержит члена
О (Re Ах3). При практическом использовании этого метода (см.
п. 6.5.8) расходимости процесса не возникает.
Отметим, что приведенное в конце п. 6.5.5 замечание,
касающееся расчета течения в полости, относится к упомянутой выше
дискретизации в консервативной форме независимо от того,
берутся ли центральные или нецентрированные разности (Ру и др.,
1980).
В общем виде поправочный член, соответствующий оператору
Ал, стоящему в правой части уравнения (6.5.30), записывается
следующим образом:
ЛЛ OF,-, /) (ùi, i = -j-Axe" y àxx (u(ù)i ,j + — A№. / &yy (w>)*, / +
+ C, AxxCû/, / + C2 A^cû/, /, (6.5.42)
где Ci и C2 определяются согласно соотношениям (6.5.32) при том
же выборе коэффициентов сри, ф^, %и, %v.
Другим способом дискретизации нелинейного члена V-(Vœ)
в центрированной форме является следующее представление:
Vä • (V©)/. / = A* (и©),, j + &l {m)it /, (6.5.43)
где A1 и A1 определяются как
Air _ ^- + '/2, j—fi-Чг, I
lf _ fi, /+i/a—ff, /-'/2
tifi.I
при
'i + '/2,/""" 2 ('i+l,/"'"'i./)' li,i+42~ 2 ('*,/+! ''*./)•
Схема с направленными против потока разностями для
уравнения, записанного в консервативной форме, была введена Ранчелом
и др. (1967, 1969) и Торренсом (1968). Она более сложна, нежели
схема с разностями против потока первого типа, но обладает тем
преимуществом, что дает матрицу с диагональным преобладанием.
195

ui
(и
и-
+ !/а
£ + 1.
+ »/2,
/°/ + 1
l-Ui-
2 Ал
/®/ + i.
Дл:
/—
Д*
-1.
/~"
• "*-
г) <»£.
М/-
"Ь
/
Va,
. /°*. /
»
/®*-1.
»
»
/
Принцип построения этой схемы станет ясным, если рассмотреть,
например, аппроксимацию производной
\ дх )i,j-
если tt/ + I/fi/>0 и и/-|/ь/>0
если и/ + ./1§/<0 и ut_4t tf< О
если Mi + l/fi/>0 и и._1/2 у.<0
А -,если и,,,. ,<0ии, ,, ,>0.
Две последних конечно-разностных формулы согласуются только
в том случае, если величина \и\ достаточно близка к нулю, чтобы
ею можно было пренебречь (это возможно, так как и меняет
знак).
Аналогичным образом аппроксимируя производную d(v(ù)/dy,
можем записать в сокращенном виде конечно-разностное
выражение для V- (Vco)
Va • (Vco)/, / = Д* (u(ù)i, i ~ Ал: Ai (г}, jUit / äU/, /) +
+ к), (v(ù)i, 1 —j-ky Aly (e?f pi, i kyiùi, /). (6.5.44)
Оператор A/t определяется следующим образом:
ЛА (Vi, /) (ùi, / = ~y Л* Ах (et, ,щ, , Ахт,/)+-§-А# Л^ (8^ iVi. 'д^' ■ ') +
+ С, Д**со/, 7 + С2 Д^со/, /, (6.5.45)
где Ci и С2 находятся из (6.5.32).
В заключение отметим, что добавление члена Ci AxxG),-,/ +
+ С2 Ayyiùi, j, описывающего вязкость, нарушает консервативность
схемы. В п. 6.5.8 мы рассмотрим результаты применений
перечисленных выше схем. Критическую оценку этих схем с
центральными и нецентрированными разностями, а также схем с
направленными против потока разностями («схемы со взвешенными
разностями против потока» Рейсби и Торренса, 1974; «схемы,
асимметричные по потоку» Рейсби, 1976а) можно найти в
работах Торренса (1968), Ранчёла (1972), Де Валь Дэвиса, Малинсона
(1976) и Рейсби (1976b).
6.5.7. Уравнения для нестационарного случая
Для решения уравнений нестационарной задачи
J^ + V.Vû)-jgL = 0, (6.5.46)
v*¥ + » = 0 (6.5.47)
196

могут быть использованы различные численные методы,
предназначенные для решения уравнений параболического типа. Однако
какой бы метод не применялся, на каждом шаге по времени
приходится решать уравнение Пуассона (для функции тока). Для
этого можно использовать явные схемы, полученные на основе
схем, представленных в главе 2 (Фромм, 1964, 1969; Томен и Шев-
чик, 1969). Однако, как об этом уже говорилось выше,
предпочтительнее использовать неявные схемы, среди которых можно
выделить метод чередующихся направлений, обладающий
следующими преимуществами:
1) второй порядок точности аппроксимации по времени и
пространственным переменным;
2) хорошая устойчивость;
3) решение легко получается путем обращения трехдиагональных
матриц.
Метод чередующихся направлений и его свойства уже
обсуждались в главе 2 и предыдущих параграфах этой главы. Здесь
мы рассмотрим итерационную процедуру, применяемую для
решения поставленной задачи.
Допустим, что для аппроксимации уравнения (6.5.46)
используется схема (2.8.4), где /, А и В заменены соответственно
величинами со, и и v. Параметры, входящие в уравнения (2.8.4),
выбираются следующим образом:
Со = —, с1 = с2 = 01 у0 = — , Yi = V2 = 0 (Пирсон, 1966);
с0 = 0, с, = с2 = g", Yo = 0, Yi = Y2= 2~ (Брайли, 1971);
_ 1 — —п — 1
<Y,=Y2 = 0 (Азиз и Хеллумс, 1967).
Схема чередующихся направлений применительно к уравнениям
(6.5.46) и (6.5.47) может быть записана в символической форме
Л, (и?,+, ') S, t, + Mi (v?+-1) со?, i = 0, (6.5.48а)
Л2(<У)со?,У + M2(vî,y)&itJ = 0, (6.5.486)
vMV + <ö?.V = 0, (6.5.49а)
uiy = Л>?,У, itf.V = -A^F?,V. (6.5.496)
Отметим, что в соответствии с указанным выше выбором аппрок-
симационных выражений для составляющих скорости
конечно-разностные операторы Ai(h*+?), M\(vn+}) и т. д. очевидным
образом зависят от решения в момент времени, соответствующий
(п+ 1)-му шагу.
197

Предположим, что решение задачи определяется в квадратной
области Q, 0<х< 1, 0<у< 1, представленной в виде сеточной
области Q/t при Xi = iAx, у,=]Ау, i, /=1, ..., N. Задача решается
при начальном условии
V(*. у, 0) = V°(*> У), (х, у)€=а, (6.5.50)
и граничных условиях
¥(*, у, t) = f(xt у, t) (6.5.51а)
W(x^y, t) =g(^ ^ ^ (6.5.516)
Из (6.5.50) можно получить начальное условие для со
©(*, у, 0)=co0(x, у). (6.5.51b)
Условие Дирихле (6.5.51а) относится к уравнению (6.5.49). Для
решения (6.5.48а) необходимо иметь значения со/,/ на границах
х = 0 и х=1, а для решения (6.5.486)—значения со™*1 на
границах у = 0 и у = 1. Для определения этих значений мы можем
использовать метод, изложенный в п. 6.5.3. Окончательные
формулы в символической форме записываются так:
<V = /4<tf.V, 4tffV)-FS + 1.
©7.V+ ! = F«V, 4tf.V)- tffti, (6.5.52)
где / = 0 соответствует у = 0 и' j = N+l соответствует у = \.
Для получения промежуточных значений о/, у на границе
следует использовать формулы (2.8.5) в тех случаях, когда это
возможно, именно при условии, что на обоих шагах по времени
используются одинаковые аппроксимации и. В этом
предположении мы получим
"-V + </ , Д* IV до 1
. At Г/ .0 1 . \ га+1
©г,/ = -
-(vtA°y gi-A« )©"./] (6.5.53)
для / = 0 (х = 0) и / = N+1 (х=1). Величины v\ и и2
представляют собой аппроксимации v (см. п. 2.8.2). При расчетах (6.5.53)
в окрестности угловых точек можно использовать нецентрирован-
•ные разности с целью избежать необходимости определения со
в этих точках.
Заметим, что можно воспользоваться простым способом
определения вихря на границе, который дает достаточно точные
результаты (Бонту, 1978):
&i.i = ±№.Y + <i)- (6-5-54)
198

Входящие в уравнения (6.5.53) или (6.5.54) значения юп. .
и (ùV-y на границе определяются по формулам, аналогичным
(6.5.52). Поэтому можно записать в символической форме
~ г^ ( п +1 я \ /^,П + 1
СОо, / = G((Ö|,/ , (х)1г]) = и0 ,
<ùn+ 1, у = G (cdî^/, 0)w, /) — oîvr+\. (6.5.55)
С использованием всех этих формул итерационное решение
данной задачи строится следующим образом. Зная t/?>y-, и"/, со"/>
определяем решение и?,У> t>7,V» CÖ?.V посредством следующей
итерационной процедуры, шаг которой обозначается индексом m:
1) из уравнений (6.5.48а) и (6.5.55) находится со™*1
Л/ п +1, т\ ~т +1 , дуг / n+l,m\ n ^
©о,/ =yGo +(1— Y) ^о, /,
Sîvrîi1. / = yCT^-tV m + (1 — Y) ®îv+1. /. i=U ..., N; (6.5.56a)
2) из уравнений (6.5.486) и (6.5.52) находится ю*+1,т+1
Л/ я+1,т\ /г+1,т + 1 | %ж ( п + \,т\ ~т + 1 Л
2№,/ ; со,, / r + Af2(öi,/ )©/,/ =0,
©7,V'w + ,=^ô+1'm + (i--Y)<+o1,m.
co?,V+T + 1=Y/7UVm + (l-Y)<V+?, /— 1 Л^; (6.5.566)
3) из уравнений (6.5.49а) и (6.5.51а) находится <ф^"К1»m+1
^+1,т + 1=/Гд ^ y^Vh, (6в5>б7)
4) из уравнения (6.5.496) находятся м*уН-m+1 и у™.+?- ,n+1
a?.+/,,m + ,=oAX+/l,m + , + (l-o)u?.V,m,
n + 1, m + 1 Л 0 iTPn + 1 m + 1 i /i \ Ai+l,m /с с сo\
о/,/ =-аДЛ,/ +(1—a)üif/ . (6.5.58)
Входящие в (6.5.56) и (6.5.58) величины у и а суть параметры
релаксации (0<Y, a^l). Отметим, что четвертый этап не нужен,
если в качестве и и v в (6.5.56) используются только их значения
на предыдущем шаге по времени, как это сделано у Брайли
(1971). Кроме того, в действительности вовсе не обязательно
искать точное решение системы (6.5.57) при каждом обращении
к процедуре глобальной итерации. В том случае когда для
решения этой системы используется какой-либо из итерационных
методов, достаточно для каждого полного итерационного цикла
ограничиться лишь несколькими итерациями.
Обычно в качестве начальных значений для итерационной
процедуры используются величины, относящиеся к временному
199

уровню п. Можно применить другой подход, основанный на
использовании величин, экстраполированных с уровней nun—1.
Такая инициализация эффективна, если в действительности
решение нестационарно, однако, как показали исследования, ее
эффективность падает по мере приближения к стационарному
решению.
Вопросы устойчивости, связанные с постановкой граничных
условий при использовании метода чередующихся направлений,
рассмотрены Бонту и др. (1980). В этой работе приведено
условие, вводящее ограничение на шаг по времени, типа At/Ах2 < а, где
а зависит от числа Рейнольдса. Подобное же условие получено
(см. п. 6.2.6.3) и для случая, когда метод чередующихся
направлений применяется к системе уравнений с использованием
переменных скорость—давление.
Можно применить метод чередующихся направлений и для
решения уравнения вихря, записанного в консервативной форме.
Схемы первого порядка точности по времени (и и v на каждом
шаге по времени берутся для уровня п) использовались,
например, Торренсом (1968) и Та Фуок Лок (1980). Результаты,
полученные с помощью схем второго порядка точности, изложены
в п. 6.6.2. Наконец, в методе чередующихся направлений могут
применяться также схемы с нецентрированными направленными
против потока разностями с учетом или без учета поправочного
члена (см. п. 2.4 и 6.5.5) (Бонне и Альзар де Рокфор, 1976, Аль-
зар де Рокфор и Грийо, 1978).
6.6. Примеры решения уравнений для вихря и функции тока
6.6.1. Стационарный поток в полости квадратного сечения
Одной из типичных задач, на которых испытываются и
сравниваются между собой различные численные методы, стал в
последние годы расчет стационарного течения в полости квадратного
сечения. В большинстве таких работ (см., например, Бурграф, 1966,
Гринспен, 1969, Фортен и др., 1971, Роуч, 1975, Де Валь Дэвис
и Малинсон, 1976, Рубин и Хосла, 1977, Гупта и Манохар, 1979)
скорость течения полагается равной нулю на трех сторонах
квадрата, а на четвертой стороне она постоянна, равна единице и
направлена вдоль этой стороны. Вследствие разрыва скорости в
угловых точках решение уравнений Навье—Стокса сингулярно в этих
точках (вихрь обращается в бесконечность). Фактически
получить достоверные оценки влияния этих особенностей на точность
решения весьма трудно. В частности, это касается тех случаев,
когда узлы расчетной сетки при ее измельчении все более
приближаются к угловым точкам, даже если в численной схеме
значения вихря в этих точках не учитываются, как это обычно
принято делать при введении конечно-разностных
аппроксимаций.
200

Рассмотрим решение уравнений Навье—Стокса, описывающих
течение жидкости в полости (рис. 6.6.1), которое было получено
Бурсье и Франсуа (1969). В этой задаче скорость и на стороне
AB уже не постоянная величина, а функция, определяемая по
формуле
и(х) = -16х2(1 -х2)
так, что и(0) =и{\ ) = и' (0) =и' (1) =0. Граничные условия для
функции тока определяются следующим образом:
^ = 0, -5^- = — 16а:2(1 -х2) на AB,
^ = 0,
- = 0
на ВС, CD, DA,
где N — единичная нормаль к границе.
Рис. 6.6.1 Форма рассматриваемой области и
граничные условия.
</='
A v=0
и=0
v=0
у--о
Уравнения
Навье - Стокса
v-0
х=0
к=0
v-0
x=f
С
Вычисления производились с помощью итерационного метода
(см. п. 6.5.4 и 6.5.5); ниже приведены данные о сравнении
результатов экспериментов двух типов. Первая группа результатов
была получена для уравнения вихря, записанного в различных
формах (консервативной или неконсервативной), и при разных
аппроксимациях нелинейного члена. Для расчета значения вихря
на границе области использовалась формула первого порядка
точности (6.5.10). Вторая группа результатов была получена при
различных формулировках граничных условий для вихря. В этих
экспериментах расчеты производились по численной схеме второго
порядка точности с коррекцией, полученной из (6.5.40) и (6.5.42)
при Ci = C2 = 0.
Для того чтобы проиллюстрировать характерные особенности
полученного течения, на рис. 6.6.2 и 6.6.3 показаны линии тока
и изолинии вихря для случая Re = 400. Эти карты изолиний
соответствуют результатам расчетов, проведенных для сетки с шагом
Ах = Ai/= 720 по схеме второго порядка точности (6.5.40), (6.5.42),
используемой для решения уравнения вихря в консервативной
форме при Ci = C2 = 0; значение вихря на границе вычисляется по
формуле первого порядка точности (6.5.10).
201

■0,00Û35\
4=0,0/
Рис. 6.6.2. Линии тока для течения
в полости, Re = 400.
Рис. 6.6.3. Изолинии вихря для
течения в полости, Re = 400.
Результаты расчетов для Re = 400, Ах = Ау = 1/2о представлены
в табл. 6.6.1, в которой приведены максимальные значения
функции тока Ч', осредненная по отрезку AB величина вихря со (пол-
0J5
0,50\-
0,25\
Номер эксперимента w° V
(табл 6 61) \\
о о о о 2
6
+ + + + 9
10
-1,0 -0,5 О 0,5 и(0,5у)
Рис. 6.6.4. Скорость и в сечении х =-0,5, Re = 400.

Таблица 6.6.1. Сравнение различных методов расчета течения в полости
при Re=400, kx=ày = l/2o (граничные значения вихря по (6.5.10))

Эксперимент
1
2
3
4
5
6
7
8
9
10
Форма
записи
уравнения
ДЛЯ CÙ
нка
нк
нк
нк
к
к
к
к
к
нк
Схема
Нецентрированная
(6.5.27)
С коррекцией (6.5.30),
(6.5.33)
С коррекцией (6.5.30),
(6.5.36)
С коррекцией (6.5.30),
(6.5.34), (6.5.35)
СХи = аг>=1> ßu = ßu = 0
Нецентрированная
(6.5.40)
С коррекцией (6.5.40),
(6.5.42)
С, = С2=0
С коррекцией (6.5.40),
(6.5.42), (6.5.34), (6.5.35)
au = at, = l, ßu = ßr = 0
Нецентрированная
(6.5.44)
С коррекцией (6.5.44),
(6.5.45)
с1=с2=о
Эрмитова четвертого
порядка в
maxw (х, у)6
х,у
0,0632
0,0584
0,0661
0,0652
0,0593
0,0750
0,0718
0,0677
0,0669
0,0844
Результаты
1
jj со (х, 1) dx
0
7,62
9,38
8,00
8,27
7,99
6,94
7,55
7,35
8,15
8,10
max и (0,5, у)
У
0,132
0,140
0,155
0,153
0,116
0,188
0,173
0,141
0,164
0,229
а НК — неконсервативная форма; К — консервативная форма.
6 Получено для #=0,35, # = 0,75 (эксперимент 1); л:=0,35, # = 0,70
(эксперименты 2, 4, 8), *=0,40, #=0,65 (эксперименты 3, 5, 6, 7, 9, 10).
в Бонту и др. (1978).
ное напряжение сдвига), причем интеграл берется по правилу
трапеции, при (о(0, 1 ) = со( 1, 1)=0, и максимальное значение
составляющей скорости и(0,5; у). Численные эксперименты 1—9 (см.
табл. 6.6.1) выполнены по разным схемам с применением
формулы (6.5.10) для расчета вихря на границе области. Точность
этих результатов можно оценить путем их сравнения с данными
расчета, в котором использован эрмитов метод четвертого
порядка точности (Бонту и др., 1978). Эти результаты приведены
здесь в качестве образца для сравнения (эксперимент 10).
На рис. 6.6.4 приведены разности между значениями скорости
гг(0,5; у), полученными по разным схемам.
Как можно судить на основании результатов, полученных при
решении указанной задачи, а также по данным ряда
сравнительных испытаний для более общих случаев (например, Рубин
и Хосла, 1977), использование уравнений, записанных в консер-
203

вативной форме, приводит к более точным результатам, нежели
в случае уравнений, взятых в неконсервативной форме. Кроме
того, дискретизация типа (6.5.39), к которой сводится схема,
использованная в эксперименте 6, по-видимому, предпочтительнее
дискретизации типа (6.5.43), к которой сводится схема,
использованная в эксперименте 9, если не принимать во внимание средние
значения со на AB. Однако следует отметить, что эта величина
несущественна, поскольку со меняется в значительных пределах,
принимая как отрицательные, так и положительные значения (от
—5,0 до 25,0).
Результаты, представленные в табл. 6.6.1 (эксперименты 1 —
9), соответствуют критерию сходимости max(/?W, /?^)<10"5
(см. п. 6.5.4), тогда max(#<^, RW ) <6-10~5. Для их получения
сначала применялась итерационная процедура (при значениях
параметров релаксации в (6.5.24) и (6.5.26) а=1, ß=v = 0,5), в
которой в качестве исходных данных использовались результаты
расчетов для Re=100. По этой причине нельзя дать точной
информации о скорости сходимости итерационного процесса, за
исключением того факта, что использование уравнения вихря в
консервативной форме обеспечивает лучшую сходимость; это
преимущество, кстати, отмечалось при сравнительных испытаниях,
проводившихся также и для других задач.
Проведена также оценка эффективности такого итерационного
метода для случая Re=100, Ах = Ау = [/2о (эксперимент И,
табл. 6.6.2). Если используется схема с коррекцией, определяемая
соотношениями (6.5.40) и (6.5.42) при Ci = C2 = 0, и в качестве
параметров релаксации [уравнения (6.5.24) и (6.5.26)], связанных
с применением формулы (6.5.10) для расчета граничных значений
вихря, выбраны значения а=1, ß =0,5 и 7 = 0>5 [уравнения
(6.5.26)], то требуется 138 глобальных итераций для получения
сходимости, характеризуемой следующими величинами (см.
п. 6.5.4):
/?<;> = 8 - lu"6, <> = 6 - m"4, *<? = lu"4, <2)= 5 - lu"5,
R{*] = 2 - 10"6, <3)= 1,6 . Ю-4, #(ч4) = 3 - 10~6,
^ = 2.10-4, /?(^ = 2 - 10"3, Rl] = 5 - 10"3.
На каждой глобальной итерации линейные уравнения
решаются с помощью метода последовательной релаксации, причем
параметр релаксации выбран равным 1,5 при решении уравнения
для 4я и 1,0 при решении уравнения для со. Так как эти
уравнения каждый раз решаются приближенно (процесс релаксации
прекращается, когда разность между двумя последовательными
итерациями становится меньше Ю-2), общий объем
вычислительной работы, необходимой для обеспечения сходимости, лучше
всего оценить по общему числу шагов итерационного процесса
204

Таблица 6.6.2. Сравнение способов аппроксимации вихря на границе для течения в полости при Re =100
(схема (6.5.40), (6.5.42), d = C2 = 0)

Эксперимент
И
12
13
14
15
16
17
18
19
20
21
22
23
Шаг
сетки
Ах = At/
1/10
1/20
1/10
1/20
1/10
1/20
1/10
1/20
1/10
1/20
1/20
1/20
1/20
Аппроксимация граничных
условий для со
(эксперименты (11) - (21))
Методы расчета
(эксперименты 22 и 23)
(6.5.10)
(6.5.10)
(6.5.11)
(6.5.11)
(6.5.12)
(6.5.12)
(6.5.18), Q' = Q
(6.5.18), Q' = Q
(6.5.18), Q'={(0,2;
0,9). (0,1; 0,8)}
(6.5.18), Q' = {(0,2;
0,9), (0,1; 0,8)}
(6.5.18), ö' = {(0,05;
0,95), (0,05; 0,8)}
Эрмитов четвертого
порядка д
Эрмитов четвертого
порядка е
Число
глобальных
итераций
62а
138
50
130
48
127
11
117
78
142
143
Общее число
итераций
Гаусса—Зейделя
W
71
144
80
148
58
144
86
119
84
146
147
Û)
388
737
301
719
292
865
285
635
316
697
726
Результаты
тах^ (х, у)в
х, у
0,0735
0,0806
0,0792
0,0829
0,0799
0,0829
0,0796
0,0826
0,0792
0,0825
0,0825
0,0835
0,0829
max ш (х, 1)г
X
9,84
12,61
11,63
13,07
11,95
13,14
11,99
13,01
11,89
12,99
12,95
13,31
13,16
1
§ со (х, 1) dx
0
4,44
4,80
4,85
4,94
4,85
4,93
5,17
5,01
5,11
5,00
4,98
5,14
5,20
max и (0,5; у)
У
0,133
0,153
0,145
0,158
0,146
0,158
0,145
0,157
0,143
0,157
0,159
0,163
0,162
а Проверка сходимости по max^^, /?^4))<е; e=5-10~5 для шага Vioî е= 10~5 для шага У2о.
6 Проверка сходимости до 10~2.
11 Получено для *=0,4; # = 0,8.
г Получено для x=0ß.
л Функция тока—вихрь (Бонту и др., 1978).
е Скорость»—давление (Эльзассер и Пейре, 1979).

типа метода Гаусса—Зейделя (144 итерации при решении
уравнения для Ч* и 737 итераций при решении уравнения для со). Время
работы центрального процессора составило 18 с при решении
задачи на компьютере IBM 3033.
Используя ту же вычислительную схему при тех же значениях
параметров релаксации, мы сравнили между собой несколько
способов расчета вихря на границе (см. п. 6.5.3). Напомним, что
такого рода численная схема в случае, когда решение
устанавливается, превращается в схему центральных разностей (6.5.39).
Сравнение производилось для случая Re =100 и двух сеток с ша-
pi
У2
У<
а'
г
г'
X'Û Х<
х2
Рис. 6.6.5. Область интегрирования Q' в формуле
:~1 Грина.
гами Ax = Ay = i/\<x и Ax = Ay = i/2o. В экспериментах 11 —16 (см.
табл. 6.6.2) для расчета граничных значений вихря
использовались формулы первого и второго порядка точности. Результаты
экспериментов 17—20 были получены Сеа и др. (1981) путем
применения формулы Грина (6.5.18) при значении параметра
сходимости у = 8 [уравнение (6.5.19)]. В этом случае область Û' либо
совпадает с й, либо представляет собой кольцевую область
(рис. 6.6.5). Интегралы, входящие в формулу Грина, определяются
по правилу трапеций с расчетом dW/dN на Г' по схеме
центральных разностей. Полученные результаты сравниваются с данными,
полученными путем применения метода Эрмита четвертого
порядка точности (эксперименты 22 и 23) к уравнениям для вихря
и функции тока (Бонту и др., 1978) или к уравнению для
переменных скорость—давление (Эльзассер и Пейре, 1979).
В данном случае, когда число Рейнольдса сравнительно мало
(Re=100), значения вихря со на стороне AB (см. рис. 6.6.1)
меняются в диапазоне от —1,50 до 13,31, так что среднее и
максимальное значения вихря на AB выше, нежели для случая Re =
= 400.
Из разнообразных данных, представленных в табл. 6.6.2, видно,
что формулы второго порядка точности (6.5.11), (6.5.12) и
формула Грина (6.5.18) дают сравнимые результаты. Однако важно
отметить, что результаты, полученные с помощью функции Грина,
зависят от способа расчета интегралов. К тому же выводу
относительно точности формулы (6.5.11) пришли Гупта и Манохар
(1979), рассматривая случай вынужденного движения жидкости
в полости при и (х, 1)= — 1. Те же авторы нашли, что формула
206

Вудса (6.5.12) не очень точна и завышает максимальные
значения функции тока и вихря на AB. Однако полученные здесь
и в других работах (Роуч, 1975, Деннис и др., 1979) результаты
показывают, что это не так.
Из табл. 6.6.2 видно также, что скорость сходимости при
различных способах определения граничных значений вихря
изменяется мало (расчеты с использованием формулы Грина требуют
наибольших затрат машинного времени). Однако нельзя считать,
что этот вывод справедлив для общего случая, поскольку
указанная скорость сходимости зависит от нескольких факторов и, в
частности, от числа Рейнольдса и параметра релаксации у или от
способа решения линейных уравнений на каждой глобальной
итерации. Гупта и Манохар (1979) получили, что формуле второго
порядка точности (6.5.11) соответствует наибольшее число
итераций, требуемое для достижения стационарного состояния.
В заключение отметим, что мы не проводили сравнения
эффективности итерационного метода, использованного в данном
примере, и метода чередующихся направлений [уравнения (6.5.4)
и (6.5.5)]. Возможно, что метод чередующихся направлений
обеспечит более быструю сходимость к конечному состоянию, если
параметры At и а изменяются в соответствии с правилом выбора
оптимальных параметров (Вакспресс, 1966).
6.6.2. Нестационарное обтекание кругового цилиндра
В качестве примера расчета нестационарного течения с
использованием уравнений для функции тока и вихря изложим теперь
результаты, полученные в работе Та Фуок Лок (1980). В этой
работе исследовано явление возникновения вторичных вихрей
Рис. 6.6.6. Обтекание цилиндра.
в потоке, обтекающем круговой цилиндр, с помощью изложенного
в п. 6.5.2 и 6.5.7 численного метода чередующихся направлений
с применением эрмитовой формулы четвертого порядка точности
для аппроксимации уравнения для функции тока.
Схематически плоскость течения показана на рис. 6.6.6.
Круговой цилиндр радиуса а располагается в жидкости, находящейся
при ^<0 в состоянии покоя. При /^0 жидкость движется с
постоянной скоростью Uoo на бесконечности. Нестационарные
уравнения Навье—Стокса решаются для бесконечной области,
внешней по отношению к границе Г, при отсутствии скольжения на
этой границе и условии постоянства потока на бесконечности.
207

Кроме того, течение считается симметричным относительно
направления набегающего потока.
Особенность данной задачи состоит в том, что
рассматриваемая область неограниченна. Такого рода трудность встречается
при расчете многих видов течений, например в рассмотренной
в п. 6.4 задаче расчета течения жидкости в канале, которая
решается с использованием уравнений для скорости и давления
Сошлемся также на главы 10 и 11, в которых эта задача
обсуждается более подробно в применении к течению сжимаемой
жидкости. В рассматриваемом случае для решения задачи вводятся
новые координаты g, rj, определяемые из соотношений
г=аеп1у е = лг], (6.6.1)
/ 1
£ов £ Рис. 6.6.7. Расчетная область.
так что уравнения, полученные в результате этого
преобразования, решаются для полуполосы 0^£ < оо, 0<г]<1 (рис. 6.6.7).
Фактически же рассматривается ограниченная область
протяженности goo и соответствующие граничные условия ставятся при
Та Фуок Лок (1980) вводит условие, что при £ = £«> имеет
место потенциальное течение без вязкости. Поэтому расчет
проводится только для первой стадии процесса, а именно до того
момента, когда вихрь, возникший при обтекании тела, достигнет
внешней границы области. Кроме того, принятая гипотеза о
симметрии движения может также наложить ограничение на время
возможного развития возмущений, вызывающих колебания спут-
ной струи. Очевидно, что это последнее ограничение может быть
снято, если отказаться от условия симметрии. Что касается
первого ограничения, то его можно обойти, если использовать
какое-либо условие, описывающее конвекцию вихря со через
некоторую часть границы, где жидкость вытекает, например:
-gr + v.vo) = o при £ = £оо, е0<е<2я-е0. (6.6.2)
В качестве переменного по времени краевого условия для Y
можно взять уравнение, аналогичное (6.6.2), в котором вместо со
используется производная по нормали от функции тока д^/д^.
208

Такого рода условия успешно применялись Лугтом и Хослингом
(1974) для расчета нестационарного течения вокруг цилиндра
эллиптического сечения при набегании на него потока жидкости.
Отметим, что при расчетах стационарных течений часто с
успехом используются условия д2(о/д£2 = d2XV/д£2 = 0. Однако следует
указать, что самый лучший метод, который, правда, не так прост
в реализации, состоит в том, чтобы воспользоваться
асимптотическими решениями, как это сделали Таками и Келлер (1969) для
расчета обтекания кругового цилиндра стационарным потоком при
малом числе Рейнольдса. Неизвестные, определяющие
асимптотический режим движения, рассматриваются как сопротивление
и находятся вместе с решением задачи с помощью итерационной
процедуры.
Кроме введения новых координат (6.6.1), искомые переменные
приводятся к безразмерному виду путем введения характерных
величин a/Uco для времени, U^a для функции тока и lfoo/a для
вихря скорости. Тогда уравнения движения примут вид
да . d(U(ù) . d(V(ù) 2_
dt ^ ду\ "• д£ Re
■(■S-+-3F-)-0' (6-6-3)
где Re = 2at/0o/v, g = n2e2"t и
Эти уравнения решаются для области 0<|<£оо, 0<г]< 1 при
начальном условии V(|, т), 0)=0. Поэтому оо(£, т|, 0)=0 и
граничные условия имеют вид
при £ = 0, 0<ïi< 1, (6.6.6)
J при £ = !<», 0<т|<1- (6.6.7)
При условии симметрии
\р = со = 0прит1 = 0иг1=1, Q <£<£«,• (6-6-8)
Вычислительная область разбивается на ячейки узлами £г=/Д£,
m = jAy (/, / = 0, ..., N+l). Численное решение в точке g,-, т],
и момент времени tn = nAt обозначается через Ч?" ., ©7/* ^ля
дискретизации уравнения вихря (6.6.3) используется схема
чередующихся направлений, аналогичная схеме (6.5.4а) и (6.5.46), за
исключением того, что нелинейные члены представлены в
консервативной форме.
Ч^ =
(0 =
W
= 0
■2shn£
- =
sin
0
ЛУ\
209

схема
схема
схема
1:
2:
3:
С/«£/п;
"«-J-
иъ-L
На первом шаге производные по г\ рассчитываются по неявной
схеме, а величина U, входящая в аппроксимационное выражение
d(U(ù)
для —- , может определяться тремя различными способами:
(3Un-Un-1);
JL(un + x + Un).
На втором шаге по неявной схеме рассчитываются
производные по g, а величина V, входящая в d(l/co)/d£, определяется по
одной из трех указанных выше схем. Аппроксимация,
отвечающая схеме 1, имеет первый порядок точности по времени, а
схемам 2 и 3 — второй порядок точности. Граничные условия в дис-
кретизированной форме получены из (6.6.6) — (6.6.8) с
использованием формулы второго порядка точности (6.5.12) для
определения значения вихря на поверхности обтекаемого тела. Значение
функции тока, входящей в эту формулу, берется для уровня п
в схемах 1 и 2 и для уровня п+1 в схеме 3.
Для расчета функции тока W7}*1 используется эрмитова
аппроксимация уравнения (6.6.4) четвертого порядка и
применяется итерационная процедура метода чередующихся
направлений. Неизвестными здесь являются значения Ч^.1 и производных
( -тг-2 ) . , ("7Р"). • Ниже в этих обозначениях для простоты
будет опущен верхний индекс /г+1. Пусть m — номер итерации
в процедуре чередующихся направлений. На первом шаге
решаются следующие уравнения:
«•, / - (-^Л, , = *•*№. I + {-W)t, J + 8&W' (6-6-9а)
^-Й./ + 1-2Т,/ + Ч?,/-,)-[(-^)</ + 1 +
Уравнения для второго шага имеют вид
12 Лтгт + 1. 2„fm + l , 1Fm + l \ Г / &V V" + ' ,
На каждом из этих шагов задача сводится к решению системы
уравнений с (2x2)-блочной трехдиагональнои матрицей, которая
210

путем исключения вторых производных, как это указано в п. 2.5.1,
может быть сведена к обычной трехдиагональной системе
уравнений относительно неизвестной функции тока. Граничные уело
~ ( д2у¥
вия на первом шаге записываются в виде Wit /
( д2Ч ^ _
Л drf Ji,i~
О
в соответствии с условиями симметрии, полученными на основе
(6.6.8) и уравнения (6.6.6). Граничные условия на втором шаге
для Ч^.1 и (ö247d£2)m+1 получаются из (6.6.6) и (6.6.7). Пара-
180 б
Рис. 6.6.8. Распределение вихря на поверхности
цилиндра, Re = 300, Д£ = 0,954/40, Дг|=1/40, Д/ = 0,05.
(Любезно представлен Та Фуок Лок.)
метры Хш и |Lim, входящие в уравнения (6.6.9) и (6.6.10),
рассчитываются по формулам, полученным Вакспрессом (1966).
Наконец, величины Un+j = (dW/dl)ff и 1Л+1 = — (дЧ/дц)^
определяются по значениям W7}*} из эрмитовых формул типа
(2.59).
В случае когда используются схемы 1 и 2, значения вихря
и функции тока вычисляются последовательно одно за другим.
После того как (опМ определено, необходимо выполнить восемь
итераций в процедуре чередующихся направлений (6.6.9)
и (6.6.10), чтобы обеспечить сходимость с невязкой меньше 10~5.
При применении схемы 3 величины со и W находятся совместно
с помощью итерационной процедуры. Фактически эта же процедура
используется и при определении Ч^*1 с помощью метода
чередующихся направлений, так что величины Un+l и Vn+]
пересчитывайте через каждые четыре итерации, отвечающие процедуре
чередующихся направлений (6.6.9) и (6.6.10).
На рис. 6.6.8 показано распределение вихря на поверхности
цилиндра, рассчитанное по схемам 1, 2 и 3 для случая Re = 300,
211

£оо = 0,954 (т. е. Гоо = 20а), Дё = 0,954/40, Лг) = у4о и Д/ = 0,05.
Следует отметить, что для области перед цилиндром отличия в
расчетах неразличимы, если их изобразить в масштабе рис. 6.6.8. Эти
различия невелики и для остальных частей обтекаемого тела
и с увеличением времени стремятся к нулю.
Однако заключение о подобии результатов, полученных с
помощью схем первого и второго порядков точности, нельзя рас-
Рис. 6.6.9. Сравнение полученных
экспериментальным путем (Кутансо и Буйяр, 1979) и
рассчитанных линий тока при / = 5,0; Re=550.
(Любезно предоставлен Кутансо и Буйяром и
Та Фуок Лок.)
пространять на случай любого течения, к тому же оно касается
главным образом изменения во времени ошибки аппроксимации.
Рисунок 6.6.9 относится к случаю Re = 550 при £<» = 0,954, Д£ =
= 0,954/50, Ат] = 75о и At = 0,04. Время работы центрального
процессора на ЭВМ UNIVAC 1110 составляет 1,5 с для каждого шага
по времени. На рисунке представлены рассчитанное (по схеме 1)
распределение линий тока в момент t = 5 и для сравнения
приведена фотография, полученная Кутансо и Буйяром (1979). Наличие
вторичного вихря на рисунке может служить иллюстрацией того,
что с помощью численных методов можно описать отдельные
особенности сложных нестационарных течений.
Список литературы
Дородницын А. А., Меллер Н. А. О некоторых подходах к решению
стационарных уравнений Навье—Стокса.— Журнал вычислительной математики и
математической физики, 1968, 8, № 2, с. 393—402.
Яненко H. Н. Метод дробных шагов решения многомерных задач математической
физики.— Новосибирск: Наука, 1967.
Alziary de Roquefort, T., and Grillaud, G. Comput. Fluids 6, 259—269 (1978).
Amsden, A. A.,' and Harlow F. H. The SMAC Method: A Numerical Technique for
Calculating Incompressible Fluid Flows. Los Alamos Research Laboratory
Report No. LA-4370, May (1970).
Aziz, К., and Heliums, J. D. Phys. Fluids 10, 314—324 (1967).
Barakat, H. Z., and Clark, J. A. Analytical and Experimental Study of the
Transient Laminar Natural Convection Flows in Partially Filled Liquid Containers.
In: Proceedings of the Third International Heat Transfer Conference, Vol. 2,
p. 152, AICE, New York, (1966).
Bercovier, M., and Engelman, M. /. Comput. Phys. 30, 181—201 (1979).
Blanschong, G. P., and Hartmann, С. /. Méc. 18, 713—744 (1979).
Bonnet, J P., and Alziary de Roquefort, T. /. Méc. 15, 373—397 (1976).
Bontoux, P. Contribution à l'Etude des Écoulements Visqueux en Milieu Confiné
Thèse Doctorat d'Etat, IMFM, Université d'Aix-Marseille (1978).
212

Bontoux, P., Gilly, В., and Roux, В. /. Comput. Pfiys. 15, 417—427 (1980).
Bourcier, M., and Françous, С. Rech. Aérosp. No. 131, 23—33 (1969).
Bozeman, J. D., and Dalton, С J. Comput. Phys. 12, 348—363 (1973).
Bramble, J. H., and Hubbard, В. E. Numer. Math. 4, 313—327 (1962).
Briley, R. N. /. Fluid Mech. 47, 713—736 (1971).
Bryan, K. /. At mos. Sei. 20, 594—606 (1963).
Burggraf, О. R. /. Fluid Mech. 24, 113—151 (1966).
Céa, J., Lhomme, В., and Peyret, R. The use of Green's formula for vorticity
boundary values. Rapport IMAN, P-28, Université de Nice, June (1981).
Childress, S., and Peyret, R. /. Méc. 15, 753—779 (1976). [Erratum: 16, 803
(1976)].
Chorin, A. J. /. Comput. Phys. 2, 12—26 (1967).
Chorin, \. J. Math. Comput. 22, 745—762 (1968).
Coutanceau, M., and Bouard, R. С R. Acad. Sei. В 288, 485—488 (1979).
Cushman-Roisin, В. /. Comput. Phys. 53, 227—239 (1984).
Daube, О., and Та Phuoc Loc. A Mixed Compact Hermitian Method for the
Numerical Study of Unsteady Viscous Flow Around and Oscillating Airfoil. In:
Proceedings of the 3rd GAMM Conference on Numerical Methods in Fluid
Mechanics, p. 56—66 Vieweg & Sons, Cologne, (1979).
Dennis, S. С R., and Chang, G. Z. Phys. Fluids 12, Suppl. II, 1188—1193 (1969).
Dennis, S. С R„ Ingham, D. В., and Cook, R. N. /. Comput. Phys. 33, 325—339
(1979).
De Vahl Davis, G., and Mallinson, G. D. Comput. Fluids 4, 29—43 (1976).
Deville, M. O. /. Comput. Phus. 15, 362—374 (1974).
Deville, M. O. /. Méc. 14, 161—187 (1975).
Douglas, J., and Gunn, J. E. Numer. Math. 6, 428—453 (1964).
Easton, С R. /. Comput. Phys. 9, 375—379 (1972).
Elsaesser, E., and Peyret, R. Métodes Hermitiennes pour la Résolution Numérique
des Equations de Navier-Stokes. In: Méthodes Numériques dans les Sciences
de l'Ingénieur, E. Absi and R. Glowinski, Eds. p. 249—258, Dunod, Paris
(1979).
Fortin, M. Calcul Numérique des Ecoulements des Fluides de Bingham et des
Fluides Newtoniens par la Méthode des Eléments Finis. Thèse d'Etat,
Université Paris VI (1972).
Fortin, M., Peyret, R., and Temam, R. J. Méc. 10, 357—390 (1971). [See also
Lecture Notes in Physics, Vol. 8, pp. 337—342, Springer-Verlag, New York,
1971)].
Fromm, J. E. The time dependent flow of an incompressible viscous fluid. In:
Methods in Computational Physics, Vol. 3, pp. 345—382, Academic Press, New
York (1964). (Фромм Дж. Неустановившееся течение несжимаемой вязкой
жидкости. Вычислительные методы в гидродинамике. М.: Мир, 1967).
Fromm, J. Е. Phys. Fluids 12, Suppl. II, II113—III 19 (1969).
Ganoulis, J., and Thirriot, C. Lecture Notes in Physics, Vol. 59, pp. 191 — 196,
Springer-Verlag, New York (1976).
Gosman, A. D., Pun, W. M., Runchal, A. K., Spalding, D. В., and Wolfshtein, M.
Heat and Mass Transfer in Recirculating Flows, Academic Press, London and
New York (1969). (Госмен А. Д., Пан В. M., Ранчел A. К., Сполдинг Д. Б.,
Вольфштейн М. Численные методы исследования течений вязкой жидкости.—
М.: Мир, 1972, 323 с.)
Greenspan, D. Comput. J. 12, 89—96 (1969).
Gupta, M. M., and Manohar, R. P. /. Comput. Phys. 31, 265—288 (1979).
Harlow, F. H., and Welsh, J. E. Phys. Fluids 8, 2182-2189 (1965).
Hughes, T. J. R., Liu, \V. T., and Brooks, A. /. Comput. Phys. 30, 1—60 (1979).
Israeli, M. Stud. Appl. Math. 49, 327—349 (1970).
Israeli, M. Stud Appl. Math. 51, 67—71 (1972).
Kao, T. W., Park, C, and Pao, H. P. Phys. Fluids 21, 1912—1922 (1978).
Kreiss, H. O. Math. Comput. 26, 605—624 (1972).
Kuznetsov, B. G. Fluid Dynam. Trans. 4, 85—89 (1968).
Ladevèze. J., and Peyret, R. /. Méc. 13, 367—396 (1974).
Liu, N. Lectwe Notes in Physics, Vol. 59, pp. 300—305, Springer-Verlag, New
York (1976).
213

Lugt, H. J., and Haussling, H. J. /. Fluid Mech. 65, 711—734 (1974).
Mallinson, G. D., and De Vahl Davis, G. I. /. Comput. Phys. 12, 435—461 (1973).
Marshall, R. S., Heinrich, J. C, and Zienkiewicz, О. C. Numer. Heat Trans. 1,
315—330 (1978).
Morchoisne, Y. AIAA Paper No. 81-0109 (1981).
Orszag, S. A., and Israeli, M. in Annual Review of Fluid Mechanics, Vol. 6,
pp. 281—318, Annual Reviews Inc., Paolo Alto CA (1974).
Orszag, S. A., and Kells, L. С /. Fluid Mech. 96, 159—205 (1980).
Peaceman, D. W., and Rachford, H. H. /. Soc. Indus. Appl. Math. 3, 28—41
(1955).
Pearson, С. E. /. Fluid Mech. 21, 611—622 (1965).
Pearson, С. E. /. Fluid Mech. 28, 323—336 (1966).
Peyret, R. C. P. Acad. Sei. A, 272, 1274—1277 (1971).
Peyret, R. J. Fluid Mech., 28, 49—63 (1976).
Peyret, R. C. Numerical Studies of Nonhomogeneous Fluid Flows. In: Advances
in Fluid Mechanics. Lecture Notes in Physics, Vol. 148, pp. 330—361, Springer-
Verlag, New York (1981).
Peyret, R., and Rebourcet, B. In: Proceedings of the 2nd International Conference
on Numerical Methods in Laminar and Turbulent Flow, pp. 1229—1239. Pine-
ridge Press, Swansea, U. K. (1981).
Peyret, R., and Rebourcet, B. /. Méc. Théor. Appl. 1, No. 3 (1982).
Pracht, W. E. /. Comput. Phys. 7, 46—60 (1971).
Raithby, G. D. Comput. Meth. Appl. Mech. Eng. 9, 75—102 (1976a).
Raithbv, G. D. Comput. Meth. Appl. Mech. Eng. 9, 153—164 (1976b).
Raithby, G. D., and Torrance, К. E. Comput. Fluids, 2, 191—206 (1974).
Richtmyer, R. D., and Morton, K. W. Difference Methods for Initial Value
Problems, Interscience, New York (1967). (Рихтмайер P., Мортон К. Разностные
методы решения краевых задач.— М.: Мир, 1972, 418 с.)
Roache, P. J. Computational Fluid Dynamics, Hermosa Publishing. Albuquerque,
NM (1972). (Роуч П. Вычислительная гидродинамика.— M.: Мир, 1980.)
Roache, P. Comput. Fluids 3, 179—195 (1975).
Roux, В,. Bontoux, P., Ta Phuoc Loc, and Daube, O. In: Approximation Methods
for Navier-Stokes Problems. Lecture Notes in Mathematics, Vol. 771, pp. 450—
468, Springer-Verlag, New York (1980).
Rubin, S. G., and Khosla, P. K. /. Comput. Phys. 24, 217—246 (1977).
Runchal, A. K., Spalding, D. В., and Wolfshtein, M. The Numerical Solution of
the Elliptic Equations for transport of Vorticity, Heat, and Matter in Two-
Dimensional Flows. Imperial College, London, Dept. Mechanical Engineering
Rept. No. SF/TN/2 (1967).
Runchal, A. K., Spalding, D. В., and Wolfshtein, M. Phys. Fluids 12, Suppl. II,
1121—1128 (1969).
Runchal, A. K. Int. J. Numer. Meth. Eng 4, 541—550 (1972).
Sills, J. AIAA J. 7, 117—123 (1969) (PTK, 7, № 1, с 137—144).
Takami, H., and Keller, H. В. Phys. Fluids 12, Suppl. II, 1151—1156 (1969).
Та Phuoc Loc. /. Méc. 14, 109—134 (1975).
Ta Phuoc Loc. /. Fluid Mech 100, 111 — 128 (1980).
Ta Phuoc Loc, and Daube, О. In Vortex Flows, N. L. Swift and P. S. Barna, Eds.,
p. 155—171, ASME, New York (1981).
Taylor, T. D., and Murdock, J. W. In: Approximation Methods for Navier-Stokes
Problems. Lecture Notes in Mathematics, Vol. 771, pp. 519—537, Springer-
Verlag, New York (1980).
Taylor, T. D. and Ndefo, E. In: Lecture Notes in Physics, No. 8, pp. 356—364,
Springer-Verlag, New York (1971). (Тэйлор, Т. Д., Ндефо Э. Расчет течения
вязкой жидкости в канале при помощи метода расщепления.— В кн.:
Численные методы в механике жидкостей. М.: Мир, 1973, с. 218—229.)
Temam, R. Bull. Soc. Math. Fr, 96, 115—152 (1968).
Temam, R. Archiv. Ration. Mech. Anal. 32, 135—153 (1969a).
Temam, R. Archiv. Ration. Mech. Anal. 32, 377—385 (1969b).
Temam, R. Navier-Stokes Equations, Norch-Holland, Amsterdam (1977). (Темам P.
Уравнения Навье-Стоксэ.— M.: Мир, 1981.)
Thorn, A. Proc R. Soc. Lond. Л 141, 651—666 (1933).
214

Thoman, D. С, and Szewczyk, A. A. Phys. Fluids 12, Suppl. II, 1176—1186 (1969).
Torrance, K. E. /. Res. Natl. Bur. Stand. В 72B, 281—301 (1968).
Upson, C. D., Gresho, P. M., and Lee, R. L. Finite-Element Simulation of Thermally
Induced Convection in an Enclosed Cavity. Lawrence Livermore Laboratory
Rept. UCID-18602, March (1980).
Veldman, A. E. P. Comput. Fluids 1, 251—271 (1973).
Viecelli, J. A. /. Comput. Phys. 8, 119—143 (1971).
Wachspress, E. L. Iterative Solution of Elliptic Systems. Prentice-Hall, Englewood
Cliffs, NJ (1966).
Wilkes, J. O. The Finite-Difference of Natural Convection in an Enclosed
Rectangular Cavity, Ph. D. Thesis University of Michigan, Ann Arbor (1963).
Williams, G. L. /. Fluid Mech. 37, 727—750 (1969).
Woods, L. С Aeronaut. Q. 5, 176—184 (1954).
Wu, J. C, and Wahbah, M. M. In: Lecture Notes in Physics. Vol. 59, pp. 448—
453. Springer-Verlag, New York (1976).
Zabusky, N. J., and Deem, G. S. /. Fluid Mech. 47, 353—379 (1971).
Глава 7
Использование) метода
конечных элементов
для решения задач механики
несжимаемой жидкости
При решении двумерных задач механики жидкости
с помощью методов конечных элементов, которые применяются
совместно с методом наименьших квадратов или методом Галеркина,
используются либо уравнения для вихря и функции тока, либо
уравнения для исходных переменных. Число возникающих при
этом возможных разновидностей методов, связанных с
использованием различных конфигураций элементов, способов
аппроксимации функций и записи уравнений, становится чрезвычайно
велико. Поэтому изложить все такие методы, появляющиеся в
литературе, весьма затруднительно. Наиболее подробно они
рассмотрены в обзорных работах Бейкера и Солимена (1979), Бейкера
(1979), Жиро и Равьяра (1979), Томассета (1981), а также Чанга
(1978). Мы же, не вдаваясь в излишние подробности, попытаемся
изложить лишь самые существенные моменты, имеющие
наиболее важное значение для практического применения метода
конечных элементов. При исследовании этого метода выявляется
целый ряд важных фактов. Первый из них заключается в том,
что в отношении эффективности и простоты применения метода
конечных элементов уравнения с физическими переменными имеют
несомненное преимущество перед системой уравнений для вихря
215

и функции тока. В случае течений идеальной жидкости это
очевидно, поскольку уравнения с физическими переменными
содержат производные более низкого порядка, нежели уравнения для
функции тока. Для вязкой жидкости этот вывод также
справедлив, поскольку постановка граничных условий для вихря скорости
вызывает определенные трудности. В частности, Хаттон (1975)
обнаружил, что для обеспечения сходимости итерационного
процесса требуется неизмеримо больше времени, чем для решения
задачи с переменными давление—скорость. Хаттон рекомендовал
в качестве искомых переменных брать давление и скорость, а не
вихрь и функцию тока.
Следует ожидать, что при использовании метода конечных
элементов возникнут проблемы, аналогичные тем, которые связаны
с применением метода конечных разностей. Так, например,
естественно предполагать, что стандартные аппроксимации с
применением конечных элементов приведут к таким же результатам,
что и конечно-разностные схемы с центральными разностями.
Поэтому, как можно ожидать, применение метода конечных
элементов к задачам расчета течений идеальной или сильно
инерционной жидкости вызовет определенные трудности. В большинстве
опубликованных работ по применению этого метода уравнения
Навье—Стокса решаются для чисел Рейнольдса, не
превышающих 1000. Для того чтобы выйти за пределы этих значений,
необходимо использовать либо элементы чрезвычайно малых
размеров, либо аппроксимационную схему с конечными элементами,
направленную против потока. Имеются и другие аспекты этой
проблемы: 1) в применении к нелинейным задачам метод
наименьших квадратов оказывается более устойчивым, чем метод
Галеркина (Флетчер, 1976); 2) прямоугольные элементы
обеспечивают более эффективное решение задачи нежели треугольные
элементы, независимо от того, используются ли при этом
линейные или квадратичные базисные функции; 3) при применении
квадратичной базисной функции для прямоугольных элементов
семейства Серендипити ошибка в два раза меньше, чем в случае
использования треугольных элементов с линейной базисной
функцией. Для тех, кто незнаком с терминологией, относящейся
к квадратичной аппроксимации Серендипити, укажем, что в
данном случае речь идет просто о прямоугольном элементе с восемью
узлами (рис. 7.1)*. Базисные функции для угловых точек имеют
вид
* Изопараметрические элементы с квадратичной аппроксимацией, подобные
изображенному на этом рисунке, могут быть трансформированы в
криволинейные четырехугольные элементы с тем, чтобы можно было решать задачи для
области произвольной формы.
216

а для узлов, расположенных в серединах сторон, записываются
следующим образом:
Ni = -ö-(l-l*)(l+m) при |£ = 0,
(7.2)
N,=
<=-2-(l+^)(l-ri2) при т|, = 0.
(7.3)
Отметим, что величины g* и гц принимают значения (—1, 0, 1)
в зависимости от того, где расположена узловая точка. Кроме
того, о чем уже было сказано выше, Флетчер обнаружил, что, не
снижая точности результатов, можно почти в 10 раз уменьшить
затраты машинного времени, если использовать более грубые
Рис. 7.1. Система нормализованных
координат, используемых в методе конечных %-~1
элементов. tl-'f
квадратурные формулы при расчетах интегралов, содержащих
базисные функции, например J J N.Njdxdy.
Еще одно обстоятельство, на которое следует обратить
внимание при использовании метода конечных элементов, заключается
в том, ^что для обеспечения устойчивости решения задачи расчета
течений идеальной жидкости можно ввести искусственную
вязкость в какой-либо форме. Для этого можно использовать
односторонние разностные аппроксимации. Однако Грешо и Ли (1980)
показали, что для сохранения точности решения такой подход
следует применять с крайней осторожностью. Кроме того, во
многих случаях может оказаться, что целесообразнее использовать
нестационарные уравнения и искать решение для стационарного
состояния, нежели пытаться применять какой-либо итерационный
метод или метод релаксации для решения системы
алгебраических уравнений, получаемых из уравнений для стационарной
задачи. Флетчер (1977) отметил, что при решении уравнений
движения идеальной жидкости с помощью метода конечных
элементов следует применять метод наименьших квадратов, а не метод
Галеркина, с тем, чтобы избежать неустойчивости решения
алгебраических уравнений с помощью итерационных методов.
217

На основании изучения работ, посвященных методу конечных
элементов, можно сделать вывод, что наиболее эффективный
с практической точки зрения способ получения решения состоит
в следующем:
использовании уравнений для физических переменных;
применении метода последовательной релаксации для решения
этих уравнений;
использовании квадратичных базисных функций;
использовании прямоугольных или четырехугольных
элементов;
применении, где это возможно, более простых методов
численного интегрирования.
Перечисленные правила отнюдь не следует рассматривать как
непреложный закон — они предлагаются читателю лишь в
качестве практического руководства. Область математики, о которой
здесь говорится, быстро развивается, появляются новые
результаты, которые могут привести к пересмотру этих рекомендаций.
При решении задач механики несжимаемой жидкости
применяются как способ наименьших квадратов, так и метод Галеркина.
Существуют различные варианты использования этих методов
для определения давления. Одни пытаются обойти эту проблему,
решая задачу для переменных функция тока—вихрь, другие
используют метод введения функции штрафа, рассмотренный выше
(см. п. 6.3.4). Как показывают исследования, выполненные в
последние годы Грешо и др. (1979), Берковье и Пиронно (1979),
Гловински и Пиронно (1979), если в уравнения, используемые
в методе Галеркина, входит давление, наилучшие результаты
получаются в том случае, когда порядок величины базисной
функции для давления на единицу меньше порядка величины базисной
функции для скорости, причем первая из этих функций
используется в качестве весовой функции для уравнения
непрерывности, а вторая — в качестве весовой функции для уравнений
движения.
7.1. Метод Галеркина
Если учесть все, что было сказано выше о конечно-элементной
схеме Галеркина, мы должны начать с представления искомых
функций в виде рядов
N
a=Z Ui(t)Fi(x, у), (7.1.1а)
i = \
N
v=Z Vi{t)Fi{x9 у), (7.1.16)
i = l
N
P=S Pi(t)Oi(x9 y). (7.1.1b)
t = i
218

Затем эти разложения подставляются в соотношения,
используемые в схеме Галеркина для исходных переменных и
записываемые в следующем виде:
+^\Frfudxdy, (7.1.2)
+ -jr\F1y*vdxdy, (7.1.3)
|(-£+4)°'^-°- (?л-4)
Применяя формулу Грина к интегралам, стоящим в правых
частях (7.1.2) и (7.1.3), и подставляя разложения для и, v и р,
получим систему конечно-элементных уравнений
А>> / 4г + &'- / + С'. /) щ + Di> iVi + Ki> № = S F*î* ds> <7'l 5)
г
Д., у -^f- + Д. ,и, + (Bi, у + С. у) vt + Lit ip\ = J F,f y ds, (7.1.6)
/C./^ + I/./l^O, (7.1.7)
Л/, у = \ FtFj dx dy,
B. .-\J-(2^L^±+dF' dFi)dxdy,
a Re V dx dx ^ dy dy ) y
Ci. / = Z ("* \ FkFi -^rdxdy + vk\ FkFi -^- dx dy\,
С \ dF ; я/7.
Ki.i = l^Gidxdy, fx=nx(-p + ^r^L-) +
. 1 (du , Jo\
+ л» Re V dy + ox ) •
_L_ 1 / sfa . rfp \
-1" n*~RT v ^ + <** ;•
219
где

Эти уравнения представляют собой обычные уравнения
конечно-элементной схемы с применением метода Галеркина. Их
решение может быть получено, например, с помощью метода
предиктор—корректор. Благодаря уравнению неразрывности схема,
соответствующая предиктору, может быть явной по времени, однако
корректор должен быть записан в виде неявной схемы. Главная
трудность заключается в решении системы уравнений, отвечающей
неявной части схемы. Грешо и др. (1979) решали эту систему
уравнений для задачи об обтекании цилиндра при числе Рей-
нольдса, равном ПО, используя в качестве предиктора схему
Адамса—Бэшфорта
/ + '_/ + ^_[(2+^7.)Ä--_^-Ä-'], (7.1.8)
а в качестве корректора — модифицированную схему Эйлера
у =у +Мп -4} , (7.1.9)
где под у подразумевается ut либо и,-, а в h входят члены без
производных. Эти соотношения применялись к уравнениям
(7.1.5) — (7.1.6). На этапе коррекции указанные уравнения
решались совместно с уравнением неразрывности путем одношаговой
итерации по Ньютону для нахождения результирующих значений
uV-+\ v71*1 и р™.+1. Результаты расчета функции тока показаны на
рис. 7.1.1. Для этих расчетов использовалась представленная на
рис. 7.1.2 сетка с девятиузловым элементом для биквадратичной
аппроксимации скорости и четырехузловым элементом для
билинейной аппроксимации давления. Сетка включала 196 элементов
и 850 узлов. На рис. 7.1.2 представлены также граничные условия
задачи. Величины fn и /т определяются по формулам *
t — п 1 2 дип
Тп— р+ Re дп •
f _ 1 ( дип . àux \
Гх~ Re V дх "1" дп )*
где индексами п и т обозначены составляющие соответствующих
величин по нормали и касательной. Приведенные результаты
дают общее представление о методе Галеркина. С помощью этого
метода были исследованы также течения в полости и обтекание
уступов и цилиндров при числах Рейнольдса, близких к 100. Мы
не будем останавливаться на результатах этих исследований,
поскольку пока еще нельзя указать на сколько-нибудь существенные
достижения или расширение вычислительных возможностей в этой
области. Однако существует другое направление развития метода
* Здесь индекс п использован для обозначения составляющей по нормали
в соответствии с обозначениями, принятыми в работе Грешо.
220

a)
Рис. 7.1.1. Линии тока для вихревого потока,
обтекающего цилиндр, при Re—110. (Любезно предоставлен
Грешо.)
a) /=532i00; б) /=533,55; в) /=535,10 и г) /=536,65.
221

конечных элементов, в котором достигнуты заметные успехи. Речь
идет о применении в конечно-элементных схемах метода
наименьших квадратов. Этот метод сейчас интенсивно развивается, однако
ввиду его сложности мы рассмотрим его очень кратко.
Ф
Ф
iL-U v-0
Р~тт
»
1 1 JJ
щ
f~f~
г
_i Li l_
12
16
С Л>Т
"[ \Л/ 1 ♦—•—f
I- \^ \ * • А
H Л -M i—•—4
У
в
6
20 X
Рис. 7.1.2. Сетка и граничные
условия, примененные Грешо
и др. для расчета обтекания
цилиндра (a), a также сетка
вблизи цилиндра и
распределение узлов в элементе (б).
(Любезно предоставлен Грешо.)
7.2. Метод наименьших квадратов
Схема конечных элементов с применением метода наименьших
квадратов получила развитие в работах группы французских
ученых: Гловински и Пиронно (1979), Бристо и др., (1978, 1979,
1980). Рассмотрим систему нестационарных уравнений Навье—
Стокса
dV
dt
V2V
Re
+ (V.V)V+Vp = f„
vv = o,
V = V° при * = 0,
V = g на Г,
где Г — граница области Q. Решение этих уравнений определяется
с помощью схемы чередующихся направлений по начальному рас-
222

пределению V°. Для /г^О по значениям V71 последовательно
находятся (Vn+,/2, pn+l/2) и Vn+1 по двухшаговой схеме:
2vn + v,_vn_^_vV+l/2 + v/+1/2 =
= |» + ■/,_ (г . v)у" + (1-е> V2V",
V- V" + ,/2 = 0 внутри Q,
v» + v, = g» + v, на г,
и затем
= f" + 1 + -fe-V2Vn + ,/2-VP" + ,/2 внутри Q,
V" + 1=g" + 1 на Г.
Оптимальное значение 0 равно 72- На первом шаге задача Стокса
решается с помощью метода искусственной сжимаемости. На
втором шаге для того, чтобы найти решение нелинейных уравнений,
с помощью метода наименьших квадратов строится нелинейная
функция полезности для уравнения более общего вида:
aV-ßV2V + (V- V)V = f внутри Q,
V = g на Г
при а, ß>0, a затем используется метод сопряженных градиентов
с масштабированием для минимизации функции полезности.
Такой способ реализации метода конечных элементов изложен в
работах Гловински (1984) и Гловински и др. (1981). Для того чтобы
получить решение уравнений Навье—Стокса с помощью этой
процедуры, необходимо многократно решать задачу Дирихле. Более
подробные сведения можно найти в работах, указанных в списке
литературы, однако перед тем как обратиться к этим работам,
следует детальнее познакомиться с методом сопряженных
градиентов, методом матричной факторизации Холески и сведениями
о пространствах Соболева и Гильберта.
Представляет несомненный интерес применение способа
наименьших квадратов в сочетании с методом сопряженных
градиентов к задачам, решение которых уже демонстрировалось ранее.
Приведем некоторые результаты расчетов, выполненных Гловински
и Перио. Первый результат касается расчета течения жидкости
над уступом (рис. 7.2.1 а). Расчетная сетка включала 619 узлов
и 1109 элементов. Отметим, что изображенная на рисунке сетка
обрезана справа, хотя в действительности расчеты велись для
сетки, продолженной более чем на 100 таких прямоугольников.
223

Числа Рейнольдса были приняты равными Re=100 и Re =191.
На входе в рассматриваемую область задавалось течение Пуа-
зейля с V = 0 на стенках. Использовались линейные базисные
функции.
Для получения в конечном счете стационарного решения
использовалась нестационарная схема* с Д/ = 0,4. Типичное распре-
а)
е)
Рис. 7.2.1. Сетка для расчета потока над уступом (а), распределение линий
тока при Re=100 (б) и Re=191 (в). (Любезно предоставлен Гловински
и Перио.)
деление линий тока показано на рис. 7.2.1 бив. Полученные
результаты были сопоставлены с расчетами, выполненными Хат-
тоном (1975) независимо от этих исследований для уравнений
с переменными функцией тока и вихрем скорости. Оказалось,
что эти результаты хорошо согласуются между собой. Более
интересный результат получен при решении задачи о потоке,
натекающем под некоторым углом атаки на сопло (рис. 7.2.2). Расчеты
были выполнены на сетке с 1458 элементами и 795 узлами при
угле атаки 40° и числе Рейнольдса, равном 250. В качестве
начальных условий задавалось течение Стокса. Для расчета на
100 шагов по времени при А/ = 0,1 требуется несколько часов
машинного времени на компьютере IBM 370/168. Рассчитанные рас-
* С применением упомянутой выше методики, но для одношаговой схемы
(Бристо и др., 1980).
224

пределения линий тока для моментов времени от / = 0 до /=100
показаны на рис. 7.2.3. Как свидетельствуют приведенные
результаты, метод позволяет получить разделение потока при
сравнительно небольших числах Рейнольдса. Однако, как указывают
авторы этой работы, при увеличении числа Рейнольдса возникают
трудности при использовании данной схемы, и поэтому они
исследовали возможность применения аппроксимаций с нецентрирован-
Рис. 7.2.2. Сетка для расчета обтекания сопла при Re = 250.
(Любезно предоставлен Гловински и Перио.)
ными разностями. Это равносильно, как показали ранее
специалисты по конечно-разностным методам, введению сглаживающего
эффекта.
Примеры, приведенные в данном параграфе, дают отчетливое
представление о том, какое развитие получил метод конечных
элементов в настоящее время. Основными задачами, как и в методе
конечных разностей, по-прежнему являются уменьшение объема
вычислений и обеспечение устойчивости решения для чисел
Рейнольдса, превышающих 1000. Так как в большинстве
практически важных задач рассматривается движение в диапазоне
больших чисел Рейнольдса, ясно, что метод конечных элементов
нуждается в дальнейшем усовершенствовании, с тем чтобы его можно
225

было применить к более широкому классу задач механики
несжимаемой жидкости.
t « 0 t -20At
t =40 At t =S0At
t=80At t =100 At
Рис. 7.2.3. Распределение линий тока в разные моменты времени при
обтекании сопла, Re=250. (Любезно предоставлен Гловински и
Перио.)
Список литературы
Baker, A. J., and Soliman, M. О. /. Comput. Phys. 32, 289—324 (1979).
Baker, A. J. Finite Element Computational Fluid Mechanics. Short Course Notes,
University of Texas, Austin, (1979).
Bercovier, M., and Pironneau O. Numer. Math. 33, 211—224 (1979).
Bristeau, M. O., et al. IRIA Report No. 294, LeChesnay, France, April (1978).
Bristeau, M. O.. et al. Comp. Meth. Appl. Mech. Eng. 17/18, 619—657 (1979).
Bristeau, M. O., et al. In: Approximation Methods for Navier-Stokes Problems.
226

Lecture Notes in Mathematics, Vol. 771, pp. 78—128, Springer-Verlag, New
York (1980).
Chung, T. J. Finite Element Methods in Fluid Dynamics. McGraw-Hill, New York
(1978).
Fletcher, C. A. J. Dept. of Defence Weapons Research Establishment Rept. WRE-
TN-1606 (WR&D), Salisbury, S. Australia, May (1976).
Fletcher, С A. J. Dept. of Defence Weapons Research Establishment Rept. WRE-
TR-1858(W), Salisbury, S. Australia, August (1977).
Giraut, V., and Ravi art, P. A. Finite Element Approximation of the Navier-Stokes
Equations. Lecture Notes in Mathematics. Vol. 749, Springer-Verlag, New York
(1979).
Glowinski, R., and Pironneau, O. Numer. Math. 33, 397—424 (1979).
Glowinski, R. Numerical Methods for Nonlinear Variational Problems. 2nd ed.
Spiinger-Verlag. New York (1984).
Glowinski, R., Mantel, В., and Periaux, J. Proceedings of Conference on
Numerical Methods in Aeronautical Fluid Dynamics. University of Reading, March
(1981).
Gresho, P. M., Lee, R. L., and Sani, R. L. Lawrense Livermore Laboratory Rept.
UCRL-83282, September (1979).
Gresho, R. M., and Lee, R. L. Don't Suppress the Wiggles They are Telling You
Something. UCRL Preprint 82979. April (1980). Comput. Fluids. 9, 223—253
(1981).
Hutton, A. G. A General Finite Element Model for Vorticity and Stream Function
Applied to a Laminar Separated Flow. Central Electric Generating Board
Rept. RD/B/N3050, August (1975).
Thomasset, F. Implementation of Finite Element Methods for Navier—Stokes
Equations, Springer-Verlag, New York (1981).
Глава 8
Спектральные методы
решения задач механики
несжимаемой жидкости
Исследования в области применения спектральных
методов к решению задач механики жидкости в основном
находятся пока еще на стадии своего развития, и умение обращаться
с этими методами до сих пор является своего рода искусством.
До настоящего времени спектральные методы использовались для
решения уравнений с физическими переменными, системы
уравнений для функции тока и вихря скорости или одного лишь
уравнения для функции тока. В каждой из этих задач
рассматривались нестационарные уравнения и главная трудность состояла
в постановке краевых условий. В некоторых случаях вопрос о
граничных условиях можно упростить, поставив на границе условия
периодичности движения, которые будут естественным образом
удовлетворены, если использовать разложения в ряд Фурье.
Однако если исследуются течения с заданными условиями на
границе рассматриваемой области, то непосредственное
использование рядов Фурье может оказаться неприемлемым.
227

В данной главе мы изложим схемы, которые успешно
применялись для решения двумерных задач механики как идеальной,
так и вязкой жидкости с помощью спектрального метода.
8.1. Идеальная жидкость
Рассмотрим сначала задачу о течении идеальной несжимаемой
жидкости, описываемом уравнениями для функции тока и вихря
скорости:
*t- L- А
+ со
W
Л -L
Dt
= 0,
v2xF=— û).
(8.1.1)
(8.1.2)
Эти уравнения были использованы
Майерсом и др. (1981) для
решения задачи о движении двух вихрей
в ограниченной области методом
разложения по полиномам Чебы-
шева. В силу симметричности
движения достаточно решать задачу
лишь для одной из половин
рассматриваемой области (рис. 8.1.1).
В начальный момент
распределение завихренности задается
Рис. 8.1.1. Вихрь в прямоугольной области.
согласно соотношению (8.1.13а). В других точках завихренность
равна нулю. Функция тока на границе также считается равной
нулю. Это избавляет от необходимости ставить граничные условия
для со. Можно искать решение задачи двумя способами, каждый
из которых основан на представлении решения в виде
лг м
со= S S an.m{t)TUx)Tm(y), (8.1.3)
n=0m=0
TV M
f=ZE bntm(t)fn(x)fm(y)1 (8.1.4)
n=0m=0
где T*n—полином Чебышева, заданный на промежутке O^x^l.
Коэффициенты а и Ъ можно определить двумя способами. Первый
заключается в том, что эти ряды непосредственно подставляются
в уравнения (8.1.1) и (8.1.2), в результате получаем
dan.m (8.1.5)
dt — 'm*
-аа.т = (Ьхх + Ьу»)п,
(8.1.6)
228

где bx* т и byy т удовлетворяют соотношениям
NM MM
д2Ч? д2
Z Z 1>п,тТ*п(х)Т*т(у)= £ £ ЬХп*тТ*п(х)Т*т(у),
дх2 - дх2 - Л __ л _л _
d2*F
-Z Z ЬУпУ тТ*п{х)Т*т{У)>
* n=0m=0
а сп, m получаются в результате разложения выражения
л diù , dco d*F do) № dû) с,, ,v /0 , «v
" ^г + 0-эг=^-"аГ~^гж=^{x' y' '> (8-1J)
в двойной ряд Чебышева
N Ni
F(x,y,t)=Z Z с». тГ; (х) Г; (у). (8.1.8)
п=0 m =0
Заметим, что сп,т можно рассчитать лишь в том случае, если
в момент времени t известны значения F. Поэтому для того, чтобы
проинтегрировать уравнение (8.1.5), следует воспользоваться
процедурой интегрирования по времени типа схемы
предиктор—корректор. Существует большое количество такого рода схем,
причем наиболее широко используются схемы, являющиеся
разновидностями метода Рунге—Кутта. Простейшая из них имеет вид
ап, m (?) = un. m (t) + — ЫСП, m (t),
аПш m{t + M) = an, m (t) + Mcnt m (t). (8.1.9)
Наряду с такими схемами успешно применялся метод Адамса—
Бэшфорта
antm(t + At) = antm(t)^^Atcnfm(t^àt)+^-àtcnttn(t). (8.1.10)
После того как значение an,m(t) найдено, необходимо решить
уравнение (8.1.6) для Ьхх и Ьуу и обеспечить выполнение
граничных условий для функции тока. Эти условия сводятся к
следующему:
N M
Z Z Ьп. тТт(У)Тп {0) = 0, 0<у<1, (8.1.11а)
п=0 т=0
IV M
Z Z ЬЯ.тГт (») Г; (1) = 0, 0<*/<1, (8.1.116)
п=0 т=0
N M
Z S bn,mT*m(0)T*n(x) = 0, 0<х<1, (8.1.11b)
n=0 т=0
N M
Z Z bntmT*m(l)T*n(x) = 0, 0<x<\. (8.1.Иг)
fi=0m=0
220

Приведенные соотношения служат для определения неизвестных
постоянных величин Ьп,т для n = N—1, N и т=М—1, га, так
как из уравнения (8.1.6) можно найти значения bn, m лишь для
n<CN— 1 и т<М— 1 (см. главу 3). Объединяя уравнение (8.1.6)
с граничными условиями (8.1.11), получим замкнутую систему
уравнений для нахождения Ьп,т. Чтобы завершить процесс
построения решения задачи, нужно указать вычислительный
алгоритм перехода от ô**m и Ь**т к Ьп,т. Такой переход
осуществляется с помощью приведенного в работе Готлиба и Орзага
(1977) соотношения, которое после преобразования к промежутку
О^х^ 1 дает
f(x)=Z bjl(x),
откуда
f= £ b'n'T'nix),
где
с»
ъпЪп* = 4 2 р(р2 — п) ьр> а0 = 2, ап = 1 для п > 0.
р=п + 2
р + п — четные
Для решения этих уравнений необходимо обратить матрицу с
элементами bn,m. Существующие эффективные численные методы
решения этой задачи достаточно подробно описаны в работе
Готлиба и Орзага (1977) или в недавно появившейся статье Хедфо-
геля и Занга (1979). Здесь же обсуждение такого рода деталей
привело бы к излишнему усложнению изложения.*
После того как получены значения bn,m, можно, используя
разложения со (х, у, t) и Ч1* (х, у, t), построить функцию F (х, у, t)f
определяемую согласно (8.1.7). Это делается следующим образом.
Используя указанные разложения, вычисляем значения F (х, у, t)
в точках xi, yi, в которых функции T*N(x) и Т*м(у) соответственно
принимают экстремальные значения. Теперь с помощью
полученных таким образом величин F (*,, yit t) можно рассчитать cn,m,
воспользовавшись разложением
N M
F(xiy yht)= Z Z cntm{t)TUxt)Tm(y,) (8.1.12)
n = 0 m=0
и применив для обращения матрицы процедуру быстрого двойного
преобразования Фурье (согласно работе Кули и Тьюки, 1965).
* Недавно было установлено, что эффективным способом решения таких
уравнений является метод сопряженных градиентов. Кроме того, оказалось,
что если при использовании этого метода привести упомянутую матрицу к
треугольному виду на первом шаге по времени, то это ускорит прямое решение
задачи для остальных временных шагов [см. Тейлор и др. (1981) и Хёрш
и др. (1982)].
230

Зная Сп,т, можно вычислить ип, m для следующего момента
времени t + At и, продолжая этот процесс шаг за шагом, найти
значения как 4я, так и со, составляющие решение задачи.
Второй способ построения решения 4х и со состоит в том, что
значения со находятся непосредственно, а не через коэффициенты
разложения. Для реализации этого метода можно по-прежнему
воспользоваться теми же разложениями для W и со. При этом
способ определения ^ может быть прежним. Для расчета же со
используется уравнение
t + м
<ù(x,y,t + U)-<ù(x,y,t) = - J (u^+v-^-)dt9 (8.1.13)
a разложения для W и со подставляются только в правую част
этого уравнения. Процедура решения состоит из следующих
этапов:
1) задать начальное распределение 4я и со;
2) вычислить и, ды/дх, v и ды/ду с использованием разложений
начальных распределений W и со по полиномам Чебышева;
3) проинтегрировать уравнение (8.1.13) по описанной ранее явной
схеме интегрирования по времени;
4) разложить со (х, у, / + Д/) в ряд по полиномам Чебышева по
данным значениям со (х/, у/, t + At)\
5) по данным значениям со (х, у, t + àt) определить 4я, как было
показано ранее *.
Оба описанных подхода были применены для решения задачи
о движении вихря. Начальное распределение завихренности
задавалось в виде
(0= г ехг (х-х.)' + а,-1,.)'-| (8ЛЛЗа)
znr0 L 2ro J
где Г = 13,76 м2/с, я'о=15 м, г/о = —70 м и г0 = 5 м. Ширина
расчетной прямоугольной области была принята равной 45 м, ее
высота составляла 90 м, шаг по времени был взят равным At =
= 0,2 min (Ajc//I t/t, /1, àyj/\vi, /|). При разложении в ряд
учитывалось по 17 гармоник для каждой из независимых переменных.
Для того чтобы в полученном решении не проявлялось заметных
осцилляции гиббсовского типа, необходимо, как правило,
фильтровать результаты либо в процессе расчетов, либо после их
завершения. При выполнении расчетов можно использовать
различные фильтры. Хедфогель и др. (1980) применяли фильтр
следующего вида:
an,m = Cln1mfnfm, (8.1.14)
* Заметим, что для получения 4я можно использовать конечно-разностный
предиктор и спектральный корректор, аналогично тому, как это сделано Орзагом
(1980) и Моршуазном (1981).
231

таи
Рис. 8.1.2. Трехмерное изображение поля завихренности при движении
вихря в прямоугольной области (вихрь движется вверх).

Рис. 8.1.3. Трехмерное изображение поля завихренности при движении
вихря в прямоугольной области (вихрь достиг верхней границы области и
начинает двигаться вниз).

Рис. 8.1.4. Поля завихренности в один и тот же момент
времени, полученные без применения фильтра (а) и с применением
фильтра (б) (вихрь движется вверх).

где fn = 1,0 ехр[—В (N2— n2)], а В — специально подобранный
параметр. Орзаг и Готлиб (1980) задавали fn в виде
Г1 для п < /г0,
fn = \ r D/ ЧП ^ (8.1.15)
(ехр[—ß (n — /г0)4] для п > n0j v '
причем м0 составляло от V2 до 7з от максимального значения м,
а 5 было выбрано таким образом, чтобы гармоники высших
порядков подавлялись в отношении от е~1 до е-10. Майерс и др.
(1981), испытав различные способы, нашли, что наилучшая
процедура расчета течения идеальной несжимаемой жидкости
заключается в том, чтобы вычислять значения ш непосредственно из
уравнений (8.1.13), а затем применять процедуру фильтрации для
несжимаемой жидкости, описанную в п. 3.6.
Результаты расчета поля завихренности при движении вихря
в прямоугольной области для четырех различных моментов
времени без применения фильтра показаны на рис. 8.1.2 и 8.1.3.
В процессе этих расчетов меньше всего трудностей встретилось
при вычислении вихря по уравнению (8.1.13). На рис. 8.1.4 для
сравнения даны результаты расчетов с применением и без
применения фильтра для одного и того же момента времени.
Было проведено также сопоставление спектральных и конечно-
разностных методов решения этой задачи. Как показали расчеты,
спектральный метод решения задачи по сравнению с
конечно-разностным методом дает выигрыш во времени счета в 10 раз, а в
некоторых случаях в 30 раз при обеспечении той же точности
решения. Аналогичное сравнение методов конечных разностей,
конечных элементов и спектрального разложения по полиномам Чебы-
шева провели Хедфогель и др. (1980) на примере решения задачи
о течении идеальной жидкости в неограниченном океане с
использованием уравнений для функции тока и вихря. Авторы этой
работы также подтвердили преимущество спектральных методов
перед методами конечных разностей и конечных элементов. Было
также обнаружено, что для сохранения устойчивости численного
решения необходимо периодически фильтровать результаты,
получаемые в процессе расчетов.
8.2. Вязкая жидкость — ламинарные и турбулентные течения
Спектральные методы расчета двумерных течений вязкой
несжимаемой жидкости находятся на стадии развития, и до сих пор
не разработаны некоторые вопросы, связанные с аппроксимацией
граничных условий. Тем не менее в области практического
применения этих методов достигнут существенный прогресс. В
настоящее время проведены исследования течения в прямоугольной
области (Моршуазн, 1981), потока в канале (Девиль и Орзаг, 1980,
Орзаг и Келс, 1980), течений над пластиной (Мёрдок и Тейлор,
1977, 1979, 1980) и течений в слое сдвига скорости (Райли и Мет-
каф, 1980, Меткаф и Райли, 1981). Расчеты этих течений
выполнены как на основе уравнений с физическими переменными, так
235

и с применением системы уравнений для функции тока и вихря
скорости. При решении трехмерных задач часто используются
периодические граничные условия по одной или нескольким
независимым переменным. Полученные решения дают хорошее
представление о принятом методе исследования течений и их
фундаментальных свойствах.
Наиболее явным преимуществом спектрального метода
являются большие скорость расчетов и разрешения моделей по
сравнению с конечно-разностными схемами и классическим
методом конечных элементов. Это преимущество побудило
исследователей попытаться предвычислить с помощью данного метода
переход от ламинарного потока к турбулентному и рассчитать
характеристики турбулентного течения. Если для изучения
движения вязкой жидкости применять спектральный метод, то
оптимальный подход состоит в использовании физических переменных,
поскольку это позволяет обойти проблемы, связанные с
постановкой граничных условий при использовании уравнений для функции
тока и вихря скорости. К тому же в уравнения с физическими
переменными входят производные более низкого порядка, чем в
уравнение для функции тока. Тем не менее и при использовании
физических переменных могут возникнуть трудности, связанные с
постановкой граничных условий.
Наиболее сложно сформулировать и обеспечить выполнение
двух видов граничных условий:
1) на границе, расположенной вниз по потоку;
2) для давления на твердой граничной поверхности.
В настоящее время нельзя указать оптимальных способов задания
краевых условий на границе, расположенной вниз по потоку, т. е.
условий вытекания жидкости для случая вязкой несжимаемой
жидкости, если решение для последующих моментов времени нам
заранее неизвестно.
В большинстве случаев вопрос о постановке краевых условий
на границе, расположенной вниз по потоку, решается следующими
способами:
1) пренебрегают диффузионными членами, из-за которых
приходится ставить краевое условие на границе, расположенной вниз
по потоку (приближение пограничного слоя), вследствие чего
эти условия вообще не ставятся;
2) вводят такое граничное условие, которое обеспечивает
вытекание жидкости через границу с минимальным возмущающим
эффектом;
3) ставят условие периодичности движения.
Наиболее просто применять спектральные методы в тех
случаях, когда используются первый и третий способы постановки
граничных условий. Второй способ является наименее
ограничительным в физическом отношении, однако вызывает наибольшие
трудности в реализации указанных методов. Этот подход, как
правило, требует постановки таких краевых условий, при которых не
нужно вводить пограничный слой на границе, через которую жид-
236

кость вытекает. Однако практически это сделать весьма трудно.
До сих пор нет четких представлений о том, как реализовать
такого рода подход, и этот вопрос остается пока предметом
дальнейших исследований (см. Хедфогель, 1979).
Определение поля давления в потоке несжимаемой жидкости
вызывает трудности из-за того, что нет достаточно отчетливых
представлений о том, каковы должны быть граничные условия
для давления. Раньше многие исследователи использовали
уравнение Пуассона для определения давления, но для этого нужно
было задавать граничные условия для давления на всей границе
рассматриваемой области течения. Однако недавно Мойн и Ким
(1980) показали, что если рассматривается двумерное течение
и используются уравнения для исходных переменных с
разложением в ряд всех искомых величин, то нет необходимости ставить
граничные условия для давления. Требуется лишь выбрать
некоторое значение давления для приведения этой переменной к
нормализованному виду. Задача, которую решают Мойн и Ким,
ставится для спектральной области, и это несколько усложняет ее
анализ в тех случаях, когда возникает необходимость ставить
непериодические граничные условия для скорости потока. Для того
чтобы такие непериодические условия надлежащим образом
удовлетворялись, можно обратиться либо к итерационной процедуре
с применением явной схемы релаксации по времени, либо к
решению системы уравнений, получающихся при использовании
неявного метода. Это дает возможность более полно использовать
идею, аналогичную той, которая была предложена Мойном и
Кимом, и применить псевдоспектральный метод для решения задачи
как в физическом пространстве, так и в спектральной области.
Такой подход и будет изложен ниже.
Особенно заманчивой выглядит идея об исключении
граничных условий для давления в тех случаях, когда поле давления
в данной задаче определяется из уравнения Пуассона. В этих
случаях для нахождения решения задачи необходимо задать на всей
границе такие краевые условия для давления, которые должны
быть строго согласованы с полем скорости. Поэтому если
скорости, на основе которых определяются краевые условия для
давления, будут рассчитываться по явной схеме интегрирования по
времени, это может привести к нарушению устойчивости решения,
если не прибегать каждый раз к сглаживающему итерационному
методу. Тем, кто собирается решать задачу с использованием
уравнения Пуассона, можно рекомендовать воспользоваться
приведенной ниже и уже испытанной на практике процедурой
решения задачи с помощью псевдоспектрального метода. Отметим,
что здесь для определения одной из составляющих скорости
используется не уравнение движения, а уравнение
неразрывности.
1. Определить и путем интегрирования уравнения движения для
и с помощью псевдоспектрального метода при заданных в
предыдущий момент времени значениях и, v и р.
237

2. Вычислить v, используя уравнение неразрывности и
спектральное разложение функции и.
3. Используя вновь полученные значения и и vy вычислить
правую часть уравнения для давления и значения градиентов
функции р на границах области.
4. Решить уравнение Пуассона для функции р.
5. Заменить прежнее значение р его новым значением и снова
вернуться к первому шагу процедуры, если новое и прежнее
значения р недостаточно хорошо совпадают одно с другим.
Такой подход может показаться слишком сложным, однако
опыт показывает, что если на первом шаге по времени может
потребоваться много итераций, то на следующих шагах по
времени для получения решения с точностью до четвертого знака
будет, как правило, достаточно двух итераций.
В отличие от изложенной выше процедуры можно попытаться
рассчитать давление непосредственно из уравнений с физическими
переменными, не прибегая к решению уравнения Пуассона, но
сделать это можно иначе, чем делали Мойн и Ким (1980).
Предлагаемый псевдоспектральный метод сводится к следующему:
1) вычислить и из уравнения движения для составляющей
скорости вдоль оси х\
2) вычислить v из уравнения неразрывности;
3) вычислить др/ду из уравнения движения для составляющей
скорости вдоль оси у с использованием неявной схемы
интегрирования по времени
v(t + M)-v (t) = -^lF(t + M) + F (Щ Af,
с ( àp х dv , dv \ . 1 / d2v . d2v \ /0 0 14
4) вычислить p путем интегрирования спектрального разложения
др/ду. При этом может возникнуть необходимость в
вычислении интеграла от др/дх при некотором значении у = уо> для
того чтобы определить значение р на одном из пределов
интеграла *.
Орзаг и Келс (1980), а также Девиль и Орзаг (1980)
применили другой подход.
Шаг I (с использованием псевдоспектрального метода)
Из уравнений движения идеальной жидкости, в которых пре-
небрегается градиентами давления, определяется поле скорости
* + д*
ul(t + M)-u(t) = - J (u-^- + v^f)dt, (6.2.2а)
t +At
* Для этого требуется, чтобы давление было задано в какой-либо одной
точке на прямой у = уо.
238

При этом обычно используется явная схема интегрирования по
времени, так что члены в скобках представлены в виде
спектральных разложений для момента времени /, а интегралы вычисляются
по формуле Адамса—Бэшфорта.
Шаг II (с использованием спектрального метода)
Производится коррекция скорости по давлению таким
образом, чтобы выполнялось уравнение неразрывности
t +ы
uu{t + M)-ul{t + M) = - J -^-Л. (8.2.3а)
t +д*
vll(t+\t)-vl(t + M) = - J М-dt, (8.2.36)
du11 , dv
На этом шаге задача решается с использованием неявной схемы
интегрирования по времени и для спектральной области,
поскольку здесь используются линейные уравнения. При этом
необходимо определить давление, которое можно получить, либо
решая совместно систему уравнений (8.2.3а) — (8.2.3в), либо
непосредственно из уравнения Пуассона, причем в последнем случае
для получения согласованных полей необходимо, чтобы на гра-
нице выполнялось условие, включающее связанные между собой
значения скорости и давления. Хотя это условие линейно, оно все
же затрудняет получение поля скорости. Девиль и Орзаг
упростили решение задачи на этом шаге, использовав граничное
условие для давления в идеальной жидкости Vp-N.
Шаг III (с использованием псевдоспектрального или
спектрального метода)
Производится коррекция поля скорости с учетом вязкости
t +At
u(t + At)-uu(t + At) = J ^rdt* (8.2.4a)
v(t + At)-üU(t + At)= j -^Tdt- (8.2.46)
Коррекция может производиться как по неявной, так и по явной
схеме, поскольку используются линейные уравнения.
Как видно из предыдущего, приведенная процедура не снимает
вопроса о граничном условии для давления, и пока остается
неясным, в чем состоит ее преимущество перед другими подходами.
При реализации описанных выше спектральных и
псевдоспектральных методов использовались упрощенные схемы
интегрирования по времени. Однако можно применить и более сложную
процедуру интегрирования по времени, используя разложение в ряд
по полиномам Чебышева как функциям времени (Моршуазн,
239

1981) или в ряд Тейлора по времени с сохранением членов более
высокого порядка (Газдаг, 1973, Рой, 1980) вида
Значения производных по времени от искомых функций
определялись путем последовательного дифференцирования уравнений
Навье—Стокса по времени, причем эту процедуру можно
организовать в виде каскадного процесса
ft = L(f),
îtt = L(ft) = L(Lf),
где L — дифференциальный оператор по пространственным
переменным, связанный с производной по времени. Отметим, что
повышение точности результатов может быть достигнуто лишь за
счет уменьшения скорости вычислений. Поэтому для ускорения
расчетов предпочтительнее использовать простые схемы
интегрирования по времени, но если необходимо повысить точность
решения, то для получения желаемых результатов следует
воспользоваться схемами интегрирования по времени, основанными на
разложении искомых функций в ряды Чебышева или Тейлора.
В исследованиях, упомянутых в начале этого параграфа,
спектральные методы применялись главным образом для изучения
процесса перехода от ламинарного потока к турбулентному.
Методика проведения каждого из этих исследований состояла в том,
что выбирался случай обтекания плоской пластины или течения
в канале определенной конфигурации и решались уравнения
ламинарного движения, записанные для физических переменных.
Затем на ламинарный поток накладывались возмущения, снова
решалась та же задача и изучалось поведение возмущений с тем,
чтобы определить, будут ли эти возмущения расти или ослабевать.
Ниже обсуждаются результаты одного из таких исследований,
выполненного Тейлором и Мёрдоком (1980).
В задаче Тейлора—Мёрдока был использован метод
псевдоспектральной коллокации, с помощью которого находилось
решение уравнений для исходных переменных скорость—давление,
записанных в форме
» = -]-ЪГ*У. (8-2.5)
\*Р =
Ш+Чг-Й-К-Ё-Я- <8">
240

Схема интегрирования этих уравнений по времени имела
следующий вид:
«(* + *)-«(0 +^fl(Q_^fl(<_A0__j^L+
V2P (?) = ~ 4 8 W + 4" * <' - Af>• <8'2-9)
причем v рассчитывалось путем численного интегрирования
уравнения (8.2.5), а уравнение Пуассона для функции р решалось
с помощью метода тензорных произведений (Мёрдок, 1977). Для
получения решения задачи каждая из искомых функций
разлагалась в ряд вида
Л' M
f=E £ fn.^fni^rtrjTUn (8.2.10)
п = 0 m =0
где
у — ехР (—У/Уе) — ехР (Утах/Уе)
1 — ехр (Утах/Уе)
Здесь r/max соответствует внешнему краю сетки, а г/е — масштаб,
выбираемый таким образом, чтобы обеспечить достаточно
надежное разрешение для описания результатов расчетов. Обычно уе
имеет порядок 0(1). Функции Т*(х) есть полиномы Чебышева
для отрезка O^x^l.
Эти разложения используются в основном как
интерполяционные формулы для более точного расчета производных и
интегралов от искомых функций. В качестве функции / берутся
величины и, v или р. Для получения соответствующих коэффициентов
разложения эти ряды записываются для (N+1) (Af-f 1) точек,
в которых известны значения и, v или р. Таким образом
получаем (А/+1)(М+1) уравнений для определения неизвестных
коэффициентов fn.m. Для решения полученной системы уравнений
можно воспользоваться каким-либо методом обращения матриц;
в этой задаче была использована процедура быстрого
преобразования Фурье, позволяющая ускорить вычисления. С помощью
указанных рядов в процессе расчетов вычислялись величины a(t),
у
g(t) и J—rr-dy. Рассматривалась задача исследования течения
у ох
о
над плоской пластинкой с границами (рис. 8.2.1). Граничные
условия определялись следующим образом. На границе,
расположенной вверх по потоку, профиль скорости задавался в виде суммы
241

решения уравнения Блазиуса и периодического по времени
решения уравнения Орра—Зоммерфельда, т. е.
и = иБЛ+ A Real [q^ (*, у) ехр (—кот)], (8.2.11)
Р = Рбл + Ро-з,
где ф — решение уравнения Орра—Зоммерфельда для волнового
числа а и частоты со. Величина т — безразмерное время,
определяемое по формуле i = tVoolU где Уоо — характерное значение
скорости, а / — расстояние от переднего края плоской пластинки до
^у^Граница
у^ вверх по"*'
yS потеку
Граница
-*~8низ по
потоку
vuvuuv\\vuuu\m\muuu\\\\\\uu\\u\uv0v\
**х,
Re
*г
Рис. 8.2.1. Течение над плоской
пластинкой.
границы расчетной области. Кроме того, используются другие
граничные условия:
dp 1 ô2u
u = v==Oi
dy
Re dx dy
при 0 = 0, (8.2.12)
u= 1, Р = Рбл при y-
OO.
(8.2.13)
При решении этой задачи на границе, расположенной вниз по
потоку, не требовалось задавать граничное условие для и, поскольку
из уравнения движения для переменной и было исключено д2и/дх2
с целью избавиться от необходимости ставить указанное условие.
В качестве граничного условия для давления на границе,
расположенной вниз по потоку, использовалось условие
д2р
дх2
-0 при х = х2.
(8.2.14)
Решение поставленной задачи находится сравнительно просто,
если не считать того, что из-за граничного условия (8.2.12) на
поверхности пластинки возникает взаимодействие между
скоростью и давлением. С целью исследовать вопрос о том, насколько
существенное значение имеет это взаимодействие, наряду с
решением задачи при граничном условии (8.2.12) на поверхности
пластинки был проведен расчет при другом граничном условии:
др
ду
0.
(8.2.15)
Указанная выше процедура была использована для расчета
двумерного течения над плоской пластинкой для чисел Рей-
нольдса, меняющихся в диапазоне 1,2- 105^Re.x^3,8-105. Возму-
242

щения вводились в передней части потока. Эти возмущения
задавались в виде отклонений от профиля скорости по Блазиусу, как
это показано на рис. 8.2.2. Скорость была представлена как
и = иБЛ + и'. (8.2.16)
Амплитуда возмущений составляла 5 % от скорости набегающего
потока. Частота начальной волны была принята равной côv/V2 =
= 56-Ю-6.
0,561 1
45*
OjSO
Рис. 8.2.2. Рассчитанная ско- Öfö
рость и как функция х при
фиксированном значении у,
Rey-784,f^ =0, tV /х=
\dyJy=o °° 0А2
= 4,0. f,2 1,Ь 1,6 1,8 10sRex
На рис. 8.2.2 представлен результат расчета скорости и как
функции х. Приведено также распределение скорости по
Блазиусу. Как видно из рисунка, амплитуда волнового возмущения
профиля скорости по Блазиусу уменьшается по мере перемещения
этой волны вниз по потоку, однако никаких сколько-нибудь
значительных ее деформаций вследствие нелинейных эффектов не
наблюдается. Результаты расчета амплитуды первой гармоники
ряда Фурье для и\ полученные с использованием уравнений для
переменных v — р, показаны на рис. 8.2.3 и 8.2.4. На этих-же
рисунках представлены результаты расчетов, выполненных для
условия др/ду = 0 на поверхности пластинки. Видно, что хотя
результаты и отличаются один от другого, но эти различия
незначительны. Вместе с тем важно отметить, что при использовании
последнего граничного условия затраты машинного времени
уменьшились почти вдвое.
В процессе выполнения данного исследования Тейлор и Мёрдок
обнаружили, что значительно проще приведенные выше
уравнения решать с учетом граничных условий в физическом
пространстве, нежели пытаться искать решение в спектральной области,
243

и использовать т-метод для того, чтобы это решение
удовлетворяло поставленным граничным условиям.
В качестве другого примера применения псевдоспектрального
метода укажем на работу Моршуазна (1981), использовавшего
комбинированный подход с учетом конечно-разностных
аппроксимаций и спектральных разложений для расчета течения в
полости и обтекания крыла двумерным потоком жидкости. Моршуазн
0,032
!
!
0Ш\
0?СОв
OMh
2,0 /0~*Кеа
Рис. 8.2.3. Амплитуда колебания
скорости и' относительно решения Блазиуса
как функция х при Rey=196 (только
для первой гармоники).
— fr*
№П
Рис. 8.2.4. Амплитуда колебания
скорости относительно решения
Блазиуса как функция параметра
пограничного слоя r\ = y(Rex/2)2 /х (только
для первой гармоники), Re.x- = 2-105.
применил этот подход к решению как уравнения для функции
тока, так и системы уравнений для скорости и давления.
Мы остановимся лишь на решении последней задачи и
приведем некоторые результаты, полученные при исследовании
течения в полости. Схема Моршуазна состоит в следующем.
Шаг I
Запишем уравнения Навье—Стокса для двумерного течения
в виде
ди
ди2
duv
dp
vf"__ _
dt
dv
дх
duv
ду
âv2
âx
dp
ât
dx
ày
ày
Re
Re
.=0,
= g2 = 0,
du | âv n
(8.2.17a)
(8.2.176)
(8.2.17b)
244

Шаг II
Введем глобальные итерационные значения для всех искомых
переменных, рассчитываемых как функции пространственных
координат и времени:
£7 = um+1-um, (8.2.18а)
V = vm + x-vm> (8.2.186)
Р = рт + 1-/Л (8.2.18b)
где m — номер глобального шага итерации, причем т+\
соответствует новому результату, полученному по значениям
соответствующей функции на шаге га. Используя эти новые переменные,
мы можем записать уравнения, описывающие течение, в виде
тг + 4r^2+2"mt/)+w{uv + Uvm + y"m) +
■ àP y2U __ ( дит , д(ит)' , d(umvm) ,
"i" дх Re ~ V dt "г дх "+" ди +
<?рот V
&t Re
gl)-g;(e",0", pm) (8.2.19а)
и аналогично этому
^-JSL = ^Um,Um,pm). (8.2.196)
<fy Re
*-TC—ftUm.O. (8.2.19b)
Шаг ///
Комбинируя уравнения (8.2.19a) и (8.2.196) с (8.2.19в), вместо
уравнения неразрывности можно получить уравнение Пуассона
для давления
^ + ^ + ^ + v2P-^--^ + -^ (8 2 20*
dt + дх + ду +V/^ Re — ах + ду ' lö-^u>
где Л и ß — выражения, получающиеся путем комбинирования
нелинейных членов уравнений (8.2.19а) и (8.2.196).
Это уравнение решается при обычных граничных условиях для
градиента давления, направленного по нормали к границе
-ЗГ = Ф*. (8.2.21)
где <çn находится из уравнений (8.2.19а) и (8.2.196).
Шаг IV
Вводятся конечно-разностные аппроксимации производных от
А, В, Р, U и V. Эти аппроксимации строятся для неравномерной
245

сетки, определяемой точками коллокации (jc£-, *//, tn)y связанными
с псевдоспектральными аппроксимациями и, v и р. Для
дискретизации производных по времени используется двухуровенная схема,
а аппроксимация производных по пространственным переменным
осуществляется с помощью центральных разностей [см.
уравнения (6.4.6) и (6.4.7)].
ШагУ
Интегрирование полученных уравнений и построение решения
задачи осуществляется по следующей схеме.
Рис. 8.2.5. Поле давления,
рассчитанное с помощью спектрального метода,
Re=100.
Изобары проведены через Др = 0,025.
(Любезно предоставлен Моршуазном.)
Рис. 8.2.6. Поле вихря, рассчитанное
с помощью спектрального метода,
Re=100. (Любезно предоставлен
Моршуазном.)
а. Вычисляются значения g*k{um, vm, рт) путем разложения
функций в ряды по полиномам Чебышева как по
пространственным переменным, так и по времени. Берутся производные от
этих рядов и затем находятся значения производных и
нелинейных членов в реальном физическом пространстве.
б. После определения значений g* левые части уравнений
аппроксимируются с помощью конечно-разностных выражений,
причем диффузионные члены и слагаемые с давлением
учитываются неявным образом по времени.
в. Находится решение для U, V и Р на каждом шаге по времени
с использованием итерационного метода, аналогичного методу,
описанному в п. 6.3.1.3.
г. Если \U\y \V\ и \Р\ недостаточно малы, из уравнений (8.2.18)
определяются ит+\ uw+1 и pm+1 с возможной релаксацией,
далее следует обращение к п. «а».
Это процедура была использована Моршуазном для расчета
течения в полости квадратного сечения (см. п. 6.6.1). При этом ис-
246

пользовались ряды с 17 членами разложения по обеим
пространственным переменным и 5 членами разложения в ряд по времени.
Конфигурация области и граничные условия приведены на
рис. 6.6.1. Число Рейнольдса было выбрано равным 100, и
решение определялось с точностью до Ю-4. Полученные распределения
давления и вихря показаны на рис. 8.2.5 и 8.2.6.
Список литературы
Cooley, J. Y\\, and Tukey, J. \V. Math. Comput. 19, 297—301 (1965).
Deville, M.f and Orszag, S. A. In: Approximation Methods for Navier—Stokes
Problems, Lecture Notes in Mathematics, Vol. 771, pp. 159—176, Springer-
Verlag, New York (1980).
Gazdag, J. /. Comput. Phys. 13, 100—113 (1973).
Gottlieb, D., and Orszag, S. A. Numerical Analysis of Spectral Methods, SIAM,
Philadelphia (1977).
Haidvogel, D. В., and Zang, T. /. Comput. Phys. 30, 167—180 (1979).
Haidvogel, D. В., Robinson, A. R., and Schulman, E. E. /. Comput. Phys. 34,
1—53 (1980).
Haidvogel, D. В /. Comput. Phys. 33, 313—324 (1979).
Hirsh, R. S., Taylor, T. D., Nadworny, M. N., and Kerr, J. L. Techniques for
efficient implementation of pseudo spectral methods and comparison with finite
difference solutions of the Navier—Stokes equations. Eighth International
Conference on Numerical Methods in Fluid Dynamics, Aachen (1982).
Metcalfe, R. W., and Riley, J. J. Proceedings of the 7th International Conference
on Numerical Methods in Fluid Dynamics. Lecture Notes in Physics, Vol. 141,
pp. 279—284, Springer-Verlag, New York (1981).
Myers, R. В., Tavlor, T. D., and Murdok, J. \V. /. Comput. Phys., 43, 180—188
(1981).
Moin, P., and Kim, J. /. Comput. Phys. 35, 381—392 (1980).
Morchcisne, Y. AIAA Paper 81—0109, January (1981).
Murdok, J. W. AIAA J. 8, 1167—1173 (1977) (PTK, 8, № 8, с 139).
Murdock, J. W., and Taylor, T. D. AGARD Symposium on Laminar Turbulent
Transition, Copenhagen, Denmark, May (1977).
Murdock, J. W. IUTAM Proceedings of the Symposium on Laminar-Turbulent
Transition, Stuttgart, Germany, September (1979).
Orszag, S. A. /. Comput. Phys. 37, 70—92 (1980)
Orszag, S. A., and Kells, L. С /. Fluid Mech. 96, 159—205 (1980).
Orszag, S. A., and Gottlieb, D. In: Approximation Methods for Navier—Stokes
Problems, Lecture Notes in Mathematics, Vol. 771, pp. 381—398. Springer-
Verlag, New York (1980).
Riley, J. J., and Metcalfe, R. W. AIAA Paper No. 80-0274, January (1980).
Roy, P. Rech. Aerosp. 1980-6, 373—385 (1980).
Taylor, T. D., and Murdock, J. \V. In: Approximation Methods for Navier—Stokes
Problems, Lecture Notes in Mathematics, Vol. 771, pp. 519—537, Springer-
Verlag, New York (1980).
Taylor, T. D., Hirsh, R. S., and Nadworny, M. N. FFT vs conjugate gradient
method for solutions of flow equations by pseudo spectral methods. Fourth
GAMM Conference on Numerical Methods in Fluid Mechanics, Paris (1981).

Глава 9
Модели и расчеты
турбулентных потоков
Уравнения Навье—Стокса служат для описания как
турбулентных, так и ламинарных течений. Однако вопрос о том,
достаточно ли полно эти уравнения описывают турбулентное
движение, нуждается еще в дополнительной проверке. Тем не менее
мы будем считать, что эти уравнения адекватны рассматриваемым
физическим процессам. Расчет турбулентных течений на основе
использования уравнений Навье—Стокса является трудной
задачей, так как, даже если мы интересуемся только осредненными
по времени величинами, следует учитывать существенно
нестационарный характер турбулентности. В результате приходится
сталкиваться с проблемой решения полных уравнений, описывающих
движения различных пространственных масштабов. Расчеты по
полным уравнениям с использованием вычислительных машин пока
находят ограниченное применение из-за большой их стоимости.
Однако в ближайшие несколько лет положение должно
существенно измениться. Ниже излагаются некоторые из работ,
выполненных в этой области в последнее время.
Вместо нахождения чисто нестационарных решений основное
развитие получил другой подход к решению прикладных задач
расчета турбулентных движений. Такой подход является отчасти
эмпирическим, однако для определенного класса задач он
оказался весьма полезным. Перейдем к изложению основ этого
метода и используемых уравнений.
9.1. Замыкание уравнений турбулентного движения
Вывод уравнений турбулентного движения, предназначенных для
решения прикладных задач, осуществляется путем осреднения по
времени пульсационных колебаний относительно среднего
движения жидкости. Соответствующие рассуждения приводятся во
многих книгах (см., например, Роди, 1980)*, посвященных
исследованию турбулентных движений, и здесь мы лишь вкратце
изложим этот вопрос.
Предположим, что все переменные характеристики течения
можно представить в виде f = f + f\ где f — среднее значение f,
a Y—отклонение от этого среднего значения. Тогда можно
показать, что
-^ = 0, (9.1.1)
dÜl ' и^=-4г4^+±^-^-. (9.1.2)
dt ^ ' дх}- — р dxi: ^ р v ' dxj
* Обстоятельное изложение предмета содержится в книге Монина А. С. и
Яглома А. М. «Статистическая гидромеханика», т. I (1965) и II (1967), М.:
Наука.-— Прим. перев.
248

где
Rij=u'iUj. (9.1.3>
Очевидно, что величину р/?,, в последнем уравнении можно
рассматривать как напряжение. Для того чтобы построить модель
турбулентного движения, более простую по сравнению с моделью,
описываемой с помощью указанных полных уравнений, необходимо
выразить это напряжение через переменные щ и, может быть,
некоторые постоянные, которые «настроены» на решение данной
задачи. Построению такого рода соотношений посвящено множество
опубликованных работ и вряд ли целесообразно излагать все
возможные подходы. Остановимся лишь на основных принципах
решения этой проблемы. Первое и главное условие заключается
в том, что на каком-то этапе построения модели необходимо
принять гипотезу относительно корреляционных моментов, которая
обеспечивала бы замыкание системы уравнений модели.
Замыкание первого уровня сводится к определению вида /?;,/. По
аналогии с ламинарным течением примем
где \xt — коэффициент турбулентной вязкости, а 6 ц— символ Кро-
некера. Подставляя это выражение в уравнение (9.1.2) при
постоянном \xtу получим
dR" =J^-v2"<. (9.1.5),
dxj
Это весьма простой подход, который сводится к добавлению
турбулентной вязкости к молекулярной. К сожалению, модель с
постоянным значением \it обычно недостаточно точна, однако с ее
помощью можно получить некоторое представление о характерных
особенностях течения. Чтобы точнее предсказать развитие
процесса, необходимо ввести более совершенную модель,
позволяющую уточнить Rij. В исследованиях используются модели
различной степени сложности от так называемых двухпараметрических
моделей до моделей с полным учетом напряжений Рейнольдса
(см. Брэдшоу и др., 1967, а также работу Смагоринского, 1963).
С практической точки зрения наиболее сложные модели не всегда
лучше двухпараметрических моделей, поскольку все они основаны
на использовании эмпирических констант и постулатов.
Вследствие этого вопрос о законности применения тех или иных моделей
замыкания к конкретным задачам расчета течений неизменно
вызывает полемику. В настоящее время в большинстве инженерных
расчетов используются параметризации типа двухпараметрических
моделей пограничного слоя, поэтому кратко рассмотрим такой вид
модели. Для ее построения необходимо ввести некоторое
соотношение, связывающее Rij с характеристиками среднего течения.
249^

Эти соотношения могут различаться по форме; одно из самых
простейших выражений выглядит следующим образом:
Р _ и ( dût , àa, \ 26,/fe
где ixt — коэффициент турбулентной вязкости, a k — кинетическая
энергия турбулентности —и'м'.. В этом определении содержится
две неизвестных величины \\t и é, и для замыкания системы
необходимы два уравнения.
Однако трудно получить уравнение для \xt, не принимая
дополнительных предположений. На основе анализа размерностей для
течений при больших числах Рейнольдса принимается (гипотеза
приближенного подобия Прандтля—Колмогорова):
где б — скорость диссипации энергии. На этом основании
вводится соотношение
-&- = сх —, (9.1.8)
где С\ может быть функцией числа Рейнольдса. Теперь, используя
некоторые предположения, логические умозаключения и
эмпирические данные, можно получить уравнения для k и г.
Эти уравнения строятся по аналогии с классическими
уравнениями переноса энергии и имеют вид
-ST-V-^-Ç-V^ + O-e, (9.1.9)
4r-V-(,3^Ve) + c4^ü-,5-f. (9.1.10)
где левые части определяют конвекцию, а правые части —
диффузию, источники и стоки. В этих уравнениях величина G
определяет генерацию кинетической энергии турбулентности и в
наиболее общей форме может быть представлена аналогично члену,
описывающему генерацию энергии в уравнении сохранения
энергии. Общий вид этого члена сложен, и мы не будем его
выписывать. Наиболее часто используются уравнения для двумерного
движения
Dt дх
где
(9.1.12)
о--^[*(4У+»(-ЗгМ-£-+-|-Л- (»•'•»>
250

Величины Си, входящие в эти уравнения, являются эмпирическими
функциями, которые в простейшем случае считаются
постоянными. В часто используемой модели Лаундера и Сполдинга (1974)
для этих безразмерных постоянных приняты следующие значения:.
с, = 0,09, с3 = 0,769, с5= 1,92.
с2=1,0, с4=1,44.
Любой исследователь может выбрать более подходящие
(приспособленные для конкретной задачи) значения этих постоянных или
даже считать их функциями зависимых или независимых
переменных. Этим определяется точность самой модели, меняющаяся,
согласно некоторым данным (Лаундер и Морзе, 1979), на 10—
50 % в зависимости от вида течения.
Численное интегрирование уравнений (&, е) -модели может
также вызвать определенные трудности в связи с тем, что
последние два члена в правой части уравнения для е имеют
особенности вблизи стенки, где кинетическая энергия турбулентности k
обращается в нуль. В результате при расчете течения вблизи
твердой стенки приходится применять специальные методы.
Дополнительные трудности при использовании моделей этого типа
возникают в связи с формулировкой начальных или граничных
условий для k и е. Способы преодоления этих трудностей зависят
от конкретного вида решаемой задачи.
Построение моделей замыкания следующего уровня
осуществляется путем выписывания уравнений непосредственно для
напряжений Рейнольдса /?;/. Сделав это, мы получим более
сложную систему уравнений, поскольку совместно с уравнениями для
средних величин приходится решать дифференциальные
уравнения для каждого /?,-/• Степень сложности этих уравнений зависит
от уровня и способа замыкания. Более подробно эта проблема
рассмотрена в работах Меллора и Ямады, 1974; Дональдсона, 1973;
Роди, 1980; Меллора и Херринга, 1971; Рейнольдса, 1976.
Выбор метода численного решения уравнений замыкания
в значительной мере зависит от характера самой задачи и поэтому
не является однозначным. Завершая обсуждение моделей
замыкания, отметим, что Роди (1980) указал на возможность
упрощения моделей замыкания путем введения в (к, е)-модель
алгебраических соотношений для корреляций скорости.
После построения модели турбулентности с замыканием для
всех Ru следующей по сложности задачей является
использование полной системы уравнений движения жидкости совместно
с гипотезой замыкания, применяемой только для движений
малых масштабов. Такой подход позволяет обойти трудности,
связанные с разрешением модели, и сэкономить машинное время
благодаря усечению полного спектра движений, определяемых
решением общей системы уравнений. В результате для всего спектра
устанавливается минимальный масштаб длины и вместо точного
описания движений, масштаб которых меньше этого минимального
251

значения, вводится модель замыкания для учета турбулентных
движений всех масштабов, не превосходящих выбранного
минимального масштаба длины. Такие модели, используемые при
моделировании крупномасштабного вихревого движения, именуют
схемами с параметризацией процессов подсеточных масштабов.
Ниже излагаются основные идеи такого подхода.
9.2. Моделирование крупномасштабных вихрей
Для моделирования движения крупномасштабных вихрей в
турбулентном течении используется полная система уравнений,
однако пытаться детально рассчитать мелкомасштабную
турбулентность было бы слишком расточительно. Поэтому для флуктуации,
размеры которых меньше выбранного масштаба усечения /,
строится модель замыкания. Для этого к уравнениям движения, в
которые входят напряжения Рейнольдса для флуктуации масштаба,
меньшего, чем /, применяется оператор фильтра. Существует
много фильтров, которые могут быть использованы для этих
целей, начиная от функций, зависящих от шага сетки, и кончая
фильтром Гаусса. Рассмотрим результаты, полученные с
использованием фильтра Гаусса в работе Ферцигера (1977). Этот фильтр
применяется для осреднения крупномасштабного поля согласно
.формуле:
f(x) = Jtf(x, x')f(x')dx'f
где H — фильтр, выбранный следующим образом:
и ( 6 Y/2 Г —6(х —X7)2 1
н=\-ж) ехР[ /» J'
I — масштаб длины и х= (х\, х2у х$).
Осредняя уравнения движения, получим
dût , àuiui _ 1 dp , I* „2,-
dt "Г dxj ~ p dxi T" p v "'*•
Полагая т = щ + и'. имеем
Щи i = UiUj + UiÜj + UiUj + UiUj.
Как отметил Ферцигер, эти средние величины нельзя упростить
так, как это делается в случае полной замкнутости. Поэтому
величина UiUj для наиболее простой модели замыкания
записывается в виде
ад^= щщ + -gj- V2ûiûi + -Ц- UiV2ûj + "24" û}si2ui + -^ Su,
где \it — коэффициент турбулентной вязкости. Во многих
использовавшихся ранее моделях принималось предположение о том, что
252

коэффициент турбулентной вязкости может быть представлен
в виде (Смагоринский, 1963)
где
ç _ 1 ( àûi , äuj }
°" — 2 V dxj + dxi )•
а с — постоянная, которая находится эмпирическим путем.
В последнее время в связи с растущим интересом к моделям
с параметризацией процессов подсеточных масштабов в ряде
работ (Кларк и др., 1979; Лесли и Кварини, 1979; Лав и Лесли,
1979) были выдвинуты новые предположения относительно
коэффициента турбулентной вязкости. Он был представлен в виде
самых различных соотношений, включавших либо энергетические
характеристики, либо вихрь скорости, и мы даже не будем
пытаться выбрать из этих подходов самый оптимальный, ибо это
очевидно является задачей будущего. Как и в задачах полного
замыкания, можно также повышать порядок моделей замыкания для
процессов подсеточных масштабов аналогично тому, как указано
выше.
Расчеты, связанные с моделированием крупномасштабных
вихрей, по степени своей сложности не будут сильно отличаться
от расчетов по моделям полного замыкания, за исключением того,
что в первом случае следует ожидать получения более
реалистичной картины изменений турбулентных флуктуации со временем.
Поэтому возникнет проблема повышения точности начальных
полей и схемы интегрирования. Кроме того, такой подход связан
с увеличением затрат машинного времени и памяти, так как
масштаб усечения / становится малым по сравнению с характерной
длиной, определяемой конфигурацией потока. Некоторые из этих
проблем будут рассмотрены на примерах, приведенных в п. 9.3
и 9.4.
9.3. Расчеты турбулентных потоков с использованием модели
замыкания
В начале данной главы уже обсуждались различные модели
турбулентности, которые могут быть использованы для расчета
течения несжимаемой жидкости. В этом параграфе мы рассмотрим
некоторые из результатов, полученных в последнее время.
Для расчетов течений с применением моделей турбулентности
используются численные методы двух типов: конечно-разностные,
обычно применяемые при расчетах с моделями замыкания, и
псевдоспектральные, используемые при моделировании
крупномасштабных вихрей и среднего движения. До сих пор метод конечных
253

элементов не использовался для расчетов турбулентных потоков.
Возможно, в будущем псевдоспектральный метод по мере его
совершенствования, как и конечно-разностные методы, займет
важное место в расчетах с использованием моделей замыкания.
Представленные ниже результаты расчетов получены с
применением конечно-разностного метода. Основные вопросы,
возникающие при решении с помощью конечно-разностных методов задач,
в которых используются модели замыкания, связаны с выбором
разностной аппроксимации для инерционных членов и с тем,
какая схема, явная или неявная, используется при расчете
диффузионных членов. Дело в том что для обеспечения устойчивости
решения при больших числах Рейнольдса в случае, когда
используется явная схема с центральными разностями, приходится
выбирать очень маленькие шаги сетки. Существует тенденция
использовать односторонние разности для аппроксимации
производных по пространству, входящих в конвективные члены. Это
эквивалентно введению искусственной вязкости для подавления
осцилляции.
Такой подход приводит к повышению устойчивости, но не
точности решения. Неявные по времени аппроксимации членов,
описывающих вязкость, при использовании которых проблема
устойчивости решения не возникает, нашли широкое применение при
исследовании турбулентных течений *.
Большинство других трудностей вычислительного характера,
возникающих при расчетах с применением моделей замыкания,
обусловлены не столько недостатками вычислительных схем,
сколько неадекватностью самой модели. Например, в двухпара-
метрической (&, е)-модели члены, в которые входит величина
e/k, могут иметь особенности в плохо описываемых моделью
областях течения, и результаты расчетов для такой задачи
интерпретировать весьма сложно. Мы не будем здесь затрагивать
такого рода проблемы, связанные с моделированием турбулентных
процессов. Полезные сведения о свойствах тех или иных моделей
можно найти в недавно опубликованных исследованиях
турбулентных течений со сдвигом скорости (Дёрст и др., 1979; Роди, 1980).
В качестве двух показательных примеров современного
развития методов расчетов течений жидкости с привлечением моделей
замыкания, приведем работу Ха Мина и Чассенга (1979), а также
исследование Гранта и др. (1980). Ха Мин и Чассенг
использовали иерархию моделей замыкания для расчета осесимметричного
турбулентного потока. Ими были проведены исследования с
применением различных моделей, начиная от двухпараметрической
(£, е)-модели, основные положения которой изложены выше,
и кончая обобщенной моделью переноса с учетом напряжений
Рейнольдса. Помимо указанной двухпараметрической модели,
авторы рассмотрели трехпараметрическую модель, описанную Лаун-
* Альтернативой такого рода схем могут быть явные, но не согласованные
схемы (см. главу 11).— Прим. перев.
254

дером и др. (1973), в которой используется следующее
соотношение:
( k -s duv \
Duv Ci д ( k — duv \ kw2 uv
~DT T~dF^r~v "^ьг-J — Cl
_(l_a)^^__.-ÇL, (9.3.1)
где U и V — средние значения составляющих скорости в
направлениях х и у, а и, и и w — флуктуации составляющих скорости
в направлениях л\ гиб соответственно. При этом предполагается,
что u2 = a\k, v2 = a2k, w2 = a^k так, что
Duv 1 д ( k2 duv \ k2 u~v
-~пг=с^-чг\г—-дГ)-с^—-т2--
_(l_a)a2fe^_.J^Lf (9.3.2)
где постоянные имеют следующие значения: ai = 1,0; a2 = 0,5; a3 =
= 0,5; Ci = 0,25; a = 0,4; ß = 2,5. Были проведены также расчеты
по модели более общего вида, предложенной Роди (1972). Эта
модель включала пять уравнений и записывалась в следующей
форме:
Dû2 1 д ( u v2 дТГ2 \ 0— dU е (— 2k \ ,
\ д ( u 1? dv~2\ е (-2 Ы \
= C2 — ihVk — ^)-c>irV)--—)-
Dv2
Dt
Dw2
Dt
0— dV 2c4 — dU 2e m 0 ,4
~2ü -d? з-и°-ЗГ—3"» (9-3-4>
-^^('»-f^-^-î-e-f)-
_-&-="-* ,9.3.5)
где постоянные имели следующие значения: с2 = 0,25; с3 = 2,75;
с4 = 0,42.
Эллиптические уравнения, входящие в эту систему, решались
с помощью метода поточечных итераций, аналогичного
релаксационной процедуре, предложенной Госменом и др. (1969) (см.
п. 6.5.4 и 6.5.5). Для этой цели можно использовать более
эффективные методы, такие, как метод полной редукции или метод
сопряженных градиентов. При решении уравнений параболиче-
255

ского типа на первых семи шагах по времени использовалась схема
центральных разностей, а затем осуществлялся переход к нецент-
рированной схеме Дюфорта—Франкела.
С помощью указанных моделей исследовались три различных
случая течения жидкости: течение над уступом, течение в рас-
Рис. 9.3.1. Средняя скорость турбулентного потока над
уступом в Т£убе. (Любезно предоставлен Ха Мином и
Чассенгом.)
— V*
7 — модель с использованием [it/ç)=L^k и e=0,09fc L, 2 —
полная (k, е)-модель; эксперименты с использованием трубки Пито
{3) и манометра (4).
7гаЛ i i L
Рис. 9.3.2. Средние скорости турбулентной струи
кругового сечения, рассчитанные по модели
напряжений Рейнольдса. (Любезно предоставлен
Ха Мином и Чассенгом.)
ширяющейся круглой трубе и движения в виде струи кругового
сечения. Для сравнения авторы провели также соответствующие
эксперименты и выполнили ряд измерений. На рис. 9.3.1 и 9.3.2
показаны результаты сравнения расчетных и экспериментальных
данных для случаев течения в трубе с расширением и течения
в виде круглой струи. При расчете течения в трубе с
расширением использовалось два вида (k, е) -моделей. Результаты
расчетов по изложенной выше модели представлены в виде сплошной
кривой, пунктирная кривая соответствует гипотезе е =0,09£3/2L,
256

где L — заданная величина. Для расчета струи использовалась пя-
типараметрическая модель. Для случая течения в трубе с
расширением было принято Re0 = 7,2-104 и ô/7?0 = 0,3*, где ô—толщина
пограничного слоя над уступом, а /?0 — радиус трубы перед
уступом. Высота уступа была также равна R0. При расчетах струи
было принято Reo = 11 • 104 и о//?0=1,0. Отметим, что в целом
рассчитанные значения хорошо согласуются с экспериментальными
данными. Эти результаты показывают достигнутый в настоящее
время уровень моделирования турбулентных процессов с
привлечением моделей замыкания. Детальная проверка методов
численного моделирования была проведена Грантом и др. (1980).
Авторы этой работы применили усовершенствованную пятипарамет-
рическую модель для изучения стратифицированных течений. Эта
модель была «приспособлена» для решения задачи о разрушении
слоя перемешивания в стратифицированной жидкости. В данном
исследовании не применялось никаких новых численных методов
и точность полученных результатов была того же порядка, что
и в работе Ха Мина и Чассенга. Как сами использованные
уравнения, так и полученные с их помощью результаты требуют
более внимательного изучения, и поэтому мы отсылаем читателя,
интересующегося этим вопросом, непосредственно к самой
работе.
Наряду с исследованиями в области применения моделей
замыкания начинают появляться работы по непосредственному
моделированию турбулентности. Однако развитие такого рода
исследований сдерживается ограниченными возможностями
вычислительной техники. Тем не менее, в этом направлении уже
достигнуты некоторые успехи, о них будет сказано ниже.
9.4. Моделирование турбулентности
Построение численного решения уравнений Навье—Стокса без
использования гипотез замыкания для больших чисел Рейнольдса
с теоретической точки зрения является решением задачи о
моделировании полностью турбулизированного течения. Для
реализации такого подхода необходимо использовать очень густую сеть
точек, что в свою очередь непомерно повышает стоимость
выполнения таких расчетов. Однако по мере снижения стоимости
вычислительных работ и повышения эффективности вычислительных
методов начинают появляются работы, в которых делаются
попытки прямого моделирования турбулентных течений. В недавно
опубликованной работе Райли и Меткафа (1980) был выполнен
расчет турбулентного потока в свободном слое со сдвигом
скорости. Ранее выполненные исследования Шумана и Паттерсона
(1978 а, Ь), Лесли и Кварини (1979), Рогалло (1977), Орзага
и др. (1969, 1972, 1974) и Паттерсона (1971) были посвящены
* Re0 есть число Рейнольдса на входе в расширяющийся участок трубы,
рассчитанное по /?о-
257

моделированию процесса затухания турбулентности при
периодических граничных условиях. В этих исследованиях для решения
уравнений задачи был использован псевдоспектральный подход.
В ряде других работ (Кларк и др., 1979; Мак-Миллан и Ферци-
гер, 1979; Дирдорф, 1970, 1972, 1974а, Ь) применялся конечно-
разностный метод с использованием моделей замыкания при
параметризации процессов подсеточных масштабов для упрощения
задачи.
Проведенные исследования показали, что псевдоспектральный
метод является наиболее перспективным для непосредственного
моделирования турбулентных
течений без использования гипотез
замыкания. Это объясняется тем, что
псевдоспектральный метод более
эффективен по сравнению с
конечно-разностным. Однако этот
оптимистический вывод основан на
результатах, полученных при
решении задач с периодическими
граничными условиями, и для того,
и}х чтобы судить о его преимуществах
при расчетах конвективных потоков
с непериодическими граничными
условиями, необходимо провести
дополнительные исследования.
w,z .
"*
"в
. и
i и
t»
*►
**
*;
s"V'y
/
и X
Рис. 9.4.1. Эпюра течения в слое сдвига
скорости.
В большинстве случаев как конечно-разностный, так и
псевдоспектральный подход применяется для решения уравнений
движения жидкости, записанных для исходных переменных, и
давление обычно определяется из уравнений Пуассона. В случае
задания периодических граничных условий задачу можно решать
с помощью как конечно-разностных, так и псевдоспектральных
методов, и при этом не возникает никаких особых проблем, если
удовлетворяются стандартные требования к величине шага по
времени и сеточному значению числа Рейнольдса. Однако задание
непериодических граничных условий сразу же приводит к
вычислительным трудностям, связанным с тем, что вблизи границ могут
возникать большие градиенты. В настоящее время опыт решения
таких задач еще невелик, и сколько-нибудь надежная информация
по этому вопросу пока отсутствует. Вследствие этого мы- не
можем представить результаты расчетов по полной модели
турбулентного пограничного слоя вблизи твердой стенки. Примером,
наиболее близким к такого рода задачам, может служить расчет
свободного слоя со сдвигом скорости, выполненный Райли и Мет-
кафом. Область течения показана на рис. 9.4.1. Задача состоит
в том, чтобы по заданному начальному полю движения рассчи-
258

тать, как будет развиваться турбулентность в последующие
моменты времени. Начальное состояние было получено путем
построения случайного поля (Орзаг и Рао, 1974) с заданными
характеристиками
й(г) _ 1 ±и ( 0,55г
Au
Y th (—!—— J (средняя скорость),
n iQ / —0,536г2 \ , Ä ч
0,18 ехр | 5 I (интенсивность турбулентности),
V гг/2 ;
Au
причем остальные составляющие скорости равны нулю. Величина
Au характеризует перепад средней скорости в слое, z
—расстояние от уровня 2 = 0 до такого уровня, где й составляет половину
скорости свободного потока. Начальное значение числа Рей-
нольдса, рассчитанное по тейлоровскому микромасштабу
турбулентности, приблизительно равно 50.
В качестве расчетной области был выбран куб с длиной ребра
L = 22,8z,/2.
Для построения решения при исследовании свободного слоя со
сдвигом скорости Райли и Меткаф использовали
псевдоспектральное разложение с 32x32x33 гармониками. Искомые переменные
разлагались в ряды Фурье по х (долгота) и у (широта). По
переменной z (высота) решение было представлено в виде рядов по
синусам и косинусам. Переход из области физических переменных
в спектральную осуществлялся с использованием процедуры
быстрого преобразования Фурье. Для нелинейных членов
использовалась центрально-разностная схема интегрирования по времени,
а для диффузионных членов — неявная схема Кранка—Николсона.
В связи с этим важно отметить, что при использовании неявной
аппроксимации диффузионных членов целесообразно выполнять
интегрирование в спектральной области. При использовании рядов
Фурье такой подход является оптимальным, так как
дифференциальные операторы второго порядка приводят к диагональным
матрицам в спектральной области, поскольку d2eikx/dx2 = —k2eikx
и, следовательно, элементы матрицы вне диагонали равны
нулю. Разложение по полиномам Чебышева в данном случае не
применяется, поскольку неявная схема интегрирования по времени
затрудняет реализацию метода. В процессе вычислений для
расчета нелинейных членов использовались разложения функций
в ряд с целью определить значения этих слагаемых в области
физических переменных. Затем полученные значения переводились
в спектральную область для последующего численного
интегрирования по времени. Важно отметить, что это интегрирование
можно было бы провести и в физической области, если
использовать для диффузионных членов схему предиктор—корректор.
Периодические граничные условия по переменным х и у
автоматически выполняются благодаря использованию рядов Фурье. Раз-
259

F T=0
M III I Ill HI II III II II
/ x/KF
ложения функций в тригонометрические ряды по переменной z
строились таким образом, чтобы обеспечить результирующий
перепад скорости поперек слоя
z/Kf сдвига. Шаги сетки по прост-
с г ранственным переменным
были выбраны одинаковыми, что
также было удобно для
построения рядов Фурье и
использования быстрого
преобразования Фурье. Прогноз на один
шаг по времени продолжался
4 с. Результаты расчета
завихренности для трех различных
моментов времени показаны
на рис. 9.4.2. Представленные
результаты даны в масштабе
времени (0,275Ди/zi/,)-1. Рай-
ли и Меткаф показали, что
эти результаты неплохо
согласуются с экспериментальными
и теоретическими данными.
Они провели также расчеты
двумерного течения с
использованием сеток с 64x64 и
128X128 узлами.
Начальные условия были
выбраны такими же, как и в
трехмерном случае, однако
в качестве возмущения в
начальное поле скорости была
введена наиболее
неустойчивая, согласно линейной
теории, гармоника с длиной
волны XF. Полученное в
результате расчетов поле вихря для
трех моментов времени
показано на рис. 1.2. Отметим, что
Рис. 9.4.2. Широтная (у)
составляющая вихря в плоскости (*, z) для
различных моментов времени Т.
(Любезно предоставлен Райли и Мет-
кафом.)
начальное возмущение растет и, закручиваясь, образует
завихрения. Не приходится говорить о том, что, несмотря на многие
недостатки такого рода моделей, они открывают весьма перспективное
направление моделирования турбулентных движений жидкости.
260

Следует ожидать, что в ближайшие годы благодаря
совершенствованию вычислительной техники и снижению стоимости
расчетов работы по прямому моделированию турбулентности получат
дальнейшее развитие и в этой области будут достигнуты
значительные успехи.
Список литературы
Bradshaw, P., Ferriss, D. H., and Atwell, N. P. /. Fluid Mech. 28, 593—616
(1967).
Bradshaw, P. Aero. J. 76, 403—418 (1972).
Clark, R. A., Ferziger, J. H., and Reynolds, W. С. /. Fluid Mech. 91, 1—16 (1979).
Daly, B. J., and Harlow, F. H. Phys. Fluid 13, 2634 (1970).
Deardorff, J. W. Workshop on Micrometeorology, pp. 271—311. American
Meteorological Society, Boston (1973).
Deardorff, J. W. /. Fluid Mech. 41, 453—480 (1970).
Deardorff, J. W. Boundary Layer Meteor. 7, 81—106 (1974a).
Deardorff, J. W. Boundary Layer Meteor. 7, 199—226 (1974b).
Deardorff, J. W. J. Attn. Sei. £9, 91—115 (1972).
Donaldson, С du P., and Rosenbaum, H. Calculation of Turbulent Shear Flows
through Closure of the Reynolds Equations by Invariant Modeling, ARAP Inc.
Rept. 127, Princeton, NJ (1-968).
Donaldson, C. du P. Workshop on Micrometeorology, pp. 313—392, American
Meteorological Society, Boston (1973).
Durst, F., Launder, B. E., Schmidt, F. W., and Whitelaw, J. H. (eds.) Turbulent
Shear Flows I. Springer-Verlag, New York (1979). (Турбулентные сдвиговые
течения. I.—M.: Машиностроение, 1982).
Ferziger, J. H. AIAA J. 15, 1261—1267 (1977). (PTK, 15, № 9, с 56).
Gosman, A. D., Pun, W. M., Runchal, A. K., Spalding, D. В., and Wolfshtein, M. Y.
Heat and Mass Transfer in Recirculating Flows, Academic Press, London
(1969). (Госмен, А. Д., Пан В. M., Ранчел A. К., Сполдинг Д. Б., Вольф-
штейн М. Численные методы исследования течений вязкой жидкости.— М.:
Мир, 1972, 323 с.)
Grant, J. R., Innis, G. E., and Shaw, W. Y. A Computational Model for Turbulent
Wake Flows in a Stratified Fluid, SAI Rept. 200-80-483-LJ, La Jolla, CA,
August (1980).
Ha Minh, H., and Chassaing, P. Turbulent Shear Flows, I, pp. 178—197, Springer-
Verlag, Berlin, Heidelberg, New York (1979).
Hanjalic, K., and Launder, B. E. /. Fluid Mech. 52, 609—638 (1972).
Harlow, F. H., and Nakayama, P. I. Phys. Fluids, 10, 2323—2332 (1967).
Jones, W. P., and Launder, B. E. Int. J. Heat and Mass. Tans. 15, 301—314
(1972).
Launder, B. E., and Spalding, D. В. Сотр. Methods Appl. Mech. Eng. 3, 269
(1974).
Launder, B. E., Reece, G. J., and Rodi, W. Progress in Development of a Reynolds
Stress Turbulence Closure, Rept. HTS/73/31. Imperial College of London.
December (1973).
Launder, B. E., Reece, G. J., and Rodi, W. J. /. Fluid Mech. 68, 537 (1975).
Launder, B. E., and Morse, A. Turbulent Shear Flows /, pp. 279—294, Springer-
Verlag, Berlin, Heidelberg, New York (1979).
Leslie, D. C, and Quarini, G. L. /. Fluid Mech. 91, 65—91 (1979).
Love, M. D., and Leslie, D. С Turbulent Shear Flows /, pp. 353—369, Springer-
Verlag, New York (1979).
Lumley, J. L., and Khajeh-Nouri, B. Proceedings of the 2nd IUGG-IUTAM Sum-
posium on Atmospheric Diffusion, Academic Press, New York (1974); Adv.
Geophys. 18, 169—192 (1974).
McMillan, O. J., and Ferziger, J. H. AIAA Paper 79-0072, New Orleans (1979).
Mellor, G. L., and Herring, H. J. A Study of Turbulent Boundary Layer Models
Part II, Sandia Corp., Rept. SC-CR-70-6125B, January (1971).
261

Mellor, G. U and Yamada, T. J. Attn. Sei. 31, 1791—1806 (1974).
Metcalfe, R. W., and Riley, J. J. In: Proceedings of the 7th International
Conference on Numerical Methods in Fluid Dynamics. Lecture Notes in Physics
No. 141, pp. 279—284, Springer-Verlag, New York (1981).
Orszag, S., and Pao, Y. J. Adv. Geophys. 18A, 225—236 (1974).
Orszag, S. A., and Patterson, G. S. In Statistical Models and Turbulence. Lecture
Notes in Physics No. 12, pp. 127—147, Springer-Verlag, Berlin, Heidelberg,
New York (1972).
Orszag, S. A. Phys. Fluids Suppl 12, 250—257 (1969).
Patterson, G. S., and Orszag, S. A. Phys. Fluids 14, 2538—2541 (1971).
Reynolds, W. С Ann. Rev. Fluid Mech. 8, 183—208 (1976).
Riley, J. J., and Metcalfe, R. W. AIAA Paper 80-0274, Pasadena (1980).
Rodi, W. The Prediction of Free Turbulent Boundary Layers by Use of a Two-
Equation Model Turbulence, PhD Thesis, University of London (1972).
Rodi, W. Turbulence Models and Their Application in Hydraulics, International
Association for Hydraulic Research, Delft (1980). (Contact W. Rodi, Univ.
of Karlsruhe, Karlsruhe, West Germany).
Rodi, W., and Spalding, D. B. Wärme und Stoff Übertrag 3, 85 (1970).
Rodi, W. On Ihe Equation Governing the Rate of Energy Dissipation Imperial
College Rept. No. TM/TN/A/14, London (1971).
Rogallo, R. S. An ILLIAC Program for the Numerical Simulation of Homogenous
Incompressible Turbulence NASA Document No. NASA TM-73, 203 (1977).
Rotta J. С Z. Phys. 129, 547—572 (1951).
Saffman, R. G. Proc. R. Soc. Lond. A 317, 417—433 (1970).
Schumann, V., and Patterson, G. S. /. Fluid Mech. 88, 711—735 (1978a).
Schumann, V., and Patterson, G. S. /. Fluid Mech. 88, 685—709 (1978b).
Smagorinski, J. Mon. Weather Rev. 91, 94—165 (1963).

Часть III
Течения сжимаемой
жидкости
Общие замечания
о расчете течений
сжимаемой жидкости
В двух последующих главах представлен расчет
течений сжимаемой жидкости, а также рассмотрены методы
расчета идеальной и вязкой жидкости с учетом ее сжимаемости.
Материал относится к обширной области вычислительной
гидродинамики; мы попытались, насколько возможно, представить основные
работы этого направления. Краткость изложения и отказ от
воспроизводства деталей могут побудить читателя обратиться к
библиографии для более полного ознакомления с предметом.
Зоны невязкого течения
Задачи о течениях сжимаемой жидкости имеют свою специфику.
Наиболее существенным отличием от случая несжимаемой
жидкости является модифицированная форма уравнения
неразрывности, включающая производные от дополнительной неизвестной
величины— плотности, что упрощает численную реализацию задачи,
допуская расчет эволюции всех искомых характеристик потока.
Наряду с этим в уравнениях возникает дополнительный
параметр— число Маха (М), характеризующее тип течения: при М<С
<1—течение дозвуковое, при М>\—сверхзвуковое. В
последнем случае расчет может быть связан с серьезными трудностями
в связи с возникновением ударных волн, сильных волн
разрежения, звуковых линий, контактных разрывов. При наличии такого
рода особенностей может возникнуть необходимость в разработке
специальных способов расчета. Для расчета ударной волны,
например, в уравнения движения, чтобы сгладить высокочастотные
возмущения, обычно вводится искусственная вязкость; звуковая
линия в стационарном потоке оказывается линией звуковых
особых точек, каждая из которых является седлом, и в этом случае
интегрирование уравнений требует применения специальных
методов (Холт, 1977); при расчете волн разрежения, а также
контактных поверхностей (скачков плотности) могут возникать
значительные осцилляции решения разностных уравнений.
Звуковая линия, являясь важным элементом структуры
течения невязкой сжимаемой жидкости, разделяет область решения на
263

дозвуковую зону, где уравнения потока имеют эллиптический
характер, и зону сверхзвукового потока, описываемого
эволюционными гиперболическими уравнениями. Для описания различных
режимов течения в некоторых случаях могут потребоваться
различные методы численной реализации для повышения
эффективности расчета.
Зоны течения вязкой жидкости
Течения сжимаемых жидкостей имеют еще одну черту,
затрудняющую их расчет. Как правило, размеры зоны, в которой
необходимо учитывать вязкость, весьма небольшие по сравнению с
размером области невязкого течения, исключение составляют потоки
газа малой плотности. Однако требования, предъявляемые к
расчету течения в этой узкой зоне, являются наиболее жесткими
и определяют степень разрешения пространственно-временной
сетки. Использование мелкой сетки во всей области оказывается
расточительным и неэффективным. Альтернативой является
отдельное рассмотрение области невязкого течения и вязкого
пограничного слоя. Такой подход, однако, неудовлетворителен при
наличии зон отрыва течения или сильного взаимодействия течения
в пограничном слое с ядром потока. В этом случае возникает
необходимость «сшивания» различных решений аналогично
сращиванию внутреннего и внешнего асимптотических разложений. Это
легко реализуется в спектральных методах, использующих
функциональные разложения перекрывающихся решений, полученных
в областях различного масштаба. Внутреннее решение описывает
течение в пограничном слое, а внешнее — потенциальный поток,
причем происходит их взаимное приспособление: внешнее
решение служит граничным условием для внутреннего, а внутреннее —
определяет граничное условие для получения внешнего решения.
Заметим, что эти условия не обязательно должны применяться
в одних и тех же точках. Подробно этот подход рассмотрен в
работе Ле Баллёра и др. (1980).
Задачи не сплошной среды
Другим трудным для моделирования классом течений является
расчет течений разреженного газа. Для описания возникающих
эффектов обычно привлекаются уравнения кинетической теории,
решение которых может быть связано с большим объемом
сложных вычислений. Здесь эти исследования не затрагиваются. Тем,
кто интересуется состоянием вопроса, рекомендуем монографию
Берда (1978).*
* См. также: Белоцерковский О. М., Яницкий В. Е. Статистический метод
«частиц в ячейках» для решения задач динамики разреженного газа.— ЖВМ
и МФ, 1975, т. 15, № 5, 6; Белоцерковский О. М., Ерофеев А. И., Яницкий В. Е.
О нестационарном методе прямого статистического моделирования течений
разреженного газа,—ЖВМ и МФ, 1980, т. 20, № 5.—Прим. перев.
264

Искусственная вязкость при расчете течений сжимаемой
жидкости
При расчете движения невязкой сжимаемой жидкости может
возникнуть необходимость в использовании некоторого механизма
демпфирования, способствующего устойчивости вычислительного
алгоритма и позволяющего выполнить расчет ударных волн. Этой
цели служит ряд приемов — от способа «коррекции потока»
(Борис, Бук, 1976) до непосредственного включения в уравнения
движения члена, описывающего искусственную вязкость в виде aV2/.
Многие методы интегрирования нестационарных уравнений
движения идеальной жидкости обладают собственной аппроксимаци-
онной вязкостью и не требуют введения дополнительного члена.
Среди подходов, реализуемых в разностных методах, способ
«коррекции потока» привлекателен тем, что вязкость вводится лишь
в тех зонах, где это необходимо; другие формы псевдовязкости
воздействуют на решение глобально. Залесак (1979) обобщил
алгоритм переноса с «коррекцией потоков» на многомерный случай.
Предложенный способ прост и заключается в том, что
псевдовязкость не включается в уравнения, где это не требуется для
устойчивости. Как указывалось в работах Бориса и Бука, этот метод
может применяться в различных формах. Затруднение состоит
в том, что не ясно, в чем состоит его оптимальная модификация
и выбор ее определяется субъективной оценкой. Очевидно, что
наилучшим образом псевдовязкость используется в случае, когда
она, в некотором смысле, минимальна.
Члены, описывающие турбулентность
Выше при расчете течений несжимаемой жидкости обсуждались
различные модели турбулентности и методы их численной
реализации. Применительно к сжимаемой жидкости такие модели
должны учитывать пульсации плотности. Это приводит к появлению
в соответствующих уравнениях дополнительных корреляционных
членов, число которых уменьшается, если используются осреднен-
ные по массе переменные (Фавр, 1965). Можно замкнуть
уравнения на различных уровнях аппроксимации либо моделировать
турбулентность непосредственно. Однако, за исключением моделей
пограничного слоя, включающих одну-две компоненты тензора
напряжений Рейнольдса, модели замыкания применительно к
несжимаемой жидкости не получили должного развития. Пока мы еще
не имеем содержательной иерархии моделей турбулентности,
одной из определяющих черт которых был бы учет пульсаций
плотности. Брэдшоу (1977) отмечает, что для чисел Маха М<5 учет
флуктуации плотности для большинства течений, по-видимому, не
существен и поэтому модели замыканий применимы для случая
турбулентных течений несжимаемой жидкости. Это утверждение
имеет общий характер, и выбор модели предоставляется
исследователю. К сожалению, можно или нельзя применять эти поло-
265

жения к инженерным задачам без пограничного слоя будет з
значительной степени определяться представлениями, относящимися
к течению несжимаемой жидкости.
Кроме обращения к моделям замыкания существует
возможность непосредственного моделирования турбулентности. В
настоящее время эти перспективные исследования еще не вышли за
рамки численного эксперимента.
Поскольку вопросы моделирования турбулентных сжимаемых
течений в основном относятся к области теории пограничного слоя
и соответствующие модели подробно описаны в монографии Че-
беки и Смита (1974), здесь мы не будем останавливаться на этих
вопросах.
Список литературы
Bird, G. A. Ann. Rev. Fluid Mech. 10, 11—31 (1978).
Boris, J. P., and Book, D. L. /. Comput. Phys. 20, 397—431 (1976).
Bradsha^, P. Ann. Rev. Fluid Mech. 9, 33—54 (1977),
Cebeci, T., and Smith, A. M. O. Analysis of Turbulent Boundary Layers,
Academic Press, New York (1974).
Favre, A. J. /. Méc. 4(3), 361—390 (1965).
Holt, M. Numerical Methods in Fluid Dnyamics, Springer-Verlag, New York
(1977).
LeBalleur, J. C, Peyret, R., and Viviand, H. Сотр. Fluids 8, 1—30 (1980).
Zalesak, S. T. J. Comput. Phys. 31, 335—362 (1979).
Глава 10
Течения невязкой
сжимаемой жидкости
Современные практические задачи аэродинамики
невязкой сжимаемой жидкости включают в себя расчеты истечения
газа из сопла ракеты, обтекания самолетов и летательных
аппаратов, расчеты взрывов при различных формах высвобождения
энергии, аэродинамические расчеты с целью оптимизации
элементов летательных конструкций. Перечень легко продолжить, однако
уже представленные задачи могут служить примерами
вычислительных методов, используемых в этой области.
Методы решения уравнений сжимаемой жидкости (историю
развития см. Тейлор, 1974) можно условно разбить на три группы.
К первой группе относятся методы интегрирования
нестационарных уравнений движения для моделирования как
нестационарных, так и установившихся течений. Их развитие способствовало
преодолению многих трудностей, связанных с расчетом ударных
волн и трансзвуковых течений. Вторую группу составляют
релаксационные методы расчета потенциальных трансзвуковых течений,
266

третью — пошаговые методы интегрирования уравнений
установившегося сверхзвукового движения. В настоящее время все эти
методы в основном относятся к конечно-разностным. Некоторые
методы используют конечно-элементную аппроксимацию (Бристо
и др., 1978; Бристо, 1977; Перио, 1975; Чен идр ., 1975; Флетчер,
1977, 1979), однако они применяются не так часто, как
разностные методы. В силу природы околозвуковых течений совсем не
очевидно, что методы конечных элементов являются
оптимальными в случае, когда течение имеет перемежающиеся дозвуковые
и сверхзвуковые зоны. При использовании этих методов трудность
расчетов течений, описываемых смешанными эллиптико-гиперболи-
ческими уравнениями, связана с необходимостью использования
единообразной центрально-разностной аппроксимации
производных. В этом случае устойчивость вычислений контролируется путем
введения псевдовязкости — подход, принятый Бристо и др. (1978),
однако для оптимизации вычислительной процедуры необходимы
еще значительные усилия. Что касается спектральных методов, то
они не нашли применения в связи с трудностями расчета ударных
волн. В главе 3 отмечалась возможность применения
псевдоспектрального метода в таких расчетах. В ближайшем будущем можно
ожидать, что спектральные методы будут применяться и при
решении задачи гидродинамики сжимаемой жидкости.
При расчете невязких течений возникают две категории
трудностей. Первая относится к случаю, когда ускоряющийся
свободный дозвуковой поток переходит в сверхзвуковой под влиянием
возникающих возмущений течения. Вторая связана с расчетом
свободного сверхзвукового течения, замедляющегося при
взаимодействии с телом. Вообще говоря, оба случая относятся к задачам
трансзвукового течения, и существенное различие между ними
определяется тем, что дозвуковое установившееся течение имеет
эллиптический характер. Решение соответствующих задач может
оказаться чувствительным к виду граничных условий, и тогда
в процессе численного интегрирования возникают трудности. Это
ограничивает область применения методов первой группы —
нестационарных разностных методов,— поскольку генерируемые при их
применении высокочастотные волны, отражаясь от границы,
усиливаются и возмущают поле течения. Необходимо учитывать
возможность появления таких эффектов при расчете на длительный
срок потоков с Моо< 1. Магнус и Иошихара (1970, 1975),
Гроссман и Моретти (1970), Мессон и Фридмен (1972) отмечали эту
особенность расчета трансзвуковых течений.
Еще одно направление исследований связано с отображением
областей сложной геометрии на простую область. Перспективность
этих методов растет, и аргументация в пользу
конечно-элементного подхода в областях со сложными очертаниями становится
менее убедительной. В приводимых ниже примерах техника
отображений играет ведущую роль при практической реализации
вычислений разностными методами, однако и применимость
спектрального подхода может сильно возрасти при использовании его
267

совместно с методами преобразования области решения. После
этих замечаний обратимся к примерам использования
упомянутых расчетных методов для случаев установившихся и
неустановившихся течений.
10.1. Применение нестационарных методов
Общая процедура решения задач движения невязкой жидкости
нестационарными методами распадается на следующие шаги.
Шаг I
Рассматриваются нелинейные нестационарные уравнения
невязкой жидкости, записываемые в следующем виде (см. главу 1):
*+-£-+-£-• <■«•'•»
при некоторых дополнительных — начальных и граничных—
условиях,
Шаг II
Если область решения имеет сложную конфигурацию, то
используется ее численное или аналитическое отображение на
некоторую правильную область, например, цилиндр,
прямоугольник или пластина. В двумерном случае это производится путем
построения потенциального решения для правильной области,
близкой к рассматриваемой. Для этого существует ряд методов:
от панельного, обсуждавшегося выше, до известного
преобразования Кристоффеля—Шварца. Весьма общая вычислительная
программа была разработана Томпсоном и др. (1974); описание
соответствующего метода можно найти в последующих публикациях
тех же авторов.
Шаг III
Осуществляется численное или аналитическое преобразование
уравнения (10.1.1) к новой координатной системе либо
дискретизация уравнения в декартовой системе координат для
интегрирования его каким-либо методом из рассмотренных в п. 11.4.2.
Шаг IV
Выбирается любой метод интегрирования уравнений
нестационарного движения невязкой жидкости при граничном условии
отсутствия потока, нормального к твердому контуру и заданным
условиям на границе внешнего потока.
Расчет по явной схеме выполняется шагами по времени
аналогично интегрированию дифференциального уравнения первого
порядка. При использовании неявной схемы исходную систему
уравнений удобно расщепить на одномерные задачи, как это
показано в п. 6.4. Процедура решения расщепленных локально
одномерных задач зависит от используемого метода. Если
неизвестные в каждом из уравнений связаны в точках i—1, /, /+1, то
можно воспользоваться методом непосредственного решения
системы алгебраических уравнений (см. главу 2). В случае когда
каждое разностное уравнение отвечает сеточному шаблону, пре-
268

восходящему трехточечный, можно воспользоваться методом
сопряженных градиентов (Кершоу, 1978); возможны и другие
подходы, однако упомянутый метод исключительно эффективен (Хо-
сла и Рубин, 1981).
В ходе вычислений возможно выделение, «подгонка» скачков,
как было предложено Рихтмайером и Мортоном (1967), а также
Моретти (1974), однако это требует дополнительного времени
счета и громоздко для сложных течений. При этом, конечно,
расчет уточняется, однако для многих инженерных целей
предпочтительнее использовать методы «размазывания» скачка путем
введения некоторой формы искусственной вязкости. Для повышения
точности можно предварительно выделить разрывы.
Прежде чем перейти к обсуждению примеров использования
методов расчета нестационарных течений, сделаем важное
замечание относительно интегрирования уравнения энергии в случае,
когда представляет интерес только установившееся течение. В
таких задачах можно предположить постоянство общей энтальпии
(что справедливо только в стационарном случае). Для гладких
течений или течений со слабыми разрывами можно пользоваться
допущением о постоянстве энтропии в форме p~pv (что
справедливо и в нестационарном случае). Оба эти допущения
способствуют стационированию уравнения энергии и приводят к
корректным в стационарном режиме решениям (Вивиан, Вейо, 1978).
При расчете внешних течений можно также воспользоваться
представлением решения в виде внутреннего и внешнего
разложения, что облегчает реализацию граничного условия и сокращает
время счета. Концепция асимптотического представления решения
может опираться как на аналитические, так и на численные
методы расчета течения в дальней области (Мурман, Коул, 1971;
Эврар, Турнемин, 1973). Полученное решение определяет
граничное условие для нелинейных уравнений в ближней области,
заменяющее условие на свободной границе. Такой подход,
позволяющий уменьшить расчетную область и сократить время счета,
использовали Холт и Мессон (1971) при изучении околозвуковых
течений методом интегральных соотношений. Наряду с краевыми
условиями следует выбрать подходящие начальные условия.
Гроссман и Моретти (1970) нашли, например, что задание начальных
условий в форме импульса нарушает устойчивость расчета
трансзвукового течения, тогда как при плавном начальном разгоне
трудностей не возникает.
10.1.1. Конечно-разностные решения
10.1.1.1. Примеры для М00<1. В п. 2.7 и 2.8 были приведены
примеры использования нестационарных методов на основе принципа
установления для расчетов при 7Иоо<1, 0. Здесь мы рассмотрим
три примера, демонстрирующих общие возможности подхода.
Первый из них относится к истечению газа из сопла (Чанг, 1980).
При расчете используется схема Мак-Кормака; интегрирование
269

нелинейных уравнений выполняется с добавлением разностного
оператора вязкости четвертого порядка до выхода решения на
стационар. Оператор, добавляемый на втором полушаге к
корректору схемы, имеет вид
Dl /= -a, [f?+2. , + f!_2t, _ 4(/?+I., + f?_,, ,) + 6f?. ,] -
~«Л/" / + 2 + f?. /-2-4(fJ, / + , + f?, ,-.)+ 6ft /], (10.1.2)
где ai, a2 — коэффициенты вязкости, принимавшиеся равными
0,01. Расчет выполнялся в криволинейной системы координат с
построением сетки методом отображения (Томпсон и др., 1974). Как
упоминалось выше, генерируемая сетка отвечает структуре линий
тока и потенциала скорости решаемой задачи. Чанг рассматривал
три области разной конфигурации (рис. 10.1.1), причем для
каждой из этих трех областей была построена своя сетка. Граничные
условия вверх по потоку определялись предварительным расчетом
потока в камере сгорания, а вниз по потоку — экстраполяцией
сверхзвукового течения. Расчеты были выполнены для потока как
чистого газа, так и газа с примесью твердых частиц. Оказалось,
что их можно использовать в технике.
Истечение газа из сопла — классический случай внутреннего
течения, а двумерное обтекание крыла — классическое внешнее
течение. В литературе содержится множество примеров
применения рассматриваемых методов для решения последней задачи;
и здесь мы не будем их перечислять. Рассмотрим только пример,
демонстрирующий результат, который можно ожидать. Пример
заимствован из отчета Магнуса (1978), использовавшего двухша-
говый метод (Томмен, 1966) для решения полной системы
уравнений Эйлера в консервативной форме с добавлением
искусственной вязкости. Расчет выполнен на неравномерной сетке,
содержащей 5000 узлов. Сетка сгущалась в стреловидной части крыла,
а в остальной зоне, составляющей 0,04 толщины хорды крыла,
была регулярной; вне зоны обтекания, примыкающей к крылу,
использовалась грубая сетка с шагом в несколько хорд.
Тангенциальные граничные условия, верхнее и нижнее давление, а также
направления потоков удовлетворялись, если в качестве предиктора
использовалось условие для простои волны, предложенное Аббе-
том (1973). Внешние границы располагались на расстоянии семи
хорд вверх и вниз по потоку и на 10,4 длины хорды по вертикали.
На этих границах задавалось распределение диполей и вихрь,
а также параметры набегающего потока. Вычисления на машине
CDC 7600 заняли около 2400 циклов, или 580 с, до выхода на
начальную стадию стационирования, установившееся состояние было
достигнуто за 2200 с счета. Очертания крыла и распределение
давления представлены на рис. 10.1.2 и 10.1.3. Отметим, что число
Маха свободного потока Моо = 0,7. Результаты сравнивались с
решением уравнений установившегося потенциального течения,
полученного Бауэром и др. (1975); оба решения не совпадают только
у подошвы ударной волны. В заключение отметим, что при
интегрировании уравнений на длительный срок необходимо обратить
270

внимание на возможность возникновения кумулятивного эффекта
малых возмущений потока, приводящего к неустойчивости,
г дюймы
2,5 г
1,5 х дюймы
ОСЬ симметрии
Выток
х=5 дюймов
Рис. 10.1.1. Конфигурация областей и сетки для
конечно-разностного интегрирования уравнений Эйлера. (Любезно
предоставлен Чангом.)
В последнем примере расчета трансзвукового нестационарного
течения при Moo^l используем допущения о постоянстве
энтальпии и энтропии для уменьшения времени процесса установления.
Влияние этих допущений на течения в различных областях с раз-
271

ными числами Маха изучалось Вивианом и Вейо (1978) (см..
также п. 11.4.2). Для случая Моо<;1 ими рассматривалось обте-
С 0,5 1,0 х/С
Рис. 10.1.2. Профиль крыла самолета NLR7301.
-2,0
-1,5
4,0
-0,5
к
\.
\
?
+ — +2
0,2
4*
0,6
0,8 х/С
Рис. 10.1.3. Распределение давления на
профиле крыла самолета NLR 7301 при ^^ = 0,7
и угле атаки а = 3° (Магнус, 1978).
/ — решение уравнений Эйлера, 2 — потенциальное
приближение Бауэра-Корна
кание полукруглого профиля толщиной 8,4 % в канале;
расстояние между центральной линией профиля и стенкой канала
составляло 2,073 длины хорды. В области, аппроксимирующей канал,
сетка имела 81x26 узлов. В качестве граничного условия вверх
272

по потоку задавалось давление для течения, параллельного
стенкам канала при М = 0,85, а вниз по потоку принималось р2/роо =
= 0,6235. На рис. 10.1.4 показаны линии тока для различных М.
Одно решение, отвечающее постоянству энтальпии, получено при
использовании установившегося значения энергии: h-\ q^ = h0\
0,85 0,8750,90 0,325 0,875
Рис. 10.1.4. Изолинии чисел Маха при обтекании
профиля в канале; Мто =0,85; ДЛТ = 0,25; е/с = 8,4 %, h/c =
= 2,073. (Любезно предоставлен Вивианом.)
а ~ решение при постоянной энтальпии, б — решение при
постоянных энтальпии и энтропии.
второе решение, отвечающее постоянству энтальпии и энтропии,
использует наряду с этим условие р/рт = const. Уравнения
движения и неразрывности записывались относительно переменных
завихренности со и угла потока 0 = arctg (v/u), причем
дб ( dv du \
dt — 0)~~ \дх ~ЩГ)-
Это уравнение следует из первоначальных допущений. Из рисунка
видно, что второе решение имеет тенденцию к осцилляции вблизи
273

скачка. Возможно, что другие формы уравнения движения
окажутся предпочтительнее и подавят этот эффект.
Таковы некоторые двумерные решения свободного потока при
Моо<1. Рассмотрим теперь примеры расчета сверхзвукового
свободного потока.
10.1.1.2. Примеры с Моо>1. Использование нестационарных
методов для расчета сверхзвуковых свободных потоков
ограничивается нестационарными течениями или стационарными — при
наличии зон дозвукового течения. Если такие зоны отсутствуют, то
следует обратиться к пошаговым методам интегрирования стацио-
У^ Рис. 10.1.5. Зубчатый профиль.
нарных уравнений, которые обсуждаются в следующем разделе.
Значительный прогресс в вычислениях был достигнут, когда
в нестационарном случае при Мто:>1 стали применяться
разностные методы. Важной в этой области явилась работа Бохачевского
и Рубина (1966). Для интегрирования уравнений Эйлера с целью
расчета обтекания затупленного тела авторы использовали схему
Лакса (1954), которая обладает большой аппроксимационной
вязкостью и здесь не приводится. Затем появились расчеты Моретти
и его сотрудников, опиравшиеся на схему Лакса—Вендрофа
(1960, 1964) и ее двухшаговую модификацию Мак-Кормака (1969).
Одновременно численные решения нестационарных задач
получил Русанов (1968, 1970), использовавший собственные методы
решения.*
Схемы Лакса—Вендрофа, Мак-Кормака и Русанова оказались
удовлетворительными для расчета обтекания тел простой
конфигурации, например шарового сектора, однако их применение
встречает трудности при расчете обтекания профилей сложной
конфигурации типа зубчатого профиля (рис. 10.1.5). Схема,
предложенная Моретти и названная А-схемой (1978, 1979, 1980),
по-видимому, вполне пригодна для расчета нестационарных и
установившихся сверхзвуковых течений. Конструкция этой схемы.
* См. также: Любимов Л. Н., Русанов В. В. Течения газа около тупых
тел.— М.: Наука, 1970.— Прим. перев.
274

как и метод Годунова, в значительной степени опирается на
физические представления. Отмечая простую причину ограниченных
возможностей наиболее часто применяющихся схем, Моретти
указывает, что присущая им единообразная аппроксимация
производных не соответствует физике распространения сигнала в
гиперболическом случае. Моретти строит схему, учитывающую
направление характеристик, определяющих аппроксимацию уравнений.
Рис. 10.1.6. Поле изобар при обтекании зубчатого
осесимметричного профиля; Af00 = 12. (Любезно
предоставлен Моретти.)
В сущности та же процедура используется и в методе Годуноза,
что обеспечивает его успешное применение.
В методе Моретти уравнения движения невязкой жидкости
записываются в нормальном виде, т. е. каждое из уравнений
дифференцируется по одному характеристическому направлению. Это
приближает их к системе обыкновенных дифференциальных
уравнений. Моретти использует метод расщепления, обобщающий
нормальную форму уравнений таким образом, что аппроксимация
производных согласовывается с направлением характеристик.
Граничные условия при этом ставятся наиболее просто, и точность
метода, как показал Аббет (1973), повышается. Метод доказал
свою применимость для расчета сверхзвукового обтекания
профилей типа профиля, изображенного на рис. 10.1.5, и др., расчет
которых мог быть выполнен раньше только по схеме Годунова.
На рис. 10.1.6 представлено поле изобар при обтекании сложного
профиля потоком при М=12; сетка, построенная в конформно
275

отображенной области, содержала 31 узел вдоль профиля и 16
узлов между фронтом скачка и поверхностью тела (Моретти, 1977).
Схема применялась также для расчета установившегося
сверхзвукового обтекания сложного профиля; соответствующие результаты
обсуждаются в п. 10.2.2.
Расчет гладких невязких течений по схеме Моретти или
апробированной схеме Мак-Кормака приводит к хорошим результатам.
Для получения установившегося решения можно заменить
нестационарное уравнение энергии стационарным уравнением,
выражающим постоянство энтальпии. Следуя такому подходу, Вивиан
и Вейо (1979) рассчитали стационарное обтекание сферы при
Моо = 3 на сетке с числом узлов 41X21 (позднее было показано,
что та же точность достигается на сетке с числом узлов 21x21).
Использовавшаяся сетка, изолинии чисел Маха и поле изобар
приведены на рис. 10.1.7.
276

Эти примеры демонстрируют эффективность нестационарных
разностных методов расчета сверхзвуковых течений. К сожалению,
реализация рассмотренных методов относится к обтеканию лишь
простых профилей. Расчет обтекания профилей произвольной
формы остается делом будущего, и для наиболее перспективных
схем типа схемы Моретти желательна дополнительная
проверка.
10.1.2. Применение методов ячеек и конечных объемов
В главе 3 рассматривались методы ячеек Годунова и Глимма,
а также методы конечных объемов. Напомним, что метод Годунова
является двухшаговым: предиктор состоит из решения задачи Ри-
мана о распаде разрыва на сторонах прямоугольной ячейки сетки,
а на корректирующем шаге неизвестные в центре ячейки
определяются потоками через границы ячейки. Метод Глимма также
опирается на идею пересчета и использует предиктор схемы
Годунова. Однако для оценки потока на границе прямоугольной
ячейки принимается решение задачи о распаде разрыва в
случайно выбранной точке основания прямоугольника;
корректирующий шаг просто повторяет процедуру предиктора уже с этими
найденными потоками, что существенно отличается от корректора
схемы Годунова. Метод зарекомендовал себя хорошо в
одномерном случае, однако для многомерных задач возможности его
оптимизации, по-видимому, остались не использованными. Ниже мы
обсудим результаты применения этих методов для расчета
установившихся и нестационарных течений.
Метод Годунова (1959) оказался одним из лучших при
решении задач движения невязкой несжимаемой жидкости со сложной
структурой ударной волны или большими градиентами. Он
неизменно приводил к успеху там, где большинство других методов,
использующих разложение решения в ряд Тейлора, оказывалось
непригодным. Успех метода объясняется двумя причинами.
Во-первых, его конструкция связана с локальной физической задачей
и опирается на локальное поведение характеристик. Во-вторых,
метод обладает достаточной схемной вязкостью для подавления
тенденции к неустойчивости в области больших градиентов
течения.
В главе 3 метод Годунова изложен применительно к решению
одномерных задач. В двумерном случае используется метод
расщепления уравнений. Область течения разбивается на ячейки, не
обязательно прямоугольные, и по локально-одномерным схемам
определяются потоки массы, импульса и энергии через границы
ячеек. Эти промежуточные значения используются затем для
аппроксимации пространственных потоков, позволяющих получить
решение уравнений невязкой жидкости на следующем временном
шаге. В основе всей процедуры лежит оригинальный метод
Годунова, однако существуют и его модификации повышенной точности
(см. Холт, 1977; Ван Леер, 1979). Однако эти модификации не
277

Эксперимент
Расчет
всегда оправдывают себя. Хороших результатов, по-видимому,
можно ожидать от сочетания модифицированной Ван Леером
схемы Годунова с методом Глимма. Такой подход успешно
опробовали Глаз и Колелла (неопубликованное сообщение, 1980) для
расчета течений с сильными скачками. Ниже мы рассмотрим
некоторые результаты расчета как нестационарных, так и
установившихся течений методами
Годунова и Глимма для случаев
Моо<1 И Моо>1.
10.1.2.1. Примеры для Моо<1.
В случае дозвуковых течений
можно выделить два класса
задач. К ним относятся
расчеты течений позади или
внутри конструкций и течений,
распространяющихся во
внешнюю среду. Примером задач
первого типа может служить
околозвуковое обтекание тела
или профиля. Рассмотрим
результаты расчета осесиммет-
ричного профиля методом
Годунова, выполненного Мессо-
ном и Фридменом (1972).
Авторы использовали
криволинейную сетку, отвечающую
очертаниям профиля;
граничные условия для свободного
/ 2
Ссебая координата x/L
Рис. 10.1.8. Распределение
поверхностного давления при
трансзвуковом обтекании оживала; М^ = 0,9
(Мессон и Фридмен, 1972).
потока получены путем решения задачи в дальней области. Один
из результатов, относящихся к обтеканию осесимметричного
цилиндра оживальной формы, приведен на рис. 10.1.8, где
рассчитанное давление сравнивается с данными эксперимента. Решение
выглядит приемлемо, однако требует длительного счета и
большого числа итераций до сходимости.*
* Расчет дозвукового и трансзвукового обтекания плоских и осесимметрич-
ных тел по схеме Годунова выполнен в ряде работ (см., например, Иванов М. Я.
К решению двумерных и пространственных задач обтекания тел околозвуковым
потоком — ЖВМ и МФ, 1975, 15, № 5; Фоиарев А. С. Расчет обтекания осесим-
метричных тел и несущих крыловых профилей трансзвуковым потоком газа.—
Уч. зап. ЦАГИ, 1973, 4, № 3; Тагиров Р. К. Расчет обтекания кормовых частей
тел вращения дозвуковым и трансзвуковым потоком.— Изв. АН СССР МЖГ,
1972, № 6.— Прим. ne рве.
278

Среди других расчетов свободных дозвуковых потоков отметим
работу Тейлора и Лина (1980) по истечению газа из ствола ружья,
а также работу Реддала (1980), относящуюся к течениям,
возникающим при запуске ракеты «Титан». В этих работах метод
Годунова применялся для решения двумерных нестационарных
уравнений. Схема задачи о взрывной волне дана на рис. 10.1.9. Здесь
по заданной скорости потока в стволе и скорости вылета пули
определяется поле скорости во внешней, прилегающей к стволу,
Воздушная Волна
Контактная
"поверхность
Диен Маха
Снаряд
F х,и
Рис. 10.1.9. Область расчета течения
при выстреле.
Е — невозмущенный свободный поток,
С или А — границы при условии v=0, D —
граница с заданием us, F — граница с
условием симметрии, В или G — границы
с условиями на концах ствола.
tMKC
103-
10*
10
Диск
я Маха
Расчет
т \ Эксперимент
_I I I 1111
10
50x/D
Рис. 10.1.10. Сравнение параметров
течения при выстреле с данными
Шмидта и Шира (1974).
области. Трудность решения задачи связана с резким
пространственным изменением давления, значения которого в соседних
ячейках сетки отличаются на два порядка. Перепады давления
возникают при распространении потока вблизи оси симметрии
и у выхода из ствола. Типичное поле течения, возникающее после
выстрела из винтовки М-16 и выброса гильзы, было показано на
рис. 1.5. Результаты, относящиеся к движению взрывной волны,
и сравнение с экспериментом даны на рис. 10.1.10.*
Расчет Реддалом течений, возникающих при запуске ракеты
«Титан III», выполнен с меньшей точностью, но интересен тем, что
демонстрирует гибкость нестационарных схем. Задача о выхлопе
* Расчет течений при взрыве осесимметричного заряда на подвижной
разностной сетке методом Годунова выполнен в работе Шуршалова Л. В.
Численное исследование задачи о взрыве цилиндрического заряда конечной длины.—
ЖВМ и МФ, 1973, т. 13, № 4; см. также: Коробейников В. П., Чушкин П. И.,
Шуршалов Л. В. О зоне наземных разрушений при воздушном взрыве крупного
метеорита.—Изв. АН СССР, МЖГ, 1974, вып. 32.— Прим перев.
279

газа из ракеты решалась методом Годунова на прямоугольной
сетке; моделируемое двумерное поле течений приведено на
рис. 1.5. Результаты служат примером применения метода для
области со сложной геометрией когда трудно проводить
измерения.
Остановимся теперь на применении метода Глимма. Он
изучался в работах Чорина (1976, 1977), Сода (1978, 1980), Колеллы
(1978) и Глаза (1979). Результаты исследований оставляют
некоторое сомнение относительно пригодности метода для расчета
двумерных течений с сильными скачками. Глаз попытался
применить метод Глимма для расчета обтекания затупленного тела
сверхзвуковым потоком и нашел, что метод не вполне отвечает
специфике задачи. Колелла отметил трудности, с которыми он
столкнулся при выделении скачков, и для их преодоления
предложил ввести в уравнения искусственную вязкость. Очевидно, что
для применения метода для решения двумерных задач
потребуются дополнительные усилия. Вместе с тем, как показал Сод
(1980), в случае слабых разрывов, таких, как в двигателях
внутреннего сгорания, этот метод пригоден.
Наряду с обсуждаемыми разностными методами в
вычислительной гидродинамике сжимаемой жидкости успешно
развивается подход на основе метода конечных объемов. Одна из схем
была предложена и опробована Лера и Сайдсом (1981) для
расчета обтекания профиля трансзвуковым потоком. В этой схеме
потоки на границах ячейки вычисляются непосредственно с
осреднением по пространственным переменным. В общих чертах метод
представлен в п. 3.7. В данном случае он используется в двухша-
говой модификации с пересчетом. Предиктор определяет потоки
через границы ячейки, а корректор — значения компонент
искомого вектора в центре ячейки (см. рис. 3.7.1). Значения
предиктора вычисляются на сторонах ячеек, сдвинутых на половину их
ширины, и таким образом граница ячейки, соответствующая
первоначальному разбиению области, проходит через центр ячейки
предиктора. Согласно п. 3.7, для аппроксимации потоков при
сдвиге вправо имеем
НпА>в> = FÏ+\, i Ьул>в> - GÏ+1, / Дхлчг, (Ю. 1.3)
—lT(Gl , + C7?+i>/+C77+ii/ + i + 0?l/ + i)A^c'. (Ю.1.4)
Напомним, что А'В' и В' С являются гранями сдвинутых ячеек;
при начальном разбиении области ячейка центрирована в точке
(i, /). Сдвинутая ячейка предиктора центрирована в (1+Ч2, /)•
Аналогично записываются потоки через границы CD' и D'A'.
Заметим, что в этих выражениях потоки в направлении /, т. е.
направлении, перпендикулярном сдвигу, осредняются по четырем
280

точкам, в отличие от нео^редняемых потоков в направлении
сдвига. Если сдвиг осуществляется в направлении /, то осредняе-
мыми будут только потоки в направлении L Потоки, найденные
на каждой из границ сдвигаемых ячеек, определяют в уравнении
движения неизвестный вектор на следующем временном шаге.
Уравнение в точке (1 + V2, /) записывается следующим образом:
~2~(Si + l, j + Si, j)fi + 42, i = -2~\Sit jfit 1 + Sf+i, jfi + \, j) —
-aM{HnA.B> + HnB>c' + Hnc.D.-\ HnD'A'\ (10.1.5)
где a — доля используемого временного шага, Si,,- — площадь
ячейки, центрированной в точке (/, /).
На корректирующем шаге потоки через границы AB и ВС
ячейки с центром в (/, /) имеют вид
иав = -?£- [(<* — 72) (FÏ+1, / + Fït j) + Fit*,, /] &Уав —
—k t(a - V«) (07+1. / + Gl ;) + ОПъ, /] &хАВ, (10.1.6)
Яве = -^ [(а - '/Ж. /+1 + П /) + FlY+42] Аувс -
—w 1(а "1/2)(G'> '+■ + G?- /) + °?.'"/?'/.] A**c. (10-1J)
где Fn.+" . = /7 (/".+?, ) и т. д. Аналогично записываются потоки
*~г /2, / *+ /2, У
через границы CD и /ЗЛ. Уравнение на шаге корректор имеет вид
Si. ///Л1 = Si, jfl, j - M [Hab + H ВС + H cd + HDA]. (10.1.8)
В вычислениях принималось a=l + y5/2, что отвечает
оптимальному значению параметра а в соответствующей одномерной
разностной схеме (см. п. 2.7.1). Заметим, что на равномерной сетке
эта схема сводится к разностной схеме (2.8.9) при всех значениях
параметров, кроме а = 7г (схема типа схемы Томмена). Лера
и Сайде (1981) выполнили расчет обтекания профиля NACA 0012
под углом атаки 1,25° и М = 0,8 на сетке 298x34 (рис. 10.1.11).
Результирующее распределение давления и изолинии чисел Маха
показаны на рис. 10.1.12, 10.1.13. На рис. 10.1.14 представлены
изолинии энтропии. Все эти результаты свидетельствуют в пользу
метода.
10.1.2.2. Примеры для Моо>1. Применение нестационарных схем
расчета сверхзвуковых свободных течений и, в частности, течений
с дозвуковыми зонами привело к значительным успехам. Одной из
знаменательных работ этого направления была работа Бохачев-
281

ского и Рубина (1966).* В рассматриваемом случае применяется
та же схема, что и для Моо<1, за исключением постановки
граничных условий. Увеличение эффективности метода достигается
выделением разрывов на границе области (Тейлор и Мессон, 1970,
Рис. 10.1.11. Профиль NACA0012 и расчетная сетка (Лера и Сайде, 1981).
1974; Мессон и др., 1969, 1971). Для расчета сверхзвуковых
течений с успехом применялись методы ячеек и собственно
разностные методы.
При моделировании сверхзвуковых течений, имеющих зоны
с дозвуковой скоростью, хорошо зарекомендовали себя методы
ячеек и наилучшим образом — метод Годунова. С помощью
последнего Тейлор и Мессон рассчитали обтекание затупленных тел
сверхзвуковым потоком. В настоящее время этот метод является
единственным, позволяющим успешно и без затруднений имитиро-
* Впервые рас-"- таких задач методом установления выполнен в работе
Годунова С. К-, Зсброднна А В , Прокопова Г. П. Разностная схема для
двумерных нестационарных задач газовой динамики и расчет обтекания с
отошедшей ударной волной. ЖВМ и МФ, 1961, т. 1, № 6.— Прим. перев.
282

вать сложные течения со скачками, контактными разрывами и
звуковыми линиями. Конкурентоспособной может оказаться л-схема
Моретти. Остановимся на применении метода; вместе с модифи-
Рис. 10.1.12. Распределение давления
на профиле NACA 0012; ^=0,8;
а=1,25°. (Любезно предоставлен
Лера и Сайдсом.)
кацией Ван Леера он представляется оптимальным для решения
сложных задач. Следует отметить, что для расчета стационарных
сверхзвуковых течений без областей дозвукового потока не
рационально пользоваться методами установления по времени,
поскольку уравнения являются в этом случае гиперболическими,
а потому могут решаться пошаговыми методами. Для
стационарного случая пока не существует схемы, аналогичной схеме Году-
283

Рис. 10.1.13. Изолинии чисел Маха; Mœ =0,8; а=1,25°.
(Любезно предоставлен Лера и Сайдсом.)
Рис. 10.1.14. Изолинии энтропии; М^ =0,8; а=1,25°. (Любезно предоставлен
Лера и Сайдсом.)

нова, хотя такое ее обобщение представляет большой интерес*
При решении задач обтекания методом Годунова используют
переменный шаг по времени, адаптирующийся к профилю тела
и форме скачка. Расчетная сетка для двумерных течений
показана на рис. 10.1.15.
Область расчета покрывается системой лучей, приблизительно
нормальных к ее границе. Каждый луч характеризуется углом 0*,
который он образует с осью симметрии. Лучи разбивают область
на равновеликие сегменты между поверхностью тела и головной
Волна,
бегущая^
влево
Состояние(N/\
рпРп"п
Рис. 10.1.15. Сетка для расчета
двумерных течений методом Годунова.
Грань
ячейки
Контактна^'
{поверхность Шщ ^егуЦМ
Ê >'£/**"
HyP7l+f,UnHr
X
Рис. 10.1.16. Разрыв на границе
ячейки в схеме Годунова.
&.
ударной волной. Расстояние вдоль луча i до точки с координатой/
обозначим /;, /. Интегрирование уравнений движения по
элементарной ячейке приводит к их разностной аппроксимации в виде
М^./И) +Д.(Я5)(/, ь + А,(Нз)и, о + С-у-),,,,, о = 0, (Ю.1.9)
где
Я =
pu (qN -
VN)
- VN) + p sin 6
pv (qN — VN) + p cos 0
LpE + P
Q =
Г pu ~|
puv
pv2
[_pv(E+p/p)J
Avf = fv + l—fv, v = i, j, t
E = e + -^-(u2 + v*)
* Аналог схемы С. К. Годунова для расчета двумерных стационарных
сверхзвуковых течений предложен в работе Иванова М. Я., Крайко А. Н.,
Михайлова Н. В. Метод сквозного счета для двумерных и пространственных
сверхзвуковых течений. I.— ЖВМ и МФ, 1372, т. 12, № 2; обобщение на
пространственный случай и развитие метода содержится в работах: Иванов М. Я-,
Крайко А. Н. Метод сквозного счета для двумерных и пространственных
сверхзвуковых течений. II.—ЖВМ и МФ, 1972, т. 12, № 3; Луцкий А. Е.,
Прокопов Г. П., Черкашин В. А. Расчет стационарных течений смешанного типа.—
ИПМ АН СССР. Препринт 87, 1980.— Прим. перев.
285

и символ </, /> означает осреднение по промежуткам (/, /+1)
и (/, /+1), т. е. /</, />=Л-1 J J fdxdy, а </, О— осреднение по
(/, /+1) и по промежутку Д*. В рассматриваемой постановке
qN — скорость, нормальная к границе, VN — скорость движения
самой границы по нормали к ней, А — площадь элементарной
ячейки, 5 —длина дуги границы (в плоском случае Q = 0).
У/Л
0,8
0,1
0,6
0,5
0,±
0,3
0,2\
Q.1
-О/ 0 0,1 0,2 Oß X/D
Рис. 10.1.17. Расчет невязкого
обтекания колоколообразного
профиля по схеме Годунова;
картина течения после 1200Д/.
Головная
ударная ~
1 волна
-Сверх-
звуковая.
область^
- / /n
/ \Звуковая
I \линия
1 Доз в у ко \
1$ая области
1 Кон m акт- £$ï
\ная поверяк^
г \иость /&
^у""* Звуковая
у линия
Тело
_| 1 1
О 0,2 0,ч- пву/р
Рис. 10.1.18. Распределение
поверхностного давления при обтекании
колоколообразного профиля.
Конечно-разностные уравнения описывают поведение
пространственно осредненных величин /</>;^в каждой ячейке области. Для
решения уравнений требуется соотнести значения граничных
потоков #<;, *>, //</, ^. к осредненным по ячейке значениям /<;, ;>.
Такое соответствие определяется аналогично схеме Годунова, т. е.
на каждой границе ячейки решается одномерная задача Римана,
позволяющая получить осредненные по границе значения
параметров течения, через которые выражаются потоки #</,*>, //</, />
Решение такой одномерной задачи в узле границы определяет все
волны, выходящие из этого узла в результате распада
произвольного разрыва (рис. 10.1.16). Параметры волн вычисляются по
соотношениям, приведенным в главе 3.
Метод использовался для расчета обтекания затупленного
колоколообразного профиля при Моо = 8,0. Результат для
установившегося состояния, достигнутого после 1200 шагов интегрирования
286

по времени, представлен на рис. 10.1.17. Заметим, что течение
выявляет ряд существенных особенностей, описание которых
связано с серьезными вычислительными трудностями. Так, поле
течения содержит, например, сверхзвуковую зону, тройную точку
и контактную поверхность. Каждая из этих структур, как изве-
у/- Внешняя головная ^f Внутренняя головная
У/ffref ударная волна \у' о^« уударная волна
3 г Хл
Начальное ' 9** 9у
положение у #И
ударной \s ••
волны / -•
X//?ref
Рис. 10.1.19. Осциллирующий поток,
рассчитанный по методу Годунова для колоколооб-
разного профиля, А/^ =5,01 ; у = 7/5.
Рис. 10.1.20. Распределение
осредненного по времени
давления в осциллирующем
течении, Afoo = 10, у = 7/5.
J — невязкое течение. 2 — вязкое
осредненное по времени течение.
f2 s/AVef
стно, осложняет расчет сверхзвуковых течений. Распределение
поверхностного давления показано на рис. 10.1.18, по которому
можно оценить воздействие вторичного скачка на поверхность
тела.
Аналогичный расчет выполнен для такого же профиля в
случае осциллирующего течения; положение скачка показано на
рис. 10.1.19. Трудность расчета заключается в том, что метод
обнаруживает тенденцию к подавлению длительных осцилляции,
представлявших реальный фактор и установленных
экспериментально (Холден, 1975). Сопоставление распределения давления
в случае невязкого течения и с учетом вязкости представлено на
287

рис. 10.1.20. Тот же подход применялся для расчета обтекания
со вдувом (Мессон и Тейлор, 1971).
Все результаты, представленные выше, получены методом
Годунова. Насколько известно, другие методы ячеек в двумерном
случае не оказались столь же приемлемыми. Метод Лера и Сайдса
(1981) представляется перспективным. Существуют также, как
отмечалось, некоторые возможности развития метода Годунова,
однако соответствующие попытки не достигли уровня,
допускающего публикацию.
10.2. Разностные методы решения стационарных уравнений
Методы расчета стационарных течений сжимаемой жидкости с
использованием непосредственно стационарных схем получили
значительное развитие в двух направлениях. К ним относятся
разностные методы расчета потенциальных течений при Моо<1 и
пошаговые схемы для Моо>1. Методы интегрирования уравнений
потенциального движения развивались в основном применительно
к задачам трансзвукового обтекания профилей, и повышение их
эффективности достигается переходом к нестационарным схемам.
Допущения об отсутствии завихренности и постоянстве энтропии
становятся менее корректными с приближением MTO к единице;
методы нахождения потенциальных решений стационарных задач,
по-видимому, наилучшим образом применимы для интервала
OJ^Afoo^ 1. Конечно-элементные и спектральные методы не
представляются пока достаточно эффективными для нахождения
решения таких задач. Обратимся к описанию методов расчета
потенциального движения.
10.2.1. Примеры для М00<\
Методы решения задач с потенциальными движениями
совершенствовались с развитием релаксационных методов интегрирования
уравнений неразрывности и энергии в виде
_djgul_ +^£L = 0 (1021)
дх ' ду v 7
(v_1)p +?2/2 = fto, (Ю.2.2)
и = дфху ю = дц/ду, (10.2.3)
где q = (u2 + v2)i/2. Присоединим к этому соотношения для изэнтро-
пического течения в безразмерной форме: p/poo = pv, р<х> =
= 1/(уМ2оо). В декартовой системе координат имеем
2 2 у— \ 2
с = со Hj— Я >
9у-] = М
2 2
288

где скорость звука с=У YP/p. В каждой из областей течения —
дозвуковой и сверхзвуковой — требуется надлежащая разностная
аппроксимация уравнения. В области дозвукового течения для
аппроксимации производных можно использовать центральные
разности, которые в области сверхзвукового течения следует
заменить направленными разностями для того, чтобы схема была
устойчива. Такая конструкция конечных разностей в зависимости от
типа уравнений была предложена Мурманом и Коулом (1971).
Подход, автоматизирующий вычисления, заключается в
использовании центральных разностей наряду с искусственной вязкостью,
переключающей тип аппроксимации при М>\.
Член с искусственной вязкостью, добавляемый обычно в
правую часть уравнения неразрывности, имеет вид
где \л — регулятор включения вязкости в зависимости от значения
числа Маха. Джеймсон (1975) предложил для \л следующее
выражение:
jj, = const • max (0, 1 — M ~2),
отключающее вязкость при М<\. Возможны и другие удобные
формы определения этого члена.
Такой способ стабилизирует расчет течения при появлении
скачков и в интервалах переключения от дозвукового режима
к сверхзвуковому. После того как тип аппроксимации выбран,
остается решить получающуюся систему алгебраических
уравнений. Здесь исследователю предоставляется две возможности:
искать непосредственно решение полной нелинейной системы
уравнений, либо попытаться упростить ее, обратившись к
классическим методам малых возмущений в теории околозвуковых
течений. Первому направлению следовали, например, Джеймсон
(1974, 1975, 1979), Кофи и Джеймсон (1977а, Ь, 1979а, Ь), Шатто
и Куломбе (1978), тогда как Мурман и Коул (1971), Боппе
и Эйдала (1980), Боппе и Стерн (1980), Болхауз (1972, 1978)
и другие (см. Шмидт, 1978) развивали альтернативное
направление. При разработке численных алгоритмов основное внимание
уделялось повышению их эффективности. В настоящее время
в этой области не существует метода, которому следовало бы
отдать предпочтение. Для повышения точности применялся метод
последовательности сеток (Саут и Джеймсон, 1973; см. также
приложение Б). Так, при решении алгебраических уравнений
используются разнообразные релаксационные методы, такие, как
последовательная релаксация, релаксация по линии, неявные методы
чередующихся направлений и др. (см. обзор Ломэкса и Стегера
(1975)). Отметим, что в этой области метод сопряженных
градиентов с факторизацией (см. приложение В), по-видимому, не
нашел применения.
289

^Для ряда задач уравнение (10.2.4) записывалось в
криволинейной системе координат, определяемой формой обтекаемого тела.
Так, координатными линиями для расчета трансзвукового потока
могут служить линии функций тока, отвечающие потенциальному
движению несжимаемой жидкости. Для общего преобразования
£ = £(*, У)> rl=rl(^ У) уравнение (10.2.4) имеет следующий вид
(Шатто, Куломбе, 1978):
+^-(ртг)]+0-°' <10-2-5>
где
D= (% дг\ . dl дц
дх дх ~*~ ду ду *
G = \др' + ~W)9 Iff + Кдх1' +~дуг)9 "Э?Г '
Добавление искусственной вязкости в случае ориентирования
координатной линии по потоку будет непосредственно
воздействовать на адвекцию. Для решения уравнения (10.2.5) используются
следующие граничные условия:
1) на поверхности тела dq>/dN = 0y N — нормаль к поверхности;
2) условие Кутты, требующее, чтобы тангенциальная скорость
у задней кромки была конечной; нормальная к линии
скольжения скорость у задней кромки должна быть непрерывной;
3) на внешней границе задается вихрь внешнего поля скорости
либо подъемная сила и скорость свободного потока.
Решения различных задач, отвечающих этим условиям,
получены для полных уравнений и в редуцированных постановках
теории малых возмущений. Их обзор выполнил Кофи (1982). Здесь
мы приведем лишь несколько примеров расчета,
демонстрирующих прогресс в этой области.
В качестве первого примера обратимся к работам Боппе
и Эйдала (1980) и Боппе и Стерна (1980), в которых дается
решение ряда задач обтекания тонкого крыла потенциальным
потоком. Расчетная область со сложными очертаниями покрывалась
сеткой, имевшей различные шаги; две сетки перекрывались таким
образом, чтобы обеспечить аппроксимацию внешнего и
внутреннего разложения решения. Вычисляемые значения функций в зоне
сопряжения на одной из сеток служили граничными условиями
290

для функций, вычисляемых на другой сетке (рис. 10.2.1). Мелкая
сетка покрывала область, прилегающую к профилю, а грубая —
внешнюю зону. Уравнение потенциального движения в виде
[l - Ml - (y + 1) Mlq>x - -J- (Y + 1) Л&ф!]ф** -
- 2M2ooWxy + [l - (Y - 1) Ml<çx] <pyy H- ф22 = 0 (10.2.6)
решалось методом последовательной релаксации по схеме
Мурмана—Коула с переключением от центральных разностей в зоне
Точки грубой ce m m
1 X i 1 M
-<
-ч
-
То
' '<
<
, /
Г т / -
чки сгущенной.
сетки
(л
^
А
^
<У
Г<>
1
3f
rv;
с—<
^
1 I
>_ Внешняя граница
jfc^^~ Внутренняя
- граница
гг4 ^^ U0J]acmb
1 ^^ перекрытия
- Граничная
поверхность
Рис. 10.2.1. Наложение сеток. (Любезно
предоставлен Бонпе.)
дозвукового течения к направленным разностям — в зоне
сверхзвукового течения. На рис. 10.2.2 представлены некоторые
результаты, относящиеся к расчету распределения давления на профиле
КС 135. Отмечается хорошее в целом совпадение с
экспериментом, за исключением нижней стороны поверхности. Боппе и Эйдала
выполнили также расчет обтекания космического корабля сложной
конфигурации (рис. 10.2.3). Распределение поверхностного
давления показано на рис. 10.2.4. Для такой сложной формы расчет
разумно повторяет экспериментальную кривую давления и требует
около 10—12 мин работы ЭВМ CDC 7600.
В качестве второго примера мы выбрали работу Шатто и Ку-
ломбе (1978), в которой уравнение потенциального движения
решалось по схеме Мурмана—Коула с добавлением искусственной
вязкости в форме, предложенной Джеймсоном (1974). Уравнение
решалось методом верхней релаксации с расщеплением по
вязкости. Для интегрирования уравнений в неконсервативной и
консервативной формах использовались сетки соответственно с 128X
Х32Х16 и 96X32X16 узлов. Время счета 15—30 мин на ЭВМ
CDC 7600. На рис. 10.2.5 дана сетка, использовавшаяся для
291

°} Зксперимент
*} Теория
*****
Рис. 10.2.2. Распределение давления на крыле самолета
КС 135, рассчитанное Боппе и Стерном (1980), ^^,=0,78;
а=2°. (Любезно предоставлен Боппе.)
L
4Щ^|р2£
ощщ^
Рис. 10.2.3. Конфигурация и сеточное разрешение в моделях обтекания
шаттла. (Любезно предоставлен Боппе.)
А — модель внешней ступени шаттла, Б — модель орбитального корабля.

расчета обтекания профиля NACA 0012, а на рис. 10.2.6 предвы-
численное давление сравнивается с результатами эксперимента.
Интересно, что экспериментальный скачок давления при M = 0,85
и нулевом угле атаки располагается между результатами, полу-
СР
-1,200 г-
- 0,800 V-
-о,ш\
ср о о о Эксперимент
-1200г + + + Расчет
-0,800
-OfiOO
0
0,400
0,800
1,200
У- <Ь
£\о °
о©
h о
(S
Верхняя центровая линия
Нижняя центровая линия
Рис. 10.2.4. Распределение давления, рассчитанное Боппе и Эйдалой, М=
= 0,9; а=0. (Любезно предоставлен Боппе.)
Рис. 10.2.5. Сетка в расчете
трансзвукового обтекания профиля
NACA 0012, проведенном Шатто
и Куломбе. (Любезно
предоставлен Шатто.)
ченными по двумерным моделям в консервативной и
неконсервативной формах.
Наконец, в качестве последнего примера результатов,
полученных при интегрировании полного уравнения потенциального
движения, обратимся к работам Кофи (1978), Чена и Кофи (1980),
в которых рассматривалось обтекание осесимметричного капота
с затупленной сердцевиной. Геометрия области и отвечающая ей
разностная криволинейная сетка, конформно отображаемая на
293

прямоугольник, показаны на рис. 10.2.7. Решаемое уравнение
имело вид
Г д(Ри) , а (Dp) 1 пГи д . , о д Л ■
L~~3Öf ' ЭТ J ~ ^ L"2" дХ Я + 2 <ЭГ * _| +
öc2o
= 0,
Рис. 10.2.6. Давление на
профиле, рассчитанное по
неконсервативной схеме Мурмана—
Коула (/) и консервативной
схеме Джеймсона (2), Af00 =
= 0,85; а=0. (Любезно
предоставлен Шатто.) ; 3 —
эксперимент.
1,0 X
Рис. Ю.2.7. Геометрия и сетка расчета
воздухозаборника, проведенного Кофи. (Любезно предоставлен
Кофи.)
где q2 = u2 + v2, D — коэффициент преобразования к новым
координатам X, У, определенный выше. Производные в уравнении
аппроксимировались центральными разностями, причем при
расчете в сверхзвуковой зоне течения использовалась искусственная
вязкость. Система алгебраических уравнений решалась методом
последовательной релаксации по линиям. Решение, полученное
294

Кофи при небольшом числе Маха свободного потока, приведено
на рис. 10.2.8.
Обсуждаемые результаты относились к решению стационарных
задач. При этом отмечались три основные характеристики их
реализации: геометрия области, аппроксимация и вычислительная
процедура. Выбор среди разработанных подходов определяется
конкретными особенностями практических задач. Перспектива
дальнейших исследований заключается в решении полной нели-
(P-Pûo)/ff
-J
-2
ч
Рис. 10.2.8. Распределение давления
на поверхности двигателя, М\ = 0,256,
М^ =0,235. (Любезно предоставлен
Кофи.)
Эксперимент на поверхности втулки (/) и и
на поверхности входной кромки (2).
нейной системы уравнений Эйлера с тем, чтобы ослабить
ограничения, вытекающие из предположений о потенциальности течения
и постоянстве энтропии.
10.2.2. Примеры для М00>\
Стационарные схемы для расчета стационарных сверхзвуковых
течений применяются только для течений, имеющих полностью
сверхзвуковой характер. Процедура при этом состоит в
интегрировании уравнений по потоку так, как если бы его направление
совпадало с осью времени. Таким образом, любая разностная
схема, пригодная для расчета нестационарных течений, может
быть применена и для стационарного случая при интерпретации
производных по времени как производных в направлении потока.
В общем случае криволинейных координат уравнения Эйлера (см.
главу 1 ) преобразуются к виду
El + Flï + Gl+H = 09
0,4 0,8 x/D
295

где
Е = höh*
р + ри2
puv
\puw J
G = hxh2
F = hxh,
fpw ^
puw
pvw
^ p + pw2 /
(puvhz -|*!_ -f- 9uwh2 -Щ (p + pü2) A3 -Щ-
H =
— (p + pw2) h2
dl
puvhs
puwh2
dh2
dh2
dhx
dl
dh*
pvwh{ -^- — (p + pu2) A3 -щ
-(p + pw2)^-^-
dh,
dhx
dl
+. pVWhx -^- — {p+ pu2) h2 -g±
dh2
(p + pv2)hx^
Здесь Ль h2i hs — метрические коэффициенты, принимающие,
например, в случае цилиндрических координат (х, г, ф) значения
/zi = /г2 = 1, Нъ = г. Эти уравнения по маршевой переменной
интегрируются каким-либо апробированным пошаговым методом,
подходящим для расчета особенностей течения, связанных с
возникновением скачков. Такой подход последовательно разрабатывали
Катлер и др. (1971, 1973, 1974, 1975, 1978), Томмен и Д'Атторре
(1965), Томас и др. (1972), Бабенко и др. (1964). Другое
направление исследований определили работы Уолкдена и др. (1978)
и Моретти (1979). В них осуществляется преобразование
криволинейных координат, такое, что координатные линии являются
линиями тока невязкого течения, и вдоль этих линий уравнения
интегрируются методом характеристик. Представляется, что А-ме-
тод Моретти весьма удобен, поскольку его можно применять к
задачам обтекания затупленных тел в сверхзвуковом и
околозвуковом режимах по единой вычислительной программе. Возможно,
метод Уолкдена и др. (1978) столь же универсален, однако это
нуждается в подтверждении. Во всяком случае применение
методов типа Уолкдена—Кэйна—Лоуса и Моретти должно приводить
к хорошим результатам, ибо они допускают естественную
аппроксимацию граничных условий. Это подтверждается и работой Аббета
(1973), в которой показано, что оптимальную точность на границе
296

Фюзеляж
ДР =0,05
е)
Головная
^ударная
волна
АР =0,02
Рис. 10.2.9. Упрощенная конфигурация сверхзвукового
самолета (а), расчет давления в сечении АА (б) и сечении ВВ (в)
по Я-схеме Моретти. (Любезно предоставлен Моретти.)

обеспечивают схемы характеристического типа; что же касается
условий на твердой стенке, то применимы и разностные методы
типа предиктор—корректор. В последнем случае предиктор у
границы использует одностороннюю разность, и полученное значение
уточняется на шаге корректор, согласно следующей процедуре:
1) компоненты искомого вектора, подлежащие расчету на границе,
Рис. 10.2.10. Сетка сечения ВВ. (Лю- Рис. 10.2.11. Сравнение с эксперимен-
безно предоставлен Моретти.) том рассчитанных значений СР в
сечении ЛЛ, х=0,5. (Любезно
предоставлен Моретти.)
определяются какой-либо формой предиктора (например,
первым полушагом схемы Мак-Кормака);
2) предсказанные значения функций корректируются по
известным на границе значениям энтропии, энтальпии и разложению
типа простой волны для приспособления давления к
пристеночному течению.
Для случая границы, являющейся ударной волной, Аббет
установил возможность применения ряда методов, например методов
Кенцера (1971), Барнуэлла (1971) и метода характеристик
Томаса и др. (1972). Отметим, что в этих методах граничные
процедуры для скачков основываются на тех же представлениях, что
и более общие схемы типа схемы Моретти. Из анализа Аббета
вытекает, что лучшей схемой расчета сверхзвуковых течений
будет такая, которая имеет характеристическую структуру, но
непосредственно не следует интегрированию вдоль характеристик.
298

Именно такими являются схемы Уолкдена с соавторами и Мо-
ретти.* Возможности ^-схемы Моретти можно показать при
расчете обтекания сложной летательной конструкции (рис. 10.2.9)
для двух значений числа Маха набегающего потока M»: 2.36
и 4.63. На рис. 10.2.9 бив представлены изобары в сечениях АА
и ВВ. В первом случае расстояние между изобарами Ар = 0,05
и угол атаки равен нулю, во втором — Др = 0,2 и угол атаки
равен 10°. На рис. 10.2.10 дана сетка в сечении ВВ\ по окружности
сетка содержит 48 узлов, между телом и скачком—12 узлов.
В сечении АА (рис. 10.2.11) используется аналогичная сетка
с 24 узлами по окружности. Сравнение вычислительных значений
коэффициента давления Ср с экспериментом показано на
рис. 10.2.11. Результат убедителен.
Задачи, сравнимые по сложности с приведенной, решались
и методом «размазывания» скачка по схеме типа Мак-Кормака
(Катлер и др., 1973; Рэкич и Катлер, 1972; Маркони и Кох, 1979).
На основе имеющихся результатов можно заключить, что в
моделировании трехмерных сверхзвуковых течений имеется заметный
прогресс; существующие трудности связаны лишь с
возможностями учета сложной геометрии расчетной области.
Список литературы
Бабенко К. И., Воскресенский Г. П., Любимов А. М., Русанов В. В.
Пространственное обтекание гладких тел идеальным газом.— М.: Наука, 1964.
Годунов С. К. Разностный метод численного расчета разрывных решений
уравнений гидродинамики.— Матем. сб., 1959, 47, вып. 3, 271—306.
Русанов В. В. Пространственное обтекание затупленного тела сверхзвуковым
потоком газа.— ЖВМ и МФ, 1968, 8, № 3, с. 616—633.
Abbett, M. J. Proceedings of the AIAA Computational Fluid Dynamics Conference»
pp. 153—172, Palm Springs, July (1973).
Ballhaus, W. F., and Bailey, F. R. AIAA Paper 7—677, July (1972).
Ballhaus, W. F. Recent Progress in Transonic Flow Calculation. In: Numerical
Methods in Fluid Dynamics, H. J. Wirz and J. J. Smolderen, Eds., pp. 155—
236, Hemisphere Publishing, Washington, D. С (1978).
Barnwell, G. AIAA Paper 71—56, January (1971).
Bauer, F., Gaiabedian, P., Korn, D., and Jameson, A. Supercritical Wing
Sections IIу Springer-Verlag, New York (1975).
Bohachevsky, I. O., and Rubin, E. L. AIAA J. 4, 600—607 (1966). (PTK, 4, № 4,
с 33—42).
Boppe, С W., and Stern, M. A. AIAA Paper 80-0130, January (1980).
Boppe, С W., and Aidala, P. V. Complex Configuration Analysis at Transonic
Speeds. AGARD Conference on Subsonic/Transonic Configuration
Aerodynamics, Preprint No. 285, May (1980).
Bristeau, M. O. Application of Optimal Control Theory to Transonic Flow Com-
mupations. In Proceedings of the 3rd IRIA Symposium on Computational
Methods in Applied Science and Engineering, Versailles, France, December (1977).
Bristeau, M. O.. et al. Application of Optimal Control and Finite Element Methods
to the Calculation of Transonic and Incompressible Flow. IRIA Rept. No. 294,
LeChesnay, France, April (1978).
* Сеточно-характеристические методы рассмотрены в обзорной работе Чуш-
кина П. И. Метод характеристик для пространственных сверхзвуковых течений.
М., ВЦ АН СССР, 1968.— Прим. перев.
299

Caughey, D. A., and Jameson, A. Transonic Flow Problems in Turbomachinery,
Т. C. Adamson and M. Platier, Eds., pp. 274—291, Hemisphere Publishing,
Washington, D. C. (1977a).
Caughey, D. A., and Jameson, A. AIAA J. 15, 1474—1480 (1977b). (PTK, 15,
N 10, с 123).
Caughey, D. A. Lecture Notes, University of Tennessee Space Institute, Tullahoma,
TN, December (1978).
Caughey, D. A., and Jameson, A. AIAA J. 17, 175—181 (1979a). (PTK, 17, N 2,
с 61—69).
Caughey, D. A., and Jameson, A. AIAA Paper No. 79—1513 (1979b).
Caughey, D. A.: "A (Limited) Perspective on Computational Aerodynamics".
Presented at the 13th AIAA Fluid and Plasma Dynamics Conference, July (1980);
also Cornell University Rept. FDA-80-07, July (1980).
Caughey, D. A. "A Review of Transonic Flow Computation", Ann. Rev. Fluid
Mech. 14, 261—283 (1982).
Chan, S. T. K., Brashears, M. R., and Young, V. Y. С AIAA Paper 75—79,
Pasadena, (1975).
Chang, I. S. AIAA Paper 80-0272, Pasadena, (1980).
Chen, L. T., and Caughey, D. A. /. Aircraft 17, 167—174 (1980).
Chattot, J. J., and Coulombeix, С Calcus D'Ecoulements Transsoniques Autor
D'Ailes. ONERA Rept. T. P. No. 1978—125 Chatillon, France (1978).
Chorin, A. J. /. Comput. Phys. 22, 517—533 (1976).
Chorin, A. J. /. Conput. Phys. 25, 253—272 (1977).
Colella, P. The Effects of Sampling and Operator Splitting on the Accuracy of
Glimm's Scheme. PhD Thesis, University of California, Berkley (1978).
Euvrard, D., and Tournemine, G. /. Niée, 12, 419—461 (1973).
Fletcher, С A. J. Subsonic Inviscid Flow by the Finite — Element Method. Dept.
of Defence, Weapons Research Establishment Rept. WRE-TR-1858 (W),
Salisbury, S. Australia, August (1977).
Fletcher, С A. J. /. Comput. Phys. 33, 301—312 (1979).
Glaz, H. M. Development of Random Choice Numerical Methods for Blast Wave
Problems. NSW3 Report/WOL TR 78-211, March (1979).
Glaz, H. M., and Colella, P. Private communication results can be obtained from
P. Colella at LLL, Livermore, CA (1980).
Grossman, R., and Moretti, G. AIAA Paper 70-1322 (1970).
Holden, M. Studies of Transitional Flows, Unsteady Separation Phenomena, and
Partial Induced Augmentation Heating on Ablated Noise Tips. AFOLL Rept.
TR-76-1066, October (1975).
Holt, M., and Masson, B. S. Lecture Notes in Physics, Vol. 8, pp. 207—214.
Springer-Veriag, New York (1971).
Holt, M. Numerical Methods in Fluid Dynamics, Springer-Verlag, New York,
(1977).
Jameson, A. Commun. Pure Appl. Math. 27, 283—309 (1974).
Jameson, A. In: Proceedings of the 2nd AIAA Computational Fluid Dynamics
Conference, pp. 148—161, Hartford, CT, June (1975).
Jameson, A., and Caughey, D. A.: In: Proceedings of the 3rd AIAA Computational
Fluid Dynamics Conference, pp. 35—54, Albuquerque, N. M., June (1977c).
Jameson, A. In: Proceedings of the 4th AIAA Computational Fluid Dynamics
Conference, pp. 122—146, Williamsburg, VA, July (1979).
Kentzer, С. P. Lecture Notes in Physics, Vol. 8, pp. 108—113, Springer-Verlag,
New York (1971).
Kershaw, D. С /. Comput. Phys. 26, 43—65 (1978).
Khosla, P. K-, and Rubin, S. G. Comput. Fluids, 1, 109—121 (1981).
Kutler, P., and Lomax, H. /. Spacecraft Rockets 8, 1175—1182 (1971).
Kutler, P., Lomax, H., and Warming, R. F. AIAA J. 11, 196—204 (1973) (PTK,
11, N 2, с 86).
Kutler, P., Reinhardt, W., and Warming, R. F. AIAA J. 11, 657—664 (1973).
(PTK, 11, N 5, с 102.)
Kutler, P. AIAA J. 12. 557—578 (1974). (PTK, 12, N 5, с 3.)
Kutler, P., and Sakell, L. AIAA Paper 75—49, January (1975).
Kutler, P., Chakravarthy, S. R., and Lombard, С. К. AIAA Paper 78—213 (1978).
300

Lax, P. D. Commun. Pure Appl. Math. 7, 159—193 (1954).
Lax, P. D., and Wendroff, B. Commun. Pure Appl. Math. 13, 217—237 (1960).
Lax, P. D., and Wendroff, B. Commun. Pure Appl. Math. 17, 381—398 (1964).
Lerat, A., and Sides, J. In: Proceedings of the Conference on Numerical Methods
in Aeronautical Fluid Dynamics, University of Reading, March 29—April 1
(1981).
Lomax, H. and Steger, J. L. Ann. Rev. Fluid Mech. 7, 63—80 (1975).
Magnus, R., and Yoshihara, H. AIAA J. 8, 2157—2162 (1970). (PTK, 8, N 12,
с 53)
Magnus, R., and Yoshihara, H. AIAA J. 13, 1622—1628 (1975). (PTK, 13, N 12,
с 93.)
Magnus, R. J. Some Numerical Solutions of Inviscid, Unsteady, Transonic Flows
over the NLR 7301 Airfoil. Convair Dynamics Rept. CASD/LVP 78-013,
January (1978).
Marconi, F., and Koch, F. An Improved Supersonic 3-D Externall Inviscid Flow
Field Code. NASA Contractor Rept. 3108, Grumman Aerospace, Bethpage, NY
(1979).
Masson, B. S., Taylor, T. D., and Foster, R. M. AIAA J. 7, 694—698 (1969).
(PTK, 7, N 4, с 148.)
Masson, B. S., and Taylor, T. D. Polish Fluid Dyn. Trans. 5, 185—194 (1971).
Masson, B. S., and Friedman, G. Axisymmetric Transonic Flow Calculations. Pica-
tinny Arsenal Tech. Rept. No. 4271, Dover, NJ (1972).
MacCormack, R. W. AIAA Paper 69-354, May (1969).
Moretti, G. In: Proceedings of the 1974 Heat Transfer and Fluid Mechanics
Institute, pp. 184—201, Stanford University Press, Stanford (1974).
Moretti, G. Computation of Shock Layers about Ablated Blunt Nosed Bodies.
Polytechnic Institute of New York Rept. 77—14, August (1977).
Moretti, G. An Old Integration Scheme Refurbished and put to Work. Polytechnic
Institute of New York Rept. M/AE 78-22, September (1978).
Moretti, G. Comput. Fluids 7, 191—205 (1979).
Moretti, G. A. A Numerical Analysis of Muzzle Blast—Precursor Flow. Polytechnic
Institute of New York Rept. M/AE 80-10, May (1980).
Murman, E. M., and Cole, J. D. AIAA J. 9, 114—121 (1971) (PTK, 9,№ 1, с 137.)
Periaux. J. Int. J. Numer. Meth. Eng. 9, 775—831 (1975).
Rakich, J. V., and Kutler, P. AIAA Paper 72-191, January (1972).
Reddall, W. Private communication of result (1980).
Richtmyer, R. D., and Morton, K. W. Difference Methods of Initial-Value
Problems, 2nd ed., Interscience, New York (1967). (Рихтмайер P., Мортон К.
Разностные методы решения краевых задач.— М.: Мир, 1972).
Rusanov, V. V. J. Comput. Phys. 5, 507—516 (1970).
Schmidt, W. Progress in Transonic Flow Computations; Analysis and Design
Methods for 3-D Flows. In: Numerical Methods in Fluid Dynamics, H. J. Wirz
and J. J Smolderen, Eds., pp. 299—338, Hemisphere Publishing, Washington,
D. С (1978).
Schmidt, E. M., and Shear, D. D., The Flow Field About the Muzzle of an M-16
Rifle, BRL Report No. 1692, U. S. Army Ballistic Research Laboratory,
Aberdeen Proving Ground, Md., January (1974).
Sod, G. A. /. Comput. Phys. 27, 1—31 (1978).
Sod, G. A. Computational Fluid Dynamics with Stochastic Techniques. Princeton
University Technical Rept. MAE 1479, March (1980a).
Sod, G. A. Automotive Engine Modeling with a Random Choice Hybrid Method,
II. SAE Technical Paper 800288, February (1980b).
South, Jr., J. C, and Jameson, A. In: Proceedings of the AIAA Computational
Fluid Dynamics Conference, pp. 8—12, July, AIAA, New York (1973).
Taylor, T. D., and Masson, B. S. /. Comput. Phys. 5, 443—454 (1970).
Taylor, T. D. AGARDograph, No. 187 (1974).
Taylor, T. D., and Lin, Т. С AIAA J, 19, 346—349 (1981) (PTK, 19, № 4, с 88.)
Thomas, P. D., Vinokur, M. Bastianon, R. A., and Conti, R. J. AIAA J. 10, 887—
894 (1972), (PTK, 10, N 7, с 77.)
Thommen, H. U. Z. Angew. Math. Phys. 17, 369—384 (1966).
Thommen, H. U., and D'Attore, L. AIAA Paper 65—25, January (1965).
301

Thompson, J. R, Thames, F. С, and Martin, С. W. /. Comput. Phys. 15, 299—
313 (1974).
VanLeer, В. /. Comput Phys. 32, 101—136 (1979).
Viviand, H., and Veuillot, J. P. Pseudo-Unstationary Methods for Calculation of
Transonic Flows (in French). ONERA Publication No. 1978-4, Chatillon,
France (1978).
Walkden, F., Caine, P. and Laws, G. T. /. Comput. Phys. 27, 103—122 (1978).
Глава 11
Течения вязкой
сжимаемой жидкости
11.1. Введение
При расчете стационарных вязких течений обычно используют
нестационарные уравнения Навье—Стокса, интегрируемые на
большом интервале времени до асимптотического стационирования
решения. Большинство решений получено при использовании
явных разностных схем, типа схем Томмена (1966) и Мак-Кормака
(1969). Такие методы легко реализуемы, что существенно при
большом числе зависимых переменных и сложных уравнениях,
интегрируемых в областях со сложной геометрией. Однако
ограничения на временной шаг, налагаемые явными методами, приводят
к излишним вычислительным затратам. В связи с этим предметом
внимания всегда оставались схемы с менее ограничительными
условиями устойчивости. Одну из первых таких работ выполнил
Крокко (1965), предложивший несогласованную схему с
аппроксимацией второй производной:
/ ä2f У
Разностные уравнения оказываются согласованными с
дифференциальной задачей при достижении стационарного состояния.
Такую же несогласованную аппроксимацию диффузионного
члена предложили Аллен и Ченг (1970) для двухшаговой схемы
Браиловской (1967). Эта последняя схема близка к схеме Томмена
(см. п. 2.7 и 2.8), но предвычисляемые и скорректированные
значения определяются в одних и тех же узлах. Схема Браиловской
не подпадает под общее описание схем (2.7.11) или (2.8.9).
Схема Аллена—Ченга является безусловно устойчивой, если
сеточное число Рейнольдса Rec<2 (Пейре, Вивиан, 1975); для
Rec^2 устойчивость определяется условием Куранта—Фрид-
рихса—Леви. Это означает, что в несогласованных
аппроксимациях вида (11.1.1) вязкость не влияет на устойчивость схемы.
Однако, как показали Пейре и Вивиан (1975), интегрирование не-
302

стационарных уравнений по схеме Аллена—Ченга замедляет
процесс установления по сравнению с интегрированием на основе
согласованных аппроксимаций. Медленное установление
стационарного состояния компенсируется возможностью использования
большого шага по времени.
Опираясь на идею построения несогласованных аппроксимаций
с улучшенными условиями устойчивости для приближения к
стационарному состоянию, Пейре и Вивиан выполнили расчеты
течений при небольших числах Рейнольдса. Использовалась простая
одношаговая схема, позволяющая последовательно определять
сеточные функции методом Гаусса—Зейделя при аппроксимации
производных:
1аГЛ-"2аГ^ + 1""^-^ VdP-Ji- 5? • (1М-2)
Заметим, что схема «чехарда» Дюфорта—Франкела, которую
применяли, например, Викториа и Уидхоф (1973), может также
интерпретироваться как несогласованная аппроксимация,
допускающая шаг по времени больший, нежели тот, который следует
из условия устойчивости явной аппроксимации, согласованной
с дифференциальным уравнением (см. п. 2.6.3).
Такого рода схемы интегрирования нестационарных уравнений
относятся к типу псевдонестационарных методов, опирающихся
либо на несогласованные аппроксимации, включающие
дополнительные по сравнению с дифференциальной задачей приближения
производных по времени, либо на преобразование исходных
уравнений, обеспечивающее эффективный выход решения на
стационар. Обзор методов второго направления, применявшихся для
расчета трансзвуковых невязких течений, выполнен Вивианом
(1980).
Другую возможность ослабления условия устойчивости явных
аппроксимаций многомерных задач представляет метод
расщепления (см. п. 2.8.4). Для расчета сжимаемой вязкой жидкости
Мак-Кормак (1971) предложил схему расщепления, которая стала
широко использоваться, в частности, в методе конечных объемов
(Дейуэрт, 1975, 1976; Болдуин и др., 1975; Ханг и Мак-Кормак,
1977).
Большие усилия, предпринятые в последние годы для развития
неявных методов, оказались весьма плодотворными. Такие методы
эффективны, если: 1) они основываются на расщеплении или
процедуре чередующихся направлений, что позволяет свести
многомерную задачу к системе локально одномерных задач, и 2) не
требуют итераций на каждом временном шаге. Использовать
метод чередующихся направлений без итеративного процесса первым
предложил, по-видимому, Полежаев (1967). Обобщение процедуры
чередующихся направлений для расчета движения вязкой
сжимаемой жидкости получило успешное развитие в работах Березина
и др. (1972, 1975 а, Ь), Брайли и Макдональда (1973, 1975, 1977);
несколько позже Бим и Уорминг (1978) расширили сферу прило-
303

жений неявного метода, разработанного ими для гиперболических
уравнений и реализующегося процедурой чередующихся
направлений (Бим, Уорминг, 1976).
В заключение остановимся на двух неявных схемах
Мак-Кормака. Первая схема (Мак-Кормак, 1976 а, Ь) содержит
расщепление по координатным направлениям, а также дополнительное
расщепление оператора дифференциальной задачи на вязкую и
невязкую части. Для решения расщепленных уравнений без
вязкости применялся метод характеристик в сочетании с явной двух-
шаговой схемой Мак-Кормака, а для уравнений с членами
вязкости— схема Кранка—Николсона. Вторая схема Мак-Кормака
представляется более интересной, в связи с простотой ее
реализации (решение линейных уравнений с бидиагональной структурой)
и хорошими свойствами устойчивости. Неявная часть разностного
оператора основывается на пошаговом поочередном
использовании разностей вперед и назад, аналогично явной схеме
Мак-Кормака, а аппроксимация оператора вязкости производится по схеме
Саульева (см. Рихтмайер и Мортон, 1967). Анализ этой схемы
применительно к решению гиперболических задач выполнен Хол-
ландерсом и Пейре (1981).
Все обсуждавшиеся методы являются конечно-разностными,
либо методами конечных объемов. К настоящему времени для
очень небольшого числа расчетов применяются другие описанные
выше методы: метод конечных элементов (Оден и Уэлфорд, 1972;
Бейкер, 1978; Куке и Бланшар, 1979) или спектральные методы
(Бохари и др., 1981). Мы их рассматривать не будем, так как они
еще только формируются.
В настоящей главе обсуждаются общие черты явных и
неявных разностных аппроксимаций вместе с вопросами задания
области расчета и постановки граничных условий. Основное
внимание при этом уделяется интегрированию на неравномерной сетке.
Более подробно эти методы проанализированы в обзорных
работах Пейре и Вивиана (1975), Вивиана (1978), Холландерса и Ви-
виана (1980), Болдуина и др. (1975), Мар-Кормака и Ломэкса
(1979), Мета и Ломэкса (1981), в которых представлены общие
подходы и ссылки.
11.2. Граничные условия
Уравнения Навье—Стокса, описывающие нестационарное
движение сжимаемой жидкости, относятся к смешанному параболо-ги-
перболическому типу (иногда их называют не вполне
параболическими уравнениями). Их параболический характер определяется
наличием в уравнениях движения и энергии (температуры)
вторых производных по пространственным переменным, которые
описывают диссипативные эффекты; уравнением неразрывности
определяются гиперболические черты поведения общей системы
уравнений. Стационарные уравнения Навье—Стокса представляют
эллиптико-гиперболическую систему.
304

Задачи, представляющие практический интерес, являются
краевыми задачами, либо нестационарными с задаваемыми
начальными условиями для вектора решения (р, pV, р£), либо не
зависящими от времени. Строгие результаты, относящиеся к
корректности краевых задач движения несжимаемой жидкости, получены
лишь для некоторых частных случаев. В результате многие задачи
ставятся эвристически, основываются на физических
представлениях и характере решаемых уравнений. Так, можно полагать, что
каждое из уравнений для импульса и энергии требует в
простейшем случае, т. е. в области, ограниченной непроницаемыми
стенками, задания лишь одного условия на каждой из границ, где и
задаются соответственно компоненты V и Г. Уравнение
неразрывности, рассматриваемое как уравнение для р, в котором значения
вектора скорости V предполагаются известными, выражает
изменение плотности частицы жидкости вдоль траектории ее
движения. Следовательно, если частица входит в рассматриваемую
область через границу, ее плотность должна быть задана как
граничное условие, и наоборот: если частица выходит из области
расчета, плотность должна определяться как часть решения и ее
нельзя произвольно задавать.
В случае когда границей является непроницаемая стенка и при
отсутствии эффектов разрежения обычное условие прилипания
заменяется условием
V = VW, (11.2.1)
где Vw — скорость движения стенки. Для температуры обычно
принимают либо условие
T = TW (11.2.2)
(Тги — температура стенки), либо условие
dT/dN = Oy (11.2.3)
где N— единичный вектор нормали к стенке. Для совершенного
газа с постоянной удельной теплоемкостью это приводит к
условию для внутренней энергии e = cvT. На непроницаемой стенке
условие для плотности не ставится, и она должна там
определяться.
Общее обсуждение постановки граничных условий на
нематериальных границах содержится у Холландерса и Вивиана (1980);
некоторые вопросы корректности краевых задач исследованы Гус-
тафсоном и Сандстрёмом (1978).*
Рассмотрим область расчета и граничные условия на ней для
двух типичных примеров: (1) взаимодействие ударной волны с
пограничным слоем и (2) обтекание тела конечного размера.
В задаче взаимодействия скачка с пограничным слоем
(рис. 11.2.1), решавшейся, например, Болдуином и Мак-Кормаком
* См. также: Белов Ю. А., Яненко H. Н. Влияние вязкости на гладкость
решений не вполне параболических систем.— Матем. зап., 1971, т. 10.— Прим.
перев.
305

(1974), область интегрирования уравнений Навье—Стокса
перекрывала область невязкого сверхзвукового течения (/) и зоны
пограничных слоев (2) и (<?). Параметры течения задавались на
линиях AB и ВС: граничные условия для течения в пограничном
слое ставились на АА''; для равномерного внешнего потока
условия на A'S, SB и ВС согласовывались с заданным косым скачком
уплотнения. Вдоль CD значения потока принимались равными
значениям соседнего ряда узлов (т. е. условие df/dx = 0
аппроксимировалось с первым порядком точности). Это условие ставилось
в связи с тем, что поток вниз от CD не оказывал влияние на ре-
Косой
скачок
уплотненш
ILL
Область решения
уравнений Навье-Стокса
/ ' '
ft)
\\\\\\\\\\\\m х
А В
Рис. 11.2.1. Область расчета в задаче
взаимодействия скачка с пограничным слоем.
шение в области интегрирования уравнений Навье—Стокса,
поскольку на CD течение было сверхзвуковым либо типа
пограничного слоя. Более корректным был бы расчет плотности на этой
границе по нестационарному уравнению неразрывности с
аппроксимацией пространственной производной разностным отношением
против потока. Возможность применения простой экстраполяции
объясняется специальным типом течения на границе.
В некоторых случаях (см. пример в п. 11.4.2) значения потока
вдоль AB получались предварительным расчетом течения на
передней кромке пластины.
Второй пример постановки граничных условий относится к
обтеканию конечного тела равномерным потоком с условиями на
бесконечности. В этом случае необходимы процедуры,
позволяющие выполнить интегрирование уравнений Навье—Стокса в
ограниченной области. Для таких задач можно применить
преобразование координат, отображающее всю плоскость в некоторую
замкнутую вычислительную область. Классическим примером этого
является конформное отображение внешней к телу области на
круг. Однако обычно пользуются более простым способом — рас-
306

тяжением координат. Другой близкий прием состоит в
использовании такого преобразования, в результате которого внешняя
граница вычислительной области является периферией физической
области, на которой выполняются условия равномерного течения
или некоторые асимптотические условия. В последнем случае
асимптотическое решение для больших расстояний связано со
свойствами потока вблизи тела, и для получения окончательного
результата требуются итерации. Такая техника успешно
применялась для расчета несжимаемого вязкого течения (Таками и
Келлер, 1969) и сжимаемых невязких трансзвуковых течений (Мурман
g
Равномерный ^\
поток ^r \
/ \^~ Экстраполяция
Ai j^j \с
Рис. 11.2.2. Область расчета обтекания тела.
и Коул, 1971; Эврар и Турнемин, 1973). Поскольку метод очень
сложен, для расчета сжимаемых вязких течений он не
применялся.
Третий и наиболее простой метод иллюстрируется рис. 11.2.2,
где внешняя граница располагается на некотором расстоянии от
обтекаемого тела и разделяется на два участка: 1) границу BAD
вверх по течению, сквозь которую равномерный поток входит в
область расчета, и 2) границу BCD вниз по течению, сквозь которую
поток выходит из области расчета и на которой требуются
некоторые экстраполяционные процедуры. Однако и в этом случае
успех зависит от характера граничного течения. В случае
дозвукового потока может оказаться необходимым обращение к более
сложному методу, типа метода краевых условий «поглощения»,
основанного на подавлении возмущений, распространяющихся
вдоль приходящих в область характеристик. Эту процедуру
разработали Энквист и Майда (1977), а также Хедстром (1977) для
гиперболических краевых задач; Руди и Стрикверда (1980)
применили ее к уравнениям Навье—Стокса. Аналогичный прием
использовал Пейре (1971) для расчета простых течений
несжимаемой жидкости.
В случае сверхзвукового потока поле течения вверх от
головной ударной волны остается невозмущенным, и верхняя граница
вычислительной области может быть поставлена вблизи скачка
307

либо на самом скачке, в зависимости от интерпретации самого
скачка как зоны резких, но конечных градиентов (методы
«улавливания», или «размазывания» скачка), либо действительного
разрыва (методы выделения скачка). В первом случае на выбранной
границе ставятся условия равномерного потока. Во втором —
локализация скачка и поле течения за ним являются
определяемыми элементами решения (Моретти и Салас, 1969; Таннехилл
и др., 1975; Вивиан и Гацци, 1976).
Что касается задания условий на материальной границе
(плоскость на рис. 11.2.1, поверхность тела на рис. 11.2.2), то
единственным затруднением является задание на ней плотности или
давления. Когда уравнения Навье—Стокса в консервативной форме
аппроксимируются конечно-разностной схемой на сетке, где все
параметры течения определяются в каждом узле, причем стенка
совпадает с линией узлов, то граничные значения давления на ней
требуются только для центрально-разностной аппроксимации
производной от давления в проекции уравнения количества движения
на нормаль к стенке. Для задания этого граничного условия
применяются различные способы. Иногда из уравнения неразрывно-
ности вычисляют плотность, а затем из уравнения состояния
получают давление на стенке, однако такая процедура может
повлечь сильные осцилляции и даже неустойчивость, если не
применять искусственного сглаживания. В частности, в случае
отрывных течений при этом могут получаться отрицательные
значения плотности (Роуч, 1972; Пейре, Вивиан, 1973). Вместе с тем
некоторые типы аппроксимации уравнения неразрывности на
стенке приводят к приемлемым результатам (явная схема — Вик-
ториа и Уидхоф, 1973; неявная — Полежаев, 1967; Скала и
Гордон, 1970; Брайли и Макдональд, 1973). Другой способ
заключается в определении давления на стенке путем квадратичной
(Картер, 1973; Таннехилл и др., 1974) или линейной
экстраполяции в узлы на полушаге за стенкой (Аллен и Ченг, 1970).
Часто и успешно используется способ, заключающийся в
определении давления на стенке из проекции уравнения движения на
нормаль к ней при односторонней аппроксимации производных.
Допустим, что стенка совпадает с координатной линией у = 0;
уравнение количества движения в проекции на нормаль к стенке
имеет на ней вид
(ар \ _, 1 г ü / »и . , а»р \ .
V ду Â/=o~~ Re L 3 \ дхду ^ ду2 /^
, ф/4 dv дТ . ди дТ\1 (U2 4)
При больших числах Рейнольдса получим
(др/ду)у==0 = 0. (11.2.5)
308

11.3. Разностные схемы на равномерной сетке
в декартовых координатах
В этом разделе обсуждаются некоторые разностные методы
интегрирования уравнений движения вязкой сжимаемой жидкости.
Ограничимся рассмотрением методов интегрирования уравнений
в декартовой системе координат на равномерной сетке. Это
делается только в целях упрощения изложения, ибо, как
упоминалось в главе 1, уравнения Навье—Стокса можно записать в
любой криволинейной системе координат в консервативной форме.
Для плоского двумерного течения имеем
dt
дх
ду
= 0,
где
/ = (р, pu, pü, р£), F = FÎ
Re
G = GY
Gy
Re
Выражения Fj, Gi, отвечающие невязкому течению, и FYi Ол
течению при учете вязкости, определены в главе 1.
11.3.1. Явные схемы
Применение двухшаговых явных методов, представленных в п. 2.8,.
для решения системы уравнений (11.3.1) не вызывает затруднений.
Остановимся на аппроксимации
смешанных производных,
отсутствовавших в модельном уравнении. Ее- j+i
тественно, что наличие этих членов
изменит критерий устойчивости
схемы.
Рассмотрим аппроксимацию
смешанной производной J ф-
Ф-
"--е-ИтВ
(11.3.2) Jj±
Рис. 11.3.1. Сетка для схемы Томмена.
Ф
1-1
Ф-
гф-
Т
-Ф-
Ф"
-Ф-
-Ф-
1+1.
добавленной к модельному уравнению (2.8.1). Для
«центрированной» версии схемы (2.8.9), возникающей при ß =7 = ^ = 72,
смешанную производную D следует вычислять в точках Q и R
(рис. 11.3.1) на шаге предиктор и в точке Р — на шаге корректор.
В точке Q (i+l/2, /), примем
Df+'h, 1 = д*(v"+1/,, iAyf1+,ht j),
(11.3.3)
309-

где, как обычно,
Alm, .„==
Дл:
Ахф/, m = "XT" (W + '/2. m — Ф/ - '/2, m),
Д|/Ф/, m =-удГ-(ф/, ro+i — ф/.m-i)
и v—значение v(/) в точке Q; можно принять, например,
^+»/1./= ~2"[v (/«+!,/)+v (//,/) ]. Аппроксимация D в точке
#(*'. / + V2) определяется аналогично:
D?./ + '/. = AÎK / + '/.Aif" / + '/2). (И.3.4)
В точке Р (/, /) имеем
D?./ = AÏ(v?,/AÎtf./). (11.3.5)
В схемах типа схемы Мак-Кормака (2.8.8) (или (2.8.9)) при
значениях параметров ах, о^, не равных нулю или единице,
смешанная производная D обычно представляется комбинацией
направленных и центральных разностей. На первом полушаге в схеме
(2.8.8а) для D имеем
Dli^AiivlfAlfli) (11.3.6а)
и на втором полушаге в схеме (2.8.8в) —
А-, / = А7 (Я J A°yfit Д ( 11.3.66)
где
Л?Ф/, m = ± (ф/ ± 1, m — ф/, т)/Д*.
В работе Ле Баллёра и др. (1980) для аппроксимации
смешанной производной использовались формулы
D?i/ = AÎ"(v?i/A;f?i/)f
Dl9! = bï(vi9,bïJi,i), (Н.3.7)
которые, как и (11.3.6), имеют второй порядок точности.
В случае сжимаемой вязкой жидкости строгий критерий
устойчивости методов (2.8.8) или (2.8.9) отсутствует. Для разностных
уравнений движения без диссипации необходимый критерий
устойчивости следует из условия того, что интервал зависимости для
разностного уравнения должен быть не меньше интервала
зависимости для дифференциального уравнения (Курант и др., 1928;
Лаке и Вендроф, 1964). Для схемы (2.8.8) или (2.8.9) это
приводит к условию КФЛ:
310

где с — скорость звука. Подробности вывода этого условия
содержатся в работе Мак-Кормака (1971), который показал, что
применительно к его схеме условие (11.3.8) не является достаточным.
Для разностных аппроксимаций уравнений Навье—Стокса
максимально допустимый шаг по времени определяется анализом
собственных чисел матрицы перехода. Однако приближенную оценку
временного шага можно получить при расщеплении разностного-
оператора (см. п. 2.8.4) на одномерные операторы Мак-Кормака
(Мак-Кормак и Болдуин, 1975). Результаты показывают, что для
оператора в направлении х оценкой шага по времени является
выражение
A'*<4lM| + c+w(T^Wïib-)r' (1L3-9a)'
а для оператора в направлении у —
^^^О^ + ^ + ^р-С-Дг + л/х-Ег)]"'- (1КЗ-9б>
Следует отметить, что эти критерии получены при законе
Стокса (À =—2/з(1) и что ограничения на шаг по времени,
накладываемые термическими эффектами, более существенны нежели
те, которые возникают при учете вязкости (присутствие члена
с Ar/ в (11.3.9а) и с Ах — в (11.3.96) обязано наличию в схеме
смешанных производных).
С помощью эвристических соображений, основывающихся на
связи между критериями устойчивости одномерных и двумерных,
задач, из (11.3.8) и (11.3.9) при Дл: = Д*/ можно получить
следующую оценку временного шага:
A^A^^^I + hl + cV^ + ^y^ + V^]"1-
(11.3.10)
Это условие относится к устойчивости схемы Мак-Кормака (2.8.8)
или к «центрированной» версии схемы типа схемы Томмена (2.8.9),.
где ах, аУ произвольны, а все прочие параметры равны 7г-
11.3.2. Неявные схемы
Эффективные неявные схемы интегрирования уравнений
движения сжимаемой вязкой жидкости строятся на основе
дискретизации (2.7.22) в сочетании с линеаризацией (2.7.24) и обобщенной
процедурой чередующихся направлений, описанной в п. 2.8.5.
Такие методы развивали Брайли, Макдональд (1973, 1975, 1977)
и Бим, Уорминг (1978). Эти методы близки между собой и
реализуются путем решения блочно-трехдиагональных линейных систем
уравнений. Некоторое различие между ними заключается в том,
что в методе Бима—Уорминга искомым является вектор <p = f =
= (р, pV, р£), а Брайли и Макдональд используют дополнительную
311

линеаризацию и решают уравнения относительно неизвестного
вектора ф = (р, V, Т).
Рассмотрим в общих чертах метод Бима—Уорминга, обратив
особое внимание на аппроксимацию диссипативных членов;
представление их в уравнениях Навье—Стокса сложнее, чем в
модельном уравнении (2.7.1), где коэффициент вязкости принимался
постоянным и смешанные производные отсутствовали. Ограничим
рассмотрение трехуровенной схемой, возникающей из (2.7.22) при
8=1, 6=2. Для уравнения (11.3.1) имеем
1
2 M
.(Г + '-4Г + Г1) + (-^Г' + (^)П + 1=0. (11.3.11)
Обратимся к аппроксимации производной (dF/dx)n+i\
производная (dF/dy)n+{ имеет аналогичное разностное представление.
Слагаемое Fj9 отвечающее недиссипативной части суммарного
вектора F=Fi — Fv/Re, линеаризуется способом, представленным
в п. 2.7.4. Имеем
F?+ | ~ F? + Ля^я + ! — fn),
где A=dFi/df — матрица Якоби. Слагаемое Fv, включающее
смешанные производные, представим в виде
Fv = Fvl(fy df/dx) + Fw2(f> df/ду).
Линеаризуем первый член правой части
Ftf^F«vl + Mn(r + l-r) + Pn[(^)n+l-(^r)n],
Fiïl^F"vl + [Mn-(^r)n](r + l-f)+
+ -|Г[/>п(Г+1-Г)]. (11.3.12)
где M = dFYi/dx, P = dFYi/d(df/dx). Неявная аппроксимация
слагаемого Fy2 приводит к осложнениям, в связи с чем для него
используется экстраполяция
тлП + 1 о j-i/l Т}П — 1
rV2 = *JTv2 — -Tv2 .
Это не снижает второго порядка точности схемы по Д/ и не
нарушает ее безусловной устойчивости в случае модельного
скалярного уравнения (Бим и Уорминг, 1978, 1980).
Выполнив аналогичные преобразования с членом G и
аппроксимируя пространственные производные в (11.3.11), имеем схему
в символической записи (2.8.18)
(1 + Ах + Ау)(П^ -fi9 }) = Rfl h (И.3.13)
312

где / — тождественный оператор, Л*, Л^, R — операторы,
определяемые выражениями:
-ЙН^иЧ,,-
^u--¥-(*{[*--^-(*'4B]'}),/-
-!&■[■& Щ. г
+ШШ^-^-,Я,1+Ша"--а"г'Я,1}+
+-f(r-r-')i./
- а/ ' v д (df/dy) •
Ov-OVI(f,^-) + 0„(f.^-).
В приведенных выражениях разностные операторы,
аппроксимирующие операторы дифференцирования по пространственным
переменным, не конкретизируются. С этой целью можно
воспользоваться различными формулами, но окончательный вид уравнений
должен оставаться блочно трехдиагональным. Так, Бим и Уор-
минг (1978) использовали обычную трехточечную
центрально-разностную аппроксимацию пространственных производных.
Поскольку коэффициенты вязкости À, ц и коэффициент
теплопроводности k зависят от температуры, то матрицы M и N
оказываются весьма сложными. Если эти коэффициенты не зависят
от времени, то матрицы имеют более простой вид; кроме того,
сумма M — дР/дх оказывается однородной функцией первых
производных от коэффициентов вязкости и, если пренебречь этими
производными, то M — дР/дх = 0. В частности, это выполняется
в случае постоянных коэффициентов. Аналогичное равенство
N — dQ/dy = 0 при тех же условиях имеет место для GV2. Члены,
содержащие операторы Ах, Ау, представимы при этом в виде
при обозначениях
Re
313

Отметим, что для получения стационарных решений этими
выражениями можно пользоваться без потери точности независимо от
вариации, коэффициентов вязкости, поскольку в установившемся
состоянии fn+i = fn . =fn-j = fitf и уравнение (11.3.13)
редуцируется к виду Rfi, / = 0, т. е.
(-*-'),,+(-£ <»),.,-°-
В общем случае схема (11.3.13) реализуется обобщенным
методом чередующихся направлений (см. п. 2.8.5). На практике, где
представляет интерес лишь установившееся состояние,
использование схем второго порядка точности по времени не является
необходимым и описанная процедура может применяться к схеме
первого порядка точности, следующей из (2.7.22) при 6=1, 6 = 1;
при этом смешанные производные вычисляются на п-временном
'Слое.
11.3.3. Искусственная вязкость
Схемы, представленные в п. 11.3.2, устойчивы при ограничениях,
получаемых путем анализа методом фон Неймана, т. е. в
линейном случае с постоянными коэффициентами без учета граничных
условий (или с периодическими граничными условиями). В
расчетах реальных течений при больших числах Рейнольдса может
возникнуть неустойчивость, обязанная источникам различной
природы: 1) нелинейным эффектам, 2) быстрому изменению
направления потока в зоне отрыва, 3) большим градиентам давления,
4) наличию стенок и других граничных поверхностей в
вычислительной области. Неустойчивость, которая вызывается этими
факторами и которую можно назвать «слабой», не обязательно
проявляется в быстрой расходимости вычислительного процесса —
часто она вызывает осцилляции решения, амплитуда которых
сохраняется постоянной.
Обычным способом подавления таких осцилляции, равно как и
тех, появление которых вызвано иными причинами (см. главу 2),
является введение искусственной вязкости.
Искусственная вязкость четвертого порядка точности в форме
Рихтмайера, Мортона (1964), добавляемая к уравнению (11.3.1),
имеет вид
D=-a1Ax4-g—а2Дг/4-^ (а, > 0, а2 > 0). (11.3.14)
В расчете невязких течений эту формулу использовали, например,
Барнуэлл (1971) и Чанг (1980); в расчетах движения вязкой
жидкости ее апробировали Гноффо (1974), Бим и Уорминг (1978),
Стегер (1978), Ле Баллёр и др. (1980). Ее дискретный аналог
Di,i — уравнение (10.1.2) — включается в общую схему (2.8.8)
:314

либо (2.8.9) на корректирующем шаге или осуществляется третий
шаг, сглаживающий значения функции f^+f по формуле
Ш=П^+Оп^\ (11.3.15)
Анализ устойчивости такой схемы в одномерном случае приводит
к ограничению на коэффициенты: O^ai, a2^Ve.
Для неявной схемы предыдущего раздела вязкость (11.3.14)
расщепляется: D = Di+D2
Dx = -a^xAd*fldx\
D2 = -a2&y4d4f/dy\
Аппроксимация этих выражений на временном слое п включается
в правую часть соответствующих уравнений (2.8.17а, б),
представляющих два шага обобщенного метода чередующихся
направлений, который применяется для решения уравнения (11.3.13)
в соответствии с описанием, содержащимся в п. 2.8.5.
Другую форму подавления нежелательных осцилляции
применили Мак-Кормак и Болдуин (1975) в явной расщепляющейся
схеме (см. п. 2.8.4), которая основывалась на схеме (2.7.10) при
a = ß=Y = l; искусственная вязкость, например, в направлении х
имеет вид
Разностный аналог этого выражения добавляется на каждом из
двух шагов схемы таким образом, что D7} . =At(Sn. . —S7} А . ) и
с» . — Art (\ /,? . I 4- //? Л 1 PÏ+\,I— 2Pl /+ P?-l. /1 (fn t сn \
P/ + 1, /+ 2pt-f j+ pt_K j
на первом шаге; Bi, j=At(Si+\,j — Si,j) и
Si,j = 4a(\ui,j\ + citj) ft + li/ + 2ft>/ + ft_|f/ lft./-fi-ij
на втором шаге. Для устойчивости необходимо выполнение
условия: O^a^Ve. Вместе с тем, как указывается в работе,
неустойчивость может индуцироваться адвективным членом при
изменении знака скорости, т. е. в зонах возвратного течения.
Неустойчивость устраняется при замене адвективного члена и71. ер? . на
2 ("«•,/ +"/+!,/) в предикторе и йГ+i,/Ф?+1, / на 72(ß?, / + S/ +i, /)Х
ХФ?+1,у в корректоре.
11.4. Разностные схемы в криволинейных координатах
Задачи расчета невязких течений в областях сложной геометрии
обсуждались в главе 10. В случае вязкой жидкости многие
стороны этих задач трактуются аналогично. Вместе с тем наличие
315

тонких слоев с доминирующими вязкостными эффектами
(пограничный слой и «вязкий скачок») делает необходимым адаптацию
сетки не только к геометрии области, но и к самому решению.
Заметим, что последнее требование не является спецификой
задач движения вязкой жидкости — оно относится и к расчетам
движения идеальной жидкости в области возникновения больших
градиентов. Задачи на адаптирующихся сетках являются весьма
сложными, если рассматривать их во всей общности. Интересные
способы построения самоадаптирующихся сеток как
функционалов решения предложили Гауф и др. (1975), Яненко и др. (1979),
Шёнауэр и др. (1980), Дуайер и др. (1980) для, различных
специальных случаев, допускающих обобщения.
До настоящего времени методы, используемые на практике
для расчетов в областях сложной конфигурации, строятся на
менее общих принципах и обычно апеллируют к априорным
представлениям о поведении решения. При этом сетка может быть
построена с различной степенью сложности, например: 1)
аналитически с помощью формул преобразования координат; 2) с
помощью методов конформных отображений или некоторых общих
приемов (Моретти, 1976, 1977; Чу, 1971; Томпсон и др., 1974;
Айземан, 1978, 1980) наряду с растяжением координат (Соренсон,
Стегер, 1977); 3) путем дробления сетки (Вивиан и Гацци, 1976;
Ле Баллёр и др., 1980).*
При рассмотрении течений в криволинейной области расчет
может быть выполнен либо непосредственно в заданной физической
области, либо в преобразованной вычислительной области. В этом
разделе обсуждаются оба подхода и приводятся примеры
расчетов.
11.4.1. Дискретизация в трансформированной области
При отображении физической области существования решения на
каноническую область уравнения Навье—Стокса записываются
в криволинейных координатах и аппроксимируются некоторой
разностной схемой. Для представления векторных и тензорных
величин существуют две возможности.
Согласно одной из них, в качестве локального базиса можно
выбрать какую-либо из обычных ортогональных криволинейных
систем координат, например полярную (Моретти и Салас, 1969;
Таннехилл и др., 1975), параболическую (плоский случай: Пейре
и Вивиан, 1972, 1973; осесимметричный: Вейльмунстер и Грейвс,
* Одной из первых в этом направлении была работа Годунова С. К-, Про-
копова Г. П. О расчетах конформных отображений и построении разностных
сеток.— ЖВМ и МФ, 1967, т. 7, № 5; изложение развитого подхода содержит
работа Годунова С. К-, Забродина А. В., Прокопова Г. П. Численное решение
многомерных задач газовой динамики в подвижной криволинейной системе
координат.— ИПМ АН СССР, препринт № 66, 1976; подходы к построению
оптимизированных сеток и библиография содержатся в обзоре Номофилова Е. В.,
Пирогова Э. П., Тревгоды В. М. Анализ численных методов моделирования
задач гидродинамики, 1983, ФЭИ—1400, Обнинск.— Прим. перев.
.316

1981), сферическую (Викториа и Уидхоф, 1973). Результаты,
полученные Пейре и Вивианом (1973) на основе такого подхода,
представлены на рис. 11.4.1. В области расчета показан фронт
вязкого скачка и звуковая линия для случая сверхзвукового
потока (Моо = 2), обтекающего плоское тело при низких числах Рей-
нольдса (Re = 25 и 50 при характерной длине, определяемой
протяженностью тела), числе Прандтля Рг = 0,72 и показателе
адиабаты 7=1 А Уравнения Навье—Стокса (с постоянным коэффи-
4| Вязкий скачок
Рис. 11.4.1. Вязкий скачок и звуковая линия при
обтекании параболического тела, Моо = 2,0.
циентом вязкости) интегрировались псевдонестационарным
методом, рассмотренным в п. 11.1, на основе формул
дифференцирования (11.1.2). Граничными условиями вверх по потоку являлись
условия равномерного потока, а параметры течения на границе вниз
по потоку определялись линейной экстраполяцией. Отношение
температуры поверхности тела к температуре внешнего потока
принималось равным 1,2. На контуре тела давление не
вычислялось, поскольку для градиента давления по нормали к контуру
использовались направленные разности.
Вместо локального базиса обычно удобнее задавать векторы
и тензоры в фиксированной декартовой системе координат,
сохраняя уравнения записанными в криволинейных координатах.
Отметим, в частности, выполненный в такой постановке расчет
обтекания полусферы—цилиндра сверхзвуковым потоком по явной
схеме Мак-Кормака (Вивиан и Гацци, 1976), в приближении
317

пограничного слоя —расчеты обтекания крыла (Стегер, 1978; Сте-
гер и Бейли, 1980), оживала и полусферы — цилиндра (Шифф
и Стегер, 1980; Пуллиам и Ломэкс, 1979; Пуллиам и Стегер,
1980). В этих работах уравнения интегрировались по явной схеме
Бима—Уорминга (1978) (см. п. 11.3.2); в некоторых расчетах для
описания турбулентности использовались модели вихревой
вязкости.
Рис. 11.4.2. Расчет трехмерного обтекания
полусферы—цилиндра при M00 = l,2, а=19°, Re© =
= 4,45-105. (Любезно предоставлен Пуллиамом.)
Течения: основное —5р, вторичное — Ss.
Результаты, полученные Пуллиамом, Стегером (1980) и
Пуллиамом, Ломэксом (1979), относятся к обтеканию полусферы—
цилиндра под углом атаки (рис. 11.4.2). Уравнения
преобразовывались к криволинейной системе координат (g, т], £) с
координатами (g, г]), меняющимися в направлении тела, так что его
поверхность соответствовала уравнению £=const. Вязкостью в
направлениях g, т] пренебрегалось. На рисунке для сравнения
приводятся рассчитанные значения давления и параметров отрывного
течения и полученные экспериментально. Несмотря на принятые
допущения, результаты представляются вполне приемлемыми.
Что касается полных уравнений Навье—Стокса, то Вивианом
(1978), а также Шамротом и Гибелингом (1979) отмечалось, что
в случае больших деформаций сетки их квазиконсервативная
форма (см. уравнения (1.31а), п. 1.2.3) является более
предпочтительной, нежели консервативная форма (1.31). Дело в том, что
318

при вычислении производных по вводимым криволинейным
координатам необходимо обратить особое внимание на исключение
ошибок аппроксимации в выражениях для метрики, содержащих
якобианы преобразования (Вивиан и Вейо, 1978). Расчеты
обтекания цилиндра и профиля NACA 0012 выполнены Шамротом
и Гибелингом (1979) по уравнениям Навье—Стокса в
квазиконсервативной форме, которые интегрировались по схеме Брайли—
Макдональда (1973) на сетке, построенной методом Айземана
(1978).
11.4.2. Дискретизация в физической области
Другой подход к решению задач для уравнений Навье—Стокса
заключается в численном интегрировании уравнений в декартовых
Рис. 11.4.3. Разностные операторы на
криволинейной сетке.
координатах на нерегулярной сетке, адаптированной к сложной
геометрии области и, возможно, к характеру решения. Для
нахождения решения можно использовать различные методы: конечно-
разностные (Вивиан и Вейо, 1978; Ле Баллёр и др., 1980),
конечных объемов (Дейверт, 1975) или конечных элементов (Бейкер,
1978; Куке и Бланшар, 1979). Отметим, что результаты,
полученные с помощью различной аппроксимационной техники, близки
между собой.
11.4.2.1. Разностная схема. Опишем конечно-разностный
метод, предложенный Вивианом и Вейо (1978) для расчета
невязких течений и развитый для течений с вязкостью в работах Хол-
ландерса и Вивиана (1980), Ле Баллером и др. (1980). Метод
представляет обобщение явной схемы Мак-Кормака (2.8.8).
Рассмотрим плоскую неравномерную сетку (рис. 11.4.3), узлы
которой Р определяются индексами (/, /). Сетка обычно строится
путем преобразования координат, и локализация узлов (/, /)
определяется декартовыми координатами (х, у). Аппроксимация
производных ду/дх, ду/ду некоторой функции ф(д:, у) в точке Р
319

определяется через значения ф в Р и двух соседних точках Q и /?,
не лежащих с ней на одной прямой (рис. 11.4.4). Имеем
(JS-\ = , д V = АФр* byPQ - AcppQ AyPR
Аг/pQ àxPR — &yPR l±*Pq
A<pPR kxPQ — AcppQ AxPR
AxPQ AyPR — Дхря A^/pQ
(11.4.1a)
(11.4.16)
где
q>p-
АфР^ = (pR — фр, AxP# = xR — xP, &yPR = yR — yPi
■значение ф в точке Р с координатами (хР, уР) и т. д.
Рис. 11.4.4. Ячейка сетки.
Эти формулы можно вывести различными способами: 1)
разложением ф в ряд Тейлора относительно точки Р с первым
порядком точности; 2) в предположении, что ф (х, у) —
кусочно-линейная функция в каждом из треугольников PQR; 3) воспользоваться
формулами (3.7.11) при аппроксимации производных по |, ц
направленным разностям.
Рассмотрим точку Р и четыре соседних с ней точки N, 5, Еу W
(см. рис. 11.4.3) и определим разностные операторы типа (11.4.1):
А*, Д* — использующие точки Р, N, Е и Д*х*, А** —
использующие точки W, Р, S. Дискретизация уравнений Навье—Стокса
(11.3.1) в декартовых координатах осуществляется по двухшаго-
вой схеме
Гit I = fi f - А* (АХ / + a;G7. /), ( 11.4.2а)
f 7.7 = -y (f?. / + h i) - ^r (A"^. / + A^' /) • <11 A26)
где Fitf = F(fitj)9 Gi,f = G (/*,/)• Диссипативные слагаемые Fv, Gv
в векторах F и G содержат первые производные составляющих
скорости и, и, а также внутренней энергии е. Эти производные
аппроксимируются с привлечением операторов А*^*, А** на
промежуточном шаге и операторов Д*Л, Д*^ на окончательном шаге.
В случае равномерной прямоугольной сетки схема (11.4.2)
представляет схему Мак-Кормака (2.8.8); входящие в уравнения
смешанные производные дифференцируются согласно (11.3.7).
320

Ошибка аппроксимации схемы (11.4.2) в скалярном случае
имеет порядок 0(АЕи AtAE2, At2, А£22)> где
Д£, = max (| РЕ + PW |, | PN + PS |),
ДЯ2 = тах(|РЕ|, |PW|, |PN|, |PS|),
т. е. схема имеет второй порядок точности, если A£i = 0(A£2).
Для устойчивости должно выполняться условие (11.3.10), где
Ax = min(|PE|, |PW|, I PN I, |PS|).
I w
- Зона (r+f)
2
1=/
Зона г
Зона (r-f)
Рис. 11.4.5. Сгущение сетки и
сращивание соседних зон.
11.4.2.2. Метод сгущения узлов сеточной области. При
дискретизации уравнений Навье—Стокса в физической области часто
требуется дробление сетки с тем, чтобы получить достаточно
подробное описание эффектов в пограничном слое. Параллельно
с растяжением координат или в сочетании с этим используется
способ, основанный на разбиении области расчета на зоны, в
которых шаги сетки отличаются вдвое (Вивиан и Гацци, 1975;
Ле Баллер и др., 1980). Такому разбиению отвечает
последовательная процедура сращивания решений в соседних зонах в
процессе интегрирования по времени.
Опишем этот метод для случая, когда дробление сетки
осуществляется в направлении у; пусть граница у = 0 является
стенкой, у которой развивается пограничный слой. Область
разбивается на R зон: yir^y^y{Q А* = 1, 2, ..., R. В каждой зоне
шаг AyW постоянен и при переходе к следующей зоне подчинен
условию А#с+1) = 2Ду(г), т. е. Ay(r+v = 2r Ду(1). Зоне 1 соответствует
вязкий подслой, прилегающие к стенке у = 0; зоне R отвечает
область внешнего течения с шагом Ау. Таким образом, Дг/=Д#(Н) =
= 2R~iAyW. Отношением AyW/Ay = 2i-R характеризуется степень
сгущения сетки в вязком подслое.
321

Для сращивания решений в соседних зонах они перекрываются
(рис. 11.4.5) так, что строки каждого столбца представляют
линии узлов у = у(? =у([)+(/— 1)Л#(Г), /=1, 2, ..., Lr для зоны г.
В схеме (11.4.2) решение на временном слое t + At в точке Р
использует решение слоя t в двух рядах узлов, прилегающих к Р.
Следовательно, в каждой зоне г две нижние и две верхние
узловые линии должны рассматриваться как граничные, и решение на
момент t + A№ определяется только на внутренних узловых
линиях. Решение /<г) в момент t + A№ на граничных линиях /=1, 2;
Lr-u Lr зоны г получается сращиванием значений в соседних
зонах согласно условиям
fir) r(r-l) .(Г) c(r-l) ni iQv
П =Дг-|-4, Ï2 =fLr_i-2 (11.4.da)
и
/Ç-fir+l). fÇ-i=^(-/ïr+I4 9(^+1) + fr+1))-/r+1)).
(11.4.36)
Шаг по времени А№ и число шагов ЛЛГ> в зоне г, необходимых
для перехода от t к f + Д* при Д/ = Д/<Д), определяется
соотношениями
дг(г)=2(г)д;(1), г>1,
N{r)=2R~r, (11.4.4)
где шаг Д^1) в зоне 1 должен удовлетворять условию
устойчивости (11.3.10). Изменение временного шага в (11.4.4) отвечает
максимально допустимым значениям в каждой зоне г>1, если
устойчивость схемы определяется условием Куранта—Фридрихса—Леви
(11.3.8).
Продвижение решения от t к / + Д/(Д> осуществляется двумя
шагами в зоне 1 и одним шагом в зоне 2. На границе зон
решения сращиваются по формулам (11.4.3), что дает новые
граничные условия на момент t + 2 Д/(1) = ^ + Д^2). Процесс продолжается
до нахождения решения во внешней области R. Важно отметить,
что получаемое решение не согласовано во времени с решением
нестационарных уравнений. В стационарном случае это
несущественно, если схема устойчива. Для получения удовлетворительных
нестационарных решений необходимо уточнение процедуры
расчета на границах между зонами.
11.4.2.3. Примеры. Приведем два примера использования
схемы (11.4.2) совместно с процедурой дробления сетки для
расчета стационарных течений. Работы выполнены группой Вивиана
(ONERA) и относятся ко взаимодействию скачка с пограничным
слоем и обтеканию профиля. В обоих случаях средой является газ
с y = 1,4 и вязкостью, вычисляемой по формуле Сазерленда.
На стенке течение принимается адиабатическим и скольжение от-
322

сутствует. Значения внутренней энергии ew и давления pw на
стенке определяются путем использования односторонних
разностных отношений соответственно в условии адиабатичности
de/dN и в уравнении количества движения, нормальном к стенке.
Взаимодействие скачка с пограничным слоем на пластине
рассматривалось для потока с Моо = 2 и Reoo,*s =2,96-105, где xs —
расстояние от передней кромки пластины до точки воздействия
невязкой ударной волны. Для интенсивности скачка принималось
Рис. 11.4.6. Область расчета и сетка в задаче
взаимодействия скачка с пограничным слоем на пластине.
а — фронт скачка, б — косой скачок уплотнения (без учета
вязкости).
Р//роо=1,4 (pf — теоретическое значение давления отраженной
ударной волны вниз по потоку); число Прандтля принималось
равным 0,72. Падающая ударная волна рассматривалась как
разрыв во внешнем потоке. В расчете скачок улавливался
(«размазывался») схемой (11.4.2) с добавлением искусственного
демпфирования на третьем шаге в соответствии с (11.3.15) при ai=a2 =
= 10_3. Область расчета взаимодействия скачка с пограничным
слоем представлена на рис. 11.4.6. На основе вспомогательного
расчета, не представленного здесь, определяется обтекание
пластины в области от границы свободного потока до точки л: = 0,7
вниз по потоку. Этот расчет дает краевые условия на границе
вверх по потоку, на противоположной границе используется
линейная экстраполяция; верхняя граница вычислительной области
расположена в области свободного потока.
Опишем конструкцию сетки, изображенной на рис. 11.4.6. Она
априорно адаптирована к особенностям задачи, включающей
преобразование координат (х, у)^-(х, у), где
323

Функция уе(х), определяющая внешнюю границу
вычислительной области, и функции ßi(x), ß2 (х) должны удовлетворять
следующим условиям:
1) внешней границе пограничного слоя, определяемой как уь =
= 7x/yRex, отвечает (/ = 0,025;
2) фронту скачка, оцениваемому координатой ys(x)=x/8,
отвечает // = 0,8;
3) внешней границе области уе(х) отвечает линия //=1,07.
Рис. 11.4.7. Распределение изобар для взаимодействия
скачка с пограничным слоем на пластине.
Далее используется дополнительное преобразование (#, у) ->•
-*-(Х, У), дающее равномерное распределение узлов сетки с
шагами АХ, ДУ:
J^±_. = ±X(X+1), y=±Y(3Y+l),
где хо, х\ — боковые границы области. Тем самым сетка
разрежается в направлении х и сгущается в направлении у. Это
позволяет обойтись всего тремя зонами в непосредственной
близости у стенки, используя процедуру, описанную в п. 11.4.2.2, число
узловых линий: Li = 17, L2=13, L3=20. Обращением
используемых преобразований определяются декартовы координаты узлов,
относительно которых записана схема (11.4.2). Рисунок 11.4.7
представляет карту изобар отрыва и отошедшей ударной волны;
линии тока в зоне отрыва показаны на рис. 11.4.8.
Второй пример относится к расчету сверхзвукового обтекания
крыла NACA 0012 при Mœ = 2 и числе Рейнольдса, вычисленном
по хорде крыла, Re =106 и Рг = 0,723. Расчетная сетка части
области приведены на рис. 11.4.9. Сетка построена путем решения
обыкновенных дифференциальных уравнений, определяющих
ортогональные траектории / = const семейства кривых / = const;
324

/=1—контур профиля. Общее число узлов составляет 101x23,
процедура дробления сетки осуществлялась в трех зонах с Li =9,
L2 = 7, /,з = 3, причем последняя зона по сеточным параметрам
уже не отличалась от* остальной области.
У
от
0,0/
Рис. 11.4.8. Линии тока отрывного течения при
взаимодействии скачка с пограничным слоем на пластине.
Рис. 11.4.9. Сеточная область расчета обтекания
профиля NACA0012.
На границе вверх по потоку ставились краевые условия,
отвечающие равномерному течению, а вниз по потоку условия
определялись линейной экстраполяцией. На рис. 11.4.10а, б приведены
изолинии плотности (р/роо = const), рассчитанные и полученные
экспериментально д-ром Аллегре (лаборатория Аэротермики, Ме-
дон). Область счета составляла половину всей области с
использованием условия симметрии при нулевом угле атаки
набегающего потока. На рис. 11.4.11 показаны изолинии чисел Маха при
325

Ofi 1ft Iß
Рис. 11.4.10a. Изолинии относительной плотности (р/р^) при
обтекании профиля NAC А 0012 при ^=2,0; а=0. (Любезно
предоставлен ONERA.)
Рис. 11.4.106. Измеренное поле изолиний р/Роо при обтекании
профиля N АСА 0012; ^4^=2,0; а=0. (Любезно предоставлен
д-ром Алегре.)
326

обтекании того же профиля с углом атаки 10°. Вычисления
выполнялись во всей области, ибо симметрия в этом случае
отсутствует.
Рис. 11.4.11. Изолинии чисел
Маха при обтекании профиля _jq
NAC А 0012; ^=2,0; а-0. " '
Список литературы
Березин Ю. А., Ковеня В. М., Яненко H. Н. Об одной неявной схеме расчета
течения вязкого теплопроводного газа.—* Численные методы механики
сплошной среды. 1972, 3, № 4, 3—18.
Allen, J. S., and Cheng, S. I. Phys. Fluids 18, 37—52 (1970).
Baker, A. J. Finite-Element Analysis of Turbulent Flows. In: Proceedings of the
1st International Conference on Numerical Methods in Laminar and Turbulent
Flow, pp. 203—229, Pentech Press, Swansea (1978).
327

Baldwin, В. S., and MacCormack, R. W. AIAA Paper No. 74-558 (1974).
Baldwin, В. S., MacCormack, R. W., and Deiwert, G. S. Numerical Techniques
for the Solution of the Compressible Navier—Stokes Equations and
Implementation of Turbulent Models. In: AGARD-LS-73, Computational Methods of
Inviscid and Viscous Two- and Three-Dimensional Flow Fields, pp. 2.1—2.24,
Von Karman Institute, Rhode-St.-Genèse, Belgium (1975).
Barnwell, R. W. A Time-Dependent Method for Calculating Supersonic Angle of
Attack Flow about Axisymmetric Blunt Bodies with Sharp Shoulders and
Smooth Non-axisymmetric Blunt Bodies. NASA-TND-6283, Wash., D. C, August
(1971).
Beam, R. M., and Warming, R. F. /. Comput. Phys. 22, 87—110 (1976).
Beam, R. M., and Warming, R. F. AIAA J. 16, 393—402 (1978). (PTK, 16, N 4,
с 145.)
Beam, R. M., and Warming, R. F. SIAM J. Sei. Statis. Comput. 1, 131—159
(1980).
Berezin, Yu. A., Kovenja, V. M., and Yanenko, N. N. Lecture Notes in Physics,
Vol. 35, pp. 85—90, Springer-Verlag, New York (1975a).
Berezin, Yu. A., Kovenja, V. M., and Yanenko, N. N. Comput. Fluids 3, 271—281
(1975b).
Bokhari, S., Hussaini, M. Y., Lambiotte, J. J., and Orszag, S. A. A Navier—Stokes
Solution on the CYBER-203 by a Pseudospectral Technique. ICASE Rept.
No. 81—12 (1981).
Brailovskaya, I. Yu. Fluid. Dyn. 2, 49—55 (1967).
Briley, W. R., and McDonald, H. An Implicit Method for the Multidimensional,
Nonstationary Navier—Stokes Equations. United Aircraft Research Laboratory
Rept. M911363-6, November (1973).
Briley, W. R., and McDonald, H. J. Comput. Phys. 24, 372—397 (1977).
Carter, J. E. Lecture Notes in Physics, Vol. 19, pp. 69—78, Springer-Verlag, New
York (1973).
Chu, W. H. /. Comput. Phys. 8, 392—408 (1971).
Chang, J. S. AIAA Paper No. 80-0272 (1980).
Cooke, С H., and Blanchard, D. К. Int. J. Numer. Eng. 14, 271—286 (1979).
Courant, R., Friedrichs, К. О., and Lewy, H. Math. Ann. 100, 32—74 (1928).
[English translation: IBM J. Res. Dev. 11, 215—234 (1967)]. (Курант P.,
Фридрихе K.-O., Леви Г. О разностных уравнениях математической физики.—
У. M. Н., 1940, VIII.)
Crocco, L. AIAA J. 3, 1824—1832 (1965). (PTK, 13, N 10, с. 430.)
Deiwert, G. S. AIAA J. 13, 1354—1359 (1975). (PTK, 13, N 10, с 120.)
Deiwert, G. S. Lecture Notes in Physics, Vol. 59, pp. 159—163, Springer-Verlag,
New York (1976).
Dwyer, H. A., Kee, R. J., and Sanders, В. R. AIAA J. 18, 1205—1212 (1980).
(PTK, 18, N 10, с 70.)
Eiseman, P. R. J. Comput. Phys. 26, 307—338 (1978).
Eiseman, P. R. Coordinate Generation with Precise Controls over Mesh Properties.
ICASE Rept. No. 80—30 (1980).
Engquist, E., and Maida, A. Math. Comput. 31, 629—651 (1977).
Euvrard, D., and Tournenmine, G. /. Méc. 12, 419—461 (1973).
Gnoffo, P. A. Solutions of the Navier—Stokes Equations for Supersonic Flow
Over Blunt Bodies in a Generalized Orthogonal System. M. S. Thesis,
Polytechnic Institute of Brooklin, New York (1974).
Gough, D. O., Spiegel, E. A., and Toomre, /. Lecture Notes in Physics, Vol. 35,
pp. 191—196, Springer-Verlag, New York (1975).
Gustaffson, В., and Sundström, A. SIAM J. Appl. Math. 35, 343—357 (1978).
Hedstrom, G. W. /. Comput. Phys. 30, 222—237 (1979).
Hollanders, H., and Peyret, R. Rech. Aérosp. No. 1981—4, 287—294 (1981).
Hollanders, H., and Viviand, H. The Numerical Treatment of Compressible High
Reynolds Number Flows. In: Computation Fluid Dynamics, Von Karman
Institute Book, Vol. 2, pp. 1—65, Hemisphere Publishing, Washington, D. С (1980).
Hung, G. M., and MacCormack, R. W. AIAA J. 15, 410—416 (1977). (PTK, 15,
N 3, с 150).
Lax, P. D., and Wendroff, B. Commun. Pure Appl. Math. 17, 381—398 (1964).
328

LeBalleur, J. С, Peyret, R., and Viviand, H. Comput. Fluids 8, 1—30 (1980).
MacCormack, R. W. AIAA Paper No. 69-354 (1969).
MacCormack, R. W. Lecture Notes in Physics, Vol. 8, pp. 151 — 161,
Springer-Verlag, New York (1971).
MacCormack, R. W. An Efficient Numerical Method for Solving the
Time-Dependent Compressible Navier—Stokes Equations at High Reynolds Number. NASA
TM.73129; also in: Computing in Applied Mechanics, Applied Mechanics
Division, Vol. 18, ASME, New York, (1976a).
MacCormack, R. W. Lecture Notes in Physics, Vol. 59, pp. 307—317,
Springer-Verlag, New York (1976b).
MacCormack, R. W. Lecture Notes in Physics, Vol. 148, pp. 254—267, Springer-
Verlag, New York (1981a).
MacCormack, R. W. AIAA Paper No. 81-0110 (1981b).
MacCormack, R. W., and Baldwin, B. S. AIAA Paper No. 75-1 (1975).
MacCoimack, R. W., and Lomax, H. Numerical Solution of Compressible Viscous
Flow, In: Annual Reviews of Fluid Mechanics, Vol. 11, pp. 289—316, Annual
Reviews Inc., Palo Alto, CA (1979).
Menta, U., and Lomax, H. Reynolds Averaged Navier—Stokes Computations of
Transonic Flows: The State of the Art. In: Symposium on Transonic
Perspective, Ames Research Center, NASA, February (1981).
Moretti, G. Conformai Mappings for computations of steady, Three-dimensional,
supersonic flows. In: Numerical/Laboratory Computer Methods in Fluid
Mechanics, A. A. Pouring and V. I. Shan, Eds., pp. 13—28, ASME, New York
(1976).
Moretti, G. Computation of Shock Layers About Ablated Blunt-Nosed Bodies,
Polytechnic Institute cf New York, Rept. 77-14, August (1977).
Moretti, G., and Salas, M. D. AIAA Paper No. 69-139 (1969).
Murman, E. M., and Cole, J., AIAA J. 9, 121—141 (1971). (PTK, 9, N 1, с 137.)
Oden, J. T., and Wellford, L. С. AIAA J. 10, 1590—1599 (1972). (PTK, 10, N 12,
с 47.)
Peyret, R. Rech. Aérosp. No. 1971-3, 133—138 (1971).
Peyret, R., and Viviand, H. Rech. Aérosp. No. 1972-3, 123—131 (1972).
Peyret, R., and Viviand, H. Lecture Notes in Physics, Vol. 19, pp. 228—229,
Springer-Verlag, New York (1973).
Peyret, R., and Viviand, H. AGARDograph, No. 212, September (1975).
Polezhaev, V. I. Fluid Dyn. 2, 70—74 (1967).
Pulliam, T. R, and Lomax, H. AIAA Paper 79-0206 (1979).
Pulliam, T. R, and Steger, J. L. AIAA J. 18, 159—167 (1980). (PTK, 18, N 4,
с 39.)
Richtmyër, R. D., and Morton, К. W. Stability Studies with Difference Equations.
(1) Nonlinear Stability, (2) Coupled Sound and Heat Flow. Courant Institute
of Mathematical Sciences, New York University Rept. NYO-1480-5 (1964).
Richtmyer, R. D., and Morton, K. W. Difference Methods for Initial Value
Problems, Interscience, New York (1967) (Рихтмайер P., Мортон К. Разностные
методы решения краевых задач.— М.: Мир, 1972). ,
Roache, P. J. Computational Fluid Dynamics, Hermosa Publishing, Albuquerque,
NM (1972) (Роуч П. Вычислительная гидродинамика.— M.: Мир, 1980).
Rudy, О., and Stiikwerda, J. /. Comput. Phys. 36, 55—70 (1980).
Scala, S. M., and Gordon, P. Solution of the Navier—Stokes Equations for
Viscous Supersonic Flows Adjacent to Isothermal and Adiabatic Surfaces. In:
Proceedings of the 1969 Symposium on Viscous Interaction Phenomena in
Supersonic and Hypersonic Flow, pp. 319—391, University of Dayton Press,.
Dayton, OH (1970).
Schiff, L. В., and Steger, J. L. AIAA J. 18, 1421—1430 (1980). (PTK, 18, N 12,
с 16.)
Schönauer, W., Glotz, G., and Raith, К. The solution of the laminar boundary
layer equations by variable self-adaptive difference methods. In: Recent
Advances in Numerical Methods in Fluids. С Taylor and K. Morgan, Eds. Vol. 1,
pp. 81—118. Pineridge, Swansea, U. K. (1980).
Shamroth, S. J., and Gibeling, H. J. A Compressible Solution of the Navier—Stokes
Equations for Turbulent Flow about an Airfoil. NASA-CR-3183 (1979).
329

Sorenson, R., and Steger, J. L. Simplified Clustering of Nonorthogonal Grids
Generated by Elliptic Partial Differential Equations. NASA-TM-73252 (1977).
Steger, J. L. AIAA J. 16, 679—686 (1978), (PTK, 16, N 7, с 51.)
Steger, J. U and Bailey, H. E. AIAA J. 18, 249—255 (1980). (PTK, 18, N 4,
с 151.)
Takami, H., and Keller, H. В. Phys. Fluids 12, Supp. II, 1151—1156 (1969).
Tannehill, J. C, Mohling, R. A., and Rakich, J. V. AIAA J. 12, 129—130 (1974).
[See also AIAA Paper No. 73-200 (1973)]. (PTK, 12, N 2, с 3.)
Tannehill, J. С, Holst, T. L., and Rakich, J. V. AIAA Paper No. 75-154 (1975).
Thommen, H. U., Z. Angew. Math. Phys. 17, 369—384 (1966).
Thompson, J. F., Thames, F. С, and Mastin, С. M. /. Comput. Phys. 15, 299—
319 (1974).
Victoria, K. J., and Widhoff, G. F. Lecture Notes in Physics, Vol. 19, pp. 254—
267, Springer-Verlag, New York (1973).
Viviand, H. Traitment des Problèmes d'Interaction Fluide Parfait — Fluide Vis-
quex en Ecoulement Bidimensionel Compressible à partir des Equations de
Navier—Stokes. AGARD-LS-94 on Three-Dimensional and Unsteady Separation
of High Reynolds Numbers, pp. 3.1—3.21, Von Karman Institute, Rhode-St-
Genèse, Belgium (1978).
Viviand, H. Lecture Notes in Physics, Vol. 141, pp. 44—54, Springer-Verlag, New
York (1981).
Viviand, H., and Ghazzi, W. Lecture Notes in Physics, Vol. 59, pp. 434—439,
Springer-Verlag, New York (1976).
Viviand, H., and Veuillot, J.-P. Méthodes Pseudo-Instationnaires pour le Calcul
d'Ecoulements Transsoniques. Publication ONERA No. 1978—4, (1978).
Weilmuenster, K. J., and Graves, Jr. R. A. AIAA J. 19, 1089—1090 (1981). (PTK,
19, N 10, с 3.)
Yanenko, N. N., Lisseikin, V. D., and Kovenja, V. M. Lecture Notes in Physics,
Vol. 91, pp. 48—61, Springer-Verlag, New York (1979).
Список дополнительной литературы
Белоцерковский О. M. Численное моделирование в механике сплошных
сред.—M : Наука, 1984, 520 с.
Воскресенский Г. П., Чушкин П. И. Численные методы решения задач
сверхзвукового обтекания тел.— Итоги науки и техники. Механика жидкости
и газа. II. М., 1978, с. 5-65.
Годунов С. К., Забродин А. В., Иванов М. Я., Край ко А. Н.,
Прокопов Г. П. Численное решение многомерных задач газовой динамики.—
М.: Наука, 1975, 400 с.
Русанов В. В., Поспелов В. В. Исследование течений жидкости и газа.—
Итоги науки и техники. Математический анализ, М., 1975, с. 57—98.
Теоретические основы и конструирование численных алгоритмов задач
математической физики/Под ред. К. И. Бабенко.— М.: Наука, 1979.
Чушкин П. И., Шмыглевский Ю. Д. Обзор исследований по газовой
динамике.—М,., 1980, 62 с.
330

Заключительные замечания
В этой книге авторы попытались дать обзор
численных методов, используемых для решения гидродинамических
задач в Европе и США. К сожалению, в этом обзоре не освещены
методы, разработанные в СССР; мы приводим лишь тот материал,
который оказался нам доступным и не вошел в монографию
М. Холта, опубликованную в этой же серии.
Стремительный прогресс вычислительной гидродинамики
позволяет легко допустить, что существуют результаты, нам еще не
известные, несмотря на то, что при подготовке книги мы стардлись
поддерживать тесные контакты с различными исследовательскими
группами. Среди других подходов следует, по-видимому, отметить
перспективы развития приложений конечноэлементных и
спектральных методов.

Приложение А
Устойчивость
Рассмотрим разностную схему
Clui + l + CoUnh+C^lunh-l = 09 (АЛ)
где Ci, Со, C-i — конечно-разностные операторы, Uh^u(xhy nAt),
u=(ui, ..., «m), x=(xi, ..., Xd)y & узлами Xft выражается
пространственная дискретизация: Xh=(y\Ax, ..., уааха), уь • • •> Yd—
целые числа; tn = nAt, п — целое число.
Устойчивость схемы (АЛ) обычно изучается с применением
дискретного преобразования Фурье к функции и£ ; член ряда
имеет вид
unh = Un(k)exp(\k'Xh) (А.2)
где i = V—1, k=(&i, ..., ko) — волновой вектор. Подстановка
этого выражения в (АЛ) после сокращения на exp (ik-x^)
приводит к уравнению
QxUn + ' + O0Un + G-xUn-l= 0. (А.З)
Такая трехслойная схема преобразуется в двухслойную путем
введения вспомогательной переменной Vn = Un-{. Получим
QxUn + ' + G0Un + 0-Уп = 0, (А.4)
vn+x -ип = о,
что можно записать в виде
фп + 1 = ОФп, (А.5)
где Ф=(£/, V) — 2га— компонентный вектор, G — матрица
размерности 2га X 2т.
Для устойчивости схемы (условие фон Неймана) необходимо,
чтобы спектральный радиус матрицы перехода G не превышал
единицы, т. е.
p(G) = max|A,/|<l, 0 < ft/А*/< 2л, /=l,...,d, (А.6)
где Ki — собственные числа матрицы С* Эти собственные числа
являются корнями алгебраического уравнения
det(G — М) = 0,
где / — единичная матрица, т. е. К — корни многочлена степени
q = 2га
f(K) = a0 + alK+. . . + aqKq = S в/*/. (AJ)
причем коэффициенты a/ могут быть комплексными числами.
* Точнее 1 + 0 (АО (см. примечание на с. 45).
332

Заметим, что если схема является двухслойной (C_i = 0), то
в скалярном случае матрица G состоит из одного элемента g,
называемого множителем перехода, и, согласно (А.6):
|#|<1, (ХбуДх/^л, /=1,..„ d. (А.8)
Исследование корней /(À)=0 упрощается при использовании
результатов Миллера (1971). Приведем формулировки теоремы,
содержащей условия того, что нули полинома f (X) удовлетворяют
условию (А.6); доказательство теоремы вместе с некоторыми
другими интересными фактами содержится в работе Миллера.
Определим полином (а0Ф0, аяФ0)
f(l) = a*olq + ... + a*q= £ aq-,k!, (А.9)
/-о
где а* — числа, комплексно сопряженные а/. Рассмотрим
полином fi (X):
fiM = ±U(0)f(X)-f(0)r№ (АЛО)
степени не выше, чем q—1. Утверждается, что нули X полинома
f (X) таковы, что |А,|^1 в случае, если либо (1): \f(0) | > |/(0) |,
причем нули fi (X) не выходят за пределы единичного круга, либо
(2): /i^eO и нули df/dX не выходят за пределы единичного круга.
Согласно этой теореме изучение нулей / сводится к
нахождению нулей полинома меньшей степени; такая процедура при
повторном воспроизведении последовательно упрощает анализ.
Вместе с тем при больших q проверка условий теоремы может
оказаться весьма сложной; тогда определение устойчивости схемы
может быть выполнено численно.
Такая возможность заключается в нахождении собственных
значений матрицы G численными методами. Вычисления
выполняются при различных параметрах задачи, после чего поведение X
в зависимости от этих параметров можно представить графически.
Полезно выполнить предварительное аналитическое исследование
устойчивости в простых случаях: при уменьшении размерности
задачи, обращении в нуль некоторых физических параметров,
задании связи между компонентами волнового вектора, фиксировании
гармоник. Такой предварительный анализ зачастую позволяет
определить приближенную форму критерия устойчивости, который
можно уточнить вычислением собственных значений матрицы
перехода.
Список литературы
Miller, J. J. H. /. Inst. Math. AppL 8, 397—406 (1971).
333

Приложение Б
Метод последовательности сеток
Численная реализация конечно-разностных и конечно-
элементных аппроксимаций может встретиться с трудностями
получения приемлемо точных решений при ограниченных
вычислительных возможностях. Метод, предложенный Федоренко (1964)*,
позволяет, вообще говоря, находить решения, отвечающие мелкой
сетке, используя численные решения на более грубых сетках, что
приводит к экономии времени и стоимости расчета.
Метод анализировался Бахваловым (1966) и применялся
Брандтом (1977), Саутом и Брандтом (1977), Джеймсоном
(1979)**. Метод использовался в расчетах сверхзвуковых течений,
но может применяться и в других задачах.
В линейном случае метод последовательности сеток
формулируется следующим образом. Пусть разностное уравнение
LU = F (Б.1)
аппроксимирует дифференциальную краевую задачу относительно
неизвестной вектор-функции U на сетке й^ с шагом h. Пусть uh —
приближение к Uh, полученное в результате всего нескольких
итераций какого-либо процесса, например, простых итераций.
Обозначим через vh возникающую на сетке Ùh погрешность
vh = Uh - и. (Б.2)
Известно, что в процессе итераций высокочастотные гармоники
конечного ряда Фурье погрешности vh эффективно гасятся.
Каждая итерация уменьшает вклад высокочастотных гармоник
погрешности почти вдвое и для нахождения сглаженной сеточной
функции vh можно воспользоваться сеткой более грубой,
например, вдвое более крупной сеткой ßH. Относительно поправки vH
на сетке йя, согласно (Б.1), имеем уравнение
LHvH = iïfh (Б.З)
* Метод последовательности сеток предложен в более ранней работе
Р. П. Федоренко.— ЖВМ и МФ, 1961, т. 1, N° 5.— Прим. перев.
** См. также Астраханцев Г. П. Об одном итерационном методе решения
сеточных эллиптических задач.— ЖВМ и МФ, 1971, т. 11, № 2.
Астраханцев Г. П., Руховец Л. А. Метод релаксации на последовательности сеток для
эллиптических уравнений с естественными краевыми условиями.— ЖВМ и МФ,
1981, т. 21, № 4; Оганесян Л. А. Метод Федоренко—Бахвалова для двумерного
эллиптического уравнения в случае задачи Дирихле.— Изв. АН АрмССР,
Математика, 1983, 18, № 2.— Прим. перев.
Относительно другой формы метода ' последовательности сеток, обобщающей
экстраполяцию Ричардсона, см. Волков Е. А. Решение задачи Дирихле методом
уточнений разностями высших порядков.— Диф. уравнения, 1965, 1, № 8; Шай-
дуров А. В. Об одном методе повышения точности разностных решений.—
Численные методы механики сплошной среды, 1972, 3, № 2. Щербаков А. В.,
Кочергин В. П. Метод вложенных сеток в задачах динамики океана.—
Численные методы механики сплошной среды, 1977, 8, № 2.— Прим. перев.
334

с однородными граничными условиями, где Л* —оператор
интерполяции с Qh на Qh, fh — невязка, определяемая подстановкой
uh в (Б.1)
th = Fh-Lhuh. (Б.4)
После нескольких итераций интерполируем поправку vH на
исходную сетку и определим исправленную функцию и\
u^uh + lhHhH, (Б.5)
где IhH—оператор интерполяции с QH на Qh. Интерполяция
поправки вносит некоторую погрешность в новое значение и\,
Фурье-разложение которой будет содержать высокие гармоники.
Их можно эффективно погасить несколькими шагами исходного
итерационного процесса, приняв и\ за начальное приближение.
В случае большого числа узлов сеточной области решение
задачи на одной вспомогательной крупной сетке может все еще
оставаться достаточно трудоемким, ибо основные затраты связаны
с интегрированием до сходимости уравнения (Б.З) на QH.
Рассмотрим конечную последовательность равномерных сеток; сетку
с минимальным шагом обозначим М, с максимальным — N. Общий
алгоритм представляется следующим образом.
1. На исходной М-сетке выполним несколько итераций
уравнения
LMUM = FM, (Б.6)
чтобы погасить высокочастотную компоненту еще неизвестной
погрешности. Результат обозначим им.
2. Для определения поправки vM = UM — им рассмотрим задачу
LM + lvM + l + IÜ + xfM (Б.7)
на укрупненной (Af+1) -сетке. После нескольких итераций
«поправка к погрешности» сглаживается. Такая процедура
повторяется на последовательности сеток с увеличивающимся шагом
до конечной Л^-сетки. На ней vN итерируется до сходимости.
3. Начинаем возвращение на мелкую сетку. Интерполируем
последнюю поправку vN на более мелкую (N — 1 ) -сетку,
корректируем значение Vм-1 и, приняв исправленное значение v% 1 за
начальное приближение, делаем несколько итераций, чтобы
сгладить погрешность интерполяции. На некоторой Ä-сетке при
переходе к ней от более грубой (*+1) -сетки коррекция к поправке
имеет вид
На последнем этапе интерполируем поправку vM+l на исходную
Af-сетку, находим коррекцию: и* = им + /*J+, vM+l и после
335

нескольких сглаживающих итераций получаем окончательный
результат.
В нелинейном случае для решения на &-сетке, использующем
значения на более мелкой (k—1)-сетке, Брандт (1977)
предложил следующую форму:
LV = L*(/ft-i«*-I) + /*-i(/?*-I-L*-,a*-'). (Б.9)
Значения uk~x получаются при переходе k-*k— 1 по схеме
ил =и +Ik [и —Ik-\ti ). (Б.10)
Обоснование процедуры отсутствует, но Брандт (1977) и Джейм-
сон (1979) показали ее пригодность.
В заключение отметим, что приведенная стратегия
монотонного движения k-+k+l (k = M, Л4+1, ..., N—1, N) и обратно
допускает модификацию. Порядок переходов на сетках может
иметь эвристический характер, определяясь эффективностью
сглаживания промежуточных невязок (Брандт, 1977).
Метод последовательности сеток исключительно эффективен.
Число арифметических действий, необходимых для получения
решения общего эллиптического уравнения с точностью е, имеет
порядок 0(-р-1п—J, т. е. в расчете на узел не зависит от шага
сетки (Бахвалов, 1966).
Список литературы
Бахвалов Н. С. О сходимости одного релаксационного метода при естественных
ограничениях на эллиптический оператор.— ЖВМ и МФ> 1966, 6, 5, 101—135.
Федсренко Р. П. О скорости сходимости одного итерационного процесса.— ЖВМ
и МФ, 1964, 4, 3, с. 227—235.
Brandt, A. Math. Comput. 31, 333—390 (1977).
Jameson, A. AIAA Paper No 79-1458 (1979).
South, J. C, and Brandt, A. In: Transonic Flow Problems in Turbomachinery,
Т. C. Adamson, and M. F. Platzer, Eds., pp. 180—207, Hemisphere Publishing*
Washington, D. С (1977).
Приложение В
Метод сопряженных градиентов
В ходе изложения неоднократно упоминалось о
высокой эффективности использования метода сопряженных градиентов
для решения систем алгебраических уравнений, возникающих
в результате дискретизации исходной дифференциальной задачи.
В работе Хослы и Рубина (1981) показано, что реализация
разностной схемы, аппроксимирующей уравнение Лапласа методом
сопряженных градиентов, обеспечивает более быструю сходимость
по сравнению с широко употребляющимися методами: точечной
336

релаксации, последовательной релаксации по линиям, неявным
методом чередующихся направлений и полностью неявной
процедурой (Стоун, 1968).
На преимущества этого метода указывает также Кершоу
(1978), отметивший, что он в 6000 раз быстрее метода поточечных
итераций Гаусса—Зейделя, в 200 раз быстрее метода
чередующихся направлений и в 30 раз быстрее последовательной блочной
релаксации.
В работе Гловински и др. (1980) указывается на
преимущества использования метода сопряженных градиентов для решения
систем уравнений, порождаемых конечно-элементными
аппроксимациями. Следует ожидать, что он окажется столь же
эффективным и для спектральных аппроксимаций. Вывод метода
сопряженных градиентов приведен в работе Бекмана (I960)*. Опишем его.
Запишем систему алгебраических уравнений в матричном виде
Ax = ky
где х — вектор. Метод является итеративным и применяется в
следующей последовательности.
1. Задается начальное приближение xq.
2. Вычисляется ро = r0 = k — Axq.
3. Вычисляется а,- = | п |2/ (pt, Api).
4. Вычисляется хi+i = xi+ <XiPi.
5. Вычисляется r/+i = n — айр*.
6. Вычисляется ß* = | rf+i |2/1 п |2.
7. Вычисляется p/+i==ri+i + ßiPi.
Здесь (р/, Api)—скалярное произведение векторов р, и Лр/.
Заметим, что для определения а/, ßf возможна и другая
(усложненная, но более точная) форма:
п _ (Р*. п) R _ (п + i, Apj)
Щ~ (Pi, APi) ' Р<— (pit APi) *
Эта техника основывается на процессе ортогонализации
Грама—Шмидта последовательности векторов. Возможности
метода обычно ограничены симметричными и положительно
определенными матрицами, однако его можно использовать и в случае
любой положительной матрицы Л, симметризуя ее
преобразованием
(АТА) х = ATk, Ат {Ах - k) = ATri,
где Ат — матрица, транспонированная к А. При этом алгоритм
решения выглядит следующим образом:
r0 = k — Ax0t ро = ATr0y
OLi
xi + l = Xi + aipi
_ \ATrt\2
— \APt\* •
-a
= J
iApi,
ATri + l\*
\A'nf
Pi+l =
* См. также: Бахвалов H. С. Численные методы, I.— М.: Наука, 1973.
Марчук Г. И., Кузнецов Ю. А. Теория и применение обобщенного метода
сопряженных градиентов.— Новосибирск, 1980.— Прим. перев.
337

Приведенная процедура обеспечивает быструю сходимость
итерационного процесса решения алгебраических уравнений,
порождаемых различными схемами дискретизации уравнений
гидродинамики.
Список литературы
Beckman, F. S. In: Mathematical Methods for Digital Computers, A. Ralston and
H. S. Wilf, Eds., pp. 62—72, John Wiley & Sons, New York (1960).
Glowinski, R., Periaux, J., and Pironneau, O. Appl. Math. Modelling 4, 187—192
(1980).
Khosla, P. K., and Rubin, S. G. Comput. Fluids 9, 109—122 (1981).
Kershaw, D. S. /. Comput. Phys. 26, 43—65 (1978).
Stone, H. L. SI AM J. Numer. Anal. 5, 530—558 (1968).

Именной указатель
А
Аббет (Abbett. M J.) 270 , 275 , 296
Адам (Adam Y.) 39 , 40 , 41
Азиз (Aziz К.) 139 , 197
Айземан (Eiseman P. R.) 316
Аллен (Allen J. S.) 64 , 302 , 308
Альберт (Albert J.) 109
Альзар де Рокфор (Alziary de Roquefort) 200
Амсден (Amsden A. A.) 163
Ансельм (Enselme M.) 12
Анучина H. H. 52
Апсон (Upson С. D.) 171
Атвелл (Atwell N. P.) 261
Б
Бабенко К. И. (Babenko К. I.) 296
Баракат (Barakat H. Z.) 192
Барнуэлл (Barnwell R.) 298
Батлер (Butler D. С.) 137
Бауэр (Bauer F.) 270
Бахвалов H. С. 334 , 336
Бейкер (Baker A. J.) 131 , 215 , 304
Бейли (Bailey H. Е.) 318
Бекман (Beckman F. S.) 337
Бергер (Berger A. E.) 42 , 43
Березин Ю. A. (Berezin Yu. A.) 79 , 303
Берковье (Bercovier M.) 171 , 218
Бернар (Bernard P. S.) 132
Бёрд (Bird G. A.) 264
Бёрстейн (Burstein S. Z.) 55
Бим (Beam R. M.) 52 , 66 , 69 , 70 , 79 , 303 , 311 , 318
Биркгоф (Birkhoff G.) 131
Бланшар (Blanchard D. K.) 304
Бланшон (Blanshong G. P.) 169
Боземан (Boseman J. D.) 186
Болдуин (Baldwin В. S.) 303 , 304 , 305 , 310 , 315
Болхауз (Ballhaus W. F.) 289
Бонне (Bonnet J. P.) 200
Бонту (Bontoux P.) 41 , 72 , 183 , 198 , 203 , 205
Боппе (Ворре С. W.) 289 , 290
Борис (Boris J. P.) 109 , 265
Бохари (Bokhari S.) 304
Бохачевский (Bohachevsky I. О.) 274 , 282
Браиловская И. Ю. (Brailovskaya I. Yu.) 64 , 302
Брайен (Bryan К.) 185
Брайли (Briley W. R.) 69 , 79 , 80 , 186 , 197 , 199 , 303 , 308 , 311
Брамбль (Bramble J. H.) 65 , 149
Брандт (Brandt А.) 334 , 336
Бристо (Bristeau M. О.) 90 , 222 , 224 , 267
Броше (Brochet J.) 12
Брэдшоу (Bradshaw P.) 249 , 265
Буассо (Boisseau J. P.) 12
Буйяр (Bouard R. С.) 212
Бук (Book D. L.) 109 , 265
Бурграф (Burggraf О. R.) 82 , 200

Бурсье (Bourcier M.) 139 , 201
Бэтчелор (Batchelor G. К.) 129
В
Вабах (Wahbah) 130 , 189
Вайнберг (Weinberg В. С.) 82
Вакспресс (Wachspress Е. L.) 207 , 211
Ван Леер (VanLeer В.) 277
Варга (Varga R. S.) 28
Вейльмунстер (Weilmuenster К. J.) 316
Вейо (Veuillot J. P.) 269 , 272 , 276
Вельдман (Veldman A. E. P.) 35 , 193
Вендроф (Wendroff B.) 52 , 58 , 274 , 310
Вивиан (Viviand H.) 7 , 269 , 272 , 276 , 302 , 303 , 304 , 308 , 316 , 318 , 321
Викториа (Victoria K. J.) 303 , 308 , 317
Вичелли (Viecelli J. A.) 170
Вольфштейн (Wolfshtein M. Y.) 213 , 214 , 261
Воскресенский Г. П. (Voskresenskii G. P.) 299
By (Wu J. C.) 129 , 130 , 189
Вудс (Woods L. C.) 207
Г
Газдаг (Gazdag J.) 240
Ганн (Gunn J. E.) 71 , 79 , 182
Ганулис (Ganoulis J.) 143
Гарабедян (Garabedian P. R.) 29 , 30
Гауф (Gough D. O.) 316
Гацци (Ghazzi W.) 308 , 316 , 317 , 321
Гиа (Ghia K. N.) 41
Гиа (Ghia U.) 41
Гибелинг (Gibeling H. J.) 318
Гиро-Валле (Guiraud-Vallée) 132
Глаз (Glaz H. M.) 278 , 280
Глимм (Glimm J.) 118 , 280
Гловински (Glowinski R.) 218 , 222 , 223 , 337
Гноффо (Gnoffe P. A.)
Годунов С. К. (Godunov S. К.) 9 , 31 , 115 , 277
Гордон (Gordon P.) 308
Госмен (Gosman A. D.) 195 , 255
Готлиб (Gottlieb D.) 14 , 88 , 89 , 99 , 107 , 108 , 230 , 235
Грант (Grant J. R.) 254 , 257
Грейвс (Graves Jr. A.) 316
Грешо (Gresho P. M.) 217 , 218 , 220
Грийо (Grillaud G.) 200
Гринспен (Greenspan D.) 185 , 190 , 192 , 200
Гросман (Grossman R.) 267 , 269
Гупта (Gupta M. M.) 186 , 187 , 200 , 206
Гурлей (Gourlay A. R.) 78 , 79
Густафсон (Gustaffson B.) 64 , 305
Д
Дальтон (Dalton C.) 186
Д'Атторе (D'Attore L.) 296
Де Валь Дэвис (De Vahl Davis G. J.) 139 , 182 , 196 , 200
Дэвиль (Deville M. O.) 163 , 235 , 238
340

Дейверт (Deiwert G. S.) 113 , 115 , 303
Деннис (Dennis S. С. R.) 35 , 140 , 193 , 207
Дёрст (Durst F.) 254
Джеймсон (Jameson А.) 289 , 290 , 291 , 334 , 336
Дим (Deem G. S.) 145
Дирдорф (Deardorf J. W.) 258
Доб (Daube О.) 41 , 74 , 183
Дональдсон (Donaldson С.) 251
Дородницын А. А. 187
Дуайер (Dwyer H. А.) 316
Дуглас (Douglas J.) 71 , 79 , 182
Ж
Жиро (Giraut V.) 215
3
Забуски (Zabusky N. J.) 145
Залесак (Zalesak S. T.) 109 , 265
Замир (Zamir M.)
Занг (Zang T.) 230
Зенкевич (Zienkiewicz О. C.) 96 , 214
и
Изааксон (Isaacson E.) 27 , 82
Израэли (Israeli M.) 12 , 186 , 187
Ингэм (Ingham D. В.) 213
Иннис (Innis G. E.) 261
Инуе (Inouye M.) 113
Иошихара (Yoshihara H.) 77 , 267
Истон (Easton C. R.) 163
К
Kao (Kao T. W.) 177
Картер (Carter J. E.) 308
Катлер (Kutler P.) 55 , 60 , 137 , 296 , 299
Кашмен-Русин (Cushman-Roisin B.) 155
Кварини (Quarini G. L.) 253 , 257
Келлер (Keller H. В.) 27 , 209 , 307
Келлог (Kellog О. D.) 126
Келс (Keils L. С.) 165 , 235 , 238
Кенцер (Kentzer С. Р.) 298
Кершоу (Kershaw D. С.) 269 , 337
Ки (Кее R. J.) 328
Киллин (Killeen J.) 68 , 79
Ким (Kim J.) 237
Клайн (Cline M. С.) 137
Кларк (Clark R. A.) 192 , 253 , 258
Ковеня В. M. (Kovenja V. M.) 82 , 330
Колелла (Colella P.) 118 , 278 , 280
Коллатц (Collatz L.) 38
Кордулла (Kordulla W.) 83
Коул (Cole J.) 269 , 289 , 307
Кофи (Caughey D. A.) 289 , 290 , 293
341

Кох (Koch F.) 299
Краузе (Krause E.) 42
Крейс (Kreiss H. О.) 58 , 64 , 187
Кристиансен (Christiansen J. P.) 132 , 133
Крокко (Crocco L.) 302
Крэгс (Craggs J. W.) 127
Кузнецов В. Г. (Kuznetsov В. G.) 153
Кук (Cook R. N.) 213
Куке (Cooke С. H.) 304
Кули (Cooley J. W.) 230
Куломбе (Coulombeix С.) 289 , 290
Курант (Courant R.) 49 , 52 , 310
Кутансо (Coutanceau M.) 212
Л
Лав (Love M. D.) 253
Лаваль (Laval P. C.) 74 , 78
Ладевез (Ladevéze J.) 159 , 166
Лаке (Lax P. D.) 43 , 51 , 52 , 58 , 274 , 310
Ланцош (Lanczos C.) 104 , 108 , 111
Лаундер (Launder В. E.) 251 , 255
Ле Баллёр (Le Balleur J. С.) 264 , 310 , 316 , 321
Левенталь (Leventhal S. H.) 81
Леви (Lewy H.) 48 , 82 , 328
Леконт (Lecointe Y.) 41 , 42
Леонард (Leonard A.) 131
Лера (Lerat A.) 54 , 55 , 56 , 58 , 69 , 70 , 74 , 75 , 76 , 77 , 81 , 280 , 288
Лесли (Leslie D. C.) 253 , 257
Ли (Lee R. L.) 217
Лин (Lin T. C.) 279
Линдемат (Lindemuth J.) 68 , 79
Липманн (Liepmann H. W.) 137
Лисейкин В. Д. (Lisseikin V. D.) 330
Лиу (Liu N.) 170
Ломэкс (Lomax H.) 55 , 60 , 84 , 289 , 304 , 318
Лоус (Laws G. T.) 302
Лугт (Lugt H. J.) 209
Любимов A. H. (Lyubimov A. N.) 299
M
Магнус (Magnus R.) 77 , 267 , 270
Майда (Majda A.) 307
Майерс (Myers R.) 12 , 107 , 109 , 228
Мак-Гир (McGuire G. R.) 55 , 78 , 79
Макдональд (McDonald H.) 69 , 79 , 80 , 303 , 308 , 311
Мак-Кормак (MacCormack R. W.) 54 , 55 , 74 , 78 , 113 , 302 , 303 , 304 , 305 ,
311 , 315
Мак-Миллан (McMillan О. J.) 258
Малинсон (Mallinson G. D.) 139 , 182 , 196 , 200
Манохар (Manohar R. P.) 186 , 200 , 206 , 287
Маркони (Marconi F.) 299
Маршалл (Marshall R. S.) 171
Меллер H. A. 187
Меллор (Mellor G. L.) 251
Мессон (Masson B. S.) 267 , 269 , 278 , 282 , 288
Мета (Mehta U. B.) 41 , 304
Меткаф (Metcalfe R. W.) 9 , 235 , 257 , 258
342

Мёрдок (Murdock J. W.) 12 , 104 , 107 , 165 , 235 , 240
Милинаццо (Milinazzo F.) 131 , 132
Миллер (Miller J. J.) 67 , 333
Митчелл (Mitchell A. R.) 63 , 71 , 73
Михалке (Michalke A. J.) 10
Мойн (Moin P.) 237
Моретти (Moretti G.) 53 , 267 , 269 , 274 , 296 , 299 , 308 , 316
Морзе (Morse A.) 251
Моррис (Morris J. L.) 55 , 78 , 79
Мортон (Morton K. W.) 14 , 43 , 53 , 58 , 66 , 169 , 269 , 304
Моршуазн (Morchoisne Y.) 107 , 139 , 165 , 231 , 235 , 240 , 244 , 246
Myp (Moore D. W.) 131
Мурман (Murman E. M.) 269 , 289 , 307
(Mangier K. W.) 127
H
Ндефо (Ndefo E.) 142 , 171
Нейман , фон (von Neumann J.) 58 , 332
Нерон (Néron M.) 80
О
Оден (Oden J. T.) 304
Олейннк О. А. 51
Олигер (Öliger J.) 58
Орзаг (Orszag S. А.) 12 , 14 , 67 , 88 , 89 , 99 , 107 , 108 , 165 , 186 , 230 , 231 ,
235 , 238 , 257 , 259
п
Пан (Pan W. M.) 213 , 261
Паркер (Parker I. В.) 98
Паттерсон (Patterson G. S.) 257
Пейре (Peyret R.) 12 , 35 , 41 , 54 , 56 , 58 , 70 , 74 , 81 , 157 , 166 , 169 , 175 , 180 ,
205 , 302 , 304 , 307 , 316
Перио (Periaux J.) 90 , 267
Перье (Perrier P.) 120
Пике (Piquet J.) 41 , 42
Пиронио (Pironneau O.) 120 , 218 , 222
Пирсон (Pearson С. E.) 185 , 197
Писмен (Peaceman D. W.) 71 , 182
Полежаев В. И. (Polezhaev V. I.) 303 , 308
Поллей (Paullay A. J.) 113
Прахт (Pracht W. E.) 163 , 165
Пуллиам (Pulliam T. H.) 318
P
Рабберт (Rubbert P. E.) 125
Равьяр (Raviart P. A.) 34 , 215
Райли (Riley J. J.) 9 , 235 , 257 , 258
Рандл (Rundle K.) 125 , 127
Ранчел (Runchal A. K.) 186 , 190 , 192 , 195 , 196 , 213 , 261
Ребах (Rehbach С.) 132
Ребурсе (Rebourcet В.) 175 , 180
Реддал (Reddall W.) 279
343

Рейнольде (Reynolds W. С.) 251
Рейсби (Raithby G. D.) 196
Ривлин (Rivlin T. J.) 98
Рис (Rees M.) 82
Рисе (Reece G. J.) 261
Рихтмайер (Richtmyer R. D.) 14 , 43 , 53 , 54 , 55 , 58 , 66 , 169 , 269
Рицк (Rizk Y. M.) 130
Риччи (Rizzi A. W.) 103
Роберте (Roberts A. L.) 125 , 127 , 133
Робинсон (Robinson A. R.) 12 , 120
Рогалло (Rogallo R. S.) 257
Роди (Rodi W.) 248 , 251 , 254 , 255
Розенхед (Rosenhead L.) 131
Рой (Roy P.) 240
Роуч (Roache P.) 14 , 33 , 139 , 186 , 190 , 200 , 207 , 308
Рошко (Roshko A.) 137
Py (Roux B. J.) 82
Рубин (Rubin S. G) 12 , 35 , 39 , 41 , 55 , 200 , 203 , 269 , 274 , 282 , 336
Руди (Rudy О.) 307
Русанов В. В. (Rusanov V. V.) 274 , 299
Рэкич (Rakich J. V.) 137 , 299
Рэчфорд (Rachford H. H.) 71 , 182
Рябенький В. С. 31
С
Саарис (Saaris G. R.) 125
Сайде (Sides J.) 77 , 280 , 288
Саймент (Ciment M.) 39 , 42 , 81
Салас (Salas M. D.) 308 , 316
Сандерс (Sanders В. R.) 328
Сандстрём (Sundström А) 305
Саульев В. К. 304
Саут (South Jr. J.) 289 , 334
Сафмен (Saffman P. G.) 131 , 132
Cea (Céa J.) 189 , 206
Силе (Sills J.) 177
Скала (Scala S. M.) 308
Смагоринский (Smagorinski J.) 249 , 253
Смит (Smith A. M.) 125 , 128 , 130 , 266
Сод (Sod G. A.) 118 , 280
Солимен (Soliman M. O.) 215
Соломон (Solomon J. M.) 81
Соренсон (Sorenson R.) 316
Сполдинг (Spalding D. В.) 213 , 251 , 261
Стегер (Steger J. L.) 52 , 289 , 316 , 318
Стерн (Stern M. A.) 289 , 290
Стоун (Stone H. L.) 337
Стрикверда (Strikvverda J.) 307
Стрэнг (Strang G.) 78
т
Таками (Takami H.) 209 , 307
Таиг (Tang С.-М.) 67
Таннехилл (Tannehill J. С.) 308 , 316
Ta Ovok Лок (Ta Phuoc Loc) 35 , 41 , 74 , 183 , 193 , 200 , 208
Тейлор (Taylor T. D.) 12 , 89 , 104 , 107 , 109 , 118 , 142 , 165 , 171 , 230 , 235 ,
266 , 279 , 282 , 288
344

Темам (Temam R.) 143 , 158 , 164 , 170
Тиррио (Thirrio С.) 143
Том (Thorn А.) 185
Томас (Thomas P. D.) 296 , 298
Томассет (Thomasset F.) 215
Томен (Thoman H. V.) 197
Томмен (Thommen H. U.) 60 , 64 , 74 , 76 , 77 , 270 , 296 , 302 , 311
Томпсон (Thompson J. F.) 130 , 270 , 316
Торренс (Torrance К. E.) 192 , 195 , 196 , 200
Турнемин (Tournemine G.) 269 , 307
Тьюки (Tukey J. W.) 230
У
Уидхоф (Widhoff G. F.) 303 , 308 , 317
Уилкс (Wilkes J. О.) 185
Уильяме (Williams G. L.) 140 , 158
Уолкден (Walkden F.) 296 , 299
Уорминг (Warming R. F.) 52 , 55 , 56 , 58 , 60 , 66 , 69 , 70 , 79 , 303 , 311 , 318
Уэлфорд (Wellford) 304
Уэлш (Welsh J. E.) 143 , 158 , 161
Ф
Фавр (Favre A. J.) 265
Фасел (Fasel M. J.) 140
Федоренко P. П. 334
Фейрвезер (Fairweather G.) 63 , 73
Ферри (Ferri A.) 137
Феррис (Ferris D. H.) 330
Ферцигер (Ferziger J. H.) 252 , 258
Фишер (Fisher J.) 131
Флетчер (Fletcher CA.) 216 , 217 , 267
Фокс (Fox L.) 98
Форестье (Forestier В.) 82
Фортен (Fortin M.) 145 , 153 , 158 , 159 , 163 , 166 , 172 , 200
Франсуа (Francois С.) 139 , 201
Фридман (Friedman G.) 247 , 278
Фридрихе (Friedrichs К. О.) 82 , 328
Фромм (Fromm J. E.) 197
X
Хаббард (Hubbard В. E.) 65
Хайет (Hyett В. J.) 56 , 58
Хаймен (Hyman J. M.) 82
Xa Мин (Ha Minh H.) 254 , 257
Ханг (Hung С. M.) 303
Харлоу (Harlow F. H.) 143 , 158 , 161 , 163
Хартен (Harten А.) 58
Хартманн (Hartmann С.) 169
Хаттон (Hutton A. J.) 216 , 224
Хедстром (Hedstrom G. W.) 307
Хедфогель (Haidvogel D. В.) 12 , 108 , 230 , 231 , 235 , 237
Хеллумс (Heliums J. D.) 139 , 197
Херринг (Herring H. J.) 251
Xecc (Hess- J. L.) 125 , 126 , 127 , 130
Хёрт (Hirt С. W.) 58

Хёрш (Hirsh R. S.) 12 , 40 , 41 , 107 , 140 , 230
Хирасаки (Hirasaki G. L.) 139
Хиршель (Hirschel E. H.) 83
Холд (Hald O. H.) 131
Холден (Holden M.) 287
Холландерс (Hollanders H.) 81 , 304 , 305
Холт (Holt M.) 14 , 86 , 137 , 263 , 269 , 277 , 330
Хосла (Khosla P. M.) 12 , 35 , 39 , 41 , 200 , 203 , 269 , 336
Хослинг (Haussling H. J.) 209
Хофман (Hoffman J. D.) 137
Хьюз (Hughes T. J.) 171
4
Чайлдрес (Childress S.) 169
Чанг (Chang J. S.) 193 , 269
Чанг (Chang T. J.) 215
Чанг (Chang J.-Z.) 35
Чассенг (Chassaing P.) 254 , 257
Чебеки (Cebeci T.) 139 , 266
Чен (Chan L. T.) 267
Чен (Chan S. Т. К.) 293
Ченг (Cheng S. I.) 35 , 64 , 302 , 308
Чепмен (Chapman D. R.) 10
Чорин (Chorin A. J.) 118 , 131 , 132 , 142 , 152 , 155 , 158 , 159 , 163 , 170
Чу (Chu W. H.) 316
Ш
Шамрот (Shamroth S. G.) 318
Шанкс (Shanks S. P.)
Шатто (Chattot J. J.) 289 , 290
Шевчик (Szewczyk A. A.) 197
Шёнауэр (Shönauer W.) 316
Шин (Shin С. T.) 82
Шифф (Schiff L. В.) 318
Шмидт (Schmidt W.) 289
Шокин Ю. И. (Shokin Y. I.) 52 , 58
Шоу (Shaw W. Y.) 261
Шубин (Shubin G. J.) 35
Шульман (Schulman E. E.) 12 , 120
Шуман (Schumann V.) 257
э
Эврар (Euvrard D.) 269 , 307
Эйдала (Aidala P. V.) 289 , 290
Эллис (Ellis M. A.) 139
Эльзассер (Elsaesser E.) 41 , 205
Энгельман (Engelman M.) 171
Энквист (Engquist E.) 307
Я
Ямада (Yamada T.) 251
Яненко H. H. (Yanenko N. N.) 52 , 58 , 63 , 71 , 79 , 142 , 171 , 316
346

Предметный указатель
Аппроксимации ошибка 30 , 32 , 37 ,
44 , 49 , 56 , 65 , 68 , 75 , 145 , 151 , 155 ,
166 , 178 , 192 , 321
Вязкость
аппроксимационная 56 , 117 , 254 ,
265
искусственная 35 , 37 , 58 , 194 , 265 ,
270 , 289 , 290 , 294 , 314
Граничные условия 63 , 73 , 137 , 187
в замкнутой области 171 , 201 , 305
в методе
двухшаговом 63
искусственной сжимаемости 148
«отражения» 148 , 151 , 165
проекционном 159 , 165
спектральном 88
чередующихся направлений 63 ,
79 , 80 , 184
для вихря 129 , 186 , 198 , 203 , 208 ,
290
давления 152 , 162 , 164 , 236 , 242 ,
245 , 308
скорости 141 , 305
вверх по потоку 241 , 270 , 272 ,
307 , 317 , 323 , 325
вниз по потоку 236 , 242 , 270 ,
272 , 290 , 307 , 317 , 323 , 325
функции тока 184 , 201 , 208 , 211 ,
228
на сетке
разнесенной 143 , 148 , 153
совмещенной 153
периодические 227 , 236 , 258
«поглощения» 307
Метод
взвешенного остатка 85
Галеркина 84 , 89 , 106 , 216 , 218
Гаусса—Зейделя 28 , 146 , 165 , 168 ,
170 , 178 , 206 , 303
дискретных вихрей 131 , 133
дробных шагов 158 , 163
исключения Гаусса 128
искусственной сжимаемости 141 ,
151 , 154 , 158 , 165 , 169
итерационный 28 , 35 , 143 , 166 , 169 ,
189 , 192 , 197 , 201 , 245
коллокаций 40 , 86 , 240
компактного оператора 38 , 39 , 43
конечных объемов 111 , 277 , 280 ,
303 , 304 , 319
конечных элементов 86 , 89 , 92 , 102 ,
121 , 215 , 304 , 319
А , (Я-метод Моретти) 274 , 283 , 296
М-метод 38 , 42
маркеров и ячеек 148 , 158 , 161 , 170
моментов 86
наименьших квадратов 86 , 90 , 216 ,
222
облака в ячейках 133
обобщенный чередующихся
направлений 80 , 182 , 303 , 315
последовательной релаксации 28 ,
147 , 186 , 204 , 289 , 291 , 294
последовательности сеток 289 , 334
проекционный 158 , 170
псевдонестационарный 142 , 182 ,
244 , 303 , 317
псевдоспектральный 91 , 106 , 237 ,
240 , 244 , 258 , 267
расщепления 63 , 78 , 113 , 137 , 161 ,
165 , 171 , 303
Рунге-Кутта 229
Рэлея-Ритца 84
скачка
выделения 53 , 269 , 308
улавливания (размазывания) 53 ,
137 , 269 , 299 , 308 , 323
сопряженных градиентов 108 , 223 ,
269 , 336
спектральный 9 , 86 , 89 , 98 , 103 ,
108 , 122 , 227 , 235 , 264 , 267
т (т-метод) 89 , 104
факторизации 26 , 69 , 157 , 183 , 268 ,
311
характеристик 134 , 298 , 304
чередующихся направлений 63 , 71 ,
73 , 156 , 182 , 183 , 197 , 200 , 207 , 209 ,
289 , 303 , 337
штрафа 170 , 218
Эрмита 12 , 38 , 40 , 203 , 206 , 210
Якоби 28 , 47 , 174
ячейковый 84 , 106 , 111 , 277
Обтекание
космического корабля 291
полусферы — цилиндра 318
профиля
зубчатого 274
крыловидного 244 , 270 , 290 , 318
КС 135 291
NAC А 0012 281 , 324
NLR 7301 270
сферы 276
цилиндра 207 , 220 , 278
Пограничный слой 31 , 264 , 305 , 321
Схема
Адамса—Бэшфорта 67 , 107 , 164 ,
220 , 229
Аллена—Ченга 64 , 302
асимметричная по потоку 48 , 75 ,
157 , 196
347

Бима—Уорминга 66 , 303 , 312 , 318
Браиловской 64 , 302
Брайли—Макдональда 69 , 311 , 319
Глимма 118 , 135 , 277 , 280
Годунова 115 , 124 , 135 , 275 , 277 ,
278 , 282 , 285
двухшаговая (предиктор —
корректор) 54 , 59 , 62 , 74 , 113 , 220 , 280
девятиточечная 76
Дюфорта—Франкела 50 , 154 , 256 ,
303
Кранка—Николсона 66 , 67 , 164 ,
166 , 177 , 259 , 304
Лакса 52 , 274
Лакса—Вендрофа 53 , 54 , 58 , 60 ,
76 , 274
мажорантная 52
Мак-Кормака 54 , 55 , 60 , 63 , 64 ,
74 , 77 , 269 , 274 , 299 , 302 , 303 , 304 ,
317 320
Мурмана—Коула 289 , 291
несогласованная 50 , 302 , 303
неявная 40 , 65 , 71 , 122 , 163 , 169 ,
210 , 268 , 304 , 311
Писмена—Рэчфорда 71 , 81 , 182
пятиточечная 60 , 62 , 63 , 178
Рихтмайера 54 , 76 , 79
Русанова 274
Саульева 304
с весом 34
с разностями против потока
(ветра) 33 , 48 , 52 , 73 , 155 , 192 , 200
с разностями против потока с
весом 33 , 34 , 48 , 49 , 196
с разностями против потока с
коррекцией 35 , 36 , 109 , 193 , 194 , 200 ,
204 , 265
семиточечная 60
согласованная 44 , 50 , 151
Томмена 60 , 76 , 77 , 270 , 281 , 302 ,
309
трехслойная 50 , 66 , 155 , 169
центральноразностная 58 , 154 , 173
четвертого порядка точности 40 ,
43 , 178
явная 41 , 43 , 52 , 70 , 74 , 78 , 89 ,
143 , 170 , 268 , 309
явно — неявная 182
Течение
в канале 171 , 174 , 235
возвратное 194 , 315
из сопла 224 , 266 , 269
изэнтропическое 135
жидкости
несжимаемой 21 , 128 , 139
вязкой 235
невязкой 115 , 134 , 207 , 228
нестационарное 9 , 115 , 134 , 175 ,
196 , 207
стационарное 145 , 171 , 175 , 181 ,
200 , 224
сжимаемой 115 , 134
вязкой 14 , 17 , 51 , 59 , 264 , 302 ,
309
дозвуковое 263 , 278
околозвуковое 266
сверхзвуковое 263 , 317 , 324
турбулентное 265
невязкой 263 , 266
дозвуковое 263 , 269 , 278 , 288
нестационарное 266 , 268
околозвуковое 266 , 271 , 282 ,
290
сверхзвуковое 77 , 134 , 263 , 274 ,
280 , 281 , 286 , 295
стационарное 136 , 266 , 276 , 285 ,
288 , 295
над пластиной 235 , 241
отрывное 13 , 318 , 324
потенциальное 125 , 268 , 270 , 288 ,
291
при взрыве 279
при выстреле 13 , 279
при запуске ракеты 8 , 263 , 279
разреженное 264
стратифицированное 13 , 175 , 257
струйное 175 , 256
турбулентное 9 , 13 , 235 , 248 , 257 ,
265
Ударная волна 51 , 57 , 110 , 118 , 263
Уравнение
гиперболическое 51 , 53 , 104
Лапласа 100 , 125
нелинейное 35 , 51 , 67 , 74
Орра—Зоммерфельда 242
параболическое 29 , 43 , 51 , 60 , 106 ,
147 , 182
Пуассона 22 , 65 , 125 , 151 , 158 , 161 ,
170 , 237 , 245
Уравнения
Буссинеска 176
газовой динамики 70 , 135 , 136
в криволинейных координатах
295 , 315
потенциального движения 288 ,
291
Навье—Стокса 14 , 140 , 158 , 175 ,
244 , 304 , 318
не вполне параболические 304
эллиптико-гиперболические 264 , 267 ,
304
Условие
диагонального преобладания 27 , 28 ,
36 , 47 , 69 , 72 , 157 , 195
Кутты 290
348

Рэнкина—Гюгонио 53
совместимости 134
согласованности 43 , 63 , 145 , 151
сходимости итераций 168 , 178 , 191
сходимости к стационарному
состоянию 145 , 147 , 276
устойчивости
аппроксимации 30 , 43 , 66 , 68 ,
146 , 157
уравнения адвективно-диффузи-
онного 46 , 49 , 71 , 75 , 155
Куранта—Фридрихса—Леви 48 ,
51 , 53 , 67 , 75 , 78 , 146 , 155 , 302 ,
310
Навье—Стокса 72 , 146 , 169 , 310 ,
321
параболического 46 , 71
фон Неймана 45 , 51 , 146 , 332

Оглавление
Предисловие переводчиков 5
Предисловие 7
Часть I. Численные методы 8
Глава 1. Введение. Общие уравнения 8
1.1. Уравнения Навье—Стокса 14
1.2. Различные формы уравнений Навье—Стокса 17
1.2.1. Уравнения в безразмерной форме 17
1.2.2. Ортогональные криволинейные координаты 18
1.2.3. Плоские течения 19
1.3. Уравнения Навье—Стокса для несжимаемой жидкости ... 21
1.3.1. Уравнения в переменных скорость—давление 21
1.3.2. Уравнения в переменных вихрь—функция тока .... 22
Список литературы 23
Глава 2. Конечно-разностные методы 24
2.1. Дискретные аппроксимации 24
2.2. Решение обыкновенного дифференциального уравнения ... 26
2.2.1. Метод факторизации 26
2.2.2. Итерационные методы 28
2.2.3. Аналогия между итерационными процедурами и
решением эволюционных уравнений 29
2.3. Аналитическое решение конечно-разностной задачи 30
2.4. Схемы направленных против потока разностей с коррекцией 35
2.5. Методы повышенного порядка точности 38
2.5.1. Эрмитов метод 38
2.5.2. VW-метод и неявный метод компактного оператора ... 42
2.6. Решение одномерного линейного параболического уравнения 43
2.6.1. Эффект неустойчивости 47
2.6.2. Схемы с нецентрированными разностями 47
2.6.3. Центрально-разностная схема Дюфорта—Франкела 50
2.7. Решение одномерных нелинейных параболических и
гиперболических уравнений 51
2.7.1. Методы решения уравнений при отсутствии вязкости 52
2.7.2. Методы решения уравнений при наличии вязкости . . 59
2.7.3. О граничных условиях 63
2.7.4. Неявные методы 65
2.8. Многомерные уравнения 70
2.8.1. Явные схемы для адвективно-диффузионного
уравнения 70
2.8.2. Неявный метод чередующихся направлений 71
2.8.3. Явные схемы для нелинейных уравнений в
консервативной форме 74
2.8.4. Явные методы расщепления 78
2.8.5. Обобщенные методы чередующихся направлений ... 79
Список литературы 81
Глава 3. Интегральные и спектральные методы 84
3.1. Методы конечных элементов и спектральные 86
3.2. Примеры применения метода конечных элементов для
решения стационарных задач 91
3.3. Примеры применения спектрального метода для решения
стационарных задач 98
3.4. Пример применения метода конечных элементов в
нестационарном случае 102
3.5. Пример применения спектрального метода в
нестационарном случае 103
3.6. Псевдоспектральные методы 106
3.7. Методы конечных объемов (ячеек) 111
3.7.1. Метод Годунова 115
350

3.7.2. Метод Глимма 118
Список литературы 120
Глава 4. Сопоставление численных методов 121
4.1. Конечно-разностный аналог метода конечных элементов ... 121
4.2. Конечно-разностный аналог спектрального метода 122
4.3. Простейший разностный аналог метода Годунова 124
Глава 5. Некоторые специальные методы 125
5.1. Метод решения задач потенциального течения 125
5.2. Функция Грина и уравнения в переменных вихрь—функция
тока 128
5.3. Метод дискретных вихрей 131
5.4. Метод облака в ячейке 133
5.5. Метод характеристик 134
Список литературы 137
Часть II. Несжимаемая жидкость 139
Глава 6. Конечно-разностные методы решения уравнений Навье—Стокса 140
6.1. Уравнения Навье—Стокса для физических переменных . . . 140
6.2. Уравнения Навье—Стокса для стационарного случая:
метод искусственной сжимаемости 141
6.2.1. Описание метода 141
6.2.2. Дискретизация 143
6.2.3. Сходимость к стационарному состоянию 145
6.2.4. Аппроксимация граничных условий 148
6.2.5. Уравнение Пуассона для давления 151
6.2.6. Другие варианты метода искусственной сжимаемости 154
6.3. Уравнения Навье—Стокса для нестационарного случая . . . 158
6.3.1. Проекционный метод и метод маркеров и ячеек .... 158
6.3.2. Итерационный метод 166
6.3.3. Сопоставление различных методов 169
6.3.4. Метод возмущений (штрафа) 170
6.4. Примеры решения задач для физических переменных
скорость—давление 171
6.4.1. Стационарный поток над уступом 171
6.4.2. Нестационарная горизонтальная струя в
стратифицированной жидкости 175
6.5. Уравнения для переменных вихря и функции тока и методы
их решения 181
6.5.1. Уравнения для стационарного случая 181
6.5.2. Псевдонестационарные методы 182
6.5.3. Граничные условия 184
6.5.4. Итерационный метод 189
6.5.5. Решение задачи для больших чисел Рейнольдса . . . 192
6.5.6. Аппроксимация уравнения вихря, записанного в
консервативной форме 194
6.5.7. Уравнения для нестационарного случая 196
6.6. Примеры решения уравнений для вихря и функции тока . . 200
6.6.1. Стационарный поток в полости квадратного сечения 200
6.6.2. Нестационарное обтекание кругового цилиндра .... 202
Список литературы 212
Глава 7. Использование метода конечных элементов для решения задач
механики несжимаемой жидкости 215
7.1. Метод Галеркина 218
7.2. Метод наименьших квадратов 222
Список литературы 226
Глава 8. Спектральные методы решения задач механики несжимаемой
жидкости 227
8.1. Идеальная жидкость 228
8.2. Вязкая жидкость — ламинарные и турбулентные течения . . 235
Список литературы 247
351

Глава 9. Модели и расчеты турбулентных потоков 248
9.1. Замыкание уравнений турбулентного движения 248
9.2. Моделирование крупномасштабных вихрей 252
9.3. Расчеты турбулентных потоков с использованием модели
замыкания 253
9.4. Моделирование турбулентности 257
Список литературы 261
Часть III. Течения сжимаемой жидкости 263
Глава 10. Течения невязкой сжимаемой жидкости 266
10.1. Применение нестационарных методов 268
10.1.1. Конечно-разностные решения 269
10.1.2. Применения методов ячеек и конечных объемов . . 277
10.2. Разностные методы решения стационарных уравнений . . 288
10.2.1. Примеры для М0О<\ 288
10.2.2. Примеры для Afro>l 295
Список литературы 299
Глава 11. Течения вязкой сжимаемой жидкости 302
11.1. Введение 302
11.2. Граничные условия 304
11.3. Разностные схемы на равномерной сетке в декартовых
координатах 309
11.3.1. Явные схемы 309
11.3.2. Неявные схемы 311
11.3.3. Искусственная вязкость 314
11.4. Разностные схемы в криволинейных координатах. . . . 315
11.4.1. Дискретизация в трансформированной области . . . 316
11.4.2. Дискретизация в физической области 319
Список литературы 327
Заключительные замечания 331
Приложение А. Устойчивость 332
Приложение Б. Метод последовательности сеток 334
Приложение В. Метод сопряженных градиентов 336
Именной указатель 339
Предметный указатель 342
Переводная монография
Роже Пейре,
Томас Д. Тейлор
Вычислительные методы
в задачах механики жидкости
Редактор О. Д. Рейнгеверц.
Художественный редактор В. В. Быков.
Технический редактор Т. В. Павлова. Корректор А. В. Хюркес.
ИБ № 1663. Сдано в набор 29.01.86. Подписано в печать 03.06.86. Формат 60X90Vie. Бумага
книжно-журнальная. Литературная гарнитура. Печать высокая. Пел. л. 22,0. Кр.-отт. 22,0.
Уч.-изд. л. 24,05. Тираж 2240 экз. Индекс МОЛ-141. Заказ № 80. Цена 4 р. 40 к.
Гидрометеоиздат. 199053, Ленинград, 2-я линия, д. 23.
Ленинградская типография № 8 ордена Трудового Красного Знамени Ленинградского
объединения «Техническая книга» им. Евгении Соколовой Союзполиграфпрома при
Государственном комитете СССР по делам издательств, полиграфии и книжной торговли.
190000, Ленинград, Прачечный переулок, 6.