Текст
ОНТИ•НКТП•СССР
ВОЕННАЯ ВОЗДУШНАЯ ОРДЕНА ЛЕНИНА АКАДЕМИЯ РККА
им. Н. Е. ЖУКОВСКОГО
В. С. пышнов
АЭРОДИНАМИКА САМОЛЕТА
ЧАСТЬ ТРЕТЬЯ
ДИНАМИКА УПРАВЛЯЕМЫХ ДВИЖЕНИЙ
САМОЛЕТА
Утверждено в качестве учебника Главным
управлением учебных заведений НКТП СССР
Отзыв проф. А. Н. Журавченко
Цена 2 р. 20 к., перей. 1 р. 50 к.
ОНТИ НКТП СССР
ГЛАВНАЯ РЕДАКЦИЯ АВИАЦИОННОЙ ЛИТЕРАТУРЫ
МОСКВА 1937 ЛЕНИНГРАД
Книга представляет собой третью часть учебника „Аэро-
динамика самолета* для авиационных втузов. В ней рассмотре-
ны вопросы динамики полета: взлет, посадка, неустановившееся
прямолинейное движение, а также вираж, спирали, петли и
другие фигуры.
Книга является также пособием для расчета перечисленных
движений самолета.
Редактор С. Г. Бошенятов.
Технич. редактор Р. Г. Нейман,
Сдано в набор 21/1 1937 г. Подписано к печати 1/IV 1937 г. Автор, дог. № 170.
Инд. 20-5-2. Тираж 8000. Количество бум. лист. б3/8. Учетно-авт. лист. 11,5.
Формат бум. 62 x 94. Уполн. Главл. № Б-9498. Зак. № 1896. Кол. печ. зн. в 1 б. л. 101504.
2-я типогр. ОНТИ имени Евгении Соколовой. Ленинград, просп. Красных Командиров, 2Э.
ОГЛАВЛЕНИЕ
Предисловие ......................................................... 5
Введени е ........................................................... б
Взлет и посадка самолета
Взлет........................................................... 7
Тяга винта..................................................... 11
Сопротивление воздуха........................................ 20
Силы трения.................................................... 21
Аналитический расчет пути и времени разбега.................... 22
Расчет разбега численным или графическим интегрированием .... 27
Приближенный расчет разбега................................ . . 33
Наивыгоднейший угол атаки для разбега.......................... 34
Расчет размеров взлетной площадки.............................. 37
Посадка самолета............................................... 40
Расчет пробега самолета при посадке............................ 43
Расчет посадочной площадки..................................... 49
Взлет и посадка на высокогорном аэродроме...............• . . 49
Неправильные посадки........................................... 51
Некоторые особые виды посадки.................................. 58
Воздушные тормоза............................................ 61
Влияние близости земли на аэродинамические силы................ 64
Основы устойчивости и управляемости при движении самолета по
земле.......................................................... 69
Разгон и торможение в прямолинейном полете
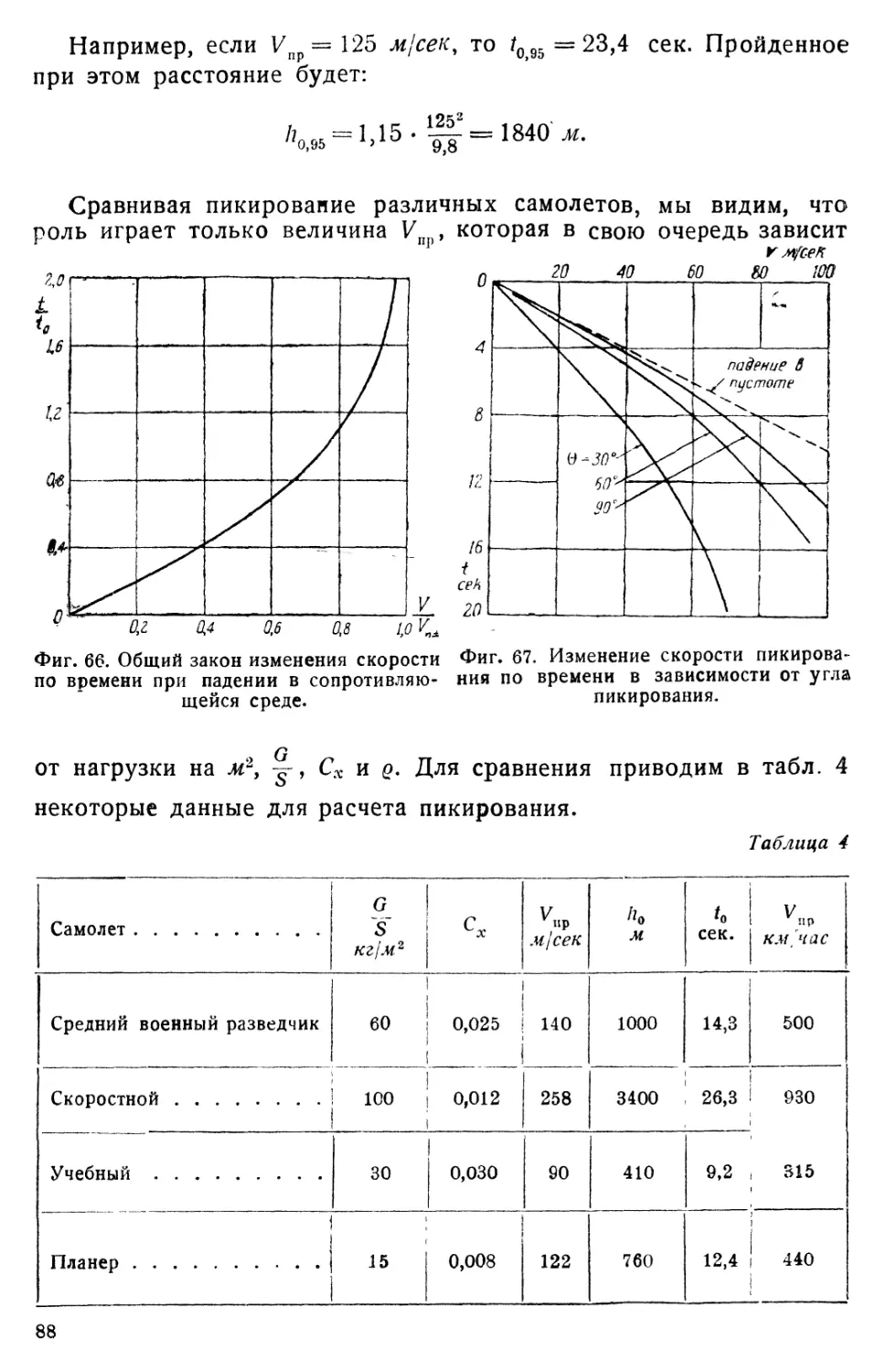
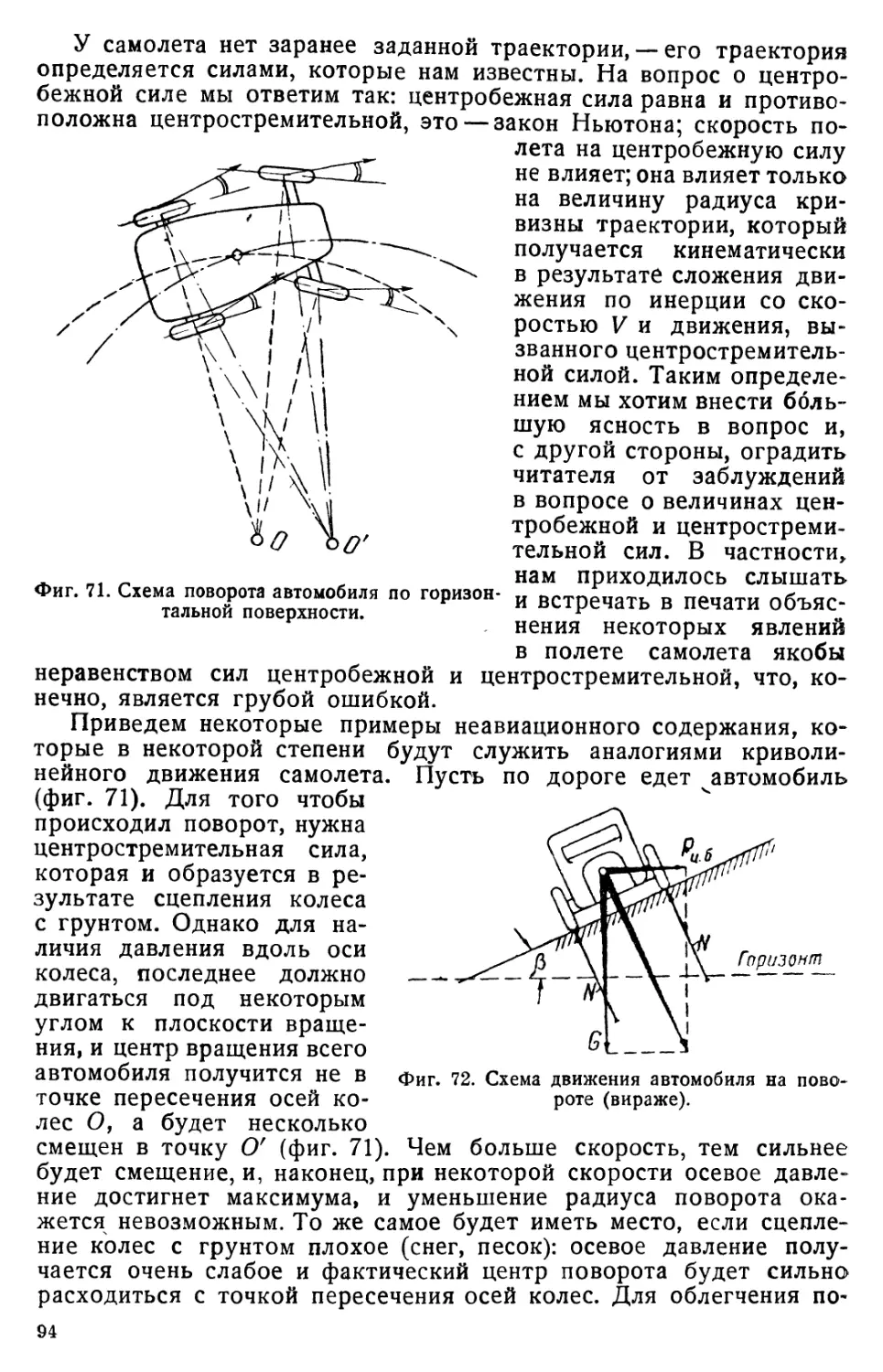
Общий случай расчета........................................... 76
Разгон самолета при пикировании................................ 81
Пикирование в среде переменной плотности....................... 89
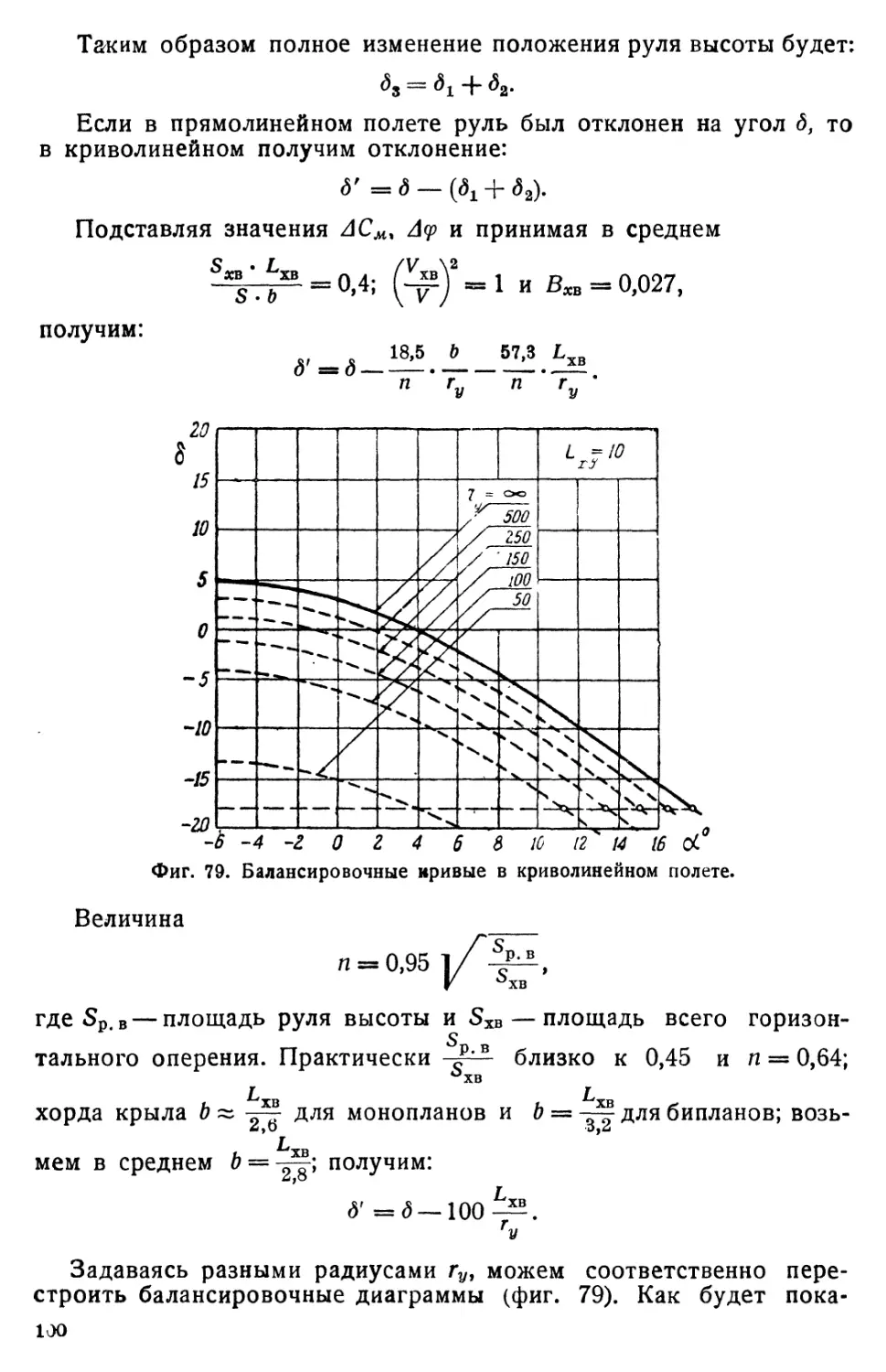
Криволинейный полет
Общие сведения................................................. 92
Особенности криволинейного движения самолета................... 96
Равновесие продольных моментов................................. 97
Равновесие моментов поперечных и пути..................... ... 101
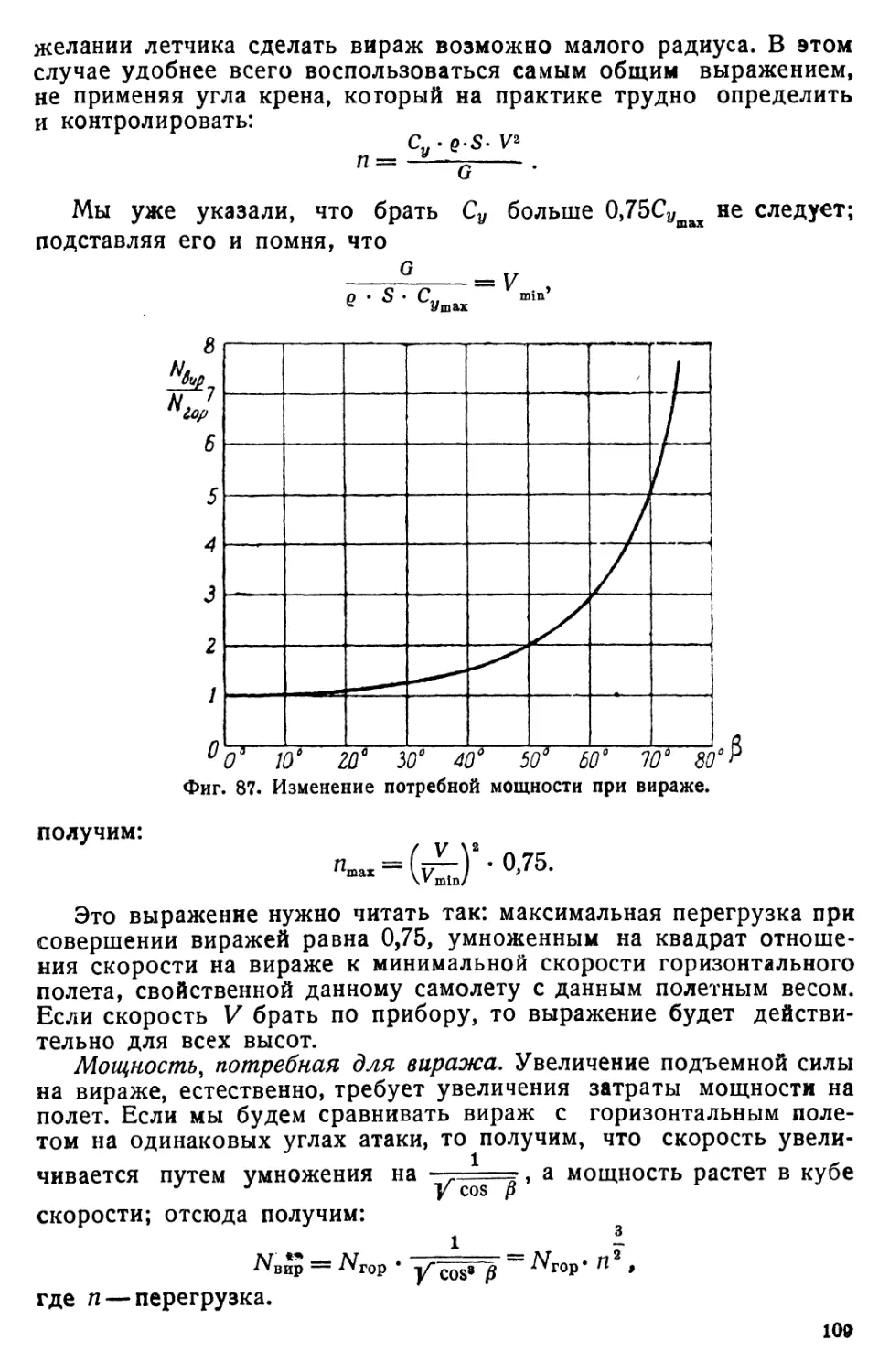
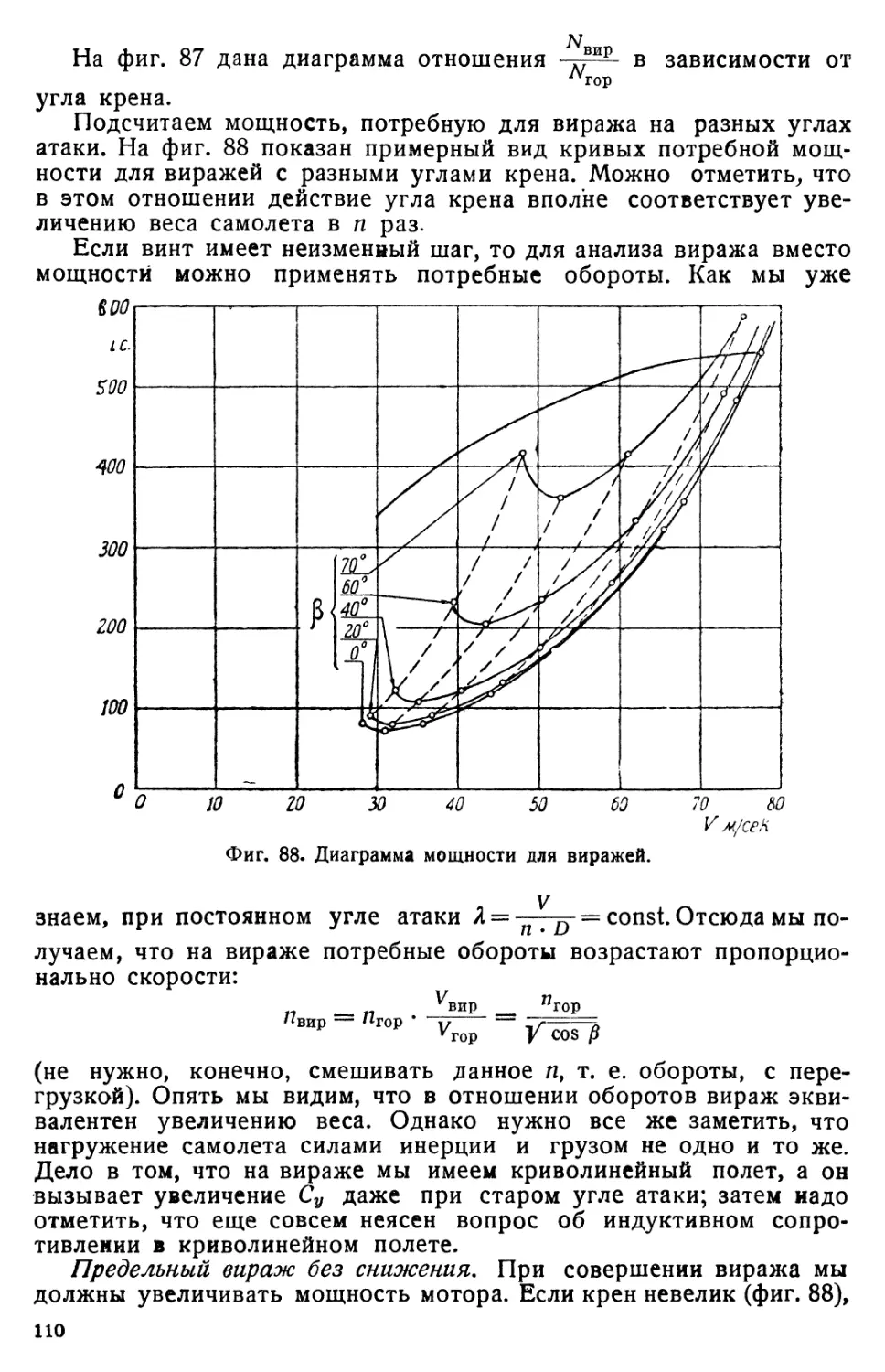
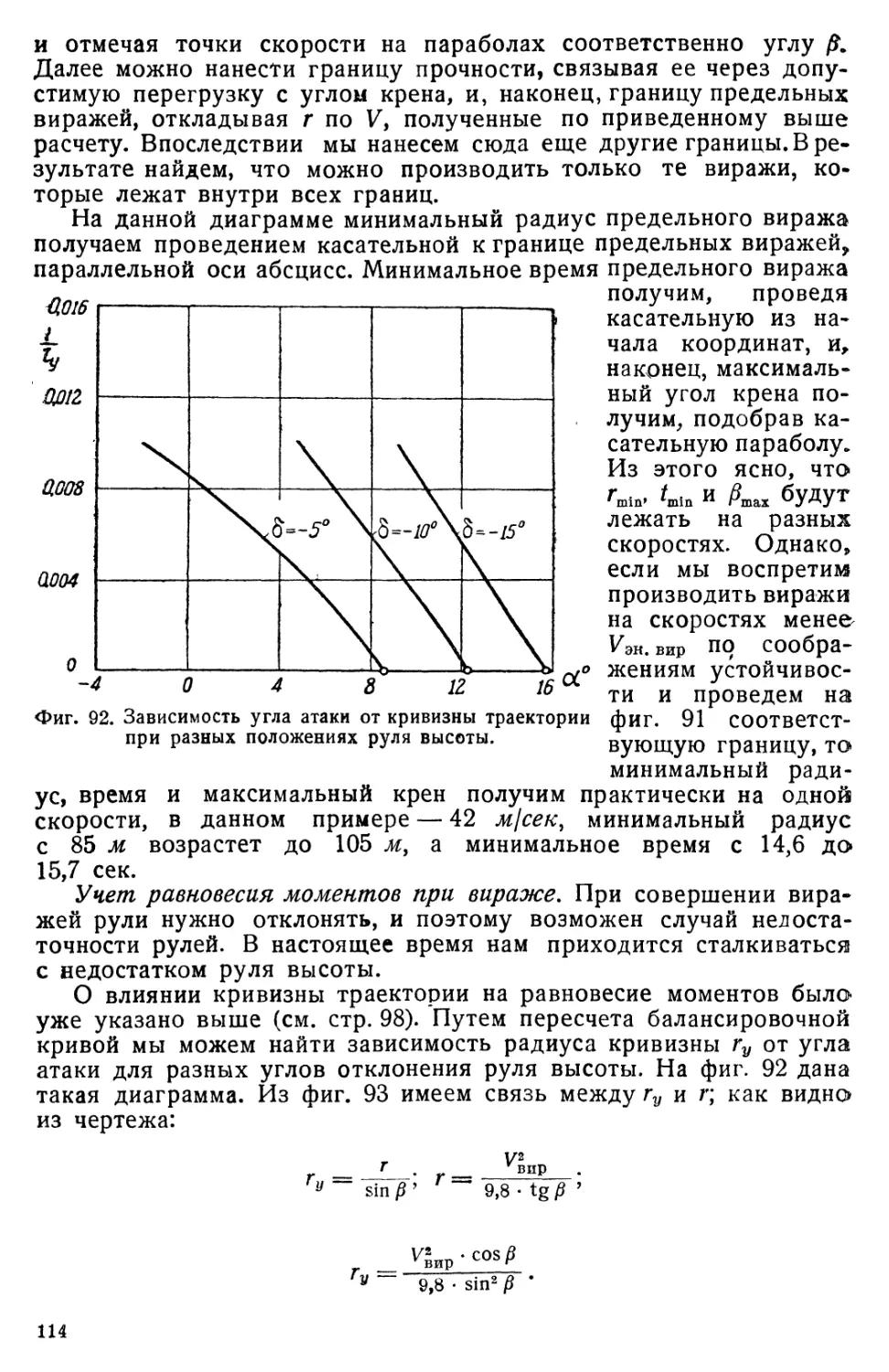
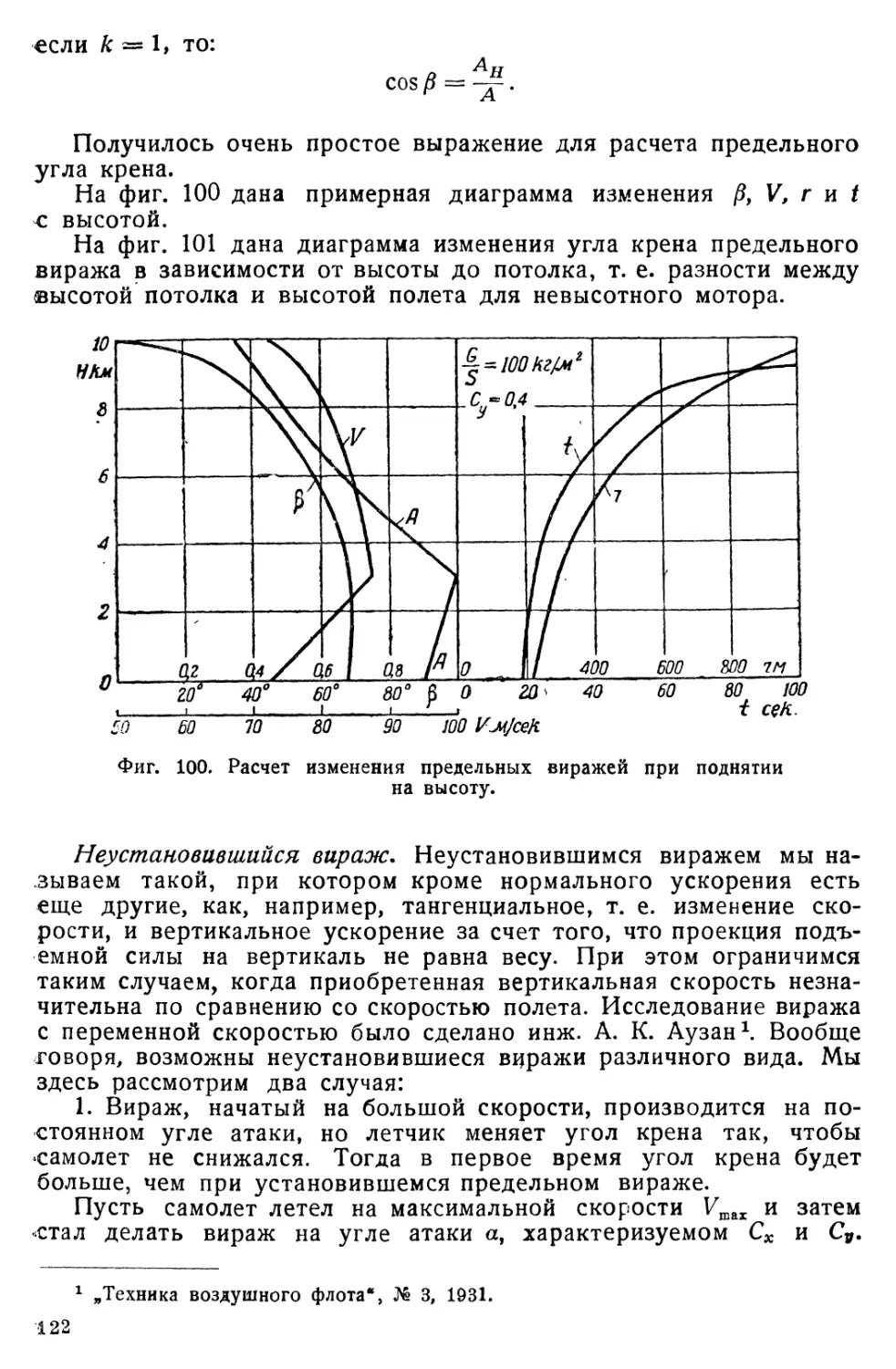
Вираж......................................................... 103
Прямолинейный полет с креном............................... . 136
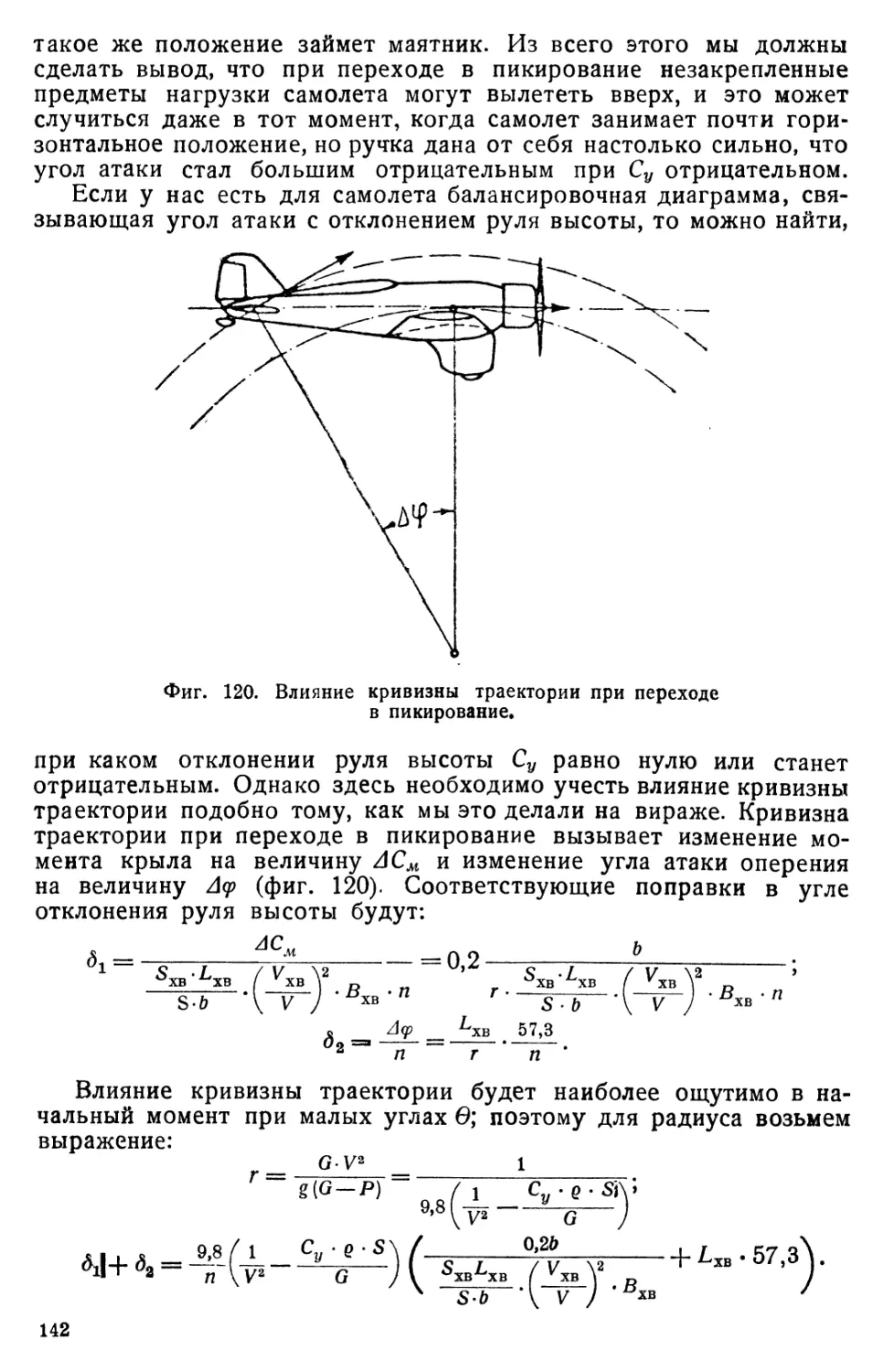
Переход в пикирование и выход из него......................... 137
!♦ 3
ОГЛАВЛЕНИЕ
Фигурные полеты
Общие сведения................................................... 150
Управление самолетом............................................ 151
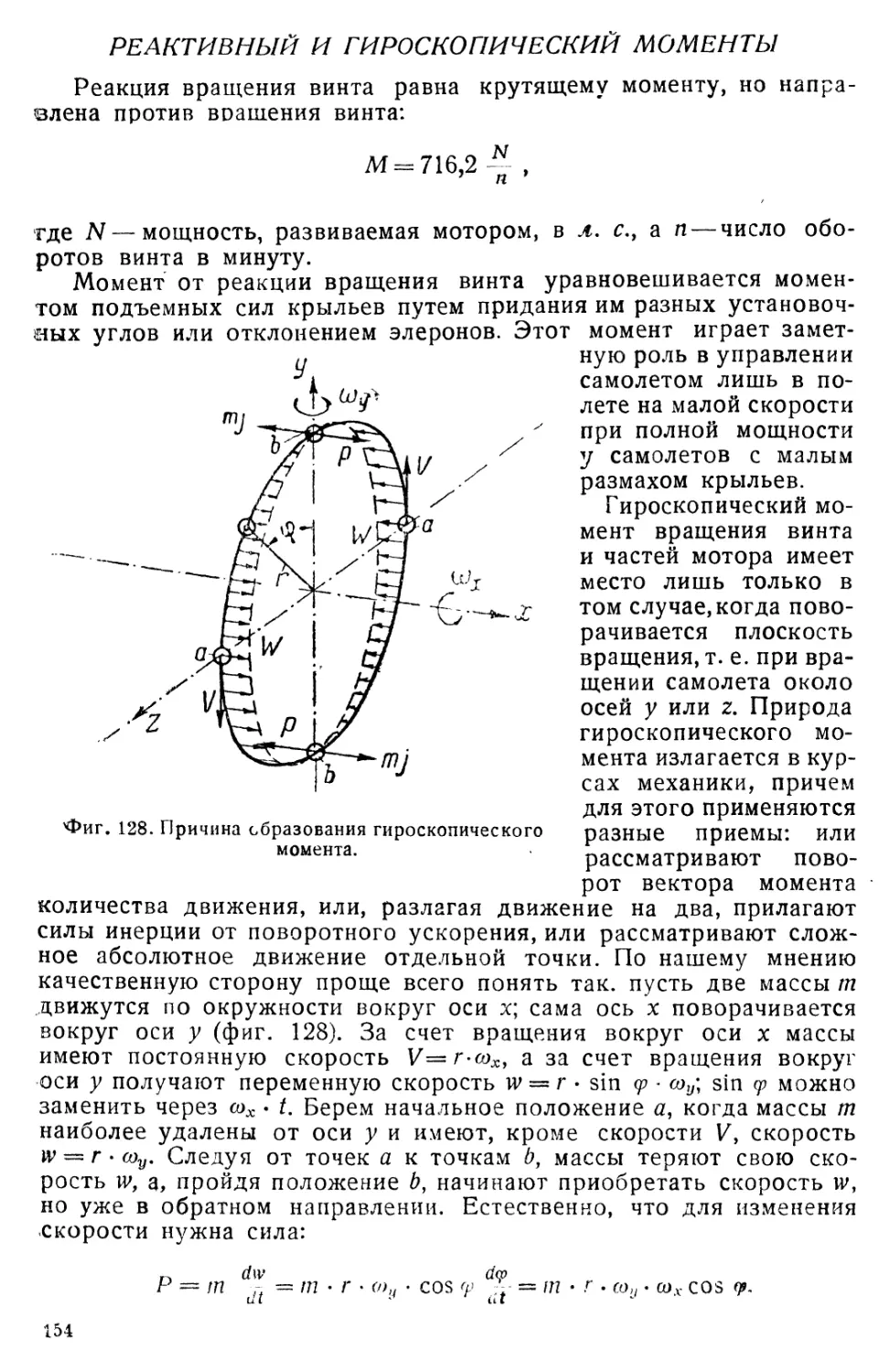
Реактивный и гироскопический моменты ............................ 154
Вопросы прочности при фигурных полетав........................... 157
Измерение перегрузок в полете.................................... 160
Описание основных фигурных полетов............................... 160
ПРЕДИСЛОВИЕ
Термин—динамика управляемых движений самолета — применя-
ется, быть может, впервые, однако, мы считаем его удачным для
объединения большого количества случаев полета самолета, в
которых самолет вполне повинуется воле пилота в отношении
величины углов атаки, скольжения и величины тяги винта. Время,
необходимое на желаемое изменение углов атаки, скольжения и
тяги винта, считается очень малым и во внимание не принимается.
В самом деле, современный самолет при выполнении нормаль-
ного полета и при правильном выполнении большинства фигурных
полетов настолько послушен, чтб, по выражению летчиков, самолет
„идет за ручкой".
Не нужно думать, что существует какая-то динамика неуправ-
ляемых движений. Просто есть вопросы динамики, в которых
управляемость играет важную роль в отношении времени, или где
самолет не повинуется летчику прямым образом, а требует косвен-
ных воздействий, или, наконец, где рассматривается полет самолета
без управления летчиком.
Такие вопросы будут рассмотрены в главах: потеря скорости,
штопор и динамическая устойчивость, которые будут изложены в
дальнейших частях настоящего труда.
Курс динамики управляемых движений рассматривает взлет,
посадку, неустановившееся прямолинейное движение и криволиней-
ное движение; в последнее входят: вираж, петля и некоторые
близкие к ним эволюции самолета.
При рассмотрении каждого вопроса выясняется физическая
сущность явления, а затем дается способ расчета данного движе-
ния, имеющий достаточную практическую точность.
Настоящая книга написана в значительной мере под влиянием
работ проф. В. П. Ветчинкина. Кроме прямых заимствований,
указанных в тексте, ряд вопросов изложен в развитие мыслей и
соображений, высказанных В. П. Ветчинкиным в его работах или
на лекциях. Поэтому я считаю долгом выразить В. П. Ветчинкину
свою глубокую благодарность. Из иностранной литературы мной
заимствовано очень мало, так как там вопросы динамики рассмат-
риваются очень кратко и неполно.
Настоящая книга не имеет цели заменить „Динамику самолета"
В. П. Ветчинкина, будучи изложена более элементарно и с большим
уклоном в практическую сторону, что необходимо для подготовки
инженеров, особенно инженеров-эксплоатационников.
Доцент В. Пышное
ВВЕДЕНИЕ
В первой части курса, содержащей аэродинамический расчет
самолета, мы рассматривали установившееся движение самолета,
т. е. движение равномерное и прямолинейное.
При рассмотрении движения мы полагали, что скорость самолета
иногда меняется, но ускорение было при этом столь незна-
чительно, что силами инерции мы могли пренебречь. Во второй
части курса мы рассматривали равновесие моментов опять-таки для
случая равномерного движения. В настоящей, третьей, части курса
мы разбираем неустановившееся движение самолета. Порядок рас-
смотрения задач вызывается методическими соображениями, хотя
мы придерживались его не очень строго, так как было нежелатель-
но возвращаться к одному и тому же вопросу по нескольку раз.
В первую очередь рассматриваются задачи, в которых движение
прямолинейно, но скорость переменна. Сюда относятся: разбег при
взлете, пробег при посадке и ряд случаев разгона и торможения
в полете. Затем идут задачи, в которых скорость постоянна, но
траектория криволинейна: вираж, спираль и, наконец, наиболее
общий случай движения, когда скорость переменна и траектория
криволинейна,— петля и другие фигуры. Для большей полноты
рассмотрения фигурных полетов мы даем фигуры, содержащие
штопорные перевороты через крыло, хотя теория штопорного
вращения самолета будет изложена нами в дальнейших частях
курса.
В четвертой части курса „Аэродинамика самолета" намечено
изложить такие вопросы:
1. Равновесие поперечное и пути.
2. Управляемость в неустановившемся движении.
3. Устойчивость при движении по земле.
4. Потеря скорости и основы штопора самолета.
5. Теоретические основы слепого полета.
ВЗЛЕТ И ПОСАДКА САМОЛЕТА
Самолет обладает способностью двигаться в трех измерениях.
Однако на его движение наложено очень серьезное ограничение:
самолет неспособен лететь, если скорость его упадет ниже некото-
рого предельного значения; на этой минимальной скорости мы уже
останавливались в первой части настоящего труда. Дело в том,
что у самолета крылья жестко связаны с фюзеляжем, и если
медленно движется фюзеляж, то и крылья обдуваются слабым
потоком воздуха, неспособным создать достаточную подъемную
силу. Существуют летательные машины, у которых скорость движе-
ния крыльев сильно отличается от скорости движения фюзеляжа:
автожир, орнитоптер, минимальная скорость которых значительно
меньше, чем у самолета. Наконец, есть такие машины, у которых
при полной неподвижности фюзеляжа крылья движутся настолько
быстро, что дают подъемную силу, достаточную для полета, хотя
для этого и требуется затрата очень значительной мощности.
Мы сейчас интересуемся только самолетом. Чтобы взлететь,
самолет должен уже иметь скорость не менее минимальной, а от-
сюда встает проблема разгона самолета перед взлетом.
Посадка на землю без сильного удара может быть сделана
только в том случае, если в момент соприкосновения с землей
скорость будет не менее минимальной.
Желание достичь большой быстроходности заставляет умень-
шать крылья самолета. В результате минимальная скорость боль-
шинства современных самолетов превосходит 100 км/час. Самолетов
с минимальной скоростью менее 50 км/час почти не существует.
Естественно, что проблема разгона и торможения для взлета и
посадки, является весьма важной и стеснительной. Условия взлета
и посадки приводят к необходимости создания специальных аэро-
дромов, т. е. ровных площадок протяжением от 500 до 1000 м в
разных направлениях.
ВЗЛЕ1
Краткая история. Самые первые полеты (Лилиенталь) произ-
водились на балансирных планерах. Человек бежал, держа на себе
планер против ветра, и обычно с горы. Взлетная скорость была
около 8—10 м/сек. Если взять скорость бега около 3 м/сек (вслед-
ствие большого лобового сопротивления бежать можно только под
гору), взлет можно произвести при ветре не менее 5 м/сек. По-
добным образом летали братья Райт, причем у них бежал не пилот,
7
а помощники, в то время как пилот в лежачем положении управлял
рулями. Когда на планер был поставлен мотор, нести его на себе
стало невозможно. Французские конструкторы (Сантос-Дюмон, Бле-
рио, Вуазен и др.) поставили самолеты на колесное шасси и про-
изводили разбег по земле, пока под действием тяги винта самолет
не набирал достаточной скорости.
Братья Райт сделали для взлета своего самолета специальное
приспособление, которое позволяло взлетать с очень маленькой
площадки. Для этой цели был сделан деревянный рельс; на рельс
ставилась тележка, а на тележку — самолет, у котррого колес не
было и имелись только лыжи для посадки. При взлете тележка
оставалась на земле. Сзади лыжи был установлен пилон с блоками
и грузом 700 кг, который тянул трос, а последний через блок, на-
ходившийся в передней части лыжи, тянул за тележку. Таким об-
разом разбег при взлете происходил не только под действием тяги
винта, но и под действием тяги троса. В дальнейшем бр. Райт от-
казались сначала от груза, удлинив рельс, а затем выбросили рельс
Разгон
Подъел
1
Фиг. 1. Схема взлета самолета.
и поставили на самолет колеса. Это произошло по той причине,
что самолет стал совершать все более дальние полеты, делать пе-
релеты, и пользование взлетным приспособлением стало неудобным.
В настоящее время громадное большинство самолетов взлетает за
счет силы тяги винта. Специальные взлетные машины, называемые
катапультами, применяются там, где нельзя иметь взлетной пло-
щадки, как, например, на кораблях. Для взлета планера, не имею-
щего своего мотора, приходится применять постороннюю тягу. Обычно
взлет планера производится людской тягой посредством резино-
вого амортизатора; применяется также буксировка планера автомо-
билем или чаще самолетом.
Весь взлет самолета можно разбить на три стадии: разбег по
земле, выдерживание или разгон над землей для набора скорости
и самый подъем (фиг. 1).
Скорость при. отрыве от земли. Процесс разбега самолета по
земле имеет целью набрать скорость, на которой самолет может
нормально лететь. Эту скорость мы и называем скоростью отрыва.
Самолет может лететь и на минимальной скорости, однако эту
скорость нельзя принять за взлетную по следующим причинам:
во-первых, при полете на минимальной скорости самолет имеет
плохую поперечную устойчивость; во-вторых, на минимальной ско-
рости велико лобовое сопротивление, и если запас мощности невелик,
то взлет получается очень вялым.Если мы посмотрим на диаграммы
тяги потребной и располагаемой (фиг. 2), то увидим, что на мини-
мальной скорости избыток тяги невелик. При увеличении скорости
избыток тяги резко увеличивается, и поэтому гораздо выгоднее
взлетать на скорости, при которой имеется достаточный избыток
тяги. Однако совсем нет необходимости взлетать при максималь-
ном избытке тяги. Таким образом, имея диаграммы потребной и
располагаемой тяги, нетрудно решить вопрос о взлетной скорости.
Берем скорость, при которой избыток тяги уже велик, хотя и ме-
нее максимального; практически для обычных самолетов эта ско-
рость процентов на 10—15 больше минимальной:
Уотп =1,1 4-1,15 Vmln.
Принимая СУшах в среднем равным 0,6 и плотность воздуха
р= 0,125, получим: __ _________
Уотр = 4 j/Z- 4- 4,2 jZ у MjceK.
Составление уравнений движения для разбега. Разбег предста-
вляет собой ускоренное движение. Тяга винта Ф тянет самолет
вперед; сопротивление воздуха и трение колес препятствуют дви-
жению. Вычитая из тяги винта сопротивления движению, получим
силу R, идущую на создание ускорения /, и тогда по закону Нью-
тона:
где т — масса самолета.
Величина ускорения переменна, и, зная ее зависимость от ско-
рости, путем интегрирования можно найти путь и время разбега.
Перейдем к более детальному составлению уравнений движения.
На фиг. 3 изображен самолет, совершающий разбег, причем для
общего случая аэродром взят наклонным под некоторым углом
в
К самолету приложены силы: тяжести G, тяга винта Ф, трение ко-
лес F, лобовое сопротивление Q, подъемная сила Р и реакция
земли N.
Берем координатные оси, направляя ось х вдоль движения, а
ось у перпендикулярно ему; так сделать удобнее, чем направлять
оси горизонтально и вертикально. Для простоты будем считать,
что направление тяги совпадает с направлением движения; можно
было бы этого и не делать, но большое отклонение тяги винта от
направления движения встречается лишь у специальных само-
летов.
Напишем сумму проекций сил на оси х и у;
2х = ф- Q — F — G-sin0,
2 У = Р — G-COS0+N.
Фиг. 3. Действие сил на самолет при разбеге.
Так как в направлении оси х имеем ускоренное движение, то
2 X приравниваем массе, умноженной на ускорение mj; ввиду того,
что наклоны аэродрома бывают очень незначительны, sin0 можно
заменить углом 0, выраженным в радианах, a cos 0 считать равным
единице; тогда:
Ff — Ф — Q — F—G-& = mj.
В направлении оси у ускорения нет, и потому 2и = 0. Уско-
рение вдоль оси у могло бы быть в случае криволинейной формы
аэродрома, чего, конечно, на практике не бывает. Ускорения, вызы-
ваемые небольшими кочками, во внимание не принимаются.
Имеем:
Р—G + N = 0,
откуда
Р + N = G,
т. е. сумма подъемной силы и реакции земли равна весу само-
лета и, следовательно, является величиной постоянной. В процессе
разбега подъемная сила возрастает, а реакция земли соответственно
убывает.
ю
Для определения пути и времени разбега нужно произвести ин-
тегрирование выражения R = mj, однако перед этим уравнение
нужно обработать так, чтобы в нем было не более двух перемен-
ных. Силу R выражают в функции скорости V, а выражение для
ускорения берут в виде / = для определения времени и в виде
dV _
j = V для определения пути. В зависимости от того, как вы-
ражены Ф, Q и F в функции скорости, получаем интеграл боль-
шей или меньшей трудности. Мы дадим ниже несколько примеров
интегрирования, предварительно же остановимся подробнее на
силах.
ТЯГА ВИНТА
Зависимость тяги винта от скорости может быть определена
обычным методом, как это делается в аэродинамическом расчете \
но только надо продолжить расчет в сторону малых скоростей;
имея характеристику мощности мотора и винтовой график, это
всегда легко сделать, причем можно найти тягу на месте.
Обычно при расчете тяги мы поступаем так: зная коэфициент
мощности (3, находим обороты, развиваемые мотором для задан-
ного режима работы винта л = ; это делается или построе-
нием кубической параболы
на характеристике мотора, или иным графическим способом, или
аналитически, выражая характеристику мотора некоторой функцией,
близкой к фактической характеристике в нужном диапазоне обо-
ротов. Наиболее часто пользуются законом:
где No и п0 — известные мощность и обороты для полной мощ-
ности.
Приравнивая мощность мотора мощности, затраченной на вра-
щение винта, получим:
75‘N°(x)ft==|3'^n3’D5’
отсюда обороты мотора:
_______k 1
„ з-fc I 75NO \з-й
п~п° •
Для многих моторов к= 1; тогда:
п = т/...75-2У».--
п V n0-f}-Q.Dt ’
1 В. С. П ы ш н о в, Аэродинамика самолетов, ч. I, ОНТИ, 1934.
11
по оборотам определяем мощность мотора, а затем располагаемую
мощность:
N расп = А/»/.
Скорость полета
и, наконец, тяга винта
75-Npacn _ 75-N-4
V “ Лп-D •
Однако, если взять Л = 0, то »? = 0, и отсюда получим неопреде-
ленность вида -у. Эта неопределенность раскрывается таким об-
разом, что вместо отношения у- берется производная , т. е.
тангенс угла наклона диаграммы ц по Л. Тяга на месте Фо будет:
Л 75 N dr)
где обороты и мощность нужно подставить соответственно вели-
чине /? при Л = 0.
При определении можно сделать значительную ошибку; по-
этому для расчета тяги на месте следует взять специальный ко-
эфициент тяги а0 для Л = 0; тогда
Фо = ао-е-п2-04.
Наконец, выведем относительный коэфициент полезного дей-
ствия винта
0o=(/7.94,2.%.N-D) т,
где N—мощность мотора в л. с. при оборотах, развиваемых на
месте (зная /?0) легко определить число оборотов, развиваемых на
месте).
К сожалению, у большинству графиков испытания винтов нет
данных для малых Л. Кривые оканчиваются обычно при к. п. д.,
равном ~0,4, что соответствует скорости около 0,3 максимальной
скорости, считая при последней у максимальным.
Вообще говоря, с увеличением скорости тяга винта падает и,
следовательно, наибольшая тяга должна быть при работе винта на
месте. Для винтов сравнительно небольшого относительного шага
изменение тяги винта происходит по закону, очень близко отвечаю-
щему прямой линии. Поэтому проф. В. П. Ветчинкин в своей книге
„Динамика самолета' предлагает брать изменение тяги винта по
прямой, выражая ее аналитически. Из фиг. 4 мы можем написать
уравнение тяги в виде:
Ф==Ф0(1-4г)-
Для получения Фо и V рекомендуется взять диаграмму тяги
винта из аэродинамического расчета и затем экстраполировать ее
12
до V = 0 и V; Фо означает тягу винта при работе на месте, а
V— скорость, при которой тяга винта обращается в нуль.
Если винт подбирается с целью получения наибольшего к. п. д.
^шах на расчетной скорости Vp, то тяга на расчетной скорости
будет:
rf, ________________________
«Рр — — у------ •
Р
Обычно расчетная скорость составляет от 90 до 100% макси-
мальной скорости.
Величина V' равна приблизительно 2,2VP, а ФО = 1,8ФР; эти зна-
чения определены с учетом изменения оборотов винта и пригодны
для скоростей меньше Vp для винтов с относительным шагом не
более Л = S1.
Фиг. 4. Упрощенное изменение тяги винта по скорости.
Посмотрим, как выглядит диаграмма тяги винта фактически.
На фиг. 5 дана диаграмма коэфициентов тяги а для серии винтов
Уэйка 4412 с разными углами установки лопасти ср на г = 0,75-^- .
Переход от угла <р к относительному шагу можно сделать по
формуле:
Н = 2 пг • tg <р = 1,5л -5- tg 99;
Л = ~ — 0,75л • tg ср = 2,35 tg ср.
Для удобства перевода даем диаграмму фиг. 6. Как видно,
только при h ^0,9 изменение величины а близко к прямой линии.
Однако величина а характеризует тягу только при условии со-
хранения оборотов. Найдем величину а’, отнесенную к оборотам
полной мощности пъ учитывая изменение оборотов от перемены Я
и коэфициента мощности Изображая характеристику в виде
1\п1 / ’
13
получим для расчетной скорости, на которую подобран винт при
мощности Ni и оборотах
Л
Фиг. 5. Характеристика винта с разными углами
установки лопасти.
Для некоторого другого режима:
n = nA ^^p-Q-n^D5.
Из последних двух выражений, разделив второе на первое, по-
лучим:
( 2L\k = A (—\3
\ «1 / ft \7
14
и
Мы обозначаем
гф
as==
вместо
Ф
a~—n*-Dr>
отсюда
2
Если взять к = 1, то
а' = а-|-,
т. е. тяга винта пропорциональна а'. Зная тягу Фр на расчетной
скорости, мы можем найти тягу на любой скорости из выражения:
Ф = ФР^.
Из условия Я определяем:
V = A-n-D.
Умножая и деля правую часть на nlf получим:
7 = ЯП-л-^-=Л,.л1-Р,
«1 1 ’
где
или при fc=l:
я' = я —
П1
Я'
Л'
Теперь построим диаграммы, откладывая по оси абсцисс -у,
V а'
что соответствует -тг~, а по оси ординат —, что соответствует
•р ai
отношению . По этой диаграмме (фиг. 7) мы видим, как ме-
няется тяга винта, и, зная расчетную скорость Vp и тягу на расчет-
ной скорости
хь __ 75N*f?max
Фр — -----у-----
можем найти тягу и на других скоростях. Как видно, лучшее от-
ношение тяги на месте к тяге на расчетной скорости дал винт
с относительным шагом, равным ~0,65. Для других серий резуль-
тат может получиться несколько иным.
15
У винтов с очень большим относительным шагом тяга на малых
скоростях значительно ниже (фиг. 7).
Для выбора наилучшего
Фиг. 7. Зависимость тяги винта от скорости
у винтов с разными углами установки лопасти.
винта как в отношении по-
лета, так и взлета нужно,
конечно, сделать специаль-
ное исследование, из кото-
рого надо найти лучший диа-
метр и соответствующее ему
число оборотов. Если число
оборотов не подходит, то
отчасти положение можно
улучшить изменением ши-
рины или числа лопастей;
подходящее число оборотов
является важнейшим услови-
ем подбора хорошего винта.
В последнее время в прак-
тику стали входить винты
с изменяемым шагом. По-
смотрим, насколько они по-
лезны для взлета. Регулируя
шаг винта, мы можем сохра-
нять величину р, а с этим
обороты и мощность мотора.
С другой стороны, уменьшая
шаг на малой скорости для
сохранения мы получаем
винт, более выгодный на малых скоростях. Для иллюстрации мы даем
расчет для винтов американского стандарта 4412 с поворотными ло-
пастями. На фиг. 8 дана
диаграмма изменения
тяги винта по скорости
для винтов с постоян-
ным и изменяемым ша-
гом, причем один винт
на расчетной скорости
имеет лопасти с накло-
ном в 35° (что соответ-
ствует относительному
шагу около 1,65), а вто-
рой— с наклоном ло-
пастей в 20°(что соот-
ветствует относитель-
ному шагу 0,857). Как
видно, для первого
винта на малой ско-
рости тяга винта удвой- фиг. 8. Сравнение тяги винтов с постоянным и изме-
лась; ДЛЯ винта малого няемым в полете шагом.
шага улучшение не так
значительно, но все же существенно. Отсюда мы видим, что для
винтов с относительным шагом на максимальной скорости более 1,0
16
поворотные лопасти являются элементарным условием получения
короткого старта.
Проанализируем еще вопрос в таком направлении. Для увели-
чения тяги винта применяется форсирование мотора. Пусть после
форсирования характеристика мотора поднялась, так что отноше-
ние ординат при постоянных оборотах получено постоянным:
где N' относится к форсированному мотору. Если положить = 1,
то сила тяги изменится в отношении квадрата оборотов при усло-
Фиг. 9. Изменение тяги винта на месте от угла поворота
лопасти.
вии Л = const. Изменение оборотов получим из условий затраты
мощности на вращение винта для обоих условий:
N — ft-Q-n3‘D5;
Сравнивая эти выражения между собой, получим:
п \ п / ’ \ п ) Ф ’
таким образом тяга изменилась в той же степени, что и мощность
мотора при постоянных оборотах.
Другое дело получим при винте с изменяемым шагом. Предпо-
ложим, это у нас винт автоматически изменяет шаг так, что обо-
роты остаются постоянными, т. е. при увеличении мощности уве-
ничивается шаг. Очевидно, что на постоянных оборотах затрата
мощности пропорциональна величине /?, а тяга винта — величине а.
1а фиг. 9 построена диаграмма а0 по при 2 = 0 и разных углах
наклона лопастей. Иначе говоря, эта диаграмма дает зависимость
2 В. С. Пышнов.
17
тяги от мощности при постоянных оборотах. Как видно, при уве-
личении мощности тяга сначала немного растет, а потом падает.
Поскольку винты с углом лопастей менее 20° на практике приме-
няются очень редко, увеличение мощности мотора при постоянных
оборотах не только не увеличивает тяги, но даже уменьшает ее.
Возьмем еще такой случай: изменяя шаг винта и действуя дрос-
селем, будем менять обороты, сохраняя мощность мотора. При
изменении оборотов на постоянной мощности величина Д будет
Фиг. 10. Изменение тяги винта на месте при
изменении оборотов путем поворота лопасти
при постоянной мощности.
обратно пропорциональна ку-
бу оборотов, а тяга винта про-
порциональна а и квадрату
числа оборотов. Выбрав винт
с некоторым углом лопастей
будем дальше менять обороты
и найдем соответствующий
ему наклон лопастей <р, вели-
чину а и, наконец, тягу. На
фиг. 10 дана диаграмма изме-
нения тяги по оборотам для
исходного наклона лопасти
(р — 35° и (р = 20°. Как видно,
при увеличении оборотов тяга
сильно возрастает, особенно
для винта большого шага. Та-
ким образом, не меняя мощ-
ности, за счет уменьшения шага
винта мы много выигрываем
в тяге.
Настоящие расчеты носят
иллюстративный характер, но
они указывают на важность
подбора винта для улучшения
взлета самолета.
Рассматривая вопрос о тяге винта и мерах к ее повышению,
необходимо помнить о максимальной теоретически возможной вели-
чине тяги, получаемой по теории идеального, т. е. не имеющего
потерь, винта.
Приведем краткие выводы из этой теории1. Пусть F— пло-
щадь, ометаемая лопастями винта:
F = (D2 — d2),
где D — диаметр винта; d— диаметр нерабочей части, близкой к оси
вращения (величина d берется приблизительно); о — плотность воз-
духа; V — скорость полета и v—скорость подсасывания.
Тягу Ф получим, исходя из изменения секундного количества
движения воздуха, проходящего через ометаемую площадь, а за-
трату энергии — по изменению живой силы:
и Ф=о.?(у + и)2о
F(V +v)22v.
1 Подробное изложение см. Б. Н. Юрьев, Воздушные винты, ОНТИ, 1935.
18
Преобразуем выражения:
Нас интересует связь Ф с N, поэтому следует сделать подста-
новку у-; однако сделать это очень неудобно, так как корни
кубического уравнения
очень громоздки. Для
получения практически
удобного решения будем
V
задаваться величинами у
и подсчитаем В и А. По-
строив диаграмму В по А,
можно пользоваться ею
для всевозможных задач,
если известны N, В и V.
Заметим также, что отно-
шение В к А представляет
собой идеальный к. п. д.
винта:
_ в _ Ф • V
~А ~ 75 • N'
Для практического
приложения удобнее по-
ступить еще так. По оси
абсцисс отложим:
3 3
1/л = v 1/7ZL
У А У 75 • N’
т. е. величину, пропорци-
ональную скорости при
постоянной мощности.
По оси ординат отло-
жим:
В _ Ф _________
~2 ~ 3 ________*
л'з /е • В • (75N)2
Фиг. 11. Зависимость тяги идеального винта
от скорости.
Фиг. 12. Зависимость относительного к. п. д. винта
от скольжения.
Эта величина пропорциональна тяге при постоянной мощности.
В результате мы получим диаграмму, которая при постоянной мощ-
ности дает закон изменения идеальной тяги по скорости. Если
взять случай V = 0, то, пользуясь исходными выражениями для
Ф и N, получим:
н 3 -
=1^2= 1,26.
\A3Z
2*
19
На фиг. 11 построена диаграмма — по
ею можно пользо-
ваться для расчета идеальной тяги винта, но можно воспользо-
ваться ею также для расчета действительной тяги, если мощность
N взять за вычетом потерь:
N = NM •
где if— относительный к. п. д., учитывающий потери винта на
профильное сопротивление лопастей и потери на вращение струи.
На фиг. 12 дано примерное значение t]' в функции относительного
динамического скольжения (йд — А); йд равно относительной поступи
при т] — 0. Вводя переменное (Лд — А,) мы делаем диаграмму при-
годной для винтов разного относительного шага. Из диаграммы
мы видим, что при винтах большого относительного шага на малой
скорости (йд — Я) велико, а »?'— мало, — это и объясняет малую
тягу. Для удобства расчетов даем табл. 1.
Таблица 1
1 ! 10 2 1 ; 1 0,5 0,2 Г 0,1 0,05 0,01 j i
6 4
1 Со II s. 220 84 ! j 40 12 1 ! 4 1,5 ! 0,48 I 0,22 0,105 j 0,020 [ ।
А==._"__ 2420 588 200 1 1 1 36 8 i 2,25 0,576 1 0,242 0,110 0,0204
е • f • v3
I II 0,091 0,143 0,20 0,33 0,50 0,667 0,833 0,91 0,952 0,99
1 3 Кд 0,0744 0,12 0,171 0,302 0,5 0,765 1,2 1,6 2,08 3,65
А 1,22 1,2 1Д7 1,1 1,0 0,872 0,696 0,568 0,455 0,271
СОПРОТИВЛЕНИЕ ВОЗДУХА
Величину сопротивления воздуха при разбеге можно предста-
вить в виде:
Q—Cx- о • S • V2
или через подъемную силу:
Q=P-^
20
В большинстве случаев считают, что угол атаки на разбеге
постоянен, и поэтому Сх можно считать постоянным. Обычно на
взлете держат угол атаки близким к экономическому; ниже мы
приведем исследование угла атаки, наиболее благоприятного для
взлета. Из аэродинамики известно, что вблизи земли индуктивное
сопротивление уменьшается, и, следовательно, в Сх нужно внести
поправку. Подробности по этому вопросу мы приведем далее,
здесь же нужно отметить, что на расчете введение поправки
сказывается очень мало; к тому же остается неизвестным фактор
зависимости Сх от ускоренного движения.
Если во все время разбега сохранять угол атаки постоянным,
то самолет взлетит сам собой по достижении скорости Уо:
В момент взлета сила сопротивления будет:
л р
Q = G- р-.
у
На скоростях V, меньших Vo, сопротивление будет:
Это выражение очень удобно и мы его дальше будем при-
менять.
СИЛЫ ТРЕНИЯ
При взлете силы трения имеют место у колес и костыля. Если
на костыле колеса нет, то летчик старается возможно быстрее
поднять хвост, чтобы избавиться от сильного трения костыля, и
практически нормальный самолет производит разбег с поднятым
хвостом, имея угол атаки, близкий к экономическому. При таком
разбеге силу трения колес можно выразить:
F = j • N,
т. е. сила трения равна реакции земли N, умноженной на коэфи-
циент трения /. Подставляя в это выражение величину реакции N,
получим:
F = f(G — P) = f(G —Cyo-S- V2).
На скорости Уо имеем:
Су • о • S • Vi = G,
отсюда
21
АНАЛИТИЧЕСКИЙ РАСЧЕТ ПУТИ И ВРЕМЕНИ РАЗБЕГА
Подставив выражение для сил в уравнение движения, получим:
т1 = Ф0(1 — yrj — Сх- q -S • V2 — q -S- V2) — Gsin6>= R;
Систематизируя части выражения, можно получить: 1) постоянные
члены, 2) члены, зависящие от скорости в первой степени, и
3) члены, зависящие от скорости в квадрате. Схематично можно
написать:
/ = а + bV + eV2.
Длина и время разбега выразятся:
= а + bV + eV2;
dt = i‘/v. ...
a + bV + cV-
v отр
J ~a^~bV +cv^
о
V - a + bV + cV\
ax
dx =_______
X a + bV + cV*
VdV
a bV 4- c V~
Интегрирование полученных выражений и их практическое при-
менение довольно сложны, так как получаются тригонометрические
и гиперболические функции. Само интегрирование мы здесь не
приводим; оно изложено в книге В. П. Ветчинкина „Динамика
самолета". Для практического пользования мы даем графики (фиг. 13
и 14) коэфициентов, при помощи которых весь расчет можно
сделать сравнительно просто. Уравнения, полученные в результате
интегрирования, по которым построены графики, имеют вид:
V- _ V
_ ¥отр у. , г отр у,
X-2g(p-/)’A’ ?~g(p-/) l-
32
24
Величины X и Т являются некоторыми безразмерными коэфи-
циентами; их можно выразить так:
In
1
1 + — <52)
Как видно, выражения очень громоздки и требуют наличия
таблиц натуральных логарифмов и гиперболических функций.
Однако, если есть таблица или диаграмма значений X и Т, то
пользоваться формулами не нужно.
Для расчета длины и времени разбега поступаем следующим
образом.
1. Подсчитываем величины и <32 по формулам:
р ^отр
Р~1 * ~V'
*2=
м — / ( V2
р-1 ‘ \ V.7 ’
Фл S
где р = ~причем Фо должно включать в себя потерю на об-
дувку (это обычно бывает уже сделано в расчете
характеристики винтомоторной группы);
/ — коэфициент трения;
сх
р,—~ — величина, обратная качеству самолета;
7
Котр — скорость отрыва;
Ко— скорость, при которой самолет взлетит, если не
менять угла атаки:
— о • S • С,
здесь Су нужно взять для того угла атаки, под которым происходит
разбег;
V — скорость, при которой тяга винта равна нулю.
2. Находим £=^ + ^2 и затем, интерполируя по диаграмме,
находим X и Т.
25
3. Подставляя X и Т, получаем путь в м и время в секундах:
v
f _ ОТР -тг.
g (Р - /)
Если взлет происходит при встречном ветре, то разгон само-
лета начинается не от нуля, а от скорости w ветра и до взлетной
скорости Готр, которая не отличается от скорости взлета при без-
ветрии. Длина пути разбега при ветре сокращается, во-первых, за
счет уменьшения времени разбега, а во-вторых, за счет уменьшения
скорости по отношению к земле.
Графики В. П. Ветчинкина позволяют сделать расчет разбега
при ветре. Для этого сначала ищем др d3, s, X и Т при безветрии.
Затем находим д' и д' для ветра:
е — дх + д2;
по d't и е', пользуясь теми же графиками, находим X» и Tw.
Сначала находим время разбега tK:
, _ ^отр w ’
w g(p~/)
Затем находим путь:
Сравнивая взлеты при безветрии и ветре, нужно обратить вни-
мание на то, что длина разбега меняется в значительно большей
степени, нежели время.
В расчете разбега по графикам В. П. Ветчинкина не учиты-
вается наклон аэродрома; однако его легко туда ввести, вычитая
составляющую веса Gsin© из тяги винта. Произведя такое вычи-
тание, мы получим новые значения для характеристики тяги Ф' и
V’:
Ф'0=Ф0 — G • sin 0;
V" = V (1 ——s—
\ Фо I
Практически наклоны аэродрома бывают очень незначительны,
однако, для среднего самолета наклон аэродрома в 1° меняет длину
разбега примерно на 10°/о.
Кроме расчета, предложенного В. П. Ветчинкиным, есть еще
другие способы, в которых для упрощения интегрирования прини-
9^
мается изменение тяги по параболе или тяга считается постоянной
(некоторой средней величины). Однако упрощения не так велики,
и поэтому мы эти расчеты не приводим; ниже мы дадим более
простой приближенный расчет времени и пути разбега.
РАСЧЕТ РАЗБЕГА ЧИСЛЕННЫМ ИЛИ ГРАФИЧЕСКИМ
ИНТЕГРИРОВАНИЕМ
Во многих отраслях техники, а особенно в авиационной тех-
нике, приходится оперировать, с исходным материалом в виде
диаграмм, полученных или прямо из эксперимента, или несколько
обработанных математически, например по кривым Лилиенталя.
Это происходит из-за отставания теории, которая не успевает
давать достаточно точных закономерностей.
Если исходные данные представлены в виде кривых, то и все
дальнейшие результаты обрабатываются в виде кривых. Часто
стараются под кривые подобрать аналитические выражения, и тогда
получается аналитический расчет; нередко он оказывается менее
точным, так как аналитические выражения стараются брать воз-
можно более простыми (иначе с ними крайне трудно оперировать).
Работа по обработке кривых для перехода от одних величин
к другим почти не зависит от вида кривых. Недостатком метода
обработки кривых является длительность расчета, причем перемена
некоторых параметров требует полного повторения работы. В ана-
литическом же расчете нужно только раз вывести окончательное
выражение и в дальнейшем можно более или менее легко произ-
водить вариации в целях исследования.
Применим способ обработки кривых для расчета разбега. Пусть
мы имеем зависимость Ф, Q и Г от скорости в виде диаграммы
фиг. 15, причем тяга винта может быть взята из расчета характе-
ристики винтомоторной группы, сила Q может быть построена
с учетом изменения угла атаки, а сила F—с учетом трения костыля.
Затем находим
Р=Ф—Q—F
и ускорение
Время разбега найдем, исходя из следующих соображений.
Имеем:
^’отр
/= f dv.
dt m ] ’ J ]
Зная ускорения при разных скоростях, можно произвести числен-
ное интегрирование любым методом, причем простейший расчет
будет состоять из разделения разбега на интервалы скоростей AV;
взяв среднее ускорение в интервале /ср, получим промежуток вре-
мени:
27
и, наконец, все время разбега будет:
Для расчета пути будем иметь:
^отр
' = v = *= J -fdv-
б
Фиг. 15. Изменение сил по скорости при разбеге самолета.
При расчете пути разбега при ветре интегрирование нужно
вести по скорости по отношению к земле, а ускорения брать соот-
ветственно воздушной скорости:
^отр
Г V — W
х~ J i
dV.
W
Этот интеграл разделим на два:
'7отр
xj= У* X dV — w
^отр
W
Второй интеграл представляет собой время разбега при ветре,
умноженное на скорость ветра, т. е. путь, пройденный ветром
в течение разбега. Таким образом для расчета пути разбега при
ветре интегрирование производим в пределах от скорости ветра
до скорости взлета, а затем вычитаем путь, пройденный ветром;
это требует предварительного расчета времени разбега.
28
Разделив разбег от скорости ветра w до скорости взлета Уотр
на интервалы ЛУ, находим среднюю величину /ср в каждом интер-
вале; тогда часть пути будет:
Лх=-^-ЛУ,
^ср
и весь путь разбега:
'X — 2 Ах.
Величину интервалов AV нужно брать небольшую, однако, и
очень мелких интервалов следует избегать: достаточно от пяти до
десяти интервалов.
Подобную же работу можно сделать, заменив интегрирование
измерением площади диаграммы. Для расчета времени строим
диаграмму Д- = ~ по V (фиг. 16). Элементарная площадка диаг-
раммы df = у dz соответствует элементу времени dt = . Вся пло-
щадь диаграммы в пределах от скорости ветра до скорости взлета
Уотр соответствует времени разбега. Если масштаб по оси абсцисс
1 мм соответствует А м]сек, а 1 мм по оси ординат соответствует
В сек2/м, то для получения времени в секундах площадь диаграммы
/ мм2 надо умножить на масштабы А и В:
t — f.A.B,
Для расчета пути разбега строим диаграмму Д- (фиг. 17); тогда
элементарная площадка df = у dz соответствует элементу пути dx,
а вся площадь диаграммы соответствует пути х. Если масштаб
скорости 1 мм соответствует A м!сек и 1 мм масштаба X соответ-
29
ствует С сек., то весь путь разбега получим, умножив площадь
/ мм2 на масштаб А и на С:
x = А-С.
При расчете времени разбега учет ветра производим, перенося
границу расчета площади на скорость ветра w. При расчете пути
разбега при ветре мы также интегрируем от скорости ветра w до
скорости взлета Иотр, но из полученного пути вычитаем путь w • t,
пройденный ветром за время разбега, как это было показано выше.
Можно было бы, конечно, произвести интегрирование по земной
скорости, но это потребовало бы перестроения диаграммы.
Приведем еще способ графического интегрирования, применяе-
мый немецким инженером Маделунг. Взяв конечный интервал вре-
мени 3/, мы можем написать:
_ Z1V
I т ~ At ’
AV Al.
Задаваясь некоторой величиной At, например 1 сек., мы можем
найти изменение скорости за время At путем графического умно-
жения / на At. Графическое умножение производят путем построе-
ния треугольника, один катет которого представляет множимое /,
тангенс прилежащего угла в некотором масштабе выражает мно-
житель At, а найденный второй катет дает произведение AV. Пов-
торяя такое построение несколько раз, мы можем дойти до ско-
рости взлета, и тогда число построенных треугольников, умножен-
ное на взятое At, даст время разбега. Практически работа сводится
зо
к построению зигзагообразной линии между кривыми Ф и Q + F
(фиг. 18). Для построения нужно найти угол наклона линий
отсюда:
io- m = о . —
г> q •
Задаваясь некоторой произвольной силой /?0, подсчитываем:
Фиг. 18. Графический расчет времени разбега.
Полученные значения RQ и AVg наносим на диаграмму, отсчи-
тывая их от начала координат (фиг. 18); найденную точку соеди-
няем с началом координат и получаем искомый наклон; соединив
точки Rg и AVg, на осях координат получим обратный наклон.
Само построение ведется с помощью треугольника и линейки и
занимает немного времени. Чем меньше At, тем лучше; однако,
очень малые At брать не следует, так как тогда может произойти
накопление чертежных ошибок. Вообще говоря, точность выше,
когда линии проводятся попеременно то в одну, то в другую сто-
рону, а не все время в одну сторону, но в сочетании с вертика-
лями. Затем tg <р не следует брать более одной пятой минималь-
ного тангенса углов наклона касательных и интегрируемых кривых.
Если кривая имеет ветвь, уходящую в бесконечность, то такой
способ интегрирования следует признать неудобным.
Перейдем к расчету длины разбега. После расчета времени
разбега указанным выше способом весь разбег у нас разделится
на равные отрезки времени разбега At', путь, пройденный за каж-
дое At, будет равен:
Ах — Vср * At,
1
где Vcp — средняя скорость в данном отрезке; ее мы можем полу-
чить, разделив каждую наклонную линию пополам; тогда абсциссы
этих середин будут выражать собой в некотором масштабе путь,
пройденный в данный интервал времени. Для получения всего вре-
мени разбега нужно сложить все абсциссы средних точек вплоть
до отрыва и умножить их на At. Проще всего, если At — 1 сек.;
тогда Уср даст непосредственно путь за интервал времени At.
Однако длину пути можно найти и сразу путем интегрирования
подобным же способом. Выразим ускорение в виде:
Фиг. 19. Графический расчет пути разбега.
Задавшись некоторым интервалом пути Ах, например 10—20 м,
получим изменение квадрата скорости:
А V2 = 2 • / • Ах = 2 • g • • Ах.
Строим диаграмму Ф, Q и F по V2 и интегрируем опять построе-
нием зигзагообразной линии, каждый кусок которой соответствует
пути Ах. Нужный наклон ср построим, задаваясь величиной Ах и
некоторым /?0; тогда:
(АУ2)0 = 2 • g • Ах;
нанося на диаграмме 7?0 и (AV2)0, получим нужный угол (фиг. 19).
Интересно отметить, что если разбег происходит на постоянном
угле атаки, то сопротивление воздуха Q и трение Fjia диаграмме
изобразятся в виде прямых линий. Трение F обращается в нуль
на некоторой скорости Уо, при которой самолет взлетел бы,
если бы угол атаки в процессе разбега не менялся. Интегрирова-
ние может быть прекращено на фактической скорости отрыва, но
тогда надо подразумевать, что летчик в момент отрыва увеличит
угол атаки.
32
При наличии ветра интегрируем от скорости ветра до скорости
взлета, а затем из полученного расстояния вычитаем путь ветра.
ПРИБЛИЖЕННЫЙ РАСЧЕТ РАЗБЕГА
Ускорение при разбеге имеет вид:
mj — Ф — Q— F-^-G • sin 0.
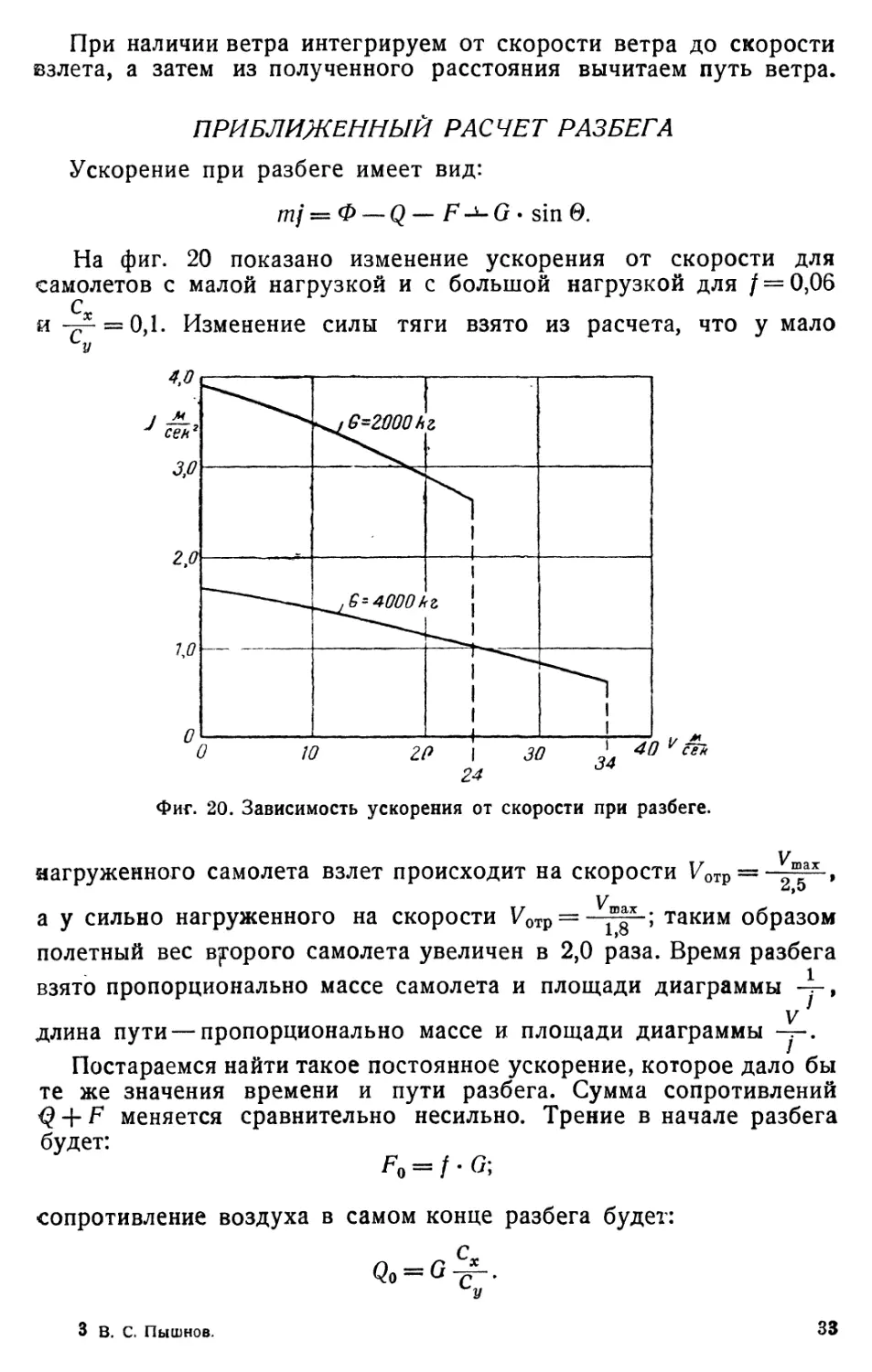
На фиг. 20 показано изменение ускорения от скорости для
самолетов с малой нагрузкой и с большой нагрузкой для / = 0,06
Сг
и yF = 0,l. Изменение силы тяги взято из расчета, что у мало
су
Фиг. 20. Зависимость ускорения от скорости при разбеге.
нагруженного самолета взлет происходит на скорости Уотр = —
у
а у сильно нагруженного на скорости УОтр = —таким образом
полетный вес второго самолета увеличен в 2,0 раза. Время разбега
взято пропорционально массе самолета и площади диаграммы Д-,
V}
длина пути — пропорционально массе и площади диаграммы —.
Постараемся найти такое постоянное ускорение, которое дало бы
те же значения времени и пути разбега. Сумма сопротивлений
Q + F меняется сравнительно несильно. Трение в начале разбега
будет:
F0 = f.G;
сопротивление воздуха в самом конце разбега будет:
<~х
Qo @ с
3 В. С. Пышное.
33
Очевидно, что можно подобрать такую постоянную тягу винта
и такие постоянные F и Q, которые дадут искомое постоянное
ускорение; однако нужно иметь в виду следующее:
1) нужно стараться подобрать такие доли, чтобы величина их
сохранялась для разных самолетов с разными нагрузками;
2) значения средних ускорений для времени разбега и пути
не равны друг другу.
Если для расчета времени взять ускорение при V = 0,6 • V0Tp и
для расчета пути V = 0,75 • V0Tp, то получаются хорошие резуль-
таты. Для расчета времени получим:
Д = 9,8 135 - Nr ^- /1 — 0,27-^А — 0,36 — 0,64/ — sin ©| ;
G • VP \ Vp ) СУ J'
135 ”ах (1 — 0,34 — 0,56 - 0,44 / — sin 6
G • vp \ vp 7 су
/i
Для расчета пути:
7*2 = 9,8
„ ; (УОТР-^
2 • /2 ’
где Vp—расчетная скорость винта при ??mas, обычно близкая к мак-
симальной скорости горизонтального полета.
Величина
1 q К N ' ?7тах Фо
о• vp -
если известно Фо, то его можно прямо подставить в формулу.
Точно также
0,27 = 0,6 0,34 = 0,75 ^р-.
vp v vp v
Примерные расчеты по этому методу для разнообразных вари-
антов показали отличие от расчета по графикам В. П. Ветчинкина
не более, чем на 1 —2%, а чаще меньше 1%. Напоминаем обозна-
чения: IV — мощность мотора в полете на расчетной скорости при
положении дросселя на взлете; Vp — расчетная скорость, т. е. ско-
рость, на которой к. п. д. винта максимален; т) — максимальный
к. п. д. винта; V0Tp—скорость при отрыве от земли.
НАИВЫГОДНЕЙШИЙ УГОЛ АТАКИ ДЛЯ РАЗБЕГА
Наивыгоднейшим углом атаки для горизонтального полета будет
Сх
тот, при котором качество имеет максимальное значение; наи-
су
выгоднейший угол атаки для разбега будет иной. От угла атаки
зависит сопротивление воздуха Q = Сж • q • S • V2 и трение колес»
поскольку, меняя угол атаки, мы меняем подъемную силу и, следо-
вательно, нагрузку на колеса. Изменения сил Q и F имеют обрат-
ные знаки; например, при увеличении угла атаки сила Q увеличи-
вается, а сила F уменьшается. Величина этих изменений неоди-
34
накова, и можно найти такой угол атаки, при котором сумма со-
противлений будет минимальной:
Q + F=CX- e-S - V2 + (G-Cy.e-S. V2)-/.
Угол атаки связан с величиной Cv; поэтому для отыскания мини-
мума Q4-F продиференцируем последнее выражение по Су.
d(Q + F} „ „ dCr
_L—2 = в . S - V*-^-Q • S • V2 • / = 0.
uui/
Отсюда найдем, что наивыгоднейший угол атаки для разбега
такой, на котором величина ,гх — Л Чтобы найти искомый угол
dCx
атаки, можно, конечно, построить предварительно диаграмму
ису
по а. Однако можно решить задачу и проще: берем кривую Лилиен-
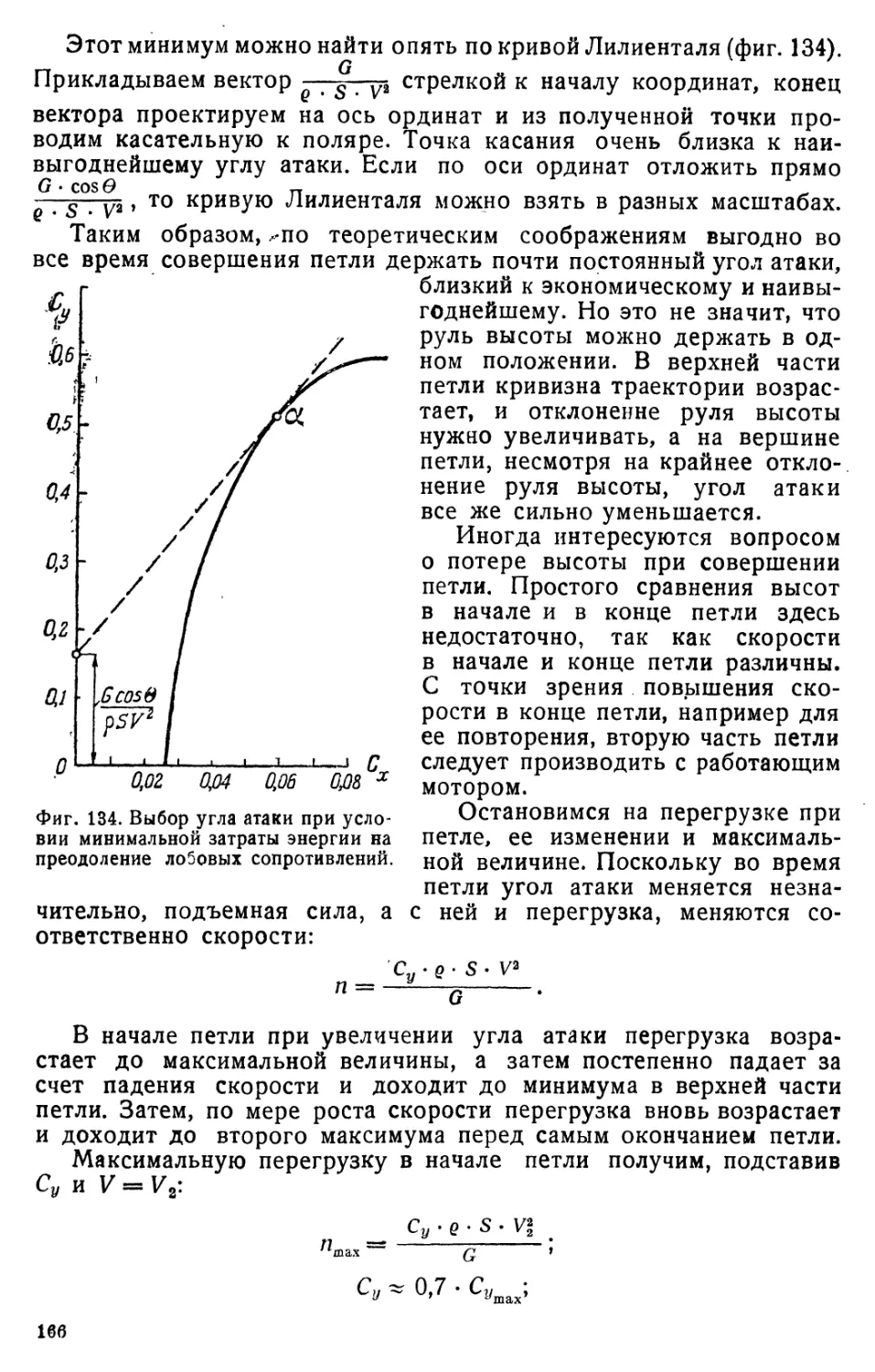
таля самолета (фиг. 21), берем произвольный Су, например 0,5, и на-
ходим Сх = j-Cy, наносим эту точку на диаграмму. Соединив точку с
и
у —
Фиг. 21. Определение угла атаки для крат-
чайшего разбега.
Как
трения
видим, наивыгоднейший Су пропорционален коэфициенту
и удлинению крыла; например, при Я = 7 и / = 0,05
Су = 0,262.
з*
35
Таким образом в решении задачи главную роль играло индук-
тивное сопротивление. Однако при взлете крылья самолета нахо-
дятся близко к земле, и это дает заметное уменьшение индуктив-
ного сопротивления. Для расчета можно вводить как бы фиктивное
удлинение. За счет влияния земли индуктивное сопротивление
нужно умножить на (1—<т), где:
»=0,29.1g[l + (i)!].
Имеем:
отсюда
где Л — расстояние до земли, I — размах крыла, Я' — фиктивное
удлинение, заменяющее влияние земли.
Например, для Л =7;-^- = 8; а =0,36 найдем:
Г=0'64=10>9-
Если теперь найдем наивыгоднейший Су для разбега, то полу-
чим Су = 0,428. Таким образом разбег происходит на сравнительно
большом Су. При большом коэфициенте трения Су выгодно еще
увеличить. Нужно только иметь в виду, что аналитический расчет
пригоден до такого Су, при котором начинается увеличение про-
фильного сопротивления; графический расчет годен во всех случаях.
При отыскании оптимальных условий инженер никогда не должен
ограничиваться одним математическим нахождением максимума или
минимума путем взятия производной. Всегда нужен анализ: что
будет при отклонениях от оптимальных условий. В данном случае
посмотрим, как меняется величина Q + F при перемене Су.
Q + F=G-]+Cx-q-S- V2— С,, . . S • V2 • / =
= G-/ + e-s. v2(Ca,-7.cy).;
Вообще говоря, угол атаки играет роль лишь тогда, когда ско-
рость достаточно велика. Возьмем V = 0,7 V0Tp и, поскольку нас
интересует относительное изменение сопротивлений движению, при-
ведем последнее выражение к безразмерной форме, поделив обе
части его на q • S • Уотр:
= /(Ср отр 0’5 • Су) + Сх‘
если при взлете нет подрыва, то
Су отр —
В табл. 2 даны примерные значения f(Cy отр — 0,5С„)+Сж для
Су от нуля до Су отр = 0,5 при / = 0,08.
36
Таблица 2
0 0,1 0,2 0,3 0,4 0,5
/ (Су отр О’5 Су) | 1 0,065 0,0616 0,0595 0,0588 0,059 0,061
Как видно, даже при очень сильном изменении угла атаки сум-
марное сопротивление меняется мало, и поэтому роль угла атаки
следует считать незначительной.
РАСЧЕТ РАЗМЕРОВ ВЗЛЕТНОЙ ПЛОЩАДКИ
Длина разбега самолета по земле еще не определяет всех усло-
вий взлета. Оторвавшись от земли на сравнительно небольшой
скорости, самолет должен увеличить скорость до взлетной, соот-
ветствующей максимальной вертикальной скорости, и затем перейти
на подъем и перелететь препятствия, окружающие аэродром, на
некоторой высоте. Таким образом весь взлет распадается на три
этапа: 1) разбег, 2) разгон и 3) подъем (фиг. 22). Разгон может
Фиг. 22. Схема расчета взлетной площадки.
быть произведен по некоторой наклонной траектории, угол кото-
рой должен быть во всяком случае меньше угла подъема на взлет-
ной скорости.
Пусть нам уже известны: длина разбега по земле хх, скорость
отрыва Ротр, взлетная скорость Квзл и вертикальная скорость цшах.
Угол подъема после достижения взлетной скорости определим &из
выражения:
Sin0 =
*взл
Путь подъема будет равен:
___ h
Хз sin 0 ’
Остается найти путь разгона. Вопросу разгона в воздухе посвя-
щена в нашем труде специальная глава, здесь же мы приведем
упрощенное решение, пригодное для данной задачи.
При взлете на скорости 70т₽ самолет имеет некоторый избыток
тяги в виде разности между тягой винта и сопротивлением (фиг. 23).
37
Избыток тяги может быть использован для подъема или дальней-
шего увеличения скорости. В последнем случае получим ускорение:
Разгон будем производить до взлетной скорости, дающей наи-
больший избыток мощности
... ЛФ- V
Л -•
Фиг. 23. Изменение избытка тяги при разгоне.
В интервале от ЕОтр до Евзя величина ДФ меняется очень мало
и поэтому ускорение можно считать постоянным. Найти его можно
по вертикальной скорости, взятой из аэродинамического расчета:
____AN • 75 _ АФ ,7 / ,Л
U — q q • Гвзл — g ' ‘взл.
откуда
/ = Sin е.
v взл
Таким образом ускорение в горизонтальном полете равно уско-
рению силы тяжести, умноженному на синус угла подъема, с кото-
рым мог бы подниматься самолет. Если бы самолет стал подни-
маться с углом 0, ускорения не было бы, а при подъеме с углом,
меньшим 6, ускорение будет, но небольшое.
Получив /, можем найти путь и время разгона:
# _ ^взл ^отр , _ ^взл ^отр
Г2 - , XS------.
38
Зная высоту, необходимую для перехода границы аэродрома,
получим расстояние х = хх 4- х2 + х3, на котором самолет должен
начать разбег.
В случае взлета при ветре путь разгона х2 следует геометриче-
ски сложить с путем, пройденным воздухом xw за время /2:
xw = w • Г2Л3
Угол подъема по отношению к земле получим геометрическим
сложением векторов Увзл и w. Однако при расчете / угол подъема О
нужно брать как при безветрии. Если угол подъема невелик,
можно взять путь х3 при безветрии и затем геометрически приба-
вить к нему путь, пройденный ветром за время подъема w • t3.
Если ветер встречный, получим:
х'3 = х3 — w • t3.
Если разгон происходит с некоторым углом подъема 02< то
величину ускорения получим:
ДФ — G • sin 02
, =------ ------
’ т
Подставляя ЛФ = G • sin 0, получим:
/ = g (Sin 0 — sin 02),
V2 ___ V2
х2 = взл2 у отр-• COS 02.
Путь разгона получается больший, но зато при разгоне самолет
наберет высоту h2 = х2 • tg 02, и путь подъема будет:
h — /?2
Х3 — "tg © •
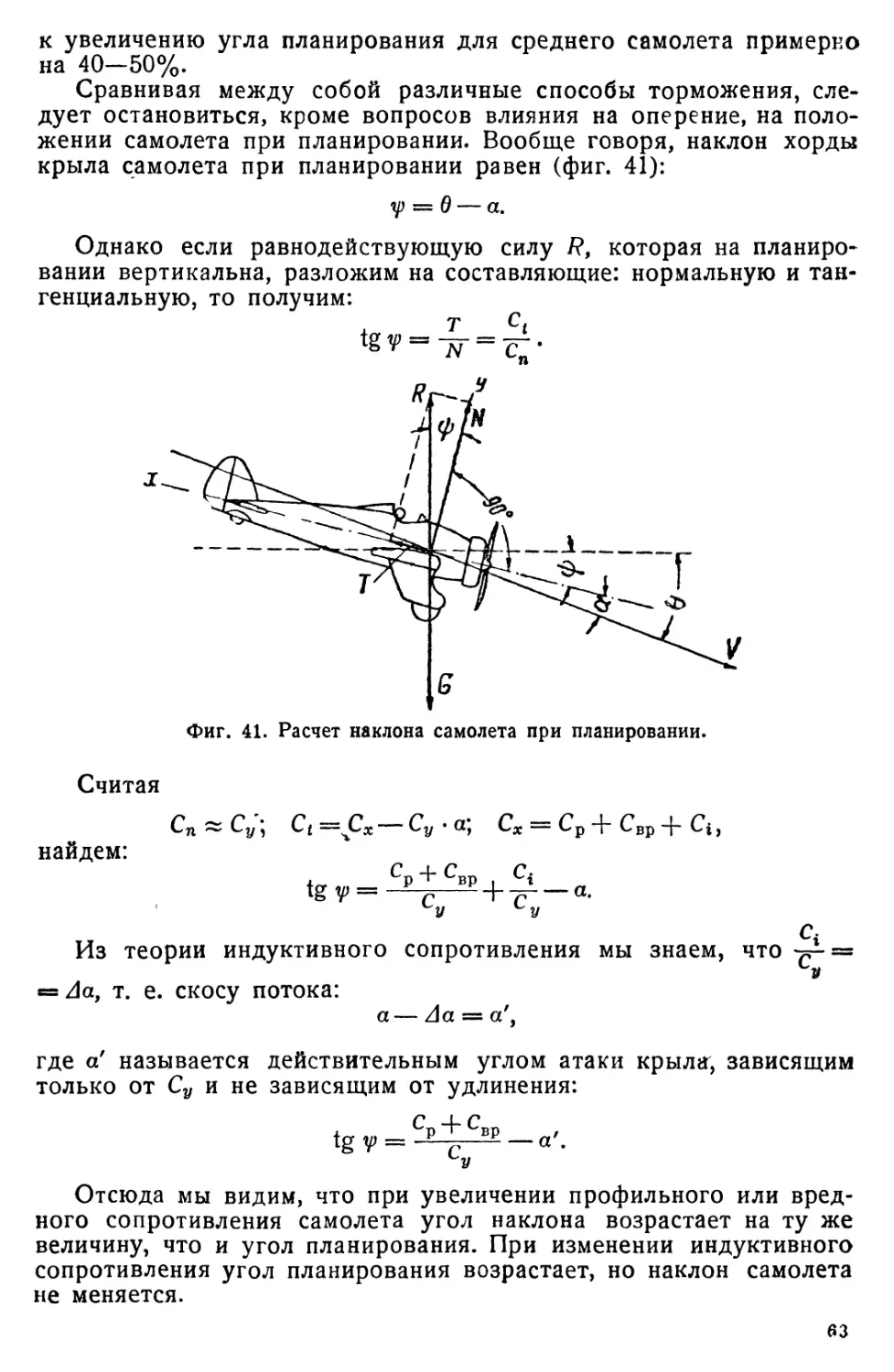
Естественно возникает вопрос о том, как же выгоднее произ-
водить разгон. Для этой цели составим выражение для х2 + х3:
V2 ___ V2 h h.
v I у — B3JI 0TP . СОЧ 0 4- —_____________
X2-1-X3— 2 g. (Sin©_sin©2) UJi,J2Ttg0 tg0,
подставляем й2 и делаем приведение:
Y ' V = <V^-^otp)cos02 f _ tg 0Л ft
2 ' 3 2 • g • (sin 0 — sin 02) \ tg 0/"* tg 0
(ya ___уз \ (
_ ' ’ взл 'отрЦ1 tg 0 / f h
= + tg® ‘
8 8 \cos0, tg©/
Вопрос о размерах взлетной площадки наиболее важен для са-
молетов, имеющих сравнительно небольшой угол подъема; в этом
случае можно с достаточной степенью точности считать cos 0 =
= cos 02 = 1. Тогда получим:
1 /V- — V2 \
Y 4- х — —- - ( взл отр 4- h 1
X2-t-X3 — 2 ,g -t-11 J-
39
Оказалось, что угол 02 роли не играет, а само выражение имеет
у2 _______________________________ у2
интересный механический смысл: • взл2 . g °ТР|—эт0 высота свобод-
ного падения для набора скорости от Уотр до УВзл.
ПОСАДКА САМОЛЕТА
Общие сведения. Перед посадкой на землю самолет спускается
с мотором, работающим на малых оборотах, или в более редких
случаях планирует с вращающимся от воздушного потока или ос-
тановленным винтом. Приблизившись к земле, самолет выравни-
вается по кривой линии до горизонтального полета, далее летит
Фиг. 24. Схема посадки самолета.
некоторое время параллельно земле, теряя скорость, затем, дойдя
до посадочной скорости, опускается на землю и, наконец, бежит
некоторое время по земле. Соответственно этому посадку самолета
можно подразделить на: 1) спуск или планирование, 2) выравни-
вание, 3) выдерживание над землей, 4) парашютирование и 5) про-
бег по земле (фиг. 24). Нас интересует площадка, необходимая для
посадки; очевидно, она сложится из частей, соответствующих эта-
пам посадки. Рассмотрим все эти этапы в отдельности.
Спуск. Подходя к земле под некоторым углом спуска, самолет
должен перелететь препятствия, окружающие аэродром, на неко-
торой высоте, например 20 м. Очевидно, что чем выше препятст-
вие и чем положе спускается самолет, тем дальше от препятствия
он подойдет к земле и тем больше будет неиспользованная пло-
щадь аэродрома (фиг. 25). Это обстоятельство (или, как говорят^
подходы к аэродрому) сильно влияет на величину аэродрома. По
мере повышения качества самолетов их угол планирования стано-
40
вился все более и более пологим и это, естественно, заставило
задуматься о мероприятиях к увеличению угла планирования при.
подходе к аэродрому.
Из аэродинамического расчета определим угол планирования:
сг
Как видно, угол планирования мы можем увеличивать повыше-
нием Сх или уменьшением Су. При планировании для увеличениям
угла планирования обычно прибегают к уменьшению угла атаки,
когда Су сильно уменьшается, а Сх хотя и уменьшается, но в мень-
шей степени. Однако этот способ при посадке негоден, так как
за счёт увеличения угла планирования самолет разгоняется и длина
выдерживания над землей возрастает.
Выравнивание. При спуске скорость самолета V можно разло-
жить на горизонтальную и вертикальную составляющие. Подойдя
к земле, нужно во избежание удара уничтожить вертикальную*
составляющую u = V sin 0. Для этой цели нужно временно увели-
чить подъемную силу для создания некоторого ускорения jy, на-
правленного вверх. Считая его для простоты постоянным, опре-
делим время выравнивания и вертикальный путь выравнивания:
Увеличить подъемную силу можно увеличением Су, но это воз-
можно только в том случае, если планирование происходит на*
Су Сутах.
В процессе выравнивания скорость самолета падает, и поэтому
перед началом выравнивания нужно иметь запас скорости.
Выдерживание над землей. Самолет подходит к земле, имея запас
скорости против посадочной. Чтобы не катиться по земле с боль-
шой скоростью, летчик старается еще в воздухе уменьшить ско-
рость насколько возможно. Для этой цели он постепенно увели-
чивает угол атаки для сохранения подъемной силы путем увеличе-
ния Су соответственно уменьшению скорости. Искусство посадки за-
ключается в том, чтобы вести самолет параллельно земле на высоте
около 1 м. Когда Су дойдет до максимальной величины, дальней-
ший горизонтальный полет станет невозможным, и самолет сам
собой опустится на землю. Если скорость самолета была велика,,
то выдерживание над землей может оказаться длительным.
Парашютирование. Достигнув СУшаж, самолет начинает опускаться,
так как подъемная сила становится меньше веса и появляется-
ускорение, направленное вниз и создающее вертикальную скорость.
Это движение самолета мы называем парашютированием. Если
высота небольшая, самолет не успевает приобрести значительной
вертикальной скорости и сила удара о землю невелика. Чем больше
высота парашютирования, тем больше вертикальная скорость и
сильнее толчок. При некоторой высоте парашютирования шасси
самолета может быть поломано. Однако обойтись совсем без
парашютирования очень трудно, так как для этого нужно выдер-
41
живать самолет, почти касаясь земли колесами; но в этом случае
небольшая неровность почвы или неправильность движения рулями
может вызвать небольшой толчок о землю, за которым последует
так называемый „козел", приводящий затем к парашютированию
со значительной высоты.
Положительная сторона парашютирования заключается в том,
•что во время парашютирования самолет теряет горизонтальную
составляющую скорости, и от этого сокращается последующий
пробег по земле.
Посадочная скорость. Посадочной скоростью мы называем ско-
рость самолета в момент начала движения по земле при посадке.
Величина посадочной скорости является одной из важнейших
характеристик самолета. Всегда стараются сделать посадочную
скорость возможно меньшей, однако, желание увеличить быстро-
ходность самолета заставляет итти на увеличение посадочной
скорости.
Подходя к вопросу о величине посадочной скорости, нужно
условиться, какую посадку самолета следует считать правильной.
Обычно считают, что самолет должен садиться на землю без тол-
чка, поэтому в момент соприкосновения с землей траектория должна
плавно переходить в горизонтальную прямую и подъемная сила
должна держать на себе вес самолета; следовательно, мы можем
написать:
P = G = CV- q •£V2.
Поскольку мы желаем иметь возможно малую скорость, Су
нужно взять максимальный:
у — -\/-----2— .
пос V
Величиной Cj,mai мы называем максимальный коэфициент подъем-
ной силы всего самолета в условиях близости земли. Обычно счи-
тают, что под влиянием близости земли Су возрастает, и даже было
принято такое выражение:
где СУалх — только для крыла по продувке вне близости земной
поверхности. Мы здесь не будем обсуждать вопрос о величине
^т/max, так как это вопрос аэродинамики крыла и в нем еще нет
достаточной ясности как в отношении перехода от модели к на-
туре, так и в отношении влияния земной поверхности.
Таким образом величина посадочной скорости определяется во-
все не невозможностью уменьшить скорость торможением, а тем,
что летчик не может допустить уменьшения скорости, пока машина
не коснется земли, и в результате на величину посадочной скорости
влияют нагрузка на квадратный метр крыла и величина СИшах. Оче-
видно, что увеличение сопротивления не будет сказываться на вели-
чине посадочной скорости.
Л П
Иначе нужно отнестись к вопросу о посадочной скорости при
рассмотрении посадки с ударом, т. е. когда самолет уже стал
парашютировать. Подобным образом садятся автожиры, и были
попытки построить специальные самолеты, у которых нормальная
посадка происходит с значительной вертикальной скоростью
и шасси рассчитано на восприятие энергии удара. При парашю-
тировании горизонтальная составляющая скорости сильно падает,
а вертикальная нарастает. Шасси воспринимает вертикальную
скорость, и у самолета остается одна горизонтальная составляю-
щая, значительно меньшая, чем при нормальной посадке без удара.
Более подробно о посадке с парашютированием мы скажем далее.
Напомним только, что так садятся птицы: во время парашютиро-
вания они очень сильно увеличивают угол атаки и этим почти
полностью уничтожают горизонтальную составляющую скорости.
Пробег по земле. Коснувшись земли, самолет бежит по ней,
уменьшая постепенно скорость. Процесс пробега после посадки
похож на разбег, но только отсутствует тяга винта, а прочие силы
меняются в обратном порядке, т. е. подъемная сила и сопротив-
ление воздуха уменьшаются, а сила трения нарастает. Кроме того
коэфициент трения и качество самолета сильно отличаются от та-
ковых при взлете. При посадке стремятся увеличить силы тре-
ния, для чего или стараются прижать костыль к земле, или при-
меняют тормозные колеса.
РАСЧЕТ ПРОБЕГА САМОЛЕТА ПРИ ПОСАДКЕ
Способ расчета пробега самолета при посадке вполне аналоги-
чен расчету разбега, только здесь мы не имеем тяги винта, коэфи-
циенты трения и Сх больше, чем при взлете, и, наконец, интегри-
рование ведется в обратном порядке, т. е. от посадочной скорости
Фиг. 26. Действие сил на самолет при пробеге после посадки.
до остановки. Для составления уравнений движения берем схему
самолета на посадке (фиг. 26). Прикладываем силы: тяжести G,
подъемную Р, сопротивление воздуха Q, реакцию колес Nx, реак-
цию костыля ЛГ2, трение колес и трение костыля F2. Ось х на-
правляем параллельно поверхности земли, которая в общем случае
может быть наклонена под некоторым углом 0 к горизонту. Пишем
проекции сил на оси координат:
— (Q -|- Fi -|- F2 Ч- G • sin 0) = mj,
2Y = Ni + N2 + P— G-COS0 =0.
43
Опять, как и при взлете, ввиду малости угла 6 берем cos 6=1
и sin 6=0; получим:
j = - 9,8 -g + F. + F,+0-» = _ 9 8 «
Л г (j
G
G = N1+N2 + P.
Перед интегрированием раскроем выражения для сил:
Q = Сх • о S • V2; Р = Су q • S-V2.
Величины Сж и Су нужно взять для угла атаки соответственно
стоянке самолета на земле, причем следует принять во внимание
влияние близости земли:
F1 = /1-N1; F2 = /2.N2;
f = f1 + f2 = n(/1^ + /2^) = /n
JV = N1 + N2; +
Величина / представляет собой некоторый приведенный коэфи-
N, Nz
циент трения для всего самолета. и ~ дают распределение ре-
акции между колесами и костылем. Вообще говоря, распределение
реакции может меняться в процессе пробега по земле за счет при-
жатия хвоста рулем высоты. Однако современные самолеты цент-
рируются в большинстве случаев таким образом, что перед со-
прикосновением с землей
при максимальном отклоне-
нии руля высоты моменты
находятся в равновесии и
нарастание реакций проис-
ходит пропорционально; к
моменту остановки имеем
нагрузки на колеса и на
г Na
костыль о2; отсюда и
Gi G2
можно заменить и
(j (j 1
Фиг. 27. Распределение нагрузки между коле- получим.
сами и костылем. / — / 41 । / 41
/ g T/2G '
Величины G± и G2 можно найти, имея чертеж бокового вида са-
молета и зная положение центра тяжести (фиг. 27). В результате
получаем:
/ = — 9,8 [|+^+9].
Q и Р еще удобно представить так:
Q = Сх • о • S V2; Р Су о . S • V2.
44
Умножим и разделим выражение для Q на Су • G:
Q = £? . G • Vs
СУ
G
С
=п,
где У1—скорость, на которой самолет мог бы еще лететь горизон-
тально при том же Cv, что и в положении стоянки на земле. Этот
Су может отличаться от CUm„, хотя часто он близок к нему. В резуль-
тате получаем:
Схематично можно написать:
j = -(a + c- V2); а = 9,8(/ + 0);
Уравнение интегрируем в пределах от воздушной посадочной
скорости VB0C до скорости ^етра w:
^пос
Г dV _ f dV .
- “ J a + c- V2 J a-\-c- V2’
ПОС W
Г ' arc tg (,/Z. . 1A.
J а-\-с-У г V a с \ у a }
Подставляя пределы, значения а, с и преобразуя, получим:
у
'= 9^7 (А-А^
где
45
Произведя аналогичный расчет для пути, получим:
V1
где
In
Bv> —
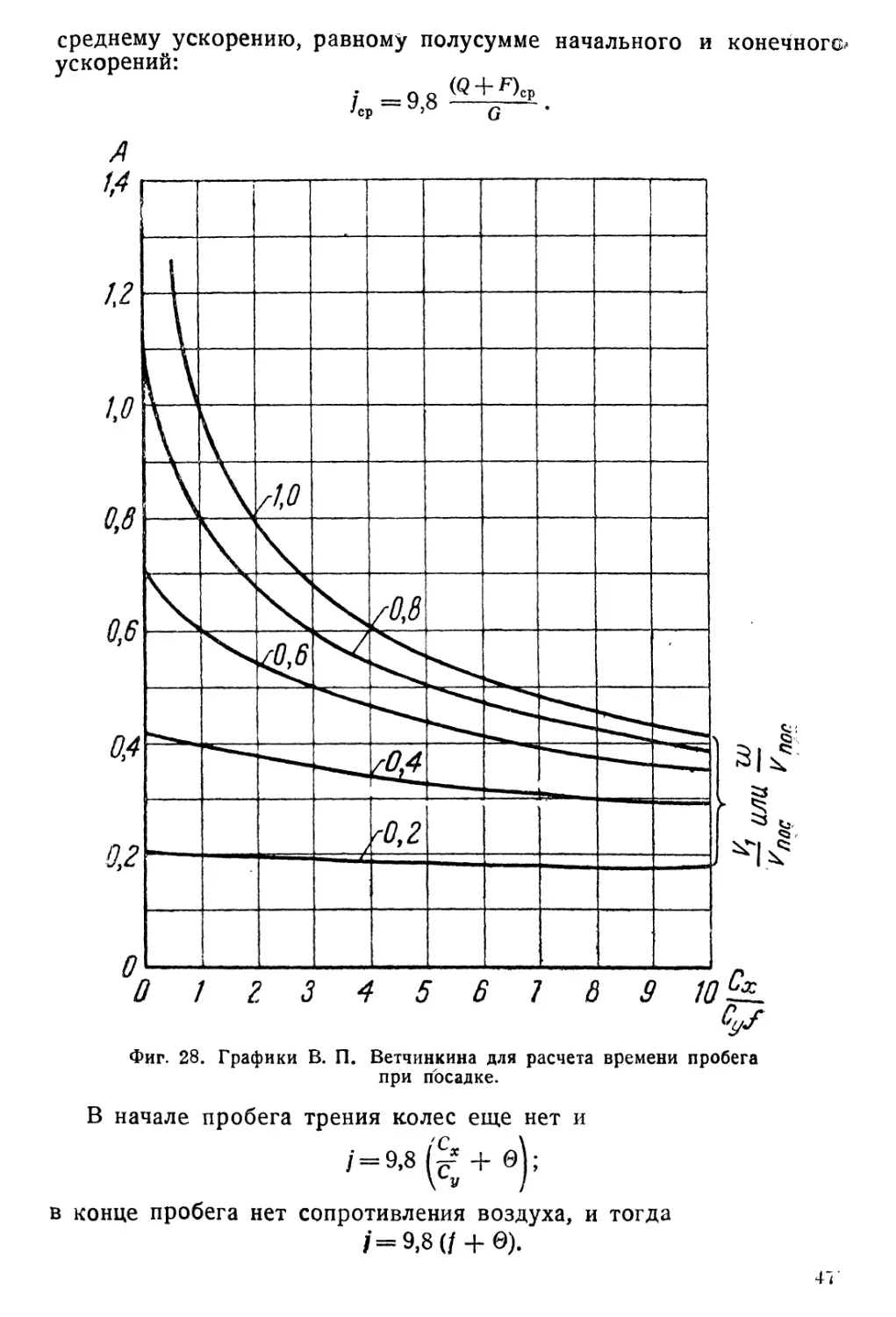
Для того чтобы не затрудняться вычислением значений A, Aw,
В и BW) проф. Ветчинкиным были сделаны вычисления в вероят-
/ Vj \2 / W \2 /Г \ ,
ных границах -р— ) —) и (7^-77 — 1 . На фиг. 28 и 29
\ 'пос / ’ у 'пос J у *~у * / )
мы приводим эти данные в виде диаграмм.
Таким образом для практического расчета пробега нам нужно
знать: посадочную скорость Кпос, скорость ветра w, величину
Сх
гг для угла атаки соответственно стоянке самолета на земле с уче-
том влияния земли, приведенный коэфициент трения /; затем нужно
подсчитать скорость Ер
^==1/^----
q • S • Су
взяв Су соответственно углу стоянки самолета на земле (желательно
Сх V1
с учетом влияния земли). Далее по величинам , -р—
’ J *пос
w
И -у
г пос
находим A, Aw, В, Bw и, наконец, по формулам t и х.
О коэфициенте трения колес уже было сказано. Если на коле-
сах стоят тормоза, коэфициент трения возрастает до 0,2 и даже
больше. Коэфициент трения костыля около 0,5. В итоге приведен-
ный коэфициент трения без применения колесных тормозов будет
с
около 0,1, с тормозами — около 0,2—0,25. Величина у обыч-
ного самолета составляет около 0,1, а в случае применения щит-
ков возрастает примерно до 0,15. Отсюда мы видим, что величины
С
f и ~ близки между собой, ускорение в процессе разбега меняется
незначительно и расчет можно вести с достаточной точностью по
46
среднему ускорению, равному полусумме начального и
ускорений:
конечного'
'ср-9’8 G------
Фиг. 28. Графики В. П. Ветчинкина для расчета времени пробега
при посадке.
В начале пробега трения колес еще нет и
/==9,8 (& + 0
в конце пробега нет сопротивления воздуха, и тогда
/=9,8 (/ + ©).
47
В результате среднее ускорение будет:
L = 9,8 [о,5 (} + + &
L \ у/
Фиг. 29. Графики В. П. Ветчинкина для расчета пути пробега
при посадке.
X - (Vnoc.~ w)2
/ср
48
РАСЧЕТ ПОСАДОЧНОЙ ПЛОЩАДКИ
Подобно расчету взлетной площадки найдем посадочную пло-
щадку, учитывая планирование после перехода через препятствия
на границе аэродрома, выдерживание над землей и пробег по земле.
Длина пробега по земле хх нами уже найдена. Путь планирования
получим, зная угол планирования 0 и высоту полета h при пролете
через границу аэродрома:
_ ft
Х3— tg© •
Расчет пути торможения приведен далее, здесь же мы дадим
приближенный расчет. Планирование происходит на угле атаки,
близком к наивыгоднейшему. По кривой Пэно самолета легко ви-
деть, что на больших углах атаки сопротивление самолета меняется
очень мало, и только вблизи CVmat происходит быстрое увеличение
сопротивления. Отсюда в первом приближении движение можно
считать равномерно замедленным, принимая ускорение
тогда
где — скорость планирования.
с
Величину можно брать минимальной, предполагая, что уве-
личение Ск на углах, близких к CUmax, отчасти компенсируется влия-
нием земли.
ВЗЛЕТ И ПОСАДКА НА ВЫСОКОГОРНОМ АЭРОДРОМЕ
В некоторых случаях самолету приходится производить взлет
и посадку на плоскогорья или даже в ущельи, расположенном на
значительной высоте над уровнем моря. Вообще говоря, в этих ус-
ловиях требуется аэродром больших размеров, нежели на уровне
моря.
Имеются аэродромы, расположенные на высоте около 2 км, в
условиях же Памира возможны взлет и посадка на высоте 5 км.
На таких высотах мы имеем значительное уменьшение плотности
воздуха и падение мощности мотора (кроме случаев применения
моторов с большой высотностью). Трудность взлета еще усугу-
бляется тем, что на плоскогорьях мы часто имеем температуру
воздуха более высокую, нежели на той же высоте в свободной
атмосфере, а это приводит к дополнительному снижению плотности
воздуха и мощности мотора. Поэтому для расчета взлета и посадки
в высокогорных условиях не следует пользоваться стандартными
значениями плотности и мощности, а надо подсчитывать их для
4 В. С. Пышное.
49
конкретных значений температуры и давления. Для относительной
плотности имеем такое выражение:
где давления берутся в любых мерах, а температура — по абсолют-
ной шкале.
Изменение мощности мотора без наддува можно подсчитать:
Для мотора с нагнетателем мы пока не можем предложить
формулы.
Скорость при отрыве от землиги при посадке мы можем под-
считать обычным способом или, взяв соответствующие скорости
для малых высот, разделить их на корень квадратный из относи-
тельной плотности. Качество самолета оставляем без изменений,
коэфициент трения берем соответственно грунту. Тягу винта полу-
чаем из тяги для работы на малой высоте, умножив ее на отноше-
ние плотностей и квадрат отношения числа оборотов; при этом
скорость можно оставить без изменения, хотя правильнее было бы
получить скорость на высоте путем умножения скорости на уровне
моря на отношение чисел оборотов. Последнее можно найти по
выражению, которое уже не раз нами применялось:
1
, . з - k
2
При взлете с высокогорного аэродрома удлинение разбега про-'
исходит за счет повышения скорости при отрыве и за счет сниже-
ния тяги винта. Однако дать простую пропорциональность здесь
не представляется возможным, так как в выражение для ускорения
входит разность.
При посадке пробег удлиняется только за счет повышения
посадочной скорости и поэтому здесь мы получаем простое соот-
ношение: длина пробега обратно пропорциональна плотности воз-
духа, а время пробега обратно пропорционально корню квадрат-
ному из отношения плотностей.
С точки зрения работы пилота следует отметить, что на высо-
когорном аэродроме отрыв от земли при взлете, планирование
и посадка производятся на такой же скорости по прибору, как
и в нормальных условиях.
50
НЕПРАВИЛЬНЫЕ ПОСАДКИ
Как мы уже указывали, принцип посадки большинства совре-
менных самолетов заключается в том, чтобы коснуться земли без
толчка с минимальной скоростью. Следовательно, нужно удовлет-
ворить сразу двум условиям: довести самолет до минимальной
скорости как раз в тот момент, когда траектория плавно коснется
земли. Это, конечно, требует большого уменья и навыка, выра-
ботки глазомера и, естественно, может привести к ряду ошибок.
Фиг. 30. Правильная посадка на три точки.
Поэтому приходится, с одной стороны, обучать летчиков соверше-
нию посадки и тренировать их, а с другой стороны, предусматри-
вать возможность поглощения определенного удара конструкцией
шасси. Величина энергии удара была выработана опытным путем
и задается в нормах прочности.
Исходя из условий правильной посадки, нетрудно представить
себе возможные ошибки: 1) траектория коснулась земли, но ско-
рость еще не минимальна, — получается так называемая „посадка
Фиг. 31. Посадка на колеса.
на колеса"; 2) самолет достиг минимальной скорости, но траекто-
рия еще не коснулась земли; после этого самолет хотя и будет
иметь малую скорость, но плавное касание земли окажется невоз-
можным и произойдет так называемое парашютирование. Третий
вид ошибки — комбинированный, когда самолет, имея скорость
больше минимальной, коснется земли не плавно, а с ударом; прои-
зойдет „козел" с последующим парашютированием. На фиг. 30—33
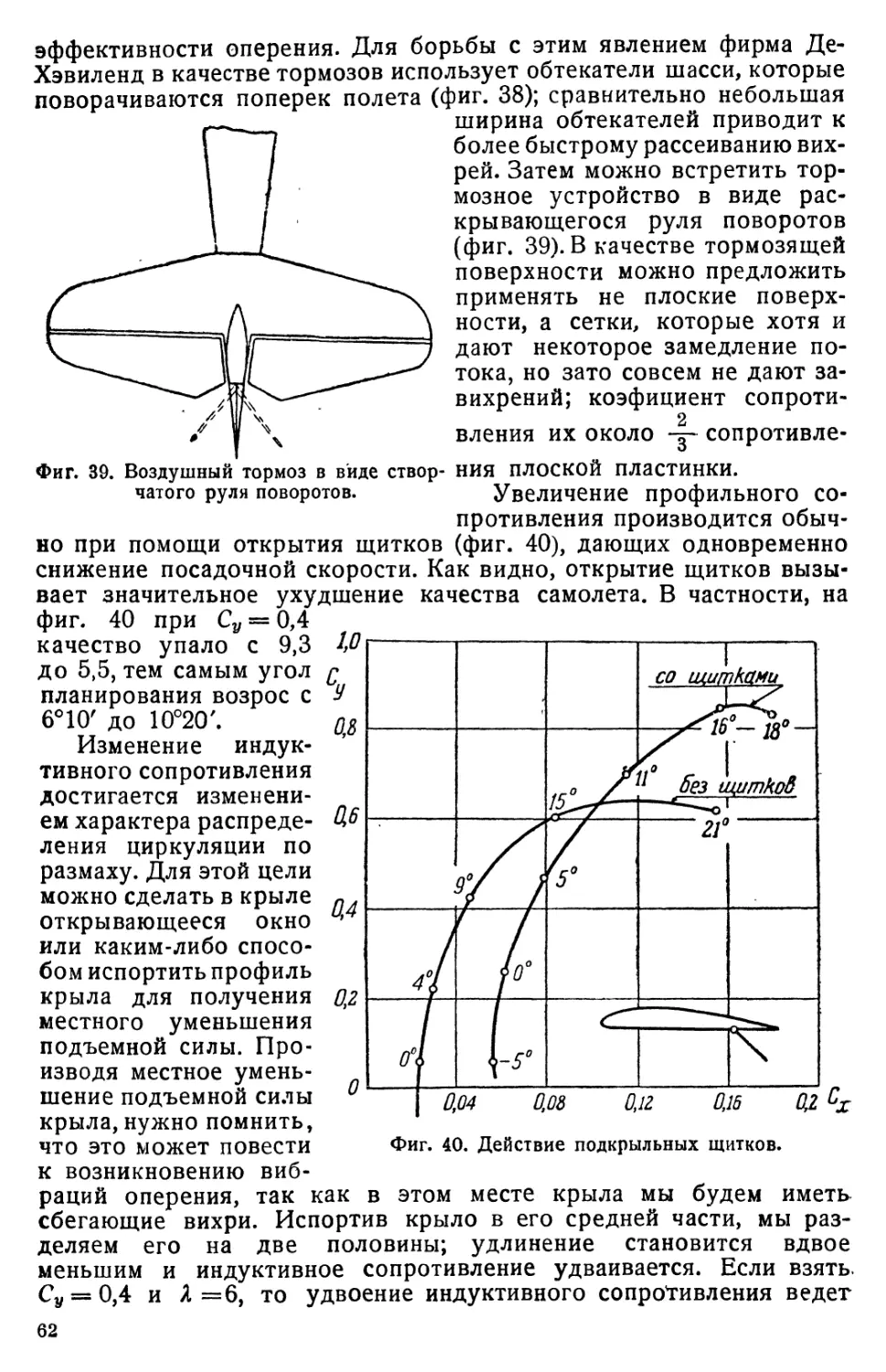
представлены типичные посадки.
Посадка на колеса может пройти без особых последствий, если
летчик достаточно опытен и аэродром ровный. Дело в том, что
коснувшись земли колесами, хотя бы без толчка, самолет стре-
мится опустить хвост; если это допустить, то в результате увели-
чения угла атаки возрастет подъемная сила и самолет вновь взле-
4* 51
тит. Для предупреждения этого летчик должен рулем высоты удер-
жать самолет от опускания хвоста, пока скорость не дойдет до
минимальной.
Кочка или канавка может дать толчок в колеса, который лет-
чик не успеет парализовать, и тогда получится „козел". Более
подробно вопрос о посадке на колеса будет рассмотрен в главе об
устойчивости при движении по земле в четвертой части настоящего
курса.
Вопрос о парашютировании самолета был подробно исследован
В. П. Ветчинкиным и изложен в его труде „Динамика самолета".
Фиг. 32. Посадка с парашютированием.
Мы здесь рассмотрим этот вопрос лишь приближенно, интересуясь
физической картиной явления и примерной энергией удара.
При достижении критического угла атаки, соответствующего
Ctfmax’ величина подъемной силы не может быть увеличена и даже
сохранена, так как скорость продолжает падать, а увеличение или
уменьшение угла атаки вызывает лишь уменьшение Су. В резуль-
тате подъемная сила будет меньше веса, появится вертикальное
ускорение, горизонтальная составляющая скорости будет умень-
шаться, а вертикальная — нарастать.
| В отношении удара о землю нас интересует вертикальная
составляющая скорости. Для упрощения расчета примем следую-
щие допущения, вполне справедливые для обычного самолета. При
небольшой высоте парашютирования:
1) будем считать, что Cv остается без изменения; это имеет
место для большинства профилей, применяемых на современных
самолетах;
2) будем считать Сх постоянным, объясняя это тем, что увели-
чение Сх от увеличения угла атаки компенсируется уменьше-
нием Сх за счет влияния приближения земли;
52
3) будем считать, что скорость по траектории равна горизон-
тальной составляющей; это допустимо для углов наклона траекто-
рии не более 15°.
Теперь без труда можно составить уравнения движения:
CxqSV*
= ---G---
при t = 0 имеем Vx — Уш!п; тогда:
G - P ( P\ I
1v~ О Q — ~~S Q/~ V “
P—G p g cv^.
ix Q Q Q Cx ’
с,, . -e-s-v2
3/max g ____
О
Проинтегрируем полученные выражения:
min
— ± f dx — J-/'—___1 \
“ к J V*~ k\V VaJ
v
Мы получили связь скорости со временем; теперь получим связь
скорости с пройденным расстоянием:
У>--= — ЛУ2- dx------- - •
v dx v ’ AV’
Y____.1 fdV l . Vmln
x~ к J V - A 111 V •
V
v min
Так как мы приняли, что величина воздушных сил зависит лишь
от горизонтальной составляющей скорости, то для расчета верти-
кальной скорости и и вертикального пути у разложим движение
на две составляющие: а) движение по инерции по горизонтали со
скоростью Уш1п со свободным падением по вертикали; б) движе-
с,.
ние под действием воздушных сил назад-вверх с наклоном ~ к го-
ризонтали (фиг. 34). Согласно принятому допущению, движение под
действием силы тяжести, давая только вертикальную скорость, не
будет сказываться на величине воздушных сил. Это соображение
и позволило прибегнуть к разложению движения.
Результирующее движение получим сложением составляющих.
Скорости и перемещения под действием воздушных сил по гори-
зонтали и вертикали будут относиться друг к другу, как Сх к Су.
53
Скорости и перемещения по горизонтали под действием воздушных
сил можно найти как разности найденных V и х и получающихся
при движении по инерции ИШ1П и Vmtn-/. Вертикальная скорость,
Фиг. 34. Расчет парашютирования.
вызванная воздушными
силами, будет:
с«
^ = (^-7)--^,
так как (Vmln—V) пред-
ставляет изменение
скорости за счет гори-
зонтального ускоре-
ния.
Полная вертикаль-
ная скорость будет:
и = 9,8 • t — нх =
су
=9,8/--
Аналогично для
пройденного пути по-
лучим:
=х ^mln* t
СУм
У1=^1-С~ =
= -^(VmlB-/-x);
/2
У = 9,8‘—
По полученным выражениям можно легко получить все эле-
менты; задаваясь промежутками времени, например 1 сек., сначала
находим скорость:
у —-------1-------•
1 ~nCx‘SS
---4-9 8 . t
* mm и
затем, имея t и V, находим н:
tz = 9,8-f
далее, зная V, находим х:
Y ________In ~min — 94 ____—____1 ст ^rotn
Х — 9,8-е-'$-Сх 1 V “z,o9,8^-s-cx V
54
и, наконец:
y = 9,4‘-^(Vmtn.f-x).
X
Результаты подобного расчета даны на фиг. 35.
Как видно, в приведенном примере через 3 сек. скорость
самолета упала на 15%, вертикальная скорость дошла до
4,7 м/сек и была пройдена высота 5,4 м. К сожалению, данный
метод расчета хотя и прост, но имеет малую точность, так как
все выражения содержат
разности близких величин.
Для повышения точности х
и у лучше подсчитывать по
средним скоростям V и и за
интервал времени.
Однако можно пойти
еще на дальнейшее упро-
щение. При коротком пара-
шютировании скорость V
не успевает значительно
упасть, поэтому ускорение jx
меняется не сильно и его
можно считать постоянным:
C-e-s-v*,
♦ П о х min
;Ж = У,8---Q----.
Фиг. 35. Изменение элементов движения при
парашютировании.
Было бы лучше взять
не Уш1а, а меньшую ско-
рость— среднюю между на-
чалом и концом парашютирования, но тогда придется прибегнуть
ко второму приближению; можно примерно для небольших пара-
шютирований принять: V'mln — 0,95 Kmln; имеем:
V = V min------jx ’ С
. t®
X ‘ 7х ‘ 2 9
ускорение по вертикали:
/« = 9,8(1
Cy-e-S-v*
a
Диференцируя по времени, получим:
diy... noC«gSV-2 dV.
dt ~ 3,0 G 'at’
тогда
dv . c„-e-S (v' . )s
; _ ex q X « \ min'
dt =/«-y>8 G
G
esc
*max
2
mln*
Cx
ix=9,8c-y
= v
5
подставляя jx, получим:
djv 9’82 • 2 ' Vmin Сх / Уш1~п X2 192 Сх /Ут1п\2 172^ Сх '
dt ^Г'СУ ’ ” Vmin’ Су W " Vmin ’ Су ’
172 С„
dlv = у~~ ’ с~
* тт
dt-,
• _ I72 С« /_ ЛЦ.
1у— v . 'с,,~ dt ’
тт У
U =
86 Сг Л
____ х . /2.
V 5 С ‘ ’
min У
29 Сх .
у = —т-'-
min У
Полученные выражения хотя и грубы по абсолютным величинам,
но дают достаточное представление о закономерностях. Выразим и2
через у (энергия удара пропорциональна и2):
подставляем /:
и2
При падении в пустоте с высоты h получаем:
и2= 19,6й.
Приравнивая оба выражения для и2 друг другу, получим высоту
падения в пустоте, которая даст тот же удар, что и парашютиро-
вание с высоты у:
4 Л
^4,234- (1;/.
3 у
V 4
min
В табл. 3 приведены значения/! для разных упри VBin = 25м/сек
и ~ = 6,5.
Таблица 3
у, м 1 2 3 4
h, м 0,14 0,355 0,606 0,895
2 h 7,15 5,62 4,95 4,47
56
Как видно, в данном примере парашютирование с высоты 2 м
дало такой же удар, как падение с высоты 0,355 м, т. е. в 5,62 раза
меньший. Из выражения для и2 видим, что самолеты с разной Ут1ж
и разным качеством при парашютировании с одной высоты дают
различную удельную энергию удара, а именно: чем больше мини-
мальная скорость и больше качество самолета, тем слабее удар.
Возьмем, например, два самолета: первый с Vmin = 15 м/сек и
С с
7^ = 5, второй с УШ1П = 30 м/сек и ^=10; величину и2 для у = 2 м
получим:
щ2 = 83~-0,23’=11,1 м2/сек2,
163
J I
и! = 83 • • 0,1 = 4,63 м2)сек2.
30 3
Как видно, у второго самолета удар получился в 2,4 раза сла-
бее. Чтобы получить такой же удар, как первый самолет, второй
самолет должен был бы спарашютировать с высоты:
Л 1
83-^0,13= 11,1; у= 3,8 м.
зо3
Интересная мысль о сравнении парашютирования с падением
в пустоте принадлежит В. П. Ветчинкину.
Аналогичным образом можно было бы исследовать вопрос о
парашютировании в случае изменения Су скачком, как это иногда
наблюдается на практике. Тогда в расчет нужно ввести другой С9,
а также ввести начальное ускорение за счет падения Су.
Если по какой-либо причине высота парашютирования оказа-
лась очень велика и есть опасность аварии, то полезно включить
мотор. Тогда скорость падать не будет и посадка может быть сде-
лана плавной.
Анализ посадки с преждевременным ударом о землю и после-
дующим „козлом" представляет огромные трудности. Здесь мы
имеем явление удара, направление которого не проходит через
центр тяжести, вследствие чего происходит образование угловой
скорости у самолета, появление сил инерции самолета, действие
воздушных моментов, изменение Су и Сх вследствие перемены угла
атаки и, наконец, фактор вмешательства летчика.
Точный расчет этого случая не имеет особой практической цен-
ности, так как исходные данные достаточно произвольны. Но нужно
обратить внимание на те мероприятия, которые способствуют
ослаблению наклонности самолета к „козлам" и позволяют наибо-
лее удачным образом исправить создавшееся положение.
В отношении самого толчка о землю можно сказать следующее.
Для уменьшения „козла" нужно, чтобы под действием толчка
57
в колеса самолет приобрел возможно меньшую угловую скорость
в направлении кабрирования. В этом отношении наиболее важно
уменьшать плечо силы удара, однако, здесь нельзя перейти оп-
ределенной границы, так как, если направление реакции земли
пройдет позади центра тяжести, то самолет поднимет хвост и оп-
рокинется. Другое дело, если самолет имеет впереди предохрани-
тельное шасси. Тогда главное шасси можно поставить под центром
тяжести или даже немного сзади. Коснувшись земли, самолет умень-
шит угол атаки и никакого „козла", кроме небольшого подпрыги-
вания от амортизации, не получится. Если шасси вынесено вперед,
„козел" можно уменьшить, применяя более мягкую амортизацию
с большим ходом, а главное амортизацию, поглощающую удар.
Таким свойством в лучшей мере обладает масляная амортизация.
Высота „козла" зависит от скорости в момент толчка, степени
увеличения угла атаки при ударе, устойчивости и управляемости
самолета. При большой скорости „козел" может получиться очень
высоким, тогда у летчика больше возможности выправить самолет
рулями и дачей тяги винта.
Сравнивая „козел" с парашютированием, нужно указать, что
удар после „козла" получается сильнее, чем при парашютировании
с той же высоты, так как на вершине „козла" самолет уже будет
иметь вертикальное ускорение и, следовательно, за время спуска
накопит бдльшую вертикальную скорость.
НЕКОТОРЫЕ ОСОБЫЕ ВИДЫ ПОСАДКИ
При рассмотрении парашютирования мы видели, что чем боль-
ше высота парашютирования, тем больше падает горизонтальная
составляющая скорости, но зато приобретается вертикальная со-
ставляющая, дающая удар при посадке. Таким образом, если пойти
на посадку с ударом, посадочную скорость можно снизить. Вос-
пользуемся приближенными формулами для парашютирования
и найдем связь между степенью падения горизонтальной скорости
и нарастанием вертикальной, или, лучше, с фиктивной высотой
падения в пустоте. Изменение скорости выражается:
V = 7mln-/x-f;
=
V min
. Cx-e-s-(<ln)2.
/х = у,a------Q-------,
умножая и деля на С„ и замечая, что V2,
J ашах 1 min
_ G
e-sc
‘'max
CY /V' с
/х = 9,8р- = 8,8 а-.
'’min' У
получим:
Связь вертикальной скорости с временем имеет такой вид:
и = -р— — • Р; t= 1/ и' Vmln,‘ СУ-
Су “ 86СХ ’
К~ = 1
v min
8,8 сх -1/ и • Vmln • Су
Vmin • Су' V 86 сх
1 — 0,95
“-Сх
Уш1п ’ Су
58
Если подставить вместо вертикальной скорости фиктивную
высоту падения, то получим:
и2 = 19,6й; и = 4,43//Г;
V’
Vh
С ’
1_2 V,л
\г______________1 х, г mln
’'min
Согласно нормам прочности шасси безопасная работа аморти-
зации должна быть:
А = 0,4G.
Это соответствует падению с высоты h = 0,4 лс; определим
v
V min
V . 1,6
--- = 1---------.
m,n 1/V . Cv
у У min 'TV-'
Для Vmln = 25 м/сек и -# = 6,5 получим = 0,875.
Из этого выражения видно, что самолеты с малой посадочной
скоростью и плохим качеством сильнее теряют скорость; например,
при УШ1п= 18,5 м/сек и ~ =4,5 имеем -^— = 0,825. Таким образом
'-'X *ш!п
увеличение Сх при посадке представляет выгоду.
Фиг. 36. Посадка птицы.
Очень интересен метод посадки птиц. Подойдя к земле, птица
выравнивается на некоторой высоте, затем резко увеличивает угол
атаки почти до 90° и опускается на ноги (фиг. 36). Благодаря
этому маневру достигается следующее: после увеличения угла
атаки почти до 90° птица, не имея подъемной силы, начинает
падать как в пустоте, поэтому высота выравнивания не может
быть велика; однако за время этого падения, благодаря огромному
Сх, птица успевает почти совсем потерять поступательную скорость.
Примерные подсчеты показывают, что такой метод посадки мало
пригоден для самолета, даже если бы удалось достичь нужного
увеличения угла атаки. В самом деле, высота проваливания не
может быть велика по условиям прочности шасси; не имея подъ-
емной силы, самолет провалится очень быстро и не успеет заметно
59
потерять скорость. Интересно отметить, что по примерному расчету
при подобной посадке посадочная скорость оказывается такой же,
как при посадке с парашютированием с некоторой высоты, дающей
тот же самый толчок о землю.
Есть еще метод посадки, когда самолет, планируя на втором
режиме на равномерной скорости иногда со значительной высоты,
подходит к земле и, не выравниваясь (чего он сделать и не может),
ударяется о землю. Для совершения такой посадки самолет дол-
жен обладать амортизацией, способной поглощать значительно
бблыпую энергию, нежели это требуется по нормам для обычных
шасси.
Кроме того, ввиду близости к срыву обтекания и, следовательно,
к срыву в штопор, самолет должен быть оборудован специальным
устройством, повышающим поперечную устойчивость на больших
Фиг. 37. Посадка с работающим мотором.
углах атаки. В качестве таковых применяются предкрылки, распо-
ложенные у концов крыла, которые обеспечивают поперечную
устойчивость до углов атаки 25—27°.
Наконец, остановимся еще на одном способе посадки без толчка,
могущем дать очень сильное снижение посадочной скорости. Пред-
положим, самолет совершает посадку на большом угле атаки и
перед парашютированием увеличивает обороты мотора так, что
появляется сила тяги, которая все же меньше силы сопротивления.
Тогда самолет продолжает терять скорость, но вертикальная со-
ставляющая тяги винта дает подъемную силу, снижающую поса-
дочную скорость (фиг. 37). Для расчета посадочной скорости в этом
случае можно написать соотношения:
где л < 1;
Ф cos (а 4- у) < Q = п • Q = п • Сх • q S • V2,
Р = Су Q • S • V2+ Ф sin (а + у) = G;
Су • Q • S • V2 +п • Сх • е • S • V2 • tg (а + у) = G;
Г е • s [С,, + п • Сх • tg (а + у)] *
Если взять обычный самолет, имеющий Сж = 0,1; а + у =14°;
п = 0,8 и С = 0,65, то уменьшение посадочной скорости за счет
" ТПП т
60
тяги винта получается около 1,5 — 2%. Если же взять самолет со
щитками и предкрылками, имеющий посадочный угол около 25°;
Сх ~ 0,3; Су =1,0, то снижение посадочной скорости получается
около 8—10%.
Если добиться еще большего увеличения лобового сопроти-
вления, то тягу винта можно довести до максимальной, равной
примерно 1,5—2 кг)л. с. При нагрузке около 5 лгг/ж с., как у раз-
ведывательного самолета, это даст вертикальную составляющую
тяги винта (при а + у — 20°) около 20% веса и снижение посадочной
скорости на 10%. У истребительного самолета это могло бы дать
соответственно до 30% веса и снижение посадочной скорости около
15%.
Работы по изысканию методов снижения посадочной скорости
ведутся очень интенсивно и поэтому можно ожидать появления
новых способов.
О пользе применения закрылков, щитков и других способов
увеличения Су мы уже говорили в первой части настоящего
труда.
ВОЗДУШНЫЕ ТОРМОЗА
Как мы уже указывали ранее, при посадке самолетов часто
очень желательно сделать траекторию более крутой, не увеличивая
скорости. Это вызывается требованиями повышения точности по-
садки. Увеличение угла планирования без повышения скорости,
т. е. без уменьшения Су, может быть достигнуто увеличением
коэфициента сопротивле-
ния самолета Сх: л
tg 6 = •
У
Увеличение Сх всего
самолета может быть до-
стигнуто тремя различ-
ными способами: увеличе-
нием вредного сопроти-
вления, увеличением про-
фильного сопротивления
крыла и увеличением ин-
дуктивного сопротивле-
ния крыла.
Увеличение вредных
Фиг. 38. Применение обтекателей шасси как
сопротивлений самолета воздушных тормозов.
осуществляется путем от-
крытия или выдвижения каких-либо заслонок, работающих как
плоские пластинки и дающих значительное сопротивление. Однако,
несмотря на кажущуюся простоту подобного устройства, мы на-
талкиваемся здесь на большие неприятности. Дело в том, что
эти устройства, будучи близко расположенными к фюзеляжу, дают
струю завихрений, попадающую на оперение или проходящую
вблизи него; в результате мы получаем вибрации и ослабление
61
эффективности оперения. Для борьбы с этим явлением фирма Де-
Хэвиленд в качестве тормозов использует обтекатели шасси, которые
полета (фиг. 38); сравнительно небольшая
ширина обтекателей приводит к
более быстрому рассеиванию вих-
рей. Затем можно встретить тор-
мозное устройство в виде рас-
крывающегося руля поворотов
(фиг. 39). В качестве тормозящей
поверхности можно предложить
применять не плоские поверх-
ности, а сетки, которые хотя и
дают некоторое замедление по-
тока, но зато совсем не дают за-
вихрений; коэфициент сопроти-
2
вления их около у- сопротивле-
ния плоской пластинки.
Увеличение профильного со-
противления производится обыч-
(фиг. 40), дающих одновременно
поворачиваются поперек
Фиг. 39. Воздушный тормоз в виде створ-
чатого руля поворотов.
со щитками
Пб
0,4
0,2
О
ю
СУ
0,8
0,2 Cj
Фиг. 40. Действие подкрыльных щитков.
0,04 0,08 0,12 0,16
но при помощи открытия щитков
снижение посадочной скорости. Как видно, открытие щитков вызы-
вает значительное ухудшение качества самолета. В частности, на
фиг. 40 при Су — 0,4
качество упало с 9,3
до 5,5, тем самым угол
планирования возрос с
6° 10' до 10°20'.
Изменение индук-
тивного сопротивления
достигается изменени-
ем характера распреде-
ления циркуляции по
размаху. Для этой цели
можно сделать в крыле
открывающееся окно
или каким-либо спосо-
бом испортить профиль
крыла для получения
местного уменьшения
подъемной силы. Про-
изводя местное умень-
шение подъемной силы
крыла, нужно помнить,
что это может повести
к возникновению виб-
раций оперения, так как в этом месте крыла мы будем иметь
сбегающие вихри. Испортив крыло в его средней части, мы раз-
деляем его на две половины; удлинение становится вдвое
меньшим и индуктивное сопротивление удваивается. Если взять.
Су = 0,4 и Л =6, то удвоение индуктивного сопротивления ведет
62
к увеличению угла планирования для среднего самолета примерно
на 40-50%.
Сравнивая между собой различные способы торможения, сле-
дует остановиться, кроме вопросов влияния на оперение, на поло-
жении самолета при планировании. Вообще говоря, наклон хорды
крыла самолета при планировании равен (фиг. 41):
у = 0 — а.
Однако если равнодействующую силу R, которая на планиро-
вании вертикальна, разложим на составляющие: нормальную и тан-
генциальную, то получим:
Считая
Сд ~ Су,
найдем:
. Ср + Свр ।
tg V = -----l-p---«•
' СУ с У
С.
Из теории индуктивного сопротивления мы знаем, что тЛ =
«= Аа, т. е. скосу потока:
а— Аа = а',
где а’ называется действительным углом атаки крыл», зависящим
только от Су и не зависящим от удлинения:
. Ср + Свр
tg V = р г — а’.
у
Отсюда мы видим, что при увеличении профильного или вред-
ного сопротивления самолета угол наклона возрастает на ту же
величину, что и угол планирования. При изменении индуктивного
сопротивления угол планирования возрастает, но наклон самолета
не меняется.
63
ВЛИЯНИЕ БЛИЗОСТИ ЗЕМЛИ НА АЭРОДИНАМИЧЕСКИЕ
СИЛЫ
При детальном рассмотрении взлета и посадки самолета, а осо-
бенно равновесия моментов и устойчивости, следует учитывать
влияние близости поверхности земли на аэродинамические силы.
Ниже мы приводим некоторые основные положения и способы
расчета, оговариваясь, что все это носит характер первого прибли-
жения и современем будет уточнено и пополнено. Если в отно-
шении крыла мы располагали некоторым материалом, то в отно-
шении оперения пришлось прибегать просто к применению выра-
жений, которые верны только в своих крайних значениях, а
в промежуточных возможны
большие или меньшие откло-
нения.
Влияние поверхности земли
сводится в основном к умень-
шению скоростей, направлен-
ных перпендикулярно к зем-
ле, т. е. к спрямлению потока.
Для математического анализа
1 вопроса применяют метод зер-
Фиг. 42. „Зеркальное отражение" для расчета
влияния земли.
кального отражения, т. е.
вместо поверхности земли на
том же расстоянии снизу в
опрокинутом виде помещают
крыло или целый самолет
(фиг. 42) и затем рассматри-
вают их влияние друг на друга
обычными методами теории
крыла, заменяя последние си-
стемами вихрей.
Если взять только одно
крыло, то взаимное влияние
двух симметрично расположенных крыльев сводится к уменьшению
скосов потока, а отсюда к повышению истинного угла атаки при умень-
шении сопротивления; кроме того, взаимное действие циркуляции
скорости вокруг крыльев приводит к уменьшению скорости. Мы
будем принимать во внимание только изменение скоса потока. Это
.изменение по формуле Бетца имеет вид:
с» • 0-291g [1 + (±)!] = • С,
c=0,29 1g[l+(2?)!],
где I—размах крыла, a h — расстояние присоединенного вихря,
положение которого принимается на одной трети хорды от носка
до земли (в формуле логарифм десятичный).
Изменение индуктивного сопротивления будет:
лс. = С„-Аа = CJ • 0,29 1g [1 + (i)'] .
84
Изменение скоса потока и индуктивного сопротивления можно
свести как бы к фиктивному увеличению удлинения:
с-=Л. • М1 - °.29 + Ш’]1 - А с»;
отсюда получим:
при движении по земле мы имеем -^- = 5-^10, и тогда -у- =
= 1,33 +1,7. Летчики иногда пользуются влиянием близости земли
для улучшения качества самолета с целью повышения дальности
полета. Если полет производить на высоте, равной трети размаха,
т. е. = 1,5, то
£11
= 1,17;
Л
так, например, вместо Я = 6 получим Л = 7; конечно, такой полет
возможен над ровной местностью, например, степью или морем.
Рассматривая диаграмму фиг. 43, мы к своему удивлению вместо
сложной кривой, какую можно было бы ожидать по уравнению
для Ц- = 2^-10, видим прямую линию. Нужно сказать, что этот
диапазон вполне обеспечивает практические потребности. Рас-
стояние менее требует учета еще других факторов, которые
5 В. С. Пышнов.
65
в выражение не вошли вовсе, а при расстояниях более по-
правка настолько мала, что ею можно пренебречь. Тогда получим:
4 = 1 +0,08(4- - 1).
Если же пойти на то, чтобы в данном диапазоне значений 4~
ошибка не превышала 3%, можно выражение упростить еще более;
получим:
4 = 1 + 0,065 4-
или
ff = l--------1_ .
1 4- 0,065 —т—
h
на фиг. 43 это соответствует пунктирной линии.
При расчете равновесия и устойчивости нужно иметь величину
dc„ „
В — . Учитывая влияние земли, получим:
1 _ 1 . 2. 1 _ 1 । 2
В ~ Вй + и • Я ’ В' ~ Во + п • Лф ’
отсюда
= J____Ml-—V
В' В Яф/’
71 • Л \ Лф /
ЯЛ
Подставляя новое выражение для -у-, получим:
о,_____________________________в____________
"1—^-/1_____________I______V
П Я ( 1 + 0,065 • 4- J
\ ’ h /
Совершенно аналогичные рассуждения можно приложить к опре-
делению величины наклона диаграммы Су^ по углам атаки хвоста,
или пользуясь обозначениями, принятыми во второй части нашего
труда:
dCy
R — хв
хв rfaxB •
Значение В'хв, исправленное на влияние земли, получим:
Вхв
хв
1
2Вхв /
1-------/ 1 -
Я • Лхв
хв I 1 + 0,065
66
Перейдем к вопросу о скосе потока у оперения. К сожалению,
детального исследования данного вопроса еще не сделано и по-
этому мы рассмотрим его в грубом приближении. Вообще говоря,
скос потока за крылом рассчитывается, исходя из скоростей,
вызванных вихрями, сбегающими с крыла. Возьмем более простой
случай, когда с крыла сбегают два вихря, расположенные на
некотором расстоянии 1г, вообще говоря, не равном размаху крыльев.
В случае полета вблизи земли
ных и два фиктивных от-
раженных (фиг. 44). _
Зная циркуляцию вих-
рей, можно найти скос
потока. Пусть от одной
пары вихрей в плоскости
ее действия получается
вертикальная скорость и0.
Тогда при удалении от
плоскости вихрей полу-
чим изменение вертикаль-
ной скорости вследствие
увеличения расстояния на
величину cos <р и измене-
ния направления скорос-
ти, вызванной вихрем,
тоже на cos <р; в итоге
получим четыре вихря, т. е. два реаль-
Фиг. 44. Расчет скоса потока у хвоста при полете
вблизи земли.
получим:
и — и0 • cos2?>.
Складывая алгебраически влияние обеих пар вихрей, получим:
и — и0 (cos2 — cos2 ?>2).
Заменяя косинусы через тангенсы и замечая, что
Л — ftXB h + ftXB
tg ----• tg <р2 = —----,
ТГ Т
получим:
U У° 4 (ft - ftXB)2 4 (ft + ftXB)2 = U° ’ ffxB’
/+ 1+ I -
Вместо /zXB подставим h — yXB:
— Г 1 1 I
U~y° , 4(2Л-УХЕ)2 •
1 + 1 +------------,3---
L *1 J
Разделив и на скорость полета V, получим скос потока:
5
Если взять ухв = 0, получим:
1
Это выражение при /х = I дает величину а, значительно большую,
чем дают другие, проверенные на опыте выражения. Отсюда делаем
вывод, что вихри нужно считать сближенными, так как на самом
Фиг. 45. Зависимость скоса потока у хвоста от близости
земли.
распределенных по размаху, расстояние между которыми в среднем
меньше I. Практически хорошее совпадение мы получим, приняв
= 0,5 I:
О' ==
1
Скос потока у хвоста будет:
1________________1
. , ,ft f Ухв¥ . j-iaf Ухв \'
1 + 16^-J 14-16^-------г)
На диаграмме фиг. 45 даны значения — в зависимости от —~
г 0 П
h
для разных -у .
У -
Как видно по диаграмме, если -jp положительно, т. е. если
хвост находится ближе к земле, нежели крылья, что обычно имеет
место при полете вблизи земли или при движении по земле, то
<>8
зависимости можно принять за прямые линии, уравнения для которых
примерно примут такой вид:
JL = 4 /z ~Ухв = 4 /*хв
€0 I Z
причем — не может быть больше единицы.
£0
Таким образом оказывается, что если хвост ниже крыла, то
влияние земли на скос потока у хвоста не зависит от высоты
крыльев над землей, а зависит лишь от отношения высоты хвоста
к размаху крыльев, при условии, что
^-< 0,25,
т. е. это относится к случаям близкого к земле положения хвоста
и может быть использовано для анализа равновесия и устойчивости
при движении по земле.
ОСНОВЫ УСТОЙЧИВОСТИ И УПРАВЛЯЕМОСТИ ПРИ
ДВИЖЕНИИ САМОЛЕТА ПО ЗЕМЛЕ
Обычный самолет при стоянке на земле имеет три точки опоры:
два колеса и костыль. Ось колес расположена сравнительно близко
к центру тяжести самолета. Сделано это для того, чтобы в процессе
разбега летчик мог управлять углом атаки, поднимая хвост. Однако
это порождает опасность переворачивания самолета через нос или,
как говорят, капотирования. Мы остановимся на вопросе об обеспе-
чении подъема хвоста на взлете, с одной стороны, и достаточной
гарантии против капотирования—с другой.
Шасси и костыль самолета располагаются с таким расчетом,
чтобы: 1) при стоянке на трех точках самолет имел угол атаки аст,
близкий к Сушах, с учетом влияния земли; практически это дает
угол на 2—3° меньший, чем апос по продувке вдали от поверхности
земли; 2) при горизонтальной оси винта конец лопасти не был
ближе 0,25 м от поверхности земли; 3) устойчивость и управляемость
обеспечивались наличием некоторого угла выноса шасси <р, обра-
зуемого линией, соединяющей центр тяжести с осью колес и
вертикалью.
Угол выноса шасси в положении горизонтальной оси винта
берется от 12 до 18°; тогда в положении на трех точках он возра-
стает до 25—30° (фиг. 46). Если к самолету нужно поставить шасси,
то порядок работы рекомендуется такой: 1) из центра тяжести
проводим линию под углом <р соответственно выбранной величине
при горизонтальном положении оси винта; 2) проводим горизон-
тальную линию соответственно наиболее близкому положению
земли, исходя из условия минимального расстояния конца лопасти
до земли; 3) проводим наклонную линию соответственно положе-
нию земли 'при стоянке. Теперь, поднимая или опуская наклонную
линию, подбираем высоту шасси и костыля (фиг. 47). Вообще
нужно стараться сделать шасси пониже, но препятствием этому
60
может быть костыль, так как для создания нужного угла на стоянке
приходится конец фюзеляжа выгнуть вверх, а это в свою очередь
нежелательно по аэродинамическим соображениям.
Перейдем теперь к некоторому обоснованию угла выноса шасси.
Желательно сделать так, чтобы при взятой на себя ручке самолет
не поднимал хвоста, даже в том случае, когда колеса уперты или
заторможены. Это необязательно, но желательно. Посмотрим, как
этого можно достичь. Для простоты будем считать, что при взятой
на себя ручке действие стабилизатора и действие руля высоты
взаимно погашаются и никакого момента хвоста нет. Тогда, для
Фиг. 47. Расчет расположения шасси.
того чтобы хвост не поднялся, момент от тяги винта Ф относитель-
но центра тяжести самолета должен быть меньше момента от
реакции шасси, приложенной на оси колес, если колеса просто
уперты, и в точке касания колес с землей, если колеса заторможены
(фиг. 48). Однако удобнее рассматривать равновесие моментов не
вокруг центра тяжести, а вокруг точки приложения реакции шасси.
Пусть Ф — тяга винта, G — вес самолета, ув—плечо тяги винта от-
70
носительно центра тяжести, I — расстояние от центра тяжести до
точки приложения реакции шасси и <р— угол выноса. Условие при-
жатия хвоста будет:
G • I • sin <р > Ф (I • cos <р + ув);
sin 9?
cos <р Н—y
У
Если пренебречь величиной -j-, то:
Ф
Фиг. 48. Равновесие моментов при пробе мотора.
Если <р = 30°, то:
< 0,58.
Следовательно, хвост поднимается, если тяга винта превышает
половину веса.
Перейдем к вопросу поднятия хвоста при разбеге. Выясним
приблизительно, в каком случае самолет сможет поднять хвост на
месте. Поскольку колеса не уперты в подкладки, а имеют лишь
силу трения, моменты удобнее брать вокруг центра тяжести самолета.
Пользуясь опять фиг. 48, получим условие поднятия хвоста:
Ф • Ув + Р • I • cos 9? + Мхв > N • I • sin
где угол <р нужно взять в положении стоянки.
В момент подъема хвоста можно считать N = G; момент хвоста
можно выразить так:
А1ХВ = СУхв • §хв • i'XB • Q • ^хв>
71
где Sxb — площадь горизонтального оперения в струе винта;
СУхв можно брать примерно 0,25—0,30;
Vxb —скорость отброшенной струи:
Vxb — 20 р2 J ; Q • Vxb = 2,5 • pj >
%- (ув + 2,5 с„хв • • LXB ') > I (sin <Р — / cos <р).
По этому неравенству можно подобрать величину угла <р.
Если считать, что коэфициент трения мал, получим:
. Ф ( Ув > о г Л' ^хв ^хв
sin <р < 4- 2,5 CVxB • l j •
У самолетов с большой нагрузкой на л. с. трудно добиться
подъема хвоста при нормальной величине угла <р. Тогда нужно
постараться, чтобы хвост поднялся еще на сравнительно небольшой
Фиг. 49. Условие капотирования.
скорости, иначе тре-
ние костыля будет
сильно мешать раз-
бегу самолета. Если
костыль имеет коле-
со, подъем хвоста на
малой скорости не
так необходим. Если
стояночный угол не
очень велик, взлет
может быть сделан
без подъема хвосто-
вого колеса.
Расчет подъема
хвоста при движе-
нии подобен расчету,
приведенному выше, но нужно ввести еще момент от аэродинами-
ческих сил. Решение этой задачи будет приведено в четвертой части
настоящего труда.
Займемся рассмотрением вопроса о возможности капотирования
самолета. Решим эту задачу в наиболее простом случае, когда
скорость относительно воздуха невелика, струи винта нет и, следо-
вательно, аэродинамическими силами можно пренебречь. Если
хвост самолета приподнялся, на самолет будут действовать: сила
тяжести G, реакция земли N, сила трения F и сила инерции. Вокруг
центра тяжести силы N и F будут давать моменты (фиг. 49).
Капотирование произойдет, если момент силы F больше момента
силы N:
F • I • cos <р > N • I • sin <р.
Однако вместо моментов сил F и N можно брать момент от их
равнодействующей, проходящей через ось колеса (фиг. 50, а).
72
Очевидно, что капотирование произойдет тогда, когда равнодей-
ствующая пройдет позади центра тяжести и наклон равнодействую-
щей будет больше угла <р:
arctg-^ > 9»; 4
Но представляет собой коэфициент трения /. Следовательно,
условие капотирования будет:
/ >tg?.
В случае применения тормозов равнодействующую нужно про-
вести не через ось колес, а сзади нее, так чтобы произведение /?•/'
равнялось тормозному моменту Л4Торм:
_ ^торм
Г— R .
Фиг. 50. Точка приложения реакции земли на колесе.
Однако проще рассуждать так: тормозящий момент Л1торм пре-
одолевается силой F, действующей по касательной к окружности
колеса, и следовательно, равнодействующую нужно приложить в
точке касания земли колесом (фиг. 50, Ь). Если имеется трение
качения и одновременно торможение, поступаем так: 1) через ось
колеса проводим линию, наклоненную к вертикали под углом тре-
ния, т. е. arc tg /, и отмечаем точку на ободе колеса; 2) в этой точке
проводим равнодействующую, наклонив ее так, чтобы она прошла
на расстоянии г = —от оси вращения (фиг. 50, с).
Подобным образом можно решать обратные задачи, выбирая
предельный момент торможения колеса во избежание капотиро-
вания.
Посмотрим, когда может получиться коэфициент трения, опас-
ный для капотирования. Трение качения происходит, когда жест-
кое колесо катится по мягкому грунту, или мягкое колесо по
твердому грунту. Поскольку исправное колесо бывает довольно
жестким, обычно трение получается за счет мягкости грунта. Однако,
если шина спущена, получается сильное трение даже по твердому
грунту.
7»
Катясь по мягкому грунту, колесо несколько погружается ниже
поверхности земли, причем сзади или остается колея, или грунт
опять приподнимается, но вследствие несовершенной упругости
запаздывает, и между колесом и грунтом сзади получается просвет.
Если для простоты считать, что давление колеса на грунт равно-
мерно, то соприкосновение с землей будет происходить по не-
которому сектору, а равнодействующая разделит этот сектор
пополам (фиг. 51). Взяв тангенс угла наклона равнодействующей,
получим коэфициент трения.
При движении самолета с поднятым хвостом угол выноса шас-
си в среднем составляет около 15°. Следовательно, капотирование
произойдет при наклоне равнодействующей более 15° при секторе
соприкосновения с землей более 30°. Отсюда можно найти глубину
погружения колеса:
h = г (1— cos30°) = 0,14г = £ .
Фиг. 51. Зависимость коэфициента трения от глубины увязания
колеса.
Для капотирования с трех точек наклон равнодействующей дол-
жен быть около 30°, угол сектора 60° и
h — г (1 — cos 60°) = 0,5 • г = ~ .
Таким образом для капотирования колесо должно сильно про-
валиваться в грунт.
Кроме увязания колеса причиной капотирования может быть
попадание самолета на трамплин, наклон которого больше угла
выноса шасси, так как в этом случае реакция колеса пройдет
позади центра тяжести.
Рассмотрение устойчивости поперечной и пути требует деталь-
ного анализа действующих сил; здесь мы приведем лишь при-
ближенное решение задачи, полагая, что скорость мала, и потому
пренебрегая воздушными силами. Колеса самолета легко движутся
в плоскости вращения, но оказывают сильное сопротивление всяким
боковым движениям.
Если самолет при движении по земле завернул и движется с
некоторым углом скольжения, то на колеса начнет действовать
74
большая боковая сила Fz (фиг. 52). Эта сила является центростре-
мительной, и траектория движения станет криволинейной. Так как
колеса находятся впереди центра тяжести, то сила Fz будет стре-
миться развернуть само-
лет еще сильнее. Сила
трения костыля, наобо-
рот, будет препятствовать
развороту; если ее мо-
мент меньше момента си-
лы Fz, то самолет будет
неустойчив, и для выпра-
вления движения летчик
должен будет действо-
вать рулем поворотов.
Однако на малой скоро-
сти руль работает слабо,
и бывали случаи, когда
летчик не был в состоя-
нии удержать самолет от
разворота. С целью улуч-
шения устойчивости и уп-
равляемости рекоменду-
ется: уменьшать вынос
шасси, ставить на хвосте
управляемый костыль или
колесо, управляемое или
Фиг. 52. Причина разворота при качении по земле.
жестко закрепленное, но
не свободно поворачивающееся; для улучшения управляемости сле-
дует применять тормозные колеса с раздельным торможением.
Интересно отметить, что очень хорошая устойчивость пути
была получена у самолета, имеющего шасси с одним колесом в
середине и двумя костылями
у концов крыльев. При слу-
чайном завороте под действи-
ем центробежных сил самолет
валится на бой} но тогда тре-
ние костыля автоматически
его выравнивает.
От действия сил Fz само-
лет имеет стремление валиться
Фиг. 53. Условие заваливания на крыло. на бок. Опрокидывание на
крыло произойдет в том слу-
чае, если равнодействующая сил Fz и N пройдет ниже центра тя-
жести (фиг. 53). Во избежание этого шасси должно быть доста-
точно раздвинуто в стороны. Боковой угол выноса шасси между
линией, соединяющей центр тяжести с точкой прикосновения ко-
леса к земле, и вертикалью нужно брать (на виде самолета спе-
реди) не менее 25°.
РАЗГОН И ТОРМОЖЕНИЕ В ПРЯМОЛИНЕЙНОМ
ПОЛЕТЕ .
Современные самолеты обладают большим диапазоном скоро-
стей. Максимальная скорость превышает минимальную в три и
даже в четыре раза. При крутом планировании мы имеем скоро-
сти, которые превышают минимальную скорость горизонтального
полета в пять-шесть раз. Отсюда понятно, что режим перехода
с малой скорости на большую и обратно представляет большой
интерес. Особенно важны вопросы разгона и торможения при испы-
тании самолетов и решении некоторых военных задач.
ОБЩИЙ СЛУЧАЙ РАСЧЕТА
С точки зрения механики вся работа сводится к интегрирова-
нию одного уравнения движения, но так как величина сил задается
в виде диаграмм, то приходится применять графическое решение.
Вводя некоторые упрощения, можно решать задачи и аналити-
чески.
Пусть мы имеем самолет (фиг. 54), который летит по прямой,
и в общем случае его траектория наклонена под некоторым уг-
лом 0. Вдоль траектории мы имеем ускорение, и следовательно,
силы не должны быть в равновесии, как это имеет место при
обычном подъеме. По мере изменения скорости меняются силы,
меняется ускорение. В случаях разгона мы всегда имеем предель-
ную скорость, к которой самолет стремится, но достигает ее тео-
ретически лишь за бесконечно большое время. При инженерном
подходе к задаче нужно брать разгон не до самой предельной ско-
рости, а до скорости несколько меньшей, например на 3—5%.
При торможении минимальная скорость определяется способно-
стью самолета лететь по прямой. В прямолинейном движении нор-
мального ускорения нет, а потому в этом направлении силы должны
быть в равновесии. Для оформления задачи возьмем оси коорди-
нат, направив ось х вдоль движения, и напишем уравнения
проекций сил на координатные оси:
= ф. cos (а у)— Q — G-sin 0 = mj\
2 У = Р + Ф- sin (а +у) — G-cos 6 — 0.
Как видно, 2-^ мы приравняли массе, умноженной на ускоре-
ние, а 2 У приравняли нулю. Пусть зависимость тяги винта от
76
скорости нам известна из аэродинамического расчета. Силы Р и
Q зависят от скорости и угла атаки. Величину угла атаки, Сх и
Су мы можем найти из второго уравнения, причем угол атаки вы-
разим через Су, как мы это уже делали:
с
Су-= В (а — а0); а = -g- + а0.
Ввиду малости угла (а + у) вместо синуса возьмем угол в ради-
анах:
Су(>-8. У2 + ф(Ь^ + «о + y)=G-cosO;
Су( e-S" V2 + = G-cos 6 — ф(ао + у);
р __ G-COS 0 — Ф (а0 -|- у)
V 6
Фиг. 54. Действие сил в прямолинейном неустановившемся полете.
Если наклоном тяги винта к линии полета пренебречь, то вы-
ражение упростится:
Су = “Т^Туз--
Получив Су, по характеристике крыла найдем а и Сх, необходи-
мый для подсчета сопротивления Q = Cx-q-S-V2. Если наклоном
тяги винта пренебрегают, то величину Q удобнее подсчитать из
выражения:
С,. Л „ Сх
Q=P- = G • cos О ~ .
Ly
Теперь мы можем получить все действующие силы на желаемых
скоростях и затем найти ускорение:
.__ Ф-cosfa + y)—Q — G*sin0
J — - .
Из зависимости ускорения от скорости мы путем интегрирова-
ния можем получить зависимости: скорости от времени, скорости
77
от пути и пути от времени. Интегрирование будем производить
графически путем подсчета площадей трапеций. Прежде всего
находим последовательно Ф, Су, Сх, a, Q и Ф-соз(а + у) для разных
значений скоростей с таким расчетом, чтобы охватить нужный диа-
пазон скоростей. Нет нужды брать точки очень часто, так как
кривые идут довольно плавно. Затем строим диаграмму R=
= [Ф• cos (а + у) — Q—G-sin6] по V (фиг. 55). В случае разгона
пересечение кривой R с осью абсцисс даст нам предельную ско-
рость.
Фиг. 55. Изменение сил по скорости при разгоне.
Для получения времени воспользуемся соотношением:
откуда
• = dV _ _R_
’ dt т ’
dt = - dV = 4- • dV;
R j
dt есть произведение двух величин -4- и dV. Построив диаграмму
у по V (фиг. 56) и интегрируя ее последовательно, передвигая пре-
дел интегрирования (скорость), получим время для разных скоро-
стей и сможем построить диаграмму V по t (фиг. 57). Практиче-
ски разбиваем диаграмму -4- по V на ряд трапеций с таким расче-
том, чтобы у каждой из них отношение сторон было не более 1,5.
Это особенно относится к скоростям, близким к предельным, где
трапеции приходится брать узкие. Затем находим время, соответ-
ствующее каждой трапеции, путем умножения интервала скоростей
на среднее -4-, или умножая площадь трапеции на масштабы.
Складывая последовательно отрезки времени, строим диаграмму V
по t.
78
Фиг. 56. Расчет времени разгона.
Фиг. 57. Изменение скорости по времени
при разгоне.
Фиг. 58. Расчет пути разгона.
Расчет зависимости скорости от пути производим подобным же
образом, но исходя из соотношения:
dV .
ds ’
/= V-
ds=~~ -dV.
I
Строим диаграмму Л- по V (фиг. 58) и, интегрируя ее совер-
шенно так же, получим данные для построения диаграммы V по s
(фиг. 59)._ Если нужна диаграмма s по t, то ее можно построить
из диаграмм V по t и V по s, беря значения t и s для одинако-
вых скоростей; если же нет
диаграмм V по s и t по s, то
можно построить ее из диа-
граммы V по t, интегрируя по-
следнюю графически на осно-
вании соотношения:
V=-£-; ds=V-dt.
dt
Если траектория наклонна,
то строят еще диаграмму зави-
симости скорости V от высо-
ты Я; для этой цели пройден-
ный путь умножают на sin 0:
Н = s-sin0.
Кроме интегрирования путем подсчета площадей, можно вос-
пользоваться методом интегрирования путем построения зигзагооб-
разной линии, который был уже изложен в расчете разбега. Зада-
ваясь промежутками времени At, находим:
где т — масса самолета; tg <р должен быть отложен с учетом мас-
штабов, для чего удобно задаться некоторой произвольной вели-
чиной Rq, тогда:
= Ro- ~
^Откладывая в масштабе Ro и АУ0, получим треугольник, кото-
рый и даст нам нужный наклон линий (р (фиг. 60). Для расчета
пути каждую наклонную линию делим пополам, и абсциссы этих
точек дадут нам среднюю скорость в интервале. Умножая Уср на
At, получаем As, а затем, суммируя все As, получим весь путь s.
Можно также подсчитать путь графическим интегрированием диа-
граммы сил по V2, как это мы делали в расчете разбега.
На практике приходится рассчитывать ряд случаев разгона и
торможения; например: разгон по горизонтали от минимальной
30
скорости до 0,95% максимальной скорости; торможение от макси-
мальной скорости до минимальной; разгон по наклонной вниз тра-
ектории под разными углами 0 с работающим мотором и без мо-
Фиг. 60. Графический расчет разгона.
тора; торможение под разными углами подъема с работающим
мотором и без мотора. Все эти данные желательно уложить в одно
минимальное количество удобных графиков.
РАЗГОН САМОЛЕТА ПРИ ПИКИРОВАНИИ
Обычно пикированием называют вообще крутой спуск самолета.
В теории часто под пикированием подразумевают спуск по верти-
кали. Мы будем называть пикированием вообще крутой спуск и
будем указывать угол наклона траектории. При пикировании са-
молет быстро набирает скорость, стремясь к некоторой предель-
ной скорости, величину которой мы определяли еще в первой ча-
сти настоящего труда при построении указательницы глиссад пла-
нирования. Однако на самом деле, если учитывать перемену
плотности воздуха за время спуска, то мы найдем, что скорость
вначале возрастет, а затем несколько убывает за счет увеличения
плотности воздуха. Мы рассмотрим сначала пикирование в посто-
янной плотности, что приемлемо для пикирований с потерей вы-
соты не более 1000—1500 м, а затем значительно более сложный
случай пикирования в переменной плотности.
При пикировании роль силы тяги винта невелика, так как ве-
личина силы тяги на большой скорости мала по сравнению с си-
лой тяжести самолета. Если же летчик при пикировании умень-
шает газ мотора, то в этом случае винт не только не тянет, но
даже оказывает сопротивление. Поэтому, рассчитывая пикирование
6 В. С. Пышнов. 81
с работающим мотором, мы не будем учитывать тягу, а при пики-
ровании без мотора будем добавлять сопротивление винта.
Итак, при пикировании мы имеем силы: вес самолета G, неболь-
шую подъемную силу Р и сопротивление воздуха Q (фиг. 61). По-
лагая, что движение ускоренное, но
прямолинейное, и проектируя силы,
получим:
G-sin & — Q == zn/,
G-cosG — Р — 0.
Второе выражение позволяет нам
найти Су и, следовательно, угол атаки:
п __ G-COS0
q-S-V* •
При пикировании cos О мал, а ско-
рость велика; поэтому Су мал.
Глядя на кривую Лилиенталя само-
лета, мы убеждаемся в том, что Сх
можно считать при малых Cv постоян-
ным и равным СЖо, соответствующим
Су = 0 (фиг. 62). Исключение может
Фиг. 61. Схема сил при
пикировании.
представить лишь случай применения сильно вогнутых профилей
крыла, когда наблюдаются срыв обтекания и резкое увеличение Сх,
но такие профили почти не встречаются на современных самолетах
и даже планерах. Если счи-
тать Сх постоянным, расчет
сильно упрощается и его
можно провести аналити-
чески. Уравнение движения
приобретает вид:
G-sin0 — Cx,-g-S-V2=~ J-,
j =^(sin 0- —) =
= g sin 0(1 —
G-sin0 /
Если плотность воздуха
постоянна, самолет будет
стремиться к предельной
скорости, которая наступит
при условии / = 0 или
Фиг. 62. Коэфициент сопротивления при малых
коэфициентах подъемной силы.
G-sin 0 = CXo-e-S-Vnp,
отсюда
,/9 ___ G-sin 0
G-sin Э
V пр
82
Обращаясь к выражению для ускорения, мы можем подставить
Vnp и получим:
/ V2 \
J = £-sin 0(1----г^-).
' пр '
В случае вертикального пикирования G-cos0=O, и, следова-
тельно, подъемная сила должна быть равна нулю. Остаются только
две силы G и Q.
Обычно крылья, применяемые на самолетах,
при Су = 0 дают крутящий момент:
MQ = C^.Q.S-V^b,
с которым приходится иметь дело в расчете рав-
новесия самолета и прочности; это случай С.
Обычно мы говорим, что пару сил Мо уравнове-
шиваем нагрузкой на оперение, хотя знаем, что
пару сил можно уравновесить только парой сил.
В качестве второй силы уравновешивающей пары
будет небольшая подъемная сила крыла (фиг. 63):
р__р —
* - • ХВ--г
Таким образом при вертикальном пикировании,
вообще говоря, подъемная сила крыльев не равна
нулю, хотя подъемная сила всего самолета, ко-
нечно, равна нулю. Подставляя Р и Мо, получим:
P = Cy.Q-S-V2:, Mo = CMo-e-S-V2b;
Фиг. 63. Равнове-
сие моментов при
пикировании.
у ~ j ,
Величина равна примерно 0,4—0,3; СМо ред-
^ХВ
ко бывает больше 0,05; отсюда при пикировании Су
крыла не превышает 0,02, а угол атаки при пикировании отлича-
ется не больше, чем на 0,6° от а0, когда СУкр равен нулю. Но,
конечно, когда самолет пикирует по вертикали, хорда крыла имеет
уже обратный наклон, так как а0 отрицательно. Наклон оси фюзе-
ляжа, считая его по оси мотора, будет еще более отрицателен, так
как хорда крыла имеет еще некоторый установочный угол.
Для получения зависимости скорости от времени или пройден-
ного пути проинтегрируем уравнение движения, взяв его в общем
виде для некоторого угла пикирования 0.
Начнем с расчета пути. Возьмем производную в виде:
.. dV . , V2
/ = (/-^=^0(1---
dx =
v-dV
9,8-sin О
V2 \
Пр /
6*
83
В левой части выражения стоит диференциал пути, а в правой
должен быть диференциал некоторого выражения, зависящего от
скорости. Для определения этого выражения нужно или уметь
узнавать функции по виду их производной, или проще обратиться
к справочнику. Если мы обозначим
то
dc = -2-^L: VdV =------------------V-^-dz.
пр 2
Подставив z и V-dV, получим:
V2 /Ут V2
dx =_______________ — =___________.d (In zl
2-g-sinO z 2-g-sin0 u
Производя интегрирование от начальной скорости до конеч-
ной V2 и считая, что при V = Уг в начальный момент х = 0, по-
лучим:
V2 /I V2 Zl
х =-----—/ d(lnz) = ——и.р In z.
2-g-sin0 J v } 2-g-sin0
Z1 22
Подставляя пределы и величину г, получим:
. In______
111 у2
1-----2__
У2
пр
V2
V — ИР
2-g-sin6
Переходя к десятичным логарифмам, получим:
V2
1-~ уГ"
пр
у2
пр
х = 1,15—^Цу-lg
’ g-sin0 5
Если вместо пройденного пути
то получим:
взять потерю высоты h = x-sin 0,
V'2
/2 = 1,15 J
V2
V2
пр
!g
1
пр
Этим выражением удобно пользоваться, если известны V\ и V2-
Если же даны Vi и й, то определять V2 довольно неудобно.
Произведем некоторые преобразования:
V2 J У2 ч V2 / V2 \
-lg(l -
84
где /?! — высота пикирования для набора скорости от V = 0 до
а Л2 — соответственно для набора скорости У2. Определяем:
9Q.V2 1 ч
('“vt)
9 Q. У2 1 1
'is - • ig. т- -Ц;,_ 2,3.Л°. Ig—
х пр ' \ *пр '
Величина h0 —..А'1' представляет собой высоту свободного па-
дения в пустоте, необходимую для набора скорости УПр.
Обозначим:
/г. =/г0-Д1; /г2=й0-А2; h = hQ(A2 — A1).
Величины А можно заранее подсчитать и построить диаграмму,
в которой по оси абсцисс
нат ~. Подобная диа-
/?0
грамма дана на фиг. 64.
По ней легко решать раз-
нообразные задачи на пи-
кирование. Например, да-
ны и V2; требуется
найти h. По отношениям
v, V, hi л-.
У- и -тт- находим у и 7Г,
VBP vnp "» по
а затем /г = й2—/гг.
Если приходится иметь
дело постоянно с одним
самолетом, то следует по-
строить диаграмму V по
/г, что можно сделать или
по начальному выраже-
нию, задаваясь Vi = О,
а для Vt беря разные
значения, или прямо
перестроить диаграмму
V
отложить значения у^, а по оси орди-
Фиг. 64. Общий закон изменения скорости по пути
при падении в сопротивляющейся среде.
фиг. 64, умножив на нужное й0 и на свое Vnp (фиг. 65).
Если рассматривать пикирование для набора скорости Упр и
взять V2 = Vnp, то нетрудно видеть, что х = ос, и это имеет место
лишь при условии постоянства плотности q. Сравнивая пикирование
в постоянной плотности с падением в пустоте, мы видим на
фиг. 65, что вначале кривые изменения скорости идут одинаково,
а затем расхождение между ними постепенно увеличивается. Пройдя
расстояние й0> в пустоте мы набрали бы уже скорость, равную Уир;
фактически же будет набрана скорость только 0,8 Уир.
85
Подсчитаем, какой путь должен пройти самолет при пикиро-
вании для набора скорости Va = 0,95 Упр, если Vx = 0.
Подставляя эти значения в формулу для h, получим:
1 V2
h— 2,3 • h0 • lg t _ 0>952 = 2,3 • /z0 = ,
0
при Упр = 140 м1сек и /г0 — 1000 м получим h. — 2300 м\ очевидно
что при такой высоте пикирования пренебрегать изменением плот-
ности воздуха не следует; однако все же мы видим, что для
набора скорости, близ-
кой к предельной, пи-
кирование должнобыть
довольно длительным.
Перейдем к вопросу
о связи скорости с вре-
менем пикирования. Бе-
рем ускорение в виде:
/=-
7 dt ’
7 dt
= g sin © 1 — yr ,
пр/
dV
200
400
600
300
h м
WOO
Г м/се ft
20 40 60 83 WO 120 140
Г?-----1
Фиг. 65. Изменение скорости в зависимости
от высоты пикирования.
dt =
g • sin 0
np.
dV .
величина----пред-
i — ——
1 v2
пр
ставляет собой дифе-
ренциал некоторой величины z, которую можно представить в двух
видах:
V
Z = • In
пр .
1--L’
%
z=V -Arth-^-;
пр
dt =
g • sin 0 ’
Z2
r 1
g • sin 0 ^2
t = --Цу . и<
g • sin 0 J
zi
Подставляя zx и z2, получим:
V ! V., V, '
t ~ Лп <л I Ar th 7--Аг th тг-
g-sm0 vnp vnp
86
или
V I “ V / I V
f _____nP 1 n др/ V др/
2-g-sin0'* , Vj_\ '
\ v ) \ l + V )
\ F пр/ \ v пр/
Переходя к десятичным логарифмам, будем иметь:
V (1
t = 1,15 —- • 1g
’ g-sin 0 & /
V
/2= 1,15 ------
4 g • sin 0
Если есть таблицы гиперболических тангенсов, расчет удобнее
вести по ним.
Преобразуем полученное выражение подобно тому, как мы это
делали при расчете высоты:
t= h ti,
1 + 1 + ^
V 1 15 V
. ig___. f . ig_______________s. •
g _ Vg sin 0 ° g _ v2 ’
% vnp
1 + ^
V°p _ 1,15 . t • \q V°P
Vi “ sin 0 0 & Vj_ •
v 1 V
*np np
v
Величиной t0 мы обозначили ; нетрудно видеть, что она пред-
ставляет собой время падения в пустоте от V = 0 до V == Vnp. Для
удобства расчета подсчитаем:
G = 1,15 V°p n 1g-
1 ’ g • sin 0 &
t _ J.J5
f0 sin Й
1 + 7“
ig—7-
1 V
др
о V t
Задаваясь разными значениями р- , построим диаграмму в за-
висимости от (фиг. 66). Для определенного самолета следует
*пр
построить диаграмму V по 1, начиная от = 0, подобно тому, как мы
поступали при расчете высоты Л (фиг. 67). По этой диаграмме можно
решать разные задачи. Если не равно нулю, отсчет времени
ведем от точки кривой, соответствующей начальной скорости
Если взять t = t0, получим, что самолет наберет скорость 0,76 Vnp.
Если же взять V2 = 0>95 Vnp и 0 = 90°, получим, что для набора
такой скорости самолет должен пикировать:
/0)95 = 1,15 • /0 • 1g = 1,83 • f0= 1,83
87
Например, если Vnp=125 м)сек, то /095 = 23,4 сек. Пройденное
при этом расстояние будет:
Ло(95 = Ы5-^- = 184О' м.
Сравнивая пикирование различных самолетов, мы видим, что
Фиг. 66. Общий закон изменения скорости Фиг. 67. Изменение скорости пикирова-
ло времени при падении в сопротивляю- ния по времени в зависимости от угла
щейся среде. пикирования.
от нагрузки на л*2, у, Сх и д. Для сравнения приводим в табл. 4
некоторые данные для расчета пикирования.
Таблица 4
Самолет G S кг/м2 Сх Vnp mJ сек ^0 м ^0 сек. Vnp км, час
Средний военный разведчик I 60 1 0,025 i i i 140 1000 14,3 500
Скоростной : i I 100 1 0,012 258 3400 ' 26,3 930
Учебный 30 0,030 90 410 9,2 , 315
i Планер | 15 0,008 122 760 12,4 ! 440 1
88
У некоторых гоночных самолетов $-=150 кг1м- и Сх — 0,01-
это дает скорость пикирования Vnp = 347 м)сек, т. е. скорость звука,
однако, пикировать для этого нужно было бы около 10000 м.
ПИКИРОВАНИЕ В СРЕДЕ ПЕРЕМЕННОЙ ПЛОТНОСТИ
Если изменение плотности с высотой представить в виде неко-
торого закона, задачу можно разрешить в аналитическом виде.
Такое решение сделано проф. В. П. Ветчинкиным 1 для изменения
плотности воздуха по закону:
где z — высота, Н— фиктивная высота атмосферы, если бы плот-
ность ее была постоянна и равна @0. Даже при таком сравнительно
простом выражении плотности интеграл получается очень сложный,
требующий для своего решения разложения в ряд или наличия
специальных таблиц. С целью получения более простого метода,
пригодного для решения задач при любом законе изменения плот-
ности с высотой и позволяющего учитывать даже изменение Сх от
скорости или числа Рейнольдса, мы предлагаем следующий метод
графического интегрирования. Уравнение движения напишем
в виде:
g / CY • О . S . V2 \ ,
dV2 = 2 • -7Г- • sin в G------п---------- dx;
G \ sin ’
dx • sin 0 = d/z;
g f C-^S-V*\ /?
= 19,6-fl — ~ Й.
\ *пр/
Теперь интегрирование можно произвести путем построения зиг-
загообразной линии. Для этого строим диаграмму, в которой по
оси абсцисс отложим V2, а по оси ординат
„ Сх о . S V2
G — - -..." " а- •
sin 0
Вместо бесконечно малой величины dh берем некоторый конеч-
ный интервал высоты J/z, например 50 или 100 м. Наклон можно
получить, задавшись некоторым произвольным /?0, например рав-
ным G, и затем подсчитывая:
AV02 = ^-2-g-Ah.
1 В. П. Ветчинки н, Динамика самолета, ОНТИ, 1935.
89
Cr-e-S-V2
Диаграммы G--------------- по получаются в виде прямых
линий, идущих от G при V2 = 0 до скорости Vnp для соответствую-
Фиг. 68. Графический расчет пикирования в среде переменной плотности.
И м/сеК
Фиг. 69. Сравнение пикирования в пустоте, в постоянной и переменной
плотности.
щих высот. Высоты берем: начальную—Но; Яо — 3 zl/i
и т. д., как это сделано на фиг. 68, где Яо = 5О00 м\ Л Л = 200 м и
затем взяты высоты 4800, 4400, 4000 м и т< д. Интегрирование
производим построением наклонных линий; первая линия пойдет
от V = 0 до линии — d/z; вторая идет вниз, третья к Н2 =
= Н0 — З-J/z и т. д. Получается ряд треугольников, каждый из ко-
торых соответствует изменению высоты на 2Ah, а вершина доходит
до линии, соответствующей средней высоте для данного интервала
скорости. Подобный расчет произведен на фиг. 68, где пикирова-
ние взято с высоты 5000 м от начальной скорости, равной нулю.
Следует обратить внимание на момент, когда скорость пошла на
убыль и треугольники стали строиться вниз. Подобную задачу
можно было бы решать и для случая, когда начальная скорость не
равна нулю. В этом случае начало построений зигзагов нужно
взять на соответствующем V2.
На фиг. 69 дана диаграмма изменения скорости при пикирова-
нии в переменной плотности. Кроме того, на той же диаграмме
приведены значения: скорости падения в пустоте, предельной ско-
рости пикирования, скорости пикирования в постоянной плотности,
равной плотности на начальной высоте Но = 5000 м, и при плот-
ности q0. Как видно, при пикировании в сопротивляющейся среде
переменной плотности скорость растет, доходит до максимума, а
затем опять убывает; скорость пикирования доходит до максимума
на той высоте, где она равна предельной скорости для соответ-
ствующей высоты, а далее скорость пикирования хотя и убывает,
но остается больше скорости установившегося пикирования на со-
ответствующих высотах, и следовательно, в случае отвесного пи-
кирования лобовое сопротивление превышает вес самолета.
КРИВОЛИНЕЙНЫЙ ПОЛЕТ
ОБЩИЕ СВЕДЕНИЯ
Анализ криволинейного движения тела можно провести двумя
способами: 1) рассматривать движение по отношению к некоторым
неподвижным в пространстве осям координат и 2) рассматривать
движение в отношении величины скорости, кривизны траектории и
плоскости кривизны траектории. Применение той или иной схемы
зависит от содержания задачи и дает определенные облегчения
в работе, хотя применение и иного метода ошибки не повлечет.
В более сложных-задачах приходится рассматривать одновременно
движение координат в пространстве и кривизну траектории.
В методическом отношении первый способ наиболее прост для
усвоения. Все движение мы заменяем изменением трех координат
тела, а действующие силы раскладываем на направления осей.
В результате вся задача сводится к расчету трех совместных пря-
молинейных движений. По отношению к движению вдоль каждой
из осей координат мы пишем выражение закона Ньютона:
-V d2* х? tz d2y х? 7 d2z
2иХ = т-^-,
Полученные уравнения интегрируем совместно, что обычно не
удается сделать в общем виде и приходится применять численные
методы интегрирования, принцип которых обычно очень прост, но
самый расчет требует большого внимания и занимает много вре-
мени.
Во многих задачах координаты тела в пространстве нас не ин-
тересуют, но зато интересуют величина скорости и кривизна тра-
ектории. В этом случае для анализа движения мы применяем прин-
цип д'Аламбера, вводя, кроме действующих сил, силу инерции — mj,
где /— полное ускорение. Затем требуем равновесия всех сил,
включая силу инерции; это условие часто выражают геометрически.
Введение силы инерции в выражение для равновесия сил вовсе
не говорит о реальности сил инерции, а является лишь удобным
приемом для решения инженерных задач. Мы вводим условную
силу инерции — mj для того, чтобы свести динамическую задачу
к статической, помня всегда о том, что сила инерции не является
92
причиной движения. Для лучшего понимания физической стороны
движения самолета мы будем вести рассуждения, исходя из дей-
ствия реальных внешних сил и вводя силы инерции только для
расчета. Точно так же мы не изображаем сил инерции на чертежах.
В тех случаях, когда нам известен характер движения, например
известны скорость и радиус кривизны, отыскание сил, вызывающих
данное движение, удобно вести, исходя из сил инерции, которые
в данном случае легко подсчитать. К счастью, при рассмотрении
полета самолета к этому прибегать почти не приходится, так как
обычно нам бывают известны
силы и приходится искать тра-
екторию.
Рассматривая задачу о вели-
чине скорости и кривизне траек-
тории, мы разлагаем действую-
щие силы на: составляющую, на-
правленную по касательной к
траектории, и составляющую, ле-
жащую в плоскости, перпенди-
кулярной к касательной (фиг. 70).
Первую силу будем называть
ускоряющей силой и применять
ее для расчета величины ско-
рости независимо от ее напра-
вления:
n dV
Руск — tn • ~di~
Фиг. 70. Разложение силы на ускоряю-
щую и центростремительную.
Вторую силу будем называть центростремительной и применять
для расчета кривизны траектории:
Рц.с — №• jn,
где ]'п — нормальное ускорение, которое, как мы знаем из механики,
может быть выражено так:
V2 „ V2
/п — —у > Рц.с — т .
V2
Сила — mjn = —т~у~ называется центробежной силой инерции.
Люди, недостаточно глубоко изучившие механику, считают силу
инерции какой-то особенной силой, противящейся криволинейному
движению. На самом деле она ничем не отличается от обычной
силы инерции и ее формально иное выражение произошло исклю-
чительно по причине указанного выше разложения сил. Напоми-
наем, что вывод центробежной силы сделан, исходя из сложения
двух независимых движений: одного по инерции со скоростью V,
другого — нарождающегося ускоренного движения в перпендику-
лярном к первому направлении.
На вопрос, от чего зависит центробежная сила инерции, при-
выкли отвечать: от квадрата скорости и радиуса кривизны траекто-
рии, и это методически верно, пока мы рассматриваем движение
машин по заранее заданной траектории.
93
У самолета нет заранее заданной траектории, — его траектория
определяется силами, которые нам известны. На вопрос о центро-
бежной силе мы ответим так: центробежная сила равна и противо-
положна центростремительной, это — закон Ньютона; скорость по-
Фиг. 71. Схема поворота автомобиля по горизон
тальной поверхности.
лета на центробежную силу
не влияет; она влияет только
на величину радиуса кри-
визны траектории, который
получается кинематически
в результате сложения дви-
жения по инерции со ско-
ростью V и движения, вы-
званного центростремитель-
ной силой. Таким определе-
нием мы хотим внести боль-
шую ясность в вопрос и,
с другой стороны, оградить
читателя от заблуждений
в вопросе о величинах цен-
тробежной и центростреми-
тельной сил. В частности,
неравенством сил центробежной и
нечно, является грубой ошибкой.
нам приходилось слышать
и встречать в печати объяс-
нения некоторых явлений
в полете самолета якобы
центростремительной, что, ко-
Приведем некоторые примеры неавиационного содержания, ко-
торые в некоторой степени будут служить аналогиями криволи-
нейного движения самолета,
(фиг. 71). Для того чтобы
происходил поворот, нужна
центростремительная сила,
которая и образуется в ре-
зультате сцепления колеса
с грунтом. Однако для на-
личия давления вдоль оси
колеса, последнее должно
двигаться под некоторым
углом к плоскости враще-
ния, и центр вращения всего
автомобиля получится не в
Пусть по дороге едет автомобиль
Фиг. 72. Схема движения автомобиля на пово-
роте (вираже).
Чем больше скорость, тем сильнее
точке пересечения осей ко-
лес О, а будет несколько
смещен в точку О' (фиг. 71).
будет смещение, и, наконец, при некоторой скорости осевое давле-
ние достигнет максимума, и уменьшение радиуса поворота ока-
жется невозможным. То же самое будет иметь место, если сцепле-
ние колес с грунтом плохое (снег, песок): осевое давление полу-
чается очень слабое и фактический центр поворота будет сильно
расходиться с точкой пересечения осей колес. Для облегчения по-
94
ворота дорогу делают наклонной, стремясь
действующая сил тяжести и сил инерции
поверхности грунта. Необходимый наклон
(фиг. 72):
к тому, чтобы равно-
была перпендикулярна
легко найти из схемы
Как видно, угол /3 зависит от радиуса
и скорости движения; если угол /? не
соответствует требуемому углу, выте-
кающему из последнего выражения, то
потребуется использовать осевое давле-
ние колес. В частном случае, если нак-
лон пути слишком велик, осевое давле-
ние нужно направить наружу, т. е. об-
ратно случаю поворота на горизонталь-
ном пути. Возможен даже такой случай
поворота, когда движение будет проис-
ходить по вертикальной цилиндрической
Фиг. 73. Схема движения авто-
мобиля по цилиндрической по-
верхности.
стенке (фиг. 73); в этом случае осевое
давление колес должно быть направлено
вертикально вверх, и при достаточной
скорости и малом радиусе эти осевые
давления F смогут удержать вес автомобиля. Как нетрудно сообра-
зить, в этом случае руль должен быть повернут в сторону, обратную
повороту на горизонтальной плоскости. Итак, мы видели три случая
поворота автомобиля: 1) по горизонтальному пути, когда сила тя-
жести удерживалась реакцией земли, а центростремительную силу
Фиг. 74. Неправильная схема поворота корабля.
давало трение колес; 2) поворот по наклонному пути, когда реакция
земли N давала центростремительную силу и удерживала вес, и
3) поворот по вертикальной цилиндрической стенке; когда центро-
стремительную силу давала реакция поверхности N, а вес удержи-
вался силами трения F, т. е. обратно первому случаю. Нужно от-
метить, что данный пример с автомобилем имеет много общего
с виражем самолета при разных скольжениях.
95
Приведем еще характерный пример с поворотом корабля. Иногда
поворот корабля рисуют, как показано на фиг. 74. Но это совер-
шенно неверно, и нужно представлять себе дело так: 1) под дей-
ствием момента, вызванного поворотом руля, корабль поворачи-
вается на некоторый угол и начинает двигаться несимметрично,
т. е. со скольжением (фиг. 75); 2) под действием скольжения ме-
няется давление на борта корабля, так что создается сила, дей-
ствующая поперек движения, аналогичная подъемной силе крыла;
эта сила будет служить центростремительной силой и величина ее
определит радиус поворота; 3) в течение всего поворота корабль
должен сохранять угол скольжения для сохранения центростреми-
тельной силы; стоящим на палубе корабля будет казаться, что од-
новременно с поворотом их несет вбок. Это явление тоже имеет
аналогию в вираже самолета.
Фиг. 75. Правильная схема поворота корабля.
В итоге нужно обратить внимание на следующее: искривле-
ние траектории происходит под действием центростремительной
силы, величина которой в зависимости от скорости и массы тела
определяет радиус кривизны траектории; поворот тела вокруг
центра тяжести еще необязательно дает искривление траектории;
это имеет место только в том случае, если в результате поворота
вокруг центра тяжести создастся центростремительная сила.
ОСОБЕННОСТИ КРИВОЛИНЕЙНОГО ДВИЖЕНИЯ САМОЛЕТА
Испытание моделей самолетов в лабораториях производится
в прямолинейном потоке воздуха; поэтому материалы этих испы-
таний пригодны лишь для расчета прямолинейного полета. В слу-
чае криволинейного движения мы имеем отличие от прямолиней-
ного движения в величинах сил и моментов. К сожалению, эти
изменения пока не удается достаточно надежно найти лаборатор-
ным путем ввиду отсутствия специальной аппаратуры; поэтому,
для расчета, в силы и моменты прямолинейного полета мы вводим
поправки, полученные теоретическим путем и по некоторым кос-
венным испытаниям. Нужно сказать, что влияние криволинейного
D6
полета на величину сил незначительно, и поэтому мы ограничимся
рассмотрением изменения моментов. Для упрощения работы (без
особого ущерба для точности расчетов) можно считать, что радиус
кривизны траектории лежит в плоскости, перпендикулярной оси х
самолета. Тогда на виде самолета спереди мы будем иметь радиус
кривизны в натуральную величину. Пусть самолет движется по
кривой траектории некоторого радиуса г (фиг. 76); тогда ось вра-
щения 00 будет перпендикулярна радиусу. Продолжив ось 00 до
пересечения с осями у и z, определим радиусы гу и гг:
Фиг. 76. Разложение кривизны траектории на координатные
плоскости самолета.
Это будут радиусы кривизны проекции траектории на плоско-
стях ху и xz.
ДЛя рассмотрения йзменения моментов сделаем допущение, что
кривизна траектории в плоскости xz не влияет на моменты вокруг
оси z, а кривизна в плоскости ху не влияет на моменты вокруг
оси у. Это допущение справедливо в случае, когда размеры само-
лета невелики по сравнению с радиусами кривизны.
РАВНОВЕСИЕ ПРОДОЛЬНЫХ МОМЕНТОВ
Берем проекцию самолета и траектории на плоскость ху, т. е.
вид сбоку (фиг. 77). Как видим, самолет находится теперь в кри-
волинейном потоке воздуха. Естественно, что это вызовет измене-
ние подъемной силы крыла, и затем, как нетрудно видеть из чер-
7 В. С. Пышное.
тежа, угол подхода потока к оперению возрастает на величину Лер,
и следовательно, при расчете момента хвоста нужно, кроме скоса
потока от крыла, учесть угол Лер. Иногда для пояснения влияния
кривизны траектории производят такую операцию: разгибают тра-
ектории в прямолинейные, а самолет соответственно искажают
с таким расчетом, чтобы угол подхода воздушных струй к отдель-
ным частям самолета остался такой же, как в криволинейном по-
лете. На фиг. 78 показан пример такого выпрямления траектории.
Фиг. 77. Влияние кривизны траектории на равновесие продольных
моментов.
Как видно, изменился профиль крыла в сторону увеличения кри-
визны средней линии и загнулся вниз фюзеляж, увеличив тем са-
мым установочный угол стабилизатора на величину Лер.
Величину изменения коэфициента момента крыла можно подсчи-
тать по формуле Глауэрта х:
dC„ / х„ \ b
dCu
где = В— зависит от удлинения крыла,
—центровка по средней аэродинамической хорде,
b — средняя аэродинамическая хорда.
* R. & М. № 1216.
98
Если взять в среднем В — 2,0 и -у- = 0,3, то получим:
ЛСМ = Ъ2±
У
Величину Ду можно найти так: из фиг. 77 мы видим, что 4<р
является углом между радиусами, проведенными к одной трети
хорд крыла и горизонтального оперения. За малостью угол можно
считать:
Д<р° = 57Д
ги
Можно получить Д<р и иначе: зная угловую скорость сог вокруг
оси z, определим скорость опускания хвоста а>х • LXB:
Фиг. 78. Фиктивное искривление самолета.
Расчет равновесия самолета заключается в построении балан-
сировочной диаграммы. Для расчета балансировочной диаграммы
для криволинейного полета можно проделать новый расчет, но го-
раздо проще внести поправки в уже имеющуюся балансировочную
диаграмму для прямолинейного полета. Проделаем такой расчет.
Пусть у нас имеются балансировочная диаграмма для прямолиней-
ного полета (фиг. 79) и необходимые данные о самолете. Увели-
чение момента крыла нужно уравновесить поворотом руля высоты
на себя из условия:
* Q 1 / V \2
откуда
Увеличение угла установки хвоста Ду тоже нужно компенсиро-
вать поворотом руля высоты на угол <32:
<32 = ——.
2 п
99
Таким образом полное изменение положения руля высоты будет:
<^3 = + ^2-
Если в прямолинейном полете руль был отклонен на угол 8, то
в криволинейном получим отклонение:
8' = 8 — (81 + 82).
Подставляя значения ДСМ. Ду и принимая в среднем
= 0,4; = 1 и Вхв = 0,027,
получим:
Величина ____
Sp, в
^хв
где£р<в — площадь руля высоты и SXB — площадь всего горизон-
тального оперения. Практически -^-5- близко к 0,45 и п = 0,64;
^ХВ
хорда крыла b х для монопланов и b = —~ для бипланов; возь-
мем в среднем Ь — получим:
8' = <5 — 100—.
rv
Задаваясь разными радиусами гу, можем соответственно пере-
строить балансировочные диаграммы (фиг. 79). Как будет пока-
100
зано далее, для определенного вида криволинейного движения гу
зависит от а; принимая эту зависимость, можно построить балан-
сировочную диаграмму для криволинейного полета с учетом реаль-
ных радиусов. Величина-^ доходит до 0,06 — 0,1 и даже более.
гу
Отсюда нетрудно видеть, что на больших углах атаки мы можем
столкнуться с нехваткой руля высоты, так как полезная эффектив-
ность сохраняется до <5 ——18 — 20°. Задаваясь предельной вели-
чиной <5шах, можем найти минимальный радиус гу, в зависимости от
угла атаки определяемый условием управляемости:
принимая <5шах = 18°, получим:
Фиг. 80. Изменение угла атаки при постоянном положении руля
высоты в зависимости от кривизны траектории.
Величину 8 берем для разных углов атаки по балансировочной
кривой прямолинейного полета. Примерный расчет приведен на
фиг. 80.
Как видно, если в прямолинейном полете, отклоняя руль на
—18°, мы достигали угла атаки 17,7°, то при гу = 100 мы могли
достичь только 11,3°. У самолетов с большим LXB изменение будет
еще сильнее. Однако вопрос может заключаться не только в от-
клонении руля высоты, но и в давлении на ручку.
РАВНОВЕСИЕ МОМЕНТОВ ПОПЕРЕЧНЫХ И ПУТИ
Рассмотрим вращение самолета по некоторому радиусу rz (фиг. 81).
Мы можем отметить следующее: самолет обтекается криволиней-
ным потоком, в результате чего углы подхода потока к фюзеляжу
и оперению изменяются; в отношении крыла криволинейный поток
особой роли не играет, но зато скорость в разных частях крыла
будет различна, а отсюда различными будут лобовое сопротивле-
ние и подъемная сила.
101
Подсчет моментов и сил в данном случае получается довольно
затруднительным. К тому же по этому вопросу у нас нет никаких
опытных данных. Применим такой же способ, как и при рассмот-
Фиг. 81. Влияние кривизны траектории на равновесие заворачивающих моментов.
рении равновесия вокруг оси z, т. е. превратим движение в прямо-
линейное, исказив соответственно самолет. Кроме искривления фю-
зеляжа, для учета перемены скоростей вдоль размаха крыльев,
условно увеличим
хорды крыльев про-
порционально квад-
рату расстояния их
от центра вращения
(фиг. 82). Не касаясь
количественной сто-
роны вопроса, мы
все же можем за-
ключить, что: 1) при
криволинейном дви-
жении в плоскости xz
самолет под дейст-
вием вертикального
оперения обнаружит
тенденцию повора-
чиваться против ос-
новного направле-
ния поворота, и по-
тому для сохранения
Фиг. 82. Фиктивное искажение самолета. правильного движе-
ния, при котором
фюзеляж совпадал
бы с касательной к траектории центра тяжести, необходимо руль
поворотов отклонить в сторону поворота; 2) по причине разности
скоростей в разных частях крыла самолет проявит тенденцию к на-
102
кренению в сторону поворота, и если накренение нежелательно,
летчик должен отклонить элероны, опустив находящийся со сто-
роны центра вращения и подняв противоположный. Более подробно
этот вопрос будет рассмотрен в четвертой части настоящего
труда.
ВИРАЖ
Вираж представляет собой наиболее распространенный и наибо-
лее простой вид криволинейного полета. Применяется он для изме-
нения направления полета в горизонтальной плоскости и соответ-
ственно повороту траектории ука-
зывается угол, например: вираж на
90°, на 180° и т. д. (фиг. 83); с тре-
нировочной целью выполняются ви-
ражи на 360 и более градусов, т. е.
самолет непрерывно кружится.
В дальнейшем нам часто придется
применять термин — правильный ви-
раж; оговорим, что мы под этим по-
нимаем. Правильным виражем мы
называем полет по кривой, лежащей
в горизонтальной плоскости с по-
стоянным радиусом, причем самолет
накренен, но не имеет скольжения,
т. е. размах крыльев перпендикуля-
рен касательной к траектории. Го-
воря о других видах виража, мы
будем указывать, чем они отличаю-
тся от правильного, т. е. вираж со
снижением и т. п.
Правильный вираж. Основным параметром при всяком криво-
линейном движении является центростремительная сила. Нам нужно
некоторую силу направить к желаемому центру поворота, т. е. го-
ризонтально в сторону поворота.
При правильном вираже в каче-
стве центростремительной силы
используется подъемная сила
крыльев Р. Для этой цели само-
лет накреняют на некоторый
угол р, тогда наклоняется и подъ-
емная сила (фиг. 84). Разлагая
подъемную силу на вертикаль-
ную и горизонтальную составляю-
щие, получим, что вертикальная
составляющая должна продол-
жать удерживать вес самолета,
а горизонтальная — служить цен-
тростремительной силой. Таким образом подъемная сила должна
быть увеличена с таким расчетом, чтобы вертикальная проекция ее
равнялась весу самолета. Этого можно достичь увеличением угла
атаки или увеличением скорости. Чем круче крен, тем больше цен-
Фиг. 84. Действие сил на вираже.
103
тростремительная сила, тем меньше радиус поворота. Увеличение
подъемной силы, естественно, вызывает увеличение сопротивления,
а отсюда и увеличение потребной мощности.
Как видим, для совершения виража самолет нужно только на-
кренить; однако возникающее вслед за этим криволинейное движе-
ние требует для равновесия моментов отклонения рулей.
Радиус виража. Имея центростремительную силу, нетрудно
найти радиус кривизны траектории. Из фиг. 84 имеем:
Рц. с = Р • sin /?.
Приравнивая Рц.с центробежной силе и подставляя аэроди-
намическое выражение для подъемной силы, получим:
т у- = Су • q • S • V2 • sin /?,
• _ G • v2 _ о
1 ~~ g • е • $ • V2 • су sin р ~ s • у • Су sin р ’
где
T = Q.
Как видим, в выражение для радиуса скорость не входит, но это,
конечно, не значит, что вообще для виража величина скорости не
имеет значения. Радиус виража зависит от нагрузки на квадрат-
ный метр крыла, от плотности воздуха, угла атаки и угла крена.
Обычно мы интересуемся радиусом виража в отношении его мини-
мального значения. Для уменьшения радиуса мы должны лететь на
большом Су, но не на СУтат, так как при этом сильно возрастает Сх
и ухудшается устойчивость самолета. Практически применяется Су
не более экономического, что соответствует Су = 0,75 Cv . С уве-
личением угла крена радиус меняется обратно пропорционально
синусу угла крена. Практически правильный вираж удается совер-
шать с креном не более 60—70°, когда sin/3 ~ 0,865— 0,94, т. е.
мало отличается от единицы. В среднем можно взять: sin = 0,9 и
у = 1,22 • А, где А— отношение плотностей на высоте и у земли.
Минимальный радиус виража:
г =____________9___________= 121____-___—
'mm S • 1,22-Л-0,75-С„ -0,9 ’ S Л • С„ '
wmax ^max
Можно дать еще такое выражение; мы знаем, что для экономи-
ческой скорости:
n G • 8 , 2
Р . 5'."с-> = S • Л • 0,75 • с = (1,15 Vmin);
е Уэк
отсюда
Гш!п= 0,113 • = 0,15Vmin,
где Уэк и Ут1п должны быть взяты для соответствующей высоты.
Взяв в среднем СУтах = 0,65, получим приближенное выражение для
минимального радиуса виража:
'„.-=1,86.4.4.
104
Это выражение показывает нам, что минимальный радиус виража
в основном зависит от нагрузки на квадратный метр крыльев. Это
выражение пригодно, конечно, только в том случае, когда в криво-
линейном полете руль высоты способен дать Cv — 0,75 Су . Ра-
счет виража с учетом равновесия моментов будет приведен далее.
В табл. 5 приведены значения минимального радиуса виража»
подсчитанные указанным способом для самолетов различных типов,
и для птицы.
Таблица 5
Самолет G / 2 кг/м2 о С« "max Лп1п
Гоночный . . . 180 — 200 0,5 435 — 485
Истребитель . . 80—120 0,6 160 — 240
Разведчик . . . 60—100 0,65 110 — 185
Учебный .... 25 — 35 0,65 47 — 65
Планер 15—20 0,7 26 — 35
Птица 2 — 3 0,8 3 — 4,5
Расчет для птицы сделан, исходя из полета с неподвижными
крыльями, так как при полете с машущими крыльями может
быть значительно больше, а у малых птиц, способных висеть на
месте, радиус поворота может быть равен нулю.
Табл. 5 очень наглядно иллюстрирует роль нагрузки на квад-
ратный метр крыла; затем мы видим тесную связь минимального
радиуса вцража с минимальной скоростью полета.
При выводе радиуса виража мы взяли проекцию подъемной
силы на горизонталь, не проверив предварительно, будет ли вер-
тикальная проекция равна весу. Поэтому выражение для радиуса,
содержащее sin /3, пригодно не только для правильных виражей.
Теперь примем, что Р cos /?=G; тогда из отношения катетов по-
лучим:
V2
Рц. С = G tg р = т ,
_ mV2 _ V2
Г~ G-tg 0 “ 9,8 - tg jg •
Мы получили совершенно иное выражение для радиуса, которое
на первый взгляд дает другие результаты. В частности, в первом
выражении при увеличении р радиус стремится к некоторой вели-
чине; в последнем выражении при увеличении Р как будто бы tg р
стремится к бесконечности, а радиус—к нулю. Но это не так;
дело в том, что в данном выражении нельзя брать какую угодно
скорость. Если же мы подставим скорость, потребную для виража,
то получим выражение с синусом р.
Скорость на вираже. В горизонтальном полете самолет мог ле-
тать на разных скоростях в интервале от минимальной до макси-
мальной. На вираже тоже можно иметь разные скорости, но только
диапазон скоростей сужается тем сильнее, чем больше крен. Для
105
рассмотрения вопроса мы поступим так же, как это делали при
рассмотрении нормального полета, т. е. будем производить сравне-
ние при постоянном угле атаки. Приравнивая вес вертикальной
проекции подъемной силы, получим:
G = Р • cos Д = Су • q • S • V2 • cos /?,
откуда ___________
у —1Л G__________.
v Г а • S • cv- cos 0
Скорбеть горизонтального полета на том же угле атаки, а сле-
довательно, на том же Су, будет:
Vrop-]/ Q-S-Cy
Отсюда, сравнивая скорости, потребные для виража и горизон-
тального полета, получим:
у
17 = _ Го-Р_
V вир ---п •
у cos Р
Поскольку cos р меньше единицы, делаем вывод, что вираж
требует скорости большей, нежели горизонтальный полет. Это
совсем не значит, что для совершения виража мы должны увели
Фиг. 85. Изменение экономической скорости в зависи-
мости от угла крена.
чить скорость поле-
та. Мы можем делать
вираж на ином угле
атаки, лишь бы он
не был слишком бли-
зок к критическому
углу при С„шах. Одна-
ко, если мы уже ле-
тели на большом
угле атаки, то для
совершения виража
скорость нужно уве-
личить. Иа эту сто-
рону вопроса и нуж-
но обратить внима-
ние.
Если мы летели
горизонтально на
экономической скорости УЭк, которая практически должна счи-
таться минимальной скоростью полета, то экономическая скорость
на вираже будет:
V
V — - эк
v эк. вир — г— .
у cos р
Начиная делать вираж, мы должны уже иметь скорость не
менее Кж. вир для предполагаемого угла крена. На фиг. 85 пока-
зана для наглядности диаграмма изменения Кж. вир в зависимости
от крена, если Уэк принято за 100%- Как видно, при /3 = 45° мы
106
имеем 119%, а при /3 = 60° соответственно 141%; таким образом
имеем довольно существенное увеличение скорости.
Для понимания важности вопроса посмотрим, что случится,
если скорость будет недостаточна. В этом случае проекция подъ-
емной силы будет меньше веса, некоторая доля веса останется
неуравновешенной, и к криволинейному горизонтальному движению
на вираже добавится ускоренное движение вниз — именно ускорен-
ное движение, а не просто опускание. Поскольку траектория по-
степенно склоняется вниз, самолет в силу своей устойчивости
будет опускать нос, переходя в пикирование, задержать которое
будет невозможно, даже выровняв крен, если самолет уже успел
достаточно наклониться. Набрав скорость, самолет выровняется,
но дело в том, что сваливание в пикирование и последующее вы-
равнивание дадут значительную потерю высоты, и если это слу-
чится на малой высоте, то неизбежна катастрофа. Одно время
такие катастрофы были очень часты и объяснялись они недостат-
ком теоретических знаний и недисциплинированностью. Борьба
с этим велась такими путями: популяризацией теории, запрещением
делать развороты на малой высоте, запрещением летать на эконо-
мической скорости на малой высоте, установлением некоторой
эволютивной скорости, позволяющей в случае нужды безопасно
сделать пологий вираж.
Особое внимание на скорость при вираже нужно обратить
в случае полета перегруженного самолета, когда УЭк. вир должна
быть увеличена пропорционально корню квадратному из отноше-
ния весов:
%к. вир = Уэк. вир ~\/ •
На практике самолеты перегружаются иногда на 30—50% про-
тив среднего веса при тренировочных полетах й это дает увели-
чение скорости на 15—20%.
При совершении виража на высоте скорость должна быть уве-
личена путем
умножения на
Со
е
Однако на самом деле
этого делать не нужно, так как если летчик контролирует полет
по указателю скорости, основанному на измерении скоростного
напора, то прибор автоматически учтет необходимую поправку,
и поэтому по прибору скорость на высоте и у земли может быть
одинакова.
Вопрос о максимальной скорости на вираже определяется или
мощностью винтомоторной группы, или условием прочности, о чем
будет сказано далее.
Перегрузка. Из сказанного выше уже ясно было видно, что
вираж требует большей подъемной силы, нежели горизонтальный
полет. Перегрузкой мы называем отношение подъемной силы к весу
самолета; в горизонтальном полете перегрузка, очевидно, равна
единице. Во всяком другом полете, а следовательно, и на вираже,
перегрузка будет:
р су • g • s • v2
п ~ g ~ о 8
107
Это наиболее общее и пригодное для всех случаев выражение.
Для правильного виража перегрузка может быть выражена как
отношение гипотенузы к вертикальному катету в силовом тре-
угольнике (фиг. 84):
п= ‘
COS0
Это выражение очень просто и часто применяется при рассмо-
трении виража. Однако здесь нужно быть последовательным, ого-
варивая, что вираж правильный. Так, например, неверно думать,
что перегрузка возникает от простого накренения самолета. Пере-
грузка п = s д- получается при условии соблюдения всех условий
правильного виража, особенно в отношении угла атаки и скорости.
Фиг. 80. Изменение перегрузки при правильном вираже
в зависимости от угла крена.
Например, при крене 90° перегрузка не будет бесконечно велика,
что следует по формуле, так как такой вираж никогда не будет
правильным (по той причине, что правильный вираж с креном в 90°
потребовал бы бесконечно большой скорости).
На фиг. 86 дана перегрузка на вираже, вычисленная по фор-
муле 'СОз~д~- Как видно, при увеличении р она растет сначала
медленно, а потом все более и более резко. Можно составить еще
такое выражение для перегрузки, складывая геометрически вес G
с центробежной силой т -у-:
p’ = g2 + (-^)‘ = g(i + ~),
" = V' + ^-
Это выражение для некоторых задач представляет известное
удобство, но зато имеет тот недостаток, что радиус г не может
быть подставлен менее определенной величины. На практике нас
редко интересует перегрузка вообще в каком-то случае. Обычно
нас интересует максимальная перегрузка, которая получается при
108
желании летчика сделать вираж возможно малого радиуса. В этом
случае удобнее всего воспользоваться самым общим выражением,
не применяя угла крена, который на практике трудно определить
и контролировать:
су. &-S- Vs
п = —-—-------
И G
Мы уже указали, что брать Су больше 0,75СИт^ не следует;
подставляя его и помня, что
----------= V
е • s ’ с»№ ш1“
Фиг. 87. Изменение потребной мощности при вираже.
получим:
"тх = (у^-п) - °’75-
Это выражение нужно читать так: максимальная перегрузка при
совершении виражей равна 0,75, умноженным на квадрат отноше-
ния скорости на вираже к минимальной скорости горизонтального
полета, свойственной данному самолету с данным полетным весом.
Если скорость V брать по прибору, то выражение будет действи-
тельно для всех высот.
Мощность, потребная для виража. Увеличение подъемной силы
на вираже, естественно, требует увеличения затраты мощности на
полет. Если мы будем сравнивать вираж с горизонтальным поле-
том на одинаковых углах атаки, то получим, что скорость увели-
чивается путем умножения на г 1 , а мощность растет в кубе
у cos р
скорости; отсюда получим:
Nвир = Nгор * у СО5» 0 ^гор • Л 2 >
где п — перегрузка.
10»
На фиг. 87 дана диаграмма отношения -д.вир в зависимости от
^гор
угла крена.
Подсчитаем мощность, потребную для виража на разных углах
атаки. На фиг. 88 показан примерный вид кривых потребной мощ-
ности для виражей с разными углами крена. Можно отметить, что
в этом отношении действие угла крена вполне соответствует уве-
личению веса самолета в п раз.
Если винт имеет неизменный шаг, то для анализа виража вместо
мощности можно применять потребные обороты. Как мы уже
V
const. Отсюда мы по-
знаем, при постоянном угле атаки Л— п д
лучаем, что на вираже потребные обороты возрастают пропорцио-
нально скорости:
V п
„ — „ вир __ "гор
''вир — "гор • "Т7 — - Г—---о
*гор V cos fi
(не нужно, конечно, смешивать данное п, т. е. обороты, с пере-
грузкой). Опять мы видим, что в отношении оборотов вираж экви-
валентен увеличению веса. Однако нужно все же заметить, что
нагружение самолета силами инерции и грузом не одно и то же.
Дело в том, что на вираже мы имеем криволинейный полет, а он
вызывает увеличение Су даже при старом угле атаки; затем надо
отметить, что еще совсем неясен вопрос об индуктивном сопро-
тивлении в криволинейном полете.
Предельный вираж без снижения. При совершении виража мы
должны увеличивать мощность мотора. Если крен невелик (фиг. 88),
но
мы будем иметь избыток мощности, который позволит нам совер-
шать вираж с подъемом, причем величина вертикальной скорости
может быть подсчитана обычным способом. Увеличивая крен, мы
можем дойти до такого момента, когда придется использовать всю
мощность мотора, и дальнейшее увеличение крена без перехода на
снижение станет невозможным. Вираж, при котором для сохране-
ния высоты мы вынуждены использовать всю мощность мотора
мы будем называть предельным виражем. На разных углах атаки
получаются разные величины предельного угла крена и соответ-
ственно разные скорости. Максимальный угол крена соответствует
предельные виражи, дающие минимальный радиус и минимальное-
время виража, и все они будут соответствовать разным углам
атаки, что будет доказано в дальнейшем,
Поскольку мы вначале еще не знаем, каким углам атаки соот-
ветствуют предельные виражи с максимальным углом крена, мини-
мальным радиусом и минимальным временем, расчет приходится
вести для серии углов атаки, а потом путем интерполяции можно
будет найти искомые величины. Расчет можно расположить, как
это сделано на фиг. 88: предельные виражи будут соответствовать
точкам пересечения кривых потребной и располагаемой мощностей.
Однако удобнее поступить несколько иначе: берем диаграммы
потребной и располагаемой мощностей для горизонтального по-,
лета на нужной высоте (фиг. 89). Если мы будем делать вираж на
постоянном угле атаки, но на переменном угле крена, то потреб-
ная мощность будет меняться по кубу скорости, так как
N = Cx-q.S-V3>-±
4 «х
На чертеже проводим ряд кубических парабол, начиная их из то-
чек кривой потребной мощности с отмеченными углами атаки. Эти
и»
кубические параболы будут соответствовать виражам на взятых
углах атаки, а предельные виражи будут соответствовать точкам
пересечения кубических парабол с кривой располагаемой мощности.
Таким образом для каждого угла атаки мы будем знать скорость
горизонтального полета Угор и скорость на вираже Увир с еще не-
известным нам углом крена. Найти теперь угол крена труда не
представит. В самом деле, мы знаем:
у
IZ г°р
V вир- ~ ’
У COS 0
отсюда
Фиг. 90. Радиус, крен и время поворота на 380° для предельного
виража.
По cos/? находим /? и tg/?; тогда получаем радиус:
Увир
9,8-tg 0
& время поворота на угол <р:
4__ 2-л-г <р
1 ~ ~Т зао3-'
Подсчитав 0, г и t для всех парабол, можем построить гра-
фики 0, г и t по Увир (фиг. 9Э) и найти rmln и fmln. Построенные
кривые дадут нам /?тах, гт1п и tmIn на разных скоростях, и это может
показаться случайным. Тогда можно построить другой график, на
первый взгляд несколько запутанный, но который дает более чет-
кое соотношение между элементами виража (фиг. 91). На фиг. 91
по оси абсцисс отложена скорость, по оси ординат — радиус; время
поворота на некоторый угол, например 360°, можно изобразить
112
в виде прямых, идущих из начала координат, наклон которых
можно подсчитать по выражению:
, ,2-л-г
задаваясь разными значениями времени t. Линии равных углов
крена получим из условия
Фиг. 91. График виражей.
подставляя разные tg Нетрудно видеть, что это — параболы.
Полученная сетка для t и /3 несколько затемняет чертеж, и ее
лучше иметь отдельно на прозрачной кальке. Затем на этом чер-
теже могут быть нанесены различные линии, ограничивающие вираж.
Например, можно нанести границу экономической скорости, под-
считав ее по условию
у
и — эк
V ЭК. вир -- /---:
8
В. С. Пышнов.
ИЗ
Фиг. 92. Зависимость угла атаки от кривизны т]
при разных положениях руля высоты.
и отмечая точки скорости на параболах соответственно углу /J.
Далее можно нанести границу прочности, связывая ее через допу-
стимую перегрузку с углом крена, и, наконец, границу предельных
виражей, откладывая г по V, полученные по приведенному выше
расчету. Впоследствии мы нанесем сюда еще другие границы. В ре-
зультате найдем, что можно производить только те виражи, ко-
торые лежат внутри всех границ.
На данной диаграмме минимальный радиус предельного виража
получаем проведением касательной к границе предельных виражей,
параллельной оси абсцисс. Минимальное время предельного виража
получим, проведя
касательную из на-
чала координат, и,
наконец, максималь-
ный угол крена по-
лучим, подобрав ка-
сательную параболу.
Из ЭТОГО ЯСНО, ЧТО'
гш1п, *Ш1П и /9тах будут
лежать на разных
скоростях. Однако,
если мы воспретим
производить виражи
на скоростях менее
Van. вир ПО сообра-
жениям устойчивос-
ти и проведем на
рии фиг. 91 соответст-
вующую границу, то
минимальный ради-
ус, время и максимальный крен получим практически на одной
скорости, в данном примере — 42 м/сек, минимальный радиус
с 85 м возрастет до 105 м, а минимальное время с 14,6 до
15,7 сек.
Учет равновесия моментов при вираже. При совершении вира-
жей рули нужно отклонять, и поэтому возможен случай недоста-
точности рулей. В настоящее время нам приходится сталкиваться
с недостатком руля высоты.
О влиянии кривизны траектории на равновесие моментов было
уже указано выше (см. стр. 98). Путем пересчета балансировочной
кривой мы можем найти зависимость радиуса кривизны гу от угла
атаки для разных углов отклонения руля высоты. На фиг. 92 дана
такая диаграмма. Из фиг. 93 имеем связь между гу и г; как видно
из чертежа:
, V2
r = _L_- г — __•
у sin ft ’ 9,8 • tg /? ’
г /bhp-C0S^
у 9,8 • sin2 fl
114
Подставляя эти значения, получим:
V2 V2
172 _ __ГОр . __ ___•'гор
вир cos р ’ у 9,8 • sin р ’
1/2
sin В =
Для каждого угла атаки нам известны гу (фиг. 92) и Угор (фиг. 94);
у
отсюда находим sin р, а затем г = гу • sin р и Увир = —--Г01>— . На
J/COS0
фиг. 95 дана диаграмма г по V, аналогичная фиг. 91, на которой
нанесены пограничные линии из условий управляемости для откло-
Фиг. 93. Кривизна траектории в плос-
кости симметрии при вираже.
нений руля высоты <5 =—15°;
— 10° и —5°. Если произвольно
задаваться величиной гу, то можно
получить sin р > 1, что абсурдно.
Поэтому лучше построить диа-
/ У2
грамму у ^-8г°р - по гу или Vrop
и брать только значения, мень-
шие единицы (фиг. 96). По по-
строенным примерным диаграм-
мам мы видим, что управляемость
может дать значительное ограни-
чение для маневренности само-
лета. Вопрос об управляемости
в криволинейном полете будет
нами освещен в дальнейшем.
С поднятием ла высоту гра-
ница управляемости остается, а
граница мощности поднимается
вверх. В итоге на высоте вопросы
управляемости играют меньшую
роль.
Расчет предельного виража методом оборотов. Если на само-
лете установлен винт с неизменяемым шагом и деформации его
при перемене нагрузки невелики, то можно рассчитать предельный
вираж методом оборотов. Мы уже получили скорость и число
оборотов на вираже:
v п
JZ ____ гор . „ _ “гор
v вир — _ . ——п , 1 \ г--з •
У cos $ у cos Р
диаграммы потребных и располагаемых оборо-
возьмем некоторую скорость горизонтального
накренении самолета и сохранении угла атаки
Если мы имеем
тов (фиг. 97) и
полета то при
скорость и обороты будут расти в одинаковой степени, и точка
на диаграмме будет перемещаться по прямой, идущей из начала
координат. Предельный вираж будет в точке V'v когда будут
использованы максимальные обороты. Угол крена получим:
cos/? = (-^r Г-^^-
р \ v; / ’ g - tg# •
8*
115
Фиг. 95. График виражей с учетом управляемости.
116
Проводя ряд лучей из начала координат, получим предельные
виражи на разных скоростях и затем можем построить границу
Фиг. 96. График к расчету влияния управляемости.
Предельный вираж на высоте. Поскольку предельный вираж
определялся запасом мощности, то, очевидно, с поднятием на
высоту мы должны ожидать значительных изменений в вираже.
V км]час
Фиг. 97. Расчет предельного виража по диаграмме
оборотов.
Для расчета мы могли бы поступить так: построить серию кривых
потребной и располагаемой мощностей на разных высотах, про-
вести кубические параболы и подсчитать cos/9 и г. Затем то же
самое можно было бы проделать методом оборотов. В результате
окажется,s что с поднятием на высоту предельный угол крена умень-
шается, а радиус растет. На потолке мы имели бы касание кривых
117
и для этой точки cos/? = l; /5 = 0; г — оо, т. е. на потолке нельзя
сделать виража без снижения.
Теперь возьмем и исследуем данный вопрос аналитически. Для
расчета угла крена мы брали квадрат отношения скоростей:
(V \2
-у"0-) •
вир /
Вместо отношения скоростей можно взять отношение мощностей
или оборотов:
V / N \ 3 п
v гор _/ гор \ __ "гор
V \ W ) П *
вир \ вир / вир
£
\ 3 /и \2
вир / \ "вир /
Отношение мощностей мраС11 часто называют запасом мощности
^потр
и обозначают:
N in
2 расп ________________________/ "расп
^потр \ лпотр
3
= £,
причем мощности нужно брать на одной кубической параболе,
а обороты на одной прямой, проходящей через начало координат.
Это является условием сохранения угла атаки и к. п. д. винта.
Следовательно, задача расчета виража на другой высоте или
при другом полетном весе сводится к расчету запаса мощности
или запаса оборотов.
Вспоминая основные соотношения из аэродинамического рас-
чета, можно сказать: если в полете у земли при полетном весе Go
потребная мощность была Мютр, то на другой высоте и при дру-
гом полетном весе будем иметь:
V' /AV’5- (-М0,5
Если в полете у земли полная располагаемая мощность была
2VpaCn, то на другой высоте будем иметь изменение мощности за
N„
счет величины А — и изменения оборотов мотора:
Nрасп = Nрасп • А • ( — ) ,
где к — показатель степени параболы, заменяющей внешнюю харак-
теристику мотора.
Из условия сохранения Я = имеем:
Wpacn = Nm • *7 = /? • е0 • п30 • О5 . V,
Npacn = NM • П • А • = р-е-п3- D5 .q;
118
отсюда
ь
в результате:
з ________k
Nрасп = Nрасп * (-А) * (^)
Если в полете у земли при весе Go запас мощности был е0, то
на высоте при весе G получим:
3 к
М Л 3~к Л 3—к , 1 5 3 3~~3fe
^расп’А _ F.fCo\’ . (Ь\3~к . (/h6~2fe
N .(^.д-и °^о) ( ) ( ) •
потр \GJ
Если в полете у земли для некоторого угла атаки при весе Оо
мы нашли угол крена /?0, скорость Vo и радиус г0 для предельного
виража, то теперь мы можем найти иг для любой другой
высоты и другого полетного веса. В самом деле, определив е0 из
условия
1
ео 3 >
(cos Р) 2
находим е по приведенной выше формуле, и тогда:
cosj5 = (—V; V =
г Хе/’ и Г G0-e-cosp ’
— у2
r “ g • tg р •
Для расчета виражей можно предложить два порядка.
1. Построив кубические параболы на диаграмме мощностей
(фиг. 88), найти значения £0 = Для разных углов атаки, затем
^*потр
построить диаграмму е0 по Су и подсчитать е для других высот и
весов (фиг. 98):
3 3—3fe
По e находим скорости и радиусы виражей (фиг. 99).
2. Второй способ можно принять такой: построить границу
виражей г по V без снижения обычным способом; пересчитать
границу на другие высоты или веса, пользуясь отношениями:
но
Фиг. S9. График виражей на разных высотах.
120
Выражение для скорости получилось довольно простое, и еще
более упростится, если взять Л=1:
1
/ Д \3-fe
Можно напомнить, что множитель ( представляет со-
бой коэфициент изменения располагаемых оборотов по высоте.
Если нас интересует только предельный вираж с наибольшим
углом крена и мы уже нашли cos т. е. для виража у земли
при весе Go, то на другой высоте при весе G получим:
2
cos /?шах= cos/?0mai = cos /?Ошах
2
Go
1 — fe.
3— k
Если взять Л = 1, то выражение сильно упрощается:
cos — COS в0 • 4- .
rmax rumax А
На потолке е = 1 и 0°; при спуске с потолка s растет,
а вместе с этим растет угол крена предельного виража. Следова-
тельно, можно найти связь между предельным углом крена и вы-
сотой до потолка, т. е. разностью между высотой потолка и высо-
той, на которой находится самолет. То же самое можно сделать
для минимального радиуса и минимального времени совершения;
полного круга.
На высоте полета имеем запас мощности:
3 3—3ft
е = е0 • А3-'й •
на потолке:
3 3—3k
отсюда
3 3—3ft
\Ан) \АН ) 9
2 2 1 — k
Скорость, радиус и время найдем, полагая, что полет происхо-
дит на угле атаки, близком к наивыгоднейшему:
““ 1/ Q • s • Су • C0S/3 ’
V ^наив г
• = V2 •
1 ” g * tg £ ’
. _ 2лг .
1 ~ V ’
121
если к = 1, то:
Ан
COS/5 = -^.
Получилось очень простое выражение для расчета предельного
угла крена.
На фиг. 100 дана примерная диаграмма изменения /?, V, г и t
с высотой.
На фиг. 101 дана диаграмма изменения угла крена предельного
виража в зависимости от высоты до потолка, т. е. разности между
высотой потолка и высотой полета для невысотного мотора.
Фиг. 100. Расчет изменения предельных виражей при поднятии
на высоту.
Неустановившийся вираж. Неустановившимся виражем мы на-
зываем такой, при котором кроме нормального ускорения есть
еще другие, как, например, тангенциальное, т. е. изменение ско-
рости, и вертикальное ускорение за счет того, что проекция подъ-
емной силы на вертикаль не равна весу. При этом ограничимся
таким случаем, когда приобретенная вертикальная скорость незна-
чительна по сравнению со скоростью полета. Исследование виража
с переменной скоростью было сделано инж. А. К. Аузан1. Вообще
говоря, возможны неустановившиеся виражи различного вида. Мы
здесь рассмотрим два случая:
1. Вираж, начатый на большой скорости, производится на по-
стоянном угле атаки, но летчик меняет угол крена так, чтобы
самолет не снижался. Тогда в первое время угол крена будет
больше, чем при установившемся предельном вираже.
Пусть самолет летел на максимальной скорости и затем
«стал делать вираж на угле атаки а, характеризуемом Сх и С9.
1 „Техника воздушного флота*, № 3, 1931.
122
Тогда в зависимости от скорости будем иметь угол крена и ра-
диус;
cos = су • е • s • Vl 2 ;
_ уг
Г~ 9,8 • tg j? •
Ускорение движения будет:
Фиг. 101. Зависимость предельного угла крена от высоты
полета.
Интегрируя последнее выражение, получим зависимость ско-
рости по времени, а затем и г.
Возьмем для примера Ф = 0, т. е. вираж, выполняемый без
снижения за счет сил инерции:
__ G dV ,
ai — 9,8 • е • S • Gx ’ V2 ’
у
max
/ = G Г ~ •
1 9,8 • Q S • cx J V2 ’
V
l~ ЙЗ-8-S-CxU Vm„/’
отсюда
123
На фиг. 102 и 103 даны результаты примерного расчета для
Vmax — 80 м[сек', о = 0,125; — 60; Сх — 0,04 и Су — 0,4. Как видно,
самолет успел совершить поворот на 370° за 20 сек., угол крена
Фиг. 102. Изменение элементов неустановившегося
виража.
Фиг. 103. Изменение элементов неустановившегося
виража.
менялся от 79 до 0°; радиус — от 128 м бесконечности и пере-
грузка— от 5,1 до 1,0.
2. Второй пример неустановившегося виража возьмем такой:
самолет совершает вираж на постоянной скорости с постоянным
креном, но проекция подъемной силы на вертикаль меньше веса.
124
Тогда получим по вертикали ускорение:
du no G— Pcos/5 п о Л Р о\
Hi = 9,8-----Q----р- = 9,8 (1 - -G- cos Д) .
Если в начале виража самолет имел некоторую вертикальную
скорость и0, направленную вверх, то, исходя из постоянного уско-
du
рения получим перемещение самолета по высоте в зависимости
от времени:
Л1г = и0 • t —
Затем подсчитываем радиус виража:
._____________________________G________.
1 9,8 • е • s • Су • sin 0 ’
получим угловую скорость
и угол поворота
Q =а> •
в выражение для Ah вместо t подставляем угол поворота в в гра-
дусах:
..__ 0 du 02
ЛЛ-И|> о - 57,3 ~~dF‘ 2 • со2 57,32 '
Возьмем для примера: V = 50 м/сек-, Су = 0,5; -у- == 60 кг/м2-, q =
= 0,12; u0 = 5 м/сек-, угол крена 75°. Определим перегрузку:
В установившемся вираже это должно соответствовать углу
крена 66°,5, а мы имеем крен 75°. Получим ускорение по верти-
кали:
= 9,8 (1 — 2,5 • cos 75°) = 3,47.
Радиус виража
60
Г 9,8-0,12-0,5-0,965 105,5 М’
(О
50
105,5
= 0,473;
М = 5 TOTS' 3'47 = 0,185- 0 - 0,00237 • 0\
Результаты расчета приведены в табл. 6.
125
Таблица 6
0 0° 30° 60° 90° 120° 150° 180°
t 0 1,1 2,2 3,3 4,4 5,5 6,6
и 5 1,2 — 2,6 — 6,4 — 10,2 — 14,0 — 17,8
Ah 0 3,4 2,7 — 2,6 — 12,0 — 25,7 — 33,7
Как видно из табл. 6, при вираже до 90° изменение высоты
было ничтожно.
Возьмем другой пример, когда самолет перед виражем сделал
„горку", набрав вертикальную скорость 15 м]сек, а затем стал
делать вираж с креном 90°; остальные данные — как и в преды-
дущем примере. Тогда
~dt~ ЭД Г = 9,8-0,12-0,5-1,о = м’
50 л лп
°> = 102 =°>49-
Результаты расчета приведены в табл. 7.
Таблица 7
0 0° 30° 60° 90° 120е
t 0 1,06 2,12 3,18 4,24
и I 15 4,6 — 5,8 — 16,2 — 26,6
Ah 0 10,4 9,8 — 1,8 — 24,5
Как видно из табл. 7, самолет, повернув на 90°, почти не потерял
высоты. Если бы крен 90° был более длительное время, самолет
приобрел бы такую большую вертикальную скорость, что его
траектория была бы круто наклонена вниз.
Такие виражи, при которых вначале делается горка, а затем
вираж с креном больше предельного, называются „боевым разво-
ротом". Из всего этого мы видим, что при наличии запаса скорости
виражи с углом поворота 90—120° и даже 180° могут быть выпол-
нены с очень большим креном без снижения и без соблюдения
правил, полученных для правильных виражей.
126
Фиг. 104. Вираж без крена с внешним
скольжением.
Виражи со скольжением. При скольжении на самолет действует
некоторая боковая сила Z, которую можно выразить:
Z = G-e-S-V2,
где Сг—коэфициент боковой силы, зависящий от формы самолета
и угла скольжения у. Одновременно скольжение вызывает изме-
нение лобового сопротивления и даже иногда подъемной силы.
При совершении виражей нередко имеет место скольжение
умышленное или неумышленное, которое довольно сильно отра-
жается на характеристике виража. Углом скольжения мы будем
считать угол между осью х
и проекцией касательной к
траектории центра тяжести
на плоскость х — z; по-
скольку мы рассматриваем
вираж на углах атаки не бо-
лее 12°, угол скольжения
можно считать между осью
и самой касательной к тра-
ектории центра тяжести.
Сила направлена по нормали
к траектории и может быть
использована как центро-
стремительная сила или на
поддержание веса самолета,
хотя бы частично.
Различаются виражи с
внешним и внутренним
скольжением. При вираже
с внешним скольжением са-
молет получает боковое дви-
жение, направленное в сто-
рону крыла, идущего по
большому радиусу и выдвинутого вперед (фиг. 104); при внутреннем
скольжении — картина обратная. Нужно заметить, что эти опреде-
ления не совсем четки и более правильно говорить, при каком ви-
раже и на какое крыло получается боковое движение.
Рассмотрим несколько примеров виражей со скольжением. Пер-
вым примером возьмем вираж без крена. Поворачивая самолет
рулем поворотов в желаемом направлении и удерживая его от на-
кренения, мы получим скольжение у и боковую силу Z. Так как
сила Z остается неуравновешенной, то она сообщит самолету нор-
мальное ускорение, и мы получим криволинейное движение, ра-
диус которого не трудно определить:
_ G-V2 _ G
Г~ 9,8-Z “ 9,8-Сг-е-« *
Имея зависимость Cz от у и зная величину угла у в зависимо-
сти от отклонения руля поворотов с учетом криволинейности дви-
127
жения, находим Cz и затем г. Обычно величина С2 невелика и ра-
диус получается большой.
По данным, помещенным в „Handbook of Aeronautics", при
у = 20° для самолетов-бипланов военного типа Сг = 0,06— 0,07. Од-
нако практически едва ли удается достичь у = 20°, и для расчета
величину Cz не следует брать более 0,03—0,04. Тогда, если для
примера взять
~ = 60 и е = 0,12,
получим:
Как видно, радиус получился очень большой. Величина Сг полу-
чается относительно большей у самолетов, имеющих высокий плоский
фюзеляж, широкие стойки и подкосы, т. е. части с большой боко-
вой поверхностью. Значительную
I
Фиг. 105. Вираж со скольжением.
боковую силу дают самолеты с
крыльями типа „чайка". Наобо-
рот, нужно ожидать малой боко-
вой силы у самолетов со сво-
боднонесущими крыльями, тон-
кими круглыми фюзеляжами и
убирающимися шасси.
В расчете виража без крена
нами сделана некоторая ошибка,
которую мы сейчас исправим. Из
фиг. 104 видно, что при вираже
со скольжением тяга винта на-
правлена не по линии полета и
потому ее можно разложить на
две составляющие: по полету и перпендикулярно к нему. Соста-
вляющую, направленную перпендикулярно линии полета, нужно
прибавить к силе Z. В установившемся полете Ф • cos 0 = Q; тогда
перпендикулярная составляющая будет:
Фг = ф-siny = Q.tgy = Cx-q-S- V2-tgу,
__ G-V2 _ G
“ 9,8 (Z + Q.fgy) ~ 9,8е-$(Сг+Сж-18У )•
Если взять на средних режимах: Су = 0,4; =8; Сх = 0,05;
7 = 10°; tgу = 0,267, то получим Сх-tgу = 0,0133, но при у =10°
получим Cz = 0,03; отсюда видно, что добавок за счет проекции
тяги винта довольно существенен и составляет около 45% от Cz.
Рассмотрев этот наиболее простой пример виража со скольже-
нием, перейдем к более общему случаю.
Пусть самолет совершает вираж с некоторым углом крена и
скольжением у (фиг. 105). Условимся считать силу Z положитель-
ной, когда она действует внутрь виража, т. е. скольжение внешнее.
Для рассмотрения виража с внутренним скольжением изменим знак
силы Z.
128
Проектируя силы на вертикаль, касательную к движению, и ра-
диус, получим:
Фиг. 106. Скорость, потребная для виража со скольжением.
Обратим внимание вначале на первые два выражения, которые
дадут нам потребную скорость и радиус. Подставим выражения
для Р и Z:
P = Cv-q-S-V2-, Z = Cz-q-S-V^
(Cy-cos0— Cz •sin^)e-S.V2 = G(.
у = 1/_______ _____g—
r e-S (Cy-cos0-Cz-sin0) •
Из этого выражения мы видим, что вираж с внешним скольже-
нием требует увеличения скорости; при вираже с внутренним
скольжением, когда Cz отрицательно, скорость может быть умень-
шена. На фиг. 106 дано примерное значение зависимости скорости
от угла крена и угла скольжения при некотором угле атаки. Как
видно, скольжение позволяет значительно изменять угол крена при
одной и той же скорости полета. Отсюда нетрудно сделать такой
вывод: если на вираже крен дан больше, чем это допустимо с точки
зрения правильного виража, то можно прибегнуть к внутреннему
скольжению, действуя рулем направления в сторону, обратную по-
вороту. Если же вираж совершается на скорости, близкой к ми-
нимальной при данном угле крена, внешнее скольжение, т. е. пе-
редача руля направления в сторону виража, не допустимо, так как
сила Z дает составляющую, направленную вниз, проекция подъем-
ной силы на вертикаль окажется недостаточной, и у самолета по-
явится ускорение, направленное вниз.
9 в. С. Пышнов. 129
Посмотрим, что происходит с радиусом виража:
G-V*____________
9,8 (Р-sin/? + Z-cosФ-sin у • cos/?)
Подставим значения Р, Z и Ф. Силу тяги винта получим из вы-
ражения (А) на стр. 129:
Ф. sin у — Сх • о -S. V2 • tg у.
Величину Сх приближенно можно выразить через Су и Cz:
Сх = Сх„ + Ar Су + А2 • С* = СХ1+А2 • С*.
Фиг. 107. Влияние скольжения на радиус виража.
Л2 = 0,12. Если мы возьмем постоянный Су,
Величину А2 можно
подобрать по продув-
кам; СХ1 — коэфициент
сопротивления самоле-
та без скольжения.
Затем можно ввести
еще такие аналитиче-
ские выражения:
Су = (а — а0),
где
Углы а и у берутся
в радианах.
Фиктивное удлине-
ние Л2 можно подо-
брать, пользуясь про-
дувками на С2. При-
мерно можно принять
а угол скольжения бу-
дем менять, выражение для радиуса виража примет вид:
______________G___________
Г ““ 9,8-e-S (Су.sin ft + C2-cos ft -f- Сх- tgy-cos ft) ’
_________________G________________.
Г v C„ v A2 ’
9'8'-sc.si"4i+b-^+^--&+-c7w4
здесь мы считали tgy= у, так как угол у обычно не превышает 10°.
Для иллюстрации полученного результата дана диаграмма (фиг. 107)
г по /3 для постоянного угла атаки и переменного у. Здесь мы ви-
дим, что внешнее скольжение сокращает радиус г, а внутреннее—
130
его увеличивает. Из диаграммы г по /? видим, что при внешнем
скольжении можно лететь по кривой без крена. Наоборот, при
внутреннем скольжении можно лететь прямолинейно, но с креном
и скольжением.
Для выяснения преимуществ виража со скольжением посмотрим,
какой вираж при заданной скорости полета дает меньший радиус.
Примерный подсчет показывает, что если мы будем делать вираж
с заданными скоростью и углом атаки, а крен будем менять, на-
сколько это допустимо при разных скольжениях, то величина ра-
диуса получается одинаковой. Объяснение этому явлению будет
дано далее.
Для более детального сравнения виражей найдем предельные
виражи без снижения при разных скольжениях. Для этой цели бе-
рем Сх соответственно углу атаки и углу скольжения, подсчиты-
V3
ваем TV = CX’O-S для разных скоростей и наносим на диаграммы
I о
N по V, где имеется еще и диаграмма располагаемой мощности
(фиг. 108). Тогда по пересечениям получаем максимальные скоро-
сти, достижимые при вираже с данным углом атаки и данными
углами скольжения. Полученные точки отмечаем на диаграмме V
по (3 (фиг. 109), аналогичной диаграмме фиг. 106, затем переносим
на диаграмму г по /3 (фиг. ПО) и, наконец, зная V и г, можем под-
считать время виражей при повороте, например на 360° (фиг. 111).
Рассматривая полученные результаты, мы можем сделать такие вы-
воды о предельном вираже со скольжением: 1) скольжение вызы-
вает увеличение Сх и потому происходит уменьшение скорости на
предельном вираже; 2) при внешнем скольжении угол крена умень-
шается, при внутреннем — немного растет; 3) при внешнем сколь-
жении, несмотря на уменьшение угла крена, радиус виража не уве-
личивается; при внутреннем скольжении, несмотря на увеличение
крена, радиус виража возрастает; 4) при разных скольжениях, не-
смотря на различие в скоростях и углах крена, время совершения
поворота почти не меняется, и только при сильном скольжении оно
несколько возрастает.
Общие выводы о вираже со скольжением. Прежде видели в сколь-
жении самолета что-то ненормальное и даже опасное. Это проис-
ходило в силу смешения понятий скольжения и падения на крыло,
когда проекция сил на вертикаль вверх оказывается меньше веса
самолета. При скольжении самолет движется несимметрично и эта
несимметрия движения создает боковую силу Z и моменты вокруг
осей х и у, которые приходится уравновешивать элеронами и ру-
лем поворота. Обратно, скольжение всегда можно получить дей-
ствием элеронов и руля поворотов. Совершая вираж со скольже-
нием, самолет может сохранять свою высоту, *• т. е. описывать
замкнутую окружность, лишь бы тяга винта преодолевала сопро-
тивление.
Складывая подъемную силу Р с силой Z, получим равнодей-
ствующую, которая будет наклонена на некоторый угол к пло-
скости симметрии (фиг. 112). Величина равнодействующей больше
силы Р, но если сила Z невелика, то можно считать, что скольже-
ние вызывает как бы боковое наклонение равнодействующей.
9* 131
Фиг. 108. Изменение максимальной скорости
от скольжения.
132
Фиг. 111. Зависимость времени виража от скольжения.
183
Анализируя вираж со скольжением, нетрудно решить, что сколь-
жение эквивалентно изменению крена, и если мы возьмем наклон
равнодействующей к вертикали ft = ± ft, то можем воспользоваться
всеми формулами правильного виража, применяя ft вместо ft Отли-
чие будет только в величине сопротивления. Отсюда понятно, что
Фиг. 112. Наклонение равнодействую-
щей при скольжении.
Фиг. ИЗ. Виражи с разным скольжением, но
с одинаковым радиусом.
скольжение не могло дать улучше-
ния виража и только при том же
наклоне равнодействующей давало
разный крен самолета (фиг. 113).
Таким образом дело сводилось лишь
к внешнему эффекту, если не рас-
сматривать вопроса о времени на-
кренения.
Если боковая поверхность у са-
молета велика и сила Z значитель-
на, нужно учесть увеличение рав-
нодействующей от сложения сил.
Тогда уже вираж со скольжением
начинает давать значительное пре-
имущество в поворотливости само-
лета. В частности, при большой силе Z самолет сможет делать верти-
кальный вираж без снижения или описывать вираж небольшого ра-
диуса без крена. Существовали самолеты, как, например, биплан
Вуазен, у которого между крыльями были специальные перегородки
для возможности со-
вершать вираж без
крена, а элероны или
другие аналогичные
приспособления отсут-
ствовали.
Рассмотрим еще во-
прос о положении ма-
ятника при вираже са-
молета или о показа-
нии поперечного укло-
номера. Этот вопрос
имеет весьма большой
теоретический и прак-
тический интерес.
Пусть у нас имеет-
ся некоторое тело
(фиг. 114), на которое
действуют сила тяжести
может представлять результат сложения нескольких сил. Приме-
няя принцип д'Аламбера, мы должны к телу приложить силу инер-
ции — mj так, чтобы получилось равновесие сил. Для этой цели
мы складываем силы Р и G и уравновешиваем их силой инерции.
Ввиду того что силы инерции поступательного движения распре-
деляются между частицами тела пропорционально весам и по харак-
теру своего действия сила инерции не отличима от силы тяжести,
нам удобно сложить силу инерции с силой тяжести. Тогда нетрудно
и еще сила Р; последняя сама по себе
G
134
видеть, что равнодействующая сил G и —mj равна и противопо-
ложна силе Р.
Теперь мы можем сформулировать общее правило, пригодное
для решения многих вопросов: равнодействующая силы тяжести и
силы инерции равна и противоположно направлена равнодействую-
щей прочих сил; для тела в целом это применимо всегда, а для
отдельных его частей применимо лишь для частей, расположенных
вблизи центра тяжести; для частей, удаленных от центра тяжести,
нужно принять во внимание сг
общего центра тяжести. Посколь-
ку кабина летчика расположена
вблизи центра тяжести, а ускоре-
ния от вращения самолета обычно
невелики (кроме штопорных вра-
щений), можно считать, что укло-
номер, стоящий вблизи центра
тяжести самолета, показывает на-
правление равнодействующей
внешних сил без силы тяжести;
это применимо для любого слу-
чая полета. Величина и направле-
ние внешних сил, кроме силы тя-
инерции от вращения вокруг
6
жести, ДЛЯ Самолета зависят ОТ Фиг. 114. Схема сил, действующих
скорости, угла атаки, угла сколь- на тело.
жения и режима работы мотора;
отсюда мы делаем заключение, что показание уклономера зависит
лишь от угла атаки, угла скольжения и режима работы винта I -уз~) >
скорость же влияет лишь на величину равнодействующей. Пере-
ходя к показанию поперечного уклономера, работающего в плоско-
сти у— z (фиг. 115), куда проектируются лишь силы Р и Z, мы
можем сказать, что поперечный уклономер показывает направле-
ние равнодействующей сил Р и Z. Если вираж происходит без
скольжения и сила Z отсутствует, маятник будет стоять в плоско-
сти симметрии, а уклономер покажет 0°. Если есть скольжение,
то уклономер покажет угол
, д z _ С
tg Pl 'p Q '
Подставляя
C: = B2-y и Су = Bi(a — а0),
получим:
Отсюда мы видим, что поперечный уклономер показывает со-
отношение между углом скольжения и углом атаки. Если угол
атаки держать постоянным, то угол будет зависеть от скольже-
ния у, т. е. уклономер окажется показателем не крена, а сколь-
жения.
135
Человек обладает инстинктом равновесия, по которому его ту-
ловище стремится направиться по равнодействующей сил тяже-
сти и сил инерции. Отсюда летчик инстинктивно отгибается в сто-
Фиг. 115. Положение маятника и уклономера при вираже
со скольжением.
рону, обратную скольжению. Если скольжения нет, то летчик
будет сидеть прямо по отношению к самолету и будет ощущать
прижатие к сиденью. Все это имеет важное значение для слепого
пилотирования самолета.
ПРЯМОЛИНЕЙНЫЙ ПОЛЕТ С КРЕНОМ
Как частный случай виража со скольжением можно рассмотреть
прямолинейный полет с креном. В этом случае равнодействующая
сил Р и Z должна быть вертикальна и равняться весу самолета.
Из фиг. 116 мы видим, что наклон равнодействующей к верти-
кали равен /3 + Ру отсюда в прямолинейном полете
Р = -Ъ,
т. е. скольжение на опущенное крыло; имеем:
tg0 = §-*
и
G = q.S-V2-VC2v+C2z.
Задаваясь разными углами атаки и скольжения, можем найти
р и V.
136
На фиг. 117 дана примерная диаграмма /3 по V для разных у. Как
видно, с увеличением скорости угол крена растет и на некоторой,
скорости доходит даже до 93°. В этом расчете следует учесть также
составляющую от тяги винта Сх • tg у, добавляя ее к Cz. Если найти.
Фиг. 116. Прямолинейный полет со скольжением.
мощности, потребные для полета с креном N = Сх • q • S • V8 •
то можно получить максимальные скорости,’’развиваемые само-
летом при разных углах
скольжения. Тогда мы бу-
дем иметь максимальный
крен для длительного по-
лета. На фиг. 117 проведе-
на граница, найденная из
условия достаточной мощ-
ности; предельный угол
крена получился 27,5°.
Для полета с креном в 90°
самолет должен был ра-
зогнаться до скорости
92 м)сек и лететь со сколь-
жением у = 15°, однако
полет был бы непродол-
жителен, так как самолет
будет терять скорость.
В некоторых схемах с
большими боковыми по-
верхностями или с крыль-
ями типа „чайка* си-
лы Z довольно велики,
Фиг. 117. Расчет угла крена в прямолинейном пс
лете со скольжением.
и мощность мотора может оказаться достаточной для полета
с креном в 90°.
ПЕРЕХОД В ПИКИРОВАНИЕ И ВЫХОД ИЗ НЕГО
Пусть перед переходом в пикирование самолет летит на некото-
рой скорости V горизонтально и силы находятся в равновесие
(фиг. 118).
137
Для перехода в пикирование траектория должна опуститься
вниз по некоторой кривой, обращенной выпуклостью вверх, а это
требует уменьшения подъемной силы. Пусть летчик уменьшил
угол атаки и подъемная сила стала меньше веса. Избыток силы
тяжести G — Р будет служить центростремительной силой, и ра-
диус кривизны траектории мы получим из условия:
G— Р = т • jn = mV-;
Фиг. 118. Переход (плавный и резкий) в пикирование.
По мере склонения траектории силы, действующие по нормали
к траектории, будут изменяться. Вместо полной силы тяжести
будем иметь G • cos 0, т. е. уменьшение, а подъемная сила будет
расти за счет увеличения скорости. В результате выражение для
радиуса примет вид:
г= ________-______.
9,8 (cos 0-
От увеличения V и Р и уменьшения cos 0 величина радиуса
будет расти, т. е. траектория будет распрямляться и после неболь-
ших колебаний перейдет в прямолинейный равномерный спуск под
Сх
углом 0, причем tg 0 = ~- для случая полета без мотора; в слу-
чае полета с мотором расчет угла 0 более сложен.
Если бы мы желали перейти в вертикальное пикирование, то
угол атаки нужно уменьшить до величины а0, т. е. Су = 0; тогда
в начальный момент получим радиус кривизны траектории
138
Однако по мере дальнейшего пикирования радиус кривизны
траектории будет расти за счет нарастания скорости и уменьшения
cos 0:
_ v~
Г 9,8 cos © ’
При подходе к вертикали радиус стремится к бесконечности,
и следовательно, траектория лишь асимптотически приближается
к вертикали. Форма траектории в этом случае будет близка к пара-
боле падения в пустоте при начальной горизонтальной скорости
Ух, но все же будет от нее отличаться.
Наконец, можно было бы уменьшить угол атаки настолько, что
подъемная сила станет отрицательной. Это даст наиболее интен-
сивный переход в пикирование. Радиус кривизны траектории
будет:
г_ ________________
9,8 (cos 0 —
Силу Р нужно брать отрицательной. В этом случае радиус кри-
визны траектории будет меняться мало и траектория может быть
получена почти постоянного радиуса.
В связи с переходом в пикирование можно рассмотреть такие
практические задачи: 1) расстояние по вертикали и горизонтали
для перехода в вертикальное пикирование; 2) нагрузка на самолет;
3) работа руля высоты.
Для точного расчета траектории перехода в пикирование обычно
прибегают к численному интегрированию уравнений движения.
Здесь мы ограничимся приближенным решением задачи, считая
скорость постоянной, равной некоторой средней скорости в про-
цессе перехода в пикирование. Начнем со случая, когда Р =0.
В некотором месте траектории (фиг. 119) при изменении угла 0
на величину d& самолет проходит дугу ds = г • d&; тогда
dx = ds • cos ©; dy = ds • sin 0;
dx = r • cos 0 • d0;
dy — r
Ранее мы получили:
v2
Г = ------7Г
g • COS 0
V2
dx= — • d&; x
если 0 = ~ , то:
di
V-n
x=^=0,16-v*.
• sin 0 • d0.
; r • cos 0 — —;
e b
= rv- • d0 = r.0;
J g g
0
Получилось очень простое выражение
пути, пройденного самолетом для перехода
для горизонтального
в отвесное пикирова-
139
ние, при Р=0; его можно использовать при расчете расстояния,
с которого нужно начать пикирование для того, чтобы оказаться
на вертикали над определенным объектом. Путь по вертикали
тоже можно найти, подставив вместо sin 0 — tg & • cos 0:
dy = ~ ’t§ 0 ‘ d0;
получим:
Фиг. 119. Элемент траектории при переходе в пикирование.
При приближении 0 к 90°, cos 0 подходит к нулю, a 1g —
к бесконечности, и путь у для перехода в отвесное пикирование
окажется бесконечно большим. Это показывает, что для перехода
в отвесное пикирование, хотя бы в последней его стадии, нужно
дать отрицательную подъемную силу.
Случай перехода в пикирование с отрицательной подъемной
силой можно также решить аналитически при условии допущения
постоянства скорости:
g ^COS 0 — -J ) g (cos 0—7?)
P
где n «= -g-— перегрузка;
, V2 cos 0 • d0
ax — — •;—.
g (cos 0— n)
Интеграл этого выражения получается сравнительно сложный и
вид его меняется при переходе через п =—1. На практике едва ли
140
летчик станет применять перегрузку более —1, и если взять п = —1,
то получим более простое выражение:
В отношении величины у дело обстоит лучше:
, _ V2 sin О dG .
g (cos О — п) ’
е
/sin OdO ___. 1 . 1
(cose —и) ~~ П (cose — n) П (1 — n) ’
° va- ln (1~n) = 23 va lr (1~n) •
y g 1 (cos О— n) ’ 9,8 ° (cos©— n) ’
если 6=90° и n ——1, то получим:
y = 0,69^; x = 0,57^.
Еще раз отмечаем, что предположение о постоянстве скорости
очень грубо и дает только первое приближение.
Обращаем внимание на сильную зависимость х и у от скорости.
Если скорость полета велика, то переход в пикирование будет
происходить очень медленно, сопровождаться большой потерей
высоты и нарастанием скорости. Расчет у и х в этом случае лучше
производить путем последовательных приближений, определяя
сначала у по начальной скорости; затем по у и диаграмме пикиро-
вания находим скорость для h = у; далее повторяем расчет, взяв
среднюю скорость, находим новое у и снова ищем скорость. Если
летчик желает перейти в пикирование наиболее быстро, следует
прибегнуть к потере скорости путем совершения предварительной
„горки" на малом газе.
Разберем вопрос о нагрузке самолета при переходе в пикиро-
вание. На летящий самолет действуют воздушные силы и сила
тяжести. Инерционные силы возникают только соответственно
величинам воздушных сил и силы тяжести, что вытекает из прин-
ципа д'Аламбера. Равнодействующая силы тяжести и сил инерции
уравновешивается равнодействующей воздушных сил. Отсутствие
воздушных сил потребовало бы равновесия силы тяжести и сил
инерции и произвело бы впечатление отсутствия сил вообще.
Если переход в пикирование происходит при Р = 0, то остается
небольшая сила сопротивления воздуха, и в итоге нагрузка само-
лета будет совсем незначительна. На экипаж самолета это произ-
водит впечатление почти полной невесомости, и у летчиков остается
лишь слабое стремление двигаться вперед, т. е. против силы со-
противления. Маятник, на который действуют только сила тяжести
и сила инерции, займет положение по направлению против силы
сопротивления. Если же при переходе в пикирование подъемная
сила отрицательна, то равнодействующая сил тяжести и инерции
направится против равнодействующей воздушных сил, т. е. по
отношению к самолету вперед—вверх, и все части, не подвержен-
ные воздушной нагрузке, будут иметь стремление двигаться в этом
направлении. В частности, летчика будет тянуть вперед — вверх и
141
такое же положение займет маятник. Из всего этого мы должны
сделать вывод, что при переходе в пикирование незакрепленные
предметы нагрузки самолета могут вылететь вверх, и это может
случиться даже в тот момент, когда самолет занимает почти гори-
зонтальное положение, но ручка дана от себя настолько сильно, что
угол атаки стал большим отрицательным при Су отрицательном.
Если у нас есть для самолета балансировочная диаграмма, свя-
зывающая угол атаки с отклонением руля высоты, то можно найти,
Фиг. 120. Влияние кривизны траектории при переходе
в пикирование.
= 0,2
при каком отклонении руля высоты Су равно нулю или станет
отрицательным. Однако здесь необходимо учесть влияние кривизны
траектории подобно тому, как мы это делали на вираже. Кривизна
траектории при переходе в пикирование вызывает изменение мо-
мента крыла на величину АСМ и изменение угла атаки оперения
на величину Дд> (фиг. 120). Соответствующие поправки в угле
отклонения руля высоты будут:
а __=02____________________________________-___________•
1 $хв4в /VxbY ’ SXB-£XB ( ^xbY
AP Ao / Ad 1 R y> r I I D
S-b \~v~J ' XB ’n Sb
о —a
2 3=8 n — r ‘ n ‘
Влияние кривизны траектории будет наиболее ощутимо в на-
чальный момент при
выражение:
хв ‘ п
малых углах О; поэтому для радиуса возьмем
GV2 _ 1
g(o-p)~ /i cy-e.si\;
9,8 \V2 G )
6 (~s L /2? \2---------4- Ьхв • 57,зА .
dXBbXB ( VXB \ p ]
S-b A V J XB 7
г =
444=4А—в
142
Пусть для примера имеем балансировочную диаграмму для
горизонтального полета, диаграмму Су по а (фиг. 121), а также
п = 0,65; е = 0,1; S=100 л/2; 0 = 6000 кг; Ь = 4 LXB = 10 м;
Q Г / 17 \9
-^2-= 0,4; =0,8; = 0,025.
В балансировочную диаграмму внесем исправления для ско-
ростей 30, 40 и 50 м!сек. Как видно, поправка получилась довольно
Фиг. 121. Расчет положения руля высоты при переходе
в пикирование.
значительной; если при Су = 0 и а = —3° в прямолинейном полете
<5 = 4°, то при V = 50 м]сек 8 = 8°,3, при V = 40 м]сек 8 = 10°,5 и
при V = 30 MfceK 8 = 15°,5.
Перейдем теперь к вопросу о выходе из пикирования. Для
выхода из пикирования летчик увеличивает угол атаки, появляется
подъемная сила, под действием которой траектория самолета ста-
новится криволинейной, постепенно переходящей в горизонтальную.
Радиус кривизны траектории мы можем подсчитать, найдя центро-
стремительную силу путем проектирования сил на направление
нормали (фиг. 122):
P-Gcos0 = ^- г=__________________
н ucosn— „ , Г g(p_Gcos0) •
Г =
143
Траектория выхода из пикирования зависит от изменения угла
атаки крыльев в процессе выхода. Можно, например, держать
постоянный угол атаки, можно сохранять постоянную перегрузку
р
-Q- или применять постоянное отклонение руля высоты, или давле-
ние на ручку. Траекторию выхода из пикирования наиболее точно
можно построить численным интегрированием, однако, вначале мы
произведем более простые приближенные расчеты, которые хорошо
иллюстрируют вопрос.
Фиг. 122. Выход из пикирования.
Поинтересуемся вопросом о том, какую высоту теряет самолет
при выходе из пикирования. Этот вопрос имеет большую практи-
ческую важность, поскольку из-за неправильного расчета высоты,
потребной на выход из пикирования, может произойти катастрофа,
а это на практике не раз и случалось. Если мы желаем вырав-
няться возможно скорее, подъемную силу нужно увеличивать путем
увеличения угла атаки и, следовательно, Cv. Однако брать
не следует, так как при этом самолет близок к потере управляе-
мости, и мы рекомендуем для расчета применять Cv S0.7 Сушы-
Подставляя подъемную силу, получим:
G V»
Г g (С„ • е • S • V2 —G • cos 0) /С • q • S cos0\
U О I и _____ I
G V* )
rmin / 0,7 • С„ • е • S COS в
I “max
Минимальная скорость горизонтального полета
144
отсюда можем сделать подстановку:
1
7 min —у- -~s v .
а I _1___ )
Н У2 • у2 I
\ v min /
В процессе выхода из пикирования меняются cos 0 и скорость;
поэтому меняется и радиус. Если в начале выхода из пикирования
скорость самолета значительно больше минимальной, величина
будет значительно меньше , и потому для расчета можно
V *inin
взять некоторое среднее значение и найти средний радиус
выхода гср; среднее значение для 6 будет:
в
(cos 0)Ср = i y*cos 6 d& = ° ,
о 0
где 0О— наклон траектории пикирования:
г =_________________________________1 ______
ср / 0,7 sin (~)0 '\'
Му2. а . у2 )
\ mm уо v ср /
Потерю высоты получим:
, ,, \ 1 — cos 0п
/z = rcp(l—cos 0О) = ° .-•
14 07 о„/ 0,7 sin (%
У’ \ V2 • 0 • V2 )
\ v in in уо у ср/
Среднюю скорость при выходе из пикирования получим так:
вначале считаем скорость постоянной, равной начальной, и на-
ходим Л; затем по диаграмме пикирования находим прираще-
h
ние скорости за время потери высоты и, приняв эту скорость
за среднюю, находим новое й; после этого можно сделать еще
одно приближение. Из расчета минимального радиуса выхода из
пикирования мы видели, что по мере увеличения начальной ско-
рости радиус сокращается, приближаясь по своей величине к мини-
мальному радиусу виража. Однако, если бы мы подсчитали вели-
чину подъемной силы, она оказалась бы весьма велика и опасна
для прочности самолета. Пусть в начале выхода из пикирования
самолет имел скорость Vv Взяв Су, получим подъемную силу Р =
= СУ • q • S • Vp коэфициент перегрузки будет:
р c-e-s- v-
п-----— ___________
Максимальная перегрузка будет при Су = Су
10 В. С. Пышное.
145
Это выражение можно представить еще в других видах. Напри-
Т/2 G
мер, подставим V?nin = ---:
Р • о • с
утах
^max I I/
' y min
Читать это выражение нужно так: если при скорости V мы да-
дим Сушйх, то величина перегрузки будет равна квадрату отноше-
ния скорости полета к минимальной скорости полета самолета
с данным весом на данной высоте. Это выражение очень просто и
позволяет очень быстро определить, какое условие полета может
быть опасным в отношении прочности. Для исследования вопроса
лучше применить другое выражение. Умножим и разделим пере-
грузку на CXo, соответствующее Су = 0:
„_£« C»o-g'S- V2 - Q St
СХВ' ° G'C^
где Q—сопротивление самолета при пикировании.
Умножим и разделим правую часть выражения на предельную
скорость пикирования, заметив, что СХд q S • V„p = G'-
Это выражение уже хорошо иллюстрирует нам, до какой сте-
пени мы можем увеличивать Су при известной скорости пикирова-
ния, если задана величина перегрузки.
Максимальная перегрузка будет при Cj, = Су :
Су I v\2
~_____Jmax • f |
'*max r» ’ l и I ‘
ux0 и пр/
Наконец, максимум максиморум будет иметь место при V=VDp:
CV СУ
л ____ ~тах _ утах
тах ~ сХл сх
х° xmin
Таким образом самая большая перегрузка может получиться
при увеличении угла атаки до Су на скорости установившегося
пикирования; она равна отношению максимального Су к минималь-
ному Сх. Эта перегрузка обычно получается настолько большой,
что говорить о ее реальности не приходится. У самолета средних
СУ
качеств равно около 25; у самолетов с высоким аЭрОДИНаМИ-
^пап
ческим качеством оно доходит до 50, а у планеров до 80 и даже 100.
Таких перегрузок не может выдержать не только самолет, но
и человек. Найдем радиус выхода из пикирования, если перегрузка
задана.
146
~T
9,8
Опять подставим средние значения cos© и (V2)cp:
(V2)cp _ . h = (1 —cos 6>o)(V3)cp .
1 918(п_^у
0O / к ©0 J
для ©c — 90 :
9,8 (n —0,64)
(^)ер
„ _ sin 0о \ '
"дсн © у
Среднюю величину квадрата скорости находим опять путем
последовательных приближений, беря из диаграммы пикирования
скорость после дополнительного пикирования на высоту-^ .
Для определения радиуса выхода из пикирования, допустимого
по соображениям прочности, в расчет нужно вставить допустимую
перегрузку пдоп:
ГДОП —
9,8
Обычно допустимой принимается перегрузка, равная половине
разрушающей. Разрушающая перегрузка предусматривается нор-
мами прочности, где задаются: 1) разрушающая перегрузка Па при
угле атаки, соответствующем Сушах’, 2) разрушающая перегрузка Пв
при угле атаки, соответствующем Су — 0,2 Cv ; 3) надежность nG
в случае пикирования при Су — 0. Следовательно, прочность само-
лета зависит от угла атаки. Построим диаграмму прочности само-
лета в зависимости от угла атаки. Скорость полета в случае А
получим из условия:
отсюда
/ С-пА __
Рл =1/ е.§:ст = Vmin’V4па ;
подобным образом получим скорость в случае В:
рв 2-с -q-sv*
_______________________ угоах
ПВ--д= Q-------,
/ G-/7r .---
Vb==]/ .
r ymax
Скорость для разрушения в случае С получим из условия:
пс ! Vс = Vп-рУ'Пс .
Нужно заметить, что По не является перегрузкой, а представляет
лишь коэфициент надежности по отношению к нагрузке, имеющей
место при предельной скорости пикирования. Перегрузка в слу-
чае С вообще равна нулю, так как Су = 0. Взяв координатные оси:
перегрузка и скорость, строим диаграмму, на которую наносим
10* 147
точки пл при Vа, п13 при V в и Vс, и получаем границу разрушаю-
щей перегрузки (фиг. 123). Границу допускаемой перегрузки полу-
Уг
. Эта
/2
Фиг. 123. Зависимость разрушающей и допускаемой
перегрузок от скорости.
граница также нанесена нафиг. 123. Наконец, по диаграмме можно
нанести границу максимальной перегрузки, подсчитанной по фор-
муле:
— ( v \2
^тах (у . ) *
v v min /
Фиг. 124. Зависимость радиуса выхода из пикирования
от начальной скорости при допускаемой перегрузке.
Пользуясь построенной диаграммой допустимой перегрузки, мы
можем произвести расчет допустимого радиуса выхода из пикиро-
вания и потери высоты для разных начальных скоростей выхода.
1Фв
На фиг. 124 дана диаграмма Лдоп по V, построенная по приведен-
ным материалам. Если скорость близка к предельной, то можно
последовательных приближений не делать, так как скорость будет
меняться очень мало.
Расчет диаграммы допустимого радиуса выхода из пикирования
удобнее вести, задаваясь не начальной скоростью, а средней; тогда
никаких последовательных приближений производить не прихо-
дится. Зная VCp и Пдоп, находим гдоп и йдоп; затем на диаграмме
пикирования от точки Vcp откладываем вверх и вниз высоты ~ и тогда
можем прочесть начальную и конечную скорости.
Имея диаграммы минимального и допустимого радиусов выхода
из пикирования, мы можем найти радиус для нужного примера,
взяв из двух указанных больший.
Не следует стремиться к очень большой точности расчета
радиуса выхода из пикирования, но, с другой стороны, необходимо
предусматривать значительный запас высоты, так как режим выхода
трудно контролировать, а еще труднее уловить момент начала
выхода, так как' промедление на каждую секунду будет давать
потерю высоты 50—100 м и даже более.
ФИГУРНЫЕ ПОЛЕТЫ
ОБЩИЕ СВЕДЕНИЯ
Фигурный полет самолета складывается из отдельных элемен-
тов: 1) прямолинейный, наклонный или горизонтальный полет са-
молета с разгоном или торможением; 2) полет по криволинейной
траектории; 3) вращение самолета. В зависимости от порядка ком-
бинации этих элементов и положения самолета, прямого или пе-
Фиг. 125. Действие сил в горизонтальном полете.
ревернутого, получаются
все фигуры.
Изменение скорости про-
изводит сила, действующая
в направлении движения,
и ее мы можем назвать ус-
коряющей силой; замедле-
ние движения будет проис-
ходить под действием тор-
мозящей силы или отрица-
тельного ускорения. Для
криволинейного движения
нужна центростремительная
сила, действующая перпен-
дикулярно скорости и на-
правленная к центру кри-
визны. Вращение самолета
вокруг оси, совпадающей
с направлением полета, бу-
дет происходить под дей-
ствием вращающей пары
сил.
Рассматривая какую-либо фигуру, мы в первую очередь должны
оценить роль сил, как ускоряющих, так и центростремительных.
Оказывается, что в отношении сил, действующих на самолет, такое
разделение сил на ускоряющие и центростремительные может быть
произведено. Например, сила тяги винта почти совпадает с напра-
влением скорости полета, и во всяком случае этим несовпадением
мы обычно пренебрегаем. Отсюда силу тяги винта нужно рассма-
тривать как силу ускоряющую. Сопротивление воздуха направлено
всегда против скорости и потому является чистой тормозящей
силой. Подъемная сила направлена перпендикулярно скорости и
потому она безусловно есть сила центростремительная. То же
150
самое относится к боковой силе Z, возникающей при скольжении,
это — сила центростремительная. Теперь осталась только сила тя-
жести, роль которой переменна в зависимости от направления
движения: если траектория горизонтальна, — сила тяжести дей-
ствует как центростремительная; если траектория вертикальна,—
сила тяжести действует как тормозящая или ускоряющая; при на-
клонном движении мы силу тяжести раскладываем на две состав-
ляющие по траектории и перпендикулярно к ней, тогда одна со-
ставляющая будет ускоряющей, другая — центростремительной.
Равномерный горизонтальный полет мы можем рассматривать
теперь так (фиг. 125): сила тяги ускоряет движение, сила сопро-
тивления замедляет, и их действие взаимно нейтрализуется. Сила
тяжести дает криволинейную траекторию с центром, лежащим
ниже самолета; подъемная сила дает криволинейную траекторию
с центром, лежащим выше самолета. Сложение этих движений
в случае одинаковой кривизны дает прямолинейную траекторию.
Но стоит только появиться несоответствию между величиной
подъемной силы и веса, как траектория искривится в сторону
большей силы. Конечно, такое разложение движений применимо
на малых участках траектории, когда скорость не успевает заметно
измениться.
УПРАВЛЕНИЕ САМОЛЕТОМ
При движении машин по земле или при движении отдельных
частей машин траектория бывает задана. Самолет в воздухе может
выбирать разные траектории, но, управляя самолетом, летчик воз-
действует лишь на величину сил, а силы определяют траекторию
и скорости по ней. Для управления самолетом летчик имеет такие
органы управления: руль высоты, руль поворотов, элероны и упра-
вление мотором. Рулем высоты летчик меняет угол атаки, а с этим
и подъемную силу, которая, как мы уже указали, служит центро-
стремительной силой. Следовательно, руль высоты служит как
средство создания кривизны траектории в плоскости симметрии ху
самолета. Величина подъемной силы может меняться до некоторой
максимальной положительной величины. Величина подъемной силы
ограничивается, с одной стороны, скоростью полета, поскольку
р = Су • q • S • V2, с другой стороны, при большой скорости полета,
ограничивается прочностью самолета, когда подъемная сила могла
бы быть очень большой, но летчик не должен этого допустить.
Подъемная сила играет важнейшую роль при фигурных поле-
тах; двигая ручкой «от себя», «на себя», летчик имеет в своих
руках эту мощную и очень послушную центростремительную силу,
неразумное пользование которой может привести к разрушению
самолета.
Сопротивлением воздуха летчик обычно никогда специально не
управляет; оно получается само собой в зависимости от углов
атаки и скольжения в процессе воздействия на подъемную и бо-
ковую силы. Непосредственное управление силой сопротивления
.мыслимо путем специальных воздушных тормозов.
При помощи руля поворотов, давая скольжение, мы можем
управлять также боковой силой Z, используя ее как пентростре-
151
мительную, что мы уже показали в вираже со скольжением.
Тягу винта мы регулируем при помощи сектора газа мотора,
меняя число оборотов. Тягу винта мы можем менять по своему
усмотрению от нулевой и даже несколько отрицательной величины
до некоторой максимальной величины, зависящей от скорости полета.
Для использования силы тяжести с той или иной целью мы
должны поставить самолет в соответствующее положение. Напри-
мер, желая набрать скорость, мы должны траекторию сравнительно
круто наклонить вниз. Говоря о действии руля высоты и руля по-
воротов, следует помнить, что, когда траектория криволинейна,
эффективность рулей снижается по причине скоростей, вызванных
вращением самолета вокруг центра тяжести. Об этом мы уже го-
_ ворили подробно при описании ви-
♦ Zj \ ража и выхода из пикирования и
учитывали в расчете путем внесе-
—А А —ния поправок в балансировочную
б б | кривую.
Вращая самолет вокруг напра-
Фиг. 126. Действие элеронов. вления полета, мы меняем напра-
вления действия подъемной силы
и силы Z, а с этим меняем плоскость кривизны траектории. Вра-
щение самолета может быть произведено тремя способами: 1) дей-
ствием элеронов, 2) действием скольжения и 3) переводом само-
лета на режим авторотации.
Действие элеронов, вообще говоря, очень просто и понятно.
Следует остановиться только на изменении момента элеронов
в зависимости от угловой скорости. Если мы отклоним элероны,
то получится пара сил (фиг. 126), которая дает угловое ускорение,
равное моменту пары, деленному на момент инерции. Под дей-
ствием ускорения появится угловая скорость сох, постепенно воз-
растающая. При наличии угловой скорости траектории частей
крыла будут уже не прямолинейными, а спиральными. Наклон
траектории в любом месте крыла, считая по размаху, можно по-
лучить, складывая скорость полета V со скоростью • z, выз-
ванной вращением. В результате получаем увеличение углов атаки
в опускающейся части крыла и уменьшение у поднимающейся.
Появление разницы в углах атаки дает противодействующую пару
сил, которая, нарастая вместе с угловой скоростью мХ) в конце
концов приведет к равновесию моментов и, следовательно, к уста-
новившейся скорости вращения. Практически под действием эле-
ронов самолет довольно быстро приобретает определенную угловую
скорость. Ее величина более подробно будет определена в четвертой
части настоящего труда.
Вращение самолета под действием скольжения происходит
так. Создавая скольжение при помощи руля поворотов, мы
получаем несколько косое обтекание самолета, в результате
которого, например, получилась боковая сила Z, Косое обте-
кание крыла вызывает боковое смещение центра давления
(фиг. 127). Придание крыльям поперечного угла усиливает боковое
смещение центра давления. Момент от бокового смещения центра
давления приводит самолет сначала в ускоренное вращение, кото-
152
рое затем быстро приходит к установившейся угловой скорости
по тем же причинам, что и при действии элеронов. Вращающий
момент от скольжения имеет свои положительные и отрицатель-
ные стороны. Положительно то, что это дает летчику дополни-
тельный способ управлять самолетом, например в случае порчи
элеронов. Используя этот эффект, можно летать, вообще не тро-
гая элеронов, и есть даже самолет „Небесная блоха", не имею-
щий элеронов, а управляемый скольжением. Отрицательная сторона
заключается в том, что если сколь-
жение случайно или мы его даем
ради получения боковой силы Z, то
поперечный момент от скольжения
приходится погашать элеронами,
давая последним иногда значитель-
ное отклонение и прилагая соответ-
ственное усилие к ручке или штур-
валу. Это обстоятельство застав-
ляет ограничивать поперечный угол
крыльев, особенно на тяжелых са-
молетах, где держать элероны в от-
клоненном положении для летчика
особенно тяжело.
Вопрос о вращении самолета на
режиме авторотации будет подроб-
но изложен в главе о штопоре (ве-
роятно, в пятой части настоящего
труда), а сейчас мы дадим лишь ос-
новные понятия. Приводя самолет
Фиг. 127. Возникновение накреняю-
щего момента от скольжения.
во вращение, например элеронами,
мы испытываем противодействие со стороны крыльев. Оказыва-
ется, что если угол атаки сделать больше критического, соответст-
вующего Cv когда происходит срыв обтекания, то крыло не только
не препятствует вращению, но, наоборот, стремится перейти во вра-
щение по причине неодинакового срыва обтекания на обеих сторонах
крыла. Для получения авторотации следует быстро увеличить
угол атаки насколько можно, а затем дать начальный момент при
помощи элеронов или, лучше, скольжения. Вращение в этом случае
получается чрезвычайно быстрое и применяется на некоторых фи-
гурах и при штопоре.
При действии элеронами на больших углах атаки начинает
сказываться заворачивающий момент от разницы сопротивления
элеронов, однако, только в очень редких случаях летчик исполь-
зует этот момент с целью управления самолетом.
Усвоив роль сил, действующих на самолет, и способ управле-
ния ими, можно разобраться во всех фигурах как в отношении
сил, так и в отношении способов пилотирования.. Перед тем как
перейти к фигурам, остановимся еще на некоторых факторах,
влияющих на управление самолетом, которые необходимо учиты-
вать для правильного выполнения фигур. Это относится к реакции
вращения винта и к гироскопическому моменту винта и вращаю-
щихся частей мотора.
153
РЕАКТИВНЫЙ И ГИРОСКОПИЧЕСКИЙ МОМЕНТЫ
Реакция вращения винта равна крутящему моменту, но напра-
влена против вращения винта:
М = 716,2 -- ,
7 п
где N — мощность, развиваемая мотором, в л. с., а п — число обо-
ротов винта в минуту.
Момент от реакции вращения винта уравновешивается момен-
том подъемных сил крыльев путем придания им разных установоч-
ных углов или отклонением элеронов. Этот момент играет замет-
Фиг. 128. Причина образования гироскопического
момента.
ную роль в управлении
самолетом лишь в по-
лете на малой скорости
при полной мощности
у самолетов с малым
размахом крыльев.
Гироскопический мо-
мент вращения винта
и частей мотора имеет
место лишь только в
том случае, когда пово-
рачивается плоскость
вращения, т. е. при вра-
щении самолета около
осей у или z. Природа
гироскопического мо-
мента излагается в кур-
сах механики, причем
для этого применяются
разные приемы: или
рассматривают пово-
рот вектора момента
количества движения, или, разлагая движение на два, прилагают
силы инерции от поворотного ускорения, или рассматривают слож-
ное абсолютное движение отдельной точки. По нашему мнению
качественную сторону проще всего понять так. пусть две массы т
движутся по окружности вокруг оси х; сама ось х поворачивается
вокруг оси у (фиг. 128). За счет вращения вокруг оси х массы
имеют постоянную скорость V=r-cox, а за счет вращения вокруг
оси у получают переменную скорость w = r • sin у • соу\ sin 99 можно
заменить через а>х • t. Берем начальное положение а, когда массы т
наиболее удалены от оси у и имеют, кроме скорости V, скорость
iv — г • ajy. Следуя от точек а к точкам Ь, массы теряют свою ско-
рость w, а, пройдя положение Ь, начинают приобретать скорость w,
но уже в обратном направлении. Естественно, что для изменения
скорости нужна сила:
Р = tn = т • г • о,. • cos (р --- = т • г • соч • сох cos у.
til ill и '
154
Силы Р направлены параллельно оси х, но в разные стороны,
и достигают своего максимума при ср — О° и <р=180°, т. е. при
прохождении масс через ось у. Силы Р образуют пару:
Mz — 2 • Р • г • cos <р — 2 • т • г2 cos2 <р • сох • a>y.
Но 2m-r2-cos2 ср является моментом инерции масс вокруг оси z:
2 • т • г2 • cos2 <р — Iz = 1х - cos2 у.
Заменяя cos2 = 1 — sin2 ср и замечая, что 2 • т • г2 • sin2 ср = [у,
получим:
Л4г = • сс>у (Iх 1У).
Это и есть формула для расчета гироскопического момента.
Если направление момента сил Р по отношению к оси z отрица-
тельно, то направление момента инерционных сил будет положи-
тельно, как и дано в формуле.
Если винт двухлопастный, величина 1У переменна:
1у = 1Х • sin2 ср
и будет меняться от нуля до максимальной величины, равной 1Х.
Следовательно, гироскопический момент будет меняться два раза
за один оборот от нуля до Mz = 1Х • шх • соу. Среднюю величину
момента получим, взяв среднюю величину для sin2 ср от 0 до 360°:
2л
I sin2 <р - (кр
(sin2 9?)Ср = °----------- 0,5;
<’ср о)х ’ ™у ’
Если винт имеет более двух лопастей:
I — — г
1 у — 2 ‘г’
то выражение получается то же самое, но оно будет постоянно
по величине.
Направление действия гироскопического момента получаем со-
гласно знаку моментов и угловых скоростей: если знаки сох и со.
одинаковы, то момент положителен; если знаки разные — момент
отрицателен. Если вращение происходит вокруг оси z, то момент
будет вокруг оси у; его мы получим, произведя круговую подста-
новку, т. е. после z подставив еще х, а потом у:
Му = coz • СОХ (/г /х) = г, • сох • со. • I х.
Пользуясь принятыми нами обозначениями направления осей:
ось х назад, ось у вверх и ось z влево, будем иметь сох положи-
тельным при вращении влево, глядя по полету, соу—положитель-
ным при повороте влево, coz— положительным при опускании носа.
По ivH’j I таблицу направления гироскопических моментов (табл. 8).
1,5^
Таблица 8
Движение самолета Вращение винта вправо — Вращение винта влево ; 4- W.,.
Поворот влево Стремление поднять нос — Mz Стремление опустить нос 4- М,
— Поворот вправо i Стремление опустить нос • Стремление поднять нос — Mz
+ с,)- ! Опускание носа Стремление повернуть ' влево ! + ми | Стремление повернуть вправо дл
Поднятие носа j Стремление повернуть вправо -м. Стремление повернуть влево + ™у
Фиг. 129. Направление действия гироскопического
момента.
Следует запомнить еще такое правило: если направление пово-
рота совпадает с направлением вращения винта, самолет стремится
опустить нос; если направления разные, самолет стремится поднять
нос. Если самолет поднимает нос, то гироскопический момент
стремится повернуть
его в сторону враще-
ния винта; а при опу-
скании носа стремит-
ся повернуть против
вращения винта.
При всяких бо-
лее сложных случа-
ях для определения
направления дейст-
вия гироскопическо-
го момента следует
поступать так:вдоль
оси винта отклады-
ваем вектор угловой
скорости вращения
винта, направив его
так, чтобы, глядя
вдоль вектора, ви-
деть вращение по
часовой стрелке, т. е. вправо. Вектор угловой скорости вращения
самолета откладываем вдоль оси вращения самолета, тоже напра-
вив его так, чтобы, глядя вдоль вектора, видеть вращение вправо
(фиг. 129). Складываем угловые скорости по правилу параллело-
грама;тогда гироскопический момент будет стремиться совместить
ось винта с результирующей осью вращения. Этот прием также удо-
156
бен для объяснения причины возникновения и расчета величины гиро^
скопического момента. В самом деле, сложив геометрически угловые
скорости, мы получаем, что винт вращается не вокруг оси х, а во-
круг оси 00. Центробежные силы, действующие по радиусам, иду-
щим от оси 00, создадут момент, который и будет являться гиро-
скопическим моментом.
* Для подобных винтов момент инерции 1Х пропорционален пятой
степени диаметра. Для деревянных винтов английского типа имеем
примерно:
1Х = 0,001 • D5 •
где i—число лопастей.
Для металлических винтов типа Уэйк:
/* = 0,00185 • Z)5 • z.
У английских винтов относительная ширина лопасти ~ =0,082,
у винтов Уэйка =0,065. В случае уширения винта при сохра-
нении подобных сечений момент инерции растет в квадрате. При
утолщении лопасти момент инерции растет в первой степени
утолщения.
Диаметр винта обычно выбирается с таким расчетом, чтобы
окружная скорость конца лопасти не превышала некоторой вели-
чины Vp, следовательно,
Подставляя все в выражение для гироскопического момента,
получим:
Mz = 0,5 • сох . ojy • 0,001 • D3 • i — 0,002 • оуу • D4 • V\.
При уменьшении числа оборотов винта путем устройства ре-
дукции диаметр винта повышается, а с этим повышается и гиро-
скопический момент.
ВОПРОСЫ ПРОЧНОСТИ ПРИ ФИГУРНЫХ ПОЛЕТАХ
Вопрос прочности является важнейшим фактором, который
необходимо учитывать при рассмотрении фигурных полетов. Если
самолету в порядке выполнения фигуры приходится двигаться по
кривой при наличии большой скорости, прочность самолета может
не позволить этого, и тем самым фигура окажется недопустимой.
Для суждения о нагрузке на самолет мы рассматривали пере-
грузку, т. е. отношение подъемной силы к весу. Большая перегрузка
получается при большом Су на большой скорости. В главе о выходе
из пикирования мы остановились подробно на возможных пере-
грузках и допустимой перегрузке, исходя из прочности самолета.
Диаграмму допустимой перегрузки по скорости (см. фиг. 123)
необходимо иметь перед собой при рассмотрении теории фигурных
полетов.
157
Если запас прочности самолета невелик, а совершение фигур
очень желательно, то прибегают к уменьшению полетного веса
путем снятия части оборудования, уменьшения запаса горючего
и т. д. Определение запаса прочности при уменьшенном полетном
весе может быть проделано путем специального расчета, причем
интересно отметить, что не всякое уменьшение нагрузки дает уве-
личение запаса прочности. Грузы, находящиеся на крыле вдали
от фюзеляжа, дают разгружающий момент и потому повышают
прочность.
Если взять наиболее обычную схему самолета с центрально
расположенной нагрузкой, перерасчет запаса прочности может быть
сделан сравнительно просто. Пусть при некотором весе Go запас
прочности самолета будет л0, а вес крыльев GKp. Поскольку вес
крыльев дает разгрузку, разрушающая подъемная сила будет иметь
величину:
= "о (<?0 ^кр)-
Вводя вместо Go вес G, получим запас прочности:
Рр = nQ (Gq GKp) = и (G GKp);
^кр
Go — GKP _ 1 ~ Go
G—GkP G GKP
Go Go
G
Величина колеблется в пределах 0,12—0,15. Получив отно-
шение , вносим поправки в запас прочности случаев А и В.
^0
Однако скорости VA и Гв, соответствующие новым запасам проч-
ности, останутся почти без изменения, так как произведение G • п
изменится очень мало. На это следует обратить внимание: увели-
чив запас прочности путем разгрузки самолета, мы вовсе не полу-
чаем права делать фигуры на большей скорости. Польза разгрузки
G
самолета заключается в том, что от уменьшения -g- уменьшаются
возможный радиус кривизны траектории и минимальная скорость
полета. В результате относительный запас скорости возрастает,
фигура становится меньше, и, если ранее скорость полета была
недостаточна для совершения фигуры, то с уменьшенным весом
скорость станет уже достаточной.
У каждого самолета есть некоторая наибольшая безвредная
для конструкции скорость, при которой летчик может доводить
угол атаки до Су . Поскольку при Су шах нагрузка соответствует
случаю А, а допускается перегрузка не более половины запаса
прочности, величину искомой скорости получим из выражения:
V _ 1 /" G«' пл _ v . f пл
V max. безвр — I/ р . S • С -2 — У min I/ 2 ’
г ’ '“'Утах - Г
где Go — некоторый исходный полетный вес, для которого известен
запас прочности пЛ, a Су следует взять, конечно, без применения
158
щитков и других устройств, применяемых только на посадке. Если
ввести другой вес G, то нужно пА умножить на ; получим:
\Г _ Ъ 1 / ' и КР'
У max. безвр — 1 шах. безвр Go .’(G_ G ) *
Преобразуя корень, получим:
------------- Г . GKP
, Г° JG°- GKP> Я /
I/ Go • (G —- GKp) I / ___£KP_ Go
r Go ‘ G
r-r GR .
Принимая = 0,13, получим:
Г 0,87
I/ 1-0,13-^?-
r G
Если
= 0,8,
Go
TO
1/ZZ^KZZZ=1O2
F 1-0,13-1,25
Оказалось, что разгружение самолета на 20% повысило макси-
мальную безвредную скорость лишь на 2%. Следовательно, можно
ее считать независящей от веса самолета.
Максимальную безвредную скорость самолета необходимо знать
инженеру и летчику. На скорости, меньшей максимальной безвред-
ной, летчик может позволить себе любое движение рулями без
риска создать нагрузку, превышающую предел упругости конструк-
ции. Если скорость полета превышает максимальную безвредную,,
летчик должен воздерживаться от сильного увеличения угла атаки,,
рискуя получить остаточные деформации, что выражается в нару-
шении регулировки. Если скорость полета превышает максималь-
ную безвредную больше, чем в ]/2 раза, то летчик должен быть
еще более осторожен, так как чрезмерное увеличение Су может
привести к поломке самолета. Какой именно Су может быть до-
пущен на больших скоростях полета, можно определить, взяв до-
пускаемую перегрузку по диаграмме фиг. 123.
Вопрос о предохранении самолета от неумышленных перегрузок,
могущих вызвать остаточные деформации или даже поломку, пред-
ставляет большую практическую важность, тем более что многие
быстроходные самолеты имеют максимальную и даже крейсерскую
скорость, превышающую максимальную безвредную скорость. По-
дробнее на этом вопросе мы остановимся в дальнейших частях
настоящего труда, а сейчас укажем лишь на контроль над пере-
грузкой.
Необходимо отметить также, что при совершении фигурных по-
летов скорость не должна приближаться к критической в отноше-
нии вибраций.
159
ИЗМЕРЕНИЕ ПЕРЕГРУЗОК В ПОЛЕТЕ
При всех фигурных полетах происходит то или иное измене-
ние перегрузки. Перегрузку нужно знать по соображениям проч-
ности самолета; кроме того, характер изменения перегрузки по
времени служит хорошей иллюстрацией действия сил на самолет
при фигурах, а также отражает правильность совершения фигур
и поэтому пригоден для контроля пилотажа.
Можно предположить, что для измерения перегрузки следует
включить динамометр (т. е. измеритель усилий) в силовую кон-
струкцию крыльев. Это, конечно, возможно, но достаточно сложно.
Однако в этом, как будет показано ниже, нет никакой необходи-
мости. Увеличение подъемной силы передается по всей конструк-
ции и передается на все детали, так как под действием увеличен-
ной подъемной силы меняется характер движения самолета и инер-
ционные силы действуют на все части самолета, распределяясь
пропорционально весам частей.
Если в самолете мы подвесим груз на пружинных весах, то
весы будут измерять равнодействующую сил тяжести и инерции.
Мы уже указали, что отношение этой равнодействующей к весу и
есть перегрузка. Пусть мы подвесили груз в 1 кг\ тогда пружинные
весы будут нам показывать перегрузку. Именно таким образом и
были впервые получены величины перегрузок при фигурных поле-
тах проф. В. П. Ветчинкиным в 1918 г.
В дальнейшем строились специальные приборы, в принципе
сходные с пружинными весами, но более удобные в пользовании,
более точные и, наконец, самопишущие.
Несмотря на простоту принципа работы прибора, измеряющего
перегрузки и называемого перегрузочным прибором, или измерите-
лем ускорений, или акселерометром, в нем есть некоторые прин-
ципиальные недостатки. Дело в том, что груз связан с самолетом
упруго и, следовательно, имеет некоторые собственные движения,
создающие новые силы инерции, искажающие правильность показа-
ний. Практически это сводится к раскачиваниям, так что действи-
тельная перегрузка в начале действия больше, чем показывает
прибор, а затем при убывании — меньще, чем показывает прибор.
Иными словами, прибор реагирует на нагрузку не статически, как
это было бы желательно, а динамически.
Для уточнения показаний прибора стремятся к тому, чтобы он,
во-первых, не отставал (это достигается повышением частоты соб-
ственных колебаний), а во-вторых, принимают меры к погашению
получающихся колебаний.
ОПИСАНИЕ ОСНОВНЫХ ФИГУРНЫХ ПОЛЕТОВ
Ниже мы приводим описание основных фигур: петля, перево-
роты через крыло и полет на спине. В описании обратим внима-
ние на действующие силы, их изменение, перегрузку, способ упра-
вления самолетом,условия выполнения. Точного расчета траекторий
мы не даем и приведем это в четвертой части настоящего труда.
Петля. Петля является наиболее известной и эффектной фигу-
рой, в которой самолет весьма наглядно показывает свою свободу
1(50
перемещения в пространстве. Совершенная впервые русским лет-
чиком Нестеровым в 1913 г. петля послужила родоначальницей
фигурного летания вообще.
Способ выполнения петли нетрудно понять, исходя из общих
соображений, приведенных выше.
Пусть в начальный момент самолет летит горизонтально и силы
находятся в равновесии (фиг. 130). Затем летчик, взяв ручку на
себя, увеличивает угол атаки, вследствие чего подъемная сила
становится больше веса (положение 2 на фиг. 130). Под влиянием
избытка подъемной силы самолет начинает двигаться по кривой,
радиус которой будет:
г G'V* -
2~ g(P-G) g(n-l) •
Через некоторое время (положение 3 на фиг. 130) самолет, двига-
ясь по кривой, наберет некоторую высоту и траектория примет
наклон 0 Самолет будет двигаться по кривой радиуса:
G • VI VI
3 g (Р — G • cos 0) g (п — cos ©) •
Если взять проекции сил на направление движения, то будем
иметь изменение скорости с ускорением:
Ф — Q — G-sinO
/=£----------------.
Постепенно поднимаясь, самолет будет терять скорость. В по-
ложении 4 (фиг. 130) радиус и ускорение будут:
r4 = -^L- Ф —G—Q
4 gn ’ ' ° G
К положению 4 (фиг. 130) самолет успеет сильно потерять ско-
рость. В положении 5 сила тяжести уже начинает играть роль
центростремительной силы и, наконец, в положении 6 радиус кри-
визны траектории будет:
Г- G'V*
9(P + G)
В итоге в точке 6 радиус кривизны очень мал. Во второй по-
ловине петли явления следуют в обратном порядке: в точке 7
сила тяжести энергично разгоняет самолет, в точке 8 благодаря
увеличению скорости вырастает подъемная сила и, наконец, в точке 9
самолет приходит в положение горизонтального полета.
Таким образом о роли сил можно сказать следующее: подъем-
ная сила все время содействовала искривлению траектории, т. е.
она главным образом и давала петлю. Сила тяжести в первой по-
ловине петли уменьшала скорость, на вершине содействовала ма-
лой кривизне траектории и во второй половине вновь разгоняла
самолет. Сила тяги винта способствовала сохранению скорости и
тем помогала совершению петли. Сила сопротивления, конечно,
все время мешала совершению петли.
11 В. С. Пышнов.
161
162
Фиг. 130. Схема петли.
Рассмотрим такие вопросы: 1) какова форма петли; 2) каковы
условия ее выполнения; 3) какой угол атаки следует иметь; 4) ка-
кая получается перегрузка.
В отношении формы петли прежде всего нужно указать, что
она не получается круглой, а действительно похожа на веревочную
петлю.
Радиус кривизны траектории — вначале наибольший, затем убы-
вает, доходя до минимума в верхней части петли, после этого ра-
диус опять нарастает. Приближенно можно считать, что высота
петли равна диаметру очень крутого виража на том же угле атаки.
Если на петле угол атаки был переменный, то можно для расчета
взять средний. Зная средний угол атаки и соответствующий Су,
получим высоту петли:
При совершении петли самолет должен в очень короткий срок
набрать высоту /г. Очевидно, что за короткий срок это не может
быть сделано за счет тяги винта, а придется израсходовать часть
кинетической энергии самолета; на вершине петли скорость полета
будет очень невелика. Если кинетическая энергия самолета ока-
жется недостаточной для подъема на высоту h, то петля вообще
не получится. Таким образом важнейшим условием совершения
петли будет наличие определенной скорости V2 вначале.
Подсчитаем приблизительно, какую скорость У2 должен иметь
самолет перед петлей, чтобы на вершине петли иметь еще некото-
рую скорость Ve. Если взять условный случай, когда нет сопроти-
вления и тяги, то расчет скорости можно сделать, исходя из вы-
соты подъема за счет перехода кинетической энергии в потенци-
альную:
m-Vl _r . 2'Gl
2 2 -u-«- g.e.S-Cv ’
V2 I/» — *'9. ... • _9 — 1/2
V2 e.S.Cy > e.S.Cy V°’
где Vo — скорость горизонтального полета на данном Су;
V2 = V 4-V° + V‘ = 21/01 + 0,25 (^-)2 .
Поскольку Су довольно большой, скорость Уо близка к мини-
мальной скорости Vmln. Следовательно, при отсутствии тяги и со-
противления скорость в начале петли должна превосходить мини-
мальную по крайней мере вдвое, или, если ъ1 = 1, то:
" •'о
V2 = 2,24 Vo.
На самом деле тяга и сопротивление имеются. Если тяга пре-
восходит лобовое сопротивление, то полная энергия самолета
продолжает возрастать и потому запас скорости можно уменьшить.
и* 1вз
Практически это мы имеем у многих самолетов, и у средних само-
летов, учебных и тренировочных, У2 = 2 • Уш1п будет достаточным.
Истребительные самолеты обладают относительно еще большей
тягой и потому требуют начальную скорость V2=1,6VB)M и даже
меньше.
Если петля совершается без мотора, то за счет лобового сопро-
тивления расходуется кинетическая энергия и поэтому начальный
запас скорости нужен еще больший. Практически это дает для
обычного самолета V2 ~ 3 • Vmin, а для планера,
имеющего сравнительно малый Сх, будет:
V2 2,8 4- 2,6 . Vmin.
Рассмотрим вопрос об угле атаки при петле.
С точки зрения сокращения радиуса выгодно
увеличивать Су. Однако это влечет увеличе-
ние Сх и, следовательно, более быстрое падение
скорости. Исследуем вопрос об угле атаки,
Фиг. 131. Действие сил на элементе петли.
Фиг. 132. Расчет
наилучшего угла
атаки при совер-
шении петли.
наиболее благоприятном для выполнения петли. Поставим себе за-
дачу сделать петлю в ее первой части с минимальным уменьшением
скорости. Для этой цели поворот траектории на угол dO должен
сопровождаться минимальным уменьшением скорости dV по абсо-
лютной величине. Найдем соотношение dV и d6:
._ dV _ Ф — G • sin О — Q
j __ — — z
dO _ _ V —G • cos9
— г m- V ~ ‘
Деля j на co, получим:
dV _ v Ф— G • sinG — Q
dO ~~ ’ P-—G • cos 9 ’
Нужно найти максимум величины
Ф —G • sin О — Q
Р — G • cos О
164
в алгебраическом смысле, т. е. если эта величина положительна,
интересно иметь ее возможно большей, а если отрицательна, то —
возможно меньшей.
Эта задача может быть разрешена графически без диференци-
рования. Если мы возьмем силы Ф, Q, Р и G, то указанное отно-
шение будет тангенсом угла наклона <р равнодействующей этих
сил к нормали к траектории (фиг. 131). Поскольку нас интересует
начало петли, когда скорость падает, нам интересен минимум tg <р.
Его мы можем найти таким построением: разделим все силы на
q • S • V2; тогда получим:
Ф
G • sin Q
, q-s-v1 — е • s • V2
tg Ч> = ---------G . cos0
\J * Lvo С/
e • s • v2
Берем кривую Лилиенталя (фиг. 132) в одинаковых масштабах
Наносим силу стрелкой к оси ординат, а затем —g—
под углом 0 к оси ординат, стрелкой к началу силы - • Из на-
чала вектора проводим касательную к кривой Лилиенталя
и получаем искомый угол. Нетрудно видеть, что этот угол больше
наивыгоднейшего и ближе к экономическому.
По мере увеличения 0 скорость падает, а ?
G \ ।
— g растет; в результате угол атаки уве- х.
личивается, однако, незначительно. Если на- г
чало вектора - g- окажется внутри кри-
вой Лилиенталя, то угол <р может быть взят /7
положительным, но менее 90°, иначе траекто- /
рия будет прямолинейной. /и
Можно поставить задачу немного иначе, *
причем Она будет пригодна И ДЛЯ второй ПО- Фиг. 133. Работа сил со-
ловины петли. Поставим задачу сделать пет- противлен“еятлина элементе
лю, затратив минимальную работу на пре-
одоление лобовых сопротивлений. Работа лобовых сопротивлений
на элементарном участке будет (фиг. 133):
dE = Q • dS = Q • г • dO.
Найдем минимум :
dE _п _ Q G • У2 _ G • V2 Q
de —Q’r~~ g(p — g cose) — g ’ P — G cose ’
Минимум величины p _G^ cos0 можно заменить минимумом ве-
личины
Сх
с G • COS О ‘
су~ е • s • v2
165
Этот минимум можно найти опять по кривой Лилиенталя (фиг. 134).
Прикладываем вектор $ стрелкой к началу координат, конец
вектора проектируем на ось ординат и из полученной точки про-
водим касательную к поляре. Точка касания очень близка к наи-
выгоднейшему углу атаки. Если по оси ординат отложить прямо
g~'~s'T~ya > то КРИВУЮ Лилиенталя можно взять в разных масштабах.
Таким образом, -по теоретическим соображениям выгодно во
все время совершения петли держать почти постоянный угол атаки,
Фиг. 134. Выбор угла атаки при усло-
вии минимальной затраты энергии на
преодоление лобовых сопротивлений.
чительно, подъемная сила, а
ответственно скорости:
близкий к экономическому и наивы-
годнейшему. Но это не значит, что
руль высоты можно держать в од-
ном положении. В верхней части
петли кривизна траектории возрас-
тает, и отклонение руля высоты
нужно увеличивать, а на вершине
петли, несмотря на крайнее откло-
нение руля высоты, угол атаки
все же сильно уменьшается.
Иногда интересуются вопросом
о потере высоты при совершении
петли. Простого сравнения высот
в начале и в конце петли здесь
недостаточно, так как скорости
в начале и конце петли различны.
С точки зрения повышения ско-
рости в конце петли, например для
ее повторения, вторую часть петли
следует производить с работающим
мотором.
Остановимся на перегрузке при
петле, ее изменении и максималь-
ной величине. Поскольку во время
петли угол атаки меняется незна-
: ней и перегрузка, меняются со-
Cy-f>-S-V*
В начале петли при увеличении угла атаки перегрузка возра-
стает до максимальной величины, а затем постепенно падает за
счет падения скорости и доходит до минимума в верхней части
петли. Затем, по мере роста скорости перегрузка вновь возрастает
и доходит до второго максимума перед самым окончанием петли.
Максимальную перегрузку в начале петли получим, подставив
Су и V = V2:
_ су • е • s • V* .
^шах Q 1
Су ~ 0,7 • Су ;
V ’ утах’
166
тогда получим:
Если
то
«max - 0,7 (-jJ, ) .
= 2Vmin,
лшах = 2,8.
Иногда прижатие летчика к сиденью на вершине петли объясняют
наличием центробежной силы, большей веса. По существу это
правильно, но такое рассуждение неточно. Мы уже раньше ука-
зывали, что равнодействующая силы тяжести и силы инерции
равна и противоположна равнодействующей внешних сил, не счи-
тая силы тяжести. Следовательно, для прижатия летчика к сиденью
вполне достаточно наличия подъемной силы. Отставание от сидения
получается тогда, когда подъемная сила направится обратно при
сильно отрицательном угле атаки. Практически это может быть
в таком случае: летчик делает петлю так, что на вершине ско-
рость очень мала и поэтому траектория
круто заворачивает (фиг. 135); самолет не М
успевает поворачиваться вслед за траекто- । ---
рией, а угол атаки падает до сильно отри-
цательной величины и самолет начинает \
парашютировать на спину: дальше самолет // \
все же поворачивается на нос и петля по- / / I
лучается, но, как говорят, с зависанием. ' / |
Перевороты через крыло. Переворотами j 6
через крыло называются фигуры, при ко- '
ТОрЫХ самолет поворачивается вокруг на- Фиг. 135. Зависание на петле,
правления полета на угол 180° или более.
Перевороты часто комбинируются с другими фигурами, как, на-
пример, с петлей. Имеются такие фигуры: 1) одинарный переворот
с последующим переходом в пикирование и выходом в обратную
сторону (фиг. 136); 2) переворот Иммельмана, начинающийся с по-
лупетли и заканчиваемый переходом в нормальный полет путем
переворота на 180° (фиг. 137); 3) двойные и многократные перево-
роты или „бочки", представляющие собой перевороты на 360® или
кратные ему углы (фиг. 138).
По способу выполнения перевороты разделяются на быстрые
или штопорные и медленные или управляемые. Штопорные пере-
вороты совершаются за счет перевода самолета на режим авторо-
тации; для этого самолету обязательно придается угол атаки
больше критического, соответствующего Су , затем самолету при-
дается вращение элеронами и внешним скольжением путем дачи
ноги в сторону желаемого вращения. Имея угол атаки больше
критического, самолет легко и быстро вращается, летчик продолжает
держать ручку на себя и в сторону вращения и ногу в сторону
вращения. Для прекращения вращения ручка ставится нейтрально,
а нога дается в обратную сторону. Искусство совершения фигуры
заключается в своевременной остановке вращения, что не так
просто сделать вследствие быстроты вращения.
167
Фиг. 136. Одинарный переворот через крыло.
168
Для успешного выполнения штопорных Переворотов необхо-
димо: 1) иметь достаточную скорость; 2) достаточную прочность
самолета; 3) самолет не должен иметь чрезмерного запаса устой-
чивости, иначе увеличение угла атаки затруднительно; 4) большой
поперечный угол крыльев облегчает начало вращения самолета пу-
тем дачи скольжения.
Для выяснения величины
скорости необходимо иметь
в виду, что по причине боль-
шого угла атаки Сх очень
велик и его следует брать
не менее 0,15 — 0,20. Изме-
нение скорости во время
вращения можно найти
обычным методом, опреде-
ляя ускорение из условия:
Ф-C^e-sv2
Интегрирование можно
провести графически. Запас
скорости должен быть та-
ков, чтобы за время враще-
ния скорость упала до вели-
чины не меньше экономиче-
ской скорости.
На фиг. 139 приведен при-
мерный расчет, причем гра-
фическое интегрирование
велось от меньшей скорости
к большей. Это сделано для
того, чтобы получить диа-
грамму времени вращения
в зависимости от начальной
скорости, если конечная ско-
рость равна экономической
(фиг. 140). Теперь остается
связать время вращения с
числом сделанных оборотов.
Теория авторотации указы-
вает, что угловая скорость
может быть выражена при-
мерно:
Фиг. 139. Расчет потерь скорости при што-
порном перевороте.
Фиг. 140. Диаграмма потребной в начале пере-
ворота скорости в зависимости от времени
вращения.
где V — скорость полета, I — размах крыльев.
Время полного оборота или, как говорят, витка будет:
2л
со
12,5-4-.
169
Подбирая среднюю скорость, мы на Диаграмме фиг. 140 можем
разметить начальные скорости для совершения переворотов с же-
лательным числом витков. Если скорость будет больше указанной
величины, то после переворота скорость самолета будет больше
экономической. Примерные значения скоростей получились: для
одинарного переворота V = l,45VmIn; для двойного V = 1,75 Vmln;
для полутора витков V = 2,l Vmln; для двух витков V = 2,5 7ш1п.
При расчете скорости для совершения переворота Иммельмана
нужно учитывать потерю скорости на полупетле. Разгон самолету
нужно дать такой, чтобы, дойдя до вершины петли, самолет имел
запас скорости около 1,5 Vttin, в то время как при обычной петле
запас скорости бывает менее Vm!n. Поэтому вначале скорость на
истребительных самолетах доводят до 2,3—2,5 Vroin; самолеты
с меньшим запасом мощности потребуют еще большего разгона.
Однако некоторые мощные истребительные самолеты после зна-
чительного разгона, сделав переворот Иммельмана и набрав при
этом большую высоту, непосредственно выполняют еще петлю и
описывают таким образом вертикальную восьмерку.
Подсчет перегрузки при штопорных переворотах очень прост.
Дело в том, что угол атаки сильно увеличивается и Су доходит
до максимальной величины; имеем:
/ V V
шал I I
б - k :
Принимая во внимание значения скорости, необходимые для
совершения переворотов, указанных выше, получим перегрузки:
при одинарном, т. е. на 180°, перевороте л = 2,1; при двойном,
т. е. на 360°, перевороте п = 3,05; при выполнении двух витков
п = 6,25. Как видно, при выполнении двух витков перегрузка до-
вольно велика; она требует от самолета запаса прочности свыше
12 и, кроме того, уже тяжела для летчика. Нужно, конечно, пом-
нить, что величина перегрузки зависит не от числа оборотов, а от
скорости, на которой перевороты начинаются.
При совершении переворота Иммельмана наибольшая перегрузка
получается не во время переворачивания через крыло, а в начале
полупетли. Учитывая разгон самолета в этом случае и Су ~ 0,7 CVjnax,
получаем перегрузку около 4,5—5.
Для многих разведывательных и учебных самолетов эта пере-
грузка велика, и поэтому фигура не допускается.
В последнее время при фигурных полетах штопорные перево-
роты применяют все реже и реже, так как на устойчивых самоле-
тах увеличение угла атаки затруднительно и, кроме того, большая
перегрузка утомляет летчика. Большим распространением стал
пользоваться медленный переворот, совершаемый при помощи
элеронов. На первый взгляд выполнение его очень просто, но на
самом деле это не так. Дело в том, что при этом необходимо
всемерно поддерживать прямолинейность траектории, непрерывно
действуя рулями высоты и поворотов. Необходимо стремиться
к тому, чтобы равнодействующая подъемной силы Р и боковой
силы Z оставалась вертикальной и но возможности равной весу
170
при медленном
перевороте.
Фиг. 141. Действие
сил
самолета (фиг. 141). Для этой цели летчик должен по мере уве-
личения крена уменьшать угол атаки, увеличивая отклонение руля
поворотов в сторону, обратную накренению; при крене в 90°Су
должен равняться нулю, а отклонение руля поворотов должно
быть максимальное. Затем руль поворотов постепенно убирается,
а ручка дается дальше от себя для создания об-,
ратной подъемной силы; при положении 180° рулы
поворотов — нейтрален, руль высоты — до отказа
от себя. Дальше руль высоты постепенно идет
в нормальное положение, а руль поворотов —в об-
ратную сторону. Фигура не дает значительных пе-
регрузок и может быть выполняема многократно.
Перевернутый полет. Сам по себе перевернутый
полет (фиг. 142) обычно считают фигурным, хотя
в перевернутом виде совершаются все те фигуры,
что и в нормальном положении. Фигурами в пере-
вернутом положении называются такие, при кото-
рых на самолет действует обратная подъемная
сила на сильно отрицательных углах атаки. Необ-
ходимо вспомнить, что на самолете можно крат-
ковременно находиться вверх колесами при пря-
мом действии подъемной силы, как, например, на
вообще говоря, перевернутое положение самолета нужно брать не
в отношении его положения в пространстве, а в отношении напра-
вления действия подъемной силы.
петле, и потому.
Фиг. 142. Действие сил при полете на спине.
Отличие перевернутого полета от нормального заключается
в следующем:
1. Особенность работы крыла обратной стороной,что приводит
к сильному ухудшению качества и, следовательно, к низким полет-
ным качествам.
Для специально фигурных. самолетов этот недостаток устра-
няется применением симметричного профиля крыла, чем несколько
ухудшается полет в нормальном положении, но зато сильно улуч-
шается в перевернутом.
2. Изменение управляемости самолета. Прежде всего летчику
приходится делать ручкой обратные движения, что требует трени-
171
ровки. Затем самолет, будучи сбалансирован стабилизатором на
нормальный полет, для получения сильно отрицательного угла
атаки требует сильного отклонения руля высоты от себя, причем
иногда руля высоты может и не хватить. В последнем случае
самолет сам собой из положения на спине переходит в пикиро-
вание.
Во второй части настоящего труда мы останавливались на рав-
новесии в перевернутом полете и рекомендовали применять более
заднюю центровку. Однако можно хорошо летать на спине и
с обычной центровкой, но для этого нужно снабдить самолет ста-
билизатором, быстро переставляемым соответственно балансировке
в перевернутом полете. Это устройство и делается на специально
фигурных самолетах.
3. Третье условие длительного перевернутого полета—это
работа мотора. Следует предусмотреть питание мотора горючим и
маслом в перевернутом положении, а также устранить возможность
выливания горючего и масла из баков.
Теория перевернутого полета и фигур ничем не отличается от
теории полета в обычном положении, только нужно применять
участок кривой Лилиенталя для сильно отрицательных углов атаки.
Величины перегрузок примерно такие же, но нужно учитывать
обратное направление их действия. В отношении самолета это тре-
бует замены случая А случаем D; для летчика вместо прижатия
к сиденью получается повисание на ремнях. Это требует придания
ремням достаточной прочности и удобного прилегания к телу
летчика. Необходимо закрепить ноги пилота к педалям и вообще
обеспечить удобство работы летчика в положении вниз головой.
В физиологическом отношении раньше полагали, что длительный
полет вниз головой невозможен, однако, впоследствии оказалось,
что при известной тренировке можно совершать длительные по-
леты. Перевернутые полеты совершаются даже группами по три и
пять самолетов в строю, причем производятся перестроения и
групповые виражи.
Из фигурных полетов обычно совершаются: виражи, штопор и
петли, хотя выполнение петель колесами внутрь петли для летчика
очень тяжело.
Переход в перевернутый полет можно сделать различными спо-
собами, но предпочтительны такие способы, при которых летчик
оказывается в перевернутом положении с нужной скоростью.
В этом отношении можно рекомендовать медленный полупереворот
через крыло и применение полупетли, но с таким предварительным
разгоном, чтобы на вершине петли самолет имел скорость, доста-
точную для перевернутого полета.