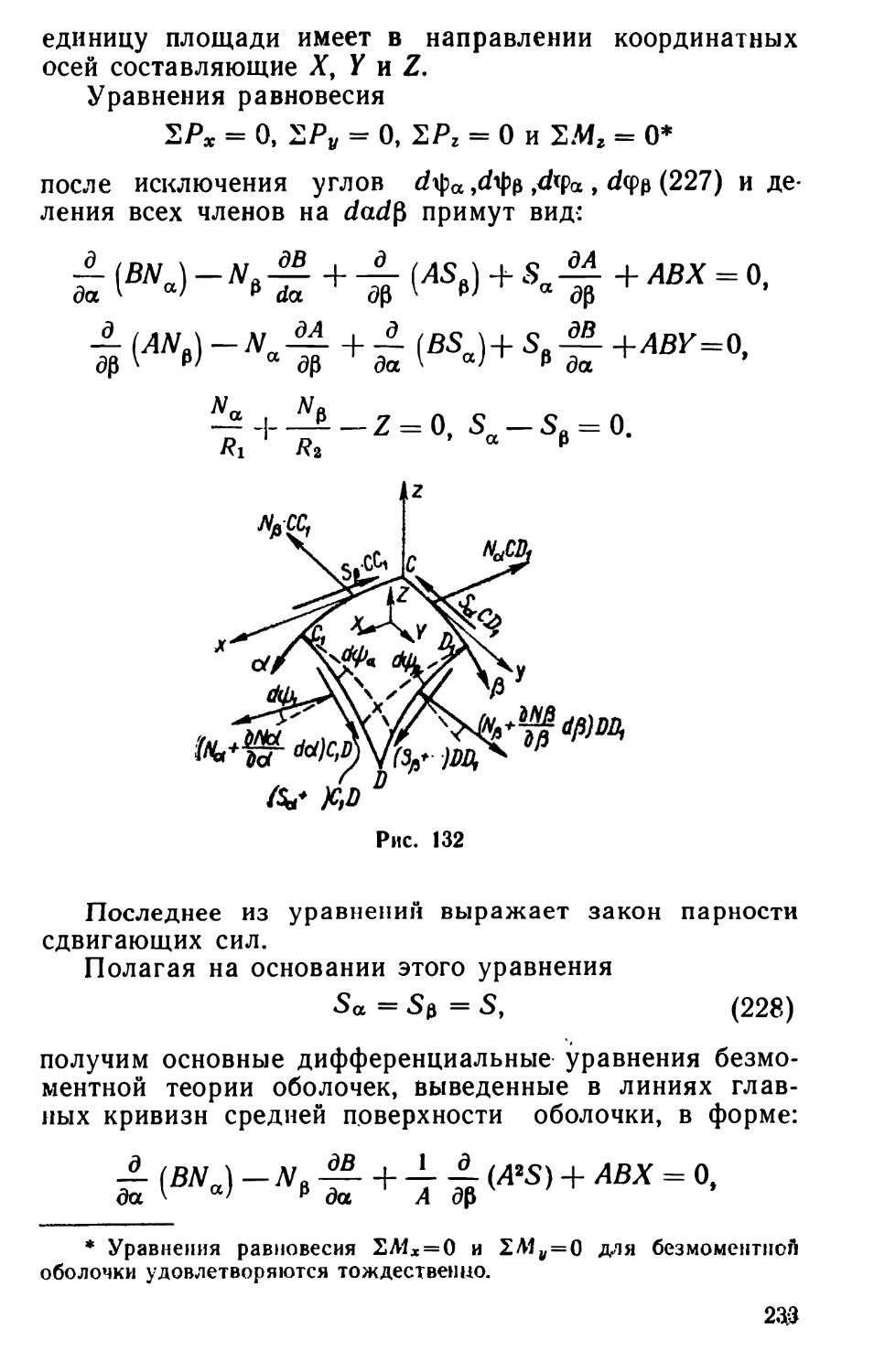
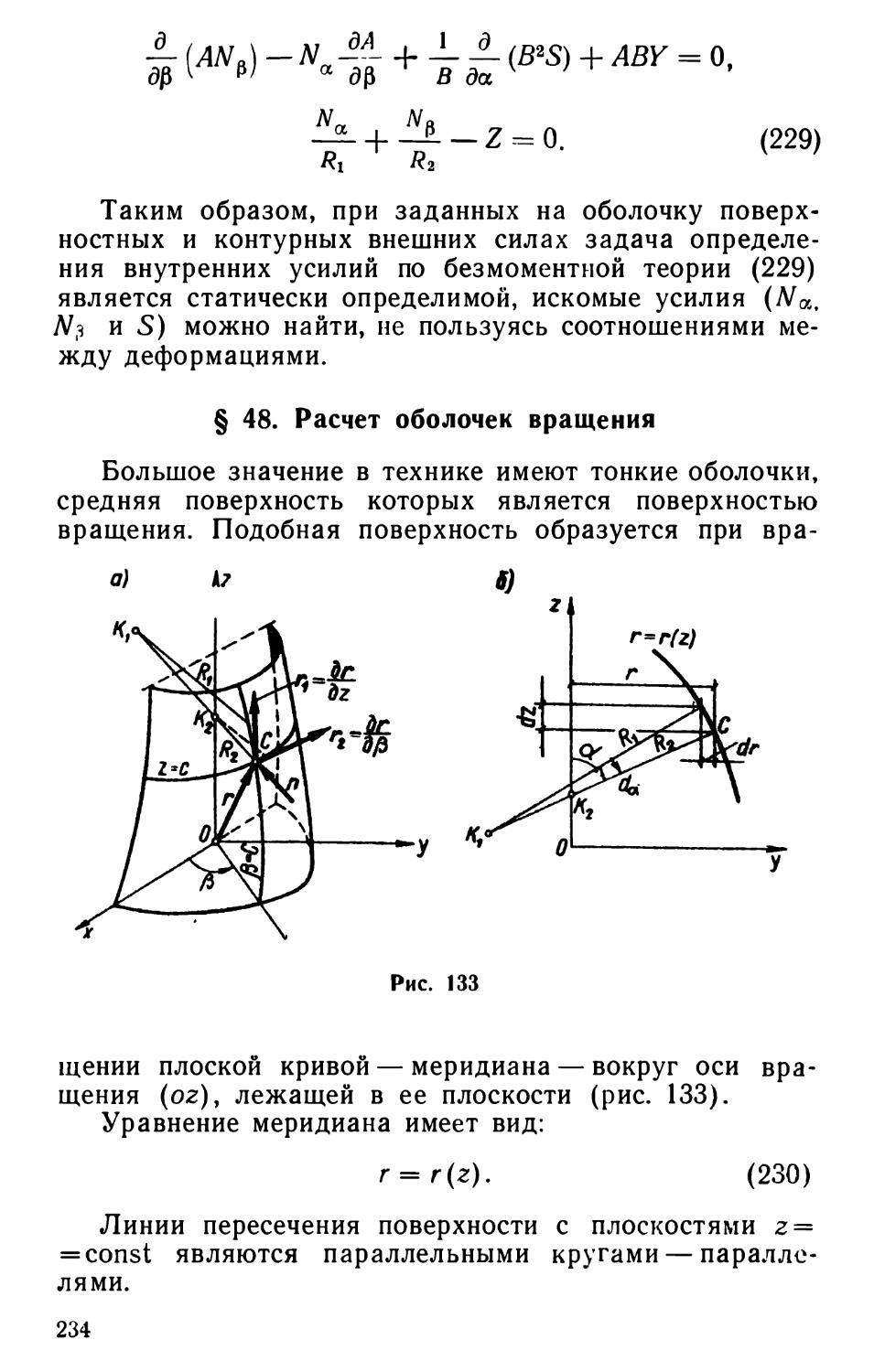
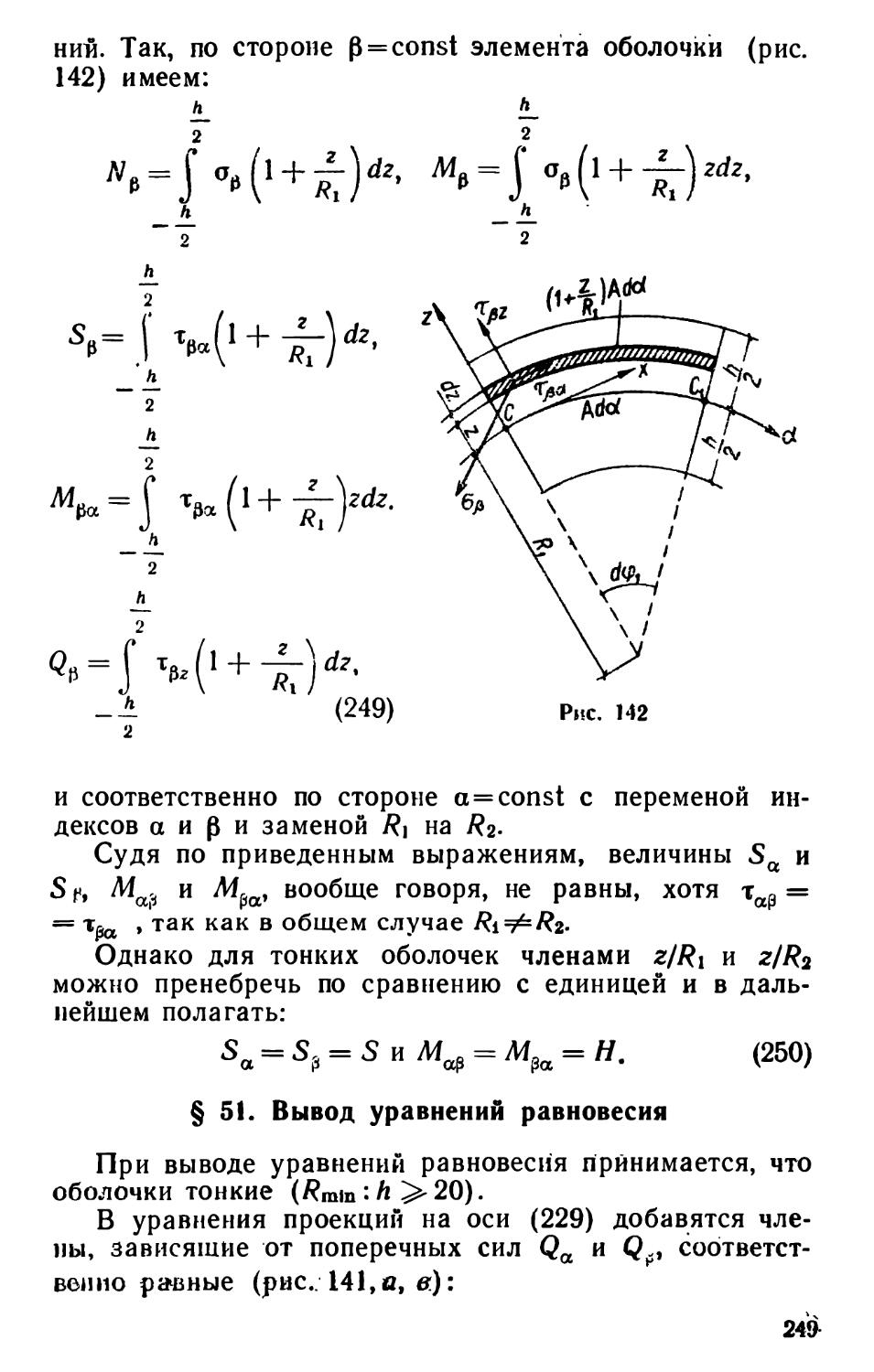
Текст
Г. К. КЛЕЙН, В. Г. РЕКАЧ, Г. И. РОЗЕНБЛАТ
РУКОВОДСТВО К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО КУРСУ СТРОИТЕЛЬНОЙ МЕХАНИКИ
(ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ, ДИНАМИКИ СООРУЖЕНИЙ И РАСЧЕТА ПРОСТРАНСТВЕННЫХ СИСТЕМ)
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством высшего и среднего специального образования СССР в качестве учебного пособия для студентов строительных специальностей вузов
ИЗДАТЕЛЬСТВО «ВЫСШАЯ 111 КОЛ А Москва — 1972
6С1
К48
УДК 624.04
Клейн Г. К. и др.
К48 Руководство к практическим занятиям по курсу строительной механики. Учеб. пособие для втузов. М., «Высш. школа», 1972
320 с. с илл.
Перед загл. авт.: Г. К. Клейн, В. Г. Р е к а ч, Г. И. Р о з е н б л а т.
Учебное пособие по курсу строительной механики для студентов строительных высших учебных заведений по специальности «Промышленное и гражданское строительство» состоит из трех разделов: «Основы теории устойчивости», «Основы динамики сооружений» и «Основы расчета пространственных систем».
Руководство содержит большое число наиболее характерных типовых задач с подробными решениями, которым предшествует краткое, но в то же время достаточно полное изложение теории.
По сравнению с предыдущим изданием заметно дополнен раздел динамики сооружений.
ПРЕДИСЛОВИЕ
Руководство по специальному разделу курса строительной механики предназначено для студентов строительных вузов по специальности «Промышленное и гражданское строительство». Все три раздела руководства отвечают действующей в настоящее время программе.
Прослушав лекции по соответствующему разделу курса, студент может приступить к решению задач, пользуясь руководством, в котором приведены многочисленные задачи с решениями; задачам предшествует краткое, но довольно полное изложение теории.
Раздел I «Основы расчета стержневых систем на устойчивость» написан канд. техн. наук, доц. Г. И. Р о з е н б л а т;
раздел II «Основы динамики стержневых систем» — докт. техн. наук, проф. Г. К. К л е йн о м;
раздел III «Основы расчета пространственных тонкостенных конструкций.» — докт. техн. наук, проф. В. Г. Р е к а ч е м.
По сравнению с первым изданием раздел «Основы динамики стержневых систем» дополнен изложением расчета статически неопределимых систем по методу сил и особенно по методу перемещений. Внесены некоторые изменения и в порядок расположения ма¬
1*
з
териала этого раздела. Переработаны и два других раздела руководства.
При переработке книги для второго издания учтены ценные замечания, сделанные коллективом кафедры строительной механики Ленинградского инженерно-строительного института, руководимой проф. И. И. Гордан о в ы м.
РАЗДЕЛ I
ОСНОВЫ РАСЧЕТА СТЕРЖНЕВЫХ СИСТЕМ НА УСТОЙЧИВОСТЬ
ГЛАВА 1
ПОНЯТИЕ О ПОТЕРЕ УСТОЙЧИВОСТИ, КРИТИЧЕСКОЙ НАГРУЗКЕ И МЕТОДАХ РАСЧЕТА НА УСТОЙЧИВОСТЬ
§ 1. Введение
Системы, применяемые в качестве строительных конструкций, под действием нагрузки должны находиться в состоянии устойчивого равновесия. Это означает, что если какие-либо случайные причины выведут систему из состояния равновесия, то после удаления этих причин система должна вернуться в первоначальное положение.
Если вертикальный тонкий столб, свободно опирающийся на землю, находится в равновесии под действием центрально приложенной силы Р (рис. 1 , а) и при небольшом отклонении вернуться в исходное положение не может, то равновесное состояние является неустойчивым.
Если упругий тонкий стержень, жестко защемленный в основании (рис. 1,6), после отклонения, поколебавшись вокруг вертикального положения, вернется в первоначальное положение, то его равновесие является устойчивым.
При заданной схеме сооружения и заданной схеме нагрузки устойчивость равновесного состояния зависит от величины нагрузки. В каждом отдельном случае можно найти ту нагрузку (или параметр, определяющий всю данную систему нагрузок), при которой первоначальная форма равновесия становится неустойчивой и возможно
5
другое, качественно новое деформированное состояние, тоже являющееся состоянием равновесия. Выход системы из первоначального состояния равновесия называется потерей устойчивости, а нагрузка, при небольшом превышении которой возможно осуществление новой устойчивой формы равновесия (так называемое раздвоение,
или бифуркация, форм равновесия), называется критической нагрузкой.
Обеспечение устойчивости строительных конструкций особенно важно потому, что самый процесс потери устойчивости происходит очень быстро и практически ведет к разрушению сооружения. Ряд случаев катастроф крупных инженерных сооружений, происшедших в результате потери устойчивости, описан в работе [4].
В зависимости от того, является действующая нагрузка статической или динамической, можно рассматривать вопросы статической или динамической устойчи-
Рис. 1
г)
*р
вости сооружений. В дальнейшем рассматривается влияние только статических нагрузок.
На рис. 2, а, б, в, г сплошными линиями показана первоначальная форма равновесия стойки, кольца, арки и рамы при центральном сжатии, пунктиром — новая, изогнутая форма равновесия после потери устойчивости. Это есть потеря устойчивости центрального сжатия.
На рис. 2, д изображена потеря устойчивости плоской
6
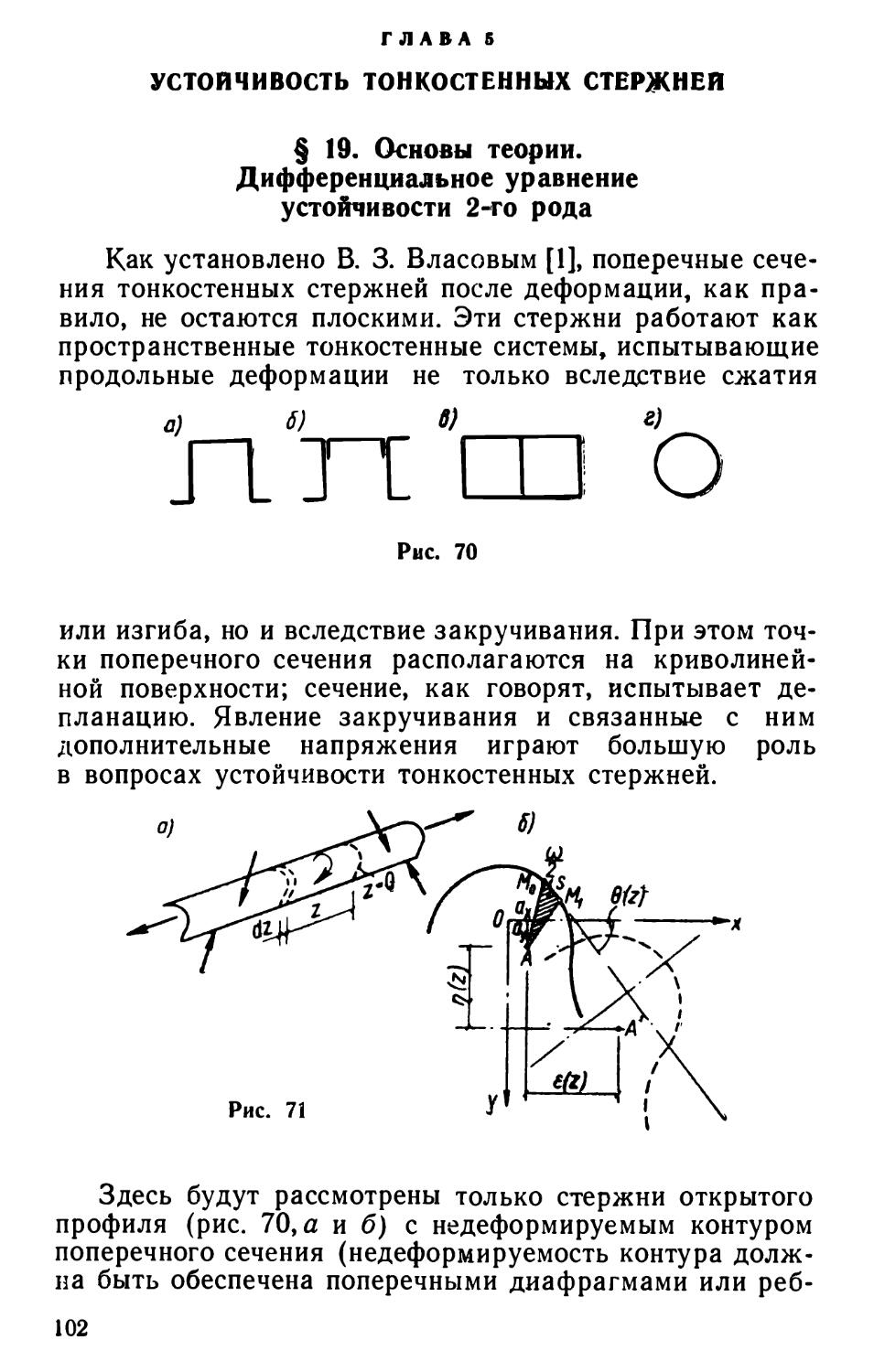
формы изгиба балки с поперечным сечением в виде узкой полосы. Могут быть рассмотрены и другие виды потери устойчивости.
Все приведенные на рис. 2 примеры характерны тем, что в момент потери устойчивости появляется новый вид деформации, качественно отличный от первоначальных деформаций сооружения (первоначально сжатые стойка, арка, рама получили деформации изгиба; первоначально изогнутая в вертикальной плоскости балка закрутилась и изогнулась в горизонтальной плоскости). Принято потерю устойчивости, характеризуемую внезапным появлением качественно новых деформаций, называть потерей устойчивости 1-го рода (потеря устойчивости по Эйлеру). Именно к этому случаю и относится определение критической силы, данное выше.
В инженерной практике весьма часто встречается и другой класс задач: на рис. 3,а, б, в в качестве примера изображены внецентренно сжатая стойка, рама и арка, элементы которых с самого начала находятся под воздействием продольных сил и изгибающих моментов. При малых нагрузках влияние продольных сил на деформации невелико и приращения перемещений Дь Лг и т. д. почти пропорциональны приращениям нагрузок. С увеличением нагрузки влияние продольных сил возрастает и в какой-то момент пропорциональность между деформацией и нагрузкой резко нарушается — деформации начинают расти во много раз быстрее, чем нагрузка. Может наступить такой момент, когда увеличения нагрузки не требуется для роста деформаций, они будут расти даже при уменьшении нагрузки; при этом никаких «разветвлений» состояния равновесия не будет — явление развивается все время в одном направлении и меняется только в количественном отношении.
Рост деформации при отсутствии приращения нагрузки может рассматриваться тоже как потеря устойчивости (так называемая потеря устойчивости 2-го рода), связанная с потерей несущей способности сооружения. Нагрузка, соответствующая началу деформации без прира¬
7
щения нагрузки, называется критической силой при потере устойчивости 2-го рода *.
Следует отметить, что и потеря устойчивости в эйлеровском смысле, и потеря несущей способности могут произойти как при упругих деформациях, так и при работе сооружения за пределами упругости.
Большая часть задач, решаемых в данном курсе, относится к задачам о потере устойчивости 1-го рода, причем явление рассматривается только в упругой стадии.
§ 2. Устойчивость 1-города; постановка задачи; методы расчета
При определении критической нагрузки 1-го рода постановка задачи такова: система (например, рис. 2, а, б, в, г, д) при нагрузке, равной РКр, потеряла устойчивость и перешла в новое деформированное состояние; требуется определить ту нагрузку (РКр), при которой это новое состояние будет состоянием равновесия. Таким образом, для расчета на устойчивость можно использовать все методы, которые применяются для расчета равновесных систем; эти методы делятся на статические и энергетические.
Сущность статического метода заключается в следующем: поскольку система находится в равновесии, в равновесии находится и любой бесконечно малый элемент этой системы; записав дифференциальные уравнения равновесия бесконечно малого элемента в деформированном состоянии под действием всех внутренних и внешних сил и проинтегрировав эти уравнения, находим форму потери устойчивости и критическую нагрузку.
Энергетические методы делятся в основном на две разновидности:
А. Непосредственное применение принципа возможных перемещений: поскольку деформированное состояние есть состояние равновесия, критическая нагрузка определяется путем приравнивания нулю суммарной работы внешних и внутренних сил на малых возможных перемещениях из деформированного состояния.
Б. Использование энергетического критерия равно¬
* Не следует смешивать это явление с явлением ползучести материала, которое в данной работе не рассматривается.
8
весного состояния: полная потенциальная энергия системы, находящейся в равновесии, имеет экстремальное значение, поэтому, записав выражение полной потенциальной энергии системы в деформированном состоянии, критическую силу определяем из условия экстремума этой функции.
Точный расчет на устойчивость более или менее сложной системы встречает большие математические трудности, поэтому
во многих случаях задачи
решаются
приближенно.
Упрощение мо- % J **”1
жет быть достиг- Шй j—
нуто: g)y EJ*oo
упрощением рас- четной схемы сооружения;
Jz,
J»oo
ближенных методов 1а. ■■ ' m~i
расчета. шя т*0
Рис. 4
Назовем степенью свободы т системы число независимых геометрических параметров, полностью определяющих возможные перемещения всех ее точек. Реальная упругая система всегда будет иметь степень свободы т = оо; чтобы полностью определить деформацию, например, балки конечной жесткости (рис. 4,а), надо задать прогибы во всех точках; если же очень жесткая балка опирается на весьма податливую в вертикальном направлении опору (рис. 4,6), то при решении вопросов устойчивости изгибом балки можно пренебречь, и тогда перемещения всех точек определяются одним параметром— углом а или осадкой опоры Д; степень свободы т = I.
Для схем (рис. 4, в, г) имеем соответственно т = 2 и т = 0.
Система будет иметь столько возможных форм потери устойчивости и соответствующих им критических сил, сколько она имеет степеней свободы; естественно, что с увеличением числа степеней свободы трудность определения минимальной критической нагрузки возрастает.
9
Рассмотрим детально указанные выше методы определения критической нагрузки и вопрос о точных и приближенных методах расчета на примере системы с двумя степенями свободы.
§ 3. Устойчивость системы с двумя степенями свободы.
Точные и приближенные методы расчета
Рассмотрим балку, состоящую из трех абсолютно жестких звеньев, шарнирно соединенных между собой (рис. 5,а). Опоры А и В не допускают вертикальных перемещений, опоры С и D унругоподатливые с одина-
а 61 ptmd
j(2o,+az) га, гаг f(a,+2az) Рис. 5
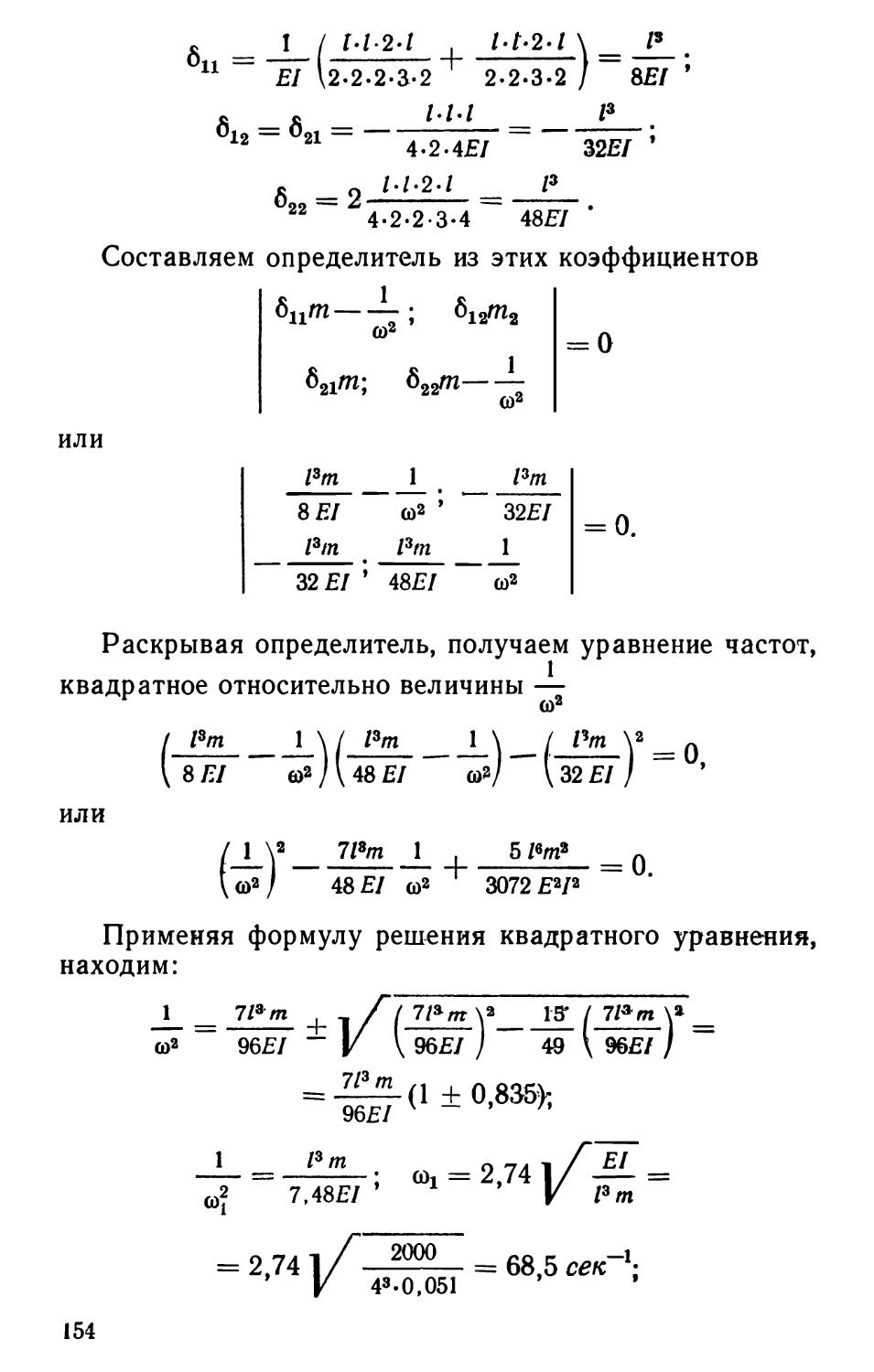
ковым коэффициентом жесткости г (г — реакция, возникающая при единичном вертикальном смещении). Балка находится под действием продольной силы Р. Требуется определить ту нагрузку, при которой, кроме горизонтального положения равновесия, возможно какое-то отклоненное равновесное состояние, характеризуемое двумя неизвестными параметрами (степень свободы т = 2), например, вертикальными перемещениями точек С и D—аг и а*2. Опорные реакции нового равновесного состояния показаны па чертеже.
Решаем задачу тремя способами:
Статический способ
Поскольку система имеет две степени свободы, достаточно составить для всей системы два уравнения рав¬
* Все рассуждения ведутся в предположении малых перемещений.
10
новесия, в которые войдут два неизвестных параметра cti и а2:
2Л1?*В = 0 -j- (2а, + а2)1 — Р -а, = 0,
=0 -у(а, + 2а2) / — Р-а2 = 0,
откуда имеем систему двух однородных линейных уравнений относительно ai и аг:
(2 rl — 3 Р) at + rla2 = 0, . „
rlai + (2rl — 3P)a2 = 0.
Система (1) может иметь нулевое решение для неизвестных ai=a2=0, что соответствует горизонтальному равновесному состоянию; ненулевое решение получим, если приравняем нулю определитель, составленный из коэффициентов при неизвестных
2г1 — ЪР; rl
D =
= 0.
rl 2/7 — ЗР
Раскрывая определитель, получаем квадратное уравнение для определения критической силы
(2ri — 3/)2 — (г/)2 = о и два значения Ркр: = --; Р$ =rl, из которых рас¬
четным будет минимальное значение Рр = — .
3
Форма потери устойчивости определится, если полученные значения критических сил подставить в одно из уравнений (1): при PKp=Pi имеем
(2/7— rl)ai + rla2 = 0,
т. е. ai = —a2 (рис. 5,6); при ЯКр=Рп имеем (2/7—3rl)cii + + г/*Я2=0, т. е. ai = a2 (рис. 5,в).
Таким образом, статический способ расчета дает все возможные для данной системы формы потери устойчивости и соответствующие им критические силы.
При решении системы с бесконечным числом степеней свободы, интегрируя дифференциальные уравнения равновесия бесконечно малого элемента, получаем бесконечное множество возможных форм потери устойчивости и соответствующих им критических сил; практи¬
11
чески важно найти наименьшее значение критическои нагрузки.
Давая всю совокупность решений, статический способ является точным способом расчета на устойчивость.
Энергетические способы
А. Рассматривая деформированное равновесное состояние, приравняем нулю сумму работ внешних и внутренних сил на перемещениях из деформированного состояния обратно в первоначальное. При этом работа внешних сил А = —ЯД; работа внутренних сил W =
I
\4«
I
I
Ркс. 6
= у К + 4-
При повороте жесткого стержня смещение его конца Ai (рис. 6) определяется так:
Дх = / — / cos ос = / (1 — cos а) 1
tg2 а
__ 1у'2 ~ 2 “ 2 *
Таким образом, полное горизонтальное перемещение точки приложения силы Я, зависящее от поворотов всех трёх звеньев,
(а1-а2у
А = —(— + —
2 \ Р Р Р
Записав уравнение
А + W = 0 и решив его относительно Р, получаем
°i — Oj-a2 4-
I
Р — — КР 2
aj + al
(2)
(3)
Выражение (3) дает точные значения критических сил, если известны формы потери устойчивости, т. е. зависимости между ai и й2; (в самом деле, при а\ = а2 получаем
Я,ф = rl,
при di=—аг получаем Якр=-“.
12
дР г I
да% 2
2а, ( 4 - ava2 а]) - (2д1 - а2) ( а\ + 4)\ _ Q
Поскольку формы потери устойчивости неизвестны, для получения решения надо составить условие минимума выражения (3); при двух параметрах ai и а2 следует приравнять нулю частные производные по каждому из параметров:
■=0; «0;
daL да2
п
(-ага2 + а)2 J
откуда а\ = ±аг.
Второе выражение --=0 дает тот же результат.
да2
Энергетический способ в качестве приближенного весьма часто употребляется при расчетах на устойчивость.
При этом задаются возможной формой потери устойчивости и определяют соответствующую ей критическую силу. Прием, предложенный С. П. Тимошенко, для общего случая системы с любым числом степеней свободы заключается в следующем:
1) на основании опытных данных или рассмотрения аналогичных задач задаемся формой потери устойчивости, причем уравнение кривой обязательно должно удовлетворять условиям на границах и содержать один или несколько произвольных параметров. Следовательно, полагаем y = f{x, ait «2, ап)\
2) составляем выражения работ внешних и внутренних сил А и W и, решив уравнение (2) относительно Р, находим
Р = F(au аъ ..., ап);
п, „ дР Л дР Л -
3) при помощи уравнении —— = 0,...,—— = 0 подои-
дй\ ийп
раем параметры аи ..., ап таким образом, чтобы сила Р имела минимальное значение.
Заставляя систему деформироваться по заранее заданному закону, мы тем самым как бы накладываем на нее дополнительные связи, и найденная таким образом критическая сила будет выше действительной критической силы.
Б. Вернемся к рассматриваемому случаю системы
13
с двумя степенями свободы и определим полную потенциальную энергию системы
U = A + W = -P д1~а + а2 + г_ (а\+а\),
которая является функцией двух параметров ai и а* Условия экстремума этой функции запишутся так:
.ба1 = 0; f--taa = О,
ddi оа%
или
= 0; «L-0.
даг да
откуда получаем
—j- (2ах — а2) + гах = 0; — у (— ах + 2as) + га2 = 0,
ИЛИ
(т—г)“‘ та‘~0’’
— -J- а1 + (у —'•j а* = 0-
(4)
Приравняв нулю определитель, составленный из коэффициентов при неизвестных ах и а2, получаем квадратное уравнение для определения критических сил; решая это уравнение, находим
Pip=T; Pif = r/-
Уравнения (4) можно получить также, применяя непосредственно принцип возможных перемещений и записывая возможную работу внешних и внутренних сил на перемещениях, отвечающих бесконечно малому изменению каждого из параметров.
Если форма потери устойчивости при вычислении потенциальной энергии U задана с точностью до такого количества параметров, какова степень свободы системы, то изложенный здесь способ дает точное решение задачи. Если задать форму потери устойчивости с точностью до числа параметров меньшего, чем число степеней свободы системы, то решение будет приближенным, и минимальное полученное значение нагрузки будет несколько выше действительной критической силы.
14
Одним из приближенных способов решения задач устойчивости путем варьирования функции U является способ Ритца. Для системы с произвольным числом степеней свободы он заключается в следующем:
1. Задаемся формой потери устойчивости в виде ряда
У = aifi(x) + + +CLnfn(x), где аи а2, ап —
неопределенные коэффициенты, a fu /2» ••• fn — функции, каждая из которых должна удовлетворять граничным условиям и представлять по возможности близко предполагаемую форму кривой изгиба.
2. Составляем выражение потенциальной энергии, которая будет функцией параметров а{, ..., ап. U = = F(fli,ctn).
3. Из условий экстремума функции U = 0, =
д(1\ да2
= 0... получаем систему уравнений линейных и однородных относительно аи ..., ап. Для того чтобы она имела решение, отличное от нуля, необходимо, чтобы определитель этой системы обращался в нуль. Составляя определитель и приравнивая его нулю, получаем уравнение для определения критической силы D(P)= 0.
К решению сложных задач с успехом применяется вариационный способ И. Г. Бубнова и Б. Г. Галеркина, не требующий записи выражения потенциальной энергии системы. Этот способ изложен в работе [2]. Применяется также и ряд других вариационных приемов; с некоторыми из них читатель может познакомиться по книге [13].
В следующих главах рассматриваются некоторые частные задачи устойчивости упругих систем.
ГЛАВА 2
УСТОЙЧИВОСТЬ ЦЕНТРАЛЬНО СЖАТОГО ПРЯМОГО СТЕРЖНЯ
§ 4. Прямой стержень с упругой заделкой на одном конце и упругоподатливой опорой на другом
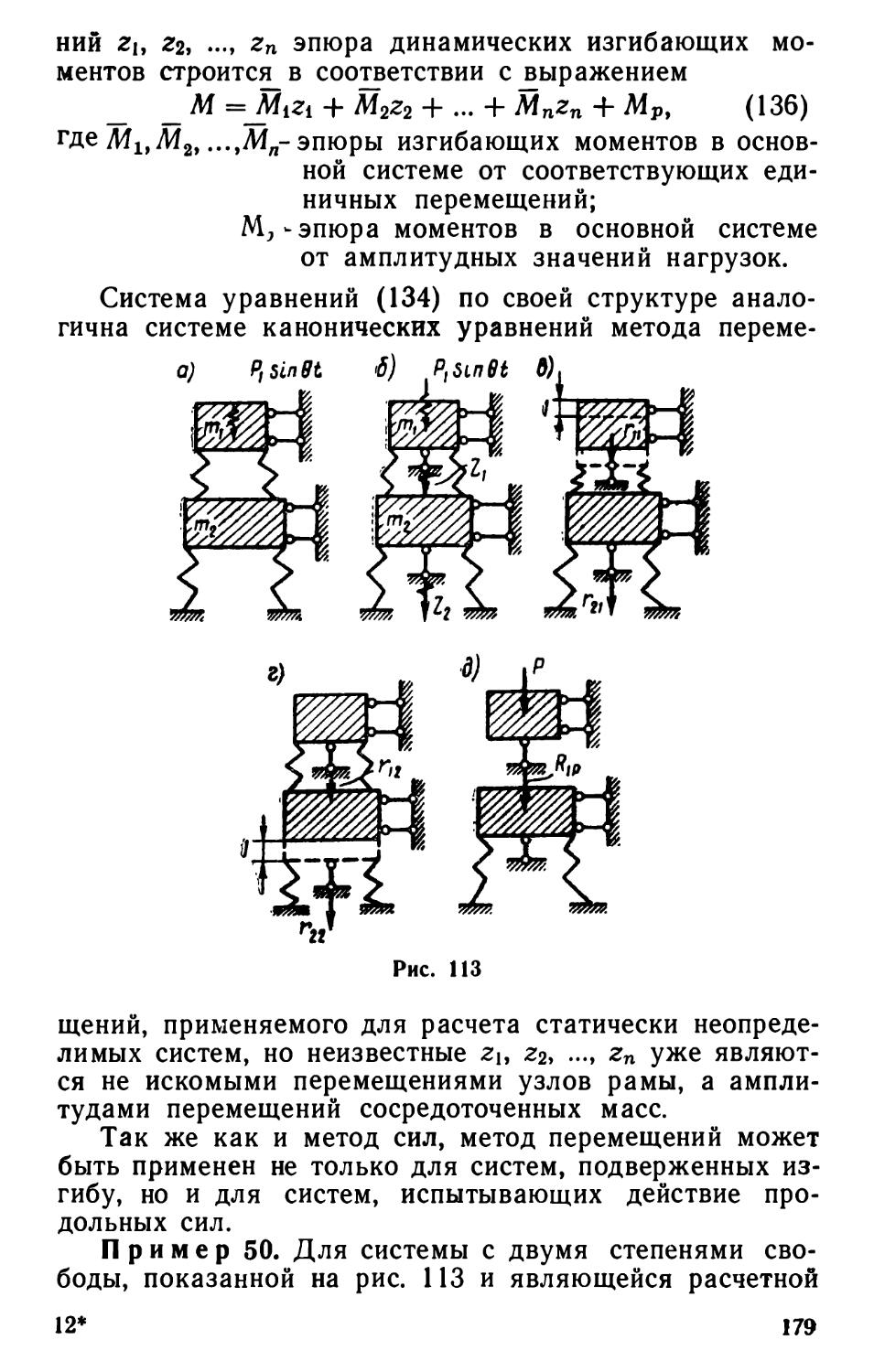
Прямолинейный стержень АВ (рис. 7) имеет упругую заделку в точке А и шарнирную, упругоподатливую в горизонтальном направлении опору в точке В.
15
гii — горизонтальная реакция, возникающая в точке В при горизонтальном смещении этой точки на единицу;
г22—реактивный момент в_заделке Л, возникающий при повороте заделки на угол ф = 1.
Пусть стержень, потеряв устойчивость, изогнулся, как показано на рис. 7 пунктиром. При этом на опорах возникли реакции, показанные на чертеже. Найдем критическую нагрузку точным статическим способом.
Дифференциальное уравнение изгиба имеет вид
Е1у" = М = -Р(6 + у) +
+ fii6(l —х),
или
Ely" + Ру = 6[гц(1-х)-Р]
— интеграл этого уравнения у = Acosnx+ В sin пх + 6р~(/ — х) — lj , (5)
где
Vi-
Для определения А, В и 6 имеем три граничных условия:
1) при jc=0 г/ = 0;
dy
М,
2) при х = 0 — = Ф dx Т 22
6 (ГП1-Р)
г22
3) при х = 1 у=—6.
Подставляя граничные условия в выражение (5), получаем систему трех однородных алгебраических уравнений:
Так как нас интересует ненулевое решение для А, В и б, приравниваем нулю определитель, составленный из коэффициентов при этих неизвестных
Гц1
D =
1:
0:
0:
— 1
« -(т+)
lg til;
= 0.
1; tg nl; 0
откуда после небольших преобразований, подставив Р = —п2Е1, получаем уравнение aj $ у
устойчивости
Г ц1
tg fll — nl-
r?Ei
•1
Гц1 (Гц1 — rfiEl) I пгЕ1 r22
IV
rn=°
(6)
Рис. 8
г„‘0
Из формулы (6) при известных величинах гц, Г&, EI,
I путем подбора определяется величина п и после этого Ркр=п2Е1. Частные случаи:
1) (рис. 8,а): избавляясь от неопределенности, по формуле (6) получаем
tgn/ = 0, nl = in(i = 1,2,3...), PZa = L.t
2) (рис. 8,6): по формуле (6) получаем
откуда:
при гц=0 (что соответствует свободному верхнему концу) получим tg«/=oo или n/=t —(i = 1, 2, 3, ...),
ркР = VlEL.
min 42 f
при лц = оо (что соответствует жесткому опорному стержню) получим tgnl=nl; наименьший отличный от
нуля корень этого уравнения «/=4,493; = 20,19-;
3) (рис. 8,в): по формуле (6) получаем tgnl= .
пЕ/
2—949
17
Пр им ер 1. Определить критическую нагрузку для системы» показанной на рис. 9, а. Расчетная схема будет иметь вид стойки, упруго защемленной внизу (рис. 9, г)
и уравнение устойчивости tgn/=--.
nEI
Величина г-в зависит от формы потери устойчивости всей системы; при симметричной форме потери устойчи-
JD)
6)
б)
гЦ
1 1
1
* г,
1 1
/ \
i
/ \
/
I \
i
1
% Ж.
I,-*»»
12 ш4,0м
Рис. 9
вости (рис. 9,6) величина Г22 определится из условия:
Г ММ , 1.1, El
Ф = I -Jfds= 7r22-4 Y = !. откуда r22 = —;
при кососимметричной форме потери устойчивости
(рис. 9, в) г22 определится из условия р= ( ds =
J EI
= —• • • " = 1» откуда Г22=1,5/. Минимальная критическая сила будет иметь место при минимальном значении Г22.
EI
Таким образом, tgn/i =
= — = = —. Решая
2 nEI 2 п 2 nli nli
путем подбора полученное уравнение, находим til =1,19 и критическая нагрузка, соответствующая симметричной форме потери устойчивости
18
Ркр = 1'19у./- = -1-1?*-- = 0.0394Я/(/ в г*г).
/j 62
Пример 2. Требуется определить критическое значение вертикальной силы, действующей в точке В (рис. 10, а) на стойку АВУ связанную жесткой фермой с двухэтажной рамой CDEF. Стойку АВ можно рассматривать как защемленную внизу и упруго опертую вверху (рис. 10,6). Коэффициент жесткости упругой опоры г и определится из расчета рамы CDEF. Так как реакция от
J-2J,
единичного смещения есть величина, обратная смещению от единичной силы гп = —найдем величину 6ц, приложив горизонтальную единичную силу к узлу D (рис. 10,в). Эпюра М от этой силы показана на рис. 10,г:
Л v С М* ds 26 EIt
6“-sJ— --щ-l-
Используем полученное выше уравнение устойчивости для этого частного случая
Помножив числитель и знаменатель второго члена в скобках на /2, подставив в знаменатель 1=8 м и учитывая, что /-=2/i, получаем
tgnl = nl[l — 0,101 (я/)2].
2* 19
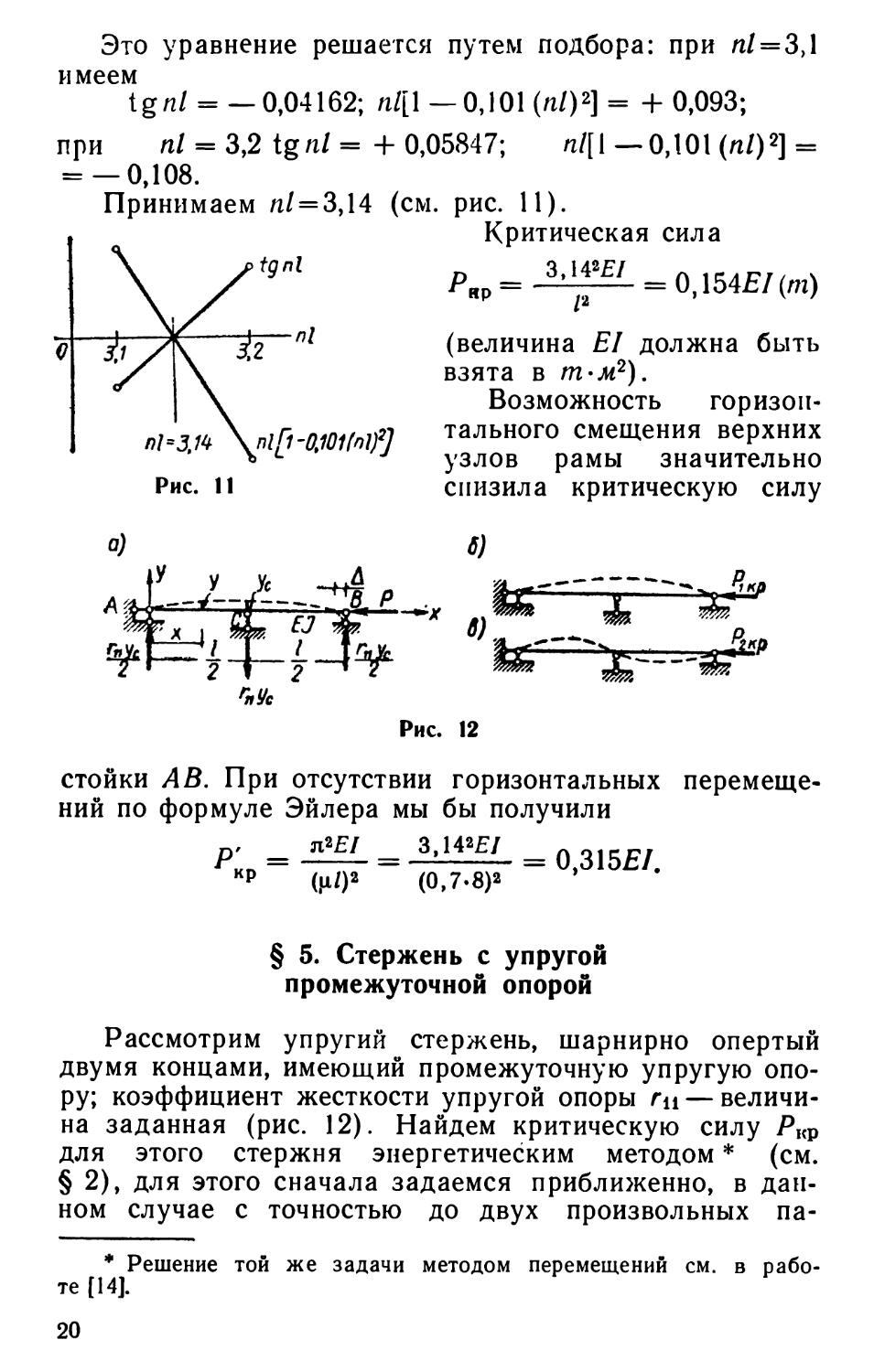
Это уравнение решается путем подбора: при «/=3,1 имеем
tgnl = —0,04162; nl[ 1—0,101 (я/)2] = + 0,093;
при nl = 3,2 tgnl= + 0,05847; nl[ 1—0,101 (л/)2] = = —0,108.
Принимаем «/ = 3,14 (см. рис. 11).
Критическая сила п 3,14 2/ Л 1С/С,/ ч
= —Ч: = 0,154/ (т)
(величина EI должна быть взята в ГП'М2).
Возможность горизонтального смещения верхних узлов рамы значительно снизила критическую силу
б)
Рис. 12
Ри
«Р
йЙ
стойки А В. При отсутствии горизонтальных перемещений по формуле Эйлера мы бы получили
3,1427
р’ =JEL
кр (А/)а
(0,7-8)2
= 0,315/.
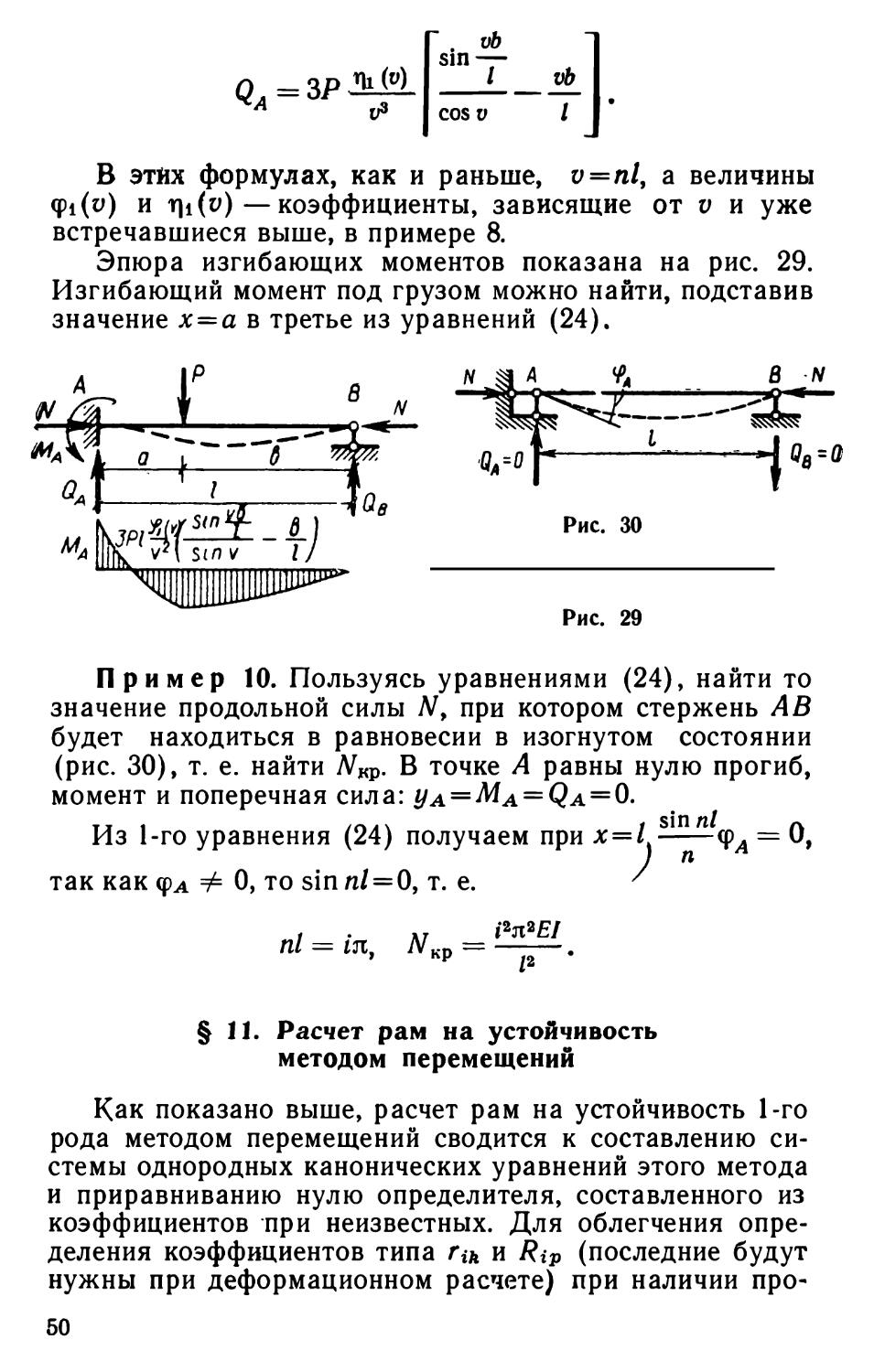
§ 5. Стержень с упругой промежуточной опорой
Рассмотрим упругий стержень, шарнирно опертый двумя концами, имеющий промежуточную упругую опору; коэффициент жесткости упругой опоры г а — величина заданная (рис. 12). Найдем критическую силу Р1ф для этого стержня энергетическим методом * (см. § 2), для этого сначала задаемся приближенно, в данном случае с точностью до двух произвольных па¬
* Решение той же задачи методом перемещений см. в рабо те [14].
20
раметров, уравнением упругой линии в изогнутом равновесном состоянии
. лх . . 2лх
y = atsin — + а2 sin —.
Это уравнение удовлетворяет граничным условиям:
У (0) = 0; у' (0) = 0; у" (0) = 0;
У (0 = 0; У'ЩФО; /(/) = 0;
»(т)* °-
Приравняем нулю сумму работ внешних и внутренних сил на перемещениях, соответствующих приращению одного, а затем другого параметра; в уравнения работ войдет энергия изгиба балки (энергией сжатия и сдвига пренебрегаем), работа, производимая реакцией упругой опоры, и работа внешней силы Р:
77 7- бд1dx + ги0с б°х —
дах El J cai дах
_р_ба1 = 0;
дйх
Ьаг = ± Г М Sa2dx + гиУс Ьаг -
да2 El J да2 да2
— Я — 6о2 = 0.
да2
(7)
Используем зависимость
ш. г? г " Г/ /я2 . пх , 4ла . 2лх \
М = Ely =—alSiny+ —a2sin—j;
dM
daj
/л2
. ЛХ
sin— ; / *
дМ
EI • 4л2
/2
да2
/*
II
II
J_ = аи
2
дус ,
даг
дУс = да2
sin-
2jix
~r
Величину Д определяем следующим образом: если для бесконечно малого элемента (см. рис. 13, а) имеем при его повороте на угол а вертикальное перемещение
верхней точки на dA = dx t-~~- = , то для изогну-
21
того стержня длиной / укорочение вертикальной проекции (рис. 13,6)
Подставив найденные выражения в уравнения (7) и произведя интегрирование, получим:
Так как нас интересует тот случай, когда aiO, а2=т0. находим соответственно из первого и второго уравнений:
Сила Р1кр соответствует симметричной форме потери устойчивости (см. рис. 12,6). Второй член формулы показывает, что наличие промежуточной опоры увеличивает критическую нагрузку; в частности, при гц=оо (жесткая опора) получим PiKp = oo, т. е. такая форма потери устойчивости становится невозможной; при отсутствии
д2 Е1
средней опоры гц = 0, Рцр= .
1г
В нашем случае
л)
р JlIZi , tTn e р 1кр /а яа ’ 2kP Р
л2Е/ 21гц р 4лаУ
14 —п » 2КР «о
22
Сила Ягкр соответствует искривлению по двум полуволнам (см. рис. 12,в).
Расчетной критической силой будет Ртщ.
Найдем то значение Ги, при котором Рмъ=Рш?
я27 . 2/-Гц 4л2Е1
I2
1,5л4/ 146Я/
откуда Гц = .
Рис. 14
146 EI
Таким образом, при гц упругая линия при поте-
146/
ре устойчивости имеет одну полуволну, при Гц I3
две полуволны.
ПримерЗ. Найти критическую силу и форму потери устойчивости для двух систем, показанных на рис. 14, а и б. Расчетная схема стойки АВ представлена на
рис. 14,в. Величину гц= — найдем из условия работы на изгиб стойки CD
для случая а
3 EI = 3 Е/ = 24 Е1 146/
/3 /3 1* ’
D л*/ , 2124EI EI / „ . 48\ 14,7/
р _ _ — /я2 I j —! Р /2 /3Л2 /2 \ Я2 ) 12
— изгиб с одной полуволной, сопровождаемый изгибом стойки CD;
23
для случая б
3 EI = ЗЕ/ __ 192Е/ 146Е/
/3 "" /з/з*
D 4я*/ 39, 4/
кр ~ I* - I*
— изгиб по двум полуволнам, стойка CD неподвижна.
§ 6. Стержень в упругой среде. Устойчивость сжатого пояса открытого моста
Рассмотрим шарнирно опертый двумя концами стержень, находящийся в сплошной упругой среде, характеризуемой коэффициентом жесткости р(р— реакция на погопную единицу длины стержня при единичном смещении в направлении, перпендикулярном его оси) (рис. 15). Если такой стержень, нагруженный на конце осевой силой Р после потери устойчивости находится в изогнутом равновесном состоянии, то в число сил, обеспечивающих равновесие, входят и реакции упругой среды, интенсивность которых равна ру, где у — величина прогиба.
Применим к этой задаче энергетический метод, приравняв нулю сумму работ внешних и внутренних сил на перемещениях из изогнутого состояния в прямоли-
А + W = 0. (9)
Работа внешней силы
/
А = -РА = -(у')Ых. (9а)
о
Пренебрегая потенциальной энергией сжатия и сдвига, получим работу внутренних сил, как сумму работ изгибающих моментов и реакций упругой среды:
Ъ
Г
т
Рис. 15
неиное:
24
/ I
jV)2d* + -jV-** (96)
о о
(следует хорошо уяснить, что при переходе из криволинейного в прямолинейное состояние сила Р остается постоянной, работа ее равна РД; внутренние же силы уменьшаются до нуля, поэтому в выражение их работы
входит коэффициент Подставив выражения (9а) и (96) в условие (9), получаем
/ /
EI f (y")2dx + $ \y2-dx
Р«р = ——i - . (10)
f (yV-dx
0
Как видно из формулы (10), наличие упругой среды повышает критическую силу. Чтобы определить величину РКр, надо задаться формой упругой линии y=f(x). 0 . knx
Задаемся уравнением у = а sin —у— , которое удовлетворяет граничным условиям: при* = 0 у — 0 у" = 0; при х = 1 у = 0 у" = 0.
При этом
j' (уУ .dx = ; J (y'Y-dx = ;
о о
W-T-
о
Подставляя полученные значения в формулу (10) и произведя небольшие преобразования, получаем
р Р\ kWEI )
Нас интересует минимальное значение ЯКр, поэтому встает вопрос, при каком числе полуволн kPuр будет минимальным. Очевидно, это зависит от конкретного значения коэффициента жесткости упругой среды р. Найдем те граничные значения р, при которых становится равновозможной потеря устойчивости по двум формам (с од-
25
ной и с двумя полуволнами, с двумя и тремя полуволнами и т. д.). Для этого составим равенства:
1\ pk=\ _ pk=2, л2Е1 Л , р/4 \ _ (л I Р*4 \
' кр к* ’ /2 \ п*Е1 ) /2 \ + 4я4/ / ’
откуда $ = --Л*Е- .
/4
4+5--9+Г’
0 36л4/
откуда р=—— ит.д.
Отсюда получается следующая таблица: при
*-1;
при
4п*Ш „ 36л*Е1 k=
/4 /4 '
36 л4/ д Л44л4/ , Q
р Я = о
/* /4
И Т. Д.
Определив число /г, соответствующее заданному значению р, находим Р„р по формуле (11).
Пример 4. Найти критическую нагрузку для сжатого пояса открытого моста (задача Ясинского).
Сжатый верхний пояс открытого моста (рис. 16) при потере устойчивости из плоскости фермы работает как стержень, нагруженный сосредоточенными горизонтальными силами (DiXcosa) в точках прикрепления раскосов и опертый на упругие опоры, которыми являются работающие на изгиб стойки (рис. 16,в).
При большом числе панелей можно:
1) упругие опоры заменить сплошной упругой средой
с коэффициентом жесткости Р=—, где г а — горизон-
d
тальная сила, смещающая верхний конец стойки на единицу (рис. 16,6, г); d — длина панели;
2) сосредоточенные силы D* cos а заменить сплошной нагрузкой, меняющейся по треугольному закону
26
(рис. 16). Максимальная интенсивность нагрузки 70 определится из условия
2- = Dcosa; q0 = -y-Dcosa.
1/2
1/2
*) i
D,coso(DjCosat
ъЬя. vhz jJL
г;
4/.
1 " * fly ' ' ' 4 9 9 Эпюра нагрузок
ТПШПВртППгтг—rtrTTTrrnTllIlfinl
Рис. 16
Применяя энергетический метод, получаем? работа внешних сил
А = - J qe-dxj[ (y'Y-dx = -J[*(l-»*.. X 0 0 о
х
X J (y'Y-dx -dx;
работа внутренних сил
i i w = *LUyy.dx + ±V jV-d*.
О о
Приравнивая нулю сумму работ внешних и внутрен-
27
них сил, находим критическую интенсивность нагрузки на опоре
i i
El (y")2-dx + JpУ-dx
р=7г
I [„_«
Критическая продольная сила посередине пролета
Тимошенко дал решение этой задачи, задавшись формой упругой линии y=f(x) в виде бесконечного ряда
оо
V. knx
*k sm—.
п=1
При этом критическая сила посередине пролета запи-
п2Е1
сывается в эйлеоовской форме NKT)= , где коэффи-
р (ц/)2
циент свободной длины и зависит от жесткости /, пролета I и коэффициента жесткости упругой среды р. Эта зависимость приведена в табл. 1.
Таблица 1
р/4
16/
0
5
10
15
22,8
56,5
0,696
0,524
0,443
0,396
0,363
0,324
р/4 16 EI
100
162,8
200
300
500
1000
И
0,29
0,259
0,246
0,225
0,204
0,174
§ 7. Стержень переменного сечения
Для общего случая стержня переменного сечения с переменными по длине продольными силами Nx (рис. 17) дифференциальное уравнение изогнутой оси при потере устойчивости имеет следующий вид:
(Е1ху'')"+ (Nxy')' = 0 (12)
(см. работу 17).
J (y')2-dx Vdx
28
Если стержень нагружен осевыми силами только у концов, то Nx = P = const, и уравнение (12) приобретает вил
(Е1ху")" + Ру" = 0 (13)
или
М" + — м = о.
Е1Х
Для некоторых частных законов изменения жесткости вдоль стержня (например, при Е1 = Аха, где А и
а — постоянные коэффициенты и т. д.) уравнение с переменными коэффициентами (13) решено и, таким образом, получены точные значения критических нагрузок. Эти решения приводятся в работах [14], [19] и др. и связаны с применением Бесселевых и других специальных функций или с численным интегрированием дифференциальных уравнений.
Рассмотрим простейший случай стержня, жесткость которого меняется по длине уступами (рис. 18). Нагрузка приложена вверху (Р) и на уровне уступа (рР). Покажем решение статическим и энергетическим способами.
Статический способ расчета
Записываем дифференциальные уравнения изгиба по участкам:
Е11у[ + РУг = ЬР,
ЕГ + и+МР-ур + ЩР.
29
Интегралы этих уравнений:
ух = Ai sin пгх + Аа cos ntx + б,
у2 = Вх sin п2х -f В2 cos пгх + —i- (б + рб,
1 + Р
где
1f* + Vp,
у Е1г V Eh
Для определения Аи А2, В и В2, б, 61 имеем шесть ус¬
ловий:
У2 (°) = °; у\ (°) = 0; у г («0 = а,; у2 («0 = ух («0;
у\ («0 = у\ («0; Ух (0 = у[ (0 = О-
Из граничных условий находим 5i = 0 и, исключив 6 и б 1, получаем следующие три однородных уравнения для определения Аи Л2 и В2:
Ai sin nial + А2 cos ntal — B2 (1 + P) cos n2al = 0;
Ai cos tiial — A2 sin пкх/ + B2 — sin n2al = 0;
nx
Ai sin /11/ + A2 cos /it/ = 0.
Приравняв нулю определитель из коэффициентов при неизвестных, получаем характеристическое уравнение
для определения критического параметра нагрузки РКр:
tg «1 (1 — а) / tg n2al = — (1 + Р). (15)
П2
Из уравнения (15) при а = 0 имеем tg nj = 00; (m0m,n = Y; jVikp =
что соответствует стойке с постоянной жесткостью 7ь при а--=1 имеем tgn2l=oof откуда N2kv = 71 Е1г, что соот-
4/2
ветствует стойке с постоянной жесткостью Е12,
30
Энергетический способ расчета
Приравняем нулю сумму работ внешних и внутренних сил на перемещениях из изогнутого состояния в прямолинейное.
Работа внешних сил
г al
— А = SPA = Р-Г00*Л + РР- -у §(у')21х.
о о
Работа внутренних сил
al /
и? = Е J r = Y [EI* I{уУ dx + E/l I{уУ dx] •
О al
Из условия A + W=0 находим
al I
EI2\(y"Ydx + EI1 J (y"Ydx
Ркр=- . (16)
pj (y'Y d* +J (y’Ydx
Для получения приближенного решения зададимся формой потери устойчивости в виде полинома
у = а0 + atx2 + а-\ а2пп,
из которого удержим только три первых члена; величины Яо и й2 определим из граничных условий:
у(0) = у'(0) = 0; у(1)Ф0; у'(1)=0; у"(1)=0.
_ at
, 1*;' нии принимает вид
При этом а0=0; аг — и уравнение упругой ли-
Задавая упругую линию с точностью до одного параметра аи мы как бы превращаем заданную систему в систему с одной степенью свободы.
Находим
31
и, внося эти выражения в формулу (16), после интегрирования и подстановки пределов, получаем:
р _Mh -fe + (a-T“,+ -H(f-1) m
"■ '■ ■ +»(*-!-+*) '
при а=0 формула (17) дает
р = МЬ. . ®ll®? = 2,47065-
р 12 15-68 12
EI
(точное решение Р1ф = 2,4674 —относительная точ-
/2
иость составляет 0,13%).
Если задать уравнение y=f(x) с точностью до двух параметров:
то формула (16) ири а = 0 дает
16 4
р g/i 42 +T2+T
кр I2 17 * 348 404 .
1 + 153г+ 935г
(см. работу [14]), где z= — .
а
Наименьшее значение РКр определится из условия dP Л
—— = 0, которое приводит к квадратному уравнению dz
z2+1,06232+0,1604=0 с корнями Zt~—0,1822, г2=
= —0,8802.
Е1
При Zi = —0,1822 получаем Ркр=2,4674 , что прак-
I2
ткчески совпадает с точным решением.
Пример 5. Найти критический параметр нагрузки РКр для стойки, показанной на рис. 19.
Имеем
При решении задачи статическим методом получаем характеристическое уравнение
tg0,5ni/ • tg 0,79/4/ = 0,633 • 5 = 3,16.
Подбором находим «t/ = 1,59; при этом
tg 0,795= 1,014;
tg(0,79-1,59)= tg 1,26 -3,11;
1,014-3,11 « 3,16.
Таким образом, критический параметр нагрузки
кр
2,53 Е1г
/2
При решении задачи энергетическим методом по формуле (17) получим
Рис. 19
Р —
г кр —
ЗЕТ
/2
2
с
2,61 Е1Х
/2
(расхождение с результатом статического расчета 3%).
Сниженная точность энергетического расчета по сравнению с приведенным выше расчетом для случая а=0 объясняется тем, что уравнения упругой линии для верхней и нижней части ступенчатой стойки в действительности будут различны.
§ 8. Составные стержни
Рассматривая вопросы устойчивости стержней со сплошным поперечным сечением, мы учитывали до сих пор только деформации изгиба стержня, потерявшего устойчивость, пренебрегая деформациями сжатия и деформациями сдвига. В стержнях, составленных из отдельных ветвей, соединенных между собой какими-то связями (решеткой, планками, шпонками, гвоздями и т. д.) (рис. 20, а, б, в), деформация связей при потере
3—949
33
устойчивости создает дополнительную деформативность всей конструкции, что может существенно снизить величину критической нагрузки.
Общая постановка задачи об устойчивости составного стержня дана в работах проф. А. Р. Ржаницына (см. [18], [19] и др.), который делит связи между ветвями
на связи сдвига, пере-
0) дающие касательные
напряжения, и поперечные связи, передающие нормальные напряжения, действующие перпендикулярно оси стержня (рис. 20, г).
Для частного случая шарнирно опертого двумя концами стержня, состоящего из двух ветвей, далеко отстоящих друг от друга (жесткость каждой ветви на изгиб мала по сравнению с жесткостью всего поперечного сечения) с жесткими поперечными связями и податливыми связями сдвига (например, изгибаемые, но сохраняющие свою длину планки, рис. 20,6), минимальная критическая сила определяется по следующей формуле:
111
Связи сдвига
Поперечные
связи
Рис. 20
кр —
п*Е1
/2
1
п*Е1
1
С02
(18)
I де
EI— жесткость всего сечения;
(о— расстояние между осями ветвей;
§—коэффициент жесткости шва на сдвиг* Тслт / кг \ # бед [cjfl/9
1 =
7\д— сдвигающее усилие, приходящееся на одну связь;
34
т—число связей на единицу длины шва;
6СД—деформация взаимного сдвига смежных волокон по обе стороны разделяющей плоскости шва.
Величина —— в этом случае эквивалентна удельно-
со2!
му углу сдвига сплошного стержня
k
GF
(k — коэффициент, зависящий от формы поперечного сечения, см. [16]) и при такой замене формула (18) совпадает с приближенной формулой Энгессера, данной им в 1891 г. и учитывающей влияние сдвигов в сплошном стержне:
Ркр = Рэ \ .
где Рэ —эйлеровская критическая сила при данных граничных условиях.
Формула (18) показывает, что при увеличении жесткости связей критическая сила возрастает и при стремится к эйлеровской критической силе для сплошного стержня: при -4), т. е. при отсутствии связей, получаем РКр = 0, так как в этой формуле жесткость отдельных ветвей на изгиб принята равной нулю.
Решим энергетическим методом задачу об устойчивости стержня, состоящего из двух поясов, соединенных между собой реш ткой в виде раскосов и cr ек. Пус . ь, например, это буд ,т колонна, жестко защемленная BHHjy и свободная вверху (рис.21).
До потери устойчивости пояса стержня сжаты, решетка не работает. При потере устойчивости ось стержня изгибается, не меняя своей длины; поперечные сечения стержня поворачиваются, при этом один пояс укорачивается, другой — удлиняется, суммарная работа первоначальных продольных сил в поясах равна нулю. Работу производят дополнительные усилия в поясах, возникающие благодаря изгибу, усилия в элементах решетки, также возникающие 3* 35
Рис. 21
при потере устойчивости, и внешняя сила. Следует отметить, что элементы решетки в реальных конструкциях прикрепляются к поясам какими-то более или менее податливыми связями (заклепки, болты и т.д.). Дефоомативность этих связей также может влиять на величину критическои нагрузки. В данном случае этих деформаций мы не учитываем. н
Задаемся упругой линией в форме
у = а( 1 — cos —) ,
V 21 j’
которая удовлетворяет граничным условиям: при * = 0 у = 0, у'= 0; при х = I уф 0, у'фо, у" = 0.
Опускание верхней точки колонны
о
_ а»л» _ 21_ ' я __ а2я*
8/2 л 4 16?'
Работа внешней силы на перемещениях из криволинеиного состояния в прямолинейное
А = —Р.А = _
161 ’
Работу внутренне сил найдем как работу продольных сил, пренебрегая изгибом каждой панели пояса в
отдельности:
1,2 - — -2 ' 1/2
р
Kd
2EF,
где первая сумма относится к поясам, вторая — к стойкам и третья — к раскосам *, с— длина панели пояса; h—длина стойки; d— длина раскоса.
Усилие в каждой панели пояса определяется, как мо¬
* Учитывая работу продольных сил и в стойках, и в раскосах мы тем самым учитываем деформативность и связей сдвига, и поп«-’ речных связей. ’
36
мент относительно соответствующей моментной точки, деленный на расстояние между поясами h
М — Р (а — у) -- Ра cos ;
\т М г» а лх
N п = — = Р — COS — . h h 21
Решетка воспринимает перерезывающую силу. Усилия в стойках и в раскосах равны:
dM
= ±
Рал
-sin
лх
dx
21
21'
= ±
Рал
21
d
• — -sin h
лх
2Г*
Таким образом, суммарная работа внутренних сил
W = Vp2-—cos2 — • -- +Ylsin2— • -2- + Li ft* 21 2EFi -1 At1 21 2EFi П С
+2
P2a2n2 d3 . 2 лх 1
— Sin2 —
8/2 h2 21 EFt p
Приравняв нулю сумму работ внешних и внутренних сил, получаем
л2Е 21
Р кр —
4с VI 1 я* n2h 1 лх
JT+—1т;5шг¥ +
(19)
Ft 21 ' I* i-J Fi
п О
л 2Е 21
пЧ* \Л 1 . лх
+ /2/j2 Fl Sm 21 P
здесь x—координата моментной точки, соответствующей определению усилия в поясе каждой панели.
Формула (19) показывает, что деформативность решетки уменьшает критическую силу. Если площади раскосов или стоек стремятся к нулю (т. е. отсутствуют либо связи сдвига, либо поперечные связи), критическая сила составного стержня с пренебрежимо малой жесткостью отдельной ветви на изгиб стремится к нулю. Если уве¬
37
личить жесткость решетки, критическая сила возрастает иприЯ-оо и Я-оо
с р
n2Eh2
р
г кр
S1 „ ях ’
7Г ¥
п
что при постоянном сечении поясов равно
Р _ л2Е1_
КР “ 4/2 ’
где I=--Fh2—момент инерции монолитного стержня,
состоящего из двух поясов с общей площадью 2F.
Если сечения поясов, стоек и раскосов не меняются по длине стержня, то формулу (19) удобно преобразовать следующим образом: вынося из-под знака суммы
постоянные площади и учитывая, что —Fuh2 = It полу¬
чаем
X
я2Е/ 4/2
1
кр = -Ё~ х
&
2с пх я2/ Г h пх
— • 2 cos2 — 4- — 2 sin2 — 4- 2 sin2
I 21 P L 21FC 21 2lh*Fp
ЛХ 1
2/"J
Под знаком каждой суммы в знаменателе стоит столько членов, сколько панелей длиной с имеется в составном стержне; разделим все члены в знаменателе на с, помножим на dx и заменим суммирование интегрированием.
При этом
= Г cos2 — -dx =
21 Г , 1 . пх , ях 1
= — + — sin я 4 / 4/J
Введя обозначения
я2 EI
р* =
9 W
38
где и- — коэффициент свободной длины, получаем формулу, действительную при любых граничных условиях *:
1 (20)
1 +
-[ Е [
1
+ '
Fc tg a Fр sin
— г
sin a cos2 aj
здесь a— угол между направлениями раскоса и стойки; Рэ—критическая сила монолитного стержня;
Fc— площадь сечения стойки;
Fp—площадь сечения раскоса.
Пример 6. На рис. 22 показаны поперечное сечечие и г анель со связями сжатого пояса Ki ебекского места (США), обрушившегося во время сборки 29 августа 190/ г. Авария произошла из-за потери устойчивости в связи с тем, что не было учтено влияние деформативности решетки на величину критической силы.
Требуется определить критическую силу составного стержня данных размеров и сравнить ее с критической силой монолитного стержня того же момента инерции**. Имеем:
площадь сечения одного уголка 204x162x24 F1 = (20,4 + 13,8)2,4 = 34,2 см2;
площадь сечения одного уголка 204x89x23,8 F2 = (20,4 + 6,52) 2,38 = 64 см
* Формула (20), выведенная другим способом, приведена в книге [14] и др.
** Данные взяты из книги [4].
ЗЭ
площадь сечения одного уголка 89X76X9,5
F3 = (8,9 + 6,65)0,95 = 14,8 см2; площадь сечения одного уголка 102 X 76X 9,5
Fk = (10,2 + 6,65)0,95 = 16,0 см2;
площадь сечения всего пояса
Fn ■( 8,74 + 8,92)2-138,4 + 4-34,2 + 8-64 —
-6.42,5-2,4 = 4926,8 см2;
площадь стоек на длине одной панели
Fст = 2 -14,8 = 29,6 см2;
площадь сечения раскосов на длине одной панели
FpacK = 4» 16,0 = 64 см2.
Угол наклона раскосов а«45°; sin a=cos а=0,707; tg а= 1,0.
Критическая нагрузка по формуле (20)
введем в пол/ченную формулу величину критического напряжения
При = 2,1 • 106 кг!см2 и ОкР =хПц=2400 кг!см2 по-
Р = Р3
кр — Г
= РЭ
рэ
I +— 0.0779
Тогда
°ко
1 + -Fn-0.0779
лучим
2-4-10»
1 + 2AAV -0'0779-4926'8
= Р3
= 0,697Р3,
1+0,438
40
Таким образом, в данном случае (при а*р = = 2400 кг/см2) деформативность решетки снизила критическую силу в 1,44 раза. В действительности гибкость потерявшего устойчивость стержня Квебекского моста была мала, и эйлеровские критические напряжения значительно превышали предел пропорциональности материала, что еще более усилило влияние деформативности решетки.
ГЛАВД3
УСТОЙЧИВОСТЬ ПЛОСКИХ РАМ*
§ 9. Постановка задачи
При рассмотрении вопросов устойчивости рам так же, как и других систем, необходимо различать два типа задач:
потеря устойчивости 1-го рода (потеря устойчивости в Эйлеровском смысле) и
потеря устойчивости 2-го рода (потеря несущей способности сжатоизогнутой рамы).
Постановка задачи и схема решения при расчете на устойчивость 1-го рода
Для исследования устойчивости рамы принимаются следующие допущения: 1. Рассматривается только узловая нагрузка, не вызывающая поперечного изгиба стержней рамы.
2. Стержни считаются нерастяжимыми и несжимаемыми.
3. Изменением растояния между концами стержня, которое получается благодаря его изгибу, пренебрегаем **.
4. При работе учитываются нормальные силы, возникающие до потери устойчивости. Влияние приращений нормальных сил Д/V, возникающих в момент потери устойчивости, не учитывается.
5. При определении поперечных сил в изогнутых
* Наиболее полно вопросы устойчивости рам разработаны п монографии [8].
** Это допущение неприменимо при определении работы внешних сил, если задача решается энергетическим методом.
41
стержнях не учитывается изменение угла наклона сечения за счет изгиба стержня.
Рассмотрим раму, представленную на рис. 23. Пока нагрузка меньше критической, единственной возможной формой равновесия будет прямолинейная форма, показанная на рис. 23 сплошной линией. Существует такое критическое значение нагрузки (Ркр — критический параметр этой нагрузки), при котором, кроме прямолинейного (являющегося при данной нагрузке неустойчивым) положения равновесия, возможно еще другое, изогнутое равновесное состояние (на рис. 23 показано пунктирной линией). Задачей расчета является определение критической нагрузки, по которой при заданном коэффициенте запаса можно определить расчетную нагрузку.
Поскольку новое, изогнутое состояние есть состояние равновесия, расчет может быть произведен любым из методов, применяемых к расчету равновесных систем, в том числе методом сил или методом перемещений. При вы-
а)
1
Jf
я
дЛ
ШИ
Га
Рис. 24
боре основной системы следует всегда стремиться к тому, чтобы в основной системе не возникало изгибающих моментов от заданной нагрузки; например, для рамы, показанной на рис. 23, это условие удовлетворяется при основных системах, показанных на рис. 24, а, б, и не удовлетворяется для основной системы в *. При отсут¬
* Более подробно о выборе основной системы при решении методом сил см. § 12.
42
ствии моментов от нагрузки в основной системе все свободные члены канонических уравнений равны нулю и система уравнений приобретает вид: для метода сил
6 11*1 + 612*2 + + 6ln*n = о,
621*1 + 622*2 + + б2п*п = О,
6nl*l + 6п2*2 +
для метода перемещений Гу г 1 + rl2z2 + Г2&1 + /22Z2 +
+ 6 nn*n — Oj
+ rlnZn = О, + 2 п%п — О,
Г nlZl + Т n2Z2 + + Г nnZn = 0.
В этих уравнениях 6ш и г,-* соответственно перемещения и реакции по направлению i от единичных лишних неизвестных при наличии продольных сил в стержнях. Таким образом, в 6гл и rih входит параметр нагрузки Р.
В ИЗОГНУТОМ раВНОВеСНОМ СОСТОЯНИИ Х{ф0 и
система же линейных однородных уравнений дает ненулевое решение для неизвестных только при равенстве нулю определителя, составленного из коэффициентов при неизвестных. Составляем определитель и, приравняв его нулю, получаем так называемое уравнение устойчивости, из которого и определяется критический параметр нагрузки
= 0.
В расчетах на устойчивость для большинства типов рам метод перемещений требует более простых и менее трудоемких вычислений, чем метод сил. Это имеет место особенно потому, что усложняются вычисления коэффициентов канонических уравнений по деформированной схеме с учетом продольных сил в стержнях (см. § 10,12). Н. В. Корноуховым в работе [8] показано, что метод сил может оказаться целесообразным при расчете устойчивости рам с большим числом стержней, из которых только немногие имеют продольные силы, отличные от нуля.
«и;
S12! *
• Ап
Гп'у
Г12*, • •
•Гщ
D =
2l
22; '
* *®2л
= 0 или D=
Г2Ь
Г22*. * ’
* Г2 г
Л2 *
• 'бЯЯ
ГпЬ
•Гпп
43
Более детальный разбор обоих методов и примеры расчета см. ниже.
Постановка задачи и схема решения при расчете на устойчивость 2-го рода.
Так называемый «деформационный расчет»
Пусть дана рама (рис. 25,а), в стержнях которой даже при малых нагрузках возникают и продольные силы, и изгибающие моменты. График зависимости какого-либо перемещения (например, горизонтального перемеще-
ста раздвоение форм равновесия, имеется только одна изогнутая форма равновесия, и прогибы растут с увеличением нагрузки. В этом случае критической или предельной нагрузкой будет нагрузка, соответствующая исчерпанию несущей способности рамы.
Поскольку при росте деформаций и изгибающих моментов в элементах рамы возникнет текучесть, предел несущей способности будет достигнут раньше, чем в предположении упругой работы (см. пунктирную линию на рис. 25,6), и определение действительной предельной нагрузки всегда связано с расчетом рамы за пределом упругости. Этот вопрос выходит за рамки настоящего курса и здесь не рассматривается.
При расчетной нагрузке обычный расчет рамы на прочность производится по недеформированной схеме; при этом нагрузки, направленные вдоль оси стержней и передающиеся непосредственно на опоры (силы Р и \лР на рис. 25, а) и вообще продольные силы в стержнях, не влияют на величины изгибающих моментов; в действительности, благодаря изгибу эти нагрузки вызывают дополнительные усилия и перемещения, которые при больших осевых силах и больших гибкостях стержней могут достигать значительной величины. Расчет с учетом этих дополнительных факторов, который ведется уже по де¬
ния верхнего узла Д) от нагрузки Р в предположении неограниченной упругой работы системы показан на рис. 25, б сплошной
линией. Здесь не про-
Рис. 25
исходит потери устойчивости в эйлеровском смысле, не имеет ме-
44
формированной схеме рамы, называется «деформационным расчетом».
Система канонических уравнений при деформационном расчете имеет тот же вид, что и при обычном расчете на прочность, например, при решении методом перемещений
Гц%1 + Т 122 + + rinZn + Rip = О,
nli + п22 + + Г-ппп + Rnp — О,
но здесь гik, Rip соответственно реакции в связи i от единичного смещения связи k и от нагрузки при наличии постоянных продольных сил в стержнях.
Таким образом, для решения задач устойчивости I и
II рода необходимо уметь определять усилия и перемещения в сжатоизогнутых стержнях. Переходим сейчас поэтому к рассмотрению дифференциального уравнения изгиба сжатоизогнутого стержня.
§ 10. Дифференциальное уравнение изгиба сжатоизогнутого стержня и его интеграл
Пусть первоначально прямолинейный стержень АВ под действием сосредоточенных сил Р* равномерной нагрузки q, моментов и поперечных сил по ко щам jМА, Qa, Мв, Qb и постоянной продольной силы N изогнулся и переместился, как показано на рис: 26.
Изгибающий момент в произвольном сечении будет равен
Рис. 26
Mg = N(y-yA) + MA + QA-x-
(21)
где под знаком суммы стоят только те силы, которые находятся левее сечения х.
Дифференциальное уравнение изгиба Е1у" = —М по-
45
еле подстановки значения изгибающего момента по формуле (21) примет вид:
у"+-у=-[ма + -уа-
_S--Z/((*-a,)]. (22)
Введя обозначение получаем общее реше-
ние дифференциального уравнения (22) в следующей форме:
у = Cj cos пх + С2 sin пх + уА — [МА + QA дг) +
+ SPj [п (х — а,) — sin п (х — а;)] —
— Г1 — — cos пх 1. (23)
п*Е1 [ 2 J к '
В выражении (23) первые два члена представляют собой общий интеграл однородного уравнения у" + N
Н у = 0, а остальные члены — частный интеграл неод-
EI
нородного уравнения (22), что легко проверить непосредственной подстановкой в уравнение. С{ и Сг — произвольные постоянные, определяемые из граничных условий:
МА
1) при дг = 0 у = УА, откуда Сх = —;
2) при лг - 0 - Члг откуда С,= -Цф„+ А.).
Подставив полученные значения произвольных постоянных в выражение (23), получаем после небольших преобразований окончательную формулу для прогиба и путем ее последовательного дифференцирования — формулы для углов поворота, моментов и поперечных сил в произвольном сечении сжатоизогнутого стержня:
, sin/i* . cosnx — 1 АЛ ,
У = Ул+—оЛ~г"Л + "?- + »■
46
dtt
ф = — = cos пх*цАdx
Sinn*
nEI
мл+
. cos nx — 1 ~ , —
-I ——Q + ф,
nEI
M = — EI = nEI sin ПХ'cp, + cos nxM, +
dx2 л л
+ !i.Q +м,
dM
Q = — = n?EI cos nx-го. — n sin nxM. +
dx
+ cos nxQ . + Q.
(24)
(25)
В этих формулах у, ф, М, Q представляют собой влияние пролетной нагрузки на соответствующую функцию и для нагрузки, показанной на рис. 26, определяются по следующим формулам:
У = -jzr [п (х — at) — sin п (х — а,)] + V
rrEI
. q I n2x2 , t \
—— f cos nx — 1 ,
n*EI \ 2 ) 9
Ф = Zpi [1 — COS «(x a,)] +
+ -r— {nx — sin nx), n3EI
M 5- 2Рг sin n{x — a,) + — (cos nx — 1),
Q = — 2Pt cos n(x — ai) — sin nx.
n
Во всех случаях под знаком 2 стоят только те силы, которые находятся левее сечения х.
Пример 7. Рассмотрим балку, защемленную двумя концами, в которой при наличии постоянной продольной силы N произошел поворот левой заделки на угол, равный единице (рис. 27).
Из четырех начальных параметров два известны: Фа=1; Уа = 0; остальные два определяются из условий
У в = 0; фв = 0. (а)
47
Подставляя значение х=1 и условия (а) в первые два из уравнений (24), получаем для определения МА и Q* следующие два уравнения:
sin nl , cos nl — 1 . sin nl — nl _ g
~n riW A A~ ’
, sin /2/ w .cos nl — 1 Л Л
cos nl M.-{ Q. = 0.
nEl A n*EI A
Решая совместно полученные уравнения и вводя обозначение
(26)
получаем после небольших преобразований
Мл= =■4-f
Л / I 4 tg о о I I
~~2~ °
о =-OL
Ча /2
Г—•
4t go
[v tgv — v v e v sin у I
2 tg у v 2 sin с/ v I
2tgy-i 2 tg — 0 J
6El , 4
= ГФ4(Р).
Подставив значения Л1А и QA в третье из уравнений (24), найдем изгибающий момент на правой опоре Мв■
2EI Г v v — sin v П 2EI
/ I 2 sin t; л v I I
L
ZC.1 I V V — Sin V I / v
MB = 7-1 ;ГТТГТ : I = — p3 (l).
Эпюра изгибающих моментов показана на рис. 27. Пример 8. Рассмотрим балку с заделкой на одном конце и шарниром на другом, в которой при наличии постоянной продольной силы N произошло смещение правой опоры в направлении, перпендикулярном оси балки на величину Д=1 (рис. 28),
48
Из четырех начальных параметров два известны: Уа= 0; фл = 0; остальные два определятся из условий:
У в = 1; Мв = 0. (б)
Подставляя значение х=1 и условие (б) в первое и третье из уравнений (24), получаем для определения МА и Qa следующие два уравнения:
cos/i/ — 1 . sinnl—nl w
■Мд+ X
пт А пт х Qa = 1,
cosnl‘MA -f smnl-.QA = о.
Вводя величину v = ln и решая совместно полученные уравнения, находим:
м 3/ 3El . .
М. = 2 .m, (t»V
А I* 3 (tg о — v) Р
п п 3EI V3 ZEI , .
Qa~Qb— р ’ 2(tgv — v) ~ Р
Эпюра изгибающих моментов показана на рис. 28.
Пример 9. Рассмотрим балку, находящуюся под действием сосредоточенной вертикальной силы в пролете и постоянной продольной силы N (рис. 29).
Для этой балки #а = Фа=0. Момент и поперечная сила в заделке определяются из условий: ув = 0; Мв = 0. Подставляя эти условия в первое и третье из уравнений (24), получаем:
cos nl — 1 .. . sin nl — nl Л . P , , . ,. »
~Г'МЛ+ -„,и -Q, + n--(»-sin)-o.
cosЫ-М. + slnnf Q. —— -sinrtb = 0.
A п л n
Решая совместно эти уравнения, находим
мА =
— ZPI-1--1 1- -1 ’
к* sin t» I I
4—949 49
В этйх формулах, как и раньше, v=nl, а величины Pi(y) и ti(u)—коэффициенты, зависящие от v и уже встречавшиеся выше, в примере 8.
Эпюра изгибающих моментов показана на рис. 29. Изгибающий момент под грузом можно найти, подставив значение х = а в третье из уравнений (24).
Пример 10. Пользуясь уравнениями (24), найти то значение продольной силы N, при котором стержень АВ будет находиться в равновесии в изогнутом состоянии (рис. 30), т. е. найти NKl. В точке А равны нулю прогиб, момент и поперечная сила: i/a = Ma = Qa = 0.
Как показано выше, расчет рам на устойчивость 1-го рода методом перемещений сводится к составлению системы однородных канонических уравнений этого метода и приравниванию нулю определителя, составленного из коэффициентов при неизвестных. Для облегчения определения коэффициентов типа гг* и /?гр (последние будут нужны при деформационном расчете) при наличии про-
§ 11. Расчет рам на устойчивость методом перемещений
дольной силы в стержне однопролетные балки различных типов рассчитаны заранее при помощи формул (24) на различные виды воздействий (см. примеры 7, 8, 9 предыдущего параграфа).
Таким образом получена таблица реакций сжатоизогнутых стержней от единичных перемещений и нагрузок (табл. 2), которой и надлежит пользоваться при практических расчетах.
Таблица 2
Реакции сжато изогнутых стержней от единичных перемещений и нагрузок
Продолжение табл. 2
„f й , Зф4(о) \b — a . . bo .toll
qa =я(т+_7ГГ I™“0+smT" sinTj
QC — P(-f- У* + sin-2-sln-7-))
4B [I o2sint) V I I I I)
(W)
M.
V "-Ik,
I V V Ivvf I/ f
(MJ
©
N * A
В N
.— *CT
©i
в у
Pbj4d_ i ~ i1
JVh
j® 3 IT
rmnft»ut .»
f Ql Cf* Ed N
2 ~iT" liiyej
г U~
Mi
E3
vtgv
ТШТПТ0"""-
MlllTm
Значения функций, а также других вспомогательных величин приведены в табл. 3—5.
Все детали расчета будут ясны из разобранных ниже примеров.
Примеры расчета рам на устойчивость методом перемещений
Пример 11. Требуется найти критическую нагрузку Ркр для рамы, показанной на рис. 31, а. Основная система метода перемещений и эпюра изгибающих моментов
52
от единичного поворота узла 1 показаны на рис. 31,6. При построении эпюры продольная сила в ригеле (в соответствии с принятым выше допущением) считалась равной нулю, продольная сила в стойке равна силе Р. Каноническое уравнение метода перемещений имеет, вид: 1=0. Так как мы ищем нагрузку, соответствующую изогнутому равновесному состоянию рамы, то гх ф 0,
'Рис. 31
4Ely , л . 37а п
следовательно, гц= —Ф2(рН—з~ ’ откУДа
/1(ф2(«) +2) =0 и фг(г) =—2.
Из табл. 3 при фг(у)=—2 находим по интерполяции о=5,66. Критическая нагрузка Ркр= —= —662 Е!г =
=2Eli(m). Коэффициент свободной длины стойки может быть найден при приравнивании полученного значения критической силы критической силе по формуле Эйлера:
v2 EI п2 EI зх
, откуда \х = — .
/а ((л/)2
В нашем случае =0,555, т. е. стойка работа¬
ет в условиях, близких к полному защемлению верхнего конца (как и следовало ожидать, ввиду большой жесткости ригеля).
Расчетная длина стойки /о = (ш/ = 0,555 «4 = 2,22 л* является исходной величиной для нахождения коэффициента продольного изгиба ф в зависимости от расчетной гибкости и материала стержня по таблицам из соответствующих СНиП.
Пример 12. Требуется определить ЯКр для рамы, показанной на рис. 32, а. До потери устойчивости стерж¬
53
ни рамы не испытывают изгиба. При достижении нагрузкой критического значения узлы рамы могут получить как угловые, так и линейные смещения (возможная форма потери устойчивости показана на рис. 32, а пунктиромИри расчете рамы методом перемещений имеем 1фи неизвестных — два угла поворота и одно линейное смещение. Сгруппировав повороты крайних узлов в симметричную и кососимметричную группы (что возможно
Рис. 32
ввиду симметрии рамы и нагрузки), получаем эпюры от единичных смещений, показанные на рис. 32, б, в, г, и систему канонических уравнений следующего вида:
7) rnZi = О,
2) r22z2 + /*232з = О,
3) Т322 + г 333 = 0.
Так как в крайних стойках нет продольной силы, главный коэффициент Гц не может обратиться в нуль, следовательно, i = 0 и рама теряет устойчивость по кососимметричной форме; находим по единичным эпюрам коэффициенты второго и третьего уравнений:
г22 = 3EI • 2 = 6EI (тм) (если EI в тм2), гзз = -2 + 41 (V) = EI [0,375 + 0,111гц (v)) (-2-) ,
гга = r«—JSJ- .2 = -0,75/(m).
4а
54
Условие z2 Ф 0, zs=f= 0 удовлетворяется, если равен нулю определитель, составленный из коэффициентов при этих неизвестных:
D=
22, '23
'32, '33
= 0, или Гагю — 4 = 0.
Подставляя в полученное уравнение значения коэффициентов и сокращая на (EI)2, находим: 6[0,375 + +0,1111 ()1—0,752 = 0, откуда (v) =— 2,53.
Рис. 33
По найденной величине тиС) из табл. 3 по интерполяции определяем v =2,88, и критическая нагрузка
*кр= = 0,92 / (ш).
Коэффициент свободной длины средней стойки л 3,14 t пп
ц = — = —1— = 1,09.
v 2,88
Пример 13. Та же рама, что и в предыдущем примере, загружена несимметрично (рис. 33,а). Требуется определить критический параметр нагрузки Ркр. Из-за отсутствия симметрии в нагрузке решаем задачу без
группировки неизвестных. Эпюры от единичных поворо¬
тов узлов и от единичного горизонтального смещения показаны на рис. 33,6, в, г. Во всех трех стойках будут различные величины v, так как продольные силы и длины различны.
Для левой стойки
65
для средней стойки v2=3 р/~=0,75v,
Г 2 Р
для правой стойки v3 = 41/ — = 1,410.
На единичных эпюрах при коэффициентах фг(а), Фз(у), ... поставлены в скобках те значения v, которым эти коэффициенты соответствуют. Так как до потери устойчивости изгиба не было, канонические уравнения однородны и система уравнений для данной рамы имеет вид:
г 111 + f 122 + Г13Z3 = 0; r2\Zl + Г 222 + Г23?3 = 0;
rsiZt + Г 322 +3323 = 0.
Значения коэффициентов:
AEI
Гц =
Т22 —
—
4 EI
4
12 Е\
Ф2 (Ui) + 2Е/ = EI [ф, (и) + 21; Ф2 (v3) + 2EI = EI [ф,(1,41о) + 2];
ha fa) + Чг (*»«)] + т1 (Ъ) =
43 33
= / [0,187 (ть(о) + Л. (1,41о)) + 0,111% (0,75о)];
12
— r2i — 0; г13 — г31 =
6/
42
= —EI «0,375ф4 (и); 6EJ
32
42
Ф4 (v3) = — 0,375/ф4(1,41а).
D =
= 0.
Составляем определитель из коэффициентов при неизвестных и приравниваем его нулю
Г11\ Г12\ Г13 Г2\\ Г22\ Г2 ГЗЪ Г32\ Г33
В развернутом виде, принимая во внимание, что гj2 = = ?2\ = 0, получаем гпг22г33—Лъ r22—rh /’и®5!).
Подставив в это уравнение найденные значения коэффициентов и произведя небольшие преобразования, получим сложное трансцендентное уравнение (так назы¬
56
ваемое уравнение устойчивости), которое надо решать путем подбора:
12 [th(i») + л. (1,41о)] + 7,11% (0,75о) = +
Фа W + *
[2ф2(1,4Ь) + Ф8(М1)12 ф2(1,4Ь) + 2
Раньше, чем задаваться каким-то значением v, целесообразно посмотреть, в каких а* Пределах оно может изменяться. Левая стойка рамы находится в таких условиях, что ее верхний конец может смещаться по горизонтали (но смещению сопротивляется жесткость других стоек) и упруго поворачиваться (повороту сопротивляется жесткость ригеля); следовательно, критическая сила стойки рамы будет выше, чем для стержня, показанного на рис. 34, а, и ниже, чем для стержня, показанного на рис. 34, б.
Находим значение v для этих двух случаев:
для случая а
п я2 Е[ v2 EI я 1 г 7 Рис. 34
= — = — ’ откУда и= Т = ’ '
для случая б
п 4л2 EI v2 EI ос ПО
'р = —Р— = —~ ОТ,УД'1 v = 2л = 6.28-
Таким образом, в нашем сл/чае 6,28 v 1,57.
Так как диапазон все еще достаточно широк, отметим, что возможность горизонтальных смещений значительно уменьшает жесткость системы и поэтому целесообразно задаться значением, более близким к нижнему пределу, чем к верхнему.
1. Задаемся значением v = 2,0; 1,41 = 2,82; 0,75и=1,5.
По табл. 3 находим: фг() =0,8590; фг(1,41а) =0,7016; фз(1,41а) = 1,1744; ф4(о) = 0,9313; Л1(0,75у) = 0,0893;
r)2(v) = 0,598; ri2(l,41c;) = 0,1965.
Обозначив левую часть уравнения устойчивости буквой Л, а правую — буквой В, получаем:
А = 12[0,598 + 0,197] + 7,11-0,0893 = 10,167;
57
в = 9-0.93138 , (2-0,7016+ 1,1745)*
0,8590 + 2 0,7016 + 2
7,82 . 6,64
= 2,74 + 2,46 = 5,20;
2,859 2,702
АФВ.
2. Задаемся v = 2,50; 1,41 v = 3,52; 0,75i = 1,88;
ФгИ = 0,772; ф2(1,41и) = 0,495; фз(1,41и) = 1,327; ф4(о) = = 0,8909; t]i(0,?5i) =—0,4420; т]2 (о )= 0,3701;
кя(1,410) = —0,2602;
А = 12[0,3707 —0,2602] +
+ 7, И (—0,4420) = — 1,84;
Рис. 35
9 0.8909. . .(0,990+1,327). _ 3
0,7720 + 2 0,495 + 2
АфВ.
Построим график изменения величин А и В, считая их меняющимися по прямолинейному закону в небольшом диапазоне v (2,5а2,1) (рис. 35).
Принимаем и = 2,23.
Критический параметр нагрузки
Ркр= —- = 2,238 Е1 = 0,311 El (т).
КР /2 42 * ' 7
Коэффициенты свободных длин стоек рамы JX 3,14 , л,
iii = — = —1— = 1,41;
Vi 2,23 ’ ’
я 3,14 Q7
ц — — = = l.oi;
™ v2 0,75-2,23
л 3,14 in
„ _ _ ! ~ 1 И,
r3 v3 1,41-2,23
Сравнивая результаты этого примера с примером 12, видим, что наличие сил в крайних узлах значительно
58
уменьшило критическую нагрузку и ухудшило условия работы средней стойки (л= 1,87 вместо fi=l,09 в примере 12).
§ 12. Расчет рам на устойчивость методом сил.
Выбор основной системы и лишних неизвестных
Выше (см. § 9) уже указывалось, что для получения однородной системы канонических уравнений основная система должна быть выбрана так, чтобы в ней не возникало изгибающих моментов от заданной нагрузки. Помимо этого, при расчете на устойчивость первостепенное значение будет иметь упрощение вычисления коэффициентов бih — перемещений по направлению отброшенных связей. (Напоминаем, что при вычислении бгь учитывается влияние продольных сил, которые имели место до потери устойчивости, на изгибные деформации при потере устойчивости). Если, пользуясь формулой Мора, ограничиться только членом, содержащим изгибающие моменты, то бih = '2\±dst где эпюра М* будет
J EI
состоять из прямолинейных участков, а эпюра Л* будет криволинейна на тех стержнях, где есть продольная сила. Наиболее просто интеграл Мора вычисляется в тех основных системах, в которых сжатые стержни представляют собой простые балки с шарнирно опертыми несмещающимися концами или балки, защемленные одним концом.
Например, для расчета рамы, представленной на рис. 38, выбрана основная система, показанная на рис. 39, а. Здесь сжатый стержень представляет собой шарнирно опертую двумя концами балку. Значительно сложнее оказалась бы основная система по рис. 39, б.
Для расчета рамы, показанной на рис. 40, а, выбрана основная система, в которой сжатый стержень — балка, защемленная одним концом (рис. 40,6). Основная система по рис. 40, д будет значительно более трудоемка.
* Эпюра от единичной силы, приложенной по направлению искомого перемещения в системе, где заданные воздействия отброшены.
** Эпюра от единичной силы k при наличии заданных осевых
сил.
59
Лишними неизвестными при расчете на устойчивость по методу сил являются те малые усилия в отброшенных связях, которые появляются при потере устойчивости. В результате расчета эти силы остаются неопределенными.
Выведем окончательные формулы для требуемых в случае простейших основных систем интегралов Мора.
Стержень, защемленный одним концом
Рассмотрим стержень, защемленный одним концом и нагруженный на другом конце произвольной поперечной
силой Qa= произвольным 1 моментом Ма = с и продоль-
подставляя полученное значение qu в третье из уравнений (24), после небольших преобразований находим
В прямолинейной эпюре Mi момент в произвольном сечении
ч/ будет криволинейна, причем момент в заделке
ной силой N (рис. 36).Эпюра изгибающих моментов
Мв — С + el + Nt/A — = d + NyAi
где d—момент от поперечной нагрузки; е= .
Рис. 36
Выражение изгибающего момента в произвольном сечении х получим,воспользовавшись формулами (24). Составляя условие фдг=/ = = 0, получаем:
v Е/
cos V — 1 /2
я л v М* = с cos — * /
с (i;«sin р— 1) -\- d v cos v
]
Mf = а + -я
60
Таким образом,
i i
J Mi Mk dx = с J cos -у- (a + * j dx -f
о о
cMinv-D + d Гsjn «_ L + b=±x) dx.
и cos 0 J / \ / /
0
Произведя интегрирование и подставив пределы, получаем:
i
JM, мкdx = -у- -0! -у- е2 (о) +
О
+ (-Т" +(27)*
где
1);
+ 7 + ф
e,C)=-r-L-—!iil.
и2 L COS j V J
(Величины 0 для различных значений у даны в табл. 4.)
Таким образом, в этом частном случае стержня с жесткой заделкой на одном конце интеграл берется как сумма интегралов «одноименных» (имеющих вершины с одной и той же стороны) треугольников I—/' и II—//' с поправками 0i(fl) и 02(a) и «разноименных» треугольников /—//' и /'—II с поправкой 0з(). Ординаты берутся из эпюр от поперечной нагрузки; влияние продольной силы заключено в коэффициентах 0.
* Тот же результат несколько другим способом получен в книге: Прокофьев И. П. и Смирнов А. Ф. «Теория сооружений». Ч. III, 1948. Там же рассмотрен случай шарнирно опертого стержня.
61
Стержень шарнирно опертый
Для частного случая шарнирно опертого стержня, показанного на рис. 37, подставив в уравнения (24) граничное условие ув = 0, получим
фл = [(l р-)с —(l —) d\ —-—
L\ tg ti / \ sin v) J v*EI
и из третьего уравнения (24) после небольших преобразований получим
i
N г
-t
-const *—»«
M
Рис. 37
Mxk = с cos ——f- ( — k / \ Sinv
с \ . vx
:— sin — .
/ I
Таким образом,
i
j M, Mkdx = cj cos -y~(a +
+
, b — a \
(— -) Г X
\sini; tg t / J
X Sin
vx [ in — la
l \
+
b — a \ i
x dx.
i !
После взятия интегралов и подстановки пределов получаем
i
(28)
f М, Mkdx= 64 (v) + (у + -у") е. (Р).
О
где
04(0) = 05(О)=— L).
v \ v tgu / v \sinw v /
Как видим, в этом частном случае «одноименные» треугольники /—/' и II—//' интегрируются с коэффициентом 04(v), «разноименные» треугольники — с коэффи-
62
циентом 05(у). Коэффициент 04 и 05 учитывакгг_влияние продольной силы на бтбетствующую эпюре М* деформацию.
Примеры расчета рамы на устойчивость методом сил
Пример 14. Определить критический параметр нагрузки для рамы, показанной на рис. 38. Ввиду симметрии рамы и нагрузки в случае выбора симметричной ос-
Е3= Const J
счГ
j, V
Рис. 38
новнои системы получим следующие уравнения метода сил:
Sii-i + 6122 = 0;
621*1 + 622*2 = 0;
6зз*з = 0
и, таким образом, следующие уравнения устойчивости:
1) для симметричной формы потери устойчивости
D=
б п; б12 62lJ б22
= 0 ИЛИ бп 622 — б12621 = 0;
2) для кососимметричной формы потери устойчивости б33=0. Основная система и эпюры от единичных лишних неизвестных показаны на рис. 39.
Определяем коэффициенты бгл, пользуясь формулой 28.
i-2]2=
- 10,670,(0)+ 7,52;
63
El6“ = 2J [T19(t,) + 4- ■ f]2“
33
=si
= 2,6704( + 2,67;
Ma Ma El
ds = EIbn = 2,6704 (r) -f 2,67;
mH = j ds = EIb21 = -04 (o)2 =
= 5,3304 (0). _ _
На рис. 39 не показаны эпюры М2 и М3, они имеют тот же вид, что и эпюры М2 и М$, но все участки прямо-
о)
Р *!__ 1Р *mt »Р tP. .
Рис. 39
линейны, так как силы Р отсутствуют. Для симметричной формы уравнение устойчивости принимает вид:
[10,6704(0) + 7,52]-[2,6704 (у) + 2,67] — 5,332* 0*0) =0,
откуда находим 04 () =—0,41 и по табл. 4 0 = 4,03.
Таким образом, критическая сила, соответствующая симметричной форме потери устойчивости,
рст = &]Ц_ = _4.032.i-/ = 1(02/
/2 42
Для кососимметричной формы „имеем 2,67 04(0) + -}-2,67 = 0; 04,(0) =—1 и по табл. *4 0 = 3,72.
Таким образом, критическая сила, соответствующая кососимметричной форме потери устойчивости,
РЦ = -3,7/- = 0,862/ РкГ-
64
Опасной является кососимметричная форма потери устойчивости, сопровождающаяся перекосом верхней части рамы (пунктирная линия на рис. 38).
Пример 15. Определить Р«р для рамы, показанной на рис. 40, а. Основная система и эпюры от лишних неизвестных при наличии продольной силы Р в левой стойке показаны на рис. 40, б, в, г*.
Вычисляем коэффициенты 6ц, пользуясь формулой 27 (при этом эпюры Mi и AJ2 на стойках будут прямолинейны, как показано пунктиром на эпюрах Afi и М2)
+ 2 0з (у) = 32 [0,666 + 6Х (у) + 0, (к) + 03 (V)};
О
/622= А.6+6-4.6+ §-01(D) = 72[3 + et(p)J;
2 о о
* Следует отметить, что здесь, как и при расчете методом перемещений, мы пренебрегаем теми приращениями продольных сил, которые получаются при потере устойчивости.
Рис. 40*
Уравнение устойчивости!
5—949
U ГА 4*4 /Ч 4*6-6л/ж 4*6*6 Д / V
EI 6i2= — -6 — 02 И —03 (о) =
L 6 о
= _ 24(2 + 20,(0) + 03 (о)].
После подстановки полученных значений коэффициентов уравнение устойчивости принимает вид:
4[0,666 + 01 (и) + 02 (о) + 0з(о)ЫЗ + 0г(о)] —
— [2 + 202 (о) + 03(о)]2 = О.
Подбором находим то значение о, при котором это уравнение удовлетворяется.
При о = 3,12 по табл. 4 находим: 0i(o) =—0,31; 02(о) = = 0,902; 03(о)=—0,612.
4[0,666 — 0,31 + 0,902 — 0,612] - [3 + 0,902] —
— [2 + 2 - 0,902 — 0,612]2 = 10,1 — 10,2 да 0.
Таким образом, критическая нагрузка
Р = *!L = _lil*!L = 0,27 EI,
Р /2 62
а коэффициент свободной длины сжатой стойки
Л = АН = 101.
r v 3,12
§ 13. Примеры деформационного расчета рам.
Таблицы функций
Пример 16. Требуется проверить напряжение в месте заделки стойки П-образной рамы, показанной на рис. 41 у а с учетом влияния продольных сил на деформацию рамы, и найти горизонтальное перемещение верхних узлов.
Дано: сечение всех стержней — двутавр № 30а, 1Х = = 8950 см4;
Wx = 597 см3; F = 61,2 см2; i = 12,1 см.
EI = 2,1 • 10? • 8950 • 10-8 = 1880 тм\
Обычный расчет рамы без учета влияния продольных сил на деформацию дает эпюру изгибающих моментов М*у показанную на рис. 41,6, и эпюру продольных сил N' (рис. 41,в).
6ь
По эпюре N' в качестве первого приближения определяем величины v: 1) для левой стойки v*T = I -jj- = 8 /"= = 1,29;
а) 6)
Р=50т Р=50г
EJ-caisf
§
Q923 №3
Рис. 41
2) для правой стойки = 8 \/ —— = 1,31;
ст V 1880
3) для ригеля 1риг = 4 у 0,5 =0,065.
f 1880
Полученные значения v показывают, что при больших осевых силах, действующих на стойки (Я = 50т), приращением продольных сил от изгиба можно пренебречь.
Таким образом, для дальнейшего расчета принимаем:
для стоек v = 8 \/ —= 1,3;
V 1880
для ригеля а=0.
Рассчитывая раму методом перемещений, получаем (в силу кососимметричности деформации) два уравнения с двумя неизвестными
raZi + ri2z2 + Rip = 0; r2izi + r22z2 + R2p = 0
Основная система и* эпюры от единичных смещений показаны на рис. 42. Построение этих эпюр и вычисление ординат произведены в соответствии с табл. 2 и 3 при принятых величинах v.
5*
67
Коэффициенты канонических уравнений:
Гп
4EI
Фг (°)
6 EI
2 =
= -1 0,9424 + 1,б) Eh2 = 3,94/;
= -ir ч. (») = -iF0)8307 = °-0388/;
'is = =- -2Ц- ф4 (v)-2 =- -1ML .0,9715 = - 0.182Е/;
t2 82
?ip — 0; /?2р = — 1
т.
Таким образом, получаем следующие два уравнения:
3,9421 — 0,182 = 0;
— 0,1822! + 0,0388г. = 0;
. I'*. 2 Е/ откуда
*1 =
1,525 . El ’
33
EI
Окончательные эпюры изгибающих моментов, поперечных и продольных сил показаны на рис. 43. Как видим, окончательная эпюра N мало отличается от принятой для деформационного расчета, поэтому первое приближение можно считать окончательным решением. Изгибающий момент в заделке возрос по сравнению с недеформационным расчетом на
2,61 —2,15 2,15
• 100 = 21,4%.
68
Проверяем напряжение в месте заделки стойки:
Отт
_ N , М 51400 , 261000
-'max I Л
F W 61,2 597
= 840 + 438 = 1278 кг,!см2.
Горизонтальное перемещение верхних узлов без учета влияния продольных сил
д=УГ
М-М'
jLJj EI
ds (эпюры М и М! на рис. 41),
__ГМ_/А .25 - • 1,85)1 = — .
ГА [ 2 V 3 ’ 3 ' }\ EI
С учетом влияния вертикальных сил Р горизонталь-
33
ное перемещение верхних узлов Д = z2= — (прирост деформации на 27%).
Пример 17. Требуется построить эпюру изгибающих моментов в раме, показанной на рис. 44, с учетом дополнительного изгиба от продольных сил.
Дано: сечение стойки — двутавр № 12, /* = 436 смА; сечение ригеля—двутавр № 16, /jc =1130 смА. Жесткости:
Eli = 2,1 • 107 • 436 • 10"8 = 91,5 тм2;
Eh
Е12 = 2,1* 107« 1130* 10~8 = 237 тм2; =
237
= 2,58.
EIt 91,5
1. Производим расчет без учета влияния продольных сил. Единичная эпюра, эпюра от нагрузки и окончательные эпюры М и N показаны на рис. 45
Гп = 3,08 EI 1 j Rip = — 2,67 тм;
2,67 0,865
*1 =
3,0 8EIt
Eh
69
2. Производим деформационный расчет, при этом продольной силой в ригеле можно пренебречь и считать для ригеля у = 0;
для стойки получаем
v = I л/ — =8,0 л[-1®. = 3,04.
У Eh V 91,5
Из табл. 3 интерполированием находим: фг() =
= 0,645; ф3() = 1,213; единичная эпюра показана на рис. 46, а; эпюра от нагрузки в основной системе осталась без изменения, поскольку мы пренебрегли продольной силой в ригеле
г и = (2,58 + 0,25 • 1,29) Eh = 2,902/i; Rip = — 2,67;
= 2,67 _ 0,92
Zl _ 2,902/, Elt ’
Естественно, что при учете дополнительной деформативности от продольных сил угол поворота возрастает
, 0,2 — 0,865 1пч с \
(в данном случае на •10)=6,4%).
0,865
Окончательные эпюры М и N показаны на рис. 46, б и в. Из-за увеличения податливости стойки момент на левом конце ригеля уменьшился по сравнению с недеформационным расчетом, а на правом конце — увеличился.
Момент на нижнем конце стойки увеличился на 0,28-0,216 .Ю0 = 29,6%.
0,216
Воспользовавшись уравнениями (24), найдем местоположение и величину максимального изгибающего момента в стойке. Для этого сначала составим условие
——- =Q. Подставив в четвертое из уравнений (24) значения фл = 0, Ма= 0,28, Qa = —0,071, получаем:—nsintix•
•0,28—0,071 cosnx=0 in = —V или tgпх = —а,’071'8 == \ / / & 0,28-3,04
= —0,666, т. е. пх = 2,55 (табл. 5).
Сечение с максимальным изгибающим моментом в
2,55 2,55-8 с _
стоике находится на расстоянии х= = ~з1н =
от нижней заделки.
70
Р-101
А
q= lljnm
ШШП
ТиП
У— +
Рис. 44
Рис. 45
б)
J.071 шшпввшш
ш
71
Таблица 3
Значения функций метода перемещений для сжатоизогиутых стержней
t»2tgl» v(tgv — v)
Pl (v) = — — ' Ф2 (v) = Рз (») =
3 (tg у — v)
v (v — sin v)
••(• f-f)'
ч4 (») = Ф1 ;
*ii («) =
4 sin v (tg -j- )
=4t -‘Vt'
3 (tg v — V)
•; Л2 (v)
ф2(»)
Ф.(С')
ф4(0)
Л()
Th(w)
0,0
0.2
0.4
0.6
0.8
1,00
1,10
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9 2.0 2.1 2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
3.1
3.2
3.3
3.4
1.0000
0.9973
0.9895
0.9856
0.9566
0.9313
0.9164
0.8998
0.8814
0.8613
0.8393
0,8153
0.7891
0.7609
0.7297
0.6961
0,6597
0.6202
0,5772
0.5304
0.4793
0.4234
0.3621
0,2944
0.2195
0,1361
0.0424
-0.0635
-0.1847
—0.3248
1.0000
0.9980
0.9945
0.9881
0,9787
0,9662
0.9590
0.9511
0.9424
0.9329
0.9226
0.9116
0.8998
0.8871
0.8735
0.8590
0.8437
0,8273
0.8099
0.7915
0.7720
0.7513
0.7294
0.7064
0.6819
0.6560
0.6287
0.5997
0.5691
0.5366
1.0000
1.0009
1.0026
1.0061
1.0111
1.0172
1,0209 1.0251 1.0298 1.0348 1.0403 1.0463
1.0529
1.0600
1.0676
1.0760
1.085Э
1.0946
1,1050
1.U64
1.1286
1417
1559
1712
1.1878
1,2057
1,2252
1,2463
1.2691
1.2940
1,0000
0,9992
0,9973
0,9941
0.9895
0,9832
0.9798
0,9751
0,9715
0.9669
0.9619
0.9566
0.950Э
0,9448
0,9382
0,9313
0.9240
0,9164
0.9083
0.8998
0,8909
0.8814
0,8716
0,8613
0,8506
0.8393
0.8275
0.8153
0.8024
0.7891
1.0000
0,9840
0,9362
0,8557
0,7432
0,5980
0,5131
0,4193
0,3181
0,2080
0,0893
—0,0380
—0,1742
—0.3191
—0.4736
—0,6372
—0,8103
—0.9931
—1,1861 —1.3895 —1,6040 —1,8299 —2.0679 —2,3189
—2.5838
—2.8639
—3.1609
—3,4768
—3,8147
—4,1781
1.0000
0.9959
0,9840
0,9641
0.9362
0.8999
0.8789
0,8557
0,8307
0,8035
0,7743
0,7432
0.7100
0,6747
0.6374
0.5980
0.5565
0.5131
0.4675
0.4198
0,3701
0.3181
0.2641
0.208Э
0,1498
0.0893
0,0207
—0,0380
—0,1051
—0.1742
72
Продолжение табл. 3
pi(u)
ф2(у)
Фэ(У)
4a(v)
*ni(o)
Tfe(u)
3,5
—0,4894
0,5021
1,3212
0,7751
—4,5727
—0,2457
3,6
—0,6862
0,4656
1,3508
0,7609
—5.0062
—0,3191
3.7
-0,9270
0,4265
1,3834
0,7457
—5.4903
—0,3951
3,8
-1,2303
0,3850
1,4191
0,7297
—6.0436
-0,4736
3.9
—1,6268
0,3407
1,4584
0,7133
—6,6968
—0,5542
4.0
—2,1726
0,2933
1,5018
0,6961
—7,5058
—0,6372
4.1
—2,9806
0,2424
1,5501
0,6783
—8,5836
—0,7225
4.2
—4,3155
0,1877
1,6036
0,6597
—10,196
—0,8103
4.3
—6,9949
0,1288
1,6637
0,6404
—13,158
—0,9004
4,4
—15,330
0,0648
1,7310
0,6202
—27,781
—0,9931
4.5
227,80
—0,0048
1,8070
0,5991
+221,05
—1,0884
4.6
14,669
—0,0808
1,8933
0,5772
7,6160
—1,1861
4,7
7,8185
—0,1646
1,9919
0,5543
0,4553
—1,2865
4,8
5,4020
—0,2572
2,1056
0,5304
—2,2777
—1,3895
4,9
4,1463
—0,3612
2,2377
0,5054
—3,8570
—1,4954
5.0
3,3615
—0,4772
2,3924
0,47§3
—4,9718
—1,6040
5.1
2,8130
—0,6100
2,5757
0,4520
—5,8570
—1,7155
5,2
2,3986
—0,7630
2,7961
0,4234
—6,6147
—1,8299
5,3
2,0668
—0,9423
3,0648
0,3935
—7,2965
—1,9473
5.4
1,7884
—1,1563
3,3989
0,3621
—7,9316
—2,0679
5.5
1,5455
—1,4181
3,8234
0,3291
—8,5379
—2,1917
5.6
1,3265
—1,7481
4,3794
0,2944
—9,1268
—2,3189
5,7
1,1235
—2.1804
5,1346
0,2580
—9,7056
—2,4495
5.8
0,9302
—2,7777
6,2140
0,2195
—10,283
—2,5838
5,9
0,7421
—3,6678
7,8726
0,1790
—10,863
—2,7218
6,0
0,5551
—5,1589
10,727
0,1361
—11,445
—2,8639
6.1
0,3659
—8,2355
16,739
0,0906
—12,038
—3,0102
6,2
0,1700
—18,591
37,308
0,0424
-12,643
—3,1609
2я
0,0000
— oo
+ «
0,0000
—13,033
—3,2898
Таблица 4
Значения функций метода сил
01» 02» 08» 04» 05
01 (v) = -J- —i); 02 (v) = -у (— + v f8 v — +i)
V2 \ V J V2 \ v cosy /
V \COSV V J V \ V tgy/
05 (V) = — —)
o \sino V )
73
Продолжение табл. 4
0i(o)
в9(0)
в.(0)
0,00
0,10
1,0000
1,0000
1,0000
1,0000
1,0000
0,20
0,30
1,0163
1,0065
1,0178
1,0027
1.0042
0,40
0,50
1,0683
1,0252
1,0768
1,0107
1,0188
0,60
0,70
1,1686
1,0622
1,1901
1,0249
1.0437
0,80
0,90
1.3456
1,1256
1,3900
1.0455
1.0800
1,00
1,6722
1,2395
1,7605
1,0737
1,1304
1,10
1,9491
1,3344
2,0750
1,0912
1,1617
1,20
2,3822
1,4806
2,5677
1.1114
1,1979
1,30
3,1435
1,7342
3,4347
1.1345
1.2396
1,40
4,8082
2,2832
5,3332
1.1610
1,2878
1,50
11,2013
4,3740
12,6292
1,1915
1,3534
л
о
оо
оо
оо
1,2159
1.3880
1,60
—26,2445
—7,8214
—30,1204
1,2266
1,4078
1,70
—5,7378
—1,1299
—6,7141
1,2673
1.4830
1,80
—3,1308
—0,8271
—3,7410
1,3147
1,5710
1,90
—2,1133
+0,0701
—2,5805
1,3704
1,6750
2,00
—1,5694
0,2575
—1,9658
1,4365
1.7993
2,10
—1,2342
0,3788
—1,5872
1.5158
1,9494
2,20
—1,0069
0,4659
—1,3323
1.6124
2,1336
2,30
—0,8431
0,5336
—1,1504
1.7325
2,3641
2,40
—0,7196
0,5897
—1,0151
1.8854
2,6596
2,50
—0,6234
0,6385
—0,9114
2,0864
3,0502
2,60
—0,5465
0,6828
—0,8304
2,3618
3,5890
2,70
—0,4836
0,7246
—0,7663
2,7619
4,3766
2,80
—0,4313
0,7654
—0,7151
3,3963
5,6315
2,90
—0,3870
0,8063
—0,6742
4,5550
7,9343
3,00
—0,3492
0,8483
—0,6417
7,3486
13,5057
3,10
—0,3165
0,8926
—0,6165
23,5659
45,9234
я
—0,3040
0,9119
—0,6079
оо
оо
3,20
—0,2876
0,9401
—0,5976
—15,7398
—32,7063
3,30
—0,2621
0,9920
—0,5846
—5,4154
— 12,0770
3,40
—0,2394
1,0499
—0,5772
—3,0787
—7,4248
3,50
—0,2187
1,1152
—0,5751
—2,0433
—5,3769
3,60
—0,1997
1,1907
—0,5797
—1,4572
—4,2292
3,70
—0,1821
1,2795
—0,5908
—1,0787
—3,4990
3,80
—0,1654
1,3861
—0,6099
—0,8128
—2,9961
3,90
74
—0,1493
1,5174
—0,6392
—0,6147
—2,6314
Продолжение табл. 4
0i(»)
e2(i)
e9(a)
e4(y)
4,00
—0,1332
1,6838
—0,6823
—0,4603
—2,3570
4,10
—0,1165
1,9030
—0,7449
—0,3355
—2,1454
4,20
—0,0981
2,2057
—0,8378
—0,2317
—1,9792
4,30
—0,0760
2,6529
—0,9821
—0,1430
—1,8475
4,40
—0,0459
3,3836
—1,2265
—0,0652
—1,7429
4,50
+0,0045
4,7980
—1,7110
+0,0044
—1,6603
4,60
0,1314
8,7218
—3,0745
0,0682
—1,5962
4,70
2,1964
75,9101
—26,5889
0,1279
—1,5483
3/2 я
oo
oo
oo
0,1351
—1,5434
4,80
—0,4390
—10,2705
+3,5933
0,1851
—1,5152
4,90
—0,2593
—4,5743
1,6085
0,2412
—1,4963
5,СО
—0,2011
—2,8355
1,0083
0,2975
—1,4914
5, Ю
-0,1707
—1,9912
0,7211
0,3555
—1,5014
5,20
—0,1512
—1,4908
0,5541
0,4169
—1,5280
5,30
—0,1370
—1,1585
0,4458
0,4838
—1,5738
5,40
—0,1261
—0,9209
0,3706
0,5592
—1,6436
5,50
—0,1171
—0,7417
0,3158
0,6470
—1,7446
5,60
—0,1096
—0,6010
0,2745
0,7538
—1,8886
5,70
-0,1030
—0,4868
0,2426
0,8901
—2,0961
5,80
—0,0972
—0,3917
0,2176
1,0750
—2,4050
5,90
—0,0921
—0,3105
0,1976
1,3476
-2,8924
6,00
—0,0874
—0,2398
0,1817
1,8015
—3,7455
6,10
—0,0831
—0,1769
0,1689
2,7289
—5,5609
6,20
—0,0791
—0,1200
0,1588
5,8812
—11,803Э
2л;
—0,0760
-0,0760
0,1520
oo
oo
Таблица 5
Значения функции , , vtgu, cos и, sin и, igv
tg V sin V
V
V
V tg V
tg V
tg V
sin V
0,0
1,0000
1,0000
0,0000
1,00000
0,00000
0,00000
0,10
0,9967
1,0017
0,0100
0,99500
0,09983
0,10033
0,20
0,9866
1,0067
0,0405
0,98007
0,19867
0,20271
0,30
0,9698
1,0152
0,0928
0,95534
0,29552
0,30934
0,40
0,9461
1,0272
0,1691
0,92106
0,38942
0,42279
0,50
0,9152
1,0429
0,2731
0,87758
0,47943
0,54630
0,60
0,8770
1,0626
0,4105
0,82534
0,56464
0,68414
0,70
0,8311
1,0866
0,5896
0,76484
0,64422
0,84229
0,80
0,7770
1,1152
0,8237
0,69671
0,71736
1,02964
0,90
0,7142
1,1489
1,1341
0,62161
0,78333
1,26016
75
Продолжение табл. 5
V
V
V tg V
sin 0
tgo
tgo
sin v
1,00
0,6421
1,1885
1,5574
0.54030
0,84147
1,55741
1,10
0,5599
1,2343
2,1612
0,45360
0,89121
* 1,96476
1,20
0,4665
1,2875
3,0866
0,36236
0,93204
2,57215
1,30
0,3609
1,3493
4,6827
0,26750
0,96356
3,60210
1,40
0,2415
1,4207
8,1170
0,16997
0,98545
5,79788
1,50
0,1064
1,5038
21,1521
0,07074
0,99749
14,10142
1,60
—0,0467
1,6007
—54,7721
—0,02920
0,99957
—37,23253
1,70
—0,2209
1,7143
—13,0842
—0,12884
0,99166
—7,69660
1,80
—0,4199
1,8483
—7,7153
0,22720
0,97385
—4,28626
1,90
—0,6491
2,0078
—5,5615
—0,32329
0,94630
—2,92710
2,0
—0,9153
2,1995
—4,3701
—0,41615
0,90930
—2,18504
2,10
—1,2282
2,4328
—3,5907
—0,50485
0,86321
—1,70985
2,20
—1,6014
2,7211
—3,0224
—0,58850
0,80850
—1,37382
2,30
—2,0550
3,0843
—2,5742
—0,66628
0,74571
—1,11921
2,40
—2,6201
3,5531
—2,1984
—0,73739
0,67546
—0,91601
2,50
—3,3466
4,1773
—1,8675
—0,80114
0,59847
—0,74702
2,60
—4,3218
5,0436
—1,5642
—0,85689
0,51550
—0,60160
2,70
—5,7115
6,3176
—1,2764
—0,90407
0,42738
—0,47273
2,80
—7,8756
8,3585
—0,9955
—0,94222
0,33499
—0,35553
2,90
—11,7690
12,1212
—0,7146
—0,97096
0,23925
—0,24641
3,00
—21,0452
21,2585
—0,4276
—0,98999
0,14112
—0,14255
3,10
—74,4888
74,5533
—0,1321
—0,99914
0,04158
—0,04162
3,20
54,7289
—54,8227
0,1871
—0,99829
—0,05837
0,05847
3,30
20,6573
—20,9192
0,5272
—0,98748
—0,15775
0,15975
3,40
12.8632
—13,3052
0,8987
—0,96680
—0,25554
0,26432
3,50
9,3435
—9,9778
1,3111
—0,93646
—0,35078
0,37459
3,60
7,2953
—8,1352
1,7765
—0,89676
—0,44252
0,49347
3,70
5,9226
—6,9832
2,3115
—0,84810
—0,52984
0,62473
3,80
4,9123
—6,2106
2,9395
—0,79097
—0,61186
0,77356
3,90
4,1164
—5,6705
3,6949
—072593
—0,68777
0,94742
4,00
3,4548
—5,2854
4,6313
—0,65364
—0,75680
1,15782
4,10
2,8802
—5,0105
5,8365
—0,57482
—0,81828
1,42353
4,20
2,3625
—4,8188
7,4667
—0,49026
-0,87158
1,77778
4,30
1,8811
—4,6934
9.8291
—0,40080
—0,91617
2,28585
4,40
1,4210
—4,6238
13,6238
—0,30733
—0,95160
3,09632
4,50
0,9704
—4,6034
20,8680
—0,21080
—0,97753
4,63733
4,60
0,5192
—4,6292
40,7568
—0,11215
-0,99369
8,86017
4,70
0,0582
—4,7004
379,350
—0,01239
—0,99992
80,71276
4,80
—0,4216
—4,8185
—54,6474
0,08750
—0,99616
—11,3849
4,90
—0,9302
—4,9875
—25,8107
0,18651
—0,98245
—5,26749
5,00
—1,4791
—5,2142
—16,9026
0,28366
—0,95892
—3,38052
5,10
—2,0821
—5,5087
—12,4919
0,37798
—0,92581
—2,44939
5,20
—2,7577
—5,8860
—9,8053
0,46852
—0,88345
—1,88564
5,30
—3,5303
—6,3681
—7,9567
0,55437
—0,83227
—1,50127
76
Продолжение табл. 5
V tg V
V
sin v
v igo
sin V
tg v
5,40
—4,4352
—6,9879
—6,5747
0,63469
—0,77276
—1,21754
5,50
—5,5244
—7,7954
—5,4757
0,70867
—0,70554
—0,99558
5,60
—6,8801
—8,8710
-4,5581
0,77557
—0,63127
—0,81394
5,70
-8,6399
—10,3506
—3,7605
0,83471
—0,55069
—0,65973
5,80
—11,0546
—12,4839
—3,0431
0,88552
—0,46460
—0,52467
5,90
—14,6362
—15,7805
—2,3783
0,92748
—0,37388
—0.40311
6,0
—20,6178
—21,4731
—1,7461
0,96017
—0,27942
—0,29101
6,10
—32,9263
—33,4867
—1,1301
0,98327
—0,18216
—0,18529
6,20
—74,3604
—74,6184
—0,5170
0,99654
—0,08309
—0,08338
Величину максимального момента в стойке найдем, подставив пх=2,55 в третье из уравнений (24),
AW = cos (2,55) -0,28 - sin (2,55). =
3,04
=—0,83-0,28— 0,567■•0’071 = —0,338 тм.
3,04
ГЛАВА 4
УСТОЙЧИВОСТЬ АРОК
§ 14. Устойчивость круговой арки постоянного сечения с упругозащемленными пятами и радиальной нагрузкой
Рассмотрим арку кругового очертания, находящуюся под действием гидростатической нагрузки (рис. 47). Если пренебречь незначительными изгибающими моментами, возникающими при обжатии оси, то при нагрузке, равной критической, может произойти потеря устойчивости 1-го рода, потеря устойчивости центрального сжатия. При этом форма потери устойчивости может оказаться симметричной (рис. 47, а) или кососимметричной (рис. 47,6). Опыты и теоретические расчеты показыва-
77
ют, что для арки без промежуточного шарнира кососимметричной форме изгиба соответствует меньшая критическая нагрузка, а следовательно, эта форма и является наиболее опасной. Поэтому определение критической нагрузки производим именно для этой кососимметричной формы потери устойчивости.
Пусть круговая арка радиуса R с центральным углом
2а и с постоянной жесткостью EI упруго защемлена на опорах, причем жесткость упругого защемления характеризуется коэффициентом ги — реактивным моментом, возникающим в упругой заделке от единичного поворота. Пусть при критической радиальной нагрузке 7кр ось арки приняла новую изогнутую равновесную форму, показанную на рис. 48 пунктиром.
Решая задачу статическим способом, необходимо записать дифференциальное уравнение изгиба и проинтегрировать его. Дифференциальное уравнение изгиба бруса кругового очертания имеет вид:
Рис. 48
d2 w d02
М
ш
R2*,
(29)
* Это уравнение было выведено Буссинеском в работе 1. Boussinesq, Comptes rend us, т. 97, стр. 843, 1883.
См. также работы [12] и [21].
78
где w — прогиб в произвольном сечении;
0—угловая координата, отсчитываемая от оси симметрии;
М— изгибающий момент.
Изгибающий момент в сечении в деформированном состоянии складывается из влияния продольной силы N = qR и момента т, являющегося следствием упругого защемления (см. рис. 48,в). Влияние моментов заделки изображено на эпюре (рис. 48,6), на которой видно, что
гц Ф = -гц ф.
/ /?sina sin a
Таким образом,
M = qRw — гп ф. (30)
sin CL
Подставив полученное значение М в дифференциальное уравнение изгиба и перенеся все члены, содержащие значение прогиба w, в левую часть уравнения, получаем
d2w , /, . qR3 \ гХ1 фR2 . п
f 1 + -— w= — sin 0.
\ El j sin a El
d02
Вводим обозначения
n-Y
С =
1 + S5-
El гц ФR2 sin a El
(31)
Дифференциальное уравнение приобретает вид: d2 w
d№
+ n2w = с sin 0,
и его общий интеграл может быть получен в следующей форме
w = A cos я0 + В sin лг0 —-— sin 0. (32)
л2 —1 v 7
Выражение (32) дает форму потери устойчивости с
точностью до трех неизвестных параметров А, В и С
(С содержит угол поворота заделки ф), для определения которых надо составить граничные условия.
Записываем три граничных условия (см. рис. 48,а).
1) при 0 = 0 w = 0, откуда получаем А — 0;
79
2) при 0 = а w = 0, откуда получаем
Q
В sin па Н sin а = 0;
Л* — 1
3) при 0 = а =р или, используя (31),
ds
dw sin а EIC
RdQ гп R* ‘
Дифференцируя выражение (32), имеем
dw О л - С п
—— = пВ cos /70Н COS0
Л2 — 1
и, следовательно,
Q
п В cos па Н cos а =
/12—1
sin а/С
rn R
Таким образом, для определения трех параметров прогиба имеем три однородных алгебраических уравнения:
Одно из возможных решений этой системы уравнений— нулевое решение (А = В = С = 0)—дает для всех точек w — 0, т. е. соответствует тому случаю, когда при нагрузке, равной критической, потери устойчивости не произошло. Из этого решения нельзя найти величину критической нагрузки.
Ненулевое решение для А, В, С получится в том случае, если определитель, составленный из коэффициентов при неизвестных, обращается в нуль. Приравнивая нулю определитель, получим так называемое уравнение устойчивости, из которого и определяется значение критической нагрузки.
В нашем случае, так как Л=0, имеем
1) А= 0;
2) sin паВ + С = 0; ’ я*—1
D=
80
откуда после небольших преобразований получаем уравнение устойчивости в следующем виде:
п
tg па =
ctga-
(п2— \)Е1'
'и Я
(33)
Определив значение п, надо критическую нагрузку найти из формулы (31)
(34)
Пример 18. Пусть требуется определить критическую интенсивность нагрузки для круговой арки с пролетом / = 20 м и стрелой подъема f = 4 м, жестко связанной с Г-образными рамами (см. рис. 49,а).
Определяем радиус арки R и центральный угол 2а (рис. 49, б)
*2 + у2 = R2.
Ю2+ (R — 4)2 =
откуда
R — 14,5 м; sin a =
10,0
14,5
= 0,69;
a = 43°30' = 0,241 я = 0,758;
ctg 43°30' = 1,055.
Подставляя полученные значения R, a, ctg а в уравнение 33, получаем
п
tg 0,758/г =
1,055
(п*— \)Е1 14,5г1
Для определения гц рассчитываем Г-образную раму методом перемещений (рис. 50). Каноническое уравне¬
6—949
81
ние будет иметь вид: 2Eh%i—/*н=0, откуда угол поворота узла
Zi = = 1 и гп = 2 /х = EI.
2 Е1Х
После подстановки гц и небольшого преобразования из формулы (33) получаем:
tgO,758/г= - . (а)
s ’ 1,125 — 0,069л2 '
Уравнение (а) решаем путем подбора: задаваясь различными значениями п, находим то значение п, при котором уравнение удовлетворяется. На
„ графике (рис. 51) показаны кривые
tgO,758M и правой части уравнения (а), которую мы обозначили буквой А. Абсцисса точки пересечения этих кривых и есть корень нашего уравнения.
Для примера покажем вычислеРис. во ние, соответствующее одному значе¬
нию я = 6,5. При этом
tg 0,758л = tg4,92 = tg282° = — 4,7;
А = = =—3,64.
1,125 — 0,069/12 1,125 — 0,069-42,2
При п = 6,58 получаем критическую нагрузку
««. - - 1) -5Г = I6.58’—1) - «,з .
Пример 19. Требуется определить критическую нагрузку для двухшарнирной арки радиуса R с центральным углом 2а, показанной на рис. 52.
Уравнение устойчивости для данной задачи получается как частный случай из уравнения (33) при коэффициенте жесткости упругого защемления /*н = 0. При этом получаем
tg па = 0, т. е. па = in (/ = 1, 2, 3,...).
Минимальная критическая нагрузка соответствует 1=1, при этом я= — и из формулы (34) получаем
-(-')#" б)
82
Например, для центрального угла 2а=60° имеем
я2
а = 30° = ; qKf) =
EI
EI
El R5
= (36—1) — =35 ' R* R3
Для приведенной арки с центральным углом 60° от-
f 1
ношение стрелы подъема к пролету составляет —= —;
/ 3,8
при этом, как видно из расчета [см. формулу (б)], первый член, стоящий в скобках, —, уже в 36 раз больше
а2
единицы.
6* S3
При увеличении пологости арки величина — возрастает, и единицей по сравнению с этой величиной можно пренебречь. Таким образом, для пологих двухшарниркых арок получаем критическую нагрузку
_ л2 EI а2 ’ R3
и критическую продольную силу
лС/
Лкр *7кр R
л2 F.I
а2 R2
где 5 — половина длины дуги арки.
Пример 20. Требуется определить критическую нагрузку для арки с защемленными пятами радиуса R с центральным углом 2а (рис. 53). Уравнение устойчивости для данной задачи получается как частный случай из уравнения 33 при коэффициенте жесткости упругого защемления гц=оо.
При этом получаем tg па =
ctg а
, или п = ctg а-tg па.
(В)
Характеристическое уравнение (в) решается в каждом частном случае путем подбора. Возьмем, как и в предыдущем примере, арку с центральным углом 2а = 60°. Тогда ctg а = ctg 30°= 1,73 и уравнение (в) приобретает вид:
п = 1,73 tg па. (г)
Обозначив правую часть полученного уравнения буквой А и давая п различные значения, получаем:
при п = 7 А = 1,73 tg 210° = 1,73-0,578 = 1,0;
при /1 = 8 А = 1,73tg240° - 1,73-1,73 = 3,0;
при /2 = 9/4 = tg—-rcj 1,73 = оо;
при п = 8,625 А = 1,73 tg 258°45' - 8,7.
84
На рис. 54 представлен график решения уравнения (г). Приняв tt-"8,625, получаем критическую нагрузку, равную
(8.625« -1) 73,3-2-.
Сравнивая результаты этого примера с предыдущим,
видим, что при 2а = 60° бесшарнирная арка оказалась в 2,09 раза устойчивее двухшарнирной (см. рис. 55).
А. Н. Динником показано, что для трехшарнирной круговой арки наиболее опасной формой потери устойчивости является симметричная форма, характеризую¬
щаяся опусканием среднего шарнира (см. рис. 56, а и б). При этом критическая нагрузка также определяется по
формуле qKP = {п2 — 1) — f где п находится из следующего уравнения:
tgu—u _ 4 (tgа — а) / _ па \
и* а3 \ 2 / *
85
Таким образом, во всех случаях для круговой арки с гидростатической нагрузкой имеем: критическая интенсивность нагрузки
KEI
?кр
R3
критическая сжимающая сила KEI
N Кр=
R2
(35)
где К — коэффициент устойчивости.
В табл. 6 даны коэффициенты устойчивости, вычисленные А. Н. Динником для ряда значений а.
Приведенная таблица показывает, как уменьшается критическая нагрузка при уменьшении жесткости системы.
Рис. 56
Таблица 6
2а
Бесшарнирная арка
Двухшарнирная
арка
Трехшариирная
арка
30°
294,0
143,0
108,0
60°
73,3
35,0
27,6
90°
32,4
15,0
12,0
120°
18,1
8,0
6,75
150°
11,5
4,76
4,32
180°
8,0
3,0
3,0
Интересна зависимость между величиной критической нагрузки и отношением стрелы подъема арки к ее пролету. Если использовать соотношения / = 2# sin а и
2f х a . KiEI
-у- = tg—, то легко получить формулу вида qKp=—,
где коэффициент Ki зависит только от -у- График коэффициента Ki представлен на рис. 57, из которого видно, что арка является наиболее устойчивой при отношении
стрелы подъема к пролету -у- «0,3.
86
О Щ 02 03 йМ а) Кру гобоя арка
)
/
1
/
Л
h
/
4XN
О 0) 0,2 03 Q4 05 Qfi 0.7 Од 09 6) Параболическая арка
Рис. 57
§ 15. Устойчивость круглых колец и труб под действием равномерной радиальной нагрузки
Если круглое кольцо находится под воздействием радиальной равномерно распределенной нагрузки, то оно (при 77кр) испытывает только напряжения сжатия и продольная сила равна N = qR. При достижении нагрузкой критического значения может произойти потеря устойчивости и кольцо примет слегка изогнутую форму, которая при 7 = 7кр будет формой равновесия. Рассмотрим изогнутую равновесную форму с двумя осями симметрии, показанную на рис. 58. Дифференциальное уравнение изгиба бруса кругового очертания, как показано выше, имеет вид
d2w , М
—— + w R2.
dO2 El
В силу симметрии задачи первоначальная ось кольца может рассматриваться как веревочная кривая от равномерной радиальной нагрузки и изгибающий момент
87
в точке А' будет равен M{s = qRwo, а изгибающий момент в произвольной точке kM = qRw*
Подставляя это выражение в дифференциальное уравнение изгиба, получаем после небольшого преобразования
d62
обозначив через
л = /
1 +
qR3
EI
получим общее решение этого однородного дифференциального уравнения в следующем виде
щш
Рис. 59
w = A cos п 0 + В sin п 0.
dw ~dQ
= 0.
Граничные условия: 1) при 0=0 Jt!L j = (—лЛ sin nQ + лВ* ccs я0)0==о = пВ = 0,
откуда В = 0;
о\ Л dlS) л
2) при 0 = = 0;
} v 2 d0
л . пл . D пл - . лл л
—яЛ sin f- пВ cos =— пл sin = 0,
2 2 2
л=0, 4=0, так как о; не обращается тождественно в нуль, следовательно, sin --=0, что дает минимальное
2
значение
min 2.
* Более строгое доказательство см. в [22].
88
Таким образом, минимальная критическая нагрузка, соответствующая данной форме потери устойчивости, определится из условия
/
II R3 О ЗЕ/ /0V
1 + Якр— =2, или 7кр = -Г‘ 36)
Результаты, полученные для круглого кольца, могут быть применены также при расчете на устойчивость длинных труб круглого поперечного сечения. При этом для определения quv на погонную единицу длины трубы надо в формулу (36) подставить вместо Е величину Е
(где ы— коэффициент Пуассона) и вместо I ве-
Л3
личину — (где Л — толщина стенки).
Таким образом, для труб получаем
тгггда- т
Пример 21. Дана стальная труба диаметром D = = 2 м, толщина стенок h = 3 см. Модуль упругости Е= = 2,1 • 10е кг/см2, коэффициент Пуассона ц = 0,3 (рис. 59).
Требуется определить, на какую глубину можно опустить эту трубу под воду, чтобы коэффициент запаса на устойчивость равнялся двум (ввиду малого диаметра трубы по сравнению с глубиной, неравномерностью давления можно пренебречь). Определяем критическую нагрузку по формуле (37)
Е h3 2,Ы0«-33 ---- / о
7ко = —- = 1 = 15,55 кг см?.
VkP 1_2 4ДЗ (1 — OM-lOO* 1
что дает критическое напряжение
Л7Кр 15,55*100 ГОЛ , о ак1) = — = — =520 кг см2 апц;
кР р 3 1 пц,
7кр= 15,55 кг/см2= 155,5 т/м2, т. е. труба потеряет устойчивость при погружении ее на глубину 155,5 м. Для по¬
89
лучения коэффициента запаса, равного двум, ее надо погрузить на глубину 77,7 м.
Для параболической арки, несущей вертикальную равномерно распределенную нагрузку, так же, как и для
круговой арки с радиальной на-
Используя общее уравнение устойчивости плоского кривого стержня см. ни
* и вертикальной равномерно распределенной нагрузки
(+1)(с“*е)+т(л,8ес,е,-°’ з8
q— вертикальная нагрузка на единицу длины пролета;
а — радиус кривизны параболы в вершине. Уравнение (38) интегрировалось численным методом
для различных соотношений — и одновременно удовлетворялись граничные условия, соответствующие данному типу арки (двухшарнирная, бесшарнирная и т.д.)
§16. Устойчивость параболической арки постоянного сечения с равномерно распределенной вертикальной нагрузкой
грузкой, потеря устойчивости характеризуется появлением изгиба причем наиболее опасной формой потери устойчивости для двухшарнирной и бесшарнирной арки будет кососимметричная
форма (рис. 60).
Рис. 60
7 = —т- -j получил дифференциальное уравнение рав¬
новесия в деформированном состоянии:
где
90
и данной форме потери устойчивости. Таким образом, окончательное решение для критической интенсивности нагрузки приведено к форме
7кр = -, (39)
где К — коэффициенты устойчивости, даны в табл. 7 и на рис. 57, б.
Как видно из таблицы, симметричная форма потери устойчивости является опасной для трехшарнирной арки
до -L « 0,3.
Таблица 7
_L
i
Бесшарнирная арка
Двухшарнирная арка
Трехшарш
симметричная
форма
«рная арка
кососимметричная форма
0,1
60,7
28,5
22,5
28,5
0.2
101,0
45,4
39,6
45,4
0,3
115.0
46,5
47,3
46,5
0.4
1И.0
43,9
49,2
43,9
0.5
97,4
38,4
—
38,4
0,6
83,8
30,5
38,0
30,5
0.8
59,1
20,0
28,8
20,0
1.0
43,7
14,7
22,1
14,1
Рис. 61
При определении критической нагрузки для данной арки из таблицы должен быть взят меньший коэффициент устойчивости.
Пример 22 *. Найти критическую нагрузку qiiv для двухшарнирной и трехшарнирной параболических арок
* Пример взят из книги А. Н. Динника «Устойчивость арок». ГТИ, 1946.
91
постоянного сечения при размерах, показанных на рис. 61. Площадь сечения арки F=325 см2. Момент инерции /170000 см\ = 2,1 • 10е кг/см2. Отношение стре-
f
лы подъема к пролету — = 0,1.
В табл. 7 находим: для двухшарнирной арки К = 28,5; для трехшарнирной арки К = 22,5. Критическая интенсивность нагрузки по формуле (39):
1) для двухшарнирной арки
28.5-2,Ы0«* 170000 о, о , , ею/
7ко = —■—1 = 81,2 кг пог-см = 8,12 т пог-м\
4 р 50003
2) для трехшарнирной арки
22.5-2,1.106.170 000 0 , а ас ,
Dun = —!—1 = 64,2 кг пог*см = 6,42 m пог-м.
чк? 5000з / »
Критическая величина распора и, следовательно, критическая сжимающая сила в замке и соответствующие критические напряжения равны:
1) для двухшарнирной арки
NKP = Нкр = 3J&JL = j’12'.502- = 507 m.
8/ 8-5
NKp 507 000 ~F~ ~ 325
aKp = = 1560 кг/см2;
2) для трехшарнирной арки
гт Аг 6,42 • 502
Нкр — — g g — 401 /71.
401 000 , ЛОС , о
aKD = = 1235 кг;см2.
кр 325
И в том, и в другом случае критические напряжения ниже предела текучести, что говорит о том, что потеря
устойчивости происходит в условиях упругой работы ма¬
териала и наши вычисления являются законными.
§ 17. Устойчивость весьма пологих арок
В предыдущих параграфах данной главы рассматривались арки с нерастяжимой осью. Условие нерастяжимости оси и приводило к тому, что в двухшарнирной и бесшарнирной арке наиболее опасной формой потери
92
устойчивости оказывалась кососимметричная форма. В весьма пологих арках при малой стреле подъема нельзя пренебрегать изменениями длины оси арки при ее обжатии.
В этом случае арка потеряет несущую способность, деформируясь по симметричной кривой с одной полуволной (рис. 62), причем при одних геометриче- У А
ских характеристиках м ♦ М ♦ ♦ УГ1 f ГГ'М *
кривизна будет оста- 1 f
ваться того же знака, У~~ ==rr==*‘x # »
что и в недеформиро- ванном состоянии (см. пунктирную кривую), рис 62
при других геометрических характеристиках в критическом состоянии произойдет так называемое прощелкивание, арка выпучится в другую сторону (точечная кривая на рис. 62) и из сжатой станет растянутой.
Решение задачи о потере устойчивости весьма пологих арок с учетом изменения длины осевой линии было дано С. П. Тимошенко [22], который рассмотрел арку с шарнирно опертыми концами, очерченную по синусоиде, имеющей уравнение
С. П. Тимошенко выведена формула для величины критической нагрузки, при которой арка будет выпучиваться вниз
и — отношение прогиба посередине пролета шарнирно опертой балки при заданной нагрузке к стреле подъема арки; например, при равномерно распределенной нагрузке интенсивностью q
/пх
sin —
(40)
где
4/
пг =
Ff2
и =
384 El f
93
Лри сосредоточенном грузе посередине пролета
PI3 1
и =
4 8/
f
Формула (40) действительна при m 1.
При т1 имеется только одна форма равновесия, которая будет устойчивой. Критическое значение распора, соответствующее моменту выпучивания арки вниз, определяется по формуле
H=\i
я 2/ /2
т 4-2
где i= —— является одним из корней выражения
(!-«)*= (Г-т.О-ц)2.
На рис. 63 показано изменение и и ц в зависимости
QiHH ГН IIUII
1 = 50 м Рис. 64
0} OZOJMQfQfiOJOtW
* li
Рис. 63
Рис. 65
от т. При расчете по приведенным здесь формулам коэффициент и должен быть меньше 4, так как при х=4 происходит выпучивание арки с точкой перегиба посере-
/ « я2/\
дине эилеровская критическая сила Якр= 2)») и допущение, что арка остается симметричной относительно середины, больше не выполняется.
94
Найдем то значение т, при котором u = 4: = 4
3 т
откуда т = 0,182. Таким образом, если т0,182, следует определять критическую нагрузку по формулам, приведенным в § 14 и 16 и соответствующим кососимметричной форме потери устойчивости.
Пример 23. Рассмотрим арку, рассчитанную в примерев (рис. 61). Для этой арки имеем
= 4-170000 = 0 00837 0,182,
325-5002
т. е. наиболее опасной формой потери устойчивости должна явиться кососимметричная форма.
Для проверки подсчитаем критическую нагрузку по формуле (40)
«=-!-..-L = i + l/lHZ =
384 El f V 27 m2
= j /4(1 -0,00837)3 = 4g
V 27-0,008372 ’ ’
_ 384‘/«/-46,4 _ 384-2,1-lQe-170 000-500-46,4 _
9кр _ 51* ~ 5-50004 ”
= 1015 кг/см = 101,5 т/пог-м 8,12 т/пог-м.
Таким образом, действительно расчетной критической нагрузкой является нагрузка
7кр = 8,12 т/пог-м,
найденная из условия кососимметричной формы потери устойчивости. Здесь следует оговориться, что в сравниваемых результатах взяты различные очертания оси: в одном — параболическая, в другом — синусоидальная арка, но это не должно дать значительной разницы в критической нагрузке.
Пример 24. Рассмотрим арку тою же пролета и того же поперечного сечения, что и в предыдущем примере, но со стрелой подъема /=1,0 м (рис. 64). При этом
m — 4,170000 =0,21. Из табл. 8 по интерполяции на-
325-ЮО2 ’ к
ходим и = 2,32; (и = 3,56.
95
Критическая нагрузка
_ 384/-/«2,32 _ 384• 2,Ы0* 170000-100-2,32
!*р~ /«-5 ~ 5.5000*
= 10,2 кг!пог‘СМ.
Критическая величина распора
и &EI „ 3,142.2,Ы0».17000Э
/7 KD = Ц = ,00 =
КР ~ /2 ’ (ПП2
5*5000*
= 501000 кг = 501 т.
Критические напряжения
#кр 501000 глг\ / о
aKD= — 1540 кг саг , что меньше
р F 325 '
что меньше
предела пропорциональности.
А. Р. Ржаницыным.в работе [19] рассмотрена весьма пологая круговая арка постоянного сечения, нагруженная постоянной радиальной нагрузкой (рис. 65). Путем интегрирования дифференциального уравнения изгиба такой арки с учетом обжатия оси получено сложное трансцендентное уравнение, из которого способом подбора можно найти величину критической нагрузки. Кроме того, в работе предлагается приближенное решение, основанное на том, что форма изгиба оси арки прини-
определяется при помощи метода Бубнова — Галеркина. Не приводя вывода, приведем только окончательные формулы, необходимые для определения критической таI рузки.
Для двухшарнирной арки критическая нагрузка определяется по формуле
мается за синусоиду
стрела прогиба
Якр~ n*R3
4/2 EF
[а±2(П
где
g _ я« 2 /?2 _ 240,4 #
4/4 (2а)2 А»2 в
96
I— радиус инерции сечения арки;
Я— гибкость арки (% = ;
а—половина центрального угла.
Для бесшарнирной арки критическая нагрузка определяется по формуле
/2 EF
7кр
64л2 R3
36j — 30 ± + -у/~19-6. . — 38 j /г EF
64я2 Я?
(42)
где
61 =
64я4 Р R*
6234 t (2а)2 Я.2 ’
половина центрального угла; к— гибкость арки.
Зависимость между нагрузкой и прогибом двухшарнирной арки посередине пролета при фиксированных значениях б показана на
рис. 66 (качественно эта картина полностью совпадает с результатами исследования Т имошенко). Критическая нагрузка соответствует экстремальным точкам на кривых q(w), причем верхняя точка (точка В на кривой при 6 = 0,5) соответствует кр ит ическо м у состоянию, достигаемому при монотонном возрастании нагрузки (в формуле 41 для определения величины этой нагрузки следует взять знак плюс). После перехода через критическое состоя¬
7—949
97
ние деформация будет расти без увеличения нагрузки (прямая В—D). Нижняя точка (точка С на кривой 6 = = 0,5) соответствует критическому состоянию, достигаемому при монотонном уменьшении нагрузки (прямая С—А характеризует прощелкивание арки в обратном направлении). Обе экстремальные точки сливаются в одну для двухшарнирной арки при 6=1, а для бесшарнирной арки при 8i = 19.
Таким образом, при б1 в двухшарнирной арке и
при 6i19 в бесшарнирной арке не будет происходить потери устойчивости, арка будет плавно деформироваться под нагрузкой. Для удобства вычислений в табл. 9 и на рис. 67 даем коэффициенты формул (41), (42), 9* и 9** для ряда значений б и 6i. Пример 25. Опреfj) f делить критическую нагрузку 7кр для круговой двухшарнирной арки, показанной на
ТШШЩЩМк 'ЧТ \
Рис. 67
рис. 68. Поперечное сечение арки двутавровое: вертикальная стенка 500X 12 мм, четыре уголка 90х90х12лш и четыре горизонтальных листа 380X 12 мм (см. рис. 61):
F = 325 см2; /= 170000 см4;
98
У F у 325
Гибкость
% = — = = 219.
i 22,8
Радиус арки R находим из уравнения
-yj2 + (R — f)2 = R2, откуда R = 313 м.
Половина центрального угла
-Ц- -0.08.
8 „ Jfi. = «М _096
(2а)2 А,2 (2*0,08)2‘2192
Из табл. 9 находим 7* = 0,473 и по формуле (41) — критическую нагрузку, соответствующую монотонному возрастанию нагрузки
4PEF * 4• 50002-2,1 • 10е• 325 Л лпо
qит\ = q* = *0,473 =
чкр эх*/?3 4 3.144-313005
= 10,8 кг/пог.см = 1,08гп/пог.м.
Как видим, результат мало отличается от результата предыдущего примера. Этого следовало ожидать, так как арка весьма пологая, радиальная нагрузка при этом близка к вертикальной и круговое очертание — к синусоидальному.
§ 18. Устойчивость арки с затяжкой
Задача об устойчивости арки с затяжкой отличается от задачи об устойчивости рассмотренных выше арок тем, что еще до потери утойчивости имеет место явление изгиба, арка является сжатоизогнутой. В работе [15] рассмотрена параболическая арка постоянного сечения, нагруженная вертикальной равномерно распределенной нагрузкой q, имеющая гибкую (рис. 69, а) или жесткую (рис. 69, б) затяжку.
7*
99
Дифференциальное уравнение изгиба такой арки имеет вид:
(■ + ‘) (cos’е* ■L)+m [(п _+sec*01 sec*0 + + т [ft— l) + 4sec20] tg0*sec,0*A1 = 0, (43)*
где
т _ . _ н» .
Ш Т) = !
Е1 ’ 1 // *
Мх—дополнительный момент, возникающий при потере устойчивости; а— радиус кривизны арки в вершине;
Н— распор двухшарнирной и параболической арки; //3 — распор такой же арки с затяжкой.
Потеря устойчивости арки с затяжкой так же, как и арки с неподвижными пятами, сопровождается изгибом по двум полуволнам, что дает для арки с гибкой затяжкой следующие граничные условия:
в ключе М(0) = 0; (-Ц = 0,
в пяте М (а) = 0.
(а)
Численное интегрирование уравнения (43) с учетом граничных условий дало следующие результаты:
_ K-EI
19 9
Таблица 8
п
1.0
0.9
0,8
к
45,4
50,5
57
Рис. 69
* Уравнение (43) выведено проф. И. Я. Штаерманом.
100
где' К — коэффициент устойчивости, для отношения -у- =
= 0,2, приведен в табл. 8
Вывод, казалось бы, парадоксален: если при данной жесткости арки Е1 мы будем уменьшать жесткость затяжки E3F3 (при этом г]= -f будет уменьшаться), т. е.
н
будем уменьшать жесткость системы — критическая нагрузка будет возрастать. Это объясняется тем, что с уменьшением распора уменьшается и осевая сжимающая сила в арке; может быть найдено то относительное значение жесткости затяжки, при котором потеря устойчивости в эйлеровском смысле станет вообще невозможной; при этом с увеличением нагрузки арка будет плавно деформироваться до потери несущей способности.
В запас прочности часто считают критическую нагрузку для арки с шарнирно прикрепленной затяжкой, равной критической нагрузке для двухшарнирной арки.
Для арки с жесткой работающей на изгиб затяжкой граничные условия в замке остаются те же, что и при гибкой затяжке [М(0)=0; М"(0)= 0], а условие в пяте, выражающее неразрывность деформаций арки и затяжки, принимает вид:
+а
( tg ф sec3 (pMdq = —р— tg аМ (а),
J 6а /зах
о
где М(сс)— момент в пяте;
а—половина центрального угла.
Критическая нагзка, как и раньше, определяется по формуле 7кР= —, где К для —=0,2 и г] = 1 име¬
ют следующие значения:
Таблица 9
7ар
Бесшарнирная арка 0
Арка с затяжкой
Двухшарнирная арка оо
'зт
0,28
1.60
4,45
К
101
82
61.5
53
45,4
101
ГЛАВА 5
УСТОЙЧИВОСТЬ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
§ 19. Основы теории.
Дифференциальное уравнение устойчивости 2-го рода
Как установлено В. 3. Власовым [1], поперечные сечения тонкостенных стержней после деформации, как правило, не остаются плоскими. Эти стержни работают как пространственные тонкостенные системы, испытывающие продольные деформации не только вследствие сжатия
или изгиба, но и вследствие закручивания. При этом точки поперечного сечения располагаются на криволинейной поверхности; сечение, как говорят, испытывает депланацию. Явление закручивания и связанные с ним дополнительные напряжения играют большую роль в вопросах устойчивости тонкостенных стержней.
Здесь будут рассмотрены только стержни открытого профиля (рис. 70, а и б) с недеформируемым контуром поперечного сечения (недеформируемость контура должна быть обеспечена поперечными диафрагмами или реб-
Рис. 70
102
рами жесткости). Сечения с замкнутым профилем {рис. 70,6, г) при отсутствии деформации контура могут, как известно, рассчитываться по обычной теории сплошного бруса с применением гипотезы плоских сечений.
На рис. 71 у а изображен тонкостенный стержень с недеформируемым профилем, находящийся в равновесии под действием произвольных продольных и поперечных нагрузок.
На рис. 71,6 показано поперечное сечение стержня и его перемещение в плоскости хОу после деформации.
Здесь О—центр тяжести сечения;
А— центр изгиба, г], 0— соответственно перемещения центра изгиба по направлению осей х и у и угол поворота всего сечения в плоскости хОу (угол закручивания); все эти величины являются функциями координаты г сечения вдоль образующей стержня. Кроме того, точки сечения перемещаются в направлении оси z\ эти перемещения являются функциями координаты s(M0—Mi) по дуге контура.
В рассматриваемом случае потеря устойчивости не связана с появлением новых форм равновесия, так как и до потери устойчивости стержень и изгибается, и закручивается, и депланирует; следовательно, речь идет о потере устойчивости 2-го рода.
Поведение тонкостенных стержней в задачах прочности описывается системой трех дифферен циальных уравнений, составленных стояния:
Рис. 72
для недеформированного со-
Ely-l = qx,
/о • 0IV — GI$" = tti,
(44)
103
где первые два уравнения — это уравнения изгиба стержня, как балки, в направлении осей леи у, а третье — уравнение стесненного кручения тонкостенного стержня; Qjx и qv — интенсивности погонных поперечных нагрузок; т — интенсивность внешнего крутящего момента, определяемого относительно центра изгиба.
Если рассмотреть равновесие бесконечно малой полоски длиной dz (рис. 72) тонкостенного стержня в деформированном состоянии, то уравнения (44) приобретают следующий вид ([1] и [10]):
здесь N— продольная сила;
Мх, Муу В—соответственно изгибающие моменты относительно осей х и у и бимомент; аху ау—координаты центра изгиба; ех еу—координаты точки приложения заданной
г, Рх, ру рсо — геометрические характеристики, определяемые по следующим формам:
и секториально-полярный моменты инерции;
1Х, 1у—осевые моменты инерции;
/© = fa2dF— секториальный момент инерции;
Е/,114 - {N (' + ау%’))’ + (MXQ)" = 0; EIX VV - [N (л' - 0')]' + (М„ О)" = 0;
Е/а 01V _ Gld 0" - [(rW + 220, M + (45)
+ Ра, В?Г]- + [яЛе*-ах)+%{еу-ау)}*-
- ау №')' + ах (АЧ)' + МХ + Му г," = 0.
погонной нагрузки в плоскости поперечного сечения;
(46)
Ux= jyp2dF; /„ = j xp'dF;
F
F
иы= — полярно осевые
F
F
104
Ia—момент инерции чистого кручения, определяемый для поГгеречных сечений, состоящих из отдельных прямоугольников или криволинейных полос со сторонами bi и б* по формуле
(а» 1,3 — для двутавров; сх « 1,12 — для швеллеров; а«1,0 — для уголков и т. д.).
Уравнения (45) являются наиболее общими уравнениями устойчивости тонкостенного стержня.
§ 20. Потеря устойчивости 1-го рода.
Внецентренное и центральное сжатие
Если поперечная нагрузка и реакции тонкостенного стержня проходят через линию центров изгиба, то до потери устойчивости стержень не испытывает кручения, депланация отсутствует, она проявляется только в результате потери устойчивости. Таким образом, потеря устойчивости будет характеризоваться появлением качественно нового деформированного состояния, новой формы равновесия и уравнения (45) при бимоменте В —О будут описывать явление потери устойчивости 1-го рода*.
Для такого внецентренно сжатого стержня (рис. 72) имеем:
В - 0;
N = —Р\
Мх = — Реу\
Му = Рех
(при определении знака Мх и Му поступаем так: при взгляде от положительного направления оси к центру момент по часовой стрелке считается положительным).
Уравнения устойчивости (45) при внецентренном сжатии принимают вид:
* В таком виде эти уравнения и были выведены нроф. В. 3. Власовым. Вывод уравнений (45) см. работу [10].
105
ei Л™ + ?? + (м* + Рау)0" = °;
Е1Х ц1 v + /У + (Му - Рах) 0" = 0;
(Мх + Рау) Г + (Му - Рах) rf + /. 01 v + + (r2P + 2РХ - 2pv М, - G/d) 0" = 0.
(47)
Рассмотрим детально случай центрального сжатия, когда сила приложена в центре тяжести сечения, но центр тяжести не совпадает с центром изгиба; в этом случае
вх = = 0; А1х = Му — 0; Qx ~~ 0; dy -j— 0
и уравнения устойчивости принимают вид:
Е1и1™ + РЪ + PauQ = 0;
Elx r)IV -f Рц — Рах 0 = 0;
Рау I" - Рах тГ + EIa 0,v + (г2 Р - GId) 0* = 0.
Дифференциальными уравнениями (48) и условиями закрепления стержня по концам определяются все формы потери устойчивости невесомого стержня при его центральном сжатии. В каждое из уравнений (48) входят одновременно поступательные перемещения g, г] и углы закручивания 0; это показывает, что, если центр изгиба не совпадает с центром тяжести (ахф0, ауФ0), то эйлеровская изгибная форма потери устойчивости при центральном сжатии становится невозможной. В частном случае, когда центр изгиба совпадает с центром тяжести (например, в сечении с двумя осями симметрии) ах = ау = 0 и уравнения (48) распадаются на три отдельных уравнения
/„lIV + PI" = 0;
EIxr\lv + Рц" = 0;
Е1УУ + {r2P — GId)Q = 0.
Решения первых двух уравнений дают две эйлеровские критические силы, соответствующие изгибу относительно осей х и у, решение третьего уравнения дает критическую силу Р(о, соответствующую чисто крутильной форме потери устойчивости.
Уравнения (48) характеризуют наличие одновремен¬
на)
106
но изгиба и кручения при потере устойчивости, или, как говорят, изгибно-крутильную форму потери устойчивости.
Рассмотрим случай, когда концы стержня закреплены от перемещений в плоскости поперечного сечения и свободны от нормальных напряжений, вызываемых изгибом и кручением, т. е.
при z = 0 и при г = 1
5 = П = 0 = О, I" = л" = 0" = 0.
Этим граничным условиям и дифференциальным уравнениям (48) будет удовлетворять решение в виде
л • inz о . inz л ~ . inz
I = A sin — ; Г] = В sin — ; 0 = С sin — , (49)
где -4, В, С—некоторые постоянные коэффициенты;
i—любое целое положительное число (/ = = 1,2, 3...).
Подставляя значения (49) в уравнение (48) и вводя обозначение
in
I
(50)
получаем после сокращения на общий множитель A2sinz следующую систему линейных однородных алгебраических уравнений:
(Е1у1*-Р)А-РауС = 0;
(EIxV-P)B + PaxC = 0; (51)
-РауА + РахВ + [Е/ш12 + G/d-r2 Р]С = 0.
Ненулевое решение для неизвестных Л, В и С получим, если приравняем нулю определитель, составленный из коэффициентов при этих неизвестных. Условие D = 0 и есть уравнение устойчивости, из которого определяется критическое значение нагрузки. Это уравнение может быть записано так:
Р —Р-
1 У *9 0;
—ауР;
0;
Рг-Р:
ах р\
ауР
агР
(К-Р)г
= 0.
10Г
где
(а)
РХ = Е1Х№ —эйлеровские критические СйЛй;
Ру = Е1у№ i —критическая сила для чисто кру-
1)2+ QJ тильной формы потери устойчиli) = —~ 2 вости.
Раскрывая определитель, получаем
(р,-р) (р-р)\р.-рУ--“1р‘(р.-р) -
-Я) — 0, (52)
пли, располагая по степеням Я
(- г» + al + a]) Р + [(Р + Pt + PJ - о; Р, _
- М Р* —* (Р. Р, + Р, р. + Р. Р.) Р +
+ p,p,pj'- = b. (5.3)
Уравнение (53), кубическое относительно силы Я, имеет три корня Ри Р2, Яз соответствующие трем степеням свободы поперечного сечения с недеформируемым контуром в своей плоскости. Каждый из этих корней Ри Яг, Я3 будет зависеть от числа полуволн п (п= 1, 2, 3, ...,
оо), т. е. будет иметь бесконечное множество значений б соответствии с бесконечным числом степеней свободы упругой оси стержня.
Пусть Р\Р2Рг, а из эйлеровских критических сил минимальной будет Рх
Я Я Я
л X у (0 '
Представим уравнение (53) в виде /(Я)=0 и исследуем характер функции / (Я), произвольно изображенной на рис. 73. Из уравнения (53) видно, что при малых значениях Я знак / (Я) должен совпадать со знаком свободного члена, т. е. при РР\ f(P)0. Из уравнения (52) находим, что
1) приЯ = Я* f(P)=—alPx (Яу—Я*) 0, т. е. значение Р = РХ располагается где-то между Я4 и Я2;
2) при Ру=Р f(P) —(Рх-Ру)4 0;
3)при Р=Рв f(P) (Рх—Рп) а2уР1—(Ру—Рш)Х
Ха*Рп0, т. е. значения Р=РУ и Р=РШ располагаются между корнями Рг и Рг-
208
При больших значениях Р знак f(P) будет совпадать со знаком старшего члена
_f2 + a2 + a2 = __V±A_ о, т. е. f(P) 0.
Основной, практически очень важный вывод, который следует из этих рассуждений, заключается в следующем: для несимметричного тонкостенного стержня, в котором центр изгиба не совпадает с центром тяжести, критическая сила, соответствующая изгибно-крутильной форме потери устойчивости, всегда меньше минимальной эйлеровской критической силы.
kJMeLk
I -2,1 Юб**/см* G-0/tE-4M 10*«Чем* Рис. 74
В частном случае, если центр изгиба совпадает с центром тяжести сечения, имеем ах = ау = 0, и уравнение (52) принимает вид
(РУ-Р) (Р*-Р)(Р*-Р)г2 = °-
откуда получаем три решения:
1) Рх-Р = 0, Pi = Px,
2) Ру-Р = 0, Р2 = РУ,
3)Р„-Р = 0, Р3 = Р
т. е. в этом случае имеем или чисто изгибную, или чисто крутильную форму потери устойчивости, что уже было показано выше непосредственно на дифференциальных уравнениях.
При внецентренном сжатии чисто изгибные и чисто крутильные формы потери устойчивости имеют место, если сила приложена в центре изгиба. В этом случае ех =
109
=ах\ еу=ау и уравнения (47) тоже распадаются на три самостоятельных уравнения
EIytlV+PZ= 0;
/жт,1У + /т,’ = 0;
Elm* + [Р(r2 + 2М* + M ~°Ц 0’ = 0-
Первые два уравнения определяют изгибные формы потери устойчивости и дают эйлеровские критические силы РХ = Е1ХК2 и Ру = Е1уХ2\ третье уравнение определяет крутильную форму потери устойчивости, при которой поперечные сечения стержня поворачиваются вокруг центра изгиба; при этом величина критической силы [10] определится по формуле:
Р г2
р кР г* + 2фхах + Щау *
Расчетной будет минимальная из трех критических сил.
Пример 26. Найти критическую силу РКр для шарнирно опертого двумя концами стержня длиной 1 = 5 м, находящегося под действием постоянной продольной, центрально приложенной силы Р. Поперечное сечение стержня—неравнобокий уголок, показанный на рис. 74,а.
Для каждой полоски, составляющей уголок, проводим срединную линию (рис. 74) и все дальнейшие расчеты ведем для этой линии. Площадь поперечного сечения
F = 30-1+20-1=50 см2.
Координаты центра тяжести
sar ЗД-15 Уо= ~y~ = 50 =
SAC 20-10 *. = -Г- = “i5“ = 4 «*•
Моменты инерции относительно случайных центральных осей
/ = 20-92 + + 30-6* = 4950 см\
*1 12
/ = 30*4® + + 20-62 = 1867 см*
vi 12
1 , = -20.9-6 -30.4-6 = — 1800 см\
110
Угол наклона главной оси
tg 2а0 . 2‘1800 = 165,
60 К— /„ 4950 —1867 ’
Ух
откуда
ао = 2440'; tg ао = 0,46; sin ао = 0,418; cos а0 = 0,91. Главные моменты инерции
1я--!атл-±т'г1'--,-У+*р~-
= 4950 + l867. ± _L 1/(4950 — 1867)2 +'4-1800® ;
/тах = 1Х = 3408 + 2365 = 5773 сл4;
/тш = 1У = 3408 — 2365 = 1043 см\
Момент инерции при свободном кручении
ld -&63 = —(30-13 + 20-1*)= 16,7 с*4-
3 3
Центр изгиба лежит на пересечении полок (точка А на рис. 74, б).
Поэтому секториальный момент инерции /© = 0. Координаты центра изгиба относительно центра тяжести
ах = 7,4 см; ау = 6,5 см\
Г* = а2х + а1 + -±1у_ = 7,4* + 6,5* +
5773+1043_ = 233 ,
50
Эйлеровские критические силы и критическая сила свободного кручения
Р. = Е1Л2 = 2,1 • 10е*5773* biii = 478000 кг = 478 т-
X X 5QQ2 »
Р„ = Е1и № = 2,1 • 10е • 1043 biii = 86300 кг = 86,3 т; » у • 5002 » »
EIaW + Gld _ Gld
Р = (О г2 г2
0.84-106.16,7
= 60200 кг = 60,2 т.
233,4
111
Подставляя все полученные значения в уравнение (53), имеем следующее кубическое уравнение для определения критической силы: —Р3+885,4 Р2—128000Р +
+ 4 200 000 = 0. Минимальный из трех корней этого уравнения и является расчетной критической силой, соответствующей изгибно-крутильной форме потери, устойчивости. Решая уравнение, получаем Pmin=Лер=47,6 Т* что меньше минимальной из трех ранее найденных критичес59 4 47 6
ких сил на —’ 59~4~"~~ ’ и меньше эйлеровской изгибной критической силы на
86,3 — 47,6
86,3
100 = 45%.
Следует отметить, что неравнобокие уголки прокатного сортамента имеют значительно большую относительную жесткость на кручение, чем в данном примере, из трех сил Рх Ру, Ра минимальной для них является эйлеровская критическая сила Ру и окончательная критическая сила, соответствующая изгибно-крутильной форме потери устойчивости, мало отличается от Ру.
После определения критической силы, как всегда, необходимо проверить, находятся ли критические напряжения в пределах упругости материала. В нашем примере:
Ркр _ 47600
1 50
FKT 4/bUU лгл t « 7Кр = Нг = ~~5Г = 950 Кг'СМ апа.
что подтверждает законность произведенного расчета.
Пример 27. Найти величину критической нагрузки центрально нагруженного продольной силой, шарнирно опертого двумя концами стержня длиной / = 9,0 м\ поперечное сечение стержня — сварное, из стальных листов 300X12 и 200X12 мм (рис. 75, а). Площадь сечения F = = 2-30-1,2 + 20• 1,2 = 96 см2. Положение центра тяжести
„ _ Snm _ 30.1,2.15.2 _ Ц'25 см.
F 96
Главные моменты инерции и момент инерции свободного кручения
1Х = + 2.30-1,2 • 10а = 8000 см4t
112
lu = 20.1,2 -Ц.254-2-1 + 2-30.1,2.3,75* = 9450 см*;
= И см".
Определяем положение центра изгиба на оси х, которая является осью симметрии (рис. 76, б).
_ J ав ydF
bh b
2 2
•6-2
6/i3 e № — + 265 —
12 4
h
~3 +
302
20
T+2-30
= — 13,5 CM:
°) f 30_
Пщ-
ци
S)
6=1,2
w
tfjf
0/r
и
'Ц
8 ©
штПТШПШ
А__А—»
/5.
-ЩЩЩ
Рис. 76
О)
мгЫ-
м
■a
cw52H
7& \
niniim nn it —i
Рис. 75
Рис. 77
* Коэффициент а здесь принят равным единице. 8—949
113
о* = a* 4- хо = 13,5 + 11,25 = 24,75 см\ ау =-- 0.
Вычисляем секториальный момент инерции при помощи эпюры секториальных площадей, показанной на рис. 76,в
= Г со* dF=2.1,2 \'™- . J. +
а .) [ 2 3 2-3
1630 . _2 _ 2 13530 les-l _ 700000 сл.;
2 3 2 3 J
г2 = а\ + al + = 24,75* +
8000 + 9450
У F ’ 96
= 612 + 182 = 794 см2.
Эйлеровские изгибные критические силы и критическая сила при свободном кручении:
Р=Е1Л2=2,МО".8000.— = 204000 кГ=204 Т;
х X I доог ’
Р =Е1Л2=2,\.10*.9450— = 241 000 кГ = 241 Т;
у У 900а *
3.142
р/ »2j-n 2.1.10«.700 000 —— + 0,84.10*.46
/(0+0/ 90Q2 /■г 794
= 71 200 «/'=71,2 7'.
Ввиду того, что сечение имеет одну ось симметрии и ау=0, система уравнений (51) распадается на две системы:
(Ру—Р)А = 0, откуда при А ф 0 Р\ = РУ = 2А\ 7’; {Рх-Р)В-ахРС = 0, а.
Рх-Р)В-ахРС = 0, \ Рх-Р-, *ХР
. РВ+ {Р0-Р) г2 С = 0, ) °ТКуда а, Р; {Ра—Ру
= 0.
Раскрывая определитель, получаем для определения критических сил, соответствующих изгибно-крутильной форме потери устойчивости, следующее квадратное уравнение
Р — (Рж + РЛ——Р + Р р —= 0.
V* */ 2 2 лег со 2 2
2 2 ‘ х (О 2 2
г -а$ г -а*х
114
Подставляя в это уравнение найденные выше значения Рх, Л», г2, al, получаем
Р2— 1200Р + 63200 = 0, откуда Р = 600± V360 ООО—63 200 = 600 ±545;
Рmin = 55 Т; Рщах =1145 Т.
Таким образом, расчетной критической силой является Pmin=55 т, критические напряжения
*кр= = 574 кГ/см* апц.
§ 21. Потеря устойчивости плоской формы изгиба балки
Одним из частных случаев потери устойчивости 1-го рода является потеря устойчивости плоской формы изгиба; при этом в первоначальном состоянии ось стержня от действия продольных или поперечных нагрузок изгибается в одной какой-то плоскости, а при нагрузке, равной критической, становится возможной новая форма равновесия, с изгибом в двух плоскостях и закручиванием (см. рис. 76, а, б).
1. Рассмотрим сначала случай потери устойчивости при наличии только поперечных нагрузок (см. рис. 76,а); пусть сечение стержня имеет две оси симметрии (например, двутавр). Для этого случая из общих уравнений (45), приняв N = ах = С1у = ех = еу = $х = $у = $а =МУ = 0У получаем два совместных дифференциальных уравнения, описывающие дополнительные деформации при выходе из первоначальной плоскости изгиба
+ (М9)" = 0,
/ше'у — GIdB" + Mg = 0 1
При произвольной нагрузке уравнения (54) имеют переменные коэффициенты, так как M=f(z). Наиболее простое решение получаем при чистом изгибе, когда М = = const (рис. 77,а).
При М = const уравнения (54) приобретают вид
EI.F + MST- о,
Е1Ш eIV _ GIj Q" + Ml" = 0.
8*
115
Граничные условия могут быть различными; рассматривая, как и в § 20 данной главы, шарнирное закрепление обоих концов стержня, имеем граничные условия: при z=0 и при z=l, =0=0, "=0"=О решение системы уравнений (55) в виде
sin—; 0 = Csin—.
Подставляя это решение в уравнения (55), после сокращения на
I2 я2 . im
— sin —
/2 /
получаем два однородных линейных уравнения для определения постоянных А и С
Е1У№А — МС = 0; -МА + (EI„V + Gld) С = 0, где К =
Приравнивая нулю определитель, составленный из коэффициентов при неизвестных А и С, получаем уравнение для определения критического значения момента М
/,*•; -М -М-, EIaV + GId U’
EIyV(EIaW + GId)-M* = 0,
откуда критическое значение момента М
мкр = ± Я /E/'(E1J* + GI4 )=±r VJT. (56)
Для балки на двух опорах, загруженной равномерно распределенной нагрузкой (рис. 77,6), изгибающий момент в произвольном сечении равен
м= у у - г
2
и уравнения (54) принимают вид:
EJyllv + -Lq[z(l-z)QY = 0,
ЕГ e‘v - GId 6'+ i- qz (I - z) r = 0.
(57)
116
В результате интегрирования уравнений (57), которое можно выполнить либо одним из вариационных методов, либо в бесконечных рядах, находим, что критическая интенсивность нагрузки имеет следующее значение:
7кр —
/с Vf.Iu Gig
18
(58)
Величина /С, являющаяся функцией параметра т2=
Cld /2 , 1Л
— —-Tj— , приведена в табл. 10.
Таблица 10
т2
0,4
16
24
32
48
64
80
96
160
240
320
400
К
143
53,3
42.6
36,3
33,8
32.6
31,5
30,5
30.1
29 29
28.8
28.6
28.6
Влияние различного вида поперечных нагрузок рассмотрено в работе [10].
2. Рассмотрим случай потери устойчивости плоской формы изгиба стержня с сечением, имеющим две оси симметрии, при действии постоянной продольной силы, внецентренно приложенной по одной из осей симметрии (рис. 76, б).
Для этого случая из уравнений устойчивости при внецентренном сжатии (47), положив ах=ау = ех = $х = = ру=Л1у=0 и Мх = —Peyt получаем следующие уравнения, описывающие дополнительные деформации при выходе из первоначальной плоскости изгиба
/,eIV + Ps'-e' = o,
- Реу Г + Eiyv + (г* Р - GId) в" = 0.
(59)
Для шарнирно опертого концами стержня с граничными условиями g = g" = 0 = 0"=O при z=0 и z=l имеем
l = Asinkz\ 0 = CsinA,2 и, подставляя это решение в уравнения (59), после сокращения на Я,2 sin Кг получим (Е1УХ2—Р) А + РеуС=0, РеуА + (/© Х2+GId—г2Р) С=0.
Используя введенные выше [см. (а)] обозначения и
117
приравнивая нулю определитель, составленный из коэффициентов при неизвестных, получаем
D =
Р —Р-
У 1 I
Ре..
Р*у' (Рш-П*
= 0.
Таким образом, для определения критической силы, соответствующей потере устойчивости плоской формы изгиба, имеем следующее квадратное уравнение:
Р*-{Ру + Р»)-ГЧ Р + Ру Р»-г = ° 60
(0 о 2
г —р
г еу
(аналогичное уравнение было выше получено при рассмотрении центрального сжатия сечения с одной осью симметрии).
Решая уравнение (60) относительно Р, найдем
кр-
•и*
1-Г
+ ш)2
(61)
-+*-4
Пример 28. Однопролетяая шарнирно опертая балка с двумя короткими кон1 солями изгибается в плос* I кости yOz (рис. 78). Пролет балки /=10,0 м\ поперечное сечение — двутавр № 60а. Пренебрегая влиянием кон-
I
2,2см
‘О
100 см
-4
Рис. 78
Рис. 79
солей, найти критическое значение момента М = Ра, соответствующее потере устойчивости плоской формы изгиба балки. Модули упругости
118
Е = 2,Ы0« кГ/см2,
G = 0,4 Е.
Геометрические характеристики поперечного сечения
— 83860 см 1 по сортаменту ГОСТ 8239—56 Iy = 1700 см* I
Ia= аБ — = ЬЗ(556.1,Зз + 2.17,6-2,23) = 215сл«*.
3 3
, bh Ь 2 bh Afi 6 tph*
/ = — . — . — . — .4о, = — =
“ 4 4 3 4 2 24
= 2,2‘17’68'58-- = 1670000 СМ\
4
По формуле (56), приняв i= 1 и вынося модуль упругости Е из-под знака радикала, имеем
М” = Т 'EV'»('-7- + м/') “
= Ы12,Ы0« 1/ 1700 (1670000--+0,4-215) =
1000 V \ 10002 ’ /
= 2750000 кг ■ см —- 27,5 тм.
Критическое краевое напряжение
g = = -70000'30 = 983 кГ/см2.
р Wx 83860 '
Пример 29. Найти критическую интенсивность нагрузки и критический изгибающий момент, соответствующие потере устойчивости плоской формы изгиба, для шарнирно опертой балки /=10,0 м, нагруженной равномерно распределенной нагрузкой по всей длине. Поперечное сечение — двутавр № 60а.
Геометрические характеристики берем из предыдущего примера. Определяем параметр
т2 = ———————— = 51,6.
Е'п 16700000
Из табл. 12 по интерполяции находим
К = 31,3.
119
Критическая интенсивность нагрузки (по формуле 58) _ EKVlyO,4ld _ 2,Ь10*-31.3 1/7700-0,4-215
~ 13 ~ 10003 =
= 25,2 кГ/пог- см.
7„р = 2,52 Т/пог-м.
Критический максимальный изгибающий момент
Дтах = ЯкрЛ _ 2,52-10» = 315 Тм.
КР 8 8 ’
Критические краевые напряжения
а = = 315000°-30 = 1125 кГ/см2.
р Wx 83860 '
Пример 30. Найти критическую силу для внецентренно сжатой стальной полосы с размерами, показанными на рис. 79.
Е = 2,1 • 10е кГ/сж2; G = 0,84.10« кГ/см*. Геометрические характеристики:
_ 2 _ 1333 сж4;
* 12 = = 13’33сЛ4;
Л/ = ~ 53,3 сж4;
/,0 = 0;
г2 = l*±h = 1333+ 13.33 = 33 6 F 40
Критические силы чистого изгиба и чистого кручения при выходе из плоскости yOz
Ри = Е1и — =2,1- 10е-13,33--- = 27700 кГ = 27,7 Т.
У У 12 1 * 1002 *
Р =- = 0,84‘10в~53'3- = 1330000 кг = 1330 т.
“ /•* 33,6
120
згибно-крутильные критические силы при лотере устойчивости плоской формы изгиба (формула 61):
кр =' ~/ у **" х x[l±l/,-4(l-i)TA-7
(27,7+ 1330) X
*(-)
*[.± !/-«(.-)• 27'7-,3“
(27,7+ 1330)» J = 2657(1 ±0,9897).
Минимальная критическая сила Рнр = 2657 (1 — 0,9897) = 2657 • 0,0103 = 27,36 Р„. Критические краевые напряжения (- _ Р Реу _ 27360 акрах~Т + ¥7~ 40 +
27360.5.10 = 6g4 1023 = т7кГ см,
1333 ' пц
§ 22. Потеря устойчивости при растяжении
При внецентренном действии продольной силы потеря устойчивости может возникнуть не только при сжимающей, но и при растягивающей продольной силе. Неустойчивые формы равновесия возникают здесь потому, что при внецентренном приложении растягивающей силы часть сечения оказывается сжатой.
Математически возможность иотери устойчивости при растяжении подтверждается уравнениями (45), которые могут быть решены для N=+P при эксцентриситетах, лежащих за пределами некоторой области, которая называется областью устойчивости при растяжении. В самом деле, если, например, растягивающая сила приложена в ядре сечения, во всех точках возникнут только
121
растягивающие напряжения и первоначальная форма равновесия будет устойчивой при всех значениях нагрузки.
Анализ уравнений, проведенный В. 3. Власовым, показывает, что область устойчивости при растяжении независимо от формы поперечного сечения стержня представляет собой круг, так называемый круг устойчивости,
радиус которого и координаты центра в самом общем случае определяются по формулам:
R2 = 4- 4- ,х + 'у .
* .9 1 . .9 1 г »
4/
4/
kx = -Qt- = а р • ku - = а, + 6
21 у х х у 21 х и«Гу
(Vx, И у, Р*, Р у см. формулы 46)
(62)
122
Если поперечное сечение стержня имеет одну ось симметрии, то Ux=Uy=0, центр круга устойчивости совпадает с центром тяжести и радиус его равен полярному радиусу инерции
2 __ + 1у
При одном и том же эксцентриситете растягивающая критическая сила всегда оказывается больше сжимающей. Эта разница убывает с увеличением эксцентриситета.
На рис. 80 даны графики критических сжимающих и растягивающих сил, построенные для таврового стержня с размерами: di = 10 см\ d2 = 5 см\ 61 = 62 = 0,5 см\ /= = 167 см и силой, действующей на оси ох (еу = 0). На графике значение каждой силы отложено в точке, соответствующей ее эксцентриситету (график взят из книги [1]).
РАЗДЕЛ II
ОСНОВЫ ДИНАМИКИ СТЕРЖНЕВЫХ СИСТЕМ
ГЛАВА в
СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
§ 23. Основные понятия
Динамика сооружений, являющаяся одним из разделов строительной механики, занимается разработкой принципов и методов расчета сооружений на действие динамических нагрузок, т. е. таких нагрузок, величина, направление или положение которых изменяются во времени. При действии на сооружение динамических нагрузок возникают и играют существенную роль силы инерции масс этих нагрузок и самого сооружения.
Динамические нагрузки разделяются на следующие основные виды:
а) вибрационная нагрузка, создаваемая стационарными машинами и механизмами с движущимися частями, например, электромоторами, турбогенераторами, станками и др. Нагрузки этого вида почти не зависят от свойств конструкций, на которые они действуют, но являются основным источником колебаний этих конструкций;
б) ударная нагрузка, создаваемая падающими грузами и падающими частями силовых установок (молотов, копров и др.). Эти нагрузки характеризуются небольшой продолжительностью их действия и зависят от упругих и инерционных свойств конструкций, воспринимающих удар;
в) подвижная нагрузка, положение которой в пролетах сооружения изменяется во времени, например,
124
нагрузка от подвижного состава железных дорог, от автомобилей, от кранов и др.
Динамические нагрузки могут быть и комбинированными, например ударно-вибрационная нагрузка от копров периодического действия.
К числу динамических нагрузок относятся ветровая, от взрывной волны и сейсмическая нагрузки, проявляющиеся в виде одного или ряда, иногда периодических, толчков.
Все динамические нагрузки вызывают колебания конструкций, на которые они действуют.
Здесь будет в основном рассмотрено действие вибрационной нагрузки в виде периодически действующих сил, изменяющихся во времени по гармоническому закону, т. е. по закону синусоиды или косинусоиды.
Динамический расчет производится как с целью проверки сооружения на прочность, так и с целью определения величин динамических перемещений, скоростей и ускорений, которые при воздействии на людей и на некоторые виды оборудования, например на измерительные приборы, не должны превосходить допустимых пределов.
Для решения задач динамики сооружений применяются два основных способа:
А. Статический способ, основанный на применении уравнений динамического равновесия, которые отличаются от уравнений статического равновесия дополнительным учетом, согласно принципу Даламбера, сил инерции в виде произведения масс или их моментов инерции на ускорения, т. е. на вторые производные линейных или угловых перемещений по времени.
Б. Энергетический способ, основанный на применении закона сохранения энергии М. В. Ломоносова, согласно которому сумма потенциальной и кинетической энергии упругой системы является величиной постоянной во времени.
Трудоемкость динамического расчета той или иной упругой системы зависит прежде всего от степени свободы этой системы, т. е. от количества независимых геометрических параметров, определяющих положение всех масс при любых возможных упругих перемещениях системы.
Следует иметь в виду, что в понятие степень свободы в динамике сооружений вкладывается другой смысл, чем
J25
в статике сооружений. Подсчет степеней свободы при кинематическом анализе в статике сооружений производится без учета собственных деформаций дисков и стержней, которые считаются абсолютно жесткими. В динамике же сооружений при определении степени свободы системы рассматриваются именно ее упругие или упруго-пластические деформации.
о) 6)
Так, например, показанная на рис. 81,а, невесомая балка с одной точечной массой т имеет одну степень свободы, так как положение этой массы определяется одним параметром у. Невесомая балка с тремя точечными массами, показанная на рис. 81,6, несмотря на бесконечное число возможных форм упругой линии, имеет только три степени свободы, так как положение трех масс ти т2, m3 определяется тремя прогибами уи у2 и Уг соответствующих точек балки.
Рама, показанная на рис. 81, в, с тремя сосредоточенными массами имеет четыре степени свободы, так как положение каждой из масс тх и т2 характеризуется только ее горизонтальным перемещением, а положение массы Шз характеризуется уже двумя ее перемещениями— горизонтальным и вертикальным.
Если же учесть продольные деформации стержней, то раму, показанную на рис. 81, в, следует считать системой с шестью степенями свободы, так как массы т\ и т2 в этом случае могут иметь не только горизонтальные, но и вертикальные перемещения. Однако в большинстве случаев колебания масс, связанные с продольными деформациями стержней, можно не учитывать.
Абсолютно жесткая балка (рис. 81,г), могущая совершать перемещения, вращаясь вокруг неподвижной точки О, является системой с одной степенью свободы,
Рис. 81
126
независийЩчисла масс и упругих опор, так как положение всех масс определяется одним параметром — углом поворота а балки относительно центра О.
Если массы рассматриваются не как точечные, то приходится учитывать инерцию их вращения, и тогда во всех рассмотренных примерах число степеней свободы оказывается большим, так как положение масс в этом случае определяется уже не только прогибами, но и углами поворотов.
Так, например, плоская система, показанная на рис. 81,в, будет в этом случае иметь семь степеней свободы.
Если учитывать собственную распределенную массу упругой системы, то степень свободы такой системы окажется уже равной бесконечности. Строго говоря, поскольку все сооружения имеют распределенную массу, они всегда являются системами со степенью свободы, равной бесконечности, однако во многих случаях удается свести расчет таких систем к расчету систем с конечным числом или даже с одной степенью свободы.
§ 24. Свободные колебания
Если упругая система в результате взаимодействия с каким-либо другим физическим телом оказывается выведенной из состояния равновесия, то после прекращения указанного взаимодействия система будет совершать свободные колебания.
Свободные колебания системы с одной степенью свободы рассмотрим на примере балки, жестко заделанной одним концом с точечной массой на свободном конце (рис. 82). Из основного уравнения динамики (второй закон Ньютона) масса выражается как частное от деления силы веса груза Q на величину ускорения силы тяжести g = 981 см/сек2у т. е.
т = — у или Q = mg. (63)
8
Таким образом, в технической системе единиц размерность массы выражается в кГсек2/см.
Под действием груза Q точка его приложения переместится вниз на величину уст. На рис. 82 упругая линия балки от статической силы Q изображена сплошной кривой линией.
127
Силу веса можно исключить из рассмОТщия, так как она уравновешивается начальной силой реа1одМстемы.
При свободных колебаниях балки в любой'щКдот времени на массу т, отклонившуюся от положения CTifcтического равновесия на величину у, будет действовать восстанавливающая сила /?, сила сопротивления F и сила инерции X.
Рассмотрим каждую из этих сил, считая положительными силы, перемещения, скорости и ускорения, направленные вниз.
Восстанавливающая сила R—это сила упругой реакции системы, возникающая при отклонении массы m от положения статического равновесия. Эта сила, стремящаяся вернуть массу в положение статического равновесия, направлена в сторис 82 рону, противоположную пе¬
ремещению и, в соответствии с принятым правилом знаков должна считаться отрицательной. Восстанавливающая сила пропорциональна величине отклонения у точки, в которой сосредоточена масса, т. е.
R = — Гу. (64)
Коэффициент пропорциональности г представляет собой реакцию балки в рассматриваемой точке при перемещении этой точки, равном единице. Эта величина, зависящая от упругих и геометрических характеристик системы, может быть найдена из общего выражения для перемещения, вызванного силой г и приравненного единице, т. е.
У = бг = 1, или r=-i- ,
где б — перемещение рассматриваемой точки, вызванное единичной силой.
Так, например, для рассматриваемой балки, жесткость которой равна EI, при действии силы Q = 1 имеем:
с Q/3 /3 3 Е/
о = = — и г = .
3 Е/ 3 Е/ Р
Сила сопротивления F возникает из-за сопротивления внешней среды, т. е. воздуха или воды, а также от вяз¬
128
кости или неполной упругости материала самого сооружения и от трения в опорных устройствах. При всех этих неупругих сопротивлениях происходит поглощение энергии.
Для упрощения математической стороны задачи обычно принимают, что сила сопротивления F пропорциональна скорости колебаний v=y\ что она приложена к массе и направлена в сторону, противоположную ее движению. Последнее обстоятельство учитывается знаком «минус»
F = -kjL = -ky'. (65)
Здесь k—коэффициент пропорциональности, физический смысл которого мы установим ниже; t— время.
Сила инерции X в соответствии с принципом Даламбера равна произведению массы т на ее ускорение, т. е. на вторую производную пути или перемещения у по времени t. Эта сила направлена в сторону, противоположную ускорению, и считается отрицательной
X = -т = -ту" (66)
Уравнение динамического равновесия всех сил, действующих на массу,
2У = * + + /? = 0.
Сила Q в это уравнение не входит, так как ее действие уже учтено тем, что перемещения отсчитываются не
от уровня нуля, а от уровня статического равновесия.
Подставляя вместо сил /?, F и X их выражения (64) —
(66), деля уравнение на т и меняя знаки, получим такое обыкновенное однородное линейное дифференциальное уравнение второго порядка
у” + — у' + — у = о. (67)
т т
Решение этого дифференциального уравнения будет таким
kt
у = а0е 2т sin (со/ + р0). (68)
9—949
129
Здесь е—основание натуральных логарифмов (е = = 2,72);
(о — круговая частота свободных колебаний, т. е. число циклов колебаний в течение 2л сек
—VT-Ш т
а0—начальная амплитуда свободных колебаний:
а = У\ + (
k \ 2 Vo + Уо — \
— ) (70)
(0 /
р0— начальная фаза свободных колебаний, характеризующая отклонение массы в начале движения;
Ф0 = arctg — arcsin —; (71)
k а0
00 + 00
ttt
tf0— начальное перемещение tfo = а о sin ро» v0— начальная скорость колебаний.
Период, т. е. продолжительность полного цикла колебаний в секундах, составляет
Т = —. (72)
График свободных затухающих колебаний показан на рис. 83.
Найдем натуральный логарифм отношения двух последовательных однозначных амплитуд свободных колебаний, который обозначим через б
мп
6 = In = In е 2-- = \пе»“(1п+1~*п) = ся+1 _ ыя+1
е 2гп
= \пМ = — = пТ. (73)
2/п
Эта величина, характеризующая скорость затухания колебаний, называется логарифмическим декре-
130
ментом затухания, а величина п= коэф-
2т
фициентом затухания.
В системе с затуханием зависимость между силой Р и перемещением у нелинейна, поэтому при каждом цикле колебаний на диаграмме Р— у получается замкнутая кривая, называемая петлей гистерезиса (рис. 84).
Можно принять, что при гармонических колебаниях петля гистерезиса имеет форму эллипса с центром в
начале координат. Отношение работы неупругих сопротивлений AW за цикл к работе W упругих сил за четверть цикла, т. е. на пути от ненагруженного до крайнего деформированного состояния системы, называется коэффициентом поглощения.
На графике рис. 84 работа AW выражается площадью эллипса, а работа W—площадью заштрихованного треугольника.
Коэффициент поглощения
t+T t+T
1) = — = — Г — = 2 Г — = 2 In -2i- = 26. (74) У V J W ,) у Oa+t
В расчет обычно вводятся значения коэффициента неупругого сопротивления материалов в конструкции у» равные коэффициентам поглощения, деленным на 2я, и представляющие собой отношения амплитуд неупругой и упругой деформации, т. е.
Т= — =
Ун
Уу
2л
kT
2л m
= — . (75)
rtKD
Значения этого коэффициента для разных материалов и для разных величин амплитуд инерционных сил машин приведены в табл. 11.
Из формулы (75) можно выразить первоначально принятый коэффициент пропорциональности k через дру-
9*
13!
гие характеристики затухания
k = = ту со = 2 тп = у V гт. (76)
Таблица И
Амплитуда инерционной силы в кГ
Железобетон
Кирпичная
кладка
Дерево
Сталь
прокатная
100
100
0,05
0,1
0,04
0,08
0,03
0,05
0,01
0,025
Таким образом, коэффициент k не является физической постоянной материала, а зависит еще от массы и жесткости конструкции.
Более общей является зависимость, предложенная Е. С. Сорокиным,
= тсоу(ео), (77)
где ео — амплитуда деформации.
Иногда силу сопротивления принимают постоянной
Рис. 84
или пропорциональной величине перемещения массы. Если не учитывать затухания колебаний, т. е. принять k = 0, то из формул (68) — (71) получается:
у = a sin (со/ + фо),
(О
a~V
Ф0 - arctg — - arc sin — .
io a
У о
(78)
(79)
(80) (81)
132
При этом t/cT = 6Q — статическое перемещение системы от груза Q = mg.
Дифференцированием выражения (78) можно получить такие формулы для скорости и ускорения гармонического колебательного движения:
График уравнения (78) представлен на рис. 85.
Величина а характеризующая размах колебания, называется амплитудой колебаний. Величина ф0, характеризующая отклонение точечной массы в начальное мгновение, называется начальной фазой колебаний.
Уравнение (78) приводит к одинаковым значениям у при
поэтому период, т. е. продолжительность полного цикла колебаний, выражается формулой (72):
На графике рис. 85 эта величина, имеющая размерность времени, показана как отрезок времени между двумя соседними однозначными амплитудами.
Частота колебаний, т. е. число полных циклов колебаний в 1 сек, выражается в герцах и составляет
При этом Т должно быть выражено в сек.
Из формул (79) видно, что частота уменьшается с увеличением статического прогиба упругой системы, т. е. с уменьшением ее жесткости. Частота убывает также с увеличением массы.
Технической частотой п называют число колебаний в минуту. Техническая частота выражается следующими формулами:
= (85)
Г я я у у
Как показывает формула (69), затухание приводит к уменьшению частоты свободных колебаний. Однако вто-
v = у' = a® cos (at + фо); w = у" = — асо2 sin (cat + фо).
(82)
(83)
со
133
рои член под корнем этого выражения, как правило, во много раз меньше первого, поэтому практически можно считать, что затухание не оказывает влияния на частоту свободных колебаний.
Пр и мер 31. Требуется определить круговую и техническую частоту, а также период собственных колебаний сосредоточенного груза Q = = 1200 кГ, приложенного на свободном конце балки, жестко заделанной другим концом (рис. 82). Балка пролетом / = = 1 м9 из прокатного двутавра 20в с моментом инерции поперечного сечения относительно горизонтальной оси / = 2500 см\ Собственный вес балки не учитывается.
Приняв модуль упругости Е = 2,1 10е кГ/.см2у найдем
статический прогиб свободного конца балки от заданного груза
QP 1200-ЮО3
Рис. 86
Уст 3 EI
■■ 0,0762 см.
3*2,Ы0в «2500
Круговая частота свободных колебаний находится ло формуле (79) при g=981 см/сек2.
со
= = 1 f -9—— = 113 сек~1.
V Уст V 0,0762
Период колебаний по формуле (72) т = 2л = 628 = 0 0555
о 113
Техническая частота по формуле (85) составляет _ 60 _ 60 ~ Т ~ 0,0555
= 1080 минг1.
Если бы требовалось найти только этот результат, то его проще было получить непосредственно по другой формуле
300 300
п =
V Уст /0.0762
= 1080 мин
—1
134
Пример 32; Требуется определить круговую частоту собственных колебаний сосредоточенного груза Q = = mg = 3 Ту приложенного на расстоянии а = 1,5 м от левой опоры балки (рис. 86). Пролет балки #=6 м. Собственный вес балки (двутавр 30а) не учитывается'. Момент инерции поперечного сечения- балки / = 8950 смА.
Статический прогиб балки под грузом Q от действия этого же груза находится путем перемножения эпюр по способу А. Н. Верещагина
— _1 /3(3* 11 , 3Q/ 3/ / У
~~ EI \ 16 4-2 * 8 16 8 8 )
3Q/3
3-3000-600»
256EI 256-2, Ы0в.8950
= 0,404 СМ.
Рис. 87
Круговая частота по формуле (79)
со = / \/ — --- 49,2 сек-1.
V Уст V 0,404
Пример 33. Требуется определить круговую частоту свободных колебаний массы т= — сосредоточенной
S
посредине пролета ригеля рамы, показанной на рис. 87,а, если Q = 1000 кГу 1 = 2 м, А = 3 му EI = 1010 кГсм2 и — = 2.
Собственную массу стержней рамы не учитывать.
Пользуясь данными из книги проф. Д. В. Бычкова «Формулы и графики для расчета рам» (Госстройиздат,
135
М., 1957, стр. 70), получаем в готовом виде эпюру изгибающих моментов в раме от действия груза (рис. 87,6). Вычисляем момент в узле В по готовой формуле
Статический прогиб под силой Q определяем путем перемножения эпюр. При этом эпюра М от единичной
силы, приложенной по направлению искомого перемещения, построена для статически определимой основной системы (рис. 87,в).
Произведя перемножение эпюр по способу А. Н. Верещагина, найдем
Пример 34. Требуется определить техническую частоту собственных вертикальных колебаний фундамента (рис. 88), передающего равномерное давление на грунт, равнодействующая которого Q = 200 Т. Площадь подошвы фундамента составляет F=10 м2, а коэффициент упругого сжатия грунта k = 2,5 кГ/см3.
M„=W ! :5±2
в л
3-1-2
ТЩЯ I#
т
Рис. 88
Рис. 89
Круговая частота свободных колебаний
136
Давление на грунт основания составляет
q =-9-= = 20 Т/м2 = 2 кГ/см2.
При таком давлении упругая статическая осадка фундамента, которая войдет в расчетную формулу для частоты вместо статического прогиба, будет равна
Техническая частота свободных колебаний
Пример 35. Требуется найти круговую частоту свободных колебаний массы т, входящей в состав системы, показанной на рис. 89. Жесткость стержней и пружины соответственно равны Е1= оо иг.
Статическое перемещение массы равно статическому укорочению пружины и составляет
Круговая частота свободных колебаний
Вынужденными называются колебания системы, на массу которой, кроме восстанавливающей силы, силы сопротивления и силы инерции, действует еще возмущающая сила, изменяющаяся по времени.
Наибольшее практическое значение для расчета промышленных сооружений имеет вибрационная гармоническая нагрузка, т. е. нагрузка, изменяющаяся во времени по закону синуса или косинуса, например сосредоточенная сила
п = ——.
Vs/ст У 0.8
§ 25. Вынужденные колебания при действии вибрационной нагрузки
P(t) = Р sin 0/,
где Р — амплитуда возмущающей силы;
0— круговая частота возмущающей силы.
(86)
137
По гармоническим законам изменяются вертикальная (Ру) и горизонтальная (Рх) составляющие центробежной силы, возникающей при наличии неуравновешенной массы т равномерно вращающейся части машины (рис. 90).
I Pit)
EJ
/ Рис. 90 Рис. 91
Если к системе с одной степенью свободы, например, к балке, рассмотренной в предыдущем разделе и показанной на рис. 82, приложена гармоническая возмущающая сила (рис. 91) P(t), то в дополнение к силам R и X в уравнение динамического равновесия войдет и сила P(t) и тогда вместо однородного дифференциального уравнения (67) мы получим неоднородное, т. е. уравнение с правой частью
У" + — у' + (о2 у = — sin 0/. (87)
т т
Полное решение этого уравнения состоит из общего решения соответствующего однородного уравнения (67) и частного решения уравнения (87)
_ kt_
у = а0е 2m sin (со/+ф0) + цуСТ sin (0/ — е). (88)
Первый член этого уравнения выражает свободные колебания, а второй — вынужденные.
Как было показано выше, свободные колебания быстро затухают благодаря силам сопротивления и тогда устанавливаются вынужденные колебания с частотой 0.
Во второй член формулы (88) входят следующие величины: е — сдвиг фазы вынужденных колебаний по отношению к колебаниям возмущающей силы, характеризующий величину опережения
— 0
138
(а—динамический коэффициент гармонической нагрузки, показывающий, во сколько раз ее динамическое действие превышает статическое действие ее амплитуды
1 1
/(-№)■ /(-S)4v)‘
(90)
Амплитуды вынужденных колебаний и динамические коэффициенты благодаря затуханию уменьшаются и при резонансе в бесконечность уже не обращаются. Тем не менее они могут достигнуть опасных значений.
При совпадении частот (0 = со) из формулы (90) получается
(91)
Наибольшего достигает при
значения динамический коэффициент
йма
fV4-T*
(92)
Однако разница между результатами по формулам
(91) и (92) очень мала. График динамического коэффициента при наличии затухания показан на рис. 92.
Таким образом, при резонансе амплитуда вы- р нужденных колебаний об- 5 ратно пропорциональна логарифмическому декременту затухания. Сдвиг же фазы колебаний по отношению к возмущающей силе составляет при
этом 8 = —j, т. е. периода.
При очень большом значении коэффициента поглощения гр4л, например при колебаниях в
У*'в
ft
\г0-2
i
жга5
0.5 1
15 2 25
'Рис. 92
139
вязкой жидкости, частота со по формуле (69) может получиться мнимой. Это означает, что колебаний не будет происходить и что упругая система, выведенная из первоначального состояния равновесия, медленно вернется в это состояние.
При k = 0, т. е. без учета затухания, формула (90) получает следующий вид
Однако эта формула оказывается недостаточно точной в области, близкой к резонансу, в которой особенно велико влияние затухания. При равенстве частот 0 = со формула приводит к значениям [х=± оо, которые в действительности не могут быть достигнуты.
Особенностью вынужденных колебаний при резонансе является то, что перемещения сдвинуты по фазе на
= -j- относительно возмущающей силы, т. е. перемещения достигают наибольшей величины в те моменты, когда эта сила обращается в нуль.
При 0со величина ц по формуле (93) становится отрицательной. Это означает, что колебания возмущающей силы и самой массы происходят в противоположные стороны.
Пример 36. Определить динамический коэффициент, амплитуду вынужденных колебаний и наибольшие нормальные напряжения в балке, рассмотренной в примере 32,если сосредоточенный груз Q = 3 Т является двигателем, совершающим 400 об/мин и дающим вертикальную составляющую центробежной силы P(/)=Psin0/. При этом Р = 0,8 Г. Найти также величину динамического коэффициента при резонансе.
Круговая частота свободных колебаний была найдена в примере 32 и равна со = 49,2 сек~х. Круговая частота вынужденных колебаний, равная частоте возмущающей силы
Так как балка стальная, а амплитуда вертикальной составляющей центробежной силы превышает 100 кГ, то
(93)
0 = 400— = 41,8 сек~\
60
140
по табл. 11 принимаем коэффициент неупругого сопротивления материала у = 0,025.
Динамический коэффициент по формуле (90)
_ 1 _
'7нШ’
= 1 Г7 41,82 \2 / „ 41,8 2
У ( “ 49,22 ) +(0,02 49,2)
= 1 — = 3,56.
V"0,2732 + 0,0212
Динамический коэффициент по формуле (93)
и - —Ц— ! = з,бо.
‘-(т)
Таким образом, учет затухания при отсутствии резонанса почти не изменил величину динамического коэффициента. При резонансе же, т. е. при 0 = со, с учетом затухания по формуле (91) получим
Таким образом, хотя с учетом затухания динамический коэффициент при резонансе и не получается бесконечно большим, он все же оказывается весьма высоким. Это обстоятельство заставляет избегать в конструкциях явления резонанса.
Статический прогиб от силы Р = 0,8Г найдем, используя результат, найденный в примере 32 для силы Q = 3 Т
у:т = 0,404 = 0,404 — = 0,107 см.
Q 3,0
Амплитуда вынужденных колебаний будет равна динамическому прогибу
Ул,ин = №Уст = 3,56*0,107 = 0,381 см.
Полный прогиб балки под силой будет равен статическому прогибу от силы Q плюс динамический прогиб от силы Р
1/полн = 0,404 + 0,381 = 0,785 см.
141
Максимальный прогиб, находящийся около пролета, может быть несколько больше.
Наибольший изгибающий момент с учетом динамического действия силы Р
Ммакс = (Q+fiP)- = (з+ 3,56 • 0,8) L’LUi =
/ о
= 6,56 Тм = 656 ООО кГсм.
Наибольшие нормальные напряжения в опасном поперечном сечении балки
Омакс = = 1 ЮО кГ/СМ2.
В случае же, когда двигатель стоит неподвижно:
.м Qab 3*1,5*4,5 0
макс Y~ g 3,37 tYlM\
337 000 ссс г, о
Омакс = —— = 565 КГ/СМ2.
Таким образом, наличие динамической нагрузки, даже при отсутствии резонанса, может привести к сильному увеличению напряжений в сооружении по сравнению со статическими.
§ 26. Действие других возмущающих нагрузок
Внезапно приложенная возмущающая сила постоянной величиш
Если к упругой системе, находящейся в состоянии покоя, в момент времени to прикладывается возмущающая сила то уравнение динамического равновесия
без учета затухания для tU будет таким
у" + 0*у=±-. (94)
m
Полное решение этого уравнения, включающее свободные и вынужденные колебания системы при /о=0, имеет следующий вид
р
у = a sin (oi + q0) -f (1 —cos (at) (95)
mco2
p
Так как =Уст, то динамический коэффициент
mco2
142
силы Р при вынужденных колебаниях будет
[х = 1 — cos соt. (96)
Наибольшее значение этого коэффициента при е)/ = я, Зя,... достигает Лмакс = 2.
На рис. 93 показан график колебательного движения точки приложения силы Р.
Внезапно приложенная и внезапно прекратившая свое действие сила постоянной величины
Принимается, что сила Р прикладывается внезапно в момент времени /0 и сохраняет постоянное значение в течение периода Тр.
Для периода /о//о+Гр действительно предыдущее решение, а в период tt0 + TPy т. е. после прекращения действия силы Р система будет совершать свободные колебания в соответствии с первым членом выражения (95). При этом начальные условия этого движения (при t=t0+Tp), совпадающие с условиями движения в конце предыдущего периода, позволяют определить амплитуду колебаний и динамический коэффициент силы Р
(а = ± 2 sin = + 2 sin (97)
Величина этого коэффициента зависит от соотношения между периодом Тр действия нагрузки и периодом Т свободных колебаний системы. В табл. 12 приведены значения [i в зависимости от величины Тр/Т.
Таблица 12 Значения динамического коэффициента fi
туг
0
0.01
0,02
0,05
0,1
0,167
0,2
°’3.
0,4
0,5
и
более
и
0
0,52
0,126
0,313
0,618
1,00
1,175
1,617
1,902
2,0
143
Кратковременный импульс силы
Если импульс сосредоточенной силы P(t) имеет величину S и действует в течение малого промежутка времени (периода) T°pi то среднее значение силы за этот период будет
Р = —. (98)
Т1
Приняв вместо силы P(t) ее среднее значение Я, можно воспользоваться формулой (97) для динамического коэффициента. Обе части этого выражения умножим на Р и, кроме того, правую часть умножим и одновременно ыТ°в
разделим на Тогда в левой части мы получим ста¬
тическую силу, эквивалентную данному импульсу по своему действию
*Т°р .
Sin— sin —
Рзк = ЦЯ = ± р*т; —f- = ± (OS —(99)
toТр toТр
2 2
Так как для любого угла а отношение 1 и это
а
отношение при стремлении а к нулю стремится к единице, то наиболее опасным из всех ударных импульсов, имеющих заданную величину S, является мгновенный импульс, для которого
Яэк = ±coS. (100)
§ 27. Ударная нагрузка
1
дт
i с
При ударе движущегося тела по упругой системе, например в случае свободного падения груза Q = mg на конец балки, показанной на рис. 94, происходит передача кинетической энергии движения груза балке, сопровождающаяся деформацией последней и Рис. 94 возникновением равных между
I
144
собой сил взаимодействия груза и балки. Каждая из этих сил называется силой удара. Сила удара имеет вполне определенную продолжительность или период действия Т обычно измеряющийся сотыми или тысячными долями секунды и в течение этого периода изменяется по величине. Примерный график силы удара показан на рис. 95 (сплошная линия).
Сила удара характеризуется ее наибольшей величиной Я, периодом Т°р и импульсом, равным площади диаграммы удара
То
S=$PP(f)dt. (101)
0
В то же время импульс силы удара равен количеству движения ударяющей массы m
S = mv, (102)
где v — скорость движущейся массы т.
Если сила в течение периода Тр остается постоянной и равной Я, то импульс такой силы будет выражаться простым произведением
S = PTp. (103)
Сила удара, период ее действия и закон изменения во времени зависят не только от величины массы тела и скорости его движения, но также и от упругих свойств самого сооружения и его поверхности в месте удара.
В настоящее время мы можем получить график силы
удара только экспериментальным путем, например с помощью осциллографа. График силы удара можно приближенно заменить равновеликим прямоугольником, например исходя из равенства наибольших ординат, как это показано на рис. 95 пунктиром, или исходя из равенства периодов Тр = Тр.
Зная величину импульса S ударной нагрузки, период ее действия Тр и круговую частоту со собственных колебаний системы, можно воспользоваться формулой (99) для нахождения статической силы, эквивалентной силе неупругого удара.
Не зная периода действия ударной нагрузки, будем считать ее импульс мгновенным. Тогда эквивалентная статическая сила выразится формулой (100), а динами¬
10—949
145
ческий коэффициент ударяющего груза Q = mg окажется равным
р,=
_ Рэк WS _ У Уст __
Q
VtmV
Л
Уст
-=—=. (104)
V ёУст
Эта формула справедлива при движении массы m в любом направлении. Формула показывает, что эффект ударной нагрузки зависит не только от величины ее импульса, но также и от частоты собственных колебаний самой системы. Чем жестче сооружение, тем больше будет динамический коэффициент удара при одном и том же импульсе.
ь.
Рис. 96
Рис. 95
Если принять скорость v равной скорости свободного падения груза Q с высоты h + \iycт, т. е. v = V 2g(h + + МЛ/ст), то после подстановки этого выражения в формулу (104) из решения квадратного уравнения получим
ц = 1 + т/1 + (105)
У Уст
В случае, если величина h много больше, чем величина уСъ можно пренебречь единицами, стоящими под кор-
2 h
нем и перед корнем по сравнению с величинами — и
Уст
/ 2h 7огда получается приближенная формула У Уст
ш
(106)
При наличии на сооружении в месте удара сосредоточенной массы т статический прогиб от весов обеих масс будет уже равным
Подставляя в формулу (106) вместо уст величину У\ст, получим
Таким же путем могут быть уточнены формулы (104) и (105).
Равномерно распределенная масса приводится к сосредоточенной в месте удара путем умножения ее на некоторый коэффициент р, зависящий от условий опирания концов стержня.
В табл. 13 приведены коэффициенты приведения равномерно распределенной массы к точке удара, обозначенной буквой С.
(107)
Таблица 13
Коэффициенты приведения масс
№ п. п.
Схема стержня
П р и м е р 37. На железобетонную балку пролетом
1 = 6 м падает посредине пролета груз Q = 200 кГ с высоты А = 20 см (рис. 96). Определить силу удара, если модуль упругости бетона =340000 кГ/см2, момент инерции поперечного сечения балки /=360 000 см4, собственный вес балки 2,0 Т.
Статический прогиб балки от груза весом Q
уст = -У— = - --0-°03 = 0,0074 см.
а 48 EI 48-340000-360000
Собственный вес балки, приведенный к точке удара, принимается равным половине действительного собственного веса, т. е.
Qi = 0,5 • 2,0 = 1,07\
По формуле (107) определяется динамический коэффициент удара. При этом отношение масс заменяется отношением соответствующих весов
IV
2*20
0074
/ 1000\ (1 + 200)
= 31.
Сила удара оказывается равной
Р = [ivQ = 31 • 200 = 6200 кГ.
Если бы мы пренебрегли собственной массой балки, то динамический коэффициент и сила удара получились бы по расчету значительно большими:
»«=1/Ж-7за
Р = \yyQ = 73,5 • 200 = 14700 кГ.
Га* т.
Рис. 97
Таким образом, сила удара груза, даже при падении его с небольшой высоты, оказывается значительно больше, чем вес этого груза. При этом сила удара увеличивается с увеличением жесткости сооружения.
Пример 38. Определить силу удара льди-
148
ны весом Q = 1 ООО кГ о железобетонную сваю-оболочку, погруженную в дно реки на глубине Я = 6 м (рис. 97). Скорость течения v =1,5 м/сек. Внутренний диаметр оболочки D0 =1,5 м при толщине стенки 6=14 см. Модуль упругости железобетона *=340 000 кГ/см2. Защемление свай в грунт принимается на уровне дна.
Момент инерции кольцевого сечения при радиусе срединной поверхности г = 0,82 м.
/ = ягзб = 3,14-0,823.0,14 = 0,24 л*4 = 2,4• 10 смК
Собственный вес оболочки, приведенный к точке удара, принимается равным одной четверти полного веса ее наземной части, т. е.
Qi = 0,25• 2яг6#ye = 0,25-2-3,14 X)
X 0,82-0,14.6,0.2,5 = 2,7 Т.
Статический прогиб верха сваи от силы Q, равной весу льдины и приложенной горизонтально,
QH3 1000-6003 Л ллоо
уст = —— = = 0,0088 см.
3 EI 3-3,4 -10® * 2,4•107
Динамический коэффициент удара по формуле (107)
v 150 л/»
\ху — ■ ■ 26,7.
/Ц'+Ю »•«.««(■+й)
Сила удара
Р = [ivQ = 26,7.1,0 = 26,7 m = 26,7.1,0 = 26,7 Т.
гл а в А 7
СИСТЕМЫ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
§ 28. Свободные колебания
Число возможных форм свободных колебаний упругой системы равно числу степеней ее свободы. Каждой форме колебаний соответствует своя частота. Совокупность частот данной системы составляет ее спектр частот.
149
Для практических целей часто бывает достаточно найти наименьшую частоту, представляющую наибольшую опасность в смысле возможности возникновения резонанса с вибрационной нагрузкой. Дело в том, что, во-яервых, резонанс на низшей частоте приводит к наибольшему динамическому эффекту. Во-вторых, если даже частота возмущающей силы значительно превышает низшую частоту собственных колебаний системы, то ре-
Щ /Т?2
V/ V?
Рис. 9f
зонанс на этой частоте все же будет возникать при разгоне машины во время ее пуска. Поэтому низшую частоту иногда называют частотой основного тона колебаний. Следующий по порядку тон колебаний называется первым обертоном.
В качестве примера системы с несколькими степенями свободы рассмотрим простую балку с тремя точечными массами mu т2 и т3 (рис. 98). Такая балка имеет три степени свободы, поэтому она характеризуется тремя частотами свободных колебаний — соь 002 и 003.
Для определения этих частот можно составить следующие выражения перемещений точек приложения сосредоточенных масс под действием сил инерции этих масс:
Ух = — 6Пт1 у\ — 6J2m202 — б13т.Л.
У2 = 2111 2222 ®2333
Уз = — б31т1 — V"a02 — бззшзу
(108)
Перемещения 6ц, 612 = 621, 613 = 631, 622, 623=632» бзз вычисляются как обычно способом О. Мора или А. Н. Верещагина от единичных сил, приложенных в местах действия сил инерции, т. е. в сечениях, где находятся точечные массы.
Система дифференциальных уравнений (108) имеет следующее частное решение:
у! = ах sin (со/ + Фо),
у2 = at sin (оat + ср0), У О09)
у3 = а3 sin ((at + фо).
150
Здесь alta2 и Од— амплитуды колебаний соответствующих масс;
Ф0 — начальная фаза колебаний.
Вторые производные этих перемещений по времени, т. е. ускорения, выражаются так:
у" = — to2**! Sin (со; + р0), '
у" = — со2а2 sin (со/ + ф0), (НО)
У” = — #а3 sin (соt + ф0). ,
Подставив в систему уравнений (108) выражение
(109) и (110) и сократив на co2sin(cof+9o), получим:
ii™i — j + б12т2а2 + &i3m/i3 = 0, + 1б22т2 — а2 + б23т3а3 = 0, 63i/nifl!i + Ь.2т$,2 + (b33m3 —-i-joj = 0.
(Ill)
Тривиальное решение этой системы уравнений а\ = = а2 = аз=0 соответствует равенству нулю амплитуд колебаний, т. е. случаю, когда система находится в покое.
Существование отличных от нуля амплитуд а и а* и а3 возможно только в том случае, если определитель, составленный из коэффициентов при амплитудах, равен нулю, т. е.
©2
D =
бц/Пх — б пт2 б 13т3
®ззтз
_1_
6)2
= 0. (112)
Если этот определитель раскрыть по известному правилу Саррюса, то получится одно уравнение третьей степени относительно _, которое при решении даст три
положительных значения частей’ ©. Каждому значению со соответствует одна определенная система уравнений, решив которую, можно найти соотношения между амплитудами колебаний.
В общем виде определитель частот, называемый ве-
151
новым уравнением, для системы с п степенями свободы записывается так:
1
D =
бц/П! — ■ (
ЬцЩ
(0
б12т2-*' 1
б,„т,
22ПЬ ~Т *
G)2
1 пиьп
6nlmi
б«22
= 0. (113)
Уравнение частот, полученное в результате раскрытия определителя второго или, в крайнем случае, третьего порядка (п=2 или п = 3), может быть решено строго непосредственно. В случае, когда п 3, это уже может оказаться затруднительным или даже невозможным.
Если направления перемещений у и Уг, уп выбраны так, что побочные перемещения бik обращаются в нуль, то система дифференциальных уравнений (108) и соответствующее ей уравнение частот распадаются на отдельные уравнения,содержащие только главные перемещения. В этом случае перемещения уи Уь уп называются главными координатами, а соответствующие формы колебаний — главными формами колебаний. Главные формы колебаний обособлены друг от друга и каждая из них происходит со своей определенной частотой, которая выражается простой формулой.
(0 i = —±—. (114)
V
Эта формула по своей структуре аналогична формуле (79) для системы с одной степенью свободы.
Однако выбрать главные координаты для системы с числом степеней свободы больше двух-трех в общем случае весьма затруднительно.
о
Рис.
99
152
Для системы с двумя степенями свободы это всегда оказывается возможным.
Для симметричных систем с симметрично расположенными массами возможны прямо симметричные и обратно симметричные формы колебаний, при которых силы инерции будут прямо симметричны и обратно симметричны. В этом случае перемещения вычисляются как групповые от парных прямо симметричных или обратно симметричных единичных сил. Побочные же перемещения, связывающие прямо симметричные и обратно симметричные силы инерции, обращаются в нуль.
Это также приводит к распаду уравнения частот на два независимых уравнения, из которых одно позволит найти частоты прямо симметричных колебаний, а другое — обратно симметричных.
При этом, так как групповые перемещения находятся от парных единичных сил, то соответствующая масса должна входить в вековые уравнения с коэффициентом
Пример 39. Определить частоты собственных колебаний невесомой консольной балки с двумя равными сосредоточенными массами (рис. 99)
т = 0,051 —, если */=2000 т-м2;
I = 4,0 м.
Вычисляем перемещения от единичных сил путем перемножения построенных от них эпюр изгибающих моментов
Рис. 100
153
5а = -4
11 EI V
14 24 . /-Г-2-/
2-2.2-3-2 2-2
.2./ \ _ J*_ в .3-2 / 8/ ’
12 — 21 —
4-2.4/
14-24 _
4*2.2-3*4 ~~
32Е/ 1
/3
487
Составляем определитель из этих коэффициентов
6nm —
О)2 ’
122
62i; 622т—
= 0
или
13т
8EI
1Ьп
J_ со2 *
Рт
Рт
32 / 1 48/
32EI
О)2
= 0.
Раскрывая определитель, получаем уравнение частот, квадратное относительно величины —
(0й
/ lBm 1\ I Isт 1\ / Pm \2 _ q
\ 8EI щ2 j V 48 / ю»/ \32еГ/ ~~ ’
или
7l3m 1 48 / со2
+
5 1*т? 3072 2/2
= 0.
Применяя формулу решения квадратного уравнения, находим:
1 _ 7/а m У"/ 7l*m \2 Iff / 7/a m \2 _
со2 “ 96EI - V \ 96EJ ) 49 \ 96Е/ )
7/3 т 96 EI
(1 ± 0,836);
1 /Зт 0 7/ 1 Г EI
ю2 “ 7,48/ ’ 0)1 “ ’ К S"
= 2,74 l/—
’ у 43«(
2000
•0,051
= 68,5 сек
154
1 _ Pm
w2 _ 83.2El ’
= 9,12]/=228
J/ 4s-0.051
сек *.
Пр и мер 40. Определить частоты свободных колебаний балки с тремя равными сосредоточенными массами т, расположенными так, как показано на рис. 100, а. Жесткость балки равна EI.
Так как система и расположенные на ней массы симметричны, то задача может быть решена с учетом и использованием симметрии. Построив эпюры изгибающих моментов от единичных гил инерции (рис. 100,б,в, г), находим перемещения путем перемножения эпюр:
с II I 1 21-2 . I I 1 \ 1 /3
Oii= ( — • — • — — • — 1 = I
\ 4 4 2 3-4 4 2 4 ) EJ 24/ ’
8 -. — 2 +(— + -)—•- -2] —=
13 [ 8 4 2 3-4 \ 8 4 / 2 4 4 J /
II/3
384/
б = — • _L . J_ . Z1L2 — — —— •
33 4 * 2 * 2 ’ 3*4 El ~ A№ ’
g _ J_ m _l 1_ # JM 4 _J_ = /3
22 8 4 2 3.8 / 192/
Перемещения 612 и 623 обращаются в нуль.
Определитель для симметричных колебаний составляем с учетом того, что перемещения от групповой силы Хи состоящей из двух сил, получились удвоенными, поэтому соответствующая масса вводится с коэффициентом 7г
с т 1
11 ~2 ~ ©з"’
с т «31 т;
■*13
т
б33/71 1_
СО2
= 0.
155
или
I* т
24EI ~2
_1_
О)2
11- I3 m
384EI
11I3 m 384 1Г
/ lzm 1_\
V 48/ со2 /
= 0.
Раскрывая определитель, получаем уравнение частот,
j Is т 1_\2 /
\ 4SEI о2 / 2 \
(i
Ilf3m \2
384/
= 0;
-L + ±(JHL)2=0.
1_\2 /3 0)2 j 24/ О)2 2 \384EI /
Решая это уравнение, находим
о)2 48/Г/ ” Г V
8/3 т \ 2 / /зт \2 384EI ) ~\384EI ) 2 ~~
Is т
348EI 15,78/3 т 384EI
(8 + 7,78);
/3 т
24,35/
/ 24,35/:/ , по 1 / /
—= = 4,98 1/ —;
г т г /3 т
*3
0,22/Зт 384EI
/Зт
С0
= ,/msa =42 01/и.
V /3 га у /3 т
1745/
42J
Уравнение частот для обратно симметричных колебаний
1
— 0:
©с
= /б—=l/=19-6/: у о22 m f I3 т V
EI 13 m
156
Пример 41. Определить частоты свободных колебаний неразрезной балки с двумя сосредоточенными массами (рис. 101, а).
Так как система и расположенные на ней массы симметричны, то используем связанные с этим упрощения.
Построив эпюры М\ и М2 (рис. 101,6 и в) от единичных групповых сил, найдем перемещения путем перемножения эпюр по способу А. Н. Верещагина
* /3 * 14/3
11 22 а
24EI 9 22 768EI
а)
Рис. 101
Уравнение частот для обратно симметричных колебаний
с т 1 л
«ну Г = 0,
2 0)2
отсюда
' ' " EI
»1 = л! ~г~ = л/ = 6-93 ]/ -
V fill т V 13т У Is
т
Уравнение частот для прямо симметричных колебаний
157
отсюда
Каждой из частот coi и сд2 соответствует своя форма изгиба при колебаниях. Первой частоте соответствует изогнутая ось в виде двух полуволн с точкой перегиба над средней опорой (рис. 101,г). Второй частоте соответствует изогнутая ось, симметричная относительно средней опоры (рис. 101,(9). В обоих случаях форма изгиба не зависит от времени, а отношение между ординатами эпюры прогибов колеблющейся балки остается постоянным. Подобные упругие линии образуют так называемые стоячие волны.
Пример 42. Определить частоты свободных коле-
Система имеет две степени свободы и может совершать симметричные и обратно симметричные колебания.
формулами из книги Д. В. Бычкова «Формулы и графики для расчета рам», Госстройиздат, 1957, стр. 101 и 102.
Для эпюры Мх\
Для построения эпюр Мх и М2 пользуемся готовыми
мс = 3
Ith
hi
МА = (1—0,473) -у = 0,527*2 = 1,054 м.
Для эпюры М2:
— =0,2— =0,2— = 0,133 м;
4 4 ’ 3-4
158
МА = 0,5Me = 0,5*0,133 = 0,067 м;
м JJU7_ __о 133 = о 533 м ь 4 * ’
Ординаты получаются в м9 так как эпюры построены от безразмерных единичных сил Х\ и Х2.
Умножив эпюры М\ и М2 на соответствующие эпюры М\ и (рис. 102), построенные для простейшей основной системы, получим перемещения:
6U= —1—(2.4-1,054 —0,946-4) =
6 Eli Eh
А 0,033-1.33-4 . 0,133-1.33-0,67
и„ M EIt 2/,
0,67-1,33-0,445 _ 0.136 2-2 EIt ~ Eli ’
Побочное перемещение 612 = 621=0, поэтому получаем два независимых уравнения частот:
159
йц т — =0 и 622 т = 0.
ю, щ
Отсюда можно найти частоты обратно симметричных и симметричных колебаний
Пример 43. Определить частоты собственных колебаний рамы с тремя равными сосредоточенными массами, показанной на рис. 103, а если Л = 0,6 и h!h = 1,5.
Рама имеет четыре степени свободы.
Расчет ее производим с использованием симметрии.
Построив эпюры изгибающих моментов от единичных сил, показанные на рис. 103, в, г, д, е, находим перемещения:
Определитель системы уравнений для симметричных колебаний напишется так:
Раскрывая определитель, получим такое уравнение ча стот
Подставив вычисленные значения перемещений и решив уравнение, получим частоты симметричных колебаний:
©! = \/ —= 1 [= 0,57 \f • V т Г 3,11m V т 9
61а = б21 = - 0,00352 б31 = б43 = 0,0695
Е1Х Е1г
622 = 0,00738 ; б44 = 0,056 .
LI] t,i i
= 0.
m2
2
СО2 со4
160
0,31 J G31
“■=‘°'57
Для обратно симметричных колебаний имеем такой определитель
6 л __LV. 83 2 0)2/’
с т «43 у;
834 т
о)
т
г111! " т;
/7?
I
14
т X,
3f
О,Л к1
W -ггтГТШ51 051 in
т
ш
Рис. 103
11—949
161
Отсюда уравнение частот
Из решения этого уравнения находятся частоты обратно симметричных колебаний:
о3 = ■„„„ = 3,14; ®4 = 33,43 У.
Следует иметь в виду, что в отличие от балок частоты различных форм колебаний рам могут быть близкими друг к другу. Такое совпадение частот может привести к сдвоенному резонансу, представляющему повышенную опасность для сооружения.
В тех случаях, когда раскрытие определителя приводит к уравнению частот третьей степени или выше, для нахождения корней такого уравнения может быть применен графический способ. Для этого на горизонтальной оси прямоугольной системы координат откладываются
1
различные произвольно взятые значения — , а по вертикальной оси — соответствующие значения суммы всех членов уравнения частот. Абсциссы нулевых точек графика дадут искомые значения .
Для определения частот свободных колебаний систем со многими степенями свободы может быть также применен и другой метод (перемещений), сущность которого состоит в том, что силы инерции выражаются как функции перемещений. Так, например, для системы с тремя степенями свободы, показанной на рис. 98, силы инерции масс mi, т2 и т3 выражаются так:
у\ = Ух гхх + у2 г\2 + Узг is;
т2 У2 = У\ Г2Х “Ь У2 Г22 “Ь Уъ Г23 *
Щ Уз = Ух гзх “Ь У2 Г32 “Ь Уз Г33 •
Реакции г1Ь r22, r33, г12 = г2ь г13=г31, г23=г32 вычисляются как обычно от единичных перемещений, приложенных в сечениях, в которых находятся точечные массы.
Для перемещений и их вторых производных остаются в силе выражения (109) и (110), которые подставляются в последние уравнения, в результате чего получается следующая система однородных уравнений
162
(г И — mica2) ai + rl2a2 + ri3a3 = 0; Г21Я1 + (r22 — т2(о2)а2 + r23a3 = 0; гз№ + Г32Я2 + (*зз— 3(02)Д3 = 0.
Составляя из коэффициентов этого уравнения определитель и раскрывая его, можно найти частоты собственных колебаний системы.
По этому же принципу можно найти частоты собственных колебаний системы с любым числом степеней свободы п. При этом определитель записывается в такой форме:
Уравнение частот при использовании этого метода имеет для данной системы тот же порядок, как и при применении метода, рассмотренного выше.
Так как стержень, к которому приложена сосредоточенная масса, далеко не во всех случаях может быть сведен к одному из случаев, представленных в таблице реакций, применяемой для расчета рам на действие статической нагрузки, то реакции приходится определять через перемещения. Поэтому данный метод оказывается более трудоемким, чем предыдущий.
Пример 44. Определить по методу перемещений частоты свободных колебаний неразрезной балки, рассмотренной в примере 41.
Исходя из найденных ранее перемещений от единичных сил, можно найти реакции, вызванные единичными перемещениями:
Уравнения частот для обратно симметричных и симметричных колебаний:
(гп—т1 соа) г12 Гл (22 2
Ги
(fan Мп ®2)
= 0.
гпХ п2
(115)
384EI
11*
163
Отсюда можно определить соответствующие частоты.
Полученные результаты, естественно, совпадают с теми, которые были получены в примере 41.
Как было показано выше, расчет системы с произвольным числом степеней свободы на действие вибрационной нагрузки требует нахождения частот свободных колебаний этой системы, что связано с составлением и
радикалах. Такие уравнения могут быть решены подбором корней или графически. Во многих случаях определение всех частот свободных колебаний системы оказывается излишним и достаточно отыскать только первую, т. е. низшую, частоту. Это может быть, например, в том случае, когда частота возмущающей нагрузки ниже первой собственной частоты колебаний конструкции и, следовательно, резонанс с более высокими частотами уже исключен. Для отыскания первой частоты могут быть применены различные приближенные методы, не требующие решения векового уравнения и приводящие к более или менее простым вычислительным действиям. Мы рассмотрим некоторые из приближенных методов.
§ 29. Приближенная оценка частоты основного тона колебаний
Рис. 104
решением уравнения частот. При числе степеней свободы системы больше двух-трех процесс раскрытия определителя (113) третьего, четвертого и более высоких порядков усложняется. Решение же полученного в результате этого уравнения третьей, четвертой степени и выше в большинстве случаев не может быть получено в
164
Исходя из свойств определителя уравнения частот, проф. С. А. Бернштейн установил пределы, между которыми заключена частота основного тона колебаний. Эти пределы называются двусторонними оценками частоты сомин и могут быть записаны в следующем виде:
1 «„„„ ; 1 . (116)
Vb.,
где
*i = 26„m,; (117)
В2 = Щт* + 2Жшт,тк. (118)
Здесь 6и II bik—главные и соответственно побочные перемещения системы от действия единичных сил в точках приложения сосредоточенных масс 1Щ и т&.
Суммирование распространяется на все массы и соответствующие им перемещения системы. Для верхнего предела частоты основного тона А. Ф. Смирновым предложена более простая формула
(119)
Пример 45. Определить низшую частоту свободных колебаний балки, показанной на рис. 104, а, если
т2 = 2т1
и
rtiz = mi = т.
Жесткость балки равна 7.
По единичным эпюрам, показанным на рис. 104,6, б и г, найдены перемещения
8/3 я 713 * 8/3
с с 01" с /I" д
Оц - о22 - —— ; 012 = —— ; 013 =
486EI ’ “ 486/ * 486EI
я _ Ю/3 * 24/з
23 лоагг * °33
486Е/ ’ 00 486Е/
Находим значения параметров, входящих в формулу (116)
165
Вг = bnmi + 622m2 + 633/n3 = L + L +
i 486У 486/ 486/
48 l3m
486EI ’
B2 = 62, m2 + 62, m2 + 623 m2 + 2 (62, m, m2 +
. S2 , ss 4 / 8/3/n \2 . (8l32m ,a .
+%тл+6?»т1''ь)-Ыёг) +(шг) +
+ /W +2Г/_те_\»л12т+ fJ2?2™n +
\486/ ; [\486/ ) \486/ )
__ l 8/3 Vmm] = 1620 ( m/3 У
\4867 ,/ J \486/ /
Искомая частота лежит в пределах
«мин -J-ZT ~7' 1 = 3*48 л/— •
/«. l/,620(-f У т13’ у \486/ /
1
Юмин , ■ . ZZT =
=3'52/-S- _
Приняв среднее, получим оМин=3,50 1/ JE.
* ml3 *
Более простая формула (119) дает для верхнего предела такой результат
*». l/ - V--" T-gg-f = 3.70 l/ 1l.
/ В3 г 4867 1620 { ml3 ) у ml3
При этом среднее значение уже составит оМин =
-3'59/1-
§ 30. Энергетический способ
Как было указано в п. 1, по закону сохранения энергии сумма потенциальной (U) и кинетической (V) энергии колеблющейся системы (без учета потерь, связанных с затуханием) является величиной постоянной, т. е.
(/+ V = const, (120).
166
В каждом цикле колебаний происходит переход энергии одного вида в другой. В момент наибольшего отклонения массы от положения статического равновесия потенциальная энергия достигает наибольшего значения, а скорость и вместе с ней кинетическая энергия убывают до нуля (рис. 105).
В момент перехода массы через положение статического равновесия потенциальная энергия деформации
Ihr:
имя.
И - У/пак V--0 U=0; v=vmax
Рис. 105 Рис. 106
(точнее приращение потенциальной энергии по сравнению с той, которая соответствует положению статического равновесия) равна нулю, а кинетическая энергия достигает наибольшего значения Vm&kc (рис. 106).
Так как минимальные значения потенциальной и кинетической энергий равны нулю, то из условия (120) можно сделать вывод, что
макс = 1Лмакс- (121)
Это уравнение при подстановке в него выражений энергий дает возможность определить частоты колебаний. Если форма колебаний, т. е. вид упругой линии был бы нам заранее известен, то уравнение (121) привело бы к строгому решению задачи. Для приближенного решения задачи можно задать динамическую упругую линию, т. е. кривую стоячей волны любым уравнением y=f(x)j удовлетворяющим граничным условиям, например уравнением изогнутой оси стержня при действии на него статической нагрузки, соответствующей приложенным массам. Потенциальную энергию деформации изгиба стержня с сосредоточенными массами можно выразить через работу внешних сил Qi = rmg на перемещениях ус
п п
макс = (122)
о о
где п — число масс.
167
Для определения наибольшей величины кинетической энергии нужно найти наибольшее значение скорости. Для этого примем, что в соответствии с выражением (82) скорость любой массы в произвольный момент выражается так:
Vi = УгСО COS (со/ + фо) .
Наибольшая скорость, соответствующая cos (со/+ ■+фо) = 1,
макс = УгСО. (123)
Искомая кинетическая энергия будет равна
024)
О о
Приравняв друг другу величины UMакс И Умакс, получим следующую формулу для определения низшей частоты колебаний
Для балт с распределенной массой т суммирование заменяется интегрированием по длине балки. В этом случае
¥ к
mydx
■„„„ = / -г-_ . (126)
my2dx
При постоянстве массы m по длине балки она выносится за знаки интегралов и на нее производится сокраЗЁцение выражения (126). В этом случае интегрзл,-€Тёвщий в числителе подкоренного выражения, будё'г равен площади эпюры прогибов, а интеграл, стоящий в знаменателе,— площади эпюры квадратов ординат прогиба.
Пример 46. Решить предыдущую задачу, пользуясь энергетическим методом.
Исходя из заданных величин масс, находим соответствующие силы (рис. 107)
168
Qi = Q3 = Q = mg\ Q2 = 2Q = 2 mg.
При этом сила Q3 считается направленной вверх, так как это приводит к большим значениям прогибов, кривая которых показана на рис. 107 пунктиром. Про-
ЗА,
Рис. 107
гибы вычисляются с использованием перемещений от единичных сил, приведенных в примере 45.
л=!_(8 + 2.7 + 8)=«:
У 486EI 486EI ’
-(7 + 2-8+10)=;
486/ V ' 486/
S,= W1_,8 + 2.0+24)=
486/ v 486/
Частота основного тона колебаний находится по формуле (125)
сом
= “l/g 30 + 2.33 + 52 # 486EI f Я/
V 302 + 2.332 + 522 Q/з ’ V ml3'
Пример 47. Найти частоту основного тона свободных колебаний балки, свободно лежащей на двух опорах с равномерно распределенной нагрузкой q = mg.
Приближенное решение задачи производится энергетическим методом. При этом принимается, что основная форма колебаний совпадает с упругой линией от
статической нагрузки q.
Эта линия выражается уравнением прогибов, отнесенным к началу координат на левой опоре:
»-Йг[т-*(Я+(тП-
Вычисляем интегралы, входящие в формулу (126) при /72 = const
Г ydx= — ; Г y2dx = — (-—\2 ;
J 120 7 * У 630 V24EI ) 9
о о
169
л f gql*63Q /24El \* _ 9,87 f~Elg Й““ “ v 120E/.31 { gl* ) I* V q
Этот результат почти не отличается от строгого решения, приведенного ниже
.. _ 1 / Elg
©мин- 3 У q •
§ 31. Определение вынужденных колебаний при действии вибрационной нагрузки методом сил
При действии на упругую систему со многими степенями свободы вибрационной гармонической нагрузки
изгибающие моменты, поW) перечные и продольные
силы также будут изменяться во времени, а их
I P,W-
mm yt
фх наибольшие значения
(амплитуды) будут зависеть от частот возмущающих сил. Если все возмущающие силы, действующие на систему, имеют одну и ту же частоту 0 и изменяются в одной фазе, то силы инерции, а следовательно, и изгибающие моменты, поперечные и продольные силы достигают наибольших значений в о) Lp
i
одно и то же время.
Для системы со многими степенями \ xt
свободы возможны несколько случаев резонанса, которые наступают при совпадении частоты с теми или Рис. 109
иными частотами свободных колебаний системы.
В задачу динамического расчета входит определение амплитуд внутренних усилий и напряжений, а также проверка системы на резонанс. При этой проверке в большинстве случаев достаточно определить частоту основного тона свободных колебаний.
170
Для этого может быть применен метод сил или метод перемещений.
Рассмотрим упругую систему, показанную на рис. 108, с точечными массами, на которую действуют вибрационные силы Pk(t) =PkS\n 0/.
Перемещение любой массы тх в произвольный момент времени t выражается так
у г = + 6122 + ... + biiXi + ... +6tnn + At p, (127)
где XltX2t...Х[9...9Хп—силы инерции соответствующих масс;
—перемещения по направлению силы инерции Х{, вызванные единичными силами Хи Х2,...у Х{,..., Хпу приложенными в точках нахождения соответствующих масс; для вычисления этих перемещений применяется обычный способ строительной механики;
Aip—перемещение точки i от амплитудных значений вибрационных нагрузок. При определении этих перемещений эпюра от нагрузок (эпюра Мр) интегрируется (перемножается) с соответствующими единичными эпюрами.
При гармонических вынужденных колебаниях с частотой 0 перемещение массы mt* и ее ускорение выражается так:
у. = а,8т0/; у] = — a,02sin0/ = —у{№. (128)
Сила инерции массы т* может быть представлена в таком виде: Xi = —miy'miyfi2. Отсюда
(129)
Подставив это выражение в исходное каноническое уравнение, получим
6il *1 + 612 Х2 + ' * • + Х1 + * • • + 6Ш Хп + = 0
здесь
А* А 1
Таким же путем составляется любое уравнение. В результате получается система уравнений, позволяющая определить наибольшие (амплитудные) значения сил инерции:
б;1Х1 + 612Х2 + ...+ 61яХп + Д,р = 0;
621 Х1 + в22 *2 Н Ьб21Х#1 + Д2р = 0;
*й1 + в-2+--+в« + -о.
Сама система уравнений по форме аналогична системе канонических уравнений метода сил. Однако неизвестными в ней являются не реакции отброшенных связей в статически неопределимой системе, а амплитуды сил инерции масс, которые могут возникать как в статически определимой, так и в статически неопределимой системе.
После нахождения наибольших значений сил инерции Хи Х2..., Хп из решения системы уравнений эпюра динамических изгибающих моментов строится путем сложения единичных эпюр, предварительно умноженных на найденные значения соответствующих инерционных сил, с эпюрой Мр, т. е. в соответствии с выражением (132) _ _
М = MiXi + М 2X2 + + МпХп + Мр. (132)
Использование симметрии системы при ее динамическом расчете оказывается возможным только при симметричном расположении масс. При несимметричной вибрационной нагрузке разложение сил инерции на симметричные и обратно симметричные группы, как это показано на рис. 109, приводит к распаду системы канонических уравнений на две независимые системы.
В этом случае вычисление главных перемещений по направлению парных неизвестных нужно делать по формуле
,зз
При симметричной вибрационной нагрузке все обратно симметричные силы инерции равны нулю, а при обратно симметричной вибрационной нагрузке симметричные силы инерции равны нулю. Симметричная вибрационная нагрузка может привести к резонансу толь-
172
ко при совпадении ее частоты с собственными частотами симметричных колебаний системы и, наобо- aj рот, обратно симметричная нагрузка может дать резонанс только с частотами обратно симметричных свободных колебаний.
Пример 48. Построить эпюру динамических изгибающих моментов для невесомой балки пролетом / = 4 му рассмотренной в примере 39 при действии вибрационной нагрузки P(t) = Psin0/
(рис. 110, а), если Р =
==0,2 Т\ 0 = 57,5 сек-'.
Эпюры от единичных сил для данной балки были построены в примере 39. По этим эпюрам найдены перемещения 8
Рис. 110
8Е!
EI ’
21
32 EI
2_
Е1
622 —
/3
48 EI
4
3 Е/
Эпюра от статической нагрузки, равной амплитуде вибрационной силы, показана на рис._110, Путем перемножения этой эпюры с эпюрами Mi и М2 находим: 0,1 1-1-21 , 0.1 Ы-21 = L6
/ '
= 0,4 EI ‘
2р
2-2-3-2-EI 14-0,1 I
2-S-2-EI 0,1 /3
4-2-2-EI
16 EI
Частоты свободных колебаний балки уже найдены в примере 38 и равны:
©1 = 68,5 сект1; ©2 = 228 сек-1.
Для определения главных перемещений нужно предварительно вычислить величину
173
El 2000
m02 0,05b 57,52
Тогда
6* = 629—= 22 22 m02
11-11 mO2
6
После подстановки полученных значений для перемещений и умножения уравнений на EI получим:
Решив эти уравнения, получим:
Xt = 0,491 Т\ Х2 = — 0,132 7\
Умножив эпюры Mi и М2 (см. пример 39) на соответствующие значения инерционных сил и сложив полученные эпюры с эпюрой MPt получим окончательную эпюру динамических моментов (рис. 110,в).
Кроме того, балка подвергается действию изгибающих моментов от статических грузов Q=mg.
Пример 49.* Построить эпюру динамических изгибающих моментов в симметричной раме, показанной на рис. 111, при действии на нее симметричной динамической нагрузки P(/)=6sin0/ и (/)=3sin0/. Частота возмущающих сил 0=0,6 соь Массы сосредоточены по-
Q
средине каждого стержня и равны пг =
Так как вибрационная нагрузка симметрична, то формы вынужденных колебаний также будут симметричными. Групповые симметричные неизвестные силы инерции показаны на рис. 111, б. _ __ _
Эпюры моментов от единичных сил Xu Х2 и Х3, действующих по направлению сил инерции, показаны на
* Заимствован из книги И. П. Прокофьева и А. Ф. Смирено в а. «Теория соор женин». Ч. III, Трансжелдориздат, 1948.
—3,81 — 2Х2 + 1,6 = 0; —2Xi—10,472 —0,4 = 0.
174
Рис. Ill
176
рис. Ill в,г, д. Для их построения можно было применить любой метод расчета рам, например метод перемещений или способ уравновешивания узлов.
Перемещения 6ц, 612, 613, 622, 623 и бзз можно определить путем перемножения этих эпюр. Однако проще перемножать эпюры Мь М2 и М3 не между собой, а с эпюрами М[, М'2 и М'3, построенными для основных систем и показанными на рис. 111, е9 ж, з.
Перемещения получаются равными:
Для определения частот собственных колебаний со ставляется уравнение частот:
Подставив вычисленные перемещения в уравнение частот, раскрыв определитель и решив полученное в результате этого кубическое уравнение, найдем частоты свободных колебаний
Построив для заданной системы эпюру Мр от нагрузок Я = 6Г и q = 3 Т/м (рис. 111, и) иеремножгтэту эпюру с вспомогательными эпюрами M'v М\ и М'г (рис. 111,6, ж, з), получим перемещения от амплитуд динамических нагрузок:
/Дip = 12,37; /Д2р = 20,25; /Д3р = — 2,25.
При заданной частоте возмущающих сил 0 = О,6Х
Xo)i = 0,319 главные перемещения с учетом зави-
Е16ц = 1,88; /6i2 = — 1,13; /6i3 = — 0,75; /622 = 5,63; /62з=1,13; Шзз = 3,00.
176
симости инерционных сил от частоты 0 будут равны:
Канонические уравнения, умноженные на 7, будут такими
— 7,94*1 — 1,13*2 — 0,75*з + 12,37 = 0;
— l,13*t — 14,01*2 + 1,13*з + 20,25 = 0;
— 0,75*t + 1,13*2— 16,64*3 — 2,25 = 0.
Решив эти уравнения, найдем наибольшие значения сил инерции масс:
*! = 1,390 Т\ *2 = 1,327 Т\ *3 = —0,108 Т.
Для построения эпюры динамических моментов (рис. 111, к) изгибающие моменты в характерных сечениях стержней рамы вычисляются по формуле
М = l,39Mi + 1,327Л?2 — 0,108Яз + Мр.
На рис. 111, к пунктиром показана эпюра М для 0 = = 0, т. е. эпюра от амплитуд динамических нагрузок.
Для заданной системы, показанной на рис. 112, основная система получается путем введения связей по направлению неизвестных перемещений гь 22,..., г*,..., %п соответствующих масс ть т2,..., т*,.., тп.
При этом уравнение, выражающее равенство нулю динамической реакции введенной связи по направлению любого перемещения z* с учетом силы инерции — тп(г\% выражается так
14,01 EI ’
16,64 Е! '
§ 32. Метод перемещений
— mt *\ + rn + ri2 Z2 + • • * + ril Zi Н Ьг/л Zn + Rip = °*
12-949
177
Учитывая, что при гармонических колебаниях г,= = —2г*02, получим такую систему уравнений:
г\\ г\ + ri2 г2 н н Ты гп + Rip=
Г2121 + Г22г2 + ,,‘+Г2п 2л + 2р = 0‘
''nl г1+Гп2г‘2 Ь Г\п Zn + КР — °*
где
r\l = rU-mi 0*-
П34)
(135)
Строго говоря, неизвестные zu z2,..., гп и свободные члены Rip, R%p,.,,, R„p являются величинами перемен ны-
о)
S)
lilt)
Pit) w
m,
P(t)
Zfr-ilO
2n(tf
Рис. 112
ми, изменяющимися одновременно и по одному и тому же закону, характеризуемому множителем sin[0(/) + + Фо] к их амплитудным значениям. Так как этот множитель присутствует во всех членах системы уравнений (134), то на него может быть произведено сокращение. Тогда неизвестные и свободные члены уравнений должны рассматриваться в качестве соответствующих амплитудных значений.
Реакции г
ti, ггг» •••» rin определяются от единичных перемещений основной системы, приложенных в тех сечениях, где находятся точечные массы, т. е. так же, как и при определении частот свободных колебаний.
Реакции от амплитудных значений вибрационных нагрузок /?1Р, /?2р, Rnp определяются в основной системе.
После нахождения неизвестных амплитуд перемеще¬
178
ний Z[, гг, zn эпюра динамических изгибающих моментов строится_в соответствии с выражением
М = MtZi + M2Z2 + ... + Mnzn + (136)
где МЪМЪ ...,Мп- эпюры изгибающих моментов в основной системе от соответствующих единичных перемещений;
-эпюра моментов в основной системе от амплитудных значений нагрузок.
Система уравнений (134) по своей структуре аналогична системе канонических уравнений метода переме¬
щений, применяемого для расчета статически неопределимых систем, но неизвестные гь гг, гп уже являются не искомыми перемещениями узлов рамы, а амплитудами перемещений сосредоточенных масс.
Так же как и метод сил, метод перемещений может быть применен не только для систем, подверженных изгибу, но и для систем, испытывающих действие продольных сил.
Пример 50. Для системы с двумя степенями свободы, показанной на рис. 113 и являющейся расчетной
12*
179
схемой виброгасителя, требуется определить соотношение между жесткостями С\ и с2 пружин и основания, при котором масса гп\ двигателя будет находиться в состоянии покоя за счет гашения ее колебаний массой фундамента т2.
Применяя метод перемещении и переходя к основной системе, показанной на рис. 113,6, мы сумеем найти амплитуды колебаний Z\ и z2 масс т\ и т2 сразу же из решения системы канонических уравнений:
Г11 21 “Ь Г12 г2 "I" &ip =
Г21 г\ ”1“ r22 Z2 2р =
Считая перемещения и реакции, направленные вниз положительными, найдем из рассмотрения основной системы при действии единичных перемещений (рис. 113, в и г) коэффициенты при неизвестных. При этом главные реакции вычисляются по формуле (135)
ги = ги — т1 02 = сх — пг, 62; г 12 = Г21 = с,;
г*2 = г22 — тг 62 = с, + С2 — т2 02.
Свободные члены системы уравнений находятся из рассмотрения рис. 113, д.
Rip = — Р\ Rip = 0.
Подставив коэффициенты при неизвестных и свободные члены в систему уравнений и решая ее, найдем амплитуды колебаний масс
= (gi + с2 — т2 62) Р # -
(с1 + с2-т2 0*) (с1-т1 в*)-е?’
z2 = с-— .
(с, + С2 - т2 02) (ct - тх 02) - с?
Наибольший эффект виброгасителя будет достигнут в том случае, когда амплитуда колебаний двигателя, т. е. массы ти будет равна нулю, поэтому приравняем нулю числитель первой из формул (137). Это позволит найти требуемую жесткость пружин, при которой двигатель будет находиться в состоянии покоя
Cl = ш202 — с 2- (138)
При этом фундамент будет колебаться с амплитудой
180
р
(139)
*2 =
Отметим, что величина С\ по формуле (138) не зависит от массы двигателя гп\ и что при совпадении частоты 0 с одной из собственных частот колебаний масс m\ и т2 виброгаситель может сыграть даже отрицательную роль и привести к увеличению амплитуд колебаний массы т\.
Определитель (112), который служит для нахождения частот собственных колебаний системы со многими степенями свободы, может быть записан в матричной форме так:
Е—единичная диагональная матрица;
С—матричное произведение четырех матриц;
здесь Ьт—матрица влияния изгибающих моментов в
п—число участков, на которые разбивается стержень; d — длина участка;
(л_1) — матрица, симметричная относительно обеих диагоналей;
L*m—матрица влияния моментов в фиктивной балке;
— модулированная якобиева матрица упругих грузов;
Ж* — диагональная матрица масс.
§ 33. Матричная форма расчета
\\C-hE\l
(140)
где
(141)
заданной системе от сил Р%= 1, приложенных раздельно в сечениях, совпадающих с массами
Для простой балки
т — А- I — hi
(142)
181
На основании теоремы Перрона характеристические числа вычисляются по формуле
= *2(6т?-4у,), (143)
где yi — характеристические числа матрицы 7(Л-1, для которых имеются готовые значения, вычисленные для матриц разного порядка и приведенные в табл. 14.
Таблица 14 Характеристические числа матрицы /n-i)
Порядок матрицы (п — 1)
к
1
2
1 3
4
5
6 1
1 т
1
1.000
3.000
6,828
13,090
22,393
35,21
52,67
2
—
1.000
2,000
3,618
6.000
—
—
3
—
—
1.172
1,910
3.000
—
—
4
—
—
—
1.382
2,000
—
—
5
—
—
—
—
1,607
—
—
Пример 51. Представить в матричной форме решение примера 40.
Находим все исходные матрицы, входящие в произведение (141).
Разобьем балку на четыре участка (п = 4) длиной
Матрицу влияния изгибающих моментов Lm найдем по формуле (142).
L = — / = —
т 4а 3 16
3
2
1
2
4
*1
1
2
з 1
В нашем случае L*m=Lm = — /3,
% = —= -L_
1 6El 24 /’
1 0 0 М*= отВ0 1 о
0 0 1
182
Модулированная якобиева матрица упругих грузов
а
р
0
4
1 0
Вг =
р
а
Р
1
4 1
0
Р
а
0
1 4
Подставив в (141), получим выражение для С в таком виде
C-tf/jfli/*
где
Как известно, произведение матриц С представляет собой функцию матрицы /3, которая может быть записана так
C=k2 [(а+2р)/з — Р(3+1)/3],
где а и р — элементы модулированной матрицы В\.
В нашем случае а = 4 и 3=1.
Характеристические числа матрицы /4-1) = /з находятся по табл. 14 г
Yi = 6,828;
Y2 = 2,000;
Y3 = М72.
Характеристические числа матрицы С находятся по формуле (143)
?vol = k2 (6*6,828* — 4-6,828) = — -252,414;
16
= ft*(6.2-4.2) =-.16;
*03 = ** (6-1,172*-4-1,172) =..3,553.
Частоты собственных колебаний, как и в примере 38, оказываются равными:
о»! = 1[ —— - ~\/ 24Е1‘т ■ = 4,98 ]/~—
У ткхкох У mil2 *252,414 \ ml3
183
(0.
0,
,-у
-■/
02
-V
24 М6» Ы/2.16
24 /-16» т//а-3,553
=i9-6/-«v7
/ ML
ml3
ГЛАВА 8
СИСТЕМЫ С БЕСКОНЕЧНО БОЛЬШИМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
§ 34. Свободные колебания балок с равномерно распределенной массой
В качестве примера системы с бесконечно большим числом степеней свободы рассмотрим балку с равномерно распределенной массой интенсивностью т=-- и с
о)
Рис. 114
постоянной жесткостью EI (рис. 114,а).
Спектр частот такой системы состоит из бесконечного множества частот, для определения которых будем исходить из дифференциального уравнения упругой линии балки, известного из курса сопротивления материалов
д*у дх2
М
EI 9
(144)
где М — изгибающий момент в произвольном сечении балки, который на основании теоремы Д. И. Журавского может быть выражен через интенсивность инерционной нагрузки р
д2М дх2
= Р.
(145)
184
Обозначения частных производных приходится применять потому, что перемещение у является функцией двух переменных — координаты х и времени t.
Из выражения (144) и (145) следует
Р = хг- (146)
дх4
Вместе с тем интенсивность инерционной нагрузки балки может быть выражена через погонную массу т
и через ускорение при колебаниях
p = — m*L. (147)
и dt* к '
Приравнивая выражения (146) и (147) для нагрузки, получим дифференциальное уравнение свободных колебаний балки
+ 42. iSL = 0. (148)
dt2 т дх4
Это уравнение линейное, четвертого порядка, в частных производных.
Ограничимся отысканием только таких решений этого дифференциального уравнения, которые определяют стоячие волны, т. е. форму изгиба, не зависящую от времени.
При такой форме колебаний решение дифференциального уравнения (148) может быть представлено в виде произведения двух функций, каждая из которых зависит от одного переменного
у = X(x)T(t).
Для нахождения функций Х(х) и T(t) служат обыкновенные дифференциальные уравнения:
+ ш2Т (0 = о,
dt2
— 2
ЛТ(ЛГ) =0.
dx* El
(149)
Эти дифференциальные уравнения имеют следующие решения:
T(t) = a sin (со/ + ф0) (150)
X (х) = Ci sin kx + С2 cos kx + C3 sh kx +
+ Ct ch kx, (151)
185
где
(152)
Значение k должно быть определено из условий на концах балки, которые зависят от способа закрепления этих концов. Всего для определения Сь С2, Сз и С4 имеем 4 условия — по два на каждом конце.
Так как рассматриваемая балка имеет шарнирные опоры, то прогибы и изгибающие моменты на опорах должны быть равны нулю, поэтому:
Из выражения (151) при этих условиях определяем:
С2 = С3 = С4 = 0 и sin kl = 0.
Но если sin kl = 0, то kl = nn, где п — произвольное целое число. Следовательно,
Приравнивая (152) и (154), получим выражение частот
Таким образом, спектр частот действительно содержит их бесконечное множество. При этом частоты относятся друг к другу как квадраты целых чисел натурального ряда. Каждой частоте соответствует своя форма колебаний, т.е. своя форма стоячей волны.
На рис. 114,6 показаны формы стоячих волн, соответствующие трем низшим частотам.
Частота основного тона свободных колебаний выражается такой формулой
при х = 0 Х(*) = 0;-- = 0,
при х = I X (х) = 0; d*X = 0.
W ’ dx*
Х(х) = С1 sin kx,
(153)
(154)
rm
л2 , f El = 03мин = — I/ — /2 V tn
—
~F
186
где q = mg — интенсивность равномерной нагрузки на балку
Для балки же с одной сосредоточенной силой Q посредине пролета частота свободных колебаний выражается такой формулой
~Yz-/W 0671
Приравнивая выражения -л . . . ,
(156) и (157), найдем сосредо-
точенную силу Q3KB, эквива- f—-—J {
лентную равномерно распреде- * 1
ленной нагрузке по частоте Рис. П5
свободных колебаний балки
Q*ю = = 0,493qlz&0,5ql. (158)
Таким образом, для нахождения частоты основного тона колебаний балки с равномерно распределенной нагрузкой можно заменить эту нагрузку половиной ее равнодействующей, приложенной посредине пролета.
Пр и мер 52. Определить частоты свободных колебаний балки, жестко заделанной одним концом с равномерно распределенной нагрузкой (рис. 115).
В этом случае для определения Си С2, Сз» и С4, входящих в выражение (151), имеем следующие условия на концах балки:
при х = 0 X (х) = 0- dxM = о,
dx
, d*X (х) л d3X (х) л
Из выражения (151) при этих условиях получается: С2 + С4 = 0;
Ci + С3 = 0.
Это дает возможность найти из выражения (151)
cos klchkl = — 1.
Корни этого уравнения будут:
. 1.875 , 4,694 , 7,855
«1 — —”— #2 — j 1 " —~—
187
Этим корням соответствуют частоты:
3,515 , [ШГ 22 , f Elg
;Щ=У Я •Юз=
Elg
Приравнивая выражение частоты основного тона частоте колебаний балки с одной эквивалентной точечной
массой т = на свободном конце, получим, испольЯ
зовав результат примера 31, следующее уравнение
д-тд
I Ш Н11 п
Рис. ив отсюда
Qskb = 0,244 Ч1'
4
Пример 53. Определить частоту основного тона колебаний балки с обоими жестко заделанными концами при равномерном распределении нагрузки. В этом случае условия на концах балки будут такими (рис. 116):
ПРИ* = °)л(,)_0;“М=0.
при X = I \ dx
Это дает:
Ci + Сз = 0, С2 + С4 = 0
cos kl ch kl = 1.
Отсюда
. 4,73 22,4 , f Elg
ki = И (О, = 1 / —
l * V Q
Частота колебаний балки, жестко заделанной обоими концами при действии эквивалентного сосредоточенного груза Qaкв посредине пролета, составляет
и- W
_ .Г19» Е/е
V QskbP
Приравнивая это выражение предыдущему, найдем величину эквивалентного сосредоточенного груза
Qokb = 0,3857/ « 0,4//.
188
Рама представляет собой систему с распределенными и сосредоточенными массами, и строгий, или так называемый «точный», метод расчета как системы с бесконечно большим числом степеней свободы оказывается чрезвычайно сложным и громоздким. Поэтому на практике почти исключительно применяются различные приближенные методы. Среди них основным является метод приведения рамы к системе с конечным числом степеней свободы.
Приведение рамы к системе с конечным числом степеней свободы производится путем замены массы, распределенной по длине стержней, массами сосредоточенными. Эта замена делается путем приведения масс.
Часто половину массы каждого элемента рамы считают сосредоточенной посредине его длины, а по одной четверти этой массы переносят в узлы, к которым примыкает данный элемент.
Примеры расчета рам с одной и тремя сосредоточенными массами как систем с двумя и четырьмя степенями свободы уже были приведены ранее (примеры 42 и 50).
§ 35. Колебания балок при подвижной нагрузке
Рассмотрим случай движения сосредоточенного груза постоянной величины Р по балке с погонной массой т (рис. 117,а). Массу груза будем считать очень малой по сравнению с массой балки, а скорость v движения груза настолько большой, что задачу уже нельзя свести к статической.
Если принять, что в начальный момент времени о=0 груз входит на балку, то в мгновение t он будет находиться на расстоянии a=vt от левой опоры.
Уравнение колебаний может быть получено из уравнения (148) путем добавления в правой части Р(х, t)
Рис. 117
189
ш 1& + т1*=р{хл (169)
Несмотря на то, что величина силы Р остается постоянной при движении, ее составляющие по главным формам колебаний непрерывно изменяют свою величину, поэтому принимается Р(х, /).
Для нахождения этих составляющих разложим силу в тригонометрический ряд по синусам
оо
/(*,/) = Л, (0 sin (160)
п=\
Для вычисления коэффициентов ряда An(t) необходимо представить силу Р, распределенной равномерно по малому участку длины 2е (от а — е до а + е). Тогда коэффициенты ряда будут выражаться интегралами
I а+е
А 2 С п / • njlX Л PC- ППХ J
Ап = — I Р (х, t) sm — ах = — I sm — dx =*
/ J I el J I
0 a—
2 P . пла . fine
= sin sm . (161)
e/m I I
Уменьшая e до предела, равного нулю, и имея в виду, что a = vt, получим:
- 2 Р . nnvt
A. = — sm — .
Тогда
оо
П/ 4\ 2Р V! . пШ . ппх /1ЛП,
р(*0 = —2j Sin—sin—. (162)
п=\
Подставим п-ный член этого ряда в уравнение (159) вместо силы Р\
EI*yn+JhdHb=*L sin sin . (163)
дх* dt2 I I I
Решение этого дифференциального уравнения, соответствующего п-ой главной форме колебаний, можно представить в следующем виде
Уп = Т„ (0 sin . (164)
190
Тогда:
?У»=Тпп™ sin;
дх* п I* I '
дгУп _ дгТ„ sjn ппх_
dt* dt* I
Подставив эти выражения в уравнение (159) и со. пп X
кратив на sin -у-, получим:
EITn + т‘?Ь=™- sin. (165)
l* п dt* I 1 к '
Решение этого дифференциального уравнений можно привести к виду
Тп = Вп sin к* + К)+ ~ , (166)
ml
где
0),
/2
nnv
Постоянные Вп и Яп можно найти из граничных условий: при /=0 уп = 0 это дает BnsinA.n = 0 и так как
Вп Ф О, то Ап = 0; при t=0: Щт- = 0.
ot
Отсюда
В 2Рп 1
mlsn —
Следовательно,
2Рф/, . . . ппх ,
Уп =-- 7J7 т: sin (0„ t sin — +
+ —-rf-irsin ♦«* sin т~ • 169
(«2—■♦2) 1
Первый член этой суммы выражает свободные колебания балки с частотой сэп, а второй — вынужденные с частотой tn.
191
Совпадение частот (оп = г)?г приводит к резонансу, который возможен при такой критической скорости движения
/
= — «V*
JI
(170)
Оказывается, что даже при п= 1 эта скорость настолько велика, что резонанс практически невозможен. Наибольшее значение прогиба под грузом Я, стоящим в середине пролета, оказывается равным
где
у:т— статический прогиб под грузом;
(л — динамический коэффициент подвижной нагрузки, выражающийся такой формулой
Пример 54. Определить динамический коэффициент подвижной нагрузки, движущейся по балке пролетом /=10 м со скоростью v=80 км/ч = 22,2 м/сек, если частота собственных колебаний балки составляет со = = 40 сек~\
По формуле (172) находим
Если масса груза велика по сравнению с массой сооружения, то данное решение оказывается уже недостаточно точным.
Критическая скорость, соответствующая резонансу по формуле (170), составляет при п= 1
Если, наоборот, массу балки можно считать очень малой по сравнению с массой т движущегося груза, то его динамическое воздействие на балку оказывается переменным. Своего максимального значения динамический коэффициент достигает при нахождении груза все-
У = УстМм
(171)
ц =
(172)
ц =
22,2-3,14 1—0.174
40-10
= 1,21
I
V = (О =
п
10 ■ 40 = 127 м/сек = 455 км/ч. 3,14 ' 1
192
редине пролета балки. Для этого сечения динамический коэффициент выражается такой формулой
И=1+- = 1+ (-)*. (173)
§ 36. Вынужденные колебания балок с равномерно распределенной массой при действии вибрационной нагрузки
__ Если на балку с равномерно распределенной массой т действует возмущающая сила P(i)=Ps\x\Qt, то вместо однородного дифференциального уравнения (148) мы будем иметь неоднородное
т?т д4 у . — д2ц п • /w
EI + m —= Р sin 0/.
(174)
i/г
P(t) q = mg
dx4 dt2
Решение этого уравнения без правой части, выражающее свободные колебания, было рассмот- Црено в § 34. Вынужденные колебания балки при действии вибрационной нагрузки определяются Рис. 118
частным решением уравнения (174).
Если балка свободно лежит на двух опорах, а сила P(t) действует посредине пролета (рис. 118), то частным решением уравнения (174) для левой половины пролета является:
Р1*(с..,оВ „—А„
где
' (Си/2В x~Au/2D х\
\ “т
2El(Ali2-Cl/2)
« = / l/—.
У EI
(175)
(176)
Л х =
“Т
X X
ch и — + cos и -у-
13—949
193
Для этих гиперболо-кругсьвых функций имеются таблицы значений.
Соответствующие изгибающие моменты выражаются такой форму.гюй
При совпадении частот 0 и ео, иа которыя последа»» выражается формулой (155), настукает? резонанс.
Пример 55. Определить наибольший изгибающим момент в стальной балке на двух опорах с учетом ее ешбсгвеншм* расиределен ной, массы, если воередане, шролета 1 = 2 м действует сосредоточенная. в&бредиотвая сила P(t) = Psm ft, круговая частота ььотою» ft= = 425 се/с-1, а амплитуда Р = 500 к Г. Равшхмерная ивагрузка на балку 9=100 кГ/м=1 кГ/см, а момент инерции балки /=8950 см*.
Распределенная масса балки
Для еередивьс
М =
(178)
т = — = = 0,00102 —1—
g 981 см2
По формуле (176) находится параметр
т = — g
От = -2. = — = 0,00102 к["‘сек8 g 981 см2
По формулам (177) с помью таблиц круговых и гиперболических функций находятся значения функций,
соответствующие иояученншгу значеншо аргумента и — =2.
*4-1,0 = 1,042; Bi,o — 1,008; Ci,o — .0,503;; D*p =
Изгибающий момент посредине пролета находится по формуле (178) при х= —
м S00-200 (1.042.1,008-,501.0,167), = р
2-2 (1,0422 — 0,5012)
Так как статический изгибающий момент составляет
Л4 Р1 500-200 осглал г,
AfCT= = = 25000 кГ см,
4 4
то динамический коэффициент вибрационной нагрузки оказывается р;аетым
М 2900Э - 1С
XI = — = = 1 ,16.
-Мет 25000
Если же при приближенном расчете рассматривать балку как систему с одной степенью свободы с эквивалентной тачечной массой т ='0,493 md, дряложеидой посредине пролета, то частота собственник колебаний и динамический коэффициент ло -формулам (157) и (93) оказываются равными:
ЛГ 48Е1Я Г 48.2,1.10е.8000-981 -1
со = 1/ «- = 1/ = 1000 сек ,
V Оэкв/3 V 0,493*200*2003
и = = - = 1,19.
1_Ш* 1 _/ 400 Ч‘
О) / \ J'000
Разница составляет всего 2,5?/0.
Г а А (В А 9
РАСЧЕТ СТАТИЧЕСКИ НЕОИРЕДЛИМЬГХ СИСТЕМ
§ 37. Определение перемещений и реакций от динамической нагрузки
Основные теоремы строительной механики о работе упругих сил, о перемещениях и ре-акциях имеют обобщение в динамике сооружений, сделанное Н. И. Безуховым.
13* ш
i
I 4.;
Теорема о взаимности работ состоит в том, что работа сил состояния i на перемещениях состояния k равна работе сил состояния k на перемещениях состояния /, т.е.
Tih = Тм. (179)
При этом динамичеРяш$г ские силы и перемещения
считаются изменяющимися по гармоническому закону с одинаковой частотой 0 и в одной и той же фазе.
Взаимность перемещений относится к амплиРис 19 тудам перемещений от
единичных сил в состояниях ink и выражается
такой формулой
bik = б/л*. (180)
Аналогично выражается взаимность амплитуд динамических реакций
rih = rhi (181)
и взаимность амплитуд динамических перемещений и реакций
bik — fhi- (182)
Приравнивая возможную работу статической внешней единичной силы состояния i на перемещениях состояния k, вызванных динамической нагрузкой PftSinG/, соответствующей потенциальной энергии системы (рис. 119), получаем следующую формулу для амплитуды динамического перемещения
Д;*=1 MiE,kds’ (183)
где М( — выражение изгибающих моментов от силы
Pi = 1;
Mk— выражение изгибающих моментов от динамической нагрузки с учетом сил инерции.
Основная трудность применения формулы (183) состоит именно в определении изгибающих моментов от динамической нагрузки с учетом сил инерции.
196
§ 38. Расчет рам по методу сил
На рис. 120 показана заданная статически неопределимая система, па которую действуют вибрационные гармонические нагрузки, имеющие одинаковую частоту 0 и находящиеся в одной фазе. Как уже было указано выше, при установившихся колебаниях все внутренние
силы и перемещения системы будут изменяться по тому же закону. Переходя к основной системе, показанной на рис. 120,6, заменим отброшенные связи неизве¬
стными динамическими реакциями, которые также будут изменяться по тому гармоническому закону, которому следует нагрузка.
Условия равенства нулю полных динамических перемещений по направлению отброшенных связей можно записать в виде канонических уравнений метода сил, которые после сокращения на sin0/ примут такой же вид, как и в случае статической нагрузки
111 + 122 + р = ® \ (184)
621*1 + 822*2 + 4 = 0. I
Здесь61Ь 612, 622— амплитудные значения перемещений по направлению неизвестных от динамических сил Xi= 1 sin 0/ и Хг= = 1 sin0/;
AjP и Д2р—амплитудные перемещения по направлению неизвестных сил от динамической нагрузки.
Коэффициенты при неизвестных и свободные члены канонических уравнений определяются по формуле
107
(183). При этом возникают трудности, связанные с определением изгибающих моментов от динамической нагрузки с учетом инерционных сил.
Поэтому метод сил оказывается мало эффективным для динамического расчета рам. Для неразрезных же балок вычисление коэффициентов не представляет затруднений.
Для определения частот свободных колебаний рам свободные члены канонических уравнений {184) принимаются равными нулю, а вместо частоты 0 возмущающей нагрузки перемещения бн, 612 и 622 определяются от динамических неизвестных Asincot и J2 = sin(o/, где
о — неизвестная частота свободных колебаний рамы.
Для нахождения частот свободных колебаний рамы составляется определитель из коэффициентов системы уравнений. Этот определитель приравнивается нулю, раскрывается и дает уравнение частот. Это последнее уравнение оказывается трансцендентным и сложным. Единственным способом его решения оказывается подбор.
§ 39. Расчет рам по методу перемещений
Перейдем от заданной системы, показанной на рис.
121, я, к основной иутем наложения связей с одновременным приложением динамических неизвестных перемещений Z\{t) =2!sinef,
z2(t) = z2smBtt Zz(t) =2:3sin0/.
Условие отсутствия полных динамических реакции введенных связей выражается системой канонических уравнений метода перемещений:
Г11 21 Н~ Г12 22 + Г13 + Rip = О,
Г21 г1 + Г22 г2 + r23 z3 + R*p = 0, 05)
Г31 1 4" -Гад "тЬ *3 Н“ #3р = О*
Неизвестными в этой системе уравнений являются амплитуды вибрационных перемещений Zj, z2, г3.
Коэффициентами при неизвестных служат амплитудные значения реакций введенных связей от единичных вибрационных перемещений, а свободными членами — амплитудные реакции связей от вибрационной нагрузки. И те и другие величины отличаются от соответству-
198
Амплитуды динамических реакций
Таблица 15
к*
п.п.
Расчетная схема и эпюра изгцбаюших моментов
Расчетные формулы для амплитуд реакций
МА = 4(,ф2 (и)-, Мв = 21% (и) Qa =6■)"%(«); Qfi-6yt)e(u)
МА = -у- % (и); Мв=-% (“)
12 i i
Qb = i 2—V(“)
§
Продолжение табл. /5
Продолжение табл. /5
MA=MB= f-V“
Qa=Qb=-t %p «)
MA=MB = q~\g(u) Qa=Qb= ~.J M
К (“) = ■
, U U
sh — + sin — 2 2
, и . и , и и
ch — sin — Н- sh — cos —
2 2 2 2
И= —
л . и и
— 2 sh — sin —
2 2
, и , и и и
ch — sin — + sh — cos —■
2 2 2 2
Значения функций, входящих
и 2sh и sin и
ti (“) = — •
'Ь (и) = — •
3 ch и sin и—sh и cos и'
и ch и sin и — sh и cos и
4 1 — ch и cos и
и sh и—sin и *’(u) = T'l-chUcosV
и2 ch и sin и 4- sh и cos и
♦4 (и) = X * “Т—: 5
3 ch и sin и — sh и cos и
и2 sh и sin и
\Ь5 (и) = — . ;
Уэ v 6 1— chwcosa
и2 ch и — cos и
(") = — •: г :
6 1 — ch и cos и
и
(м)
12 (и)
(и)
4 («)
(«)
Фв (и)
0
1,0000
1,0000
1,0000
1,0000
. 1,0000
1,0000
0.1
1,0000
1,0000
1,0000
0,9999
0,9999
1,0000
0,2
0,9999
К. 0000
1,0000
0,9999
0,9999
1,0000
0,3
0,9999
0,9999
1,0001
0,9998
0,9998
1,0001
0,4
0,9998
0,9999
1,0001
0,9993
0,9997
1,0002
0,5
0,9996
0,9999
1,0002
0,9982
0,9995
1,0003
0,6
0,9992
0,9997
1,0005
0,9964
0,9989
1,0007
0,7
0,9985
0,9994
1,0009
0,9931
0,9979
1,0012
0,8
0,9974
0,9990
1,0015
0,9883
0,9964
1,0021
0,9
0,9958
0,9984
1,0023
0,9812
0,9943
1,0034
1.0
0,9936
0,9976
1,0036
0,9313
0,9913
1,0052
1.1
0,9906
0,9965
1,0052
0,9580
0,9872
1,0076
1.2
0,9867
0,9950
1,0074
0,9403'
, 0,9818
1,0108
1.3
0,9817
0,9932
1,0103
0,9176
, 0,9750
1,0148
1.4
0,9752
0,9908
1,0138
0,888а
; 0,9663
1,0200
1.5
0,9672
0,9878
1,0182
0,8529
Q„9555
1,0265
1.6
0,9573
0‘, 9842
1,0237
0,8086
0„9422
1,0343
1.7
0,9453
0,9798
1,0304
0,7546
! 0J.9262
1,0439
1.8
0,9306
0,9745
1.С384
0,6892
0,9069
1,0555
1.9
0,9130
0,9682
1,0479
0,6Ю7
0,8840
1,0693
2,0
0,8919
0,9608
1,0592
0,5170
0,8569
, 1,0857
2.1
0,8667
0,9521
1,0725
0,4055
0,8252
1,1051
2,2
0,8368
0,9419
1,0885
0,2733
0,7881
1,1278
2,3
0,8012
0,9300
1,1064
0,1168
0,7451
1,1544
202*
Таблица 16
в формулы метода перемещений
ik («) = -j и*
8 (“) = -J
sh и + sin и
.(«) =
12
ch и sin и — sh w cos и 2 ch и cos и chasm u— sh и cos-м ch и + cos и ch и sin и — sh и cos и ch и sin и + sh и cos и 1 — ch и cos и
Фи (и) =
и3 sh а + sin и 12 1 — *ch u cos и *
1 + ch Я1 cos и ch usrns — sh и cos a
ф, {и)
iu)
*9 ( «)
lo (!U)
Фи (w)
4,0000
1.0000
J.0000 '
1,0000
1,0000
1,0000
1,0000
0,9999
1,0001
0,9999
1.0000
0,9999
1 ,€001 «
0,997 ;
a, oo 02
0,9999
1,0000
0,9999
•1 ;00€2
0,9087 1
1,0007
0,9997
1,0001 1
0,9994
1,0004
0,9958
1,0014
0,9992
1,0004 ;
0,9980
1,0008
0.19899 !
4,0029 :
t) ,9981
1,0007 :
0,9951
J„0017
0,9790 к
1,0060 .
0,9960
1,0014
0,9898
1,0031
0/9611
*1,0111
0,9926
1,0026 ,
0,9811
1,0054
0,9336 '
1,0190
0,9873
1,0044
0,9678
1,0086
0,8936
1,0306
0,9797
1,0070
0,9484
1,0132
0,8377
1,0467
0,9690
1,0107 '
0,9213
1,(0198 !
0,7621 i
J.,;0685
0,9546 ;
*,0157
0,3846
1,0274
0/6626 ,
4,0973
O.J9357
1,0223 -
0,8363
Ц0379
0,5345 .
1,1346
0.9113
1,0308
0,7741
1,0512
0,3724
1,1820
0,8806
1,0416
0,6955
1.0679 ;
0* 1705 j
1,5414 ,
),M25
d 0549
0,5976
1 ,886 '
—.0,0777
1,3150
0,7958 ,
1,07J4 ,
0,4772
1 ,U39 ;
—0,3794 ,
1 „ 4054
0,7393
1,0914
0,3309
1,1447 1
—0,7430 1
1.5T55
0,6716
1,1155
0,1547
1, Ш9
—0,1775
1 ,49
0,5913 ;
1,1444
-0,0539
\лш
— 1,6936 ;
1,8098
0,4967
1,1757
—0,3059
1 /2806
—2,3035 1
2,0034 ‘
t),3861
1,2192
—0,6012
1,3450
—3.0212
2,2862
0,3574
1,2668 '
—0,94«7
1,4222
—3,8638 ;
2,5160
0,1087
\
1,3227
—1,3563
203
и
(и)
(и)
*М«)
(«)
% («)
(и)
2.4
0.7589
0,9162
1,1277
—0,0684
0,6953
1,1853
2.5
0,7085
0,9002
1,1525
—0,287$
0,6379
1,2215
2.6
0,6484
0,8819
1.1813
—0,5488
0,5718
1,2635
2.7
0,5761
0,8606
1,2146
—0,8604
0,4958
1,3122
2.8
0,4886
0,8362
1,2534
—1,2350
0,4086
1,3691
2.9
0,3817
0,8080
1.2984
— 1,6895
0,3084
1,4352
3.0
0,2494
0,7754
1,3509
—2,2482
0,1934
1,5124
3.1
0,0826
0,7377
1,4121
—2,9464
0,0609
1,6028
3.2
—0,1325
0,6940
1,4840
—3,8388
-0,0920
1,7091
3.3
—0,4185
0,6430
1,5687
—5,0147
—0,2691
1,8349
3,4
-0,8150
0,5832
1,6693
—6,6306
—0,4753
1,9844
3,5
—1,3590
0,5126
1,7896
—8,9890
—0,7172
2,1640
3,6
—2,3415
0,4284
1,9349
—12,762
— 1,0032
2,3816
3,7
—4,1148
0,3269
2,1127
—19,808
— 1,3453
2,6487
3,8
—8,6838
0,2027
2,3335
—37,845
—1,7603
2,9817
3,9
—47,556
0,0478
2,6131
— 190,69
—2,2730
3,4048
4,0
19,468
—0,1501
2,9758
72,589
—2,9217
3,9557
4,1
9,1701
—0,4110
3,4615
32,016
—3,7687
4,6961
4,2
6,3934
—0,7700
4,1402
20,984
—4,9232
5,7342
4,3
5,0927
—1,2950
5,1472
15,743
—6,5952
7,2795
4.4
4,3307
—2,1357
6,7817
12.607
—9,2489
9,7956
4,5
3,8236
—3,7021
9,8635
10,460
—14,155
14,552
4.6
3,4560
—7,6655
17,734
8,8476
—26,492
26,725
4.7
3,1721
—37,947
78,238
7,5480
— 120,37
120,43
4.8
2,9412
18,304
—34,332
6,4399
53,839
—53,975
4,9
2,7452
8,3439
— 14,483
5,4496
22,905
—23,252
5.0
2,5722
5,7486
—9,3710
4,5288
14,786
—15,362
ющих величин, используемых в статических расчетах, тем, что при их определении учитываются силы инерции сосредоточенных или равномерно распределенных масс, стержней рамы. Это делается с помощью поправочных функций к формулам для статических реакций.
Если массы стержней приняты равномерно распредг ленными по их длине, то амплитуды динамических реакций выражаются формулами, приведенными в табл. 15. Влияние сил инерции распределенных масс учитывается с помощью поправочных функций гэ(и) к формулам для статических реакций. Числовые значения этих функций зависят от аргумента н, выражаемого формулой (176)
204
Продолжение табл. 16
! чч ii)
!
(и)
(«)
'he («)
4и(м)
12 («)
1,5148
-4,8513
2,5830
—0,0626
1,3879
—1,8337
1,6263
—6,0086
3,2601
—0,2592
1,4641
—2,3928
1,7610
—7,3665
3,7543
—0,4840
1,5530
—3,0482
1,9248
—8,9647
4,3582
—0,7405
1,6565
—3,8189
2,1257
— 10,855
5,1028
—1,0327
1,7775
—4,7296
2,3747
— 13,108
6,0312
— 1,3651
1,9187.
—5,8136
2,6880
— 15,823
7,2056
— 1,7432
2,0842
—7,1176
3,0891
— 19,142
8,7185
—2,1736
2,2789
—8,7095
3,6150
—23,284
10,714
—2,6641
2,5087
—10,693
4,3262
—28,605
13,430
—3,2245
2,7817
—13,236
5,3294
—35,725
17,285
—3,8671
3,1083
—16,631
6,8316
—45,833
23,091
—4,6079
3,5020
—22,442
9,2938
—61,587
32,657
—5,4678
3,9819
—28,918
13,991
—90,280
50,994
—6,4756
4,5742
—42,510
26,227
— 162,26
98,945
—7,6716
5,3165
—76,545
131,08
—764,08
510,82
—9,1145
6,2652
—360,80
—50,020
269,20
—201,00
— 10,894
7,5072
127,06
—22,351
108,35
—92,452
— 13,157
9,1857
51,053
—15,002
63,467
—63,776
—16,158
11,552
29,793
—11,654
41,210
—50,990
—20,388
15,092
19,210
—9,7781
27,086
—43,734
—26,925
20,883
12,461
—8,6096
16,701
-39,428
—38,725
31,873
7,4703
—7,8395
8,2554
—36,721
-67,821
60,093
3,3879
—7,3194
—0,8683
—35,036
—286,43
277,75
0,2033
—6,9700
—5,9531
—34,067
117,88
— 127,58
—3,5364
—6,7457
— 12,451
—33,642
45,470
—56,284
—6,7568
—6,6193
— 19,024
—33.661
26,034
—38,052
-9,9639
где I—длина стержня;
т — погонная масса стержня;
EI — жесткость стержня;
i—погонная жесткость стержня; в—частота вынужденных колебаний, равная частоте возмущающих сил.
В табл. 16 приведены значения функций гэ(н).
При рассмотрении собственных колебаний в формулу (176) вместо величины 0 входит частота собственных колебаний со, а в канонических уравнениях (185) свободные члены принимаются равными нулю.
205
Для получения уравнения частот составляется, приравнивается нулю и раскрывается определитель, составленный из коэффициентов при неизвестных канонических уравнениях.
Так как стержни рамы могут иметь разные значения и, то их все следует привести к одному из элементов.
Окончательная эпюра динамических .изгибающих моментов строится, как и в случае статических нагрузок, т. е. ш формуле (136).
Для симметричных систем с симметрично расположенными массами принимаются групповые неизвестные перемещения, а определение симметричных -и обратно симметричных форм колебаний производится независимо друг от друга.
Пр и мер 56. Определить собственные част®ты колебаний рамы, рассмотренной в примере 49, считая массы стержней равномерно распределенными по их длине (рис. 122, а).
Основная система рамы, соответствующая методу перемещений, показана на рис. 122,6. При этом неизвестные динамические угловые перемещения узлов разложены на симметричную и обратно симметричную группы Zi'(t) и z2(t).
Эпюры амплитуд динамических изгибающих моментов от единичных перемещений Zj и z2 показаны на рис.
122, в и г.
Так как рама симметричная, то симметричные и обратно симметричные формы ее колебаний обособляют-
™ Ij&Lndt P4&ln&t
Рис. 121
206
ж
Рис. 122
ся, неизвестные разделяются, а уравнения распадаются на два независимых:
rZi = 0 и /'222 = О.
Так как определяются собственные частоты колебаний, то свободные члены уравнений /?1р и R2p равны нулю.
Неизвестные Z\ и z2 не равны нулю, поэтому для определения искомых частот имеем два уравнения:
Г и = О И /*22 = 0. _
Величина гц определяется по эпюре М\ с помощью формул табл. 15 и приравнивается нулю
гц = 2[3п1 (и) + Щ2{и) + Щ2(и) — 2i3(u)] = 0.
Отсюда, после приведения подобных членов и сокращений на 2i получим
3\fi (и) + 82 (и)— 2\)з (и) = 0.
Это трансцендентное уравнение решается подбором с помощью табл. 16, в результате чего находятся следующие значения аргумента:
«1 = 3,34; «2 = 4,25; и3 = 4,73.
Из формулы (176), заменив 0 на со, можно выразить частоту колебаний 1/¥
Подставляя /=6 м и три значения м, получим собственные частоты симметричных колебаний
“■=()'1/С=°’318 i/’t=
—тУч -ws
Если распределенные массы т считать эквивалентными сосредоточенными m=TL посредине стержней, то частоты будут такими: ®. = 0,55 1[Щ, -щ = 0,87 л/Шг ; (о3 = 1,08 л/~—
j т f т \ т
208
Эти результаты отличаются от полученных в примере
50 соответственно на 3,5 6,2 и 15%.
Частоты обратно симметричных колебании определяются из уравнения
г 22 = 2[3/i(w) + 4п)2(и) + 4пг(и) + 2пз(«)] = 0
или
3ii(w) + 82 (и) + 2ф3(и) = 0
Подбором находим:
и[ = 3,60; и2 = 4,53.
Этому соответствуют такие частоты обратно симметричных колебаний: “Ит-T/f
При расчете на вынужденные колебания величина аргумента и находится по формуле (176), так как частота оказывается заданной, например
0 = 0,6 сох = 0,6*0,55 1/=0,331/
V т у т
Тогда
и = I = б froW = 3,45.
Соответствующие значения поправочных функций находятся по табл. 16:
t?i (и) = — 1,0775; \з2 (и) = 0,5498; % (и) = 1,7260.
Для определения неизвестных при действии только симметричной возмущающей нагрузки служит неоднородное уравнение
rnZt + Rip = 0.
После подстановки значений гц и /?iP и решения уравнения находится Z\ и строится эпюра динамических изгибающих моментов.
М = MiZi + Мр.
Пример 57. Требуется найти основную частоту собственных колебаний и построить эпюру динамичес-
14—949 209
imx изгибающих моментов в ракге, потеаззтгок на* рис. 123,а, от действия возмущающей силы P(t) =Psin&t, есяю ее частота в составляет 0,& от собственной частоты основного тона колебаний рамы. Основная спсгешз иетода веремедедогй показана иа рис. 123*6* а эпюры М\
Рис. т
и М2— на рис. 123,в, г. Система канонических уравнений в общем виде записывается так:
TuZi + rl2Z2 + Rip = О,
r2JfZl Hr Г222 + Rzp = Or.
Если для стойки аргументом функций гэ является велжчижг м, то для ригеля это будет величина и
= 0,707и. Кроме того, необходимо учесть продольную силу инерции распределенной, массы т самого ригеля
С помощью табл. 15 выражаются реакции ru=i*)+121:(0,707.U).; г12 = га = —-у= — «р1в(й)т1-—Ф12/Ы.) ~ы*; Rip=0; /?4р= Я.
Для определения собственной частоты колебаний свободные члены уравнений принимаются равными ну„лю, а из коэффициентов при неизвестных составляется он ре делитель:
D =
Г11 Г12
= 0.
' 21 ' 22
Раскрывая этот определитель, получаем урадеыи&е частот
Г11 Г22 ГП =
После подстановки выражений реакций и решения уравнения частот подбором иаходим «1 = 1,68 и вычисляем частоту основного тона собственных колебаний
2 25 /El
По условию 9 = 0,8 toi = —t—1/ -=- следовательно,
I2 у т
u = VX25 = 1Д
Находим значения функций t)i(0,707
ю(м); i2(w) и величину и4. Подставив их в канонические уравнения, после их решения находим: Zi =
Pi pi2
=Д,0759 —; 2 = 0,210 —. Окончательная эпюра дина-
i i
мичееких изгибающих моментов, показанная на рис.
123, е, строится по формуле (136)
М = MiZi + M*z2.
Для сравнения на рис. 125, «оказана апюра моментов от статической нагрузки, равной амплитудному значению силы P(t). Наибольший динамический коэффициент оказывается равным
§ 40. Применение готовых формул
Для многоэтажных и многопролетных рам Э. Е. Сигаловым получены простые формулы для низших частот их собственных горизонтальных колебаний, являющихся наиболее опасными (рис. 124),
*!=-==, (186)
У Уст
где у т — горизонтальное перемещение верхних узлов рамы от горизонтальных сил, соответствующих точечным массам в узлах рамы, заменяющих ее распределенную по стержням массу;
К1— коэффициент, зависящий от числа этажей. Значения этого коэффициента приведены в табл. 17.
Таблица 17
Значения коэффициента К\
Число этажей рамы п »
4
5
б
7
8 и более
/Cl
34,5
35,1
35,8
36,4
49,2л/
V 2п
Для нахождения перемещений уст служит формула
= (wi
k=\ k—\
П
где Qk = Е gi — поперечная сила в стойках k-ro
i=k
этажа, равная сумме всех вышележащих сил gi\
с* = + — j—линейный перекос Л-го этажа вы¬
сотой / от единичной силы;
212
i
i
—i
и
0
mL
I
\
¥
az _.
2
*U
n
/
Рис. 124
sk и rk— соответственно суммы погонных жесткостей стоек и ригелей fe-ro этажа.
Для нижнего и верхнего этажей перекосы составля¬
ют:
/2/1 С'-Т2 Х +
Чг): с""тНт + )'
’• + ъ) .
Для определения двух следующих частот служит формула
*2.3
“2.3 =
(188)
"Vmin k=\
Ck
где mk—этажные точечные массы;
ск—соответствующие линейные перекосы этажей. Значения коэффициентов К2 и Кз приведены в табл. 18.
•Таблица 18
Значения Кг и Кз
Число этажей рамы п
4
5
6
7
8 и более
Kt
4
4,35
4,55
4,65
4,72
Кз
6,15
7,10
7,60
7,80
7,85
Пример 58. Найти первую частоту собственных горизонтальных колебаний железобетонной рамы, показанной на рис. 125. Этажные нагрузки, приведенные к перекрытиям, составляют: gi = 43,3 Т\ g2= п = 44,1 Т\ §з = 43,0 Т; g,= 3
= 38,1 Т. Действительная погонная жесткость стоек первого этажа / = 5,04Х ХЮ8 кГсм. Относительные погонные жесткости стержней рамы показаны в кружках на ее схеме.
Для определения про- 1IJfni ..
гиба верха рамы находим суммы погонных жестко- Рис. 125
И
в®
5
1®®
0®
5
$
213
стен стоек и ригелей по этажам, а также соответствующие поперечные силы:
Sl = 3.1 = 3; S2 = 3.0.8 = 2,4; s3 = 3 • 0,6 = 1,8;
Si = 3-0,4 = 1,2;
П = 2-2=4; Гг = 2• 1,6 = 3,2; r* = 2-1,2 = 2,4;
П = 2-0;8 --= Ц6;
QA = 38,1 T; Q3 = 38,1 + 43,0 = 81,1 Г;
Q2 = 81,1 + 44,1 = 125,2 T; Qt = 125,2 + 43,3 = 168,5 T.
Перекосы этажей, уменьшенные в Р _ 450а _ J
121 _ 12-б,0в-.108 ~~ 30000 РЭЗ’
1 I 1 1 I 1 «С7
?1 = — + —= -Г- + г- = 0,57;
1 I S1 1 I °
Г1+и 4+ 12
с2 = J_ +—=— + — = 0,73;
2 S2 г2 2,4 3,2
С3 = —-—1—-— = — + — = 0,97;
* s3 г3 1,8 2,4
с4 = — + —= — + —— = 0,99.
4 s4 4 г4 1,2 4-1,6
Горизонтальное перемещение верха рамы, соответствующее этажным нагрузкам, которые для этого принимаются приложенными горизонтально:
+ Qt С2 + Qs сз + Qt ct —~ "Ь “Ь
2 V г, Гг
+ _ftL + _lJ] = _J_ri68,5-0,57+ L25,2- 0,73 4гя r4 JJ 30000 [
+ 81,1-0,97 + 38,1 -0,99 - -L +
-i-Y] 1000 = ——271,5-1000 = 9,04 см.
2.4 )\ 30000
Для четырехэтажной рамы коэффициент К\ *то табл. 17 равен 34,5.
По формуле (186) первая круговая частота обставляет
Кг _ 34,5
Вторая частота оказывается* равной со2=29,4 сек~1.
Длш п§убишжешшш ощецрявжт чейпии? к®пе(*аний ферм применяется способ перехода к эквивалентной балке. При этом прогиб посредине пролета фермы от узловой нагрузки, соответствующей массам, приложенным в узлах фермы, находится по формуле Мора — Максвелла для шарнирно стержневых систем:
г = у1 iVpflys ф 2-1 EF у
где Мр—усилие а любом стержые от заданной» ыагрузки;
— усилие Bi том же стершие: qit едтгопнв&ск»лы,. приложенном в еередаие проаета
S n EJ? — доиша и жесткость tqfo лее схеракня.
Суммирование распространяете* н» все стертом фермы.
Для балки на: двух опорах щпг дайстяш р*я«ягерной нагрузки q соответствующий ирогаб выражается? известной формулой
f 5ql
16 384 EJ "
Из условия равенства прогибтж фермы и балктг, обладающих одним и тем же модулем упругости , можно определить эквивалентную жееткостчг последаей
ЕI =
384 [ф '
Подставляя в формулу (156) для основного тона колебаний балки последнее выражение, получим следующую формулу для фермы
я2 [~Ёгй 36,2'
Щ-ТУТ-У1- 189
Пример 59. Определить частоту основного тона колебаний балачвой фермы, если' от действие заданной равномерной нагрузки расчетный прогиб составляет ф=1,5 см.
Искомая частота свободных колебаний фермы по формуле (189) будет
35,2 по 0 —1
со, = ■ = 28,8 сек .
/,5
215
ГЛАВА 10
МЕРЫ БОРЬБЫ С ВИБРАЦИОННЫМИ ЯВЛЕНИЯМИ
§ 41. Характеристики физиологического и других воздействий вибраций
Колебания могут оказать вредное влияние на организм человека и помешать работе оборудования производственных зданий. Колебания конструкций в зависимости от частоты и амплитуды могут оказать различное физиологическое воздействие на людей. На основании имеющегося опытного материала сделан вывод, что критерием чувствительности людей к колебаниям с низкими частотами (от 1 до 10 гц, т. е. кол/сек) может служить ускорение колебаний, а к колебаниям с высокими частотами (выше 10 кол/сек) — скорость колебаний.
Характеристики воздействия на людей гармонических колебаний с амплитудами до 1 мм приведены в табл. 19.
Таблица 19
Характеристики физиологического воздействия гармонических колебаний
Характеристики воздействия
Для частот от 1 до 10 гц
Для частот от 10 до 100 гц
колебаний на людей
предельное ускорение в мм/секЛ
предельное ускорение в мм/сек2
Не ощутимы
10
0.16
Слабо ощутимы
40
0,24
Хорошо ощутимы.
125
2
Сильно ощутимы (мешают) Вредны при длительном воздей¬
400
6,4
ствии
1000
16
Безусловно вредны
более 1000
более 16
Допустимую амплитуду ао динамических перемещений определяют по формулам:
я0 = ; 190
2л п0
«О = -тг. (191)
4л щ
216
гдеа0и&»0—допускаемые пределы скорости (в мм/сек) и ускорения (в мм/сек2), принимаемые по табл. 19; п0 — частота колебаний, гц.
В качестве допускаемых должны приниматься колебания с характеристикой безвредного воздействия их на людей.
Для различных машин и оборудования, монтируемых на фундаментах и перекрытиях, нормами установлены допустимые значения амплитуд и скоростей колебаний.
§ 42. Способы уменьшения резонансных явлений
В тех случаях, когда в результате динамического расчета конструкции требования прочности, жесткости или характеристики воздействия на людей и оборудование не удовлетворяются, следует принимать меры борьбы с колебаниями. Эти меры довольно разнообразны и эффективны при условии правильного выбора их в каждом конкретном случае. Мы перечислим основные из них.
Целесообразная расстановка машин
Путем той или иной расстановки машин, служащих источником колебаний, можно уменьшить или даже избежать резонансных явлений. Так, например, придвинув такую машину ближе к опоре несущей балки, можно увеличить частоту собственных колебаний последней. Машины, создающие горизонтальные силы инерции, следует располагать так, чтобы эти силы действовали в том направлении, для которого жесткость здания больше или частота собственных колебаний сильнее отличается от числа оборотов машины.
Изменение жесткости конструкции
Увеличение жесткости конструкции путем увеличения размеров ее поперечных сечений, путем уменьшения пролетов или с применением других мероприятий приводит к повышению частот собственных колебаний и может быть использовано для удаления низшей из этих частот вверх от частоты возмущающих нагрузок.
217
Уменьшение жесткости конструкций может быть. целесообразным лтсшь в редких случаях, так как приводит к снижению прочности и создает возможность резонанса с более высокими тонами колебаний изменешгой конструкщш.
Изменение режима работы машины
Понижение или повышение числа оборотов может привеети к такому же эффекту, как и повышение или соответственно понижение жесткости конструкции, т. е. к уменьшению» динамического коэффициента.
Колебания, создаваемые машинами с вращающимися массами с возвратно-поступательным ходом, можно значительно уменьшить путем уравновешивания» инерционных сил. Урв-новешивание м*ашины может быть достигнута за счет уравновешивания' ее движущиеся мжх, а также путем встречного сдааиваюи» ииги стрвтавия, при которож две или три одинаковые мажига* ставятся 1гя одном валу и работают с относительными едтггтг фз 1та 1*80 ргли 129. Для это» же цел» к мгавне может быть добавлен специальный антивибратор.
Применение виброгасителя
Динамический виброгаситель представляет собой дополнительную систему,, которая устанавливается на конструкции, совершающей вынужденные колебания с целью нейтрализовать своими реакциями возмущающую нагрузку. Для этого частота собственных колебаний виброгасителя должна быть равна частоте возмущающей нагрузки.
Виброизоляция
Виброизоляция оказывается одним иа наиболее простых средств для уменьшения вредного действия колебаний. Различают активную &и6роизолщию, назначением которой является уменьшение динамических сил, передаваемых машиной на несущую конструкцию, и пассивную виброизоляцию, которая имеет целью изолировать те или иные места работы или приборы от колебаний несущих конструкций.
21»8
§ 43. 'Расчет виброидоляцм
Расчет активенюй виброизоляции ведется, жждм из рассмотрения (расчетной схемы, показанной на шс. d36. При этом массу т на амортизаторах можно рассматривать в качестве системы с одной степенью свободы, могущей совершать только вертикальные колебания, и для которой динамический коэффициент выражается формулой (90).
Эффективность виброизоляции оценивается коэффициентом передачи силы, который выражается такой формулой
ц=
Vi
+
402 62
О2
О)4
(о2 (4л2 -- 62) j 92)
402 б2
(О2 (4л + 62)
где б— логарифмический декремент затухания амортизаторов.
Величина D=— называется коэффициентом
Y Ап*+ Ь*
демпфирования и в большинстве случаев меньше 0,05. Тогда можно пользоваться приближенной формулой
Т) =
)■-
(193)
Для эффективности виброизоляции отношение частоты возмущающей силы 0 к частоте свободных колебаний со подрессоренной массы должно быть не меньше 4. В этом случае величина ц будет не выше 1/15 и эффективность виброизоляции достигнет 93,5%-
При малых значениях 0 ц~1 и виброизоляция оказывается бесполезной.
0
При — 1,41 т 1 и тогда виброизоляция оказываем
ет даже вредное действие.
При — 1 наступает резонанс, который может быть опасен для пружинных амортизаторов.
210
Для гашения колебаний со средними частотами (6— 25 герц) наиболее подходят стальные пружинные изоляторы, которые допускают большую статическую осадку и дают возможность понизить частоту собственных колебаний изолируемой массы.
РАЗДЕЛ III
ОСНОВЫ РАСЧЕТА ПРОСТРАНСТВЕННЫХ ТОНКОСТЕННЫХ КОНСТРУКЦИИ
ГЛАВА 11
ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ ПОВЕРХНОСТИ
§ 44. Аналитическое выражение поверхности
Поверхность есть геометрическое место точек, радиус-вектор которых г, направленный из фиксированного центра 0, является функцией двух независимых параметров а и р. В векторной форме уравнение поверхности имеет вид:
X =г(«, Р)
или
г = х(а, P)i +у{a, p)j + z(а, P)k. (194)
Поверхность можно определить в параметрической форме с помощью трех уравнений вида:
х = ft (а, Р), у = /г(а, 0), г = f3(а, р), (195)
где х, у% г— декартовы координаты точки поверхности — известные функции (fi) параметров аир.
Если из уравнения (195) исключить а и р, то получается уравнение поверхности в неявной
F(x, у, z) = 0 (196)
или явной форме
Z=f(x,y). (197)
Любое соотношение между параметрами вида ф(а, Р) представляет кривую линию на поверхности.
221
Кривые на поверхности, вдоль которых один из параметров остается постоянным, называются координатными линиями. Поверхность полностью определяется двумя семействами координатных линий — криволинейными координатами поверхности.
Положение любой точки на поверхности определяется значениями криволинейных координат
а = const и р = const
в этой точке.
§ 45. Линейный элемент поверхности
Рассмотрим две соседние точки поверхности С и D (рис. 127), определяемые радиус-векторами г и r + dr и
соответственно криволинейными координатами
а, р и a + da, p + dp.
В пределе длина элемента дуги, соединяющей точки С и ), стремится к дифференциалу ds и равна модулю \dr\ вектора
= ~-da Н—ф, (198)
ool ар
а квадрат дифференциала дуги
ds2 = \dr\2 = dr-dr = Eda2 + 2Fdadp + Gdfl2, (199) где согласно (194)
Выражение (199) называется первой квадратичной
222
формой поверхности* а величины Е3 F и 6 ее хоэффициентами.
Из (200) следует, что rL = = V Е, г2 = =
да др
= Vc
F = -J-'S- =VE-VGcos х, (201)*
dot др
где х—угол между векторами JE и 1f G (рис. 128).
Согласно (199)* вдоль координатной линии а = С, da=Q длина элемента CD\
ds2 = VGd$t (202)
вдоль координатной линии р = С, dp = 0 длина элемента
ссъ
dsl = VEda. (203)
Если координатные линии образуют на поверхности ортогональную сетку то (199) примет вид:
ds2 = ds\ -f ds\ = A2 da2 + Я® d32, (204)
где
A = VE9 B=VG. (205)
§ 46. Кривизна линии на поверхности
Если через точку С[г(х, у, г)] провести на поверхности различные кривые, то касательные к ним в точке С, как правило, располагаются в одной плоскости — касательной плоскости к поверхности в точке С.
Прямая, проходящая через точку С перпендикуляр¬
* Согласно фермуле евалярвого вревзаедеяв* в агатов А п В: j4ZJ = [AJ-[B] cos х.
223
но к касательной плоскости, называется нормалью к поверхности в точке С (рис. 128).
Нормальным сечением поверхности в точке С называется сечение некоторой плоскостью, содержащей нормаль к поверхности в этой точке. Такое сечение представляет собой плоскую кривую, главная нормаль* к
-нормаль
Рис. 123
которой совпадает по направлению с нормалью к поверхности в данной точке С.
Касательная плоскость проходит через
ч плоскость
векторы:
дг дг
гх = и г2 = .
да 2 д$
касательные кайр линиям в точке С.
Вектор нормали /V параллелен вектору, образованному векторным произведением** векторов п и г2, а его орт дг
дг
__ ГДХГ2 __ да
ар
I ГХ X г2 I
Н
где знаменатель является модулем векторного произведения
Я
дг дг
— X — да dfi
дг
да
дг
д$
Используя (201), получим
sin х = Kl — cos2 х =
= VE,
EG — F2
EG
dr
da
* Нормаль, перпендикулярная к касательной в точке С и лежащая в соприкасающейся плоскости.
** Векторное произведение векторов А и В имеет вид: АУ,В = С. где С — вектор J_ к плоскости, проходящей через А и В, модуль его равен площади параллелограмма, построенного на этих векторах: )СI = Л • в -sinх.
224
и окончательно
П=7Г7Х1Г- (20б)
Н да др
где
Н = VEG — F2. (207)
Нормали, проведенные в соседних точках поверхности, как правило, не пересекаются между собой, но для любой точки С имеется два таких направления на поверхности— линии кривизны, для которых это пересечение имеет место.
Если обозначить через г радиус-вектор точки поверхности С, через п орт нормали, через r+dr радиусвектор соседней с С точки, лежащей на расстоянии da или dp, а через n + dn орт нормали в этой точке, то необходимым условием пересечения этих двух смежных нормалей является компланарность векторов n, dп и dr, что в векторной записи имеет вид:
п• dn X dr = 0. (208)
Подставляя (198) и аналогичное ему выражение для dn в уравнение (208), получим после группировки*:
(п1гх1г)" + [(п1гхж) + (пЖ*)]х
X dadf. + (n-Jjj- х) d? = 0, (209)
квадратное уравнение относительно
da dp
или —— .
dfi da
Корни уравнения (209) определяют два направления на поверхности, для которых нормали, проведенные в соседних точках, пересекаются между собой. Преобразуем уравнение (209).
гг дг дт
Так как векторы гА= и г2 = касательны к ко-
да ар
ординатным линиям p = const и a = const в точке С и перпендикулярны к нормали у» то:
"• = 0ипЖ=0- (210)
* Для векторных произведений справедлив распределительный закон: А X (Д+С) =А ХВ+А ХС.
15—949 225
Дифференцируя уравнение (210) по а и получим:
дп дг п д2г да да да2 *
—= -п-~ = —М,
др да д&др
*L.iL = _n=
да ap dadfl
дп дт
др ' др
(211)
= —п-
а2г
ар2
= —N.
Величины L, М, N представляют собой проекции век-
д2г дт д2г
торов , — , на направление нормали к поверх-
да2 оадр др2
ности и называются коэффициентами второй квадратичной формы
drdn = Lda2 + 2Mdadfi + Ndp2. (212)
Подставив (194) и (206) в уравнения (211) и проделав необходимые выкладки, получим коэффициенты второй квадратичной формы, выраженные в декартовых координатах:
д2х
д2у
д2г
д2х
д*у
дЧ
да2
да2
да2
lip2
др2
дР2
дх
ду
дг
• JV--L
дх
ду
дг
да
да
да
’ N ~ н
да
да
да
дх
ду
дг
дх
ду
дг
IjT
дР
ар
дР
1р~
м = — н
д2х
д*у
д2г
дадр
дадр
дадр
дх
ду
дг
да
да
да
дх
ду
дг
~дР
др
др
(213)
где Н определяется формулой (207).
Так как п вектор постоянной длины, то первые производные от п должны быть перпендикулярны к п и па-
226
dr dr
раллельны плоскости, содержащей векторы и ,
да
через которые они и могут быть выражены посредством уравнений:
дп дг , , дг дп л дт , , дт /01
= а \-Ь , =ах h &i , (214)
да dot dp ’ ар да 1 dp * v 7
где а, 6, а\, Ь\— постоянные, подлежащие определению. Умножая последовательно первое уравнение (214) dr dr
скалярно на векторы и и учтя (200) и (211),по-
da dp
лучим:
— L = аЕ + bFt — М = aF + bG,
откуда
FM—GL , FL — EM
а = , о = //2 ’ я*
Окончательно получим
dn _ FM —GL дг , FL — ЕМ дт (с.
~да “ Н2 да /Я ар ' '
и аналогичным путем
dn FN — GM дг , FM — ЕМ дг
dp ” TP IT2 dp" ‘ ' '
С помощью зависимостей (215), (216) и уравнения (206) можно доказать равенства:
EM
—
FL
H
%
FM
—
GL
H
•
EN
—
FM
H
FN
—
GM
П да Х да ~ dn dr П да Х dp ~~
dn dr in „
a-5fx-=—z—- (217»
dn dr
n
dp dp H
15* 227
Сравнение (209) после деления на dp примет вид:
+ (FN — GM) = 0. (218)
По двум корням уравнения (218) можно доказать ортогональность линий кривизны
(F = 0).
Полагая, что бесконечно близкие точки С и D лежат на линии кривизны, проведем через них нормали к поверхности, точка пересечения которых дает центр кривизны (рис. 129).
Расстояние от центра кривизны — k до точки С, измеряемое в направлении единичной нормали — п, называется главным радиусом кривизны поверхности в точке С и обозначается
R = Rn.
Величина, обратная главному радиусу кривизны, называется главной кривизной поверхности в точке С и обозначается
Для каждой точки поверхности есть две главные кривизны, которые являются нормальными кривизнами поверхности в направлении линий кривизны.
Главная нормаль к линии кривизны, вообще говоря, не совпадает с нормалью к поверхности и, следовательно, нормальная кривизна поверхности в направлении линии кривизны в общем случае не является кривизной этой линии. Из всех возможных кривизн линий кривизны одна главная кривизна имеет минимальное, другая— максимальное значения. Полагаем, что центр кривизны определяется вектором р (рис. 129)
р = Г + Rn; dp =d (г + Rn) = (dr + Rdn) + n dP.
Рис. 129
228
Вектор dr+Rdn касателен к поверхности, а из условия, что вектор dr расположен вдоль линии кривизны, следует, что вектор dp должен иметь направление п. Таким образом,
ar + Rdn = О и получаем в векторной записи формулу Родрига;
kar + dn = 0. (219)
Подставляя (198) и аналогичное выражение для da в уравнение (219), получим:
(*+)"“+(*-!+ж)*-0'
Составляя скалярное произведение этого уравнения от дг
на векторы — и ,соответственно получим два урав-
да др
иения:
(kE—L)aa + (kF — M)a р = О,
(kF — M)da + (kG — N)dp = 0. (220)
Исключая из уравнений (220) da и dp, получим уравнение второй степени относительно k:
//2*2 _ (ДГ _ 2 FM — GL)k + (LM — М*) = 0, (221)
два корня которого дают значения двух главных кривизн kt и кг.
Если поверхность отнесена к линиям кривизны, что часто делается в теории оболочек, toF=M=0 и из уравнения (220) непосредственно получаем:
ь L — — — k — 1 = N — N 1222)
Ri ~ E ~ A* ’ a_ R* G ~ B* ' UZ2)
В этом случае коэффициенты первой квадратичной формы (А и В) связаны с главными кривизнами поверхности (kt и 1&2) уравнениями Кодацци — Гаусса;
“г»
229
Величина
k k-yk Ri R2
(224)
называется гауссовой кривизной поверхности. Если гауссова кривизна равна нулю, что справедливо для случая развертывающейся поверхности (один из главных радиусов кривизны равен бесконечности), то геометрия поверхности совпадает с евклидовой; если гауссова кривизна отлична от нуля, то поверхность обладает своей геометрией, отличной от геометрии плоскости.
Величина
называется средней кривизной поверхности. Поверхности, для которых средняя кривизна во всех точках равна нулю, называются минимальными.
При расчете оболочек по безмоментной теории пренебрегают крутящими и изгибающими моментами и поперечными силами, возникающими в сечениях оболочки. Это можно сделать, если напряжения от изгиба и кручения малы в сравнении с напряжениями от нормальных и сдвигающих сил.
Рассмотрим оболочку постоянной толщины А, очерченную по произвольно заданной поверхности. Пусть Nа и 5а будут нормальная и сдвигающая сила в точке
*‘+4’-т (т+тЬ)- (225
ГЛАВА 12
БЕЗМОМЕНТНАЯ (МЕМБРАННАЯ) ТЕОРИЯ РАСЧЕТА ОБОЛОЧЕК
§ 47. Основные дифференциальные уравнения
230
С по нормальному сечению, совпадающему с координатной линией а = const, N$ и S3 нормальная и сдвигающая силы по нормальному сечению, совпадающему с координатной линией р = const.
За координатные линии аир примем линии кривизны средней поверхности оболочки. Силы отнесены к единице длины линии средней поверхности оболочки, положительное направление сил показано на рис. 130.
Вырежем из средней поверхности ортогональной криволинейный четырехугольник CD{DCА со сторонами
(рис. 131).
Для углов dpa и Лрз, лежащих в двух взаимно перпендикулярных главных нормальных плоскостях, проходящих через точку С, и углов dxи d\(эр, лежащих в касательной плоскости и образованных касательными к линиям кривизны в точках С, Di и С\ (рис. 131), получим формулы:
На выделенный элемент оболочки CD\DC\ будут действовать силы, показанные на рис. 132.
Уравнения равновесия запишем для осей подвижного ортогонального трехгранника Cxyz в котором оси Сх и Су направлены по касательным к координатным линиям а и р в сторону возрастания параметров, ось Cz направлена по внешней нормали.
Оси трехграника образуют правую систему координат. Интенсивность внешней поверхностной нагрузки на
СС1 = Ada, DDl
(л + j- dp) da, (226)
231
232-
единицу площади имеет в направлении координатных осей составляющие X, У и Z.
Уравнения равновесия
2Рх = О, ZPV = 0, = 0 и ЪМг = О*
после исключения углов аГфа ,drpa , Рэ (227) и де¬
ления всех членов на dadfi примут вид:
* (вЛ'«)-Л'э+-№) + *«-+'4в;( = 0’
да
_д_
да
i мо ■-N«+ +ABV=°’
0.
/V KD
Рис. 132
Последнее из уравнений выражает закон парности сдвигающих сил.
Полагая на основании этого уравнения
Sa = = S, (228)
получим основные дифференциальные уравнения безмоментной теории оболочек, выведенные в линиях главных кривизн средней поверхности оболочки, в форме:
(“.)-» + 75и+ АВХ = °'
а ар
* Уравнения равновесия 2М* = 0 и 2Л1/ = 0 для безмомеитной оболочки удовлетворяются тождественно.
233
iw-'v4- + T-fi!5)+'4Si'-0'
N„ No
— + —t — Z = 0. (229)
Ri R 2
Таким образом, при заданных на оболочку поверхностных и контурных внешних силах задача определения внутренних усилий по безмоментиой теории (229) является статически определимой, искомые усилия (jVa, Л/3 и S) можно найти, не пользуясь соотношениями между деформациями.
§ 48. Расчет оболочек вращения
Большое значение в технике имеют тонкие оболочки, средняя поверхность которых является поверхностью вращения. Подобная поверхность образуется при вра¬
щении плоской кривой — меридиана — вокруг оси вращения (oz), лежащей в ее плоскости (рис. 133). Уравнение меридиана имеет вид:
г = г (г). (230)
Линии пересечения поверхности с плоскостями 2 = = const являются параллельными кругами — параллелями.
234
Декартовы координаты точки С будут х, у, г, причем
х = г (г) cos р, у = г (z) sin р.
Радиус-вектор точки С, согласно (194), равен:
г = г (г) cos pi + r(z) sin pj + zk.
Принимая параллели 2=const и меридианы p = =const за координатные линии поверхности, получим:
= r' (z) cos pi + г' (z) sinPj+ к,
дг
-- = —/• (г) sin pi + г (г) cospj,
ар
где штрихами обозначены производные по г. Коэффициенты первой квадратичной формы
А2 = — • — = (г')2 cos2 р + (г')2 sin2 р + 1 = 1 + (г')2, дг дг
Б2 = = т2 sin2 р + т2 cos2 р = г2,
ар ар
откуда
А = [1 + (г')2]1'2, B = r, Н = AB = r [ 1 + (г')2].1'2,
F = — = 0.
дг ар
(231)
Для подсчета коэффициентов второй квадратичной формы определим величины:
а*г
дг2
= г" cos pi + г" sin pj,
= — г cos pi — r sin Pj,
o p2
n =
dr dr
dz * ap
H
H
i j k
r' cos p f sin p 1 — rsin prcos p 0
— ~~ ( cos pi sin Pj ,k),
П
откуда
L = n (r* cos2 p + л» sin2 p) = —rj- ,
дг2 И п
235
(,W! + r‘s",= fi) = 7f ■
(232)
Так как величины F и M одновременно обращаются в нуль, то координатные линии являются линиями кривизны и для определения кривизн можно воспользоваться формулами (222):
А* [1 + (г')Ч3/2 ’
**-4- 1
(233)
Уравнения (229) после подстановки в них величин (231) и (233) и замены а на г, примут вид:
-Иа)-г'ЛГЭ+ [1 +(г')*]1/2-.+г[1+(гГ],/2Х= О,
[1 + (0*],/2р + - Т-{r2S) +г [1 + 1,2у = °* (234)
ар г ог
1/2,
■Na + Nt-r[l+(rV]l"Z = 0.
1+(0»
Для случая однородной задачи X=Y=Z=0 (общее решение) усилия могут быть выражены через одну функцию усилий по формулам [2]:
V —i-it N. = 1(1. (235)
* г* др р Ar dp ’ dz \ г )
В этом случае первое и третье уравнения (234) удовлетворяются при любом выборе функции р, а второе примет вид:
3-т(*+)-* 236'
Таким образом, расчет безмоментной оболочки, очерченной по произвольной поверхности вращения при отсутствии поверхностной нагрузки, приводится к определению функции усилий р=ф(г, р) из дифференциального уравнения (236), удовлетворяющей заданным тангенциальным граничным условиям. Тангенциальные гра-. ничные условия могут быть поставлены в силах Na, N$
236
S — статические граничные условия, когда задачу определения усилий можно выделить в самостоятельную задачу, и в перемещениях иа, ии зависящих от тангенциальных усилий, когда подобного выделения сделать нельзя.
В главе 2-й будут рассматриваться лишь задачи первого характера.
Для случая осесимметричного загружения оболочки вращения (У=0) усилия не зависят от угла р, S=0 и надо определить только Na и N
В последнем случае уравнения (229) примут вид:
da
— (NaR2 sm a) — cos a + 12 sin = 0,
-Z = 0.
Na JVp Ri
откуда получаем решение:
о
Л/ =
TV,
“ = /? sjn2a [j S'n “ C0S a— sin dX +C0] ,
a
в = /?2г — ! — I f RiR% sin a (2 cos a— Asm a) da+cj,
aj sin a _J j
a*
(237)
где Co — произвольная постоянная.
Внутренние силы могут быть определены и без рассмотрения дифференциальных соотношений.
Обозначим равнодействующую всех сил, действующих на оболочку вращения выше сечения z=c через Q*, тогда из суммы проекций на вертикальную ось oz следует (рис. 134) Qz+2nrNasin a = 0, откуда меридиальное силие
237
(238)
2 яг sin а
Кольцевое усилие iVp проще всего определить из 3-го уравнения (234).
Решения (237) и (238) эквивалентны.
Пр и м е р 60. Определить усилия в замкнутом шаровом куполе постоянной толщины А, опертом по экватору (рис. 135) [3]
Ri = R2 = R, cos а = — , sin а = — ,
R R
А (а) = R, А (г) = — ; В (a) = R sin а = r,
Г
В (г) = VR2 — z2 = r.
Эпюры /V*
¥
щ
ш
и
=
Rg
a) От собственного веса g {Т/м2 поверхности) Q, = F:g = 2nR (R — z)g = 2nR2g (1 — cos a),
N =
Ог _ /?* (fi-g)g
N6 =
2лr sin a g COS a
1 + cos a
D 1 — cos a — cos2 a D
i i
1 + cos a
Эпюры усилий приведены на рис. 135.
Т
б) От снеговой нагрузки — р (— горизонтальной
проекции)
Qz = nr2p, jVa= —
л r2P
2лг sin a
0.
2
238
Nq = — lp cos2 a — R = —cos 2a.
Эпюры усилий приведены на рис. 135.
Пример 61. Определить усилия от симметричной нагрузки (У = 0) в псевдосферической оболочке постоянной толщины Л, опертой по параллельному кругу (рис. 136) [4].
Геометрия псевдосферической поверхности определяется следующими соотношениями:
2 = а 1„ a + ]/fl2-'2. =
Г
= a arch — Va2 —г2
т
дифференцирование по z дает:
/•'=— = — г (а2 — г2Г1/2, г" = — = а2г (а2 — г2)'2, dz ' dz2 v ’
Согласно формулам (233),
Ri = — -j (а2 - r2)1/2, R2 = га (a2 - г2)~щ Гауссова кривизна
k=-L-==_±.
R1R2 я2
Согласно формулам (231),
А = а{а2 — г2Г1/2, В — г.
230
Для симметричной задачи (У = 0) уравнения равновесия (234) примут вид:
4 И«) -гЩ + га (а2 - гТ'/2Х = О,
02
— г2 (a2-r*)-lNa + jVp — га (а2 - r2)-1/2 Z=0, откуда
дг
= 177 + —ш f(1 -x*)m{X-r'Z) dx,
x (1 — x*)U2 X (1 — J
w» = irrJjvr + “(1-r,'!z +
Jf
+ Г (1 — *2),/2 (X — r1 Z)dx,
(I—X2) J
С
где
x = — 1, rl = —x(l— x*ru\ a
Co — произвольная постоянная общего решения (Х = = Z=0).
tgP = -j- = —*0 — *2Г‘/2, sinq = x,
az
cos
ф = — (1 — jc2)1aj
а) от собственного веса — поверхности).
Составляющие нагрузки g равны:
X = gcosp = — g(l — x2)1/2, Z = -gsinqi = — gx. Краевые условия задачи имеют вид: при х2= -f Na = 0;
(при xi=~Y иа~0 — вторая часть задачи — определение
перемещений).
Согласно первому краевому условию,
9° g Гп — jrV/2'
*(i-4У/2 x2{i-4У/2Г
X [хг (1 — х2Г1/2 + (1 — дг2)1/2] dx = О,
240
или после преобразований
Со — agx 2 = О,
1 г а откуда при *2= — Lo = — •
Окончательные значения усилий выражаются формулами:
Эпюры Na и Np приведены на рис. 136;
б) от действия сил Na = —pcos р, приложенных к верхнему краю оболочки (рис. 137). Уравнение (236) для псевдосферической оболочки примет вид:
Полагаем р(г, Р) = Е jTO(z)sinmp и для qm(z) по¬
лучаем обыкновенное дифференциальное уравнение вида:
Для данной обратно симметричной задачи (т = 1) разрешающее уравнение для pi(z) примет вид:
+ а* (а* - г*Г2 (m‘ - 1) Ф, ,=0.
Д2а
откуда
ф1 (г) = Ci + Diz и ф»(г, Р) = (Ci + Di2)sin p. Согласно формулам (235),
N* = -ra*-~rW (Cl + °1 2) C°SP’
S= - f(a2J,2)1/y [Cl + (г + V*-*) A] sin p,
16—949
где
л 1 а + "/ а2—г2 1 /-о 5
2 = а In —! у а2—г2.
г
Произвольные постоянные Ci и Д определяются из краевых условий:
при 2 = г2 Ла = — р cos р, 5 = 0.
Принимая размеры, показанные на рис. 136, получим
22=1,11 а, гг=0,25 а, и краевые условия примут вид: Сг + 1,11 aDx = — 0,0625 а2 (1 — 0,0625)1/2 р, C1-j-[l,lla + a(l — 0,0625)1/2] Dt = 0
или
С, + \,UaDi = —0,0606 ра\
Ci + 2,0825aDi = 0,
откуда
Ci = — 0,1305 pa2, Dt = 0,0625 ра.
Окончательно усилия будут равны:
.г 0,0625 2 — 0,1305 а « п N„ = — — pa2 cos р,
а г* (а2—г2)1/2 ’
.г 0,0625 г — 0,1305 а « 0
(д2 Г2)3/2 C0S3’
242
S == -j-2—172 [iz + V— r2) 0,0625 —0,1305 a] pa sin (5. Эпюры усилий приведены на рис. 137.
§ 49. Расчет цилиндрических и конических оболочек
Цилиндрическая и коническая оболочки являются
оболочками нулевой гауссовой кривизны k=—=0.
Ri R2
Произвольная цилиндрическая поверхность с образующими параллельными оси х определяется уравнениями:
* = сс, у'=У(Р) 2 = 2(р)
или векторным уравнением:
r=ai+r/(p)j + z(p)k. (239)
Произвольная коническая поверхность, вершина которой совпадает с началом прямоугольных координат, определяется уравнениями:
Jt = acos0, у = asin0 sin р, 2 = asin0cosp
или векторным уравнением:
г = a cos 0i + a sin 0 sin pj + a sin 0 cos pk, (240)
где 0 = 0(p)—функция, зависящая от геометрического очертания конуса
а2 = хг + уг + г2, -j = tg р (241)
(рис. 138).
Для цилиндра
А = i/IF= 1,
У да да
B=Y*w = Vr(*f+(wf-F-°- (242)
L = 0, М = 09 N =
в щ ар2 ар ар*/
Для конуса
А= 1, В = сс sin20 F = 0,
16* 241
L = О, M = О,
N = —— [cos 0 sin* 0 + 2 cos 0 — — sin в]. (243)
В i \ор dp* J
Главные кривизны равны:
а) для цилиндра
N_ _ у' г” — * у"
В* ~ [(Л2 + (г')2]3/2’
кг = 0, = -2L =
(244)
Ряс. 138
б) для конуса t_ п L N cos 0 sin2 0 + 2 (0')2 cos 0 — 0" sin 0 /Гме\
*1 = 0,*, = - = a [sin2 0 + (0')*]3/2 * (245)
где производные берутся по переменной р.
Уравнения равновесия для оболочек нулевой кривизны примут вид:
(™«)-+д+вх=°
да dp dNa 1 д
Sf—s--(B*S) + BK = °,
(246)
В да iVp — R2Z = 0.
Представим уравнения (246) в следующем виде [5]:
Л'* = R2Z,
f)hl~
(247)
— — (В2 S) = — — — BY, В да К ' ар
244
Интегрируя уравнения (247), получим:
ЛГ„ = R2Z = RZ,
-F Л И-F[В-5-(ад +
а,
f -2- Г Aft к. + А®. + ± Г (Ж RZ_
“ в J sp [ да J т в в Д *
ai at
-ВХ)Л. + ± {J-j[S JL (RZ) +
оц а,
-j- В2 hJ daj da,
(248)
Ul
Ш.
Зпюра
ШППТГГгт
stnfl
Зпюра
cos а
«■
Рис. 139
где fi (Р) и /г(Р) — произвольные функции общего решения однородной системы (247), ai — выбранный постоянный предел.
Пример 62. Определить усилия в цилиндрической оболочке полукруглого поперечного сечения от собственного веса g опертой по краям а = + —рна диафрагмы
абсолютно жесткие в своей плоскости и, гибкие из плоскости (рис. 139).
245г‘ч
В настоящем случае У = О, X = g sin р, Z = — g cos р, А = 1, В = а. Согласно формулам (248),
Л/ = ап гпс А
Краевые силы S воспринимаются продольными бортовыми элементами, работающими только на растяжение
Пример 63. Определить внутренние усилия в оболочке постоянной толщины Л, имеющей форму кругового конуса, опирающегося в вершине на колонну. На оболочку нормально поверхности действует ветер, который изменяется пропорционально cos р (рис. 140) [6].
В настоящем случае
МШ
При а=±- Na=О, откуда /4(р) =0,/2(Р) =—
iXcos р.
Окончательно усилия будут равны
ZpCosQ Cos ft
Рис. 140
Na = ---(l*- 4a’)cosp, 4 a
Np=— ga cosp,
S = — 2gasin p.
Эпюры усилий приведены на рис. 139. На свободных прямолинейных краях Лр = 0; 5 = ± 2ga.
(N„ = 0).
0 = const, X = У = 0, Z = — р cos 0 COS р,
246
где р — давление ветра на вертикальную плоскость.
Согласно (243),
Л = 1, В = asin6.
Согласно (245),
Ri = оо, /?2 = R = a tg 0.
Согласно формулам (248),
Np = —pa sin 0 cos р,
S = — Г a (a cos P) da = — - ~ a sin P,
a2 J dp 3 a2
i
A,__peacosP(te_SSJ[rJct,A,](fa =
I I I
p (I3 — a3 /2 — a2 2Д
= —-— COS2 0 I COS P.
sin p \ 3a2 2a /
При a = / Na = S = 0—край свободен от усилий и произвольные функции jfi О) =/г(Р) =0.
Для сокращения записи они не показаны. При а=0 N и 5 стремятся к бесконечности. Чтобы это устранить, надо задать для некоторого конечного значе¬
ния a = ao параллельный круг, по которому коническая оболочка укреплена на колонне.
ГЛАВА 13
МОМЕНТНАЯ ТЕОРИЯ РАСЧЕТА ОБОЛОЧЕК
§ 50. Общие положения
Теория расчета тонких оболочек (7?тт:й20) была впервые рассмотрена Г. Ароном 17], который вывел выражение для потенциальной энергии оболочки и уравнения равновесия и деформаций в криволинейных координатах средней поверхности оболочки.
247
Подробный вывод уравнений равновесия и движения оболочек с исправлением ряда существенных неточностей, допущенных Ароном*, был дан английским ученым А. Лявом [8].
Теория оболочек была построена Лявом по аналогии с кирхговской теорией пластинок [9] и основана на тех же допущениях.
Рис. 14
Непоследовательное обращение А. Лява с малыми относительно единицы членами порядка А: R и А2: R2 привело к несимметричным уравнениям теории тонких оболочек, что противоречило основным теоремам теории упругости (теорема взаимности и др.). Эти недостатки были устранены в работах зарубежных ученых, например Е. Райсснера (1941), и работах советской школы теории оболочек, например В. 3. Власова (1949).
При расчете оболочек по моментной теории, помимо
тангенциальных сил — Nа, Sa, Sp, учитываются также поперечные силы — Qa, Qp изгибающие момен¬
ты— Ма и Мр и крутящие моменты — Ма AfSa (рис. 141).
Усилия ,в сечениях оболочки появляются от суммирования касательных — т и нормальных — а напряже¬
* Пренебрег членами, зависящими от иа и в формулах иа, и кар, т. е. принял допущения теории пологих оболочек.
248
ний. Так, по стороне р = const элемента оболочки (рис. 142) имеем:
h_ Л_
и соответственно по стороне а = const с переменой индексов а и р и заменой R\ на /?2.
Судя по приведенным выражениям, величины Sa и S f, и МраУ вообще говоря, не равны, хотя та(3 =
= та , так как в общем случае
Однако для тонких оболочек членами z/Ri и z/R2 можно пренебречь по сравнению с единицей и в дальнейшем полагать:
Sa = S? = SnMaft = M?a = H. (250)
§ 51. Вывод уравнений равновесия
При выводе уравнений равновесия принимается, что оболочки тонкие (Rm\n : Л 20).
В уравнения проекций на оси (229) добавятся члены, зависящие от поперечных сил Qa и Q., соответственно равные (рис.. 141,я, в):
249
n лх
t— Qa-z- aadfi,
Al
— Q? +
-*)(
A + ~d)da
Ada
~rT
Bd$
Rt
*— Qp -—- dccdfi,
A2
+
da
«*«.)
л+ -У-#)««-?„
Ada =
djAQp) da ' dp
+
dadfi.
Уравнения проекций на оси х, у и г после сокращения на dadfi примут вид:
— (BN\ —Ыл— + — — (Аг 5)— ?_ — -f АВХ = 0. да ' р да А 30 ' “Я,
-k(Жр) -1v- ■Ж+Т ib(B2 S) - Q* «Г+ влк=°’
I1 + "4; + (*.)+-№)- 51
При составлении уравнений моментов относительно осей представим каждый сосредоточенный момент в виде вектора по правилу правого винта (рис. 141,6). Моменты относительно оси х определятся как проекции векторов на ось л'-ов:
МВф
-MtMa+M,+ -d(A + dt,)da-
{B+ddc‘)dll'-B%da-
250
=[-■(“«)+1 (“»)-"4-
-AVsf]**
Момент поперечной силы Q относительно оси х равен:
-($3 + ф)(л+) с1аВф«_QpЛВаЫр.
Окончательно приняв во внимание (250), получаем для 2Л1* = 0 и 2Afy = 0 уравнения:
т (М) - и**»)+ +л,°*=°-(252) t('4‘h-(b"“)+"»S+'4SQ»=0-
Условие равновесия 2М*=0 приводит к уравнению
М„а Ма„
s —sft + — = о,
которое в теории оболочек полагают удовлетворяющимся тождественно*.
Таким образом, в моментной теории имеем 8 силовых неизвестных: Na, Afp, 5, Ма, УИр, Я, Qa и Qp и пять уравнений статики (25Ь) и (252). Задача в бесконечно малом трижды статически неопределима, и необходимо рассмотрение деформаций оболочек.
§ 52. Определение компонентов деформации
Для получения общих выражений компонентов деформации, отнесенных к ортогональным криволинейным координатам а, р и у, рассмотрим две точки С (a, р, y)
♦ Для длинных оболочек это положение может привести к значительному накоплению ошибок.
251
и D(a+da, p+'dp, y+dy), находящиеся на расстоянии ds друг от друга (рис. 143).
Пусть Сх, Су и Cz будут касательными к координатным линиям а, р, у и направляющие косинусы отрезка
CD по отношению к этим касательным будут /, т, п.
Обозначим через А и В1, Г1 множители, которые преобразуют криволинейные координаты в линейные отрезки, тогда проекции отрезка ds на направления х, у, г будут равны:
Ids = Aida, mds = /Мр, nds = tidy. (253)
Квадрат линейного элемента будет равен:
ds2 = А\ da* + В\ dp2 + Г\ df. (см. 204)
Допустим, что после деформации точки С и D переместятся в положение Сi и Di. Пусть проекции перемещения и = СС на направления х, у, z равны иа, ир, иу криволинейные координаты в точке Ci —
а, =- « + И«. Pi = Р + Vi = Y + Иу
Полагая перемещения малыми — иа, и иу Л, получим, согласно (253),
«а = Л(а1—а) = А1 и» = В1 “у = /у 254
Криволинейные координаты в точке D{ а2 = ®1 + dCLl = «1 *М« + = а + На + da +
На ~i%~ 1т"
Рг = Pi "Ь Pi = Pi + Р + = Р + Ия + d$ +
+ Са + + ,
dot др ду
?2 = V! + dyt = Y, + dy + dfiv = Y + + df+
252
Значение коэффициентов первой квадратичной формы для точки Ci получим по формулам:
в„ = в, + щ = в1 + к + ьЛ. га-г, + «-,-г, + 3-к + !ЬГ' + {Ь'г
Обозначим через dsi длину элемента С4/)ь а через /ь mu П\ — направляющие косинусы отрезка C\D\ к касательным координатных линий а, р, у, проведенным через Cj.
Проекции отрезка C\D\ на эти касательные можно с достаточной точностью, пренебрегая членами высшего порядка, выразить с помощью трех формул типа:
/, ds, = Ап (а2 - а,) = (л, + м-р + nv j х
X (da -f da + dp + - d? ) ~ Ada +
\ da dp dy J
dAx t dAt вЛ dAx + __}laCfa+__flpdp+ _ n?dv +
+ p A,da + Adp + S- A,dy. da dp dy
Подставляя (253) и (254) в написанное уравнение и принимая во внимание правило дифференцирования произведения
дА1 A I dna a j .
—- u da4 A. da = —i—- da,
да да 1 да ’
* В этих формулах da*:a1— а«"цв. *р « Pj - р = , dy .
окончательно получим первую формулу и аналогичным путем две другие:
IА - Ш (1 + -L + JL Jh- + Ji_ +
11 \ аа ар л,/4! av /
+ (шЬЫ + яЛ1Ы,
вх ар \ л/ ГъЪ\А1Г
* tit , 1 а“з , иУ ев . иа as, \
m.dSi - tnds (14 I -f*
1 \ ap ay 51/4i da }
+ nds-~ (] + lds- 1- (255)
rldy\BlJ At да \ В )
(1 ди„ дГ, d/'t \
1 H — H 2 1— I +
rt dY Г 1.Л, aa ар /
+ MslJ. Л) + т*±±Ы
U,/ в, df\rj
Две последние формулы (255) также получаются из первой круговой заменой индексов.
Обозначая е относительную линейную деформацию элемента CiDu найдем
CiD, = CD{ 1 +e) = ds(l +е).
Но, с другой стороны,
(СА)2 = (1 + е)2 ds2 = (UdsJ2 + (msj2 + (M*i)2, откуда, пренебрегая квадратами и произведениями иа, Мр и му, получим
е = ваР + Н"1* + 67 ”2 + ap/m +
Pv Bt ар \Л / Гг ду\В1 I ’
= LJi I ux \ 4- — —
8V“ Гг dy\ At J Ax da \A / ‘
Сравнивая (256) с уравнениями теории упругости, выражающими деформации в точке, убеждаемся в том, что еа, ер, 8 у являются компонентами относительной линейной деформации в направлении а, р, у» 3 величины е . гг . е —компонентами относительной деформа-
C6,j pv * V»
ции сдвига.
Вывод компонентов деформаций для тонких оболочек основан на следующих допущениях Кирхгофа [9].
1. Нормальный к средней поверхности прямолинейный элемент оболочки после деформации остается прямолинейным, нормальным к деформированной поверхности и сохраняет свою длину, т. е.
2. Компоненты напряжений, направленные по нормали к средней поверхности (сх7), малы по сравнению с другими составляющими напряжений и в уравнениях не учитываются.
Примем для оболочек у=2, в этом случае
A'-A{l + i)- в‘=г(1+)' Л = 1-259)
где А и В — коэффициенты первой квадратичной формы средней поверхности.
Согласно (257), (258), (259),
е = = 0, откуда иг = иг (а, Р). (260)
v ду дг
Используя другие два уравнения (258), получим
= j_dUa_ + А (Ч ) = о, (261)
“V Fl дг АХГг дг ' Ах да \ Гг/
= и? дв' =0
Bt d$\rt) Гг дг дг
255
Подставляя (259) в (261) при 2 = 0, найдем
/ диа \ = _*& 1_
\ дг /2=э Ri Ад а ’
диь \ и\ 1 ди\
().
дг ] z=о /?а В др
откуда, применяя разложение Тейлора и взяв два первых члена, получим:
(262)
К »
U О = и а 4“ 2 [ — 1 ,
р •* \ r% в ар /
где показатель 0 соответствует перемещениям средней поверхности.
Учитывая далее соотношения
dAt __ A dBt В
дг Ri ' дг Rt
и пренебрегая отношениями z/R\ и z/Ri по сравнению с единицей, получим из формул (257):
Величины е°, и е3 являются относительными линейными и угловой деформациями средней поверхности оболочки, величины , х° и — изменениями кривизн изгиба и кривизны кручения.
Используя второе допущение (сху=0), получим согласно (263), для компонентов напряжения выражения
Подстзчтяя (265) в (249) и пренебрегая величинами г/Ri и г//?2 по сравнению с единицей, получим:
= С ( еа + v8fj). Ма = —° («а + VJtp).
Nft = C{h + VBa)y Мй = — D («р + v*a) (266)
О,
а
тРа — 2 (1 + v) ( 8“Р + 2гК«э)-
S = -jO-v)eafJ, H = D( l-v)xa/
где С = —— цилинлоическая жесткость оболочки
* В формулах (266) и в дальнейшем индекс 0 у деформаций опущен, так как речь будет идти только о перемещениях средней поверхности.
D цилиндрическая жёсткость оболочки
12(1—v2)
на изгиб.
При получении основных уравнений моментной теории использован вывод Е. Райсснера [10].
§ 53. Расчет оболочек вращения на осесимметричную нагрузку
При осесимметричной нагрузке оболочек вращения (У=0) усилия и деформации не зависят от угла долготы р и, кроме того,
S = Q = Н = 0, Ug = еар = хар = 0.
Уравнения равновесия (251) и (252) при угловой координате а (рис. 133), когда Л=/?1 и B = r = /?2Sina, примут вид:
(Nа 2 sin a) — Wp /?J cos а* —
— Qa R2 sin a + /?!&, sin aX = 0,
(Qa R2 sin a) -f Na R2 sin a +
+ sin a — Rt R2 sin aZ = 0, (267)
■- [Ma R2 sin a) — Mp Rx cos a — QaRl R2 sin a = 0. Деформации (264) примут вид:
i ( dua 1 d 1 / duz\
'“"«rUr+N’ =
‘» = (v‘e “ + “•)• (“•-')■ m
Следуя E. Майсснеру [11], введем неизвестные
(269
где V — угол поворота касательной к меридиану при деформации.
Старые неизвестные уравнений (267) выразятся через новые неизвестные посредством соотношений:
Л'"=-Тс'+Л'«- JV»“-*ril+'v
* = s¥Lv’ I270)
fli da ’ Яг
Л*а = — Df— — + v),
a \/?t da R2 Г
Me = — D(-- V + — —), ** V /?, tfi da Г
(271)
деЛ7 аоиэо—значение нормальных сил по безмоментной теории от нагрузки (237).
Если подставить (270) в (267), то первые два уравнения удовлетворятся тождественно.
Согласно уравнениям (266) и (268),
И. с‘8“+“,-If
Исключая из уравнений (271) uz, получим:
- «actg a = ± [(/?, + vR2) Na -
— (R2 + vRl)Nfi]. (272)
Дифференцируя последнее уравнение (271), получим:
Lctga——+ --=——viVl. (273)
da sin2 a da da\_Eh' -*
Исключая из уравнений (272) и (273) производную
du
—-, найдем: da
“ Rl V = *пГ KR, + ’*«) - № + vRi) -
274
17* 259
Подставляя значение (270) в третье уравнение (267) и в уравнение (274), приходим к следующим двум уравнениям:
— [-ctg2a-v --ctga]u = ERlhV + d(a)t
lR2 h da J
Система (275) для сферических оболочек использовалась Экстремом И. Э. [12] и другими; для конических— Ф. Дюбуа [13] и другими; для тороидальных — Г. Висслером [14] и другими.
При постоянной толщине h уравнения (275) примут вид:
где Ф=р(а)—функция усилий и перемещений, тождественно удовлетворим первому уравнению (276), а второе примет вид:
3v ctg a dh h da
+ &ctg2a]v = “% 275)
Ri d2U Ri da?
где
-ctga [(/?, + vR2) Na0 - (R2 + v/?,) Лд.
b(U) + -U = EhV+± Ф(а), (276)
Hi Hi
где
Полагая
U = L(i p)--«p, V = --j-9, (278)
Al Lf
ф= —Ф(а). (279)
Если радиус кривизны tfi=const (сфера, конус, тор), то уравнение (279) принимает вид:
1/.(ф) + ц*ф = --Ф(а), (280)
где
Eh v2 1 12(1—v2) R\ А2 li2 = — —— —— — = —, 281)
Р ° R\ R\ h2 R\
12(1 -v2)
— основная характеристика оболочки.
h2
Уравнение (280) может быть представлено в виде: [L + i] [L (ф) — 1’цф] = J- Ф (а) (282)
и общее решение получено в комплексной форме.
Для получения частного решения уравнения (280) надо решить уравнение
(ф)+1ф = -!-Ф(а),
О
которое получается, если задать частное решение ф в комплексной форме
Ф = г + ik,
где г и k — действительные функции от а.
Сферическая оболочка постоянной толщины
В случае сферической оболочки Ri=Rz=R однородное уравнение (282) примет вид:
(V? + Ф1.а = (283)
где
V2(...) = fll(...) = i + ctga-) —(•••),
V ' da* е da sina'
1*1.2 = 1 ± bi = v,.2(v,2+ 1),
vi,2 — комплексные числа.
Уравнение (283) может быть представлено в виде:
— + ctg а- + Ivj 2 (vj 2 + 1) —1 ф = 0 (284)
da2 6 da _ ' 1 ’ ' sin2 а Г
и интегрируется в присоединенных функциях Лежандра
261
первого и второго родов, комплексной степени vi,2, первого порядка, которые соответственно обозначаются pv, 2 (cos а) и QVj 2 (cos а).
Заменяя в уравнении (284) переменную а по формуле
х = cos а, (285)
получим уравнение (284) в следующем виде:
0 ~*2) iS - 2хЪ+[v*-2 к* +!) —t=tJ ф=0- (286)
Наиболее полно теория функций Лежандра изложена в монографиях И. Лензе [15] и Е. В. Гобсона [16].
Решение уравнения (284) было дано Е Майсснером в гипергеометрических рядах [6]; подсчеты проводились Л. Боллем [17] и Экстремой [18] и показали, что при R :Н55 число членов ряда, подлежащих суммированию, 18.
Решение в присоединенных функциях Лежандра комплексной степени и техника их табулирования в зависимости от величины b=j-13(1—v2) приводится в
работах автора [19] и [20].
Решение уравнения (284) можно принять в форме:
Ф = Ci Фи* + Di Фп* + С2 + °2 Фг?\ 287) гдеф}—гипергеометрические ряды, через которые выражаются присоединенные функции Лежандра
PV 2(cos а) = ф{ + QVj 2(cosа) = $ + ф* I (288)
и которые при отношении R :h= 100 и v = 0,25 табулированы вместе со своими первыми производными.
Вторые производные получаются путем подстановки (288) в (284) и приравниваем нулю действительной и мнимой частей полученного уравнения:
(ф{1’ + фУ’ 0 + cts а (ф!!’ + Фя’ 0 +
+ [(1 ± bi) ~ + ф*’ = 0 и аналогично для Qv12 (cosа). Из приведенного уравнения получим:
262
da2
- -ctg “ “ST + (Г -')ф"’ - S!1
dlL—cgctM!. + (_L—iWj + 4»j.
doC2 S da \ sin2 a / 21 11
и аналогичные формулы для Qv{ 2 (cos a).
Производные более высоких порядков получаются последовательным дифференцированием с учетом полученных уже соотношений, т. е. будут выражаться через функции и их первые производные.
Приведенные в уравнениях (287) и (288) гипергеометрические ряды выражаются формулами:
оо
фЦ’ = tg-f-f1 +an(1— C0Sa)“].
п=1
оо
Ф2Р = *g — cosa)"
п=1
оо
Я? = фЦ» In Sin2 у + tg -J- 2 Ь’п (1 — cos a)n, (289)
л=0
оо
Ф* = ф() In sin2 -у + tg-J J] bn (1 — cos a)»,
/1=0
где числовые коэффициенты рядов определяются по рекурентным формулам:
ап+\ ~ 2(я+1)(л + 2) л+1
Q = 2+iHn + i)+ia;TK)’
л+l — 2 (п + 1) (п + 2) [п+1 ~ Ьп~~
— (2« + 3) an+i + (2га + 1) а],
bn+l ~ 2(n+ 1) (л+ 2) Ь" + ЬЬ,‘ —
- (2га + 3) ап+1 + (2га + 1) ая] (290)
263
Л„+1 = (Я + 1) Л — 1, «о = 1. “о = °K = -J, bl = o, b=2fv3(N=V),
V1.2(Vi,2+ 1) = 1 ± W.
Ниже приводятся таблицы присоединенных функций Лежандра первого и второго родов, комплексной степени vi,2, первого порядка и их первых производных для /? : А = 100 и v = 0,25
Таблица 20
1,2 =
Qv 1,2 "
\
II
а
а
А
р
А
Р
А
Р
А
р
90
1,362
7
1,217
7
90
—7,016
7
5,451
7
80
1,058
6
3,189
5
80
-4,909
6
2,437
6
70
6,402
4
6,098
4
70
—2,708
5
—3,055
5
60
9,325
2
8,490
2
60
—3,287
3
—1,106
5
Б0
6,795
2
—5,263
1
50
—1,005
3
—3,021
4
40
1,342
1
6,698
1
40
—3,348
1
—6,596
3
30
—4,431
0
—3,298
0
30
1,718
1
—8,465
2
20
0,739
0
—0,191
0
20
—2,194
0
—5,237
1
10
—0,041
0
0,102
0
10
■ 0,085
0
—0,837
0
0
0,000
—
0,000
—
0
— оо
—
— оо
—
Продолжение табл. 20
* %
8 I
II
1 —
+i
4i\
da
о
II
-*1?
da
¥!«
1+ 1
1 -ЛЮР
— =АЮР
(2)
ЛУП =АЮР
— =А ЮР
а
da
da
а
da
da
А
1 Р
А
1 р
А
1 Р
А
р
90
2,438
8
2,081
8
90
— 1,031
9
1,106
9
80
1,120
7
5,234
6
80
—6,995
7
5,888
7
70
1,361
6
6,519
5
70
—5,092
6
—4,767
5
60
4,081
5
2,533
5
60
—6,615
5
—1,119
6
50
6,299
3
5,092
3
50
—3,476
3
—2,454
5
40
0,943
3
0,910
3
40
—2,198
3
—6,494
4
30
—9,718
4
0,104
3
30
2,744
2
—1,176
2
20
6,190
0
—1,172
1
20
—3,429
0
— 1,029
3
10
1,271
0
1,520
0
10
—7,417
0
—2,061
1
0
0,000
—
0,000
—
0
оо
оо
264.
Числовые подсчеты показали, что для R:h = 100 при ограничении относительной точности одним процентом надо брать 22 члена рядов (289).
При увеличении отношения R : h сходимость рядов ухудшается, однако подсчет их производится по рекурентным формулам (290) и является, хотя и большой, но простой вычислительной задачей, особенно при современной вычислительной технике.
Методика нахождения частных решений уравнения (280) приводится в [19].
Перемещения иа и иг определяются из уравнений (271) или из уравнения (272) и последнего уравнения (271):
da “ 6 Eh \ R da
-d&U+Nrt-vN, (291)
и ctg a+u = — /vctgCT U — -j- Nm — vAL,,),
a 6 2 Eh \ R R da & a0/’
при этом уравнение (274) удовлетворяется тождественно. Решая уравнения (291), получим:
иа = Alsina + l-±?U +
+ (1+v)/? sin а Г Afa0~VjVp° da, (292)
Eh J sin a
--ctg a - -» с tg at/)+
+ Ж (293)
где A i — константа.
Произвольные постоянные решений (287), (292) и (293) определяются из краевых условий, число которых для каждого из краев оболочки, равно трем.
Например, для неподвижного шарнирного опирания края оболочки а = а\ на жесткую опору при a = ai
и = и = М =0*
а г ot »
265
для жесткого защемления при а = ои
для свободного края при а = а\
Na = Qa = Ма = 0 и т- Д-
§ 54. Приближенные расчеты оболочек вращения на осесимметричную нагрузку
Трудности использования математически точного решения оболочек вращения на осесимметричную нагрузку привели к разработке приближенных методов интегрирования уравнений равновесия оболочек вращения. Одним из таких методов является метод асимптотического интегрирования.
При асимптотическом интегрировании данное дифференциальное уравнение заменяется другим со специально подобранными коэффициентами, мало отличающимися от заданных, решение которого может быть получено точным методом и выражено через элементарные функции.
Метод асимптотического интегрирования был предложен О. Блюменталем в 1912 г. [21], применение его к интегрированию уравнений оболочек было дано С. П. Тимошенко в 1913 г. [22] и детально разработано в трудах И. Я. Штаермана [23], В. В. Новожилова [24], А. Л. Гольденвейзера [5] и других.
Большое распространение имеет расчет оболочек вращения по безмоментной теории с учетом краевого эффекта.
Этот метод был предложен И. В. Геккелером [25] и с успехом разрабатывался П. Л. Пастернаком [26] и другими авторами.
Явление краевого эффекта заключается в том, что сосредоточенные силовые факторы, приложенные к границам, вызывают усилия изгиба лишь в области, непосредственно примыкающей к границе.
Существование краевого эффекта в симметрично загруженных оболочках вращения позволяет заменить точные уравнения приближенными уравнениями Геккелера. Однородные уравнения (276) с учетом соотношений
266
(277) и (269) для сферической оболочки (Ri = R2=R) примут вид:
PV , * dv / , 2 , М, WQa
+ ctga — — (ctg2 a+v) V = —,
tQ dQ 294
—— + ctg a — — (ctg2 a — v) Q = da2 s da ' 6 a
С увеличением расстояния от края оболочки Qa и V быстро затухают и, кроме того,
da* " da v 1
Поэтому уравнения (294) можно заменить следующей упрощенной системой:
— = — — Qa и - EhV. (295)
da2 D а da*
Исключая из этих уравнений V, получим:
d* Qa . R2 Eh da* D
или, так как
R»F.h R* Eh 12 (1 — v2) 12a R* _ y
D f/i3 V '
получаем уравнение краевого эффекта Геккелера VQa ,
Qa = 0,
dal . 4X*Qe = 0. (296)
где
4A.4 = Ьг = 12(1 — v2) . (297)
Общим решением этого уравнения будет Qa = (С, cos A,a + С2 sin tax) +
+ e-Xa (С3 cos ка + С4 sin ка.) (298)
или в другой форме
Qa = С, eta sin [%а + б,) + C2e_to sin (to + в2), (299) где Ch и 6л— произвольные постоянные.
267
Далее усилия определяются по формулам (270) с учетом (295) и (269) и характера затухания функций и их производных или по формулам (270) определяются
изгибающие моменты, а нормальные силы берутся согласно безмоментной теории.
Пример 64. Найти напряженное и деформированное состояние сферической оболочки постоянной толщины Л, которая изгибается силой — Н и моментом — М, равномерно распределенными по краю (рис. 144) [6].
Решение уравнения (296). берем в форме
Qa = С, еы sin (Ла + б,).
Для удобства введем угол
гэ = ai — a,
в этом случае решение примет вид:
Qa. = ”Ь ®)
где С и б — новые произвольные постоянные.
Согласно (295),
1 d2Qa Eh da2
V =
=-—Се'1» Eh
cos (Хгр + б).
Откуда по формулам (270)
Na = — ctg aQa =—Cctg (a, — ip) е-Ъ’ sin (Xip + 6), dQa =— %V2 Ce-M,sin (xy + b — ,
da
M =
a R da
Ma
: VM„ =
(X
Ce-»sin( + 8 + i).
. Горизонтальная составляющая смещения и, согласно рис. 144 и формул (292) и (293),
268
г , sin a I dU ri i \
6 = и sin a -f и cos a = xU ctg a
a Eh \ da b /
/? .
« — sin a —
Eh da
VT KR
С sin (*! — if) e sin Ал) + 6 —j.
Eh
Краевые условия задачи имеют вид при гр=0 ма = м, Na=—H cosa,.
Разбиваем задачу на две части, рассматривая вначале действие только М, а потом только Н.
В первом случае при (Ма)ф=0=М и (Na)=Q =0 получим:
= 0. С = — М.
/1 /ч 4А»® ■ ш /л v 2А.2 sin 0Cj пм
=0=- 1ШГМ (бЛ=о = —rLM-
(300)
Во втором случае при (МДО н (Ла),+=0 = —Н cosai получим:
5= — , С =—l/2 sinax Н,
4
(Юф=0=р-Я, (301)
Как и следовало ожидать, на основании теоремы о взаимности коэффициент второй формулы (300) равен коэффициенту первой формулы (301).
Формулы для коэффициентов влияния (300, 301) при М = Н= 1 с различной степенью точности были получены рядом авторов: П. Л. Пастернаком [26], Б. С. Жармагамбетовым [27] и другими.
Формулами (300) и (301) можно пользоваться при решении различных задач с гладкой нагрузкой.
Пример 65. Рассчитать сферическую оболочку с заделанным краем при a = ai от действия внешнего рав-
т
номерного нормального давления р — [6].
Мембранные силы для соответствующей безмоментной задачи (237)
269
дг =N = —
аО iV(30 2 *
Край безмоментной оболочки не поворачивается (V = = 0), а его горизонтальное перемещение
К = - «.■
Прикладывая по краю равномерно распределенные усилия моментного состояния М и Н (рис. 144), потребуем, чтобы при a = ai V = 6h = 0. Пользуясь формулами (300) и (301), получим эти условия в следующем виде:
4Х3
ERh Eh
2А.Д sin at 2 RX sin8 щ pR2 (I — v) = { g =Q
Eh Eh 2 Eh 1
из которых находим:
AT
pR2 (1 —v) _ pRh
4X* 4 V 3(1+ v)
H 2X M_ pft(l-v)
R sin ax 2X sin aj
Отрицательные знаки показывают, что направление М и Н противоположны указанным на рис. 144. Полный распор и вертикальную реакцию купола получим по формулам:
и. - с»з «, - н - -f-(cos а, - ,
У. = Na0 sin Cti.
Подобным образом можно рассчитать сферические оболочки на нагрузки примера (60).
Пример 66. Рассчитать оболочку в форме шарового сегмента, нагруженную распределенным моментом М
(-) по шарнирно закрепленному краю при ai = 80°, при \ М }
двух значениях отношения R:h= 10 и 100 и v = 0,25 (рис. 145) [19].
Решение (287) берем в форме:
Qa = (С1 cos + С2sin ax) .
270
Вводя вместо а угол = «1—а и не меняя обозначений произвольных постоянных, получим:
Qa = (Cj cos -f C2 sin X1J3) e-x't.
Усилия и перемещения, согласно формулам (270), (295), (292) и (293), примут вид:
Na =— (С, cos Л-ф + С2 sin Алэ) х
dQg
v =
Xctg (а, -ф)
p da
= К [C2 — Ct) cos Xij) —
- (C2 + Cx) sin Ц] e"**,
I &Qa 1 d"-Q«
Этра Мы для Rh-10
Eh da*
Eh d$2
2K2
—
Af
= (C2 cos Ллэ — C\ sin tyX) e
Eh
D dV D dV R un n v . * u
= = \(Ct — C2) Sin Ы —
R da R dx 2X LV 1 2/ Y
ua = у4, sin (a, — t) -ь (1 +р’ь - (Cl cosfop + -f- C2 sin e
Eh
R dQrr
U2 Ax cos a + — —— = — Ax cos (a! — Ф) +
Eh dty
+ — [(C, - CJ cos Xi) - (C, + Cj) sin Xty] TH
Краевые условия задачи имеют вид:, при ф = 0 иа = = wz=0, Ма =М или в развернутом виде:
Ai sin ai +-(1 ~p-V) С, = 0,
Eh
Решив эту систему, найдем:
- 2*2(1 +v)Af г _ 2У?М
Л] — , Li — ,
Eh sin Д /?Д
с 2МА-Х) м
2 ЯД
где А = 2Я. — (1 + v)ctgai.
Дальнейшие расчеты сведены в табл. 21.
Таблица 21
Величина
к
А.2
А.4
Л
At
1 с.
Сг
10
4,095
16,771
281,25
7,87
М
54,10 — ER
М
-4,262-
м
3,928— R
100
12,95
167,71
28,125
25,67
М
1668 — ER
м
-13,07 — R
М
-,2-83Т
Для изгибающих моментов получим: при R : А = 10
ма = м (cos 4,095— 0,0408 sin 4,095i) е-4'095'1’,
при : Л = 100
Ма = М (cos 12,95t) — 0,00927 sin 12,95яр) е-12,95
Сравнение результатов асимптотического интегрирования с точным решением, полученным в [19], дано в табл. 22.
Таблица 22
R:h = 10
а °
асимптотическое интегрирование
точное решение
at
a2
ai
а2
0
— 52,8
0,0029
—48,8
-0,0000
20
— 46,1
-0,0053
—37,2
—0,0056
40
— 46.8
-0,0560
—43,0
—0,0823
60
-105,7
0,0271
— 12,9
0,0240
80
— 0
1,000
0
1,000
272
Продолжение табл. 22
R:h = 100
а°
асимптотическое интегрирование
точное решение
а%
а-л
*1
%
0
—1,658
0.0000
—1,632
0,0000
20
— 1,558
0.0000
— 1,533
0.0000
40
—1,268
0.0001
—1,251
0,0001
60
—1.192
0.0021
—0.932
0.0089
80
0
1,000
0
1,000
аг
М
RR
Ма = а2М*.
Таблица 22 показывает хорошее совпадение метода асимптотического интегрирования с точным решением. Для величины иа при а = 0 (в полюсе) асимптотический метод дает физически неверный результат иа=0 ф 0.
§ 55. Расчет цилиндрических оболочек — общая теория
Пусть координата а = х изменяется вдоль образующей, р = 5 — вдоль дуги, а г — в направлении внешней
нормали к средней поверхности оболочки (рис. 146).
В этом случае
А = В — 1, da = dx, dp = ds, Rt = oo
R2 = R (s), d(Pa = dq) = .
R
и уравнения (251) и (252) примут вид: дых , as , v Л aws { as
ад: дН
+ —+ х = о, a* as
I dQx R дх
+
dQs
ds
dH
ds
ds
Z = 0
dM
= 0,
R
dMs
dx
dx
* +Qx = °.
as
+ Qs = 0,
(302)
Из последних двух уравнений находим:
0 = dMx dH Q = dMs _ дН
х dx ds * 5 ds дх
—. (303)
Эпюру Ма см. на рис. 145.
18—949
273
Подставляя (303) в первые три уравнения (302), получим:
dNs
ds
N,
+ -f- + x = o,
дх ds dS 1 dMs 1 дН у = Q
dx R ds R dx ’
(304)
a2 ai.
' R dx»
2 d*H d'Ms
dxds
ds2
z = o.
v-l?*/ X /
/ X -
Nt*ytd$
fs dVi'dV Рис. 146
Согласно уравнениям (264):
дих dus - uz dus , ды*
1 "г p — I
a* ’ ~5 as /г ’ Л8 dx ds ’
d2 д I us du
dx2 5 ds
1 d / ws \ d2 u2
(JL-i). «305,
X rs 2 dx \ R j dxds
Подставляя (305) в (266), получим:
л'-с(+-+)’ s = i-vc(.+) (306)
274
М.:
мх
н = (1 — v) D — (Лг- — .
дх [2R ds )
Подставляя (306) в (304) и полагая R = const, получим, в частности, для круговых цилиндрических оболочек три уравнения:
Симметричная система похожих уравнений приводится также В. 3. Власовым [28].
Уравнения (307) являются симметричными относительно главной диагонали, что находится в согласии с основными теоремами теории упругости.
Любая задача для круговой цилиндрической оболочки сводится к решению системы (307).
В случае осесимметричной нагрузки (У = 0) Qs=S = = Н = и8 = 0, а величины их и иг, как и другие, зависят лишь от координаты х. Система (307) в этом случае примет вид:
d2ux _v_ du _j. = q.
(308)
гают.
18*
275
При X = 0 интегрирование первого уравнения (308) дает:
— + — иг = С„ (309)
dx R ' '
N
т. е., согласно (306), С5 = -4-.
С»
Второе уравнение (308) принимает вид:
+4/и, = 4“(31°)
dx* ' * D RD
где
4_3(1-у2)
R2 Л2
Общее решение уравнения (310) будет иметь вид: иг = e”v* (Сх cos ух + С2 sin ух) +
-f eVJt (С3 cos V* + С4 sin 7л:) + / (дг), (311)
где Ck — произвольные постоянные,
f (х) — частное решение неоднородного уравнения (310), которое содержит произвольную константу С5.
Шестая константа получается из интегрирования уравнения (309):
X
ux = Ct + C6x J ыг dx. (312)
О
§ 56. Теория круговых ортотропных* цилиндрических оболочек
(оболочки средней длины -j- = 2 -г- 8j
В 30-х годах настоящего столетия Г. Элерсом [29), И. Грубером, Г. Грюнингом и И. Финстервальдером [30] за границей и А. А. Гвоздевым [31], В. 3. Власовым [32] и П. Л. Пастернаком [33] в Советском Союзе был предложен упрощенный метод расчета цилиндрических оболочек по полумоментной теории.
* Оболочки с различными физическими свойствами во взаимно перпендикулярных направлениях: в продольном ехф0 и поперечном ев=0.
276
При расчете по полумоментной теории, на основании опытных данных для цилиндрических оболочек средней длины, пренебрегают влиянием продольных изгибающих моментов Мх, поперечных сил Qx и крутящих моментов Н (рис. 146) и вводят геометрические гипотезы.
8s = О И &xs = 0. (313)
В этом случае уравнения (302) и (305) принимают вид:
+J* +х = 0,
дх ds j dS Qs_ _j_ у
ds dx R
h. л. _ z = 0
R ds
Q$_iL = o. (314)
OS
дих
е, =
dus ,
“г
дх 9
ds
R
dus .
дих
0,
хъ
dx
ds
i
d2 иг
л/ —
“s
dx2
* к» -
ds \
R
(315)
Исключая из уравнений (314) S, Na и Q«, а из уравнений (315) ux, иви uz и заменяя Nx через ah, В. 3. Вла-
J о М \
сов при v=0le* = —, х,= —1 приводит задачу о рас¬
чете цилиндрической оболочки средней длины к системе двух разрешающих уравнений:
+ QM,=- + ж.__sl(R2),
дх2 дх ds ds2
nw_ ■»(■-»■) *«■_(). (316,
' h2 dx2 X 1
где
fi= + jL\_ (3i7)
ds2 V ds2) ds \R ds ) K '
оператор В. 3. Власова.
При h и R = const (круговая оболочка постоянной толщины) уравнения (316) будут иметь постоянные коэф¬
277
фициенты и приводятся к одному разрешающему уравнению
QQF + b? —- = R2 (— ——), (318)
р. ф дх* \ дф дх дф* /
где
S “ X
Ф = — и х = — безразмерные координаты,
,2 12 (1 — v2) R2
= ——/2 основная характеристика оболоч¬
ки (см. 281),
й = —- + —- ) — оператор В. 3. Власова,
ф я* \ дф* _ дф* I к
(* ф) — функция напряжений, через которую неизвестные аиМ« выражаются по формулам:
_ 12(1— у) R d2F Н? дх2 1
M=QmF = — (F+—). (31?)
s * аф* \ дф ' '
Уравнение (318) решается разложением в одинарные ряды по переменной х.
При D= оо (xs = 0) получается недеформированный жесткий контур поперечного сечения оболочки (es=xs = = 0) и из второго уравнения (316) при A = const следует закон секториальных площадей, который является основой теории оболочек с жестким контуром (тонкостенных стержней) см. [34, 35]
ds2 ds2 ) ds \ R ds )
По полумоментной теории имеются многочисленные исследования: С. И. Стельмаха (1938), Н. Д. Левитской (1949, 1950), Б. С. Василькова (1950), И. Е. Милейковского (1950, 1956), В. С. Бартеньева (1957), Н. Н. Леонтьева (1958) и др.
Пример 67. Рассчитать круговой цилиндрический резервуар постоянной толщины Л, жестко заделанный в основании и наполненный жидкостью с объемным весом
gfy (рис. 147) [11.
Давление Z = g(l—х).
278
Уравнение (310) примет вид:
+ 4,=
dx* * г D
При x=l Nx = 0 и, следовательно, Cs= — =0.
С
Решая уравнение, получим:
аг = е T*(Cx cos ya'+ +C2sm ух) +
-f еух(С3 cos ух + С4 sin ух) +
g(l — x) R2 Eh
Рис. 147
и согласно (312)
их = — j М* + С6 = е“7ЛГ (Cj (cos y* —
о
— sin Y*) + с2 (cos ух + sin Y*)] — eyx [C3 (cos yx+
2y R
+ sin yx) + Ct sin yx — cos yx)] + + ct-
2 h
Оставшиеся краевые условия задачи имеют вид: при ЛГ=0 их = 0,иг = 0, — = О;
dx
при x=l MX=D = 0, Q = = 0.
дх* д dx»
Из этих пяти краевых условий определяются все произвольные постоянные Си
Если длина резервуара / велика по сравнению с /?, то цилиндр можно рассматривать как бесконечно длинный.
В последнем случае С3=С4=0 и краевые условия примут вид:
при х = 0 их = 0, иг = 0 и -у2- = О,
279
откуда
("A-о - (Ci+с) + 'f- + с. ■= °.
Ч- ' с + -«ir = »• (L “ * с. - СО - - о
(!-)•
и окончательно получим:
Cl = —I»L,C,—M-
Eh 9 2 7i
/г» I г* \ У’*2Я
~ ” (Ci + С2)
2yR " 2 Eh
Uz = u{l~x~e VJ:pcos'’•*' + (*— sin T*] ’
v—*.\ =С
V2
■0
dx )
u
R
V
' /?
—2,ms =
vD
d2u2
Qx
= D—2.
dx2 ’ S
’
Л
dx3
MX = D
Наибольший изгибающий момент при *=0 будет
мх= — — IV * \y/ У 2 к з (1 — V2)
Характер эпюр Ns и Af* приведен на рис. 147.
Пример 68. Рассчитать замкнутую круговую цилиндрическую оболочку постоянной толщины Л, шарнирно опертую по краям *=0 и х = 1 и частично наполненную жидкостью с объемным весом g (рис. 148) см. [36].
Краевые условия задачи имеют вид: при х = 0 и x = l us = uz = Nx=Mx = 0.
Эти условия вместе с условиями симметрии деформаций относительно плоскости ог удовлетворяются, если составляющие перемещения задать в виде рядов:
оо оо
VI VI л тпх
«л- = 2j 2j тп cos щ *cos ~г ’
/и=1 п =0
оо оо
VI VI г» тл*
«. = 2j 2j тпsinщ'sm~T'
1 п= 0
dux v dux v
* Согласно (309): + — и2 — 0, откуда —— = — — и2.
ах R dx R
280
».=SSc;
'Cosmp'sm
mnx
T
m=1 n =0
Интенсивность давления Z выразится следующим образом:.
Z = gR (cos ф — cos а) при 0 ф a,
Z = 0 при a ф я.
о) 6)
Последние выражения представляются в форме следующего ряда Фурье:
оо оо
2 = 2 S Ап л cos пР • sin -у-,J
т=1 п=0
где коэффициенты Dmn вычисляются обычным приемом по следующим формулам:
о а]?
Ann — 7Т~,—77 (cos a • sin я a — я cos rta • sin a),
тпл2(п2 — 1)
где m= 1, 3, 5, ... и n = 2, 3, 4, причем
4 ER
Ало = —г- (s'n a — a cos °0
/яяг
Ani = 7 (2a — sin 2a).
/72 Jl*
В случае цилиндра, заполненного жидкостью вместе с призматической вертикальной областью (рис. 148,6),
обозначая через gd давление на уровне оси оболочки, получим:
Z = g(d + R costp).
Коэффициенты разложения нагрузки
n п 4У? п- Л
Ь'шо = , Dml = , Dmn = 0 При Я 1
тя тл
т = 1,3, 5,...
Пренебрегая во втором уравнении (307) величиной Л2/12/?2 по сравнению с единицей, получим эти уравнения после подстановки в них соответствующих рядов для. перемещений и нагрузки в следующем виде:
Атп[2т2п2 + (1 — v) Х2п2] — Втп (1 + v) Хтап +
+ Cmn2vXmn = 0,
АтпЗ (1 4- v) ктпп — Втп[з (1 — v) т2л2 + 6А,2п2] —
— Стп2к2п[3 + г)2(т2я2 + Х2п2)] = 0,
Amn3v7ittm — ВтпХ2п2 [3 + т]2 (т2п2 + %2п2)] —
_ - Стп [3V + rf (mW + Vn*)] = - ,
где
Пользуясь этими уравнениями, можно вычислить величины Атпу'Втп и Стп при любых значениях т и /г, подсчитать составляющие перемещения и по формулам (306) — усилия.
Числовые расчеты показывают [1], что коэффициенты Атт Втп И Стп быстро затухают и при расчете можно ограничиться 2—3 первыми членами рядов.
ГЛАВА 14
РАСЧЕТ ПОЛОГИХ ОБОЛОЧЕК
§ 57. Вывод основных расчетных уравнений
В 1938 г. на V Конгрессе прикладной механики К. Марквер [37] сделал доклад о теории пластинок с
282
большими прогибами, которые были названы пологими оболочками (l:f 5 и Rm\n' h20).
Общая теория пологих оболочек была разработана В. 3. Власовым [38] на основе следующих допущений:
1. На средней поверхности пологих оболочек, вследствие малой гауссовой кривизны (k = kxk2)y риманова геометрия заменяется евклидовой геометрией на плоскости. Таким образом, третье уравнение (223)—уравнение Гаусса — заменяется приближенным:
±(± + «±Ч_0. (320)
да да У dp I S
2. Изменение кривизны изгиба (х0 и хр) и кручения (иар) средней поверхности пологой оболочки принимается, как и в теории Кирхгофа изгиба тонких плит, не зависящим от тангенциальных перемещений иа и ир.
На основании этих допущений уравнения (264) примут вид:
1 диа 1 дА
“ А да АП ар р 1 *’
1 j as . ,
ей = - Н и -f км,
р В ар АВ да а 2 г’
а6 А да \ В } В д$\ Л /'
Ha=-±±(-L*±\ (321)
“ А да \ А да] АВ2 ар ар
1 / 1 диг \ 1 дВ ди2
хр ~ В a.) ("s’ "ар-/ ~ ЛаВ ~да ' ~да ’
_1 / д2иг 1 дВ диг 1 дА диг \
*otP _ ~АВ 1 дадр —~В да ~д(Г Л ~дР На ) *
Уравнения равновесия (251) с учетом (252) и принятых допущений запишутся в форме:
д /окт \ м дВ . 1 д /Д2С\Л_ Л D V п
— Мй —1 + (АМЛ — — — (В2Н) —
* да J ар АВ [ар *• е; В да ’
= (322)
Зависимость между внутренними силами и деформациями выражается шестью формулами (266). Статические уравнения (322) вместе с физическими (266) образуют полную систему 9 уравнений с 9 неизвестными функциями: Na, S, Nэ, Ма, Я, иаУ и иг.
Вводя в рассмотрение скалярную функцию напряжений ф(а, р), через которую тангенциальные усилия выражаются по формулам:
N — — — I _1_ J*!.
а В д [ В dfi / А2В да да
N — — — (J- \ I 1 дЛ ар
э “ ~А да [ А да j ~АВ2 ~df ~др 9 _ _J__ 1_д2ф_ 1_ дВ_ _5ф_ 1_ _аЛ_
лд \ ааар в аа ар л ар а а / ’ 1
аналогично последним формулам (321) можно, учтя формулу (320), тождественно удовлетворить первым двум однородным (Я=К=0) уравнениям (322).
Уравнения неразрывности деформаций для пологих оболочек — уравнения Кодацци — Гаусса — для деформированного состояния, где отброшены члены с множителями k\f k2 и k (39), имеют вид:
(*“•» = 0'
АВ (*,*» + - ± {-i- [-i е„-± (А.) +
+ т (*4)--=• (i[f(в‘» +
+is-(-4'M-°- (324)
* Уравнение разделено на АВ.
284
Первые два уравнения (324) удовлетворяются тождественно, что следует из аналогии формул для Л/а, S (323) и ха, иар (321) и аналогии этих уравнений с первыми уравнениями (322).
Последние уравнения (322) и (324) после необходимых преобразований примут вид:
± V* ф + Dy2y\ = Z, (325)
vVp + Eflvluz =
где
у2 = —[А- — эллиптический
АВ [да \ А да ) д(5 \ В др /
оператор Лапласса,
=т» [ (f1*•)+1 (4 *«-)] - оп'ратор
смешанного типа (326).
В общем случае, когда координатные линии неортогональны (х Ф я/2) и, следовательно, не являются линиями кривизны (F Ф О, М ф 0), дефференциальные операторы усложняются см. [40].
Согласно уравнениям (252), (266), (321) и (326), ~ Од 2
(327)
Для получения тангенциальных усилий служат формулы (323), для остальных усилий— (266) и (321), тангенциальные перемещения определяются из первых трех уравнений (321), однако решение их можно получить лишь для частных случаев (см. примеры 69 и 70).
Для случая круговой цилиндрической оболочки уравнения (325) применялись до 1944 г. С. М. Файнбергом [41] и В. В. Новожиловым [24].
В комплексном виде, как показал В. В. Новожилов в 1951 г. [24], система (325) имеет вид:
— + i —— vV = Z-
2 V 3(1 —V2)
* Нижние знаки соответствуют направлению иг и Z по внутренней нормали.
285
Полагая в последнем уравнении
Eh2
¥-р + /-
2 V 3 (1 — v2)
и отделяя в нем вещественные и мнимые части, получим систему (325).
В. 3. Власовым были выведены также уравнения для расчета пологих оболочек на действие температуры [42]:
V2V2«Z — у1ч = о, vVp + v*«2 + “v2i + (i + k2)Y = °* (328)
где
t = t'—t" — температура при неравномерном нагреве оболочки по толщине,
. V +1"
h = — средняя температура нагрева,
t'(а,Р) — температура на внешней поверхности оболочки,
Г (а, Р) — то же на внутренней,
а—коэффициент линейного расширения.
§ 58. Частные случаи расчетных уравнений
В случае декартовых координат, употребляемых при расчете пологих оболочек с прямоугольным планом,
а = х, = у,А = В = 1. (32Э)
дих I I dll и , *
~ I" 12» ~ “Г— “Ь U2j
дх * ду
д2иг д2иг
ду* ’ Ях№ ~~ дхду *
уравнения (322) примут вид
dNx , dS
причем кривизны могут быть выражены приближенными формулами:
**-• 332)
Тангенциальные усилия будут равны:
N X=*V, N =L,S = -5, (333)
d*/2 у дх2 дхду
иприХ=К=0, согласно (331),
о d*S _ fd*Nx My) дхду \ дх2 ду2 /
Уравнения (324) примут вид:
*,-«•„=«.-»=■ 334 *,*, + + 4т + Й - 2 - 0.
1 * 2 * ду2 дх* дхду
Дифференциальные операторы (326) будут равны:
V2 = J!. + 1 = *_ +2 (335)
v дх2 %2 ’v v дх* д*2ду2 ду* ' у
S' ,ь 3*
di/2 2 Эх2 ’
Остальные усилия определяются по формулам:
=d(S+'v’M‘--d- v4,
= + (336)
Н = —D(1 — \)дг“2
дхду
В случае полярных координат а = г, Э — полярный угол, /4 = 1*, В=г (рис. 133).
Деформации и усилия определяются по формулам (321), (323) и (266)
I U 1 I Ur I L
®- + БВ-— 1р- + — + *А»
* Сравии с формулами (231) при lr1.
287
е =гаЫ+-
rf дг V г / г ар ’
г дг* р г \ г др дг )'
•*—НЗ—rt)- ю7
#'-т+т5)-*.-5-
5 = tf±Jv)
дг \ г ар }'
мг = о\ + (± + Щ,
дг* г \ г ар* дг )\ ’
М. = о\±(± + ) + 1
р [ г \ г ар* дг I дг* ]
И—Dll-O ±±(%.-f),
Qr=-D±V\, Qfi=-D-L±v\, (338) где, согласно (326),
*-НЮ+*(*)1- «»
Разрешающие уравнения имеют вид (325).
Как указал В. 3. Власов [28, стр. 315], безмоментная теория пологих оболочек описывается первым уравнением (325), если в нем отбросить член Dy2y2u2, учитывающий влияние моментов, это уравнение будет иметь вид:
I—*2—W-M—*1 —Vl=-Z. (340)
Ав [аа а 2да I ар \ в 1 ар /J ' '
Практический интерес это уравнение имеет при положительной гауссовой кривизне (&0), когда изгибающие моменты достигают наименьшей величины по сравнению со случаями 0.
Безмоментная теория пологих оболочек рассматривалась за границей в работах Пухера А. [43], Чонки П. [44], Флюгге В. [45] и в СССР в работах А. Р. Ржаницына[46], В. М. Никиреева [47] и др.
288
Наконец, в последнее время появились интересные исследования по вопросу суммирования решений безмоментной теории и уравнений краевого эффекта (П. Л. Пастернак, В. М. Никиреев).
Расчетные уравнения пологих оболочек можно получить и в форме метода перемещений, подставив в уравнения (322) значение усилий через деформации по уравнениям (266) и значение деформаций через перемещения по формулам (321). В последнем случае получается система трех дифференциальных уравнений равновесия в перемещениях, которая в случае симметричной задачи приводится к двум уравнениям.
Не приводя общего вида системы в перемещениях, дадим ее для частного случая пологих оболочек двойной кривизны с прямоугольным планом, см. [48] и [42]:
*+v *4
V дх2 2 ду2 ) * 2 дхду
+ {ktv + k1)=-±,
дх С
1 + у д*их
2 дхду
+ (klV + k2) = -, (341)
(ktV+ k,) + (klV+ kA +
дх ду
+ (V4 + *?+*i + 2v*A)«,=--,
где
V4 = — + 2 *-+-*.
v дх* дх*ду* ду4
Сравни (341) с уравнениями (307) при s=y и k = 0.
Пример 69. Определить напряженное состояние пологой круговой цилиндрической оболочки, которая имеет по всем краям шарнирно подвижное закрепление и нагружена радиальной нагрузкой интенсивностью Z =
(рис. 149) см. [28].
Обозначая aR расстояние по образующей (х), а р— центральный угол, получим:
19—949
289
A = B = R, *i = 0, k=— = const,
e“” г да ’ * R\d& + 2 }’
1 ldU,x 11
} R l д$ да I ’
=
OS
R \ d$
1 д*»г 1 a«ug
R* da2 ' Xp_ tf* ap* ’
исф —
1 дгиг R* dad$
(342)
Согласно (326),
V‘ =
_ _L I dt -L aa \
i a*
V* = — — • (343)
v* fi da* 7
Разрешающие уравнения (325) примут вид:
у2у2ф — REh
д*иг
да2
= 0.
д2
Здесь и далее V2 = + арг Вводя функцию Ф(а, Р) по формулам:
иг = у2у2ф, ф = REh
(344)
(345)
тождественно удовлетворим второму уравнению, а первое уравнение примет вид:
290
vVvVo + = Zi
(346)
где
Уравнение (346) является основным разрешающим уравнением пологой цилиндрической оболочки.
Краевые условия задачи имеют вид:
при а = 0 и а ■= а{ ыр = иг = Na = Ма = О,
при Р = О и Р = Р, иа = иг = iVp = Мр = 0.
Усилия через основную функцию Ф(а, р) выразятся по формулам (323):
Решив первые три уравнения (342) с учетом (345) и первых трех уравнений 347), получим:
Учитывая то обстоятельство, что если функция на каком-либо краю равна нулю, то и все частные производные вдоль этого края по другому аргументу также будут равны нулю, запишем граничные условия в следующем виде
д2ф _ Eh д*Ф
“ R*dр* R даЩ* ’ д, _ 1 (foy _ Eh d4»!) р ~ R* ~да? ~ ~R да* ’
1 д\ _ Eh д*Ф
R* dadfi R д&др
(347)
“ даЭр*
19*
291
Этим условиям удовлетворяет функция Ф(а, 0), взятая в виде двойного тригонометрического ряда:
® = f.sin = si„S. (349)
m=l п=1
Внося (349) в уравнение (346), получим:
оо оо
. шла . ялВ
cm cm —
тп '
т=1 л=1
где
2в;,,л51П5т = 2(а,Р), (350)
D_
R4
Из уравнения (350)
а* 3
= ~г П 2 (о, р) sin — -sin dadp «iPi J J ax pi
о о
1n
= при Z =—p = — ■
л2тп
Окончательно искомая функция Ф(а, Р) примет вид:
Ф (а, Р) -
шла ллб
ш 00 00 sin -sin-—
!М1_ у у а Pi (351)
Далее по формулам (347) определяются усилия. Подробное исследование пологих цилиндрических оболочек дано в работе [49].
Пример 70. Определить напряженное состояние пологой сферической оболочки, заделанной по опорному краю и подверженной действию сосредоточенной силы Р, приложенной в верхней точке [28],. рис. 150.
Пусть а — г и р — полярные координаты точки оболочки на горизонтальной плоскости.
В этом случае Л = 1, B = r, kx=k2 = k= — = const,
R
292
er = + kuz, ep = ~ + kuz 8rp — °
d2u
1 duz
Xa = , Xrft = 0.
dr* ' P Ad/-’ rP
Согласно (326),
(352)
Согласно (325) и (328), основные дифференциальные уравнения задачи примут вид:
Dy2y2ut + — У2Ф = 0,
*\
— vVp —— v2“*=
Eh Я V г
Из последнего уравнения (353)
R_
Eh
v4 = v2v2(p.
откуда
иг = Аь + Ав lnr + —У2Ф
(353)
или, отбрасывая решение бесконечное в полюсе (г = 0), получим
Uz = Л + VV
(354)
293
При полученном значении и2 второе уравнение (353) удовлетворяется тождественно, а первое ттримет вид: V*V2V24p + c*V 2ф = О,
где
с - л/= l/-12(1 V (355)
У DR2 У h*R* \mJ ' ’
Полагая в последнем уравнении
ф (356)
и вводя безразмерную величину
JC = сг,
приведем уравнение (355) к виду:
tfv5* + * = 0f (357)
где
о d2--- . 1 d-.. 1 2
V;* • • = 1 — v * • *
dx2 дс dx c*
Следуя В. 3. Власову {28], берем общий интеграл уравнения (357) в форме:
\э = AJi (х) + 4 2/2 00 + А313(х) + Л4/4 (х), (358)
где Ai — постоянные интегрирования,
1( (х) — частные интегралы уравнения (357), которые имеют вид
.. ГЛ(° = 1,1 [/;(0) = о J-
Г /.(0) = о, 1 [/'0)=0 ’
/1(х) = 1 ——+ — = h
7 2242 2242«6282 2242 — 122
у2 ув уЮ
/ (х) = - 1 i 2W 22 224262 2242« • • 102
/3 (*) = -L Л (дг) + j- [ (in + С ) /, (x)-Rx (X) ] [/8(0)=0,5, /; (0) = 0] ,
Л М = - у h (х) + [(in ~+C)h (дг) + Rz (*)]
f/4(0) = oo, /;(0) = оо], (359)
при значении
*lW = Wl_/i + _L + _L\*W +
1V 1 U-1)2 \ 2 3 / (3!)2
294
1 N (*/2)«* ) (5t)2
+ (l + ~y + -j + -j + -g-}
-(1 + -С + т+т + +
\ JC/g«
/ (6!)2
+(' + t+t+t+t + t)№‘
C=0,577215 — эйлерова константа,
я = 3,1415... (360)
Таблица функций (359) и их первых производных для значений лс=0ч- 6, составленная с использованием таблиц цилиндрических функций [50], приведены в приложении I к книге [28].
Для нахождения высших производных имеют место следующие дифференциальные зависимости
Vl1l = —I*VVi=I* (361)
v?'2 = 'i. V = -'3-
Откуда получаем
= зв2)
И т. д.
Согласно уравнениям (354), (356) и (358),
иг = \ = ~§r (Ail 1 + Al2 +
Eh th
+ A$Iз + AJ4) -f- Л5. (363)
Учитывая формулы (356) и (357), получим
= — 'ф = —г (i 1 "I" 2з + з + AJ4). (364)
с2
Учитывая соотношения (361), найдем интеграл уоавнения (364)
ф = ~ (4i/2 — A211 — Л3/4 + AJз + Л6 In х -\-А-) (365)
са
Для определения тангенциальных перемещений надо удовлетворить первым двум уравнениям (352). Заменяя тангенциальные деформации ег и ер усилиями N, и а
295
последнее и нормальное перемещение иг через функцию Ф, по формулам (338) и (354), получим:
иг = ±Х irCH' (366)
Rc Eh dx
или учтя формулу (365), получим
= —-/42—-
Rc Ehc \ dx dx
— Аг~ + А + —Л. (367)
dx dx х J
Полученный результат (366) является новым, так как обычно касательное перемещение ит определялось из уравнения закона Гука:
е' + * = Чт (Л,' + Л'«) (Ш)
при неудовлетворении первых двух уравнений (352).
Для определения шести произвольных постоянных At имеем шесть условий:
1. Краевые условия
при г = b(x = cb) иг=аг= = о.
dr
2. Условия симметрии
при г —0 (jc 0) иг = - = 0, (369)
dr
Zn
j Q/ф = P.
о
Определим величины, входящие в условия симметрии:
*h_ = c&h_ =_!LIAi*Ll + A2-l +
dr dx Eh \ dx dx
+ А3. + А,--). (370)
dx dx )
Согласно формулам (338),
d „2.. Поя d DRc3 ( л dli
Из второго условия симметрии
Ak =0;
из первого условия симметрии
Л» = Неполученная зависимость следует из выражения
-т';+;'+И+‘)''+*
и предельного соотношения
ХГI = — •
4 [jc—►О „ *
из третьего условия симметрии 2nDRc2
(372)
a* d* dx ] I jco
Л
EhP
откуда Л3 =
4 DRC2
Произвольные постоянные Au A2 и Л5 определяются из краевых условий (369), усилия — по формулам (338).
Расчет сферических оболочек на осесимметричный нагрев см. в [51].
Расчет пологих оболочек двойной кривизны прямоугольных в плане и опирающихся по контуру на диафрагмы абсолютно жесткие в своей плоскости и гибкие из плоскости, что соответствует шарнирно неподвижному в вертикальной плоскости и шарнирно подвижному в касательной плоскости закреплениям, рассмотрен в [28], стр. 439 и в [52].
В последнем случае краевые условия будут иметь вид (см. пример 69):
при х=0 и х = а uy = uz = Nx=Mx = 0,
при у = 0 и y = b ux = uz=Ny=My = 0*
или для функции напряжений (349):
д2Ф
__ д*Ф
__ а«Ф
= 0,
дх2
~ Ite*
дх6
вт
а4Ф
__ д«Ф
= 0.
ду2
“ ду*
ду8
при у=0 и у=Ь Ф= —• = —- = -— = 0. (373)
* В работе [52] краевые условия иу= 0 и ил=0 заменяются соответственно, на еу = 0 и е*=0.
297
ГЛАВА IS
РАСЧЕТ ПРОСТРАНСТВЕННЫХ ПРИЗМАТИЧЕСКИХ РАМ (МЕТОД ПРОФ. В. 3. ВЛАСОВА)
§ 59. Общие положения
В настоящей главе рассматриваются пространственные тонкостенные конструкции, имеющие в поперечном сечении произвольный профиль, состоящий из одного или нескольких замкнутых контуров (рис. 151).
мальные, сдвигающие, поперечные силы и изгибающие моменты. Таким образом, в отношении внутренних сил принимается гипотеза оболочек средней длины. Из геометрических гипотез принимается гипотеза нерастяжимости контура ев = 0 и вводится гипотеза плоских сечений для каждой из пластинок, образующих призматическую раму, т. е. предполагается, что поперечное сечение (сечение, перпендикулярное оси л:-ов) для каждой пластинки остается плоским.
В поперечном сечении рассматривается плоская стержневая система с конечным числом степеней свободы, в продольном направлении — система с бесконечным числом степеней свободы. Таким образом, расчетная система является дискретно-континуальной.
Расчет таких систем был разработан в 1949 г. В. 3. Власовым (53].
Рис. 151
Призматическая рама рассматривается как совокупность бесконечного множества бесконечно узких полосок, имеющих вид плоских рам, соединенных между собой стержнями, передающими от одной рамы к другой нормальные — а и касательные — т напряжения. На площадках продольного сечения возникают нор-
298
§ 6®. Напряженное и деформированное состояние рамы-полоски
В плоскости поперечного сечения степень свободы шарнирной схемы рамыг характеризующая независимые смещения ее узлов, равна:
п = 2У— С — Со, (374)
где Y — число узлов (включая опорные),
С — число стержней рамы,
С0— число опорных стержней, лежащих в плоскости рамы.
Степень свободы шарнирной схемы рамы из плоскости в направлении оси л;-ов равна
mY — C*, (375)
где С — число опорных стержней в направлении оси х.
Например, для поперечной рамы снстемыг изображенной на рис. 151, a Y=5, С = 4, Со=4, Со =2, поэтому
степень свободы в ее плоскости /1 = 2*5—4—4=2, степень
свободы из ее плоскости т = 5—2=3.
Положение точки С на средней поверхности призматической рамы определяется координатами х и s (рис. 151,а). Деформированное состояние можно полностью описать, если известны ux(x, s) —перемещения точки С в направлении образующей (оси лс-ов) и u8(x, s) —поперечное (тангенциальное) перемещение в направлении касательной к контуру поперечного сечения.
Эти перемещения можно представить в виде разложений:
т
“х (х, s) = иi (ж) фм (s) (376)
/ =1
оо
M*,s)= ***) !*(«), (377)
k=l
где Ui (х) и Vk(x)—неизвестные пока функции, которые выражают закон изменения перемещений по длине системы,
Ф; (Ф* (s) — элементарные перемещения, выбирае¬
мые из числа возможных.
Выбранные тем или иным способом линейно независимые между собой непрерывные функции pi(s) общим
Ш
числом m представляют собой заданные обобщенные координаты деформации элементарной поперечной полоски из плоскости поперечного сечения *=const.
Выбранные тем или иным способом линейно независимые между собой непрерывные функции \?a(s) общим
Рис. 152
числом п представляют собой заданные обобщенные координаты деформации элементарной поперечной полоски в ее плоскости х=const.
Примеры выбора этих функций даны на рис. 152.
§ 61. Дифференциальные уравнения равновесия рамы-полоски
На раму-полоску действуют нормальные и касательные напряжения постоянные по толщине стенки, которые определяются по формулам:
т
o(x,s) = E = E'u'i (X).ф,- (s), (378)
т т
= G [ и( (х) Ф; (s) + 5Х (х) 4»*(s)I. (379)
i=l k=l
На элементарную площадку dF рамы-полоски (рис. 153, а) при *=const действует нормальная сила odF, а
при x+d.x:=const — нормальная силача + dxjdF и соответственно силы сдвига тdF и + -с*д/\Проекции
внешней нагрузки, отнесенной к единице площади, на направление образующей и касательной к линии контура поперечного сечения обозначим соответственно через р и q.
300
Для нахождения (т+п) искомых функций Ui(x) и Vk(x) составляется (т + п) уравнений равновесия рамыполоски. Для этого раме-полоске дается (т+п) независимых возможных перемещений, и сумма работ внешних и внутренних сил на этих перемещениях приравнивается нулю.
Каждое возможное перемещение можно рассматривать как результат бесконечно малого изменения (вари-
о) 6) 5)
ации) одной из обобщенных координат деформации, определяющих положение узлов и стержней рамы. Такое применение принципа возможных перемещений называется вариационным методом.
Интегральные условия равновесия элементарной рамы-полоски после сокращения на dx представляются в следующем виде:
J "аГ Ф/ dF ~~ J %4idF + J p(fids = 0 (380)
F F s
/ = 1,2, 3
f -Jj %dF - J] ds -f- j' qtyhds = 0 (381)
F k=1 s s
h = 1, 2, 3, ..., n.
Каждое из уравнений (380) выражает равенство нулю суммы работ всех сил элементарной рамы-полоски шириной dx= 1 при перемещении из ее плоскости. За возможные перемещения в уравнении номер j этой груп¬
301
пы приняты продольные перемещения иХ] = ф{ (s), определяемые одним членом номера / разложения (376) при
К,- -1.
Средним членом выражена работа сдвигающих сил (рис. 153). Каждое из уравнений (381) выражает равенство нулю суммы работ всех сил элементарной рамыполоски шириной dx= 1 при перемещении в ее плоскости. За возможные перемещения в уравнения номер h этой группы приняты поперечные контурные перемещения «sft =4'ft(s)» определяемые одним членом номер Л в разложении (377) прны*„ = 1.
Средним членом выражена работа внутренних сил— изгибающих_моментов {НУлМь) на деформациях изгиба (Mbds\
полоски 1 I, соответствующих я-му элементарному
состоянию (рис. 153).
Момент инерции 1=1 (s) подсчитывается, как для обычной плоской рамы шириной dx=1 (при отсутствии
поперечных связей — рам =
Подставляя в (380) и (381) вместо а и т их значения по формулам (376) и (377), получим систему (т+п) линейных дифференциальных уравнений:
т п
~ S w -2 ci‘v+т р=*•
t=i /=1 k=\ (382)
т п п
cjj',+2 - т 2 +j- «* -0
1=1 *=1 fe=l
j = 1,2Л = 1,2 п,
где
Т= Y = 2(1+ v); ан = Оц = I ф/ф
V
cjk = ckj = J’ %%dF; rHk = rkh = J
skk — s»h — J j к ds’ Pi — J PWjdS) (383)
s s
qh = j ‘W/A
S
Если отказаться от гипотезы нерастяжимости контура поперечного сечения (ев = 0), та
В этом случае надо учесть изменение числа степеней свободы.
Теория расчета плоских рамных систем представляет частный случай теории расчета тонкостенных призматических систем, а канонические уравнения метода перемещений являются частным случаем дифференциальных уравнений (382). Если в уравнениях (382) все коэффициенты shh(h9 k=l9 2, ..., п) равны нулю, то система (382) будет относиться к призматической системе, пластинки которой на линиях контакта соединены между собой цилиндрическими шарнирами (безмоментная призматическая система). Система дифференциальных уравнений (382) приводится к одному дифференциальному уравнению порядка 2 (т + п). Интеграл этого уравнения содержит 2(т + п) постоянных, которые определяются из кинематических, статических или смешанных условий на концевых сечениях х = 0 и х = 1.
При изложении настоящей главы мы следовали [53] и [54].
Пример 71. Определить напряженное состояние симметричной пространственной рамы, которая имеет цилиндрические опорные шарниры (полная линейная неподвижность опорных точек) и опирается по торцам на диафрагмы, жесткие в своей плоскости и гибкие из плоскости.
Рама нагружена горизонтальной равномерно распределенной нагрузкой д, расположенной в плоскости верхней грани (рис. 154) см. [53].
Разложим известные функции Ui(x)t Vh(x) и нагрузку q(x) =q в тригонометрические ряды:
303
иЛх) = ]и1п cos (
Л=1
оо
V* W = vkn sin &п.Г1)пх, (384)
П=1
i?V —!—sin(2n~1)jl*. (385)
4 n 2л — 1 I
Выражения (384) удовлетворяют краевым условиям: при л:=0 и х = 1 их%Ф0, м8л=0.
Продольные перемещения ux(xs) в сечении * = const для двух точек симметричных относительно оси г будут
в)
v,=/
шЙ*'
/©
Рис. 155
равны по величине и противоположны по знаку. Степень свободы шарнирной схемы рамы из плоскости, согласно (375), равна т = 4—2 = 2, но принимая во внимание, что нагрузку можно представить как обратно симметричную, получаем один параметр U{(x)t за который примем продольное перемещение верхнего правого угла. Эпюра перемещений, представленная при и\ = 1 функцией pi(s),
304
показана на рис. 155, а. На рис. 155,6 приведена эпюра % (s).
Степень свободы шарнирной схемы рамы в плоскости, согласно (374), равна:
п = 2-4 —3 — 4= 1,
т. е. определяется тоже одним параметром V\(x), за который примем прогиб горизонтальной пластинки в ее
плоскости. Эпюра контурных перемещений, представленная при V\=\ функцией tfi(s), показана на рис. 155,в.
Для подсчета коэффициентов Злли) надо построить эпюру изгибающих моментов Мн(М\) от перемещения tpi и эпюру от У* =1—Мл, которая совпадает с Ми.
На рис. 156, а представлена эпюра изгибающих моментов поперечной рамы от единичного горизонтального смещения ригеля с неизвестным моментом Mh=Mi.
На рис. 156,6 представлена эпюра изгибающих моментов в статически определимой системе — трехшарнирной раме от единичной горизонтальной силы, приложенной в правом углу.
Интегрируя эти эпюры и приравнивая результат единице (i?i=l), получим значение неизвестного момента М\
Ail = - 6 . (386)
2df//j + dxd2II2 d*
Уравнения (382) примут вид:
УацИ i cni = О»
CnU'i + rnVl-ySnV-L-O.
(387)
20—949
305
Подставляя (384) в их производные и (385) в урав-
(2/1—1) ЯДЕ
нения (387), сокращая последние на cos — и
sjn2lZlil5 получим систему алгебраических уравнений:
я® (2л — I)2 , и гг I я(2я— 1),/ п
уап — р Ullt + buUu -f clt Vln = О,
я(2я—1) ,, . я2(2п — I)2 „ . „
Си-5— 1 Vin + гп ~J2 Vin + TSnin —
Aq = 0.
Gn (2n — 1)
Коэффициенты уравнений, согласно (383), будут равны:
ап = j Ф\dF = (2d,6, + d262) = d8 = 0,1 d\
F
*ц,да-2(А + 2.)_б-1,о,в,
F
cu j" = 262 = 26 = 0,2 d,
F
rn= dF = d2b2 = db = 0,\d\
., _ J_ f = Л (_L д} + _L .-L Ж _
11 E J И V 3 El, Eh 3 2 I
s
1
= 6* IQ-3 (cm. 386).
di (2di/6i + «V6*) 3d* 3
Подставляя эти коэффициенты в уравнения, принимая Е = 2,1 -10е кПсм2, у = 2 и ограничиваясь первым членом разложения (384) и (385) при n= 1, получим:
[1,974 (d//)2 + 0,6]t/n + 0,628d//V'i* = 0,
0,628 d/lUn + [0,987 (d, If + 10-3J Vu =
= 1,213-10~V (388)
Решив уравнения (388) при любом принятом отноше-
306
нии d/l, найдем величины f/ц и Уп, после чего перемещения примут вид:
«ж (*»«) = 1Хф1 (s) cos -у-,
ы, (л:, s) = Vnг)! (s) sin у-. (389)
Согласно формулам (378), продольное нормальное напряжение будет равно:
а (*, s) = — 6,597 • 106 И. щ (s) sin — . (390)
i i
Наибольшие моменты возникнут в углах рамы. Согласно формуле (386), с учетом формулы (389) при
ф,(5) = 1
я л 2Е1 § г . тех
Мг = -Уп sin у- =
Исследования показывают, что при увеличении отношения Ijd оба перемещения (389) сначала возрастают — жесткость пространственной рамы уменьшается и деформации растут. При отношении /Д/ = 20ч-25 продольное перемещение /ц достигает наибольшего значения и затем убывает, стремясь в пределе к нулю, что соответствует вырождению пространственной конструкции в плоскую.
Рост перемещения V\\ постепенно уменьшается, и оно как бы стремится к максимуму.
Пр имер 72. Определить напряженное состояние в безмоментной пространственной раме, которая получится при введении цилиндрических шарниров во всех узлах системы примера 71.
Нагрузка и размеры сохраняются.
*
Для безмоментной пространственной рамы следует в уравнениях (388) положить $ц = 0, т. е. отбросить во
2
втором из этих уравнений член — 10~3 в коэффициенте
3
при V\\.
Уравнения (388) в этом случае примут вид:
20* 307
[ 1,974(d/l)» + 0,6] Uи + 0,628d/lVu = 0,
0,628d/lUu + 0,987 (d/l)2Vu = 1,213 • lO"6?. ( ’
Если уравнения (388) и (392) записать в форме:
AUu + BVu = 0, BUn + CVn = Q, (393) то неизвестные определяются по формулам:
Uи , Vn = —. (394)
АС — В* ’ АС —В* ' '
Уравнения (388) и (392) различаются между собой только коэффициентом С, который для моментной теории больше. Таким образом, перемещения (389) и напряжения (390) безмоментной системы будут в К раз больше, чем моментной, где
К = -ЛСмом~ В- 1. (395)
Лбезм В2
Исследования показывают [53], что К увеличивается при возрастании отношения l/d. При l/d = 2--5 /С«1.
Расчет тонкостенных пространственных систем с замкнутым контуром см. [53].
ЛИТЕРАТУРА
к первому разделу
1. В. 3. Власов. Тонкостенные упругие стержни. Госстройиздат, 1940.
2. Б. Г. Галеркин. Стержни и пластинки. Собр. соч., т. 1, изд-во АН СССР, М., 1952.
3. А. Н. Д и н н и к. Избранные труды. Т. 1, изд-во АН УССР, Киев, 1952.
4. А. Н. Дин ник. Устойчивость арок. Гостехиздат, 1946.
5. Ф. Д. Дмитриев. Крушения инженерных сооружений. М.,
1953.
6. М. Я. Дьяков. Устойчивость двухшарнирной арки с затяжкой и подвесками. Строительная механика и расчет сооружений. № 2,
1961.
7. В. И. Заборов. Об устойчивости несимметричной трехшарнирной арки. Сб. Исследования по теории сооружений. М., 1954.
8. Н. В. К о р н о у х о в. Прочность и устойчивость стержневых систем. Стройиздат, 1949.
9. П. И. К о ч у г о в. Устойчивость арок переменного сечения. Вестник инж. и техн., № 7, 1937.
10. Н. Л. Кузьмин, П. А. Лукаш, И. Е. Милейковс к и й. Расчет конструкций из тонкостенных стержней и оболочек. Гос. изд-во по стр-ву и архитектуре. М., 1960.
11. А. П. Локшин. Об устойчивости стержня с криволинейной осью. Прикл. мат. и мех. Т. 2, вып. 1, 1934.
12. Е. Л. Н и к о л а и. Об устойчивости кругового кольца и арки. Изв. Петрог. политехи, ин-та. Т. XXVIII, 1918.
13. Я А. П р а т у с е в и ч. Вариационные методы в строительной механике. Гостехиздат, М., 1948.
14. И. П. Прокофьев, А. Ф. Смирнов. Теория сооружений. Ч. 3. Трансжелдориздат, 1948.
15. Г. Л. Павленко, А. Б. Моргаевский. Устойчивость упругой параболической арки с затяжкой. Сб. Исследования по теории сооружений. Т. 5. М., 1951.
309
16. А. А. Пи ко век ий. Устойчивость и деформационный расчет стержневых систем. Справочник проектировщика. М., 1960.
17. И. М. Рабинов ич. Курс строительной механики. Т. 2, М.,
1954.
18. А. Н. Раевский. Основы расчета сооружений на устойчивость. Высшая школа, 1962.
19. А. Р. Ржаницын. Теория составных стержней строительных конструкций. Стройиздат, 1948.
20. А. Р. Ржаницы н. Устойчивость равновесия упругих систем. Гостехтеориздат, М., 1955.
21. А. Ф. Смирнов. Устойчивость и колебания сооружений. Трансжелдориздат, 1958.
22. Н. К- С н ит к о. Устойчивость стержневых систем. Гос. издво по стр-ву и архит., М., 1956.
23. С. П. Тимошенко. Устойчивость упругих систем. Гостехиздат. 1955.
24. И. Я. Ш т а е р м а н, А. А. П и к о в с к и й. Основы теории устойчивости строительных конструкций. Госстройиздат, 1939.
ко второму разделу
1. И. В. Ананьев. Справочник по расчету собственных колебаний упругих систем. Гостехиздат, 1946.
2. Н. И. Б е з у х о в, О. В. Л у ж и и, Н. В. К о л к у н о в. Устойчивость и динамика сооружений в примерах и задачах. Стройиздат. 1969.
3. С. А. Бернштейн. Основы динамики сооружений. Стройиздат, 1941.
4. В. В. Болотин. Динамическая устойчивость упругих систем. Гостехтеориздат, 1956.
5. И. И. Гольденблат, А. М. Сизов. Справочник по расчету строительных конструкций на устойчивость и колебания. Госстройиздат, 1952.
6. К. С. 3 а в р и е в. Динамика сооружений. Трансжелдориздат, 1952.
7. В. А. Киселев. Строительная механика (специальный курс). Стройиздат, 1969.
8. Б. Г. Коренев. Динамика сооружений. Справочник проектировщика. Раздел 22, Расчетно-теоретический. Госстройиздат, 1960.
9. И. Л. Корчи некий. Расчет строительных конструкций на вибрационную нагрузку. Стройиздат, 1948.
10. Б. Н. К у ту к о в. Упругие колебания (основы динамического расчета элементов конструкций). ВЗПИ, Государственное издательство «Высшая школа», 1961.
310
11. А. Лисовский. Колебания прямых стержней и рам. Госстройиздат, 1961.
12. Ю. А. Ни лен дер. Современное состояние динамики сооружений и практическое значение внутреннего сопротивления материалов. Сб. «Динамические свойства материалов». Гоестройнздат, 1940.
13. И. П. Прокофьев, А. Ф. Смирнов. Теория сооружений. Ч. 3, Трансжелдориздат, 1948.
14. Я- Г. Паыовко. Основы прикладной теории упругих колебании. Машгиз, 1957.
15. И. М. Рабинович. Основы строительной механики стержневых систем. Госстройиздат, 1960.
16. Э. Е. Сигалов. Практический метод расчета рам на колебания. Труды Московского института инженеров городского строительства Мосгорисполкома. Строительная механика и конструкции. Сб. 7, Госстройиздат, 1957.
17. А- Ф. Смирнов. Устойчивость и колебания сооружений. Трансжелдориздат, 1958.
18. Е. С Сорокин. Динамический расчет несущих конструкции зданий. Госстройиздат, 1956.
19. Н. К. Снитко. Методы расчета сооружений на вибрацию и удар. Госстройиздат, 1953.
20. С. П. Тимошенко. Теория колебаний в инженерном деле. Изд-во «Наука», 1967.
21. А. П. Филиппов. Колебания упругих систем. Изд-во АН УССР, 1956.
22. В. Г. Ч у д н о в с к и й. Методы расчета колебаний и устойчивости стержневых систем. Изд-во АН УССР, 1952.
23. ЦНИИСК. Инструкция по расчету несущих конструкций промышленных зданий и сооружений на динамические нагрузки. Стройиздат, 1970.
к третьему разделу
1. Ван-цзи-де. Прикладная теория упругости, гл. 12, ГИФМЛ, М., 1959.
2. Е. R е i s s п е г I. Math. Phys. 26, 290, 1947.
3. Ф. Д и шин гер. Оболочки. ГНТИ, М.—Л., 1932.
4. В. Г. Р е к а ч. Беэмоментная теория расчета псевдосферическнх оболочек. Изв. Арт. инж. Ак. Т. 109, М , 1958.
5. Л. Л. Гольденвейзер. Теория упругих тонких оболочек. ГИТТЛ, М., 1953, стр. 127.
6. С. П. Т и м о ш е и к о. Пластинки и оболочки. ГИТТЛ, М.—Л.,
1948, §78, стр. 411,443.
7. Н. А го n. I. f. reine u. angew. Math. Bd. 78, § 196, 1874.
3!1
8. A. Love. Philosofical Transactions Roy. Soc. V. 179(A), p. 491, 1888, перевод А. Ляв, Математическая теория упругости гл. XXIV, ОНТИ НКТП, М.—Л., 1935.
9. G. Ki rchhoff. Vorlesungen fibermathematische Physik, Bd. 1, Mechanik, 1876.
10. E. R e i s s n e r. A. new derivation of the eguations for the deformation of elastic, shells, Am. * Math. T. 63, № 1 1941, p. 177— 184.
11. E. Meisner. Physik Zeitschr. Т. XIV, 343, 1913.
12. И. Э. Экстрем. Тонкостенные симметричные купола. ОНТИ, Харьков — Киев, 1936.
13. F. Dubois. Ober die Festigkeit der Kuqelschale d. d. Цюрих, 1917.
14. H. Wissler. Festigkeitsberechnung von Ringflachenschalen, d. d. Цюрих, 1917.
15. I. Lense. Kuqelfunktionen, Leipzig, 1950.
16. E. В. Гобсон. Теория сферических и эллипсоидальных функций. ИЛ., М., 1952.
17. L. Boll е. Schweiz. Bauzeiteung, Т. 66, 1915, см. также 6.
18. I. Е. Е k strom. Ing. Vetensk. Akad. Т. 121, Стокгольм, 1933.
19. В. Г. Р е к а ч. Расчет сферических оболочек, д. д. 1954.
20. В. Г. Р е к а ч. Расчет тонких сферических оболочек. Научн. докл. высш. шк., Строительство. № 1, 1958.
21. Труды 5-го Международного математического конгресса. Кембридж, 1912, см. также статью О. Блюменталя в Z. Math. Phys. Т. 62, стр. 343, 1914.
22. С. П. Тимошенко. К вопросу о расчете сферических оболочек. Вестник общества технологов, № 17, СПБ, 1913.
23. И. Я. Ш т а е р м а н. О применении метода асимптотического интегрирования к расчету упругих оболочек, 1924 и другие статьи в Изв. Киевского политехнического и сельскохозяйственного ин-тов.
24. В. В. Новожилов. Теория тонких оболочек. Судпромгнз,
1962.
25. I. W. Geckeler, Forschungsarbeiten, № 276, Берлин, 1926.
26. P. Pasternak. Z. ang. Math. u. Mech. T. 6, 1926, см. также, Vorhandlung d. 2 Int. Kongr. fur techn. Mech., Zurich, 1927.
27. Б. С. Ж a p м а г а м б e т о в. Практический метод расчета железобетонной сферической оболочки. Изв. АН Каз. ССР, сер. горное дело, вып. 8, 1956.
28. В. 3. Власов. Общая теория оболочек. ГИТТЛ, М.—Л., стр. 257, 329, 420, 439, 1949.
29. G. Ehlers. Beton und Eisen, JVb 13, 14, 1929. Перевод см. в сб. Складчатые железобетонные конструкции, Харьков, 1934.
312
30. Dr. Ing. Finsterwalder, Die Theorie der Zyhndrischen Schalengewolbe Sistem Zeiss-Dywidag u..., Abhandlungen der Intern. Gesellschaft f. Вгйскеп и. Hochbau, В. I. Zurich, 1932.
31. А. А. Г в о з д е в. К расчету тонкостенных цилиндрических оболочек, Строит, промышленность, № 1, 1932.
32. В. 3. В л а с о в. Новый практический метод расчета складчатых покрытий и оболочек. Строительная промышленность, № 11,
12, 1932.
33. П. Л. Пастернак. Практический расчет складок и цилиндрических оболочек с учетом изгибающих моментов. Строительный бюллетень, № 9, 10, 1932.
34. В. 3. В л а с о в. Строительная механика оболочек, ОНТИ, 1936.
35. В. 3. В л а с о в. Тонкие упругие стержни. Стройиздат, 1940.
36. L. A. W о j t a s z a k. Deformation of thin cylindrical shells subjected to intemel loading, Phil, Mag. ser. 7, p. 18, 1934, p. 1099— 1116, см. также 1, стр. 391.
37. К. Marquerre. Zur Theorie der Gekriimmten Platte Grosser Formanderung. Proceedings of the Fifth Int. Congress for Appl. Mech. 1938, p. 93—101.
38. В. 3. Власов. Основные дифференциальные уравнения общей теории упругих оболочек. ПММ, Т. VIII, № 2, 1944. См. также [28], стр. 301—309.
39. А. Л. Гольденвейзер. Дополнения и поправки к теории тонких оболочек Love. Сб. пластинки и оболочки. Госстройиздат, 1939, см. также [5], стр. 59.
40. В. Г. Р е к а ч. Расчет пологих винтовых (геликоидальных) оболочек. Сб. трудов МИСИ, № 27, М., 1957.
41. С. М. Ф а й н б е р г. Проект и стандарт, № 12, 1936.
42. В. 3. Власов. Некоторые задачи сопротивления материалов, строительной механики и теории упругости. Изв. АН СССР, отд. техн. наук, № 9, 1950.
43. Р и с h е г A. Ober die Spannungsfunktion belibig gekrummter dimer Schalen, Proceedings of the V Int Congress for Appl. Mech. p. 134, 1938.
44. P. С s о n k a, Ober doppelt gekrummte Schalen, Acta, techn. Acad, scient. Hung; 1959, 26, № 1—2, Там же приведен перечень его
11 работ периода 1955—1958 гг.
45. W. F 1 u g g е. Statik und Dinamik der Schalen Springer— Verlag, 1957; перевод В. Флюгге, Статика и динамика оболочек. ГСИ, М., 1961.
46. А. Р. Ржаницын. Расчет тонких безмоментных оболочек вращения малой кривизны. Труды лаб. строит, механики ЦНИПС,
1949.
313
47. В. М. Н и к и р е е в. Расчет безмоментной пологой оболочки на постоянную вертикальную нагрузку. Строит, механика и расчет сооружений, АСиА СССР, № 6, 1959.
48. В. С. Бартенев. Расчет пологих оболочек двоякой кривизны с прямоугольным планом для произвольной нагрузки. Научные доклады высшей школы. Строительство, № 2, 1959. См. также [42].
49. Т. Т. Хачатурян. Пологие цилиндрические оболочки. Сообщения института, мат. и механ. АН Арм. ССР, вып. 4, 1949.
50. Е. Я н к е, Ф. Э м д е. Таблицы функций с формулами и кривыми. Харьков — Киев, 1934, 1959.
51. В. Г. Рекач. Симметричный нагрев пологих сферических оболочек, Сб. трудов МИСИ, № 8, 1954.
52. В. В. Д н к о в и ч. Пологие, прямоугольные в плане, оболочки вращения, ГСИ, М., 1960.
53. В. 3. Власов. Строительная механика тонкостенных пространственных систем. Гл. Ill, IV. Стройиздат, 1949 или 1958.
54. И. М. Р а б и н о в и ч. Основы строительной механики стержневых систем. Стройиздат, 1956.
ОГЛАВЛЕНИЕ
Стр.
Предисловие ...... 3
Раздел I
Основы расчета стержневых систем на устойчивость
Глава 1. Понятие о потере устойчивости, критической нагрузке
и методах расчета на устойчивость 5
§ 1. Введение 5
§ 2. Устойчивость 1-го рода; постановка задачи; методы
расчета 8
§ 3. Устойчивость системы с двумя степенями свободы.
Точные и приближенные методы расчета 10
Глава 2. Устойчивость центрально сжатого прямого стержия 15
§ 4. Прямой стержень с упругой заделкой на одном конце и упруго лодатливой опорой на другом .... 15
§ 5. Стержень с упругой промежуточной опорой . . , 20
§ 6. Стержень в упругой среде. Устойчивость сжатого
пояса открытого моста 24
§ 7. Стержень переменного сечения 28
§ 8. Составные стержни 33
Глава"3. Устойчивость плоских рам 41
§ 9. Постановка задачи 41
§ 10. Дифференциальное уравнение изгиба сжатоизогнутого стержня и его интеграл . 45
§ 11. Расчет рам на устойчивость методом перемещений 50
§ 12. Расчет рам на устойчивость методом сил. Выбор основной системы и лишних неизвестных 59
§ 13. Примеры деформационного расчета рам. Таблицы
функций 66
Глава 4. Устойчивость арок . . „ 77
§ 14. Устойчивость круговой арки постоянного сечения с упруго защемленными пятами и радиальной иагр узкой 77
315
Стр.
§ 15. Устойчивость круглых колец и труб под действием
равномерной радиальной нагрузки 87
§ 16. Устойчивость параболической арки постоянного сече¬
ния с равномерно распределенной вертикальной нагрузкой 90
§ 17. Устойчивость весьма пологих арок 92
§ 18. Устойчивость арки с затяжкой 99
Глава 5. Устойчивость тонкостенных стержней 102
§ 19. Основы теории. Дифференциальное уравнение устойчивости 2-го рода 102
§ 20. Потеря устойчивости 1-го рода. Внецентренное и
центральное сжатие 105
§ 21. Потеря устойчивости плоской формы изгиба балки 115
§ 22. Потеря устойчивости при растяжении 121
Раздел II Основы динамики стержневых систем
Глава 6. Системы с одной степенью свободы 124
§ 23. Основные понятия , 124
§ 24. Свободные колебания 127
§ 25. Вынужденные колебания при действии вибрационной
нагрузки 137
§ 26. Действие других возмущающих нагрузок .... 142
§ 27. Ударная нагрузка 144
Г лава 7. Системы со многими степенями свободы 149
§ 28. Свободные колебания 149
§ 29. Приближенная оценка частоты основного тона колебаний 164
§ 30. Энергетический способ 166
§ 31. Определение вынужденных колебаний при действии
вибрационной нагрузки методом сил ...... 170
§ 32. Метод перемещений 179
§ 33. Матричная форма расчета 181
Глава 8. Система с бесконечно большим числом степеней свободы 184
§ 34. Свободные колебания балок с равномерно распределенной массой 184
§ 35. Колебания балки при подвижной нагрузке .... 189
§ 36. Вынужденные колебания балок с равномерно рас¬
пределенной массой при действии вибрационной на* грузки 193
316
Стр.
Глава 9. Расчет статически неопределимых систем . . . . 15
§ 37. Определение перемещений и реакций от динамической нагрузки 195
§ 38. Расчет рам по методу сил 197
§ 39. Расчет рам по методу перемещений 198
§ 40. Применение готовых формул 212
Глава 10. Меры борьбы с вибрационными явлениями . . . 216
§ 41. Характеристики физиологического и других воздействий вибраций 216
§ 42. Способы уменьшения резонансных явлений ... 217
§ 43. Расчет виброизоляции 219
Раздел III
Основы расчета пространственных тонкостенных конструкций
Глава 11. Элементы дифференциальной геометрии поверхности 221
§ 44. Аналитическое выражение поверхности 221
§ 45. Линейный элемент поверхности 222
§ 46. Кривизна линии на поверхности 223
Глава 12. Безмоментная (мембранная) теория расчета оболочек 230
§ 47. Основные дифференциальные уравнения .... 23Э
§ 48. Расчет оболочек вращения 234
§ 49. Расчет цилиндрических и конических оболочек . . 243
Глава 13. Моментная теория расчета оболочек 247
§ 50. Общие положения 247
§ 51. Вывод уравнений равновесия 249
§ 52. Определение компонентов деформации 251
§ 53. Расчет оболочек вращения на осесимметричЕ1ую
нагрузку 258
§ 54. Приближенные расчеты оболочек вращения на осесимметричную нагрузку 266
§ 55. Расчет цилиндрических оболочек — общая теория . 273
§ 56. Теория круговых ортотропных цилиндрических
оболочек (оболочки средней длины — =2+8) . . 276
Глава 14. Расчет пологих оболочек 282
§ 57. Вывод основных расчетных уравнений . . . . . 282
§ 58. Частные случаи расчетных уравнений 286
317
Глава 15. Расчет пространственных призматических рам (метод проф. В. 3. Власова) . 298
§ 59. Общие пбложения 298
§ 60. Напряженное и деформированное состояние рамы-
полоски 299
§ 61. Дифференциальные уравнения равновесия рамы-полоски 300
Литература 309
Сдано в набор 8/VI—71 г. Подписано к печати 8/XII—71 г. Формат 84Х1081/з2 Объем 10 печ. л. 16,8 уел. п. л. Уч.-изд. л. 13,86 Изд. № ОТ—122/69 Тираж 48 000 экз. Зак. 949 Цена 50 коп.
План выпуска литературы для вузов и техникумов издательства «Высшая вдкола» на 1972 г. Позиция № 76
Москва, К-51, Неглинная ул., д. 29/14, Издательство «Высшая школа»
Владимирская типография Главполиграфпрома Комитета по печати при Совете Министров СССР Гор. Владимир, ул. Победы, д. 18-6
РУКОВОДСТВО к ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО КУРСУ СТРОИТЕЛЬНОЙ МЕХАНИКИ
Редактор Л. Н. Чупеева Художник Л. М. Чернышев Художественный редактор Н. К: Гиторов Технический редактор 3. В. Нуждина Корректор Г. Н. Брхенова