SL2(R) - Ленг С.

Автор: Ленг С.
Теги: анализ физико-математическая литература
Год: 1977
Похожие
Краевые задачи математической физики
Методы современной математической физики. Том 2. Гармонический анализ
Пространства С.Л. Соболева
Абстрактный гармонический анализ. Том I. Структура топологических групп. Теория интегрирования. Представления групп
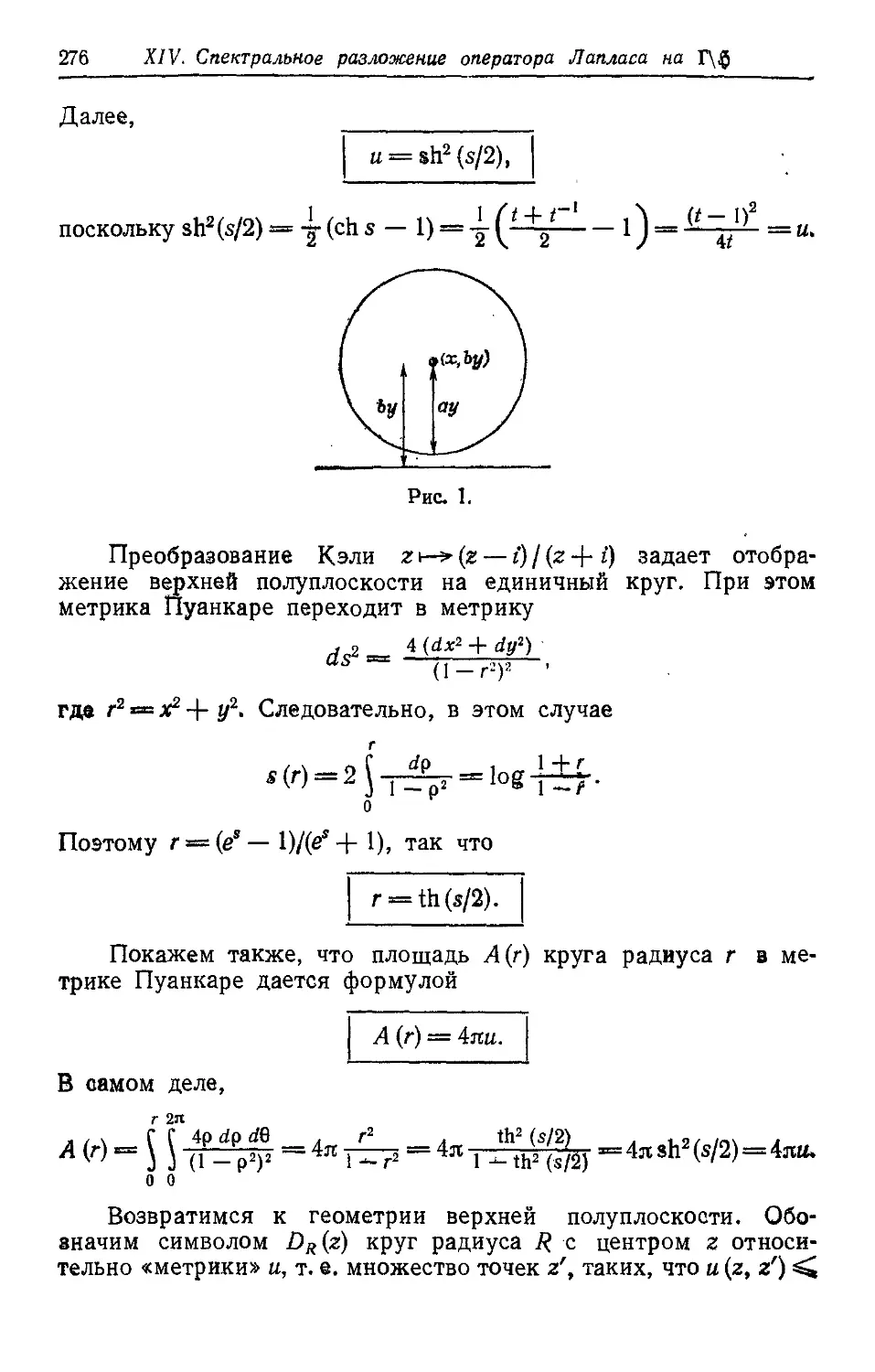
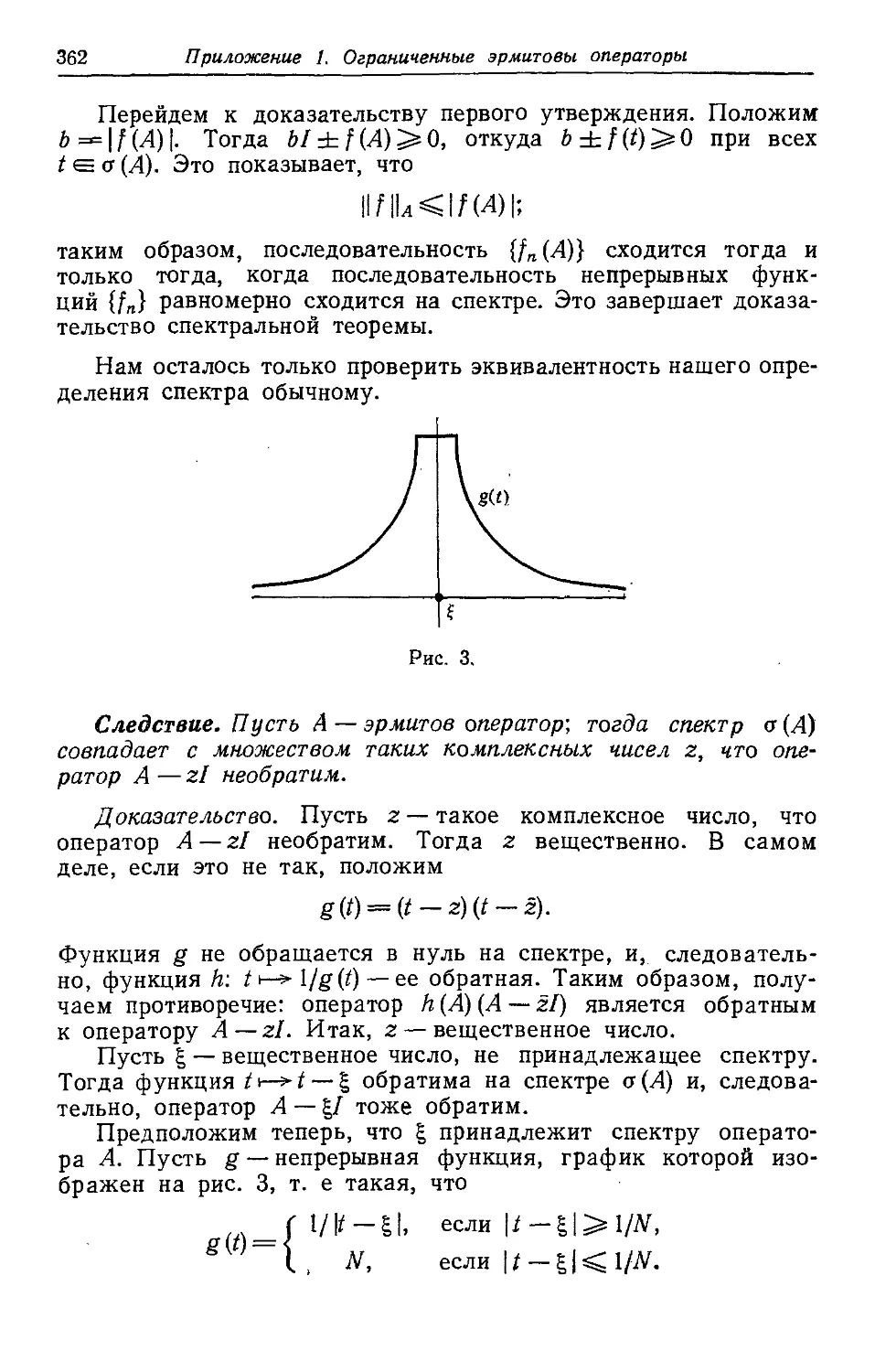
Текст
                    Serge Lang
Yale University
Mew Haven, Cenaeotieei
ADDISON-WESLEY
PUBLISHING COMPANY
Read!no, Maseaohusetts
Menlo Park, California-London-Ameterdam
Don Mills, Ontario-Sydney
1975

с. ЛЕНГ
Перевод с английского
В. И. Васюнина и М. А, Семенова-Тян-Шанского
Под редакцией
А. А. Кириллова
Издательство «Мир» Москва 1977

УДК 517
Книга с таким кратким, но выразительным
названием написана известным американским
математиком, автором около двадцати учебников н
монографий по алгебре, теории чисел, анализу,
дифференциальной геометрии и другим областям современной
математики. Некоторые нз них известны советским
читателям по русским переводам.
Новая книга С. .Яенга посвящена гармоническому
анализу иа группе SZ,2(R) вещественных матрип
второго порядка с определителем, равным 1. Эта группа
имеет много важных реализаций и встречается в
различных разделах математики и физики. Наряду с
классическими результатами автор приводит и совсем
новые.
Написанная очень живо и четко, доступная для
читателей с минимальной математической
подготовкой, книга будет интересна как специалистам, так
и начинающим математикам и физикам.
Редакция литературы по математическим наукам
© 1975 by Addlson-Wesley Publishing Company, Itn,
20203-004
Jl „хгтттТГтт *"'^ ® Перевод на русский язык, «Мир», 1977

Предисловие редактора перевода
Новая книга Сержа Ленга, перевод которой предлагается
читателям, посвящена теории представлений группы SL2(R).
Стандартное наименование этой группы (которое
расшифровывается как «специальная линейная группа порядка 2 над полем
R»), возможно, не дает ясного представления об этой группе
и о т»й роли, которую она играет в различных областях
математики и ее приложений. Повтому я приведу некоторые пояснения.
Во-первых, это некомпактная простая группа Ли
минимальной размерности, т. е. простейший представитель большого
семейства, включающего линейные, ортогональные, унитарные и
симплектические группы над полями вещественных и
комплексных чисел и телом кватернионов. Теория представлений этих
групп составляет одну из самых трудных, красивых и богатых
приложениями областей современного функционального
анализа. Началась эта теория с исследования группы SL2(R),
предпринятого Баргманном 30 лет назад. И до сих пор эта группа
является «пробным камнем» для всех новых методов и понятий
в теории представлений.
Во-вторых, группа SL2(R) имеет несколько геометрических
реализаций. А именно: она является группой движений
плоскости Лобачевского, группой симметрии теории относительности
в трехмерном пространстве-времени (так называемая
«укороченная группа Лоренца»), группой автоморфизмов любой одно-
связной области на комплексной плоскости, в частности
единичного круга и верхней полуплоскости, группой конформных
(дробно-линейных) преобразований в одномерном вещественном
пространстве. Каждая из перечисленных реализаций сама по
себе является достаточным поводом для детального изучения
группы SZ,2(R) и ее представлений.
В третьих, группа SL2(R) и тесно связанные с ней группы
SZ,2(Z) и SL2(A) (состоящие из унимодулярных матриц второго
порядка с коэффициентами из кольца Z целых чисел или из
кольца А аделей соответственно) попали в последнее время
в центр внимания специалистов по алгебраической теории чисел.
Оказалось, что давно уже известные глубокие связи этой теории
с теорией автоморфных функций и эллиптических кривых
допускают наиболее полное и естественное изложение на языке
теории представлений. В настоящем предисловии нет возможно-

предисловие редактора перевода
сти подробно рассказать об этой новой теории, получившей
название «некоммутативного закона взаимности» и обобщающей
классическую теорию полей классов. Интересующиеся этим'
вопросом читатели могут обратиться к книге Э. Жаке и Р. Ленг-
лендса «Автоморфные формы на GLi» («Мир», М., 1975) и к
шестому выпуску серии «Обобщенные функции» И. М. Гельфанда
и др. («Наука», М., 1966).
Содержание книги С. Ленга можно разделить на три части.
Первая часть (главы I—XI) является введением в теорию
бесконечномерных представлений на примере группы SL2(R). Во
второй части (главы XII—XIV) строится гармонический анализ
на пространстве Г\'0, где G = SL2(R), а Г — дискретная
подгруппа в G. Для теории чисел оказался очень важным частный
случай этой задачи, когда Г — арифметическая подгруппа в G
(например, r = SL2(Z)). Интересно, что эта же задача тесно
связана с совсем другой областью функционального анализа —
теорией рассеяния в математических моделях квантовой
механики. На эту связь обратил внимание И. М. Гельфанд, а полное
решение задачи было получено Л. Д. Фаддеевым. По существу,
вся вторая часть книги С. Ленга является подробным
изложением работы Л. Д. Фаддеева.
Третью часть составляют пять приложений, в которых
излагаются сведения из различных областей математики, не
входящие пока в стандартные программы вузов, но необходимые для
излагаемой теории. С присущей автору четкостью, краткостью
и полнотой доказательств здесь строится спектральная теория
ограниченных и неограниченных самосопряженных операторов,
доказываются основные теоремы теории эллиптических
уравнений, изучаются мероморфные семейства операторов и
аналитические вектор-функции.
Я полагаю, что книга в целом будет полезна очень широкому
кругу математиков всех уровней и специальностей.
Л. Кириллов

Предисловие автора
Начиная с работы Баргманиа о бесконечномерных
представлениях группы SL2(R), теории представлений полупростых
групп Ли было посвящено очень большое число исследований.
Назовем здесь тех, кто внес наиболее значительный вклад в
развитие теории. В конце 40-х годов И. М. Гельфанд, М. А. Най-
марк и Хариш-Чандра изучили неприводимые представления
группы Лоренца. Затем И, М. Гельфанд и М. А. Наймарк
рассмотрели классические комплексные группы, а Хариш-
Чандра, опираясь на исследование производного представления
алгебры Ли, изучил общий вещественный случай. (Этому
случаю посвящено также несколько работ И. М. Гельфанда и
М. И. Граева.) Э. Картан, И. М. Гельфанд и М. А. Наймарк,
Р. Годеман,' Хариш-Чандра построили теорию сферических
функций (Годеман сделал несколько докладов на семинаре Бур-
баки, в которых содержатся доказательства ряда спектральных
результатов, отсутствующие в других источниках). А, Сельберг
рассмотрел факторпространство группы по ее дискретной
подгруппе и получил формулу следа; И. М. Гельфанд, С. В. Фомин,
И. И. Пятецкий-Шапиро и Хариш-Чандра установили связь
теории представлений полупростых групп Ли с теорией авто-
морфных форм. Жаке и Ленглендс связали теорию
представлений с теорией L-рядов и теорией Гекке. История развития теории
представлений настолько сложна и насыщена, что я чувствую
себя недостаточно компетентным для того, чтобы ее хорошо
изложить; за дальнейшей информацией я отсылаю читателей
к библиографиям в книгах Г.- Уорнера, И. М. Гельфанда,
М. И. Граева и И. И. Пятецкого-Шапиро и С. Хелгасона. Ряд
дополнительных исторических замечаний будет сделан в
соответствующих местах книги.
Неспециалисту, особенно тому, кто интересуется в основном
теорией чисел, разобраться в теории представлений не так-то
легко. Это объясняется многими причинами. Во-первых, обилие
теоремы о многомерных группах существенно опираются на
теорию Ли. Во-вторых, необходима хорошая подготовка в целом
ряде стандартных и не очень стандартных разделов анализа.
В третьих, специалисты так долго писали друг для друга, что
литература стала напоминать лабиринт.

Предисловие автора
Я заинтересовался теорией представлений из-за ее очевидных
связей с теорией чисел, в особенности из-за гипотезы Ленгленд-
са, связывающей теорию представлений с теорией эллиптических
кривых (Ленглендс [2]). Эта гипотеза относится к теории аделей
и глобальному гармоническому анализу. Довольно быстро я
обнаружил, что прежде, чем заниматься аделями, лучше всего
как следует разобраться с вещественным случаем. Я думаю, что
большинство людей, занимающихся теорией представлений,
начинали с изучения группы SL2(R), и я знаю, что именно так
поступали Ленглендс и Хариш-Чандра.
Поэтому, когда я сам выучил теорию представлений, мне
показалось, что написать книгу о представлениях группы
SZ,2(R) —хорошая идея. Содержание этой книги таково.
1. Сначала мы исследуем, как ведут себя представления
группы SL2(R) при сужении на ее максимальную компактную
подгруппу К, и показываем, что кратность, с которой
представление группы К входит в разложение сужения неприводимого
представления 5L2(R) на К, не превосходит 1.
2. Мы описываем разложение Ивасавы G=ANI{, из которого
вытекает большая часть теорем о структуре и свойствах группы
G. В частности, мы получаем представления группы G,
индуцированные характерами подгруппы AN.
3. Мы подробно исследуем случай, когда неприводимые
представления группы G содержат тривиальное представление
подгруппы К. Это — теория сферических функций. При этом
мы используем только меру Хаара, что делает наш подход более
доступным, чем в других изложениях, где применяются также
теория Ли, структурная теория и дифференциальные уравнения.
4. Мы описываем представления непрерывной серии, часть
которых унитарна.
5. Мы переходим к инфинитезимальной теории, обсуждаем
производное представление алгебры Ли и доказываем, что в
пространстве неприводимого представления можно ввести не
более одной эрмитовой структуры, превращающей это
представление в унитарное. Мы перечисляем также все случаи, когда
такая унитаризация возможна, и получаем тем самым
классификацию Баргманна. Хотя этот результат и не требуется для
вывода формулы Планшереля, все же приятно узнать, что любое
неприводимое унитарное представление инфинитезимально
эквивалентно подпредставлению представления основной серии,
индуцированного квазихарактером треугольной подгруппы. Цен-
ральную роль при доказательстве этого факта играет
производное представление алгебры Ли на подпространстве /С-конечных
вектйфов, использование которого, по существу, сводит задачу
к алгебраической.

предисловие автора
6. Различные представления связаны формулой обращения
Планшереля. Следуя Хариш-Чандре, мы получаем эту формулу
при помощи интегрирования по классам сопряженных
элементов.
7. Мы приводим принадлежащий Хариш-Чандре метод уни-
таризации представлений дискретной серии, т. е. представлений,
имеющих вектор старшего или младшего веса в пространстве
/С-конечных векторов.
8. Мы обсуждаем структуру алгебры дифференциальных
операторов и приводим для группы SLiiR) частный случай
теорем Хариш-Чандры, описывающих централизатор подгруппы К
и центр универсальной обертывающей алгебры. На этом этапе
у нас уже имеется достаточно информации о дифференциальных
уравнениях, чтобы получить тот единственный результат о
сферических функциях, который мы не могли доказать раньше, а
именно, что примеры, приведенные в гл. IV, исчерпывают все
сферические функции.
Перечисленные темы составляют, в некотором смысле,
первую часть книги. Во второй части рассматривается
гармонический анализ на факторпространстве группы по ее дискретной
подгруппе. Классическим примером такой подгруппы является
SZ.2(Z). Наша основная цель — получение теоремы разложения
для пространства L^{T\G) и различных формул обращения.
Их доказательству и посвящены остальные главы этой
книги.
Первоначально я предполагал включить формулу Сельберга
для еледа над полем вещественных чисел, но в случае
дискретных подгрупп с некомпактным факторпространством это
потребовало бы заметного увеличения объема, а книга и без того уже
стала довольно большой. Поэтому я решил отказаться от этой
мысли в надежде когда-нибудь позже еще вернуться к этому
предмету.
В первой части книги мы в основном используем только меру
Хаара и разложение Ивасавы и почти не привлекаем инфини-
тезимальные соображения. В тех случаях, когда они все-таки
затрагиваются, мы в состоянии вывести формулу Планшереля
и изучить свойства различных представлений, не заботясь о
вопросах полноты, т. е. о том, построены ли нами «все»
неприводимые унитарные представления, «все» сферические функции
и т. п. (хотя, кстати сказать, мы доказываем, что это так).
Теоремы, в которых используется теория уравнений в частных
производных (необходимая для изучения оператора Казимира),
собраны в отдельную главу. Мы привлекаем в этой главе также
аналитические соображения, связанные с теоремой локальной
регулярности для эллиптических дифференциальных уравнений.

10 Првдивловие автора
Такая структура книги долж»а обеспечить максимальную
гибкость и предполагает минимум предварительных знаний.
Методы и обозначения, которые мы используем, подобраны с таким
расчетом, чтобы они подсказывали подход, пригодный для про-'
извольных полупростых групп.
Поскольку эта книга преднааначеиа для тех, кто — подобно
мне самому, до тех пор, пока я ее не написал, — совсем не знает
теории представлений, я приложил значительные усилия, чтобы
сделать изложение независимым. Для удобства читателя я
воспроизвел доказательства целого ряда фактов из анализа, а
также привел в конц« книги пять приложений, посвященных
различным разделам анализа (спектральная теорема для
ограниченных и неограниченных эрмитовых операторов, эллиптические
дифференциальные уравнения и т. д.). Если добавить сюда мою
книгу «Real Analysis», то этого материала будет достаточно для
чтения настоящей книги')•
Работа Л. Д. Фаддеева о спектральном разложении
оператора Лапласа на верхней полуплоскости представляет собой
пр«краеное введение в анализ, облеченный в красивую геометри-
чеекую форму. Большая ее часть должна быть доступна любому
хорошему старшекурснику, и я воспроизвел эту работу в гл. XIV
(с добавлением ряда деталей, опущенных Фаддеевым, который
ориентировался на более искушенного читателя). Методы
Фаддеева берут свое начало в теории возмущений и теории
рассеяния и представляют самостоятельный интерес; они могут быть
интересны и специалисту, который знаком с аналитической
частью работы и хочет узнать, как она используется в теоретико-
групповой задаче. В недавней книге Куботы о рядах
Эйзенштейна (которая появилась в то время, когда эта книга была
в печати) использован другой подход (Сельберга—Ленг-
лендса); кроме того, применяемые в ней факты из
функционального анализа предполагаются известными. Поэтому ни книга
Куботы, ни моя не делает другую ненужной.
Включение в эту книгу глобального гармонического анализа
и аделей нарушило бы ее единство. Я надеюсь, однако, что,
познакомившись с группой 5L2(R), читатель будет хорошо
подготовлен для того, чтобы двигаться дальше в этом направлении.
Весьма полезна в этом отношении книга И. М. Гельфанда,
М. И. Граева и И. И. Пятецкого-Шапиро.
Мне принесли большую пользу дискуссии со многими людьми
в течение последних двух лет, в частности на конференции по
теории представлений в Вильямстауне в 1972 г. Среди них
я хочу особо поблагодарить Годемана, Харйш-Чандру, Хелга-
') Из книг, имеющихся на русском языке, назовем следующие: Иосида
(1], Рудин [1], [2].—Ярил, перев.

предисловие автора 11
сона, Лабесса, Лашо, Ленглендса, К. Мура, Салли, Уилфрида
Шмида, Стейна. Питер Лаке и Ральф Филлипс помогли мне
изучить уравнения в частных производных. Я благодарю также
участников семинара в Йельском университете, контакты с
которыми во время работы над книгой оказались очень полезными.
В особенности я признателен Р. Браггеману за внимательное
чтение рукописи. Я хотел бы также поблагодарить Джо Репка
за помощь при чтении корректуры.
Серж Ленг
Нью Хейвен, Коннектикут
Сентябрь 1974

Обозначения
Будем писать /==0(1), если / — ограниченная функция.
Пусть f, g — две функции на некотором пространстве X,
причем g^O. Мы пишем /«0(g), если существует такая
константа С, что |/(л)|^Ся(л) для всех леХ. Если Х—К —
вещественная прямая, то возможен случай, когда это
неравенство выполняется лишь для достаточно больших х, скажем для
x'^Xq. в этом случае мы будем писать: /■=0(g) при л-»-оо.
Вместо обозначения /-«0(g) мы будем использовать Tajrace
обозначение И. М. Виноградова:
f<8'
Пусть X — топологическое пространство; С{Х) обозначает
пространство непрерывных функций на X. Если X — гладкое
(С") многообразие (в этой книге мы не встретим ничего
худшего, чем открытые подмножества евклидова пространства или
простые многообразия типа Sl2(R) с очевидными
координатами), то С°°{Х) обозначает пространство гладких функций на X.
Индексом с мы будем отмечать пространства функций с
компактным носителем; таким образом, Сс{Х) и СГ (Х) —
соответственно пространства непрерывных и гладких функций с
компактным носителем.
Нелишне напомнить, что SL2(R) — это группа вещественных
2Х2-матриц с определителем 1.
Изоморфизмом называется морфизм (в некоторой категории),
для которого существует обратный в той же категории.
Изоморфизм объекта с самим собой называется автоморфизмом.
Например, непрерывный линейный автоморфизм нормированного
векторного пространства Н есть непрерывное линейное
отображение А: Н^-Н, для которого существует такое непрерывное
линейное отображение В: Н-*Н, что АВ^^ВА-^!.
Диффеоморфизм — это изоморфизм в категории гладких
многообразий, т. е. гладкое отображение, для которого существует гладкое
обратное.
Пусть Н — банахово пространство. Обозначим End Н
банахово пространство непрерывных линейных отображений Я в себя.
Если Н — гильбертово пространство, обозначим AutJIT группу
его унитарных автоморфизмов; группу всех непрерывых
линейных автоморфизмов пространства Я будем обозначать GL(H).

14 Обозначения
Пусть С — подгруппа группы G; символом G'\G обозначается
множество правых смежных классов группы О'. Если группа Г
действует справа на пространстве X, мы обозначаем символом
Г\Х пространство орбит. В некоторых работах авторы
помещают дискретную группу справа. И. М. Гельфанд с соавторами
и Р. Ленглендс пишут ее слева. Я согласен с ними и надеюсь
склонить к этому читателей.
Для удобства в конце книги помещен также краткий
перечень часто используемых символов вместе с их краткими
определениями.

I. ОБЩИЕ РЕЗУЛЬТАТЫ
§ 1. Представления алгебры Cc{G)
Пусть G — локально компактная группа, которую мы всегда
будем предполагать хаусдорфовой. Пусть Я—банахово
пространство (в большинстве наших приложений оно будет
гильбертовым). Представление группы G в пространстве Я есть
гомоморфизм
я: Q^GL{H)
группы G в группу непрерывных линейных
автоморфизмов.пространства Я, такой, что для любого вектора у из Я
отображение G ъ Н, задаваемое формулой
х>-^п{х) V,
непрерывно. Иначе говоря, этот гомоморфизм непрерывен
в сильной операторной топологии, т. е. в топологии,
определяемой нормой банахова пространства. [Напомним, что слабая
топология в Я—это самая слабая (т. е. имеющая наименьшее
семейство открытых множеств) топология, в которой непрерывны
все линейные функционалы на Я.]
Представление называется ограниченным, если существует
такое число С > О, что | я (л) | ^ С для всех л е G. Если Я —
гильбертово пространство и операторы л{х) унитарны при всех
значениях аргумента, т. е. сохраняют норму в Я, то
представление я называется унитарным; унитарные представления,
очевидно, ограничены (С=1).
Проверять условие непрерывности представления достаточно
на плотном подмножестве векторов; другими словами:
Пусть я: G-*GL (Я) — некоторый гомоморфизм;
предположим, что отображение x>—^n,{x)v непрерывно для плотного
множества векторов у s Я. Предположим также, что некоторая
окрестность единичного элемента е в группе G переходит при
отображении л в ограниченное подмножество пространства GL (Я).
Тогда я — представление.
Доказательство этого утверждения совсем просто.
Достаточно проверить непрерывность отображения я на единичном
элементе. Пусть уеЯ; выберем достаточно близкий к v
вектор Vi^H, такой, что отображение x*—*'n{x)vi непрерывно.

16 /■ Общие результаты
Теперь для доказательства нашего утверждения воспользуемся
неравенством треугольника:
I я (а:) о — о КI л (а:) о — я (а:) oi I + I я (а:) Oi — Oi I + I о, — о |.
Представление я: G-*-GL[H) локально ограничено: если
К c^G — компактное подмножество, то множество я (К)
ограничено в GL(H).
Доказательство. Пусть KczG — компактное подмножество.
Для любого вектора v из Н множество я(Д)о компактно и,
следовательно, ограничено. По теореме о равномерной
ограниченности (Ленг [1, гл. VHI, § 3]) отсюда вытекает, что я (Д)—
ограниченное подмножество GL{H).
Для удобства читателя мы напомним здесь вкратце теорему
о равномерной ограниченности.
Пусть {T'ilfe/—семейство ограниченных операторов в
банаховом пространстве Б; предположим, что для любого вектора v
из Е множество {7'iW},^^ ограничено. Тогда семейство {Г^}^g^
ограничено как подмножество в пространстве End Е.
Доказательство. Пусть С„ — множество таких векторов о
из Е, что
I TiV I ^ п при всех i е /.
Тогда множества С„ замкнуты и их объединение совпадает
с Е. По теореме Бэра одно из множеств С„ содержит открытый
шар. Перенесем этот шар в начало координат. Получим
открытый шар В, такой, что объединение множеств Т{ (В), i е /,
ограничено; следовательно, семейство \Ti]^^J ограничено, что
и требовалось доказать.
Обозначим символом C<,(G) пространство непрерывных
функций с компактным носителем на группе G. Это пространство
представляет собой алгебру относительно свертки, т. е.
относительно произведения, задаваемого формулой
(ф * 1|)) (;с) « j ф {ху-') ^ (у) dy,
TA&dy— мера Хаара на G. Мы будем предполагать, что группа О
унимедулярна, т. е. что правая мера Хаара совпадает с левой
мерой Хаара. Для любой функции / на G обозначим
символом /~ функцию ATI—>/(а:~'). Тогда
^fix)dx^^f (х~') dX'^^r {x)dx.

§ 1. Представления алгебры Ce(G) 17
Замечание. Если группа G не унимодулярна, то, в силу
единственности меры Хаара, на G существует модулярная
функция, т. е. непрерывный гомоморфизм А, отображающий группу G
в мультипликативную группу положительных вещественных
чисел R"*", такой, что
\f{xa)dx = ^{a)\f{x)dx.
а а
Тогда стандартное рассуждение показывает, что
^f[x-^)^{x)dx=^f{x)dx.
о ^, о
Отсюда следует, что А(а:)с?а: —правая мера Хаара. Типичная
неунимодулярная группа, с которой нам придется иметь дело
(начиная с гл. III), — это группа треугольных матриц вида
b
(о d) «-^^ (о !-')
В этой главе мы можем забыть про неунимодулярный случай.
Модулярная функция встречается и в несколько более общей
ситуации, чем рассмотренная выше. Пусть т: G-*G —
топологический и групповой автоморфизм группы G или ее
антиавтоморфизм, т. е. такое отображение, что {xyY = у'^х^. Результат
действия отображения т на элемент л: е G мы обозначаем х^
или '^х. В силу единственности меры Хаара, существует
положительное число Д(т), такое, что
\^f[x')dx = ^[x)^f{x)dx.
поскольку выражение слева есть нетривиальный инвариантный
положительный функционал на C<,(G). Выполняется очевидное
правило композиции:
А (та) = А (т) А (а).
Во многих приложениях T^ = id и, следовательно, А(т)= I, т. е.
автоморфизм т унимодулярен. Для матричных групп это имеет
место, например, если т — транспонирование.
Важный пример унимодулярной группы — полная матричная
группа:
G = GL„{R).

1& 1. Общие результаты
Формула замены переменных показывает, что мера Хаара на G
равна
Idetjcl" '
где d'^x — мера Лебега на линейном пространстве п X
«-матриц. Приведенная мера на GL„(R) есть, таким образом, дву-
сторонне инвариантная мера Хаара. Поскольку
GL2+(R) = SL2(R)XR^,
где GLt (R) — группа 2 X 2-матриц с положительным
определителем и R"*"—группа положительных вещественных чисел, левая
мера Хаара на SL2(R) инвариантна также и справа, т. е. группа
SL2 (R) унимодулярна. Можно привести и более красивое
доказательство: заметим, что правая и левая меры Хаара
отличаются на непрерывный гомоморфизм данной группы в группу
положительных вещественных чисел, однако у группы SLzCR)
не существует таких нетривиальных гомоморфизмов
(рассматривая классы сопряженных элементов и используя различные
разложения SL2(R). приведенные далее в этой книге, читатель
сможет доказать это в качестве упражнения). Позднее мы дадим
явное описание меры Хаара на SL2(R) при помощи различных
координат и поэтому не будем сейчас обсуждать эти вопросы
более подробно.
Вернемся к произвольной локально компактной группе G.
Пусть я — представление G в пространстве Я, ф е €^{0).
Определим отображение
я': С, (G) —End Я,
полагая
я' (ф) о = \ Ф {х) л (х) V dx.
Интеграл сходится, поскольку x*-^(f{x)n{x)v — непрерывное
отображение с компактным носителем из группы G в
пространство Я. (По поводу интегрирования функций со значениями
в банаховом пространстве см., например, Ленг [!]')•)
Пусть a^^G; положим ХаЩ{х) = (^{а~^х) (это обозначение
сохранится до конца параграфа). Тогда из левоинвариантности
меры Хаара немедленно получаем
(1) я (а) я'(ф) = я'(тдф).
') На русском языке изложение теории векторного интегрирования можно
найти в книге У. Рудина «Функциональный анализ», «Мир», М., Г975. —
Прим. ред.

§ I. Представления алгебры Cc(G) 19
Более того, отсюда следует, что я' есть кольцевой гомоморфизм,
т. е. что
(2) я' (ф * ij)) = я' (ф) я' (ij)).
В самом деле,
I = У(ф * ij)) (а;) я (х) dx =
я' (ф * lj)) = \ I
-\у
= \ \ Ф [ху-^) ^ {у) ^ {X) dx dy.
Переставим порядок интегрирования и заменим х на ху\ тогда
последний интеграл запишется в виде
\ \ ф (д;) ij) (г/) я (а:) я (г/) dx dy = я' (ф) я' (ij)).
аа
В приведенном доказательстве мы для простоты опустили
вектор V, к которому применяются оператор я' (ф * ij)) и все
операторы под знаком интеграла, однако все интегралы мы
понимаем в сильном смысле').
Поскольку функция ф имеет компактный носитель и
представление я локально ограничено, то оператор я' (ф) ограничен,
т. е. я' (ф) е End Я.
Если я — ограниченное представление, то вместо функции ф
с компактным носителем мы могли бы взять функцию/eL'(G);
формулы (1), (2) останутся при этом сгграведливыми. Другими
словами, представление я' продолжается на пространство L' (G)
и, более того, имеет место неравенство
(3) - |яЧ/)1<С||/||,.
Следовательно, я' — непрерывный линейный гомоморфизм
нормированной алгебры V (G) в алгебру всех ограниченных
операторов в пространстве Я, т. е. представление алгебры L' (G)
в пространстве Я.
EcMi Я — гильбертово пространство и представление л
унитарно, то справедлива также формула,
(4) я'(ф-) = я'(фГ,
где ф' —такая функция, что ф*(а:) = ф(а:-''). Это утверждение
непосредственно вытекает из определений.
Зная операторы я'(ф) при феСд(О), можно следующим
образом восстановить операторы я (а) для a^G. Назовем ио-
') То есть как интегралы от вектор-функций со значениями в
пространстве операторов снабженном сильной операторной топологией. — Прим. ред.

20
/. Общие результаты
следовательностью Дирака последовательность вещественных
функций с компактным носителем, удовлетворяющих
следующим условиям:
DIR 1. Фп^О при всех п.
DIR 2. \ф„(а:)^а:=1 при всех п.
а
DIR 3. При достаточно большом п носитель функции ф_
содержится в любой наперед заданной окрестности единицы в и.
Последнее условие показывает, что при больших п площадь,
ограниченная графиком функции ф„, сосредоточена в
окрестности начала. Последовательность Дирака выглядит так, как
Рис. 1.
показано на рис. 1. Очевидно, что последовательности Дирака
существуют. Если группа G имеет, подобно SLjCR), гладкую
структуру, то можно построить последовательность Дирака,
состоящую из бесконечно дифференцируемых функций. Часто
бывает удобнее пользоваться вместо DIR 3 следующим более
слабым условием:
DIR 3'. Пусть V — произвольная окрестность единицы в G,
Z — ее дополнение, 8 > О — любое вещественное число. Тогда при
достаточно больших п
\ ф„ {х) dx < 8.
Другими словами, вместо того чтобы предполагать, что
носители функций ф„ стягиваются к единице, мы накладываем
соответствующее интегральное условие. Более сильное условие
несколько нагляднее; его достаточно для большинства прило-

§ 1. Представления алаебры Cc(G) 21
жений. Когда иам понадобится условие DIR 3', мы будем
предполагать, что читатель может самостоятельно проверить
требуемые утверждения о сходимости и убедиться в том, что
доказательства проходят без изменений.
Как будет упомянуто впоследствии, при изучении
аналитических векторов, условие DIR 3' становится существенным,
когда мы хотим, чтобы функции ф„ были аналитическими (они
не могут иметь компактный носитель).
На протяжении нескольких первых глав этой книги мы будем
заниматься, в основном, общими свойствами представлений,
связанными с интегрированием и гладкой структурой на группе.
Поэтому все, что нам потребуется знать о последовательностях
Дирака,— это их определение. Однако полезно знать, что в
некоторых хорошо известных операторах свертки используются
последевательности Дирака. Приведем примеры таких
последовательностей на вещественной прямой.
(i) Пусть ф —гладкая положительная функция на R с
компактным носителем, такая, что
5 Ф(0й/==1.
Тогда ф„(/) = пф (ni) — последовательность Дирака.
(ii) Пусть ф(/) = я~'/2е~'' и ф„ задается той же формулой,
что и выше. Тогда {ф„} — последовательность Дирака.
(iii) Положим
Фе(0=4-"?ТР'-
Тогда {фг}^ ^ Q — семейство Дирака (в очевидном смысле;
чтобы получить последовательность Дирака, достаточно
положить е„ = 1/п).
В примерах (ii) и (iii) множитель, содержащий л, введен для
нормировки. Проверка того, что приведенные
последовательности— действительно последовательности Дирака, доступна
первокурснику. Заметим, что носители функций в примерах (ii)
и (iii) не компактны. Пример (ii) будет полезен нам при
изучении аналитических векторов. Примером (iii) мы воспользуемся
в § 3 приложения 2. Примеры последовательностей Дирака
дают также ядро Фейера и ядро Пуассона в теории рядов
Фурье. Для изучения общих свойств последовательностей
Дирака явные формулы несущественны. Мы напомним сейчас эти
свойства и воспроизведем некоторые основные теоремы об
аппроксимации из книги Ленга [1].

22 /. Общие результаты
Пусть {ф„} — последовательность Дирака. Тогда для любого
вектора V ^ Н последовательность {л^ (ф„) v} сходится к v.
Доказательство. Имеем
\ ф„ {х) n{x)v dx — v = \ [ф„ (х) л (х) — ф„ (х)] V dx =
о о
= ^(fn(x)[!i(x)v — v]dx,
где S„ — носитель функции ф„. Из условия непрерывности
представления ясно, что последний интеграл стремится к О при
п-уоо.
Пусть a^G. Если {ф„} — последовательность Дирака, то
{таФп} — последовательность Дирака в точке а (в очевидном
смысле). Из (1) ясно, что
"' (т^аФп) v->'n{a)v
при п->оо. Таким образом, вектор n(a)v можно получить как
предел я'(ф)о при подходящем выборе феС<,(0).
Пусть W cz Н — подпространство. (Термин подпространство
мы будем употреблять только для замкнутых подпространств;
в противном случае мы будем говорить линейное подмножество.)
Под плотным подмножеством мы всегда подразумеваем плотное
линейное подмножество. Подпространство WczH будем
называть G-инвариантным, если n{x)W czW для всех лгеО.
Аналогично определяется С(,(0)-инвариантность.
Можно дать и более общее определение. Пусть S —
семейство операторов в банаховом пространстве Я. Будем говорить,
что подпространство W cz Н S-инвариаитно, если AW cz W для
всех операторов А из S. Пусть Wo — плотное линейное
подмножество W. Если оно S-инвариантно, то, очевидно,
подпространство W тоже S-инвариантно.
Из полученного нами результата об аппроксимации
заключаем:
Подпространство W cz И является G-инвариантным в том и
только в том случае, когда оно Сс{0)-инвариантно.
Пусть si- — плотное подмножество в L' (G). Предположим,
что представление я ограничено. Подпространство W czH является
G-инвариантньш в том и только в том случае, когда оно зФ-ин-
вариантно.
Для удобства читателей напомним свойства операторов
свертки в пространстве L' (G), задаваемых последовательностью
Дирака.

§ 1. Представления алгебры C^(G) 23
Пусть f е О {G) и Z — компактное множество, на котором
функция f непрерывна. Пусть {ф„} — последовательность Дирака.
Тогда последовательность функций ф„ * / сходится к функции f
равномерно на множестве Z.
Доказательство. Имеем
(Ф„ * /) (х) = 5 Ф„ {ху-^) f {у) dz/ = J ф„ (у) f iy-^x) dy,
fix)=\<(>niy)f(x)dy.
Следовательно,
(ф„,* /) W - / W = 5 [/ iy-'x) - f ix)] ф„ iy) dy.
Существует такая окрестность единицы U cG, что если у eU,
то для всех а: е Z имеем
\f{y-'x)-fix)\<B.
При большом п носитель функции ф„ содержится в U;
следовательно, можно интегрировать по области U и наш интеграл
не превосходит е. Утверждение доказано.
Носитель функции ф„ * / содержится в области (supp ф„) X
X (supp /), поскольку подынтегральное выражение в свертке
отлично от нуля только при А:г/-'е5иррф и г/е supp/.
Следовательно:
Если f — непрерывная функция с компактным носителем, то
последовательность {ф„ * /} равномерно сходится к функции f на
компактном множестве (supp ф„) • (supp /) и равна нулю на его
дополнении. Таким образом, {ф„ * /} сходится к f в топологии
L4G).
Поскольку множество С^. (G) плотно в О (G), мы получаем
также следующее утверждение:
Пусть / S L' (G). Тогда последовательность {ф„ * /} сходится
к функции f в топологии 0{G).
Доказательство. Найдем сначала такую функцию ф из CdG),
что IIФ — f 111 < е. Тогда
II Фп * f — / 111 < II Фп * f — Фп * Ф 111 + II Фп * Ф — Ф 111 + IIФ — / 111-
Так как для любых функций g, Л е L' (G) справедлива оценка
ll^*A||i<||g||i||A||| и, в силу условия DIR2, ||ф„||1=1, наше
утверждение становится очевидным.

24 /. Общие результаты
Аналогичные рассуждения пригодны для любого
пространства L'', 1^р<оо. Для наших целей будет достаточно
рассматривать пространство L^.
§ 2. Критерий полной приводимости
Пусть я: G-yQL (Я) и я': G-*- GL [Н') -^ представления. Мор-
физмом представления я в представление я называется
непрерывное линейное отображение А: Н-*Н', такое, что для любого
ж S G следующая диаграмма коммутативна:
{В литературе морфизмы иногда называют сплетающими
операторами.) Будем говорить, что А — вложение, если А —
линейный топологический изоморфизм пространства Я на
подпространство в Я'. Будем говорить, что А — изоморфизм, если
существует такой морфизм В представления я' в
представление я, что АВ и ВЛ —единичные операторы в пространствах Я
я я' соответственно. Изоморфизм называют также эквивалеит-
«остью. Если Я, Я' — гильбертовы пространства, а
представления я, я' унитарны, мы можем ограничиться унитарными
отображениями, т. е. потребовать, чтобы оператор А был унитарным.
Из контекста всегда будет понятно, накладывается или нет это
дополнительное ограничение. Мы будем говорить, что
представление я входит в я', если существует вложение я в я'.
Представление р: G-*GL(E) называется неприводимым, если
пространство Е не содержит инвариантных подпространств,
отличных от {0} и самого В. Пусть S — некоторый набор
операторов в Е. Будем говорить, что пространство Е является S-не-
лриводимым, если в £ не существует S-инвариантных
подпространств, отличных от {0} и Е.
Пусть пространство Я гильбертово и представляется в виде
прямой суммы инвариантных подпространств:
H = Ei®E2® ... ®E„®F.
Если каждое подпространство Ei неприводимо и G-изоморфно
(относительно я) пространству (р, Е), а F не содержит
подпространств, я (О)-изоморфных Ei, то мы будем говорить, что
подпространство В входит в Я с кратностью т. Легко видеть,
что в этом случае если
Я = Е[®Е'^® ... ф£;фГ

§ 2. Критерий полной приводимости 25
— любое разбиение Н в прямую сумму, причем
подпространства E'l я(0)-изоморфны подпространствам Ei и представление
(р, Е) не входит в F', то г = т. Доказательство этого
утверждения сводится к стандартным алгебраическим фактам о
полупростых эндоморфизмах; см. по этому поводу Ленг [1, гл. VIII,
упр. 19]'). Число т мы будем называть кратностью
представления р в разложении представления я (или пространства Е
в разложении Н).
Пусть Н — гильбертово пространство, я — представление
группы G в Н. Будем говорить, что пространство Н вполне
приводимо относительно я или что представление я вполне
приводимо, если Н разлагается в ортогональную сумму
неприводимых подпространств. Мы будем записывать эту прямую сумму
в виде
Я= ФЯ„
i el
где / пробегает множество индексов /, Hi — взаимно
ортогональные инвариантные подпространства я Н — замыкание
линейной оболочки подпространств Hi. Замыкание мы обозначаем
крышкой над знаком прямой суммы, который обозначает
прямую сумму в алгебраическом смысле. Мы будем говорить также,
что семейство {Hi} есть ортогональное разложение
пространства Н.
Пусть А: Я-> Я —оператор (непрерывное линейное
отображение). Напомним, что оператор называется компактным, если
он переводит ограниченные множества в относительно
компактные (т. е. множ-ества, замыкание которых компактно).
Эквивалентное определение: оператор А компактен, если для всякой
ограниченной последовательности {о„} последовательность {Ло„}
содержит сходящуюся подпоследовательность. Вектор v^H
называется собственным вектором оператора А, если Ao^^Xv
для некоторого комплексного числа %. Зафиксируем некоторое
Я, S С; множество всех векторов v ^Н, включая О, таких, что
Ах = iv, образует подпространство Н^ — собственное
подпространство оператора А, соответствующее собственному
значению X.
Спектральная теорема для компактных операторов. Пусть
А — компактный эрмитов оператор в гильбертовом
пространстве Е. Тогда семейство его собственных подпространств {Ef},
где Я, пробегает множество всех собственных значений
{включая 0), есть ортогональное разложение пространства Е.
') См. также А. А. Кириллов, Элементы теории представлений, «Наука»
М.. ]»972. — Прим. мрев.

26 /. Общие результаты
Доказательство. Пусть F — замыкание линейной оболочки
всех подпространств £>,. Пусть Н — ортогональное дополнение F.
Тогда подпространство Н инвариантно относительно
оператора А и А индуцирует на Н компактный эрмитов оператор,
не имеющий собственных значений. Нужно показать, что Я = {0}.
Это вытекает из следующей леммы.
Лемма. Пусть А — компактный эрмитов оператор в
гильбертовом пространстве Н=}^{0}. Положим с:=|Л|. Тогда по
крайней мере одно из чисел си — с является собственным
значением оператора А.
Доказательство. Существует последовательность векторов {х„}
из Я, такая, что |а:„| = 1 и |(А>с„, а:„)|->|Л|. Переходя, если
это необходимо, к подпоследовательности, мы можем
предположить, что
{Ах„, x„) -> а
для некоторого числа а, причем а = ± | Л |. Тогда
О ^ t Ах^ — аХп Р = {Ахп — ах„. Ах^ — a,v„) =
^\AxJ-2a{Ах,,, ^„) + а^I x„ Р^а^ - 2а(Ас„, x„> + а^.
Правая часть неравенства стремится к О при п-*оо. Так как
оператор А компактен, то, переходя к подпоследовательности,
можно считать, что последовательность {Ах„} сходится к
некоторому вектору у\ тогда последовательность {ад;„} также должна
сходиться к этому вектору. Если а = О, то | Л | =»= О, так что
Л = О, н утверждение леммы тривиально. Если а ^ О, то
последовательность {Хп) сама должна сходиться к некоторому
вектору X, и тогда Ах = ах, так что а — искомое собственное
значение. Это доказывает нашу лемму, а вместе с ней — и
теорему.
Заметим, что в каждом подпространстве Е\ существует
гильбертов базис, состоящий из собственных векторов. В самом
деле, таким свойством обладает любой гильбертов базис Яд,,
поскольку все ненулевые векторы из Е^ — собственные. Поэтому
в пространстве Е также существует гильбертов базис,
состоящий из собственных векторов. Таким образом, мы получили
точный аналог спектральной теоремы для конечномерных
пространств. Более того, мы получаем ряд дополнительных фактов,
которые тривиально вытекают из доказанной теоремы.
Все подпространства Е^ при % ФО конечномерны; в
противном случае существование счетной последовательности ввйторов
из гильбертова базиса в Е^ противоречило бы компактности
оператора. По той же причине для любого фиксированного
числа г > О суи^ествует лишь конечное множество собственных

§ 2. Критерий полной приводимости 27
значений Я,, таких, что |Я, |^г. Таким образом, если оператор А
имеет бесконечное множество ненулевых собственных значений,
то нуль является единственной точкой сгущения этого
множества. Поэтому если Я — гильбертово пространство и Л
^эрмитов компактный оператор, то пространство Н разлагается
в ортогональную сумму собственных подпространств:
оо
А, (-1 '
где собственные значения занумерованы в порядке убывания
модулей: |Я,{+11^1 Я,; ] и limA,i = 0.
Подалгебра ^ операторов в пространстве Н называется
♦-подалгеброй, если вместе с любым оператором Л s j^ она
содержит также и сопряженный оператор А*.
Теорема 1. Пусть бФ есть *-подалгебра компактных
операторов в гильбертовом пространстве Н. Тогда Н вполне
приводимо относительно зФ и каждое неприводимое подпространство
входит в разложение Н с конечной кратностью.
Доказательство. Пусть {Е^ — максимальное ортогональное
семейство л^-неприводимых подпространств, а /="
—ортогональное дополнение линейной оболочки семейства {£;}. Так как зФ
есть *-подалгебра, то подпространство F тоже J^-инвариантно.
Поэтому достаточно доказать, что в предположениях теоремы
существует л^-неприводимое подпространство. Сделаем это
следующим образом.
Если А^бФ, то
А = —^^-^ + г
2( '
и, значит, в ^ существует элемент Л = Л* ^^ 0. Пусть М —
инвариантное подпространство, отличное от {0}. Тогда сужение
алгебры зФ па М удовлетворяет условиям теоремы. Пусть
% ФО — собственное значение самосопряженного оператора Л.
Среди всех ^^инвариантных подпространств М Ф {0} выберем
то, для которого собственное подпространство
А/>, = {о е М\ Av = Я,у}
имеет наименьшую положительную размерность. Выберем
ненулевой вектор о из подпространства Mj,. Тогда sФv<zlM и
.я^о—инвариантное подпространство. Мы утверждаем, что это
подпространство неприводимо. Предположим, что £ =7^ {0} —
инвариантное подпространство, Е cz зФ-п. Можно написать
« == 0£ + ■о'е.

28 /■ Общие результаты
где ve^E, v'eJ-E. Заметим, что
Хо = Av = Ave + Ave = Xve + ^v'e-
Таким образом, Ve и v'e — собственные векторы оиерагора А
с собственным значением X. Если один из них, скажем ve,
равен нулю, то у s £, откуда j>^v = Е. Если же оба этн
вектора отличны от нуля, то приходим к противоречию: Ej^aMi^
и dim £■>, < dim Мд,. Следовательно, подпространство s4-v непри-
водимо, и наша теорема доказана.
Замечание. Для того чтобы найти неприводимое
подпространство, достаточно, чтобы в алгебре зФ содержался хотя бы
один компактный эрмитов оператор.
§ 3. Квадратично интегрируемые ядра и операторы
Гильберта — Шмидта
Один тип ядер и операторов будет встречаться нам
достаточно часто, так что стоит отдельно упомянуть их здесь, а не
в приложении или тогда, когда они понадобятся нам в
первый раз. Они дадут нам примеры компактных операторов.
Теорема 2. Пусть {X, ЗЯ, dx) и (Y, 31, dy) — пространства
с мерой; предположим, что пространства L^(X) и L^(y) сепа-
рабельны. Пусть q^^ L?{dx®dy). Тогда оператор f*-^Qf, такой,
что
Qf{x)^\q(x,y)f{y)dy,
у
есть ограниченный компактный оператор из L^ (F) в L? {X), причем
IQKIklli.
Доказательство. Пусть f ^ L? (7). Из условий теоремы
вытекает, что при почти всех значениях х функция Qx, определяемая
равенством qx{y) = (){x, у), также принадлежит L^(Y).
Следовательно, их произведение fqx принадлежит V (У). В силу
неравенства Шварца
IQfWP^II/IIMkxI.
Интегрируя это неравенство, получаем
\\Qf\?,= \\Qf{x)fdx<\\f\^\\\q{x,y)fdydx^\\q\Uf\l
Отсюда следует, что IQI^IUlk; таким образом, оператор Q
ограничен.

§ 3. Квадратично интегрируемые ядра и операторы Гильберта — Шмидта 29
Пусть {фг}, {гр/} — ортонормнрованные базнсы в L^{X) и I*(F)
воответственно. Положим
^tiix,y) = if{{x)ylf,{y).
Тогда {9j/} — ортонормированный базис в L^ (^ X Y). Чтобы
убедиться в этом, заметим, во-первых, что векторы 9^/ взаимно
ортогональны н нормированы. Предположим, что g&L^{XXY)
ортогональна ко всем 9,-;. Тогда
J 9j (х) dx J ij)/ (у) g {x, y)dy = 0
X Y
при всех значениях i и /. Следовательно, функция
x'-*'\^j{y)g{x, y)dy
равна нулю при всех х, за исключением точек, принадлежащих
некоторому множеству S czX нулевой меры. Если хф8, то
g{x, у) = 0 для почти всех у. Следовательно, по теореме Фубини,
six, г/) = О для почти всех {х, у)е.ХУ^У.
Пусть q=Yj cLifiii — разложение функции q в ряд в 1?{ХУ^У)
с коэффициентами ац. Пусть
— конечный отрезок этого ряда. Немедленно проверяется, что
оператор Q„ с ядром q^ имеет конечномерный образ. В самом
деле, если 9 — функция на X XY, такая, что 9{х, г/) = ф(х)ij)(у),
то образ соответствующего оператора имеет размерность 1.
Мы уже доказали неравенство
\Qn-Q\<\\qn-q\\2,
выражение справа стремится к О при л->оо. Итак, компактные
операторы Q„ сходятся по операторной норме к оператору Q.
Следовательно, Q тоже компактен. Теорема доказана.
Сделаем теперь несколько замечаний формального характера
о свойотвах следов операторов, задаваемых ядрами. Заметим,
что Фг ® ф/ — ортонормированный базис в пространстве L^ {ХУ,Х).
Напишем разложение Фурье ядра q относительно этого базиса:
Формально можно ожидать, что след оператора Q задается
формулой
tr Q = 2] <<3ф„, Ф»> = 2 2 S 5 с</ф< (д;) фу (у) ф„ (у) фд (д;) dy dx.

30 1- Общие результаты
В силу ортогональности функций ф/, ф„ ясно, что последнее
выражение сводится к
trQ=Sc„„-
п
С другой стороны,
\^qix,x)dx = Y,Cij^ Фг (х) ф/ (х) dx = JJc^».
i.t п
Таким образом, мы получаем формально:
tTQ^Y,^nn=\q{x,x)dx.
Для того чтобы придать смысл этим вычислениям, нужно
указать достаточные условия, которые гарантировали бы
сходимость всех рядов и независимость суммы
S (Qfm Фп)
от выбора ортонормированного базиса. Мы вернемся к этим
вопросам при обсуждении формулы Планшереля. Пока же мы
будем рассматривать интеграл
\ q {х, х) dx
X
как определение следа всякий раз, когда оператор может быть
определен при помощи непрерывного ядра q.
§ 4. Меры Планшереля
Пусть Z, У— пространства с мерами dx и dy.{y)
соответственно. Пусть ф = ф(а:, г/) — функция на их произведении.
Тогда ф задает оператор Ф из пространства функций на X
в пространство функций на Y, действующий по формуле
X
и транспонированный оператор
m){y)=\f{x)<f{x,y)dx,
(Фё) W = 5 Ф (*. у) giy)d\i iy).
(Иногда мы будем использовать противоположное соглашение,
меняя местами 'Г' и 'Ф.) Оператор 'Ф обозначается также Ф*, т. е.
К"-^ ё) l-t) = ^ Ф {х, у) g {у) dn [у).

§ 4. Меры Планшереля 31
Тогда Ф* — сопряженный оператор к Ф относительно скалярных
произведений, задаваемых формулами
</i. f2}=\fi{x)fz{x)dx на X,
(gu g2)vL = 5 §1 (у) SAy) с^Ц (у) на Y;
иначе говоря, справедливо равенство
Это немедленно вытекает из следующего формального
вычисления:
<Ф/. -?)^ = 5 5 /(х)Ф{х, у)g{y)dxdy.{у) =
Y X
S / W 5 Ф {X, у) g{у) dn {y)dx = (/. Ф*^).
Все эти формулы применимы в различных ситуациях, когда
входящие в них интегралы абсолютно сходятся, например когда
(f^L^(XXY) и f^L^X) или феСЛХХП и feC,{X).
В каждом конкретном случае нужно точно указывать область
определения оператора.
Равенство ф* = Ф''^ имеет место в том и только в том
случае, когда оператор Ф унитарен. Доказательство очевидно.
В некоторых приложениях мы будем сначала доказывать, что
оператор Ф унитарен, а затем на основании изложенного
формализма делать вывод, что действие оператора Ф"' на
функции g, для которых все рассматриваемые интегралы сходятся,
например на функции с компактным носителем на локально
компактных пространствах, задается эрмитово сопряженным
ядром.
В приложениях мы всегда будем указывать конкретные
функциональные пространства, на которых все интегралы
сходятся. В теории представлений мы начинаем с X = G (в этой
книге G = SL2(R)), а в качестве dx берется мера Хаара.
Пространства с мерой {X, dx) и {Y, dy) всегда будут заданы
«еетественным» образом. Наша задача будет состоять в том,
чтобы найти такую положительную функцию Р на У, что для
меры dn (у)'^ Р{у)dy справедливо равенство ф* = Ф~'. Другими
словами, пусть транспонирование определяется относительно
меры d^iy), т. е.
{'Фg){x) = \q>{x,y)g{y)P{y)dy.

32
/. Общие результаты
Тогда мы требуем, чтобы Ф*Ф = id в подходящем пространстве
функций на X. Если это условие выполнено, мы будем
называть P{y)dy мерой Планшереля для функции ф; формула
Ф*Ф = id называется формулой обращения Планшереля.
В действительности ситуация с формулой Планшереля для
некоммутативных групп (в частности, для SL2 (R)) несколько более
сложная, хотя формально вполне аналогичная. Дело в том, что
в этом случае функция ф операторнозначная и в формулу
обращения нужно включить операцию взятия следа. Ср. конец
гл. VIII, посвященной формуле Планшереля.
ws
-3
-1
-+—I—*—i—h
Рис. 2.
Пусть G — множество классов эквивалентности
неприводимых унитарных представлений группы G. Обычно G или какое-
нибудь его подходящее подмножество можно параметризовать
при помощи аналитического пространства Y (множества корней
аналитических уравнений), снабженного «естественной» мерой dy
(например, если Y — кусок евклидова пространства, то dy —
мера Лебега). Мы увидим, что для группы Sl2(R)
пространство Y состоит из двух вертикальных прямых н изолированных
точек, как это изображено на рис. 2. В действительности это
пространство параметризует только' часть множества G. В этом
случае мера dy на прямых совпадает с мерой Лебега, а точки
имеют диснретную меру.
Прежде чем рассматривать формулу Планшереля в полной
общности, мы займемся несколько более простой задачей —
вычислением меры Планшереля только для специального класса
функций, двусторонне инвариантных относительно
максимальной компактной подгруппы группы G. Для этого нам
потребуется сначала рассмотреть представления компактных групн,
что будет сделано в следующей главе.

II. КОМПАКТНЫЕ ГРУППЫ
§ 1. Сужение представлений группы S£j(R)
на ее максимальную компактную подгруппу
Важную роль в теории представлений полупростых групп Ли
играют максимальные компактные подгруппы.
В этом параграфе мы рассмотрим представления
максимальной компактной подгруппы К группы SIjCR), группы
вращений окружности, т. е. группы матриц вида
/ cos 9 sin9N
'(^^ = l-sin9 cos9j-
Излагаемая нами теория представляет собой частный случай
общей теории представлений компактных групп. Она послужит
хорошим введением в рассматриваемый круг вопросов.
Характером группы К называется непрерывный
гомоморфизм К в единичную окружность; характеры нумеруются
целыми числами:
Возьмем в качестве G группу SLjIR) или GL^(R) (группу
матриц с положительным определителем). Для любого элемента
у е G и для любой функции / s С^ (G) положим
Г(9, 90 = f(r(9)z/r(9')).
Обозначим символам 5„,;„ подпространство пространства €^{0),
состоящее из всех функций f, удовлетворяющих условию
при всех г/ е G и при всех вещественных значениях 9, 9'.
Лемма 1. Линейная оболочка подпространств Sn,m плотна
в C^{G) в топологии равномерной сходимости. Более точно, для
любого 8 > О ы любой функции f ^С^ (G) найдется такая
функция g ^ zl ^п, т> ''^о ее носитель содержится в множестве
/C(SUppM U||/-gL<8.
Доказательство. Пусть
я я
fn. т{у)=^\ 5 / (г (9) уг (90) е'^ве^-б' dd d9'
—я —я
2 Зак, 5S9

34 77. Компактные группы
— коэффициент Фурье функции f. Тогда носитель функции /„,„
содержится в множестве /C(suppf)/C- Ядра Чезаро —Фейера
от одной переменной
( М-1 \
IE ZH
'^ N=0 inKAf ^
образуют последовательность Дирака. Произведения двух таких
ядер от переменных 9 и 9' образуют последовательность Дирака
от двух переменных. Обозначим ее {Cjv((6, 6')}^^|. Пусть
Р« Сл{ — свертка функции f с ядром С^ (мы рассматриваем
f и См как функции на произведении двух окружностей). Из
определений ясно, что {f * C^f) (О, 0) представляется в виде
суммы членов вида c„^„f„^„{y) с коэффициентами с„,„,
появляющимися из суммы в ядре Чезаро. Последовательность
(/" * Cjvf) (О, 0) сходится к функции f (О, 0) = f (г/). Проверим,
что сходимость равномерна по у. Нам нужно оценить разность
\ \ {!" (6, ео Сл,(- е, - 60 - f (о, о) с^(- е, - е')] de de'.
Зафиксируем е > 0; существует такая окрестность U точки
(О, 0), что
где 'S'f/— дополнение U. Напомним, что
Таким образом, наша разность не превосходит
sup 1Г(в, 90-/^(0, 0)| + 2||flLUcM.
<в, e')st/ ^jJ
Так как f имеет компактный носитель, неравенство
lf(r(e)r/r(e'))-f(i/)l<e
справедливо для всех (6, 6')ef/ равномерно по у, если окрест
ность и достаточно мала. Доказательство закончено.
Лемма 2. Справедливы следующие соотношения:
(О 'S„,m*5j,, = {0}, если тф1;
(и) Ьп^ т =^ «Ьт» п\
(Hi) S„.„*5„.,cS„.,.

§ I. Сужение представлений группы SLzCR) 35
Напомним, что для любой функции ф на группе G мы
определили функцию ф* формулой
Ф*и) = фи-').
Доказательство. Пусть f^S„,m, g^Si^^. Рассмотрим свертку
функций f, g:
{f*g){x)=\f{xy-')giy)dy.
Сделаем в этом интеграле замену переменной y^—^r{Q)y. Так
как группа G унимодулярна, интеграл инвариантен относительно
преобразования у>-^у~^. Отсюда и из двусторонней
инвариантности меры Хаара вытекает, что значение {f*g){x) не меняется
при умножении на е''»^е-''^. Это возможно, лишь если
if*g){x) = 0; таким образом, утверждение (i) доказано.
Остальные два утверждения доказываются аналогично, и мы
предоставляем сделать это читателю.
Из леммы 2 следует, что подпространство S„.„ является
алгеброй относительно свертки. Доказательство этого
утверждения очевидно. Мы рассмотрим сейчас более тонкое свойство.
Лемма 3. Алгебра 5„,„ коммутативна.
Так как мы рассматриваем сейчас алгебру 5„, „ при
произвольных п, а не только алгебру 5о,о, мы приведем
доказательство в полной общности. Читателю полезно взглянуть на более
простое доказательство для случая биинвариантных функций,
приведенное в начале гл. IV. Это доказательство принадлежит
И. М. Гельфанду. Обобщение, которое мы приводим здесь,
было дано Силбергером (А. Silberger, Proc. Amer. Math. Soc,
21 (1969), 437—440). Этот результат был предназначен для
использования в теории представлений р-адических групп.
Пусть (т —автоморфизм или антиавтоморфизм унимодуляр-
ной группы G. В силу единственности меры Хаара существует
положительное число А((т), такое, что для любой функции f из
Cc{G) справедливо равенство
^f{x")dx = ^ia)\^f{x)dx.
Ясно, что А (сг^) = А ((т) А ((т); таким образом, если а^ = 1, то
А((т)= 1. Итак, мера Хаара инвариантна относительно
преобразования xi-^x°. Вместо х^ мы будем иногда писать "л.

36 fl- Компактные группы
Теорема I. Пусть G — локально компактная унимодулярная
группа и К — ее компактная подгруппа. Предположим, что
выполнены следующие условия:
(i) существует антиавтоморфизм х порядка 2 группы G,
такой, что k' = /е~' для всех k е К;
(ii) пусть S — множество элементов s^G, таких, что s^ = s;
тогда G = SK',
(iii) существует автоморфизм а порядка 2 группы G, такой,
что k° = /е~' для всех k^K, а для всех s е 5
выполнено равенство s° = k\skT^ tipu некотором /е, е К.
Пусть р: /С -»■ С — характер К', обозначим символом 5р, р
множество функций f из Cc{G), таких, что
f{kiXki) = f>{k{)fix)f>{k2)
при всех x^G, ki, k^^K- Тогда алгебра Sp, р коммутативна.
Доказательство. Положим /* (;с) = / (;с^). Тогда if * g)* = £**[*•
С другой стороны, положим f (х) — f (л°). Тогда (f * g)' = f'* g'.
Докажем первое равенство (доказательство второго проще).
Имеем
{g * fT W = (g * f) (X') = \ g ix^y-') f (y) dy.
Аналогично
(f * * Л W = \ r ixy-') g* iy) dy=\f i-y-^x^) g iy-) dy.
Сделаем во втором интеграле последовательные замены
переменных у*—* у'', у<'-^х^у, у^-^у~^. Это и завершает доказательство
нашей формулы. Для функций fe5p, р имеем, кроме того,
f*=f'. В самом деле, достаточно проверить, что f (х") = f (х'^).
Напишем x = sk. Тогда
f(/) = f(/e-'s^) = p(/er'f(s),
f{x") = f{s4-') = f{kiskT'k-') = (>{k)-'f{s);
тем самым наше утверждение доказано. Получаем
f*g = g*f,
что и требовалось доказать.
Пример. Пусть G — GLtiR) или SL^CR), /С —группа враш,е-
ний окружности. Положим
X'' = *х (транспонированная матрица),
xf = Y*Y» где Y
< -D-

§ f. Сужение представлений группы SIzfR) 37
В силу стандартного полярного разложения матриц все условия
теоремы 1 выполнены. Напомним, как строится полярное
разложение. Пусть xsGL„(R); положим у = х^х; таким образом,
у — симметричная положительно определенная матрица. В
пространстве R" существует базис, состоящий из собственных
векторов матрицы у:
yVi=XiVi, Xi>0.
Пусть S — симметричная матрица, такая, что s^ = i/;
собственные значения матрицы s равны ± V^i- Выберем s так, что
sign det S == sign det х. Положим /j = s"'x. Тогда x = sk и
eet/e=l. Кроме того, *kk = h^s~^s~^x = ^xy-^x = *x^x-h-^x=l.
Таким образом, k — ортогональная матрица, и наше
построение окончено.
Вернемся снова к случаю G'^SL^iR) или GLtiR). Пусть
я: G~*GL{H)
— представление группы Q в банаховом пространстве Н. Для
любого целого п обозначим символом Я„ множество
элементов « е Я, таких, что
л (г (6)) V = e^^^^v.
Ясно, что Я„ —замкнутое подпространство.
Лемма 4. Предположим, что пространство Я гильбертово,
а представление я унитарно на подгруппе К- Тогда при тфп
подпространства Я„ и Я„ ортогональны.
Доказательство. Сужение л на /С унитарно. Это означает,
что я (г (6))* = л (г (— 6)) при всех 6. Пусть о е Я„, w ^ Н^ —
произвольные векторы. Имеем
(л(г(6))«, w) = e'"^{v, w) = {v, я(г(—6))аи) = е""^(о, w).
Теперь результат очевиден.
Лемма 5. Справедливы следующие соотношения:
(i) n'{S„,^HczH„;
(ii) если тфд, то я' (5„, т) Я, = {0}.
Доказательство. Пусть тф q и « — произвольный вектор
из подпространства Я^. Воспользуемся инвариантностьк.
интеграла
5 / (г/) л {у) V dy
а

38 //■ Компактные группы
относительно преобразований y>-^yr(Q). Если / е 5„ „,, то
значение интеграла не меняется при умножении на e~*'^^e*i^ и,
следовательно, равно нулю. Доказательство первого
утверждения леммы также несложно. Пусть « е Я, /е5„ „• Тогда при
/е = г(е)
л (k) л' if)v = л (k) ^fiy)л{y)v dy = \^f {у) л{ку) vdy =
а а
= \f{k-'y)лiy)vdy = e"^\'{f)v.
а
Лемма доказана.
Если вектор w принадлежит прямой сумме конечного
множества подпространств Я^, мы будем обозначать ш^ его
компоненту в Нд. Лемма 5 показывает, что при f sXs„,„
оператор л' (f) отображает пространство Я в такую прямую сумму.
Лемма 6. Предположим, что представление л неприводимо.
Тогда подпространство Я^ неприводимо относительно
подалгебры 5,.,, и если Я, =5^ {0}, то я'(5,.,) Я, ¥= {0}.
Доказательство. Пусть W — подпространство в Я^,
инвариантное относительно л' (5,, ,), причем W ф {0}, W' ф Я,.
Пусть ffi) е W, и пусть / — конечная сумма функций /„, „ eS„. „.
Тогда, по лемме 5,
Алгебра ^ = Х'5я,от плотна в пространстве Cc{G) в топологии
равномерной сходимости, согласно лемме 1. Для любой
функции f е^ проекция вектора л^{f)w на Н^ принадлежит
подпространству W. Это противоречит предположению W Ф Н^,
так как любой вектор из Нц можно аппроксимировать при
помощи последовательностей Дирака (см. § 1 гл. I).
Теорема 2, Пусть я — неприводимое представление группы G
в банаховом пространстве Н. Пусть Н„ — подпространство И,
состоящее из таких векторов v, что
л (г (6)) V = е'«««.
Если подпространство Н„ конечномерно, то его размерность
может быть равна только 1 или 0. Это всегда так, если л —
унитарное неприводимое представление в гильбертовом
пространстве.
Доказательство. Мы знаем, что подпространство Я„
неприводимо относительно л'(5„, „); так как алгебра 5„. „
коммутативна, стандартные алгебраические соображения показывают,

§ 1. Сужение представлений группы SLjCR) 39
ЧТО dim//„ = 0 или 1. Предположим, что я унитарно, и пусть
/е5„,„; тогда я'(/)* = я'(П, где функция/* определена
равенством Г W = f U"')- Немедленно проверяется, что /*е5„,„
(ср. с леммой 2, (ii)). Следовательно, я'(5„,„) является *-алгеб-
рой; теперь утверждение теоремы вытекает из леммы Шура
(см. приложение 1).
Теорема 3. Пусть л — неприводимое представление группы G
в банаховом пространстве Н. Тогда сумма подпространств Н„
плотна в Н. Если Н — гильбертово пространство и сужение
представления и на подгруппу К унитарно, то эта сумма
является ортогональным разложением пространства Н.
Доказательство. Пусть Е — замкнутая линейная оболочка
подпространств Я„. Из леммы 5 и того факта, что сумма
подпространств S^,„ плотна в Cc{G), следует, что
подпространство Е является Сс(0)-инвариантным, а значит, и G-инвариант-
ным. Поскольку представление л неприводимо, Е совпадает с Я.
Если сужение я на подгруппу К унитарно, то из леммы 4
следует, что подпространства Я„ взаимно ортогональны. Теорема
доказана.
Теоремы 2 и 3 подсказывают возможные приложения
полученных результатов к изучению представлений группы SL^iR).
Мы можем классифицировать их в зависимости от присутствия
или отсутствия подходящих подпространств Я„. В теории
сферических функций мы изучим случай, когда в разложении
пространства Я содержится подпространство Но- это равносильно
существованию инвариантного вектора относительно подгруппы К,
т.е. такого ненулевого вектора «еЯ, что n{K)v = v. Если
в пространстве представления нет такого вектора,
представление входит в дискретную серию.
В этом параграфе мы изучали разложение представления
относительно подгруппы К, используя только формальные
свойства меры Хаара и операторов свертки. В гл. VI мы вернемся
к этому разложению и воспользуемся для его изучения
свойствами производного представления алгебры Ли. Применяя
экспоненциальное отображение, мы получим гораздо более
точную информацию о действии группы. Глава VI, в основном,
логически не зависит от теории сферических функций, и
читатель сможет без труда прочесть большую ее часть
непосредственно вслед за данной главой, если он хочет понять, как
используется дифференцируемость.
Пусть л — представление группы G в банаховом
пространстве Я; предположим, что Я разложено в прямую сумму
Я=0Я«,

40 //. Компактные группы
где Я„ есть га-е собственное подпространство относительно
действия подгруппы К, которое было определено выше. Тогда
линейная оболочка подпространств Я„ плотна в
пространстве Н. Можно охарактеризовать ее чисто алгебраически.
Будем говорить, что вектор оеЯ /(-конечен, если множество
n{K)v порождает конечномерное векторное пространство.
Линейная оболочка подпространств Н„ — это множество
всех К-конечных векторов.
Доказательство. Ясно, что любой элемент из линейной
оболочки 2 ^п Д'-конечен. Обратно, предположим, что некоторый
элемент а е Я является /(-конечным. Пусть W — линейная
оболочка множества я(/() о. Конечномерное пространство W
распадается в прямую сумму подпространств W„, неприводимых
относительно я{К), причем W„cH„. Отсюда ясно, что вектор v
содержится в 2_, Я„.
Множество /(-конечных векторов мы будем обозначать Н {К).
Теорема 2 показывает, что важно знать, что размерности
подпространств Я„ конечны. Введем поэтому следующее
определение. Будем говорить, что представление я допустимо, если
пространства Я„ конечномерны при всех п. Теорема 2
означает, что каждое неприводимое унитарное представление
допустимо. Будем говорить, что представление строго допустимо,
если размерности подпространств Я„ ограничены.
§ 2. Общая теория представлений компактных групп
Максимальная компактная подгруппа группы SL,, (R), с
которой мы имели дело в предыдущем параграфе, коммутативна;
поэтому нам не потребовалась общая теория представлений
компактных групп (которая, впрочем, строится по той же схеме,
что и в коммутативном случае). Однако особенности теории,
связанные с некоммутативностью, позволяют проиллюстрировать
другие общие принципы, например формализм следов, с
которыми нам придется встретиться в гораздо более сложной
ситуации при изучении некомпактной группы SL2(R). Поэтому имеет
смысл рассмотреть теорию представлений компактных групп
в качестве введения в общую теорию.
Пусть К — компактная группа; мы предположим, что ее
мера Хаара равна единице. Пусть
я: K->GL{H)

§ 2. Общая теория представлений компактных групп 41
— представление группы К в гильбертовом пространстве Н.
Из замечания в начале § 1 гл. I мы знаем, что представление я
ограничено.
Покажем, что в пространстве Я можно ввести
эквивалентную норму, относительно которой представление л унитарно.
Для произвольного вектора « s Я положим
\vtn=\\a{k)vfdk.
к
Пусть С == max | л [k) |. Тогда | « £ < С^| о р и, следовательно,
I ^' 1„^ С| « |. С другой стороны, для любого /е S /<" имеем
|о| = |я(/е)"'л(/е)«|<С|л(/е)« I,
откуда
\n{k)v\>C-'\v\, \vL^C-'\v\.
Это показывает, что нормы | • | и | • |^^ эквивалентны; ясно,
что представление л унитарно относительно нормы | • Ij^. Таким
образом, наше утверждение доказано.
В пространстве L^iK) (относительно меры Хаара) введем
оператор правого сдвига, действующий по формуле
T{y)fix)^f{xy).
Тогда Г —унитарный оператор, поскольку
\\f{xy)fdx^\\f{x)fdx,
ибо любая компактная группа унимодулярна (любой
гомоморфизм компактной группы в мультипликативную группу
положительных чисел тривиален). Мы будем называть Т (правым)
регулярным представлением.
Пусть ф — непрерывная функция на К. Тогда
P{4')f{x) = [f{xy)q>{y)dy =
к
= 5 / (i/) Ф (^"'г/) dy = (f * ф-) {х),
к
где мы положили ф- (л:) = ф(л;~')- Мы видим, что оператор Г' (ф)
задается ядром
(х, y)'r^(f{x-'y).

42 //. Компактные группы
которое непрерывно на КУ,К. По теореме Стоуна — Вейер-
штрасса, любую непрерывную функцию на АГХ^С можно
равномерно приблизить последовательностью конечных сумм вида;
Z Фг W i'i (у)-
При любом / оператор, соответствующий ядру Ф< ® t|)<, т. е.
функции (;с, г/)|—»-фг М^фИ^/). имеет одномерный образ.
Следовательно, оператор Г'(ф) есть предел последовательности
конечномерных операторов в равномерной топологии. Таким
образом, оператор Г' (ф) компактен. Из теоремы 1 § 2 гл. I получаем
следующее утверждение:
Теорема 1. Пространство L^{K) разлагается в
ортогональную прямую сумму подпространств, неприводимых относительно
регулярного представления группы К; другими словами,
регулярное представление вполне приводимо.
Теорема 2. Пусть л; К^- Aut Я — унитарное неприводимое
представление компактной группы К. Тогда пространство Н
конечномерно.
Доказательство. Пусть ы —единичный вектор в Я, Р —
ортогональный проектор на одномерное подпространство,
порожденное вектором и. Пусть Q: Н -^ Н — непрерывное линейное
отображение, определенное формулой
Qt) = \ л {х) 'Рл {х) V dx.
Тогда оператор Q коммутирует со всеми операторами л (у),
у ^К (это сразу вытекает из двусторонней инвариантности
меры Хаара). Кроме того, Q = Q*, поскольку
(Qv, ау> = \ (л {х) 'Рл (л:) v, w) dx =
к
= \ (о, л {х)~^Рп (х) w) dx = {v, Qw).
Из теоремы 4 приложения 1 мы заключаем, что Q = XI для
некоторого вещественного числа X; константа X отлична от
нуля, поскольку подынтегральное выражение в формуле для
квадратичной формы (Qu, и) неотрицательно и строго больше
нуля в окрестности единицы. Пусть {«J — ортонормированный
базис в Н. Тогда
п
2J \ (л {х)~^Ря {х) щ, U{) dx = пХ.

§ 2. Общая теория представлений компактных групп
43
Для любого хе/С множество {я{х)и{}—тоже ортонормиро-
ванный базис. Следовательно,
п оо оо
"Z (РЯ (Х) Ui, Л {Х) Щ) < Z {Рп {Х) Щ, Л {Х) Щ) = Y. (PU{, Ui),
i-l t=l /-I
где мы положили «< = Ji(x)«;. Но Pv={v, и)и. Таким образом,
(Pu{, u'l) = ( (ы'г, и) р.
Отсюда вытекает, что
п оо
Y, (-Рл (л:) щ, я {х) ЫгХ 2 I {щ, м) Р = 1.
1-1 t-i
Интегрирование этого неравенства по К завершает
доказательство теоремы.
Замечание. Пусть л (x) = (n^ (.«)) —матричное представление
группы в конечномерном пространстве. Пусть {е\ е„} —
базис в пространстве представления, а Я,; — линейный
функционал, сопоставляющий вектору его г-ю координату. Тогда
матричный элемент представления ji</(x) равен %i{n{x)ej).
Действие операторов представления на векторы в матричной
записи выглядит следующим образом:
It,l .
^nl •
•• "ln\
•
•
•• ^ппУ
0
•
1
0
^—
"]/'
•
Я//
"nf
Вообще, если л — представление группы G в банаховом
пространстве Н, V — вектор из Я и Я, — линейный функционал на Я,
мы будем называть функцию
Х I—5- Я, (л {х) V) = Ло, л, {х)
матричным элементом представления. Если пространство Я
гильбертово, мы можем, разумеется, представить функционал %
при помощи элемента w ^ Н; матричные элементы задаются
S этом случае формулой
л: н-^ (я (л:) V, w) = п„, „, {х).

44 '/ Компактные группы
Если Пространство Н конечномерно, {е{} — ето базис и {A,J—
дуальный базис, то след представления задается формулой
Хп W = tr я W = S Kt (л (л:) et).
i
Мы использовали след в доказательстве теоремы 2. В случае
бесконечномерных представлений вопрос о сходимости рядов,
определяющих след, становится нетривиальным; мы будем
обсуждать его впоследствии в связи с конкретными
представлениями.
Пусть л, а — представления компактной группы К в
банаховых пространствах Н„ и Нд. Пусть К — линейный функционал'
на На- Тогда для любых а^ К, w ^ Н^ отображение
(1) L: V 1-^ [ X {а {ах) v) л {х'^) W dx
к
пространства На в пространство Н„ есть /С-гомоморфизм.
Доказательство. По определению,
La{y)v= [х {а (а) а (х) а {у) v) л (д;-') w dx.
к
Сделаем замену переменной X'i—^xy~^, Выражение справа
переходит при этом в л{у)Ьо, что и требовалось.
Теперь из леммы Шура (приложение 1) вытекает
Теорема 3. Пусть л, а — неэквивалентные неприводимые
представления группы К- Тогда для любых v е Нд, w s Я„,
а еЛ;
(2) \k{a{ax)v)a{x~^)wdx = 0,
к
т. е. л' {а:^^ \ == 0; матричные элементы одного представления
тривиально действуют в другом. Пусть ц — линейный функционал
на Н„; тогда
(3) \^X{a{ax)v)[i.{n{x-^)w)dx = 0.
к
Замечание. Чтобы получить формулу (3) из (2), достаточно
применить к обеим частям функционал \i. Интегрирование
перестановочно с непрерывными линейными отображениями
в пространствах значений.
Удобно иметь дело с симметричным скалярным
произведением, которое задается интегралом
[f,g\--\f{x)g{x-^)dx.

§ 2. Общая Теория представлений компактных групп 45
Теорема 3 показывает, что матричные элементы двух
неэквивалентных представлений ортогональны относительно этого
скалярного произведения. По этой причине теорему 3 называют
соотношением ортогональности.
Следствие. В предположениях теоремы 8 имеем
{Напомним, что XJ" (а:) = х„(а:-')-)
Доказательство.
я' (х7) да == J 2] Я, (а (х-1) е,) я {х) да dx —= 0.
к i
Пусть X — характер конечномерного представления а, а d^,
da ИЛИ d (cr) — размерность' а. Для любого представления л
определим оператор Р" или Р" формулой
р^ = d^n' (Х~) = dx \ X {х~') л (л:) dx = d^ \ х W я (х"') dx.
к к
Если представления л и а унитарны, то оператор /•"
самосопряжен, поскольку в этом случае х~ == Х-
Заметим, что оператор Pj коммутирует со всеми
операторами л{у), y^G, т. е.
PU{y)=n{y)Pl
В самом деле,
P"л{y)=\x{x)л{x-^y)dx =
к
(замена переменной Xi—>yx)
'^^x{yx)я{x-^)dxг==
к
(замена х^—^ху-^)
= 5 X {уху-') л (у) л {х- ^)dx=л (у) Р".
к
Из леммы Шура вытекает, что если представление л непри-
водимо, то
Р^=^Са1
для некоторого комплексного числа Сд, которое мы сейчас
вычислим.

46 //. Компактные группы
Если представления л и ст не эквивалентны, то €„ = 0 и
Ра = 0 в силу теоремы 3.
Лемма. Пусть X — ненулевой линейный функционал на
конечномерном пространстве Н. Положим
9x.oH = A.(w)o.
Тогда
Доказательство. Если « = О, то утверждение очевидно. Пусть
«=5^0, {«I, «2> ■••> «п}—базис в Я, такой, что «i = o. Тогда
<?},.« {V\)=X{Vi)Vu
Фя. о («/) = >-(0/)«1 при/>1.
Только первая строка матрицы ф^,, о отлична от нуля, и мы
получаем для следа нужное выражение.
Так как след — непрерывный линейный функционал на
пространстве операторов, мы получаем
(4) tr ^ я (л;-') фх. оЯ (х) dx = tr ф^, „ = Я, («).
к
Теорема 4. Пусть л — неприводимое представление группы К
в пространстве Н. Пусть о, w ^ Н — произвольные векторы,
% — линейный функционал на Н. Тогда
\ Я, (л (jc-') ay) п {х) vdx = ., .'k{v) w.
к
Доказательство. Зафиксируем вектор о s Я и рассмотрим
отображение L: Н^-Н, задаваемое левой частью формулы,
которую мы хотим доказать. Тогда
Lw=\n {х) qpj^. о [л {х~^) w] dx.
След оператора L совпадает со следом ф^..^ и равен X{v). Кроме
того, L является /(-гомоморфизмом и, следовательно, по лемме
Шура L = tl для некоторого числа t. Таким образом,
Л («) = / dim n^=td (я),
откуда
Теорема доказана.

§ 2. Общая теория представлений компактных групп 47
Следствие 1. Для любого а^К и для любого функщюнала
\i на Н справедливы следующие соотношения:
^ Я, (л (а) л (х-') w) л (х) vdx = -^т^ А, (я (а) v) w,
к
\К{л (а) л (х-') w) ц (л {х) v) dx = ^, Я, (л (а) «) ц (ау).
Доказательство. Возьмем я (а) о вместо о в формулировке
теоремы, сделаем замену переменной х^-^ха~^ и применим
к обеим частям равенства функционал ц.
Предположим теперь, что представление л унитарно; пусть
{е,} — ортонормированныи базис в пространстве Я. Положим
Я,, (о) = (о, е,), лц {х) = {л W е,, в/).
Тогда из теоремы 4 и следствия 1 вытекает, что
[лц, ^ki] = -j^ (б/. е<) (б/, fife) = О,
за исключением случая 1 = 1, j = k. Таким образом, скалярное
пpJИЗвeдeниe равно нулю, если матричные элементы лц и я^;
не совпадают. Но для унитарных представлений
яд(л;) = я,|(х-')
[л,/, Щ1] = \ "<7 (^~') "fe/ W ^^ = \ "/< W "fe/ W ^^•
Таким образом, мы получаем соотношения ортогональности для
матричных элементов одного представления;
Следствие 2. Предположим, что представление я унитарно,
и пусть л,-/ — его матричные элементы по отношению к
некоторому ортонормированному базису в Н. Тогда все эти матричные
элементы взаимно ортогональны относительно эрмитова
скалярного произведения
к
Теорема 5. Пусть я — неприводимое представление группы К.
Тогда

48 //. Компактные группы
Доказательство. Имеем
л' (%-)« = 5 X(х-^) я (х) vdx=^
= \ V Я,< (л (jc~') ei) я {х) V dx =
к. i
= V \ Л; (я (;с~') ei) п {х) v dx =
i К
что и требовалось доказать.
Мы можем теперь следующим образом суммировать
полученные нами соотношения ортогональности:
f 0.
если пф а,
если л ~ о.
во всех случаях, когда представления лист иеприводимы.
Теорема 6. Каждое неприводимое представление группы К
входит в разложение регулярного представления в пространстве
ЩК).
Доказательство. Из полной приводимости регулярного
представления вытекает, что
Пусть а — неприводимое представление /С, ^Ф — его характер.
Если а не входит в разложение, то для любых л, входящих
в L^{K), получаем
л'(г|з") = 0.
Следовательно, если Т — регулярное представление (правыми
сдвигами), то оператор Г' (■ф~) равен нулю на каждом
подпространстве Н„ и, значит,
как оператор в L^ {К). Но тогда для всех f s L^ (/С) имеем
О = f (ф-) f {X) = 5 ^- {у) Т {у) f ix) dy =
= \'if{y-')t{xy)dy = {l*^){x).

§ 2. Общая теория представлений компактных групп 49
Это невозможно, например, в силу существования
последовательностей Дирака; полученное противоречие доказывает
теорему.
Теорема 7. Пусть л, а—неприводимые представления группы К.
Тогда
( О, если а Ф ZI,
^*^""°1 /ir'OC„, если а~п.
Доказательство, Пусть X. 'Ф — характеры неэквивалентных
неприводимых представлений группы К, действующих в
пространствах Н п Н' соответственно (для краткости мы будем
опускать соответствующие индексы). Пусть {ej —базис в Н,
{б/} — базис в Н', {Ki} и {Я,/} — дуальные базисы. Тогда
(X * г|з) (а) = J X (ах) г|з (х-') dx =
к
== У [l{{n (а) л {х) et) %'j (я' {х-') e'j) dx = 0.
i,i к
С другой стороны,
(Х * Х) (а) === J] \Xi{n (а) л; {х-') ej Я,/ (я {х) е,) dx ■■
i.i к
-2-^^Я,г(я(а)е|)Я,|(ег)^
■.-^Y,^,in{a)ed =
i
' %{а).
Теорема доказана.
Следствие, Для любого неприводимого представления л
группы К функция d„%„ — идемпотент в кольце С^. (/<")
{совпадающем с С {К)).
Пусть, как и выше. Г —правое регулярное представление
группы К, действующее по формуле
T{y)f{x) = f{xy).
Для любого характера х конечномерного представления группы/С
положим
p, = r'(d,x-).

50
//. Компактные группы
Тогда
Г {dyTT) f(y)'=d^\t {х-') / {ху) dx •
= dy:\^%{yx-^)f{x)dx.
Таким образом,
{P^{y)^d^{X*f){y).
Мы видим, что проектор Р^ задается сверткой с функцией d^.

III. ИНДУЦИРОВАННЫЕ ПРЕДСТАВЛЕНИЯ
§ 1. Интегрирование на однородных пространствах
При изучении группы 5L2(R) мы будем представлять ее
в виде произведения некоторых замкнутых подгрупп (не
являющихся нормальными). Поэтому здесь мы напомним основные
свойства интегралов по множествам смежных классов.
Пусть К — замкнутая подгруппа локально компактной
группы G; мы предполагаем, что обе группы унимодулярны. Тогда G
действует как группа топологических автоморфизмов на
множестве левых смежных классов GjK по правилу
х: уК^-^хуК-
Мера \к на пространстве GjK называется G-инвариантной, если
ц (Л) = ц [хА) для любого борелевского подмножества А сг GjK
и для любого элемента х^О. По поводу соответствия между
мерами и интегралами см. Ленг [1, гл. XIII, § 4].
Пусть fsC(,(G). Обозначим символом /^ функцию
\f{xk)
dk.
Тогда, в силу правоинвариантности меры Хаара, f^^CdG/K).
Отображение
С AG) ^ С AG/К): f^f^
есть отображение «на» (доказательство имеется у Ленга [I,
гл. XIII, § 4, теорема 3]).
Теорема 1. Пусть К — замкнутая подгруппа группы G.
Предположим, что G и к унимодулярны. Существует единственная
инвариантная мера ^iQ^^^ на пространстве GJK, такая, что для
любой функции f sCg (G) справедливо равенство
QIK а
где \iq — мера Хаара на G.
Доказательство. Единственность меры ^iQ,^^ очевидна.
Выберем произвольную функцию Ф е Cj (G//C), и пусть / S Cj (G) —

///. Индуцированные представления
такая функция, что /^ = ф. Мы можем определить
инвариантный интеграл по G/K формулой
OIK
если проверить, что
\ vd\^a/к==\f^i^G
^f{x)dx = 0,
когда f^ = 0. Пусть рг: G->G/i*C —каноническая проекция.
Выберем функцию of) ^Cc{GlK), равную 1 на множестве pr(supp/).
Пусть ge Cc{G)— такая функция, что ^•^ = 'ф. Тогда,
предполагая, что /^ = 0, получаем
О = 5 \g{x)f{xk)dk dx = ^^ g{x)f{xk)dxdk
а к к Q
^f{x)g^{x)dx=\^f{x)dx.
в
Теорема доказана.
Замечание. Хотя это нам и не потребуется, отметим, что
аналогичные рассуждения позволяют доказать существование
инвариантной меры и в том случае, когда группы G, К не
обязательно унимодулярны, если только сужение модулярной
функции Aq на К совпадает с Aj^.
Пусть Р, К —замкнутые подгруппы группы G, такие, что
G'=PK и отображение
{р, k)^—^pk
задает топологический {не групповоШ) изоморфизм пространства
Р X. К на G. Предположим также, что группы G и К
унимодулярны. Тогда интеграл Хаара на G задается формулой
fy-^\\f{pk)dpdk.
к Р
В самом деле, на пространстве G/K существует G-инвариант-
ная мера; как Р-пространство, G(K изоморфно самой группе Р,
рассматриваемой как однородное пространство относительно
левых сдвигов. Следовательно, эта мера совпадает с мерой
Хаара на Р. Таким образом,
(1> dx^dpdk.

§ I. Интегрирование на однородных пространствах 53
Порядок множителей pk. существен при вычислении
значения fipk), но, по теореме Фубини, мы можем написать также
\f{x)dx==\\^f{pk)dkdp,
р к
т. е. изменить порядок интегрирования.
В приложениях группа Р также представляется в виде
произведения
P^AN,
еде А и N — замкнутые унимодулярные подгруппы. Другими
словами, отображение
AXN-*P: {а,п)^-^an
есть топологический изоморфизм. Кроме того, подгруппа А
нормализует N (см. пример ниже), т. е. апа'^ е N для любых а^А,
п^ N. Группа G, которая.допускает такое разложение G = ANK,
называется группой Ивасавы, а соответствующее разложение —
ее разложением Ивасавы.
Пусть da, dn, dk — меры Хаара на группах Л, N, К
соответственно. Тогда
(2)
dp = da dn.
т. е. если мера Хаара на Р подходящим образом нормирована,
то справедливо равенство
\ / (р) dp = \ \ / (а/г) dtt da == \ \ / {an) da dn.
Р AN NA
Доказательство. Ясно, что мера da dn левоинвариантна
относительно А. Пусть ni^N. Получаем
\ \ f (/Ziare) dnda = [ \f (oa-'/Zion) dn da.
AN AN
Ho a~'«ia e N, поэтому мы можем опустить этот сомножитель,
делая во внутреннем интеграле замену переменной а~^П\ап^—^ п
и пользуясь левоинвариантностью меры Хаара на N. Наше
утверждение доказано.
Объединяя (1) и (2), мы видим, что если задано разложение
Q = ANK, X = ank = а^п^кх,

5,4
///. Индуцированные представления
группы в произведение ее замкнутых унимодулярных подгрупп,
причем А нормализует N, то
(3)
dx = da dn dk.
Предположим, что А нормализует N. Тогда при
фиксированном а^ А отображение
п t—3- alla~'^
есть автоморфизм группы N; следовательно, существует
непрерывный гомоморфизм
а: Л->Я+,
такой, что
\ / {апа-^) dn = a{а)~^ \ / (ге) dn.
N N
Заменяя функцию / ее правым сдвигом на а, получаем
эквивалентную формулу
(4) \ / (an) dn=^a {а)~^ \ / (па) dn.
Объединяя (4) и (3), получаем формулу
(5)
dx = a (а) dn da dk.
Можно также вычислить модулярную функцию для группы
P = AN; мы утверждаем, что
(6)
Д (р) = Д {an) = а (а).
В самом деле, интеграл
\ \ / {an) da dn.
N А
очевидно, инвариантен относительно правых сдвигов из
подгруппы N. Пусть ai е А. Тогда
\ \ / (areaj) dadn = \\f (^аа^а'^па^) da dn = а (а^) [\ f {an) da dn.
Тем самым наше утверждение доказано.

§ I. Интегрирование на однородных пространствах 56
Пример. Пусть G = Git (R) (группа 2 X 2-матриц с
положительным определителем).
fai О \
Л — группа диагональных матриц I _ \, а^ а2> 0.
/1 Ь\
iV — унипотентная группа матриц вида I I.
Р — группа верхних треугольных матриц вида I I.
Пересечение подгрупп Р а А с SL2(R) состоит из матриц, для
которых 02 = aj"'. Справедливо коммутационное соотношение:
/ai 0\/1 6^/1 а^а-'Ь\/а, 0\
U ОаЛо iJ-U 1 ){о aj'
Сделаем замену переменных t = a^a^^b, dt = а^а^^ db; получим
»начение модулярной функции а:
Таким образом, для группы 5L2(R)
(7) а((^" ^^,))=.a^
Трудно устоять перед искушением ввести некорректное
обозначение
а (а) = а'.
/а О \
Правильнее было бы положить, например, /za = l„ -i ) ^
ватем писать
а (Лд) = а-
= /у2
Реализация на верхней полуплоскости. Пусть § — верхняя
полуплоскость, т. е. множество комплексных чисел
z = x->riy, у>0.
Тогда группа G = GLt (R) действует на ф. А именно, пусть
'-Сс d)^G^^'(R)-

56 ///. Индуцированные представления
Положим, ПО определению,
аг-
Несложное вычисление показывает, что сг (сг'(г)) ■« (сгсг') (2).
Заметим, что матрицы вида
а О'
С )
Ко а)
действуют тривиально. Далее, простое вычисление
показывает, что
г Im 2 (ad — be)
Im az = —I I . 12 .
\cz + dv
Таким образом, условие ad —be > О гарантирует, что если
Z S ф, то и (Т2 S |). Поскольку скалярные матрицы действуют
на § тривиально, действие группы GLt (R) сводится к действию
ее факторгруппы 5L2(R).
Пусть К а SL2 (R) — стационарная подгруппа точки /, т. е.
подгруппа таких' матриц, что
ai+b
с1-\- d
Это требование налагает следующие условия на матричные
элементы:
а2 + й2^1, c^ + (f = \, ad-bc = l.
Другими словами, К есть группа матриц вида
/ cos 8 sin 8 "Ч
^(6) = (,_sin8 cos8j-
Отображение cri—^•cri группы SLjCR) на ф задает биекцию NA
на ф. В самом деле, ясно, что если у = а^, то
(о 0(о а-0^^ + '^-
Заметим здесь, что в разложении подгруппы Р удобен
следующий порядок сомножителей:
P=-NA,
поскольку тогда а->оо при г/->оо. Пусть d'^a —мера Лебега
на прямой. Тогда
dy =" 2ad'^a

§ 2. Индуцированные представления 57
И, следовательно,
—-Г- = -, = 2а (а) dx d*a.
где
d*a--
d+a
— мера Xaapa на мультипликативной группе положительных
чисел.
Параметризуем матрицы из подгруппы А при помощи
переменной aeR"*". Тогда из формул (5), (6), (7) следует, что при
изоморфизме G/K ^ §
(8) мера 2а {а)~Ып da переходит в dxdy/y^.
Вывод. При вычислениях, использующих меру Хаара на
группе G, особенно удобны разложение ank и мера dadndk.
Разложение nak и мера а{а)~ dndadk удобны тогда, когда
мы имеем дело с однородным пространством GjK и его
реализацией на верхней полуплоскости.
§ 2. Индуцированные представления
Пусть К — замкнутая подгруппа группы G; предположим,,
что G и К унимодулярны. Предположим также, что существует
такая замкнутая подгруппа Р, что G = РК и отображение
PXK-*G: (p,k)y^pk
есть топологический изоморфизм.
Тогда мы можем рассмотреть пространство P\G правых
смежных классов; при этом пространства P\G и К изоморфны
как правые /(-пространства.
Пусть а — представление группы Р в гильбертовом
пространстве V. Обозначим символом Н{а) пространство
отображений
/: G-*V,
которые удовлетворяют условию
f{py)=^h{pta{p)f{y)
и сужение которых на подгруппу К принадлежит пространству
L?(K,V). (Здесь А = Ар — модулярная функция на Р.) Пусть
\ff^-^\\f{k)fdk

58 III- Индуцированные представления
— обычная L^-норма на К- Обозначим буквой л представление
группы G в пространстве Н{а), задаваемое правыми сдвигами,
т. е. действующее по формуле
л {у) f{x) = f {ху).
Говорят, что представление л индуцированэ представлением а
подгруппы к. Дополнительный множитель Д(р)''« введен в
определение для нормировки.
Теорема 2. Если представление а ограничено, то
индуцированное представление л также ограничено. Если а унитарно, то
представление л тоже унитарно.
Доказательство. Зафиксируем y&G. Напишем ky = p\k'\
таким образом,
/ {ky) = f {p',k') = А (р^)'/. а (р;) / {k').
Тогда
\\!{ky)?dk^\^{p\)\a{p',)f{k')fdk.
к к
Если представление а унитарно, то правая часть равна
\^{p',)\f{k')?dk;
к
если а ограничено, то она оценивается сверху этим интегралом,
умноженным на константу. Проверим теперь, что для любой
функции il) е Сс (К)
(1) \Mp{k')A{p',)dk^\^{k)dk.
к к
Пусть fe^CciG). Так как группа О унимодулярна, получаем
J \^f{pk)dkdp== \^f{x)dx== ^f{xy)dx=-\ \^f {pky)dkdp =
p к 0 a p к
^\\f {pp',k') dpdk=^\\f ipk') Д (p;) dp dk =
к P к P
\ \f{pk')A{p',)dkdp.
p к
Мы получим нужный нам результат, если положим / (pk) ■
= 'Ф(*)ф(р). где ^sCciK), феСЛР) и
\ Ф (р) dp ■■
1.

§ 2. Индуцированные представления 59
Заметим, что, кроме того, мы доказали и ограниченность
представления л, если от представления а тоже требовать лишь
ограниченности.
Предположим для простоты, что представление а
одномерно, т. е. является roMOjviop(j)H3MOM в мультипликативную
группу комплексных чисел. Тогда определены также
одномерные представления сг"', а~\ где а — комплексно сопряженное
представление. Мы будем писать
Чтобы избежать комплексных сопряжений, определим
симметричное скалярное произведение на L^{jK) формулой
[f,g] = \f{k)g{k)dk.
к
Теорема 3. Пространства Н{а) и Н{а-^) двойственны
относительно этого скалярного произведения. Цля любых y^G^
/еЯ((т), ^еЯ(ст~') справедлива формула
[^{y)f,8] = [f,^{y-')g].
Доказательство состоит в несложном вычислении;
\n{y)f{k)g{k)dk= \f{ky)g{k)dk=:
К к
= \^{p',y''<r{p',)f{k')g{k)dk =
к
= 5 Д [р'.У' а(р',) / ik') g {p',k'y-^) dk =
к
= \ Д (p;) a [p',) f {k') a {p',)-' g {k'y-') dk =
к
= \f{k)g{ky-^)dk,
К
ЧТО и требовалось показать.
Если рассматривать эрмитово скалярное произведение,
следует заменить сг"' на сг*. В этом случае нространство Я((т'')
эрмитово двойственно к Н {а).

60 ///. Индуцированные представления
§ 3. Ассоциированные сферические функции
Пусть, как и выше, G = РК и Р = AN, причем А
нормализует N. Предположим, что группа К компактна, и ее мера
Хаара равна 1. Как и раньше,
Д (р) = Д (а/г) = а (а).
Введем обозначение
р(а)==а(а)'/».
Пусть S — комплексное число^ Положим
9s (х) -= Ps iank) = р («)"+'.
Тогда ps (^5) = 1 = Pj (n). Функция
И.: Р-*С\
задаваемая формулой
цЛап) = р(а)',
есть, очевидно, характер группы Р (непрерывный гомоморфизм
в С*). Если I fAj I = 1, то мы будем говорить, что ц^ — унитарный
характер.
Пример. Для группы SL2(R)
Обозначим символом H{s) пространство представления щ
группы G, индуцированного представлением Hj. Это
пространство функций / на G, таких, что
(i) / {any) = р (а)^+'/ {у), а^А, n^N;
(ii) сужение f па К принадлежит L?{K).
Обычная норма в D{K.) наделяет H{s) структурой гильбертова
пространства.
Мы утверждаем, что функция Ps — единичный вектор в
пространстве Н {s).
Доказательство. Сначала покажем, что функция р^
нужным образом преобразуется при левых сдвигах из
подгруппы Р. Имеем
Ps {nay) = Ps {папуау) = р, {папуа'^аау) == pj (а) р^ {у) =
= р (а) р {af Ps {у) = Д {nayi' р,, (а) Ps {у).

§ 3. Ассоциированные сферические функции 61
что и требовалось.. Далее,
iiP.iP^ = Sip.(*)Pdfe = l.
к
Таким образом, Ps — единичный вектор в пространстве
представления Jtj. Кроме, того,
Щ (*) Ps = Ps.
поэтому Ps называется инвариантным вектором относительно
подгруппы К или, короче, iC-инвариантным вектором.
Несмотря на то что мы здесь имеем дело с
бесконечномерными представлениями, мы можем рассмотреть матричный
элемент
{щ {х) Ps, Ps) = 5 «s {х) Ps {k) p7(F) d/j = ^ Ps {kx) dk.
к к
Как мы увидим, это весьма важная функция, ассоциированная
с характером \is', она будет подробно изучена в главе,
посвященной сферическим функциям. Мы будем пользоваться
следующим обозначением:
<fs{x) = \p{kxf^'dk.
Характер fij унитарен тогда и только тогда, когда число s
чисто мнимое. В этом случае, как мы увидим позднее, сдвиги
функции (fs порождают неприводимое подпространство Hs',
сужение представления л^ на это подпространство —
неприводимое унитарное представление группы G. Мы будем
называть (fs сферической функцией, ассоциированной с характером [i^-
Семейство представлений itj часто называют основной серией
представлений группы SLjCR). В некоторых работах термин
«основная серия» используется только для унитарных
представлений, когда S чисто мнимое. Пользуясь этим термином,
мы всегда будем указывать, какая область значений s
подразумевается в каждом конкретном случае. Кроме того, как мы
увидим, эти индуцированные представления 5L2(R) распадаются
на две неприводимые компоненты в соответствии с четностью
функций из пространства представления; здесь опять-таки
термин «представления основной серии» иногда используют
только для этих неприводимых компонент (см. § 3 гл. VII).

62 III. Индуцированные представления
§ 4. Ядро, задающее индуцированное представление
Пусть S е С. Определим пространство H{s), как в
предыдущем параграфе, и пусть «j — представление группы G в ti{s)
правыми сдвигами, т. е.
Щ{х)!{у) = !{ух), f^H{s).
Пусть tj)eCc(G). Найдем выражение для оператора л^ (i|3):
К (^) / (г/) = S ^ W ^s W f{y)dx=\^ (дг) / {ух) dx =
в в
= \ \ {■^{ку^Пу^йу^ ank)f{ank)dadndk =
АПК
= 5 \ \'^{ky^ny^ay^ank)p{ay^^f{k)dadndk='
АПК
==\q^{k,y)f{k)dk,
К
где
(1) 9i|)(*.«/)=\ \'^{ky'tiy^ay^ank)p{af'^^ dadn.
А м
В частном случае при y = k'
(2) <7,„(/г, k')=^ ^ tl) {k'~'ank) р (а)'+' da dn.
л iV
Разумеется, функция я^Ст]))/ полностью определяется своими
значениями на К, и мы имеем
(3)
nl(^)f{k')=\q^{k,k')f(k)dk.
Таким образом, мы видим, что оператор n^(T|3) задается ядром
<7i|)(^. у)- В данный момент мы не станем заниматься вопросами
сходимости следа, определенного при помощи матричных
элементов оператора; мы предпочитаем, не вдаваясь в детали,
как можно скорее окунуться в теорию сферических функций.
Поэтому сейчас мы определим след оператора л^(г|)) ad hoc,
положив
(4) tvnl{Mf)=^q^{k,k)dk,

§ 4. Ядро, задающее индуцированное представление 63
где
(5) q^(k,k)=^ Jtl)(/5~'are/5)p(a)''^'dad/z.
А N
(Связь ЭТОГО определения с обычным мы обсудим впоследствии,
когда будем заниматься формулой Планшереля.)
Предположим, что функция a|3 инвариантна относительно
внутренних автоморфизмов из подгруппы К, т. е.
г1)(/гдг/г~') =•*(•«)
для всех дг е G, k^ К. Пространство таких функций мы будем
обозначать CdG, К). Тогда формула для ядра q^ еще больше
упрощается, а именно справедливо следующее утверждение:
Если tj) S С(, (G, К), то функция
(6) ^ф(/г,/г)=-= J Jtl)(a/z)p(a)'+'dad/z
А N
— постоянная, не зависящая от k.
Будем по-прежнему предполагать, что полная мера
подгруппы К равна 1. В гл. V мы подробно изучим
преобразование Хариш-Чандры на пространстве CdG, К), определяемое
формулой
Нф (а) »= р (а) \ it (an) dn, где р 11 i )) ^^ '''•
Приняв это определение, мы получаем следующий результат:
Теорема 4. Для любой функции tj) е Q (G, К) и любого
SS.C
1тп1(М?) = \Щ(а)р(аУс1а.
А
Интегралы такого вида, зависящие от параметра s, мы
будем в дальнейшем называть преобразованием Меллияа и
обозначать буквой М. Теперь мы можем еще сократить нашу
формулу для следа и написать
trjti(i|3) = MHtl)(s).
Если функция ij3 биинвариантна относительно К, т. е. ip{kxk') =
= 1{)(л:) для всех k, k' е.К и всех atsG, то последний интеграл
равен
\^{x)p{xf^' dx.
о
Случай биинвариантных функций будет систематически изучен
в следующей главе.

IV. СФЕРИЧЕСКИЕ ФУНКЦИИ
в этой и следующей главах мы изучим алгебру функций на
группе G, которые инвариантны при правых и левых сдвигах
из подгруппы К, и установим связь характеров этой алгебры
с теорией представлений. Последний вопрос сводится к
изучению тех представлений, которые содержат Я'-инвариантный век-,
тор. Наше изложение охватывает § 3 и § 4 последней главы
книги Хелгасона [2]. Мы опираемся только на абстрактные
свойства меры Хаара и свертки и не используем
дифференциальных операторов. Преимущества такого подхода отмечал
Годеман [6]; см. также статью Там агавы [1], которой мы
частично следуем. Чтобы доказать, что все сферические функции
исчерпываются теми, которые мы явно построим, нам
понадобятся дифференциальные уравнения, и доказательство этого
факта будет отложено до § 3 гл. X.
По поводу р-адической теории см. статью Макдональда [l].
На протяжении всей этой главы мы предполагаем, что G —
унимодулярная группа, К — ее компактная подгруппа, и мера
Хаара на К нормирована, т. е.
§ 1. Двусторонне инвариантные функции
на группе
Функция / на группе G называется двусторонне /С-инва-
риантной (или, для краткости, просто двусторонне
инвариантной, или биинвариаитной), если
. / (feiAT/sa) = f (дг)
для всех ku k^^ К ъ всех л;еG. Пространство двусторонне
инвариантных непрерывных функций на G с компактным
носителем мы будем обозначать С^ОЦК). Для любой функции /на
группе G положим
к
функция ^/ определяется аналогично при помощи усреднения
по левым сдвигам. Тогда в силу инвариантности меры Хаара,

§ 1. Двусторонне инвариантные функции на группе 65
функция /^ npaBO-i<'-HHBapHaHTHa, а функция ^f лево-^С-инва-
риантна. Если исходная функция / право-ТС-инвариантна, то
р = f; поэтому отображение / ь-»f^ — проектор на пространство
правоинвариантных функций. Аналогичное утверждение
справедливо и для отображения /•—*^/. Таким образом, функция
^/^ двусторонне инвариантна.
Пусть / — правоинвариантная функция. Тогда для любой
функции ф
\f{x)<f{x)dx= \f{x),f'^{x)dx.
а о
В самом деле,
^fix)(f(x)dx=^ \fix)(fix)dxdk =
в ко
= 5 \f{x)(f(xk)dxdk= [fix)<f'<{x)dx.
ко о
(Мы сделали замену переменной x^■^*■xk и воспользовались
теоремой Фубини.) Аналогичное утверждение справедливо и для
левоинвариантных функций. В частности, если функция /
двусторонне инвариантна, то
\f{x)<pix)dx==\f{x)i^<p^{x)dx.
Эти соотношения выполняются во всех случаях, когда
интегралы абсолютно сходятся, например если функция / непрерывна,
а ф имеет компактный носитель или / принадлежит
пространству V, а ф ограничена. На практике подобные условия
сходимости всегда будут тривиальным образом выполнены, и с этой
точки зрения теория, которую мы здесь излагаем, не содержит
каких-либо тонкостей.
Пусть л: G->GL (Я) — представление группы G в
гильбертовом пространстве Н. Обозначим Н^ подпространство,
состоящее из /"С-инвариантных векторов, т. е. из таких векторов
оеЯ, что
a{k)v = v для всех k ^ К.
Зададим отображение Pj^: Н -^ Н формулой
P/fV = \п (k) V dk.
к
Тогда Pj^ есть ортогональный проектор на подпространство Н^.
Пусть V е Н^, Ф е С(, (G). Тогда
я' (ф) ц = л' (ф^) V.

66 IV, Сферические функции
Обратно, если функция ф принадлежит пространству CdGJ/K)
и V — произвольный вектор из Н, то
л' (ф) V е Н^.
Бели V, wgH^ и л(К)*=-п{К) {например, если сужение
представления п на К унитарно), то
(л' (ф) V, w) = (я' (^ф^) V, w).
Эти утверждения тривиально проверяются при помощи
определений и будут свободно использоваться в дальнейшем без
специальных ссылок.
Пространство С с {G//K) является алгеброй относительно
свертки. Важнейшее свойство этой алгебры — ее
коммутативность, которая была впервые открыта И. М. Гельфандом.
Теорема 1. Пусть G — локально компактная унимодулярная
группа, К — ее компактная подгруппа. Пусть х —
антиавтоморфизм группы О порядка 2, такой, что для любого дг е G
существуют элементы /г,, k2^K, для которых
Тогда алгебра CdGJ/K) коммутативна.
Доказательство. Мера Хаара инвариантна относительно
отображения дгн-э-дг^; в самом деле, 1 = Д (т^) = Д (т)^, откуда
Д(т) = 1. Кроме того, /(дг)=/(дг^) для любой функции / е
еС(, {G//K). Рассмотрим теперь свертку произвольных функций
/, g ^Cc{G/lK). Воспользуемся инвариантностью этих функций
относительно автоморфизма т и сделаем в интеграле замену
переменной у^-^ух. Получим
(hg)(x) = \f{xy-')g{y)dy =
= \ f {'у- ^x') g {у') dy^\f Сг/->) g {х^у') dy.
Сделаем в последнем интеграле замену переменной у*-^у~^
и подставим kixk2 вместо х''; пользуясь инвариантностью меры
Хаара, получаем
{f*g){x) = {g*f){x);
теорема доказана.
Пример. Предположения теоремы 1, разумеется, выполнены,
когда G=5L2(R), а /"С —группа вращений окружности. В
качестве преобразования т возьмем транспонирование матриц.
Разложение x = sk произвольной матрицы дгеО в произведение
симметричной и ортогональной немедленно показывает, что
*x = *ks = k~^xk~\ поскольку *k = k~^.

§ 2. Неприводимость 67
§ 2. Неприводимость
Одним из приложений теоремы 1 будет изучение
неприводимых представлений группы G, и в особенности ее унитарных
представлений. Вместо того чтобы предполагать, что
представление я: G-*GL{H) унитарно, иногда достаточно предположить,
что оно *-зам1шуто, т. е. n{G) = n{G)*, или что этим свойством
обладает сужение представления л на подгруппу К, т. е. я (К) =
= л(Д')', Кроме того, ясно, что замыкание линейной оболочки
множества я(0)Я^ является G-инвариантным
подпространством Н; следовательно, если представление неприводимо и
Н^ ф О, то это замыкание совпадает со всем пространством Е.
Теорема 2. Пусть я: G-*GL (Я) — представление группы G
в гильбертовом пространстве Н. Предположим, что
представление я и его сужение на К *-замкнуты. Допустим, что Н'^ФО
и что замыкание линейной оболочки множества я{(})Н'^
совпадает с Н. Тогда пространство Н^ является Cc(Gf/H)-Henpueodu-
мым в том и только в том случае, когда С^фУнеприводимо
пространство И {и, следовательно, представление я неприводимо).
Доказательство. =^ Пусть W cz Н ~ ненулевое G-инвариант-
ное подпространство; в силу условия *-замкнутости,
подпространство W^ тоже G-инвариантно. Пусть Р = P^( — ортогональный
проектор на подпространство Я^. Рассмотрим два случая.
Сначала предположим, что PW = 0. Из равенств
H==W®W^ и PH = PW®PW^
получаем, что PW^=^H'^; таким образом, h'^czW^, откуда
W^'=H, tr = 0, и наше утверждение доказано. С другой
стороны, если PW == W^ ф Н^ — нетривиальное подпространство,
то оно Сс (С/Д)-инвариантно; в самом деле, если ф е С^ (G(/K),
W ^W, то
я^ {(f)w^W
и, кроме того, вектор л'(ф)ш инвариантен относительно
подгруппы К. Таким образом, и в этом случае наше утверждение
доказано, и тем самым доказана первая половина теоремы.
4= Обратно, предположим, что пространство Н неприводимо.
Пусть W CZ Н^ — ненулевое подпространство, инвариантное
относительно алгебры CciGjlK)- Предположим, что W ф Н^; тогда
существует ненулевой вектор а е Н^, ортогональный этому
подпространству. Мы покажем, что
я'(СЛО)) f 1 й^.
откуда следует, что замыкание линейного подмножества
л' {Се{0^ V не совпадает со всем пространством Н. Пусть ш е IF

68 /V. Сферические функции
И ф е Cc(G). Тогда
(л'(ф)ц, ш)=\ \ \ ф (дг) (л (дг) а, w)dxdkidk2.
к к о
Сделаем замену переменной лг»—э-дгД^,. Оператор лСдгй)) равен
л{х)п{к{); множитель n(ki) можно опустить, поскольку вектор v
принадлежит подпространству Я^. Сделаем теперь замену
переменной x^—^k2X. Тогда я (k^x) = я (k2) я{х); перенесем оператор
я{к^ на вектор ш, заменив его на эрмитово сопряженный. Так
как ш е Я^, этот оператор тоже действует как единичный. Это
показывает, что наше выражение равно
\ ^ф^ (дг) {я {х) V, ш) ^дг = (я' (^ф^) V, ш) = О,
а
поскольку ортогональное дополнение подпространства W в Я^
инвариантно относительно операторов я' (/) для любых функций
f ^Сс {G//K)- Это противоречит неприводимости пространства Я.
Теорема 3. Пусть я: G ->■ GL (Я) — неприводимое унитарное
представление. Если алгебра CdG Ц К) коммутативна, то
(11тЯ^<1.
Доказательство. Предположим, что dim Я^ ¥= 0. Из теоремы 2
мы знаем, что пространство Я^ неприводимо. Алгебра Cc\gЦК)
коммутативна и «-замкнута. Теперь лемма Шура показывает,
что (ЛтЯ^== 1, что и требовалось.
Теоремы 2 и 3, естественно, применимы, когда G = SL2(R),
а К—группа вращений окружности. Однако ни одно из
доказательств, которые мы привели, в этом частном случае не
упрощается.
§ 3. Определение сферических функций
Мы по-прежнему предполагаем, что группа G унимодулярна,
а. К — ее компактная подгруппа. Будем говорить, что функция f
на группе G является Д'-сферической, или, для краткости,
просто сферической, если она обладает следующими свойствами:
SPH 1. Функция f двусторонне инвариантна и непрерывна.
SPH 2. Функция f — правая собственная функция алгебры
CAG//K), т.е.
f*a|) = A(f, at)/
для любой функции ■^^Cc{GIIК) и некоторого комплексного
числа X(f, 1|з).

§ 3. Определение сферических функций 69
SPH 3. /(е)=1, где е —единичный элемент G.
Последнее условие есть условие нормировки. Произвольную
функцию, удовлетворяющую первым двум условиям и такую,
что / (е) ф О, можно поделить на / (е) и получить функцию,
удовлетворяющую всем трем условиям.
Заметим, что собственное значение X{f, a|3) равно {f*'^){e);
это вытекает из второго условия, если воспользоваться им
в точке е.
Следующая теорема дает основной пример сферических
функций.
Теорема 4. Предположим, что G = РК, где Р — замкнутая
подгруппа, и Р У(. К-^РК^G — топологический изоморфизм.
Пусть
р: Р^С
— характер группы, Р (т. е. непрерывный гомоморфизм);
продолжим его до функции на G, полагая р (pk) = р (р). Тогда р —
правая собственная функция алгебры CdG/fK), т.е.
(р*11))(д:)=А(р, ^)р{х),
и функция f, такая, что
f{x)=\p{kx)dk,
к
является К-сферической с собственными значениями X{f, 113) =
= (р * a|5) (е) = X (р, ф).
Доказательство. Положим x=^pik^. Тогда для любой
функции ■\Sf eCc{G//К) получаем
(р*а|?)(д:)= J p{xy-^)ilf{y)dy=\^p{p^y)'\}f{y-^)dy.
в а
Пусть y = pk; тогда р (Pir/) = p(pip) = p(p,) р(р) = р (р,) р(г/).
Таким образом, наше последнее выражение равно
Р (Pi) \ Р (2/)Ф (г/~') dy^X (р, а|з) р (д;).
о
Итак, мы доказали, что р — собственная функция, и получили
явное выражение для соответствующего собственного значения.
Рассмотрим теперь функцию /:
(/ * а|)) W = \f (ху-') ^{y)dy=\\p (kxy-') ^ (у) dy dk =
а к а
= 5а(р, ^!f)p{kx)dk=X{p, ф)/(д:);

70 IV. Сферические функции
таким образом, / — тоже собственная функция с тем же
собственным значением. Ясно, что /(e) = 1; кроме того, / двусто-
ронне инвариантна, так как функция р правоинвариантна, а
после усреднения она становится также и левоинвариантной.
Итак, теорема 4 доказана.
Пример. Абстрактное утверждение теоремы 4 принимает
конкретную форму для группы G=SL2(R), которую мы постоянно
имеем в виду в этой книге. Группа Р состоит в этом случае
из треугольных матриц
Р(л«) = р((о ^-)) = «.
Пусть S — произвольное комплексное число. Тогда функция
р^: pt-^a^ есть непрерывный гомоморфизм грзшпы Р в С*; таким
образом, мы получаем сферические функции
Мы систематически изучим эти функции в следующей главе.
Пока же приведем еще несколько теорем, справедливых для
групп G я К общего вида.
Теорема 5. Пусть f — непрерывная функция на группе G, не
равная тождественно нулю. Тогда функция f сферическая в том
и только в том случае, когда
\f{xky)dk = f{x)f(y)
к
для всех X, у ^G.
Доказательство. Предположим, что функция f сферическая.
Для произвольного элемента xeG положим
FAy)=^\fixky)dk.
к
Пусть ф е С^ {GfJK). Тогда
{fx * ф) {у) = \ Рх (г/z-') Ф (z) dz =
а
= \ \ / {xkyz~^) ф (Z)dk dz.
в к

§ 3. Определение сферических функций 71
Изменим порядок интегрирования и сделаем последовательные
замены переменных zv-^zy, zt—^zk. Получаем, что наше
последнее выражение равно
к о
где
J J f {xz-^) ф (zky) dz dk = (f* ф^) (д:),
Ф^ (z) = 5 Ф (zky) dk.
к
Так как функция ф^ двусторонне инвариантна, находим
окончательно
iF,*<p){y) = X{f, ф;)/(;с),
где Я,(/, ф^) — собственное значение. Положим д: = е. Тогда
Fe{y) = fiy),
т.е. /■«="/. Следовательно,
(f*9)(r/) = A(f, ф;)/(е) = А(/, ф'Д
и поэтому
{F,*(f)iy) = if*cf){y)f{x).
С другой стороны, пусть {ф„} — последовательность Дирака;
применим только что полученную формулу к функции ф = ф„.
Как мы знаем,
Fx*Vn-*Px и /*Ф„-*/ при п-*оо.
Так как функЦии Fx а f двусторонне инвариантны, мы можем
заменить ф^ на "^ф^. Следовательно,
\f{xky}dk = FAy)^f{y)fix).
Это доказывает первую половину нашей теоремы.
Обратно, предположим, что функция / удовлетворяет
сформулированному функциональному уравнению. Пусть Xq^G — такая
точка, что f{Xo) Ф 0. Тогда
f Ы f (г/) = 5 / {4kk,y) dk = f (дго) / ikiy).
к
Таким образом, f{y) = f{kiy) для всех ki^K, т.е. функция /
левоинвариантна. Аналогичное рассуждение показывает, что
функция / правоинвариантна; итак, она двусторонне
инвариантна. Тогда
f(Xo) = \f{xok)dk = f{xo)f{ey,
к

72 IV. Сферические функции
таким образом, f(e) = l. Наконец, пусть фе CclG/Z^C)
—произвольная функция. По определению,
if * ф) (;с) = J f (ху- •) ф (у) dy.
а
Умножим правую часть равенства на 1 = \ dk, сделаем замену
к
переменной y\~^yk ' и поменяем порядок интегрирования.
Получим
(/* ф) (х) == J J f (л/г^^-1) Ф (г/) d/г dr/==
ак
= \f{x)f{y-')<9iy)dy^{f*<^){e)f{x).
а
Следовательно, f — собственная функция алгебры С^ {0//К), н
мы доказали вторую часть нашей теоремы.
Теорема 6. Пусть f ^С {G//K)- Тогда f — сферическая функция
в том и только в том случае, когда отображение
L: фь-з>- \ (:p{x)f{x) dx
о
есть гомоморфизм алгебры С^ОЦК) в С.
Доказательство. По определению,
L (ф * ф) == J J Ф (ху-^) ф (г/) f (х) dy dx.
а а
Поменяем порядок интегрирования и сделаем замену
переменной xi-^xy. Получим
L
(ф*Ф) = 5 '^((>{x)'^iy)fixy)dxdy.
а а
Умножим это выражение на 1 = \ dk, сделаем замену пере-
к
менной Xi—^xk и поменяем порядок интегрирования. Получим
(1) L (ф*1|з) = J J Ф(х)^{у) 5 f (xky) dk dx dy.
a a к
С другой стороны,
(2) L (ф) L (ф) = 5 5 ф (х) ф (у) fix) f (у) dx dy.
а а

§ 3. Определение сферических функций 73
Итак, утверждение теоремы б в одну сторону доказано: если / —
сферическая функция, то отображение L является
гомоморфизмом.
■ Обратно, предположим, что L—гомоморфизм алгебр, т. е. что
L(9*il3) = L(9)L(i|3)
для всех функций ф, '^sCdG/jK). Тогда из равенства
выражений (1) и (2) немедленно вытекает функциональное уравнение
для функции f, что и требовалось доказать.
Замечание. Если в условиях теоремы 6 предположить, что
функция f ограничена, то отображение
L: ф ь-3^ \ ф (jc) f (х) dx
а
продолжается до гомоморфизма алгебры L'{G//K) в С.
Теорема 7. Всякий непрерывный гомоморфизм алгебры V (G/JK)
в С имеет вид
ф1-^(/*ф-)(е),
где f — некоторая ограниченная сферическая функция.
Доказательство. Как известно из теории меры, для любого
ненулевого характера L алгебры L^G/JK) существует такая
ограниченная измеримая функция f, что
L (ф) = 5 ф {х) f{x)dx, ф S L • {GIIK).
Подставим в это равенство (^{к^хк^ вместо ф(^с),
проинтегрируем по К У, К и сделаем замену переменной х>—^к~\к2^- Это
показывает, что мы можем заменить функцию / функцией
XI—?- \ \ / {kixk2) dki dki,
к к
т. е. можем предположить, что f двусторонне инвариантна.
Из формул (1) и (2) получаем
\f{xky)dk = f{x)f{y)
к
для почти всех пар {х, y)^GX,G. Чтобы показать, что можно
заменить f непрерывной функцией, выберем такую функцию
i|)eC,(G), что
а

74 IV. Сферические функции
и предположим, без потери общности, что этот интеграл
равен 1 (если потребуется, можно умножить функцию ф на
константу). Тогда
J Ф(д;)/ (д;) dx J ^{y)f(y)dy^\ J ф(д;)ф(г/) \ f{xky) dk dy i
a a a a к
a ко
J dx.
5 a S a к
Воспользуемся теоремой Фубини и сделаем последовательные
замены переменных r/i—>-/г""'г/, у*—^х~^у. Мы получим, что
последний интеграл равен
5 J J Ф {X) г|з {k-'x-'y) f (у) dy dk dx =
= 5 ^ ^ ф (л:) г|з (kx-^y) f (у) dk dy dx.
a a к
Таким образом, вместо f можно взять непрерывную функцию g,
которая задается формулой
g{x)^[ \^{kx-^y)f{y)dkdy.
а к
Теорема доказана.
Замечание. Если G —группа Ли, снабженная структурой
гладкого многообразия, то мы можем взять г|зеСГ(0), и наша
функция будет бесконечно дифференцируемой.
§ 4, Связь с унитарными представлениями
Пусть л: G-^AwiH — унитарное представление группы Q
в гильбертовом пространстве Н. Пусть и е Н^ — единичный
вектор. Мы изучим матричный элемент представления
f{x) = n^,^{x)={n{x)u, и).
Очевидно, функция f двусторонне инвариантна и f(e)=l.
Будем говорить, что вектор о е Я топологически порождает
пространство Н (относительно представления л), если замыкание
линейной оболочки множества n{G)v совпадает со всем
пространством Н.
Теорема 8. Пусть я: G -> Aut Н — унитарное представление',
предположим, что суи{ествует единичный вектор и, топологически
порождающий подпространство Н^ с: Н. Тогда пространство Я^
одномерно в том и только в том случае, когда функция f: х^—>-
у—>{л,{х)и, и) сферическая.
Доказательство. Мы видели, что функция f двусторонне
инвариантна и /(е) = 1. Предположим, что подпространство

§ 5. Положительно определенные функции 75
Н^=Си одномерно. Для любой функции (р^С^ОЦК) вектор
я'(ф)ы инвариантен относительно подгруппы К', таким образом,
я'(ф)ы = Я((р)ы для некоторого числа Я(ф)еС, и отображение
ф1-^Я(ф)
есть гомоморфизм алгебр. Но
(f * ф-) (е) = J f (х) (:pix)dx^ J ф (х) (л {х) и, и) dx = (л' (ф) и, и),
а а
Это означает, что отображение Ф i—^ (f * Ф~) (е) есть
гомоморфизм алгебры CciG/JK) в С; поэтому, согласно теореме б,
функция f сферическая. Заметим, что при доказательстве этой
части утверждения теоремы мы не использовали того, что
вектор и — порождающий.
Обратно, предположим, что / — сферическая функция. Пусть
Р: V I—>- \n{k)v dk
— проектор на подпространство Н^. Для любого b ^G имеем
<Ря (д;) и, л (ft) ы) = (я (ft"') Ря (х) и, и) =
= 5 f {b~'kx) dk = f (ft-') f (x) = (/ {x) u, я (&) и),
к
(Мы воспользовались теоремой 5.) Так как векторы п{Ь)и, b ^G,
порождают плотное линейное подмножество в Н, отсюда
следует, что
Ря {x)u = f {х) и.
Таким образом, РН = Си и с11тЯ^=1. Теорема доказана.
§ 5. Положительно определенные функции
Ненулевая функция f на группе G называется положительно
определенной, если она непрерывна и для любого набора точек
Последнее условие можно также записать в виде
Zf{xr^x^)a.aj^O,
заменяя Xj на х'К

76 IV. Сферические функции
Пример. Пусть л: 0->Аи1Я — унитарное представление
группы G в гильбертовом пространстве Я, и^Н — единичный
вектор. Тогда функция
/: Х''—^{я{х)и, и)
положительно определена, поскольку
Y, (я (^x^xJ^"ja^йjU, ы) = /^ «;" {x^'j и, X a^л; [х^) и\ >0.
Мы увидим, что этот пример, по существу, исчерпывает все
положительно определенные функции.
Перечислим сначала три простых свойства положительно
определенных функций:
(1) fie)>0;
(2) f(^-')=rw;
(3) \fix)\^fie).
Для доказательства первого свойства возьмем га=1, Xi==e,
Oi = 1. Чтобы доказать второе, возьмем Xi = е, X;f=x, Oi ==а2=1.
Напишем
fix) = rix) + itix).
Мы знаем, что
f (е) aiCJ, + f (х-^) а,а2 + / (х) aacii + f (е) Огйг > 0.
Отсюда ясно, что число f {х~^) + f (х) вещественно; таким
образом, t{x~^) = — tix)- Возьмем теперь ai==i, 02=!. Тогда
число
г (х-^) 0102 + г (х) ОгО, = г (jc~') i — г {х) i
должно быть вещественным, откуда г{х~^) = г{х). Итак, второе
свойство доказано. Для доказательства последнего положим
«2== —ifWI, ai = f{x).
Получим
f{e)\f{x)f-2\fix)f + fie)\fix)f^0,
откуда
\fix)?<fie)\fix)r.
Если f{x) = 0, то все доказано, поскольку f(e)^0; если же
f{x)^0, то мы можем разделить обе части неравенства на
\fix)f.
Обращая конструкцию из нашего примера, мы построим
сейчас по заданной положительно определенной функции ф
унитарное представление. Обозначим символом F^ векторное про-

§ 5. Положительно определенные функции 77
странство, порожденное функциями л (а) ф —правыми сдвигами
функции ф. Напомним, что, по определению,
я (а) ф (х)--Ф (;са), х, a^G.
Ясно, что л (aft) = я (а) я (6). Если f, g-sF^, то
Определим скалярное произведение функций /, g равенством
if, Я) = Z агР,Ф (^"'aj = Z а,Р; Ф (^Г'^) =
Если задано выражение для функции g- в виде линейной
комбинации сдвигов функции ф, то приведенная цепочка равенств
показывает, что величина (f, g) не зависит от того, как
функция f представляется в виде линейной комбинации сдвигов
функции ф. Поскольку f я g в предыдущем утверждении можно
поменять местами, величина (f, g) определена корректно и,
очевидно, задает положительную эрмитову форму в
пространстве Уф, возможно, вырожденную.
Пусть У° с: У —ядро этой эрмитовой формы, Н
—пополнение факторпространства VJV^', таким образом, Н^ —
гильбертово пространство. Тогда операторы сдвига, которые оставляют
нашу эрмитову форму в пространстве Уф инвариантной,
индуцируют унитарные операторы в пространстве VJV°^ и,
следовательно, продолжаются до унитарных операторов в
пространстве Яф. Значит, мы получаем групповой гомоморфизм
Яф: 0->Аи1Яф.
Проверим теперь, что для гомоморфизма Яф выполнено условие
непрерывности, т. е. что Яф — представление группы G в
пространстве Яф. В начале книги мы уже отмечали, что
достаточно проверить это условие на плотном множестве; таким
образом, достаточно проверить его иа элементах fе V^.
Пусть f (л;) = 2^а<ф(ха;), так что
" (у) f W = Z «гФ (хущ), y^G.
Тогда
\\n{y)f-f\f^(n{y)f-f,n{y)f-r) =
= 2(f,/)-(я(г/)/. f)-(f, я(г/)/) =
= 2 2a^d^ф(a-'a;) — Еага,ф(аГ'У~'й/) — Zaгa^ф(af^r/a^).

78 IV. Сферические функции
Это последнее выражение стремится к нулю при г/->е.
Следовательно, отображение
y\-^n{y)f
непрерывно в окрестности единичного элемента. Отсюда
вытекает, что это отображение непрерывно всюду и я — унитарное
представление.
Возьмем в качестве единичного вектора и функцию ф;
получим
ф(л:) = (я(л:)ф, ф).
Таким образом, ясно, что любую положительно определенную
функцию можно получить при помощи конструкции из нашего
примера. Более формально, рассмотрим тройки (л, Я, и),
состоящие из унитарного представления л: G->Aut/f,
гильбертова пространства Н и единичного вектора и^Н. Две тройки
(л. Я, и) и (л'. Я', «О называются эквивалентными, если
существует унитарный изоморфизм пространства Я иа Я',
перестановочный с действием группы и переводящий вектор и в и'.
Теорема 9. Отображение
ф^-^(л;ф, Я<р, ф)
устанавливает взаимно однозначное соответствие между
множеством положительно определенных функций на группе G и
множеством классов эквивалентности троек (л, Я, и), состоящих
из унитарного представления
л: 0->Аи1Я,
гильбертова пространства Я и единичного вектора и^ Н,
топологически порождающего Я относительно л.
Следствие. Пусть К — компактная подгруппа группы G, такая,
что алгебра CdG/JK) коммутативна. Тогда существует взаимно
однозначное соответствие между положительно определенными
сферическими функциями на группе G и классами
эквивалентности неприводимых унитарных представлений группы G,
содержащих К-инвариантный вектор.
Доказательство немедленно получается из теоремы 8 § 4 и
теоремы 2 § 2.
Предыдущие результаты, разумеется, применимы к группе
51^ф). Однако переход к этому конкретному случаю не
упростил бы дела по сравнению с абстрактным подходом.

V. СФЕРИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ
В этой главе мы изучим спектральное разложение алгебры
CT{G//K), состоящей из гладких функций с компактным
носителем, двусторонне инвариантных относительно подгруппы К.
Мы также найдем все ограниченные сферические функции. На
протяжении всей главы G = SL2(R).
§ 1. Интегральные формулы
Из работ Хариш-Чандры стала ясной важная роль
подгрупп А и К группы G и однородных пространств A\G и
K\G при выводе формулы Планшереля. В этой главе мы
рассматриваем только пространство A\G; изучение взаимосвязи
между группой G и пространствами A\G, K\G мы отложим
до гл. VIII, посвященной формуле Планшереля.
Функции на пространстве A\GIK, т. е. функции,
постоянные на двойных смежных классах по А vi К, однозначно
определяются своим сужением на подгруппу N. Поэтому мы начнем
с интегральных формул, связывающих интегралы по
пространствам A\G и N. При докавательстве первой формулы нам не
удастся обойтись только абстрактными соображениями, так как
здесь требуется вычислить якобиан. Поэтому мы докажем ее,
используя конкретную матричную реализацию группы SL2(R).
Для любой функции f &Сс (G) и любого а^ А, такого, что
а{а) ф 1, имеем
II. 5 f {апа-'п-') dn = ^ '_ ^. J f (га) dn.
N Ы
Доказательство. Перемножение матриц показывает, что
/а О \П га\/а-' 0\/1 —п\_^1 {с^-1)п\
\0 a-'JU iJvO а)\0 lJ~U 1 )'
Сделаем в интеграле замену переменной га>—>(а^—1)га. Теперь
наше утверждение очевидно.
(По поводу доказательства этой формулы для произвольных
полупростых групп Ли см. Хелгасон [2, гл. 10, предложение
1.13]. Аналогам перемножения матриц служит более тонкое
вычисление в алгебре Ли.)

80 V. Сферическое преобразоеание
Следующую формулу, к счастью, можно доказать, пользуясь
только формулой I 1 и абстрактным разложением Ивасавы
Ь = AN К, dx = da dn dk. Хотя переменную на множестве
смежных классов, скажем на A\G, следовало бы обозначать х, для
простоты мы будем иногда писать х. Однако мы всегда будем
обозначать символом dx инвариантную меру на пространстве
A\G, такую, что dx = dadx.
Пусть f S CJfi), матрица а^А удовлетворяет условию
а.{а)ф1. Тогда функция x>—^f{x~^ax) на пространстве A\Q
имеет компактный носитель и справедлива формула
12. [ f{x~^ax)dx=^ , \ \\\{kank~')dndk===^
.L |а(а-')—1 I ^ J
v^ хп \ \fikank~^)dndk.
А\а ■ ' ' • к N
а (а)'''
I а iaf' -а {а
Доказательство. Положим ф(;с) = /(х-'ох). Ясно, что
носитель функции ф в пространстве A\G компактен. Согласно
общим теоремам об однородных пространствах, если g — такая
функция из CciG), что '*я = ф, то
^ (p{x)dx= ^g (х) dx.
А\а а
Используя разложение dx=^dadndk, получаем
\ (р{х) dx= \ \ ф (nk) dndk = \\f{k' 'га 'ага/г) dn dk ■■
\ [f{k~^aa~^n~^ank)dndk =
'К
—.—г:——г \ \ f{k~^ank) dndk
а \а~ ) — \\ J •?
А\а ПК N к
N К
К N
(в силу формулы I 1). Наше утверждение доказано,
Введем обозначение
D (а) = а {а)''' - а [аГ'^' = р (а) - р (а)"'.
Тогда
|D(a)| = |D(a-')|.
а (а)''' а (аУ'
I а (а)'/'- а (а)-'/Ч \D(a)\ '
В зависимости от обстоятельств часто бывает удобно заменить
множитель перед интегралом в формуле 12, пользуясь этим
тождеством.

§ 2. Преобразование Хариш-Чандры 81
§ 2. Преобразование Хариш-Чандры
Пусть CciG, iC) — пространство функций на группе G с
компактным носителем, инвариантных относительно сопряжений
из подгруппы К, т. е. таких, что
f{k~^xk) = fix), k^K, x^G.
Для функции f^CciG, К) определим ее преобразование
Хариш-Чандры формулой
Н/(а) = р(а) 5 /(an)dn = \D{a)\ J /{х-'са)dx.
и А\а
Первое интегральное в^)Ipaжeниe пригодно при всех а^А,
второе — только для тех элементов а, для которых р(а)Ф1.
Позднее мы определим преобразование Хариш-Чандры для
другой подгруппы Картана iCcrG; поэтому мы будем
обозначать только что введенное преобразование символом H^f, чтобы
подчеркнуть зависимость от А. В этой главе мы почти всюду
будем использовать выражение для преобразования Хариш-
Чандры в виде интеграла по N, а ие по A\G. Из этой
формулы ясно, что если f^CT{G, К), то hfeCT {А).
Назовем матрицей Вейля матрицу
W ■■
а :)•
Она порождает группу из четырех элементов: 1, w, —1, — w.
Ее факторгруппа W по подгруппе (1, —1} называется группой
Вейля. Матрица w действует на группе А следующим образом:
1-1 оЛо a-'Ju oj~lo а)'
при этом а'" = а~\ Пространство орбит A/W параметризуется
точками множества А'^, состоящего из матриц аеД для
которых р(а)^1, т. е. из матриц вида
С :-)•
а>1.
Очевидным образом определяется также действие группы Вейля
на функции на группе А
Теорема 1. Функция Hf инвариантна относительно группы
Вейля, т. в.
lil{a)=Hf(a-').

82 V. Сферическое преобразование
Доказательство. В силу непрерывности функции Н/,
достаточно доказать это утверждение, когда 0{а)ФО и,
следовательно, I D (а) I = ID (а~') |. Заметим, что отображение
есть внутренний автоморфизм группы G порядка 2, причем на
подгруппе А оно совпадает с отображением ai—*-а~'. Это
отображение сохраняет меру на пространстве A\G; теперь
инвариантность функции Н/ относительно группы Вейля очевидна
из второй интегральной формулы для преобразования Хариш-
Чандры.
Итак, преобразование Хариш-Чандры есть линейное
отображение
Н: C,(G, Ю->CЛЛ)^
где индекс W обозначает пространство функций, инвариантных
относительно группы Вейля.
Теорема 2. Если f, g^Cc{G//K), то
Hif*g)^Hf*Hg,
т. е. сужение преобразования Хариш-Чандры на пространство
CciGj/K) есть гомоморфизм алгебр.
Доказательство. Имеем
Н (/* g) (а) == р (а) J (/« g) (а«) rfra =
N
= Р(а) 5 5 / {any)g(г/-') dydn='
N а
= р (а) J J / {ay) g(г/-'«) dy dn.
N a
(Мы сделали замены переменных у^-^у~\ у*-^п~^у.) Пусть
у ==Ь/га/г — разложение Ивасавы; тогда
Н (/ * g^) (а) = р (а) 5 5 5 f {abm) g{m-'b-'n) db dm dn =
NAN
==P(^) \ \ \ f{ab~^tn)g{nr^bn)dbdmdn =
N A Ы
== p (a) p {b)~^ \\\ f {ab'^tn) g (m~'nb) db dm dn ==
= p (a) p (6)'"' \ \\ f (ab'^m) g (nb) db dm dn =
= p (a) \ U / (ab'^m) g (bn) db dmdn.

§ 2. Преобразование Хариш-Чандры 83
Но
(Н/ * Hg) (а) = J Н/ (aft-') Hgr(ft) db =
\\\piab-')f {ab-'m) p (ft) g (ft«) i/m dn db,
что совпадает с только что полученным выражением. Теорема
доказана.
Сформулируем основную теорему о преобразовании Хариш-
Чандры,
Теорема 3. Отображение
Н: CTiG//K)->CT{Af
есть изоморфизм алгебр.
Из доказательства будет следовать явная формула обращения
для преобразования Хариш-Чандры, принадлежащая Годе-
ману [6]; см. также статью Хариш-Чандры [6].
Обозначим буквой Р множество положительно определенных
симметричных 2Х2-матриц. Любую матрицу реР можно
привести к диагональному виду, и в пространстве R^ существует
ортоиормированный базис, состоящий из собственных векторов
матрицы р. Следовательно,
p = k~^ak
при некоторых k^K, а^А.
С другой стороны, произвольную матрицу ;csG можно
записать в виде произведения
x = pki,
где р^Р, ki^K. Следовательно,
xx = ki pk\==k\ k~ а kk\.
Если функция / двусторонне инвариантна, то
/(^)«./(р) = /(а) = /(а-'),
так как матрица w принадлежит подгруппе К и шаш-' = а~'.
Таким образом, функция f зависит только от величины а (а);
заметим, что собственные значения матрицы *хх равны а (а) и
а (а-'). Поэтому, в частности.

84 V. Сферическое преобразование
Введем ряд обозначений для того, чтобы использовать
координаты на группе G. Пусть
Если матрица х диагональна, она имеет вид
^"=(0 а-)'
причем а(йа) = а^. Функция
а'^ + а-^ а(а)+а(а-')
взаимно однозначно отображает интервал [1, оо) на себя.
Если /о — двусторонне инвариантная функция на группе G,
то она зависит только от величины tr';cx; поэтому мы будем
пользоваться новой переменной
1 , / а2 + 6^ + с2 + ^2
о == — tr 'л:л: == —^—^—^— .
Если ;с — диагональная матрица, как выше, то
функция /о соответствует функции вещественной переменной,
определенной иа интервале [1, оо):
при помощи этих координат можно записать
преобразование Хариш-Чандры следующим образом:
nfQ{h) = a{K)^'\fa{hn)dn^
N
Тем самым мы получаем обычный интеграл от функции
вещественной переменной
оо

§ 2. Преобразование Хариш-Чандры
85
что дает, после замены переменной,
(1)
Лемма. Если
оо
Fiv)=\f(v + ^u')du, v>l,
— 00
то
оо
—оо
и обратно.
Доказательство. (Упражнение из элементарного курса
анализа.) Дифференцирование под знаком интеграла дает
оо
Г(о)= J /'(^о + у«2)^ы;
— оо
таким образом,
]F{v + -Lr^)dw==] ]r{v + ^^^)dudw =
—оо —оо —оо
2Я оо
о о
оо
= 2я J/'(о + ;с) ^л: == - 2я/(о),
что и требовалось показать (обратное утверждение также
очевидно).
Заметим, что из этой леммы вытекает также теорема 3,
поскольку, используя координаты на группе, мы получаем
явную формулу обращения для преобразования Хариш-Чандры.
В литературе иногда используется другая замена переменной,
которая соответствует параметризации элементов группы А при
помощи экспоненциального отображения из алгебры Ли. В
нашем конкретном случае положим
а == е"^, откуда v ■
е' + е-'
= ch/.

86 V. Сферическое преобразование
Напомним, что
sh/=^ , ch2/-sh''/==l.
В терминах переменной t мы получаем следующее выражение
для преобразования Хариш-Чандры:
оо
<2) Н/о {К) = f (о) = Ф (О = 5 / (^Ч^ + Т "') ^"-
Очевидно, что
Ф'(/) = Г(о)зК/.
Следовательно,
оо
{3) -2л/а(1о)= \ F'{\ +1ш2)^ш.
— оо
Положим ffi)==e"2—е~''2. Получаем следующий результат:
Формула обращения. Если f^CT{G/JK) и функция Ф
задается формулой (2), то
2я/о(1о)= S Ф'(0-7713-^
е "2
—оо
Эта формула представляет собой частный случай формулы
Планшереля для произвольных (не обязательно двусторонне
инвариантных) функций, которую мы докажем позднее.
§ 3. Преобразование Меллина
Пусть, как и выше. Л —группа диагональных матриц
с определителем 1 и положительными диагональными
элементами. Преобразование Меллина функции д&С^{А) определяется
формулой
fAgis)='^g{a)(){ayda, seC.
А
Ясно, что это целая функция s. Если g^CdA)'^, т. е. g{a) —
= §■(0"'), то замена переменных а>—^-д-' в нашем интеграле
показывает, что
mg{s) = Mg{-s).
Мы будем говорить, что четные функции комплексной
переменной инвариантны относительно группы Вейля, и будем
использовать обозначение
Но1 (С)^

§ 3. преобразование Меллина 87"
для пространства голоморфных функций А, удовлетворяющих
условию h (s) = h {—s). Тогда преобразование Меллина задает
линейное отображение
М: СЛ^Г->Но1(СГ.
Группа А, очевидно, изоморфна мультипликативной группе
положительных чисел R , и мы можем определить
преобразование Меллина функций на R"*" = (О, оо) формулой
оо
Mfis)^\fia)a''^. /sC,(R+).
о
Мы хотим охарактеризовать образ пространства С^Я.'^) при
этом отображении. Пусть P1F (С) — пространство Пэли —
Винера, состоящее из целых функций /, для которых существует
такая постоянная С > О, что при всех натуральных N
справедлива оценка
константа в этой оценке может зависеть от / и от Л/
(например, можно взять ее в виде с'^). Иными словами, функция /
имеет не более чем экспоненциальный рост по переменной а и
быстро убывает по переменной /, равномерно в любой полосе
конечной ширины.
Если функция / бесконечно дифференцируема и имеет
компактный носитель, то ее преобразование Меллина принадлежит
пространству Пэли-Винера. Чтобы убедиться в этом,
проинтегрируем по частям в формуле для функции Mf:
оо оо
о с
Так как / имеет компактный носитель на открытом интервале
(О, оо), то внеинтегральный член равен нулю. Продолжая
интегрировать по частям, мы будем получать все более высокие
производные функции /; ясно, что все они также имеют
компактный носитель. При этом перед интегралом появляются
множители вида
1 ,
s(s+l)(s + 2) ... (s + n) •
ЭТО показывает, что преобразование Меллина быстро убывает
в любой полосе фиксированной ширины. Экспоненциальная
оценка по переменной а очевидна.

88
V, Сферическое преобразование
Дифференцирование под знаком интеграла показывает, что
л-я производная функции Mf задается формулой
со
(M/r(s) = J f {а) а'(log аТ^',
таким образом, если f еСГ(0, оо), то все производные
функции Mf тоже принадлежат пространству Пэли — Винера.
г-
-г-
'
<^1
'
,
"*
Рис. 1.
Мы хотим получить формулу обращения для
преобразования Меллина; при этом будет доказано следующее утверждение.
Теорема 4. Преобразование Меллина
М: C?{Af->PWiCf
есть изоморфизм.
Доказательство. В действительности мы докажем, что
преобразование Меллина задает изоморфизм пространств СТ{А)
и PW (С). Для любой функции F s PW (С) и для любого
вещественного числа а положим
^MaFia) = -i J F{s)a'ds.
Re s=a
Ha самом деле функция *M„F не зависит от а. Действительно,
пусть 01 < 02, и пусть R — прямоугольный контур,
изображенный на рис. 1; тогда интеграл
Jf (s)a^rfs.

§ 3. преобразование Меллина
89
очевидно, равен нулю. Если s = ai + //, то ds==idt (это
объясняет, зачем мы ввели множитель — I). С другой стороны,
справедливы оценки
5 \Р{а±1Т)\аЫа
J gO log о
Т" log а
ЭТО показывает, что интегралы по верхней и нижней сторонам
прямоугольника R стремятся к нулю при Г->оо. Таким
образом, *MaF не зависит от а.
Функция *Mf,F имеет компактный носитель на R"*". Чтобы
доказать это, зафиксируем число а > 0. При всех а и при всех
натуральных N справедлива оценка
Предположим, что а < 1/С, и устремим а к бесконечности.
Мы видим, что *М.аР{а) = а. Если а велико, то нужно
рассмотреть предел при (т-> —оо; мы снова получим, что ^Af^f (а) = 0.
Итак, функция *M(,F имеет компактный носитель.
Нам осталось доказать формулу обращения. Положим, по
определению.
*М~
F(a)-=-i J F{s)a~'ds.
Мы покажем, что
Res=(T
'М~М/= 2я/
для всех функций /eCc(R ). В самом деле, с точностью до
замены переменной это просто формула обращения Фурье.
Действительно, положим а = е*; тогда
Ml (s) = 5 / (е*) е-^^е"^ dx = Fa (- t),
FAx)==fie'')e<"'.
оо
F{a) = -i 5 f (s)a~Vs= 5 f ((T-f й)а~"~"^/ =
Re s™(T — oo
oo
a-" J Fia + it)a-»dt,
где
С другой стороны.
'М"

90 V. Сферическое преобразование
И мы видим, что оператор М~ сводится к обратному
преобразованию Фурье. Теорема доказана.
§ 4. Сферическое преобразование
Положим, как и прежде.
Ф« W = ^Р (kxf^^ dk = (p {х, s),
где К — группа вращений окружности, а переменная х
принимает значения в группе G = SL2(R). Для произвольной функции
f^CciG/IK) определим ее сферическое преобразование формулой
Sf(s)= \f{x)cpAx)dx.
Q
Теорема 5. Следующая диаграмма коммутативна:
\ /
s\ /м
РГ(С)'*'
т. е. S = МН, причем все отображения являются изоморфизмами.
Доказательство. Имеем
Sf (s) == 5 / (х) ф, {x)dx=^^^f (х) р {kxY+' dx dk =
Q КО
= \\\f (an) p (/га)*+' da dn dk = MHf (s).
A N к
Мы уже показали раньше, что отображения М и Н —
изоморфизмы. Итак, наша теорема доказана.
Следствие 1. ф^ = ф_з.
Доказательство. Для любой функции f ^СТ {G//K)
выполняется равенство Sf(s) = S/(—s). Поэтому ф^ и ф_^ совпадают
как функционалы на пространстве C^iG/jK). Следовательно,
Следствие 2. При всех значениях s из полосы — 1 ^Res^l
функции фз не превосходят 1.
Доказательство. Мы приведем два доказательства, каждое
из которых иллюстрирует полезные методы. Первое принадлежит

§ 4. Сферическое преобразование 91
Хелгасону и Джонсону [1], которые рассматривали
сферические функции на произвольных компактных полупростых
группах Ли. Пусть f sL'(G) — двусторонне инвариантная функция.
Тогда
\^\fix)\dx^\^\ f{kan)\piafdkdadn= J р(а)(Н 1 /|) {a)da.
А
Если — 1 < (Г = Re S < 1, то
51 ^pAx)fix)\dx^ 5 ^p„ix)\f{x)ldx = {fAH\f\){a) =
= 5(H|f|)(a)(p(ar + p(an)da<
А+
<2 5 p(a)(H|/l)(a)da<oo.
А+
Таким образом, функция фз задает непрерывный функционал
на пространстве L^{G) и, следовательно, ограничена.
Второе доказательство принадлежит И. Стейну. Зафиксируем
точку ае Л и будем рассматривать Фз(а) как функцию
переменной S. При (г==—1 получаем оценку |фз(а)|^1. В силу
следствия 1, эта оценка справедлива также при (г=1. Очевидно,
что рост в полосе — 1 ^ а ^ 1 не более чем экспоненциальный.
Из теоремы Фрагмена — Линделефа вытекает, что функция ф^
ограничена в этой полосе, что и требовалось доказать.
В следующем параграфе мы докажем, что справедливо и
обратное утверждение: функция ф^ ограничена, только если s
лежит в указанной полосе.
Для удобства читателя мы воспроизводим здесь
доказательство теоремы Фрагмена — Линделефа.
Теорема Фрагмена — Линделефа. Пусть f — голоморфная
функция в полосе Ст] ^ ст ^ (Тг. че превосходящая по модулю 1
на границе этой полосы. Предположим, что существует такое
число а ^ 1, что f{s) = 0 (е' ^'") в нашей полосе. Тогда | / (s) К 1
во всей полосе.
Доказательство. Пусть А, > а; тогда при всех достаточно
больших I /1 справедливо неравенство
|/((T-f Й)|<е1'|\
Выберем целое число /и ^ 2 (mod 4), такое, что от > А,. Если
S =■ ге'^, то S'" = г'" (cos /иЭ -\- i sin /пЭ), причем угол /иЭ близок
к (2^-1-1) я. Зафиксируем число е>0 и рассмотрим функцию
g{s) = e,{s) = f{s)e^'^.

«2
V. Сферическое преобразоеание
Тогда для всех s из нашей полосы получаем
|g(s)Kei'iV'"=°^'»e.
Следовательно, найдется достаточно большое число Т, такое,
что функция \g\ не превосходит единицы на горизонтальных
^1
Рис. 2.
отрезках t=±T, di^a^a^- Ясно также, что она не
превосходит единицы на боковых сторонах прямоугольника,
изображенного на рис. 2. Следовательно, внутри этого прямоугольника
/(s)Ke-«^'"=°»
me
Это неравенство справедливо при всех е > О, и, значит, внутри
прямоугольника
l/(s)l<l.
Теорема доказана.
Мы закончим этот параграф выводом явной формулы
обращения для сферического преобразования. Существование такой
формулы вытекает из теоремы 5. Мы покажем, что ядром
обратного преобразования служит функция ф(л:, s), причем
переменная s пробегает прямую (г = 0. Поэтому мы будем
писать ф(л:, //) вместо ф(л:, s).
Напомним формулу для сферического преобразования:
Sf(s)= \nx)^{x,s)dx.
а
Теорема 6. Пусть / е СГ {G//K). Тогда
/(1)= 5 S/(/T)TthM^.

§ 4. Сферическое преобразование 93
Доказательство. Мы сохраняем наши старые обозначения и
полагаем
" U a-'J' 2 ' «-^ '
/^(и) = Ш(Л„).
По формуле обращения Меллина получаем
— ОО —ОО
Следовательно,
ОО
F{cht)= 5 S/(/t)cos(/t)-
2я
/^'(ch/)= 5 S/(/T)^i2jM(_^)
2я
Из определания преобразования Хариш-Чандры вытекает, что
ОО ОО
2я/(1) = - ^F'[l+ju')du=~ ^ F{cht)chJdt-=
— ОО —ОО
ОО ОО
— ОО —ОО
Внутренний интеграл равен
ОО
Ssin /т J, ..
в'" — е
— ОО
Теорема доказана.
Георелеа 7. Определим меру Планшереля формулой
PW</« = i-lh(if)|l.
Если функция q четна и принадлежит пространству Пэли —
Винера, то
S"'gW= 5 g{s)^{x, s)P{s)ds;
Res-O
другими словами, S~ = S , где S — эрмитово сопряженный
оператор относительно меры P{s)ds.

94 V. Сферическое преобразование
Доказательство. Мы сведем обшую формулу обращения
к доказанной только что формуле для f (1), пользуясь свойствами
сферических функций. Для произвольной функции f ^СТ (G//^)
определим функцию fx равенством
fx(y)= \f{xky)dk.
к
Тогда f^&C^iG//К) и f^{l) = f{x). Применим к функции f^
формулу обращения из теоремы 6; ясно, что общая формула
обращения вытекает из следующей леммы:
Лемма. Sfx{s) = Sf{s)((){x, s).
Доказательство. Имеем
Sfx (s) = 5 fx (у) Ф {у, S) dy =
а
= 5 \f(xky)(fiiy, s)dydk = ^fixy)(fi(y, s)dy =
а к о
= \f{y)^{x~''y, s)dy = ^fiy)(()ix-^ky, s)dy;
последнее равенство справедливо при всех k^K. Усредняя
обе части равенства по группе К и используя функциональное
уравнение для сферических функций, получаем
Щх (5) "= S / iy) Ф(•^~'' 5) ф (г/, s) dy = S/ (s) ф{x, s),
a
что и требовалось доказать.
§ б. Явные формулы и асимптотические разложения
Представим произвольную матрицу x^G = SL2 (R) п виде
/а Ь\ /у О \П и Л/ cose sine\
^^\с dj^yo v-^)K0 iJl-sine osQJ'
Тогда a{x)=^v^. Перемножая матрицы, получаем
Следовательно,
sin 9 , cos 9
V ' V
ч(* d))=^^-

§ 5. Явные формулы и асимптотические разложения
96
Далее, пусть
/а О \ ( cose sine\
^^•=10 a-'j' ^(Q) = Usine cosej-
тогда справедлива явная формула
(1)
а (г (е) Л J = „2 3in2e + „-2cos^e
Таким образом, полагая a = a(Aa) = a^, мы получаем для
сферических функций на группе SL^ (R) интегральное выражение
{2)
■''' J (а si;
db
sm^e + a-'cos^e)*^^"'^
В силу симметрии подынтегрального выражения можно
вычислить интеграл по промежутку [— я/2, я/2] и умножить его на 2.
Сделаем в интеграле замену переменных. Пусть
du
« = tge, e = arctg«, ^9 = T+U'
тогда
<3)
Ф2;
Замечание. Переменная и связана с матрицей
п(«)=(^ i);
формула (3) дает выражение для сферической функции в виде
интеграла по подгруппе N нижних треугольных матриц.
Сделаем в интеграле (3) подстановку у = (ш; получим
(4)
2/^2)^-1
Л-v^Y
dv.
По модулю этот интеграл ограничен величиной
Ой
г>2/о.2\а-1
Г (1+оУау-
I (1 + v'f
dv.

96
У, Сферическое преобразование
Предположим теперь, что а>\. Только что написанный
интеграл убывает при возрастании а, а^1. При а=1 он равен
dv
1 +о2
Поэтому можно воспользоваться теоремой об ограниченной
сходимости. Мы получим
lim \
(l+oVa^)
|2/о.2^«-1
1
„^оо . (l+t^r ^"= S (ГТ^^^-
Последний интеграл выражается через Г-функцию Эйлера:
оо
(5) \
1 , /— г (S - Va)
Чтобы доказать это тождество, рассмотрим произведение
— ОО —ОО о
1
Сделаем замену переменной /ь-5»(1-(-y^)i и воспользуемся
инвариантностью меры dtii относительно растяжений. Получаем
искомое выражение.
Вычисленный нами предел не равен нулю (напомним, что
(г>1). Следовательно, мы получаем асимптотическую формулу
для функции фя при а(а)->оо, справедливую в полуплоскости
(г>1:
(6)
Ф« {а) 7= Р {af
41)
Из этой формулы вытекает следующий результат.
Теорема 8. Если число s не принадлежит полосе — 1 <Re s^l,
то сферическая функция ф^ не ограничена.
Доказательство, которое мы дали, взято из работы Хелга-
сона и Джонсона [1], где оно проведено для произвольных
некомпактных полупростых групп Ли; в случае 5^2 (R)
возникающие интегралы легко выражаются через специальные функции.
В теории линейных дифференциальных уравнений второго
порядка при построении разложения по собственным функциям

§ 5. Язныв формулы и асимптотические разложения 97
важную роль играют некоторые асимптотические оценки. Это
обстоятельство в явной форме использовано Баргманном в его
работе [1]. Хотя мы не будем здесь касаться этих вопросов, для
удобства читателя мы приведем в теореме 9 два первых члена
асимптотического разложения сферических функций (4). В общем
виде такое разложение получено Хариш-Чандрой [7, лемма 37]
и представляет собой, по существу, один из центральных
результатов его работы. Я признателен И. Стейну, которому
принадлежит приводимое ниже элементарное изложение
заключительной части этого параграфа.
Пусть с (s) — аналитическое продолжение функции,
задаваемой в полуплоскости Res>0 интегралом
оо
dv.
J (1 +o2)(S+l)/2
Формула (5) выражает этот интеграл через Г-функцию.
Теорема 9. При е->0 справедлива асимптотическая формула
оо
1
S
dv = с (it) + с (- it) е" + О (е''^.
Доказательство. Нам потребуются некоторые леммы.
Лемма 1. Существует такая функция С{, зависящая только
от t, что при N —>оо
SlTT^^ —^+'' + °(^-)-
Доказательство. Разобьем интеграл на два слагаемых:
N а N
\=\ + 1
0 0а
где а > О —фиксированное число. Преобразуем интеграл по
промежутку [а, N] следующим образом:
N N N
] (1 + „2)(1+г«/2 = ] [ (1 + „2)(1 + ")/2 - "^IT+TrJ d° + ] -;г+1г ■
а а а
Первый интеграл в правой части предатавим в виде разности
двух интегралов:
HS-$-
4 Зак. 589

N-^* , а-"
98 V. Сферическое преобразование
По теореме о среднем,
Ц(.+Да^Ь,д-7П:7г]^"°'0(^-')-
С другой стороны,
лг
f dv
а
Положим
"^^J (i+t,2)<i+»)/2 + i [(1 + o2)(i+it)/2 --;;i+7rj^^-^—t
0 a
Лемма доказана.
Лемма 2. Справедливо равенство
с^ = с (It),
Доказательство. Рассмотрим интеграл
-it
и WW
—»
s
Очевидно, этот интеграл аналитически завиеит от параметра *
в окрестности прямой s^it (на самом деле во всей
полуплоскости Res>—1, S'^O). При Res>0 интеграл
:(.)-5
dv
1+»)/2
О ^• + "^)
абсолютно сходится. Следовательно, Cg = c{s) в этой полупло-
акости, а по принципу аналитического продолжения, и всюду.
Обратимся теперь к доказательству теоремы 9. Разобьем
интеграл на два слагаемых:
\^\ +\ »1 + П.
в о 8-Vi
в первом интеграле О^у^е"''*; таким образом, е^у^^е<<1.
Следовательно,
(l+eV)"+"'"-.l + 0(eV).

§ 5. Явные формулы и асимптотические разложения 99
Поэтому
8-'/.
^ ^ J (l+o2)a + ")/2(l + g2o2)(I-«)/2 ^^ =
е-'/. /- 8-V. ч
= -■£^ + <:. + 0(в''.)
При е-»о в силу леммы 1.
Далее,
"-S
g-Vi
cfy ■
=s
(l+o2)<t+")/2(e2 + o2)a-«)/2
da
(мы сделали замену переменной v ^-^ \/v). Положим и = v/e;
снова в силу леммы 1 получаем
= e"[--~J- + c-< + 0(eV.)].
Таким образом,
I + П = с, + е''с_, + О {е'''),
что и требовалось доказать.

VI. ПРОИЗВОДНОЕ ПРЕДСТАВЛЕНИЕ
АЛГЕБРЫ ЛИ
До сих пор мы пользовались в наших рассуждениях, по
существу, только теорией меры. В этой главе мы впервые
начинаем использовать гладкую') (или вещественно аналитическую)
структуру на группе. Мы увидим, каким образом
представление произвольной группы Ли G порождает представление ее
алгебры Ли, определенное на плотном линейном подмножестве
пространства представления группы G. В случае группы SLgCR)
это представление имеет особенно простой вид (§ 2)»
§ 1, Производное представление
Пусть G — группа Ли. Для наших целей достаточно
предположить, что G^SLaCR), или GL} (R), или GL^ (R). Важно,
что на группе G можно ввести бесконечно дифференцируемые
координаты. Напомним, что на SLiiK) мы ввели координаты
{х, у, 9), связанные с действием на верхней полуплоскости. Для
группы GLt (R) потребовались бы 4 координаты (и, х, у, Э), где
ы — скалярная матрица. Разумеется, для GLjCR) можно
использовать также 4 элемента 2 X 2-матрицы.
Пусть G-—замкнутая подгруппа группы GL„(R). Алгебра Ли
группы G определяется как множество таких матриц X, что ряд
ехр/Х = 2,^^
Принадлежит G при всех / s R, Алгебра Ли группы О
обозначается д. Если G = SL2(R). то алгебра Ли g состоит из всех
вещественных 2 X 2-матриц со следом 0. (Чтобы это проверить,
воспользуйтесь, к примеру, жордановой нормальной формой.)
Таким образом, для группы SLziK) базис алгебры Ли над R
состоит из трех матриц
1о oj' li oj' U -ij-
') Термин «гладкий» всюду в этой книге означает «бесконечно
дифференцируемый». — Прим. ред.

§ 1. производное представление 101
Если Z —элемент алгебры Ли, то отображение
/|—s-exp/J
называется однопараметрической подгруппой группы G. Мол<но
доказать, что для произвольных групп Ли отображение
ехр: g-^G
является вещественно аналитическим диффеоморфизмом (но,
конечно, не групповым изоморфизмом) в некоторой окрестности
нуля. Это утверждение тривиально проверяется для группы
SLolR). Если Z, У е g и матрицы X, Y коммутируют, то
ехр (J + Г) = ехр J-ехр 7.
В частности, рассмотренная выше параметризация
однопараметрической подгруппы есть групповой гомоморфизм.
Функция на группе бесконечно дифференцируема в том и
только в том случае, котда она бесконечно дифференцируема
как функция локальных координат. Смысл этого утверждения
для группы SL2(R) ясен, и мы не станем сейчас утомлять
читателя общими определениями многообразий и групп Ли. Пусть
он опирается на свою интуицию или обратится к другим
источникам. По поводу отображений в банаховы пространства и их
дифференцируемости см. Ленг [1]. Этот случай не содержит
существенных отличий от случая скалярных функций.
Пусть G —группа Ли, Я — банахово пространство. Пусть
/: G-^ Я —гладкое отображение. Для любых элементов J eg,
J/ е G определим производную Ли формулой
2J(y) = l-/(yexp(a))|,.o.
Тогда 2^/ -— тоже гладкое отображение; таким образом, мы
получаем линейный оператор
S;f: С°° (G, Я) -^ С°° (G, Я).
Ясно, что оператор 2^ левоинвариантен, т. е. коммутирует с
левыми сдвигами. Если Я = С — поле скаляров, то легко
проверить, что 8^- — дифференцирование, т. е.
Зафиксируем у ^ G а положим
Fy{X) = f{yexpX).
Тогда Fy — гладкая функция на алгебре Ли g и, по определению,
^xf (у) = Itm J .

102 yj- Производное представление алгебры Ли
Для любого гладкого отображения F, заданного в окрестности
нуля в 3, справедлива формула Тейлора
F[X)^F{0) + F'{iS)X+O{\Xf),
где F'{Q): g-^ Я — производная отображения F в точке О
(линейный оператор). Следовательно,
и отображение Ji—s-S^- линейно, т.е. для любых X, У s д,
с S R имеем
^л-к = ^х + 2у, Sgjr^cSjf.
Обозначим Зд множество линейных комбинаций элементов
алгебры Ли g с комплексными коэффициентами; таким образом,
элементы д^ — это матрицы вида
Х + гУ, Х.Уед.
Если a. = a-\-ib, а, & е R, то положим, по определению,
Kx=Kx-^ihx-
Тем самым мы распространили определение производной Ли
на элементы комплексной алгебры Ли д^,.
Рассматривая гладкие функции и интегральные
представления, мы часто должны будем переходить к пределу или
дифференцировать под знаком интеграла. Для удобства читателя
приведем здесь несколько лемм, обосновывающих эти операции.
Лемма 1. Пусть X — пространство с положительной мерой j*.
Пусть f/сR" — открытое подмножество. Пусть f: ХУ^О->Е —
отображение в банахово пространство Е. Предположим, что
{{) для любого у^и отображение хi—s-/(х, у) принадлежит
пространству L'(n, £■);
(ii) для любых х& X, Уо^и справедливо равенство
lim f(x,y) = f{x, у о);
У-*-Уй
(iii) существует такая функция /teL'(n), что
\f{x,y)\<\h{x)\
для всех у^^и.
Тогда отображение
У ^-^ \ f ix, у) dvi (х)
X
непрерывно.

§ 1. производное представление 103
Доказательство. Достаточно показать, что для любой
последовательности {у^}, сходящейся к точке у ^U,
последовательность интегралов \f{x,yk)d\x{x) сходится к \f{x, у)с1ц{х).
X X
Положим fk{x)='f{x,yk). Тогда последовательность {f^}
поточечно сходится к функции xt-^f{x, у). В силу (iii) мы можем
воспользоваться теоремой об ограниченной сходимости, что и
завершает доказательство.
Лемма 2. Пусть X — пространство с положительной мерой ц.
Пусть и а 9!^ — открытое подмножество. Пусть f: Xy^U -*Е —
отображение в банахово пространство Е. Предположим, что
(i) для любого у ^U отображение xi-^ f{x, у) принадлежит
пространству V (ц, £■);
(ii) для любого у ^U каждая частная производная Djf{x, у)
(вычисленная по отношению к j-u координате
переменной у ^U) принадлежит пространству L' (ц, Е);
(iii) существует такая функция fi s L' (\х), что для всех y&U
\ОДх,у)\<\и{х)\.
Положим
0{y) = \f{x,y)dix(x).
X
Тогда производная DjO{y) существует и
Di^{y)^\Dif{x,y)dvi{x).
X
Доказательство. Имеем
Ф(у + he,) — Ф (i/) г 1 .
-^ f = i"^ [/ (^, У + he,) - f (х, у)] dix(х).
X
Пользуясь теоремой о среднем и условием (iii), заключаем, по
теореме об ограниченной сходимости, что правая часть при
А->0 имеет предел, равный
^Dif{x,y)dn{x).
X
(Как и в предыдущем доказательстве, для того чтобы
воспользоваться теоремой об ограниченной сходимости в ее
стандартной форме, нам следует перейти к последовательности {/г^}.)
Основное предположение в лемме 2, которое позволяет нам
дифференцировать под знаком интеграла, — это существование

104 ^i- Производное представление алгебры Ли
суммируемой мажоранты у частной производной по у;
остальные предположения сделаны для того, чтобы все встречающиеся
символы имели смысл.
Пример. Пусть / S L' (R"), ф е СГ (r"). Покажем, что
функция f * ф бесконечно дифференцируема и для любого
дифференциального оператора D^^Df'' ... Z)^" справедливо равенство
Z)P(/*ф) = /*£)"ф.
В самом деле, по определению,
(/*ф)(г/)= \^f[—x)(^{x-\-y)dx.
Очевидно, что условия леммы 2 выполнены, и мы можем
последовательно дифференцировать функцию ф под знаком интеграла,
что и дает приведенную выше формулу.
Лемма 3, Пусть G — группа Ли, И — банахово пространство,
f^V (G, Я). Пусть ф S С^ (G, С), X s g,,- Тогда функция f * ф
бесконечно дифференцируема и
2.V (/ * ф) = / * ЙхФ-
Доказательство не отличается от случая пространства R"»
По определению,
if*(p)iy)='\fix-')(p{xy)dx.
а
В окрестности точки у ^G можно ввести локальные
координаты, отождествляющие эту окрестность с открытым
подмножеством евклидова пространства. Условие равномерной
ограниченности из леммы 2, очевидно, выполнено.
Пусть G — группа Ли, п: G-^GL (Я) — ее представление
в банаховом пространстве. Линейное подмножество Я" с: Н,
которое состоит из всех векторов аеЯ, таких, что отображение
X 1—> п [х) V
бесконечно дифференцируемо, называется пространством
С°°-векторов (или пространством Гординга). Оно инвариантно
относительно действия группы G, т. е. если a^G и а е Яд, то
п (а) а е Ял;
кроме того, оно инвариантно относительно действия гладких
функций с компактным носителем. В действительности
справедливо более сильное утверждение:

§ 1. Производное представление 10В
Если (f^CT{G) и у S Я, то п' (ф) v е Ял •
Доказательство. По определению,
п (х) п'(ф) У = J ((>{y)n{xy)vdy =
= ^cpix-^y)n{y)vdy.
В силу леммы 2 мы можем дифференцировать по переменной х
под знаком интеграла. Доказанное утверждение есть, по
существу, частный случай леммы 3.
Напомним, что если {9„}—последовательность Дирака, то
для любого вектора vmH последовательность п'(9„)а сходится
к V. Так как можно выбрать последовательность Дирака,
состоящую из гладких функций с компактным носителем, то
отсюда вытекает, что
пространство Ял плотно в Н.
Другими словами, существует большой запас С°°-векторов,
и даже С°°-векторов вида л' (ф) у, где ф е СГ (G).
Перейдем теперь к определению производного представления
алгебры Ли. Если v s Ял, то положим
dn{X)v = -^ n{exptX)v\f^Q.
Мы докажем, что вектор в правой части принадлежит
пространству Ня, и, более того, получим формулу
DER 1. Если f {х) = я (х) v, то для всех а(= С% о ен Ял
dn{X)v== (ZJ) (е), л (а) ал (Х) v = (S.^/) (а).
Так как функция / бесконечно дифференцируема по
предположению, из этой формулы вытекает, что вектор dn (Х) v
также бесконечно дифференцируем. Для доказательства
формулы заметим, что, по определению,
(S.J)(a) = -^f(aexp/X)Uo,
поэтому достаточно применить к выражению
я (ехр tX) у — у
t
непрерывный оператор л (а) и перейти к пределу при ^->0.

106 VI. производное представление алгебры Ли
Из сказанного ясно, что dn{X): Я^-> Яп — линейный
оператор, линейно зависящий от X е д^,. Мы будем называть
отображение Xy-^dn{X) производным представлением
представления я.
DER 2. Для любых X,Y е<з, и функции f: х^-^п {х) v, аеЯл >
Доказательство. Имеем
n{x)dn{Y)v'==^^yfix)
в силу DER 1. Кроме того, еоли w&H^ и /^ (х) — Jt (х) т>, то
dn{X)w = {SJJie)
(достаточно в предыдущую формулу подставить je = e). Чтобы
получить bER 2, нужно воспользоваться этой формулой при
т> = dn{Y) V.
Пусть X,Y т%. Существует единственный элемент [X, Y] s 0,
такой, что для всех функций feiC"'{G, Н) справедлива
формула
^[х,у]!'-^хЫ-ЬЫ.
Скобку можно вычислить, используя произведение матриц,
а именно
[X, Y\^XY — YX.
Мы докажем это утверждение ниже. Из формулы DER 2
получаем тогда для представления dn соотношение
DER 3. du ([X, Y]) = [du {X), dn (V)],
где скобка в правой части означает коммутатор операторов,
т. е. dn{X)dn{Y) — dn{Y)dn{X).
Чтобы доказать формулу для коммутатора производных Ли,
нам потребуются две леммы. Заметим, что если g — обратимая
матрица, то
^-'(ехр X) ^ = ехр (,^^-'ад.
Это очевидно, поскольку g~^X"'g = {g~^Xgf'.
Лемма 4. Пусть s — вещественное число; положим gs = ехр sY.
Пусть
ф(Х) = /(ехрХ).
Тогда
-h^ie;'^s;)U-¥iX){XY-YX).

§ 1. Производное представление 107
Доказательство. Имеем
g;^Xg^ ^{I-sY + 0 (s^)) X{I + sY-^0 {s")) =
= X + s(Zy-7Z) + 0(s2).
Следовательно,
Ф {S7'^S,) = Ф (X) + Ф' (X) s (X7 - rZ) + 0 {s\
Отсюда немедленно вытекает утверждение леммы.
Заметим, что в лемме 4 можно было рассматривать
функцию Ф^ (X) = / (г/ехр X). Мы воспользуемся этим в лемме 5,
имея в виду приложение к доказательству формулы для
коммутатора производных Ли.
Лемма 5. Пусть и — фиксированное вещественное число;
положим y^expuY. Пусть
J {и, S, t)==f(yexp{igj^Xg^)).
Тогда
D,DJ{u, 0,0) = <(>'^{0){XY-YX).
Доказательство. Левая часть нашей формулы равна
I- D^ {и, О, О li=o = 4f [ф; (tX) t {XY - YX)^ 1,^3.
Утверждение леммы немедленно следует из правила
дифференцирования произведения.
Положим теперь, как и прежде, ^^ = ехр5У, и пусть
F [и, s,t) = f (ехр (uY)ехр(tgj'Xg^)).
Тогда
/ (ехр itX) ехр (uY)) = / (ехр (uY) ехр (tg^'Xg^)) = F (и, и, i).
Таким образом,
{2.ад)(е) = /)зА/='(0, О, 0) + D,D^F{0, О, 0).
Кроме того,
/(ехр(иУ)ехр(а)) = /^(и, О, t),
так что
{^y^xf){e)=D^D,F{0,0, 0).
Следовательно,
(2;,gyf) {е) - (S^ySiJ) (е) = D.D^F (О, О, 0).
Из леммы 5 вытекает, что
D,D/ {и, О, 0) = ф' (0) {XY - YX).

VI. производное представление алгебры Ли
Получаем
Оф2р (О, о, 0) = ф' (0) {XY - YX) = {i^xY-YK)f) {е).
Итак, мы доказали справедливость приведенного выражения
для коммутатора производных Ли.
Установим, каким образом ведет себя производное
представление при композиции с операторами я (ф), ф s СГ (G)- Введем
правую производную Ли
(9?.,/)(x) = -^f(exp(^J)x)|,,o,
которая коммутирует с правыми сдвигами.
Пусть (s^CT {G). Следующая формула справедлива для
произвольных векторов а е Я, а не только для v е Н^:.
DER 4. du (АО я' (ф) = я' (8?_хго).
Доказательство. Имеем
п (ехр tX) я' (ф) а ^ я (ехр ^/Y) \ ф (х) я (х) и dx =
= \ Ф (;с) я (ехр [tX) х) v dx =
^ \ Ф (ехр (— tX) х) 31 ix) V dx;
мы сделали замену переменной хг--^ гкр{—tX) х. Рассмотрим
полученное выражение при малых t и продифференцируем его
под знаком интеграла; это допустимо, так как функция ф имеет
компактный носитель. Положим
Ф (ехр (— iX) х) = F (/, .1')-
Функция Xi-^DiF{t, х) имеет компактный носитель. Применяя
оператор d/dt к нашему выралсению, получаем интеграл
\ -^ Ф (ехр (— iX) х) я (х) V dx.
При ^ = 0 этот интеграл в точности равен п'(8?_хф) а; итак,
формула DER 4 доказана.
DER 5. я' (ф) dn {X) = п' (£-хф).
Доказательство совершенно аналогично предыдущему и будет
опущено.
Из-за знака минус, появляющегося в формулах DER 4 и
DER 5, а также по некоторым другим причинам иногда удобно

§ 1. Производное представление ЮЭ
пользоваться следующими обозначениями:
{X * ф) (^/) = -|. ф (ехр (- tX) у) \tJ, = - {Шх<р) (у),
(Ф * J) (г/) = А ф {у ехр (_ tX)) Uo = - (Sx<P) (у) •
Легко проверить, что
(ф * J) * г}) = ф * (X * ij3)
для любых ф, -ф е СГ (G). В этих обозначениях получаем
rJ (ф * X) = л' (ф) cfn (X), п' (X * ф) = dn (Z) п' (ф).
Для краткости иногда пишут п{Х) и я(ф) вместо dn(X) и зт'(ф)
(обозначения, котор'ые сильно смущали меня, когда я изучал
теорию представлений, но которые очень удобны, если к ним
привыкнуть). При этом л рассматривается как
мультипликативный гомоморфизм алгебры (относительно свертки), порожденной
элементами алгебры Ли и функциями из пространства С" (и).
Другими словами, в этих обозначениях
я (ф * X) ^ п (ф) л (Х), я (X * ф) ^ п (Х) я (ф).
На этом мы покончим с формализмом С°°-векторов; скажем
дополнительно несколько слов по поводу аналитичности. Пусть
Я — банахово пространство. Отображение f: G ^-Н называется
аналитическим (т. е. вещественно аналитическим), если оно
как функция локальных координат допускает разложение в
степенной ряд в окрестности каждой точки.
Форлгула Тейлора. Пусть f: G —>- Н — аналитическое отобра-
Пусть у ^ G. Для всех достаточно малых X ^ %
(относительно любой нормы в конечномерном векторном
пространстве^ и для всех t, Q^t^X, справедлива формула, Тейлора
оо
1
f(t/exp^J) = j;^(2xf)(i/)^
п=0
Доказательство. По определению,
Sx/ {у ехр uX) = -j^f (у ехр ((и -f t) X)) \i=u = ^f(y ехр иХ).
Рассуждая по индукции, положим F = ixf и допустим, что
/?(i/exp«X) = (-|j-) fiyexpuX).
Тогда
^xF {у ехр uX) = -^F{y ехр uX) = (-j^j f {у ехр иХ).

lie VI. Производное представление алгебры Ли
Другими словами, мы доказали формулу
(*) m{yexpuX) = (-^yfiyexpuX).
Пусть {хи ..., Хг) — координаты вектора X по отношению к
фиксированному базису алгебры Ли g над R. Так как функция /
аналитическая, то при достаточно малых | X | имеем
fiyexpX) = Pixi Хг),
где Р — сходяш,ийся степенной ряд в окрестности нуля.
Следовательно,
/(irexpMZ) = J]a„^, a„eR,
при всех и, 0^и^1. Применяя формулу (*) при и^О,
получаем
(«х/)(^) = а„.
Положим теперь u^t', формула Тейлора доказана.
Пусть я: G-*-GL{H) — представление в банаховом
пространстве. Вектор V ^ Н называется аналитическим, если
отображение X v-^ Я (л:) V аналитическое.
Следствие. Если вектор v аналитический, то
оо
п (ехр Z) о = JI -^ dn (Z)" V.
Доказательство. Это немедленно вытекает из формулы
Тейлора.
Ясно, что аналитические векторы образуют в пространстве Я
линейное подмножество. Мы будем обозначать его Яя".
Теорема 1. Пусть G — связная группа Ли, я: G->GL (Я) —
ее представление в банаховом пространстве Я. Пусть VаН —
линейное подмножество, состоящее из аналитических векторов
и инвариантное относительно йя (д). Тогда его замыкание G-ин-
вариантно.
Доказательство. Пусть v sV. Для любого достаточно малого
вектора Z s g можно применить наше следствие к
аналитическому отображению x*~^a{x)v. Получим
я (ехр J^O о = JI-^ dn (Z)" о S К.

§ J. Производное представление П1
Экспоненциальное отображение переводит окрестность нуля
в алгебре Ли g в окрестность единицы в группе G.
Следовательно, замыкание V инвариантно относительно некоторой
окрестности единицы в G. Но произведения элементов из этой
окрестности порождают всю группу. Теорема доказана.
Теорема 1 дает важный критерий неприводимости
представления. Впоследствии мы увидим, что примеры множества V
из теоремы 1 можно получить, рассматривая множество К-ко-
нечных векторов в некоторых представлениях или другие
подходящие линейные подмножества.
Как мы увидим ниже, в конкретных ситуациях имеются
прямые способы доказательства того, что некоторые векторы
являются аналитическими. Это связано с тем, что некоторые
представления можно реализовать в функциональных
пространствах на группе G, причем в этих пространствах имеется
большой запас аналитических функций. Нам нужно будет в этом
случае доказывать, что эти функци!^ рассматриваемые как
элементы пространства представления, являются аналитическими
векторами.
Существование плотного подмножества аналитических
векторов для совершенно произвольных групп Ли было доказано
Нелсоном [1].
Для произвольных полупростых групп Ли существует другое
доказательство, основанное на идеях Хариш-Чандры. Для
случая группы SLziR) методы этого доказательства блкэки к тем,
которые использовались в этой книге. Достаточно построить
последовательность Дирака, состоящую из аналитических
функций ц удовлетворяющую ослабленному интегральному
условию DIR 3'. Как аналитическое многообразие группа G
эквивалентна прямому произведению ЛХ^^Х-^. где А изоморфна R"*",
N изоморфна R, а Д" —группа вращений окружности.
Последовательность Дирака на К можно построить при помощи
рядов Фурье. Рассмотрим функцию
и образуем последовательность функций
ф„ (О = Иф (nt).
Эти функции положительны, интеграл от них равен единице,
и, как легко проверить, они удовлетворяют условию DIR 3'.
Нетрудно показать, что для любого вектора w « Я вектор
я'(ф„) о аналитический. Таким образом, во всех практически
интересных случаях у нас не возникает затруднений при
использовании аналитических векторвв, совершенно так же, как

112 VI. Производное представление алгебры Ли
И при использовании С°°-векторов. Впоследствии мы увидим,
что во всех важных для нас случаях Л^-конечные векторы
являются аналитическими (см. теорему 7 § 2 гл. X). Это даат
еще более удобный способ построения аналитических векторов.
§ 2. Сужение производного представления
на алгебру Ли подгруппы К
Вернемся к вопросам, которые рассматривались в § 1 гл. II,
где было описано, как разлагается произвольное представление
группы G = SL^ (R) при сужении на подгруппу К. Мы
исследуем связь этого разложения со свойствами производного
представления. Как обычно, положим
/ cos б sinQN
'•(e) = l,_sine cosej-
Для удобства читателя напомним, что /eS„,„ в том и
только в том случае, когда y^CdG) и справедливо
функциональное уравнение
для всех г/ S G и всех 8, 9' е R. Заметим, что множество всех
гладких функций из пространства S„,;„, которое мы будем
обозначать S^, „», плотно в Sn, т- Это утверждение, по
существу, очевидно: любую непрерывную функцию с компактным
носителем можно равномерно аппроксимировать гладкой
функцией со сколь угодно близким носителем. Заметим также, что
в формулировке леммы 1 § 1 гл. II можно заменить
пространство S„,,n на S^^. В дальнейшем при ссылках на указанную
лемму мы всегда будем иметь это в виду.
Мы сохраняем обозначения § 1 гл. П. Пусть я: G-^GL (Я) —
представление в банаховом пространстве; Я„ с: Я —
подпространство, состоящее из таких векторов v, что
я{r(Q))v=e^'^^v,
т. е. п-е собственное подпространство подгруппы К в Н.
Так как подпространство S^ ^ плотно в Sq q, ясно, что если
л' (S,,,) Я, Ф О, то
я' {Sl,) Я, Ф 0.
Положим, как и прежде.
W
<л ;)•

§ 2. Сужение производного представления на алгебру Ли подгруппы К ИЗ
Однопараметрическая подгруппа группы G, порожденная
матрицей W, совпадает с группой К.
Лемма 1. Пусть я: G~^GL{H) — некоторое представление,
^ е д. Предположим, что v е Яп — собственный вектор
оператора с1я{Х) с собственным значением X, т. е.
Тогда для всех / s R
я (ехр tX)v = е'-'о.
Доказательство. Положим f{t) = я{exptX)v. По
предположению, функция / дифференцируема. Имеем
f{t + h)-f{t) __п (ехр {t + h)X)v-n (ехр iX) v
h ^ h ~
==я(ехр/Х)"^^"Р\^)°-°.
Переходя к пределу при /г-^0, получаем я{eyi^tX)dя{X)v =
= я (ехр ^Х) Ао. Следовательно, f {t) = Xf{t). Отсюда вытекает,
что f{t)^e'**v, что и требовалось доказать.
Мы будем пользоваться этой леммой, когда X^W, / = 9,
expGr = r(G).
Теорема 2. Пусть я: G-^GL{H)— допустимое неприводимое
представление группы G = SL2 (R) в банаховом пространстве.
Пусть п — целое число, такое, что Нп Ф {0}. Тогда
пространство Нп одномерно, любой элемент v ^ Нп является С°°-вектором
и Я„ — собственное подпространство оператора йя (W),
соответствующее собственному значению in.
Доказательство. Из теоремы 2 § 1 гл. II мы знаем, что
пространство Я„ одномерно. Ясно, что я'(S^ „) Я^ #= 0; поэтому
если о„ S Я„ — ненулевой вектор, то
я' {Sn, п) Vn — CVn.
Следовательно, о„ есть С°°-вектор. Из определения
пространства Я„ ясно, что векторы о е Яд преобразуются по
представлению г (6) v-^ е'"^ подгруппы К и что Я„ — собственное
подпространство оператора йя(1^) с собственным значением in.
Из предыдущей леммы следует, что, и обратно, каждый такой
собственный вектор должен принадлежать Я„. Теорема
доказана.
Замечание. Как уже упоминалось, тот факт, что
пространство Я„ состоит из аналитических векторов, будет доказан
в гл. X (теорема 6 § 2).

114 VI. Производное представление алгебры Ли
Исследуем, как действуют в пространствах Я„ остальные
базисные элементы алгебры Ли. Удобно выбрать в качестве
базиса комплексные матрицы. Положим
Е'
=(-.' :';)• ^--ч; -О-
Перемножая матрицы, получаем
[£+,£-] = -4гГ, [г, £+] = 2г£+, \W, Е~'\-= -2iE~.
Коммутатор с элементом X s g — это линейный эндоморфизм
алгебры Ли; он обозначается adZ. Приведенные формулы
показывают, что Е"^, Е~ — собственные векторы оператора ad W.
(Заметим, что отображение Zi—> ad Z — это регулярное
представление алгебры Ли на самой себе. Его называют
присоединенным представлением. Выло бы лучше обозначать его reg X,
однако уже слишком поздно изменять общепринятые
обозначения.)
Иногда мы будем также писать Е+ и £_ вместо £"*■ и Е~,
в особенности тогда, когда нам придется употреблять эти
символы с показателями степени.
Теорема 3. Пусть я: G-^GL (Я) — неприводимое
представление группы G в банаховом пространстве. Пусть т — целое
число. Тогда прямая сумма
паЕШ (mod 2)
инвариантна относительно dn(g). Более того,
dn(£+): Я„->Я„+2,
dn(E-): Н,^Н,-2.
Доказательство. Пусть о е Я„. Формула DER 3 показывает,
что
dn (W) dn (£+) о = dn ( [Г, £"*■]) о + dn (£+) dn {W) v =
= 2j dn (E'^) V + in dn (£■+) о = г (л + 2) dn {e'^) v.
Таким образом, dn(E'^) v — собственный вектор оператора dn (W)
с собственным значением г (и+ 2). Теорема 2 или
предпосланная ей лемма показывает, что с?я(£'*') о еЯ„+2- Доказательство
для матрицы Е~ аналогично. Теорема доказана.
Приведенные рассуждения, принадлежащие Баргманну [1],
показывают, как алгебра Ли действует в пространстве
неприводимого представления группы SL2(R).

§ 2. Сужение производного представления на алгебру Ли подгруппы К Пб
Предположим, что Н^^О для некоторого целого т.
Рассмотрим' прямые суммы
q > m q < m.
no всем целым ^^/n(mod2). Тогда Нт, Яй — инвариантные
линейные подмножества относительно представления (1я(%Л.
Пусть мы уже знаем, что пространство Я„ состоит из
аналитических векторов. Тогда можно воспользоваться теоремой 1,
из которой вытекает, что если пространство Нт ненулевое, то
его замыкание инвариантно относительно n(G); так как
представление я неприводимо, то отсюда следует, что это замыкание
совпадает с Я.
Рассуждая аналогичным образом, Баргманн [1] доказал
также единственность неприводимого унитарного представления
группы SL2(R), производное представление которого обладает
описанными выше свойствами. Часть этих теорем
единственности будет доказана ниже. Остальные будут рассмотрены
в следующем параграфе.
Из того что мы знаем о действии алгебры Ли, ясно, что
неприводимые бесконечноме'рные представления группы G можно
разбить на 4 класса в соответствии с характером спектра
сужения представления йя на подалгебру f, порожденную
матрицей W.
Случай 1. Существует такое целое т, что пространство Я
совпадает с замыканием прямой суммы
Z Я,;
q^m (mod 2)
при этом Нт ф 0.
Случай 2. Существует такое целое т, что пространство Я
совпадает с замыканием прямой суммы
Z Я,;
17 < m
17 ^m (mod 2)
При ЭТОМ Нт Ф 0.
Случай 3. Пространство Н^ ненулевое, и Я совпадает с
замыканием прямой суммы
L, fig.
q четно
Случай 4. Пространство Я совпадает с замыканием прямой
суммы
Z Я,.
q нечетно

116 VI. Производное представление алгебры Ли
В случае 1 мы будем называть число т младшим весом '),
а ненулевой вектор v е Я^ — вектором младшего веса. В
случае 2 мы будем называть число т старшим весом, а ненулеаой
вектор V е Я^ — вектором старшего веса. Отметим также, что
в случае 3 пространство Нц состоит из ЛГ-инвариантных
векторов. Неудивительно поэтому, что теория представлений этого
типа тесно связана с теорией сферических функций. В
остальных случаях двусторонне инвариантные функции тривиально
действуют на Я, т. е. единичное представление подгруппы К
не входит Б разложение представления Д" в Я.
Наглядно прямую сумму ненулевых подпространств Я„
в перечисленных четырех случаях можно представить таким
образом:
пт® "т+2^J^т+А® • • • ,
... ®Н^.,@Н,„-2@Н^,
... ея-4ея_2еяоея2®я4е...,
... ея_зея-1фя,еязея5ф....
Кроме этого, у группы G существуют еще конечномерные
представления (веса которых удовлетворяют условию —т^а^т).
Мы займемся ими позднее в связи с доказательством формулы
Планшереля.
Так как весовые векторы заданного представления ~-это
функции с определенной четностью, удобно ввести разложение
функций из групповой алгебры на четные и нечетные. Для
произвольной функции f на группе G положим
Тогда функция f^ четна, а /~ нечетна. (Из контекста всегда
будет ясно, означает ли /~ нечетную функцию, определенную
выше, или же /~ (х) = f (х~').)
Пусть я — представление группы G в банаховом
пространстве Я. Пространство
Я"*" = ш lin
п четно
МЫ будем называть четным подпространством Я, а
пространство
Я" = 0 Я„
'п.
п нечетно
нечетным подпространством.
') Заметим, что вообще номер пространства ffg называется весом, а
лектор V ^ Нд ~ весовым вектором. — Прим. перев.

§ 2. Сужение производного представления на алгебру Ли подгруппы К И 7
Леяма 2. Если функция ij)eCr(G) нечетна {соответственно
четна), то оператор n'i|) переводит пространство Н в Н~
{соответственно в Я"^'), а его сужение на Н'^ {^соответственно на Н~)
равно нулю.
Доказательство. Это немедленно следует из определения
оператора я' (i|)).
Разложив функцию »ф на четную и нечетную компоненты,
мы можем затем изучать действие оператора я'(i|)) на каждом
из подпространств Н , Н~ в отдельности.
В заключение этого параграфа рассмотрим вопрос о
единственности производного представления в различных случаях.
Пусть л — представление группы G в банаховом
пространстве Н. Пусть
H{K)^ZHn
— линейное подмнолсество ^<'-конечных векторов; здесь Я„ есть 'г-е
собственное подпространство подгруппы К. Мы называли пред-
ставлет-'ие я допустимым, если размерности пространств /■/„
конечны. Если это условие выполнено, то рассуждения,
аналогичные тем, которые были использованы при доказательстве
теоремы 2 § 2, показывают, что- элементы пространства .'Y„
представляют собой С°°-векторы. Проверку этого свойства мы
поедоставляем читателю в качестве упражнения. (В дейстзи-
тельБссти они являются даже аналитичаскими векторами.)
Доказательство будет проведено в § 2 гл. X для случая
uimh\= 1.
Пусть у ^G, Л~ е g. Положим, по определению,
Ad{y)X = yXy-'-
таким образом, Ad (г/) — линейный эндоморфизм аягебры Ли g.
Отображение y-^^A.d{y) мы бз^дем называть присоединенным
представлением группы G. Напомним, что
exp(t/Zz/-') = ;/(expA')t/-'.
Если у ^G, то, как легко видеть, я (у) dn {X) = dn (Ad (у) X) я (у).
Пространство Н[Ю инвариантно относительно dn(^).
Доказательство. Пусть k ^ К, v ^ Н (К), X е д. Тогда
я {k) dn (Х) v = dn (Ad {k) X) я {k) v.
Таким образом, К-орбита вектора dn{X)v содержится в
конечномерном подпространстве — образе пространства,
порожденного i\-op6HTOE вектора v, при действии представления йя(д).

118 VI. Производное представление алгебры Ли
Следовательно, эта орбита конечномерна, что и требовалось
доказать.
Пусть rti, Лч — допустимые представления группы G в
банаховых пространствах Ни Н^- Будем говорить, что эти
представления иифинитезимально эквивалентны, если существует
линейный изоморфизм
L: Hi(K)^HAK),
коммутирующий с производным представлением, т. е. такой, что
L о drti {X) = drt2 {X) о L на Hi {Ю-
В этом случае мы будем также говорить, что оператор L
является ((-изоморфизмом или инфииитезимальиой
эквивалентностью.
Пусть S°° = YjSn,m — TO же пространство, что и выше.
Будем говорить, что представления rti и Яг являются 5°°-экви-
валеитными, если существует такой линейный изоморфизм
L: Hi{K)-^HAK),
что для всех функций ф ^ S°°
L о Я1 (ф) = Я2 (ф) о Z, на Я| {К).
Если оператор L есть 8°°-аквивалентность, то L есть ^уизо-
морфизм.
Доказательство. Пусть v ^ Hi {К). Существуют такая
функция ф е S°° и такой вектор w ^ Hi {К), что о = Я] (ф) w. Для
любого элемента X^% получаем
Lrt] (Х) V == Lui (Х) Я1 (ф) W = Ья1 (Х*ф) w =
= Я2 (X * ф) Lw = Я2 (X) Я2 (ф) Lw =
= Я2 (X) Lni (ф) ш = Я2 (X) Lv,
что и требовалось показать.
Заметим, что, так как д-изоморфизм, заданный на
пространстве Н{К), коммутирует с оператором da{W), он заведомо
коммутирует с действием подгруппы К, т. е. сохраняет градуировку
в пространстве Н {K) = ^ Я„.
Теорема 4. Пусть я, я' — допустимые неприводимые
представления группы G в банаховых пространствах Н, Н'.
Предположим, что существует такое целое число т, что представле-

§ 2. Сужение производного представления на алгебру Ли подгруппы К 119
ния Л, я' имеют младшие векторы веса т. Обозначим эти
векторы и^, и'^. Если пространства Н, Н' оба бесконечномерны
или имеют одинаковую конечную размерность, то существует
инфинитезимальная эквивалентность
L: H{K)-^H'{K),
причем i^u^==u'^.
Доказательство. Для простоты будем писать Xv вместо
dn {X) V и аналогично Xv' вместо dn' {X) v', v' е Н'. Положим
Um+2r == E+Um, Um+2r = -E+M/n-
В силу неприводимости представлений векторы и^_^_^, и'^_^^ не
равны нулю и образуют базис в пространствах Н^^^, Н'^_^^^
соответственно. Определим оператор L формулой
Тогда L коммутирует с операторами W, Е+. Остается
проверить, что L коммутирует с оператором Е_. Это доказывается
по индукции при помощи коммутационного соотношения
E+E- = E-E+~4iW.
На первом шаге индукции следует воспользоваться тем, что,
по предположению, £_м,„ = 0, E-Um = 0. Теорема доказана.
Теорема 4 имеет аналог для неприводимых представлений
со старшим вектором веса — т, где m по-прежнему целое
положительное число. Если т^2, такие представления
называются представлениями дискретной серии, потому что онл
инфинитезимально эквивалентны неприводимым
подпространствам L^{G), на которых группа G действует сдвигами. Мы
докажем это позднее, построив соответствующее инвариантное
подпространство пространства L^{G), содержащее вектор
младшего веса. Что касается конечномерного случая, то мы
получаем такой результат.
Следствие. Для любого положительного целого числа d
существует одно и, с точностью до эквивалентности, только одно
неприводимое представление группы SLiiR) размерности d.
Доказательство. Существование будет доказано в конце § б.
Единственность с точностью до инфинитезимальной
эквивалентности вытекает из теоремы 4. Итак, пусть

120 VI. Производное представление алгебры Ли
— инфинитезимальная эквивалентность. В конечномерном
случае автоматически справедлива формула Тейлора
n(expZ)y=J]^dn(J)"y,
поэтому L коммутирует с действием группы, что и требовалось
доказать.
§ 3. Унитаризация представлений
Пусть я — представление группы G в банаховом
пространстве Е. Мы будем говорить, что представление я уиятаризуемо,
если я инфинитезимально эквивалентно некоторому унитарному
представлению в гильбертовом пространстве Н.
Инфинитезимальная эквивалентность
L: Е{К)-^Н{К)
индуцирует скалярное произведение в линейном
пространстве Е{К.). Обозначим символом Е{К)п п-е собственное
подпространство Е{К) (которое совпадает с пространством £„);
различные такие подпространства должны быть ортогональны
относительно этого скалярного произведения. В частности, если
dim£(/C)„ = ciim£'„='1, то скалярное произведение на £„
полностью определяется значением {и, и) для любого
фиксированного ненулевого вектора u^E^- Если м —единичный вектор
относительно одного скалярного произведения, т. е.
{и, m)i = 1,
а (•, •)2 — другое скалярное произведение, такое, что {и, м)2==с^,
с > О, то с~'м—единичный вектор относительно второго
скалярного произведения. Если {«„} — семейство единичных
векторов {относительно первого скалярного произведения) из
пространств £„, причем dim£„=l, то векторы (с~'и„} образуют
семейство единичных векторов относительно второго скалярного
произведения. Таким образом, унитаризация представления я
определяет набор положительных чисел {с„}.
Существует простое инфинитезимальное условие,
необходимое для того, чтобы представление было унитарным.
Лемма 1. Пусть л — унитарное' представление группы G.
Тогда для любого X е g оператор йя {X) кососимметричгн на
пространстве Гординга представления я.
Доказательство. Утверждение очевидно, если вспомнить
определение производного представления.
Следующие леммы приводят к теореме, обеспечивающей
единственность унитарного представления, инфинитезимально
эквивалентного данному.

§ 3, Унитаризация представлений 121
Лемма 2. Пусть я — допустимое неприводимое представление
в банаховом пространстве Н, s^ — алгебра операторов в
пространстве Н {К), порожденная над С элементами множества dn (g).
Тогда, если и — произвольный ненулевой вектор из некоторого
подпространства Н^ <=^ Н, то Н (К) = s4'U. Другими словами^
алгебра s4- транзитивно действует на H{K).
Доказательство. Утверждение с очевидностью вытекает из
теоремы 3 § 2 и теоремы 1 § 1.
Лемма 3. Пусть 1^ = zl -^п ~ комплексное векторное
пространство, представленное в виде прямой суммы своих
подпространств. Пусть $Ф — алгебра линейных операторов в
пространстве V с образующими Хх, ..., Х^. Пусть т —целое число,
такое, что (11тЯ^=1, и^Н„—ненулевой вектор. Предположим, что
^и = V {т. е. что алгебра $Ф транзитивно действует на V). Тогда
любые два положительно определенных скалярных произведения
на V, относительно которых подпространства Я„ взаимно
ортогональны, а операторы Х^, ..., Х^ кососимметричны, отличаются
одно от другого положительным скалярным множителем.
Доказательство. Умножив одно из скалярных произведений
на постоянную, мы можем считать, что на подпространстве Н^
они совпадают. Нам нужно показать, что скалярное
произведение, удовлетворяющее условиям теоремы, определяется своими
значениями на Я„. Достаточно рассмотреть скалярное
произведение векторов V, W ^V, для которых существуют такие
операторы Z, Z'е л^, что Zu = v и Z'u^w; при этом
Z == Zi ... Zt, Z == Ъ\ .,. Zs,
где операторы Zi, Z] принадлежат множеству \Х\, ..., Ха\
образующих алгебры 2Ф. Тогда
<о, w) = (-!)'■ {и, ZZ' и), где Z^Zr ... Zy.
В силу ортогональности подпространств Я„, скалярное
произведение в этой формуле зависит только от проекции вектора ZZ'u
на Н^. Поэтому скалярное произведение на Я^ определяет
скалярное произведение на всем пространстве V, что и
требовалось доказать.
Лемма 4. Пусть я — допустимое неприводимое представление
группы G в банаховом пространстве Я. Любые два
положительно определенных скалярных произведения, определенные на
Н {К) с: Я, относительно которых операторы производного
представления алгебры Ли g кососимметричны, отличаются на
положительный скалярный множитель.

J 22 ^^- Производное представление алгебры Ли
Доказательство. Возьмем в качестве s^ алгебру,
порожденную операторами da{X), Zeg, и воспользуемся леммами 2 и 3.
Теорема 5. Пусть Я), л^ — неприводимые унитарные
представления группы G, и пусть L: Hi {К) —>■ Н^ {К) — инфинитезимальная
эквивалентность. Тогда существует такое -число с > О, что
оператор cL унитарен и продолжается до унитарной
эквивалентности представлений щ, Яд.
Доказательство. Первое утверждение немедленно следует из
леммы 4. Умножив оператор L на положительное число, мы
можем считать, что он унитарен. Для достаточно малых X е g
справедлива формула Тейлора
{п (ехр X) v,w)^Yj ^<^" W" "' ^>-
Положим п = Я1. Тогда эта формула показывает, что для всех
элементов х из окрестности единицы
{Lzii (х) V, Lw)2 = (яз {х) Lv, Lw)^.
Таким образом, оператор L коммутирует с действием группы
в окрестности единицы, а значит, и глобально, так как группа G
связна. Теорема доказана.
Замечание. В предыдущих рассуждениях мы существенным
образом опирались на то, что в разложение пространства Н{К)
по представлениям подгруппы К одно из представлений
входило с кратностью 1. Обобщением этого предположения
является существование /С-инвариантного положительно
определенного скалярного произведения на одной из компонент этого
разложения. Рассуждая аналогичным образом, можно
распространить нашу теорему на этот более общий случай.
Пусть я — представление группы G в гильбертовом
пространстве Я. Мы не предполагаем, что я унитарно. Пусть о е Я —
ненулевой вектор; рассмотрим матричный элемент представления
/„ {х) = <я {х) и, и),
где и — единичный вектор в направлении v. Если
пространство Я„ одномерно, то мы можем определить и-й матричный
элемент /„, положив fn {х) = f„^ (х), где Vn — ненулевой вектор из
пространства Я„.
Теорема 6. Пусть я, я' — инфинитезимально эквивалентные
представления группы G в гильбертовых пространствах Н, Н'.
Предположим, что сужения этих представлений на подгруппу К
унитарны и пространства Нп, Н'п одномерны. Тогда матричные
элементы /„, /^ этих представлений совпадают.

§ 3. Унитаризация представлений 123
Доказательство. Пусть м —единичный вектор в
пространстве Я„; тогда
fn {х) = (я {х) и, и).
Как мы впоследствии докажем, функция /„ аналитична; для
всех достаточно малых X е g справедлива формула
п (ехр X) м = V —J- dn (Х)^ и.
Полагая x = expX, мы получаем
Каждое слагаемое {da{X)''u, и) однозначно определяется, если
представление da задано с точностью до эквивалентности.
Таким образом, функция /„ однозначно определена в окрестности
единицы. В силу ее аналитичности, функция /„ однозначно
определена на всей группе.
Замечание 1. Мы воспользовались аналитичностью
матричного элемента представления. Этот результат уже упоминался
и будет доказан в § 2 гл. X.
Замечание 2. Впоследствии мы воспользуемся теоремой 6,
чтобы доказать, что след представления зависит только от его
класса (инфинитезимальной) эквивалентности. В самом деле,
мы увидим, что как обобщенная функция на группе след
представления равен сумме матричных элементов
X<nW "«,«„),
и можно воспользоваться теоремой 6.
Матричные элементы представления можно иногда
использовать для того, чтобы построить инфинитезнмальное вложение
заданного представления в пространстве L}(G). Пусть я
—представление группы G в банаховом пространстве Н и Я, —
ненулевой функционал на Я. Пусть w е Я. Положим
Функционал X будет в дальнейшем фиксирован, поэтому мы
опускаем индекс X у функции /.
Чтобы доказать следующий результат, нам потребуется ряд
формул. Пусть феС,(0); положим, как обычно, ф~(л;) = ф(л;~').
Тогда
(1) fnw« = f.*«P~-

124 VI. Производное представление алгебры Ли
Пусть X е I], / е L^ (G), ф е СТ (G). Тогда
(3) (^*ф)~=2^г(ф~),
(4) /лтя(ф) o'^^x(/я(ф)o)•
Bce эти формулы немедленно следуют из определений.
Лемма 5. Пусть я — правое регулярное представление в
пространстве L^ (G), т. е. n{x)f(y) = f (ух). Пусть f ^ L^ (G),
Ф s СГ (G). Тогда функция / * ф принадлежит пространству Гор-
динга представления я и
(*) йяШ(Г*ф) = 2ИГ*ф)-
Доказательство. Достаточно доказать, что отображение
xi—s-n(x)/ бесконечно дифференцируемо в окрестности единицы
группы G. Положим
n<x/(i/)==/(i/expa).
Мы начнем с доказательства формулы (*). Нам нужно
показать, что отношение
t
стремится в пространстве L^{G) к пределу, равному 2^(/*ф).
Таким образом, нам нужно исследовать предел функции
Г f (у (ехр т х-') ф (л:) - / (ух-') ф fx) ^^
а
в пространстве L?{G). Сделаем замену переменной л; ь—*■ л;{/ехр^Х
в интеграле от первого слагаемого и х^—^ху в интеграле от
второго. Тогда приведенное выражение примет вид
г }(x-')<f(xy№ptX)-f{x-')^(xy) ^^
а
Положим '^{t) = (^{xye.x^tX). По теореме о среднем
ij) (О - -ф (0) = ^' (to) t = 2;^ф {ух ехр ^0^) t,
где to — некоторое число из интервала [О, t]. Таким образом,
наше выражение равно
/ {х~^) 2хФ {ху ехр toX) dx;

§ 3. Унитаризация представлений 126
МЫ рассматриваем его как функцию переменной у. Нам нужно
показать, что при ^-^0 эта функция стремится в пространстве
L^{G) к пределу, равному
а
а
Для этого достаточно показать, что интеграл
ехр ^0^) — 2;сф (ху)] dx
2
dy
а а
стремится к нулю при ^о~*0- Так как f^L'^^G), а функция ф
финитна и бесконечно дифференцируема, то функция
\F[y)f= 5 / {х-') [а;,ф {ху ехр t,X) - 2;,ф {ху)\ dx ^
а
имеет суммируемую мажоранту при /о-^0')"> поэтому можно
перейти к пределу под знаком интеграла. Теперь
доказательство леммы завершается по индукции при помощи формулы (2).
Теорема 7. Пусть я — допустимое неприводимое
представление группы G в банаховом пространстве Е. Пусть X —
ненулевой функционал на Е,
/о (х) = Х{я(х) v), v^E(К),
— соответствующий матричный элемент представления п.
Зададим, действие группы G в пространстве L^{G) правыми сдвигами.
Если функция fu принадлежит пространству L^ (G) для
некоторого ненулевого вектора и из Е{К), то f„^L^{G) при всех
') Обозначим S = supp ф. Тогда
I F [у) ?<\\ «хФ llj А I /~ Uy-') fdx+^r (х ехр (- toX) (/-') Р dx^ <
<4^X<^t\\rixy-^)fdx,
s
где S=» М {StxptoX}. Ясно, что volS < оо. Функция г/(—* \ I Г {ху~^) fdx,
очевидно, суммируема. В самом деле,
5 \\r'{xy-')fdxdy = \\riyo\^-
а S
— Прим. nevea.

126 V/. Производное представление алгебры Ли
V ^Е (К) и отображение v»—* /о есть %-эквивариантное вложение
пространства Е{К) в L? (G). В частности, это вложение задает
унитаризацию представления я.
Доказательство. Так как представление я неприводимо,
алгебра 2 " (•^т, п) транзитивно действует в пространстве Е{К).
Из формулы (1) ясно, что f„^L^{G) при всех v^E{K). Лемма 5
и формулы (2), (3) и (4) показывают, что отображение vy—>fo
коммутирует с производным представлением алгебры Ли. В силу
неприводимости представления я это отображение инъективно,
т. е. является вложением. Теорема доказана.
§ 4. Производные Ли на группе G
В этом параграфе мы явно вычислим производные Ли
функций на группе G. Как мы знаем, группа SLziK) действует на
верхней полуплоскости. Нам сейчас удобнее иметь дело с
группой GLt (R), поскольку можно использовать координаты (л:, у)
для параметризации элементов группы; в этом случае
скалярные матрицы действуют, разумеется, тривиально.
Итак, пусть G ^ GL2 (R), и пусть
g
=(::)
— произвольный элемент группы G. Пусть z = x-{- iy, у>0,—
такая точка верхней полуплоскости •§, что gi=^z. Тогда
матрица g допускает единственное разложение вида
/и 0\/t/ х\/' cos 6 sin9\
^ = U JU JUsine cosej' "'^>0'
причем матрица
an
переводит точку г e § в точку z = л: -f iy. Перемножая матрицы,
получаем
(1) uei^^d-ic, е'в= '^-^''
\d-ic\'
(2) x+/t/=-i-e'9(a + ift).
Любзто функцию Ф на группе О можно выразить при
помощи введенных нами координат («, х, у, 6):
Ф{§) = ф{и(^1 l)r{Q)^^F{u,x,y,Q).

§ 4. Производные Ли на группе G
127
Так как нас интересует группа SI2 (R)> то для простоты мы
предположим, что функция Ф не зависит от и; поэтому
опустим переменную и и будем писать просто F (х, у, 0).
Пусть X S д; положим
Тогда
ЩеЛ))-=р{хМ У At), Mt))
d ^ , /,\ч I dF dx,
■jfO{gAt))\uo^-9r-ir
<=0
I dF dy,
"^ dy dt
, dF d9.
t=o~'' эе dt
i=o
Мы получим явные формулы для производных Ли,
соответствующих элементам алгебры Ли
(о о)' »"-(-? J)'
X'
"=(1 \\ «=(J Л)
Заметим, что
(3) V^2X-W,
E-^H-iV, £+ = Я + гУ-
Докажем следующую формулу, дающую явное выражение
для производной Ли 2^:
(4)
Доказ
S^ = i/cos 29 ^ + {/sm2e-^ + sirf 9-|-.
ательство. Имеем
ехра = (о j);
таким образом.
/ а at + Ь\
8At)i'=f^f^^zAt)'=^xAt) + iyAt).
кт^^^^уе^-.
/о /A^lnrr ct + d-ic
^^*^^^ '°^((c< + rf)' + .^)'/. •

128
VI. Производное представление алгебры Ли
Следовательно,
л^^О) = t/cos 29,
/,(0) = i/sin29,
е^ (0) = siri" 9 ==
I — cos 29
Наша формула доказана.
Очевидно, что
(5)
аи.=-
Э9
Так как V=2X — W, то
(6)
S,, = 2ifcos2e^ + 2t/sin2e-^ —COS29 ^
дх
эе
Так как
е' О
получаем для соответствующей матрицы g^{t) выражение
откуда
Кроме того.
аеН + be~^
сеЧ + rfe~'
/9, (О = log-
de"
Отсюда мы находим для производной Ли выражение
(7)
йя = - 2{/sin 29 ^ + 2{/cos 29-^ + sin 29 4-•
дх
эе
Поскольку Е = Н — iV, имеем
(8)
le
-2ie
о9
= _4/j/e-2'9_£__L ,>-2гв. ^

§ 5. Неприводимые компоненты индуцированных представлений 129
Заметим, что в это выражение входит оператор d/dz, т. е.
оператор Коши — Римана. Функция / аналитична в том и только
в том случае, когда df/dz = 0. На этом мы-заканчиваем
перечень формул для производных Ли на группе G.
§ 5. Неприводимые компоненты индуцированных
представлений
Пусть S — комплексное число. Обозначим символом H{s)
пространство функций на группе G = SL2 (R), сужение которых на
подгруппу К czG принадлежит пространству L^ {К) и которые
удовлетворяют условию
f{ank)^p{aY+'f{k),
где x = ank — разложение Ивасавы матрицы xsG. Пусть я —
представление группы G в пространстве H{s), действующее
правыми сдвигами.
Из разложения матрицы g е G вида
Q l)r{% и, у>0,
вытекает, что функция f ^ Н (s) удовлетворяет условию
/(g) = j/(.+i)/2/(r(e)).
Пусть ф„ е я (s) — такая функция, что
Ф„(г(е)) = е-9.
Тогда
Ф„(и(о ^)г(9)) = {/(^+')'2е"'«.
и по формулам для производных Ли, которые были выведены
в предыдущем параграфе, получаем
(1)
Докажем теперь две важные леммы, которые позволяют
отождествить производную Ли 2;f с оператором представления
ёл{Х), а аналитические функции, принадлежащие
пространству H{s), — c аналитическими векторами.
Лемма 1. Пусть я — представление группы G в
пространстве H{s), действующее правыми сдвигами. Пусть Х^^Ч, /еЯ(5)
5 Зак. 589

130 VI. производное представление алгебры Ли
и, кроме того, f ^С" (G). Тогда функция f, рассматриваемая
как элемент пространства L^{K), есть С^-вектор для
представления я и справедлива формула
dniX)f==iJ.
Доказательство. Рассмотрим функцию ntxf ig) = fig exp tX).
Нам нужно проверить, что
В пространстве L^iK), т. е. что интеграл
ntmjnjzm^f^z^f^k)
^ dk
стремится к нулю при t-*Q. Положим i|)(0 = f (^exp/Z). По
теореме о среднем, существует число t^ s (О, /) (мы можем
считать, что / > 0), такое, что
±MLZ1M. = ^' (^ = (2^/) (Л ехр t,X).
Значения производной (2;^/)(/г ехрfo-X') ограничены при всех As/C
и при всех малых ^о- По теореме об ограниченной сходимости,
мы можем перейти к пределу под знаком интеграла. Лемма
доказана.
Лемма 2. Пусть f — аналитическая функция на группе G,
Пусть п {х) — оператор правого сдвига:
n{x)f{y) = f{yx).
Тогда отображение
XI—» n{x)f\K
есть аналитическое отображение группы. G в пространство О (К).
Доказательство. Пусть Xq е G. Если мы уже доказали, что
отображение х^-^п{х)1\К аиалитично в окрестности единицы,
то ясно, что отображение
x^n(x-'x)f\K = n{x^')n{x)f\K
аналитическое, поскольку оператор я(л;~') непрерывен. Таким
образом, достаточно доказать наше утверждение в окрестности
единицы. Пусть (xj л;„) — локальные координаты точки х
из окрестности единицы, причем
xi{e)= ... =х„{е) = 0.
Так как группа К компактна, найдутся такие числа
О = 00 < е, < ... < е^ == 2я,

§ 5. Неприводимые компоненты йпдуцированнык представлений 131
что на каждом интервале [6/, 9^+l) справедливо разложение
в степенной ряд
Положим
fir (9) ^) = Z Z см, д (9 - Q,fx\^ .. . ху
^f.,(e)=i:c,,,j9-9/.
и пусть 1|3(^, — функция от 9, совпадающая с ^lf^^^^ на интервале
[9/, e/+i). Тогда
/(r(9)x)=g^,^,(e)<. ... ху,
Иначе говоря,
лix)f=Zx^:^ ... X>J.,
(V)
т 'V^чy
Из абсолютной сходимости этого ряда вытекает, что он сходится
в пространстве L^{K); таким образом, мы получили для
функции я {х) f выражение в виде степенного ряда с коэффициентами
из 1ЦК).
Неприводимые подпространства
Как мы только что показали, функции ф„ являются
аналитическими векторами в пространстве H{s)- Вычисленные нами
значения производньлх Ли функций <p„ задают действие на эти
функции операторов представления йя^, а именно
(2)
dns(E~) ф„ = (s-f 1 — я)ф„-2,
dns (Е'^) ф„ = (s -f 1 -f я) ф„+2.
Пользуясь теоремой 1 § 1, мы можем теперь без труда найти
неприводимые подпространства пространства H{s). Сужение
f*-*f\K позволяет отождествить H{s) с L?{K).
Случай 1. S не есть целое число. Пусть Н' c:H{s) —
неприводимое подпространство. Тогда Н' разлагается в ортогональную
прямую сумму одномерных подпространств, неприводимых
относительно подгруппы К. В частности, пространство Н' содержит
функцию ф„ для некоторого п; так как числа s -f 1 ± « не равны
нулю, то отсюда следует, что пространству Я' пpинaдлeжat
либо все функции ф„ с четными номерами, либо все функции ф„

132 VI. Производное представление алгебры Ли
С нечетными номерами. Подпространства
е Сф„, е Сф„,
пчетно п нечетно
очевидно, неприводимы.
Случай 2. « = 0. в этом случае пространство Н (s) содержит
три неприводимых подпространства:
е Сф„,
п четно
Ф Сф„,
п нечетно
п>1
Ф Сф„.
п нечетно
п<- 1
Случай 3. s==nt—1, где т^2 —целое число. Заметим,
что в этом случае функция ф„ принадлежит ядру оператора
dns{E~) и является собственной функцией оператора dn^iW),
а оператор dn^iE'^) переводит ее в функцию, кратную ф^+г-
Следовательно, подпространство
Я^'"*= Ф Сф„
пштт
неприводимо. (Мы пишем п^пг вместо n^sm(mod2).) По
аналогичной причине подпространство
Я^"'"*= Ф Сф„
пштт
также неприводимо, ибо dn^{E'*')(f_^=0.
Существует также неприводимое подпространство, состоящее
из функций противоположной четности, а именно
Ф Сф„.
п^ т
Факторпространство
У(т-1) = Я(т-1)/Гя<'"> + Я<-'"Ч ф СфЛ
L пщьт J
конечномерно и имеет размерность /п— 1, В нем имеется базис,
порожденный образами элементов
ИЗ пространства Я(/п—1). Действие алгебры Ли показывает,
что это факторпространство неприводимо. Оно содержит векторы
старшего и младшего веса.
Построенные выше бесконечномерные неприводимые
подпространства (в случае 3) содержат младший вектор веса т или
старший вектор веса —т. Позднее мы докажем, что при т^2
существует унитарное представление группы G, производное

§ 5. Неприводимые компоненты индуцированных представлений 133
представление которого линейно эквивалентно представлениям
алгебры Ли g в этих подпространствах.
Напомним, что в случае 2, когда s = 0, мы построили два
неприводимых унитарных представления со старшим вектором
веса — 1 и младшим вектором веса 1 соответственно.
Говорят, что унитарное представление принадлежит
дискретной серии, если оно входит в разложение регулярного
представления в пространстве L?{G). Как мы увидим, унитарные
представления группы G, соответствующие представлениям
алгебры Ли, построенным в случае 3 при /п^2, принадлежат
дискретной серии. Представления, для которых s = 0, не
принадлежат дискретной серии, хотя во многих отношениях похожи
на представления дискретной серии. Их можно было бы назвать
«ложнодискретными представлениями».
Случай 4. S = — m -+- 1, где m ^ 2 — целое число. Этот случай
аналогичен случаю 3 и в действительности является
двойственным к нему. В самом деле, из общей теории индуцированных
представлений мы знаем, что для любого комплексного числа s
пространство H{s) двойственно пространству H{—s). (Мы
обозначаем символом H{s) пространство представления,
индуцированного характером ц,, как в теореме 3 § 2 гл. III.) Из действия
алгебры Ли ясно, что в этом случае пространство H{s) содержит
неприводимое конечномерное подпространство У(—m-f-l),
причем соответствующие ему веса (относительно подгруппы К) —
те же самые, что и в факторпространстве V {т—1). Далее,
факторпространство Я(—m-f 1)/У (—m-f 1) содержит два
неприводимых подпространства, в одном из которых есть старший
вектор веса — т, а в другом — младший вектор веса т. Пусть,
как и выше, {ф„} — ортонормированный базис пространства
Н{т— 1), и пусть {ф1„} — соответствующий ортонормированный
базис пространства Н {— т+ 1). Тогда эти базисы дуальны
друг другу относительно двойственности, определенной в
теореме 3 § 2 гл. III. В частности, конечномерные пространства
V{т— I) и V{— т+ I) дуальны друг другу. По поводу
дальнейшего использования этой двойственности см. § 4 гл. VII, и
в особенаости лемму 2, которая описывает пространство
У(—/n-fl) более точно.
Пусть Я*""* и Я *"** — подпространства с младшим вектором
веса т в пространствах Я(т —1) и Я(—m-f-1)/У (—m-+-1)
соответственно. Мы явно зададим инфинитезимальную
эквивалентность
L: Я<'"'(Ю->Я'^'"ЧА1.
Пусть фд, ф^ —весовые векторы в пространетвах Я„, Я^, причем
я^/п и я ^/п (mod 2). Мы хотим задать такой изоморфизм L,

134 VI. Производное представление алгебры Ли
ЧТО 1ф„ = Ь„ф^, где Ь„ —некоторые постоянные. Зная действие
операторов £"*" на векторы ф„, ф„, нетрудно получить
рекуррентную формулу
h h —"1 + 2 + 11
'п+2 — "» ^ ц. „
Таким образом, выбор числа Ь„ однозначно определяет
постоянные 6„ при всех п.
§ 6. Классификация всех
неприводимых унитарных представлений
Хотя это и не существенно для тех вопросов, которые
рассматриваются в настоящей книге, иногда бывает необходимо
иметь полное описание всех неприводимых унитарных
представлений группы G. Например, представления, которые не дают
вклада в формулу Планшереля для группы G, могут встретиться
в разложении пространства L^(r\G) для различных дискретных
подгрупп Г с: G,. причем ни одно из этих представлений а priori
нельзя исключить. Поэтому мы приведем здесь классификацию
Баргманна; ее можно без труда получить из уже доказанных
нами результатов.
Пусть я — допустимое неприводимое представление группы G
в пространстве Я, dv. — производное представление,
определенное на H{K)czH. Имеет место разложение в прямую сумму
где п пробегает некоторое множество целых чисел заданной
четности (т. е. принадлежащих одному классу вычетов mod 2).
Предположим сначала, что в пространстве Н нет векторов
старшего и младшего веса.
Чтобы пояснить идею рассуждения, допустим сначала, что
НоФО. Пусть Оо — ненулевой вектор из подпространства Hq.
Определим векторы о„ е Я„ {п четно) при помощи рекуррентной
формулы
(для краткости мы пишем E+Vn вместо йя(£'+)о„). Ясно, что
векторы Vn определяются этой формулой однозначно при всех
четных п, положительных и отрицательных. Определим числа с„
формулой
Нас интересует, при каких условиях в пространстве H{K)
существует положительно определенное скалярное произведение,
согласованное с заданным представлением алгебры Ли д^,, т. е.

§ 6. Классификация всех неприводимых унитарных представлений 135
такое, что операторы dniX) кососимметричны при всех J eg.
Очевидно, длину вектора Vq можно выбрать произвольной;
положим
Ш К Оо> = «?. «о>0.
Из формулы
вытекает соотношение
(2) с„ - Сп+2 = 4/г.
Условие кососимметричности
показывает, что
(3) «'„+2=-^„+2«^
Таким образом, числа с„ должны быть вещественными и
отрицательными. Кроме того, из формулы (2) видно, что выбор Cq
полностью определяет с„ при всех п. А тогда по формуле (3)
однозначно определяются также все числа а^. Итак, унитари-
зация представления, если она существует, полностью
определяется выбором отрицательного числа Cq.
Аналогичные рассуждения можно провести для представления
противоположной четности, выбирая базисный вектор о, в
пространстве Н^. Условия (2) и (3) остаются без изменений, и уни-
таризация представления однозначно определяется выбором
отрицательного числа Cj.
Рассмотрим индуцированиое представление я, в
пространстве Н (s), где S — произвольное комплексное число. Так как
йя, (£•+) ф„ = (S + 1 + я) ф„+2, djls (£_) ф„ = (S 4- 1 — ft) Фи-2.
то условие отрицательности Cq эквивалентно неравенству
(s+l)(5-l)<0.
Это неравенство выполняется, когда s чисто мнимое или когда s
вещественное и — 1 < s < 1. Мы уже знаем, что чисто мнимым s
соответствуют неприводимые унитарные представления.
Представления, для которых — 1 < S < 1, также допускают унитари-
зацию; для этого нужно пополнить пространство Н{К)
относительно скалярного произведения, определяемого условиями (2)
и (3). Получаемые неприводимые представления называются
представлениями дополнительной серии.
Заметим, что для представлений противоположной четности
условие на постоянную С\ приводит к неравенству Cj = s^ < 0.

136 VI. Производное представление алгебры Ли
Таким образом, в этом случае показатель s может иметь только
чисто мнимые значения.
Рассмотрим, наконец, при каких условиях допускают унйта-
ризацию представления со старшим или младшим вектором.
Пусть, например, в пространстве Н существует старший вектор
веса т. Мы утверждаем, что тогда m < 0. В самом деле, если
E+v„ = 0, то аналог соотношения (2) имеет в данном случае вид
с„ == 4т;
число Cm должно быть отрицательным. Аналогично, если в
пространстве Н существует младший вектор веса т, то m > 0.
-4 -3
Рис. 1
Классификацию Баргманна можно резюмировать следующим
образом:
Теорема 8. Всякое неприводимое унитарное представление
группы SLiiR) инфинитезимально эквивалентно одному из под-
представлений представления щ в пространстве Н (s) при
следующих значениях s:
(i) представления дискретной серии, s=m—1, m^ 2 —целое;
(ii) ложнодискретные представления, s = 0; существует одно
представление со старшим вектором веса — I и одно
представление с младшим вектором веса 1;
(iii) представления основной серии; при s == /т, т ^ О,
существуют представления обеих четностей] при s = О
существует только четное представление;
(iv) представления дополнительной серии, —l<s<l, s^O;
(v) одномерное представление, s = — 1.
Теорема 8 оправдывает наш рисунок части пространства G,
приведенный в § 4 гл. I. Полная параметризация
пространства G изображена на рис. 1. Вертикальная линия является
двойной (по одному экземпляру для представлений каждой чет-

§ 7. Разделение представлений при помощи их характеров 137
ности), а горизонтальный отрезок н целые точки — одинарные.
Точки соответствуют старшему или младшему весу представления.
Из теоремы 8 видно также, что неприводимые унитарные
представления реализуются как подпредставления
индуцированных представлений. Единственность обеспечивается
теоремой 5 § 3.
§ 7. Разделение представлений при помощи их характеров
Как известно, представление компактной группы определяется
своим характером, т. е. следом представления. Нас интересует
аналогичное утверждение для неприводимых унитарных
представлений в гильбертовом пространстве. Грубо говоря, у нас нет
надежды отделить одно из представлений, входящих в
непрерывное семейство, от всех остальных. Однако можно попытаться
Рис. 2.
отделить представление, входящее дискретно. Мы покажем
сейчас, как это сделать для представлений, описанных в § 5.
Для любого отличного от нуля целого числа m обозначим
символом Я*"" пространство представления я„, обладающего
старшим вектором веса т, если m < О, или младшим вектором
веса т, если m > 0. Тогда Нт — старшее (соответственно
младшее) весовое подпространство в пространстве Я*"". Как и в гл. V,
мы обозначаем буквой Н преобразование Хариш-Чандры.
Теорема 9. Пусть, как и выше, т —целое, тФО. Существует
такая функция 1|з е СГ (G), что
(ii) Лт (ф) 1 Яп"" = о, если пфт, и п\ (ф) = О, если qфm•,
(Ш) Hi|3 = 0.
Доказательство. Пусть, к примеру, m^l. Для любой
функции f^Sm,m справедливы равенства
я1„{ПН''::^=^НТ или О,
n],{f)H'i?^ = 0, если пфд.
Для наглядности старшие веса наших представлений изображены
на рис. 2. Сначала мы рассмотрим представления, старшие вес?;,

138 VI. Производное представление алгебры Ли
которых лежат между 1 и т. Чтобы разделить эти представления,
поступим следующим образом. Для любой функции f^S^^^
образ оператора я' (f), самое большее, одномерен, и поэтому
имеет смысл говорить о следе этого оператора. Рассмотрим
функционалы 6i, ..., Q„ на пространстве
m
2-1 "^Я, пг
задаваемые формулами
е/(/) = 1гя'(/), / = 1, ..., т.
Ясно, что эти функционалы линейно независимы. Значит,
отображение
m
переводит пространство J^Sn. п в С"*. Следовательно, сущест-
m
вует функция / е J^ S^ „, такая, что
tr<(f) = l.
^г ^1 if) — О' 6СЛИ 1 ^ л < m.
Из того, как преобразуются элементы пространства S„, „, и из
соотношений ортогональности мы автоматически получаем
^liif) = О, если я^ — 1 или п> т.
Итак, нам удалось построить функцию, отделяющую
представление Пт ОТ всех остальных представлений Пп{пф О, пФ пг),
имеющих вектор старшего или младшего веса.
Осталось показать, что построенную нами функцию / можно
изменить так, что преобразование Хариш-Чандры обратится
в нуль. Наша функция принадлежит пространству СГ(0, К),
т. е. инвариантна относительно сопряжений элементами
подгруппы К. В силу фундаментальной теоремы о сферическом
преобразовании, т. е. в силу сюръективности преобразования
Хариш-Чандры (теорема 3 § 2 гл. V), существует функция
/, е СГ {G//K), такая, что
Hf=Hf,.
Так как функция /i двусторонне инвариантна, то справедливо
равенство
<(/.) = О

S 7- Разделение представлений при помощи их характеров 139
И, следовательно, оператор яЦ/j) аннулирует все собственные
подпространства группы К с ненулевыми собственными
значениями, т. е. при пФО
nn{fi)H^^^ = 0 для всех q.
Положим i|) = f —fj. Тогда Hi|) = 0 и я^, (i|)) = я^ (/). Теорема
доказана.
Теорема 9 принадлежит Дюфло и Лабессу [1]. Приведенным
доказательством я обязан Хариш-Чандре.
Теорема 9 вместе с теоремой 4 § 4 гл. III позволяет
разделять различные представления при помощи их следов;
теорема 9 содержит даже несколько больше, поскольку она
позволяет разделять представления на операторном уров-не.

VII. СЛЕДЫ
В этой главе мы систематически рассмотрим следы
бесконечномерных представлений, и в особенности тех
представлений, которые мы явно построили. Мы покажем, что след
индуцированного представления, определяемый как интеграл от
сужения ядра оператора представления на диагональ, можно
отождествить с обычной суммой диагональных матричных
элементов. После этого мы вычислим следы различных
представлений.
В качестве технического отступления мы рассмотрим ряд
интегральных формул, связанных с различными разложениями
группы G, некоторые из которых приспособлены к изучению
классов сопряженных элементов. За исключением множества
меры нуль, состоящего из унипотентных матриц, классы
сопряженных элементов параметризуются точками подгрупп А и К;
следы представлений можно выразить в виде интегралов по
таким классам. Придерживаясь этого систематического подхода,
развитого Хариш-Чандрой, мы выведем формулу Планшереля.
Это объясняет название, которое я выбрал для преобразования
Харига-Чандры.
Как мы увидим, следы представлений дискретной серии
входят в формулу Планшереля парами. Теорема Хариш-Чандры,
в которой вычислен след каждой из компонент, будет опущена;
см. замечания к теореме 5 § 4. Стоит подчеркнуть этот аспект
доказательства Хариш-Чандры (которое пригодно для
произвольных полупростых групп Ли): вычисление следа представляет
собой более сложную задачу, чем вывод формулы Планшереля;
для групп более высоких размерностей существуют примеры,
в которых следы представлений все еше не вычислены, хотя
формула Планшереля уже получена.
§ 1. Ядерные операторы
Пусть А — оператор в гильбертовом пространстве Н (в этом
параграфе мы рассматриваем только ограниченные операторы).
Оператор А называется оператором Гильберта—Шмидта, если
для некоторого ортонормированного базиса {ы;} в пространстве
Я. В этом случае то же самое справедливо для любого дру-

§ 1. Ядерные операторы j4]
гого ортонормированного базиса {vj}. В самом деле, заметим,
что для любого вектора w ^ Н
\ni)f=L\{w,v,)f;
таким образом,
Z i ^i Р = Z i (Ащ, vi) р = Z i («i. A*vi) P = E i A'v, p.
i i, ! i, t f
Оператор A называют ядерным, если его можно представить
в виде произведения двух операторов Гильберта—Шмидта,
скажем А==В*С, где В и С — операторы Гильберта — Шмидта.
В таком случае след оператора А определяется формулой
tr Л = Z (Aui, щ) = Z (C"i, Вщ).
Первое равенство показывает, что след не зависит от выбора
операторов В, С. Из второго равенства следует, что ряд
абсолютно сходится; достаточно два раза воспользоваться
неравенством Шварца.
Пусть теперь /С—группа вращений окружности, {ф„}—обычный
ортонормированный базис в пространстве L^{K), Фя('" (9))==^'"^.
Пусть q — гладкая функция на КУ.К- Разложим ее в двойной
ряд Фурье
Интегрируя по частям, легко показать, что коэффициенты Фурье
быстро убывают. В самом деле, для любого положительного
целого d справедлива оценка типа
<
(\ + \т\ + \п\У
(постоянная в этом неравенстве, которая подразумевается
символом <С зависит от d). Таким образом, ряд Фурье функции q
быстро сходится V. q ти можно воспользоваться вычислениями
§ 3 гл. I. В дополнение получаем такую теорему.
Теорема 1. Пусть q — гладкая функция на КУ(.К- Тогда
интегральный оператор Q, задаваемый ядром q, — ядерный.
Доказательство. Нам нужно представить Q в виде
произведения двух операторов Гильберта—Шмидта. Пусть d—большое
положительное число. Пусть P„_ „ — интегральный оператор
с ядром фда ® ф„; таким образом,
Рт. ,ф/ = О, если / ф п.

142 V'//. Следы
Пусть Pj — Проектор на одномерное подпространство Сф/.
Положим
т.п i
Ряды, определяющие В и С, быстро сходятся и задают
операторы Гильберта—Шмидта. Ясно, что BC=Q. Теорема доказана.
Пусть G = SL2(R), я; — представление группы G в
гильбертовом пространстве Я. Для любого целого п обозначим Н„
весовое подпространство, соответствующее я-му характеру
подгруппы К- Таким образом.
Будем говорить, что представление я строго допустимо, если
размерности подпространств Я„ ограничены равномерно по п.
Из теоремы 2 § 1 гл. II мы знаем, что неприводимые
унитарные представления группы G строго допустимы (при всех п
размерности подпространств Я„ равны О или 1).
Теорема 2, Пусть л — строго допустимое представление
группы G в гильбертовом пространстве Я. Если f ^ С7 (G), то
оператор я' (/) ядерный.
Доказательство. Основная идея аналогична той, которую
мы использовали при доказательстве теоремы 1. Пусть
G = y4iViiC— разложение Ивасавы; положим B = AN. По
определению,
я' (f) = 5 / {х) n{x)dx='^\^ f{bk) я (Ь) я (k) dkdb =
о в к
2я
= ^л{Ь) \fibkQ)n{k(,)dQdb.
в а
(Для нас сейчас несущественно, что при такой нормировке
полная мера подгруппы К равна 2я.) Так как л{кд) допускает
разложение
п
где Р„ — ортогональный проектор на подпространство Я„, то
2Я
я' (/) = 5 я ф) 5 5] e^'-9f {bk,) deP„ db =
в on
==\n{b)Y,fn{b)Pndb,

§ 1. Ядерные операторы 143
где
2я
о
Зафиксируем целое число d > 0. Интегрируя по частям, легко
показать, что
/„(6) К
1 + п^'* ■
Кроме того, носитель функции /„ компактен. Положим
Q„ = ( я (6) /„ (&) db; таким образом, 1 Q„ |< ' ^ .
а ' +'*
(Напомним, что представление я локально ограничено; см. § 1
гл. I.) Получаем
п
Пусть
л, = Е(1+я^'*)р„р„,
п
п
\+п^
Ряды, задающие А^ и А^, быстро сходятся; поэтому А^ и А^ —
операторы Гильберта—Шмидта. Кроме того, rt'(f) = >li^2.
Теорема доказана.
Пусть я — строго допустимое представление группы G
в гильбертовом пространстве Н. Тогда отображение
■^H-^tr я' (Мр)
задает линейный функционал на пространстве С^ {G). Легко
проверить, что он представляет собой распределение в смысле
Л. Шварца (определение см. в конце приложения 4). Хотя мы
и не будем в дальнейшем пользоваться этим утверждением,
для удобства читателя докажем его в том случае, когда
представление я унитарно. Если ф s С^ (G), то для простоты будем
писать Wij) вместо й^р-т];; здесь W — обычная образующая
алгебры Ли подгруппы К- Достаточно показать, что для всех
функций 1|з, носитель которых лежит в компактном множестве Q,
справедлива оценка
Цгя'(^з)1<СЛ(1-1Г2)^||^^
Пусть Un — единичный вектор в пространстве Я„ и

144 VII. Следы
— соответствующий матричный элемент представления я. Мы
докажем нашу оценку для каждого слагаемого
S
о
откуда и будет следовать наше утверждение. Интегрируя по
частям, получаем
( (1 - W')if{x) Ux) dx= \^{х) (1 - ^)!Лх)йх==
а о
= (l+ft')5^W/«WdA;..
о
Следов ательно,
5 ^ (X) /„ {х) dx <-(ГТ713)- S i (1 - "^'Ш^) fn{x)ldx.
а Q
По предположению, представление я унитарно; поэтому | /„ (д:) |:^1.
Теперь нужное нам неравенство очевидно.
Для представлений, рассматриваемых в этой главе,
функционал trji' задается обычной функцией Гл. а именно
tr л' (ф) = ( 1|з {х)Т„ {х) dx.
Так как в правой и в левой части этого равенства стоит одна
и та же мера Хаара, ясно, что функция Г„ не зависит от
выбора меры Хаара. Если такая функция существует, то
а priori она определена только почти всюду. Однако, как мы
увидим, эта функция непрерывна на открытом множестве,
а вне этого открытого множества ее можно положить равной
нулю. Таким образом, даже эта неоднозначность устраняется.
В этой главе нам не встретятся другие типы распределений.
Предположим, что пространство Н конечномерно. Тогда
задающая след сумма
tr я' (ф) = ^ J 1|) {х) (я {х) Ui, щ) dx
i О
конечна и ее можно внести под знак интеграла. Таким
образом, Г„(л;) есть обычный след в смысле элементарной алгебры.
Для простоты мы часто будем писать я (ф) вместо я' (г|)).
До конца этого параграфа мы будем предполагать, что все
представления являются строго допустимыми.

§ 1. Ядерные операторы 145
Инвариантность относительно сопряжения
Пусть л — представление группы G в гильбертовом
пространстве Н. Пусть ■^Sp^CT (G). Пусть у е G и ф^ — такая функция
на G, что
у1рУ{х) = ^^{у-^ху).
Тогда -
tr л (ф) = tr я (i|:^).
Доказательство. Это следует из соотношений ji(i|j^) =
=л{у)п (i|)) л (г/)"' и tr {XAX~^)=tT А (см. приложение к этой главе).
Предположим, что мера группы К равна 1. Пусть
'^к W = \ ^ {k~^xk) dk.
к
Тогда tr я (iji) = tr я (фд^).
Доказательство. Рассмотрим интеграл
tr л (1|)д^) = У] \ \ "^{k'^xk) (я {х) щ, Ui) dk dx.
I о к
Изменим порядок интегрирования и вынесем интеграл по К за
знак суммы. Модулярная функция преобразования xy-^kxk~^
равна 1. Поэтому искомый след равен
\ V \'^(х) {л{к)л{х) я(А~') щ, щ) dxdk.
к i о
Теперь наше утверждение вытекает из того факта, что trя(l|)) =
= trя(V)•
В силу доказанных утверждений, при вычислении следа
операторов я' (a|3) мы можем предполагать, что i|) s С" (G, К), т. е.
что ij) — гладкая функция с компактным носителем,
инвариантная относительно сопряжений элементами подгруппы К-
Хариш-Чандра доказал, что след произвольного
неприводимого унитарного представления полупростой группы Ли является
распределением. Это сводится к проверке условия строгой
допустимости, т. е. к оценке размерности /С-неприводимых
подпространств пространства /С-конечных векторов. (На самом
dim Я „ й.^ о
деле равномерно ограничена величина -г^. р-, ред.! Он
доказал также, что след представляется локально суммируемой
функцией. При изучении группы SL2(R) мы будем, следуя
Хариш-Чандре, разбивать интегралы по группе на интегралы

146 VU. Следы
по различным классам сопряженных элементов. Элемент группы G
будем называть регулярным, если он имеет различные
собственные значения; множество всех регулярных элементов
Обозначим символом G'. Если S — подмножество группы G, то
символ S' будет обозначать множество регулярных элементов 5,
а символ S^ — множество элементов, сопряженных элементам
множества S, т. е. элементов вида g~^xg, g^G, x^S.
Лемма 1. Пусть G = AN К — разложение Ивасавы. Тогда
G' = ± Л'« и К'°.
Дополнение множества G' в G имеет меру нуль.
Доказательство. Если элемент g s SL^ (R) имеет одно
собственное значение кратности 2, то по теореме Жордана он
сопряжен некоторому элементу подгруппы ± N. Так как
группа AN нормализует N, образ группы N при сопряжении
относительно G имеет размерность 2; следовательно, его мера
равна нулю. Если матрица g имеет различные вещественные
собственные значения, то ее можно привести к диагональному
виду (над R); таким образом, она сопряжена некоторому
элементу подмножества ± А'. Если собственные значения
матрицы g не вещественны, то простые алгебраические соображения
показывают, что она сопряжена некоторому элементу
подмножества К', что и требовалось доказать.
Из приведенного описания классов сопряженных элементов
вытекает, что
^f(x)dx= J f (х) dx+ J f {x) dx.
+ A
Мы будем пользоваться этим разложением при вычислении
следов. В § 2 будут приведены различные формулы для этих
интегралов, которые получаются при разных п^аметризациях
множества классов сопряженных элементов.
Инфинитезимальная инвариантность
Напомним, что две нормы называются эквивалентными,
если каждая из них оценивается через другую. Два скалярных
произведения называются эквивалентными, если эквивалентны
соответствующие им нормы.
Лемма 2. Пусть щ — представление группы G в
гильбертовом пространстве Н^, а Яг — то же самое пространство, снаб-
женное эквивалентным скалярным произведением. Пусть щ — то же

§ 1. Ядерные операторы 147
самое представление, рассматриваемое как представление в
пространстве Hi- Тогда
tr Я] (i|)) = tr Яа W-
Доказательство. Пусть Г: Н^-^-Н^— тождественное
отображение. Ясно, что операторы Г, Т~ непрерывны. Тогда
л^{к) = Т%,{х)Т~\
и равенство следов вытекает из общей теории следов
операторов (см. последнюю теорему в приложении к этой главе).
В частности, предположим, что сужение представления ji==jii
на подгруппу К. не унитарно. Усредняя скалярное
произведение по К, можно получить новое скалярное произведение и
новое гильбертово пространство Hi, такое, что сужение
представления Ji2 на подгруппу К унитарно. Следы обоих
представлений одинаковы.
Лемма 2 представляет собой частный случай следующей
теоремы.
Теорема 3. Пусть щ, щ — представления группы G в
гильбертовых пространствах. Предположим, что весовые
подпространства каждого из этих представлений не более чем одномерны
и что представления п\ и л^ инфинитезимально эквивалентны.
Тогда
trjii(ifi) = trn;2(il3)
для любой функции i|) е С^ (G).
Доказательство. Согласно предыдущему замечанию, мы можем
считать, что сужения представлений jii, яг на подгруппу К
унитарны. Воспользуемся теперь теоремой 5 § 3 гл. VI, в которой
мы доказали, что матричные элементы обоих представлений
совпадают. Следовательно, их суммы тоже совпадают и равны
Yj S ^ W ^" W "'■' "') '^^'
I о
где я — любое из представлений Я], яг, а (•, •) —
соответствующее ему скалярное произведение.
Из теоремы 3 вытекает, что для вычисления следа
унитарного представления можно использовать любую его реализацию
(не обязательно унитарную), инфинитезимально эквивалентную
данной. Это замечание полезно, в частности, при работе с
унитарными представлениями, для которых существует реализация
в виде индуцированного представления, когда след задается
просто как интеграл от сужения ядра представления на
диагональ.

148 VII. Следы
§ 2. Интегральные формулы
Предварительные замечания
В этом параграфе мы сведем воедино различные формулы
замены переменных; для удобства читателя напомним сначала
некоторые элементарные факты о многообразиях и
интегрировании на них. Мы предполагаем, что читатель знаком с
основами теории, изложенными, например, в книге Ленга [1, гл. XVI>
XVII и часть гл. XVIII], где приведены общие теоремы об
интегрировании на многообразиях и о мерах, связанных с
дифференциальными формами.
В этом параграфе многообразия, с которыми мы будем
иметь дело, — это ЗЦ (R) или произведение ее одномерных
подгрупп типа А, N, К (т. е. аддитивной и мультипликативной
групп вещественных чисел и группы вращений окружности).
В качестве карты на этих многообразиях мы будем
использовать касательное пространство к единице вместе с
экспоненциальным отображением. Если G — одна из перечисленных
групп Ли и g — ее алгебра Ли, то для любого элемента g^G
карта окрестности точки g задается отображением
ехр: U—>G, Ху-^gexpX,
где X принадлежит окрестности нуля в алгебре Ли д. Если
G' —другая группа Ли с алгеброй Ли д' и F: G'-»■ G — гладкое
отображение (не обязательно гомоморфизм), то для любой точки
g' е G' определен соответствующий дифференциал
dF{gy. g'-^g,
т. е. касательное отображение функции F в точке g^. Пусть
{Jj, ..., ZJ —базис д, а {J', ..., J^} — базис д'. В
приложениях d=3 и группы G, G' имеют одинаковую размерность,
поэтому будем считать, что эти условия выполнены. Поливекторы
Xj л ... л X., X', А ,.. л Х^
образуют базис в пространствах Л'^д и Л'^д' соответственно.
Если Fi, ..., F^eg, то
Г,л...лГ^ = ш(Г1, ..., Г^)Х,л... аХ^,
где u)(Fi, ..., Fj) — вещественное число, а отображение
(F„ ..., F,)b-*(D(Fb..., FJ
представляет собой дифференциальную форму. Аналогично,
заменяя векторы F/, Xj на F/, X'j, мы получаем
дифференциальную форму ш' на д'. Разумеется, эти формы зависят от выбора
базисов {Xj} и {X'j},

§ 2. Интегральные формулы I4&
Предположим, ЧТО отображение f —локальный
диффеоморфизм в каждой точке открытого подмножества группы G'
(в наших примерах это всегда выполнено). Тогда отображение
A'dFig'): AV-^A'^g
есть изоморфизм и поэтому задается умножением на число,
зависящее от точки g\ скажем на c(g'), т. е.
dF (gO X'iA...AdF ig') Z'i = с (/) Zi л ... л Zi.
По определению, прообраз дифференциальной формы ш при
отображении F задается формулой
(Гш) (§0 = с (gO ©'(/)•
Число c{g') называется якобианом преобразования F; если [i
и ц' — положительные меры, ассоциированные с
дифференциальными формами ш и соответственно ©', то локально в
каждой точке
(Г|г)(яО = к(я01|*'(яО.
В терминах интегралов это означает, что в открытом
множестве V\ на котором F представляет собой локальный
диффеоморфизм, справедливо равенство
\ f is) d|i ig)=\f if is')) I ^ is') I dvi' iS%
F (V) v
Если F — накрытие степени m, отображающее открытое
подмножество V с: G' на открытое подмножество V с:0, то для
того, чтобы это равенство осталось справедливым, правую часть
следует разделить на т.
Оставшаяся часть этого параграфа посвящена вычислению
якобианов в четырех специальных случаях. Дифференциал dF {^)
можно вычислить при помощи производных Ли. Пусть X' е д'.
Мы хотим найти вектор dF {g') X' = X. Этот вектор
характеризуется следующим свойством. Пусть феСГ(О). Тогда
'ix^iFig')) = ^x'i'^°F)ie')-
Вычисление якобианов
До конца этого параграфа выберем в качестве базиса
алгебры Ли g группы SL2(R) = G матрицы

150 Vll. Следы
Тогда вектор Я л Х"*" л Х~ — ненулевой вектор из Л ^8 и
существует единственная левоинвариантная дифференциальная форма©
на группе G, такая, что
со(Я, Z+, Z-)=l.
С этой дифференциальной формой связана положительная
мера Цщ. Мы будем сравнивать другие меры на группе с этой
стандартной мерой, что позволит нам также установить связь
их друг с другом.
Однопараметрическая подгруппа, для которой Я —
касательный вектор, совпадает с А; если мы запишем ее элементы в виде
/е' О \
то мере Хаара da на группе А соответствует мера Лебега dt.
Аналогично, однопараметрическая подгруппа с касательным
вектором Х"^ есть подгруппа N, и если записать ее элементы
в виде
1
"="" = (о ")'
то мере Хаара dn на подгруппе N соответствует мера Лебега du.
Аналогичное утверждение справедливо для группы /V,
состоящей из матриц вида
«"=С i)'-
Отображение ■ ^ь-> Ad g есть представление группы G; его
называют присоединенным представлением. Заметим, что
мере Хаара dn соответствует мера du.
Если g е G и Z е д, то, по определению,
Z« = g^-'Zg^ = Ad{g-')Z.
■Adg есть представление
иным представлением. 3:
g--'(ехр Z) g = ехр (g-'Zg).
Следовательно,
(ехр Z) g = g- ехр Z^ = g- ехр (Ad {g-') Z).
Это показывает, как «принести» элемент группы через
экспоненту.
Как обычно, мы полагаем
W
-U :)■

§ 2. Интегральные формулы 351
Матрица W является образующей алгебры Ли группы К;
матрицы ехрбй^' задают параметризацию этой группы. При такой
параметризации мера Хаара на К переходит в меру йЬ.
Мы будем считать, что меры Хаара на подгруппах А, N, К
выбраны при помощи описанной параметризации. Меры на
прямых произведениях AXNXK и КХАХК — произведения мер
на сомножителях da = dt, dn = du, dk = d6.
INT 1. Зададим отображение F: AXN XK-*-G формулой
p {a, n, k) = ank. Тогда для любой функции ф е СГ (G)
справедливо равенство
^ Ф (g-) d\i^ (§■) = 5 \ W ^""^^ ^" ^" '^^'
а А N к
Доказательство. Пусть ф — гладкая функция на группе G.
Тройка векторов {Н, А'+, W} образует базис касательного
пространства к единичному элементу в AXN ХК. Для того чтобы
вычислить действие дифференциала отображения F на векторы Н,
Х'^, W, воспользуемся производными Ли. Рассмотрим сначала
производную
-^ф{аехр(/Я)/г^)|^^о.
Ясно, что
Ф {а ехр (/Я) nk) = ф {ank ехр (^Я"*)).
Это означает, что
dF[a, п, k) Н = Ad (k-^) Ad {п-')Н.
Аналогично
dF{a, п, k)X+=^Ad{k~^)x+,
dF{a, п, k)W^W = X+-X-
С другой стороны, нетрудно проверить прямым вычислением,
что если
1
" = (о ")'
то Ad («"') Я = Я + 2mZ+. Следовательно,
Н^-^Н + 2иХ+,
Ad ik) dF {а, п, k): ■ ^+ ^ Х^,
W^^X"^-X~.
Отображение ^b->A^Adfe задает представление группы К
в мультипликативной группе вещественных чисел и поэтому

152 ^Ч- Следы
Тривиально. Значит, отображение A^dF{a, п, k) переводит
вектор Н hX'^ ^W в — Н а Х'^ а Х~. Это показывает, что
локально прообраз меры [Лщ есть в точности dadndk. Так как
отображение F взаимно однозначно, наша формула доказана.
Выведем теперь интегральную формулу, связанную с так
называемым разложением Картана. Обозначим Л"*" множество
всех матриц вида
Ко а-7'
а> 1.
Рассмотрим отображение
действующее по правилу (^i, а, k^^^—^kyak^. Это отображение
сюръективно, поскольку полярное разложение матрицы х по
зволяет однозначно записать ее в виде
где S — положительная симметричная матрица, /г е /С. Кроме
того, если собственные значения матрицы s различны, ее можно
привести к диагональному виду ортогональным
преобразованием. Сопрягая полученную диагональную матрицу, если это
необходимо, при помощи матрицы w, можно перевести ее в
элемент множества Л"*". Наконец, если а=?^±1, то в выражении
s = k\^ak\ для положительной симметричной матрицы s, где
а е Л"*" и /si е К, элемент ^i определен с точностью до
умножения на ± 1. Следовательно, разложение
где а е Л"*", k^, k^ е /С, определено однозначно с точностью до
умножения матриц ^i, k^ на ±1.
Отображение
F: KXA'^XK^G, [k^, а, k^)^-^k^ak2
называется разложением Картана. Приведенные замечания
показывают, что отображение F двулистно накрывает свой
образ, который в действительности совпадает с дополнением
к подгруппе /С в G. В самом деле, если а е Л"*", то двойной
смежный класс КаК не пересекается с подгруппой К (так как
ЛП/С = {±1}); с другой стороны, мы уже видели, что любую
матрицу л; е G можно представить в виде х = k^ak^ для
некоторых ^1, ^2^^. аеЛ. В частности, образ множества
/С X Л"*" X ^ открыт в G, а его дополнение имеет меру нуль.

§ 2. Интегральные формулы 153
INT 2. Пусть F: К X Л^ X К-* G — разложение Картана.
Для любой функции феС(;{0) справедливо равенство
\^<f(x)dix^{x)=^ \ ^^{k,ak2)^M^z3l2l!}.cLk,dadk2.
о КА+ к
Положив a = hi, /г, = г (Bj), k^^r (62), можно записать эта
равенство в виде
J Ф (л;) d\ji^ W = 5 \ \ Ф (г (Bi) A<r (62)) sh 2/ dB, dt ^02.
G 0 0 0
Интеграл no переменной / берется от О до оо, поскольку
интервал (О, оо) параметризует множество Л"*". Напомним, чта
а(а) = е2*.
Чтобы вычислить дифференциал отображения F, возьмем
в качестве базиса алгебр Ли групп /Cj = /С, Л, /С2 == /( матрицы-
Wi = W, Н, W2 = W соответственно. Этот выбор фиксирует
меру на произведении КХЛХК. Нам нужно определить,
образ 3-вектора WiA Н AW2 при отображении F,. Как и выше,
возьмем произвольную функцию феСГ(О) и преобразуем
выражения
q)(kiexp{tWi)ak2), ф (^iQ ехр (/Я) ^2). qi{kiak2exp{tW2)),
пользуясь правилами коммутации экспоненты с элементам»
группы и пронося ее направо. В результате вычислений
получаем, что дифференциал отображения F действует по
следующему правилу:
Г Г1 ^^ Ad (а-') W = а-Ч+ - аЧ-,
Adk2-dF{k^, а, ^2): i ^^~^Н,
[W2^-^W = X+-X-.
Перемножая эти векторы, находим
F,{Wi А Н AW2) = {a-^~- а^) Н А Х+ А Х-.
Это означает, что локально прообраз меры d\x^ дается формулой.
F* {d\xj = (а (а) — а (а"')) dki da dk2.
Так как F — двулистное накрытие, то для того, чтобы
получить интеграл по всему произведению /СХ^^Х^> нужно
разделить нашу меру на два.
Следующие две формулы связаны с интегрированием пО'
множеству классов сопряженных элементов. Обозначим
символом G' множество элементов группы G с различными собственными.

154 W/. Следы
значениями; аналогично определяются множества А', К!• Мы
■будем называть такие элементы регулярными.
Рассмотрим сначала множество X.. Множество л' ,
состоящее из всех элементов вида g~^ag, где а е Л', g е G, открыто
в G. В самом деле, предположим, что элемент geG таков,
что матрица g~^ag также принадлежит Л. Тогда матрицы а и
g~^ag имеют одинаковые собственные значения, откуда
g~'ag = a или g—^ag = a-K
В первом случае матрица g централизует а; мы предоставляем
читателю проверить, что §еЛ^Л, где М = {±1}. Во втором
случае gw е МА, поскольку сопряжение матрицей- w переводит
а в а~К Чтобы пояснить эти замечания, рассмотрим
отображение
F: Л' X A\G -* G\ {а, g) ^ g-'ag.
Из сказанного выше следует, что это отображение представляет
собой накрытие степени 4; в самом деле, четыре элемента
(а, ±1), {а-\ ±w)
имеют один и тот же образ в группе G при отображении F.
Разложение
G ^ AN К
позволяет параметризовать множество A\G точками (п, k) е
е yv X /С; мы воспользуемся этой параметризацией в нашей
следующей интегральной формуле.
INT 3. Зададим отображение F: А''К N'К К-* G' формулой
F [а, п, k) = k~'n~^ank.
Положим D{a) = a {а)''' — а {а) . Тогда для любой функции ф
с носителем в множестве А справедливо равенство
\(f{g)dii^{g) = ^^^^fp{k-'n-'ank)\D{a}fdadndk.
а А N к
Доказательство. Множитель 1/4 связан с тем, что
отображение F — накрытие степени 4. Остается показать, что локально
прообраз меры d\i^ при отображении F равен \ D {а) f da dndk.
Рассмотрим сначала выражение
Ф (^"'rt"'a ехр (^Я) rt^).
Легко проверить, что, если пронести экспоненту направо, оно
лримет вид
Ф (ife~'rt-'artife ехр (Ad/г-'• Adrt-'• Я)).

§ 2. Интегральше формулы 155
Отсюда после несложных выкладок получаем
Ad k-dF{а, п, k) Н = Adп-'Н = Н+ 2иХ+,
где «=Q ;;).
Далее, рассмотрим функцию
/ ь-> ф (й-' ехр (— tX+) п-'апехр (tX+) k) =
= ф(^-'/г-'а/гехр(—^Adrt-' -Ada-' ■ kdn- X+)&vg{tX+)k).
Чтобы вычислить ее производную при / = 0, заменим
переменную t на втором месте новой переменной v. Затем,
воспользовавшись правилом дифференцирования сложной функции,
сложим частные производные по / и по а и сделаем подстановку
/ = а=0. Для вычисления производной по / заметим, что
kdn-X+ = X+
(так как группа Л^ коммутативна!) и
Ada-'Z+ = a-2^+.
В результате получаем
Adk-dF {а, п, k)X+ = {\-a-'-)X+.
Наконец, рассмотрим функцию
t Н-» ф (ехр (— т) k-^n-^ank ехр {tW)) =
= ф(^^-'/г-'а/гехр (- / Ad«"' Ada"' Adn-W)ехр (/Г) • k}
и воспользуемся снова правилом дифференцирования сложной
функции, заменив переменную / на втором месте новой
переменной V. Получим
kdk-dF {а, п, k)W = -Ad {«"'а-'/г) -W + W.
Нас будет интересовать внешнее произведение векторов ^,Я,
F,X+, FJ^. Заметим, что вектор F^X+ есть скалярное кратное
вектора Х+. Поэтому нам достаточно вычислить вектор F^H^
лишь с точностью до слагаемых, кратных А'+, а вектор F^W—
с точностью до линейной комбинации векторов Я, Х+.
Вычислим явно матрицу g = n~'a~^n, а затем определим проекцию
вектора gWg~^ на Х-. Получим
Ad k ■ F,W = (а^ - 1) Х- (mod (Я, Х+)).
Отсюда
F^(H hX+AW) -= (1 - а-'^){с^ - 1)Я л J+ л J_.
Но
(1 - а-2) {а^-\) = (а- a~Y = | Z) (а) Р.
Итак, наша формула доказана.

156 VJl- Следы
Пусть Л_ — класс смежности подгруппы А, состоящий из
всех матриц вида —а, аеЛ. Положим /п = — 1. Тогда
справедлив следующий аналог формулы INT 3.
INT 3'. Зададим отображение F: А-"Х N У^ К -^ G формулой
F{a, п, k) = k-^n~^ank.
Тогда для любой функции Ф е С,, (G), носитель которой
содержится в множестве А , справедливо равенство
5 Ф (8) d\i^{8) = ^\\\(p {k-'n-'mank) | D (а) Р da dn dk.
f[Q A N К
Эта формула немедленно вытекает из INT 3.
Последняя формула этого параграфа будет связана с
однородным пространством /C\G. В общей теории полупростых
групп Ли аналогом группы К в данном контексте является
подгруппа Картана, которую обозначают В. В данном случае
В = К, но иногда мы будем писать В вместо К.
Разложение Картана G = KA'^K позволяет указать
параметризацию множества (/C\G)' = К\КА'^К; в самом деле, из него
следует, что
{K\G)'c=,A+K/M,
где, как и прежде, М = {±1}- Рассмотрим теперь отображение
F: ICXA^XK^G',
действующее по правилу
(k', а, k)^-^k-^a-^k'ak;
здесь К' — множество регулярных элементов группы К, т. е.
множество всех элементов из К, отличных от ±1. Из
разложения Картана следует, что если k' ^К' и матрица g е G
удовлетворяет условию
то g е /с. Отсюда немедленно вытекает, что отображение F
представляет собой двулистное накрытие (так как образ точки
{k', а, k) не изменяется при замене матрицы k па — k).
Пусть k = kQ = r (6); положим, по определению,
D (fee) = Z) (6) = е'9 - е-^9 = 2/ sin 6.
Эта величина представляет собой разность собственных
значений матрицы kfi.

§ 2. Интегральные формулы 157
При выводе формулы замены переменных сейчас будет
удобнее использовать комплексный базис алгебры Ли, состоящий
из собственных векторов операторов Ad^, k^K- Выше мы уже
вводили матрицы
V--
{::). ^-С-О. -Ч-,':!)^
ясно, что матрицы {Я, V} образуют базис в пространстве
симметричных 2 X 2-матриц со следом 0; кроме того,
E+ = H + iV, E- = H-iV.
Матрица W образует базис в пространстве кососимметричных
матриц; справедливы коммутационные соотношения
{W, Е+] = 2iE+, [W, Е-] = - 2iE-.
Следующая лемма показывает, что элементы Е+, Е- являются
также собственными векторами операторов Adfe, fe е/С. Эта
лемма справедлива для произвольных групп Ли, хотя при ее
доказательстве мы будем пользоваться матричной реализацией.
Пусть У, Z е Mat„(С) — комплексные п X «-матрицы, и пусть
g е GLn (С). По определению,
adZ-y = [Z, У], Aug-Y=^gYg-K
Итак, adZ есть линейный эндоморфизм пространства матриц.
Определим эндоморфизм ехр ad Z при помощи обычного
степенного ряда:
ехр ad Z = / + ad Z -1- -^ (ad Z)2 -f
Ясно, что матрица ехр Z принадлежит группе GL„{C), и,
значит, определен эндоморфизм Ad (ехр Z).
Лемма. Ad (ехр Z) = ехр (ad Z).
Доказательство. Положим
/ (t) = Ad (ехр (tZ)), g (t) = ехр (ad (tZ)).
Тогда fug — гомоморфизмы аддитивной группы вещественных
чисел в группу GL(Mat„(C)), причем их значения в точке/=0
совпадают, а именно
/(0) = g(0) = /.
Мы покажем, что их производная при / = 0 равна adZ, откуда
и будет следовать, что f{t) = g{t) при всех ^ е R. Имеем
Ad (ехр (tZ)) Y = {I + iZ + 0 (Z^)) Y{I-tZ + 0 {f)) =
= Y + t\Z,Y]+0{i').

158 VII- Следы
Это показывает, что f (0) = ad Z. Далее,
exp{ad^Z)-y = K + /adZ-y 4-0{/2),
откуда немедленно следует, что g' (0) = ad Z, Лемма доказана.
Приведем пример приложения доказанной леммы. Допустим,
что У е 9 — собственный вектор оператора adZ, т.е.
adZ-Y = XY.
Тогда ясно, что
Ad (ехр Z) У ^е'-У,
и, таким образом, У есть собственный вектор оператора Ad (ехр Z).
Воспользуемся этим замечанием, когда У = Е+ или Е~ и
Z = W. Имеем
Следовательно,
Adk^■E+=e^^^E+, Ad к^Е-=е-^'^Е-.
INT 4. Зададим отображение F : К' "Х А'^ У, К-*■ G' формулой
F{k', а, k) = k-'^a-^k'ak.
Тогда для любой функции ц>, носитель которой содержится в
множестве К'^, справедливо равенство
\ \ \^(k-'a-'k'ak)\D{k')f °^'^^~"(^"'^ dk'dadk =
к А+ к
2л оо 2Л
= 5 S 5 f(fe^'Ar'A:e'Me)|Z){e')P-^^^-=^^^de'd/de.
'" °° '" .и .-п
0 0 0
Доказательство. Схема наших рассуждений та же, что и
прежде. Нам нужно определить, как дифференциал
отображения F действует на векторы W' = W, Н и W.
Для того чтобы вычислить вектор FJ^', рассмотрим функцию
f{fe-'a~'fe'exp{^U^")a/5); нам нужно пронести множитель ехр (/11^')
направо. Получаем
Aia-AdkdF{k', а, k)W' = W.
Используя ту же технику, что и выше, можно вывести
соотношения
Ada-Ad k-dF{к', а, А!)Я ={/ —Ad fe'-') Я,
Ada-Ad к-dF{k', а, k)W ^ {I - Ad к'-') Ada-Wi

§ 2. Интегральные формулы 159
ДЛЯ ЭТОГО нужно проносить множители ехр{—tH) или ехр(—tW)
направо. Как и при доказательстве формулы ШТ 3, такие
экспоненциальные множители встречаются в двух местах;
поэтому при вычислении производной следует заменить переменную t,
стоящую на втором месте, новой переменной v и воспользоваться
правилом дифференцирования сложной функции. Отсюда
немедленно получаются приведенные выше формулы.
Перейдем к вычислению внешнего произведения FJ^' л F,H л
aF,W. Перемножая матрицы, получаем
/ О 0^4
Ada.r = (_^_, J;
запишем это равенство следующим образом:
Ada . Г = a^Z+-a-2J_ = ^i^ F+ ^i±-^r.
При вычислении внешнего произведения слагаемое,
пропорциональное W, можно опустить. Поэтому
ЛMAdaA:)F.(^'лЯлr) =
= Г л (/ - Ad k'-') Я л (/ - Ad k'->) "'-^"^ V.
Воспользуемся равенствами H = E+--iV = E- + iV, или, иначе
говоря, тем, что
2 ' " Ш
Так как Е+ и Е- —собственные векторы оператора Ad ^', наше
внешнее произведение равно
-j"'~°"' (1-б2'в')(1_е-2«')й^'л£_л£+
(мы пишем k' = expQ'W). Пользуясь равенствами
W = X+-X-, E±=^H±iV, F=X+ + J_,
получаем
Г л £•-л £+= —4гЯ л ^+л А"-.
7Т я -TTf>f>
(1 - е2«') (1 - е-2'в') = ID (в') ?.
Таким образом, с точностью до множителя, по модулю
равного 1, якобиан преобразования кй. а АЛ. k dF {k', а, k) равен

160 Vn. Следы
Отображение gi—* A^Adg есть одномерное представление
группы G в пространстве Л^9- Мы уже знаем, что оператор A^Ad k
действует тривиально. Так как группа G = Si2(R) не имеет
нетривиальных непрерывных гомоморфизмов в
мультипликативную группу вещественных чисел, то оператор A^{AdaAd^) —
тождественный оператор на f\\, поэтому вычисленный нами
якобиан совпадает с якобианом преобразования dF{k', а, k).
Итак, формула INT 4 доказана.
Замечание 1. Мера dk на группе /С нормирована так, что
при параметризации ^ = ^Q = r(G) она переходит в d6. Это
означает, что в приведенных выше формулах полная мера группы/С
равна 2я. Для нормировки мы можем поделить все интегралы
на 2я. Однако в тех формулах, где содержатся два интеграла
по К, например в формуле INT 2, связанной с разложением
Картана, и в формуле INT 4, только один из этих интегралов
окажется нормированным, а второй останется без множителя
(2я)~'. Ввиду этой асимметрии я предпочел использовать
ненормированную меру d6; мы будем переходить к нормированной
мере только в конкретных случаях, когда такая нормировка
возникает естественным образом.
Замечание 2. Следуя рассмотренной схеме, можно
систематическим образом получать различные интегральные формулы.
Например, при изз^ении отображения
K'XK\G-*G',
определяемого формулой
которое мы рассматривали при выводе формулы INT 4, мы
могли бы воспользоваться однозначным разложением G = KAN
и группами AN или NA для параметризации множества K\G.
Так как читатель сможет теперь без труда вывести
соответствующую формулу, если она ему потребуется, и так как нам эта
формула не понадобится, мы не будем приводить ее здесь.
§ 3. Следы индуцированных представлений
Пусть S — комплексное число; напомним, что Н (s) —
гильбертово пространство функций f на группе G, сужение которых
на подгруппу К принадлежит пространству L^{K) и таких, что
f{ank)^p{ay+'f(k).
Группа G действует в пространстве Н (s) правыми сдвигами;
в § 4 гл. III мы видели, что для любой функции ф е СГ {G, К)

§ 3. Следы индуцированных представлений 161
оператор ns{^) есть интегральный оператор с ядром
А N
Т. е. что сужение функции л^ (г!)) f на подгруппу К задается
формулой
ns{^)f{k')=:=\^q^{k, k')f{k)dk.
к
Мы предполагаем, что мера Хаара dx на G нормирована так,
что dx^==^dadndk, и что мера подгруппы К равна 1, т. е.
dkQ == -^ dB.
Тогда, как мы видели,
1тщ{'^) = ^д^{к, k)dk.
к
Как и прежде, определим преобразование Хариш-Чандры
формулой
НЩа)=\0{а)\ ^ г|з(х-^ах)di = р(а) ^ г|з {an)dn.
А\а N
Пусть fi = fis —характер группы А, задаваемый формулой
ц {а) = fi, (а) = р {а)\
Обозначим символом % представление группы G в пространстве
His). Получим
(1) !г%(ф)=5нлг|)(а)ц(а)^а.
А
Согласно теореме 1 § 2 гл. V, функция Н'*г|з инвариантна
относительно преобразования а»—^а-Ч Таким образом, справедлива
также формула
(2) tr я, № = 5 Н^ (а) '^<^>+/(^-'> da.
А
Напомним, что символом G' мы обозначаем множество
регулярных элементов (т. е. множество матриц с различными
собственными значениями).
Теорема 4. След представления л^ совпадает [в смысле теории
распределений) с функцией 7^, определяемой формулами
^^(") = 2Ji(5^+^|^. есша^А',
7'nW='0, еслихф.А"^,
T^^{x-^ax)==Ty_{a) для всех л; е G, а^^А'.
6 Зак. 589

162 V//. Следы
Иначе говоря,
а
Доказательство. В соответствии с формулой INT 3 имеем
J ■\!f{x)dx'^j^ J г|)(д;-'ал;)|/)(а)Р^а^;с =
л'О А А\а
■j\H'^Mf{a)\D{a)\da.
Существует функция f на группе G, постоянная на классах
сопряженных элементов, равная нулю в дополнении к множеству
Л'° и такая, что
f (^\ — ц(а) + Ц(Д~')
'W- \г)(а)\
1^орректность нашего определения вытекает из того, что х-^ах е А
в том и только том случае, когда д;=±1 или ±w{modA)',
ясно, что f (а;-'аоу) = /(а-') = /(а). Выражение для функции Н'*'ф
в виде интеграла по классам сопряженных элементов
показывает, что
Заменяя ^ф на fij), получаем
[^{x)f {X) йл: -1 5 H^t (а) [ц(а) + fi (а"')] da.
А'а А
Сравнение с формулой (2) завершает доказательство теоремы.
Появление множителя 2 в формуле для следа
индуцированного представления связано с тем, что мы не разделили
подпространства H+{s) и H~(s). Чтобы устранить его, поступим
следуюш,им образом.
Пусть (i — непрерывный гомоморфизм группы А в С* —
мультипликативную группу комплексных чисел. Пусть е-характер
группы М = {± 1}. Тогда пара {ц, е) определяет характер группы
MAN по формуле
zanн->-е(г) \i(а), г еЛ!, а е Л, п^ N.
Мы можем образовать индуцированное представление группы G
при помощи этого характера подгруппы MAN. Пространство
представления Н (s, г) или Н(ц, е) совпадает с подпространством
четных или нечетных функций в пространстве Н (s) в зависимости
от того, тривиален характер е или нет. Обозначим два
возможных представления символами я„ + и Яц -, а их следы Г^ +

§ 4. Следы представлений дискретной серии 163
Следствие. Пусть я (ц, е) — представление группы G в
пространстве Н{ц, е). Тогда след этого представления совпадает, в
смысле теории распределений, с функцией T^.g, определяемой
формулами
7'ц.8(za) = е(2) ^ ^"i^'(Г)i""'^ ■ «^^ Z&M, as А',
Гц,g(л:) = О, если х0± А'°,
r^,g(^;~'ax).= 7'^. g(a) для всех x^G, а^А'.
Доказательство. Для определенности рассмотрим случай, когда
характер е нетривиален. Пусть f — та же функция, что и в
теореме 4. Тогда
tr«,(^l.-)= \±i^U^^f±lll2f{x)dx^
= J ^{x)f{x)dx~ J ^{-x)f{x)dx =
= \ i|3 {;c) 8 (x) f (x) dx.
Итак, наше утверждение доказано. Второй случай
рассматривается аналогично.
§ 4. Следы представлений дискретной серии
Пусть /п —целое число, /п^2. Положим s = m — l. В § 5
гл. VI мы видели, что пространство Н{т—\) разлагается на
несколько неприводимых подпространств; сейчас нас интересуют
подпр остр анств а
n>m n<-m
И факторпространство К (m — 1) = Я (m — 1, е) (mod [Я*"" +/^*"'"']);
здесь 8 —характер группы iVf = {± 1}, задаваемый формулой
■»-я<-»')-*| [- V(w-1) -[ [-i—tf(«)—-
.Н 1 1 1 1 1 1 1 1 1 1
-*i-2-m |-« + 4...0...m-4i wm + 2
-m+3 ni-2
Рис. 1.

!64 V//. Следы
е(— 1) = (— l)"*. Из изучения производного представления
вытекало, что пространства Я*"»', Я*-"*), V{m—l) неприводимы;
кроме того, пространство V{m—\) конечномерно. Весовые
диаграммы этих пространств изображены на рис. 1.
Мы вычислим след представления группы G в прямой сумме
пространств
Я("" + Ж-"»),
используя выражение для следа в пространстве Я(/п—1),
полученное в предыдущем параграфе, и вычитая из него след
конечномерного представления в пространстве V{m—l).
Положим
± 1.
Лемлш 1. Пусть п —целое число, п^1; положим /п = /г4- 1,
8(—1) = (—l)"*. След представления группы G в пространстве
Я {п, е.) совпадает, в смысле теории распределений, с функцией Т,
постоянной на классах сопряженных элементов и такой, что
ent + е-'Ч
\е — ^ I
Т{х) == О, если хф± А'°.
Доказательство. Это частный случай формулы, полученной
в предыдущем параграфе для произвольного индуцированного
представления.
Лемма 2. Для любой пары неотрицательных целых чисел р, q,
таких, что р -\- q = n— I, определим функцию fp,^ на группе G
формулой fp^ ^ (х) = c''d'', если
'<: :)■
Тогда fp^^Q Н(—• п, е). Функции fp,, образуют базис
конечномерного неприводимого подпространства
V' (rt) == I/ (- «) = F (- /п + 1)
размерности П'==т— 1. Пусть р' — представление группы G в
пространстве V (п). Тогда
„-nt
trp'(zA,) = 8(z)
е'-е-'
Доказательство. Очевидно, что функции /р., принадлежат
пространству Н{—п), линейно независимы, и их линейная
оболочка инвариантна относительно действия группы. Каждая из

§ 4. Следы представлений дискретной серии 165
ЭТИХ функций является собственным вектором однопараметри-
ческой подгруппы p'(Af); в самом деле, нетрудно проверить, что
Поэтому след представления р' легко вычисляется, и мы
получаем приведенную выше формулу.
Из теоремы 4 § 2 гл. VI мы знаем, что два конечномерных
неприводимых представления одинаковой размерности инфините-
зимально эквивалентны, а согласно следствию этой теоремы —
даже эквивалентны, хотя для равенства следов достаточно инфи-
нитезимальной эквивалентности. Поэтому представление,
построенное в лемме 2, или же представление в пространстве
V (т— 1) можно использовать как модель представления данной
размерности.
Лемма 3. Пусть V — конечномерное неприводимое
пространство размерности п = т — 1, р — соответствующее представление
группы G. Тогда
е« _ g-ie
Доказательство. Мы знаем, что пространство V порождается
собственными векторами подгруппы К с собственными
значениями
р1{~т+2)в z,((-m+4)e z,i(m-2)e.
с- , с- ,...,& ,
чтобы вычислить след представления на элементе k^ е К, нужно
сложить эти собственные значения, т. е. просуммировать
геометрическую прогрессию. Теперь наше утверждение очевидно.
Лемма 4. Пусть п — ц^лое число, п^\; положим т = п+ 1.
Пусть е(—1) = (—l)"*. Тогда след представления группы G
в пространстве Я*'" + Я*~"'' совпадает, в смысле теории
распределений, с функцией Т, постоянной на классах сопряженных
элементов и такой, что
T{zh,) = B{z)
2е-
\nt\
Т{х) = О, если хф±А'°[}К'^.
Доказательство. Это утверждение с очевидностью вытекает
из лемм 1, 2, 3; достаточно вычесть след конечномерного
представления, вычисленный в леммах 2 и 3, из следа, полученного
в лемме 1.

166 УН Следы
Мы ВЫЧИСЛИЛИ след представления группы G в пространстве
^Ы) _|_ /^(-'">_ Нам нужно теперь разделить эти неприводимые
подпространства. Окончательный результат таков:
Теорема 5. Пусть п —целое число, пфО; положим /п =
= |rt|+l- Пусть z=±l, 8(—1) = (—l)"*. Пусть о„
—представление группы G в пространстве Я*""*"", если /г > О, ив
пространстве Я "~", если «< 0. Тогда tr а„ совпадает, в смысле
теории распределений, с функцией S„, постоянной на классах
сопряженных элементов и такой, что
Sn (fee) = - sign п -jQ Г7в
5„(гЛ,) = е{г)-
е
е — е
\nt\
е'-е-'
S„ (х) = О, если л; ^ ± Л'о и Я'«.
Доказательство. Доказательство этой теоремы довольно
сложное; оно принадлежит Хариш-Чандре. Основная трудность
состоит в том, чтобы исключить возможность вклада от
сингулярного множества, т. е. от множества G — G', который
сокращается при суммировании следов представлений дискретной
серии с положительным и отрицательным весом. Я опускаю это
доказательство (может быть, я включу его во второй том,
в котором будут рассмотрены различные вопросы, связанные
с дифференциальными уравнениями и распределениями на
группе SL2(R)). Легко проверить, что на множестве регулярных
элементов (т. е. на функциях с компактным носителем,
содержащимся в множестве G') след представления совпадает с
описанной выше функцией. Это простое следствие наших
интегральных формул и выражений для преобразования Хариш-Чандры
на подгруппах Л и /С, которые мы получим в § 2 следующей
главы. Для вывода формулы Планшереля теорема 5
несущественна, поскольку в нее входит сумма следов представлений
дискретной серии. Однако для дальнейшего изучения группы
SL2(R) эта теорема очень важна.
Заметим также, что из интегральных формул вытекает, что
след является локально суммируемой функцией.
§ б. Связь между преобразованиями Хариш-Чандры
на подгруппах А \л К
Для произвольной функции г|з S СГ (G, К) мы определили
преобразование Хариш-Чандры на А формулой
(1) Н^1() (а) = IZ) (а) I \^^ {х-^ах) dJt,
А\а

§ 5. Связь между преобразованиями Хариш-Чандры на А и К 167
где di —такая мера на A\G, что dx = dadx; мера Хаара dx
нормирована так, что
dx = da dn dk, dk^ = -g—.
Таким образом, по определению, для любой функции /
справедливо равенство
J ^f{ait)dadx= ^f{x)dx.
A\Q А a
в силу Ьормулы INT 3 получаем
(2) \^{g)dg={\^\A^{a)\D{a)\da.
A'Q А
Аналогично определим преобразование Хариш-Чандры на
множестве /С' = /С —(±1}, полагая
(3) Н^1|) (k) = D{k) J я|) {х-1 kx) dJt,
где dx теперь — такая мера на пространстве K\G, что
J \^f{kx)dkdx== [f{x)dx,
к\ак а
и
Z)(A!e) = e'9_g-i9.
Из формулы INT 2 ясно, что пространство K\G однозначно
параметризуется точками множества Л"^/С/{± 1} и что поэтому
(4) Н^г|) {k)==D{k) 5 я|) (а-'ka) «(^)-°'(^"') da.
А+
Согласно формуле INT 4, получаем
2я
(5) J я|) (л;) йд; = 5 Н^г|) (feg) Щй^) dB.
(Если разделить обе части формулы INT 4 на 2я, в ней Bct
еще останется один интеграл по /С, в котором полная мера
группы К равна 2я.)

168 VII. Следы
Для любого целого п^'О обозначим символом S„ функцию,
постоянную на классах сопряженных элементов и такую, что
„tee
Sn. (^e) = — sign n -^—Г7Г
e — e
S„(Z/Z<)X=8(Z)-— Г7Т.
S„ (x) = 0, если хф±А'°\} /('".
Как и выше, здесь z = ±l, e(z) = z"+'. Мы снова будем
рассматривать S„ как функционал; таким образом, для любой
функции f »
S,(f)^]f{x)SAx)dx.
а
Теорема 6. Справедливо соотношение
S„W = —signrtj H^^'^ikQ)e''^ЧQ +
о
оо
+ \\ [НЧ(АЛ + (- 1Г+'Н^я|,(-/ч)]е-1»М di.
о
Доказательство. С точностью до множества меры нуль G =
= /С'° и ± Л'°. Вычислим сначала интеграл по множеству К,'^.
Мы получим для этого интеграла выражение
] ^ W (- sign п) ,9(.) -т(х) dx,
где элемент л; е G сопряжен матрице ^в(х) s /С. Применим теперь
к подынтегральной функции формулу INT 4. Из формулы (4)
следует, что наш интеграл равен
2я
-sign«J HH(A!e)e^"«de.
о
Это выражение является первым членом нашего соотношения.
Перейдем к интегралу по множеству ±Л'°:
J 'ф(д;)8(д;)
■dx =
^t{x) _ -t{x)
= S Иix)+(- 1г^ч (-^)], n'.) _,-^w I ^^ ==
oo
= ~ 5 [H^it)(A<) + (-l)"+'H^it)(-Ai)]e-l'"ld/,

Приложение. Общие сведения о следах операторов 169
где элемент л; s G сопряжен матрице dzht^x)- Для завершения
доказательства достаточно заметить, что функция Н^
инвариантна относительно преобразования а^—^а~-.
Приложение. Общие сведения о следах операторов
в гильбертовом пространстве
Полярное разложение
Пусть Я — сепарабельное гильбертово пространство, А —
линейный оператор в пространстве Н (все операторы, которые
рассматриваются в этом приложении, предполагаются
ограниченными). Оператор А*А симметричен и положителен; существует
единственный положительный оператор Р^==(Л*Л)''' (квадратный
корень из А*А), т.е. такой оператор, что Ра^А'А. Зададим
оператор U = Ua на образе оператора Ра формулой
U{A'Ai''v^Av, v^H.
Чтобы проверить корректность этого определения, достаточно
показать, что если (А'А)'' v =0, то и Av==0. Но при сделанном
предположении
О = I (A'Af V f = {A*Av, v) = (Av, Av),
что и требовалось показать. Немедленно проверяется, что
отображение и изометрично, и, значит, его можно продолжить по
непрерывности на замыкание образа оператора Р^. В
ортогональном дополнении ImP^ доопределим оператор U нулем (такой
оператор называют частичной нзометрией). Тогда имеют место
очевидные соотношения
UV^I на 1т Ра, Ш* = /на1тА
Разложение Л = f/P оператора Л в произведение частичной
изометрии и и положительного оператора Р однозначно. В самом
деле, если А = WQ, то А* = QW* и
откуда P = Q, поскольку положительный квадратный корень из
положительного оператора определен однозначно (спектральная
теорема!). Построенное разложение называется полярным
разложением оператора А. Полярное разложение оператора А*
легко построить, исходя из разложения для оператора А, а именно
A*^Ua*Pa; где Ua*^U\ P^'^UPaU*.
Чтобы проверить это, заметим, что оператор UPU*
положителен и
(UPUy = UPU*UPU* = иРЮ* = АА*.

170 VII. Следы
Таким образом, мы построили оператор Ра*; выражение для
оператора Ua* теперь очевидно.
Операторы Гильберта—Шмидта
Оператор А называется оператором Гильберта—Шмидта,
если
Si ащ^<оо
для некоторого ортонормированного базиса {и;} в пространстве Я.
То же самое справедливо тогда и для любого другого
ортонормированного базиса {Vj}. В самом деле, заметим, что для
любого вектора w имеет место равенство \wf^'^\{w, Vj)f;
таким образом,
(*) ZI Ли. Р = SI {Ащ, V,) Р = ZI («й A'v,) Р = ZI A'vi р.
i i.l и I I
Определим скалярное произведение двух операторов
Гильберта — Шмидта Л и В формулой
{А, В) = Т.{Ащ, Вщ),
где {ut) — некоторый ортонормированный базис. Написанный ряд
абсолютно сходится, что нетрудно увидеть из неравенства
Шварца (примененного дважды):
Z\{Aui, Bui)\^Z\M\\But\.
Таким образом, В*А есть оператор Гильберта — Шмидта и
величина {А, В) не зависит от выбора базиса {и,}.
Соответствующая норма обозначается символом || • Цг-'
\\Ai = Z\Aui\\
Операторы Гильберта — Шмидта образуют полное относительно
этой нормы гильбертово пространство, которое иногда
обозначают символом ®^. В следующих утверждениях мы предполагаем,
что А и В —операторы Гильберта — Шмидта, а X
—произвольный ограниченный оператор.
HS1. М*|Ь = М1Ь.
HS 2. ХА и АХ —операторы Гильберта — Шмидта, и
||ХЛ|Ь<|Х|М1Ь, \\AXl^\X\\\A\k.
HS 3. Всякий оператор Гильберта — Шмидта компактен.
Прежде чем продвинуться дальше, докажем
сформулированные выше утверждения. Первое из них, по существу, уже
доказано (см. формулу (*)).

приложение. Общие сведения о следах операторов 171
Утверждение HS2 следует из очевидного неравенства
|ХЛиг К| Х|| Лиг I и того факта, что {АХ)*=К*А*. Перейдем
к доказательству компактности операторов Гильберта — Шмидта.
Зафиксируем число N, столь большое, что
S \Auif<s.
i>N
Пусть Pfj — проектор на подпространство, натянутое на
векторы «1, ..., «jv- Тогда предыдущее неравенство можно
записать так:
^\(А-АР!,)щГ= Z \АщГ<е.
i-\ i>N
Ясно, ЧТО ДЛЯ любого оператора Т мы имеем ITI^XlT'w^F-
Это показывает, что А можно равномерно аппроксимировать
конечномерными операторами, и, следовательно, оператор А
компактен.
HS4. 1\А + ВЦ-\\АЩ-\\В\Г, = 2Яе{А, В).
Это поляризационное тождество немедленно вытекает из
того, что
{{А + В)щ, {A + B)ui) = {Aui, Aui)-\-2Re{Aui, Вщ)-\-{Вщ, Вщ).
Так как || А Цг = || А* Цг, получаем
HS 5. Re 2 {Aui, Вщ) = Re S (^Ч, В\).
HS6. {А, В) = {А*, ВУ
HS7. (ХЛ, В) = (ЛГ5) и {АХ, В) = (А, ВГ).
Утверждения HS 5 и HS 6 немедленно следуют из HS 4.
Первая из формул HS 7 очевидна; для доказательства второй
формулы заметим, что
{АХ, В) = {Х*А*, В') = {А\ ХВ^ = {А, ВХУ
Ядерные операторы
Оператор А называется ядерным, если его можно
представить в виде произведения двух операторов Гильберта — Шмидта.
Чтобы избежать появления сопряженных операторов в
следующих ниже формулах, мы будем записывать это разложение
оператора А в виде А = В'С, где В, С — операторы Гильберта-
Шмидта. Если А — ядерный оператор, то его след определяется
формулой
tvA = Z{Aui, щ) = ^{Сщ, Вщ) = {С, В).

172 VIL Следы
Первое из этих равенств показывает, что след не зависит от
выбора операторов В а С. Справедливо очевидное неравенство
TR1. ИгЛ|<||В||2||С|Ь. .
TR 2. Если оператор А ядерный, то операторы ХЛ и АХ
тоже ядерные и при этом
tr АХ = tr ХА.
В самом деле, ядерность операторов АХ и ХА вытекает из
HS 2; далее,
trAX = trB*CX = {CX, В) = {С, ВХ') =
= tr {ВХУ С = tr ХВ'С = tr ХА.
Вернемся к полярному разложению
A^U^P^^UP,
где и — частичная изометрия, а. Р — положительный оператор.
Оператор Р мы будем называть абсолютной величиной Л;
иногда его обозначают P = AbsA. Так как P^U*A, то мы
получаем следующее утверждение:
TR 8. Оператор А ядерный в том и только в том случае,
когда оператор Р^ ядерный, и при этом
tr Ра = tr Ра*.
Последнее тождество вытекает из того, что
tr Ра = tr и*А = tr AU* = tr UA* = tr Pa*.
Вообще говоря, неверно, что оператор А ядерный тогда и
только тогда, когда сходится ряд
SI {Au{, щ) |.
С другой стороны, имеет место такое утверждение:
TR 4. Пусть Р — симметричный положительный оператор.
Тогда Р ядерный в том и только в том случае, когда сходится
ряд Yj{Pui, Ui).
Для доказательства достаточно воспользоваться
существованием оператора Р . В частности, оператор А ядерный тогда
и только тогда, когда его абсолютное значение ядерно.
Если А — ядерный оператор, положим
M||, = tr/>^ = |l/>v.|.

приложение. Общие сведения о следах операторов 173
TR б. Ядерные операторы образуют линейное пространство]
функция Л ь-^ IIЛ 111 есть симметричная норма на stom
пространстве {т. е. такая, что IIЛ ||i ==|| Л^Ц])').
Доказательство. Пусть P^+g = (У* (Л + В), где U — частичная
изометрия. Предположим, что оба оператора Л и В ядерны.
Их сумма есть ядерный оператор в том и только том случае,
когда
Однако эта сумма равна
ZiU'Aui, Ui) + Z{U*Bui, щ) =
= 1г^/*Л + 1гС/*В<||Л||, + ||В||,.
Тем самым доказано, что ядерные операторы образуют
линейное пространство и что || • ||i — норма на этом пространстве
(однородность функции II • 111 очевидна). Наконец,
симметричность нормы доказана в утверждении TR 3.
TR 6. Если оператор А ядерный, то операторы ХА и АХ
тоже ядерные и справедливы неравенства
||ХЛ||,<|Х|||Л||„ ||ЛХ||,<|Х|||Л||,.
Доказательство. Достаточно рассмотреть оператор ХА, так
как ЛХ = (Х'Л*)'. Существует такая частичная изометрия V,
что /'^^1 = У*ХЛ. Положим A = UPa, получим
P^^ = V*XA = V*XUPa = YPa, где Y = V*XU.
Ясно, что I F КI XI. Далее,
\\XA\^Z{YP,u„ щ) = {Р'1^, Р'1Г)<
< II р''а 1II p'kY* I < II р'к 11 у I < II л II, 1XI,
что и требовалось доказать.
TR 7. Если оператор А ядерный, то НгЛ КЦЛЦ].
Доказательство. Пусть A^^^UP^. Тогда
|1гЛ| = |Е№., p'!^u\)\ = \{pl p''iu*)\<
^\\pn,mu'i<\\pn,=irPA.
Теорема 7. Пусть {Г„} — последовательность операторов
в пространстве Н, слабо сходящаяся к оператору Т. Другими
') Пространство ядерных операторов обычно обозначается &. — Прим.
перев.

174 VII. Следы
словами, для любых векторов V, w^H пусть (Г„о, w)-*(Jv,w).
Пусть А — ядерный оператор. Тогда
tr ТА = Ит tr ТпА.
П->оо
Доказательство. Предположим сначала, что А =
Р—симметричный положительный оператор. Так как А компактен (это
следует из HS 3, поскольку Л —оператор Гильберта —Шмидта),
существует ортоиормированный базис {щ} в пространстве Я,
состоящий из собственных векторов оператора А, Aut^^^CiUi.
При заданных векторах v,w^H множество {(Т„о, ау»
ограничено. Зафиксируем вектор о и будем рассматривать вектор w
как переменный; из теоремы о равномерной ограниченности
вытекает, что множество {Г„о} ограничено. Отсюда, снова по
теореме о равномерной ограниченности, следует, что нормы |Г„|
ограничены. Теперь из ядерности оператора А, т. е. из того, что
i
МЫ получаем
lim tr Г„Л = lim £ (Jn^i, щ) =
n->oo П-*оа i
= lim 2 С{ {TnUi, щ) = Yj lim Ci {Т^Щ, щ) = tr ТА,
n-*oo I i n-*oa
И наше утверждение в рассматриваемом частном случае
доказано. Перейдем к общему случаю; пусть А = UP — полярное
разложение оператора А, (У —частичная изометрия, Р —
положительный оператор. Тогда TA^TUP и последовательность
{TJJ) слабо сходится к TU; таким образом, дело свелось к
разобранному выше частному случаю.
Следствие. Пусть А — ядерный оператор в гильбертовом
пространстве Hi. Пусть Т: Hi-*Н2 —топологический линейный
изоморфизм между пространством Hi и другим гильбертовым
пространством Яг. Тогда trTAT~^=irA.
Доказательство. Пусть {ui} — ортоиормированный базис
в пространстве Я], /*„ —проектор на подпространство,
порожденное векторами щ, ..., ы„. Тогда
tr Л = lim tr РпЛРп, tr ТАТ'^ = lim tr TP^APJ~\
Поскольку наше утверждение справедливо для конечномерных
пространств, предельным переходом оно переносится на общий
случай.
Это следствие показывает, что след не зависит от выбора
скалярного произведения в заданном классе эквивалентности,

приложение. Общие сведения о следах операторов 175
Т. е. среди скалярных произведений, определяющих
эквивалентные нормы.
Замечание. Обозначим символом ®°° банахово пространство
компактных операторов. Легко показать, что отображение
®1Х(5~^С: {А, К)^-^\гАК
индуцирует сохраняющий норму изоморфизм пространства <3'
на сопряженное пространство к ®°°. Мы не будем пользоваться
этим фактом в настоящей книге и предоставляем его
доказательство в качестве упражнения.

VIII. ФОРМУЛА ПЛАНШЕРЕЛЯ
в этой главе все факты о следах представлений, с которыми
мы познакомились выше, будут собраны вместе н использованы
для доказательства формулы Планшереля, дающей разложение
произвольной функции на группе по характерам.
Доказательство, которое будет приведено, принадлежит Хариш-Чандре [6].
Сначала мы разложим в ряд Фурье функцию H^a|3, пользуясь
соотношением между следами представлений дискретной серии
и преобразованием Хариш-Чандры на А, которое было
получено в теореме 6 предыдущей главы. Чтобы вывести
окончательную формулу, нужно сделать преобразование Фурье
некоторых членов. Оказывается, что функция Н^г|з не является
непрерывной: она терпит разрыв в тех точках подгруппы К,
которые принадлежат также и подгруппе А, т. е. в точках ±1.
Первая аналитическая лемма служит для определения скачков
функции Н^ф в этих точках; эта лемма показывает также,
что производная (Н^г|з)' непрерывна в рассматриваемых точках
и что ряд Фурье для производной в этих точках сходится.
Это позволяет представить значение a|3(l) в виде ряда,
содержащего следы представлений основной и дискретной серий.
Л. Пуканский [1] доказал формулу Планшереля для
универсальной накрывающей группы SL2(R). По поводу р-адиче-
ского случая см. книгу Гельфаида, Граева и др. [1] и статью
Салли и Шалика [2]. По поводу связей с теорией специальных
функций см. Виленкин [1].
В статье Баргманна [1] приведены различные соотношения
полноты, однако явная формула Планшереля там не выписана.
Баргманн осознавал связь этих вопросов с некоторыми
асимптотическими разложениями (ср. § 5 гл. V). Сама мера
Планшереля просто выражается через функцию c{s), которая
возникает в этих разложениях. Связь между разложением по
собственным функциям и асимптотическим разложением была
известна уже давно в связи с теорией линейных
дифференциальных уравнений второго порядка. Намеченный в статье
Баргманна вывод формулы Планшереля для группы SL^i^,
следующий общей схеме построения разложений по собственным
функциям для дифференциальных операторов второго порядка,
приведен в книге Виленкина [1, стр. 335—340]. Однако
Виленкин не проводит подробно всех вычислений, а просто

§ 1. Аналитическая лемма 177
отсылает читателя к монографиям Б. М. Левитана и Э. Титч-
марша и ограничивается такими словами: „Применяя обычную
технику разложения по собственным функциям
самосопряженных операторов, получаем следующий результат" (формулу
Планшереля). Неискушенному читателю приходится
самостоятельно восстанавливать детали.
Первоначальное доказательство Хариш-Чандры основано на
совершенно ином подходе, однако в своих недавних работах
он возвратился к методам, основанным на изучении
асимптотики. Оценки, необходимые для доказательства формулы
Планшереля для произвольных групп, довольно сложны. См. по
этому поводу статьи Хариш-Чандры [7, стр. 576, 682] и
[3, стр. 71] ')• По поводу связи этих оценок с другими
вопросами см. также статью Кнаппа и Стейна [1].
Подход, связанный с изучением асимптотики собственных
функций, мы используем в последней главе для построения
спектрального разложения пространства L^(T\G). Идея этого
метода состоит в том, чтобы сравнить асимптотику точных
собственных функций с асимптотикой собственных функций
простой модельной задачи. Для получения теоремы разложения
используется теория возмущений.
§ 1. Аналитическая лемма
Лемма. Пусть FeCr(R^). Положим
g (0) = J F {QeK Qe-') (e' - e-^) dt.
0
Тогда
(i) lim Qg{Q)=\F{u, 0)du;
0
(ii) lim eg (9) = - [ F{u, 0)aY
9->-0 J
— oo
(iii) lim-^(eg(e)) = -2F(0, 0).
9-*0 "°
(iv) Существуют такие постоянные a, b > О, что при всех В,
О < 0 ^1, справедливо неравенство
d
М
(0gr(e)) + 2/='(o, 0) <a|ei + *ieiog0!.
') Формула Планшереля для произвольных вещественных редуктивных
групп Лн доказана в работах Хариш-Чандры [9], [10], [11]. Краткое
изложение этих результатов содержится в его лекциях [8]. (См. также
приложение 2 к книге Хариш-Чандры [\].) — Прим. перев.

178 VIU. Формула Планшереля
Доказательство. Заметим сначала, что
оо
(1) 0 J f (9е', ее-Ое-'Л-^О при в-*"0.
о
Чтобы доказать (i), рассмотрим интеграл
оо
5 QF{Qe\ Qe-*)e*dt
о
при 0 > 0. Сделаем замену переменной, положив ы=«6е*; тогда
du = Qe*dt, e~* = Q/u и интеграл принимает вид
9
При 0-»-О этот интеграл стремится к нужному пределу,
указанному в (i). Утверждение (ii) доказывается аналогично. Чтобы
доказать (iii), заметим, что
^(eg(e))=er(0) + 0gr'(0) =
оо оо
= 5 F{Qe^ Qe-')e4t-\ F{Qe', Qe-*)e-*dt +
о о
оо
+ 0 J [D^FiQeK Qe-')e' + D2F{Qe*, &е-^)е-*]{е^-e-*)dh
о
При 0-^0 второй интеграл стремится к — ^'(0,0). Любой
интеграл, имеющий множитель 0 снаружи и не содержащий
множителя е^ внутри, стремится к нулю при 0-»-О. Поэтому
достаточно рассмотреть интегралы, не принадлежащие к этим двум
типам. Имеем
-~[e'F{ee\ 0e-O]=-e'i?(0e', Qe-') +
+ Qe'^'DiFiQe*, 0e-') - QD2F [QeK ве-').
Подставим это выражение в наши интегралы; после всех
сокращений оставшиеся интегралы дают нужный вклад, равный —F{0, 0).
Чтобы получить оценку производной, приведенную в (iv), выберем
такое число Т, что D2F{х, у) = О, если \х.\'^Т или \у\'^Т.
Если I 0еЧ < Т, то е' < Г/1 0 |, т. е. ^ < log (Г/| 0 |). Таким образом,
мы получаем оценку вида
\ D,f{<de\ Qe-')dt
< IIА^ III log Г/1 01

§ 2. Скачки преобразования Харши-Чандры 179
И аналогичную оценку для интеграла от производной О^Р.
Теперь утверждение (iv) очевидно.
Оценка (iv) понадобится нам для доказательства сходимости
некоторого ряда Фурье.
Замечание. При вычислении различных пределов, которые
мы рассматривали в лемме, можно заменить 0 на sinG, поскольку
эти функции совпадают с точностью до величин 3-го порядка
малости, не влияющих на наши пределы.
§ 2. Скачки преобразования Хариш-Чандры
Запишем элемент x&SLziK) в виде
X = ank = hitiuk^,
где мы пользуемся параметризацией
/е' О \ /^1 «^ ( COS0 sin0\
^-^^-\0 e-'j' " = "« = U ij' *« = l-sin0 cosej-
Меру Xaapa на G нормируем так, что
dx = da dn dk = dt du -к—
таким образом, мера подгруппы К равна 1. Положим
£)jf(0) = e'9_g-.-9==,2isin9
и определим, как и выше, преобразование Хариш-Чандры на К
функции f^CT{G, К) формулой
(1) (H'^f) {ke) = (H'^f) (0) = Dk (0) 5 / (ЛГ'ЫО ^-=f^ dt,
0
С точностью до постоянного множителя это выражение
совпадает с интегралом
Ок{к) 5 f{g-'kg)dg.
Придадим выражению для преобразования Хариш-Чандры на К
несколько иную форму, которая позволит воспользоваться
доказанной выше леммой. Для этого представим элемент a~^ka
в виде экспоненты:
hT'keht = /гГ' exp{QW)ht = ехр(/гГ'0ГЛО

180 VIII. Формула Плашиереля
И заметим, что
Сделаем замену переменной 2/ь-^^. Пределы интегрирования
при этом не меняются, и мы получаем
оо
(2) (H^f) (0) = 1Dj,(0) \ FW, Qe-*){e*-e~^)dt,
где
F(«,.)^/(exp(_'^ о))
Очевидно, F(0, 0)=f(l), 1 = Iq.
С другой стороны, мы определили преобразование Хариш-
Чандры на А:
(Н^/) (а) = I D (а) I J I (л:-1 ал) rfi = р (а) J f {an) dn.
A\a N
Нам были нужны значения функции Н"*/ только на подгруппе А.
Однако можно рассмотреть ее значения также и на
множестве — А. При любом а е Л имеем
{l\^f){-a) = 9{a)\t{-an)dn.
N
Теорема 1. Пусть f s СГ (G, К). Тогда
H«f \tl =■ (H^f) (+0) - (H^f) (- 0) = {(H^f) (1),
H^/i:;!^=(H^/)(n + 0)-(H^f)(n-0) = i(H^f)(-l).
wnuW~^ = n~u> получаем
Доказательство. Пользуясь леммой из § 1 и соотношением
получаем
(H-m+o)=i[/((J ;)).«
,„.„(-0)—i S,((; ;)).„.

§ 2. Скачки преобразования Хариш-Чандры 181
Следовательно,
оо
(H^/)(+o)-(H^f)(-o) = i \f(J^^ О)'^"'"
N
Для доказательства второго утверждения заменим функцию f
функцией x^-^f{—x) и заметим, что f{—-x)'=f{xk^).
Точки 0 = 0 и 0 = л —точки разрыва преобразования
Хариш-Чандры на К; предыдущая теорема дает выражение для
скачков в этих точках через преобразование Хариш-Чандры
на А.
Из нашей аналитической леммы мы знаем, что производная
преобразования Хариш-Чандры (H^fY {Q) непрерывна в нуле.
Теорема 2. Для любой функции f ^С^ (G) справедливо
соотношение
(H^fr(0) = -i7(i).
Доказательство. Это немедленно следует из утверждения (iii)
леммы предыдущего параграфа.
Теорема 3. Ряд Фурье функции (Н^/)' сходится к ее
значению в нуле.
Доказательство. Из утверждения (Iv) нашей леммы мы знаем,,
что
(HKfY (0) =^ const + О (I 0 log 10 11).
Ядро Дирихле, свертка с которым дает частную сумму ряда
Фурье, с точностью до постоянного множителя равно
sin
{п + Гу
2пп . е
sm-g-
Сходимость ряда Фурье зависит только от поведения функции
в окрестности заданной точки; для сходимости достаточно,
чтобы интеграл
sin (п + -^)&
)g|e|—^ е ^9
sin-g-
±Je,o,

182 VIII. Формула Планшереля
стремился к нулю при е-^О. Но этот интеграл не превосходит
JiogieirfG
<8|l0g6|,
И наша теорема доказана.
§ 3. Некоторые леммы
Чтобы не прерывать затем доказательство формулы
Планшереля, мы собрали в этом параграфе некоторые простые леммы.
Первая из них сводится к суммированию геометрической
прогрессии.
Лемма 1. Справедливы следующие соотношениях
Z- /• р I л\ -\пм 2 sin 6 ch ^
sin(|«|0)e-i»M=-^-^^___,
п. ■" 1 (mod 2)
Y, sin(|n|0)e-l'»l' =
sin 26
ch 2^ —cos 26 ■
n i> 0 (mod 2)
Суммы берутся no всем нечетным и четным целым числам, как
положительным, так и отрицательным.
Доказательство. Пусть п нечетно и положительно, n==2d+ 1.
Имеем
ОО ОО
Epi (2d+l) 9p-(2d+l) t __ plu-t V p2d ('6-0 = !
^ ^ ^ Zj g-«e-0 _ e(«e-0 •
d-0 d-O
Умножив числитель и знаменатель на комплексно сопряженное
к знаменателю число, получим для нашей суммы следующее
выражение;
е'+ге _ g-{.t+m _ gt ^(.Qg g ^ ■ з,-д e) - e~' (cos6 - / sin 6)
2 (ch 2t — cos 26) 2 (ch 2< - cos 26)
Мнимая часть числителя равна e'sinG+ 6"'sin0 = 2ch^sin0, и
тем самым наше первое равенство доказано.
Для доказательства второго заметим, что
1 4- 9 > /.2<de„-2 di _- 1 I ^^ .£ ^ ^

§ 3. Некоторые леммы
183
Умножим снова числитель и знаменатель этой дроби на
комплексно сопряженное к знаменателю; это даст для правой части
выражение
в2' + е"в-
,2«e _ ^-219 _ -2t
е "~ — е
sh 2t + (• sin 26
2(ch2<-co3 2e)
ch2< —соз2е •
Отсюда получится наше второе соотношение, если рассмотреть
мнимые части.
Теперь нам придется вычислить преобразование Фурье
некоторых функций.
-С + /С
c + te
Лемма 2. При любых 9 из промежутка О < 9 < л ы при всех
%>0
lim
jxt
sh
ch 2t — cos 26
Л =
(t-0
sin 26
sh
пК
Доказательство. Вычислим интеграл по контуру, изображен*
ному на рис. 1. Интеграл
f
dz
2nl д ch2z —cos2e
равен сумме вычетов подынтегрального выражения. Имеем
ch 2г >-= cos 29 4ф2 = {яп ± 0) /.
Кроме того,
d
de
Значение этого выражения в точках 2„ = (лп±9)^ равно
sfc2isin2e. Следовательно, вычет подынтегральной функции
в точке 2„ равен
в
-\ (ЯП ±9)
2tsln(±26)

-Д.9 J-e„~\n
a с
184 VIIl. Формула Планшереля
Поэтому предел нашего интеграла при с-»-оо равен
^"'' Г V р-^ (яп+9) _ у р-Д. (яп-9) "1 _
2/sin2e i Zj Zj '^ }■
^ я г 8-^Q
"^ sin 26 L 1 - e""''" 1 - e"''" J *
Умножение числителя и знаменателя на е^'^ завершает
доказательство.
Разумеется, при вычислении предела мы выбираем с так,
чтобы полюс подынтегральной функции не попал на контур
интегрирования.
Лемма 3. При любых 6 из промежутка О < 0 < л и при всех
lim \ ..1 "'\.dt =
ch 2t — cos 26 2 sin e , nX
с ch-g-
Доказательство. Рассмотрим интеграл
1 с e'^^chz .
2iti Т ch2z-cos26 "^
no тому же контуру, что и раньше. Вычет подынтегральной
функции в точке 2„ = (я;п±9)/ равен
g-^'"''^S)ch(nn±6)t- _ .„ cos6e-^<"'»±9'
2(sin(±26) ^ '' 2/ sin (± 26)
Наше преобразование Фурье равно сумме вычетов, т. е.
2то
4/ sin в
^- п-О ifl -'
2 sin е L 1 + е"'-" 1 + е-^" J 2 sin 6 " „^ i^
°" 2
ЧТО и требовалось доказать.
Приведенные выше леммы будут применяться для
доказательства формулы Планшереля в следующей ситуации. Пусть
Ф^СГ(Н), и пусть g —одна из двух функций, преобразования
Фурье которых вычислены в леммах 2 и 3; таким образом,
в частности, функция g вещественна. Обозначим gc функцию,
равную нулю вне интервала [— с, с] и совпадающую с g на
этом интервале. Тогда преобразование Фурье функции g^ по

§ 4. Формула Планшереля 185
существу, вычислено в предыдущих леммах и равно частной
сумме вычетов с точностью до слагаемого, стремящегося к нулю
при с-^оо. Так как носитель функции ф компактен, мы
получаем
\ Ф^= \ Ф^.= \ ^йс-
Из лемм 2 и 3 ясно, что при с-^оо функция ^^ стремится к
непрерывной ограниченной функции переменной К. Мы получаем
формулу Планшереля
5 Ф^== \^й
§ 4. Формула Планшереля
Объединим полученные нами результаты. Напомним, что^
по определению,
Пусть S = iK, где К — вещественное число. Представление л^
в пространстве Я (Л) —это представление основной серии; как
мы видели, при %Ф Q оно распадается в прямую сумму двух
неприводимых представлений, в соответствии с четностью
функций. По формуле (1) § 3 гл. VII, след этих представлений дается
такими выражениями:
оо
(1) Tt{t)== \ {HY)ilii)e"-'dt,
— ОО
оо
(2) ГГ(Г)= \ {HY)ilit)e^'-'dt.
— ОО
Можно рассматривать их как преобразование Фурье функции
при о < 9 < л для любой функции f^CT{G) справедливы
разложения Фурье
2Я
п о

186 VIIl. Формула Планшереля
Найдем разность этих выражений:
т) (в)=Y KH'^f) (9) - (H'^f) (- 6)].
Теорема 4. Пусть S„ — функция, определенная в теореме 6
§ 5 гл. VII. Тогда для любой функции f ^Cf (G, К) при О < 9 < л
справедливо соотношение
-у-(/^/)(е) = - j;s„(f)sinui0 +
+ т\ Ttif) ^\/ dK + ^\ nif) ^' / dK.
т i ^J^^
Доказательство. При вычитании приведенных выше рядов
Фурье постоянные члены сокращаются, и мы получаем
2Я
(3) Щ- {Щ) (9) = - X sin пб \ (H^f) (ф) e^'^^^ ^ф.
Подставляя в эту формулу значение, найденное в последней
теореме предыдущей главы (теорема 6 § 5 гл. Vlf), получаем
(4) ^(/'^f)(e) = - j; S„(f)sin|n|9 +
оо
n^iO О
Разобьем последнюю сумму на две, по четным и нечетным п
соответственно. В силу леммы 1 § 3 эта сумма равна
О о
Воспользуемся тем, что функция H^f имеет компактный
носитель, и формулой Планшереля для обычного преобразования
Фурье, которую мы обсуждали в конце предыдущего параграфа.
Наше выражение примет вид
0 2 0 2
A
-dK.

§ 4. Формула Планшереля J87
Заметим, что функции, преобразование Фурье которых мы
вычисляем, четны по переменной /; поэтому интеграл по всей оси
можно заменить удвоенным интегралом от О до оо. Тем самым
мы получаем требуемое разложение, и теорема доказана.
Формула Планшереля. Пусть f ^ СТ (G). Тогда
2я/(1)= j;|n|S„(/) +
оо оо
о о
Доказательство. Продифференцируем выражение, полученное
в теореме 4, и положим 0 = 0.
Замечание. Как мы знаем, характеры Т^ связаны с
унитарными представлениями. В следующей главе мы покажем, что
характеры S„ тоже связаны с унитарными представлениями.
Таким образом, в формулу Планшереля входят только
унитарные представления. Для наших предыдущих рассуждений это
было несущественно,' но в дальнейших построениях мы этим
воспользуемся.
Обозначим символом G множество классов эквивалентности
неприводимых унитарных представлений группы G. Определим
на множестве G меру \х следующим образом.
На множестве дискретных серий пусть эта мера дискретна;
|т|-1
точке веса т припишем меру -—д .
На множестве четных представлений основной серии,
параметризованных числом S = iX, Я > О, положим
dii{K) = ^-^ih^dK.
На множестве нечетных представлений основной серии
положим
di.il) =^-^cihf-dl.
Меру дополнения к перечисленным множествам положим равной
нулю.
Меру [X мы будем называть мерой Планшереля. Вместо того
чтобы использовать параметры п и X, мы будем писать d\i (я),
jtsG, рассматривая множество Q как пространство с мерой.
На произведении GXG зададим операторнозначное
отображение
Ф (л, х) = я {х).

188 ^Ш- Формула Планшереля
Соответствующее отобр ажение на функциях f ^СТ (G) действует
по правилу
Ф: (я, f) t-» f (л) = W (л) л (л;) ^л: = л'(/).
С другой стороны, пусть (Л (л)} — семейство операторов, причем
оператор Л (л) действует в пространстве Н„. Определим
(формально) сопряженный оператор Ф*, положив
(ФМ) (х) = J hA (л) л (х)* d\i (л).
Как мы сейчас увидим, из формулы Планшереля вытекает
формула обращения
Ф*Ф = 1с1 на CTiG).
Формулу Планшереля можно записать следующим образом:
PL1. f{l) = ^trn'{f)dii{ny,
а
она справедлива для любых функций f ^СТ(G) или f&CT(G, К).
В самом деле, если / е СГ (G), то положим
fj^{x)=\^f{k~^xk)dk.
•Обе части формулы PL 1 не изменятся, если / заменить на fj^.
Пусть r{x)f — правый сдвиг функции /, т. е.
r{x)fiy) = fiyx).
Заменяя / на r{x)f в формуле PL 1 и замечая, что
лЧг(.г)П = л1(/)л(л:-'),
мы получаем формулу обращения в произвольной точке:
PL 2. / W = 5 tr л' (/) л (х)* d\i (л).
Далее, пусть ф, ij)eCr(G) и ф*(л:) = ф(л;-'). Применим
формулу PL 1 к функции /==ф*г|з*. Тогда
я1(/) = л'(ф)я'(ФГ,
(ф * г|з*) (1) = (ф, 1|))о == J ф (х) Щх) dx,
а
tr л' (ф * 1|5*) = tr n^ (ф) л' (г|з)* = (л' (ф), л' (\|))) = (ф, ^).

§ 4. Формула Планшереля 189
Таким образом, мы получаем следующее соотношение полноты:
PL 3. (ф, г|з)а = J tr я' (ф) п' (г|з)* d[x (я) = (ф, ф>
5
для любых функций ф, г|з е СГ (G).
Итак, различные варианты формулы Планшереля выводятся
из формулы PL 1 при помощи простых формальных рассуждений.
В предыдущих формулах мы часто вычисляли след
произведения операторов. Пусть {щ} — ортонормированный базис
пространства Н. Если А, В —операторы в пространстве Н, то
положим Aii = {Aui,Uf). Тогда, как и в конечномерном случае,
tr ЛВ == 2] ЛцВц. В самом деле, ряд
Вщ = 2 ВцН/
сходится в Н; таким образом,
(ABUi, щ) = Yj (ABifUf, щ)
I
и
trAB^'ZBiiA.i.
1,1
На практике такие разложения иногда нужны для оценки
некоторых следов; в этих случаях базис {щ} состоит из ТС-конеч-
ных векторов.

IX. ПРЕДСТАВЛЕНИЯ ДИСКРЕТНОЙ СЕРИИ
в этой главе мы приводим различные реализации унитарных
представлений дискретной серии, т. е. неприводимых
представлений, содержащих старший вектор веса ^ — 2 или младший
вектор веса ^2. Оказывается, что представления одного из этих
типов комплексно сопряжены представлениям второго типа,
поэтому достаточно рассматривать только представления с
вектором младшего веса. Мы увидим, что эти представления
допускают инфинитезимальное вложение в пространство L^iG),
в котором группа действует левыми сдвигами, и что они могут
быть реализованы в некоторых пространствах функций на
верхней полуплоскости.
Теорема единственности из § 3 гл. VI показывает, что уни-
таризация этих представлений определена однозначно, и
позволяет установить унитарн)по эквивалентность их различных
реализаций.
§ 1. Вложение представлений дискретной серии в 1^(6)
Основной результат этого параграфа принадлежит Хариш-
Чандре.
Положим
Пусть
Сделаем замену переменных, перейдя к рассмотрению
матричных элементов матрицы ТхТ~\ а именно положим
<" М-\ -"Ж :)w(; 'i)=(; D-
(Мы выбираем параметры а, р так, чтобы в дальнейших
формулах было как можно меньше черточек.) Тогда
(2) a = ^(a + d-ic + ib), ^=^~{с + b ~ ia +id).

§ 1. Вложение представлений дискретной серии в L^(G) 191
Заметим, что а и р—функции на группе, поэтому мы можем
писать а(д:), Р(д:). Для элементов подгрупп А и К эти функции
легко вычисляются;
Кроме того, эти функции просто преобразуются при действии
подгруппы К справа и слева. Заметим, что сопряжение
элементов подгруппы К при помощи матрицы Т дает
_, / cose sme\ _, /е'9 о \
Отсюда ясно, что
(5) а (к^х) = е^^а (х), а (xk^) = а (х) е'^,
(6) р(М) = е-'9р(х), р(д;йе) = Р(А:)е«.
Из разложения Картана Gr=KA'^K видно, что значения
функций аир полностью определяются приведенн-ыми выше
формулами; в частности, их абсолютные величины равны
соответственно ch^ и sh^, если матрица х сопряжена матрице hf.
Заметим, что | а (д:) | ^ 1 при всех д; s G.
Лемма 1. Пусть т—целое, /и^2. Тогда функция а~'"
принадлежит L^{G).
Доказательство. Из интегральной формулы ШТ 2 мы знаем,
что с точностью до постоянного множителя
оо
5 I а Г"" dx = 5 (ch /)~"" sh 24 dt.
а о
Так как sh2t'={e* + е~*){е'— е-*)/2, последний интеграл равен
оо
2 \ u-zm+i du.
1
Этот интеграл сходится при /и^2, что и требовалось доказать.
Пусть я — левое регулярное представление группы G ъ L? (G),
т в
n{y)f{x)^t{y-^x).

192 IX. Представления дискретной серии
Для краткости будем писать fy вместо n{y)f. Тогда
(7) ^, = а(у-)а + Р(у-)Р,
(8) ^ = P(i/-')a + a(i/-')p.
Теорема 1. Положим Фт+2г = "~'"~'^P^ г = 0, 1, 2, ... . Тогда
функции <fm+2r — собстввнные векторы подгруппы К с
собственными значениями ^^("+2^)8 Порожденное ими замкнутое
подпространство в L? (G) инвариантно относительно левых сдвигов из G,
неприводимо и содержит вектор младшего веса, равный а"".
Доказательство. Из формул (5) и (6), т. е., по существу,
непосредственно из определения функций а, р, ясно, что (fm+2r ~
весовые векторы подгруппы К. Заметим, что IР (г/)/а («/) I < 1 для
любого y^G. Функция п(г/~')фп,+2г принадлежит линейному
пространству, порожденному функциями
К "^ а{у) а )
Пусть Х = Р(у)Р/а(г/)а; тогда | Я, К | р (t/)/a (у) |< 1. Функцию
Q-m (1 _|_ Х)"'""'" можно разложить в ряд по степеням X; в силу
леммы 1 этот ряд сходится в ^-^(0). Это показывает, что
замкнутое подпространство, порожденное нашими функциями,
инвариантно относительно сдвигов; тем самым доказательство
теоремы закончено.
§ 2. Представления на верхней полуплоскости
Опишем здесь другую модель унитарных представлений
дискретной серии. Мы реализуем их в некотором пространстве
функций на верхней полуплоскости.
Пусть т —целое число, /и ^2. Напомним, что инвариантная
мера на верхней полуплоскости ф равна
dn {х, у)
Положим
dx dy
i72
#.= t/'"^
Пусть
^ = ^Li(§. О

§ 2. Представления на верхней полуплоскости 193
— пространство голоморфных функций на §, квадратично
интегрируемых по мере Цп,. Скалярное произведение в Я —
обычное эрмитово скалярное произведение, задаваемое интегралом
по ф. Следующая лемма показывает, что пространство Н полно.
Лемма 1. Если последовательность голоморфных функций {/„}
сходится в топологии L^ на открытом подмножестве
комплексной плоскости, то она равномерно сходится к голоморфной
функции на любом его компактном подмножестве. Более того, для
любого компакта К справедлива оценка
Доказательство. Достаточно доказать лемму в окрестности
некоторой точки; без ограничения общности можно считать ее
началом координат. Наши оценки зависят от выбора круга
фиксированного радиуса б с центром в произвольной точке;
достаточно опять-таки оценить |f(0)| через L'- и L^-нормы
функции f в круге радиуса б с центром в точке 0. Из формулы
Коши следует, что
2л
откуда
Так как
19
2л
fm\<-^\\f(re^^\dQ.
о
l/(0)l-^ = Slf(0)|rdr,
б 2л
l/(0)l-y<i5^S \mre^')\rdrdQ:
о о
= i-11^11., .oc<2!rll^'l..locimi2, (ОС
(последнее неравенство следует из неравенства Шварца). Итак,
лемма доказана.
Пусть
a-i=(^ ^)eG = SL2(R).
7 За к. 589

194 IX. Представления дискретной серии
Определим оператор л„ в пространстве Н формулой
(n„(a)f)(z) = f(a-z)(cz + d)-'".
Непосредственно проверяется, что п„ — гомоморфизм группы G
в группу линейных автоморфизмов пространства Н.
Теорема 2. п^ есть унитарное представление.
Доказательство. Проверим сначала унитарность. Пусть w =
= a~^z. Напомним, что
поэтому
оо оо
dy
N„(a)f||^=5 5 \fia-^z)f\c2 + dr'"y'"^
О —оо
оо оо
5 5 1/(ш)Р(1тшГ^ц(ш)=||/||,
о —оо
что и требовалось показать.
Условие непрерывности представления достаточно проверить
на плотном множестве элементов гильбертова пространства.
Наше представление действует в подпространстве пространства
L^(§, Цп,), поэтому достаточно проверить непрерывность
представления в этом большем пространстве. Возьмем
произвольный вектор /, принадлежаш,ий пространству С<,(Ф), и
проверим, что
1|я(а)/-/|Ь->0
при а->1. Это немедленно вытекает из теоремы об
ограниченной сходимости.
Лемма 2. Пусть п — целое неотрицательное число; положим
Тогда i|)„ е Я.
Доказательство. При | z | -> оо функция t)3„ (z) стремится к 0;
для всех Z из верхней полуплоскости справедливо неравенство
Z — i
z + i
<1.
Пусть б > 0. Для доказательства леммы мы покажем, что
сходятся интегралы по полуплоскости Im z>6 и по полосе 0<Imz<6.

g 2. Представления на верхней полуплоскости 196
Для первого интеграла имеем оценку
б —оо б —оо '
оо оо
б —оо
„т-2
Г f 1 у
б
оо оо
^\ \ (,2+1).+в „л. ^«^i/-.
интеграл в правой части сходится. Второй интеграл
оценивается так:
О -00 ' О -00 ^ ' О
Последний интеграл сходится, если m > 1. Лемма доказана.
Теорема 3. Представление п^ в пространстве ff =' ^loi{^, 1^^)
неприводимо. Пусть Нт+2п — одномерное подпространство,
порожденное функцией ij)„. Тогда Я„+2„ — собственное
подпространство подгруппы К с весом т-\-2п и
Я= ф Пт+2п
— ортогональное разложение; i|)o — вектор младшего веса т.
Доказательство теоремы 3 лучше всего провести при помощи
другой модели для представления п^, которая получается, если
перейти от верхней полуплоскости к единичному кругу. Мы
сделаем это в следующем параграфе.
Теорема 3 дает нам еще один пример представления с
младшим вектором любого веса т^2. Чтобы получить
аналогичные представления с вектором старшего веса ^ — 2, достаточно
рассмотреть действие группы 5/^2 (R) на антиголоморфные
функции в нин<ней полуплоскости.
7*

19b IX. Представления дискретной серии
§ 3. Реализация представлений в единичном круга
Часто бывает удобнее работать с единичным кругом, где
упрощается выражение для функций i|)„. Положим
2 — 1
^ Z + i
Отображение z^—^w есть аналитический изоморфизм верхней
полуплоскости и единичного круга D с центром в начале
координат'). Обратное отображение задается формулой
. w + \
z = — I-
w — i '
Если f — функция на ^, то положим
Тогда Тт- S^('&)^-^(D) есть линейное отображение
пространства функций на $ в пространство функций на D. Пусть
W = и-{■ iv ^ D\ положим
dv.
= —Ц- (1 -1 ш IT —^"'"' , = —Ц- (1 - лТ"' г dr d%.
• Лемма 1. Отображение
есть изометрия.
Доказательство. Имеем dw ^ dw == — 2i du л dv, dz \dz='
= — 2г dx л dz/. Получаем
4 rfu rfo dxdy
Для доказательства изометричности отображения Г„ достаточно
проверить, что
Последнее равенство очевидно.
Теперь ясно, в чем состоит преимущество перехода к
единичному кругу:
') Это отвбражение называется преобразованием Кэли. — Прим. перев

§ 3. Реализация представлений в единичном круге 197
Таким образом, наши функции переходят в степени
независимой переменной в единичном круге; легко проверить, что эти
функции ортогональны.
Теорена 4. Функции {1, w, w^, ...} образуют полную
ортогональную систему в пространстве lXo\ (D, v^)-
Доказательство. Пусть / е Ihoi (D, v^); тогда функцию /
можн© разложить в степенной ряд
оо
Достаточно доказать, что этот ряд сходится в топологии L^ (v„).
Пусть г'—-вещественное число, 0<г'<1; обозначим
символом D;.' круг радиуса г'. Тогда
В;.' q. п D,.'
1-0 о
поскольку
О
если n=fi=q. Перейдем к пределу при л'->1. Получим
D О
^cY,\an\Чw'^i,^,
где с — некоторая постоянная. Следовательно, ряд Х'^п®"
сходится в 1?(Ут) при т> 1. Теорема доказана.
Действие группы при переходе от верхней полуплоскости
к единичному кругу изменяется следующим образом. Группа
8ЩЖ) переходит в группу матриц вида
^-* = (ё ^)' ««-Р3=1.
Обвзначим символом п^ ее представление, полученное из
представления я„ группы 5L2(R). Тогда
ft„ (а) f И = фш + аГ" f (|—^).
Vpai» + а/

198 fX- Представления дискретной серии
Пусть Я == Lhoi (D, Vm). Тогда одномерное подпространство,
порожденное функцией ш", совпадает с подпространством
Нт+2п- в самом деле,
ЭТО сразу ясно из формулы для представления п^- Поэтому
Hm+in есть весовое подпространство группы К с весом т + 2п.
Вес постоянной функции 1 равен т.
Чтобы закончить доказательство теоремы 2, осталось
проверить следующее утверждение:
Лемма 2. Элементы 1, w, w^, ... пространства Н являются
аналитическими векторами.
Доказательство полностью аналогично доказательству
сходного утверждения для представлений основной серии (лемма 2
§ 5 гл. VI) и предоставляется читателю.
Теперь для завершения доказательства теоремы 2 можно
воспользоваться результатами § 2 гл. VI, где обсуждалась
неприводимость представлений.
§ 4. Поднятие веса т
В этом параграфе показано, как установить изоморфизм
между реализациями представлений дискретной серии,
рассмотренными в § 1 и в § 2, 3, связывая функции на -g» с
функциями на G при помощи формальной процедуры поднятия.
Пусть ф — верхняя полуплоскость, т— фиксированное целое
число. Всякой функции ф на ф сопоставим функцию Ф на
группе G = GL} (R), положив
/и OWi/ х\Г cos9 sin9\ /а b\
^^\0 и)\0 iJV-sine cos9J""U d)
— наше обычное разложение элемента группы GL2 (R), и, у >0.
Построенная нами функция Ф не зависит от ы и определяет*,
таким образом, функцию на группе SL2(R), однако нам больше
нравится пользоваться координатами {х, у), которые имеют
удобную интерпретацию на верхней полуплоскости.
Функция Ф удовлетворяет следующим условиям:
^„ 1. Ф ме зависит от и.
где

§ 4. Поднятие веса т ]99
Обозначим символом ^„(G) пространство всех функций
на группе G, удовлетворяющих этим двум условиям, и пусть
^ (§) — пространство всех функций на •§>. Мы определили
поднятие
которое сопоставляет функции ф новую функцию Ф по
описанному выше правилу. Это отображение взаимно однозначно, так
как у него есть обратное, которое сопоставляет каждой
функции Ф, удовлетворяющей условиям ^т 1 и ^^ 2, функцию ф
на •£>:
Каждой матрице
сопоставим оператор Пт{о), действующий в пространстве ^(•£>),
полагая
я„ (а) ф (2) = (Y2 + бГ" ф(a-'z).
Тогда а ь-»• п^ (а) есть групповой гомоморфизм. Пусть L„ —
оператор левого сдвига на элемент а, т. е. (Ь„Ф)(^) = Ф(а-'^) для
любой функции Ф на группе G. Тогда следующая диаграмма
коммутативна:
Г(§)->^„(0)
Доказательство. Перемножая матрицы, легко проверить, что
d — ic
\d-ic\ •
(1) ue^^==d — ic, e^^ =
(2) x+iy = -e^^{ai-]-b).
Рассмотрим матрицу
"'^ = "'(о i)''(^'^ = (y« + 6c yblbd)
а
и положим

200 !Х Представления дискретнт! серии
Формулы (1) и (2), примененные к матрице a-'g, показывают,
что 9'= 9 — arg (yz + 6)- Получаем
ф (ag) = ф (a-'g/) /"«/Zeime' ==^
= ф (z') г/'"'2 I Y2 + б Г'" e«nj9g-im arg (уг+-в) =
= Ф (а-'г) (yz + б)~'"у'"/2е«'"9 ==
= л„ (а) ф (z) у'^'^е'"^ = /,; Лш-(а) /^„Ф (g),
и наше утверждение доказано.
§ Б. Голоморфность
Ясно, что при описанном выше соответствии между
функциями на ф и функциями на G гладкие функции переходят
в гладкие функции. Обсудим теперь, какое условие на
функцию Ф соответствует аналитичности ф. Как и прежде,
обозначим буквой g алгебру Ли группы SL2(R); напомним, что с
каждым элементом Х^% связана производная Ли
(8хФ)(§) = -^Ф(^ехра)|<=о.
В § 4 гл. VI мы вычислили производные Ли в координатах
{х, у, 9); в частности, мы получили формулу для производной
Ли й^-, которую мы сейчас применим к функции
Ф (g) = f {и, X, г/, 9) = ф (л; + iy) у"Ч^е^'^^,
не зависящей от и. Получим
(3) (^B-f) (^. J/. 0) = - 4гг/'"/2+>е2' ""«-D 9||. _
Итак, мы доказали следующее утверждение:
Теорема 5, Функция ф голоморфна тогда и только тогда,
когда

X. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
До сих пор мы, в основном, избегали вопросов о действии
производных Ли на функции. При построении теории
сферических функций мы рассматривали собственные векторы
операторов свертки. Теперь пришло время связать некоторые из
инвариантов, построенных нами в теории представлений, со
свойствами инвариантных дифференциальных операторов на группе.
Баргманн [1] впервые понял, что матричные элементы
представлений являются собственными функциями таких операторов.
Хариш-Чандра полностью разъяснил вопрос, описав структуру
центра алгебры инвариантных операторов и централизатора
подгруппы К в этой алгебре. Гельфанд охарактеризовал
сферические функции как собственные функции этого
централизатора. В этой главе мы докажем для случая SLzlR) теорему
Хариш-Чандры, утверждающую, что все сферические функции
исчерпываются описанными в гл. IV. Доказательства в этом
частном случае простые и короткие.
§ 1. Универсальная обертывающая алгебра
Пусть (} — алгебра Ли группы SL2 (R). Матрицы
^+ = (о oj* ^-^(1 о)' ^==(о -l)
образуют базис в д. Мы будем также использовать следующий
базис комплексификации vjc алгебры д:
Напомним коммутационные соотношения
[Я, Х+] = 2Х+, [Н, Х-] = - 2Х-, [Х+, XJi = Я,
[W, Е+] = 2iE+, [W, Е^] = - 2i£_, [Е+, Е-] = - 4iW.
С каждым элементом X е% свяжем образующую L^ и
построим универсальную ассоциативную алгебру над С,
порожденную этими образующими. Рассмотрим идеал этой алгебры,
порожденный элементами вида
i-xLy — LyLx — L[x, У],

202 X. Дифференциальные операторы
где коммутатор \Х, К] = ХУ — YX определяется при помоши
матричного умножения. Факторалгебра по этому идеалу
называется универсальной обертывающей алгеброй алгебры Ли ди
обозначается 41 (а,).
Ясно, что использование дополнительного символа L только
усложняет обозначения. С другой стороны, существует
естественный гомоморфизм алгебры ^(д) в любую ассоциативную
алгебру, образующие которой параметризуются элементами g
и удовлетворяют приведенному выше соотношению. Пусть,
в частности, 2^ обозначает леноинвариантный
дифференциальный оператор в пространстве C°°{Q), который мы уже
определили выше в гл. VI; тогда существует канонический
гомоморфизм алгебры ^(й) в алгебру, порожденную этими
операторами, который переводит L^ в 2^.
Аналогично, пусть я — представление группы G в
банаховом пространстве Я; как и прежде, обозначим символом Я"
пространство Гординга этого представления. Пусть End Я" —
алгебра его эндоморфизмов. Тогда определен канонический
гомоморфизм
^{g)->EndW~,
такой, что Lj(t-^^ dn{X).
Первый из описанных гомоморфизмов является на самом
деле изоморфизмом. Прежде чем доказать это утверждение,
упростим наши обозначения. Для произвольного X е дс
обозначим буквой X оператор 2^. Таким образом, ЛГ/ = 2^/.
Теорема 1. Отображение алгебры 41 (д) в алгебру
дифференциальных операторов на С°° (G) инъективно. Если отождествить
алгебру 41 (д) с ее образом, то 41 (д) имеет базис, состоящий из
элементов AifЛГг .Хз, где р, q, г — неотрицательные целые числа,
а [Xi, Х2, Xi) — базис алгебры g над R или дс над С.
Доказательство, Без ограничения общности достаточно
доказать утверждение теоремы для какого-либо конкретного базиса,
скажем {Е+, E-,W]. Пусть Л — ассоциативная алгебра, л;еЛ—
произвольный фиксированный элемент. Тогда отображение
y-^U, у]=ху — ух
есть дифференцирование, т. е. удовлетворяет условию D(yz)^
= yDz + (Dy) z. Вообще,
г
D {х^х^ ... Х;.) = X ^1 • • • Dxj ... х^.
Определяющие соотношения алгебры 41 (д) показывают, что
одночлены, указанные в теореме, порождают 'Ui^) над С. Для

^ /. Универсальная обертывающая алгебра 208
доказательства теоремы достаточно проверить, что если
/j Cpqfb + W t,-
— нулевой оператор, то все коэффициенты Ср^^ равны нулю.
Запишем этот оператор в виде полинома
fo(£+, W) + f,(£+, W)E- + ... +1 {Е+, W)EL.
В обозначениях § 5 гл. VI положим s = n— I и применим наш
оператор к функции ф„, «^1. Оператор Е_ аннулирует
функцию ф„; из формул (I) § 5 гл. VI ясно, что оператор fo{E+, W)
тождественно равен нулю как полином от В+ и W. Рассуждая
по индукции и используя функции ф„+2. Фгц-4. • • •. мы получаем,
что и остальные полиномы ff{B+, W) тождественно равны нулю,
что и требовалось доказать.
Пользуясь теоремой I, мы можем, когда это необходимо,
отождествлять ^{%) с алгеброй дифференциальных операторов.
Теорема 2. Централизатор оператора IF е ^(д) состоит из
всех линейных комбинаций одночленов E+WEl, р, q'^0.
Доказательство. Правило дифференцирования произведения
показывает, что
(I) [W, ElWEL] = 2i (р - г) ElV^'E'-.
Отсюда следует, что наши одночлены коммутирз^от с W.
Обратно, предположим, что линейная комбинация
Zcp.rElWEL
коммутирует с W. Вычисляя ее коммутатор с W, получаем
Zcp,rip-r)ElW''EL=0.
Пользуясь линейной независимостью входящих в это равенство
одночленов, мы получаем, что Ср^^ = 0 при рфг; теорема
доказана.
Централизатор W в алгебре '2/='^(д) обозначается 2^(W).
Центр алгебры ИХ обозначается Xill) или ^(д). Ясно, что
^(W)rD^(g). Так как матрица W порождает алгебру Ли
группы К, мы будем также писать 5C(f) вместо 2^(W).
Перейдем к определению центра алгебры 'U{^ = 'U.
Существует единственное линейное отображение
Л: 3^(W)->C[Wl
такое, что
О, '
W\ если p=Q,
если р> Q.

204 X. Дифференциальные операторы
Образ /г (У) элемента У при отображении Л характеризуется
сравнением
Y =h{Y) mod ЧгЕ-.
Ленча 1. Отображение h есть кольцевой гомоморфизм.
Доказательство. Пусть У;, Y2^.3£{W); тогда
y, = /i(y,)mod^£_, Y^ = h{Y.,)moi<UE-,
откуда
У2У1 = h (У2) h (У1) mod {<UE-W + 'UE-).
Воспользуемся правилами коммутации £-, W и тем
обстоятельством, что £_ —собственный вектор оператора ad ТТ. Теперь
наше утверждение очевидно.
Ленма 2. Сужение отображения h на ^{^) инъективно.
Доказательство. Пусть
Y^^Y^c^^WEL + Z c^.ElW'^E'L,
И предположим, что г ^ 1 и некоторые из коэффициентов Срд
отличны от нуля. Мы покажем, что У не может коммутировать
с Е-. Рассмотрим неприводимое представление с младшим
вектором веса m ^ 1, как в § 5 гл. VI; мы можем
воспользоваться полученными там формулами для производного
представления dn{X), полагая в них s^m—1. Нас интересует
действие наших одночленов на функции (fm+2r- При р> г
одночлен Е+W''E- аннулирует функции (fm+2r и^Б-ф^+2r•
Поэтому действие слагаемых, содержащих только г-ю степень Е+
и Е-, совпадает с действием У и имеет вид
Уфш+2г = ^('-)Ес<,(гт)Чт+2г> где Я(г)еС, Х{г)фО.
Применяя к обеим частям равенства при подходящем
значении т. оператор Е-, мы получим ненулевой вектор. С другой
стороны, УЕ_ф„+2г^0- Таким образом, У и £- не
коммутируют. Следовательно, если Y^2C{41) и h{Y)^0, то У = 0,
что и требовалось доказать.
Укажем в явном виде элемент центра алгебры 16 —так
называемый оператор Казимира
й = Д« + 2(Х+Х- + Х-Х+).
Несложным прямым вычислением проверяется, что оператор ю
коммутирует с Я, Х+, Х- и, следовательно, принадлежит
центру. Можно нормировать (л, умножив его на постоянный

§ 1. Универсальная обертывающая алгебра 205
множитель; этот множитель часто выбирают равным —1/4,
чтобы сделать оператор «положительным», однако сейчас мы
в этом не заинтересованы, и поэтому сохраним наше более
простое определение. Положим
< 1\
<й =
<й =
= № 4- у2 _
= -\-{W
\F = 2iW —
-if+E^E-
W^
■
+ £+£-,
Тогда оператор Казимира имеет также следующие выражения
(проверяемые прямым вычислением):
(2)
В частности,
(3) -Л(<» + 1)==(й^-0'-
Теорема 3. Центр алгебры 'Ы {%) является алгеброй поли-
номов от одной переменной С [<»]. При отображении h она
переходит в алгебру С {{W — if\.
Доказательство. Так как h инъективно на ^{Щ, а
оператор (W — if, как мы уже видели, принадлежит образу центра
при этом отображении, то достаточно проверить, что в образе
содержатся только полиномы четной степени от {W — i). Иначе
говоря, достаточно проверить, что если У принадлежит центру
алгебры 11 и
у = 2 с, (1Г - iY + Z c^^ElWEt,
то в первой сумме с jt? = О встречаются только четные степени q.
Рассмотрим действие универсальной обертывающей алгебры
в пространстве индуцированного представления п = щ, где
s==—т+1, т —целое число, /п^2. Тогда конечномерное
подпространство V {—т-\- 1), порожденное весовыми векторами
Ф-т+2> Ф-т+4. ■••> Фт-2>
инвариантно относительно действия алгебры Ли. Так как
оператор dniy) коммутирует со всеми операторами производного
представления и так как пространство V (-—т+ 1) неприводимо
относительно dn(g), то отсюда следует, что оператор dn(Y)
кратен единичному. Рассмотрим действие оператора dn(F) на
весовой вектор ф-т+г! этот вектор аннулируется оператором £-,
и мы получаем
Уф-т+2 = Р (- m + 1) ф^„+2. где Р (Г) = Z c.iT.

206 X. Дифференциальные операторы
С другой стороны, так как, по предположению, Y
коммутирует с Е~ и так как функция £_ф„ отлична от нуля и
пропорциональна функции фп,-2, мы получаем
£_Уф„ = YE-<f„ = Р (- m + 1) ^-ф„ = £-Р (- m + 1) ф„.
Поскольку Е- инъективен на подпространстве Я(—/n+l)m
(собственном подпространстве пространства Н{—т+1).
соответствующем весу т), отсюда следует, что Уф„^Р(—m + 1)фт-
Другими словами, Р(—т+ О есть также собственное значение
оператора dn{Y) в пространстве Я(—т+!)„,.
Положим теперь s = m — 1 вместо s = — m + 1. и пусть
я^Л;;,-!. Тогда ^я(£_) аннулирует подпространство Н {т — !)„,
(весовое подпространство, отвечающее младшему весу
представления я). Заметим, что 1^ф„^1тфп,. Следовательно,
Y(Pm = S с,,/' (т — 1)'' ф„ == Р (/п — 1) фп,-
Отсюда вытекает, что Р{—т-{-1) = Р{т—I) для бесконечно
многих /п; поэтому полином Р четный, и наша теорема
доказана.
Теорема 4. Централизатор подалгебры t [иначе говоря,
централизатор W) в 11 есть коммутативная алгебра полиномов от
двух образующих С [<», W].
Доказательство. Выражение оператора «о через операторы W,
Е+, £- показывает, что наша алгебра содержит
произведение Е+Е-, а значит, и {Е+Е-У при любом целом р'^0.
Пользуясь коммутационными соотношениями
[W, Е+] = 2iE+, [W, Е-] = - 2iE-,
легко проверить по индукции, что ему принадлежат все
одночлены вида E+WEt. Теперь из теоремы 2 следует, что
С [<й, IF] =^(0, что и требовалось доказать.
Присоединенное представление группы G в алгебре Ли g
канонически продолжается до представления в ^(з). Если
X = Х1Х2 . ■ . Х„,
где Xi=9:x^, Xi eg, то
л — Л1Л2 ... Лп,
где Xf'^g^^Xig. Мы будем писать также
X^'^{Adcug)X.

§ I. Универсальная обертывающая алгебра 207
Лемма 3. Для любого X ^ % справедливо равенство
Adq^ (ехр X) = ехр (ad X),
где (ad X) (У) = ХУ- YX.
Доказательство совершенно аналогично доказательству леммы
из § 2 гл. VII. Мы предоставляем его читателю.
Теорема 5. Пусть Y ^11 {%); предположим, что Y
коммутирует с некоторым оператором X, соответствующим элементу X
из д. Тогда Y коммутирует с правыми и левыми сдвигами на
ехр X (мы рассматриваем Y как оператор в пространстве
С°° (G, Н), где Н — некоторое банахово пространство). Если Y
принадлежит центру алгебры ^{%), то Y коммутирует со всеми
правыми и левыми сдвигами.
Доказательство. По определению, оператор Y левоинвариан-
тен, и нам нужно лишь проверить, что он также и правоинва-
риантен. Пусть g^expJ. Тогда
/ (х (ехр /У) g) = f {xg ехр (tg- ^Yg)),
поэтому, обозначив Rg правый сдвиг на элемент g, получим
YRgf=RJ4.
Из предыдущей леммы мы знаем, что У* ^(Ad<2^g)y = У.
Теорема доказана.
Замечание. Эта теорема для функций со значениями в
банаховом пространстве вытекает из аналогичной теоремы для
числовых функций: достаточно применить к доказываемому
соотношению произвольный линейный функционал и
воспользоваться теоремой Хана — Банаха»
Пусть л — представление группы G в банаховом
пространстве Я, у е Я — бесконечно дифференцируемый вектор.
Зададим отображение /„ формулой
f^,ix) = n{x)v;
таким образом, по определению, /„—гладкое отображение
из G в Я.
Если У — элемент алгебры '^{%), то его образ в End Я"
(в пространстве эндоморфизмов пространства С°°-векторов)
естественно обозначить dn (У). Для простоты мы часто будем
пользоваться сокращенным обозначением и писать
У„=^я(У)о.

208 X. Дифференциальные операторы
Если Z е д, то из наших определений немедленно следует
формула
( V ^Х'о ^ ' dn (X) о-
По индукции эта формула распространяется на произвольные
элементы алгебры 4^(д). В наших сокращенных обозначениях
она записывается так:
(5) ^^« = ^V
В частности, если v — собственный вектор оператора У, то
/о — тоже его собственный вектор.
Теорема 6. Пусть я — представление группы G в банаховом
пространстве Н. Если У е <2^ {%), Z е g ы У коммутирует с X,
то оператор dn{Y) (определенный на пространстве Нп)
коммутирует со сдвигом я (ехр X).
Доказательство аналогично доказательству теоремы 5. Мы
предоставляем его читателю.
§ 2. Аналитические векторы
Мы будем пользоваться координатами [х, у, Э) на группе G,
введенными в § 4 гл. VI, где мы представили элемент группы
в виде
/ы ^Л^У л:\ / cos 9 sin9\
^^\Q u)\Q lJv-sin9 соз9У'
Вычисления, проведенные в гл. VI, позволяют найти следующее
выражение для оператора Казимира в этих координатах:
(1)
^., .... - , д^\ ... д^
-^^{-§^+Ь)-'у
ду^ J ^ (Jjc ав
В частности, на функциях, которые не зависят от 9, т. е.
постоянны на левых смежных классах по К (иначе говоря, на
функциях на верхней полуплоскости), оператор Казимира с
точностью до постоянного множителя равен
У V <Эд:2 ■+■ ду^ ) ■
И теоремы 5 следует, что ои коммутирует с правыми сдвигами
и, следовательно, является инвариантным дифференциальным
оператором на верхней полуплоскости. Мы подробно исследуем
этот оператор в последней главе.

§ 3. Собственные функции кольца Z{t) 209
Пусть / — гладкая функция на группе G, такая, что
Тогда df/de = inf. Из формулы (1), выражающей оператор
Казимира в координатах (х, у, 9), ясно, что действие
оператора (Л на функцию / совпадает с действием оператора
который является эллиптическим (см. приложение 4).
Теорема 7. Пусть л — представление группы G в банаховом
пространстве Н. Предположим, что для некоторого целого п
весовое подпространство Я„ одномерно, и пусть (у) —его базис.
Тогда v — аналитический вектор.
Доказательство. Положим /„ (g) = я (g) v. Тогда
h{gk,) = e'-^fAg)-
Отсюда следует, что /„ — собственная функция оператора W
с собственным значением in. Поскольку <л коммутирует с
операторами п{к) при всех k ^ К, то <лу е Я„; так как, по
предположению, пространство Я„ одномерно, то у — собственный
вектор оператора Казимира, т. е.
й)у = CV
для некоторого комплексного числа с. Таким образом, (©—с)и^О,
и, в силу формулы (5) предыдущего параграфа,
((й-с)/„ = 0.
Следовательно, /„ есть решение эллиптического
дифференциального уравнения. Для любого функционала Я на
пространстве Н функция Я о /„ есть решение того же
дифференциального уравнения и, в силу теоремы регулярности (приложение 4),
является вещественно аналитической. Так как из слабой
аналитичности вытекает сильная аналитичность (приложение 5),
то функция /о — аналитическая, что и требовалось доказать.
§ 3. Собственные функции кольца 3C(t)
Как и в гл. IV, рассмотрим сначала сферические функции.
Напомним, что, по определению, сферическая функция — это
непрерывная функция на группе G, двусторонне инвариантная
относительно подгруппы К, которая является собственной
функцией операторов правой свертки с элементами кольца CTiGj/K)
и нормирована так, что она равна 1 на единичном элементе
группы. Так как операторы свертки являются сглаживающими,

210 X. Дифференциальные операторы
ТО сферическая функция, очевидно, бесконечно
дифференцируема.
Теорема 8. Пусть f — гладкая функция на G, двусторонне
инвариантная относительно подгруппы К и такая, что /(е)=1.
Тогда функция f является сферической в том и только в том
случае, когда существует такое комплексное число Я, что ©f = Xf.
Доказательство. Предположим сначала, что функция f
сферическая. Пусть (f^CT{G//K). По определению,
{/ *<i>)ix)=\f {ху-')Ф(у)dy = 5 /(у-')Ф(ху) dy.
а а
Так как оператор <л левоинвариантен, то ясно, что (д(^*ф) =
= /*((дф). С другой стороны, поскольку оператор <л также и
правоинвариантен, получаем
(Й (/ * ф) = (©f) * ф.
(Дифференцирование под знаком интеграла, очевидно,
допустимо, так как функция ф имеет компактный носитель.) Пусть
{■ф„} — последовательность Дирака из С^ (G). Положим ф„ = '^ф^.
т. е. усредним функции i|3„ справа и слева по подгруппе К.
Тогда
((л/)*ф„ = /*(<йф„)=Я„/,
где
Я„ = (/ * (йф„) (е) = (©/= * ф„) (е).
Так как подпоследовательность {<л/ * ф„} поточечно сходится
к ft>/, отсюда следует, что последовательность {Я„} сходится
к (ft>/)(e), и мы видим, что &f^Xf, где Я = (<л/)(е). Итак,
первая половина теоремы доказана.
Обратное утверждение будет выведено из свойств
собственных функций оператора Казимира, к обсуждению которых мы
теперь переходим. Свойства двусторонне инвариантных
функций вытекают из более общих результатов о функциях,
инвариантных относительно сопряжения элементами подгруппы Kl
поэтому мы займемся сейчас изучением таких функций.
Напомним, что собственная функция оператора Казимира,
постоянная на правых смежных классах по К (т. е. функция
на GJK), заведомо является аналитической в силу теоремы ре*
гулярности (см. § 2).
Выше мы определили присоединенное представление группы Q
в алгебре '2/(д). Если
Х = Xi ... х„
и Xi = 2х;, Xi е д, то
yg VS vS

§ 3. Собственные функции кольца aC{l) 211
где Xf = g Xig. Отображение Уь^-У^ есть автоморфизм
алгебры li (g) при .любом g е G.
В частности, взяв g = k е /С, можно усреднить элемент
У е ^ (д) по группе К- Положим, по определению,
к
Легко проверить, что У^ е .^ {t), т. е. что У^ коммутирует с W.
Для любой функции / определим функцию /* формулой
f'ix)^fikxk-').
Положим также x^^g~^xg. Пусть J е д. Имеем
f''ixexptX)=^f{kx{&xptX)k~') = fikxk~'expitkXk~%
Отсюда по индукции получаем формулу
(1)
{Yr){x') = {Yf){x)
для всех Уе'?/(д). В частности, если f^C°°{Q, К), то
(2) {Y^f){e) = {Yf){e).
Теорема 9. Пусть X: ЗС {t) -> С — характер, т. е. гомоморфизм
кольца ЗС (f) в поле комплексных чисел. Пусть f —
аналитическая функция на группе G, инвариантная относительно
сопряжений элементами подгруппы К, т. е. такая, что
f (fejcfe"') = / (х) для всех jc S G, k ^ !(■
Предположим, кроме того, что
Yf^k{Y)f
для всех Y ^2^ (f). Тогда при всех достаточно малых Z е g
справедливо разложение
/(expj)= j;M^/(^).
Доказательство. Это немедленно следует из формулы
Тейлора
И полученной выше формулы (2), так как, по предположе-
^1ию, f — собственная функция кольца 2^ (f), соответствующая
характеру Я.

212 X. Дифференциальные операторы
Теорема 9 определяет значения фу?жции / в окрестности
единицы группы G и, следовательно, однозначно определяет ее
на всей группе ввиду аналитичности. В частности, имеет место
Теореча 10. (i) Пусть f, g<=C°°{G, К) — собственные
функции кольца ^{t), соответствующие одному и тому же характеру
и нормированные так, что f{e)^g{e) = l. Тогда эти функции
совпадают.
(ii) Пусть f, g ^С"^ {G//K) — собственные функции оператора
Казимира, отвечающие одному и тому же собственному
значению и нормированные так, что f{e) = g{e)^l. Тогда эти
функции совпадают.
Доказательство. Первая часть теоремы уже была доказана.
Вторая часть вытекает из следующих замечаний.
Пусть /еС°° [ОЦЮ—гладкая двусторонне инвариантная
функция. Тогда Wf^Q. Если, кроме того, f — собственная
функция оператора <л, то, по теореме 4, для любого элемента Y из
кольца ^ (f) ^ С [<л, W] существует такое комплексное число А, (У),
что
Yf = h{Y)f;
при этом отображение Уь-г-Я(У) является гомоморфизмом
кольца 2^{t) в поле комплексных чисел, т. е. характером
кольца ^(О- Далее, так как 'k(W)^Q, этот характер
однозначно определяется своим значением на операторе Казимира,
т. е. числом Я (<й).
Аналитичность наших функций можно или потребовать
а priori, или вывести из теоремы регулярности, так как они
являются собственными функциями эллиптического оператора.
Теперь мы в состоянии завершить доказательство теоремы 8.
В самом деле, явная формула для сферических функций
Фя W = \ Р {k^Y dk
дает нам функции, которые двусторонне инвариантны, являются
собственными функциями оператора Казимира с собственным
значением Я ^ s(s — 1), где s — произвольное комплексное число,
и нормированы так, что 9s(e) = l. Одновременно с
завершением доказательства теоремы 8 мы закончили также
принадлежащее Хариш-Чандре доказательство его классификационной
теоремы для сферических функций:
Теорема 11. Все сферические функции исчерпываются теми,
которые были построены выше, т. е. функциями 9s, s е С.

§ 3. Собственные функции кольца ЗС(1) 2i3
Замечание. Существует другой подход к классификации
сферических функций. Мы начинаем с исследования
нелинейного дифференциального уравнения второго порядка для дву-
сторонне инвариантной функции f:
«/ = s(s-l)f.
Поскольку функция / двусторонне инвариантна, ее можно
рассматривать как функцию от переменной а <= Л в разложении
Картана G = /C^'*'/C. Таким образом, мы получаем для
функции / обыкновенное дифференциальное уравнение 2-го порядка;
оно имеет два линейно независимых решения. Пусть заданы
число Я и сферическая функция /, такая, что <л/ = Я/. Мы
всегда можем найти такое число s, что s{s — 1) = Я. Итак,
специальная сферическая функция ф, удовлетворяет тому же
самому дифференциальному уравнению, что и f. [Решения этого
уравнения выражаются через классические специальные
функции.] В теореме 1 § 2 гл. XIV мы построим другое решение
того же уравнения; это решение выражено там через другую
переменную, однако легко видеть, что как функция
переменной у на верхней полуплоскости оно имеет логарифмическую
особенность. Так как функция / должна быть линейной
комбинацией (ps и функции, построенной в § 2 гл. XIV, и так как f
не имеет особенностей, то / должна быть кратна фа, что и
требовалось доказать.

XI. ПРЕДСТАВЛЕНИЕ ВЕЙЛЯ
в теории представлений группы 5Z,2 (R) существует большой
круг вопросов, которых мы не будем касаться, а именно
построение различных моделей представлений из данного класса инфини-
тезимальной эквивалентности и возможность выбора
канонической модели, например модели Унттекера, в данном классе.
Мы отсылаем читателя к книге Жаке и Ленглендса [1] и
к статьям Стейна [2] и Кнаппа и Стейна [1]'), где можно найти
более подробную информацию по этому поводу и обсуждение
сплетающих операторов между различными моделями. Хелга-
сон [3] приводит очень интересную модель представлений
в собственных подпространствах оператора Лапласа. Я включил
в эту книгу только специальную модель представления Вейля,
поскольку это представление особенно важно в
теоретико-числовых приложениях н позволяет строить примеры автоморфных
форм (см., например, Шалика и Танака [1]). Кроме того, так
как работа Вейля [1] написана в чрезвычайно большой
общности, может оказаться полезным иметь в качестве введения
наивное изложение частного случая. Наконец, способ
построения представления Вейля дает повод упомянуть разложение
Брюа и привести образующие и соотношения для группы SL2 (R).
Я не предполагал слишком глубоко вдаваться в
рассматриваемые здесь вопросы, и поэтому выбор материала в этой главе
несколько произволен.
§ 1. Преобразование Фурье и свертки
Пусть & е R, & =5^ 0. Рассмотрим функцию на R",
определенную формулой
ftj {х) = е-"'""',
где лг^ = л: • л: — скалярное произведение. Эта функция равна 1
по абсолютной величине, и поэтому ее преобразование Фурье
в «наивном» смысле не существует. Однако при помощи
подходящей предельной процедуры мы сможем обращаться с ней
так же, как с функциями из пространства Шварца в обычной
теории сверток н преобразований Фурье. (См. Ленг [1, гл. XIV].
') См. также Годеман [7]. — Прим. перев.

§ I. Преобразование Фурье и свертки 215
Мы предполагаем, что читатель знаком с изложенной в этой
книге элементарной теорией, и будем использовать
соответствующие понятия н теоремы без специальных ссылок.) Заметим,
что функция hb четна, h^ (— х) = hf, (х).
Мы покажем, что ее преобразование Фурье «естественно»
определить формулой
Кроме того, мы покажем, что если функция / принадлежит
пространству Шварца, то функция h^ * f, определенная
обычной формулой
{hb*f){x)= 5 hb{x-y)f{y)dy,
н функция hbf тоже принадлежат пространству Шварца и
справедливы следующие формулы, в которых символом f
обозначено обычное преобразование Фурье функции f:
Нх)=\ f{y)e-^^"'^-ydy.
h2. {hb*ir = hbl
h 3. {htr = fi,*f.
h4. h,*f = hb{{hbfr oM-b),
где для любого ненулевого ft е R мы обозначаем символом М,,
оператор в R", действующий по формуле МьХ = Ьх (оператор
умножения на Ь); при этом {foMb){x)^f{bx). В частности,
h5. h^,{hb*f) = {hbfroM-b.
Другими словами, наше определение h 1 таково, что для
функции hi, выполнены все обычные свойства свертки и
преобразования Фурье.
Перейдем к доказательству этих формул. Зафиксируем число b
и положим, для краткости,
Ф(х) = (?-"'**'.
Для вещественного а, а> О, положим
фд {Х) = ip-'^'*-^'e^''^^*^
Таким образом, мы умножили функцию ф на одну из
стандартных функций из пространства Шварца. Поэтому ясно, что

216 XL Представление Вейля
функция Фа быстро убывает, и мы можем вычислить ее
преобразование Фурье:
ф^(г/) == ( е-я (a+<ft) x^g-2nixy fix.
Положим g{x) = e-^''\ Функция g совпадает со своим
преобразованием Фурье, g^u- Д-'1я любого комплексного а положим
g^{x) = e-^''\
Если а вещественно и положительно, то
1
йЛх) = -7[пе
-пл'/а
а
По принципу аналитического продолжения, то же самое
соотношение справедливо прн комплексных а с положительной
вещественной частью, т. е. для а = а -j- /ft, а > 0. Следовательно,
^"^ ' (а+ (6)"'^
Естественно теперь рассмотреть предел этого выражения прн
а->0. Этот предел существует, хотя к нему и нельзя перейти
под знаком интеграла, и мы получаем нашу формулу для
функции ф = йь, что оправдывает принятое определение.
Пусть f(=S. Тогда /♦фе5.
Доказательство. Имеем (f *Фд) =f^a- Ниже мы проверим,
что в этом равенстве можно перейти к пределу при а->0 под
знаком интеграла; поэтому (/*ф) =/ф. Ясно, что произведение/ф
быстро убывает; сделав преобразование Фурье, мы видим, что
функция f*ф является фурье-образом некоторой функции из
пространства Шварца. Следовательно, она сама принадлежит
пространству Шварца, что и требовалось доказать.
Заменяя f на f и ф на ф, получаем аналогичное
соотношение
Мы должны теперь обосновать предельный переход под
знаком интеграла, т. е. показать, что
lim \ if * Фа) (х) е-2я<д:!/ dx==[if*(p) (х) е-гжАгг/ dx.
Для ЭТОГО нужно найти суммируемую функцию, которая
мажорирует / *фо равномерно по а; достаточно доказать, что функция
x^-^xPif* ф J (X)

§ 2. Образующие и соотношения для группы Si-j 217
ограничена при всех р. Обозначим оператор умножения на
одночлен символом М'':
(M''f)W = <' ... <"fW.
Из теории преобразования Фурье следует, что
Заменим функцию f на f~. Имеем, кроме того, (Фа)~=(ф^)">
ф-=Ф^; следовательно, достаточно показать, что функция
{D''{fq)a)y ограничена. Но функция 1)''{/фо) представляется
в виде суммы
причем функции D'f = /, быстро убывают. Кроме того.
(а + tb) \ а + lb J
-nx4{a+lb)
И справедлива оценка
1 (D"/) {X) /.—"^/«"+^'' I ^ I {ВЦ) {x)/\^\h W I,
где /г — функция из пространства Шварца. Таким образом»
каждая функция
f,., = (D'f)(Z)4J
ограничена быстро убывающей функцией g равномерно по а;
при этом
Это оправдывает сделанный нами предельный переход под
знаком интеграла.
Те формулы, которые мы привели в начале этого параграфа
и еще не доказали, теперь очевидны.
§ 2, Образующие и соотношения для группы SLj
Пусть F — поле. Мы приведем образующие и соотношения
для группы 512(Л- Пусть Ь^Р, a^F, афО. Введем
следующие обозначения:
иф) = {\ \), sia) = [l 1_), ш = (_' \).

218 XI. Представление Вейля
Тогда
<*) s{a) = wu{a~^)wu{a)wu{a~^).
SL 1. ftb-г-м{&) есть аддитивный гомоморфизм.
SL 2. а ь-*• S (а) есгб мультипликативный гомоморфизм.
SL 3. оу2 = 5(-1).
SL4. s{a)u{b)s{a-') = u{ba^).
Предположим, что G — произвольная группа с образующими
и [Ь) [b^F) и w, такая, что если определить элемент s (а) для
а =5^ О формулой {*), то выполнены условия SL 1 — SL 4. Из
условий SL 3 и SL 4 вытекает тогда, что s{—1) принадлежит
центру G и что ш* = 1. Кроме того,
SL 5. WS [а) = S {а~')w.
В самом деле,
■w~^{a) ■=u{a-^)wu{a)wu{a~^),
откуда
oys{a)oy~'s(a) = oys(a)«{a-')s{a~')a(— а)ш)~' = 1,
что и требовалось (мы воспользовались формулой SL 4,
положив в нен.Ь.^а"').
Пусть (3 —группа с образующими и{Ь), w и соотношениями
SL 1 — SL 4, в которых элемент s (а) определен формулой (*).
Тогда существует естественный гомоморфизм группы G на
SL^iF).
Теорема 1. Естественный гомоморфизм описанной выше
группы на SL^{F) является изоморфизмом.
Доказательство. Любая группа с образующими и{Ь) [b^F)
и W, которые удовлетворяют приведенным соотношениям,
состоит из элементов вида
и [Ь) S [а) или и {Ь) S (а) wu {с),
тле элемент s{a) определен формулой (*). В самом деле, пусть
N — подгруппа всех элементов и{Ь) и А — подгруппа всех
элементов s{a). Тогда SL 4 показывает, что NA=^AN. Рассмотрим
подмножество G' = NA [} NAwN группы G. Умножение справа
на элемент w или на элемент u^N отображает подгруппу NA
в G'. То же самое произойдет, если подмножество NAwN
умножить справа на элемент v ^ N. Из тождества
wu{c)w = u{— c-^)w~^s{c)u{— c-^)

§ 2. Образующие и соотношения для группы SLi 219
(которое немедленно следует из определения s{c)) и формулы
SL 5 вытекает, что
NAwNw CZ NAwN.
Следовательно, G' = G. Чтобы проверить, что в группе SL2{F)
нет других соотношений, достаточно доказать следующую лемму.
Ленна. Каждый элемент группы 5^2 (^) допускает
однозначное разложение вида
и (а) S ф) или и (а) s (b) wu {с),
т. е. группа SLiiF) представляется в виде объединения
непересекающихся подмножеств
NA и NAwN.
Доказательство. Пусть F^ — пространство вектор-строк под
полем F; зададим на F^ естественное правое действие группы
SL2{F). Пусть ^2 —циничный вектор, е2 = {0, 1). Очевидно, что
группа Л^ есть стационарная подгруппа вектора ^2, т. е.
подгруппа матриц geSLiiF), таких, что e2g===e2. Следовательно,
отображение g^-^e^g задает изоморфизм пространства N\SL2{F)
и G-орбиты вектора ^2- Образ матриц з{а) при этом
отображении есть
^25 (а) = (О, а-'),
т. е. состоит из всех векторов, первая компонента которых
равна нулю. При этом элемент а(= F* определяется тачкой
орбиты однозначно. Если подействовать на нашу точку
матрицей W, она перейдет в точку (—а-', 0). Подействовав на нее
справа матрицей «(с), получим вектор вида
{—а-', -са-'),
т. е. вектор с ненулевой первой компонентой. При этом его
первая компонента однозначно определяет элемент а <= f*,
а затем элемент с е f однозначно определяется по второй
компоненте. Это показывает, что наше разложение единственно.
Тем самым лемма, а вместе с ней и теорема 1 полностью
доказаны.
Разложение, описанное в лемме, называется разложением
Брюа.
Замечание. Для произвольного поля не имеет смысла
говорить о положительных и отрицательных элементах; поэтому мы
определили подгруппу А как образ всей мультипликативной
группы поля при гомоморфизме s. Разумеется, над полем ве-
ш;ественных чисел можно ввести более тонкое деление,
учитывающее знак чисел.

220 XI. Представление Вейля
§ 3. Представление Вейля
Теорема 2. Пусть 5 = 5 (R^) — пространство Шварца на
плоскости R^. Существует единственное линейное представление г
группы 5^2 (R) в пространстве 5 {мы не налагаем на это
представление никаких условий непрерывности), такое, что
<1) r{w)f=-if;
<2) r{uib))f = h,f, где ftiW = e-*»«', Ь е R.
Для этого представления справедлива также формула
<3) r{sia))fix) = afiax), афО.
Представление г унитарно относительно обычного скалярного
произведения в 5.
Доказательство. Достаточно проверить, что операторы,
соответствующие матрицам w, u{b), s{a), удовлетворяют
соотношениям из § 2. Заметим, что
Для доказательства оставшихся соотношений проще всего
проверить сначала, что если оператор r{s{a)) определен формулой (3),
то выполнено соотношение
r{w)r(u{b))r(w)r{u{b-'))^r(u{-b-'))r{w-')r{s{b)),
соответствующее формуле (*) из § 2. Проверка этого
соотношения основана на формулах hi — Ь4из§1и является
стандартной, хотя и несколько утомительной. После этого остальные
утверждения теоремы становятся очевидными; например, из
формулы (3) для оператора r{s{a)) немедленно следует, что
отображение аг—^г(s(а)) — гомоморфизм.
Отождествим теперь пространство R^ с комплексной
плоскостью С. Обозначим С мультипликативную группу
комплексных чисел, равных 1 по модулю. Пусть % — характер
группы С, 5 (С, х) — подпространство в 5(C), состоящее из
функций, которые удовлетворяют функциональному уравнению
/(а2) = х(аГ'/(2), аеС', геС.
Лемма 1. Пространство 5 (С, х) инвариантно относительно
представления г.
Доказательство. Комплексно сопряженное число к а е С
будем обозначать а'. Если аа' = 1, то h^{uz)==h^{z); таким об:

§ 3. Представление Вейля 221
разом, если / е 5 (С, х). то функция г (и [Ь]) f тоже принадлежит
этому пространству. Далее,
f (ал:) =\f{y) е-"' " ("*"'' dy.
Сделаем замену переменной у*—^ау. Мера на R^ = C остается
инвариантной, так как |а|=1. Следовательно,
f (си) = 5 f [ay) е-"' " ('!'') йу = г (а)"' f (х).
Лемма доказана.
Мы хотим продолжить наше представление на группу GLt (R).
Начнем с некоторых алгебраических замечаний.
Пусть G — группа, Л и В — ее подгруппы, такие, что G = АВ.
Пусть ф: A-*G\, i|3: В-♦ Gj—гомоморфизмы в другую группу.
Предположим, что всякий раз, когда элемент g^^G можно
записать в виде
g = ab = b'a', а,а'^А, Ь, Ь'^В,
справедливо соотношение
ф(а)аК&) = а1з(&')ф(а');
предположим также, что сужения гомоморфизмов ф и ф на
А{\В совпадают. Тогда ф и ф можно однозначно продолжить
до гомоморфизма h группы G в Gx, положив
h (ab) = ф (а) ^ф {Ь).
Проверка этого утверждения тривиальна и предоставляется
читателю.
Предположим, кроме того, что подгруппа В — нормальный
делитель G и ЛПВ = {1}. Тогда из соотношения ab-=b'a'
следует, что аЬа-^ =b'a'a~^, откуда а' = а и ab-=b'a. Итак, чтобы
установить существование продолжения гомоморфизма Л,
достаточно проверить, что если b' = aba~\ то
ф(а)а1,(й)ф(а)-'=1|)(&').
Применим эти соображения к представлению г. Пусть
(О — характер С* (мультипликативной группьл поля комплексных
чисел), сужение которого на С' совпадает с х- Для а > О
положим
/а 0\
Определим оператор r^{v{a)) формулой
(4) А^(У1а))/(2) = |а|(о(а)/(аг),

222 XI. Представление Вейля
где а —любое комплексное число, такое, что аа' = а. Это
определение корректно, т. е. не зависит от выбора а. Мы
утверждаем, что формула (4) задает продолжение представления г
на группу Gl2"{R); мы будем обозначать это представление Гщ,
В силу сделанных выше алгебраических замечаний, для
проверки нашего утверждения достаточно доказать для х е 512 (R)
соотношение
'•((о \))'^^^'AV ?))-'-((о iWr ?))■
Если это соотношение доказано для матриц х, J:'e5Z,2(R), то
оно выполняется и для их произведения. Поэтому достаточно
проверить его для
X'
(о i) « ^ = ^ = (-1 I)-
Эта проверка проводится непосредственно на основе
определений с использованием равенств
(а 0\/ О 1\/а-' 0\_/а О Ч/ О 1\
U \)\-\ оЛо ij-U а-'Д-1 OJ'
Заметим, что представление Г(д унитарно, т. е. все операторы
r^ix), x^Gbt(R), унитарны по отношению к обычному
скалярному произведению в пространстве 5(C).
Теорема 3. Обозначим символом L? (С, ©) пополнение 5 (С, со)
относительно LP-нормы. Тогда пространство L?{C со) непри-
водимо относительно представления Гщ.
Доказательство. Линейное подмножество 5 (С, со) плотно
в L^(C, со). Зададим отображение Г на функциях из 5 (С, со)
формулой
(5) {Tf){z) = \z^{z)f{z).
Заметим, что ijf) (ez) = {Tf) (z) для любого комплексного числа е,
по модулю равного 1. Таким образом, функция Tf зависит
только от расстояния до начала координат, и ее можно
рассматривать как функцию на положительной полуоси.
Далее, положим
ri-=Tor^oT~\ т. е. г1{х)1 = Т{г^{х){Т~'!)).

§ 3. Представление Вейля 223
Тогда, если / — такая функция, что / (вг) = f (2) для всех е,
|8|=1, то действие на нее операторов представления г^
задается формулами
(6)
'^((о 0)^^^^=^^""'*"'^^^^'
(7) г^((о ^))f(2) = f(a2),
где а — любое комплексное число, такое, что аа' = а > 0.
Сопоставим функции Г/ функцию (Г/)* на полуоси R""",
положив
(8) (ПГ(/) = {Г/)(/''0 = (Г/)(2).
где Z — любое комплексное число, такое, что zz' = /.
Немедленно проверяется следующее утверждение:
Лемма 2. Отображение f ь-»- (rf)* продолжается до
изометрического изоморфизма пространства L^(C, ш) на i*(R"^)
относительно меры л1~ dt.
Доказательство очевидно и предоставляется читателю.
Мы свели изучение представления г^ к изучению
представления Га в пространстве TS{C, о»), которое плотно в L^(r"'").
Обозначим символом В"*" (R) группу матриц вида
(^Q jj, а>0, ftsR.
Сужение представления Гш на подгруппу B"^(R) обозначим л.
Это представление продолжается до унитарного представления
в пространстве L (R"*"), которое задается формулами
(9) я(^(^д 1 ))/(/) = в—*'/(/),
(10) я((д J ))/(/) =/(о/).
Для доказательства теоремы 3 достаточно проверить
следующее утверн^дение:
Теорема 4. Представление я группы B''"(R) в пространстве
L (R"""), заданное формулами (9), (10), неприводимо.
Доказательство основано на двух леммах из
функционального анализа.

224 ^1- Представление Вейля
Лепма 3. Пусть {X, \и) — измеримое а-конечное пространство
с мерой. Пусть
Л: L2(Z, (i)->L2(Z, (i)
— непрерывное линейное отображение, которое коммутирует со
всеми операторами умножения на функции из пространства
L°° {X, \i). Тогда А есть оператор умножения на некоторую
функцию g ^ L°° {X, \и).
Доказательство. Пусть ф s L^ (X, ц) — в существенном
положительная функция. Например, представим пространство X
в виде объединения
л
непересекающихся подмножеств конечной меры и положим
Ф I Х_ = п- = const.
Для любой функции f^L"'(]L^ имеем Л(ф/) =ф^4(/) = М(ф).
Следовательно,
Положим § = Лф/ф. Достаточно доказать, что функция g
ограничена. Если это не так, то для любого наперед заданного
числа N найдется такое множество Е конечной положительной
меры, что \g{x)\>N для всех х^Е. Пусть Хв
—характеристическая функция множества Е. Положим
(напомним, что g ФО в точках Е). Тогда
"^ (т1г ^0 ^ |¥г ^^ ^' ^' ^^ ^ ^^^'
/Лнорма этой последней функции равна N\i{E)'''. Но, с другой
стороны,
^ёц = ц{Е).
' %Е
\\\8\ ""=fe n\g\
Е
Это противоречит ограниченности отображения А; лемма
доказана.
Рассмотрим, в частности, в качестве пространства X
полуось R""" с мерой Хаара Г^ dt.
Ле.чна 4. Пусть
А: L4R^)->i4R-')

§ 3. Представление Вейля 225
— ограниченный линейный оператор, коммутирующий с
операторами умножения на экспоненты е"'*, & е R. Тогда А
коммутирует со всеми операторами умножения на функции ф е L°° (R"*")
и, по лемме 3, сам является оператором умножения на
некоторую функцию g^ L°° (R"*").
Доказательство. Докажем сначала утверждение леммы для
функций ф е crfR"*"). Пусть N — большое целое число, i|3;v —
периодическое продолжение функции ф на полуось R"*" с
интервала (О, N]; таким образом, график функции ■фд, выглядит так,
как показано на рис. 1.
Рис. 1.
Пусть Е — некоторый интервал, содержащийся в (О, N], н
Xj; — его характеристическая функция. Тогда
Л (фХя) = А (^.vXfi) = "Фл^^ (%е)-
Зафиксировав Е и устремив jV->oo, получаем
Это равенство справедливо прн любом выборе интервала Е на
полуоси. Линейные комбинации характеристических функций
таких интервалов плотны в L*. По непрерывности мы
получаем, что
Л(ф/) = фЛ(/)
для всех f е L^.
Распространим доказанное равенство на все измеримые
ограниченные функции. Пусть фе2,°°. Существует равномерно
ограниченная последовательность гладких финитных функций {ф„},
сходящаяся к функции ф почти всюду. (Например, можно
сначала аппроксимировать ф на конечном интервале [1/Л^, Л^], а
затем увтремить N->oo.) Если f ^ L^, то, по теореме об
ограниченной сходимости, последовательность {ф„/} сходится в L-
к функции ф/. Следовательн©,
Ф„^/ = Л(ф„П-^Л(ф/=);
с другой стороны,
Ф„Л/->ф^/.
Лемма доказана.
8 Зак. 589

2i3e XI. Представление Вейля
Докажем теперь неприводимость представления я из
теоремы 4. Пусть Л —проектор на инвариантное подпространство.
Обозначим f°a функцию x*—^f(ax). Тогда, по лемме 3, при
фиксированном а > О
A{foa)^g{foa)^{Af)oa,
или, иначе,
A{foa){t) = g(i)f{at)^g{at)f{ai).
Отсюда вытекает, что g{t)=^g (at) для почти всех /. По теореме
Фубини, функция g{at) — g{t) равна нулю при почти всех (а, t).
Таким образом, функция g в существенном постоянна;
следовательно, либо А = 1, либо Л = 0, что и требовалось доказать.

XII. ПРЕДСТАВЛЕНИЕ В ПРОСТРАНСТВЕ оь'(Г\еу
При изучении представлений в пространствах V (T\G), где
Г с: G — некоторая дискретная подгруппа, становятся
ощутимыми алгебраические и арифметические свойства группы SLj.
В этой главе, после того, как мы обсудим структуру фактор-
пространства T\G или r\G/K = T\^ (этот материал является, по
существу, классическим), мы докажем, что сужение
представления в L^(r\G) на некоторое подпространство '^L^{r\G) вполне
приводимо. Доказательство будет проведено для случая Г =
= SZ.2{Z); оно пригодно также для любых «арифметических»
подгрупп, т. е. подгрупп конечного индекса в SLj (Z). В нем
используется формула суммирования Пуассона и некоторые
оценки. Его преимущество в том, что оно быстро приводит
к цели н использует минимум сведений из анализа.
С другой стороны, этот метод непригоден для более общих
дискретных подгрупп. Мы обсудим общий случай в гл. XIV на
основе одного метода Л. Д. Фаддеева.
Основной результат этой главы о том, что пространство
"L^(r\G) вполне приводимо, принадлежит И. М. Гельфанду и
И. И. Пятецкому-Шапиро. (См. книгу Гельфанда, Граева и
Пятецкого-Шапиро [1], в которой приведен адельный вариант
этой теоремы.) При изложении я следую практически без
изменений заметке Годемана [5]. Годеман рассматривает более общий
случай, однако в соответствии с нашим подходом в этой книге
нам кажется, что проще сначала познакомиться с
доказательством для случая SZ.2 (Z), а затем убедиться, что оно проходит
в большей общности.
§ 1. Вершины и вершинные подгруппы
Пусть Г —дискретная подгруппа группы SLj (R)- Однопара-
метрическая подгруппа N группы G = SL2(R) называется уни-
потентной, если она состоит из всех элементов вида exp/Z,
где Z —некоторая нильпотентная 2 X 2-матрица, / е R. Будем
говорить, что М — вершинная подгруппа ') для Г, если
') в литературе по теории представлений уже утвердился термин
«каспидальная подгруппа». Ясно, что предложенный переводчиком вариант
гораздо уместнее. — Прим. ред.

228 X!J- Представление в пространстве '^L^(V\G)
факторпространство NjN П Г компактно, или, что эквивалентно,
N содержит неединичный элемент подгруппы Г.
Типичный пример унипотентной подгруппы—это подгруппа jVq,
состоящая из матриц вида
а О
R.
Простое перемножение матриц показывает, что нормализатор
подгруппы Л^о в группе GLjCR) состоит из матриц вида
ь-
(о dj'
Нормализатор подгруппы N в SLziR) мы будем обозначать
Norm N.
Теорема 1. Все однопараметрические унипотентные подгруппы
группы SL2 (R) сопряжены. Две унипотентные подгруппы N и N'
совпадают в том и только в том случае, когда Norm Л^ = Norm N'.
Доказательство. Пусть X — нильпотентная матрица. Тогда по
теореме Жордана существует такая матрица AfeGLgCR), что
Если понадобится, можно умножить М слева на матрицу
(о Л>
таким образом, без ограничения общности можно считать, что
М. принадлежит GLt (R). Умножив матрицу М на
положительное число, мы можем даже считать, что MeSLjlR); при этом
МХМ'
U о;
Тогда подгруппа (ехрШХМ '}, ^ е R, сопряжена подгруппе
(ехр^Х} в SL2{R). Это показывает, что все однопараметрические
унипотентные подгруппы группы SLjCR) сопряжены.
Пусть S — подгруппа Бореля группы SLjCR), т. е. подгруппа
матриц вида
b
VO а-Ч
Множество унипотентных однопараметрических подгрупп есть
орбита группы Л/'о относительно сопряжения в 5L2{R); поэтому

§ I. Вершины и вершинные подгруппы 229
ОНО находится во взаимно однозначном соответствии с
множеством смежных классов SL2{R)/B. Для любого л;еК обозначим
символом
подгруппу, сопряженную Nq при помощи матрицы
с:)
Группа Nx состоит из матриц вида
{ \ —их и \
(1^ I ^и 1+их)^ ^^^-
Так как любую 2 X 2-матрицу можно записать в виде
Га Ь\ /1 0\/а р\
\с d)^\x 1Д0 ь)'
в предположении, что а =И= О {х = с/а), то группы Nx {х е R)
образуют семейство представителей для смежных классов из
пространства SLjCRVB, содержащих матрицу, у которой а =И= 0.
Немедленно проверяется, что существует только один смежный
класс, не удовлетворяющий этому условию. Представителем
этого класса является матрица
W
<-: 1У
и ему соответствует унипотентная подгруппа
^~ = {(i ?)} = ^-
Таким образом, множество RU{°o} взаимно однозначно
параметризует унипотентные подгруппы группы 5^2 (R).
Теорема 2, Подгруппа Nx является вершинной подгруппой
для Г = 5^2 (Z) в том и только в том случае, когда х —
рациональное число или оо.
Доказательство. Это немедленно следует из явного описания
матриц подгруппы Nx, приведенного в формуле (1). Если
пересечение подгрупп Nx и SL2 (Z) содержит элемент, отличный от 1,
то и ^п —целое и 1 —ил; тоже целое; таким образом, х
рационально. Обратное утверждение также очевидно.

230 XIf. Представление в пространстве ''l.^{T\G)
Пусть Г — подгруппа группы SL2 (Z) конечного индекса. Тогда
N — вершинная подгруппа для Г в том и только в том случае,
когда она вершинная для 8Ц (2).
Доказательство. Если пересечение подгрупп Л^ и SL2 (Z)
содержит элемент, отличный от единицы, то некоторая степень
этого элемента принадлежит Г. Кроме того, подгруппа N не
содержит элементов конечного порядка, поэтому N —
вершинная подгруппа для Г. Обратное утверждение очевидно.
Две унипотентные подгруппы N и N' называются Г-сопря-
женными, если существует такой элемент у^Г, что yNy-^ = N'.
Рассмотрим множество всех унипотентных подгрупп, которые
являются вершинными для Г. Группа Г действует на этом
множестве при помощи сопряжения, и класс Г-сопряженных
подгрупп (т. е. орбита группы Г) называется вершиной группы Г.
Пример. Если rc:5L2(Z), то вершины находятся во взаимно
однозначном соответствии с двойными смежными классами
T\SU iQ)/B (Q),
где Q —поле рациональных чисел, В (Q) — подгруппа
треугольных матриц в SL^iQ). Это немедленно вытекает из
параметризации вершинных подгрупп точками множества QU{°o}-
Подгруппа Г == 5^2(2) имеет только одну вершину. В общем случае
число вершин не превосходит индекса [SLj (Z): Г].
Теорема 3. Пусть Г—дискретная подгруппа группы G =
= SL2(R), такая, что факторпрост ранет во V\G компактно. Тогда G
не содержит вершинных подгрупп для Г.
Доказательство. Нам нужно показать, что группа Г не
содержит унипотентных матриц, отличных от единичной.
Докажем сначала, что класс сопряженных элементов,
соответствующий любой матрице Y ^ Г, замкнут в SLj (R). В самом деле,
пусть W — компактное множество, такое, что SL2 (R) = WV.
Рассмотрим отображение группы SL2(R) в себя, задаваемое
формулой
Его образ состоит из матриц, сопряженных при помощи
элементов, принадлежащих W, элементам множества
S={0Y0-'; (теГ}.
Множество S содержится в Г и является замкнутым и
дискретным. Предположим, что заданы последовательности элементов
gn^W и 0„ е Г, такие, что
S о yo~^s —* h,

§ I. Вершины и вершинные подгруппы 231
ДЛЯ некоторого элемента h е 5^2 (R). Переходя, если это
необходимо, к подпоследовательности, мы можем считать, что g„
сходится к элементу g^W. Тогда
и так как множество S дискретно, то последовательность
(cr^Ycfj'} стабилизируется при достаточно больших п (мы не
утверждаем, что сама последовательность {(т„} стабилизируется).
Таким образом,
en<^„УO-^g-^-*gaya-^g-K
Это показывает, что класс сопряженных элементов замкнут.
Для завершения доказательства достаточно заметить, что класс
сопряженности любого отличного от единицы унипотентного
элемента в SL2(R) не замкнут. В самом деле, в любом таком
классе содержится матрица
СО.
ифО.
Сопрягая ее при помощи диагональной матрицы, мы видим,
что при а-*О
/а О \/1 u\/a-^ 0\ /1 0\
Ко a-'JVO ljv.0 aj~*U ij'
т. е. наш класс сопряженных элементов не замкнут. Теорема 3
доказана.
Происхождение термина «вершина» (cusp) связано с
геометрией верхней полуплоскости. Пусть G = 5L2(R); положим, как
обычно, I» = G/K- Пусть Г — дискретная подгруппа группы G.
Рассмотрим факторпространство Г\§. Фундаментальной областью F
в ф относительно подгруппы Г назовем такое подмножество ф,
которое содержит представитель каждой Г-орбиты в §
(относительно обычного левого действия) и обладает тем свойством,
что если две точки z, z' ^ F лежат на одной орбите, то они
принадлежат границе F. Если r=SL2(Z), то легко доказать,
что фундаментальной является область, изображенная на рис. 1
(см. например, Серр [1] или любую книгу по теории
эллиптических функций, например мою).
Единственная вершина подгруппы Г =5^2(2) задается
стандартной унипотентной подгруппой Л^о- Можно присоединить
к пространству Г\ф вершинную точку, задав в нем топологию
при помощи системы окрестностей вершины; по определению

232
ХП. Представление в пространстве ''Z,^(r\G)
базис окрестностей вершины образуют подмножества Г\§,
представители которых принадлежат подмножествам
Fa = {x + ly\ -72<^<72, У>а}
(ср. Шимура [1, гл. 1]). Элемент
W
=(-::)
переводит фундаментальную область в фигуру, изображенную
на рис. 2(b), т. е. отражает ее относительно дуги окружности.
е2тп'/з'
••Й«!*'
••••••у
Щ
л>у.
1:%?
ш
ш
Ш
I
2
♦.v.;
:♦:•:•:
<•»:•
%::?
•'••••л
•>t'X«
Ш
1
1
2
Рис. 1.
Эта фигура теперь напоминает острие (две ее стороны,
примыкающие к вещественной оси, имеют общую вертикальную
касательную в точке 0). Это и объясняет происхождение термина
вершина {cusp'); лат. cuspls — острие; рог луны).
Как показал Зигель [1], в общем случае, если Г —
дискретная подгруппа группы SL2(R), такая, что объем факторпростран-
ства Г\§ конечен, то всегда можно построить для Г
фундаментальную облдсть F следующего вида. Она является конечным
объединением областей f„:
а=0
') В последнее время термин «каспидальный» стал употребляться и в
русских работах. Как указал А. Вейль, с латинским произношением лучше
согласовано написаине «куспидальный». — Прим. перев.

§ 1. Вершины и вершинные подгруппы
233
причем
(i) область Fo компактна и имеет кусочно-аналитическую
границу;
(ii) существует такое число Хо > О, что F содержится в
полосе — Xq^x^Xq;
(iii) существуют (большое) число а и элементы ga (" = 1 > • • ■. ^)
группы SLalR), такие, что Fa, = gaPa-
(См. Гельфанд, Граев, Пятецкий-Шапиро [1, гл. 1].) В этой
книге нас интересуют в первую очередь вопросы анализа и
теории представлений, а не геометрия римановых поверхностей;
Ш
(а)
Рис. 2.
поэтому МЫ не включили доказательство этого результата. По
поводу других фактов относительно фундаментальных областей
и римановых поверхностей см. также статью Петерсона [2]. Мы
вернемся к этим вопросам при обсуждении работы Л. Д. Фад-
деева в гл. XIV.
Обсудим теперь условия роста, налагаемые на функции
в окрестности вершины. Нас будет интересовать, в частности,
как преобразуются эти условия при поднятии функций с
верхней полуплоскости на группу (ср. § 4 гл. IX).
Рассмотрим сначала частный случай. Пусть Fq — группа
матриц вида
с:).
Эта группа есть пересечение 5Z,2(Z) с нашей стандартной уни-
потентной подгруппой No- Предположим, что функция f на
верхней полуплоскости инвариантна относительно Го. Это означает,
что
f{z + l) = f(z), ze^.

234
ХП. Представление в пространстве °L^(T\G)
Предположим также, что f голоморфна на §. Отображение
комплексно аналитично, и его можно рассматривать как ofo-
бражение факторпространства Го\ф. При фиксированном
значении у оно переводит отрезок
— 72<л:<72, У^Уй
в окружность
При у^-оо радиус круга уменьшается. Значит, отображение
zi-^Qz задает комплексно аналитический изоморфизм
пространства
{2еГо\§; Imz^B)
(см. рис. 3) на проколотый круг
■ 0<l9l<e-2"B.
Пусть f — голоморфная функция на верхней полуплоскости,
инвариантная относительно Fq. При отображении Z'r-^ q^ эта
ш
к-х-ЩЩ
» 1
Рис. 3.
функция переходит в функцию f, определенную в проколотой
окрестности нуля на плоскости переменной q. Если функция f*
имеет полюс в нуле, мы будем говорить, что функция f меро-
морфна на бесконечности. Если /* голоморфна в нуле, то мы
будем говорить, что f голоморфна на бесконечности. В первом
случае имеет место разложение
f(2)=r(9)=i;a„^, г>о.
—г
Если функция f* голоморфна в нуле, этот ряд начинается с
постоянного члена или с более высоких степеней q. Если у функ-

§ 2. Параболические формы 235
ции есть полюс, то первый член ряда
a^q-'' = а^е-'^Уе-'^'^''''', а^ ф О,
экспоненциально растет при у-*оо как е'^-'°'У. Таким образом,
условие отсутствия полюса означает, что функция f ограничена
на бесконечности, т. е. при у—>-оо.
Рассмотрим теперь функцию Ф на группе, полученную
поднятием функции ф, заданной на верхней полуплоскости, т. е.
определяемую формулой
Предположим, что функция ф голоморфна на § и инвариантна
относительно Fq.
Функция ф голоморфна на бесконечности в том и только в том
случае, когда
Другими словами, Ф имеет не более чем полиномиальный рост
на бесконечности.
Это утверждение немедленно вытекает из нашего
предыдущего обсуждения.
Аналогичные соображения применимы и к .Ш^ой подгруппе
группы Го конечного индекса; любая такая по^руппа состоит
из матриц вида
/1 dn\
lo 1 )'
2,
где d — некоторое фиксированное натуральное число. Вместо
единичной полосы в этом случае нужно использовать полосу
ширины d. В остальном все рассуждения совершенно аналогичны.
Условия на рост функций в окрестности произвольной
вершины сводятся к уже рассмотренному случаю при помощи
внутреннего автоморфизма группы SL^iR),
§ 2. Параболические формы
Пусть Г — дискретная подгруппа группы G = SL2 (R);
предположим для простоты, что Г имеет лишь конечное число
вершин, т. е. что существует лишь конечное^ число классов Г-со-
пряженных унипотентных подгрупп, имеющих с Г нетривиальное
пересечение.
Пусть/п —натуральное число. Обозначим символом ^(Г\0,/п)
пространство гладких функций на группе G, удовлетворяющих

236 XJI. Представление в пространстве "L^iVXG)
следующим условиям (при всех g е G и всех y ^ Г):
AUT1. f{gr{e)) = e""ef(g).
AUT2. f{yg) = f(g).
AUT3. 8E_f = 0.
AUT 4. В каждой вершине функция f имеет не более чем
полиномиальный рост.
Третье условие соответствует условию аналитичности на
верхней полуплоскости и показывает, что функция f во всяком
случае вещественно аналитична на группе G (см. § 4 гл. IX).
Четвертое условие означает, что наша функция голоморфна на
бесконечности. Условия AUT 1 и AUT 2 можно
интерпретировать в терминах процедуры поднятия, определенной в § 4 гл. IX.
Эти условия означают, что если функция f = Q получена из
функции ф на верхней полуплоскости при помощи поднятия, то
ф(Y2) = (cг + dГф(2)
для всех Y ^ Г; здесь
Y-'
=(: :)■
Чтобы избежать перехода к обратной матрице, во многих
классических работах действие элемента y ^ Г записывается
справа. При таком соглашении, если
=(::).
мы пишем
Фl[Y]ш{2) = Ф(Y2)(c2 + dГ'";
при этом справедливо правило композиции
[YYlm=[YL[Y']m-
Подпространство в ^(Г\0, т), состоящее из функций f,
удовлетворяющих дополнительному условию
\ f{ng)dn = 0
ДЛЯ любой вершинной подгруппы N группы G, называется
пространством голоморфных параболических форм ') и
обозначается ssf-°(r\G, т). Мы использовали сокращенное
обозначение Fjv для подгруппы Г П Л/'.
') В оригинале: cusp forms,—Яр«л, ред.

§ 2. Параболические формы 237
Рассмотрим также пространство L^(r\G) и обозначим
символом °L^(r\G) его замкнутое подпространство, порожденное
всеми ограниченными непрерывными функциями f, для которых
выполнено следующее условие:
CUSP1. J f{ng)dn = 0
rjv\w
для всех элементов g^G и для всех вершинных подгрупп N,
Пусть
я: G^AutL2(r\G)
— унитарное представление правыми сдвигами, т. е.
^(s)f{g) = f{gs).
Заметим, что подпространство °L^(r\G) инвариантно
относительно представления п, поскольку
J (n(s)f)(ng)dn= J f{ngs)dn = 0.
rjv\JV rjv\JV
Заметим также, что если условие CUSP 1 выполнено для одной
вершинной подгруппы N, то оно выполняется и для подгруппы
yNy~\ Y ^ Г. В самом деле,
Y(rnA^)Y-J = rnYA^Y-';
таким образом, полагая уМу-^ = М, мы, по предположению,
получаем
J f(mg)dm= J f{yny-^g)dn =
Тм\м rjv\A;
= \ f(ny-^g)dn = 0.
Vn\N
Вплоть до конца параграфа мы будем предполагать, чт©
r = 5L2(Z), чтобы упростить разложение функций в
окрестности вершины (в общем случае необходимо переводить
произвольную вершину в стандартную при помощи внутреннего
автоморфизма). Таким образом. Го — подгруппа матриц вида
а:>
Пусть функция Ф е ^ {r\G, т) соответствует функции ф на
верхней полуплоскости. Из условия AUT 3. вытекает, что
функция ф голоморфна на ф, а условие роста Aut 4 показывает, что

238 XII. Представление в пространстве "1^(1^0)
функция ф голоморфна на бесконечности, т. е. допускает
разложение
п=0
где ^ = е^"'^ = е""-'"*'е^". Это разложение представляет собой,
по существу, ряд Фурье. Коэффициенты а„ задаются формулой
1
е-^Уа^ = ^ Ф (л: + iy) e~^'^^'^'^ dx;
о
в частности, ,
1
flo = J Ф (л: + iy) dx.
о
Воспользуемся определением поднятия веса т\
Ф (« ( Q \У (е)) = Ф (^ + iy) y-^Ч^"^\
Получим
Оо = \ е-'"'«г/-'"«ф Ги Г ^ Mr (0) j dx =
^^-'v-'i'^fti i)(o \y^^))^^-
,0
где С (g) — некоторое число, зависящее от g. Таким образом,
мы получаем следующее условие, эквивалентное первому
условию параболичности:
CUSP 2. Пусть Фе,5^(Г\0, т) и <^ — соответствующая
функция на верхней полуплоскости. Тогда постоянный член
разложения функции ф в окрестности вершины равен нулю в том
и только в том случае, когда для всех g^G
1
l^iil l)^)'^ = °-
Разумеется, приведенное условие можно переписать в виде
\ O{ng)rfn==0.
^n\n

§ 2. Параболические формы 239
Теорема 4. Имеет место включение ^° (Г\0, т) с "L^ (Г\0).
Доказательство. Пусть ф — функция на §, соответствующая
поднятой функции Ф из пространства ^°(Г\6, т). Так как
коэффициент flo ее разложения в окрестности вершины равен
нулю, это разложение начинается с члена a,e-2we^"'*;
следовательно,
\<f{x + iy)\<^e-^^y,
т. е. функция ф экспоненциально убывает при f/-»-oo. функция Ф
растет не быстрее, чем у'"'-\ ^ (х-\-iy) \, и, следовательно,
ограничена. Так как мера пространства Г\0 конечна (если мера
подгруппы К равна 1—она совпадает с площадью
фундаментальной области группы Г на верхней полуплоскости по мере
dxdy/y^), то функция Ф квадратично интегрируема, что и
требовалось доказать.
В заключение этого параграфа приведем принадлежащую
Гекке классическую оценку коэффициентов Фурье
параболических форм.
Теорема 5. Пусть f — голоморфная функция на верхней
полуплоскости, такая, что
f\[y]tn = f «Р« всех Y^r.
Предполоэюим, что постоянный член ее разложения в
окрестности вершины равен нулю, т. е. что
Тогда (i) | f (2) |< у-'"'^ при у-*оо,
(И) |а„| = 0(п«/2).
Доказательство. Из определения оператора [у]т. Y ^ Г,
немедленно следует, что функция h {z) = \ f {z) \ у"Ч^ инвариантна
относительно Г. Кроме того, при у->-оо функция h{z)
стремится к нулю. Следовательно, она ограничена на
фундаментальной области группы Г. Тем самым первое утверждение
теоремы доказано. Далее, имеем
где интеграл берется по маленькой окружности с центром
в нуле на плоскости переменной q. Заметим, что dqlq = 2nidx.
Следовательно,
1
\ап\ < 5 I f (^ + iy) 1 е-""» dx < е^пуу-тп

240 ХП Представление в пространстве 'Ч,2(Г\0)
при всех г/ > О (мы воспользовались первым утверждением
теоремы). Чтобы получить отсюда оценку (ii) для коэффициентов q„,
достаточно положить у = 1/п.
§ 3. Признак компактности операторов
В этом параграфе доказывается несколько абстрактных
лемм, которыми мы воспользуемся в следующем параграфе.
Приведем один признак компактности операторов.
Теорема 6. Пусть X — локально компактное пространство,
снабженное конечной положительной мерой ц- Пусть Н —
замкнутое подпространство пространства L^{X, \i) = L^{X), Т ~
линейное отображение пространства Н в линейное пространство
ограниченных непрерывных функций на X. Предположим, что
существует такая постоянная С > О, что
lirflKCIIfIb при всех f^H,
где \\ • II — обычная 5Щ-норма. Тогда оператор
Т: Н^ЬЦХ)
компактен и его можно задать при помощи ядра из пространства
LHXXX).
Доказательство. Как мы знаем, оператор, который можно
задать квадратично интегрируемым ядром, компактен (см. § 3
гл. I). Чтобы доказать существование ядра у нашего оператора,
воспользуемся тем, что, по условию теоремы, отображение
f^Tfix), f^H,
линейно и непрерывно при всех х^Х. Следовательно,
существует такая функция д^^ е Я, что
Tf{x) = {f,q,)=\f{y)qAy)dy
при всех f^.H. Так как Г/— непрерывная функция на X, это
показывает также, что отображение xi-^q^ пространства X
в Я слабо непрерывно, а значит, и слабо измеримо. Кроме
того, образ X в пространстве LP-{X) ограничен. Поэтому наша
теорема вытекает из следующей леммы:
Лемма 1, Пусть X, Y — пространства с конечной мерой,
причем а-алгебра измеримых подмножеств Y порождается своей
счетной подалгеброй. Предположим, что задано слабо измеримое
отображение
q: X^L^Y),

§ 3. признак компактности операторов 241
образ которого в пространстве L^{Y) ограничен. Тогда
существует такое ядро Q^Lr{X X Y), что
qxiy) = Qix, у)
для почти всех х^Х и для всех уфЗх, где S^ — некоторое
зависящее от X подмножество Y нулевой меры.
Доказательство. В нашей следующей лемме мы покажем,
что функция
x^-*{qjc, qx) = \\Qx{y)fdy
измерима. Она ограничена, и потому принадлежит
пространству Z.'. Пусть g — ступенчатая функция на Xy^Y, постоянная
на «прямоугольниках» (т. е. на произведениях измеримых
подмножеств из Z и У соответственно). Тогда
I \ \ g{x, y)'qAy)dy dx \<\\gf,\\\qAy) f dydx
(это обычное неравенство Шварца), Итак, отображение
g*-* \ё{х, y)~qAy)dydx
непрерывно в топологии L^. Следовательно, существует ядро
Q^.L^{Xy^Y), такое, что для всех характеристических
функций ф, ф измеримых подмножеств в пространствах Z и У
соответственно справедливо равенство
5 Ф W 5 Ф {у) яАу) dydx=\^(f, (x)S^ ф iy)Q{x, у) dydx.
Для любой функции ф существует такое подмножество Z^
меры нуль в X, что если x^.Z^, то
\ Ф(у)Qx(у)dy=\^yi?(y)Q{х, y)dy.
Выберем счетную систему образующих 0-алгебры измеримых
подмножеств Y. Существует такое подмножество Z меры нуль
в пространстве Х, что при хф1 предыдущее соотношение
выполняется одновременно для всех характеристических
функций этих образующих. Следовательно, при х ф.Ъ
gxiy) = Q(x, у)
при всех уфЗх, где S^; — некоторое подмножество Y меры
нуль. Лемма доказана..
Нам осталось проверить только несложное утверждение об
измеримости.

242 XII. Представление в пространстве 'Ч^(Г\0)
Лемма 2. Пусть Н — сепарабельное гильбертово
пространство, X—пространство с мерой. Если отображения f, g: Х—>-Н
слабо измеримы, то функция x^—^{f{x), g{x)) измерима.
Доказательство. Пусть {щ} — ортонормированный базис в Я.
Рассмотрим разложения Фурье
fix)=^T.fi{x)Ui,
six) = l,gi{x)Ui
функций f и g. По предположению, все функции fi, gi
измеримы. Функция
(fix), g{x)) = Zfi{x)Iilx)
есть предел измеримых функций, а потому сама измерима,
что и требовалось доказать.
§ 4. Полная приводимость пространства '^U{r\G)
Пусть Г = SL2 (Z), я — представление группы G = SL2 (R)
в пространстве °L^(T\G), действующее правыми сдвигами;
таким образом,
л (у) f{x) = f {ху).
Если ф е СГ (G), то
я' (ф) f (х) = J я (у) f {х) (f{y)dy=\f (ху) ф (у) dy.
а а
Для простоты мы будем писать я (ф) вместо я' (ф). Основной
результат этого параграфа состоит в следующем:
Теорема 7. Если феСГ{0), то существует такое число С^,
что для всех функций [^°L^'(r\G) справедлива оценка
\\n{^)f\\<CJf\^,
еде II • II — обычная snp-норма.
Из теоремы 6 предыдущего параграфа вытекает такое
Следствие, Оператор я(ф) компактен.
Пользуясь теоремой 1 § 2 гл. I, мы получаем следующее
утверждение:
Теорема 8. Представмние я группы G в пространстве °L^ (Г\0)
вполне приводимо, и каждая неприводимая компонента входит
в его разложение с конечной кратностью.

§ 4. Полная приводимость пространства "L'{T\G) 243
Перейдем к доказательству теоремы 7. Как обычно, мы
полагаем Tfj^rflN. Мы будем пользоваться разложением
Ивасавы G = NAK. Имеем
-]
п (ф) f(x)= \f (у) ф {х-^у) dy =
где
= \ Z 'P(^"''nj/)f{nj/)cfj/= \ 1^{х, y)f(y)dy,
rjv\0 пеГл, rjv\(J
Для краткости обозначим общий член этой суммы фд;,у(/п).
Пользуясь формулой суммирования Пуассона, получаем
/ф {Х, У)= Yi Фл;. у (/и) = Z Ч'х. у itn).
meZ msZ
Итак, оператор я(ф) задается ядром 1^{х, у). Перейдем к оценке
этого ядра.
Запишем разложение Ивасавы элемента л; е G в виде
^< П("о "')'.-
t, и, >0;
таким образом, на верхней полуплоскости G//C
л; ■ г ==Ид. + ivx-
Мы будем писать также х^Пха^кх-
Зафиксируем число с > О и рассмотрим область Зигеля Р^,
которая состоит из всех элементов л; е G, таких, что п^
принадлежит компактному подмножеству Qjy группы N и Vx'^c.
При достаточно малом с справедливо разложение
G^TF,.
Проекция области F^ на верхнюю полуплоскость изображена
на рис. 4(a). Чтобы оценить я{ф)/(л;), мы можем без
ограничения общности считать, что х е F^, так как функция f левоин-
вариантна относительно Г. Заметим, что интеграл \ можно
Гл,\0
рассматривать как интеграл по фундаментальной области
группы Fjv; в качестве такой области можно взять прообраз
в группе G множества, изображенного на рис. 4(b). Нам нужно
оценить ядро !^{х, у) при xef^.
Для удобства мы будем ниже обозначать одной буквой Q
различные компактные множества, а индексом внизу указывать
пространство, которому принадлежит данное множество;

244
ХП. Представление в пространстве °L^{V\G)
например, Qq есть компактное подмножество группы G. Все такие
множества будут предполагаться фиксированными. Константы
в неравенствах зависят от выбора этих множеств.
т
О) (Ь)
Рис. 4.
Заметим сначала, что
(1) если x^Ff., то д;е Q;y,ajc/C с: ajcQ(3.
В самом деле, перемножая матрицы, легко проверить, что
(о ж ПЧ°о 'X 0=(о" °f)
и, следовательно, vj/ = и, u'^v~^u. Так как v^^c, то отсюда
вытекает, что Qn^^x с= UxQn, и наше утверждение очевидно.
Пусть (йх=х-^ах. Тогда
(2)
Сй«
Qn.
Более того, пусть й>^; „^Qi"'!/; мы утверждаем, что если
X. у
ф(л;~'т11/) =И= О для некоторого т] е Г^/, то можно считать, что
(3) щ, у е Q(j.
Чтобы доказать это, воспользуемся разложением
Левая часть равенства ^принадлежит компактному множеству^
мы уже видели, что элемент х'^а^ тоже лежит в компактном
множестве. Элементы '^"'■пПуа^ и a'^a^k принадлежат N и АК
соответственно и должны лежать в компактных множествах.
Следовательно, йу sa^jQ^, у е Na^Qj^K- Так как у можно
умножить слева на произвольный элемент из подгруппы Т^, то наше
"/тверждение теперь очевидно.

§ 4. Полная приводимость пространства "L^iVyO) 245
Лемма 1. Для любого натурального числа d существует
такая постоянная С(ф, d, F^), что
Доказательство. По определению,
R
Сделаем замену переменной, положив
W = v~'u, dw = и j' du.
Получим
Фх. у (^) = f л; S Ф (_«>л; (^ Q ^ ) <^х. у J е"^"'^"*'" Й^Ш = V^^^, д.. у (и^^Я,),
где
Ф<о. «. у {") = Ф I ®« I Q ij^x.yj, <^х, «>х. у ^ ^0-
Эта последняя функция бесконечно дифференцируема по и и
зависит от параметров, принадлежащих компактному множеству.
Интегрируя по частям d раз, получаем оценку
Чтобы вывести отсюда лемму, достаточно заменить X на v^X.
Воспользуемся полученным неравенством, чтобы оценить
сумму для ядра 1^{х, у), используя условие параболичности
CUSP1:
\ f [пу) dn = 0 для почти всех у ^G.
Как мы уже видели,
1^(ф)/(^)= S Yj ^x,y{fn)f{y)dy.
Член с /п = 0 равен
J \^(f,{x-^y)f{y)dndy= J J \^(f,{x~^nn'y)f{n'y)dndn'dy.

246 XII. Представление в пространстве ''L^{T\G)
Так как интеграл инвариантен относительно сдвигов, можно
заменить ф(х~'пп'г/) на ф(х~'пг/); таким образом, наше
предыдущее выражение равно
\ dy \dnc(i{x-^ny) \ dn'f{n'y)='Q,
N\G N Tf^\N
поскольку / — параболическая форма.
При тфО воспользуемся оценкой из леммы 1; получим
|я(ф)/(х)|< Y, \ v',-''-rir\f{y)\dy<
< «Г" \ \f{y)\dy< v^-'li {a^Qaf И / %>
гц\а
В силу неравенства Шварца. Итак, наша теорема доказана.

XIII. НЕПРЕРЫВНЫЙ СПЕКТР
В ПРОСТРАНСТВЕ LHTjG)
в этой главе мы изучим ортогональное дополнение
пространства параболических форм и получим для него спектральное
разложение, следуя работе Годемана [2]. Это доказательство
основано на формуле суммирования Пуассона; оно применимо
к арифметическим подгруппам Г. Его преимуществом является
краткость и простота, однако оно не годится для более общих
дискретных подгрупп; поэтому в следующей, последней главе
мы вновь рассмотрим этот вопрос, используя другие методы.
Спектральное разложение осуществляется при помощи
преобразования Эйзенштейна, которое отображает ортогональное
дополнение к пространству °1^(Г\С) и одномерному пространству
констант в пространство L^ на полуоси; при нашей нормировке
эта полуось будет верхней частью прямой Re s =: '/2-
Для простоты на протяжении всей главы мы будем считать,
что r=^SL2(Z). Ее максимальная унипотентная подгруппа
Гдг = Г П Л^ состоит тогда из матриц вида
ат).
/п е Z.
Факторпространство Г\С имеет конечный объем. Полезно иметь
в виду, что с точностью до сомножителя К справа
пространство r\G совпадает с пространством Г\^, где ф — верхняя
полуплоскость, ■& = G/K.
§ 1. Одно соотношение ортогональности
Тэта-преобразование
Пусть G=^NAK — разложение Ивасавы группы G=:SL2(R).
В § 2 гл. XI мы уже изучали однородное пространство N\Q.
Зададим в пространстве R^ правое действие группы G.
Стационарная подгруппа единичного вектора ^2=^(0' 1) ^сть в
точности N. Таким образом, пространство N\G изоморфно R^ — {0},
т. е. плоскости R^ с удаленным началом координат. Обозначим
символом S(N\G) (пространство Шварца на N\G) пространство
функций, полученных сужением на N\G быстро убывающих
гладких функций на R^. Таким образом, можно отождествить S {N\G)

248 XIII. Непрерывный спектр в пространстве 1'{Т\0)
н S(R^) (по ПОВОДУ определения пространства Шварца см.
Ленг [1]')).
Определим тэта-преобразование, переводящее функции на N\G
в функции на r\G, положив
Гф(х)= X ф(ух)
(ряд в правой части называется тэта-рядом). Преобразование
определено только для тех функций, для которых этот ряд
абсолютно сходится. Рассмотрим условия его сходимости. Если
С :)■
то е^у = (О, 1) Y = {с, d). Если Y ^ Г, то ad — be =1, (с, d) —
примитивный целочисленный вектор, т. е. числа с, d взаимно просты.
Обратно, любую пару {с, d) взаимно простых чисел можно
дополнить до 2Х2-матрицы игз группы SLziZ). Таким образом,
множество смежных классов Гдг\Г находится во взаимно
однозначном соответствии с множеством примитивных векторов
tn = {mi, Wa) решетки 7?.
Если ф — функция на N\G, обозначим символом ф [ • ]
соответствующую функцию на R^. Тогда
Гдг\Г m^Z' (с, d)-\
т prim
Ясно, ЧТО если функция ф принадлежит пространству Шварца
и, следовательно, быстро убывает на бесконечности, то этот
ряд сходится.
Пусть ф — функция на N\G с компактным носителем. Тогда
при любом у ^ G ряд
T(f(y)=^ S Ф(уг/)
содержит только конечное число ненулевых членов.
Доказательство. Пусть Q — компактный носитель функции ф.
Если ф (yj^) Ф о, то уу е Q. Существует элемент y' ^ Г^у. такой,
что y'yj^ ^ QjvQ, где Q^v — фиксированное компактное
подмножество группы N. Следовательно, у'у ^Qf/Qy-\ и наше
утверждение доказано.
Ясно, что если cfi^C^{N\G), то функция Гф непрерывна
на Т\0.
'') См. также любой kv^c функционального анализа, например Иосида [1].—
Прим. перев.

§ 1. Одно соотношение ортогональности 249
Если феС^(#\С), то функция Гф имеет компактный
носитель.
Доказательство. Пусть Q — компактное подмножество
группы G, такое, что носитель функции ф содержится в
множестве N\NQ. Если ф (yj^) Ф О, то yj^ ^ ^^- Существует
элемент y'^Tjv, такой, что у'уу ^Q[jQ, где Од, — фиксированное
компактное подмножество группы .V. Следовательно, у е rQo>
где Qq — компактное подмножество группы G, что и
требовалось показать.
Из доказанных утверждений ясно, что тэта-преобразование
можно рассматривать как отображение
Т: CAN\G)->CAr\G).
Так как группа Г содержит матрицу —1, то сумма по
примитивным элементам решетки Z^ симметрична относительно
начала координат. Представим функцию ф в виде суммы
четной и нечетной функций на R* — {0}; ясно, что если ф нечетна,
то Гф^^О. Итак, в дальнейшем при рассмотрении
тэта-преобразования можно без потери общности предполагать, что
функция ф четна, т. е. ф(х) = ф(—jc).
Сопряженный оператор к тэта-преобразованню
Рассмотрим отображение Г", сопоетавляющее функциям-
на r\G функции на N\6 и действующее по формуле
П(г/)= \ f{ny)dn.
Таким образом, оператор Г® задается интегралом,
участвовавшим в определении параболических форм. В каждой
конкретной ситуации мы всегда будем указывать, в каком
функциональном пространстве рассматривается этот оператор. Обычно
это будет L^(r\G), и тогда подпространство параболических форм
°1^{Г\0) совпадает с ядром оператора Т°.
Отображения Т и Т° являются сопряженными. Другими
словами, если выполнены условия абсолютной сходимости, то
(1) {Tcf,f)^^^ = {cf,TOf)^,^,
где скалярное произведение определяется при помощи обычного-
интеграла.
Замечание. Приведенное соотношение справедливо для любой
пары замкнутых подгрупп Г и Л^ группы G. По существу, оно-
представляет собой абстрактное соотношение, пригодное для

250 XIII. Непрерывный спектр в пространстве L^{T\G)
любой локально компактной группы и двух ее замкнутых
подгрупп. В частности, не используется дискретность Г. Сначала
мы проведем формальное вычисление, не уточняя условий
сходимости интегралов. Меры на группах и факторпространствах
нормируются согласованно, в соответствии с
последовательностью групп
Имеем
<^Ф. /)г\о = \ ^Ф (^) f (У^ ^У =
= ] ] ^{ny)f{ny)dndy =
== 5фЫ 5 JJny)dndy^{^,rf\^g.
N\e Гдг\^
Теорема 1.
(i) Приведенное соотношение справедливо для f ^ L? (Г\0)
(ii) Функция Гф ортогональна подпространству °1^(Г\0).
(iii) Если f ^. L? (Г\С) и функция f ортогональна всем
функциям вида Гф, феС<.(Л^\С), то fs''L^{r\G).
(iv) Пусть ф — преобразование Фурье функции ф,
рассматриваемой как функция на R . Тогда ф [0] = О в том и
только в том случае, когда функция Гф ортогональна
константам на Г\0.
Доказательство. Все эти утверждения немедленно следуют
из соотношения (1). Напомним, что преобразование Фурье
функции на R^ задается формулой
ФИ= 5ф[|]e-^«'^*4•
Правоинвариантная мера на однородном пространстве N\Q
совпадает с мерой Лебега на R^, поэтому
ф[0]= 5 cf{y)dif.
N\a

§ 2. Ряды Эйзенштейна 251
Условие ф[0]=0 эквивалентно тому, что
Таким образом, функция Гф ортогональна константам на Г\С_
§ 2. Ряды Эйзенштейна
Для любой функции ф на N\G и для любого числа s, для
которых написанный ниже интеграл сходится, определим дзета-
преобразование формулой
оо
2(ф; у, 2s) = ^ф(аг^)р(а)~'^ da=^ (f> (кау) а--'-^.
А О
Мы используем наши обычные обозначения, т. е.
К
(а О Л
Если ф е S {N\G) ц ff = Re S > О, то интеграл, определяющий
дзета-преобразование, абсолютно сходится.
Доказательство. Заменим функцию ф ее правым сдвигом на
элемент у и будем рассматривать ф как функцию на R^. Тогда
наш интеграл примет вид
оо
\ /[(0. а-')]а-2^^.
о
Сделаем замену переменной ау-*а~^ и воспользуемся
инвариантностью меры daja при этом преобразовании. Теперь
сходимость интеграла очевидна.
Прежде чем переходить к другим признакам сходимости,
заметим, что функция г(ф) удовлетворяет функциональным
уравнениям
Z (ф; пу, 2s) = Z (ф; у, 2s), n^N,
Z (ф; ay, 2s) == Z (ф; ^, 2s) p (a)^,. a e Л,
T. e. принадлежит пространству индуцированного представления
//(2s—1). Если функция / на группе G удовлетворяет
условиям
f{ny) = f{y), fiay)=^f{y)9{aY%

252 XIП. Непрерывный спектр в пространстве L'{T\G)
ТО будем говорить, что она имеет тип 2s. Мы воспользуемся
понятием типа при доказательстве теоремы 3 в § 7.
Изучим теперь аналитические свойства
дзета-преобразования при различных условиях на функцию ф.
Лемма 1. Если ф е Q {N\G), то Z (ф; у, 2s) — целая функция
переменной s.
Это утверждение практически очевидно, так как
подынтегральное выражение не имеет особенностей ни в нуле, ни на
Рис. 1.
бесконечности. Мы уже встречались с такой ситуацией в § 3
гл. V.
Лемма 2. Для любой функции ф е S {N\G) ряд Эйзенштейна
Е (ф; у, s)= X Z (ф; yj^, 2s) == TZ (ф; у, 2s)
абсолютно сходится при Res> 1.
Доказательство. Функцию ф можно заменить ее правым
сдвигом на элемент у ^G; поэтому достаточно доказать
утверждение леммы при у = е, т. е. рассматривать сумму
Z 2(ф; Y, 2s).
Но если
/ * * \
^==U d)'
со
г(ф; Y, 2s) =^ ^[е2Ку]а--^-^==
о
оо во
= \ ф[(с/а, u«/a)]a-2«-^=^ Ф [(ас, ad)]a^'-^
то
da

§ 3. Аналитическое продолжение и функциональное уравнение 253
Пусть т = {с, d) пробегает все пары взаимно простых целых
чисел (или даже все пары целых чисел). Разобьем сумму по
всем таким т, просуммировав сначала по тем точкам, которые
лежат в кольце радиуса п и ширины 1 (например, по
отношению к обычной евклидовой норме). Пусть т — точка из этого
кольца, т е Z^. Мы хотим оценить соответствующий ей член
ряда. Выберем число С, такое, что если | s R^ и || | > С, то
I ф [|] I "С 1/11 Р""*"*. Разобьем наш интеграл на два слагаемых:
С/п
\+\
_2ff
Cm
Первый интеграл не превосходит
с/п
\ I ф [am] I а"-' da < а"-" Р < 4
о "■
Второй интеграл не превосходит
оо оо
5|ф[а;п]|а-'^а< l.^^da«^.
с in С/п '
Число точек решетки в нашем кольце по порядку величины не
превосходит п. Таким образом, сумма по всем этим точкам не
превосходит 1/п°. Суммирование по п завершает доказательство
леммы.
§ 3. Аналитическое продолжение и функциональное
уравнение
Пусть ф е S (N\G) = S (R^). Будем рассматривать ф как
функцию на R^; ее обычное преобразование Фурье задается
формулой
где d| — мера Лебега. Тогда ф=:ф-, где ф-[2]=ф[—z]. (По
поводу преобразования Фурье и связанных с ним элементарных
вопросов см. Ленг [1].)
Для произвольного элемента y^G положим д='*у~К
Замена переменных показывает, что преобразованием Фурье
функции
I >-» Ф [lay]
служит функция
|^ф[|а-'Р]а-».

254 XIII. Непрерывный спектр в пространстве U(T\0)
Поэтому ИЗ формулы суммирования Пуассона следует, что
(1) Z ф[/паг^]= Е фltna~^g]a-^
т eZ' m е Z'
Мы воспользуемся этим соотношением при доказательстве
следующей теоремы.
Заметим, что если феС^(Л/^\0), то ф[0] = 0. Отсюда, конечно,
не следует, что ф [6] = 0. В некоторых приложениях следующей
теоремы мы будем иметь дело с функциями ф^ С(.(Л/^\0); однако
нам нужно, чтобы эта теорема была применима и к функции ф.
Теорема 2. Пусть ф е S (N\G) — четная функция;
предположим, что ф [0] = ф [0] = 0. Положим
Г(ф; у, 5) = $(25)£(ф; у, s).
Тогда Е* — целая функция переменной s, и справедливо
функциональное уравнение
Г(ф; у, 5) = Г(Ф; д, 1 -s).
Доказательство. По определению,
оо
da
Z (ф; у, 2s) = ^ ф (h^y) а
о
Пусть
-2s
а
/ * * \
'^Кс dj-
Тогда
оо оо
Z (ф; уу, 2s) = 5 ф [{ас, ad) y]a^^^=\cf> [may] а^" -^
о о
и
оо
£(ф; j^, s)= Yj \^['пау]а'''-^.
m е Z', о
m prim
Умножим обе части этого равенства на S(2s) и воспользуемся
формулой
S(2s) = ^
п2а

§ 3. Аналитическое продолжение и функциональное уравнение 255
Получим
\2s da_
а
l{2s)E{^; У, s)=^Y, Е \^{may\{alnf
rt—1 т prim О
оо
= 5 Е '^{may]d^'-^-=
О m S Z'
00 I
1 /п - От
оо ]
= J. 2 Ф [/па//] а2. ^ + J J^ ф [^0-1^] «2.-2 ^ _
i m От
оо оо
\ т \ т
на последнем шаге мы сделали во втором интеграле замену
переменной ау-^а~^. Каждый из двух последних интегралов
является целой функцией от s, и их сумма инвариантна
относительно преобразования
(ф, у, 5)ь^(ф, ^, 1 —s).
(Мы воспользовались тем, что ф = ф- и ф~=ф, так как, по
предположению, ф — четная функция.) Теорема доказана.
Положим, по определению,
ф (j^) = Ф {е2У] == Ф [e^yw],
где, как обычно,
^ = (-1 о)-
Заметим, что wyw~^ =^Q. Кроме того, отображение т^—^тха
переводит решетку Z^ в себя. Поэтому
X ф[/паг/]= Yu ф [/пш^ш-'аш]= 2] ^[тау\.
Отсюда получаем
Следствие.
Е* (ф; у, s) = Е* (ф; у, 1 — s).
Преимуществом этой записи является то, что аргумент у
одинаковый в обеих частях формулы.

256 Kill. Непрерывный спектр в пространстве V^{T\G)
§ 4. Дзета-преобразование и преобразование Меллина
Пусть f — гладкая быстро убывающая функция на R. В гл.. V
мы уже рассматривали преобразование Меллина
ао
da
Mf{2s) = ^ f(a)a2*-
для функций с компактным носителем, не содержащим точки 0.
В этом случае функция Mf — целая. Для / е S (R) написанный
интеграл абсолютно сходится в полуплоскости Re s > 0. Кроме
того, интеграл
сходится при всех комплексных s и определяет целую функцию.
Возможные полюсы преобразования Меллина связаны с
поведением функции f в окрестности нуля.
Лемиа 1. Если f е S (R) и f (0) = О, то Mf (2s) — мероморф-
ная функция переменной s, которая имеет разве лишь простые
полюсы в точках
__1 _1 1
Доказательство. Так как, по предположению, f (0) = О, то
f{a) = afi{a), где fj —гладкая функция. Интегрирование и@
частям в интеграле
1 1
\f(a)a'^^^\fia)a'^-^da
о о
приводит к выражению
2s+1
' 1_
о 2s +
1
J 5 /; (а) а2^+' da.
Последовательное интегрирование по частям завершает
доказательство.
Применим доказанную лемму к функции f, которая задается
формулой
/(а) = ф[(0, а) у],
где ф е СГ {N\G) = СТ (R^ — {0}), у е G. В этом случае функция
М/(2з) = 2;(ф; у, 2s) — целая. Однако, если перейти к
преобразованию Фурье, то носитель функции ф не обязательно отделен

§ 4. Дзета-преобразование и преобразование Меллина 257
ОТ куля. Тем не менее наша лемма по-прежнему применима
к функции
Z (ф; у, 2s) = Mf (2s), где f (а) = ф [(О, а) yw\,
если предположить, что ф [0] = 0.
Рассмотрим функцию g, определенную в полосе
ffo^cr = Res ^ 01.
Будем говорить, что эта функция быстро- убывает на каждой
вертикальной прямой равномерно в полосе, если для любого
натурального числа d существует такая постоянная С, что
|£(0 + /т)|<
для всех а + ix из нашей полосы. (Мы пишем 2d, чтобы
показатель степени был четным и оценка имела смысл при любом
знаке т.) Мы будем рассматривать также функции, которые
имеют в полосе конечное число полюсов и для которых
приведенная оценка справедлива в полосе с удаленными
окрестностями этих полюсов.
Лемма 2. Пусть / s S (R); предположим, что f (0) = 0. Тогда
функция Mf{2s) быстро убывает на любой вертикальной прямой
равномерно в каждой полосе Оо^а ^ CTi, за исключением
окрестности полюсов.
Доказательство. Предположим сначала, что Re s > 0. Для
любого целого п> О мы получаем, после интегрирования по
частям,
{2s+[){2s + 2) ... (2s + п) Mf (2s) = Mf'"' (2s + n),
где f'"' есть п-я производная функции f. Это выражение
ограничено. Следовательно, функция Mf убывает быстрее любой
степени. По принципу аналитического продолжения, это
справедливо при всех S, за исключением окрестности полюсов.
Действительно, если S — точка полосы, всегда можно выбрать столь
большое п, что Re s + « > 0.
8 гл. V мы уже видели, что замена переменных превращает
преобразование Меллина в преобразование Фурье. Имеет место
следующая
9 За к. 589

258 Xlll. Непрерывный спектр в пространстве L'(r\G)
Лемма 3. Пусть ст = Re s > 1. Предположим, что функции f, g
на полуоси таковы,, что функции f{a)a^^~^ и g(a)a~^^
принадлежат пространству 1^ Tr"''; -j-J fl Ь' (ж^', -^J . Тогдл
оо оо
\!{а)Ш)а-'^=\! (а) a^'"^g{a)a--^ -^ =
о о
= -1- \ Mn2s-2)Mgi-2s)ds.
Res-o
,•-1
{На вертикальной прямой ds = i dx, поэтому мера i ' ds
вещественна. )
Доказательство. Положим а2 = е*; таким образом, а = е*®.
Тогда
da 1_ ,.
а 2 ■
Пусть S = (т + /т. Положим
f, (Ь) = / (е»й) gb (0-0 ^ g, (6) = g (е»/2) е-бв.
Тогда fl, gi S L^ (R) П L'(R), и применима обычная формула
Планшереля:
<fi, gi) = (fi, ^i).
В этом доказательстве мы пользуемся следующей нормировкой
преобразования Фурье:
^'(^)=vk 5мь)в-'ь^^ь.
и аналогично для g'l. В терминах преобразования Меллина это
означает, что
f, (т) = -^ Mf {2s - 2), й, (т) = -^Mg (-25).
Следовательно, скалярное произведение функций fj и ^] равно
оо
-f \fA-^)IJ^)dt = ^ \ Mf{2s-2)Mg{-2s)ds,
Res—о
ЧТО И Требовалось доказать

§ 5. Некоторые теоретико-групповые леммы 259
Предостережение. При переходе от преобразования Меллина
к дзета-преобразованию нужно внимательно следить за
знаками. Если 6 — функция на N\G и f (а) = 6 (Л^г/), то
оо
Mf (2s) = 5 9 {h,y) а2. ^ = z (6; у, - 2s).
§ б. Некоторые теоретико-групповые леммы
Двойные смежные классы
Как и прежде, мы полагаем Т^/==ГГ\М. Представим группу Г
в виде объединения двойных смежных классов:
Г=иГлгУгГл,.
i
Если TffyiTf/ ф ± Yif, то элементы {угЛ}. Л ^ Г^у, образуют
систему представителей множества правых смежных классов,
принадлежащих двойному классу Гл^у^Гд^; другими словами,
множество TffytTff представляется в виде объединения правых
смежных классов:
i\srf,
Доказательство. Если цфц', ц, л'^ Гу, то Гл^у<Л=7^Гл^угЛ'-
Действительно, в противном случае нашелся бы такой элемент
TjiSFjv, что Ц\У1'г\ = У1У\' и, следовательно.
УГ'Л]У, = Л'Л-' ^Tj^,
откуда У1^± Tff.
Немедленно проверяется также, что множества Tf/yTf/ и
— Гд^уГ'лг различны при всех у ^ Г; таким образом, двойные
смежные классы разбиваются на пары.
Разложение Брюа
Напомним кратко разложение Брюа, которое было подробно
изучено в § 2 гл. XI.
Группа G допускает однозначное разложение
G=^±NA{j± NAwN,
где
W
-и :)•
9*

260 XIII. Непрерывный спектр в пространстве L^(T\G)
Доказательство основано на изучении пространства N\G,
которое естественно вкладывается в R^, так как стационарная
подгруппа точки 62 = (О, 1) S R^ совпадает с Л^. Запишем элемент
у е NAwN в виде
у = n'yhywn'y',
это разложение однозначно, и элемент hy ееть Л-компонвнта
матрицы t/ в разложении Брюа.
Заметим, что если
/1 «'Wl/c 04/0 -U/1 и"\
^ = U iJU Jll oJU 1 )'
то
Следовательно,
§ 6. Выражение для функции Г«Гср
Пусть ф е С^(Л^\0)| предположим, что функция ф четна, т. а.
ф(д;) = ф(—л;), Обозначим симво^юм (у) нетривиальные пары
двойных смежных классов'.
Пусть hy есть А-компонвнта разложения Брюа матрицы Y-
Рассмотрим функцию
ГОГф(г/)=- \ Y. ^{yny)dn.
V^\N Глг\Г
В предыдущем параграфе мы установили связь между
множеством представителей правых смежных классов из пространства
Tif\T и множеством представителей двойных смежных классов
по подгруппе Г^у. В написанной выше сумме член,
соответствующий смежному классу матрицы ± 1, дает вклад
2 J ф (nj^) rfn = 2ф (j^).

§ 6. Выражение для функции РГф
261
Таким образом,
-i Г«Гф {y)=cf{y) + J]\cf (упу) dn =
(Y) N
^<fiy) + Yj \^ {hywn'yny) dn =
(Y) ЛГ
= Ф (J^) + 5] S Ф (hywny) dn =
(Y) ЛГ
(Y) ЛГ
-.<.)+zM4; ?)(:- .;j^)
^u.
lY) R
После замены переменных получаем
(1)
Сумма 2c(y) следующим образом связана с ^-функцией
Римана. Положим
(Y) ^^'
тогда имеет место тождество
(3)
_ V *М. —iJ^izLlL
F{s)^Y.
„is
m-l
;(2s)
где <j> — функция Эйлера. Чтобы доказать это, заметим, что
каждая пара (с, d) взаимно простых целых чисел (с > О,
O^d < с) соответствует в точности одной паре двойных
смежных классов; это ясно из формул
/1 т\/' а Ь\ /* *^
VO 1 )\с dj'^yc d)
и
/а b\/'l т\ /* * Ч
\с dJKO 1 J'^Kc d + mcj'
Отсюда следует, что F (s) = X ^ {m.)/ni^\

262 XUl. Непрерывный спектр в пространстве L'(r\0)
С другой стороны, пусть / — функция на множестве
положительных целых чисел, такая, что / (т) = ш, и ц — функция
Мёбиуса; тогда свертка
(M.*/)(m)-Eix(d)/(m/d)
переводит / в функцию Эйлера, т. е. у^*! = <!>. Так как
£(2»-')-Z^-Z
т" '—' т^
отсюда вытекает наше выражение для F (s) через
дзета-функцию, поскольку умножение рядов Дирихле соответствует свертке
их коэффициентов.
Замечание. Функция Мёбиуса, функция Эйлера и функция /
мультипликативны. При вычислении сверток таких функций
достаточно проверять формулы только для степеней простых
чисел, а в этом случае проверка не представляет труда. Далее,
функция Мёбиуса и постоянная функция, равная единице,
взаимно обратны относительно свертки; таким образом,
-I
„2s
S(2s) ^ m
Пользуясь этими замечаниями, читатель может легка проверить
соотношение / = ^*1, нужное для доказательства формулы (3).
§ 7. Аналитическое продолжение дзета-преобразования
функции ГТср
Мы собираемся исследовать функцию 2(Г°Гф; у, 2s). Начнем
с некоторых замечаний о функциях вида 2(Г°9; у, 2s), где не
обязательно 9 = Гф.
Будем рассматривать оператор Г° как отображение
7°: Q(r\G)-> ВС (iV\G),
т. е. как отображение в пространство ограниченных
непрерывных функций.
Лемма 1. Если 6еС(.(Г\С), то Т°&{каУ) = 0 при достаточно
больших а.
Доказательство. По определению,
T%{h„y)= 5 Q{nh„y)dn.
Vn\N
При а-*оо элемент nh^ стремится к бесконечности (т. е. при
достаточно больших а этот элемент попадает в дополнение лк>»

§ 7. Аналитическое продолжение дзета-преобразования функции Т'Тц) 263
бого наперед заданного компактного подмножества). Таким
образом, подынтегральное выражение равно нулю при
достаточно больших а; лемма доказана.
Лемма 2. Интеграл
оо
Z {Т% 1/, 2 - 2s) = 5 rQ {hay) а2*-2 -^
о
абсолютно сходится при Res> 1.
Доказательство. В силу леммы 1 интеграл в действительности
берется по компактному промежутку; поэтому можно оценить
его сходящимся интегралом
Q20-2 ii. _ _£!"
„ia-2
о
а 2а —2
о
лемма доказана.
Теорема 3. Пусть ф е СГ {N\G) — четная функция;
предположим, что ф [0] = ф [0] = 0. Тогда при Re s > 1 справедливо
равенство
12(Г»Гф; у, 2-25) = 2(ф; у, 2 - 2s) + i|^ Z (ф; у,.2-2s).
Правая часть этого равенства — мероморфная функция на всей
плоскости; таким образом, она дает аналитическое продолжение
левой части. Эта функция голоморфна при Res^72-
Для доказательства этой теоремы мы проведем ряд
вычислений и преобразований, итогом которых будут приведенные ниже
соотношения (1), (2) и (3). Мы будем пользоваться следующими
обозначениями.
Пусть Res> 1; А-компоненту разложения Брюа элемента у
будем обозначать h^. Если а — положительное вещественное
число, то соответствуюи^ую матрицу из подгруппы А мы
обозначаем ha-
/а о Ч
Это не может привести к недоразумениям, так как а и \
принадлежат различным множествам.

264 XIII. Непрерывный спектр в пространстве IJ{T\Q)
Применим дзета-преобразование к соотношению, полученному
в предыдущем параграфе. Пользуясь леммой 2, мы получаем
для произвольной функции (f^Cc(N\G):
^ Z {РТг, г/, 2 - 2s) = у ^ РГф (hy) а (ЬУ'-'- dh =
А
= Z (ф; у, 2 — 2s) + ^ с (у)~^ \ \ ф (wnlt^^hy) а {hf^~^ dn dh.
(V) N А
Сделаем во втором члене замену переменной h\-^h^h (заметим,
что a{h^ = c{y)~ ), Он примет следующий вид:
S с (y)"^' \ \ Ф {wnhy) а (hf'-' dn dh =
(V) Af A
'F{s)\ J Ф (whny) a {hf' dn dh =-
JV A
■■F{s)^ J Ф (h-^wny) a {hf dn dh ■■
N A
■ P{s) \ \ Ф {hwny) a {h)~^^ dn dh.
N A
Таким образом, мы доказали формулу
(1)
4 Z (ГГф; у, 2-2s) = Z (ф; у, 2-2s)+F (s) J Z(ф; wny, 2s) dn,
справедливую в полуплоскости Res>l для всех (р ^Cc{N\G).
Заметим, что функции Z(Г°Гф•, у, 2 — 2s) и Z(ф•, у, 2 — 2s)
имеют тип 2 —2s; таким образом, второе слагаемое в
правой части формулы (1) имеет тот же тип по крайней мере
при Res>I. Мы получим сейчас, используя другой подход,
аналитическое продолжение этого слагаемого. Нашей целью
является доказательство приведенной ниже формулы (2).
Как мы видели, в полуплоскости Res> 1 справедлива
формула
^(ф; у, s) = ГZ(ф•, у, 2s) = Z 2(ф; уу, 2s).
Следовательно,
T°TZ{q>; у, 2s)== \ J] Ъ{,^; упу, 2s)dn,
Tfj\N Гл,\Г

§ 7. Аналитическое продолжение дзета-преобразования функции Т°Т(р 265
Как и выше, разобьем сумму по двойным смежным классам
на две части, разделив вклады от тривиального и
нетривиальных классов. Получим
}r'TZ{<pi у, 25)=2(ф; у, 2s)+ Y, ^^(ф; упу, 2s)dn^
(V) JV
= Z (ф; у, 2s) + ^ \ Z (ф} hywrC^ny, 2s) dti =
(V) JV
= Z(ф; у, 2s) + ^ ^ 2(ф; h^wny, 2s)dn.
(V) 'V
Воспользуемся тем, что функция 2(ф; у, 2s) имеет тип 2s:
2(ф; Л,шлг/)=c(Y)"^*Z(ф, хюпу).
После этогр сумма по двойным смежным классам легко
вычисляется, и формула принимает следующий вид:
(2)
\ ТЧЪ (ф; у, 2s) = Z (ф; у, 2s) + f (s) J Z (ф; mny, 2s) dn.
Докажем теперь соотношение, которое заканчивает
доказательство теоремы 3: при Res> 1
(3)
F{s)\l (ф; wny, 2s) dn = Щщ^ Z (ф; у, 2- 2s).
Доказательство. Кроме уже известных нам фактов об
аналитическом продолжении рядов Эйзенштейна, необходимо будет
дополнительно исследовать тип функций, входящих в эту
формулу.
Умножим обе части формулы (2) на С (2s) и положим
L (ф; у, 2s) = у S (2s) T°TZ (ф; у, 2s).
Из результатов § 3 об аналитическом продолжении рядов
Эйзенштейна следует, что L (ф; у, 2s) — целая функция, инвариантная
относительно преобразования
(ф, s) ь-з- (ф, 1 — s)
(см. следствие из теоремы 2).
Выражение
1(ф; у, 2s)-e(2s)Z(ф! Z/. 2s)

266 XIП. Непрерывный спектр в пространстве L'(r\G)
равно последнему члену в формуле (2), умноженному на S(2s).
Это выражение мероморфно и, в силу формулы (1) и принципа
аналитического продолжения, имеет тип 2 — 2s при всех
комплексных S. Сделаем преобразование (ф, 5)ь-5-(ф, 1 — s). Из
сказанного ясно, что функция
L (ф; г/, 2 - 2s) - S(2 - 2s) 2(ф; у, 2- 2s)
имеет тип 2s. Непосредственно из определения мы знаем, что
функция Z (ф; г/, 2 — 2s) имеет тип 2 — 2s. В силу результатов
§ 4 эта функция мероморфна. Получаем
1(ф; у, 2-2s)-S(2-2s)Z(ф; г/, 2 - 2s) =
= L (ф; у, 2s) - S (2 - 2s) Z (ф, у, 2- 2s).
Другими словами, левая часть формулы (2), умноженная на t,{2s),
равна
1(ф; у, 2s) = S(2 —2s)Z(ф; у, 2 — 2s) + члены типа 2s.
Поскольку такое разложение в сумму членов типа 2s и 2 — 2s
однозначно, отсюда следует, что члены типа 2 — 2s в обеих
частях формулы равны, а это как раз и есть соотношение (3).
Доказательство теоремы 3 закончено.
Теорема 4. Пусть ф е С" {N\G), и предположим, что ф [0] =0.
Тогда функция
1{Т<Г(р; у, 2-2s)
мероморфна и не имеет полюсов в полуплоскости Re s ^ '/2- ^'^^^
функция, а также функция
Z(ф;г/, 2-2s)
быстро убывает на любой вертикальной прямой в полуплоскости
Res^72 равномерно в любой полосе конечной ширины.
Доказательство. Дзета-функция Римана g(2s) не имеет нулей
при Re2s^l или, иначе говоря, при Res^72- Поэтому
знаменатель t,{2s) в теореме 3 не приводит к появлению
особенностей в рассматриваемой области. Быстрое убывание на
вертикальных прямых вытекает из леммы 2 § 4.
Мы воспользуемся теоремами 3 и 4 при выводе теоремы
разложения. Для доказательства этой теоремы необходимо
сместить контур интегрирования в формуле Планшереля из
леммы 3 § 4 на прямую Res = 72- Теоремы 3 и 4 как раз и
позволяют это сделать, так как из них следует, что
подынтегральная функция антиголоморфна по s и быстро убывает при
Ims->-oo.

§ 8. Теорема разложения 2вТ
Заметим, что если Res ==0 = 72. то I — S'^s; таким
образом, формула в теореме 3 принимает вид
(4)
|2(Г0Гф; у, 2s)=Z(9; у, 2з) + ^Щ-Ъ{ф; у, 2s).
§ 8. Теорема разложения
Пусть / — функция типа 2s на группе G. Тогда f Фпредв-
ляется своим сужением на подгруппу К в разложении G = NAK.
Поэтому такую функцию можно рассматривать только на /С;
ее сужение на подгруппу К мы будем обозначать той же
буквой, опуская переменную у ^ G. L^ норму на К будем ©бозна-
чать \\-\\к; по определению,
e/l^-Jl/WN^.
Мы будем пользоваться аналогичным обозначением для L^-нормы
и скалярного произведения на любой другой группе или
однородном пространстве.
Как мы знаем из теоремы 1 § 1, тэта-преобразование
переводит пространство СТ {N\G) в ортогональное дополнение
пространства параболических форм; кроме того, из
дополнительного условия ф [0] = О вытекает, что функция Гф ортогональна
постоянным. Сейчас мы докажем, что коядро тэта-превбразова-
иия этим и исчерпывается. Это будет вытекать из соотношения
полноты.
Теорема 5. Пусть ф, ifi s СГ (iV\G) — четные функции, такие,
что
ф[0]=ф[0]==0.
Тогда
{Тер, Щ^^а-4й S <2(Г°Гф; 2s), ZCrTif; 2s))jcd*.
lms>0
Доказательство. Формальное вычисление, предпосланное
теореме 1 § I, в данном случае оправдано и дает
(Гф, riij)r^о = {^Тч>, ^)„^о « 5 ГТф (у) ^ (у) dy =
N\a
J 5 Г^Гф {ak) ^^Щ р (а)"' da dk.
к А

268 XI[I. Непрерывный спектр в пространстве L^{r\G)
Воспользовавшись выражением для формулы Планшереля,
которое было получено в лемме 3 § 4, преобразуем это скалярное
произведение к виду
(1) (Гф, Га|))гдо = ^ 5 5 Z (Г^Гф! k,2- 25) Ъ{^1 k, 2s) ds dk.
к Re s-o,
Внутренний интеграл в этой формуле берется по вертикальной
прямой Re 5=00 с некоторым 0о>1- Как мы уже отмечали, по
теореме 4 из предыдущего параграфа контур интегрирования
можно сместить на прямую 0 = 72. поскольку подынтегральная
функция антиголоморфна и быстро убывает в полосе между
прямыми 0 = V2 и 0 == Сто > 1.
С другой стороны, при Re S > 1
EW, s) = rZ(a|); 2§).
Пользуясь формальным выражением для сопряженного опера»
тора к тэта-преобразованию, получаем
{Гф, £(ф; 5))г\о = {Гф, ТЪ{^- 2s))r^o =
= {Г''Гф, Ъ{^; 2s))^^^ =
= J J Г^Гф {ak) Z (a|); afe, 2f) p (a)"^ da dfe.
к A
Ясно, что в рассматриваемом случае проведенные выкладки
корректны. Так как функция Z (ijj; у, 2s) имеет тип 2s, последнее
выражение равно
(2) J Z (Г»Гф; А;, 2 - 2s) Z(i|5; k, 2s) dk,
К
Это равенство доказано первоначально при Res>l, но по
принципу аналитического продолжения оно справедливо вплоть
до прямой Re 5 = 72- Умножим обе части этого соотношения
на t,{2s). При Re5=72 имеем 1 — s = l. Поэтому, вспоминая
наше определение
Е'{^\ s)^l{2s)EW, 8),
мы получаем при Re s = 72
(3) <Гф, Е*(lij; s)\^a = \ 2(ГТф; k, 2§)I(2s)ЪЩХЩdk,
к
Из инвариантности функции Л* относительно преобразования
(•ф, s)i—^(ф, s) (на прямой Res = '/2) вытекает, что интеграл

§ 8. Теорема разложения
В формуле (3) тоже инвариантен относительно этого
преобразования. Поэтому его можно переписать в виде
(4) \ Ъ{Г«Гф; k,1s)l(2s) t{^\ k, 2s)dk\
к
таким образом, разделив формулы (3) и (4) на t,{2S), мы
получаем
5 Z(Г°Гф; k, 2а)l{p, k, 2s) = J Z(Г°Гф! k, 2s)^Щ-2(-^; k,2s)dk.
к к
Заметим, что в интеграле (1) для скалярного произведения
(Уф, Г'Ф)г\а можно изменить порядок интегрирования, поскольку
подынтегральное выражение быстро убывает. Следовательно,
(Гф, 7''Ф)г\о="-^Г i \'^(Т^т k, 2s)Z(i|); k, 2s)dkda.
Ho
J f{s)ds=- J f(§)£/s
(интегралы берутся по полупрямым s = 1/2 -|- h, т s (О, оо) и
te(—оо, 0)). Таким образом,
<Гф, Щ^^а = ^1 \ \'Z'iT°T^ k, щЩГкГЩйкйз-]-
ч, к
-f-Jr 5 \г(Г«Гф5 k, 2S)Z(i|3; jfe, 25)dA:dsi
у« /с
в силу теоремы 3 (ем. также конец предыдущего параграфа),
это выражение равно
1/j + iOO
-1- J 5 Z (ГОГф; k, 2s) [Z (ij,; fe, 2s) +1||- Z (of.; k, 2s)] d& ds =
l/j + iOO
: -gij- 5 J Z (Г°Гф5 ;fe, 2s) Z(rOfi|)| Й, 2s) dA; ds =
V. к
'/«+<■«>
-J- 5 (Z(Г''Гфl 2s), Z(7oriij; 2s))i^d9.
55
Теорема доказана.

270 XIII. Непрерывный спектр в пространстве L^(T\G)
Замечание. В предыдущих рассуждениях мы могли бы
с тем же успехом интегрировать и по нижней половине прямой
а = 72-
Полученная нами теорема показывает, что оператор Т" изо-
метричен на образе оператора Т. Более того, имеет место
Следствие. {Гф, Т^)^,^^ = {Г>Т((>, Т°Т^)^,а-
Доказательство состоит в формальных выкладках и
предоставляется читателю.

XIV. СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ
ОПЕРАТОРА ЛАПЛАСА НА г\^
В этой главе мы в основном следуем статье Л. Д. Фаддеева [1];
добавлен лишь ряд деталей, опущенных в его работе.
Собственные функции оператора Лапласа на верхней
полуплоскости, инвариантные относительно дискретной подгруппы
группы 5L2 (R). были введены Маасом [1], [2] как аналог
классических автоморфных форм. Затем они были исследованы
в двух работах Рёльке [1], [2] и, совсем недавно, в работе
Эльстродта [2]. Эти функции нашли важное приложение в
работе Сельберга [2] о формуле следа. Связь теории автоморфных
функций с теорией бесконечномерных представлений групп Ли
была впервые замечена в работе И. М. Гельфанда и С. В.
Фомина [1] и исследовалась затем в работах И. М. Гельфанда,
И. И. Пятецкого-Шапиро и М. И. Граева (см. список
литературы в конце книги).
Пусть Г —дискретная подгруппа группы SLjCR). такая, что
объем пространства Т\^ конечен. Фундаментальная область F
этой группы состоит из компактной части Fq и конечного числа
«вершин», конформно эквивалентных верхней части полосы.
Оператор Лапласа L можно расширить до самосопряженного
оператора А в гильбертовом пространстве V{r\^). Нашей
задачей является построение спектрального разложения
оператора А. В гл. XII мы построили инвариантное подпространство
°1^(Г\ф) — так называемое пространство параболических форм —
и показали, что спектр сужения оператора А на это
подпространство дискретен. Оказывается, что, кроме этого, оператор А
имеет непрерывный спектр конечной кратности (кратность
спектра равна числу вершин фундаментальной облэ'ти) и
конечное число собственных значений, принадлежащих интервалу
[— 1/4, 0]. Мы хотим описать все собственные подпрсстранства
оператора А и найти ядро 'ц{г, s) преобразования, которое
переводит А в простой оператор умножения (в нашем случае это
будет оператор умножения на функцию ^li-ht^, действующий
в пространстве вектор-функций; / — вещественная переменная).
Ядро Т1 (z, s), где z^F и S принадлежит подходящему
пространству, называют функцией Эйзенштейна, а соответствующее
преобразование—преобразованием Эйзенштейна. Функция
Эйзенштейна удовлетворяет некоторому функциональному уравнвито,
которое тесно связано с рассматриваемой теорией. Этим
вопросам посвящена книга Куботы [1].

272 XIV. Спектральное разложение оператора Лапласа на Г\ §
Наиболее важные и изученные дискретные подгруппы
SL^ (R) — это группа SL2 (Z) и ее конгруэнц-подгруппы. Как
заметил Рёльке, для того, чтобы доказать теорему разложения
для произвольных дискретных подгрупп с конечным объемом
фундаментальной области, достаточно показать, что
соответствующие функции Эйзенщтейна имеют аналитическое
продолжение того же типа, что и функции, связанные с SL^iZ). Такая
теорема разложения была приведена без доказательства в
стокгольмском докладе Сельберга [1].
Годеман доказал теорему разложения для арифметических
подгрупп, пользуясь классическими методами, основанными на
формуле суммирования Пуассона; это доказательство все еще
не охватывает общий случай. Подход Сельберга был развит
в неопубликованной рукописи Ленглендсом [1], который дал
доказательство для произвольных полупростых групп Ли. Метод
Сельберга и Ленглендса не использует формулы суммирования
Пуассона и близок к теории операторов. Краткое изложение
этого подхода дано в работе Ленглендса [2|. Подробное
изложение результатов Ленглендса (не охватывающее, однако, цо-
следней главы его работы) содержится в книге Харищ-Чандры [1].
Л. Д. Фаддеев вновь рассмотрел эти вопросы с совершенно
новой точки зрения, основанной на теории возмущений
непрерывного спектра, построенной Фридрихсом [1] и развитой
А. Я. Повзнером [1]. Мы дадим набросок метода Фаддеева.
Функциональное уравнение для функции Эйзенштейна и ее
аналитическое продолжение могут быть получены исходя из
тождества Гильберта (резольвентного уравнения)
R{s)-R is') - (s (1 - s) - s' (1 - sO) R (s) R is')
для резольвенты оператора Лапласа. Параметр .? в этом тождестве
такой же, как и в обычной теории рядов jДиpиxлe;
соответствующие собственные значения равны Я^ = s (1 — s). При
выбранной нормировке критическая прямая совпадает с вертикальной
прямой Res = 1/2.
Зададимся большим числом х > О и исследуем резольвентное
уравнение при s' = x как функцию переменной s. Положив
R = R{yi), получаем уравнение
R{s)-R=<i,{s)RR{s).
Затем выберем подходящую функцию Грина qsiy, г/О для
уравнения
на полуоси у'^а, удовлетворяющую некоторому граничному
условию при у = а. Пусть Q (s) — соответствующий оператор.

Спектральное разложение оператора Лапласа на Г\5 273
Вместо того чтобы изучать R{s) непосредственно, сделаем
преобразование:
R{s) = Q (s) + (/ + а) (s) Q is)) В {s) (/ + ю (s) Q (s)).
Можно показать, что это уравнение разрешимо относительн9
оператора B{s), который оказывается мероморфной функцией
от S в полосе О < Res < 2. Уравнение для оператора B{s)
вытекает из резольвентного уравнения для /? (s). Построим оператор
TF(s)x=(o(s)(/ + (o(s)Q(s))5(s),
который будем рассматривать как возмущение единичного
оператора.
Функция Грина qs имеет вид
Э(г/, 5)г/''-^ если у<у',
0(/. s)y^-\ если у>у%
где
в (г/, s)^y' + c{s)y^-^
из (г, 2') = ^~г{
с is)
S + X— 1
Эти функции удовлетворяют функциональным уравнениям
Эйзенштейна
Q{y, 5) = е(г/, l-s)c(s),
c(s)c(l-s)=l.
Если положить
т,(г, s)^[I + W{s)]Q{z, S),
то функции Эйзенштейна ц^ будут удовлетворять аналогичным
функциональным уравнениям, которые, как и аналитическое
продолжение функций 1]з, получаются из резольвентного уравнения
для оператора B{s) и аналитических свойств оператора W (s).
Общая схема приведенных рассуждений вполне аналогична
использованной самим Фаддеевым по другому поводу в его
работе [2].
Аналитическое продолжение семейств операторов
производится одновременно с аналитическим продолжением их ядер.
Важно отличать области, где ядро резольвенты имеет
аналитическое продолжение, которое уже не связано с резольвентой.
В общем случае про эти области почти ничего не известно.
Если r = SL2(Z), то, как можно показать, полюсы аналитического
продолжения ядра резольвенты совпадают с нулями ^-функции
Романа С(2s). Таким образом, прямая Res = '/4 — это еще одна
критическая прямая (гораздо более критическая!); это было
отмечено еще Сельбергом [1].

274 XIV. Спектральное разложение оператора Лапласа на Г\ф
Если бы мне нужно было выучить кого-либо анализу, я
посоветовал бы ему во всех деталях разобрать статью Фаддеева,
где в содержательной конкретной ситуации использовано
множество технических приемов анализа в рамках единого и
впечатляющего подхода. Как я уже сказал в предисловии, чтобы
облегчить задачу читателя, в приложения к настоящей книге
включены все вспомогательные результаты из общего курса
анализа.
Доказательства будут проведены сначала для случая Г =
= 5L2(Z), когда фундаментальная область имеет только одну
вершину. В заключительном параграфе указаны те места, в
которые необходимо внести изменения при переходе к общему
случаю. В основном эти изменения не идут дальше введения
в нужных местах матричных индексов. Функция c{s)
превращается при этом в матрицу (оператор) порядка п., где п — число
вершин дискретной подгруппы Г. Как показано в недавней
работе Павлова и Фаддеева [1]'), эта матрица тесно связана
с оператором рассеяния в физике.
Метод Фаддеева был использован Лашо [1] при
доказательстве теоремы разложения для так называемых групп ранга I.
Можно надеяться, что этот метод переносится также на группы
более высокого ранга.
Я включил в изложение целый ряд деталей, опущенных
'Фаддеевым. Быть может, из-за неизбежного увеличения объема
читателю будет трудно уследить за общим ходом мысли. Поэтому
рекомендуем ему обратиться к оригинальной работе Фаддеева.
§ 1. Геометрия и дифференциальные операторы на ф
Геометрия
Группа G = SLi (R) действует на верхней полуплоскости ф
обычным образом:
az + b /' '^ * ^
'-" ^=U J-
функция пары точек z==x-\- iy, z' ■=х,' ■\- iy'
Y'- 2^77ТТ' «^™
и {z, z')
iyy'
очевидно, инвариантна относительно G, т. е. для у &Q
uiyz, yz') = u{z, z').
') См. также книгу Лакса н Фнллипса [1]. — Прим. перев.

§ 1. Геометрия и дифференциальные операторы на ^ 275
В дальнейшем мы будем иметь дело в основном с функцией
u{z, zO; поэтому читатель может пропустить нижеследующее
обсуждение метрики Пуанкаре. Однако полезно познакомиться
с геометрией Пуанкаре для развития интуиции.
Метрика Пуанкаре на верхней полуплоскости задается
формулой
JJ2 __ dx" + dy^ dzdz
~ У^ ~ У^ '
Так как d (yz) = {cz + d)~^ dz и Im yz=\m z/\ cz-\- d f, эта метрика
G-инвариантна; ей соответствует функция расстояния p(z, z'),
равная длине кратчайшей кривой, соединяющей z и z'. Если
z{f)='x{t) + ly{t), a^t^b,
— кривая в Ф, то, по определению, ее длина равна
J y(t)
а
Для любых точек z, z' е § существует элемент у группы G,
такой, что yz = i и yz' = iyo для некоторого вещественного
числа Уо'^1. Ясно, что
р (z, z') = р {i, iyo).
Мы дадим краткое доказательство того, что среди кривых,
соединяющих точки / и гг/о, вертикальный отрезок имеет
минимальную длину. Пусть x{t)-^iy{t) — OKaa из таких кривых.
Тогда ее длина не меньше, чем
Г \y4t)\
J у it)
■dt>
f у' H)
J у it)
dt
Если кривая имеет минимальную длину, то в предыдущей
формуле должно выполняться равенство: в противном случае
кривая iy{t), соединяющая i и гг/д, имела бы меньшую длину.
Следовательно, x{t)^Q, и доказательство закончено.
Расстояние между точками И {t> \) vi i теперь легко
вычислить:
t
Таким образом, расстояние равно
s = \ogt и t=e?.

276 XIV. Спектральное разложение оператора Лапласа на Дф
Далее,
и = sh^ (s/2),
поскольку sh2(s/2) = ^ (ch s - 1) = -i (^4^ ~ О =° "^Чг^ = "•
Рис 1.
Преобразование Кэли z н-^ (z — г) / (z + О задает
отображение верхней полуплоскости на единичный круг. При этом
Метрика Пуанкаре переходит в метрику
ds2:
4 {dx^ + dy^)
где r^ = x^ + y^. Следовательно, в этом случае
1 ~f
Поэтому г = (6"— 1)/(е*+ 1), так что
r = th(s/2).
Покажем также, что площадь А{г) круга радиуса г в
метрике Пуанкаре дается формулой
А (г) = 4пи.
В самом деле,
г 2л
A{r)^\\^^^4nj^,^in-^^^^^^sh4sl2) = inu.
о о
Возвратимся к геометрии верхней полуплоскости.
Обозначим символом Dniz) круг радиуса /? с центром z
относительно «метрики» и, т. е. множество точек z', таких, что и (z, z') ^

§ 1. Геометрия и дифференциальные операторы на ^ 277
^ R. Множество Вц является обычным евклидовым кругом и
задается неравенством
{х'-хГ + iy'-byY^aY,
где i = 2/?+l, a2 = 2/?(2i? + 2) (рис.1). Когда R
увеличивается, этот круг подходит все ближе и ближе к вещественной
оси.
Дифференциальные операторы
Пусть g — алгебра Ли группы SL2 (R), т. е. множество
вещественных матриц со следом 0. Произвольному Z е g соответствует
дифференциальный оператор 2^ на С°(ф), задаваемый формулой
Sxf(2)'=J-f(exp/Z.2;)^ .
Операторы, соответствующие матрицам
^'""(о о)' ^^^li oj' -^^"U -ij'
обозначим Si, 2j, 83. В координатах x=^{x, у) они задаются
формулами
^1 ах •
Получить эти выражения совсем просто. Мы проделаем это,
скажем, для ^2 и Йг • Положим
где
«^^^ t(x + ly)+\ '
Тогда
g'{0) = y'^-x'' — 2ixg.
Жсли g{t) = u it) + iv it), то
f'//4\ ELjfil _lJL_EL|
1*^^' du dt \t=f)'^ dv dt |f=o'
откуда и следует искомая формула.

278 XIV. Спектральное разложение оператора Лапласа на Г\$
Мы будем заниматься изучением оператора Лапласа
Знак минус введен для того, чтобы сделать оператор L
«положительно определенным» в следующем смысле. Пусть ф, ij)
принадлежат С^ {Щ, и пусть эти функции вещественны. В
скалярном произведении
{1Ф,Ц,)=5$^Ф-^-^^
ifi
можно проинтегрировать по частям и перенести одну
производную с ф на ifi; изменение общего знака уничтожает минус
в определении L. Таким образом,
<1ф, ф)= \\ [(-^у Н- (|2-y]d;cdr/> О, если ф ^ 0.
Мера dxdy/if инвариантна относительно 5L2(R); мы будем
обозначать ее в дальнейшем просто dz.
Оператор L является G-инвариантным. Это означает, что если
и Т(, —оператор сдвига, tj{z) = f{az), то
То о L = L ° То.
Это можно показать прямым вычислением, применив несколько
раз правило дифференцирования сложной функции. С другой
стороны, мы уже знаем это из гл. X (теорема 4 § 1), т. е. из
общих соображений о структуре алгебры дифференциальных
операторов на группе SLgCR)-
В нашем случае оператор Лапласа будет применяться
к функдиям, зависящим только от инварианта и; поэтому для
него можно получить выражение в виде обыкновенного
дифференциального оператора по переменной и. А именно,
справедливо следующее утверждение:
Пусть ф — гладкая функция на положительной полуоси,
Zq — некоторая точка ■§. Положим / (z) ^ ф («(z, Zq)). Тогда
Lf = h,
/ф (и) = _ («2 Ц_ „) ф" („) _ (1 + 2и) ф' (и).

§2. Решение уравнения 1(р = s(l — s)(p 279
Доказательство. Имеем
-y'[S^ + TJ^] = -y'^<Р"t«^ + '41 + Ф' [«- + Uyy]};
нам нужно показать, что
Ф (и** + Uy^ = 1 + 2и.
„ , ,, (X - х'У Л-{у - у'?
Но и (2, 2') = -i '-^^—^-^, откуда
2уу' • "-У 4у^у'
1 „ _ у" + (х- хУ
"■XX =
2уу' ' --УУ 2у^у'
Теперь результат очевиден.
§ 2. Решение уравнения /ф = в(1 — в)ф
В конце предыдущего параграфа мы вычислили оператор
Лапласа на функциях, зависящих только от расстояния. Теперь
мы построим рещение однородного дифференциального
уравнения для этого оператора. Оно дается классическим
интегралом
ф, («) = ф («, 5) = -^ 5 [/ (1 - t)]'-' it -f и)-' dt,
О
который абсолютно сходится при комплексных значениях s =
= 0 + /т, о > О, и при U > 0.
Теорема 1. В описанной выше области функция ф аналитична
по S, принадлежит классу С°° по и, и
(i) /ф = 5(1 —5)ф;
(ii) ф (и, s) = — (4я)~' log и + О (1) при фиксированном s, и-*0»
(iii) ф' («, s) = — (4я)~' и~' -Ь О (1) при фиксированном s, и -> 0;
(iv) ф (и, s) ^ О («"") при фиксированном а, и->оо.
Доказательство. Утверждение (iv) очевидно. Чтобы доказать,
что ф удовлетворяет дифференциальному уравнению,
продифференцируем подынтегральное выражение; оказывается, что
применение оператора /„ превращает его в полный
дифференциал с нулевыми граничными значениями. Более точно,
несложное прямое вычисление показывает, что если
Mu = iu'-hu)-£r + {l+2u)-^ + s{l-s),

280 XIV. Спектральное разложение оператора Лапласа на Г\ф
ТО
Ми [t (1 - t)]'-' it + иГ = 5 -I (р (1 - t)Y it + И)-^-'} . •
Так как функция в правой части равенства имеет нулевые
граничные значения при /^0 и ^=1, отсюда следует, что
(/_5(1-5))ф=0.
Замечание. Рассмотрим более общую ситуацию. Пусть
S'a — дифференциальный оператор по переменной и,
пробегающей некоторое многообразие,^ и пусть со (/, и) — функция
переменной и и дифференциальная форма по переменной t,
пробегающей некоторое многообразие с краем Т. Назовем со
разрешающей формой для S", если существует такая форма ti {t, и),
что Г1 {t, и) = О при / S аг и
S'tfii {t, и) = di^] {t, и),
где di — обычная внешняя производная. Теорема Стокса
показывает, что
Jco(/, и)
есть решение уравнения 5'ф = 0. Ниже в этой главе мы снова
воспользуемся этой техникой разрешающих форм в связи
с уравнением Уиттекера. Было бы интересно изучить ее более
подробно для подходящих дифференциальных операторов на
многомерных многообразиях.
Докажем теперь, что
iS-l
[t (1 - 0] {t + «) Л = - log « + О (1)
о
при и->0. Ясно, что интеграл от '/г ДО 1 ограничен как
функция и при и, близком к нулю. Поэтому рассмотрим интеграл
по промежутку (О, '/г)
о
и вспомогательную функцию
г _

§ 2. Решение уравнения кр = slj —s)(p 281
Замена переменных t = ur дает
где
^W-)11+tJ ~-[ 0(1) при х<1.
Имеем
V.
л«-1 «/Л (^, и)
о
■А
= ( 1 - ^)'"' Л ('/2. «) - S 4 (^ - ^)"' ^ (^' «) '^^'
Заметим, что Л(1/2, и)=Л(1/2и)=-=— loga + О(1). Разобьем
интеграл следующим образом:
'/2 " 'Л
о о U
Если О :</=<«, то функция Л (/, и) = Л (//и) ограничена, и
поэтому интеграл /i ограничен при и—>-0. Чтобы оценить
интеграл/г, используем вторую оценку для функции A{t, u) = A{tlu)i
h=-\ -lf{\-tr-'{\ogt-\ogu+0{\)\dt =
и
Чг
и
= log « [(1 - 1)'"' - (1 - «Г"'] + 0(1).
Члены (log«i)(l — Уг)^" сокращаются, и поэтому
/ = - (logu) (1 - иу-' + О (1) -= - log и + О (1),
что и требовалось доказать. (Приведенное доказательство
принадлежит П. Лаксу.)
Асимптотическая опенка для ф' (и, s) при и -> О получается
аналогичным образом после дифференцирования под знаком
интеграла.

282 XIV. Спектральное разложение оператора Лапласа на Г\$
§ 3. Резольвента оператора Лапласа на Ф при <т>1
Обозначим ВС°°{^) пространство ограниченных гладких
функций на •&.
Теорема 2. Пусть f е ВС°° (•&). Для Re s > 1 положим
RQ{s)f{z) = \cfAu{z,z'))f{z')dz',
где dz' = dx' dy'jy'^ — инвариантная мера на •&. Тогда функция
R^{s)f также гладкая и ограниченная, и
{L-s{l-s)I)R^(s)f = f.
Другими словами, мы нашли правый обратный для
оператора L — s{l — s)I {I — единичный оператор). Он задается ядром
n^iz, z'\ 5) = ф(и(2, z');s),
которое мы будем записывать также в виде rj5(s) = fiOM, если
захотим опустить аргументы z, z'.
Доказательство будет проведено в три этапа.
Во-первых, мы покажем, что функция R^{s)f ограничена.
Во-вторых, при помощи теории потенциала мы докажем
частный случай теоремы, когда f имеет компактный носитель.
В-третьих, мы докажем теорему в общем случае, опираясь
на фундаментальную теорему из теории эллиптических
операторов, доказательство которой, для удобства читателей,
приводится в приложении.
Лемма 1. Пусть f е ВС°° (•&). Тогда функция Rt^ (s) f
ограничена при а > 1.
Доказательство. Положим
hiz) = \cpAu{z,z'))f{z')dz'.
Тогда
\h{z)\^\\f\\\\<f,{u{z,z'))\dz',
причем интеграл справа не зависит от z. В самом деле, если
Y S G, то
5 I ф, {и {yz, z')) 1 dz' = 5 I ф, {и {z, y-V)) I dz' = 5 1 ф, {и (z, z')) 1 dz'.

§ 3. Резольвента оператора Лапласа на ф при а > 1 283
так как мера dz' является G-инвариантной. Мы можем поэтому
положить Z = /. Пусть D — небольшой кружок вокруг точки г;
напишем
© ©-D D
При малых и имеем 9s(u)~ log ы; эта функция локально
интегрируема, так что интеграл по кружку D сходится. С другой
стороны, интеграл по дополнению не превосходит
I
\
dz'.
Таким образом, достаточно доказать следующую оценку:
Лемма 2. Интеграл
(• ' -dzf
J (1 -Ь « (г. г')Г
сходится при а > 1.
Доказательство. Мы можем положить z = L Тогда указанный
интеграл можно записать в виде
„0-2
И
^ dydx.
(х^ + (у- \Yf
—оо О
Разобьем внутренний интеграл на два:
HS+S-
Оценки этих интегралов стандартны; в действительности мы
уже полностью провели их в § 2 гл. IX.
Теория потенциала
Для удобства читателя мы напомним Некоторые
элементарные факты теории потенциала на плоскости. Пусть f,g — две
функции на R . Пусть U czft^ — область с . кусочно-гладкой
границей. Для любого векторного поля F на U справедлива
формула Грина — Стокса
\{di\Fdxdy= [ F -nds.
и dU
Положим f =-= g- grad f == {gfx, gfy) или f grad g = (fg^, fgy). Пусть-
A-divgrad = ^+^.

§84 XIV. Спектральное разложение оператора Лапласа на Г\ф
Мы получаем формулу
и dU
Пусть 2о —точка на плоскости; обозначим U = U{e) внешность
окружности S(e) радиуса е с центром в точке Zq. Предположим,
что носитель функции f компактен; тогда
\\(gAf-fAg)dxdy = - 5 (g^-f^)Us.
и (8) S (8)
Эта формула называется формулой Грииа.
Пример. Пусть точка Zq фиксирована; положим
В полярных координатах df/dn==df/dr, если / = /(г, 9), где
г ==\z — Zq\. Параметризуем окружность при помощи
отображения 9^-^(ecos9/8, esin9/8), 0^9^2ле. Тогда ds==dQ. Ясно,
что Ag==0. Правая часть формулы Грина дает
При 6-^0 первое слагаемое стремится к / (О, 0), а второе
к нулю. Следовательно,
^\^gAfdxdy = fizo).
Аналогичное рассуждение будет проведено для верхней
полуплоскости.
Лемма 3. Пусть а> 1, feCT{^- Положим
h{z)=\^<pAu{z,z'))fiz')dz'.
Тогда h s С°°. Если обозначить М^ == L — s (1 — s) /, то MJi = f и
MJi = 5 фЛ« (3, /)) (Msf) iz') dz' = \ r^ {z, z'; s) {MJ (z')) dz'.
Доказательство. Зафиксируем переменную s и не будем ее
писать. Предположим, что z меняется в маленьком открытом
подмножестве •£>, и пусть гi—>y{z)^G — гладкое отображение,

§ 3. Резольвента оператора Лапласа на ф при а > 1 285
такое, что y{z)i^='Z (таким образом, 21—* у (2) — гладкое
сечение). Положим, для краткости, (f(u{z,zy,s) = k{z,z). Тогда
h{z)^\k {у (2) 1, z') f (zO dz'=^\k и, у {zГ^ г') / (z') dz' =
^\k{i,z')f{y{z)z')dz'.
Так как носитель функции / компактен, мы можем
дифференцировать под знаком интеграла; отсюда ясно, что h s С°°.
Лелша. %h (z) = J й (z, z') Ц (z') dz'.
Доказательство. Имеем
h (exp {tXj) z) = J yfe (exp {tXj) z, zf) f {z') dz'.
Поскольку k {yz, yz') = k (z, z') для всех преобразований у из G
к мера dz' G-инвариантна, получаем
h (exp (tXf) z) = 5 fe (z, z') f (exp (/J,) z') dz'.
Так как функция f имеет компактный носитель, мы можем
дифференцировать под знаком интеграла; теперь утверждение
леммы очевидно.
В частности, мы получаем промежуточную формулу
Msh iz)=^k (z, z') Ms! (z') dz'.
Применим ее к соотношению из теории потенциала
\\{fLg- gLf)dz^\\{gM - ! ^g)dxdy ^ \ (g|t.-/|f-)d5.
dU
Пусть и = и{л) — внешность маленького евклидова круга
радиуса е с центром в точке z, так что df/(е) = S (е) —
окружность. Для простоты опустим индекс s в обозначении
оператора М. Получим
\\ k{z, z')Mf {z') dz' - J J Мг'к(z, z') f (zOdz' =
V (8) и (e)
S(e)
Ho Mz'k{z,z') = Q вне диагонали; таким образом, слагаемое,
содержащее Mz'k{z, z'), исчезает. Поскольку при z', близких

286 XIV. Спектральное разложение оператора Лапласа на Г\$
К Z, k{z,zf) ведет себя, как \ogu{z,z'), то интеграл по
окружности от kdfjdn стремится к О при е-^0. Наконец, из
теоремы 1 § 2 мы знаем, что ф'(ы)==(4лы)~'+ О (1). Так как.
-Qp-{Z,Z )=ф (и)-^,
отсюда немедленно следует, что интеграл от dkldn стремится
к 1, когда е-^0. Это завершает доказательство теоремы 2 для
функций f с компактным носителем.
Рассмотрим, наконец, общий случай, когда носитель
функции f не обязательно компактен, но / е ВС°° (•&). Из леммы 1
мы знаем, что функция /?§ (s) f = Л ограничена. Далее, М = М^—
эллиптический оператор на •&. Пусть "^^£7 (•&) — вещественная
функция; тогда
(Л. Мг|з> == ^ J ;fe (z, z') М^ (z) f (zO dz dz',
и мы можем воспользоваться теоремой Фубини. Из частного
случая теоремы 2 для функций с компактным носителем
получаем
^ k (z, z') Мг|з (z) dz = г|з (z').
Следовательно,
(/г,Мг|з> = (/,г|з>.
По теореме о регулярности для эллиптических операторов
отсюда следует, что h s С°° и Mh = /. Доказательство теоремы 2
закончено.
§ 4. Симметричность оператора Лапласа на Г\ф
Мы уже кратко упоминали в § 1, что оператор Лапласа
на ф симметричен. Теперь мы хотим показать, что оператор
Лапласа на Г\"& тоже симметричен. Для этого нам понадобится
срезающая функция 1,у, график которой изображен на рис. 2:
1) Ск(г/) = 1 при г/<У, У{у)=^ при y>2Y;
2) ry(г/)<l/i'^
Такую функцию легко построить. Пусть функция г|з(^) имеет
график, изображенный на рис. 3. Тогда if' и ij)" ограничены.
Ясно, что функция
удовлетворяет нашим требованиям.

§ 4. Симметричность оператора Лапласа на Т\^
287
Пусть Г = SL2 (Z). Фундаментальная область Р группы Г
изображена на рис. 4. Мы опускаем доказательство этого факта;
его легко найти в многочисленных учебниках. Пространство Г\ф
можно отождествить с F.
Г
Рис. 2.
2Y
\,Ф{Т)
1
Рис. 3.
Как и раньше, положим
^^-y^i-^+w) и
Напомним, что оператор L инвариантен относительно
действия группы G == SL2 (R). Поэтому если / е С°° (Г\'£>), т. е.
язЙЙЯ^
ш
vKvl
а
йй
*
1^
Рис. 4.
f — гладкая функция на •&, инвариантная относительно Г, то
L/ — также гладкая Г-инвариантная функция.
Лемма 1. Пусть f — вещественная функция, такая, что
/, LfeBC~(r\§).
Тогда интеграл по фундаментальной области
if.fi=n((fr+(f)>^*
р
конечен и
{Lf,f) = [f.f].
Доказательство. Пусть Y — большое положительное число,
t,==t,y — срезающая функция, описанная выше. Нашей первой

288 XIV. Спектральное разложение оператора Лапласа на Т\^
целью будет доказательство формулы (*) ниже. Положим
Поскольку поверхность Г\ф не имеет края, то по формуле
Грина имеем
г\©
Г\ф Г\©
Г\ф г\©
(При желании можно работать только на области F, используя
периодичность производной dfjdti, а также тот факт, что куски
границы фундаментальной области переходят друг в друга
с изменением ориентации под действием группы Г.) Мы
воспользовались также тем, что д^/дл;==0. Заметим теперь, что
Так как число Y велико, то производная dt^jdy. равна нулю
всюду, где dx Ф 0. Следовательно,
F
I 2У
F О У
При Y-^oo второй член в правой части стремится к нулю,
поэтому
F Р
Когда 7->9о^-71евая~часть возрастает, оставаясь ограниченной,
MocKojjbKy правая часть стремится к
F -
Это завершает доказательство леммы.
Теорема 3. Пусть fug — вещественные функции из ВС°° (Г\4^),
такие, что Lf и Lg также принадлежат ВС°°{Т\^). Тогда
{Lf,g)={Lg,f).

§ 4. Симметричность оператора Лапласа на Г\ф
289
Доказательство. Пусть а—большое положительное число.
Fa — срезанная фундаментальная область, изображенная на
рис. 5. Положим
I=={L!,g)-{Lg,!).
Тогда по формуле Грина имеем
''а ^''а
Интегралы по участкам границы, сопряженным относительно Г,
а
• I * • ■
ftii
Рис. 5.
взаимно уничтожаются. Поэтому не исчезает только интеграл
по верхнему куску границы, т. е
Так как функции fag ограничены, то из неравенства Шварца
вытекает оценка
Интегрируя обе части неравенства по интервалу А^а^В,
получаем
SV.N»< П"[Ш"+(!!-)>'^^-
А А -Чг
Из леммы 1 мы знаем, что этот интеграл ограничен равномерно
по Л и по В. С другой стороны, интеграл
/а= \\{g^f-f^g)dxdy
10 Зак. 589

290 XIV. Спектральное разложение оператора Лапласа на T\Q
имеет предел при а-^оо, поскольку функции Lf и Lg
ограничены, а область F имеет конечную инвариантную меру. Этот
предел должен быть равен нулю, ибо в противном случае
найдется такое положительное число с, что I /а Р ^ с > О для
достаточно больших а; следовательно, интеграл
в
\^\1^Ыа>с{В-А)
А
не ограничен, что противоречит предыдущей оценке. Это
завершает доказательство теоремы 3.
§ б. Оператор Лапласа на Г\ф
Пусть £>£— пространство всех функций f еВС°°(Г\ф), таких,
что Lf — также гладкая ограниченная функция. Обозначим
буквой Н гильбертово пространство 1^{Г\ф). Мы будем
пользоваться этим обозначением на протяжении всей главы. Тогда
£>£,— плотное подмножество в Н. Оператор L будем считать
определенным на этом подмножестве; из теоремы 3 известно,
что он симметричен. Как мы увидим, на самом деле оператор L
в существенном самосопряжен (см. приложение 2). Чтобы
убедиться в этом, построим его резольвенту, усредняя по Г
резольвенту оператора L на всей верхней полуплоскости. Нам
потребуется следующая оценка:
Лемма 1, Если а > 1, то ряд
^^у []+«(2,Y2')f
сходится равномерно по z, г' на любом компакте.
Доказательство. Пусть Мц — число элементов Y ^ Г, таких,
что u{z, yjf)-^R. Мы утверждаем, что Мц <€. R. В самом деле,
пусть D/- круг фиксированного малого радиуса с центром z',
такой,/что D П Y-b = 0, если yz" Ф г'. Пусть Dj^ — множество
точеь? z", таких, что m(z, z")^R. Как мы знаем, площадь Dj^
пропорциональна R (см. § 1). Если уг' '^Dj^, то yD cz D^r для
достаточно больших R. Следовательно, число элементов у ^Т,
таких, что yD cz D^r и yz' ф z', в существенном ограничен^
=(вличиной
площадь D„D
=^ <С R
площадь D
Число элементов у ^ Г, таких, что yz' = zf, равномерно
ограничено (легко доказать, что для Г = SLz (Z) это число не
превосходит шести и в действительности равно двум для всех

§ 5. Оператор Лапласа на Г\$ 291
точек, за исключением тех, которые эквивалентны / или е^""^).
Итак, наше утверждение доказано.
Разобьем теперь нашу сумму на частичные суммы по таким
элементам \, что yz' лежит в кольце
Пусть m=^[log2R]. Тогда эта сумма не превосходит
R , R/2 , ^ R/2'" ^
14-2*4-22*4- 4-2™* <>(т+\)г
< '+2 +2^+ ■••+2 «2___ = 0(1).
Очевидно, все оценки равномерны по z, / на компактных
подобластях. Это завершает доказательство леммы.
Для а > 1 положим
г (г, г'; s)=^jYj ф("(2. Y^O; s).
vsr
Мы будем иногда писать f^(z, z') вместо r{z,z';s).
Множитель '/2 введен для того, чтобы учесть тривиальное действие
элементов ± 1. Если z^Vz', то из леммы 1 заключаем, что ряд
абсолютно сходится при а> 1. Для 1&ВС°°{ТЩ имеем
\ г (Z, Z'; s)f{z')dz'=±\ JI• ф{и(Z, yzy, s) f {z') dz'.
F P Y^r
В силу леммы 1 можно переставить суммирование и
интегрирование; поэтому предыдущее выражение равно
5 Ф{и{Z, Z'); S) I {Z') dz' = {R^(5) /) (z).
Таким образом, мы получили старое выражение для резольвенты
на всей верхней полуплоскоети. Вспоминая теорему 2, видим,
что нами доказана
Теорема 4. Пусть сг> 1. Ядро r{z, z'; s) задает оператор
R{s): ВС" {ТЩ ^ ВС^ {ТЩ,
такой, что
{L-si\-s)I)R{s)f = f.
Из теоремы 4 следует, что
Dj,=>R{s)BC'-{T\^,
1в*

292 XIV. Спектральное разложение оператора Лапласа на Г\$
т. е. ЧТО область определения оператора L содержит образ
оператора R (s), а также что линейное подмножество (L—s(l —s) /) D^
плотно в я. Из общих свойств неограниченных операторов
(приложение 2) вытекает следующий результат:
Теорема 5. Оператор L, заданный на области Di, допускает
замыкание. Обозначим это замыкание буквой А, и пусть D^ — его
область определения. Оператор [А, Dj^ самосопряжен.
Используя подходящие оценки, мы докажем в § 7 следующее
утверждение;
Теорема р. Если а > ^U, то R (s) — ограниченный оператор
в пространств H = L'{T\v).
В ходе доказательства нам потребуется разбить ядро г (z, z'; s)
на несколько \различных компонент. Теорема 6 показывает, что
оператор /?(s)\ecTb в точности резольвента оператора А.
Из теоремы ^ вытекает, что R{s) Н с. Da, т. е. что образ
оператора R (s) соХержится в области определения оператора А.
В самом деле, nycm,/„->-f в Я, /„ s 5С°° (Цф). Положим А=«
= s(l—s). Из равенства
Li?(5)f„ = Ai?(5)f„ + /„
следует, что LR{s)f„-^KR{s)f + f. Следовательно, вектор i?(s)f
принадлежит области определения оператора Л, и при всех f ^ Н
справедливо равенство
{A-s{l-s)I)R{s)f^f.
(Мы предполагаем по-прежнему, что Res>Va-)
§ е. Функции Грина и уравнение Уиттекера
В этом параграфе мы напомним некоторые факты из анализа?
это подготовит почву для изучения резольвенты R{s). Будут
рассмотрены некоторые специальные линейные
дифференциальные уравнения 2-го порядка; этого достаточно для приложений,
которые мы имеем в виду.
Пусть (а, Ь) — открытый интервал (случай 6 = оо не
исключается). Положим

§ 6. функции Грина и уравнение Уиттекера 293
где р —гладкая функция на (а, Ь). Функцией Грина
дифференциального оператора М назовем функцию g, заданную на
квадрате (а, Ь) X (<2, Ь), такую, что
My 5 g {у, у') f (г/О dy' = / (у), f ffi СТ {а, Ь).
а
Другими словами, оператор Грина есть правый обратный к
оператору М. В этом параграфе мы будем предполагать, что
функция Грина удовлетворяет следующему дополнительному
условию:
GF 0. Функция g непрерывна и принадлежит классу С°° по
каждой переменной вне диагонали.
Как мы сейчас увидим, существенно, что частные
производные ядра g терпят разрыв на диагонали. В самом деле,
предположим, что g удовлетворяет еще такому условию:
GF1. Если у фу', то Mygiy, у')=0.
Другими словами, вне диагонали функция g удовлетворяет
однородному дифференциальному уравнению.
Предположим, что функция g удовлетворяет условиям GF О
и GF 1. Тогда g есть функция Грина оператора М в том и
только в том случае, когда g удовлетворяет также следующему
условию на скачок производной:
GF2. Dig{y,y + 0)-D,g{y, у-0)^1.
Как обычно.
Dig {у, у + 0)= lim D,g {у, г/0;
у'->у
у >У
аналогично, D^giy, у — О) вычисляется как левый предел.
Для доказательства приведенного утверждения напишем
ь у ь
S=S + S
а а у
Возьмем производную по у а воспользуемся непрерывностью g.
Получим
g{y,y)f(t/) + ]D,g{y,y')f{y')dy'-
а
Ь
- Р. (У, у) !(у) + \ D,g {у, г/0 / (г/0 dy'.

294 XIV. Спектральное разложение оператора Лапласа на Г\$
Таким образом, член g{y, y)f{y) сокращается. Вычисление
второй производной приводит к выражению
у
D,g {у, г/ - 0) f (г/) + 5 D\g (г/, /) / {у') dy' -
а
Ь
- Dig {у, y + 0)f{y)+\lfxg {у, у') f (г/') dy'.
Следовательно,
My \ g {у, у') I (г/О dy' = {Dig (у, у + 0)- Dig (у, y-Q))f (у) +
а
Ь
+ ]Myg{y,y')f(y')dy'.
а
В силу условия GF 1 второй член в правой части исчезает.
Поэтому условие GF 2 эквивалентно тому, что g — функция
Грина, что и требовалось показать.
Пусть J, К — два линейно независимых решения однородного
уравнения, т. е.
_/" + р/ = 0,
-К" + рК=-0.
Существует единственная функция Грина, такая, что
^^У'У>-\В{у')К{у), если у'>у.
Функции А, В определены, этими условиями однозначно и будут
вычислены ниже.
Чтобы доказать это, заметим, что если g{y, у') имеет такой
вид, то условие GF 1 выполнено автоматически. Условие
непрерывности ядра g и условие GF 2 сводятся к системе
линейных уравнений
A(y)]{y)-B{y)K{y)^Q,
-А{у)Г{у) + В{у)К'{у)^\.
Положим W == JK' — J'K (эта билинейная форма называется
вронскианом). Заметим, что W=0 (это немедленно вытекает
из дифференциального уравнения) и, следовательно, вронскиан
постоянен; он не равен нулю, поскольку J к К линейно
независимы. Отсюда
A = KIW, B = JfW.

§ в. функции Грина и уравнение Уиттекера 295
Таким образом, для функции Грнна мы получаем выражение
ГШШИ, если ,'<,,
'^«■"'^-[iMl^iWl. если />,.
Следующие два примера будут использованы в приложениях.
Пример 1. Рассмотрим оператор
Соответствующее однородное уравнение имеет вид
При S ф '/г мы можем взять в качестве линейно независимых
рещений lj'^~^ н у^. Вронскиан этих решений равен 2s—1, и,
следовательно, функция Грина задается формулой
's„l-s при у> <- у^
I Г у''у''
^(г/./;s)=2F=T•(г/Y'-
пpи у' > у.
Мы сохраним это обозначение до конца главы.
Пример 2. (Уравнение Уиттекера.) Пусть sgC, Res>0,
с — вещественное число, с^1. Положим
Однородное уравнение, отвечающее оператору My, имеет вид
Г(у)=(с'-^^^)^{у).
При больших у его можно рассматривать как возмущение более
простого уравнения Tf)"^c^i|;, имеющего независимые
решения е±''^. Мы покажем, что у возмущенного уравнения
существуют решения с аналогичными асимптотическими свойствами.
Более точно, мы покажем, что существуют два решения
уравнения Уиттекера:
J = Js.c и K=Ks.o
со следующим асимптотическим поведением:
При у-^оо, с> 1
Ну)^е-'=У, Г (у) се-'У,
К {у) — е'^У, К' (у) — се'У

296
XIV. Спектральное разложение оператора Лапласа на Г\ф
равномерно по s в любом фиксированном компакте в
полуплоскости Re S > О (для У (у) — в полуплоскости Re 5 > 1).
При у> О и фиксированном с
Js,c{y)
^^w^^^yy-
равномерно по s на любом компакте в полуплоскости Re s > '/2,
Ks.ciy}'
r(s)
{2суУ
равномерно no s на любом компакте в полуплоскости Re s > 0;
здесь
Р(5)=5[^(1-/)Г'л=^^-
г (2s)
Из асимптотики при у-*-оо вытекает, что вронскиан функ-
гбй J, К асимптотически стремится к 2с; так как вронскиан
не зависит от у, то он равен 2с тождественно. Поэтому
существует функция Грина, задаваемая формулами
К Ю J (у)
' —г ^^
gs,c(y, У) = '\ J (у>) j( (у)
2с
если у' < У,
если У <у'-
Это единственная функция Грина, удовлетворяющая условиям
GF О и GF I и имеющая вид A{y')J{y), если у' <у,и К (у) В {у'),
если у < у'. Из равномерных оценок, сформулированных выше,
следует, что функция Грина удовлетворяет неравенству
\gs,AУ,У')\<■^г^-'""-'''^
(где Ci — константа) равномерно по 5 на любом компакте в
полуплоскости ReS> О и по i/, / в области 0<а<у, / < оо.
Доказательство. Нам остается доказать существование
решений /j,, и Ks.ey имеющих нужные свойства. Напомним для этого
некоторые классические результаты.
Положим
со
WAy)'=T^^ye-y''\ e-*nt{i+t)r'dt.

Пу)-={^-^^)^(у1
§ 6. Функции Грина и уравнение Уиттекера 297
После замены переменных этот интеграл можно также
переписать в виде
оо
о
Тогда функция (Tj удовлетворяет уравнению Уиттекера
1 5(1 -S)
В самом деле, если мы подействуем на функцию
y'e-«'^iв-^y[t{l-\-t)Y~^
дифференциальным оператором
то она превратится в полную производную (по переменной t)
граничные значения которой при /=0 и ^ = оо равны нулю.
Дифференцирование под знаком интеграла показывает, что
функция Wg удовлетворяет уравнению Уиттекера.
Положим
4 Лу) = WA2cy)=^e-'^y \ e-'f (l + ^)^"' f.
о
В силу теоремы Лебега об ограниченной сходимости ясно, что
при !/-»•«> интеграл в правой части стремится к величине
оо
J е~' t'~'' dt = r (s)
равномерно по с ^ 1 и по s на любом компакте в полуплоскости
Re 5 > 0. Следовательно,
h.ciy)'^e-'=y
равномерно при сделанных ограничениях на параметры.
Дифференцирование под знаком интеграла дает
оо
Мы снова получаем нужную нам равномерную асимптотику J's, с{у)
при I/-*•<».

298 XIV. Спектральное разложение оператора Лапласа на Г\$
С другой стороны, имеем также
оо
о
Зафиксируем *. Ясно, что при i/->0 интеграл в правой части
стремится к Г (2s—1) равномерно по 5 на любом компакте.
Следовательно,
Это завершает исследование первого решения.
Второе решение изучается аналогичным образом. Пусть
1
о
Та же техника, что и раньше, основанная на построении
разрешающей формы, показывает, что Vs — решение уравнения
Уиттекера. В самом деле, оператор Уиттекера переводит
фу1}КЩ1Ю
в полную производную
с нулевыми граничными значениями.
При 1/->0 немедленно получаем
1
V.(t/)~^/, где р(5)=5И1-0]
s-\.
dt.
о
Положим
1
Ks. с (у) = V, (2ct/) =^ (2ct/r е-'=У \ е^'^У [t (1 ~ О]'"' dt.
о
Тогда функция Kg, с имеет нужное поведение при у -^0. Сделаем
замену переменных tt—^l — t и затем u^2cyt, du = 2cydv-
Ks.Ay)-=^e^"\e~^[u{l-^)]'- du.
о
При у-^оо этот интеграл стремится к Г (s) равномерно в
требуемой области. Следовательно, при у—*-оо
Ks.c{y)-e^'

§ 7. Разложение резольвенты на Г\5 при а > 3/2
•299
равномерно при сделанных ограничениях на параметры. С другой
стороны, дифференцирование функции V^^су) по у дает
K'..c{y)'=jKs.c{y)-cKs.c{y) +
1
+ ~ {2еуУ е-'=У J е^'=у' [t (1 -1)]"-' 2ct dt.
о
Заменим снова t на 1—/ и положим u = 2cyt. Тогда третий
член в правой части равенства примет вид
2су
о
Этот интеграл имеет при у-^оо равномерную асимптотику 206"".
Так как —cKs.dy)'^ — се*^^, мы получаем, что
Ks. с (у) — се^"
равномерно по s, что и требовалось доказать.
§ 7. Разложение резольвенты на Г\ф при а>3/2
В этом параграфе мы будем исследовать резольвенту, когда
а > 72 или даже сг > 3. Разобьем сумму по всем элементам
уеГ на две части. Пусть Го — группа матриц вида
\ О ±lj'
Напишем
r{z, z'\ s) = ~Y, ф("(2, YZ'); s)+\ Yj ^^^^^' ^^)' ^^•
(Множитель Va введен для того, чтобы учесть, что матрицы
± 1 е Г действуют тривиально.) Первое слагаемое мы будем
называть вершинной частью резольвенты, а второе слагаемое —
незершинной частью резольвенты. Займемся сначала
исследованием вершинной части. Мы увидим, что ее тоже можно
разбить на несколько слагаемых, причем соответствующие ядра
удовлетворяют различным условиям ограниченности. В
частности, мы введем, помимо L^(V\^), и другие функциональные
пространства, более удобные для изучения этих ядер.
Разобьем фундаментальную область на 2 части. Пусть
а — большое положительное число. Обозначим символом р.^ ту
часть фундаментальной области, где у ^ а, и пусть F^^=F — Fq

300
XIV- Спектральное разложение оператора Лапласа на Г\ф
(рис. 6). В соответствии с этим функции на фундаментальной
области мы будем разлагать на две компоненты:
часто нам будет удобнее записывать это разбиение в виде
столбца
/ =
(,';)•
чтобы можно было действовать на / операторами слева. Если,
к примеру, /о и fi рассматриваются как элементы некоторых
Рис. 6.
функциональных пространств, то любой оператор Q можно
записать в виде 2 X 2-матрицы:
'^Ht. ЖУ
Мы будем рассматривать следующие функциональные
пространства. Во-первых, естественно, пространство
Я = L^m) == L2 (Fo) ф 1МЛ).
(Скалярное произведение берется по мере dz = dxdy/y^.)
Во-вторых, для любого вещественного числа ц определим
пространство

§ 7. Разложение резольвенты на Г\Ф при а > 3/2
301
здесь ^^ (Fq) — пространство непрерывных функций на Fq
с обычной sup-нормой, а Jf^ (/=■!)— пространство непрерывных
функций / на F,, удовлетворяющих условию
l/(A: + гt/)|<t/^
снабженное нормой
llfll.= sup-^.
Таким образом, пространство Я гильбертово, а
пространства ^у,{Р) банаховы. Заметим, что
т. е. любая ограниченная функция принадлежит пространству
Р(Г\'&), так как объем Г\Ф конечен. То же самое верно и для
пространотва J^-i <= SS^.
Пусть k (z, 2') — функция, определенная на произведении
FiXff- Мы будем обычно использовать обозначение ktf{z, z'),
чтобы подчеркнуть, что переменные (z, z') изменяются в
областях Ft, Ff соответственно. Будем говорить, что наше ядро
имеет тип ^ц, если оно непрерывно и выполняется оценка
\k(z,z')\<(yy'f.
Пусть, к примару, fe = ^oi; тогда переменная z (а значит, и
переменная у) изменяется в компактной области; следовательно,
это неравенство имеет значение только для второй переменной.
Таким образом, в рассматриваемом случае наша оценка
эквивалентна неравенству
I ^01 {Z, z') I < у'К
Будем говорить, что оператор имеет тип .^^, если он задается
ядром этого типа. Такие операторы, очевидно, удовлетворяют
некоторым условиям непрерывности как отображения
пространств ^р. Например:
Лемма 0. Пусть k{z,z') — Hdpo типа 3S-^; тогда
соответствующий оператор К определен на пространстве ^n+i-g "
непрерывно отображает его в J^-^.
Доказательство тривиально и основано на простых
манипуляциях G интегралами. Например, на Fi справедливо очевидное
неравенство
оо

302 XIV. Спектральное разложение оператора Лапласа на Пб
Мы используем также тот факт, что некоторые отображения
пространств ^^ компактны. Чтобы доказать это, нам
потребуется несколько дополнительных замечаний в духе теоремы
Асколи. Для удобства читателя мы напоминаем здесь
формулировку этой теоремы.
Теорема Асколи. Пусть X — компактное метрическое
пространство, Ф — семейство непрерывных функций на X. Тогда Ф
относительно компактно в пространстве непрерывных функций
на X (с обычной топологией равномерной сходимости) в том и
только в том случае, когда Ф равностепенно непрерывно и
ограничено.
Доказательство см., например, в книге Ленга [1].
Равностепенная непрерывность семейства функций означает, что для
любой точки jcq е X и любого е > О существует такое б > О,
что если \x — Xq\<8, то \f{x) — f{xo)\<e для всех /еф.
При доказательстве компактности отображений мы будем
пользоваться теоремой Асколи вместе со следующим
утверждением:
/
Пусть V <у^1 Множество Е равностепенно непрерывных
функций наБ\, ограниченное в пространстве ^^, относительно
компактноув пространстве ^^.
Доказательство. Достаточно проверить, что множество Е
вполне ограничено в ^^, т. е. может быть покрыто конечным
числом шаров заданного радиуса г > 0. По предположению,
существует такое положительное число С, что для любой
функции f^E выполняется неравенство
\f{y)\<Cy\ т. е. \f{y)\y--^C.
Выберем столь большое число Y, что если y'^Y, то i fiy) \у~^<е
для всех feE. Напишем
где f~ — сужение функции f на область г/<К, г f^ — на
область y'^Y. Имеет место включение
^^{F,)c:^y{FV)X^v{Ft).
Функция f^ лежит в шаре радиуса в в пространстве ^ii{Fy)-
С другой стороны, семейство функций {/"; f^E} равностепенно
непрерывно и ограничено на FV- Поэтому, согласно обычной
теореме Асколи, оно относительно компактно в пространстве
^'»{Fy), Наше утверждение доказано.

§ 7. Разложение резольвенты на Г\ф при о > 3/2
303
В Приложениях семейство равностепенно непрерывных
функций возникает при действии оператора К, задаваемого ядром
k{z, z'), на единичный шар в пространстве ^^. Рассмотрим,
к примеру, ядро, определенное на произведении Fj X ^^i- Пусть
х'у
Рис. 7.
/ — Произвольная функция нз единичного шара в ,^v
Зафиксируем точку ZflS/^'i; тогда
dy'
Kf (z) - Kf (zo) \<\\k{y,y')-k (г/о, г/О 11/^ f
Так как f принадлежит ограниченному множеству в
пространстве ^^, она совсем выпадает из оценки, и все нужные
неравенства вытекают только из свойств ядра. Таким образом, мы
докажем равностепенную непрерывность для любого ядра, для
которого можно перейти под знаком интеграла к пределу при
г/-*г/о- На практике нужная оценка будет очевидной, если
k — ядро типа .^^, но для ядер других типов, возникающих
в вершинной части, потребуются дополнительные усилия.
Вершинная часть
Мы займемся сейчас суммой
г°{г, z'; s)=Y ^ ф(«(2, yz'); s) =
уеГ,
= 2] Ф (гг(г, г'-Ь п)! .) = j; ф (1^.=|^ ; s) .

304 XIV. Спектральное разложение оператора Лапласа на Г\5
Ясно, что г° — периодическая функция по переменнойjc и четная
функция от X — xf. Следовательно, она имеет разложение Фурье
вида
00
(1) г° (z, z'\ s) = /По (у, у'; s) + 2 Z т« (г/, г/'; s) cos 2як (д; — д/).
где коэффициенты Фурье для к^О задаются формулой
(2)
/"к (У> у'; s) = \ г° (z, z'; s) cos 2як (д; — д/) dx.
Функция тк{у, у'', s) симметрична по переменным у, у' и
удовлетворяет принципу симметрии по переменной seC:
гПк {у, у'; s) = m« {у, у'; s).
Кроме того, из интегрального представления для т^ ясно, что
ГПк — непрерывные функции, в том числе и на диагонали.
Рис. 8
Мы явно вычислим функцию щ и покажем, что она
совпадает с ядром J из примера 1 в конце § 6. Мы покажем также,
что при к ^ 1 функции Шц — это в точности функции Грина из
примера 2. Наконец, мы приведем оценки, из которых будут
следовать свойства соответствующих операторов в различных
функциональных пространствах.
Ядру /""(z, z'; s) соответствует оператор R°{s), определенный
в пространстве ВС°°(Го\Ф). Нетрудно показать, что
{L-s{l-s)I)R°{s)f=^f
для всех функций f^BC°°{To\^. Доказательство этого
утверждения аналогично доказательству формулы
{L-s{l-s)DR{s)f = f

§ 7. Разложение резольвенты на Т\^ при в > 3/2 305
для функций f е ВС°° (Г\|>). Фундаментальная область группы
Го — это полоса 5, изображенная на рис. 8.
Лемма 1. При к>0 функция тк{у, у'; s) есть функция Грина
дифференциального оператора
1..у--£г + {2пк?-1^^
на интервале (О, оо). Кроме того, функция Шк непрерывна и вне
диагонали удовлетворяет однородному уравнению. Таким образом,
Шк удовлетворяет условиям GF О, GF 1, GF 2.
Доказательство. Положим, для краткости,
Af, = L-s(l-s)/.
Пусть f, ^еСГСГо^Ф) —пробные функции. Формула обращения
для оператора /?°(s) показывает, что
5 5 гО (Z, z"; s) f (z") M,g (z) dz" dz=\^f {z") g {z") dz".
s s s
Изменив порядок интегрирования, получаем
JrO(z, z"; s)Msg{z)dz = g{z").
s
Зафиксируем точку z' и возьмем в качестве g функцию вида
g (z) = cos 2пк {х — x^)h (у),
где AeCCR"^). Тогда
M,g (z) = - г/2 [_ (2лк)2 cos 2пк (а; - л/) А (г/) + cos 2пк (х-У) h" (г/)]—
— S (1 — s) COS 2як {х — х') h (у).
Напомним, что dz — dxdy/y^ и
S -Ч2 о
поэтому, интегрируя сначала по л: и замечая, что g{z') = h{y'),
мы получаем
оо
(*) 5 Шк {у, г/0 /«Л (у) dy=h (г/О-
о
Зафиксируем значение у' и выберем пробную функцию Л
так, чтобы ее носитель не содержал точку г/'; тогда (*) дает
5 т» (у, г/О /«Л (г/) dz/ = 0.

306 XIV. Спектральное разлоокение оператора Лапласа на Т\$
По теореме регулярности для эллиптических операторов, отсюда
следует, что функция /п» бесконечно дифференцируема вне
диагонали и удовлетворяет однородному дифференциальному
уравнению 1к.утк{у, г/') = 0-
Далее, проинтегрируем обе части формулы (*) с пробной
функцией ofieCrlR"^)- Получим
\ \ т« (у, г/О Ufi (у) a|3 (у') dy dy'=\^h (у) г|) (у) dy.
0 0 о
Изменяя порядок интегрирования в левой части, получаем для
нее выражение
оо г оо 1
\ 1к.у\гп^{у, у')'^(у')dy' h{у)dy.
о ■- о -•
Отсюда вытекает, что
/.
.у\тк{у, г/0•Ф(г/0dy' = -^(у).
О /
Таким образом, Шк -уфункция Грина, что и требовалось
доказать.
Лемма 2^^J}peдnoлoжuм, что Res> 1. Тогда
1 Г у'^У^~^, 2слгг г/' < у,
mo{y,y;s) = t{y,y;s)^^^::rr[yn-sys^ если у'> у.
Кроме того, при к > О ядро Шк {у, у'; s) совпадает с
функцией Грина §^_1пк^У' У''^' определенной в примере 2 § 6.
Доказательство. Имеем
Щ{у, /; s)= ^ r°{z, z'; s)dx.
-'Л
Зафиксируем значение у'. Пусть у> у'. Так как вне диагонали
ядро щ удовлетворяет однородному дифференциальному
уравнению, оно должно иметь вид
Щ {у, г/'; s)=^a (г/0 у'-' + Ь (г/0 У'
^ и-*^ при и-^оо, то r°{z,2';s)
Ь(г/О = 0- Пусть теперь у<у'.
то (г/, г/'; s) — с (г/0 У'-' + d (/) У
Так как ф(гг)'~гг-<' при и-^оо, то r°{z, z'\ s)->0 при у-»-оо.
Следовательно, Ь(г/О^0- Пусть теперь у<у'. Тогда

§ 7. Разложение резольвенты на Г\ф при в > 3/2 307
Так как u{z, г')-»- оо при г/-*-0, то и в этом случае r°{z, z'\ s) -»-0.
Следовательно, с(^) = 0. Таким образом.
если у' < у,
если г/ < у'.
Теперь из общей теории функций Грина вытекает, что
функция /Пв совпадает с ядром t из примера 1 § 6. В точности
те же рассуждения показывают, что при к^1 ядро т»
совпадает с функцией Грина ^^ 2лк- Заметим, что для того, чтобы
отождествить гПк с определенной функцией Грина оператора /«,
нам нужно было знать асимптотическое поведение решений
однородного уравнения как при у-*оо, так и при г/->0.
Из общих оценок, доказанных ранее для функций Грина gs,^,
мы получаем равномерные оценки для ядер тк{у, у'; s), k^'i.
Эти оценки сформулированы ниже.
При а > 1 определим ядро т (z, z'; s) формулой
т (z, z'; s) == 2 2] /Пк (г/, г/'; s) cos 2пк {х — х').
Лемма 3. Для всех а > 1 справедлива оценка
-2Л1С \у~!/'\
\1Пк{у, у'; s)\^C- ,
равномерная, когда s изменяется на компактном множестве и
у, у' е [а, оо), а > 0. Поэтому ядро т» принадлежит
пространству L? {Fi X ^i) и соответствующий оператор
компактен.
Обозначим символом M{s) оператор, единственная ненулевая
компонента которого vWn(s) задается ядром m(z, z'; s). Таким
образом,
mii(z, z'; s)^m{z, z'; s),
irioi = ruio = moo = 0-
MjjI получили следующее разложение:
(3)
г" (z, z'; s) = / (г/, у'; s) + m (z, z'; s).
В следующих леммах мы докажем ограниченность операторов,
соответствующих этим ядрам, в различных функциональных
пространствах.

308 XIV. Спектральное разложение оператора Лапласа на Г\4)
Операторы, возникающие из вершинной части, будут иметь
только компоненту (1, 1). Это выполняется, в частности, для
операторов T{s) и M{s), Таким образом, матричное ядро tij{s)
оператора T{s) имеет ненулевую компоненту
tniz, z'; s) = t{y, г/'; s),
в то время как компоненты iij{z, г'; s) равны нулю, если i ф j
илн г = / = 0. То же самое верно для оператора M{s).
Ленма 4. Пусть а > '/г. 1 — ст < ц < а. Тогда для всех у'^а
справедлива оценка
\\iiy, у':
и соответствующий оператор
ограничен.
Доказательство
на два слагаемых:
Они оцениваются
—- —-^
T{s): ^,
. Разобьем
оо
s)\y'^^
ЛРх)-^%
интеграл \
у оо
а У
CBeprjcy выражением
-VY-^^
оо
■<^^
(Fi)
в левой части
'-/^ '/. .
неравенства
Написанные интегралы легко берутся и оцениваются сверху
функцией y^^, что и требовалось показать.
Лемма 5. При а > '/г оператор Т (s) с ядром t {у, у'; s)
является ограниченным оператором в пространстве L^{Fi).
Доказательство. Выберем показатель ц, как в лемме 4. Вез
ограничения общности мы можем взять какую-нибудь функцию
feL^([a, оо)) и подействовать на нее оператором T{s).
Применим неравенство Шварца к функциям
U(y, г/Ог/'М''' и U(y, г/Ог/'-'^|''Ч/(/)|.
Получим
оо оо
|Г/(г/)Р<5 \t{y,/)\y'^^\\t{y,y^)\y'->4f(y')^^.

§ 7. Разложение резольвенты на Г\ф при а > 3/2 309
Воспользовавшись леммой 4, получим
оо
\Tf{y)f<\y>^\t{y,y')\y'->4f{y')r^.
а
Проинтегрируем обе части этого неравенства по г/ и еще раз
применим лемму 4:
00 00
\т\\1<\ \y-^HCy,у01/-'^|/(/)р|т--р1-<11/11|.
а а
Доказательство закончено.
Лемма 6. Пусть с^1. Тогда для любого вещественного
числа |i справедлива оценка
оо
J e-''\y-y'\y'^dy'^C,-\y^,
а
где Ci — постоянная, не зависящая от с и у.
Доказательство. Разобьем наш интеграл на два интеграла
по промежуткам [а, у] и [у, оо). Рассмотрим, к примеру, первый
интеграл. Интегрирование по частям дает
у ^
^ + ^\e-o(y-y')^^/^^-Ыy\
y'V.g-o{y-y')
Первое слагаемое не превосходит C^^jc. Второе слагаемое снова
разобьем на два интеграла по интервалам [а, р] н [р, у]. Первый
из этих интегралов ведет себя как e~'^yjc, а второй не
превосходит исходного интеграла, умноженного на \ilpc. Выберем число р
так, что |i/pc < V2, и перенесем этот интеграл в левую часть.
Доказательство закончено.
Лемма 7. Пусть ст > 1. Тогда оператор М (s), задаваемый
ядром m{z, z'\ s), непрерывно отображает L^{Fi) в ^-^(F^.
Доказательство. Пусть /—произвольная функция нз L?([a, 00)).
В силу неравенства Шварца и леммы б, можно написать цепочку
неравенств
^-' к к'*у у
к—1
Полученная оценка доказывает нашу лемму.

310 XIV. Спектральное разложение оператора Лапласа на Г\ф
Лемма 8. Пусть ст > 1, |i — произвольное вещественное число.
Тогда оператор М{з) с ядром m{z, z'; s) задает непрерывное
линейное отображение
Mis): ^ЛЛ)^^^-2(Л)5
соответствующее отображение пространства J?_i в себя
компактно.
Доказательство. Нам снова достаточно рассматривать
функции! f ^^y^i^a, оо)). Чтобы, доказать первое утверждение, оценим
сумму
Y,\ ^-(У' y';s)t/^-^dy\
к=1 а
ПОЛЬЗУЯСЬ тем, что
g-2me\y-y'\
\т,{у,у; s)\< ^^
Теперь неизбывность отображения
M{s): %(F,)-^^^-^(F,)
вытекает из леммы 6. При доказательстве компактности мы
будем следовать схеме, которая уже упоминалась в начале
этого параграфа, и докажем следующее утверждение:
Оператор M{s) переводит единичный шар пространства ^^(Fi)
(v < 1) е равностепенно непрерывное подмножество.
Доказательство. Функция, принадлежащая единичному шару
пространства ^3v, ограничена. Зафиксируем точку Zq е Fi.
Получим оценку
\М
(s) f{z)-M is) f (го) К j 2 I тЛу, у'; s) - m« (г/о, у[\ s) \ ^
В этом неравенстве можно перейти к пределу под знаком
интеграла. Это и доказывает равностепенную непрерывность.
Заметим, что действие ядра свелось к тому, что функция f исчезла
из правой части неравенства.
Невершвнная часть
Наше исходное ядро г (г, z'\ s) при а > 1 получалось
усреднением ядра Tjg {z, г'; s) по подгруппе Г. Мы рассмотрим сейчас

§ 7. Разложение резольвенты на Г\ф при в > 3/2 311
ядро n{z, z'; s), компоненты которого задаются следующим
образом:
«11 (z, z'; s) = Y J] ф(«(г, y^O; s).
Обозначим операторы, задаваемые этими ядрами,
соответствующими прописными буквами:
, (Rmis) /?ш(s)^
^''''К Rio is) Nnis))'
Лемма 9. При а > ^2 все ядра п// (z, z'; s) принадлежат
пространству i С^"/ X ^/); гак«л< образом, N (s) —
компактный оператор в 1} (F). В действительности, если (/, j) Ф (О, 0),
ff > 1 и 8 > О достаточно мало, ядра пц {z, z'\ s) имеют тип
^2+8-0. ^- е.
I Г«1 (Z, Z';S)\^ /2+в-а^
|r,o(z, z'; 5)|<г/2+в-а_
|nii(z, z';s)|<(i//f+^-".
Гоо (z, z'; s) = —-^ log I z — z' I + непрерывная функция от (z, z').
Доказательство. Ясно, что из приведенных оценок вытекает
квадратичная интегрируемость всех ядер. Для доказательства
этих оценок нам потребуется еще одна лемма.
Лемна 10. Пусть г/о > 0. Тогда в полуплоскости а > 1
справедлива следующая оценка, равномерная при у, у''^Уй,
Доказательство. Запишем матрицу у ^ Го в виде
Тогда
4уу'^и (г, Y^O = C2:z' + dz — az'^ — b^ = {cxx' + dx — ax' — bf +
+ y' {ex' + df + y'^ {ex - af + cYy'^ ~ 2yy'.

312 XIV. Спектральное разложение оператора Лапласа на Т\^
Пусть 2о»=ж + %, z^ = a:' + /z/o (см. рис. 9). Выражение для
величины 4уоУ^и(г^, yz'^) получается из написанного выше
заменой у и у' нг уп- Заметим, что первый член зависит только
Zo
i-
/^
Рис. 9.
ОТ X, д/ И одинаков в обоих выражениях. Воспользуемся, кроме
того, очевидными неравенствами типа
Получим
4уу'и (г, угП - 4г^„« (z„. у<) > cYlT - <?у1 - 2уу' + 2у1
16
откуда
4уу' [1+ «(г, yz')] > 4у1 [I + «(г,, у<)] + т^ с^ (г/г/О'*
Поделив на {уу'^, получим
1 + и
УУ'
>4
У5
(^^[1+«о]
(обозначения очевидны). Это неравенство не нарушится, если
возвести его левую часть в степень а, а правую — в степень
I + 8 и умножить ее затем на достаточно большую постоянную
(зависящую от 8, а и г/о). Таким образом, справедлива оценка
\ <_^ !
Доказательство завершается ссылкой на лемму 1 § 5.
Оценки в лемме 9 получаются комбинированием леммы 10
с оценками типа
Y. |Ф(И(2, ут!); 5) К/'-",

§ S. Уравнение — ф" (у) »=»—■—j—-^ ф (г/) не промежутке [а, во)
ЯГ* о1о
когда Z меняется в компактной подобласти. Эта оценка вытекает
нз неравенства
/о
/1-0
3)0 " у
Ряды такого вида и аналогичные нм интегралы мы уже
рассматривали при изучении представлений дискретной серии.
Лемма It. Пусть а > 3. Тогда оператор N (s) отображает
пространство ^1 в J?_i-e для некоторого б > 0. Оператор
N{s): ^i-^J?-,
компактен. Кроме того, оператор N {s) непрерывно отображает
пространство Н в SS-i.
Доказательство. Ядра рассматриваемых операторов имеют
тип ^2+8-0. Доказательство сводится к оценке элементарных
интегралов. Например, если f е ^i {F^, нам нужно оценить
интеграл
\{ууТ'-''у'^<у'^'-''-
Отображение N(s): ^i-^^-i компактно по той же причине,
что и выше. Применяя оператор к единичному шару, мы
получаем равностепенно непрерывное семейство функций. Чтобы
показать, что оператор N {s) отображает пространство Н в ^_,,
достаточно воспользоваться неравенством Шварца.
§ 8. Уравнение —^"(у)= ^^ 'Ф (у) на промежутке [а, оо)
Для того чтобы исследовать указанное в заголовке
дифференциальное уравнение на полупрямой, потребуется ввести еще одни
оператор. Мы будем предполагать, что а^1. Пусть %>3.
Положим
Q(y, s) = y' + c{s)y^-'.
Тогда 6 (jr, s) — решение нашего дифференциального уравнения,
удовлетворяющее краевому условию 9(а) = ак~'9'(а). Как легко

314 XIV. Спектральное разложение оператора Лапласа на Г\5
Проверить непосредственно из определений, справедливы
следующие соотношения:
c(s)c(l — s)= 1,
е(г/. s) = Q{y, l-s)c(s).
Мы будем называть эти соотношения функциональными
уравнениями Эйзенштейна.
Решения Э(г/, s) н г/'~* линейно независимы, и их вронскиан
равен 2s—1. Из общих свойств функций Грина, которые мы
обсуждали в § 6, вытекает, что
-^ , 1 / 6(г/', s)г/'~^ если г/'< г/,
'/(г/, у; s)-2._i \9(г/, s)/'-, если ц<ц',
— функция Грина нашего уравнения. Ясно, что функция q{y,y'; s)
симметрична по переменным у, у' и удовлетворяет условию
q{y, у'; s)=q{y, у'; S).
Пусть Q(s)— оператор, единственная ненулевая компонента
которого задается ядром
quiz, z'\ s)=^q{y, у'; s);
таким образом, для подходящей функции f на. F имеем
Q{s)f{z)= \q{y,y'; s)f{z')dz'.
F,
Заметим, что Q (s) / не зависит от х.
Мы опишем сейчас свойства оператора Q{s) в различных
функциональных пространствах.
Лемма 1.
(i) При а > '/г оператор Q (s) — ограниченный оператор
в пространстве Н.
(и) При О < ff < 2 оператор Q (s) непрерывно отображает
пространство ^-i{Fi) в Ji-o(Fi); отображение
компактно.
Доказательство. Непрерывность операторов Q{s)
доказывается так же, как и соответствующие утверждения для
оператора T(s) в леммах 4 и б § 7. Из рассмотрения тех же
элементарных интегралов ясно, что оператор Q,{s) отображает
пространство ,^-1 в ^i-g. Компактность оператора Q{s)\ ^-i-^^\
вытекает теперь из следующего утверждения:

§ 8. Уравнение — it" (у) = -i—2~^^4> (у) на промежутке [а, ж)
У о I о
Единичный шар пространства 3S-i под действием оператора
Q{s) переходит в равностепенно непрерывное множество.
Доказательство. Пусть f — произвольная функция из ^_i.
Тогда
IQ(s)f(y)-Q(s)f(yo)l< \\q(y, у'; s)-q(y„ у'; s)\\f{z')\dz'.
Оценим правую часть, заменив |/(z')| на / ~^; подынтегральное
выражение не превосходит
Последняя функция интегрируема на промежутке [а, оо). Теперь
наше утверждение очевидно.
Соотношения для ядра q(s)
Пусть kiiy, у'), kziy, Z/') —два ядра. Определим нх свертку
формулой
(*1 **2){у, у') = \k,(y, у")Й2(у", г/0
dy"
у'" '
В конкретных приложениях нам нужно будет проверять
абсолютную сходимость этого интеграла при тех или иных значениях
параметров. Свертка ядер соответствует композиции операторов,
задаваемых этими ядрами. Если операторы действуют на функции
слева, то ядро ^1*^2 соответствует оператору /Ci^^2 (при цравом
действии порядок операторов заменяется на обратный). Это
верно во всех пространствах, где рассматриваемые интегралы
абсолютно сходятся.
Перечислим некоторые свойства сверток ядер q{s) и t{s).
Как обычно, мы считаем, что « > 3, и полагаем
(i){s) = s{l — s) — %{l—к).
Для краткости мы будем также писать Г вместо Т{%).
Пусть ff > 1 — к. Тогда справедливо соотношение
оо
ql. <7(у. у'; s)-tiy, у'; и) = со (5) ^ t {у, у"; %) q{у", у'\ s) -^.
а
Это соотношение можно также записать следующим образом:
qs — t^^^ (s) t^ * qs,
или, в операторной форме,
Q1. Q{s)-T^<o{s)TQ{s).

316 XIV. Спектральное разложение оператора Лапласа на Г\ф
Соотношение q 1 проверяется при помощи непосредственных
вычислений, исходя из определения ядер qs и ^^. Пусть, к
примеру, у' < у. Разобьем интеграл по промежутку [а, оо)
следующим образом:
оо у^ у оо
\~\+\+\-
а а у' у
Подставим сюда определения ядер t{y, у"; к) и q{y", у'; s) и
возьмем все интегралы. Мы получим требуемое соотношение.
Пусть, как и выше, Т = Т{%). Соотношение Q 1 эквивалентно
следующему соотношению:
Q2. (/-со (s) Г) (/ +со (s)Q(s)) = /, a>l—yi.
Чтобы проверить это, достаточно раскрыть скобки. Кроме того,
так как ядра qs и ^^ симметричны, они коммутируют:
q 3. t.^*qs = qs*tw о> 1—%.
Следовательно, операторы Т(к) и Q{s) также коммутируют:
Q3. T{%)Q{s)==Q{s)T{%), а>1-%.
Отсюда вытекает также, что операторы
I — <o{s)T и / + (u(5)Q(s)
взаимно обратны на любых пространствах, где их композиция
определена.
Ленча 2. Операторные соотношения Q 1, Q 2, Q 3
справедливы при сяедуюи^их условиях:
(i) в пространстве Н при а > '/г;
(ii) в пространстве 3^-^ при 0< ст <2.
Доказательство. В силу лемм О, 4 и 5 § 7, интегралы,
содержащие ядра qs, /и> абсолютно сходятся в соответствующих
областях.
В следующем параграфе нам потребуется также формула
q4. q{y,y'\s) — q{y, у'; 1 — s) =-gjrrr^(У. s)Q{y', \ — s).
Эта формула немедленно вытекает из определений и
справедлива без всяких ограничений на значения параметра s.
Соответствующее операторное равенство (Q 4) показывает, что
разность Q{s) — Q(\—s) представляет собой одномерный оператор;
мы не будем выписывать это соотношение явно.

§ 8. Уравнение — ij)" (у) = —~—^— ^ (У) "^ промежутке [а, оо> -
Соотношения, приведенные ниже, не потребуются нам вплоть
до § 11; мы выпишем их здесь только для того, чтобы иметь
полную таблицу соотношений, в которые входит ядро q^.
q 5. q{y, ц'\ s) — q {у, у'; s') =
оо
- [(D(S) - со (sO] \ q {у, у"; S) q{у", у'; s')^
а
при а, а' > Уг-
Заметим, что
©(s)-cu(«') = s(l-s)-s'(l-/).
Это соотношение снова проверяется прямым вычислением.
Ограничение а, а' > '/г здесь существенно, так как иначе, скажем,
для s' = 1 — S мы получили бы (В {$') =■ (О (s), и вся правая часть
равенства обратилась бы в нуль. С другой стороны, заметим,
что формула q 4 выражает разность ядер qs и qis через
функции 9д. Отметим, что операторная форма соотношения q 5 имеет
следующий вид:
Q 5. Q{s)-Q(sO = [со(s) - (О(s')] Q(s)Q(s').
Наконец, справедливо такое соотношение:
оо
q 6. \q{y, у'; s) 9 {у', s') ^ = ^ (,,) 1 ^ (,) Э (|,, sO
а
при а' <а.
Это соотношение тоже проверяется прямым вычислением;
эквивалентная операторная формулировка:
другими словами, если выполнено условие ст' < а, то в^' —
собственная функция оператора Q{s).
Лемма 3. Пусть и > 3; положим М'=М{%). Произведения
операторов MQ{s) и Q{s)M определены на пространствах ^_i
и ^1 соответственно и
A[Q(s) = 0, Q(5)M = 0.
Доказательство. Ядро оператора М{%) представляется в виде
ряда Фурье, содержащего cos 2л,к {х — х'); следовательно, оно
ортогонально ядру оператора Q{s), которое не зависит от х.
На этом заканчивается наш список соотношений для
операторов Q{s). В прилагаемой таблице мы свели воедино основные
результаты о непрерывности рассмотренных нами операторов

318 XIV. Спектральное разложение оператора Лапласа на Г\©
В различных пространствах н некоторые соотношения между
этими операторами.
T{s), а> '/г; единственная ненулевая компонента (1,1),
(i) Непрерывен как оператор в Я.
(ii) Непрерывен как оператор в ^^ при 1 — ст < |i < ст.
M{s), ст> 1; единственная ненулевая компонента (1, 1).
(i) Компактен как оператор в Я; ядро m{z, z'; s)
принадлежит L^ {Fi X ^i)-
(ii) Непрерывно отображает 3§^ в .^y,-2; компактен как
оператор из ^_i в 3§-i.
(iii) Непрерывно отображает Я в ^_i.
N (s); ядро имеет тип 2 + е — ст
(i) При а > ^2 компактен как оператор в Я; ядро п (z, z'; s)
принадлежит I? {F X ^)-
(ii) При ff>3 непрерывно отображает J?i b-J?_[_j, S > 0;
компактен как оператор из ^i'b 3S-i.
(iii) При ff > 3 непрерывно отображает Я в 3S-i.
V := Л1 (и) + ]V (х), X > 3; единственная ненулевая
компонента (1, 1).
(i) Компактен как оператор в Я; непрерывно отображает
Я в ^_1.
(ii) Непрерывно отображает ^i в ^-i, компактен как
оператор из ^-1 в k-i.
Q(s); единственная ненулевая компонента (1, 1).
(i) Непрерывен как оператор в Я при а > '/а-
(ii) Непрерывно отображает ^_i в ^\-ф компактен как
оператор из ^-х в i^i (О < ст < 2).
Г = Г {%), М^М {%), N = N{k)
§ 9. Собственные функции оператора Лапласа
в пространстве £''(Г\ф) = Я
Напомним, что А — зам'ыкание оператора Лапласа с областью
определения D^ с: Я. Нас интересуют собственные функции
оператора А, т. е. такие элементы ofi s D^, ij) =5^ О, что Л-ф = A,ij).

§ 9. Собственные функции оператора Лапласа в пространстве L' (Т\^) 319
Предположим, как обычно, что и > 3. Заметим, что если 'феЯ —
ненулевой вектор и /?(>c)a|3 = aa|3 для некоторого комплексного
афО, то ■^^Ол и
ylaa|3 = (l—>с(1 — ,н)а)'ф;
таким образом, ofi — собственная функция самого оператора А.
Мы исследуем собственные векторы оператора R{k) в Н я
покажем, что они соответствуют собственным векторам
некоторого компактного оператора в пространстве ^-i-
Пусть О < ff < 2. Положим, как и раньше,
(О = со (s) == S (1 — s) — и (1 — и).
Пусть
K{s)^V + т (s) VQ (s) = 1/ (/ + coQ (s)).
Рассмотрим последовательность отображений:
Q(s) V
Мы знаем, что оператор V компактен. Отсюда ясно, что
оператор
K{s): ^_,^^_,
тоже компактен. Мы используем его для аналитического
продолжения резольвенты в полосу О < ст < 2. Однако в данный
момент мы интересуемся только дискретным спектром, и
поэтому мы будем рассматривать его только в области справа
от прямой а = '/г-
Пусть '/2^ог<2. Обозначим символом ,^_i(cu(s), K{s))
собственное подпространство оператора K{s) в пространстве ,®_i,
отвечающее собственному значению cu(s)~', т. е. пространство
функций /е^_1, таких, что
co(s)/C(s)/ = f.
Аналогично, пусть Я (со (s), /?) = Я(со (s), R {%)) — собственное
подпространство оператора R в пространстве Я, отвечающее
собственному значению co(s)~', т. е. совокупность таких функций
ф е Я, что
(О (s) /? (и) of) = of).
Теорема 7. При '/г ^ ст < 2 и s =ф ^2 отображения
/ + cu(s)Q(s) и / —(й(5)Г(>с)
вадают взаимно обратные изоморфизмы пространств
^_,((о(5),/C(s)) и H{a{s),R{%)).

320 XIV. Спектральное разложение оператора Лапласа на Пф
Доказательство теоремы 7 содержит формальные выкладки,
основанные на соотношениях между различными операторами,
а также оценки, которые мы докажем как отдельные леммы.
Начнем с формальной части. Мы будем для краткости писать Q
вместо Q{s).
Предположим сначала, что f е.^_, и <i)K{s)f = f, т. е. что
(ol/(/ + (oQ)f = /.
Поскольку R = T + V, то
(О/? (/+ coQ) / = (О (Г + 1/) (/+ (oQ) / =
= (соГ + co^TQ+ /)/ = (/ +(oQ) f;
тем самым первая половина теоремы доказана.
Обратно, предположим, что феЯ и (u/?ij) = i|). Тогда Kofie^.j
и
(иТ'ф + cuFa|3 == г|);
таким образом,
(/ — (оГ) a|3 == coya|3 е ^_i.
Тогда
а>К (S) {I — (оГ) a|3 = col/ (/ + coQ (s)) (/ — соГ) г|) =
= (ul/a|3 = (/ — ©Г) a|3.
Мы проверили обратное утверждение; тем самым формальное
доказательство теоремы 7 закончено.
Нижеследующие леммы обосновывают эти вычисления.
Заметим, что для первой части нашего рассуждения нам нужно
было знать, что если f^3§-i, то функция Q{s)f принадлежит
пространству Я. Это утверждение очевидно, когда Res =
= (Т > '/г- При а = Уз оно будет доказано в леммах 1 и 2. Во
второй части доказательства мы пользовались тем, что
отображение
(/ + (oQ)(/-(or)
действует на функцию ofi как тождественный оператор. Это
будет доказано ниже в теореме 8.
Лемма 1. Пусть 5 = '/2 + '^ причем t^O. Пусть f^^-i —
собственная функция оператора K{s), т. е.
co(s)/C(s)f = /.
Тогда сужение фунщии f на Fx ортогонально функции 8 (г/, s),
т. е.

§ 9. Собственные функции оператора Лапласа в пространстве Ь^(Г\,§) 321
Доказательство. Положим ofi == (/+ ©Q (s)) f. Тогда, в силу
наших предположений н определения оператора K{s), f = coFa|3.
Функция 'ф(2)/(2) принадлежит пространству L^ {F), так как
/s,^_i H.ijjs^i. Интегрируя ее по фундаментальной области,
получаем
J ^ф (г) / (г) dz = (О (s) J ф {z) V^ (г) dz ==
F F
=«= CO (5) f f t (z) У (г, г'; и) a|3 (z') dz' dz.
F p
Заметим, что ядро v{z,z'; и) оператора V вещественно и
симметрично. Кроме того, так как сг = 72. то 5 = 1—s; поэтому
функция cu(s):=(o(f) вещественна. Отсюда немедленно следует,
что мнимая часть интеграла в правой части равенства равна
нулю. Таким образом,
\ (•Ф/ — •Ф/) dz = 0.
Но of/ = [f + со (I) Q(5) f] / н a|3f = [f + (i){s)Q{s) f\ f. Следовательно,
0 = J 5 [?(г/, у'; s) -q{y, /; 1 - s)] f{z) W) dz dz' =
= S \B{y,s)W7bf{2)W)dzdz'=^ \Q{y,s)f(z)dz\
F, F, F,
ЧТО И Требовалось доказать. В наших выкладках мы
воспользовались соотношением q 4.
Лемма 2. Пусть О < ст < 2 « 5 =7^ '/г- Если f s i^_i, то
(*) Q (s) f (z) = ^j^ г/'-^ j e iy', s) f (z') dz' + 0(1).
Если s Ф '/2, о'^^12 и
TO функция Q{s)f ограничена и, в частности, принадлежит
пространству Н.
Доказательство. Воспользуемся определением ядра q{y,y';s)
и соотнвшением
■А «>
(25 - 1) Q (S) / (Z) = 5 \q {у, у'; s)t{x + iy') ^ dx.
11 Зак. 589

322 XIV- Спектральное разложение оператора Лапласа на Г\©
Напишем
со I/ со
а а у
Интегралы по переменной у' принимают вид
у <х>
а у
Легко видеть, что второй из этих интегралов ограничен. Интеграл
оо
У^-'\ Hy',s)f(z')f^
у
сходится и оценивается следующим выражением:
оо
г/'-" 5 (/" + с(S)/'-") Л-^ = О (1).
у
Таким образом, главный вклад вносит первый интеграл и мы
можем заменить в нем предел интегрирования на оо.. Первое
утверждение леммы доказано. Обратимся к второму
утверждению. Если о > 'li, то из интегрального представления ясно, что
функция Q (s) / ограничена. Пусть а = %, по s ф '/aJ тогда из
леммы 1 следует, что если
co(s)K(s)f=f,
то интеграл в оценке (*) обращается в нуль. Это завершает
доказательство.
Теояема 8. (Маас.) Пусть Res = '/2. * ?^'/2- Бели а))еЯ="
= 1^(Г\-&) и
A-^'^s{l — 5)1)),
то функция -ф аналитична и удовлетворяет оценке
\^{х + 1у)\< 6-2"^/.
В частности, функция f = {I — ш (s) Г {%)) a|3 принадлежит
пространству ^-\. Если ■фе^ц для некоторого ц>0 и La|3 = s(l — s)a|3,
то существуют такие постоянные Ь^, Cq, что
^ (х + iy) -= Ьоу" + ад' -' + 0 (е-^^У).
Доказательство. Для любой пробной функции g s СТ (Г\ф)
имеем
{{А - S (1 - S)) а|з, g) = (aj), (Л - s (1 - s)) g).

af^(y)={4n'n'-^^^)ajy),
§ 9. Собственные функции оператора Лапласа в пространстве L^(T\^) 323
Следовательно, по теореме регулярности для эллиптических
операторов, функция ф аналитическая и
(Л — S (1 — s)) а|) = 1а|) — S (1 — s) ф.
Поэтому ф разлагается в сходящийся ряд Фурье:
где
■л
ап(у)= 5 ^{x + iy)e-^^''^''dx.
-V.
Так же как и для ряда Фурье резольвенты, легко видеть, что
„2 ^ О - S)
у'
т. е. функция а„ есть решение уравнения Уиттекера.
Следовательно, существуют постоянные 6„, с„, такие, что
an (у) = b^Ws{4л\п\у) + CnVs{4л\п\у),
где Ws — экспоненциально убывающее решение уравнения
Уиттекера, а Vj — экспоненциально растущее решение. Если
функция ij) принадлежит пространству L^ или ^^, то ее коэффициент
Фурье имеет, самое большее, полиномиальный рост на
бесконечности; таким образом, экспоненциально растущий член должен
отсутствовать, т. е. с„ = 0. Зафиксируем точку у\, такую, что
при у^Уг выполнено неравенство
\WAy)\>je-y'K
Так как ряд Фурье — всюду сходящийся, его коэффициенты
ограничены. В частности, существует такая постоянная С] > О,
что
|а„Ы1 = |г'„1ГЛ4я|л|г/,)|<С,
при всех пф О, откуда
I 6„ К е2"1" I»'.
Если у'^2уи получаем
\ii{x + iy) — До (г/) К Z e^^l^l^e--"!»i» < е-^"»;
таким образом,
^{x + iy) = aAy) + 0{e--''y).
Далее, функция Оо есть решение уравнения
11*

324 XIV. Спектральное разложение оператора Лапласа на Г\©
Поэтому существуют такие постоянные Ьа, Cq, что
ао(у) = Ьоу' + Соу^-\
Если Res = V2> это совместимо с условием ijjeL^ лишь когда
i>o = Co — 0. Итак, теорема 8 доказана.
Замечание. Рассуждения аналогичного типа использованы
самим Маасом в работе [1].
Из определения оператора Q{s), который отображает
пространство ^-1 в ^1-0, и компактности оператора V мы
получаем следующие свойства семейства операторов K{s):
Теорема 9, Отображение s»—*- К (s) есть аналитическая
функция в полосе О < а < 2 со значениями в пространстве
компактных операторов на ^-i, за исключением, возможно, полюса
в точке 5 = 1/2, который появляется из-за множителя (2s— 1)~'
в определении оператора Q{s). Во всяком случае, отображение
SI—?-(2s— l)i'C(s) аналитично во всей полосе. Множество точек s
в полосе, в которых оператор
I-(u{s)K is)
необратим, дискретно, и отображение
s^^(/-<B(s)K(s)r'
имеет лишь полюсы в этих точках.
Доказательство. Аналитичность отображения s i—^ К (s)
очевидна. Свойства операторов и ядер, аналитически зависящих
от параметра, подробно исследованы в приложении 5 и в конце
следующего параграфа. Мероморфность отображения
s^^(/-(u(s)K(s)r'
вытекает из абстрактных теорем об аналитических семействах
компактных операторов, доказательство которых приведено
в приложении 5.
Будем называть точки s, в которых оператор / — (nKis)
необратим, сингулярными. Как показывает теорема 8,
множество сингулярных точек в полосе О < Re s < 2 дискретно. Из
теоремы 7 мы анаем, что сингулярные точки, лежащие на
прямой а =1/2 (за исключением точки s = l/2) или на отрезке
1/2 < 5^1, соответствуют собственным значениям оператора
Лапласа.
§ 10. Резольвентное уравнение в полосе О < а < 2
Мы по-прежнему считаем, что х > 3, и используем
обозначения
R = Rb<), V = V(x), Г = Г(х).

§ 10 Резольвентное уравнение в полосе О < а < 2 325
Справедливо разложение
Напомним также, что
(В = (В (s) = S (1 — s) — X (1 — х).
Мы хотим найти аналитическое выражение для ядр?
резольвенты, которое было бы пригодно во всей полосе С < а < 2
и представляло бы резольвенту при а > '/г- Основное
резольвентное уравнение имеет вид
(1) R{s)-R = ii^{s)RR{s).
Рассмотрим сначала вопрос о единственности.
Лемма 1. Пусть ^2^0 <2, s Ф '/г- Предположим также, что
точка S несингулярна. Тогда сущзствует не больше одного
ограниченного оператора X в пространстве Н = L^{T\^), такого,
что
X — R==a{s) RX.
Доказательство. Пусть X, X' — два решения приведенного
уравнения. Тогда
X-X' = (Si{s)R{X-X').
Если X — X'ф О, то любой ненулевой вектор ■ф = (Х—X')h,
he. Н, удовлетворяет уравнению
это означает, по определению, что точка s сингулярна
(противоречие).
Заметим, что ядро г {z, z'; s) представляет резольвенту, когда
а > '/г и S не принадлежит интервалу ('/г, !]• Хотя мы найдем
выражение для ядра, пригодное в полосе, оно не будет
представлять резольвенту при других значениях параметра s
Проделаем сначала алгебраические преобразования, чтобы
привести резольвентное уравнение к более удобному виду, и
для этого выполним формальные вычисления. В конечном итоге
мы хотим получить для резольвенты следующее выражение,
справедливое, когда s — несингулярная точка нашей полосы;
(2) R{s)^Q (s) + (/ + coQ (s)) В (s) (/ + (oQ (s)),
где B{s) — некоторый оператор. Посмотрим, каким
необходимым и достаточным условиям должен удовлетворять этот
оператор, чтобы было выполнено равенство (2). Воспользуемся
формально соотношениями
(Г-сйГ) = (/,+ «д(5))
-1

326 XIV. Спектральное разложение оператора Лапласа на Г\©
и Т + Q(s)T = Q{s); получим
(3) Х-Я=(йЯХ<^Х-Я = (йТХ + а>УХ
(4) ^{I-(oT)X = R + (uVX
(5) ^^X = (I + mQ(s))R + (oiI-ha»Q{s))VX
(6) ^X^Q{s) + {I + (oQ{s))V + со{1 + (oQ {s))VX.
Предположим, что X = Q (s) + (/ + coQ (s)) В (s) (I + ©Q (s)); тогда
это эквивалентно следующим равенствам:
(7) <^S(s) = V + (oV(/ + (oQ(s))5(s)
(8) ^B{s) = V + a)K{s)B{s)
(9) фф[/-(0Л(5)]В(5) = 1/.
Мы хотим свести исследование резольвенты к изучению
компактных операторов. Как сейчас будет видно, наша
подстановка как раз и подходит для этой цели.
Лемма 2. Пусть s — несингулярная точка полосы О < а < 2.
Тогда оператор
I — (oK{sy. ^-i-ySS-i
обратим, и существует единственный оператор
В is): а-1-*3§-1,
такой, что
[I-(oK{s)]B{s)=V.
Более того, оператор B{s) компактен.
Доказательство. Мы знаем, что оператор K{s), а значит, и
(йК {s), компактен. Следовательно, оператор / — аК (s) фред-
гольмов. Так как, по предположению, точка s несингулярна, то
оператор / — (йК{з) имеет нулевое ядро. Отсюда вытекает, что
он обратим. (Мы используем тот факт, что индекс фредголь-
мова оператора — локально постоянная функция и что для
компактного К отрезок I—iK, 0^/^1, соединяет оператор I — K
с единичным оператором в пространстве фредгольмовых
операторов. См. Ленг [1].) Так как оператор V компактен в
пространстве Зё-и то и оператор B{s) компактен.
Оператор V задается ядром v, которое имеет
логарифмическую особенность на диагонали и, следовательно, не может
быть непрерывным. По этой причине удобно еще немного
преобразовать оператор B(s), а именно, положить
(10) Bi(s) = B(s)-y.
Тогда уравнение
ll-(i>K{s)]B{s)=^V

§ 10. Резольвентное уравнение в полосе О < ст < 2 327
эквивалентно уравнению
(И) [/-(u/C(s)]B,(s) = Bo(s).
где
(12) 5o(s) = (uV(/ + (oQ(s))V.
Вернемся немного назад и определим ядро, соответствующее
последнему равенству. Для любого несингулярного s из нашей
полосы определим ядро 6о,* оператора Bq{s) формулой
(13)
\ S == <ВУ * У + (В^У * (fs* V,
где v = v{%) и ^j — ядра операторов V и Q(s). Это определение
применяется покомпонентно к ядрам, соответствующим
произведению Fi X fj двух частей нашей фундаментальной области.
Лемча 3. Пусть О < а < 2; предположим также, что точка
S несингулярна. Тогда
(i) Все компоненты ядер v * v и v * qs* v имеют тип ,^_i, и,
следовательно, все компоненты ядра &о, $ имеют тот же тип.
(и) Семейство функций bo, z, s. задаваемое формулой
bo. г, S (z') == bo {z, z'; s),
равностепенно непрерывно для всех zeFt(/ = 0, 1).
Доказательство. Рассмотрим сначала компоненту ядра v*v,
действующую на Fq X Fo- Заметим, что соответствующая
компонента ядра V равна
гоо (z, z'; х) = у ^ Ф (u (z, yz'y, к).
С точностью до постоянного множителя это ядро имеет вид
logl Z — z' 1 + непрерывная функция от (z, z^),
где Z, z' s Fq. Особенности ядра Гоо * гоо могут возникнуть от
свертки двух логарифмов. Итак, нам нужно показать, что ядро
l{z, z') = 5 log 12 - z" I log I z' - z" I dz"
непрерывно. Разобьем этот интеграл на 3 слагаемых, выделив
в нем вклад от окрестностей точек z, z'. Ясно, что интеграл
по дополнению является непрерывной функцией. Интегралы по

328 XIV. Спектральное разложение оператора Лапласа на Г\^
маленьким кружкам | г" — z |< е, \z" — z' \<г сходятся и не
превосходят величины
8^ \ I log \z" - z I logl z" - z' 11 dz" <
< 8^ Д i0g21 Z - Z" I dz'^y j' J iOg21 Z' - Z" I dz"Y < e2
(мы воспользовались неравенством Шварца). Теперь
непрерывность ядра Гоз * Гоо очевидна.
Оператор V имеет вид V = М + N, причем компоненты «о,,
«10, Пц ядра оператора Л^ имеют тип ^~i, а оператор Мц
задается ядром
т (z, z'; х) = J] /"f (l/. i/'; >«) cos 2п/ (л: — л:'),
где
Остальные компоненты Моо, Мю, Mgi равны нулю. Легко
проверить, что ядра операторов Л^Л^, MN, и NM имеют нужный
тип. Мы приведем детали вычислений для последнего
остающегося ядра т*т.
Лемма 4. Пусть т {г, z'; %) — то же ядро, что и выше. Тогда
ядро т*т имеет тип ^_i.
Доказательство. При / Ф I имеет место соотношение
ортогональности
'Л
[ cos 2п/ {х — х") cos 2%1 {х — х") dx" — 0.
Следовательно,
I (/п * /п) (г/, i/) К Е I (/п/ * /п/) (i/, у') I;
кроме того,
\{mi*mi){y,y)\<:\^ р ^.
а
Пусть, к примеру, у' < у. Разобьем интеграл, как и раньше,
следующим образом:
а а у' у

§ 10. Резольвентное уравнение в полосе О < ст < 2 329
Получаем оценку
Если у^2у', то слагаемое, содержащее константу а,
экспоненциально убывает при у-\- у' ->оо и, таким образом, ведет себя
даже лучше, чем нужно. Первое слагаемое ведет себя, как
1/у'^, или, что то же самое, как 1/уу'. Если у'^2у', то в ядро
входит обший экспоненциально убывающий множитель е~'^^<У.
Проверку того, что ядро v*qs*v имеет тип ^-i, мы
предоставляем читателю. Напомним только, что
MQ(s) = Q(s)M = 0,
благодаря тому, что косинусы ортогональны постоянным и,
в силу определения, оператор Q{s) имеет лишь одну ненулевую
компоненту Q,,, которая зависит только от у.
Итак, мы доказали первую часть леммы 3.
Что касается второй части, то я не вижу другого способа
доказательства, кроме проверки возможности предельного
перехода под знаком интеграла в выражениях для компонент ядра
bo (г, г'\ s). Тем самым будет доказана равностепенная
непрерывность соответствующего семейства функций. Чтобы
проверить это, нужно провести чуть больше таких же утомительных
стандартных оценок, что и выше. Мы предоставляем сделать
это читателю. (Так же поступает и Л. Д. Фаддеев в своей
статье [1].)
Лемма 5. Пусть О < а < 2; предположим, кроме того, что
точка S несингулярна. Тогда оператор Bj (s), определяемый
формулой
B,(s) = [/-coK(s)]-'So(s),
задается ядром Ь^ {z, г'; s) типа J-j.
Доказательство. Из леммы 4 мы знаем, что ядро Ьо {г, г'; s)
оператора fio имеет тип ^-i. Напишем
Ьо (2, Z';s) = bo, г'. S (z)
и будем рассматривать ядро Ьо как функцию от z,
принадлежащую пространству ^-i. Тогда имеют место оценки
\bo.z'.s{z)\<-^
И
II [/ - СК (S)]-' bo, г', S IL, < II bo, г', s ||_, < ~ .
Положим
6, (2, /; S) - ((/ - (ОК (S))-' Ьо, г', s) (2).

830 XJV- Спектральное разложение оператора Лапласа на Г\©
Полученное неравенство означает, что
|6,(2, z';s)|<-^,
так как для любой функции / е ^_i
llfL,=SUp|f(2)i/|,
И поэтому если ||f ||_, <! 1/t/', то | / (г) | <С l/i/i/'. Мы получили
нужную нам оценку асимптотического поведения ядра 6]. Чтобы
доказать его непрерывность, напишем
b,{z,,z\)-b,{z^,z'^) =
= 6, (2,, z\) - b, [z^, z\) + b, [z^, z\) - 6, {z^, z'^).
Зафиксируем точки (г,, 2j), и пусть {z^, z'^ стремится к (г,, z[y
Так как функция 6, ^/ непрерывна, то первая разность в
правой части предыдущего равенства стремится к 0. Вторая
разность также стремится к 0; в самом деле, согласно
второй части леммы 3, аналогичная разность для ядра &и
стремится к О, и это свойство не нарушится при применении
ограниченного оператора в пространстве ^-j.
Мы полностью исследовали непрерывность ядер 6о и 6].
Изучим теперь их зависимость от s.
Теорема 10. Определим для любого несингулярного s из
полосы о < а < 2 оператор В (s) формулой
B(s) = [/-(o(s)K(s)]~'y.
Тогда
(i) Отображение si—> В (s) является мероморфной функцией,
заданной в полосе О < (т < 2 и принимающей значения
в банаховом пространстве ограниченных операторов,
действующих в ^-1. Полюсы этого отображения совпадают
с сингулярными точками.
(ii) Имеет место разложение
B{s)=^M + №{s),
где оператор №{s) задается ядром типа ^-i, а М'=М{%),
х>3.
(lii) При а > '/21 зф S справедливо соотношение
R{s)^Q is) + (/ + coQ (s)) В (s) (/ + coQ (s)).

§ 10. Резольвентное уравнение е полосе О < (Т < 2 331
Доказательство. Первое утверждение немедленно следует
из теоремы 9 предыдущего параграфа. Второе вытекает из
доказанных лемм, если принять во внимание соотношение
fi (s) = В, (S) + У = В, (s) + М + Л^.
Третье очевидно из цепочек эквивалентных формул (3) — (9) и
единственности решения резольвентного уравнения, доказанной
в лемме 1. Теорема доказана.
В заключение этого пераграфа выпишем уравнение для
оператора B\s), которое вытекает из резольвентного уравнения.
Теорема 11.
(i) Пусть О < а < 1 и точки s и I — s несингулярны. Тогда
имеет место соотношение
В (S) - ВЦ - s)=(i>isf B{s)[Q{s) -Qil - s)]B{l - S),
где все операторы рассматриваются в пространстве .^-j.
(ii) При о, а' > '/г и,меет место соотношение
В _ В' = (и - (о') В (/ + (bQ) (/ + ffl'Q') В',
где B = B(s), B' = B(s'), (u = (b(s), (u'=(b(s') и т. д., все
операторы рассматриваются в пространстве Н.
Доказательство. Начнем с равенства В = (1 —■ аКУ^ V. Пусть
а, а' е (О, 2). Будем рассматривать все операторы в
пространстве 3S-1. Тогда справедливо равенство
В-В'-=[{1- шД')-' - (/ - ш'Г)-'] V =
= (/ - шЛ:)-' (шД - ffl'iC') (/ - ш'Д')-' У-
Так как i<- = У (/ + (oQ), К'= V Ц + (o'Q'), то
(*) B-B' = B((u-(u' + (b2Q_u)'2Q')S'-
Положим s' = 1 — s; в этом случае ш = а', и мы получаем
наше первое соотношение. С другой стороны, формулу (*),
которая представляет собой операторное равенство в
пространстве ^_1, когда S, s' лежат в полосе О < а < 2, можно
рассмотреть в более узкой полосе 1/2 < а < 2, в этом случае
входящие в нее операторы ограничены как операторы в
пространстве Н и формула (*) справедлива как операторное равенство
в Я. Воспользуемся соотношением
Q-Q' = ((u-(o')QQ',
справедливым как операторное равенство в Я; мы видим, что
формулы (ii) и (*) эквивалентны. Теорема доказана.

332 XIV Спектральное разложение оператора Лапласа на Г\§
В дальнейшем мы будем пользоваться только первым из
доказанных соотношений; его можно рассматривать как
«функциональное уравнение» для оператора B{s). Из
доказанного соотношения будет непосредственно следовать
функциональное уравнение для функций Эйзенштейна (которые мы
определим в § 12).
§ 11. Ядро резольвенты в полосе О < а < 2
В этом параграфе мы увидим, что, хотя резольвенту
оператора Лапласа нельзя аналитически продолжить левее прямой
сг=1/2, можно, однако, аналитически продолжить лЗро
резольвенты как функцию параметра s во всю полосу О < сг < 2.
Мы построим это продолжение, используя уравнение для ядра
b{jz.,zf;s). Я признателен Р. Браггеману, которому
принадлежит изложение настоящего параграфа.
Теорема 12. Пусть U — открытое подмножество комплексной
плоскости, [1, V — вещественные числа. Предположим, что для
любого set/ определен непрерывный оператор
R(s): ^^->^v,
задаваемый ядром r{z,z';s), причем (z', s)^-^ г (г, z'; s) —
измеримая функция на произведении РУ\и при всех z^ F.
Предположим, кроме того, что для каждого компактного подмножества
К'^и существует такой ограниченный оператор
с ядром гк, что для почти всех {z, z')^ FyiF и для всех s ^ К
справедлива оценка
\r{z,z'; S)|<rjc(2, 2').
Тогда ядро r{z,z'\ s) аналитично по s при почти всех {z,z')
в том и только в том случае, когда отображение s^-^^R{,s)
аналитическое.
Доказательство. Мы используем теорему 1 приложения 5,
а также утверждение, аналогичное теореме 2 из этого
приложения. А именно, мы докажем сначала следующее утверждение:
Лемма 1. В предположениях теоремы 12, ядро г {z, z'; s)
аналитически зависит от s при почти всех {z, z'\ в том и только
в том случае, когда для всех функций f ^^^^ и для всех
Z ^ F отображение
st-^R{s)f{z)
аналитическое.

§11. Ядро резольвенты в полосе О < ст < 2 333
=Ф Пусть С—любая окружность, целиком лежащая в области U.
Предположим, что / е ^^, z^F. Функция
z'^rc{z,z')\f{z')\
интегрируема и мажорирует функцию z'^-^ r(z, z'; s)f{z') при
всех s^C. Следовательно, отображение s>-^ R{s)f {z)
непрерывно по теореме об ограниченной сходимости. Далее, функция
(z', s) 1-^ г {z, г'; s) измерима и ограничена интегрируемой
функцией
(2',S)H-»rc(2,20|/(2')|;
таким образом, функция (г', s)-—* г {z, z'\ s) интегрируема, и
5;? (S) / (z) ds = J J г (2, z'; s) f (zO dz' ds =
с с F
= \f{z')^riz,z';s)dsdz' = o.
F С
Итак, мы показали, что отображение s*—^ R{s)f (z)
аналитическое.
ф: Предположим, что отображение s^—^R (s) f{z) аналитично
для всех / и Z. Ясно, что мы можем снова поменять порядок
интегрирования и получить, таким образом, что
J/CzOjrCz, z';s)dsdz'=0
для всех z^F и для всех функций / е J^. Тогда для почти
всех (z, z')e FX.F получаем
\ г (z, z'; s) ds = 0.
Из леммы §1 приложения 5 вытекает, что ядро r{z,z';s)
аналитически зависит от S.
Теперь мы проверим, что для некоторого подходящего
множества функционалов выполняются условия теоремы 1
приложения 5.
Так как для любого компакта К ядро г мажорируется
ядром Tjf, получаем
sup|^?(s)|<|^?^cl• .
seK
Для любой точки 2 из F и любой функции / из единичного
шара в пространстве 3§^ определим линейный функционал Я^, ^
на банаховом пространстве
Е = Нот {3§^, 3S^)

334 XIV. Спектральное разлооюение оператора Лапласа на Г\5
формулой
Таким образом, Xf^^ есть композиция двух непрерывных
линейных отображений
A^Af и gy^^,
у
норма которых не превосходит единицы. Ясно, что множество Л
всех таких функционалов — нормирующее^ Это позволяет
воспользоваться теоремой I приложения 5, что и завершает
доказательство теоремы 12.
Следствие. Предположим дополнительно, что для всех z^ F,
s^U функция z' ь-> г (г, z'; s) непрерывна, а функция z'»—>
н-> r^{ (2, z') локально ограничена. Тогда функция Si—^r{z, z'; s)
аналитична при всех {z, z') в том и только в том случае, когда
отображение s н-> i? (s) аналитическое.
Доказательство. Наше дополнительное предположение
необходимо только для доказательства импликации ф.
Достаточно показать, что если
{\riz,z';s)f{z')dz'ds=0
с F
для всех z^F и всех f е .^„, то
\
с
1»>
r{z, г'', s)ds=0
для всех Z, /. Зафиксируем точку z, и пусть g — функция от г',
задаваемая последним интегралом. Для любой вещественной
функции f ^.Сс {F) (в этом случае, очевидно, / е if д) мы
получаем
{g,f)^\\r{z,2'',s)f{.z')dsdz'^Q.
ГС
Следовательно, функция g равна нулю почти всюду. Из
сделанных предположений вытекает, что она непрерывна, откуда g = 0.
Итак, наше утверждение доказано.
Пусть Q — компактное подмножество полосы О < а < 2.
Пусть О < ai < а < СГ2 < 2; мы можем определить
мажорирующее ядро
, d/^' + c^-"')/'""', если у<у\
(Z z')==c Я^°' + ''^
Ц-Сз/'-"'), если / <у.

§ п. Ядро резольвенты в полосе О < сг < 2 335
где Ci, сз — подходящие постоянные, такие, что для всех seQ
справедлива оценка
U(2,/;s)|<?2(2, 2').
Пусть
— ограниченный оператор, единственная ненулевая компонента
которого (Qq),, задается ядром д^. Так же как и для
оператора Q (s), легко видеть, что если 0< ц< Oi <2, то
оператор Qq непрерывно отображает пространство 3§о в .^[з.^; поэтому
мы напишем
Следующие две Леммы содержат оценки, необходимые для
применения теоремы 12.
Лемма 2. Пусть Q — компактная окрестность точки Sq из
нашей полосы. Пусть т — порядок полюса оператора
[/-u)(s)K(s)]-'
в точке Sq. Тогда существует такая постоянная С > О, что для
всех se.Q справедливо неравенство
\s-s,r\b,{z,z';s)\^C{yyr\
где, как и раньше, Ь^ {z, z'; s) — ядро оператора Bj (s).
Доказательство. Рассуждения, проведенные при
доказательстве леммы 5 предыдущего параграфа, проходят без изменений.
Достаточно заметить, что все оценки равномерны, когда s
меняется в компактном множестве Q.
Введем обозначение для функции, которая является
аналитическим продолжением ядра резольвенты в нашей полосе.
Положим
Ps=(fs+ (^ + «s^s) *Ь,* (1+ (n^qs).
Мы пишем Ps (z, z') = Р (2, z'; s). По теореме 10, (iii), при '/г <
< а < 2, зф§ ядро р(2, z'; s) задает резольвенту оператора
Лапласа. За исключением, возможно, диагонали и границ
областей Fi, на которые мы разбили фундаментальную область,
ядра р (z, z'; s) и г {z, z'; s) непрерывны по (z, z') и совпадают
в полосе 1 < а < 2.
Лемма 3. Пусть Q — компактная окрестность точки Sq из
нашей полосы. Предположим, что Q содержится в полосе
О < ai < а < аз < 2. Определим число т., как в лемме 2. Тогда

336 XJV. Спектральное разложение оператора Лапласа на Г\©
существуют такие постоянные Ci, что для всех seQ справедливо
неравенство
< c,q^ (2, 2') + c,{yyУ^ + с,\т {z, г') | + с,{уу')'-".
Доказательство. Это вытекает из простых оценок интегралов,
входящих в определение ядра p{z,z';s).
Теперь мы в состоянии воспользоваться теоремой 12. Зная,
что некоторые семейства операторов мероморфны, а также что
соответствующие им ядра удовлетворяют подходящим условиям
локальной ограниченности, мы можем сделать вывод, что сами
ядра являются мероморфными функциями от параметра. Более
точно, справедлива
Теорема 13. Если гфг' и тонки г, z' не лежат на границе
областей Fq и f j, то функции
st—^p{z,z';s) и st-^'b{z, z'; s)
мероморфны в полосе О < а < 2 и имеют полюсы только в
сингулярных точках.
Порядки полюсов и главные части в этих полюсах мы
определим, основываясь на самосопряженности оператора, который
задает ядро р (z, z'\ s) при о > '/г- Будет установлен следующий
результат.
Теорема 14. Пусть Sq — сингулярная тонка, такая, нто Oq"^ '/з,
ЗаФЧ^' Пусть al)], ..., ■^п — полная ортонормированная система
собственных функций самосопряженного оператора А в
пространстве Н, отвечающих собственному значению Xq = Sq{\ —So). Мы
будем предполагать, что функции of,- вещественны. Положим
f^ = {I-(^{so)T)b.
Тогда функции f; принадлежат пространству 3S-i. Более того,
справедливы разложения
п
1
г (2, Z'; S) = j^ J] ^i (z) aj), {z') + r+ (2, z'; s),
n
b (z, z'; s) = 5^ Y. f' (^) f' (^') + *^ (^' ^'' ^)'
i-i
где функции s 1—^ Гз, s 1—^ bt голоморфны в о/срестности точки
Sq] мы используем обозначение X^^s{l —s) и не различаем ядра
г и р.

§11. Ядро резольвенты в полосе О < сг < 2 337
Доказательство. Осложнение, которое не позволяет нам иметь
дело исключительно с операторами, состоит в том, что на
прямой а = '/2 оператор А имеет также непрерывный спектр; таким
образом, его резольвента (как оператор) не допускает
разложения в степенной ряд в окрестности сингулярной точки, лежащей
на этой линии, несмотря на то что, как мы докажем,
аналитическое продолжение ядра резольвенты допускает такое
разложение. Отсюда следует, что наши операторы снова придется
рассматривать в других пространствах, например в пространствах
^ ■ в то же время мы будем использовать свойства резольвенты
справа от прямой а = '/2 и, в частности, оценку
1^(5)яК^(Я^, зресЛ)'
где diXs, spec Л) — расстояние от точки Х^ = з{1 — s) до спектра
оператора А. Напомним, что этот спектр расположен на
вещественной прямой и соответствует значениям s, для которых
'/г < S < 1 или Re S == '/2-
Мы пишем R {s)ff, чтобы подчеркнуть, что рассматриваем
резольвенту как оператор в пространстве Я. Приведенная оценка —
это просто переформулировка в терминах переменной s
очевидной оценки
(см. приложение 2, § 1, теорема 2).
Обратимся теперь к самому доказательству. Пусть (х^О.
При ц < а < 2 определен оператор
Ris): ^о->^1-^,
задаваемый обычной формулой
R{s) = Q is) + (/ + со (s) Q (s)) В (s) (/ + ш (s) Q (s)),
и отображение s 1-^ R (s) мероморфно. Выберем конкретное
значение (х, которое позволит нам работать в полуплоскости
а^'/г. например (х = 74-
Лемма 4. Пусть Sq — сингулярная точка, такая, что Sq Ф '/а
" сго ^ '/г- Пусть
R{s): Jo->^'A
— оператор, задаваемый ядром r(z, z'; s). Тогда отображение
S н-^ R (s) имеет в точке Sq полюс первого порядка.
Доказательство. Пусть {s„} — последовательность
несингулярных точек полуплоскости Res>'/2. еходящаяся к So и такая.

338 XIV- Спектральное разложение оператора Лапласа на Г\©
что Re (Xs^ — ^s^) = 0. Таким образом, мнимая часть Xs
стремится к нулю с той же скоростью, что и разность (s„ — Sq).
Положим
S->S|i
где т — порядок полюса. Нам нужно показать, что /?_^==0,
если /п> 1. Пусть f — произвольная функция из 3Sq; покажем,
что ^?_„/ = 0. Допустим противное: R_^t=^Q и положим
en^{Xs^-Uj^R{Sn)t.
Тогда последовательность {§•„} сходится к R_Ji в пространстве
Jisy^. Следовательно, для некоторой положительной постоянной
С] и всех у из некоторого открытого множества справедливо
неравенство
\R.J{z)y-''^>c,.
По определению нормы в пространстве J/„ мы получаем также,
что при всех достаточно больших п имеет место оценка
\lgn{z)-R_J{z)-]y-'i'\<B
равномерно по i/ в некотором открытом множестве. Отсюда при
больших п мы получаем неравенство
\gn{z)y-'i*\>Ci>Q\
таким образом, для некоторой постоянной Сз > О и для всех ц
из некоторого открытого множества верна оценка
1^«(2)|>Сз.
Так как iMo^z Н и Re s„ > '/г- отсюда следует, что R {s„) f ^ Н,
а значит, и g^^ Н. Неравенство, которое мы только что
получили, показывает, что существует постоянная с^ > О, такая, что
при всех достаточно больших п
Но, с другой стороны,
11^112<1Ч-^оГ1^(5„)я111/1Ь.
что противоречит оценке для резольвенты в гильбертовом
пространстве Я. Лемма доказана.
Из леммы 4 вытекает, что ядро г (z, z'; s) имеет в точке 5о
полюс первого порядка. Действительно, из леммы 2 мы знаем,
что порядок этого полюса не превосходит т (т. е. порядка полюса
оператора (/ — ш(s)К(s))"')- Допустим, что он равен 1'^2. Для

§ 11. Ядро резольвенты в полосе О < ст < 2 339
любого малого контура С вокруг точки Sq, соответствующего
окружности с центром в точке Xq, и для любой функции f ^^о
имеем, согласно лемме 4,
5 5 (Яо - К)'~' г (z, z'; s) t {z') dz' ds = 0.
Оценка, полученная в лемме 3, показывает, что мы можем
изменить порядок интегрирования. (Заметим, что абсолютная
величина |Яо —Я^! постоянна на контуре С.) Таким образом,
получаем
^(Яо-Я,^/"'г(2, z';s)ds = 0
для почти всех точек (z, z'), а значит, для всех (z, z'),
удовлетворяющих условиям теоремы 13. Отсюда следует, что /=1.
Теперь мы должны определить главную часть ядра в полюсе.
Рассуждения будут проводиться по той же схеме: сначала мы
будем рассматривать семейство операторов, а затем переходить
к их ядрам.
Умножим обе части- уравнения
R{s)-Q(s) = (/ -f coQ(s)) В(s) (/ + (oQ (s))
справа и слева на оператор / — шГ; получим
В (s) = (/ - шГ) {R (S) - Q (s)) (/ - (оГ).
Итак, отображение s и-> В (s) имеет в точке Sq полюс первого
порядка; мы рассматриваем В (s) как линейное отображение из
.^0 в Js/,. Из теоремы 12 следует, что ядро b{^,z';^, которое
задает этот оператор, также имеет в точке Sq полюс первого
порядка. Но то же самое ядро определяет в действительности
и оператор
^7. -> J_,;
следовательно, по той же теореме, этот оператор тоже имеет
полюс первого порядка в точке Sq.
Лемма 5. Пусть 3§-i(so} cz iM-i — собственное
подпространство оператора K{so), отвечающее собственному значению
co(so)~^ Положим
В-1 = lim (ш (so) — (О (s)) В is);
s->s„
мы рассматриваем B{s) как отображение из ^,^ в J_j. Тогда
отображение
В ,; i®,, —> X .
— 1 и — i

340 XIV. Спектральное разложение оператора Лапласа на Г\©
переводит пространство ^y^ в упомянутое выше подпространство
^-l(So)-
Доказательство. Имеем
fi(s) = [/-(u(s)K(s)]->y.
Умножим обе части этого равенства на ((a(so) — o>(s)) и
устремим S к Sq. Ясно, что этот предел существует. Теперь наше
утверждение очевидно.
Лемма 6. Положим
R-1 = lim (ш (So) — co(s)) R (s);
мы будем рассматривать ^?_, как отображение из ^q в ^,..
Тогда оператор R_^ переводит пространство ^д в собственное
подпространство Н (sq) оператора А, отвечающее собственному
значению Xs„ и индуцирует тождественное отображение на
этом подпространстве.
Доказательство. Умножим обе части равенства
/? (S) = (/ + (О (S) Q is)) В (S) (/ + (О (S) Q (S))
на (b(so) — (b(s) и устремим s к Sq. В левой части мы получим
оператор R-i. Предел правой части равен
(/ + (О (So) Q (So)) S-, (/ + (О (So) Q (So)).
Из предыдущей леммы и из фундаментальной теоремы о
собственных векторах оператора А (теорема 7 § 9) мы получаем,
что оператор ^?_i переводит пространство ^о в Н (sq). Кроме
того, если ij) е Я (Sq) и, следовательно, по теореме 8 § 9, а|) е ^о>
то мы знаем, что при а > '/г справедливо равенство
((u(So) —co(s))i?(s)a|) = a|3.
Это соотношение имеет смысл и в пространстве ^»/,. Устремим
S к So и вычислим предел в этом пространстве. Мы получим
R_i 013 = 11); итак, лемма доказана.
Лемма 7. Оператор R-i отображает подпространство %f\
nЯ(so)-^ в нуль.
Доказательство. Пусть gs^of\H (so)"*", а|) s Я (so). При а >
> '/г имеем
ПК - К) R (s) g, il3) = {g, (Яо - Xs) R (s) oj)) = 0.
Левая часть этого равенства имеет вид
\{Xo-X,)R{s)giz)^dz;,
р

§ 12. Оператор Эйзенштейна и функции Эйзенштейна 341
функцию R{s)g МОЖНО рассматривать как элемент
пространства ^v^. Устремив S к So в полуплоскости а > '/г, получаем,
что
Но из леммы 6 мы знаем, что R-ig е Я (sq). Следовательно,
R-ig = 0, что и требовалось доказать.
Пусть {а))1, ..., а))„} — ортонормированный базис
пространства Н (so); мы можем предположить, что все функции ajji
вещественны. Ядро
п
задает проектор из пространства Я на подпространство Н {Sq).
Можно рассматривать его и как проектор из ^q на Н (sq),
поскольку имеет место ортогональное разложение
^о = Я(5о)е[^оПЯ(5о)^].
Ядро
r{z, Z'\ S) — Яо-я/-' (^' ^')
задает оператор
R{s)- j;^R-x- ^o-^^v..
Семейство этих операторов голоморфно по s в точке Sq. Отсюда
следует, что для любого маленького контура С вокруг точки Sq
\\r{z,z!; s)-j^-^r_,(2,2')]ds = 0.
с
Чтобы доказать это, нужно снова воспользоваться оценками
из леммы 3 и тем, что аналогичное равенство имеет место
для нашего операторного семейства в сильном смысле — в
применении к произвольной функции / е ^0- Это завершает
доказательство той части теоремы 13, которая относится к ядру
г (Z, z'; s).
Чтобы доказать утверждение теоремы о ядре Ь {z, z'\ s),
нужно свернуть ядро г {z, z'; s) с ядром 1 — ш (s) t.
§ 12. Оператор Эйзенштейна и функции Эйзенштейна
Обозначим символом 6 (z, s) функцию на F, сужение которой
на Fq равно нулю, а сужение на f, задается формулой
е,{2, s) = e(i/, s) = г/-+c(s)i/^-^

342 XIV. Спектральное разложение оператора Лапласа на Г\©
где
S + х— 1
Эта функция принадлежит пространству ^^, где jj,=max((T, 1—а).
Обозначим символом W (s) оператор
r(s) = (D[/ + (DQ(s)]fi(s).
где, как и раньше, © = ©(s) = s(l—s) — %{\—и). Этот
оператор определен для всех несингулярных точек s полосы О < а < 2
и отображает пространство ^2-в в ^i_<j. Оператор
I + W{s)
мы будем называть оператором Эйзенштейна. Применяя его
к функциям ^s'- 2 *—* 9 (2, s), мы получим функции Эйзенштейна
Л (2, S) = (/ + г (s)) 8 (2, s) = 8 (2, s) + Г (s) 8 {z, s),
определенные в полосе О < а < 2.
Теорема 15. При фиксированном г функции s ь-^ т| (z, s)
аналитичны в полосе О < а < 2, за исключением сингулярных
точек, лежащьа в полуплоскости а<}12 или на отрезке '/г ^ s ^ 1.
В окрестности прямой а = '/г, за исключением, возможно, точки
S = '/г. ^гы функции ана^штические.
Доказательство. Если а ^^ 72» то наше утверждение
немедленно следует из аналитических свойств рассматриваемых ядер
и функций. Рассмотрим прямую а = '/г- Пусть Sq — такая точка,
что СТо = '/2> но So =7^'Л- Из аналитического выражения для ядра
b {z, z'l s) (теорема 13 §11) и определения собственных функций
l|5i=(/ + (DQ(s))/i
ясно, что
п
" "i-l F
где функция Tji аналитична в окрестности точки Sq. В силу
леммы 1 § 9, интеграл в правой части равен нулю для всех
значений s вида '/г + ^Л где t близко к ^о- Так как интеграл
аналитичен по s, он равен нулю тождественно. Теорема доказана.
Мы будем использовать прежние обозначения для свертки
ядер, но теперь свертка берется по всей фундаментальной
области F. Другими словами, пусть ft, (z, z'), ^2 (2, 2') — функции
от аргументов z, z' е F. Тогда, по определению,
(А, * Аа) (2, г') = \ k, {z, z") k, (2", /) dz\

§ 12. Оператор Эйзенштейна и функции Эйзенштейна 343
Аналогичные обозначения мы будем использовать для свертки
ядра с функцией от одной переменной:
{k,*t){z)=\k,{z,z')t{z')d2',
F
(/*ft,)(2)= \f{z')k,{z',z)dZ^.
F
Пусть bs — ядро оператора В (s); положим
c(s) = c(s) + f^e,*6,*e,.
в более подробной записи
е^ * 6^ * 9^ = J J 6 (Z, S) 6 (z, z'; s) 9 (z', s) dz dz'.
F F
Дадим теперь асимптотическое описание функций Эйзенштейна.
Теорема 16. Зафиксируем несингулярную точку s из полосы
О < ст < 2. Тогда при у ^>- ао имеет место асимптотическая
формула
T,(2,s)=/ + c(s)|/'-^+0(l).
Доказательство. По определению,
т), = [/ + ©(/ + ©Q (s)) В (S)] е, = 8, + ©6, * 8, + ©2^3 *bs*Qs-
Как мы знаем, В (s) = М + N^ (s); напомним, что разложение
оператора М в ряд Фурье по косинусам не содержит
постоянного члена, в то время как функция 9^ не зависит от х.
Следовательно,
УИ8, = О и В (s) 8, = N^ is) 8„
в силу ортогональности косинусов константам. Так как оператор
№ (s) имеет тип J_i, а тип функции 9^ равен max (ст, 1 — а) < 2,
то функция №{s)Qs принадлежит пространству J_i и, в
частности, ограничена. Тем самым мы оценили второе слагаемое
в формуле для Tjj. Чтобы оценить третье слагаемое,
воспользуемся снова тем, что функция S (s) 9^ = Л^-^ (s) 9^ принадлежит
пространству J-i. Из леммы 2§9 вытекает, что
Q is) В (S) е, = ~ У'-']\^ (2. S) b (2, z'; s) 9 {z', s) dz dz' + 0 (1).
F F
Теорема доказана.
Теорема 17. Пусть s — несингулярная точка. Если О < ст < 1,
то уравнение
© (S) /? (и) Т| = Т1

344 XIV. Спектральное разложение оператора Лапласа на V\Q
имеет одно и только одно решение с асимптотикой
л(2)=/+с(5)г/'-^+0(1);
S фиксировано, у->ао. Если ст> 1, то у этого уравнения есть
одно и только одно решение с асимптотикой
Л (2) = / +0(1).
Доказательство. Существование решений будет доказано
позднее; сейчас мы докажем только их единственность. Пусть
сначала 0<ст<1. Если t)i, tjj — два решения приведенного
уравнения на собственные функции оператора R (х), то их
разность i|) ограничена, а значит, принадлежит пространству
L^ {Т\ф) = Я и удовлетворяет тому же уравнению. Если ijj =7^ О,
то, по определению, это означает, что точка s сингулярна, что
противоречит нашему предположению. Аналогичное рассуждение
проходит и в случае, когда а>1.
Следствие. При а > 1 справедливо равенство
х\ (2, s) = Х Im {yzf.
УеГо\Г
Доказательство. Ряд в правой части абсолютно сходится
при а> 1. Оператор Лапласа коммутирует с действием группы
SL2 (R) в пространстве Н; следовательно, этот ряд определяет
функцию т), такую, что
Ltj ==s(l — s) Tl.
Слагаемое с v = 1 Дает член у^. Все остальные члены ряда
имеют вид
^ если Y = l wj' ^^ '
\cz + d\
и, следовательно, ограничены при у-^оо. Так как ряд
равномерно сходится, то сумма этих членов есть также
ограниченная функция. Таким образом, мы можем воспользоваться
теоремой единственности. Доказательство закончено.
Покажем теперь, что наша функция 1^5 = (/+ lF(s))8j,
определенная в полосе О < а < 2, удовлетворяет уравнению на
собственные функции из теоремы единственности и тем самым
при а > 1 совпадает с приведенным выше рядом. Это уравнение
будет первым из формальных свойств функций Эйзенштейна,
которые непосредственно следуют из соответствующих
формальных свойств операторов Эйзенштейна. Общим источником этих
свойств является, по существу, резольвентное уравнение.
Лемма. При %> 3, 0<б<2 справедливо соотношение
(й(5)г(и)9, = е,.

§ 12. Оператор Эйзенштейна и функции Эйзенштейна 345
Доказательство сводится к элементарному интегрированию
(заметим, что все интегралы в этом равенстве — сходящиеся).
Эта лемма позволит нам заменять оператор ©Г на
единичный оператор при действии на функции 8^.
Справедливо операторное равенство
(1) ©/?(/ +Г) = ©Г + Г;
как обычно, мы пишем R = R (и), Т = Т {%), W = W (s). Чтобы
получить это равенство, воспользуемся определением оператора IF(s)r
r = ©(/-|-©Q)fi,
а также равенствами R = T + V я
Получим
<uRiI + W) = (uT + (u{I + (oQ)B^aT + W;
следовательно, согласно нашей лемме,
©/?(/-}-Г) 8, = (/-}-Г) 9,.
Отсюда вытекает первое соотношение
ES1. ©(s)i?(x)Tt==V
Таким образом, функция Эйзенштейна — собственная функция
резольвенты оператора Лапласа.
ES 2. т) {yz, s) = т) (2, s) для всех v ^ Г.
Доказательство. В силу равенства ES 1,
т) [уг, s) == © (s) R {%) т) {yz, s) =
= © (5) J г {yz, z'\ %) T) {z', s) dz' = T| (2, s),
F
так как г {yz, z'; %) = r {z,z'\ v).
ES 3. L-(\s = s (1 — s)'r\s-
Доказательство. Достаточно доказать это равенство в слабом,
смысле, так как потом можно будет воспользоваться теоремой,
регулярности для эллиптических операторов. Как и раньше,
положим Ms = L — s{\ —s). Для любой функции f ^С'^ (Г\'&) имеем
© (S)-' 5 т| (2. S) MJ {z)dz==\^r (г, 2'; и) т| {z', s) MJ (2) dz dz' =.
F F P
i\ {z', s) \r^ {z, z'; h) Msf (г) dz dz'^
\

346 XIV. Спектральное разложение оператора Лапласа на Г\^
Воспользуемся равенством Ms = M^ — (ii{s), леммой 1 § 3 и
теоремой 2 § 3. Наше предыдущее выражение равно
\r\{zf,s){Rb<.)Mj){z')dz'-
F
— © (s) \ \ т| [z', s) Г [z, z'; к) / (z) dz dz' =
F F
= J T, (2', S) / (20 d2'- 5 T, (2, S) / (2) d2 = 0.
/■■ F
Утверждение доказано.
ES4. ;u^)='ri(2,7).
Это равенство очевидно, так как все ядра и функции,
которые мы рассматриваем, обладают этим свойством.
Покажем теперь, каким образом различные формы
резольвентного уравнения из предыдущего параграфа можно
интерпретировать как соотношения для функций Эйзенштейна. Мы
будем рассматривать резольвентные уравнения как операторные
равенства или как равенства для ядер.
Рассмотрим сначала резольвентное уравнение для
оператора R{s). Как мы знаем, если а, а'>1/2, то справедливо
равенство
/?-/?' = (со-©О/?/?'.
где мы пишем (для краткости) R=^R{s), R' = R{s'), ©' = ©(s').
Ниже мы используем также обозначения S = fi(s), B' = B{s')
и т. д. Напомним две формулы для ядра оператора Q, которыми
мы будем постоянно пользоваться в дальнейшем.
Q5. Q — Q'=-{iii-(Si')QQ' при а, а'> 1/2.
где 6^ = 8^(2) и 95_j=9,_j(2'). Переменные 2, z' — это аргументы
ядер ^^(z, z') и q^_^{z,z').
ES 5. Пусть S лежит в полосе О < а < 1, причем точки s и
1 — S несингулярны. Тогда
г (Z, z'\ s) — г{г, z'\ 1 - s) == 271ГГ ^С'^' «) Л(2', I — s).
Доказательство. Воспользуемся соотношением
/?-=Q + (/ + a)Q)S(/ + (DQ).

§ 12. Оператор Эйзенштейна и функции Эйзенштейна 347
Получим
+ (©-©О (/+ ©Q) й (/+ ©Q) Q'+
+((й - ©О Q (/ + <oQ') В' (/ + a'Q') +
+ (© - ©') (/ + ©Q) fi (/ + ©Q) (/ + ©QO fi' (/ + ©'Q').
Заметим, что произведение, составленное из операторов fi и Q,
в котором В и Q чередуются, задает при 0<а<2 непрерывное
отображение из пространства Jf_i в Jfi; если же мы рассмотрим,
скажем, произведение QQ', то оно имеет смысл лишь при
а, а'>1/2 как отображение пространства Н в себя.
Воспользовавшись соотношением Q 5, мы можем разбить предыдущее
выражение на два слагаемых, первое из которых не содержит
множителя (© — ©0. а второе слагаемое Z пропорционально
(© — ©О, причем операторы В и Q входят в него, чередуясь, как
описано выше. Таким образом,
i? -/?'= Q - Q'+ (/+ ©Q) ©fi (Q - Q0 ffl'fi'(/+ ©V)+
+(© — ©') Z.
Подставим в правую часть равенства s' = l—s. В этом случае
©(5) — ©(1 — s) = 0;
таким образом, слагаемое, пропорциональное © — ©', исчезает.
Что касается остальных членов, то мы интерпретируем
полученное равенство как соотношение для ядер и воспользуемся
формулой q 4, которая справедлива при всех значениях s. В силу
симметричности ядер b{z,z';s) и q{z,z';s), мы получаем
нужное нам соотношение. Заметим, что правая свертка ядер
соответствует композиции операторов в обратном порядке.
Следующие соотношения для функций Эйзенштейна
аналогичны соотношениям, которым удовлетворяет функция 6(2, s).
Напомним, что
е(2, s) = / + c(s)г/^-^
где
c(s) = a2^-'-4^^.
Тривиально проверяется, что
с is)
8(2,
с(1
s) =
-s)-
= 8(2,
= 1,
1-
s) с [s).

348 xrv. Спектральное разложение оператора Лапласа на Г\^
Мы докажем аналогичные формулы для функций r\{z, s) и c(s).
А именно: в полосе О < ст < 1 справедливы соотношения
ES 6. c(s)c(l — s) = l,
ES 7. т) (z, s) == т| (z, 1 — s) с (s).
Доказательство. Пусть, как и раньше, 6^ —ядро
оператора B{s). Введем для краткости обозначение
где S — точка полосы О < а < 2. Мы покажем, что
p(s)c(l — s) —р(1 — s)c(s) = —p(s)p (1 —s).
Отсюда немедленно следует тождество ES 6, так как
c(5) = c(s) + p(s).
Приведенное соотношение немедленно вытекает из
резольвентного уравнения для оператора B(s), доказанного в
теореме И § 10. Перепишем его как соотношение для ядер;
bs — bi-s = © {sf bs * {qs — qi-s) * &1-5 =
мы воспользовались очевидным обозначением: (6i-s * 9i-s)' есть
функция переменной z', если z, 2'— аргументы ядра Ь^(2, г').
Свернем это соотношение с функцией Э^ слева и с функцией
6i_5 справа. Воспользовавшись формулами
e, = ei-,c(s) и c{l-s) = c(s)-\
лолучим
Qs*bs*esC{l—s) — c(s)Qi_s*bi-s*Qi-,='p(s]p{l —s)~^-
Теперь искомое соотношение между p(s) и р(1—s) следует
непосредственно из определений.
Соотношение ES 7 можно доказать по той же схеме,
используя резольвентное уравнение для ядра 6j. С другой стороны,
теперь мы можем вывести его из теоремы единственности.
В самом деле, в силу теоремы 16, в полосе О < а < 1
справедливы асимптотические формулы
r\,{z)^y^ + c{s)y'-^ + Oil),
Л1_Л2) = с(1-5)г/- + у-^ + 0(1).
Для доказательства формулы ES 7 достаточно умножить
второе равенство на c(s), воспользоваться формулой ES 6 и при-
иеять теорему единственности.

§ 13. Непрерывный спектр оператора Лапласа 349
§ 13. Непрерывный спектр оператора Лапласа
Обозначим Символом Н^ пространство L' (^+, —di\ где
d^—мера Лебега. Определим оператор Aq в пространстве На
формулой (^,(,) = (i + <=)|„)
для тех функций |, для которых это произведение принадлежит
пространству i^. Тогда оператор Aq самосопряжен. Мы
докажем, что сужение оператора А на ортогональное дополнение к
прямой сумме его собственных подпространств в пространстве
Я = L^(r\'S>) унитарно эквивалентно оператору Ло. Чтобы
проверить это, мы явно укажем ядро оператора, осуществляющего
унитарную эквивалентность. Это ядро есть не что иное как
функция Эйзенштейна ц {z, 1/2 + it), рассматриваемая на
произведении пространств (Г\Ф) X [О, оо). Зададим преобразование
Эйзенштейна Е, определенное на пространстве ограниченных
функций на Г\'&, формулой
iEf){t)=\i,][2,^ + it)fiz)dz.
Теорема 18.
(i) Ядром преобразования Эйзенштейна является
подпространство, натянутое на собственные функции
оператора Л.
(ii) Преобразование Эйзенштейна можно продолжить до
частичной изометрии, образ которой есть пространство Hq,
(iii) Преобразование Эйзенштейна переводит оператор А в
оператор Ло, т. е.
ER{k) = RoME, £Лс=Ло£,
где R {%) — резольвента оператора А, и > 3, а
Ro{s) = iAo-s{l-s) IaГ^.
Доказательство. Пусть f ^С^ (Г\ф). Пусть [а, Ь] — такой
интервал на оси(0, оо), что интервал {'/г + i^; /е[а, 6]} не
содержит ни одной сингулярной точки. Тогда
а
Ь
а F Р
Ь
=h \ 2'^ ^^ и [' С"'' ^'^ т + ''0~' (^' ^''' т -") ] ^ (^) ^ ^^') "^^ "^^'^
Р Р

350 XIV. Спектральное разложение оператора Лапласа на Г\й
Мы воспользовались формулой ES 5; ясно, что если s= 1/2 + it,
то 2s — 1 = 2it. Имеем
K = s{\-s) = ^ + f, d% — 2tdt.
Нам будет удобнее выразить ядро резольвенты через
переменную %, поскольку мы собираемся сейчас воспользоваться
спектральной теоремой для неограниченных операторов.
Напишем
г (2, z'; s) = р (z, z'; А).
Когда переменная t меняется в интервале [а, Ь], переменная А
пробегает интервал
4 ~> —> 4 '
Значения ст + //, для которых а > '/г. соответствуют значениям
А. с отрицательной мнимой частью, а значения а — it, а > 'Д
соответствуют значениям А с положительной мнимой частью.
Следовательно, наше последнее выражение равно
Ч ■
ij- 5 i dA И [р (2,2'; А - Ю) - р (2,2'; А + /0)] / (г) / (2') dz dz',
где
р (2, 2'; А — /0) = lim р (z, z'; А — is),
е->0
р (2, z'; А + /0) = Ига р (z, z'; А + is).
е->0
Мы можем также записать это выражение как предел при 8-*-0
интеграла
Ч
i 5 dA 5 5 [р (z, z'; А + /8) - р (Z, z'; А - /е)] / (2) / (2') d2 dz\
Если s = a±it, причем сг >'/2, то функция r{z,z^;s) является
ядром резольвенты. Следовательно, последнее выражение можно
переписать таким образом:
^ lim ^ ([R (А + /е) - /? (А - /в)] /, /) dA;

§ 13. Непрерывный спектр оператора Лапласа 351
согласно формуле обращения для резольвенты (см.
приложение 2), этот предел равен
где (If. f ~ спектральная мера оператора А.
Разобьем полуось 5 = '/г + '^. / > О на отрезки, не
содержащие сингулярных точек, и сложим интегралы по этим отрезкам.
Из приложения 2 мы знаем, что результат равен
{{I-P)f,f),
где Р — проектор на подпространство, порожденное
собственными функциями оператора А. Таким образом, функция Ef
принадлежит пространству Нд и собственные векторы
оператора А переводятся преобразованием Эйзенштейна в нуль.
Кроме того, если функция / ортогональна ко всем собственным
функциям оператора А, то
11/112= 11^/Иг
Тем самым утверждения (i) и (ii) нашей теоремы доказаны.
Формула ES 1 показывает, что функция Эйзенштейна т]^ —
собственная функция оператора R (х), отвечающая собствен-
нОхМу значению ©(s)"'. Это, по существу, переформулировка
последнего утверждения теоремы. Более того, формула ES 1
показывает, что
ЕА CZ АоЕ,
где символ с: означает, как обычно в теории неограниченных
операторов, что область определения оператора ЕА содержится
в области определения оператора AqE и сужение AqE на эту
область совпадает с ЕА.
Отсюда следует, что для любой ограниченной измеримой
функции А на вещественной оси справедливо равенство
EhiA) = h{Ao)E.
(Мы предполагаем, что читатель знаком со спектральной теорией
неограниченных операторов; см. приложение 2.)
Нам остается только доказать, что образ пространства
ограниченных функций на Т\^ при отображении Е плотен в Hq.
Отсюда будет следовать, что замыкание оператора Е
осуществляет изометрию подпространства Ц — Р)Н на Яо-
Зафиксируем число ^о > О- Мы знаем, что
Л(2, s) = / + c(s)|/i-- + 0(l).

352 XIV. Спектральное разложение оператора Лапласа на Г \$
Пусть f — функция, которая в окрестности некоторой точки Zq
с достаточно большой мнимой частью Imzo совпадает с
функцией т) (2, Уг + i^o). а затем быстро стремится к нулю.
Преобразование Эйзенштейна
{Ef){t)=\y\{z,s)f{z)d2
не исчезает в точке ^о"> в самом деле, его значение в точке /о
положительно. Выберем теперь функцию h так, что
1
Мт+'=)^
(£/) {t)
в окрестности точки ^о и равно нулю вне этой окрестности.
Тогда функция
h{Ao)Ef = Eh{A)f
есть характеристическая функция маленького интервала,
содержащего точку /о- Это показывает, чго образ отображения Е плотен
в пространстве Яд; теорема доказана.
§ 14. Случай нескольких вершин
На протяжении всей главы мы предполагали, что r = SZ,2(Z).
Это ограничение в действительности несущественно; теперь
пришло время показать, какие дополнительные особенности
возникают' в общем случае произвольной дискретной подгруппы Г,
такой, что пространство Т\^ имеет конечный объем. Мы
будем предполагать, что —1еГ. Как обычно, полагаем G =
= SL2(R)-
В гл. XII уже упоминалось, что у подгруппы Г существует
фундаментальная область F, обладающая следующими
свойствами:
(i) F лежит в полосе —Хо^лг^Хо для некоторого xq.
(И) Существует такое вещественное число а, что F
представляется в виде объединения областей
^=/^ou(U/„),
причем Fq компактна и имеет кусочно-гладкую границу,
а. Fa. есть образ верхней части полосы Fi, определенной
неравенствами
— Y ^^ ^ 2" > i/ ^ ".
п.ри отображении zi—^-^„з, где g'o — некоторый элемент
группы G = SL^ (R).

§ 14. Случай нескольких вершин 353
Сопоставим каждой функции / на фундаментальной области F
[п -\- 1)-компонентный вектор (вместо двухкомпонентного
вектора, когда r = SZ,2(Z)). Положим
k{z) = f{z), Z^Po,
/a(2) = /(^aZ), zeF,.
Аналогично, ядро k {z, z') па РУСР имеет компоненты й„р (z, z'),
определяемые следующим образом:
koo (z, z') = k {z, z'), z, z' e Fo,
Йоа (Z, Z') = k (Z, ^„Z'), ? e ^='o, 2' e Fi,
K^ (2, z') = k {ga.z, g^z'), z, 2' e Fi.
Для a ^ 1, ... , n положим
Подгруппу группы Го, состоящую из элементов вида
Y
<::у
мы будем обозначать Fq. Она совпадает с нашей прежней
подгруппой Го.
Группа Г, по существу, в первый раз появлялась в
вычислениях при доказательстве симметричности оператора
Лапласа на Г\ф, т. е. в лемме 1 § 4. Как это будет типично для
наших последующих рассуждений, доказательство при переходе
к общему случаю остается практически без изменений; нужно
лишь заменить р на /^ в правой части формулы (*) и
просуммировать по а. Таким образом, с каждой вершиной связан один
интеграл по верхней части полосы.
При доказательстве сходимости ряда
1
Z-
^^Г [i + u{z,yz')f
в лемме 1 § 5 мы пользовались только тем, что группа Г
дискретно действует на верхней полуплоскости.
Несколько более серьезно утверждение, необходимое для
доказательства оценки
Z
1 " / .л2+е-<1
^^^Ji + uiz,yz')r
Wf
(лемма 9 § 7). Нам нужно знать, что в любом подмножестве
матриц
а
12 Зак. 58§
1;

354 XIV. Спектральное разложение оператора Лапласа на Г\©
ИЗ Га, Аа ИЛИ Аар, не пересекзющемся с Го, величина | с \
ограничена снизу. Фаддеев отсылает по этому поводу к статье
Петерсона [2[; я поступлю таким же образом.
Все рассуждения, связанные с поведением в окрестности
вершины, буквально переносятся на общий случай, поскольку
элементы g^ переводят стандартную область Fi в
соответствующую часть фундаментальной области. Отметим лишь, что
некоторые ядра имеют только диагональные компоненты, т. е.
все их компоненты, за исключением
taa{z,z'; s) = t{y,y'\ s),
maa(z, z'\ s) = miz, z'; s),
9aa (z, 2'; s)=-q (y, y'; s),
равны нулю. Вплоть до § 12 не требуется больше никаких
изменений, за исключением замены области F^ на Fi.
В § 12 нам потребуется ввести у наших функций ряд
индексов. Для любого р^1, ..., п определим кусочно-гладкую
функцию 8 (z, s) на области F, компоненты которой задаются
формулами
в^2,5) = 6аз9(г/, S), eg(2,s) = 0.
Здесь бар—обычный символ Кронекера. Для любого р мы
получаем функцию Эйзенштейна
Т,е(2,5) = вР(2,5)+Г(5)9в(2,5),
где оператор W {s) определен прежними формулами (но теперь
это матричный оператор). Теорема 15 применима к каждой
функции Эйзенштейна т)Р. В доказательстве нужно просто
заменить т) и 8 на т]^ и 9^. Каждая функция т|^ — это в
действительности вектор-столбец, и мы получаем матрицу размера
(« + 1)Х«
л^ • • • 11Г
чТ1* ... Tl",
составленную из компонент функций т|а, а=0, ...,«, р==1, ..., л.
функция c(s) превращается теперь в матрицу — матрицу
рассеяния'), элементы которой равны
С„в is) = с is) б„р + |У4 ^s * «. * е.'-
') По поводу связи с теорией рассеяния см. Павлов и Фаддеев [1], Лаке
и Филлипс [1]. — Прим. перев.

§ 14. Случай нескольких вершин 355
(Мы могли б-ы написать bs вместо п^, поскольку B{s)^ М-\-
-\-№{s) и оператор М переводит функции 9^ в нуль, т. е.
S(s)eP = jV^(s)eP.)
Теорема 16, описывающая асимптотическое поведение
функции т1 (z, s), остается без изменений, не считая того, что,
как и выше, функция т| становится теперь матрицей.
Слагаемое if нужно интерпретировать как ^^^7, где / — единичная
матрица.
В следствии, приведенном после теоремы 17, дающем
выражение для функций Эйзенштейна в виде ряда, нужно писать
^^{gpz, s)= D Im(Yz)^
Утверждения ES 1—ES 4 остаются без изменений и
справедливы для каждой компоненты вектор-столбца ti^. В формуле
для резольвенты ES 5 следует ввести суммирование
п
ES 5. г (2, z';s) - г {г, г'; 1 - s) = ^^ ^ т|^ (2, s) т)^ (z', 1 - s).
0=1
Формулы ES б и ES 7 остаются без изменений, но
интерпретируются теперь как матричные равенства. Другими словами,
матрица c(s) является обратной к матрице с(1 — s). Имея в виду
предстоящее обобщение, мы поместили в формуле ES 7
матрицу c(s) справа от матрицы t)(z, 1 — s).
В спектральном разложении для непрерывного спектра нам
нужно ввести многокомпонентные функции. Пусть Н^ —
пространство векторнозначных функций
таких, что |^eZ,^(0, оо). Скалярное произведение в Hq зададим
формулой
{bi)=^^Y.Wt)i^t)dt.
а-1 О
Оператор Д) — по-прежнему оператор умножения на функцию
/1—> 1/4 -[- f. Преобразование Эйзенштейна Ef. определяется
покомпонентно:
{E^f){t)=\^4z,\ + it)f{z)dz,
F
И теорема 18 справедлива без дальнейших изменений.
12*

Приложение 1
ОГРАНИЧЕННЫЕ ЭРМИТОВЫ ОПЕРАТОРЫ
И ЛЕММА ШУРА
§ 1. Непрерывные функции от операторов
Мы предполагаем, что читатель знаком лишь с наиболее
элементарными фактами о гильбертовом пространстве; поэтому
приведем доказательство следующего вспомогательного
результата:
Лемма. Пусть А — линейный оператор в гильбертовом
пространстве Н, с— положительное число, такое^ что
\{Ах,х)\^с\х\'
для всех х^Н. Тогда для всех векторов х, у из Н справедливо
неравенство
\{Ах,у)\ + \{х,Ау)\^2с\х\\у\.
Доказательство. Из поляризационного тождества следует, что
2\{Ах,у)+{Ау,х)\^с\х + у\' + с\х-у\' = 2с{\х\'+\у\').
Таким образом, \{Ах, у) +{Ау, х)\^с{\х\^ + \yf). Умножим у
на комплексное число е'®; мы получим в левой части
неравенства выражение
\{e-''{Ax,y) + e^^{Ay,x)\.
Правая часть останется при этом неизменной; при подходящем
выборе 9 левая часть примет вид
|<Ac,i/)|4-|<^i/,^)|.
(Другими словами, мы поворачиваем одно комплексное число на
угол 8, а второе — на угол — 9, пока они не попадут на одну
прямую.) Заменим теперь вектор х на tx, а у — яа y/t, где ^ — поло-
Рис. 1.

§ 1. Непрерывные функции от операторов 357
жительное вещественное число. При этом левая часть
неравенства не изменится, а правая примет вид
e{t) = f\x\^ + ],\yf.
Точка, в которой производная g'(0 равна нулю, —
единственный минимум функции g; нетрудно видеть, что ее значение
в этой точке ^0 есть g{t,^= \х\\у\. Лемма доказана.
Теорема 1. Пусть А — эрмитов оператор. Тогда его норма
IАI есть точная нижняя грань множества всех чисел с, таких,
что
I {Ах, л;) К с I л: р, х^Н.
Эквивалентно, \А\ есть точная верхняя грань множества
значений величины \{Ах, х)\, когда вектор х пробегает единичную сферу
в пространстве Н
Доказательство. Пусть А — эрмитов оператор; тогда для
любых X, у ^ Н справедливо неравенство
\{Ах,у)\^с\х\\у\;
таким образом, число \А\ не превосходит константы с из
предыдущей леммы. С другой стороны, ясно, что с = | Л | —
допустимое значение для с в силу неравенства Шварца.
Теорема доказана.
Теорема 1 позволяет нам ввести частичную упорядоченность
в множестве эрмитовых операторов. Пусть А — эрмитов
оператор; мы будем писать Л^О и говорить, что Л —
положительный оператор, если {Ах, л:) ^ О для всех х ^ Н. Если А, В —
эрмитовы операторы, мы будем писать А^В, когда А — В^О.
Это в самом деле задает частичную упорядоченность, поскольку
выполнены обычные правила: если Ai^Bi и Ао^В2, то
Л,-f Л2>Д,-f fia.
Если с — положительное число и Л^О, то сЛ^О. Пока мы
ничего не сказали о произведении положительных эрмитовых
операторов АВ, даже когда АВ = ВА. Мы займемся этим
вопросом позднее.
Пусть с —верхняя грань для оператора Л. Тогда |(Лл:, л:)|^
:^с|л:р и, следовательно,
-с1^А<,с1.
Если а — вещественное число, то для простоты мы будем иногда
писать а^Л вместо а/^Л и, аналогично, будем писать Л^р
вместо Л^р/. Положим
а = inf {Ах, х), р = sup {Ах, х);

358 Приложение I. Ограниченные эрмитовы операторы
тогда
а < Л < р,
и из теоремы 1 вытекает, что
|Л| = гаах(|а|, |р|).
Пусть р — произвольный полином с вещественными
коэффициентами, Л —эрмитов оператор. Если
р(/) = а„Г+...+ао,
то положим, по определению,
p{A) = a,A'^+...+aol.
Обозначим R [Л] алгебру, порожденную оператором Л над полем
вещественных чисел R, т. е. алгебру всех операторов р (Л), где
p{t) ^R[t]. Мы хотим исследовать замыкание алгебры R[A]
в вещественном банаховом пространстве всех операторов. Мы
покажем, что это замыкание может быть реализовано как кольцо
непрерывных функций на некотором подмножестве множества
вещественных чисел. Заметим сначала, что эрмитовы операторы
образуют замкнутое подпространство в End Я и что R [Л] —
замкнутое подпространство пространства эрмитовых операторов.
Мы покажем, что если р — вещественный полином,
принимающий положительные значения на интервале [а, р], то
оператор р(Л) положителен. Нам потребуется для этого одна чисто
алгебраическая лемма.
Лемма 1. Пусть р — вещественный полином, такой, что p{t)'^0
при всех ^е[а, р]. Тогда полином р можно представить в
следующем виде:
pa)==4ZQaO^ + Za-a)Q/(0^4-i;(p-OQ.(0'],
где Qi, Q,-, Q,, — вещественные полиномы и с^О.
Доказательство. Разложим сначала полином р на линейные
и неприводимые квадратичные сомножители. Если у полинома р
есть корень у в интервале (а, р), то его кратность четна (в
противном случае р менял бы знак в окрестности точки у, что
противоречит сделанному предположению) и, значит,
множитель {t — у) входит в разложение р в чётной степени. Если
корень Y таков, что у^а,'то в разложение р входит линейный
сомножитель t — у; мы запишем его следующим образом:
/ - Y = (^ - а)-f (а - Y).
Заметим, что число (а — у) — квадрат вещественного числа.
Аналогично, если р имеет корень у, такой, что Y ^ Р, мы запишем
соответствующий линейный множитель в виде

§ 1. Непрерывные функции от операторов 359
ЧИСЛО Y ~ Р также есть квадрат. Итак, в разложение полинома р
входят множители вида {t — yf" *^*, если y ^ (а, р); остальные
линейные множители имеют вид ^ — Y, если Y^a, и y —/, если
Y ^ р. Квадратичные множители имеют вид {t — af + ьК При
таком соглашении константа с (постоянный множитель)
положительна, так как полином р неотрицателен на интервале [а, р].
Перемножим все эти множители и заметим, что произведение
суммы квадратов на сумму квадратов — снова сумма квадратов.
Мы получим для р выражение нужного нам вида, за
исключением того, что еще присутствуют члены вида
(^-a)(p-OQ(0^
где Q — вещественный полином. Чтобы избавиться от них,
воспользуемся тождеством
(^ - а) (р - О = ^^^=^^^^fc^^^^^=^^HPz:^.
Лемма доказана.
Чтобы исследовать К[Л], заметим, что отображение
р*-^р{А)
есть гомоморфизм алгебры R[^] на R[A]. Кроме того, если
В, С — эрмитовы операторы, такие, что ВС = СВ и fi ^ О, то
оператор ВС^, очевидно, положителен, ибо
{ВС% х) = {СВСх, х) = {ВСх, Сл:)>0.
Сумма двух положительных эрмитовых операторов положительна.
Таким образом, из выражения для полинома р, полученного
в лемме 1, вытекает
Лемма 2. Если полином р положителен на интервале [а, р],
то оператор р (Л) положителен. Если q, р — такие вещественные
полиномы, что p^q на интервале [а, Р], то p{A)^q (А).
Наконец, пусть \\р\\= sup \p{t)\; тогда
1р(Л)|<||р||.
Доказательство. Первое утверждение вытекает из замечаний,
предшествовавших лемме. Второе немедленно следует из первого:
достаточно применить его к полиному q — р. Наконец, положим
qjt) = \\p\\±p{ty,
тогда полиномы q^ неотрицательны на интервале [а, Р] и,
следовательно, q^iA)'^0. Теперь последнее утверждение леммы
вытекает из теоремы 1.

360 Приложение 1. Ограниченные эрмитовы операторы
Мы доказали, что р ►—* р (Л) — непрерывное линейное
отображение из пространства полиномиальных функций на интервале
[а, р] в алгебру R [Л]. По теореме о продолжении, мы можем
распространить его по непрерывности на все банахово
пространство непрерывных функций на [а, р]. Таким образом, по
теореме Стоуна — Веиерштраеса, мы можем определить оператор
/(Л) для любой непрерывной функции / на [а, р]. Пусть {р„}—
последовательность полиномов, которая равномерно сходится к /;
тогда, по определению,
f{A) = \impAA).
Более того, снова по непрерывности, получаем
1/(Л)|<||/||,
где 11/11= sup 1/(01- Пусть {р„}, {g„} — две равномерно схо-
i S [«, В]
дяшиеся последовательности полиномов, / = limp„, g' = limg„.
Тогда РпЯп-^fe- Таким образом, мы получаем
(fg){A)^f{A) g{A)
для любых непрерывных функций /, g. Другими словами,
наше отображение есть также гомоморфизм.
Теорема 2. Бели оператор А положителен, то существует
такой оператор В еК[Л], что В^ = А. Произведение двух
коммутирующих положительных эрмитовых операторов—также
положительный оператор.
Доказательство. Непрерывная функция t^-^i'' переходит при
нашем отображении в квадратный корень из оператора Л
в кольце R [Л]. Ясно, что любой элемент кольца R [Л]
коммутирует с Л. Если операторы Л и С коммутируют и Л = Б- для
некоторого fi е R [Л], то операторы В и С также коммутируют,
поскольку С коммутирует со всеми операторами р(Л), где р —
вещественный полином, а значит, и со всеми элементами кольца
W[A]. Но, как мы видели, если С^О и В и С коммутируют, то
В^С^О. Теорема доказана.
Ядро нашего отображения /1—>- / (Л) — замкнутый идеал
в кольце непрерывных функций на интервале [а, р]. Забудем
иа время обычное определение спектра оператора и определим
спектр а (А) как замкнутое множество нулей этого идеала.
Пусть / — любая непрерывная функция на множестве а {А)\
продолжим ее с сохранением нормы до непрерывной функции
/i на интервале [а, р] и положим, по определению,
/(Л)=:/,(Л).

§ 1. Непрерывные функции от операторов 361
Если g —другое продолжение / на [а, р], то функция g — fi
обращается в нуль на множестве а (А) и, следовательно, g{A) =
=-fi{A). Таким образом, /(Л) не зависит от конкретного
продолжения функции / на интервал [а, р], и наше определение
корректно. Обозначим || • ||^i норму в кольце непрерывных
функций иа множестве а (А), т. е.
imu= sup i/(/)i.
Мы получаем гомоморфизм кольца непрерывных функций на
спектре а (Л) в кольцо R [Л]; при этом
1/(Л)1<||/1и.
Сформулируем теперь спектральную теорему.
Теорема 3. Отображение f г-^ / (Л) есть банахов
{сохраняющий норму) изоморфизм кольца непрерывных функций на
спектре а (А) на банахову алгебру R [Л]. Непрерывная функция f
неотрицательна на множестве о (А) тогда и только тогда, когда
f{A)>0.
Доказательство. Мы только что вывели неравенство для
норм, воспользовавшись тем, что положительным функциям
соответствуют при нашем отображении положительные
операторы. Докажем теперь противоположное неравенство. Итак, пусть
/(Л)^0; мы докажем, что функция / неотрицательна на
спектре оператора Л. Предположим, что это неверно; тогда /
отрицательна в окрестности некоторой точки с из спектра. Пусть
g — непрерывная функция, график которой изображен на рис. 2.
Таким образом, функция g неотрицательна и имеет
положительный пик в окрестности точки с. Тогда fg^O и f{c)g (с) < 0.
Следовательно, —fg'^0 и, значит, — /(Л)g{A) ^ 0. Но /(Л) ^О,
и g{A)'^0; таким образом, по теореме 2, f{A)g{A)^0. Отсюда
следует, что / (Л) g (Л) = О, но это невозможно, так как функция
fg не обращается в нуль на спектре. Таким образом, /^0 на
множестве а (А). Итак, второе утверждение теоремы доказано.

362
Приложение I. Ограниченные эрмитовы операторы
Перейдем к доказательству первого утверждения. Положим
й=|/(Л)|. Тогда й/±/(Л)>0, откуда й±/(/)>0 при всех
/ е ст (Л). Это показывает, что
|1/|1л<1/(Л)|;
таким образом, последовательность {/„(Л)} сходится тогда и
только тогда, когда последовательность непрерывных
функций {fn} равномерно сходится на спектре. Это завершает
доказательство спектральной теоремы.
Нам осталось только проверить эквивалентность нашего
определения спектра обычному.
Следствие. Пусть А — эрмитов оператор; тогда спектр а (Л)
совпадает с множеством таких комплексных чисел z, что
оператор А — zl необратим.
Доказательство. Пусть z — такое комплексное число, что
оператор A — zI необратим. Тогда z веш;ественно. В самом
деле, если это не так, положим
g{t)^{t-z){t-z).
функция g не обращается в нуль на спектре, и,
следовательно, функция h: t>—^l/g{t) — ee обратная. Таким образом,
получаем противоречие: оператор h (Л) (Л ~ zl) является обратным
к оператору Л — zl. Итак, z — вещественное число.
Пусть I — вещественное число, не принадлежащее спектру.
Тогда функция^!—^/ — | обратима на спектре а {А) и,
следовательно, оператор Л — |/ тоже обратим.
Предположим теперь, что | принадлежит спектру
оператора Л. Пусть g — непрерывная функция, график которой
изображен на рис. 3, т. е такая, что
git)
н:
N,
если
если
■1\>\IN,
■1\<\IN.

§ I. Непрерывные функции от операторов 363
Предположим, что оператор Л —|/ обратим, и пусть S —era
обратный, т. е.
В{А-11) = {А-11)В^1.
Так как | (t —|) g(0 I ^ I, получаем
1(Л-|/)^(Л)|<1.
откуда
\g{A)\ = \B{A-lI)g{A)\^\B\.
Но норму ||g||=iV можно выбрать сколь угодно большой, и,
следовательно, норма |§(Л)| тоже сколь угодно велика
(противоречие). Теорема 3 доказана.
Основная идея — использовать положительность для
доказательства спектральной теоремы — принадлежит ф. Риссу.
Однако в большинстве изложений основной целью является
получение для оператора А интегрального представления,
которое мы обсудим в приложении 2. Дж. фон Нейман всегда
подчеркивал, что го]раздо более эффективно доказывать сразу
утверждение теоремы 3, которое достаточно для большинства
приложений и может быть совсем просто выведено из теоремы
о положительных операторах. Эти рассуждения заимствованы
из заметок семинара фон Неймана 1950 г. Следующую
теорему и ее следствие, обычно называют леммой Шура.
Теорема 4. Пусть S — множество операторов в гильбертовом
пространстве Н, не имеющее в Н замкнутых инвариантных
подпространств, за исключением {0} и самого Н. Пусть А —
эрмитов оператор в Н, такой, что АВ = ВА для всех операторов В
из S. Тогда А = с1, где с — некоторое вещественное число.
Доказательство. Достаточно доказать, что спектр А состоит
только из одной точки. Допустим, что найдутся две различные
точки С] ф С2, принадлежащие спектру А. Существуют
непрерывные функции f, g, ни одна из которых не обращается
Рис. 4.

364 Приложение I. Ограниченные эрмитовы операторы
В нуль на спектре, такие, что их произведение fg тождественно
обращается в нуль. Например, в качестве функций f и g мы
можем взять функции, графики которых изображены на рис. .4.
При всех S е S имеем f {А) В^ Bf (А) (поскольку оператор
В коммутирует с вещественными полиномами от А, а значит, и
с их пределами). Следовательно, линейное подмножество f{A)H
инвариантно относительно всех оператйров из S, так как
Bf{A)H = f{A)BHczfiA)H.
Пусть f —замыкание множества f{A)H. Тогда F ф {0},
поскольку / (Л) ф 0. Кроме того, F фН, поскольку g{A) f (Л) Н = {0}
и, значит, §(Л)/' = {0}. Инвариантность подпространства F
относительно S противоречит условию теоремы. Теорема
доказана.
Следствие. Пусть S — множество линейных операторов в
гильбертовом пространстве Н, не имеюи^ее в Н нетривиальных
инвариантных подпространств. Пусть А — такой линейный
оператор в Н, что ЛЛ* = ЛМ и АТ = ТА, А*Т = ТА* для всех T^S.
Тогда Л = с1, где с — некоторое комплексное число.
Доказательство. Представим оператор А в виде A^B-\-iC,
где S = (Л + Л')/2, С={А — Л')/2г — коммутирующие
эрмитовы операторы. Чтобы доказать наще утверждение,
достаточно применить теорему 4 к каждому из операторов S и С.
§ 2. Проекторнозначные функции от операторов
Нам необходимо распространить понятие функции от
оператора на более широкий класс функций, включающий по
крайней мере характеристические функции интегралов. В нашем
изложении мы, в основном, следуем Б. Секефальви-Надю и
Ф. Риссу.
Лемма 1. Пусть а — вещественное число, {Л„} —
последовательность эрмитовых операторов, таких, что An^al при всех
п и Л„^Л„+1. Тогда для любого вектора аеЯ
последовательность {Л„а} сходится в Н. Обозначим ее предел Av; тогда
отображение v и-* Av — ограниченный эрмитов оператор.
Доказательство. Из неравенства
(Л„а, а)>а(а, а>
вытекает, что последовательность (Л„а, а) сходится при любом
а е Я. Так как
(Л„а, ге;) = -^<Л„(а+гг»), а + ш) —-^ (Л„(а —ш), v — w).

§ 2. Проекторнозначные функции от операторов 365
ТО последовательность (Л„а, w) сходится для любых элементов
V, w^H. Определим функционал А.^ на Я равенством
А,о (ш) = lim (Л„а, ш).
ге->оо
Функционал А,„ антилинеен; существует такая постоянная С, что
для всех V, w^H справедливо неравенство {A^v, w)^C\v\\w\.
Следовательно, существует такой оператор Л в Я, что {Av, w) =
= lim (Л„а,ш). Так как (Л„а, ш)^(а, Л„ш), то оператор А эр-
митов.
Лемма 2. Пусть f — ограниченная снизу функция на спектре
оператора А. Предположим, что функция f есть поточечный
предел монотонно убывающей последовательности непрерывных
функций {fi„}. Тогда предел ИтЛ„(Л) не зависит от выбора
последовательности {Л„}.
Доказательство. Пусть {g„} — другая убывающая
последовательность, поточечно сходящаяся к функции /. Зафиксируем
числа кие. Тогда для всех достаточно больших номеров п
max(g„, AfeXAfe + e;
таким образом, при всех t справедливо неравенство g„(0^
^ Afe (t) + 8. Следовательно,
g„{A)^h,{A) + eI.
Это показывает, что
limg„H)<Afe(^) + 8/,
откуда
lim g„ (А) < lim h^ {А) + &I.
Это неравенство справедливо при всех 8>0, поэтому можно
устремить 8 к нулю. Так как функции g я h входят в наше
рассуждение симметрично,, то справедливо и противоположное
неравенство. Лемма доказана.
Из леммы 2 видно, что отображение
можно продолжить на линейное пространство, порожденное
полуограниченными снизу функциями, которые можно
представить как пределы убывающих последовательностей непрерывных
функций. Продолженное отображение по-прежнему линейно,
сохраняет порядок и мультипликативно, т. е.
i!g){A) = f{A)g{A)
для любых функций /, g из нашего векторного пространства.

^66
Приложение t. Ограниченные эрмитовы операторы
Наиболее важные функции, к которым мы применим это
продолжение, — это характеристические функции, подобные
функции TJJc, график которой изображен на рис. 5. Она может
быть получена как предел функций Л„, графики которых
изображены на рис. 6.
>/'cU)
Л/ч(')
п
Рис. 5.
Рис. 6.
Лемма 3. Обозначим % (А) = Р^. Предположим, что а/ < Л ^
^^1; тогда
(i) Р(. = 0, если с^а; Рс=^1, если с^р.
(И) Если с<с', то Рс<:Р^,.
Эта лемма непосредственно вытекает из леммы 2.
2
Заметим, что Pc = Pg, т. е. Р^ —проектор. Совокупность
лроекторов {Р^ мы будем называть спектральным семейством,
Рис. 7.
ассоциированным с оператором А. Мы сохраняем прежние
обозначения; нам потребуются еще две функции f^, gc, графики
которых изображены на рис. 7. Таким образом, f<, {t) -\- g^ (t) =
= \t — c\. Справедливо равенство
Следовательно,
(1)
(2)
(3)
{t-c){i-^SfAt))=^fAt).
{A-cI){I-P,)=^fAA),
A-cI = UiA)-gAA),
(A - cl) Pc=-gc{A) Pc=~gc(A).

§ 2. Проекторнозначньш функции от операторов Зб/
Теорема 5. Пусть {Р^} — спектральное семейство,
ассоциированное с оператором А. Если Ь^с, то в подпространстве
{Рс — Р/,) Н справедливо неравенство
■ Доказательство. Из формулы (1) следует, что сужения
операторов А — Ы и fb {А) на ядро проектора Pj совпадают. Так
как fft^O, то в этом подпространстве справедливо неравенство
Ы-^А. Из формулы (3) следует, что сужение операторов А — с1
и — gci'^) на образ проектора Р,. тоже совпадают. Так как
— g^j^O, то в этом подпространстве A^cl. Теорема доказана.
Теорема 6. Семейство {Р^} сильно непрерывно справа.
Доказательство. Пусть а е Я — произвольный вектор. Наше
утверждение означает, что Pc+gV ->■ P^v при е ^ 0. Достаточно
доказать, что
{Рс+г^, v)-^{P,v, v),
так как
Но квадратичная форма {PgV, v) близка к (Л (Л) а, а), где h —
функция, график которой изображен на рис. 8.
Определим функцию Ад равенством h^it) = h{t — 6). Тогда
г!зЛО<Л(/)<Лв(0,
Так как последовательность функций Ад равномерно сходится
к функции h при б-^О, то последовательность операторов Ад (Л)
сходится к оператору Л (Л). Тогда
Р^<А(Л)<А(Л) + 8/,
Таким образом, мы получаем следующие неравенства для
квадратичных форм:
{P,v, а^<<Л(Л)а, а)«Л(Л)а, v) + b{v, v),
{P,v, v)^{Pc+zV, v)^{h{A)v, a)+ 8(a. a).

368 Приложение 1. Ограниченные эрмитовы операторы
Так как {h{A)v, v) сколь угодно близко к {PcV, v), то теорема
доказана.
Теорема 7 (Лорх). Предел слева
lim(P^-P^J = Q^
8->0
— проектор на собственное подпространство оператора А,
отвечающее собственному значению с.
Доказательство. Из теоремы 5 вытекает, что
(с - г) {Ра - Рс-г) <А{Ра- Ра-г) < С (Р, - Р,-е),
откуда
|(Л-С/)(Р,-Р,_е)1<в.
Но для любого вектора а е Я существует предел lim(P^ ~ Pg-g) v.
е->0
Обозначим этот предел ш. Из доказанного неравенства следует,
что Aw^cw; таким образом, если шфО, то w — собственный
вектор оператора А.
Обратно, пусть ф — непрерывная функция; тогда для любого
замкнутого Л-инвариантного подпространства F cz Н имеем
(p{A\F)==q>{A)\F.
Пусть Не — собственное подпространство оператора Л,
отвечающее собственному значению с. Мы хотим показать, что
сужение проектора Q<, на это подпространство есть единичный
оператор. Без ограничения общности можно предположить, что
Н=Нс- Тогда Р<, = 0, так как /<, = 0 на спектре оператора А.
Предположим, что b < с; тогда оператор
f,iA)=^A-bI = ic-b)I
обратим и, следовательно, Pj = 0. Теорема доказана.

Приложение 2
НЕОГРАНИЧЕННЫЕ ОПЕРАТОРЫ
§ 1. Самосопряженные операторы
Пусть Я — гильбертово пространство, А — линейное
отображение
А: Da->H,
определенное на плотном линейном подмножестве в Я.
Рассмотрим точки (а, w) произведения НУ^Н, удовлетворяющие
условию
(1) {Аи, о) = (ы, w) для всех и^Ол.
Так как линейное подмножество Da плотно в Я, то элементы w
однозначно определяются элементами а. Поэтому соотношение (1)
определяет некоторый линейный оператор А*: A*v=^w.
Оператор А* называется сопряженным к А. Его область определения 1)л»
представляет собой совокупность всех векторов а е Я, для
которых существует вектор w, удовлетворяющий условию (1).
Ясно, что это множество линейно. Чтобы выяснить, при каких
условиях оператор А* является плотно определенным,
рассмотрим отображение
/: НХН-^НХН,
задаваемое равенством / (х, у) = (— у, х). Ясно, что Р ^ — L
Исходя из определения сопряженного оператора, нетрудно
проверить, что график Ga* оператора А* задается формулой
Ол» = (/С/л) ,
где ± обозначает ортогональное дополнение. Следовательно,
график оператора Л* —замкнутое подмножество в Я X Я.
Будем говорить, что оператор А замкнут, если его график
замкнут в Я X Я.
Если А — замкнутый оператор, то линейное подмножество Da*
плотно в Я.
Доказательство. Пусть h е Da'', тогда
(Л, О)е(0л»)^ = (/0л)^^=/0л,
так как, по предположению, оператор А замкнут. Отсюда
вытекает, что (О, Л) е Ga, следовательно, Л = 0, и наше утверждение
доказано.
13 Зак. 589

370 Приложение 2. Неограниченные операторы
Если А — замкнутый оператор, то А** = А.
Доказательство. Ga**^=^{JGa*)'^ =^0 {JGj^ ) = G^.
Рели операторы А и А* плотно определены, то график Ga**
есть замыкание Ga-
Доказательство. Ga** = (/G^»)""" = (/ (/G^)""") = G^.
Предположим, что оператор А определен на множестве Da,
оператор В — на D^, причем DaCzD^ и сужение В на D^
совпадает с Л. В этом случае говорят, что оператор В есть
расширение оператора А, и пишут Acz В. Приведенное
утверждение показывает, что А cz А**.
Будем говорить, что оператор А симметричен, если {Аи, а) =
= (ы, Av) для всех и, v^Da- Будем говорить, что оператор А
самосопряжен, если, кроме того, области определения
операторов А и А* совпадают.
Если оператор А симметричен, то Acz А*.
Это утверждение очевидно. Напомним, что, по
предположению, область определения оператора А плотна в Я.
Если операторы А, В самосопряжены и Acz В, то Л = В.
Это тоже очевидно, поскольку из включения Acz В следует,
что В* CZ А*, и так как операторы А и В самосопряжены, то
В czA, откуда А = В.
Пусть Л — симметричный оператор, заданный на плотном
множестве D^. Предположим, что число А,еС не является
вещественным. Тогда оператор Л — А,/ инъективен на D^. В
самом деле, допустим, что Аи^Ы для некоторого u^Da- Так
как {Аи, и)^{и, Аи), то
А, {и, и) = {%и, и) = {и, ки) = X {и, и),
откуда ы^О. Таким образом, можно определить оператор
U = UA.x^iA + il) {А + МУ\
заданный на многообразии (Л + ^Л ^л- M>>^ утверждаем, что
оператор U изометричен. Для доказательства достаточно
проверить, что для любых и, V^Da
{Аи + 1и, Av -f Xv) = {Аи + Хи, Av + Xv).
Но это очевидно.

§ 1. Самосопряженные операторы 371
Лемма 1. Пусть А — замкнутый симметричный оператор,
% ^Х — комплексное число. Тогда {А -j- А,/) Дд — замкнутое
подпространство .
Доказательство. Пусть векторы ы„ из Da таковы, что
{(Л + А,/)ы„} — последовательность Кощи. Так как оператор U
изометричен, то {(А + Щ м„} — тоже последовательность Коши.
Поэтому последовательность {(А, — А,)ы„} сходится. Так как
X ^ %, последовательность {ы„} также сходится; пусть и — ее
предел. Но
{2Л«„ + (^ + Я) «„}
— тоже последовательность Коши; значит, последовательность
{Aun} — сходящаяся. Мы предположили, что график оператора А
замкнут; поэтому и е D^ и последовательность {(ы„, Лы„)}
сходится к некоторому элементу (ы, Аи) е G^; последовательность
{{A + Xl)Un\
сходится к {А-{-%1)и. Отсюда вытекает, что множество (Л + А./)Дд
замкнуто.
Теорема 1. Пусть А — замкнутый симметричный оператор и
существует комплексное число %фХ, такое, что линейные
подмножества {А + Я-О ^А W (-Л + А./) Da плотны в Н {и,
следовательно, совпадают с Н, по лемме 1). Тогда оператор А
самосопряжен.
Доказательство. Пусть аеДд*. Нам нужно показать, что
а S Дд. По определению, для всех u^D^ справедливо
равенство
{Аи, v) = {u, A*v).
Так как {A-\-kI)DA^Н, то существует такой вектор MjSD^,
что
A*v + А,а = Ащ + Xui.
Тогда
{Аи, v) = {и, Ащ + Щ — Щ
для всех u^Da, откуда
{{А + Я/) и, V) = ((Л + И) и, щ)
для всех u^Da- Так как {А -\-XI)Da = ff, то v = Ui, что и
требовалось показать.
Замечание. Коразмерности подпространств {A-\-%I)Da и
{А-\-XI)Da называются в литературе индексами дефекта. Мы
13*

372 Приложение 2. Неограниченные операторы
рассматриваем сейчас ситуацию, когда индексы дефекта
оператора А равны нулю.
Следствие. Пусть А — симметричный плотно определенный
оператор. Предположим, что существует комплексное число
ХфХ, такое, что подпространства {A-\-XI)Da и {А-\-XI) Da
совпадают с Н. Тогда оператор А допускает самосопряженное
замыкание.
Доказательство. Так как оператор А симметричен, то область
определения А* также плотна в Я. Мы уже доказали выше,
что график Ga** совпадает с замыканием графика G^; таким
образом, оператор А допускает замыкание. Ясно, что это
замыкание— тоже симметричный оператор. Теперь мы можем
воспользоваться теоремой 1.
Оператор А, заданный на линейном подмножестве DaCzH,
называется в существенном самосопряженным, если замыкание
его графика есть график самосопряженного оператора.
Приведенное выше следствие дает достаточное условие суш;естзен-
ной самосопряженности.
Теорема 2. Пусть А — самосопряженный оператор. Пусть
Z Ф Z — произвольное комплексное число. Тогда оператор А — zl
имеет нулевое ядро. Существует единственный ограниченный
оператор
R{z)^{A-zI)-': H-^Da,
взаимно однозначно отображающий пространство Н на область
определения Da- Справедливо равенство
R{zr = R(z).
Если Z и W — два любых невещественных комплексных числа,
то имеет место резольвентное уравнение
iz-w)Riz) R (w) = R{z) -Riw) = (z- w) R (w) R (z);
в частности, операторы R{z) и R (w) коммутируют. Справедлива
оценка
Доказательство. Пусть z = x + iy. Если вектор и
принадлежит области определения оператора А, то выполняется
неравенство
\{A-zI)uf^^\iA-xI)uf + y'\uf>y'\uf,
так как оператор А симметричен, и поэтому перекрестные
члены в скалярном произведении йокраш1аются. Это показы-

§ I. Самосопряженные операторы 373
вает, что оператор А—zl имеет нулевое ядро и что обратный
оператор, определенный иа подпространстве {А — гГ}Ол,
непрерывен. Предположим, что вектор v ортогонален к образу
оператора А — zl, т. е.
{Аи — zu,v) = 0
для всех u^Da- Тогда {Аи, v) = {u, zv). Так как оператор А
самосопряжен, то отсюда следует, что вектор v принадлежит
области определения оператора А и что Av = zv. Однако
Кег(Л —2/) = 0, поэтому w = 0. Следовательно, образ
оператора А — zl плотен в Я. Но тогда, по теореме 2, он
совпадает со всем Я. Итак, оператор R{z) определен на всем
пространстве и равен {А — z/)"\ Имеем очевидное тождество
[{А — wl) — (Л — zl)] R (w) = (2 — ш) /? (w).
Умножив обе части слева на Я (г), получаем резольвентное
уравнение. Теорема доказана.
Напишем
R(i) = (A-iir^ = C + iB,
где В, С — ограниченные эрмитовы операторы. Ма
резольвентного уравнения для R(i) и R{—/) следует, что операторы В
и С коммутируют. Оператор В можно назвать мнимой частью
оператора {А — Я)~':
B^lm{A-iI)-\
Лемма 2. Сохраним предыдущие обозначения. Тогда С = АВ
и ВА CZ АВ. Оператор В имеет нулевое ядро; справедливо
неравенство O^B^I.
Доказательство. Из равенства R (/)* = i? (— i) вытекает, что
(А - И)-' - (Л + иг' =. 2/S.
Умножим обе части этого равенства слева на оператор А и
заметим, что
Л (Л - г7)~' = i{A- г/)~' + /,
Л{А + Я)~' = - / (Л + Я)~* + /.
Получим С = АВ. Чтобы доказать второе утверждение,
умножим обе части того же равенства на оператор Л справа и
воспользуемся тем, что
(Л-г/)-'(Л-Я) = /|£>л,
и аналогичным соотношением для оператора А-\-И. Отсюда
немедленно вытекает, что В А сг АВ. Любой вектор v из ядра

374 Приложение 2. Неограниченные операторы
оператора В принадлежит также ядру оператора С = АВ,
а значит, и ядру оператора (Л — г/)~'; следовательно, w = 0.
Неравенство В^1 вытекает из неравенства |i?(/)l^l,
которое представляет собой частный случай оценки, доказанной
в теореме 2. Проверку положительности оператора В мы
предоставляем читателю.
Приведем теперь пример самосопряженного оператора. Мы
увидим позднее, что любой самосопряженный оператор имеет
ту же природу.
Теорема 3. Пусть (Я„} — последовательность гильбертовых
пространств. An — ограниченный самосопряженный оператор
в Я„. Пусть Н = @Нп, таким образом, пространство Н состоит
п
из всех рядов вида /] «и, где ы„ е Я„, таких, что 21"« Р < °° •
п п
В пространстве Н суи^ествует единственный самосопряженный
оператор А, область определения которого содержит каждое из
подпространств H^cz Н и сужение которого на Н^ совпадает
с An- Область определения оператора А состоит из всех рядов
вида u=Y^Un, м„ S Я„, таких, что
п
Еи„и„Р<оо;
п
при этом Лы = 2j Л„ы„.
п
Доказательство. Единственность оператора А вытекает из
того, что самосопряженные операторы не допускают
нетривиальных расширений: если А, В — самосопряженные
операторы и AczB, то А = В. Поэтому достаточно показать, что
если Dji с: Я — линейное подмножество, описанное выше, и для
любого u = 2lun^Dji оператор А определен формулой Аи =
= ^A„Un, то оператор {А, D^) самосопряжен. Ясно, что
оператор А симметричен. Пусть w е Дд* — произвольный вектор.
Тогда для любого вектора и^ D^
{и, A*v) = {Аи, v).
Пусть ы == 2 Иц, «п ^ ^п- Тогда
Z {и„, A*v) = 2 {A„Un, v).
Ясно, что для всех ы„ е Я„
{ы„, A*v) = {AnUn, v),
{ы„, (Л*о)„) = (Лл, w„).

§ 1. Самосопряженные операторы
375
Отсюда следует, что {A*v)„ = Л„г)„. Но тогда
следовательно, v е Da, т. е. Da* с: Da, и оператор А
самосопряжен. Теорема доказана.
1-'
1о
1
при других t
1
1_
л
Рис. 1
в предположениях теоремы 3 мы будем использовать
обозначение
Л = УЗ Afi.
п
Рассмотрим обращение теоремы 3. Пусть А — произвольный
самосопряженный оператор в гильбертовом пространстве Н;
положим, как и выше,
{/4-i/)~' = C-f/S.
Мы собираемся разложить гильбертово пространство при
помощи спектральных проекторов, связанных с оператором В.
Пусть %с — функция, график которой изображен на рис. 1.
Ht)
vW
(а)
(b)
Рис. 2,
Пусть {Р} — спектральное семейство, связанное с оператором 5.
Положим
Q„ = e„(S) = P,/„-P,/(„+i);
тогда Qn — проектор. Пусть Hn = QnH. Очевидно, что
п
— ортогональная прямая сумма. Пусть бит) — функции,
графики которых изображены соответственно на рис. 2(a) и (Ь).

376 Приложение 2 Неограниченные операторы
Тогда 1 — 6 = т) и т) (В) = О, так как, в силу леммы 2 и теоремы
Лорха, спектральное семейство оператора S непрерывно в пул?
оператор В имеет нулевое ядро).
(lltr:p.±.<t<l
-*-
1/ГПрИ-—r<г%•
I о при других t
1 i
Рис. 3
Пусть s„ —функция, график которой изображен на рис. 3.
Гогда
ss„(s) = e„(s) = Q„.
Теорема 4. Пусть А — самосопряженный оператор. Положим
В = Im (Л — И)~ . Пусть Q„ = 9„(В) — проектор, определенный
выше. Тогда оператор А определен на образе оператора Q„ и
д„лс:лд„=5„(в)с.
Положим Нп = Qn.H- Тогда Н — ортогональная прямая сумма
подпространств Нп- Пусть Л„ — сужение оператора А на Нп-
Тогда оператор An ограничен и
Л = ф Л„.
п
Доказательство. Так как /s„(0 = 9„(/), мы получаем BSn{B) =
= 9„(S) = Q„. Тогда, в силу леммы 2,
Лд„ = ABsn (В) = Csn (В) = sn (В) С.
В частности, оператор AQn определен на всем пространстве.
С другой стороны,
д„Л = s„ (В) В А а SniB) ЛВ = s„ (В) С.
Это показывает, что р„Л с: Лр„. Другими словами, пусть
W е /)д — произвольный вектор, о = X ^л — ^го разложение на
составляющие w„ е Я„ и Ло = 2 ^"(11 тогда
QnAv = Wn = AQnV = Avn = AnVn,
Таким образом, Av = 2JiAnV„; теорема доказана.

§ 2 Спектральная мера 37,
§ 2. Спектральная мера
Рассмотрим сначала ограниченный самосопряженный
оператор А в гильбертовом пространстве Я. Для любого вектора
оеЯ определим линейный функционал в пространстве ^(R),
положив
К{Ч') = {Ч'{А)У, V).
Ясно, что этот функционал положителен. Следовательно,
существует единственная положительная мера ц^ на прямой,
такая, что
{ф(Л)г), v)=\^(fdn^.
Воспользовавшись поляризационным тождеством, мы получаем,
что для любых двух векторов v, w ^ Н существует такая
комплексная мера ц^, а,, что
{ф(Л)о, ау> = ^фйц^,,
Ясно, что отображение (w, w)>-^\i„^^ линейно по w и ^нтили
нейно по W. Кроме того, из теоремы 3 § 1 приложения 1
следует, что
Кф(Л)о, ш)|<||ф1и|о||ш|.
В частности, HoW^^I^P! таким образом, мера fi», конечна.
Пусть SM(R) — банахово пространство ограниченных боре-
левских функций на R. Для любой функции f е ВМ (R)
отображение
линейно по W и антилинейно по w. Кроме того,
|Sf#^,t«|<llflUlfll^|;
чтобы проверить это неравенство, достаточно построить после
довательность функций ф„ е Q (R), поточечно сходящуюся к j
почти всюду (по мере |(Хо,а,1) и такую, что I Фп I^ II f IU.
Следовательно, наше отображение непрерывно, и существует
единственный ограниченный оператор, который мы обозначим fiA),
такой, что
{f{A)v, ш)=5/<и„.^.

378 Приложение 2. Неограниченные операторы
Для любых функций /, geSAf(R) справедливы следующие
утверждения.
SPEC1. {lg){A) = f{A)g{A).
SPEC 2. f{A') = }{A).
SPEC 3. Если f 1 = 1 —постоянная функция, то fj (Л) =/.
SPEC 4. Если g {t) = tf {t) и функции fug измеримы и
ограничены, то g (А) = Af (А).
SPEC 5. f (А) ^ II f ||оо. Кроме того, если {/„} — ограниченная
последовательность в BMCR), поточечно сходящаяся к f, то
последовательность операторов {/„(Л)} сильно сходится к
оператору f{A).
Перечисленные утверждения либо очевидны, либо могут быть
получены при помощи теоремы Лебега об ограниченной
сходимости. Например, для доказательства первого утверждения
достаточно взять две последовательности непрерывных
финитных функций, которые сходятся соответственно к f и g.
Мы воспользуемся структурной теоремой из предыдущего
параграфа, чтобы распространить эти результаты на
неограниченные самосопряженные операторы. Пусть А —
самосопряженный оператор, такой, что
Л = срЛ„, л=Шл„,
п п
где Л„ — ограниченный самосопряженный оператор в
пространстве Я„. Пусть f — ограниченная борелевская функция, w е Я —
произвольный вектор. Так как | f (Л„) w„ |^||/||оо| w„ |, то
существует единственный ограниченный оператор f (А), такой, что
/(Л)о = Е/(Л„)о„.
Как и выше, с каждым подпространством Я„ и вектором v^^Hn
мы можем ассоциировать меру Цо"'. Пусть \i„ — единственная
положительная мера, такая, что
п п
Так как
К/(Л)о„, t>„)|<||fLit>„P,
полученная мера конечна, и утверждения SPEC 1 — SPEC 5
немедленно переносятся на случай неограниченных самосопряженных
операторов. Другими словами, справедлива
Теоре.па 5. Пусть А — самосопряженный оператор. Существует
единственное отображение f i-^ / (Л) из кольца ВМ (R) в алгебру

§ 3. Формула обращения для резольвенты 379
ограниченных операторов на Н, обладающее свойствами SPFC 1 —
SPEC 5.
Доказательство. Существование такого отображения вытекает
из сказанного выше. Сделаем лишь небольшое замечание по
поводу доказательства SPEC 4. Заметим, что, поскольку
Mf(^)t>j<||gLit>j,
вектор 2 f (^) ^п принадлежит области определения оператора А;
теперь наше утверждение очевидно. Единственность указанного
отображения вытекает из результатов следующего параграфа.
§ 3. Формула обращения для резольвенты
Предположим, что нам задано отображение /|-^/(Л), для
которого выполнены пять утверждений предыдущего параграфа.
Для любых векторов v, w ^ Н существует единственная мера
ц„.^, такая, что
Пусть 2 — комплексное число, г^фг. Функция/: t^-^{t—z)~^
измерима и ограничена, функция t^-^tf{t) тоже ограничена;
кроме того, (/ —2)/(/)=1. Следовательно,
(Л-2/)/(Л) = /.
Это означает, что для резольвенты справедливо интегральное
представление
{{A-zI) 'w, ш)= J j3:jdno,^(0.
Заметим, что мера Цо положительна. Мы пишем ц^, вместо ц.„, j,.
Теорема б. Пусть А — самосопряженный оператор в
гильбертовом пространстве Н, v — произвольный вектор из Н. Для
комплексного числа гфг положим R{z)=^{А — zl)~\ Тогда для
любой функции г|з S Q (R) выполняется соотношение
lira ^ W [R {X + /8) - /? (Л - ге)] v, v) ip (?.) dX = U (X) dii, (Л).
Если Xi Ы A,2 — вещественные числа, Xj < A,2, и \х^-мера
одноточечных множеств {Х|}, {Xj} равна нулю, то
Ига ijjf- 5 <[/? (^ + ie) -R{X- /е)] v, v)dX = \^ йц^ (X).

приложение 2. Неограниченные операторы
Доказательство основано на следующей лемме.
Ленча. Пусть ц — регулярная положительная конечная мера^
на прямой. Тогда для любой функции ij) е Q (R) справедливо,
равенство
lim ^ S S ]731уг+1г Ф W dii it) dX = J ф (к) dii {%),
— оо —оо —оо
Кроме того, если Ху иХ^ — вещественные числа, А,| < Xj ы \i-Mepa
.^тожества {А,|, Хг} равна нулю, то
^1 — 00 л,]
Доказательство. Заметим сначала, что при е-»-О функции
образуют семейство Дирака на прямой. (Функции Фв не финитнц,
так что в рассматриваемом случае выполнено условие DIR 3',
а не более сильное условие DIR 3.) Интегралы в левой части
доказываемых равенств можно записать в виде
J 5 (f^{t~X)h{X)dii{t)dX,
— 00 —оо
рде k совпадает с функ1шей ij) или с характеристической
функцией интервала [А,,, Xj]. По теореме Фубини, написанное
выражение равно
5 {(f^*h){t)dii{t).
Заметим, что функции Фе * Л ограничены и сходятся к h при
8->0 поточечно, если /г = 1|з; если /г— характеристическая
функция интервала, то функции фр * Л сходятся к h поточечно всюду,
за исключением концов интервала. Поскольку мы выбрали наш
интервал так, что его конщ^а имеют нулевую меру, мы »|ожем
воспользоваться теоремой об ограниченной сходимости. Лемма
доказана.
Поскольку
1 1 _ g<
t — X — ie t-X + ia (t — %Y + 8^ '
H3 доказанной леммы вытекает теорема 6.

§ 5, Формула обращения для резольвенты 381
Теорема 6 позволяет установить единственность отображения
ft—^ f (А) в теореме 5. В самом деле, мы восстановили меру ц„
непосредственно по резольвенте оператора, как это видно из
первой формулы в теореме.
Иногда построение спектральной теории начинают с прямого
доказательства теоремы 6, непосредственно проверяя
существование предела левой части равенств. После этого определяется
спектральная мера, ассоциированная с соответствующим
функционалом, и устанавливаются остальные свойства. См. Ахиезер и
Глазман [I, гл. VI], а также новую книгу Л. Хёрмандера,
который дает очень изящный споеоб построения спектральной меры
Непосредственно из формулы обращения для резольвенты.

Приложение 3
МЕРОМОРФНЫЕ СЕМЕЙСТВА ОПЕРАТОРОВ
§ 1. Компактные операторы
Пусть Е — банахово пространство. Обозначим символом К {Е)
пространство компактных операторов в Е. Напомним, что
оператор Т называется компактным, если Т переводит
ограниченные множества в относительно компактные. В гл. II мы уже
напоминали некоторые свойства компактных операторов в
гильбертовом пространстве. Пусть Г — компактный оператор. Если
множество ненулевых собственных значений оператора Т
бесконечно, то нуль является его единственной точкой сгущения.
Можно упорядочить эти собственные значения таким
образом, что
Предположим, что Лд —отличное от нуля комплексное число,
такое, что оператор T — XqI необратим. Тогда Я,о — собственное
значение. Более того, для достаточно большого целого,п имеет
место прямое разложение
E = Ker{T-Xoir®W,
где подпространство Кег (Г — Яд/)" конечномерно, оператор Т — XqI
отображает подпространство W в себя и его сужение на W
обратимо (в таких случаях мы будем говорить, что оператор T—XqI
обратим на W). Доказательство этой основной теоремы о
компактных операторах можно найти в большинстве книг по
анализу; см., например, Лент [1]. Далее, нетрудно показать, что
оператор Т — Я,/обратим на W (а также на Е) при всех Я,,
достаточно близких к точке Xq, X ^Xq. Подпространство Кег (Г — Яо/)" мы
будем называть корневым подпространством оператора Т,
отвечающим собственному числу Xq. Опишем естественный способ
построения проектора на это подпространство.
Теорема 1. Пусть Т — компактный оператор в банаховом про-
отранстве Е. Предположим, что Х^ФО —точка спектра
оператора Т. Пусть W — прямое дополнение корневого
подпространства Е, соответствующего точке Xq. Положим

§ 1. Компактные операторы 383
где с — достаточно малый контур, охватывающий точку Xq. Тогда
сужение оператора Р на корневое подпространство Е%^ —
тождественный оператор и PW = 0. Таким образом, оператор Р
проектирует Е на Е%„ параллельно W.
Доказательство. Заметим сначала, что если (Г — Я,о/)"у = О,
то Ру = у. Действительно, так как
с
^^ - " = i S t(^/ - Г)"' - (Я - Яо)-'] vdX =
с
_ 1 гг 1 L_lydx =
2яг jL^ — А,о + ^о—?" Я, — loJ
С
= JL(
2ni J
TO
С
11 у dA,.
С
1 + ^°
л — Л|
Так как, по предположению, вектор v принадлежит корневому
подпространству, то функция
Г 1
1 +
Ло ■
- 1 \v
представляет собой полином по степеням {X—Яд) ', причем
свободный член этого полинома равен нулю. Таким образом,
вычет подынтегрального выражения в точке Я,о обращается в нуль,
и первое утверждение теоремы доказано.
Рассмотрим теперь сужение оператора Т на подпространство
W czE. Это обратимый оператор. Нам достаточно доказать
следующее утверждение:
Если оператор А = Т— XqI обратим, то Р = 0.
В самом деле, если оператор А обратим, то функция
-^ (Г — Я,)"' регулярна в окр'
это, заметим, что формально
1_
{■к-Ха)А-
Xv-^ {Т — X) ' регулярна в окрестности точки Xq. Чтобы показать
(я-гг' = л~' ^—,— = -Т (я-ЯоГл-"-';
«=0
степенной ряд в правой части сходится в круге \Х—Х^\<\ А |.
Интеграл голоморфной функции по замкнутому контуру равен
нулю. Теорема доказана.

384 Приложение 3. Мероморфные семейства операторов
Говорят, что семейство операторов A{z) мероморфно в точкеZq,
если существует разложение в ряд
A{z)^ S AAz-z,r
п'^—т
С операторными коэффициентами Л„. Вообще, пусть
/: и-^Е
— отображение открытого подмножества U аС в банахово
пространство Е. Будем говорить, что отображение f мероморфно
в точке Zq s и, если в окрестности Zq оно допускает
разложение в ряд
/(2)= S a„(z-Zo)"
С коэффициентами а„ е Е.
Следующая теорема принадлежит Стенли Стейнбергу {Arch.
Rat. Mech. Anal., 31(1968), 372-379).
Теорема 2. Пусть Е — банахово пространство, U — открытое
связное множество в С, Г: U-^K{E) — голоморфное
отображение. Предположим, что существует такая точка Zq е U, что
оператор I — Т (zo) обратим. Тогда отображение
z^{I-T{z))-'
мероморфно.
Доказательство, Множество точек z^.U, в которых наше
отображение мероморфно, открыто и непусто в силу
предположения про точку z = Zo. Мы покажем, что его дополнение
также открыто, а потому пусто, так как множество U связно.
Пусть Zj е и. Так как собственные значения компактных
операторов изолированы, существует маленькая окружность С с
центром в точке 1, внутри которой нет собственных значений
оператора r(zi), кроме, возможно, самой точки 1. Тогда оператор
XI — Т (zi) обратим при всех Х^С. Образ окружности С при
отображении
X^^XI-T{z{)
компактен в открытом множестве всех обратимых операторов;
следовательно, операторы Я,/— Г(z) обратимы при всех Х^С
и при всех Z, достаточно близких к точке Zj. Положим
Р(^)-4й\^^^-^^''^^~''^^'
Тогда отображение zi—^P(z) голоморфно в окрестности точки z,;
из теоремы 1 мы знаем, что Р {zf==P (z) (это проектор на
корневое подпространство).

§ t. Компактные операторы 385
Заметим, что Р (zi) — проектор на подпространство £],
корневое подпространство оператора T{Zi), соответствующее
собственному значению 1. Рассмотрим разложение
Тогда оператор I — T{zi) обратим на W. Заметим, что операторы
P{z) и T{z) коммутируют. Положим
Q{z) = I-P{z);
таким образом, Q{zi) — проектор на W параллельно £[. Пусть
S{z)^P{zi)Piz) + Q{z,)Q{z).
Тогда S{zi) = I; поэтому оператор S{z) обратим в окрестности
точки Z]. Положим
A{z) = S{z){I-T{z))S{zr';
оператор A{z) определен в окрестности точки Zj. Очевидно, что
S(z)P(z) = P(z,)S(z);
следовательно, оператор P{zi) коммутирует с A{z); это же верно
для оператораQ (zi). Таким образом, оператор A{z) «расщепляется»
на два оператора, действующие в подпространствах Е^ и W
соответственно. Положим
^(z), = ^(z)|£„ A{z)^^A{z)\W;
тогда
A{z) = A{z)i@A{z)^.
Оператор I — T{zi) обратим на W', отсюда следует, что в
окрестности точки Zi оператор A{z)^ тоже обратим, поскольку A{z)
близок к Л (г,) = / — Г (zi). Обозначим символом Л
(z)^'оператор, который совпадает с обратным к A{z)^ на 117 и равен
нулю на £■[. Заметим, что подпространство £[ конечномерно.
Если определитель det Л (z,) тождественно равен нулю в
окрестности точки Zj, функция ZI—*(/— r(z))~' не может быть меро-
морфной. Напротив, если его нули изолированы, то функция
zt-^(/— r(z))~ мероморфна. Так как множество U связно и
оператор I — T{Z(,) обратим, мы видим, что реализуется вторая
возможность.
Мы получили также дополнительную информацию, поскольку
теперь мы знаем, что определитель det Л (z)i не обращается
тождественно в нуль. Обозначим символом .4(z)r' оператор, который
совпадает с обратным к A{z)i на подпространстве EyCzE и равен
нулю на подпространстве W. Он определен для тех точек z в
окрестности точки Zi, где такой обратный оператор существует. Так

386 Приложение 3. Мероморфные семейства операторов
как оператор A{z)i действует в конечномерном пространстве £,,
отображение
мероморфно в обычном смысле, и его полюсы совпадают с нулями
определителя detA(z)i. Тогда
{1-Т (z))-' = S{z)A{z)VS (z)-' -\-S{z)A(z)^'S(z)"'-
Итак, локально, после применения голоморфного семейства
внутренних автоморфизмов, наше семейство операторов расщепилось
на мероморфное семейство в фиксированном конечномерном
подпространстве и голоморфное семейство обратимых операторов
в дополнительном подпространстве.
§ 2. Ограниченные операторы
Теорема 3. Пусть S — замкнутое подмножество открытого
множества U czC и С — простая замкнутая кривая в U,
охватывающая множество S. Пусть
Рис. 1.
— голоморфное семейство операторов в банаховом пространстве Е,
удовлетворяющее соотношению
R{).)-R (ЛО = (Я' - Л) i? (Л) R (Я').
Для любой голоморфной в U функции f положим
R(f)^-^\f{X)R{X)dX.
с
Тогда отображение f i—* R (f) — кольцевой гомоморфизм, т. е. это
отображение линейно и
R(fg) = R{f)R{g)-

§ 2. Ограниченные операторы 387
Доказательство. Пусть С — замкнутая кривая, охватывающая
контур С, как показано на рис. 1. Тогда
с с
с с
Таким образом, оператор R{f)R{g) представлен в виде разности
двух интегралов. Имеем
с
так что первый интеграл равен R{fg) по определению. С другой
стороны.
с
так что второй интеграл обращается в нуль. Теорема доказана.
В частности, положим / = g'=l. Мы получаем, что оператор
с
удовлетворяет условию Р^^Р; это проектор на подпространство,
соответствующее «спектру», лежащему в S.

Приложение 4
ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
§ 1. Пространства Соболева
Мы будем рассматривать функции на торе, хотя некоторые
предварительные замечания верны и для функций в евклидовом
пространстве. Итак, положим T'* = R'*/Z'*. Пространство L^(T'*)
мы будем обозначать просто L^. Произвольная функция f ^. L^
порождает линейный функционал в пространстве С°°(Т''),
действующий по правилу
Этот функционал называется распределением, ассоциированным
с /, и обозначается (/). Элементы пространства С°°(Т'*)
называются пробными функциями. Пусть Di=^dJdXi —ouepaTQp
дифференцирования. Определим функционал Di{f) формулой
Di (/):. ф ь-» - ^f{x) Di(f (х) dx.
Знак минус введен для того, чтобы согласовать наше
определение с формулой интегрирования по частям в случае, когда / а С,
Функционал Diif) совпадает тогда с (Af). Как обычно, мы
полагаем для любого набора p = (pi, ..., р^) неотрицательны*
целых чисел
D^^Df' ... D^/',
целое число
\p\===Pi+ ... + Ра
мы будем называть порядком оператора В''. Любая конечная
линейная комбинация
с коэффициентами а-, S С°°(Т'') называется дифференциальным
оператором.
Мы будем пользоваться скалярным произведением
(I,g)=lfix)W)dx.

§ 1. Пространства Соболева Э89
Относительно этого скалярного произведения можно очевидным
образом определить сопряженный оператор D* для любого
дифференциального оператора D. Если ф, -ф s С°° (Т**), то
В пространстве С°° (Т*) можно ввести гильбертову норму по
формуле
11|ф11С= Е {D\,D\).
Практически более удобно иметь дело с эквивалентной нормой,
которая определяется при помощи рядов Фурье, как будет
описано ниже.
Пусть ф S С°° (Т'*). Тогда ф допускает разложение в ряд Фурье
п
где суммирование производится по всем точкам п s Z''.
Интегрируя по частям в формуле для коэффициентов Фурье, легко
показать, что для любого положительного числа k справедлива
оценка
1^«1^Т~;1 при п-^оо.
Следовательно, ряд Фурье абсолютно сходится к исходной
функции. Пусть S — положительное целое число; тогда из
определений непосредственно вытекает, что
ДЛЯ любой функции ф S С°° (Т**).
Пусть S — целое число. Зададим дискретную меру ц^ на Z''
формулой
цЛ/г) = (1 + /гТ
Тогда С°° (Т**) с: L? [Х^, ц^) для всех s s Z, Более того, очевидно,
что при любом S пространство С°° [1^) плотно в этом
гильбертовом пространстве, которое мы обозначим Я^, Таким образом,
по определению, Hs — пространство функций на Z^, которые мы
будем записывать в виде последовательностей (с„} или
«формальных рядов Фурье»
таких, что ряд
1(1 + /гТк„р

390 Приложение 4. Эллиптические уравнения
СХОДИТСЯ. Сумма этого ряда равна тогда, по определению, \\f\\l.
Скалярное произведение в пространстве Н^ задается формулой
где fn, ёп — «коэффициенты Фурье» функций f я g
соответственно. Нормы \\-\ и 111 • |IL на С°° {Т") эквивалентны. По
определению, Hs — полное пространство. Заметим, что
Тригонометрические полиномы, т. е. конечные суммы вида
образуют плотное подмножество в Н^. Им соответствуют
последовательности, в которых все члены, за исключением конечного
числа, равны нулю.
Очевидно, что если s <.t, то
II • II, < 11 • II, и Я.гзЯ,.
Промежуточное неравенство. Пусть г < s <^ — целые. Для
заданного 8 > О существует такое число С (г), что для всех f ^ Н^
llflb<8||f|k + C(e)||f||,.
Доказательство, Пусть а -
поскольку
а^<
-Произвольное
8а' + С (г) а',
положительное число
Применим это неравенство к а = (1 -j- л^) из определения нормы;
получим
11/1Г;<е||П|2 + С(8)||е|Г-.
Добавим в правую часть перекрестный член и извлечем
квадратный корень; неравенство доказано.
Спаривание (/, g)i—*{f, Я)=1] fngn задает антилинейное
отображение пространства Я_5 в сопряженное пространство Hs\
в самом деле, неравенство Шварца показывает, что ряд
СХОДИТСЯ. Также при помощи неравенства Шварца получаем
оценку
К/, ^)I<II/IUI^IU, /еЯ„ g^H-s.

§ 1. Пространства Соболева 391
Следовательно, отображение
задает линейный функционал {g) в пространстве Hs- Его норма
не превосходит НяП-^; мы увидим сейчас, что она в точности
равна II^ILs-
Определим оператор D^^ = df^/dx\ формулой
Далее, положим А = XI £>?; таким образом, для функции
/ = 2/„е'"'' имеем, по определению,
(Л/)„ = -«2/„.
Для произвольного целого s определим оператор (1 — Л)*
формулой
Тогда
II (1 - А)-' ^1? = Z I (1 + пГ' ёп Г (1 + пГ = II g 111,
-s'
Это показывает, что если geH-s, то функция (1 —Л) g
принадлежит пространству Я,. Более того,
<я, (i-Ar^) = Eu„f(i + «r'=iuii'U.
Положим / = (1 —A)~^g; теперь ясно, что норма функционала (g)
есть в точности II |г||_^. Таким образом, спаривание
if,g)^{f,g)
задает изометрическое вложение
Предположим, что ряд Y,\fnl сходится; тогда ряд Фурье
для функции f равномерно сходится к непрерывной функции,
которую можно отождествить с /; при этом
iifii<Ei/j,
где II / II = sup If (л;) |.
Неравенство Соболева. Предположим, что s > d/2. Тогда
существует непрерывное вложение пространства Hs в С(Т'*);
другими словами, для любой f е Hs норма || /1| конечна и
существует такая константа С, что
II f II < СП/11,
для всех / е //,.

392 Приложение 4. Эллиптические уравнения
Доказательство. В силу неравенства Шварца, справедлива
оценка
l\ft<iZ\L\f<Zii + nrifnfZii+mr'.
п т
Неравенство s > d/2 гарантирует сходимость ряда по т. Итак,
наше утверждение доказано.
Пусть Dif — формальный ряд Фурье, полученный формальным
дифференцированием ряда Фурье для функции /. Имеем
очевидную оценку
ll£'.flL-.<C||fL
Следовательно, если s— 1 > d/2, то функция DJ непрерывна и f
получается интегрированием ряда Фурье для Dif. Таким
образом, функция / принадлежит пространству С. Рассуждая по
индукции, получаем следующий результат:
Лемма Соболева. Пусть k — положительное целое число.
Если S > /г + dj2, то существует непрерывное вложение
пространства Hs в пространство С*; для любого p = (pi, ..., р^,
такого, что \p\-^k, справедлива оценка
wonw^^wfWs.
в качестве следствия получаем
оо
11
s=\
Hs
(Т'^) =
= с°=
(Т'*).
Объединение пространств Я-^ для всех s^O называется
пространством распределений на торе. Теорема регулярности для
эллиптических операторов утверждает, что некоторые
распределения принадлежат пространствам Я^ при всех s и,
следовательно, совпадают с гладкими функциями.
Мы закончим этот параграф несколькими замечаниями,
которые не будут использоваться в дальнейшем, но помогут лучше
представить себе пространства Я^. Пусть / е L^. Тогда
функция f порождает в пространстве С°°(Т'*) линейный функционал
(/): ф1-> \^f{x)(f{x)dx.
T-rf
функционал
D^it): фь-*!-!)'"' ^l{x)D\{x)dx

§ 1. Пространства Соболева 393
называется обобщенной производной функционала (f). Мы хотим
непосредственно показать, не используя рядов Фурье, что для
положительного целого s пространство Н^ есть пополнение
пространства С°° по норме
IpKs
Для этого мы будем рассматривать Я^ как пространство
функций из L?, обобщенные производные которых до порядка s
также принадлежат L^. Нам нужно проверить, что некоторые
последовательности гладких функций сходятся по норме Я^; это
сделано в следующих двух замечаниях.
Замечание 1. Пусть {ф„} — последовательность гладких
функций, такая, что D''qi„~^gp в L^ для всех |р |^5 ы ф„->/ в L^.
Тогда
D4f) = {§,).
Доказательство.
{g„ ф) = Ит<ДЧ, ф) = Ит<ф„, £»"» = </, D"».
Наше утверждение доказано.
Замечание 2. Пусть f ^. L^ — произвольная функция;
предположим, что D'' (/) ^ (g) для некоторой функции g из L^. Если
{а„} — последовательность Дирака в С°°, то
D''{an*f)-*g
в L\
Доказательство. Мы покажем, что D''{а„ * f) = {а„ * g). Из
элементарных свойств последовательностей Дирака мы знаем,
что а^*g сходится к функции g в L^. Это доказывает наше
утверждение, если предварительно проверить, что для любог
функции а е С°°
D'{a*f) = {a*g).
Пусть D = D'', Имеем
{a*f,D'4')='^'^a{x-y)f{y)D'((,{x)dydx= ,
= \\a{-y)f{y + x)D\ (х) dy dx =
(замена переменной у у-^ у -\- х)
= \ \ а (" г/) / (х) 0*ф (х -^у) dy dx —
(замена переменной ху-^х — у)
= ]o.{~y)g{x)cp{x — у)dxdy = {a*g, ф>,
что и требовалось показать.

394 Приложение 4. Эллиптические уравнения
Смысл замечания 2 состоит в том, что оператор
обобщенного дифференцирования перестановочен со сверткой. Как и
следует ожидать, справедливо равенство
D" {a*g) = (D^a) * g
(это доказывается, по существу, дифференцированием под знаком
интеграла, см. Ленг [1, гл. XIV, § 4, теорема 7]). Поскольку
а — гладкая функция, то функция а*g тоже гладкая, несмотря
на то что g — только распределение.
§ 2, Априорные оценки
Пусть а е С°° (Т**) — гладкая функция. Мы будем доказывать
оценки с константами С„, зависящими только от а, и будем
в этих случаях использовать обозначение Оц.
Пусть ф, 1|) е С°° (Т'*); тогда
<DV 1|)) = (-1)1'"<Ф, £>»■
Таким образом,
(Д^Рф,'ф) = <ф, D^"-*),
т. е. оператор D'^" симметричен. В частности,
<Лф, 1|)) = <ф, Л1|)).
Более того,
<(1-Л)>, а|)) = <ф, (1-ЛГа|,)
для произвольного целого s, положительного или отрицательного.
Заметим, что скалярное произведение, задаваемое формально
рядом
<Ф, i^) = Е ФпФп,
совпадает с обычным скалярным произведением в L^, когда ф,
■ф — гладкие функции. Поэтому симметричность оператора (1 —Л)*
не зависит от того, в каком смысле мы понимаем скалярное
произведение. Разумеется, если определять скалярное
произведение при помощи формальных рядов Фурье, то
симметричность оператора (1 — Л)* очевидна. Из неравенства Шварца и
обычной интегральной формы скалярного произведения мы
получаем также неравенство
I <D'aD>, D4) I < II D'a \\ \\ D\ W, \\ D^ Но < II D'a || || Ф II,, , И ||,,,.
Мы установим теперь различные неравенства для операторов
диф(()еренцирования и умножения на функции и их
сопряженных. Доказательство этих неравенств несложно, но несколько
утомительно.

§ 2. Априорные оценки 395
Пусть
— дифференциальный оператор. Если сумма берется по всем
точкам р, для которых | р | ^ /г, мы будем говорить, что
порядок D не превосходит k {ovdD^k). В этом случае
(1) {D (аф), i|5) = (а £)ф, ^) + <£ф, ^),
где £ —дифференциальный оператор, порядок которого не
превосходит k — 1; коэффициенты оператора £ зависят только от
производных функции а.
Для любых 5^0 справедлива оценка
Е 1. <( 1 - Л)^ (аф), 1|)) = (а (1 - АУ ф, ^) + 0„ (|| ф |L_, || i|) у.
Доказательство. Положим в формуле (1) D^(l—Л)^ Тогда
ord D = 2s, ord Е = 2s — 1. Пусть pD'' — одно из слагаемых
оператора Е; предположим, что | р | ^2s— 1. Напишем p = q -\- p — q,.
где I (? I = S — 1. Тогда
Далее, D''~''^'^=Y, Yr-O''"''"''^, где сумма берется по всем г, для
которых ri^Pi^qt, г=1, ..., d, а коэффициенты Уг
—производные функции р. Следовательно,
(рД'ф,^) = Ор(||ф||,-,ИУ.
Слагаемые с номерами р, для которых | р |< 2s — 1, оцениваются
аналогично и не дают вклада того же порядка. Оценка Е I
доказана.
Для любых S S Z справедливы также оценки
Е 2. (аф, 1|)), = (ф, ai|)), + О„(IIФIL-1И1У•
Доказательство. Рассмотрим сначала случай, когда s^O.
Имеем, по определению,
(аф, 'ф), = ((1-ЛГ(аф),-ф),
и нужное неравенство вытекает из Е 1. Перейдем к случаю
отрицательных показателей. Пусть s > 0; положим
ы = (1-Л)"Ч, у = (1-Л)"'1|).
Тогда, в силу Е 1,
(аф, ^)_s = (аф, (1 - А)-Ч) = <а (1 - Af и, v) =-
= ((1-ЛГаи, o)-f 0„(ll"IL-il|oy.

398 Приложение 4. Эллиптические уравнения
Далее,
((1 - hf (т), v) = <(Ш, (1 - Д)' «>=<(!- Д)-' ф, ait) = <ф, а^)_^.
Преобразуем теперь остаточный член:
II"iiL. == <". (1 - Д)'"'«)=<(1 - Д)~' Ф. а - Д)"' Ф>=
==<(1-дГ-'ф,ф) = 11ф111,_,.
Аналогично, II о 11^" II i|3 IL^. Итак, оценка Е2 доказана.
ЕЗ. 11аф|^<С||а||||ф||,+ 0Л11ф11а-.).
Доказательство. Пусть сначала s ^ 0. Если | р | ^ s, то
D" (аф) = I b^D'aD"-V
и, в силу неравенства треугольника,
\\D''{ac(,)i<snplD''aD'-\i.
Если I р I = S и <7 = О, то соответствующий член оцениваетоя
величиной II а |Н| ф iL- Члены | р | = s и <? =j^ О имеют порядок || ф ||^_ i
с точностью до множителя, зависящего только от а. Это
завершает доказательство оценки для положительных показателей.
Рассмотрим теперь отрицательные показатели. Пусть ф,
\|1 — гладкие функции; положим
ы = (1-Д)~'ф, v = {l-^Г'^.
Тогда
<аф, i|))_, = (аф, (1 - Д)~' -ф) = (а (1 - Д)^ и, v) =
= ((1-ДГ(Ш, о) + 0„(||ы||,_,||ау==
= <(Ш, v}s+OA\\u\\s-i\\v\\s).
Мы предполагаем, что s > 0. В силу неравенства Шварца,
справедлива оценка
|(аи, a)J<l|a«IU|f|l.<[lla||||«||, + OJ||«|L_,)]||a|L.
Но
11«11,-11ф1и, 11«1и = 11ф1и_р llfi = HIL^
Следовательно,
|(аф, г1>)_,|<[||а||||ф1и + СЛф||_^_,]И1|_^,
и поэтому
1|аф1и<||а||||ф||., + СЛф|1_,_„
что и требовалось показать.

§ 2. Априорные оценки 397
Е 4. Пусть D — дифференциальный оператор, порядок кото-
роао не превосходит к. Тогда
11£'ф|1.<Со1|ф|и„
sde константа С^ зависит только от оператора D. В частности,
11£'''Ф11. <11ф1и,р|.
Доказательство. Пусть ф = XI Ф«^'"''- Тогда
£'''ф = Еф«г""Л'"^!
отсюда сразу получается оценка для оператора £>". Из нее
непосредственно следует оценка для операторов вида D = aD^,
а значит, и для произвольных операторов.
Из Е 4 мы видим, что для любого целого 5, положительного
или отрицательного, оператор D можно продолжить до
непрерывного линейного отображения
(мы сохраняем для него прежнее обозначение). В
действительности из Е 3 и Е 4 вытекает более точное неравенство, в
котором учтена выделенная роль коэффициентов при старших
членах оператора по сравнению со всеми остальными. Если
£>= Z apD",
МЫ будем называть коэффициенты Ор, для которых |р| = /г,
коэффициентами при старших членах. Следующая оценка
немедленно вытекает из Е 3 и Е 4:
Е 5. II ДфIL< Со (D)II фIU, -f С, {D)II фIU,-,.
еде Со (D) = sup | Ор {х) \, а константа Сх {D) зависит от всех
I р | = А, jcs Т
коэффициентов D.
Е 6. Для любого дифференциального оператора D, порядок
которого не превосходит к, справедлива оценка
{D (аф), 1|)), = (аДф, 1|)), -f Од, „ (IIФ Ws+k-1II ^ lis)-
Доказательство. Если D — оператор умножения на функцию,
оценка очевидна. Достаточно доказать ее для D^='D''. Заметим,
что
D''{aff)-aD\'= Е C-D'aZ)""" (аф);
При ЭТОМ \р — q\-^s-\- к— \. В силу неравенства Шварца,
I {D'aD"-" (аф), ^\ \ < 1 D'aD"-" (аф) |L \\ ^ Ь <
<^''o,allaфlL+*-lll'Фlls<C^,,J|ф||,+ft_,|j1i)|U

398 Приложение 4. Эллиптические уравнения
Мы воспользовались также оценками Е 4 и Е 3. Итак,
утверждение Е 6 доказано.
Е 7. Пусть D, D' — дифференциальные операторы, порядок
которых не превосходит к. Тогда
<Д(аф), Д», = <Дф, D'(ail3)).+
+ Oo,B',„(lklUfeHIUfe-i + lk IL+fe-ill'^l'lls+fe)'
Доказательство. Этот результат получается
последовательным применением оценок Е 2 •— Е 6.
§ 3. Априорные оценки для эллиптических операторов
Пусть
— дифференциальный оператор с гладкими коэффициентами,
определенный в открытом подмножестве U пространства R** или
тора Т**. Мы будем называть выражение
\p\=k
старшим членом оператора D, а число k — порядком оператора.
Для произвольной точки х^и пусть
— однородный полином от переменных li, ..., 1ф полученный
подстановкой переменной |/ вместо D/ и ар{х) вместо Ор в
старшем члене оператора D.
Если сто,д;(|) ф О для всех ненулевых векторов | е R^, то мы
будем называть оператор D эллиптическим. Функция а^
называется символом оператора D.
Пример. Оператор
эллиптичен: его символ равен |^ +12^
Пример. Оператор
д . . д
-Z—f- г ^-
дх ду
.адлиптичен, и его символ равен |i + г|а.

§ 3. Априорные оценки для эллиптических операторов 399
Пример. Оператор
эллиптический порядка 2 в верхней полуплоскости.
Пусть L — эллиптический оператор порядка k. Тогда ясно,
что для любой точки X из и существует такое число Сх > О, что
\<rD(x,l)\>Cx\lf
для любого ненулевого вектора | е R**. Здесь 11| — евклидова
норма в R**.
В этом параграфе мы докажем оценку для эллиптических
операторов, которая, грубо говоря, противоположна
неравенству Е 4.
Основная априорная оценка. Пусть L — эллиптический
оператор порядка k, действующий на торе Т**, So — произвольное
целое число. Тогда для любой функции ф е С°° (Т**) справедлива
оценка
11ф1и<С,(||£ф||, + ||фу.
Доказательство будет состоять из трех шагов; прежде чем
привести доказательство, заметим, что число Sq обычно
выбирают большим отрицательным. Более того, мы увидим
впоследствии, что на подпространстве конечной коразмерности в оценке
можно опустить член ||ф|Ц. Во всяком случае благодаря этому
члену теорема нетривиальна, только если So^s-f/г — 1. Мы
будем предполагать, что это условие выполнено. Заметим также,
что константа в неравенстве зависит от оператора L.
Решающее место в доказательстве — получение основной
априорной оценки для операторов с постоянными
коэффициентами. Это будет сделано в следующей лемме.
Ленма 1. Предположим, что L — однородный оператор
порядка k с постоянными коэффициентами. Тогда для любой
функции ф е С°° (Т**) справедлива оценка
Доказательство. Имеем
II ^^Ф11^ = Е I Ф„ РI ^L in) I ■ (1 + пГ > S I Ф„ р in')'{I + n'Y;
bU-ZlVnHl+nT.
Следовательно,
II ^Ф1^' + IIФ III» Zi Ф„ Г (1 + пТ^*=IIФ \Lk.
Лемма 1 доказана.

400 Приложение 4. Эллиптические уравнения
Лемма 2. Пусть L — эллиптический оператор порядка k,
действующий на торе Т**. Тогда существует такое положительное
число б = б (L), что для всех гладких функций q) на Т' с
носителем в шаре радиуса меньшего, чем б, имеет место оценка
11ф1и<||/.ф||, + ||ф1и.
Доказательство. Пусть L= ^apD''. Так как коэффициентыОр
равномерно непрерывны, мы можем выбрать столь малое число б,
что колебание каждой из функций Ор в шаре радиуса б не
превосходит 8. Пусть ф — произвольная гладкая функция, носитель
которой содержится в некотором шаре радиуса б, Xq — центр
этого шара. Пусть
\pT=k
— однородный эллиптический оператор с постоянными
коэффициентами, полученный «замораживанием» коэффициентов в
старшем члене оператора L. По предположению, для всех точек х
из шара 5в(^о) выполнено неравенство
I Ор (х) — Ор {хо) I < е.
В силу леммы 1,
Заметим, что || ф 11^^ ^11 ф Ws+k-i IIФ \\$+к- ^^^ нужно сравнить нормы
II Lcp \\i и II Lfjcp lli Их разность равна
{{Lo — L)((,, Lo((,\ + {Lcp, (Lo —1)ф)^.
Первое слагаемое можно оценить при помощи неравенства
Шварца. Положим ар{хо) = ар. Абсолютная величина члена
с номером р оценивается следующим образом:
I ((ар - ар) D\, 1оф). I ^ II (ар - «р) £»> II. II /-оФ II. <
<[е||ф1и4-С,||ф||,^,_,]||1оф11,<
<вСз (L)II ф t+k -f Сз (L)II ф ||.+fe-, II ф \\s+k.
Мы воспользовались при этом также оценкой Е 5. Выберем
числа б и 8 так, что гС^ {L) ^ 1/2; тогда
т11ф1Р,,.<С411^:ф11^ + С51|ф1и,.,!1ф1и,.
Разделим обе части неравенства на ||ф||^^^^ и воспользуемся
промежуточным неравенством из § 1 для показателей Sq < s-{-
-\-k—l<s-{-k. Мы получаем в правой части слагаемое II фЦ^^^
с малым коэффициентом; его мол<но перенести в левую часть;

§ 3. Априорные оценки для эллиптических операторов 401
после этого в правой части останется только слагаемое ||ф||
что и требовалось.
Чтобы завершить доказательство иашей^ оценки,
воспользуемся разбиением единицы. Пусть {aj — конечное семейство
гладких функций на Т**, таких, что
(Обычная конструкция разбиения единицы показывает, что из
функций, образующих это разбиение, можно извлечь
квадратный корень, и полученные функции снова будут г;;а1кими.)
Предположим, кроме того, что носитель каждой функции Of
содержится в шаре радиуса 6 = 6(L), как в лемме 2. Для любой
функции феС°°(Т'^) произведение а^ф сосредоточено в том же
шаре. Символ <! мы будем использовать для обозначения
неравенств с константами, зависящими от оператора L и от
разбиения единицы (само это разбиение единицы строится по
оператору L). Итак, имеем
II ф Wl+k = <Ф. 4')s+k ^ Е <«?*Р' *P>s+A =
= ;^<а,ф, а,ф),+, + 0£( II ФIUJIФ IU,_,) <
< XII ^(«^ф) llf + Ell«'ф IU* II«^ф IU*-. + II фIU*IIф IU.-..
Мы воспользовались оценкой Е 2. В силу Е 7, полученное
выражение не превосходит величины
Сб ЩЩЬ (а!ф), ЬФ>, + IIФ IU, IIФ IU,_,) <
<си/.)1|/.ф111 + С8(1)||ф||,^Лф1Ц,_,.
Заметим, что ||/.фЦ ^:< С9(^)||ф||^^^,. Разделим обе части
полученного неравенства на ИфИ^^^,. Выберем такое 8 > О, что
eCs (L) ^ 72> и воспользуемся неравенством
lklU_,<8b|^,-f С(е)||ф||,^.
Вычтем из обеих частей'полученного неравенства у ||ф|К^. Мы
получаем основную априорную оценку; доказательство закончено.
Замечание. Наша оценка по непрерывности продолжается
на элементы пространства H^+k- В самом деле, пусть h е Hs+ii>
{ф„} — последовательность гладких функций на торе, сходящаяся
к Л в топологии пространства Н^+к- Неравенство
11^Ф«'1, <11ф«1и,
14 Зак. 589

402 Приложение 4. Эллиптические уравнения
показывает, что последовательность 1ф„ сходится в Н^, и мы
получаем
Это неравенство можно переписать также в эквивалентной
форме:
llfl<ll^flU + llflU, /ея,.
§ 4. Теоремы вложения для пространств Я^ и теорема
регулярности для эллиптических уравнений на торе
В этом параграфе мы исключим из основной о-цеики член || ф ||^^
за счет перехода к подпространству конечной коразмерности.
Лемна 1. Предположим, что г < s. Тогда единичный шар
пространства Hs относительно компактен в Н^.
Доказательство. Пусть функция
п
принадлежит единичному шару пространства Н^, т. е.
Zl/„P(l+nT<l.
Выберем такое число N, что (1 + N^Y'^ < е. Разобьем
функцию f на два слагаемых:
\n\^N \n\>N
Тогда норма второго слагаемого в пространстве Я^ близка
к нулю:
Ul >Af \n\>N \ -r I
Первое слагаемое принадлежит ограниченному подмножеству
конечномерного пространства, состоящего из функций,
коэффициенты Фурье которых отличны от нуля только при I п I ^ Af.
Такое множество можно покрыть конечным числом щаров
радиуса е в метрике пространства Я^. Таким образом,
единичный шар пространства Я^ вполне ограничен в Н^. Лемма
доказана. По существу, мы получили даже несколько более сильный
результат:
Теорема 1. Пусть г <s. Обозначим символом Ms (N)
подпространство всех функций f S Hs, таких, что коэффициенты
Фурье fn = О,если\п\^Ы. Для любого в > О существует такоеN,

§ 4. Теоремы вложения для пространств Н, 403
что для всех f ^ Н^ {N) справедливо неравенство
llflKellft
Вложение пространства Н^ в Н^ компактно.
Отметим, что подпространство Hs{N) замкнуто и имеет
конечную коразмерность в Н^. Кроме того, оно порождается
гладкими функциями.
Замечание. Теорема 1 была доказана при помощи обычных
формальных манипуляций с рядами Фурье. Полезно заметить,,
что она справедлива в несколько более общей ситуации.
Пусть Н, Е — гильбертовы пространства,
А: Н-^Е
— компактный оператор. Пусть {е^} (г^1,2, ...) — ортонорми-
рованный базис в пространстве Н. Обозначим символом Н (TV)
замкнутое подпространство Н, порожденное векторами е,- с
номерами i'^N. Для любого е > О существует такое N, что для
всех векторов he Н {N) справедливо неравенство
||ЛЛ||я<е||Л||я.
В самом деле, предположим, что это не так. Тогда для
любого п найдется единичный вектор hn^ Н («), такой, что
\\Ahn\\E^^- fio последовательность {Л„} слабо сходится к нулю,
следовательно, Л/г„^-0 в сильном смысле (противоречие).
Мы воспользовались тем обстоятельством, что оператор
А: Н -* Е компактен тогда и только тогда, когда он переводит
любую слабо сходящуюся последовательность в сильно
сходящуюся. К^роме того, если оператор А компактен и
последовательность {Vn} слабо сходится к нулю в Н, то
последовательность {Avn} сильно сходится к нулю в Е.
Напомним несложное доказательство этого факта.
Предположим, что оператор А компактен. Предположим, что
последовательность {у„} слабо сходится к вектору у е Я. Без
ограничения общности можно считать, что у ^ 0. Тогда для любого
weH имеем {w, t'„)-^0. Так как оператор А компактен,
последовательность {Avn} содержит сильно сходящуюся
подпоследовательность. Если ее предел w не равен нулю, то существует
такой функционал X на Е, что X{w) ¥=0. Но Я о Л — функционал
на пространстве Н и, по предположению, Л(Лу„)^-0
(противоречие). Таким образом, точка О — единственная предельная
точка последовательности {Лу„}, что и требовалось показать.
Обратно, предположим, что оператор Л переводит слабо
сходящиеся последовательности в сильно сходящиеся. Пусть {и„} —
14*

404 Приложение 4. Эллиптические уравнения
ограниченная последовательность, | у„ | ^ 1 для всех п. Так как
единичный шар в гильбертовом пространстве слабо компактен,
наша последовательность содержит слабо сходящуюся
подпоследовательность {frtj}; последовательность {^««Л сходится в
сильном смысле. Итак, оператор А компактен.
После этого небольшого отступления вернемся снова к
нашей конкретной ситуации.
Теорена 2. Пусть L — эллиптический оператор порядка k на
торе. Для любого показателя s существует такое число N, что
оператор L индуцирует топологический линейный изоморфизм
пространства Hs{N) на его образ в пространстве Н^-к\ другими
словами, для всех h^ Н^{N) справедлива оценка
IIЛII. < \\Lhl_^<\\hl.
Кроме того, подпространство таких функций f s Н~g+i^, что
(/, 1ф)^0 для всех феС°°(Т ), конечномерно; таким образом,
замыкание образа LC°° (Т ) в пространстве Н^~к имеет
конечную коразмерность.
Доказательство. В силу теоремы 1 и основной априорной
оценки, по заданному е > О найдется такое N, что для всех
функций h^H, (N) справедлива оценка
II h I < С, II Lh IU, + Сг IIЛ II,, < С, II Lh ||,_, + С^е || h ||,.
Выберем е столь малым, что Cge ^ '/г^ Мы получаем нужное
нам неравенство. Так как, очевидно, имеет место и
противоположная оценка:
1|М1и,<1|Л||„
то первое утверждение теоремы доказано. В частности, ядро
оператора L в пространстве Н^ конечномерно. Покажем теперь,
что L переводит пространство гладких функций на торе в
линейное подмножество конечной коразмерности. Пусть f^H-s+k\
предположим, что
<f, 1ф) = 0, феС~(т^)-
Тогда {L*l, ф)==0; следовательно, L*f=^0. Таким образом,
вектор f принадлежит конечномерному ядру оператора L*. Итак,
второе утверждение теоремы тоже доказано.
Теорема 3. Пусть L — эллиптический оператор порядка k на
торе, функция h принадлежит пространству Ht для некоторого t.
Если

§ 5. Теорема регулярности в евклидовом пространстве 405
{равенство понимается как равенство линейных функционалов на
С°° {V)) и функция g принадлежит пространству Hs, то к^Н^+к-
В частности, если g^C"{Т\ то и h^C"(Т").
Доказательство. Для достаточно больших N справедлива
оценка
llflL,<ll^^7IU_„ f^H_,{N).
в силу теоремы 2, для любой функции ф из Я-^(ЛГ) имеем
{h, Гф) = <g, ф)<IIgII,IIФIL, < II^ 11,II^*ФIL,-,-
Следовательно, функционал {И) непрерывен на множестве
L*C°°(J'^). По теореме 2, это множество имеет конечную
коразмерность в пространстве H-s-k- Следовательно, пространство,
порожденное множеством L*C°° (Т**) и конечным набором гладвдх
функций, образует плотное подмножество в Н-^-к- Таким
образом, функционал {h) непрерывен на плотном подмножестве
в H-s-k и, следовательно, индуцирован элементом
двойственного пространства, которое есть не что иное, как Hs+k- Итак,
h е Hs+k, что и требовалось показать.
Замечание. В приведенном доказательстве мы в основном
следовали статье П. Лакса «О задаче Коши для
гиперболических уравнений и днфференцируемости решений эллиптических
уравнений» {Сотт. Риге Appl. Math., 8 (1955), 615—633). Однако
Лаке использует несколько иное (ныне забытое) определение
эллиптичности и только намечает отдельные этапы
доказательства. Хорошее и замкнутое в себе изложение дано Л. Нйрен-
бергом в докладе «Об эллиптических уравнениях в частных
производных» (CIME Conference, II principio di minimo e sue
applicazioni alle equazioni funzionali, Rome^ 1959, pp. 1—58).
Однако вместо простых рассуждений, использованных нами при
доказательстве теоремы 3, Ниренберг пользуется аппаратом
«конечных разностей», который мне не нравится. Кроме того,
в обеих работах не выделена конечномерность ядра и коядра
эллиптического оператора. Изложение Ниренберга впоследствии
воспроизводилось несколько раз, например в книгах Л. Берса
и Ф. Джона и А. Фридмана по теории дифференциальных
уравнений в частных производных и в книге Уорнера о
гладких многообразиях. Все же, как мне кажется, имело смысл
привести здесь полное доказательство.
§ б. Теорема регулярности в евклидовом пространстве
Пусть и — открытое подмножество евклидова
пространства R''. Мы будем рассматривать дифференциальные
операторы на и. Если функция / локально квадратично интегри-

406 Приложение 4. Эллиптические уравнения
руема на U, она порождает, как обычно, непрерывный
функционал в пространстве пробных функций, т. е. в
пространстве СТ {U). Мы покажем, что теорему регулярности легко
перенести с тора на область U.
Теорема 4. Пусть f — локально квадратично интегрируемая
функция на открытом подмножестве U czj^''. Пусть g^C°°{U);
предположим, что L — эллиптический оператор порядка k на U
с гладкими коэффициентами. Пусть LQ) = {g). Тогда f^C°°{U).
Доказательство. Пусть Хц е U. Положим
Достаточно доказать, что f — гладкая функция в окрестности
точки Хо- Пусть функция a^C7{U) равна 1 в шаре малого
радиуса г вокруг точки х^ и равна нулю вне шара радиуса 2г.
Положим
Al = aL-4-(l-a)Lo.
Тогда оператор М эллиптичен и имеет постоянные коэффициенты
вне маленького шара. Пусть Oi —гладкая функция, которая
равна 1 в окрестности точки Xq и обращается в нуль вне шара
радиуса г/2. Тогда для любой функции феСГ(^/) имеем
<М<а,/), ф)=^а,/М> =
= 5 cti/L* (аф) + ^ OifLo ((1 — а) ф) =
= ^ aJL* (аф) = ^ /L* (а1аф) + ^ /£)>,
где D* — оператор порядка меньшего, чем k, коэффициенты
которого суть финитные функции, сосредоточенные на
множестве supp а; интегрирование производится по всему
пространству R'', однако все подынтегральные функции финитны. Таким
образом, написанное выражение равно
(cxig, Ф) + (/, £>»•
Равенство
5 a.JM\={aig, ф) + <f, D\)
справедливо и для периодических функций ф, так как обе части
зависят только от значений функции ф на множестве supp а.
Пусть функция р е С°° (Т'') равна 1 на множестве supp а и равна
нулю вне шара малого радиуса. Тогда для всех периодических
функций ф
<Р/, Д*Ф) = </, Д'Ф).

§ 5. Теорема регулярности в евклидовом пространстве 407
Мы можем «периодически продолжить» все наши срезанные
функции на тор Т**; другими словами,, мы можем найти
функции g„ е С°° (Т''), {fif)„ е L^ {Т'), эллиптический оператор М„ на
торе, оператор £)„, порядок которого не превосходит k — 1,
функцию {aJ)„^L^T'), которые совпадают с g, р/, М, D, aj
соответственно в малой окрестности точки х^; при этом
М„ <(a,f )„) = ((a,g)„) + D„ <(pf)„) = (h),
где функция h принадлежит пространству H-k+^iT').
Следовательно, по теореме регулярности, (а,/)„еЯ].
Повторяя наше рассуждение, мы получим, что
Л1д((сч/)д) = (Л)
для некоторого Л е/fi_(ft_i)=^ Яг-*. Следовательно, {aif)„^ Н^-
Рассуждая по индукции, заключаем, что (aif)„ е Н^. Другими
словами, функция (ai/)„ совпадает с гладкой функцией как
функционал на С"* (Т'') и, стало быть, совпадает с такой
функцией почти всюду. Далее, функция (ai/)„ равна / в окрестности
точки Хй- Таким образом, мы получили нужный результат:
функция f бесконечно дифференцируема в окрестности точки хц.
Если в теореме регулярности предположить, что функция g
вещественно аналитическая, то функция f также будет
вещественно аналитической. Доказательство, принадлежащее Морри
и Ниренбергу, кратким и изящным образом воспроизведено
в книге Л. Берса и др. «Дифференциальные уравнения в
частных производных» (Proceedings о! the summer seminar,
Boulder, Colorado, Interscience, N. Y., 1964, pp. 207—210).
Доказательство занимает всего три страницы; оно состоит из серии
оценок, показывающих, что построенная гладкая функция
разлагается в сходящийся степенной ряд. По существу, это
доказательство использует только теорию уравнений с гладкой правой
частью и основное неравенство.
Мы сформулировали теорему регулярности для локально
квадратично интегрируемых функций. В действительности наше
доказательство годится и для произвольных распределений.
Напомним, что распределение Т в открытом множестве U —
это линейное отображение
Т: C7{U)^C,
обладающее следующим свойством. Для любого компактного
подмножества К czU существует конечный набор
дифференциальных операторов Dj, ..,, D^, такой, что если ф —гладкая
функция и supp ф с: /С, то
|Гф|<тах||Аф11,

408 Приложение 4. Эллиптические уравнения
где II ф II = sup I ф (О 1- Распределения на торе определяются совер-
шенйо аналогично, за исключением того, что там не нужно
рассматривать компактных подмножеств и пробные функции
принадлежат пространству С°° (Т**). Ясно тогда, что
распределения — это элементы пространств Н^ при всевозможных s.
Теорему регулярности в евклидовом пространстве можно
сформулировать следующим образом:
Теорема 5. Пусть Т — распределение, g — гладкая функция
на и. Пусть L — эллиптический оператор с гладкими
коэффициентами, который имеет порядок k. Предположим, что LT = g.
Тогда Т^Т^ для некоторой функции h^C" (U).
Доказательство остается практически без изменений, нужно
только несколько изменить обозначения. Например, вместо
\ а^ЛГф мы пишем Т {щМ*(^) и т. п.

Приложение 5
СЛАБАЯ И СИЛЬНАЯ АНАЛИТИЧНОСТЬ
§ 1. Комплексный случай
Теорема 1. Пусть Е — комплексное банахово пространство,
Л — нормирующее подмножество двойственного пространства Е',
т. в, такое подмножество, что для любого и е £
1.1= sup JAJli.
Пусть и czC — открытое подмножество, f: U -^ Е — такое
отображение, что
(i) для любого ЯеЛ функция s*-^Xof[s) аналитическая;
(ii) для любого компактного подмножества К cz U
справедливо неравенство
sup I f (s) К оо.
Тогда отображение f аналитическое.
Доказательство (см., например, Иосида [1]). Нам нужно
показать, что отображение f сильно дифференцируемо. Мы
проверим, что отношение приращений f к приращениям
аргумента образуют последовательность Коши. Достаточно
покачать, что
f{s + h)-l{s) f(s + k)-l(s) \_^AM\h-k\
h k \^ г' '
где М = sup I f (О I. a h, k — такие комплексные числа, что
\h\, \k\<. r/2. Так как множество Л нормирующее, достаточно
доказать наше неравенство для скалярной функции A,of, где А,еЛ.
Поэтому без ограничения общности можно считать, что f —
ограниченная комплекснозначная аналитическая функция. В этом
случае формула Коши и интегральная форма теоремы о
среднем показывают, что нужное неравенство в самом деле
выполнено. Это вытекает из тождества
/ (S + Й) - ? (S) :(s + k)-f (s)
^ _L ( f(z)(h-k) .
2я/ J {z-s-k)(z-s-k)(z-s) "'^'

410 Приложение 5. Слабая и сильная аналитичность
где С — окружность радиуса г вокруг точки s. Значение
константы в неравенстве, разумеется, несущественно.
В некоторых приложениях, например в §11 гл. XIV, нам
нужно было доказать, что ядро оператора аналитически
зависит от параметра s, исходя из того, что сам оператор —
аналитическая функция этого параметра. При этом заранее
неизвестно, является ли зависимость ядер от s непрерывной.
Поэтому требуется дополнительная лемма.
Лемма. Пусть D с: С — открытый круг радиуса 1, f —
локально суммируемая функция в D. Предположим, что для почти
всех {по мере Лебега) пар {а, г), таких, что а е С, л > О и
I а I -j- г < 1, равен нулю интеграл по окружности радиуса г
с центром в точке а:
J fds^O.
С^ (а)
Тогда суи^ествует голоморфная функция, которая совпадает с f
почти всюду в D.
Доказательство. Для произвольного натурального числа л ^2
определим функцию
/„:(1-1)d^C
формулой
fniw) = ~Wf{x+ iy -f ay) dx dy.
— D
Легко видеть, что
\ fnds = 0
с,(a)
для почти всех пар {а, г), таких, что \a\-\- г <1 — 1/п, г > О
(Чтобы показать это, достаточно воспользоваться теоремой Фу-
бини и изменить порядок интегрирования.) Так как функция f
локально суммируема, мы можем перейти к пределу под
знаком интеграла и доказать, что функция /„ непрерывна в круге
(l ] D. Согласно обычному критерию, отсюда вытекает,
что /„ в действительности голоморфна в этом круге. В круге

§ 1. Комплексный случай
411
-o-D справедлива следующая оценка;
^\^\f-fjdxdy=\\^ '{^^[f(w)-f{w + x+iy)]dxdy
1 „
— D
dw ■
\ \^\f{w) — f(w + x+iy)\dw
-°
dxdy ^
<
sup \^Yf{w) — f{w-\-x-\- iy) I dw.
X+tyi _
По теореме об ограниченной сходимости, при п-^оо
выражение справа стремится к 0. Таким образом, {f„} есть
последовательность Коши в пространстве 0\-^1)\. Легко показать, что
тогда последовательность {/„} сходится равномерно на
компактных подмножествах, а значит, сходится к голоморфной
функции, которая совпадает с / почти всюду в круге -^ D. Тем самым мы
доказали наше утверждение локально, в окрестности любой
заданной точки. Этого достаточно для доказательства нашей
леммы, так как мы можем заменить функцию / ее сдвигом.
(Приведенным доказательством я обязан Д. Петерсону.)
Этой леммой пользуются тогда, когда нужно доказать
аналитичность ядра, задающего оператор, как, например, в
теореме 12 § И гл. XIV.
Заметим, что множество Л, о котором шла речь в теореме 1,
не обязано быть линейным (это не очень существенное
обстоятельство) и — что более серьезно — оно не обязательно замкнуто.
В этом отношении теорема 1 отличается от ее вещественного
аналога, который будет приведен в следующем параграфе; эти
две теоремы имеют различные области применимости, причем
ни одна из них, по-видимому, не перекрывает другую.
Хотя следующая теорема и не используется в этой книге,
все же полезно привести ее здесь. Я обязан этой теоремой
Дж. Гамлену. По образцу ее доказательства построено
доказательство теоремы 12 § 11 гл. XIV.
Пусть Z — локально компактное пространство с
положительной мерой fi. Мы будем писать dz вместо rf[i (2). Пусть t/ с: С —
открытое подмножество; предположим, что задано семейство
R, = R{s), s^U,
ограниченных операторов в пространстве L^{Z, ц). Мы будем
предполагать, что каждый оператор R, можно задать при

412 Приложение 5. Слабая и сильная аналитичность
помощи ядра r{z, г'\ s), где г. ZX-^X^^-C—борелевская
функция; другими словами, для всех f ^ L^ (Z, ц)
Rsf{z)==\r(z,z'; S) l{2f)dzf.
z
Теорема 2. Предположим, что
(i) для почти всех (относительно меры ц ® Ц) пар [z, г')
функция
s^-^r{z, z'\ s)
аналитическая;
(ii) для любого компактного подмножества К czU
существует ядро Мк, удовлетворяюи^ее неравенству
Мк (2, 2') > sup I г (2, z'; s) I
и задающее ограниченный оператор в пространстве L^{Z, ц).
Тогда отображение s t—^ R^ слабо аналитическое в том смысле,
что для любых f, g S L^ (Z, \i) функция
s ^^ {Rsf, 8)
аналитична.
Доказательство. Функция
(2,2')H^r(2,2';s)f(2')g(2)
мажорируется суммируемой функцией
{z,z')^MK{z,z')\f{z')\\g{z)\i
из теоремы об ограниченной сходимости следует поэтому, что
отображение s>-^{RJ, g) непрерывно. Таким образом,
достаточно показать, что для произвольной окружности С, лежащей
в и,
(1) ^ds\\^r{z,z'; s)J(z)f(z')dzdz'=:^0.
с Z Z
Подынтегральное выражение не превосходит
Afc(2,2')|f(2')IU(2)|.
Согласно предположению, ядро Ы.с задает ограниченный
оператор в 1} (Z, ц); следовательно, интеграл
55Mc(2,zO|f(2')l|g(2)|d2'd2
Z Z

§ 2. Вещественный случай 413
сходится. По теореме Фубини, подынтегральная функция
принадлежит пространству L' (Z X Z), и поэтому тройной
интеграл (I) можно вычислять в любом порядке. Воспользовавшись
предположением (i), мы видим, что этот интеграл равен нулю.
Теорема доказана.
Следствие. В предположениях теоремы 2 отображение s н-> R^
аналитическое в сильном смысле.
Доказательство. Это частный случай теоремы 1.
Для комплексных отображений из комплексной дифференци-
руемости вытекает существование разложений в степенной ряд.
Доказательство для отображений со значениями в банаховом
пространстве такое же, как и для скалярного случая.
Вещественную аналитичность нужно определять при помощи
степенных рядов.
То обстоятельство, что в теореме 2 мы рассматривали
функции комплексной переменной, существенно. Я обязан Дж. Гам-
лену следующим контрпримером для вещественного случая.
Пусть Н = Р{1). Положим для т, пфО
J (m+rt) s
T(jn,n\S)=^ ^^5^^~'
Для любых последовательностей f, g^Р(Z) имеем
EJ (m+rt) s ,
^2^2 f{m)g{n).
m, пфй
Положим / = (...,0,1,0, ,..), g{n) = lln. Тогда {R{s)f,g) =
5—. Функция $*-^R{s) не аналитическая,
§ 2. Вещественный случай
С другой стороны, имеет место следующая теорема,
принадлежащая У. Браудеру («Аналитичность и дифференциальные
уравнения в частных ■ производных», Атег. J. Math., 84 (1962),
666-710).
Теорема 3. Пусть U — открытое подмножество
пространства t(f. Пусть
f: и-^Е
— отображение в вещественное или комплексное банахово
пространство. Пусть Hi, Яг — вещественные или комплексные бана-

414 Приложение 5. Слабая и сильная аналитичность
ховы пространства. Предположим, что задано линейное по всем
аргументам отображение
£■ X Я, X /^2 -^ R ("лы С): {и, V, w) н-^ {и, v, w),
которое индуцирует изометрическое вложение пространства Е
в банахово пространство билинейных форм Bil (Я,, Яг). Другими
словами, мы предполагаем, что для любого вектора и е £
|u| = sup{K«, v,w)\; уеЯ„ |уК1, w ^ Н^, |ауК1}.
Предположим, что для любого вектора (у, ш) е Я, X -^2 функция
Xi-^{f (х), V, w)
аналитична. Тогда отображение f вещественно аналитическое.
Доказательство. Утверждение теоремы локальное; поэтому
мы можем предположить, что U — полидиск с центром в точке
OsR'' и координатами Xj, ..., х^. Напомним тривиальный факт,
что степенной ряд
с коэффициентами ар в банаховом пространстве абсолютно
сходится в окрестности нуля тогда и только тогда, когда существуют
такие постоянные г > О, С > О, что для всех значений р
справедливо неравенство
|aJ<Cri''l.
Если это условие выполнено, степенной ряд определяет
бесконечно дифференцируемую функцию g; при этом
где pl = Pi\ ... Pal
Пусть В — единичный шар в пространстве Я, X Яг (с нормой
I (у, w) I = max (I у I, I ш |). Для любых элементов [v, w)^ В
определим линейный функционал A^_^ формулой
Я„,„(ы) = <и, v,w).
По предположению, для всех (у, на) е S функции ^v.w°f
аналитические и потому допускают разложение в степенной ряд;
следовательно, их производные удовлетворяют оценкам
|Д''(Яо/)(ОЖС(Я)г(Я)"'У
Константа С (Я) и радиус сходимости г (Я) а priori зависят от Я.
Мы покажем прежде всего, что их можно выбрать независимо
от Я. Для любой пары положительных целых чисел т, п обозна-

§ 2 Вещественный случай . 415
чим символом В„ „ подмножество таких векторов (у,, w) е В,
что для всех р справедливо неравенство
Мы утверждаем, что это множество замкнуто. Достаточно
показать, что для любого х^и отображение
X^-^D''{Xof){x)
непрерывно (фактически достаточно доказать это при х = 0).
Проведем доказательство индукцией по \р\. При \р\==0
утверждение очевидно. Предположим, что оно выполнено для
некоторого I Ро I; пусть \q\ = \po\+l. Пусть e^R" — единичный
вектор, такой, что
D\{x) = {j^)^_DP'if{x + ie).
Тогда
D^A о/) (;с) = 1 im-^^^i^^iH£+^f:z£liAluM..
Устремим Л-^О по последовательности {/г„}. Каждое из
отображений
. . , Di"{X'>l){x + hne)-D'"(Xof){x)
А I—^ ;
линейно и непрерывно, в силу предположения индукции. По
теореме о равномерной ограниченности, предел этой
последовательности— также непрерывное отображение. Таким образом,
наше утверждение доказано.
Итак, множество В представлено в виде объединения
счетного числа замкнутых подмножеств В„. „. По теореме Бэра, одно
из них содержит открытый шар пространства Н^ X -^2 (см. Ленг [1]).
Если нужно, сделаем сдвиг и будем считать, что центр этого
шара лежит в точке (О, 0). Отсюда следует, что мы можем
выбрать константы С{Х}, г{Х) независимо от величины А^,, „, когда
вектор (у, w) лежрт в маленьком шаре в Я) X -^г-
Зададим билинейное отображение Ь^: Я1Х-^2"*К (или С)
формулой
Ьр. (V, W) v-^ -^ .
Из доказанной выше равномерной оценки следует, что
отображение Ьр непрерывно, т. е.
6реВ11(Я,ХЯ2).
Кроме того, существуют константы Сиг, такие, что
I 6р I ^ Сг^р^ для всех р.

416 Приложение 5. Слабая и сильная аналитичность
Следовательно, ряд
р
сходится в окрестности нуля в R"*. Таким образом, для всех
векторов (о, ш) S Я] X -^2 и для всех точек х в достаточно малой
окрестности нуля в R** справедливо равенство
{f{x), v,w) = Jlbp{v, w)x''.
Иначе говоря, f аналитично как отображение {/-»• Ви(Я1 Х^а).
В частности, отображение f бесконечно дифференцируемо и
По предположению, Е — замкнутое подпространство пространства
BiliHi'XH^. Следовательно, Ьр^Е. Теорема доказана.
Замечание. Эта теорема используется в различных ситуациях.
Во-первых, когда Е == End Н — банахово пространство
эндоморфизмов гильбертова пространства Я, а трилинейное отображение
задается естественной формулой: {А, v, w)i—^{Av, w) для Ле
Во-вторых, в теории представлений, когда нужно доказать,
что некоторые векторы в пространстве представления —
аналитические. Обычно эти векторы удовлетворяют некоторому
эллиптическому дифференциальному уравнению, например, в слабом
смысле. В этом случае можно сначала воспользоваться
аналитическим вариантом теоремы регулярности, чтобы доказать
аналитичность функций, полученных композицией данного
отображения с линейными функционалами, а затем применить теорему 3
для доказательства того, что исходное отображение x\-^n{x)v
в гильбертово пространство —- также аналитическое.

Список литературы')
Артур (Arthur J.)
[1] Harmonic analysis of tempered distributions on semisimple Lie groups of
real rank one. Thesis, Yale Univ., 1970.
[2*] Some tempered distributions on semisimple groups of real rank one, Ann-
Math., 100 (1974), 553—584.
{3*] The Selberg trace formula for groups of f-rank one, Ann. Math., 100
(1974), 326—385.
Ахиезер H. И., Глазман И. М.
[1] Теория линейных операторов в гильбертовом пространстве, 2-е изд.,
«Наука», М., 1966.
Баргманн (Bargmann V.)
[1] Irreducible unitary representations of the Lorentz group, Ann. Math., 48
(1947), 568—640.
Березин Ф. A., Гельфанд И. М., Граев М. И., Наймарк М. А.
[1] Представления групп, УМН, 11 :6 (1956), 19—40.
Брюа (Bruhat F.)
[1] Representations des groupes localement compacts, Universite de Paris, 1969—
1970, 1971 (mimeographed).
Вейль (Weil A.)
[1] Sur certains groupes d'operateurs unitaires. Acta Math., Ill (1964), 143—
211. [Русский перевод: сб. Математика, 13! 5 (1969), 33—94.]
Венков А, Б.
[1*] Разложение по собственным функциям оператора Лапласа — Бельтрами
в классических симметрических пространствах ранга 1 и формула следа
Сельберга, Труды Матем. ин-та им. В. А. Стеклова АН СССР, 125
(1973), 6—55.
[2*] О формуле следа Сельберга для 51з(2), ДАН СССР, 228 (1976), 273—
276; Записки научных семинаров ЛОМИ, 63 (1976), 8—66.
Венков А. Б., Калинин В. Л., Фаддеев Л. Д.
[1*] Неарифметический вывод формулы следа Сельберга, Записки научных
семинаров ЛОМИ, 87 (1973), 5—42.
Виленкин Н. Я.
[1] Специальные функции и теория представлений групп, «Наука», М., 1965.
Гелбарт (Gelbart S.)
[1*] .Automorphic forms on adele groups, Ann. Math. Studies, № 83, Princeton
Univ. Press, Princeton, N. J., 1975.
') Работы, отмеченные звездочкой, добавлены при переводе.— Прим. ред.

418 Список литературы
Гельфанд И. М.
[1*] Automorphic functions and theory of representations, Proc. Int. Congr. of
Math. (Stockholm, 1962), Inst. Mittag-Leffler, Djursholm, 1963, pp. 74—
85.
Гельфанд И. M., Граев М. И., Виленкии Н. Я.
[1*] Интегральная геометрия и связанные с ней вопросы теории
представлений (Обобщенные функции, вып. 5), «Наука», М., 1962.
Гельфанд И. М., Граев М. И., Пятецкий-Шапиро И. И.
[1] Теория представлений и автоморфные функции (Обобщенные функции,
вып. 6), «Наука», М., 1966.
Гельфанд И. М., Наймарк М. А.
[1] Унитарные представления классических групп. Труды Матем. ин-та им.
В. А. Стеклова АН СССР, 36 (1950).
Гельфанд И. Л1., Пятепкий-Шапиро И. И.
[1] Теория представлений н теория автоморфных функций, УМН, 14:2 (1959),
171—194.
Гельфанд И. М., Фомин С. В.
[1] Геодезические потоки на многообразиях постоянной отрицательной
кривизны, УМН, 7: 1 (1952), 118—137.
Гиндикин с. Г., Карпелевич Ф. И.
[1*] Мера Планшереля для римановых симметрических пространств
неположительной кривизны, ДАН СССР, 145 (1962), 252—255.
Годеман (Godement R.)
[1] Analyse spectrale des fonctions modulaires, Sem. Bourbaki, exp. 278
(1964), Paris.
[2] The decomposition of L^{G1V) for Т = 8и{1), Proc. Symp. Pure Math.,
vol. 9, Amer. Math. Soc, Providence, R> I., 1966, pp. 211—224. [Русский
перевод в сб. «Арифметические группы и автоморфные функции», «Мир»,
М., 1969, стр. 127—145.]
[3] La formule des traces de Selberg, Sem. Bourbaki, exp. 244 (1962), Paris.
[4] Introduction aux travaux de A. Selberg, Sem. Bourbaki, exp. 144 (1957),
Paris.
[5] The spectral decomposition of cusp forms, Proc. Symp. Pure Math., vol. 9,
Amer. Math. Soc, Providence, R. I., 1966, pp. 225—234. [Русский перевод
в сб «Арифметические группы и автоморфные функции», «Мир», М., 1969,
стр. 146—158.]
[6] А theory of spherical functions. Trans. Amer. Math. Soc, 73 (1952), 496—
556.
[7*] Заметки no теории Жаке — Ленглендса, сб. Математика, 18:2 (1974),
28—72; 18:3 (1974), 3—45.
Дюфло, Лабесс (Duflo М., Labesse J. P.)
[1] Sur la formule des traces de Selberg, Ann. Set Ecole Norm. Sup., 4-e se-
rie, 4, f. 2 (1971), 193—284.
Жаке и Ленглендс (Jacquet Н., Langlands R. P.)
[1] Автоморфные формы на GL2, «Мир», М., 1973.
Зигель (Siegel С. L.)
[1] Some remarks on discontinous groups, Ann. Math., 46 (1945), 708—718.

Список литературы 419
Иосида (Yosida К.)
[1*] Функциональный анализ, «Мир», М., 1967.
Като (Kato Т.)
{1] Perturbation of continuous spectra by trace class operators, Proc. Japan
Acad., 33 (1957), 260—264. '^
Кнапп и Стейн (Knapp A. W., Stein E.)
tl] Intertwining operators for semisimple Lie groups, Ann. Math., 93 (1971),
489—578. [Русский перевод: сб. Математика, 18:5 (1974), 42—121.]
Кубота (Kubota Т.)
[1] Introduction to Eisenstein series, Halsted Press, New York, 1973.
Лаке и Филлипс (Lax P. D., Phillips R. S.)
[1*] Scattering theory for automorphic functions, Ann. Math. Studies, № 87,
Princeton Univ. Press, Princeton, N. J., 1976.
Лашо (Lachaud G.)
{1*] Spectral analysis of automorphic forms on rank one groups by
perturbation methods, Proc. Symp. Pure Math., vol. 26, Amer. Math. Soc,
Providence, R. I., 1973, pp. 441—450.
Ленг (Lang S.)
[1] Real Analysis, Addison Wesley, Reading, Mass., 1969.
Ленглендс (Langlands R. P.)
[1] On the functional equations satisfied by Eisenstein series (mimeographed).
[2] Eisenstein series, Proc. Symp. Pure Math., vol. 9, Amer. Math. Soc,
Providence, R. I., 1966, pp. 235—252. [Русский перевод в сб. «Арифметические
группы и автоморфные функции», «Мир», М., 1969, стр. 186—220.]
[3] Euler products. Lecture Notes, Yale University, 1967. [Русский перевод: сб.
Математика, 15: 1 (1971), 14—43.]
[4] Problems in the theory of automorphic forms. Lectures in Modern Analysis
and Applications, Lecture Notes in Math., vol. 170, Springer-Verlag,
Berlin— Heidelberg — New York, 1970, pp. 18—46. [Русский перевод: сб.
Математика, 15:2 (1971), 57—83.]
Маас (Maas Н.)
[1] Lectures on modular functions of one complex variable, Tata Inst. Lecture
Notes, Bombay, 1964.
[2] Ober eine neue Art von nichtanaiytischen automorphen Funktionen und die
Bestimmung Dirichletscher Reihen durch Funktionalgleichungen, Math. Ann.,
121 :2 (1949), 141—183.
Макдональд (McDonald I. G.)
[1] Spherical functions on a group of p-adic type, Ramanujan Inst.
Publications, Madras, 1971. [Русский перевод: УМН, 28:5 (1973), 153—224.)
Нелсон (Nelson Е.)
[1] Analytic vectors, Ann. Math., 70 (1959), 572—615. [Русский перевод: сб.
Математика, 6:3 (1962), 89—131.]
Павлов В. С, Фаддеев Л. Д.
[1*] Теория рассеяния и автоморфные функции, Записки научных семинаров
ЛОМИ, 27 (1972), 161—193.

420 Список литературы
Петерсон (Peterson Н.)
[1] Uber den Bereich absoluter Konvergenz der Poincareschen Reihen, Acta
Math., 80 (1948), 23—63.
[2] Zur analytischen Theorie der Grenzkreisgruppen, I, Math. Ann., 115 (1937)',
23—67.
Повзнер A. Я.
[1] 0 разложении произвольных функций по собственным функциям
оператора —Аи + си, Матем. сб., 32 (1953), 109—156.
Пуканский (Pukanszky L.)
[1] The Plancherel formula for the universal covering group of SL{R,2), Math.
Ann., 158 (1964), 96—143.
Рёльке (Roelcke W.)
[1] Uber die Wellengleichung bei Grenzkreisgruppen erster Art, Sitzungsbe-
richte Heidelberger Akad. Wiss., Math. — Nat. Kl., 1953—1955 (1956),
S. 159—267.
[2] .'^alytische Fortsetzung der Eisensteinreihen zu den parabolischen Spitzen
von Grenzkreisgruppen erster Art, Math. Ann., 132 (19Б6), 121—129.
[3] Das Eigenwertproblera der automorphen forraen in der hyperbolischen Ebene
I, II, Math. Ann., 187 (1966), 292—337; 168 (1967), 261—324.
Розенблюм (Rosenblura M.)
[1] Perturbation of the continuous spectrum and unitary equivalence, Pacific J.
Math., 7 (1957), 997—1010.
Рудин У.
[1*] Основы математического анализа, «Мир», М., 1976.
[2*] Функциональный анализ, «Мир», М., 1975.
Салли и Шалика (Sally Р., Shalika J.)
[1] The Fourier transform of SL2 over a non-archimedean local field (to ap«
pear).
[2] The Plancherel formula for SL(2) over a local field, Proc. Nat. Acad. Sci.
USA, 83 (1969), 661—667.
Сатаке (Satake I.)
[1] Theory of spherical functions on reductive algebraic groups over p-adic
fields, Publ. Math. I. H. E. S., 18 (1963), 1—69.
Сельберг (Selberg A.)
[1] Discontinuous groups and harmonic analysis, Proc. Int. Gongr. of Math.
(Stockholm, 1962), Inst. Mittaff-Leffler, Djursholm, 1963, pp. 177—189.
[Вольный русский перевод в сб. «Арифметические группы и автоморфные
функции», «Мир», М., 1969, стр. 71—79.]
[2] Harmonic analysis and discontinuous groups in weakly symmetric Rieman-
nian spaces with applications to Dirichlet series, /. Indiun Math. Soc, 20
(1956), 47—87. [Русский перевод: сб. Математика, l!4 (1967), 3—28.]
Серр (Serre J.-P.)
[1*] Курс арифметики, «Мир», М., 1972.
Силбергер (Silberger А.)
[1*] PGLi over the p-adics: its representations, spherical functions and
Fourier analysis, Lecture Notes in Math., vol. 166, Springer-Verlag, Berlin —
Heidelberg - New York, 1970.

Список литературы 421
CTeiiH (Stein Е.)
[1] Analysis in matrix spaces and some new representations of SL(N,C), Ann.
Math., 88 (1967), 461—490.
[2] Analytic continuation of group representations. Adv. Math., 4 (1970) 172—
207.
Такахаси (Takahashi R.)
[1] Sur les fonctions spheriques et la formule de Plancherel dans le groupe
hyperbolique, Jap. J. Math., 31 (1961), 55—90.
[2] Sur les representations unitaires des groupes de Lorentz generalises. Bull.
Soc. Math. France, 91 (1963), 289—433.
Тамагава (Tamagawa T.)
[1] On Selberg's trace formula, /. Fac. Sci. Tokyo, Sec 1, 8 (Ft. 2, 1960),
363—386.
Уоллак (Wallach N.)
[1*] Harmonic analysis on homogeneous spaces (Pure and Applied
Mathematics, vol. 19), Marcel Dekker, Inc., New York, 1973.
Уорнер (Warner G.)
[1] Harmonic analysis on semisimple Lie groups (Die Grundlehren der mathe-
matischen Wissenschaften, Bd. 188, 189), Springer-Verlag, Berlin —
Heidelberg — New York, 1972.
Фаддеев Л. Д.
[1] Разложение по собственным функциям оператора Лапласа на
фундаментальной области дискретной группы на плоскости Лобачевского, Tpi/dbiAlo-
сковск. матем. об-ва, 17 (1966), 323—350.
[2] О модели Фридрихса в теории возмущений непрерывного спектра. Труды
Матем. ин-та им. В. А. Стеклова АН СССР, 73 (1964), 292—313.
Фридрихе (Friedrichs К)
[1] On the perturbation of continuous spectra, Comm. Pure Appl. Math., 1
(1948), 361—406.
Хариш-Чандра (Harish-Chandra)
[1] Автоморфные формы на полупростых группах Ли, «Мир», М., 1972.
[2] Discrete series for semisimple Lie groups I, Acta Math., 113 (1965),
241—318.
[3] Discrete series for semisimple Lie groups П, Acta Math., 116 (1966),
1-111.
[4] Harmonic analysis on semisimple Lie groups. Bull. Amer. Math. Soc.,
76 (1970), 529—551. [Русский перевод: приложение 2 к книге [1],
стр. 204—234.]
[5] Invariant eigendistribution on а semisimple Lie algebra, Publ. Math. I.
H. E. S., 27 (1965), 1-54.
[6] Plancherel formula for 2X2 real unimodular group,/'/'oc. Nat. Acad. Sci.
USA, 4 (1952), 337—342.
[7] Splierical functions on a semisimple Lie group I, II, Amer. J. Math., 80
(1958), pp. 241—310, 553—613.
[8*] On the theory of tlie Eisenstein integral. Lecture Notes in Math., 266,
Springer-Verlag, Berlin — Heidelberg — New York, 1972, pp. 123—150.
[9*] Harmonic analysis on real reductive groups I. The theory of the constant
term, /. Fund. Anal., 19:2 (1975), 104—204.
[10*] Harmonic analysis on real reductive groups П. Wave-packets in the
Schwartz space, Inv. Math., 38 (1976), 1—56.

422 Список литературы
[11*] Harmonic analysis on real reductive groups III. The Maas—Selberg le-
lations and the Plancherel formula, Ann. Math.. 104 (1976), 117—201.
Хелгасон (Helgason S.)
{1] Analysis on Lie groups and homogeneous spaces, Regional conference
series, № 14, Amer. Math. Soc, Providence, R. I., 1972.
(2] Дифференциальная геометрия и симметрические пространства, «Мир», М.,
1964.
fS] А duality for symmetric spaces with applications to group representations.
Adv. Math., 4 (1970), 1—154.
Хелгасон и Джонсон (Helgason S., Johnson K)
*1] The bounded spherical functions on symmetric spaces. Adv. Math., 3, № 4
(1969), 586—593.
Шалика (Shalika J.)
[1] Representations of the 2X2 unimodular group over local fields (to
appear).
Шалика и Танака (Shalika J., Tanaka S.)
[1] On an explicit construction of a certain class of automorphic forms, Amer.
J. Math, 91 (1969), 1049—1076.
Шимура (Shimura G.)
[1] Введение в арифметическую теорию автоморфных функций, «Мир», М.,
1973.
Эльстродт (Elstrodt J.)
[1] Die Resolvente zum Eigenwertproblem der automorphen Formen in der hy-
perbolischen Ebene I, Math. Ann., 203 (1973), 295—330; II, Math. Zeitschr.,
132 (1973), 99—134.
Замечание. Приведенный список литературы не претендует на полноту.
Хорошая подробная библиография имеется в книгах Н. Я. Виленкина
(работы, опубликованные до 1964 г.) и Уорнера."

Часто используемые обозначения
стр. 16 ф*'ф(л;) = ^ф(л;г/-')'ф(г/)йг/.
а
стр. 16 f~W=f (л;"') или/(—л;) (в зависимости от контекста),
стр. 18 п' (ф) ц = \ ф (л;) л (х) v dx.
стр. 19 ф*(л;) = ф(л;-').
стр. 33 Sn т — пространство функций f на 5^2 (R). таких,
что f (г (6) у г (60) = e-'"9f {у) е-'«9'.
(cos 6 sin 6 \
■а о •
— sin 6 COS 6/
стр. 37 Н„ — весовое подпространство, состоящее из
векторов и е Я, таких, что 1т;(г (6))и^е'«9и.
"Р-55 «((о а-0)="'-
стр. 60 р{а)=а{а)'', р(д;) = р(а), если х = anfe —
разложение Ивасавы.
стр. 60 Us (а/г) = р (a)^
стр. 60 Н (s) — пространство измеримых функций / на G,
таких, что
(i) сужение f на/С принадлежит пространству L^ (/С);
(ii) f {any) = р (а)*"*"' f (у) для любых а^А, n^N,
y^G.
lis ~ естественное представление группы G в
пространстве Н {s).

424 Часто используемые обозначения
стр. 61 ф5 (л;) = \ р(^л;)*''"' dx — сферическая функция; пр.п
к.
обсуждении рядов Фурье ф„(9) = е''»*.
стр. 63 Сд(0, /Q — пространство непрерывных функции
с компактным носителем, инвариантных
относительно сопряжения на элементы k е К.
стр. 64 Сс {ОЦЮ — пространство непрерывных функций
с компактным носителем, двусторонне
инвариантных относительно К-
стр. 80 D(a)==p(a) —р(а-').
стр. 81 ®=(_1 oj'
стр. 81 Преобразование Хариш-Чандры
Hf(a) = p(a)^f(art)drt = D(a) J !{x-^ax)di.
N A\Q
стр. 81 A'^ = {a^ A; p (a) > 1}.
стр. 86 Преобразование Меллина
Mg (s) = J g (a) p {of da.
A
стр. 90 Сферическое преобразование
Sf(s) = MHf(s) = 5f(;c)(p,Wdx
стр.
стр.
стр.
стр.
100
101
105
114
expZ = 2.i^"-
п-О
8jr/(y) = ^f(|/exp(/J))[_^.
йя(Z) и = -j^ я(ехрtX)v\
^Н\ -■)■ -=(J :'■)•
[£+, £_] = -4/Г, [Г, £±] = ±2/£±.

Часто используемые обозначения 425
стр. 114 adX-Y = [X, Y].
стр. 116 1Г = ф я„, я-= ф Я„.
n=0(mod2) nMil(mod2)
стр. 117 МуХ = уХу-\
стр. 145 ^к W = J а|з (^~'xfe) dk.
к
стр. 146 G' —множество регулярных элементов в G, т. е.
множество матриц с различными собственными
значениями.
стр. 162 Я(^i, е) или H{s, е) — подпространство Н {s),
соответствующее характеру е группы М^{±1}.
стр. 163 Н"''^ ф Я„, Я'-'">= ф Я„.
п>/п п<1—т
n=m (mod 2) n=m (mod й
стр. 202 ^ (g) — универсальная обертывающая алгебра
алгебры Ли д.
стр. 203 Х{-) — централизатор.
стр. 237 ''L^(r\G)— пространство параболических форм,
состоящее из всех функций f, таких, что
J f(rtg)drt = 0
г^\лг
для всех g S G и для всех вершинных подгрупп N
(относительно Г).
стр. 251 Z (ф, у; 2s) = J ф {ay) р (а)~^* da.
А
стр. 252 Е{ф, у; s)= Ц 2(ф, уу; 2s) = TZ{(f, у; 2s).
гл\г

УКАЗАТЕЛЬ
Алгебра Ли 100
Аналитическое отображение 109
Аналитичность 409
Асимптотическое разложение 97
Вектор аналитический 110
— бесконечно
дифференцируемый 104
— весовой 116
— инвариантный 39, 61
— /(-конечный 40
— младшего веса 116
— порождающий 74
— старшего веса Пб
Верхняя полуплоскость 55
Вершина 230
Вершинная подгруппа 227
— часть резольвенты 299, 303
Вложение 24
Группа Вейля 81
Дзета-преобразование 251, 256
Изоморфизм 24
Й-изоморфизм 118
Инвариантная мера 51
Интегральные формулы 79, 148
Компактные группы 40
Кратность 25
Лемма Шура 363
Линейное подмножество 22
плотное 22
Матрица Вейля 81
Матричные элеменгы представления
43, 61
Мероморфиое семейство операторов
384
Морфизм 24
Область Зягеля 243
Образуюш,ие и соотношения 218
Однородные пространства 51
Оператор Гильберта — Шмидта 140,
170
— замкнутый 369
— Казимира 204
— компактный 25, 240,
— Лапласа 278
— ограниченный 356
— самосопряженный 370
в существенном 372
— симметричный 370
— сопряженный 369
— сплетающий 24
— частично изометрический 159
— эллиптический 398
— ядерный 141, 171
Ортогональное разложение 25
Основная априорная оценка 399
Параболическая форма 236
Подгруппа однопараметрическая 101
— унимодулярная 16
— унипотентная 227
Поднятие веса т 198
Подпространство 22
— весовое 116
— инвариантное 22
Полиномиальный рост 235
Полярное разложение 169
Последовательность Дирака 20
Представление 15
— Вейля 220
— вполне приводимое 25
— допустимое 40, 117
— индуцированное 58
— неприводимое 24
— ограниченное 15
~ присоединенное 114, 117, 150
— производное 106
— регулярное 41
— строго допустимое 40, 142
— унитарное 15
Представления группы SLi{R)
дискретной серии 119, 133, 136
— дополнительной серии 135, 136
— ложнодискретные 133, 136
— основной серии 61, 136

Указатель
427
Преобразование Меллина 63, 86, 256
— сферическое 90
— Хариш-Чандры на А 63, 81,
161, 166, 180
К 167, 179
Проекторы 366
Производная Ли 101
Пространство Гординга 104
— Пэлн — Винера 87
— H(s) 60
33
259
Разложение Брюа 219,
— Ивасавы 53
— Картана 152
Разрешающая форма 280
Распределения 388, 392, 407
Расширение операторов 370
Регулярный элемент группы 146
Резольвента оператора Лапласа
Резольвентное уравнение 372
282
Симметричность оператора Лапласа
288
Слабая аналитичность 407
— топология 15
След 30, 141
Следы представлений дискретной
серии 165, 166
индуцированных 62, 161
Собственные функции оператора
Казимира 209
— Лапласа 318
Спектральная мера 377
— теорема для компактных
операторов 25
— — — неограниченных
операторов 378
ограниченных
операторов 361
Спектральное семейство 366
Теорема регулярности 404,
Тип оператора 301
— функции 252
Тэта-преобразование 248
406, 408
Уиттекера уравнение 295
Универсальная обертывающая
алгебра 202
Унитарнзация 120
Формула Планшереля 32, 187
Фундаментальная область 231
Функции Грина 293
Функция быстро убывающая 257
— двусторонне инвариантная 64
— положительно определенная
75
— сферическая 61, 68, 212
Характеры 33, 60
Централизатор 203
Эйзенштейна оператор 342
— преобразование 349
— ряд 252
— функциональное
254, 314
Эквивалентность 24
— иифинитезимальная
уравнение
118

Оглавление
Предисловие редактора перевода 5
Предисловие автора 7
Обозначения 13
I. Общие результаты 15
§ L Представления алгебры Сс (G) , 15
§ 2. Критерий полной приводимости 24'
§ 3. Квадратично интегрируемые ядра и операторы Гильберта —
Шмидта 28
§ 4 Меры Планшереля 30
II. Компактные группы 33
§ 1. Сужение представлений группы SLj (R) на ее максимальную
кбмйаетаую подгруппу 33
§ 2. Общая теория представлений компактных групп 40
ill. Индуцированные представления 51
§ 1. Интегрирование на однородных пространствах 51
§ 2. Индуцированные представления 57
§ 3. Ассоциированные сферические функции 60
§ 4. Ядро, задающее индуцированное представление 62
IV. Сферические функции 64
§ 1. Двусторонне инвариантные функции на группе 64
§ 2. Неприводимость • 67
§ 3. Определение сферических функций 68
§ 4. Связь с унитарными представлениями 74
§ 5. Положительно определенные функции 75
V Сферическое преобразованиэ 79
§ 1. Интегральные формулы 79
§ 2. Преобразование Харнш-Чандры У 81
§ 3. Преобразование Меллнна 86
§ 4. Сферическое преобразование 90
§ 5. Явные формулы н асимптотические разложения 94
VI. Производное представление алгебры Ли 100
I 1. Производное представление 100
I 2. Сужение производного Представления иа алгебру Ли
подгруппы ^ ..... . ........... 112

Оглавление 429
§ 3. Унитаризация представлений • 120
§ 4. Произв^иые Ли на группе G 126
§ 5. Неприводимые компоиеиты индуцированных представлений . . .129
§ 6. Классификация всех неприводимых унитарных представлений 134
§ 7. Разделйние представлений при помощи их характеров 137
VII. Следы ,140
§ 1. Ядерные операторы 140
§ 2. Интегральные формулы 148
§ 3. Следы индуцированных представлений 160
I 4. Следы представлений дискретной серии 163
§ 3. Связь между преобразованиями Хариш-Чаидры на
подгруппах А а К • . . .166
Приложение. Общие сведения о следах операторов в гильбертовом
пространстве 169
Viil. Формула Планшерелл 176
S 1. Аналитическая лемма 177
I 2. Скачки преобразования Хариш-Чандры 179
I 3. Некоторые леммы 182
§ 4. Формула Плаишерели 185
IX. Представления дискретной серии 190
§ 1. Вложение представлений дискретиой серии в Z,^ (G) 190
§ 2. Представления на верхней полуплоскости 192
§ 3. Реализация представлений в единичном круге 196
§ 4. Поднятие веса т 198
§ 5. Голоморфность 200
X. Дифференциальные операторы . 201
§ 1. Универсальная обертывающая алгебра 201
§ 2. Аналитические векторы 208
§ 3. Собственные функции кольца ЗС (t) 209
XI. Представление Вейля 214
§ \, Преобразование Фурье и свертки 214
§ 2. Образующие и соотношения для группы SL^ 2l7
§ 3. Представление Вейля 220
XII. Представление в пространстве '>L'^(T\G) . . 227
§ 1. Вершины и вершинные подгруппы . . . 227
§ 2. Параболические формы 235
§ 3. Признак компактности операторов 240
§4. Полная приводимость пространства "i^ (Г\0) 242
Xlli. Непрерывный спектр в пространстве L^(r\G) 247
§ 1. Одно соотношение ортогональности 247
§ 2. Ряды Эйзештейна 251
§ 3. Аналитическое продолжение и функциональное уравнение . . , . 253
§ 4. Дзета-преобразование и преобрадовйВИе Меллина 2б6
§ б. Некоторые теоретико-групповые леммы 259

430 Оглавление
§ 6. Выражение для функции Г°Гф 260
§ 7. Аналитическое продолжение дзета-преобразования функции
ГТф V. . . .262
§ 8. Теорема разложения 267
XiV. Спектральное разложение оператора Лапласа на Г\ф .... 271
§ 1. Геометрия и дифференциальные операторы на § 274
§ 2. Решение уравнения /ф = 5(1—5)ф 279
§ 3. Резольвента оператора Лапласа на © при а>1 282
§ 4. Симметричность оператора Лапласа на Г\§ 286
§ 5. Оператор Лапласа на Г\§ 290
§ 6. Функции Грина и уравнение Уиттекера 292
§ 7. Разложение резольвенты на Г\§ при а>3/2 299
s(\ — s)
§ 8. Уравнение — i|)" (у) = —^—^—- i|) (у) на промежутке [а. оо) 313
У
§ 9. Собственные функции оператора Лапласа в пространстве
ЛЧГ\&) = Я 318
§ 10. Резольвентное уравнение в полосе 0<а<2 324
§ И. Ядро резольвенты в полосе 0<а<2 332
§ 12. Оператор Эйзенштейна и функции Эйзенштейна 341
§ 13. Непрерывный спектр оператора Лапласа 349
§ 14. Случай нескольких вершин 352
Приложение 1. Ограниченные эрмитовы операторы и лемма
Шура 356
§ 1. Непрерывные функции от операторов 356
§ 2. Проекторнозначные функции от операторов 364
Приложение 2. Неограниченные операторы 369
§ 1. Самосопряженные операторы 369
§ 2. Спектральная мера 377
§ 3. Формула обращения для резольвенты 379
Приложение 3. Мероморфные семейства операторов 382
§ 1. Компактные операторы 382
§ 2. Ограниченные операторы 386
Приложение 4. Эллиптические уравнения в частных производных 388
§ 1. Пространства Соболева 388
§ 2. Априорные оценки 394
§ 3. Априорные оценки для эллиптических операторов 398
§ 4. Теоремы вложения для пространств Н^ и теорема регулярности
для эллиптических уравнений иа торе 402
§ 5. Теорема регулярности в евклидовом пространстве 405
Приложение 5. Слабая и сильная аналитичность 409
§ 1. Комплексный случай 409
§ 2. Вещественный случай 413
Список литературы • 417
Часто используемые обозначения 423
Указатель' 426

Уважаемый читатель!
Ваши замечания о содержании книги, ее
оформлении, качестве перевода и другие просим присылать по
адресу:129820. Москва. И-110, ГСП, 1-й Рижский пер.,
д. 2. издательство «Мир».