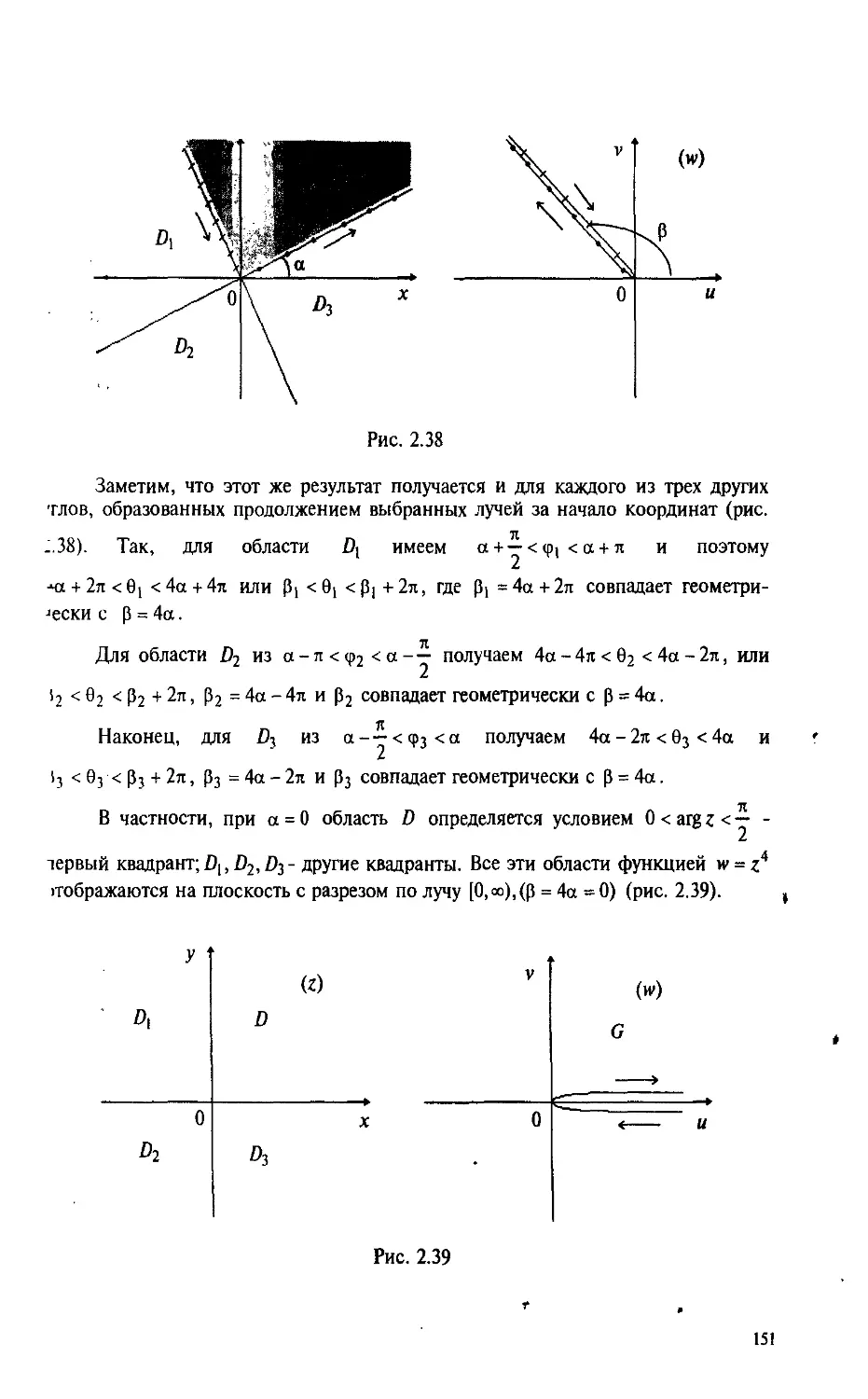
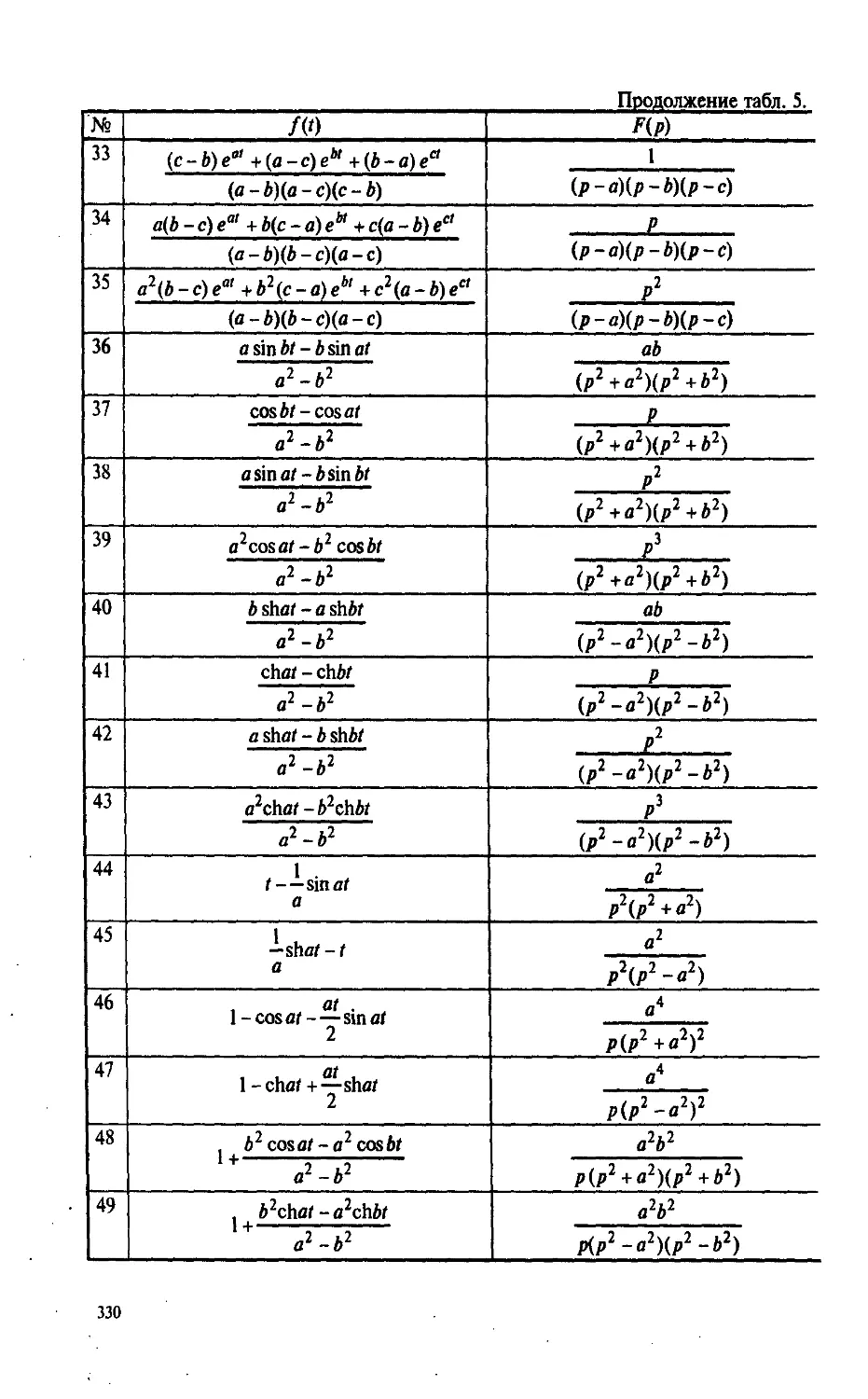
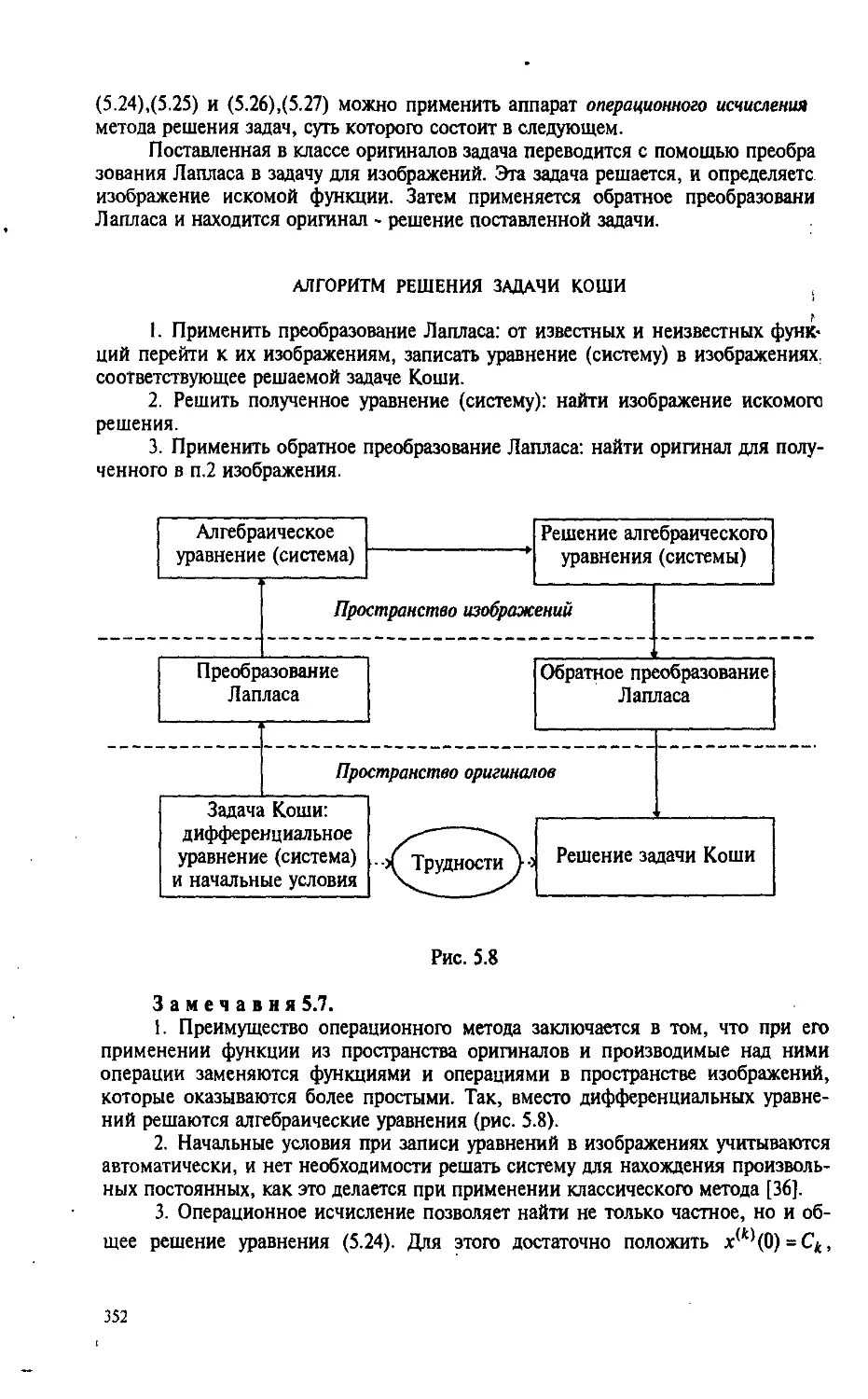
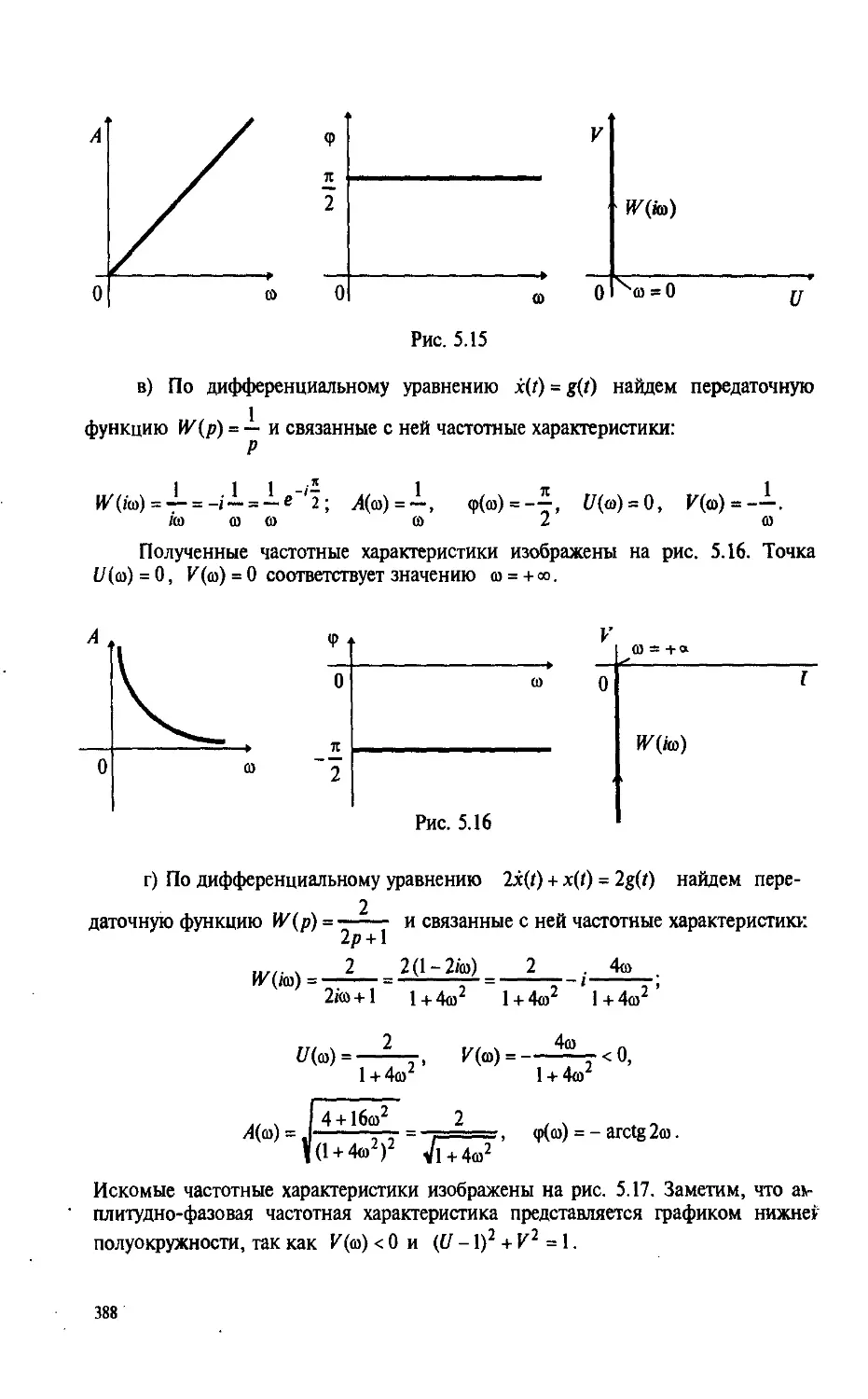
Автор: Пантелеев А.В. Якимова А.С.
Теги: анализ математический анализ функциональный анализ физика математика математическая физика компьютерные науки издательство высшая школа
ISBN: 5-06-004135-2
Год: 2001
ПРИКЛАДНАЯ МАТЕМАТИКА
для ВТУЗов
А.В. Пантелеев А.С. Якимова
Теория функций
комплексного переменного
и операционное исчисление
в примерах и задачах
Рекомендовано Учебно-методическим объединением
высших учебных заведений Российской Федерации
по образованию в области авиации, ракетостроения
и космоса в качестве учебного пособия для студентов
высших технических учебных заведений
Москва
'Высшая школа"
2001
Рецензенты:
доктор физ.-мат. иаук, профессор А.Ю. Аржененко,
заслуженный деятель науки РФ, доктор физ.-мат. неук,
профессор В.Ф. Формалев
Пантелеев А.В., Якимова А.С.
П 16 Теория функций комплексного переменного и операциош
исчисление в примерах и задачах: Учебное пособие. — М.: Вые
шк., 2001. — 445 с: ил.
ISBN 5-06-004135-2
Пособие охватывает классические разделы теории функций комплексного i
ременного: дифференцирование, интегрирование, разложение в функциоиальи.
ряды, анализ особых точек и вычисление вычетов. Рассмотрено применение прес
разования Лапласа и z-преобразования для решения линейных дифференциальш
и разностных уравнений. Особое внимание уделено специфике решения задач ан
лиза выходных процессов и устойчивости линейных одномерных и многомернь
непрерывных и дискретных динамических систем, исследуемых в теории управл
ния.
По казкдому разделу кратко изложены основные теоретические сведения, npi
ведены решения типовых примеров, даны упражнения и задачи для самостоятель
ной работы с ответами.
Для студентов высших технических учебных заведений.
«Издательство «Е
УДК 517.3
ББК 22.161.6
ISBN 5-06-004135-.. «Издательство «Высшая школа», 2001
Орнгинап-макет данного издания является собственностью издательства «Высшая
школа», и его репродуцирование (воспроизведение) любым способом без согласия
издательства запрещается.
ОГЛАВЛЕНИЕ
Предисловие 5
Введение 6
Глава 1. Комплексные числа 10
1.1. Формы задания комплексных чисел 10
1.1.1. Комплексные числа в алгебраической форме 10
1.1.2. Комплексные числа в тригонометрической
и показательной формах 16
1.2. Множества на комплексной плоскости 31
1.2.1. Основные определения 31
1.2.2. Кривые на комплексной плоскости 32
1.2.3. Области 38
1.3. Числовые последовательности и ряды с комплексными членами 45
1.3.1. Последовательности комплексных чисел 45
1.3.2. Анализ сходимости рядов с комплексными членами 48
Задачи для самостоятельного решения 55
X. Функции комплексного переменного 57
2.1. Дифференцирование функций комплексного переменного 57
2.1.1. Основные определения 57
2.1.2. Элементарные функции комплексного переменного 71
2.1.3. Свойства дифференцируемых функций 88
2.1.4. Аналитические функции 100
2.1.5. Простейшие отображения 120
2.2. Интегрирование функций комплексного переменного 158
2.2.1. Основные определения 158
2.2.2. Вычисление интегралов 162
2.2.3. Основные теоремы интегрального исчисления 169
2.2.4. Вычисление интегралов по замкнутому контуру
от функций комплексного переменного 173
Задачи для самостоятельного решения 179
. Функциональные рады в комплексной области 181
1 3.1. Анализ сходимости функциональных последовательностей
и радов 181
'* 3.1.1. Основные определения 181
3.1.2. Нахождение области сходимости рядов. Исследование рядов
на равномерную сходимость 183
3.1.3. Степенные ряды 187
3.1.4. Ряды по целым степеням 194
3.2. Разложение функций в ряды 198
• 3.2.1. Разложение функций в степенные ряды. Ряд Тейлора 198
• 3.2.2. Нули аналитических функций. 214
3.2.3. Разложение функций в ряды по целым степеням.
Ряд Лорана 218
Задачи для самостоятельного решения 232
Глава 4. Особые точки функций комплексного переменного. Вычеты 234
4.1. Изолированные особые точки функций 234
4.1.1. Классификация особых точек 234
4.1.2. Ряд Лорана в окрестности особой точки 241
4.1.3. Правила определения порядка полюса 247
4.1.4. Определение типа особых точек для суммы, разности,
произведения и частного функций 257
4.2. Вычеты и их применение 263
4.2.1. Определение вычета 263
4.2.2. Вычисление вычетов в полюсе и устранимой
особой точке 270
4.2.3. Вычисление контурных интегралов с помощью вычетов 277
4.2.4. Применение вычетов к вычислению интегралов
от функций действительной переменной 286
4.2.5. Применение вычетов к исследованию расположения
нулей многочлена на комплексной плоскости 302
Задачи для самостоятельного решения 314
Глава 5. Операционное исчисление 316
5.1. Преобразование Лапласа 316
5.1.1. Основные определения _ 316
5.1.2. Свойства преобразования Лапласа 319
5.1.3. Нахождение изображения по оригиналу 328
5.1.4. Нахождение оригинала по изображению 339
5.2. Области применения преобразования Лапласа 351
5.2.1. Решение линейных обыкновенных дифференциальных
уравнений с постоянными коэффициентами 351
5.2.2. Анализ выходных процессов линейных непрерывных
стационарных динамических систем 371
5.2.3. Анализ устойчивости линейных непрерывных стационарных
динамических систем 383
5.3. Z -преобразование 396
5.3.1. Основные определения 396
5.3.2. Свойства Z -преобразования 398
5.3.3. Нахождение изображения по оригиналу 399
5.3.4. Нахождение оригинала по изображению 400
5.4. Области применения Z-преобразования 406
5.4.1. Решение линейных разностных уравнений с постоянными
коэффициентами 406
5.4.2. Анализ выходных процессов линейных дискретных
стационарных динамических систем 415
5.4.3. Анализ устойчивости линейных дискретных стационарных
динамических систем 427
Задачи для самостоятельного решения 436
Ответы и указания 438
Литература 443
ПРЕДИСЛОВИЕ
Факт сам по себе - ничто. Он приоб-
приобретает ценность только в том случае,
когда он подкрепляет какую-то идею
или подтверждает доказательство.
К. Бернар
Книга представляет собой учебное пособие по курсам "Теория функций
Комплексного переменного", "Специальные главы высшей математики". Пред-
молпгается, что читатель владеет основными понятиями математического анализа
и линейной алгебры.
Книга состоит из пяти глав, которые охватывают основные разделы курсов
пгкций, читаемых авторами на факультетах Московского государственного авиа-
авиационного института.
Первая глава посвящена описанию трех эквивалентных форм задания
комплексных чисел, заданию множеств на комплексной плоскости, анализу схо-
йимоети последовательностей и радов с комплексными членами.
Вторая глава содержит описание функций комплексного переменного и
шишшых операций над ними: дифференцирования и интегрирования.
В третьей главе рассматриваются вопросы сходимости функциональных
Последовательностей и разложения функций комплексного переменного в ряды.
Четвертая глава содержит алгоритмы исследования особых точек функций
Комплексного переменного и нахождения вычетов, используемых для вычисле-
вычислении интегралов.
Пятая глава посвящена основам операционного исчисления и его приме-
применению к решению обыкновенных дифференциальных и разностных уравнений
у постоянными коэффициентами. Особое внимание уделено применению опера-
операционного исчисления для решения основных задач анализа линейных непрерыв-.
Них и дискретных стационарных динамических систем: анализа выходных про-
unrnn и устойчивости.
Описанные методы решения задач используются в ряде смежных дисцип-
дисциплин, тпких как теория управления и теория устойчивости [4,8,9,16-18,22-24,
.11, И,М>,51,54], дифференциальные уравнения, гидромеханика [26] и др.
Книга входит в серию "Прикладная математика в примерах и задачах".
Они может быть использована для самостоятельного изучения предмета, так как
весь необходимый теоретический материал и большое количество де-
разобранных примеров.
Апторы выражают глубокую признательность редактору серии Е.В. Лисовец
И постоянную поддержку, внимание и терпение, а также М.Ф. Татаринцевой,
И J1.. Калинину, Л.Л. Улашенко, Е.О. Пранц, Т.Ю. Жудиной, Д. В. Копошко
М содействие, оказанное при подготовке оригинала-макета.
ВВЕДЕНИЕ
Известно, что не на любом числовом множестве выполнима любая алгеб-
раическая операция. Так, на множестве Z (целые числа) не выполнима операция
деления (например, —tZ). Но множество Z является частью множества Q-
множества рациональных чисел, т.е. Z с Q, и на множестве Q операция деле-
деления выполнима. Однако на нем не выполнима операция извлечения корня, на-
например, на множестве Q не имеет решения уравнение х2 - 2 = О . Множество Q
является подмножеством множества R - множества действительных чисел. Но на
множестве R операция извлечения корня также не выполнима, например, не
имеют решений уравнения х2 + 2 = О и х2+1 = 0. Множество комплексных чисел
вводится как расширение множества R таким образом, чтобы на нем эта опера-
операция была выполнима, т.е. чтобы было определено число, квадрат которого равен
-1, и, следовательно, существовало решение простого уравнения х2 +1 = 0.
С другой стороны, множество комплексных чисел можно ввести из геомет-
геометрических соображений. А именно действительные числа интерпретируются точ-
точками числовой прямой: каждому числу х е R соответствует точка на оси, а каж-
каждой точке - действительное число. Если рассмотреть эту задачу на плоскости
хОу , то точке М, принадлежащей оси Ох, соответствует пара (х,0). В общем
случае любой точке плоскости соответствует пара (х,у) действительных чисел, а
множество таких пар можно рассматривать как расширение множества пар (х,0).
Если в таком множестве ввести алгебраические действия, так чтобы в частном
случае, т.е. для (х,0), они совпадали с операциями в R, а в общем случае позво-
позволяли выполнить операцию извлечения корня (в том числе извлечения корня чет-
четной степени из отрицательного числа), то множество - искомое.
Итак, рассмотрим множество упорядоченных пар (х,у) действительных
чисел. Элемент множества обозначим z = (х,у). Пары, образующие множество, -
упорядоченные, т.е., например, пара B,1) не совпадает с парой A,2).
Два элемента назовем равными, если у них равны соответствующие компо-
компоненты, т.е. для Z\ =(*i,.Vi) и ц =(х2,У2) равенство Z\ =Zi выполняется тогда и
только тогда, когда xj = xi, у\ = уг-
Суммой элементов Z\=(xx,y\) и Zi={xi,yi) назовем элемент z = (x,y)
такой, что х = Xj + х2, у = у\ + у^, а операцию сложения обозначим z = Z\ + г2 •
Произведением элементов Z\=(x\,y\) и 1г=(хъУг) назовем элемент
Z = (х, у) fакой, что х = х(х2 - у(у2. У = ЩУг + У\хг. а операцию умножения обо-
обозначим Z = Z\ -Zi-
Можно убедиться, что введенные таким образом операции сложения и ум-
умножения удовлетворяют свойствам этих операций, известным на множестве R.
Например, ^1+^2=^2+^1, Z\ ■ Zi = г2 • Z| - переместительные законы сложения
и умножения и др. Поэтому можно считать, что знаки, принятые в обозначениях
суммы и произведения, - обычные знаки сложения и умножения.
Рассмотрим произведение г, =@,1) на гг = @,1) - Результатом умножения
Оудет число z = (x,y), где х = -\,у = 0, т.е. г = (-1,0) или @,1) - СОД) = — 1. Следо-
нительно, элемент @,1) построенного множества есть тот элемент, квадрат кото-
которого равен -1. Этот элемент обозначается буквой /, т.е. i = @,1) и /2 = -1.
Таким образом, решены обе поставленные задачи:
- множество R является подмножеством построенного;
- в построенном множестве есть элемент, квадрат которого равен -1.
Это множество называется множеством комплексных чисел и обозна-
чкется С. Элементы z множества называются комплексными числами: zsC.
Для удобства выполнения операций вводится алгебраическая форма записи
комплексного числа следующим образом. В результате умножения чисел i = @,1)
и .V ■ @, у) получаем i ■ у = @, у), а сумма чисел х = (х,0) и iy = @, у) дает
IE t ly = (х, у). Поэтому любое комплексное число можно записать в виде
С • л f iy.
На множестве С вводятся понятия функции, предела таким образом, что
Ооотпетствуюшие понятия действительного анализа рассматриваются как част-
частный случай. Естественно, при этом сохраняются известные свойства функций
действительного переменного: теоремы о пределах, правила дифференцирования,
формулы интегрирования и т.д. Однако, благодаря расширению класса функций,
чинным случаем которых являются функции действительного переменного, по-
кшжются новые свойства. Например, доказывается, что из существования произ-
производной функции следует существование ее производных я-го порядка в области.
Усмжавливается, что все элементарные функции связаны между собой: тригоно-
мпрические функции выражаются через показательную функцию, а обратные
Пнионометрические - через логарифмическую. Значительно глубже, чем в анали-
« функций действительного переменного, развита геометрическая теория - кон-
конформные отображения. Благодаря сочетанию аналитических и геометрических
мг и шоп теория функций комплексного переменного находит широкое примене-
применение и других разделах математики и прикладных задачах.
Одним из важных приложений теории функций комплексного переменного
иилнется операционное исчисление, рассмотренное в гл. 5. Описано его приме-
МРние для решения обыкновенных линейных дифференциальных и разностных
уриинений с постоянными коэффициентами. Они могут быть решены с помо-
1Ш.и> классических методов [9,36], но применение операционного исчисления по-
'Шолист упростить процедуру решения за счет перехода к решению более простых
йЛ1?браических уравнений.
Примером рассматриваемых математических моделей может служить диф-
дифференциальное уравнение первого порядка [36,45]
RC^ + uc=g(t), 1^.@) = 0, (В.1)
at
описывающее изменение напряжения на емкости С в схеме, изображенной
ни рис. В.1,а. Здесь R - сопротивление, g(t)- закон изменения входного напря-
жгния; t- время, / = 0 - момент подачи входного напряжения на схему, ис@) -
Мочильное напряжение на емкости (предполагается, что она не заряжена). Реше-
Решением уравнения является функция uc(t) , которая при подстановке обращает его
и тождество.
git)
с -L- uc(t) sit)
с -==. "с С)
Рис. B.I
Другим примером может быть система обыкновенных дифференциальных
уравнений первого порядка [36,45]:
^L = _l,_ifL+iW ;(O) = o
dt L L L '
-2t = —, и @) = 0,
Л С
(В.2)
описывающая изменение тока и напряжения на емкости С в схеме, изображен-
изображенной на рис. В. 1,6. Здесь R - сопротивление, L - индуктивность, git)- закон
изменения входного напряжения, t - время, t = 0 - момент подачи входного
напряжения на схему, /@)- начальный ток, ыс@) - начальное напряжение на
емкости. Решением системы являются функции i(t), uc(t).
В теории автоматического регулирования и управления используется поня-
понятие непрерывной одномерной динамической системы, описываемой одним диф-
дифференциальным уравнением я-го порядка, характеризующим поведение выход-
выходного сигнала x(t) в зависимости от изменения входного сигнала и заданных на-
начальных условий (рис. В.2). Так, в уравнении (В.1) входным сигналом может
считаться входное напряжение g(t), а выходным сигналом - напряжение на ем-
емкости, т.е. x(t) = uc(t).
1
—
\ ► t
Вход
Начальные условия
Непрерывная
динамическая
система
у
-\ ►
Выход
Рис. В.2
Наряду с одномерными динамическими системами в теории управления
также изучаются непрерывные многомерные динамические системы, которые
описываются системами обыкновенных дифференциальных уравнений и имеют
суммарное число входных и выходных сигналов больше двух. Система уравнений
(В.2) может трактоваться как модель многомерной динамической системы с од-
одним входом g(t)- входным напряжением и двумя выходами i(t),uc(t), состав-
составляющими вектор х@ = (i(t),uc(t))T. Поэтому в гл. 5 вместе с проблемой решения
дифференциальных уравнений рассматривается весьма близкая к ней проблема
анализа непрерывных динамических систем.
Одновременно с описанными выше задачами рассмотрено применение
операционного исчисления к решению разностных уравнений. Примером разно-
разностного уравнения может служить уравнение
х(к + I) = A + а) х(к) + g(k), к = 0,1,2
(В.З)
описывающее состояние х(к) балансового счета в банке в начале каждого к -го
месяца. Здесь а - месячная процентная ставка, х0 - начальный капитал, к -
дискретное время, g(k) - сумма взносов и изъятых денег в течение к -го месяца.
Предполагаем, что величина капитала вычисляется ежемесячно на основании ба-
линса на начало месяца. В результате получаем последовательность х(к),к =0,1,...
В теории управления вместе с непрерывными одномерными и многомер-
многомерными динамическими системами изучаются одномерные и многомерные дис-
дискретные динамические системы. Они функционируют в дискретном времени, а
входной и выходной сигналы представляются последовательностями (рис. В.З).
Начальные условия
Вход
I
Дискретная
динамическая
система
-»- к
Выход
Рис. В.З
Дискретная динамическая система преобразует входной сигнал в выходной
при заданных начальных условиях. В уравнении (В.З) входным сигналом можно
считать g(k)- сумму взносов и изъятых денег в течение к -го месяца, а выход-
выходным х(к) - состояние балансового счета. Поэтому наряду с проблемой решения
ри шостных уравнений в пособии изучается близкая проблема анализа дискрет-
дискретных динамических систем. Последняя является более общей, имеет свою специ-
специфику и встречается во многих практических приложениях.
Глава 1. КОМПЛЕКСНЫЕ ЧИСЛА
1.1. ФОРМЫ ЗАДАНИЯ КОМПЛЕКСНЫХ ЧИСЕЛ
1.1.1. Комплексные числа в алгебраической форме
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
1. Комплексным числом называется выражение вида
х + iy,
где х, у - действительные числа (х s R, yeR); i - число, квадрат которого равен
минус единице \i2 = -Ij; число обозначается z = х + iy.
Числа х к у при этом называются соответственно действительной и мни-
мнимой частью комплексного числа и обозначаются jc = Re г, у = Im г; ' - мнимая
единица.
Выражение z = x + iy называется алгебраической формой записи комплекс-
комплексного числа; знаки между составляющими числа - обычные знаки операций сло-
сложения и умножения, которые обладают теми же свойствами, что и в действи-
действительной области.
Множество комплексных чисел обозначается С, a z e С - элемент мно-
множества.
Из определения следует, что действительные числа можно рассматривать
как частный случай комплексных, т.е. R с С, а именно при у = 0 получаем
Z = х - действительное число.
Число i = iy называется чисто мнимым.
Пример 1.1. Записать действительную и мнимую части чисел:
г, = 3 - 2/, zi = 5, zi = -3/, Zt, = 1 + /' •
□ Re^i =3, Inui =-2; Re^2 =5, 1тг2 =0; Re?3 =0,1тгз =-3;
Re^4 =1, lm4 =1. ■
2. Комплексные числа называются равными, если у них соответственно
равны действительные и мнимые части:
Re г, =Rez2, ,. п
3. Комплексные числа называются сопряженными, если у них равны дейст-
действительные чисти, и мнимые противоположны по знаку. Число, сопряженное чис-
числу 1-х + 1у, оботачпется z = x-iy. Определение сопряженных чисел можно
мписйть и пиле рпненств:
A.2)
1A
Из определения, в частности, следует, что число, сопряженное действи-
действительному числу, совпадает с ним: 3c = jc, xeR.
ра 1.1.
Пример 1.2. Записать числа, сопряженные комплексным числам из приме-
приме□ Используя A.2), получаем: ^=3-2», Zi=3 + 2i;
= -3/, г3 = 3/; ц = -1 + /, г4 = -1 - / .■
^=5, ?2=5;
4. Из определения комплексного числа как упорядоченной пары действи-
действительных чисел (см. введение) получаем, что задание комплексного числа z мож-
можно рассматривать как задание точки на плоскости, абсциссой которой является
х •• Re z, ординатой у = 1тг, т.е. числу г = x + iy соответствует точка Af(jc,у).
Между множеством точек плоскости хОу и множеством комплексных чисел
(множество С) устанавливается взаимно однозначное соответствие: каждой точ-
точке М(х, у) соответствует единственное число z = х + iy, каждому числу z = x + iy
соответствует единственная точка М с координатами (х,у) ; плоскость хОу при
«пш называется комплексной плоскостью (плоскость (z))- На рис. 1.1 отмечены
точки, соответствующие комплексным числам из примера 1.2.
(Z)
* х = Rez
Рис. 1.1
Используя геометрическую интерпретацию комплексных чисел как точек
Плоскости, убеждаемся в справедливости утверждения, что комплексные числа не
цчшниваются, т.е. на множестве С не определены операции сравнения (не име-
имени места знаки <,<,>,>). Это следует из того, что множество точек плоскости
нр упорядочено.
5. Как и в действительной области, на множестве комплексных чисел вво-
читси понятие бесконечности, бесконечно удаленной точки.
'Это можно сделать по аналогии с множеством R действительных чисел из
Неметрических соображений.
Рассмотрим числовую прямую и окружность S, которая касается прямо?
в точке О; точку, диаметрально противоположную точке О, обозначим/N (рж.
1.2,6). /
Рис. 1.2
Будем соединять прямыми различные точки оси с точкой N; точки перс
сечения прямых с окружностью будем обозначать X. Очевидно, каждой точке
х е R соответствует точка X е S. Обратное справедливо для всех точек окружно-
окружности, за исключением точки N. Но по мере удаления х по прямой от точки О
(с увеличением расстояния, равного |jc|), ее образ на окружности приближается
к точке N. Для последовательности такого вида в анализе принято название
бесконечно большая последовательность (величина). Ее предел обозначается
lim х„ = оо и называется бесконечностью или бесконечно удаленной точкой.
Л->оо
Поэтому точку N можно рассматривать как образ бесконечно удаленной точки
на окружности, а бесконечность - как "точку" оси Ох, образом которой на ок-
окружности является точка N.
По аналогии рассмотрим плоскость С (плоскость хОу) и сферу S, ка-
касающуюся ее в начале координат, т.е. в точке О (рис. 1.2,в). Лучи, соединяющие
точки zeC с точкой N пересекают сферу в точках ZeS. При этом любой
точке z е С соответствует единственная точка Z e S, и наоборот, любой точке
ZeS\N соответствует единственная точка zeС. Очевидно, чем дальше рас-
расу\ - длина
положена точка z е С от начала координат (lim р„ = оо, р„ = Jj
и-»»
радиуса-вектора точки z = х + iy), тем ближе ее образ Z e S к точке N (см. да-
далее разд. 1.3, Нтгя=°о)- Чтобы соответствие было полным, вводится
л-юо
"несобственный" элемент (символ оо) , бесконечно удаленная точка как точка
плоскости, образом которой на S является точка N.
Плоскость С , дополненная элементом оо , называется расширенной
комплексной плоскостью и обозначается С=Си {оо}.
Построенное взаимно однозначное соответствие точек сферы и множества
С называется стереографической проекцией, а сфера S - сферой Романа.
12
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ,
ЗАДАННЫМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
1. Суммой двух комплексных чисел Z\ = xt + iy{ и z2 = х2 + 'Уг называется
число z=\x + iy такое, что справедливы равенства x = xt + х2, у = у\ + у2, т.е.
Z = Zi + Z2 Щ(jcj + х2) + <СУ1 + у2) = х + iy. Обозначение: z = Z\ + z2.
Правил» сложения. При сложении комплексных чисел складываются дей-
действительные и мнимые части соответственно.
Пример 1.3. Найти сумму чисел Z\ и z2, z2 и гз > гае Z\ = 3 - Ъ,
Z2 = 5 + 2/, г3 = 1 -' ■
□
2. Разностью чисел Zt и г2 называется число z такое, что Z\ =
Обозначение: z = Zi - z2. Используя правило сложения, получаем для нахожде-
нахождения разности z = Z\-Z2, z = x + iy равенства x = xl-x2, у = У\~Уг-
Правило вычитания. При нахождении разности Z\ - Zj из действительной
и мнимой частей уменьшаемого Z\ вычитаются соответственно действительная и
мнимая части вычитаемого:
Пример 1.4. Найти разность Z\ - z2, z2 - Zi для чисел из примера 1.3.
□ Zi -г2=C-20-E + 2»)=C-5)+(-2/-2»)=-2-4/;
3. Произведением чисел Z\ = JC| + iy\ и z2 = х^ + iy2 называется число
z = x + iy такое, что выполняются равенства х = х{х2-у{у2, у = х1у2 + х2у1)
Обозначение: z = Z\ -z2.
Нетрудно убедиться, что эти равенства имеют место, если произвести фор-
формальное перемножение выражений (jct +/yt) и (jc2 +iy2) , как двучленов:
(х, +о>|)(х2 +iy2) = х,х2 +ixiy2+iy{x2 +i2yty2 = (х,х2 -
Правило умножения. Комплексные числа перемножаются, как двучлены,
при этом учитывается, что /2 = -1.
Пример 1.5. Найти произведение чисел Zi =1-2/ и z2 = 3 + 4/.
х □ z, z2 = О - 2/)C + 4/) = 1 • 3 +1 - 4/ - 3 - 2/ + 4/ (- 2/) = 3 - 2i - 8/2 = 11 - 21.И
13
Пример 1.6. Найти сумму и произведение пары комплексных сопряженных
чисел
□ Дли чисел z = х + iy, z = x-iy получаем
jc-i>) = 2x ,т.е. z + z = 2Rez;
-о')=х2 +ixy-ixy-i2y2 = х2 + у2. ■
" Результат решения примера можно сформулировать как свойство: сумма и
произведение сопряженных комплексных чисел - числа действительные. /
4. Частным от деления числа Z\ на ti {zi * 0) называется чи^ло z , такое,
что справедливо равенство z ■ z2 =Z\- Обозначение: z = —. Задача нахождения
частного сводится к определению Rez и 1тг из системы .
При нахождении частного удобно использовать свойство произведения
сопряженных чисел.
Правило деления. Чтобы разделить число Z\ на ?2 (г2 *0), следует числи-
числитель и знаменатель дроби — умножить на число г2, сопряженное знаменателю.
Пример 1.7. Найти частное от деления числа z\ = 3 + 2/ на z2 = 2 - /.
Z\ 3 + 2f C + 2/)B + /) F-2)+/C + 4) 4 ^ 7. и
Z2 = 2-/ ~ B-/)B + /) ~ 4 + 1 ~5"V'
S. Возведение комплексного числа z в степень п — это нахождение произ-
произведения п сомножителей, каждый из которых равен z, т.е. z" = Z-Z---Z-
И
Правило возведения в степень. При возведении в степень л числа z
(нахождении Re г" и 1тгя) используется правило возведения в степень двучле-
двучлена (х + iy), в общем случае применяется формула бинома Ньютона:
Пример 1.8. Найти различные степени числа /', т.е. /".
□ Имеем i2 = -1, /3 = i1 ■ i = -/, /4 = (Z2J = (-1J = 1. Замечая законо-
закономерность, получаем для n = 4k, n = 4Jk + l, n = 4k + 2, n = 4Jk + 3 следующие зна-
значения:
Пример 1.9. Найти Im(l - if, ReB - if.
О \ (\-iL4l-ifJ=(l-2i-\f=(-
B-if = 2Л+ 3 22 ■ (-1) + 3 ■ 2 ■ (-02 + (-03 = 8 -12/ - 6 + / = 2 -11/; ReB-if =2.
Пример 1.10. Возвести число B + /) в пятую степень.
D Испбльзуем формулу бинома Ньютона при л = 5:
""' B +/У = 25 +5-24 .,Ч^ ^ 1±11
2!
2¥ + 2 / +
2! 3! 4!
=32 + 80;-80-40/ + 10 + ; =
6. Корнем п -й степени из комплексного числа z называется число w,
Такое, что w" = z ■ Обозначение: v> = Щ1.
Правило извлечения корня. Для извлечения корня tfz (нахождения
х = Rttfz и у = Imtfz) следует, используя определение корня и правило возве-
возведения в степень, составить и решить систему уравнений относительно искомых
.«; и у:
[ = lm(jc + iy) .
Пример 1.11. Извлечь корень V3 - 4/.
D Обозначим V3 - 4» = х + iy, тогда (x + iyf =3-4/, или
- у2 + /2ху = 3 - 4/. Используя условие равенства комплексных чисел, записы-
U-v2=3
наем систему \ ' '
Решая ее, находим jq = 2, х2 = -2, у{ = -1, у2 = 1. В результате получаем два
значения квадратного корня: V3 - 4» = 2 - / и V3 - 4г = -2 + / .■
7. Используя определение сопряженных чисел и правила нахождения сум-
суммы, произведения, частного комплексных чисел, можно установить справедли-
справедливость следующих свойств операции комплексного сопряжения.
1) z\±z2 = zi±z2; 2) (zi-z2)=zl-z2;
3) Ы = 4; 4) Pn(zhPn(z);
(Pn(z)
В двух последних равенствах Pn(z) и Qm(z) - многочлены с действитель-
действительными коэффициентами степени пит соответственно.
15
Пример 1.12. Вычислить P(lo) + P(Zo) , если Р(г)» 2*2 + 3? +1 и
1 + 2/
го=тт-
D Используя свойство 4 из п.7, находим
Р(Хо) + P(z0) =P(Zo) + P(zo) = 2Re Р(ю) ■
Далее, производя деление, записываем число Zq в алгебраической форме:
1 + 2/ A + 2/)A + /) -1 + 3/ 1. . „
Zo = = = и подставляем в выражение для fl(z) . Полу-
1-/22
_. . -C/-1J 3C/-I) . -9-6/ + 1 + 9/-3 + 2 9 .3
чаем P(zo) = 2y 4 + 2 +1= ^ ""I"'! ' П0Этому
а
Re P(zo) = — • Окончательно имеем: P(zo) + P(Zo) = 2Re P(zo) = -9 •■
1.1.2. Комплексные числа в тригонометрической и показательной формах
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
1. Каждому комплексному числу z = x + iy геометрически соответствует
точка М(х,у) на плоскости xdy. Но положение точки на плоскости, кроме де-
декартовых координат (х,у), можно зафиксировать другой парой — ее полярных
координат (/-,ф) в полярной системе (рис. 1.3,в).
М
Рис. 1.3
Величина г является неотрицательной и для данной точки определяется
единственным образом, а угол <р может принимать бесчисленное множество зна-
значений (при этом z * 0): если точке соответствует некоторое значение <ро , то ей
также соответствуют значения ср = ф0 + 2кж, к = 0,±1,... Например, если для точки
Z = -1-/ (см. рис. 1.1) выбрать (р0 =—, то ей соответствует любое
4
16
да = — + 2кя,к =0,±1,..., в частности ю = при к = -\. Если же выбрать
4 \ 4
Фо = \ то и = + 2Ля, А; = 0,±1,..., а при А; = I получаем ф = —.
4 4 4
ИспоЛьзуя связь декартовых и полярных координат точки М:
jc = г - cos ф, y = rsm<p (рис. 1.3,6), из алгебраической формы записи комплекс-
комплексного числа i = х + iy получаем тригонометрическую форму.
Z = r(cos(f + isinif). A.3)
Если обозначить комплексное число z, у которого Rez = coso, a
lmz = sin(p, через е'ф, т.е. cos(p + /sin(p = e"p , то из A.3) получим показатель-
показательную форму записи комплексного числа:
z = rei<r. A.4)
Равенство
e'v = cos ф + / sin ф
называется формулой Эйлера (доказательство формулы см. в разд. 2.1.2).
Заметим, что геометрически задание комплексного числа z = {r,y) равно-
равносильно заданию вектора ОМ, длина которого равна г, т.е. ОМ = г, а направ-
направление - под углом ф к оси Ох (рис. 1.3,6).
2. Число г — длина радиуса-вектора точки М(х,у) называется модулем
комплексного числа z = х + iy. Обозначение: |г| = г.
Из рис. 1.3,6 получаем формулу для нахоадения модуля числа, заданного
и алгебраической форме z =
A.5)
Очевидно, что |z| S: 0 и \z\ = 0 только для числа z = 0 (jc = 0,у = 0).
С помощью правила вычитания запишем модуль числа z = Z\ - Zi, где»
<;, = х, + iy{ и zi = х2 + iy-i: \z\ - Zi\ = V(*i - X2 f + (У\ ~ У2 f ■ A это> как известно,
есть формула для расстояния меаду точками М((х,,у,) и ^fo,.)^)-
Таким образом, число \zi -гг| есть расстояние между точками z\ и zi на
комплексной плоскости.
Пример 1.13. Найти модули комплексных чисел:
a) zi = 2, z2 =-2 + V3; б) г3 = -Ъ, г4 = (г-S)i; в) г5 =-1 + 2/.
D Найдем решение для каждого из трех случаев:
а) числа z\ и z2 действительные, причем Z\ = хх = 2 > 0,
«2 =x2=-2 + V3<0. Поэтому |z,| = zi=2, \z2\ = -z2=2-S (рис. 1.4);
17
б) числа Z3 и г4 — чисто мнимые, причем £з=»>з. Л=/-2<0;
Z4='>4> У4 = 2 - V3 > 0. Поэтому |гз| = \у$\ = -Уз = 2, т.е. |/2ij = 2;
|z4| = l^l= У4 = 2-v3, или B — v3J/1 = 2-V3 (рис. 1.4);
в) для числа гз=-1 + 2/ имеем xs=Rezs=~l, ys=lmzs=2j Поэтому
у
\
|\
; \
Z3
2/
1
Z4
0
-2/
2
Рис. 1.4
3. Полярный угол ф точки М(х,у) называется аргументом комплексного
числа г = х + iy. Обозначение: ф = arg z ■
В дальнейшем, если нет специальных оговорок (см. разд. 2.1.1), под argz
будем понимать значение ф, удовлетворяющее условию - к < ср <, к. Так, для
точки г = -1-/ (см. рис. 1.1) aigz = .
4
Формулу для нахождения аргумента комплексного числа z = х + iy, задан-
заданного в алгебраической форме, получаем, используя связь декартовых и полярных
координат точки М(х,у) (см. рис. 1.3,6). Для точек, не лежащих на мнимой оси,
т.е. для z , У которых х*0, получаем tgф = —; для точек мнимой положитель-
х
ной полуоси, т.е. для z, у которых jc = 0,у > 0 , имеем ф = —; для точек мнимой
отрицательной полуоси, т.е. для z, у которых х = 0, у < 0, соответственно
п
ф=--.
Аргумент числа z = 0 - величина неопределенная.
Нахождение аргумента при jc * 0 сводится к решению тригонометриче-
тригонометрического уравнения tgq = —. При у = 0, т.е. когда z = x — число действительное,
JC
имеем (р = 0 при jc > 0 и ф = л при jc < 0. При у * 0 решение уравнения зависит
18
от четверти плоскости хОу. Четверть, в которой расположена точка г , опреде-
определяется по знакам Rez и lm z-
В результате получаем:
arctg-, x>0,
х
у
л + arctg—, jc < 0, > > 0,
- л + arctg-, jc<0, y<0, A.6)
£,
При решении примеров удобно пользоваться схемой, которая изображена
на put. l.s.
II
Ф = я + агс^—
X
Ф = -я + ап^—
X
III
У А
0
/
Ф = arctg—
JC
X
Ф = arctg—
JC
IV
Рис. 1.5
Пример 1.14. Найти аргументы чисел из примера 1.13.
D Как и в примере 1.13, решим задачу для каждого из трех случаев:
а) числа z\ = 2 и Zi = -2 + & - действительные, причем
Zi = jci >О, Z2 = Х2 <®> поэтому argzi = 0, argZ2 = я (см. рис. 1.4);
б) числа гз=-2/ и ^=B-^3)/ - чисто мнимые (jc3=jc4=0), причем
Уз =1пиз =-2<0, у4 = Imz4 =2-fi>0, поэтому arg?3 =-т> argZ4=- (см.
рис. 1.4);
в) для числа 25=-1 + 2/ Rez5=-l*0, поэтому из tg(p = — находим
JC
tg ф = -2; так как при этом Im z$ > 0. Re zs < 0 (точка z$ находится во второй
четверти, рис. 1.4), то получаем ф = я + arctg (- 2) (рис. 1.5) или ф = п - arctg2.
19
Пример 1.15. Найти модуль и аргумент числа i = 2-i. ]
j22+(-lf =&. Так как Rez = 2>0, lmz = -litO, т.е.
Q Находим
1
1
точка расположена в четвертой четверти, то из равенства tg<p = — получаем
Ф-arctg -- (рис. 1.5). ■
4. Аргумент комплексного числа определяется неоднозначно. Это следует
из неоднозначности задания величины угла ф для данной точки, а также из
тригонометрической формы записи комплексного числа и свойства периодично-
периодичности функций sin ф и cos ф.
Всякий угол, отличающийся от arg z на слагаемое, кратное 2к, обознача-
обозначается Arg z и записывается равенством:
A.7)
где arg z - главное значение аргумента, -n<aigz^ л.
Пример 1.16. Записать arg z и Arg г для чисел z{ = 1, Zz = -1.
D Числа Z\ и ф - действительные, расположены на действительной оси
(рис. 1.6), поэтому
числа Zi и Z* - чисто мнимые, расположены на мнимой оси (рис. 1.6), поэтому
-1
(Z)
Рис. 1.6
Пример 1.17. Записать числа из примера 1.16: а) в тригонометрической
форме; б) в показательной форме.
D Модули всех чисел, очевидно, равны 1. Поэтому, используя решение
предыдущего примера и формулы A.3) и A.4), получаем:
20
Пример 1.18. Записать в тригонометрической форме числа ц =-1-/\
B =cos-j-/sin-^, zj = /lcos^-/sin-| .
О Числа Z\ и Zi записаны в алгебраической форме (заметим, что заданная
мпись числа гг не является тригонометрической формой записи (сравните
с A3)). Находим модули чисел по формуле A.5): fal^yi-l?+(-lf =Л,
I 7 ~J
= Jcos2 — + - sin— = 1. Далее находим аргументы.
Для числа Z\ имеем tg<p = l и, так как Rezi <0, \mz\ <0 (точка располо-
я Зя
жена в третьей четверти), получаем argzi = -я+—= (см. рис. 1.5). Для числа
4 4
Ъ имеем tg<p = -tg—, или tg<p = tg -—1, и, так как Re?2 >0, Imz2 <0 (точка
5 \ 5)
расположена в четвертой четверти (см. рис. 1.5)), получаем argZ2 = -—•
Записываем числа Z\ и Zi в тригонометрической форме
Заметим, что для числа z2 решение можно найти иначе, а именно исполь-
используя свойства тригонометрических функций: cos a = cos (-а), -sin а = sin (-а).
Число Zi является произведением двух чисел. Выполнив умножение, полу-
получим алгебраическую форму записи (найдем Re?3 и Inu3): г3 =sin— + icos—.
Здесь, как и для числа ц. при решении удобно использовать преобразования
тригонометрических выражений, а именно sin—=cos — -— , cos—= sin —- — I.
Рассуждая, как выше, найдем |гз| = 1. Щ>Ц = = — • Для числа
21
Zi =sin—+ /COS—, записанного в алгебраической форме, получаем тригономет-
тригонометрическую форму. 2з = cos -^ + 2fet + i sin — + 2fot , к = 0,± 1,± 2,... ■
5. Условия равенства комплексных чисел получаем, используя геометриче-
геометрический смысл модуля и аргумента комплексного числа, заданного в тригонометри-
тригонометрической форме. Так, для чисел Z\ = /i(costpt + /sin<p|), ti = r2(cos<P2+'sinq>2) из
условия Z\ = z2. очевидно, следует:
1 =Ъ <Pi-<P2=2b, A = O^t 1,± 2,...
или
Ы 1Ы * = 0,±1,... A.8)
Аргументы равных комплексных чисел либо равны (в частности равны
главные значения), либо отличаются на слагаемое, кратное 2л.
Для пары сопряженных комплексных чисел z и z справедливы следующие
равенства:
|| || A.9)
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ, ЗАДАННЫМИ
В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ
1. Умножение. Зададим два комплексных числа в тригонометрической
форме Z\ = /i(cos<p[ +/siri(p1) и z2 = r2(cosy2 +isia(f2) и перемножим их по пра-
правилу умножения двучленов:
Z\ ?2 =ri ^(cosq»! +/sin<p1)(cos<p2 +/sin
или
cos<p2 - sin ф[ sin q>2 +' (cos<Pi sin ч>2 + s'n <Pi C0S<P2))
zx -Z2=n r2{cos(<fx +<p2)+'sin(<p1
Получили новое число z, записанное в тригонометрической форме:
£ = r(cos<p + isin<p), для которого г = /[ -г2, <p = <Pi +ч>2-
Правило умножения. При умножении комплексных чисел, заданных
в тригонометрической форме, их модули перемножаются, а аргументы склады-
складываются:
кгггНЫЫ . Axg(zxZ2) = aigZi+aiSZ2. (UO)
В результате умножения чисел может получиться аргумент произведения,
не являющийся главным значением.
22
Пример 1.19. Найти модули и аргументы чисел:
а) z = -2i (cos у - / sin у]; б) z = (l + i)(i/3 - 0.
D Каждое из заданных чисел записано в виде произведения. Найдем мо-
дши и аргументы сомножителей и воспользуемся правилом A.10) умножения
Чисел, заданных в тригонометрической форме:
a)z = zrz2, Zi=-2i, z2=cosy-ismy = cos -yl + isml-yl.
Для чисел Z\ и г2 находим модули и аргументы: \z\\ = 2, arg^i =—;
|t]| = 1, arg^2 =——. Используя формулы A.10), получаем
я 4л 15я Л 15я 13л
---y = -—; xgz = 2n- — = —;
б) z = Zi -Zi, Z\ =(l + 0> Z2 =V3-/. Для числа z\ имеем:
|?:i|=V2, argzi =-; для числа г2: |г2| = 2, tg(p2=-jr, и так как
Re?2 >0, Inu2 <0 (точка расположена в четвертой четверти), то arg^2 =—г-
о
Используя формулы A.10), получаем |г| = 2^2, arg^ = — ~7 = ~^-
Заметим, что для решения этой задачи можно раскрыть скобки, записать
каждое число в алгебраической форме, а затем найти |г| и arg z, используя фор-
формулы A.5), A.6). ■
2. Деление. Рассмотрим частное комплексных чисел — , заданных в три-
г2
гонометрической форме. Из определения частного z = — имеем Z\=z-Zi и,
г2
применяя к произведению правило умножения (формулы A.10)), получаем
г,
/•=—, ф = я>1-ф2.
гг
Правило деления. Модуль частного, полученного в результате деления чи-
чисел, заданных в тригонометрической форме, равен частному от деления модуля
числителя на модуль знаменателя, а аргумент частного равен разности аргумен-
аргументов делимого и делителя:
Z\
Arg— = argzi -argz2- A-11)
1
В результате деления чисел по формуле A.11) может получиться аргумент
честного, не являющийся главным значением.
23
Пример 1.20. Записать в тригонометрической форме число -=—
□ Обозначим г = -Ц Zi =l + i, Z2=S-i. Для чисел Z\ и г2 находим
модули и аргументы: |zi|=V2, arg^ =j; |?2| = 2> ОД^ =-7 (см. пример 1.19).
О / \ *
По формуле A.11) получаем \А=-= = Л, arg?= —- -— =— и
V2 4 ^ 6) 12
4^L = V2fcosf%
V3-/ I, U2
inf-^ + 2Jbt)l> Л = 0,±1,±2,...
U2 yj
3. Возведение в степень. Из определения степени z" и правила умножения
чисел, записанных в тригонометрической форме (формула A.10)), получаем
\zn
где z = г (cos <р + i sin <p).
Правило возведения в степень. При возведении в степень комплексного
числа в эту степень возводится модуль числа, а аргумент умножается на показа-
показатель степени:
A12)
Записывая число z" в тригонометрической форме z" = /-"(cos«q> + /sin/Kp) ,
получаем формулу возведения в степень:
[/•(coscp + z'sincp)]" =r"(cosn<p + /sin n<p). A-13)
При г = 1 это равенство принимает вид
(cos <р + / sin <p)" =cosn<p + /sinn<p. A.14)
Равенство A.14) носит название формулы Муавра.
Пример 1.21. Найти модуль и аргумент числа (l + if.
О Обозначим z = Zi5, Zi=l + '- Находим модуль и аргумент числа z\-
|zi| = Vl.arg^i =—. Поэтому |?| = (V2| и Arg? = 5argzi =5j. Так как по опре-
определению для главного значения аргумента выполняется условие - ж arg z £ я, то
.я - Зя _
>--2я = -т..
24
Пример 1.22. Записать в тригонометрической форме число A + /дч/3-/) .
D Обозначим z=Z\-l2, Z\ =(l+if,Z2 =\S-i) . Находим модули и аргу-
аргументы чисел z\ и zi- Для числа Z\ имеем: |zi| = (V2|, arg^i =—- (см. пример
1.2!). Для числа г2 последовательно находим: W3-z| = 2, arg(V3 -/)=-— (см.
пример 1.19), 1*21 = 27 , Arg?2 =7aig(V3-/j=—-, или, находя главное значение
аргумента: arg<:2 =-т-- Таким образом, по формуле A.10) получаем
6
Ы = (VIM • 27 = 29VI и Argz= — - =—. Записываем число z = Z\l2 в три-
6 4 12
гонометрической форме:? = 29V2 cos — + Ikn + /sin — + 2fat , к = 0,± 1,±2,...*
Пример 1.23. Используя формулу Муавра, найти выражения для cos3<p и
sin Зф через тригонометрические функции угла <р.
D Из формулы A.14) при п = 3 имеем (cos<p + /sin<pK = cos Зф + / sin Зф. Воз-
нсдем левую часть в степень, учитывая, что /3 =-/ (см. пример 1.8):
cos3 <р + /3cos2 (р sin (р - 3coscp sin2 (р + /3 sin3 <р = cos3(p + / sin3<p,
(cos3 ф - 3 «Кф sin2 ф) + /'Ccos2 ф sin ф - sin3 ф) = совЗф + isin Зф.
Используя условие равенства комплексных чисел, получаем:
cos Зф = cos3 ф - 3 ажф sin2 ф, sin Зф = 3cos2 ф • sin ф - sin3 ф .
4. Извлечение корня. Рассмотрим задачу извлечения корня из комплекс-
комплексного числа, заданного в показательной или тригонометрической форме z ~ re"*,
или ; = r(cosq> + isinq>). Искомое число w = <jf? также запишем в показательной
форме: tv = pe'e, p=|tv|, 6 = argw. Используя определение операции извлечения
корня z = w" и условия A.8), получаем соотношения
р"=г, п6 = ф + 2Ьг, £ = 0,±1,...,
или
P = fr, e«i±^, k = o,±\,... A.15)
я
Правило извлечения кория. Чтобы извлечь корень из комплексного числа,
нужно извлечь корень (арифметический) той же степени из модуля данного чис-
числа, а аргумент (Argz) разделить на показатель корня:
25
Теперь можно записать число w - yz в показательной форме:
Если записать это соотношение в тригонометрической форме, то, учитывая
периодичность тригонометрических функций, нетрудно убедиться, что выраже-
выражение щг принимает только л различных значений. Для их записи достаточно в
формуле A.15) взять и последовательных значений к, например к = 0,1,2,...,л-1.
В результате получаем формулу извлечения корня из комплексного числа в три-
тригонометрической форме:
„г пг( <р + 2)Ьг . . <в+2кп\ , „. . ,. ,_,
Щ1=Щг cos- + /sin- , * = 0,1,...,л-1, A.17)
V я п )
где r = \z\, <p = arg<:.
Замечания 1.1.
1. Рассмотренная задача извлечения корня степени п из комплексного
числа равносильна решению уравнения вида z" - а = 0, где, очевидно, г = ^а .
Для решения уравнения нужно найти л значений Ща, а для этого необхо-
необходимо найти г =|я|, ф = argc и использовать формулу извлечения корня.
2. Исследование формулы A.17) показывает, что все комплексные числа
wk,k = 1,...,я (значения Щг) имеют равные модули, т.е. геометрически располо-
расположены на окружности радиуса R = &, г = \z\. Аргументы двух последовательных
2я Ъ.
чисел отличаются на —, так как aigtv^+i -argw* = —, т.е. каждое последующее
я л
значение и^+| может быть получено из предыдущего и>ц поворотом радиуса-
вектора точки wk на —.В этом заключается геометрический смысл формулы
я
A.17), что можно сформулировать следующим образом.
Точки, соответствующие значениям ^z , расположены в вершинах пра-
правильного л-угольника, вписанного в окружность с центром в начале координат,
радиус которой R = ^\z\, причем аргумент одного из значений wk равен
= ^ (рис. 1.7).
л
Алгоритм решения уравнений вида z" - а = 0
1. Найти модуль и аргумент числа а : г-\а\, <р = argo.
2. Записать формулу A.17) при заданном значении п :
Ща =
( ф 2Ля . .
г cos- -tnvn.
-tnvn. .
п п )
3. Выписать значения корней уравнения Zk , придавая значения
Jk = 0,1 я-1.
fe>
Рис. 1.7
Пример 1.24. Решить уравнения: а) г6 -1 = 0; б) г3 -1 = О.
О Задача равносильна задаче нахождения всех значений корня из ком-
комплексного числа. Решаем в каждом случае по алгоритму,
а) Найдем z = vf.
1. Определим модуль и аргумент числа 1: г = 1, <р = 0.
2. При полученных значениях г и <р записываем формулу A.17):
6/7 6г ( 2Ь . . 2кп
Z = V1 =vl • cos-—+ i sin-—
^6 6
Чвметим, что справа стоит %{ — арифметический корень, его единственное зна-
значение равно 1.
3. Придавая к последовательно значения от 0 до 5 , выписываем решения
уравнения:
Zi со 3 + i шз = 2+/ 2 ,
=cosO + /sinO = l,
= COS +(SU1 = + / ,
3 3 2 2
4я . . 4я I .i/3
= cosh + /suih = -1;
_5я ... 5я I .i/3
>
Геометрически соответствующие точки расположены в вершинах правиль-
правильного шестиугольника, вписанного в окружность радиуса R = I, одна из точек
(соответствует к = 0) z\ = I. Строим шестиугольник (рис. 1.8,в). Отметим свойст-
nu корней этого уравнения с действительными коэффициентами - его комплекс-
комплексные корни являются попарно сопряженными: г6 = гг, Zs = ?з> ^1 и U - действи-
действительные числа.
б) Найдем z = VJ.
1. Определим модуль и аргумент числа / : г = |i) = 1, <р = arg / = —.
27
2. По формуле A.17) имеем
Hi =1-
cos
+ / sin
Рис. 1.8
isinfi+ijbiV Л = 0,1,2.
3. Выписываем корни i{,ii,lv zi=~Z~ + i~5> *2=~~2~ + ''2' zi=~L
Для геометрического представления решения уравнения достаточно изо-
изобразить одно значение, например ц = cos- + /sin — (при Jfc=0) - это точка ок
6 б
ружности Ы = 1, лежащая на луче <р = —• После этого строим правильный трс-
6
угольник, вписанный в окружность |г| = 1 (рис. 1.8,6). ■
Пример 1.25. Найти корень уравнения z4 -1 + / = 0, для которой
<0, Inu>0.
D Задача равносильна задаче нахождения z = ^1-/ при условие
Re?<0, 1шг>0.
I. Находим модуль и аргумент числа 1 - /: г = |l - /j = Л, <р = arg(l - /) = —
:^+1=СЛ = ^2.е^16+4 ", к = 0,1,2,3.
2. По формуле A.17) имеем:
3. Для нахождения искомого решения нет необходимости выписывать вес
значения корня. Нужно выбрать значение к (А: =0,1,2,3) , при котором arg
п
удовлетворяет условию — < arg z < я (соответствующая точка - точка второй ч&
верти). Удобно при этом использовать чертеж (рис. 1.9).
28
1.7.
S
fc)
Рис. 1.9
Условию поставленной задачи удовлетворяет корень г3 (при к = 2):
Упражнения
1. Найти ImF , если z = ;
Ответ: - ^.
2. Найти Re z , если z =
Ответ: - %.
3. Доказать справедливость равенств Z[Z2 = ZiZ2, — ==,
\Z2J Z2
2
4. Найти Re z, Im z, если z = — и Z\ = 1 +» •
Ответ: Re z = 1, Im z = -1.
5. Даны комплексные числа z\=i-1, ?2 = '"> гз = 3/ + 2. Какие из следующих
равенств верны: a) Re^i = Im?2, б) Z\2 =—; в)
г)
Ответ: верными являются все указанные равенства.
6. Найти модули и аргументы комплексных чисел z\ = 1 - 3i, Zt = -1 - 2/.
Ответ. \z\ \ = V^ aig^, = arctg (- 3); |г21 = V5, arg г2 = - n + arctg 2.
7. Даны комплексные числа z\ = 1 - 4l, Z2 = 1 + VI/, ?3 = A - VI) / .
Какие из следующих равенств верны:
v I I __ /i^ on* • Л\ I I _ /О 1 ^1
^з 2
в) argZj = я, |z2| = V3; г) Ы = 1/з, arg^ = arctg(-VI).
29
Ответ: б) и в) .
8. Даны комплексные числа Z\ = \1 + v2)i, z2 = (l - VI)/, г3 = 2 + VI.
Какие из следующих равенств верны: a) |z, • ?2| = 1, arg— = -—;
Z\ 2
6) arg?3 = ^; в) argzi = arctgV3; r) argfoz^O; д) |zi| = V3, arg?3 =0.
Ответ: а) и г).
9. Найти модуль и аргумент (главное значение) комплексного числа
л
7
ie
л
Ответ: |г| = е 7, aigz=—•
Ю. Найти |г| и arg?, если ? = г, гг, Zi = (l-Sji,
Ответ: |г| = 2 (i/з -1), argz = Y-
I I e
11. Найти \z\ и aigz,ecjiH a) z = 2/e 5 ; 6) г = -3е5 .
Ответ: a) 2,-^; 6) 3,- j.
12. Найти |?| и argz , если z = —, Z\=i, z2=l + 'V3.
n ! 5jt
Ответ: —,—■
2 6
13. Найти модули и аргументы комплексных чисел Z\ = -2, г2 = 3/, г3 = -1 - /.
Ответ: |?i| = 2, argzi=n; |?г| = 3, arg^2=—; |zj| = V2
14. Пусть Z\,Zi,Zi — корни уравнения г3 -2/ =0, причем
0 < arg ?[ < —, arg г3 < 0. Какие из следующих равенств верны:
—/
a) Zi = - ?i; б) arg ?2 = arg ^1; в) г3 = г2 • е 3 ;
г) arg Zj = я - arg г2; д) z3 = Z\ ■ е 3 ; е) -j—т = 1.
Ответ: а), в), г), е).
15. Дано уравнение z1 +1 - / = 0. Выписать все корни этого уравнения, ко-
которые изображаются точками третьей четверти.
_3п.
Ответ: z = Xfle 4 .
30
1.2. МНОЖЕСТВА НА КОМПЛЕКСНОЙ ПЛОСКОСТИ
:'.;Г« I
1.2.1. Основные определения
Напомним известные из анализа функций двух действительных перемен-
переменных основные геометрические понятия, связанные с расположением точек на
плоскости. Определения будем давать в терминах комплексной плоскости, т.е.
ючка М(х,у) плоскости - это точка z комплексной плоскости.
1. Множество точек z, удаленных от заданной точки Zq на расстояние,
меньшее чем заданное число е, называется е - окрестностью точки zo, будем
обозначать ее 0E(zo). Используя понятие расстояния между точками плоскости
(|г Zo\), определение можно записать в виде соотношения:
Oz(z0)={z:\z-Zo\<s\.
Очевидно, что геометрически 0E(zo) - круг с центром в точке ю и радиу-
радиусом г..
2. Множество точек z, удовлетворяющих неравенству 0 < \z - Zq\ < е, обра-
аует проколотую окрестность точки iu: Oc{zo)\zo-
3. Точка называется внутренней точкой множества, если она принадлежит
•му вместе с некоторой своей окрестностью, т.е. Zo - внутренняя точка множест-
М М , если го е М и Эе > 0, что ОЕ(г0) с М.
4. Множество, состоящее только из внутренних точек (множество, все точ-
точки которого являются внутренними), называется открытым.
5. Точка называется граничной точкой множества, если в любой ее окрест-
окрестности есть точки, принадлежащие множеству, и точки, не принадлежащие ему,
r.e. Zo - граничная точка множества М, если для Ve>0 3 точки ^ и Zj,
1\ « °еЫ, Zi е Ot{z0), такие, что ц е М, z2 £ М.
Совокупность граничных точек множества образует границу множества.
Направление обхода границы называется иоложнтельным, если область,
огриниченная контуром, при обходе расположена слева. \
6. Множество, содержащее все свои граничные точки (множество вместе
е границей), называется замкнутым. Оно обозначается М, т.е. М = MkjC , где
Г граница множества М (С = &М).
7. Множество называется связным, если любые две его точки можно
соединить непрерывной кривой, все точки которой принадлежат множеству.
8. Открытое, связное множество называется областью. Область с присое-
присоединенной границей - замкнутая область, D = D и С, С = &D.
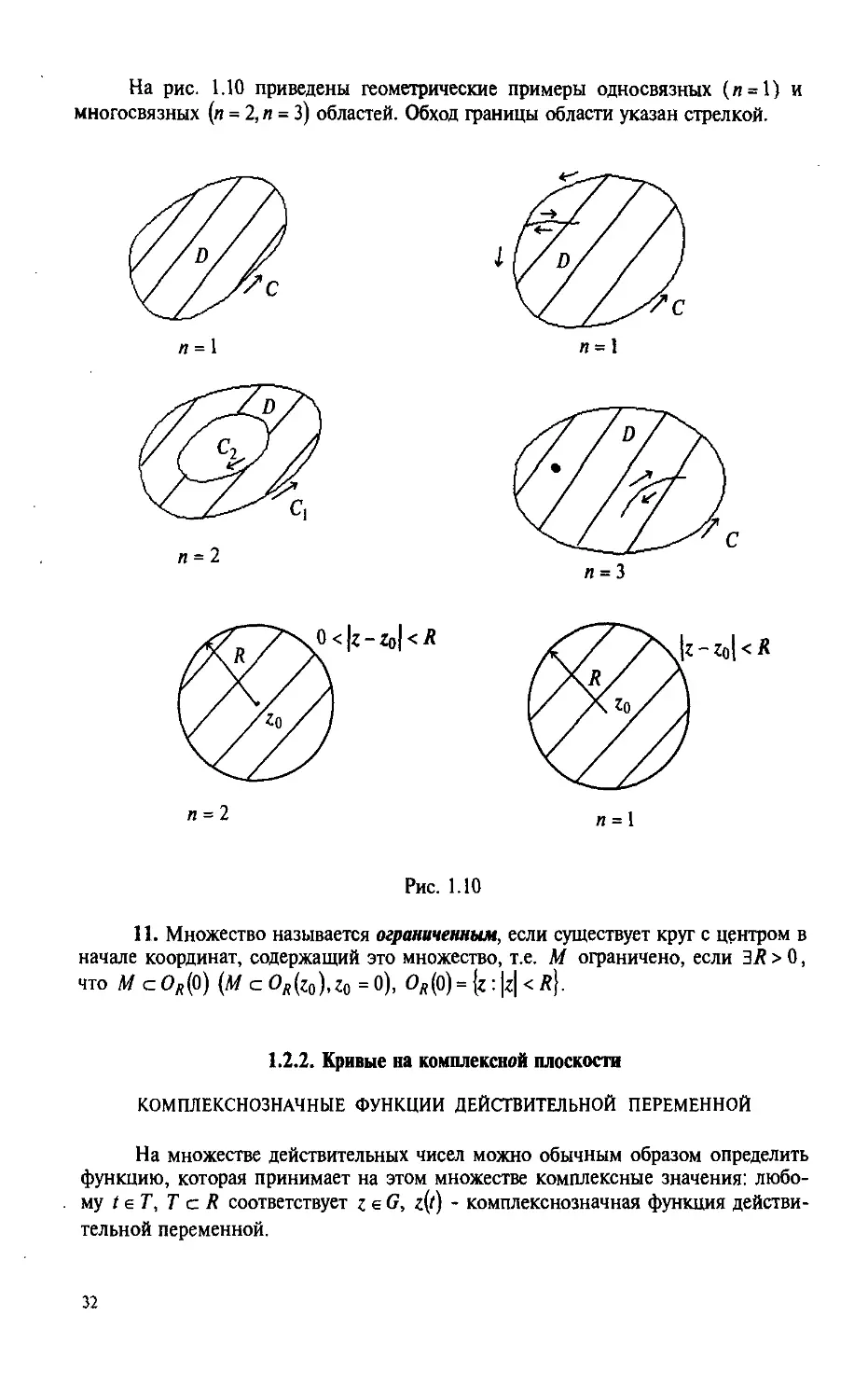
9. Область (множество) называется односвязнон, если для любой замкнутой
Ириной, принадлежащей области, точки множества, границей которого является
кривая, также принадлежат области. В противнрм случае - область многосвязная.
10. Многосвязная область называется н - связной, если ее граница состоит
т п компонент. Порядок (и) связности многосвязной (л - связной) области
определяется числом (и) связных компонент границы области.
31
На рис. 1.10 приведены геометрические примеры односвязных (л = 1) и
многосвязных (и = 2, п = 3) областей. Обход границы области указан стрелкой.
Рис. 1.10
11. Множество называется ограниченньш, если существует круг с центром в
начале координат, содержащий это множество, т.е. М ограничено, если ЗЛ > 0,
что Л/сОЛ@) (M<zOR(z0),z0=0), OR@)={z:\z\<R].
1.2.2. Кривые на комплексной плоскости
КОМПЛЕКСНОЗНАЧНЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
На множестве действительных чисел можно обычным образом определить
функцию, которая принимает на этом множестве комплексные значения: любо-
любому t е Т, Т с R соответствует z e G, z{t) - комплекснозначная функция действи-
действительной переменной.
Например, i(t) = it + 2t, i(t)= , z(t) = - комплекснозначные функ-
t+i t-l
ции, первые две определены для любого t ((е Л), последняя - для любого t * 1.
Для функции z(t), так же как для действительной функции действительной
переменной, вводится понятие предела в точке, а на его основе - понятия непре-
рынности, производной, интеграла.
Так как для любого значения t из области определения число z(t) являет-
ия комплексным числом, то, записав его в алгебраической форме z = х + iy, по-
«учим, что задание комплексной функции z(t) действительной переменной на
некотором множестве Т(Т с R) равносильно заданию на этом множестве двух
действительных функций x(t)= Rez(t) и y(t) = lm z(t).
Используя соответствующие определения, нетрудно убедиться в справедли-
иости следующих утверждений и формул:
1. Для непрерывности функции z(t) в точке fy необходимо и достаточно,
Чтобы в этой точке были непрерывны функции x(t)= Rez(t) и y{t)= \mz{t).
2. lim z(t)= lim x(t)+ i lim y(t).
1->IO Г->Г0 l->«o
3. z'{t)=x'{t) +iy'{t), dz = dx + idy.
b b b
4. \z{f)dt=\x{t)dt +
УРАВНЕНИЯ КРИВЫХ НА КОМПЛЕКСНОЙ ПЛОСКОСТИ
Одним из способов задания кривой на плоскости является параметриче-
«Кос задание:
1л (>
У = УЧ),
\
Будем рассматривать гладкие и кусочно-гладкие кривые.
Кривая называется гладкой на множестве Т, если функции x(t),y(t) имеют
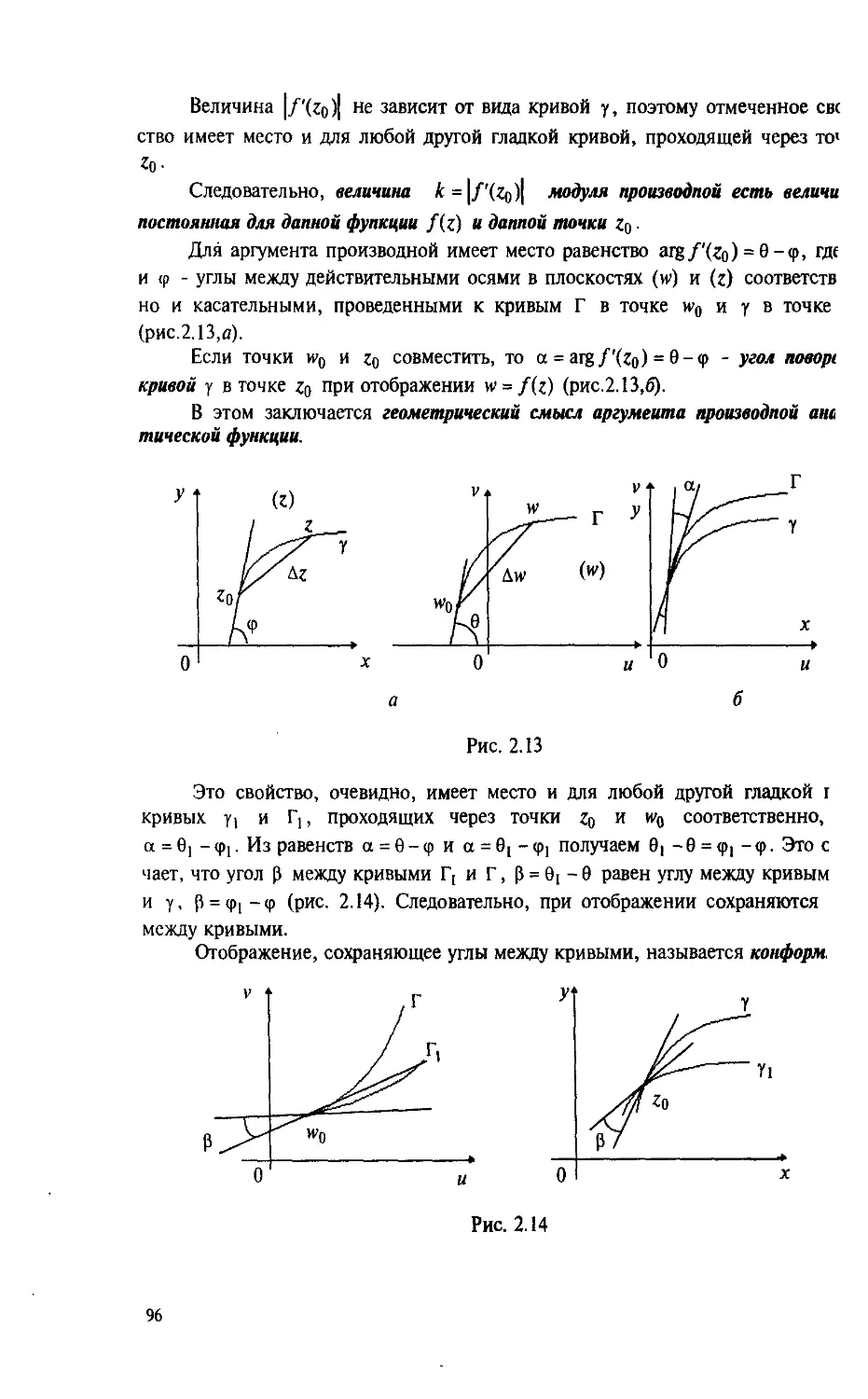
ни '/' непрерывные производные x'(t),y'(t). Геометрически гладкая кривая харак-
1сри)уется существованием касательной к этой кривой в каждой точке, причем
направление касательной изменяется непрерывно при движении точки по кри-
нпй.
Кривая называется кусочно-гладкой, если ее можно разбить на конечное
число гладких кривых.
На рис. 1.11 изображены кривые, которые являются кусочно-гладкими на
(«,<■) и гладкими на каждом из интервалов (а,Ь) и (Ь,с).
Из определения функции z(t), данного йыше, следует, что геометрически
се задание определяет кривую на плоскости (и обратно): по формуле A.18) лю-
Оому значению t еТ соответствует точка (х,у), т.е. число z = х + iy.
1 Пантелеев А.В.. Якимова А.С. * 33
Рис. 1.11
Следовательно, параметрическое задание кривой в форме A.18) равно-
равносильно заданию z(t) = x(t) + i y(t). Равенство
* = #),/еГ A.19)
называется уравнением кривой в параметрической форме.
Пример 1.26. Записать в параметрической форме уравнение окружности,
центр которой находится в точке С{х0<у0) , а радиус равен R.
□ Используем известные параметрические уравнения окружности:
x-x0+Rcost, te{ }
Отсюда получаем z{t) = x(t) + / y(t) - х0 + R cos t + / (y0 + R sin t) или
Ф)=£о + Л (cos? +/sin/), где Zq =xo+iyo - центр окружности. Используя фор-
формулу Эйлера, окончательно запишем уравнение окружности в параметрической
форме:
z(t) = Z0+Re", fe[0,2«]. A.20)
Заметим, что если переписать A.20) в виде z-Zo = Re", то получим ра-
равенство |г-го| = Л, которое определяет окружность как геометрическое место
точек плоскости (точек z), равноудаленных (на заданное расстояние R) от за-
заданной точки (го). Очевидно, уравнение A.20) определяет гладкую кривую, что
соответствует геометрическому виду этой кривой. ■
Уравнение плоской кривой, как известно, можно также записать в виде
F(x, у) = 0 , т.е. соотношения, связывающего декартовы координаты (х, у) точек,
принадлежащих этой линии; в частности, у = f(x) - явное задание линии. Но так
как пара (дг, у) определяет комплексное число z = х + iy, то, выразив х и у через
Z , можно записать соотношение в комплексной форме. Из z = х + iy и
Z = x-iy получаем х = и у = . Поэтому равенство
2 2/
34
есть уравнение кривой на плоскости, записанное в комплексной форме. Используя
тригонометрическую форму задания комплексного числа, можно получить и
другие виды уравнений кривых на комплексной плоскости.
Пример 1.27. Записать в комплексной форме уравнения:
а)прямой; б) окружности.
П а) Общее уравнение прямой на плоскости имеет вид Ах + Ву + С = 0.
Подставляя в это уравнение х = и у = ——, находим
—(г + г)-'—(z~z)+C = 0, или z\ —'—\ + z ~7 + ' +^ = 0- Введя обозначе-
нис — + i—=M, окончательно получим Mz + Mz+C = 0 — уравнение прямой
r комплексной форме.
б) Используем уравнение окружности в общем виде
Ах2 ¥ Ау2 + Вх + Су + F = 0. Подставляя в это уравнение х=^-^-, у=-—- и
2 2/
ti + y2=zz, получаем Лг? + г—«'— +F — + «'— +/" = 0, или, обозначая
О Q _ _
М-— +/—, Azl+ Mz + Mz + F = 0, - уравнение окружности в комплексной
форме. Заметим, что при Л = 0 получаем задачу, рассмотренную в п. "а". ■
Замечание 1.2. Утверждение, что уравнение прямой на плоскости
иилиется частным случаем уравнения окружности на комплексной плоскости
имеет более глубокий смысл: прямые как геометрический образ являются част-
частным случаем окружности (их можно рассматривать как окружности
"бесконечного" радиуса, Л = оо). Обоснование этого можно получить, используя
стереографическую проекцию - геометрическое изображение комплексных чисел
(множества С) точками на сфере Римана.
Имеет место утверждение: окружности и прямые плоскости при стереогра-
стереографической проекции отображаются в окружности, причем образом окружности
иидяется окружность на сфере Римана, не проходящая через точку N, а образом *
прямой - окружность, проходящая через N.
Для доказательства используем формулы связи координат точки плоскости
С и ее образа на сфере (см. рис. 1.2,а).
Если положить диаметр сферы равным единице (ON = l) и ввести систему
координат E,ti,<p), направив по лучу ON ось ftp, а плоскость С выбрав за плос-
плоскость feOn), гДе ось О£, совпадает с Ох, а ось Оц - с Оу, то, используя коллине-
нрность векторов zN и ZN, получим выражение координат точки z{x, у) плос-
плоскости С через координаты ее образа Z(^,ri,(p) на сфере. Эти формулы имеют вид
1 -ф ] -ф
Подставляем их в уравнение окружности Ах2 + Ay2 +Bx + Cy + D = 0 и учи-
учитывая, что точка Z(£,,r\,q>) лежит на сфере, т.е. ее координаты удовлетворяют
35
1V 1
или §2 +2 +ф2 =
( 1V 1
уравнению §2+ti2+U — =- или §2 +п2 +ф2 = ф, после преобразований по-
I 2) 4
лучаем уравнение плоскости B£, + Cr) + (A-D)q>+ D = 0. Следовательно, образом
окружности является линия пересечения сферы этой плоскостью, т.е. окруж-
окружность на сфере. При /4 = 0 на плоскости имеем прямую с уравнением
Вх + Су + D = 0; ее образом на сфере будет окружность
1
проходящая через точку N, так как координаты точки N@,0,1) удовлетворяют
этой системе.
Аналогично доказывается обратное утверждение: окружностям на сфере,
не проходящим через точку N, соответствуют окружности плоскости С, а ок-
окружностям, проходящим через N, - прямые.
Пример 1.28. Записать в комплексной форме уравнения: а) координатных
осей; б) биссектрисы первого и третьего координатных углов.
□ а) Для уравнения оси Ох из _у = О и у= получаем z - Z = 0; для
2/
z + ? ~
оси Оу из х = 0 и х = следует z + Z = 0.
б) Уравнение биссектрисы у = х принимает вид —— = .
Z-Z = (z + z)i, или z(\-i)-Z (l + 0= О-
Если умножить уравнение на A + 0, то его можно записать иначе:
Пример 1.29. Записать в комплексной форме уравнение:
а) дуги окружности единичного радиуса с центром в начале координат,
расположенной в первой четверти;
б) биссектрисы первого координатного угла;
в) отрезка ОА биссектрисы первого координатного угла, где АA,1).
□ Для решения удобно использовать задание комплексного числа в три-
тригонометрической форме, т.е. через \z\ и arg z:
а) любой точке дуги соответствует число z, для которого \z\ = 1, а аргумент
удовлетворяет условию 0 < arg z ^ — ■ Соотношения
я определяют со-
2
ответствующую дугу. Полученный результат можно записать в комплексной
форме: zz-\ = 0, Rez^O, Irn^O или в параметрической форме: z = e",
~2'
36
б) используя результат примера 1.28 , ответ можно записать в виде
Более удобной является запись argz = -;
4
в) используя результат предыдущего пункта, ответ можно записать в виде
/М
Пример 1.30. Определить вид кривой, заданной соотношением:
I a)|z-2|=|z + 2j|; б) |г + з| = |г-5|.
D а) Подставив z = х + iy, запишем числа в алгебраической форме:
\(\ 2) + iy | = | х + i{y + 2)|. Далее по определению модуля запишем квадраты мо-
jiviii'H полученных комплексных чисел: (x-if +у2 =х2 +{у + 2) . Отсюда после
преобразований имеем у = -х - уравнение биссектрисы второго и четвертого ко-
координатных углов. Задачу можно решить иначе, геометрически, если воспользо-
шиьеи геометрическим смыслом модуля \zi -*г| как расстояния между точками.
Переформулируем условие следующим образом: найти геометрическое место то-
точек z, равноудаленных от двух заданных точек 2 и - 2/. Очевидно, что геомет-
геометрическое место точек есть прямая, которая перпендикулярна отрезку, соеди-
ниюшему заданные точки, и проходит через его середину. Такой прямой являет-
I И )' = -X.
б) Решим задачу геометрически. На оси Ох отмечаем точки - 3 и 5 и через
гередину отрезка их соединяющего (точку х = 1) проводим перпендикулярную
прямую; ее уравнение х = 1 .■
Пример 1.31. Определить вид кривой, заданной уравнением:
a) Im- = -; б) Re-Ul.
z 1 z
1 1 x-iy m „. , 1 »
n а) Используя правило деления — = = —, находим Im —:
Z x + iy x2+y Z
Получаем уравнение кривой в действительной форме:
2у = 0, или х2 + {у +1J = 1. Это уравнение окружности
радиуса R = 1 с центром в точке С@,-1).
б) Производим действия, как в предыдущем пункте:
— — кр ь— —
.,2'
V
37
В результате получено уравнение окружности радиуса R = Yi с центром
в точке C(y2fi). ш
1.2.3. Области
Будем рассматривать области, границы которых состоят из конечного чис-
числа кусочно-гладких кривых, в частности простых кривых, т.е. не имеющих точек
самопересечения, а также отдельных изолированных точек.
Приведем аналитические выражения для областей простейшего вида, гра-
границами которых являются простейшие линии - прямые, окружности.
1. Круг радиуса R с центром в точке ^о задается неравенством |г-£о| < R.
Это - открытое, связное множество, т.е. область. Область - ограниченная, одно-
связная; ее границей является окружность \z-Zo\ = R (рис. 1.12,а). В частности,
круг |z-Zo|<e есть окрестность точки ^о: OE(z0). Заметим, что неравенство
\z - го| ^ R определяет замкнутую область, т.е. область вместе с границей.
2. Проколотая окрестность точки z0 : Oe(zo)\zo - круг с выброшенным
центром задается неравенством 0 < \z - Zo\ < e. Это двусвязная, ограниченная об-
область, граница которой состоит из двух компонент - окружности |z-Zo| = e и
точки го (рис. 1.12,6).
3. Окрестность бесконечно удаленной точки определяется как множество
точек плоскости С, образами которых на сфере Римана являются точки, при-
принадлежащие окрестности точки N (см. рис. 1.2,а). Эта окрестность получается
отсечением от сферы некоторой области плоскостью, перпендикулярной лучу
ON. Границей этой окрестности на сфере является окружность - пересечение
сферы и плоскости. На плоскости С этой окружности соответствует также ок-
окружность, центр которой, очевидно, находится в точке О ; ее уравнение \z\ = R.
Сферической окрестности точки N будет соответствовать часть плоскости, гра-
границей которой является окружность \z\ = R и которая содержит бесконечно уда-
удаленную точку (образ точки N), эта область - внешность круга \z\> R (рис.
1.12,в).
4. Кольцо с центром в точке г0, радиус внешней окружности которого R и
внутренней г, задается неравенством л<|г-го|<Л (Рис- 1-12,г). Это - ограни-
ограниченная, двусвязная область, граница которой состоит из двух окружностей
C,:|z-«o| = * и С2:|г-го| = г.
5. Верхняя полуплоскость плоскости С - множество точек, для которых
^>0, т.е. в комплексной форме Im^>0 (рис. 1.12,д); соответственно 1тг<0 -
нижняя полуплоскость. Неравенство Re z > 0 определяет правую иолуплоскость
(рис. 1.12,е), Re г <0 - левую полуплоскость. Это односвязные, неограниченные
области.
Заметим, что на расширенной комплексной плоскости С граница
односвязной области состоит либо только из одной замкнутой кривой,
38
шбо её границей является единственная точка z - «(область С), или граница не
■одержит ни одной точки (сама расширенная плоскость С).
Замкнутая кривая на С может быть неофаниченной (кривая "проходит"
'ерез бесконечно удаленную точку). Например, на рис. 1.12,д фаницей одно-
•иииной области Im z > 0 является прямая Im г = 0, которую рассматриваем
ш С как окружность радиуса R = а>; её образом на сфере Римана является
жпужность (см. замечание 1.2).
\z-Zo\<R
У ж Im z > О
у Rtz>0
Рис. 1.12
39
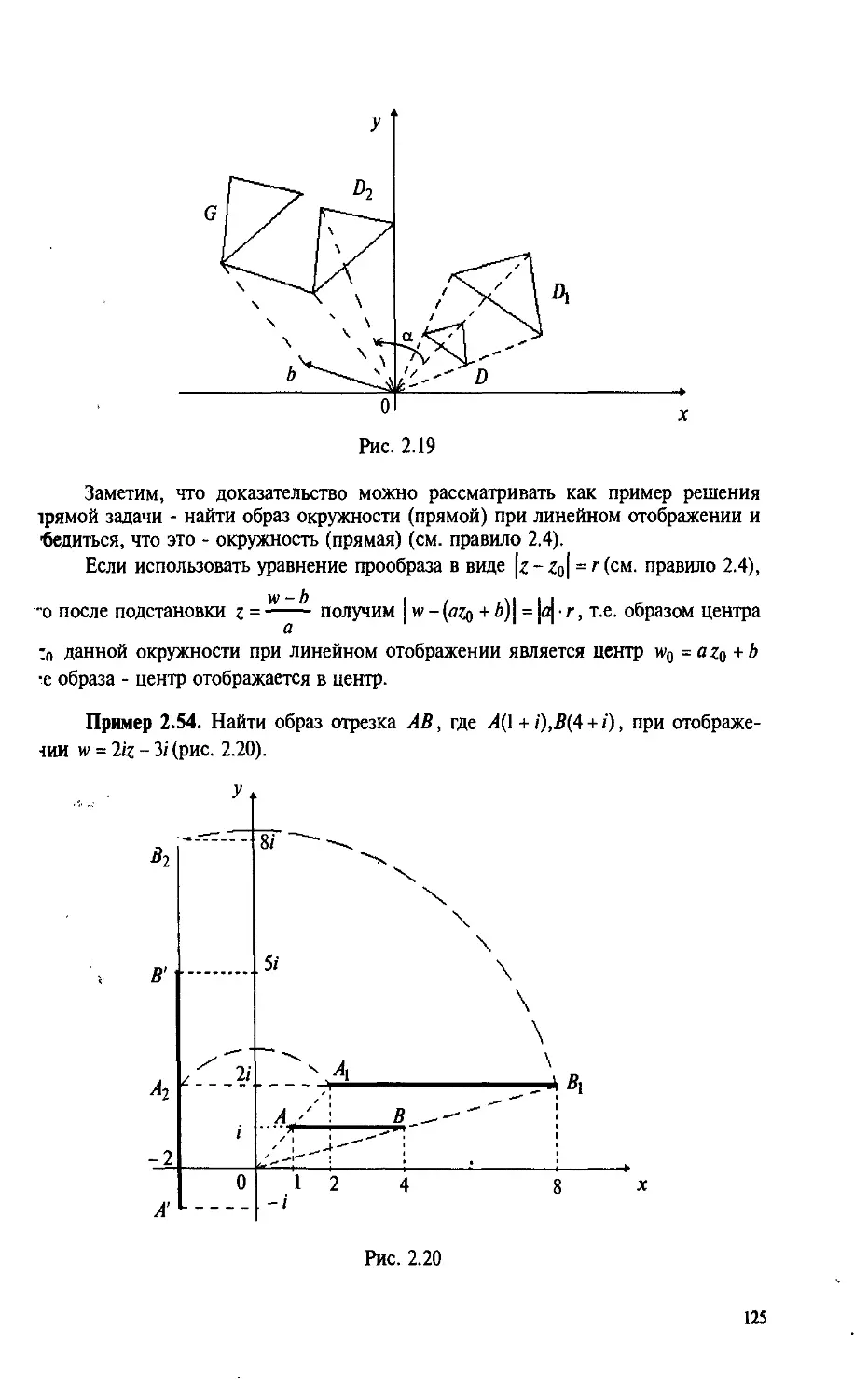
Утверждение 1.1 (теорема Жордана). Простая замкнутая непрерывная кри-
кривая разбивает расширенную комплексную плоскость на две области.
Если граница - ограниченная кривая, то области называются внутренней у.
внешней; внутренняя - та из двух областей, которая не содержит бесконечш
удаленную точку, внешняя - другая область. Так, на рис. 1.12,в область |г| > Р
внешность круга; а множество |г| < R - внутренняя часть круга, или просто круг
Пример 1.32. Определить вид множеств, заданных соотношениями:
а)
1пи<0;
б)
в)
■#-!■
D а) Искомым множеством является пересечение кольца 1 < \z\ < 3 и ни>
ней полуплоскости - нижнее полукольцо (рис. 1.13,а). Это - ограниченная одн<-
связная область.
б) Искомым множеством является пересечение круга \z - /j < 1 и правор
полуплоскости - правый полукруг (рис.1.13,6). Область огоаниченная. опног.ия--
ная.
(г)
Рис. 1.13
1 1
в) Определяем вид границы множеств - линий Im- = —- и |argz| = -r- bTi-
п к
рое равенство определяет два луча argz = — и argz =— и, следовательно, мнь
мую ось. Чтобы определить вид другой линии, запишем уравнение в действь
тельной форме, производя указанные действия с г = х + iy :
1 х- iy
-У
Z xz+y x +y xL+yL Z x +y
Поэтому уравнение Im—= -—, т.е. x2 +y2 =2y, есть уравнение окружно-
окружности x2 +{y-\J =1, а неравенство Im—<— - круг, который можно записан
40
иниче |z - i\ < 1. Ответом является та же область, что и в предыдущем пункте
(рис. 1.13,6). ■
Пример 1.33. Определить вид множеств, заданных неравенствами:
stl 14Г". 7-4>|1П7^11" (II I Kf 7 I f i ' HI (
Imz <2.
a)
>0; б) Re*
в)
□ Для выяснения вида множества в каждом случае сначала определяем вид
Границы:
а) границей множества является линия Re^ + Jm^ = 0, или х + у = 0, т.е.
у - х. Она разбивает плоскость на две полуплоскости - верхнюю (содержит,
например, точку /') и нижнюю (не содержит точку /'). Условию задачи удовле-
удовлетворяет верхняя полуплоскость (рис. 1.14,я). На рисунке указан обход границы и
точки, принадлежащая множеству. Множество, очевидно, является односвязным
и неограниченным;
i
/
-1
I
У
/у
/
/о
/
/
/
/ /
(z)
г х
-1
т,
/о/
-2/
а б в
Рис. 1.14
б) граница области состоит из двух компонент - прямых | Re z \ = 1, т.е.
х - 1 и х = -1. Условие | Rzz \ = \х\ < 1 определяет полосу на плоскости (условию
удовлетворяет, например, точка г = 0). На рис. 1.14,5 указан обход границы.^
Множество является неограниченным односвязным;
в) граница области состоит из отрезков прямых х = ±1 и у = ±2. Контур
прямоугольника, сторонами которого являются эти отрезки, разбивает плоскость
МП дна множества: внутреннюю часть и внешнюю. Условию задачи удовлетворя-
f I Re г | < 1,
ет, например, точка г = 0, поэтому система ^|1__i - описывает внутреннюю
чисть прямоугольника (рис. 1.14,в). ■
Пример 1.34. Записать в виде неравенств множества точек:
а) угла АОВ; б) сектора АОВ, если A^l), В^,-1г\ 0@,0).
□ Чтобы получить неравенства, определяющие эти множества, сначала со-
итиним уравнения, описывающие их границы:
41
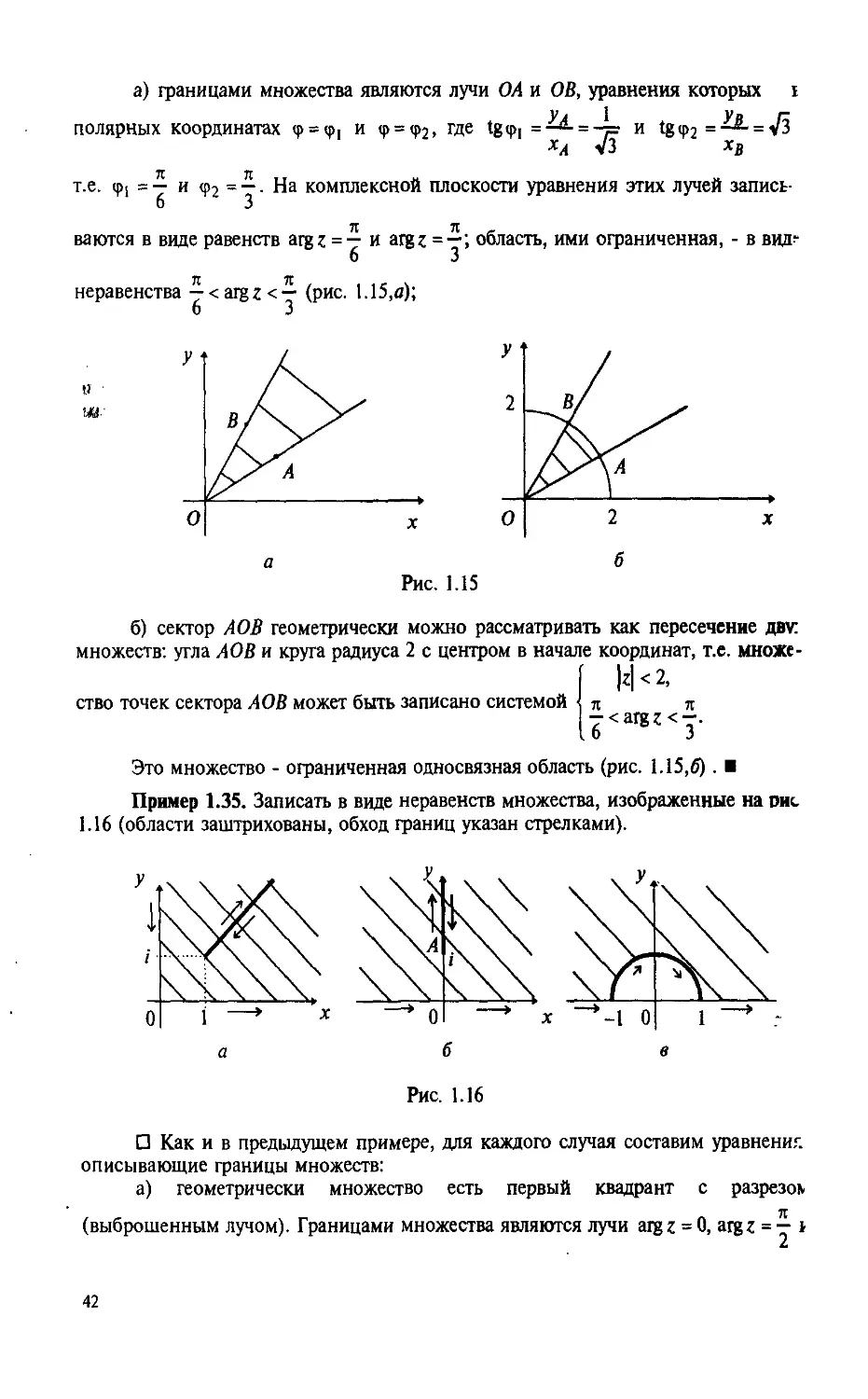
а) границами множества являются лучи ОА и ОВ, уравнения которых i
полярных координатах ф = Ф[ и <p = q>2, где tgtp, =—— = -р и tgq>2 =—— = V3
хл V3 хв
т.е. ф[ = — и ф2 = —. На комплексной плоскости уравнения этих лучей запись-
6 3
я t ,
ваются в виде равенств argz = — и argz =—; область, ими ограниченная, - в вид?
6 3
неравенства -<argz<— (рис. 1.15,д);
6 3
» ■
У 1
О
У 1
2
О
Рис. 1.15
б) сектор АОВ геометрически можно рассматривать как пересечение двг.
множеств: угла АОВ и круга радиуса 2 с центром в начале координат, т.е. множе-
ство точек сектора АОВ может быть записано системой
Это множество - ограниченная односвязная область (рис. 1.15,6). ■
Пример 1.35. Записать в виде неравенств множества, изображенные на ож.
1.16 (области заштрихованы, обход границ указан стрелками).
\
\
\
r
-1
У
\
0
^\
1 ~*
D Как и в предыдущем примере, для каждого случая составим уравнениг.
описывающие границы множеств:
а) геометрически множество есть первый квадрант с разрезок
(выброшенным лучом). Границами множества являются лучи argz = 0, argz =— i
42
луч по биссектрисе от точки A(l,l) в бесконечность. Уравнение этого луча можно
агаг = —,
«писать в виде
\>А.
Следовательно, множество, изображенное на рис. 1.16,д, можно описать
соотношениями: 0<argz<-,argz*- для точек z, у которых ld>V2 или
2 4
п
,i я arg 7 —
2 1Ф
б) геометрически множество есть верхняя полуплоскость с разрезом по лу-
[а =-
чу от точки j4@,1) в бесконечность; уравнение луча: \ ™ 2'
Следовательно, множество, изображенное на рис. 1.16,5, можно описать
соотношениями 1тг>0, zi- ™г~2'
|г| > 1;
в) на рис. 1.16,в изображена верхняя полуплоскость с "выброшенным" по-
полукругом. Точки полукруга описываются системой \ ' ' '
[О < arg z < я.
Следовательно, изображенное множество можно описать соотношениями
1m i > 0, z £ \ ' ' ' или ] ' ' ■
lO<argz<t [Imz>0.
Упражнения
I. Какие из следующих уравнений являются уравнениями:
а) оси Ох; б) оси Оу:
I) г = 0; 2) г + г = 0; 3)г = г; 4) argz = O; 5)
; 7) argz = -^; 8) Re? = 0; 9)
Ответ: а) 3,6,5; б) 2,8,9.
2. Записать в комплексной форме уравнение окружности единичного ра-
радиуса с центром на биссектрисе угла третьей четверти и касающейся осей коор-
ЛИШ1Т.
О/иве/и:|г + 1 + /| = 1.
3. Какое геометрическое место точек плоскости определяется каждым из
следующих соотношений: a) \z - 2| = |г + 4|; б) \z - 2 + /| > 2.
Ответ: а) прямая Rez = -1 (x = -l);
б) внешность круга с центром в точке го B,-1), Л = 2 .
4. Каким из следующих неравенств описывается множество точек нижней
полуплоскости:
43
a) Imz<0; б) -я <aigz <O; в) Re?<0; r) n<argz<2n;
д) Rez>0; e) г<0.
Ответ: а) и б).
5. Описать в виде соотношений множество точек, изобоаженных на пи:
1.17: а) отрезок DC; б) дугу AD.
\
I
\
H
Fy
\
/
\
К
у'
с
л
\м
/2
l ч
/3 х
Рис. 1.17
Рис. 1.18
Ответ: а)
б)
N1 = 2,
6. Какое из множеств точек, изображенных на рис. 1.17, описывается ох-
ним из следующих соотношений:
2<|г|<3,
а)] я б)
--<argz<0;
Ответ: а) сектор АМО; б) часть ABCD кольца.
7. Описать в виде соотношений множества точек, изображенных на ри;.
1.18: а) внутренность полосы; б) отрезок АВ.
(Rez>1,
Ответ: а) \ . . б) <, ,
[ | Im г | < я; [ | Im z | < я.
8. Определить вид множества точек г, удовлетворяющих неравенств1
г + 2
г + 4
Ответ: правая полуплоскость, Re г >-3.
9. Какие из следующих уравнений являются уравнениями оси Ох:
аIшг = 0; б)
=i; в) г-г = 0; г) |г-<| = |
Ответ: все уравнения определяют ось Ох.
10. Какие из следующих уравнений являются уравнениями оси Оу:
a)Rez = 0; 6)|aigz| = i; в) г + г = О ; г) |г-1| = | |
Ответ: все уравнения определяют ось Оу.
44
1.3. ЧИСЛОВЫЕ ПОСЛВДОВАТЕЛЪНОСТИ И РЯДЫ
С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
1.3.1. Последовательности комплексных чисел
Основные понятия, связанные с последовательностями комплексных чи-
чисел, вводятся так же, как в действительной области.
1. Если каждому натуральному числу л (Уле N) поставлено в соответст-
иие комплексное число zn (zn eC), то говорят, что задана последовательность
комплексных чисел (последовательность с комплексными членами): {г„}"=1-
2. Последовательность zn называется ограниченной, если существует число
М >0, такое, что для любого пе N выполняется неравенство |г„| < М. После-
доиательность, не являющаяся ограниченной, называется неограниченной: для
\IM(M eR) Эи°,что |г„о|>М.
3. Последовательность zn называется бесконечно малой, если для любого
числа е > 0 найдется номер Л^е), такой, что для всех л, удовлетворяющих усло-
нию п > N(s), выполняется неравенство |г„| < s:
Zn — бесконечно малая о Ve > 0 3N(e): п > N(e), \zn\ < e .
Правило 1.1. Чтобы по определению доказать, что данная последователь-
последовательность zn является бесконечно малой, следует:
1) записать неравенство |г„| < £, где к - любое, г > 0;
2) решить это неравенство относительно п;
3) из полученного решения и > N(e), определить N(e).
4. Последовательность zn называется бескоиечпо большой, если для любого
числа М (М е R) найдется номер N(M), такой, что для всех л, удовлетворяю-
удовлетворяющих условию n>N(M), выполняется неравенство |г„|>М. Геометрически это
спнпчает, что члены последовательности zn для и > N(M) расположены в окре-
сиюсти бесконечно удаленной точки, в области | z \ > М. »
Из определений бесконечно малой и бесконечно большой последователь-
последовательностей легко установить связь между ними. Если а„ - бесконечно малая после-
последовательность, то zn =— - бесконечно большая, и наоборот, если zn - беско-
нечно большая последовательность, то а„ = бесконечно малая.
5. Число А (А*ю,АеС) называется пределом последовательности zn,
гели последовательность а„ = zn - А является бесконечно малой (обозначается
А - шп г„):
Л-»ос
А= lim Zn <=> Ve>0 M{e):\zn -A\<e для п> N{e).
Из определения получаем правило.
45
Правило 1.2. Чтобы доказать, что заданное число А является пределом
данной последовательности ztt, следует:
1) составить последовательность а„ =zn- А;
2) доказать, что а„ — бесконечно малая последовательность (см. правило
1.1).
6. Последовательность, имеющая предел, называется сходящейся, а после-
последовательность, не имеющая предела, - расходящейся.
Расходящейся последовательностью является любая неограниченная по-
последовательность, в частности бесконечно большая. Для бесконечно большой
последовательности принято обозначение lim zn = <».
И-»оо
Интерпретация комплексных чисел точками сферы Римана придает этому
равенству большую наглядность. Действительно, образами точек последователь-
последовательности zn на сфере Римана являются точки Мп с координатами
? *" „ Уп « №
1+Ы2 1+Ы2 1+Ы2
где xnR 1
Эти соотношения получаются из равенств х = —*—, >" = —^— и уравнения
1-ф 1-ф
сферы 42 + л2 = фA - ф) (см. замечание 1.2). Поскольку \хп \ < |г„ |, \у„ \ £ \zn \, то ус-
условие lim ztt = « означает, что последовательность точек Л/„ сходится к точке N
сферы Римана, так как при этом lim £,„ = 0, lim г\„ = 0, lim ф„ = 1.
Л-»оо Л->00 Л-ЮО
Пример 1.36. Записать пять первых членов последовательностей:
а)гй=(л;б)(оп=A + /Г.
П Подставляя последовательно значения п = 1,...,5, получаем:
а) ^| = /; z-i = -1; г3 = -»; г4 = 1; г$ = /;
б) ш, = 1 +;, <о2 = A + /J = 2/, и3 = A + if = 2/ A +') = -2 + 2/,
<о4 =A + /L =((l + /Jf =B/J =-4, ш5 =(l + /f = A + /LA + /) = -4-4/. ■
Пример 1.37. Исследовать на ограниченность последовательности:
г„= Л »„=(! + ,■)".
□ Так как |г„| = /" = 1, то для любого пе N выполняется, например, не-
неравенство |г„| < 2. По определению последовательность zn =/'" — ограниченная.
Для второй последовательности, используя свойство модуля, находим
|ги| = A + /)"= (|l + /| f = Щ) ■ Далее рассматриваем неравенство (VI)" > М при
любом М и решаем его относительно и: /ilgV2>lgM, л>—-—. В качестве
Ig2
46
/i° можно взять любое N(M) = —-—. По определению
последовательность не-
офнниченная. ■
Пример 1.38. Доказать, что последовательность zn вида zn = q" является
бесконечно малой, если \q\ < 1, и бесконечно большой, если |<?| > 1.
□ Пусть \q\ <1. Воспользуемся правилом 1.1:
1) составляем неравенство |г„| < £, т.е. \q" = \q\" < e ;
2) решаем его относительно п: п>-т-г;
Щ
• 3) обозначив N(e) = -Д^г +1 ([х] - целая часть числа х), получим, что для
[Щ\
п > N(k) выполняется неравенство |г„|<£ для любого е>0. По определению zn
- бесконечно малая последовательность.
Учитывая связь бесконечно малых и бесконечно больших последовательно-
последовательностей, заключаем, что zn - q" при \q\ > 1 является бесконечно большой.
Так, бесконечно малыми являются, например, последовательности:
т) Ш Ш) (t^J ;б~чнобольшими: A+/)й{тгт] •■
Пример 1.39. Применяя определение, доказать, что lim = 1-2/.
я-»» л+ 2
П Используем правило 1.2:
I) составляем последовательность
. n-2ni ... 4;-2
«n=Zn-A, „„=-^--A-2/) =
2) доказываем, что а„- бесконечно малая. Находим |ot_| = "• = .
л+2 л+2
Гик как Пт|аи|=0, то |а„|<£, n>N(e) и, следовательно, ая - бесконечно
милая. ■
Исследование сходимости последовательности комплексных чисел и нахо-
нахождение ее предела (в случае сходимости) можно свести к соответствующей задаче
дли последовательностей с действительными членами. А именно имеет место
следующее утверждение.
Утверждение 1.2. Для сходимости последовательности zn необходимо и дос-
достаточно, чтобы сходились две последовательности Rezn = хп и ImZn= Уп, причем
lim zn = lim Re zn +' Hm Im zn, иначе
H »«i Л-MG И-»оо
lim zn = li
п-
lim xn = а,
= *.
с = а + Ы.
47
Из утверждения 1.2 и свойств сходящихся последовательностей действи-
действительных чисел вытекают следующие свойства последовательностей с комплекс-
комплексными членами. Эти свойства приведем в виде утверждения.
Утверждение 1.3. Если lim zn = a, lim и„ = Ь, то
Л->ао Л-»оо
\\m(zn+un) = a + b; lim zn и„ =ab;
lim ^- = y, ип*0, /1 = 1,2,...; b*0.
П-хх> Un О
Пример 1.40. Вычислить lim .
п-ке / - П
□ Первый способ. Используем утверждение 1.2. Обозначим zn = и
i-л
найдем х„ = Re г„ , у„ = Im zn, выполняя операцию деления комплексных чисел:
2 + Зи/ B + Зл;)(л + ;) -я + /(Зи2 + 2) п ,Зя2+2
i-n -(n-i)(n + i) -(п2 + 1) л2 + 1 л2+Г
Получаем х„=——, уп=—~ -■ Найдем пределы последовательностей
и +1 и +1
действительных чисел:
lim—-^— = 0 ,
1
= 0 , lim = 3,т.е.а = 0, Ь = 3.
п^«>п +1 "->» л +1
Следовательно, lim zn =a + bi = -3/.
Второй способ. Используем утверждение 1.3, применяя соответствуюище
методы, как в действительном анализе. Находим
v 1
,. 2 + Зл/ ,. 3(+л ..
lim = lim т- = -3i,
И->00 i—П П-VD . I
п
так как здесь - и - бесконечно малые. ■
и л
1.3.2. Анализ сходимости рядов с комплексными членами
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Основные понятия, связанные с рядами в комплексной области, вводятся
так же, как в действительной области.
1. Выражение вида Z\ +Z2+--- + Zn +.-., где Z\,Zi,—,zn~- - последователь-
последовательность комплексных чисел, называется числовым рядом с комплексными членами
00
(обозначается ]Гг„).
л=|
48
и
2. Сумма Z\ +Z2 +-.. + £„ = "YjZk называется п-й частичной суммой ряда,
к=\
обозначается Sn\ последовательность SltS2 Sn,... — последовательность час-
частичных сумм ряда.
СО
3. Ряд £ zn называется сходящимся, если сходится последовательность его
я=1
частичных сумм, т.е. существует WmSn. Этот предел называется суммой ряда:
00
S = lim Sn, S - сумма ряда; S - Sn = £ яи+* ~ остаток ряда.
Л->оо Jt = l
00
4. Ряд J]zn называется абсолютно сходящимся, если сходится ряд, состав-
составлю
00 00
ленный из модулей его членов, т.е. ряд ^|zn|. Заметим, что ряд ^\zn\ - ряд
и=1 и=1
с действительными положительными членами.
Ц* ПРИЗНАКИ СХОДИМОСТИ РЯДОВ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
00
Критерий Коши. Дня сходимости ряда ]Г zn необходимо и достаточно, что-
бы для любого е > 0 можно было найти N(e), такое, что для любого n > N(e) и лю-
любого т (натурального) выполнялось неравенство |ги+[ +... + Zn+m\ <e-
00
Необходимый признак сходимости ряда. Если ряд ^Zn сходится, то
Ншг„=0.
й-»со
Отсюда следует, что условие limzn*0 является достаточным условием
Л->оо
»
расходимости ряда £г„.
Исследование сходимости ряда с комплексными членами можно свести к
соответствующей задаче для рядов с действительными членами.
Утверждение 1.4. Дня сходимости ряда с комплексными членами необходимо и
достаточно, чтобы сходились два ряда с действительными членами:
00 00 00 00
*=1 и=1 к=\ л=1
причем
f,Zn=S о !>„=о, ^Уп=Ь,
49
Правило 1.3. Чтобы исследовать ряд на сходимость, необходимо:
00
1) для данного ряда £zn найти Rezn = х„ и Im zn=yn;
Q0 00
2) составить ряды £ х„ и £ Уи и исследовать их на сходимость, как ряды
Л = 1 Л = 1
ОС
с действительными членами. Если оба ряда сходятся, то ряд ^ги сходящийся,
если хотя бы один из рядов ^х„ или ^уп расходится, то ряд ^г„ расходя-
щийся.
Правило 1.4. Чтобы исследовать ряд на абсолютную сходимость, необходи-
необходимо:
1) составить ряд ^|ги|, членами которого являются модули членов дан-
ОС
ного ряда £г„;
я=]
2) исследовать полученный ряд на сходимость, как ряд с действительными
положительными членами. Для этого могут быть использованы признаки сходи-
сходимости таких рядов: признак Даламбера, Коши, признаки сравнения, интеграль-
интегральный признак.
QO 00
Если ряд £|г„| сходится, то ряд £г„ сходится абсолютно.
Если ^|г„| расходится, то ^zn может быть либо расходящимся, либо
сходящимся; в последнем случае он называется условно сходящимся.
Признаки абсолютной сходимости ряда.
А. Признак Даламбера.
Если lim
и-юо
= |^|, \q\ < 1, то ряд £ 1П сходится абсолютно.
Б. Признак Коши.
Если lim <(\zn\ = |?|, \q\ < 1, то ряд £ in сходится абсолютно.
В. Признак сравнения.
00 00
Если \zn\ < \an\ Vn и ряд ^|а„| сходится, то ряд £г„ сходится абсолютно.
л=1 и=1
50
Замечание 1.3. При исследовании на сходимость рядов ]Гг„ , где гп
л=1
дробно-рациональное, или дробно-иррациональное выражение от и, использу-
етея признак сравнения; при этом в качестве ряда ]Га„ выбирается ряд вида
л=1
* 1
£—, который, как доказывается в действительном анализе, сходится при
*»| я"
а > 1 и расходится при а < 1.
Пример 1.41. Исследовать на сходимость ряды; в случае сходимости найти
суммы рядов:
«=1W л=1
D а) Так как \zn\ = \— , то, применяя признак Коши, получаем
lim 4J\zn\ = - < 1, следовательно, ряд сходится абсолютно.
" (О*
Составляем последовательность частичных сумм ряда Sn = ]Г — и обо-
■шачаем q = — . Тогда Sn = 2^q - сумма я членов геометрической прогрессии:
Sn =!Lll— = Л—1—. так как \q\<\, то lim q"*1 =0 (см. пример 1.38) ,
\-q \-q \-q л^«о
поэтому lim Sn =——. Полученный результат можно сформулировать следую-
л-юо \-q
QO СО
щим образом: ряд ^zn вида ^q" при |^| < 1 сходится и сумма его вычисляется
но формуле S = —*—. В данном случае q - —, поэтому S = ^ _
\-q 2 -.-»-•
б) Используем правило 1.3:
1) из zn - — +i— имеем х„ =—,у„ = —;
00 СО
2) составляем ряды ^]хл = £ - и ^Уп - X ~ • ^яды сходятся, как
л=1 fl=lV3/ л=1 л=Л2/
у 1 У)
ряды вида 2] ^", |^| < 1, и их суммы равны S\ •= •: . = —, S^- ., = 1 • Сум-
Суммой данного ряда является число S = 5j +1 ^ = — +1. ■
51
Пример 1.42. Исследовать на сходимость ряды:
а) У —; б) У =-.
D Для этих рядов нахождение хп и у„ затруднительно, поэтому будем
пользоваться другими признаками:
а) здесь lim zn= — * 0, ряд расходится, так как не выполняется необходи-
л-юо 2/
мый признак сходимости;
б) для этого ряда lim zn = 0, необходимый признак выполняется, но в силу
Л-ЮО
его недостаточности требуется дальнейшее исследование. Воспользуемся замеча-
замечанием 1.3. Применим признак сравнения с рядом У—г:
п=1 Я
lim —f- = lim
Л-»со
я4+3я3/-я2
«4-я2+Зш3
= lim ■
1
/V
По признаку сравнения ряд сходится абсолютно. ■
Пример 1.43. Доказать, что сходится абсолютно ряд
D Используя признак Даламбера, рассмотрим lim
lim
(я + 1)! B/)"
= lim
2/
я + 1
= lim —=— = 0 < 1.
Я->оо Я + 1
Так как lim
< 1, то ряд сходится абсолютно.
Заметим, что сходится абсолютно любой ряд вида £ —, где z — любое
комплексное число. ■
СВОЙСТВА АБСОЛЮТНО СХОДЯЩИХСЯ РЯДОВ
Как и в действительной области, для абсолютно сходящихся рядов с ком-
комплексными членами справедливы те же правила действий, что и с конечными
суммами.
1. В абсолютно сходящихся рядах допустима любая перестановка и группи-
группировка членов (даже бесконечного их числа).
52
Например, если ряд £г„ сходится абсолютно, то сходятся и ряды,
я=1
00 00
полученные группировкой членов этого ряда, например ]Гг2п и У^2П-1 — ря-
я=1 я=1
ос оо оо
ды членов с четными и нечетными номерами, причем £г„ = Y.z2n-i + £г2л •
п--\ n=t л=1
2. Абсолютно сходящиеся ряды можно перемножать по правилу перемно-
перемножения многочленов.
оо _ Я оо ^ Я
Пример 1.44. Найти произведение рядов У— и У-^--
я=1 nl я=1 я!
00 _Л
D Как отмечено в примере 1.43, ряды вида Yj— абсолютно сходятся при
любом фиксированном z ■ Поэтому сомножителями являются абсолютно схо-
сходящиеся ряды. Перемножим их по правилу перемножения многочленов:
Z|+ 2! +"+(п-кI+"+ п\ '
Перепишем последнее выражение следующим образом:
Общий член этого ряда имеет вид — 'УСп*-\"~к%г > ши> согласно формуле
«!*to
бинома Ньютона, —(z\ +ггГ- Таким образом, окончательно получаем
и!
_ я=л Я-
Упражнения
1. Какие из следующих утверждений справедливы для последовательности
а) ограничена; б) сходится; в) lim in = 0; г) не ограничена;
Я-»оо
д) lim zn = 1 + i', e) расходится; ж) бесконечно большая.
Л-»°°
Ответ: г), е).
2. Вычислить lim zn '■
Ответ: а) 1; б) cos 1 +1sin 1 или е(.
3. Какие из следующих утверждений справедливы для последовательности
'"•
а) ограничена; б) сходится; в) lim zn = 1; г) не ограничена;
Л-ЮО
д) бесконечно малая; е) расходится; ж) бесконечно большая.
Ответ: а), е).
. „ • 1-ш
4. Вычислить lim in, если zn = .
л-юо 1 + in
Ответ: -1.
5. Исследовать сходимость рядов:
00 1 СО 1
а) 2-~г Г> "' 2j 7 ТР'
V ()
Ответ: а) расходится; б) сходится абсолютно.
6. Доказать, что последовательность zn = i—L— ограничена, но расхо-
расходится.
( 9 VV
7. Найти Rec, где а= lim 1+ .
Ответ: е1 cos3.
8. Исследовать на сходимость ряды:
. 2,( . 1 .2"
а) £ sin —+ 1—
„tit я п
Ответ: а) расходится; б) сходится условно.
00 И °° ffl
9. Доказать абсолютную сходимость рядов V , У——.
.„ о „ . ,. ( . 1 .2я + П ,. .. f . . 2 fl + i
10. Найти пределы: a) lim и sin—+1 ; б) lim nisin— +
^ И П ) 1 П \ П
+1; б) lim nisin +
И П ) л->«1 П \ П )
Ответ: а) 1 + 2/; б) 2/.
11. Исследовать на сходимость рады: ,,
л=1 1- я=1 J
Ответ: а) расходится; б) сходится абсолютно.
1
12. Найти сумму ряда У
„to B - 3i)"
г, с
Ответ: S =
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Зшисать в алгебраической форме число z , если z - \ ~—: | •
L 1 X I ,
2. Даны комплексные числа ц =' • е 5 и z2 - е 5 • Какие из следующих
равенств верны:
a) arg^i г2) = 0; б) ln|zi| = arg*2; в) arg?,2 =2arg?2;
=1; д) arg^i2 =5argz2-
Л-
3. Даны комплексные числа t\ = 2/ • е 5 , ?2 = « -'' ■ Найти
г) —
4. Записать в показательной форме комплексные числа
.± . п . . п »
1\ =1+1, Zi =COS- + lSin-.
11.
5. Найти |?i ■ Z2| и arg—, если z\ = 2i • e 5 , z2 = " ~' •
?2
6. Найти модуль и аргумент комплексного числа A + /'г(«3 - ij .
7. Сколько корней уравнения г8 +1 = 0 расположены в верхней полуплос-
полуплоскости? Выпишите эти корни.
8. Описать в виде соотношений множества точек, принадлежащих:
а) дуге DE; б) отрезку GH на рис. 1.17.
9- Какие из множеств, изображенных на рис. 1.17, описываются одним из
следующих соотношений:
55
jlarsz|<^;
10. Записать в виде неравенств множество точек, принадлежащих кольцу
с центром в точке (-1,2), границы которого касаются осей координат.
11. Каким из следующих неравенств описывается множество точек правой
полуплоскости:
a)|argz|<-; 6)argz<-; в) Rez>0; r)Imz>0;
:-; е) 0 <argz< n.
1
12. Вычислить lim — -е
13. Вычислить lim nsin —+ » 1 + —
14. Какие из следующих утверждений справедливы для последовательности
а) офаничена; б) сходится; в) lim zn = 1 -1; г) не ограничена;
д) lim zn = 1 + i; e) расходится; ж) бесконечно большая.
=0 2" - 5" 1
15. Для ряда ^ укажите все верные утверждения:
а) ряд сходится, так как сходится ряд
б) рад сходится, так как сходятся ряды ]ГКег„,
в) ряд сходится абсолютно;
г) сумма ряда равна — 2/;
4
д) сумма рада равна - - i.
4
56
Глава 2. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
2.1. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО
2.1.1. Основные определения
Основные понятия, связанные с функцией комплексного переменного,
вводятся так же, как и в действительной области.
Пусть заданы два множества D и G комплексных чисел.
1. Если каждому значению z e D ставится в соответствие число и> е G, то
творят, что на множестве D задана функция w = f(z) комплексного переменно-
переменного, т.е.
/: V? б Д DcC ->• wsG, G с С о и> = f(z).
Если записать числа z и w в алгебраической форме: z = х + iy , w = u + iv ,
го замечаем, что действителъпая и = Re f(z) и мнимая v = Im/(z) части функ-
функции f(z) являются функциями переменных х и у: и = и(х,у) и v = v(x,y).
Задание функции w = f(z), ze. D эквивалентно заданию на множестве D
яиух функций и = и(х,у), v = v(x,y) двух действительных переменных.
Кроме того, если для числа и> записать модуль |w| = su2 + v2 и аргумент
argw = ф, tg(p = — для ифО и ф = ±— при и = 0 ( <р = — при v>0 и <р = — при
и 2 2 2
v < 0 ), то получим аналогичное утверждение. Задание функции комплексного
переменного w = /(г) равносильно заданию двух функций двух действительных
переменных. Первая из функций определяет модуль функции: |/(г)| = F(x, у) =
Ju2(x,y) + v2(x,y), вторая - аргумент функции: arg f(z) = Ф(х, у), где
v(x v) 7t
щФ(х,у)- в точках, в которых u(x,y)*Q; Ф(х,у) = — при
и(х,у) 2
и(х,у) = 0, v(x,у) >0 и Ф(х,у) = — при и(х,у) = 0, v(x,y)<0.
Пример 2.1. Найти значение функции f(z) = it2 - Z в точках Zi = 1 +' и
*2=2f.
2A-') = '-2/-1 + i = -3 + i ;
=.- • B/J -(-2/) = -4i + 2/ = -2;. ■
Пример 2.2. Найти Re/(г), 1т/(г) , если а) /(г) = г2;б)
D a) z2=(x + iyJ=x2-y2+i2xy, Rt f(z) = х2 - у2, lmf(z) = 2xy;
57
6)
z-i
г + 2
x + iy-i _ x + i(y -1)
x + iy + 2 (x
)- xy]
т.е. Re f(z) =
x2 + y2 + 2x - у
(x + 2J+y2
(x + 2J+y2
2y-x-2
2J+y2
2. Задание функции комплексного переменного f{z) с областью определе-
определения D и областью значений G есть отображение множества D на множество G,
f: D-> G (рис. 2.1).
Рис. 2.1
Точка w е G называется образом точки z при отображении w = /(г), точка
Z е D - прообразом.
По определению предполагается однозначность отображения, т.е. каждому
числу z e D соответствует единственное значение w e G, но при этом может
оказаться, что точка w является образом двух или более точек z б D (на рис. 2.1
это точка и>0, так как w0 = f(Z\) и и>0 = /(г2)).
Если любое значение weG является образом только одной точки z&D,
то отображение называется однолистным в Д в противном случае - неоднолист-
неоднолистным. Из определения следует, что однолистное отображение является взаимно
однозначным отображением.
Простейшими однолистными (во всей комплексной плоскости) отображе-
отображениями являются отображения и> = z, w = z. Первое отображает любую область, в
том числе и всю комплексную плоскость, на себя, второе - верхнюю полуплос-
полуплоскость на нижнюю, а нижнюю на верхнюю.
Примером неоднолистного в С отображения является w = z2 ■ Действитель-
Действительно, различным точкам, например z\ = 1 и Zi = -1, соответствует одно значение
и> = 1, а точкам ± i - одно значение w = -1. Неоднолистным отображением яв-
является и w = z" ■ Каждой точке w, w *■ 0, w *■ оо, соответствуют я значений
Zk, к = 0,1,...,п-1. В силу этого отображение
н -листным, а отображение w = z2 - двулистным.
= z" при я>1 называют
58
Из определения получаем и условие однолистности отображения, отобра-
отображение является однолистным на множестве D, если для любых точек Z\ и гг,
принадлежащих D , равенство f(Z\) = f(Zi) выполняется тогда и только тогда,
когда Z\ = Zi • Иначе: отображение однолистно на множестве D, если множество
не содержит ни одной пары чисел Z\ и Zi, таких, что Z\ *■ Zi и выполняется ус-
ЛО11ИС f() f)
Пример 2.3. Найти область однолистности функции w = z2 ■
D Во всей комплексной плоскости отображение не является однолистным.
Но можно найти множество, где условие однолистности будет выполняться, т.е.
множество, которое не содержит двух различных точек z\ и Zi, для которых
Рассмотрим две произвольные точки г, и zi и разность значений функции
й них: и>! -и>2 = Z2-Ii =(Z\ -Z2)(Z\ +1г)- При Z\*Z2 равенство wt=w2 вы-
выполняется, если Z\ + Zi = 0 • Таким образом, отображение w = z2 будет однолист-
однолистным в любой области, в которой не лежат одновременно две точки Z\ и г.г, гн ■
;ие, что г2 = -Z\ ■ Эти точки нужно расположить на границе области. Так как
■кшшнному условию удовлетворяют точки, симметрично расположенные относк-
■ельно начала координат, то в качестве границы можно выбрать любую прямую,
доходящую через z = 0.
Отображение однолистно в любой полуплоскости, границей которой явля-
является прямая, проходящая через начало координат, например Im z > 0 или
ш z < 0. При этом каждую такую полуплоскость w = z2 отображает на всю
1ЛОСКОСТЬ.
Рассмотрим подробнее отображение области Imz >0. На границе выберем
"очки Л(—1,0), 0@,0), 5A,0) (рис. 2.2,с), а обход границы в направлении от А
; В . Образами точек А и В на плоскости w является одна точка w = 1 (рис.
~..2,б). При этом и левая, и правая полуоси действительной оси отображаются в
действительную положительную полуось. Любая область D, принадлежащая
юрхней полуплоскости, взаимно однозначно отображается на соответствующую
.юласть G. '
(и-)
Рис. 2.2
59
Взаимная однозначность отображения нарушается на границе. Чтобы ото-
отображение было взаимно однозначным (однолистным) и на границе, сделаем
"разрез" действительной положительной полуоси. Будем считать, что эта полуось
состоит из двух "частей" - верхнего "берега" и нижнего "берега" (рис. 2.2,6).
Полуось как граница пробегается точкой дважды, скачала по нижнему "берету" в
направлении от точки А к О, потом по верхнему - от О к В.
Функция w = z1 взаимно однозначно отображает верхнюю полуплоскость
на плоскость с разрезом по действительной положительной полуоси.
Также на всю плоскость с разрезом по действительной положительной
полуоси функция и> = z2 отображает и нижнюю полуплоскость (на рис. 2.2,с
обход от В к А), только при этом образом точки В будет точка нижнего "берега"
разреза (Л на рис. 2.2,6). Заметим также, что правая (Rez > 0) и левая (Re? < 0)
полуплоскости переходят при отображении и> = z2 в плоскость с разрезом по от-
отрицательной действительной полуоси.
В силу указанной особенности отображение является двулистным в D. ■
Пример 2.4. Исследовать на однолистность отображения:
a) w = az + b, a * 0;
6) w = — ;
z
D а) Отображение однолистно во всей комплексной плоскости, так как
для tV[ = az\ + b и и>2 = azi + b равенство wx - щ = 0 выполняется тогда и только
тогда, когда ц = z2 ■
б) При z * 0 для Wj = — и и>2 = — имеем w\ - щ - ~—~ • Поэтому для
любых Z\ и ?2 ПРИ *i * *2 получаем и^ * w2 и wl ф и>2 только при условии
Z\ *Zi- Отображение однолистно всюду в С (г * 0).
в) Во всей плоскости отображение не является однолистным, так как, на-
пример, для точек z\ и ц - Z\ ■ е " значения функции совпадают: и>, = г," и
w2=Zlnl.
Однолистным отображение будет в любой области, принадлежащей углу
раствора — с вершиной в начале координат. Каждый такой угол функция
л
w = z" отображает на всю плоскость с разрезом по лучу [0,а>), в частности по
действительной положительной полуоси (рис. 2.3).в
(Z)
(w)
Рис. 2.3
60
3. Понятие обратной функции для функции комплексного переменного
инодится, как и в действительной области.
Пусть задана функция w = f(z), f:D-*G. Тогда по определению любому
числу w из области G соответствует одно или несколько значений z из области
/) тпких, что f(z)= w, т.е. для любого weG уравнение f(z)= w имеет решения
и области D. В таком случае говорят, что уравнение f(z) = w определяет функ-
функцию i = /"'(w) , обратную функции w = /(г).
Существование функции, согласно определению, предполагает ее одно-
однотипность, т.е. для случая обратной функции - это единственность решения
уршшения f(z)=w при всяком фиксированном w из G. Очевидно, в общем
случае уравнение определяет неоднозначную функцию.
Достаточным условием однозначности обратной функции является одно-
однолистность функции f(z).
Пример 2.5. Найти функции, обратные к следующим однолистным функ-
функциям: a) w = a-z + b, a*0; 6)w=—, fl*0; b)w = z-
Z
wj А
D а) Из равенства w = az + b получаем z = , или z = aiw + b\. Обратная
а
к линейной функции также является линейной, однозначной. Линейная функ-
функции взаимно однозначно отображает комплексную плоскость на себя: С -*С.
Ьсли положить Цда) = да, то можно говорить о взаимно однозначном отображе-
отображении расширенной плоскости на себя: С -+С.
б) Из w = ~, а* О, получаем г = —. Функция сама себе обратная, одно-
Z w
ишчная; осуществляет взаимно однозначное соответствие плоскости с выбро-
выброшенной точкой z = 0 на всю комплексную плоскость. Если положить w@) = оо, а
tv(oo) = 0, то получим отображение /: С -> С.
в) Отображение w = г, очевидно, однолистное, так как из wj - w2 = Z\ - ?2>
или иначе w, - w2 = z\ ~Zi , получаем, что для любых значений Z\ и Zi, Z\ * Z2
шичения функции не совпадают, т.е. w, * w2. Функция z = v>, обратная к функ-
функции w-z, является однозначной.
4. Функции, обратные к неоднолистным. Выделение однозначных ветвей.
С неоднозначными функциями приходится встречаться в математическом
ннализе. Например, уравнение х2 + у1 = 1 на множестве jjcj < I определяет дву-
шачную функцию у = ±vl -х2, точнее, две функции: у = \1-х2 и у = -vl -х2 .
Геометрически - это две части окружности, верхняя и нижняя полуокружности.
)ти функции можно назвать двумя однозначными ветвями функции, определяе-
определяемой неявно уравнением х2 + у2 = 1. Отделение этих функций - выделение одно-
ншчных ветвей - здесь не представляет затруднений. Говоря о верхней полуок-
полуокружности, подразумеваем то решение уравнения х2 + у2 = 1, где у > 0, поэтому
нетвь у = \\-х2 можно выделить, задавая значения функции во внутренней
61
точке промежутка |х| < 1, например yifi) = 1; говоря о нижней, можем задаъ
Аналогично в комплексной области предполагаем однозначность функцик
однако термин "функция" применяем и к случаю неоднозначных отображений.
Примерами неоднозначных отображений являются функции, обратны?
к неоднолистным. Например, функция w = уг, обратная к функции w = z2,
неоднозначная.
Вопрос о возможности выделения в соответствующих областях однозна1-
ных ветвей - однозначных, непрерывных функций и построении таких функцир
связан с исследованием простейшей многозначной функции w = Argz.
5. Функция w = Argz является многозначной, что следует из способа вве-
введения полярных координат, а именно аргумент числа z (z * 0) определяете;,
с точностью до слагаемого, кратного 2я.
При перемещении любой точки z(z * 0) по произвольной непрерывной
кривой аргумент числа z непрерывно изменяется. При этом, если кривая зам:-
нутая, то возможны два случая. В одном случае точка после обхода возвращается
в исходное положение с прежним значением аргумента. Так будет для любо»
кривой, не совершающей обхода вокруг начала координат (рис. 2.4,й). В друго\
случае аргумент изменяется на 2я или (- 2я) в зависимости от направления об-
обхода, а при я-кратном обходе - на 2kn, k = n или к = -п. Это имеет месте
в случае, когда точка при перемещении обходит начало коошинат (пис. 2.4.6.
Рис. 2.4
Аргумент как функция точки будет однозначной функцией в области, ю-
торая не содержит кривых, совершающих обход точки z = 0. В качестве таког
области можно взять плоскость с разрезом по любому лучу, выходящему из нь
чала координат, в частности, с разрезом по действительной отрицательной
оси - область £>2> -t < arg? < я; можно выбрать разрез по действительной
62
«итсльной полуоси - область Dx, где главное значение аргумента определяется
«рпвенством 0 < arg г < 2л (рис. 2.5). Заметим, что аргументы числа, геометри-
■ееки соответствующего одной и той же точке областей D\ и D2 могут быть раз-
1ичны. Напоимео. в области £>(: arg(-/) =— , а в области D2: arg(— i) = —.
+ /
(z)
1!
Я.
:0
<argz<
У
0
2л
(z)
<—
-i
D2: - ж < arg z < я
Рис. 2.5
Границами каждой из областей £>) и £>2 являются два "берега" соответст-
чуюшей полуоси, обход границ на рисунках указан стрелками.
Пример 2.6. Исследовать возможность выделения однозначных ветвей не-
щножачной, функции w = Jz.
О Функция является неоднозначной как обратная к неоднолистной w = г2.
!е неоднозначность (двузначность), согласно правилу извлечения корня, связана
/ 2Sit)
■ Неоднозначностью аргумента: 4z = у |г| • е *■ 2 ', к = 0,1.
Для каждого г(г*О) получаем два значения w, для одного из которых
arg г are z n
imci'm argw, = , для другого argw2 = +n. При этом в силу равенства
'"
-I эти значения функции отличаются только знаком,
= W[ • e , т.е.
*j -w,. Например, значению z = -1 (точка С в плоскости г на рис. 2.6 и 2.7)
•ответствуют два значения w: w = i и w = -j (точки С в плоскости w на рис.
.(> и 2.7).
В плоскости с разрезом по лучу [0,°о) (£>, на рис. 2.5) возможно выделение
^позначных ветвей аргумента. Можно рассмотреть две функции:
г 2 и w = \JIJ= J\z\ • е ^ 2 , 0 < arg z < 2л.
Первая из них переводит область Z), - плоскость с разрезом - в область G,,
де lmiv>0 (на рис. 2.6 точка С принадлежит области Gt), так как для
arg z
щи>= —г— имеем неравенство 0<argw<%.
Положительный обход границ указан стрелками. В точках границы области
J, однозначность нарушается, но в силу сделанного разреза действительные по-
63
ложительные значения (z = х, х > 0) рассматриваются дважды: на верхнем
"берегу" и на нижнем "берегу". Например, при z = 1 это точки А - верхнего
"берега" и В - нижнего, а при z = 2 точки Е - верхнего "берега" и F - нижнего
(рис. 2.6). При отображении w = {Jzj] точкам верхнего "берега" соответствуют
положительные значения уг (точки А и Е), а точкам нижнего - отрицательные
(точки В и F).
-1 О
(Z)
F В
В F
-V2-1
(w)
А Е
О 1 42
Рис. 2.6
Вторая функция \<JzJ2 переводит область D^ - плоскость с разрезом [0,°о)
на нижнюю полуплоскость lmw<0 (рис. 2.7), так как для argw= + % им<*-
ем неравенство п < arg w < 2%. На рис. 2.7 точка С принадлежит области 6.
-1
(Z)
в
-1 *~
-'■
0
с
(и>
А
1
G2
Рис. 2.7
Граничным точкам верхнего "берега" соответствуют отрицательные значениг
4z (точка В), а точкам нижнего "берега" - положительные (точка А). ■
Из приведенных рассуждений сформулируем следующее утверждение.
Утверждение 2.1. Двузначная функция уг отображает плоскость с разрезал
по действительной положительной полуоси (область D) на верхнюю полуплоскост*
64
(область G\) и нижнюю (область G2). В области D возможно выделение однознач-
однозначных ветвей - двух однозначных функций, одна из которых отображает D на G{,
другая - D на G2. Однозначное отображение всей плоскости (z * 0) 0 < \z\ < да
невозможно.
Замечание 2.1. Проведение разреза в плоскости позволило получить
однозначные функции, с которыми можно производить обычные операции
(нахождение значений функции, дифференцирование, интегрирование). Указа-
Указание определенной ветви осуществляется заданием функции в некоторой точке
области. Например, при задании условия V-T = / рассматривается ветвь (yzji;
при условии V-T = -i - ветвь \4zJ(на рис. 2.6 и 2.7 точка С ). Но, с другой
стороны, проведение разреза нарушило непрерывность отображения. Нарушен-
Нарушенную непрерывность можно восстановить следующим образом. На основе приве-
приведенных рассуждений имеем, что значения (yzji на верхнем "берегу" границы
области D совпадают со значением функции [fzJ на нижнем "берегу" той же
области, и наоборот (точки А и В на рис. 2.6 и 2.7). Поэтому можно построить
следующую модель.
Возьмем два экземпляра (листа) плоскости D (плоскость с разрезом), а
именно £>, и D2, и "склеим" верхний "берег" разреза Dx с нижним для D2, a
нижний D2 - с верхним для Dx. В плоскости (w) при этом получим полную
плоскость С. Построенная модель называется римановой поверхностью функции
Если в плоскости (z) точка описывает простую замкнутую кривую, обходя
начало координат, то в плоскости (w) ей будет соответствовать кривая, совер-
совершающая дважды обход вокруг w = 0, а на римановой поверхности - простая кри-
кривая, по которой точка, взятая, например, на первом листе, перемещается по это-
этому листу, потом по второму и возвращается в исходное положение, совершив
один обход. Непрерывность и однозначность отображения соблюдены.
Точка го = 0, при обходе вокруг которой по замкнутой кривой точка пере-
переходит с одного листа на другой, называется точкой ветвления уг • Также точкой
ветвления 4z является точка z = да. '
Утверждение 2.2. Функция w = z2 взаимно однозначно и непрерывно отобра-
отображает полную плоскость (г * 0, z * да) на риманову поверхность этой функции.
Обратная функция z = vw также взаимно однозначно и непрерывно отображает
риманову поверхность функции w = г на полную плоскость (z *■ 0, z * да)-
Аналогично можно исследовать я -листную функцию w = г" и обратную
к ней w = <fz ■
6. Число А (А £ С) называется пределом функции f(z) в точке го, если
для любого числа е > 0 найдется число 8(е) такое, что для z, удовлетворяющих
неравенству 0 < |г - го| < 8(е) , выполняется неравенство | /(г) - А | < в :
3 Пантелеев А.В., Якимова А.С.
lim f(z) = А о Ve>0 35(Е):|/(г)-Л|<Е для zeOs(z0), z*Zo-
г-»гь
Геометрически это означает, что для точек из проколотой 8-окрестности
точки Zo(zeOb(zo),z *Zo) соответствующие значения функции принадлежат е-
окрестности точки A (f(z) e Ог(А)).
Напомним (см. разд. 1.3), что окрестность точки на комплексной плоско-
плоскости - это круг с центром в этой точке. Так, OZ(A) или | /(г) - А \ < е есть крут ра-
радиуса е с центром в точке А, а проколотая окрестность точки г0: 05(го), z*Zq
или 0S(го) \ Zq , или 0 < \z -Zo\ < 8 - крут радиуса 8 с центром в точке го за ис-
исключением точки го ■
Если записать числа в алгебраической форме, то нетрудно доказать спра-
справедливость следующего утверждения.
Утверждение 2.3 (необходимое и достаточное условие существования пре-
предела функции комплексного переменного).
Для того чтобы в точке zq существовал предел функции f(z), необходимо и
достаточно, чтобы в точке (хо,,уо), го = хо + Щ существовали пределы двух функ-
функций действительных переменных и(х, у), v(x, у), где и = Re /(г), v = Im /(г); при
этом имеет место равенство
lim /(г)= lim u(x,y) + i lim v(x,.y), /(x, у) = и + iv, го =*о+'>о •
Иначе:
3lim f{z) = A о 31im Яе/(г) = ЯеЛ, 3lim
г-»го г->гь г-»го
Замечания 2.2.
1. Из сформулированного критерия следует, что в комплексной области
имеют место правила и свойства пределов такие же, как и в действительной об-
области (за исключением, разумеется, свойств, связанных со знаками неравенств).
Например, Нт(с1/,(г) + с2/2(г)) = с, lim f\(z) + c2 lim /2(г) (при условии,
г-»го г->го г-»го
что существуют пределы в правой части равенства ).
2. Можно определить понятие предела функции в точке, рассматривая не
всю окрестность этой точки, а только некоторое связное множество точек из
этой окрестности - предельный переход по множеству:
lim =ЛоУе>0 38(Е):|/(г)-Л|<Е для г £ {^П05(г0)\го} •
Здесь точки г принадлежат пересечению множества М и проколотой окре-
окрестности точки го • В частности, это имеет место, если М - множество точек кри-
кривой, или U - замкнутое множество М = /). Так, на рис. 2.8,а множество М -
кривая /, функция /(г) определена на / и {М П О8(г0) \ го} - дута АВ, за исклю-
исключением точки го- На рис. 2.8,5 множество М- множество D = DuC, функция
определена в области D (или D), {МC\Os(zo)\zo} - заштрихованная часть об-
области D.
66
7 /
Рис. 2.8
7. Функция называется непрерывной в точке Zo, если бесконечно малому
приращению аргумента в точке соответствует бесконечно малое в этой точке
приращение функции, т.е. lim (f(zn + А г) - f(Zn)) = 0.
дг-»0
Это эквивалентно следующему определению: функция f(z) непрерывна
* точке ю, если предел функции в точке равен ее значению в этой точке, т.е.
Ит/(г) =/(го).
г ->4)
Так как понятие непрерывности определяется через понятие предела, то,
учитывая сформулированный выше критерий существования предела функции
(утверждение 2.3), нетрудно убедиться в справедливости следующего утвержде-
утверждения.
Утверждение 2.4 (необходимое и достаточное условие непрерывности
функции в точке).
Для того чтобы функция f(z) была непрерывна в точке z§, необходимо т
достаточно, чтобы в точке (*о>.Уо)> (Zo=xo+')'o) были непрерывны функции
и - и(х, у), v = v(x, у), где и = Re f(z), v = Im f(z).
Функция, непрерывная в каждой точке области D , называется непрерывной
в этой области.
Замечание 2.3. Как и в действительной области, справедливы свойст-
свойства непрерывности в точке для суммы, произведения, частного двух функций, а
также свойство непрерывности сложной функции.
Пример 2.7. Исследовать функцию w = z" на непрерывность.
D Функция w = z, очевидно, непрерывна во всей комплексной плоскости.
Поэтому непрерывными во всей плоскости являются функции w = z" при любом
я , согласно свойству непрерывности произведения. ■
67
Пример 2.8. Исследовать на непрерывность многочлен я-й степени
= anz" +an,lz"~l +...+ alz + a0 - где ак (к = 0,1,...,я) - любые комплексные
числа.
D Функция w = c (c = const), очевидно, непрерывна во всей комплексной
плоскости. Поэтому, учитывая непрерывность суммы и произведения непрерыв-
непрерывных функций и результат примера 2.7, заключаем, что многочлен
P{z) = anz" +an_xzn~x +...+ ajz + OQ есть функция, непрерывная во всей комплекс-
комплексной плоскости. ■
Пример 2.9. Исследовать на непрерывность рациональную функцию
P(z)
R(z) = —^ , где P(z) и Q(z) - многочлены.
Q(z)
P(z)
О Согласно замечанию 2.3 рациональная функция R(z) = —— непрерывна
Q(z)
во всей комплексной плоскости, за исключением точек, где Q(z) = О.и
Пример 2.10. Исследовать на непрерывность функции z, \z\, Re z, Ini z ■
О Функции z, \z\, Re z, 1гл z непрерывны во всей комплексной плоскости
(всюду в С), что нетрудно установить, используя утверждение 2.4. ■
Пример 2.11. Исследовать на непрерывность функции и ——.
2г -1 z +1
D Функция непрерывна всюду в С, за исключением точки -, а
2г-1 . ^
функция — за исключением точек i и-i. Этот вывод следует из решения
г2 + 1
примера 2.9. ■
Пример 2.12. Найти пределы: Шп , lim ——, lim ——.
г->1 2г -1 i-*i 2z -1 г-»' z +1
D В первых двух случаях в силу непрерывности функций в предельных
,. г2+1 1 + 1 „ ,. z2 + l -1 + 1 „
точках получаем lim = = 2; hm = = 0.
г-и2г-1 2-1-1 z-*>2z-\ 2/-1
z + l .
Так как функция f(z) = является бесконечно малой в точке /, то об-
2г-1
ратная ей дробь - функция = —— бесконечно большая в этой точке. По-
f(z) z2 +1
,. 2г-1
этому hm —— = да .■
г-*' z + 1
68
8. Производная функции комплексного переменного в точке го е С вводит-
вводится так же, как и в действительной области, а именно
fiZo)= lim /ta+AO-/ta)tHmп)= lim a/Uo). B.0
1 ;;■"' Аг-+о Дг <и-»о дг
Здесь Д г стремится к нулю по любой кривой, по любому направлению.
Функция, имеющая производную в точке, называется дифференцируемой
# лпой точке, функция, дифференцируемая в каждой точке области, называется
дифференцируемой в области.
Из равенства B.1) и свойств пределов получаем, что приращение диффе-
дифференцируемой в точке функции можно записать в виде
где а(го,Лг) - бесконечно малая при Дг -> 0.
Очевидно, справедливо и обратное утверждение. Поэтому равенство B.2)
ннляется необходимым и достаточным условием дифференцируемости функции
и точке го.
Кроме того, из равенства B.2) следует, что непрерывность функции в точке
является необходимым условием дифференцируемости ее в этой точке, т.е. если
функция дифференцируема в точке, то она непрерывна в этой точке.
Упражнения
1. Найти Re/(г), 1ш/(г), если /(г) = г2 + iz.
Ответ: Re /(г) = х2 - у2 + у, Im /(г) = 2ху + х.
2. Найти Re /(г), Im /(г), если /(г) =
г-2/
, D ... г3+8г ,. .. (г2+1)(г2-3/г + 2)
3. Вычислить пределы: a) lim ; б) hm -—-—i '.
г-2/ z - 2/ z->/ z2 + Z(l - i) - i
Ответ: а) -12; б) 4 +4г.
4. Найти функцию, обратную к данной:
х 1 ,, 2г + 3
а) w = — ; б) w = -.
г - Ъ г - 3;
_ . l + 2/w ,. 3A + iw)
Ответ: a) z = ; б) z = — ■
w w-2
5. Найти образ точки го при данном отображении:
= г2-2/г-8/, z0 =2 + 3/; б) £±1
Ответ: а) /(г0) = 1; б) f(z0) = | A + 3/).
6. Найти образы координатных осей при отображении:
a) w = -; б) w = 2/'г.
г
Ответ: а) образом действительной оси является действительная ось, обра-
образом мнимой - мнимая; б) образом действительной оси является мнимая ось, об-
образом мнимой - действительная.
Указание: в уравнение прообраза, записанное в комплексной форме,
подставить z = /~'(w), где f~l(w) - функция, обратная к заданной.
7. Найти образы координатных осей при отображении w = ■
Ответ: Образом действительной оси является окружность w — + i = —,
образом мнимой - прямая 2и - v = 2.
8. Допускает ли выделение однозначных ветвей заданная многозначная
функция в окрестности указанной точки:
a) w = tfz~^i, Zo = '; б) w = Jl^Jz, Zi=Q, Z2 = 1 ?
Ответ: а) нет; б) в окрестности zi = 0 - нет; в окрестности z2 = 1 возмож-
возможно выделение однозначной функции для случая той ветви двузначного выраже-
выражения Jz, для которой vl = -1; для другого случая невозможно.
9. Найти точки ветвления функции w = $P(z), где P(z) - многочлен
Ответ: точкой ветвления является любой нуль многочлена при условии,
что его порядок не является числом, кратным порядку корня, т.е. я.
10. Определить точки ветвления функции w = y(z- 1K(г + О2 .(г * «) •
Ответ: z = 1 - точка ветвления; z = -«' не является точкой ветвления.
11. Найти Re/(/), если f(z) = J7^l и /@) = -«.
_ зл
Ответ: - cos — =
8
8 2
70
2.1.2. Элементарные функции комплексного переменного
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
В действительной области показательная функция ех вводится обычно
в связи с обобщением понятия степени а". В комплексной области функцию
требуется определить так, чтобы при z = х ее свойства совпадали с известными
свойствами функции ех. Одно из важнейших свойств функции ех - представ-
представление ее рядом Тейлора: она является суммой сходящегося на всей числовой
ОО уП
прямой ряда Yj —.
оо -П
Учитывая это, рассматриваем ряд У — и убеждаемся (см. разд. 1.3), что
„to n\
он абсолютно сходится при любом z , т.е. во всей комплексной плоскости С
определена некоторая функция - сумма этого ряда. Так как при г = х имеем
]Г — = ех , то вводим следующее определение: показательной функцией ez
л-о "•
и комплексной области называется функция, которая является суммой сходяще-
оо Я
гася во всей комплексной плоскости ряда £ —:
е —у —, < € с . \>--Э/
«=о "■
Из определения следует, что показательная функция определена во всей
комплексной плоскости. В частности, при z = ix, где х - действительное число,
СО ,' ft v ft
имеем е'х = У . Используя свойства абсолютно сходящихся рядов
/1=0 "■
(иозможность перестановки и фуппировки членов ряда, см. разд. 1.3), ряд мож-
можно записать в виде алгебраической суммы двух рядов с действительными членами^
отделить действительную и мнимую части ряда :
JO :ft „tt X :Zk у.Ik со :lK — \ „2л —1 со /_1\^ „2л со / 1\"-"*"l уа/С"~1
*-о
B*)!
Полученные ряды являются рядами Тейлора для функций cos л: и sinx.
В результате имеем равенство е'х =cosx + /'sinx, или, обозначив х через <р:
е'ф = cos ф + /' sin ф. B.4)
Формула B.4) - формула Эйлера была использована для записи комплекс-
комплексного числа в показательной форме (см. разд. 1.1).
Функция е1 обладает, очевидно, рядом свойств, справедливость которых
установлена в действительной области, т.е. для ех.
71
С другой стороны, в силу расширения множества, следует ожидать, что
имеют место и другие свойства, аналога которых в действительной области нет.
К свойствам первой группы нужно отнести прежде всего формулу сложе-
сложения :
ег,+г2 =€г, .еъ B 5)
Доказательство формулы сводится, согласно определению показательной
функции, к доказательству справедливости при любых z\ и z-i равенства
У — ■ У —= У— — , которое устанавливается путем перемножения
„Го «! „to n\ „f0 n!
абсолютно сходящихся рядов, записанных слева (см. пример 1.44 ).
Если в равенстве B.5) положить zj = 2Ш, z\-z- любое комплексное чис-
число, то, учитывая тождество e2la" = cos2fc7t + isin2fc7t = l, можно записать
ez*ikn =ег егы _ег.] ^т равенство, справедливое при любых значениях z,
означает, что функция ez является периодической и ее период - чисто мнимое
число Т = 2тн. Аналога этому свойству в действительной области нет, функция
ех- непериодическая.
Так же, как и в действительной области, иоказательиая функция ez не об-
обращается в нуль ни при каком значении аргумента. Действительно, если предпо-
предположить противное, что существует Z\, при котором eZl =0, то из тождества
ег =eZl+z~zi =eZl -ez~z>, где z- любое комплексное число, получили бы, е1 =0
при любом z , что неверно. Однако это единственное исключение, т.е. нуль -
единственное значение, которое не может принимать функция е1 . В отличие от
ех значение функции в комплексной области может быть отрицательным, на-
например е'" = cosn + /sin7t = -l. Вообще г1 может принимать любые значения в
С, за исключением нуля. Это свойство доказывается просто, если в формуле
B.5) положить Z\ =x,zi=iy и сравнить равенство ех+'у = ех е'у с показательной
формой записи комплексного числа (см. разд. 1.1). В результате получим, что
при фиксированном z , т.е. при фиксированных х и у, модуль числа ez равен
ех (г = ех), а аргумент равен у(<р = у), т.е.
arge* = у =
B.6)
Отсюда получаем, что ez может принимать любые значения (ег #0), так как
arge* = у - любое число.
Пример 2.13. Найти Re г, Inu, |г|, argz для чисел: а) е1'1 ; б) -е'2+1.
D а) Находим модуль числа г= е2"' =е2 и аргумент <p = arg(e2~') = -l.
После этого можно записать Re г = х = /-cos<p, Imz = y = rsiny, т.е.
72
Можно записать решение иначе, используя формулу сложения B.5) и фор-
формулу Эйлера B.4): z = е1'1 = е2е~' = e2[cos(-l) + /sin(-l)] = e2(cosl — / sin 1). По-
Полому Rez = e2cosl, Imz = -e2sinl, а из показательной формы записи числа
г*е~' находим \z\ = r = е2, argz = <p = -l.
б) Представим число в виде произведения z = -1 е~2+' , а множитель (-1) в
показательной форме: -1 = е™. Тогда г = -1 • е'2+' = е™ • е+; = е~2*'ы*1) =
(, 2 е/(и+о Поэтому имеем \z\ = e~2,ar%z = л + 1, или argz = -n + l, так как для
данного значения аргумента имеет место ограничение -n<argz£^. После
чтого записываем Re^ = e 2cos(n + l) = -e 2cosl,Imz = e"sin(n +1) = -e 2sin 1.1
Пример 2.14. Найти Re f(z\ Im f(z) , если f(z) = ez .
П Применяя последовательно формулы B.5),B.6), находим ez = е(х*'у) =
= ех~у , argeJ =2xy. Поэтому Reez =
, \mez =ex y sin2xyM
Пример 2.15. Показать, что функция e'z является периодической и ее пе-
период - действительное число.
D Нужно показать, что существует число Т е С такое, что е'*г+Г) = e'z для
любого z . Но из формулы B.5) имеем е'*г+Г) =е'г е'т , поэтому число Т
должно быть таким, чтобы выполнялось равенство е =1 , а это верно при
/' *■■ 2л. Следовательно, период функции еп - действительное число Т = Ъ. .■
Пример 2.16. Доказать, что функция w = ez является неоднолистной
ни множестве С. Найти область однолистности.
D Неоднолистность функции следует из определения, так как существуют
не равные значения аргумента, такие, что в них совпадают значения функции. >
Например, для Z\=2m и Z2=4w получается eZ] = eZ2=l.
Чтобы определить область однолистности, запишем разность
wt- w2= ez>-eZl или w[~w2= eZl(l-eZl'Zl).
Значения функции совпадают для тех *i и гг, для которых выполняется
равенство eZl~Zl =1 , т.е. ^2 -£| =2Ы, fe = 0,±l,±2,
Однолистным отображение будет в любой области, принадлежащей гори-
юнтальной полосе ширины 2л, о<1тг<о+2я, в частности полосе
it < Im z < я или 0 < Im z < 2л (рис. 2.9).
73
У t
(z)
-X X *-
(w
Рис. 2.9
Любая прямая z - х + ic (у = const = с), параллельная действительной oci.
отображается в луч arg w = с , так как из w = ez - ех- е'с получаем |w| = ех > О
arg w = с. В частности, действительная ось Inu = 0 , т.е. z = х, переходит в лу1
argw = 0 - действительную положительную полуось, а прямая 1пи = 2я , T.t
г = х + i -2я,- в луч arg w = 2л, геометрически это - та же действительная полуось
Для однозначности отображения на границе проведем разрез по лучу. flpi.
этом точкам прямой Im z = 0 будут соответствовать точки нижнего "берега" оа
Im w = 0, а точкам прямой Im z = 2я точки верхнего "берега".
Такой же результат получим и для следующей полосы 2л < Im z < 4n. Ohi
отображается также в плоскость с разрезом [0, да).
Вообще любая полоса 2(fc-l)n < Im z < Ikn, k= 0,±l,±2,... с помощью функ
ции w = е1 переходит в плоскость с разрезом по действительной положительно*
полуоси.
Нарушенную разрезом непрерывность отображения можно восстановит,
построением римановой поверхности функции w = ez по такому же принцип'
как сделано для w = z2.
Полученный результат запишем в виде утверждения: функция w = eJ взе
имно однозначно отображает:
1) любую полосу a <lm z < о+2п - в плоскость с разрезом по луч*
arg w =a;
2) полосу Bfc-l)Tt < Im z < Bк + \)п, fe=0,±l,±2,..., в плоскость с разрезол
по действительной отрицательной полуоси;
74
3) полосу 2(fe-l)n < Im z < 2fen, fc=0,±l,±2,..., во всю комплексную плос-
плоскость с разрезом по действительной положительной полуоси. ■
ТРИГОНОМЕТРИЧЕСКИЕ И ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Функции sin z, cos z, sh z, ch z вводятся аналогично показательной функ-
функции - как суммы соответствующих абсолютно сходящихся во всей комплексной
плоскости рядов:
tg£='
thz =
sm z
cosz
sh z
chz
— . B.8)
2«)!
На основе этих функций определяются и другие:
i c°s Z
ctg^= ,
sin z
cthz=—,
sh z
Из определений следует, что функции cos z, ch z являются четными, а ос-
остальные - нечетными.
Сравнивая формулы B.7) и B.8) с формулой B.3) - определением функции
«1 , получаем следующие формулы, справедливые при любом z '■
e'z =oosz + isinz, B.9)
eJ = chz + sh*. B.10)*
Формулы B.9) и B.10) - формулы Эйлера; они связывают тригонометриче-
тригонометрические и гиперболические функции с показательной.
Формула B.9) при z = х (г = <р), где х - действительная переменная, рас-
рассмотрена выше (см. формулу B.4)).
Так как формулы B.9) и B.10) верны при любых значениях z , то, заменяя
Z на "-z" и учитывая, что sin г и shz - нечетные, a cosz и chz - четные
функции, можем записать
е'г =cosz-i sin z,
e~z =chz - sh z-
75
Комбинируя эти формулы с B.9) и B.10), получаем представление три-
тригонометрических и гиперболических функций через показательную:
eiz-e-iz
sin*= -—, cosz = — , B.11)
B.12)
Эти формулы позволяют использовать при исследовании гиперболических
и тригонометрических функций в комплексной области свойства показательной
функции и не обращаться к определениям B.7),B.8), т.е. не рассматривать более
сложные операции - действия с рядами.
Так, с помощью B.11) и B.12) устанавливается справедливость таких
формул сложения, как
) i sin ^
и других формул, в частности формул тригонометрии.
Кроме того, что тригонометрические и гиперболические функции выража-
выражаются через ez, они еще и связаны между собой.
Соответствующие формулы получаются из B.11) и B.12):
ch iz = cosz,
.« ...
sin iz = i sh г, sh iz = i sin z.
Отсюда, в частности, получаются такие формулы, как
Как и в действительной области, тригонометрические функции sin г и
cosz являются периодическими и их период равен 2п. Это следует из формул
B.11) (см. пример 2.15). А гиперболические функции, не будучи периодическими
в действительной области, в комплексной области являются периодическими, их
период, как и у функции е1, - мнимое число 7 = 2я/ (это следует из рассмотре-
рассмотрения равенств B.12)).
Замечательным свойством, не имеющим аналога в действительной области,
является свойство неограниченности (по модулю) функций sin г и cos г. Эти
76
функции могут принимать любые значения, в частности большие единицы. На-
пример, для числа cos/ по формуле B.11) имеем: cos/ = —-—> 1.
Можно показать и в общем виде, что для любого числа М > 0 найдется та-
такое число 5 (М), что для всех z , удовлетворяющих условию \z\ > 5 (М), выпол-
выполняется неравенство |cos ^j > A/, |sin^|>M. Для доказательства следует исполь-
ювать формулы B.11).>
Пример 2.17. Найти |г| и aigz для чисел:
а) z - sin 2/; б) z = / sin2-.
□ а) Используем формулу B.13): sin2/ = /sh 2, поэтомуRe г = 0, Inu = sh2,
• так как sh 2 = > 0 , то Im z > 0 и, следовательно, \z\ = sh 2, aig z =—.
б) Учитывая равенство - = - / , используем, как и выше, формулу B.13):
/'
/ sin2- = / sin 2(-/) = / sin2/ = / (/ shlJ= - / sh 21.
/
Поэтому Re г = 0 , Inu = -sh2l<0 и, следовательно, |z| = sh2l, aig г = -—•■
Пример 2.18. Найти Re f(z), 1т/(г). если
a) f(z) = sinz; б) /(г) = сЬг.
□ Для решения используем формулу сложения, обозначая z = х + iy, а так-
также формулу B.13). '
а) Решим первый пример:
fit) = sin z = sin(x + iy) = sinx • cos iy + sin iy ■ cosx = sinx • chy + / sh у ■ cos x,
поэтому Re/U) = sin x ■ chy, lmf(z) = shy • cos x.
б) Решим второй пример:
f(z) = спг = cos iz = cos / (x + iy) = cos (ix -y) = cos ix ■ cos у + sin ix ■ sin у =
= cos у ■ chx + i shx ■ sin y,
поэтому Re/(z) = cos у ■ ch x, Im/(z) = shx • sinj^ .
Для решения можно использовать формулу сложения непосредственно для
гиперболической функции:
77
dnz = ch(x + iy) = chx • ch iy + shx ■ sin iy =
= cos у ■ chx +1 shx ■ sin у. ■
Пример 2.19. Найти модуль и аргумент числа/(/), если
a) f{z) = xgz; 5) 1
О а) Используем определение функции tg ^ = и формулу B.13):
cos z
..... . . sin/ /shl .... n .... n . .... ... sh 1 e'-e
/(i) = tg(= : = —- = /thl; Re/@ = 0, Im/(/)= th 1 = —- = - ->0,
cos» chl chl e'+e
поэтому |/(i)| = th 1 = —-, arg/(O = ^ .
e +1 !■
б) Представим число /(/) = A - /') • cth i2 в виде произведения двух чисел:
и найдем модуль и аргумент каждого .
Для числа Z\ =\-i имеем |zi|= Jl, are^i = - — • Число zi является
1 ' 4
действительным, причем отрицательным, так как
sh(-l) "~ shT~ e-'-el <
Поэтому |^2| = с
= cthl = r,
е -1
Окончательно, используя правило умножения комплексных чисел в триго-
тригонометрической форме (см. разд. 1.1), получаем
Пример 2.20. Найти мнимую часть числа ch a , где a - тот корень уравне-
уравнения z4+ 4 = 0, который расположен в третьей четверти.
D Корнями уравнения z4+4 = 0, или г4=-4, являются четыре комплекс-
комплексных числа, которые могут быть найдены по правилу извлечения корня из ком-
плексного числа (см. разд. 1.1): z = tf-4, Zk=fie 4 , fe = 0,1,2,3.
78
..^Для того чтобы отобрать корень, которому соответствует точка в третьей
четверти, нужно взять к = 2 . Искомым корнем будет число а =^2е 4 , или
г( Л Л)
В алгебраической форме а =,/2 --— ;'— = - A + /) .
Вычислим теперь ch(-1 - /) или, что то же, ch(l + /'). Можно перейти
К показательной функции по формуле B.12) или использовать формулу сложения
для гиперболической функции и формулу B.13) :
сп A + /) = ch 1 • ch; + sh 1 • sh; = ch 1 • cos 1 +;' sh 1 • sin 1.
Получаем ответ: Imcho = sh lsinl.i
ОБРАТНЫЕ ФУНКЦИИ В КОМПЛЕКСНОЙ ОБЛАСТИ
Логарифмическая функция
1. Понятие функции, обратной показательной функции, как и в действи-
действительной области, связано с понятием логарифма числа.
Логарифмом числа z * 0 называется число А такое, что справедливо ра-
исмство ez=A ; обозначается А = Inz ■ Таким образом, In z =А<z>eA=z, z * 0.
Для нахождения логарифма числа z , т.е. для нахождения действительной
и мнимой частей числа А ( А = In z ), запишем число z в показательной форме,
н число А будем искать в алгебраической форме: А = u+iv.
Тогда равенство eu+lv = /■е'ф или e"-e'v = /-е'ф есть равенство чисел, запи-
записанных в показательной форме, и из него находим м и v , а именно еи=г , т.е.
// - In г, (г > 0); v = ф + 2кп, к =0,±1,... Для искомого числа А получаем выраже-»
мис: А = In г = In r +/'(<p+2fcn), fe = 0,±l,..., где /■ = |z|, <p = argz. Из этого следует,
что логарифм комплексного числа определяется неоднозначно; полученное вы-
рижение определяет множество значений логарифма данного числа z ', обознача-
обозначается Lnz'-
Ln z = Ш | z\ + i (arg z + 2fat), к = 0,±l,±2,... B.14)
Для каждого фиксированного значения fe=0,±l,... получаем определенное
число - значение логарифма числа z ; при к =*0 оно называется главным значе-
значением логарифма:
Inг = 1п|г| + iargz, -norgz^n. B.15)
79
Пример 2.21. Найти In z - главные значения и Ln z для следующих чисел:
а) z = 1; б) z = 1 + i; в) z = 2 - /.
D а) Находим модуль и аргумент числа z = 1 •' |<:| = 1, arg г = 0. По формулам
B.14) и B.15) получаем: In 1 = 0; Lnl = 2b/, fc = 0,±l,...
б) Для числа z = 1 + 1 находим модуль и аргумент: |г|=^2, argz= —. По-
Поэтому имеем результат: In A + /') = ln^/1 + <—; Ln A + i) = ln^/I + /' Uh- 2fot I fc = 0,±l,...
в) Находим модуль и аргумент числа г = 2-/: |г|=чР, arg г = arctg— .
Получаем ответ:
Ln B - 0 = 1п^5 + ; arctg j - - )+2Ь I к = 0,±l,...
ln B - /) = In S + i aretgf- - j. ■
Пример 2.22. Найти модуль, аргумент, действительную и мнимую части
числа 1п2(.
D Находим модуль и аргумент числа 2/': |г| = 2, argz = —. По формуле
B.14) получаем In 2/ = In 2 + /' —. Поэтому:
Re (In 2») = ln 2, Im (In 20 = -, I In 2/1 = Jin2 2+— = -Jln24+7t2.
2 1 4 2
Точка о = 1п2; расположена в первой четверти, так как Reo>0 и
Im а > 0. Поэтому arg Aп2/) = arctg = arctg . ■
Замечание 2.4. Введение понятия логарифма числа позволяет опреде-
определить в комплексной области степень с любым комплексным показателем za и
показательную функцию с любым комплексным основанием а1 .
При а = п и а=— , где л - натуральное число, степени z" и 8f? pac-
п
смотрены выше; при а = к и а = — ,где£- целое число (к*0), определение
к
также очевидно.
80
В общем случае при любом комплексном а степень определяется форму-
формулой
Za=eaLaz, z*0. B.16)
Аналогично вводится функция а1 с любым комплексным основанием
<;*0:
az = ezUla. B.17)
В силу бесконечной значности логарифма, каждому числу z (z * 0) соот-
соответствует бесконечное множество значений степени za, определяемой по фор-
формуле B.16), и бесконечное множество чисел, определяемых по формуле B.17)
при я*0. Среди этих множеств выделяются главные значения, которые соот-
мстствуют главным значениям логарифмов.
Пример 2.23. Показать, что выражение /' принимает только действитель-
действительные значения.
О Используя определение для az, запишем выражение /' в виде i' = elLm.
Найдем значения для Ln i :
Ln i = In 1 + i {- + 2fo ], т.е. Ln i = i[- + 2fcn|, к = 0,± 1...
. ;(+2n*) -+2nk
Поэтому i'=e y '-e 2 - действительное число при любом целом к .■
Пример 2.24. Найти In а , где а - корень уравнения г6+8 = 0 , удовлетво-
ряющии условию — < arg г < л .
О Корнями уравнения г6+8 = 0 являются числа
Z*«tfT-e 6 ', ^ = 0,1,2,3,4,5.
5я .
Условию — <argz<n удовлетворяет Zi=j2-e(> . Для найденного числа zi=a
имеем \а\ =^2, arg а = ~ . Поэтому получаем ответ: In а - 1п^2 + -£. ■ i .и
6 6
Замечание 2.5. Введение понятия логарифма комплексного числа
позволяет решать в комплексной области показательные уравнения. Простейшим
таким уравнением является уравнение вида ег+а = 0 . Решение этого уравнения
сводится к нахождению значений выражения Ln (- а), т.е. z - Ln (- a).
81
Пример 2.25. Решить уравнения: a) ez-2 = 0 ; б) ег + 2 = О; в) ег + 2/ = О.
О а) Из равенства ег=2 по определению логарифма получаем ? = Ln2.
Далее, учитывая равенства |2| = 2, arg2 = 0, по формуле B.14) находим
z = Ln2 = ln2 + / Bкж), fc=0,±l,±2,.... Уравнение имеет бесчисленное множество
решений, которые геометрически изображаются точками, расположенными на
расстоянии 2л друг от друга на прямой Re z = In 2, параллельной мнимой оси.
Среди решений есть действительное число ?0= In 2 - точка на оси Ох.
б) Все решения уравнения получаются, как значения выражения Ln(-2),
т.е. z = Ln (- 2) = In 2 + i (л + 2кж), к = 0,±1,...
в) Из равенства el =-2i получаем z = Ln(-2<). Находим модуль и аргу-
аргумент числа (-2i): г = 2, ф = —. Множество решений уравнения описывается ра-
равенством z = Ln (- Ъ) = In 2 + / (- ^ + 2Ь), к = 0,±1,...
В случаях "б" и "в" уравнения не имеют действительных решений, так как
ни при каких значениях к среди полученных множеств нет действительных чи-
чисел. Геометрически же соответствующие точки расположены на той же прямой
Re г = In 2, что и в случае "а", на расстоянии 2л друг от друга; начальными зна-
значениями (при к = 0) для них являются го= In 2 + /я и zо = In 2 - i—.
У1
3m
3m/2
(л
о
-к/2
-in
In 2!
Рис. 2.10
(г)
i-j/2
(Л
и/2
(г)
ln(V5
Рис. 2.11
Решения уравнений "б" и "в" изображены на рис. 2.10 (по осям масштабы
разные).!
82
Пример 2.26. Найти z из уравнения ch z = -2i.
D Используя формулу B.12), сведем задачу к решению показательного
уравнения ег + е~г= - 4/. Получим квадратное уравнение относительно функции
#': е2г + 41ег +1 = 0, корнями которого являются числа (-2+^5)i и
(-2 /5)<. Далее нужно найти значения выражений Ln(-2+/5)< и Ln(-2-/5)i.
Для этого используем формулу B.14):
Ln (-2 + /5)i = In(/5 -2) + i[- + 2жк\, к = 0,±1,...
Получили два множества решений исходного уравнения:
2 / ' '
Геометрически - это точки, лежащие на прямых Re z = In(^5-2) =
1
= ln-=— = -ln(v5 + 2) и Re z = ln(^5+ 2), параллельных мнимой оси; расстоя-
V5+2
ние между любыми соседними точками на каждой прямой равны 2л ; начальные
значения (при fc = 0): го=1п(/5-2) + (- или zo=-ln(j5 +2) + <— и
2 2 f
2. Логарифмическая функция вводится, как функция, обратная к показа-
показательной, т.е. как решение уравнения ew=z, w = Lnz ', значения функции при
любом z*0 определяются по формуле B.14).
Функция, очевидно, многозначная и отображает плоскость на каждую из
полос: 2(fc-lOr < Im z <2kn, fc=0,+l,... или Bfc-l)n< Im z <Bk + 1)л, Jt=O,±l,...
В плоскости с разрезом по лучу [О,») возможно выделение однозначных
ветвей, каждая из которых однозначно отображает эту плоскость на одну из по-
полос 2(fc—1Oг < Im z < 2kn, k =0,±l,..., в частности функция In z - главное значение
логарифмической функции отображает плоскость на полосу 0 < Im z < 2л (см.
рис. 2.9). В плоскости с разрезом (-°о,0] также возможно выделение однознач-
однозначных ветвей, каждая из которых однозначно отображает эту плоскость на одну из
полос B£-1)л< 1тг <B& + 1)л, fc=0,+l,..., в частности функция In г- главное
83
значение логарифмической функции отображает плоскость на полосу
- ж lm z < п. Выделение ветви определяется заданием значения функции
в одной из точек области.
Пример 2.27. Найти решение уравнения ez+2i = 0 при условии
In (-1) = Зги.
Q Так как дополнительное условие задает значение функции в точке дей-
действительной отрицательной оси, то рассматриваем плоскость с разрезом по
[О, «>), где главное значение аргумента определяется неравенством 0 < arg z < 2л .
Из дополнительного условия определяем значение к , соответствующее выбран-
выбранной ветви Arg z, а следовательно и Ln z '■ In (-1) = (я + 2кп) i = Зл/, к = 1.
—+2кп .
При к = 1 получаем ответ: z = In 2 + —i .■
Обратные тригонометрические и гиперболические функции
Функции, обратные к тригонометрическим и гиперболическим функциям,
определяются, как и в действительной области.
Например, обратным тригонометрическим синусом числа z называется
число w такое, что выполняется равенство sinw = z. Отображение обозначается,
как и в действительной области, w = arcsin z.
Аналогично определяются и другие функции:
arccos z, arctg z , arcctg z , arch z , arsh z, arth z, arcth z ■
Из определений могут быть получены формулы для нахождения числа w по
заданному числу z.
Рассмотрим эту задачу на примере нахождения w = arcsin z ■ По определе-
определению имеем z = sin w . Заменим sin w по формуле Эйлера B.11), и из соотноше-
ния z- ; или е -2ize'w-l = 0, т.е. квадратного уравнения относи-
относительно e'w, находим e'w: e'w=iz + V('?J+l • Перед радикалом записан только
знак плюс, так как в комплексной области Ja - двузначное выражение. Далее,
используя определение логарифма, находим
84
Для каждого числа г получаем бесконечное множество значений для w
I силу двузначности yl-г2 и бесконечной значности логарифма. Все это мно-
множество значений w обозначается Arcsin z ■ Окончательный результат:
Arcsin z = т Ln (iz + Jl-Z2) ■ B.18)
Формулы, аналогичные B.18), могут быть получены и для других функций:
. 1. , / i ,. . i , 1 + iz 4 i т z-i
Arccosz =-Ln(z+yr-l); Arctgz=--Ln ; Arcctgz=-Ln-—;
i 2 \-iz 2 z + i
Arsh z = Ln (z + J\+z2); Arch z = Ln (z +
= -Ln —; Arcth?=-Ln —.
2 \-z 2 z-\
Все эти формулы, как и B.18), дают бесконечнозначные выражения -
определяют многозначные функции. Выделяя однозначную ветвь выражения
\.п А, можно получить однозначные функции в каждом случае.
Большого практического значения эти формулы, как и B.18), не имеют.
Для нахождения значений обратных тригонометрических и обратных гиперболи-
гиперболических функций можно использовать их определения и формулы связи тригоно-
тригонометрических и гиперболических функций с показательной функцией (формулы
•)йлера B.11)-B.12)), т.е. применять метод, с помощью которого выведена фор-
формула B.18). Этим методом решен пример 2.26, где найдено значение Arch (- 2 /').
Замечание 2.6. Рассмотрим уравнения, содержащие тригонометриче-
тригонометрические и гиперболические функции. Простейшими из них являются уравнения:
sin z = о, cos z ~ о, tg z = a, ctg z - a,
sh z = a, ch z = a, th z = a, cth z = a.
Решение их, согласно определению, сводится к нахождению обратных
тригонометрических и обратных гиперболических функций.
Пример 2.28. Решить уравнение: sin z = 2.
□ Множество решений уравнения определяется выражением z — Arcsin 2,
или с помощью формулы B.18): z = -' Ln Bi + Jl - 4). Выражение в скобках,
в силу двузначности корня, записывается в виде а = 2i+fii и b = 2i-Jbi . Для
каждого из этих чисел по сформулированному выше правилу находим логарифм:
а) для числа а = B+^/3)г имеем |a| = 2 + V3, arga =—, поэтому
85
LnB +1/3)/ = InB + 1/З) + /1 у + 2Ь ], Jt = 0,±l,...;
б) для числа b = B-fi)i имеем |*| = 2-^3, arg6 =—, поэтому
Ln B - V3) (= ln B - V3) + / — + 2къ , к = 0,±l,.. Получаем два множества реше-
решений уравнения: г*= —+2fot -ПпB + ^3) или zk= — + 2£я +/lnB-V3) и
!
или
,*=0,±l,...
Геометрически - это множество точек, расположенных на расстоянии 2я
друг от друга на прямых Imz = lnB-V3) = In =r = -lnB + V3) и
2 + V3
Im z = In B + ^3) = ln = = - ln B - ^3) , параллельных мнимой оси (рис. 2.12).
2-V3
у.
1Ы2 + Я)
-'У °
-ilnB + S)
го
У
гГ
5У х
Z\
Рис. 2.12
Действительных решений уравнение не имеет, так как ни при каком зна-
значении к среди чисел zk нет действительных. Это соответствует известному свой-
свойству функции sin х в действительной области Isinjcl < 1 .■
1. Какие из следующих функций являются периодическими:
а) f\(z) = Z-sinz; б) f2(z) = zs\ni; в) /3U) = z--Sin«;
Ответ: никакие.
2. Какие из следующих функций являются периодическими:
a) /i (z) = /sin iz; 6) f2(z) = icosz;
в) /3(г) = sin(l + i)z; г) /4(г) = A + /) • cos(l - о? ?
Для периодических функций определить период.
Ответ: все представленные функции являются периодическими с перио-
периодами: а) Г, = 2да ; б) Т2 = 2тс; в) Г3 = тсA - /); г) Т4 = лA + /).
3. Являются ли периодическими функциями следующие функции:
а) /, (z) = 2; ■ ей; б) f2(z) = 2Z ■ eiz; в) /3(?) = z ■ е21 ?
Ответ: /j (z) — периодическая, Т = 2к.
4. Найти |/Ы|, arg/(z0) если f(z) = zez+\ zo=2i.
Ответ: г = 2е, ф = — + 2.
5. Какие из следующих равенств верны для значения функции f(z) = z-ez
■ Точке со ='у: а) |/Ы| =■?■■; б) Re/(?0) = -^; в)
г) 1т/(го) = О; д) arg/(zo) =
Ответ: все.
6. Записать в показательной форме число z = Z\ -z2, где Zi = /, z2 = е1'.
Г2'
Ответ: z = e-ey ' .
1. Для чисел Z\ =l + ( и ?2 =е1+' среди следующих соотношений выбрать
верные: a) z2>Z\\ б) Re г, = Re г2 ;в) Re г2 = Im z2 ;r) Re ?i = Im z\; д) Im z2 >\mz\-
Ответ: г), д).
8. Записать в показательной форме число /((), если f(z) = z-chz-
Ответ: /(/) = cos 1 ■ е2 .
9. Найти Re z, Im г, если: a) z = cos(l - /); б) sh2/.
Ответ: a) Re? = coslchl, Im? = sin 1 - shl; 6) Rez = 0, Inu = sin2.
10. Найти Re г, 1тг,если z = e' (cos 1 + ch/).
Ответ: Re? = 2cos2l, Im? = sin2.
11. Найти Re /(я), где f(z) = sin(l + z) и а — корень уравнения
г4 + 5z2 + 4 = 0, удовлетворяющий условию |<з| = 1. t
Ответ: Re/(a) = chl ■ sin 1.
12. Найти arg/(?0), где /(?) = 2г, ?0 = 1 +' •
Ответ: ф = In 2.
13. Найти |г|, arg?, Rtz, Inu для чисел ?i =ln(-l) и z2 =ln/.
Oweew: Re?, =Re?2 =0, |z,| = lmzi =я, |?2|
14. Решить уравнения: a) ln(z + l) = ni; б) ег+1 =7t;.
Ответ: a)? = -2; 6) z = ln- + ([-+2ufc), к = 0;±l;±2....
e U j
+ ([+2ufc),
e U j
15. Решить уравнения: а)ег+1 = 0; б)ег-3 = 0.
: a) ? = Bfc + 1)л/,it = 0; ± 1; ± 2...; б) z = In 3 + 2Ы, fc = 0,±l,±2...
87
2.1.3. Свойства дифференцируемых функций
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Так как производная функции комплексного переменного определяется,
как и в действительной области, т.е. в виде предела f'(zn) = lim , то, ис-
дг-+о Д z
пользуя это определение и свойства пределов, несложно убедиться в справедли-
справедливости правил дифференцирования, известных из математического анализа.
А именно имеет место следующее утверждение.
Утверждение 2.5.
I. Сумма, произведение функций, дифференцируемых в точке, есть функция,
дифференцируемая в этой точке, и справедливы равенства:
(Л (г) + /г(г)У = /i'(г) + Л (г),
(Л (г) • /2 W)' = /,'(г) • Ш + h(z) ■ h(z).
Из этого свойства и очевидного равенства с' - 0 (с = const) следует
2. Частное функций, дифференцируемых в точке, есть функция, дифференци-
дифференцируемая в этой точке, при условии, что знаменатель в точке не равен нулю:
" tiiz)
3. Сложная функция /(ф(г)) дифференцируема в точке za, w* в этап точке
дифференцируема функция ф(г), а функция f(u) дифференцируема в точке и0 , где
и0 = ф(го) и и = ф(г). При этом в точке Zo имеет место формула
Пример 2.29. Доказать дифференцируемость во всей плоскости функций:
a) w - г; б) w = z" ■ Найти их производные.
D а) По определению производной для любой точки z e С записываем
lim -^ U-1. = ]; предел существует для любой точки z е С и z' = I.
дг->о дг
б) Для любой точки Zo e С и любого приращения Л z рассмотрим
lim —= lim — ' 2_. Выражение (го+Аг)" раскрываем по формуле
Дг>0Д£ дг->0 Л?
fit ц(л-1)
бинома ' Ньютона: (г0 + Дг)" = го" + «• го + ., faJ ■ z$~2 +...+(лг)",
и результате получаем
Дг-»0
= lim я-г?
lim яг?+Лг + ...
Дг-*0 ^ 2!
Предел существует, следовательно, функция дифференцируема в точке го.
Гак как г0 - произвольная точка плоскости, то доказана дифференцируемость
г" (я - натуральное) при любом z и получена формула (z") = n-z"'1 -Ш
Пример 2.30. Исследовать дифференцируемость функций:
а) Pn(z) - многочлен степени и; б) R(z) - рациональная функция.
О а) Дифференцируемость многочлена в любой точке геС следует из
дифференцируемое™ функции z" (пример 2.29) и п. 1 утверждения 2.5.
р (z\
б) Дифференцируемость рациональной функции R(z) = — отношения
диух многочленов в любой точке из области определения, т.е. за исключением
нулей знаменателя, получается из результата п. "а" и п. 2 утверждения 2.5. ■
Пример 2.31. Найти модуль и аргумент производной f'(z) в точке ?0, если
a) f(z) = Hz - 3/; б) /(г) = i^L, го = 1 _ /; в) f(z) = z2.
D а) Используя правила дифференцирования, находим /'(г) = li ■ Поэтому
'(г0) = 2/ для любой точки г0 и |/'(го)| = 2, аг§/'(го) = -j.
б) Используя правила дифференцирования частного, находим
(г + 2/J (г + 2/J (го + 2()
Поэтому в результате имеем | /'(l - /)| = 3, arg /'A - /) = 0.
в) Используя результат примера 2.29, находим (г2) =2г, поэтому
) = 2го и
УСЛОВИЯ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ. УСЛОВИЯ КОШИ-РИМАНА
Очевидно, между свойствами дифференцируемое™ функции комплексного
переменного как функции точки плоскости и дифференцируемостью ее действи-
действительной и мнимой частей как функций двух действительных переменных сущест-
существует тесная связь.
Утверждение 2.6.
1. Если функция f(z) дифференцируема в точке, то в этой точке существу-
существуют частные производные ее действительной и(х, у) и мнимой v(x, у) частей и вы-
выполняются условия Коши-Римана:
ди_ _ dv_
f"*' B.19)
ди dv
ду дх'
2. Если и(х,у) и v(x,y) дифференцируемы в точке (х(,,У(,) ив этой точке
выполняются условия B.19), то функция f(z) = u + h> дифференцируема в точке
Zo=x0+ iy0.
3. Производная дифференцируемой функции может быть записана по одной из
формул'.
ди .dv г,. ч dv .ди
—+'—, /(*)=—-'т'
дх дх су ду
ди .ди ги . dv .dv
— "'т. Аг) = г-+'—•
дх ду ду дх
Доказательство этих утверждений не представляет трудностей и опирается
только на определения дифференцируемости функций f(z), и(х, у), v(x, у).
Анализ утверждения 2.6 позволяет сделать следующие полезные для иссле-
исследования функций на дифференцируемость замечания.
Замечания 2.7.
1. Выполнение условий B.19) является необходимым условием дифферен-
дифференцируемости функции f(z) в точке. Следовательно, их невыполнения достаточно
для утверждения о том, что функция не является дифференцируемой в соответ-
соответствующей точке.
2. Условия B.19) не являются достаточными. Согласно п.2 утверждения 2.6
в соответствующей точке должны быть дифференцируемы функции и(х,у) и
v(x,у). Напомним, что условием дифференцируемости функции двух действи-
действительных переменных в точке является существование и непрерывность частных
производных в этой точке.
Из утверждения 2.6 и замечаний 2.7 следует правило исследования функ-
функции на дифференцируемость.
Правило 2.1. Для исследования функции на дифференцируемость и нахож-
нахождения ее производной следует выполнить следующие операции.
1. Для заданной функции f(z) найти действительную и мнимую части:
v= Im/(z), u = u(x,y), v = v(x,y).
90
2. Найти частные производные функций и(х,у) ,v(x,y).
3. Проверить выполнение условий Коши-Римана. Точки, в которых эти ус-
ЛОПия не выполняются, являются точками, где функция не дифференцируема.
Томки, в которых условия B.19) выполняются и частные производные являются
непрерывными, принадлежат области, где функция дифференцируема.
4. Записать выражение производной в точках дифференцируемости по од-
одной из формул B.20).
Пример 2.32. Исследовать на дифференцируемость функцию f(z)
□ Для решения выделим два случая.
Первый случай. Рассмотрим произвольную точку z * 0. Исследование про-
Ввдгм по правилу 2.1.
1. По условию и(х, у) = J\x\ ■ J\y\, v(x, у) = 0.
dv dv
2. Очевидно, — = 0, — =0 для любой точки. Находим частные производ-
дх ду
ные функции и(х,у). Для нахождения — положим у = const и, учитывая опре-
дх
целение модуля, рассмотрим два случая: х>0 (тогда |х| = х) и х<0 (тогда
|«| = -х). Получаем— = «/Ы—;= прих>0 и — = «/Ы-—р=прих<0.
дх " 2Ух дх Ч1 2V-X
Аналогично при любом х = const имеем
flu гт 1 „ ди ГТ -1 п
— = J]x\—= приу>0 и — = Jjc—■== приу<0.
ду У1 ify ду " 2f^y
3. Проверяем условие B.19). Условие — = — выполняется в точках пря-
дх ду
мой у = 0 при любом х*0. Условие — = выполняется в точках прямой
ду дх
х = 0 при любом у ф 0. Вместе эти условия не выполняются ни в одной точке.
Согласно п.2 замечаний 2.7 функция не является дифференцируемой.
Второй случай. Рассмотрим точку z = 0.
1,2. Найдем частные производные функции " = у|х-.у| в точке A/q @,0) ,
используя определение:
дх
любом х.
ди
Аналогично —
ду
.. ы(Дх,0) - ы@,0) .. и(х,0) - м@,0) „ . „. „
= lim ————^-*- = lim -^-^—i-i-i = 0, так как и(х,0) = 0 при
д^->о Дх х^о х
dv dv
= 0. Так как v(x,у) = 0,то — = 0 и — = 0.
дх ду
3. Условие B.19) в точке Мо (т.е. г = 0) выполняется.
Согласно п.2 замечаний 2.7 следует проверить дифференцируемость функ-
функций и(х, у), v(x, у) в точке Mq . Это можно сделать, установив непрерывность
91
частных производных в точке г = 0, для чего следует рассмотреть пределы всех
найденных в п. "а" производных при г -> 0, т.е. х -> 0, у -> 0.
В данном случае удобнее проверить дифференцируемость /(г) в точке
z = 0 по определению производной. В точке го = 0 рассмотрим произвольное
приращение Дг и составим приращение функции Д/@) = /(Дг)-/@) = /(Дг).
Далее записываем предел lim —-—- = lim ——- = lim -^-i = lim — . Про-
л:-»о tii д:-+о &z :->« Z i-»o x + iy
изводная в точке z = 0 существует, если этот предел имеет одно и то же значение
при любом стремлении z к 0 , при этом нельзя ограничиться никаким специ-
специальным классом путей.
Выберем сначала в качестве пути простейший - прямую у = кх или в ком-
комплексной форме z - x(l + ki). Тогда выражение для предела принимает вид
VfoJ ЫJj
lim = limJ——-, из чего следует, что значение предела зависит от к,
г-»0 хA + ik) г-»0 хA + ik)
от наклона прямой - т.е. от выбранного пути. В частности, при к = 1, т.е. для
,. Д/@) ,. V? .. И
прямой у = х , можно записать lim —^^—= lim = lim———, поэтому
дг-»о Дг х->о х(\ + /) х->о х(\ + ')
прих>0 M0)J
lim)anpHX<0 lim .
Лг-»О Д^ 1 + / Дг^О Дг 1 + /
По определению lim ■ не существует и функция /(г) = «Лл: - зН не
Аг-»о Дг 4 1
дифференцируема в точке z = 0.
Объединяя результаты пп. "а" и "б" , получаем окончательный ответ: дан-
данная функция не дифференцируема всюду. ■
Пример 2.33. Исследовать на дифференцируемость функции:
а)/(г) = |г|2; б) /(*) = ?.
D а) Найдем решение, используя правило 2.1.
1. Находим « = Re f{z), v= 1т/(г), и = х2 + y2,v = 0.
2. Определяем частные производные: — = 2х, — = 2у, — = 0, — = 0.
дх ду дх ду
3. Условия B.19) выполняются только в точке г = 0,гдех = 0и>' = 0.
Непрерывность частных производных очевидна. Следовательно, функция
f(z) = \z\2 дифференцируема только в одной точке z = 0.
б) Найдем решение, используя также правило 2.1.
1. Находим Re г и 1т?,т.е. и = х, v = ~y .
2,3. Условия B.19) не выполняются ни в одной точке, так как
— = 1, — = -1. Следовательно, функция не дифференцируема всюду. ■
дх ду
Пример 2.34. Исследовать на дифференцируемость функцию е1. Найти
производную.
D 1. Из равенства ег = ex(cos у +1 sin у) находим и = е* cos у, v = ex sin у.
92
2. Находим частные производные:
ди х ди г . dv x . dv r
— = е cosy, — = -е sin у, — = е sin у, — = е cosy.
йс ду дх ду
3. Условия B.19) выполняются в любой точке zeC, и частные производ-
ИЫс, очевидно, непрерывны всюду. Поэтому функция е1 дифференцируема всю-
всюду н с.
4. Надо полагать, что (ez) =ez. Действительно, записываем производную
По формуле B.20), используя найденные частные производные
f'(z) =—+' — = ex(cosy + isinу)= ех е'у -е1 М
дх дх
Пример 2.35. Записать условия Коши-Римана в полярных координатах.
D Пусть f(z) = и(х,у) + iv(x, у) дифференцируема в точке z и z = г ■ е'*.
Ниходим частные производные сложных функций и = и(х,у), v = v(x,y), где
X -> rcos<p, у = /• sin tp:
ди ди дх ди ду ди ди .
— = + — = cos<p + Sin<p;
дг дх дг ду дг дх ду
ди ди дх ди ди ди, . ч ди
— = + = —(- г sin ср) +—rcoscp,
dv) дх дч> ду dv) дхУ ду
„ ,„ ... ди (dv . dv \
или, в силу условии B.19), — = -'" —sin9 + — cosip ;
9ip {ду дх )
dv dv дх dv ду dv dv .
— = + — = cosffl + — вшф;
дг дх дг ду дг дх ду
dv dv дх dv ду dv, . \ dv
— = + - = —(-/^икри—rcoscp,
ар дх ар ду ар эх ду
._ ... dv (ди ди . \
или, используя условия B.19): — = г\ — сскф + — sin<p .
ар {дх ду )
_ ди dv dv ди ди
Сравнивая равенства для — и — , имеем — = г —, а из равенств для —
5г йр ар дг ' йр
dv ди dv
и — получаем — = -г—
дг йр дг
ар
Выписываем результат:
ди__1 dv_
А** *• An
B-21)
дг
ди_
ар
г ар
Sv
f» __
— — г ' ^^
дг
Это и «сть искомые условия Коши-Римана в полярных координатах.
93
Пример 2.36. Записать производную функции f(z) для случая z = r-ei<*
в полярных координатах.
D Пусть f(z) = u + iv, u = u(r, <р), v = v(r, <р) и г = удг + у , <р = arctgА За-
х
пишем частные производные по правилу дифференцирования сложной функции:
ди ди дг ди 5ш ди ди дг ди д® .. ,„„,,
— = + -,— = + -. Используя условия B.21), запишем
дх дг дх 9ip дх ду дг ду ftp ду
выражение для /'(г): /'(г) = i —. Получим
дх ду
дг{дх ду) дг\дх ду
Далее находим производные функций r(x,y) = Jx2 +y2, <p(x,;y) = arctg— и
х
выписываем выражения, стоящие в скобках:
У I.
Эф_ .dtp у . х Kx-iy) _-'-Z _ i-Z
дх ду х2\у2 х2+у2 х2+у2 Z-Z г2'
Для производной получаем выражение
,,. z(du .dv~] ,,. . г(ди .dv\
f(z) = -\ — + i—\ или /(*) = -—+(—•■ B.22)
г {дг дг) z\dr дг)
Пример 2.37. Исследовать на дифференцируемость функцию
f(z) = In z, 0 < arg z < 2л. Найти производную.
D В области D : 0 < arg z < 2л - плоскости с разрезом по действительной
положительной полуоси, функция однозначная (см. рис. 2.5). Исследуем ее на
дифференцируемость по правилу 2.1, используя запись в полярных координатах.
1. Из равенства In г = In г + ир имеем u(r, <p) = In r, v(r, <p) = <р.
. „ ди 1 ди dv n Sv
2. Находим частные производные: — = -, — = 0, — = 0, — = 1.
дг г 9ф дг Sip
3. Условия B.21) выполняются в любой точке области D, следовательно,
функция дифференцируема в области D. Заметим, что, очевидно, дифференци-
дифференцируемой в соответствующей области будет любая однозначная ветвь логарифма,
In г = In г + i(arg z + 2кп\ к - любое, к = 0,+1,... Используя формулу B.22), записы-
записываем производную
Z \r
94
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ МОДУЛЯ И, АРГУМЕНТА ПРОИЗВОДНОЙ
Производная /'(г) как функция комплексного переменного определяет
отображение некоторой области D - области дифференцируемое™ функции /(г)
пи область G. В каждой точке z$eD определено комплексное число /'(го),
ши-допательно, определены |/'(го)| и arg/'Uo), если /'(го)*О. Геометрически
число |/'(го)| - длина радиуса-вектора точки /'(го), a arg/'U0) - угол наклона
нот радиуса-вектора к действительной оси.
Возникает вопрос, как характеризуют эти величины само отображение
w - У (г) в точке го • Как известно, для функции действительной переменной
аналогичный вопрос решается просто: производная /'(х0) определяет угловой
коэффициент касательной, проведенной к кривой у = f(x) в точке (хо,/(хо)).
Рассмотрим геометрические свойства величин £ = |/'(го)| и a = arg/'(Zo)>
1ЮЛИП1Я /'(го) * 0, а функцию /(г) дифференцируемой в окрестности точки го-
Тек как по определению производной /'(го)= Нт — предел в точке не зави-
Дг->0 Дг
вит от направления и способа стремления Дг к нулю, то можно взять произ-
произвольную гладкую кривую у, проходящую через точку Zo, и на ней любую точку
I и 1 окрестности точки го •
Образ кривой у при отображении w = /(г) обозначим Г, образы точек го
и г через w0 и w соответственно; из непрерывности отображения очевидно, что
и»,, i г и wеГ. Приращения переменных Дг = г-го и bM = vi-w§ геометриче-
гки есть векторы (рис. 2.13,о), их длины - |Дг|, |Aw|.
Из определения производной и свойства предела lim — = /'(г) имеем
дг-»о д г
~ = /'(го) + а. следовательно, — = | /'(го) + а < | /'(го) | + |а|, или
<|а|<Е для геО(го)- Последнее неравенство, согласно опре- *
лг
делению, означает |/'(го)
= lim
дг-»о
Aw
Дг
. Перепишем его следующим образом:
Аг
А/Г dlr
= lim —- = —-, где Д/г и Д/„ - длины соответствующих
дг->од/у dly '
avr кривых Г и у , как известно, эквивалентных при |д г| -> 0 стягивающим их
чордам |aw| и |Дг|; dlr и dly - элементы длин дуг Г и у в точках w0 и го co-
coin нетственно.
Отношение —- определяет изменение масштаба (растяжение, сжатие)
dly
и точке го при отображении w = /(г). В этом заключается геометрический смысл
модуля производной.
95
Величина |/'(го)| не зависит от вида кривой у, поэтому отмеченное свс
ство имеет место и для любой другой гладкой кривой, проходящей через то<
г0-
Следовательно, величина £ = |/'(го)| модуля производной есть величи
постоянная для данной функции /(г) и датой точки г0
Для аргумента производной имеет место равенство arg/'(^o) = 0-<p, где
и <р - углы между действительными осями в плоскостях (w) и (г) соответств
но и касательными, проведенными к кривым Г в точке w0 и у в точке
(рис.2.13,о).
Если точки w0 и го совместить, то <x = arg/'(Zo) = 0-<p - угол noeopi
кривой у в точке zo при отображении w = f(z) (рис.2.13,6).
В этом заключается геометрический смысл аргумеита производной аш
тической функции.
f
0
w
Aw
— Г
(w)
V ■
У
и
/
0
7
X
и
Рис. 2.13
Это свойство, очевидно, имеет место и для любой другой гладкой i
кривых у, и Г15 проходящих через точки го и vc0 соответственно,
a = 6[ -ф[. Из равенств а = 6-ср и а = 01-<р1 получаем 6| -6 = ф| -<р. Это с
чает, что угол |3 между кривыми Г( и Г, р = 6i -6 равен углу между кривым
и у, р = ф] — ф (рис. 2.14). Следовательно, при отображении сохраняются
между кривыми.
Отображение, сохраняющее углы между кривыми, называется конформ,
Рис. 2.14
96
Полученные результаты сформулируем в виде утверждения.
Утверждение 2.7.
1. Модуль |/'(го )| производной функции /(г), дифференцируемой в окрестно-
окрестности точки го , есть коэффициент линейного растяжения кривой в точке Zq при
отображении w = f(z).
2. Аргумент производной в точке есть угол поворота кривой в этой точке при
отображении w = /(г).
3. Отображение с помощью дифференцируемой в окрестности точки г0
функции f(z), удовлетворяющее условию f'(Zo) * 0> является конформным в точке
Ли. Оно обладает свойством постоянства растяжения и сохранения углов. Причем
ты сохраняются как по величине, так и по направлению отсчета.
Пример 2.38. Найти коэффициент растяжения и угол поворота в точке
2/ при
D
г + 1
отображении w = .
z + i
Находим производную и
., z + i-z
(z + i)
-1
2
ее значение в точке
(г + 'Г
ll:w'Bi) = . Коэффициент к растяжения равен модулю производной,
ill - |w'B/)| = -■ 1/2, угол поворота - аргументу производной argw'Bi) = --.■
Пример 2.39. Определить, какая часть плоскости при отображении w = z2
растягивается, а какая - сжимается.
D Находим производную w' = 2г , коэффициент растяжения в любой точ-
точке равен м/(го)| = 2|го|> к = 2|го| • Множество точек ?о. для которых к > I, т.е.
2|jo| > I, |го| >—, очевидно, образует часть плоскости, которая при отображении
растягивается. Следовательно, при отображении w = z2 внешность круга |г|>-
растягивается, а внутренняя часть \z\ < — сжимается. ■
Пример 2.40. Показать, что при отображении w = z2 координатная сетка
плоскости (w) соответствует двум ортогональным семействам кривых плоскости
(г).
D Так как /'(г) = 2г, то отображение w = z2 конформно всюду, кроме точ-
точки г = 0. Координатная сетка плоскости (w) - это совокупность линий
I/ = const, v = const. Очевидно, любая пара таких линий в точках пересечения об-
образует прямой угол (рис. 2.15,о). Прообразами этих линий в плоскости (г) будут
два семейства гипербол: х1 - у2 = с, с * 0 и 2ху = с, с * 0 (рис. 2.15,6). Они полу-
получаются из равенства w = z2, т.е. u + iv = (x + iyf или и = х2 -у2, v = 2xy. Линии
рассматриваются при любых значениях с * 0. Заметим, что при с = 0 линии
у = х, у = -х, у = 0, х = 0 проходят через точку z = 0, где /'@) = 0.
I Пантелеев А.В., Якимова А.С.
97
(w)
В
0
V
« = c2
A
v = q
u
Рис. 2.15
Покажем, что гиперболы х2 - у2 = с2 и 2ху = q при любых ci
C2(q *0,ci *0) пересекаются под прямым углом, т.е. прямой угол образуют ка-
касательные к этим кривым в точке пересечения кривых (например, точка А н
рис. 2.15,6). Угловой коэффициент кривой первого семейства - производную
точке А(хо,уо) - находим по правилу дифференцирования неявной функци
-; для кривой второго семейства
- Щ Уо
пересечения (хо>.Уо) верно равенство 2хо>"о =q, поэтому у\
Условие ортогональности касательных выполнено: _yj(x0)
в точк
2^оУо
' 2x1
= -1 .i
Упражнения
1. Найти /'@), если f(z) = 1пBг + 0.
Ответ: -2(.
2. Найти |/(го)|, arg/'(?0), f(z) = ez\zQ=l + i.
Ответ: ъп, -+2.
4
3. Для /'(^о) гДе /(г) = /sin2 г и го =2(, выбрать верные соотношения
следующих:
а)/'Ы<0; б) 1т/'(г0)<0; в) Re/'(jo) = sin4; г) |/'(го)| = -Re/(г,
Ответ: а), г).
4. Определить, в каких точках дифференцируема функция:
a) f(z) = z-Rez; б) Дг) =
Ответ: только в точке го = 0.
5. Проверить условия Коши-Римана в произвольной точке, и в случае их
выполнения найти f'(z) для функций:
а) /(г) = Зг ■ е2г ; б) /(г) = cos(* + 2i).
Ответ: условия выполняются в любой точке г;
4 a) f(Z) = 3e2HU2z); б) /'(г) = -ап(г + 2/).
6. Определить, в каких точках дифференцируема функция:
Ответ: ни в одной точке.
7. Найти |/'(го)|, atgfizo), если f(z) = e2z и г0 =«•
• Ответ: 2; 2.
8. Для /'(го), где /(г) = sin 2z и го =', выбрать верные соотношения среди
следующих:
а) /'(() > 0; б) Re f'(i) = 2 ch 2; в) Im /'(С) = 0; г) arg /'(») = 0.
Ответ: все.
9. Найти Re/(г), если:
a) f(z) = rz + 2z2; б)/(г)=4 +=-
' г
О/иве/и: а) у + г(х2 - у2}, 6) -у —-2—.
х1 + У1
10. Найти |/(го)|, arg/Ы, если:
1 L
1
а) /<г) = е* sin|, г0 =-; б) /(г) = е« -ап^, го =1.
Ответ: a) sin 2, -я + —; б) shl, 1—.
11. Найти |/(го)|, aig/(z0), если /(г) = -|—, г0 =1 + '-
г +1
Ответ: —, л +1.
12. Найти образ точки го при отображении w = /(г), если:
а) го=1-|,/(г) = (г+2г3; б)го=2-/,
6
Ответ: a) w = -5-3/'; б) w = г.
13. Для функции f(z) = e2z'' среди следующих соотношений выбрать вер-
верные: а) |/(г)| = е2^+У2); б) |/(г)| = е2х; в) /@) > 0; г) aig/(») = -i;
д) arg /(/) = -3; е) Re /(() = cos 3.
Ответ: б), д), е).
99
2.1.4. Аналитические функции
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
В теории и практике применения функций комплексного переменного ин
терес представляют дифференцируемые функции, причем имеющие производные
не в отдельных точках, а на множествах - в областях. Такие функции называюга
аналитическими.
Имеют место следующие определения.
1. Функция, дифференцируемая в каждой точке области, называется ста
литической в области.
2. Функция, аналитическая в окрестности некоторой точки, называете)
аналитической в этой точке.
3. Функция называется аполитической па замкнутом множестве \D), есл(
она является аналитической в некоторой области (В), содержащей это множест-
множество (F с в).
4. Точки, в которых нарушается аналитичность функции, называются ei
особыми точками.
Дифференцируемость функции в точке, согласно утверждению 2.6, прове-
проверяется по правилу 2.1. Но аналитичность функции по определению связана <
дифференцируемостью в области, в частности, в окрестности точки. Для иссле-
исследования дифференцируемое™ в области (аналитичности) используется следую-
следующее обобщенное утверждение [5].
Утверждение 2.8. Если функция непрерывна в области и в каждой ттк<
области выполняются условия Коши-Римана, то функция является аналитически
в области.
Правило 2.2. Для исследования функции на аналитичность требуется вы-
выполнить следующие операции.
1. Найти действительную и мнимую части функции /(г):
и = Re/(г), v = lmf(z).
2. Найти частные производные функций и = и(х,у) и v = v(x,y) или функ
ций « = «(г,ср) и v = v(r,(p) в полярных координатах.
3. Если условия Коши-Римана B.19) или B.21) выполняются в юждо£
точке непрерывности функции, то функция в этой области аналитическая.
Производная аналитической функции может быть найдена с помощью оп
ределения, т.е. по формуле B.1) или по формулам B.20) или B.22).
Пример 2.41. Исследовать на аналитичность функции:
а) /,(г) = г, /2(г) = |г|2; б) /,(г) = с, f2(z) = г", /3(г) = ez;
в) /[ (z) = In z в плоскости с разрезом по [0, °о).
D а) Функции w = z и w = |г| - не аналитические всюду, что следует и
решения примера 2.33.
100
б) Функция /| (г) = с = с, + с2/, где и(х, y) = q и v(x, у) = с2, очевидно, яв-
/-. ди ди dv dv . , п
лиется аналитической всюду в С, так как — = — = — = — = 0; и с = 0.
дх ду дх ду
Аналитичность функций w = z" и w = ег всюду в С следует из решения приме-
примером 2.29 и 2.34 , где установлена их дифференцируемость; кроме того, там же
нпйлсны их производные (ez) =ez,(z") = n-z"~l-
в) Аналитичность и- = 1пг,0<ф<2л (см. область О, на рис. 2.5) следует
hi решения примера 2.37, где получена и производная (Inг) = —.■
Z
Пример 2.42. Является ли функция и(х,у) двух действительных перемен-
переменных аналитической ?
□ Функция и(х,у) как функция комплексного переменного имеет вид
f(l)-u(x,y) + i-0 и является дифференцируемой на линиях или в точках -
решениях системы
дх
не образующих область (см. разд. 1.2). Поэтому она
ду
не является аналитической.*
Пример 2.43. Доказать аналитичность функции sin z во всей комплексной
плоскости. Найти производную.
D Запишем решение по правилу 2.2.
1. Действительную и мнимую части функции находим, используя формулу
sin(x + iy) = sin x ■ cos iy + cos x ■ sin iy = sin x ■ chy + / cos x ■ shy.
Получаем и = sin x ■ chy, v = cosx • shy.
2. Находим частные производные:
dv . . dv , du , du
— = - sin x ■ shy, — = cos x ■ chy; — = cos x ■ chy, — = sin x ■ shy.
dx dy дх ду
3. Условия B.19) выполняются для любой точки (х,у), поэтому функция »
w = sin z дифференцируема при любом z ■ Кроме того, по формуле B.20) получа-
получаем производную
.... . ди dv . . . . .... / . \
/ (z) = — + / — = cosx ■ chy -1 sin x ■ shy = cos x ■ cosiy - sin x ■ sin iy = coslx + ty),
dx dx
re. f'(z) = cosz-
Здесь использованы формулы cosiy = chy, siniy = i-shyM
СВОЙСТВА АНАЛИТИЧЕСКИХ ФУНКЦИЙ
Результаты примеров 2.41 и 2.43 не являются случайными. Более того, по-
поскольку понятие аналитичности функции определяется через понятие дифферен-
дифференцируемое™, то, учитывая утверждение 2.5 о свойствах функций, дифференци-
дифференцируемых в точке, убеждаемся в справедливости следующего утверждения.
101
Утверждение 2.9.
1. Сумма, произведение функций, аналитических в точке, есть функция, ана-
аналитическая в этой точке. Поэтому, в силу аналитичности функции w = c
(см.пример 2.41), линейная комбинация функций, аналитических в точке, является
аналитической функцией.
2. Частное функций, аналитических в точке, есть функция, аналитическая
в этой точке, если знаменатель в ней отличен от нуля.
3. Суперпозиция аналитических функций - функция аналитическая.
4. Если f(z) - аналитическая в точке го и /'(?о) *0, то обратная функция
f'](w) является аналитической в wo(f(zo) = и"о)-
Эти свойства используются в большинстве случаев при исследовании
функции на аналитичность. При этом отпадает необходимость проверять условия
Коши-Римана. Правила нахождения производной такие же, как в действитель-
действительном анализе (см. утверждение 2.5). Очевидно, совпадают и табличные производ-
производные и нет необходимости использовать формулу B.20).
Пример 2.44. Доказать аналитичность во всей комплексной плоскости
функций shz, chz, Pn(z).
в*" — €~^ 1 1 б^ + €~^
О Аналитичность функций shz= — = -ez--e'z и chz = — =
= -ег +--e'z всюду в С следует из аналитичности функции ег(пример 2.41)
и п. 1 утверждения 2.9. Аналитичность многочлена Pn(z) всюду в С является
следствием аналитичности функции г" (пример 2.41) и п. 1 утверждения 2.9. ■
Пример 2.45. Исследовать на аналитичность функции tgz, ctgz, Л(г)-
рациональная функция.
D Каждая из заданных функций представляет собой частное аналитических
функций. Особыми точками этих дробей, согласно определению и п. 2 утвер-
утверждения 2.9, являются только нули знаменателя .
р (^)
Для рациональной функции R(z) = —-— эти точки - нули многочлена
Qm(Z)
Qm(z), т.е. решения уравнения Qm(z)= 0; для tgz = особыми точками яв-
cos*
ляются точки Zk = — + kn, для ctgz = ——точки zk = kn, k = 0,+l,+2,.... Всюду
2 sin z
в С, кроме найденных особых точек, функции являются аналитическими."
Пример 2.46. Найти особые точки функций:
-T^ . /3W = #k4
102
D а) Особыми точками этих рациональных функций являются только нули
знаменателей. Для /](г) это, очевидно, точки Z\ =1, Zj =-l + i, Zy = -l-i; для
/2 (г) - корни уравнения г6 +1 = 0, т.е. Zk =е 6 , к = 1,2,3,4,5,6, и точка г0 = 0.
б) Особыми точками функции fx(г) являются нули знаменателя, это точки
lk =кп, к = 0,+1,..., г ='. и особая точка числителя z = 1 ■
Для функции /2 (г) особые точки - нули знаменателя и z = 0 - особая точ-
точка знаменателя. Найдем нули знаменателя, как решения уравнений sin—= 0 и
г
cosz + l=0. Получаем в результате - = кп или Zt =—• k = ±l,±2..., и
z кп
1т =п + 2тл, т = 0,±1,...
Особыми точками функции /з(г) являются только нули знаменателя, т.е.
Z=0, и точки, для которых ег=-1, т.е. ez = eGI+2fa'', или
Zk =(n + 2kn)i, Jfc = 0,±l,... ■
Отметим одно важное обстоятельство, связанное с определением произ-
производной функции комплексного переменного. В определении производной со-
содержится требование, чтобы предел lim — — не зависел от способа
z->*o z-Za
стремления z к го. т.е. если существует производная /'(го). то отношение
—-—— имеет один и тот же предел (при &z -»0) по любому пути и, в частно-
AZo
сти, по любому из бесконечного множества различных лучей, выходящих из точ-
точки Zo ■ Заметим, что для функции действительной переменной таких направле-
направлений только два - производная в точке слева и справа.
Указанное обстоятельство накладывает на дифференцируемую функцию
комплексной переменной (а следовательно, и на аналитическую) более сильные
ограничения, чем на дифференцируемую функцию действительной переменной,
и является причиной появления некоторых дополнительных свойств этих функ- v
ций.
Важным отличительным свойством аналитической функции комплексного
переменного является следующее. Кроме того, что функция, согласно определе-
определению, имеет производную первого порядка в точке, она имеет в этой точке и
производную любого порядка. А из существования производных любого порядка
следует их непрерывность, так как непрерывность функции в точке является не-
необходимым условием дифференцируемое™. Так, из существования в точке про-
производной второго порядка от некоторой функции следует непрерывность первой
производной от этой функции в указанной точке и так далее.
Можно сформулировать следующее утверждение, доказательство которого
основано на материале, излагаемом в разд. 2.2.
Утверждение 2.10 (о бесконечной дифференцируемое™ аналитической
функции). Функция, аналитическая в точке, имеет в этой точке производные лю-
любого порядка, которые являются непрерывными в этой точке.
103
СВЯЗЬ АНАЛИТИЧЕСКИХ ФУНКЦИЙ С ГАРМОНИЧЕСКИМИ. ВОССТАНОВЛЕНИЕ
АНАЛИТИЧЕСКОЙ ФУНКЦИИ ПО ЗАДАННОЙ ЕЕ ДЕЙСТВИТЕЛЬНОЙ
ИЛИ МНИМОЙ ЧАСТИ
Другая отличительная особенность аналитической функции связана с диф-
ференцируемостью ее действительной и мнимой частей как функций двух дейст-
действительных переменных. Во-первых, из формулы B.19) и утверждения 2.10 следу-
следует, что эти функции имеют непрерывные частные производные любого порядка
в области, где функция является аналитической. Во-вторых, нетрудно убедиться,
что функции и(х,у) = Re/(г) и v(x,y) = lmf(z) являются гармоническими в об-
области аналитичности f(z) ■
Напомним, что гармонической в области D называется функция и(х,у)
двух действительных переменных, которая имеет в D непрерывные частные
производные до второго порядка включительно и удовлетворяет в D уравнению
^ + ^ = 0. B.23)
дх2 ду2
Для доказательства справедливости равенства B.23) для функций и = Re f(z) и
v = \mf(z) достаточно продифференцировать одно из равенств B.19) (условия
Коши-Римана) по х, другое - по у и воспользоваться равенством смешанных
производных, которое имеет место в силу непрерывности этих производных.
Уравнение B.23) называется уравнеиием Лапласа, его можно записать в ви-
д2 д2
де Дм = 0, где Д = —- + —г - оператор Лапласа. Уравнение имеет важное зна-
дх2 ду2
чение при решении плоских задач математической физики.
Две гармонические функции, связанные между собой условиями Коши-
Римана, называются сопряженными гармоническими функциями.
Полученное свойство аналитических функций запишем в виде утвержде-
утверждения.
Утверждение 2.11. Действительная и мнимая части любой аналитической
в области D функции являются в D сопряженными гармоническими функциями.
Учитывая, что действительная и мнимая части аналитической функции не
являются независимыми друг от друга, а связаны условиями Коши-Римана, сле-
следует ожидать, что, используя эти условия, можно, зная одну из них, найти дру-
другую, а тем самым и аналитическую функцию, т.е. восстановить аналитическую
функцию по заданной ее действительной или мнимой части.
Для функции, заданной в односвязной области, эта задача сводится к ин-
интегрированию полного дифференциала. Действительно, если и(х,у) - гармони-
„ _ _ д2и д2и , .„ _,. „ .
ческая в односвязной области D, то условие —- = - (см. B.23)) будет
дх2 ду2
,, ди , ди .
являться условием полного дифференциала для выражения ах +—ау, т.е.
ду дх
104
существует однозначная в области D функция v(x,y), такая, что имеет место
, ди , ди
равенство dv = dx +—dy, и, следовательно,
ду дх
' *'r dU dU
v(x,y)= -—dx +—dy + c. B.24)
J» ду дх
С помощью B.24) определяется функция v(x,y) по заданной гармониче-
гармонической функции и(х,у). Кроме того, сравнивая подынтегральное выражение
к B.24) с формулой полного дифференциала dv для функции v, т.е.
, dv , dv , , „ . .
civ = —dx+—dy, получаем, что для частных производных функции и(х,у) и
дх ду
v(x,y) выполняются условия Коши-Римана, т.е. функция v(x,y) является
сопряженной с и(х,у). Из этого следует, что v(x,y)- мнимая часть f(z),
v(x,y) = Im f(z) и и + /v = f(z) - аналитическая функция.
Полученный результат запишем в виде утверждения.
Утверждение 2.12. Для любой гармонической в односвязной области D функ-
функции можно найти с точностью до постоянного слагаемого сопряженную с ней гар-
гармоническую функцию; задача решается интегрированием полного дифференциала по
формуле B.24). Постоянная определяется из дополнительного условия - задания ис-
искомой функции в некоторой точке.
Замечания 2.8.
1. Если область D многосвязная, то функция v(x,y), определяемая инте-
интегралом B.24), а также функция f(z) = u + iv могут оказаться многозначными.
2. Интеграл в B.24) не зависит от вида кривой. Если выбрать в качестве пу-
пути интегрирования ломаную, звенья которой параллельны координатным осям,
то задачу можно свести к вычислению двух определенных интегралов:
)^)^ c. B.25)
Точка (хо,уо) может быть выбрана любой из области определения функ-
функции. Заметим также, что в первом подынтегральном выражении значение пере-
переменной у при вычислении интеграла заменяется на у0 = const.
Пример 2.47. Проверить, что функция и = -\п[х2 +у2} является гармони-
гармонической. Найти сопряженную с ней функцию: а) в области с разрезом по лучу
- оо < х < 0; б) в плоскости с выколотой точкой @,0).
□ Находим частные производные второго порядка от функции и(х,у) и
проверяем равенство B.23):
ди х д2и х2+у2-х-2х у2-х2 д2и х2 - у2
= = = ^
поэтому —- + —г = 0 для любой точки плоскости, исключая точку @,0).
дхг ду1
105
а) В односвязной области - плоскости с разрезом по действительной отри-
отрицательной полуоси в соответствии с утверждением 2.12 существует однозначная
сопряженная с данной и(х,у) гармоническая функция. Определим ее по форму-
формуле B.25):
Точку (хо,уй) можно выбрать произвольной в указанной области, напри-
например A,0). Поэтому получаем
у
f
у х \ у
v(x,y)= \0dx+ f — -dy + c = x—arctg—
/ &хг+уг x x
/ &хг+у
+ c = arctg— + c.
Нетрудно проверить, что полученная функция v(x,y) - гармоническая.
В частности, при задании дополнительного условия v(l,0) = 2, находим значение
с: arctgO + c = 2, т.е. с = 2 и, следовательно, определенную гармоническую
функцию v(x, у) = arctg— + 2. Запишем функцию f(z), для которой заданная
х
функция и(х,у) является действительной частью, а найденная v(x,y) - мнимой
частью:
f(z) = и + iv = -In [х2 + у2)+1 • arctg— +1 • с = In |г| + i • arg z +' • с,
или f(z) = In z +' • с - функция, аналитическая в плоскости с разрезом по лучу,
б) Область D здесь не является односвязной (двусвязная).
Находим функцию v по ее полному дифференциалу: v = f dx + —dy + с.
i дУ дх
Если путь интегрирования - произвольная кривая, соединяющая точки Мо
и М, не проходящая через начало координат и не совершающая обхода вокруг
@,0), в частности ломаная МОМХМ (рис. 2.16), то результат получен в предыду-
у
шем пункте v = arctg— + с.
х
Выберем теперь в качестве пути интегрирования кривую /, которая, выхо-
выходя из точки Мо, совершает один раз обход вокруг начала координат по произ-
вольной замкнутой кривой, например по окружности радиуса R =
ОМй\, и
] ду дх I ду дх J ду дх
заканчивается в точке М (рис. 2.16). Интеграл можно представить в виде двух
слагаемых:
г ди . ди , е ди . ди , Ме ди , ди ,
dx +—ay + c = q fl!x + —dy+ dx + —dy + c.
' Яч Яг J Яи Яг ' Яv Яг
«О
106
(г)
•'«. ' Рис. 2.16
Второе слагаемое вычислено выше. Найдем интеграл по контуру - по ок-
окружности радиуса R, для которой запишем параметрические уравнения
х = R cos /, у = R sin /. Вычисляем криволинейный интеграл второго рода через
определенный для случая параметрического задания кривой:
-у
х2+у2
о
Таким образом, получаем результат f dv = arctg— + 2л + с.
1 х
Если / совершает обход к раз вокруг начала координат по часовой стрелке или
против часовой стрелки, то результат, очевидно, принимает вид
v(x, у) = arctg-+ 2кп + с, к = 0,±1,±2...
л:
При задании дополнительного условия находим значение с, например, при ус-
условии v(l,0) = 0 имеем с = О. Получена многозначная функция (см. замечание»
2.8) v = arctg— +2£л, при этом f(z) = u + iv, очевидно, также многозначная,
х
f(z) = In |г| + / (arg z + 2£л) или f(z) = Ln i. ■
Пример 2.48. Найти аналитическую функцию f(z) = u + iv по заданной ее
действительной части и(х,у) = х3 -Злу2 + 2у.
D Находим частные производные данной функции:
ди
дх
ду
д2и
дх'
=-6х.
f) и Ли
Так как равенство —- + —- = 0 выполняется для любой точки (х, у), то и{х, у)
дх1 ду2
- гармоническая в любой области D. Находим сопряженную с ней функцию по
формуле B.25):
107
v(x,у) = ](бху0 - 2)dx + )(зх2 - 3y2)dy + с, = (зУйх2 -2х)\ (зх2у - у3) ' + с, =
= Зуох2 -2х- Зуох$ + 2х0 + Зх2у -уг - Зх2у0 + у$ + q = Зх2.у - уг - 2х + с,
С| = const, с = const.
Этот же результат можно получить, взяв при интегрировании х0 = 0, у0 = О,
т.е.
J (- 2dc)+ J (Зх2 - 3y2)afv + с = -2* + Зх2у -уг + с.
о о
Записываем функцию /(г): f{z) = u + iv = x3 - Зху2 +2y + i \3x2y - уъ - 2х + с).
В правой части равенства нужно заменить х и у их выражениями через пере-
переменную z:x = , у = ——; для удобства можно использовать равенство
г3 = (х + iyf = х3 + Зх2у ■ i - Зху2 - /у3, которое, очевидно, присутствует в выра-
выражении для f(z) ■ Получаем
/(г) = х3 - Зху2 + / (з*2у -yi)+2y-2ix + ic = zi - 2/ (к + />) + /с = г3 - 2iz + ic,
или f(z) = zi - 2iz + с, где с - комплексная константа.
Задачу можно решить иначе, используя непосредственно условия Коши-
Римана. А именно из равенства — = = 6ху-2 находим
дх ду
v= \^d ()
1 дх
Заметим, что здесь интегрируется по одной из переменных (по х) функция
5v
двух переменных —, поэтому постоянная интегрирования, не зависящая от пе-
дх
ременной интегрирования, является функцией параметра, т.е. у.
Далее, для нахождения функции ф(у) используем другое условие Коши-
„ dv ди „ dv
Римана — = —. Находим производную — от полученного выше выражения
ду дх ду
для v(x, у), — = Зх2 + ф'(у) и приравниваем известной производной
ду
—, — = Зх2 - Зу2. Из полученного равенства - Зу2 = <р'(у) определяем <f(y):
дх дх
М I 'МФ + с = \~ 3У2(Ь> + с = -уг +с.
Таким образом, найдена функция v(x,у) = Зх2у - 2х + (-уъ + с)
108
Пример 2.49. Пусть v = v{x,y) - гармоническая в области D функция. Най-
Найти сопряженную с ней функцию и(х,у), такую, что и = Re f(z), v - Im f(z), где
f(z) - аналитическая в области D функция.
□ Поставленную задачу можно сформулировать, как задачу восстановления
аналитической функции по заданной ее мнимой части. Будем рассматривать слу-
случай односвязной области D.
Функцию и(х,у), согласно утверждению 2.12, находим интегрированием
полного дифференциала: и(х,у)= \ du + c = ( —dx +—dy + c, или, исполь-
1 J дх ду
Wo *о.Л
зуя условия Коши-Римана для пары сопряженных гармонических функций:
и(х,у)= '( ^dx-^-dy + c. B.26)
1 ду дх
Если, как и выше, в качестве пути интегрирования, соединяющего точки (xo.j'o)
и (х,у), выбрать ломаную, звенья которой параллельны координатным осям, то
из B.26) получим два определенных интеграла:
Ф,У) = )^(x,yo)dx-)^(x,y)dy + c. Ш B.27)
Iду 1дх
Обобщая изложенный материал и рассмотренные примеры, можно сфор-
сформулировать следующее правило нахождения аналитической функции по задан-
заданной ее действительной или мнимой части.
Правило 2.3. Для нахождения аналитической функции по заданной ее дей-
действительной или мнимой части необходимо выполнить следующие операции.
1. Найти частные производные до второго порядка заданной функции двух
переменных и(х,у) или v(x,y). Проверить, если требуется, что заданная функ-
функция гармоническая, т.е. выполняется в некоторой области D равенство Аи = О
или Ду = 0.
2. Найти по заданной гармонической функции сопряженную с ней функ-
функцию, используя формулы B.24) или B.25) для нахождения v = Im f(z) или B.26),
B.27) для нахождения u = Ref(z). Можно воспользоваться непосредственно
условиями Коши-Римана (см. пример 2.48).
3. Записать функцию /(г) = м + /у, где одна из функций (и(х,у) или
v(x, у)) - заданная гармоническая, другая - гармоническая, сопряженная с ней.
В односвязной области функция f(z) - аналитическая (однозначная) и опреде-
определена с точностью до постоянного слагаемого.
4. Если задано дополнительное условие - значение искомой функции f(z)
в некоторой точке из области аналитичности функции, то следует использовать
его для определения постоянной с, получившейся при нахождении сопряженной
функции.
109
Пример 2.50. Найти аналитическую функцию f{z), если
Im f(z) = x ■ shx ■ sin у + у ■ chx ■ cos у и /(l) = ch 1.
Q Запишем решение по правилу 23.
1. Находим частные производные функции
v(x, у) = х ■ shx • sin у + у ■ chx • cos у:
dv , . , .
— = shx • sin у + л: • chx • sin у + у ■ shx ■ cos у,
дх
dv ■ i ■
— = x ■ shx • cos у + chx • cos у - у ■ chx • sin y.
dy
2. Находим функцию и(х, у) по формуле B.27):
х у
и(х,у)= j((x-shx + chx)-cos,y0 -у0 -smy0 -chx)dx- f (shx + x ■ chx) • sin у dy -
*o Уо
У
- jshx • cos у ■ у dy = cosj/0 x ■ chx
- Jchxflbc +cosy0-shx
-JVsinj/0-shx
У ( У у, )
-shxb-siny - Jsinydy =cosy0 xchx-x0-chx0 cosy0-
» I "> Уо j
-chx)cosy
- shx- cos y0 +shx0 -cosj/0 + cos уй ■ shx - cos уй ■ shx0 - y0 ■ sin y0 ■ shx + y0 -sin,yox
xshx0 + shx- cosy + x-chx-cos,y-shx-cos)>o -xchx-cosy0 -shx-siny-y +
+ shx • уо • s'n ^o - cosy • shx + cosy0 • shx = x ■ chx • cosy - у • shx • sin у + с.
Можно проверить, что полученная функция и(х,у) является гармониче-
гармонической. Заметим, что при интегрировании можно взять х0 = 0, у0 = 0. Можно, как
записано в правиле 2.3, при нахождении функции и(х,у) использовать условия
Коши-Римана непосредственно:
\—
где i|/(x,y)- определенная, полученная при интегрировании функция, а функцию
ф(у) требуется определить. Она находится из равенства, получаемого при сравне-
ди ди dv .
нии выражения для — ( известного из условия — = , где v(x,y) - заданная
ду ду дх
ди
функция) с выражением для —, получаемым при дифференцировании по у
ду
функции \]/(х,у)+ф(у).
ПО
3. Записываем функцию f(z) = u + iv = х- chx ■ cos у - у ■ shx • sin у + с +
+ /(xshxsinj' + >'chxcosj'). Преобразуем полученное выражение к функции
переменной z , используя формулы Эйлера cos iz = chz, sin it = i • shz и тригоно-
тригонометрическую формулу для cos(a + р). Получаем
f{z)= z{cosix ■ cosy + sinix ■ siny) + с = z-cos(ix-y) = z-cosi(x + iy)+c =
*' = z ■ cos iz + с,
или окончательно: f(z) = z ■ ch z + с, где с - действительная постоянная. ■
Ч.г
Пример 2.51. Показать, что функция arctg— является гармонической в об-
х
ласти определения. Найти аналитическую функцию f(z) = u + iv, для которой
у
и = arctg—
X
U 1.
и/(-0=у + 2/.
Находим частные производные
ди -у
дх х2+у2'
Далее находим производные
д2и у■2х
дх2 (х2 + у2
ди
ду
второго
г
функции
X
х2+у2
порядка:
д2и
V (,
arctg—:
X
при х*
-х-2у
■2 + y2Y
_ . . ди ди
При х = 0 и v * 0 частные производные — и — равны нулю, так как при
дх ду
7U V
этом и = ±—. Тем самым убеждаемся, что функция и(х, у) = arctg— удовлетворяет
2 . х
уравнению Лапласа —- + —- = 0 для любых (х,у), за исключением точки @,0) >
дх2 ду2
т.е. всюду в области определения.
Согласно утверждению 2.12, в комплексной плоскости с выколотой точкой
Z = 0, т.е. в 0 < \z\ < оо, существует функция f(z), для которой данная функция
является действительной, как в данном случае, или мнимой частью. При этом в
любой односвязной области Z), в частности в плоскости с разрезом по лучу
[0,оо) (см. рис. 2.5), определяется однозначная аналитическая функция.
2. Находим функцию vfoy), сопряженную с функцией и = arctg—. Ис-
х
пользуем условие Коши-Римана. Получаем:
v(x,y)= } —
' дх
111
дх ' ау х + у
Отсюда находим производную —, — = — . + у'(у) и приравниваем
ду ду х2 + у2
Эй у v
ее —. Получаем равенство -—г1—т- + <?'(у) = — , из которого определя-
дх х2+у2 х2+у
ем ?
В результате с точностью до произвольной постоянной с найдена функция
v(x,y)-—1п(х2 +у2)+с, сопряженная с данной функцией и(х,у), причем
v(x,y) является мнимой частью аналитической в указанной области функции
/(г), для которой и(х,у) = Re/(г).
3. Записываем аналитическую функцию
/(г) = и + /V = arctg— - /'-ln|x2 + уг)+ ic,
или, переходя к переменной z: f(z) = arg z - i In |г| + ic.
Можно записать иначе: /(г) = -j'(ln|z| + /argz) + C[ или окончательно
f(z) = -1 In г + q, где ct - комплексная константа.
4. Используем условие /(-/') = — +2/ для нахождения су:
—
или, вычисляя значение ln(-z') (см. разд. 2.1.2.),
Получаем с, =2/ и /(г) = -Ппг+2/. ■
Пример 2.52. Существует ли аналитическая функция /(г) = и + /V, для ко-
которой
2 2
х — у у
a)v=- ~r; 6)u = cos—;
В случае положительного ответа найти /(г).
□ а) Ответ на поставленный вопрос сводится к выяснению, является ли
гармонической заданная функция двух переменных. Для гармонической функ-
функции и(х,у) или v(x,y) находим решение по правилу 2.3.
1. Находим частные производные до второго порядка заданной функции
двух переменных v(x, у):
112
5v 2х(х2+Л-(х2-у2)-2(х2+у2)-2'х' x2+y2-2x2+2y2
дх= '
= Ъу2-х2 9v Ъхг-у2
" > =У
32v
дх2
22
92v
(у2-х2){х2+у2)-2х{зу2х-х1)
Условие Av = 0 выполняется всюду, кроме точки @,0). Следовательно, функция
v(x, у)- гармоническая в области определения.
2. Находим сопряженную с v(x, у) функцию:
•■■ "k'Mi
Л ..2
-x2
Полагаем ^о=О, тогда остается одно слагаемое —2x1— T'fy. которое
преобразуем следующим образом:
Лз^-Л.. ,.Лз,2 + з*2-4*2,.. ,.Л » ...yf ^
о
л £ у{ dy 0Л
dy = -6x\- ^—-- + 8x3 —- .
(x2+y2j o(x2+y2f o(x2+y2j
Для полученных интегралов применяем рекуррентную формулу:
, е dx х 2л-3 ,
/„ = +ПРИ
В данном случае удобнее переписать выражение, применив эту формулу
сначала для второго слагаемого (и = 3):
Таким образом, получена функция и(х, у) = —-г- + с.
(x2+y2f
3. Записываем /(г) = и + /V, преобразуя выражение к переменной г:
113
= (Г?ГГ ' •~V/T"~<2?2"'~*2
Окончательный ответ: f(z) = — + с - функция аналитическая всюду кроме
Г ■<
г = 0 (при любом с).
б) Находим производные при х * О:
ди у . у ди 1 . у
— = -4г sin—, — = —sin—,
дх х х ду хх
д2и у (, . у у) д2и 1 у
—- = —— 2xsm — + ycos— , —- = —j-cos—.
Условие Аи = 0 выполняется на отдельных линиях вида у = ах, а е R, следова-
следовательно, и(х, у) не является гармонической. Поэтому не существует аналитиче-
аналитической функции /(г), для которой и(х,у) является действительной (и мнимой то-
тоже) частью.
=2 32
О V С? V
в) Находим производные второго порядка: —r = -ycosx,—т = 0- Условие
9х2 ду2
Ды = 0 выполняется на прямых у = О,х= — +кп. Функция v(x,y) не является
гармонической. Поэтому не существует аналитической функции f(z), для кото-
которой v(x,y) является мнимой (и действительной тоже) частью.*
Пример 2.53. Найти все аналитические функции, для которых действи-
действительная часть имеет вид и = ф(х2 + у2).
□ Задача нахождения аналитической функции по ее действительной части
решается, если Re/(г) = и(х,у) является функцией гармонической. Здесь функ-
функция ы(х, у) задана, как сложная функция переменных х и у: и = ф(/),
t = х2 + у2. Для решения задачи сначала определим вид гармонической функции
и = ф@ из условия Аи = 0. Найдем частные производные второго порядка. По
, , „ . ди d® dt
правилу дифференцирования сложной функции получаем: — = —-— , т.е.
дх at дх
— = ф'@■ 2х или — = ф'(х2 + у2) ■ 2х. Далее дифференцируем это произведение
Эх дх
по переменной х, учитывая, что ф'(х2 +у2)- сложная функция переменной х :
дх2
114
В силу симметрии переменных производная —- имеет вид
» ду2
Записываем уравнение Лапласа: (х2 +у2]-(р"[х2 + у2)+(р'\х2 +у2)=0. Обозначив
х2 + у2 = t, получим для функции ф@ дифференциальное уравнение второго
порядка /ф"(/)+ф'(/)=0, которое допускает понижение порядка с помощью
замены ф'(/) = v(/). Для нахождения вспомогательной функции v(t) получаем про-
простейшее дифференциальное уравнение t ■ v' + v = 0; разделяя переменные, нахо-
находим v(/): v(/) = -, t * 0. Далее, интефируя равенство q>'(f) = —, получаем функцию
ф(/) = q • In t + с2. Гармонические функции вида щх2 + у2) записываются в форме
и(х,y)=Ci -щх2 +у2]+с2, х2+у2*0.
Далее, обычным образом находим сопряженную с и(х, у) функцию. Можно
использовать результат примера 2.47. Получим v(x,y)=2c, ■ arctg— + C3. В одно-
х
связной области - плоскости с разрезом [0,°о) соответствующая аналитическая
функция записывается в виде f(z) = u+iv = cl ■ \п\х2 + у2]+ с2 + /2с, • arctg— + /с3 =
= 2q In ух2 + у2 + / arctg— + с2 + щ = 2cj In z + с2 + ic$. Вводя новые обозначения
для постоянных, окончательно получаем f(z) = с, • In z + c2, q e R,c2eC M
АНАЛИТИЧЕСКИЕ ФУНКЦИИ В ЗАДАЧАХ ТЕОРИИ ПОЛЯ
Известные из интефального исчисления функции многих переменных за-
задачи векторного анализа - вычисления работы, потока векторного поля, нахож-
нахождения потенциальной функции и потенциала, с физической точки зрения явля-
являются важнейшими задачами электростатики и гидродинамики, так называемыми
задачами теории потенциала - исследования стационарных полей.
При исследовании плоских векторных полей в таких задачах применяются
методы теории аналитических функций, так как задание функции в плоской об-
области есть задание функции комплексного переменного.
Задание векторного поля (например, поля скоростей течения жидкости, га-
газа) "а = axi + ayj означает, что в некоторой плоской области D каждой точке
Мо^О'УоN D соответствует вектор а =aV +ay0J или паРа (ало>вД))> т-е- каж"
дому комплексному числу zo = *о+ 'Уо > Zo e D соответствует число
115
Следовательно, задание векторного поля а - axi + ayj эквивалентно зада-
заданию функции комплексного переменного f(z), Re /(г) = ах, Im /(г) = ау.
При исследовании установившихся стационарных течений идеальной жид-
жидкости (газа) рассматриваются поля, безвихревые и без источников и стоков. Если
поле а", а'= Р i +Q- j или "a =axi +ayj - потенциальное (безвихревое), то по
свойству таких полей выполняется условие
ИЖ „ли ^.«Ь, B.28)
ду дх ду дх
которое является условием потенциальности поля д. При выполнении условия
B.28) существует функция и(х,у) - потенциальная функция, для которой
а" = grad и и выражение Pdx + Qdy или axdx + aydy является полным дифферен-
дифференциалом, т.е.
du = Pdx + Qdy или du = axdx + aydy. B.29)
Если поле И к тому же соленоидально (без источников и стоков), то по
определению таких полей дивергенция поля равна нулю, dive" = 0, т.е.
— + —= 0 или —£■ + —*-= 0. B.30)
дх ду дх ду
Условие B.30) - является условием полного дифференциала некоторой
функции v(x, у), для которой справедливо равенство
dv = -Qdx + Pdy или dv = - ау dx + ax dy. B.31)
Равенства B.29) и B.31) определяют для заданного поля а, а= Pi +Qj
или а" = axi + ayj две функции и(х, у) и v(x, у).
ди dv ди
Из этих условий следуют равенства ах =— и ах = —, а также а =—,
дх ду ду
dv ди dv ди dv
av = , и поэтому — = — и —= . Эти равенства, полученные для
у дх дх ду ду дх
функций и(х,у), v(x,y), являются не чем иным, как условиями Коши-Римана
некоторой аналитической функции /(г), для которой и = Re/(г), v = 1т/(г).
Рассмотрим физический смысл функций и(х,у) и v(x, у) как характери-
характеристик поля а". _ _
Функция и = и(х, у) - потенциальная функция поля а , Ъ~ = grad и; линии
уровня и = const представляют собой семейство линий равного потенциала или
семейство эквипотенциальных линий.
Линии уровня v = const образуют семейство линий, ортогональных линиям
семейства и - const, т.е. любая пара пересекающихся линий этих семейств обра-
образует в точке пересечения прямой угол, иначе линии уровня функций и(х,у),
v(x,y) - два семейства и(х, у)= const и v(x, y)= const образуют в плоскости
(хОу) ортогональную сетку. Это связано с тем, что образами этих линий в плос-
116
кости (uOv) являются два ортогональных семейства и = const и v = const прямых,
параллельных координатным осям 0« и Ov , а отображение с помощью аналити-
аналитической функции f(z) = и + iv является конформным отображением, так как при
таком отображении сохраняются углы (см. утверждение 2.7).
Вектор поля а", как градиент скалярного поля и , a" = grad«, по свойству
градиента направлен по нормали к линии уровня и = const и , следовательно, по
касательной к линии v = const. Поэтому линии уровня v = const являются век-
векторными линиями поля "а , и если вектор а" с физической точки зрения опре-
определяет скорость течения жидкости, то v = const - траектории жидких частиц.
Поэтому линии v = с называются линиями тока поля а.
Сформулируем результат приведенных рассуждений в виде утверждения.
Утверждение 2.13.
1. Исследование потенциального и соленоидального поля ~а, "а = Р i +Q- j или
~a=axi +ayj связано с исследованием функций и(х,у), v(x,y), которые определя-
определяются для заданного поля а по формулам B.29) и B.31).
2. Линии и(х, у) = const - эквипотенциальные линии, линии v(x, у) = const -
линии тока поля ~а. Они образуют два ортогональных друг другу семейства.
3. Функции и(х,у) и v(x,y) являются сопряженными гармоническими функ-
функциями и определяют некоторую аналитическую функцию f(z) = и + iv. Тем самым
подтверждается, что исследование поля а~ связано с исследованием функции f(z).
Функция f(z), построенная таким образом, называется комплексным потенциалом
поля а".
4. Для исследования потенциально-соленоидальных полей может быть успешно
использован хорошо разработанный аппарат аналитических функций, в частности
теория конформных отображений.
АНАЛИТИЧЕСКИЕ ФУНКЦИИ В ПРИЛОЖЕНИЯХ
Остановимся подробнее на свойстве конформности как геометрическом
свойстве отображения.
Учитывая определение аналитической функции, утверждение 2.7 можно
сформулировать следующим образом.
Утверждение 2.14 (о геометрическом свойстве конформного отображения).
Отображение с помощью аналитической функции является конформным всюду
в области аналитичности, где производная функции отлична от нуля, т.е. если
f'(zo) * 0, ото отображение w - f(z) обладает свойствами постоянства растяже-
растяжения и сохранения углов (по величине и направлению отсчета) в бесконечно малой ок-
окрестности точки г0 аналитичности функции. Это означает, в частности, что оно
сохраняет бесконечно малые окружности, т.е. окружность у, имеющая уравнение
\z - Zq\ = r, где г достаточно мало, при отображении w = f(z) переходит в кри-
кривую Г, которая с точностью до бесконечно малых величин может быть заменена
окружностью \w - wQ\ = R, где R = kr, k = \ /'(го)| * 0 (рис. 2.17).
117
х О
Рис. 2.17
Отображение с помощью аналитической функции можно рассматривать
как преобразование подобия в бесконечно малом, так как сохраняется пропор-
пропорциональность линейных размеров сходственных линий, в частности границ фи-
фигур, и имеет место равенство соответствующих углов. Так, треугольник плоскости
(г) переходит в подобный ему криволинейный треугольник плоскости w .
Теория и практика конформных отображений имеет широкое применение
в различных областях: в теории потенциала, при решении краевых задач уравне-
уравнений математической физики, прежде всего первой краевой задачи для уравнений
Лапласа и Пуассона - задачи Дирихле и Неймана, в задачах гидродинамики и
электростатики, теории упругости.
Во многих случаях возникает проблема сведения задачи, решаемой в неко-
некоторой заданной области, к решению ее в другой области, в частности в простей-
простейшей канонической области. Это - проблема нахождения отображения областей.
Для плоских областей такое отображение
\и = и{х,у),
\v = v{x,y)
может определяться в виде w = f(z), и = Re f(z), v = Im f{z), т.е. сводится к на-
нахождению соответствующей аналитической функции.
Каноническими областями при этом являются верхняя полуплоскость
Aтг>0) и круг единичного радиуса с центром в начале координат (J?|<l).
Принципиальным становится вопрос о самой возможности конформного ото-
отображения произвольных областей, а также о практическом осуществлении такого
отображения, причем по возможности с помощью сравнительно простых функ-
функций.
Хорошо разработанная геометрическая теория [10,20,25,46] функций ком-
комплексного переменного - теория конформных отображений дает ответы на эти
вопросы. Первый вопрос решает теорема Римана, согласно которой для любой
односвязной области, за исключением двух тривиальных случаев - всей плоско-
плоскости С и плоскости с одной удаленной точкой, существует конформное отобра-
отображение ее на единичный круг.
Кроме того, простое дробно-линейное отображение (см. разд. 2.1.5. и
[3,25,46,53]) w = е'а =г- переводит круг в себя, т.е. отображает круг Ы < 1 на
I-Z-Zq
118
круг |wj < 1, так, что заданная точка круга Zo(|zo|<l) переходит в центр круга
w(zo) = O. Это позволяет утверждать, что для любых двух односвязных областей
(за исключением двух упомянутых случаев) существует конформное отображе-
отображение, переводящее одну область в другую.
Упражнения
1. Существует ли аналитическая функция f(z) такая, что:
2_ 2 -
a) Re/(g)= * У ; б) 1тД1) = у-еУ1
■< \Х2+У2)
В случае положительного ответа найти сопряженную с заданной функцию
И функцию f(z).
2xv I
Ответ: а) существует в С, z * 0; Im /(г) = - —;г + с, /(г) = — + с.
{2 2f 2
б) не существует.
2. Найти гармоническую функцию, сопряженную с заданной:
a) f(x,y) = e'y(xcosx-ysinx); б) Дх,у)= У +у.
х + у
( х )
Ответ: а) ±е y(xsinx +ycosx) + c; 6)±\x+— +с.
I *2+У )
3. Найти аналитическую функцию /(г), если:
a) Ref(z)=e~y(xcosx-ysinx); б) Imf(z) = x+— -.
х +у
Ответ: a) f(z) = Z ■ еп + с; б) /(г) = iz + — + с.
4. Найти гармоническую функцию, сопряженную с заданной:
а) Дх,у) = х—-1—; 5)Дх,у) = у + —^-.
х +у х +у
. Ответ: а) ±\у-——- +с; б) ±\х+ У \ + с
{ x2+/J I, ^+/J
5. Найти аналитическую функцию f{z), если:
a) \mf(z) = e~y(xzosx-ysmx);
' б) Re/(г) =_£—. + *.
Ответ: а) /(г) = /г ■ е'г + с; б) /(г) = г + - + с.
Z
6. Найти аналитическую функцию f(z), если
Re f(z) = х sin x ■ chy - у cos x • shy.
Ответ: f(z) = Z sin г + с.
119
*ti 7. Найти все гармонические функции вида:
а) « = ф(х2-^2); б) v = cp(x2+/!).
Указание. Задача сводится к решению обыкновенного дифференци-
дифференциального уравнения вида a(t) ■ /'(/) + b(t)f"(t) = О.
Ответ: а) и = сДх2 -у2]+с2; 6) v = ci\n[x2+у2)+с2.
8. Найти аналитическую функцию f(z), для которой:
а) Re f(z) = ф(х2 ~У)~ гармоническая функция;
б) Im f(z) = (fix2 + у2) - гармоническая функция.
Ответ: a) f(z) = cxz2 +с2; б) f(z) = с, In г + с2.
2.1.5. Простейшие отображения
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Рассмотрим подробнее геометрические свойства отображений с помощью
аналитических функций.
Исследование геометрического смысла модуля и аргумента производной
аналитической функции показало, что отображение с помощью аналитической
функции является конформным в любой точке zq аналитичности функции, где
выполняется условие /'(го) * 0. По определению конформного отображения оно
обладает в такой точке свойствами сохранения углов и постоянства растяжения.
Взаимно однозначное в конечной области D отображение, т.е. отображе-
отображение, осуществляемое однолистной функцией, конформное в каждой точке облас-
области, называется конформным в области D.
Можно показать, что условие f'(z)*0, jeD является следствием
(необходимым условием) однолистности функции w = /(г) в D.
Действительно, отображение w = f(z) можно записать в виде
= «M> B32)
= v{x,y), {x,y)eD,
где u = Re/(z), v=Im/(z).
Из свойств отображения B.32), изучаемого в действительном анализе, из-
известно, что условием его взаимной однозначности в D является условие
1(х,у) * 0, (х,у) eZ), где 1{х,у) - якобиан отображения, определяемый равенст-
равенством
ди
дх
dv
дх
ди
ду
dv
ду
120
Отображение B.32), удовлетворяющее условию I(x,y)*0, (x,y)eD, обла-
дяст в D следующими свойствами: переводит внутреннюю точку во внутреннюю,
граничную - в граничную.
Для функции w = f(z) , аналитической в D, условие 1{х, у) * О в силу ус-
условий Коши-Римана принимает вид
нмь ■'.'■
[л
—
дх
ди_
ах
dv
~дх
dv
дх
ди
дх
/я \
+ — * О. Это последнее условие означа-
{дх)
ет, что |/'(г)|*0, так как производная аналитической функции f(z) =
может быть записана в виде f'(z) = — + ('— (см. B.20)).
дх дх
Утверждение 2.15. Отображение с помощью аналитической, однолистной
в конечной области D функции является конформным в D.
Если функция w = f{z), аналитическая в D, осуществляет взаимно одно-
шачное отображение, то точки w называются образами точек г, а точки z -
прообразами. В силу свойств взаимно однозначного отображения образом облас-
области D как открытого множества, состоящего из внутренних точек, является
область G, а образом кривой у - границы области D (у = 5/))- является кривая
Г - граница области G (г = 5G).
В теории и практике конформных отображений ставятся и решаются две
■щдачи.
Первая задача заключается в нахождении образа данной линии или области
при заданном отображении - прямая задача.
Вторая - заключается в нахождении функции, осуществляющей отображе-
отображение данной линии или области на другую заданную линию или область - обрат-
обратная задача.
При решении прямой задачи учитывается, что образом точки го пРи ото-
отображении w = f(z) является точка w0 , такая, что w0 =/(?o) , т.е. результат
подстановки значения го в f(z). Поэтому для нахождения образа множества
нужно решить систему, состоящую из двух соотношений. Одно из них задает
отображающую функцию и> = /(г), другое - уравнение линии, если решается за-
задача нахождения образа линии, или неравенство, определяющее множество то-
точек прообраза, если решается задача отображения областей. В обоих случаях
процедура решения сводится к исключению переменной г из двух заданных со-
соотношений.
Рассмотрим подробнее задачу отображения линин. Чтобы исключить z из
заданных соотношений, следует выразить z из первого уравнения и подставить
во второе, либо наоборот.
Если уравнение линии задано в параметрической форме: х = x(t), у = y(t),
teT, то, записав уравнение г = г(О (см. разд. 1.3) и подставив его в отобра-
отображающую функцию w = f(z), получим соотношение, содержащее параметр t и
121
связывающее координаты точек, принадлежащих соответствующему образу, т.е.
уравнение образа данной линии.
Если линия задана уравнением F(x, у) = О, что в комплексной форме соот-
соответствует равенству Л ,—— =0 (см. разд. 1.3), то в последнее соотноше-
соотношение подставляются z и z , полученные из w = f(z), т.е. z = /"' (w) и г = /"' (w).
В результате получаем соотношение <D(w,iv) = 0, или после подстановки
w = u + iv, w = u-iv: ср(м, v) = 0. Это соотношение будет искомым уравнением об-
образа.
Таким же методом можно решить задачу отображения области. Для этого
в неравенство, определяющее заданную область, следует подставить z , получен-
полученное из отображающей функции w = f(z).
Можно решать эту задачу иначе. Известно, что любая замкнутая кривая
разбивает плоскость на две области (см. утверждение 1.1). По свойству кон-
конформного отображения граница области переходит в границу, а любая внутрен-
внутренняя точка во внутреннюю. Поэтому для нахождения образа области достаточно
найти образ ее границы, а затем по соответствию пары внутренних точек опреде-
определить, какая из двух областей, имеющих полученную линию своей границей, яв-
является искомой.
Результаты приведенных рассуждений сформулируем в виде правил реше-
решения прямой задачи для линии и области соответственно.
Правило 2.4. Для нахождения образа данной линии при отображении
w = f{z) необходимо:
1. Записать уравнение линии в параметрической форме z = z(t) или
в комплексной форме F , —— = 0.
2. В зависимости от вида уравнения линии, заданного или выбранного в
п.1, рассмотреть соответствующий случай:
- если линия задана в параметрической форме, подставить выражение г@
в w = f(z) . Полученное соотношение w = /(г@) - уравнение образа линии
z = z(t) при отображении w = f{z);
- если линия задана в комплексной форме, то выразить z из w = f(z), т.е.
z = f~l(w), и найти ? = /"'(w)- Затем следует подставить г и г в уравнение
линии. Полученное соотношение - уравнение образа данной линии.
Правило 2.5. Для нахождения образа данной области следует воспользо-
воспользоваться одним из двух способов.
Первый способ.
1. Записать уравнение границы заданной области.
2. Найти образ границы заданной области по правилу 2.4.
3. Выбрать произвольную внутреннюю точку заданной области и найти ее
образ при заданном отображении. Область, которой принадлежит полученная
точка, является искомым образом заданной области.
122
Второй способ.
1. Выразить z из соотношения w = f(z).
2. Подставить полученное в п.1 выражение z = f~l{w) в неравенство, опре-
определяющее заданную область. Полученное соотношение - искомый образ.
Замечания 2.9.
1. На практике при нахождении образов с помощью отображений
w = , w = z", w = ez и других используются свойства этих отображений,
cz + d
например круговое свойство дробно-линейного отображения или свойство функ-
функции w = z" увеличивать углы в и раз.
2. При решении обратной задачи используются свойства простейших ото-
отображений и некоторый набор известных отображений - "таблица" отображений
121].
Рассмотрим отображения с помощью простейших функций.
ЛИНЕЙНОЕ ОТОБРАЖЕНИЕ
Линейная функция w = az + b, где а и b - любые комплексные числа,
а * 0, определена в С, а если положить w(a>) = да, то в С . Отображение являет-
является однолистным в С, что вытекает из равенства W] -w2 = a(z\ -Zi), так как при
а * 0 из условия z\ * Z2 следует w, ф щ (см. также пример 2.4).
Функция является аналитической в С. Исходя из сказанного заключаем,
что линейное отображение является конформным всюду в С.
Выясним геометрический смысл отображения. Для этого запишем пара-
параметр а в показательной форме: а = |а|е'а и рассмотрим следующие частные
случаи отображения как составляющие:
Первому из этих отображений соответствует изменение длины радиуса-
вектора любой точки в \а\ раз, а именно растяжение, если \а\ > 1, и сжатие при
\а\ < 1. Это следует из соотношений |w,| = \a\\z\, aigw, = aigz-
Для второго отображения из соотношений jw( | = |w2|, aig w2 = arg Щ + a
получаем, что оно определяет преобразование поворота - радиус-вектор любой
точки W| поворачивается относительно начала координат на угол а по часовой
стрелке, если a > 0, и против - если a < 0.
Геометрический смысл отображения w = w2+b получается из геометриче-
геометрического смысла сложения комплексных чисел, как векторов, или, что то же, из со-
соотношений Re w = Re w2 + Re b, Im w = Im w2 + Im b. Отображение w = щ + b есть
параллельный перенос радиуса-вектора любой точки w2 в направлении вектора b
на его величину.
123
На рис. 2.18 проиллюстрированы операции, соответствующие всем рас-
рассмотренным отображениям; для наглядности все плоскости (z,wl,W2,w) совме-
совмещены (совмещены их действительные и мнимые оси).
Представляя линейное отображение w = az + b как суперпозицию рассмот-
рассмотренных отображений, можно сформулировать утверждение.
Утверждение 2.16.
1. Отображение w = az + b геометрически сводится к последовательному вы-
выполнению над радиусом-вектором любой точки плоскости z следующих операций:
растяжению (сжатию) в |я| раз, повороту на угол а = arg а и смещению
(параллельному переносу) в направлении вектора Ь на величину \b\.
2. Отображение w = az + b изменяет линейные размеры любой фигуры плоско-
плоскости в \а\ раз (гомотетия - подобие с центром в начале координат и коэффициен-
коэффициентом подобия к = \а\), поворачивает эту фигуру на угол а = arg а вокруг начала ко-
координат и смещает ее в направлении вектора b на его величину (рис. 2.19).
3. Линейное отображение обладает круговым свойством, т.е. переводит ок-
окружности плоскости z в окружности плоскости w (и обратно); прямые переводит
в прямые.
Справедливость последнего утверждения следует из геометрических свойств
составляющих, так как они, очевидно, обладают круговым свойством. Оно также
может быть доказано аналитически.
А именно запишем в комплексной форме уравнение прообраза - окружно-
окружности в плоскости z (см. пример 1.27): Azz + Mz + Mz + D = 0 (Л, D e R) и подста-
■ш h
вим в него выражение для z, полученное из w = az + b, т.е. z = . Будем
а
а
иметь A(w-b)tp> -6)+M(iv -bja + M(w-b)a + Daa" = 0 или после преобразова-
преобразований: A wiv + N w + Л^ w + L = 0, где А и L e R (L = Dяя). А это и есть уравне-
уравнение окружности в плоскости w.
При А = 0 и прообраз, и образ определяют прямые (см. разд. 1.2).
124
Заметим, что доказательство можно рассматривать как пример решения
лрямой задачи - найти образ окррсности (прямой) при линейном отображении и
■бедиться, что это - окружность (прямая) (см. правило 2.4).
Если использовать уравнение прообраза в виде \z - Zq\ = г (см. правило 2.4),
w-b I , ,ч| и
-о после подстановки z = получим | w -(azo + b)\ = щ • г, т.е. образом центра
;п данной окружности при линейном отображении является центр w0 = a zq + Ь
•е образа - центр отображается в центр.
Пример 2.54. Найти образ отрезка АВ, где ЛA + /),5D + /), при отображе-
1ИИ w = 2iz - 3/ (рис. 2.20).
У *■
Вг
В'
-2
А'
8/
Si
\
\
\
\
\
А / !
1 2
\
\
Рис. 2.20
125
D Для решения используем круговое свойство, согласно которому образом
прямой при линейном отображении является прямая. А так как прямая опреде-
определяется двумя точками, то достаточно найти образы концов отрезка. Точке
ЛA + /) соответствует точка А, для которой w = 2/A + /)- 3/ = -2 - /, а точке В -
точка B'(-2 + 5i). Образом отрезка АВ будет отрезок А'В'(рис. 2.20).
Используя геометрический смысл составляющих линейного отображения,
можно проиллюстрировать этапы решения геометрически. Запишем составляю-
составляющие: и>! = 2z, w2 = w,, w = w2 - 3/.
Образом отрезка АВ при отображении w, = 2z будет отрезок А1В1, кото-
который получается из АВ гомотетией с центром в начале координат и коэффициен-
коэффициентом к = 2 (растяжение радиуса-вектора любой точки в два раза).
Далее, образом отрезка Л, В\ при отображении w2=iwt будет отрезок
А2В2, который получается из А{В] поворотом относительно начала координат на
угол a = arg/ = —. Наконец, отрезок А'В' получается из А2В2 при отображении
w = w2 - 3/ смещением на 3 единицы вниз. Все этапы построения показаны на
рис. 2.20. ■
Пример 2.55. Найти образ окружности |г| = 1 при отображении w = 2iz - 3/.
D Первый способ. Приведем решение согласно правилу 2.4.
1. Уравнение данной окружности задано в комплексной форме: |г| = 1.
w + 3i
2. Выражаем z из w = 2k-3/, т.е. г= , и подставляем полученное
2/
выражение для z в уравнение |г| = 1: —-— = 2, или \w + 3/'| = 2.
Второй способ. Как и в предыдущем примере, используем круговое свойст-
свойство. Образом данной окружности будет окружность, радиус которой равен
|д| ■ г = 2, а центром является образ точки г0 = 0, т.е. w0 = -3/. Следовательно,
искомый образ - окружность \w + 3ij = 2.
Выделив составляющие отображения: w, = 2г, щ = щ, w = w2 - 3/, мож-
можно получить геометрическое решение.*
Пример 2.56. Найти образ окружности: a) \z\ = 1; б) \z -1| = 1 при отобра-
отображении w = 2z.
О а) Так как |w| = 2 • \z\ и |г| = 1, то образом окружности |г| = 1 является
окружность |w| = 2.
б) Решаем в соответствии с правилом 2.4.
1. Уравнение окружности задано в комплексной форме \z -1\ = I.
2. Выражаем z из w = 2z и подставляем полученное выражение z = —
в уравнение \z -1| = 1: = 1, т.е. \w - 2| = 2. Образом окружности \z -1\ = 1
является окружность \w - 2| = 2.
126
У '
х О
Рис. 2.21
На рис. 2.21 дана геометрическая иллюстрация решения.*
Пример 2.57. Найти образ оси Оупри отображении w = 2iz - 3/.
D Первый способ. Решаем по правилу 2.4. Уравнение оси Оу выберем в па-
шметрической форме.
1. Так как в действительной форме уравнение имеет вид х = О, -«><у <со,
"о в комплексной форме запишется как z = iy, -<x><y<<x>. Это - параметриче-
•кое уравнение, в качестве параметра выбран у.
2. Выражаем г из w = Ъг - 3/ и подставляем в уравнение оси Оу или, что
0 же, подставляем z = iy в выражение w = 2iz - 3/. Получаем уравнение образа
1 параметрической форме: w = -2у - 3/, - да < у < а>; параметром является у. От-
1елив действительную и мнимую части, получим уравнение в действительной
норме: v = -3, и = -2у или v = -2,-v<u<co. Это есть уравнение прямой в
носкости w, параллельной действительной оси.
Второй способ. Решаем по правилу 2.4, но уравнение оси Оу выберем
i комплексной форме.
1. Записываем комплексное уравнение оси Оу: г + г = О (см. разд. 1.2.).
„ „ , w + 3/ - iv-3/
2. Выражаем z из w = 2iz - 3/ и подставляем z = и z =
2/ - 2/
> уравнение z + Z = 0. Получаем в комплексной форме уравнение образа оси Оу:
+ = 0, или +3 = 0. В действительной форме результат запи-
2/ - 2/ 2/
иется в виде Im w + 3 = 0 или v = -3.
Третий способ. Используем для решения круговое свойство линейного ото-
тажения - образом прямой является прямая. Так как прямая определяется дву-
w точками, то достаточно на оси Оу выбрать любые две точки и найти их обра-
:ы. Прямая, проходящая через найденные точки, и будет искомой. Выберем точ-
127
ки Z\ = 0, z-i = i', их образы W| = -3/, w2 = -2 - 3/ при отображении лежат на пря-
мой Im w = -3. Следовательно, образом прямой Оу является прямая v = -3.
Четвертый способ. Можно привести геометрическое решение, как и в при-
примере 2.54. Так как из условия w = 2iz - 3/ следует, что \а\ = 2, aiga = -, b = -3/, те
нужно заданную линию (ось Оу) повернуть на — (относительно начала коорд>
нат), а затем сместить вниз на 3 единицы. Растяжение в 2 раза не меняет геоме^
рического вида исходной линии (оси Оу), так как она проходит через началг
координат.*
Пример 2.58. Найти какую-либо линейную функцию, отображающую лтг
нию Re z + Im г = 0 на линию Im w = 0.
□ Поставленная задача есть обратная задача теории отображений - по зь
данным образу и прообразу найти соответствующее отображение. Без дополнг-
тельных условий задача не имеет единственного решения. Действительно, сущ
ствует множество функций, осуществляющих искомое отображение. Для нахож-
нахождения любой из них достаточно выбрать две точки Z\ и г2 в плоскости z, при-
принадлежащие прообразу (т.е. линии Re z + Im z = 0), и две любые точки w, и w2 t
плоскости w, принадлежащие линии Imw = 0 (т.е. два действительных числа), i.
из двух соотношений wt = az\ + b и w2 = azi + Ъ определить величины а и b.
Одно из отображений можно просто получить из рассмотрения рис. 2.22.
Для геометрического решения достаточно повернуть луч ОА, принадлежа-
принадлежащий прообразу, на угол а =— против часовой стрелки, т.е. выбрать отображение
4
,71
w = е 4г. При этом образом точки А(-1 + /) будет точка Лц- V2], а образом то^
г --<
ки В(\ - i) - точка В\ (V2). Можно выбрать отображение w = e 4 z - поворот hl
угол а = — по часовой стрелке. Тогда точке А будет соответствовать tomkl
4
ВЛ42], а точка Ах будет образом точки 5A -/').
Рис. 2.22
128
.* .3*
I— -/—
Заметим, что ответом может быть также w = ke*z, w = ke 4г, где к -
.Я
иобое положительное число, и w = ke 4z + b, где к и b - любые действитель-
действительные числа.*
Пример 2.59. Найти какую-либо линейную функцию, отображающую ок-
эужность |г - (| = 1 на окружность \w - 3| = 2.
□ Как и предыдущая, это - обратная задача отображений. Решать её будем,
1спользуя свойства линейного отображения - геометрический смысл его состав-
1ЯЮШИХ. В связи с этим при решении удобно выделить следующие этапы (см.
У
0
м
1 х
V
Г
Рис. 2.23
Первый этап. Переместим центр окружности в начало координат. Для
.того применим отображение щ =z-i.
Второй этап. В плоскости w, применим отображение, дающее растяжение
i 2 раза, w2 = 2w,. Окружность изображена в плоскости w (считаем плоскости
v2 и w совмещенными) пунктиром.
Третий этап. Окончательный результат получаем, применяя преобразова-
преобразование смещения, w = щ + 3, т.е. w = 2(г - /')+ 3 или w = 2z + 3 - 2/.
Здесь, как и в примере 2.58, ответ не единственный и можно рассмотреть
другой порядок выполнения операций. Из геометрических соображений ясно,
■то можно сначала применить не смещение, а поворот или растяжение и полу-
■ить в результате соответствующее отображение.
Можно получить общий вид линейной функции, осуществляющей задан-
заданное отображение, используя тот факт, что окружность определяется положением
лентра и величиной радиуса, и свойство линейного отображения, переводящего
лентр окружности в центр.
Поэтому, подбирая искомое отображение в виде w = az + b, из соотноше-
соотношения w0 = azo + b, т.е. 3 = ai + b, получаем w = az + C - ai) или w - 3 = я(г - /).
Далее из \w - 3| = \а\ ■ \z - i\, учитывая условие задачи, находим \а\ = 2 и а = 2е'а,
i - любое действительное число.
Окончательный результат w = 2е'а(г-/)+3, что также объяснимо из рис.
-.23 , так как геометрический вид окружности с центром в начале координат (см.
.. Пантелеев Л.В., Якимова Л.С.
129
(w,) или пунктир в плоскости w) не изменяется в результате поворота
(умножения на е'а ).Ш
Пример 2.60. Найти образ полосы 0 < Re z < 2 при отображена
w = 2iz - 3/.
П Заданная область - неограниченная односвязная область, границей её т
С является линия, состоящая из двух параллельных прямых (образами эти:
прямых на сфере Римана являются две окружности, пересекающиеся в точке N.
Эта линия делит С на две области - внутреннюю (полоса) и внешнюк
(внешность полосы).
Образом полосы является полоса, так как при линейном отображение
прямые переходят в прямые, а- в силу конформности отображения параллел>-
ность прямых сохраняется.
Решаем по правилу 2.5 первым способом.
1. Границу области образуют две прямые с уравнениями Re z = 0 \
2. Находим образы прямых Rez = 0 и Rez = 2. Образ прямой
получен в примере 2.57. Его уравнение Imw = -3. Образ прямой Re? = 2 можш
получить так же или, учитывая параллельность линий, достаточно найти обра:
одной точки. Например, точке z = 2 соответствует w = 4/ - 3/ = /. Поэтому o6pt
зом прямой Re z = 2 будет прямая Im w = 1, проходяшая через точку w = /.
3. Выбираем внутреннюю точку полосы 0 < Rez < 2, например z = 1, её of-
раз w = 2/ - 3/ = -/ . Эта точка должна принадлежать искомому образу. Ответо:
является множество - 3 < Im w < 1 - полоса, границами которой являютсг
Im w = 1 и Im w = -3 (рис. 2.24).
Очень простое решение задачи - геометрическое, которое сводится к пово-
повороту на — против часовой стрелки, растяжению в два раза и смешению внич m
мнимой оси на 3 единицы (рис. 2.24).*
(г)
-3/
Рис. 2.24
130
Пример 2.61. Найти линейную функцию, отображающую область D:
\е z + Im z < 0 на область G: Im w > 0.
D По свойствам искомого отображения как взаимно однозначного отобра-
отображения граница области D, прямая Re z + Im z = 0, переходит в границу области
i: Im w = 0. Функция, устанавливающая соответствие границ, получена в при-
иере 2.58. Это - либо w = ке 4г, либо w = ke 4 г, к>0. Одна из них отобража-
■т область Re z + Im z < 0 на Im w > 0 (a Re z + Im z > 0 соответственно на
m w < 0), другая - область Re г + Inu < 0 на Im w < 0. Чтобы выбрать необходи-
иую функцию, достаточно установить соответствие двух пар граничных точек
ши пары внутренних.
Выберем две граничные точки области D - точки А и В (см. рис. 2.22).
Направление обхода границы области D от точки В к точке А (область при об-
;оде расположена слева), области G - от точки А\ к точке В\. Поэтому искомая
.Зл
-I—
оункция - та, которая переводит точку В в точку А\, т.е. w - ке 4 z, к > 0 или,
Зи
-/—
ч частности, w = е 4 z (см. пример 2.58). Можно выбрать внутреннюю точку,
.л
«пример z = -2б D. Ее образом при отображении w = ke *Z, k>0 является
.л .л 5л. .Зл
v = ке 4(-2) = £е *2е"' =2кед> =2ке 4 , wе Imtv<0, т.е. и-еG. При отобра-
::ении
же
w = ке 4 z, А: > 0 образом точки
= 2А:е4 , welmw>0M
z = -2
является
Пример 2.62. Найти какую-либо линейную функцию, отображающую об-
1асть D: Re z > 1 на область G: Reiv + Imiv + l<0.
D Как и в предыдущем примере, нужно найти функцию, устанавливающую
•оответствие границ: прямой Re z = 1 в плоскости (z) и прямой
\ew + Imiv + l = 0 в плоскости w (рис. 2.25,« и г).
Применим геометрический способ решения (см. пример 2.59), используя
еометрические свойства составляющих.
Рис. 2.25
131
Первый этап. Сдвинем границу области D на единицу влево, т.е. рассмот-
рассмотрим отображение wx = z -1. Образом области D будет область G\ (рис. 2.25,6).
Второй этап. Повернем границу области Gl на угол а = — по часовой
4
_3*.
стрелке, т.е. рассмотрим отображение щ = е 4 wl. Образом области G\ будет
область О2(рис. 2.25,8).
Третий этап. Сдвинем границу области G2 на единицу вниз, т.е. рассмот-
рассмотрим отображение w = tv2 - i. Образом области G2 будет область G. Искомое
отображение получим как суперпозицию составляющих, т.е.
з*. з*. ( ЗиЛ
tv = e 4 (г-1)-/ = е 4 г- / + е 4 |
Напомним, что задачи такого типа без дополнительных условий имеют не-
неединственное решение, что в данном случае очевидно из рассмотрения рис. 2.25.
Зл.
Например, решением будет также функция w = е 4 (г-1)-1идр.
ДРОБНО-ЛИНЕЙНОЕ ОТОБРАЖЕНИЕ
Дробно-линейным называется отображение с помощью функции w = ,
cz + d
где a,b,c,d- произвольные комплексные числа (параметры).
Полагаем с * 0, так как при с = 0 получается рассмотренная выше линей-
линейная функция, и ad-bc*u, иначе, в силу пропорциональности числителя и зна-
знаменателя, w = к = const.
Функция определена в С \ —. Если положить w — = lim w(z) = »,
с К с) ^_±
с
tv(oo) = lim /(г) = - , то получаем функцию, которая определена на всей расши-
г->» с
ренной комплексной плоскости С .
Функция является однолистной в С и аналитической в С за исключением
точки —. Аналитичность вг=« следует из определения, так как аналитиче-
с
ской в £ = 0 является функция т — = -, с ф 0.
Так как однолистное отображение с помощью аналитической функции яв-
является конформным, то заключаем, что дробно-линейное отображение кон-
конформно в С, конформно в любой области D с С. Заметим, что
,/ \ ad - be „ ^ „ _ d
w(z) = * 0 для любой точки z е С, z*—•
(cz + df с
Исследуем геометрические свойства отображения. Как и в случае линейной
' функции, выделим составляющие. Выделяя целую часть дроби, получаем
132
a be-ad . , a „ bc-ad
tv = - + или, вводя обозначения А = — , В = , имеем
с (cz + d)c с с
D
w = А + , из чего следует, что дробно-линейное отображение есть суперпо-
cz + d
зиция линейного отображения и отображения w = —. Действительно, можно за-
Z
писать цепочку составляющих w, =cz + d, w2= —, w = A + Bw2.
Рассмотрим отдельно отображение w = — как частный случай дробно-
Z
линейного отображения (а = 0, d = О, b = 1, с = 1). Его также можно записать в ви-
виде более простых для исследования составляющих wl =—, w = ^. Особенность
Z
первого отображения заключается в соотношениях |wt| = р=т, aigtv! =-aig£", ко-
которые, учитывая, что | z \ = |4 и aig г = - arg z, можно переписать в виде
|tv, ||z| = l, argw, =aigz. B.33)
Геометрически эти соотношения означают, что точки W) и Z\ расположены
на одном луче, а произведение длин их радиусов-векторов равно единице. Точки,
обладающие таким свойством, называются точками, симметричными (или
сопряженными) относительно окружностн единичного радиуса с центром в начале
координат.
Функция и>, =— отображает любую точку, лежащую внутри единичного
Z
круга, в точку, лежащую вне единичного круга, так как из \z\ < 1 следует
Iv^i | = т-г > 1 и обратно.
Следовательно, функция w = — переводит внутренность единичного круга
* ♦
во внешность и наоборот. Преобразование такого вида называется инверсией от-
относительно единичной окружностн.
Заметим, что для построения точки tvj по заданной точке z(\z\ <l) нужно
сначала провести луч из центра окружности \z\ = 1, а затем к этому лучу в точке
Z восставить перпендикуляр и провести касательную к окружности в точке её
пересечения с перпендикуляром. Точкой пересечения касательной и луча будет
tvj. Обоснование построения следует из рассмотрения подобных треугольников
(рис. 2.26). Очевидно, проводя построение в обратном порядке, можно построить
по точке, лежащей вне круга (на рис. 2.26 точка wl), симметричную относитель-
относительно окружности точку z, которая будет расположена внутри круга.
Вторая составляющая отображения w = — функция w = ivj геометрически
есть симметрия относительно действительной оси (рис. 2.26).
133
(z)
w,
Рис. 2.26
Результат приведенных рассуждений запишем в виде утверждения.
Утверждение 2.17.
1. Отображение w = — геометрически сводится к построению инверсии отно-
относительно окружности \z\ = \ и симметрии относительно действительной оси.
2. Дробно-линейное отображение геометрически сводится к преобразованиям
растяжения, поворота, сдвига (см. линейное отображение), симметрии относи-
относительно окружности \z\ = 1 и симметрии относительно действительной оси.
Дробно-линейное отображение обладает круговым свойством. Достаточно
доказать это свойство для функции w = —, так как для линейных составляющих
Z
дробно-линейного отображения оно установлено.
Доказательство проведем в соответствии с правилом 2.4 решения прямой
задачи.
1. Записываем уравнение произвольной окружности в комплексной форме:
A z Z + Mz + Mz + D = 0. Заметим, что при А = 0 уравнение определяет прямую.
При D * 0 линия не проходит через начало координат (точку z = 0), при D = 0 -
проходит.
1 1-1
2. Выражая z из и> = — , получаем z = —, z =>— и подставляем в уравне-
z
W
W
ние прообраза. Преобразуем полученное равенство: А— — + М—+ М — +Z) = 0,
w w w w
или D w w + Mw + M w + А = 0. Полученное уравнение есть уравнение окружно-
окружности, в частности, при D = 0 - прямая.
1 d
Для отображения w = роль точки z = 0, очевидно, играет z = —.
cz + d с
Утверждение 2.18 (круговое свойство дробно-линейного отображения).
1. Окружности и прямые, не проходящие через особую точку (z = —), ото-
с
бражаются в окружности, а окружности и прямые, проходящие через эту точку, -
в прямые.
134
2. Дробно-линейное отображение переводит окружности расширенной ком-
комплексной плоскости в окружности С , так как прямые на расширенной комплексной
плоскости рассматриваются как окружности.
Пример 2.63. При отображении w = — найти образы:
'" г
'■ а) окружностей х2 + у2 - 2х = 0 и (х -1J + у2 = 4;
' б) прямых х = 1 и х = О.
□ а) Первая окружность проходит через точку z = 0 - особую точку функ-
функции, поэтому её образом будет прямая. Образом второй окружности, уравнение
которой можно переписать как х2 + у2 - 2х - 3 = 0, является окружность.
Решаем согласно правилу 2.4.
1. Записываем уравнения окружностей в комплексной форме:
{ ) = Q и zz( ) 3
2 2
2. Подставляем в эти уравнения выражения z = — и z = —■ Для первой ок-
w w
ружности получаем —= - — + — = 0, или w + w = 2, что можно записать
ww \w w)
w + w
=1, или Retv = l. Это - уравнение прямой, параллельной мнимой оси
(рис. 2.27,а). Для второй окружности имеем 3tviv +2(tv + iv)-4 = 0. Наличие
слагаемого w w говорит о том, что образом является окружность. Чтобы опреде-
определить её центр и радиус, перейдем к действительной форме уравнения, используя
равенства ww = u2+v2, w + w = 2u. Получим уравнение 3u2+3v +4u-4 = 0,
. ( 2J 2 16 -
или, выделив полный квадрат переменной и, u+— +v' = —• Это - уравнение
4 ( 2 }
окружности радиуса — с центром в точке —, 0 (рис. 2.27,«).
Рис. 2.27
135
б) Образом первой прямой является окружность, второй - прямая.
„ с * 2-2
Чтобы получить уравнения соответствующих образов, подставим z = — и z = —
w w
в уравнения данных линий, записанных в комплексной форме: z + z = 2 и
Z + Z = 0. Получим w iv - (tv + iv) = О - образ первой прямой и w + w = 0 - второй.
Первая линия - окружность (u2 + v2)- 2и = 0 или (и -1J + v2 = 1; её радиус R = 1,
центр в точке A,0) (рис. 2.27,6). Уравнение » + йГ=О или Retv = 0 определяет
мнимую ось (рис. 2.27,6).*
2
Пример 2.64. Найти образ полосы 0 < Re z < 1 при отображении w = —.
г
□ Решаем по правилу 2.5 первым способом.
1. Запишем уравнения, описывающие границы данной области D: Re z = 0
и Re г = 1.
2. Найдем образ границы. Уравнения соответствующих линий найдены в
предыдущем примере (п. "б"). Граница образа области D состоит из мнимой оси
и окружности (рис. 2.27,6). Она разбивает плоскость w на две области - образ
полосы G и дополнение этого образа до С. Чтобы определить, какая часть
плоскости является образом области D, достаточно установить соответствие двух
пар граничных точек (на рис.2.27,б указано направление обхода) или пары внут-
внутренних.
3. Выберем произвольную внутреннюю точку заданной области, например,
Z = — .Ее образом является точка w = 4, которая должна принадлежать искомо-
искомому образу - области G. Следовательно, G - правая полуплоскость с выброшен-
выброшенным кругом.*
Пример 2.65. Найти образ области D
1
1 при отображении
> —
'■I
□ Область D есть пересечение полуплоскости и внешности круга - полу-
полуплоскость Re z < 1 с выброшенным кругом (рис. 2.28).
В соответствии с правилом 2.5 решения задач для областей, как и в преды-
предыдущем примере, найдем прежде образ границы области D, которая состоит из
двух линий, описываемых уравнениями Rez = l и
1
= —. Так как обе
линии проходят через особую точку z = 1, то их образами будут прямые. Для
каждой линии решаем задачу по правилу 2.4.
Найдем образ прямой Re z = 1 •
1. Запишем уравнение Re г = 1 в комплексной форме: z + Z- 2 = 0.
2. Выражаем z из w = : wz-w = iz, т.е. z= , z=-=—. Подстав-
г-l w-i w + i
ляем эти значения в уравнение z + z-2 = 0. Получаем iw-iw + 2 = 0, или
w - iv = 2/. Это уравнение определяет прямую Im w = I, параллельную действи-
действительной оси (рис. 2.28).
136
(г)
.■ i Ж
Рис. 2.28
Найдем образ окружности
1. Запишем уравнение окружности в виде |2z -1| = 1.
2. Выразим г из w = и подставим z = в уравнение \2z - ll = 1.
Z-\ w-i
Получаем |w + z] = |w-i]. Это равенство определяет уравнение прямой, проходя-
цей перпендикулярно отрезку, соединяющему точки / и (-/), через его середи-
iv. Этой прямой является действительная ось Im w = 0 (рис. 2.28). В результате
юлучили, что образ границы области D состоит из двух параллельных прямых:
mw = 1 и lmw = 0.
Далее в соответствии с п.З правила 2.5 выберем произвольную точку, на-
1ример z = -\eD. Так как ее образом при заданном отображении является
v = —, то образом области D будет полоса 0 < Im и>< 1. ■
Пример 2.66. Найти какую-либо дробно-линейную функцию, отображаю-
дую круг единичного радиуса с центром в начале координат:
а) на левую полуплоскость; б) на нижнюю полуплоскость.
□ Решается обратная задача отображения областей. Требуется найти ото-
^ажение области D : \z\ < 1 на область G: a) Re w < 0; б) Im w < 0. Границей об-
|асти D является окружность |z| = 1. Так как в обоих случаях ее образ - прямая,
-о, согласно утверждению 2.18, искомая функция должна иметь особой точкой
>дну из точек окружности - окружность проходит через особую точку.
Используя это свойство, "распрямим" окружность, т.е. на первом этапе
^шения подберем функцию, переводящую одну из точек окружности в беско-
бесконечно удаленную точку.
137
Первый этап. Рассмотрим wx = , где wx -ю> при z-*-\ (W|(-l)) = x.
Найдем уравнение прямой, в которую переходит |г| = 1 при отображении
1
1-й-,
i =—-, т.е. решим прямую задачу: z = -, |l-*t'i| = ||Vi|- Получено уравне-
iv, =
ние прямой, проходящей перпендикулярно отрезку, соединяющему точки v/\ = 1
и Wj =0, через его середину, т.е. Rew, =-. Образом области D будет G\.
Re W| > —, так как, например, точка г0 = 0 е D переходит в точку и>, = 1 б G,.
Второй этап. Сравнивая полученный результат и вид области G, заключа-
заключаем, что нужно применить преобразование смещения (сдвиг) влево на —, т.е. ли-
линейное отображение w2 =W\ —. Образом RetV[ =— будет RetV2 =0. Соответст-
Соответствие границ установлено функцией и>2 = -
или
Но при
Z+1 2 2{z+l)
этом отображении образом области D является правая полуплоскость Retv2 >0,
так как точка z = 0 , принадлежащая D , переходит в точку w = 1, w e Re w2 > 0 .
Третий этап. Чтобы получить искомое отображение и для случая "а" , и
для случая "б", достаточно сделать поворот.
Решим задачу для случая "а". Применим преобразование поворота на угол
л против часовой стрелки, т.е. линейное отображение w = ет ■ w2 = -щ'■
г + Г
B.34)
Таким образом, найдено отображение, переводящее круг \z\ < 1 на полу-
полуплоскость Reiv<0 (рис. 2.29):
(Z)
W
Z-
Z +
1
1
(Н-)
Рис. 2.29
Заметим, что в силу взаимной однозначности обратная функция z -
1 + tv
отображает левую полуплоскость Re w < 0 на круг \z\ < 1. Отсюда следует вид
отображения, переводящего левую полуплоскость Rez<0 на круг |и>| < 1 (рис.
2.30):
w =■
B.35)
138
1-г
Рис. 2.30
Решим задачу для случая "б". Чтобы получить отображение круга |г| < 1 на
нижнюю полуплоскость Imiv<0 (рис. 2.31), достаточно в плоскости щ рас-
-I-
смотреть поворот на а = -, по часовой стрелке, т.е. w = е 2 w2=-iw2:
IZ-I
" г + Г
И". Г
г + 1
B.36)
V (И-)
0
ш
Рис. 2.31
Пример 2.67. Отобразить область D: \) У на область G : 0 < Re w < 1.
□ Так как образами окружностей - границы области D являются прямые,
то нужно применить отображение, "распрямляющее" прямые. Для этого следует
использовать отображение, переводящее общую точку окружностей z = 0 в а>.
Первый этап. Применяем преобразование w{ = -.
Найдем образ области D при этом отображении. Для этого, как и при ре-
решении предыдущих примеров, в уравнения границы - окружностей \z - i\ = 1 и
|z-2/j = 2 подставляем z= —, т.е. |l-/'tvi| = |tv,| и |l-2/tv,| = 2|tv,| или
= |tv,|. Эти уравнения определяют прямые, уравнения
которых в действительной форме имеют вид
=— и
2
=-—, или
4
v, =—, V! =—. Эти прямые, параллельные мнимой оси, определяют границу
2 4
области G\; область G, - внутренность полосы, так как, например, образом точ-
точки 3/ е D является точка —i, принадлежащая полосе (рис. 2.32).
139
Рис. 2.32
Второй этап. Сравнивая вид областей G, и G, убеждаемся, что следуе"
увеличить ширину области G[ в 4 раза и повернуть ее на угол а = — против ч*
.л
I—
совой стрелки, т.е. применить преобразование w2=4e 2 wl =4ivf1. Образом G
будет полоса Gi.
Третий этап. Окончательный результат получаем смещением на единиц'
влево, w = 4/ivI -1, т.е. w = .■
Пример 2.68. При отображении, полученном в примере 2.67, найти образь
прямых Re z = 0, Im z = 0, Im z = 2.
□ Воспользуемся правилом 2.4.
уравнения прямых в комплексной
1. Записываем
Z=0, z-Z = O, Z-Z
4/
4/
2. Выражаем z из tv = 1,
z
получаем z=
4/
Подставляем z
z = —— в уравнения данных прямых, получаем их образы.
w +1
Прямой z + z = 0 соответствует прямая w - w = 0, т.е. Im w = 0 (рис. 2.33).
Прямой z - z = 0, проходящей через z = 0, также соответствует прямая. Ьг
уравнение tv + iv =-2, или Rew = -1 (рис. 2.33).
Прямой z - Z = 4/, не проходящей через z = 0, соответствует окружносп.
Ее уравнение w ■ w = 1, или и2 + v2 = 1 (рис. 2.33).
Примеры 2.67 и 2.68 иллюстрируют круговое свойство отображения у
свойство конформности. Так, прямая Im z = 0 касается окружностей в плоскосго
Z и параллельна прямой Im w = 2, т.е. образует с кажцой из них угол а = 0. Е-
образ в плоскости (и>) с соответствующими линиями также образует угол а = I
140
Прямая Rez = O перпендикулярна любой из рассматриваемых здесь линий - и
юямым Im г = О , 1т г = 2, и окружностям, так как проходит через их центры.
)браз этой прямой (действительная ось v = 0) также перпендикулярен соответст-
зующим линиям - трем прямым и окружности.
4/
(w)
I
Л' Рис. 2.33
Прямая Imz = 2 образует угол а = 0 с окружностью |г-'| = 1 и прямой
m z = 0, ас другой окружностью \z - 2/| = 2 и прямой Re z = 0 - угол р = —. Та-
:ие же углы образует окружность - образ этой прямой в плоскости w с соответ-
■твующими линиями.*
Дробно-линейное отображение рассматривается, как отмечено выше, при
а Ь
), поэтому можно записать w = 4—j- или w = ■
-, т.е. оно определяет-
с »
я тремя параметрами. Следовательно, для задания дробно-линейного отображе-
•шя достаточно задать три условия, например соответствие трех пар точек. При
:том, так как отображение рассматривается на С , одна из точек может быть
1есконечно удаленной. Имеет место утверждение.
Утверждение 2.19 (условия,определяющие дробно-линейное отображение).
Каковы бы ни были три различные точки Z\,Z2,Zi плоскости z и три различ-
ше точки м>\,м>2,щ плоскости w, существует единственное дробно-линейное ото-
az + b
юажение w = -
, такое, что w(Zk) = щ,к = 1,2,3.
c-z + d
При этом справедливо соотношение
w- W[ w3 - и>1 Z-Z\ . Zj-Z\
w - w2 ' vc3 - w2 Z - Zi ' Zi ~ Zi
Равенство B.37) называется аигармоническим отношением.
B.37)
141
Если переписать B.37) в виде произведения: -
w - щ щ - tv, z - Zi Zi - Z\ '
то, рассматривая предельный переход в B.38) при Zk -»°° или tv* -»да
(Л = 1,2,3), замечаем, что предел частного, содержащего соответствующие вели-
величины, равен единице. Например, lim 1- = 1. Можно сделать заключение.
Zi -*«> Z3 ~Z\
Если одна из точек zk или wk (к = 1, 2, 3) есть бесконечно удаленная точ-
точка, то в B.37) (или B.38)) соответствующая разность заменяется единицей.
Справедливость утверждения о единственности отображения, определяе-
определяемого указанными условиями, и справедливость отношения B.37) могут быть
„ _ а, ■ Zk + b\
установлены из рассмотрения линейной системы tvt =—!—-—- или
4+d\
"\Zk+b\-»>kd\=WkZk, A: = 1,2,3.
Отметим некоторые особенности отображения B.37), запишем их в виде
утверждения.
Утверждение 2.20.
1. Дробно - линейное отображение переводит круг, граница которого прохо-
проходит через три данные точки Zk,k = 1,2,3, в круг (или во внешность круга), граница
которого проходит через три точки wk,k = 1,2,3. Это следует из того, что поло-
положение любой окружности (на плоскости) однозначно определяется тремя точками.
2. Любое дробно-линейное отображение, переводящее точку z\ в 0 и Zi в бес-
бесконечно удаленную точку, имеет вид
w = A-^^i-, B.39)
Z-Z2
что следует из формулы B.38).
С учетом этого утверждения можно сократить процедуру решения примера
2.66. А именно, так как граница области G - прямая Re w = 0 проходит через
vfi = 0, w2 = оо, то, полагая Z\ = 1 A —> 0),?2 =-' (-1 ->°°)i отображение ищем в
виде tvi -А (на первом этапе). Можно взять щ = , так как наличие
г+l г+1
множителя А в таких случаях будет определять только поворот на а = aig A, a
растяжение в |Л| для геометрического положения прямых, проходящих через на-
начало координат, не имеет значения. Далее, для решения задачи в случае "а" убе-
убеждаемся, что искомое отображение уже получено: w = w\ = -—, а для решения
г + 1
в случае "б" нужно еще сделать поворот.
Пример 2.69. Найти дробно-линейную функцию w = f(z), такую, что
w(i) = 2i, tv(oo) = l, tv(-l) = oo.
□ Обозначим £i = i, ц = <*>, Zi = -1 и W| = 2/,Wi = l,w-j = °o. Запишем фор-
формулу B.38), заменяя разности, содержащие Zi и щ , единицей. Получим
142
т.е. = ,
tv-1 -1-/
или, после преобразований, w = - искомое отображение.■
Z + 1
В утверждении 2.20 сказано, что дробно-линейное отображение переводит
любой круг (внутренность, внешность) на любой крут (внутренность, внешность)
заданием соответствия трех пар граничных точек. Так как прямые на С рас-
рассматриваются как окружности (Л = оо), то речь здесь идет и о прямых, т.е. любой
круг (внутренность, внешность) переводится на любую полуплоскость и обратно
заданием соответствия трех граничных пар (для прямой одна из точек z - °°).
По формуле B.38) при условии w^ = f(z{),k = 1,2,3 будет получено опреде-
определенное отображение области D (ее граница - окружность, прямая) на область G
(граница - окружность, прямая). При этом любой внутренней точке го е О будет
соответствовать определенная tv0 e G.
Представляют практический интерес задачи, где образом данной точки
Zn e. D должна быть заранее заданная w0 e G.
Задание соответствия внутренних точек накладывает ограничение на выбор
других соответствующих пар. Это связано со следующим свойство дробно-
линейного отображения.
Утверждение 2.21.
1. Дробно-линейное отображение переводит любые две точки, симметричные
относительно окружности расширенной комплексной плоскости, в точки, симмет-
симметричные относительно образа этой окружности при данном отображении.
Свойство называется свойством сохранения симметричных точек.
2. Точки, симметричные границе области (окружности или прямой) при дроб-
дробно-линейном отображении, переходят в точки, симметричные относительно ее об-
образа при этом отображении.
Свойство означает, что если точки гиг* симметричны относительно
линии у (окружности или прямой) в плоскости (г), а точки w и w* и линия Г-
их образы при дробно-линейном отображении, то точки w и w* симметричны
относительно Г. Линия Г, согласно круговому свойству отображения, также яв-»
ляется окружностью или прямой. Симметрия точек относительно прямой пони-
понимается в обычном смысле. Симметрия относительно окружности единичного ра-
радиуса с центром в начале координат рассматривалась при исследовании отобра-
отображения w = — (формула B.33)). В общем случае имеет место следующее определе-
определение.
Точки гиг* называются симметричными (или сопряженными) относи-
относительно окружности |г-го| = Я, если они лежат на одном луче, выходящем из
центра окружности, и произведение их расстояний от центра окружности равно
квадрату ее радиуса, т.е. справедливо равенство
Мо|-|г*-го| = К2. B.40)
Точкой, симметричной точке го ~ центру окружности, очевидно, является
бесконечно удаленная точка.
143
Пример 2.70. Отобразить область |г - 2i\ < 2 на область \w + 2/| > 2 так, что-
чтобы точки 0 и 2/ остались неподвижными.
D Задание неподвижной точки го для отображения w = /(г) означает ус-
условие w(zq) = zo, те- Zo-*Zo- В данном случае имеет место соответствие двух
пар точек: 0 -> 0, 2/ -> 2/, причем первая пара - пара граничных точек, вторая -
внутренних. Третью пару, необходимую для применения формулы B.37), нахо-
находим, используя свойство сохранения симметричных точек.
Найдем точки, симметричные точкам г = 2/ и w = Ъ относительно соот-
соответствующих окружностей.
Для точки z = 2/ точкой, симметричной относительно окружности
\z - 2/| = 2, будет z* = « , так как 2/ - центр круга. Для точки w = Ъ точку,
симметричную относительно окружности \w + 2i\ = 2, находим, используя форму-
формулу B.40), |2/ - (-2/)| • \w * -(-2j)| = 4, или \w * +2i\ = 1. Из полученного равенства
следует, что w* расположена на расстоянии d = 1 от центра круга (-2/) и, по
определению симметричных точек , на одном луче с центром и точкой 2/. Из
этих рассуждений очевидно, что w* = -i. Таким образом, имеем соответствие
трех пар точек: 0 -> 0, 2/ -> 2/, а> -> -/.
Применяя формулу B.37), получаем — = , или после преоб-
— / — 2/ w z
разований w = . ■
3/-Z
Пример 2.71. Отобразить область D на круг |wj<l так, чтобы w(zo)=O,
Z0eD, если: a)D: 1тг>0; 6)D:\z\<\.
О Так как точка го отображается в w = 0, т.е. в центр круга |wj < 1, то
точка го , сопряженная точке го относительно границы области D , отобража-
отображается в w = оо. Имеем соответствие двух пар точек, причем го ~* 0 и го -> °° ■ Мо-
Можем искать отображение в виде w = A (см B.39)). Нужно найти величи-
z-zo
ны го и А.
1. Найдем го ~" точку, симметричную точке го относительно границы об-
области D в каждом случае:
а) так как граница области Im г > 0 — действительная ось, то го = го i
б) здесь го симметрична точке го относительно окружности |г| = 1, по-
поэтому го = = (см. B.33)).
to
2. Значение А определяем из соответствия граничных точек: г| -> и»|, где
Z{ eSZ), и>, e6G. Так как |vf|| = l, то получаем условие для нахождения А:
•=14^
144
Получим решение для каждого из рассматриваемых случаев.
|г, -<
а) Имеем 1 = |л|-4—'—=4. Так как Z\ e 1тг = 0, то z\ — действительное
число и поэтому \z\ -Zo\ = \Z\ - Zo • Получаем \А\ = 1 и /4 = е'а. Искомое ото-
отображение w = е'а ==, где а - любое число.
г-г0
Заметим, что неоднозначность ответа, вызванная произволом выбора а,
связана с неопределенностью соответствия Z\ -*щ. Указана принадлежность
этих точек границам соответствующих областей, но не заданы определенные
значения. Каждому фиксированному значению Z\ е 50 можно поставить в соот-
соответствие произвольное значение W|s6C, удовлетворяющее условию |tV|| = l.
Отображение найдено с точностью до поворота окружности |tv| = 1, что геомет-
геометрически очевидно. При задании дополнительного условия для нахождения а
решение поставленной задачи единственное.
б) Отображение ищем в виде w = A р, т.е. w = -Azo ==> или>
го
если обозначить В = -A Zo. то w = В ==.
Из условия |vc,| = 1 для Z\ е 60 получаем 1 = |Я| ~—=Ут.
Так как |г|| = 1 для Z\ e 50, то, подставляя z\ = е'ф, перепишем равенство
Ф - zo\ ,., е ф - го
=±т, или 1 = |
В последнем равенстве е'ф-го = е 'ф-го как модули комплексных }
сопряженных чисел и е'ф = 1. Поэтому |fi| = 1 и В = е'а.
Искомое отображение w = е'а =, а € R. Как и в предыдущем случае,
1-гг0
оно не является единственным. ■
Полученные при решении примера 2.71 результаты запишем в виде утвер-
утверждения.
Утверждение 2.22.
1. Любое дробно-линейное отображение полуплоскости Im z > 0 на круг \w\ < 1
имеет вид
г-г0'
где lm го > 0 и а — любое, а € R.
145
2. Любое дробно-линейное отображение круга |г| < 1 на круг |tv| < 1 имеет вид
л*е |го| < 1, а - любое, а е Л.
3. Значение а определяется из дополнительного условия. Это, как правило,
задание аргумента производной искомой функции в некоторой точке, например
()
Формулы B.41) и B.42) дают решение двух канонических задач (см. разд.
2.1.4). Для удобства использования изобразим их на рис. 2.34 и рис. 2.35 соответ-
соответственно.
w = е
/a
Z-Zo
Рис. 2.34
(w)
Рис. 2.35
Пример 2.72. Отобразить область Rez-Inu>0 на |tv-3<|>2 так, чтобы
выполнялись условия vf(l) = да, argtv'B)=%.
D По условию точка г = 1 отображается в tv = oo, следовательно, точка
Z=i, симметричная точке z = 1 относительно прямой Re z - Im Z - 0, отобража-
отображается в центр окружности | w - 3( | = 2, т.е. в точку w = 3/ (рис. 2.36,о).
Задача, очевидно, эквивалентна задаче нахождения отображения полуплос-
полуплоскости Яег-1тг<0 на круг |tv-3/|<2, при условии, что данная точка / полу-
полуплоскости переходит в центр круга (незаштрихованная область на рис. 2.36,о).
Эта задача отображения полуплоскости на круг может быть приведена к
канонической. Но чтобы воспользоваться формулой B.41), нужно применить
предварительно два линейных отображения, переводящих область Re z - Im z < О
в верхнюю полуплоскость, а круг \w - 3/| < 2 в единичный круг с центром в нача-
начале координат (рис. 2.36,6).
146
Рис. 2.36
Первый этап. Первое из этих преобразований — поворот на угол у. по ча-
часовой стрелке осуществляется функцией Z\ = z-e ''4; при этом точка z =' пе-
• ->Ул 'У, ->Уа >Ул
)еходит в го = ' • е /4 = е /2 е /4 = е /4.
Для второго преобразования используем функцию и»( ={w-3i)— - смеще-
смещение и сжатие; при этом центр круга перейдет в tv0 = 0.
Второй этап. Для переменных Z\ и W) используем формулу B.41), т.е. за-
w-3/
шшем щ = е
■ = е"
-, или после сокращения
Полученная функция при любом а € R осуществляет отображение
Яе z - Im z > 0 на \w - 3/| > 2, при этом tv(l) = °о.
Третий этап. Для определения параметра а используем условие
irgvf'B) = %. Находим производную w'(z)=2e'a и ее значение в точке
= 2, т.е. w'B) = 2e'a (-1+/). По правилу нахождения аргумента произведения
:омплексных чисел из последнего равенства получаем argw'B) = a + arg(-l + /),
-.е. arg tv'B) = a + ^% . Из этого равенства и условия arg w'B) = % находим а:
х = -у^- Подставляя а = -% в полученное выше выражение, находим оконча-
147
тельный результат: w = 3i + 2e ' '2 , или tv = 3i-2 -. Искомое отображе-
ц-B + Зр „
ние w = i . ■
Пример 2.73. Найти образ прямой Re z + Im г = 0 при отображении, полу-
полученном в примере 2.72.
П Заметим, что данная прямая перпендикулярна границе области D
из примера 2.72, поэтому, по свойству отображения ее образ — линия, перпен-
перпендикулярная окружности \w - 3(| = 2. Кроме того, так как данная прямая не про-
проходит через особую точку функции, то, по круговому свойству, ее образом будет
окружность. Эта окружность ортогональна окружности \w - 3/| = 2 в точке их пе-
пересечения. Найдем ее уравнение. Решается прямая задача по правилу 2.4.
z + z z — z
1. Запишем уравнение линии Rez + Ini£ = 0 в форме -—- + = 0, или
2 2/
после преобразований: z +' Z = 0.
2. Из w = —— + выражаем z, получаем z-——■ • Подставляем z
Z-\ w-i
- w + 3/ - 2 _ w - 3/ - 2 . w + 3i - 2 .
и z - —= в уравнение и преобразуем равенство ;— +1 —= = 0:
VC + /
w (w + /) + i w (w - i) - C/ + 2) w + 3 - 2/ + / C/ - 2) w + 3/ - 2 = 0,
w w(\ + 0 + w (/ - 3 - 2/) + w A - 3/ - 2) + i +1 = 0,
- 3+/ - 3/ + 1 , .
ww-w w +1 = 0,
1+/ l+i
3 + / _ .
■ = 2-i,
2/, 2+/,
1+/ l+i
ww-B-i)w-wB + i) + \ = 0,
ww- 2(и> + w) + i(w - w) +1 = 0,
ww-4 + /——-2i + l = 0.
Полученное уравнение - уравнение окружности, так как в нем присутствует
слагаемое w w. Запишем это уравнение в действительной форме:
иг + v2 - 4м - 2v +1 = 0, или (и - 2J + (v -1J = 4, где и = Re w, v = Im w. Центр
окружности в точке B,1), радиус равен 2 (рис. 2.37).
148
(г)
Рис. 2.37
Заметим, что эта окружность пересекает окружность из примера 2.72 под
юямым углом, так как касательная к одной совпадает с радиусом другой и на-
юорот. Под прямым углом пересекаются и их прообразы (рис. 2.37), что иллю-
трирует конформность отображения в точке z = 0. ■
**■ ОТОБРАЖЕНИЕ w = z"
Рассмотрим пример не всюду конформного отображения с помощью
пункции, которая не является однолистной в С. В разд. 2.1.1. исследовалась
акая функция: w - z", в частности w = z2 ■ Напомним полученные результаты. k
Утверждение 2.23.
1. Отображение w = z" неоднолистно в С; областью однолистности являет-
я любая область, принадлежащая углу раствора — (сектору), т.е. а < р < а + —,
п п
i - любое.
2. Функция w = z", аналитическая в С и w' = nz"'1, т.е. w\z)*0 для лю-
1ого z * 0.
Отображение является конформным в С, за исключением, быть может,
•почки z = 0.
3. Функция w = z" конформно и взаимно однозначно отображает любой сек-
■пор к— < argz < (к +1)—;(к = 0,1,...,/? -1) на плоскость с разрезом по лучу [0,со),
/? /?
1 плоскость С с выброшенной точкой z = 0 -на риманову поверхность этой функ-
лии.
149
4. Функция w = yi - обратная к неоднолистной (п -листной) функции
w - г" яв1лется неоднозначной (п -значной). В областях, не содержащих точек
г = 0 и z = «> (точек ветвления функции), возможно выделение однозначных вет-
ветвей. Каждая ветвь отображает плоскость с разрезом [О, а>) на один из секторов
к—< argг < (Л +1)—;{к = О,1,...,/г-1). Риманову поверхность функции w = z"
п п
функция w = ljlz отображает на С с выброшенной точкой.
Выясним геометрические свойства отображения в точке z = 0. Запишем
переменные в показательной форме: tv = pe'9, z = r-e'v и из равенства
р-е'9 = г"-е* получим: р = /•", 9 = /г<р, или |w| = |г|" и argtv = naigz- При
отображении w = z" увеличивается в п раз аргумент - угол наклона радиуса-
вектора точки к действительной оси, а при отображении w = lgz - уменьшается
в п раз. Можно сделать заключение.
Утверждение 2.24.
1. При отображении w = z" увеличиваются в п раз углы между любыми пря-
прямыми, проходящими через начало координат.
Поэтому отображением w = z" пользуются, если нужно увеличить углы при
переходе от прообраза к образу.
2. При отображении w = lgz уменьшаются в п раз углы между любыми пря-
прямыми, проходящими через начало координат.
Поэтому отображением у/ = Щт. пользуются, если нужно уменьшить углы при
переходе от прообраза к образу.
3. Используя комбинацию дробно-линейного отображения и отображений
w - г" и w = $z , можно конформно отобразить любую "луночку" - область, огра-
ограниченную двумя дугами пересекающихся окружностей, на верхнюю полуплоскость.
Пример 2.74. При отображении w = г4 найти образ области, ограниченной
двумя лучами, выходящими из начала координат и образующими угол —.
□ Область D a<arg^<a + — есть угол раствора —, и при отображении
w = iA переходит в угол раствора 2л. Границами области D являются лучи
argz = а и arg£ = a+ —, их параметрические уравнения имеют вид z = re'a и
z = re 2 , где г - любое, г > 0 - параметр. Образами этих прямых будут пря-
прямые-лучи w = rV4a и w = гУ<4а+2*> или w=Reifi и w = Re'®*2*), где р = 4а.
Геометрически линии совпадают. Для однозначности отображения на границе
проводим разрез по лучу р (рис. 2.38). Образом области D является плоскость с
разрезом по лучу arg w = Р; угол а < <р < а + — отображается в угол р < 9 < р + 2л.
X
(w)
Рис. 2.38
Заметим, что этот же результат получается и для каждого из трех других
тлов, образованных продолжением выбранных лучей за начало координат (рис.
:.38). Так, для области D, имеем
л
а+--
и поэтому
■чх + 2л < 0! < 4а + 4л или р4 < 0j < Pi + 2ti , где P! = 4а + 2л совпадает геометри-
геометрически с р = 4а.
Для области D2 из а-л<ф2<а— получаем 4а-4л < 62 < 4а-2л, или
12 < 02 < р2 + 2л, р2 = 4а - 4л и р2 совпадает геометрически с р = 4а.
Наконец, для
13 < б3 < рз + 2л, р3 = 4а - 2л и Рз совпадает геометрически с р = 4а.
из а — <фз<а получаем 4а-2л<6з<4а и
В частности, при а = 0 область D определяется условием 0 < arg z < — -
первый квадрант; D\, D2, Dy - другие квадранты. Все эти области функцией w = z4
чображаются на плоскость с разрезом по лучу [0,°о),(р = 4а = 0) (рис. 2.39). ,
(Z)
(w)
D
D2
Z>3
Рис. 2.39
151
(z)
(w)
G
Рис. 2.40
При а =- соответствующие области отображаются на плоскость с разр».
зом по лучу (-«,0], (р = 4<х = л) (рис. 2.40). ■
Пример 2.75. Отобразить "луночку" < на верхнюю полуплоскости.
□ Границу "луночки" образуют дуги двух окружностей, пересекающихся t
точках г =0 и z = 1 + < под утлом a = —, а границу ее образа - два луча, o6pt
зующие действительную ось, угол между ними равен п (рис. 2.41).
Рис. 2.41
Так как нужно увеличить угол вдвое, применим отображение w = z2- Hi
прежде надо "распрямить" дугу, т.е. применить преобразование, переводящее oct
окружности в прямые. Для этого достаточно, чтобы одна из их общих точек oti-
бражалась в бесконечно удаленную точку (см. пример 2.67).
Первый этап. Применяем дробно-линейное преобразование wx =A —,
Z-Z2
где, например, Z\=0, г2=1+'\ те- переводим 0 в 0 @->0), A + /) в м
152
Образами дуг при отображении w = А будут два луча, пересекаю-
z - A + /)
щиеся в начале координат под прямым углом. Положение лучей (наклон) опре-
определяется параметром А.
Для определенности отображения на этом этапе зададим значение А или
найдем его, задав третью пару - соответствие внутренних точек. Из соображений
- 1 + / 1 + / _.. 1 + /
симметрии удобно взять, например, > . Образом точки , принад-
принадлежащей "луночке", будет точка , принадлежащая первая квадранту.
IJ 1+' ■• 2 А 1+'
Из равенства =Л-—— находим А = и получаем отобра-
жение и>[ =-
Образом "луночки" будет первый квадрант, а образами дуг - действитель-
. „ 1 + / 1 + /
ная и мнимая полуоси, так как из соответствия 0-»0 и > следует, что
образом прямой, соединяющей точки г = 0 и Z= , будет биссектриса пер-
первого координатного угла в плоскости и^.
Второй этап. Применяем преобразование w = wf, удваивающее углы, и
iz2
получаем окончательный ответ: w =—\ или w = ,. -
2U-0 + 0J (г-d + OJ
Пример 2.76. Отобразить полукруг |г| < 1, Im z > 0 на верхнюю полуплос-
полуплоскость.
□ Рассуждая, как и в предыдущем примере, замечаем, что нужно прежде
"распрямить" окружность; при этом образом прямой |г| < 1, Imz = 0 должна
быть также прямая. Поэтому нужно взять преобразование, переводящее одну из
точек пересечения дуги и прямой в бесконечность.
Первый этап. Пусть 1 -»со,-1 -> 0 (на рис. 2.42,о точки D и В) , т.е. выби-
выбираем отображение w, = А . При А = -1 это w = и w = при А = \.
z-1 \-z Z-1
Второй этап. Определим образ полукруга при выбранном отображении.
Для этого достаточно взять еще по одной точке на каждой из частей гра-
границы полукруга, например, z = 0 (точка А на рис. 2.42,о) и z =' (точка С на рис.
2.42,о), найти их образы и по направлению обхода границы определить вид об-
области.
Так, в случае и>, = точке г = 0 соответствует и^ = -1, точке z =' со-
соответствует и1, = -/. Образом полукруга будет третий квадрант (рис. 2.42,6)
153
Если взять А = -1, т.е. отображение W\ =
1 + 1
1-z'
то из соответствиг.
О —> 1» / —> / находим, что образом полукруга будет первый квгигоант (dhc. 2.42.e
4
-1
(г)
D
А 1
Рис. 2.42
Третий этап. В случае выбранного выше отображения при А = -
wl = ответом, очевидно, будет w = wf, т.е. w =
В случае и>! = -— отображение w = wf приводит к тому же результат.
Можно предварительно применить преобразование поворота W2=e"Iw1, в pt
зультате чего получим первый квадрант и окончательный ответ: w = w\ = w}, T.t
Пример 2.77. Найти образ плоскости с разрезом по лучу [0, °о) при отобра
S.
жении w=yz с условием и>(-1) =—A-/).
□ Заметим, что поставленную задачу можно рассматривать как обратнук
рассмотренной в примере 2.74 (см. рис. 2.39). Каждой точке границы z = х, х > (
соответствуют четыре значения w, определяемые по формул!
.2*71
wk = $[х- е 4 ,к = 0,1,2,3. Образом луча z = х, где х - параметр, будет каждый иг
лучей, параметрические уравнения которых w = r, w = re 2 =/■/, w = re'* =-.
■h
w = re 2 =-ri, г = У~х >0- параметр. Они делят плоскость на четыре квадрант;.
Выражение w = yz определяет в любой области, не содержащей точе:
Z = 0 и z = °°, четыре однозначные ветви. В данном случае такая область - плос-
плоскость с разрезом [0,°о>. Каждая из ветвей отображает эту область на один иг
154
;вадрантов. Выбор ветви определяется заданием функции в одной из тгчек об-
_,»
1асти. Из условия и>(-1) = е 4 следует, что образом заданной области будет чет-
четвертый квадрант: Re w > О, Im w < О (область Х>3 на рис. 2.39). ■
Пример 2.78. Отобразить плоскость с разрезом | Re z \ > 1, Im ? = 0 на верх-
-шю полуплоскость.
□ Из свойств отображения w = 4fz и анализа решений примеров 2.74 и
1.77 замечаем, что для отображения плоскости с разрезом по лучу [О,») на верх-
верхнюю полуплоскость нужно применить функцию w = 4l ■ В данном случае грани-
ja области состоит из двух лучей, пробегаемых дважды и соединяющихся в бес-
;онечности (рис. 2.43). Чтобы получить плоскость с одним разрезом, i .а,ло сна-
■ала применить преобразование, соединяющее разрезы - сдвиг. При этом одна
43 точек границы должна отображаться в бесконечно удаленную точку. Оледова-
~чьно. тоебуется применить дробно-линейное отображение.
-•й этап. Применим преобразование w = А-—— , где, н"" \v:?.p,
Z-Z2
. z-) = 1, т.е. -1 -»0,1 -> да. Запишем отображение vt\ = . Прк этом по-
j -> -1 и да -»1, так как lim iV] = 1. Образом данной области буте™ плос-
• разрезом [0,оо) (рис. 2.43).
Рис. 2.43
~1 этап. Применяем w = Jw[ при условии и>(-1) = /. Получим ото-
..^пш, w - ,| , переводящее заданную область в верхнюю полуплоскость.и
lz-1
Упражнения
1. При отображении w = iz + \- 2/ найти образы прямых:
a) Rez = l; б) Imz = l.
Указание. Решить задачу геометрически, используя геометрический
мысл составляющих линейной функции, и аналитически, записав уравнения
данных прямых в комплексной или параметрической форме.
f • 155
Ответ: a) Im w - 1; б) Re w = 0.
2. Найти образ области D: \ при отображении w = iz +1 - 2/.
[Im г > 1
Указание. См. указание к задаче 1.
fRew<0
Ответ: <
3. Найти какую-либо линейную функцию, отображающую область D:
Re z + Im z < 0 - на область G: Re и> > 2.
12; 2i,
Ответ: w = e* z + 2,w-ke* г + 2Д > 0.
Зл.
4. Найти образ прямой Re г - Im г = 0 при отображении w = е 4 2г + 2.
Ответ: Im w = 0.
5. Проверить, что образ прямой Re г - Im z = 0, перпендикулярной границе
2",-
области D из упражнения 3, при отображении w = 2ze4 +2 есть прямая, пер-
перпендикулярная границе области G, т.е. прямой Re w = 2 (см. упражнения 3 и 4).
6. Найти какую-либо линейную функцию, отображающую область |г| < 1 на
область | w -1 +11 < 2.
Указание. Решить задачу геометрически, используя геометрический
смысл составляющих линейной функции, и аналитически, используя круговое
свойство линейной функции.
Ответ: w = 2z +1 - /', w = 2emz +1 - / •
7. При отображении w = — найти образы областей:
z
a) \z -1| < 1; б) \z - \\ < v3; в) 1 < \z -1| < v3.
Ответ: a) Re w > 1; 6) | w +11 > &; в) полуплоскость Re w < 1 с выбро-
выброшенным кругом |iv + l|<i/3.
8. При отображении w - —— найти образы прямых:
a) Im z = 0; б) Im z = I •
v + — = —, т.е.
2) 4
9. Найти образ полосы 0 < Re z < 1 при отображении w = .
Ответ: полуплоскость Re w < 1 с выброшенным кругом « — + v2 й —.
V 2 4
156
/I, -
10. Проверить, что при отображении w = образы прямых Imz = 0,
г-1
Im z = 1, перпендикулярных границе полосы 0 < Re z < 1, ортогональны границе
образа этой полосы.
Указание. См. упражнения 8 и 9, сделайте чертеж.
11. Найти образ области 0 < Inu < 1 при отображении w = .
г-1
V + — £—.
2) 4
г 12. При отображении w =—— найти образы следующих линий:
а) окружности |г| = 3; б) мнимой оси.
*> ■■ 1
^ Ответ: a) v = —; б) и = 0.
13. Проверить ортогональность прообразов и их образов при отображении
из упражнения 12.
14. Найти дробно-линейную функцию, отображающую область \z -1| > 1 на
область Re iv > 1 при условии и>A) = /, aig w'(l) = 0.
Указание. Задача эквивалентна задаче отображения круга \z -1| < 1 на
полуплоскость при условии, что центр круга отображается в данную точку полу-
полуплоскости. Используйте каноническую задачу.
Ответ: w=
Z
15. Найти образ точки, симметричной точке /' относительно окружности
\z~ l| = 1 , при отображении из упражнения 14.
Указание. Используйте свойство сохранения симметричных точек.
Ответ: w = 3;.
16. Найти дробно-линейную функцию, отображающую область
D: Re z + Im i > 0 на область G: Im w > 0 при условии, что точка ? = 0 отобража-
отображается в бесконечно удаленную, а точка г = 1 + / остается неподвижной при ото-
отображении.
п z -1 + i
Ответ: w = .
г
17. Показать, что при отображении из упражнения 16 образом прямой
Re z - Im z = 1, перпендикулярной границе области D, является окружность, ор-
ортогональная образу этой границы, т.е. прямой Im w = 0. Найти уравнение этой
окружности.
Ответ: |и>| = 1.
18. Показать, что при отображении из упражнения 16 образом окружности
\z -1 + i\ = S., ортогональной границе области Д, является прямая, перпендику-
перпендикулярная образу этой границы, т.е. прямой Ira w = 0. Найти уравнение этой пря-
прямой.
Ответ: и = J^.
157
2.2. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
2.2.1. Основные определения
1. Понятие интеграла от функции комплексного переменного вводится (так
же, как и в действительной области) как предел последовательности интеграль-
интегральных сумм; функция при этом определена на некоторой кривой /, кривая пред-
предполагается гладкой или кусочно-гладкой:
^, B.43)
/ к=\
где \к - точка, выбранная на дуге А1к разбиения кривой; А zk - приращение ар-
аргумента функции на этом участке разбиения, X = max|A?t| - шаг разбие-
разбиения, |Дг*| - длина хорды, соединяющей концы дуги А1к; кривая / разбивается
произвольным образом на п частей А1к,к = 1,2,...,л. На кривой выбрано направ-
направление, т.е. указаны начальная и конечная точки. В случае замкнутой кривой
[[f(z)dz = l$f(z)dz\ интегрирование происходит в положительном направле-
/ с )
нии, т.е. в направлении, оставляющем слева конечную область, ограниченную
контуром.
Формула B.43) определяет криволинейный интеграл от функции комплекс-
комплексного переменного.
Если выделить действительную и мнимую части функции f(z), т.е. запи-
записать ее в виде /(г) = и + /V, и = Re f(z), v = Ira f(z), и = и{х, у), v = v(x, у), то ин-
интегральную сумму можно записать в виде двух слагаемых, которые будут являться
интегральными суммами криволинейных интегралов второго рода от функций
двух действительных переменных. Если f(z) предположить непрерывной на /,
то и(х,у), v(x,y) будут также непрерывны на /, и, следовательно, будут сущест-
существовать пределы соответствующих интегральных сумм. Поэтому, если функция
f(z) непрерывна на /, то предел в равенстве B.43) существует, т.е. существует
криволинейный интеграл от функции f(z) по кривой / и имеет место формула
f f(z) dz- Jи dx - v dy + z' fи dy + v dx. B.44)
/ / /
Используя определение интеграла или формулу B.44) и свойства криволи-
криволинейных интегралов второго рода, нетрудно убедиться в справедливости следую-
следующих свойств криволинейного интеграла от функций комплексного переменного
(свойства, известные из действительного анализа).
1- J[c,/ifc) + c2/2te)R = c, lA(z)dz + c2 \h(z)dz.
i i i
2. \f(z)dz = -\f{z)dz.
AB BA
3- lf(z)dz= [f{z)dz+ [f(z)dz.
AB AC CB
158
4. | \dz\ = IAB - длина дуги АВ.
АВ
*
5.
\f(z)dz
I
<
I
it частности, [/(гШ < М 1дв , если функция ограничена по модулю на кривой
АВ I
Л#, т.е. \f(z)\ < M, zel. Это свойство называется свойством оценки модуля
интеграла.
6. \dz = zB-zA.
АВ
Формулу B.44) можно рассматривать и как определение криволинейного
интеграла от функции комплексного переменного, и как формулу его вычисле-
вычисления через криволинейные интегралы второго рода от функций двух действитель-
действительных переменных.
Для использования и запоминания формулы вычисления отметим, что ра-
вснству B.44) соответствует формальное выполнение в левой части под знаком
интеграла действий выделения действительной и мнимой части функции f(z),
умножения на dz = dx + idy и записи полученного произведения в алгебраиче-
алгебраической форме:
\f(z)dz =|(и + iv)(dx + idy) =judx - vdy + i(udy + vdx) = \udx - vdy + i\udy + vdx.
II I ii
Пример 2.79. Вычислить интегралы [zdz и izdz, где ОА :
OA OA
i а) отрезок прямой, соединяющей точки z\ = 0 и Z2 = 1 + >',
б) ломаная ОВА, где 0@,0), А(\,\),В(\,0).
D 1. Вычислим интеграл \z~dz. Здесь f(z) = Z-x-iy, dz = dx + idy.
OA
Записываем интеграл через криволинейные интегралы второго рода:
f zdz = [(х-iy)(dx + idy) = f xdx + ydy + z' fxdy -ydx,
OA OA OA OA
что соответствует формуле B.44). Вычисляем интегралы:
а) путь интегрирования - отрезок прямой у - х, 0 < х < 1, поэтому
i
\\
ОА 0
б) путь интегрирования - ломаная, состоящая из двух отрезков
ОВ{у = 0,0 < х < 1} и ВА{х = 1,0 <у < 1}. Поэтому, разбивая интеграл на два и
1 1 1
производя вычисления, получаем j zdz = \zdz + f zdz = \xdx + ^ydy + i ^dy = 1 + i.
OA OB BA 0 0 0
159
Интеграл от функции /(г) = z зависит от выбора пути интегрирования, соеди-
соединяющего точки О и А.
2.Вычислим интеграл [г<&.3десь f(z) = z = x + iy. Записываем интеграл че-
ОА
рез криволинейные интегралы второго рода \zdz = ^xdx-ydy + i \xdy + ydx.
ОА ОА ОА
Подынтегральные выражения полученных интегралов второго рода являются
полными дифференциалами (см. условие B.30)), поэтому достаточно рассмотреть
один случай пути интегрирования. Так, в случае "а", где уравнение отрезка
у = х, 0 < х < 1, получаем ответ
ОА о
В силу независимости интеграла от формы пути интегрирования, задание в
данном случае можно сформулировать в более общем виде: вычислить интеграл
| z dz от точки Z\ = 0 до точки z-i = 1 + /. ■
/
В следующем пункте рассмотрим подробнее подобные случаи интегрирова-
интегрирования.
2. Пусть интеграл от непрерывной функции в некоторой области не зави-
зависит от вида кривой, соединяющей две точки этой области. Зафиксируем началь-
начальную точку, обозначив z0, конечная точка - переменная, обозначим ее z. Тогда
значение интеграла будет зависеть только от точки z, т.е. j f{z)dz определяет
/
некоторую функцию в указанной области.
Ниже будет дано обоснование утверждения, что в случае односвязной области
интеграл определяет в этой области однозначную функцию. Введем обозначение
)№dt, = F(z). B.45)
го
Функция F(z) - интеграл с переменным верхним пределом.
Используя определение производной, т.е. рассматривая lim — , нетрудно
Лг-0 Дг
убедиться, что F(z) имеет производную в любой точке области определения, а
следовательно, является в ней аналитической. При этом для производной полу-
получим формулу
F'{z) = f{Z). B.46)
Производная интеграла с переменным верхним пределом равна значению по-
подынтегральной функции при верхнем пределе.
Из равенства B.46), в частности, следует, что подынтегральная функция
f(z) в B.45) является аналитической функцией, так как производная F'(z) ана-
аналитической функции F(z) по свойству таких функций (см. утверждение 2.28) -
функция аналитическая.
160
3. Функция F(z), для которой выполняется равенство B.46), называется
первообразной для функции f(z) в односвязной области, а совокупность перво-
первообразных Ф(г) = F(z) + с, где с = const, - неопределенным интегралом от функции
/<*)■
Из пп. 2 и 3 получаем следующее утверждение.
д
Утверждение 2.25.
, 1. Интеграл с переменным верхним пределом {f(£,)d£, от аналитической
го
в односвязной области функции есть функция, аналитическая в этой области; эта
функция является первообразной для подынтегральной функции.
2. Любая аналитическая в односвязной области функция имеет в ней первооб-
первообразную (существование первообразной).
Первообразные аналитических функций в односвязных областях отыски-
отыскиваются, как и в случае действительного анализа: используются свойства интегра-
интегралов, таблица интегралов, правила интегрирования.
Например, jeldz = ez +c, \cc&zdz = sin? + c.
Между криволинейным интегралом от аналитической функции и ее перво-
первообразной в односвязной области имеет место формула, аналогичная формуле
Ньютона-Лейбница из действительного анализа:
)f(z)dz =
F(z)
ii
B-47)
4. Как и в действительном анализе, в комплексной области рассматрива-
рассматриваются, кроме интегралов, содержащих параметр в пределах интегрирования
(формула B.45) дает простейший пример таких интегралов), интегралы, которые
зависят от параметра, содержащегося в подынтегральной функции: \f(t,,z)d£,.
Среди таких интегралов важное место в теории и практике комплексного интег-
интегрирования и приложениях занимает интеграл вида f ■i^d\.
Полагая/(г) непрерывной на /, получаем, что для любой точки z, не при-
принадлежащей /, интеграл существует и определяет в любой области, не содержа-
содержащей /, некоторую функцию
\ B-48)
2л/ \ \-z
Интеграл B.48) называется интегралом типа Коши; множитель — введен
2л/
для удобства использования построенной функции.
Для этой функции, как и для функции, определяемой равенством B.45),
доказывается, что она является аналитической всюду в области определения.
Причем в отличие от интеграла B.45) здесь не требуется, чтобы порождающая
6 Пантелеев А.В., Якимова А.С. 161
функция f(z) была аналитической, т.е. по формуле B.48) на классе непрерыв-
непрерывных функций комплексного переменного строится класс аналитических функ-
функций.
Производная интеграла B.48) определяется по формуле
Для доказательства формулы B.49) и, следовательно, утверждения об ана-
аналитичности интеграла типа Коши достаточно, согласно определению производ-
производной, установить справедливость неравенства
Дг »-м - М<«(е)
для любого е > 0 и при любом z из области определения функции F(z).
Таким же методом можно показать, что существует производная от функ-
функции, определяемой равенством B.49), т.е. F"(z), и справедлива формула
Процедуру можно продолжить и доказать по индукции формулу для произ-
производной любого порядка от функции F(z) ■
<150)
Анализируя формулы B.48) и B.49), нетрудно убедиться, что производную
F'(z) можно получить формально, производя дифференцирование по параметру
под знаком интеграла в B.48):
Применяя формально правило дифференцирования интеграла, зависящего от па-
параметра п раз, получим формулу B.50).
Результаты, полученные в этом пункте, запишем в виде утверждения.
Утверждение 2.26. Интеграл — [ ■* *?' а\ от функции f(z), непрерывной
на кривой I, есть функция, аналитическая в любой области D, не содержащей I ;
производные этой функции могут быть получены дифференцированием по параметру
под знаком интеграла.
2.2.2. Вычисление интегралов
В предыдущем разделе получены формулы вычисления интегралов от
функций комплексного переменного - формулы B.44) и B.47).
162
Если кривую / в формуле B.44) задать параметрически: z = z(t),a<t^В
или, что соответствует действительной форме: \ ~ , а < t < В, то, используя
[У = У@
правила вычисления интегралов второго рода в случае параметрического задания
кривой, можно преобразовать формулу B.44) к виду
р
\f(z)dz=\f(z{t))z'(t)dt . B.51)
/ а
Полученный результат и результаты разд. 2.2.1 запишем в виде последова-
последовательности действий.
Способы вычисления интегралов \f(z) dz ■
i
Первый способ. Вычисление интегралов jf(z)dz от непрерывной функции
путем сведения к криволинейным интегралам от функций действительных пере-
переменных - применение формулы B.44).
1. Найти Яе/(г) = ы, \mf(z) = v.
2. Записать подынтегральное выражение f(z) dz в виде произведения
(и + iv)(dx + idy) или, перемножая, udx - vdy + i{udy + vdx).
3. Вычислить криволинейные интегралы вида ^Pdx + Qdy, где
Р-Р{х,у), Q = Q(x,y) по правилам вычисления криволинейных интегралов
второго рода.
Второй способ. Вычисление интегралов \f(z)dz от непрерывной функции
путем сведения к определенному интегралу в случае параметрического задания
пути интегрирования - применение формулы B.51).
1. Записать параметрическое уравнение кривой z - z(t) и из него опреде- *
лить пределы интегрирования: / = а соответствует начальной точке пути интег-
интегрирования, / = Р - конечной.
2. Найти дифференциал комплекснозначной функции z(t): dz = z'(t)dt.
3. Подставить z(t) в подынтегральное выражение, преобразовать интеграл
Р Р
к виду \f(z(t))l'{t)dt^\v,{t)dt .
а. а
4. Вычислить полученный в п.З определенный интеграл от комплексно-
комплекснозначной функции действительной переменной.
Заметим, что интегрирование комплекснозначной функции действительной
переменной не отличается от интегрирования действительнозначной функции;
единственным отличием является наличие в первом случае множителя /', дейст-
действия с которым, естественно, рассматриваются, как с постоянной.
163
elit
elit
Например, f e2ltdt =
, 2i
Третий способ. Вычисление интефалов от аналитических функций в одно-
связных областях - применение формулы B.47).
1. Найти первообразную F(z), используя свойства интефалов, табличные
интефалы и методы, известные из действительного анализа.
2. Применить формулу B.47): | f(z)dz = F(z2) - Ffa).
ц
Замечания 2.10.
1. В случае многосвязной области проводятся разрезы так, чтобы можно
было получить однозначную функцию F(z).
2. При интефировании однозначных ветвей многозначных функций ветвь
вьшеляется заданием значения функции в некоторой точке кривой интефирова-
ния. Если кривая замкнутая, то начальной точкой пути интефирования считает-
считается та точка, в которой задано значение подынтефальной функции. Значение ин-
тефала может зависеть от выбора этой точки.
Пример 2.80. Вычислить J Re z dz, где / - линия, соединяющая точку ц = 0
с точкой zi = 1 + /: а) / - прямая; б) / -ломаная ОВА, где О@;0), В(Г,0), ДГД).
□ а) Применяем первый способ - (формулу B.44)).
1,2. Подынтефальное выражение имеет вид Rezdz = x(dx + idy). Поэтому
JKezdz= \xdx + i\xdy.
i i i
3. Вычисляем интефалы при у = х, 0 < х < 1 (уравнение отрезка ОА,
соединяющего точки г, и г2 )■ Получаем
f Rez<fe= jxdx + i jxdy= jxdx + i jxdx = ——.
I I I 0 0
б) Так как путь интефирования состоит из двух отрезков, записываем ин-^
тефал в виде суммы двух интефалов: \Rzzdz~ |Яег^г+ JRezdz и каждый
; ов ва
вычисляем, как в предыдущем пункте. При этом для отрезка ОВ имеем
W,i,a^OTpe3KaMl()^i.
Производим вычисления:
1 1 |
f Re z dz = jx dx + / x dy + \xdx + ixdy=jxdx + ijldy = — +i.
I OB BA 0 0
Заметим, что подынтефальная функция в данном примере - функция не
аналитическая, поэтому интефалы по двум различным кривым, соединяющим
две данные точки, могут иметь разные значения, что и проиллюстрировано
в этом примере, и
164
Пример 2.81. Вычислить
, где /- верхняя полуокружность
обход кривой / против часовой стрелки.
□ Кривая имеет простое параметрическое уравнение г = е",0</<л, по-
поэтому удобно использовать второй способ (формулу B.51)). Подынтегральная
функция здесь - непрерывная функция, аналитической не является.
1,2. Для z = e" находим z=e~", \z\ - l,dz = ie"dt.
3,4. Подставляем в подынтегральное выражение. Вычисляем интеграл
/О О
Пример 2.82. Вычислить интегралы от аналитических функций:
a) f sin2 zdz; б) j -, путь интегрирования не проходит через точку /.
о -I (z - i)
П а) Применяем формулу B.47) (третье правило); первообразную нахо-
находим, используя методы интегрирования действительного анализа:
о
'О
>и
1 . 1 . „. 1 . .sh2
= -/—sin It = — i-i
2 4 2 4
= iB-sh2).
б) Подынтегральная функция является аналитической всюду, кроме точки
i. Проведя разрез плоскости по лучу от точки /доя , получим односвязную об-
область, в которой функция является аналитической и интефал можно вычислить
по формуле B.47). Поэтому для любой кривой, не проходящей через точку /,
можно вычислить интефал по формуле B.47), при этом для двух заданных точек
он будет иметь одно и то же значение.
На рис. 2.44 показаны два случая проведения разрезов. Направление обхода
фаницы односвязных областей, где подынтефальная функция является аналити-
аналитической, указано стрелками. I
(z)
\
I
Вычисляем интефал: J -
dz
Рис. 2.44
-1
*~ z-i
J 1_
1 - i 2/
u; ; -i
~+2=Т
16S
1+1
Пример 2.83. Вычислить интеграл | zdz.
о
П Подынтегральная функция - аналитическая всюду в С. Применяем тре-
третий способ, формулу B.47):
]'*■£
о
Этот результат получен в примере 2.78 согласно первому способу.и
Пример 2.84. Вычислить интеграл с| , где С - окружность \z - а| = R.
П Применим второй способ.
1. Записываем уравнение окружности в параметрической форме:
l-a= Re" или z=a+Re", 0</<2л.
2. Находим дифференциал dz = Rie"dt.
3. Подставляем z-a+Re" и dz в подынтегральное выражение:
l(z-af lRnelnt R"-1 }
Вычисляем полученный определенный интеграл.
При п*\ получаем Г e'<'-")rft , —■!— е"М * = . '. (l - е2"^
о Ч1-") |о ("-О-'
Так как е2"'^) = е2Ы' = 1, поэтому j—-— = 0 при л * 1.
d 2lt
При я = 1 получаем cf = / f dt = 2л/.
сг~в о
Выпишем полученный результат в виде формулы:
Л _А_ в0,И*1; < -^- = 2л/. B.52)
В частности, <( — = 2л/.
W-* z
Заметим, что если окружность С :|г-о| = R обходится точкой к раз, то ар-
аргумент (параметр) изменяется от 0 до Ink (к > 0, если обход в положительном
направлении, т.е. против часовой стрелки, и к < 0 - обход по часовой стрелке).
Поэтому <(—— = / \dt = 2km, cf —=2Ы .
сz а о с г
7 — /J
z а
166
Z (#
Пример 2.85. Вычислить интеграл f — :
а) путь интегрирования не проходит через точку z = 0 и не обходит ее,
- я < arg z < л;
б) путь интегрирования не проходит через точку z = 0, но обходит ее п раз
ю окружности против часовой стрелки.
□ а) Этот интеграл - интеграл с переменным верхним пределом - опреде-
1яет в любой односвязной области однозначную аналитическую функцию (см.
2.45)). Найдем аналитическое выражение этой функции - первообразной для
(г) = —. Отделяя действительную и мнимую части интеграла f— (применяя
z j z
эормулу B.44)), нетрудно убедится, что подынтегральные выражения интегралов
тгорого рода являются полными дифференциалами и, следовательно, интеграл
dt
— не зависит от вида кривой, соединяющей точки Z\ = 1 иг- Выберем путь,
остоящий из отрезка оси Охот точки Z\ = 1 до точки z2 = г, где г = \z\, и дуги /
|коужности. соединяющей zi с z (рис. 2.45,а).
Рис. 2.45
Интеграл запишем в виде суммы: f = f— + f • Д™ вычисления ин-
1 \ , х i \
-еграла по дуге окружности применяем формулу B.51), дуга при этом имеет
'равнение % = re", 0</^arg?. Получаем f— = f
; ^- о
dt = iaigz; в результа-
—
~е | — = In г + / arg z, - л < arg г ^ л. Правая часть равенства определяет одно-
:начную функцию In г - главное значение логарифма (см. разд. 2.1.2.).
167
Ответ получаем в виде
J^ = liU. B.53)
Заметим, что полученное равенство можно принять за определение однозначной
функции In z в односвязной области - плоскости с разрезом по отрицательной
действительной полуоси (-°о,0].
б) Интеграл можно записать в виде суммы: { =^— + J > где с "
п -раз пробегаемая против часовой стрелки окружность |г| = 1, а / - кривая, со-
соединяющая точки z\ и z и не охватывающая точку z - 0 (рис. 2.45,6).
Первое слагаемое равно 2ля/ (см. пример 2.84), второе - In г- формула
B.53). Получаем результат |— = ни + 2дат/.И
1 ^
Пример 2.86. Вычислить интеграл f -j= по верхней дуге окружности \ц -1
при условии: a) vl =1; б) vl = -1.
□ Задание значений функции 4z в точке контура интегрирования позво-
ляет вьщелить однозначные ветви выражения 4l = уИ е v ;, А: = 0,1
(см. пример 2.6). Разрез можно провести, например, по мнимой отрицательной
полуоси. Так как при z = 1 имеем 41- е'ы,к = 0,1 , то в первом случае выделя-
выделяется ветвь с к = 0 , во втором - с к = 1. Подынтегральная функция на контуре
интегрирования непрерывна. Для решения используем формулу B.51), кривую
задаем уравнением z = e",0<,t£п .
а) Ветвь определяется при ifc=0, т.е. из z = e" для подынтегральной
функции получаем 4z =e 2. Вычисляем интеграл:
*
о 7
= 2 Л-1 =2(/-1).
о
б) Ветвь определяется при к = 1, т.е. из z = e" для подынтегральной функ-
функции имеем 4l =е^2 ' = -е 2. Вычисляем интеграл:
2.2.3. Основные теоремы интегрального исчисления
В теории и практике, в приложениях интегрального исчисления функций
комплексного переменного, при исследовании поведения функций в ограничен-
ограниченных областях или в окрестностях отдельных точек рассматриваются интефалы по
замкнутым кривым - границам областей, в частности окрестностей точек. Будем
рассматривать интефалы <$f(z)dz, где f(z) - аналитическая в некоторой
с
области, за исключением отдельных точек, С - фаница области или внутренний
контур в этой области.
ОСНОВНАЯ ТЕОРЕМА КОШИ
Теорема 2.1 (теорема Коши для простого контура). Если f(z) аналитиче-
аналитическая в односвязной области, то для любого контура С, принадлежащего этой об-
области, справедливо равенство
O . B.54)
Доказательство теоремы нетрудно получить, опираясь на свойство аналити-
аналитических функций, согласно которому аналитическая функция имеет производные
любого порядка (см. утверждение 2.28). Это свойство обеспечивает непрерыв-
непрерывность частных производных от Re f{z) и 1т/(г), поэтому, если использовать
формулу B.44), то легко видеть, что для каждого из подынтефальных выражений
в криволинейных интефалах второго рода выполняются условия полного диффе-
дифференциала, как условия Коши-Римана аналитических функций. А интефалы
по замкнутым кривым от полных дифференциалов равны нулю.
Заметим, что все теоретические положения, излагаемые ниже, опираются в
конечном счете на эту важную теорему, в том числе и упомянутое выше свойство
аналитических функций. Чтобы не было сомнения в корректности изложения,
заметим, что теорема может быть доказана без ссылки на существование ее про-,
изводных только на основании определения аналитической функции.
Следствия из теоремы 2.1.
1. Теорема справедлива и в случае, если С- фаница области D, а функция
f(z) является аналитической в области и на фанице, т.е. в D , так как, согласно
определению, аналитичность в D предполагает аналитичность функции в неко-
некоторой области В, содержащей D [В э D), а С при этом будет внутренним кон-
контуром в В.
2. Интефалы по различным кривым, лежащим в односвязной области ана-
аналитичности функции и соединяющим две точки этой области, равны между со-
собой, т.е. ^f(z)dz = ^f(z)dz , где /j и /2 - произвольные кривые, соединяющие
'i h
точки Z\ и Zi (рис. 2.46).
Рис. 2.46
Для доказательства достаточно рассмотреть контур С, состоящий из кри-
кривой /| (от точки i\ к точке ц) и кривой 1^ (от точки ц к точке z\). Свойство
можно сформулировать следующим образом. Интеграл от аналитической функ-
функции не зависит от вида кривой интегрирования, соединяющей две точки области
аналитичности функции и не выходящей из этой области.
Это дает обоснование данного выше утверждения 2.25 о свойствах интегра-
г
ла |/D)й^ и о существовании первообразной аналитической функции.
го
Теорема 2.2 (теорема Коши для сложного контура).
Если функция f(z) является аналитической в многосвязной области, ограни-
ограниченной сложным контуром, и на этом контуре, то интеграл по границе области от
функции равен нулю, т.е., если С - сложный контур - граница области, то справед-
справедлива формула B.54).
Сложный контур С для (я +1) - связной области состоит из внешнего
контура Г и внутренних - С,-, /' = 1,2,...я; контуры попарно не пересекаются, об-
обход границы - положительный (на рис.2.47, я = 3).
Рис. 2.47
Рис. 2.48
170
Для доказательства теоремы 2.2 достаточно провести в области разрезы (на
рис. 2.47 пунктир ) так, чтобы получились две односвязные области и воспользо-
воспользоваться теоремой 2.1.
Следствия из теоремы 2.2.
1. При выполнении условий теоремы 2.2 интеграл по внешнему контуру ра-
равен сумме интегралов по внутренним; обход на всех контурах в одну сторону (на
рис. 2.48, й = 2):
*=1 С,
B.55)
2. Если f(z) является аналитической в односвязной области D и на грани-
границе области, за исключением, быть может, точки а этой области, то интегралы по
различным замкнутым кривым, которые лежат в области D и ограничивают об-
области, содержащие точку а, равны между собой (рис. 2.49):
= jf(z)dz.
B.56)
Доказательство очевидно, поскольку каждый такой контур можно рассмат-
рассматривать как внутреннюю границу двусвязной области, внешней границей которой
является граница области D. В соответствии с формулой B.55) при п = 1 любой
такой интеграл равен интегралу по границе D.
Рис. 2.49
Сравнение формулировок теоремы 2.2 и следствия 1 из теоремы 2.1 позво-
сделать обобщение, которое запишем в виде следующего утверждения.
Утверждение 2.27. Если f(z) аналитическая в D, то
где С - граница области D (простой или сложный контур).
171
ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
В следующей теореме, в отличие от двух предыдущих, рассматривается ин-
интеграл от функции, которая, не являясь аналитической в области, ограниченной
контуром интегрирования, имеет специальный вид.
Теорема 2.3. Если функция f(z) является аналитической в области D и на ее
границе С, то для любой внутренней точки а области (а е D) имеет место равен-
равенство
Т< *■ B-57)
2ш I z-a
Область D может быть односвязной или многосвязной, а граница области -
простым или сложным контуром.
Доказательство для случая односвязной области опирается на результат тео-
теоремы 2.1, а для многосвязной - приводится к случаю односвязных областей (как
при доказательстве теоремы 2.2) путем проведения разрезов, не проходящих че-
через точку а.
Следует обратить внимание на то, что точка а не принадлежит границе об-
области и поэтому подынтегральная функция является непрерывной на С и инте-
интеграл существует.
Теорема представляет собой важный прикладной интерес, а именно по
формуле B.57) решается так называемая краевая задача теории функций: по зна-
значениям функции на границе области определяется ее значение в любой внутрен-
внутренней точке.
Замечание 2.11. В условиях теоремы интеграл —4 ■ а\ определяет
2та £ \ - z
аналитическую функцию в любой точке z, не принадлежащей контуру С, при-
причем в точках конечной области D, ограниченной контуром, он равен f(z) (по
формуле B.57)), а вне О - равен нулю в силу оснований теоремы Коши. Этот
интеграл, называемый интегралом Коши, является частным случаем интеграла
типа Коши B.48). Здесь контур замкнутый, в отличие от произвольного в B.48),
а функция f(z) является аналитической, в отличие от непрерывной на / в
B.48). Для интеграла Коши, следовательно, справедливо сформулированное для
интеграла типа Коши утверждение 2.26 о существовании производных. Можно
сформулировать на основании этого следующее утверждение.
Утверждеиие 2.28.
1. Аналитическая функция в любой точке аналитичности может быть записа-
записана в виде интеграла
/w=i^fS^'?6°' B58)
2. Аналитическая функция имеет производные любого порядка, для которых
справедлива формула
Формула B.59) дает интегральное представление производных аналитической
функции.
172
2.2.4. Вычисление интегралов по замкнутому контуру
от функций комплексного переменного
Будем рассматривать интегралы вида i^-^-dz , где функция <р(г) аналити-
l ()
ческая 'в D , а у(г) - многочлен, не имеющий нулей на контуре С. Для вычисле-
вычисления интегралов применяются теоремы разд. 2.2.3 и следствия из них.
Правила 2.6. При вычислении интегралов вида <if(z)dz в зависимости от
с
характера (кратности) нулей многочлена у(г) и их расположения относительно
контура С можно выделить четыре случая.
1. В области D нет нулей многочлена ц/(г). Тогда /(г) =-"-^- функция ана-
4<(г)
литическая и, применяя основную теорему Коши, имеем результат
2. В области D расположен один простой нуль z = о многочлена v/(z) ■
а записываем дробь в виде , где /(г) - фун
г-а
Применяя интегральную формулу, получаем результат:
Тогда записываем дробь в виде , где /(г) - функция, аналитическая в D.
г-а
B.60)
3. В области D расположен один кратный нуль z = а многочлена y(z)
(кратности и). Тогда записываем дробь в виде , где f(z)- функция, ана-
(г-а)"
литическая в D. Применяя формулу B.59), получаем результат
4. В области D расположены два нуля многочлена у(г): Z\ = а и z-i = -
Тогда, используя следствие 1 из теоремы 2.2, запишем интефал в виде
jf(z)dz=jf(z)dz+jf(z)dz,
С С, С2
где С, и С2- фаницы непересекающихся окрестностей точек Z] и zi- Для каж-
каждого из полученных интефалов проводим далее вычисления в соответствии
с пп. 2 и 3. Очевидно, можно рассмотреть и случаи большего числа нулей y(z)
в области D.
Пример 2.87. Вычислить 4 —— , где С - произвольный контур, офаничи-
}z-a
вающий область, содержащую точку а.
173
Р Рассмотрим двусвязную область, одна граница которой - контур С,
другая - окружность \z - о| = R. По следствию 2 из теоремы 2.2 (см. B.56)) им^ем
<f = <f . Учитывая результат решения примера 2.84 (формула B/52)),
}l-a \zXRz-a f
получаем ответ
Z-a
Заметим, что решение можно получить, применив интегральную формулу
Коши с f(z) = 1. В частности, получаем <f — = 2п/, так как контур С один раз
с *
обходит точку z = 0. Если контур С обходит точку z = 0 к раз в положительном
(к > 0) или отрицательном направлении (к < 0), то <{ — = Ikni. ■
с ^
Пример 2.88. Вычислить [ —, где / - кривая, соединяющая точки 1 и z,
1 *■
один раз обходящая начало координат.
Р Подынтефальная функция непрерывна на кривой - интефал существует.
Для вычисления используем результаты предыдущего примера и примера 2.85.
Для этого рассмотрим замкнутый контур, соединив, например, точку А с точкой
1 (рис. 2.50). Путь интефирования из точки 1 в точку z через точку А можно
представить теперь состоящим из двух кривых - замкнутого контура С (кривая
BDEFAB) и кривой /q, соединяющей точки 1 и z через точку А :
| — =4 — + \ — ■ Используя результаты примеров 2.85 и 2.87, получаем ответ:
z z z
z z
E
У
D
f
0
V
С \^
F
■
(z)
\B
T
l
k 1
z
A
/
X
Рис. 2.50
174
Без изменения геометрической картинки, можно рассмотреть случай, когда
кривая и раз обходит начало координат. Получим результат
= f— = In z + 2rmi. Полученное выражение определяет многозначную
функцию Ln z = f — , путь интегрирования не проходит через начало коорди-
координат. Выбор ветви многозначного выражения определяется заданием значения
функций в некоторой точке. ■
I 2'dZ
Пример 2.89. Найти 1п 2; = j —, если In 1 = 4л/.
D Из формулы Ln z = In z + 2rmi = ln |г| +1 (arg z + 2kn) при z = 1 получаем
Ln 1 = 2Ы, а учитывая условие, находим к =2. Поэтому
*
1 1 ( А, * \-
. = In 2 + 4ля + — i.
,2 )\ыг { 2)
Пример 2.90. Вычислить <i—■ dz в следующих случаях задания контура
с г +16?
С: а) |г-2-/| = 2;
D Находим нули знаменателя - особые точки подынтегральной функции.
Это точки £i =0, ii =4/, Z3 =-4i. Далее нужно определить расположение точек
относительно контура интефирования. В обоих случаях ни одна из точек не вхо-
входит в область, ограниченную контуром. В этом можно убедиться, использовав
чертеж. Оба контура - окружности, центр первой г0 = 2 + / и радиус R = 2; центр
второй Zo = -2i и R = 1. Можно определить принадлежность точки области ина-
иначе, а именно определить ее расстояние от центра круга и сравнить с величиной
радиуса. Например, для точки ц = 4/ это расстояние равно
|4г - 2 - i| = |3г - 2| = i/Гз, что больше радиуса (i/Гз > 2), поэтому z-i = 4/ не при-
принадлежит кругу |г - 2 - ij < 2. В обоих случаях подынтегральная функция является,
аналитической в соответствующих кругах. Следовательно, согласно теореме
Коши (п. 1 правил 2.6), интеграл равен нулю. Заметим, что заданный интеграл
равен нулю и для любого другого контура, ограничивающего область, в которую
не входят ни одна из особых точек - нулей знаменателя. ■
Пример 2.91. Вычислить^ — dz в следующих случаях задания контура:
с г +16г
а)|*| = 2; б)|г + 1 + /| = 2.
□ Рассуждая, как в предыдущем примере, находим, что в обоих случаях
внутри кругов расположена только одна из особых точек z\ = 0. Поэтому, при-
применяя п.2 правил 2.6 (интегральная формула Коши) , записываем подынтеграль-
sin z
ную функцию в виде дроби -2—^— , где числитель f(z) - —; - функция,
г г2+ 16
175
аналитическая в указанных кругах. Ответ для обоих случаев одинаковый:
[\1
sin? I _.
?2 + 1бЛг=о
Пример 2.92. Вычислить^ — dz в следующих случаях задания
с z +16?
a)|?+4i| = 2; б) |г-1+3/| = 2.
П Контуры интефирования - окружности, как и выше, причем в случае "а"
центр находится в точке zo = - 4/, R = 2, в случае "б" - в точке ^о = 1—3/, Л = 2.
В обоих случаях внутрь соответствующих кругов попадает одна точка to =-4/.
Применяя п.2 правил 2.6, записываем подынтефальную функцию в виде
sin?
г'г~ '*, где числитель f(z) = ~r г является аналитической функцией в рас-
Z + 4/ z(z - 4/)
сматриваемых областях. Применяя интефальную формулу, получаем ответ:
sin? , . . sinz
dz = 2tu
. - sin 4/ iu ■ i sh 1
Пример 2.93. Вычислить интефал о - dz в следующих случаях
задания контура: a) \z + /j = 1; б) j? + 2 + /| = 2.
□ Находим особые точки подынтефальной функции - нули знаменателя
2| = I, zi = -2. Определяем принадлежность точек соответствующим областям. В
случае "а" в круг \z + /| < 1 не входит ни одна точка. Следовательно, интеграл в
этом случае равен нулю.
В случае "б" в круг |? + 2 + \ < 2 радиуса 2 с центром в точке ?о = -2 - i вхо-
дит одна точка: ? = -2. Записываем дробь в виде -^—'J—, где /(?) =
(г-if _ . ,, . е-
(г-/J
аналитическая функция в круге |г + 2 + /j <: 2. Вычисляем интефал:
ALL 2lil
dz = 2„- _LL = 2li
) B + .f 25
е1
Пример 2.94. Вычислить интефал а ; dz в следующих случаях
с (z -i) (z + 2)
задания контура: а) |? - г| = % б) |? + 2 - /j = 3.
176
И а) В круг \z - /| < 2 попадает точка z = i- Записываем функцию г и
применяем п. 3 правил 2.6 при т = 1 и а = i. Вычисляем интеграл:
ч
ег
(z-i?(z<
„ j- 7ti
= 2^
( e*
i)
2tti(l + i
= B + -f
■е'.
2)-ег
б) В круг |г + 2 - /| < 3 входят обе точки z\ = i, 1г=-1. Решаем в соответст-
соответствии с п. 4 правил 2.6. Записываем интеграл в виде суммы двух интегралов:
jf(z)dz=JAz)dz+jf(z)dZ,
с с, сг
где каждый из контуров С] и С2 охватывает только одну из точек. В частности,
в качестве контура С1 можно взять окружность из предыдущего случая "а";
С2- окружность из примера 2.93 п. "б", т.е. можно воспользоваться полученны-
полученными результатами. Записываем ответ:
i -
е
Упражнения
1. Вычислить интегралы /, = f z2dz и /2 = f l}dz для следующих случаев
задания кривой /:
а) / — дуга окружности единичного радиуса с центром в начале координат,^
расположенная в первой четверти; направление обхода - против часовой стрел-
стрелки;
б) хорда, соединяющая концы дуги, заданной в пункте "а".
Ответ: а) 1Х = —A +'). h = 1 +'!> б) 1\ = —A + 0, /2 = —A + 0 •
2. Вычислить \ezdz, где / - отрезок АВ, А@,-п), 5(тс,О).
Ответ: - i \е" +1).
t 3. Вычислить J Rez2dz, где / - задана свотношениями: z + Z = 2, |lmг| £ 1.
/
4
Ответ: — i.
177
4. Вычислить je2zdz, где С - контур треугольника АОВ, Д-1,1), 0@,0),
5A,1).
Ответ: 0.
5. Для интефала Г— dz рассмотреть различные контуры ni/гефи-
}cZ2-z-2 /
II ■'« I JI
рования, т.е. с\ :\z-A + 0| = 1'> с2:г = 1 + ' + е , 0^<р^2п; с3:\z-М = 3,1;
с4:|г + з| = 1. Интефалы соответственно обозначим /], /2, /3, /4. Цакие из
этих интефалов равны нулю? /
Ответ: все. '■
г е2* '
6. Для интефала J—-—dz рассмотреть различные контуры интефирова-
с 4г +1
ния с: с, - контур треугольника АОВ, /4A,1), 0@,0), 5A,-1);
с2 - контур, образованный кривыми у = х2, у = \;
с3 — контур, образованный кривыми х = у2, х = \;
: с4 - контур, образованный кривыми у2 = х +1, х = 1;
с5 - контур, образованный кривыми х2 =у + \, у = \.
Интефалы обозначим соответственно 1Х, /2, /3, /4, /5 ■ Среди следующих
равенств выбрать верные:
а) /,=0; б) /2=0; в) /3=0; г)/4=/5; д) /2=/3.
Ответ: а), в), г).
7. То же, что и в упражнении 6 для интеграла f— dz и контуров
[; z4 +1
J
а) /,=/2; б) /3 = /4; в) /5=/6; г) /,=-/,; д)/2=-/4-
Ответ: в), г), д).
8. Вычислить f dz, где:
с 2? + i
а) с - контур квадрата с центром в начале координат, сторона квадрата
равна 0,5;
б) с — фаница области D: ■
Ответ: а) 0; б) iti ■ е~'.
9. Вычислить интефал J Re z dz: а) по лучу АВ, где /4@,0), 5B + /);
б) по верхней дуге окружности |г| = 1, /4A,0).
Ответ: а) 2 + /; б) */2.
178
• \ 10. Вычислить интефал f-p, где / — правая полуокружность |z| = l,
:, \ ' *г
Re z \ 0, направление против часовой стрелки при условии а) VI = 1; б) VI = -1.
Ответ: а) 2^2 i; б) -2jTi.
11. Вычислить {-j=, где АВ- дуга окружности |г| = 1> Л@,1), 5A,0), для
\ ABSI
случаев^ a) vT = 1; 6)vT = -l.
Отрет: а) B - 41) - ivT; б) (Д- 2) + /vT.
12. 'Зычислить ^-?=, С - окружность |г| = 1 для случаев:
с *г
а) VI = 1, начало в точке 1; б) V-1 = /, начало в точке -1.
Ответ: а) / = -4; б) / = 4/.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти /Bг) , если f(z) = i[i^Z и /@) = -/.
2. Найти /(-/), если f{z) = 1Щ и /(-2) = -fi .
|г + 1
3. Доказать, что приращения аргументов функций f(z) и <р(г) при одно-
однократном обходе точкой z замкнутой кривой С совпадают, если f{z) = (f(z) + g(z)
Для точек z e С.
4. Доказать, что не существуют пределы при z -> 0 функций ег ,ег , ег .
1+— -
п)
6. Найти lm/(*o):a) f(z) = ez,zQ =3-2/; б) /(г) = cos г, г0 = 1 - '•
• 7. НайтиагвЛго): а)/(г) = Зг,го = 1 + ' ;б)/(г) = ег,г0 = 2-1 .
8. Сколько корней имеет уравнение ez +1 = 0:
. а) в правой полуплоскости; б) в левой полуплоскости?
i 9. Найти Re z , где z- корень уравнения cos& = / .
■> 10. Где расположены корни уравнения cos iz = i '■
а) на оси 0х ; б) на оси Оу ; в) на прямой, параллельной оси Ох ;
г) на прямой, параллельной оси Оу ; д) на двух прямых, параллельных оси Ох ;
е) на двух прямых, параллельных оси Оу .
11. Какие из следующих равенств верны для числа z , удовлетворяющего
уравнению In z = -3 + 4/:
а) |г| = 5;б) argz = arctg --J ; в) |г|<1 ; г) Rez<0 ; д) Inu>0; e)
12. Найти область, где функция f(z) = р - у2\ + 2/|ху| является аналитиче-
аналитической, и записать ее как функцию z ■
179
13. Найти гармоническую функцию, сопряженную с заданной:
a) f(x,y) = x2-y2+ У ; б) f(x,y) = e'y(ysiax-xcosx) .
х1 + jr
14. Найти аналитическую функцию f(z) , если
X +у
б)
15. Доказать, что образом координатной сетки при отображении w * ez яв-
является полярная сетка - совокупность лучей, выходящих из начала координат и
окружностей с центром в этой точке.
16. Найти область однолистности функции Жуковского: w = — \z +— •
21 z)
17. Найти образ полосы D при отображении w = ez :
О < Im z < л
18. Отобразить на верхнюю полуплоскость область D - верхнюю полуплос-
полуплоскость с разрезами по лучам [0, /] и [2/, да).
19. Отобразить на верхнюю полуплоскость область
20. Отобразить область — < arg г < л на область 0 < arg w < — .
2 4
21. Отобразить на правую полуплоскость область 0 < arg(z -1 -/) <—.
22. Отобразить область \z + 2/| < 2 на область \w - 2/| > 2 так, чтобы точки 0
и - 2/ остались неподвижными. Найти образ окружности \z\ = 3 при получен-
полученном отображении.
23. При отображении, полученном в задаче 22, найти:
а) прообраз прямой Re w - Im w ; б) прообраз окружности |>v| = 1 .
24. Отобразить область Im z + Re z < 0 на область \w - 3/| > 2 при условиях
Tt
/(-1) = да, arg w'(-2) = — . Найти образ прямой Re z - Im z = 0 при полученном
отображении.
25. Отобразить область Im z + Re z > 1 на область \w - A +1)| < 1 при условии
w(l +1) = 1 +1 , arg w'(\ + i) - —. Найти образ точки, сопряженной точке w = 2/
4
относительно границы.
26. Найти функцию, отображающую квадрат с вершинами в точках
/1C + 3/), 5C-3/),С(-3-3/), О(-3 + 3») на квадрат с вершинами /4,(-1), 5,(-/),
С] (—1 — 2/), Dl (-2 - /).
27. Найти Re г, где z удовлетворяет уравнению ch/z = /.
28. Решить уравнение sin z = — ■
180
Глава 3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
В КОМПЛЕКСНОЙ ОБЛАСТИ
3.1. АНАЛИЗ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
3.1.1. Основные определения
Основные понятия, связанные с функциональными последовательностями
и рядами в комплексной области, вводятся так же, как и в действительной.
1. Рассмотрим функции f\{z)Ji{z),---,fn{z),-~, определенные на некотором
множестве М. Для любой точки zo этого множества (г0 е М) получаем последо-
последовательность комплексных чисел {сл},я = 1,2,..., где с„ =/„(го)- Если последова-
последовательность с„ сходится, т.е. существует предел последовательности (см. разд. 1.3)
lim с„ = А, или, что то же самое, lim fn(zo) = Л, то говорят, что функциональная
Л-»со Л-»со
последовательность \fn{zo)\ сходится в точке z0.
Множество точек z , для которых существует предел последовательности
{fn{z)\ п = 1А•• •, называется областью сходимости функциональной последова-
последовательности (область D).
Пределом функциональной последовательности является функция, которая
называется предельной функцией последовательпости: lim /„(?)= f{z), Z e D, что
Л-»оо
можно записать, учитывая определение сходимости числовой последовательности
(см. разд. 1.3), следующим образом:
пт/л(г)=/(г),ге0о Vs>0 3N{e,z)-\fn{z)-f{z)\<e для n> N{e,z),Ze D.
п-то
Заметим, что в отличие от числовой последовательности (см. соответст-
соответствующее определение) номер N зависит не только от е, но и от г ■
Это естественно, так как для каждого фиксированного z e D получает
определенная числовая последовательность и для нее номер N, начиная с кото-
которого выполняется соответствующее неравенство, свой при одном и том же
выбранном значении е. Для различных значений ц е D получаем различные
N(e,Zi) < те- последовательность номеров Nk, k = 1,2,...
2. Если последовательность Nk,k = \,2,... ограничена, т.е. существует
N - N(e), такое, что Nk < N для любого к, то говорят, что функциональная ио-
следователыюсть fn(z) сходится к f(z) на множестве D равномерно, что обо-
обозначается /л(г)=> f{z)- Таким образом,
/»U) => /(г). Z е D о Vs > 0 3JV(e): | /„(*)- /(г)| < s для п > N{e) и V* б D.
Л*-
181
3. Ряд, членами которого являются функции комплексного переменного
un(z), я = 1,2,..., определенные на некотором множестве М комплексной плоско-
плоскости, называется функциональным рядом в комплексной плоскости и обозначается
4. Последовательность {£„(£)}, л = 1,2,..., где Sn(z) = £и*(г)> называется
последовательностью частачиых сумм ряда C.1), где Si(z)=ul(z),
5(z)= Mj(z)+ u2{z),- - частичные суммы.
5. Ряд C.1) называется сходящимся на множестве D, если на множестве
D сходится последовательность его частичных сумм, т.е. существует предел этой
последовательности, который называется суммой ряда S(z):
lim £„(*)= S(z),z е Д; Х>„(г) = .У(г),г£1>. C.2)
6. Множество точек z e D, для которых сходится ряд, называется обла-
областью сходимости ряда C.1).
Очевидно, для суммы S{z) ряда в области сходимости D справедливо
неравенство
| ■?»(*)-■?(*)! <s ДЛЯ n>N{z,z),zeD. C.3)
7. Ряд C.1) называется равномерно сходящимся на множестве D, если на
этом множестве равномерно сходится последовательность {5„(г)}, т.е.
I Sn{z)-S(z)\<e для и > N(e) и \/z e D. C.4)
Равномерно сходящиеся ряды (и последовательности) непрерывных функ-
функций комплексной переменной, как и аналогичные ряды в действительной облас-
области, обладают свойствами конечных сумм, в частности сумма такого ряда являет-
является функцией, непрерывной на множестве, где ряд сходится равномерно. Кроме
того, ряд можно почленно интегрировать. Это означает, что полученный ряд, т.е.
ряд, членами которого являются интегралы от членов данного ряда, сходится и
его сумма равна интегралу от суммы данного ряда:
11 »*(z)dz = I £ «„(г)* = JS(z)dz. C.5)
л=1 л=1
8. Для исследования функционального ряда на равномерную сходимость и
нахождения области его равномерной сходимости можно использовать, как и в
действительной области, достаточный признак равномерной сходимости.
Теорема 3.1 (признак Вейерштрасса). Если ряд C.1) на множестве D
мажорируется сходящимся числовым рядом с положительными членами, то он схо-
сходится на D равномерно, т.е. из условия
оо
I "я(*)| <cn,n>k,k>l,zeD; £с„ сходится, сп > 0 C.6)
л=1
следует равномерная сходимость ряда C.1) на множестве D.
182
ччн' 9. Для равномерно сходящихся рядов аналитических функций справедливы
отмеченные выше свойства непрерывности суммы ряда и почленного интегриро-
интегрирования. Кроме того, имеет место свойство, связанное с почленным дифференци-
дифференцированием ряда.
Теорема 3.2 (теорема Вейерштрасса для рядов аналитических функций).
Если ряд C.1) аналитических в области D функций un(z) равномерно сходится
внутри D, т.е. на любом замкнутом подмножестве В с D, то сумма S(z) ряда
аналитична в D; ряд можно почленно дифференцировать любое число раз, причем
ряд, членами которого являются производные и„ (z), равномерно сходится на любом
BcD, и сумма такого ряда равна производной S^k\z) от суммы исходного ряда,
т.е.
£«<*>(?)= Л). * = 1,2,3,... C.7)
л=1
3.1.2. Нахождение области сходимости рядов. Исследование рядов
на равномерную сходимость
Так как по определению ряд C.1) сходится в точке г0, если сходится чи-
ос
еловой ряд £и„(го)> то Для нахождения всех таких точек, т.е. области сходимо-
л=1
сти ряда, можно использовать известные признаки сходимости числовых рядов
(признаки абсолютной сводимости, изложенные в разд. 1.3).
Так, можно найти пределы:
lim
Л —>CO
или 1пп^|ия(г)|=|/(г)|. C.8)
Согласно признакам Даламбера (в первом случае) и Коши (во втором слу-
случае) область D абсолютной сходимости ряда образуют те точки z, для которых
Граничные точки, т.е. точки, для которых выполняется равенство
I /(г)|= 1> могут быть как точками абсолютной или условной сходимости, так и
точками расходимости.
Пример 3.1. Исследовать сходимость рядов:
00 00 _Л 00 00 _Л
*)!<"; 6I^; в)Х«!г"; г) ?i-.
в=1 л=1 2" л=1 „.J и!
D Все ряды, очевидно, сходятся в точке г = 0, так как lim Sn(Q) = O.
Л-»оо
Исследуем их сходимость в других точках. Для первых двух рядов используем
183
признак Коши (найдем HmW| м„(г)| = | f{z)\ ), а для других - признак Даламбера
Я—ЮО
(найдем lim ifa±lM =|/(г)|).
Л-»оо Un[Z)
а) Имеем lim й/|«„(г)| = lim в Ы" = Ы; неравенство Ы < 1 определяет об-
Л-»оо * л-»оо '
ласть сходимости ряда. Границей области является окружность \z\ = 1 или, в
комплексной форме, z = е'ф, 0<q><2я. Для точек границы получаем числовые
00 00 00
ряды вида У^е"", или y^cosmp + zy^sinrnp, очевидно, расходящиеся, так как
л=1 л=1 л=1
lim cos/icp и lim sin жр не существуют. Область сходимости ряда - круг |^| < 1.
б) lim
л-»00! 2"
U
= —. Неравенство Ы<2 определяет область
2 м
сходимости ряда. В точках границы, уравнение которой z = 2e'v, получаем рас-
расходящиеся ряды. Область сходимости ряда - круг |г| < 2.
(л + 1)! Z
л+1
в) lim
Л-»оо
только в одной точке z = 0.
г) lim
= |г| lim (я +1) = да для любого z * 0. Ряд сходится
Zn+Xn\
1
= Ы lim = 0 < 1 для любого z * 0. Ряд сходится
л->оо л+ 1
всюду, во всей комплексной плоскости.■
Пример 3.2. Исследовать сходимость рядов:
001 00 ЛЛ 001 QD „ I
a)y-L; б) У—; в) У—; г) У—.
hi" hi" txn\zn tz"
П В отличие от предыдущего примера точка г = 0, очевидно, не входит
в область сходимости этих радов. Сходимость в других точках исследуем, как
в предыдущем примере.
a) limi
= т-г; область сходимости |г| > 1 - внешность круга с центром
в точке г=0 и радиусом 1. На границе круга ряд расходится.
б) lim i
= т-г; область сходимости \z\>2 - внешность круга с центром
в точке z = 0 и радиусом 2 . На границе круга рад расходится.
184
-tk>
в) lim
п\г"
-Л + 1
= т-r lim = 0 < 1 при любом z * 0. Ряд сходится
\z\ я-»оо л + 1
всюду, кроме точки г = О (С \ 0).
г) lim
1 ,.
lim (я +1) = оо . Ряд расходится всюду.1
Пример 3.3. Найти области сходимости рядов:
•)£(*-.Г-3"; б)£—^-г.
D Используем для решения Нт^|и„(г)| = |/(г)|.
a) lim я |(г - if ■ 3" I = lim в 3" ■ |г - А" = 3 к - А; область сходимости нахо-
дим из неравенства 3|г - /| < 1, получаем |г - /| < — круг с центром в точке i = i
и радиусом —
б) lim
1 «и
lim — = 0 < 1 при любом г * -' ■ Следователь-
Следовательно, областью сходимости ряда является вся плоскость с выколотой точкой
z = -i. При решении использован известный из курса математического анализа
предел lim *я = 1 .■
Л-»со
Пример 3.4. Исследовать сходимость ряда
00 ' 1П 7П
- +
2" 7Л
D Общий член данного ряда имеет вид u.(z) = — + —, т.е.
г" 3"
6 +г2
36 +г4
Рассмотрим два вспомогательных ряда У— и У —, найдем их области
я.| г" я-| 3"
сходимости. Первый ряд сходится в области |г| > 2, второй - в круге |г| < 3 (см.
п. "б" примеров 3.1 и 3.2). Пересечение областей сходимости рядов образует
кольцо 2 < |г| < 3. В любой точке этого кольца сходятся оба ряда, т.е. сходятся
соответствующие числовые ряды. По свойствам числовых рядов сходящиеся ря-
ряды можно складывать, общий член полученного при сложении ряда равен сумме
185
общих членов рядов - слагаемых. В данном случае, складывая два ряда, сходя-
сходящиеся при любом z, принадлежащем кольцу 2<|г|<3, получим ряд с общим
членом — + — . Следовательно, исходный функциональный рад сходится в
кольце 2 <|г| < 3.1
Пример 3.5. Найти область сходимости ряда
D Находим предел lim^jf | ы„(г)|, т.е. lim
г-2/
г + г
г-2/
Z + l
. Область
сходимости определяем из неравенства
г-2/
< 1, т.е. |г - 2i| < |г +1|. Границей
множества является линия, комплексное уравнение которой |г - 2ij = |г + /| ■
Геометрически - это прямая, проходящая через середину отрезка, соединяющего
точки z = 2/ и z--i перпендикулярно этому отрезку. Уравнение этой линии
у = -, т.е. lmz=-- Эта линия разделяет плоскость на две части: 1тг>- и
1тг < - ■ Областью сходимости ряда будет 1тг > -, так как, например, для точки
г = /, принадлежащей этой области, неравенство |г - 2г| < \z + /| выполняется.!
J0 -Л
Пример 3.6. Доказать, что ряд £ — сходится равномерно в круге |г| < 1.
л=1 3
D Для точек г, удовлетворяющих неравенству |г| < 1, выполняется нера-
венство
<—, т.е. функциональный ряд в круге Ы < 1 мажорируется число-
тЛ ' '
и=1
п=\
вым рядом У —. Так как ряд У - сходится, то по признаку Вейерштрасса
данный функциональный ряд в круге |г| < 1 сходится равномерно.
Заметим, что, очевидно, ряд сходится равномерно и в большей области, а
именно в любой области В вида |г| й г, 0 < г < 3, так как мажорируется в этой
области сходящимся числовым радом:
s з "'
,апри q<\ ряд
сходящийся. Как отмечено выше, в таком случае говорят, что ряд сходится рав-
равномерно внутри круга |г| < З.и
186
1 е
*S. Пример 3.7. Найти область равномерной сходимости ряда Z<~~T-
п=\ я
D Воспользуемся признаком Вейерштрасса. Поскольку числовой ряд
00 |
У— сходится, то область равномерной сходимости данного ряда будут состав-
составлю «
лять те z, для которых справедливо неравенство \еп1\ < 1, так как при этом спра-
<——. Учитывая равенство \ег =eReJ, получаем
п
ведливо неравенство
\е"Ч = ею. Для нахождения области равномерной сходимости нужно рассмотреть
неравенство е"* < 1, которое, очевидно, выполняется при любых отрицательных
значениях х. Поэтому областью равномерной сходимости данного ряда является
множество Re г < 0 - левая полуплоскость, или любое множество вида
Re г <а, а<0М
3.1.3. Степенные ряды
КРУГ СХОДИМОСТИ СТЕПЕННОГО РЯДА
Степеииым рядом называется функциональный ряд C.1), члены которого
образованы степенями z" или (г-^о)", те- Р™ виДа
00
^niz-zof =c0+c^z-zo)+c2{z-zof +--+cn{z-ZoT +■■■ C-9)
л=0
или
Хслгл=со + с1г + с2г2+...+сл^+... . (ЗЛО)
л=0
Ряд C.9) называется рядом по степеням разности (z-Zq); ряд C.10) -
рядом по степеням г.
Очевидно, один ряд к другому можно преобразовать простой заменой.
Особенностью степенного ряда, как частного вида ряда C.1), является ана-
аналитичность его членов во всей комплексной плоскости.
Другая особенность связана с видом его области сходимости. В общем слу-
случае функционального ряда, областью сходимости может быть множество произ-
произвольного вида (см. примеры 3.1-3.5). Это и вся плоскость, и плоскость с выколо-
выколотой точкой, и круг, и внешность круга, и полуплоскость, и кольцо, и пустое
множество (ряд расходится всюду). В случае степенного ряда последнего случая
быть не может - ряд имеет хотя бы одну точку сходимости. Так, ряд C.9), оче-
очевидно, сходится в точке го. а ряд C.10) - в точке г = 0.
В примере 3.1 определялась область сходимости степенных рядов вида
C.10). Кроме двух тривиальных случаев области сходимости - вся плоскость и
только одна точка, в двух других областью сходимости оказывается круг, как и
для ряда вида C.9) из примера 3.4, п."а". Полученный результат не является слу-
случайным. Действительно, областью сходимости степенного ряда является круг.
187
При этом область сходимости, состоящую из одной точки, можно рассмат-
рассматривать как круг радиуса R = 0, а в случае сходимости ряда во всей комплексной
плоскости как круг радиуса R = «>.
Доказательство этого утверждения получается из основной теоремы теории
степенных рядов - теоремы Абеля, которая формулируется и доказывается так
же, как и в действительной области.
Теорема 3.3 (теорема Абеля). Если степенной ряд C.10) сходится в точке
Zq * 0, /ио он сходится, и притом абсолютно, для любого z, удовлетворяющего
неравенству \z\ <|го|-
Как следствие этой теоремы устанавливается существование положитель-
положительного числа Л, такого, что ряд C.10) при |г| < Л сходится, а при |г| > R расходит-
расходится, т.е. окружность \z\ = R разделяет плоскость на две части: внутри окружности
ряд сходится, вне - расходится. Радиус этой окружности - число R - называется
радиусом сходимости, круг \z\< R - кругом сходимости ряда.
Радиус сходимости определяется по формуле Коши-Адамара:
Я=— 'п-г- C.11)
Ы
Здесь lim (jf \с„\ =1 - верхний предел последовательности а„ =^\с„\. Он всегда
существует (конечный или бесконечный), и притом единственный. В случае
/ = +оо полагают R = 0, а в случае / = 0 полагают R = оо.
Замечания 3.1.
1. Для ряда C.9) имеем такое же утверждение: он сходится в круге
\z - Zq\ < R, где радиус сходимости R определяется по формуле C.11).
2. Радиус сходимости ряда можно определить иначе. Например, найти об-
область сходимости ряда, используя формулы C.8), а затем - радиус. Так, в приме-
примере 3.1 рассматриваются степенные ряды. Для первого из этих рядов найдена об-
область сходимости |г| < 1, поэтому R = 1, для второго из |г| < 2 получаем Л = 2.
Для двух других рядов имеем соответственно R = 0 и R = оо.
Пример 3.8. Доказать, что для ряда ]£слг", где сп ф 0 для любого п, ра-
71=0
диус сходимости можно определить по формулам:
1
R=\im
л-
сл+1
C.12)
D Найдем область сходимости ряда, используя формулы C.8):
\f{z)\ = lim e\un{z)\ = lim «fkz"j = \z\ ■ lim (Щ. Если lim afjc^j = 0, то нера-
Л—>со Л—>°0 1 I I Л—>00 Л—«0
венство \f{z\ < 1 выполняется при любом z, т.е. ряд сходится всюду и R = °о.
Если lim а(|ся| =оо, то неравенство |/(г)|<1 не выполняется ни для ка-
Л-*со
кого значения z * 0 и ряд сходится только в одной точке z = 0, т.е. R = 0.
188
В случае, когда предел является конечным и не равен нулю, обозначим его
/, lim tf\cn\ = I. Тогда неравенство |/(г)|<1, т.е. |г|-/<1 выполняется для г,
удовлетворяющих условию |г|<-, а это есть круг сходимости, следовательно,
R = -. Первая из формул C.12) доказана. Аналогично доказывается вторая. ■
Пример 3.9. Найти области сходимости рядов £ —, £ —, £z".
л=1 Л л=1 " л=1
D Радиус сходимости каждого из рядов R = 1, так как для первого ряда
с„ =— и согласно C.12) Л= lim
2 И»оо
И-»оо
(Я + 1)
Я
2
, 1
= 1; для второго ряда имеем с„ = —
я
и Л = lim
Л-» со
и+1
= 1; для третьего из с„ = 1 получаем R = lim -= = 1. Поэтому
п "'
областью сходимости каждого из этих рядов является круг |г| < 1.
Исследуем сходимость рядов на границе круга сходимости - на окружно-
окружности |г| = 1, или, что то же, г = е"*.
Для первого ряда в точках границы, т.е. при \z\ = 1, получаем абсолютно
оо Ы" «о j °° 1
сходящиеся ряды, так как £?-= Х~Т' а Рад X ~Т СХ°ДИТСЯ- Следовательно,
л=1« л=1«2 ИЛ
оо -Л
ряд £ — сходится во всех граничных точках. Поэтому он сходится абсолютно ~
л=1 Л
круге |г| < 1.
00
Ряд ^z" на границе расходится (см. пример 3.1, п."а").
л=1
00 _Л
Ряд У— , очевидно, расходится в точке z = 1 (точке границы z = е'ф при
лТ| И
оо j
Ф = 0) как гармонический ряд У— и сходится в точке z = -1 (точке г = е'ф при
(-1)"
(-1)
Ф = л) как знакочередующийся ряд Y, Заметим, что сходимость послед-
л=1 "
него ряда неабсолютная.
Можно показать, что ряд расходится на границе z = e"f только при ср = О,
т.е. z = 1, а во всех других точках границы, т.е. при q> * 0, он сходится.
Заметим, что данные в примере рады могут быть получены один из другого
оо _Л
с помощью дифференцирования или интегрирования. Так, из ряда ^—т полу-
л=1Я
189
да «Л-l j oo _П да _И
чаем дифференцированием ряд £ или -£—, а из ряда £— также
л=1 я гЛж| я л=1 я
00 1 00
дифференцированием - ряд £г"~' или - • £г" •■
Пример 3.10. Найти радиус сходимости рядов:
оо оо _2л
а)£(г-1Гзл; б) XV-
л=0 л=0 3
D а) Здесь сл=3", и по формуле C.12) находим: Л=-, где
/ = lim WcJ = lim чЗ" = 3. Следовательно, Д = - и |г -1| < — круг сходимости
Л-»оо Л-»оо 3 3
ряда.
«о 2 4
б) Ряд имеет вид £ctz* =1+ — + -г- + ... + с*г* +...
3 З2
Коэффициенты при нечетных степенях z равны нулю, т.е. ск = О при
А; = 2я — 1 и ct =— при к = 2п. Радиус находим по формуле C.11): /? = -,
3" /
/ = lim шкI = lim Щ— = -р. Следовательно, R = V3 и |г| < v3 - круг сходимо-
*->оо* л-»оо уз" уз
сти ряда.
Можно, как отмечено в п.2 замечаний 3.1, поступить иначе. Найдем об-
=
ласть сходимости ряда, используя формулу C.8): lim июл .....
Л-»оо ' л->оо | 3" 3
112
Из неравенства ■LJ— < 1 находим \z\ < V3 - круг сходимости и R = V3 -
сходимости.
СВОЙСТВА СТЕПЕННЫХ РЯДОВ
1. Если Л*0, т.е. ряд C.10) сходится в круге |г| < R, то, используя при-
признак Вейерштрасса, нетрудно установить, что ряд сходится равномерно в круге
|г| < г, где г - любое положительное, меньшее R число, 0 < г < R. Это означает,
что степенной ряд сходится равномерно внутри круга сходимости.
2. В силу аналитичности членов степенного ряда и свойств равномерно
сходящихся рядов получаем (см. теорему 3.2), что внутри круга сходимости сум-
сумма степенного ряда есть функция аналитическая.
3. Степенной ряд можно почленно интегрировать и дифференцировать лю-
любое число раз внутри круга сходимости.
190
Последнее свойство означает, что ряд, полученный из ряда £ V ДИФ"
л=0
00 00
ференцированием, т.е. ряд X(v") = 5] и • Ся-г" или, что удоб-
л=0 л=1
нее, £(« + 1)сл+| х.", и ряд, полученный интегрированием, т.е. ряд
л=0
'« 00 «
У \cnz"dz- Y —"—гл+11 сходятся внутри круга сходимости исходного ряда,
„=oJ л=о« + 1
а потому их радиусы сходимости не меньше радиуса сходимости исходного ряда.
Покажем, что радиус сходимости при дифференцировании и интегрирова-
интегрировании не меняется.
00
Обозначим радиус сходимости данного степенного ряда £с„ z" через R,
л=0
R = -, где / = lim ale. . Рассмотрим ряд, членами которого являются производ-
/ Л-»оо f
ные от членов данного ряда, т.е. ряд, полученный почленным дифференцирова-
00
нием: £(л + 1)сл+1г". Общий член этого ряда (л + 1)-сл+1гя запишем в виде
л=0
anz", где а„ =сл+1 (и + l), а ся+1 - коэффициент исходного ряда. Радиус сходи-
сходимости полученного ряда определим по формуле Коши-Адамара, т.е. Л, = —, где
/] = lim Я |сл+1|(и+1) = Нт(я|сл+|| ЙДл + 1) 1= lim щ|сл+|| = lii
Л-ЮО п-*ао Л-ЮО л->оо '
Следовательно, Ri=R. Здесь использован известный предел
lim Щап + b = 1, частный случай которого lim Цп = 1 был использован при реше-
М-+00 Л-+СО
00 . 00
нии примера 3.3. Так как ряд ^cnz" получается из ряда ^(л+ 1)-сл+1 г" ин-
л=0 л=0
тефированием, то из доказанного следует, что при интефировании ряда радиус
сходимости не изменяется.!
Пример 3.11. Найти суммы следующих рядов:
ОС ОС Л ОС ОС
л=0 л=0 2 л=1 л=1
00
П В первых двух случаях имеем ряды вида ^q". Для \q\ < 1 - такой ряд
л-1
сходящийся. Последовательность частичных сумм Sn = ^q = l+q+...+q"
Jt=O
может быть записана по формуле суммы членов геометрической прогрессии
Sn - ——. При Ы < 1 находим S = lim S. = сумма членов бесконечной
1 - q л->оо 1 - q
191
убывающей геометрической прогрессии, для которой первый член Ь\ = 1 и зна-
менатель q. Сумма ряда вида £и*г", к>\, к- целое, может быть получена
последовательным дифференцированием рада £г" , а рады £г" ,к >0, отли-
я=0 я=*
00
чаются от 'Yjl" на конечное число слагаемых.
со
а) Для ряда ]Г 7," имеем
1г"-Г7' |z|<1- C13)
оо -Я J со /Ч^"
б) Для рада У —- или - У - аналогично п. "а" находим:
л=0 л ^ /i=OV^y
l-z
в) Для решения используем свойство дифференцирования рада 2,7,
/1=0
Получаем ^иг" = или ^nz" ' = г-
я=о \l-zj л=1 0-г)
1 °° 1 °° z
Окончательно находим - £ ит," = или ^ иг" = -г, |q < 1.
*я=1 V-Z) я=1 V~Z)
СО СО 00
г) Используя формулу C.13) для ряда £*" = £*" -Z0 = ]£*" ~1» имеем
л=1 я=0 я=0
00 1 -
ДЕЙСТВИЯ НАД СТЕПЕННЫМИ РЯДАМИ
Кроме упомянутых выше свойств дифференцирования и интегрирования
степенных рядов внутри круга сходимости как рядов, равномерно сходящихся,
они обладают в круге сходимости общими свойствами сходящихся, в частности
абсолютно сходящихся, рядов (см. разд. 1.3): ряды можно складывать и пере-
перемножать, т.е. рассматривать сумму и произведение радов; можно также рассмат-
рассматривать их отношение - деление рядов.
Рассмотрим подробнее арифметические действия над степенными рядами.
СО СО
Обозначим R\ и R2 - радиусы сходимости двух рядов ^ояг" и ^йягл-
я=0 л=0
192
1. В общей области сходимости, т.е. в круге |*|<г, где г = mm(Rl,R2),
со
можно рассматривать сумму (разность) рядов: ряд £с„гя , сп=а„±Ь„. Радиус
сходимости полученного ряда не меньше г: R>r. Сумма S нового ряда равна
5| ±S2, где S\ и S2 - суммы радов - слагаемых.
2. В круге \z\ < г можно рассматривать произведение рядов (см. разд. 1.3):
л=0 л=0
= a0b0+z(a0bi+alb0) + z2(a0b2+albi +02*0)+••• + £„*" + ■•••
QO
Получаем рад £слг", где с„ =а0Ь„ +афпА +... + akbn_k +... + а„Ь0, или
я=1
л
с„ = ^о*Ал-* • Радиус сходимости полученного ряда не меньше г, R>r, его
*=о
сумма S равна ^ • 52, где S\ n Si - суммы радов - сомножителей.
3. В некоторой окрестности точки го = 0 можно рассматривать отношение
00 00
рядов ^onzn (делимое) и ^bnzn (делитель) при условии Ь$ *0. Частным этих
л=0 л=0
00
рядов будет ряд J/nz", такой, что выполняется равенство
л=0
со со аз
Xfl«z" = X*«z" ■ Хслг" • Коэффициенты с„ определяются, как и в случае
л=0 л=0 л=0
многочленов, методом неопределенных коэффициентов или делением "углом".
Замечание 3.2. При сложении и умножении рядов, как отмечено вы-
выше, может получиться рад, сходящийся в большей области, чем общая часть
кругов сходимости двух исходных радов: R > г, г = m\n(R\,Ri).
Приведем пример, подтверждающий это свойство. При сложении радов
f(_i) ^ f(-i) ^
Y, \ —п 1 к" и Yj\ —^-+1 г" для которых, как нетрудно проверить,
л=о \ У ) ^ 2" J
f(-l) (-1)^
имеем R]=R2=\, получим ряд V •*——-*—'-г". Радиус сходимости этого
л=0 V 1 •> )
ряда R = 2.
Рассмотренные арифметические операции- над радами используются при
решения задач разложения функции в степенные ряды (см. разд. 3.2): функций
вида f(z) = Mz) + f2(z), f(z) = A(z)-f2(l), /W #
7 ЙЬнтелеев А.В.. Якимова А.С. . 193
4. Еще одно действие - подстановка ряда в ряд связано с разложением
00
в ряд сложной функции. Пусть ряд ]Г с„и" сходится в круге |u| < R, его сумма
л=0
00
равна 5| = /(м); а ряд £бяг" " в кРУ1"е И <г и его сумма в этом круге равна
л=0
$2 = ф(г)- Тогда в некоторой окрестности точки го = 0, т.е. в круге |г| < р, можно
« (. \"
рассматривать ряд ]£с„ ^bnz" ■ Заметим, что для возможности выполнения
л=0 U=0 )
действия требуется, чтобы имело место условие ф@) = 0, т.е. Ь^ =0, в противном
случае, как правило, не удается привести подобные члены. Поэтому записываем
ряд в виде
Произведя действия возведения в степень (как умножение ряда на ряд) и
приведение подобных членов, можно записать любое число членов ряда:
Суммой нового ряда будет функция /(ф(г)).
Обобщим свойства степенных рядов и действия над ними в виде утвержде-
утверждения.
Утверждение 3.1.
00 00
1. Степенной ряд ]£сяг" сходится в круге \z\ < R; ряд ^cn(z-Zo)" схо-
л=0 л=0
дится в круге \z - za\ < R ■
2. Радиус сходимости ряда определяется по формулам C.11) и C.12).
3. На границах круга сходимости могут быть как точки сходимости, так и
точки расходимости ряда.
4. Внутри круга сходимости ряд сходится равномерно; для ряда C.10) это
круг \z\ < г, для C.9): \z - Zo\ ^ г , г^е г - любое число, 0 < г < R.
5. Сумма степенного ряда внутри круга сходимости - функция аналитиче-
аналитическая.
6. Внутри круга сходимости ряд можно интегрировать почленно и дифферен-
дифференцировать почленно любое число раз. Радиус сходимости ряда при этом не меняется.
Сходимость в отдельных точках границы может измениться.
3.1.4. Рады по целым степеням
ОС 00 L
Рассмотрим два ряда ^an(z-ZoY и X 2—«"■ Первый ряд - степенной
и, если он сходится не только в одной точке го, но и не всюду, то сходится
194
в круге |z-zo|<r. Второй ряд - не степенной, но, после замены =и>,
Z-Zq
00
получим степенной ряд ]£6nw", область сходимости которого: |w|</-i, i\ *0.
л=1
1
< Г, ИЛИ \Z - Zo\ > — = R ■
Поэтому для ряда £-—2-^-имеем
Если г < R, то исходные ряды имеют общую область сходимости - кольцо
г < \z - Zo\ < R ■ Для каждого z, принадлежащего этому кольцу, получаем два схо-
сходящихся числовых ряда, которые, по свойству сходящихся числовых рядов (см.
разд. 1.3.2), можно складывать. Следовательно, в области /•<|г-го|<^ можно
рассматривать ряд вида
C.14)
Х^гоГ + ЕЦг bnizZof-
л=0 n=\\Z-Zo) л=-°о
Ряд C.14) - ряд по целым степеням, он состоит из двух частей: первое
00
слагаемое £я„(г-го)" С0СТавлЯ1°т члены ряда с положительными степенями;
л=0
00 b
второе слагаемое £ 2 с отрицательными. Вторую часть можно записать
„=\{z-ZoY
-1
в виде Х*-л(г~го)", после чего становится понятней возможность записи
Л=-оо
суммы двух рядов в виде одного ряда, а именно по формуле C.14), где полагаем
с„ = а„ для л > 0 и с„ - Ь_„ для и < 0.
00 00
Используя для составляющих ряда C.14) - рядов £оя(г-гоГ и S*«w"
я=0 я=1
свойства степенных рядов (см. утверждение 3.1), можно сформулировать сле-
следующее утверждение для рядов по целым степеням.
Утверждение 3.2.
00
1. Ряд ^cn(z-ZoY сходится в кольце г <\z-Zo\ < R■
Л = -оо
2. В кольце I] < \z - Zo\ ^ R\, где Г\ > г, R\ < R, ряд сходится равномерно.
3. В кольце r\ < \z - Zq\ ^ R\ сумма ряда C.14) - функция аналитическая и ряд
можно почленно интегрировать и дифференцировать любое число раз.
« _л -I .л
Пример 3.12. Найти кольцо сходимости и сумму ряда £ —+ £ — •
л=1 3 л=-о>2
□ Запишем ряд в виде У — + — и, повторяя решение примера 3.4
л=Н J Z J
195
находим кольцо сходимости ряда 2 < \z\ < 3. Сумму ряда S(z) можно записать в
= S!(?) + 52(z), где S, -сумма ряда л- , S2 -ряда £ - • Для на-
Л3> Л*
виде 5^ = ЗД + ,
хождения суммы этих рядов применим формулу суммы членов бесконечно убы-
1 1
вающей геометрической прогрессии. Получаем 5j = для \z\ < 3 и S2 = *
U3 l~~z
для Id > 2. Окончательный ответ: S(z) = —■— + = -, 77 г •
11 3-z i-2 (г-2)C-г)
Заметим, что функция S(z) яаляется аналитической всюду, кроме точек
1 = 2 и z = 3, суммой данного ряда она является только в кольце 2 < \z\ < 3.
Отметим также, что в данном ряде отсутствует свободный член. Ряд
00 Я -1 Я
]Г — + £ —. гДе свободный член равен 1 (при и = 0), очевидно, сходится в
л=0 3 л=-оо 2
том же кольце, а сумма его равна 5(г)=51(г)+5'2(^) = + —г = т;—п \-
Она действительно отличается только на величину свободного члена, т.е. на еди-
единицу от найденной выше. ■
Найти области
Ответ:
л-1
Ответ:
л=1 (" Н
Ответ:
г + 2/|
г-/)"
3"
,-/|<
сходимости
! + /
<1.
3.
Упражнения
рядов.
со
9 V
Ответ:
00
4 V
л=1(и
Ответ:
6 у(и
Ответ:
-Зл+1
+»Г
И<1.
+ i)(z + if
(\ +if
00
7. У
Ответ: \z - i| > 3.
Ответ: Re z + Im г < 0.
196
9.;
Ответ: \z + /| > 1.
cc in+z
11.
Ответ:
л=1
Ответ: 2 < \z +1| < 3.
Ответ: \z +1 - /| < 2.
10. £■
Ответ: \z + <| > 2.
л=1
Ответ: Re г <-In 2.
*2"{z + \Y Зи + 1
14. ) —s '
h «+1 3-(z+o
Ответ: — < \z +1| < —.
Ответ:
Доказать, что данный ряд сходится равномерно на указанном множестве.
17.
„tlC«-lJ.3"
Найти радиусы сходимости рядов.
(я+ 0B + 0*
A+0"
Ответ: Л = ^.
,9 у
20. I.
Ответ:
22. £«
Ответ: Н = ы2.
Найти сумму ряда.
оо л
л=1 3"
Ответ: S = -
Ответ: Л = 0.
24.
Ответ: S =
25. У-2-.
Ответ: S = -
197
3.2. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯДЫ
3.2.1. Разложение функций в степенные ряды. Ряд Тейлора
Общая постановка задачи разложения функции в ряд в комплексной об-
области формулируется так же, как и в действительной области. А именно, для за-
заданной функции f(z), определенной в области D и удовлетворяющий в ней не-
него
которым дополнительным условиям, требуется найти ряд вида £«„(*)> который
бы сходился в области D и его сумма в этой области совпадала с f(z).
ПОСТАНОВКА ЗАДАЧИ РАЗЛОЖЕНИЯ ФУНКЦИИ В СТЕПЕННОЙ РЯД
СО
Для функции /(г), аналитической в области D, найти ряд ^cn(z-ZoT >
сходящийся к f(z) в круге \z - го| < R, принадлежащем области D, т.е.
1 ||
Равенство C.15) означает, что f(z) является суммой ряда в круге
|г-го|<Д.
Для решения задачи нужно, очевидно, найти коэффициенты ряда по за-
заданной функции f(z); найти круг сходимости ряда и установить сходимость ряда
именно к f(z). Последнее, напомним, означает, что для точек круга выполняет-
выполняется неравенство | Sn (z) - f{z) \ < е для любого е > 0 и п> N(e, z).
Все поставленные вопросы решаются с помощью следующей теоремы.
Теорема 3.4 (теорема Тейлора о разложении функции в степенной ряд).
Функция, аналитическая в области D, в окрестности каждой точки Zo
этой области представляется в виде степенного ряда C.15), радиус сходимости R
которого не меньше, чем расстояние от точки Zo до границы области D.
Коэффициенты ряда вычисляются по формуле
где у - произвольный контур, принадлежащий области D и охватывающий точку
Zq , в частности, у - окружность \z - Zo\ = P> или по формуле
.,,.-Щ (ЗЛ7)
п\
На основании теоремы можно сформулировать алгоритм решения постав-
поставленной выше задачи и вывод - утверждение.
198
АЛГОРИТМ РАЗЛОЖЕНИЯ АНАЛИТИЧЕСКОЙ ФУНКЦИИ В СТЕПЕННОЙ РЯД
1. Найти производные от данной функции: /'(?), /"(*),-, f^"\z),.-
2. Вычислить значения производных в точке ю', записать коэффициенты
по формуле C.17). Составить ряд по степеням г-го с этими коэффициентами,
QO
который соответствует данной функции /(г): f{z) ~ Хся(г ~ го)" ■
3. Найти область сходимости полученного ряда и записать разложение
C.15).
Если функция не имеет конечных особых точек, то ряд сходится к ней во
всей плоскости, R = °о.
Утверждение 3.3.
1. Функция, аналитическая в точке г0, раскладывается в окрестности этой
точки в степенной ряд.
2. На границе круга сходимости ряда есть хотя бы одна особая точка функ-
функции, т.е. радиус сходимости круга равен расстоянию от центра разложения г0 до
ближайшей особой точки функции.
3. Степенной ряд в круге сходимости является рядом Тейлора для своей сум-
суммы, т.е. коэффициенты ряда вычисляются по формулам C.16), C.17).
Пример 3.13. Записать разложения по степеням г функций ег, sin г,
cos z, sh z, ch z ■
□ Задачу решаем по алгоритму,
к Найдем производные:
3
/4(z) = sh z, fl"\z) = sh z при n = 2k, /4(л'(г) = ch z при n = 2k -1;
fs(z) = ch z, /5(я)(г) = ch z при n = 2k, f\n\z) = sh z при n = 2k -1.
2. В поставленной задаче го = 0. По формуле C.17) имеем
/2(z)=sinz, с„=0 при п = 2к, с„=- _ '= у >_ при п = 1к-1
/3(z)=cos7,, ся=0 при п = 2к-\,
cos?- уЬ1I7
1 „to B«)! " '
199
i оо „2л-1
, с„=0 при п = 2к, с„=— при и = 2£-1,
и!
1 оо «2л
при п 2кch г У
1 оо «2л
/5(г) = ch ?, с„ = 0 при п = 2к - 1, с„ = — при п = 2к, ch г ~ УТГТГ-
"■ л=Д2й)!
3. Нетрудно убедиться, что все составленные рады сходятся во всей ком-
комплексной плоскости, R = да. В результате получаем формулы, которые ранее
(в разд. 2.1.2) были приняты за определения соответствующих функций:
оо / |\л
4
+1 2л-1 оо / ]\л 2л
_2п-1 оо 2л
Фи1 Ch!-,?.M
В результате получены так называемые основные разложения.
Пример 3.14. Записать разложения по степеням z функций:
) L
1-г г-1
П Задачу можно решать, пользуясь алгоритмом, а можно использовать
формулы C.13) для суммы членов геометрической профессии. Заданные функ-
функции являются аналитическими во всей комплексной плоскости за исключением
одной точки z = 1. Для каждого случая получаем:
rSk|
l'z л=0
б) -l— = -z2--±- = -z2-fJz"=-'Zz"+2, |г|<1; заметим, что здесь
*"' l~Z л=0 л=0
с0 = 0, с{ = 0, с„ = -1 для и > 2 .■
Пример 3.15. Записать разложения по степеням (z - zo) функций:
a) lnz, го=1, In 1 = 0; б) ln(l + z), го=О, 1Ш = 0.
П Разложения записываются для однозначных ветвей многозначного вы-
выражения. Выбор ветви определяется заданием функции в точке го ■
а) Функция определена во всей комплексной плоскости за исключением
z = 0, т.е. в двусвязной области 0 < |г| < оо. Чтобы получить односвязную область
из 0 < |г| < оо, проведем разрез, соединяющий точки г = 0 и г=оо. Из условия
In 1 = 0 следует, что точка го = 1 должна быть внутренней точкой области. По-
Поэтому выбираем разрез, не проходящий через Zo, например по лучу (-оо,о]. В
полученной односвязной области, где - к < arg г < я, функция In г является
однозначной аналитической функцией.
Далее решаем задачу по алгоритму.
200
112
1. Находим производные: f'(z) = -, f"{z) = —7 > /'"(*) = Т •
г z z
^ -2-3 ,/„), v (-1Г'("-1)! ^
г) = —т—,-, /w«)= — — (формулу устанавливаем по индукции).
г4 г"
2. По формуле C.17):
/(")(!) = (- 1)"+I (л -1)!, сп =
3. Находим радиус сходимости ряда: R=-, где /=1нпи —= 1, Л = 1.
/ л->«> I п
В результате получаем In z = £/—-—*—*—, \z -1| < 1 •
б) Функция ln(l + z) определена всюду в С за исключением z = -1, т.е.
в двусвязной области. В односвязной области, полученной из С путем разреза
по лучу (-oo,-l], функция является однозначной , аналитической. Задачу можно
решать, как и выше, т.е. по алгоритму, а можно использовать полученный выше
результат, введя обозначение l+z = f. Для t, удовлетворяющих неравенству
ж I ал+1
|/ - lj < 1, имеем разложение In / = £•*—'—(t -1)". Заменяя t на (l + z), получа-
п
ем результат ln(l + z) =
/ ЛЯ + 1
~-—z".
ОСНОВНЫЕ РАЗЛОЖЕНИЯ
Разложения, полученные в результате решения примеров 3.13-3.15, носят
название основных (табличных) разложений. Выпишем их:
«о .л <х> I Ал+1 2л-1 « /_iyi_2B
„То"! я.1 Bл-О' £о
л=1
Основные разложения позволяют при решении примеров на разложение
функции в ряд Тейлора не пользоваться сформулированным выше алгоритмом,
сложность которого связана с техникой дифференцирования и составления фор-
формулы общего члена.
201
Утверждение 3.4. При разложении функции в ряд Тейлора используются
основные (табличные) разложения и действия над рядами. Радиус сходимости ряда
может быть получен по виду раскладываемой функции без использования формулы
общего члена ряда и формул для нахождения радиуса. Радиус сходимости ряда, полу-
полученного при разложении данной функции в окрестности точки Zo, равен расстоя-
расстоянию от центра разложения - точки Zq до ближайшей особой точки функции. Если
функция является аналитической всюду, то R - °о.
Пример 3.16. Разложить по степеням z функции:
а) сЬЗг; б) ег+2; в) sin2 г; гIпC + г).
□ а) Обозначим Зг через t и, используя табличное разложение для функ-
00 fin 00 ПП _2й
ции chr, получим ответ: ch3z = cht = У-—г-, т.е. спЗг= У-т—г-, Л = °о.
п=о12и)! „=0 12л)!
б) Запишем функцию в виде произведения е2 -е1 и, используя разложение
ОО -Л 00 О1
для е1, получим ответ: ег*2 = е2 • У —, т.е. ег*2 = У — z" , R = »•
«То"! „То"!
в) Чтобы воспользоваться одним из основных разложений, применим
тригонометрическую формулу - формулу "понижения". Получим:
.2 1-C0S2* 11.1 l^BzJ"(-l)" I I £22"(-l)V"
Заметим, что свободный член разложения в этой записи встречается дваж-
дважды, поэтому нужно привести подобные члены. Для этого в записи рада отделим
1 1 1 ^22"(-1)л72"
слагаемое при п = 0 - свободный член: £,—/—\ •
В результате имеем sin2 z = ^—т—т z2n, R = °о.
Из этого разложения можно найти значение производной любого порядка
функции sin2 z в точке г0 =0, так как эти значения связаны формулой C.17)
с коэффициентами разложения: f^"\zo)=cn -и! . Поэтому, учитывая, что в раз-
разложении присутствуют только четные степени, заключаем, что все производные
нечетных порядков от sin2 z в точке Zo = 0 равны нулю, а производная, напри-
например, десятого порядка не равна нулю. Найдем ее, используя равенство
/(|0)@) = с10 10!, где с10 - коэффициент в разложении f(z)=sin2z при г10, т.е.
в записанном выше разложении нужно взять п = 5. Получим
[sin2J'0)| =29.
202
г) Функция определена всюду, кроме z = -3. В односвязной области,
например в плоскости с разрезом по лучу (- °о,-3], где - тс < arg z < я, возможно
выделение однозначных ветвей многозначного выражения
Ln (z + 3) = In \z + 3| +1 [arg(? + 3) + 2кж] (рис. 3.1). Выбираем ту ветвь, для которой
/(О) = In3, т.е. из Ln3 = In3 + j(arg3 + 2лЛ) = In3 получаем к=0. Разложим ана-
аналитическую функцию In (z + 3) по степеням z в круге \z\ < 3; радиус круга R = 3
- расстояние от центра разложения го = 0 до граничной точки z = -3.
(z)
Рис. 3.1
Чтобы воспользоваться основным разложением, преобразуем функцию
следующим образом: 1пC
через t и используя
1+— =ln3 + ln
1+— .
Тогда, обозначая —
основное разложение для ln(l+f), получаем
In (з + г)=in з +
.-, и-Э"
I при условии
< 1, т.е. в круге \z\ < 3.1
Пример 3.17. Разложить в окрестности точки го =0 ветвь функции
In [z2 - z - б), для которой /@) = In 6 + / я.
О Функция 1п(г2 -г-б)=1п(г + 2)(г-3) определена всюду в С, кроме
точек Z\ = -2, Zi - 3, т.е. в трехсвязной области - плоскости с выколотыми точ-
точками Z\ и Zi ■ Чтобы получить односвязную область, проведем разрезы по лучам,
выходящим из этих точек. Например, луч из точки Z\ = -2 выберем параллель-
параллельным мнимой оси, {Rez = -2, Im z 2 0}, а луч из точки Zi - 3 - по действительной
оси: {imz = 0, Re г ^3}. В полученной односвязной области (рис. 3.2) каждая
ветвь является аналитической функцией и раскладывается в ряд в круге \z\ < 2
(R = 2 - расстояние от Zo=O до границы). Здесь ветвь задается условием:
/(О) = In 6 + / я, т.е. из Ln (- 6) = In 6 + i (n + 2кп) = In 6 + т при к = 0.
203
1'
У
(z)
Рис. 3.2
Далее, чтобы использовать основное разложение, преобразуем функцию:
In [(z + 2)(z - 3)] = In l(z + 2) (-1) C - z)] = In (z + 2)+ In (-1)+ In C - z). Для числа
In (-1) в силу выбора ветви берем ln(-l) = nt(A =0), а функции In (г+2) и
In C - z) раскладываем в ряды, как в предыдущем примере:
]in3 +%и£1{-#=ыз-3:-£-, м<з-
«=1 «■ 3 л=1Л-3
В области \z\ < 2, принадлежащей выбранной односвязной области, схо-
сходятся оба ряда. Используя свойство сложения рядов (см. разд. 3.1.3), получаем
окончательный результат:
2" 3"
При разложении функции в ряд в окрестности точки zo * 0, т.е. по степе-
степеням (z-Zo)< удобно использовать замену (z-Zo)=t и полученную после замены
функцию раскладывать по степеням t.
Пример 3.18. Разложить по степеням (г-2) функции:
a) sin г; б) ег\ в) 1пA + г).
□ а) Обозначим (z-2) через t, z-2 = t,n, используя тригонометрическую
формулу для функции sinB + f), получим: sinB + f)=sin2-cosf + cos2-sin/. Здесь
sin2 и cos2 - постоянные величины, а для функций cosr и sin/ используем
основные разложения. В результате получим
B-1)!
■Ц. ряд вида ]Рс„(г-2)" , где коэффициент с„ определяется следующим обра-
(-1)* (- if
зом: с„ = ■i—i—sin 2 для я = 2к и с„ = ^ ' cos 2 для я = 2к -1.
б) Можно, как и выше, использовать вспомогательную переменную, а
можно сделать то же самое, применив простое преобразование:
ez =ez'2*2 =e2 ez~2. Здесь е2 - постоянная величина, функция ег~2 расклады-
00 (z — 2)"
вается в ряд как функция е' по степеням /. Получаем ответ: ez =е2^ »
или ez = ^—(z - 2f , R = oo.
в) Обозначая {z - 2) через t, получаем функцию ln(/ + 3). Разложение этой
функции по степеням t найдено в примере 3.16: 1п(/ + 3) = 1пЗ+У-^—'—t",
n=i л-3"
\t\ < 3. Возвращаясь к исходной переменной, получаем разложение исходной
функции в круге \z - 2| < 3 (рис. 3.3):
я-3
(z)
Рис. 3.3
Пример 3.19. Разложить по степеням z функции:
/(*) =
1
\-aZ'
f(z) = -
1
/(?)■
205
D Данные- функции являются простейшими рациональными
(элементарными) дробями. Для их разложения используется формула суммы
1 GO
членов бесконечно убывающей геометрической прогрессии = £д" , \q\ <1.
В первом случае формула используется непосредственно, при д = az, во втором -
после преобразования = получаем д = — . Разложение заданных
az a £ а
у д
a-z a ._£ а
функций имеет вид
C.19)
1 « . .
Соотношения C.18),C.19) обобщают формулу = £г , ]Ц<^> кото"
1 -Z л=о
рая получается из них при а = 1.
При разложении дроби замечаем, что она является производной от
, т.е. = -, поэтому ее разложение можно получить, используя
„=о
дифференцирование ряда:
л=0 л=1
1 °О
Ответ удобнее записать в виде = ^ (я +1) z", \z\ < 1.
A - z) л=о
Очевидно, повторяя процедуру дифференцирования, можно получить раз-
разложение элементарных дробей вида — при любом натуральном к. ■
Рассмотрим примеры на разложение в ряд Тейлора рациональных дробей
R{z)-ofy
где Pm{z) и Qm(z) - многочлены. Первые этапы решения задачи аналогичны эта-
этапам интегрирования этих дробей. Приведем полный алгоритм.
206
АЛГОРИТМ РАЗЛОЖЕНИЯ РАЦИОНАЛЬНЫХ ДРОБЕЙ В РЯД ТЕЙЛОРА
1. Если дробь неправильная (т>п), следует выделить целую часть дроби -
многочлен.
2. Правильную рациональную дробь разложить на элементарные дроби:
А
а) записать дробь в виде суммы элементарных дробей вида —
{z-af
с неопределенными коэффициентами Ак, где а - корень знаменателя, к - его
кратность;
б) найти неопределенные коэффициенты.
3. Разложить элементарные дроби в степенные ряды. Основными приема-
приемами при этом являются применение формул C.13),C.18),C.19) и правила диффе-
дифференцирования ряда (см. пример 3.19)).
При разложении по степеням (z-Zo), Zo *0 можно предварительно ввести
вспомогательную переменную z-Zo=t (см. пример 3.18).
Пример 3.20. Разложить по степеням z функции:
•& 27-1 72 - 7 + 3
а) «-2 ; б)*-4р.
z+2 z+2
.>■(> □ а) Воспользуемся алгоритмом.
1. Дробь неправильная, поэтому выделяем целую часть:
2т,-1_2(т, + 2)-5_2 5_.
z + 2 z + 2 z+2'
•л) 2. Полученная правильная дробь является элементарной дробью.
3. Записываем разложение элементарной дроби и получаем:
, w<2.
„to 2«+1 ' '
Для разложения дроби можно было использовать формулу C.19) при
Z + 2
а = -2.
Для нахождения окончательного ответа нужно сделать преобразование
приведения подобных членов, так как в полученном выражении свободный член
встречается дважды. Имеем
2 t\ 2"+1 Z + 2 t\ 2"+1 2' "
б) Воспользуемся алгоритмом.
1. Дробь неправильная, выделяем целую часть. Можно, как и выше, при-
применить преобразование дроби:
(г + 2J-5г-1
Z + 2 ~ Z + 2 ~ z + 2 =U + 2M +
207
-<3+r.
z + 2
Можно для выделения целой части применить метод деления "углом",
или, обозначая i + 2 = t, произвести почленное деление на одночлен:
г + 2
2,3. Записываем разложение заданной функции, используя формулу C.19)
для правильной дроби:
-2 , , 1 0 е0 (_\\п7п Q Q Q °° f—lVy"
——т—= г-^+-2, =г-^+---г+-2, •
Окончательный ответ: — = — тг + 92] ~~f ^" - N < 2•
00 3 5 9 • (- О"
ряд вида Ycnz", где с0 =-, q =—, с. =—»—^- и ^2. Нетрудно проверить
я-о 2 4 2Л+1
равенство: с0 =/@) = —. ■
Пример 3.21. Функцию -: разложить в ряд Тейлора в окрестности
г -2г-3
точки го, если а) го = 0; б) го = 1 ■
О а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем ее на элементарные дроби. Для этого представим дробь
в виде
г + 2 А В
где А и В - неопределенные коэффициенты, которые находим из тождества
г + 2 = Л(г-3)+Я(г + 1).
Полагая последовательно г = -1 и z = 3 , получаем А = —, В = — .
4 4
о с с » г + 2 -1/4 5/4
Записываем дробь в виде суммы дробей: -. г-. г = + —-.
(г + 1)(г-3) г + l г-3
3. Раскладываем по степеням г каждую элементарную дробь:
„=0
208
CO / _\Я 00 ,Л
В общей области сходимости - круге \z\ < 1 - записываем сумму рядов
разложение исходной дроби:
б) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Разложение дроби на элементарные получено в предыдущем пункте:
Z + 2 -1/4 5/4
z2-2z-3 г + l г-3
3. Раскладываем по степеням (z -1) каждую элементарную дробь:
1 ^-\ ч v. ч 'т-1| < 2'
-L_=—1—=-1 !_=_Jk^Dls М<2.
г-З г-1-2 2 ^г^ „ti 2"+I ' '
2
Записываем разложение исходной дроби в круге \z - \\ < 2:
При разложении по степеням, (г-1) можно было сделать замену z-\=t
в исходной дроби.
Радиусы сходимости в обоих случаях можно определить заранее, до записи»
разложения - по виду функции. Ее особыми точками являются точки Z\ =-l и
Zi = 3. В первом случае ближайшей к точке г0 = 0 является точка ц, расстояние
между точками равно единице и, следовательно, R = 1; во втором - обе особые
точки удалены от го = 1 на расстояние, равное двум, и R = 2. ■
Пример 3.22. Разложить по степеням z функции:
□ а) Воспользуемся алгоритмом.
1. Дробь правильная.
2. Раскладываем правильную дробь на элементарные дроби, предваритель-
предварительно разложив знаменатель на множители:
z2 - 2z + 2 = (z - z\ ){z - Zi), где z\ = 1 - /, Zi = 1 + /'.
209
Представим дробь в виде
А В
■ + -
' {z-zi)(z-z2) z-zi z-z2'
Находим коэффициенты А и 5 из тождества A{z-Zi)+B{z~Z\)= 2, т.е. из сис-
темы
= 0,
Ь =-2
или
В = -А,
2 2
Получаем /4= = = i и B = -i.
Zi-Z2 -2/
Дробь представлена в виде суммы:
2 /
3. Раскладываем элементарные дроби по степеням г:
1
l-i
jj 1_
1+1 ',
.у
< 1, т.е.
Записываем ответ:
1 V1 Z
1 -1 Д г i±iy_il__Iy
= 2 4j(lГ+ 2 ГA +/Г S 2
1 -1 Д
2
yilI
2 ГоA +/Г 2
i-i)"-1+(i+ir' '
б) Воспользуемся алгоритмом.
1,2. Раскладываем дробь на элементарные:
г + 1 А_ В С
(z-if(z + 2)~ z-l + (z-lJ + z + 2'
где А, В,С- неопределенные коэффициенты.
Находим коэффициенты из тождества
Приравнивая коэффициенты при одинаковых степенях z , имеем
Л+С = 0, А + В-2С = \, -2A + 2B + C = 1.
Отсюда /4 = 1/9, 5 = 2/3, С = -1/9.
3. Раскладываем элементарные дроби по степеням z '■
1 1 00
1 1 V И II .,.
210
fe-1
2 -n 2"
Для исходной дроби получаем разложение:
или, складывая ряды: fe_^ + 2) = 11 [6(« + 0 " >+
Окончательный ответ:
Пример 3.23. Разложить по степеням z функции:
а)—*-=■; б)-^-.
П Обе дроби правильные; раскладывать на более простые нет необходимо-
необходимости. Используя основные разложения, получаем ответы:
_2я+1
i
г2-/ -'
или
г -' я=о
Пример 3.24. Используя разложение функции ег +г по степеням z , найти
значение производной седьмого порядка в точке го = 0 ■
D Искомая величина находится по форйуле C.17):/^@) = с7 -7!, где c-j -
коэффициент слагаемого, содержащего степень z1 в разложении функции в ряд
Тейлора. Разложение функции можно получить, используя правило умножения
211
2 2
рядов. Функцию для этого представим в виде произведения ez +z =ez -ez. При
этом нет необходимости находить первые члены разложения, достаточно опреде-
определить коэффициент при степени z1, которая получается при перемножении.
Запишем произведение рядов:
.2Z4Z6.Z«. )L._.Z2.J.ZA.Z5.Z6.Z1 )
+++... 1 + г+++ +++.
2! 3! 4! Д 2! 3! 4! 5! 6! 7!
1 1 1
Вычисляем коэффициент с7 = — (l + 6-7 + 2-5-6-7 + 4-5-6-7) =
и
7! 7!
получаем ответ: /G)@)= 1303.
Можно убедиться, что нахождение /^7^@) непосредственным дифференци-
дифференцированием более громоздко. ■
Пример 3.25. Записать разложение функций a) esmz и б) tgz no степеням
Z до члена, содержащего z5 ■
О а) Применим метод подстановки ряда в ряд, используя основные разло-
г3 г5
жения для функций ez и sin z- Имеем и = sin г, н@) = 0, u = z +—+...;
11 ( z1 z5
и2 +—н3 + или подставляя: ешг1+ г+
11 ( z1 z5 1
е" = 1+Н +—и2 +—н3 +..., или, подставляя: ешг=1+ г + ... +
2! 3! ^ 3! 5! J
z1 z5 f l( г3 г5 f l( г3 V if 1 f
z+"- +u++... +u + --- + г
2! 3! 5! 3! 3! 5! 4! 3! 5! 3!
f г3 г5 I
где а = + .... Записывать большее число слагаемых нет необходимости,
так как уже у следующего (первого отброшенного) младшая степень равна г6.
Возведение в степень рядов, как и перемножение рядов, производится по
правилам действий с многочленами, в частности применяется формула бинома
Ньютона:
212
( тъ z5 )
Так как младшая степень z выражения а = \ + -—... равна трем а,
I 3! 5- )
следовательно, а2- шести, то для записи результата следует взять из первых двух
ш>бок по два слагаемых, а из остальных по одному, т.е.
-■s ■
Приводя подобные члены, получим окончательный ответ:
,2 I , J I . I
3! У.) [ 2! 3! 4!j 15! 3! 3! 5!
sin 7 1 » 2 3 4 1 5
или е и=1 + г + — Z —Z Z +....
2! 4! 15
Разложение, очевидно, можно получить, вычисляя коэффициенты разло-
разложения по формуле C.17), что более громоздко.
б) Разложение tgz можно получить, используя формулу C.17) для коэф-
zl z5
фициентов либо произведя деление ряда sin z = z-—■ + — -... на ряд
z2 z4
cos? = l + ... методом деления "углом" или методом неопределенных
2! 4!
коэффициентов.
Применим последний прием. Разложение tg z по степеням z ищем в виде
sin z
cosz
По определению деления имеем тождество
2 3 4
3, ■ 5, ••■ I- 2! ' 4! 6! '"'|ги ■-^■"C2* +сЗг +С1г
Перемножаем ряды справа и приравниваем коэффициенты полученного
ряда известным коэффициентам при соответствующих степенях ряда, записан-
записанного слева. Получаем систему уравнений
л , «О л £l ' 1 С0 С3 С, 1
Cn=0, Ci = 1 , С-) ^-=0, Ст. L = , Сл Ci+ —= 0, С< — + —- = —,
о ' ' 2 2 3 2 3! 4 2! 2 4! 5 2! 4! 5!
1 2
из которой находим коэффициенты с0 = 0, С] = 1, с2 = 0, с^ = —, С4 = 0, с5 = —.
Ответ получаем в виде tg^ = г: + —г: +—г +...
3 15
Это разложение справедливо в круге |г|<—, так как z = ближайшая
к zo = 0 особая точка функции tg z. ■
213
3.2.2. Нули аналитических функций
Пусть функция /(г) является аналитической в точке го •
Точка го называется нулем функции /(г), если ее значение в этой точке
равно нулю, т.е. /(го) = О.
В разложении функции в ряд Тейлора в окрестности нуля этой функции
отсутствует свободный член: cq = f(zo) = O-
Если при этом в разложении отсутствуют и слагаемые, содержащие степе-
степени разности (z-Zo) Д° л"й степени, т.е. разложение имеет вид
/(*) = I с* («-*>)* .или f(z)=cn(z-ZoT+cn+l(z-Zor1+-, cn*0, C.20)
то точка го называется нулем порядка п функции /(г).
Нуль первого порядка называется простым нулем.
Правую часть равенства C.20) можно записать в виде произведения:
/(г) = (г-г0У[сп+сп+1(г-г0)+...], или f(z) = (z-zo)n■[bo+bl{z-zo)+..],
где второй множитель можно рассматривать как степенной ряд, сходящийся
в точке го > поэтому его сумма - функция, аналитическая в точке го; обозначим
ее ф(г). Таким образом, из C.20) получаем представление функции /(г) в виде
/(г) = (г-го)"-<р(г), <рЫ = с„*0. C.21)
Кроме того, используя формулу коэффициентов ряда Тейлора
с„ = *-^, находим, что для нуля порядка п функции /(г) в точке го спра-
ведливо условие
() W) O,* = O,l,...,(/i-l), C.22)
т.е. порядок нуля функции определяется порядком первой отличной от нуля
в этой точке производной.
Пусть функция /(г) задана в виде произведения /(г) = f\[z)• fi(г) и точка
го является нулем порядка к для fx{z) и нулем порядка т для /2(г). Тогда, ис-
используя условие C.21) для этих функций, можно записать
или
Это означает, что порядок нуля в точке го функции, полученной в резуль-
результате перемножения аналитических функций, равен сумме порядков нуля в этой
точке функций-сомножителей.
214
Сформулируем вывод в виде следующего утверждения.
Утверждение 3.5.
1. Точка zo является нулем функции f(z), если /(zo) = O; нулем порядка п -
если для коэффициентов ряда Тейлора ее разложения по степеням (z-Zo) справед-
справедливы равенства
ct=0, * = 0,1,...,(я-1),ся*0.
2. Следующие условия являются необходимыми и достаточными условиями
нуля порядка п функции f(z) в точке го '■
. а) условие C.22): /(и>(г0)*0> /<%,) = 0, к =0,1 (и-1);
б) представление функции в виде произведения C.21):
/(г) = (г-г0)" <р(г),
,; Замечания 3.3.
1. Если функция не определена в точке Zq, но lim /(г) = 0, то после
г-» го
доопределения функции в точке го^ /(го) = шп f(z)> точку zo тоже называют
г->го
нулем функции.
Например, для функции f(z) = , доопределенной в точке Zq =0:
•i-l
точка го = 0 является нулем.
2. Пусть /(г) представлена в виде отношения ^Щ аналитических в точ
'* п\ч
го функций и точка го является нулем порядка к для числителя и нулем г
ка т - для знаменателя. При условии к> т, доопределив функцию /(г),
выше, получим, го - нуль функции /(г).
Используя условие C.21) для функций /((г) и /г(г), получаем равенство
f(z)=] °.„ ,.. или /(г)=(г-го)*"тф(г). Здесь ф(г)- аналитическая в точке
го, так как ф|(г) и ф2(г) - аналитические в этой точке и ф2(го)*О. Кроме того,
<р(го)* 0, так как ф,(г0)* 0. Поэтому для функции /(г) точка го является нулем
порядка (к-т)(см. C.21)). Порядок нуля частного равен разности - из порядка
нуля числителя вычитается порядок нуля знаменателя.
215
АЛГОРИТМ НАХОЖДЕНИЯ НУЛЕЙ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
И ОПРЕДЕЛЕНИЯ ИХ ПОРЯДКОВ
1. Найти нули аналитической функции /(г), решая уравнение /(г) = 0.
2. Определить порядок каждого полученного нуля го • Для этого выполнить
одно из следующих действий:
а) разложить /(г) в ряд по степеням (г-го)- Младшая степень разности
(z - го), присутствующая в разложении C.20), определяет порядок нуля го ;
б) найти производные /**'(г) и их значения в нуле функции, т.е. /**'(го)-
Порядок нуля го функции /(г) определяется порядком первой, не равной нулю
в точке производной;
в) записать функцию в виде произведения C.21); степень разности (г-го)
в этом произведении определяет порядок нуля го;
г) записать функцию в виде произведения более простых функций и для
каждой из них определить порядок нуля го по одному из изложенных в преды-
предыдущих пунктах правилу. Порядок нуля го произведения равен сумме порядков
нуля сомножителей.
3. Для функции /(г), не определенной в точке го, но удовлетворяющей в
этой точке условию lim /(г) = 0, порядок нуля го определить по правилам, из-
изложенным в п. 2 или в соответствии с замечанием 3.3.
Пример 3.26. Найти все нули функции /(г)=г5-г4+4г3-4г2, опреде-
определить их порядок.
□ Воспользуемся алгоритмом.
1. Раскладываем многочлен на множители: /(г)=г4(г-1)+4г2(г-1), или
/(г) = г2(г-1)(г2+4). Находим нули функции: г] =0. г2=1, гз=2/, г4=-2/.
Разложение многочлена на линейные множители имеет вид
/(г)=г2(г-1)(г-2/)(г + 2/).
2. Определяем порядок каждого нуля. Удобнее использовать для этого
формулу C.21). Для точки z\ =0 из равенства /(г)= г2 ф(г), ф@) * 0, получаем,
что г = 0- нуль второго порядка; для точки z-i = 1 из равенства/(г) = (г -1)- ф(г),
фA) * 0, получаем, что г = 1 - нуль первого порядка (простой нуль); для точек
z-} = 2/ и Zi, = -2/ аналогично находим, что это нули первого порядка (простые
нули) данной функции. ■
Пример 3.27. Определить порядок нуля го = 0 для функций:
a) f(z) = ег -1-г2; б) /(г) = sin3 г -1 + cos г ■
□ а) Для определения порядка нуля го = 0 удобно использовать определе-
определение, т.е. разложить функцию по степеням г (п. 2"а" алгоритма). Получаем
4 ~\ 4 6
-1-г'!=|1 +г2+— + ••• -1-г2 = — +—+.... Так как в полученном разло-
216
жении коэффициент с^=~, т.е. не равен нулю, а предыдущие равны нулю
(с0 =q =с2 = с3 =0), то заключаем, что точка го = 0 является нулем порядка
п = 4 для данной функции.
б) В данном случае используем формулу C.22), т.е. п. 2"б" алгоритма. На-
Находим значения производных функции в точке го = 0:
„I f'{z) =3 sin2 г -cos г -sin z, /'@) = 0;
f"{z) = 6 sin г ■ cos2 z - 3 sin3 z - cos z, /"(°) = -1*0.
t ■■ ■
Следовательно, точка го =0 является нулем второго порядка (я = 2) дан-
данной функции. ■
Пример 3.28. Определить порядок нуля функции f(z) = (ez -1 - г2) • sin3 z
в точке го = 0.
D Функция записана в виде произведения двух функций. Для первого
множителя fl(z)=ez -1-г2 порядок нуля в точке го =0 определен в предыду-
предыдущем примере: к = 4. Для функции sin г точка го = 0 - нуль первого порядка, так
как согласно п. 2"б" алгоритма /'@) = cos@) = 1*0. Поэтому, учитывая, что
/2{г) = sin3 г = (sin гK = sin г ■ sin г ■ sin г и пользуясь п. 2"г" алгоритма, получаем,
что го = 0 - нуль третьего порядка (т = 3). Поскольку /(г) = /J (г) • f2 (г), то по
правилу 2"г" алгоритма получаем результат - точка го = 0 является нулем седь-
седьмого порядка заданной функции, так как п = к + т = 7.
Пример 3.29. Найти нули функций а) и б) ; определить их
г sin г
порядок.
□ а) Равенство /(г) = 0 в области определения функции выполняется для
точек г, таких, что sin3г = 0, г*0, т.е. г* =кп, £ = ±1,±2,... . Эти точки, оче-
очевидно, простые нули функции sin г, а потому нули третьего порядка для функ-
функции sin3 г. Поэтому для каждого нуля г*, используя необходимое условие (см.
п. 2 утверждения 3.5), можно записать sin3 г = (г - г*K4>t (г), <pifc*)*0 и, следо-
следовательно, = (г - Zk) ф(?). ф(г*) * 0 • Из этого, в силу достаточного условия
C.21) (см. п. 2 утверждения 3.5), заключаем, что точки zk -кк, к = ±1,±2,... яв-
являются нулями третьего порядка данной функции. Кроме того, так как выполня-
.. sin3 г ,. sin г ■ i л ^
ется условие hm = lim sin г = 0, то, после доопределения функции
г->о г г->о г
(см. п.1 замечаний 3.3 ), получаем, что го =0 является нулем функции. Чтобы
определить порядок нуля, используем результат, полученный в п.2 замечаний 3.3.
А именно, для функции, стоящей в числителе, точка г = 0 - нуль третьего по-
порядка (к = 3), а для знаменателя, очевидно, простой нуль {т = 1). Поэтому г = 0
- нуль второго порядка данной функции.
217
б) Нулями функции в области определения z*kn, k = Q,±l,... являются
точки zk -Ы, к = +1,... - корни уравнения e2z = 1, г * 0. Эти точки - простые
нули числителя и е1г -1 = (г-г*)-ф|(г), «Pi (^) ^ 0. Поэтому из равенства
kibeM „ли f{z)={z-zkHz), фЫ*0 заключаем, что zk=kni.
smz
к = ±1,+2,... - простые нули данной функции.
В точке z = 0, которая также является нулем числителя, функция не опре-
определена. Найдем предел функции в этой точке. Для раскрытия неопределенности
,. е*-\
hm можно использовать свойства пределов, или разложить по степеням
г->0 sin г
z числитель и знаменатель:
lim- -= limi -х -—= lim-i f = 2.
г->о sin г г->« г г"»0 2
Так как lim f(z) * 0, то точка г = 0 не является нулем данной функции.
г-»о
3.2.3. Разложение функций в ряды по целым степеням. Ряд Лорана
В разд. 3.2.1. рассматривалась задача разложения функции в степенной ряд
со
£сл(г~го)", при этом функция предполагалась аналитической в точке го,
а ряд сходящимся в круге \z - Zo| < R. О < Л < да.
Другим частным случаем функциональных рядов, наряду со степенными,
со
является ряд £ся(г-го)" " Ряд по целым степеням разности (z-Zo). Такой
ряд сходится в кольце г<|г-го|<Л, г>0, /?<оо и его сумма - функция анали-
аналитическая внутри этого кольца (см. разд. 3.1.4).
Можно рассматривать задачу разложения функции, аналитической в коль-
кольце г < \z - zq\ < R ■ Имеет место теорема, аналогичная теореме 3.3.
Теорема 3.5 (теорема Лорана о разложении функции в ряд по целым сте-
степеням). Функция f(z), аналитическая в кольце, представляется в этом кольце схо-
сходящимся рядом по целым степеням, т.е. имеет место равенство
/(г)= tc«k-zo)n- <3-24>
218
Коэффициенты ряда вычисляются по формуле
где у - произвольный контур, принадлежащий кольцу и охватывающий точку Zo >
в частности, у - окружность |г - ?о| = Р> г <р< R.
Имеют место следующие определения.
1. Ряд £ся(г-гоУ > коэффициенты которого вычисляются по формуле
л=-оо
C.25), называется рядом Лорана функции f(z).
Заметим, что формула C.16) получается из формулы C.25) при л^О, но
для коэффициентов ряда Лорана не имеет места формула вида C.17), так как
функция в точке г0 может быть не определена.
2. Совокупность членов ряда с неотрицательными степенями -
00
£ся(г-го)" называется правильной частые ряда Лорана; члены с отрицатель-
отрицательно
ными степенями образуют главную часть ряда Лорана: 2]ся(г-гоГ или
Л = -оо
у С-я
3. При г = 0 получаем частный случай кольца - вырожденное кольцо
О < \z - Zu\ < R- Это - круг с выколотым центром. Точка го - особая точка функ-
функции, и разложение в этом случае называется разложением функции в окрестности
особой точки.
4. При R = да область \z - Zq\ > г есть внешность круга. В частном случае
при го = 0 - внешность круга |г| > г. Разложение в этом случае называется
разложением в окрестности бесконечно удаленной точки и имеет вид '
Я=-оо Л=0 Л=-00
или, что то же,
/(г)=Усяг" + У—• C.27)
^ Здесь совокупность неотрицательных степеней £сяг" образует главную
л=0
часть ряда Лорана в окрестности бесконечно удаленной точки; совокупность
-1
отрицательных J^cnz" - правильную часть ряда Лорана в окрестности беско-
Я = -оо
нечно удаленной точки.
219
Пример 3.30. Исследовать возможность разложения функции
в ряды Тейлора и Лорана.
D Функцию /(г) = Jt п \ нельзя разложить в ряд по степеням г ни
К(г + 1)(г2)
в окрестности точки го = 0 (ряд Тейлора), ни в окрестности точки го = °° (ряд
Лорана), так как эти точки являются точками ветвления функции и в их окрест-
окрестностях невозможно выделение однозначных ветвей.
Невозможны также разложения этой функции в ряды по степеням (г +1) и
(z - 2), поскольку точки г = -1 иг = 2- также точки ветвления. Разложения по
степеням (г - го) , где го * 0, го * -1. Zo * 2, возможны.
Функция же f{z) = -( w г раскладывается по степеням г и в ряд
(г + 1)(г-2)
Тейлора в круге |г| < 1 ив ряд Лорана в области |г| > 2 (окрестность бесконечно
удаленной точки), а также в кольце 1 < |г| < 2. Возможны разложения и по сте-
степеням (г + 0 и (г - 2) в кольцевых областях, а также в окрестностях особых точек
г = -1, г = 2.ш
Так как ряды по целым степеням обладают свойствами степенных рядов
(см. утверждение 3.2), то, учитывая теорию и практику решения задачи разложе-
разложения функции в степенной ряд (см. утверждения 3.3 и 3.4), можно сформулиро-
сформулировать следующее утверждение.
Утверждение 3.6.
1. Функция, аналитическая в кольце г <\z-Zo\< R> r>0, R<«>, разлагает-
разлагается в этом кольце в ряд Лорана C.24), коэффициенты которого вычисляются по
формуле C.25),
2. Для коэффициентов ряда имеет место формула оценки коэффициентов -
неравенство Коши:
|ся|<-^-, Я-0Д1Д2,... C.28)
где М = тах|/(г)|, р - радиус окружности (частный случай контура у), по кото-
рой производится интегрирование в C.25).
3. На границах кольца сходимости ряда Лорана есть хотя бы по одной особой
точке функции /(г) - его суммы.
4. Частными случаями рядов Лорана являются разложения функции в окрест-
окрестности особой точки Zo(r = 0) и окрестности бесконечно удаленной точки (го =0,
220
5. Разложение в ряд Лорана сводится к разложению в ряд Тейлора, использу-
отся основные разложения и действия над рядами.
6. При разложении рациональных дробей, как и в случае рядов Тейлора, выде-
выдерется целая часть неправильной дроби, а правильная записывается в виде суммы
•.лементарных дробей, для разложения которых используется формула суммы членов
•есконечно убывающей геометрической прогрессии. При этом элементарные дроби
теобразуются следующим образом:
- для получения правильной части, т.е. ряда, сходящегося в круге \z-Zq\<R,
/изложение элементарной дроби записывается в виде
1
a-[z-Zo)
л=0
\z-zo\<\a\,
- для получения главной части, т.е. ряда, сходящегося вне круга \z-Zo\>r>
изложение элементарной дроби записывается в виде
Z-Zo
z-zo
Пример 3.31. Разложить функцию f{z) = -
Z + 2
в ряд Лорана по степе-
степеням z.
□ Функция является аналитической всюду, кроме точек ц =-1 и Zi =3,
i частности: в круге \z\ < 1, в кольце 1 < |г| < 3 ив окрестности бесконечно уда-
1енной точки 1г| > 3 (рис. 3.4).
Рис. 3.4
Рис. 3.5
В круге ]г] < 1 функция раскладывается в ряд Тейлора (см. пример 3.21).
~1олучим разложения в двух других областях.
Рассмотрим разложение в кольце. Дробь правильная, ее разложение на
элементарные дроби получено в примере C.21):
221
£±2
-1/4 5/4
Чтобы получить разложение в кольце, первое слагаемое раскладываем
в области \z\ > 1, т.е. записываем главную часть ряда, второе - в круге \z\ < 3 -
правильная часть. Получаем разложения:
1 1
1
г + l
ul ,-f-i
_ ^,(-1)" "(-I)"-'
л=1 Z"
n=0
1
_£ л=о
I 1 7
3.
1
Записываем окончательный результат:
£; f; w
72 77 1 I 4 7П п 4-3Л+1
Здесь первое слагаемое - главная часть, а второе - правильная часть ряда
Лорана в кольце 1 < \z\ < 3.
Чтобы получить разложение в области \z\ > 3 - окрестности бесконечно
удаленной точки, нужно и второе слагаемое разложить по отрицательным степе-
степеням:
1 I 1 00 ХП
""'
или
1 °° 1"'
J-=yi—, Ы>3.
г-3 „t, <" М
В результате получаем:
Z2-2z-3~k4z» *k Z" ~h 4 >• KI>J
- разложение в окрестности бесконечно удаленной точки. Заметим, что главная
часть ряда отсутствует, так как в разложении присутствуют только члены с отри-
отрицательными степенями. ■
Пример 3.32. Разложить функцию f(z) =
в ряд Лорана:
г -2г-3
а) по степеням (z - 2); б) по степеням (z -1).
□ а) Особыми точками функции являются точки z\ = -1 и z-i = 3, причем
вторая - ближайшая к центру разложения, т.е. к zo =2 (рис. 3.5,о); расстояние
между Zo = 2 и Zi = 3 равно единице, поэтому в круге |г - 2| < 1 функция раскла-
раскладывается в ряд Тейлора. Расстояние от го = 2 до другой особой точки Z\ = -1
равно трем, и в кольце 1 < \z - 2| < 3 данная функция является аналитической и
раскладывается в ряд Лорана. Аналитической она является и в области \z - 2J > 3
222
и раскладывается в ней также в ряд Лорана по степеням (г-2). Оба разложения
получаем, как в предыдущем примере, причем замену z - 2 = / можно сделать в
исходной дроби, а можно не вводить обозначения (см. пример 3.21). Запишем
разложения в каждой из двух областей, учитывая представление функции в ввде
суммы элементарных дробей (см. примеры 3.21 и 3.31):
, ч Z + 2 z + 2 -1/4 | 5/4
Разложение в кольце 1 < \z - 2\ < 3:
11 1 1 00 / |\Л ( *у\П
X ' \+l ' , |г-2|<3;
3
1111
г_3 г-2-1 z-2
Получаем ответ: г + 2 = V ЬЯИ-^)" + V 5 1<|г-2|<3.
223 t43"+lV ^ 4B)" ' '
г-2
И-^)" + V
lV ^ -2)"
Разложение в области \z - 2\ > 3:
1 11 11
г + 1
<:-2
к
(z-гу
б) Задача решается так же, как и в предыдущем пункте. Различие заключа-
заключается в том, что в данном случае обе особые точки расположены на одном рас-
расстоянии от центра - точки г0 = • • Поэтому разложения по степеням (г-1) могут
быть получены в круге \z -1| < 2 и в вырожденном кольце - в области
|г-1|>2(рис. 3.5,6). Разложение в круге |г-1|<2 - ряд Тейлора - получено в
примере 3.21. Запишем разложение в области \z-1| > 2:
223
п
Получаем ответ:
Пример 3.33. Записать разложения функции /(г) = —: в окрестно-
z - 2г - 3
стях особых точек.
П Особыми точками дроби являются Z\ = <», г2 = -1. ?з = 3. Решим задачу
для каждой особой точки го •
Разложение в окрестности бесконечно удаленной точки (го =«) получено
в примере 3.31:
Заметим, что в разложении отсутствует главная часть - совокупность чле-
членов с положительными степенями z ■
Запишем разложение в окрестности точки zo = -1 • Расстояние до другой
особой точки z = 3 равно четырем, поэтому окрестность точки zo = -1 - проко-
проколотая окрестность, которая записывается в виде 0 < \z +1| < 4 (рис. 3.6).
В разложении
Рис. 3.6
-1/4 5/4
z2-2z-3 г + l г-3
г + 2
исходной дроби на элементарные
первое слагаемое записано по степеням (г +1) (уже разложено). Это разложение
содержит только главную часть, состоящую из одного члена: здесь все ск = 0,
кроме с_|, с_| =-1/4, и разложение имеет место в области |г + 1|>0. Второе
слагаемое раскладываем в окрестности Zo = -1 и, так как для него эта точка
224
не является особой, получим ряд Тейлора в круге \z +1| < 4. Для исходной дроби
это будет правильная часть ряда Лорана:
г-3 г+1-4
4- 1--
л=0
z + l
4
|г + 1
I j j
Л+2 ' I I
Получаем ответ: —
z2-lz-Ъ i + i B=o
Для точки ?о = 3 задача решается аналогично (рис. 3.6):
Z + 2 _ 5/4 1 1 5/4 1 2, (- 1>"(г - ЗУ
z2-2z-3 г-3 4 (г-3)+4 г-3 4~0 4Л+1
Получаем ответ:
/ +
z2-2z-3 г-3 „Го 4
+V 1Л_(г_з)л 0<|г-3|<4 - раз-
Го 4Л+2 '
тожение функции в окрестности особой точки Zo = 3. Заметим, что в получен-
полученных разложениях в окрестности каждой особой точки главная часть содержит
~олько одно слагаемое. ■
Пример 3.34. Исследовать разложения функции
f(z)= | + *
ю степеням (z-Zo)- Записать разложения в окрестностях особых точек.
D Функция может быть разложена в ряд Тейлора по степеням (z-Zo)
•. окрестности любой конечной точки zo, *o *-l. *о *^> окрестностью будет
:оуг \z - zq\ < r, где г = min{|?o +1|, \zq - 3)} - наименьшее из расстояний от точки
:п до особых точек (рис. 3.7,я).
Рис. 3.7
' Пантелеев А.В.. Якимова А.С.
225
В ряд Лорана по степеням (г - ю) функция может быть разложена в коль-
кольце r<\z-Zo\<R, где r = min{|*o + l|,|zo-3|}, Л = тах{|г0 + 1|,|го -3|}, и
Rez0 * I, а также во внешности крута, т.е. в области \z -Zo\ > R(рис. ИЛ,а). Если
Re zq = 1. то разложение будет иметь место только в вырожденном кольце вида
\z-Zq\ > Л, так как в этом случае точка zo одинаково удалена от обеих особых
точек и г - R (рис. 3.7,6).
Особенностью примера является наличие в знаменателе множителя
(z +lJ, поэтому в разложении дроби на элементарные присутствует дробь
г, а именно имеет место равенство
(г + 02
г + 2 -5/16 -1/4 5/16
3)= г + 1 +(г + 1J+г-3'
Для разложения дроби по степеням {z-Zo), Zq*-2 используется
(г + 0
правило дифференцирования рядов (см. пример 3.22).
Запишем разложение функции в окрестности г0 - особой точки.
В случае г0 =-1 в разложении дроби на элементарные две первые дроби
представляют собой слагаемые требуемого вида (уже разложены): = (z +1),
г = (z +1)'2 ■ Эти разложения справедливы во всей плоскости с выколотой
(г + 1J
точкой zo = -1. т.е. в области \z +1| > 0.
От третьего слагаемого получаем правильную часть ряда Лорана:
tir, М<4.
Окончательный ответ:
В главной части разложения присутствуют два члена, при этом с_{ = -5/16,
с_2=-1/4.
В случае разложения в окрестности ^о = 3 главная часть разложения со-
содержит одно слагаемое ——; правильная получается от разложения дробей
и по степеням (г - 3).
226
Найдем эти разложения:
1 И V уГ(-0"-(г-зГ
~ U J" t I
уГ(-0-(г
" to I 4"+1
(z + \J~ U + lJ" „to I 4"+1 J ~£, 4"+1
или
_J уШ"±!к3у. u_3|<4
Записываем ответ:
Пример 3.35. Разложить функцию г3ег в окрестностях точек ю = 0 и
D Оба разложения - разложения по степеням z и получаются из основ-
основного разложения, а именно
2!г2
или
. Различие разложений заключается в записи правильной и главной частей.
Так, в случае точки г0 = 0 правильная часть содержит конечное число
слагаемых - четыре и ответ записывается в виде
ж В случае ю - °° конечное число слагаемых образует главную часть и ответ
записывается в виде
Пример 3.36. Разложить по степеням z функции:
а) Ь£°£1; б)
г2 г
С помощью полученных разложений найти lim f(z).
z->o
П Применяем основные разложения для cos г и sin г и записываем ряды
для заданных функций:
227
M
Таким образом, получаем результат
l-cos; I z^_ £^_
г2 ~ 2~ 4! + 6! ~"'
Справа записан степенной ряд, сходящийся всюду, его сумма при z * О
1 - cos г . 1
равна —, а при г = 0 , очевидно, равна —.
Г 2
„ ,. 1-COS£ 1 ,. l-COS? , „
Получаем lim — = - или lim ——.— = 1. Результат можно записать
г->0 il 2 г->0 г2/2
в виде асимптотической формулы:
l_cosZ~Iz2, z->0;
бIуГ
6) z zh B—1I
Получен результат:
3!
Отсюда lim —- = 1. Результат, как и в случае "а", можно записать в виде
г->0 z
асимптотической формулы: sin г ~ z, z -* 0. ■
Упражнения
Разложить данную функцию в ряд в указанной области, или в окрестности
указанной точки. В последнем случае указать область сходимости ряда.
1 ■ f{z) = -5 , го = 0 ■ Записать все разложения по степеням z ■
г2+2г-3
( (\У\
Ответ: а) 1+У 1-^-\z" , Ы<1;
Н-1
228
|;(гз--1)-7' М>з.
я=1 Z
2 _ л_ _ т
2. f(z) = — в окрестности нулей функции.
г + 2г - 3
Ответ: а) £ ''"^Чг +1)", |г +1| < 2;
я=1 2
я=1
3. f(z) = ——-— в окрестности особых точек.
« Ответ: л) f 3'^" (г-1)"+-——, 0 <|г-1| <4;
и=1 4 4 £-1
б) yil±2L + l-^-, 0<|г + 3|<4.
Д 4"+I 4 г + 3' ' '
г2-2г-з
а) в невырожденном кольце по степеням z',
б) в окрестности г0 = 1.
Z) = г B окрестности бесконечно удаленной точки.
(г-03
Ответ: f(z) = ^ —, |г| > 1.
л=1 z"
6. Разложить f(z) = -. г-, г по степеням z в невырожденном кольце.
229
Ответ: f(zhijz+1^j, ±
7. Разложить f(z) = - в окрестности нуля функции.
A - 2/ - гг
Ответ: f{z) = £ n {z + 2/)" , \z + 2/j < 1.
8. Разложить f(z) = г в окрестности нуля функции. Результат срав-
C-г)
нить с результатом задачи 23 (см. с. 197).
Ответ: £ п—, |г|<3.
и=1 J
9. Разложить /(г) = — в ряд Тейлора по степеням z ■ Результат срав-
(l-z2f
нить с результатом задачи 24 (см. с. 197).
Ответ: f(z)=fjnz2n,\z\<l.
л=1
10. Разложить /(г) = -г в окрестности бесконечно удаленной точки.
Результат сравнить с результатом задачи 25 (см. с. 197).
Ответ: f{z)=fJ^-,\z\>\.
и=1 Z
11. Разложить f(z) = — в окрестности точек: а) го =', б) го = 0.
Ответ: a) f{z) = J /"+1 • «(г - if1, \z - »| < 1; б) f{z) = г~2, |г| > 0.
2. Разложить f(z) = — в окрестностях точек: а) г0 = 0; б) г0 =»>
Z2{z + i)
12.
в) го=с°;Г) го=-'-
Ответ: а) /(*) = ---+ Х/"+1г'1, \z\ <1;
и=0
230
л=0
id J_
13. Разложить функции е г , г' в окрестности конечных особых точек.
Ответ: a) f(z) = е + У —*—' , Ы > 0;
л=1 "! ^"
111 _L
« 14. Записать несколько членов разложения функций е z , ег"' врядТей-
Ijppa в окрестностях нулей этих функций.
)=1 + (г-1)-|(г-1J+1(г-1)'+1(г-1L+...,
\z2-±z3+\zU..., \z\<l.
15. Разложить /(г) = —^- в окрестностях точек: а) го = 0; б) го = -2.
Г
1 л
Ответ: а) /(г) = - + -г, Ы > 0;
г z
16. Разложить f(z) = г в окрестностях особой точки и нуля функции.
(г-О
4'-
17. С помощью разложения функции е ■z в рад Тейлора найти/'5^(о).
Ответ: /*5'@) = 81.
231
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Найти области сходимости рядов.
1.'
6. ]Г2"<>+гЬ 7. £- ; 8. У/ \<ТУ + ^ ; 9.
Доказать, что данный ряд сходится равномерно на указанном множестве.
Ю- S-^Г' |г|<г<^2; 11.
Найти радиусы сходимости рядов.
СО П СО СО СО и |
12. I-2—гг"; 13. 5>л!; 14. ^"-sinto; 15. £-^г".
л=1 (л + 1)" л=1 л=1 л=1 "
Найти сумму ряда.
(Я (Я 2 (Я
l6.Ii,.fr + 2/)-. П. Е^. 18. Z
Указание. Результаты сравнить с условиями упражнений №7,5,6 на
с. 229,230 .
19. Допускает ли функция /(?) = ,/ разложение в ряд по степеням
К + 1
а) г; б) г-1.
В случае положительного ответа записать три ненулевых члена разложения.
20. Разложить в ряд Тейлора по степеням z ветвь функции /(?), для кото-
которой /@)=0: a)/(z) = arcshu; б) /(*)=arctgz. Указать радиусы сходимости ря-
рядов.
21. Возможно ли разложение функции f(z) = J-, г,—тг в ряд Лорана
в окрестности z = °° ?
22. Исследовать возможность разложения функции /(г) = \1 + 4l в ряд
в окрестности Zq ■
23. Исследовать возможность разложения функции /(г)=1п в ряд
Z + i
окрестности г0-
24. Найти нули функции P(z)= г4 -2г3 +5z2 -8г + 4 и определить их по-
порядок.
232
25. Определить порядок нуля г0 = 0 Д™ функций:
a) f{z) = (ez -I? -sin2 z; 6)(V-ll2+(cos*-lJ;
в) (e*2 -lj -4A-cosгJ.
26. Найти все нули функции и определить их порядок:
а) /(г)= *"* ' ; б) P(z)
z(z-nf
27. Записать разложение функции из задачи 24 в окрестности нуля второго
порядка этой функции.
28. Определить порядок нуля z-О функции f(z) = sin2z-\ez -I] . Разло-
Разложить функцию по степеням z ■ С помощью полученного разложения найти зна-
значения производных /G>@), /W@), /(9>@).
29. Разложить f(z) = sin z + — в окрестности Zo = я.
1 г2-2
30. Разложить /(г) = - + в ряд:
а) в окрестности г0 = -1; б) в кольце 4 < \z -1| < 2.
31. Разложить /(г) = z — + г в ряд:
а) в окрестности г0 = 1; б) в кольце 1 < \z + ll < 2.
4
32. Разложить /(г) = —— в окрестности:
V -\
a) Zo = 0; б) г0 = со.
33. Разложить в ряд:
а) f(z) = sinz по степеням (г-1);
б) f(z) - sin(z -1) по степеням z ■
233
Глава 4. ОСОБЫЕ ТОЧКИ ФУНКЦИЙ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО. ВЫЧЕТЫ
4.1. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ ФУНКЦИЙ
4.1.1. Классификация особых точек
Важное место в изучении и применении теории функций комплекс-
комплексного переменного занимает исследование их поведения в особых точках,
где нарушается аналитичность функции. В частности, это точки, где функция
не определена.
Исследование функции в особой точке г0 определяется поведением ее
в окрестности этой точки, т.е. исследованием lim f(z) ■ Очевидно, имеют
Z->Zo
место три возможности:
а) lim /(г) не существует;
г-»го
б) lim /(г) существует и равен конечному числу;
г-»го
в) lim f(z) равен бесконечности.
г-»го
Исследование пределов функции в комплексной области - задача бо-
более сложная, чем в действительной области, так как, согласно определению
(см. разд. 2.1.1), переменная z стремится к z0 (z-*Zo) по любому на-
направлению. Вычисление пределов в точках аналитичности не представляет
интереса, так как в этих случаях lim f(z) = /(?o) •
Z->Zo
Будем рассматривать lim /(г), где г0- особая точка.
I _!_
Пример 4.1. Исследовать существование lime*, lime* в случаях
г_»о г->о
a) z = xeR; б)
Da) В действительной области lime* не существует, так как не
г-»о
I I
равны односторонние пределы lim ех =«>, lim ех = 0, но существуем
х->0+0 х->0-0
_1_
предел второй функции: lime* =°o.
х-»0
б) В комплексной области, очевидно, lime* не существует, так как
г->0
он не существует в частном случае z = х.
234
«г А.
Но для второй функции полученного выше результата lime* =oo
х->0
не достаточно, так как рассмотрены только два направления на плоскости
- по действительной положительной и действительной отрицательной полу-
полуосям.
Рассмотрим еще какое-нибудь направление, например по мнимой оси,
_L _!_ _-L
т.е. z = iy, y->0: lime* =lime('r) =lime y = 0. Сравнивая этот результат
г_»о >■->() у->0
J_
с полученным выше lime*2=oo, заключаем, что в комплексной области
х->0
lime* не существует. ■
г->о
Аналогично можно показать, что не существует lira ez , хотя lim ег = ю
г->0 г-»0
для случаев z = x и z = iy (по действительной и мнимой осям).
Эти простые примеры показывают, что исследование функции в особой
точке с помощью lim f(z) может представлять большие сложности. Но,
г-»го
с другой стороны, в примере 3.36 при вычислении пределов функции в особых
точках было использовано разложение функции в ряд.
Представление функции в виде ряда как один из способов ее
аналитического задания, может быть использовано для исследования
функции, в частности, в особых точках.
Будем рассматривать изолированные особые точки функций, т.е. осо-
особые точки, для каждой из которых существует такая ее окрестность,
в которой нет других особых точек функции.
В частности, конечная особая точка г0 е С является изолиро-
изолированной особой точкой функции f(z) , если существует число г > 0,
такое, что в круге |г-го|<'' эта точка- единственная особая точка(
f(z), а в проколотой окрестности, т.е. в 0<|г-г0|<'' > функция /(г) анали-
аналитическая.
Бесконечно удаленная особая точка го = °° является изолирован-
изолированной особой точкой функции f(z) , если существует число R > 0 , та-
такое, что в области \z\ > R эта точка - единственная особая точка
/(г), а в кольце R < \z\ < °о функция f(z) - аналитическая.
Согласно теореме Лорана (см. разд. 3.2.3.) , функция, аналитическая
в кольце, в частности, в проколотой окрестности особой точки, может
быть представлена рядом Лорана. Это позволяет свести исследование
функции в изолированной особой точке к исследованию соответствующего ряда.
Особенности рядов как представления аналитических функций можно
заметить, проанализировав некоторые примеры из гл. 3.
235
Пример 4.2. Исследовать поведение и вид ряда Лорана в окрестности
особой точки z = 0 функций:
ч sin? ,ч sin? , . ,
а) ; б) , л>1; в) ez .
z ?"
D Так как особая точка z - 0 - конечная особая точка, то в разложениях в
ряд Лорана этих функций главную часть ряда образует совокупность членов с от-
отрицательными степенями, а правильную - с неотрицательными. Пределы для
первых двух функций рассмотрены в примере 3.36, а для третьей - в приме-
примере 4.1.
а) Особенностью ряда для функции является отсутствие
Z
главной части в разложении ее в окрестности точки z = 0 - особой точки
этой функции; особенностью поведения функции в этой точке - существование
,. sin? .
конечного предела hm = 1.
г-»0 z
б) Для функции —— в соответствующем разложении главная
?
часть содержит одно слагаемое, а предел функции равен бесконечности,
si
—
г
функции :
Z"
sin? 1 1 (-1)Л+У-1
слагаемых: = —; - + ... + -—■ + ... и функция может
Zn z 3!?"~3 Bл-1)!
быть записана в виде
.. sin? „ . ,
hm—— = °o. Этот результат можно обобщить: главная часть разложе-
разложения функции —— ,л>1 по степеням z содержит конечное число
.. sin? ,
а поэтому hm = °о, л > 1.
г-»0 in
в) Разложение функции еz , как и еz , в окрестности точки z = О
содержит бесконечное множество членов в главной части. Пределы этих функ-
функций в точке ? = 0 не существуют (пример 4.1). ■
Эти простые примеры показывают, что поведение функции в особой
точке связано с видом главной части ряда Лорана: трем отмеченным выше
случаям нахождения предела функции в точке ?0 соответствуют три различных
случая вида главной части ряда Лорана в окрестности точки. В примере 4.2
исследовалась конечная особая точка. Такой же результат можно получить, рас-
\_
сматривая точку ? = ю, например, для функций ez, z2 +— и ez.
?
В зависимости от трех случаев поведения функции в особой точке
(исследования lim /(?)) особые точки функций делят на три типа - произво-
236
дится классификация особых точек. В качестве определения типа особых точек
можно выбрать либо поведение функции в особой точке, либо вид ряда Лорана.
Выберем первый подход.
Изолированная особая точка zo еС функции /(г) называется:
- устранимой особой точкой, если
lim /(?) существует и конечен; D.1)
- полюсом, если
Urn /(?) = » ; D.2)
- существенно особой точкой, если
lim /(?) не существует . D.3)
Замечание 4.1. Если в случае устранимой особой точки ?0 поло-
положить /(го)= lim /(z) , то /(?) будет аналитической в 0&(Zq) и точку ?0
можно считать правильной, т.е. не особой. В этом случае говорят, что в точке ?о
устранена особенность.
Пример 4.3. Определить тип особой точки г = 0 для функций
1 J.
sin? sin? . 1ш г2
Z ' z" '
О На основании результатов решения примеров 4.1, 4.2 заключаем,
что z = 0 является устранимой особой точкой функции ; полюсом
для —— при любом л>1; существенно особой точкой для функций ег
ne'.l
Пример 4.4. Определить тип особой точки ? = ю для функций
1
}■ □ Рассмотрим lim f(z)■ Для удобства введем обозначение — = %. Для
г-»» Z
функции /j(?) получим lim/i(z)= lim—- = к (л>1) (см. пример 4.2), по-
этому г = 00 является полюсом функции f\(z) = Zn sin-, л>1. Для функ-
функции /2(г) = ez точка г = ю является существенно особой, так как
I
Hmez = lime!' не существует (см. пример4.1).
г» 4>0
237
Пример 4.5. Найти все конечные особые точки функций:
а) /i(г) = —т—; б) /2(г) = —т и определить их тип.
7+1 ■ '
*• sin —
г
D Особыми точками дробей являются особые точки числителя, осо-
особые точки знаменателя и нули знаменателя.
а) Так как числитель и знаменатель функции /j (г) - функции анали-
аналитические, то ее особыми точками являются только нули знаменателя, т.е.
%+2кж.
корни уравнения г4+1 = 0. Это четыре точки Zk=e 4 , к = 0,1,2,3 , или
Jj «/2 V2
в алгебраической форме: Z\ =—A + 0. Z2 =—(-1 + 0. ?з =—(-1-0.
?4 =—A-0- Заметим, что точки расположены в вершинах квадрата,
вписанного в окружность радиуса R = 1 с центром в начале координат,
и справедливы равенства т,2 = ii\, Z3 = -Z\, Z4 = ?i •
Очевидно, все точки изолированные и являются полюсами, так как
lim /i(z) = м для любой точки Zk . Л = 1 , 2 , 3 , 4.
б) Особыми точками функции /2(г) являются нули знаменателя,
т.е. точки, для которых — = кп или Zt = —, Л = ±1,±2,..., а также z = 0 -
г* кп
особая точка знаменателя. Точки Zk являются полюсами, так как lim /2(г) = °°-
Точка z = 0 - неизолированная особая точка функции, так как в любой ее
окрестности \z\<r (г- любое число, г > 0 ), кроме этой точки, располо-
расположено бесконечное множество особых точек вида Zk = —, £ = ±1,±2,...
кп
Точку z = 0 в таком случае называют предельной точкой полюсов г* = —,
кп
так как lim Zk =0.>
Для исследования поведения функции в существенно особой точке имеют
место следующие две теоремы [5,25,40].
Теорема 4.1 (теорема Сохоцкого). Если Zo - существенно особая точка-
функции f(z), то для любого А еС существует последовательность {zn},
сходящаяся к точке Zq , такая, что lim /(?„) = А.
Л->со
Теорема 4.2 (теорема Пикара). В любой окрестности существенно особой
точки функция f(z) принимает любое значение (причем бесконечное число
раз) кроме, быть может, одного.
238
Пример 4.6. Исследовать поведение следующих функций в существен-
существенно особых точках, проиллюстрировать теоремы Сохоцкого и Пикара:
ez\ *o=O; б) /3(г) = ez, z0 =».
D В примерах 4.3 и 4.4 показано, что точки го =0 и г0 =°° являются
существенно особыми точками соответствующих функций. Исследуем пределы
функций.
а) Для иллюстрации теоремы Сохоцкого выбираем А = 0 и А = ю.
]_
Используя результат примера 4.1, имеем lime* =0 , если z-x, х<0,и
г->0
lim е* =ю, если z = х, х > О, т.е. lira /ife) = 0 для последовательности zn=xn,
г-»о л-»°о
такой, что lira х„ =0 и х„ <0, и lira /,(?„) = оо для последовательности
zn =хп, такой, что lira хп = 0 и х„ > 0.
Аналогично исследуем функцию /2(г). Для числа Л = 0 выбираем
zn=iyn, П№ Ит}>„=0 и тогда Ига/2(г„) = 0 , а для Л = оо выбираем
/J-+GO Л-*0О
гл = хя, где lim дг„ = 0 и тогда lira f2(zn) = ».
Справедливость теоремы Пикара для этих функций следует из
I -L
{иссмотрения уравнений ег=^, ег =А , которые, как известно, имеют
бесконечное множество решений для любого А е С , Л * 0.
Например, для функции f\(z) = ez имеем ег =А. Отсюда получаем
1пЛ 1
win
Ы| + i(aigу4
Z Z
В частности, функция е1 в любой" окрестности точки го=О при-
принимает значение Л = 1 бесконечное множество раз: в точках Zk = >
2kit
Л=±1,±2...(рис. 4.1).
239
(Z)
У*
Рис. 4.1
б) Точка z = оо является существенно особой точкой функции ег (пример
4.4). Обозначив z = - , можно повторить рассуждения предыдущего пункта
для функции
и точки £ =
Упражнения
1. Найти все конечные особые точки функций:
Ответ: а) ц = -1, Z2 = ', ZiA =^±-J''' Zs>6 = ±~~''"l'
6) zk=\-+2kn\i, Jfc=0,±I,...; zm = 2mti, m = 0,±l...
2. Определить тип конечных особых точек для функций из упражнения 1.
Ответ: все конечные особые точки - полюсы.
3. Определить тип точки z = °о для функций из упражнения 1.
Ответ: а) устранимая особая точка; б) неизолированная особая точка.
4. Для каких из следующих функций точка z - 0 является полюсом:
240
Ответ: Mz), f2(z), Mz)-
5. Для каких из следующих функций точка z = 0 является устранимой осо-
особой точкой:
/(*) 'Ж) /(г) Л(г) -
е1 -1 ez -1 е -1 ег -1 + г
: /,(г), /3(г), /4(г).
6. Найти все конечные особые точки функций, определить их тип:
Ответ: а) г = 1 - полюс; б) г = 0 - существенно особая точка,
Z = 2Ы, к * 0, - полюсы.
7. Для каких из следующих функций точка z = 0 является существенно
особой точкой:
Ответ: /2(г),/4(г)-
8. Определить тип точек z = 0 и z = °° для функций из упражнения 7.
Ответ: z = 0 - полюс для /j(z) и /3(г) и существенно особая точка для
/2(г) и/4(г); г = °° - полюс для /2(г) и /4(г) и существенно особая точка
для /,(г) и /3(г).
4.1.2. Ряд Лорана в окрестности особой точки
В предыдущем разделе на примере простых функций (см. пример 4.2)
было высказано предположение, что вид ряда Лорана в окрестности осо-
особой точки зависит от типа особой точки и потому задача исследования
функции в особой точке может быть сведена к исследованию соответст-
соответствующего ряда Лорана . Подтверждением этого предположения в общем
случае является доказательство соответствующих утверждений [3,25] .
Утверждение 4.1.
1. Для того чтобы особая точка функции была ее устранимой особой
тонкой, необходимо и достаточно, чтобы в разложении функции в ряд
Лорана в окрестности этой точки отсутствовала главная часть. Это озна-
означает, что если Zo - устранимая особая точка, то ряд Лорана функции f(z)
имеет вид
£св(г-го)", 0<\z-z0\<r D.4)
для Zo - конечной точки Zo e С, и
241
c0 + fi±f, R<\Z\<oo D.5)
n=I Z
для zo - °° •
2. Для того чтобы особая точка функции была полюсом, необходимо
и достаточно, чтобы главная часть ряда Лорана функции в окрестности
этой точки содержала конечное число членов.
Ряд Лорана функции f(z) в случае г0 полюса имеет вид
Z \o\<r, D.6)
если Zo eC, и
f(z)= £ckzk, R<\z\<°° , D.7)
если zo - °° •
3. Для того чтобы особая точка функции была ее существенно особой
точкой, необходимо и достаточно, чтобы главная часть ряда Лорана
функции в окрестности этой точки содержала бесконечное число членов.
Ряд Лорана функции f(z) в случае Zo - существенно особой точки имеет
вид
f(z)= £с„(г-?„)", O<\z-zo\<r, D.8)
если Zo eC, и
№= £сп1п, R<\z\<*, D.9)
л=-°о
если Zo = °° •
Замечания 4.2.
1. Номер старшего члена главной части ряда Лорана функции в ее
разложении в окрестности полюса называется порядком нолюса.
Так, точка zo^C является полюсом порядка п ( Щи) ) функции
f(z), если в разложении D.6) с_„ * 0 , ск = 0 при к <-п.
Точка Zo = °° является полюсом иорядка п ( Щи)) функции f(z) ,
если в разложении D.7) с„ * 0 , ск = 0 при к > п.
2. Главная часть ряда Лорана в случае нолюса порядка и записыва-
записывается следующим образом:
"' " с
а) в случае zo^C в виде Yck(z-Zo)" . или У, ^Т >
к--. k=i(z-zo)k
или, подробнее:
С С1 £! с „о; D.10)
242
б) в случае ?0=°о в виде Y_cnz > или S * (см-D-7)) ,
или, подробнее:
l е„*0. D.11)
3. Главная часть ряда Лорана в случае существенно особой точки записы-
записывается так:
-1 » с_
а) в случае zo^C в виде Yc^z-Zq)" , или У 2— (см.D.8)),
«-о» л=1(г-го)"
или, подробнее:
D.12)
-1 с х
б) в случае го=0° в виде £ -=s- или £с„г" (см.D.9)),
л=-оо Z п=\
или, подробнее:
2... + с„г"+... D.13)
Пример 4.7. Определить тип особых точек функций:
а)Ш= / + 2 ; б) /2(г)= ^2 ■
Г-2г-3 (г + 1J(г - 3)
□ Особыми точками функций являются z\ = -1, Z2 = 3, £3 = °° • Чтобы
определить тип особой точки, используем разложения функций в окрестности
каждой точки, полученные в примерах 3.31 , 3.33 , 3.34.
a) f.(z) = —'-2-- Y-i—J— t 0<k + l|<4 . В главной части разложения
г+1 «То 4"+2
-1/ j
один член ряда: —— , здесь с. = — ^0 , все с„=0 для п<-1.
г + 1 4
Следовательно, в точке г = -1 - полюс первого порядка, т.е. простой полюс
функции /,(г).
у А оо (_ПЯ + 1
у А оо (_ПЯ + 1
Аналогично из разложения fi(z) =-^-*-+ Y^ г (г-3)", 0<|г-3|<4
2~3 я=0 4"+
получим такой же результат: точка г = 3 - простой полюс функции /j (г).
00 (— П" + S • 3""' 1
Разложение /|(г)=У^— '■ .к|>3 функции в окрестности
«и 4 г"
г = да не содержит главной части - разложение имеет вид D.5). Следова-
Следовательно, точка z = «| - устранимая особая точка функции /, (г).
243
б) Из разложения /2(z) = —+У( 1)"*'(" + 6)(г-3)", 0<lz-3|<4
г-3 „to 4Я+3 ' '
следует, что г = 3 -простой полюс функции
Из разложения /2(г) = -*& + —^- + f " 5(^+31) , 0 < |г +1| < 4 , где
и все с„=0 для и<~2 .получаем, что z = -\ - полюс вто-
второго порядка функции f2(z)-
Разложение f2(z) в окрестности z = °° не содержит положительны)
степеней, в чем можно убедиться, проанализировав разложения элемен-
элементарных дробей (см. пример 3.34). Поэтому z = °° - устранимая особая
точка функции /2(г) •■
Пример 4.8. Определить тип конечных особых точек для функций:
i
, 7 . 1 1 ,. Sin Z 1 - COS Z
а) е' , sin , cos ; б) , —.
Z-a z-a z" Z
D а) Используем разложения функций по степеням (z-a):
1 _. 1 1 1
Убеждаемся, что для всех указанных функций точка z = а является
существенно особой точкой, так как в разложениях главная часть содержит
бесконечное число членов, т.е. имеется бесконечное число членов с отрицатель-
отрицательными степенями (см. п.1 утверждения 4.1).
б) Запишем разложения функций по степеням z :
smz_ I L zl. )_ 1 1 . .
2! 4! JJ l\z 4!
Для первой функции при и = 1 в разложении отсутствует главная часть -
совокупность членов с отрицательными степенями. Следовательно, согласно п.1
утверждения 4.1, точка г = 0 для является устранимой особой точкой.
Z
При и > 1 главная часть разложения содержит конечное число членов, по-
поэтому точка z = 0 для является полюсом (см. п.2 утверждения 4.1). Кроме
z"
того, так как при п > 1 в разложении старшая отрицательная степень равна
(я -1) , то, согласно п. 1 замечаний 4.2, заключаем, что г = 0 для при
z"
244
я > 1 является полюсом порядка(и-1). Рассуждая аналогично, получаем, что
Z = О является полюсом первого порядка - простым полюсом для функции
l-cos; в
г3
Сравнивая разложения функций по степеням z в окрестности
го=О (формулы D.4),D.6),D.8) при го=О)и ? = °о (формулы D.5), D.7),
D.9)), можно сделать следующее заключение.
Утверждение 4.2.
1. Чтобы z = °° была устранимой особой точкой функции f(z), необ-
необходимо и достаточно, чтобы точка \ = О была устранимой (или не особой)
для Ф(^ =
2. Чтобы z = °° была полюсом порядка и функции f(z) , необходимо и
достаточно, чтобы точка {, = 0 была полюсом порядка п функции
3. Чтобы z = °° была существенно особой точкой функции f(z) , необ-
необходимо и достаточно, чтобы точка {, = 0 была существенно особой точкой
функции ф(£) /
Замечание 4.3. Как и в случае конечной особой точки zo ,
в которой функция не определена, но lim f(z) = 0 (см. утверждение 3.5) ,
г-»*о
так и для z = «| в случае lim f(z) = 0 , устранимую особую точку z = »
можно считать нулем функции /(г). Порядок нуля можно определить как
порядок нуля функции фD) в точке % = 0.
Пример 4.9. Исследовать точку z = °° для функций:
а) /(?) = -=-!—; б) /и) = -Ц±Ь, в)
г2(г-2) k зг2-2
Ц, ) /()
зг2-2 г
□ Для определения типа особой точки рассмотрим пределы lim f(z) ■
г-» оо
Ч7 а) Так как lim f(z) = 0 , то точка z = °° - устранимая особая точка
Z -юс
функции. Доопределяя ее /(<») = 0 , получим, что z = » - нуль функции.
Определим порядок нуля. Сделаем замену % = — и рассмотрим функцию
z
\\ I2 Е3
- = -р— , т.е. ф(^) = —2— . Так как % = 0 является нулем третьего
порядка функции ф(^) , то z = <*> - нуль третьего порядка для f(z).
245
б) Точка г = да является устранимой особой точкой, так как
— 1
,2+1 1 (Л Е2+ 1 + £2
lim —: = - . Заметим, что для функции / - = ■* , т.е. <рD) = ■Чг ,
г-*Зг2-2 3 \£) Ъ__2 3-2^2
точка % = О не является особой.
в) Точка z = °° является устранимой особой точкой и для этой
функции, так как £ = 0 - устранимая для <р(^) = -—^ . ш
Упражнения
1. Определить тип особой точки z = 0 для функций:
-\ 2
1 ег +1 1 -. ,/ \
)=—; ; б)/(г)=
3 г
г3
Ответ: а) полюс третьего порядка; б) полюс второго порядка.
2. Для каких из следующих функций точка z = 0 является существенно
особой точкой:
3. Определить тип особых точек z = 0, z = °° для функций из упражнения 2.
Ответ: z = 0 - простой полюс для f{(z); полюс второго порядка для /3(?)
и существенно особая точка для fi(z) и /4(z); z = <*> - устранимая особая точка
Л1 /г(^) и ЛОО и существенно особая точка для fx(z) и /з(г).
4. Для каких из следующих функций точка г = О является устранимой осо-
особой точкой:
az 1 ог I о7- 1 »г _ 1 _ 7
/M = £_li /■ (-) _ е ~ ' / (-) _ ~ / (;) _ Z ?
г z z2 z
Ответ: /,(г),/2(г),/4(г).
5. Определить тип особых точек z = 0 и г = да для функций:
н— ; б) /(г) = sin .
z) z z
Ответ: для обеих функций z = 0 - существенно особая точка, a z = <*> -
устранимая особая точка.
6. Для каких из следующих функций точка z = 0 является полюсом второго
порядка
9
О/иве/и: /2(г),/3(г).
246
7. Для каких из следующих функций точка z = 0 является полюсом первого
порядка:
,() Ю? ,()
г г г2
Ответ: /|(г).
8. Определить тип особой точки г = 1 для функций:
Ответ: а) полюс третьего порядка; б) полюс первого порядка.
9. Определить тип особой точки z =i для функций:
г
a) f{z) = г cos—; б)/(?) =—.
Ответ, а) и б) - существенно особая точка.
10. Определить тип конечных особых точек функции:
Ответ: z = -1 - существенно особая точка, z = -7 - полюс первого порядка.
4.1.3. Правила определения порядка полюса
Используя формулу D.6) разложения функции в ряд в окрестности
полюса, можно получить практически удобные правила определения поряд-
порядка полюса, не требующие записи разложений в ряд в каждом конкретном
случае.
Пусть zq (го еС)-полюс порядка и (Щи)) функции f(z). Раз-
Разложение D.6) , где главная часть имеет вид D.10) , преобразуем следую-
следующим образом: f(z)= -[с_„ +с_„+, .(z-Zo) + ... + co(z-zo)n +■■■] или
(г-го)
f(z) = —2L2— ) Где ф(г). функция, аналитическая в точке г0 , как
(г-го)"
сумма степенного ряда, записанного в скобках, и
1 G — 7 )"
Далее рассмотрим функцию F(z) = , т.е. F(z) = ~ или
f(z) ф(г)
F(z) = (z-Zq)"<?\(z) , где ф)(г) - аналитическая в точке г0 и
Из этого, согласно утверждению 3.5, следует, что Zq является нулем по-
порядка и функции F(z)- Можно доказать и обратное утверждение.
247
А именно, если функция представлена в виде /(г) =—^^—, где
(г-го)"
<р(г) - функция, аналитическая в точке го, и ф(го)*О, то го-полюс поряд-
порядка п функции /(г), а также, если го - нуль порядка п функции F(z),
то для функции f(z) = эта точка является полюсом порядка и.
F(z)
Кроме того, как и в разд. 3.2.2, рассмотрим частное /(г) = ' ,
/г (г)
где точка го является нулем порядка к для функции /,(г) и нулем по-
порядка т для функции /г(г), т.е. /(г)=- При т > к полу-
(г-го)тФ2(г)
чаем f(z) = —-"-^—г> из чего, с учетом приведенных выше рассуждений,
(z-zo)m-k
находим, что г0 - полюс порядка (т-к). Заметим, что при т-к точка
Zo - устранимая особая точка; случай т < к рассмотрен в разд. 3.2.2.
Результаты приведенных рассуждений запишем в виде утверждения.
Утверждение 4.3.
1. Для того чтобы точка г0 была полюсом порядка н функции f(z),
необходимо и достаточно, чтобы ее можно было записать в виде
f(z)= Ф(г) , <p(Zo)*O. D.14)
(z-zo)"
2. Для того чтобы точка zq была полюсом порядка и функции f(z),
необходимо и достаточно, чтобы она была нулем порядка п функции
(связь нулей с полюсами).
f(z)
3. Если точка го является нулем порядка к функции /)(г) и нулем
порядка т функции А (г) (т > к), то она - нолюс порядка (т-к) для
Пример 4.10. Определить порядок полюсов функций из примеров:
а) 4.7 ; б) 4.8.
г+2 г+2
7+1 7-3
□ а) Функцию /|(г) запишем в виде fi(z)=-^— и Mz)=- , т.е.
г-3 г+1
в виде D.14) , из чего заключаем, что обе особые точки г = 3 и г = -1
- простые полюсы.
г + 2
Для функции /2(г) из /2(г)= z~ находим, что г = -1 -полюс
(г +1)
г + 2
второго порядка, а из f2(z)=- '—следует: г = 3-простой полюс.
248
sin z 1 ~~ cos 7
б) Для функции , и>1, и г—- формула D.14) не при-
применима, так как ф@) = 0. Воспользуемся п.З утверждения 4.3. В случае
, sin ^ , п
функции , п > 1, точка z = О является нулем первого порядка для чис-
z"
лителя и нулем порядка и для знаменателя (см. разд. 3.2.2) Поэтому она
С1Г| jr I __ Ofl^ 7
- полюс порядка (и -1) для дроби , и > 1. Для функции ;—
z" zi
точка z = 0 - простой полюс, так как она нуль второго порядка для чис-
числителя и нуль третьего порядка для знаменателя (см. разд. 3.2.2). ■
Замечания 4.4.
р (z\
1. Так как конечными особыми точками рациональной дроби явля-
Qm(Z)
ются только нули знаменателя, то это либо полюсы, либо устранимые особые
точки функции.
2. Такое же заключение можно сделать и для функции вида f(z) = ,
Qm\Z)
где ф(г) - аналитическая функция. При этом, используя определение устрани-
устранимой особой точки D.1) и правила определения порядка нуля и полюса
(утверждения 3.5 и 4.3), можно сделать следующие выводы относительно особой
точки г0 ~ нуля порядка к [0(/t)] знаменателя:
а) zo - полюс порядка к функции f(z), если <р(го) * 0;
б) го - полюс порядка (к-п), если г0 - нуль порядка п функции ф(г)
и к > п;
в) го - устранимая особая точка функции /(г), если г0 - нуль порядка к
функции ф(г);
Г) £о " НУЛЬ порядка (п-к) функции f(z), если г0 - нуль порядка п
функции ф(г) и п > к; при этом полагаем f(zo)= lim f(z) = 0.
г->*о
Пример 4.11. Найти конечные особые точки следующих функций и опре-
определить их тип:
□ Конечными особыми точками этих рациональных дробей являются нули
знаменателя. Чтобы для каждой их этих точек определить, является ли она по-
полюсом или устранимой особой точкой, нужно, согласно определению, найти
предел функции в этой точке. В случае полюса, т.е. когда lim f(z) = °°, далее
г-»*о
следует определить его порядок. Для этого используется утверждение 4.3.
Можно поступить иначе - согласно замечанию 4.4. Для этого нужно найти
и нули числителя.
249
а) Особые точки функции Z\=U Z2=~2- Для точки zi =-2 можно при-
щ/у\ 7 — А? + 3
менить формулу D.14) и из /(г) = ., где <р(г) =— — и ф(-2) *0, по-
(г + 2J {z-\f
лучить, что эта точка - полюс второго порядка. Для точки z\ = 1 формула D.14)
z2 - 4z + 3
не применима, так как из ш(г) = — имеем фA) = 0. Поступаем далее со-
U + 2J
гласно замечанию 4.4. Раскладываем на множители числитель и записываем
(г-3) =
2 (z-\J
Z = 1 - полюс второго порядка для f(z).
б) Особые точки функции - корни уравнения г3 + 8г = 0, т.е. z = V^8? или
6+ 3 > fc 012 Все эти точки: Z2 i
функцию f(z) = k-y-3) = (г-3) = jpUL A) „ о . Получаем, что
(l)\ 2J AJ( 2J (\J
, fc = 0,1,2.. Все эти точки: Zj=2— -i- , г2=2/,
= 2 /- - простые нули знаменателя, и так как числитель в этих точках
не обращается в нуль, то они - простые полюсы функции f(z) M
Пример 4.12. Найти конечные особые точки следующих функций и опре-
определить их тип:
?J+8/
□ Рассуждаем и производим действия, как в предыдущем примере. Заме-
Заметим при этом, что в случае "б" в отличие от предыдущего примера особая точка
Z = Ъ является нулем числителя.
а) Раскладываем числитель и знаменатель на множители, записываем
функцию /(?) = ^ 2 ' Получаем: Z\ = 1 - простой полюс функции
/(г); Zi = 3 - полюс второго порядка.
б) Конечные особые точки функции: Z\=sh-i, zi=2i, zi =-4l-i\
функцию записываем в виде /(г) = ■: г^—тт г. Получаем: г = 2г - уст-
устранимая особая точка, так как lim /(г) * <о, а точки z\ и z-r- простые полюсы."
г->2/
Пример 4.13. Найти конечные особые точки функций и определить их тип:
О Конечными особыми точками этих функций вида f(z) = , где ю(г)
04 (г)
- аналитическая функция, являются только нули знаменателя.
250
а) Особые точки функции: Z\ =—, li =—, гз =V3i, Z4 =-V3/. Точки гз
и ц - простые полюсы, так как числитель в этих точках не обращается в нуль и
функцию можно представить в виде /(г) = , (р(го)*О. го - точка гз или
г-го
г4- В точках г = ±- числитель обращается в нуль. Очевидно, это простые нули
числителя, и поэтому его можно записать в виде cos яг = (г-го)-ф(г),
го - точка г] или г2 • Тогда для функции /(г) получаем
Так как lim /(г) * °° для го = 1\ = ~ или го = гг =—> то эти точки - уст-
г->го 2 2
ранимые особые точки функции /(г).
б) Особые точки функции: г^ = ±1 > гз,4 = ±( • Точки гз =' и г4 = - /' -
простые полюсы.
Для точек г] = 1 и гг = -1 проводим рассуждения, как в предыдущем
пункте, и находим, что они - устранимые особые точки /(г) • ■
Пример 4.14. Определить тип особой точки г = 0 для следующих функций:
)/() ^ )/() |Ц
ег -1 г -sin2г2
□ В точке г = 0 и числитель, и знаменатель каждой из функций обраща-
обращается в нуль. Определим порядок нуля в каждом случае и используем п. 3 утвер-
утверждения 4.4.
а) Из разложений по степеням г функций
е<5-1=
+...|1 г+
2! J 2!
находим, что г = 0 - нуль второго порядка для числителя @B)) и нуль пятого
порядка для знаменателя @E)). Следовательно, г = 0 - полюс третьего порядка
для /(г).
б) Используя правила определения порядка нуля, в частности, как и в пре-
предыдущем пункте, раскладывая функции в ряды по степеням г , находим, что
г = 0 является 0B) для числителя и 0G) для знаменателя. Следовательно, г = 0 -
полюс пятого порядка для /(г) .■
251
Пример 4.15. Найти конечные особые точки следующих функций и опре-
определить их тип:
a) /(г) =Jr—\ б) /(г) = j-2-.
^ — 10 Z -Sin Z
П Конечными особыми точками функций, как и в предыдущих примерах,
являются нули знаменателя.
а) Особые точки функции - корни уравнения г4-16 = 0, или
(г2 -4)(г2 +4) = 0, т.е. ц^ = ±2, гз,4 =±2i. Эти точки - простые нули знамена-
знаменателя, а поскольку числитель не обращается в нуль (ег * 0), то все они - простые
полюсы функции.
б) Особые точки функции: го =0 и Zk =кп, к = ±1,±2,.... Точка го =0 яв~
ляется нулем третьего порядка знаменателя, a zk =кк, к ф 0 - нули второго по-
порядка. Так как в точках г* = к%, к *0, к *-\ числитель в нуль не обращается,
то эти точки - полюсы второго порядка для /(г). Точки го=О и г = -я являют-
являются простыми нулями числителя, поэтому г = 0 - ПB), г = -я - Щ1) Для /(г)- ■
Пример 4.16. Определить тип особой точки г = 0 для следующих функций:
а)/(г)= ""* %; б)/(г) = -
г г
cos г -1 ch z -1
в)/(г) = ""* * ,; г)/(г) = -
г г
cos г -1 + — ch г -1 + —
□ Точка г = 0 является нулем и знаменателя, и числителя для каждой из
функций. Определим порядок нуля в каждом случае, используя правило опреде-
определения порядка нуля (утверждение 3.5), в частности, раскладывая соответствую-
соответствующую функцию по степеням г.
а) Из разложений
.£+ lz-^Л,
3! "I 3! 5!
находим, что г = 0 является 0C) для числителя и 0B) - для знаменателя, поэтому
она - устранимая особая точка. Так как
()
lim /(г) = lirai —^ ; f = 0,
252
то, полагая /@) = 0, можно считать, что г = 0 - нуль для /(г), причем 0A) (см.
замечания 4.4).
б) Из разложений
,3 2 f _2 4 ^ 2 4 6
1 ^^LI jL LL
2г_1_+... „ chz^^++ + ..j^ +
находим, что z = 0 является 0A) для числителя и 0D) - для знаменателя. Поэто-
Поэтому г = 0 - полюс третьего порядка для /(г).
в) Как и в предыдущих пунктах, находим, что г = 0 является 0C) для чис-
числителя и 0D) - для знаменателя. Поэтому г = 0 - простой полюс для f(z) ■
г) Точка г = 0 является простым нулем числителя, нулем второго порядка
для знаменателя. Следовательно, это простой полюс для /(г) • ■
ОПРЕДЕЛЕНИЕ ПОРЯДКА ПОЛЮСА В БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКЕ
Рассмотрим бесконечно удаленную точку. Тип особой точки можно опре-
определить, вычисляя lim /(г) или раскладывая функцию в ряд Лорана (см. приме-
ры 4.4, 4.7). Можно свести задачу к исследованию конечной точки \ = 0 - =
(см. утверждение 4.2 и пример 4.9). В двух последних случаях определяется и по-
порядок полюса.
Практически удобное правило определения порядка полюса вг = «> можно
получить, используя п. 2 утверждения 4.2 и правила определения порядка полюса
в конечной точке (утверждение 4.3). Действительно, пусть z = <*>- Щп) для
функции /(г), тогда \ = 0 - П( и) для / — и можно записать
, /■(!;)*0 (см. D.14)). Поэтому, обозначив F[-] = <p(z), ДЛЯ /(г)
получим
ИтФ(г)*0, lim <p(z) *«• D.15)
Представление функции в виде D.15) является необходимым и достаточным
условием полюса порядка п функции f(z) в точке z = «>. ■
Замечание 4.5. Используя формулу D.15), нетрудно убедиться, что ес-
если г = °° - Щи) для /)(г) и П(£) для /г(г), то z = °°- полюс порядка (т-к)
для функции f(z) = -r . . ■
J2\Z)
Пример 4.17. Определить тип особой точки z = » для функций:
= г2(г-2); б) f{z) = z +* *'•
253
□ Так как lim f(z) = °° в обоих случаях, то z = °° для данных функций -
полюс. Определим порядок полюса.
а) Точка z = °° является полюсом третьего порядка, в чем можно убедиться
любым из следующих способов.
Первый способ. Разложение функции по степеням z имеет вид
f(z) = z -2z, C3 *0, все с„ =0, и>3, и по определению (см. формулы D.7),
D.И)) заключаем, что z = °°- ПC).
Второй способ. Обозначим z =—, получим функцию / — =—-2-, для ко-
\ \\) i?
торой \ = 0 - ПC) . Поэтому, согласно п. 2 утверждения 4.2, точка z = °° - ПC)
для /(г).
Третий способ. Запишем функцию в виде /(г) = г3- 1— и, так как
Ч Z)
функция ф(г)= 1— удовлетворяет условиям формулы D.15), получим, что
г = °о-ПC) для /(г).
б) Разложение функции в ряд по степеням г представляет некоторые труд-
трудности. Используем другие способы.
1 (\\ (?5+Е3 + 1)-?3
Первый способ. Обозначим z = —, получим / — = Lr3—, или
/-= " , ,т.е. / - =, . q*0)*0. Поэтому £ = 0 является ПB) для
UJ ^-A-2^2) UJ ^2
/ — и, следовательно, z = °° - ПB) для /(г).
5
Второй способ. Представим функцию в виде /(г) = ^—р г-^- или
{)
1
/(г) = г2 ф(г), где lim ср(г) = 1, и, согласно формуле D.15),г = »- ПB) для /(г).
Третий способ. Используем замечание 4.5. Можно определить порядок по-
полюса z = °° для дроби ' , зная соответствующие порядки полюсов числителя
/(г)
и знаменателя. Здесь, очевидно, z = °° - ПE) для числителя и ПC) - для знамена-
знаменателя (см. формулы D.7), D.11)). Поэтому г = °° - ПB) для f(z). ■
Пример 4.18. Определить порядок полюса в точке z = <*> для следующих
функций:
а)/(г) =
г2-1
254
□ Первый способ. Запишем разложения в ряд по степеням z '■
4 а) Л^) = г3 -—Ц- = г2-Г1+- + .-] = г2 + г + 1 + -,
1 I )
•« б) 4V
Из разложений следует, что z = °° - ПB) для каждой из заданных функций.
Второй способ. Обозначим z = — и определим порядок полюса функции
/ — в точке \ = 0:
В каждом случае получаем представление функции в виде / - =
UJ
следовательно, % = й -11B) для / - . Поэтому г = » - ПB) для f(z).
Третий способ. Представим функции в виде D.15):
г г z
w' б) /(г) = -f-j- = г2 • ^-j- или /(г) = г2 • —L- = г2ср(г), ср(г) = —^-.
"'" z2 z2
' Так как ср(г) удовлетворяет условиям формулы D.15), то заключаем, что
z = * - ПB) для /(г).
Четвертый способ. Используем замечание 4.5, сравним порядки полюсов в
г3 г4
точке z = °° для числителя и знаменателя дробей f(z) = и /(г) = -:—. Для
г-1 г2-1
первой функции г = °°- ПC) для числителя и ПA) для знаменателя; для второй
Z = оо - ПD) для числителя и ПB) для знаменателя. Следовательно, для каждой
из функций z = °° - ПB). ■
255
Упражнения
1. Найти конечные особые точки следующих функций. Определить их тип
а) f(z) = :—5 ; б) f(z) = —:—-, г—•
г sin z z (z -1)
Ответ: a) z = 0 - простой полюс; Zk = кп, к * 0 - полюсы второго порядка
б) Z\ = 0 и ^2,3 = ±'>^4,5 = ±'° - все точки полюсы третьего порядка.
2. Определить порядок полюсов следующих функций:
(e2z -IJ tg5z(z4 + l6)
Ответ: a) z = 0 и Zt - — + кп - простые полюсы; z = kni,к = ±1,±2.. - по-
полюсы второго порядка;
(я кп\.
—+— i
б) z = 2е^4 2' ,к = 0,1,2,3 - простые полюсы; г = 0 - полюс второго поряд-
порядка; z = кп, к = +1,+2.. - полюсы пятого порядка.
3. Найти все особые точки следующих функций. Определить их тип:
а) /(*)=Z3+- + sin—; б) /(z)=z2cos-; в) f(z) = zisin-.
Ответ: a) z = 0 - существенно особая точка, г = °° - полюс третьего по-
порядка;
б) в) z = 0 - существенно особая точка, г = °° - полюс второго порядка.
4. Определить порядок полюсов следующих функций:
sin2k + l) , (z-nJ
а) /(г)= 3 2 2; б) ^ ^^—
Ответ: а) г = 1 - полюс пятого порядка;
б) г* = — + /с—,к = 0,±1,..; zm =е^ 8 г> ,/я = 0,±1,.. - простые полюсы.
5. Определить порядок полюсов следующих функций:
Ответ: а) г = ' - полюс первого порядка, г = -»' и г = °° - полюсы второго
порядка; б) z = °о - полюс первого порядка.
6. Определить порядок полюсов следующих функций:
256
Ответ: a) zt = — + kn,k = ±1,.. - полюсы четвертого порядка, z = — полюс
4 4
третьего порядка;
• б) Zk = — + 2кп \i, к=0,±\.. - полюсы второго порядка, г = 0 и
= — + /ял - простые полюсы.
7. Определить порядок полюса г = 0 следующих функций:
.)/fc)-£dbi; б)/(г) = ^Ц..
ог _ I г
sh г - г —
6
Ответ: а) полюс третьего порядка; б) простой полюс.
8. Определить тип конечных особых точек функций:
-; б) /(*)=■
Ответ: а) г = — полюс второго порядка, г = 0 - простой полюс;
б) Zk = Ы,к = +1,.. - простые полюсы, z = 0 - полюс второго порядка.
9. Определить тип конечных особых точек функций:
; б) /(г)
Ответ: a) z = 1 - полюс первого порядка; б) г* = (л + 2fat)/' - полюсы вто-
второго порядка.
4.1.4. Определение типа особых точек для суммы, разности,
произведения и частного функций
Пусть ^о" особая точка функций /|(г) и /2(г) и тип особой точки
для каждой из функций известен. Требуется определить тип особой точки
для функций /,(г)±/2(г) ;/ife)-/2(z) ; /,(г)//2(г).
Рассмотрим следующие случаи.
Первый случай. Пусть точка го является полюсом порядка т (П(/я))
для функции /|(z) и полюсом порядка к(Щк)) для функции /2(г).
а) При исследовании суммы f(z) = /iU) + /2(z) воспользуемся формулой
(п.1 утверждения 4.3) и запишем слагаемые в виде
-го) (г-го)
9 Пантелеев А.В., Якимова А.С.
При к = т для суммы f(z) = /, (г) + /2(г) получаем Л г) =
(г-г0 Г
или /(г) = , где <р(г) = (р1(г) + Ф2(г)- Если ср(го)*О , то го - П(т) для
(Г
функции /(г)- Однако для функций /|(г),/2(г) может выполняться условие
4>i(£o) + <l>2Bo) = o и' следовательно, (р(го)=О. В этом случае формула D.14) не
применима и точка го не будет полюсом порядка т для f(z). В соответствии
с п.З утверждения 4.3 порядок полюса будет меньше, чем т , и равен (т - р)
в случае т > р, где р - порядок нуля функции <р(г). Если р = т, то го - устра-
устранимая особая точка для /(г) ■
Таким образом, при сложении функций порядок полюса в точке может
оказаться равным или меньше, чем наибольший из порядков слагаемых.
б) Для исследования произведения ff(z)-f2(l) воспользуемся формулой
связи нулей с полюсами (п.2 утверждения 4.3) и рассмотрим вспомогательные
функции F,(z) = , F2{z)= . Для первой из этих функций го - 0(/я),
/i(z) fi(z)
для второй соответственно го - 0(/с) , а поэтому для F(z) = F\(z)-Fi(z) она бу-
будет Щт + к). Согласно п.2 утверждения 4.3, го является Щт + к) для
/,()/2(г)
в) Аналогичные рассуждения для частного /|(г)//г(г) приводят к результа-
результату: при т> к точка го является П(т-к) для ——.
Второй случай. Пусть точка го является полюсом, устранимой особой
точкой или не особой для fx(z) и существенно особой для fiix)- Так
как lim/2(г) не существует, то по свойству пределов он не существует для
1г
каждой из рассматриваемых комбинаций f\{z)^fi(z)',
fj{z)lf\(z)■ Следовательно, для каждой из них го - существенно особая
точка. Заметим, что для функции эта точка является либо сущест-
/(г)
венно особой точкой, либо не является изолированной особой точкой.
Последнее проиллюстрировано в примере 4.5 для функции -.
sin —
z
Третий случай. Пусть го - полюс порядка п для /j(z) и устранимая
особая точка для /2(г). Разложения этих функций в ряд в окрестности
г0 имеют вид D.6) и D.4) соответственно.
а) При сложении рядов в общей области сходимости получится ряд,
главную часть которого будет составлять главная часть ряда функции
f\(z). Следовательно, для f(z) = f\(z)±fi{z) точка го - полюс порядка п.
б) Аналогичные рассуждения приводят к заключению, что такой же
результат получится и для Лг) = /](г)/2(г), если Нт/2(г)*0.
258
Если lim /2(г) = 0 и ZQ-Q(p)>p<n для функции /2(г), то из равенства
Z+Z
заключаем, что г0- П(я -/>).
/д Ф2(г)(гго) \
(г-г0) (г-г0)
в) Для частного при условии lim /2 (г) * 0 из равенства
/г (г) г->г<>
Лг) = — = — = ф(г) заключаем, что г0 - П(и) для /(г).
< /2« (г-го)я/2(г) (г-гь)"
Если lim /2(г) =0 и го - 0(/>) для /2(г), то, используя условие кратного
нуля, из равенства /(г) = = —— = ——— заключаем,
/(г) ()"()()' ()л+р
что го является П(и+р) для ~—, где и - порядок полюса функции /, (г), р -
/г (г)
порядок нуля функции /2(г) в точке го-
Подводя итог, запишем следующее утверждение.
Утверждение 4.4.
1. Пусть точка го является П(/я) для функции f\ (г) и П(&) для функции
а) для /1(г)±/г(г) она будет П(и), и< max(/w,fe), а при я = 0- устрани-
устранимой особой точкой;
б) для /, (г) ■ /2(г) она является П(и), п = т + к;
в) для f\(z)/f2(z) она будет П(п), п-т-к.
2. Пусть го - существенно особая точка для функции /2(г) « устранимая
особая точка или полюс для функции /j (г) ■ Тогда го ~ существенно особая точка
для /,(г) ± /2(г); /,(г) ■ /2(г); /2(г)/Л(г) •
3. Пусть точка го является П(и) для функции /|(г) и устранимой особой
точкой для функции /2(г) • 7огда:
а) для Л(г)±/2(г) ока б>дет П(п) ;
б) для /!(г) • /2(г) она является П(и), еслы lim /2(г)*0, и П(и-р), если
Ikn /2(г) = 0 и р - порядок нуля /2(г) в точке го;
г*»гь
в) для ' ■■ она будет П(и), еслы Нт/2(г)*0, и Щп + р), если
h (г) г-»го
йт /2(г) = 0 ы р - порядок нуля /2(г) в mowe го •
'* 4. £ся« /wowa го - П(и) для ф(г) , то она существенно особая точка для
сложной функции /((р(г))- В этом можно убедиться, рассматривая*ряды для
ф(г) и /(ф(г)) в окрестности го-
Пример 4.19. Определить тип особой точки г = 0 для функции f(z),
если f(z)= /|(г) + /г(г) , где /](г)= —, а функция /2(г) определяется
Z
следующим образом: а)/2 (г) = г; б)/2(г) = г; в)/2(г) = 1—.
г г2 г г2 г
□ Очевидно, точка г = 0 является ПB) для /j(z) и для /2(г) в пер-
первых двух случаях; в последнем случае г=0 - ПA) для /2(г).
Ддя каждого из указанных случаев задания /2(г) записываем разло-
разложение функции /(г) по степеням z , из которого определяем тип точки
Z = 0 для /U):
a) f(z) = \+--\ = -\+-; г = 0-пB)для /(г);
г г г2 г2 г
z2 z z2 z
в) /U) = -V + l-- = -V-- + l ; г = 0-ПB)для f{z).
z1 г г2 z
Пример иллюстрирует п. 1 утверждения 4.4. ■
Пример 4.20. Найти особые точки функции /(г) =
делить их тип.
□ Особыми точками функции являются особые точки первого слагае-
слагаемого z = 2Ы , £ = 0,±1,..., особая точка второго слагаемого z-О входит в
это множество. Точки Zk=2kni, k*0 .являются простыми нулями знаме-
знаменателя и поэтому простыми полюсами первой функции; для второго слагае-
слагаемого эти точки не являются особыми. Поэтому точки г* = 2/Ы, к * 0 -
простые полюсы /(г) (см. п. 3 "а" утверждения 4.4).
Точка z = 0 - простой полюс и ддя первого, и для второго слагаемо-
слагаемого. Для f(z) - это или простой полюс, или устранимая особая точка (см.
1-е1 +1
п.1 "а" утверждения 4.4). Преобразуем разность в дробь: /(г) = .
(ег - 1)г
Точка z = 0 является нулем второго порядка и для числителя, и для зна-
знаменателя. Следовательно, это - устранимая особая точка, в чем можно убе-
убедиться, используя определение, т.е. находя \anf(z). Действительно,
г->0
г2 z2 zl
Точка г = оо для данной функции является неизолированной особой
точкой, так как в любой ее окрестности \z\ > R содержится бесконечное
множество особых точек вида г* = 2Ш. Эта точка - предельная точка
260
полюсов. Заметим, что для знаменателя первого слагаемого функции она -
существенно особая точка. ■
Пример 4.21. Найти особые точки следующих функций, определить их тип:
. ,. z - л 1 1 ,. ,. . 1 . nz 1
а) /(г)=-~-со8—- + ——; б f(z)= ——sin—*-+ ——
in2г z-2i г6 + 1 г2_1 2г + 1 ez
; f()
sin2г z-2i г6 + 1 г2_1 2г + 1 ez+i
П Обозначим f\(z)- первое слагаемое,/2(г)-второе слагаемое функции
/(г), т.е. имеем f(z) = fi(z) + f2(z)-
а) Для /[ (г) точка z = 2/ является существенно особой точкой, так
как это существенно особая точка для cos множителя этой функции.
Z -2/
Поэтому она - существенно особая точка для /(г) (п. 2 утверждения 4.4).
Точки Zk=kn к*\- полюсы второго порядка функции /}(г) , так как
ее можно записать в виде f\(z)= , где ф(г*)*0 , а для знаменателя
sin г
эти точки - нули второго порядка . Так как для /2(г) эти точки не особые,
то ik = кп , z * л - полюсы второго порядка для /(г) (п. 3 утверждения
4.4).
С помощью аналогичных рассуждений получаем, что z = л - простой
полюс для /(г).
Особыми точками /2(г) являются корни уравнения z6 + 1=0 , т.е.
1к -е 6 , к =0,1,..., 5. Все они - простые нули знаменателя- функции
1
F(z) , а потому - простые полюсы для /2(г)=——.Так как эти точки не
r(z)
являются особыми для f\(z), то для /(г)-это простые полюсы.
Точка z = да - неизолированная особая точка /(г).
б) Точка z = полюс дроби является существенно особой
2 2г +1
точкой для sin (п.4 утверждения 4.4), поэтому она - существенно осо-
2г + 1
бая точка для /j (г) и, следовательно, для f(z) ■
Точка г = 1- простой полюс для /)(г), так как можно записать
=-2Ш. ( (рA)*0. Поскольку г = 1 не является особой точкой для
/2(г), то она- простой полюс для /(г) •
Точка г = -1 - устранимая особая точка для /)(г), так как она-
nz
простой нуль и для числителя, и для знаменателя дроби —~—. Так
г -1
как г = -1 не является особой точкой для /2(г), то она - устранимая
особая точка для /(г) •
261
Особыми точками /2(г) являются простые нули знаменателя - кор-
корни уравнения ег+/ = 0 , или ег=-( , т.е. г = Ьп(-/). Все точки
zk =ln|-ij + i(aig(-i) + 2for), или г*=' 2Ля- — к = 0,±1,... являются про-
простыми полюсами для /2(г) и, следовательно, простыми полюсами для
Точка z = °° - неизолированная особая точка f(z) .■
Упражнения
1. Определить тип конечных особых точек функций:
а) /-feb-^-e-*2 +—; б) /(г) = —!_ + i;
е'г-\ Z
я '
cos-Z
г) /(?) = -
(Z-nj- smz si
Ответ: a) z = ± ' и Zk =— + кк,к =0,±1.. - простые полюсы, г = ' -
2. JL J*
устранимая особая точка;
б) z = 0 - устранимая особая точка, z = 2Ы,к = ±1,.. - простые полюсы;
в) z = я - полюс второго порядка, Zk = — + кп ц zm=nm,
к - 0,±1..,т = 0,-1,±2,.. - простые полюсы;
г) z = 1 - простой полюс, Zk = 1 + кк,к * 0,к * 1 - полюсы второго порядка,
г = 1 + я - полюс третьего порядка, z = 0 - существенно особая точка.
2. Определить тип конечных особых точек функций:
1 1
a) f{z)'—3—+егт^ > б) /W = —7-C0Sг+Т
г3+/ (z-nf sm2z z-i z
Ответ: а) г^ = e^ 6 3 , Л = 0,1,2; ги = — + »m, m = 0,±l,.. - простые полю-
сы, z = 0 - существенно особая точка, г = я - полюс второго порядка;
б) z = е 6 ,к= 0,..Д Ь2иг = и - простые полюсы, гк=кж,к*\ -
полюсы второго порядка, z =' - существенно особая точка.
3. Определить тип особых точек функции:
г2 -16
_
Ответ: а) г = 0 - устранимая особая точка, г = » - существенно особая
точка;
262
6) Zk ,к = 0,±1,..,г = 0 и г = — простые полюсы; г = суще-
2 + &к 4 4
ственно особая точка; г = °° - устранимая особая точка.
4. Определить тип конечных особых точек:
a) f(z)=Cg , +sin—Г; б) /W
zJ+l г + 1
1 V3
Ответ: а) г = —±—i - простые полюсы; г* = Ь, i * 1 - полюсы второго
порядка; г = л - устранимая особая точка; г = -1 - существенно особая точка;
б) z = 0, Zk = — + кп - простые полюсы; zm = чш, т * 0 - полюсы второго
порядка; г = 2 - существенно особая точка.
5. Определить тип особых точек:
J
a) /(z)=sin£±i+2e*+1, б)
Ответ: а) г = 0, z = -1 - существенно особые точки; г = °° - простой по-
полюс;
б) г = 0 - устранимая особая точка; z = 1 и z = °° - существенно особые
точки.
6. Определить тип конечных особых точек:
— .
г cos г
люсы.
♦
Ответ: г = 0, г = 3 - существенно особые точки; г* = — + кк - простые по-
4.2. ВЫЧЕТЫ И ИХ ПРИМЕНЕНИЕ
4.2.1. Определение вычета
Пусть го е С - изолированная особая точка функции /(г). По опре-
определению изолированной особой точки существует некоторая окрестность
этой точки, в которой /(г) - аналитическая. Напомним, что для го е С эта
окрестность имеет вид 0 < |г - го| < R , а для го = °° - R < \z\ < °° •
Рассмотрим произвольный контур у , принадлежащий такой окрестности
и являющийся границей некоторой области, содержащей го (рис. 4.2,а).
263
Рис. 4.2
По следствию из основной теоремы Коши (см. разд. 2.2) интеграл
<\f(l)dz имеет одно и то же значение, независимо от вида кривой у ,
г
т.е. интеграл характеризует поведение функции /(г) в особой точке го
и, следовательно, может быть использован для исследования функции как
некоторая числовая характеристика.
Вычетом функции /(г) в изолированной особой точке го (Zo е С)
называется интеграл — 4f(z) dz , где у - контур, принадлежащий окрест-
ности точки го и охватывающий ее. Обход контура - положительный, т.е.
область им ограниченная и принадлежащая окрестности го при обходе
расположена слева: для го е С - обход против часовой стрелки (рис. 4.2,а),
для го = °° - по часовой стрелке (рис. 4.2,6). Обозначается вычет res /(г) (res
го
- residu (фр.) - вычитать):
1
гь
: 0<|г-г0|<Я,
D.16)
Ksf(z)=—jf(z)dz, 7е0(оо)\со: Л<|г|<со.
Так как в окрестности изолированной особой точки функция разлага-
разлагается в ряд Лорана, то, используя формулы для коэффициентов ряда Ло-
Лорана и сравнивая их с D.16), замечаем, что можно сделать следующее
заключение.
264
Утверждение 4.5. Вычет функции в изолированной особой точке равен
коэффициенту с_х при первой отрицательной степени в разложении функции
в ряд Лорана в окрестности этой точки, т.е. при для Zq^C, и
г-го
этому коэффициенту, взятому с противоположным знаком, для г0 = °° :
пя/(г) = с_,, гоеС, D.17)
res/(z) = -c_, , го=».
D.18)
С помощью вычетов можно записать в другой форме основную тео-
теорему Коши для сложного контура (см. разд. 2.2).
Действительно, пусть функция в области D имеет п особых точек
zk, k = \,2,...,n . Можно рассмотреть контуры yksD, которые являются
границами непересекающихся областей Dk, таких, что каждая из особых
точек Zk (изолированных особых точек) принадлежит одной из Dk (рис.
4.3,а), а интеграл по ук согласно определению (см. формулу D.16)) есть
(г)
Рис. 4.3
Кроме того, для любого контура С, ограничивающего область D ,
которой принадлежат все особые точки функции /(г), и контура у - гра-
границы окрестности бесконечно удаленной точки справедливо равенство
§f(z)dz = -jf(z)dz (обход на у по часовой стрелке (рис. 4.3,6)).
Y С
Из этих рассуждений и формулы D.16) получаем следующие утвер-
утверждения.
26S
Утверждение 4.6 (основная теорема о вычетах). Если функция /(г) -
аналитическая в D за исключением конечного числа особых точек Zk e D,
то справедливо равенство
if (I) dz = 2ni £ res /(г) ,ZkeD, D.19)
С *=1 ц
где С - граница области D.
Утверждение 4.7 (обобщенная теорема о вычетах). Сумма вычетов функ-
функции f(z) во всех ее особых точках, включая бесконечно удаленную точку,
равна нулю:
f O. D.20)
Пример 4.22. Найти вычеты следующих функций в их особых точках:
a) f{t)= .*■"■ ; б)/(г) =
z -lz-Ъ
D Особыми точками функций являются точки Z\ = -1, Zi = ~!>, гз=°°-
Записываем разложения функций в ряд Лорана в окрестности этих точек
(см. примеры 3.31, 3.33 и 3.34):
а)
Из этих разложений находим : res/(г) = с_, =-j/ ; res/(£) = c_] =V. ,
-1.
Полученный результат иллюстрирует обобщенную теорему о вычетах:
res f(z) + res /(г) + res /(г) = 0 .
-1 3 00
Заметим также, что здесь точки z\ и гг-простые полюсы, аг = ю -
устранимая особая точка.
266
^£ (,,,0|J|4.
Из этих разложений имеем: res/(z) = c_i = -%: \ res/(z) = c_i ~
Вычет в бесконечно удаленной точке z =» можно найти, используя
обобщенную теорию о вычетах: res /(г) = — f res /(г) + res /(г) 1 = 0 .Этот же
«о V 3 -! )
результат получим, если запишем разложение функции в области |г| > 3 -
окрестности г = °° •
Заметим, что для этой функции Z\ - ПB) , Zi - ПA) , a z = да - уст-
устранимая особая точка. ■
Пример 4.23. Найти вычеты следующих функций в особых точках:
U Особыми точками функции являются точки Z\ = 0 , г2 = °° • Нахо-
Находим разложения функций в ряд Лорана в окрестности этих точек (см.
примеры 3.35 и 3.36):
а) Лг) = г3 + г2+|+^+~ + ... , 0 <|г| <оо ;
Из этого разложения
res/(z) = c_,= —= — и res/(z) = -c_, =-— = -—.
о 4! 24 . о° 4! 24
Заметим, что г = 0 здесь - существенно особая точка, a z = » - ПC) для /(г); ,
1 г2
б) /(г)= + ... Из этого разложения получаем res/(z) = O,
2! 4! о
res f(z) = 0. Здесь z = 0 - устранимая особая точка для /(г), а г = °° - суще-
X
ственно особая точка. ■
Пример 4.24. Найти вычеты следующих функций в их особых точках:
a) sinfl+i-1; б) {z-\)e~^.
D Конечные особые точки функций являются существенно особыми
точками. Это z = 0 для первой функции и г = 2 для второй. Разложим функции
в ряды в окрестностях этих точек и найдем вычеты по формуле D.17):
a) sin 1+- = sin 1 ■ cos— + cos 1 • sin — = sin 1 1 - + ... \ +
{ z) z z { 2\z2 )
267
,(\ 1 ) . . .1 sinl 1
+ cosl — + ... = sinl + cosl --...
U г33! ) Z 2! z2
Следовательно, res f(z) = c_j = cos 1.
Так как у рассматриваемой функции других конечных особых точек
нет, то по формуле D.20) res/(z) = -cosl. Заметим, что г = °о -устранимая
особая точка для данной функции /(г);
_L J i i
б) (г-1)-ег-2 =(г
поэтому res/(;) = l+—■ = -. Поскольку нет других конечных особых точек,
то по формуле D.20) res/(z) = —. Точка г = °° является полюсом первого по-
<» 2
рядка данной /(г) .■
Упражнения
1. Найти вычеты следующих функций в точке г = 0:
, / \ sin 1 , / 1 .1 , / \ г2
Mih- Л() яп; /(г)
/iW; Mihj, Л(г) яТ; /4(г).
Ответ: 1; 0; 0; 0.
2. Найти вычеты в точке z = °° функций Л (^) > /2B), /з Сг) из упражнения 1.
Ответ: -1; 0; 0.
3. Найти вычеты следующих функций в точке г = »:
/i@=-j-; /2B)=—^-; Л(г)=—т": fw=—l—■
Ответ: 0; 0; -1; 0.
4. Определить тип особой точки г = / и найти вычеты в этой точке сле-
следующих функций:
268
1 e7(Z-i)
fl{z)=zcos—; /2(г) = ——.
Ответ: существенно особая точка; —;е.
5. Определить тип особой точки z = °° и найти вычеты в этой точке функ-
функций из упражнения 4.
Ответ: ПA), —; устранимая особая точка, -е.
6. Найти вычеты следующих функций во всех их особых точках:
a) f{z) = cos ; б) /(г) = sin2 -.
г-1 Z
Ответ: a) res f(z) = res /(г) = 0; б) res /(г) = res f(z) = 0.
7. Найти вычеты следующих функций:
/,(г) = г3+- + 5т-^-, /2(г)=г2со8-, /3(г)=г3агД.
г г г г
а) в существенно особой точке z = 0; б) в z = ».
Ответ: &) 1;0;0; б) -1; 0; 0.
8. Определить тип особых точек и найти вычеты в этих точках следующих
функций:
; б) /W = (I±>
Ответ: a) z = 0 - ПB), res/(г) = 2, г = »- устранимая особая точка
о
res/(г) = -2; б) г = 0 - ПB) , res/(г) = 3, г = °° - существенно особая точка
00 0
res/(г) = -3.
9. Определить тип особых точек и найти вычеты в этих точках следующих
функций:
ь-^г; б) ,х„
г+i г г+1
Ответ: а) г = -1 - ПA) , res/(z) = 2, г = »- ПA), res/(г) = -2;
-! 03
б) z = 0 - ПA) , res/(z) = 1, г = -1- ПA), res/(z) = 2, г = «>- устранимая
«Ьбая точка res /(г) = -3.
Эй 10. Найти вычеты во всех особых точках функций:
1 1
Ответ: res/,(г) = res/,(z) = O, res/2(z) = -^, res/2(z) = ~-
i «о 3 2! оо 2!
11. Найти вычеты в точке г = 2 следующих функций:
/i(z) = sin- ,
г-2 i-L
Ответ: res /j (г) = 3 cos I, Ttsf2(z) = —3 sin 1.
4.2.2. Вычисление вычетов в полюсе и устранимой особой точке
В рассмотренных выше примерах при нахождении вычетов использо-
использовались формулы D.17),D.18) , т.е. функции раскладывались в ряды Лорана.
При этом знание типа особой точки, в которой вычисляется вычет функ-
функции, не является обязательным. Таким методом всегда определяется вычет
в тех случаях, когда заранее предполагается, что особая точка — сущест-
существенно особая точка для функции. В случае устранимой особой точки и по-
полюсов задачу вычисления вычета по формуле D.17) можно заменить не-
некоторыми практически более удобными формулами и правилами. Вывод
этих формул и правил в общем виде, очевидно, связан с исследованием
разложения функции в ряд в окрестности особой точки, а тип особой
точки определяется по поведению функции, т.е. вычислением предела.
Так, если lim /(г) *<*> и го - конечная особая точка, то в разло-
разложении функции в ряд Лорана в окрестности го , согласно утверждению
4.1 , отсутствует главная часть. Следовательно, c_f = 0 и res/(z) = 0.
Если lim /(г) = °°, т.е. го - полюс функции /(г) , то можно опреде-
определить порядок полюса, также не прибегая к разложению функции в ряд, исполь-
используя утверждение 4.3. Пусть z0 - п(«) функции /(г), тогда разложение
функции в ряд в окрестности го имеет вид D.6). Умножив обе части
равенства на (г-го)" и продифференцировав результат (n-l) раз, полу-
получим выражение
(«-1)!с_1+«!с0(г-г0)+-.. ,
1 rf"~' Г 1
из которого определяем с_, =-. г- lim г1/(г)(г~го) •
(п - 1)! г-»го dz
В частности, при я = 1 с_( = lim (/(г) (г-го))- Последнее равенство
г*гь
принимает наиболее удобную форму для функции вида /(г) =-^тт, ГДе
ф(г),у(г) - аналитические вточке ^о функции и (р(го)*0, у(го) = О , v'
А именно: с., = шЩ^= lim
Z-Zo
270
Результат приведенных рассуждений запишем в виде утверждения.
Утверждение 4.8.
1. Если конечная особая точка Zo является устранимой особой точкой
функции f(z), то
res/(z)=O, Zo е С , Zq - устранимая особая точка. D.21)
го
2. Если Zo полюс порядка п функции f(z) , Zo e С , то
г°-п(и); D22)
Ksf(z)=lim[f(z)(z-Z0)], ZQ-n(\). D.23)
го г->го
3. Если zo -ПA) функции /(г)= ^4» где <pU)>vU) - аналитические в точке
nz)
функции и ф(го)*О,
Замечание 4.6. Формула D.22) дает следующий алгоритм вычис-
вычисления вычета функции в полюсе порядка и.
1. Умножить f(z) на (г-го)" . ГДе и-порядок полюса го , и получить
функцию ф(г) = /(г)(г-г0)"-
2. Найти производную функции ф(г) порядка (я-l) : Ч/(г)=ф(")(г) .
3. В соответствии с D.22) найти res/(z) = 7 r Hm \\i(z).
го («-1)! г-**о 1
Пример 4.25. Найти вычеты в конечных особых точках функций:
□ Конечными особыми точками /|(г) являются Z\ =-l и ?2=3 -
полюсы первого порядка, причем в каждом случае функцию можно пред-
представить в виде, допускающем применение формулы D.24). Используя эту
формулу, находим res-
Z+2 z+2
-2г-3
г+2 z+2
res—-^ = —
з г2-2г-3 2г-2
г-г
-^-J> г=-1
V
Z + 2
2z-2
-4~ 4 '
271
Для функции /2(г) точка г = 3 также является ПA) и выполняются
условия применимости формулы D.24) . При этом функцию удобно пред-
г + 2
ставить в виде
= ^ *—. Применяя формулу D.24), находим
г-3
Z+2_
2
г=з
'(z + lf
16*
Точка z = -\ для /2(г) - полюс второго порядка. Применяем фор-
формулу D.22) при и = 2. Запишем решение согласно алгоритму.
1. Умножаем f2(z) на (г + 1J и записываем функцию
2. Находим производную функции
^)=ИЬ^%^-4т=
'U-3J
(г-З)"
3. Используя D.22), получаем res/2(z) = — lim -
-I 1! z-»-i (г_зJ
—-
16
Для функции /з(г) =
l-COSJ
:—
V
единственная конечная особая точка
г = 0 является устранимой особой точкой, поэтому res/3(z) = O (согласно D.21)).
Все полученные результаты соответствуют результатам примеров 4.22
и 4.23.И
Пример 4.26. Найти вычеты следующих функций в особых точках:
a)
б)
+8/
Zb + 8/ '
□ Особыми точками функций являются нули знаменателя, т.е. корни
уравнения г3+8/ = 0 или г3-B/) =0. Раскладывая на множители левую
часть (г-2/)(г2+2г»-4) = 0 , находим Z\=2i и два других корня, как
корни квадратного уравнения г2+2г/-4 = 0, т.е. Zi=Jb-i, z-i=-4b-i.
Z + 2i
а) Для f(z)--
все три особые точки -
простые полюсы. Находим вычеты в них по формуле D.24):
1СЛ — _
2'г3+8/ 3z2
4/ _ i
г=2/~3(-4) 3
272
i &-'+2i (Уз + о (Уз+о2 _(Уз~+о(Уз~+о2 (Уз+о3 _ а
_ _
Ъг\ = 3(УЗ-/J=3(УЗ-/J(Уз + /J = 3-42 = 316 =3-1б'
г3 +2<" -Уз-/ + 2/ /-Уз
(/ - УзхУз - о2 _ о- -Уз)(Уз- /J _ (I - УзK _ 8/ _ i.
3-(УЗ + /J(УЗ-/J 3-42 342 316 6'
res /(z) = - f res /(г) + res /(г) + res /(;)! = 0,
« V *i г2 г3 ;
что можно проверить, разложив f(z) в ряд в окрестности г = да , т.е.
в области \z\ > 2.
б) Для /(г) = -^—■ точка zt=2i- устранимая особая
(Z-2l)(Z-Z2){Z-Zi)
точка, так как Шп/(г);*°° .Поэтому res/fe) = 0. Точки г2 и ^3" ПA) ,
г-Ki 2/
поэтому вычеты находим, как и в предыдущем случае или по формуле D.23):
res/(z)= lim /*-гг= li
)= lim f(z)(z-Zi)= li
(г - 2t)(^ - г2)(г - Z3) г2-*з 2V3
( - 2i)(z - г2)(г - г3) *з-г2
Вычет функции в г = « можно получить по формуле D.20):
В заключение раздела рассмотрим бесконечно удаленную точку в слу-
случае, когда она является устранимой особой точкой для f(z) . Разложение
функции в ряд Лорана имеет вид D.5). Коэффициент с_{ можно опреде-
определить из этого равенства следующим образом: c_l = \im[{f(z)-cu)-z].
Так как, очевидно, co = lim/(?), то, доопределяя функцию, положим
г-»»
/(да) = lim f(z) = Cq . Получаем формулу для вычисления вычета в z = °о
г-» оо
- устранимой особой точке функции f(z) :
res/(z)= -с., = lim [/(«)- f{z))-z . D.25)
»О 2+0
273
В частности, если z = <*> является нулем функции f(z) , т.е.
lim f{z) = 0, то формула принимает вид
гнД»= ton (-г ■/(?))• D.26)
оо г-*00
Пример 4.27. Найти вычеты в г = °° функций:
г + 2 /\ г + 2 /ч Зг2 + z
г2 -2г-з' 2 (г + 1J(г-з)' г2 + г-4'
D а) Точка z =« - устранимая особая точка для этих функций и
/(«)= 1»п Д» = 0 . Поэтому вычеты этих функций находим по формуле
D.26):
■ = 0 .
г-*°°(г + 1) (г-3)
Результат совпадает с полученным в примере 4.22.
б) Точка г = да - устранимая особая точка для /(г), так как lim/(z)=3.
Вычет находим по формуле D.25):
res/W= щ
Упражнения
. Определить тип особых точек и найти вычеты в этих точках функции
sin?
Лг) =
Ответ: z = 0 - ПB), res /(г) = 0, z = -я - устранимая особая точка,
о
res f(z) = 0, г = оо - существенно особая точка, res /(г) = 0.
-Л оо
2. Найти вычеты в конечных особых точках функций:
sin z (г + я) sin z
Ответ: res/,(г) = (-])**V(* + 1), jfc = 0,±l,±2,..;
tot
, k*-\, ies/2(z)-O.
res/2(z)\ , k*\, ies
tot (Л +1) -it
274
3. Определить тип особых точек и найти вычеты в этих точках следующих
функций:
.)/«--^Ч; б) т shu
Ответ: a) z = 0 - устранимая особая точка, z = -я- ПB), z = °° - суще-
существенно особая точка, res/(z)= res/(z)= res/(z) = 0;
О -It 00
б) г = 0 - ПA), г = -я-ПA), г = да - существенно особая точка,
«•/(*) = "Т. res/W = —Т
4. Найти вычеты в особых точках функций:
Ответ: res /[ (г) = 3, res /[ (г) = -3, res /f (г) = 0;
О I 00
res/2(z)=-, res/2U) = --, res/2U) = O.
-1 у 2 у да
5. Найти вычеты в особых точках функций:
г + 1 ег+|
Ответ: res /i (г) = 1, res /j (г) = -1;
О 00
/2(z) = l, res/2(z) = -l.
-I 00
6. Найти вычеты функции в точках нижней полуплоскости:
Ответ: res f(z) = ——.
-/ 80
7. Найти вычеты в точке z = 0 следующих функций:
Ответ: res/,(г) = ——, res/2(z) = -l, res/3(z) = —-.
275
8. Найти вычеты в конечных особых точках функций:
е"■ -1 е z -] Z
Ответ: a) res/(z) = 0; res/(z) = —-^-—, zt =^+ fat, * =0^1,..;
О % eit+z/ra_j 2
res /(г) = — th /mt, гт = ww> ю * 0;
г„ 2
б) res /(г) = 0, res f{z) = -1, г* = 2*п/, Л * 0.
0 г*
9. Найти вычеты во всех особых точках функции
Omee/n: res/(z) = —^-, res/(?) = -^-, res/(j) = -4.
10. Найти вычеты функции /(г) = ^ г в особых точках, лежащих
г(г2+4J
в верхней полуплоскости.
Ответ: г^/(г)=-—•
11. Найти вычеты функций в г = *>■"
Ответ: а) -1; 6H; в)--.
12. Найти вычеты функции /(г) = -^т—- в особых точках левой полу-
г +1
плоскости.
Ответ: res/(г =---/--—; res/(z) = -- + i -- — Ь
г, 6 I 2 6 I г2 6 12 6 1
7' -Т'
б 6
где
276
4.2.3. Вычисление контурных интегралов с помощью вычетов
Рассмотрим несколько примеров на применение вычетов к вычисле-
вычислению интегралов по замкнутому контуру, т.е. на применение основной тео-
теоремы о вычетах ( утверждение 4.6 , формула D.19)). Использование формулы
D.19) предполагает выполнение ряда действий, связанных с формой ее записи.
Алгоритм вычисления интегралов <if(z)dz с помощью вычетов
с
1. Найти особые точки функции f(z) .
2. Определить, какие из этих точек расположены в области D, ограни-
ограниченной контуром С. Для этого достаточно сделать чертеж: изобразить кон-
контур С и отметить особые точки.
3. Вычислить вычеты в тех особых точках, которые расположены в области.
4. Записать результат по формуле D.19):
с * -1 ft
Пример 4.28. Вычислить интеграл
□ Записываем решение по алгоритму.
1. Конечными особыми точками функции f(z) = —-— являются нули
Г +1
(=♦**]/
■знаменателя, г4+1 = 0, т.е. zk=e 2, £=0,1,2,3. Заметим, что все точки
- простые нули знаменателя, следовательно, простые полюсы f(z) .
2. Контуром интегрирования является окружность |г-1| = 1 , а точ-
точки Zk расположены в вершинах квадрата, вписанного в окружность
Ы = 1 (рис. 4.4) . Поэтому в область, ограниченную контуром, попадают
/
точки Z\=e4
7 . я.
—я/ —/
=e4 =e 4 .Заметим, что z% = Z\ ■
(г)
Рис. 4.4
277
3. Находим вычеты в точках Z\ и Zi по формуле D.24):
1 1 1 -;«' 1 1 1 ;«'
res-—= ~з- = -е 4 ; res-j—- = — = -е« .
i\ 7Ч +1 4?i 4 . г? 7Ч +1 Azi 4
4. Записываем ответ:
Зи/ Зя/
Зя/ Зя/А "~7~ Т~
Пример 4.29. Вычислить интегралы:
a) <f zVcfe; б)
□ Единственной конечной особой точкой каждой из подынтеграль-
подынтегральных функций является z = 0 - существенно особая точка. В обоих случаях
она принадлежит области, ограниченной контуром интегрирования. Вычеты
находим, раскладывая функции по степеням z (см. примеры 4.23, 4.24).
Получаем
з 7 1 . (. П
resz ег =—, res sin 1+— =cosl.
о ТА й \ )
ТА
\
Записываем ответ: a) cfz3eztfc=—; б) A sin 1 + — cfe = 2nicosl.
12
N-■1-2
Пример 4.30. Вычислить интегралы:
a) <f т~ ^г ; б) <( -4"^--
□ а) Воспользуемся алгоритмом.
1. Находим конечные особые точки функции f(z)= ^ ~ ' - корни
sin«
sin«
уравнения
2. В область
, nz = nk, или г^=Л , Л = 0,±1,±2,...
< 1 входят точки Z\ = 0, zi - -1, так как
-<1. Другие точки не принадлежат кругу
1
< 1 , так как
ДЛЯ НИХ
> 1. В этом можно также убедиться, сделав чертеж.
278
3. Точка z = 0 - устранимая особая точка функции, так как
lim—^ '=lim —' ' = — ; поэтому res/(j) = 0 .Точка г = -1 является
г->0 sin я^ г->0 nz n О
полюсом первого порядка f(z) , так как она - простой нуль знамена-
знаменателя, а числитель при этом не обращается в нуль, т.е. функция может
быть записана в виде f(z) = -"-*•, <р(-1) *■ 0. Вычет вычисляем по формуле
D.24):
resL
-I sin nz (sin яг)'
г=_1
2i - 2i
z=-\ я cos л
4. Запишем ответ
■ i *
Z + ~2
sin лг
б) Воспользуемся алгоритмом.
1. Особыми точками функции являются нули знаменателя, т.е. корни
уравнения ez -; = 0 , или ez =е
г =Л2
,т.е.
, Л=0,±1...
2. Из всех точек г* = / — + 2Ая , к=0,±\... кругу |г-/|<1 при-
.я
надлежит только одна точка z = i— ■
3,4. Находим вычет в точке z = i— простом полюсе f(z):
res
Записываем ответ:
-jl ez -i ez
Zdz
.Я .1С
2я/ • — = я2/ .■
2
Пример 4.31. Вычислить интегралы:
cos
а>
D а) Особыми точками функции являются простые полюсы го = -3 и
2fa.
г* = '^Г = е 15 , Л = 1,2,...,15. Точка г0 не принадлежит области \z\ < 2 , а точки
zk расположены на окружности |г| = 1 , следовательно, входят в область
|г|<2. Применяя формулу D.19), можно найти вычеты в этих точках и
получить ответ:
279
—=2n/£ res
|z| -l) t\ ft U
Чтобы не вычислять вычеты в 15 особых точках z^ , используем
обобщенную теорему о вычетах (формулу D.20)). В данном случае она
15 / \
имеет вид Yres/(z) = - res f(z)+ res f(z) и, следовательно,
t=ift ^-3 °° I
A £_ = -2»fres/(z)+ res
Wl U+ 3) (г15-l) V-з *
Точка г = -3 - простой полюс /(г) , и вычет находим по формуле
D.24):
res/(z) =
J
-1
Точка г = оо - устранимая особая точка для f(z) и Нт/(г)=0. Вычет
вычисляем по формуле D.26): res/(г) = res = lim ~ = 0.
0 ( 3)(г15 -1) *->»(г з)A51)
г, S dz 2га
Получаем ответ: q = —j—
||1(г + 3)(г|5-1) 3|5 +
-1) 3|
б) Особыми точками функции являются г = 1 - простой полюс и
=—существенно особая точка. Обе точки принадлежат кругу |г-1|<1.
Вычет в точке z = 1 находим по формуле D.24):
res f(z) = cos
z
2z-l
г=1
= cos 1. Для нахождения вычета в точке z=— -суще-
-существенно особой точке - нужно найти коэффициент с.| , т.е. записать раз-
разложение функции в ряд по степеням г— Для этого записываем раз-
разложения функций /i(z) = cos и /2B) = , перемножаем ряды и
*>Z " 1 Z ~ 1
IV1 1
находим c_i - коэффициент при степени |z-—■ -
Если, как и в предыдущем случае, использовать формулу D.20), то
задача вычисления интефала упрощается, так как нет необходимости вычислять
вычет в существенно особой точке z=— ■ Действительно, из
res/(?) + res/(г) + res/(г) = 0 следует res/(z)+res/(z) = -res/(z). Поэтому
1 1 0О I 1 00
280
res/(*)=lim
-z- cos-
cos -
= _C0SI и
2
z-\
Пример 4.32. Вычислить интеграл <f sin dz ,
lz2-\ 2* + 1
где' С - граница круга единичного радиуса с центром в точке ц '■
a) Zq = 1 ; б) zo=-l.
П Особыми точками подынтегральной функции являются ^ = 1 - полюс
первого порядка, г2 = существенно особая точка и гз = -1 - устранимая
особая точка (см. пример 4.21).
а) В круг \z -1| < 1 входит одна точка z = 1 • Находим вычет по фор-
формуле D.24): res/(?) = -
sm-
2Z
. л
sin-
п Г 1 . Я?! , ЯУЗ(
Получаем ответ: q ——sin dz = .
П« 1 2г+1 2
2z + l
б) В круг \z +1| < 1 входят две точки: z = существенно особая
точка и z = -1 - устранимая особая точка. Поэтому
Sin dz = 2я(
2 1
ге5/(г)+гю/(г)
или, применяя формулу D.20) (чтобы избежать вычисления вычета в суще-
существенно особой точке), получаем <f ——sin dz = -2яп res/(z)+ res/(г) I.
Так как lim/(?) = 0, находим resf{z) по формуле D.24):
Получаем ответ:
<f ——
м-1г -1
)m^s
г-к» г -1
sin—^—dz = -2m Ksf(z) = -2ni— = --—/.
2z+l ' 4 2
Пример 4.33. Вычислить интегралы от ' многозначных функций:
a)
/; б)
dz.
281
□ При вычислении интегралов от многозначной функции предвари-
предварительно нужно убедиться, что в области, ограниченной контуром интегри-
интегрирования, подынтегральная функция допускает выделение однозначных вет-
ветвей. Это возможно, если точка ветвления многозначного выражения не
принадлежит области. Выделение ветви определяется заданием значения
функции в некоторой точке области (случай "а")), если нет такого зада-
задания - интеграл вычисляется от всех ветвей (случай "б")).
а) Точка ветвления z = 0 функции In z не принадлежит кругу
|г + 2| < — , и в этой области выражение In z допускает выделение одно-
однозначных ветвей (inг)* = 1п|г| + i(arg?: + 2far) , к=0,±1,... Нуль знаменателя-
точка z0 = e'i!" = -1 принадлежит кругу \z + 2| < —. Эта точка будет особой точ-
точкой для одной из ветвей, а именно для той ветви, для которой In (-1) = -Зя/.
Из условия 1п(-е)=1-я1 и (in г)* =ln|?| + i'(arg? + 2fe) находим к:
!n(-e) = ln|-e| + i(cos{-е) + 2кк) = 1 + ;'(я + 2£я) = 1-я/ при к=-1. Но при этом
1п(-1)= 1п|-1| + /(гс + 2(-1)я|)= -т * -Зя/. Следовательно, для выбранной
ветви точка г = -1 не является особой. Поэтому ветвь является в круге
\z + 2\ < — аналитической и интеграл равен нулю (см. формулу B.54).
б) Точка ветвления г = -1 функции 1п(г + 1) не принадлежит кругу
|?-l|<—. В области выделяются однозначные ветви функции 1п(г + 1) :
Aп(г + l))/t = 1п|г +1| +;'(arg(?: + 1)+2А:я), к=0,±\,... Приравнивая нулю знамена-
знаменатель, находим z + l = e , т.е. z = е -1. Точка принадлежит кругу \z -1| < — . Так
как (lne)k =l-¥i2kn , то равенство 1п(г + 1)-1 = 0 выполняется при г = е-1
только для ветви, для которой к = 0. Для этой ветви точка Zo =e-l яв-
является полюсом первого порядка и вычет в ней вычисляется по формуле
D.24): res-
= е (е -1). Получаем ответ: <f = 2я/ е(е -1).
Для других ветвей подынтегральная функция является аналитической и,
следовательно, $f{z) = 0 (см. формулу B.54). ■
Пример 4.34. Вычислить интеграл от многозначной функции
□ Точка ветвления z = 0 функции V? не принадлежит области, по
границе которой вычисляется интеграл. Возможно выделение однозначных вет-
ветвей и вычисление интеграла с использованием теоремы о вычетах.
282
Каждая из двух ветвей выражения Jz=J\z\e 2 может быть
••ыделена заданием значения функции в одной из точек области. Обозна-
■им, например, [<Jz)\ - ветвь, для которой <Д = 2 , и ЩJ - ветвь, где
•4 =-2. Для каждого случая вычисляем интеграл, т.е. 4f\{z)dz, где
М-2
в
■аях в область |г-4|<2 попадает одна особая точка г = 4-пA). Запи-
Записываем результат, вычисляя вычет в точке г = 4 :
/,(«)* = 2я/
Z — 1
Z L
Т:
4я/
Пример 4.35. Вычислить интегралы:
a) j-
smz
cz'
■<fe , С - контур, состоящий из дуги окружности
г| = 2, Inu>-- и отрезка прямой Inu = —- (рис. 4.5,а);
^) 4 ~Г^~ • ^ ~ контур, состоящий из верхней полуокружности
d = /?. /?>l.Imz>0 и отрезка действительной оси (рис. 4.5,6).
Рис. 4.5
283
Da) В область, ограниченную контуром, входят две особые точки
функции: z\ = О-ПA) и z = i'-nB). Находим вычеты в этих точках:
res _ЁЕ!_=Нт
0 ( tf
_ = 1;
if
sin z
(r '
iim cos z ■ Z2{z + if - sin zfazjz + if + г2 ■ 2(z + <))
.. cos г • Z2{z + Q- sin ; ■ 2z(z + i + z) -2icosi + 6sini 2/ Csh 1 - ch I) .
" = B'f = «3
chl -3shl
Получаем результат: <f —-— tuz=—D + ch 1 — 3sh l).
с z (z +1) 2
б) В область, ограниченную контуром, попадают две особые точки
л Зл.
—I —I
функции: z\ =е4 и zi = е 4 (см. пример 4.27). Обе точки - простые по-
полюсы. Находим вычеты функции в этих точках и записываем результат:
Л * , ■{ 1 1 1 -, -С 1 1 1 2w(*i О
ж'/ ч я/ v2 _. яу2 4 4 1 -
= -у(г1 +22)=-у— 2' =~- Здесь учтено, что г4 = г4 =-1. ■
Упражнения
1. Вычислить с помощью вычетов интегралы:
a) <f .+ Zdz, С: х2 + у2 = 6у; б) (fz +Z dz, С - граница области
с Г-16 с г+16
Ответ: а) - Зя/; б) я/.
2. Вычислить с помощью вычетов интегралы по границам указанных облас-
областей:
a) iJ%-, J>:|* + /|<2; б) Ssin^-dz, D:\z\>l.
284
Ответ', а) 2я/; б) - 2я< cos 1.
3. Вычислить с помощью вычетов интегралы:
a) <f ——; б) <f—-—— , где С - контур, состоящий из дуги парабо-
лы у2 = х к отрезка прямой х = 4.
Ответ: а) 0 ; б) 0.
4. Вычислить с помощью вычетов интегралы по фаницам указанных облас-
областей:
, а) Ляп-1-dz, D:\z]<2; б)
Л г + 1 "
50 «т' 80
fc-4)fc13-l)
Ответ: a) -2nicosl; 6) —.
'; l-4b
5. Вычислить с помощью вычетов интеграл по границе указанной области
от однозначных ветвей:
г sin; J. I 3
6|,1пг + 3я1 ' 'Г 2
Однозначные ветви задаются значением In z в точке области:
а) 1п(- е) = 1 - т ; б) 1п(- е) = 1 - Зя(.
Ответ: а) 0; б) 2я< sin 1.
6. Вычислить интегралы:
л cos2 z +1 .
а) 4 —T-—-dz\ б)
Ответ: а) 2/; б) 0.
7. Вычислить интегралы:
а) <( jli5E2L4; в,
Ответ: а) 2я4/; б) 18я(.
8. Вычислить интегралы:
a) cf (\ + z2) ег-ег+| Lfe; б)
W-2 I J
со
Ответ: а) 0; б) —я/.
285
4.2.4. Применение вычетов к вычислению интегралов
от функций действительной неременной
Рассмотренные в предыдущем разделе примеры вычисления интегралов от
функций комплексного переменного по замкнутому контуру с помощью вычетов
показывают преимущество этого метода. Методу соответствует алгоритм, со-
состоящий из несложных процедур (см. разд. 4.2.3). В случае вычисления вычетов в
полюсах задача еще более упрощается и сводится к нахождению производных
(см. формулы D.22),D.24)).
Применение вычетов этим не ограничивается (см. разд. 4.2.4 и 4.2.5, а так-
также гл. 5).
Прежде всего следует ожидать, что можно использовать аппарат вычетов
при вычислении определенных интегралов от функции действительной перемен-
переменной. В самом деле, если подобрать некоторую функцию, переводящую отрезок
*
[а, Ь] в замкнутую плоскую кривую С , то вычисление интеграла \f(x)dx мож-
а
но свести к вычислению интеграла <§ F(z)dz- Простейшая задача такого вида
с
связана с преобразованием отрезка [0,2я] в окружность.
2л
ИНТЕГРАЛЫ ВИДА J R(cosx,sinx)dx
о
Здесь R(cosx,smх) = R(u,v) - рациональная функция аргументов и и v.
Для вычисления таких интегралов в математическом анализе в общем случае, за
исключением некоторых частных случаев, применяется замена tg—= /
("универсальная" подстановка ) и интеграл приводится к интегралу от рацио-
рациональной дроби, а далее применяется соответствующий алгоритм интегрирования
с простыми, но трудоемкими процедурами.
С другой стороны, отрезок [0,2я] изменения переменных можно рассмат-
рассматривать как изменение arg z точки z, принадлежащей окружности. Действитель-
Действительно, замена z = e'x переводит отрезок [0,2я] в окружность \z\ = 1, 0 ^ arg? < 2я.
При этом для переменных u = cosx и v = sinx получаются несложные,
причем рациональные, выражения через z ■ По формулам Эйлера имеем
e'*+e-ix . eix-e-ix \( \\ . 1 ( \\
cosx = и sinx = , т.е. cosx=-U + - , sinx = —\z— .
2 Ъ 2{ z) 2i{ z)
Из е'х = z получаем ie'xdx = dz, а поэтому dx = —.
iz
В результате получаем формулу, связывающую интеграл от действительной
переменной с интегралом по замкнутой кривой от функции комплексного пере-
переменного:
2}( 4 fif^WM]) D'27)
iz
286
Полученный справа интеграл есть интеграл от рациональной функции,
особыми точками которой являются только полюсы.
Пример 4.36. Вычислить интеграл f .
о E + 4cosxJ
П Обозначим е1Х = z, тогда
U П л dz , „ с л 2 2г2+5г + 2
cosx = - \г+— \, dx=—, 5 + 4cosx = 5 + 2? + - = -
2\ Z) iz Z Z
Получаем интеграл ^ — — . Особыми точками подынтеграль-
2
ной функции являются нули знаменателя - корни уравнения 2zl + 5z + 2 = 0. Это
точки Zi=-2 и zi -—. Тогда знаменатель можно записать в виде
B(г- Z\)(z-zi)f =4(z-Z\J(z-Z2J- Точка z\ не принадлежит области |г|<1, а
точка zi принадлежит и ц- ПB). Находим вычет в точке z = полюсе вто-
второго порядка:
res L 1 Um
= — lim
4/ (г_г,K
f «& , . 5 10я
■. В результате 7 = 2я'~^г = ~zr-
JE + 4cosxf B7 27
/27
ВЫЧИСЛЕНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ С ПОМОЩЬЮ ВЫЧЕТОВ
Еще больший интерес представляет возможность применения вычетов для
00
вычисления несобственных интегралов вида J f(x)dx, где интеграл понимается
—00
ю R
в смысле главного значения, т.е. f f(x)dx = lim f f(x)dx (здесь отрезок
—00 -Л
\a,b] = [-R,R] ). Будем рассматривать функцию-/(х), непрерывную на (-ю,»).
Возможность использования вычетов при решении такой задачи основана на
том, что отрезок [- R, R] действительной оси рассматривается как часть замкну-
замкнутого контура С, состоящего из этого отрезка и дуги окружности, а интеграл по
контуру записывается в виде суммы:
287
dz= j f(x)dx+ \f(z)dz,
С -R CR
где CR - дуга окружности \z\ - R, Im z z 0 .
00
Несобственный интеграл \f(x)dx определяется как предел:
\f{z)dz.
", dx
Пример 4.37. Вычислить интеграл f ——, используя вычеты.
-*х 4+1
П Рассмотрим контур С, состоящий из дуги СЛ - окружности |г| = Л.
1тг>0 и отрезка [-R, R]. Для функции f{z) = ~r
имеем
4——- =2я« res/(?)+ res/(г) = -— (см. пример 4.35 п."б"). С другой стороны,
с Z +1 V г! г2 J 2
с / \ Яг / ч г / ч Лг flbc r <fe r dz
<]f{z)dz= \f\Z)dzjr \f\z)dz, или j—— = Ч~4 j ~4—• Оценим инте-
C -R с„ -Лх +1 с Z +1 qZ +1
грал по дуге, учитывая неравенство для подынтегральной функции
1
-, т.е.
Получаем
zU\
dz
___
Cr, где ОД = R.
-
nR, и поэтому
Ihn
f
ci ^ +1
_ .. Rr dx s dz vil "r dx пЛ
В результате hm J ——=4~J— = > те- J ~— = •
Интерес, с точки зрения применения вычетов, представляют интегралы
Г/(х)а!х, где функция f(x) такова, что lim [f{z)dz = Q, как в рассмотренном
-оо С„
примере. Классы таких функций выделяются, и для всех функций рассматривае-
00
мого класса устанавливается формула | f(x)dx = <$f(z)dz ■
-00 С
288
ИНТЕГРАЛЫ ВИДА j R(x)dx
-00
Р (х)
о Здесь R(x) - рациональная функция переменной х, т.е. R(x) = , '., где
Qm\x)
Р„(х) и Qm(x) - многочлены степени п и m соответственно. Как отмечалось
выше, рассматриваем функцию Л(х), непрерывную на (-да,»), т.е. многочлен
Qm{x) не имеет действительных нулей. В теории несобственных интегралов пу-
%dx
тем сравнения таких интегралов с интегралами I —, а > О, устанавливается их
а
сходимость при условии т - п > 1, т.е. т - п > 2. При таком условии lim R(z) = 0
и функция R(z), доопределенная в точке г = °о предельным значением Л(<») = 0,
имеет в этой точке нуль порядка не ниже второго, а поэтому может быть записа-
записана в виде R(z) = —^, где lim а(г) = 0, т.е. |а(г)| <s при | z\ ->°°-
Z г-»00
Учитывая это, проводим оценку интеграла, как в рассмотренном примере,
с»
с„
и получаем lim
Таким образом, для рассматриваемого типа интегралов получаем
да
f Я(х)а!х = A f(z)dz, где С - контур, состоящий из верхней полуокружности
-СО С
|г| = Л, Ircu>0 и отрезка [-Л,Л], причем R таково, что все особые точг
функции f(z), для которых Im z > 0, расположены в полукруге \z\ < R, lm г > С
Очевидно, аналогичный вывод можно получить, рассматривая полукруг
|г|<Л, 1пи<0.
Результаты приведенных рассуждений запишем в виде утверждения.
Р (х)
Утверждение 4.9. Пусть функция R(x) = . . удовлетворяет условиям:
Qm\xl
1) т - п > 2, т.е. степень знаменателя больше степени числителя по крайней
мере на два;
2) Qm(x)*0 для х - действительных, т. e. R(z) не имеет особых точек на
действительной оси.
Тогда справедливы равенства:
\R(x)dx = 2я1 £ res R(z), Im zk > 0, D.28)
ЮПавтелеев А.В., Якимова АС. 289
f R{x)dx = -Im £ res R(z), Im zk < 0, D.29
где Zic> к = 1,2,..,/?, - все особые точки функции R(z), расположенные выше оси Ох
(imzk >0) в случае формулы D.28) и ниже оси Ox (Im Zk <0) - в случае формуль
D.29).
Заметим, что если Я(х) - четная функция, то можно, используя эти форму-
ее
лы, вычислять интегралы вида |/(х)а!х, так как для четных функций имеет ме-
о
R R
сто равенство [f{x)dx = 2 \f{x)dx.
Алгоритм вычисления интегралов \ R(x)dx с помощью вычетов
-00
1. Проверить условия применения формулы D.28) или D.29) (см. утвержде-
утверждение 4.9).
2. Найти особые точки подынтегральной функции R(z).
3. Вычислить вычеты в особых точках функции R(z), расположенных:
а) выше оси Ох, если применяется формула D.28);
б) ниже оси Ох, если применяется формула D.29).
4. Записать результат по формуле D.28) или D.29).
Пример 4.38. Вычислить интегралы:
. "с х2 + 3 сч " x2dx
а) J71 v^' ] J77T'
{2 о(х2+4/
□ а) Воспользуемся алгоритмом.
1. Проверяем условия утверждения 4.9:
- так как в числителе многочлен степени п = 2, а в знаменателе т = 4, то
условие m - п > 2 выполняется;
- уравнение х2 + 2х +17 = 0 не имеет действительных корней, так как дис-
дискриминант трехчлена D < 0. Поэтому второе условие также выполняется.
2. Особыми точками функции f(z) = -, г- являются полюсы вто-
B
рого порядка z\ =1 + 4* и г2 = 1 - 4< ■
3. Применим формулу D.28). Для этого вычислим вычет в точке
Z\ e Imz >0:
« (Z-Ztf(z-Z2?
= Шп
290
lim
(z-Z2f
-2zz2-6
(z-z2?
-217-6 -2-20
_
-83' ~82/'
а о "г лг + 3 , _ . 5 5я
4. Записываем ответ: -. г ах = 2ж — = —.
_jm (х + 2х +17) 8 | 32
б) Воспользуемся алгоритмом.
1. Условия утверждения 4.9 выполняются. Можно использовать формулу
D.28). Подынтегральная функция является четной.
-2
2. Особыми точками функции f{z) = - — являются полюсы третьего
порядка z\ = 2/ и ?2 = -2/.
3. Находим вычет в точке z\ '■
z2 1 .. { z2(z-2>? ) 1 ,. { z2
= I f2,(, + 2,f3,(, + 2,fj = I
24 fc N j 2
1 Hm D/ - 2z)(z + 2if - 4D/; - z2)(z + 2/f _ 1 2B/ - z)Bi + г)- 4;D( - z)
2 г-^-г, (г + 2/f 2
-2-2Z-2/ 8
D/M =45/"
4. Записываем ответ:
Пример 4.39. Вычислить интегралы:
СО j 00 J
. г ах f ах
_I(x2+l)(jc2-ix-lJ' jx*-2/'
□ Условия применения формул вычисления интефалов с помощью выче-
вычету? выполняются.
Заметим, что в отличие от предыдущих примеров здесь подынтефальные
СО
функции являются комплекснозначными и \f(x)dx может быть комплексным
-СО
ЧИСЛОМ.
291
а) Особыми точками функции f(z) = : г являются г, =/,
(Г + 1)Сг -й-1J
?2=-' и корни уравнения г2-/'г-1 = О , т.е. г3 = и ?4 = • Три
точки расположены в верхней полуплоскости, одна г = - i - в нижней. Будем
применять формулу D.29). Вычисляем вычет в точке z = -i - простом полюсе
подынтефальной функции по формуле D.24):
res ■
-i
l?2-iz-\?2z
-l
(-1 -1 -!)?(- 2f) ~ 18/"
Получаем ответ: f —: : = -2л/ res f(z) = —.
_{(x2+\)(x2-ix-l) -i 9
б) Особыми точками функции f(z) = —. являются корни уравнения
г42/
г4 =2/, т.е. гд. =V2eVB ^ ^ , £ = 0,1,2,3. Все особые точки - простые полюсы
функции; две расположены в верхней полуплоскости, две - в нижней. Использу-
ем формулу D.28), рассмотрим точки Z\ = v2e8 и Z2 = v2е 8 = *2е2 е8 = (Zi•
Вычисляя вычеты по формуле D.24), записываем результат (при этом учи-
учитывается, что Z\ = z\ = 2i):
f— = я/ res+ resi^ +
J4
С 1
res— + res
U 4
4-2Г ' " 8V '
i • I' °r Л я Т' .
или, так как 1 + / = е4,то J — =—е8 .1
ИНТЕГРАЛЫ ВИДА [e'XxR(x)dx
-СО
со П ^\
Выше рассматривались интефалы вида \R(x)dx, где R(x)= "\ :,
т -п>2 и 0т (х) * 0 для х g Л.
Но такими интефалами не исчерпывается класс сходящихся несобствен-
ных интефалов \f(x)dx.
292
Например, сходящимися, согласно признаку Абеля, являются интефалы
СО
jf(x)dx, где f(x) = <p(x)-g(x) и функции ф(х)и g(x) удовлетворяют условиям:
а
а) ф(х)непрерывна и имеет офаниченную первообразную на [я,+да), т.е.
л
для любого А > а справедливо неравенство
б) g(x) - непрерывно дифференцируема на [я,+ да) и, монотонно убывая,
стремится к нулю при х -> + да, т. е. lim g(x) = 0, g'{x) < 0, jc е [а, + да).
JC+ + O
Пример 4.40. Исследовать сходимость интефалов:
. мг . . ", , %dx % xdx
a) sinxtfx, \cosxdx, —,
о а в в ' +JC
г;
^rsinx, rcosx, rxsinx, г xcosx , n
6) J dx, \ dx, \ -dx, \ -dx, a>0;
a a a l+x a l+x
. °°f x cos x . % x sin x .
в) -dx, -dx.
J \+x2 ll + x2
-GO
П а) Все интефалы расходятся по определению, так как не существует
'• А
конечного предела lim \f(x)dx.
А-*+<х '
а
б) Все интефалы сходятся по признаку Абеля. Функции ф(х) = sin x или
ф(х) = cosх, g(x) = — или g(x) = удовлетворяют указанным выше условиям.
1 + х2
в) Запишем [/(*)<& в виде суммы: \f(x)dx = J/(x)dx+ \f(x)dx+ \f(x)dx.
-CO -CO -CO -1 1
1
Определенный интефал \f(x)dx есть число, а первое слагаемое заменой х - -t
-I
СО СО
приведем к виду \f{-t)dt, т.е. \<f{t)dt. Тогда на основании результата, получен-
полученного в п. "б", можно сделать вывод о том, что оба интефала, рассматриваемые
в данном пункте, сходятся. При этом | r-rfx = 0 как интефал от нечетной
-со ' "*" X
, °г х sin х , .% х sin x , „ ,
функции, а I -dx = 2 -dx как интеграл от четной функции, в
_м 1 + х2 о 1 + *
В качестве обобщения можно на основании признака Абеля сделать заклю-
заключение, что сходящимися являются интефалы вида
293
J ^(x)cos Ajc dx, J fl(x)sin Xx dx,
-CO -CO
P (X)
где R(x)= , ., m-n > 1 и Qm(:x:)*O для хе R.
vsmW
Вычисление таких интегралов и приводящихся к ним интегралов методам}
математического анализа (нахождение первообразной) представляет в большин-
большинстве случаев определенные трудности.
Воспользуемся предложенным выше приемом сведения вычисления несоб-
СО
ственного интеграла jf(x)dx к вычислению интеграла по замкнутому контуру
-СО
СО
от функции комплексного переменного: \f{x)dx = 4f(z)dz - lim <$f{z)dz ■
с к~"°ск
СО
Заметим, что запись f f(x)dx = <$f(z)dz без исследования, в частности без
-со С
доказательства равенства lim <§f(z)dz = 0 , не имеет основания и может привес-
привести к ошибкам. Так, для интеграла из примера 4.40 имеем
°г,, . , % XCOSX , п ZCO&Z ICOSI Chi Jr<\j ■ i ,
\f\x)dx= I -dx = 0, но res T = ~z— = и Qf(z)dz = inca\,
-co 1+JC i \ + z ъ 2 с
где С - контур, состоящий из дуги |г| = Д, Д>1, Imz^O и отрезка [-Д,А].
QO
Поэтому в данном случае \f(x)dx * if(z)dz.
-СО С
СО р / \
Будем рассматривать \f(x)dx, где f(x)= R(x)e'lx и R(x)= ■ . .,
-СО ^m^ '
w - я > 1 и 0m (jc) * о, леЛ, Л(х) принимает действительные значения. Такой
интеграл сходится, так как он может быть записан в виде суммы двух сходящих-
сходящихся интегралов:
^R(x)eaxdx = j R(x)cosXxdx + i ^R(x)smXxdx. D.30)
-co —со -co
Доказательство возможности применения вычетов к вычислению интеграла
^R(x)e'Xxdx основано на следующем утверждении.
Утверждение 4.10 (лемма Жордана). Пусть функция f(z) непрерывна в об-
области D: \z\zRq, 1тг>-я и lim тах|/(г)| =0, где CR - дуга окружности
\z\ = R, lm z ^ -а. Тогда для любого Х>0 справедливо равенство
lim \eazf{z)dz = 0. D.31)
294
Замечания 4.7.
1. Формула D.31) верна для любого действительного а. На рис. 4.6 изобра-
изображены контур С и дуга CR для случаев а > О, а ■ 0, а < 0.
a
У
1 Л|
-ai
>0
A
)
N
a
(z)
\
1 x
a =
y.
r\
-Rl \
M
0
Л
0 1
6
Рис. 4.6
W
a •
/^
г/ -Ш
0
= 0
/
e
(z)
\N
2. Формула D.31) верна и при любом Х<0. При этом CR - дуга окружно-
ти |г| = Л, 1тг < а. Справедливость этого заключения получается из леммы пу-
-ем замены z на (~z), что в силу {-z)=ze'" геометрически соответствует пово-
эоту на п (рис. 4.7).
йг >0
а = 0
а<0
(z)
у ■
а/
м
(Z)
N
У '
M\ ai
(Z)
\ r
а б в
Рис. 4.7
3. Большой интерес в приложениях (см. гл. 5) представляет запись леммы,
получаемая заменой /' г = Р- Геометрически это соответствует повороту на угол
—, так как p = ze 2. Для дуг окружностей С^: 1) Cr : |р| = Л, Rep^a при
> 0 и 2) CR : \р\ = R, Re р > -а при t < 0 (рис. 4.8) имеет место формула
lim \F(p)efldp = 0.
D.32)
295
, e>0
t < 0, a > 0
(г)
1
-a
У '
/^
0
'—•>. (г)
Рис. 4.8
В частном случае а = 0 (см. рис. 4.6,6 и рис. 4.7,6) лемма применяется для
со
вычисления интегралов J f{x)ea*dx с помощью вычетов. Кроме того, если
-со
функция f(x) принимает только действительные значения при xeR, то, ис-
используя равенство D.30), получаем возможность вычислять с помощью вычетов
СО СО
интегралы \f(x)cosXxdx и \f(x)smXxdx. Первый из них является действи-
-QO -ас
со
тельной частью, второй - мнимой частью интеграла | f(x)elXxdx.
-СО
СО
Для рассматриваемых в данном пункте интегралов J R(x)elXxdx функция
-СО
f{z) = R(z) удовлетворяет лемме Жордана. Подводя итог приведенным рассужде-
рассуждениям, запишем следующее утверждение.
Утверждение 4.11. Пусть R(x) -рациональная функция, не имеющая особых
точек на действительной оси (т.е. Q(x) * 0 для х е R), для которой точка г = «
- нуль порядка не ниже первого (т. е. m-ni.\). Тогда справедливы формулы:
1) при Х>0
2) npul<0
lmzk <0 ;
D.33)
D.34)
*=l zk
296
3) приХ>0
\R(x)cosXxdx =-2я1га £ Tes[R(z)eikz\ , lmzk >0, D.35)
f R(x)smXxdx = 2itRe £ res[fl(z)e'iz] , Irrut>0. D.36)
Ui Zk )
=i
Алгоритм вычисления интегралов j fl(:>c)e'X;tfl[ic
-00
1. Проверить условия для функции R(z), записанные в утверждении 4.11.
2. Вычислить вычеты функции R(z)e'kz во всех ее особых точках:
а) лежащих выше оси Ох, в случае X > О;
б) лежащих ниже оси Ох, в случае X < 0.
3. Записать результат по формуле D.33) при X > 0 и по D.34) при X < 0.
4. Для вычисления интефалов ^ R(x)cosXxdx и [RfysmXxdx в резуль-
-G0 -СО
тате, полученном в п. 3, отделить действительную и мнимую части и записать от-
ответы для указанных интефалов по формулам D.35) и D.36).
Пример 4.41. Вычислить несобственные интефалы:
,fxsinx, _ч г (jc + Ocosx
а) f -<fc; б) [*-г—« rfx.
0J 1 + jc2 ^х2-2л: + 2
CO
□ Приведем интефалы к виду ^R{x)e'Xxdx и воспользуемся алгоритмом.
-СО
а) Так как подынтефальная функция четная, то можно записать
% xsinx , 1 °°f xsinx , _ : ,, . „, . »» „ xsmx
dx = - Л. Введем функцию f(x) = R(x) e , для которой -
Й I + x2 2-il + x2 1 + x2 ^
является мнимой частью, т.е. рассмотрим j -dx.
ll + x
1. Функция R(x) = удовлетворяет условиям: m-n = 2-l = l;
1 + х
1 + х2 * 0 для действительных х.
2. Так как здесь X = 1 > 0, применяем формулу D.33) или D.36), т.е. рас-
рассматриваем только те особые точки функции /(г), которые лежат выше оси Ох.
Функция R(z) = —^-г имеет две особые точки: Z\=i и г2 = ~' • Используя
D.24), вычисляем вычет в точке z = i - простом полюсе:
„-I
res
ze'
е
2
297
z ■ е-1
3,4. Так как Re res e'z =—, то по формуле D.36) записываем ответ:
' 1 + г 2
1 °°f xsinx 1 e
" (x + i)e'x
б) Рассматриваем интеграл -1-—' dx.
_1*2-2х + 2
1. Условия применения формул выполняются: функция R(z) = .' '—
z2-2z + 2
в точке г = да имеет нуль порядка я = 1 и на действительной оси не имеет осо-
особых точек. Особые точки функции: Z\ = 1 + i, ti = 1 - i ■
2. Так как X = 1 > 0, вычисляем вычет в точке Z\ = 1 +1 - простом полюсе
функции по формуле D.24):
2z-2
B + «VU<
2/
3. Для интефала f -*;—^ dx по формуле D.33) получаем результат:
2/
4. Записываем ответ:
Используя формулу D.35), пп. 3,4 можно объединить:
2/
где 2iie'l+' = i(l - 2/)e-'(cosl + /sin l) = ie-'((cosl + 2sinl)+ j(-2cosl + sin l));
Imilie-'«=Ie-1(sinl-2cosl).
В результате получаем ответ: - 2я - е (sin 1 - 2 cos l) = пе'х B cos 1 - sin l) .■
ОС С
Пример 4.42. Вычислить несобственный интеграл f — ■ dx.
B 1Д24)
О 1,2. Находим особые точки функции R(z) = rrr ■: z = ±' и
(z2+l)Y+4)
±2i. Так как Х = 5>0, рассматриваем точки Z\=i и г2=2/: ^ = i-ПB);
298
гг = 2/ - ПA). Находим вычеты функции
в этих точках:
res
e5il E/ (z2 + 4) (z + i) -2z{z + i) - 2 (г2 + 4))
еC-5/2/ + 4-6) -32е~5 4е
9B/K =-9-8/ " 9/
9
еЬп еЫг
3,4. Используя формулу D.35), получаем
°г cos 5л:
res
36
■/.
+ res
4 .5
е
-5
Заметим, что f/(x)rfx = |
| ^г■ = 0, так как функция f(x) - не-
-=0 [х2 + lf(x2 + 4J
четная, что соответствует вычислениям по формуле D.36):
res/(?)+res/(?)=--e/-^—-/' - мнимое число и Ref resf(z) + res/(г)| = О.и
/ 2/ ■ 9 36 \ i ii )
Пример 4.43. Вычислить интефалы:
СО [у Я
г е
-*[xA+2ix-2
О а) Применяем формулу D.33), так как X = ! > 0, т.е. рассматриваем толь-
только точки верхней полуплоскости.
1 =-/ + Л
Но обе особые точки функции f(z) =
, точки Z\
z2+2iz-2
и z2=-i-Jl расположены в нижней полуплоскости. Поэтому интеграл равен
нулю.
299
б) Требуется, как и в предыдущем пункте, вычислить интеграл от
комплекснозначной функции действительной переменной. При вычислении рас-
рассматривается та ветвь двузначного выражения ■Jz + i, для которой задано значе-
значение в точке v/ = e4 .
Функция R(z) = —|— удовлетворяет условиям применения формулы
Г+1
D.33). Так как здесь X = 1 > 0 , рассматриваем вычет в точке z = i:
xes
Получаем ответ:
e-l e-l
~гГ ' ~"гГ 2/
2/
Упражнения
1. Вычислить несобственные интегралы:
Ответ: а) —; б) .
54 4
2. Вычислить несобственные интегралы:
Ответ: а) - —-; б) - .
D о
3. Вычислить несобственные интегралы:
л:-л: + 3 , ,. г ах
Ответ: а) -; б) .
2 6
300
4. Вычислить несобственные интегралы:
а) }-£*-Л; б) ] ^
12 1 i2
Ответ: а) -р е" 3 cos 1; б) - пе'1 sin 1.
З
5. Вычислить несобственные интегралы:
. "г хе2'* , „ °°f xsinx ,
а) 'Т77 ; } '/ТТ
-» х +' о (х2 +
Ответ: а) дае~2; б) -—.
4
6. Вычислить несобственные интегралы:
, Kr xe~ix , ,. "г (х-l)e'* J
a) J— dx; б) f-i- i dx.
1х2+4 ix22x + 2
_1х2+4 i
Ответ: а) - л/е~2; б) я/'е+'.
7. Вычислить несобственные интегралы:
. xrxsin2x , _. °°f (x + l)cos4x ,
a) j— dx; 6) j i—-i dx.
oJ x2+9 1 x2-4x + 6
Ответ: a) -e ; 6) -jL e-4y2Ccos8-i/2sin8) .
2 v2
8. Вычислить несобственные интегралы:
. °f x sin 6x , _. °°f x sin 3x ,
a) — <&; 6) — dx.
_ix2+4x + 13 0Jx2 + 16
Ответ: a) ^e-'8Ccosl2 + 2sinl2); 6) V12.
9. Вычислить с помощью вычетов определенные интегралы:
. 27 COSm + 1 , _. 2": sin2m ,
,; а) [ , v dp; б) J v dp.
^ sinq> + 2 J 5 + 3cos(p
_ . 2я . 2я
Ответ: а) ~=; 6) —.
10. Вычислить с помощью вычетов определенные интегралы:
2j A 2? rix
J B + 3cos2 xJ' I D-3sin2 xJ '
Ответ: а) —==; б) —.
** lOi/lO 8
301
4.2.5. Применение вычетов к исследованию расположения нулей
многочлена на комплексной плоскости
Во многих приложениях важное значение имеет задача определения числа
нулей данной функции, расположенных в определенной области. Например, при
исследовании устойчивости решений дифференциальных уравнений интерес
представляют нули характеристического многочлена, расположенные в левой по-
полуплоскости (см. гл. 5).
Нули функции f(z) являются, очевидно, полюсами функции вида
•2L2. ) есЛи ф(г) не обращается в нуль в этих точках. В частности,
в качестве вспомогательной для исследования нулей функции f(z) можно
рассмотреть функцию, полностью определяемую только самой функцией
/(г), а именно -^-^ = ^-^- . Из-за очевидного равенства ^-^- = (in f(z)),
f(z) f(z) f(z)
эту функцию называют логарифмической производиой функции f(z). Ее осо-
особыми точками являются особые точки /(г) и нули f(z). Поэтому ну-
нули функции f(z) можно исследовать как особые точки (in f(z)) ■ Можно
применить аппарат теории вычетов, в частности основную теорему
о вычетах. Имеет место следующее утверждение.
Утверждение 4.12 (теорема о логарифмическом вычете).
1. Пусть функция f(z) - аналитическая в D за исключением, быть может,
конечного числа полюсов, на С-границе области D не имеет ни полюсов, ни
нулей. Тогда справедлива формула
jj^ = N-P, D.37)
Ъа >, f(z)
где N - число нулей, Р - число полюсов функции f(z) в области D с учетом
их кратностей, т.е. каждый нуль считается столько раз, какова его крат-
кратность, а каждый полюс - такое количество раз, каков его порядок.
2. В частности, если функция f{z) в D не имеет особых точек и на С
не имеет нулей, то
T44T* = /V. D-38)
2я« I /(г)
Доказательство формулы D.37) получается следующим образом.
Пусть г0- нуль порядка п функции f(z), тогда справедливо равенство
f(z)= (z-Zo)" -ср(г), <р(го) 5s 0- Дифференцируя это равенство, получаем
f'{z)=n(z-Zo)l'~l ■ q>(z) + q>'(z) ■ (z - Zq)"■ Поэтому для логарифмической
производной имеем = + . Здесь S-i-2 . аналитическая в точ-
f(z) Z-Zo ep(z) (z)
ке zq функция, так как ф(г) аналитическая и q>(zo)*O. Поэтому в послед-
последнем равенстве слагаемое является главной частью разложения
Z
302
в окрестности Zn, из чего следует, что п = xt%^-^- , т.е. вычет логариф-
f(z) *o fix)
мической производной функции /(г) в ее нуле равен кратности этого нуля.
Аналогично, для го - Щр) функции /(г) из равенств
и fizh-p(z-ZoTp-l<piz)+(z-Zo)'p<?l{z) получаем
= —£-+ £Li. , из чего заключаем, что -/> = resJ^-^, т.е. вычет
f(z) z-zu ч>(г) % /(г)
логарифмической производной функции f(z) в ее полюсе равен порядку полюса
с противоположным знаком.
Применяя теорему о вычетах к вычислению интеграла <f ) Idz ,
с /W
устанавливаем справедливость формулы D.37).
Пример 4.44. Вычислить интеграл j Щ+dz , если
a,
П Для каждой функции находим нули и полюсы, которые принадлежат
области, ограниченной контуром С, и применяем формулу D.37):
а) функция /(г) имеет нули: Z\=\ кратности 5 и ^2,3 = ±2' каждый
кратности 2 , а также полюс в точке Z\ -1 порядка 7. Все найденные точки
расположены в круге |г| < 3 . Следовательно, jV = 5 + 2 + 2 = 9, P = 7 и
44
'■'■ с * W
и б) в круге |г| < 2 функция имеет нули: z = 1 кратности 3 и z = О
кратности 1 , а также полюс порядка 2 в точке z = i- Другие нули:
?t = kn , k*Q,z = -$ и полюс z = -5 не принадлежат области |*| < 2 и поэтому
не учитываются. Следовательно, JV = 3 + 1 = 4, P = 2 и
Формула D.38), очевидно, может быть использована для исследова-
нулей функции f(z) , если удастся получить удобный алгоритм для
1^числения интеграла, стоящего слева в D.38).
; Воспользуемся равенством Ln /(z) = In | /(г) j + / Arg /(г) . Так как f(z) -
ОНалитическая на С и на С не имеет нулей, то в некоторой области,
303
содержащей С, возможно выделение однозначных ветвей Arg f(z) , v-
следовательно, на С имеем однозначную аналитическую функции
In f(z)= In| /(г)| + /arg/(г), где arg/(z) - одно из значений аргумента, в частно-
частности главное значение. Запишем интеграл (логарифмический вычет):
с J\z> се с
Первое слагаемое в правой части равенства равно нулю как инте-
интеграл по замкнутому контуру от полного дифференциала функции дву:
действительных переменных dln|/(z)|.
Второе слагаемое определяет приращение аргумента образа точки
при отображении w = f(z) в то время, когда точка г совершает полны!-
обход контура С в положительном направлении (рис. 4.9,о), T.t
<jV/ arg f(z) = Дс arg f(z) . Если точка wo=/(t0) не совершает обхода вг-
с
круг w = 0, то Ас arg f(z)= О (рис. 4.9,6). Если точка wq = /(zq) совершает,
оборотов, то Лс arg f(z) = 2кп (на рис. 4.9,в к = 2), причем в этом равенств<-
к > 0 при положительном обходе (против часовой стрелки) и к < 0 npi-
отрицательном (по часовой стрелке). Величина —Ас arg f(z)
число оборотов вектора w = f(z), а знак - направление обхода.
= Ы
Рис. 4.9
Приведенные рассуждения отражают геометрический смысл формуль
D.38).
Утверждение 4.13 (принцип аргумента).
1. Разность между числом нулей и полюсов функции f(z) в области
ограниченной контуром С, равна числу оборотов вектора w = f(z) при nt
ремещении точки w по кривой Г - образу С при отображении w = f(z) i
однократном обходе точкой z контура С:
D.39
304
2. Если функция f{z) - аналитическая в D и на С - границе D нет ну-
нулей f(z) , то D.39) принимает вид
Цсагв/(г) , D.40)
2л
т.е. число нулей N в области D функции f(z) , аналитической в этой области,
оавно числу оборотов вектора w = f(z) вокруг начала координат.
Принцип аргумента, в частности формула D.40), имеет многочислен-
многочисленные приложения. Приведем, например, следующие две теоремы.
Утверждение 4.14 (теорема Руше). Пусть функции f(z) и ф(г) явля-
являются аналитическими в односвязной области D и на ее границе Сив
точках границы выполняются условия \f{z)\ >|ф(г)|. ZeC. Тогда число
пулей функции f(z) и F(z) = f(z) + ф(г) в области D одинаково.
Приведем доказательство. Прежде всего проверим, что функции f(z)
и F(z) удовлетворяют условиям применения принципа аргумента, а имен-
именно не имеют нулей на контуре С. Действительно, из неравенства
|/W|>|«pfc)|, геС и |cp(z)|>0 получаем |/(г)| >0, z e С, т.е. f{z)*O,
zeC. Аналогично для функции F(z): |/U) + <p(z) | =
= |/(г)-(-ер(г))|*|/(г)Н«р(г)|>0, геС, т.е. F{z)*4, z*C.
Далее покажем, что Acarg/"(?)= Acarg/(j). Для этого запишем функ-
функцию F(z) в виде произведения F(z)= f(z)+<р(г) = f(z)- '+"w~( • Тогда
AcargF(z) = Acarg/(z)+ Acargw(z), где w(*)=l + -%4. На границе С имеем
f(z)
Ш\
< 1 , т.е. образом кривой С при отображении
w = 1 + -"-i- является окружность \w -1| = 1 , из чего следует, что радиус- *
вектор точки w не обходит начало координат, поэтому Ас arg w(z) = 0. Та- •
ким образом, получаем Ас arg F(z)= Acarg/(j).
Утверждение 4.15 (основная теорема алгебры). Многочлен степени п
с комплексными коэффициентами имеет п корней.
Для доказательства представляем многочлен
V />„(г) = о„г"+оя_,г"-1+... + 0о
в" виде суммы: Pn(z)= f{z) +<?{z) , где f{z)r=anz" и tp(z)= fln_i^""' +... + o0.
Так как lim -^4 = 0. то найдется такое число R > 0, что для z, удовле-
?-« f(z)
творяющих условию \z\ > R , выполняется неравенство |/(z)|>|ep(z)|-
305
За счет выбора достаточно большого R можно получить, что все нули
многочлена расположены в круге \z\ < R. На границе круга, т.е. на \z\ = R,
выполняется условие |/(г)|>|ф(г)|. По теореме Руше многочлен имеет
в |г| < R , а следовательно, и всюду такое же число нулей, как и функ-
функция /(г). Но f(z) = anz" имеет и нулей в круге |г|<Л, так как г = 0
является нулем кратности п.
Замечание 4.8. Во введении мы построили множество комплексных
чисел С как расширение множества действительных чисел, в котором разрешимо
любое квадратное уравнение. Может показаться, что для разрешимости уравне-
уравнений более высоких степеней понадобится раз за разом расширять множество С.
Однако оказывается, что больше никаких новых расширений не нужно. Корни
многочлена какой угодно степени принадлежат множеству С, и, значит, новых
чисел, не входящих в С, для решения не требуется. Это свойство называется
алгебраической замкнутостью множества комплексных чисел.
Практическое применение формулы D.40) при решении задач опреде-
определения числа нулей аналитической функции в области D заключается
в следующем. Строится годограф - кривая, которая является образом грани-
границы области D при отображении w = f(z). Далее по рисунку определяется
число оборотов вектора w при однократном обходе точкой г границы
области D. Наконец, по формуле D.40) определяется число нулей функции
f(z) в области D.
Область D может быть неограниченной, например полуплоскость
Re z > а. С задачей определения числа нулей многочлена f(z) - P{z) в полу-
полуплоскости Re z > 0 связана важнейшая проблема механики - проблема устой-
устойчивости электрических и механических систем.
В качестве контура С в таком случае выбирается полуокружность
|;lt R, Re?>0 и ее диаметр (рис. 4.10,в), число R выбирается достаточно
большим, чтобы все нули многочлена, расположенные в правой полуплос-
полуплоскости (Rez>0), попали в полукруг |^| <: Л, Re?>0 , и рассматривается
lim Ac arg P(z). Задача определения числа нулей в левой полуплоскости решает-
Я->СО
ся аналогично. При этом рассматривается левая полуокружность |г| = Л, Re z < 0
и ее диаметр (рис. 4.10,6).
Так как контур С состоит из дуги CR : \z\ = R и отрезка, то имеем
AcargP(z)= ДС/! argP(z)+Алв argP(z) в случае Rez>0 и hcaigP(z) =
= ДСл argP{z)+ Aba arBP{z) в случае Re* < 0.
Для удобства будем считать, что а„ = 1, так как величина коэффициента
ап(а„ * 0) не влияет на число корней уравнения Pn(z) = 0 .
Для определения Ac. argP(z) многочлен P[z)=z" +an.\Zn~* +... + Oq
записывается в виде произведения P(z) = z" -ф(г), где <p(z)= 1 + -а-^-+...+-"- .
г zn)
306
Поэтому ACr arg Я(г) = AC/f argz"+ACR arg <p(z). При этом ACr argz" = w дСл argz,
а из 1игкр(г)=1 получаем ДСл arg(p(z) = O. Таким образом, имеем
ЛсЛ argP(z)=/i ДСл arg г. Величина ACjJargz определяется как разность:
дсЛ arg г = arg г2 - arg ?i, где z\ - начальная точка на дуге Сд, a z-i - конечная. В
обоих случаях, изображенных на рис. 4.10,о и 4.10,6, AcRaT%z = n и
/
-iR
Рис. 4.10
Чтобы определить приращение аргумента P(z) при перемещении точ-
точки z по мнимой оси (отрезок АВ на рис. 4.10,о или ВА на рис. 4.10,6 при
/?-><») строится, как сказано выше, годограф - образ мнимой оси при
отображении w = P(z). Для этого записываем параметрическое уравнение
мнимой оси z = it, t е (-00,00), подставляем в w = P(z) и получаем пара-
параметрическое уравнение образа. Чтобы построить годограф, отделяем в по-
полученном уравнении действительную и мнимую части Rew = M, Im»v = v.
Получаем уравнение образа в действительной параметрической форме
u = u(t), v = v{t) .
Для схематичного построения кривой в плоскости uOv достаточно найти
несколько значений переменных и и v для различных значений t, в частности
нули функций u{t),v(t) , а также их значения при t -> +00 и / -» -°о. Часто по-
лезно найти угловой коэффициент касательной при / -> да, т.е. lim
Все
данные целесообразно занести в таблицу и по точкам построить кривую. По
графику определяем число оборотов вектора w = P(z) вокруг нуля и при-
приращение аргумента w = P(z) на мнимой оси. При решении задачи определения
числа нулей в правой полуплоскости рассматривается перемещение точки по го-
годографу в направлении от( = + » к/ = -да (рис. 4.10,о), а при определении числа
307
нулей в левой полуплоскости - в направлении от f = -« к ? = +оо(рис. 4.10,6).
Результаты рассуждений запишем в виде алгоритма.
Алгоритм применения принципа аргумента
для решения задачи отыскания числа нулей
многочлена в правой и левой полуплоскостях
1. Определить приращение аргумента на дуге CR :
где п - степень многочлена.
2. Определить приращение аргумента P(z) на мнимой оси. Для этого:
а) найти u(t)=ReP(it) и v(t) = Im P(it) ;
б) построить годограф
[v = v(/), /б(-00,00);
в) определить число оборотов к радиуса-вектора вокруг нуля и при-
приращение 2кл . При решении задачи определения числа нулей в правой полу-
полуплоскости рассматривается перемещение точки по годографу в направлении от
/ = +оо к/ = -оо, а при определении числа нулей в левой полуплоскости - в на-
направлении от / = -оо к/ = +оо. При обходе нуля против часовой стрелки к > 0, а
по часовой стрелке к < 0 .
3. Вычислить ^l.argP(z)~ пп + 1кп .
4. По формуле D.40) найти N = — Дс arg P(z) = число нулей
2я 2
многочлена P(z) в полуплоскости.
Пример 4.45. Найти число нулей многочлена P{z)=z4 -2z3 +z2 -I
в правой полуплоскости.
D 1. Определим ACr arg P(z) = An, так как п = 4 .
2. Положим z = it: P(it) = t* + lit2 -12 -1 = r4 -12 -1 + lit2:
а) выаелим аействительную и мнимую части u{t) = ?4 -11 -1, v(f) = 2р;
б) исследуем поведение функций m(/),v@: v(f)=O при f = 0,v(f)>0
при / > 0 и v(/) < 0 при / < 0 ; v = v(f) - функция нечетная.
Для нахождения нулей м(/) - корней биквадратного уравнения
/4 -12 -1 = 0, введем обозначение у = ?2. Находим корни yi = —-— ,
уг= , поэтому У -у-\ = (у-У\)(у-У2)- Так как У|>0, а ^2<0,
обозначим У[=Ь2, Уг=-аг .и запишем разложение многочлена:
/4 -/2 -I =(/-/i)(/-/2)(/2 +а2), где /i,2=±J—-—• Для значений te{tut2)
имеем u(t) < 0, вне этого промежутка u(t) > 0.
308
Так как многочлены u(t) и v(f) не имеют общих нулей, то
P{z) * 0 при z = it, т.е. на границе области Re z > 0 нет нулей много-
многочлена P(z)- Поэтому можно применить принцип аргумента.
Полученные данные запишем в табл. 4.1 и построим по точкам
кривую (рис. 4.11).
Таблица 4.1
t
и
V
+ 00
+ 00
+ 00
М)
>о
>о
'i
0
«4,4
<о
>0
0
-1
0
@,<2)
<0
<0
h
0
к-4,4
('2.-°°)
>0
<0
— 00
+ 00
-00
W = P(Z)
Рис. 4.11
в) Из рис. 4.11 видно, что при однократном обходе точкой z мни-
мнимой оси сверху вниз (t изменяется от+оок -« ), радиус-вектор w = .P(z)
поворачивается на 2л против часовой стрелки, т.е. к = 1.
3,4. Получаем AargP{z)=2n и Ас argP{z) = 4л + 2л = 6л. Поэтому по
формуле D.40) находим N = с ^ = 3.
2л
Заметим, что заданный многочлен можно разложить на множители
И
выписать все его нули: Z\t2 ■
|±/
2
7з
. В правой полуплоскости расположены нули
а в левой - один нуль
309
Заметим, что для определения числа нулей в левой полуплоскости следует
изменять t в направлении от < = -<» к < = +<». При этом обход нуля осуществ-
осуществляется по часовой стрелке и к = -1. Поэтому N = = 1. ■
2я
Пример 4.46. Найти число нулей многочлена
в левой полуплоскости.
D Воспользуемся алгоритмом.
1. Находим АСл argP(z) = 5я, так как я = 5.
2. Положим z = it: P(it) = 2it5 + ?4 + б/?3 -3t2 + 4rt + 2 = (<4 -3<2 + 2) +
а) найдем действительную и мнимую части:
u{t) = Re P(it) = t* - It1 + 2 , v(f) = Im P(/V) = 2t5 + 6<3 + At;
б) исследуем поведение функций u(t), v(t):
u(t) = 0 при ?i2=±i/2, <з,4=±1;
v(<) = t B<4 + 6<2 + 4) = It (t2 + 2) (t1 +1);
v(f) = O при < = 0, v(<)>0 при<>0и v(r)<0 при t<0.
Так как v(<ij2)*0, v(<34)^0, м@)*0, то многочлен P(z) не имеет
нулей на мнимой оси и принцип аргумента применим.
Данные занесем в табл. 4.2, причем достаточно провести вычисления
только на интервале (- оо,0) , так как можно использовать свойства функ-
функций: u(t) - четная, a v(t) - нечетная.
Таблица 4.2
t
и
V
— 00
+ 00
-00
(-00,-Л)
>0
<0
-S
0
-гф
(-V2.-D
<0
<0
-1
0
-12
(-1,0)
>0
<0
0
2
0
310
V 4
24V2
12
2
-12
-24^2
Рис. 4.12
в) Из рис. 4.12 видно, что arg?(z) = - при f-»+oo и arg.P(z) =—
при г->-оо, поэтому ДargР(г) = ----= я ( Л = -, так как годограф обхо-
обходит нуль, поворачиваясь против часовой стрелки).
3,4. Acaig/>(*)= 5я + я = 6я , #= — = 3.
2я
Заметим, что для определения числа нулей в правой полуплоскости следу-
следует изменять t в направлении от / = +юк1=-«. При этом обход нуля осуще-
осуществляется по часовой стрелке и к = —. Поэтому N = = 2. ■
2 2я
Пример 4.47. Найти число нулей многочлена
в: правой полуплоскости.
11 D 1. Находим ДСа = 8я , так как я = 8 .
2. Положим z = U: P(it) = t* + 3i75 - 5f4 -15//3 + 18ft + 4 = f8 - 5f4 + 4 +
+ /Cf5-15/3+18O:
а) запишем действительную и мнимую части:
v{t) = 3r5 - 15f3 + 18r = 3t(t2 -2)(t2 - 3);
311
б) исследуем поведение функций u(t),v(t). Так как многочлены и(/) и
v(/) имеет общие корни f,2=±V2, то при z = it P(z)=0 и принцип ар-
аргумента для данного многочлена непосредственно применить нельзя.
С другой стороны, так как многочлены имеют общий множитель, то
из P(it}= u(t)+iv(t) находим P{it) = (t2 -2) («,(/) + /v,(f)). При г = /',т.е. при
t = -iz .получаем: P{z)=\z2 +2}Q(z) , и далее задача может состоять в
определении числа нулей многочлена Q(z).
Разложение P(z)=[z +2j-Q(z) можно получить непосредственно груп-
группировкой:
= (г2 + 2)((г2 - 2}{z4 -1)+ 3z{z2 + з))= [z1 + l){z6 - 2z* * Зг3 - z2 * 9z + 2).
Из разложения следует, что многочлен P{z) имеет два нуля на мни-
мнимой оси: z = ±i<H. Другие его нули определяются как нули многочлена
Q(z)= zb -2z4 +3z3 - z2 +9z + 2. Задачу далее решаем по алгоритму с при-
применением принципа аргумента. В результате получим:
= (>n-2n = 4n и N = 2.m
Пример 4.48. Найти число нулей многочлена z3 - 2z - 5 в области D:
a) D:\z\<\ ; б) /):1<ф|<3.
□ Воспользуемся теоремой Руше.
а) Обозначим f(z) = 5, <p(z) = г3 - 2z. На границе области, т.е. для точек,
удовлетворяющих условию \z\ = 1, имеем
Условия теоремы Руше выполняются и, следовательно, число нулей данного
многочлена в области | z \ < 1 совпадает с числом нулей функции f(z) в этой об-
области. Так как многочлен f(z) = 5 не имеет корней, то заключаем, что много-
многочлен г3 - 2г — 5 в области | z \ < 1 не имеет нулей.
б) В силу того, что в круге | z \ < 1 многочлен не имеет нулей, то для нахо-
нахождения нулей в кольце D: I < |^| < 3 достаточно найти их число в круге \z\ < 3.
Обозначим f(z) = г3, ф(г) = -2z - 5. На границе области, т.е. для z, удовлетво-
удовлетворяющих условию | Z | = 3, имеем
zeC
312
Условия теоремы Руше выполняются, и искомое число нулей совпадает
с числом нулей многочлена f(z) = г3 • Так как этот многочлен в области \z\ < 3
имеет корень г = 0 кратности л = 3, то получаем, что многочлен z3 -2z-5
в кольце D : I < \z\ < 3 имеет три нуля.и
Упражнения
1. Определить число нулей многочлена гэ + г4 + г3 + Зг2 - г +15 в левой
полуплоскости.
1 Ответ: 3.
2. Определить число нулей многочлена г3 - 2г + 5 в правой полуплоскости.
Ответ'. 2.
3. Найти число корней уравнения 2г4 + г3 - 4г2 + 8г + 5 = О в правой полу-
полуплоскости.
Ответ: 2.
I 4. Найти число корней уравнения г5 - 5г2 - 4г -10 = 0 в левой полуплоско-
полуплоскости.
Ответ: 2.
5. Найти число корней уравнения г6 -6г5 +5г4 +5г-5 = 0 в правой полу-
полуплоскости.
Ответ: 4.
6. Найти число корней уравнения г8 + 5г7 - г4 + 2 = 0:
а) в круге |г| < 1; б) в кольце 4 < \z\ < 6 .
Ответ: а) 7 ; б) 1 .
7. Найти число корней уравнения Зг4 + ch iz = 0 в круге \z\ < —.
Ответ: 0.
8. Найти число корней уравнения г4 + 4г + cos г = 0 в круге |z| < 1.
Ответ: 1.
313
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти все особые точки функций и определить их тип:
а)/(*)=777Л; б) Ж
2. Найти все особые точки функций и определить их тип:
1 z
a) cos- + ——ег; б)
1г 1
1+? z +1 ег-1
^-1
3. Определить порядок полюса г = 0 функции /(г)
6sinz3 +г3(г6-6)
4. Для каких из следующих функций точка z = -i является устранимой
особой точкой:
г -(
р (г)
5. Показать, что для функции г~Л, где Р„(г) и Gm(z) - многочлены сте-
Qm\4
пеней лит соответственно, точка z = °° является полюсом порядка л - /я, если
л > т, и устранимой особой точкой, если п < т.
6. Привести примеры функций, имеющих в расширенной комплексной
плоскости только следующие особенности:
а) полюс второго порядка в z = «;
б) полюс второго порядка вг = 0и простой полюс вг = «.
7. Найти все особые точки функций, определить их тип и вычислить выче-
вычеты:
i
г +1 г +1
8. Найти все особые точки функций, определить их тип и вычислить выче-
вычеты:
\_
а) ег +cosz; б) —; cos—.
г2+16 Z
9. Вычислить вычеты функций в их особых точках:
г+7
10. Доказать, что если f(z) - четная функция, то res/(j)= res/(*)=0.
0 ш
314
11. Найти вычеты во всех особых точках функций:
a) sin г sin-; б) г3 cos .
Z Z-2
12. Найти вычет res-T=—.
13. Вычислить интегралы:
2 J[
a) jz"e4z; б) j
i 1
14. Вычислить интеграл 4
И-з
15. Вычислить интеграл
2х
16. Вычислить определенный интефал с помощью вычетов (
о
17. Вычислить несобственные интегралы:
° ° dx
а)
dx; б)
18. Вычислить несобственные интегралы:
19. Вычислить несобственные интегралы:
20. Найти число корней уравнения ez + %z2 =0 в круге |z| <—■
21. Найти число корней уравнения ez - z = 2 в левой полуплоскости.
22. Найти число корней уравнения z7 + 5z4 - z2 + 2 = 0 в кольце 1 < jz| < 2.
23. Найти число корней уравнения z3 + 4z2 - 5 = 0 в левой полуплоскости.
г .
■ 315
Глава 5. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
5.1. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
5.1.1. Основные определения
1. Оригинал - комплекснозначная функция f(t) действительного аргумен-
аргумента /, которая удовлетворяет следующим условиям:
а) /(/)=0 при /<0;
б) на любом конечном отрезке [а,Ь]е [0, + а>) функция f(t) имеет не более
чем конечное число точек разрыва первого рода;
в) f(t) имеет ограниченный рост, т.е. возрастает не быстрее показательной
функции: существуют такие постоянные М > О и а £ 0, что
\f(t)\<Meal при г>0.
Замечания 5.1.
1. Величина а0 = inf сг называется показателем роста функции f(t). Для
любой ограниченной функции, являющейся оригиналом, можно принять стд =0.
2. Обозначим
/(+0)= lim /(/); /(+»)= lim f(t),
если пределы существуют и конечны.
3. Совокупность всех оригиналов называется пространством оригиналов.
4. В точке /0 разрыва первого рода функция имеет конечные односторон-
односторонние пределы: lim /@, lim /@.
f->/0+0 f-»4>-0
Пример 5.1. Проверить, являются ли функции
/,(')=if''*0' /2@=f7T?'s0' /э@={3п4'''\°'
[О, Г<0; [0> /<0; [О, Г<0
оригиналами.
П Функция fi(t) является оригиналом, так как условия пп. "а"-"в" вы-
выполнены: М = 2,а0 =5; функция /2(г) не является оригиналом, так как в точке
/ = 2 имеет разрыв второго рода (не выполняется условие "б"); функция /3(г) не
является оригиналом, так как растет быстрее показательной функции (не выпол-
выполняется условие "в", поскольку З4' > Me"' для любых М и а , t >0).l
2. Изображение функции /(/) - функция F{p) комплексного переменного
р, определяемая равенством
= +je-i"f(t)dt. E.1)
356
Область существования этой функции определяется областью сходимости
интеграла Лапласа, стоящего в правой части равенства E.1). Исследование ин-
ierpana позволяет определить эту область и установить свойства функции F(p).
Имеет место следующее утверждение.
Утверждение 5.1. Если функция f(t), является оригиналом, то интеграл
Лапласа сходится абсолютно в области Re р = о > о0 (рис. 5.1) , где о0 - показа-
показатель роста оригинала. Внутри этой области, т.е. на любом замкнутом подмноже-
подмножестве Re р = а > а > oq , интеграл сходится равномерно и определяет аналитическую
функцию F(p).
Замечания 5.2.
1. Утверждение 5.1 аналогично свойствам степенных рядов, сходящихся
в круге и равномерно сходящихся внутри этого круга, где сумма ряда является
аналитической функцией.
2. Свойство аналитичности изображения имеет важное значение в теории и
практике применения преобразования Лапласа, так как позволяет использовать
в пространстве изображений методы теории аналитических функций, в частности
разложения функций в ряды и теорию вычетов.
3. Совокупность всех изображений F[p) называется пространством
изображений.
3. Переход, определяющий изображение F(p) по оригиналу f(t), называ-
называется преобразованием Лапласа:
F(p)=L[f(t))= ]e-"f(t)dt.
E.2)
. Запись F(p) =£[/(')] означает, что оригиналу f(t) соответствует изобра-
изображение F(p).
4. Оригинал по изображению находится с помощью обратного преобразо-
преобразования Лапласа по формуле обращения
\eptFb)dp,
E.3)
где путь интегрирования - любая прямая Re р = о, параллельная мнимой оси
лежащая правее прямой Rep = og (Рис- 5.1).
Рис. 5.1
317
Непосредственное применение формулы обращения часто затруднительно.
Поэтому на практике пользуются методами, изложенными в разд. 5.1.4.
Замечания 5.3.
1. Для преобразования Лапласа используются различные обозначения, на-
например fit) = Fip) и Fip) '= fit), что означает: оригиналу fit) соответствует
изображение Fip) и изображению Fip) соответствует оригинал fit). В [34,45,51]
вместо аргумента р применяется s,T.e. F(s) = L[f{t)] и L~llF(s)] = f(t).
2. Для компактной записи оригиналов используется единичная ступенчатая
функция l(t-t):
*->-{t;::
где т - точка приложения (рис. 5.2). Так как во многих практических задачах
аргумент t имеет смысл текущего времени, то т также называется моментом
приложения единичной ступенчатой функции. В системах автоматического регу-
регулирования и управления функция /(/ -1) рассматривается как типовой входной
сигнал [45].
/t
О
Рис. 5.2
При т = 0 функция l(t - т) является функцией Хевисайда:
П, г>0,
Тогда, если функция f(t) удовлетворяет условиям "б", "в" в определении
оригинала (п. 1), но не удовлетворяет условию "а", то функция /(/)■/(/) будет
оригиналом, так как
fiAji,) _(/(')• <>0>
w у> jo, г<о.
Далее под заданной с помощью аналитической формулы функцией f(t),
там, где это не вызывает недоразумений, будем понимать произведение этой
функции на функцию Хевисайда, а множитель /(/) опускать.
3. Функции F(p), являющиеся изображениями, удовлетворяют необходи-
необходимому условию [40]: если F{p) есть изображение, то F(p) -* 0 при Re р = а -> -н».
Поэтому функции Fi(j>)=l, F2(p)= p, F-}{p) = sinp, F4(p) = —*— не явля-
р-\
ются изображениями. Однако в практических задачах функции типа
F\(p)= I, F2{p)= p и другие встречаются. Это требует расширения понятий ори-
оригинала и изображения.
Класс оригиналов можно расширить, включив в него функции, которые
могут быть не ограничены в окрестности некоторых конечных точек, но такие,
что интеграл Лапласа от них, тем не менее, сходится абсолютно в некоторой по-
полуплоскости Rep>a0. К числу таких обобщенных оригиналов относятся сте-
степенная функция /@ = 'ц при ц>-1, In/ и некоторые другие [14,21,25,40,41].
4. Во всякой точке г0, являющейся точкой разрыва функции /(/), правая
часть формулы E.3) равна —\f{t0 -0)+/(f0 +0)].
Пример 5.2. Найти изображение единичной функции Хевисайда /(/) = l(t).
□ Так как функция /(/) ограничена, то в качестве показателя роста мож-
можно положить о0 = 0.
По формуле E.2)
+ 00 1
о =7'
так как из равенства \e'pt =eRe(-^"> =е~'Кер =е'°' (см. разд. 2.1.2) следует, что
lim е'р< = 0 при Rep = a>a0=0.l
f-n-oo
Пример 5.3. Найти изображение функции /(/) = е", где а - действитель-
действительное число.
D Показателем роста можно считать о0 = а. По формуле E.2)
F(p) = 7
ев'е-
0J о а~Р\ и а~Р Р~а
так как из равенства е(а~'))' =e~'(Re/)~a) =e-'(°-fl> следует, что lim e^"'^' =0
при Rep = o>a. ■
5.1.2. Свойства преобразования Лапласа
Будем предполагать, что рассматриваемые далее функции
/(')>/|(')>-">/я(') являются оригиналами. Соответствующие им изображения
(при Rep>a,-, / = 0,1,...,л) обозначим F(p),F{(p),...,Fn{p).
319
1. Линейность. Если f\(t),--,fn(t) - оригиналы, то для любых комплексных
п
чисел с,-,/ = !,...,/», функция /@ = XC*/*W также является оригиналом и
и л
справедливо равенство Ц]£с*/*@]=Хс* ^Л@1 или
... + c^(f)] = c,Fl(p)+... + c,f1II(p). Re/>> max{(*,,...,(*„}. E.6)
л
Заметим, что для функции /(?)= Xе*/* W существенно, что все слагае-
*=1
е'-1
мыс являются оригиналами, так как, например, функция /(/)= является
е' 1
оригиналом, а слагаемые /j(f) =— и /2(/) = — не являются.
Справедливо и обратное утверждение: если ^(/^.....^„(/^-изображения, то
Здесь также важно, что слагаемые функции clFl(p) + ... + cnFn(p) являются
изображениями, поскольку из того, что F(p)-с,F](p)+... + cnFn(p) - изображе-
изображение, не следует, что F{(p),...,Fn(j>) - изображения. Например, функция
F(p) = \n-— является изображением, а слагаемые F\ (p) = In (p -1) и
Р
F2(p) = - In p не являются.
Пример 5.4. Найти изображение функции f(t) = 3 + 2еч.
О Из примера 5.2 имеем L[l(t)} = —, а из примера 5.3 при а = -1
Р
Z, е~'= . Тогда согласно свойству линейности для оригинала
р + \
/(/)=3■/(/)+ 2-е'' получаем F(/>) = 3--+2-—^-. ■
Пример 5.5. Найти изображение функции /(/)= cost.
О Используя формулу Эйлера B.11), получаем
Из примера 5.3 при a = i и a = ~i следует: L\е" = , L\е~" = .
1 p-i P + i
Тогда по свойству линейности
,г 1 I , Г ,-rl I Л -it] 1 1 1 1 p + i + p-i p _
L[cost\ = -L\e"\ + -L\e "\ = - + = - т^— = —~М
2 L J 2 l ' p-i p + i 2(/>2+l) p2 + l
320
2. Подовые (теорема подобия). Для любого а > 0 из F(p) = l\f(t)] следует
E.7)
1%братно: fl\F(ap)\ = -/(-).
а {а)
Пример 5.6. Найти изображение функции f(t)= cos at.
П Из примера 5.5 следует, что L[cost] = ~-—• Тогда по теореме подобия
£
L[cos<w] =—
а
р2+а2'
3. Смещение (теорема смещения). При любом комплексном а из
?{Р) = L\f(t)\ следует
L\etttf(t)]=F(p-a), Щр-а)>о0, E.8)
~.е. умножению оригинала на е"' соответствует смещение изображения на а.
Пример 5.7. Найти изображение функции f(i) = eat cos bt.
П Из примера 5.6 следует
рг+Ь2
Тогда по теореме смещения
е" cos bt =-
1 ш
(p-af+b1
4. Запаздывание (теорема запаздывания). Для любого т>0 из
HP) = L[f{t)\ следует *
[()]() E.9)
де /(^-т) = /(^-т)/(^-т)(рис. 5.3), т.е. запаздыванию оригинала на т>0 соот-
1етствует умножение изображения на е'рт.
f
fit)
Рис. 5.3
1 Пантелеев Л.В., Якимова Л.С.
321
Пример 5.8. Найти изображение функции
/(<) = cos(f - 3)- l{t - 3) = cos(f - 3).
□ В примере 5.5 получено L[cost] = —~—.
По теореме запаздывания при т = 3
р2+1
Пример 5.9. Найти оригиналы по изображениям:
0>-1J+4 р2
П а) Из примера 5.7 следует, что при а = 1, b = 2 изображению
0>-1J+4
соответствует оригинал е' cos It. Тогда по теореме запаздывания при т = 4
б) По формуле 3 из табл. 5.1 I —r = t. По теореме запаздывания при
IP \
т = 1 получаем /(<) = I [f(/»)] = (f -1) • /(f -1). Заметим, что для похожего, но от-
отличного от полученного, оригинала /(/) = /-1 (его можно записать в виде
1 1 е"'
(/ -1) ■ 1@) изображение имеет вид F(p)=—r—* —г-. ■
2 Р 2
Р2 Р Р2
Пример 5.10. Найти изображение функции
»*(') =
i, o<tih.
O,t<O,t>h,
график которой представлен на рис. 5.4.
h
Рис. 5.4
D С учетом E.4) представим функцию bh(t) в виде
322
Из примера 5.2 имеем l\l(t)] = —. Применяя свойства линейности и запаз-
Р
дывания, получаем
Заметим, что, находя предел при Л -» 0 в последнем выражении, можно
получить изображение 8 -фуикцци b(t) = lim 6Л(г):
А»0
= lim {-^- = lim^- = 1.
Л-»0 />Л *-»0 />
Замечание 5.4. Дельта-функция часто встречается в инженерных
приложениях как вдеализация импульса конечной длительности. В теории авто-
автоматического регулирования и управления 5-функция вместе с единичной сту-
ступенчатой являются типовыми входными воздействиями [34,45,51].
Очеввдно, изображение дельта-функции не удовлетворяет необходимому
условию (п.2 замечаний 5.3). Этот факт свидетельствует о практическом требова-
требовании расширения понятия оригинала. Дельта-функция относится к обобщенным
функциям и задается соотношением [21,45]
*";?
5. Дифференцироваиие оригинала. Если функции f{<),f'{t),...,P"\t) являют-
являются оригиналами и F(p)= £[/(')], то
L[f'(t)UpF(j,)-f(+Q),
l\f"(t)]=p2F(p)-pf(+Q)-f'(+Q), E.11)
/-'/(+0) -...-/М(+о),
где /(/)(+0)= lim /Щ, / = 0,1,2,...,п-1.
/-»+о
Пример 5.11. Найти изображение /'('), если f(t) = e~' cos3/.
□ Из примера 5.7 следует, что при а = -1, b = 3
Найдем /(+ 0) = lim e"' cos 3f = 1. Согласно E.11) L[f'(t)] = p £±J 1.1
'-►+0 (p + l) 2+9
323
Пример 5.12. Найти изображение выражения х" + Ъх + 2дс +1 с начальны-
начальными условиями дс(+ 0) = 1, дс'(+ 0) = 4.
D Пусть Х(р) = L Щ, тогда L [*'(*)] = РХ{р) -1; L [x"(t)} = р2Х{р) - р • 1 - 4.
В примере 5.2 получено £[/(*)]=—. Используя свойство линейности, имеем
Р
L[x" + Зх + 2jc +1] = ф"] + 3i[*'] + 2I[jc] + I[l] =
б. Интегрщювшаи оригинала. Если функция /@ является оригиналом и
-4/@], то
ifJ/(t)A -/ХЙ. Re/>>a0> E.12)
т.е. интефированию оригинала соответствует деление изображения на р.
t
Пример S.13. Найти изображение интеграла J /(т)Л от функции
о
f{t) = cost.
О Из примера 5.6 следует, что l[cosf] = —f-—= F(p). Тогда
\ ^те l[sin<]
L\ \ca&x(h\ = L[smt] = ^ = ——,т.е.
[oJ J BD 2l
7. Дифференцирование изображения. Если функция /(/) является оригина-
оригиналом и F(p) = I\f(t)\, то
\ } F%). E.13)
Пример 5.14. Найти изображения функций f\ (t) = t,f2(t) = t2, ...,fn (t) = tH.
D Из примера 5.2 следует, что L[l(t)] = — = F{p). Согласно E.13) при я = 1
Р
получаем L[-t]= F'(p) = —- или по свойству линейности lM = —-г. При я = 2
Р2 Р2
имеем l\2] = F"{p)=~. Аналогично 4"] = -^Г- ■
Р Рп+
324
Пример 5.15. Найти изображение функции f(t) = t cos 3t.
О Из примера 5.6 имеем l[cos3f] = —?*-—= F(p). При п = 1 из E.13) выте-
р2+9
L[(-t)f(t)]-Fb) или Ц-гссЗг]-^]'-4^-7^4-
U +9J (p2+9f (p2+9f
р2 -9
Окончательно получаем l[fcos3<] = y^ —М
8. Интегрирование изображения. Если функция ^-^- является оригиналом,
то из F(p) = Ц/@] следует
рМ] ]ф*. E.14)
Пример 5.16. Найти изображение функции .
П Функция является оригиналом, так как
sin r
t
< 1 (условие "в") и
точка t = 0 является точкой разрыва первого рода (условие "б"). Из примера 5.13
следует L[siiw] = —;— = F(p).
2l
p2+l
Отсюда L\ = -г— = arctgz = —-arctg^.
L ' J „Г+1 P 2
9. Умножение изображений (теорема Бореля). Из F\(p) = L[f[(t)] и
= Д/г@] следует
il/iW-AWl-iW-^W. E.15)
т.е. свертке оригиналов соответствует произведение изображений. Функция
/i(') */г(') определяется формулой
J J E.16)
о
и называется сверткой оригиналов f\{t) и
Пример 5.17. Найти оригинал, соответствующий изображению
U Представим F(p) в виде произведения изображений:
325
Из примеров 5.6 и 5.13 следует
т-\
1
= siiW,
Р +1
Согласно E.15),E.1б) получаем искомый оригинал:
г-1|
If . cost cos(-')l 1
-2['Sm/""T~ + ~2 J = I
. • .
10. Дифференцирование свертки (интеграл Дюамеля). Согласно свойствам 9
и 5 найдем преобразование Лапласа от производной свертки двух функций:
С другой стороны,
[ /.(О * Ш = £ J
"'о о
или, применяя правило дифференцирования интеграла, зависящего от парамет-
параметра, имеем
о
о
Здесь при дифференцировании интеграла, зависящего от параметра, при-
применялась формула Лейбница, которая для общего случая имеет вид [21]
. v(X) г, . v(X) a
— J/(x,X)<fa=/(v(X),X)—--/(и(Х)Д)--+ J— f(x,X)dx.
dXum dX dX и(Х)дХ
Объединяя полученные результаты, можно записать:
E.17)
= /l@)/2(')+ J/l'W/2(f-1)* = /2@)/lW+ J/2 W/l(f-t)A.
0
Формула E.17) называется интегралом Дюамеля. Интеграл Дюамеля при-
применяется в разд. 5.2.1 для решения дифференциальных уравнений.
326
Пример 5.18. Найти оригиналы, соответствующие изображениям:
a) F(p)-
г; б)
О»2 +!)(/+ 4)
О а) Заметим, что здесь нельзя непосредственно воспользоваться теоре-
теоремой Бореля, так как в произведении F(p)=—2— множитель Fi(p) = -E—
р-\ р-2 р-\
не является изображением (не выполняется необходимое условие).
Представим изображение в виде произведения F(p) = p -. Из
р-\ р-2
примера 5.3 вытекает
Тогда по формуле E.17) имеем
—е'+2.*.
Можно решить этот пример с помощью теоремы Бореля, представив изо-
изображение в виде
Tip)-
p-1+i 1 1 1
—=- ' + ■
(р-\)(р-гУ (р-\)(р-2) р-2 р-\ р-2-
Тогда, используя свойство линейности и теорему Бореля, получаем
Г1 \F(p)\ = e2l+et*e2t=e2t + )e2x ■ е'"'* =
о
= е21 + е') exdi =е2' + е V -1) = 2е2' - е'.
о
б) Представим изображение в виде произведения:
2 .„ 2
Из примера 5.6 при а = 1 и а = 2 следует .
Тогда по формуле E.17) получаем
-1
L*2+4j
327
=cos2/- J
0
cos Ъ - - f [sinCt - 20 + sinB/ - т)] Л = cos It + -J- cosCx -20f - - cosBf - J'
2 о о JO 2 JO
4 1
= -cos2f—cosf.«
И. Теорема о связи "начальных" и "конечных" значений оригинала i
изображения.
Начальное значение оригинала находится по формуле
/(+0)= lim pF(p). E.18)
Если существует конечный предел lim /(/) = /(+ оо), то
/(+»)= lim pF(p). E.19)
р->0
Из соогаошений E.18),E.19) следует, что для нахождения начальных и ко-
конечных значений оригинала не требуется знания оригинала, а достаточно иметь
соответствующее изображение. На практике соотношение E.19) применяется,
например, для нахождения установившегося значения выходного сигнала в сис-
системах автоматического регулирования (см. разд. 5.2.2).
Пример 5.19. Найти начальное и конечное значения оригинала, которому
соответствует изображение F(p) = —~—.
(p + lf+9
□ Согласно E.18) и E.19)
С другой стороны, из примера 5.7 следует, что
поэтому легко убедиться в правильности полученного результата. ■
Полученные решения примеров 5.2 - 5.17 позволяют сформировать табли-
таблицу преобразования Лапласа. Табл. 5.1 является фрагментом более полных таблиц
[13,21], используемых далее при решении примеров и задач.
5.1.3. Нахождение изображения по оригиналу
ПРИМЕНЕНИЕ ТАБЛИЦЫ И СВОЙСТВ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Для нахождения изображения требуется применить свойства преобразова-
преобразования Лапласа Так, чтобы к функции или ее составляющим можно было приме-
применить результаты, содержащиеся в табл. 5.1.
32S
Таблица 5.1
/М
Пр)
/С)
F(P)
17
7<
1
P(p2+a2)
£
P
18
\(eat-\-at)
1
19
shar
-a*
n\
20
-a*
6@
21
(p-flK
22
n!
23
(р-аГ
(p-af
sm at
24
P
2+2o2
p(p2+4a2)
cosar
25
sin2e/
2a2
/>(/>2+4o2)
/ sin at
2pa
26
sin-=r sh-=r
t cos or
27
pUa4
eal sin bt
28
(p-aJ+b2
—{shat - si
e"' cos bt
29
(/>-aJ+62
a2P
1
l + ap
30
■L(ea'-D
1
p(p-a)
31
—(char + cos <rt)
/-a"
a-b
1
32
(p-a)(p-b)
ае''-be1"
a-b
(p-a)(p-b)
329
Продолжение табл. 5.
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
fit)
{c-b)eal +(а-с)еы +{Ъ-а)еа
{а-Ь)(а-с){с-Ь)
а(Ь - с) еа1 + Ъ(с - а) еы + с(а - Ь) ect
{а-Ь)(Ь-с)(а-с)
аг(Ъ - с) е"' +Ь2(с- а) еы +с2(а- Ь) е"
(а-Ь)(Ь-с)(а-с)
a sin bt-b sin at
a2-b2
cos bt- cos at
a2-b2
a sin at -b sin bt
аг-Ь2
a2cos at-b2 cos bt
a2-b2
b shot - a shbt
a2-b2
chat - chbt
a2-b2
a shot - b shbt
a2-b2
a2chat-b2chbt
a2-b2
t—sinaf
a
-shat-t
a
at
1-cosflf sinflf
1 -chflf +—shat
, b2 cos at -a2 cos bt
a2-b2
, b2chat - a2chbt
al-b2
F(p)
1
(p-a)(p-b)(p-c)
P
(p-a)(p-b)(p-c)
P2
(p-a)(p-b)(p-c)
ab
(p2+a2)(p2+b2)
P
(p2+a2)(p2 + b2)
P2
(p2+a2)(p2+b2)
P3
(p2+a2)(p2+b2)
ab
(P2-a2)(p2-b2)
P
(p2-a2)(p2-b2)
P2
{p2 -a2)(p2 -ft2)
P3
(P2-a2)(p2-b2)
a2
p\P2+a2)
a2
P\p2-a2)
p(p2+a*J
a*
P(P2-*2J
a2b2
p{P2 + a2)(p2+b2)
a2b2
P{p2-a2)(p2-b2)
330
Окончание табл. 5.1
л cos at)
at
i
at cos at)
p2
)ажения функций:
, „\" = 2e~' cos 2/ - -e'1 sin Ъ; в) f(t) = ch f cos It;
" = -^rsin 2f; e) /(f) = sin2 It;
4
з) /(f)=2f4+9f3-3f2+f-3.
;тво линейности и формулу 7 из табл. 5.1 при
линейности и формулы 13 и 12 из табл. S.1 при
п + 1 1 2
у/ т i; т т - {у т I) + 4 (/» + IJ + 4
----- Эйлера B.12), запишем оригинал в виде суммы:
t —t I 1
—..I e -cos2f = -e'cos2f+ -e~'cos2f.
z 2 2
нейности и формулу 13 из табл. 5.1, находим
w 2 (р-1J+4 "
sin4 r = -A - cos2fJ = -A - 2cos2r + cos2 Ъ) =
4 4
"' 1
—) = - (cos At - 4 cos 2t + 3) и используя свойство линейно-
8
габл. 5.1, получаем
331
д) По формуле 10 из табл. 5.1 находим
е) Так как f{t) = sin2 У = - (l - cos dt), то по формулам 2 и 9 из табл. 5.1
ж) С учетом формулы Эйлера B.12) для sh/, запишем оригинал в виде
суммы:
f(t) = ^ +sh/)cos2r = j e' +^-^- Jcos2r =-e' cos 2/ -^-е"' cos2r.
1 Р + 1
—•■ ■
Аналогично п. в получаем Fy>)= *—:
2 (p-lf+4 2 (p + lf+4
з) Используя свойство линейности и формулы 2,4 из табл. 5.1, имеем
Р* Р Р Р Р
Пример 5.21. Найти изображения функций:
a) f(t) = teb sin 3f; 6) f{t) = -(l - cos/);
■>
2
ж) J— A; 3)/(f)*cosDf-8).
о г
О а) Согласно формуле 12 из табл. S.I
L[e2'sin3,] = -JL
По свойству дифференцирования изображения (формула E.13) при п = 1):
332
или
Можно решать иначе, используя формулу 10 из табл. 5.1 при в = 3 и свой-
свойство смещения при а = 2: L[rsin3f] = —, ^ , и lite2' sin3/1 = у ."■ ' ,.
О>2+9J l J П>-2J+9]2
б) Применим свойства линейности и интегрирования изображения. Так
как L[\ -cos?] = r^— в силу формул 1 и 9 из табл. 5.1 , то согласно E.14)
Р р2+\
2
~ V+l"" P2
в) По формуле 9 из табл. 5.1 L[cos4f] = -r^—. Функцию f(t) можно за-
р +16
писать, используя единичную ступенчатую функцию: /(/) = cos Mf- 2) l(t -2).
Поэтому для нахождения изображения следует применить теорему запаздывания
E.9) к оригиналу cos4/ при т = 2: L[cos4(f -2)] =
г) Согласно теореме смещения E.8) и с учетом результата п. "в" имеем
l[e-3/cos4(f-2)]=e-2(/'+3)—^—. так как в = -3.
д) По теореме запаздывания E.9) при т = 2 и по формуле 7 из табл. 5.1 при)
я ш 2, а = -1 получаем
е) Используя свойства линейности, запаздывания и формулы 6,1,8 из табл.
5.1, получаем
р-1 р р2+9
ж) По формуле 19 из табл. 5.1 находим L[shf ] = -т—. По свойству ин-
интегрирования изображения (формула E.14)):
333
*
Z2-l
1 , x-e
,- = —In
-2 2e x + a
2 Z + \
1. p-1 1. p+l
■■—In-— = -ln-—,
2 p + l 2 p-1
По свойству интегрирования оригинала E.12):
, ['г sht I I .p + l
L\ A =—In-—.
з) Используем формулу косинуса разности и запишем оригинал в вид?
суммы: /@ = cosDf-8) = cos4fcos8 + sin4fsin8. По свойству линейности пол"-
чаем: L[cosDf-8)]
r
р2+\6
+ sin8
р2+\6
Заметим, что здесь /(/) = f(t) ■ l(t) и результаты пп. "в" и "з" различны
так как оригиналами являются разные функции.ш
НАХОЖДЕНИЕ ИЗОБРАЖЕНИЙ ФУНКЦИЙ, ЗАДАННЫХ ГРАФИКОМ
При решении прикладных задач оригинал часто задан фафиком. Это w~
жет быть, например, входной сигнал, действующий на систему автоматической
регулирования. В этом случае рекомендуется сначала записать аналитическог
выражение оригинала с помощью единичной ступенчатой функции E.4), приве< -
ти полученное выражение к виду, удобному для применения табл. 5.1 и свойстг
преобразования Лапласа.
Пример 5.22. Найти изображения функций, заданных гоайшками на пи;
5.5.
/1
••. 1
Г О
/г
t О
-1
б
Рис. 5.5
33».
/1
1
0 12 3 г 0
1 2 3
-1
\
1!
/1
I
0
sin/
ж
t 0
/1
t о
-1
!2
Рис. 5.5. Окончание
□ а) Представим функцию в виде f{t) = (l -1) • l(t -1)=- {(-1) • l{t -1).
По формуле 3 из табл.5.1 и теореме запаздывания (формула E.9) при т • 1) f
б) Запишем функцию в виде
По формулам 1,3 из табл. 5.1 и E.6), E.9)
1 1 1 _,
р р2 р2
в) Запишем изображенную функцию в виде
По формулам 1,3 из табл. 5.1 и E.6), E.9)
= _±е-Р_1е-Р
Р2 Р
J35
г) Представим функцию в виде
По формулам 3 из табл. 5.1 и E.6), E.9)
е-" 2е-2" е-3"
Р Р Р
д) Запишем функцию в форме
f(t)=t{l(t)-l(t-\)] + {l(t-l)-l(t-2h(l-t)[l('
= I ■ l{t)-(l - l)l(t - l)-l(t -1)+ l(t - l)-l(t - 2)+
+B-/).;(f-2)+;(f-2)-C-<H'-3)=
= t.l(t)-(t-l).l(t-\)-(t-2)-l(t-2)+(t-3).l(t-
По формулам З из табл. 5.1 и E.6), E.9)
Р Р Р Р
е) Представим изображенную функцию в виде
По формулам 1,3 из табл. 5.1 и E.6), E.9)
rl \ ' 1 1 -в 1 -и 1 -2в
пр)=—т+~ге —е +~те •
р р2 р2 р р2
ж) Запишем функцию в форме
/(г) = sin t [l{t) - J{t - я)] = sin t- l{t) + sin(r - я) • l(t - n).
По формуле 8 из табл. 5.1 и по теореме запаздывания
p +1 p +1
з) Представим функцию в виде
е
По формуле 6 из табл. 5.1 при а = -1 и E.9) при т = 1
и) Представим функцию в виде
Используя формулы 2 из табл. 5.1 и E.6), E.9), получаем
Р Р
НАХОЖДЕНИЕ ИЗОБРАЖЕНИЙ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ
Во многих приложениях используются оригиналы, являющиеся периодиче-
периодическими функциями.
Пусть /(/) - оригинал с периодом Г (рис. 5.6,в), образованный повторени-
повторением функции /0(г)(рис. 5.6,6):
/оЫ
О, г<0,
/@. 0<Г<7\
О, Г > Т.
f
f(t)
Т 2Г ЗГ t О Г '
а б
Рис. 5.6
Для нахождения изображения F(j>) периодической функции f(f) следует
1. Найти изображение функции /0(г):
F0(p)=L[f0(t)].
2. Найти изображение F(р) по формуле [6,25,40,56]
E.20)
?•■>.'
337
Пример 5.23. Найти изображения функций, представленных на рис. 5.7.
/t
АААА
1 2 3
т 2т Зт
/■
h
0
-h
T=lc
:
с:
2с
Зс ,
/1
t О
sin r
я 2гс 3ic
в г
Рис. 5.7
□ а) По графику (рис. 5.7,в) получаем
/0@ = t • [1@-1(/ -1)] = t ■ 1@- (* -1). /(< -1)- 1(г -1).
Поэтому
) = \—^re-p --е-р.
Поскольку 71 = 1, по формуле E.20) находим
\{\-е'»-ре'Л
е'-\-р
б) По графику (рис. 5.7,6) имеем /o@='@-'('-t)» Tor«a
11 в 1
F0(p) = е'р\ По формуле E.20) при Г = 2т: F(/>) = -^ ;— = —i г.
Р Р \-е-Ър p[l + e'pjj
в) Функция, изображенная на рис. 5.7,в , имеет период Т = 2с. Запишем
аналитическое выражение для /0@ и соответствующее изображение Fq(p):
/0@ « А [7@- Iff -4-h [1A - с)-1{1 - 2с)\ =
= h ■ 1@- 2й • l{t - с)+ h ■ l(t - 2с),
p p p
По формуле E.20) получаем F(p) =
г) Для функции, изображенной на рис. 5.7,г, изображением для /0(г) явля-
является F0(p) = —-—п+е~*р) (см. пример 5.22 п."ж"). Тогда по формуле E.20) при
Р +1
Р +1
Т = к получаем F(p) = , +е—^
B Щ\-
5.1.4. Нахождение оригинала по изображению
п Непосредственное применение формулы обращения E.3) затруднительно,
поэтому для нахождения оригинала применяются теоремы разложения и правила
преобразования изображения к виду, представленному в табл. 5.1.
ПРИМЕНЕНИЕ ТЕОРЕМ РАЗЛОЖЕНИЯ
Теорема 5.1 (первая теорема разложения). Если функция F(p) аполитична
в некоторой окрестности бесконечно удаленной точки и ее разложение в ряд
по степеням — имеет вид
то функция
является оригиналом, соответствующим изображению F(p).
Теорема 5.2 (вторая теорема разложения). Если изображение F(p) является
однозначной функцией и имеет лишь конечное число особых точек Pi,p2,—,pn> ле-
лежащих в конечной части плоскости, то
[\ E.22)
Замечания 5.5.
1. Формула E.21) может быть записана в виде
л=0
339
Задача нахождения оригинала при выполнении условий теоремы сводится
к нахождению коэффициентов разложения функции в ряд Лорана в окрестности
бесконечно удаленной точки (см. гл.З).
2. Формула E.22) принимает наиболее простой вид в случае F{p) = R(p) *
рационального изображения, т.е.
где Pm{p\Qn(p) - многочлены степеней /пил соответственно, не имеющие об-
общих корней. Если все полюсы р\,Рг>-,рп Функции F(p) простые, то по форму-
формуле D.24) получаем res "/(e^ = лрЬ'.ер*, а формула E.22) принимает вид
л Qn(p) Q'«\Pk)
W'- E.23)
nKPk)
3. Если при выполнении условий п.2 коэффициенты многочлена 0„(р)-
лействительные числа, то его комплексные корни, как известно, являются по-
попарно сопряженными. Нахождение суммы вычетов в таких точках можно заме-
заменить нахождением действительной части вычета в одной из них. Действительно,
вычет в точке ~рк, используя свойства сопряженных чисел (см. разд. 1.1.1), мож-
можно записать следующим образом:
res ШеР> е 4Ш
ft Qn(p) Q'niPk) Q'n(Pk)
Это означает, что вычет в точке />*есть число, сопряженное вычету в точ-
точке рь, а сумма таких чисел равна их удвоенной действительной части:
. ' + res -^ie" = 2 Re res -^<
ft е,ы л o«(p) * Qn(p)
Пример 5.24. Найти оригиналы для функций:
а) F,[p) = —ep , /г(р)= — cos—,
Р Р Р
б) w_\ Р с/л Р + 2 ew.\ Р +Р + '
р2+4р + 5 (р + 1)(р-2)(р'!+4) (р-
D В случае "а" для решения задачи используем теорему 5.1, а в случае "б"
- теорему 5.2.
7 ( — 117
">' а) Используем типовые разложения ez = У —, cos z = У -— ,
«to л! лГо B")!
sin г = ^^— ■—(см. разд. 3.2.1). Для заданных изображений получаем:
1 СО I 00 1 1
Согласно первой теореме разложения
«о I ,2л «о ,2л
б) Представим F\{p) в виде
Р р\{р)
2 "()"
где Р| = -2 + /, p2=-2-i - простые полюсы F(р).
По второй теореме разложения
= V
t.|2ft+4 -4 + 2Z + 4 -4-2i + 4
= e ■" —e"+—-e =e ■" 2 :— =e ""[cos/-2sin/J.
Тот же результат можно получить, пользуясь пп. 2 и 3 замечаний 5.5:
/,(/)= 2Re res -—£ «" =2Re-£--e"|_2w =
2+/ 24 5 2р + 4 '
2/
2'(l + 2/)(cos/ + /sin /)] = e'[cos/- 2sin/].
Функция /'гО') имеет четыре простых полюса: р\ =-1, pi =2,рз =2/,
р4=-2/.
Так как вычет в простом полюсе находится по формуле
resF(p)= lim F(p)(p-pk),
Рк Р^Рк
то по второй теореме разложения
341
= lim [ ^Ц «"l+limf Щ
+ Hm |-_/4__eP'l+ Hm f, P + l. ."\-
1 _/ 1 21 2 + 2/ ^t 2-2/ _2
= e ' +—e + e + e
15 6 8-24/ 8 + 24/
- ' ,-/,1с2, ,-32 + 64/ 2,, ,-32-64/ 2,-,
" 15 6 640 640
1;-/,1,2, 64
15 6 640[ 2 J 640
Функция F}(p) имеет два полюса: простой pi = 1 и полюс второго порядка
По второй теореме разложения
,м (p2+p + l)ei" (p2 + p + l)^'
/з(п= res-^-—-—l-t-+ res ■«-—i:—<—-.
n-l(p-l)(p + l? »=-i(p-l)(p + lJ
Находим вычеты
^fr+p + lHp-DeO' _ы(р2+Р + 1)е" J£,
2 2 4
(р + р + 1)ер/ ,. d\(p2+p+l)e'"(p + \)) ..
res ——-—'—-= hm — ——ь—i—v% - = hm
2 *[ 2 J
>" +te'"(p2+p+l)}(p-l)-(p2 + ^ (j
(p-1J 7 ~2
получаем
ПРИМЕНЕНИЕ ТАБЛИЦЫ И СВОЙСТВ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Приведем ряд известных приемов нахождения оригинала.
1. Если изображение отличается от табличного на постоянный множитель,
то его следует умножить и одновременно поделить на этот множитель, а затем
воспользоваться свойством линейности.
342
Пример 5.25. Найти оригиналы для функций
(р + 2? р2-!
D а) Запишем изображение в виде F(p) = '—? и при а = -2, л = 2 по
2! (p + 2f
формуле 7 из табл. 5.1 получаем f{f) = -t2e~2t .
5 5 1/7
б) Представим изображение в форме F(p) = —-— = -7= г и ПРИ
Р2~1 V? p2_y?f
а = v7 в формуле 19 из табл. 5.1 получаем /(/) = -pshV7f. ■
V7
2. Изображение, заданное в виде дроби , разлагается на сумму дро-
с
бей.
Пример 5.26. Найти оригинал для функций:
-^-; б) Fb)-j*±; в)
( 5) ( 5У
О Представим дроби в виде суммы двух слагаемых, а затем воспользуемся
свойством линейности и формулами из табл. 5.1:
( 5f 5 (р + 5J
в) представим F(p) в виде
i i 2 i '
( ) р3 Р + 1'
По формулам 4,6 из табл. 5.1 находим /(/) =/2 + е"'. ■
3. Если знаменатель дроби содержит квадратный трехчлен, то в нем выде-
выделяется полный квадрат: ар2 + Ьр + с = а(р ±аJ ± и2. При этом числитель дроби
представляется в виде многочлена от (р±а).
Пример 5.27. Найти оригиналы для функций:
343
О а) Выделим полный квадрат в знаменателе дроби и воспользуемся табл.
5.1:
„п_____3 3 с- Уз
W'b lfA l'b lfi' f*
/(<) = УЗе' sin fit по формуле 12 из табл. 5.1 при а = -2, Ь = &.
б) Используем представление
Зр + 2
(р-2J-1 (p-2J-l (p-2J-l
По формулам 19,20 из табл. 5.1 и по теореме смещения (формула E.8))
Можно решить эту задачу иначе, используя вторую теорему разложения
(см. п. "б" примера 5.24):
F(p) = lElI = lEll =;, /(,) = KsF(p)ei" + KsF(p)el" =
W V4 3) 2(pl)(pl) J" I w 3
5 / И з/ И з/ 5 .
= e + e =—e" —e . ■
2(-2) 2-2 4 4
4. Если ориганал представляет собой правильную рациональную дробь, то
следует разложить ее на простейшие дроби и для каждой из полученных дробей
найти оригинал.
Пример 5.28. Найти оригиналы для функций:
1„2
(р + 2J(р-1)
D а) Представим F(p) в виде
Р р2+4р + П
где /), В, С - неопределенные коэффициенты.
Отсюда следует равенство
344
Приравнивая коэффициенты при одинаковых степенях р , получаем сис-
систему уравнений для нахождения неопределенных коэффициентов:
Решая ее, получаем А = -\, В = 4, С = 7 и
I 4р + 7 1
Р 1~
1 л р+2 1
= —+4-— -
р (р+г^ + з2 з (р+2J + з2'
По формулам 1,12,13 из табл. 5.1
б) Представим F(p) в виде
А_ +
р + 2
/(/) = -1 + 4e' cos 3/ - -е'2' sin 3/.
f/ ч р А_ В ^ С
= + +
где А, В, С - неопределенные коэффициенты.
Отсюда
1 2
Подставляя последовательно р = 1,р = -2,р = 0, получаем А=— >С=—,
1 1 1 1 2 1
+
3
1 ы ч 1
= —и поэтому Лр) =+г
9 w 9 р-1 9 р + 2 3 (р + 2J
По формулам 6,7 из табл. 5.1
в) Представим изображение в виде
«А Р2+4 А В С
W" (р1)(р + 2)(р3)" р1 р+2 р-3'
где /),Д,С - неопределенные коэффициенты.
Отсюда
Л(р + 2)(р-3)+В(р-1)(р-3)+С(р-1)(р + 2)=р2+4.
5 8 13
При р-\,р = ~2,р = Ъ получаем А = -~, В=—, С =--, поэтому
о ■ 15 10
б'/>1 + 15р + 2+10/>3'
345
По свойству линейности и по формуле 6 из табл. 5.1
г/л 5 > 8 _2» 13 !•
Можно решить эту задачу иначе, используя вторую теорему разложения
(см. п. "б" примера 5.24):
5 / 8 _2< 13 з» 5.8 _2/ 13 я/
г) Представим F(p) в ввде
F(n\ Зр Зр Л Д
W=2p2-2p4(p
где <4, В - неопределенные коэффициенты.
Из равенства А(р +1)+ В{р -2) = — при р = -1,р = 2 получаем А = 1,
D ' „, V 1 II
В = -, поэтому Др) = -+- -.
2 /»-2 2 р + 1
По формуле 6 из табл. 5.1 /(/) = е2' +—е~'.
Можно также решить эту задачу иначе, используя вторую теорему разло-
разложения (см. п. "б" примера 5.24 и п. "в" данного примера):
—r* * ^/W
V-P-2)
= 2<-з)е +Тге =е +V '"
Пример 5.29. Найти оригиналы для функций:
а) F{p) = -~z т> ^ F(p)°
О а) Решим пример различными способами.
Первый способ. Воспользуемся разложением дроби на элементарные:
1 2 1 2 1
+
По формулам 2,3,6,7 из табл. 5.1 получаем f(t) = 2 +1 - 2е' + te'.
Второй способ. Применим вторую теорему разложения, учитывая, что
= О и р2 = 1 - полюсы второго порядка функции F(p):
»']+Ы ±\ \Р~1)\е'"
= lim —.
p->° dp[(p-\)
die].. d
+ lim —
p-ti dp
:__te"'(p-\J-e'(p-l)
= lim
(P-D4
Третий способ. Обозначим Р\(р)= -. Тогда fi(t) = te'. Рассмотрим
функцию F2(p)= . По свойству интефирования оригинала (формула E.12))
Р
получаем /2(/) = |тетА = тет
Заметим, что F(p) = . Применяя еще раз свойство интефирования
Р
оригинала, имеем
/@= |(тет-ет+1)А=<е'-е' + 1-ех
= te'-2e'+2 + t.
Четвертый способ. Представим изображение в виде произведения
Р2(Р-1Г Р2 (Р-1)
(Р-1J
По формулам 3 и 7 из табл. 5.1 /,(<) = t, f2(t) = te'. Далее по теореме Бо-
реля (формула E.15))
/ tit
2
-IxV
о J о
е' -е' +\)-t2e' = te' -2e' +2 + t.
347
б) Решим пример также несколькими способами.
Первый способ. Воспользуемся разложением дроби на элементарные:
F(p) = -
1 Р 1 Р
1)(р2+4)
1)(р2+4)
По формуле 9 из табл. 5.1 получаем /(<) = -cos t —cos Ъ.
Второй способ. Применим вторую теорему разложения с учетом пп. 2,3 за-
замечаний 5.5:
/(f)=2Reres
' (
+2Reres
2'
= 2Re-
ре'
„2 L
ре
D'
+ 2Re
pi
'■71
ft (P2+4)'
= 2Re-
ре
pi
+ 2Re-
ре
pt
Третий способ. Представим изображение в виде произведения:
Р Р _L
F(p)-
Отсюда /,@ =
■=Fi(p)-F2(p).
cos2t>
sin/-
По теореме Бореля
' 1'
fit) = /1 @ • /2 @ = J«>s 2т sin(/ - т) А =- J [sin (/ + т) - sin (Зт -
= -|-cos(/ + t)
4-cosCt-0
-cos2/-—cos/s
6 6
= -cos/--cos2<.
Четвертый способ. Используем формулу 37 из табл. 5.1. При e = l,
,,. cos2<-cos< 1 1 . _
получаем /@= = -cos/—cos2/.«
1-4 3 3
348
Найти изображения по оригиналам.
1. /(O = cos3f.
Ответ: ** + 7)
(р2+1)(р2+9)
2. /(O = sh2fsin3/.
:——
Ответ: F(p) =
3. f(t) = tc\\2t.
p2+4
Ответ: F(p) = ■ _ ,.
(p2-4J
4.
5. /(<)=sh2/cos3/.
2(Р2-13)
Ответ: F(p) =
6. /(/)-- t
Jp^+ 2p + 2
Ответ: F(p) = ln^-
Найти оригиналы по изображениям.
7. F(p)= P
2
: /(/) = e|cos 2/ + ^sin 2/1
8.
Ответ: №-±е*'-~<
9.
349
л /-/л Зг + 2/ - 2 / 2< +1 _2/
Ответ: /(<)= е + е .
54 27
10. F(p) = -—-
Ответ: f(t) = -- + в' --е2' + -е3'.
6 2 3
П.
р -1
Ответ: /(<) = -(cht-cost).
12. /■(/,) = —!—
Ответ: f(t) =
13. F(p) =
t2e'
2
Ответ: /(/) = --e"' + e1 --e' t-e'.
6 2 3
P -P
Ответ: f(t) = 2e' - 4< - 3.
15.f(p) = e Р+'Я.
р + 2
Ответ: f(t) = е''» ■ /(/ - 3) + е^' • /(/ -1).
p2 + Ip + 5
Ответ: f(t) = e'1 (cos 2< - 2 sin 2/).
17.
Ответ: f(t) =-Ue-< -le-*.
4 2 4
18 V-P-1
Ответ: /(<) 2e 2i/3e sin
) = 2e"' - 2i/3e sin—<.
19. F(p)=— P— .
B lK24)
Ответ: f(t)=—cost—cos2/.
350
5.2. ОБЛАСТИ ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
5.2.1. Решение линейных обыкновенных дифференциальных уравнений
с постоянными коэффициентами
ПОСТАНОВКА ЗАДАЧИ
Рассмотрим задачу, наиболее часто встречающуюся в теории дифференци-
дифференциальных уравнений, - задачу Коши для линейных дифференциальных уравнений и
систем [36].
1. Пусть заданы:
а) линейное обыкновенное дифференциальное уравнение с постоянными
коэффициентами
^ ^ E24)
где п - порядок дифференциального уравнения; а„,...,а0- заданные коэффици-
коэффициенты; /@ - заданная функция;
б) начальные условия:
х@) = х0, х'@) = х'о,..., х(п-1)@) = хо". E.25)
Требуется найти решение x(t) дифференциального уравнения, которое
удовлетворяет начальным условиям (решить задачу Коши E.24),E.25)).
Замечание 5.6. Переменная t в задачах анализа динамических сис-
систем имеет смысл времени. Поэтому будем использовать следующие обозначения
производных: ^ = *'(') = W, ^4 = *"@ = *Ю, ^т = *"'W = *W •
dt dt2 dt1
2. Пусть заданы:
а) система линейных обыкновенных дифференциальных уравнений пер-
первого порядка с постоянными коэффициентами, записанная в нормальной форме:
f(t), E.26)
- матрица коэффи-
где х = (JC|,..., х„ )т - вектор неизвестных; А =
циентов; f(t) = {fi(t),...,fn(t)f- заданная вектор-функция;
б) начальные условия:
Х\у) — Xq, \j.ZI)
где jc0 = (Jclo,...,JcnO)r- вектор начальных значений.
Требуется найти решение x(t) = (xi(t),...,xn(t))T системы, которое удовле-
удовлетворяет начальным условиям (решение задачи Коши E.26),E.27)).
В [36] изложены классические аналитические и численные методы реше-
решения задачи Коши. Здесь будем предполагать, что заданная функция f(t) и иско-
искомая функция x(t) принадлежат классу оригиналов. Для решения задач
351
E.24),E.25) и E.26),E.27) можно применить аппарат операционного исчисления
метода решения задач, суть которого состоит в следующем.
Поставленная в классе оригиналов задача переводится с помощью преобра
зования Лапласа в задачу для изображений. Эта задача решается, и определяете
изображение искомой функции. Затем применяется обратное преобразовали
Лапласа и находится оригинал - решение поставленной задачи.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ КОШИ
1. Применить преобразование Лапласа: от известных и неизвестных функ-
функций перейти к их изображениям, записать уравнение (систему) в изображениях,
соответствующее решаемой задаче Коши.
2. Решить полученное уравнение (систему): найти изображение искомого
решения.
3. Применить обратное преобразование Лапласа: найти оригинал для полу-
полученного в п.2 изображения.
Алгебраическое
уравнение (система)
Решение алгебраического
уравнения (системы)
Пространство изображений
Преобразование
Лапласа
Обратное преобразование
Лапласа
Пространство оригиналов
Задача Коши:
дифференциальное
уравнение (система)
и начальные условия
Решение задачи Коши
Рис. 5.8
Замечавня 5.7.
1. Преимущество операционного метода заключается в том, что при его
применении функции из пространства оригиналов и производимые над ними
операции заменяются функциями и операциями в пространстве изображений,
которые оказываются более простыми. Так, вместо дифференциальных уравне-
уравнений решаются алгебраические уравнения (рис. 5.8).
2. Начальные условия при записи уравнений в изображениях учитываются
автоматически, и нет необходимости решать систему для нахождения произволь-
произвольных постоянных, как это делается при применении классического метода [36].
3. Операционное исчисление позволяет найти не только частное, но и об-
общее решение уравнения E.24). Для этого достаточно положить x'**@) = Q,
352
к = 0,...,я -1. При нахождении общего решения системы E.26) следует принять
х/@)=С„ / = 1,...,и.
4. Операционное исчисление можно применять для широкого класса ку-
кусочно-непрерывных функций fit) и функций, заданных графически; для реше-
решения уравнений с переменными коэффициентами, уравнений в частных произ-
производных, интегральных и интегро-дифференциальных уравнений; для вычисления
несобственных интегралов и суммирования рядов.
5. При решении уравнения (системы) для изображений не следует приво-
приводить дроби к общему знаменателю, так как следующий этап - нахождение ори-
оригинала - связан с представлением дробей в виде суммы.
Пример 5.30. Решить задачи Коши:
а) х' +х = l(t), х@) = -; б) х' ч- 2х = -Зг ч- 2, х@) = 0.
□ а) Воспользуемся алгоритмом.
1. Перейдем от оригиналов к изображениям:
L[x(t)} = X(p); L[x'(t)] = pX(p)-±-; ЦЩ]*--
2 р
Здесь использованы формулы E.11) и 1 из табл. 5.1. Запишем уравнение
для изображений:
--U *(/>) = -•
2 Р
2. Решим уравнение для изображений:
I ±
р 2
3. Найдем оригинал для функции Х(р). Применяя формулы 15,6 из табл.
5.1, получаем: х(г) = Г|[А'(р)] = —(е~'-1) + -е"' = 1--е"'.
б) Воспользуемся алгоритмом.
1. Перейдем от оригиналов к изображениям:
L[x(t)\ = Х(р); ЦхЩ^рХ(р)-хф) = РХ(р); Д/@] = 1[-ЗГ+2] = 4 + --
р Р
Здесь использованы формулы 3,2 из табл. 5.1. и E.11).
Запишем уравнение для изображений:
рХ(р) + 2Х(р) = 4 + ~-
Р2 Р
2. Решим уравнение для изображений:
3 2
12 Пантелеев А.В., Якимова А.С. 3S3
3. Найдем оригинал для функции Х(р). Применяя формулы 18,15 из табл.
5.1, получаем x(t) = -3-(е~2' -1 + It) -н—(е'2' -1) = 1,75 -1,5/ -1,75е' .■
4 -2
Пример 5.31. Решить задачу Коши:
х"-3х' + 2х = 2е3', х@) = 1, х'@) = 3.
П 1. Перейдем от оригиналов к изображениям:
L\x(t)\ = X(p); L[x'(t)] = рХ(р) - х@) = РХ(р) -1;
Цх'Ш = р2Х(р) - р х@) - х'@) = р1 Х(р) - р - 3; Д2е ^
р-Ъ
Запишем уравнение для изображений:
2. Решим уравнение для изображений:
Р2Х(р) - ЪрХ(р) + 2Х(р) = -^ + р =*
-3/» + 2) />2 -Зр + 2 (/?2-Зр +
3. Найдем оригинал для функции Х(р): x@ = i"'[ ] = е3'.
р3
Пример 5.32. Решить задачу Коши:
х" + 4х = cos It, x@) = 1, х'@) = -1.
D I. Перейдем от оригиналов к изображениям:
L\x(t)\ = Х(р); L[x"(t)] = р2Х(р) -рхф) - х'ф) = р2Х(р) - р +1; L[cos It] =
Запишем уравнение для изображений:
р2+4~
2. Решим уравнение для изображений:
3. Применяя формулы 10,9,8 из табл. 5.1, найдем оригинал для функции
Х(р): x(t) = -1 sin It + cos It - - sin It M
4 2
354
Пример 5.33. Решить задачи Коши:
а) х"' + х' = 0, х@) = 2, х'@) = 0, х"@) = -1;
б) х'" + 6х"+11х' + 6х = 0, х@) = 1, х'@) = -3,.
□ а) Воспользуемся алгоритмом.
1. Перейдем от оригиналов к изображениям:
L[x(t)] = Х(р); L\x"\t)] = РгХ(р)-
= />3*(/>)-2/>2+1; Ц0] = 0.
Запишем уравнение для изображений:
9.
-рх'@)-х"@) =
2. Решим уравнение для изображений:
2p2+l p2+l
= i+^L
3. Применяя формулы 1,9 из табл. 5.1, найдем оригинал для функции Jf(p):
б) Решим вторую задачу, пользуясь алгоритмом.
1. Перейдем от оригиналов к изображениям:
L[x(t)} = Х(р); L[x'(t)} = рХ(р)-дс(О)= рХ(р)-1;
L[x"(t)} = р2 Х(р) - р х@) - х\0) = р2 Х(р) - р + 3;
Цх"(!)\ = Р1Х{р)-р2х@)-рх\0)-х'\0) = Р3Х(р)-Р2+Зр-9; ДО] = 0.
Запишем уравнение для изображений:
ръХ(р) - р2 + Зр - 9 + 6р2 Х(р) - 6р +18 +1 \рХ(р) -11 + 6Х(р) - 0.
2. Решим уравнение для изображений:
Х(р) = Р2 +1Р + 2 _ 1
/>3 + 6р2 + 11/?+ 6 Р + 3
3. Найдем оригинал для функции Х{р):
1
12*
3SS
Пример 5.34. Решить задачу Коши:
х'" -Зх" + 3х' -х = е',
х@) = 1, х'@) = -1, х"@) = 1.
D 1. Перейдем от оригиналов к изображениям:
ф@] = Х(р); L[x\t)\ = рХ(Р) - х@) = РХ(р) -1;
L[x"(t)\ = р2 Х(р) - р х@) - х'@) = Р2Х(р) - р +1;
Запишем уравнение для изображений:
*)-Р2+р-\- 1Р2Х(р) + 3р-3 + 3/>*(/>)-3-Х(р) =
р~\
2. Решим уравнение для изображений:
1 1
+
1 3! [ 1 : 1 |2 2
3. По формулам 7, 6 из табл. 5.1 найдем оригинал для функции Х(р):
Пример 5.35. Решить задачу Коши:
x' = x + 2y-9t,
У = 2х + у + 4е', у@) = 2.
О 1. Перейдем от оригиналов к изображениям:
х\т = рХ(р) - x@) = PX(p) -1; L[y(t)\ = рГ(р) - уф) = рГ(р) - 2;
p2 P-l
Запишем систему уравнений для изображений:
Р
4
' р-\
356
2. Решим систему уравнений для изображений.
Из первого уравнения выразим Х(р):
и подставим во второе:
р-\ р-\ р\р-\) w p-\
Отсюда имеем
Y(p) 2(Р~Х) 6^
Разложим каждое слагаемое на элементарные дроби:
2(j?-l) 1 1 6 3 1 3 1
(р + 1)(р-2)~ р + 1 + р-3' (р + 1)(р-3)~ +
18 4 6 9 1 1 1
Р2(Р + 1)(Р~3) P p2 2 p + l 2 р-Ъ
Tom y(,)=_! 1.2.1НЦД1-11
р-Ъ 2 p + l 2 р-Ъ p nl 2 p + l 2 р-Ъ
= -i + __ + _i_+2 __
р р2 р + 1 р-Ъ'
Yt . 8 12 8 1 1
р(р1) \\) (р + Щр1) (рЗКр1) />
18 8,1 3
р-\ р(р-\)
Разложив последнее слагаемое на элементарные дроби
3 33
р\р-\)~ Р р2+
получим
Y. , 4 3 3 8 8 1
X(p) = —r г—:—7T+:—rr;—^ + 4'
р-\ р pi p(p-l) (р + Щр-1) (р-3)(р-1)"
3. По формулам 6, 2, 3, 15, 16 из табл. 5.1 найдем оригиналы для функций
Х(р) и Г(р) :
3S7
Пример 5.36. Решить задачу Коши:
О 1. Перейдем от оригиналов к изображениям:
L[x{t)\ = Х(р); ЦуA)] = Y(p); ЦхЩ = рХ{р) - х@) = рХ(р)
Д/@1 = pY(p) - № = PY(P) +1; Ц.Щ] = -.
Р
Запишем систему уравнений для изображений:
Р
= -X(p)-2Y(p).
2. Решим систему уравнений для изображений.
Умножим второе уравнение на р, а из первого выразим рХ(р):
p
> = -PX(p)-2pY(p).
Отсюда имеем
= -Y(p)-l+--2pY(p) или
P
1
р2+2р + \ p(p + lJ P+1
Из второго уравнения системы
Х(р) = -1 - (р + 2) Y(p) = -1 - (р +1) У(/>) -
Представим второе слагаемое в виде
1 A_ _B_ C_
P /> + l (p + 1
где ^, В, С - неопределенные коэффициенты.
Отсюда находим
При р = -1,р = 0,р = \ последовательно получаем С = -1, А = 1, 5 = -1:
1 1 1 1
р(р + \J Р Р + 1
358
Поэтому
■
/> + 1 + (/> + 1J'
3. По формулам 15,2,6,7 из табл. 5.1 найдем оригиналы для функций Х(р)
и Г(р):
x(t) = 2е"' - 2 + е"' + te~' = Зв"' + »"' - 2; y(t) = 1 - 2е"' - Ге~'. ■
Пример 5.37. Решить задачу Коши:
х{' =-х2 + 2, х,@) = -1,
х2' =xt +1, х2@)=0.
□ 1. Перейдем от оригиналов к изображениям:
4*2@1 =
L[x{ (t)] = pXx (p) - xx @) = pX] (p) +1; Цх'2 @1 =
4/@1 = -; 42-/@1 = -.
p p
Запишем систему уравнений для изображений:
2_
р'
»д.
р
2. Решим систему уравнений для изображений. Для этого умножим первое
уравнение на р и подставим во второе:
1+2
Р
Отсюда получим
2 1 v , ч 2р 2 2р 2
, *2(/>) = —^- + 1-1 + - = —г~ + --
р +1 р р +1 р /г+1 />
3. По формулам 8, 2, 9 из табл. 5.1 найдем оригиналы для функций Х\(р),
Замечание 5.8. Во многих практических задачах правая часть диффе-
дифференциального уравнения задается графически. В этом случае алгоритм решения
задачи не изменяется, а для нахождения изображения оригинала, заданного
графиком, используются методы, изложенные в разд. 5.1.3.
Пример 5.38. Решить задачу Коши:
х' + х = /@, х@) = 0,
где /@ - функция, изображенная на рис. 5.9, а.
359
/t
cost
0
а б
Рис. 5.9
□ 1. Перейдем от оригиналов к изображениям:
l\x(t)] = X(p), L[x'(t)} = рХ(р) - хф) = рХ(р).
Функцию /@ можно записать в форме f(t) = l(t) - /(/ - 2). Ее изображе-
изображение находится по свойству запаздывания: F(p) = е'2р.
Р Р
Запишем уравнение для изображений:
---е-2'>.
Р Р
2. Решим уравнение для изображений:
e
р(р + 1) р(р + 1)
3. Найдем оригинал для функции Х(р). Первому слагаемому по формуле
15 из табл. 5.1 соответствует оригинал 1-е"' . Оригинал для второго слагаемого
находится по теореме запаздывания E.9):
x(t) = 1 - е"' - [1 - е-{'-2)] l{t - 2). ■
Пример 5.39. Решить задачу Коши:
х" +* = /(/), *@) = 0, х'@) = 0,
где /(/) - функция, изображенная на рис. 5.9, б.
D 1. Перейдем от оригиналов к изображениям:
L[x(t)} = X(p), L[x'(t)] = РХ(р) - х@) = рХ(р);
L\x"(t)] = Р2Х(р) -рх@) - У@) = р2Х(Р).
Так как функцию f(t) можно записать в виде
/(/) = cos t ■ [7@ - l(t - л)] = cos t + cos(f - л) l{t - it),
360
то по формуле 9 из табл. 5.1 и по теореме запаздывания находим соответствую-
соответствующее изображение: F(p) = L\f(t)] = ——
2
P2 + ] pl + \
Запишем уравнение для изображений:
р2 Х{р) + Х{р) = -£— + -f-e-v.
р1 +1 р1 +1
2. Решим уравнение для изображений:
VI \ Р Р -»
Х(р)=—г-—Т + —Г-—те р.
(р2 + 1J (р2+1J
3. Найдем ориганал для функции Х{р) по формуле 10 из табл. 5.1 и с уче-
учетом теоремы запаздывания E.9):
x(t) =—t sin / + - (t - ж) sin(/ - я)/(/ - я). ■
Пример 5.40. Решить задачу Коши:
x"-x' = f(t), x@) = 0, х'@)=0,
где /@ - функция, изображенная на рис. 5.5,з .
□ 1. Аналогично примеру 5.39 перейдем от оригиналов к изображениям:
L[x(t)) = X(p), L[x'(t)] = pX(p); Дх"
Согласно результату примера 5.22,п."з":
Ч/@] = -^0-«*'"')•
Запишем уравнение для изображений:
Aе
р + 1
2. Решим уравнение для изображений:
1 11
(р + \)р(р-\) е
3. Найдем оригинал для функции Х(р). Так как
1 J_ I _1_ 1 1
р(р + 1)(р-\)~ р + 2р + 1 + 2р-
> то
361
Пример 5.41. Решить задачу К.оши:
х' + х = /(/), х@) = 0, х'@) = 0,
где /@ - функция, изображенная на рис. 5.5,«.
□ 1. Перейдем от оригиналов к изображениям:
L[x(t)) = X(P), L[xl'(t)] = p2X(p).
Согласно результату примера 5.22 п."и"
= ---*'" Д<Г2>.
Р Р Р
Запишем уравнение для изображений:
Р Р Р
2. Решим уравнение для изображений:
Х(р)= 1 \ е-"+ \ е
B \) B 1) B 1)
3. Найдем оригинал для функции Х(р). По формуле 17 из табл. 5.1 с уче-
учетом теоремы запаздывания E.9) получаем
x(t) = 1 - cos t - 2 ■ [1 - cos(? -1)] • l(t -1) + [1 - cos(? - 2)] • l{t - 2). ■
Пример 5.42. Решить задачу Коши:
/@, х@) = 0, х'@) = 1,
где f(t) - функция, изображенная на рис. 5.5,г.
□ I. Перейдем от оригиналов к изображениям:
L[x(t)\ = X(p); L[x"(t)) = р2Х(р) - р х@) - хЩ = р2Х(р) -1;
Согласно результату примера 5.22,г
Р Р Р2
Запишем уравнение для изображений:
Р2Х(р) ~ 1 + 9Х(р) = -~
Р
2. Решим уравнение для изображений:
362
3. Найдем оригинал для функции Х(р). Заметим, что
1 1 JJ 1
Согласно формулам 8, 3 из табл. 5.1 этому изображению соответствует
нал —t sin3f . Раскрывая скобки во втором слаг
меняя теорему запаздывания при х = 1, т = 2, т = 3, получаем:
оригинал —t sin3f . Раскрывая скобки во втором слагаемом Х{р) и при-
при- [|« - 2) - ^sin 3(* - 2I ■ l(t - 2) + [i(t - 3) - ^sin 3(f - 3I • l(t - 3).
ПРИМЕНЕНИЕ ИНТЕГРАЛА ДЮАМЕЛЯ И ТЕОРЕМЫ БОРЕЛЯ
Рассмотрим задачу решения дифференциального уравнения E.24) с нуле-
нулевыми начальными условиями:
х@) = 0, хЩ = 0,..., х("-1)@) = 0. E.28)
Рассмотрим два способа ее решения, применение которых не требует
нахождения изображения правой части f(t) дифференциального уравнения.
Первый способ. Наряду с уравнением E.24) рассмотрим уравнение, полу-
получающееся из него при /@ = 1@, с нулевыми начальными условиями, т.е.
й о
E.29)
А@) = 0, Л'@) = 0,..., Л("-]>@) = 0.
Решением уравнения E.29) является функция h(t), которая называется
единичной переходной функцией.
Применим к задачам E.24), E.28) и E.29) алгоритм решения задачи Коши,
описанный в данном разделе.
Перейдем от оригиналов к изображениям:
l\x{t)] = Х(р), L[h(t)] = H(p), L[f(t)} = F(p), ЦЩ} = -.
Р
Так как начальные условия нулевые, то
В результате получаем уравнения в изображениях, соответствующие урав-
уравнениям E.24) и E.29):
D(p)X(p)=F(p), D(p)H(p) = -,
Р
где £>(р) = а„р"+... + во - характеристический многочлен.
363
Исключая D(p), находим
X(p) = pH(p)F(p).
Используя интеграл Дюамеля E.17), можно найти оригинал
о
Так как в силу E.29) й@) = 0, то окончательно получаем
JtW-jA'M/e-O*. E.30)
о
На основании E.30) можно сформулировать алгоритм решения задачи
Коши:
E.31)
х@) = 0, хЩ = 0,..., х1"-1)ф) = 0.
Алгоритм решения задачи Коши E.31)
с помощью единичной переходной функции
1. Найти единичную переходную функцию h(t), решая задачу E.29). Для
этого можно применить операционное исчисление или другие методы [45].
2. Найти производную k'(t) единичной переходной функции.
3. Определить решение задачи E.31) по формуле E.30).
Второй способ. В качестве вспомогательного уравнения для решения задачи
E.24),E.28) рассмотрим уравнение с правой частью f(t) - 5@(см. пример 5.10) и
нулевыми начальными условиями, т.е.
E.32)
= 0,*'@) = 0 kinA)(Q) = 0.
Решением уравнения E.32) является функция k(t), которая называется
импульсной переходной функцией.
Рассмотрим решение задач Коши E.31) и E.32) с помощью преобразова-
преобразования Лапласа. Перейдем от оригиналов к изображениям:
Так как начальные условия нулевые, то
Цх<*>@] = /*(/>), L[k^(t)] = pkK(p), k = !,...,«.
В результате получаем
D(p)X(p) = F(p), D(p)K(p) = 1, '
где D{p) = anpn + ... + ац.
Отсюда находим изображение искомого решения
X(p) = K(p)F(p).
Согласно теореме Бореля можно найти оригинал по формуле E.16):
x(t) = J k(x)f(t - x)<h = J k(t - x)/(t)rft. E.33)
о о
Заметим, что между переходными функциями, как следует из сравнения
E.30) и E.33), имеется связь:
k(t) = h'(t). E.34)
На основании формулы E.33) можно сформулировать алгоритм решения
задачи E.31).
Алгоритм решения задачи Коши E.31)
с помощью импульсной переходной функции
1. Найти импульсную переходную функцию, решая задачу Коши E.32).
Для этого можно применить операционное исчисление или другие методы [45].
2. По формуле E.33) найти решение задачи Коши E.31).
Пример 5.43. Решить задачу Коши:
х' + х = е', х@) = 0.
□ Первый способ.
1. Составим уравнение E.29)
Л' + А = 1, А@) = 0
для единичной переходной функции и решим его, применяя операционное ис-
исчисление: ^
1 I
a) L[h{t)] = H(p), l[h'(t)) = pH(p), L[l(t)} = —; pH(p) + H(p)= — ;
Р Р
в) ACH
2. Найдем производную единичной переходной функции:
3. По формуле E.30) при fit) = e'
x(t) = ) e-V'-^dx = е') е-ъа\ = - ^е^ = |(е' - в"').
365
Второй, способ.
1. Составим уравнение E.32)
к' + к =5@,
для импульсной переходной функции и решим его:
а) ЩA)) = К(р); £[*'(/)] - />*(/>); Д8(/)] = 1; р*(/>) + Цр)
б) К(р)Ц;
B)k(t)=
2. По формуле E.33) при /@ = е'
x(t)= je-Te('-T)A = -(e'
о 2
Пример 5.44. Решить задачу Коши:
D Применим алгоритм решения задачи Коши с помощью единичной пере-
переходной функции.
1. Составим уравнение
А' + 2А = 1, А@) = 0.
для нахождения единичной переходной функции и решим его:
, l\h\t)] = рН(р), £[/@1=-; рЩр) + 2Н(р) = -;
Р Р
б) //(/>)=
в) Л(Г) = Г'[Я(рI = -i(<T2' -1) = i(l - в'2').
2. Найдем производную от единичной переходной функции:
3. По формуле E.30) при f(t) = -3/ + 2 получаем
О 0 0
-2 + 3f ..2т|' 3 _2t|' 3'f _2tj (t 3^._2, „ 3.
lo 2 lo 2> { . 2 ) 2
_2te-* _2е-2' + 2 = 1,75 -1,5? - 1,75е-2'.
2 4 4
366
Пример 5.45. Решить задачу Коши:
х@) = 0, х'@) = 0.
□ Применим алгоритм решения задачи Коши с помощью импульсной
переходной функции.
1. Составим уравнение
к" - Зк' + 2к = 8@,
Л@) = 0, fc'@) = 0
для импульсной переходной функции и решим его:
a) L\k(t)]=K(p), L[k'(t)] = pK(p), L[k"(t)\ = p2K(p),
б) Цр) = — '
2. По формуле E.33)
о о
= -2е2'+е'+2е3'-е3'=е'-2е2'+е3'. ■
Замечание 5.9. При решении прикладных задач, в частности задачи
анализа выходных процессов линейных динамических систем [34,45,51], возни-
возникает необходимость в решении задачи, более общей по сравнению с E.24),
E.25), где правая часть представляет собой линейный дифференциальный опера-"
тор над некоторой функцией:
.. + аох = />m£(m)@+.- + bog(t),
E.35)
Здесь g(t) - заданная функция; ап,...,%\Ьт,...,Ьй - постоянные коэффициенты;
п и т - числа, определяющие порядок старшей производной в левой и правой
частях уравнения.
В процедуре решения задачи используется принцип суперпозиции: эффект,
вызываемый суммой нескольких факторов (начальными условиями и функцией
g(t)), равен сумме эффектов каждого из факторов в отдельности [34,45,51].
367
Алгоритм решения задачи Коши E.35)
с помощью принципа суперпозиции
1. Найти решение однородного уравнения (при g{t) = 0), соответствующего
уравнению E.35) с заданными начальными условиями:
аях(и)+...+ а0х = 0,
E.36)
х@) = дг„. *'@) = *4,-, *("@) = x<"-1).
Для этого может применяться как операционное исчисление, так и другие
методы [34,45,51]. Полученное решение называется свободным движением и обо-
обозначается xc(t). Оно характеризует влияние начальных условий. Если начальные
условия нулевые, свободное движение отсутствует, т.е. xc{t) а 0.
2. Найти решение неоднородного уравнения с нулевыми начальными усло-
условиями:
E.37)
х@) = 0, хЩ = 0 х("-1)@) = 0.
Полученное решение называется вынужденным движением и обозначается
*«>.»(')• Оно характеризует влияние функции git). Для его нахождения следует:
а) найти импульсную переходную функцию kQ(t) для уравнения
Для этого решить задачу E.32) с применением операционного исчисления:
а„ *<"> + ... + ао*о=8(О,
E.38)
Ло(О) = ОДо(О) = О,...Д("-1)(О) = О;
б) иайти импульсную переходную функцию k(t) для уравнения
алх(й)+
по формуле
S (S-39)
в) найти вынужденное движение по формуле, аналогичной E.33):
xeblH(t)=\k(x)g(t-x)a\. E.40)
о
3. Найти решение задачи E.35) в виде суммы свободного и вынужденного
движений:
E.41)
368
Пример 5.46. Найти решение задачи:
х" - Зх' + 2х = g'(t) - g(t), g(t) = е3' • 1@,
х@) = 0, х'@) = 0.
D Решим задачу, используя алгоритм.
1. Нрйдем решение xc(t) уравнения E.36):
) х" - Зх' + 2х = 0,
х@)=0, х'@) = 0.
Так как начальные условия нулевые, то, очевидно, xc(t) = 0.
2. Найдем решение уравнения E.37):
х" - Зх' + 2x = g'-g,
х@) = 0, х'@) = 0.
Для этого:
а) найдем импульсную переходную функцию ka(t) для уравнения
х" - Зх' + 2х = /(?), решая уравнение E.38):
*о(О) = О, *о(О) = О.
Из п.1 примера 5.45 следует, что
б) по формуле E.39) определим импульсную переходную функцию:
k(t) = 2e2t -е' -е2' +е' =е2';
в) по формуле E.40) имеем
вЫИ J J IQ
о о
3. Решение задачи получается по формуле E.41):
Пример 5.47. Найти решение задачи:
х"' + 6х" + 11х' + 6х = g" + 5g' + 6g; g(t) = 1@,
x@) = 1, x'@) = -3, x".@) = 9.
D Решим задачу, используя алгоритм.
1. Найдем свободное движение xc(t) как решение уравнения E.36):
369
x'" + 6x" + Их' + 6x = 0,
x@) = 1, x'@) = -3, x"@) = 9.
Согласно результату примера 5.33,п." xc(t) = е~3'.
2. Найдем вынужденное движение как решение уравнения E.37):
х'" + вх" +1 \х' + 6х - g" + 5g' + 6g,
х@) = 0, х'(О) = 0, х'Щ = 0.
Для этого:
а) найдем импульсную переходную функцию для уравнения
х'" + вх" + Пх' + 6х = /(?),
т.е. решим уравнение E.38):
*0@) = 0, *4(О) = О,*6'(О) = О.
Перейдем от оригиналов к изображениям:
L[ko(t)\ = К0(р); 1[*0@1 = рК0(р); £[*J'(f)] = P2K0(p}; L(*0"@] = Рг
№0] = > •
Запишем уравнение для изображений и решим его:
11рК0(р) + 6К0(р) = 1 =*
1 1
11 111
+
2р+1 р+2 2р+3
Найдем оригинал:
ee+e;
б) найдем импульсную переходную функцию k(t) по формуле E.39):
*@ = *4'(О + 5*4 +6*0 =ie-' -4e-2' +|е-3' -
_Ie-' +10e' -—е'3' +3в"' -бе' +3е-3' =е-';
в) определим вынужденное движение по формуле E.40):
о
е' + 1 е~'
3. Найдем решение задачи по формуле E.41): х@ = е' + 1 -е~'.
5.2.2. Анализ выходных процессов линейных непрерывных
\ стационарных динамических систем
В теории автоматического регулирования и управления рассматривается
следующая прикладная задача.
На вход динамической системы, математическая модель которой описыва-
описывается в той или иной форме, поступает входной сигнал. Требуется найти выход-
выходной сигнал, т.е. реакцию динамической системы на входной сигнал. Эта задача
называется основной задачей анализа.
Динамические системы подразделяются на:
- непрерывные (описываются дифференциальными уравнениями) и дис-
дискретные (описываются разностными уравнениями);
- линейные и нелинейные (описываются линейными или нелинейными
уравнениями);
- стационарные и нестационарные (описываются уравнениями с постоян-
постоянными или переменными коэффициентами);
- одномерные и многомерные (в многомерных системах суммарное число
входов и выходов больше двух).
Рассмотрим особенности применения преобразования Лапласа для реше-
решения задач анализа линейных непрерывных одномерных и многомерных стацио-
стационарных динамических систем [34,45,51].
1. Одномерные системы.
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) входной сигнал g(t), / > 0;
б) линейная непрерывная одномерная стационарная система (рис. S.10),
описываемая дифференциальным уравнением
anxw(t) +... + аох(О = bmg(m\t) +... + bog(t), E.42)
где g(t) и x(t) - входной и выходной сигналы; т и и - числа; aH,...,aQ, bm,...,b0
- коэффициенты, не зависящие от времени;
в) начальные условия:
х@) = х„, х@) = *о ^"-"(О) = 4п-1).
Требуется найти выходной сигнал x(t).
Вход
Рис. 5.10
371
Будем считать, что входной и выходной сигналы принадлежат пространству
оригиналов, и применим преобразование Лапласа.
Выходной сигнал через свободное и вынужденное движение представляется
с помощью формулы E.41), которая может быть записана в форме
где функции xc(t), xmil(t) - и раз непрерывно дифференцируемы.
Обозначим X(p) = L[x{t)), Хс(р) = L[xc(t)], Хвыи(р) = L[xetlH(t)] - изображе-
изображения по Лапласу выходного сигнала, свободного и вынужденного движения соот-
соответственно.
С использованием свойств преобразования Лапласа и E.37) получаем:
Дифференцируя выражение для x(t) с учетом двух последних равенств,
имеем
L[x(n\t)\ = р"[Хс(р) + Хшн(р)} - р"\ -... -рх("-2> - 4п-1\
Так как Х(р) = Хс (р) + Хшн (р), то
Используя E.11),E.10) при т = 0, определение производной дельта-
функции [21,45] и /'@ = 8@(см. пример 5.10), можно получить равенство
Найдем преобразование Лапласа от левой и правой частей дифференциаль-
дифференциального уравнения anx(n\t) +... + аох(/) = bm\g(t)l(t)fm) +... +
I\anx(n\t) +... + aox(t)] = D(p) X(p) - DH(p),
W>m{g(t) l(t)im) +... + bo{g(t) l(t))] =
где
... + х^-2)(аяр + о,.,) + x%-l)an = р'-'а^о + р"-2[аях0 + anAx0] +...
... + [а„хо(''-1) +а„_1х0('') +... + а2х0 +flixo].
В результате получаем уравнение в изображениях, соответствующее E.42):
Обозначим W(p) = —^i. Функция комплексного переменного W(p)
Щр)
является передаточной функцией системы [34,45,51].
372
С учетом обозначений запишем выражение для изображения выходного
сигнала:
Если начальные условия нулевые, то DH(p) = 0 и выходной сигнал совпа-
совпадает с вынужденным движением: Х(р) = W(p) G{p).
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ АНАЛИЗА ВЫХОДНЫХ ПРОЦЕССОВ
1. Найти изображение входного сигнала:
00
G(p) = Llg(t)]=lg(t)e-ptdt,
о
где g(t) - сигнал; G(p) - его изображение по Лапласу.
2. Найти передаточную функцию системы
E.43)
и если начальные условия ненулевые, то функции
2 + ... E.44)
3. Определить изображение по Лапласу выходного сигнала по формуле
E.45)
4. Найти выходной сигнал, используя обратное преобразование Лапласа
Замечания 5.10.
1. Функция D(p) = anp" +... + a!p + a0 является характеристическим много-
многочленом. Передаточная функция определяется следующими двумя способами.
Первый способ [45]. Передаточной функцией W(p) стационарной линейной
системы называется преобразование Лапласа импульсной переходной функции
k(t), соответствующей уравнению E.42): W(p) = l[k(t)]. Функция k(t) находится
по формуле E.39).
373
Второй способ [34,51]. Передаточной функцией W(p) называется отношение
преобразования Лапласа выходного сигаала к преобразованию Лапласа входного
сигнала при нулевых начальных условиях:
ш
2. Первое слагаемое в E.45) представляет собой изображение по Лапласу
свободного движения (под действием ненулевых начальных условий и нулевом
входном сигнале), а второе - вынужденного (под действием входного сигнала
при нулевых начальных условиях).
3. Применяя свойства E.11) и E.19) преобразования Лапласа, можно полу-
получить установившиеся значения выходного сигнала и его производных по изобра-
изображению Х(р):
ху = lim x(t) = lim pX(p), E.46)
/-»+0О p-tO
А(р)^
/>->0 [ Р р
Пример 5.48. Найти реакцию динамической системы, описываемой урав-
уравнением х = bg, на линейный входной сигнал g(t) = / -1(/) при нулевых начальных
условиях.
□ 1. Найдем изображение входного сигаала g(t) = t: G(p)- — .
Р
2. Запишем передаточную функцию: W{p) = -&- = - = 5. Так как начальные
а0 1
условия нулевые, то функция DH(p) = 0.
3. Определим изображение по Лапласу выходного сигнала: Х(р) =—-.
Р2
4. Найдем выходной сигнал: x(t) = 5/, / > 0.
В теории автоматического регулирования и управления рассмотренная ди-
динамическая система называется усилительным звеном. Заметим, что уравнение,
описывающее поведение динамической системы, не является дифференциаль-
дифференциальным. ■
Пример 5.49. Найти реакцию динамической системы, описываемой диффе-
дифференциальным уравнением x(t) = 4g(t), на входной сигнал g(t) = sin 3/ при нуле-
нулевых начальных условиях.
□ 1. Найдем изображение входного сигнала: G(p) = —-—.
р2+9
4
2. Запишем передаточную функцию: W(p) = —. Функция DM{p) = Q , так
Р
как начальные условия нулевые.
374
3, Определим изображение по Лапласу выходного сигнала:
Р р2+9 Зр 3(р2+9)
4. Найдем выходной сигнал:
В теории автоматического регулирования и управления рассмотренная сис-
система называется интегрирующим звеном. ■
Пример 5.50. Найти реакцию динамической системы, описываемой диффе-
дифференциальным уравнением x(t) + x(t) = g(t) с начальным условием х@) = -, на
входной сигнал g(t) = l(t).
□ 1. Найдем изображение входного сигнала: С(р) = —.
Р
2. При п = 1, flj = 1, а0 = I, х0 = — из E.43),E.44) находим передаточную
функцию и функции D(p) и DH(p):
1 1
l = p + l, DH(p) = хоах =—.
:,
p +1
3. Определим изображение по Лапласу выходного сигнала:
Х( l '
ХЛР) Хвын(Р)
4. Найдем выходной сигнал:
x(t) = -e~' + 1е"' =1е~'
хс{1)
Полученное решение совпадает с найденным в примере 5.30 п."а". В тео-
теории автоматического регулирования и управления рассмотренная система назы-
называется апериодическим звеном.и
Пример 5.51. Найти реакцию динамической системы, описываемой диффе-
дифференциальным уравнением
с начальными условиями х@) = 1, х@) = 3, на входной сигнал g(t) = 2е3'/(/).
2
□ 1. Найдем изображение входного сигнала: G(p) =
р-У
375
2. При п = 2,а2 = 1,щ = -3,%=2 из E.43),E.44) находим передаточную
функцию и функции D(p) и DH(p):
p2-3p + 2'
D{p) = p2-3p + 2, Д, (p) = хо(щ + o2p) + xoa2 = 1 • (-3 + p) + 3 • 1 = p.
3. Определим изображение по Лапласу выходного сигнала:
2 в 2
р2 -Зр + 2+ (р2 -Зр + 2)(р-3) (р-\)(р-2) + (р-\)(р-2)(р-3)
12 12 1
- + н + -
р-1 /?-2 р-1 р-2 р-3
4. Найдем выходной сигнал:
x(t) = -е< +2е2[ + е' - 1еь + e3f, = е3>.
*<•(') ■'«i-» (О
Полученное вынужденное движение совпадает с найденным в примере
5.45. ■
Пример 5.52. Найти реакцию динамической системы, описываемой диффе-
дифференциальным уравнением
с начальными условиями х@) = 1, х@) = 3, на входной сигнал g(?) = е3'/(/).
□ 1. Найдем изображение входного сигнала: G(p) = .
р-Ъ
2. Получим передаточную функцию:
Щр) =
р2-3/7+2
и функции D(p) = р2 - Ър + 2, DH(p) = ХоЦ + а2р) + х0а2 = 1 • (-3 + р) + 3• 1 = р.
3. Определим изображение по Лапласу выходного сигнала:
Х()_ Р , Р-1 Р | Р-1
р2-Зр + 2 (р2
Р-1 Р-2 р-3 р-2
376
4. Найдем выходной сигнал:
+ е21 - е'.
Полученное вынужденное решение совпадает с найденным в примере 5.46. ■
Пример 5.53. Найти реакцию динамической системы, описываемой урав-
уравнением
*(/) + 6х(г) +11х(/) + 6х(/) = g\t) + 5g(t) + 6g(t)
с начальными условиями х@) = 1, х@) = -3, х@) = 9, на входной сигнал
g(t) = l(t). Определить установившиеся значения выходного сигнала и его про-
производных.
□ 1. Найдем изображение по Лапласу входного сигнала: С(р)= —.
Р
2. Получим передаточную функцию:
w{p)= /2\5р+6
р +6р + Ир+ 6
и функции D(p) = р3 + 6р2 +11р + 6 = (р + 1)(р + 2)(р + 3);
А, (Р) = хо(а\ + aiP + °зР2) + ^о(°2 + агР) + Чаъ =
= хоA1 + 6р + р2) + хоF + р) + хо= р2 + Зр + 2 = (р + 1)(р + 2).
3. Определим изображение по Лапласу выходного сигнала:
Чр) = -
р р + 3 р(р +1)'
По формулам E.46) найдем установившиеся значения выходного сигнала и
_ v, . 1 1 р2 +2р + 3
его производных. Так как л (о) = + = — , то
р + 3 р(р + \) р( \)(р + 3)
Ху - flim х(г) - ШрХ(р) - f
х,- lim х(г)=ПтР2
у
х,= lim х@=н4Ы%
о ^ Р Р
4. Найдем выходной сигнал:
х(/) = е'+1-е-'.
Результат совпадает с полученным в примере 5.47. ■
377
2. Многомерные системы.
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) входной сигнал g(t) =
б) многомерная линейная непрерывная стационарная динамическая систе-
система (рис. 5.11), поведение которой описывается:
уравнением состояния
E.47)
уравнением выхода
E.48)
где х - «-мерный вектор состояния; g - r-мерный вектор входа; у - it-мерный
вектор выхода; А, В, С - матрицы размера (их«), (пхг), (кхп) соответственно;
в) начальные условия:
х0, E.49)
где х0 = (xl0,...,xn0)T- вектор начальных состояний.
Требуется найти законы изменения вектора состояния x(t) и вектора
выхода y(t).
g(t)
= Cx(t)\
Вход Вектор Выход
состояния
Рис. 5.11
Предположим, что каждая компонента входного и выходного сигналов, а
также вектора состояния принадлежит пространству оригиналов. Применяя пре-
преобразование Лапласа к левой и правой частям уравнений состояния и выхода
E.47),E.48), имеем
р Х(р) -хо=А Х(р) + В СО»), Пр) = СХ(р),
где Х(р) = Z,[x@], Y(p) = L\y(t)], G(p) = L[g(t)] - изображения по Лапласу векто-
векторов состояния, выхода и входа. Отсюда
Y(p) = C[pE- AY хо+С[рЕ- А]А В G(p).
378
Обозначим Wx(p) = \pE-AYB, W"(p) = C\pE - Л] В. Функции ком-
комплексного переменного Wx(p), Wy(p) являются передаточными функциями сис-
системы по состоянию и выходу [34,45,51]. С учетом введенных обозначений
= [pE-A]-lx0+Wx(p)G(p),
Y{p)~C\pE-A\Axu+Wy{p)G{p).
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ АНАЛИЗА ВЫХОДНЫХ ПРОЦЕССОВ
1. Найти изображение входного сигнала:
о
где g(t) - г-мерный входной сигнал; G(p) - г-мерный вектор его изображений по
Лапласу.
2. Найти матрицы [р£-Л]~'; С[р£-Л]~' и передаточные функции по
формулам:
где Е - единичная матрица.
3. Определить изображение по Лапласу законов изменения векторов
состояния и выхода:
= \рЕ-А\ххй+\¥х{р)С(р),
E.50)
4. Найти законы изменения векторов состояния и выхода с помощью об- '
ратного преобразования Лапласа:
Замечания 5.11.
1. Первые слагаемые в E.50) представляют собой изображения по Лапласу
свободного движения (под действием ненулевых начальных условий и при нуле-
нулевом входном сигнале), а вторые - вынужденного (под действием входного сигна-
сигнала при нулевых начальных условиях).
2. Передаточная функция Wx(p) по состоянию и передаточная функция
Wy(p) по выходу представляются матрицами размера (ихг), {ку.г) соответст-
соответственно. Они определяются как преобразования Лапласа соответствующих им-
импульсных переходных функций [45].
379
Пример 5.54. Найти законы изменения векторов состояния и выхода мно-
многомерной системы:
х, = x,+2x2+g, y = xl+x2,
х2 = 2х, + х2,
с начальными условиями х,@) = 1, х2@) = -1 при входном сигнале g(t) = e'l(t).
О Перепишем уравнения системы в матричной форме:
Ж
'■• t)
А
Здесь n = 2,r = \,k = l.
1. Найдем изображение входного сигнала G(p) =■
р-\
2. Получим передаточные функции:
\
р-\ -2
-2 р-\
-{ 2
2 р-\
p-l
2
l(p-3)(p + l) (
2 \
p-l
р_3)(р + 1)
Р-ъу
p-i
(р-Жр + 1)
( = A l)[pE-A]~
■Г1-—
3. По формулам E.50) определим изображения законов изменения векто-
векторов состояния и выхода:
380
( p-l
2 ^
-1
P-l 1
p-1
f 1 ^
p+1
-1
0>+U
(P-3)(P-
2
Г l ^
-1
l
+—
1 1
l
р-Ъ p+1
1
\р-Ъ p-\ p + l)
1 1
i
1 1 1
1
р-Ъ p-l р-Ъ p-l 2(p-3) 2(/>-
4. Искомые законы изменения векторов состояния и выхода:
0,25е3'+0,75е-'
3' -2e'
е' -0,75e
-'J'
Пример 5.55. Найти законы изменения векторов состояния и выхода мно-
многомерной системы
^2=^1 +«2. у2=х1+0,5х2
с начальными условиями xt@) = —1, л:2@) = 0 при входном сигнале
П Перепишем уравнение системы в матричной форме:
1JU2J'
u
u
с
= U2«J"
1. Определим изображение входного сигнала g(t) = | ,л\: G(p) =
2. Получим передаточные функции:
381
( p -11
2+l />2+l
( 1
p + 1 p + 1
p-t-0,5 0,5p-l
[p2+l р2+\)
1 О
О 1
Г i
P2+1
0,5/,-1
3. По формулам E.50) найдем изображения законов изменения векторов
состояния и выхода:
' р -М
Х{Р):
р2+1
{р2+\ p2+l)
-1
„2+1
-1
2 +
+1
-р2+2р-1
Г-1 2 ^
+ 0,5 0,5/?-1
Р + 0,5 0,5р-1
P2+1 p2+l)
382
pip
2
P'
2
2+l)
-P
-+1 J
< 2
P
2
[P2 +
IP
P2 +
1 P2
1
L_
+ h
4. Искомые законы изменения векторов состояния и выхода:
2sin?-cos?
Найденный закон изменения вектора состояния x(t) совпадает с получен-
полученным в примере 5.37. ■
5.2.3. Анализ устойчивости линейных непрерывных стационарных
динамических систем
1. Одномерные системы.
Пусть заданы:
ПОСТАНОВКА ЗАДАЧИ
а) одномерная линейная непрерывная стационарная динамическая система,
поведение которой описывается дифференциальным уравнением E.35):
E.51)
б) начальные условия:
Требуется исследовать, является ли динамическая система асимптотически
устойчивой.
В соответствии с принципом суперпозиции выходной сигнал системы
представляется в виде суммы свободного и вынужденного движений:
Динамическая система называется асимптотически устойчивой, если при
ненулевых ограниченных начальных условиях свободное движение xc(t) ограни-
ограничено при всех ?е[/0,+ оо) и lim xc{t) = 0.
383
КРИТЕРИЙ УСТОЙЧИВОСТИ
Для асимптотической устойчивости динамической системы E.51) необходим!
и достаточно, чтобы корни р, характеристического уравнения
апр +ап_\р 4-... + OQ ~0 E.52
имели отрицательные действительные части: Rep,- < 0, / = 1,...,п, т.е. располага-
располагались в левой полуплоскости комплексной плоскости (рис. 5.12).
Imp,
Рис. 5.12
Замечания 5.12.
1. Для проверки отрицательности действительных частей корней характе-
характеристического уравнения E.52) можно использовать критерий Рауса-Гурвиис
134,45,51]:
Для устойчивости системы E.51) необходимо и достаточно, чтпбы юппвы
миноры Л, матрицы
пп-\
а„
0
0
я„-з
йл_2
ап-\
С
ая-5 •■
ал-4 •••
ап-г ■■■
а т ••■
0
0
0
0
О О
были положительны: Л, >0, / = 1,...,и, где Л, =ап_\, Л2 = " ' " и т.д.
\ о„ а„_2)
При заполнении этой квадратной матрицы порядка п отсутствующие
в уравнении E.52) коэффициенты ал_, и а, при / > п заменяются нулями.
384
Критерий Рауса-Гурвица называется косвенным, так как в этом случае
процедура анализа устойчивости не требует нахождения корней уравнения E.52).
2. Корни характеристического уравнения E.52) являются полюсами переда-
передаточной функции E.43).
Пример 5.56. Исследовать устойчивость динамических систем, описывае-
описываемых дифференциальными уравнениями:
а) Зх + х = g; б) 4х-х = g; в) х + 2х + х = g; г) х + 2х-х = g;
д) х - 2х + 4х = g; е) х + 4х + 6х + 4х = g; ж) х + х + 4х + 4х = g.
□ Для решения задачи применим критерий асимптотической устойчивости.
а) Характеристическое уравнение D(p) = Ър +1 = 0 имеет отрицательный
корень р = —, лежащий в левой полуплоскости. Согласно критерию система
асимптотически устойчива.
б) Характеристическое уравнение D(p) = 4p-1 = 0 имеет положительный
корень р = -, лежащий в правой полуплоскости. Согласно критерию система не
4
является асимптотически устойчивой.
в) Характеристическое уравнение D(p) = р2 + 2р +1 = 0 имеет отрицатель-
отрицательный (кратный) корень р = -1, лежащий в левой полуплоскости. Согласно крите-
критерию система асимптотически устойчива.
г) Характеристическое уравнение D(p) = р2 + 2р -1 = 0 имеет два корня:
Р\ =-l+V2 >0, pi =-l-v2 <0, один из которых положительный, лежащий в
правой полуплоскости. Согласно критерию система не является асимптотически
устойчивой.
д) Характеристическое уравнение D(p) = />3 - 2р + 4 = (р2 -2р + 2){р + 2) = 0
имеет корни: р{ = -2, р2 = 1 +1:, pj -1 -1i. Так как корни р2 и р3 лежат в пра-
правой полуплоскости, то система не является асимптотически устойчивой.
е) Характеристическое уравнение D(p) = р3 + 4р2 + 6р + 4 = (р2 + 2р + 2) х
х (р + 2) = 0 имеет корни: рх = -2, p2=-l + i, pj=-l-i. Так как все корни ле-
лежат в левой полуплоскости, то система является асимптотически устойчивой.
Решим эту задачу с помощью критерия Рауса-Гурвица. Составим матрицу и
вычислим угловые миноры:
= 4 > 0, Д2=20>0, Д3=80>0.
Так как все угловые миноры положительны, то система является асимптотически
устойчивой.
.385
13 Пантелеев А.В., Якимова А.С.
4
1
0
4
6
4
oN
0
4
ж) Характеристическое уравнение D(p) = ръ + р2 + 4р + 4 = (/г + 4) х
х (р +1) = 0 имеет корни: рх = -1, р2 = 2/, Рз = ~2». Так как корни р2 и р3 не
лежат в левой полуплоскости, то система не является асимптотически устойчи-
устойчивой.
Решим задачу с помощью критерия Рауса-Гурвица. Составим матрицу и
вычислим угловые миноры:
fl 4 01
1 4 0
О 1 4
Д, =1>0, Д2=0, Д3=0.
Так как не все угловые миноры положительны, то система не является асимпто-
асимптотически устойчивой. ■
Для анализа устойчивости можно применять частотные критерии устойчи-
устойчивости [34,37,45,51], не требующие нахождения корней характеристического урав-
уравнения. Их использование требует построения годографов частотной характери-
характеристики или характеристического многочлена.
Частотной характеристикой W(ksn) стационарной линейной системы на-
называется преобразование Фурье импульсной переходной функции k{t), соответ-
соответствующей уравнению E.42):
W(m) = F[k(t)\ = J k(t) e-"°'dt. E.53)
о
Частотная характеристика является комплекснозначной функцией действи-
действительного аргумента со - частоты, изменяющейся в промежутке от 0 до +«, и
может быть представлена в показательной, тригонометрической и алгебраиче-
алгебраической формах:
W(«o) = A(a) е"^ш) = Л(со) [ cos<p(e>) + / sin ср(со) ] = Щв>) + / К(со), E.54)
где А{а), ф(и>) - амплитудная и фазовая частотные характеристики:
arctg~f для I и IV четвертей,
1/И
arctg -" + п для II четверти,
К(со)
arctg——-я для III четверти,
f(co)
U(а), V(a) - вещественная и мнимая частотные характеристики.
Частотная характеристика W(ko) изображается годографом в координатах
U, Кили в полярных координатах A, q>, который называется амплитудно-фазовой
unnmnmunii Y/innvmpmirmiivnii (nur S 1 ^
частотной характеристикой (рис. 5.13).
386
W{b)
Частотная характеристика W(h>) связана с передаточной функцией W(j>),
«пределяемой по формуле E.43), соотношением [34,45,51]
р = ко
E.55)
Пример 5.57. Изобразить частотные характеристики динамических систем,
шисываемых следующими уравнениями:
a) x(t) = 5g@; б) x(t) = g(t); в) x(t) = g(/); г) 2x(t) + x@ = 2g(t);
д) 3c
= 5,
□ а) Согласно E.54), E.55):W(p) = 5;W(iw) = 5;
/(<») = 5, К(оз) = О.
Полученные частотные характеристики изображены на рис. 5.14.
= 0,
Л(оз) = 5
Ф
ф)=0
U
Рис. 5.14
б) По дифференциальному уравнению x(t) = g(t) найдем передаточную
пункцию W(p) = p и связанные с ней частотные характеристики:
Лолученные частотные характеристики изображены на рис. 5.15. Точка
/(ш) = 0, К(ш) = 0 соответствует значению ю = 0.
387
со
■ЩЬ)
U
Рис. 5.15
в) По дифференциальному уравнению x(t) = g(t) найдем передаточную
функцию W(p) = — и связанные с ней частотные характеристики:
Р
со ш
-.
со
Полученные частотные характеристики изображены на рис. 5.16. Точка
U(а) = 0, К(оз) = 0 соответствует значению со = + а>.
Я» t
Рис. 5.16
W(fa)
г) По дифференциальному уравнению 2x(f) + x(t) ~ 2g(t) найдем пере-
передаточную функцию W(p) = ——- и связанные с ней частотные характеристики
2A-2/со) 2 . 4со
1 + 4со2 1 + 4ю2 'l+4co2'
_2_
2/(й+1
ср(со) = - arctg 2co.
Искомые частотные характеристики изображены на рис. 5.17. Заметим, что аь
плитудно-фазовая частотная характеристика представляется графиком нижне*
полуокружности, так как К(со) < 0 и (U -1J + V2 = 1.
388
#}■
2
Ф1
V
0
-1
0)
/
\
\
= +00
1
<D=0
7 ^
Рис. 5.17
д) По дифференциальному уравнению х + Зх + Зх(/) = 3g(t) найдем переда-
-очную функцию W(p) = — —— и связанные с ней частотные характери-
,тики:
J
-/ш3-3оз2+3я» 9оз2+C-оз2J 9ео3+юC-(п2J
9оз2+C-оз2J
9оз3+озC-оз2J'
лмплитудно-фазовая характеристика показана на рис. 5.18. Заметим, что
lim U(a)= lim К(оз) = О и lim К(оз) = - «, lim Щоз) = -1. ■
ш-+0
ЩЬ)
<D= +00
Рис. 5.18
Для анализа устойчивости одномерных линейных непрерывных стационар-
■шх динамических систем используется критерий Михайлова [34,37,45,51].
КРИТЕРИЙ МИХАЙЛОВА
Для асимптотической устойчивости динамической системы, описываемой
шфференциальным уравнением
389
необходимо и достаточно, чтобы годограф характеристического многочяе,
2)(/со) = аи/>и+...+ ао|/»./и пРи изменении частоты со от 0 до + со охватывая нача
координат на угол ф = — п, где я - порядок характеристического многочлена.
АЛГОРИТМ ПРИМЕНЕНИЯ КРИТЕРИЯ МИХАЙЛОВА
1. Определить порядок я характеристического многочлена D(im) .
2. Построить на комплексной плоскости годограф многочлена D(ia>) npi
изменении частоты со от 0 до + а>.
3. Вычислить величину ф угла, на который годограф охватывает начало ко
ординат:
Ф = Д Arg D(im).
OSOJ<+oo
4. Проверить выполнение условия <р = — л. Если условие выполнено, то
система асимптотически устойчива, если нет - неустойчива. Если годограф ха-
характеристического многочлена проходит через начало координат, то говорят, что
система находится на границе устойчивости (оставаясь неустойчивой). На рис.
5.19 приведены примеры годографов характеристических многочленов устойчи-
устойчивых систем.
Im D(b)
Re 2) (/со)
и = 4
л = 3
Рис. 5.19
Пример 5.58. Найти все положительные значения коэффициента усиления
К, при которых динамическая система, описываемая уравнением
асимптотически устойчива.
□ 1. Характеристический многочлен D(ka) = ръ + 2рг + Zp + К + 2\pr=io
является многочленом 3-й степени, т.е. л = 3.
390
2. Построим годограф этого многочлена, вычислив значения
К + 2 - 2со2 + ийC - со2) при некоторых частотах со (рис. 5.20).
3. Как видим, при К е@;4) годограф проходит последовательно через /,
I, III четверти, охватывая начало координат на угол q> =—. При £еD; + оо)
^одограф проходит через /, IV, III четверти, a q> = —-.
4. Таким образом, система будет устойчивой при всех К е @;4). ■
7к + г
ReZ)((co)
К>4
со
0
R
S
3
00
Д(/со)
К + 2
<RH)
Л--4
JT-16-18/
-00-[00
Рис. 5.20
Пример 5.59. Исследовать на устойчивость системы, описываемые диффе-
дифференциальными уравнениями:
aJx(t)+x{t)=2g{t); б) 3f+ 3ic + 3x = 3g.
"' П а) Решим первую задачу, следуя алгоритму.
|К 1. Характеристический многочлен Z)(/co) = 2/» +11р=<и,= 2ио +1 является
многочленом первой степени, т.е. п = 1. »
2. На рис. 5.21,0 изображен годограф Z)(fe) = 1 + »2<в , так как ReZ)(»co) = l,
ImZ)(/co)=2o).
3,4. Очевидно, q> = — при изменении со от 0 до + оо, что удовлетворяет ус-
условию <р = — п при п = 1. Поэтому система асимптотически устойчива.
б) Решим вторую задачу, следуя алгоритму.
1. Характеристический многочлен Z)(/co) = р3 +Ър2 -*- Зр|р==Ав является
многочленом третьей степени, т.е. п = 3 .
2. Годограф характеристического многочлена изображен на рис. 5.21,5, так
как 0(ко) = -Зсо2 + (со(з - со2).
391
ImZ)(/co)
я
0
t
D(k>)
со =0
1 ReL
Z>(/co)
С
ImZ>(
-3
0
q> = я
2
^co = 0
ReZ)(i<B)
«0
0
1
s
00
Z)(«b)
0
-3 + 2/
-9
-00 -/00
Рис. 5.21
3,4. Угол <р = Д Arg Z)(/oo) = n*—n при n = 3. Поэтому система не являет-
Os<b<+«> 2
ся асимптотически устойчивой. ■
2. Многомерные системы.
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) линейная многомерная непрерывная стационарная система, описывае-
описываемая уравнением состояния E.47):
x(t) = Ax{t) + Bg(t), E.56)
где х - n-мерный вектор состояния; g - г -мерный вектор входа; А, В - матрицы
размера (яхв), (пхг) соответственно;
б) начальное условие
*@) = хо-
Требуется исследовать, является ли динамическая система асимптотически
устойчивой.
Динамическая система называется асимптотически устойчивой, если ее
свободное движение xc{t) (при g@ = 0) ограничено при ограниченных началь-
начальных состояниях Xf) и выполняется условие
где |с|| - какая-либо норма вектора х , например,
392
КРИТЕРИЙ УСТОЙЧИВОСТИ
Для асимптотической устойчивости многомерной динамической системы
необходимо и достаточно, чтобы корни р, характеристического уравнения
&<А(А-рЕ) =
E.57)
имели отрицательные действительные части: Rep,- <0, i = \,...,n, т.е. располага-
располагались в левой полуплоскости комплексной плоскости (см. рис. 5.12).
Замечание 5.13. Для проверки отрицательности действительных час-
частей корней характеристического уравнения E.57) можно использовать критерий
Рауса - Гурвица (см. п.1 замечаний 5.12).
Пример 5.60. Исследовать устойчивость динамических систем, описывае-
описываемых дифференциальными уравнениями:
а) х,=х,+2х2, 6) х,=х2, в) *i=-*2+£i>
i:2=4x, + 3x2+£,; x2=-x,-2x2+gi; x2=x, +g2.
D Для решения задачи применим критерий асимптотической устойчивости.
а) Здесь А =
1 2
. Характеристическое уравнение
\-р 2
4 Ъ-р
= 0 или
p2 - Ар - 5 = 0 имеет действительные корни разных знаков: рх = 5 > 0,
рг = -1 < 0. Так как корень р\ лежит в правой полуплоскости, система не явля-
является асимптотически устойчивой.
6) Здесь А = \ I. Характеристическое уравнение
1—1 —21
-Р 1
= 0
-1 -1-р
или р2 + 2р +1 = 0 имеет отрицательный корень (кратности 2): рх 2 = -1. Так как
корень лежит в левой полуплоскости, система является асимптотически устойчи-
устойчивой.
в) Перепишем уравнения системы в матричной форме:
А В
Найдем корни характеристического уравнения. Получим:
-р -1
1 -р
= 0
+1 =0.
Отсюда P\=i, Pi=-i. Так как корни не лежат в левой полуплоскости, система
не является асимптотически устойчивой.!
393
Упражнения
Решить задачи Коши.
1. x' = x + t-l, х@)=0.
Ответ: x(t) = -t.
2. x" + x = tcos2t,
хф) = х'ф) = 0.
Ответ: x(t) = —sin t +—sin It + -I -sin 2/ - / cos It1
3. x' = -3x + 3f-2, x@) = 0.
Ответ: x{t) = e~3' +/-1.
4. x" + 9x = l, x@) = x'@) = 0.
Ответ: x(t) = - A - cos 30-
5. jc" + 4x = sin 3/,
x{0) = x'@) = 0.
Ответ: x(t) = — sin Ъ - -sin 3/.
6. x"-x" = 0,x@) = 2,x'@) = 0,x"(Q) = 1.
Ответ: x{t) = \-t + e'.
1.x"- 3x' + 2x = e5'; x@) = 1, x'@) = 2.
Ответ: x(f) = — e5' +ie' t-e2'.
12 4 3
8. 3x' + 2x + y' = 1, x@) = 0,
x' + 4y + 3y = 0, y@) = 0.
А--.-*
9. x' = 2y, x@) = 2,
у' = 2х, уф) = 2.
Ответ: x(t) = ге2', y(f) = 2e2'.
394
10. x' = 3x + Ay,
Ответ: x(t) = |e5' -je'5', y(t) = |e5' + |e'.
Решить задачи анализа выходных процессов.
11. x' = 4x + g(t), g(t) = 2-t,
Ответ: x(t)A*'+±--l-.
16 4 16
П. x' = -
х@) =
Ответ: x{t) = Зе'1 + 5t - 3.
13. x"-x' = g(/), я(/) = /2,
х@) = 0,х'@) = 0.
Ответ: x(f) = 2е' - - /3 - f2 - 2/ - 2.
14. x"l + x = g(t), я@ = 1@,
1 2 L S
Ответ: x(t) = 1 —e~' —e2 cos—/.
Ответ: x(t) = e' -e~' +t2.
Ответ: x(t) = 2te'.
17. Исследовать на устойчивость динамические системы, описываемые
дифференциальными уравнениями, в задачах 3, 4, 6, 9, 10, 12.
Ответ: в задачах 3, 12 система устойчива, а в задачах 4, 6, 9, 10 - нет.
395
5.3. Z-ПРЕОБРАЗОВАНИЕ
5.3.1. Основные определения
1. Оригинал - последовательность {/(к), к = 0,1,...}, удовлетворяющая усло-
условию: | f{k)\ < Меак, где М и о - положительные постоянные (рис. 5.22).
/@)
/A)
/B)
/C)
/E)
2 3 4 5 к
Рис. 5.22
2. Изображение последовательности \f(k),k= 0,1,...} - функция F(z) ком-
комплексного переменного z , определяемая равенством
E.58)
Изображение является аналитической функцией при \ц > е".
Совокупность всех оригиналов называется пространством оригиналов, а
совокупность всех изображений - пространством изображений.
3. Переход, определяющий изображение F(z) по оригиналу
{/{к), к =0,1,...}, называется Z-преобразованием:
F{z)=Z\f(k)l E59)
4. Оригинал по изображению находится с помощью обратного Z-преоб'
разованин по формуле:
ldz, к = 0,1,... , E.60)
где С - контур, внутри которого лежат все особые точки функции F(z).
Замечания 5.14.
1. Название Z-преобразование определяется буквой г, выбранной для
обозначения переменной. Такое название противоречит существующему обычаю
называть часто применяемые преобразования по имени ученого. В некоторых
источниках Z -преобразование называется преобразованием Лорана, так как ряд
E.58) дает разложение функции F(z) в ряд Лорана в окрестности бесконечно
удаленной точки (см. разд. 3.2.3).
2. Z -преобразование можно рассматривать как частный случай преобразо-
преобразования Лапласа, а именно как преобразование в пространстве ступенчатых ориги-
оригиналов. Ступенчатая функция - это разрывная функция целочисленного аргумен-
аргумента, которая в общем случае имеет разрывы при каждом натуральном значении
аргумента, оставаясь между ними постоянной. По рис. 5.22 можно представить
такую функцию f(t) , для которой /(г) = /@) при t е [0,1), /(/) = /A) при
/ е [1,2) и т.д. Оригиналом по Лапласу такая функция является, если выполняет-
выполняется условие |/(/)| < Л/еа'(см. разд. 5.1.1), т.е. | f(k)\ < Меа1с. Ее можно представить
00
в виде ряда /(/) = ]Г f(k) [ /(/ - к) - l(t - (к +1)) ]. Тогда по теореме запаздывания
*=о *=о
т.е. нахождение преобразования Лапласа в рассматриваемом классе оригиналов
сводится к нахождению суммы ряда Тейлора:
\ ак =
1 1 - е~'
Обозначая z = ep (тогда z = —) и отбрасывая множитель , общий для всех
и р
(\Л °° Ак)
оригиналов данного класса, получаем соотношение E.58): F(z) = «и — = У ~~.
При этом обратное преобразование - есть задача нахождения коэффициентов'
разложения функции Ф(и) в ряд Тейлора по степеням и. Коэффициенты вычис-
ляются по формуле C.16): ак =—г4 к !&иЛ = 0,1,... или C.17): ак =■
При и = — получаем ряд Лорана E.58) функции F(z) = Ф(«) в окрестности z = »
с коэффициентами E.60): f(k)=—:&F(z)zkAdz, £=0,1,... (здесь учтено, что
du = —-dz, направление обхода контура при преобразовании z = — меняется на
z "
противоположное и интеграл меняет знак при изменении направления обхода
(см. разд. 2.2.1)).
397
5.3.2. Свойства Z -преобразования
Положим, что F(z)=Z[f{k)].
1. Линейность. Для любых постоянных с,, i = \,...,т, справедливо
...+ cmFm(z), E.61)
где {/,(*),* = 0,1,...},...,{/„(*), * = 0,l,...} - оригиналы, a F,(?),...,Fm(z) - их
изображения.
2. Запаздывание (формула запаздывания):
E.62)
E.63)
где
2
при к - п < 0 (рис 5.23).
f \
/(*)
12 3 4
/1
4
2
1 2 3 4
/<*-«)
.. -*. ...'... .* ....L....1
л л + 1
Рис. 5.23
3. Онережеиие (формула опережения):
n)] = z'lF{z)-znf(O)-...-zf(n-\).
4. Дифференцирование изображения:
Z\kf{k)]=-zfz.
E.64)
E.65)
E.66)
5. Умножение изображений. Свертке оригиналов соответствует произведе-
произведение изображений:
E.67)
398
где G(z) = Z[g(k)\. Сверткой оригиналов {f(k), k = 0,1,...} и {g(k), k - ОД,...) назы-
называется сумма
£/(/)•«(*-/). E-68)
6. Теоремы о предельных значениях. Если F(z) = Z[f(n)], то
E.69)
/B) = lim z2[f(z)-/@)-/(I)- Г1] и т.д.,
Z-»<x>
где z стремится к бесконечности вдоль произвольного пути.
Если lim /(А) существует, то
к-* оо
\mj(k)=\im{z-l)F(z). E.70)
Заметим, что первую формулу в E.69) можно получить из E.58):
i г2 zk
при z -» °°. Умножая обе частиf(z) на г, получаем /(l)= lim z[F(z)-/(O)] и т.д.
Z-»oo
5.3.3. Нахождение изображения по оригиналу
Для нахождения изображений используется E.58) и свойству
Z -преобразования.
Пример 5.61. Найти изображения по оригиналам:
a) f{k) = ak; б)/(*)=1; в)/(*) = —; г) f{k)=eak.
□ а) По формуле E.58) имеем
г./ \ \-i о 1 z
- о
где использована формула суммы бесконечно убывающей геометрической про-
прогрессии с первым членом щ = 1 и знаменателем <? = — при \q\ < 1, т.е. |z| > |а| .
399
б) Аналогично п. "а"
V —
, при
в)
'hk\zk
при
!' Гле использовано типовое разложение
(см. разд. 3.2.1).
*=0 Z
Заметим, что при а =0 имеем результат, полученный в п. "б". ■
В табл. 5.2 приведены наиболее часто встречающиеся в примерах соответ-
соответствия при Z-преобразовании. Формулы 1, 7, 11 получены в примере 5.61.
5.3.4. Нахождение оригинала по изображению
Для нахождения оригинала используются следующие способы:
1) разложение функции F(z) в ряд Лорана в окрестности бесконечно уда-
удаленной точки;
2) формула E.60);
3) табл. 5.2 и свойства Z-преобразования;
4) формула E.69);
5) формула
. d*F\-\
Л = 0,1,2,...
E-71)
6) если F(z) представляет собой рациональную функцию, т.е. отношение
двух многочленов:
где степень многочлена в силу аналитичности F(z) при z = » не превышает сте-
степени многочлена Q(z), то можно разделить многочлен P(z) на Q(z) одним из
обычных способов. Это хотя и не даст общего выражения для f(k), но позволит
численным путем определить сколь угодно большое число значений f(k).
400
Замечания 5.15.
1. Сравнивая E.60) с определением D.16) вычета в z = °о, получаем
/<*) = - res F(z) zk-x, № = £ res F(z) г*,
m-l г™
да zm - особые точки функции F(z) ■
2. Формула E.71) получается из формулы для коэффициентов ряда Тейлора
■Ьк =^f^CM- замечание 5.14), где «/±1 = F(z), Ф@) = f(-)\z=0 .
Таблица 5.2
№
1
2
3
4
5
6
7
8
9
10
/<*)
1
(-1)*
к
к2
ко"
С?ак
ак
(к + 1)ак
/@) - 0, f(k) —
к
(-1)*
(О)-о,/а)_ к
F(Z)
Z
z-l
z
z + l
z
(z-lJ
z(z + 1)
(г-IK
z
(z-aJ
amz
(z-aT*
Z
z2
(z-aJ
-ri
z
№
11
12
13
14
15
16
17
18
19
20
Ak)
ak
k\
k(k -1)
2
k(k-l)-(k-m+l)
m!
sinfcp
cos*p
ak sin Лр
ak cosifcp
- ak sm(k - 1)P
a*shfcp
a
Z
a-о3
г
(«-1Г1
jsinp
Z2 -2?cosp + l
z(z-cosP)
Z2 - 2z cos p +1
azsinp
^-2fl,COSP + fl2
г (г -acosp)
z2-2o?cosp + a2
zsinp(?-2ocosp)
z2 -2o?cosP + a2
ajshp
г2-2агсЬр + в2
г(г-асьр)
,2-2flzchP+a2
401
Пример 5.62. Найти оригиналы для функций:
a) t)-^fy; б) Hz)*-^; в)
1
д)
е>
(z-a)(z-b)'
л
D а) Первый способ. Разложим функцию F(z) в ряд Лорана в окрестности
1 ( 1 ч' '
бесконечно удаленной точки, учитывая, что -
-1
к-э
П z Г
</П 1 1
+т+т
г2 г3
1 2 3 1 1 2 3
+
2 3
гг~+т+т+-
г4 J г z2 г3
£ it
2
Сравнивая с E.58), имеем /(it) = it, it = 1,2,... По формуле E.69) получаем
/@) = lim F(z) = 0. Поэтому /(it) = it, it = 0,1,2,...
Второй способ. По формуле E.60) получаем
1, к = 0,1,2
В точке z = 1 - полюс второго порядка; интеграл можно брать по любому
контуру С: \z\ = R , где R > 1, так как в \z\ < R, R > 1 содержится единственная
особая точка функции F(z). По формуле D.19)
где согласно D.22)
к j
res * ■ = lim — г* = lim к zk~x
г»1 (г _ IJ г->1 <fe г-»1
A\,\ *>ттт7г !r тр flV\ — )r Ir — A19
у ^ft^ — _ Z7IJK — Л , I.e. J\K>) — К , К — \J,l,£r,...
Поэтому
Заметим, что можно было использовать п.1 замечаний 5.15:
xesF(z)z
l
kA
lim(«*)'= it.
г1
402
Третий способ. Представим F(z) в виде рациональной функции:
P(z)
1 К
'" 2
-2г + 1
Поделим числитель на знаменатель:
z
2 +
2-1
Z
~ 2-1
z
1
Z
2
+7
Z ~~
1 2
г г2
Qiz) '
lz+\
3
г3
22
1 2 3
В результате получаем />(г)=- + -г+—г- + ... и f(k) = k, Jt = 0,1,2,...
г г2 г3
Четвертый способ. По формуле E.69)
/@)=lim Z =0,
г-»« г2 - 2г +1
0| = 1,
z -
/B) = lim г'
г-»оо
-0-1- = lim-
1,3 _ ,2
=2,
ита : /(*) = *, it =0,1,2,...
б) По формуле E.60)
, к=0,1,2,...
1 + V5 1-V5
Особые точки z\ = , z% =— полюсы первого порядка (корни
уравнения г2-г-1 = 0).
По формуле D.19)
/(*)=— 1м res-
zk+1
Jfc+1
(z-Zl){Z-z2)\
403
По формуле D.23) для вычисления вычета в полюсе первого порядка полу-
получаем
/(Л) = res
.к+1
(
es ? ^ r+res? ^ -
г, {Z-Zi)(z-Z2) ii (Z-Zi){z-Z2)
Вт
rk+l
iim
.k+l
Jim -^ + lim
.k+l -k+l k+l
22 +Jl
, г^ г — uiu г iiiii
(Z-Zi)(z-Z2) i^z-Z2 г->г2 Z-Z\
в) Представим F(z) в виде суммы двух элементарных дробей и разложим
каждую из них в окрестности г = »:
1
1 ( I 1
(z-a)(z-b) a-b\i-a z-b) (a-b)z
1
1 1
z z]
i Гд(в* v
ak-bk 1 Да^'-б*-1
а*-1 _6*-i
Поэтому fik) = ■ при it г 2 . По формуле E.69) находим
a-b
/@) = lim F(z) = 0, /A) = lim z F(z) = 0. Окончательный ответ: /@) = 0,
a*-1 -A*-1
при it 21.
a-b
г) Разложим функцию —"■ на простейшие дроби:
1 111
(г1-
поэтому
По формулам 5,7 из табл. 5.2 и
rr
-*(-з)*
* z
"
=(-3)*.
Используя свойство линейности, имеем
д) Заметим, что дискриминант трехчлена в знаменателе отрицателен. Наи-
Наиболее близкими по форме записи к данному изображению являются функции,
соответствующие формулам 14 и 15 из табл. 5.2. Чтобы выделить значения sin
и cosp, представим изображение в виде
z-z + l
При cosp = -, т.е. Р = —, первое слагаемое совпадает с изображением
л S
в формуле 15 из табл. 5.2. Так как sinp = sin— = —, то преобразуем второе сла-
слагаемое к табличному. Получим
F(z)
z\Z-cos-
z2-2zcos^-
z2 -2zcos-
По формулам 15, 14 из табл. 5.2 и по свойству линейности
л/fc гг
f(k) = cos
, it = 0,1
е) Представим изображение в виде
,2
г2-
•=z-
. л
zsin-
4
4
По формуле 16 из табл.5.2 и свойству линейности
Z
T>] = z-'
По формуле опережения E.64) с учетом ф@) = 0 получаем:
403
Упражнения
Найти изображения:
. vk nk
т~ + cos—•
Ответ: F(z)= . V
2- Д*) 3|*3
3 4
Ответ:
г-3 (г-3J 4 г-\
Найти оригиналы по изображениям:
2 г/.\ - 2z -92
Ответ: f(k) = -7 + 7 ■ 2* - -it ■ 2*.
4.
Ответ: /(Jt)=i-2*+--3*.
5.4. ОБЛАСТИ ПРИМЕНЕНИЯ Z -ПРЕОБРАЗОВАНИЯ
5.4.1. Решение линейных разностных уравнений
с постоянными коэффициентами
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) линейное разностное уравнение:
, к =0,1,... E.72)
где oB,aB.i,...,a1,a0 - постоянные коэффициенты; п - целое число; последова-
последовательность {g(k), к =0,1,...};
б) начальные условия:
x(O) = xo,*O) = *i,-,*(«-l) = *„-!■ E.73)
Требуется найти решение х(к) разностного уравнения, удовлетворяющее
начальным условиям.
3 а м е ч а н н е 5.16. Аналогично формируется постановка задачи реше-
решения систем линейных разностных уравнений.
406
Будем предполагать, что последовательности {g(k),k =0,1,...} и
{х(к), к = 0,1,...} принадлежат пространству оригиналов.
Для решения поставленной задачи можно применить аппарат операцион-
операционного исчисления - метода решения задач, содержащего следующие этапы, отра-
отраженные на рис. 5.24.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ E.72),E.73)
1. От известных и неизвестных последовательностей (оригиналов) перейти
к их Z -изображениям. Записать уравнение (систему) в изображениях, соответст-
соответствующее решаемой задаче.
2. Решить полученное уравнение (систему): найти изображение искомого
решения.
3. Применить обратное Z - преобразование: найти оригинал для получен-
полученного в п.2 изображения.
Алгебраическое
уравнение (система)
Решение алгебраического
уравнения (системы)
Пространство изображений
Z - преобразование
Обратное
Z - преобразование
Пространство оригиналов
Разностное
уравнение (система)
и начальные условия
Решение разностного
уравнения (системы)
Рис. 5.24
Пример 5.63. Найти решение задачи:
D 1. Перейдем от оригиналов к изображениям, используя формулы
E.61),E.64), E.65):
Z[x(k)} = X(z); Z[x(k +1)] = zX(z) - Z *@) = zX(z) - Z;
Z[x{k + 2)] = z2Z(z)-Z2x(Q)-zx(l) = z2X(z)-Z2-2z; Z[0] = 0 .
407
Запишем уравнение для изображений:
z2X(z)-z2-2Z-zX(z
2. Решим уравнение для изображений:
5 +г .
г-г + 1
3. Найдем оригинал для X(z) :
г2г + 1 z2?cos + l ?
По формулам 14 и 15 из табл. 5.2 получаем (см. пример 5.62, п. "д")
x(fc) = cos^-- + Vising-, /fc = 0,l
Легко проверить, что при к = 0,1 начальные условия выполняются.!
Пример 5.64. Найти решение задачи:
х@)Л,хA)=£.
D 1. Перейдем от оригиналов к изображениям, используя формулы E.61),
E.64), E.65):
Z[x{k)\ = X{Z); Z[x(k +1)] = zX(z) - гх@) = zX(z) -1;
Z[x(k + 2)] = z2X(z) -Z2x@) - z x(\) = z2X(z) - у - Z y; Z[0] = 0.
Запишем уравнение для изображений:
гЛг*(г)+
2. Решим уравнение для изображений:
2
Т
3. Найдем оригинал для X(z):
л
408
По формуле 14 из табл. 5.2 и E.64) получаем (см. пример 5.62, п.
х(к) = sin v ', it =0,1
6
При использовании формулы E.64) было учтено, что
. л
zsm-
6
и/@) = 0.
Пример 5.65. Найти решение задачи:
D 1. Перейдем от оригиналов к изображениям, используя формулы E.61),
E.64), E.65):
Z[x(k)] = X(z); Z[x(k +1)] = zX(z) - zx@) = zX(z) - Зг;
2[д:(Л + 2)] = г2Дг)-г2л@)-гхA) = г2Дг)-Зг2 + г; z[o] = o.
Запишем уравнение для изображений:
z2X(z) - Зг2 + z - 3zX(z) + 9г - №(z) = 0.
2. Решим уравнение для изображений:
(г2 - Зг -10) АГ(г) = Зг2 -Юг => X(z)
1г ~
1 •
г2-Зг-10
3. Найдем оригинал для X(z):
3;2-10г
Первый способ. Запишем X(z) в виде произведения, удобного для приме-
применения формулы 7 из табл. 5.2, и разложим дробь на элементарные:
Зг2-10г Зг-10
5 г 16 г
5 1 16 1
+
7 г-5 7 г+2
По формуле 7 из табл. 5.2 получаем
х(к)Л5кЛ(-2)кМ^
409
Второй способ. Согласно п.1 замечаний 5.15
5 (?-
z ' +res7
) 2
C;2-10;)(;-5).,_|. (З;2 -10;)(; + 2) *_
* '5+ г
Пример 5.66. Найти решение задачи:
D 1. Перейдем от оригиналов к изображениям, используя формулы 1 из
табл. 5.2, E.61), E.64), E.65):
Z[x(k)} = Х(к); Z[x(k +1)] = zX(z) - Z хф) = z X(z) - z;
z-\
Запишем уравнение для изображений:
Z2X(Z) -Z2-Z + 4zX(z) - 4z + 3X(k) = -1-.
z-\
2. Решим уравнение для изображений:
3. Найдем оригинал для X(z).
К
дробей:
Как и в предыдущем примере, представим —^-L в виде суммы простейшие
X(z) _ z2+4;-4 I J_ + l J 1 J
z "(г-1)(г + 1)(г + 3) 8'z-lV '
Отсюда
vw.l _L_1 z 7
X{Z)-~SZ-1 4z + l~&
По формулам 1,2 и 7 из табл. 5.2 имеем:
х(к)=±Л(-\)к-7-(-г)
Пример 5.67. Найти решение задачи:
х(к + 2) - 5x(jk +1) + 6х{к) = 2 • 4*,
х@)=2,хA)=1.
D 1. Перейдем от оригиналов к изображениям, используя формулы 7 из
табл. 5.2, E.61), E.64), E.65):
Z[x{k)\ = X(z); Z[x{k +1)] = ZX{z) - Z x@) = zX(z) - 2z;
Z[x{k + 2)] = z2X(z)-г2х@)~Zx(l) = z2X(z)-2z2 -z; z[l■ 4*]= 2-^.
Запишем уравнение для изображений:
z2x(z)- 2z2-z- 5Zx(z)+ Юг + 6X(Z)=2-^.
2. Решим уравнение для изображений:
3. Найдем оригинал для
Разложим каждую из дробей на элементарные:
2 112
+
(z-4)(z-2)(z-3)~ z-4
2z-9 3
(г-3)(г-2) г-3 г-2"
Тогда
+ад +б5.
г г-4 г-2 г-3 г-4 г-2 г-3
По формуле 7 из табл. 5.2 имеем: х(к) = 4* + 6 • 2* - 5 • 3* .■
Пример 5.68. Найти решение задачи:
1)+4х{к)=Зк,
D 1. Перейдем от оригиналов к изображениям, используя формулы 7 из
табл. 5.2, E.61), E.64), E.65):
Z[x{k)\ = X(z); Z[x(k +1)] = zX{Z)-zx0;
411
Запишем уравнение для изображений:
Z2X(z) - z\ -zxi- 4zX(z) + 4г x0 + 4X(z) = —
2. Решим уравнение для изображений:
Yi \ Z Z xq + ;x| -4xq;
3. Найдем оригинал для X(z).
Используем разложение
г-3 z-2(z.2f
Тогда
По формулам 5, 7, 8 из табл. 5.2 получаем
X\Kj~j — Z — АС • Z +Xq\K+IjZ + \Xi
= 3*-2*+xo(Jk + lJ*+(x1-4xo-l)jk-2*. ■
Пример 5.69. Найти решение задачи:
х(к + 3)- 3x(fc + 2)+ 3x(Jk +1)- x(jk) = 2*,
х@) = 0, хA) = 0, хB)=1.
D 1. Перейдем от оригиналов к изображениям, используя формулы 7 из
табл. 5.2, E.61), E.64), E.65):
Z[x{k)] = X(z); Z[x(k +1)] = zX(z)- z x@) = zx(z);
Z\x(k + 2)] = z2X(z) - г2х@) - z x(l) = z2 X{z);
Z[x(k + 3)] = Z3X(z)- Z3x@)- ?2x(l)- z xB)= z^iz)- z; Z|2*] = -^.
Запишем уравнение для изображений:
2. Решим уравнение для изображений:
(Z-2)(Z-If
3. Найдем оригинал для X(z).
Используем представление
1 1 1 1_ 1
(z-2)(z-lf=z-2'(z-lf~z-l~(z-lf
Тогда
X(z)- Z i Z Z Z z _ Z Z Z_
(z-lf Z-2 (z-\f z-\ (Z-lf~Z-2 Z-l (z-l
По формулам 1, 3 и 7 из табл. 5.2 получаем
х(к)=2к-1-к. ш
Пример 5.70. Найти решение задачи:
D 1. Перейдем от оригиналов к изображениям, используя формулы E.64),
E.65):
Z[x(k)hX(z); Z\y{k)]=Y(z);
z[x(k +1)] = zx(z)-z 4>) = zX(z)- z;
Z[x(k + 2)] = z2X{z)- Z2x@)- Z 4) = Z2X(z) -Z2Sz\
z\y(k + 2i = z2Y(z)-z2№-zy(ihz2Y(z)-z2; z[o]=o.
Запишем систему уравнений для изображений:
z2X(Z)-z2-J2z-Y(z)=0,
Z2Y(z)-Z2+X(z) = 0.
2. Решим систему уравнений для изображений. Выражая Y(x) из первого
уравнения и подставляя во второе, получаем
z4X(z)-z*-J2z3-z2 + X{z) = 0.
Отсюда, учитывая, что г4 +1 = г4 + 2z2 +1 - 2z2 = (z2 +1J - 2г2 =
= (Z2 -J2z + \)(Z2 +42Z + 1), имеем
{ ) Z2
413
3. Найдем оригиналы для X{z) и Y(z). Как в примере 5.62, п."д" дискри-
дискриминант знаменателя отрицателен, поэтому преобразуем дроби к виду, удобному
для применения формул 14-17 из табл. 5.2:
z2-fiz
z2
:2-V2zh
. n
zsm-
<P z
'' z2-2zcos- + l
4
\-Z 2 z^-cos-j
. я
zsin-
4
+ 1 г2гсо8
4 4
По формулам 14, 15 из табл. 5.2 и E.64) получаем
= V2sin-i s
4
пк . пк
= cos sin —
4 4
Здесь было учтено, что
т-\
. п
zsin-
4
z2 -
= sin^=/(A), t-u.-.; /(o)=o.
Прюкр 5.71. Найти решение задачи:
x@)=3,y@) = 0.
D 1. Перейдем от оригиналов к изображениям, используя формулу 7 из
табл. 5.2, E.64):
Z[x{k +1)] = zX(z) -zx(Q) = zX(z) - 3*;
Запишем систему уравнений для изображений:
2. Решим систему уравнений для изображений. Умножая первое уравнение
на г и вычитая второе, получаем
Отсюда
w г-з (г-:
3. Найдем оригиналы для X(z), Y{z).
Используем представления
X(z)
z
2 _2_ 2
(*-з)(г-2)(*+1) г-2 г+1 z-У
Тогда
г-2
—2-Ц-2-Ц--3-
2 l
По формулам E.62) и 7 из табл. S.2 получаем
и >>@) = 0или
5.4.2. Анализ выходных процессов линейных
дискретных стационарных динамических систем
В разд. S.2.2. приведена классификация динамических систем. Рассмотрим
особенности применения Z -преобразования для решения задач анализа линей-
линейных дискретных одномерных и многомерных стационарных динамических сис-
систем.
415
1. Одномерные системы.
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) входной сигнал g(k), к = 0,1,...;
б) одномерная линейная дискретная стационарная динамическая систем!
(рис. 5.25), поведение которой описывается разностным уравнением
а„х(к + п)+а„^х(к + п-\)+... + аох(к) =
), к = 0,1,2,..., E.74
где а„,...,а0; bm,...,b0 - заданные коэффициенты; п>т\
в) начальные условия:
X\yf — Xq , X^l^ = Xj,..., Xyt — If = Ал_|.
Требуется найти выходной сигнал х(к).
E.75
*(*)
Вход
апх(к + и) +... + аох(к)= bmg(k
х(к)
Выход
Рис. 5.25
Предположим, что входной сигнал g(k),k = 0,1 и выходной сигна
х(к), к = 0,1,..., принадлежат пространству оригиналов.
Для решения поставленной задачи применим Z -преобразование к левой i
правой частям уравнения E.74) с учетом E.64), E.65):
(anZn +... + ao)x(z)-xo{finzn
Обозначим
\ M{z)=bmzm+-. + bo ;
" +... + a2z)+
416
' Dg(z) = g(Q)[bmZm
Из равенства /)(г)ДГ(г) = Л/(г)(?(г) + 5//(г)-^(г) находим изображение
выходного сигнала:
где функция W(?) =—— = -2 и—22. является передаточной функцией
D(z) anz"+...
[4,8,12,16,17,23,24].
Искомый выходной сигнал x(ifc) определяется с помощью обратного
Z -преобразования.
Замечание 5.17. Первое слагаемое в E.76) описывает свободное дви-
движение (под действием ненулевых начальных условий и нулевом входном сигна-
сигнале), а второе и третье - вынужденное (под действием входного сигнала при нуле-
нулевых начальных условиях). Если начальные условия нулевые, выходной сигнал
определяется вынужденным движением. Очевидно, при т = 0 функция £)^ (г) = 0.
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ E.74),E.75)
1. Найти Z-преобразование входного сигнала:
2. Определить передаточную функцию:
и функции
/)(?) = anzn-
Dg(z) = g(Q)[bmzm +Vi?ffl"' +- +
3. Найти Z -преобразование выходного сигнала:
4. Найти выходной сигнал:
14 Пантелеев А.В.. Якимова АС. 417
Пример 5.72. Найти реакцию дискретной динамической системы, описы-
описываемой уравнением x()t + l)-2x()t)=2g(jk), на входной сигнал g(k)=k при
х@)=х0=0.
□ 1. Найдем Z -преобразование входного сигнала:
2. Определим передаточную функцию:
2
Z-2'
Поскольку х0 = 0 и т = 0, то DH(z) = 0 и Dg(z) = 0.
3. Найдем Z -преобразование выходного сигнала:
z
w Z-2 b-if [z-2 (z-\f Z-\
4. Найдем выходной сигнал по формулам 1, 3, 7 из табл. 5.2 :
Пример 5.73. Найти реакцию дискретной динамической системы, описы-
описываемой уравнением x(k + 2)-2x(k + l) + x(k) = 2g(k), на входной сигнал g(k)=2k
при х@)=хA)=0.
□ 1. Найдем Z -преобразование входного сигнала:
2. Определим передаточную функцию:
Поскольку х0 = Х( = 0 и т = 0, то DH(z) = 0 и Dg(z) = 0.
3. Найдем Z -преобразование выходного сигнала:
4. Найдем обратное Z -преобразование путем деления числителя на знаме-
знаменатель:
X(z) = ^= 1ф= 2z+&z
(z-\f(z-2) zb-4z2+Sz-2
Отсюда х@)=хA) = 0, хB)=2, хC)=8, хD)=22
4*8
Пример 5.74. Найти реакцию дискретной динамической системы, описы-
юй уравнением x(k + 2)-5x(k + l)+6x(k)=g(k), на входной сигаал g(k)=l
при начальных условиях х@) = 1, х(\) - 2.
□ 1. Найдем Z-преобразование входного сигнала:
Cfe)-Z[i]-.
2. Определим передаточную функцию:
и функцию
DH(z) = xo\p2Z2 + а^)+ xxa2z = 1 ■ (l • Z2 - 5z)+ 2 ■ 1 ■ z = Z2
Поскольку m = 0, то Dg(z) = 0.
3. Найдем Z -преобразование выходного сигнала:
г2-3г . 1 z
z _ z z_ j_ г z
Z-2 (z-\)(z-2)(z-3) £-2 2 г-l Z-l 2 z
4. Найдем выходной сигаал по формулам 1, 3, 7 из табл. 5.2 :
Пример 5.75. Найти реакцию дискретной динамической системы, описы-
описываемой уравнением х(к + 2) - Ъх(к +1) + 2x(Jk) = 2g(k +1) - 2g(k), на входной сиг-
сигнал g(k) = \'~ при начальных условиях х@) = хA) = 0.
IU, AC ^ U
П 1. Найдем Z-преобразование входного сигнала. По определению по-
получаем
2. Определим передаточную функцию:
2г-2 2
и функции
419
3. Найдем Z -преобразование выходного сигнала:
4. Найдем выходной сигнал.
Представим X{z) в виде
Отсюда по формулам E.62), 1 и 7 из табл. 5.2 получаем
' х(*)=2-2*-' -2-2* +2 = 2-2*, *>1
и х@) =0 , так как согласно E.69) х@) = lim X(z) = 0. Окончательный ответ.
х(к) = 2-2к,к>0.Ш
Пример 5.76. Найти реакцию дискретной динамической системы, описы-
описываемой уравнением х(к + 2)-5х(к + l) + 6x(k) = g{k + l)-3g(k), на входной сигнал
g(k) = 1, при начальных условиях х@) = 1, x(l) = 2.
D 1. Найдем Z-преобразование входного сигнала:
<?(*)-Z[l]-^.
2, Определим передаточную функцию:
и функции
z1 - Зг (см. пример 5.74),
3. Найдем Z -преобразование выходного сигнала:
,2
*(*) =
"i-2 z-2z-l 1-2 z-Ъ'
4. Найдем выходной сигнал по формулам 1 и 7 из табл. 5.2 :
= 2* + 2* -1 + 2* -3fc = 3-2* -1 -3*. ■
Х
42»
Пример 5.77. Найти реакцию дискретной динамической системы, описы-
описываемой уравнением х(к + 2)-5х(к + l)+6x(k) = g{k + 2)-3g(k + l)+2g(k), на вход-
входной сигнал g{k)= I, при начальных условиях х@)= 1, x(l)= 2.
D 1. Найдем Z -преобразование входного сигнала:
C(,)=Z[l] = _i_
2. Определим передаточную функцию:
2 fe-l)fe-2) z-l
(см. пример 5.74), D(z) = z2 -5г + 6,
= z2 -lz + z = z2 -2z.
3. Найдем Z -преобразование выходного сигнала:
Л) z2-lz (z-i) z z2-2z
(Zh2 C)(l) 2~
z_+_z z z
z-2 г-ъ z-Ъ z-l
4. Найдем выходной сигнал: х{к) = 2*. ■
2. Многомерные системы.
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
Ш
а) входной сигнал g(k) =
UwJ
б) многомерная линейная дискретная стационарная система (рис 5.26), по-
поведение которой описывается уравнением состояния
E.77)
и уравнением выхода
Л( E.78)
где х- л-мерный вектор состояния, у- т -мерный вектор выхода; А,В,С-
матрицы размера (лхл), (лхг), (тх л) соответственно;
в) начальное условие
х@) = х0, E.79)
где xq = (хю>---.*яо) вектор начальных состояний.
421
И*)-
Требуется найти законы изменения векторов состояния х(к) и выхода
х0
x(k + l
1
)=/Ц*)н
>Bg(k)
x(k + l)
Задержка
x(k)
-Cx{k)
Вход
Вектор
состояния
Рис. 5.26
У(к)
Выход
Предположим, что входной и выходной сигналы, а также вектор состояния
принадлежат пространству оригиналов.
Применим к левой и правой части уравнения E.77) Z-преобразование
с учетом E.64) и обозначений X(z) = Z[x{k)], G(z) = Z\g{k)):
zX{z)-zxo=AX(z)+BG{z).
Тогда получим
Решая относительно X(z), получаем
X{z) = {zE- AT1 zxo.+(zE- Ay1 В G(z),
E.80)
где Е- единичная матрица.
Из E.78) следует Y(z) = CX{z) , т.е.
■.C(zE-ATxzxu+C(zE-A)ABG(z),
E.81)
Замечания 5.18.
1. Первые слагаемые в E.80), E.81) описывают свободное движение (под
действием ненулевых начальных условий и нулевом входном сигнале), а вторые -
вынужденное (под действием входного сигнала при нулевых начальных услови-
условиях).
2. Аналогично непрерывным системам (см. разд. 5.2.2) вводятся в рассмот-
рассмотрение дискретные передаточные функции по состоянию и выходу:
Wx{z)={zE-A)AB,
422
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ E.77),E.78)
1. Найти изображение входного сигнала:
G(zhZ[g(k)}.
2. Найти матрицы {zE - А)'1, C(zE~ A)'x и передаточные функции:
Wx{z) = (zE - А)'1 В, wy{z) = C{zE- А)'1 В.
3. Определить изображение законов изменения векторов состояния
и выхода:
4. Найти законы изменения векторов состояния и выхода, используя об-
обратное Z -преобразование:
y(k)=Z-l[Y(z)}.
Пример S.78. Найти законы изменения векторов состояния и выхода мно-
многомерной динамической системы:
при входном сигнале g(ik) = 3* и начальных условиях Xj@) = 3, х2@)=0.
D 1. Найдем изображение входного сигнала:
2. Найдем передаточные функции. Так как ^=1 ' *|, 5 = 1 ,
l),Xo=Q,TO
IV1 1 (г -\
2 z ~z2-z~2{-2 z-iy
423
z -lVl
г + l
3. Определим изображение законов изменения векторов состояния и выхо-
да:
1
«
Зг
)(г
6z
4. Найдем законы изменения векторов состояния и выхода:
3 z-2) г-2
г + l г-2 г-2 г-
Для дробей г и z нужно использовать формулы 2 , 7 из табл. 5.2
г+1 z-2
и, в силу наличия множителя z, формулу E.64). Получаем
-2*-
Х(г)'
г + 1
2-
г+l г-2
424
Отсюда по формулам E.64) и 7 из табл. 5.2 получаем
-( (У72\+3\
2-(-l)* -2* -3* J [2-(-l)*-2*-3*
Результат совпадает с полученным в примере 5.71. ■
Пример 5.79. Найти законы изменения векторов состояния и выхода мно-
многомерной динамической системы:
\) = ф)+2х2(к),
у[к)=-Х1(к)+х2(к)
3 9
при входном сигнале g{k)= 1 и начальных условиях Х[@) = —, х2@) = —.
D 1. Найдем изображение входного сигнала:
2. Найдем передаточные функции. Так как А=\ ,
С=(-1 1),
, получаем
U)
Z-2
-' • '--2 -1
И 0
3. Определим изображение законов изменения векторов состояния и выхо-
выхода:
425
( ziz-2) \
11
' 4 '
33
И (г-3J 4 (,.3JJ
~(
Иг 3
4. Найдем законы изменения векторов состояния и выхода.
Воспользуемся разложениями:
1 1 1 1 1
1 1
_ I
(г-3J(г-1) 4 г-3 2
2 г-3'
J I J_
_ ЧЯ + 4 ' r -1
Тогда
15 г
3
4 (г-3J 4 (г-зJ
г2 33
4 (Z-3Jj
4 г-3 2 (Z_3J 4
2
2 г-3
1 г
4
2 г-1
4 г-3 2 (г-зJ 4 г-1
2 г-3 2 г-1 2 г-3
426
По формулам 1, 7, 8 из табл. 5.2 и E.64) получаем
*(*) =
f4(*+iK*-^*H
1кЪь +23* -^*з* --з* +1*з* +-з* -1+1з* -1з
4 44 42 2423
4 4
3* -1*3* -— ^
3 4
4J
5.4.3. Анализ устойчивости линейных дискретных
стационарных динамических систем
1. Одномерные системы.
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) одномерная линейная дискретная стационарная динамическая система,
поведение которой описывается разностным уравнением:
к = 0,1,2,... ;
б) начальные условия:
х@) = х0, хA)=х, х(п-1)=х„.,.
Требуется исследовать, является ли динамическая система асимптотически
устойчивой.
Динамическая система называется асимптотически устойчивой, если при
ненулевых ограниченных начальных значениях свободное движение хс(к) (при
g(k) = 0) ограничено при всех * = 0,1,2,... и выполняется условие
*<.(*)-> 0 при *
427
КРИТЕРИЙ УСТОЙЧИВОСТИ
Для асимптотической устойчивости динамической системы E.82) необходимо
и достаточно, чтобы корни Xt характеристического уравнения
E.83)
были по модулю меньше единицы:
Это означает, что все корни должны располагаться внутри круга единич-
единичного радиуса с центром в начале координат (рис. 5.27).
InU
ReX
Рис. 5.27
Замечание 5.19. Нахождение корней характеристического уравнения,
как правило, связано с большими вычислительными трудностями. Как и для не-
непрерывных динамических систем, в качестве косвенного критерия устойчивости
можно использовать критерий Рауса-Гурвица (см. замечание 5.12). Для этого
следует выполнить конформное отображение плоскости комплексного перемен-
переменного А. на плоскость комплексного переменного w таким образом, чтобы ок-
окружность |х| = 1 перешла в мнимую ось, а внутренность круга \к\ < 1 отобразилась
на левую полуплоскость Rew<0. Такое отображение выполняется с помощью
1 + W
дробно-линейного преобразования (см. гл.2): Х = .
1-й»
Пример 5.80. Исследовать устойчивость дискретных динамических систем,
описываемых
а) Зх{к
в) х(к -t
д) х(к ч
ж) х\к ■
уравнениями:
+ \)+x{k)=g(k);
■\)+2x(k) = g{k) ;
-2)+±x(k)=g(k);
f 3)—x(k + 2)+— x(k) =
2 4
6Lx(
r) x(k
;* + 1)-дс(*) = ^);
+ 2)+2x{k + l)+x{k)=g{k)\
2
438
D а) Характеристическое уравнение 3\+1 = 0 имеет корень Х{ =—, ле-
лежащий внутри круга единичного радиуса, изображенного на рис. 5.27, так как
)Х[ j = — < 1. Согласно критерию система асимптотически устойчива.
б) Характеристическое уравнение 4Х-1 = 0 имеет корень \, =-, лежащий
4
внутри круга единичного радиуса, изображенного на рис. 5.27, так как
|\i j = — < 1. Согласно критерию система асимптотически устойчива.
в) Характеристическое уравнение \ + 2 = 0 имеет корень ^ =-2, не лежа-
лежащий внутри круга единичного радиуса, изображенного на рис. 5.27, так как
|Х|| = 2 > 1. Согласно критерию система не является асимптотически устойчивой.
г) Характеристическое уравнение Х2+2Х + \=0 имеет корни Х{ = Х2 = -1,
лежащие на границе круга единичного радиуса, изображенного на рис. 5.27. Со-
Согласно критерию система не является асимптотически устойчивой.
д) Характеристическое уравнение X1 + - = 0 имеет корни X, =-, Х2 =—,
4 2 2
лежащие внутри круга единичного радиуса, изображенного на рис. 5.27. Соглас-
Согласно критерию система является асимптотически устойчивой.
е) Характеристическое уравнение X2-Х + — = 0 имеет корни Xt =-(l + /'),
А.2=-A-/), лежащие внутри круга единичного радиуса, так как
\\{\ = \х2\ = — < 1. Следовательно, система асимптотически устойчивая.
ж) Характеристическое уравнение X3—\2+- = 0 имеет корни Х{ =—,
2 4 2
\2 =-(!+')> Х3 =—A — /), лежащие внутри круга единичного радиуса, так как
|я.)| = — < 1, |\2| = |^з|= — < 1 .Следовательно, система асимптотически устойчи-
устойчивая.
Решим задачу с помощью критерия Рауса-Гурвица. Для этого применим
_ . l + w
преобразование X = в характеристическом уравнении:
1-й»
l-w) 2{l-w) 4
, ,2 3 1 1 2 1 1 3 1' 3 3 2 1 3
+ Зи' + Зи'+и' — + -w — w + -w + w + — w — w
22 22 444 4
+ w w + w +w + w
22 22 444 4_Q
A-й-K
429
5 з 17 2 7 3 л
В результате получим -w + — w + —w + - = О или после умножения на 4 :
4 4 4 4
5
-w + w + w +
4 4 4 4
5w3+17w2+7w + 3=0.
Составим матрицу и вычислим угловые миноры:
A7 3 0\
5 7 О
О 17 3
,Д,=17>0, Д2 = 104 > 0, Д3=3104 = 312>0.
Так как все угловые миноры положительны, система асимптотически ус-
устойчивая.
з) Характеристическое уравнение \3 + 2Х1 + IX = 0 имеет корни Xt = 0,
Х2 = -1 + /, Х-$ =-l-i, первый лежит внутри круга единичного радиуса, а Х2 > ^з
лежат вне круга, так как |Х2| = |^з| = v2 > 1. Согласно критерию система не явля-
является асимптотически устойчивой.
Решим задачу с помощью критерия Рауса-Гурвица. Для этого применим
преобразование X = в характеристическом уравнении:
1-w
{l-w) {l-w) l-w
1 + 3w + 3w2 + w3 + 2 - 2w2 + 2w - 2w3 + 2 - 2w - 2w2 + 2w3
(l-wK
В результате получим w3 - w2 + 3w + 5 = 0 .
Составим матрицу и вычислим угловые миноры:
(-1 5 О'
1 3 0,Д,=-1<0, Д2=-8<0, Д3 = -40<0.
О -\ 5)
Так как не все угловые миноры положительны (они отрицательны), систе-
система не является асимптотически устойчивой. ■
Пример 5.81. Найти значения шага интегрирования, обеспечивающие ус-
устойчивость процесса численного решения явным методом Эйлера дифференци-
дифференциального уравнения
), х@)=х0,
где Т, х0 - заданные параметры, а /(<) некоторая функция.
D Параметр Г>0 называется постоянной времени [34,45,51], влияющей
не только на поведение решения уравнения, но и на параметры численных мето-
методов.
Приведем уравнение к виду, разрешенному относительно производной:
430
*_ L+Ж
dt T T .'
F{t,'x(t))
Для нахождения численного решения выпишем соотношения явного мето-
метода Эйлера [36]:
x(k + \)=x(k)+hF{hk,x(k)), к = 0,1,... , х@)=х0 ,
где А - величина шага интегрирования.
Для поставленной задачи получаем
Запишем полученное разностное уравнение в форме E.74):
Tx{k + \) + (h-T)x{k)=hf(kh), A: =0,1
Для анализа устойчивости выпишем характеристическое уравнение:
Т — h
Отсюда X = . Для обеспечения устойчивости необходимо и достаточ-
достаточно выполнения условия
' Т~h 1 или \T-h\<T .
Следовательно, имеем -Т <Т -h<T. В результате устойчивость процесса
интегрирования дифференциального уравнения обеспечивается при 0 < h < IT.
По классификации явный метод Эйлера относится к ограниченно устойчивым,
так как существует величина критического шага hKpum = 2Г. Если h > hKpum = IT,
процесс является неустойчивым [36]. ■
Пример 5.82. Найти численное решение дифференциального уравнения »
0,1 — + х = 1, х@) = 0
явным методом Эйлером.
□ В примере Т = 0,1. Следовательно, шаг интегрирования, обеспечиваю-
обеспечивающий устойчивость процесса, должен удовлетворять условию h<2T = 0,2 (см
пример 5.81). Выберем Л = 0,05 . Тогда разностное уравнение, соответствующее
методу Эйлера при f(kh)= 1, имеет вид (см. пример 5.81)
0,1 х{к +1)- 0,05 х(к) = 0,05 g(k),
mt g{k)=[, x@) = 0 .
Воспользуемся алгоритмом решения разностного уравнения, приведенным
в разд. 5.4.1 .
431
1. Перейдем от оригиналов к изображениям с учетом E.64):
Z[x(k)}=X(z), Z[x(k + \)] = ZX(z), Z\g(k)h^i
Запишем уравнение для изображений:
o,izX{z)-O,O5X(z)=o,Q5-
.
2. Решим уравнение для изображений:
*>■%
4 м>
3. Найдем оригинал для X(z)'.
По формулам I и 7 из табл. 5.2 имеем
)
х(к) = -i +1, к =0,1,... .
Подставляя различные значения к, получаем: 0; 0,5; 0,75; 0,875; 0,9375;
0,96875, 0,984375 и т.д.
По формуле E.70) находим
. 1 Z
lim х{к) = lim (z -1) X{z) = lim - • —Ц- = 1
Z~2
Заметим, что точное решение дифференциального уравнения имеет вид
x(t)= 1-е0'. При tk =kh получаем x(kh) = 1 -e~10**, it = 0,1,... Подставляя раз-
различные значения к, имеем 0; 0,393469; 0,776870; 0,917915; 0,950213 и т.д.
В [36] приведено исследование точности метода при различных h. Сравне-
Сравнение точного и приближенного решений изображено на рис. 5.28. ■
Рис. 5.28
432
2. Многомерные системы.
ПОСТАНОВКА ЗАДАЧИ
Пусть заданы:
а) многомерная линейная дискретная стационарная динамическая система,
поведение которой описывается уравнением состояния:
x(k + \)=Ax{k)+Bg{k), E.84)
где все обозначения совпадают с используемыми в E.42);
б) начальное условие:
где х0 - начальное состояние.
Требуется исследовать, является ли динамическая система асимптотически
устойчивой.
Динамическая система называется асимптотически устойчивой, если ее
свободное движение хс(к), к =0,1,2,... (при g(k) = Q) ограничено при ограничен-
ограниченных начальных состояниях х0 и выполняется условие
||хс(А:)||-»0 при к-*+ао ,
Г„
где ЦхЦ - какая-либо норма вектора х, например, |х|| = J £ х,г.
КРИТЕРИЙ УСТОЙЧИВОСТИ
Для асимптотической устойчивости многомерной динамической системы
E.84) необходимо и достаточно, чтобы корни \; характеристического уравнения
det (А - Х£) = 0
были по модулю меньше единицы:
Это означает, что все корни Х; должны располагаться внутри круга еди-
единичного радиуса с центром в начале координат (см. рис. 5.27).
Очевидно, как и для одномерных динамических систем, для анализа ус-
устойчивости многомерных систем можно применять критерий Рауса-Гурвица (см.
замечание 5.19).
Пример 5.83. Исследовать устойчивость'дискретных динамических систем,
описываемых уравнениями состояния:
-- а) х,(* +1)= -x2(k)+ gl(k), х2(к +1) = *,(
433
6)
в)
) = x,(*)+2x2(*),
П а) Здесь Л = . Найдем корни характеристического уравнения
det(A -XE) = 0:
-X -1
1 -X
= 0,или Х2+1 = 0.
Отсюда Х| =/, Х2 =-/. Так как |Xi|=|a2| = 1, т.е. корни не лежат внутри
круга единичного радиуса (они лежат на его фанице), то система не является
асимптотически устойчивой.
б) Здесь А=\° 2
. Найдем корни характеристического уравнения
-X --
1 -1-Х
= 0, или Х2+Х + -=0.
Отсюда X! = -(-1 + /'), Х2 = -(-1 - /')• Так как |Х(| = |Х2| = — < 1, то система
является асимптотически устойчивой.
Используем критерий Рауса-Гурвица. Для этого применим преобразование
1 + w fl + wAl + wl-r,
X = к характеристическому уравнению: + + — = 0 . В результа-
[-w U-W 1-w 2
l-w2+-
2
те получаем
A-й-J
Составим матрицу и вычислим угловые миноры:
(\
-w . .
— = 0 или -vf2+w + - = 0.
2 2
5_
2)
, Д,=1>0, Д2=->0.
Так как все угловые миноры положительны, система асимптотически ус-
устойчивая.
(\ 2\
в) Здесь А = . Найдем корни характеристического уравнения
14 3J
1-Х 2
4 3-Х
= 0, или Х2-4Х-5 = 0.
Отсюда Х| = 5, Х2 = -1. Так как корни не лежат внутри круга единичного
радиуса, система не является асимптотически устойчивой. ■
434
Упражнения
Применяя г - преобразование, найти решение задач.
Ответ:
2. х(к + 2) - 5х(к +1) + 6х(к) = О,
х@) = 1,хA) = 2.
Ответ: х(к) = 2*.
3. х(к + 3) - 5х(к + 2) + 8х(/к +1) - Щк) = О,
Ответ: х(к) = -7 + 7• 2* -^Л • 2*.
4. х(/к + 2) - 5x(fc +1) + 6х(к) = g(k), g(k) = 1,
Ответ: х(к) = --2к +--3*.
5. х(/к + 1)
ХА: +1) = Зх(А:) + 4у(А:),
х@) = 3,у@) = -4.
Ответ: х(к) = 1 + Iм;y(fc) = -1-3-2*.
6. x(A; + l)
Ответ: х(к) = - V3 -2* -япу + ^/з -2* -cos—,
у(к) = 2 cos— + 2 sin—.
7. Исследовать на устойчивость динамические системы, описываемые раз-
разностными уравнениями, в упражнениях 1, 2, 4, 5.
Ответ: системы не являются устойчивыми.
435
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Применяя преобразование Лапласа, найти решение задач Коши:
1. х" + Зх' = 20е2',х@) = 1,х'@) = 7.
2. xUV) - 2х" + х = sin /, х@) = х'@) = х"@) = х'"@) = 0.
3. х" - 2х - Зх = е3', х@) = х'@) = 0.
4. х" + у = 1,
у" + х = 0,
5. х' = 2х+ 3,у + 1,
у' = 4х - 2j>,
х@) = -1, у@) = 0.
6. х' = -х + 7>у +1, х@) = 1,
у, у@) = 2.
0, 0<t<\,
7. х" + 9х = /(/), х@) = 0, х'@) = 1, /(/) =
8. х" - Зх' + 2х = /(О,
х@) = х'@) = х"@)=0,
9. х"-х = —!— ,х@) = х'@) = 0.
1 + е
Решить задачи анализа выходных процессов.
10. x"-2x' + x = g@, g(t) = 2e',
х@) = х'@) = 0.
11. x" + 3x' + 2x = g, g(t) = t,
х@) = х'@) = 0.
12. x" + 2x' + 5x = g, g{f) = sin t,
x@) = l,x'@) = 2.
0, ?S 3.
436
13. x'~x + 3y + ft @, ft @ = 2, х@) = -1,
y' = x-y + g2(t),
14. х' = 2х + у, x@) = 2,
15. x' =
16. x' =
У =
x@)=0,
Применяя z - преобразование, решить задачи:
17. x(k + 3) + 7х(Л + 2) + \5x(k +1) + 9x(/k) = 0,
x@) = 2, x(l) = -10, xB) = 46.
18. x(k + 4) + 2x(/k + 2) + x(/k) = 0,
19. x(k +2)-4x(k + l) + 4x(k) = g{k), g(k) = k-2k; л@)-1, x(l)^~.
6
20. 5x(/k +1) = I2x(k) + ^(it), x@) = 2,
Решить задачу анализа выходных процессов.
21. x(fc +1) = Щк) - у(к) + g(k), g(k) = 1,
у(к +1) = x(fc) + 2у(к), х@) = 1 у@) = Н.
4 4
22. Исследовать на устойчивость динамические системы в задачах 6, 9, 11,
13, 17, 19.
437
ОТВЕТЫ И УКАЗАНИЯ
Глава 1
1. z = '■ 2. б), д). 3. 1,—. Указание: в случае затруднений повторить
4 4 15
решение примеров 6 и 11 из упражнений к разд. 1.1.
Л (
4. Z\ =v2 -е^ , Zi =—е ' . Указание: повторить решение примеров
7 и 8 из упражнений к разд. 1.1.
5. 4,—- . 6. 25V2,— . Указание: использовать правила умножения и воз-
V 15J I 4J
ведения в степень чисел в тригонометрической форме. Найти предварительно
модули и аргументы чисел A + /) и (V3-/j. 7. Четыре корня;
,« _ _ [М = 2> [2<И<3>
Zi=ei,Z2=iZi,Z)=iZl,Z4=-Zi- 8. а) ]„ Зл б) ■ Зя
-<argz< —; argz = --—.
14 4 4
9. а) правое полукольцо; б) нижнее полукольцо. 10. 1 < \z +1 - 2/j < 2. Указа-
Указание: повторить решение примера 2 из упражнений к разд. 1.2. 11. а) и в).
12. 0. 13. 1 + /е. 14. а), е). 15. в), д). Замечание: ответ б) следует из в).
Глава 2
-'- S 1 V2
1. /B/) = е 6 =-(— + 'г)- 2. /(-') = A-')- 4. Указание: рассмотреть
2a it 2.
односторонние пределы в точке z = 0 по подходящим образом выбранным на-
направлениям, например по координатным полуосям и биссектрисам координат-
координатных углов. 6. a) -e3sin2; б) sinl-shl. 7. а) 1пЗ; б)-1. 8. а),б) ни одного. Все
корни расположены на мнимой оси. 9. Rez = ln(V2±l). 10. е). 11. в),г),е).
7 + fcU = 0,-l;/(?) = z2; ^+fet<aigz< — + кп,к = 0,-1;2
4 2 4
. 14. a)
б)/(«) = -гей. 16. И < 1 ,|г| > 1. 17. a)Im z > 0 ; б) ( N <» i8.
[Imw >0
19.w = e г .20. w = VFe. 21. w = -i(z-l-iJ. 22. w =
( i8. w =
[Imw >0 I г +1
, Imw.
Z + 3/ 2
23. a)
Z--tA-'A =
. 26 -±=e%-(\+i).n.Rtz = -
3V2 2
438
,2 Л
28. z = (- + 2/btl±/lnP^—- , it = 0;±l;±2....
2. |г|<Л. 3. |z + l|<2; 4. |г|<1. 5.
6. Всюду расходится. 7. Сходится всюду. 8. Всюду расходится.
9. |Rez|>|lnu|. 12. R = e. 13. Л = 1. 14. R = ~. 15. R=e.
16.5= Z + 2> ^
. 17.5=Ц. 18.5 .1 ,,,.
/-zJ (?-IK (*-l)(l-2«)
19. а) не допускает, так как z = 0 - точка ветвления; б) в плоскости с раз-
разрезом по лучу (- <»,0] возможно разложение каждой из двух ветвей. Например,
при условии /A) = --= имеем /(г) = -— —(г -1)+—{z - \f +..., |г -1| < 1.
lQ.a) f{z) = z+^z* +-^-z5 +±^-zy +..., R = \\
2-3 j.2.2! 5 23-3!7
г3 г5
Указание: использовать свойство интегрирования степенного ряда.
21. Нет. г = °о - точка ветвления.
22. В случае го = 0 и го = °° разложения невозможны, так как эти точки -
точки ветвления функции; для го * ° и ?о * °° возможны.
Указание. Для любой го, Zo * 0 > Zo * °° > возможно выделение однознач-
однозначных ветвей и разложение функции в ряд Тейлора по степеням z-Zo в круге,
принадлежащем односвязной области - плоскости с разрезом по лучу, соеди-
соединяющему точки z = 0 и г = °о • Например, в случае го = 1 можно провести разрез
(-<», 0] и в круге |г -1| < 1 получить разложение. Для го = -2 разрез можно взять
по лучу [0, оо) и в круге |г + 2| < 2 получить разложение. Выбор ветви осуществля-
осуществляется заданием значения f(zo)- Запишите разложение по степеням (г-1) каждой
из ветвей.
23. В окрестности любой точки г0 > Zo * 1, Zo * -' возможно разложение -
в ряд Тейлора и ряд Лорана для Zo = °° •
В случае го = 1 и Zo = -i разложение невозможно, так как это - точки
ветвления.
Запишите разложение в окрестности го = 0 и Zo = °° •
24. г = ±2/ - простые нули, г = 1 - нуль второго порядка.
25. а) нуль третьего порядка; б) нуль четвертого порядка; в) нуль шестого
порядка.
26. а) г = 0 - простой нуль; г = for, fc * 0, k*\ - нули второго порядка;
Z = л - не является нулем функции;
б) z = ±i - нули второго порядка, г = 1 ± i - простые нули.
439
n.z-iv+W
28. г = 0. Нуль восьмого порядка, поэтому /7'@) = 0; /'8'@)=8!;
/(9'@) = 0, так как функция четная и, следовательно, в разложении отсутствует
слагаемое с9 z9 ■
зо.а)
2f;(l)(«l)
32.а)Л*)=-£*2"-4. И< 1; 6)/W-«2 + » + l4
д=0 n=\Z
со / 1\"+1/- |\2л—I оо / пд/
A) (*~°()(
Y
1)! „to Bи)!
+1 _2я-1 оо /
i
Д Bи-1)! „to Bи)!
Глава 4
1. Z\ = 1,^2,3 = -1 ±» - простые полюсы, z = оо - существенно особая точка
/(*)> *к =(-л + 2£л)/' - простые полюсы —г\-
2. а) г = ±/ - простые полюсы, z = 0 и г = -1 - существенно особые точки,
Z = оо - простой полюс.
б) Zk = 2Ы,£ = +1,.. - простые полюсы, z = 0 - существенно особая точка.
3. Полюс 14-го порядка. 4. /3(г).
2 о *
z2 + z + CZ +
7. а) г = ±г - простые полюсы, z = « - существенно особая точка,
,м w4 W4
res/(*) =—, res/(z) = -—, res/(^) = ——
i 2/ _j -2/ » 2/
440
6) z = -' - простой полюс, z = i - существенно особая точка, z = °° - уст-
устранимая особая точка (нуль второго порядка),
i
res/fe) = p, res/fe) = 0, ге/(г) = -1в2.
8. а) г = 0, г = °° - существенно особые точки, res f(z) = 1, res f(z) = -1;
О 00
6) z = ±4; - простые полюсы, г = 0 - существенно особая точка, z = °° -
устранимая особая точка (нуль первого порядка),
res/(*)=res/(*) = icl4, «s/fe) = -l, res/(z)= 1-ichi.
4» -4/ 2 4 oo о 2 4
9. a) res/(£) = -l--,res/(z)= 1+-. Указание: разложить z2 по степеням
/ 6 oo 0
(z - /'); разложить f(z) в ряд Лорана в окрестности существенно особой точки
z = /', найти res /(г) = С_,; res f(z) = - res f(z);
/' 00 /
6) K&f(z) = -5, res /(г) = 6e, res/(<:) = 5-6e.
~7 -1 00
11. a) res/(*)=res/(;) = O; 6) res/(*) = ^.
о oo 2 24
*<« w \ л /г . *- \ 2 я/ _. 16я/
12. res/(z)= 4 для ветви, где VI = -1. 13. а) г-; б) .
14. (-Збя/). 15. 0. 16. —. 17. а)яе-12; б) ^-. 18. а) -е;
5V5 6 4
б) -^^'(cosl + sinl). 19. а) яЛ; б)—. 20. 2. 21. 1. 22. 3. 23. 1.
2V2 8
Глава 5
1. х(/) = 2е2'-в-3'. 2..
8
. /ч 1 1,1, 1 1 Г 1 -Г
4. х(п = —cos/ +—е +—е ; v(n = —cos/—е —е
2 4 4 2 4 4
_ /4 1 9 4f 5 _4* , ,. 15 0/ 9
1 3 л, 5 _д. .. 15 ■), 3 _i» 1
—A-V +V ■ y{t)=T +Г 4-
441
7. x(t) =|sin3/• /(*) +|[<f-1)- jsin3(/-1) |■ /(r-1)
9. x(/)=sh/.ln—+-
Указание: Сначала найти единичную переходную функцию, решая E.29),
затем воспользоваться формулой E.30).
10. x(t) = t2e'.
11. x(t) = !/-- + е-'--е-21.
2 4 4
12. х(/) = е"' —■COS2/+—^sin2n cos/ + -sin/.
у(/) = e'+-e Л+-.
4 4 2
15. x(/) = 2 + 4f-2cos/-3sin/, >>(/) = 2sin/-2/.
16. x@ = 2/-y + 4e-'-3e'+|e5'; y(t)^
17. x = (-l)*+(l + 2it)(-3)*.
18. x(it) = (l + it).cosy + B + it).sin—.
19. x(k) = (l+k)-2k +k2 ■(-- + — )-2k.
20. x(it) = 2*+3*,
2l.x(k) = 2-3k--k-3k--, >(*) = 3jfc3+.
3 4 3 4
22. В задаче 11 система устойчива, а в задачах 6, 9, 13, 17, 19 - нет.
442
ЛИТЕРАТУРА
1. Алешков Ю.З., Смышляев П.П. Теория функций комплексного перемен-
переменного и ее приложения. - Л.: Изд-во ЛГУ, 1986.
2. Анго А. Математика для электро- и радиоинженеров. - М.: Наука, 1964.
3. Артемович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного пере-
переменного. Операционное исчисление. Теория устойчивости. - М.: Наука, 1969.
4. Бесекерский В.А., Попов Е.П Теория систем автоматического регулиро-
регулирования. - М.: Наука, 1975.
5. Бицадзе А.В. Основы теории аналитических функций. -М.: Наука, 1984.
6. Бугров Я.С., Никольский СМ. Дифференциальные уравнения. Кратные
интегралы. Ряды. Функции комплексного переменного. - М.: Наука, 1985.
7. Волковыский Л.И., Лунц ГЛ., Араманович И.Г. Сборник задач по теории
функций комплексного переменного. - М.: Наука, 1975.
8. Воронов А.А. Основы теории автоматического управления: особые линей-
линейные и нелинейные системы. - М.: Энергоатомиздат, 1981.
9. Гноенскш Л.С, Каменский Г.А., Эльсгольц Л.Э. Математические основы
теории управляемых систем. - М.: Наука, 1969.
10. Голузин Г.М. Геометрическая теория функции комплексного перемен-
переменного. - М.: Наука, 1972.
11. Грищенко А.Е., Нагнибида Н.И., Настасиев П.П. Теория функций ком-
комплексного переменного. Решение задач. - К.: Вища школа, 1986.
12. Данко П.Е., Попов А. Г., Кожевникова Т.Я. Высшая математика в упраж-
упражнениях и задачах: Учеб. пособие для студентов втузов. В 2-х ч. Ч. II.- М.: Выс-
Высшая школа, 1986.
13. Деч Г. Руководство к практическому применению преобразования Лап-
Лапласа и z-преобразования. - М.: Наука, 1971.
14. Диткин В.А., Прудников А.П. Руководство к практическому применению
преобразования Лапласа. - М.: Высшая школа, 1965.
15. Диткин В.А., Прудников АИ Операционное исчисление. - М.: Высшая
школа, 1966.
16. Иващенко Н.Н. Автоматическое регулирование. - М.: Машиностроение,
1978.
17. Изерман Р. Цифровые системы управления. - М.: Мир, 1984.
18. Квакернаак X., Сиван Р. Линейные оптимальные системы управления. -
М.: Мир, 1977.
443
19. Кожевников Н.И., Краснощекова Т.И., Шишкин Н.Е. Ряды и интеграл
Фурье. Теория поля. Аналитические и специальные функции. Преобразование
Лапласа. - М.: Наука, 1964.
20. Коппенфельс В., Штапшан Ц. Практика конформного отображения. -
М.: И.Л., 1963.
21. Корн Г., Корн Т. Справочник по математике. - М.: Наука,1977.
22. Краснов М.Л., Киселев А.И., Макаренко Т.Н. Функции комплексного пе-
переменного. Операционное исчисление. Теория устойчивости. - М.: Наука, 1971.
23. Кузин Л.Т. Расчет и проектирование дискретных систем управления. -
М.: Машгиз, 1962.
24. Куо Б. Теория и проектирование цифровых систем управления. - М.:
Машиностроение, 1986.
25. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного
переменного. - М.: Наука, 1987.
26. Лаврентьев М.А., Шабат Б.В. Проблемы гидродинамики и их математи-
математические модели. - М.: Наука, 1977.
27. Леонтьева ТА., Панферов B.C., Серов B.C. Задачи по теории функций
комплексного переменного. - М.: Изд-во МГУ, 1992.
28. Летова ТА., Пантелеев А.В. Экстремум функций в примерах и задачах.
- М.: Изд-во МАИ, 1997.
29. Лурье А.И. Операционное исчисление. - М.: Гостехиздат, 1951.
30. Маркушевич А.И. Краткий курс теории аналитических функций. - М.:
Наука, 1966.
31. Мартыненко B.C. Операционное исчисление. - Киев: Вища школа, 1973.
32. Методические указания для программированного обучения студентов
по курсу "ТФКП и операционное исчисление" / Р.В. Поповкина, А.С. Якимова
и др. - М.: МАИ, 1981.
33. Методы описания, анализа и синтеза нелинейных систем управления/
В.В. Семенов, А.В. Пантелеев, Е.А. Руденко, А.С. Бортаковский. - М.: Изд-во
МАИ,1993.
34. Основы автоматического регулирования / Под ред. В.В. Солодовникова.
- М.: Машгиз,1954.
35. Пантелеев А.В., Бортаковский А.С, Летова ТА. Оптимальное управле-
управление в примерах и задачах. - М.: Изд-во МАИ, 1996.
36. Пантелеев А.В., Якимова А. С, Босов А.В. Обыкновенные дифференци-
дифференциальные уравнения в примерах и задачах. - М.: Изд-во МАИ, 2000.
37. Первозванский А.А. Курс теории автоматического управления. - М.: Нау-
Наука, 1986.
444
38. Привалов И.И. Введение в теорию функций комплексного переменного.
-М.: Наука, 1984.
39. Лчелин Б.К. Специальные разделы высшей математики (Функции ком-
комплексного переменного. Операционное исчисление). - М.: Высшая щкола,1973.
40. Романовский ИИ. Ряды Фурье. Теория поля. Аналитические и специ-
специальные функции. Преобразование Лапласа. - М.: Госуд. изд-во технико-теор. ли-
литер., 1957.
41. Сборник задач по математике для втузов. Специальные разделы мате-
математического анализа / Под редакцией А.В. Ефимова и Б.П. Демидовича. - М.:
Наука, 1981.
42. Сборник задач по теории автоматического регулирования и управления
/ Под ред. В.А. Бессекерского. - М.: Наука,1978.
43. Сборник задач по теории аналитических функций / Под ред. М.А. Ев-
Евграфова. - М: Наука, 1972.
44. Свешников А.Г., Тихонов А.Н. Теория функций комплексной перемен-
переменной. - М.: Наука, 1979.
45. Семенов В.В., Пантелеев А.В., Бортаковский А.С. Математическая теория
управления в примерах и задачах. - М.: Изд-во МАИ, 1997.
46. Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций
комплексного переменного. - М.: Наука, 1982.
47. Смирнов В.И. Курс высшей математики. - Т.З, Ч. 2.- М.: Наука, 1974.
48. Совершенный В.Д. Основы теории функций комплексного переменного.
- М.: Изд-во МАИ, 1996.
49. Соломенцев Е.Д. Функции комплексного переменного и их применения.
- М.: Высшая школа, 1988.
50. Стрейц В. Метод пространства состояний в теории дискретных линей-
линейных систем управления. - М.: Наука, 1985.
51. Техническая кибернетика. Теория автоматического регулирования. Т.1/
Под ред. В.В. Солодовникова. - М.: Машиностроение, кн. 1,2, 1967, кн.З, ч.1,2,
1969.
52. Титчмарш Е. Теория функций. - М.: Наука, 1980.
53. Фукс Б.А., Шабат Б.В. Функции комплексного переменного и некото-
некоторые их приложения. - М.: Физматгиз, 1959.
54. Чаки Ф. Современная теория управления. - М.: Мир, 1975.
55. Шелковников Ф.А., Такайшвили К.Г. Сборник упражнений по операци-
операционному исчислению. - М.: Высшая школа, 1976.'
56. Шостак Р.Я, Операционное исчисление. - М.: Высшая школа, 1972.
445